TwoTypesofSingleValuedNeutrosophicCovering RoughSetsandanApplicationtoDecisionMaking
JingqianWang 1 andXiaohongZhang 2,*
1 CollegeofElectricalandInformationEngineering,ShaanxiUniversityofScienceandTechnology, Xi’an710021,China;wangjingqianw@163.comor81157@sust.edu.cn
2 SchoolofArtsandSciences,ShaanxiUniversityofScienceandTechnology,Xi’an710021,China * Correspondence:zxhonghz@263.netorzhangxiaohong@sust.edu.cn
Received:8November2018;Accepted:27November2018;Published:3December2018
Abstract: Inthispaper,tocombinesinglevaluedneutrosophicsets(SVNSs)withcovering-based roughsets,weproposetwotypesofsinglevaluedneutrosophic(SVN)coveringroughsetmodels. Furthermore,acorrespondingapplicationtotheproblemofdecisionmakingispresented.Firstly, thenotionofSVN β-coveringapproximationspaceisproposed,andsomeconceptsandproperties initareinvestigated.Secondly,basedonSVN β-coveringapproximationspaces,twotypesofSVN coveringroughsetmodelsareproposed.Then,somepropertiesandthematrixrepresentationsofthe newlydefinedSVNcoveringapproximationoperatorsareinvestigated.Finally,weproposeanovel methodtodecisionmaking(DM)problemsbasedononeoftheSVNcoveringroughsetmodels. Moreover,theproposedDMmethodiscomparedwithothermethodsinanexample.
Keywords: covering;singlevaluedneutrosophic;matrixrepresentation;decisionmaking
1.Introduction
Roughsettheory,asaatooltodealwithvarioustypesofdataindatamining,wasproposed byPawlak[1,2]in1982.Sincethen,roughsettheoryhasbeenextendedtogeneralizedroughsets basedonothernotionssuchasbinaryrelations,neighborhoodsystemsandcoverings.
Covering-basedroughsets[3–5]wereproposedtodealwiththetypeofcoveringdata. Inapplication,theyhavebeenappliedtoknowledgereduction[6,7],decisionrulesynthesis[8,9], andotherfields[10–12].Intheory,covering-basedroughsettheoryhasbeenconnectedwithmatroid theory[13–16],latticetheory[17,18]andfuzzysettheory[19–22].
Zadeh’sfuzzysettheory[23]addressestheproblemofhowtounderstandandmanipulate imperfectknowledge.Ithasbeenusedinvariousapplications[24–27].Recentinvestigationshave attractedmoreattentiononcombiningcovering-basedroughsetandfuzzysettheories.Thereare manyfuzzycoveringroughsetmodelsproposedbyresearchers,suchasMa[28]andYangetal.[20].
Wangetal.[29]presentedsinglevaluedneutrosophicsets(SVNSs)whichcanberegardedas anextensionofIFSs[30].Neutrosophicsetsandroughsetsbothcandealwithpartialanduncertain information.Therefore,itisnecessarytocombinethem.Recently,MondalandPramanik[31]presented theconceptofroughneutrosophicset.Yangetal.[32]presentedaSVNroughsetmodelbasedon SVNrelations.However,SVNSsandcovering-basedroughsetshavenotbeencombineduptonow. Inthispaper,wepresenttwotypesofSVNcoveringroughsetmodels.Thisnewcombinationisa bridge,linkingSVNSsandcovering-basedroughsets.
Asweknow,themultiplecriteriadecisionmaking(MCDM)isanimportanttooltodealwithmore complicatedproblemsinourrealworld[33,34].TherearemanyMCDMmethodspresentedbasedon differentproblemsortheories.Forexample,Liuetal.[35]dealtwiththechallengesofmanycriteriain theMCDMproblemanddecisionmakerswithheterogeneousriskpreferences.Watróbskietal.[36]
Symmetry 2018, 10,710;doi:10.3390/sym10120710
www.mdpi.com/journal/symmetry

proposedaframeworkforselectingsuitableMCDAmethodsforaparticulardecisionsituation. Faizietal.[37,38]presentedanextensionoftheMCDMmethodbasedonhesitantfuzzytheory. Recently,manyresearchershavestudieddecisionmaking(DM)problemsbyroughsetmodels[39–42]. Forexample,Zhanetal.[39]appliedatypeofsoftroughmodeltoDMproblems. Yangetal.[32] presentedamethodforDMproblemsunderatypeofSVNroughsetmodel.Byinvestigation, wehaveobservedthatnoonehasappliedSVNcoveringroughsetmodelstoDMproblems.Therefore, weconstructthecoveringSVNdecisioninformationsystemsaccordingtothecharacterizationsof DMproblems.Then,wepresentanovelmethodtoDMproblemsunderoneoftheSVNcovering roughsetmodels.Moreover,theproposeddecisionmakingmethodiscomparedwithothermethods, whichwerepresentedbyYangetal.[32],Liu[43]andYe[44].
Therestofthispaperisorganizedasfollows.Section 2 reviewssomefundamentaldefinitions aboutcovering-basedroughsetsandSVNSs.InSection 3,somenotionsandpropertiesinSVN β-coveringapproximationspacearestudied.InSection 4,wepresenttwotypesofSVNcoveringrough setmodels,basedontheSVN β-neighborhoodsandthe β-neighborhoods.InSection 5,somenew matricesandmatrixoperationsarepresented.Basedonthis,thematrixrepresentationsoftheSVN approximationoperatorsareshown.InSection 6,anovelmethodtodecisionmaking(DM)problems underoneoftheSVNcoveringroughsetmodelsisproposed.Moreover,theproposedDMmethodis comparedwithothermethods.ThispaperisconcludedandfurtherworkisindicatedinSection 7.
2.BasicDefinitions
Suppose U isanonemptyandfinitesetcalleduniverse.
Definition1 (Covering[45,46]). Let U beauniverseand C afamilyofsubsetsof U.Ifnoneofsubsetsin C is emptyand C = U,then C iscalledacoveringofU.
Thepair (U, C) iscalledacoveringapproximationspace.
Definition2 (Singlevaluedneutrosophicset[29]). Let U beanonemptyfixedset.Asinglevalued neutrosophicset(SVNS)AinUisdefinedasanobjectofthefollowingform: A = { x, TA (x), IA (x), FA (x) : x ∈ U},
where TA (x) : U → [0,1] isatruth-membershipfunction, IA (x) : U → [0,1] isanindeterminacy-membership functionand FA (x) : U → [0,1] isafalsity-membershipfunctionforany x ∈ U.Theysatisfy 0 ≤ TA (x)+ IA (x)+ FA (x) ≤ 3 forall x ∈ U.Thefamilyofallsinglevaluedneutrosophicsetsin U isdenotedby SVN(U) Forconvenience,aSVNnumberisrepresentedby α = a, b, c ,wherea, b, c ∈ [0,1] anda + b + c ≤ 3 Specially,fortwoSVNnumbers α = a, b, c and β = d, e, f , α ≤ β ⇔ a ≤ d, b ≥ e and c ≥ f Someoperationson SVN(U) arelistedasfollows[29,32]:forany A, B ∈ SVN(U),
3.SingleValuedNeutrosophic β-CoveringApproximationSpace
Inthissection,wepresentthenotionofSVN β-coveringapproximationspace.Therearetwo basicconceptsinthisnewapproximationspace:SVN β-coveringandSVN β-neighborhood.Then, someoftheirpropertiesarestudied.
Definition3. Let U beauniverseand SVN(U) betheSVNpowersetof U.ForaSVNnumber β = a, b, c , wecall C = {C1, C2, , Cm },with Ci ∈ SVN(U)(i = 1,2,..., m),aSVN β-coveringof U,ifforall x ∈ U, Ci ∈ C existssuchthatCi (x) ≥ β.Wealsocall (U, C) aSVN β-coveringapproximationspace.
Definition4. Let C beaSVN β-coveringof U and C = {C1, C2, , Cm }.Forany x ∈ U,theSVN β-neighborhood Nβ x ofxinducedby C canbedefinedas: Nβ x = ∩{Ci ∈ C : Ci (x) ≥ β}.(1) Notethat Ci (x) isaSVNnumber TCi (x), ICi (x), FCi (x) inDefinitions 3 and 4.Hence, Ci (x) ≥ β means TCi (x) ≥ a, ICi (x) ≤ b and FCi (x) ≤ c whereSVNnumber β = a, b, c .
Remark1. Let C beaSVN β-coveringofU, β = a, b, c and C = {C1, C2,..., Cm }.Foranyx ∈ U, Nβ x = ∩{Ci ∈ C : TCi (x) ≥ a, ICi (x) ≤ b, FCi (x) ≤ c}.(2)
Example1. Let U = {x1, x2, x3, x4, x5}, C = {C1, C2, C3, C4} and β = 0.5,0.3,0.8 .Wecanseethat C is aSVN β-coveringofUinTable 1.
Table1. Thetabularrepresentationofsinglevaluedneutrosophic(SVN) β-covering C UC1 C2 C3 C4 x1 0.7,0.2,0.5 0.6,0.2,0.4 0.4,0.1,0.5 0.1,0.5,0.6 x2 0.5,0.3,0.2 0.5,0.2,0.8 0.4,0.5,0.4 0.6,0.1,0.7 x3 0.4,0.5,0.2 0.2,0.3,0.6 0.5,0.2,0.4 0.6,0.3,0.4 x4 0.6,0.1,0.7 0.4,0.5,0.7 0.3,0.6,0.5 0.5,0.3,0.2 x5 0.3,0.2,0.6 0.7,0.3,0.5 0.6,0.3,0.5 0.8,0.1,0.2 Then, Nβ x1 = C1 ∩ C2, Nβ x2 = C1 ∩ C2 ∩ C4, Nβ x3 = C3 ∩ C4, Nβ x4 = C1 ∩ C4, Nβ x5 = C2 ∩ C3 ∩ C4.
Hence,allSVN β-neighborhoodsareshowninTable 2. Table2. Thetabularrepresentationof Nβ xk (k = 1,2,3,4,5).
Nβ xk x1 x2 x3 x4 x5
Nβ x1 0.6,0.2,0.5 0.5,0.3,0.8 0.2,0.5,0.6 0.4,0.5,0.7 0.3,0.3,0.6 Nβ x2 0.1,0.5,0.6 0.5,0.3,0.8 0.2,0.5,0.6 0.4,0.5,0.7 0.3,0.3,0.6
Nβ x3 0.1,0.5,0.6 0.4,0.5,0.7 0.5,0.3,0.4 0.3,0.6,0.5 0.6,0.3,0.5
Nβ x4 0.1,0.5,0.6 0.5,0.3,0.7 0.4,0.5,0.4 0.5,0.3,0.7 0.3,0.2,0.6
Nβ x5 0.1,0.5,0.6 0.4,0.5,0.8 0.2,0.3,0.6 0.3,0.6,0.7 0.6,0.3,0.5
Proof.
(1) Forany x ∈ U, Nβ x (x)=( Ci (x)≥β Ci )(x)= Ci (x)≥β Ci (x) ≥ β
(2) Let I = {1,2, , m}.Since Nβ x (y) ≥ β,forany i ∈ I,if Ci (x) ≥ β,then Ci (y) ≥ β. Since Nβ y (z) ≥ β, forany i ∈ I, Ci (z) ≥ β when Ci (y) ≥ β.Then,forany i ∈ I, Ci (x) ≥ β implies Ci (z) ≥ β. Therefore, Nβ x (z) ≥ β (3) Forall x ∈ U,since β1 ≤ β2 ≤ β, {Ci ∈ C : Ci (x) ≥ β1}⊇{Ci ∈ C : Ci (x) ≥ β2}.Hence, Nβ1 x = ∩{Ci ∈ C : Ci (x) ≥ β1}⊆∩{Ci ∈ C : Ci (x) ≥ β2} = Nβ2 x forall x ∈ U.
Proposition1. Let C beaSVN β-coveringofU.Foranyx, y ∈ U, Nβ x (y) ≥ β ifandonlyif Nβ y ⊆ Nβ x Proof. SupposetheSVNnumber β = a, b, c (⇒):Since Nβ x (y) ≥ β, T Nβ x (y)= T TCi (x)≥a ICi (x)≤b FCi (x)≤c
Ci (y)= TCi (x)≥a ICi (x)≤b FCi (x)≤c
TCi (y) ≥ a, I Nβ x (y)= I TCi (x)≥a ICi (x)≤c FCi (x)≤b
F Nβ x (y)= F TCi (x)≥a ICi (x)≤c FCi (x)≤b
Ci (y)= TCi (x)≥a ICi (x)≤b FCi (x)≤c
Ci (y)= TCi (x)≥a ICi (x)≤b FCi (x)≤c
ICi (y) ≤ b, and
FCi (y) ≤ c.
Then, {Ci ∈ C : TCi (x) ≥ a, ICi (x) ≤ b, FCi (x) ≤ c}⊆{Ci ∈ C : TCi (y) ≥ a, ICi (y) ≤ b, FCi (y) ≤ c} Therefore,foreach z ∈ U,
T Nβ x (z)= TCi (x)≥a ICi (x)≤b FCi (x)≤c
I Nβ x (z)= TCi (x)≥a ICi (x)≤b FCi (x)≤c
F Nβ x (z)= TCi (x)≥a ICi (x)≤b FCi (x)≤c
TCi (z) ≥ TCi (y)≥a ICi (y)≤b FCi (y)≤c
ICi (z) ≤ TCi (y)≥a ICi (y)≤b FCi (y)≤c
FCi (z) ≤ TCi (y)≥a ICi (y)≤b FCi (y)≤c
TCi (z)= T Nβ y (z),
ICi (z)= I Nβ y (z),
FCi (z)= F Nβ y (z)
Hence, Nβ y ⊆ Nβ x (⇐):Forany x, y ∈ U,since Nβ y ⊆ Nβ x , T Nβ x (y) ≥ T Nβ y (y) ≥ a, I Nβ x (y) ≤ I Nβ y (y) ≤ b and F Nβ x (y) ≤ F N β y (y) ≤ c
Therefore, Nβ x (y) ≥ β ThenotionofSVN β-neighborhoodintheSVN β-coveringapproximationspaceinthe followingdefinition.
Definition5. Let (U, C) beaSVN β-coveringapproximationspaceand C = {C1, C2,..., Cm}.Foreachx ∈ U, wedefinethe β-neighborhood Nβ x ofxas: Nβ x = {y ∈ U : Nβ x (y) ≥ β}.(3) Notethat Nβ x (y) isaSVNnumber T Nβ x (y), I Nβ x (y), F Nβ x (y) inDefinition 5
Remark2. Let C beaSVN β-coveringofU, β = a, b, c and C = {C1, C2,..., Cm }.Foreachx ∈ U, Nβ x = {y ∈ U : T Nβ x (y) ≥ a, I Nβ x (y) ≤ b, F Nβ x (y) ≤ c}.(4)
Example2 (ContinuedfromExample 1). Let β = 0.5,0.3,0.8 ,thenwehave Nβ x1 = {x1, x2}, Nβ x2 = {x2}, Nβ x3 = {x3, x5}, Nβ x4 = {x2, x4}, Nβ x5 = {x5}
Somepropertiesofthe β-neighborhoodinaSVN β-coveringof U arepresentedinTheorem 2 and Proposition 2
Theorem2. Let C beaSVN β-coveringof U and C = {C1, C2, , Cm }.Then,thefollowingstatementshold:
(1) x ∈ Nβ x foreachx ∈ U. (2) ∀x, y, z ∈ U,ifx ∈ Nβ y ,y ∈ Nβ z ,thenx ∈ Nβ z . Proof. (1) AccordingtoTheorem 1 andDefinition 5,itisstraightforward. (2) Forany x, y, z ∈ U, x ∈ Nβ y ⇔ Nβ y (x) ≥ β ⇔ Nβ x ⊆ Nβ y ,and y ∈ Nβ z ⇔ Nβ z (y) ≥ β ⇔ Nβ y ⊆ Nβ z Hence, Nβ x ⊆ Nβ z .ByProposition 1,wehave Nβ z (x) ≥ β,i.e., x ∈ Nβ z
Proposition2. Let C beaSVN β-coveringof U and C = {C1, C2, ... , Cm }.Then,forall x ∈ U, x ∈ Nβ y ifandonlyif Nβ x ⊆ Nβ y Proof. (⇒):Forany z ∈ Nβ x ,weknow Nβ x (z) ≥ β.Since x ∈ Nβ y , Nβ y (x) ≥ β.Accordingto (2) in Theorem 1,wehave Nβ y (z) ≥ β.Hence, z ∈ Nβ y .Therefore, Nβ x ⊆ Nβ y (⇐):Accordingto (1) inTheorem 2, x ∈ Nβ x forall x ∈ U.Since Nβ x ⊆ Nβ y , x ∈ Nβ y
TherelationshipbetweenSVN β-neighborhoodsand β-neighborhoodsispresentedinthe followingproposition.
Proposition3. Let C beaSVN β-coveringofU.Foranyx, y ∈ U, Nβ x ⊆ Nβ y ifandonlyif Nβ x ⊆ Nβ y . Proof. AccordingtoPropositions 1 and 2,itisstraightforward.
4.TwoTypesofSingleValuedNeutrosophicCoveringRoughSetModels
Inthissection,weproposetwotypesofSVNcoveringroughsetmodelsonbasisoftheSVN β-neighborhoodsandthe β-neighborhoods,respectively.Then,weinvestigatethepropertiesofthe definedlowerandupperapproximationoperators.
Definition6. Let (U, C) beaSVN β-coveringapproximationspace.Foreach A ∈ SVN(U) where A = { x, TA (x), IA (x), FA (x) : x ∈ U},wedefinethesinglevaluedneutrosophic(SVN)coveringupper approximation C(A) andlowerapproximation C ∼ (A) ofAas: C(A)= { x, ∨y∈U [T Nβ x (y) ∧ TA(y)], ∨y∈U [I Nβ x (y) ∧ IA(y)], ∧y∈U [F Nβ x (y) ∨ FA(y)] : x ∈ U}, C ∼ (A)= { x, ∧y∈U [F Nβ x (y) ∨ TA(y)], ∧y∈U [(1 I Nβ x (y)) ∨ IA(y)], ∨y∈U [T Nβ x (y) ∧ FA(y)] : x ∈ U} (5)
If C(A) = C ∼ (A),then A iscalledthefirsttypeofSVNcoveringroughset. Example3 (ContinuedfromExample 1). Let β = 0.5,0.3,0.8 , A = (0.6,0.3,0.5) x1 + (0.4,0.5,0.1) x2 + (0.3,0.2,0.6) x3 + (0.5,0.3,0.4) x4 + (0.7,0.2,0.3) x5 .Then, C(A)= { x1,0.6,0.3,0.5 , x2,0.4,0.3,0.6 , x3,0.6,0.5,0.5 , x4,0.5,0.3,0.6 , x5,0.6,0.5,0.5 }, C ∼ (A)= { x1,0.6,0.5,0.5 , x2,0.6,0.5,0.4 , x3,0.4,0.4,0.5 , x4,0.4,0.5,0.4 , x5,0.6,0.4,0.3 }
SomebasicpropertiesoftheSVNcoveringupperandlowerapproximationoperatorsare proposedinthefollowingproposition.
Proposition4. Let C beaSVN β-coveringof U.Then,theSVNcoveringupperandlowerapproximation operatorsinDefinition 6 satisfythefollowingproperties:forallA, B ∈ SVN(U),
(1) C(A )=(C ∼ (A)) , C ∼ (A )=(C(A)) . (2) IfA ⊆ B,then C ∼ (A) ⊆ C ∼ (B), C(A) ⊆ C(B) (3) C ∼ (A B)= C ∼ (A) C ∼ (B), C(A B)= C(A) C(B). (4) C ∼ (A B) ⊇ C ∼ (A) C ∼ (B), C(A B) ⊆ C(A) C(B)
Proof. (1) C(A )= { x, ∨y∈U [TNβ x (y) ∧ TA (y)], ∨y∈U [INβ x (y) ∧ IA (y)], ∧y∈U [FNβ x (y) ∨ FA (y)] : x ∈ U} = { x, ∨y∈U [TNβ x (y) ∧ FA (y)], ∨y∈U [INβ x (y) ∧ (1 IA (y))], ∧y∈U [FNβ x (y) ∨ TA (y)] : x ∈ U} =(C ∼ (A))
Ifwereplace A by A inthisproof,wecanalsoprove C ∼ (A )=(C(A)) (2) Since A ⊆ B,so TA (x) ≤ TB (x), IB (x) ≤ IA (x) and FB (x) ≤ FA (x) forall x ∈ U.Therefore, TC ∼ (A) (x)= ∧y∈U [FNβ x (y) ∨ TA (y)] ≤∧y∈U [FNβ x (y) ∨ TB (y)]= TC ∼ (B) (x), IC ∼ (A) (x)= ∧y∈U [(1 INβ x (y)) ∨ IA (y)] ≥∧y∈U [(1 INβ x (y)) ∨ IB (y)]= IC ∼ (B) (x), FC(A) (x)= ∨y∈U [TNβ x (y) ∧ FA (y)] ≥∨y∈U [TNβ x (y) ∧ FB (y)]= FC(B) (x).
Hence, C ∼ (A) ⊆ C ∼ (B).Inthesameway,thereis C(A) ⊆ C(B). (3) C ∼ (A B) = { x, ∧y∈U [FNβ x (y) ∨ TA B (y)], ∧y∈U [(1 INβ x (y)) ∨ IA B (y)], ∨y∈U [TNβ x (y) ∧ FA B (y)] : x ∈ U} = { x, ∧y∈U [FNβ x (y) ∨ (TA (y) ∧ TB (y))], ∧y∈U [(1 INβ x (y)) ∨ (IA (y) ∨ IB (y))], ∨y∈U [TNβ x (y) ∧ (FA (y) ∨FB (y))] : x ∈ U}
= { x, ∧y∈U [(FNβ x (y) ∨ TA (y)) ∧ (FNβ x (y) ∨ TB (y))], ∧y∈U [((1 INβ x (y)) ∨ IA (y)) ∨ (1 INβ x (y))∨ IB (y))], ∨y∈U [(TNβ x (y) ∧ FA (y)) ∨ (TNβ x (y) ∧ FB (y))] : x ∈ U} = C ∼ (A) C ∼ (B) Similarly,wecanobtain C(A B)= C(A) C(B) (4) Since A ⊆ A ∪ B, B ⊆ A ∪ B, A ∩ B ⊆ A and A ∩ B ⊆ B, C ∼ (A) ⊆ C ∼ (A ∪ B), C ∼ (B) ⊆ C ∼ (A ∪ B), C(A ∩ B) ⊆ C(A) and C(A ∩ B) ⊆ C(B)
Hence, C ∼ (A B) ⊇ C ∼ (A) C ∼ (B), C(A B) ⊆ C(A) C(B)
WeproposetheotherSVNcoveringroughsetmodel,whichconcernsthecrisplowerandupper approximationsofeachcrispsetintheSVNenvironment.
Definition7. Let (U, C) beaSVN β-coveringapproximationspace.Foreachcrispsubset X ∈ P(U) (P(U) is thepowersetof U),wedefinetheSVNcoveringupperapproximation C(X) andlowerapproximation C(X) of Xas:
C(X)= {x ∈ U : Nβ x ∩ X = ∅}, C(X)= {x ∈ U : Nβ x ⊆ X}. (6)
If C(X) = C(X),then X iscalledthesecondtypeofSVNcoveringroughset.
Example4 (ContinuedfromExample 2). Let β = 0.5,0.3,0.8 ,X = {x1, x2},Y = {x2, x4, x5}.Then, C(X)= {x1, x2, x4}, C(X)= {x1, x2}, C(Y)= {x1, x2, x3, x4, x5}, C(Y)= {x2, x4, x5}, C(U)= U, C(U)= U, C(∅)= ∅, C(∅)= ∅.
Proposition5. Let C beaSVN β-coveringof U.Then,theSVNcoveringupperandlowerapproximation operatorsinDefinition 7 satisfythefollowingproperties:forallX, Y ∈ P(U),
5.MatrixRepresentationsofTheseSingleValuedNeutrosophicCoveringRoughSetModels
Inthissection,matrixrepresentationsoftheproposedSVNcoveringroughsetmodelsare investigated.Firstly,somenewmatricesandmatrixoperationsarepresented.Then,weshow thematrixrepresentationsoftheseSVNapproximationoperatorsdefinedinDefinitions 6 and 7 Theorderofelementsin U isgiven. Definition8. Let C beaSVN β-coveringof U with U = {x1, x2, ··· , xn } and C = {C1, C2, ··· , Cm } Then, MC =(Cj (xi ))n×m isnamedamatrixrepresentationof C,and Mβ C =(sij )n×m iscalleda β-matrix representationof C,where sij = 1, Cj (xi ) ≥ β; 0, otherwise.
Proposition6. Let C beaSVN β-coveringof U with U = {x1, x2, ··· , xn } and C = {C1, C2, ··· , Cm }.Then Mβ C ∗ MT C =(Nβ xi (xj ))1≤i≤n,1≤j≤n,(8) whereMT C isthetransposeofMC.
Proof. Suppose MT C =(Ck (xj ))m×n, Mβ C =(sik )n×m and Mβ C ∗ MT C =( d+ ij , dij, dij )1≤i≤n,1≤j≤n Since C isaSVN β-coveringof U,foreach i (1 ≤ i ≤ n),thereexists k (1 ≤ k ≤ m)suchthat sik = 1.Then, d+ ij , dij, dij = ∧m k=1[(1 sik ) ∨ TCk (xj )],1 −∧m k=1[(1 sik ) ∨ (1 ICk (xj ))],1 −∧m k=1[(1 sik ) ∨ (1 FCk (xj ))] = ∧sik =1[(1 sik ) ∨ TCk (xj )],1 −∧sik =1[(1 sik ) ∨ (1 ICk (xj ))],1 −∧sik =1[(1 sik ) ∨ (1 FCk (xj ))] = ∧sik =1 TCk (xj ),1 −∧sik =1(1 ICk (xj )),1 −∧sik =1(1 FCk (xj )) = ∧Ck (xi )≥β TCk (xj ),1 −∧Ck (xi )≥β (1 ICk (xj )),1 −∧Ck (xi )≥β (1 FCk (xj )) =( Ck (xi )≥β Ck )(xj ) = Nβ xi (xj ),1 ≤ i, j ≤ n Hence, Mβ C ∗ MT C =(Nβ xi (xj ))1≤i≤n,1≤j≤n.
0.7,0.2,0.5 0.6,0.2,0.4 0.4,0.1,0.5 0.1,0.5,0.6 0.5,0.3,0.2 0.5,0.2,0.8 0.4,0.5,0.4 0.6,0.1,0.7 0.4,0.5,0.2 0.2,0.3,0.6 0.5,0.2,0.4 0.6,0.3,0.4 0.6,0.1,0.7 0.4,0.5,0.7 0.3,0.6,0.5 0.5,0.3,0.2 0.3,0.2,0.6 0.7,0.3,0.5 0.6,0.3,0.5 0.8,0.1,0.2
0.7,0.2,0.5 0.5,0.3,0.2 0.4,0.5,0.2 0.6,0.1,0.7 0.3,0.2,0.6 0.6,0.2,0.4 0.5,0.2,0.8 0.2,0.3,0.6 0.4,0.5,0.7 0.7,0.3,0.5 0.4,0.1,0.5 0.4,0.5,0.4 0.5,0.2,0.4 0.3,0.6,0.5 0.6,0.3,0.5 0.1,0.5,0.6 0.6,0.1,0.7 0.6,0.3,0.4 0.5,0.3,0.2 0.8,0.1,0.2
0.6,0.2,0.5 0.5,0.3,0.8 0.2,0.5,0.6 0.4,0.5,0.7 0.3,0.3,0.6 0.1,0.5,0.6 0.5,0.3,0.8 0.2,0.5,0.6 0.4,0.5,0.7 0.3,0.3,0.6 0.1,0.5,0.6 0.4,0.5,0.7 0.5,0.3,0.4 0.3,0.6,0.5 0.6,0.3,0.5 0.1,0.5,0.6 0.5,0.3,0.7 0.4,0.5,0.4 0.5,0.3,0.7 0.3,0.2,0.6 0.1,0.5,0.6 0.4,0.5,0.8 0.2,0.3,0.6 0.3,0.6,0.7 0.6,0.3,0.5
=(N β xi (xj ))1≤i≤5,1≤j≤5. Definition10. Let A =( c+ ij , cij, cij )m×n and B =( d+ j , dj, dj )n×1 betwomatrices.Wedefine C = A ◦ B =( e+ i , ei, ei )m×1 andD = A B =( f + i , fi, fi )m×1,where e+ i , ei, ei = ∨n j=1(c+ ij ∧ d+ j ), ∨n j=1(cij ∧ dj ), ∧n j=1(cij ∨ dj ) , f + i , fi, fi = ∧n j=1(cij ∨ d+ j ), ∧n j=1[(1 cij ) ∨ dj ], ∨n j=1(c+ ij ∧ dj ) (9)
AccordingtoProposition 6 andDefinition 10,thesetrepresentationsof C(A) and C ∼ (A) (forany A ∈ SVN(U))canbeconvertedtomatrixrepresentations.
Theorem3. Let C beaSVN β-coveringof U with U = {x1, x2, , xn } and C = {C1, C2, , Cm }.Then, foranyA ∈ SVN(U), C(A)=(Mβ C ∗ MT C ) ◦ A, C ∼ (A)=(Mβ C ∗ MT C ) A, (10) where A =(ai )n×1 with ai = TA (xi ), IA (xi ), FA (xi ) isthevectorrepresentationoftheSVNS A C(A) and C ∼ (A) arealsovectorrepresentations.
Proof. AccordingtoProposition 6 andDefinitions 6 and 10,forany xi (i = 1,2, , n), ((Mβ C ∗ MT C) ◦ A)(xi )= ∨n j=1(T Nβ xi (xj ) ∧ TA (xj )), ∨n j=1(I Nβ xi (xj ) ∧ IA (xj )), ∧n j=1(F Nβ xi (xj ) ∨ FA (xj )) =(C(A))(xi ), and ((Mβ C ∗ MT C) A)(xi )= ∧n j=1(FNβ xi (xj ) ∨ TA (xj )), ∧n j=1[(1 INβ xi (xj )) ∨ IA (xj )], ∨n j=1(TNβ xi (xj ) ∧ FA (xj )) =(C ∼ (A))(xi ) Hence, C(A)=(Mβ C ∗ MT C) ◦ A, C ∼ (A)=(Mβ C ∗ MT C) A
Example7 (ContinuedfromExample 3). Let β = 0.5,0.3,0.8 , A = (0.6,0.3,0.5) x1 + (0.4,0.5,0.1) x2 + (0.3,0.2,0.6) x3 + (0.5,0.3,0.4) x4 + (0.7,0.2,0.3) x5 .Then,
0.6,0.2,0.5 0.5,0.3,0.8 0.2,0.5,0.6 0.4,0.5,0.7 0.3,0.3,0.6 0.1,0.5,0.6 0.5,0.3,0.8 0.2,0.5,0.6 0.4,0.5,0.7 0.3,0.3,0.6 0.1,0.5,0.6 0.4,0.5,0.7 0.5,0.3,0.4 0.3,0.6,0.5 0.6,0.3,0.5 0.1,0.5,0.6 0.5,0.3,0.7 0.4,0.5,0.4 0.5,0.3,0.7 0.3,0.2,0.6 0.1,0.5,0.6 0.4,0.5,0.8 0.2,0.3,0.6 0.3,0.6,0.7 0.6,0.3,0.5
0.6,0.3,0.5 0.4,0.3,0.6 0.6,0.5,0.5 0.5,0.3,0.6 0.6,0.5,0.5
0.6,0.2,0.5 0.5,0.3,0.8 0.2,0.5,0.6 0.4,0.5,0.7 0.3,0.3,0.6 0.1,0.5,0.6 0.5,0.3,0.8 0.2,0.5,0.6 0.4,0.5,0.7 0.3,0.3,0.6 0.1,0.5,0.6 0.4,0.5,0.7 0.5,0.3,0.4 0.3,0.6,0.5 0.6,0.3,0.5 0.1,0.5,0.6 0.5,0.3,0.7 0.4,0.5,0.4 0.5,0.3,0.7 0.3,0.2,0.6 0.1,0.5,0.6 0.4,0.5,0.8 0.2,0.3,0.6 0.3,0.6,0.7 0.6,0.3,0.5
0.6,0.5,0.5 0.6,0.5,0.4 0.4,0.4,0.5 0.4,0.5,0.6 0.6,0.4,0.3
0.6,0.3,0.5 0.4,0.5,0.1 0.3,0.2,0.6 0.5,0.3,0.4 0.7,0.2,0.3
0.6,0.3,0.5 0.4,0.5,0.1 0.3,0.2,0.6 0.5,0.3,0.4 0.7,0.2,0.3
representationsof C(X) and C(X) ofeverycrispsubset X ∈ P(U). Definition11 ([28]). Let A =(aik )n×m and B =(bkj )m×l betwomatrices.Wedefine C = A B =(cij )n×l andD = A B =(dij )n×l asfollows: cij = ∨m k=1(aik ∧ bkj ), dij = ∧m k=1[(1 aik ) ∨ bkj ], foranyi = 1,2, , n, andj = 1,2, , l (11) Let U = {x1, , xn } and X ∈ P(U).Then,thecharacteristicfunctionofthecrispsubset X is definedas χX ,where χX (xi )= 1, xi ∈ X; 0, otherwise
Proposition7. Let C beaSVN β-coveringofUwithU = {x1, x2, ··· , xn} and C = {C1, C2, ··· , Cm}.Then, Mβ C (Mβ C )T =(χNβ xi (xj ))1≤i≤n,1≤j≤n,(12)
Proof. Suppose Mβ C =(sik )n×m and Mβ C (Mβ C)T =(tij )n×n.Since C isaSVN β-coveringof U, foreach i (1 ≤ i ≤ n)thereexists k (1 ≤ k ≤ m)suchthat sik = 1.If tij = 1,then ∧m k=1[(1 sik ) ∨ sjk ]= 1
Itimpliesthatif sik = 1,then sjk = 1.Hence, Ck (xi ) ≥ β implies Ck (xj ) ≥ β.Therefore, xj ∈ Nβ xi , i.e., χNβ xi (xj )= 1 = tij If tij = 0,then ∧m k=1[(1 sik ) ∨ sjk ]= 0.Thisimpliesthatif sik = 1,then sjk = 0.Hence, Ck (xi ) ≥ β implies Ck (xj ) < β.Thus,wehave xj / ∈ Nβ xi ,i.e., χNβ xi (xj )= 1 = tij.
Example8 (ContinuedfromExample 2) AccordingtoMβ C inExample 5,wehavethefollowingresult. Mβ C (Mβ C )T =
=(χNβ xi (xj ))1≤i≤5,1≤j≤5.
Forany X ∈ P(U),wealsodenote χX =(ai )n×1 with ai = 1iff xi ∈ X;otherwise, ai = 0. Then,thesetrepresentationsof C(X) and C(X) (forany X ∈ P(U))canbeconvertedtomatrix representations.
Theorem4. Let C beaSVN β-coveringof U with U = {x1, x2, , xn } and C = {C1, C2, , Cm }.Then, foranyX ∈ P(U), χC(X) =(Mβ C (Mβ C )T ) · χX , χC(X) =(Mβ C (Mβ C )T ) χX . (13)
Proof. Suppose (Mβ C (Mβ C)T ) χX =(ai )n×1 and (Mβ C (Mβ C)T ) χX =(bi )n×1.Forany xi ∈ U (i = 1,2, , n), xi ∈ C(X) ⇔ χC(X) (xi )= 1
⇔ ai = 1
⇔∨n k=1[χNβ xi (xk ) ∧ χX (xk )]= 1
⇔∃k ∈{1,2, , n},s.t., χNβ xi (xk )= χX (xk )= 1
⇔∃k ∈{1,2, , n},s.t., xk ∈ Nβ xi ∩ X
⇔ Nβ xi ∩ X = ∅, and
xi ∈ C(X) ⇔ χC(X) (xi )= 1
⇔ bi = 1
⇔∧n k=1[(1 χNβ xi (xk )) ∨ χX (xk )]= 1
⇔ χNβ xi (xk )= 1 → χX (xk )= 1, k = 1,2, , n
⇔ xk ∈ Nβ xi → xk ∈ X, k = 1,2, ··· , n
⇔ Nβ xi ⊆ X
6.AnApplicationtoDecisionMakingProblems
Inthissection,wepresentanovelapproachtoDMproblemsbasedontheSVNcoveringrough setmodel.Then,acomparativestudywithothermethodsisshown.
6.1.TheProblemofDecisionMaking
Let U = {xk : k = 1,2, ··· , l} bethesetofpatientsand V = {yi |i = 1,2, ··· , m} bethe m main symptoms(forexample,cough,fever,andsoon)foraDisease B.AssumethatDoctor R evaluates everyPatient xk (k = 1,2, ··· , l). AssumethatDoctor R believeseachPatient xk ∈ U (k = 1,2, ··· , l)hasasymptomvalue Ci (i = 1,2, ··· , m),denotedby Ci (xk )= TCi (xk ), ICi (xk, FCi (xk ) ,where TCi (xk ) ∈ [0,1] isthedegree thatDoctor R confirmsPatient xk hassymptom yi, ICi (xk ) ∈ [0,1] isthedegreethatDoctor R isnot surePatient xk hassymptom yi, FCi (xk ) ∈ [0,1] isthedegreethatDoctor R confirmsPatient xk doesnot havesymptom yi,and TCi (xk )+ ICi (xk )+ FCi (xk ) ≤ 3.
Let β = a, b, c bethecriticalvalue.IfanyPatient xk ∈ U,thereisatleastonesymptom yi ∈ V suchthatthesymptomvalue Ci forPatient xk isnotlessthan β,respectively,then C = {C1, C2, , Cm } isaSVN β-coveringof U forsomeSVNnumber β.
If d isapossibledegree, e isanindeterminacydegreeand f isanimpossibledegreeofDisease B of everyPatient xk ∈ U thatisdiagnosedbyDoctor R,denotedby A(xk )= d, e, f ,thenthedecision maker(Doctor R)forthedecisionmakingproblemneedstoknowhowtoevaluatewhetherPatients xk ∈ U haveDisease B.
6.2.TheDecisionMakingAlgorithm
Inthissubsection,wegiveanapproachfortheproblemofDMwiththeabovecharacterizations bymeansofthefirsttypeofSVNcoveringroughsetmodel.Accordingtothecharacterizationsof theDMprobleminSection 6.1,weconstructtheSVNdecisioninformationsystemandpresentthe Algorithm 1 ofDMundertheframeworkofthefirsttypeofSVNcoveringroughsetmodel.
Algorithm1 ThedecisionmakingalgorithmbasedontheSVNcoveringroughsetmodel.
Input:SVNdecisioninformationsystem(U, C, β, A). Output:Thescoreorderingforallalternatives.
1: ComputetheSVN β-neighborhood Nβ x of x inducedby C,forall x ∈ U accordingtoDefinition 4; 2: ComputetheSVNcoveringupperapproximation C(A) andlowerapproximation C ∼ (A) of A, accordingtoDefinition 6; 3: Compute RA = C(A) ⊕ C ∼ (A) accordingto (6) inthebasicoperationson SVN(U); 4: Compute s(x)= TRA (x) (TRA (x))2+(IRA (x))2+(FRA (x))2 ; 5: Rankallthealternatives s(x) byusingtheprincipleofnumericalsizeandselectthemost possiblepatient.
Accordingtotheaboveprocess,wecangetthedecisionmakingaccordingtotheranking.InStep 4, S(x) isthecosinesimilaritymeasurebetween RA (x) andtheidealsolution (1,0,0),whichwas proposedbyYe[44].
6.3.AnAppliedExample
Example10. Assumethat U = {x1, x2, x3, x4, x5} isasetofpatients.Accordingtothepatients’symptoms, wewrite V = {y1, y2, y3, y4} tobefourmainsymptoms(cough,fever,soreandheadache)forDisease B. AssumethatDoctorRevaluateseveryPatientxk (k = 1,2, ,5)asshowninTable 1.
Let β = 0.5,0.3,0.8 bethecriticalvalue.Then, C = {C1, C2, C3, C4} isaSVN β-coveringsof U Nβ xk (k = 1,2,3,4,5)areshowninTable 2
AssumethatDoctorRdiagnosesthevalueA = (0.6,0.3,0.5) x1 + (0.4,0.5,0.1) x2 + (0.3,0.2,0.6) x3 + (0.5,0.3,0.4) x4 + (0.7,0.2,0.3) x5 of DiseaseBofeverypatient.Then, C(A)= { x1,0.6,0.3,0.5 , x2,0.4,0.3,0.6 , x3,0.6,0.5,0.5 , x4,0.5,0.3,0.6 , x5,0.6,0.5,0.5 }, C ∼ (A)= { x1,0.6,0.5,0.5 , x2,0.6,0.5,0.4 , x3,0.4,0.4,0.5 , x4,0.4,0.5,0.4 , x5,0.6,0.4,0.3 } Then, RA = C(A) ⊕ C ∼ (A) = { x1,0.84,0.15,0.25 , x2,0.76,0.15,0.24 , x3,0.76,0.2,0.25 , x4,0.7,0.15,0.24 , x5,0.84,0.2,0.15 }
Hence,wecanobtains(xk ) (k = 1,2, ··· ,5)inTable 3
Table3. s(xk ) (k = 1,2, ,5). Ux1 x2 x3 x4 x5 s(xk ) 0.9450.9370.9220.9090.958
Accordingtotheprincipleofnumericalsize,wehave: s(x4) < s(x3) < s(x2) < s(x1) < s(x5).
Therefore,DoctorRdiagnosesPatientx5 asmorelikelytobesickwithDiseaseB.
6.4.AComparisonAnalysis
Tovalidatethefeasibilityoftheproposeddecisionmakingmethod,acomparativestudywas conductedwithothermethods.Thesemethods,whichwereintroducedbyLiu[43],Yangetal.[32] andYe[44],arecomparedwiththeproposedapproachusingSVNinformationsystem.
6.4.1.TheResultsofLiu’sMethod
Liu’smethodisshowninAlgorithm 2. Algorithm2 Thedecisionmakingalgorithm[43]. Input:ASVNdecisionmatrix D,aweightvector w and γ Output:Thescoreorderingforallalternatives.
1: Compute nk = Tnk , Ink , Fnk = HSVNNWA(nk1, nk2, , nkm ) =
m ∏ i 1 (1+(γ 1)Tki )wi m ∏ i 1 (1 Tki )wi m ∏ i=1 (1+(γ 1)Tki )wi +(γ 1) m ∏ i=1 (1 Tki )wi , γ m ∏ i 1 Iwi ki m ∏ i=1 (1+(γ 1)(1 Iki ))wi +(γ 1) m ∏ i=1 Iwi ki , γ m ∏ i 1 Fwi ki m ∏ i 1 (1+(γ 1)(1 Fki ))wi +(γ 1) m ∏ i 1 Fwi ki (k = 1,2, , l);
2: Calculate s(nk )= Tnk T2 nk +I2 nk +F2 nk ; 3: Obtaintherankingforall s(nk ) byusingtheprincipleofnumericalsizeandselectthemost possiblepatient.
Then,Algorithm 2 canbeusedforExample 10.Let nki = Tki, Iki, Fki betheevaluation informationof xk on Ci inTable 1.Thatistosay,Table 1 istheSVNdecisionmatrix D.Wesupposethe weightvectorofthecriteriais w =(0.35,0,25,0.3,0.1) and γ = 1.
Step1:BasedonHSVNNWAoperator,weget n1 = 0.557,0.178,0.482 , n2 = 0.484,0.283,0.395 , n3 = 0.414,0.318,0.347 , n4 = 0.465,0.286,0.558 , n5 = 0.578,0.233,0.486
Step2:Weget
s(n1)= 0.735, s(n2)= 0.706, s(n3)= 0.660, s(n4)= 0.596, s(n5)= 0.734.
Step3:Accordingtothecosinesimilaritydegrees s(nk ) (k = 1,2, ,5),weobtain x4 < x3 < x2 < x5 < x1.
Therefore,Patient x1 ismorelikelytobesickwithDisease B.
6.4.2.TheResultsofYang’sMethod
Yang’smethodisshowninAlgorithm 3
Algorithm3 Thedecisionmakingalgorithm[32].
Input:AgeneralizedSVNapproximationspace(U, V, R), B ∈ SVN(V) Output:Thescoreorderingforallalternatives.
1: Calculatethelowerandupperapproximations R(B) and R(B); 2: Compute nxk =(R(B) R(B))(xk ) (k = 1,2, , l); 3: Compute s(nxk , n∗)= Tnxk Tn∗ +Inxk In∗ +Fnxk Fn∗ T2 nxk +I2 nxk +F2 nxk √(Tn∗ )2+(In∗ )2+(Fn∗ )2 (k = 1,2, , l), where n∗ = Tn∗ , In∗ , Fn∗ = 1,0,0 ; 4: Obtaintherankingforall s(nxk , n∗) byusingtheprincipleofnumericalsizeandselectthemost possiblepatient.
ForExample 10,wesupposeDisease B ∈ SVN(V) and B = (0.3,0.6,0.5) y1 + (0.7,0.2,0.1) y2 + (0.6,0.4,0.3) y3 + (0.8,0.4,0.5) y4 AccordingtoTable 1,thegeneralizedSVNapproximationspace(U, V, R)canbeobtainedinTable 4, where U = {x1, x2, x3, x4, x5} and V = {y1, y2, y3, y4} Table4. ThegeneralizedSVNapproximationspace(U, V, R). Rx1 x2 x3 x4 x5 y1 0.7,0.2,0.5 0.5,0.3,0.2 0.4,0.5,0.2 0.6,0.1,0.7 0.3,0.2,0.6 y2 0.6,0.2,0.4 0.5,0.2,0.8 0.2,0.3,0.6 0.4,0.5,0.7 0.7,0.3,0.5 y3 0.4,0.1,0.5 0.4,0.5,0.4 0.5,0.2,0.4 0.3,0.6,0.5 0.6,0.3,0.5 y4 0.1,0.5,0.6 0.6,0.1,0.7 0.6,0.3,0.4 0.5,0.3,0.2 0.8,0.1,0.2
Step1:Weget
R(B)= { x1,0.6,0.2,0.4 , x2,0.6,0.2,0.4 , x3,0.6,0.3,0.4 , x4,0.5,0.4,0.5 , x5,0.8,0.3,0.5 }, R(B)= { x1,0.5,0.6,0.5 , x2,0.3,0.6,0.5 , x3,0.3,0.5,0.5 , x4,0.6,0.6,0.5 , x5,0.6,0.6,0.5 }
Step2: R(B) R(B)= { x1,0.80,0.12,0.20 , x2,0.72,0.12,0.20 , x3,0.72,0.15,0.20 , x4,0.80,0.24,0.25 , x5,0.92,0.18,0.25 }
Step3:Let n∗ = 1,0,0 .Then, s(nx1 , n∗)= 0.960, s(nx2 , n∗)= 0.951, s(nx3 , n∗)= 0.945, s(nx4 , n∗)= 0.918, s(nx5 , n∗)= 0.948.
Step4: s(nx4 , n∗) < s(nx3 , n∗) < s(nx5 , n∗) < s(nx2 , n∗) < s(nx1 , n∗)
Therefore,Patient x1 ismorelikelytobesickwithDisease B. 6.4.3.TheResultsofYe’sMethods
Yepresentedtwomethods[44].Thus,Algorithms 4 and 5 arepresentedforExample 10
Algorithm4 Thedecisionmakingalgorithm[44].
Input:ASVNdecisionmatrix D andaweightvector w Output:Thescoreorderingforallalternatives.
1: Compute Wk (xk, A∗)= ∑m i=1 wi [aki a∗ i +bki b∗ i +cki c∗ i ] ∑m i=1 wi [a2 ki +b2 ki +c2 ki ] √∑m i=1 wi [(a∗ i )2+(b∗ i )2+(c∗ i )2] (k = 1,2, ··· , l), where α∗ i = a∗ i , b∗ i , c∗ i = 1,0,0 (i = 1,2, , m);
2: Obtaintherankingforall Wk (xk, A∗) byusingtheprincipleofnumericalsizeandselectthemost possiblepatient.
ForExample 10,Table 1 istheSVNdecisionmatrix D.Wesupposetheweightvectorofthe criteriais w =(0.35,0,25,0.3,0.1). Step1: W1(x1, A∗)= 0.677, W2(x2, A∗)= 0.608, W3(x3, A∗)= 0.580, W4(x4, A∗)= 0.511, W5(x5, A∗)= 0.666 Step2:Therankingorderof {x1, x2, , x5} is x4 < x3 < x2 < x5 < x1.Therefore,Patient x1 is morelikelytobesickwithDisease B
Algorithm5 Theotherdecisionmakingalgorithm[44]. Input:ASVNdecisionmatrix D andaweightvector w. Output:Thescoreorderingforallalternatives.
1: Compute Mk (xk, A∗)= ∑m i=1 wi aki a∗ i +bki b∗ i +cki c∗ i a2 ki +b2 ki +c2 ki √(a∗ i )2+(b∗ i )2+(c∗ i )2 (k = 1,2, , l), where α∗ i = a∗ i , b∗ i , c∗ i = 1,0,0 (i = 1,2, ··· , m); 2: Obtaintherankingforall Mk (xk, A∗) byusingtheprincipleofnumericalsizeandselectthemost possiblepatient.
ByAlgorithms 5,wehave:
Step1: M1(x1, A∗)= 0.676, M2(x2, A∗)= 0.637, M3(x3, A∗)= 0.581, M4(x4, A∗)= 0.521, M5(x5, A∗)= 0.654. Step2:Therankingorderof {x1, x2, ··· , x5} is x4 < x3 < x2 < x5 < x1.Therefore,Patient x1 is morelikelytobesickwithDisease B AllresultsareshowninTable 5,Figures 1 and 2 Table5. TheresultsutilizingthedifferentmethodsofExample 10
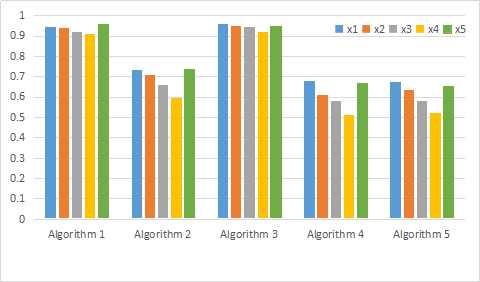
MethodsTheFinalRankingThePatientIsMostSickWiththeDisease B
Algorithm2inLiu[43] x4, x3, x2, x5, x1 x1
Algorithm3inYangetal.[32] x4, x3, x5, x2, x1 x1
Algorithm4inYe[44] x4, x3, x2, x5, x1 x1
Algorithm5inYe[44] x4, x3, x2, x5, x1 x1
Algorithm 1 inthispaper x4, x3, x2, x1, x5 x5
Figure1. ThefirstchatofdifferentvaluesofpatientinutilizingdifferentmethodsinExample 10
Figure2. ThesecondchatofdifferentvaluesofpatientinutilizingdifferentmethodsinExample 10
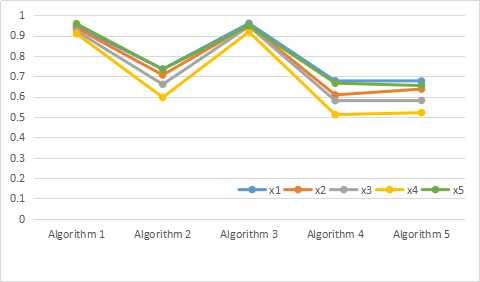
Liu[43]andYe[44]presentedthemethodsbySVNtheory.Intheirmethods,therankingorder wouldbechangedbydifferent w and γ.WeaswellasYangetal.[32]useddifferentroughsetmodelsto makethedecision.Yangetal.presentaSVNroughsetmodelbasedonSVNrelations,whilewe presentanewSVNroughsetmodelbasedoncoverings.TheresultsaredifferentbyYang’sandour methods,althoughthemethodsarebothbasedonanoperatorpresentedbyYe[44].
Inanymethod,iftherearemorethanonemostpossiblepatient,theneachpatientwillbethe optimaldecision.Inthiscase,weneedothermethodstomakeafurtherdecision.Bymeansofdifferent methods,theobtainedresultsmaybedifferent.Toachievethemostaccurateresults,furtherdiagnosis isnecessaryincombinationwithotherhybridmethods.
7.Conclusions
Thispaperisabridge,linkingSVNSsandcovering-basedroughsets.Byintroducingsome definitionsandpropertiesinSVN β-coveringapproximationspaces,wepresenttwotypesofSVN coveringroughsetmodels.Then,theircharacterizationsandmatrixrepresentationsareinvestigated. Moreover,anapplicationtotheproblemofDMisproposed.Themainconclusionsinthispaperand thefurtherworktodoarelistedasfollows.
1. TwotypesofSVNcoveringroughsetmodelsarefirstpresented,whichcombineSVNSswith covering-basedroughsets.Somedefinitionsandpropertiesincovering-basedroughsetmodel, suchascoveringsandneighborhoods,aregeneralizedtoSVNcoveringroughsetmodels.
Neutrosophicsetsandrelatedalgebraicstructures[47–49]willbeconnectedwiththeresearch contentofthispaperinfurtherresearch.
2. ItwouldbetediousandcomplicatedtousesetrepresentationstocalculateSVNcovering approximationoperators.Therefore,thematrixrepresentationsoftheseSVNcovering approximationoperatorsmakeitpossibletocalculatethemthroughthenewmatricesand matrixoperations.Bythesematrixrepresentations,calculationswillbecomealgorithmicand canbeeasilyimplementedbycomputers.
3. WeproposeamethodtoDMproblemsunderoneoftheSVNcoveringroughsetmodels.Itis anovelmethodbasedonapproximationoperatorsspecifictoSVNcoveringroughsetsfirstly. Thecomparisonanalysisisveryinterestingtoshowthedifferencebetweentheproposedmethod andothermethods.
AuthorContributions: Allauthorscontributedequallytothispaper.Theideaofthiswholethesiswasput forwardbyX.Z.,andhealsocompletedthepreparatoryworkofthepaper.J.W.analyzedtheexistingworkof roughsetsandSVNSs,andwrotethepaper.
Funding: ThisworkwassupportedbytheNationalNaturalScienceFoundationofChinaunderGrantNos. 61573240and61473239.
ConflictsofInterest: Theauthorsdeclarenoconflictofinterest.
References
1. Pawlak,Z.Roughsets. Int.J.Comput.Inf.Sci. 1982, 11,341–356.
2. Pawlak,Z. RoughSets:TheoreticalAspectsofReasoningaboutData;KluwerAcademicPublishers:Boston,MA, USA,1991.
3. Bartol,W.;Miro,J.;Pioro,K.;Rossello,F.Onthecoveringsbytoleranceclasses. Inf.Sci. 2004, 166,193–211.
4. Bianucci,D.;Cattaneo,G.;Ciucci,D.Entropiesandco-entropiesofcoveringswithapplicationtoincomplete informationsystems. Fundam.Inform. 2007, 75,77–105.
5. Zhu,W.Relationshipamongbasicconceptsincovering-basedroughsets. Inf.Sci. 2009, 179,2478–2486.
6. Yao,Y.;Zhao,Y.Attributereductionindecision-theoreticroughsetmodels. Inf.Sci. 2008, 178,3356–3373.
7. Wang,J.;Zhang,X.Matrixapproachesforsomeissuesaboutminimalandmaximaldescriptionsin covering-basedroughsets. Int.J.Approx.Reason. 2019, 104,126–143.
8. Li,F.;Yin,Y.Approachestoknowledgereductionofcoveringdecisionsystemsbasedoninformationtheory. Inf.Sci. 2009, 179,1694–1704.
9. Wu,W.Attributereductionbasedonevidencetheoryinincompletedecisionsystems. Inf.Sci. 2008, 178, 1355–1371.
10. Wang,J.;Zhu,W.Applicationsofbipartitegraphsandtheiradjacencymatricestocovering-basedroughsets. Fundam.Inform. 2017, 156,237–254.
11. Dai,J.;Wang,W.;Xu,Q.;Tian,H.Uncertaintymeasurementforinterval-valueddecisionsystemsbasedon extendedconditionalentropy. Knowl.-BasedSyst. 2012, 27,443–450.
12. Wang,C.;Chen,D.;Wu,C.;Hu,Q.Datacompressionwithhomomorphismincoveringinformationsystems. Int.J.Approx.Reason. 2011, 52,519–525.
13. Li,X.;Yi,H.;Liu,S.Roughsetsandmatroidsfromalattice-theoreticviewpoint. Inf.Sci. 2016, 342,37–52.
14. Wang,J.;Zhang,X.Fouroperatorsofroughsetsgeneralizedtomatroidsandamatroidalmethodforattribute reduction. Symmetry 2018, 10,418.
15. Wang,J.;Zhu,W.Applicationsofmatricestoamatroidalstructureofroughsets. J.Appl.Math. 2013, 2013,493201.
16. Wang,J.;Zhu,W.;Wang,F.;Liu,G.Conditionsforcoveringstoinducematroids. Int.J.Mach.Learn.Cybern. 2014, 5,947–954.
17. Chen,J.;Li,J.;Lin,Y.;Lin,G.;Ma,Z.Relationsofreductionbetweencoveringgeneralizedroughsetsand conceptlattices. Inf.Sci. 2015, 304,16–27.
18. Zhang,X.;Dai,J.;Yu,Y.Ontheunionandintersectionoperationsofroughsetsbasedonvarious approximationspaces. Inf.Sci. 2015, 292,214–229.
Symmetry 2018, 10,710
19. D’eer,L.;Cornelis,C.;Godo,L.Fuzzyneighborhoodoperatorsbasedonfuzzycoverings. FuzzySetsSyst. 2017, 312,17–35.
20. Yang,B.;Hu,B.Onsometypesoffuzzycovering-basedroughsets. FuzzySetsSyst. 2017, 312,36–65. 21. Zhang,X.;Miao,D.;Liu,C.;Le,M.Constructivemethodsofroughapproximationoperatorsand multigranulationroughsets. Knowl.-BasedSyst. 2016, 91,114–125. 22. Wang,J.;Zhang,X.Twotypesofintuitionisticfuzzycoveringroughsetsandanapplicationtomultiple criteriagroupdecisionmaking. Symmetry 2018, 10,462. 23. Zadeh,L.A.Fuzzysets. Inf.Control 1965, 8,338–353. 24. Medina,J.;Ojeda-Aciego,M.Multi-adjointt-conceptlattices. Inf.Sci. 2010, 180,712–725. 25. Pozna,C.;Minculete,N.;Precup,R.E.;Kóczy,L.T.;Ballagi,Á.Signatures:Definitions,operatorsand applicationstofuzzymodeling. FuzzySetsSyst. 2012, 201,86–104.
26. Jankowski,J.;Kazienko,P.;Watróbski,J.;Lewandowska,A.;Ziemba,P.;Zioło,M.Fuzzymulti-objective modelingofeffectivenessanduserexperienceinonlineadvertising. ExpertSyst.Appl. 2016, 65,315–331.
27. Vrkalovic,S.;Lunca,E.C.;Borlea,I.D.Model-freeslidingmodeandfuzzycontrollersforreverseosmosis desalinationplants. Int.J.Artif.Intell. 2018, 16,208–222.
28. Ma,L.Twofuzzycoveringroughsetmodelsandtheirgeneralizationsoverfuzzylattices. FuzzySetsSyst. 2016, 294,1–17.
29. Wang,H.;Smarandache,F.;Zhang,Y.;Sunderraman,R.Singlevaluedneutrosophicsets. MultispaceMultistruct. 2010, 4,410–413.
30. Atanassov,K.Intuitionisticfuzzysets. FuzzySetsSyst. 1986, 20,87–96.
31. Mondal,K.;Pramanik,S.Roughneutrosophicmulti-attributedecision-makingbasedongreyrelational analysis. NeutrosophicSetsSyst. 2015, 7,8–17.
32. Yang,H.;Zhang,C.;Guo,Z.;Liu,Y.;Liao,X.Ahybridmodelofsinglevaluedneutrosophicsetsandrough sets:Singlevaluedneutrosophicroughsetmodel. SoftComput. 2017, 21,6253–6267.
33. Zhang,X.;Xu,Z.TheextendedTOPSISmethodformulti-criteriadecisionmakingbasedonhesitant heterogeneousinformation.InProceedingsofthe20142ndInternationalConferenceonSoftwareEngineering, KnowledgeEngineeringandInformationEngineering(SEKEIE2014),Singapore,5–6August2014.
34. Cheng,J.;Zhang,Y.;Feng,Y.;Liu,Z.;Tan,J.Structuraloptimizationofahigh-speedpressconsidering multi-sourceuncertaintiesbasedonanewheterogeneousTOPSIS. Appl.Sci. 2018, 8,126.
35. Liu,J.;Zhao,H.;Li,J.;Liu,S.DecisionprocessinMCDMwithlargenumberofcriteriaandheterogeneous riskpreferences. Oper.Res.Perspect. 2017, 4,106–112.
36. Watróbski,J.;Jankowski,J.;Ziemba,P.;Karczmarczyk,A.;Zioło,M.Generalisedframeworkformulti-criteria methodselection. Omega 2018.[CrossRef]
37. Faizi,S.;Sałabun,W.;Rashid,T.;Wa¸tróbski,J.;Zafar,S.Groupdecision-makingforhesitantfuzzysetsbased oncharacteristicobjectsmethod. Symmetry 2017, 9,136.
38. Faizi,S.;Rashid,T.;Sałabun,W.;Zafar,S.;Wa¸tróbski,J.Decisionmakingwithuncertaintyusinghesitant fuzzysets. Int.J.FuzzySyst. 2018, 20,93–103. 39. Zhan,J.;Ali,M.I.;Mehmood,N.Onanoveluncertainsoftsetmodel:Z-softfuzzyroughsetmodeland correspondingdecisionmakingmethods. Appl.SoftComput. 2017, 56,446–457. 40. Zhan,J.;Alcantud,J.C.R.Anoveltypeofsoftroughcoveringanditsapplicationtomulticriteriagroup decisionmaking. Artif.Intell.Rev. 2018, 4,1–30.
41. Zhang,Z.Anapproachtodecisionmakingbasedonintuitionisticfuzzyroughsetsovertwouniverses. J.Oper.Res.Soc. 2013, 64,1079–1089.
42. Akram,M.;Ali,G.;Alshehri,N.O.Anewmulti-attributedecision-makingmethodbasedonm-polarfuzzy softroughsets. Symmetry 2017, 9,271.
43. Liu,P.Theaggregationoperatorsbasedonarchimedeant-conormandt-normforsingle-valuedneutrosophic numbersandtheirapplicationtodecisionmaking. Int.J.FuzzySyst. 2016, 18,849–863.
44. Ye,J.Multicriteriadecision-makingmethodusingthecorrelationcoefficientundersingle-valuedneutrosophic environment. Int.J.Gen.Syst. 2013, 42,386–394.
45. Bonikowski,Z.;Bryniarski,E.;Wybraniec-Skardowska,U.Extensionsandintentionsintheroughsettheory. Inf.Sci. 1998, 107,149–167.
46. Pomykala,J.A.Approximationoperationsinapproximationspace. Bull.Pol.Acad.Sci. 1987, 35,653–662.
47. Zhang,X.;Bo,C.;Smarandache,F.;Dai,J.Newinclusionrelationofneutrosophicsetswithapplicationsand relatedlatticestructure. Int.J.Mach.Learn.Cybern. 2018, 9,1753–1763.
48. Zhang,X.Fuzzyanti-groupedfiltersandfuzzynormalfiltersinpseudo-BCIalgebras. J.Intell.FuzzySyst. 2017, 33,1767–1774.
49. Zhang,X.;Park,C.;Wu,S.Softsettheoreticalapproachtopseudo-BCIalgebras. J.Intell.FuzzySyst. 2018, 34, 559–568.
c 2018bytheauthors.LicenseeMDPI,Basel,Switzerland.Thisarticleisanopenaccess articledistributedunderthetermsandconditionsoftheCreativeCommonsAttribution (CCBY)license(http://creativecommons.org/licenses/by/4.0/).

