StudyofImaginativePlayinChildrenUsing Single-ValuedRefinedNeutrosophicSets
VasanthaW.B. 1 ,IlanthenralKandasamy 1,* ,FlorentinSmarandache 2 ,VinayakDevvrat 1 andShivamGhildiyal 1
1 SchoolofComputerScienceandEngineering,VIT,Vellore,Tamilnadu-632014,India; vasantha.wb@vit.ac.in(V.W.B.); vinayak.devvrat2015@vit.ac.in(V.D.);shivam.ghildiyal2015@vit.ac.in(S.G.)
2 DepartmentofMathematics,UniversityofNewMexico,Albuquerque,NM87301,USA;smarand@unm.edu

* Correspondence:ilanthenral.k@vit.ac.in
Received:14February2020;Accepted:2March2020;Published:4March2020
Abstract: ThispaperintroducesSingleValuedRefinedNeutrosophicSet(SVRNS)whichisa generalizedversionoftheneutrosophicset.Itconsistsofsixmembershipfunctionsbasedon imaginaryandindeterminateaspectandhence,ismoresensitivetoreal-worldproblems.Membership functionsdefinedascomplex(imaginary),afalsitytendingtowardscomplexandtruthtending towardscomplexareusedtohandletheimaginaryconceptinadditiontoexistingmembershipsinthe SingleValuedNeutrosophicSet(SVNS).Severalpropertiesofthissetwerealsodiscussed.Thestudy ofimaginativepretendplayofchildrenintheagegroupfrom1to10yearswastakenforanalysis usingSVRNS,sinceitisafieldwhichhasanamplenumberofimaginaryaspectsinvolved.SVRNS willbemoreaptinrepresentingthesedatawhencomparedtootherneutrosophicsets.Machine learningalgorithmssuchasK-means,parallelaxescoordinate,etc.,wereappliedandvisualizedfora real-worldapplicationconcernedwithchildpsychology.Theproposedalgorithmshelpinanalysing thementalabilitiesofachildonthebasisofimaginativeplay.Thesealgorithmsaidinestablishinga correlationbetweenseveraldeterminantsofimaginativeplayandachild’smentalabilities,andthus helpindrawinglogicalconclusionsbasedonit.Abriefcomparisonoftheseveralalgorithmsusedis alsoprovided.
Keywords: neutrosophicsets;SingleValuedRefinedNeutrosophicSet;applicationsofNeutrosophic sets;k-meansalgorithm;clusteringalgorithms
1.Introduction
Neutrosophyisanemergingbranchinmodernmathematics.Itisbasedonphilosophyandwas introducedbySmarandacheanddealswiththeconceptofindeterminacy[1].Neutrosophiclogicisa generalizationoffuzzylogicproposedbyZadeh[2].ApropositioninNeutrosophiclogiciseithertrue (T),false(F)orindeterminate(I).Thisinclusionofindeterminacymakestheneutrosophiclogiccapable ofanalyzinguncertaintyindatasets.Hence,itcanbeusedtologicallyrepresenttheuncertainandoften inconsistentinformationintherealworldproblems.SingleValuedNeutrosophicSets(SVNS)[3]are aninstanceofaneutrosophicsetwhichcanbeusedinrealscientificandengineeringapplicationssuch asDecision-makingproblems[4–11],ImageProcessing[12–14],SocialNetworkAnalysis[15],Social problems[16,17]andpsychology[18].Thedistanceandsimilaritymeasureshavefoundpractical applicationsinthefieldsofpsychologyforcomparingdifferentbehaviouralandcognitivepatterns. Imaginativeorpretendplayisoneofthefascinatingtopicsinchildpsychology.Itbeginsaround theageof1yearorso.Itisatitsmostprominentduringthepreschoolyearswhenchildrenbegin tointeractwithotherchildrenoftheirownageandbegintoaccessmoretoys.Itiscrucialinchild developmentasithelpsinthedevelopmentoflanguage(sometimesthechildlanguagewhichcannot
Symmetry 2020, 12,402;doi:10.3390/sym12030402
www.mdpi.com/journal/symmetry
bedecipheredbyeveryone)andalsohelpsnurturetheimaginationoftiny-tots.However,thefactors determiningthelevelofimaginativeplayinchildrenarevariedandcomplicatedandastudyof themwouldhelponetoassesstheirmentaldevelopment.Itisherethatfuzzyneutrosophiclogic comesintoplay.Inthispaper,weproposeanewnotionofSingleValuedRefinedNeutrosophicSets (SVRNS)whichisamodelstructuredonindeterminateandimaginarynotions,coupledwithmachine learningtechniquessuchasheatmaps,clustering,parallelaxescoordinate,etc.,tostudythefactors thatdetermineandinfluenceimaginativeplayinchildrenandhowitdiffersinchildrenwithdifferent abilitiesandskills.
Everychildisborndifferent.Thepersonalityandbehaviourofchildrenisaninterplayofseveral differentfactors.Psychologyisacomplicatedandvariedscienceandopentosubjectiveinterpretations. Thestudyofchildpsychologyinanobjectivemannercanhelponeuncoverseveralaspectsofchild behaviourandalsoresultinearlydetectionofcertainmentaldisorders.Oneofthekeymotivationsof thisresearchistouncoverthefactorsthatdeterminethementalabilitiesofachildandtheextentoftheir imaginationwhichhelpsinpredictingtheiracademicandoverallperformanceinlaterstages.Machine Learningisslowlybutsteadilybecomingoneofthehottopicsofcomputerscience.Amalgamation ofmachinelearningalgorithmsandpsychologyonthebasisofcomplexandneutrosophiclogicis certainlyexcitingandwillhelptocovernewbounds.
Thisstudyprimarilyfocusesontheanalysisofimaginativeplayinchildrenonthebasisof neutrosophiclogicanddrawsconclusionsonthesamewiththehelpofclusteringalgorithms. Theapproachisinitializedbygeneratingafinitenumberofcomplexandneutrosophicsetsdetermined byseveralcognitive,psychologicalandbiologicalfactorsthataffectimaginativeplayinthementioned agegroup.Theprimaryadvantagehereistheabilityofsuchsetstodealwiththeuncertainty, imaginationandindeterminacypresentinthestudyofpretendplayinchildrenintheagegroupfrom 1to10years.Withthehelpofthisstudy,weaimtodistinguishthecontributionofseveralfactorsof imaginativeplayinchildrenandconcludefromthestudywhetherthechildhasanymentaldisorders ornotandaboutthegeneralcognitiveskillscoupledwithimagination.Thismodelwillalsohelpin identifyingfactorswhichmaycontributetopotentialpsychologicaldisordersinyoungchildrenatan earlystageandpredicttheacademicperformanceofthechild.
Inthisresearch,anewcomplexfuzzyneutrosophicsetisdefinedwhichwillbeusedasamodelto studytheimaginaryandindeterminatebehaviourinyoungchildrenintheagegroupfrom1to10years bygivingthemsuitablestimuliforimaginaryplay.Thedatawerecollectedfromdifferentsourceswith thehelpofaquestionnaire,observations,recordedsessionsandinterviews,andaftertransformingthe dataintotheproposednewneutrosophiclogic,theywerefittedintothenewlyconstructedmodeland conclusionsweredrawnfromthemusingachildpsychologistasanexpert.Thismodelattemptsto discovertheextenttowhichseveralfactorscontributetoimaginativeplayinchildrenofthespecified agegroupandtodetectpossibilitiesofmentaldisorderssuchasautismandhyperactivityinyoung childrenonthebasisofthetrainedmodel.
Thepaperisorganizedintosevenmajorsectionswhicharefurtherdividedintoafewsubsections. Sectiononeisintroductoryinnature.Adetailedanalysisoftheworksrelatedtoneutrosophyandits applicationstoafewrelevantfieldsarepresentedinsectiontwo.Italsoprovidesthegapsthathave beenidentifiedinthoseworks.Section 3 introducesSingleValuedRefinedNeutrosophicSets(SVRNS) alongwiththeirproperties,suchasdistancemeasuresandrelatedalgorithms.Italsointroducesand discussesseveralmachinelearningtechniquesusedforassessment.Thedescriptionofthedataset usedfortheapplicationofalgorithmssuchasK-meansclustering,heatmaps,parallelaxescoordinate isgiveninsectionfour.Italsoincludestheapproachinvolvedinprocessingthedataobtained appropriatelyintoSVRNSs.Section 5 providesanillustrativeexampleofthemethodsdescribedin theprecedingsection.Section 6 detailstheresultsobtainedfromtheapplicationofthediscussed algorithmsandtheirrespectivevisualizations.Section 7 discussestheconclusionsbasedonourstudy anditsfuturescope.
2.RelatedWorks
Fink[19]exploredtheroleofimaginativeplayintheattainmentofconservationandperspectivism withthehelpofatrainingstudyparadigm.Kindergartenchildrenwereassignedtocertainconditions suchasfreeplayinthepresenceofanexperimenterandacontrolgroup.Themethodoftheirdata collectionwasobservation.Theresultsindicatethatimaginativeplaycanresultinnewcognitive structures.Therelationshipbetweendifferenttypesofplayexperiencesandtheconstructionofcertain physicalorsocialconceptswerealsodiscussed,alongwitheducationalimplications.
Udwin[20]studiedagroupofchildrenwhohadbeenremovedfromharmfulfamilybackgrounds andplacedininstitutionalcare.Thesechildrenwereexposedtoimaginativeplaytrainingsessions. Thesesubjectsshowedanincreaseinimaginativebehaviour.Age,non-verbalintelligenceandfantasy predispositionweredeterminantsofthesubjects’responsetothetrainingprogramme,withyounger, high-fantasyandhigh-IQchildrenbeingmostsusceptibletotheinfluenceofthetrainingexercises.
Huston-Stein[21]attemptedtoestablisharelationshipbetweensocialstructureandchild psychologybyemployingmethodsofdirectobservationsoffieldexperiments.Thebehaviourwas thencategorisedonthebasisofasetofdefinedbehaviouralcategoriesandevaluatedonthebasisof suitablemetrics.Theresultsfocusonestablishingcorrelationsbetweenthesebehaviouralcategories andclassroomstructureanddrawconclusionsonhowsuchsocialstructuresimpactimaginativeplay.
Bodrova[22]relatedanotherimportantparameter,namelyacademicperformance,toimaginative play.Theyhaveestablishedimaginativeplayasanecessaryprerequisiteandoneofthemajorsources ofchilddevelopment.Theydeducedhowimaginativeplayscenariosrequireacertainknowledgeof environmentalsettingandhowitaffectstheacademicexcellenceofachild.
Seja[23]exploredanotherimportantfactorinchildpsychology—emotions.Theyattemptedto determinehowimaginativeplayhelpstounderstandtheemotionalintegrationofchildren.Thesource ofdatacollectedinthisstudyiselementaryschoolchildrenwhoweretestedonverbalintelligence andbystandardpsychologicaltests.Conclusionsweredrawnonthebasisofanextensivestatistical analysiswhichalsoattemptedtoinvestigategenderdifferences.
Neutrosophyhasgivenimportancetotheimprecisionandcomplexityofdata.Thisisanimportant reasonbehindusingneutrosophiclogicinreallifeapplications.Dhingraetal.[24]attemptedto classifyagivenleafasdiseasedorhealthybasedonthemembershipfunctionsoftheneutrosophicsets. Imagesegmentationintotrue,falseandindeterminateregionsafterpreprocessingwasusedtoextract featuresandseveralclassifierswereusedtoarriveataclassification.Acomparativeanalysisofthese classifierswasalsoprovided.
Severalresearchers[25–30]dealtwithalgebraicstructuresofneutrosophicduplets,whicharea specialcaseofneutrality.SingleValuedNeutrosophicSets(SVNS),whichisparticularcasesoftriplet followingthefuzzyneutrosphicmembershipconceptsintheirmathematicalpropertiesandoperations aredealtbyHaibin[31].
Haibin[31]gavethenotionofSingleValuedNeutrosophicSets(SVNS)alongwiththeir mathematicalpropertiesandsetoperations.Propertiessuchasinclusion,complementandunionwere definedonSVNS.Theyalsogaveexamplesofhowsuchsetscanbeusedinpracticalengineering applications.SVNShasfoundamajorapplicationinmedicaldiagnosis.Shehzadi[32]presentedthe useofHammingdistanceandsimilaritymeasuresofgivenSVNSstodiagnoseapatientashaving Diabetes,DengueorTuberculosis.Thethreemembershipfunctions(truth,falsityandindeterminacy) wereassignedsuitablevaluesanddistanceandsimilaritymeasureswereappliedonthem.These measureswerethenusedtoprovideamedicaldiagnosis.SmarandacheandAli[33]providedthe notionofcomplexneutrosophicsets(CNS).Membershipvaluesgiventothemwereoftheforma+bi. Severalpropertiesofthesesetsweredefined.Thesesetsfindapplicationsinelectricalengineeringand decision-makingfields.NeutrosophicRefinedSetswheredefinedin[34].
AmorerefinedandpreciseviewofindeterminacyisprovidedbyKandasamy[35]. Theindeterminacymembershipfunctionwasfurthercategorizedasindeterminacytendingtowards truthandindeterminacytendingtowardsfalse.Hence,resultinginDouble-ValuedNeutrosophic
Set(DVNS).Theirproperties,suchascomplement,unionandequalitywerealsodiscussedand distancemeasureswerealsodefinedonthem.Onthebasisoftheseproperties,minimumspanning treesandclusteringalgorithmsweredescribed[36].DicemeasuresonDVNSwereproposedin[37]. Theimportancegiventotheindeterminacyofincompleteandimprecisedata,asoftenfoundinthe realworld,isamajoradvantageoftheDVNSandhence,ismoreaptforseveralengineeringand medicalapplications.
ThemodelofTripleRefinedIndeterminateNeutrosophicSet(TRINS)wasalsointroducedby KandasamyandSmarandache[38].Itcategorizesindeterminacymembershipfunctionasleaning towardstruthandleaningtowardsfalseinadditiontothetraditionalthreemembershipfunctionsof neutrosophicsets.Afterdefiningtheseveralpropertiesanddistancemeasures,theTRINSwasused forpersonalityclassification.ThepersonalityclassificationusingTRINShasbeenfoundtobemore accurateandrealisticascomparedtoSVNSandDVNS.IndeterminateLikertscalingusingfivepoint scalewasintroducedin[39]andasentimentanalysisusingNeutrosophicrefinedsetswasconducted in[40,41].
Todate,thestudyofimaginativeplayinchildrenhasnotbeenanalysedusingneutrosophy coupledwithanimaginaryconcept;thus,tocoverthisunexploredarea,thenewnotionofSingle ValuedRefinedNeutrosophicSets(SVRNS)thatrepresentimaginaryandindeterminatememberships individuallyweredefined.AstudyofimaginativeplayinchildrenusingNeutrosophicCognitive Maps(NCM)modelwascarriedoutin[42].
3.SingleValuedRefinedNeutrosophicSet(SVRNS)andItsProperties
ThissectionpresentsthedefinitionofSingleValuedRefinedNeutrosophicSet(SVRNS).Thesesets arebasedontheessentialconceptsofreal,complexandneutrosophicvalueswhichtakesmembership fromthefuzzyinterval[0,1].Inawaythiscanberealizedasamixtureofrefinedneutrosophicsets coupledwithrealmembershipvaluesforimaginaryaspect.HoweverSVRNSaredifferentfrom traditionalneutrosophicsets.Theneutrosophiclogicispowerfulandcanmodelconceptsofarbitrary complexitycoveringincompleteandimprecisedata.Children’sbehaviourisonesuchcomplicated andtheimprecisebranchthatcanbemodelledasobjectivelyaspossiblebycouplingimaginaryor complexnatureofdatawithitsindeterminacy.
TheconceptofSVRNSaredefined,developedanddescribedinthefollowing.
3.1.SingleValuedRefinedNeutrosophicSet(SVRNS)
Definition1. LetXbeaspaceofpoints(objects),withagenericelementinXdenotedbyx.Aneutrosophicset AinXischaracterisedbyatruthmembershipfunction TA (x),atruetendingtowardscomplexmembership function TCA (x),acomplexmembershipfunction CA (x),afalsetendingtowardscomplexmembershipfunction FCA (x),anindeterminacymembershipfunction IA (x),andafalsitymembershipfunction FA (x).Foreach point x inX,thereare TA (x), TCA (x), CA (x), FCA (x), IA (x), FA (x) ∈ [0,1] and 0 ≤ TA(x)+ TCA(x)+ CA(x)+ FCA(x)+ IA(x)+ FA(x) ≤ 6. Therefore,aSingleValuedRefinedNeutrosophicSet(SVRNS)Acanbe
and B = TB (xi) , TCB (xi) , CB (xi) , FCB (xi) , IB (xi) , FB (xi) |xi ∈ X , where TA (xi), TCA (xi), CA (xi), FCA (xi), IA (xi), FA (xi) , TB (xi), TCB (xi), CB (xi), FCB (xi), IB (xi), FB (xi) ∈ [0,1] forevery xi ∈ X.Let wi (i = 1,2, , n) betheweightofanelement xi (i = 1,2, , n),with wi ≥ 0 (i = 1,2, , n) and n i=1 wi = 1.Then,thegeneralisedSVRNSweighteddistanceisdefinedasfollows:
dλ(A, B)= { 1 6
n i=1 wi[|TA(xi) TB(xi)|λ + |TCA(xi) TCB(xi)|λ + |CA(xi) CB(xi)|λ+ |FCA(xi) FCB(xi)|λ + |IA(xi) IB(xi)|λ + |FA(xi) FB(xi)|λ]} 1 λ
where λ> 0
TheaboveequationreducestotheSVRNSweightedHammingdistanceandtheSVRNSweightedEuclidean distance,when λ = 1,2,respectively.TheSVRNSweightedHammingdistanceisgivenas
dλ(A, B)= { 1 6
n i=1 wi[|TA(xi) TB(xi)| + |TCA(xi) TCB(xi)| + |CA(xi) CB(xi)|+ |FCA(xi) FCB(xi)| + |IA(xi) IB(xi)| + |FA(xi) FB(xi)|]} where λ = 1.
TheSVRNSweightedEuclideandistanceisgivenas dλ(A, B)= { 1 6
n i=1 wi[|TA(xi) TB(xi)|2 + |TCA(xi) TCB(xi)|2 + |CA(xi) CB(xi)|2+ |FCA(xi) FCB(xi)|2 + |IA(xi) IB(xi)|2 + |FA(xi) FB(xi)|2]} 1 2 where λ = 2.
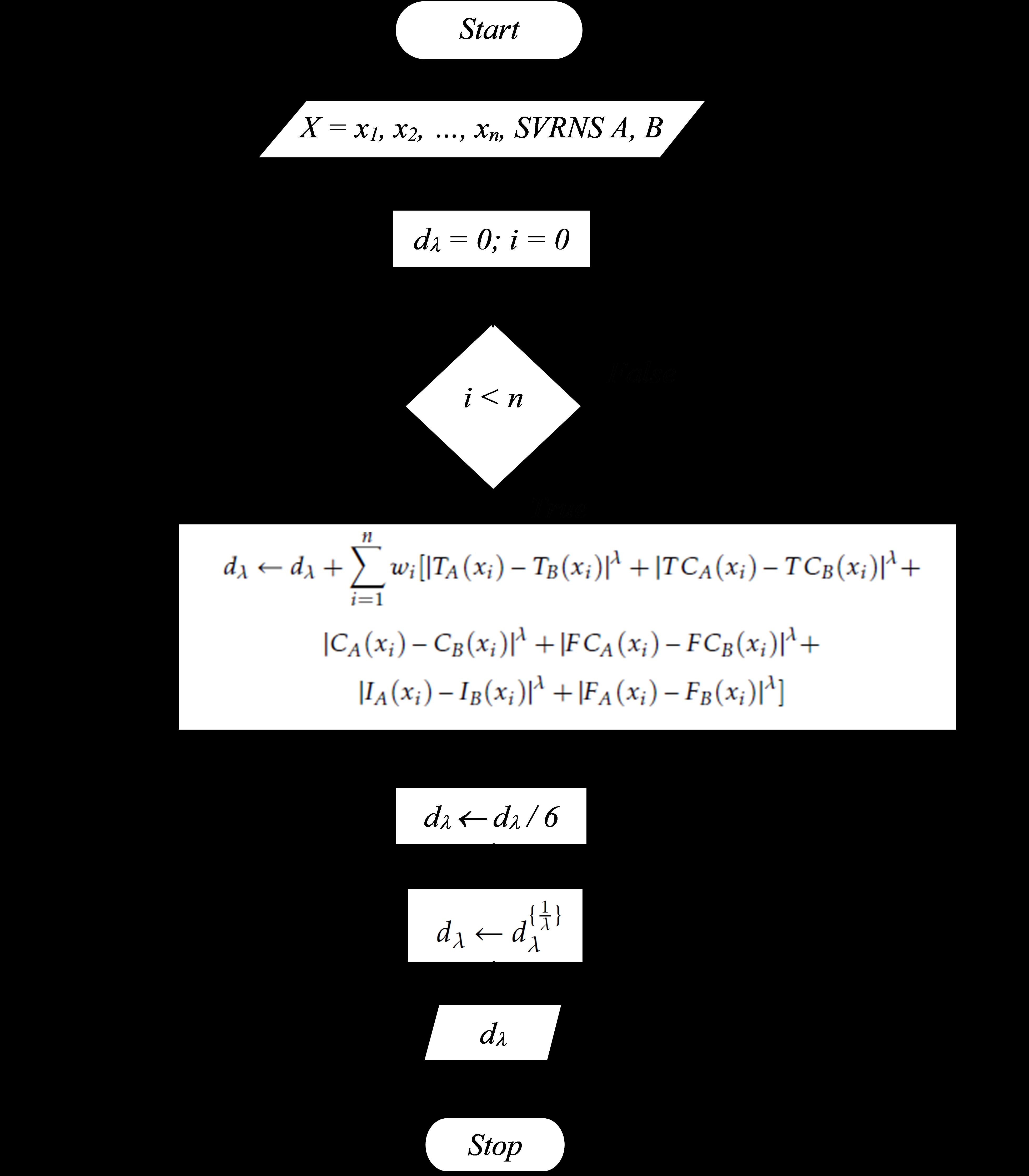
ThealgorithmtoobtainthegeneralizedSVRNSweighteddistance dλ(A, B) betweentwoSVRNS A and B isgiveninAlgorithm 1
Algorithm1: GeneralizedSVRNSweighteddistance dλ(A, B) Input: X = xl, x2, , xn,SVRNS A, B where A = TA (xi) , TCA (xi) , CA (xi) , FCA (xi) , IA (xi) , FA (xi) |xi ∈ X , B = TB (xi) , TCB (xi) , CB (xi) , FCB (xi) , IB (xi) , FB (xi) |xi ∈ X , wi(i = 1,2, , n) Output: dλ(A, B) begin dλ ← 0 for i = 1ton do dλ ← dλ + n i=1 wi[|TA(xi) TB(xi)|λ + |TCA(xi) TCB(xi)|λ+ |CA(xi) CB(xi)|λ + |FCA(xi) FCB(xi)|λ+ |IA(xi) IB(xi)|λ + |FA(xi) FB(xi)|λ] end dλ ← dλ /6 dλ ← d{ 1 λ } λ end
Algorithm2: K-meansalgorithmforclusteringSVRNSvalues
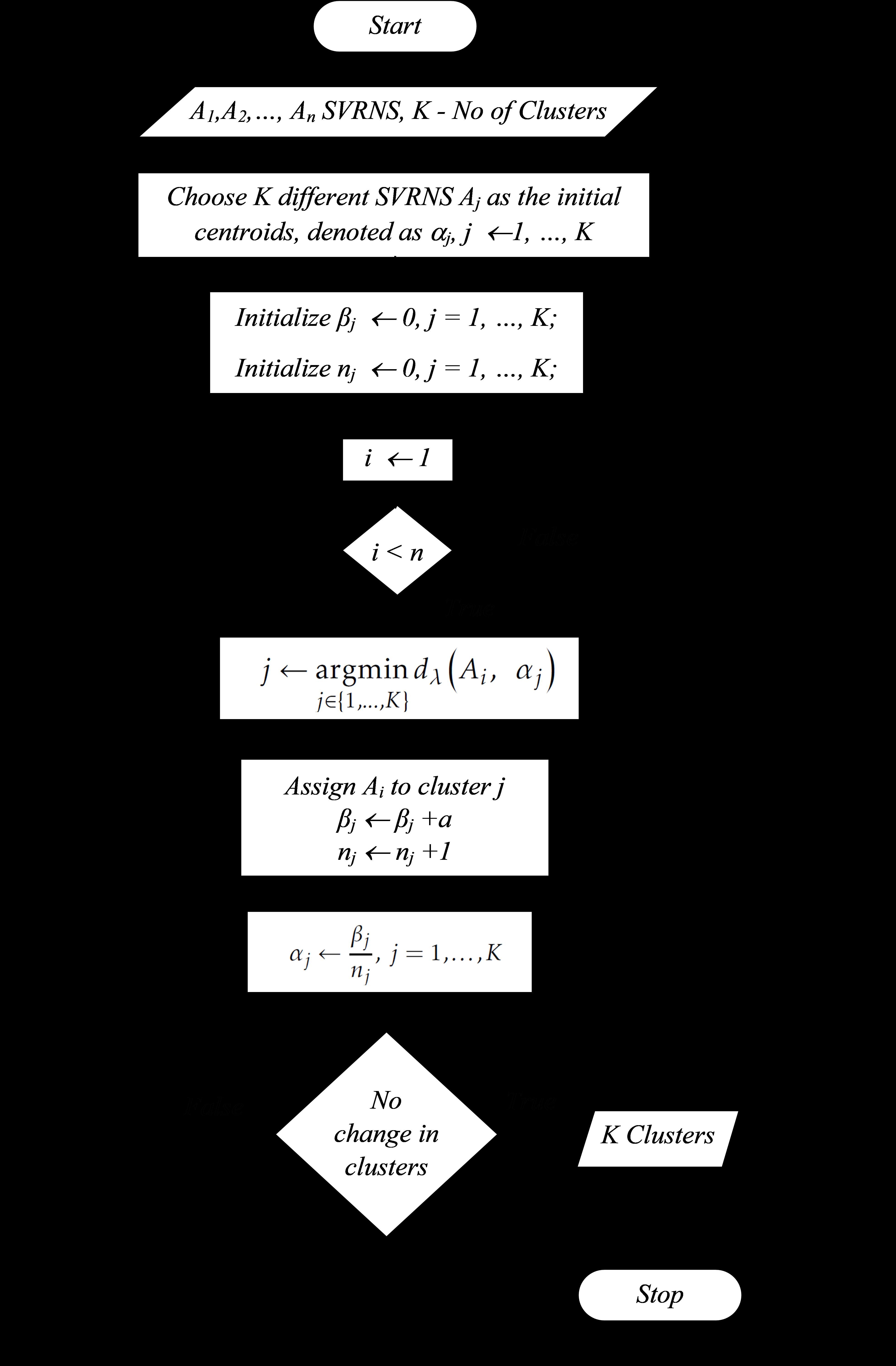
Input: Al, A2, ... , An SVRNS, K—NumberofClusters
Output: K Clusters begin
Step1: Choose K differentSVRNS A j astheinitialcentroids,denotedas α j, j = 1, ... , K Step2: Initialize β j ← 0, j = 1, , K; // 0 isavectorwithall0’s Step3: Initialize n j ← 0, j = 1, , K; // n j isthenumberofpointsincluster j Step4: CreationofClusters repeat for i = 1ton do j ← argmin j∈{1, ,K} dλ Ai, α j // FromAlgorithm 1 assign Ai toclusterj β j ← β j + a n j ← n j + 1 end α j ← β j n j , j = 1, ... , K until Clustersdonotchange end
TherelatedflowchartisgiveninFigure 2.
Figure2. FlowChartforkmeansclusteringofSVRNSvalues.
Weusedthefollowingmachinelearningtechniquesinthispaperafterobtainingandprocessing thedata.
3.4.OtherMachineLearningTechniques
TheElbowmethodisatechniqueusedtofindthevalueofappropriatevalueofK(Numberof clusters)inK-meansclustering.Itmakestheclusteranalysisdesignconsistent.Aheatmapisa datavisualizationtechniqueusedtoshowcorrelationbetweentwoattributesintheformofamatrix whereeachvalueisrepresentedascolours.ThePrincipalComponentAnalysis(PCA)makesuse oforthogonaltransformationtoconvertasetofobservationsofvariableswhichmightbepossibly correlated,intoasetofvaluesoflinearlyuncorrelatedvariablescalledprincipalcomponents.Itisa widelyusedstatisticaltechnique.Parallelcoordinates(alsoknownasParallelAxesChart(PAC))are highlyusedforthevisualizationofmulti-dimensionalgeometryandanalysisofmultivariatedata. EasyvisualizationofmultipledimensionsisaninnatefeatureofPACplot,makingitsimpletoanalyse attributeswhichareassociatedwithotherattributesinasimilarmanner.
4.DatasetDescription
Imaginativeplayisdefinedas“aformofsymbolicplaywherechildrenuseobjects,actionsor ideastorepresentotherobjects,actions,orideasusingtheirimaginationstoassignrolestoinanimate objectsorpeople”.Duringtheearlystage,“toddlersbegintodeveloptheirimaginations,withsticks becomingboatsandbroomsbecominghorses.Theirplayismostlysolitary,assigningrolestoinanimate objectsliketheirdollsandteddybears”.Ithasproventobehighlybeneficialasitresultsinearly useoflanguageandproperuseoftensesandadjectives.Itgivesthechildrenasenseoffreedomand allowsthemtobecreativeintheirownspace.Ithelpschildrenmakesenseofthephysicalworldand alsotheirinnerselves.Itcandevelopwiththehelpofthemostbasictoolssuchasatoymobileora cardboardtube.
Thedataregardingimaginativeplayinchildrenwerecollectedfromthelocalschoolandan orphanageinVellore,India.
Achildpsychologistwaspresentthroughoutthesessions,analyzedandsuggestedthevarious parametersandrecordedtheobservationsabouteachsession.Thesessionateachoftheseplacesbegan withtheexperttalkingtothechildaboutgeneralthingsandeverydaylifeasanice-breakerexercise. Thisincludedtalkingabouthis/herfavouritesubjects,parentsandtreatinghim/herwithbiscuitsor chocolates.Thesurroundingsweremadeascomfortableaspossible.Thechildwasthenaskedto conductanimaginaryphonecallinwhicheverwayhe/sheliked.Theimaginaryconversationwas thenrecordedasvideoonaphone.Theexpertmadeobservationsthatwererecordedonpaperina runninghanddescription.Thissignifiedtheendofthesession.
Overall,10suchsessionswereconductedattheschooland2wereconductedattheorphanage. Thechildrenbelongedtotheagegroupof6to8years.Additionally,inordertomakethedataset diverseassuggestedbytheexpert,7videosweretakenfromtheinternetinwhichchildrenconducted imaginaryconversationsoverthephone.Therunninghanddescriptionthuscollectedwasusedby thisexperttoassignvaluestothesixmembershipfunctionsbasedonwhichtheSVRNSisconstructed.
Table 1 providestheparameterswhichhavebeenusedtostudyimaginativeplayalongwiththeir description.Theparameters1to11areavailablein[19]andtheother4parametersfrom12to15are introducedbyus.
Table1. ParameterDescription.
S.NoParameterNameDescription
1ImaginativeTheme(IT)
2PhysicalMovements(PM)
3Gestures(G)
4FacialExpressions(FE)
5 NatureandLengthofSocial Interaction(NoI/LoI)
6PlayMaterialsUsed(PMU)
7 WayPlayMaterialswere Used(WPMwu)
8Verbalisation(V)
9ToneofVoice(ToI)
10RoleIdentification(RI)
Thethemeoftheimaginativeplayisassumedbythechildandcanbebasedon arealorimaginativesituationand/orsetting.
Themovementsachildmaymakewhiles/heconductstheimaginativeplayare alsoanimportantdeterminantofthechild’scognitivepatterns.Theyarethe waysinwhichthechilduseshis/herbodyduringtheplay.
Theyarethewaysinwhichthechildmovesapartofthebodyinorderto expressanideaorsomemeaning.Theyarethenon-verbalmeansof communicationusinghands,head,etc.
Themovementoffacialmusclesfornon-verbalcommunicationandalsoconvey theemotionsexperiencedbythechild.
Thetimedurationduringwhichthechildengagesintheimaginativeplay activitycandeterminetheextentofhis/herimagination.Thenatureofanyform ofinteractionwhichmaytakeplaceduringtheimaginativeplaybeday-to-day, meaningfulinsomeway,etc.andeventhecombinationofthetwo.
Theyaretheobjectsprovidedtothechildtoconductanimaginativeplay activity.Theplaymaterialusedherewasaplaymobilephonetoconductan imaginarytalk.
Thechild’sapproachtousingtheplaymaterialprovidedcangiveaninsight intohis/herimaginativecapabilities.
Itisthewayinwhichthechildisexpressinghis/herfeelingsoremotionsduring theimaginativeplayactivity.
Itisanimportantaspectthatchild’smoodandstateofmindasinifthechildis happy,sadornervous.Forexample,ahighpitchedvoicemayindicate happinessorexcitement.
Itistheroleachildassumesduringtheimaginativeplayandtheroles/he assignstootherpeople.
11EngagementLevel(EL)Itistheextenttowhichthechildinvolvesintheactivityofimaginativeplay.
12EyeReaction(ER)
Itreferstothemovementoftheeyesduringtheimaginativeplayactivity.Itcan giveinsightintothechild’semotionsduringtheplay.
13CognitiveResponse(CR)Itisthementalprocessbywhichthechildformsassociationbetweenthings.
14 GrammarandLinguistics (GaL)
Itreferstotheabilityofachildtomakegrammaticallycorrectsentenceswith propersentencestructureandsyntax.
15Coherence(C) Whetherthechildismakingsenseofthetalks,i.e.,ifthesentencesformedare relatedtooneanotheriscalledcoherence.
MethodofEvaluation
Therunninghanddescriptionoftheabove-mentionedparameterswastransformedintoacomplex fuzzyneutrosophicsetsbytheexpert/childpsychologist,forapplyingmachinelearningalgorithms discussedintheearliersection.Themethodsofevaluationforeachparameterassuggestedbythe expertarediscussedbelow.
1. ImaginativeTheme: Animaginativethemethatisbasedontherealsituationwillresultinthe increaseinthetruthmembershipfunctionandotherwiseifthethemeisentirelyimaginative. However,sincethereisalwaysadegreeofcomplexandindeterminacyinthisparameter,the complexandindeterminatemembershipfunctionswasalsoassignedcertainvaluesfrom[0,1].
2. PhysicalMovements: Ifphysicalmovementsaremade,thevalueoftruthmembershipfunctionwill increaseelsethefalsitymembershipfunctionwillincrease.Complexandindeterminacyvalues from[0,1]shallbeassignedvaluesifmovementsaredifficulttointerpretproperlyorhappenedto beimaginary.
3. Gestures: Similartophysicalmovements,anygesturesmadeinaccordancewiththeimaginative activitywillresultinanincreaseinthetruthmembershipvalueandinfalsityvalueotherwise. Anyindeterminateorcomplexfeaturewillresultinvaluesbeingassignedtoindeterminateand complexrespectivelyfrom[0,1].
4. FacialExpressions: Anyfacialexpressionsmadeinaccordancewiththeimaginativeactivity conductedwillleadtoanincreaseinthetruthmembershipandinfalsitymembershipfunction otherwise.Complexandindeterminacymembershipfunctionsshallbeassignedvaluesiffacial expressionsaredifficulttointerpretproperly.
5. NatureandLengthofSocialInteraction: Anyinteractionthatismadeinaccordancewiththeplay activitywillresultinanincreaseintruthmembershipfunctionsandinfalsitymembership functionsotherwise.Indeterminateandcomplexmembershipfunctionsshallbeassignedvalues iftheinteractionsaredifficulttointerpretproperly.
6. PlayMaterialsUsed: ThesearenounsandneednotbetranslatedtoSVRNS.
7. WayPlayMaterialswereUsed: Anyusageofplaymaterialsinarealisticmannerwillleadtoan increaseinthetruthmembershipandinfalsitymembershipfunctionotherwise.Complex andindeterminacymembershipfunctionsshallbeassignedvaluesifusageisdifficultto interpretproperly.
8. Verbalisation: Anyverbalisationthatismadeinaccordancewiththeplayactivitywillresultinan increaseintruthmembershipfunctionsandinfalsitymembershipfunctionsotherwise.Complex andindeterminacymembershipfunctionsshallbeassignedvaluesiftheverbalizationisdifficult tointerpretproperly.
9. ToneofVoice: Ifthetoneofvoiceisinaccordancewiththesituationofplayactivityandhigh,it willresultinanincreaseintruthmembershipfunctionsandinfalsitymembershipfunctions otherwise.Complexandindeterminacymembershipfunctionsshallbeassignedvaluesifthe interactionsaredifficulttointerpretproperly.
10. RoleIdentification: Anyroleidentificationthatisrealisticwillleadtoanincreaseinthetruth membershipandinfalsitymembershipfunctionotherwise.Complexandindeterminacy membershipfunctionsshallbeassignedvaluesifroleidentificationisdifficulttointerpretproperly.
11. EngagementLevel: Iftheengagementlevelishighbutthethemeandroleidentificationarerealistic, truthmembershipfunctionvalueincreases.Iftheengagementlevelishighbutthethemeandrole identificationareimaginative,falsitymembershipfunctionvalueincreases.Othercombinations ofengagementlevel,themeandroleidentificationwillresultinassigningvaluestotheother membershipfunctions.
12. EyeReaction: Anyeyereactionthatismadeinaccordancewiththeplayactivitywillresultinan increaseintruthmembershipfunctionsandinfalsitymembershipfunctionsotherwise.Complex andindeterminacymembershipfunctionsshallbeassignedvaluesiftheeyereactionisdifficult tointerpretproperly.
13. CognitiveResponse: Anycognitiveresponsethatismadeinaccordancewiththeplayactivity willresultinanincreaseintruthmembershipfunctionsandinfalsitymembershipfunctions otherwise.Complexandindeterminacymembershipfunctionsshallbeassignedvaluesifthe cognitiveisdifficulttointerpretproperly.
14.
GrammarandLinguistics: Ifthegrammar,sentencestructureandsyntaxarecorrect,thevalueof truthmembershipfunctionwillincrease.Anyerroringrammar,syntaxorsentencestructurewill leadtoanincreaseinthevalueoffalsitymembershipfunction.If,however,thelinguisticsare difficulttocomprehend,indeterminateandcomplexmembershipfunctions’valuewillincrease.
15. Coherence: Ifthesentencesmadearerelatedtooneanother,thevalueoftruthmembershipfunction willincrease.Anyincoherence,i.e.,makingsentencesarenotrelatedtooneanotherwillleadto anincreaseinthevalueoffalsitymembershipfunction.If,however,thecoherenceofsentencesis difficulttocomprehend,indeterminateandcomplexmembershipfunctions’valuewillincrease.
5.IllustrativeExample
Thissectionprovidesanexampleonprocessingofthedataobtainedasarunninghanddescription. Onthebasisofthisdescription,theexpertestimatedandevaluatedthechild.Thefollowingexample isbasedonavideoof3-year-oldchildandthefollowingobservationsgivenbytheexpertaremadein formofrunninghanddescriptionsofthe15parametersgiveninTable 2.
Table2. ParameterDescriptionforExample.
S.NoParameterNameDescription
1ImaginativeTheme
ThechildtalkstoMickeyMouseoverthephone.Thechildattemptstodiscuss somethingshedescribes“gross”.
2PhysicalMovementsThechilddoesnotusealotofherbodyduringtheconversation.
3GesturesThechilddoesnotuseanysignificantgesturesduringtheconversation.
4FacialExpressions
5 NatureandLengthofSocial Interaction
6PlayMaterialsUsed
7 WayPlayMaterialswere Used
8Verbalisation
Thechildischeerful,seriousandastonishedwhensheinitiatestheconversation, askssomethingtothereceiverandwhencomestoknowaboutsomething “gross”respectively.
Thechildengagesintheconversationforaboutaminute.Theinteractionis mostlyday-to-dayandthechildisratherexpressiveofheremotions.
Thechildusesatoymobiletoconductanimaginativeconversationbetween herselfandMickeyMouse.
Thechildusesthemobileinaveryrealisticway.
Thechildmakessoundandnoisesinaccordancewiththemoodofthe conversation.
9ToneofVoiceThetoneofthechild’svoiceishigh-pitched.Sheisveryexpressive.
10RoleIdentification
11EngagementLevel
Thechilddoesnotassumeanyroleotherthanherself.However,shedoes imagineherselftobeafriendofMickeyMouse.
Thechild’sengagementlevelishighandsheisattentivethroughouttheplay activity.
12EyeReactionThechild’seyeswidenandnarrowduringdifferentpointsoftheplayactivity.
13CognitiveResponseThecognitiveresponseisdirect,quickandcoherent.
14GrammarandLinguistics
15Coherence
Thechildmakesgrammaticallycorrectsentencesexceptshedoesskip supportiveverbslike“will”.
Thesentencesmadearecoherentandinsyncwiththeimaginativeconversation.
Table 2 depictsarunninghanddescriptionofthediscussedparameters.Theseparametersare thenassignedrealvaluesbytheexpert.ThesevaluesarediscussedinTable 3.
Table3. SVRNSforExample.
S.NoParameterDescriptionSVRNS
1IT
Entirelyimaginativethemethoughtheconversationwas realistic 0.75,0,0,0,0.25,0
2PMNotalot 0,0,0,0,0.25,0.75
3GNotalot 0,0,0,0,0.25,0.75
4FECheerful,confident,serious 0,0.75,0.25,0,0,0
5NoI/LoI1minute;day-to-day,verbal 0.5,0.25,0.25,0,0,0
6PMUMobileNA
7WPMwuRealistic 0.75,0,0,0,0.25
8VInaccordancewithimaginativeplay 0.5,0.25,0.25,0,0,0
9ToIInaccordancewithimaginativeplay;highpitched 0.5,0.25,0.25,0,0,0
10RISelf 0.5,0,0.25,0,0.25,0
11ELHigh 0.5,0.25,0.25,0,0,0
12ER Widening,narrowing;Inaccordancewithimaginativeplay 0,0,0.5,0,0.5,0
13CRDirect;Inaccordancewithimaginativeplay 0.75,0,0,0,0.25,0
14GaLPartiallycorrect;Inaccordancewithimaginativeplay 0.75,0,0.25,0,0,0
15CInaccordancewithimaginativeplay 0.75,0,0,0.25,0,0
LikewisetheSVRNStuplesfortheotherdatasetswasdonewiththehelpoftheexpert.Then theseSVRNSsetsareusedforanalysisusingmachinelearningalgorithms.
6.ResultsandDiscussions
Severallibrariessuchaspandas,numpy,matplotlib,sklearn,seabornandpylabassociated withPythonwereusedfordatavisualization.Programmingwascarriedoutusingpythonforthe visualizationofthepreviousdiscussedalgorithms,basedontheresultofelbowcurve,K-means clusteringwasdone.Logicalconclusionshavebeendrawnfromthesevisualizationsandtheroleseveral determinantsplayindeterminingtheimaginativecapabilitiesofthechildhasalsobeenhighlighted.
Heatmap,whichstronglydemonstratesthefactorsofcorrelationandassociativity,hasacolour scaleinwhichlightershadessignifypositivecorrelationanddarkershadessignifyanegativecorrelation. Correlationbetweenanytwoparameterssignifiestheirassociatedrelation.Positivecorrelationhappens whenanincreaseinoneattributeshowsanincreaseinanotherattributeaswell.Negativecorrelation happenswhenanincreaseinoneattributeshowsadecreaseinanotherattribute.Theheatmap,which stronglydemonstratesthefactorsofcorrelationandassociativity,hasacolourscaleinwhichlighter shadessignifypositivecorrelationanddarkershadessignifyanegativecorrelation.Forexample, inFigure 3,whichisaheatmapforfeatureT,GrammarandCoherenceshowextremelypositive correlationwhereasEyeReactionandRoleIdentificationshowanegativecorrelation.
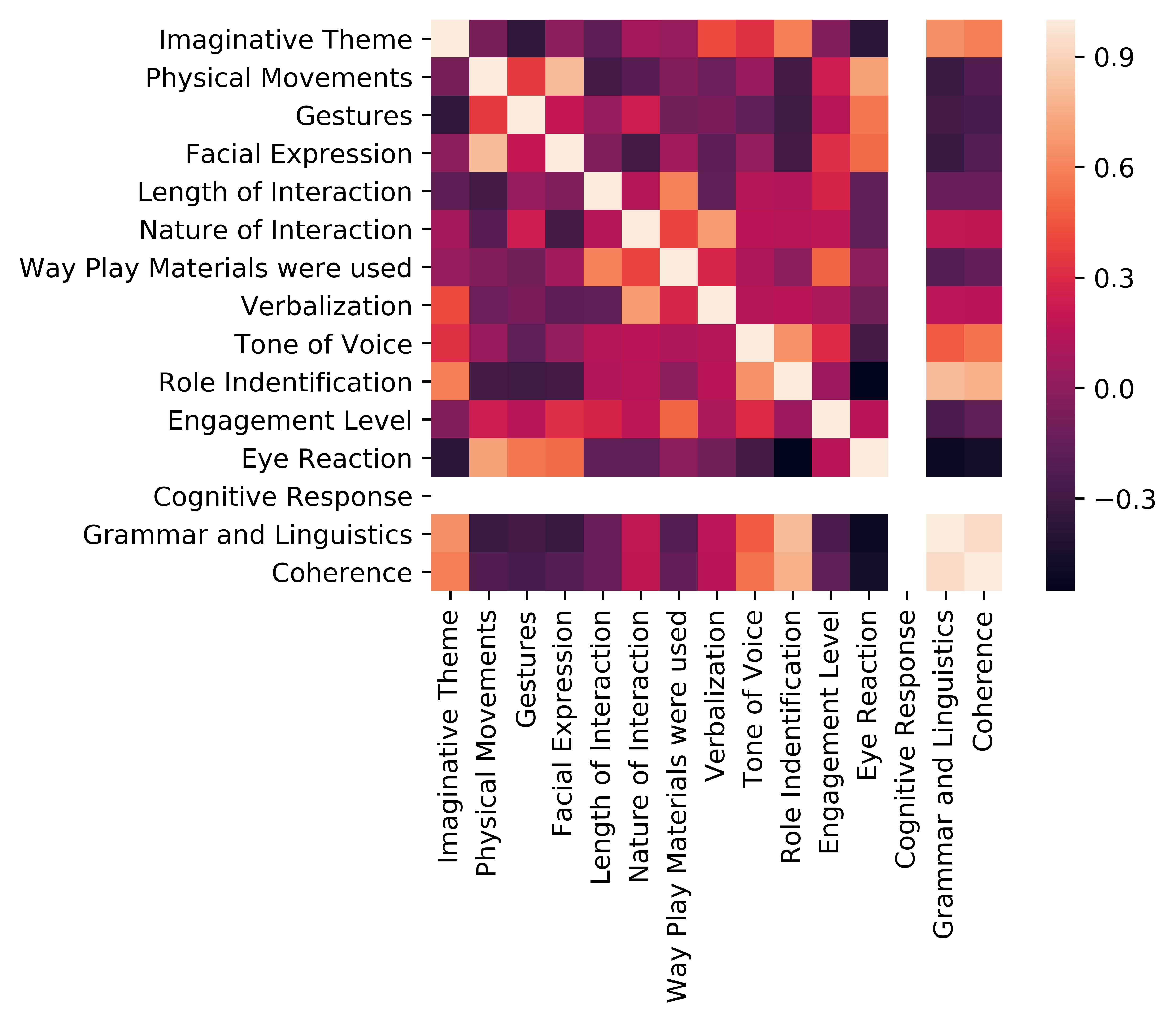
TheresultsfromtheFigure 3 showstheheatmapforfeatureT(Truthmembership).
Figure3. HeatmapforfeatureT.
AnelbowcurvewasplottedtodeterminetheoptimalnumberofclustersforK-meansandPCA K-meansclustering.Figure 4 showsourelbowcurveforfeatureTwherewecanseethatthesharp bendcomesatk = 4,thus,4clustersareoptimal.
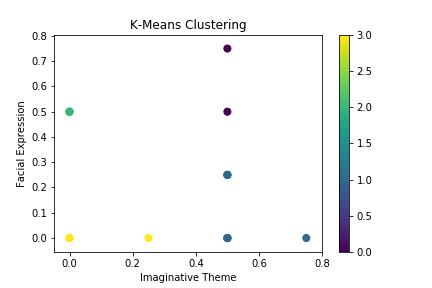
InFigure 5,whiletestingK-meansonfeatureTfortheparameters‘FacialExpression’onthe y-axisagainst‘ImaginativeTheme’onthex-axis,itwasfoundthathigherconcentrationofpointslies nearx = 0.5andy = 0.2.
Figure4. ElbowcurveforfeatureT.
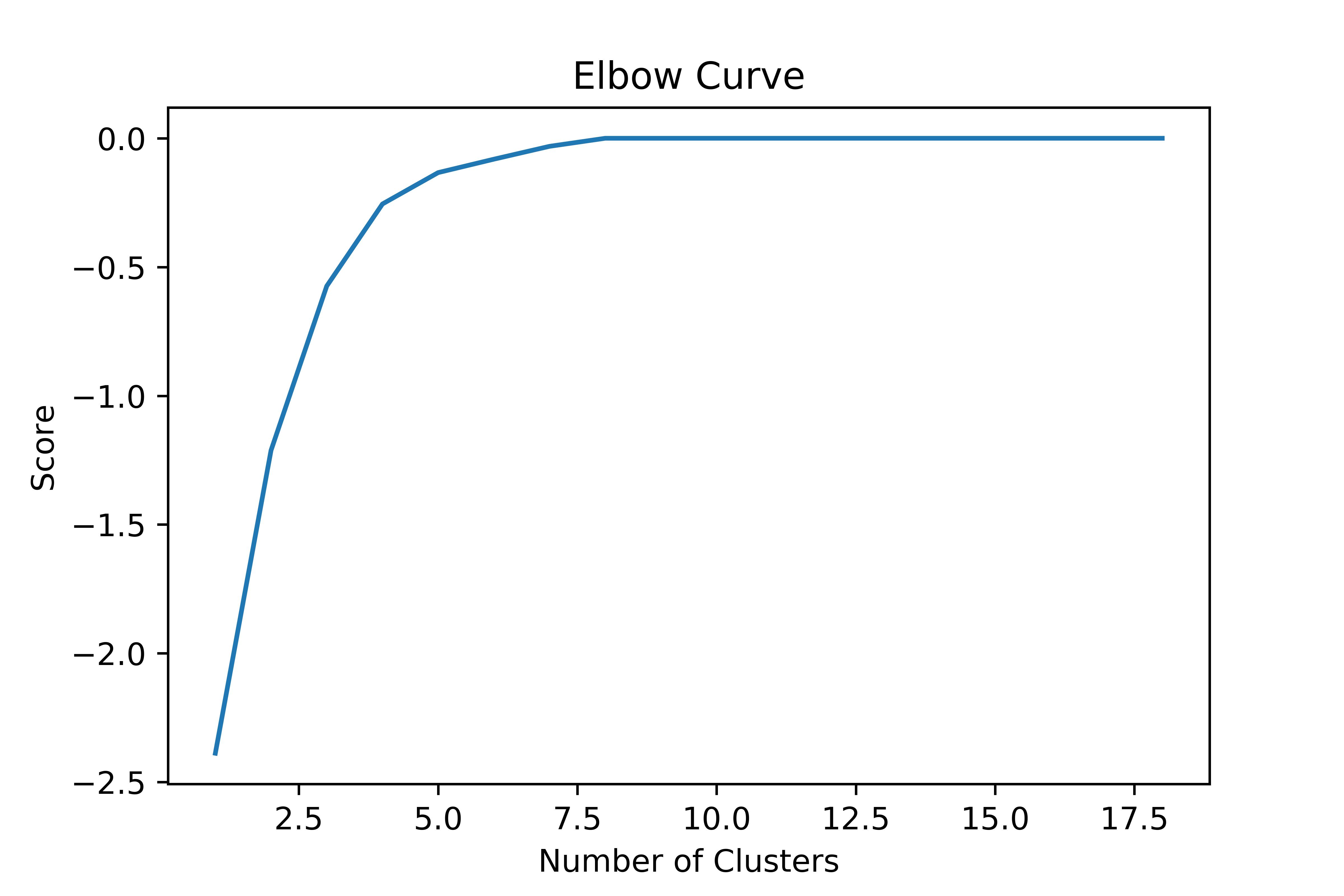
Figure5. K-meansforfeatureT.
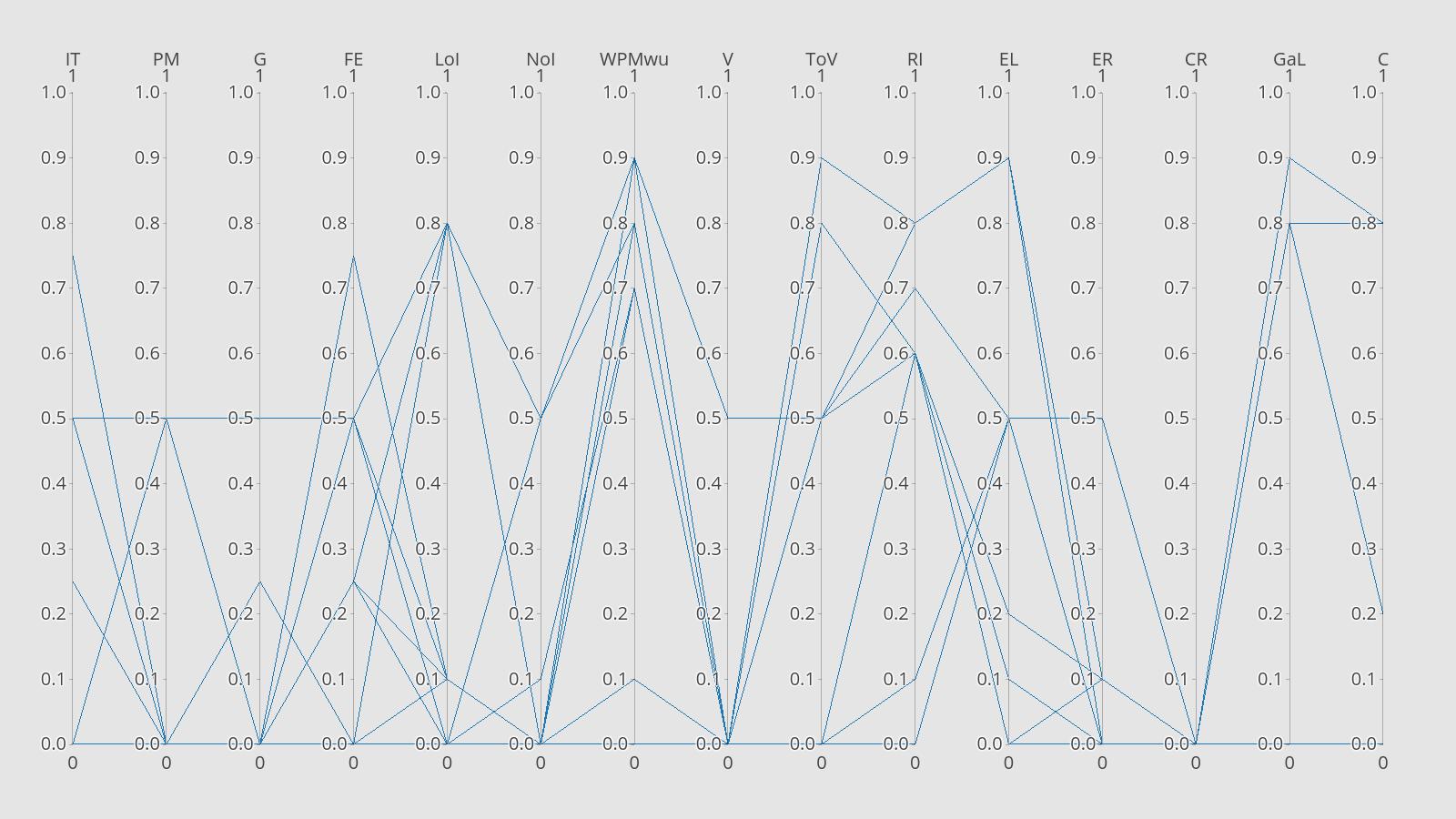
Then,thedatawasresolvedalongitsprincipalcomponents,thusgivinganewspatialarrangement ofthefeature,whichwasthenclusteredagainusingK-Means.Figure 6 showstheoutputforPCA K-MeansClusteringforT.Asignificantdeviationofthespatialarrangementofdatapointsisseen inthefigure.Now,thehigherconcentrationofpointsshifttox = 0.2,y = 0.08.‘ToneofVoice’ and‘EngagementLevel’aresimilarlyassociatedwith‘RoleIdentification’astheco-ordinateaxisis symmetricalaboutit,asshowninFigure 7
Figure6. PCAK-meansforfeatureT.
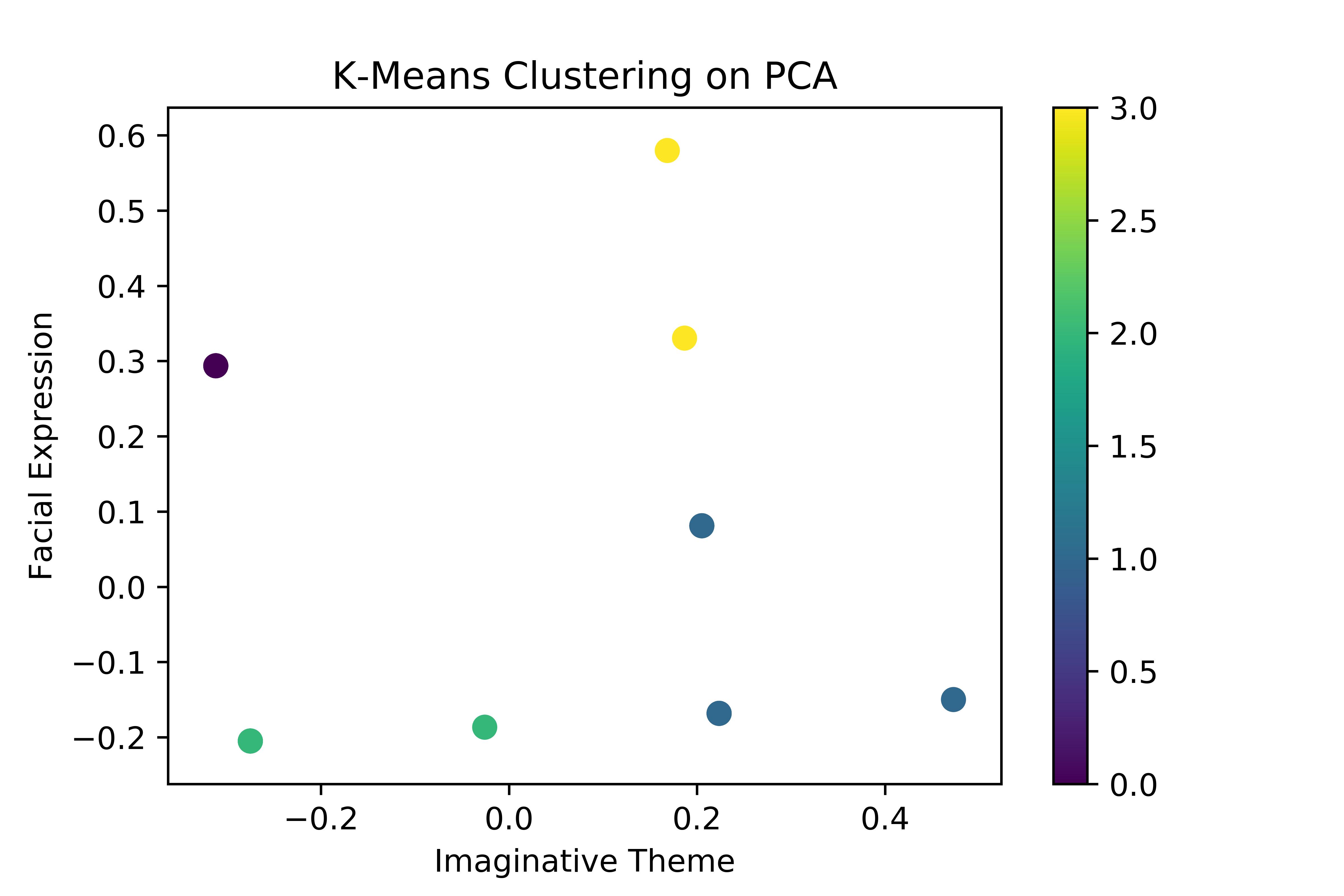
Figure7. PACforfeatureT.
ThecomparativeanalysisinTable 4 focusesonfivecommonfactorsbetweenthefouralgorithms. Thecorrelationbetweenanytwoparameterssignifiestheirassociatedrelation.Apositivecorrelation happenswhenanincreaseinoneattributeshowsanincreaseinanotherattributeaswell.Anegative correlationhappenswhenanincreaseinoneattributeshowsadecreaseinanotherattribute.Theheat map,whichstronglydemonstratesthefactorsofcorrelationandassociativity,hasacolourscaleinwhich lightershadessignifypositivecorrelationanddarkershadessignifyanegativecorrelation.Forexample, inFigure 3,whichisaheatmapforfeatureT,GrammarandCoherenceshowextremelypositive correlationwhereasEyeReactionandRoleIdentificationshowanegativecorrelation.Thevisibilityof datapointsisbestobservedinthePACgraphwhiletheleastwasobservedintheHeatMap,which focusedmoreontheirassociativity.Associativity,thereverseofthishappenedinPACGraphsandHeat Mapswhereassociativityintheformerdecreasedduetoconflictofinterestinthearrangementofaxes. ThedynamicityofPAC,unlikeforallothergraphs,isthehighestbecausetheaxescanberearranged toseewhicharrangementgivesusthebestresults.However,inK-Means,PCAK-MeansandHeat map,theaxesarestaticandrearrangingthemdoesnotshowanysignificantchange.Scalabilityisa measureofhowmanydatapointscanberepresentedinthesamegraphwithoutthelossofvisibility. ThiswasfoundtobestrongestinK-MeansandPCAK-meansaseachpointcouldbeseenuniquelyon a2DCartesianspace.
conceptofSVRNSwasusedtostudytheimaginativeplayinchildren.Themodelproposedalso consistsofdistancemeasuressuchasHammingdistanceandEuclideandistancefortwogivenSVRNSs.
Onthebasisofexpertopinion,thedatawassuccessfullytransformedintoSVRNS.Thesesetswere helpfulindrawingclusters,heatmaps,parallelaxescoordinateandsoon.Thepictorialrepresentation oftheresultsofthesealgorithmshashelpedtogainusefulinsightintothedatacollected.Wewere abletoobjectivelyinterpret,forinstance,theroleoffactorssuchasgrammarinimaginativeplay inchildren.
OnthebasisofthedatacollectedandprocessedtoformSVRNSs,wewillbeabletosuccessfully developanartificialneuralnetwork(ANN),decisiontreesandothersupervisedlearningalgorithms inthisdomainforfutureresearchandtheywillbeusefulfordrawinginsightsintotheroleofthese parametersbyvaryingthevaluesoftheparameters.Otherqualitymeasuressuchasp-value,confusion matrixandaccuracycanalsobedrawnfromit.Sincethedataunderconsiderationweresmall,we werenotabletoconstructANN.
Forfuturework,wewillstudythementallyretardedchildreninthisagegroupandperforma comparativeanalysiswiththenormalchildreninthisagegroup.
Themodelwillhelpusinidentifyingchildrenwithautismandattentiondeficithyperactivity disorder(ADHD)andotherpsychologicaldisorders.Thedetectionofsuchdisordersifanyatanearly stagewiththehelpofourmodelwillhelpparentsanddoctorstousethenecessarymeasurestotreat andcontrolthemquickly.
Themodelcanbefurtherusedforotherpsychologicalstudieslikeformodelingdestructive behavioursofalcoholicsandbulimicchildrenand/oradults.
Withthisgivendataset,crossculturevalidationwasnotdone.Forfutureresearch,weshall considerthestudyofcrosscultureamongchildrenandtrytogenerateavariationfromcrossculture anditseffectorinfluenceonthecognitiveandlanguageabilitiesofchildren.
AuthorContributions: Conceptualization,methodology,V.W.B.,F.S.,andI.K.;software,andvalidation,V.D. andS.G.;formalanalysis,investigation,I.K.,V.D.andS.G.;resources,anddatacuration,I.K.,V.D.andS.G.; writing—originaldraftpreparation,I.K.,V.D.andS.G.;writing—reviewandediting,V.W.B.andF.S.;visualization, V.D.andS.G.;supervision,V.W.B.Allauthorshavereadandagreedtothepublishedversionofthemanuscript.
Funding: Thisresearchreceivednoexternalfunding.
ConflictsofInterest: Theauthorsdeclarenoconflictofinterest.
4.
5.
6.
Liu,P.;Wang,Y.Multipleattributedecision-makingmethodbasedonsingle-valuedneutrosophicnormalized weightedBonferronimean. NeuralComput.Appl. 2014, 25,2001–2010.[CrossRef]
Liu,P.;Shi,L.Thegeneralizedhybridweightedaverageoperatorbasedonintervalneutrosophichesitantset anditsapplicationtomultipleattributedecisionmaking. NeuralComput.Appl. 2015, 26,457–471.[CrossRef]
Liu,P.;Teng,F.Multipleattributegroupdecisionmakingmethodsbasedonsomenormalneutrosophic numberHeronianMeanoperators. J.Intell.FuzzySyst. 2017, 32,2375–2391.[CrossRef]
7.
8.
Liu,P.;Li,H.Multipleattributedecision-makingmethodbasedonsomenormalneutrosophicBonferroni meanoperators. NeuralComput.Appl. 2017, 28,179–194.[CrossRef]
Ye,J.Multicriteriadecision-makingmethodusingthecorrelationcoefficientundersingle-valuedneutrosophic environment. Int.J.Gen.Syst. 2013, 42,386–394.[CrossRef]
9. Ye,J.Amulticriteriadecision-makingmethodusingaggregationoperatorsforsimplifiedneutrosophicsets. J.Intell.FuzzySyst. 2014, 26,2459–2466.[CrossRef]
10. Ye,J.Singlevaluedneutrosophiccross-entropyformulticriteriadecisionmakingproblems. Appl.Math. Model. 2014, 38,1170–1175.[CrossRef]
11. Ye,J.Similaritymeasuresbetweenintervalneutrosophicsetsandtheirapplicationsinmulticriteria decision-making. J.Intell.FuzzySyst. 2014, 26,165–172.[CrossRef]
12. Cheng,H.D.;Guo,Y.Anewneutrosophicapproachtoimagethresholding. NewMath.Nat.Comput. 2008, 4,291–308.[CrossRef]
13. Sengur,A.;Guo,Y.Colortextureimagesegmentationbasedonneutrosophicsetandwavelettransformation. Comput.Vis.ImageUnderst. 2011, 115,1134–1144.[CrossRef]
14. Zhang,M.;Zhang,L.;Cheng,H.Aneutrosophicapproachtoimagesegmentationbasedonwatershed method. SignalProcess. 2010, 90,1510–1517.[CrossRef]
15. Salama,A.;Haitham,A.;Manie,A.;Lotfy,M.UtilizingNeutrosophicSetinSocialNetworkAnalysis e-LearningSystems. Int.J.Inf.Sci.Intell.Syst. 2014, 3,61–72.
16. Vasantha,W.;Smarandache,F. FuzzyCognitiveMapsandNeutrosophicCognitiveMaps;InfiniteStudy:Phoenix, AZ,USA,2003
17. Vasantha,W.;Smarandache,F. AnalysisofSocialAspectsofMigrantLabourersLivingWithHIV/AIDSUsing FuzzyTheoryandNeutrosophicCognitiveMaps:WithSpecialReferencetoRuralTamilNaduinIndia;Infinite Study:Phoenix,AZ,USA,2004.
18. Smarandache,F.Neutropsychicpersonality.In AMathematicalApproachtoPsychology;Pons:Brussels, Belgium,2018 19. Fink,R.S.Roleofimaginativeplayincognitivedevelopment. Psychol.Rep. 1976, 39,895–906.[CrossRef] 20. Udwin,O.Imaginativeplaytrainingasaninterventionmethodwithinstitutionalisedpreschoolchildren. Br.J.Educ.Psychol. 1983, 53,32–39.[CrossRef]
21. Huston-Stein,A.;Friedrich-Cofer,L.;Susman,E.J.Therelationofclassroomstructuretosocialbehavior, imaginativeplay,andself-regulationofeconomicallydisadvantagedchildren. ChildDev. 1977, 48,908–916. [CrossRef] 22. Bodrova,E.Make-believeplayversusacademicskills:AVygotskianapproachtotoday’sdilemmaofearly childhoodeducation. Eur.EarlyChild.Educ.Res.J. 2008, 16,357–369.[CrossRef] 23. Seja,A.L.;Russ,S.W.Children’sfantasyplayandemotionalunderstanding. J.Clin.ChildPsychol. 1999, 28,269–277.[CrossRef] 24.
Dhingra,G.;Kumar,V.;Joshi,H.D.Anovelcomputervisionbasedneutrosophicapproachforleafdisease identificationandclassification. Measurement 2019, 135,782–794.[CrossRef] 25.
26.
27.
28.
29.
Vasantha,W.B.;Kandasamy,I.;Smarandache,F.NeutrosophicDupletsofZpn,× andZpq,× andTheir Properties. Symmetry 2018, 10,345.[CrossRef]
Vasantha,W.;Kandasamy,I.;Smarandache,F.AlgebraicStructureofNeutrosophicDupletsinNeutrosophic Rings. NeutrsophicSetsSyst. 2018, 23,85–95.
Vasantha,W.B.;Kandasamy,I.;Smarandache,F.AClassicalGroupofNeutrosophicTripletGroupsUsing Z2p, × Symmetry 2018, 10,194.[CrossRef]
KandasamyW.B.;Kandasamy,I.;Smarandache,F.Semi-IdempotentsinNeutrosophicRings. Mathematics 2019, 7,507.[CrossRef]
Kandasamy,W.B.;Kandasamy,I.;Smarandache,F.NeutrosophicTripletsinNeutrosophicRings. Mathematics 2019, 7,563.[CrossRef]
Symmetry 2020, 12,402
30.
Kandasamy,W.V.;Kandasamy,I.;Smarandache,F.NeutrosophicQuadrupleVectorSpacesandTheir Properties. Mathematics 2019, 7,758. 31. Haibin,W.;Smarandache,F.;Zhang,Y.;Sunderraman,R. SingleValuedNeutrosophicSets;InfiniteStudy: TamilNadu,India,2010;Volume1,pp.10–14. 32.
Shahzadi,G.;Akram,M.;Saeid,A.B.Anapplicationofsingle-valuedneutrosophicsetsinmedicaldiagnosis. NeutrosophicSetsSyst. 2018, 18,80–88. 33. Ali,M.;Smarandache,F.Complexneutrosophicset. NeuralComput.Appl. 2017, 28,1817–1834.[CrossRef] 34.
35.
36.
Smarandache,F.n-ValuedRefinedNeutrosophicLogicandItsApplicationstoPhysics. Prog.Phys. 2013, 4,143–146.
Kandasamy,I.Double-valuedneutrosophicsets,theirminimumspanningtrees,andclusteringalgorithm. J.Intell.Syst. 2018, 27,163–182.[CrossRef]
Kandasamy,I.;Smarandache,F.MulticriteriaDecisionMakingUsingDoubleRefinedIndeterminacy NeutrosophicCrossEntropyandIndeterminacyBasedCrossEntropy. Appl.Mech.Mater. 2016, 859,129–143. [CrossRef]
37. Khan,Q.;Liu,P.;Mahmood,T.SomeGeneralizedDiceMeasuresforDouble-ValuedNeutrosophicSetsand TheirApplications. Mathematics 2018, 6,121.[CrossRef]
38.
Kandasamy,I.;Smarandache,F.TripleRefinedIndeterminateNeutrosophicSetsforPersonalityClassification. InProceedingsofthe2016IEEESymposiumSeriesonComputationalIntelligence(SSCI),Athens,Greece, 6–9December2016;IEEE:Piscataway,NJ,USA,2016;pp.1–8.[CrossRef]
39.
40.
Kandasamy,I.;Vasantha,W.B.;Obbineni,J.;Smarandache,F.IndeterminateLikertScaling. SoftComput. 2019,1–10.[CrossRef]
Kandasamy,I.;Vasantha,W.;Mathur,N.;Bisht,M.;Smarandache,F.Chapter6Sentimentanalysisofthe MeToomovementusingneutrosophy:Applicationofsingle-valuedneutrosophicsets.In OptimizationTheory BasedonNeutrosophicandPlithogenicSets;Elsevier:Amsterdam,TheNetherlands,2020.[CrossRef]
41. Kandasamy,I.;Vasantha,W.;Obbineni,J.M.;Smarandache,F.Sentimentanalysisoftweetsusingrefined neutrosophicsets. Comput.Ind. 2020, 115,103180.[CrossRef]
42.
KandasamyW.B.,V.;Kandasamy,I.;Smarandache,F.;Devvrat,V.;Ghildiyal,S.StudyofImaginativePlayin ChildrenusingNeutrosophicCognitiveMapsModel. NeutrosophicSetsSyst. 2019, 30,241–252.
© 2020bytheauthors.LicenseeMDPI,Basel,Switzerland.Thisarticleisanopenaccess articledistributedunderthetermsandconditionsoftheCreativeCommonsAttribution (CCBY)license(http://creativecommons.org/licenses/by/4.0/).

