Some Root Level Modifications in Interval Valued Fuzzy Graphs

Some Root Level Modifications in Interval Valued Fuzzy Graphs and Their Generalizations Including Neutrosophic Graphs

SEE PROFILE

Kifayat Ullah International Islamic University, Islamabad 21 PUBLICATIONS 14 CITATIONS

SEE PROFILE

SEE PROFILE

SEE PROFILE

SomeRootLevelModificationsinIntervalValued FuzzyGraphsandTheirGeneralizationsIncluding NeutrosophicGraphs

NaeemJan 1,KifayatUllah 1 ,TahirMahmood 1 ,HarishGarg 2,* ,BijanDavvaz 3 , ArshamBorumandSaeid 4 andSaidBroumi 5

1 DepartmentofMathematicsandStatistics,InternationalIslamicUniversityIslamabadPakistan,Islamabad CapitalTerritory44000,Pakistan;naeem.phdma73@iiu.edu.pk(N.J.);kifayat.phdma72@iiu.edu.pk(K.U.); tahirbakhat@iiu.edu.pk(T.M.)

2 SchoolofMathematics,ThaparInstituteofEngineering&Technology,DeemedUniversity, Patiala147004,Punjab,India

4

3 DepartmentofMathematics,YazdUniversity,Yazd89195-741,Iran;davvaz@yazd.ac.ir

DepartmentofPureMathematics,FacultyofMathematicsandComputer,ShahidBahonarUniversityof Kerman,Kerman7616913439,Iran;a_b_saeid@yahoo.com

5 LaboratoryofInformationProcessing,UniversityHassanII,Casablanca20000,Morocco; broumisaid78@gmail.com

* Correspondence:harishg58iitr@gmail.com;Tel.:+91-86990-31147

Received:22November2018;Accepted:3January2019;Published:10January2019

Abstract: Fuzzygraphs(FGs)andtheirgeneralizationshaveplayedanessentialroleindealing withreal-lifeproblemsinvolvinguncertainties.Thegoalofthisarticleistoshowsomeserious flawsintheexistingdefinitionsofseveralroot-levelgeneralizedFGstructureswiththehelp ofsomecounterexamples.Toachievethis,first,weaimtoimprovetheexistingdefinitionfor interval-valuedFG,interval-valuedintuitionisticFGandtheircomplements,astheseexisting definitionsarenotwell-defined;i.e.,onecanobtainsomesenselessintervalsusingtheexisting definitions.Thelimitationsoftheexistingdefinitionsandthevalidityofthenewdefinitionsare supportedwithsomeexamples.Itisalsoobservedthatthenotionofasingle-valuedneutrosophic graph(SVNG)isnotwell-definedeither.TheconsequencesoftheexistingdefinitionofSVNGare discussedwiththehelpofexamples.AnewdefinitionofSVNGisdeveloped,anditsimprovement isdemonstratedwithsomeexamples.Thedefinitionofaninterval-valuedneutrosophicgraphisalso modifiedduetotheshortcomingsinthecurrentdefinition,andthevalidityofthenewdefinitionis proved.Anapplicationofproposedworkisillustratedthroughadecision-makingproblemunder theframeworkofSVNG,anditsperformanceiscomparedwithexistingwork.

Keywords: interval-valuedfuzzygraph;intuitionisticfuzzygraph;interval-valuedintuitionistic fuzzygraph;single-valuedneutrosophicgraph;interval-valuedneutrosophicgraph;complement

1.Introduction

Theframeworkofthefuzzyset(FS)wasintroducedbyZadeh[1]in1965asageneralization ofcrispsets,whichdescribethemembershipofanobjecttoasetbyassigningamembershipgrade from[0,1].TheconceptofFSwasfurthergeneralizedtotheinterval-valuedfuzzyset(IVFS)in[2] wherethemembershipgradeisdefinedbyclosedsub-intervals SL , SU ⊆ [0,1].TheideaofFSwas furthergeneralizedtoanenhancedframeworkoftheintuitionisticfuzzyset(IFS)in[3]byconsidering thedegreeofnon-membershipofanobjectaswellasitsmembershipgrade,suchthatthesumof thedegreesislessthanone.Lateron,AtanassovandGargov[4]extendedthetheoryofIFStoan Mathematics 2019, 7,72;doi:10.3390/math7010072 www.mdpi.com/journal/mathematics

interval-valuedIFS(IVIFS).Toconsidertheneutralopinionorabstinenceinformationintheanalysis, Smarandacheintroducedaframeworkofneutrosophiclogicandconsequentlyaneutrosophicset[5]. Aneutrosophicsetischaracterizedbythreekindsoffunctionsdescribingthedegreeofmembership, abstinenceandnon-membershipofanobject.Theconceptofthesingle-valuedneutrosophicset(SVNS) wasdevelopedbyWangetal.[6],characterizedbythreecharacteristicfunctions,namedastruth, falsityandindeterminate,witharestrictionthattheirsumisnotgreaterthan3.TheconceptofSVNS wasfurthergeneralizedtoaninterval-valuedneutrosophicset(IVNS)inWangetal.[7]wherethe membership,abstinenceandnon-membershipgradesaredefinedintermsofclosedsub-intervalsof theunitinterval.Undertheabove-mentionedsets,variousresearchershaveaddresseddifferentkinds ofalgorithmstosolvedecision-makingproblems[8–25].

Further,apartfromthis,theconceptofthefuzzygraph(FG),initiallyintroducedbyKauffman[26], wasthoroughlydevelopedbyRosenfeld[27]in1975.AgeneralizationofFGknownasthe interval-valuedFG(IVFG)wasintroducedbyAkramandDudek[28]wherethenodesandedges areintheformofinterval-valuedfuzzynumbers(IVFNs).TodealwiththestudyofFGsand IVFG,wereferthereaderstothearticlesin[29–38].Aftersuccessfulapplications,Parvathiand Karunambigai[39]introducedtheconceptofintuitionisticfuzzygraphs(IFG),whichisageneralization oftheFG.Theconceptofinterval-valuedIFG(IVIFG)isproposedin[40]andsomeotherterms andnotionsrelatedtoIVIFGcanbefoundin[41,42].Further,byfollowingthenotionofSVNS, theconceptofthesingle-valuedneutrosophicgraph(SVNG)wasintroducedbyBroumietal.[43] andhasbeenextensivelyusedinseveralproblemssuchastheshortestpathproblem[44,45], communicationproblem[46],anddecision-making[47].TheconceptofSVNGwasfurthergeneralized totheinterval-valuedneutrosophicgraph(IVNG)in[48],wherethemembership,abstinenceand non-membershipgradesaredescribedbyclosedsubintervalsoftheunitinterval.Theframeworkof IVNGisthemostsophisticatedamongallexistinggraphstructures.ForsomeotherworkonIVNG, onemayreferto[49–51].

Inthetheoryoffuzzyalgebraicstructuresandfromtheaboveliteraturesurvey,wefoundsome seriousshortcomingswhichmotivateustodevelopsomenewdefinitionsfortheexistingconcepts. Theproblemsintheexistingliteratureandstepstowardtheirsolutionarediscusseditembyitembelow.

(1) ItisobservedthattheconceptofIVFG[28]hassomelimitationswhichleadustosomeundefined results.TheloweranduppervaluesoftheedgeintervalinIVFGaredefinedas ˆ SLÄvi, vjä ≤ minÄSL (vi ), SLÄvjää and ˆ SU Ävi, vjä ≤ minÄSU (vi ), SU Ävjää.Accordingtothisdefinitionfor twoadjacentvertices (0.2,0.4) and (0.2,0.3),weobtainedanundefinededgevalueof (0.2,0.0) bytheaboveapproach.ThesametypeofproblemoccursintheframeworkofIVIFG[40]in membershipaswellasnon-membershipintervals.Further,theexistingdefinitionofIVIFGis notageneralizationofIFG;therefore,onemustdevelopadefinitionforIVIFGwhichclearly generalizesIFG.Thesetypesofflawsintheexistingliteratureleadustodevelopsomenew definitionsforIVFGandIVIFG;

(2) TheloweranduppervaluesofedgesinthecomplementofanIVFGaredefined as

(0.1,0.3) theiredge.Then,uponcalculatingthecomplement,wegetthecorrespondingedgevalue (0.1,0.0) whichisanundefinedinterval.Similartypesofflawsexistintheexistingdefinitions ofcomplementsofIVIFGs,thereforeleadingustodevelopsomenewdefinitionsforthe complementofIVFGaswellasofIVIFG.;

(3) ItisobservedthattheexistingdefinitionofSVNG[43]isnotageneralizationofIFGasclaimed intheexistingliterature.Also,theexistingnotionoftheSVNGandofitscomplementasdefined in[43]isnotwellposed,asaftertakingthecomplementofaSVNG,theresultinggraphobtained isnotaSVNG.Further,theexistingdefinitionofacomplementdoesnotsatisfytheproperty

(3) It is observed that the existing definition of SVNG [Error!

generalization of IFG as claimed in the existing literature. Also, the existing notion of the SVNG and of its complement as defined in [Error! Reference source not found.] is not well posed, as after taking the complement of a SVNG, the resulting graph obtained is not a SVNG. Further, the existing definition of a complement does not satisfy the property (�� ) =�� . These facts are described briefly in Section 5, and based on these defects, a new definition for SVNG and its complement have been developed and their validity is proved;

(Gc )c = G.ThesefactsaredescribedbrieflyinSection 5,andbasedonthesedefects,anew definitionforSVNGanditscomplementhavebeendevelopedandtheirvalidityisproved;

(4) Finally, we improve the definition of the IVNG as the existing definition contradicts the fact that IVNG is a generalization of IVIFG and IVFG. Further, the existing definition of the complement of IVNG is not well defined, which is described with the help of examples, and a new definition for complements is proposed and validated with examples.

(4) Finally,weimprovethedefinitionoftheIVNGastheexistingdefinitioncontradictsthefactthat IVNGisageneralizationofIVIFGandIVFG.Further,theexistingdefinitionofthecomplement ofIVNGisnotwelldefined,whichisdescribedwiththehelpofexamples,andanewdefinition forcomplementsisproposedandvalidatedwithexamples.

The rest of the article is organized as follows: Section 1 provides a historical background of FGs and their generalized algebraic structures. The motivation and aim of our proposed work is also discussed in this section. In Section 2, some basic concepts of FGs and IFGs are discussed and supported with examples. Section 3 is based on a description of the limitations of IVFGs and IVIFGs and some improvements in their basic definitions. In Section 4, we discuss the drawbacks of the complements of IVFG and IVIFG and propose new definitions of complements along with some examples in their support. In Section 5, the drawbacks of the existing concepts of SVNGs, IVNGs and their complements are described. Further, some new improved definitions are proposed for SVNG, IVNGs and the complement of IVNG, supported by some examples. Section 6 is based on an application of SVNGs in decision-making, while Section 7 provides a summary of the article along with some future work.

Therestofthearticleisorganizedasfollows:Section 1 providesahistoricalbackgroundof FGsandtheirgeneralizedalgebraicstructures.Themotivationandaimofourproposedworkis alsodiscussedinthissection.InSection 2,somebasicconceptsofFGsandIFGsarediscussedand supportedwithexamples.Section 3 isbasedonadescriptionofthelimitationsofIVFGsandIVIFGs andsomeimprovementsintheirbasicdefinitions.InSection 4,wediscussthedrawbacksofthe complementsofIVFGandIVIFGandproposenewdefinitionsofcomplementsalongwithsome examplesintheirsupport.InSection 5,thedrawbacksoftheexistingconceptsofSVNGs,IVNGs andtheircomplementsaredescribed.Further,somenewimproveddefinitionsareproposedfor SVNG,IVNGsandthecomplementofIVNG,supportedbysomeexamples.Section 6 isbasedonan applicationofSVNGsindecision-making,whileSection 7 providesasummaryofthearticlealong withsomefuturework.

2. Basic Concepts

2.BasicConcepts

In this section, some definitions of FG and its complement are defined and demonstrated with the help of an example. The primary definition of IFG is also discussed in this section, followed by an example for illustration.

Inthissection,somedefinitionsofFGanditscomplementaredefinedanddemonstratedwith thehelpofanexample.TheprimarydefinitionofIFGisalsodiscussedinthissection,followedbyan exampleforillustration.

Definition 1. [Error! Reference source not found.] An FG is a pair ��= (��,�� ) where �� is the set of nodes and �� is the collection of edges between these nodes such that

Definition1. [27] AnFGisapair G = (V, E) where V isthesetofnodesand E isthecollectionofedges betweenthesenodessuchthat

(1) Every ��∈�� is characterized by a function ��:��→[0,1] denoting the degree of membership of ��∈�� ;

(1) Everyv ∈ VischaracterizedbyafunctionS : V → [0,1] denotingthedegreeofmembershipofv ∈ V; (2) Every e ∈ E ischaracterizedbyafunction ˆ S: V × V → [0,1] denotingthedegreeofmembership e ∈ V × Vsatisfyingthecondition ˆ SÄvi, vjä ≤ minÄS(vi ), SÄvjää

(2) Every ��∈�� is characterized by a function Ŝ:��×��→[0,1] denoting the degree of membership ��∈ ��×�� satisfying the condition Ŝ �� ,�� ≤������ ��(�� ),�� ��

Definition2. [29] ThecomplementofFG G = (V, E) isdefinedby Gc = (Vc , Ec ) where Vc = V andthe membershipgradeofe ∈ Eisdefinedby Ĉ SäcÄvi, vjä = minÄS(vi ), SÄvjää ˆ SÄÄvi, vjää

Definition 2. [Error! Reference source not found.] The complement of FG ��= (��,�� ) is defined by �� = (�� ,�� ) where �� =�� and the membership grade of ��∈�� is defined by Ŝ �� ,�� = ������ ��(�� ),�� �� −Ŝ �� ,��

Example1. ThefollowingFigure 1 isanexampleofanFGwhileFigure 2 representsitscomplement.

(0.4) (0.2) (0.3) (0.4) (0.1)

(0.6) (0.2)

Example 1. The following Figure 1 is an example of an FG while Figure 2 represents its complement. (0.2)

Figure1. Fuzzygraph(FG)compatiblewithDefinition1.

Figure 1. Fuzzy graph (FG) compatible with Definition 1.

Figure 1. Fuzzy graph (FG) compatible with Definition 1.

(0.1)

(0.4)

(0.4)

(0.4)

(0.1) (0.2)

(0.4) (0.1) (0.1) (0.2)

(0.2) (0.6)

(0.2) (0.6)

Figure2. ComplementofFGdepictedinFigure 1

Figure 2 Complement of FG depicted in Figure 1

Figure 2. Complement of FG depicted in Figure 1

Definition 3. [Error! Reference source not found.] An IFG is a duplet ��= (��,�� ) where the set of nodes is denoted by �� and �� is the collection of edges between these nodes such that

Definition3. [39] AnIFGisaduplet G = (V, E) wherethesetofnodesisdenotedby V and E isthecollection ofedgesbetweenthesenodessuchthat

Definition 3. [Error! Reference source not found.] An IFG is a duplet ��= (��,�� ) where the set of nodes is denoted by �� and �� is the collection of edges between these nodes such that

(1) Every ��∈�� is characterized by two functions ��:��→[0,1] and ��:��→[0,1] denoting the membership and non-membership degree of ��∈�� which satisfies the condition that 0≤��+��≤1. Moreover, the term �� defined by ��=1−��−��, denotes the hesitancy level of ∈�� ;

(1) Every ��∈�� is characterized by two functions ��:��→[0,1] and ��:��→[0,1] denoting the membership and non-membership degree of ��∈�� which satisfies the condition that 0≤��+��≤1. Moreover, the term �� defined by ��=1−��−��, denotes the hesitancy level of ∈�� ; (2) Every ��∈�� is characterized by two functions Ŝ:��×��→[0,1] and Ð:��×��→[0,1] denoting the membership and non-membership degree of ��∈��×�� satisfying the conditions:

(2) Every ��∈�� is characterized by two functions Ŝ:��×��→[0,1] and Ð:��×��→[0,1] denoting the membership and non-membership degree of ��∈��×�� satisfying the conditions:

Ŝ �� ,�� ≤min ��(�� ),�� ��

Ŝ �� ,�� ≤min ��(�� ),�� ��

Ð �� ,�� ≤max ��(�� ),�� ��

Ð �� ,�� ≤max ��(�� ),�� ��

with a condition that 0≤Ŝ+Ð≤1. Moreover, the term Ř denotes the hesitancy level of ��∈�� such that Ř=1−Ŝ−Ð

with a condition that 0≤Ŝ+Ð≤1. Moreover, the term Ř denotes the hesitancy level of ��∈�� such that Ř=1−Ŝ−Ð.

(1) Every v ∈ V ischaracterizedbytwofunctions S : V → [0,1] and D : V → [0,1] denotingthe membershipandnon-membershipdegreeof v ∈ V whichsatisfiestheconditionthat 0 ≤ S + D ≤ 1. Moreover,thetermRdefinedbyR = 1 S D, denotesthehesitancylevelof ∈ E; (2) Every e ∈ E ischaracterizedbytwofunctions ˆ S: V × V → [0,1] and Ð: V × V → [0,1] denoting themembershipandnon-membershipdegreeofe ∈ V × Vsatisfyingtheconditions: ˆ SÄvi, vjä ≤ minÄS(vi ), SÄvjää ÐÄvi, vjä ≤ maxÄD(vi ), DÄvjää withaconditionthat 0 ≤ ˆ S + Ð ≤ 1.Moreover,theterm ˇ R denotesthehesitancylevelof e ∈ E suchthat ˇ R = 1 ˆ S Ð.

Example 2. The following Figure 3 is an example of an IFG.

Example2. ThefollowingFigure 3 isanexampleofanIFG.

Example 2. The following Figure 3 is an example of an IFG.

Figure 3. Intuitionistic fuzzy graph (IFG) compatible with Definition 2.

Figure3. Intuitionisticfuzzygraph(IFG)compatiblewithDefinition2.

Figure 3. Intuitionistic fuzzy graph (IFG) compatible with Definition 2.

The rest of the basic notions are discussed in Sections 3–5, in which we present a comparative analysis with our proposed work.

The rest of the basic notions are discussed in Sections 3–5, in which we present a comparative analysis with our proposed work.

TherestofthebasicnotionsarediscussedinSections 3–5,inwhichwepresentacomparative analysiswithourproposedwork.

Inthissection,first,theexistingdefinitionsofIVFGandIVIFGarereviewedandtheshortcomings ofthesealgebraicstructuresarepointedoutwiththehelpofexamples.NewdefinitionsforIVFGand IVIFGaredevelopedandtheirfitnessisverifiedwiththehelpofsomeexamples.

3. Improvements in Interval-Valued Fuzzy Graphs and Interval-Valued Intuitionistic Fuzzy Graphs

In this section, first, the existing definitions of IVFG and IVIFG are reviewed and the shortcomings of these algebraic structures are pointed out with the help of examples. New definitions for IVFG and IVIFG are developed and their fitness is verified with the help of some examples.

First,wereviewthedefinitionofIVFGdefinedin[28]andprovideanexampletoshowthe limitationofthedefinitions.

First, we review the definition of IVFG defined in [Error! Reference source not found.] and provide an example to show the limitation of the definitions.

Definition 4. [Error! Reference source not found.] An IVFG is a duplet ��=(��,��) where �� denotes a collection of nodes and �� denotes the collection of edges between these vertices such that

(1) Every ��∈�� is characterized by a function �� representing the membership degree of ��∈�� . Basically, ��= [�� ,�� ] is a closed subinterval [0, 1];

(2) Every ��∈�� is characterized by a function Ŝ denoting the degree of membership ��∈��×�� . Basically, Ŝ= Ŝ ,Ŝ satisfying the conditions:

Definition4. [28] AnIVFGisaduplet G = (V, E) where V denotesacollectionofnodesand E denotesthe collectionofedgesbetweentheseverticessuchthat (1) Every v ∈ V ischaracterizedbyafunction S representingthemembershipdegreeof v ∈ V.Basically, S = SL , SU isaclosedsubinterval[0,1]; (2) Every e ∈ E ischaracterizedbyafunction ˆ S denotingthedegreeofmembership e ∈ V × V.Basically, ˆ S = ˆ SL , ˆ SU satisfyingtheconditions:

Ŝ �� ,�� ≤min �� (�� ),�� ��

Ŝ �� ,�� ≤min �� (�� ),�� ��

Example3. ConsiderthefollowingFigure 4,whereweobservedthat,whiledeterminingtheedgevalues,weget undefinedintervalsashighlighted.ThisshowsthatthecurrentnotionofanIVFGisnotsatisfactory,which leadsustodevelopanewdefinition.

Example 3. Consider the following Figure 4, where we observed that, while determining the edge values, we get undefined intervals as highlighted. This shows that the current notion of an IVFG is not satisfactory, which leads us to develop a new definition.

Figure 4. Interval-valued fuzzy graph containing undefined intervals.

Figure4. Interval-valuedfuzzygraphcontainingundefinedintervals.

Definition 5. An IVFG is a duplet ��=(��,��) where �� denotes a collection of nodes and �� denotes the collection of edges between these vertices such that

Definition5. AnIVFGisaduplet G = (V, E) where V denotesacollectionofnodesand E denotesthe collectionofedgesbetweentheseverticessuchthat

(1) Every ��∈�� is characterized by a function �� representing the membership grade of ��∈�� . Basically, ��= [�� ,�� ] is a closed subinterval of the unit interval [0, 1];

(1) Every v ∈ V ischaracterizedbyafunction S representingthemembershipgradeof v ∈ V.Basically, S = SL , SU isaclosedsubintervaloftheunitinterval[0,1];

(2) Every ��∈�� is characterized by a function Ŝ denoting the membership grade of ��∈��×�� . The closed subinterval Ŝ= Ŝ ,Ŝ satisfying the conditions:

(2) Every e ∈ E ischaracterizedbyafunction ˆ S denotingthemembershipgradeof e ∈ V × V.Theclosed subinterval ˆ S = ˆ SL , ˆ SU satisfyingtheconditions:

Ŝ �� ,�� ≤min �� (�� ),�� �� and

Ŝ �� ,�� ≤min �� (�� ),�� �� such that Ŝ �� ,�� ≥min �� (�� ),�� ��

ˆ SLÄvi, vjä ≤ minÄSL (vi ), SLÄvjää and ˆ SU Ävi, vjä ≤ minÄSU (vi ), SU Ävjää suchthat ˆ SU Ävi, vjä ≥ minÄSL (vi ), SLÄvjää.

This definition is supported with the help of following example in which we show that none of the intervals is undefined and that Definition 5 works perfectly.

Thisdefinitionissupportedwiththehelpoffollowingexampleinwhichweshowthatnoneof theintervalsisundefinedandthatDefinition5worksperfectly.

Example 4. The following IVFG depicted in Figure 5 is in accordance with Definition 5.

Example4. ThefollowingIVFGdepictedinFigure 5 isinaccordancewithDefinition5.

Figure 5. Interval-valued fuzzy graph compatible with Definition 5.

Figure5. Interval-valuedfuzzygraphcompatiblewithDefinition5.

Next, we provide a critical study of IVIFGs with a definition which is based on IVIFG which yields undefined closed sub-intervals. First, we review the existing definition and the existing shortcomings with the help of examples. Then, the new definition is developed and supported by an example.

Next,weprovideacriticalstudyofIVIFGswithadefinitionwhichisbasedonIVIFGwhichyields undefinedclosedsub-intervals.First,wereviewtheexistingdefinitionandtheexistingshortcomings withthehelpofexamples.Then,thenewdefinitionisdevelopedandsupportedbyanexample.

Definition 6. [Error! Reference source not found.] An IVIFG is a duplet ��= (��,�� ) where the set of nodes is denoted by �� and �� is the collection of edges between these nodes such that

Definition6. [40] AnIVIFGisaduplet G = (V, E) wherethesetofnodesisdenotedby V and E isthe collectionofedgesbetweenthesenodessuchthat

(1) Every ��∈�� is characterized by two functions �� and �� denoting the membership and non-membership grades of ��∈�� . Basically, ��= [�� ,�� ] and ��= [�� ,�� ] are closed subintervals of the unit interval [0, 1] with a condition that 0≤�� +�� ≤1. Moreover, the term ��= [�� ,�� ] denote the hesitancy level of ��∈�� such that �� =1−�� −�� and �� =1−�� −��

(1) Every v ∈ V ischaracterizedbytwofunctions S and D denotingthemembershipandnon-membership gradesof v ∈ V.Basically, S = SL , SU and D = DL , DU areclosedsubintervalsoftheunitinterval [0,1]withaconditionthat 0 ≤ SU + DU ≤ 1.Moreover,theterm R = RL , RU denotethehesitancy levelofv ∈ VsuchthatRU = 1 SL DL andRL = 1 SU DU

(2) Every ��∈�� is characterized by two functions Ŝ and Ð denoting the membership and non-membership grades of ��∈��×�� . Basically, Ŝ= Ŝ ,Ŝ and Ð= [Ð ,Ð ] satisfying the conditions: Ŝ �� ,�� ≤min �� (�� ),�� �� Ŝ �� ,�� ≤min �� (�� ),�� �� Ð �� ,�� ≥max �� (�� ),�� �� Ð �� ,�� ≥max �� (�� ),�� �� provided that 0≤Ŝ +Ð ≤1 . Moreover, the term Ř= Ř ,Ř denote the hesitancy level of ��∈�� such that Ř =1−Ŝ −Ð and Ř =1−Ŝ −Ð .

(2) Every e ∈ E ischaracterizedbytwofunctions ˆ S and Ð denotingthemembershipandnon-membership gradesofe ∈ V × V.Basically, ˆ S = ˆ SL , ˆ SU and Ð = îÐL,ÐU ó satisfyingtheconditions: ˆ SLÄvi, vjä ≤ minÄSL (vi ), SLÄvjää ˆ SU Ävi, vjä ≤ minÄSU (vi ), SU Ävjää ÐLÄvi, vjä ≥ maxÄDL (vi ), DLÄvjää ÐU Ävi, vjä ≥ maxÄDU (vi ), DU Ävjää providedthat 0 ≤ ˆ SU + ÐU ≤ 1.Moreover,theterm ˇ R = ˇ RL , ˇ RU denotethehesitancylevelof e ∈ E suchthat ˇ RU = 1 ˆ SL ÐL and ˇ RL = 1 ˆ SU ÐU

Definition 6 seems to be weak in two ways. The first reason is that IVIFG is a generalization of IFG where the non-membership grade of edge is defined as Ð �� ,�� ≤������ ��(�� ),�� �� , which is not followed in defining IVIFG, raising a question regarding its perfection. Another shortcoming in Definition 6 is that we may sometimes have obtained undefined closed intervals, which should be avoided. For further illustration, consider the example as follows.

Example 5. Consider the following IVIFG in Figure 6, where it is observed that we get some undefined intervals by applying Definition 6. The undefined closed intervals are highlighted.

Definition6seemstobeweakintwoways.ThefirstreasonisthatIVIFGisageneralizationof IFGwherethenon-membershipgradeofedgeisdefinedas ÐÄvi, vjä ≤ maxÄD(vi ), DÄvjää,whichis notfollowedindefiningIVIFG,raisingaquestionregardingitsperfection.Anothershortcomingin Definition6isthatwemaysometimeshaveobtainedundefinedclosedintervals,whichshouldbe avoided.Forfurtherillustration,considertheexampleasfollows.

Example5. ConsiderthefollowingIVIFGinFigure 6,whereitisobservedthatwegetsomeundefinedintervals byapplyingDefinition6.Theundefinedclosedintervalsarehighlighted.

Figure 6. Interval-valued intuitionistic fuzzy graph (IVIFG) obtained using Definition 6 with undefined intervals.

not followed in defining IVIFG, raising a question regarding its perfection. Another shortcoming in Definition 6 is that we may sometimes have obtained undefined closed intervals, which should be avoided. For further illustration, consider the example as follows.

Mathematics 2019, 7,72 7of22

Example 5. Consider the following IVIFG in Figure 6, where it is observed that we get some undefined intervals by applying Definition 6. The undefined closed intervals are highlighted.

Figure6. Interval-valuedintuitionisticfuzzygraph (IVIFG)obtainedusingDefinition6with undefinedintervals.

Figure 6. Interval-valued intuitionistic fuzzy graph (IVIFG) obtained using Definition 6 with undefined intervals.

KeepinginmindtheweaknessofDefinition6asdemonstratedbyExample5,weproposeanew definitionofIVIFGwhichiswelldefinedandtrulyageneralizationofIFG.

Definition7. AnIVIFGisapair G = (V, E) wherethesetofnodesisdenotedby V and E isthecollectionof edgesbetweenthesenodessuchthat

(1) Every v ∈ V ischaracterizedbytwofunctions S and D denotingthemembershipandnon-membership gradesof v ∈ V.Basically, S = SL , SU and D = DL , DU areclosedsubintervalsoftheunitinterval [0,1]withaconditionthat 0 ≤ SU + DU ≤ 1.Moreover,theterm R = RL , RU denotethehesitancy levelofv ∈ VsuchthatRU = 1 SL DL andRL = 1 SU DU ;

(2) Every e ∈ E ischaracterizedbytwofunctions ˆ S and Ð denotingthemembershipandnon-membership gradesofe ∈ V × V.Basically, ˆ S = ˆ SL , ˆ SU and Ð = îÐL,ÐU ó aresuchthat ˆ SLÄvi, vjä ≤ minÄSL (vi ), SLÄvjää. ˆ SU Ävi, vjä ≤ minÄSU (vi ), SU Ävjää suchthat ˆ SU Ävi, vjä ≥ minÄSL (vi ), SLÄvjää. ÐLÄvi, vjä ≤ maxÄDL (vi ), DLÄvjää. ÐU Ävi, vjä ≤ maxÄDU (vi ), DU Ävjää suchthatÐU Ävi, vjä ≥ maxÄDL (vi ), DLÄvjää. providedthat 0 ≤ ˆ SU + ÐU ≤ 1.Moreover,theterm ˇ R = ˇ RL , ˇ RU denotethehesitancylevelof e ∈ E suchthat ˇ RU = 1 ˆ SL ÐL and ˇ RL = 1 ˆ SU ÐU .

ThefollowingexampleshowsthatDefinition7improvestheconceptofIVIFGandthatthereis nochanceofgettingundefinedintervals.

Example6. ConsiderthegraphdepictedinFigure 7 demonstratingthenewdefinitionofIVIFG.

such that Ř =1−Ŝ −Ð and Ř =1−Ŝ −Ð .

The following example shows that Definition 7 improves the concept of IVIFG and that there is no chance of getting undefined intervals.

Mathematics 2019, 7,72 8of22

Example 6. Consider the graph depicted in Figure 7 demonstrating the new definition of IVIFG.

Figure 7. Interval-valued intuitionistic fuzzy graph.

Figure7. Interval-valuedintuitionisticfuzzygraph.

The next section is based on the shortcomings of existing definitions of the complement of an IVFG and of an IVIFG together with the development of new definitions. The existing and new definitions are demonstrated with examples.

ThenextsectionisbasedontheshortcomingsofexistingdefinitionsofthecomplementofanIVFG andofanIVIFGtogetherwiththedevelopmentofnewdefinitions.Theexistingandnewdefinitions aredemonstratedwithexamples.

4. New Definitions for the Complement of the Interval-Valued Fuzzy Graph and IntervalValued Intuitionistic Fuzzy Graph

4.NewDefinitionsfortheComplementoftheInterval-ValuedFuzzyGraphandInterval-Valued IntuitionisticFuzzyGraph

It is observed that the definition of the complement of IVFG did not provide justifiable results on some occasions. The results obtained using the current definition of IVFG leads us to obtain some undefined intervals, and therefore in this section we propose a new definition for the complement of IVFG.

ItisobservedthatthedefinitionofthecomplementofIVFGdidnotprovidejustifiableresults onsomeoccasions.TheresultsobtainedusingthecurrentdefinitionofIVFGleadsustoobtainsome undefinedintervals,andthereforeinthissectionweproposeanewdefinitionforthecomplement ofIVFG.

Forthefirsttime,thecomplementofIVFGwasdefinedin[38].First,wereviewtheexisting definitionand,withthehelpofanexample,wepointoutitsshortcomings.

Mathematics 2018, 6, x FOR PEER REVIEW 8 of 21

For the first time, the complement of IVFG was defined in [Error! Reference source not found.]. First, we review the existing definition and, with the help of an example, we point out its shortcomings.

Definition8. [38]ThecomplementofanIVFG G = (V, E) isdefinedby Gc = (Vc , Ec ) where Vc = V and themembershipandnon-membershipgradesofEsatisfyingtheconditions: ˆ SL cÄvi, vjä = minÄSL (vi ), SLÄvjää ˆ SLÄÄvi, vjää ˆ SU cÄvi, vjä = minÄSU (vi ), SU Ävjää ˆ SU Ävi, vjä

Definition 8. [Error! Reference source not found.] The complement of an IVFG ��= (��,�� ) is defined by �� = (�� ,�� ) where �� =�� and the membership and non-membership grades of �� satisfying the conditions: Ŝ �� ,�� =min �� (�� ),�� �� −Ŝ �� ,��

Ŝ �� ,�� =min �� (�� ),�� �� −Ŝ �� ,��

Example 7. In the following, consider an IVFG depicted in Figure 8, then based on the existing definition 8, we compute its complement and it is given in Figure 9. It is observed from the Figure 9 that there are undefined intervals which are highlighted in red color.

Example7. Inthefollowing,consideranIVFGdepictedinFigure 8,thenbasedontheexistingdefinition8,we computeitscomplementanditisgiveninFigure 9.ItisobservedfromtheFigure 9 thatthereareundefined intervalswhicharehighlightedinredcolor.

Figure 8. Interval-valued fuzzy graph. Figure8. Interval-valuedfuzzygraph.

Figure 8. Interval-valued fuzzy graph.

Figure 9. Complement of graph depicted in Figure 8 based on Definition 8, giving us undefined intervals.

Figure9. ComplementofgraphdepictedinFigure 8 basedonDefinition8,givingus undefinedintervals.

Another definition of the complement of IVFG is defined in [11] which is described as follows:

AnotherdefinitionofthecomplementofIVFGisdefinedin[11]whichisdescribedasfollows:

Definition 9. [Error! Reference source not found.] The complement of an IVFG ��= (��,�� ) is defined by �� = (�� ,�� ) where �� =�� and the membership functions of �� satisfies the following:

Definition9. [28]ThecomplementofanIVFG G = (V, E) isdefinedby Gc = (Vc , Ec ) where Vc = V and themembershipfunctionsofEc satisfiesthefollowing:

Ŝ �� ,�� = 0 ���� �� �� ,�� ≥0 min �� (�� ),�� �� ���� �� �� ,�� =0

Ŝ �� ,�� = 0 ���� �� �� ,�� ≥0 min �� (�� ),�� �� ���� �� �� ,�� =0

ˆ SL cÄvi, vjä = 0 ifSLÄvi, vjä ≥ 0 minÄSL (vi ), SLÄvjää ifSLÄvi, vjä = 0 SU cÄvi, vjä = 0 ifSU Ävi, vjä ≥ 0 minÄSU (vi ), SU Ävjää ifSU Ävi, vjä = 0

This definition is not well defined as it is not valid for all types of IVFGs. The problem in this definition of the complement is that it does not possesses the property (�� ) =�� . This is demonstrated in the following example.

ThisdefinitionisnotwelldefinedasitisnotvalidforalltypesofIVFGs.Theprobleminthis definitionofthecomplementisthatitdoesnotpossessestheproperty (Gc )c = G.Thisisdemonstrated inthefollowingexample.

Example 8. The complement of IVFG as exhibited in Figure 8 is depicted in Figure 10 below and it is observed that all the edges have disappeared surprisingly, which seems insignificant. Now, we determine the complement of Figure 10 again and put it on display in Figure 11, which clearly indicates that the basic result of the complement, i.e., (�� ) =�� , does not hold true for Definition 9.

Example8. ThecomplementofIVFGasexhibitedinFigure 8 isdepictedinFigure 10 belowanditisobserved thatalltheedgeshavedisappearedsurprisingly,whichseemsinsignificant.Now,wedeterminethecomplementof Figure 10 againandputitondisplayinFigure 11,whichclearlyindicatesthatthebasicresultofthecomplement, i.e., (Gc )c = G,doesnotholdtrueforDefinition9. Mathematics 2018, 6, x FOR PEER REVIEW 9 of 21

Figure10. ComplementofFigure 8

Figure 10. Complement of Figure 8.

Figure 11. Complement of Figure 10 based on Definition 9.

Moreover, Definition 9 is used to find the complement of a complete IVFG in [Error! Reference source not found.] by Akram and Dudek, where this definition possesses the property of a complement; i.e., (�� ) =��. However, we need a definition of a complement which can be used for

Figure 10. Complement of Figure 8.

Figure 11. Complement of Figure 10 based on Definition 9.

Figure11. basedonDefinition9.

Moreover, Definition 9 is used to find the complement of a complete IVFG in [Error! Reference source not found.] by Akram and Dudek, where this definition possesses the property of a complement; i.e., (�� ) =��. However, we need a definition of a complement which can be used for the entire range of IVFG and not only complete IVFGs; therefore, we develop a new well-defined definition for the complement of IVFGs as follows.

Moreover,Definition9isusedtofindthecomplementofacompleteIVFGin[28]byAkram andDudek,wherethisdefinitionpossessesthepropertyofacomplement;i.e., (Gc )c = G However, weneedadefinitionofacomplementwhichcanbeusedfortheentirerangeofIVFGandnotonly completeIVFGs;therefore,wedevelopanewwell-defineddefinitionforthecomplementofIVFGs asfollows.

Figure 11. Complement of Figure 10 based on Definition 9.

Moreover, Definition 9 is used to find the complement of a complete IVFG in [Error! Reference source not found.] by Akram and Dudek, where this definition possesses the property of a complement; i.e., (�� ) =��. However, we need a definition of a complement which can be used for the entire range of IVFG and not only complete IVFGs; therefore, we develop a new well-defined definition for the complement of IVFGs as follows.

Definition 10. The complement of IVFG ��= (��,�� ) is defined by �� = (�� ,�� ) where �� =�� and the membership grades of �� satisfies the following properties:

Ŝ �� ,�� =min �� (�� ),�� �� −Ŝ �� ,��

Definition 10. The complement of IVFG ��= (��,�� ) is defined by �� = (�� ,�� ) where �� =�� and the membership grades of �� satisfies the following properties:

Ŝ �� ,�� =min �� (�� ),�� �� −Ŝ �� ,�� +min �� (�� ),�� �� .

Definition10. ThecomplementofIVFG G = (V, E) isdefinedby Gc = (Vc , Ec ) where Vc = V andthe membershipgradesofEsatisfiesthefollowingproperties: ˆ SL cÄvi, vjä = minÄSL (vi ), SLÄvjää ˆ SLÄÄvi, vjää ˆ SU cÄvi, vjä = minÄSU (vi ), SU Ävjää ˆ SU Ävi, vjä + minÄSL (vi ), SLÄvjää

Ŝ �� ,�� =min �� (�� ),�� �� −Ŝ �� ,��

In the following examples, we not only demonstrate the new definition but also verify that the basic property of the notion of the complement as presented in Definition 10 is available; i.e., (�� ) =��

Ŝ �� ,�� =min �� (�� ),�� �� −Ŝ �� ,�� +min �� (�� ),�� �� .

Inthefollowingexamples,wenotonlydemonstratethenewdefinitionbutalsoverifythat thebasicpropertyofthenotionofthecomplementaspresentedinDefinition10isavailable;i.e., (Gc )c = G.

Example 9. In what follows, Figure 12 represents the complement of Figures 8 and 13 represents the complement of Figure 12. Hence, as we claimed, the equality (�� ) =�� holds true for our proposed new definition.

In the following examples, we not only demonstrate the new definition but also verify that the basic property of the notion of the complement as presented in Definition 10 is available; i.e., (�� ) =��

Example9. Inwhatfollows,Figure 12 representsthecomplementof Figures 8 and 13 representsthe complementofFigure 12.Hence,asweclaimed,theequality (Gc )c = G holdstrueforourproposednew definition.

Example 9. In what follows, Figure 12 represents the complement of Figures 8 and 13 represents the complement of Figure 12. Hence, as we claimed, the equality (�� ) =�� holds true for our proposed new definition.

Figure 12. Complement of graph depicted in Figure 8.

Figure 12. Complement of graph depicted in Figure 8. Figure12. ComplementofgraphdepictedinFigure 8

Figure 13. The complement of graph depicted in Figure 12.

Figure13. ThecomplementofgraphdepictedinFigure 12

Figure 13. The complement of graph depicted in Figure 12.

Now, we develop the definition of the complement for IVIFGs because the existing definition does not make any sense in some cases, as we described for IVFGs.

Now,wedevelopthedefinitionofthecomplementforIVIFGsbecausetheexistingdefinition doesnotmakeanysenseinsomecases,aswedescribedforIVFGs.

Now, we develop the definition of the complement for IVIFGs because the existing definition does not make any sense in some cases, as we described for IVFGs.

Definition 11. The complement of IVIFG ��= (��,�� ) is defined by �� = (�� ,�� ) where �� =�� and the membership and non-membership grades of �� satisfied the conditions: Ŝ �� ,�� =min �� (�� ),�� �� −Ŝ �� ,�� Ŝ �� ,�� =min �� (�� ),�� �� −Ŝ �� ,�� +min �� (�� ),�� �� (Ð ) �� ,�� =max �� (�� ),�� �� −Ð �� ,�� . (Ð ) �� ,�� =max �� (�� ),�� �� −Ð �� ,�� +max �� (�� ),�� ��

Definition 11. The complement of IVIFG ��= (��,�� ) is defined by �� = (�� ,�� ) where �� =�� and the membership and non-membership grades of �� satisfied the conditions:

Ŝ �� ,�� =min �� (�� ),�� �� −Ŝ �� ,��

Definition11. ThecomplementofIVIFG G = (V, E) isdefinedby Gc = (Vc , Ec ) where Vc = V andthe membershipandnon-membershipgradesofEsatisfiedtheconditions: ˆ SL cÄvi, vjä = minÄSL (vi ), SLÄvjää ˆ SLÄÄvi, vjää ˆ SU cÄvi, vjä = minÄSU (vi ), SU Ävjää ˆ SU Ävi, vjä + minÄSL (vi ), SLÄvjää. ÄÐLäcÄvi, vjä = maxÄDL (vi ), DLÄvjää ÐLÄÄvi, vjää ÄÐU äcÄvi, vjä = maxÄDU (vi ), DU Ävjää ÐU Ävi, vjä + maxÄDL (vi ), DLÄvjää

Ŝ �� ,�� =min �� (�� ),�� �� −Ŝ �� ,�� +min �� (�� ),�� �� . (Ð ) �� ,�� =max �� (�� ),�� �� −Ð �� ,�� (Ð ) �� ,�� =max �� (�� ),�� �� −Ð �� ,�� +max �� (�� ),�� ��

Example 10. Consider the following IVIFGs whose graph is shown in Figure 14 while its complement graph is shown in Figure 15. Moreover, through some easy calculations, one can easily verify that (�� ) =��

Example10. ConsiderthefollowingIVIFGswhosegraphisshowninFigure 14 whileitscomplementgraphis showninFigure 15.Moreover,throughsomeeasycalculations,onecaneasilyverifythat (Gc )c = G.

Example 10. Consider the following IVIFGs whose graph is shown in Figure 14 while its complement graph is shown in Figure 15. Moreover, through some easy calculations, one can easily verify that (�� ) =�� .

Figure 14. Interval-valued intuitionistic fuzzy graph.

Figure 14. Interval-valued intuitionistic fuzzy graph. Figure14. Interval-valuedintuitionisticfuzzygraph.

Figure 15. Complement of IVIFG depicted in Figure 14.

Figure15. ComplementofIVIFGdepictedinFigure 14

In the next section, we discuss the limitations of SVNGS, IVNGs, and their complements. In addition, we develop some new valid definitions.

Inthenextsection,wediscussthelimitationsofSVNGS,IVNGs,andtheircomplements. Inaddition,wedevelopsomenewvaliddefinitions.

5. Improvements in Single-Valued Neutrosophic Graphs and Interval-Valued Neutrosophic Graphs

5.ImprovementsinSingle-ValuedNeutrosophicGraphsandInterval-Valued NeutrosophicGraphs

In this section, we study the SVNGs proposed in [26] and IVNGs developed in [Error! Reference source not found.] and we describe their shortcomings with some examples. Then, a new definition is proposed for both SVNGs and IVNGs, and their complement is discussed. In support of these new definitions, we present some examples.

Inthissection,westudytheSVNGsproposedin[26]andIVNGsdevelopedin[48]andwe describetheirshortcomingswithsomeexamples.Then,anewdefinitionisproposedforbothSVNGs andIVNGs,andtheircomplementisdiscussed.Insupportofthesenewdefinitions,wepresent someexamples.

Definition 12. [Error! Reference source not found.] An SVNG is a pair ��= (��,�� ) where �� is the set of nodes and �� is the collection of edges between these nodes such that

Definition12. [43]AnSVNGisapair G = (V, E) where V isthesetofnodesand E isthecollectionofedges betweenthesenodessuchthat

(1) Every ��∈�� is characterized by three functions ��:��→[0,1],��:��→[0,1] and ��:��→[0,1] denoting the membership, neutral and non-membership grades of ��∈�� which satisfy 0≤��+��+��≤3; (2) Every ��∈�� is characterized by three functions Ŝ:��×��→[0,1],Î:��×��→[0,1] and Ð:��×��→ [0,1] denoting the membership, neutral and non-membership grades of ��∈��×�� satisfies Ŝ �� ,�� ≤min ��(�� ),�� �� Î �� ,�� ≥max ��(�� ),�� �� Ð �� ,�� ≥max ��(�� ),�� �� which satisfy the inequality 0≤Ŝ+Î+Ð≤3

(1) Every v ∈ V ischaracterizedbythreefunctions S : V → [0,1] , I : V → [0,1] and D : V → [0,1] denotingthemembership,neutralandnon-membershipgradesof v ∈ V whichsatisfy 0 ≤ S + I + D ≤ 3; (2) Every e ∈ E ischaracterizedbythreefunctions ˆ S: V × V → î0,1] ,Î: V × V → [0,1ó and Ð: V × V → [0,1] denotingthemembership,neutralandnon-membershipgradesof e ∈ V × V satisfies ˆ SÄvi, vjä ≤ minÄS(vi ), SÄvjää ÎÄvi, vjä ≥ maxÄI(vi ), IÄvjää ÐÄvi, vjä ≥ maxÄD(vi ), DÄvjää

whichsatisfytheinequality 0 ≤ ˆ S + Î + Ð ≤ 3.

It is observed that this definition is not suitable and needs to be modified for two reasons. The first reason lies in the fact that as SVNG is a generalization of IFG, by exempting the indeterminacy value, Definition 12 should reduce to Definition 3. However, this does not happen, as the nonmembership degree of an edge in IFG and in SVNG are defined in a different way; i.e., the nonmembership degree for IFG is defined as Ð �� ,�� ≤max ��(�� ),�� �� while in case of SVNGs it is defined as Ð �� ,�� ≥max ��(�� ),�� ��

Itisobservedthatthisdefinitionisnotsuitableandneedstobemodifiedfortworeasons.Thefirst reasonliesinthefactthatasSVNGisageneralizationofIFG,byexemptingtheindeterminacyvalue, Definition12shouldreducetoDefinition3.However,thisdoesnothappen,asthenon-membership degreeofanedgeinIFGandinSVNGaredefinedinadifferentway;i.e.,thenon-membership degreeforIFGisdefinedas ÐÄvi, vjä ≤ maxÄD(vi ), DÄvjää whileincaseofSVNGsitisdefinedas ÐÄvi, vjä ≥ maxÄD(vi ), DÄvjää

The second reason is based on the definition of complement of SVNGs, as the complement of an SVNG needs to be an SVNG, which did not happen on some occasions. We present the current definition of the complement of an SVNG and with the help of an example describe that the complement of an SVNG is not well defined.

ThesecondreasonisbasedonthedefinitionofcomplementofSVNGs,asthecomplementof anSVNGneedstobeanSVNG,whichdidnothappenonsomeoccasions.Wepresentthecurrent definitionofthecomplementofanSVNGandwiththehelpofanexampledescribethatthecomplement ofanSVNGisnotwelldefined.

Definition 13. [Error! Reference source not found.] The complement of an SVNG ��= (��,�� ) is defined by �� = (�� ,�� ) where �� =�� and the membership, neutral value and non-membership grades of �� satisfy the conditions:

Definition13. [43]ThecomplementofanSVNG G = (V, E) isdefinedby Gc = (Vc , Ec ) where Vc = V andthemembership,neutralvalueandnon-membershipgradesofEsatisfytheconditions:

Ŝ �� ,�� =min ��(�� ),�� �� −Ŝ �� ,�� .

Î �� ,�� =max ��(�� ),�� �� −Î �� ,��

(Ð) �� ,�� =max ��(�� ),�� �� −Ð �� ,��

Ŝ �� ,�� =min ��(�� ),�� �� −Ŝ �� ,�� Î �� ,�� =max ��(�� ),�� �� −Î �� ,�� (Ð) �� ,�� =max ��(�� ),�� �� −Ð �� ,��

Ĉ SäcÄvi, vjä = minÄS(vi ), SÄvjää ˆ SÄÄvi, vjää ÄÎäcÄvi, vjä = maxÄI(vi ), IÄvjää ÎÄÄvi, vjää (Ð)cÄvi, vjä = maxÄD(vi ), DÄvjää ÐÄÄvi, vjää.

Keep in mind Definition 13 and consider the following example, where the complement of an SVNG does not remain an SVNG. All this leads to some modification in the basic definition of SVNG which not only generalizes an IFG but is also compatible to satisfy the basic properties of taking complements.

KeepinmindDefinition13andconsiderthefollowingexample,wherethecomplementof anSVNGdoesnotremainanSVNG.Allthisleadstosomemodificationinthebasicdefinitionof SVNGwhichnotonlygeneralizesanIFGbutisalsocompatibletosatisfythebasicpropertiesof takingcomplements.

Keep in mind Definition 13 and consider the following example, where the complement of an SVNG does not remain an SVNG. All this leads to some modification in the basic definition of SVNG which not only generalizes an IFG but is also compatible to satisfy the basic properties of taking complements.

Example 11. In the following figures, Figure 16 represents SVNGs and Figure 17 represents their complement. It is clear from Figure 17 that the complement of an SVNG is not an SVNG.

Example11. Inthefollowingfigures,Figure 16 representsSVNGsandFigure 17 representstheircomplement. ItisclearfromFigure 17 thatthecomplementofanSVNGisnotanSVNG.

Example 11. In the following figures, Figure 16 represents SVNGs and Figure 17 represents their complement. It is clear from Figure 17 that the complement of an SVNG is not an SVNG.

Figure 16. Single-valued neutrosophic graph.

Figure16. Single-valuedneutrosophicgraph.

Figure 16. Single-valued neutrosophic graph.

Figure 17. Complement of the SVNG depicted in Figure 16.

Figure17. ComplementoftheSVNGdepictedinFigure 16

Now, we present a new definition for SVNG as a generalization of IFG which is well-defined.

Figure 17. Complement of the SVNG depicted in Figure 16. Now, we present a new definition for SVNG as a generalization of IFG which is well-defined.

Now,wepresentanewdefinitionforSVNGasageneralizationofIFGwhichiswell-defined. Definition14. AnSVNGisapair G = (V, E) where V isthesetofnodesand E isthecollectionofedges betweenthesenodessuchthat

Definition 14. An SVNG is a pair ��= (��,�� ) where �� is the set of nodes and �� is the collection of edges between these nodes such that

Definition 14. An SVNG is a pair ��= (��,�� ) where �� is the set of nodes and �� is the collection of edges between these nodes such that

1. Every ��∈�� is characterized by three functions ��:��→[0,1],��:��→[0,1] and ��:��→[0,1] denoting the membership, neutral and non-membership grades of ��∈�� which satisfy the inequality 0≤��+��+��≤ 3.;

1. Every ��∈�� is characterized by three functions ��:��→[0,1],��:��→[0,1] and ��:��→[0,1] denoting the membership, neutral and non-membership grades of ��∈�� which satisfy the inequality 0≤��+��+��≤ 3.;

1. Every v ∈ V ischaracterizedbythreefunctions S : V → [0,1] , I : V → [0,1] and D : V → [0,1] denotingthemembership,neutralandnon-membershipgradesof v ∈ V whichsatisfytheinequality 0 ≤ S + I + D ≤ 3.;

2. Every ��∈�� is characterized by three functions Ŝ:��×��→[0,1],Î:��×��→[0,1] and Ð:��×��→ [0,1] denoting the membership, neutral and non-membership grades of ��∈��×�� satisfying Ŝ �� ,�� ≤min ��(�� ),�� ��

2. Every ��∈�� is characterized by three functions Ŝ:��×��→[0,1],Î:��×��→[0,1] and Ð:��×��→ [0,1] denoting the membership, neutral and non-membership grades of ��∈��×�� satisfying

Ŝ �� ,�� ≤min ��(�� ),�� ��

2. Every e ∈ E ischaracterizedbythreefunctions ˆ S: V × V → î0,1] ,Î: V × V → [0,1ó and Ð: V × V → [0,1] denotingthemembership,neutralandnon-membershipgradesof e ∈ V × V satisfying

Mathematics 2018, 6, x FOR PEER REVIEW

of 21

ˆ SÄvi, vjä ≤ minÄS(vi ), SÄvjää

ÎÄvi, vjä ≤ maxÄI(vi ), IÄvjää ÐÄvi, vjä ≤ maxÄD(vi ), DÄvjää

Mathematics 2018, 6, x FOR PEER REVIEW 13 of 21 Î �� ,�� ≤max ��(�� ),�� �� Ð �� ,�� ≤max ��(�� ),�� ��

providedthat 0 ≤ ˆ S + Î + Ð ≤ 3.

provided that 0≤Ŝ+Î+Ð≤3.

Example 12. In the following figures, Figure 18 represents an SVNG compatible with the new definition and Figure 19 represents the complement of the SVNG depicted in Figure 18.

Example12. Inthefollowingfigures,Figure 18 representsanSVNGcompatiblewiththenewdefinitionand Figure 19 representsthecomplementoftheSVNGdepictedinFigure 18.

Example 12. In the following figures, Figure 18 represents an SVNG compatible with the new definition and Figure 19 represents the complement of the SVNG depicted in Figure 18.

Figure 18. Single-valued neutrosophic graph.

Figure19. ComplementofthegraphdepictedinFigure 18

Figure 18. Single-valued neutrosophic graph. Figure 19. Complement of the graph depicted in Figure 18.

Figure 19. Complement of the graph depicted in Figure 18.

Likewise, in SVNGs the same kinds of flaw exist in the definition of IVNGs. First, we present the existing definition of IVNG and point out its limitation with the help of an example. Then, we develop the new definition for IVNG and support it with an example. After developing the new definition for IVNGs, we discuss the concept of complements for IVNGs by considering the defects in forming complements of IVFG and IVIFG.

Likewise, in SVNGs the same kinds of flaw exist in the definition of IVNGs. First, we present the existing definition of IVNG and point out its limitation with the help of an example. Then, we develop the new definition for IVNG and support it with an example. After developing the new definition for IVNGs, we discuss the concept of complements for IVNGs by considering the defects in forming complements of IVFG and IVIFG.

Likewise,inSVNGsthesamekindsofflawexistinthedefinitionofIVNGs.First,wepresentthe existingdefinitionofIVNGandpointoutitslimitationwiththehelpofanexample.Then,wedevelop thenewdefinitionforIVNGandsupportitwithanexample.Afterdevelopingthenewdefinition forIVNGs,wediscusstheconceptofcomplementsforIVNGsbyconsideringthedefectsinforming complementsofIVFGandIVIFG.

Definition 15. [Error! Reference source not found.] An IVNG is a pair ��= (��,�� ) where �� is the set of nodes and �� is the collection of edges between these nodes such that

Definition15. [48]AnIVNGisapair G = (V, E) where V isthesetofnodesand E isthecollectionofedges betweenthesenodessuchthat

Definition 15. [Error! Reference source not found.] An IVNG is a pair ��= (��,�� ) where �� is the set of nodes and �� is the collection of edges between these nodes such that

1. Every ��∈�� is characterized by three functions ��,�� and �� denoting the membership, neutral and nonmembership grades of ��∈�� . Basically, ��= [�� ,�� ],��= [�� ,�� ] and ��= [�� ,�� ] are closed subintervals of the unit interval [0, 1] which satisfy the inequality 0≤�� +�� +�� ≤3.;

1. Every ��∈�� is characterized by three functions ��,�� and �� denoting the membership, neutral and nonmembership grades of ��∈�� . Basically, ��= [�� ,�� ],��= [�� ,�� ] and ��= [�� ,�� ] are closed subintervals of the unit interval [0, 1] which satisfy the inequality 0≤�� +�� +�� ≤3.;

1. Every v ∈ V ischaracterizedbythreefunctions S, I and D denotingthemembership,neutraland non-membershipgradesof v ∈ V.Basically, S = SL , SU , I = I L , IU and D = DL , DU are closedsubintervalsoftheunitinterval[0,1]whichsatisfytheinequality 0 ≤ SU + IU + DU ≤ 3.;

2. Every ��∈�� is characterized by three functions Ŝ,Î and Ð denoting the membership, neutral and nonmembership grades of ��∈��×�� . Basically, Ŝ= Ŝ ,Ŝ ,Î= Î ,Î and Ð= [Ð ,Ð ] are such that:

2. Every ��∈�� is characterized by three functions Ŝ,Î and Ð denoting the membership, neutral and nonmembership grades of ��∈��×�� . Basically, Ŝ= Ŝ ,Ŝ ,Î= Î ,Î and Ð= [Ð ,Ð ] are such that:

Ŝ �� ,�� ≤min �� (�� ),�� �� Ŝ �� ,�� ≤min �� (�� ),�� �� Î �� ,�� ≥max �� (�� ),�� �� Î �� ,�� ≥max �� (�� ),�� �� Ð �� ,�� ≥max �� (�� ),�� �� Ð �� ,�� ≥max �� (�� ),�� �� which satisfy the inequality 0≤Ŝ +Î +Ð

Ŝ �� ,�� ≤min �� (�� ),�� �� Ŝ �� ,�� ≤min �� (�� ),�� �� Î �� ,�� ≥max �� (�� ),�� �� Î �� ,�� ≥max �� (�� ),�� �� Ð �� ,�� ≥max �� (�� ),�� �� Ð �� ,�� ≥max �� (�� ),�� �� which satisfy the inequality 0≤Ŝ +Î +Ð ≤3.

2. Every e ∈ E ischaracterizedbythreefunctions ˆ S, Î and Ð denotingthemembership,neutraland non-membershipgradesof e ∈ V × V.Basically, ˆ S = ˆ SL , ˆ SL , Î = ÎL,ÎU and Ð = îÐL,ÐLó are suchthat: ˆ SLÄvi, vjä ≤ minÄSL (vi ), SLÄvjää ˆ SU Ävi, vjä ≤ minÄSU (vi ), SU Ävjää ÎLÄvi, vjä ≥ maxÄI L (vi ), I LÄvjää ÎU Ävi, vjä ≥ maxÄIU (vi ), IU Ävjää ÐLÄvi, vjä ≥ maxÄDL (vi ), DLÄvjää ÐU Ävi, vjä ≥ maxÄDU (vi ), DU Ävjää whichsatisfytheinequality 0 ≤ ˆ SU + ÎU + ÐU ≤ 3.

Mathematics 2018, 6, x FOR PEER REVIEW 14 of 21

Likewise, IVFG and IVIFG are defined, and Definition 15 sometime leads to undefined closed sub-intervals as shown in the following example.

Likewise,IVFGandIVIFGaredefined,andDefinition15sometimeleadstoundefinedclosed sub-intervalsasshowninthefollowingexample.

Example 13. Consider the following example of an IVNG as exhibited in Figure 20 based on Definition 15, leading us to some undefined intervals.

Example13. ConsiderthefollowingexampleofanIVNGasexhibitedinFigure 20 basedonDefinition15, leadingustosomeundefinedintervals.

Figure 20. Interval-valued neutrosophic graph with undefined intervals.

Figure20. Interval-valuedneutrosophicgraphwithundefinedintervals.

Now, we present a new definition of IVNG as follows.

Now,wepresentanewdefinitionofIVNGasfollows.

Definition 16. An IVNG is a pair ��= (��,�� ) where �� is the set of nodes and �� is the collection of edges between these nodes such that

Definition16. AnIVNGisapair G = (V, E) where V isthesetofnodesand E isthecollectionofedges betweenthesenodessuchthat

(1) Every v ∈ V ischaracterizedbythreefunctions S, I and D denotingthemembership,neutraland non-membershipgradesof v ∈ V.Basically, S = SL , SU , I = I L , IU and D = DL , DU are closedsubintervalsoftheunitinterval[0,1]withaconditionthat 0 ≤ SU + IU + DU ≤ 3.;

(2) Every e ∈ E ischaracterizedbythreefunctions ˆ S, Î and Ð denotingthemembership,neutraland non-membershipgradesof e ∈ V × V.Basically ˆ S = ˆ SL , ˆ SL , Î = ÎL,ÎU and Ð = îÐL,ÐLó are suchthat

(1) Every ��∈�� is characterized by three functions ��,�� and �� denoting the membership, neutral and nonmembership grades of ��∈�� . Basically, ��= [�� ,�� ],��= [�� ,�� ] and ��= [�� ,�� ] are closed subintervals of the unit interval [0, 1] with a condition that 0≤�� +�� +�� ≤3.; (2) Every ��∈�� is characterized by three functions Ŝ,Î and Ð denoting the membership, neutral and nonmembership grades of ��∈��×�� . Basically Ŝ= Ŝ ,Ŝ ,Î= Î ,Î and Ð= [Ð ,Ð ] are such that Ŝ �� ,�� ≤min �� (�� ),�� �� Ŝ �� ,�� ≤min �� (�� ),�� �� Î �� ,�� ≤max �� (�� ),�� �� Î �� ,�� ≤max �� (�� ),�� �� Ð �� ,�� ≤max �� (�� ),�� �� Ð �� ,�� ≤max �� (�� ),�� �� provided that Ŝ �� ,�� ≤Ŝ �� ,�� , Î �� ,�� ≤Î �� ,�� , Ð �� ,�� ≤Ð �� ,�� and 0≤Ŝ + Î +Ð ≤3

ˆ SLÄvi, vjä ≤ minÄSL (vi ), SLÄvjää ˆ SU Ävi, vjä ≤ minÄSU (vi ), SU Ävjää ÎLÄvi, vjä ≤ maxÄI L (vi ), I LÄvjää ÎU Ävi, vjä ≤ maxÄIU (vi ), IU Ävjää ÐLÄvi, vjä ≤ maxÄDL (vi ), DLÄvjää ÐU Ävi, vjä ≤ maxÄDU (vi ), DU Ävjää providedthat ˆ SU Ävi, vjä ≤ ˆ SLÄvi, vjä, ÎLÄvi, vjä ≤ ÎU Ävi, vjä, ÐLÄvi, vjä ≤ ÐU Ävi, vjä and 0 ≤ ˆ SU + ÎU + ÐU ≤ 3.

Example 14. Consider the graph depicted in Figure 21 demonstrating the new definition of IVNGs.

Î �� ,�� ≤max �� (�� ),�� �� Î �� ,�� ≤max �� (�� ),�� �� Ð �� ,�� ≤max �� (�� ),�� �� Ð �� ,�� ≤max �� (�� ),�� �� provided that Ŝ �� ,�� ≤Ŝ �� ,�� , Î �� ,�� ≤Î �� ,�� , Ð �� ,�� ≤Ð �� ,�� and 0≤Ŝ + Î +Ð ≤3

Example14. ConsiderthegraphdepictedinFigure 21 demonstratingthenewdefinitionofIVNGs.

Example 14. Consider the graph depicted in Figure 21 demonstrating the new definition of IVNGs.

Figure 21. Interval-valued neutrosophic graph with undefined intervals. Figure21. Interval-valuedneutrosophicgraphwithundefinedintervals.

Mathematics 2018, 6, x FOR PEER REVIEW 15 of 21

Next,wediscusstheexistingdefinitionfortakingthecomplementofIVNGandshowits limitationswiththehelpofexamples.Then,weproposeanewdefinitionforthecomplementofIVNG astheexistingdefinitionleadsustosomeundefinedintervals.

Next, we discuss the existing definition for taking the complement of IVNG and show its limitations with the help of examples. Then, we propose a new definition for the complement of IVNG as the existing definition leads us to some undefined intervals.

Definition17. [48] ThecomplementofIVNG G = (V, E) isdefinedby Gc = (Vc , Ec ) where Vc = V and themembership,abstinenceandnon-membershipgradesofEsatisfy

Definition 17. [Error! Reference source not found.] The complement of IVNG ��= (��,�� ) is defined by �� = (�� ,�� ) where �� =�� and the membership, abstinence and non-membership grades of �� satisfy Ŝ �� ,�� =min �� (�� ),�� �� −Ŝ �� ,�� .

ˆ SL cÄvi, vjä = minÄSL (vi ), SLÄvjää ˆ SLÄÄvi, vjää.

ˆ SU cÄvi, vjä = minÄSU (vi ), SU Ävjää ˆ SU Ävi, vjä

Ŝ �� ,�� =min �� (�� ),�� �� −Ŝ �� ,��

Î �� ,�� =max �� (�� ),�� �� −Î �� ,�� Î �� ,�� =max �� (�� ),�� �� −Î �� ,�� . (Ð ) �� ,�� =max �� (�� ),�� �� −Ð �� ,�� (Ð ) �� ,�� =max �� (�� ),�� �� −Ð �� ,��

ÎL cÄvi, vjä = maxÄI L (vi ), I LÄvjää ÎLÄÄvi, vjää.

ÎU cÄvi, vjä = maxÄIU (vi ), IU Ävjää ÎU Ävi, vjä ÄÐLäcÄvi, vjä = maxÄDL (vi ), DLÄvjää ÐLÄÄvi, vjää. ÄÐU äcÄvi, vjä = maxÄDU (vi ), DU Ävjää ÐU Ävi, vjä.

Example15. ThefollowingIVNGdepictedinFigure 22 showsthattheDefinition17forthecomplementof IVNGleadsustosomeundefinedintervals.

Example 15. The following IVNG depicted in Figure 22 shows that the Definition 17 for the complement of IVNG leads us to some undefined intervals.

Figure22. ComplementoftheInterval-valuedneutrosophicgraphbyDefinition15.

Figure 22. Complement of the Interval-valued neutrosophic graph by Definition 15.

As the IVNG is a generalization of IVFG and IVIFG, its complement defined in [31] is not welldefined; therefore, we propose a new definition for the complement of IVNG as follows.

Definition 17. The complement of IVNG ��= (��,�� ) is defined by �� = (�� ,�� ) where �� =�� and the membership, abstinence and non-membership grades of �� are satisfying the conditions: Ŝ �� ,�� =min �� (�� ),�� �� −Ŝ �� ,��

AstheIVNGisageneralizationofIVFGandIVIFG,itscomplementdefinedin[31]isnot well-defined;therefore,weproposeanewdefinitionforthecomplementofIVNGasfollows. Definition18. ThecomplementofIVNG G = (V, E) isdefinedby Gc = (Vc , Ec ) where Vc = V andthe membership,abstinenceandnon-membershipgradesofEaresatisfyingtheconditions:

ˆ SL cÄvi, vjä = minÄSL (vi ), SLÄvjää ˆ SLÄÄvi, vjää ˆ SU cÄvi, vjä = minÄSU (vi ), SU Ävjää ˆ SU Ävi, vjä + minÄSL (vi ), SLÄvjää

ÎL cÄvi, vjä = maxÄI L (vi ), I LÄvjää ÎLÄÄvi, vjää ÎU cÄvi, vjä = maxÄIU (vi ), IU Ävjää ÎU Ävi, vjä + maxÄI L (vi ), I LÄvjää.

ÄÐLäcÄvi, vjä = maxÄDL (vi ), DLÄvjää ÐLÄÄvi, vjää ÄÐU äcÄvi, vjä = maxÄDU (vi ), DU Ävjää ÐU Ävi, vjä + maxÄDL (vi ), DLÄvjää

Example16. ConsiderthefollowingIVNGsshowninFigure 23 anditscomplementgraphisdepictedin Figure 24.Throughsomeeasycalculation,onecaneasilyverifythat (Gc )c = G.

Mathematics 2018, 6, x FOR PEER REVIEW 16 of 21

Mathematics 2018, 6, x FOR PEER REVIEW 16 of 21

Figure 23. Interval-valued neutrosophic graph.

Figure23. Interval-valuedneutrosophicgraph.

Figure 23. Interval-valued neutrosophic graph.

Figure 24. Complement of the graph depicted in Figure 23.

Figure24. ComplementofthegraphdepictedinFigure 23

Figure 24. Complement of the graph depicted in Figure 23.

So far in our study, we have developed the theory of IVFGs and its generalizations, providing examples that explained the limitations in the existing definitions and the fitness of the new definitions.

So far in our study, we have developed the theory of IVFGs and its generalizations, providing examples that explained the limitations in the existing definitions and the fitness of the new definitions.

Sofarinourstudy,wehavedevelopedthetheoryofIVFGsanditsgeneralizations,providing examplesthatexplainedthelimitationsintheexistingdefinitionsandthefitnessofthenewdefinitions.

Remark 1. The work proposed is applicable whether the graphs are directed or undirected.

Remark 1. The work proposed is applicable whether the graphs are directed or undirected.

Now, a real-life application is presented to show the feasibility of the proposed work. The process of ranking universities is explained based on SVNGs.

Now, a real-life application is presented to show the feasibility of the proposed work. The process of ranking universities is explained based on SVNGs.

Illustrative Example

Illustrative Example

Step 2: The SVNPRs form a relational matrix known as the single-valued neutrosophic relational matrix (SVNRM) denoted by Ṙ��=(��ṙ ) × where Ṙ�� =(�� ,�� ,�� ) such that Ṙ0≤�� ,�� ,�� ≤ 1 and Ṙ�� +�� + �� ≤3;

Step 3: Aggregating the different preferences by using the weighted averaging aggregation operator named as single-valued neutrosophic weighted averaging (SVNWA) operators [Error! Reference source not found.] as follows:

Remark1. Theworkproposedisapplicablewhetherthegraphsaredirectedorundirected.

��ṙ =����������(��ṙ ,��ṙ ,…,��ṙ )

Now,areal-lifeapplicationispresentedtoshowthefeasibilityoftheproposedwork.Theprocess ofrankinguniversitiesisexplainedbasedonSVNGs.

6.IllustrativeExample

= 1− 1−�� , �� , ��

where �� is the weight vector for each preference such that �� >0 and ∑ �� =1;

Step 4: Computing the score value of the aggregated number �� = (�� ,�� ,�� ) (��=1,2,…,��) by using the score function

��(�� ) = ;

Step 5: Ranking all the alternatives based on the descending order of the score values.

Now, by applying the above-mentioned steps to the considered data, we summarized their computational steps as below:

Step 1: The information from QEC of HEC Pakistan related to each university is taken in the form of SVNGs and summarized in Figure 25.

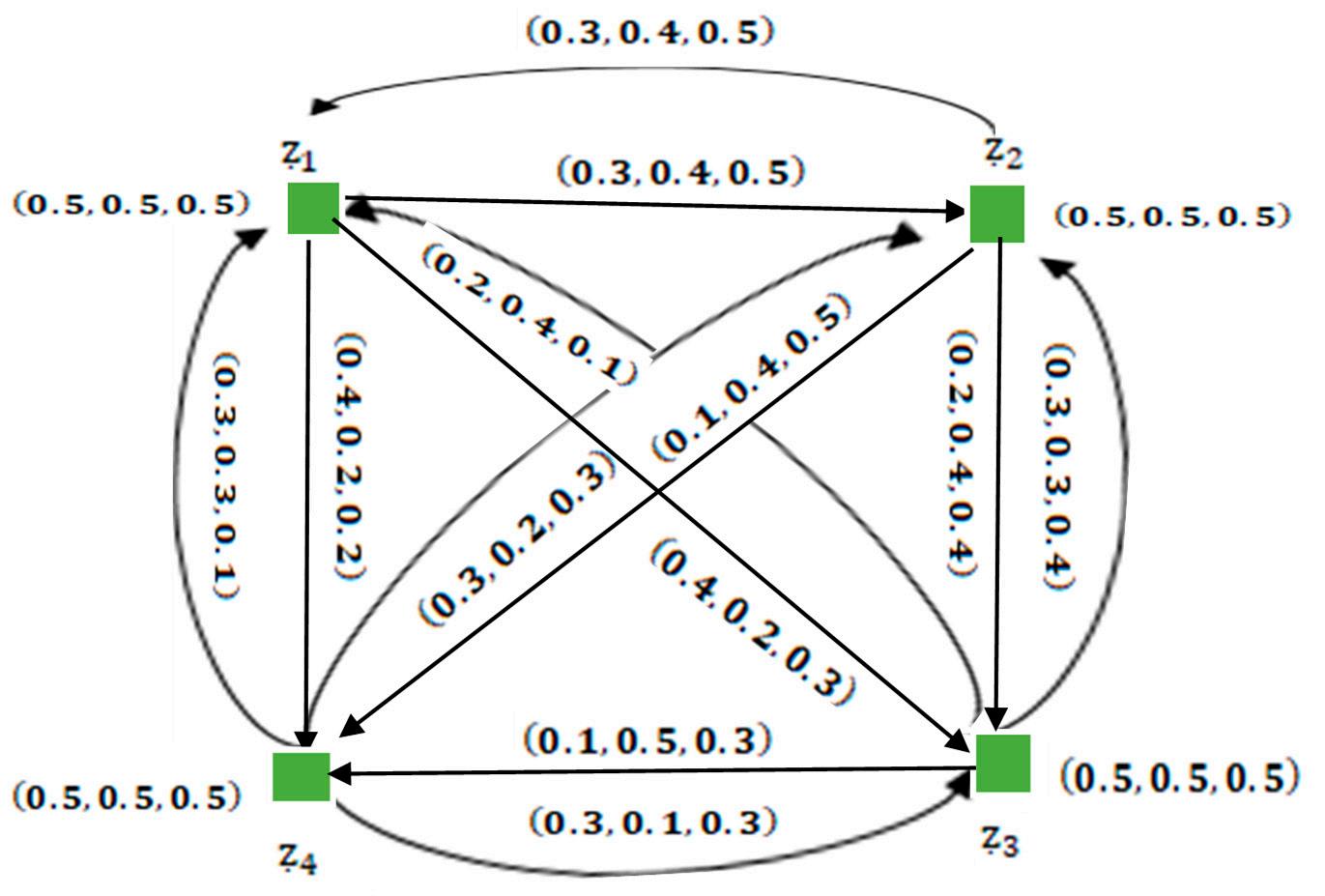
Thehighereducationcommission(HEC)ofPakistanneededtoevaluatethePakistaniuniversities fromresearchperspectives.HECPakistanplannedtogiveawaysomefinancialsupporttothose universitieswhoseresearchwascomparativelybetter.Auniversitywithagoodresearchscorewill earngreaterfinancialsupport.Here,weshalldiscussthecaseofthefederalcapitalIslamabad. Fouruniversities, z1, z2, z3 and z4,fromIslamabadarechosen,representingQuaideAzam university,NationalUniversityofScienceandTechnology,ComsatsuniversityandInternational IslamicUniversityIslamabad.Thecriterionfortherankingofuniversitiesis‘’researchproductivity”. Themembersofthequalityassurancecell(QEC)ofHECprovidetheirinformationintheformof single-valuedneutrosophicpreferencerelations(SVNPRs)asgiveninFigure 25.Theweightvector correspondingtothethemisgivenby w = (0.3,0.2,0.3,0.2)T .Thedetailedstepsofalgorithmforthis processareexplainedfollowedbystepwisecalculationsofthisproblem.

Figure25. Directednetworkwithsingle-valuedneutrosophicinformation.

Figure 25. Directed network with single-valued neutrosophic information.

Here, the importance of a new definition of an SVNG is clear. In decision-making problems, we usually have two types of attributes, known as attributes of cost type and of benefit types. In the case that the attributes are of cost types, the data is normalized using the definition of complement of SVNGs. Therefore, if we utilize the existing definition of SVNGs and their complement as we have done in Example 11, we obtain some undefined results. The case is similar with other structures. All this shows the importance of the new proposed definitions of several fuzzy graphs and their complements.

Step 2: From the SVNPRs provided in Figure 25, we have the following relational matrix.

where wj istheweightvectorforeachpreferencesuchthat wj > 0and n j=1 wj = 1;

Step4: Computingthescorevalueoftheaggregatednumber mi = (Si, Ii, Di )(i = 1,2,..., n) by usingthescorefunction

S(mi ) = Si + 1 Ii + 1 Di 3 ;

Step5: Rankingallthealternativesbasedonthedescendingorderofthescorevalues.

Now,byapplyingtheabove-mentionedstepstotheconsidereddata,wesummarizedtheir computationalstepsasbelow:

Step1: TheinformationfromQECofHECPakistanrelatedtoeachuniversityistakenintheformof SVNGsandsummarizedinFigure 25.

Here,theimportanceofanewdefinitionofanSVNGisclear.Indecision-makingproblems, weusuallyhavetwotypesofattributes,knownasattributesofcosttypeandofbenefittypes.Inthe casethattheattributesareofcosttypes,thedataisnormalizedusingthedefinitionofcomplementof SVNGs.Therefore,ifweutilizetheexistingdefinitionofSVNGsandtheircomplementaswehavedone inExample11,weobtainsomeundefinedresults.Thecaseissimilarwithotherstructures.Allthis showstheimportanceofthenewproposeddefinitionsofseveralfuzzygraphsandtheircomplements.

Step2: FromtheSVNPRsprovidedinFigure 25,wehavethefollowingrelationalmatrix.

MR = Ämrijä4×4 =

(0.5,0.5,0.5)(0.3,0.4,0.5)(0.4,0.2,0.3) (0.3,0.4,0.5)(0.5,0.5,0.5)(0.2,0.4,0.4) (0.2,0.4,0.1) (0.3,0.3,0.1) (0.3,0.3,0.4) (0.3,0.2,0.3) (0.5,0.5,0.5) (0.3,0.1,0.3)

(0.4,0.2,0.2) (0.1,0.4,0.5) (0.1,0.5,0.3) (0.5,0.5,0.5)

Step3: Usingsingle-valuedneutrosophicweightedaveragingoperatorsontherelationalmatrixto aggregatethedata,

mri = SVNWA(mri1, mri2,..., mrin ) = Ñ1 n j=1 Ä1 Sijäwj , Ñ n j=1 Iijéwj , Ñ n j=1 Dijéwj é

andtheaggregatedvaluesareobtainedas

mr1 = (0.414150269,0.3024252,0.3571309); rm2 = (0.283693469,0.4182558,0.4676242); rm3 = (0.307394227,0.4222088,0.2663957); rm4 = (0.345556087,0.2203618,0.2389762).

Step4: Thescorevaluesoftheaggregateddataareobtainedas

S(m1) = 0.584864723, sS(mr2) = 0.465937823, Ss(mr3) = 0.539596576, sS(mr4) = 0.62873936

Step5: Since S(m4) > S(m1) > S(m3) > S(m2),weobtainedtherankingorderofthegiven universitiesas z4 z1 z3 z2,where refersto“preferredto”.Thus,theranking resultsindicatethatInternationalIslamicUniversityIslamabadperformsbestinresearch productivityamongthefouruniversitiesoffederalcapitalofIslamabadintheevaluationof thequalityassurancecellofHEC.

7.Conclusions

Inthismanuscript,wesuccessfullypointedouttheshortcomingsinthecurrentdefinitionsof IVFG,IVIFGwiththehelpofexamplesanddevelopedanewimproveddefinitionfortheseconcepts. ItisalsodiscussedthatthecurrentdefinitionsofcomplementsforIVFGandIVIFGleadustosome undefinedresults;therefore,somenewdefinitionsforcomplementsofIVFGandIVIFGareproposed andsupportedbyexamples.Further,itisobservedthatthedefinitionofSVNGhassomeseriousflaws, describedbyexamples.Thus,anewmodifieddefinitionforSVNGhasbeendevelopedandsupported bysomeexamples.TheconceptofIVNGisalsomodified,andthevalidityofthemodifieddefinition istestedwithexamples.Throughoutthisarticle,wedefinedallthosetermswhichwerenotpreviously definedwell.Inthenearfuture,weshallinvestigatesomeotherresultsofIVFGs,IVIFG,IVNG,SVNGs andextendthemtosolvedecision-makingproblemsunderfuzzyoruncertainenvironments[52–58].

AuthorContributions: Conceptualization,N,J;K.U;andT.M;;Methodology,N,J;K.U;T.M.andB.D.;Validation, N.J.;K.U.;T.M.;H.G.;andA.B.S;FormalAnalysis,N.J.;K.U.;T.M.;A.B.S;andS.B.;Investigation,N.J.;K.U.;T.M.; B.D..;Writing-OriginalDraftPreparation,N.J.;K.U.;T.M.;H.G..;Writing-Review&Editing,N.J.;K.U.;T.M.;H.G.; Visualization,N.J.;K.U.;T.M.;H.G.;S.B.

Funding: Thisresearchreceivednoexternalfunding.

Acknowledgments: Theauthorsarethankfultotheeditorandanonymousreviewersfortheirusefulsuggestions regardingtheimprovementofthismanuscript.

ConflictsofInterest: Theauthorsdeclarenoconflictofinterest.

References

1. Zadeh,L.A.Fuzzysets. Inf.Control 1965, 8,338–353.[CrossRef]

2. Gorzalczany,M.B.Amethodofinferenceinapproximatereasoningbasedoninterval—Valuedfuzzysets. FuzzySetsSyst. 1987, 21,1–17.[CrossRef]

3. Atanassov,K.T.Intuitionisticfuzzysets. FuzzySetsSyst. 1986, 20,87–96.[CrossRef]

4. Atanassov,K.;Gargov,G.Interval-valuedintuitionisticfuzzysets. FuzzySetsSyst. 1989, 31,343–349. [CrossRef]

5. Smarandache,F. Neutrosophy.NeutrosophicProbability,Set,andLogic,ProQuestInformation&Learning; AmericanResearchPressRehoboth:AnnArbor,MI,USA,1998.

6. Wang,H.;Smarandache,F.;Zhang,Y.Q.;Sunderraman,R.Singlevaluedneutrosophicsets. Multisp. Multistruct. 2010, 4,410–413.

7. Wang,H.;Smarandache,F.;Zhang,Y.Q.;Smarandache,R. IntervalNeutrosophicSetsandLogic:Theoryand ApplicationsinComputing;Hexis:Phoenix,AZ,USA,2005.

8. Peng,J.J.;Wang,J.Q.;Wang,J.;Zhang,H.Y.;Chen,Z.H.Simplifiedneutrosophicsetsandtheirapplications inmulti-criteriagroupdecision-makingproblems. Int.J.Syst.Sci. 2016, 47,2342–2358.[CrossRef]

9. Garg,H.Newexponentialoperationallawsandtheiraggregationoperatorsforinterval-valuedPythagorean fuzzymulticriteriadecision—Making. Int.J.Intell.Syst. 2018, 33,653–683.[CrossRef]

10. Peng,J.J.;Wang,J.Q.;Zhang,H.Y.;Chen,X.H.Anoutrankingapproachformulti-criteriadecision-making problemswithsimplifiedneutrosophicsets. Appl.SoftComput. 2014, 25,336–346.[CrossRef]

11.

Garg,H.Somerobustimprovedgeometricaggregationoperatorsunderinterval-valuedintuitionisticfuzzy environmentformulti-criteriadecision-makingprocess. J.Ind.Manag.Optim. 2018, 14,283–308.[CrossRef]

12. Garg,H.Novelintuitionisticfuzzydecisionmakingmethodbasedonanimprovedoperationlawsandits application. Eng.Appl.Artif.Intell. 2017, 60,164–174.[CrossRef]

13. Peng,X.;Dai,J.Algorithmsforintervalneutrosophicmultipleattributedecision-makingbasedonMABAC, similaritymeasure,andEDAS. Int.J.Uncertain.Quantif. 2017, 7,395–421.[CrossRef]

14. Peng,X.D.;Dai,J.G.Approachestosingle-valuedneutrosophicmadmbasedonmabac,topsisandnew similaritymeasurewithscorefunction. NeuralComput.Appl. 2018, 29,939–954.[CrossRef]

15. Garg,H.Somepicturefuzzyaggregationoperatorsandtheirapplicationstomulticriteriadecision-making. Arab.J.Sci.Eng. 2017, 42,5275–5290.[CrossRef]

16.

Garg,H.;Kumar,K.AnovelexponentialdistanceanditsbasedTOPSISmethodforinterval-valued intuitionisticfuzzysetsusingconnectionnumberofSPAtheory. Artif.Intell.Rev. 2018,1–30.[CrossRef]

17. Smarandache,F.Subtractionanddivisionofneutrosophicnumbers. Crit.Rev. 2016, 13,103–110. 18.

Xu,Z.S.Intuitionisticfuzzyaggregationoperators. IEEETrans.FuzzySyst. 2007, 15,1179–1187. 19.

20.

Garg,H.;Arora,R.Generalizedintuitionisticfuzzysoftpoweraggregationoperatorbasedont-normand theirapplicationinmulticriteriadecision-making. Int.J.Intell.Syst. 2019, 34,215–246.[CrossRef]

Garg,H.;Kumar,K.Distancemeasuresforconnectionnumbersetsbasedonsetpairanalysisandits applicationstodecisionmakingprocess. Appl.Intell. 2018, 48,3346–3359.[CrossRef]

21. Garg,H.;Nancy.Non-linearprogrammingmethodformulti-criteriadecisionmakingproblemsunder intervalneutrosophicsetenvironment. Appl.Intell. 2018, 48,2199–2213.[CrossRef]

22. Wei,G.;Zhao,X.Anapproachtomultipleattributedecisionmakingwithcombinedweightinformationin interval-valuedintuitionisticfuzzyenvironmental. ControlCybern. 2012, 41,97–112.

23. Wei,G.W.Picture2-tuplelinguisticbonferronimeanoperatorsandtheirapplicationtomultipleattribute decisionmaking. Int.J.FuzzySyst. 2017, 19,997–1010.[CrossRef]

24. Garg,H.;Nancy.Somehybridweightedaggregationoperatorsunderneutrosophicsetenvironmentand theirapplicationstomulticriteriadecision-making. Appl.Intell. 2018, 48,4871–4888.[CrossRef]

25. Garg,H.;Nancy.Newlogarithmicoperationallawsandtheirapplicationstomultiattributedecisionmaking forsingle-valuedneutrosophicnumbers. Cogn.Syst.Res. 2018, 52,931–946.[CrossRef]

26. Kaufmann,A. IntroductiontoFuzzySubsets;AcademicPress:NewYork,NY,USA,1975;Volume1.

27. Zadeh,L.A.;Fu,K.S.;Tanaka,K.(Eds.)Fuzzysetsandtheirapplicationstocognitiveanddecisionprocesses.In ProceedingsoftheUS–JapanSeminaronFuzzySetsandTheirApplications,Berkeley,CA,USA,1–4July1974.

28. Akram,M.;Dudek,W.A.Interval-valuedfuzzygraphs. Comput.Math.Appl. 2011, 61,289–299.[CrossRef]

29. Bhattacharya,P.Someremarksonfuzzygraphs. PatternRecognit.Lett. 1987, 6,297–302.[CrossRef] 30.

Bhutani,K.R.Onautomorphismsoffuzzygraphs. PatternRecognit.Lett. 1989, 9,159–162.[CrossRef] 31.

Bhutani,K.R.;Rosenfeld,A.Strongarcsinfuzzygraphs. Inf.Sci. 2003, 152,319–322.[CrossRef] 32.

Mordeson,J.N.;Chang-Shyh,P.Operationsonfuzzygraphs. Inf.Sci. 1994, 79,159–170.[CrossRef] 33. Rashmanlou,H.;Jun,Y.B.Completeinterval-valuedfuzzygraphs. Ann.FuzzyMath.Inform. 2013, 6,677–687. 34. Pal,M.;Rashmanlou,H.Irregularintervalvaluedfuzzygraphs. arXiv,2014;arXiv:1407.6190. 35. Akram,M.Interval-valuedfuzzylinegraphs. NeuralComput.Appl. 2012, 21,145–150.[CrossRef] 36. Rashmanlou,H.;Pal,M.Balancedinterval-valuedfuzzygraphs. J.Phys.Sci. 2013, 17,43–57. 37. Pramanik,T.;Samanta,S.;Pal,M.Interval-valuedfuzzyplanargraphs. Int.J.Mach.Learn.Cybern. 2016, 7, 653–664.[CrossRef] 38. Talebi,A.;Rashmanlou,H.Isomorphismoninterval-valuedfuzzygraphs. Ann.FuzzyMath.Inform. 2013, 6, 47–58. 39. Parvathi,R.;Karunambigai,M.Intuitionisticfuzzygraphs.In ComputationalIntelligence,Theoryand Applications;Springer:NewYork,NY,USA,2006;pp.139–150. 40.

Mishra,S.;Pal,A.Productofintervalvaluedintuitionisticfuzzygraph. Ann.PureAppl.Math. 2013, 5,37–46. 41.

Mishra,S.;Pal,A.Regularinterval-valuedintuitionisticfuzzygraphs. J.Inform.Math.Sci. 2017, 9,609–621. 42.

43.

Ismayil,A.M.;Ali,A.M.Onstronginterval-valuedintuitionisticfuzzygraph. Int.J.FuzzyMath.Syst. 2014, 4,161–168.

Broumi,S.;Talea,M.;Bakali,A.;Smarandache,F.Singlevaluedneutrosophicgraphs. FlorentinSmarandache SurapatiPramanik 2015,187.

44. Broumi,S.;Talea,M.;Bakali,A.;Smarandache,F.;Kumar,P.K.Shortestpathproblemonsinglevalued neutrosophicgraphs.InProceedingsofthe2017InternationalSymposiumonNetworks,Computersand Communications(ISNCC),Marrakech,Morocco,16–18May2017;pp.1–6.

45. Broumi,S.;Bakal,A.;Talea,M.;Smarandache,F.;Vladareanu,L.Applyingdijkstraalgorithmforsolving neutrosophicshortestpathproblem.InProceedingsofthe2016InternationalConferenceonAdvanced MechatronicSystems(ICAMechS),Melbourne,VIC,Australia,30November–3December2016;pp.412–416.

46. Broumi,S.;Ullah,K.;Bakali,A.;Talea,M.;Singh,P.K.;Mahmood,T.;Smarandache,F.;Bahnasse,A.; Patro,S.K.;Oliveira,A.NovelSystemandMethodforTelephoneNetworkPlaningBasedonNeutrosophic Graph. Glob.J.Comput.Sci.Technol. 2018, 18,1–10.

47. Akram,M.;Shahzadi,S.Neutrosophicsoftgraphswithapplication. J.Intell.FuzzySyst. 2017, 32,841–858. [CrossRef]

48. Broumi,S.;Talea,M.;Bakali,A.;Smarandache,F.Intervalvaluedneutrosophicgraphs. Crit.Rev.XII 2016, 2016,5–33.

49. Akram,M.;Nasir,M.ConceptsofInterval-ValuedNeutrosophicGraphs. Infin.Study 2017, 6,22–41. [CrossRef]

50. Broumi,S.;Smarandache,F.;Talea,M.;Bakali,A.OperationsonIntervalValuedNeutrosophicGraphs; FlorentinSmarandacheSurapatiPramanik. Infin.Study 2016

51. Broumi,S.;Talea,M.;Bakali,A.;Smarandache,F.Onstrongintervalvaluedneutrosophicgraphs. Crit.Rev. 2016, 12,49–71.

52. Garg,H.;Arora,R.Dualhesitantfuzzysoftaggregationoperatorsandtheirapplicationindecisionmaking. Cogn.Comput. 2018, 10,769–789.[CrossRef]

53. Garg,H.;Rani,D.Somegeneralizedcomplexintuitionisticfuzzyaggregationoperatorsandtheirapplication tomulticriteriadecision-makingprocess. Arab.J.Sci.Eng. 2018, 10,769–789.[CrossRef]

54. Rani,D.;Garg,H.Complexintuitionisticfuzzypoweraggregationoperatorsandtheirapplicationsin multi-criteriadecision-making. ExpertSyst. 2018, 35,e12325.[CrossRef]

55. Kaur,G.;Garg,H.Multi—Attributedecision—Makingbasedonbonferronimeanoperatorsundercubic intuitionisticfuzzysetenvironment. Entropy 2018, 20,65.[CrossRef]

56. Garg,H.;Nancy.Multi-criteriadecision-makingmethodbasedonprioritizedmuirheadmeanaggregation operatorunderneutrosophicsetenvironment. Symmetry 2018, 10,280.[CrossRef]

57. Wei,G.;Garg,H.;Gao,H.;Wei,C.Interval-ValuedPythagoreanFuzzyMaclaurinSymmetricMeanOperators inMultipleAttributeDecisionMaking. IEEEAccess 2018, 6,67866–67884.[CrossRef]

58. Garg,H.HesitantPythagoreanfuzzyMaclaurinsymmetricmeanoperatorsanditsapplicationsto multiattributedecisionmakingprocess. Int.J.Intell.Syst. 2018.[CrossRef]

© 2019bytheauthors.LicenseeMDPI,Basel,Switzerland.Thisarticleisanopenaccess articledistributedunderthetermsandconditionsoftheCreativeCommonsAttribution (CCBY)license(http://creativecommons.org/licenses/by/4.0/).