SomeResultsonVariousCancellativeCA-Groupoids andVariantCA-Groupoids
ZhirouMa 1,XiaohongZhang 1,*andFlorentinSmarandache 2
1 DepartmentofMathematics,ShaanxiUniversityofScience&Technology,Xi’an710021,China; 1809037@sust.edu.cn
2 DepartmentofMathematics,UniversityofNewMexico,Gallup,NM87301,USA;smarand@unm.edu

* Correspondence:zhangxiaohong@sust.edu.cnorzhangxh@shmtu.edu.cn
Received:19January2020;Accepted:16February2020;Published:22February2020
Abstract: Cyclicassociativitycanberegardedasakindofvariationsymmetry,andcyclicassociative groupoid(CA-groupoid)isageneralizationofcommutativesemigroup.Inthispaper,thevarious cancellationpropertiesofCA-groupoids,includingcancellation,quasi-cancellationandpower cancellation,arestudied.TherelationshipsamongcancellativeCA-groupoids,quasi-cancellative CA-groupoidsandpowercancellativeCA-groupoidsarefoundout.Moreover,theconceptofvariant CA-groupoidisproposedfirstly,someexamplesarepresented.Itisshownthatthestructureof variantCA-groupoidisveryinteresting,andtheconstructionmethodsanddecompositiontheorem ofvariantCA-groupoidsareestablished.
Keywords: cyclicassociativegroupoid(CA-groupoid);cancellative;variantCA-groupoids; decompositiontheorem;constructionmethods
1.Introduction
Analgebraicstructureiscalledagroupoid,ifitiswell-definedregardinganoperationonit. Agroupoidsatisfyingthe“cyclicassociativelaw”(thatis, x(yz) = y(zx))iscalledacyclicassociative groupoid,orsimplyCA-groupoid[1,2].
Infact,asearlyas1946,whenByrne[3]studiedaxiomatizationofBooleanalgebra,hementioned thefollowingoperationlaw:(xy)z = (yz)x.Obviously,itsdualformisasfollows: z(yx) = x(zy),thisis thecyclicassociativelawmentionedabove.In1954,Sholander[4]mentionedByrne’spaper[3], andusedthetermof“cyclicassociativelaw”toexpresstheoperationlaw:(ab)c = (bc)a.Thisisthefirst literatureweknowtousetheterm“cyclicassociativelaw”.Atthesametime,Hosszualsousedthe termof“cyclicassociativelaw”inthestudyoffunctionalequation(see[5]andtheintroductionand explanationbyMaksa[6]).Later,Kleinfeld[7]andBehn[8,9]studiedtheringssatisfyingthecyclic associativelaw,andIqbaletal.[10]studiedtheAG-groupoidssatisfyingthecyclicassociativelaw.Itis onthebasisoftheseresearchesthatwestarttosystematicallystudythegroupoidssatisfyingthecyclic bindinglaw(CA-groupoids)in[1,2],inordertoprovideacommonbasisfortheresearchofrelated algebraicsystems.
Asacontinuationof[1,2],thispaperfocusesonvariouscancellationpropertiesofCA-groupoids andaspecialclassofCA-groupoids.Inmanyalgebraicsystems(suchassemigroups,commutative semigroupsandAG-groupoids),thecancellation,quasi-cancellationandpowercancellationproperties haveimportantresearchvalue(see[11 26]).In1957,TakayukiTamurastudiedcommutativenon-potent Archimedeansemigroupswithcancellativelaw(see[11]),cancellabilityisappliedtosemigroups. Sincethen,variouscancellativelawshavebeenputforwardandappliedtovariousalgebraicsystems, andaseriesofvaluableconclusionshavebeendrawn.Theriseofthesepropertiesmakesanirreplaceable contributiontothedevelopmentofalgebra.
Symmetry 2020, 12,315;doi:10.3390/sym12020315 www.mdpi.com/journal/symmetry
Semigroupwiththeidentityisnamedmonoid,theresearchofmonoidisgraduallydeepening (see[24,27]).Inaddition,AG-groupisanAG-groupoidwiththeleftidentityandinverses(see[28 32]). Throughthesepapers,weknowthattheidentityisapowerfultoolforsolvingalgebraicproblems. Therefore,wenaturallyconsiderCA-groupoidswithunitelement.However,ourstudyfindsthat CA-groupoidswithunitelementdegenerateintocommutativemonoids,andaCA-groupoidwith quasirightunitelement(i.e.,thereexists e,if x e,then xe = x;and ee e)maybenotasemigroup. Moreover,thiskindofCA-groupoids(withquasirightunitelement)notonlyhasveryinteresting properties,butalsopromotesthestudyofalgebraicstructuressuchasringsandsemirings(some examplesarepresentedinSection 5).Therefore,thispaperstudiesitindepth,andwecallthem variantCA-groupoids.
Atlast,thecontentofthispaperasfollows:inSection 2,weintroducesomebasicconcepts andcancellativepropertiesonsemigroupandAG-groupoid;inSection 3,wegivethedefinitions ofcancellativeCA-groupoids,leftcancellativeCA-groupoids,rightcancellativeCA-groupoidsand weakcancellativeCA-groupoids,anddiscusstherelationshipsaboutthem;inSection 4,wegive thedefinitionsofseveralquasi-cancellativeCA-groupoidsandpowercancellativeCA-groupoids, andanalyzetherelationshipsaboutseveraltypescancellativeCA-groupoids;inSection 5,wepropose thenewnotionofvariantCA-groupoidandsomeinterestingexamples,moreover,weprovethe structuretheoremandconstructionmethodofvariantCA-groupoids.
2.Preliminaries
ThispapermainlystudiessomespecialtypesofCA-groupoids.Inthissectionsomenotionsand resultsonsemigroupsandCA-groupoidsaregiven.Agroupoid(S,*)isanon-emptyset S together withabinaryoperation*.Traditionally,the*operatorisomittedwithoutconfusion,and(S,*)is abbreviatedto S.Foragroupoid S,anelement a∈S iscalledtobeleftcancellative(respectivelyright cancellative)ifforall x,y∈S,ax = ay implies x = y(xa = ya implies x = y); anelementiscalledtobe cancellativeifitisbothleftandrightcancellative.Agroupoid S satisfyingtheassociativelawiscalled asemigroup.Amonoid S isasemigroupwithanidentityelement.
Definition1. [1]LetSbeagroupoid.Ifforalla,b,c∈S,a(bc) = c(ab),thenSiscalledacyclicassociative groupoid(orshortlyCA-groupoid).
Proposition1. [1]IfSisaCA-groupoid,then,foranya,b,c,d,x,y∈S: (1)(ab)(cd) = (da)(cb); (2)(ab)((cd)(xy)) = (da)((cb)(xy)).
Proposition2. [1]EverycommutativesemigroupisaCA-groupoid.Assumethat(S, ·)isaCA-groupoid,ifS iscommutative,thenSisacommutativesemigroup.
Proposition3. [1]LetSbeaCA-groupoid.(1)IfShavealeftidentityelement,thatis,thereexistse∈Ssuch thatea = aforalla∈S,thenSisacommutativesemigroup(thus,Sisacommutativemonoid).(2)Ife∈Sisaleft identityelementinS,theneisanidentityelementinS.(3)Ife∈SisarightidentityelementinS,thatis,ae = a foralla∈S,theneisanidentityelementinS.(4)IfShavearightidentityelement,thenSisacommutative semigroup(thus,Sisacommutativemonoid).
Proposition4. [1]LetSbeaCA-groupoid.Ifforalla∈S,a2 = a,thenSiscommutative(thus,Sisa commutativesemigroup).
Proposition5. [1]LetS1,S2 betwoCA-groupoids.ThenthedirectproductS1 × S2 isaCA-groupoid.
Definition2. [2]AnelementaofaCA-groupoidSiscalledlocallyassociativeifsatisfied: a(aa) = (aa)a. SiscalledalocallyassociativeCA-groupoid,ifallelementsinSarelocallyassociative.
Definition3. [2]LetSbeagroupoid.Ifforalla,b,c∈S: a(bc) = (ab)c,a(bc) = c(ab), thenSiscalledacyclicassociativesemigroup(shortly,CA-semigroup).
Definition4. [18]LetSbeasemigroup.Siscalledaseparativesemigroup,ifforanyx,y∈S: (i)x2 = xyandy2 = yximplyx = y; (ii)x2 = yxandy2 = xyimplyx = y.
AsemigroupSiscalledquasi-separativeifforalla,b∈S,x2 = xy = y2 implyx = y.
3.CancellationPropertiesofCA-Groupoids
Definition5. AssumethatSisaCA-groupoid.IfeveryelementofSisleftcancellative(rightcancellative, cancellative),thenSiscalledaleftcancellative(rightcancellative,cancellative)CA-groupoid.
Example1. LetS = {0, 1, 2, 3, 4}.Forallx,y∈S,theoperation*onSisdefinedasx*y = x + y = x + y (mod5),seeTable 1.Then,(S,*)isacancellativeCA-groupoid.
Table1. Theoperation*on S. * 0 1 2 3 4 0 0 1 2 3 4 1 1 2 3 4 0 2 2 3 4 0 1 3 3 4 0 1 2 4 4 0 1 2 3
Definition6. AssumethatSisaCA-groupoid.Letx∈S,ifforanyy,z∈S,xy = xzandyx = zximplyy = z, thenxiscalledtobeweakcancellative.IfallelementsinSareweakcancellative,thenSiscalledaweak cancellativeCA-groupoid.
Obviously,foraCA-groupoidSandany x∈S,if x isaleft(orright)cancellative,then x is weakcancellative.
Example2. LetS = {1,2,3,4}.Theoperation*onSisdefinedasTable 2.Then,(S,*)isaweakcancellative CA-groupoid.
Table2. Theoperation*on S. * 1234 1 4321 2 3142 3 2413 4 1234
Theorem1. LetSbeaCA-groupoid.Then,foranyelementa, b ∈S:
(1) ifaisleftcancellative,thenaisrightcancellative,thusaiscancellative;
(2) ifaandbareleftcancellative,thenabisrightcancellative;
(3) ifaisrightcancellativeandbisleftcancellative,thenabisrightcancellative;
(4) ifabisrightcancellative,thenab = ba;
(5) ifabiscancellative,thenbiscancellative;
(6) ifabiscancellative,thenaandbarecancellative;
(7) ifaandabarerightcancellative,andbisleftcancellative,thenaiscancellative;
(8) ifaandabarerightcancellative,andbisleftcancellative,thenabiscancellative.
Proof. Supposethat(S,*)isaCA-groupoidand a,b∈S.
(1)Assumethat a isaleftcancellativeelement.If(∀x,y∈S) x*a = y*a,then(bycyclicassociation): a*(a*x) = x*(a*a) = a*(x*a) = a*(y*a) = a*(a*y).
Fromthis,applyingleftcancellationpropertyof a, a*x = a*y.Fromthis,applyingleftcancellation propertyof a onetime,wegetthat x = y.Therefore, a isarightcancellativeelementin S, so a isa cancellativeelementin S.
(2)Supposethat a and b areleftcancellative.If(∀x,y∈S) x*ab = y*ab,then: a*(b*x) = x*(a*b) = x*(ab) = y*(ab) = y*(a*b) = b*(y*a) = a*(b*y).
Since a isleftcancellative,so b*x = b*y.Moreover,fromthisand b isleftcancellative,wegetthat x = y.Therefore, ab isarightcancellative.
(3)Assumethat a isrightcancellativeand b isleftcancellative.If(∀x,y∈S) x*ab = y*ab,then: b*(x*a) = a*(b*x) = x*(a*b) = x*(ab) = y*(ab) = y*(a*b) = b*(y*a).
Since b isleftcancellative,so x*a = y*a.Moreover,fromthisand a isrightcancellative,wegetthat x = y.Therefore, ab isarightcancellative.
(4)Supposethat ab isrightcancellative.Since: ab*ab = b*(ab*a) = a*(b*ab) = a*(b*ba) = ba*ab
Since ab isrightcancellative,wegetthat ab = ba
(5)Assumethat ab iscancellative.If b*x = b*y, x,y∈S,then: x*ab = b*(x*a) = a*(b*x) = a*(b*y) = y*ab
Since ab iscancellative,so x = y.Thismeansthat b isleftcancellative.Applying(1),wegetthat b iscancellative.
(6)Assumethat ab iscancellative.Using(5),weknowthat b iscancellative.Moreover,since ab iscancellative,so ab isrightcancellative,applying(4)wegetthat ba = ab. Thus, ba iscancellative, using(5)again, a iscancellative.
(7)Supposethat a and ab arerightcancellative, and b isleftcancellative.If a*x = a*y, x,y∈S, then(applyingProposition1(1)):
b*(xa*ab) = b*(bx*aa) = b*(ab*ax) = b*(ab*ay) = b*(ya*ab).
Since b isleftcancellative,so xa*ab = ya*ab.Usingtheconditionthat ab isrightcancellative, itfollowsthat xa = ya.Since a isrightcancellative,thus, x = y.Hence, a isleftcancellative.Therefore, a iscancellative (8)Supposethat a and ab arerightcancellative, and b isleftcancellative.If ab*x = ab*y, x,y∈S,then: b*(xa*ab) = ab*(b*xa) = ab*(a*bx) = ab*(x*ab) = ab*(ab*x) = ab*(ab*y) = ab*(y*ab) = ab*(a*by) = ab*(b*ya) = b*(ya*ab).
Since b isleftcancellative,so xa*ab = ya*ab.Usingtheconditionthat ab isrightcancellative, itfollowsthat xa = ya.Since a isrightcancellative,thus, x = y.Thismeansthat ab isleftcancellative. Fromthisand ab isrightcancellative,weknowthat ab iscancellative.
ApplyingTheorem1wecangetthefollowingcorollaries.
Corollary1. LetSbeaCA-groupoid.Thenthefollowingassertsareequivalent:
(1) SisaleftcancellativeCA-groupoid; (2) SisarightcancellativeCA-groupoid; (3) Sisacancellativeandcommutativesemigroup; (4) SisacancellativeCA-groupoid.
Proof. (1) ⇒ (2):ItfollowsTheorem1(1).
(2) ⇒ (3):Forany a,b∈S,then ab∈S.Since S isrightcancellative,then ab isrightcancellative. ApplyingTheorem1(4), ab = ba.Thismeansthat S iscommutative.ByProposition2,weknowthat S isacommutativesemigroup.Moreover,since S isrightcancellative,so S isleftcancellative.Thus, S is acancellativeandcommutativesemigroup.
(3) ⇒ (4):Obviously.
(4) ⇒ (1):ItfollowsfromDefinition5.
Corollary2. LetSbeaCA-groupoid.IfthereexistsacancellativeelementinS,thenthesetH = {a∈S:ais cancellative}isasubCA-groupoidofS.
Proof. Bytheconditionthatthereexistsacancellativeelementin S,weknowthat H isnotempty. Forany a,b∈H,then a and b areleftandrightcancellative.ApplyingTheorem1(2),weknow that ab isrightcancellative.ByTheorem1(8), ab iscancellative.Thus ab∈H.Itfollowsthat H isasub CA-groupoidof S.
Corollary3. LetSbeaCA-groupoid.Ifthereexistsanon-cancellativeelementinS,thenthesetK = {a∈S:ais non-cancellative}isasubCA-groupoidofS.
Proof. Obviously, K isnon-empty.Forany a,b∈K,then a and b arenon-cancellative.ByTheorem1(5), weknowthat ab isnon-cancellative.Thus ab∈K.Itfollowsthat K isasubCA-groupoidof S.
Thefollowingexampleshowsthataweakcancellativeelementmaybenotaleft(orright) cancellativeelement.
Example3. LetS = {1,2,3,4,5},andtheoperation*onSisdefinedasTable 3,thenSisaCA-groupoid.Itis easytoverifythat3isweakcancellative,but3isnotleft(right)cancellative.
Table3. Theoperation*on S. * 12345 1 11111 2 11212 3 11422 4 11212 5 11111
OpenProblem1 (toproveorgiveacounterexample):IsanyweakcancellativeCA-groupoid necessarilycancellative?
Theorem2. LetSbeaCA-groupoidanda,b,c∈S.DefineonStherelation~as: a ∼ b ⇔ aandbarebothcancellativeornon cancellative Then~isanequivalencerelation.
Proof. Supposethat a isacancellativeelement(ornon-cancellativeelement)ofCA-groupoid S. Then a~a.Thismeansthat~isreflexive.
Suppose a~b.If a and b arecancellative,then b~a; if a and b arenon-cancellative,then b~a. Thus~ issymmetric.
Next,supposethat a~b and b~c. If a and b arecancellative,from b~c weknowthat c iscancellative, thus a and c arecancellative,i.e., a~c;if a and b arenon-cancellative,from b~c weknowthat c is non-cancellative,thus a and c arenon-cancellative,i.e., a~c. Thus~istransitive. Therefore,~isanequivalencerelation.
Example4. LetS = {1,2,3,4}andtheoperation*onSisdefinedasTable 4,thenSisaCA-groupoid.Obviously, 1and2arecancellative,3and4arenon-cancellative.H = {1,2}isasubCA-groupoidofS.
Table4. Theoperation*on S. * 1234 1 1243 2 2134 3 3443 4 4334
Theorem3. Let S1, S2 areCA-groupoids,thenthedirectproduct S1×S2 of S1 and S2 isaCA-groupoid.Ifa∈S1, b∈S2,aandbarecancellative,then(a,b) ∈ S1 × S2 iscancellative.
Proof. Supposethat S1 and S2 areCA-groupoids.ByProposition5, S1 × S2 isaCA-groupoid.Let a∈S1, b∈S2,a and b becancellative.Forany (x1, x2), (y1, y2) ∈ S1 × S2,if (a, b) ∗ (x1, x2) = (a, b) ∗ (y1, y2), then: (ax1,bx2) = (ay1,by2) ax1 = ay1,bx2 = by2 x1 = y1,x2 = y2. (since a and b arecancellative) (x1,x2) = (y1,y2). hence,(a,b)iscancellative.
4.SeparabilityandQuasi-CancellabilityofCA-Groupoids
Definition7. LetSbeaCA-groupoid.(1)Siscalledtobeleft(right)separative,forallx,y∈ S,ifx2 = xyand y2 = yx(x2 = yxandy2 = xy)implyx = y.(2)Siscalledtobeseparative,ifitisbothleftandrightseparative. (3)Siscalledtobequasi-separative,ifforallx,y∈S,x2 = xy = y2 impliesx = y.
Example5. LetS = {1,2,3,4}.Theoperation*onSisdefinedasTable 5.Then(S,*)isaseparative CA-groupoid.
Table5. Theoperation*on S. * 1234 1 4211 2 2222 3 1234 4 1244
Example6. LetS = {1,2,3,4}.Theoperation*onSisdefinedasTable 6.Then(S,*)isaquasi-separative CA-groupoid.
Table6. Theoperation*on S. * 1234 1 4321 2 3232 3 2323 4 1234
Theorem4. LetSbeaCA-groupoid.Thenthefollowingassertsareequivalent: (1) Sisseparative; (2) Sisleftseparative; (3) Sisrightseparative; (4) Sisquasi-separative.
Proof. Obviously,(1)⇒(2),byDefinition7. (2)⇒(3):Supposethat S isleftseparative.Forany x,y∈ S, if x2 = yx and y2 = xy,then(byProposition 1(1)): (xy)2 = (xy)(xy) = (xy) y2 = (xy)(yy) = (yx)(yy) = x2(yy) = (xx)(yy) = (yx)(yx) = (xy)(yx); (yx)2 = (yx)(yx) = (xy)(yx) = (xx)(yy) = x2y2 = (yx)(xy).
Since S isleftseparative,byDefinition7wehave xy = yx.Fromthis,using x2 = yx and y2 = xy, wegetthat x2 = xy and y2 = yx.Applyingtheconditionthat S isleftseparative,byDefinition7again, wehave x = y.Thismeansthat S isrightseparative.
(3)⇒(4):Supposethat S isrightseparative.Forany x,y∈ S, if x2 = xy = y2,then(byProposition 1(1)): (xy) 2 = (xy)(xy) = x2 (xy) = (xx)(xy) = (yx)(xx) = (yx)x2 = (yx)(xy); (yx) 2 = (yx)(yx) = (xy)(yx).
Since S isrightseparative,byDefinition7wehave xy = yx.Fromthis,using x2 = xy = y2,weget that x2 = yx and y2 = xy.Applyingtheconditionthat S isrightseparative,byDefinition7again, wehave x = y.ThismeansthatSisquasi-separative.
(4)⇒(1)Supposethat S isquasi-separative.Foranyx,y∈ S, then(byProposition1(1)): (xy)2 = (xy)(xy) = (yx)(xy) = (yy)(xx) = y2x2 ; (yx)2 = (yx)(yx) = (xy)(yx) = (xx)(yy) = x2y2 .
Moreover, [(yx)(xy)]2 = [(yx)(xy)][(yx)(xy)] = [(yx)(xy)][(yy)(xx)] = [(yx)(xy)](y2x2) = [(yx)(xy)](xy)2 = [(yx)(xy)][(xy)(xy)] = [(xy)(yx)][(xy)(xy)] = [(xx)(yy)][(xy)(xy)] = (x2y2)[(xy)(xy)] = (yx)2 [(xy)(xy)] = [(yx)(yx)][(xy)(xy)] = [(xy)(yx)][(xy)(yx)] = [(xy)(yx)]2 .
Ifx2 = xyandy2 = yx,then (y4)2 = (y2y2)2 = [(yx)(yx)]2 = [(xy)(yx)]2 = [(yx)(xy)]2 = (y2x2)2 = (y2x2)(y2x2) = (x2y2)(y2x2) = (x2x2)(y2y2) =x4y4 ; (x4)2 = (x2x2)2 = [(xy)(xy)]2 = [(yx)(xy)]2 = [(yy)(xx)]2 = (y2x2)2 = (y2x2)(y2x2) = (x2y2)(y2x2) = (x2x2)(y2y2) =x4y4
Fromthis,applyingtheconditionthat S isquasi-separative,wegetthat x4 =y4.Thus, (xy)2 = (x2)2 = x4 = y4 = (y2)2 = (yx)2 = (yx)(yx) = (xy)(yx).
Thatis,(xy)2 = (xy)(yx) = (yx)2.Since S isquasi-separative,byDefinition7wehave xy = yx Fromthis,using x2 = xy and y2 = yx,wehave x2 = xy = y2.Applyingtheconditionthat S is quasi-separative,byDefinition7again,wehave x = y.ThismeansthatSisleftseparative.
Similarly,wecanprovethat S isrightseparative.Therefore, S isseparativebyDefinition7.
Proposition6. LetSbeaCA-groupoid.IfSiscancellative,thenSisseparative.
Proof. Assumethat S iscancellative.Forany x,y∈ S, if x2 = xy = y2,then xx = xy and xy = yy. Usingcancellabilityof S,wehave x = y.Thismeansthat S isseparative. Similarly,wecanprovethat S isseparativewhen S isleft(orright)cancellative.
ThefollowingexampleshowsthataseparativeCA-groupoidmaybenotaleft(orright) cancellativeCA-groupoid.
Example7. LetS = {1,2,3,4}.Theoperation*onSisdefinedasTable 7.Then(S,*)isaseparativeCA-groupoid, butSisn’tcancellative,since1*1 = 2*1,1 2.
Table7. Theoperation*on S. * 1234 1 1231 2 1432 3 3333 4 1234
Definition8. LetSbeaCA-groupoid.SiscalledaCA-band,ifforalla∈S,aa = a;SiscalledCA-3-band,iffor alla∈S,a*aa = aa*a = a.
Definition9. LetSbeaCA-groupoid.Siscalledtobeleft(right)quasi-cancellative,forallx,y∈S,ifx = xy andy2 = yx(x = yxandy2 = xy)implyx = y.Siscalledquasi-cancellative,ifitisbothleftandrightquasicancellative.
Example8. LetS = {1,2,3,4}.Theoperation*onSisdefinedasTable 8.Then(S,*)isaquasi-cancellative CA-groupoid.
Table8. Theoperation*on S. * 1234 1 1111 2 1211 3 1134 4 1143
Theorem5. LetSbeaCA-groupoid.IfSisleftquasi-cancellative,thenSisrightquasi-cancellative.
Proof. Supposethat S isleftquasi-cancellative.Forany x,y∈ S, if x = yx and y2 = xy,then(byProposition 1(1)):
x2 = (yx)(yx) = (xy)(yx) = (xx)(yy) = x2y2 ; (y2)2 = y2y2 = (xy)(xy) = (yx)(xy) = (yy)(xx) = y2x2
Fromthis,applyingtheconditionthat S isleftquasi-cancellative,wegetthat x2 = y2.Thus: xy = y2 = x2 = (yx)(yx) = (xy)(yx); (yx)2 = (yx)(yx) = x(yx) = x(xy) = (yx)(xy).
Fromthis,applyingtheconditionthat S isleftquasi-cancellativeandDefinition9again,weget that xy = yx.Hence,usingtheconditionthat x = yx and y2 = xy,wehave x = xy and y2 = yx,applying thedefinitionofleftquasi-cancellative,wegetthat x = y.Therefore, S isrightquasi-cancellative.
OpenProblem2 (toproveorgiveacounterexample):Isanyrightquasi-cancellativeCA-groupoid necessarilyleftquasi-cancellative?
Theorem6. Thefollowingassertsaretrue:
(1) EveryCA-bandisquasi-cancellative.
(2) EveryCA-3-bandisquasi-cancellative.
(3) Everyquasi-separativeCA-groupoidisquasi-cancellative;
(4) Everyseparative(orleft-,right-separative)CA-groupoidisquasi-cancellative.
Proof. (1)Let S beaCA-band.Forany x,y ∈ S, if x = xy and y2 = yx, then(byDefinition8) x = x2 , y = y2.Itfollowsthat: x = x2 = (xy)(xy) = (yx)(xy) = y2(xy) = y(xy) = yx = y2 = y.
Thismeansthat S isleftquasi-cancellative.ApplyingTheorem5,weknowthat S isrightquasicancellative.Hence, S isquasi-cancellative.
(2)Let S beaCA-3-band.Forany x,y ∈ S, if x = xy and y2 = yx, then(byDefinition8) x = xx2 = x2x,y = yy2 = y2y. Furthermore:
y2 = yx = y(xy) = y(yx) = yy2 = y, x = xy = x(yy2) = y2(xy) = y2x = yx = y2 = y.
Thus, S isleftquasi-cancellative.ApplyingTheorem5,wegetthat S isrightquasi-cancellative. Hence, S isquasi-cancellative.
(3)Let S beaquasi-separativeCA-groupoid.Forany x,y ∈ S, if x = xy and y2 = yx, then: x2 = xx = x(xy) = y(xx) = x(yx) = xy2 = x(yy) = y(xy) = yx = y2
Thatis, y2 = yx = x2.ByDefinition7wehave x = y. Thismeansthat S isleftquasi-cancellative. ApplyingTheorem5,wegetthat S isrightquasi-cancellative.Hence, S isquasi-cancellative.
(4)Itfollowsfrom(3)andTheorem4.
Example9. LetS = {1,2,3,4,5}.Theoperation*onSisdefinedasTable 9.Then(S,*)isaquasi-cancellative CA-groupoid,Sisn’tseparative,because2*2 = 2*4 = 3,4*4 = 4*2 = 3,but2 4.
Table9. Theoperation*on S. * 12345 1 33533 2 33533 3 44355 4 33533 5 33533
Definition10. Let(S,*)beaCA-groupoid.Siscalledtobepower-cancellative,ifforallx,y∈S,x2 = y2 implies x = y.
Example10. LetS = {1,2,3,4,5}.Theoperation*onSisdefinedasTable 10.Then(S,*)isapower-cancellative CA-groupoid,Sisn’tcancellative,because1*2 = 1*3,but2 3.
Table10. Theoperation*on S. * 12345 1 11145 2 12145 3 11345 4 44451 5 55514
Example11. LetS = {1,2,3,4}.Theoperation*onSisdefinedasTable 11.Then(S,*)isacancellative CA-groupoid,Sisn’tpower-cancellative,because12 = 22 = 1,but1 2.
Table11. Theoperation*on S. * 1234 1 1234 2 2143 3 3421 4 4312
Theorem7. LetSbeaCA-groupoid.IfSispower-cancellative,then: (1) Siscommutative,andSisacommutativesemigroup. (2) Sisseparative.
Proof. (1)Supposethat S ispower-cancellative.Forany x,y ∈ S, since(byProposition1(1)): (xy)2 = (xy)(xy) = (yx)(xy) = (yy)(xx) = y2x2 ; (yx)2 = (yx)(yx) = (xy)(yx) = (xx)(yy) = x2y2 Moreover, [(yx)(xy)]2 = [(yx)(xy)][(yx)(xy)] = [(yx)(xy)][(yy)(xx)] = [(yx)(xy)](y2x2) = [(yx)(xy)](xy)2 = [(yx)(xy)][(xy)(xy)] = [(xy)(yx)][(xy)(xy)] = [(xx)(yy)][(xy)(xy)] = (x2y2)[(xy)(xy)] = (yx)2 [(xy)(xy)] = [(yx)(yx)][(xy)(xy)] = [(xy)(yx)][(xy)(yx)] = [(xy)(yx)]2
Applyingtheconditionthat S ispower-cancellative,wegetthat(yx)(xy) = (xy)(yx).Thus: (xy)2 = y2x2 = (yx)(xy) = (xy)(yx) = x2y2 = (yx)2
ByDefinition10,wehave xy = yx.Thismeansthat S iscommutative,and S isacommutative semigroup(byProposition2).
(2)Assumethat S ispower-cancellative.Forany x,y ∈ S, if x2 = xy = y2 , then(byDefinition10), x = y.Thismeansthat S isquasi-separative.ApplyingTheorem4,weknowthat S isseparative.
5.VariantCA-Groupoids
Inthissection,wefocusonaspecialclassofCA-groupoids,whicharecalledvariantCA-groupoids. ThereasonswhywewanttodiscussthiskindofCA-groupoidsarethat:(1)itiscloselyrelatedto thegeneralizedunitelement(i.e.,quasirightunitelement),anditistheclosesttothecommutative semigroup(seeExample12andExample13below);(2)thiskindofCA-groupoidshasmanyinteresting properties,anditcanconstructedfromanycommutativesemigroup,pleaserefertothefollowing Theorem9;(3)theresearchthiskindofCA-groupoidsisofgreatsignificancetostudysomespecial ringsandsemirings.Seeliterature[7 9]andExample14andExample15below.
Definition11. Let(S,*)beaCA-groupoid.SiscalledavariantCA-groupoid,ifexiste∈S,suchthatforall x∈S {e},xe = xande2 e.Where,eiscalledaquasi-rightuniteelementofS.
Example12. LetS = {1,2,3,4,5},Theoperation*onSisdefinedasTable 12,then(S,*)isavariant CA-groupoidand1isaquasi-rightunitelementinS.Obviously,Sisn’tcommutative.
Table12. Theoperation*on S. * 12345 1 33344 2 23344 3 33344 4 44444 5 54444
Lookingattheaboveexamplecarefully,wefindthat:(1)theelement1asaquasi-rightunit elementof S,doesnotappearintheoperationtable;(2)intheoperationtable,thefirstrowisthesame asthethirdrow;(3)ifwechangethefirstrowoftheoperationtableto{1,2,3,4,5},wewillgeta commutativesemigroup(S, +)(asshowninTable 13).Theseareallinterestingphenomena.Later, wewillanalyzethecharacteristicsofvariantCA-groupoids.
Table13. ACommutativesemigroup(S, +)correspondingto(S,*). + 12345 1 12345 2 23344 3 33344 4 44444 5 54444
Example13. LetS = {1,2,3,4,5},Theoperation*onSisdefinedasTable 14,then(S,*)isavariant CA-groupoidand5isaquasi-rightunitelementinS.Obviously,Siscommutative.
Table14. Theoperation*on S. * 12345 1 11111 2 14232 3 12343 4 13424 5 12343
Ifwechangethelastrowoftheoperationtableto{1,2,3,4,5},wewillgetacommutative semigroup(S, +)(asshowninTable 15).
Table15. ACommutativesemigroup(S, +)correspondingto(S,*). + 12345 1 11111 2 14232 3 12343 4 13424 5 12345
Example14. Let: S = a 0 00 : aisaintegralnumber ∪ 10 01 , 10 0 1 .
Definetheoperation*onSisthecommonmatrixmultiplication,then(S,*)isavariantCA-groupoidand 10 0 1 isaquasi-rightunitelementinS.Moreover,wedefinetheadditionoperation + onSasfollowing:
foranyx,y∈S,denoteS1 = a 0 00 : aisaintegralnumber ,S2 = 10 01 , 10 0 1 ,
(1) ifx,y ∈ S1,x + yiscommonmatrixaddition;
(2) ifx ∈ S1 andy ∈ S2,x + y = a + 10 00 ,wherey = a 0 00 ; (3) ifx ∈ S2 andy ∈S1,x + y = y + x(see(2)); (4) ifx = y ∈ S2,x + y = 00 00 ;
(5) ifx,y ∈ S2 andx y,x + y = 20 00
Then(S, +)isacommutativegroup,and(S; +,*)isaring,thatis,(x + y)*z = x*z + y*zandz*(x + y) = z*x + z*y,foranyx,y,z∈S.
Example15. LetS = {1,2,3,4,5,6},Theoperation*onSisdefinedasTable 16,then(S,*)isavariant CA-groupoidand1isaquasi-rightunitelementinS.Obviously,Sisnotcommutative.
Table16. Theoperation*on S. * 123456 1 333446 2 233446 3 333446 4 444446 5 544446 6 666666
Moreover,wedefinetheadditionoperation + onSasTable 17 orTable 18,then(S, +)isacommutative semigroupwithunite6.Wecanverifythat(x + y)*z = x*z + y*zforanyx,y,zinS,so(S; +,*)isasemiring (forthetheoryofsemirings,pleaseseethemonograph[33 35]).
Table17. ACommutativemonoid(S, +). + 123456 1 111111 2 123332 3 133333 4 133454 5 143555 6 123456
Table18. AnotherCommutativemonoid(S, +). + 123456 1 121451 2 222452 3 123453 4 444454 5 555545 6 123456
Theorem8. LetSbeavariantCA-groupoid:
(1) Ifeisaquasi-rightunitelementofSandee = a,a ∈ S,thenex = axforallx ∈ S. (2) Thequasi-rightuniteelementisuniqueinS.
Proof. (1)Let e beaquasi-rightunitelementof S and ee = a,a∈S. ByDefinition11,weknowthat a e Forany x∈S,if x = e,then ex = ee = a = ae = ax; if x e,then(byDefinition11): ex = e*xe = e*ex = x*ee = xa = xe*ae = e*(xe*a) = a*(e*xe) = a*(e*ex) = a*(x*ee) = a*xa = a*ax = x*aa = x*(a*ee) = x*(e*ae) = ae*xe = ax. hence, ex = ax forall x∈S.
(2)Supposethat s and t arequasi-rightunitelementsof S,s t. FromDefinition11weknowthat ss s and tt t. Since: s = st = st*ts = s*(st*t) = t*(s*st) = t*(t*ss) = t*(s*ts) = t*st = ts = t.
Thismeansthatthequasi-rightunitelementisuniquein S.
Obviously,let S = {a}and(S,*)isaCA-groupoid,then S isn’tavariantCA-groupoid.Let S = {a, b} and(S,*)isavariantCA-groupoid,denotethequasi-rightunitelement e = a (or b),thenforany x, y∈S, wehave xy = b (or a).
ThroughthestudyofthevariantCA-groupoid,wegivethefollowingconstructionmethod,thatis tosay,onthebasisofacommutativesemigroup,avariantCA-groupoidisformedbyaddingan elementwhichdoesnotintersectwithit,andavariantCA-groupoidcanalsobedecomposedtoobtain acommutativesemigroupandanindependentelement.
Theorem9. Thefollowingassertsaretrue:
(1) LetSbeavariantCA-groupoidandeisthequasi-rightuniteelementonS,thenS1 = S {e}isacommutative semigroup.
(2) LetSbeacommutativemonoidwithunitelementeandaisanelementsuchthat {a}∩S = ∅,thenS2 = S∪{a} isavariantCA-groupoidifdefinexa = x,ax = ex,aa = e,forallx∈S.
Proof. (1)Supposethat S isavariantCA-groupoidand e isthequasi-rightunitelementof S, if ∃x,y∈ S1 = S {e}suchthat xy = e,thenforall a∈S {e}, a*xy = ae = a,sowehave:
ee = e*xy = y*ex = x*ye = xy = e.
Symmetry 2020, 12, x FOR PEER REVIEW 14 of 19
for any x, y∈ S2, if x, y∈ S, then x• y = x*y; if x∈ S, then x•a = x, a•x = e•x, a•a = e.
ThisconclusioncontradictsDefinition11.Hence,forall x,y∈S {e},xy e, inotherwords, S {e}is closed,thatis, S {e}isasubCA-groupoidof S.Moreover,forall x,y∈ S1 = S {e},applyingTheorem8 (1), ex = (ee)x,and: xy = x*ye = e*xy = y*ex = y*(ee*x) = x*(y*ee) = x*(e*ye) = ye*xe = yx hence S {e}iscommutative,then S {e}isacommutativesemigroup(byProposition2). (2)Ontheotherhand,supposethat S iscommutativemonoidwithunitelement e.Let a bean elementsuchthat{a}∩S = ∅, denote S2 = S∪{a}.Defineanewbinaryoperation • on S2: forany x, y∈ S2,if x, y∈ S,then x• y = x*y;if x∈ S,then x•a = x, a•x = e•x, a•a = e. Obviously,(S2, •)isagroupoid.Forall x,y,z∈S, bythedefinitionofoperation • wehave: x•yz = x*yz = z*xy = z•xy, a•aa = a•aa, x•aa = xe = ex = ax = a•xa, a•xa = ax = bx = xe = x•ee = e•ex = a•ax, a•ax = e•ex = e•xe = xe•e = x•ee = xe = x•aa, y•ax = ax•y = ex•y = xy = x•ya, x•ya = xy = e•xy = a•xy, a•xy = (a•xa)•ya = ya•(a•xa) = y•ax. thus,(S2, •)isavariantCA-groupoidwiththequasi-rightunitelement a
Obviously, (S2, •) is a groupoid. For all x, y, z∈S, by the definition of operation • we have: x•yz = x*yz = z*xy = z•xy, a•aa = a•aa, x•aa = xe = ex = ax = a•xa, a•xa = ax = bx = xe = x•ee = e•ex = a•ax, a•ax = e•ex = e•xe = xe•e = x•ee = xe = x•aa, y•ax = ax•y = ex•y = xy = x•ya, x•ya = xy = e•xy = a•xy, a•xy = (a•xa)•ya = ya•(a•xa) = y•ax.
thus, (S2, •) is a variant CA-groupoid with the quasi-right unit element a. □ Applying Definition 11 and Definition 9 we can easy to verify that the following proposition is true.
ApplyingDefinition11andDefinition9wecaneasytoverifythatthefollowingproposition istrue.
Proposition7. (1)IfSisavariantCA-groupoid,thenSisn’tcancellative.(2)IfSisacancellativeCA-groupoid, thenSisn’tavariantCA-groupoid.
Proposition 7. (1) If S is a variant CA-groupoid, then S isn’t cancellative. (2) If S is a cancellative CA-groupoid, then S isn’t a variant CA-groupoid.
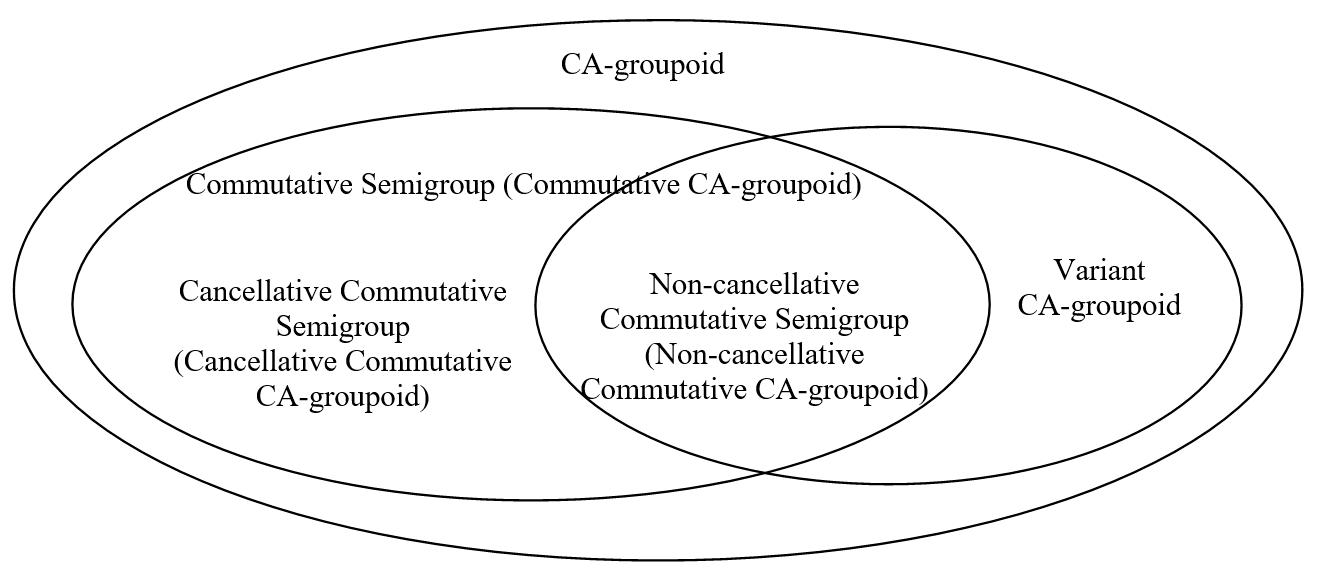
FromTheorem9,Proposition7,Examples12~15,wehaveFigure 1
Figure1. TherelationshipsamongsomeCA-groupoids.
From Theorem 9, Proposition 7, Examples 12~15, we have Figure 1. Figure 1. The relationships among some CA-groupoids
Theorem 10. Let S be a variant CA-groupoid and e be a quasi-right unit element of S. Denote a = ee, b = aa. Then the following asserts are true:
(1) If b = a, then {e, a} is a variant sub CA-groupoid of S; (2) If b≠a, then {e, a, b} is a variant sub CA-groupoid of S.
Proof. (1) Suppose b = a. For the set {e, a}, since (by Theorem 8):
Theorem10. LetSbeavariantCA-groupoidandebeaquasi-rightunitelementofS.Denotea = ee,b = aa. Thenthefollowingassertsaretrue:
(1) Ifb = a,then{e,a}isavariantsubCA-groupoidofS; (2) Ifb a,then{e,a,b}isavariantsubCA-groupoidofS.
Proof. (1)Suppose b = a. Fortheset{e,a},since(byTheorem8):
ee = a,aa = b = a,ae = a,ea = ee*a = aa = a.
Itfollowsthat{e,a}isclosedontheoperation*.Thus,{e,a}isavariantsubCA-groupoidwith quasi-rightunitelement e
(2)Assume b a. ByTheorem9(1),forall x,y∈S {e}, xy = yx.Fortheset{e,a,b},since(by Theorem8):
ee = a,aa = b,ae = a,ea = ee*a = aa = b; eb = e*aa = a*ea = a*ae = aa = b,be = b; ba = ab = ee*aa = a*(ee*a) = a*(a*ee) = a*(e*ae) = ae*ae = aa = b
Thus,{e,a,b}isclosedabout*,so{e,a,b}isavariantsubCA-groupoidof S
Theorem11. Let(S1,*1)and(S2,*2)betwovariantCA-groupoids,e1 ande2 arequasi-rightunitelementsof (S1,*1)and(S2,*2),S1 ∩S2 = {e}(e = e1 = e2).DenoteS = S1∪S2,anddefinetheoperation*onSasfollows:
(i) ifa,b∈S1,thena*b = a*1b; (ii) ifa,b∈S2,thena*b = a*2b; (iii) ifa∈S1-{e},b∈S2-{e},thena*b = b; (iv) ifa∈S2-{e},b∈S1-{e},thena*b = a. Then(S,*)isavariantCA-groupoidwiththequasi-rightunitee.
Proof. Itisonlynecessarytoprovethatthecyclicassociativelawholdin(S,*),thatis, a*(b*c) = c*(a*b) forall a,b,c∈S.Wewilldiscussthefollowingsituationsseparately:
(1) If a,b,c∈S1,ora,b,c∈S2, then a*(b*c) = c*(a*b); (2) If a∈S1 {e},b∈S2 {e}and c∈S2 {e},then a*(b*c) = b*c = c*b = c*(a*b); (3) If a∈S2 {e},b∈S1 {e}and c∈S2 {e},then a*(b*c) = a*c = c*a = c*(a*b);
(4) If a∈S2 {e},b∈S2 {e}and c∈S1 {e},then a*(b*c) = a*b = c*(a*b);
(5) If a∈S1 {e},b∈S1 {e}and c∈S2 {e},then a*(b*c) = a*c = c = c*(a*b);
(6) If a∈S1 {e},b∈S2 {e}and c∈S1 {e},then a*(b*c) = a*b = c*(a*b); (7) If a∈S2 {e},b∈S1 {e}and c∈S1 {e},then a*(b*c) = a = a*b = c*(a*b).
Then(S,*)isavariantCA-groupoidand e isthequasi-rightunitelement.
Example16. LetS1 = {1,2,3,4}andS2 = {1,5,6,7}.Defineoperations*1 and*2 onS1,S2 asfollowing Tables 19 and 21.ThenS = S1∪S2 = {1,2,3,4,5,6},and(S,*)isavariantCA-groupoidwiththeoperation*in Table 20
Table19. Theoperation*1 on S1. * 1 1234 1 2244 2 2244 3 3444 4 4444
Table20. Theoperation*on S. * 1234567 1 2244567 2 2244567 3 3444567 4 4444567 5 5555577 6 6666755 7 7777755
Table21. Theoperation*2 on S2. * 2 1567 1 5577 5 5577 6 6755 7 7755
SimilartoTheorem11,wecangetanotherconstructermethodasfollowingproposition(theproof isomitted).
Proposition8. Let(S1,*1)and(S2,*2)betwovariantCA-groupoids,e1 ande2 arevariantunitelementsof (S1,*1)and(S2,*2),S1∩S2 = ∅ andS2 iscommutative.DenoteS = S1∪S2,anddefinetheoperation*inS asfollows:
(1) ifa,b∈S1,thena*b = a*1b; (2) ifa,b ∈S2,thena*b = a*2b; (3) ifa∈S1,b∈S2,thena*b = b; (4) ifa ∈S2,b ∈ S1,thena*b = a.
Then(S,*)isavariantCA-groupoidwiththequasi-rightunitee1
Example17. LetS1 = {1,2,3,4}andS2 = {5,6,7,8}.Defineoperations*1 and*2 onS1,S2 asfollowing Tables 22 and 24.ThenS = S1∪S2 = {1,2,3,4,5,6,7,8},and(S,*)isavariantCA-groupoidwiththeoperation *inTable 23.
Table22. Theoperation*1 on S1. * 1 1234 1 3224 2 2224 3 3224 4 4444
Table23. Theoperation*on S. * 12345678 1 32245678 2 22245678 3 32245678 4 44425678 5 55558678 6 66666666 7 77777667 8 88888678
Table24. Theoperation*2 on S2. * 2 5678 5 8678 6 6666 7 7667 8 8678
Theorem12. LetS1 beavariantCA-groupoidwithordern(n ≥ 2andnisanevennumber)andthequasi-right unitelemente1 ∈ S1,letS2 beavariantCA-groupoidwithorder2andthequasi-rightunitelemente2 ∈S2.IfS = S1 ∪ S2 andS1 ∩ S2 = ∅,thenSisavariantCA-groupoid,whenitsuchthatanyofthefollowingconditions:
(1) forthevariantCA-groupoidS,thequasi-rightunitelemente = e1,ande2*e1 = e2,andforallx ∈ S,x*(e2 * e2) = (e2*e2)*x = e2*e2,x*e2 = e2*e2,e2*x = e2*e2 (x e1); (2) forthevariantCA-groupoidS,thequasi-rightunitelemente = e1 andforallx ∈ S,x*(e2*e2) = (e2*e2)*x = e2*e2,x*e2 = e2*x = e2.
Proof. (1)Supposethat S isconstructedaccordingtothemethoddescribedin(1),thenforall x,y,z∈S1, x*yz = z*xy = y*zx,and:
x*ye2 = x*e 2 e2 = e2 e2,e2*xy = e2 e 2 (xy e1) y ∗ e2x = y ∗ e2e1 = ye2 = e2e2 x = e1 y ∗ e2e2 = e2e2 x e1
Thatis, x*ye2 = e2 *xy = y*e2x.Denote e2 e2 = b,then:
x*yb = xb = b,b*xy = b,y*bx = yb = b. Thatis, x*yb = b*xy = y*bx. x*e2e2 = xb = b,e2*xe2 = e2*e2 e2 = b, e2 ∗ e2x = e2 ∗ e2e1 = e2e2 = b x = e1 e2 ∗ e2e2 = b x e1
Thus, x*e2e2 = e2*xe2 = e2*e2x. And: x*be2 = x*e2 b = xb = b,b*xe2 = b*e2 e2 = b = e2 b = e2*bx,e2*xb = e2 b = b, b ∗ e2x = b ∗ e2e1 = be2 = b x = e1 b ∗ e2e2 = b x e1
Itfollowsthat x*be2 = e2*xb = b*e2x,and x*e2b = b*xe2 = e2*bx.Obviously, x*bb = b*xb = b*bx.Hence, S isavariantCA-groupoid.
(2)Supposethat S isconstructedaccordingtothemethoddescribedin(2),thenforall x,y,z∈S1, x*yz = z*xy = y*zx,and:
x*ye2 = xe2 = e2,e2*xy = e2,y*e2x = ye2 = e2.
Then x*ye2 = e2*xy = y*e2x.Assume e2e2 = b,then:
x*yb = xb = b,b*xy = b,y*bx = yb = b.
Thatis, x*yb = b*xy = y*bx.And:
x*e2 e2 = xb = b,e2*xe2 = e2*e2 x = e2 e2 = b.
Thus, x*e2e2 = e2*xe2 = e2*e2x. Moreover:
x*be2 = x*e2 b = xb = b,b*xe2 = be2 = b = e2b = e2*bx,e2*xb = e2 b = b = be2 = b*e2x.
Itfollowsthat x*be2 = e2*xb = b*e2x,and x*e2b = b*xe2 = e2*bx.Obviously, x*bb = b*xb = b*bx.Hence, SisavariantCA-groupoid.
6.Conclusions
Inthepaper,wemainlystudyvariouscancellabilitiesofCA-groupoidsandthestructural propertiesofaspecialkindofCA-groupoids(variantCA-groupoids).Firstly,weinvestigatesome cancellabilitiesofCA-groupoids,includingleft(right)cancellation,weakcancellation,left(right) quasi-cancellationandleft(right)separation,andanalyzetherelationshipsamongthem.Secondly, fromtheviewofquasi-rightunitelement,weintroducethenewnotionofvariantCA-groupoid, illustratethecloseconnectionsamongvariantCA-groupoidwithcommutativesemigroup,ringand semiringbysomeexamples;discussdeeplythecharacteristicsofvariantCA-groupoid,andestablish itsstructuretheoremandconstructionmethods.Thispaperobtainsmanyconclusions,someimportant resultsasfollows:
(1) EveryleftcancellativeelementinCA-groupoidisrightcancellative(seeTheorem1);
(2) ForaCA-groupoid,itisleftcancellativeifandonlyifitisrightcancellative(seeTheorem1and Corollary1);
(3) ForaCA-groupoid,itisleftseparativeifandonlyifitisrightseparative,andifandonlyifitis quasi-separative(seeTheorem4andCorollary1);
(4) Everyleftquasi-cancellativeCA-groupoidisrightquasi-cancellative(seeTheorem5);everypower cancellativeCA-groupoidisseparative(seeTheorem7);
(5) ForavariantCA-groupoid,itsquasi-rightunitelementisunique;
(6) AvariantCA-groupoidcanbedecomposedintothequasi-rightunitelementandacommutative CA-groupoid;startingfromanycommutativesemigroup,onecanconstructavariantCA-groupoid (seeTheorem9);
(7) TherearemanywaystoconstructanewvariantCA-groupoidfromtheexistingvariant CA-groupoids(seeTheorems11and12).
Asadirectionoffutureresearch,wewilldiscussthestructuralcharacteristicsofCA-rings, CA-semiringsandrelatedalgebraicsystems(see[36 39]).
AuthorContributions: X.Z.,Z.M.initiatedtheresearchandwrotethepaper,F.S.supervisedtheresearchwork andprovidedhelpfulsuggestions.Allauthorshavereadandagreedtothepublishedversionofthemanuscript.
Funding: ThisresearchwasfundedbyNationalNaturalScienceFoundationofChina(GrantNo.61976130).
ConflictsofInterest: Theauthorsdeclarenoconflictofinterest.
References
1. Zhang,X.H.;Ma,Z.R.;Yuan,W.T.Cyclicassociativegroupoids(CA-groupoids)andcyclicassociative neutrosophicextendedtripletgroupoids(CA-NET-groupoids). NeutrosophicSetsSyst. 2019, 29,19–29.
2. Yuan,W.T.;Zhang,X.H.RegularCA-groupoidsandcyclicassociativeneutrosophicextendedtripletgroupoids (CA-NET-groupoids)withgreenrelations. Mathematics 2020, 8,204.[CrossRef]
3. Byrne,L.TwobriefformulationsofBooleanalgebra. Bull.Am.Math.Soc. 1946, 52,269–272.[CrossRef]
4. Sholander,M.Medians,lattices,andtrees. Proc.Am.Math.Soc. 1954, 5,808–812.[CrossRef]
5. Hosszu,M.Somefunctionalequationsrelatedwiththeassociativelaw. Publ.Math.Debrecen. 1954, 3, 205–214.
6. Maksa,G.CMsolutionsofsomefunctionalequationsofassociativetype. Ann.Univ.Sci.Bp.Sect.Comput. 2004, 24,125–132.
7. Kleinfeld,M.Ringswithx(yz)=y(zx). Commut.Algebra 1995, 23,5085–5093.[CrossRef]
8. Behn,A.;Correa,I.;Hentzel,I.R.Semiprimalityandnilpotencyofnonassociativeringssatisfyingx(yz) = y(zx). Commun.Algebra 2008, 36,132–141.[CrossRef]
9. Behn,A.;Correa,I.;Hentzel,I.R.Onflexiblealgebrassatisfyingx(yz) = y(zx). AlgebraColloq. 2010, 17, 881–886.[CrossRef]
10. Iqbal,M.;Ahmad,I.;Shah,M.;Ali,M.I.OncyclicassociativeAbel-Grassmangroupoids. Br.J.Math.Comput. Sci. 2016, 12,1–16.[CrossRef]
11. Tamura,T.CommutativenonpotentarchimedeansemigroupwithcancelationlawI. J.GakugeiTokushima Univ. 1957, 8,5–11.
12. Burmistrovich,I.E.Commutativebandsofcancellativesemigroups. Sib.Mat.Zh. 1965, 6,284–299.
13. Grillet,P.A.Cancellativecommutativesemigroups. SemigroupForum. 1970, 1,249–253.[CrossRef]
14. Neumann,B.H.Someremarksoncancellativesemigroups. Math.Z. 1970, 117,97–111.[CrossRef]
15. Goodearl,K.R.Power-cancellationofgroupsandmodules. Pac.J.Math. 1976, 64,387–411.[CrossRef]
16. Cherubini,A.;Varisco,A.Powercancellativesemigroups. SemigroupForum. 1979, 18,381–384.
17. Lezzi,D.ThePara-cancellationlawincommutativesemigroups. ActaMath.Acad.Sci.Hung.Tomus. 1980, 36,65–69.
18. Krasilnikova,Y.I.;Novikov,B.V.Onquasi-separativesemigroups. SemigroupForum 2005, 70,347–355. [CrossRef]
19. Cegarra,A.M.;Petrich,M.Therankofacommutativecancellativesemigroup. ActaMath.Hungar. 2005, 107, 71–75.
20. Cegarra,A.M.;Petrich,M.Commutativecancellativesemigroupsoflowrank. ResultsMath. 2009, 54,41–52. [CrossRef]
21. Shah,M.;Ali,A.SomestructurepropertiesofAG-groups. Int.Math.Forum. 2011, 6,1661–1667.
22.
Ali,A.;Shah,M.;Ahmad,I.Onquasi-cancellativityofAG-groupoids. Int.J.Contemp.Math.Sci. 2012, 7, 2065–2070.
23. Shah,M.;Shah,T.;Ali,A.OnthecancellativityofAG-groupoids. Int.Math.Forum. 2011, 6,2187–2194. 24. Petrich,M.Malcevproductsofweaklycancellativemonoidsandvarietiesofbands. SemigroupForum. 2015, 90,339–373.[CrossRef]
25.
Zhang,X.H.;Smarandache,F.;Liang,X.L.Neutrosophicdupletsemigroupandcancellableneutrosophic tripletgroups. Symmetry 2017, 9,275.[CrossRef]
Zhang,X.H.;Ma,Y.C.;Yu,P.OntwoconjecturesofAbelGrassmann’sgroupoids. Symmetry 2019, 11,816. [CrossRef] 27.
26.
Steinberg,B. RepresentationTheoryofFiniteMonoids;Springer:Berlin/Heidelberg,Germany,2016.
Protic,P.SomeremarksonAbel-Grassmann’sgroups. QuasigroupsRelat.Syst. 2012, 20,267–274. 29. Shah,M.ATheoreticalandComputationalInvestigationofAG-groups.Ph.DThesis,Quaidi-AzamUniversity Islamabad,Islamabad,Pakistan,2012. 30.
28.
Stanovsky,D.LinearrepresentationofAbel-Grassmanngroups. CarpathianJ.Math. 2017, 33,257–263. 31.
Zhang,X.H.;Wu,X.Y.InvolutionAbel-Grassmann’sgroupsandfiltertheoryofAbel-Grassmann’sgroups. Symmetry 2019, 11,553.[CrossRef]
32. Zhang,X.H.;Wu,X.Y.;Mao,X.Y.Onneutrosophicextendedtripletgroups(loops)andAbel-Grassmann’s groupoids(AG-groupoids). J.Intell.FuzzySyst. 2019, 37,5743–5753.[CrossRef]
Symmetry 2020, 12,315
33. Golan,J.S. SemiringsandTheirApplications;Springer:Dordrecht,TheNetherlands,1999. 34. Gondran,M.;Minoux,M.Dioïdsandsemirings:Linkstofuzzysetsandotherapplications. FuzzySetsSyst. 2007, 158,1273–1294.[CrossRef] 35. Zumbragel,J.Classificationoffinitecongruence-simplesemiringswithzero. J.AlgebraAppl. 2008, 7,363–377. [CrossRef] 36. Zhang,X.H.;Borzooei,R.A.;Jun,Y.B.Q-filtersofquantumB-algebrasandbasicimplicationalgebras. Symmetry 2018, 10,573.[CrossRef] 37. Zhang,X.H.;Hu,Q.Q.;Smarandache,F.;An,X.G.Onneutrosophictripletgroups:Basicproperties, NT-subgroups,andsomenotes. Symmetry 2018, 10,289.[CrossRef] 38. Wu,X.Y.;Zhang,X.H.ThedecompositiontheoremsofAG-neutrosophicextendedtripletloopsandstrong AG-(l,l)-loops. Mathematics 2019, 7,268.[CrossRef] 39. Zhang,X.H.;Wang,X.J.;Smarandache,F.;Jaiyeola,T.G.;Lian,T.Y.Singularneutrosophicextendedtriplet groupsandgeneralizedgroups. Cogn.Syst.Res. 2019, 57,32–40.[CrossRef]
© 2020bytheauthors.LicenseeMDPI,Basel,Switzerland.Thisarticleisanopenaccess articledistributedunderthetermsandconditionsoftheCreativeCommonsAttribution (CCBY)license(http://creativecommons.org/licenses/by/4.0/).

