Some Interval Neutrosophic Dombi Power Bonferroni Mean Operators

SomeIntervalNeutrosophicDombiPower BonferroniMeanOperatorsandTheirApplication inMulti–AttributeDecision–Making

QaisarKhan 1,PeideLiu 2,* ,TahirMahmood 1 ,FlorentinSmarandache 3 and KifayatUllah 1

1 DepartmentofMathematicsandStatistic,InternationalIslamicUniversity,Islamabad44000,Pakistan; qaisarkhan421@gmail.com(Q.K.);tahirbakhat@iiu.edu.pk(T.M.);kifayat.phdma72@iiu.edu.pk(K.U.)

2 SchoolofManagementScienceandEngineering,ShandongUniversityofFinanceandEconomics, Jinan250014,Shandong,China

3 DepartmentofMathematicsandSciences,UniversityofNewMexico,705GurleyAve,Gallup,NM87301, USA;fsmarandache@gmail.com

* Correspondence:peide.liu@gmail.com;Tel.:+86-531-8222-2188

Received:16August2018;Accepted:28September2018;Published:2October2018

Abstract: ThepowerBonferronimean(PBM)operatorisahybridstructureandcantakethe advantageofapoweraverage(PA)operator,whichcanreducetheimpactofinappropriatedatagiven bytheprejudiceddecisionmakers(DMs)andBonferronimean(BM)operator,whichcantakeinto accountthecorrelationbetweentwoattributes.Inrecentyears,manyresearchershaveextendedthe PBMoperatortohandlefuzzyinformation.TheDombioperationsofT-conorm(TCN)andT-norm (TN),proposedbyDombi,havethesupremacyofoutstandingflexibilitywithgeneralparameters. However,intheexistingliterature,PBMandtheDombioperationshavenotbeencombinedfor theaboveadvantagesforinterval-neutrosophicsets(INSs).Inthisarticle,wefirstdefinesome operationallawsforintervalneutrosophicnumbers(INNs)basedonDombiTNandTCNand discussseveraldesirablepropertiesoftheseoperationalrules.Secondly,weextendthePBMoperator basedonDombioperationstodevelopaninterval-neutrosophicDombiPBM(INDPBM)operator,an interval-neutrosophicweightedDombiPBM(INWDPBM)operator,aninterval-neutrosophicDombi powergeometricBonferronimean(INDPGBM)operatorandaninterval-neutrosophicweighted DombipowergeometricBonferronimean(INWDPGBM)operator,anddiscussseveralpropertiesof theseaggregationoperators.Thenwedevelopamulti-attributedecision-making(MADM)method, basedontheseproposedaggregationoperators,todealwithintervalneutrosophic(IN)information. Lastly,anillustrativeexampleisprovidedtoshowtheusefulnessandrealismoftheproposedMADM method.ThedevelopedaggregationoperatorsareverypracticalforsolvingMADMproblems,asit considerstheinteractionamongtwoinputargumentsandremovestheinfluenceofawkwarddata inthedecision-makingprocessatthesametime.Theotheradvantageoftheproposedaggregation operatorsisthattheyareflexibleduetogeneralparameter.

Keywords: intervalneutrosophicsets;Bonferronimean;poweroperator;multi-attributedecision making(MADM)

1.Introduction

Whiledealingwithanyrealworldproblems,adecisionmaker(DM)oftenfeelsdiscomfortwhen expressinghis\herevaluationinformationbyutilizingasinglerealnumberinmulti-attributedecision making(MADM)ormulti-attributegroupdecisionmaking(MAGDM)problemsduetotheintellectual fuzzinessofDMs.Forthiscause,Zadeh[1]developedfuzzysets(FSs),whichareassignedbya Symmetry 2018, 10,459;doi:10.3390/sym10100459 www.mdpi.com/journal/symmetry

truth-membershipdegree(TMD)in [0,1] andareabettertooltopresentfuzzyinformationforhandling MADMorMAGDMproblems.AftertheintroductionofFSs,differentfuzzymodellingapproaches weredevelopedtodealwithuncertaintyinvariousfields[2–4].However,insomesituations,it isdifficulttoexpresstruth-membershipdegreewithanexactnumber.Inordertoovercomethis defectandtoexpressTMDinamoreappropriateway,Turksen[5]developedintervalvaluedFSs (IVFSs),inwhichTMDisrepresentedbyintervalnumbersinsteadofexactnumbers.SinceonlyTMD wasconsideredinFSsorIVFSsandthefalsity-membershipdegree(FMD)cameautomaticallyby subtractingTMDfromone,itishardtoexplainsomecomplicatedfuzzyinformation,forexample,for theselectionofDeanofafaculty,iftheresultsreceivedfromfiveprofessorsareinfavor,twoareagainst andthreeareneitherinfavornoragainst.Then,thistypeofinformationcannotbeexpressedbyFSs.So, inordertohandlesuchtypesofinformation,Atanassov[6]developedintuitionisticfuzzysets(IFSs), whichwereassignedbyTMDandFMD.Atanassovetal.[7]furtherenlargedIFSsanddeveloped theintervalvaluedIFS(IVIFSs).However,theshortcomingofFSs,IVFSs,IFSsandIVIFSsarethat theycannotdealwithunreliableorindefiniteinformation.Tosolvesuchproblems,Smarandache[8,9] developedneutrosophicsets(NSs).Inneutrosophicset,everymemberofthedomainsethasTMD, anindeterminacy-membershipdegree(IMD)andFMD,whichcapturevaluesin]0 ,1+[.Duetothe containmentofsubsetsof]0 ,1+[inNS,itishardtoutilizeNSinrealworldandengineeringproblems. TomakeNSshelpfulinthesecases,someauthorsdevelopedsubclassesofNSs,suchassinglevalued neutrosophicsets(SVNSs)[10],intervalneutrosophicsets(INSs)[11,12],simplifiedneutrosophicsets (SNSs)[13,14]andsoforth.Inrecentyears,INSshavegainedmuchattentionfromtheresearchers andagreatnumberofachievementhavebeenmade,suchasdistancemeasures[15–17],entropiesof INS[18–20],correlationcoefficient[21–23].ThetheoryofNSshasbeenextensivelyutilizedtohandle MADMandMAGDMproblems.

Forthelastmanyyears,informationaggregationoperators[24–27]havestimulatedmuch awarenessofauthorsandhavebecomeverydominantresearchtopicofMADMandMAGDM problems.Theconventionalaggregationoperators(AGOs)proposedbyXu,XuandYager[28,29]can onlyaggregateagroupofrealnumbersintoasinglerealnumber.NowtheseconventionalAGOswere furtherextendedbymanyauthors,forexample,Sunetal.[30]proposedtheintervalneutrosophic numberChoquetintegraloperatorforMADMandLiuetal.[31]developedprioritizedordered weightedAGOsforINSsandappliedthemtoMADM.Inaddition,somedecision-makingmethods werealsodevelopedforMADMproblems,forexample,Mukhametzyanovetal.[32]developeda statisticallybasedmodelforsensitivityanalysisinMADMproblems.Petrovicetal.[33]developed amodelfortheselectionofaircraftsbasedondecisionmakingtrialandevaluationlaboratoryand analytichierarchyprocess(DEMATEL-AHP).Royetal.[34]proposedaroughrelationalDEMATEL modeltoanalyzethekeysuccessfactorofhospitalquality.Sarkaretal.[35]developedanoptimization techniquefornationalincomedeterminationmodelwithstabilityanalysisofdifferentialequationin discreteandcontinuousprocessunderuncertainenvironment.Thesemethodscanonlygivearanking result,however,AGOscannotonlygivetherankingresult,butalsogivethecomprehensivevalueof eachalternativebyaggregatingitsattributevalues.

Itisobviousthat,differentaggregationoperatorshavedistinctfunctions,afewofthemcanreduce theimpactofsomeawkwarddataproducedbypredisposeDMs,suchaspoweraverage(PA)operator proposedbyYager[36].ThePAoperatorcanaggregatetheinputdatabydesignatingtheweight vectorbasedonthesupportdegreeamongtheinputarguments,andcanattainthisfunction.Nowthe PAoperatorwasfurtherextendedbymanyresearchersintodifferentenvironments.Liuetal.[37] proposedsomegeneralizedPAoperatorforINNs,andappliedthemtoMADM.Consequently,some aggregationoperatorscanincludetheinterrelationshipbetweentheaggregatingparameters,suchas theBonferronimean(BM)operatorsdevelopedbyBonferroni[38],theHeronianmean(HM)operator introducedbySykora[39],MuirheadMean(MM)operator[40],Maclaurinsymmetricmean[41] operators.Inaddition,theseaggregationoperatorshavealsobeenextendedbymanyauthorstodeal withfuzzyinformation[42–46].

ForaggregatingINNs,someAGOsaredevelopedbyutilizingdifferentT-norms(TNs)and T-conorms(TCNs),suchasalgebraic,EinsteinandHamacher.Usually,theArchimedeanTNandTCN arethegeneralizationsofvariousTNsandTCNssuchasalgebraic,Einstein,Hamacher,Frank,and Dombi[47]TNsandTCNs.DombiTNandTCNhavethecharacteristicsofgeneralTNandTCNbya generalparameter,andthiscanmaketheaggregationprocessmoreflexible.Recently,severalauthors definedsomeoperationallawsforIFSs[48],SVNSs[49],hesitantfuzzysets(HFSs)[50,51]basedon DombiTNandTCN.Inpracticaldecisionmaking,wegenerallyneedtoconsiderinterrelationship amongattributesandeliminatedtheinfluenceofawkwarddata.Forthispurpose,someresearchers combinedBMandPAoperatorstoproposesomePBMoperatorsandextendedthemtovarious fields[52–55].ThePBMoperatorshavetwocharacteristics.Firstly,itcanconsidertheinteraction amongtwoinputargumentsbyBMoperator,andsecondly,itcanremovetheeffectofawkwarddata byPAoperator.TheDombiTNandTCNhaveageneralparameter,whichmakesthedecision-making processmoreflexible.Fromtheexistingliteratures,weknowthatPBMoperatorsarecombinedwith algebraicoperationstoaggregateIFNs,orIVIFNs,andthereisnoresearchoncombiningPBMoperator withDombioperationstoaggregateINNs.

Inaword,byconsideringthefollowingadvantages.(1)SinceINSsarethemoreprécisedclassby whichonecanhandlethevagueinformationinamoreaccuratewaywhencomparedwithFSsandall otherextensionslikeIVFSs,IFSs,IVIFSsandsoforth,theyaremoresuitabletodescribetheattributes ofMADMproblems,sointhisstudy,wewillselecttheINSsasinformationexpression;(2)DombiTN andTCNaremoreflexibleinthedecisionmakingprocessduetogeneralparameterwhichisregarded asdecisionmakers’riskattitude;(3)ThePBMoperatorshavethepropertiesofconsideringinteraction betweentwoinputargumentsandvanishestheeffectofawkwarddataatthesametime.Hence,the purposeandmotivationarethatwetrytocombinethesethreeconceptstotaketheabovedefined advantagesandproposedsomenewpowerfultoolstoaggregateINNs.(1)wedefinesomeDombi operationallawsforINNs;(2)weproposesomenewPBMaggregationoperatorsbasedonthesenew operationallaws;(3)wedevelopanovelMADMbasedonthesedevelopedaggregationoperators.

Thefollowingsectionsofthisarticleareshownasfollows.InSection 2,wereviewsomebasic conceptsofINSs,PAoperators,BMoperators,andGBMoperators.InSection 3,wereviewbasic conceptofDombiTNandTCN.Afterthat,weproposesomeDombioperationsforINNs,anddiscuss someproperties.InSection 4,wedefineINDPBMoperator,INWDPBMoperator,INDPGBMoperator andINWDPGBMoperatoranddiscusstheirproperties.InSection 5,weproposeaMADMmethod basedontheproposedaggregationoperatorswithINNs.InSection 6,weuseanillustrativeexample toshowtheeffectivenessoftheproposedMADMmethod.TheconclusionisdiscussedinSection 7

2.Preliminaries

Inthispart,somebasicdefinitions,propertiesaboutINSs,BMoperatorsandPAoperators arediscussed.

inreallifeorengineeringproblem,Wangetal.[8]presentedasubclassofNSbychanging ]0 ,1+ [ to [0,1] andwasnamedSVNS,andisdefinedasfollow:

Definition2. Let Ω bethedomainset[10],withanon-specificmemberin Ω expressedby v ASVNS SV in Ω isexpressedby

SV = u, t SV v , i SV v , fSV v v ∈ Ω ,(2) where t SV v , i SV v and fSV v expresstheTMD,IMDandFMDoftheelement v ∈ Ω totheset SV respectively.Foreachpoint v ∈ Ω,wehave, t SV v , i SV v , fSV v , ∈ [0,1] and 0 ≤ t SV v + i SV v + fSV v ≤ 3.

Inordertodefinemorecomplexinformation,Wangetal.[9]furtherdevelopedINSwhichis defineasfollows: Definition3. Let Ω bethedomainsetand v ∈ Ω [11].ThenanINS INin Ω isexpressedby

IN = v, TRIN v , IDIN v , FLIN v v ∈ Ω ,(3) where, TRIN v , IDIN v and FLIN v respectively,expresstheTMD,IMDandFMDoftheelement v ∈ Ω totheset IN Foreachpoint v ∈ U,wehave, TRIN v , IDIN v , FLIN v ⊆ [0,1] and 0 ≤ maxIDIN v + maxIDIN v + maxFLIN v ≤ 3.

Forcomputationalsimplicity,wecanuse in = TR L , TR U , ID L , ID U , FL L , FL U to expressanelement in inanINS,andtheelement in iscalledanintervalneutrosophicnumber(INN). Where TR L , TR U ⊆ [0,1], ID L , ID U ⊆ [0,1], FL L , FL U ⊆ [0,1] and 0 ≤ TR U + ID U + FL U ≤ 3.

Definition4. Let in1 = TR L 1 , TR U 1 , ID L 1 , ID U 1 , FL L 1 , FL U 1 and in2 =

(ii) A in = TR L + TR U 2 + 1 ID L + ID U 2 + FL L + FL U 2 .(9)

InordertocomparetwoINNs,thecomparisonrulesweredefinedbyLiuetal.[36],whichcanbe statedasfollows.

Definition6. Let in1 = TR L 1 , TR U 1 , ID L 1 , ID U 1 , FL L 1 , FL U 1 and in2 = TR L 2 , TR U 2 , ID L 2 , ID U 2 , FL L 2 , FL U 2 beanytwoINNs[42].Thenwehave:

(1) IfS in1 > S in2 , then in1 isbetterthan in2,anddenotedby in1 > in2; (2) IfS in1 = S in2 , andA in1 > A in2 , then in1 isbetterthan in2,anddenotedby in1 > in2; (3) IfS in1 = S in2 , andA in1 = A in2 , then in1 isequalto in2,anddenotedby in1 = in2

Definition7. Let in1 = TR L 1 , TR U 1 , ID L 1 , ID U 1 , FL L 1 , FL U 1 and in2 = TR L 2 , TR U 2 , ID L 2 , ID U 2 , FL L 2 , FL U 2 beanytwoINNs[15].ThenthenormalizedHamming distancebetweenn1 andn2 isdescribedasfollows. D in1, in2 = 1 6 TR L 1 TR L 2 + TR U 1 TR U 2 + ID L 1 ID L 2 + ID U 1 ID U 2 + FL L 1 FL L 2 + FL U 1 FL U 2 (10)

2.2.ThePAOperator

ThePAoperatorwasfirstpresentedbyYager[36]anditisdescribedasfollows. Definition8. Forpositiverealnumbers ℘h (h = 1,2,..., l) [36],thePAoperatorisdescribedas PA(℘1, ℘2,..., ℘l ) =

l ∑ h=1 (1 + T(℘h ))℘h l ∑ h=1 (1 + T(℘h )) ,(11) where, T(℘h ) = l ∑ y=1,h=y sup ℘h, ℘y , and sup ℘h, ℘y isthedegreetowhich ℘h supports ℘y Thesupport degree(SPD)satisfiesthefollowingproperties. (1) sup ℘h, ℘y = sup ℘y, ℘h ; (2) sup ℘h, ℘y ∈ [0,1]; (3) sup ℘h, ℘y ≥ sup(℘c, ℘d ), if ℘h ℘y ≤ |℘c ℘d |

2.3.TheBMOperator

TheBMoperatorwasinitiallypresentedbyBonferroni[38],anditwasexplainedasfollows: Definition9. Fornon-negativerealnumbers ℘h (h = 1,2, , l),and x, y ≥ 0 [38],theBMoperatoris describedas BMx,y (℘1, ℘2,..., ℘l ) = 1 l2 l l ∑ h=1

l ∑ s=1,h=s ℘x h ℘y s

1 x+y .(12)

TheBMoperatorignorestheimportancedegreeofeachinputargument,whichcanbegivenby decisionmakersaccordingtotheirinterest.ToovercomethisshortcomingofBMoperator,Heetal.[52] definedtheweightedBonferronimean(WBM)operatorswhichcanbeexplainedasfollows:

Definition10. Forpositiverealnumbers ℘h (h = 1,2, , l) and x, y ≥ 0 [52],thentheweightedBMoperator (WBM)isdescribedas

WBMx,y (℘1, ℘2,..., ℘l ) = 1 l2 l l ∑ h=1

TheWBMoperatorhasthefollowingcharacteristics:

l ∑ s=1,h=s

κhκs 1 κh ℘x h ℘y s

1 x+y ,(13) where κ = (κ1, κ2,..., κl )T istheimportancedegreeofevery ℘h (h = 1,2,..., l)

Theorem1. (Reducibility)Iftheweightvectoris κ = 1 l , 1 l ,..., 1 l T ,then WBMx,y (℘1, ℘2,..., ℘l ) = 1 l2 l l ∑ h=1

l ∑ s=1,z=s ℘x h ℘y s

1 x+y = BMx,y (℘1, ℘2,..., ℘m ) (14)

Theorem2. (Idempotency)Let ℘h = ℘, (h = 1,2,..., l).ThenBMx,y (℘1, ℘2,..., ℘l ) = ℘

Theorem3. (Permutation)Let (℘1, ℘2,..., ℘l ) beanypermutationof Z1 , Z2 ,..., Zl .Then WMBx,y Z1 , Z2 ,..., Zl = WBM(℘1, ℘2,..., ℘l ).(15)

Theorem4. (Monotonicity)Let ℘h ≥ Kh (h = 1,2,..., l).Then WBMx,y (℘1, ℘2,..., ℘l ) ≥ WBMx,y K1 , K2 ,..., Kl .(16)

Theorem5. (Boundedness)TheWBMx,y liesintheminandmaxoperators,thatis, min(℘1, ℘2,..., ℘l ) ≤ WBMx,y (℘1, ℘2,..., ℘l ) ≤ max(℘1, ℘2,..., ℘l ).(17)

SimilartoBMoperator,thegeometricBMoperatoralsoconsidersthecorrelationamongtheinput arguments.Itcanbeexplainedasfollows:

Definition11. Forpositiverealnumbers ℘h (h = 1,2, , l) and x, y ≥ 0 [53],thegeometricBMoperator (GBM)isdescribedas GBMx,y (℘1, ℘2,..., ℘l ) = 1 x + y

l ∏ h=1

l ∏ s=1,h=s (x℘h + y℘s ) 1 l2 l .(18)

TheGBMoperatorignorestheimportancedegreeofeachinputargument,whichcanbegiven bydecisionmakersaccordingtotheirinterest.InasimilarwaytoWBM,theweightedgeometric

The GBM operator ignores the importance degree of each input argument, which can be given by decision makers according to their interest. In a similar way to WBM, the weighted geometric BM (WGBM) operator was also presented. The extension process is same as that of WBM, so it is omitted here. The definition of power Bonferroni mean (PBM) and power geometric Bonferroni mean (PGBM) operators are given in Appendix A.

1 ,,....,. ll xy ll lhs hshs GBMxy xy    

(1,2,...,) h hl ,0xy      2 1 , 12 11,

BM(WGBM)operatorwasalsopresented.TheextensionprocessissameasthatofWBM,soitis omittedhere.

3. Some Operations of INSs Based on Dombi TN and TCN

Dombi

TN and TCN

ThedefinitionofpowerBonferronimean(PBM)andpowergeometricBonferronimean(PGBM) operatorsaregiveninAppendix A.

3.SomeOperationsofINSsBasedonDombiTNandTCN

Dombi operations consist of the Dombi sum and Dombi product.

DombiTNandTCN

are explained as follows:

DombioperationsconsistoftheDombisumandDombiproduct.

be any two real numbers [47] Then the Dombi TN and TCN among 

(19)

T

and

Definition12. Let and ℵ beanytworealnumbers[47].ThentheDombiTNandTCNamong and ℵ are explainedasfollows: TD ( , ℵ)= 1 1 + 1− l + 1−ℵ ℵ l 1 l ;(19) TD ∗( , ℵ)= 1 1 1 + 1− l + ℵ 1−ℵ l 1 l ,(20) where,l ≥ 1, and ( , ℵ) ∈ [0,1] × [0,1] AccordingtotheDombiTNandTCN,wedevelopafewoperationalrulesforINNs. Definition13. Let in = TR L , TR U , ID L , ID U , FL L , FL U , in1 = TR L 1 , TR U 1 , ID L 1 , ID U 1 , FL L 1 , FL U 1 and in2 = TR L 2 , TR U 2 , ID L 2 , ID U 2 , FL L 2 , FL U 2 beanythreeINNsand Φ > 0.Then,basedonDombiTNandTCN,thefollowingoperationallawsaredeveloped forINNs.

(24) Now,basedonthesenewoperationallawsforINNs,wedevelopsomeaggregationoperatorsto aggregateINinformationintheprecedingsections. 4.TheINPBMOperatorBasedonDombiTNandDombiTCN

Inthispart,basedontheDombioperationallawsforINNs,wecombinePAoperatorandBM tointroduceintervalneutrosophicDombipowerBonferronimean(INDPBM),intervalneutrosophic weightedDombipowerBonferronimean,intervalneutrosophicDombipowergeometricBonferroni mean(INDPGBM)andintervalneutrosophicweightedDombipowerBonferronimean(INWDPGBM) operatorsanddiscusssomerelatedproperties.

4.1.TheINDPBMOperatorandINWDPBMOperator

(27)

a group of INNs. Then the value obtained



1 ,1  

 l U ij j ij U j

 

                                                                                 

(28) Proof. ProofofTheorem6isgiveninAppendix B

(28)

FL FL

Proof. Proof of Theorem 6 is given in Appendix B. □

In order to determine the PWV 

, we firstly need to determine the support degree among INNs. In general, the similarity measure among INNs can replace the support degree among INNs. That is,

InordertodeterminethePWV Λ,wefirstlyneedtodeterminethesupportdegreeamongINNs. Ingeneral,thesimilaritymeasureamongINNscanreplacethesupportdegreeamongINNs.Thatis, Sup ini, inm = 1 D ini, inm (i, m = 1,2,..., l).(29) Example1. Let in1 = [0.3,0.7], [0.2,0.4], [0.3,0.5] , in2 = [0.4,0.6], [0.1,0.3], [0.2,0.4] and in3 = [0.1,0.3], [0.4,0.6], [0.2,0.4] beanythreeINNs, x = 1, y = 1, γ = 3.ThenbyTheorem6 inEquation(28),wecanaggregatethesethreeINNsandgeneratethecomprehensivevalue in = TR L , TR U , ID L , ID U , FL L , FL U whichiscalculatedasfollows:

and

be any three INNs, 1,1,3xy  

           

which is calculated as follows: Step 1. Determine the supports

. Then by Theorem (6) in Equation (28), we can aggregate these three INNs and generate the comprehensive value ,,,,, LULULU inTRTRIDIDFLFL 



0.1,0.3,0.4,0.6,0.2,0.4 in

be any three INNs, 1,1,3xy 

Step1. Determinethesupports Sup ini, inj , i, j = 1,2,3 byusingEquation(29),andthen weget Sup in1, in2 = Sup in2, in1 = 0.9, Sup in1, in3 = Sup in3, in1 = 0.933, Sup in2, in3 = Sup in3, in2 = 1. Step2. DeterminethePWVBecauseT inz = 3 ∑ s=1,s=z Sup inz, ins , and

. Then by Theorem (6) in Equation (28), we can aggregate these three INNs and generate the comprehensive value ,,,,,

        

 

by using Equation (29), and then we get

 

0.2,0.4

TinSupinin

    3

123 1 0.3269, 111 Tin TinTinTin

0.3346, 111 Tin TinTinTin

then Λ1 = T in1 + 1 T in1 + 1 + T in2 + 1 + T in3 + 1 = 0.3269, Λ2 = T in2 + 1 T in1 + 1 + T in2 + 1 + T in3 + 1 = 0.3346, Λ3 = T in3 + 1 T in1 + 1 + T in2 + 1 + T in3 + 1 = 0.3385. Step3. Determinethecomprehensivevalue in = TR L , TR U , ID L , ID U , FL L , FL U byusing Equation(28),wehave

Similarly, we can get

Proof. ProofofTheorem7isgiveninAppendix C.

  , be a group of INNs, if all   1,2,..., i inil  are equal, that is

  , 12,,...,. xy l INDPBMinininin  (30) Proof. Proof of Theorem 7 is given in Appendix C □ Theorem 8. (Commutativity) Assume that u in is any permutation of   1,2,...,, u inul  then

1 x+y , and INDPBMx,y in1, in2,..., inl =

 ,, 1212 ,,...,,,...,. xyxy ll INDPBMinininINDPBMininin   (31) Proof. From Definition (14), we have       1 12 2 ,1 1 ,,...,, xy l xy xy eij iDj ij ij INDPBMinininlinlin ll          

     

and

lΛiini x ⊗D lΛjinj y 

     

1 x+y Because, l ∑ i, j = 1 i = j

      1 , 12 2 ,1 1 ,,...,. xy l xy xy lij iDj ij ij

lΛ iin i x ⊗D lΛ jin j y = l ∑ i, j = 1 i = j

,, 1212 ,,...,,,..., xyxy ll INDPBMinininINDPBMininin

         Because,         ,1,1 llxyxy ijij iDjiDj ijij ijij linlinlinlin    , hence,

Now,weshallstudyafewspecialcasesofthe INDPBMx,y withrespectto x and y. (1)When y → 0, γ > 0,thenwecanget Symmetry 2018, 10, x 11 of 32 Theorem 7. (Idempotency) Let ,,,,,(1,2,...,) LULULL iiiiii i inTRTRIDIDFLFLil 

            . Then   12,,...,. l inINDPBMinininin   (32) Proof. Proof of Theorem 9 is given in Appendix D □ Now, we shall study a few special cases of the , xy INDPBM with respect to x and y (1) When 0,0, y   then we can get   ,0 12,,...., x lINDPBMininin

be a group of INNs, and

(37)

Proof. Proof of Theorem 10 is similar to Theorem 6. □

Similar to the INDPBM operator, the INWDPBM operator has the properties of boundedness, idempotency and commutativity.

4.2 The INDPGBM Operator and INWDPGBM Operator

In this subpart, we develop INDPGBM and INWDPGBM operators. Definition 16. Let ,,,,,,(1,2,...,) LULULL iiiiii i inTRTRIDIDFLFLil 

bea group of INNs. Then theINDPGBM operator is defined as

l(T(ini )+1) l ∑ z=1 (T(inz )+1) i + yin

l(T(ini )+1) l ∑ z=1 (T(inz )+1) j



 (38) Then, , xy INDPGBM is said to be an interval neutrosophic Dombi power geometric Bonferroni mean (INDPGBM) operator. Where     1, ,, l zzs ssz TinSupinin 

            



  

InordertosimplifyEquation(38),wecandescribe Λz = 1 + T inz l ∑ z=1 1 + T inz

    , zsSupinin isthesupport degreefor z n from , s n which satisfies the following axioms: (1)    ,0,1zsSupinin  ; (2)     ,,; zssz SupininSupinin  (3)     ,, zsab SupininSupinin  , if     ,, zsab DininDinin  , in which   , abDnn is the distance measure between INNs ain and bin defined in Definition (7). In order to simplify Equation (38), we can describe         1

z z l z z

1 , 1

,(39) andcall Λ = (Λ1, Λ2,..., Λl )T isthepowerweightvector(PWV),suchthat Λz ≥ 0, l ∑ z=1 Λz = 1. ThenEquation(38)canbewrittenasfollows:

    (39) and call   12,,..., T l is the power weight vector (PWV), such that 1 0,1. l zz z

Tin Tin

  Then Equation (38) can be written as follows:

(41)









 1 2

l U ij ij j j U j

y TR l TR

, 1

                                                                                       

then

Symmetry 2018, 10,459

Theorem14. (Boundedness)Let ini = TR L i , TR U i , ID L i , ID U i , FL L i , FL L i , (i = 1,2, , l) beagroupofINNs,and in + = l max i=1 TR L i , TR U i , l min i=1 ID L i , ID U i , l min i=1 FL L i , FL U i , in = l min i=1 TR L i , TR U i , l max i=1 ID L i , ID U i , l max i=1 FL L i , FL U i , then in ≤ INDPGBM in1, in2,..., inl ≤ in + .(44) Definition17. Let ini = TR L i , TR U i , ID L i , ID U i , FL L i , FL L i , (i = 1,2, , l) beagroupofINNs, thentheINWDPGBMoperatorisdefinedas INWDPGBM

Theorem15. Let ini = TR L i , TR U i ,

(45)

5. MADM Approach Based on the Developed Aggregation Operator

In this section, based upon the developed INWDPBM and INWDPGBM operators, we will propose a novel MADM method, which is defined as follows. Assume that in a MADM problem, we need to evaluate

alternatives

with respect to

attributes

and the importance degree of the attributes is represented by

isrepresentedby = ( 1, 2,..., v )T ,satisfyingthecondition h ∈ [0,1], v ∑ h=1 h = 1

Thedecisionmatrixforthisdecisionproblemisdenotedby D = dgh m×n ,where dgh = TR L gh, TR U gh , ID L gh, ID U gh , FL L gh FL U gh isanINNforthealternative Mg withrespecttothe

attribute Ch, (g = 1,2,..., u; h = 1,2,..., v) Thenthemainpurposeistorankthealternativeand selectthebestalternative.

Inthefollowing,wewillusetheproposedINWDPBMandINWDPGBMoperatorstosolvethis MADMproblem,andthedetaileddecisionstepsareshownasfollows:

Step1. Standardizetheattributevalues.Normally,inrealproblems,theattributesareoftwotypes, (1)costtype,(2)benefittype.Togetrightresult,itisnecessarytochangecosttypeofattribute valuestobenefittypeusingthefollowingformula:

dgh = FL L gh, FL U gh , 1 ID U gh,1 ID L gh , TR L gh, TR U gh .(47)

Step2. Calculatethesupports

Supp dgh, dgl = 1 D dgh, dgl , (g = 1,2,..., u; h, l = 1,2,..., v),(48) where, D dgh, dgl isthedistancemeasuredefinedinEquation(10).

Step3. Calculate T dgh

T dgh = u ∑ l = 1 l = h

Supp dgh, dgl , (g = 1,2,..., u; h, l = 1,2,..., v).(49)

Step4. Aggregatealltheattributevalues dgh (h = 1,2, , v) tothecomprehensivevalue Rg by usingINWDPBMorINWDPGBMoperatorsshownasfollows.

Rg = INWDPBM dg1, dg2,..., dgv ;(50) or Rg = INWDPGBM dg1, dg2,..., dgv .(51)

Step5. Determinethescorevalues,accuracyvaluesof Rg (g = 1,2,..., u),usingDefinition5.

Step6. Rankallthealternativesaccordingtotheirscoreandaccuracyvalues,andselectthebest alternativeusingDefinition6.

Step7. End.

ThisdecisionstepsarealsodescribedinFigure 1

Step 5. Determine the score values, accuracy values of using Definition (5).

Step 6. Rank all the alternatives according to their score and accuracy values, and select the best alternative using Definition (6). Step 7. End. This decision steps are also described in Figure 1 Figure 1. Flow chart for developed approach. Figure1. Flowchartfordevelopedapproach.

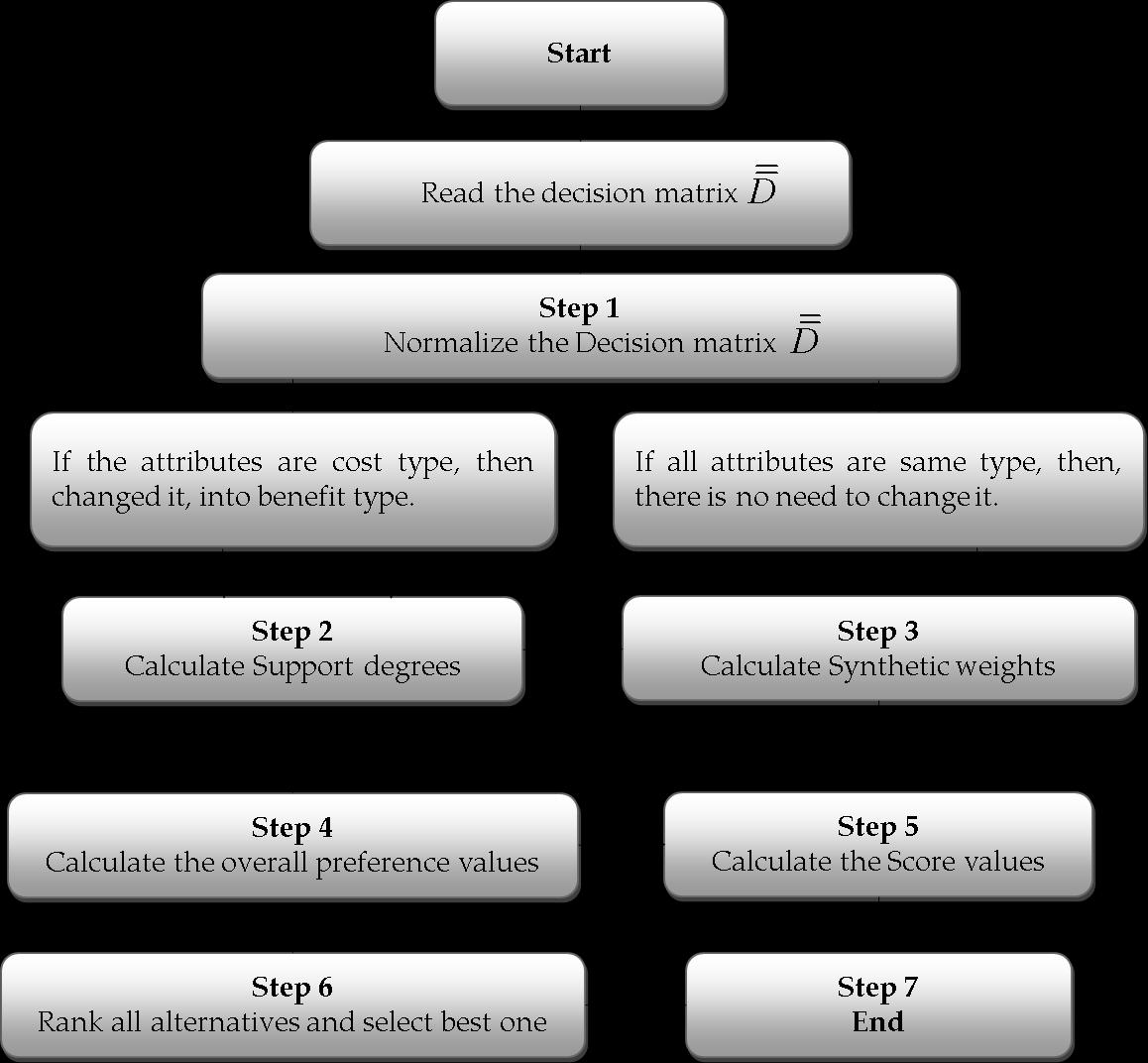
6.IllustrativeExample

Inthispart,anexampleadaptedfrom[42]isusedtoillustratetheapplicationandeffectivenessof thedevelopedmethodinMADMproblem.

Aninvestmentcompanywantstoinvestasumofmoneyinthebestoption.Thecompany mustinvestasumofmoneyinthefollowingfourpossiblecompanies(alternatives):(1)carcompany M1;(2)foodcompany M2;(3)Computercompany M3;(4)Anarmcompany M4,andtheattributes underconsiderationare(1)riskanalysis C1;(2)growthanalysis C2;(3)environmentalimpactanalysis C3.Theimportancedegreeoftheattributesis = (0.35,0.4,0.25)T .Thefourpossiblealternatives Mg (g = 1,2,3,4) areevaluatedwithrespecttotheaboveattributes Ch (h = 1,2,3) bytheformofINN, andtheINdecisionmatrix D islistedinTable 1.Thepurposeofthisdecision-makingproblemisto rankthealternatives.

Table1. TheINdecisionmatrix D.

Alternatives/Attributes C1 C2 C3

M1 [0.4,0.5], [0.2,0.3], [0.3,0.4] [0.4,0.6], [0.1,0.3], [0.2,0.4] [0.7,0.9], [0.7,0.8], [0.4,0.5] M2 [0.6,0.8], [0.1,0.2], [0.1,0.2] [0.6,0.7], [0.15,0.25], [0.2,0.3] [0.3,0.6], [0.2,0.3], [0.8,0.9] M3 [0.3,0.6], [0.2,0.3], [0.3,0.4] [0.5,0.6], [0.2,0.3], [0.3,0.4] [0.4,0.5], [0.2,0.4], [0.7,0.9] M4 [0.7,0.8], [0.01,0.1], [0.2,0.3] [0.6,0.7], [0.1,0.2], [0.3,0.4] [0.4,0.6], [0.5,0.6], [0.8,0.9]

6.1.TheDecision-MakingSteps

Step1. Since C1, C2 areofbenefittype,and C3 isofcosttype.So, C3 willbechangedintobenefit typeusingEquation(47).So,thenormalizedecisionmatrix D isgiveninTable 2

6.1 The Decision-Making

Steps

Alternatives/Attributes

Step 1. Since 1C

Table2. TheNormalizeINdecisionmatrix D.

is given in Table 2.

2 M 3 M 4 M 1C 2C 3C  0.35,0.4,0.25 T   (1,2,3,4) g Mg   1,2,3 h Ch 

Alternatives/Attributes C1 C2 C3

M1 [0.4,0.5], [0.2,0.3], [0.3,0.4] [0.4,0.6], [0.1,0.3], [0.2,0.4] [0.4,0.5], [0.2,0.3], [0.7,0.9] M2 [0.6,0.8], [0.1,0.2], [0.1,0.2] [0.6,0.7], [0.15,0.25], [0.2,0.3] [0.8,0.9], [0.6,0.7], [0.3,0.6] M3 [0.3,0.6], [0.2,0.3], [0.3,0.4] [0.5,0.6], [0.2,0.3], [0.3,0.4] [0.7,0.9], [0.6,0.8], [0.4,0.5] M4 [0.7,0.8], [0.01,0.1], [0.2,0.3] [0.6,0.7], [0.1,0.2], [0.3,0.4] [0.8,0.9], [0.4,0.5], [0.4,0.6]

D D

Step2. Determinethesupports Supp dgh, dgl , (g = 1,2,3,4; h, l = 1,2,3) byEquation(48)(for simplicitywedenote Supp dgh, dgl with Sg gh,gl ),wehave

, 2C

are of benefit type, and 3C

C1 C2 C3

1M      0.4,0.5,0.2,0.3,0.3,0.4      0.4,0.6,0.1,0.3,0.2,0.4      0.7,0.9,0.7,0.8,0.4,0.5

2 M      0.6,0.8,0.1,0.2,0.1,0.2      0.6,0.7,0.15,0.25,0.2,0.3      0.3,0.6,0.2,0.3,0.8,0.9

is of cost type. So, 3C

will be changed into benefit type using Equation (47). So, the normalize decision matrix D

3 M      0.3,0.6,0.2,0.3,0.3,0.4      0.5,0.6,0.2,0.3,0.3,0.4      0.4,0.5,0.2,0.4,0.7,0.9

4 M      0.7,0.8,0.01,0.1,0.2,0.3      0.6,0.7,0.1,0.2,0.3,0.4      0.4,0.6,0.5,0.6,0.8,0.9

Step3. Determine T dgh ; (g = 1,2,3,4; h = 1,2,3) byEquation(49),andweget

Table 2. The Normalize IN decision matrix D

Step 4. (a) Determine the comprehensive value of every alternative using the INWDPBM operator, that is, Equation (50)

R1 = [0.3974,0.5195], [0.1823,0.3023], [0.3353,0.4796] ; R2 = [0.6457,0.7954], [0.1700,0.2885], [0.2044,0.3265] ;

C1 C2 C3

1M      0.4,0.5,0.2,0.3,0.3,0.4      0.4,0.6,0.1,0.3,0.2,0.4      0.4,0.5,0.2,0.3,0.7,0.9

R3 = [0.4846,0.6503], [0.2556,0.3711], [0.3376,0.4394] ;

by Equation (48) (for simplicity we denote   , ghglSuppdd

with , g ghglS

2 M      0.6,0.8,0.1,0.2,0.1,0.2      0.6,0.7,0.15,0.25,0.2,0.3      0.8,0.9,0.6,0.7,0.3,0.6 3 M      0.3,0.6,0.2,0.3,0.3,0.4      0.5,0.6,0.2,0.3,0.3,0.4      0.7,0.9,0.6,0.8,0.4,0.5 4 M      0.7,0.8,0.01,0.1,0.2,0.3      0.6,0.7,0.1,0.2,0.3,0.4      0.8,0.9,0.4,0.5,0.4,0.6

), we have 111111222222 11,1212,1112,1313,1211,1313,1111,1212,11 333333 11,1212,1112,1313,1211,1313,1111 



0.950;0.800;0.85;0.933;0.717;0.683; 0.967;0.733;0.700; SSSSSSSSSSSS SSSSSSS

R4 = [0.6938,0.7953], [0.1062,0.2154], [0.3069,0.4278]

(b) DeterminethecomprehensivevalueofeveryalternativeusingtheINWDPGBM operator,thatisEquation(51), (Assumethatx = y = 1; γ = 3),wehave

by Equation (49), and we get 111222 111213111213 333444 111213111213





R1 = [0.4026,0.5381], [0.1570,0.2977], [0.2998,0.4520] ;

R2 = [0.6654,0.8193], [0.1558,0.2686], [0.1836,0.3035] ;

R3 = [0.5159,0.6732], [0.2366,0.3473], [0.3265,0.4279] ; R4 = [0.5159,0.8193], [0.0938,0.1952], [0.2862,0.4037]

Step5. (a) Determinethescorevaluesof Rg (g = 1,2,3,4) byDefinition5,wehave

1;3 Assumethatxy 

S(R1)= 1.8087, S(R2)= 2.2259, S(R3)= 1.8656, S(R4)= 2.2164;

(b) Determinethescorevaluesof Rg (g = 1,2,3,4) byDefinition5,wehave

1 0.3974,0.5195,0.1823,0.3023,0.3353,0.4796; R

S(R1)= 1.8671, S(R2)= 2.2866, S(R3)= 1.9254, S(R4)= 2.1781;

Step6. (a) Accordingtotheirscoreandaccuracyvalues,byusingDefinition6,therankingorder is M2 > M4 > M3 > M1. Sothebestalternativeis M2, whiletheworstalternative is M1.

(b) Accordingtotheirscoreandaccuracyvalues,byusingDefinition6,therankingorder is M2 > M4 > M3 > M1. Sothebestalternativeis M2, whiletheworstalternative is M1.

So,byusingINWDPBMorINWDPGBMoperators,thebestalternativeis M2, whiletheworst alternativeis M1.

6.2.EffectofParameters γ,xandyonRankingResultofthisExample

Inordertoshowtheeffectoftheparameters x and y ontherankingresultofthisexample,weset differentparametervaluesfor x and y,and γ = 3 isfixed,toshowtherankingresultsofthisexample. TherankingresultsaregiveninTable 3.

AsweknowfromTables 3 and 4,thescorevaluesandrankingorderaredifferentfordifferent valuesoftheparameters x and y,whenweuseINWDPBMoperatorandINWDPGBMoperator. WecanseefromTables 3 and 4,whentheparametervalues x =1or0and y =0or1,thebestchoiceis M4 andtheworstoneis M1. Insimplewords,whentheinterrelationshipamongattributesarenot considered,thebestchoiceis M4 andtheworstoneis M1. Ontheotherhand,whendifferentvalues fortheparameters x and y areutilized,forINWPBMandINWDPGBMoperators,therankingresultis changed.Thatis,fromTable 4,wecanseethatwhentheparametervalues x = 1, y = 1,theranking resultsarechangedastheoneobtainedfor x =1or0and y =0or1.Inthiscasethebestalternativeis M2 whiletheworstalternativeremainsthesame.

Table3. Rankingordersofdecisionresultusingdifferentvaluesfor x and y forINWDPBM.

ParameterValuesINWDPBMOperatorRankingOrders

x = 1, y = 0, γ = 3

x = 1, y = 5, γ = 3

S(R1)= 1.9319, S(R2)= 2.4172, S(R3)= 2.0936, S(R4)= 2.4222; M4 > M2 > M3 > M1

S(R1)= 1.8338, S(R2)= 2.2684, S(R3)= 1.9049, S(R4)= 2.2666; M2 > M4 > M3 > M1

x = 3, y = 7, γ = 3 S(R1)= 1.8169, S(R2)= 2.2398, S(R3)= 1.8777, S(R4)= 2.2327; M2 > M4 > M3 > M1

x = 5, y = 10, γ = 3 S(R1)= 1.8143, S(R2)= 2.2354, S(R3)= 1.8738, S(R4)= 2.2275; M4 > M2 > M3 > M1 x = 1, y = 10, γ = 3 S(R1)= 1.8501, S(R2)= 2.2966, S(R3)= 1.9355, S(R4)= 2.3012; M4 > M2 > M3 > M1

x = 10, y = 4, γ = 3 S(R1)= 1.8182, S(R2)= 2.2419, S(R3)= 1.8796, S(R4)= 2.2352; M4 > M2 > M3 > M1

x = 3, y = 12, γ = 3 S(R1)= 1.8285, S(R2)= 2.2592, S(R3)= 1.8958, S(R4)= 2.2557; M2 > M4 > M3 > M1

Table4. Rankingordersofdecisionresultusingdifferentvaluesfor x and y forINWDPGBM.

ParameterValuesINWDPGBMOperatorRankingOrders

x = 1, y = 0, γ = 3

S(R1)= 1.5032, S(R2)= 1.7934, S(R3)= 1.5136, S(R4)= 1.8037; M4 > M2 > M3 > M1

x = 1, y = 5, γ = 3 S(R1)= 1.8220, S(R2)= 2.2256, S(R3)= 1.8717, S(R4)= 2.1140; M2 > M4 > M3 > M1

x = 3, y = 7, γ = 3 S(R1)= 1.8539, S(R2)= 2.2686, S(R3)= 1.9094, S(R4)= 2.1584; M2 > M4 > M3 > M1

x = 5, y = 10, γ = 3 S(R1)= 1.8583, S(R2)= 2.2745, S(R3)= 1.9146, S(R4)= 2.1647; M2 > M4 > M3 > M1

x = 1, y = 10, γ = 3 S(R1)= 1.7814, S(R2)= 2.1710, S(R3)= 1.8248, S(R4)= 2.0632; M2 > M4 > M3 > M1

x = 10, y = 4, γ = 3

x = 3, y = 12, γ = 3

S(R1)= 1.8087, S(R2)= 2.2259, S(R3)= 1.8656, S(R4)= 2.2164; M2 > M4 > M3 > M1

S(R1)= 1.8671, S(R2)= 2.2866, S(R3)= 1.9254, S(R4)= 2.1781; M4 > M2 > M3 > M1

FromTables 3 and 4,wecanobservethatwhenthevaluesoftheparameterincrease,thescore valuesobtainedusingINWDPBMdecrease.WhileusingtheINWDPGBMoperator,thescorevalues increasebutthebestchoiceis M2 for x = y ≥ 1.

FromTable 5,wecanseethatdifferentrankingordersareobtainedfordifferentvaluesof γ.When γ = 0.5 and γ = 2,thebestchoiceis M4 bytheINWPBMoperator;whenweusetheINWPGBM operator,itis M2.Similarly,forothervaluesof γ > 2,thebestchoiceis M2 whiletheworstis M1

Table5. Rankingordersofdecisionresultusingdifferentvaluesfor γ

ParameterValuesINWDPBMOperatorINWDPGBMOperatorRankingOrders

x = 1, y = 1, γ = 0.5

x = 1, y = 1, γ = 2

x = 1, y = 1, γ = 4

x = 1, y = 1, γ = 7

x = 1, y = 1, γ = 10

x = 1, y = 1, γ = 15

x = 1, y = 1, γ = 20

S(R1)= 1.6662, S(R2)= 2.1025, S(R3)= 1.7606, S(R4)= 2.1972;

S(R1)= 1.7783, S(R2)= 2.2015, S(R3)= 1.8408, S(R4)= 2.2091;

S(R1)= 1.8229, S(R2)= 2.2363, S(R3)= 1.8803, S(R4)= 2.2219;

S(R1)= 1.8375, S(R2)= 2.2455, S(R3)= 1.9037, S(R4)= 2.2315;

S(R1)= 1.8418, S(R2)= 2.2477, S(R3)= 1.9160, S(R4)= 2.2365;

S(R1)= 1.8447, S(R2)= 2.2488, S(R3)= 1.9270, S(R4)= 2.2409;

S(R1)= 1.8460, S(R2)= 2.2492, S(R3)= 1.9328, S(R4)= 2.2432;

6.3.ComparingwiththeOtherMethods

S(R1)= 1.7870, S(R2)= 2.2347, S(R3)= 1.9103, S(R4)= 2.1812; M4 > M2 > M3 > M1 M2 > M4 > M3 > M1

S(R1)= 1.8491, S(R2)= 2.2786, S(R3)= 1.9213, S(R4)= 2.1799; M4 > M2 > M3 > M1 M2 > M4 > M3 > M1

S(R1)= 1.8740, S(R2)= 2.2856, S(R3)= 1.9275, S(R4)= 2.1751; M2 > M4 > M3 > M1 M2 > M4 > M3 > M1

S(R1)= 1.8747, S(R2)= 2.2763, S(R3)= 1.9331, S(R4)= 2.1669; M2 > M4 > M3 > M1 M2 > M4 > M3 > M1

S(R1)= 1.8701, S(R2)= 2.2698, S(R3)= 1.9373, S(R4)= 2.1622; M2 > M4 > M3 > M1 M2 > M4 > M3 > M1

S(R1)= 1.8642, S(R2)= 2.2637, S(R3)= 1.9414, S(R4)= 2.1582; M2 > M4 > M3 > M1 M2 > M4 > M3 > M1

S(R1)= 1.8608, S(R2)= 2.2604, S(R3)= 1.9435, S(R4)= 2.1562; M2 > M4 > M3 > M1 M2 > M4 > M3 > M1

Toillustratetheadvantagesandeffectivenessofthedevelopedmethodinthisarticle,wesolve theaboveexamplebyfourexistingMADMmethods,includingINweightedaveragingoperator,IN weightedgeometricoperator[12],thesimilaritymeasuredefinedbyYe[15],Muirheadmeanoperators developedbyLiuetal.[42],INpoweraggregationoperatordevelopedbyLiuetal.[37].

FromTable 6,wecanseethattherankingordersarethesameastheonesproducedbytheexisting aggregationoperatorswhentheparametervalues x = 1, y = 0, γ = 3,buttherankingordersare differentwhentheinterrelationshipamongattributesareconsidered.Thatiswhythedeveloped methodbasedontheproposedaggregationoperatorsismoreflexibleduetheparameterandpractical asitcanconsidertheinterrelationshipamonginputarguments.

Table6. Rankingorderofthealternativesusingdifferentaggregationoperators.

AggregationOperatorParameterScoreValuesRankingOrder

INWAoperator[12]No

S(R1)= 1.8430, S(R2)= 2.2497, S(R3)= 1.9151, S(R4)= 2.2788; M4 > M2 > M3 > M1

INWGAoperator[12]No S(R1)= 1.7286, S(R2)= 2.0991, S(R3)= 1.7751, S(R4)= 2.1608; M4 > M2 > M3 > M1

Similaritymeasure Hammingdistance[15] No D1(R∗ , R1)= 0.7948, D1(R∗ , R2)= 0.9581, D1(R∗ , R3)= 0.8805, D1(R∗ , R4)= 0.9725; M4 > M2 > M3 > M1

Generalizedpower Aggregationoperator[37] Yes λ = 1 S(R1)= 1.8460, S(R2)= 2.2543, S(R3)= 1.9163,S(R4)= 2.2799; M4 > M2 > M3 > M1

INWMMoperator[42] Yes P(1,1,1) S(R1)= 1.8054, S(R2)= 2.2321, S(R3)= 1.9172,S(R4)= 2.2773; M4 > M2 > M3 > M1

INWDMMoperator[42] Yes P(1,1,1) S(R1)= 1.6260, S(R2)= 1.9202, S(R3)= 1.7061,S(R4)= 2.0798; M4 > M2 > M3 > M1

ProposedINWDPBM

x = 1, y = 0, γ = 3 Yes S(R1)= 1.9319, S(R2)= 2.4172, S(R3)= 2.0936, S(R4)= 2.4222; M4 > M2 > M3 > M1 ProposedINWDPGBM

x = 1, y = 0, γ = 3 Yes S(R1)= 1.5032, S(R2)= 1.7934, S(R3)= 1.5136, S(R4)= 1.8037; M4 > M2 > M3 > M1

INWDPBMoperatorinthis article Yes x = y = 1, γ = 3

S(R1)= 1.8087, S(R2)= 2.2259, S(R3)= 1.8656, S(R4)= 2.2164; M2 > M4 > M3 > M1

INWDPBMoperatorinthis article Yes x = y = 1, γ = 3 S(R1)= 1.8671, S(R2)= 2.2866, S(R3)= 1.9254, S(R4)= 2.1781; M2 > M4 > M3 > M1

Fromtheabovecomparativeanalysis,wecanknowtheproposedmethodhasthefollowing advantages,thatis,itcanconsidertheinterrelationshipamongtheinputargumentsandcanrelieve theeffectoftheawkwarddatabyPWVatthesametime,anditcanpermitmorepreciserankingorder thantheexistingmethods.TheproposedmethodcantaketheadvantagesofPAoperatorandBM operatorconcurrently,thesefactorsmakesitalittlecomplexincalculations.

ThescorevaluesandrankingordersbythesemethodsareshowninTable 6

7.Conclusions

ThePBMoperatorcantaketheadvantageofPAoperator,whichcaneliminatetheimpactof awkwarddatagivenbythepredisposedDMs,andBMoperator,whichcanconsiderthecorrelation betweentwoattributes.TheDombioperationsofTNandTCNproposedbyDombihavetheedge ofgoodflexibilitywithgeneralparameter.Inthisarticle,wecombinedPBMwithDombioperation andproposedsomeaggregationoperatorstoaggregateINNs.Firstly,wedefinedsomeoperational lawsforINSsbasedonDombiTNandTCNanddiscussedsomepropertiesoftheseoperations. Secondly,weextendedPBMoperatorbasedonDombioperationstointroduceINDPBMoperator, INWDPBMoperator,INDPGBMoperator,INWDPGBMoperatoranddiscussedsomepropertiesof theseaggregationoperators.Thedevelopedaggregationoperatorshavetheedgethattheycantake thecorrelationamongtheattributesbyBMoperator,andcanalsoremovetheeffectofawkwarddata byPAoperatoratthesameandduetogeneralparameter,sotheyaremoreflexibleintheaggregation process.Further,wedevelopedanovelMADMmethodbasedondevelopedaggregationoperators todealwithintervalneutrosophicinformation.Finally,anillustrativeexampleisusedtoshowthe effectivenessandpracticalityoftheproposedMADMmethodandcomparisonweremadewiththe existingmethods.TheproposedaggregationoperatorsareveryusefultosolveMADMproblems.

Infutureresearch,weshalldefinesomedistinctaggregationoperatorsforSVHFSs,INHFSs, doublevaluedneutrosophicsetsandsoonbasedonDombioperationsandapplythemtoMAGDM andMADM.

AuthorContributions: Q.K.andP.L.visualizedandworktogethertoachievethiswork.Q.K.andP.L.wrotethe paper.T.M.,F.S.andK.U.offeredplentyofadviceenhancingthereadabilityofwork.Allauthorsapprovedthe publicationwork.

Funding: NationalNaturalScienceFoundationofChina:71771140,71471172,SpecialFundsofTaishanScholars ProjectofShandongProvince:ts201511045.

Acknowledgments: We,theauthorsofthisprojectaredeeplygratefulforthevaluablesuggestionsandcomments providedbytherespectedreviewerstoimprovethequalityandvalueofthisresearch.

Nopotentialconflictofinterestwasreportedbyauthors.

ThereforeaccordingtotheDefinition6,wehave in ≤ INDPBM in1, in2,..., inl

Inasimilarway,theotherpartcanbeproved.Thatis in ≤ INDPBM in1, in2,..., inm ≤ in + .Hence in ≤ INDPBM in1, in2,..., inm ≤ in + References

1. Zadeh,L.A.Fuzzysets. Inf.Control 1965, 8,338–353.[CrossRef] 2. Medina,J.;Ojeda-Aciego,M.Multi-adjointt-conceptlattices. Inf.Sci. 2010, 180,712–725.[CrossRef] 3. Pozna,C.;Minculete,N.;Precup,R.E.;Kóczy,L.T.;Ballagi,A.Signatures:Definitions,operatorsand applicationstofuzzymodelling. FuzzySetsSyst. 2012, 201,86–104.[CrossRef]

4. Kumar,A.;Kumar,D.;Jarial,S.K.Ahybridclusteringmethodbasedonimprovedartificialbeecolonyand fuzzyC-Meansalgorithm. Int.J.Artif.Intell. 2017, 15,24–44.

5. Turksen,I.B.Intervalvaluedfuzzysetsbasedonnormalforms. FuzzySetsSyst. 1986, 20,191–210.[CrossRef]

Therefore according to the Definition (6), we have   12,,...,. linINDPBMininin 

6. Atanassov,K.T.Intuitionisticfuzzysets. FuzzySetsSyst. 1986, 20,87–96.[CrossRef]

7. Atanassov,K.;Gargov,G.Intervalvaluedintuitionisticfuzzysets. FuzzySetsSyst. 1989, 31,343–349. [CrossRef]

8.

Smarandache,F.NeutrosophicProbability,Set,andLogic.In Neutrosophy;AmericanResearchPress: Rehoboth,IL,USA,1998.

9. Smarandache,F.Neutrosophicset—Ageneralizationoftheintuitionisticfuzzyset. Int.J.PureAppl.Math. 2010, 1,107–116.

10. Wang,H.;Smarandache,F.;Zhang,Y.;Sunderraman,R.Singlevaluedneutrosophicsets.InProceedingsof the8thjointconferenceoninformationSciences,SaltLakeCity,UT,USA,21–26July2005;pp.94–97.

11. Wang,H.;Smarandache,F.;Sunderraman,R.;Zhang,Y.Q. IntervalNeutrosophicSetsandLogic:Theoryand ApplicationinComputing;Hexis:Phoenix,AZ,USA,2005.

12. Zhang,H.Y.;Wang,J.Q.;Chen,X.H.Intervalneutrosophicsetsandtheirapplicationinmulti-criteriadecision makingproblems. Sci.WorldJ. 2014, 2014,645953.[CrossRef]

13. Ye,J.Amulti-criteriadecision-makingmethodusingaggregationoperatorsforsimplifiedneutrosophicsets. J.Intell.FuzzySyst. 2014, 26,2459–2466.[CrossRef]

14. Peng,J.J.;Wang,J.Q.;Wang,J.;Zhang,H.Y.;Chen,X.H.Simplifiedneutrosophicsetsandtheirapplications inmulti-criteriagroupdecision-makingproblems. Int.J.Syst.Sci. 2016, 47,2342–2358.[CrossRef]

15. Ye,J.Similaritymeasuresbetweenintervalneutrosophicsetsandtheirapplicationsinmulticriteria decision-making. J.Intell.FuzzySyst. 2014, 26,165–172.[CrossRef]

16. Broumi,S.;Smarandache,F.Newdistanceandsimilaritymeasuresofintervalneutrosophicsets. InProceedingsofthe17thInternationalConferenceonInformationFusion(FUSION),Salamanca,Spain, 7–10July2014;pp.1–7.

17. Broumi,S.;Smarandache,F.Cosinesimilaritymeasureofintervalvaluedneutrosophicsets. Neutrosophic SetsSyst. 2014, 5,15–20.

18. Ye,J.;Shigui,D.Somedistances,similarityandentropymeasuresforinterval-valuedneutrosophicsetsand theirrelationship. Int.J.Mach.Learn.Cybern. 2017,1–9.[CrossRef]

19. Majumdar,P.;Samanta,S.K.Onsimilarityandentropyofneutrosophicsets. J.Intell.FuzzySyst. 2014, 26, 1245–1252.[CrossRef]

20. Tian,Z.P.;Zhang,H.Y.;Wang,J.;Wang,J.Q.;Chen,X.H.Multi-criteriadecision-makingmethodbasedona cross-entropywithintervalneutrosophicsets. Int.J.Syst.Sci. 2016, 47,3598–3608.[CrossRef]

21. Ye,J.Improvedcorrelationcoefficientsofsinglevaluedneutrosophicsetsandintervalneutrosophicsetsfor multipleattributedecisionmaking. J.Intell.FuzzySyst. 2014, 27,2453–2462.[CrossRef]

22. Zhang,H.;Ji,P.;Wang,J.;Chen,X.Animprovedweightedcorrelationcoefficientbasedonintegratedweight forintervalneutrosophicsetsanditsapplicationinmulti-criteriadecision-makingproblems. Int.J.Comput. Intell.Syst. 2015, 8,1027–1043.[CrossRef]

23. Ye,J.Multipleattributedecision-makingmethodusingcorrelationcoefficientsofnormalneutrosophicsets. Symmetry 2017, 9,80.[CrossRef]

24. Yu,D.Groupdecisionmakingbasedongeneralizedintuitionisticfuzzyprioritizedgeometricoperator. Int.J. Intell.Syst. 2012, 27,635–661.[CrossRef]

25. Liu,P.Multipleattributegroupdecisionmakingmethodbasedoninterval-valuedintuitionisticfuzzypower Heronianaggregationoperators. Comput.Ind.Eng. 2017, 108,199–212.[CrossRef]

26. Mahmood,T.;Liu,P.;Ye,J.;Khan,Q.Severalhybridaggregationoperatorsfortriangularintuitionisticfuzzy setandtheirapplicationinmulti-criteriadecisionmaking. Granul.Comput. 2018, 3,153–168.[CrossRef] 27.

Liao,H.;Xu,Z.Intuitionisticfuzzyhybridweightedaggregationoperators. Int.J.Intell.Syst. 2014, 29, 971–993.[CrossRef] 28. Xu,Z.Intuitionisticfuzzyaggregationoperators. IEEETrans.FuzzySyst. 2007, 15,1179–1187.[CrossRef] 29. Xu,Z.;Yager,R.R.Somegeometricaggregationoperatorsbasedonintuitionisticfuzzysets. Int.J.Gener.Syst. 2006, 35,417–433.[CrossRef] 30. Sun,H.X.;Yang,H.X.;Wu,J.Z.;Ouyang,Y.IntervalneutrosophicnumbersChoquetintegraloperatorfor multi-criteriadecisionmaking. J.Intell.FuzzySyst. 2015, 28,2443–2455.[CrossRef] 31. Liu,P.;Wang,Y.IntervalneutrosophicprioritizedOWAoperatoranditsapplicationtomultipleattribute decisionmaking. J.Syst.Sci.Complex. 2016, 29,681–697.[CrossRef] 32. Mukhametzyanov,I.;Pamucar,D.AsensitivityanalysisinMCDMproblemsAstatisticalapproach. Decis.Mak.Appl.Manag.Eng. 2018, 1.[CrossRef]

33. Petrovi´c,I.;Kankaraš,M.DEMATEL-AHPmulti-criteriadecisionmakingmodelfortheselectionand evaluationofcriteriaforselectinganaircraftfortheprotectionofairtraffic. Decis.Mak.Appl.Manag.Eng. 2018, 1.[CrossRef]

34. Roy,J.;Adhikary,K.;Kar,S.;Pamuˇcar,D.AroughstrengthrelationalDEMATELmodelforanalysingthe keysuccessfactorsofhospitalservicequality. Decis.Mak.Appl.Manag.Eng. 2018, 1,121–142.[CrossRef]

35. Biswajit,S.;Sankar,P.M.;Sun,H.;Ali,A.;Soheil,S.;Rekha,G.;Muhammad,W.I.Anoptimizationtechnique fornationalincomedeterminationmodelwithstabilityanalysisofdifferentialequationindiscreteand continuousprocessundertheuncertainenvironment. RAIROOper.Res. 2018.[CrossRef]

Symmetry 2018, 10,459

36. Yager,R.R.Thepoweraverageoperator. IEEETrans.Syst.ManCybern.PartA 2001, 31,724–731.[CrossRef] 37.

Liu,P.;Tang,G.Somepowergeneralizedaggregationoperatorsbasedontheintervalneutrosophicsetsand theirapplicationtodecisionmaking. J.Intell.FuzzySyst. 2016, 30,2517–2528.[CrossRef] 38.

Bonferroni,C.Sullemediemultipledipotenze. Bollettinodell’UnioneMatematicaItaliana 1950, 5,267–270. 39. Sykora,S.MathematicalMeansandAverages:GeneralizedHeronianMeans. Stan’sLibr. 2009.[CrossRef] 40. Muirhead,R.F.Somemethodsapplicabletoidentitiesandinequalitiesofsymmetricalgebraicfunctionsof n letters. Proc.Edinb.Math.Soc. 1902, 21,144–162.[CrossRef] 41. Maclaurin,C.AsecondlettertoMartinFolkes,Esq.;concerningtherootsofequations,withthe demonstrationofotherrulesofalgebra. Philos.Trans. 1729, 36,59–96. 42.

Liu,P.;You,X.IntervalneutrosophicMuirheadmeanoperatorsandtheirapplicationsinmultiple-attribute groupdecisionmaking. Int.J.Uncertain.Quant. 2017, 7,303–334.[CrossRef] 43.

Qin,J.;Liu,X.AnapproachtointuitionisticfuzzymultipleattributedecisionmakingbasedonMaclaurin symmetricmeanoperators. J.Intell.FuzzySyst. 2014, 27,2177–2190.[CrossRef]

44. Li,Y.;Liu,P.;Chen,Y.SomesinglevaluedneutrosophicnumberHeronianmeanoperatorsandtheir applicationinmultipleattributegroupdecisionmaking. Informatica 2016, 27,85–110.[CrossRef]

45. Xu,Z.;Yager,R.R.IntuitionisticfuzzyBonferronimeans. IEEETrans.Syst.ManCybern.PartB 2011, 41, 568–578.[CrossRef]

46. Zhou,W.;He,J.M.IntuitionisticfuzzygeometricBonferronimeansandtheirapplicationinmulti-criteria decisionmaking. Int.J.Intell.Syst. 2012, 27,995–1019.[CrossRef]

47. Dombi,J.Ageneralclassoffuzzyoperators,theDeMorganclassoffuzzyoperatorsandfuzzinessmeasures inducedbyfuzzyoperators. FuzzySetsSyst. 1982, 8,149–163.[CrossRef]

48. Liu,P.;Liu,J.;Chen,S.H.SomeintuitionisticfuzzyDombiBonferronimeanoperatorsandtheirapplication tomulti-attributegroupdecisionmaking. J.Oper.Res.Soc. 2018, 69,1–24.[CrossRef]

49. Chen,J.;Ye,J.Somesingle-valuedneutrosophicDombiweightedaggregationoperatorsformultipleattribute decision-making. Symmetry 2017, 9,82.[CrossRef]

50. Torra,V.Hesitantfuzzysets. Int.J.Intell.Syst. 2010, 25,529–539.[CrossRef]

51. He,X.TyphoondisasterassessmentbasedonDombihesitantfuzzyinformationaggregationoperators. Nat.Hazards 2018, 90,1153–1175.[CrossRef]

52. He,Y.;He,Z.;Deng,Y.;Zhou,P.IFPBMsandtheirapplicationtomultipleattributegroupdecisionmaking. J.Oper.Res.Soc. 2016, 67,127–147.[CrossRef]

53. He,Y.;He,Z.;Jin,C.;Chen,H.IntuitionisticfuzzypowergeometricBonferronimeansandtheirapplication tomultipleattributegroupdecisionmaking. Int.J.Uncertain.Fuzz.Knowl.-BasedSyst. 2015, 23,285–315. [CrossRef]

54. He,Y.;He,Z.;Wang,G.;Chen,H.HesitantfuzzypowerBonferronimeansandtheirapplicationtomultiple attributedecisionmaking. IEEETrans.FuzzySyst. 2015, 23,1655–1668.[CrossRef]

55. Liu,P.;Liu,X.Multi-attributegroupdecisionmakingmethodsbasedonlinguisticintuitionisticfuzzypower Bonferronimeanoperators. Complexity 2017, 2017,1–15.

© 2018bytheauthors.LicenseeMDPI,Basel,Switzerland.Thisarticleisanopenaccess articledistributedunderthetermsandconditionsoftheCreativeCommonsAttribution (CCBY)license(http://creativecommons.org/licenses/by/4.0/).