AdvancesinMathematics:ScientificJournal 9 (2020),no.4,1661–1670 ISSN:1857-8365(printed);1857-8438(electronic) https://doi.org/10.37418/amsj.9.4.22Spec.IssueonNCFCTA-2020
PERIODICITYOFINTERVALFUZZYNEUTROSOPHICSOFTMATRICES

M.KAVITHA1 ,P.MURUGADAS,ANDS.SRIRAM
ABSTRACT.Inthisarticletheout-to-outdescriptionofd-periodicintervalfuzzy neutrosophicsoftmatrices(d-PIFNSMs)overfuzzyneutrosophicsoftalgebra (FNSA)isfurnishedandd-peroidicitypropertiesareproved.Delineationofthe d-periodicityofintervalvaluedfuzzysoftneutrosohicsoftmatrices(IFNSM)is interpreted.
1.INTRODUCTION
Ingenuineworld,wefacesuchalargenumberofunpredictabilityinvarying backgroundfields.Anywaythegreaterpartofthecurrentmathematicalinstrumentsforformaldisplaying,thinkingandregisteringarefreshdeterministicand exactincharacter.Therearehypothesisviz.,theoryoflikelihood,proof,fuzzy set,intervalfuzzyset,neutrosophicfuzzyset,vagueset,intervalmathematics, roughsetformanagingunreliabilities.Ingenuineworld,wefacesuchasignificantnumberofvulnerabilitiesinvaryingbackgroundsfields.Thishypotheses havetheirownchallengesascalledattentiontobyMolodtsove[13].In1999, Molodtsove[13]startedanovelideaofsoftsethypothesis,whichistotallynew approchfordisplayingambiguityandunpredictability.Softsethypothesishasa
1correspondingauthor
2010 MathematicsSubjectClassification. 03E72,15B15.
Keywordsandphrases. FuzzyNeutrosophicSoftSet(FNSS),FuzzyNeutrosophicSoftMatrices(FNSMs),IntervalFuzzyNeutrosophicSoftMatrix(IFNSM)andPeriodicityofFuzzyNeutrosophicSoftMatrix(PFNSM).
1661
1662M.KAVITHA,P.MURUGADAS,ANDS.SRIRAM
richpotentialforapplicationintacklingusefulissuesinfinancialaspects,sociology,clinicalscienceect.LateronMajiet.al,[11]haveproposedthehypothesis offuzzysoftset.Majiet.al,[10]stretchedoutsoftsetstointuitionisticsfuzzy softsets.
IntuitionisticfuzzymatrixsumsupthefuzzymatrixpresentedbyThomsom[15].In[2]Borahet.al,extentedfuzzysoftmatrixhypothesisandits application.Likewise,[14],Rajarajeswariet.al,proposednewdefinitionsfor intuitionisticfuzzysoftmatricesanditssort.SumathiandArokiarani[1]presentednewprocedureonfuzzyneutrosophicsoftmatrices.FirsttimeKavitha et.al,[3–6]presentedtheideaofoneofauniquesolvabilityofmax-minoperationthroughFNSMcondition Ax = b andclarifiedstrongregularityofFNSMs overFNSAandprocessingthegreatestX-eigenvectorofFNSM.TheyadditionallypresentedonthepowerofFNSMframework.InMurugadas[8,9]et.al, presentedMonotoneintervalfuzzyneutrosophicsofteigenproblemandMonotonefuzzyneutrosophicsofteigenspacestructureinmax-minalgebra.Uma et.al,[16],presentedtwokindsoffuzzyneutrosophicsoftmatrices.
Thepointofthispaperistoportraypurportedd-periodicityofFNSMswith vagueinformation(IFNSMs))andtoproducealgorithmsforcheckingthecorrespondingpropertiesofIFNSMs.
2.PRELIMINARIESAND BACKGROUNDS
Forbasicdefinitionandillustrationsaboutneutrosophicset,neutrosophicsoft set,FNSMssee[5,6].
TheFNSA N isthetriplet (N , ⊕, ⊗), where (N , ≤) isaboundedlinearlyorderedsetwithbinaryoperationsmaximumandminimum,denotedby ⊗, ⊕ Throughoutthepaper J representsanindexset.
Theleastelementin N willbedenotedby 0, 0, 1 , thegreatestoneby 1, 1, 0 .
For ≤ relation,stronglyconnectedcomponent K, thresholddigraph(TDG), period K andperiodforFNSMsee[7].
Forany n ∈ J, N(n,n) denotesthesetofallsquarematricesoforder n and N(n) thesetofalln-dimensionalcolumnvectorsoverFNSA.
ForaFNSM A ∈N(n,n) thesymbol G(A)=(N,EG) standsforacomplete, arc-weighteddigraphassociatedwith A, i.e.,thenodesetof G(A) is N, and thecapacityofanyare (i,j) is aT ij ,aI ij ,aF ij Let φ = N ⊂ N.G/N standsfor
thesubdigraphofdigraph G(A)=(N,EG) withthenodeset ˜ N andarcset EG/N = {(i,j) ∈ EG; i,j ∈ N } If K istrivial,thentheperiod P (K)=1 By S ∗(G) wedenotethesetofallnon-trivialstronglyconnectedcomponentsof G. Thesetofallstronglyconnectedcomponentsof G isdenotedby S(G) P (A) denotetheperiodFNSM A
Theorem2.1. [7]Let A,C ∈N(n,n) Let hT ,hI ,hF , hT 1 ,hI 1,hF 1 , hT 2 ,hI 2,hF 2 ∈N (i) If A ≤ C then G(A, hT ,hI ,hF ) ⊆ G(C, hT ,hI ,hF ), (ii) if hT 1 ,hI 1,hF 1 < hT 2 ,hI 2,hF 2 then G(A, hT 2 ,hI 2,hF 2 ) ⊆ G(A, hT 1 ,hI 1,hF 1 ).
Theorem2.2. [7]Let A ∈N(n,n),d ∈ N Then (i) P (A) | d ⇔ (∀ hT ,hI ,hF ∈N )(∀K∈S ∗(G(A, hT ,hI ,hF )))per K| d, (ii) perA = lcm{perK); K∈S ∗(A)}.
3.PERIODICITYOF INTERVAL FNSMS
InthissectionweshalldealwithFNSMswithintervalelements.Similarly to[8]wedefineanIFNSM A
Definition3.1. Let A, A ∈N(n,n),A ≤ A. AnIFNSM A withbounds A and A is definedasfollows
A =[A, A]= {A ∈N(n,n); A ≤ A ≤ A}
Definition3.2. AnIFNSM A iscalledPossiblyd-periodicifthereexistsFNSM A ∈ A suchthat P (A) | d, Universallyd-periodicifforeachFNSM A ∈ A P (A) | d holds.
3.1. Possibled-periodic(PDP). InthispartwewillproveasufficientandnecessaryconditionforanIFNSMtobepossiblyd-periodicandfindtheFNSM A ∈ A suchthat P (A) | d inpositivecase.
Theorem3.1. Let G ⊆ G, K∈S ∗(G) and K ∈S ∗(G /NK). Then P (K) |P (K ). Proof. Since {l(c); cisacyclefrom K }⊆{l(˜ c);˜cisacyclefrom K)} wehave P (K)= gcd{l(c); cisacyclefrom K}| gcd{l(˜ c;˜cisacyclefrom K )} = P (K ).
Denote H = { aT ij , aI ij , aF ij ; i,j ∈ J } = { hT ,hI ,hF 1 , hT ,hI ,hF 2 ,..., hT ,hI ,hF r} where hT ,hI ,hF 1 > hT ,hI ,hF 2 >...> hT ,hI ,hF r
Lemma3.1. Forall hT ,hI ,hF ∈ H andforevery K∈S ∗(G(A, hT ,hI ,hF )) suchthat P (K) − | d thedigraph G(A, hT ,hI ,hF )/NK beacyclic.Thenforall k,l ∈ J suchthat l ≤ k ≤ r holds P (K ) | d foreach K ∈S ∗(G(A(k) , hT ,hI ,hF (l)))
Proof. Bymathematicalinductionon k.
(i)For k =1 weshowthat P (K ) | d foreach K ∈S ∗(G(A(1) , hT ,hI ,hF )(1)) Let K1 , K2 ,..., Km ∈S ∗(G(A, hT ,hI ,hF (1))) suchthat P (Ks) | d,s =1, 2,...,m. Wehave, Ks ∈S ∗(G(A(1) , hT ,hI ,hF (1))) for s ≤ m. Moreover S ∗(G(A(1) , hT ,hI ,hF (1)))= {K1 , K2 ,..., Km}. Necessarily P (K ) | d foreach K ∈S ∗(G(A(1) , hT ,hI ,hF (1)))
(ii)If P (K ) | d foreach K ∈S ∗(G(A(k) , hT ,hI ,hF (l))),l ≤ k. Itisobviousthat G(A(k+1) , hT ,hI ,hF (l)) and G(A(k) , hT ,hI ,hF (l)) aresameforall l ∈ J,l ≤ k.
Inevitably, P (K ) | d foreach K ∈S ∗(G(A(k+1) , hT ,hI ,hF (l))),l ≤ k. The proofof P (K ) | d foreach K ∈S ∗(G(A(k+1) , hT ,hI ,hF (l))) followsfromthe factthat:
S ∗(G(A(k) , hT ,hI ,hF (k+1)))= {K∈ (G(A, hT ,hI ,hF (k+1))); P (K) | d}.
Theorem3.2. AnIFNSM A isPDPifandonlyifforeach hT ,hI ,hF ∈ H andfor each K∈S ∗(G(A, hT ,hI ,hF )) suchthat P (K) − | d thedigraph G(A, hT ,hI ,hF )/NK isacyclic. Proof. If hT ,hI ,hF ∈ H and K∈S ∗(G(A, hT ,hI ,hF )) suchthat P (K) − | d andthedigraph G(A, hT ,hI ,hF )/NK ⊆K hasacycle c. Let A ∈ A befixed.As G(A, hT ,hI ,hF ⊆ G(A, hT ,hI ,hF )), thereexists K ∈S ∗(G(A, hT ,hI ,hF )) suchthat c ∈K Since G(A, hT ,hI ,hF ) ⊆ G(A, hT ,hI ,hF ) , and K ∈S ∗(G(A, hT ,hI ,hF /NK)) byTheorem2.2weget P (K) |P (K ) and so P (K ) − | d.FromTheorem2.2, P (A) − | d.ConsequentlytheIFNSM A isnot PDP.
Forthereversepart,if G(A, hT ,hI ,hF )/NK isacyclicforall hT ,hI ,hF ∈ H andforevery K∈S ∗(G(A, hT ,hI ,hF )) suchthat P (K) − | d.Weshallsetupa FNSM A∗ ∈ A suchthat P (A∗) | d.
InitiallyraiseanauxiliarysequenceofFNSMs {A(k)}r k=0 = {( aT ij ,aI ij ,aF ij (k))}r k=0 recurrentlyasfollows. a T ij ,a I ij ,a F ij (0) = a T ij ,a I ij ,a F ij (s) foreach i,j ∈ N, a T ij ,a I ij ,a F ij (k+1) = hT ,hI ,hF (k+1) , (i,j) ∈ Us∈M EKs aT ij ,aI ij ,aF ij (k) < hT ,hI ,hF (k+1) , aT ij ,aI ij ,aF ij (k) , otherwise, foreach k ∈ J, where K1 , K2 ,..., Km ∈S ∗(G(A, hT ,hI ,hF (k+1))) aresuchthat P (Ks) | d for s =1, 2,..,m.
Bythepreviouslemma3.1.for k = r, weget P (K) | d foreach K∈S ∗(G(A(r) , hT ,hI ,hF (l))) and l ≤ r. Let A∗ = A(r) Since G(A, hT ,hI ,hF (r)) iscomplete, aT ij ,aI ij ,aF ij ∗ ≥ hT ,hI ,hF (r) foreach i,j ∈ J, then P (A∗) | d ifweshowthat P (K ) | d foreach K ∈S ∗(G(A∗ , aT ij ,aI ij ,aF ij ∗)), for i,j ∈ N suchthat aT ij ,aI ij ,aF ij ∗ > hT ,hI ,hF (r) , aT ij ,aI ij ,aF ij ∗ / ∈ H.
Evidently G(A∗ , aT ij ,aI ij ,aF ij ∗)= G(A∗ , hT ,hI ,hF (p)) where p ∈ J issuch that hT ,hI ,hF (p+1) < aT ij ,aI ij ,aF ij ∗ < hT ,hI ,hF (p) Thus P (K ) | d foreach K ∈S ∗(G(A∗ , aT ij ,aI ij ,aF ij ∗)),i,j ∈ N. Accordingly P (A∗) | d fromTheorem 2.2.ThustheIFNSM A isaPDP.
LetusconsiderthefollowingIFNSMtoillustratethePossibled-periodicity.
Example1. Let O = 0, 0, 1 ,I = 1, 1, 0 and A =[A, A] A
0, 0, 1 0 40 30 6 0, 0, 1 0 5, 0 4, 0 6 0, 0, 1 0 2, 0 1, 0 8 0, 0, 1 0 3, 0 2, 0 7 0, 0, 1 0, 0, 1 ] 0.3, 0.2, 0.7 0, 0, 1 0.2, 0.1, 0.8 0, 0, 1 0, 0, 1 0, 0, 1 0, 0, 1 0, 0, 1 0.1, 0.1, 0.9 0.2, 0.1, 0.8 0, 0, 1 0, 0, 1 0.1, 0.1, 0.9 0.2, 0.1, 0.8 0, 0, 1 ]
0, 0, 1 0 30 20 7 0, 0, 1 0, 0, 1 0, 0, 1 0 2, 0 1, 0 8 0, 0, 1 0 2, 0 1, 0 8 0, 0, 1 0, 0, 1 0 2, 0 1, 0 8 0, 0, 1 0, 0, 1 0, 0, 1 0, 0, 1 0, 0, 1 0, 0, 1 0, 0, 1 0, 0, 1 0 1, 0 1, 0 9 0, 0, 1 0, 0, 1 0.1, 0.1, 0.9 0.2, 0.1, 0.8 0, 0, 1
FIGURE 1.Thresholddigraphs hT ,hI ,hF (3) = 0 30 20 7
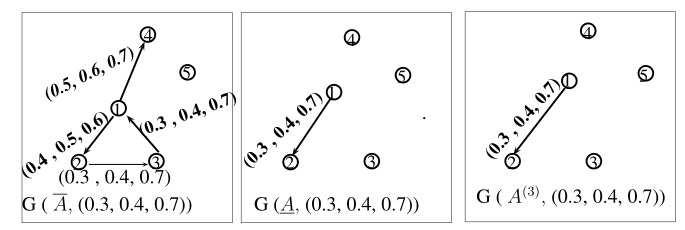
For hT ,hI ,hF (1) = 0.5, 0.4, 0.6 and hT ,hI ,hF (2) = 0.4, 0.3, 0.6 , G(A, hT ,hI ,hF (1)),G(A, hT ,hI ,hF (2)) areacyclic,so A1 = A2 = A.
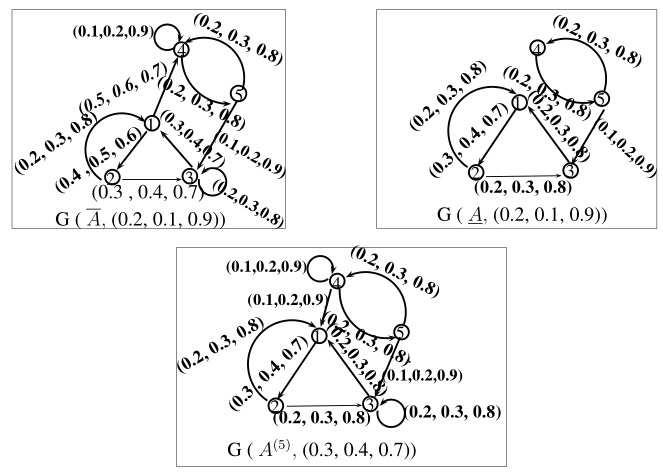
For hT ,hI ,hF (3) = 0.30.20.7 ,G(A, hT ,hI ,hF (3)) arepresentedinFigure1. Certainly G(A, hT ,hI ,hF (3)) hasexactlyoneelementin S ∗ withperiod P (K)=3 − | 4. As G(A, 3)/NK isacyclic,whichsatisfytheTheorem2.2and A(3) = A For hT ,hI ,hF (4) = 0 2, 0 1, 0 8 therearetwoelementsin S ∗(G(A, hT ,hI ,hF (4))): K1 with NK( 1) = {1, 2, 3}, P (K1)=1 and K2 with NK2 = {4, 5}, P (K2)=2 (seeFigure2).As P (K1) | 4 and P (K2) | 4 we calculatetheFNSM A(4) from A(3) byincreasingelements aT 33,aI 33,aF 33 (3) and aT 45,aI 45,aF 45 (3) to 0 2, 0 1, 0 8 InFigure3weseefor hT ,hI ,hF (5) =1 the G(A, 1) isstronglyconnectedwithperiodequaltoone,sowecomputethe FNSM A(5) from A(4) byincreasingelements aT 14,aI 14,aF 14 (4) and aT 44,aI 44,aF 44 (4) to 0.1, 0.1, 0.9 .
Weget
0, 0, 1 0.30.20.7 0, 0, 1 0, 0, 1 0, 0, 1 0 2, 0 1, 0 8 0, 0, 1 0 2, 0 1, 0 8 0, 0, 1 0, 0, 1 ] 0.2, 0.1, 0.8 0, 0, 1 0.2,0.1,0.8 0, 0, 1 0, 0, 1 0, 0, 1 0, 0, 1 0, 0, 1 0, 0, 1 0.2,0.1,0.8 0, 0, 1 0, 0, 1 0.1, 0.1, 0.9 0.2, 0.1, 0.8 0, 0, 1
A(5) =
0, 0, 1 0.3, 0.2, 0.7 0, 0, 1 0.1,0.1,0.9 0, 0, 1 0 2, 0 1, 0 8 0, 0, 1 0 2, 0 1, 0 1 0, 0, 1 0, 0, 1 ] 0.2, 0.1, 0.8 0, 0, 1 0.2, 0.1, 0.8 0, 0, 1 0, 0, 1 0, 0, 1 0, 0, 1 0, 0, 1 0.1,0.1,0.9 0 2, 0 1, 0 8 0, 0, 1 0, 0, 1 0.1, 0.1, 0.9 0.2, 0.1, 0.8 0, 0, 1
FIGURE 2.Thresholddigraphsfor hT ,hI ,hF (4) = 0 2, 0 3, 0 8
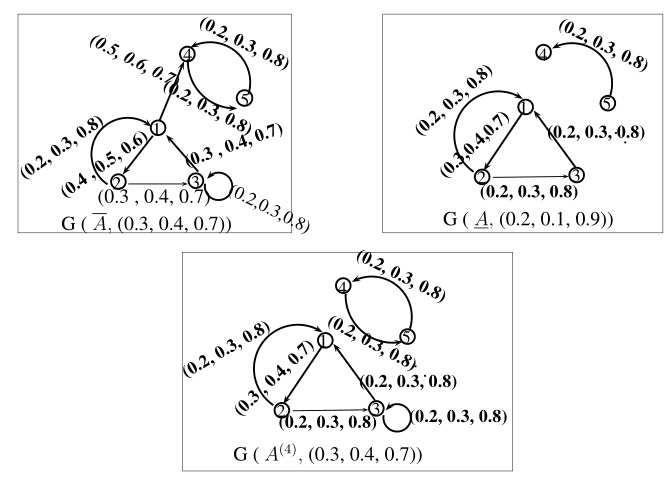
FIGURE 3.Thresholddigraphsfor hT ,hI ,hF 5 = 0 1, 0 2, 0 9
4.UNIVERSALD -PERIODICITY
InthispartweconcentrateonifandonlyifconstraintsforanIFNSMtobe universallyd-periodic(UDP).
Foragiven hT ,hI ,hF ∈ H letusdenote N h = N \ s j=1 NKj , if S ∗(G(A, hT ,hI ,hF ))= {K1 ,..., Ks}
Theorem4.1. Let A beanIFNSM.Then A isUDPifandonlyif P (A) | d and (∀ hT ,hI ,hF ∈ H )(∀c ∈ G(A, hT ,hI ,hF )/N h)[l(c) | d]. Proof. For P (A) − | d orthereexist hT ,hI ,hF ∈ H and c ∈ G(A, hT ,hI ,hF )/N h suchthat l(c) − | d.
If P (A) − | d then A isnotuniversallyd-periodic.
AsthesecondcasewesetuptheFNSM A =( ˜ aT ij , ˜ aI ij , ˜ aF ij ) asfollows: a T ij , a I ij , a F ij = aT ij , aI ij , aF ij if (i,j) ∈ c, aT ij ,aI ij ,aF ij otherwise.
Thereexists K∗ ∈S ∗G(A, hT ,hI ,hF ) containacycle c only.Since P (K∗ = l(c)) − | d byTheorem2.2, P (A) − | d. ThusanIFNSM A isnotUDP.
Converselyif A isnotUDPand P (A) | d. Weshowthatthereexists hT ,hI ,hF ∈ H and c ∈ G(A, hT ,hI ,hF )/N h suchthat l(c) − | d.
If A isnotUDPthenthereexists A ∈ A, hT ,hI ,hF ∈N and K∈S ∗(G(A, hT ,hI ,hF )) suchthat P (K) − | d. Further P (A) | d implies NK ⊆ N h From P (K) − | d impliesthatthereexistsacycle c ∈K suchthat l(c) − | d. From G(A, hT ,hI ,hF )/N h ⊆ G(A, hT ,hI ,hF )/N h itfollowsthat c ∈ G(A, hT ,hI ,hF )N h Define hT , hI , hF asfollows: hT , hI , hF = hT ,hI ,hF (r),if hT ,hI ,hF ≤ min i,j∈N a T ij , a I ij , a F ij = hT ,hI ,hF (r) , hT ,hI ,hF (k) if hT ,hI ,hF (k) ≥ hT ,hI ,hF > hT ,hI ,hF (k+1) Since N h ⊆ N h and G(A, hT ,hI ,hF (r))= G(A, hT , hI , hF ) implies c ∈ G(A, hT , hI , hF )/N h . Thusacycle c ∈ G(A, ˜ hT , ˜ hI , ˜ hF )/N h existssuchthat l(c) − | d.
NoticethatTheorem2.2impliesthatthecomputationalcomplexityofaprocedurebasedoncheckingallcyclesin G(A, hT ,hI ,hF )/ ˜ N canbeexponentially large.Theefficientalgorithmfortheintervalcirculantmatricesissuggested in[12].
5.CONCLUSION
Inthispapertheauthorspresentedd-periodicityoffuzzyneutrosophicsoft matrices(FNSMs)withintervalfuzzyneutrosophicsoftmatrices(IFNSMs).
REFERENCES
[1] I.AROCKIARANI,I.R.SUMATHI: Afuzzyneutrosophicsoftmatrixapproachindecision making, JGRMA 2(2)(2014),14-23.
[2] M.J.BORAH,T.J.NEOG,D.K.SUT: Fuzzysoftmatrixtheoryanditsdecisionmaking, InternationalJournalofModernEngineeringResearch, 2 (2012),121-127.
[3] M.KAVITHA,P.MURUGADAS,S.SRIRAM: Minimalsolutionoffuzzyneutrosophicsoft matrix,JournalofLinearandTopologicalAlgebra, 6 (2017),171-189.
[4] M.KAVITHA,P.MURUGADAS,S.SRIRAM: Onthe λ-robustnessoffuzzyneutrosophicsoft matrix,InternationalJournalofFuzzyMathematicalArchive, 2 (2017),267-287.
1670M.KAVITHA,P.MURUGADAS,ANDS.SRIRAM
[5] M.KAVITHA,P.MURUGADAS,S.SRIRAM: Computingthegreatest X-eigenvectorof fuzzyneutrosophicsoftmatrix,InternationalJournalofMathamaticsanditsApplications, 4 (2017),893-907.
[6] M.KAVITHA,P.MURUGADAS,S.SRIRAM: Onthepoweroffuzzyneutrosophicsoftmatrix,JournalofLinearandTopologicalAlgebra, 7(2018),133-147.
[7] M.KAVITHA: Astudyonfuzzyneutrosophicsoftmatriceswithrelatedaspectsoneigenvectors ofthematrices,2018.
[8] P.MURUGADAS,M.KAVITHA,S.SRIRAM: Monotoneintervalfuzzyneutrosophicsoft eigenproblem,MalayaJournalofMatematik, 5(1)(2019),342-350.
[9] P.MURUGADAS,M.KAVITHA,S.SRIRAM: Monotonefuzzyneutrosophicsofteigenspace structureinmax-minalgebra,RecentTrendsinPureandAppliedMathematics, 2177 (1) (2019),1-8.
[10] P.K.MAJI,A.R.ROY,R.BISWAS: Onintuitionisticfuzzysoftset, InternationalJournal ofFuzzyMathematics, 12(3)(2004),669-684.
[11] P.K.MAJI,R.BISWAS,R.RAY: FuzzySoftSet,J.FuzzyMath., 9 (2001),589-602.
[12] M.MOLNAROVA,H.MYSKOA,J.PLAVKA: Therobustnessofintervalfuzzymatrices, (SubmittedtoDAM),2019.
[13] M.MOLNAROVA,H.MYSKOA,J.PLAVKA: Periodicityofintervalmatricesinfuzzyalgebra,Proceedingsof30thInt.lConf.Math.Meth.inEconomics,2011.
[14] P.RAJARAJESWARI,P.DHANALAKSHMI: Intuitionisticfuzzysoftmatrixtheoryandapplicationindecisionmaking,InternationalJournalofEngineeringResearchandTechnology, 2 (2013),1100-1111.
[15] M.G.THOMSON: ConvergenceofPowersoffuzzymatrix, J.ofMath.Anal.andAppl., 57 (1977),476-480.
[16] R.UMA,P.MURUGADAS,S.SRIRAM: Fuzzyneutrosophicsoftmatricesoftype-Iand type-II,Communicated,2020.
DEPARTMENTOF MATHEMATICS
APOLLO ARTSAND SCIENCE COLLEGE
CHENNAI-602105,TAMIL NADU,INDIA E-mailaddress:
DEPARTMENTOF MATHEMATICS
GOVERNMENT ARTS COLLEGE (AUTONOMOUS)
KARUR-639007,TAMIL NADU,INDIA
E-mailaddress:
MATHEMATICS WING
DIRECTORATEOF DISTANCE EDUCATION,ANNAMALAI UNIVERSITY
ANNAMALAINAGAR-608002,TAMIL NADU,INDIA
E-mailaddress:
