Neutrosophic Actions, Prevalence Order, Refinement of Neutrosophic Entities

Neutrosophic Sets and Systems, Vol. 10, 2015

Neutrosophic Actions, Prevalence Order, Refinement of Neutrosophic Entities, and Neutrosophic Literal Logical Operators

Florentin Smaradache

Mathematics Department, University of New Mexico Gallup, NM 87301, USA. E-mail: fsmarandache@unm.edu

Abstract In this paper, we define for the first time three neutrosophic actions and their properties. We then introduce the prevalence order on {T, I, F} with respect to a given neutrosophic operator “o”, which may be subjective as defined by the neutrosophic experts; and the re-

finement of neutrosophic entities <A>, <neutA>, and <antiA>. Then we extend the classical logical operators to neutrosophic literal logical operators and to refined literal logical operators, and we define the refinement neutrosophic literal space

Keywords: neutrosophic logic, neutrosophic actions, prevalence order, neutrosophic operator, neutrosophic entities, neutrosophic literal logical operators, refined literal logical operators, refinement neutrosophic literal space, neutrosophic conjunction, neutrosophic disjunction, neutrosophic Sheffer’s stroke, neutrosophic equivalence

1 Introduction

In Boolean Logic, a proposition is either true (T), or false (F). In Neutrosophic Logic, a proposition is either true (T), false (F), or indeterminate (I). For example, in Boolean Logic the proposition : is true, while the proposition : is false.

In neutrosophic logic, besides propositions (which is true) and (which is false), we may also have proposition : which is an incomplete/indeterminate proposition (neither true, nor false).

1.1 Remark

All conjectures in science are indeterminate at the beginning (researchers not knowing if they are true or false), and later they are proved as being either true, or false, or indeterminate in the case they were unclearly formulated.

1.2 Notations

In order to avoid confusions regarding the operators, we note them as:

a. Boolean (classical) logic:

b.Fuzzy logic:

c.Neutrosophic logic:

2 Three Neutrosophic Actions

In the frame of neutrosophy, we have considered [1995] for each entity , its opposite , and their neutrality {i.e. neither , nor Also, by we mean what is not , i.e. its opposite , together with its neutral(ity) ; therefore:

Based on these, we may straightforwardly introduce for the first time the following neutrosophic actions with respect to an entity <A>:

1.To neutralize (or to neuter, or simply to neut ize) the entity <A>. [As a noun: neutralization, or neuter ization, or simply neut ization.]

We denote it by <neutA> or neut(A).

2.To antithetic-ize (or to anti-ize) the entity <A>. [As a noun: antithetic ization, or anti ization.]

We denote it by <antiA> ot anti(A).

This action is 100% opposition to entity <A> (strong opposition, or strong negation).

3.To non ize the entity <A>. [As a noun: non ization].

We denote it by <nonA> or non(A).

It is an opposition in a percentage between (0, 100]% to entity <A> (weak opposition).

Of course, not all entities <A> can be neutralized, or antithetic ized, or non ized.

Florentin Smaradache, Neutrosophic Actions, Prevalence Order, Refinement of Neutrosophic Entities, and Neutrosophic Literal Logical Operators

University of New Mexico

Neutrosophic Sets and Systems, Vol. 10, 2015

2.2

Example

Let Then,

3 Properties of the Three Neutrosophic Actions

anti(〈antiA〉) = A; anti(〈neutA〉) = 〈A〉 or 〈antiA〉; non(〈antiA〉) = 〈A〉 or 〈neutA〉; non(〈neutA〉) = 〈A〉 or 〈antiA〉.

4 Neutrosophic Actions’ Truth Value Tables

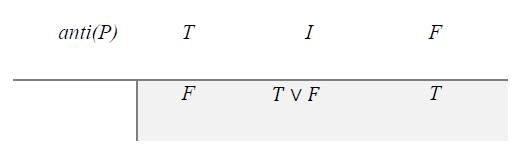
Let’s have a logical proposition P, which may be true (T), Indeterminate (I), or false (F) as in previous example. One applies the neutrosophic actions below.

4.1 Neutralization (or Indetermination) of P

, but (meaning that at least one of , or is refined in two or more sub entities). For example, if then while .

If we refine them, we get various nuances of white color: , and various nuances of black color: and the colors in between them (red, green, yellow, blue, etc.):

Similarly as above, we want to point out that not all entities <A> and/or their corresponding (if any) <neutA> and <antiA> can be refined.

6 The Prevalence Order

Let’s consider the classical literal (symbolic) truth (T) and falsehood (F)

In a similar way, for neutrosophic operators we may consider the literal (symbolic) truth (T), the literal (symbolic) indeterminacy (I), and the literal (symbolic) falsehood (F).

We also introduce the prevalence order on with respect to a given binary and commutative neutrosophic operator

The neutrosophic operators are: neutrosophic negation, neutrosophic conjunction, neutrosophic disjunction, neutrosophic exclusive disjunction, neutrosophic Sheffer’s stroke, neutrosophic implication, neutrosophic equivalence, etc.

4.2

4.3

5 Refinement of Entities in Neutrosophy

In neutrosophy, an entity has an opposite and a neutral . But these three categories can be refined in sub entities and respectively and also where m, n, p are integers

The prevalence order is partially objective (following the classical logic for the relationship between T and F), and partially subjective (when the indeterminacy I interferes with itself or with T or F).

For its subjective part, the prevalence order is determined by the neutrosophic logic expert in terms of the application/problem to solve, and also depending on the specific conditions of the application/problem.

For , we write , or , and we read “X” prevails to Y with respect to the neutrosophic binary commutative operator “o”, which means that .

Let’s see the below examples. We mean by “o”: conjunction, disjunction, exclusive disjunction, Sheffer’s stroke, and equivalence.

7 Neutrosophic Literal Operators & Neutrosophic Numerical Operators

7.1 If we mean by neutrosophic literal proposition, a proposition whose truth value is a letter: either T or I or F. The operators that deal with such logical propositions are called neutrosophic literal operators.

7.2. And by neutrosophic numerical proposition, a proposition whose truth value is a triple of numbers (or in general of numerical subsets of the interval [0, 1]), for examples A(0.6, 0.1, 0.4) or B([0, 0.2], {0.3, 0.4, 0.6}, (0.7, 0.8)).

Florentin Smaradache, Neutrosophic Actions, Prevalence Order, Refinement of Neutrosophic Entities, and Neutrosophic Literal Logical Operators

Antitheticization (Neutrosophic Strong Opposition to P

Non ization (Neutrosophic Weak Opposition to P)

Neutrosophic Sets and Systems, Vol. 10, 2015

The operators that deal with such logical propositions are called neutrosophic numerical operators

8 Truth Value Tables of Neutrosophic Literal Operators

In Boolean Logic, one has the following truth value table for negation:

8.1 Classical Negation

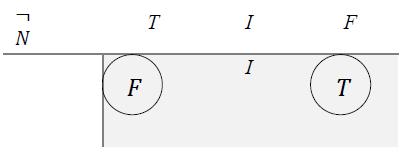
In Neutrosophic Logic, one has the following neutrosophic truth value table for the neutrosophic negation:

8.2 Neutrosophic Negation

So, we have to consider that the negation of I is I, while the negations of T and F are similar as in classical logic.

In classical logic, one has:

8.3 Classical Conjunction

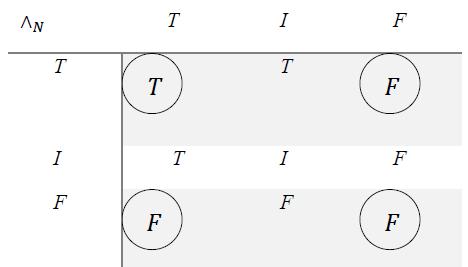
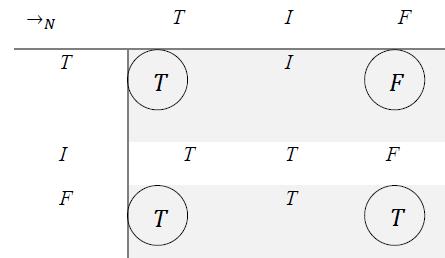
In neutrosophic logic, one has:

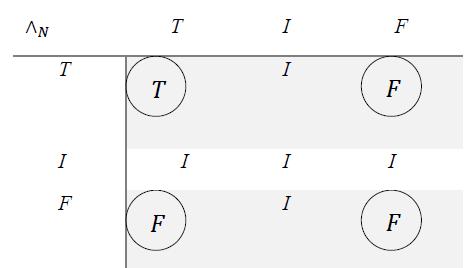
8.4 Neutrosophic Conjunction ( ), version 1

The objective part (circled literal components in the above table) remains as in classical logic, but when indeterminacy I interferes, the neutrosophic expert may choose the most fit prevalence order.

There are also cases when the expert may choose, for various reasons, to entangle the classical logic in the objective part. In this case, the prevalence order will be totally subjective.

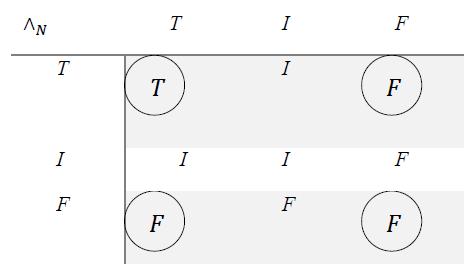
The prevalence order works for classical logic too. As an example, for classical conjunction, one has , which means that While the prevalence order for the neutrosophic conjunction in the above tables was: which means that , and Other prevalence orders can be used herein, such as: and its corresponding table would be:

8.5 Neutrosophic Conjunction ( ), version 2 which means that and ; or another prevalence order: and its corresponging table would be:

8.6 Neutrosophic Conjunction ( ), version 3

which means that and

If one compares the three versions of the neutrosophic literal conjunction, one observes that the objective part remains the same, but the subjective part changes.

Florentin Smaradache, Neutrosophic Actions, Prevalence Order, Refinement of Neutrosophic Entities, and Neutrosophic Literal Logical Operators

Neutrosophic Sets and Systems, Vol. 10, 2015

The subjective of the prevalence order can be established in an optimistic way, or pessimistic way, or according to the weights assigned to the neutrosophic literal components T, I, F by the experts.

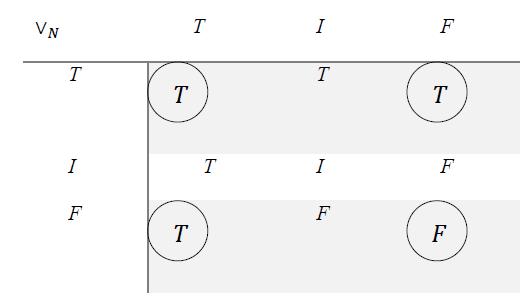
In a similar way, we do for disjunction.

In classical logic, one has:

8.7 Classical Disjunction

In neutrosophic logic, one has:

8.8 Neutrosophic Disjunction ( )

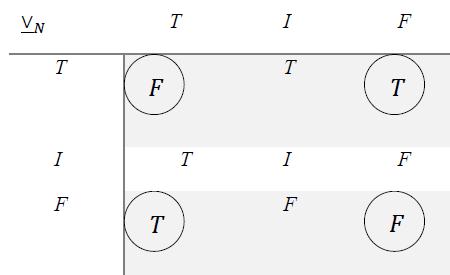
8.10 Neutrosophic Exclusive Disjunction

where we used the following prevalence order: but the reader is invited (as an exercise) to use another prevalence order, such as: or etc., for all neutrosophic logical operators presented above and below in this paper.

In classical logic, one has:

8.9 Classical Exclusive Disjunction

using the prevalence order

In classical logic, one has: 8.11 Classical Sheffer’s Stroke

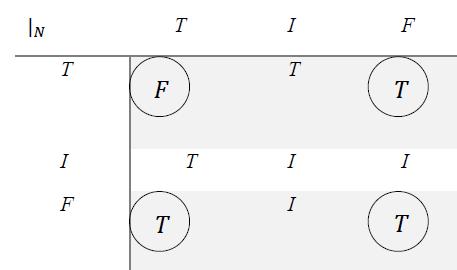
In neutrosophic logic, one has: 8.12 Neutrosophic Sheffer’s Stroke

using the prevalence order

In classical logic, one has: 8.13 Classical Implication

In neutrosophic logic, one has:

Florentin Smaradache, Neutrosophic Actions, Prevalence Order, Refinement of Neutrosophic Entities, and Neutrosophic Literal Logical Operators

Neutrosophic Sets and Systems, Vol. 10, 2015

In neutrosophic logic, one has:

8.14

Neutrosophic Implication

using the subjective preference that is true (because in the classical implication is implied by anything), and is false, while is true because is similar to the classical implications and , which are true.

The reader is free to check different subjective preferences.

In classical logic, one has:

8.15 Classical Equivalence

In neutrosophic logic, one has:

8.16 Neutrosophic Equivalence

using the subjective preference that is true, because it is similar to the classical equivalences that and are true, and also using the prevalence:

9 Refined Neutrosophic Literal Logic

Each particular case has to be treated individually. In this paper, we present a simple example.

Let’s consider the following neutrosophic logical propositions:

T = Tomorrow it will rain or snow.

T is split into  Tomorrow it will rain.  Tomorrow it will snow. F = Tomorrow it will neither rain nor snow.

F is split into  Tomorrow it will not rain.  Tomorrow it will not snow.

I = Do not know if tomorrow it will be raining, nor if it will be snowing.

I is split into  Do not know if tomorrow it will be raining or not.  Do not know if tomorrow it will be snowing or not.

Then: It is clear that the negation of (Tomorrow it will raining) is (Tomorrow it will not be raining). Similarly for the negation of , which is

But, the negation of (Do not know if tomorrow it will be raining or not) is “Do know if tomorrow it will be raining or not”, which is equivalent to “We know that tomorrow it will be raining” ( , or “We know that tomorrow it will not be raining” ( . Whence, the negation of is , and similarly, the negation of is

9.1 Refined Neutrosophic Literal Conjunction Operator where

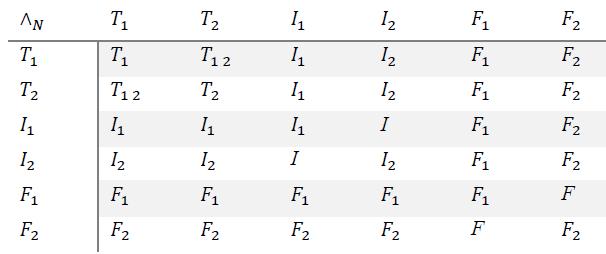
“Tomorrow it will rain and it will snow”.

Of course, other prevalence orders can be studied for this particular example.

With respect to the neutrosophic conjunction, prevail in front of , which prevail in front of , or , for all .

Florentin Smaradache, Neutrosophic Actions, Prevalence Order, Refinement of Neutrosophic Entities, and Neutrosophic Literal Logical Operators

Neutrosophic Sets and Systems, Vol. 10, 2015

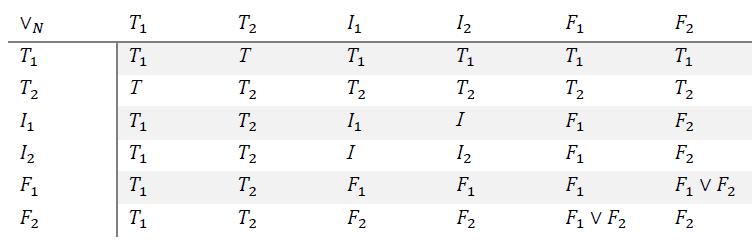
9.2 Refined Neutrosophic Literal Disjunction Operator

Conclusion

We have defined for the first time three neutrosophic actions and their properties. We have introduced the prevalence order on {T, I, F} with respect to a given neutrosophic operator “o”, the refinement of neutrosophic entities <A>, <neutA>, and <antiA>, and the neutrosophic literal logical operators, the refined literal logical operators, as well as the refinement neutrosophic literal space.

References

With respect to the neutrosophic disjunction, prevail in front of , which prevail in front of , or , for all .

For example, , but .

10 The Refinement Neutrosophic Literal Space

The Refinement Neutrosophic Literal Space is not closed under neutrosophic negation, neutrosophic conjunction, and neutrosophic disjunction.

The reader can check the closeness under other neutrosophic literal operations.

A neutrosophic refined literal space ,

where are integers , is said to be closed under a given neutrosophic operator , if for any elements one has .

Let’s denote the extension of with respect to a single by:

If is not closed with respect to the given neutrosophic operator , then , and we extend by adding in the new elements resulted from the operation , let’s denote them by Therefore, encloses

Similarly, we can define the closeness of the neutrosophic refined literal space with respect to the two or more neutrosophic operators , for

is closed under if for any and for any one has

If is not closed under these neutrosophic operators, one can extend it as previously.

Let’s consider: , which is closed with respect to all neutrosophic operators , then encloses

[1] F. Smarandache, "Neutrosophy. / Neutrosophic Probability, Set, and Logic", Am. Res. Press, Rehoboth, USA, 105 p., 1998;

Republished in 2000, 2003, 2005, A Unifying Field in Logics: Neutrosophic Logic. Neutrosophy, Neutrosophic Set, Neutrosophic Probability and Statistics (second, third, and respectively fourth edition), American Research Press, 156 p.;

Chinese translation by F. Liu, “A Unifying Field in Logics: Neutrosophic Logic. / Neutrosophy, Neutrosophic Set, Neutrosophic Probability and statistics”, Xiquan Chinese Branch, 121 p., 2003;

Russian partial translation by D. Rabounski: Hexis, Сущность нейтрософии, 32 p., 2006.

[2] Florentin Smarandache, Refined Literal Indeterminacy and the Multiplication Law of Sub Indeterminacies, Neutrosophic Sets and Systems, 58 63, Vol. 9, 2015.

Received: August 20, 2015 Accepted: September 26, 2015

Florentin Smaradache, Neutrosophic Actions, Prevalence Order, Refinement of Neutrosophic Entities, and Neutrosophic Literal Logical Operators