1
2
3
Neutrosophic Sets and Systems,Vol. 38,2020
ConvexandConcaveHypersoftSetswithSomeProperties

AtiqeUrRahman 1,∗ ,MuhammadSaeed 2 andFlorentinSmarandache 3
DepartmentofMathematics,UniversityofManagementandTechology,Lahore,Pakistan aurkhb@gmail.com
DepartmentofMathematics,UniversityofManagementandTechology,Lahore,Pakistan muhammad.saeed@umt.edu.pk
DepartmentofMathematics,UniversityofNewMexico,Gallup,NM87301,USA ∗ Correspondence:aurkhb@gmail.com

smarand@unm.edu
Abstract Convexityplaysanimperativeroleinoptimization,patternclassificationandrecognition,image processingandmanyotherrelatingtopicsindifferentfieldsofmathematicalscienceslikeoperationresearch, numericalanalysisetc.TheconceptofsoftsetswasfirstformulatedbyMolodtsovasacompletelynewmathematicaltoolforsolvingproblemsdealingwithuncertainties.Smarandacheconceptualizedhypersoftsetasa generalizationofsoftset(hS ,E)asittransformsthefunction hS intoamulti-attributefunction hHS .Deli introducedtheconceptofconvexitycumconcavityonsoftsetstocoverabovetopicsunderuncertainscenario. Inthisstudy,atheoreticandanalyticalapproachisemployedtodevelopaconceptualframeworkofconvexity cumconcavityonhypersoftsetwhichisgeneralizedandmoreeffectiveconcepttodealwithoptimizationrelatingproblems.Moreover,somegeneralizedpropertieslike δ-inclusion,intersectionandunion,areestablished. Thenoveltyofthisworkismaintainedwiththehelpofillustrativeexamplesandpictorialversionfirsttimein literature.
Keywords: ConvexSoftSet;ConcaveSoftSet;hypersoftSet;convexhypersoftset;concavehypersoftset. —————————————————————————————————————————-
1. Introduction
Thetheoriesliketheoryofprobability,theoryoffuzzysets,andtheintervalmathematics, areconsideredasmathematicalmeanstotacklemanyIntricateproblemsinvolvingvarious uncertaintiesindifferentfieldsofmathematicalsciences.Thesetheorieshavetheirowncomplexitieswhichrestrainthemtosolvetheseproblemssuccessfully.Thereasonforthesehurdles is,possibly,theinadequacyoftheparametrizationtool.Amathematicaltoolisneededfor dealingwithuncertaintieswhichshouldbefreeofallsuchImpediments.In1999,Molodtsov[1] hasthehonortointroducethesuchmathematicaltoolcalledsoftsetsinliteratureasanew
AtiqeUrRahman,MuhammadSaeedandFlorentinSmarandache,ConvexandConcaveHypersoftSets withSomeProperties
parameterizedfamilyofsubsetsoftheuniverseofdiscourse.In2003,Majietal.[2]extended theconceptandintroducedsomefundamentalterminologiesandoperationslikeequalityof twosoftsets,subsetandsupersetofasoftset,complementofasoftset,nullsoftset,absolute softset,AND,ORandalsotheoperationsofunionandintersection.TheyverifiedDeMorgan’slawsandanumberofotherresultstoo.In2005,Peietal.[3]discussedtherelationship betweensoftsetsandinformationsystems.Theyshowedthesoftsetsasaclassofspecial informationsystems.In2009,Alietal.[4]pointedseveralassertionsinpreviousworkofMaji etal.anddefinednewnotionssuchastherestrictedintersection,therestrictedunion,the restricteddifferenceandtheextendedintersectionoftwosoftsets.In2010,2011,Babithaet al.[5,6]introducedtheconceptsofsoftsetrelationsasasubsoftsetoftheCartesianproduct ofthesoftsetsandalsodiscussedmanyrelatedconceptssuchasequivalentsoftsetrelation, partition,compositionandfunction.In2011,Sezginetal.[7],Geetal.[8],Fuli[9]gave somemodificationsintheworkofMajietal.andalsoestablishedsomenewresults.Many researchers[10]-[19]developedcertainhybridswithsoftsetstogetmoregeneralizedresults forimplementationindecisionmakingandotherrelateddisciplines.
In2013,Deli[20]definedsoftcovexandsoftconcavesetswithsomeproperties.In2016, Majeed[21]investigatedsomemorepropertiesofconvexsoftsets.Shedevelopedtheconvex hullandtheconeofasoftsetwiththeirgeneralizedresults.In2018,Salihetal.[22]defined strictlysoftconvexandstrictlysoftconcavesetsandtheydiscussedtheirproperties. In2018,Smarandache[23]introducedtheconceptofhypersoftsetandin2020,M.Saeedet al.[24]extendedtheconceptanddiscussedthefundamentalsofhypersoftsetsuchashypersoft subset,complement,nothypersoftset,aggregationoperatorsalongwithhypersoftsetrelation, subrelation,complementrelation,function,matricesandoperationsonhypersoftmatrices. Convexityisanessentialconceptinoptimization,recognitionandclassificationofcertain patterns,processinganddecompositionofimages,antismatroids,discreteeventsimulation, dualityproblemsandmanyotherrelatedtopicsinoperationresearch,mathematicaleconomics,numericalanalysisandothermathematicalsciences.Deliprovidedamathematicaltoolto tackleallsuchproblemsundersoftsetenvironment.Hypersoftsettheoryismoregeneralized thansoftsettheorysoit’stheneedoftheliteraturetocarveoutaconceptualframeworkfor solvingsuchkindofproblemsundermoregeneralizedversioni.e.hypersoftset.Therefore,to meetthisdemand,anabstractandanalyticalapproachisutilizedtodevelopabasicframework ofconvexityandconcavityonhypersoftsetsalongwithsomeimportantresults.Examples andpictorialversionofconvexityandconcavityonhypersoftsetsarepresentedfirsttimein literature.
Therestofthisarticleisstructuredasfollows:Section2recallssomebasicdefinitionsand termsfromliteraturetosupportmainresults.Section3discussesthemainresultsi.e.convex
AtiqeUrRahman,MuhammadSaeedandFlorentinSmarandache,ConvexandConcave HypersoftSetswithSomeProperties
andconcavehypersoftsetsalongwithsomegeneralizedresults.Section4concludesthepaper anddescribesfuturedirections.Throughoutthepaper, G , J • , and P ( ),willplaytherole of Rn,unitinterval,universalsetandpowersetrespectively.
2. Preliminaries
Inthissection,somefundamentaltermsregardingsoftset,hypersoftsetandtheirconvexitycum-concavityarepresented.
Definition2.1. [1](SoftSet)
Let beaninitialuniversesetandletEbeasetofparameters.Apair(hS ,E)iscalleda softsetover ,where hS isamappinggivenby hS : E → P (U ).Inotherwords,asoftset (hS ,E)over isaparameterizedfamilyofsubsetsof .For ω ∈ E,hS (ω)maybeconsidered asthesetof ω-elementsor ω-approximateelementsofthesoftset(hS ,E).
Definition2.2. [2] Let(fS ,A)and(gS ,B)betwosoftsetsoveracommonuniverse , (1) wesaythat(fS ,A)isa softsubset of(gS ,B)denotedby(fS ,A) ⊆ (gS ,B)if i A ⊆ B,and ii ∀ω ∈ A,fS (ω)and gS (ω)areidenticalapproximations.
(2) the union of(fS ,A)and(gS ,B),denotedby(fS ,A) ∪ (gS ,B),isasoftset(hS ,C), where C = A ∪ B and ω ∈ C, hS (ω)= fS (ω),ω ∈ A B gS (ω),ω ∈ B A fS (ω) ∪ gS (ω),ω ∈ A ∩ B
(3) the intersection of(fS ,A)and(gS ,B)denotedby(fS ,A) ∩ (gS ,B),isasoftset (hS ,C),where C = A ∩ B and ω ∈ C,hS (ω)= fS (ω)or gS (ω)(asbotharesameset).
Definition2.3. [2](ComplementofSoftSet)
Thecomplementofasoftset(hS ,A),denotedby(hS ,A)c,isdefinedas(hS ,A)c =(hS c , ¬A) where hS c : ¬A → P ( ) isamappinggivenby hS c(ω)= − hS (¬ω)∀ω ∈¬A.
Definition2.4. [23](HypersoftSet)
Let beauniverseofdiscourse, P ( )thepowersetof .Let a1,a2,a3,.....,an,for n ≥ 1,bendistinctattributes,whosecorrespondingattributevaluesarerespectivelythesets A1,A2,A3,.....,An,with Ai ∩ Aj = ∅,for i = j,and i,j ∈{1, 2, 3,...,n} Thenthepair
AtiqeUrRahman,MuhammadSaeedandFlorentinSmarandache,ConvexandConcave HypersoftSetswithSomeProperties
(hHS ,G),where G = A1 × A2 × A3 × ..... × An and hHS : G → P ( )iscalledahypersoftSet over
Definition2.5. [24](UnionofHypersoftSets)
Let(Φ,G1)and(Ψ,G2)betwohypersoftsetsoverthesameuniversalset ,thentheirunion (Φ,G1) ∪ (Ψ,G2)ishypersoftset(hHS ,C),where C = G1 ∪ G2 ; G1 = A1 × A2 × A3 × × An , G2 = B1 × B2 × B3 × × Bn and ∀ e ∈ C with hHS (e)= Φ(e) ,e ∈ G1 G2 Ψ(e) ,e ∈ G2 G1 Φ(e) ∪ Ψ(e) ,e ∈ G2 ∩ G1
Definition2.6. [24](IntersectionofHypersoftSets)
Let(Φ,G1)and(Ψ,G2)betwohypersoftsetsoverthesameuniversalset ,thentheir intersection(Φ,G1) ∩ (Ψ,G2)ishypersoftset(hHS ,C),where C = G1 ∩ G2 ;where G1 = A1 ×A2 ×A3 × ×An , G2 = B1 ×B2 ×B3 × ×Bn and ∀ e ∈ C with hHS (e)=Φ(e)∩Ψ(e) Formoredefinitionandresultsregardinghypersoftset,see[24–27].
Definition2.7. [20](δ-inclusion) The δ-inclusionofasoftset(hS , Λ)(where δ⊆ )isdefinedby (hS , Λ)δ = {ω ∈ Λ: hS (ω) ⊇ δ}
Definition2.8. [20](ConvexSoftSet) Thesoftset(hS , Λ)onΛiscalledaconvexsoftsetif hS ( ω +(1 ) µ) ⊇ hS (ω) ∩ hS (µ) forevery ω,µ ∈ Λand ∈ J • .
Definition2.9. [20](ConcaveSoftSet)
Thesoftset(hS , Λ)onΛiscalledaconcavesoftsetif hS ( ω +(1 ) µ) ⊆ hS (ω) ∪ hS (µ) forevery ω,µ ∈ Λand ∈ J •
Formoreaboutconvexsoft,see[20,21].
3. ConvexandConcavehypersoftsets
Hereconvexhypersoftsetsandconcavehypersoftsetsaredefinedandsomeimportant resultsareproved.
AtiqeUrRahman,MuhammadSaeedandFlorentinSmarandache,ConvexandConcave HypersoftSetswithSomeProperties
Figure 1. Convex hypersoft Set
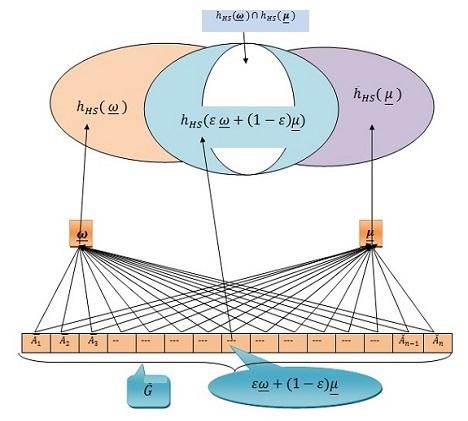
Definition 3.1. δ -inclusion for hypersoft Set
The δ inclusion of a hypersoft set (hH S , G) (where δ ⊆ ) is defined by (hH S , G)δ = {ω ∈ G : hH S (ω ) ⊇ δ }
Definition 3.2. Convex hypersoft Set
The hypersoft set (hH S , G) is called a convex hypersoft set if hH S ω + (1 ) µ ⊇ hH S (ω ) ∩ hH S µ for every ω , µ ∈ G where, G = A1 × A2 × A3 × ..... × An with Ai ∩ Aj = ∅, for i = j , and i, j ∈ {1, 2, 3, ..., n} ; hH S : G → P ( ) and ∈ J • .
Example 3.3. Suppose a university wants to observe(evaluate) the characteristics of its teach ers by some defined indicators. For this purpose, consider a set of teachers as a universe of discourse = {t1 , t2 , t3 , ..., t10 } The attributes of the teachers under consideration are the set Λ = {A1 , A2 , A3 }, where
A1 = Total experience in years
A2 = Total no. of publications
Atiqe Ur Rahman , Muhammad Saeed and Florentin Smarandache , Convex and Concave Hypersoft Sets with Some Properties
A3 =Student’sevaluationagainsteachteacher suchthattheattributesvaluesagainsttheseattributesrespectivelyarethesetsgivenas
A1 = {1year, 2years, 3years, 4years, 5years}
A2 = {1, 2, 3, 4, 5}
A3 = {Excellent(1),verygood(2),good(3),average(4),bad(5)}
Forsimplicity,wewrite
A1 = {1, 2, 3, 4, 5}
A2 = {1, 2, 3, 4, 5}
A3 = {1, 2, 3, 4, 5}
Thehypersoftset(hHS ,G)isafunctiondefinedbythemapping hHS : G → P ( )where G = A1 × A2 × A3 Sincethecartesianproductof A1 × A2 × A3 isa3-tuple.weconsider ω =(2, 1, 3),then thefunctionbecomes hHS (ω)= hHS (2, 1, 3)= {t1,t5}.Also,consider µ =(3, 2, 2),thenthe functionbecomes hHS (µ)= hHS (3, 2, 2)= {t1,t3,t4} Now hHS (ω) ∩ hHS (µ)= hHS ({2, 1, 3}) ∩ hHS ({3, 2, 2})= {t1,t5}∩{t1,t3,t4} = {t1} (1)
Let =0 6 ∈ J •,then,wehave ω +(1 )µ =0.6(2, 1, 3)+(10.6)(3, 2, 2)=0.6(2, 1, 3)+0.4(3, 2, 2) =(1 2, 0 6, 1 8)+(1 2, 0 8, 0 8)=(1 2+1 2, 0 6+0 8, 1 8+0 8)=(2 4, 1 4, 2 6) whichisagaina3-tuple.Byusingthedecimalroundoffproperty,weget(2, 1, 3)
hHS ( ω +(1 )µ)= hHS (2, 1, 3)= {t1,t5} (2) itisvividfromequations(1)and(2),wehave
hHS ω +(1 ) µ ⊇ hHS (ω) ∩ hHS µ Theorem3.4. (fHS ,S) ∩ (gHS ,T ) isaconvexhypersoftsetwhenboth (fHS ,S) and (gHS ,T ) areconvexhypersoftsets.
Proof. Supposethat(fHS ,S) ∩ (gHS ,T )=(hHS ,G)with G = S ∩ T ,for ω1,ω2 ∈ G; ∈ J • , wehavethen
hHS ( ω1 +(1 )ω2)= fHS ( ω1 +(1 )ω2) ∩ gHS ( ω1 +(1 )ω2)
As(fHS ,S)and(gHS ,T )areconvexhypersoftsets, fHS ( ω1 +(1 )ω2) ⊇ fHS (ω1) ∩ fHS (ω2) gHS ( ω1 +(1 )ω2) ⊇ gHS (ω1) ∩ gHS (ω2)
AtiqeUrRahman,MuhammadSaeedandFlorentinSmarandache,ConvexandConcave HypersoftSetswithSomeProperties
whichimplies
hHS ( ω1 +(1 )ω2) ⊇ (fHS (ω1) ∩ fHS (ω2)) ∩ (gHS (ω1) ∩ gHS (ω2)) andthus hHS ( ω1 +(1 )ω2) ⊇ hHS (ω1) ∩ hHS (ω2)
Remark3.5. If (hi HS ,Gi): i ∈{1, 2, 3,...} isanyfamilyofconvexhypersoftsets,thenthe intersection i∈I (hi HS ,Gi)isaconvexhypersoftset.
Remark3.6. Theunionofanyfamily (hi HS ,Gi): i ∈{1, 2, 3,...} ofconvexhypersoftsets isnotnecessarilyaconvexhypersoftset.
Theorem3.7. (hHS ,G) isconvexhypersoftsetiffforevery ∈ J • and δ ∈ P ( ), (hHS ,G)δ isconvexhypersoftset.
Proof. Suppose(hHS ,G)isconvexhypersoftset.If ω,µ ∈ G and δ ∈ P ( ),then hHS (ω) ⊇ δ and hHS µ ⊇ δ,itimpliesthat hHS (ω) ∩ hHS µ ⊇ δ. Sowehave, hHS ω +(1 ) µ ⊇ hHS (ω) ∩ hHS µ ⊇ δ ⇒ hHS ω +(1 ) µ ⊇ δ thus(hHS ,G)δ isconvexhypersoftset. Converselysupposethat(hHS ,G)δ isconvexhypersoftsetforevery ∈ J •.For ω,µ ∈ G ,(hHS ,G)δ isconvexhypersoftsetwith δ = hHS (ω) ∩ hHS µ .Since hHS (ω) ⊇ δ and hHS µ ⊇ δ,wehave ω ∈ (hHS ,G)δ and µ ∈ (hHS ,G)δ , ⇒ ω +(1 ) µ ∈ (hHS ,G)δ . Therefore, hHS ω +(1 ) µ ⊇ δ So hHS ω +(1 ) µ ⊇ hHS (ω) ∩ hHS µ , Hence(hHS ,G)isconvexhypersoftset.
AtiqeUrRahman,MuhammadSaeedandFlorentinSmarandache,ConvexandConcave HypersoftSetswithSomeProperties
Figure2. ConcavehypersoftSet
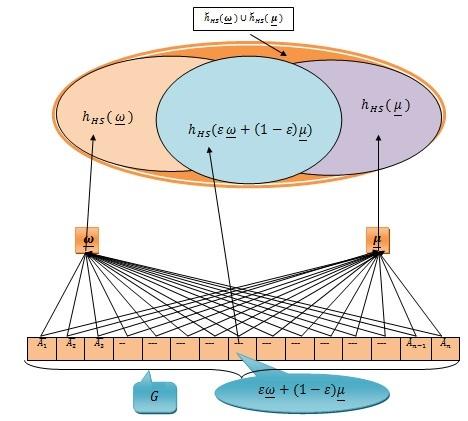
Definition3.8. ConcavehypersoftSet
Thehypersoftset(hHS ,G)onΛiscalleda concavehypersoftset if hHS ω +(1 ) µ ⊆ hHS (ω) ∪ hHS µ forevery ω =(A1,A2,A3,.....,An) ,µ =(B1,B2,B3,.....,Bn) ∈ G where, G = A1 × A2 × A3 × ..... × An with Ai ∩ Aj = ∅,for i = j,and i,j ∈{1, 2, 3,...,n} ; hHS : G → P ( )and ∈ J • .
Example3.9. ConsideringgivendatainExample3.3,wehave hHS (ω) ∪ hHS (µ)= hHS ({2, 1, 3}) ∪ hHS ({3, 2, 2})= {t1,t5}∪{t1,t3,t4} = {t1,t3,t4,t5} (3) itisvividfromequations(2)and(3),wehave hHS ω +(1 ) µ ⊆ hHS (ω) ∪ hHS µ
Theorem3.10. (fHS ,S)∪(gHS ,T ) isaconcavehypersoftsetwhenboth (fHS ,S) and (gHS ,T ) areconcavehypersoftsets. AtiqeUrRahman,MuhammadSaeedandFlorentinSmarandache,ConvexandConcave HypersoftSetswithSomeProperties
Proof. Supposethat(fHS ,S) ∪ (gHS ,T )=(hHS ,G)with G = S ∪ T ,for ω1,ω2 ∈ G; ∈ J • , wehavethen
hHS ( ω1 +(1 )ω2)= fHS ( ω1 +(1 )ω2) ∪ gHS ( ω1 +(1 )ω2)
As(fHS ,S)and(gHS ,T )areconcavehypersoftsets, fHS ( ω1 +(1 )ω2) ⊆ fHS (ω1) ∪ fHS (ω2) gHS ( ω1 +(1 )ω2) ⊆ gHS (ω1) ∪ gHS (ω2) whichimplies hHS ( ω1 +(1 )ω2) ⊆ (fHS (ω1) ∪ fHS (ω2)) ∪ (gHS (ω1) ∪ gHS (ω2)) andthus hHS ( ω1 +(1 )ω2) ⊆ hHS (ω1) ∪ hHS (ω2)
Remark3.11. If ( ˘ hiHS ,Gi): i ∈{1, 2, 3,...} isanyfamilyofconcavehypersoftsets,then theunion i∈I ( ˘ hiHS ,Gi)isaconcavehypersoftset.
Theorem3.12. (fHS ,S)∩(gHS ,T ) isaconcavehypersoftsetwhenboth (fHS ,S) and (gHS ,T ) areconcavehypersoftsets.
Proof. Supposethat(fHS ,S) ∩ (gHS ,T )=(hHS ,G)with G = S ∩ T ,for ω1,ω2 ∈ G; ∈ J • , wehavethen hHS ( ω1 +(1 )ω2)= fHS ( ω1 +(1 )ω2) ∩ gHS ( ω1 +(1 )ω2) As(fHS ,S)and(gHS ,T )areconcavehypersoftsets, fHS ( ω1 +(1 )ω2) ⊆ fHS (ω1) ∪ fHS (ω2) gHS ( ω1 +(1 )ω2) ⊆ gHS (ω1) ∪ gHS (ω2) whichimplies hHS ( ω1 +(1 )ω2) ⊆ (fHS (ω1) ∪ fHS (ω2)) ∩ (gHS (ω1) ∪ gHS (ω2)) andthus hHS ( ω1 +(1 )ω2) ⊆ hHS (ω1) ∪ hHS (ω2)
Remark3.13. Theintersectionofanyfamily ( ˘ hiHS ,Gi): i ∈{1, 2, 3,...} ofconcavehypersoftsetsisaconcavehypersoftset.
AtiqeUrRahman,MuhammadSaeedandFlorentinSmarandache,ConvexandConcave HypersoftSetswithSomeProperties
38,2020
Theorem3.14. (hHS ,G)c isaconvexhypersoftsetwhen (hHS ,G) isaconcavehypersoftset.
Proof. Supposethatfor ω1,ω2 ∈ G, ∈ J • and(hHS ,G)beconcavehypersoftset. Since(hHS ,G)isconcavehypersoftset, hHS ( ω1 +(1 )ω2) ⊆ hHS (ω1) ∪ hHS (ω2) or \ hHS ( ω1 +(1 )ω2) ⊇ \{hHS (ω1) ∪ hHS (ω2) }
If hHS (ω1) ⊃ hHS (ω2)then hHS (ω1) ∪ hHS (ω2)= hHS (ω1)therefore, \ hHS ( ω1 +(1 )ω2) ⊇ \ hHS (ω1) (4)
If hHS (ω1) ⊂ hHS (ω2)then hHS (ω1) ∪ hHS (ω2)= hHS (ω2)therefore, \ hHS ( ω1 +(1 )ω2) ⊇ \ hHS (ω2) (5)
From(4)and(5),wehave \ hHS ( ω1 +(1 )ω2) ⊇ ( \hHS (ω1)) ∩ ( \hM (ω2))
So,(hHS ,G)c isaconvexhypersoftset.
Theorem3.15. (hHS ,G)c isaconcavehypersoftsetwhen (hHS ,G) isaconvexhypersoftset.
Proof. Supposethatfor ω1,ω2 ∈ G, ∈ J • and(hHS ,G)beconvexhypersoftset. since(hHS ,G)isconvexhypersoftset, hHS ( ω1 +(1 )ω2) ⊇ hHS (ω1) ∩ hHS (ω2) or \ hHS ( ω1 +(1 )ω2) ⊆ \{hHS (ω1) ∩ hHS (ω2) }
If hHS (ω1) ⊃ hHS (ω2)then hHS (ω1) ∩ hHS (ω2)= hHS (ω2)therefore, \ hHS ( ω1 +(1 )ω2) ⊆ \ hHS (ω2) (6)
If hHS (ω1) ⊂ hHS (ω2)then hHS (ω1) ∩ hHS (ω2)= hHS (ω1)therefore, \ hHS ( ω1 +(1 )ω2) ⊆ \ hHS (ω1) (7)
From(6)and(7),wehave
\ hHS ( ω1 +(1 )ω2) ⊇ ( \hHS (ω1)) ∪ ( \hM (ω2))
So(hHS ,G)c isaconcavehypersoftset.
Theorem3.16. (hHS ,G) isconcavehypersoftsetiffforevery ∈ J • and δ ∈ P ( ), (hHS ,G)δ isconcavehypersoftset.
AtiqeUrRahman,MuhammadSaeedandFlorentinSmarandache,ConvexandConcave HypersoftSetswithSomeProperties
38,2020
Proof. Suppose(hHS ,G)isconcavehypersoftset.If ω,µ ∈ G and δ ∈ P ( ),then hHS (ω) ⊇ δ and hHS µ ⊇ δ,itimpliesthat hHS (ω) ∪ hHS µ ⊇ δ. Sowehave, δ ⊆ hHS (ω) ∩ hHS µ ⊆ hHS ω +(1 ) µ ⊆ hHS (ω) ∪ hHS µ ⇒ δ ⊆ hHS ω +(1 ) µ thus(hHS ,G)δ isconcavehypersoftset. Converselysupposethat(hHS ,G)δ isconcavehypersoftsetforevery ∈ J •.For ω,µ ∈ G ,(hHS ,G)δ isconcavehypersoftsetwith δ = hHS (ω) ∪ hHS µ .Since hHS (ω) ⊆ δ and hHS µ ⊆ δ,wehave ω ∈ (hHS ,G)δ and µ ∈ (hHS ,G)δ , ⇒ ω +(1 ) µ ∈ (hHS ,G)δ . Therefore, hHS ω +(1 ) µ ⊆ δ So hHS ω +(1 ) µ ⊆ hHS (ω) ∪ hHS µ , Hence(hHS ,G)isconcavehypersoftset.
4. Conclusion
Inthisstudy,convexitycumconcavityonhypersoftsets,isconceptualizedbyadoptingan abstractandanalyticaltechnique.Thisisnoveladditionintheliteratureandmayenable theresearcherstodealimportantapplicationsofconvexityunderhypersoftenvironmentwith preciseresults.Moreover,someimportantresultsareestablished.Futureworkmayinclude theintroductionofstrictlyandstronglyconexitycumconcavity,convexhull,convexconeand manyothertypesofconvexitylike(m,n)-convexity, φ-convexity,gradedconvexity,triangular convexity,concavoconvexityetc.onhypersoftset.Itmayalsoincludetheextensionofthis workbyconsideringthemodifiedversionsofcomplement,intersectionandunionasdiscussed in[2]-[4].
References
[1] Molodtsov,D.,SoftSetTheory-FirstResults, Comput.Math.withAppl. 1999,37,19-31.
[2] Maji,P.K.;Biswas,R.,andRoy,A.R.,SoftSetTheory, Comput.Math.withAppl. 2003,45,555-562.
[3] Pei.D.,andMiao.D.,Fromsoftsettoinformationsystem, Ininternationalconferenceofgranularcomputing,IEEE 2005,2,617-621.
[4] Ali,M.I.;Feng,F.;Liu,X.;Min,W.K.,andSabir,M.,Onsomenewoperationsinsoftsettheory, Comput.Math.withAppl. 2009,57,1547-1553.
[5] BabithaK.V.,andSunilJ.J.,Softsetrelationsandfunctions, Comput.Math.withAppl. 2010,60,18401849.
AtiqeUrRahman,MuhammadSaeedandFlorentinSmarandache,ConvexandConcave HypersoftSetswithSomeProperties
[6] BabithaK.V.,andSunilJ.J.,Transitiveclosureandorderinginsoftset, Comput.Math.withAppl. 2011, 61,2235-2239.
[7] Sezgin,A.,andAtag¨ un,A.O.,Onoperationsofsoftsets, Comput.Math.withAppl. 2011,61(5),14571467.
[8] GeX.,andYangS.,Investigationsonsomeoperationsofsoftsets, WorldAcademyofScienceEngineering andTechnology 2011,75,1113-1116.
[9] Li,F.,Notesonsoftsetoperations, ARPNJournalofsystemsandsoftwares 2011,205-208.
[10] Abdel-Basset,M.;Gamal,A.;Son,L.H.,andSmarandache,F.,ABipolarNeutrosophicMultiCriteria DecisionMakingFrameworkforProfessionalSelection, AppliedSciences 2020,10(4),1202.
[11] Abdel-Basset,M.;Mohamed,R.;Zaied,A.E.N.H.;Gamal,A.,andSmarandache,F.,Solvingthesupply chainproblemusingthebest-worstmethodbasedonanovelPlithogenicmodel, InOptimizationTheory BasedonNeutrosophicandPlithogenicSets(pp.1-19).AcademicPress 2020.
[12] Abdel-Basset,M.;Ding,W.;Mohamed,R.,andMetawa,N.,AnintegratedplithogenicMCDMapproach forfinancialperformanceevaluationofmanufacturingindustries, RiskManagement 2020,22(3),192-218.
[13] Abdel-Basst,M.;Mohamed,R.,andElhoseny,M.,Anovelframeworktoevaluateinnovationvaluepropositionforsmartproduct-servicesystems, EnvironmentalTechnologyandInnovation 2020,101036.
[14] Martin,N.,andSmarandache,F.,ConcentricPlithogenicHypergraphbasedonPlithogenicHypersoft setsANovelOutlook, NeutrosophicSetsandSystems 2020,33(1),5.
[15] Khalid,H.E.;Smarandache,F.,andEssa,A.K.,Thebasicnotionsfor(over,off,under)neutrosophic geometricprogrammingproblems, NeutrosophicSetsandSystems 2018,22,50-62.
[16] Bera,T.,andMahapatra,N.K.,NeutrosophicSoftNormedLinearSpace, NeutrosophicSetsandSystems 2018,23(1),6.
[17] Mondal,B.;Kar,C.;Garai,A.,andRoy,T.K.,OptimizationofEOQModelwithLimitedStorageCapacity byNeutrosophicGeometricProgramming, NeutrosophicSetsandSystems 2018,22(1),2.
[18] Chakraborty,A.;Mondal,S.,andBroumi,S.,De-neutrosophicationtechniqueofpentagonalneutrosophic numberandapplicationinminimalspanningtree, NeutrosophicSetsandSystems 2019,29(1),1.
[19] Chakraborty,A.;Broumi,S.,andSingh,P.K.,Somepropertiesofpentagonalneutrosophicnumbersand itsapplicationsintransportationproblemenvironment, NeutrosophicSetsandSystems 2019,28(1),16.
[20] Deli,I.,ConvexandConcaveSoftSetsandSomeProperties, ResearchGate 2013
[21] Majeed,S.N.,Somenotionsonconvexsoftsets, Ann.FuzzyMath.Inform. 2016,12(4),517-526.
[22] Salih,H.M.,andSabir,P.O.,SomeNewPropertiesofConvexandConcaveSoftSets, DiyalaJournalfor PureSciences 2018,15(9).
[23] Smarandache,F.,ExtensionofSoftSettoHypersoftSet,andthentoPlithogenicHypersoftSet, NeutrosophicSetsSyst. 2018,22,168-170.
[24] Saeed,M.;Ahsan,M.;Siddique,M.K.,andAhmad,M.R.,AStudyofTheFundamentalsofHypersoft SetTheory, InternationalJournalofScientificandEngineeringResearch 2020,11.
[25] Saqlain,M.;Jafar,N.;Moin,S.;Saeed,M.,andBroumi,S.,SingleandMulti-valuedNeutrosophicHypersoftsetandTangentSimilarityMeasureofSinglevaluedNeutrosophicHypersoftSets, NeutrosophicSets Syst. 2020,32(1),20.
[26] Saqlain,M.;Moin,S.;Jafar,M.N.;Saeed,M.,andSmarandache,F.,AggregateOperatorsofNeutrosophic HypersoftSet, NeutrosophicSetsSyst. 2020,32(1),18.
[27] Saqlain,M.;Saeed,M.;Ahmad,M.R.,andSmarandache,F.,GeneralizationofTOPSISforNeutrosophic HypersoftsetusingAccuracyFunctionanditsApplication, NeutrosophicSetsSyst. 2019,27(1),12.
Received: June 10, 2020. Accepted: Nov 25, 2020
AtiqeUrRahman,MuhammadSaeedandFlorentinSmarandache,ConvexandConcave HypersoftSetswithSomeProperties
