Bipolar fuzzy soft mappings with application to bipolar disorders

Vol.12,No.7(2019)1950080(31pages)

c WorldScientificPublishingCompany DOI:10.1142/S1793524519500803

Bipolarfuzzysoftmappingswithapplication tobipolardisorders

MuhammadRiaz∗ andSyedaTayybaTehrim† DepartmentofMathematics

UniversityofthePunjab,Lahore,Pakistan ∗mriaz.math@pu.edu.pk †tayyabatehrim126@gmail.com

Received29April2019 Revised22July2019 Accepted16August2019 Published4October2019

Bipolardisorderisaneurologicaldisorderthatconsistsoftwomainfactors,i.e.mania anddepression.Therearetwomaindrawbacksinclinicaldiagnosisofthebipolardisorder.First,bipolardisorderismostlywronglydiagnosedasunipolardepressioninclinical diagnosis.Thisis,becauseinclinicaldiagnosis,thefirstfactorisoftenneglecteddue toitsapproachtowardpositivity.Consequently,theelementofbipolarityvanishesand thediseasebecomesworse.Second,thetypesofbipolardisorderaremostlymisdiagnosedduetosimilarsymptoms.Toovercometheseproblems,thebipolarfuzzysoft set(BFS-set)andbipolarfuzzysoftmappings(BFS-mappings)areusefultotackle bipolarityandtoconstructastrongmathematicalmodelingprocesstodiagnosethis diseasecorrectly.Thistechniqueisextensivebutsimpleascomparedtoexistingmedical diagnosismethods.Achart(relationbetweendifferenttypesandsymptomsofbipolar disorder)isprovidedwhichcontainsdifferentrangesovertheinterval[ 1, 1].Aprocess ofBFS-mappingsisalsoprovidedtoobtaincorrectdiagnosisandtosuggestthebest treatment.Lastly,ageneralizedBFS-mappingisintroducedwhichishelpfultokeep patient’simprovementrecord.Thecasestudyindicatesthereliability,efficiencyand capabilityoftheachievedtheoreticalresults.Further,itrevealsthattheconnectionof softsetwithbipolarfuzzysetisfruitfultoconstructaconnectionbetweensymptoms whichminimizethecomplexityofthecasestudy. Keywords :BFS-set;BFS-mappings;operationsandpropertiesofBFS-mappings; Bipolarity;BipolarIdisorder;BipolarIIdisorder;Cyclothymia. MathematicsSubjectClassification2010:03B52,03E72

[42]broughtouttheideaoffuzzysetsin1965.Fuzzysettheoryhasbeenauspiciouslyadaptedinthefieldofmedicalsciences[10,16,24].Thetheoryhasbeen extendedwithmanyhybridstructures.Theresearchershavebeenpublishedagood numberofresearchpapersonextensionsoffuzzysets.Asanextensionoffuzzytheory,manysettheorieshavebeendeveloped,including,intervalvaluedsettheory [43],intuitionisticfuzzysettheory[5],bipolarfuzzysettheory[44],neutrosophic settheory[35],m-polarfuzzysettheory[7],etc.Allthesetheorieshavebeendevelopedaccordingtothenecessityofhandlingspecifictypeofdataanditsuseability indifferentsuitabledomains.Riaz etal. workedondifferentextensionsoffuzzyset theoryandtheirapplications[25–30,32,34].

In1999,Molodstov[21]broughtoutnewabstraction,namely,softset(amathematicaltoolwhichhandleambiguitiesandimprecisionsinparametricmanners). Theroleofparametersisanessentialpartinanalyzingandscrutinizinginformation ormakingadecision.Recently,thetheoryhasbeenaffirmedtobeanappropriateparametrizationmechanism.Inshort,theoryofsoftsetfascinatinglyovercame manyproblemsraisedonimplementingtheexistingtheories.Thetheorygotgreat attentionofthescientistsandresearchers becauseofitsmiscellaneousapplications. Inlastfewyears,thedomainofsoftsethasbeenpopularamongresearchers.Maji etal. [18,19]introducedsomeusefulbasicoperationsonsoftsetsaswellasits implementationindecisionsupportsystem.Ali etal. [1,2]presentedsomenew operationonsoftsetandalgebraicstructuresofsoftsets.

Fordataanalyzingofmanytypes,bipolarityofknowledgeisavitalparttobe consideredwhiledevelopingamathematicalframeworkformostofthesituations. Bipolarityindicatesthepositiveandnegativeaspectsofaparticularproblem.The conceptbehindthebipolarityisthatahugerangeofhumandecisionsanalysis isinvolvedinbipolarsubjectivethoughts.Forillustration,happinessandgrief, sweetnessandsourness,effectsandsideeffectsaretwodifferentaspectsofdecision analysis.Theequilibriumandmutualcoexistenceofthesetwoaspectsaretreated asakeyforbalancedsocialenvironment. Thefuzzysetandsoftsettheoriesare notenoughtohandlesuchtypeofbipolarity;forinstance,amedicinewhichisnot effectivemaynotbehavinganysideeffect.Zhang[45]introducedtheextension offuzzysetwithbipolarity,called,bipolar-valuedfuzzysets.Bipolarfuzzysetis suitableforinformationwhichinvolvespropertyaswellasitscounterproperty.Lee [17]discussedsomebasicoperationsofbipolar-valuedfuzzyset.Aslam etal. [4] broughtouttheabstractionofbipolarfuzzysoftset(BFS-set).Theydiscussedthe operationsofBFS-setsandaproblemofdecision-making.Inshort,bipolarfuzzy sethasbeenusedinmanymathematicaldomains[11,12,23,37–41].Theconcept ofmappingisausefultooltobeconsideredwhiledevelopingmodelsformany problems.Amappingisanassociationbetweentwoormoredomainsundersome specificrules.Differentfieldsincluding,mathematics,computersciences,chemistry, psychologyandlogicsadaptedconceptofmappingundertheirspecificcriteria.In 2010,MajumdarandSamanta[20]introducedmappingsonsoftsetsandtheir implementationinmedicaldiagnosis.KharalandAhmadpresentedtheideaof

Bipolarfuzzysoftmappingswithapplicationtobipolardisorders softmappings[15]andfuzzysoftmappings[14].GunduzandBayramov[9]also discussedcontinuous,openandclosedfuzzysoftmappings.BashirandSaleh[6] introducedmappingsonintuitionisticfuzzysoftclasses.Karata¸sandAkda˘g[13] discussedcontinuous,openandclosedintuitionisticfuzzymappings.

Accordingtoworldmentalhealthsurvey(WHOs),Bipolardisordershavebeen classifiedasthediseasewithsecondmajorcauseofincapabilitytoperformdaily task[3].Sincetheredoesnotexistanybiologicalmarkerforthisdisorder,thecharacterofclinicaldiagnosisofbipolardisorderisstillindispensable.Unfortunately, statisticsshowsthatonly20%ofpatientswithbipolardisorderhavingadepressive episodearediagnozedwithbipolardisorderwithinthefirstyearofseekingtreatment,sincetheylooksimilartotheoneswithunipolardepression[8].Peoplewith bipolardisordergothroughunexpectedchangesinmood.Thesechangesinclude feelingverycheerfulandhopefulwhichisrepresentedby“highs”andthenfeeling verycheerlessandhopelesswhichisrepresentedby“lows”.Theyoftenswingback tonormalmood.Thefeelingsofhighsareknownasmania,ontheotherhand, feelingsoflowsareknownasdepression.Thesecondarylevelofmaniaperiods arecalledhypomaniaepisodesandseverefeelingsofdepressionarecalledmajor depression.Bipolardisorderoccursintheratioof1inevery100adults.Bipolar disorderiscommonattheageofearly20sandrarelyusualaftertheageof40. Iteffectsbothmaleandfemaleequally.Thesymptomscanvaryfrompersonto person,dependingontheperson’shistoryofillness.Thesymptomsalsovaryfrom timetotime.Thebipolaritycanexistinotherdiseasesaswell,butinbipolar disorderitisusualratherthananomaly.Thechiefmotivationofthispaperisto developamathematicalmodelforstablebipolarityinbipolardisorderbyconsideringdomainsofbipolarity,fuzzinessandsoftness.Sincethereexistmanymodels infuzzysystemwhichhavebeenefficientlyappliedtomedicaldiagnosis,among whichbipolarfuzzysoftsetismoresuitabletodiagnosebipolardisorder.Thereis nodoubtthatthemethodspresentedby[20]and[15]aresimpleanduseful,but theyarenotcomprehensiveenoughtodiagnozesuchtypeofcomplicateddiseases, resultinginaccuracyintherealworldclinicaldiagnosis.Theareaofthebrainlinked withbipolardisordercanbeseeninFig.1Thus,weproposeanovelBFS-mapping methodtobipolardisorderdiagnosis.Byconsideringthefeaturesofbipolardisorder diagnosis,acomprehensiveBFS-mappingmethodtobipolardisorderdiagnosisis presented.TheproposedmethodisdependentondifferenttypesofBFS-mappings andtheirrelevantproperties.Theprop osedmethodismoreefficientascompared totheexistingmethodsofmedicaldiagnosis.Theadvantagesofthismethodare givenasfollows:First,achartofconditionsandtheirintensityisprovided,whichis helpfultodeterminetheseverenessofdisease.Second,thesoftsetisinvolvedwhich isefficientenoughtopresenttheparametersorattributetowholeproblemnicely. Third,BFS-mappingsandBFSmax–mincompositionareusedtocreaterelations betweentwodifferentphenomena.Fourth,arangeisprovidedforfinaldiagnosis ofthreetypesofbipolardisorderandequilibriumstateofmind.Fifth,thebest treatmentisalsodiscussedinthemethod.Last,thegeneralizedBFS-mappingis

Fig.1.Areaofbrainlinkedtobipolardisorder.

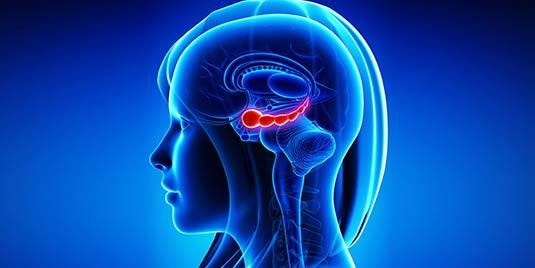
Source:UniversityofTexasHealthScienceCenteratHouston.

providedwhichishelpfultokeeparecordofimprovementofeachpatient.The motivationalworkofthispaperislistedasfollows:(1)Intheory,differenttypesof mappingtheiroperationsandpropertiesofabipolarfuzzysoftsetarediscussed. (2)Inmethodology,ahybridizationoffuzzydecision-makingmethodtobipolardisorderdiagnosisisproposed,whichishelpfultodiagnosetypesofbipolardisorder, besttreatmentandimprovementrecord.Theremainderofthispaperisstructured asfollows.InSec.2,somebasicdefinitionsarepresented.InSec.3,bystudyingthe featuresofbipolardisorderdiagnosis,themotivationtointroducethenewmethod ispresented.Second,somenovelconceptsandtheoriesaboutbipolarfuzzysoft informationareproposed.Differenttypesofmappingstheiroperationsandpropertiesarepresented.Last,ahybridmethodtobipolardisorderdiagnosisisproposed basedonBFS-mappings.InSec.4,thecomputativecaseisdiscussed.InSec.5, comparisonanddiscussionareincludedtohighlighttheuseability,reliabilityand necessityofthetheoreticalresultsobtained.ThepaperisconcludedinSec.6.

2.Preliminaries

Inthissection,wereviewsomebasicdefinitions.

Definition2.1([42]). Considertheuniversalset V andmembershipfunction f : V → [0, 1].Then, Vf isafuzzyseton V ifeachelement ξ ∈ V isassociatedwith degreeofmembership,whichisarealnumberin[0, 1]anditisdenotedby fξ .

Definition2.2([21]). Considertheuniversalset V andasetofdecisionvariables D .Let A1 ⊆D and K : A1 →P (V )betheset-valuedfunction,where P (V )isthe powersetof V .Then, KA1 or(K, A1 )denotesasoftseton V Definition2.3([45]). Abipolarfuzzyseton V isoftheform K = {(ξ,δ + K (ξ ),δK (ξ )):forall ξ ∈ V }, where δ + K (ξ )denotesthepositivemembershiprangesover[0, 1]and δK (ξ )denotes thenegativemembershiprangesover[ 1, 0].

Bipolarfuzzysoftmappingswithapplicationtobipolardisorders

Definition2.4([4]). Let A1 ⊂D anddefineamapping K : A1 →BF (V ),where BF (V )representsthefamilyofallbipolarfuzzysubsetsof V .Then, KA1 or(K, A1 ) iscalledabipolarfuzzyset(BFS-set)on V .ABFS-setcanbedefinedas

KA1 = {Kp =(ξ,δ + p (ξ ),δp (ξ )):forall ξ ∈ V and p ∈A1 }

Example2.5. Let V ={ξ1 , ξ2 , ξ3 } bethesetofthreecompaniesofhomeappliances and D = {p1 ,p2 ,p3 } bethesetofdecisionvariablesrelatedtotheirproductivity, where p1 :representsdurability. p2 :representsexpensive. p3 :representseconomical.

Supposethat A1 = {p1 ,p3 }⊂D ,nowaBFS-set KA1 canbewrittenasfollows: KA1 = Kp1 = {(ξ1 , 0.12, 0.53), (ξ2 , 0.31, 0.62), (ξ3 , 0.41, 0.23)}, Kp3 = {(ξ1 , 0 82, 0 11), (ξ2 , 0 33, 0 61), (ξ3 , 0 42, 0 32)}

Definition2.6([4]). ABFS-set KD iscalledanullBFS-set,if δ + p (ξ )=0and δp (ξ )=0,foreach p ∈D and ξ ∈ V andwewriteitas φD

Definition2.7([4]). ABFS-set KD iscalledanabsoluteBFS-set,if δ + p (ξ )=1 and δp (ξ )= 1,foreach p ∈D and ξ ∈ V andwewriteitas VD .

Definition2.8([4]). ThecomplementofaBFS-set KA1 isrepresentedby(KA1 )c andisdefinedby(KA1 )c = {Kp =(ξ, 1 δ + p (ξ ), 1 δp (ξ )): ξ ∈ V,p ∈A1 } Definition2.9([4]). ConsidertwoBFS-sets KA1 and KA2 on V .Then, KA1 isa BFS-subsetof KA2 ,if (i) A1 ⊆A2 (ii) δ + A1 (ξ ) ≤ δ + A2 (ξ ), δA1 (ξ ) ≥ δA2 (ξ ). Thenwecanwriteitas KA1 ⊆KA2 .

Definition2.10([4]). Let K1 A1 and K2 A2 ∈BF (VD ).Then,intersectionof K1 A1 and K2 A2 isaBFS-set KA ,where A = A1 ∩A2 = ∅, K : A→BF (V )isamapping definedby Kp = K1 p ∩K2 p ∀ p ∈A anditiswrittenas KA = K1 A1 ∩K2 A2 .

Definition2.11([4]). Let K1 A1 and K2 A2 ∈BF (VD ).Theunionof K1 A1 and K2 A2 isaBFS-set KA ,where A = A1 ∪A2 and K : A→BF (V )isamappingdefinedas Kp = K1 p if p ∈A1 \A2

= K2 p if p ∈A2 \A1

˜ ∪K2 A2

3.PropoundedTechnique

Inthissection,first,byconsideringthefeaturesofthebipolardisorderdiagnosis, themotivationofthepresentedtechniqueisproposed.Second,relevanttheoriesof methodtobipolardisorderdiagnosis,includingdifferenttypesofmappings,useful operationsandpropertiesunderthebipolarfuzzysoftenvironmentarepropounded. Last,dependingontheanalysis,aBFS-mappingmethodtobipolardisorderdiagnosis,besttreatmentandimprovementrecordispresented.

3.1. Investigationofbipolardisorderdiagnosisproblem

Inclinicalpsychopharmacologyandbiomedicalengineering,themodelingofmathematicsanddiagnosticstudyofpsychologicaldisordershavegreatimportance[36]. Tofindanappropriatemathematicalframework,thefeaturesofthebipolardisorderdiagnosisarestudied,andapropermathematicalframeworktotackleitis addressedasfollows:Assaidearlier,bipolarityisthemainfeatureofbipolardisorderdiagnosis.Similarly,vaguenessorfuzzinessofbipolardisorderdiagnosisis anotherfeature.Thus,itisessentialtofindaproperfuzzyframework,whichcan tackleuncertaintiesaswellasbipolarityindiagnosisofbipolardisorder.Thefollowingtableprovidesinformationonwhichsetismoresuitabletocapturebipolarity inbipolardisorderdiagnosisprocess.Ifwelookatthebipolarityfromsemantics pointofview,weobtainTable1whichisasemanticalcomparisonofdifferent settheories.Althoughinpattern,bipolarfuzzysetisequivalenttoneutrosophic set[22].Whereas,semantically,bipolarfuzzyset[46]representsequilibriumand neutrosophicsetwhichprovidedausualimpartiality.Nodoubttheneutrosophic setshavebeenauspiciouslyappliedtomedicaldiagnosis.Bythiscomparison,we concludethatbipolarfuzzysoftsetisdefinitelyasuitablecombinationtoseta frameworkforbipolardiagnostic.

Bipolarfuzzysoftmappingswithapplicationtobipolardisorders orstabilityprinciple.InChinesemedicine,symptomsareconsideredtobethelossof stabilityoftwosides.Thus,weuseZhang’sequilibriumconceptandorderrelationin ourpaper.Becausebipolardisordersareimbalanceofmoodanddisturbedharmony oftwodifferentsidesofastability,weusemultiplesymptomsandtheirconnections asparametersofsoftsettodiagnosecorrectly.Therearethreemaintypesofbipolar disorders.

BipolarIDisorder

Inthistype,apersonwashadoneormoreepisodesofhighormania,whichhasa durationofoneweekormore.Apersonmayencounterwithonlymaniaepisodes, butmostlysomepeoplealsoencounterwithepisodesofdepressionaswell.

BipolarIIDisorder

Inthistype,apersonhashadoneormoreperiodsofmajordepressionaswell asoneormoreepisodesofhypomania(lesssevereformofmania).Inthistype,a personneverencounterswithamaniaepisode.Thistypeisnotlightformoftype I,butisdiagnosedseparately.NotethatmaniaepisodesoftypeIcanbesevere andseriouswhichcancauseaseriousloss,whereaslong-termdepressionperiodsof typeIIcanalsobedangerousandmayleadtosuicidalattempt.

Cyclothymia

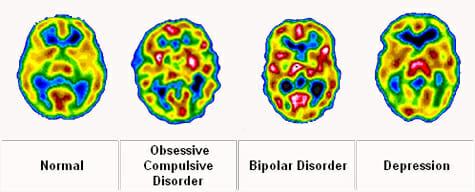
Inthistype,swingsofmoodasdescribedinprevioustypesarenotasmuchsevere asintypesIandII,butcanlastforalongtime,whichcancausefordeveloping itintotypeIortypeII.Apersonmayhavelesssevereepisodesofhypomaniaand someperiodsofdepression(lessseverethanmajordepression).Thecomparisonof normalbrainwithdisorderedbrainscanbeseeninFig.2.

3.2. Proposedtheoriesaboutbipolarfuzzysoftset

Inthissection,theBFS-mappingsandinverseBFS-mappingsaredefined.Different typesofBFS-mappings,including,BFS-surjective,BFS-injectiveandBFS-bijective mappingsarealsopresentedinthissection.Somebasicoperationsandpropertiesof

Fig.2.Comparisonofnormalbrainwithbipolardisorderbrain. Source:BrainMattersImagingCenters(2007).

BFS-mappingsareincluded.BFSmax–mincompositionisdefinedinthissection. TheseBFS-mappingsareusefulthroughoutthistechnique.

Definition3.1. Considerauniversalset V andasetofdecisionvariables D ,then BF (VD )representsthefamilyofallBFS-setson V withdecisionvariablesfrom D anditiscalledclassofBFS-sets.





(









   

) max p∈g 1 (p )∩A δ (+) Kp (ξ ), if u 1 (ς ) = ∅, g 1 (p ) ∩A = ∅, 0, otherwise,

 ξ ∈u 1 (ς ) p∈g 1 (p )∩A Kp (ξ ), if u 1 (ς ) = ∅, g 1 (p ) ∩A = ∅, 0, otherwise, (3)

Definition3.3. Supposethat u : V → W and g : D→D betwomappings. Then,wedefineamapping f : BF (VD ) →BF (WD )asfollows:if KA isaBFS-set in BF (WD )for A ⊆D ,thenwehaveaBFS-set f 1 (KA )in BF (VD ),havingform f 1 (KA )= {Kp =(ξ,δ (+) f 1 (KA ) (p)(ξ ),δ ( ) f 1 (KA ) (p)(ξ )): for ξ ∈ V and p ∈ g 1 (A ) ⊆D},

1950080-8

where

δ (+) f 1 (KA ) (p)(ξ )=    δ (+) Kg(p) (u(ξ )), for g(p) ∈A , 0, otherwise, (4) δ ( ) f 1 (KA ) (p)(ξ )= δ ( ) Kg(p) (u(ξ )), for g(p) ∈A , 0, otherwise (5)

Oncombining(4)and(5),wehave

f 1 (KA )(p)(ξ )= K(g(p)) (u(ξ )), for g(p) ∈A , 0, otherwise. (6)

Then, f 1 (KA )iscalledBFSinverseimageof KA ,whichcanbeobtainedby using(6).

Example3.4. Considertwouniversalsets V = {ξ1 ,ξ2 ,ξ3 } and W = {ς1 ,ς2 ,ς3 } Let D = {p1 ,p2 ,p3 } and D = {p1 ,p2 ,p3 } becorrespondingsetsofdecisionvariables,respectively.LetusconsidertwoclassesofBFS-sets BF (VD )and BF (WD ). Supposethatthemappings u : V → W and g : D→D aredefinedas u(ξ1 )= ς1 , u(ξ2 )= ς2 , u(ξ3 )= ς3 , g(p1 )= p1 , g(p2 )= p2 , g(p3 )= p2 .

Let KA and KA betwoBFS-setsin BF (VD )and BF (WD ),respectively.



      KA = 

Kp1 = {(ς1 , 0.51, 0.33), (ς2 , 0.32, 0.21), (ς3 , 0.22, 0.31)}, Kp2 = {(ς1 , 0 32, 0 43)



 Kp1 = {(ξ1 , 0 33, 0 54), (ξ2 , 0 53, 0 64), (ξ3 , 0 63, 0 44)}, Kp2 = {(ξ1 , 0.53, 0.44), (ξ2 , 0.63, 0.54), (ξ3 , 0.73, 0.54)}, Kp3 = {(ξ1 , 0.63, 0.24), (ξ2 , 0.23, 0.14), (ξ3 , 0.43, 0.24)}.  p∈g 1 (p1 )∩A Kp   (ξ ) = ξ ∈{ξ1 }  p∈{p1 } Kp   (ξ ) 1950080-9

        Now,weobtaintheimageof KA underthemapping f : BF (VD ) →BF (WD )as follows: f(KA )(p 1 )(ς1 )= ξ ∈u 1 (ς1 )

= ξ ∈{ξ1 } ({(ξ1 , 0 33, 0 54), (ξ2 , 0 53, 0 64), (ξ3 , 0 63, 0 44)})(ξ ) = (0.33, 0.54)=(0.33, 0.54); similarly, f(KA )(p 1 )(ς2 )=(0 53, 0 64), f(KA )(p 1 )(ς3 )=(0 63, 0 44); bysimilarcalculationweobtain f(KA )(p 2 )(ς1 )= ξ ∈u 1 (ς1 )

 p∈g 1 (p2 )∩A Kp   (ξ ) = ξ ∈{ξ1 }  p∈{p2 ,p3 } Kp   (ξ ) = ξ ∈{ξ1 } ({(ξ1 , 0.63, 0.24), (ξ2 , 0.63, 0.14), (ξ3 , 0.73, 0.24)})(ξ ) = (0.63, 0.24)=(0.63, 0.24); similarly, f(KA )(p 2 )(ς2 )=(0.63, 0.14), f(KA )(p 2 )(ς3 )=(0.73, 0.24), and f(KA )(p 3 )(ς1 )=(0, 0), f(KA )(p 3 )(ς2 )=(0, 0), f(KA )(p 3 )(ς3 )=(0, 0). Hence,weobtaintheBFS-imageof KA underthegivenmappingas f(KA )=        Kp1 = {(ς1 , 0.33, 0.54), (ς2 , 0.53, 0.64), (ς3 , 0.63, 0.44)}, Kp2 = {(ς1 , 0 63, 0 24), (ς2 , 0 63, 0 14), (ς3 , 0 73, 0 24)}, Kp3 = {(ς1 , 0, 0), (ς2 , 0, 0), (ς3 , 0, 0)}.

      

Nowwecalculatetheimageof KA underinversemappingasfollows: f 1 (KA )(p1 )(ξ1 )= K(g(p1 )) (u(ξ1 )) = K(p1 ) (ς1 ) = {(ς1 , 0.51, 0.33), (ς2 , 0.32, 0.21), (ς3 , 0.22, 0.31)}(ς1) =(0 51, 0 33), f 1 (KA )(p1 )(ξ2 )= K(g(p1 )) (u(ξ2 )) = K(p1 ) (ς2 )

= {(ς1 , 0.51, 0.33), (ς2 , 0.32, 0.21), (ς3 , 0.22, 0.31)}(ς2) =(0.32, 0.21), f 1 (KA )(p1 )(ξ3 )= K(g(p1 )) (u(ξ3 )) = K(p1 ) (ς3 ) = {(ς1 , 0 51, 0 33), (ς2 , 0 32, 0 21), (ς3 , 0 22, 0 31)}(ς3) =(0.22, 0.31).

Similarcalculationgives f 1 (KA )= 

Kp1 = {(ξ1 , 0.51, 0.33), (ξ2 , 0.32, 0.21), (ξ3 , 0.22, 0.31)}, Kp2 = {(ξ1 , 0 32, 0 43), (ξ2 , 0 51, 0 33), (ξ3 , 0 71, 0 51)}, Kp3 = {(ξ1 , 0.32, 0.43), (ξ2 , 0.51, 0.33), (ξ3 , 0.71, 0.51)}.



Definition3.5.

(i)ABFS-mapping f =(u, g)issaidtobeinjectiveifboth u and g areinjective mappings.

(ii)ABFS-mapping f =(u, g)issaidtobesurjectiveifboth u and g aresurjective mappings. (iii)ABFS-mapping f =(u, g)issaidtobebijectiveifboth u and g arebijective (injectiveaswellassurjective)mappings.

Example3.6. Let V = {ξ1 ,ξ2 ,ξ3 }, W = {ς1 ,ς2 ,ς3 } and D = {p1 ,p2 ,p3 }D = {p1 ,p2 ,p3 }.LetusconsidertwoclassesofBFS-sets BF (VD )and BF (WD ).Suppose thatthemappings u : V → W and g : D→D aredefinedas u(ξ1 )= ς3 , u(ξ2 )= ς1 , u(ξ3 )= ς2 , g(p1 )= p1 , g(p2 )= p3 , g(p3 )= p2 . Let KA and KA betwoBFS-setsin BF (VD )and BF (WD ),respectively.

BFS-intersectionofBFS-images f(KA1 )and f(KA2 )in BF (WD ),for p ∈D and ς ∈ W definedasfollows:

(f(KA1 ) ∪ f(KA2 ))(p )(ς )= f(KA1 )(p )(ς ) ∪ f(KA2 )(p )(ς ), and (f(KA1 ) ∩ f(KA2 ))(p )(ς )= f(KA1 )(p )(ς ) ∩ f(KA2 )(p )(ς ).

Definition3.8. Supposethat f =(u, g): BF (VD ) →BF (WD )beaBFSmapping.Let KA1 and KA2 betwoBFS-setsin BF (WD ),thenBFS-unionand BFS-intersectionofBFS-images f 1 (KA1 )and f 1 (KA2 )in BF (VD ),for p ∈D and ξ ∈ V definedasfollows: (f 1 (KA1 ) ∪ f 1 (KA2 ))(p)(ξ )= f 1 (KA1 )(p)(ξ ) ∪ f 1 (KA2 )(p)(ξ ), and (f 1 (KA1 ) ∩ f 1 (KA2 ))(p)(ξ )= f 1 (KA1 )(p)(ξ ) ∩ f 1 (KA2 )(p)(ξ ).

˜ ∪K2 A2 )= f(K1 A1 ) ˜ ∪ f(K2 A2 ). (iii) f(K1 A1 ∩K2 A2 ) ˜ ⊆ f(K1 A1 ) ∩ f(K2 A2 ). (iv) KA ⊆ f 1 (f(KA )).Theequalitydoesholdif u isinjectivemapping. (v) If KA1 ⊆KA2 ⇒ f(KA1 ) ⊆ f(KA2 ). Proof. (i)Obvious (ii)Supposethatfor p ∈ g(D ) ⊆D and ς ∈ W ,wehavetoshowthat f(K1 A1 ∪K2 A2 )(p )(ς )= f(K1 A1 )(p )(ς ) ∪ f(K2 A2 )(p )(ς ).Considerthelefthandside first,let f(K1 A1 ∪K2 A2 )(p )(ς )= f(HA1 ∪A2 )(p )(ς ),bydefinitionofBFS-mapping, weget          max ξ ∈u 1 (ς ) max p∈g 1 (p )∩(A1 ∪A2 ) δ (+) Hp (ξ ), if u 1 (ς ) = ∅, g 1 (p ) ∩ (A1 ∪A2 ) = ∅, 0otherwise, δ ( ) f(HA1 ∪A2 ) (p )(ς ) =

(+) f(HA1 ∪A2 ) (p )(ς )          min ξ ∈u 1 (ς ) min p∈g 1 (p )∩(A1 ∪A2 ) δ ( ) Hp (ξ ), if u 1 (ς ) = ∅, g 1 (p ) ∩ (A1 ∪A2 ) = ∅, 0otherwise, 1950080-12

f(HA1 ∪A2 )(p )(ς )

forsome p ∈ g 1 (p ) ∩ (A1 ∪A2 ).Thetrivialcaseisobvious,weonlyconsidernon trivialcase. f(HA1 ∪A2 )(p )(ς )=

K1 p (ξ ), if p ∈A1 \A2 ∩ g 1 (p ) K2 p (ξ ), if p ∈A2 \A1 ∩ g 1 (p ) (K1 p ∪K2 p )(ξ ), if p ∈A1 ∩A2 ∩ g 1 (p )

Nowforright-handside,bydefinitionofunionofBFS-mappings,wehave f(KA1 ∪KA2 )(p )(ς )= f(KA1 )(p )(ς ) ∪ f(KA2 )(p )(ς ), δ (+) f(K1 A1 ) (p )(ς ) ∪ δ (+) f(K2 A2 ) (p )(ς ) = max ξ ∈u 1 (ς ) max p∈g 1 (p )∩(A1 ∪A2 ) δ (+) K1 p (ξ ) max max ξ ∈u 1 (ς ) max p∈g 1 (p )∩(A1 ∪A2 ) δ (+) K2 p (ξ ) =max ξ ∈u 1 (ς ) max p∈g 1 (p )∩(A1 ∪A2 ) max(δ (+) K1 p ,δ (+) K2 p ) (ξ )







f [

0

9 > >

f [

˜ ∪K2 A2 )= f(K1 A1 ) ˜ ∪ f(K2 A2 ). (iii)Supposethatfor p ∈ g(D ) ⊆D and ς ∈ W andbydefinitionofintersection ofBFS-mappings,wehave f(K1 A1

˜ ∪K2 A2 )(p )(ς )= f(HA1 ∩A2 )(p )(ς ).Nowbythe definitionofBFS-mappings,weget

A



u

(ς )

  p∈g 1 (p )∩(A1 ∩A2 ) K1 A1 (ξ )    1950080-14

,

    p∈g 1 (p )∩(A1 ∩A2 ) (K1 A1 (ξ ) ∩K2 A2 (ξ ))  ⊆  ξ ∈u 1 (ς )

∩  ξ ∈u 1 (ς )

 p∈g 1 (p )∩(A1 ∩A2 ) K2 A2 (ξ )    = f(K1 A1 )(p )(ς ) ∩ f(K2 A2 )(p )(ς ) =(f(K1 A1 ) ∩ f(K2 A2 ))(p )(ς ). (iv)Straightforward. (v)Supposethatfor p ∈ g(D ) ⊆D and ς ∈ W andbythedefinitionof BFS-mappings,weget δ (+) f(KA1 ) (p )(ς )=    max ξ ∈u 1 (ς ) max p∈g 1 (p )∩A1 δ (+) K(p) (ξ ), if u 1 (ς ) = ∅, g 1 (p ) ∩A1 = ∅, (11) δ ( ) f(KA1 ) (p )(ς )=    min ξ ∈u 1 (ς ) min p∈g 1 (p )∩A1 δ ( ) K(p) (ξ ), if u 1 (ς ) = ∅, g 1 (p ) ∩A1 = ∅, (12) oncombining(11)and(12),weobtain f(KA1 )(p )(ς )= ξ ∈u 1 (ς )

 p∈g 1 (p )∩A1

KA1   (ξ ) = ξ ∈u 1 (ς )p∈g 1 (p )∩A1

KA1 (ξ ) ⊆ ξ ∈u 1 (ς )p∈g 1 (p )∩A2

KA2 (ξ ) = f(KA2 )(p )(ς ).

Theorem3.10. Supposethat KA , K1 A1 and K2 A2

˜ ∈BF (WD ) andconsideraBFSmapping f =(u, g): BF (VD ) →BF (WD ), then (i) f 1 (φD )= φD (ii) f 1 (K1 A1 ∪K2 A2 )= f 1 (K1 A1 ) ∪ f 1 (K2 A2 ). (iii) f 1 (K1 A1 ∪K2 A2 )= f 1 (K1 A1 ) ∪ f 1 (K2 A2 ). (iv) f(f 1 (KA )) ⊆KA .Theequalitydoesholdif u and g aresurjectivemappings. (v) If K1 A1 ⊆K2 A2 ⇒ f 1 (K1 A1 ) ⊆ f 1 (K2 A2 )

˜ ∪K2 A2 )(p)(ξ )= f 1 (HA1 ∪A2 )(p)(ξ )= H(g(p))(u(ς )),where(g(p) ∈ (A1 ∪A2 ), u(ς ) ∈ W ),taking

righthand-sideandbythedefinitionofinverseBFS-mapping,weget





 

 



      .

    

  , (16)

9 > > > > = > > > > ; , (17) δ ( ) f 1 (K1 A1 ) (p)(ξ ) ∪ δ ( ) f 1 (K2 A2 ) (p)(ξ )=min „δ ( ) K1 g(p) (u (ξ )),δ ( ) K2 g(p) (u (ξ ))« =

8 > > > > < > > > > :

δ (+) K1 g(p) (u (ξ )), if g (p) ∈A1 \A2 δ (+) K2 g(p) (u (ξ )), if g (p) ∈A2 \A1 max(δ (+) K1 g(p) ,δ (+) K2 g(p) )(u (ξ )), if g (p) ∈A1 ∩A2

δ ( ) K1 g(p) (u (ξ )), if g (p) ∈A1 \A2 δ ( ) K2 g(p) (u (ξ )), if g (p) ∈A2 \A1 min(δ ( ) K1 g(p) ,δ (+) K2 g(p) )(u (ξ )), if g (p) ∈A1 ∩A2 (18) 1950080-16

9 > > > > = > > > > ; ,

oncombining(17)and(18),weobtain

f 1 (K1 A1 )(p)(ξ ) ∪ f 1 (K2 A2 )(p)(ξ )=        K1 g(p) (u(ξ )), if g(p) ∈A1 \A2 K2 g(p) (u(ξ )), if g(p) ∈A2 \A1 (K1 g(p) ∪K2 g(p) )(u(ξ )), if g(p) ∈A1 ∩A2

       , (19) from(16)and(19)itisevidentthat f 1 (K1 A1 ∪K2 A2 )= f 1 (K1 A1 ) ∪ f 1 (K2 A2 ).

(iii)Supposethatfor p ∈D and ξ ∈ V andbydefinitionofintersectionof inverseBFS-mappings,wehave f 1 (K1 A1

˜ ∩K2 A2 )(p)(ξ )= f 1 (HA1 ∩A2 )(p)(ξ ).Now, bythedefinitionofinverseBFS-mappings,weobtain δ (+) f 1 (HA1 ∩A2 ) (p)(ξ )= δ (+) Hg(p) (u(ξ )), for g(p) ∈ (A1 ∩A2 ), 0otherwise, δ ( ) f 1 (HA1 ∩A2 ) (p)(ξ )= δ ( ) Hg(p) (u(ξ )), for g(p) ∈ (A1 ∩A2 ), 0otherwise, f 1 (HA1 ∩A2 )(p)(ξ )= Hg(p) (u(ξ )), for g(p) ∈ (A1 ∩A2 ), 0otherwise, where Hg(p) =(K1 g(p) ˜ ∩K2 g(p) ), f 1 (HA1 ∩A2 )(p)(ξ )= Hg(p) (u(ξ )) =(K1 g(p) ˜ ∩K2 g(p) )(u(ξ )) = K1 g(p) (u(ξ )) ˜ ∩K2 g(p) (u(ξ )) = f 1 (K1 A1 )(p)(ξ ) ∩ f 1 (K2 A2 )(p)(ξ ) =(f 1 (K1 A1 ) ∩ f 1 (K2 A2 ))(p)(ξ ).

(iv)Straightforward. (v)Supposethatfor p ∈D and ξ ∈ V andbythedefinitionofinverseBFSmappings,weget

δ (+) f 1 (K1 A1 ) (p)(ξ )= δ (+) K1 g(p) (u(ξ )), for g(p) ∈A1 , 0otherwise, (20) δ ( ) f 1 (K1 A1 ) (p)(ξ )= δ ( ) K1 g(p) (u(ξ )), for g(p) ∈A1 , 0otherwise (21)

Oncombining(20)and(21),wehave

f 1 (K1 A1 )(p)(ξ )= K1 g(p) (u(ξ )), for g(p) ∈A1 , 0otherwise, (22) f 1 (K1 A1 )(p)(ξ )=(K1 g(p) )(u(ξ )) = K1 g(p) (u(ξ )) ⊆K2 g(p) (u(ξ )) = f 1 (KA2 )(p)(ξ ).

Definition3.11. ABFS-relation V × W canbedefinedas R = {(ξ,ς ),δ (+) R (ξ,ς ),δ ( ) R (ξ,ς ), (ξ,ς ) ∈ V × W },where δ (+) R : V × W → [0, 1], δ ( ) R : V × W → [ 1, 0]arecalledpositiveandnegativemembershipfunctions. ThesetofallBFS-relationsisdenotedbyBFS-(V × W ).

Definition3.12. Let A1 ∈ BFS-(V × W )and A2 ∈ BFS-(W × Z ),aBFSmax–min composition A1 ◦A2 canbedefinedas A1 ◦A2 = {{(ξ,ρ),δ (+) A1 ◦A2 (ξ,ρ),δ ( ) A1 ◦A2 (ξ,ρ)} : ξ ∈ V,ρ ∈ Z }},where δ (+) A1 ◦A2 (ξ,ρ)=max ς ∈W {min[δ (+) A2 (ξ,ς ),δ (+) A1 (ς,ρ)]}, δ ( ) A1 ◦A2 (ξ,ρ)=min ς ∈W {max[δ ( ) A2 (ξ,ς ),δ ( ) A1 (ς,ρ)]}.

3.3. Methodology

Inthissection,wediscussourproposedmethodofBFS-mappingtodiagnosebipolar disorder,besttreatmentandprogressoftreatmentepisodes.Forbipolardisorder diagnosis

Pre-Step: Bipolardisorderdiagnosishastwodifficulties:firstdiagnosingbipolar disordercorrectlyandthendiagnosingitstypescorrectlyaswell.Itisveryhard todifferentiateamongitstypes.Becausethesymptomsformaniaandhypomania aresimilar,ontheotherhand,symptomsfordepressionandmajordepressionare similar.Asweseethatitinvolvesuncertaintiesandvagueinformation,sobipolar fuzzysoftsetissuitabletohandlesuchkindofdata.Weassociate[0, 1]interval ofBFS-setwithfeelingsof“highs”and[ 1, 0]intervalwithfeelingsof“lows”in bipolardisorder(seeFig.4).WefurtherassociatedecisionvariablesofBFS-setwith symptomsofbipolardisorder.WealsouseBFS-mappingstodiagnosethetypeof bipolardisorder(seeFig.5).WefurtherseethattheBFS-mappingsworkperfectly toknowtheprogressinthetenureoftreatment(seeFig.6).Wemakeachart forabovethreetypesandassigndifferentrangesofmembershipdegreestomania, hypomania,depressionandmajordepressionfromtheirassociatedinterval.For

Bipolarfuzzysoftmappingswithapplicationtobipolardisorders mania0.80to1(severemania),thevalue0.80to0.89isforoneweekcontinuously manicconditions,0.90to0.99isfortwotothreeweeksmanicconditionsand1 forabovethreeweeksmanicconditions.Incaseofhypomania(moderatemaniaor lessseverethanmania),thevalue0.50to0.59isforfirstweek,0.60to0.69for secondandthirdweekand0.70to0.79forthehypomanicconditionswhichlasted formorethanthreeweeks.Therange0.20–0.40(mildmania)islesssevereformof hypomaniaandsetaccordingtothesymptomswhichlastedforoneyearandabove. Similarly,formajordepression(extremedepression)conditionsofoneweek,weset 0.80to 0.89, 0.90to 0.99fortwotothreeweeksand 1forabovethree weekscontinuousepisodesofmajordepression.AsinbipolarIdisorder,feelingsof depressionormajordepressionmayormaynotoccurthereforewesettherange 1 to0(severetonildepression).Incyclothymic,thepersononlyfeelsthemildorless severehypomaniaanddepressive(lowtomoderatedepressionorlessseverethan extremedepression)forlongtimesowe settherangeaccordingly.Thegraphof mainconditionsrelevanttodifferenttypes ofbipolardisordercanbeseeninFig.3.

Now,wesetarangeofspecificvaluestoobtainthefinalresults.

Step1. Identifyandframethebipolardisorderproblem.Let V = {ξ1 ,ξ2 ,...,ξ } be thesetofpatientand D = {p1 ,p2 ,...,po } bethesetofrelatedsymptomsofbipolar disorder.Adoctormakes t numberofweeksdiagnosischarts(representedbyBFSsets)toobtainafinalcorrectdecision.TheBFS-setprovidedbydoctorat εthtime canbewrittenas Kε D =(δ ε+ k ,δ ε k ),where δ ε+ k and δ ε k arefuzzymembershipdegrees evaluationofmaniaanddepressionfor k thsymptomand thpatient,respectively, ε =1, 2,...,n, =1, 2,...,m and k =1, 2,...,o.TakeBFS-unionof ε numberof weekchartstoobtainfinalBFS-settoexaminedisorderfurther.

Step2. Consideraset D = {p1 ,p2 ,...,po } ofconnectedsymptoms(primary symptomscontainingrelevantbasicsymptoms).ConstructaBFS-set(doctor’s

Fig.3.Graphoftypesofbipolardisorderwithsymptomslevel. Source:https://meandcyclothymia.wordpress.com/2015/01/19/opening-up-to-cyclothymia/.

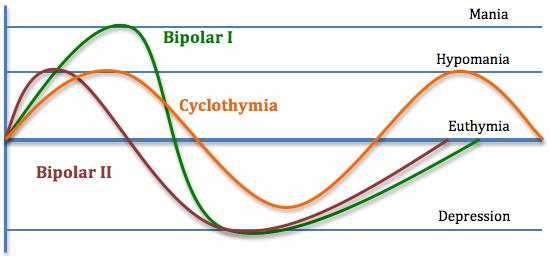
Fig.4.Flowchartofthedifferentrangesassignedtoconditions.

assigningweightsbykeepinginviewthepatient’s ε numberofweekevaluation ofbasicsymptoms)basedonprimarysymptomsandpatients.

Step3. Definemappingwhichisbasicallyarelationbetweenfinalsetobtained in Step1 andBFS-setobtainedin Step2,let u : V → V , g : D→D defined asfollows: u(ξ )= ξ and g(pk )= pk (dependsoninterrelationbetweenbasic andprimarysymptoms),considerthemapping f =(u, g): BF (VD ) →BF (VD ) definedby δ (+) f(KD ) (p )(ξ )= | δ i+ pk

Step4. ComparethevalueofobtainedsetwithTable2andprepareaTableof pre-diagnosiswhichhelpstocheckaccuracyoffinalresults.

Step5. Calculate S = δ i+ pj +δ i pj m where m isnumberofconnectedsymptoms,concludetheresultbyusingTable3. Forbesttreatment,dothefollowingsteps:

Fig.6.Flowchartofthetreatmentandimprovement.

Table2.Conditionsandtheirintensitybasedonweeklyobservationtodiagnose bipolardisorder.

Conditions ≤1week2–3weeks >3weeks

SevereMania(SM)0.80to0.890.90to0.991

Hypomania(HM)0.50to0.590.60–0.690.70to0.79

MildMania(MM)0.20to0.290.30to0.390.40to0.49

ExtremeDepression(ED) 0.80to 0.89 0.90to 0.99 1

ModerateDepression(MD) 0.50to 0.59 0.60to 0.69 0.70to 0.079

LowDepression(LD) 0.20to 0.29 0.30to 0.39 0.40to 0.49

Bipolarfuzzysoftmappingswithapplicationtobipolardisorders

Table3.Finaldiagnosischart.

TypesofdisorderDifferentrangesof[ 1, 1]

BipolarIDisorder[0 5, 1]

BipolarIIDisorder[ 0 5, 1] Cyclothymic( 0 5, 0 2] ∪ [0 2, 0 5) NoBipolarDisorder( 0 2, 0 2) where n =2, 3,... isnumberoftreatmentepisodes, p ∈ g(D ) ⊆D and ξ ∈ V 1 . α ∈ V n 1 , β ∈ (D )n 1 Step10. Repeatapplicationin Step9 untiltherequiredresultsareachieved.

4.ApplicationofBFS-MappingstoBipolarDisorders

Inthissection,weapplyourmethodtoacaseunderconsideration.

CaseStudy

Supposethatapsychiatristwantstodiagnosethebipolardisorderanditstypes inhisfourpatients.Mostly,typeofthebipolardisordercannotbediagnosedcorrectlyduetoitssymptomsmatchingwithotherdiseases.Therefore,afteracomplete physicalexam,thepsychiatristrulesoutalltheimpossiblefactors.Heconsidersall possiblefactors,suchascompleteandcarefulhistoryofmedical,genetics,family history,neurological(episodesofhighstress,suchasthedeathofasiblingorother traumaticevent,structureandfunctioningofbrainandanxietydisorder),environmental,physicalillnesses,whicharealongwithbipolardisorder(includingthyroid disease,heartdisease,migraineheadaches,diabetesandobesity)andsubstance abuse(drugoralcohol),etc.Let V = {ξ1 ,ξ2 ,ξ3 ,ξ4 } bethesetoffourpatientsand D = {p1 ,p2 ,p3 ,p4 ,p5 ,p6 } bethesetofsymptomsoftheirillnesswhichapsychiatristconductsafteracompletementalevaluationofthepatientsbyanalyzingthe dailypreparedmoodchartsaftersomevisitsanddiscussionwithfamilymembers andfriendsofthepatients.Here, p1 representsfeelingsofeuphoric,exultantandsometimesdejected,sorrowful, p2 representsfullenergizedmeanwhiledecreasedlevelsofactivity, p3 representsdisturbedsleepduetoracingthoughts,unusualactiveaswellaseat toolittleortoomuch, p4 representsfullactivatedmoodontheotherhanddisturbedmood, p5 representsmosttalkativeandtouchyaswellascannotenjoyanything, p6 representsThinkaboutriskythingsandalsosleeptoolittleortoomuch,think aboutdeathorsuicide.

Foraperfectandrightdiagnosis,constructcharts(whichareBFS-sets)ofthree consecutiveweeks Kε D ∈BF (VD )andassignmembershipdegreestothesymptoms

ofthepatientsbykeepinginviewallpossiblefactors.Firstweekchartisasfollows:

K1 p1 = {(ξ1 , 0.87, 0.61), (ξ2 , 0.52, 0.51), (ξ3 , 0.89, 0.10), (ξ4 , 0.40, 0.30)},

K1 p2 = {(ξ1 , 0 26, 0 76), (ξ2 , 0 63, 0 76), (ξ3 , 0 83, 0 15), (ξ4 , 0 60, 0 00)},

K1 D

K1 p3 = {(ξ1 , 0 15, 0 55), (ξ2 , 0 50, 0 78), (ξ3 , 0 86, 0 23), (ξ4 , 0 60, 0 30)},

K1 p4 = {(ξ1 , 0 14, 0 43), (ξ2 , 0 81, 0 87), (ξ3 , 0 31, 0 73), (ξ4 , 0 50, 0 50)},

K1 p5 = {(ξ1 , 0 23, 0 86), (ξ2 , 0 40, 0 91), (ξ3 , 0 40, 0 24), (ξ4 , 0 20, 0 10)},

K1 p6 = {(ξ1 , 0 15, 0 83), (ξ2 , 0 36, 0 81), (ξ3 , 0 31, 0 66), (ξ4 , 0 20, 0 40)}

Secondweekchartis

8

>

K2 p3 = {(ξ1 , 0 25, 0 55), (ξ2 , 0 00, 0 78), (ξ3 , 0 23, 0 13), (ξ4 , 0 00, 0 30)}, K2 p4 = {(ξ1 , 0 14, 0 43), (ξ2 , 0 10, 0 27), (ξ3 , 0 21, 0 43), (ξ4 , 0 10, 0 40)},

K2 p5 = {(ξ1 , 0 23, 0 56), (ξ2 , 0 10, 0 11), (ξ3 , 0 60, 0 44), (ξ4 , 0 40, 0 10)},

K2 p6 = {(ξ1 , 0.15, 0.73), (ξ2 , 0.66, 0.91), (ξ3 , 0.21, 0.56), (ξ4 , 0.10, 0.70)}.

9 > > > > > > > > > > > = > > > > > > > > > > > ;

>

> > > > > > > > >

> <

=

> > > > > > > > > > > ;

ConstructclassofBFS-set BF (VD )onthesameuniversalset V ,whichhasweights givenbydoctorforconnectedsymptomsandpatientscollecteddata

KD =

8 > > < > > : Kp1 = {(ξ1 , 0 60, 0 81), (ξ2 , 0 52, 0 87), (ξ3 , 0 81, 0 10), (ξ4 , 0 11, 0 54)}, Kp2 = {(ξ1 , 0.12, 0.86), (ξ2 , 0.63, 0.87), (ξ3 , 0.95, 0.25), (ξ4 , 0.41, 0.21)}, Kp3 = {(ξ1 , 0.15, 0.93), (ξ2 , 0.70, 0.81), (ξ3 , 0.89, 0.30), (ξ4 , 0.54, 0.50)}.

9 > > = > > ;

Definingmappings u : V → V , g : D→D asfollows: u(ξ1 )= ξ1 , u(ξ2 )= ξ2 , u(ξ3 )= ξ3 , g(p1 )= p1 , g(p4 )= p1 , g(p2 )= p2 , g(p5 )= p2 , g(p3 )= p3 , g(p6 )= p3 , themapping f =(u, g): BF (VD ) →BF (VD )definedby δ (+) f (KD ) (p )(ξ )= | δ i+ pj | 8 > < > : max ξ∈u 1 (ξ) max p∈g 1 (p )∩D δ (+) K(p) ! (ξ ), if u 1 (ξ ) = ∅, g 1 (p ) ∩D = ∅, 0otherwise δ ( ) f (KD ) (p )(ξ )= | δ i pj | 8 > < > : min ξ∈u 1 (ξ) min p∈g 1 (p )∩D δ ( ) K(p) ! (ξ ), if u 1 (ξ ) = ∅, g 1 (p ) ∩D = ∅, 0otherwise theimageof Kε D under f isgivenby KD =

8 > > > < > > > : K p1 = {(ξ1 , 0 52, 0 75), (ξ2 , 0 42, 0 75), (ξ3 , 0 72, 0 07), (ξ4 , 0 06, 0 27)}, K p2 = {(ξ1 , 0.03, 0.73), (ξ2 , 0.39, 0.79), (ξ3 , 0.83, 0.08), (ξ4 , 0.28, 0.12)}, K p3 = {(ξ1 , 0.03, 0.86), (ξ2 , 0.46, 0.73), (ξ3 , 0.76, 0.19), (ξ4 , 0.32, 0.35)}

9 > > > = > > > ;

OncomparingthevaluesofabovesetwithTable2,wegetachart(Table4)of pre-diagnosis,whichwecomparelater withourresultstocheckaccuracy. Calculatingthescorefunction,for i =1, 2, 3, 4and j =1, 2, 3 S = δ i+ pj + δ i pj m , where m isnumberofconnectedsymptoms,here m =3.Thus,weobtain ξ1 = 0.58, ξ2 = 0.33, ξ3 =0.65and ξ4 = 0.02.Oncomparingthescorevalues withTable3weget, ξ1 isdiagnosedwithbipolarIIdisorder, ξ2 withcyclothymic disorder, ξ3 isdiagnosedwithbipolarIdisorderand ξ4 isfreefrombipolardisorder.

Table4.Pre-diagnosischart. Pre-diagnosis ξ1 ξ2 ξ3 ξ4 K p1 (HM,MD)(MM,MD)(HM,N)(N,LD) K p2 (N,MD)(MM,MD)(SM,N)(MM,N) K p3 (N,ED)(MM,MD)(HM,N)(MM,LD)

Afterdiagnosis,thepsychiatristsuggestsbestmedicationalongwithpsychotherapy. HeconstructsanotherBFS-setwithsuggestingtreatmentandtypesofdisease. Let W = {p1 ,p2 ,p3 } bethesetofprimarysymptomsofbipolardisorderand D = {p1 ,p2 ,p3 } bethesetofrecommendedtreatments,where p1 representstreatmentwithhighpotencymedication andelectroconvulsive therapy, p2 representstreatmentwithmoderatepotencymedicationandsome psychotherapies, p3 representstreatmentwithcognitivebehaviortherapyandsomemild medications. Nowsupposethat KD ∈BF (WD ),where

KD =    Kp1 = {(p1 , 0.90, 0.50), (p2 , 0.50, 0.90), (p3 , 0.40, 0.95)}, Kp2 = {(p1 , 0 70, 0 50), (p2 , 0 90, 0 80), (p3 , 0 60, 0 50)}, Kp3 = {(p1 , 0.50, 0.25), (p2 , 0.60, 0.40), (p3 , 0.90, 0.20)},

   themembershipdegreesareassignedaccordingtohistoryofmedicalofeachpatient. Here,positivemembershipdegreesshow thateffectivenessoftreatmentsforeach typeontheotherhandnegativemembershipdegreesindicatethesideeffectsof medicationsandlesseffectivenessofthe treatmentforeachtype.Now,byapplying BFSmax–mincompositionbetween KD and KD ,

KD p1 p2 p3

Kp1 (0.90, 0.50)(0.50, 0.90)(0.40, 0.95) Kp2 (0.70, 0.50)(0.90, 0.80)(0.60, 0.50) Kp3 (0.50, 0.25)(0.60, 0.40)(0.90, 0.20), now,the KD canbewrittenas KD ξ1 ξ2 ξ3 p1 (0.52, 0.75)(0.42, 0.75)(0.72, 0.07) p2 (0.03, 0.73)(0.39, 0.79)(0.83, 0.08) p3 (0.03, 0.86)(0.46, 0.73)(0.76, 0.19), weobtainaBFS-set,whichisrelationbetweenpatientsandsuggestedtreatment accordingtotheirdisease.

KD ◦KD ξ1 ξ2 ξ3 Kp1 (0.52, 0.86)(0.42, 0.79)(0.72, 0.19) Kp2 (0.52, 0.73)(0.46, 0.79)(0.83, 0.19) Kp3 (0.50, 0.40)(0.46, 0.40)(0.76, 0.19)

Thereisnodoubtthatadoctorwantsatreatmentwithlesssideeffectsand morebenefits.So,accordingtosuitabilityofthetreatmentforeachpatient,weget p3 for ξ1 , p3 for ξ2 and p2 for ξ3 .

1

1

 V n D = f (V n 1 D )(p )(ξ ) =1/n   

 α∈

Kp1 = {(ξ1 , 0 52, 0 75), (ξ2 , 0 42, 0 75), (ξ3 , 0 72, 0 07)}, Kp2 = {(ξ1 , 0.03, 0.73), (ξ2 , 0.39, 0.79), (ξ3 , 0.83, 0.08)}, Kp3 = {(ξ1 , 0 03, 0 86), (ξ2 , 0 46, 0 73), (ξ3 , 0 76, 0 19)}



Kp1 = {(ξ1 , 0.26, 0.38), (ξ2 , 0.21, 0.38), (ξ3 , 0.36, 0.04)}, Kp2 = {(ξ1 , 0.02, 0.37), (ξ2 , 0.20, 0.40), (ξ3 , 0.42, 0.04)}, Kp3 = {(ξ1 , 0 02, 0 43), (ξ2 , 0 23, 0 37), (ξ3 , 0 38, 0 10)}

 



 Similarly,when n =3,anotherapplicationof f totheresultantsetgives

,

restrictthevaluesinpreviousphaseoftreatmentandwedothisuntilwegetan improvement.Thedurationofasingleepisodeofatreatmentcanberecommended accordingtotheseverenessofthedisease.Theeffectivenessofthemethodcanbe seenthroughouttheprocess.Sincepsychologicaltreatmentstakealongertimeto recover,sothismethodisalsohelpfultokeeprecordandhistoryofeachpatient. Themembershipdegreesarehelpfultoknowtheseverenessofthecausesandright diagnoseofthedisease.Inparticular,whenwehaveuncertainbipolarinformation ordata.

5.ComparisonandDiscussion

Inthissection,wediscussthecomparisonanalysisofourmethodanditsaccuracy. First,weexaminethatamultipleweekschartprovidedagreatfuzzyenvironment evaluationofpatientswhichisnecessary todiagnoseperfectlybecausepsychologicaldisordercannotbejudgedinasinglevisit.TheBFS-unionalsoprovided

Bipolarfuzzysoftmappingswithapplicationtobipolardisorders maximumdegreesofpatient’sbasicsymptomswhichisnecessarytoexaminefull manicepisodeandextremedepressionepisodeifoccurs.Second,weseethatthe connectionbetweenprimaryandbasicsymptomsandweightsprovidedbydoctor (accordingtoseverenessofbasicsymptoms)areveryimportant,ifweconsideronly basicsymptoms,thenwecannotcorrectlyconclude.Inthiscase,patient4alsohas bipolardisorderwhichhasnegativeresultsinourcase.Third,thepre-diagnosis chartmakessuretheaccuracyofthemethod,wecanseepatient1encounters withoneepisodeofhypomania,2episodesofmoderatedepressionand1episodeof extremedepressionwhichareindicatingaboutbipolarIIdisorderaccordingtodefinition.Wegetthesameresultaftercalculatingandcomparingthescorefunction. Asimilarevaluationcanbemadeforremainingpatients.Thisevaluationmakes surethemethod’sreliability.Insecondphase,weseethetreatmentanditsrelated degreesplayanimportantroletofinalizethemostaccuratetreatmentforapatient accordingtotheirmedicalhistory.Inthirdphaseofthemethod,ageneralizedmappingishelpfultochecktheimprovementoftreatmentthroughoutthetenure,ifa patientcannotgettheconvergencestateinnextepisodeoftreatment,theninverse BFS-mappingshiftsitautomaticallyinthepreviousepisode.Themethodisuseful totreatalargenumberofpatients.Inparticular,thismathematicalframeworkis reliableandcapabletohandlebipolardisorderefficiently.

6.Conclusion

Inthisstudy,weproposedatechniquetodiagnoseabipolardisorderanditstypes perfectly.Thesymptomsandtheirconnectionsplayanimportantsroletolessthe complexityofdiagnosisitstypes.Inthisregard,wedefinemappingsonBFS-set andsomeusefulbasicoperationsandpropertiesofBFS-mappings.Wepropose anextensivemodeltocorrectlydiagnosebipolardisorderintheenvironmentof BFS-mappings.Themethodishelpfulto suggestaperfecttreatmentaswellas improvementsintreatmentepisodes.Weintroducemappingsonbipolarfuzzysoft set,wedefineconceptsofBFS-mappings.WefindtheimageofaBFS-setunder definedBFS-mapping.WediscusscertainpropertiesofBFS-mappings.Finally,we presentanapplicationofBFS-mappingsintheareaofneurologicaldisorders.We applytheconceptofBFS-mappingtodiagnosethebipolardisorderanditstype. Theprocessisalsohelpfultotracktheprogressofthetreatmentepisodes.In short,theprocessisreliableandsuitabletotreatsuchkindofmedicalissuesin whichuncertainbipolartypeinformationisinvolved.Infuture,weextendourwork todiscussdisorderundertheenvironmentofpythagoreanfuzzysetandmultiple symptomsdisorderusingm-polarfuzzyinformation.

References

[1]M.I.Ali,F.Feng,X.Y.Liu,W.K.MinandM.Shabir,Onsomenewoperationsin softsettheory, Comput.Math.Appl. 57 (2009)1547–1553.

[2]M.I.Ali,M.ShabirandN.Naz,Algebraicstructuresofsoftsetsassociatedwith newoperations, Comput.Math.Appl. 61 (2011)2647–2654. 1950080-29

[3]J.Alonso etal.,Daysoutofroleduetocommonphysicalandmentalconditions: ResultsfromtheWHOworldmentalhealthsurveys, Mol.Psychiatr. 16 (2011)1234–1246.

[4]M.Aslam,S.AbdullahandK.Ullah,Bipolarfuzzysoftsetanditsapplicationin decisionmaking, JIntell.FuzzySyst. 27(2)(2014)729–742.

[5]K.T.Atanassov,Intuitionisticfuzzysets, FuzzySetsSyst. 20 (1986)87–96.

[6]M.BashirandA.R.Salleh,Mappingsonintuitionisticfuzzysoftclasses, AIPConf. Proc. (2013)15–22.

[7]J.Chen,S.Li,S.MaandX.Wang, m-Polarfuzzysets:Anextensionofbipolarfuzzy sets, TheSci.WorldJ. (2014)1–8.

[8]J.F.Goldberg,M.HarrowandJ.E.Whiteside,Riskforbipolarillnessinpatients initiallyhospitalizedforunipolardepression, Am.J.Psychiatr. 158 (2001)1265–1270.

[9]C.GunduzandS.Bayramov,Someresultsonfuzzysofttopologicalspaces, Math. Prob.Eng. (2013)1–10.

[10]P.R.InnocentandR.I.Jhon,Computeraidedfuzzymedicaldiagnosis, Inf.Sci. 162(2)(2004)81–104.

[11]F.Karaaslan,Bipolarsoftroughrelations, Commun.FacultySci.Univ.Ankara SeriesA1:Math.Stat. 65(1)(2016)105–126.

[12]F.KaraaslanandN.Cagman,Bipolarsoftroughsetsandtheirapplicationsindecisionmaking, AfrikaMatematika 29(5–6)(2018)823–839.

[13]S.Karata¸sandM.Akda˘g,Onintuitionisticfuzzysoftcontinuousmappings, J.New ResultsSci. 4 (2014)55–70.

[14]A.KharalandB.Ahmad,Mappingsonfuzzysoftclasses, Adv.FuzzySyst. 2009 (2009)4–5.

[15]A.KharalandB.Ahmad,Mappingsonsoftclasses, NewMath.Nat.Comput. 7(3) (2011)471–482.

[16]B.Kovalerchukab,E.Triantaphyllouab,J.F.FuizcandJ.Claytond,Fuzzylogicin computer-aidedbreastcancerdiagnosis:Analysisoflobulation, Artif.Intell.Med. 11(1)(1997)75–85.

[17]K.M.Lee,Bipolar-valuedfuzzysetsandtheirbasicopperations,in Proceeding ofInternationalConferenceonIntelligentTechnology (Bangkok,Thailand,2000), pp.307–317.

[18]P.K.Maji,R.BiswasandA.R.Roy,Anapplicationofsoftsetsindecisionmaking problem, Comput.Math.Appl. 44 (2002)1077–1083.

[19]P.K.Maji,R.BiswasandA.R.Roy,Softsettheory, Comput.Math.Appl. 45 (2003) 555–562.

[20]P.MajumdarandS.K.Samanta,Onsoftmappings, Comput.Math.Appl. 60(9) (2010)2666–2672.

[21]D.Molodtsov,Softsettheory-firstresults, Comput.Math.Appl. 37 (1999)19–31.

[22]J.Montero etal.,Pairedstructuresinknowledgerepresentation, Knowl.BasedSyst. 100 (2016)50–58.

[23]S.Naz,S.AshrafandF.Karaaslan,Energyofabipolarfuzzygraphanditsapplicationindecisionmaking, Ital.J.PureAppl.Math. 40 (2018)339–352.

[24]N.H.PhuongandV.Kreinovich,Fuzzylogicanditsapplicationsinmedicine, Int. J.Med.Inform 62(23)(2011)165–173.

[25]M.RiazandK.Naeem,Measurablesoftmappings, PunjabUniv.J.Math. 48(2) (2016)19–34.

[26]M.RiazandM.R.Hashmi,Fixedpointsoffuzzyneutrosophicsoftmappingwith decisionmaking, FixedPointTheoryAppl. 7 (2018)110.

Bipolarfuzzysoftmappingswithapplicationtobipolardisorders

[27]M.Riaz,M.R.HashmiandA.Farooq,Fuzzyparameterizedfuzzysoftmetricspaces, J.MathematicalAnal. 9(2)(2018)25–36.

[28]M.RiazandS.T.Tehrim,Certainpropertiesofbipolarfuzzysofttopologyvia Q-neighborhood, PunjabUniv.J.Math. 51(3)(2019)113–131.

[29]M.RiazandS.T.Tehrim,Cubicbipolarfuzzyorderedweightedgeometricaggregationoperatorsandtheirapplicationusinginternalandexternalcubicbipolarfuzzy data, Comput.Appl.Math. 38(2)(2019)1–25.

[30]M.RiazandS.T.Tehrim,Multi-attributegroupdecisionmakingbasedoncubic bipolarfuzzyinformationusingaveragingaggregationoperators, J.Intell.FuzzySyst. 37(2)(2019)2473-2494.

[31]S.T.TehrimandM.Riaz,AnovelextensionofTOPSIStoMCGDMwithbipolar neutrosophicsofttopology, J.Intell.FuzzySyst. (2019),doi:10.3233/JIFS-190668.

[32]M.Riaz,B.Davvaz,A.FirdousandF.Fakhar,Novelconceptsofsoftroughset topologywithapplications, J.Intell.FuzzySyst. 36(4)(2019)3579–3590.

[33]M.Riaz,F.Samrandache,A.FirdousandA.Fakhar,Onsoftroughtopologywith multi-attributegroupdecisionmaking, Mathematics 7(1)(2019)1–18.

[34]M.Riaz,N.Cagman,I.ZareefandM.Aslam,N-softtopologyanditsapplicationsto multi-criteria group decision making, J. Intell. Fuzzy Syst. 36(6) (2019) 6521–6536.

[35] F. Smarandache, A Unifying Field in Logics. Neutrosophy: Neutrosophic Probability, Set and Logic, Rehoboth (American Research Press, 1999).

[36] Y. S. Woo, et al., A diagnosis of bipolar spectrum disorder predicts diagnostic conversionfromunipolardepressiontobipolardisorder:A5-yearretrospectivestudy, J.AffectDisord. 174 (2015)83–88.

[37]N.Yaqoob,I.RehmanandM.Aslam,ApproximationsofbipolarfuzzyΓ-hyperideals ofΓ-semihypergroups, AfrikaMatematika 29(5–6)(2018)869–886.

[38]N.Yaqoob,M.Aslam,B.DavvazandA.Ghareeb,Structuresofbipolarfuzzy Γ-hyperidealsinΓ-semihypergroups, J.Intell.FuzzySyst. 27(6)(2014)3015–3032.

[39]N.Yaqoob,M.Aslam,I.RehamnandM.Khalaf,Newtypesofbipolarfuzzysetsin Γ-semihypergroups, SongklanakarinJ.Sci.Technol. 38(2)(2016)119–127.

[40]N.Yaqoob,M.AkramandM.Aslam,Intuitionisticfuzzysoftgroupsinducedby (t,s)-norm, IndianJ.Sci.Technol. 6(4)(2013)4282–4289.

[41]F.Yousazai,N.YaqoobandA.B.Saeid,Someresultsinbipolar-valuedfuzzyordered AG-groupoids, DiscussionesMathematicae-Gen.Algebr.Appl. 32 (2012)55–76.

[42]L.A.Zadeh,Fuzzysets, InformationControl 8(3)(1965)338–353.

[43]L.A.Zadeh,Similarityrelationsandfuzzyordering, InformationScience 3 (1971) 199–249.

[44]W.R.Zhang,Bipolarfuzzysetsandrelations:acomputationalframeworkforcognitivemodelingandmulti-agentdecisionanalysis,in ProceedingsofIEEEConference (SanAntonio,TX,USA,1994),pp.305-309.

[45]W.R.Zhang,(YinYang) BipolarFuzzySets,in Proc.IEEEWorldCongress onComputationalIntelligence-Fuzz-IEEE,Anchorage,AK,May,Vol.22(1998), pp.835–840.

[46]W.R.ZhangandL.Zhang,YinYangbipolarlogicandbipolarfuzzylogic, Inf.Sci. 165(3–4)(2004)265–287.