













(1, -4, 6)





- + 8 = -107 6 + = 17 3 - 5 = 89


(-5, 8, 13)
(-5, -8, 13)
(5, 8, -13)
(5, -8, -13)





4 - + 3 = 12 2 + 9 = -5 + 4 + 6 = -32



-7, -1)







(0, 1, 2)
(1, 2, 3)
(-1, 2, -3)






+ + = 7 - + 2 = 7 5 + + = 11



(1, 4, 2)
(4, 1, 2)
(4, 2, 1)
(1, 2, 4)









(-2, -1, 9)
(2, -1, -9)
(-2, -1, -9)
(2, -1, 9)



5 + 2 + = -11



2 - 3 - = 17



7 + + 2 = -4
(3, 0, -4)
(0, -6, 1)
(0, 6, -1)
(-3, 0, 4)






7 + 7 + = 1 + 8 + 8 = 8 9 + + 9 = 9



(0, 0, 1)
(-1, 1, 1)
(1, -1, 1)
(0, 1, 0)


2 + = 0 - 3 + = 0






3 + - = 0
1, 0)
0, 0)
(0, 0, 0)
Determine whether the system is consistent.




+ + = 7 - + 2 = 7





5 + + = 11













































































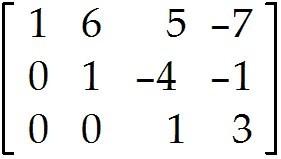
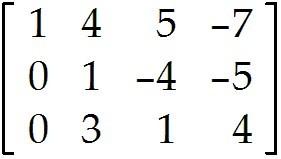
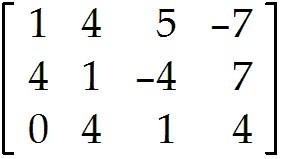
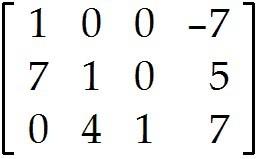
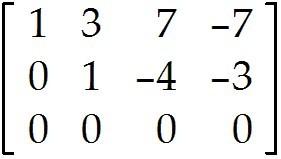
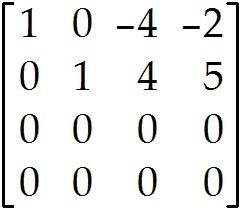

Use the row reduction algorithm to transform the matrix into echelon form or reduced echelon form as indicated. 2
Find the echelon form of the given matrix.
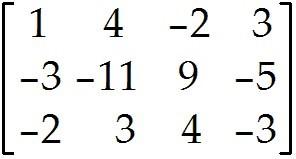
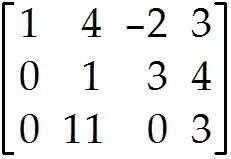



Find the reduced echelon form of the given matrix.
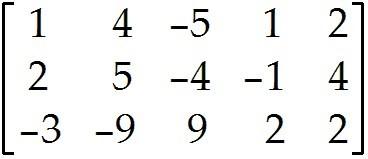
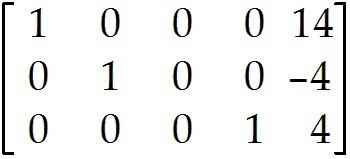
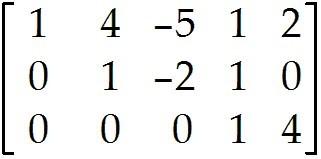
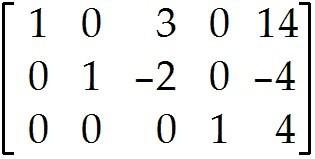

The augmented matrix is given for a system of equations. If the system is consistent, find the general solution. Otherwise state that there is no solution.
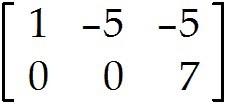






= -5 + 5

-5, 7)
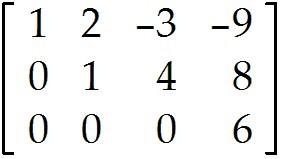



= -25 + 11 = 8 - 4 = 6





solution C) = -9 - 2 + 3 is free is free




= -25 + 11 = 8 - 4



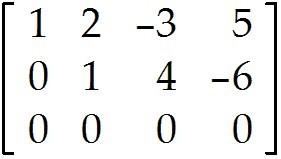













= 5 -2 + 3

= -6 - 4 is free


= 5 - 2 + 3 is free is free
= 17 + 11
= -6 - 4 = 0



= 17 + 11
= -6 - 4 is free






= 7 - 6

= -2 + 2 is free




= 7 - 6

= -2 + 2 = 0





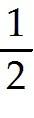

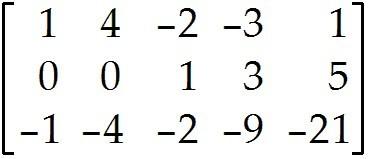
















11 - 4 - 3

3





= - 4 +2 + 3 + 1 is free = 5 - 3 is free

= 11 - 4 - 3 is free = 5 - 3 is free




= 11 - 4 - 3 = 5 - 3 is free









= -6 - 6 + 9 is free is free = -4 = -4







= -6 - 6 + 9 is free = -4 = - 1 = -4











= -6 - 6 + - 2 + 5 is free is free = - 1 = -4


Find the indicated vector. 3
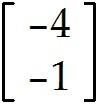

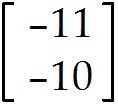

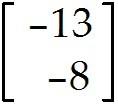


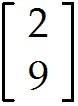



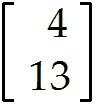

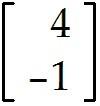



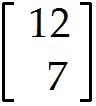

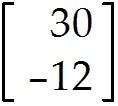
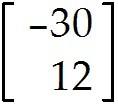
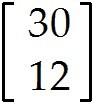
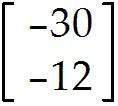

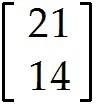
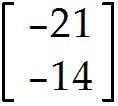

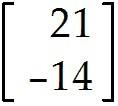
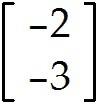
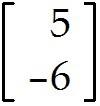
u = . Find -9u
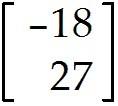
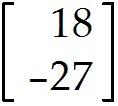
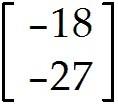



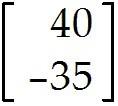



u = , v = . Find 2u + v
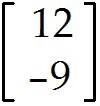


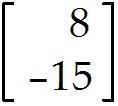
Display the indicated vector(s) on an xy-graph. 4


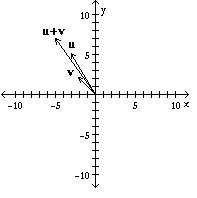
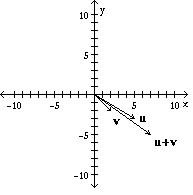
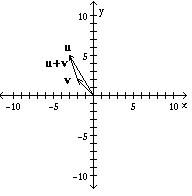
Let u = and v = . Display the vectors u, v, and u + v on the same axes.

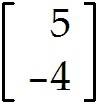
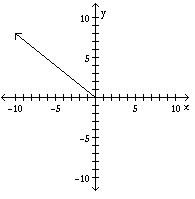
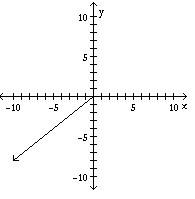
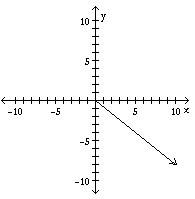
Let u = Display the vector 2u using the given axes.


Solve the problem.
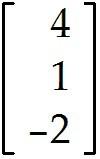

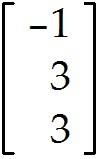

Let = , = , and b = .

Determine whether b can be written as a linear combination of and . In other words, determine whether weights and exist, such that + = b. Determine the weights and if possible.













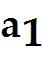
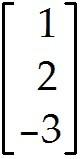


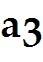

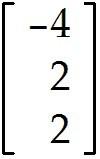
Let = , = , = , and b = .
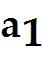

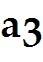
Determine whether b can be written as a linear combination of , , and . In other words, determine whether weights , , and exist, such that + + = b. Determine the weights , , and if possible.




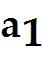



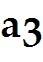






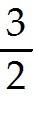






SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. 4
A company manufactures two products. For $1.00 worth of product A, the company spends $0.40 on materials, $0.30 on labor, and $0.15 on overhead. For $1.00 worth of product B, the company spends $0.40 on materials, $0.25 on labor, and $0.15 on overhead. Let a = and b = .

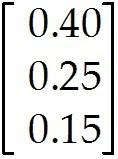
Then a and b represent the "costs per dollar of income" for the two products. Evaluate 300a + 200b and give an economic interpretation of the result. 48)
A company manufactures two products. For $1.00 worth of product A, the company spends $0.45 on materials, $0.20 on labor, and $0.10 on overhead. For $1.00 worth of product B, the company spends $0.45 on materials, $0.20 on labor, and $0.15 on overhead. Let a = and b = .



Then a and b represent the "costs per dollar of income" for the two products. Suppose the company manufactures dollars worth of product A and dollars worth of product B and that its total costs for materials are $315, its total costs for labor are $140, and its total costs for overhead are $90.



Determine and , the dollars worth of each product produced. Include a vector equation as part of your solution.
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Compute the product or state that it is undefined.
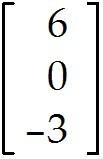
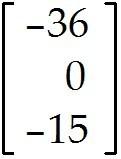
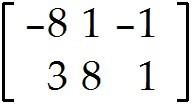

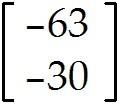

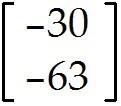
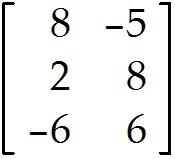
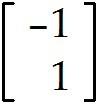

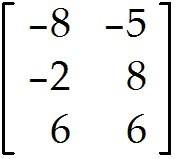
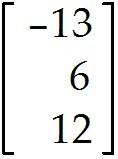

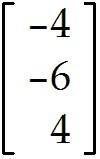

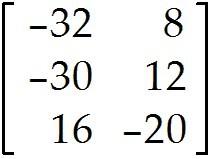
Undefined

Write the system as a vector equation or matrix equation as indicated.
Write the following system as a vector equation involving a linear combination of vectors.




5



3 - 5 - = 2


5 + 3 = 6

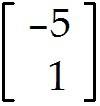

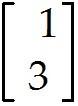


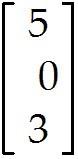
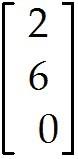











Write the following system as a matrix equation involving the product of a matrix and a vector on the left side and a vector on the right side.

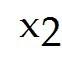

4 + - 2 = 5 2 - 3 = 1


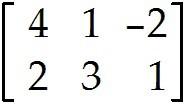



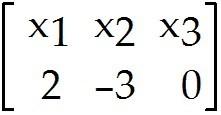




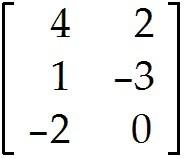
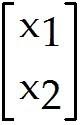

Solve the problem. 5 Let A = and b =
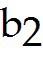
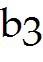
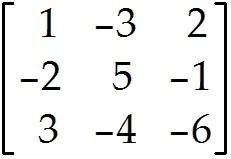

Determine if the equation Ax = b is consistent for all possible , , . If the equation is not consistent for all possible , , , give a description of the set of all b for which the equation is consistent (i.e., a condition which must be satisfied by
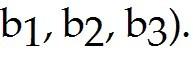
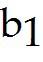
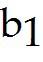
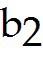
Equation is consistent for all possible , , B)
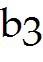
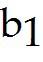
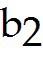
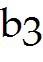
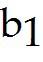
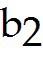
Equation is consistent for all , , satisfying 2 + = 0. C)
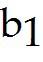
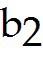
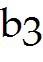
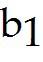
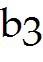
Equation is consistent for all , , satisfying -3 + = 0. D)
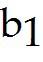
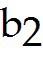
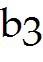
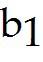
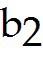
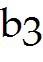
Equation is consistent for all , , satisfying 7 + 5 + = 0. 5
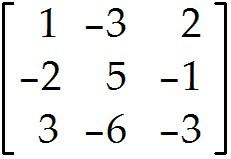
Let A = and b =

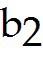
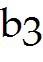
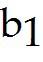
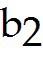
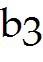
Determine if the equation Ax = b is consistent for all possible , , . If the equation is not consistent for all possible , , , give a description of the set of all b for which the equation is consistent (i.e., a condition which must be satisfied by , , ).
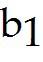
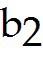
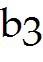
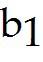
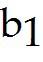
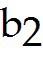
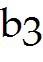
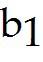
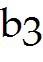
Equation is consistent for all , , satisfying -3 + = 0. B)
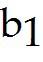
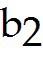
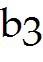
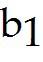
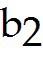
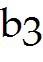
Equation is consistent for all , , satisfying - + + = 0. C)
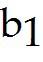
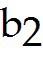
Equation is consistent for all possible , , D)
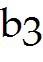
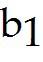
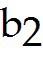
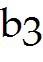
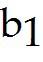
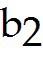
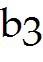
Equation is consistent for all , , satisfying 3 + 3 + = 0.


5
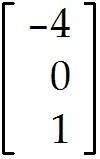
Find the general solution of the simple homogeneous "system" below, which consists of a single linear equation. Give your answer as a linear combination of vectors. Let and be free variables. -2 - 14 + 8 = 0












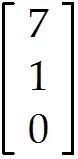

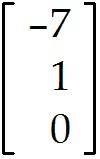





+ (with , free)

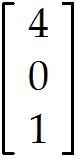


+ (with , free)

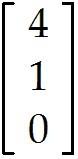
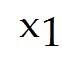



(with , free)
Find the general solution of the homogeneous system below. Give your answer as a vector.







+ 2 - 3 = 0


4 + 7 - 9 = 0 - - 3 + 6 = 0


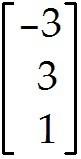

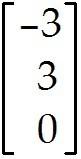



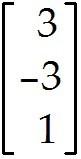
Describe all solutions of Ax = b, where
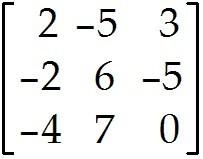
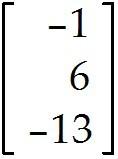
Describe the general solution in parametric vector form.

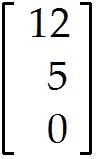

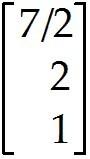



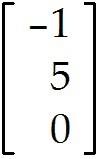







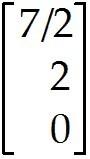
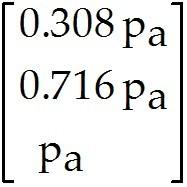
Suppose an economy consists of three sectors: Energy (E), Manufacturing (M), and Agriculture (A).
Sector E sells 70% of its output to M and 30% to A.
Sector M sells 30% of its output to E, 50% to A, and retains the rest.
Sector A sells 15% of its output to E, 30% to M, and retains the rest.


Denote the prices (dollar values) of the total annual outputs of the Energy, Manufacturing, and Agriculture sectors by , , and , respectively. If possible, find equilibrium prices that make each sector's income match its expenditures. Find the general solution as a vector, with free.

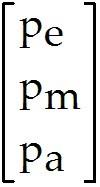

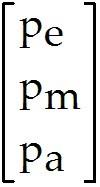
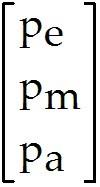

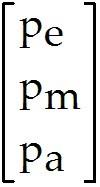

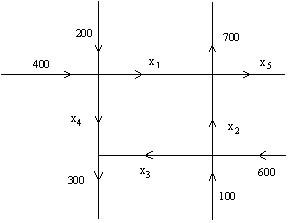
The network in the figure shows the traffic flow (in vehicles per hour) over several one-way streets in the downtown area of a certain city during a typical lunch time. Determine the general flow pattern for the network. In other words, find the general solution of the system of equations that describes the flow. In your general solution let be free.

































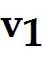

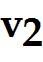
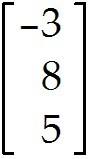
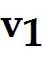
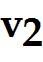


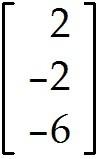
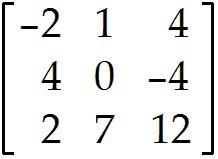
For what values of h are the given vectors linearly independent? ,
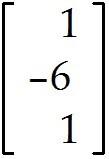
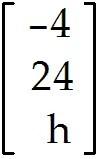
A)
Vectors are linearly independent for h = -4 B)
Vectors are linearly independent for h ≠ -4 C)
Vectors are linearly independent for all h D)
Vectors are linearly dependent for all h 6
For what values of h are the given vectors linearly dependent? , , , 66)

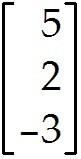

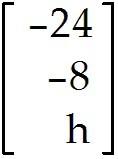
Vectors are linearly independent for all h B)
Vectors are linearly dependent for h ≠ -24 C)
Vectors are linearly dependent for h = -24 D)
Vectors are linearly dependent for all h
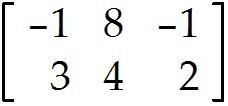
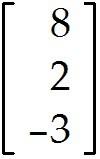
Let A = and u =

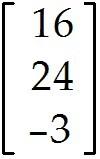
Define a transformation T: -> by T(x) = Ax. Find T(u), the image of u under the transformation T.
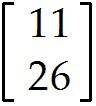
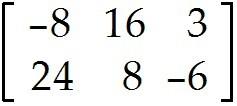



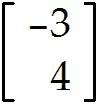


Let T: -> be a linear transformation that maps u = into and maps v = into Use the fact that T is linear to find the image of
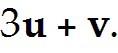
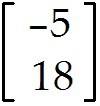

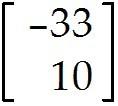
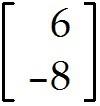


Let A = and b =
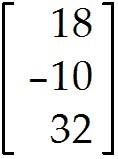
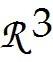
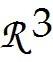
Define a transformation T: -> by T(x) = Ax.
If possible, find a vector x whose image under T is b. Otherwise, state that b is not in the range of the transformation T.
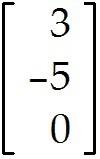
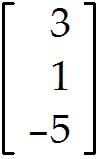
b is not in the range of the transformation T. D)
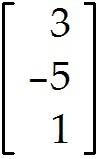
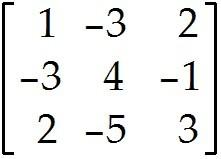
Let A = and b =
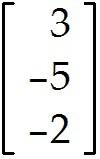
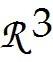
Define a transformation T: -> by T(x) = Ax.
If possible, find a vector x whose image under T is b. Otherwise, state that b is not in the range of the transformation T.
b is not in the range of the transformation T. B)
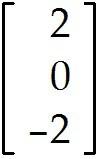

Describe geometrically the effect of the transformation T.
Let A =
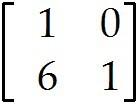
Define a transformation T by T(x) = Ax
71) ______ A)
Vertical shear
Horizontal shear C)
Projection onto -axis

Projection onto -axis

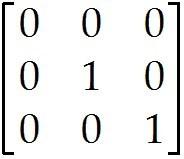
Let A = .
Define a transformation T by T(x) = Ax.
72) ______ A)
Horizontal shear


Projection onto the -plane C)
Vertical shear
Projection onto the -axis
Solve the problem.

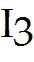
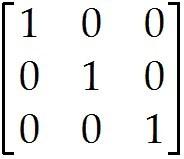
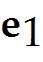

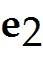

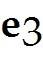
The columns of = are = , = , =


Suppose that T is a linear transformation from into such that T( ) = , T( ) = , and T( ) = .
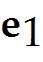
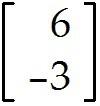
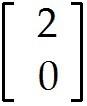
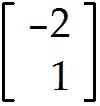

Find a formula for the image of an arbitrary x = in .

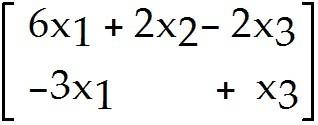

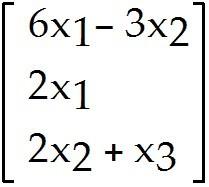



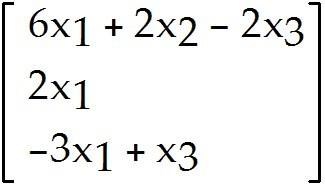


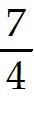
T: -> rotates points (about the origin) through π radians (with counterclockwise rotation for a positive angle).
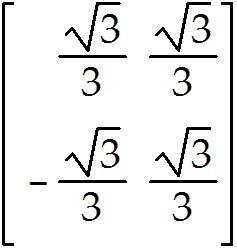
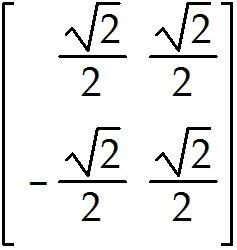

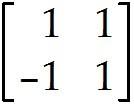


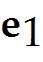
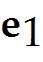
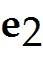
T: -> first performs a vertical shear that maps into + 5 , but leaves the vector unchanged, then reflects the result through the horizontal -axis.


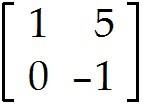
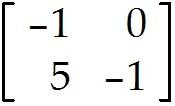

Determine whether the linear transformation T is one-to-one and whether it maps as specified. 7
Let T be the linear transformation whose standard matrix is
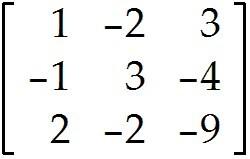
Determine whether the linear transformation T is one-to-one and whether it maps onto . 76) ______ A)
Not one-to-one; onto
One-to-one; onto C)
Not one-to-one; not onto
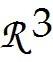
One-to-one; not onto
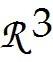












Determine whether the linear transformation T is one-to-one and whether it maps onto
______ A)
One-to-one; onto
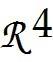
Not one-to-one; onto C)
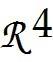
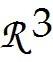
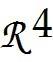
One-to-one; not onto
Solve the problem.
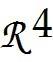
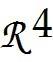
7
The table shows the amount (in g) of protein, carbohydrate, and fat supplied by one unit (100 g) of three different foods.
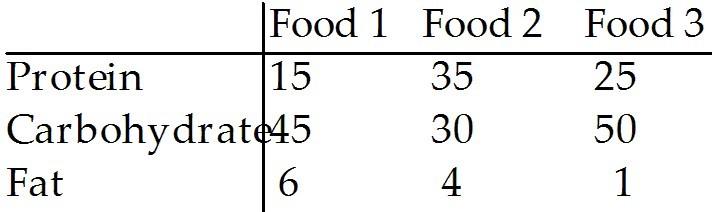
Betty would like to prepare a meal using some combination of these three foods. She would like the meal to contain 15 g of protein, 25 g of carbohydrate, and 3 g of fat. How many units of each food should she use so that the meal will contain the desired amounts of protein, carbohydrate, and fat? Round to 3 decimal places.
78)
A)
0.302 units of Food 1, 0.238 units of Food 2, 0.085 units of Food 3 B)
0.280 units of Food 1, 0.192 units of Food 2, 0.164 units of Food 3 C)
0.360 units of Food 1, 0.204 units of Food 2, 0.055 units of Food 3 D)
0.326 units of Food 1, 0.247 units of Food 2, 0.059 units of Food 3
7
The population of a city in 2000 was 600,000 while the population of the suburbs of that city in 2000 was 900,000. Suppose that demographic studies show that each year about 5% of the city's population moves to the suburbs (and 95% stays in the city), while 2% of the suburban population moves to the city (and 98% remains in the suburbs). Compute the population of the city and of the suburbs in the year 2002. For simplicity, ignore other influences on the population such as births, deaths, and migration into and out of the city/suburban region.
79) ______ A)
City: 541,500
Suburbs: 958,500
City: 588,000
Suburbs: 912,000 C)
City: 541,500
Suburbs: 864,360
300a + 200b =

300a + 200b lists the various costs for producing $300 worth of product A and $200 worth of product B, namely $200 for materials, $140 for labor, and $75 for overhead. 49)



+ b = or + =







