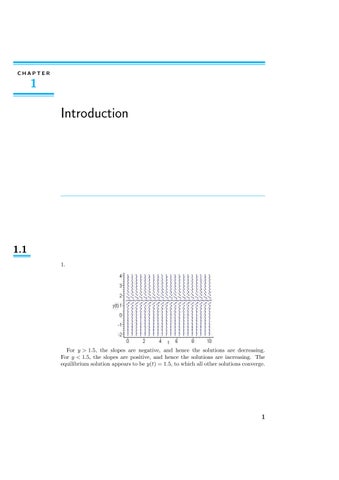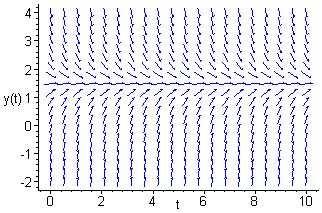
For y> 1.5,theslopesarenegative,andhencethesolutionsaredecreasing. For y< 1 5,theslopesarepositive,andhencethesolutionsareincreasing.The equilibriumsolutionappearstobe y(t)=1 5,towhichallothersolutionsconverge.
3.
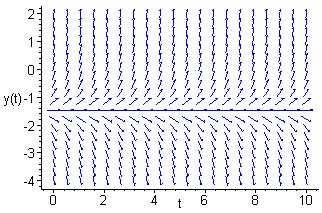
For y> 1.5,theslopesarepositive,andhencethesolutionsincrease.For y< 1 5,theslopesarenegative,andhencethesolutionsdecrease.Allsolutions appeartodivergeawayfromtheequilibriumsolution y(t)= 1 5.
5.
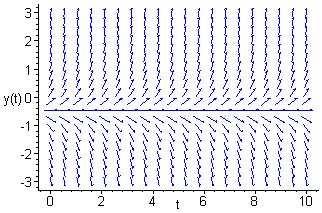
For y> 1/2,theslopesarepositive,andhencethesolutionsincrease.For y< 1/2,theslopesarenegative,andhencethesolutionsdecrease.Allsolutions divergeawayfromtheequilibriumsolution y(t)= 1/2.
6.

For y> 2,theslopesarepositive,andhencethesolutionsincrease.For y< 2, theslopesarenegative,andhencethesolutionsdecrease.Allsolutionsdivergeaway
fromtheequilibriumsolution y(t)= 2.
8.Forallsolutionstoapproachtheequilibriumsolution y(t)=2/3,wemusthave y < 0for y> 2/3,and y > 0for y< 2/3.Therequiredratesaresatisfiedbythe differentialequation y =2 3y
9.Forsolutionsotherthan y(t)=2todivergefrom y =2, y(t)mustbeanincreasingfunctionfor y> 2,andadecreasingfunctionfor y< 2.Thesimplestdifferential equationwhosesolutionssatisfythesecriteriais y = y 2.
10.Forsolutionsotherthan y(t)=1/3todivergefrom y =1/3,wemusthave y < 0for y< 1/3,and y > 0for y> 1/3.Therequiredratesaresatisfiedbythe differentialequation y =3y 1.
12.
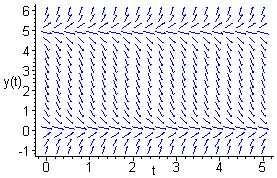
Notethat y =0for y =0and y =5.Thetwoequilibriumsolutionsare y(t)=0 and y(t)=5.Basedonthedirectionfield, y > 0for y> 5;thussolutionswith initialvaluesgreaterthan5divergefromthesolution y(t)=5.For0 <y< 5,the slopesarenegative,andhencesolutionswithinitialvaluesbetween0and5all decreasetowardthesolution y(t)=0.For y< 0,theslopesareallpositive;thus solutionswithinitialvalueslessthan0approachthesolution y(t)=0.
14.

Observethat y =0for y =0and y =2.Thetwoequilibriumsolutionsare y(t)=0and y(t)=2.Basedonthedirectionfield, y > 0for y> 2;thussolutions
withinitialvaluesgreaterthan2divergefrom y(t)=2.For0 <y< 2,theslopes arealsopositive,andhencesolutionswithinitialvaluesbetween0and2allincrease towardthesolution y(t)=2.For y< 0,theslopesareallnegative;thussolutions withinitialvalueslessthan0divergefromthesolution y(t)=0.
15.-(j) y =2 y.
16.-(c) y = y 2.
17.-(g) y = 2 y
18.-(b) y =2+ y
19.-(h) y = y (3 y).
20.-(e) y = y (y 3).
23.Thedifferencebetweenthetemperatureoftheobjectandtheambienttemperatureis u 70,u in ◦F.
Sincetheobjectiscoolingwhen u> 70,andtherateconstantis k =0.05min 1 , thegoverningdifferentialequationforthetemperatureoftheobjectis du dt = .05(u 70).
24.(a)Let M (t)bethetotalamountofthedrug(inmilligrams)inthepatient’s bodyatanygiventime t (hr).Thedrugisadministeredintothebodyataconstant rateof500mg/hr.Therateatwhichthedrugleavesthebloodstreamisgivenby 0.4M (t).Hencetheaccumulationrateofthedrugisdescribedbythedifferential equation
(b)
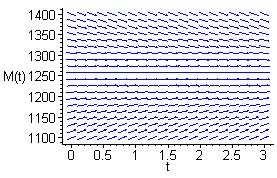
Basedonthedirectionfield,theamountofdruginthebloodstreamapproaches theequilibriumlevelof1250mg(withinafewhours).
25.(a)Followingthediscussioninthetext,thedifferentialequationis m dv dt = mg γv 2 orequivalently, dv dt = g γ m v 2
(b)Afteralongtime, dv dt ≈ 0.Hencetheobjectattainsaterminalvelocitygiven by
(c)Usingtherelation γv 2 ∞ = mg,therequireddragcoefficientis γ =2/49kg/s.
(d)
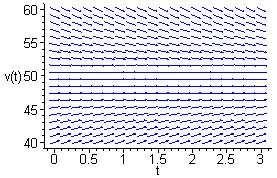
26.

Allsolutionsappeartoapproachalinearasymptote(withslopeequalto1).It iseasytoverifythat y(t)= t 3isasolution.
27.
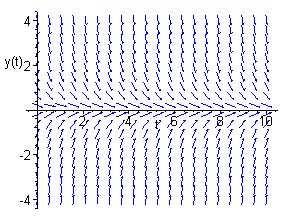
Allsolutionsapproachtheequilibriumsolution y(t)=0.
29.
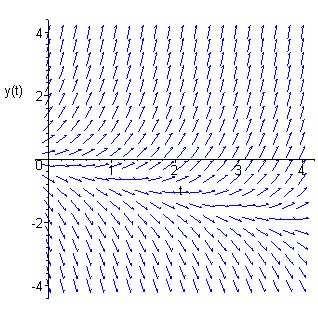
Allsolutions(except y(0)= 1/4)divergefromthesolution y(t)= t/2 1/4 andapproach ±∞
30.
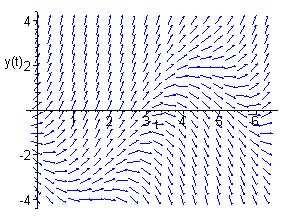
Allsolutions(except y(0)= 5/2)appeartodivergefromthesinusoid y(t)= 3sin(t + π/4)/√2 1,whichisalsoasolutioncorrespondingtotheinitialvalue y(0)= 5/2.

Solutionsapproach −∞ orareasymptoticto √2t 1.
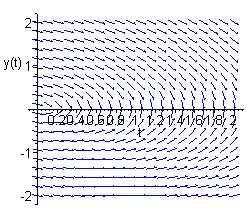
Allsolutionsappeartoconvergeto y(t)=0.Solutionsabovetheline y = 2t (butbelowthe t-axis)havepositiveslopeandincreaserapidlytomeetthe t axis. Solutionsthatbeginbelowtheline y = 2t eventuallycrossitandhavepositive slope.
33.

Thedirectionfieldisrathercomplicated.Nevertheless,thecollectionofpoints atwhichtheslopefieldiszero,isgivenbytheimplicitequation y3 6y =2t2.The graphofthesepointsisshownbelow:
8Chapter1.Introduction
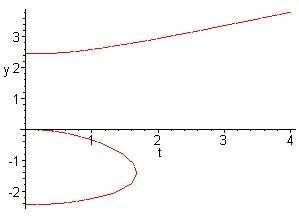
The y-interceptsofthesecurvesareat y =0, ±√6.Itfollowsthatforsolutions withinitialvalues y> √6,allsolutionsincreasewithoutbound.Forsolutionswith initialvaluesintherange y< √6or0 <y< √6,theslopesremainnegative,and hencethesesolutionsdecreasewithoutbound.Solutionswithinitialconditionsin therange √6 <y< 0initiallyincrease.Oncethesolutionsreachthecritical value,givenbytheequation y3 6y =2t2,theslopesbecomenegativeandremain negative.Thesesolutionseventuallydecreasewithoutbound.
1.2
1.(a)Thedifferentialequationcanberewrittenas dy 5 y = dt.
Integratingbothsidesofthisequationresultsin ln |5 y| = t + c1,orequivalently,5 y = ce t.Applyingtheinitialcondition y(0)= y0 resultsinthespecificationoftheconstantas c =5 y0.Hencethesolutionis y(t)=5+(y0 5)e t .
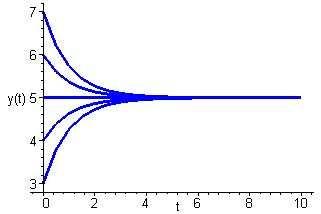
Allsolutionsappeartoconvergetotheequilibriumsolution y(t)=5.
(c)Rewritethedifferentialequationas dy 10 2y = dt.
Integratingbothsidesofthisequationresultsin 1 2 ln |10 2y| = t + c1,orequivalently,5 y = ce 2t.Applyingtheinitialcondition y(0)= y0 resultsinthespecificationoftheconstantas c =5 y0.Hencethesolutionis y(t)=5+(y0 5)e 2t
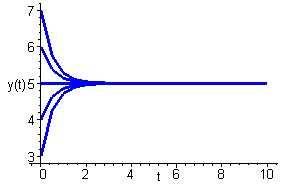
Allsolutionsappeartoconvergetotheequilibriumsolution y(t)=5,butatafaster ratethaninProblem1(a).
2.(a)Thedifferentialequationcanberewrittenas
dy y 5 = dt.
Integratingbothsidesofthisequationresultsinln |y 5| = t + c1,orequivalently, y 5= cet.Applyingtheinitialcondition y(0)= y0 resultsinthespecificationof theconstantas c = y0 5.Hencethesolutionis y(t)=5+(y0 5)et
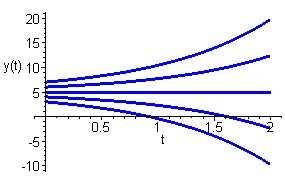
Allsolutionsappeartodivergefromtheequilibriumsolution y(t)=5.
(b)Rewritethedifferentialequationas
dy 2y 5 = dt.
Integratingbothsidesofthisequationresultsin 1 2 ln |2y 5| = t + c1,orequivalently,2y 5= ce2t.Applyingtheinitialcondition y(0)= y0 resultsinthespecificationoftheconstantas c =2y0 5.Sothesolutionis y(t)=(y0 2 5)e2t +2 5.
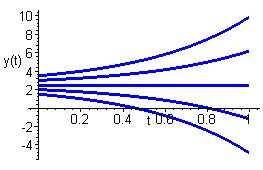
Allsolutionsappeartodivergefromtheequilibriumsolution y(t)=2 5.
(c)Thedifferentialequationcanberewrittenas dy 2y 10 = dt.
Integratingbothsidesofthisequationresultsin 1 2 ln |2y 10| = t + c1,orequivalently, y 5= ce2t.Applyingtheinitialcondition y(0)= y0 resultsinthespecificationoftheconstantas c = y0 5.Hencethesolutionis y(t)=5+(y0 5)e2t
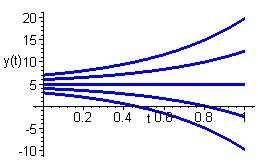
Allsolutionsappeartodivergefromtheequilibriumsolution y(t)=5.
3.(a)Rewritethedifferentialequationas dy b ay = dt , whichisvalidfor y = b/a.Integratingbothsidesresultsin 1 a ln |b ay| = t + c1, orequivalently, b ay = ce at.Hencethegeneralsolutionis y(t)=(b ce at)/a Notethatif y = b/a,then dy/dt =0,and y(t)= b/a isanequilibriumsolution.
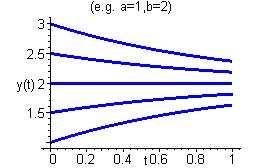
(c)(i)As a increases,theequilibriumsolutiongetscloserto y(t)=0,fromabove. Theconvergencerateofallsolutionsis a.As a increases,thesolutionsconvergeto theequilibriumsolutionquicker.
(ii)As b increases,thentheequilibriumsolution y(t)= b/a alsobecomeslarger. Inthiscase,theconvergencerateremainsthesame.
(iii)If a and b bothincreasebut b/a =constant,thentheequilibriumsolution y(t)= b/a remainsthesame,buttheconvergencerateofallsolutionsincreases.
4.(a)Theequilibriumsolutionsatisfiesthedifferentialequation
dye dt =0 .
Setting aye b =0,weobtain ye(t)= b/a
(b)Since dY/dt = dy/dt,itfollowsthat
dY dt = a(Y + ye) b = aY.
6.(a)Considerthesimplerequation dy1/dt = ay1.Asintheprevioussolutions, rewritetheequationas dy1 y1 = adt.
Integratingbothsidesresultsin y1(t)= ce at
(b)Nowset y(t)= y1(t)+ k,andsubstituteintotheoriginaldifferentialequation. Wefindthat ay1 +0= a(y1 + k)+ b.
Thatis, ak + b =0,andhence k = b/a
(c)Thegeneralsolutionofthedifferentialequationis y(t)= ce at + b/a.This isexactlytheformgivenbyEq.(17)inthetext.Invokinganinitialcondition y(0)= y0,thesolutionmayalsobeexpressedas y(t)= b/a +(y0 b/a)e at
7.(a)Thegeneralsolutionis p(t)=900+ cet/2,thatis, p(t)=900+(p0 900)et/2 With p0 =850,thespecificsolutionbecomes p(t)=900 50et/2.Thissolutionisa decreasingexponential,andhencethetimeofextinctionisequaltothenumberof monthsittakes,say tf ,forthepopulationtoreachzero.Solving900 50etf /2 =0, wefindthat tf =2ln(900/50) ≈ 5.78months.
(b)Thesolution, p(t)=900+(p0 900)et/2,isadecreasingexponentialaslongas p0 < 900.Hence900+(p0 900)etf /2 =0hasonlyoneroot,givenby
tf =2ln( 900 900 p0 )
(c)Theanswerinpart(b)isageneralequationrelatingtimeofextinctiontothe valueoftheinitialpopulation.Setting tf =12months,theequationmaybewritten as
900 p0 = e 6 , whichhassolution p0 ≈ 897 8.Since p0 istheinitialpopulation,theappropriate answeris p0 =898mice.
8.(a)Thegeneralsolutionis p(t)= p0 ert.Basedonthediscussioninthetext,time t ismeasuredinmonths.Assuming1month=30days,thehypothesiscanbe expressedas p0 er 1 =2p0.Solvingfortherateconstant, r =ln(2),withunitsof permonth.
(b) N days= N/30months.Thehypothesisisstatedmathematicallyas p0erN/30 = 2p0.Itfollowsthat rN/30=ln(2),andhencetherateconstantisgivenby r = 30ln(2)/N .Theunitsareunderstoodtobepermonth.
10.(a)Assumingnoairresistance,withthepositivedirectiontakenasdownward, Newton’sSecondLawcanbeexpressedas
m dv dt = mg,
inwhich g isthegravitationalconstantmeasuredinappropriateunits.Theequation canbewrittenas dv/dt = g,withsolution v(t)= gt + v0.Theobjectisreleased withaninitialvelocity v0
(b)Supposethattheobjectisreleasedfromaheightof h unitsabovetheground. Usingthefactthat v = dx/dt,inwhich x isthedownwarddisplacementofthe object,weobtainthedifferentialequationforthedisplacementas dx/dt = gt + v0. Withtheoriginplacedatthepointofrelease,directintegrationresultsin x(t)= gt2/2+ v0 t.Basedonthechosencoordinatesystem,theobjectreachestheground when x(t)= h.Let t = T bethetimethatittakestheobjecttoreachtheground. Then gT 2/2+ v0T = h.Usingthequadraticformulatosolvefor T , T = v0 ± √v0 +2gh g
Thepositiveanswercorrespondstothetimeittakesfortheobjecttofalltothe ground.Thenegativeanswerrepresentsapreviousinstantatwhichtheobject couldhavebeenlaunchedupward(withthesameimpactspeed),onlytoultimately falldownwardwithspeed v0,fromaheightof h unitsabovetheground.The numericalvalueis T = √2 9 8 300/9 8 ≈ 7 82s.
(c)Theimpactspeediscalculatedbysubstituting t = T into v(t)inpart(a).That is, v(T )= √v0 +2gh .Thenumericalvalueis v = √2 · 9 8 · 300 ≈ 76 68m/s.
12.(a,b)Thegeneralsolutionofthedifferentialequationis Q(t)= ce rt.Giventhat Q(0)=100mg,thevalueoftheconstantisgivenby c =100.Hencetheamountof thorium-234presentatanytimeisgivenby Q(t)=100 e rt.Furthermore,based onthehypothesis,setting t =1resultsin82 04=100 e r.Solvingfortherate constant,wefindthat r = ln(82 04/100) ≈ 19796/weekor r ≈ 02828/day.
(c)Let T bethetimethatittakestheisotopetodecaytoone-halfofitsoriginal amount.Frompart(a),itfollowsthat50=100 e rT ,inwhich r = 19796/week. Takingthenaturallogarithmofbothsides,wefindthat T ≈ 3 5014weeksor T ≈ 24 51days.
13.Thegeneralsolutionofthedifferentialequation dQ/dt = rQ is Q(t)= Q0e rt,inwhich Q0 = Q(0)istheinitialamountofthesubstance.Let τ be thetimethatittakesthesubstancetodecaytoone-halfofitsoriginalamount, Q0.Setting t = τ inthesolution,wehave0 5 Q0 = Q0e rτ .Takingthenatural logarithmofbothsides,itfollowsthat rτ =ln(0 5)or rτ =ln2.
14.Thedifferentialequationgoverningtheamountofradium-226is dQ/dt = rQ, withsolution Q(t)= Q(0)e rt.UsingtheresultinProblem13,andthefactthat thehalf-life τ =1620years,thedecayrateisgivenby r =ln(2)/1620peryear.The amountofradium-226,after t years,istherefore Q(t)= Q(0)e 0 00042786t.Let T bethetimethatittakestheisotopetodecayto3/4ofitsoriginalamount.Then setting t = T ,and Q(T )= 3 4 Q(0),weobtain 3 4 Q(0)= Q(0)e 0 00042786T .Solving forthedecaytime,itfollowsthat 0 00042786 T =ln(3/4)or T ≈ 672 36years.
16.BasedonProblem15,thegoverningdifferentialequationforthetemperature intheroomis du dt = .15(u 10) .
Setting t =0attheinstantthattheheatingsystemfail,theinitialconditionis u(0)=70 ◦F.
Usingseparationofvariables,thegeneralsolutionofthedifferentialequationis
u(t)=10+ Ce 15 t
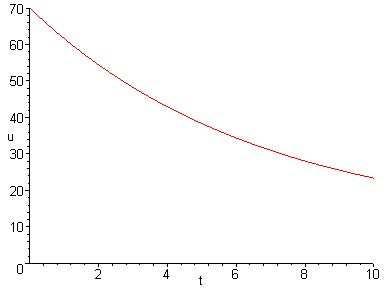
Invokingthegiveninitialcondition,thetemperatureintheroomisgivenby u(t)=10+60 e 15 t
Setting u(t)=32,weobtain t =6 69hr.
17.Thesolutionofthedifferentialequation,with Q(0)=0,is
Q(t)= CV (1 e t/CR).
As t →∞,theexponentialtermvanishes,andthelimitingvalueis QL = CV
18.(a)Theaccumulationrateofthechemicalis(0.01)(300)gramsperhour.At anygiventime t,theconcentrationofthechemicalinthepondis Q(t)/106 grams pergallon.Consequently,thechemicalleavesthepondatarateof(3 × 10 4)Q(t) gramsperhour.Hence,therateofchangeofthechemicalisgivenby
dQ dt =3 0 0003 Q(t)g/hr.
Sincethepondisinitiallyfreeofthechemical, Q(0)=0.
(b)Thedifferentialequationcanberewrittenas
dQ 10000 Q =0.0003 dt.
Integratingbothsidesoftheequationresultsin ln |10000 Q| =0 0003t + C
Takingtheexponentialofbothsidesgives10000 Q = ce 0 0003t.Since Q(0)= 0,thevalueoftheconstantis c =10000.Hencetheamountofchemicalinthe pondatanytimeis Q(t)=10000(1 e 0 0003t)grams.Notethat1year=8760 hours.Setting t =8760,theamountofchemicalpresentafteroneyearis Q(8760) ≈ 9277 77grams,thatis,9 27777kilograms.
(c)Withtheaccumulationratenowequaltozero,thegoverningequationbecomes dQ/dt = 0 0003 Q(t)g/hr.Resettingthetimevariable,wenowassignthenew initialvalueas Q(0)=9277 77grams.
(d)Thesolutionofthedifferentialequationinpart(c)is
Q(t)=9277 77 e 0 0003t
Hence,oneyearafterthesourceisremoved,theamountofchemicalinthepondis Q(8760) ≈ 670.1grams.
(e)Letting t betheamountoftimeafterthesourceisremoved,weobtaintheequation10=9277 77 e 0 0003t.Takingthenaturallogarithmofbothsides, 0 0003 t = ln(10/9277 77)or t ≈ 22, 776hours≈ 2 6years.
(f)

19.(a)Itisassumedthatdyeisnolongerenteringthepool.Infact,therateat whichthedyeleavesthepoolis200 [q(t)/60000]g/min.Hencetheequationthat governstheamountofdyeinthepoolis
dq dt = q/300(g/min)
Theinitialamountofdyeinthepoolis q(0)=5000grams.
(b)Thesolutionofthegoverningdifferentialequation,withthespecifiedinitial value,is q(t)=5000 e t/300
(c)Theamountofdyeinthepoolafterfourhoursisobtainedbysetting t =240. Thatis, q(4)=5000 e 0 8 =2246 64grams.Sincethesizeofthepoolis60, 000 gallons,theconcentrationofthedyeis0 0374grams/gallon,andtheanswerisno.
(d)Let T bethetimethatittakestoreducetheconcentrationlevelofthedyeto 0 02grams/gallon.Atthattime,theamountofdyeinthepoolis1, 200grams. Usingtheanswerinpart(b),wehave5000 e T/300 =1200.Takingthenatural logarithmofbothsidesoftheequationresultsintherequiredtime T ≈ 7 14hours.
(e)Considerthedifferentialequation dq dt = r 60, 000 q.
Heretheparameter r correspondstotheflowrate,measuredingallonsperminute. Usingthesameinitialvalue,thesolutionisgivenby q(t)=5000 e rt/60,000.In ordertodeterminetheappropriateflowrate,set t =240and q =1200.(Recall that1200gramsofdyehasaconcentrationof0 02g/gal).Weobtaintheequation 1200=5000 e r/250.Takingthenaturallogarithmofbothsidesoftheequation resultsintherequiredflowrate r ≈ 357gallonsperminute.
1.Thedifferentialequationissecondorder,sincethehighestderivativeinthe equationisofordertwo.Theequationislinear,sincethelefthandsideisalinear functionof y anditsderivatives.
3.Thedifferentialequationisfourthorder,sincethehighestderivativeofthe function y isoforderfour.Theequationisalsolinear,sincethetermscontaining thedependentvariableislinearin y anditsderivatives.
4.Thedifferentialequationisfirstorder,sincetheonlyderivativeisoforderone. Thedependentvariableissquared,hencetheequationisnonlinear.
5.Thedifferentialequationissecondorder.Furthermore,theequationisnonlinear, sincethedependentvariable y isanargumentofthesinefunction,whichisnota linearfunction.
7. y1(t)= et ⇒ y1(t)= y1 (t)= et.Hence y1 y1 =0.Also, y2(t)=cosh t ⇒ y1(t)=sinh t and y2 (t)=cosh t.Thus y2 y2 =0.
9. y(t)=3t + t2 ⇒ y (t)=3+2t.Substitutingintothedifferentialequation,we have t(3+2t) (3t + t2)=3t +2t2 3t t2 = t2.Hencethegivenfunctionisa solution.
10. y1(t)= t/3 ⇒ y1(t)=1/3and y1 (t)= y1 (t)= y1 (t)=0.Clearly, y1(t) isasolution.Likewise, y2(t)= e t + t/3 ⇒ y2(t)= e t +1/3, y2 (t)= e t , y2 (t)= e t , y2 (t)= e t.Substitutingintothelefthandsideoftheequation, wefindthat e t +4( e t)+3(e t + t/3)= e t 4e t +3e t + t = t.Henceboth functionsaresolutionsofthedifferentialequation.
11. y1(t)= t1/2 ⇒ y1(t)= t 1/2/2and y1 (t)= t 3/2/4.Substitutingintothe lefthandsideoftheequation,wehave 2t2( t 3/2/4)+3t(t 1/2/2)
Likewise, y2(t)= t 1 ⇒ y2(t)= t 2 and y2 (t)=2 t 3.Substitutingintotheleft handsideofthedifferentialequation,wehave
Hencebothfunctionsaresolutionsofthedifferentialequation.
12. y1(t)= t 2 ⇒ y1(t)= 2t 3 and y1 (t)=6 t 4.Substitutingintothelefthand sideofthedifferentialequation,wehave t2(6 t 4)+5t( 2t 3)+4 t 2 =6 t 2 10 t 2 +4 t 2 =0
Likewise, y2(t)= t 2 ln t ⇒ y2(t)= t 3 2t 3 ln t and y2 (t)= 5 t 4 +6 t 4 ln t.
Substitutingintothelefthandsideoftheequation,wehave
2( 5
Hencebothfunctionsaresolutionsofthedifferentialequation.
.
13. y(t)=(cos t)lncos t + t sin t ⇒ y (t)= (sin t)lncos t + t cos t and y (t)= (cos t)lncos t t sin t +sec t.Substitutingintothelefthandsideofthedifferentialequation,wehave ( (cos t)lncos t t sin t +sec t)+(cos t)lncos t + t sin t = (cos t)lncos t t sin t +sec t +(cos t)lncos t + t sin t =sec t.
Hencethefunction y(t)isasolutionofthedifferentialequation.
15.Let y(t)= ert.Then y (t)= rert,andsubstitutionintothedifferentialequation resultsin rert +2ert =0.Since ert =0,weobtainthealgebraicequation r +2=0. Therootofthisequationis r = 2.
16.Let y(t)= ert.Then y (t)= r2ert,andsubstitutionintothedifferentialequationresultsin r2ert ert =0.Since ert =0,weobtainthealgebraicequation r2 1=0.Therootsofthisequationare r1,2 = ±1.
17. y(t)= ert ⇒ y (t)= rert and y (t)= r2ert.Substitutingintothedifferential equation,wehave r2ert + rert 6 ert =0.Since ert =0,weobtainthealgebraic equation r2 + r 6=0,thatis,(r 2)(r +3)=0.Therootsare r1,2 = 3,2.
18.Let y(t)= ert.Then y (t)= rert , y (t)= r2ert and y (t)= r3ert.Substitutingthederivativesintothedifferentialequation,wehave r3ert 3r2ert +2rert =0. Since ert =0,weobtainthealgebraicequation r3 3r2 +2r =0.Byinspection, itfollowsthat r(r 1)(r 2)=0.Clearly,therootsare r1 =0, r2 =1and r3 =2.
20. y(t)= tr ⇒ y (t)= rtr 1 and y (t)= r(r 1)tr 2.Substitutingthederivativesintothedifferentialequation,wehave t2 r(r 1)tr 2 4t(rtr 1)+4 tr =0. Aftersomealgebra,itfollowsthat r(r 1)tr 4rtr +4 tr =0.For t =0,weobtainthealgebraicequation r2 5r +4=0.Therootsofthisequationare r1 =1 and r2 =4.
21.Theorderofthepartialdifferentialequationistwo,sincethehighestderivative, infacteachoneofthederivatives,isofsecondorder.Theequationislinear,since thelefthandsideisalinearfunctionofthepartialderivatives.
23.Thepartialdifferentialequationisfourthorder,sincethehighestderivative, andinfacteachofthederivatives,isoforderfour.Theequationislinear,since thelefthandsideisalinearfunctionofthepartialderivatives.
24.Thepartialdifferentialequationissecondorder,sincethehighestderivativeof thefunction u(x,y)isofordertwo.Theequationisnonlinear,duetotheproduct u · ux onthelefthandsideoftheequation.
25.If u1(x,y)=cos x cosh y,then
Itisevidentthat
u2(
)=ln(x2 + y2),thesecond derivativesare
Addingthepartialderivatives,
Hence u2(x,y)isalsoasolutionofthedifferentialequation.
27.Let u1(x,t)=sin(λx)sin(λat).Thenthesecondderivativesare
Itiseasytoseethat
(
)=sin(x at),wehave
Clearly, u2(x,t)isalsoasolutionofthepartialdifferentialequation.
28.Giventhefunction u(x,t)= π/te
α 2t,thepartialderivativesare
Itfollowsthat
Hence u(x,t)isasolutionofthepartialdifferentialequation.
29.(a)
(b)Thepathoftheparticleisacircle,thereforepolarcoordinatesareintrinsicto theproblem.Thevariable r isradialdistanceandtheangle θ ismeasuredfrom thevertical.
Newton’sSecondLawstatesthat F = ma.Inthetangentialdirection,the equationofmotionmaybeexpressedas Fθ = maθ,inwhichthetangential acceleration,thatis,thelinearaccelerationalongthepathis aθ = Ld2θ/dt2.( aθ ispositiveinthedirectionofincreasing θ ).Sincetheonlyforceactinginthe tangentialdirectionisthecomponentofweight,theequationofmotionis
(c)Rearrangingthetermsresultsinthedifferentialequation
30.(a)Thekineticenergyofaparticleofmass m isgivenby T = 1 2 mv2,inwhich v isitsspeed.Aparticleinmotiononacircleofradius L hasspeed L (dθ/dt), where θ isitsangularpositionand dθ/dt isitsangularspeed.
(b)Gravitationalpotentialenergyisgivenby V = mgh,where h istheheight aboveacertaindatum.Choosingthelowestpointoftheswingasthedatum (V =0),itfollowsfromtrigonometrythat h =1 cos θ
(c)Fromparts(a)and(b),
ApplyingtheChainRuleforDifferentiation,
20Chapter1.Introduction
Setting dE/dt =0anddividingbothsidesoftheequationby dθ/dt resultsin mL2 d2θ dt2 + mgL sin θ =0, whichleadstoequation(12).
31.Angularmomentumisthemoment(aboutacertainpoint)oflinearmomentum, whichisgivenby
mv = mL dθ dt
Takingamomentaboutthepivotpoint,theangularmomentumis
Mp = mL2 dθ dt .
Themomentofthegravitationalforce(aboutthesamepoint)is Mg = mg L sin θ