Chi ha paura della matematica_SKILL_BOOK

BOOK SKILL BOOK SKILL PAURA matematica della ?

COMPETENZE AZIONE in aritmetica 1 GEOMETRIA 1

SCRATCH IA

GEOGEBRA

COMPITI DI REALTÀ

TEST INVALSI

IA E PROMPTING

COMPITO DI REALTÀ 1

Micaela ha deciso di svolgere un anno di Servizio civile presso il Centro Comunale di Raccolta (CCR) del suo paese, Ferla (SR), uno dei Comuni più virtuosi d’Italia nel settore della raccolta differenziata. Ogni giorno i cittadini portano i propri rifiuti differenziati presso il CCR, dove vengono pesati per avere una riduzione sulla TARI (la TAssa sui RIfiuti).

Micaela raccoglie periodicamente i dati per il suo ufficio così da avere un riscontro sulla quantità di rifiuti che transitano per il CCR. Aiutala a riportare i dati su tabelle e grafici.

1 Nell’ultimo anno sono state raccolte 750 tonnellate (t) di rifiuti, di cui 500 t circa sono di raccolta differenziata e 250 t di indifferenziato secco.

a) Riporta i dati sulla tabella.

Raccolta differenziata

b) Crea un grafico a torta (areogramma) che permetta di visualizzare la differenza di rifiuti riciclabili (differenziati) da quelli da mandare in discarica (indifferenziati).

2 Micaela ha confrontato i dati con quelli degli ultimi 4 anni.

a) Realizza un grafico lineare (poligonale delle frequenze) per evidenziare i progressi nella raccolta differenziata.

b) Realizza un grafico lineare (poligonale delle frequenze) per evidenziare il calo progressivo della raccolta di indifferenziato secco. Raccolta

3 Il Sindaco ha voluto anche un riepilogo delle entrate che si sono avute nell’ultimo anno grazie alla vendita del materiale riciclabile.

a) Completa la tabella.

Alluminio

Carta e cartone

b) Realizza un ideogramma con la seguente simbologia:

= 2 000 = 1 000

PER RIFLETTERE

• Qual è stato il passaggio che ti è risultato più difficile? Per quale motivo?

• Ritieni che gli argomenti studiati siano realmente utili in caso ti trovassi in una situazione del genere?

• Sapevi già dell’esistenza del Servizio civile, del CCR e della TARI?

• Conosci qualche altra località particolarmente virtuosa nella raccolta differenziata?

ARITMETICA

COMPITO DI REALTÀ 2

Il volantino di un grande ipermercato pubblicizza quattro notebook in offerta:

• DreamNB: 17,3 pollici − RAM 4 GB − SSD 2 TB − Scheda grafica (449,00 €);

• Full Touch: 15, 6 pollici − RAM 12 GB − SSD 1 000 GB − Scheda grafica (499,00 €);

• Top flash: 17,3 pollici − RAM 8 GB − SSD 500 GB − Scheda grafica (449,00 €);

• Virtual Net: 17,3 pollici − RAM 8 GB − SSD 1 TB − Scheda grafica (499,00 €).

Pietro deve comprare un nuovo portatile che dovrà avere un hard disk capace di contenere, oltre al sistema operativo, ai software e ai documenti di scuola:

• la sua collezione di film, che occupa una memoria di circa 150 gigabyte;

• il suo archivio fotografico di circa 5 000 foto, che occupa 20 000 megabyte;

• il suo archivio musicale di 90 000 brani (mediamente 1 giga contiene 300 brani).

SSD: Solid State Disk

1 Quanti gigabyte occupa la memoria dei tre archivi di Pietro? Sul quaderno raccogli i dati in una tabella con 4 righe (film, foto, musica, totale).

2 Può pensare di acquistare il Top Flash con un hard disk di 500 GB? Perché?

1 TB (terabyte) = 1012 bytes

1 GB (gigabyte) = 109 bytes

1 MB (megabyte) = 106 bytes

3 Volendo acquistare un notebook con una Ram di almeno 8 GB per i videogiochi, uno schermo molto grande e la scheda grafica Intel, qual è l’offerta adatta a lui?

a) ™ DreamNB b) ™ Full Touch c) ™ Top flash d) ™ Virtual Net

ARITMETICA

COMPITO DI REALTÀ 3

Il paesino di Roccadisopra si sta preparando a ospitare la gara podistica Benvenuta Primavera per il 20 marzo 2027.

1 Tre amici si preparano all’evento allenandosi sulla pista di atletica. Mirko si allena solo il mercoledì, Chicco ogni 3 giorni e Tom a giorni alterni. Mercoledì 7 febbraio si sono allenati tutti e tre insieme e hanno calcolato che riusciranno a farlo solamente un’altra volta prima della gara.

a) In che giorno del mese di marzo si incontreranno?

b) In quali giorni si alleneranno insieme solo Tom e Chicco?

c) Chi si allenerà il 29 febbraio?

d) Quanti allenamenti farà Mirko, dopo il 7 febbraio, prima della gara?

2 La banda del paese si prepara a sfilare prima della corsa. Il direttore della banda ha a disposizione: – 20 ottoni (trombe, tromboni, flicorni, corni e tube); – 24 legni (flauti, clarinetti, oboe, fagotti e sassofoni); – 8 percussioni (tamburi, rullanti, piatti e grancasse).

Vuole disporre i musicisti allineati in modo da formare file tutte uguali per numero e per tipologia di strumento.

a) Quanti musicisti ci saranno in ogni fila?

b) Quante file farà con i legni?

c) Quante file farà con gli ottoni?

COMPITO DI REALTÀ 4

EDUCAZIONE CIVICA MATEMATICA IN AZIONE In Italia

il Presidente della Repubblica viene eletto ogni 7 anni. Le modalità dell’elezione sono descritte nell’articolo 83 della Costituzione: “Il Presidente della Repubblica italiana è eletto dal Parlamento in seduta comune dei suoi membri. All’elezione partecipano tre delegati per ogni Regione eletti dal Consiglio regionale in modo che sia assicurata la rappresentanza delle minoranze. La Valle d’Aosta ha un solo delegato.

L’elezione del Presidente della Repubblica ha luogo per scrutinio segreto a maggioranza dei due terzi dell’assemblea. Dopo il terzo scrutinio è sufficiente la maggioranza assoluta”.

1 Al suo primo mandato nel gennaio 2015, il Presidente Sergio Mattarella è stato eletto al IV scrutinio con 665 voti. Secondo la Costituzione con quanti voti avrebbe dovuto essere eletto al primo scrutinio?

a) Parlamentari votanti: 630 deputati + 315 senatori =

b) Delegati regionali: 3 × (20 − 1) + 1 =

c) Calcola il numero totale degli elettori: parlamentari + delegati regionali + 6 senatori a vita →

d) Calcola i 2 3 del numero totale dei votanti (approssima alle unità).

2 Il 29 gennaio 2022 il Presidente Mattarella è stato rieletto all’VIII scrutinio con 759 voti. Questa volta, con la riforma costituzionale del gennaio 2020, il numero dei parlamentari si è ridotto rispetto alla prima elezione. Con questa nuova riforma, quanti voti avrebbe dovuto avere per essere eletto al primo scrutinio?

a) Parlamentari votanti: 400 deputati + 200 senatori =

b) Delegati regionali:

c) Numero totale degli elettori:

d) Maggioranza dei due terzi dell’assemblea (approssima alle unità):

3 In quale anno scadrà il secondo mandato del Presidente Mattarella?

PER RIFLETTERE

• Qual è stato il passaggio che ti è risultato più difficile? Per quale motivo?

• Ritieni che gli argomenti studiati siano realmente utili per descrivere e analizzare una situazione del genere?

• Conoscevi il nome del Presidente della Repubblica?

• Sai chi sono i senatori a vita e i senatori di diritto?

• Fai una ricerca sulle funzioni svolte dalla Camera dei Deputati e dal Senato.

COMPITO DI REALTÀ 5

1 L’insegnante di musica della II F di un Istituto Comprensivo, per aiutare i suoi alunni a capire meglio il tempo di esecuzione di ogni nota, usa le frazioni. Aiutali a risolvere i seguenti esercizi.

a) Ricordando che le note puntate aumentano il loro valore della metà, scrivi sotto forma di frazione il valore di ciascuna nota o gruppo di note usando la tabella. q h . w h e q q q q q q h = w + q = h + w = q + h = w + h . = q q + q =

b) Scrivi la nota che rende vera ciascuna uguaglianza.

1) q + = 2 4 2) q + = 4 4 3) + = 8 4 4) e + = 2 4 5) h + = 4 4

INTERO w METÀ h UN QUARTO q UN OTTAVO e UN SEDICESIMO 

 + = 1 8 7) q + = 5 4 8) + = 7 4 9) h + = 3 4 10) q + = 3 8

c) Osserva le seguenti frazioni: in musica si chiamano tempo e indicano il numero di accenti in ogni battuta.

& & & & & &

Abbina a ogni battuta il tempo corretto. h h q q q qq∑∑∑∑ q ÓÓÓÓÓÓÓÓÓÓÓ q e qÓÓÓq q q h h q q q qq∑∑∑∑ q ÓÓÓÓÓÓÓÓÓÓÓ q e qÓÓÓq q q h h q q q qq∑∑∑∑ q

ÓÓÓÓÓÓÓÓÓÓÓ q e qÓÓÓq q q 1) 2) 3) Hk q q q

ÓÓÓÓÓ e e q q ÓÓÓÓq q e q q Hk q q q

ÓÓÓÓÓ e e q q ÓÓÓÓq q e q q Hk q q q

ÓÓÓÓÓ e e q q ÓÓÓÓq q e q q 4) 5) 6)

d) Ognuna delle seguenti note completa le battute di ogni spartito. Inserisci a fianco di ogni partitura la nota mancante.

(Attenzione al tempo che si trova allinizio della battuta.)

e) Una scolaresca di Liverpool sarà ospite dei ragazzi dell’Istituto per un Erasmus e l’orchestra dei flauti ha preparato l’Inno nazionale inglese.

Calcola in quanto tempo eseguiranno l’inno, considerando che una semiminima, q , ha un durata di mezzo secondo nell’esecuzione e il tempo è 3 4 . God save the King

PER RIFLETTERE

• Qual è stato il passaggio che ti è risultato più difficile? Per quale motivo?

• Ritieni che gli argomenti studiati siano realmente utili per descrivere e analizzare una situazione del genere?

• Fai una ricerca sull’inno inglese, sul suo compositore e come varia il suo testo a seconda che ci sia un re o una regina.

• Prova a suonarlo con il tuo strumento delle lezioni di musica.

• Ti vengono in mente altri Paesi che aderiscono al progetto Erasmus?

COMPITO DI REALTÀ 6

Il perlinato è il rivestimento di una parete (o altre superfici) che viene effettuato accostando lunghe e strette tavole di legno. Ognuna di queste tavole viene chiamata perlina di legno. Una superficie rivestita con un perlinato svolge uno scopo sia decorativo sia di isolante termico. Per evitare deformazioni e muffa, le tavole di legno (perline) non devono essere a contatto diretto con il muro. Per questo motivo, prima vengono fissati dei listelli orizzontali alla parete e poi a questi vengono inchiodate le perline, garantendo quindi che tra le perline e la parete possa circolare l’aria.

COOPERATIVE LEARNING Il papà di Filippo ha deciso di ricoprire con delle perline di legno di abete una parete di un locale. Prima di iniziare, vuole però sapere quanto gli costerà tutto il materiale necessario a eseguire il lavoro.

Aiutalo, tenendo conto di tutte le informazioni fornite di seguito.

• Il papà di Filippo può scegliere tra due tipi di perline di legno: 15 cm × 2,5 m oppure 15 cm × 3 m.

• Il costo di entrambi i tipi di perline di legno è di 1,85 euro al metro lineare.

• La parete da ricoprire con le perline di legno ha le seguenti dimensioni: 3 metri di altezza e 4,2 metri di lunghezza.

• Lungo la parete vengono fissati 5 listelli sui quali devono essere inchiodate le perline di legno.

• Il costo dei listelli è di 0,75 euro al metro lineare.

larghezza della parete: 4,2 metri 15 cm

altezza della parete: 3 metri

Perline

Listello

Per aiutare il papà di Filippo, risolvi i seguenti quesiti.

(Puoi svolgere l’attività collaborando con un tuo compagno di classe.)

1 Tra i due tipi di perline, qual è il più conveniente? Perché?

2 Calcola la lunghezza totale sia delle perline sia dei listelli da acquistare.

a) Utilizzando le misure date, perché non puoi dividere la misura della lunghezza della parete per la misura della larghezza della perlina?

b) Effettua l’equivalenza necessaria (4,2 m = cm).

c) Calcola il numero di perline necessarie per coprire tutta la parete.

d) Quanto è la lunghezza totale delle perline?

e) Quanti sono i listelli? Quanto deve essere lungo un listello?

f) Quanto è la lunghezza complessiva dei listelli?

3 Calcola quanto spende per acquistare il materiale occorrente.

a) Qual è il costo totale delle perline e quello totale dei listelli?

b) Qual è il costo del materiale necessario al papà di Filippo?

PER RIFLETTERE

• Qual è stato il passaggio che ti è risultato più difficile? Per quale motivo?

• Il lavoro in coppia è stato efficace?

• Vi è già capitato di svolgere realmente un compito come questo proposto?

• Gli argomenti studiati ti sono stati utili o avresti potuto usare altri metodi semplici?

• Ti eri mai chiesto come si fa a rivestire i muri delle case con il legno? Sapevi già che i rivestimenti di legno delle pareti non sono direttamente attaccati al muro?

COMPITO DI REALTÀ 7

Per indicare con precisione una posizione esiste un metodo che utilizza:

• i punti cardinali a cui vengono assegnati:

0° o 360° (Nord), 90° (Est), 180° (Sud), 270° (Ovest);

• l’ampiezza di un angolo;

• una distanza

Per indicare la posizione della nave (B) rispetto al faro (A) si procede come segue:

1) partendo dal punto A si traccia la linea che indica il Nord (linea Nord);

2) si uniscono con un segmento i punti A e B;

3) con il goniometro si misura in senso orario l’ampiezza dell’angolo formato dalla linea Nord e dal segmento che unisce A e B;

4) si misura la distanza AB

Se questo metodo si applica a un disegno ridotto o ingrandito in cui è indicata la scala, si può calcolare anche la distanza reale tra A e B.

1 Sulla mappa a fianco, partendo dalla città di Lugano, traccia la linea che indica il Nord. (Osserva la rosa dei venti.)

2 Utilizzando il metodo descritto, indica le posizioni delle seguenti località rispetto alla linea che indica il Nord: Bellinzona, Menaggio, Gravedona, Lecco, Como, Chiasso.

a) Bellinzona ( °; cm)

b) Menaggio ( °; cm)

c) Gravedona ( °; cm)

d) Lecco ( °; cm)

e) Como ( °; cm)

f) Chiasso ( °; cm)

PER RIFLETTERE

• Qual è stato il passaggio che ti è risultato più difficile? Per quale motivo?

• Se un tuo amico avesse un’altra mappa dei dintorni di Lugano su cui le città non sono indicate, potrebbe individuarle utilizzando le informazioni che hai raccolto?

• È possibile indicare le distanze reali che le località hanno da Lugano? Perché?

Faro

Nord

La posizione della nave rispetto al faro è 122° e 7 cm.

Menaggio Gravedona

Lecco Como

Chiasso

Lugano SVIZZERA ITALIA

Bellinzona

COMPITO DI REALTÀ 8

Per il suo compleanno Pietro riceve un binocolo a pantografo. Questo strumento viene utilizzato dagli astronomi perché il piedistallo consente di alzare e abbassare il binocolo attaccato mantenendo il fuoco sull’obiettivo, il che risulta molto utile quando più persone di altezza diversa osserveranno una dopo l’altra lo stesso oggetto. Pietro vuole capire come funziona il telaio (in rosso nella figura) e si pone delle domande. Aiutalo a rispondere.

1 Pietro misura i lati: AB ≅ CD = 1,30 m

e DA ≅ BC = 15 cm.

a) Che tipo di quadrilatero è ABCD? Perché?

b) Il telaio è collegato al treppiedi nei punti E e F in modo che EF ≅ AD e AF ≅ DE. Che tipo di quadrilatero è AFED? Perché?

c) Facendo scorrere il telaio lungo i punti E e F, che cosa cambia del quadrilatero AFED ?

d) Se AF ≅ AD che tipo di quadrilatero è AFED?

2 Pietro misura l’angolo D = 78°.

a) Può dedurre quanto misurano gli angoli B, C, A ?

b) Quanto misurano gli angoli

DEF, AFE ?

3 Nella posizione attuale

AF = 64 cm, calcola:

a) il perimetro del quadrilatero ABCD

b) il perimetro del quadrilatero AFED

c) il perimetro del quadrilatero

FBCE.

PER RIFLETTERE

• Qual è stato il passaggio che ti è risultato più difficile? Per quale motivo?

• I particolari a cui si è interessato Pietro pensi abbiano una utilità reale? Quali ti sembrano più utili e quali meno? Perché?

• Ritieni che gli argomenti studiati siano stati realmente utili per descrivere e analizzare una situazione del genere?

• Fai una ricerca per scoprire in quali casi è più utile un binocolo a pantografo e in quali casi è più utile un binocolo normale.

• Quando e da chi è stato inventato il binocolo a pantografo?

DI REALTÀ 9

EDUCAZIONE CIVICA COOPERATIVE LEARNING La geometria della strada

Secondo il Codice della strada la forma dei cartelli stradali dipende dal tipo di informazione che rappresentano. Esistono infatti diversi tipi di cartelli stradali:

• segnali di pericolo, di forma triangolare;

• segnali di prescrizione, obbligo o divieto, di forma circolare;

• segnali di indicazione, di forma quadrata o rettangolare.

Inoltre, ci sono segnali con forme proprie e più facili da distinguere, poiché utilizzati in situazioni particolari, per esempio la Croce di Sant’Andrea e lo STOP. Il linguaggio geometrico, quindi, è fondamentale per le norme stradali.

Come puoi vedere dal seguente testo, tratto dalla Convenzione di Vienna sulla segnaletica stradale (1968), una buona conoscenza della geometria è preziosa per descrivere e comprendere le forme dei cartelli stradali.

Segnali di pericolo generico

1) Il segnale «A» Pericolo generico è disponibile nei modelli Aa o Ab, ambedue descritti qui di seguito […].

Il modello Aa consiste in un triangolo equilatero avente un lato orizzontale il cui vertice opposto è orientato verso l’alto; il fondo è bianco o giallo, il bordo è rosso.

Il modello Ab consiste in un quadrato di cui una diagonale è verticale; il fondo è giallo, il bordo che si riduce ad un listello è nero.

I simboli che sono posti su questi segnali sono, salvo indicazione diversa nella descrizione, neri o di colore blu scuro.

2) Il lato dei segnali Aa di dimensioni normali è di circa 0,90 m; il lato dei segnali Aa di piccole dimensioni non deve essere inferiore a 0,60 m. Il lato dei segnali A b di piccole dimensioni non deve essere inferiore a 0,40 m.

1 Dal testo di legge ricava le informazioni sui segnali stradali per completare la tabella.

• Consiste in un triangolo equilatero

• Il fondo è

• Il bordo è

• I simboli che sono posti su questo modello di segnale sono

• Il lato per il modello di dimensioni normali misura

• Il lato non deve essere

• Consiste in un quadrato

• Il fondo è

• Il bordo Il bordo si riduce a un ed è

• I simboli che sono posti su questo modello di segnale sono

• Il lato non deve essere

Modello A a

Modello A b

2 Lavoro di gruppo

Produttori di cartelli stradali

• Divisi in gruppi, progettate il simbolo per un nuovo segnale che indichi “attraversamento di pedoni distratti dal telefonino”.

• Scegliete uno dei modelli descritti nella legge e, utilizzando del cartone (per esempio quello di una grossa scatola), realizzate la forma del cartello in modo che sia perfettamente a norma di legge.

• Disegnate sul modello in cartone il simbolo che avete progettato e colorate il vostro cartello. Fate attenzione: il sindaco vuole sapere i costi di realizzazione di questo nuovo cartello; quindi, durante la lavorazione dovete misurare la quantità di tempera utilizzata.

Dipendenti comunali

All’interno di ogni gruppo, ciascun componente dovrà scegliere uno dei due seguenti ruoli:

a) ufficiale del traffico: ha il compito di controllare che tutti i cartelli prodotti siano a norma, rispettino cioè le norme geometriche fissate dalla Convenzione di Vienna.

b) economo: ha il compito di calcolare quanta tempera è stata utilizzata, all’incirca, per dipingere 1 dm2 del cartello. Esaminerà poi i cartelli prodotti dagli altri gruppi raccogliendo i dati in una tabella.

Cittadini del futuro

• Sempre divisi in gruppi, immaginate di essere cittadini del futuro e di dover progettare una nuova categoria di segnali stradali, che indichino la presenza sulle strade di “dispositivi governati da Intelligenze Artificiali (A.I.)”. Quale forma utilizzereste per questa nuova categoria di cartelli?

• Ispirandovi al testo della Convenzione di Vienna riportato all’inizio, provate a scrivere un breve testo di una possibile legge che, con precisione geometrica, indichi le regole per costruire questa nuova categoria di cartelli.

• Consegnate il testo della vostra legge a un altro gruppo, che proverà a riprodurre in cartone un modello del cartello, rispettando tutte le regole indicate. La vostra descrizione geometrica è stata abbastanza precisa da permettere una realizzazione accurata del modello?

PER RIFLETTERE

• Riguarda il tuo quaderno di geometria di quest’anno e individua gli argomenti che sono stati utili per svolgere i diversi passaggi del lavoro di gruppo.

• Alla fine dell’esperienza svolta con questo lavoro, discuti con i tuoi compagni dell’importanza che ha la precisione nel linguaggio matematico.

• In quali altre situazioni reali è necessario descrivere gli oggetti “con precisione geometrica”? Fai qualche esempio.

1

GLI INSIEMI

1 Considera A = { ■; ; ; &;^} e B = {^}; indica quale affermazione è vera.

2 Osserva il seguente diagramma di Venn e stabilisci a che cosa corrisponde la parte colorata.

3 Prova nazionale classi quinte.

Gli alunni della V B, al rientro dalle vacanze estive, costruiscono questo diagramma per rappresentare i mezzi di trasporto che hanno utilizzato per recarsi in villeggiatura. Ciascun pallino nero rappresenta un alunno.

Indica se le seguenti affermazioni sono vere (V) o false (F). Metti una crocetta per ogni riga.

A Gli alunni che hanno utilizzato l’automobile sono 8.

F

B 2 alunni hanno utilizzato sia il treno che l’automobile. V F

C Gli alunni che hanno utilizzato un solo mezzo di trasporto sono 14.

D Nessun alunno ha utilizzato tre mezzi di trasporto.

4 Prova nazionale classi quinte.

Mario ha suddiviso le seguenti figure in due gruppi utilizzando un criterio.

Quale criterio ha usato Mario per suddividere le figure?

F

F

A Criterio 1: Mario ha messo nel gruppo A i poligoni e nel gruppo B le figure che non sono poligoni.

B Criterio 2: Mario ha messo nel gruppo A le figure convesse e nel gruppo B le figure concave.

C Criterio 3: Mario ha messo nel gruppo A le figure simmetriche e nel gruppo B le figure che non sono simmetriche.

D Criterio 4: Mario ha messo nel gruppo A i quadrilateri e nel gruppo B le figure che non sono quadrilateri.

IL SISTEMA DI NUMERAZIONE DECIMALE

1 Nella parola “gelsomino” il posto occupato dalle vocali:

A è sempre pari

B è sempre dispari

2 Quale fra queste disuguaglianze è falsa?

A 5,6 > 5,595

B 1,53 < 2,35

C sono il primo e l’ultimo

D è pari solo per la “e”

C 2,34 < 2,43

D 1,63 > 1,643

3 Quale gruppo di numeri è scritto in ordine crescente?

A 709; 790; 789; 798

B 31,5; 131,5; 301,5; 310,5

C 6,08; 6,80; 80,6; 60,8

D 295; 259; 952; 592

4 Qual è il numero formato da 4 decimi e 35 decine?

A 4,35

B 35,4

C 350,04

D 350,4

5 Camilla spende 3,15 in edicola e 90 centesimi al bar. Paga con una banconota da 10 €.

Quindi:

A spende meno di 5 €

B spende meno di 4 €

6 Prova nazionale classi prime.

C spende 10 €

D riceve di resto più di 6 €

Angelo, Marco, Piero e Samuel partecipano a una corsa campestre.

• Angelo taglia il traguardo alle 15:03

• Samuel arriva 10 minuti prima di Angelo

Chi vince?

A Angelo B Marco

Chi arriva ultimo?

A Angelo B Marco

7 Prova nazionale classi terze.

• Piero arriva 7 minuti dopo Samuel

• Marco arriva 2 minuti dopo Piero

C Piero D Samuel

C Piero D Samuel

La somma di un numero naturale con il suo successivo n + 1 è sempre un numero dispari?

Scegli una delle due risposte e completa la frase.

Sì, perché

No, perché

LE QUATTRO OPERAZIONI E LE LORO PROPRIETÀ

1 Prova nazionale classi quinte.

La maestra chiede alla classe di calcolare a mente 137 × 4 Riccardo risponde: “Io ho moltiplicato cento per quattro, trenta per quattro e sette per quattro e poi ho sommato i risultati’’. Alessandro risponde: “Io invece ho moltiplicato sette per quattro, tre per quattro e uno per quattro e poi ho sommato i risultati’’. Chi ha seguito un procedimento corretto per fare la moltiplicazione?

A Solo Riccardo

B Solo Alessandro

C Nessuno dei due

D Tutti e due

2 Sara ha risolto la moltiplicazione 32 × 25 in questo modo: (30 + 2) × 25 = 750 + 50 = 800; quale proprietà della moltiplicazione ha applicato?

A Associativa

B Commutativa

3 Date le moltiplicazioni:

a) 359 × 17 b) 408 × 22 c) 65 × 108 d) 48 × 159 quale affermazione relativa ai prodotti è falsa?

A b > d

B Solo a è dispari

C Seconda proprietà

D Distributiva

C Solo c è pari

D c < d

4 Quale procedimento non è corretto per risolvere la moltiplicazione 365 × 14?

A 365 × 10 + 365 × 4

B 365 × 20 365 × 6

5 Esame di Stato.

C 14 × 400 14 × 35

D 14 × 300 14 × 65

Osserva questa moltiplicazione: 17 × 36 = 612

Ora scrivi il risultato delle seguenti moltiplicazioni.

A 17 × 3,6 =

B 17 × 0,36 =

C 1,7 × 360 =

D 1,7 × 3,6 =

6 Esame di Stato.

a, b e c sono tre numeri naturali.

a × b = 2 b × c = 3 a × c = 6

Quale fra i seguenti valori corrisponde al prodotto a × b × c?

METODI PER RISOLVERE I PROBLEMI

1 Considera la seguente rappresentazione grafica e stabilisci a quale testo corrisponde.

A Anna ha il doppio dell’età di Lia e Sara ha il quintuplo dell’età di Lia. Se gli anni in tutto sono 108, quanti anni hanno Anna, Lia e Sara?

B Calcola le altezze dei tre alberi del giardino di John, sapendo che l’altezza totale è 63 m, l’altezza dell’olmo è il triplo dell’acero e quella del pino è il quintuplo dell’acero.

C Corrado spende 320 € per tre attrezzi: il secondo costa il triplo del primo e il terzo il quintuplo del secondo. Qual è il costo di ogni attrezzo?

D Il peso complessivo di tre carichi di agrumi è di 200 quintali; calcola il peso di ogni carico, sapendo che il secondo e il primo sono rispettivamente un terzo e un quinto del peso del terzo carico.

2 Una lavanderia a gettoni lavora con orario continuato dalle 9 alle 18. Ogni lavatrice effettua cicli di lavaggio della durata di 33 minuti, ai quali si devono aggiungere 10 minuti per l’operazione di carico e 5 per lo svuotamento.

Quanti lavaggi completi, comprensivi di carico e svuotamento, può effettuare al massimo una lavatrice nell’arco della giornata?

3 È stato effettuato un sondaggio su un campione di 1 500 donne di età compresa tra i 25 e i 55 anni per conoscere la loro opinione su una rivista mensile dedicata alla salute. Si sono ottenuti i seguenti risultati:

A Quante sono le donne che hanno espresso un giudizio positivo?

B Quanto sono le donne disoccupate intervistate?

4 Prova nazionale classi terze. Francesco esegue nell’ordine le seguenti operazioni:

1) scrive il numero 5

2) lo raddoppia

3) aggiunge 6

4) divide per 2

5) sottrae 5

Quale delle seguenti espressioni traduce correttamente la sequenza delle operazioni fatte da Francesco?

A (5 2 + 6) : 2 5

B 5 ⋅ 2 + 6 : 2 5

1 La seguente tabella riporta le età di un gruppo di ragazzi che ha frequentato un campeggio estivo sulle rive del fiume Dolceacqua.

Stabilisci quale serie di età rappresenta la tabella.

A 12; 13; 11; 9; 10; 10; 12; 11; 10; 11; 11; 9; 10; 11; 11; 12; 11; 12

B 9; 11; 10; 11; 9; 11; 10; 9; 10; 10; 11; 11; 11; 10; 11; 11; 12; 11

C 11; 12; 10; 9; 11; 12; 11; 10; 10; 12; 11; 10; 10; 12; 10; 12; 11; 9

D 12; 10; 11; 9; 10; 10; 12; 11; 12; 11; 11; 9; 10; 11; 11; 12; 11; 12

2 Il seguente ideogramma rappresenta i libri prestati da una biblioteca nei mesi estivi.

Stabilisci quanti libri sono stati prestati in totale.

giugno

luglio

agosto

3 Prova nazionale classi terze.

Nella tabella sono riportati i dati relativi alla raccolta differenziata dei rifiuti nelle province liguri dal 2009 al 2012. I dati sono forniti in kilogrammi.

Con i dati della tabella è stato costruito il grafico. Completa la legenda. = 20 libri

LE POTENZE

1 Quale fra le seguenti potenze ha valore minore?

A 35 0

2 Uno solo dei seguenti numeri è scritto in notazione scientifica; quale?

A 1,48 × 10 9 B 0,148 × 10 8

3 La luce viaggia nel vuoto alla velocità di circa 3 × 108 km al secondo.

La distanza percorsa in un’ora è:

A 3,6 × 10 8 km

B 1,08 × 1012 km

C 3 × 1011 km

D 2,16 × 1011 km

4 Quali numeri completano la sequenza 2; 4; 8; .....; 32; 64; 128; .....?

A 24 e 3 × 26

B 24 e 28

5 Il doppio di 29 è:

A

6 Il quadrato di 25 è:

7 Prova nazionale classi terze.

C 3 × 2 2 e 28

D 3 × 23 e 3 × 28

Elisa e Paolo stanno cercando di rispondere a questa domanda:

``Qual è la coppia di numeri interi a, b (diversi fra loro) tali che ab = ba?’’

Ecco le loro soluzioni:

Chi ha ragione?

A Solo Elisa

B Solo Paolo

8 Prova nazionale classi terze.

C Entrambi

D Nessuno dei due

Per produrre 1 kg di carne da manzi di allevamento si utilizzano 10 000 litri di acqua. Quanti litri di acqua occorrono per produrre 1000 kg di carne? Scrivi il risultato come potenza di 10, scrivendo l’esponente corretto nel quadratino.

Risposta: 10

Elisa Paolo

DIVISORI E MULTIPLI

1 Il numero la cui fattorizzazione è 22 × 3 × 5 × 11 non è sicuramente divisibile per:

A 12 B 15 C 25 D 33

2 60 è multiplo di 15; allora:

a)

b)

c)

d)

M.C.D. (15; 60) = 1 m.c.m.(15; 60) = 60

M.C.D. (15; 60) = 15 m.c.m.(15; 60) = 120

M.C.D. (15; 60) = 15 m.c.m.(15; 60) = 75

M.C.D. (15; 60) = 15 m.c.m.(15; 60) = 60

3 Sebastiano ha raccolto nella sua azienda agricola 144 kg di pomodori, 108 kg di peperoni e 210 kg di melanzane. Prepara delle cassette con lo stesso peso e con lo stessa quantità di ogni tipo di verdura per ogni cassetta.

Quanto pesa ogni cassetta e quante ne prepara?

A Una cassetta pesa 70 kg e prepara 6 cassette

B Una cassetta pesa 70 kg e prepara 7 cassette

C Una cassetta pesa 6 kg e prepara 77 cassette

D Una cassetta pesa 6 kg e prepara 66 cassette

4 Lorenzo ha scommesso con Emma che, tra (15 e 80) e (15 e 8), la seconda coppia è di numeri primi tra loro. Vince la scommessa? Spiega perché.

5 Marcella compera due biglietti della lotteria segnati con dei numeri primi; qual è la coppia di biglietti?

A 27 e 29 B 37 e 39 C 59 e 79 D 71 e 81

6 Prova nazionale classi terze.

Filippo si prepara per una gara di triathlon. Si allena nel nuoto ogni 3 giorni, nella corsa a piedi ogni 6 giorni e nella corsa in bicicletta ogni 8 giorni. Se oggi si è allenato in tutti e tre gli sport, tra quanti giorni gli accadrà di nuovo di allenarsi nei tre sport nella stessa giornata?

A 8 B 12 C 17 D 24

7 Prova nazionale classi terze.

Considera due numeri naturali qualsiasi s e t. Se a = 3 s e b = 3t, allora a + b è sempre divisibile per 3 perché...

a) a + b = 3 s + 3t = 3 × (s + t)

b) a + b = 3

c) a + b = 6 + 9 = 15

d) a + b = 3 s + 3t = 3 × s + t

LE FRAZIONI

1 La frazione 7 9 corrisponde a:

A 9 : 7

B 7 : 9

C un numero maggiore di 1

D 7,9

2 Quale frazione completa l’uguaglianza 28 5 = 5 + .................. ?

A 1 3

3 Puoi scrivere una frazione equivalente a 7 15 avente come denominatore 40?

A Sì, semplificando 15 ottieni 5 e 5 × 8 = 40.

B No, 40 non è multiplo di 15.

C No, 40 non è multiplo di 7.

D Sì, ogni frazione ha infinite frazioni equivalenti.

4 Indica la disuguaglianza falsa.

A 5 5 > 4 5 B 1 7 < 1 3

5 Data la frazione 1 4 , se si aumenta il denominatore di una unità, la frazione che si ottiene è:

A equivalente a quella data

B maggiore di quella data

6 Prova nazionale classi terze.

C minore di quella data

D impropria

Quale numero puoi inserire nel quadratino per rendere vera la seguente disuguaglianza?

2 5 < 10 < 3 5

7 Prova nazionale classi prime.

Scrivi nei riquadri i seguenti numeri, posizionandoli correttamente sulla retta:

1 2 ; 1 4 ; 2 3 .

8 Considera le frazioni proprie n d e n + 1 d ; passando dalla prima alla seconda, ottieni una frazione:

A impropria

B equivalente alla prima

C maggiore della prima

D minore della prima

OPERAZIONI E PROBLEMI

CON LE FRAZIONI

1 Quali sono i valori delle potenze ( 2 3 )4 e 2 34 ?

A Entrambe 16 81 C La prima 16 81 , la seconda 2 81

B Entrambe 2 12 D La prima 8 12 , la seconda 2 81

2 Della pizza fatta dalla nonna ne è rimasto 1 3 e i quattro nipoti se lo dividono in parti uguali per merenda.

Quale parte dell’intera pizza mangerà ognuno di loro? Spiega il procedimento che hai utilizzato.

A 1 3 B 1 9 C 1 7

1 12 Risposta:

3 Scopri il numero che sommato ai suoi 3 5 dà come risultato 48. A 18 B 30 C 80

4 Se sottrai da un numero i suoi 2 7 ottieni 14; qual è il numero?

5

5 Quale dei seguenti rappresenta il triplo di 1 3 ?

3 9

1 3 × 1 3

6 Per andare in vacanza in montagna Giorgio percorre 336 km, di cui 3 8 sono in salita e 2 7 sono in discesa. Quanti kilometri percorre Giorgio in pianura? A 111 B 210 C 240 D 114

7 Prova nazionale classi terze.

Qual è il risultato della seguente espressione: 1 2 + 1 + 1?

1

8 Prova nazionale classi terze.

Osserva questa uguaglianza: 3 + 2 5 + 1 1 000 = m

Quale fra i seguenti valori di m rende vera l’uguaglianza?

3,201

MISURA DI GRANDEZZE

1 Con un righello si vuole misurare la lunghezza di una penna. Qual è la misura corretta?

A 147 dm B 14,7 cm C 14,7 dm D 14,7 mm

2 Prova nazionale classi terze. Osserva l’immagine.

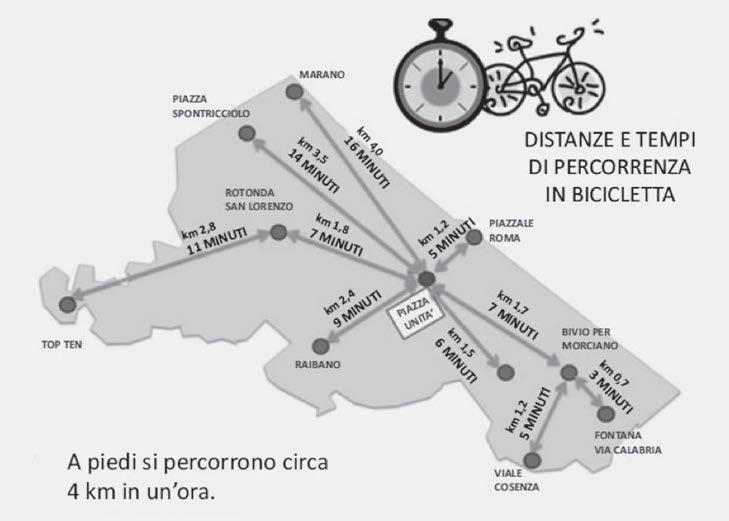
a) Secondo le informazioni riportate nell’immagine, quanto tempo ci vuole per andare in bicicletta da Piazzale Roma a Rotonda San Lorenzo passando da Piazza Unità?

Risposta: … minuti

b) Secondo le informazioni riportate nell’immagine, quanto tempo ci vuole all’incirca per percorrere lo stesso tragitto a piedi?

3 Un bicchiere contiene 1 4 di litro di acqua. Si vuole riempire una bottiglia da 750 mL. Quanti bicchieri di acqua bisogna versare nella bottiglia? A 1 B 2 C 3 D 4

4 Emma ha ordinato due torte per il suo 18-esimo compleanno. Una, al cioccolato, pesa 4,436 kg e l’altra 2 100 g. Qual è la differenza di peso tra le due torte?

Risposta:

I PRIMI ELEMENTI DELLA GEOMETRIA

1 Considera i due quadrati, ABCD e EFGH, uguali tra loro, con M, N, O punti medi dei lati. Che cosa puoi dire dei segmenti AM, OF e NH?

Giustifica la risposta:

2 In quale delle seguenti figure sono rappresentati dei segmenti adiacenti?

3 Prova nazionale classi terze.

Seguendo il percorso indicato dalla linea tratteggiata sulla mappa, Enrico parte in auto da Castro, va ad Abate a prendere un amico e riparte con lui per andare a S. Teodoro.

Dopo aver fatto 52 km dalla partenza da Castro, si ferma lungo la strada tra due località a fare rifornimento a un distributore di benzina.

Indica con una crocetta sulla mappa la posizione del distributore.

Teodoro

S.

Calliano

Valverde

Samone

Abate

Livo

Peglio

Castro

4 km

Brione

GLI ANGOLI

1 Prova nazionale classi prime.

Quale dei seguenti gruppi è costituito solo da angoli NON retti?

A tutti

B 2, 3, 4, 6

C 3, 4, 6

D 1, 3, 4, 5

2 Prova nazionale classi prime.

Quanto misura, all’incirca, l’angolo seguente?

A 5°

B 45°

C 90°

D 110°

3 Prova nazionale classi prime.

Osserva l’orologio in figura.

A Qual è l’ampiezza dell’angolo che la lancetta dei minuti, girando, descrive in mezz’ora?

…180°……

B Che ora sarà quando la lancetta dei minuti avrà descritto un angolo di 90°? …180°……

4 Nel manometro a fianco:

A gli angoli sono tutti concavi

B gli angoli sono tutti convessi

C solo l’angolo verde è concavo

D solo l’angolo verde è convesso

5 Nella seguente figura i punti A , O e B giacciono sulla stessa retta. OM divide in due parti uguali l’angolo BOC e ON divide in due parti uguali l’angolo AOC .

A Qual è la misura dell’angolo MOB ?

Risposta: 40 gradi

B Scrivi i calcoli che hai fatto per trovare la risposta.

RETTE NEL PIANO

1 Date le rette parallele m e n e due trasversali:

A l’angolo 1 misura …45°…

B l’angolo 10 misura …35°…

2 Date due rette parallele t e s, quale punto di t ha distanza maggiore da s?

A Il punto A

B Il punto B

C Il punto C

D Hanno tutti la stessa distanza

3 OQ e LN sono tratti di linee parallele. Quali tra i seguenti sono angoli supplementari?

A RPO e KMN C MPQ e PML

B LMK e OPR D RPQ e LMK

4 Due rette incidenti formano un angolo di 34°. Quale delle seguenti affermazioni è falsa?

A Formano anche un angolo ottuso.

B Formano anche altri tre angoli tutti diversi.

C Formano un angolo di 146°.

D Formano un altro angolo di 34°.

5 Prova nazionale classi terze.

Osserva la figura.

A Disegna la retta s perpendicolare a t passante per F

B Il punto R di intersezione tra la retta s e il segmento

AB ha coordinate (…4…; …4 ..).

1 Prova nazionale classi prime. La cartina a lato rappresenta una parte del percorso delle

4 linee della metropolitana

(Linea A, Linea B, Linea C e Linea D) di una grande città.

a) Quali linee della metropolitana si incontrano alla fermata di San Giovanni?

A Linea A e Linea B

B Linea A e Linea D

C Linea C e Linea D

D Linea B e Linea D

Buenos

Fiume

b) Giovanni sale alla fermata Bologna e vuole scendere alla fermata Venezia. Traccia con la penna sulla cartina il percorso con meno fermate per andare in metropolitana dalla fermata Bologna alla fermata Venezia.

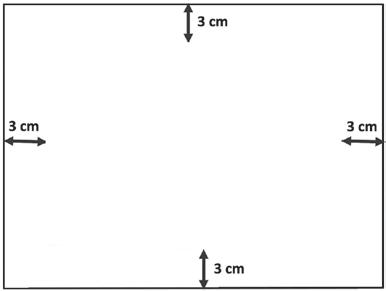
2 Prova nazionale classi prime.

Franco incolla una fotografia rettangolare di dimensioni 22 × 15 cm su un cartoncino. Attorno alla fotografia resta una cornice larga 3 cm, come vedi in figura.

Quali sono le dimensioni del cartoncino?

A 28 cm × 18 cm

B 25 cm × 18 cm

C 28 cm × 21 cm

D 25 cm × 21 cm

3 Prova nazionale classi prime.

Osserva le figure a lato.

Quale delle due ha il perimetro maggiore?

Risposta: …………………………………

4 Prova nazionale classi prime.

Osserva il poligono a lato.

Il suo perimetro è:

A 18 cm C 20 cm B

Linea C Linea B

Linea A

Linea C

Linea B

Linea D

Linea A

Linea D

Termini

Policlinico

Bologna

S.Silvestro

OttavianoLepantoFlaminio Repubblica Barberini

VittorioE.Manzoni

S.GiovanniRediRomaPonteLungo Lodi Laziali

Castro Pretorio

Piramide

Nievo

Sonnino

Chiesa Nuova

S.Pietro

Mazzini

Colosseo

Circo Massimo

Venezia Cavour

Amba Aradam

Spagna

Aires

S.Agnese/ Annibaliano

figura 1

figura 2

1 cm

I TRIANGOLI

1 Se CB ≅ DF e AB ≅ FE, quale informazione aggiuntiva ti serve per stabilire la congruenza dei triangoli ABC e DEF?

A C ≅ E

B B ≅ F

C CB ≅ FE

D AB ≅ FD

2 La figura qui a lato è composta da quattro triangoli rettangoli congruenti. Se 1 = 40°, quanto è ampio l’angolo 2 ?

A 40° C 80°

B 50° D 100°

3 Prova nazionale classi prime. La lunghezza dell’ombra di un albero varia durante il giorno a seconda dell’altezza del Sole sull’orizzonte. Quanto deve misurare l’angolo a affinché l’altezza dell’albero e la lunghezza della sua ombra diventino uguali?

Risposta: …45 °

4 Prova nazionale classi prime.

Con tre bastoncini lunghi 12 cm, 4 cm, 3 cm, che cosa è possibile ottenere?

A Un triangolo isoscele

B Un triangolo scaleno

C Un triangolo rettangolo

D Nessun tipo di triangolo

5 Prova nazionale classi prime.

Osserva la figura. Quale, tra le seguenti coppie di segmenti, rappresenta due delle altezze del triangolo ABC ?

A AD e AG

B CE e AG

C CF e AD

D CE e CF

I QUADRILATERI

1 Prova nazionale classi terze.

Osserva il rettangolo.

Sul lato DC segna il punto H in modo tale che il segmento HK divida il rettangolo in due parti uguali.

2 Di quante unità ( u ) il perimetro del rettangolo è maggiore di quello del quadrato?

A 4 u

B 6 u

C 8 u

D 10 u u

3 Prova nazionale classi terze.

Edoardo vuole disegnare un rombo con le sue diagonali.

Il segmento AB rappresenta la diagonale maggiore del rombo.

Completa il disegno di Edoardo tracciando il rombo e la relativa diagonale minore.

4 Prova nazionale classi terze.

La seguente figura rappresenta il prato davanti alla casa di Paolo.

È possibile, con i dati a disposizione, calcolare il perimetro del prato?

A Sì, misura 15 m.

B Sì, misura 30 m.

C Sì, misura 50 m.

D No, non si può calcolare.

m 5 m

IL MISTERO DELLA DATA DI NASCITA 1

Titolo Il mistero della data di nascita!

Contenuti Le 4 operazioni, il sistema di numerazione in base 10

Obiettivi Effettuare calcoli a mente, comprendere che cosa è un algoritmo

Chi gioca Mago o Maga della matematica, Spettatori e Spettatrici

Metodologia Gamification

INTRODUZIONE

Ti piacerebbe fare un numero di magia matematica? Se la risposta è “sì”, non devi fare altro che seguire minuziosamente le indicazioni qui riportate e sorprendere tutti con il trucco magico che ora ti svelerò.

FASE 1

Da questo momento tu sei il Mago o la Maga dei Numeri: individua uno Spettatore o una Spettatrice a cui proporre il gioco (un compagno o una compagna di classe, una persona di famiglia, un professore o una professoressa), disponibile a fare alcune semplici operazioni matematiche a partire da due numeri:

• quello del suo mese di nascita (M),

• quello del suo giorno di nascita (G).

FASE 2

Rivolgiti allo spettatore selezionato o alla spettatrice selezionata e impartisci le seguenti istruzioni:

1. pensa al numero che corrisponde al tuo mese di nascita (Gennaio = 1, Febbraio = 2, ..., Dicembre = 12);

2. moltiplica il numero del mese per 100;

3. aggiungi, al risultato ottenuto, il tuo giorno di nascita;

4. moltiplica il nuovo risultato così ottenuto per 2;

5. aggiungi 8 al risultato;

6. moltiplica il tutto per 5;

7. dimmi il risultato finale.

FASE 3

Quando lo spettatore o la spettatrice ti dice il suo risultato, esegui mentalmente o su un foglio il passaggio finale:

• sottrai 40 al numero che ti è stato comunicato,

• dividi il risultato per 10.

Il risultato finale ti darà la data di nascita nel formato: MMGG (Mese-Giorno).

• Le ultime due cifre (GG) sono il giorno di nascita.

• Le prime due (o una; MM o M) cifre sono il mese di nascita.

ESEMPIO

Per la buona riuscita del gioco, all’occorrenza si potrà usare anche la calcolatrice.

• Se il compleanno è il 15 Maggio (mese 5, giorno 15), il risultato finale che ti comunicherà sarà dunque 5190.

• Sottraendo 40 si ottiene 5150 (5190 – 40 = 5150), che diviso per 10 dà 515 (5150 : 10 = 515).

• Il numero 515 si legge come: 5 (mese - M), 15 (giorno - GG).

COME È POSSIBILE?

Matematica alla mano, proviamo a comprendere come mai questo trucco funziona sempre!

Indichiamo con M il mese e con G il giorno di nascita dello spettatore o della spettatrice e seguiamo l’algoritmo (il procedimento) creando, passo dopo passo, l’espressione.

ESPRESSIONE “STEP BY STEP”

Identifica il numero corrispondente al mese di nascita M.

1. Moltiplicalo per 100: M × 100

2. Aggiungi il giorno di nascita: 100M + G

3. Moltiplica tutto per 2: 2 × (100M + G)

4. Aggiungi 8 : 2 × (100M + G) + 8

5. Applica la proprietà distributiva: 200M + 2G + 8

6. Moltiplica tutto per 5: [200M +2G + 8] × 5= 1000M + 10G + 40

7. Sottrai 40 dal risultato finale: 1000M + 10G + 40 – 40 = 1000M + 10G

GAMIFICATION

MAGIA PER UN GIORNO

Quando il Mago o la Maga sottrae 40 dal risultato finale, si elimina il 40 che è sempre presente nell’espressione (indipendentemente dalla data di nascita).

8. Dividendo il risultato finale per 10 si ottiene: 100M + G quindi esattamente il mese moltiplicato per 100 e sommato al giorno, grazie al sistema di numerazione in base 10. Il trucco funziona perché il sistema decimale fa sì che “centinaia” e “unità” rappresentino posti diversi nel numero.

Come trasformare questo gioco in una sfida in classe? Inseriamo nell’attività didattica, gli elementi propri del Game design (regole, classifiche, conferimenti di badge, giochi a tempo, riconoscimento dei risultati raggiunti, motivazioni aggiuntive).

AZIONE

Regole e classifiche: gli studenti si mettono a coppie; a turno uno è il “Mago” o la "Maga" e l’altro lo “Spettatore” o la "Spettatrice". Ogni volta che il Mago o la Maga indovina correttamente la data, guadagna 10 punti.

Conferimento del badge: chi completa 5 letture della mente con successo e dimostra di conoscere l’algoritmo a memoria. Riceve il badge virtuale Principiante della Decifrazione

Gioco a tempo: lo spettatore o la spettatrice ha un tempo limitato (es. 2 minuti) per eseguire i calcoli. Chi gioca ha 10 secondi per svelare il risultato.

Riconoscimento dei risultati raggiunti: si deve riprodurre l’algoritmo del trucco usando le lettere (M per Mese, G per Giorno) e semplificarlo fino a ottenere 100M + G. La dimostrazione corretta vale 50 punti.

Motivazioni aggiuntive: ogni gruppo deve inventare un algoritmo originale, efficace e matematicamente solido.

OBIETTIVO

Riproduzione dell’algoritmo/ procedimento

Memorizzazione e fluidità nell’esecuzione

Potenziamento del calcolo mentale

Traduzione dal linguaggio naturale al linguaggio matematico e semplificazione di espressioni

Pensiero divergente e creatività

INDOVINA CHE NUMERO HO PENSATO?

Titolo Indovina che numero ho pensato?

Contenuti Le 4 operazioni, il sistema di numerazione in base 10

Obiettivi Effettuare calcoli a mente, comprendere che cos'è un algoritmo

Chi gioca Mago o Maga della matematica, Spettatori e Spettatrici

Metodologia Gamification

INTRODUZIONE

Nel mondo affascinante della matematica, anche un semplice numero di tre cifre nasconde un segreto “universale”. Per scoprirlo non occorre alcuna preparazione, è sufficiente eseguire una sequenza di operazioni, che condurrà allo stesso incredibile risultato. La vera sfida sarà quella di rispondere a questa domanda: “Come mai non ha importanza il numero che scegliamo all’inizio del gioco, visto che finiamo sempre con lo stesso risultato?”

FASE 1

Da questo momento il Mago o la Maga dei Numeri sei tu: ora hai bisogno di trovare due o tre Spettatori a cui proporre il gioco (cercali tra la classe, la famiglia o il corpo docente). Gli spettatori o le spettatrici dovranno svolgere alcune semplici operazioni matematiche: per la buona riuscita del gioco, all’occorrenza potranno usare anche la calcolatrice.

FASE 2

Rivolgiti agli spettatori e alle spettatrici selezionati e impartisci le seguenti istruzioni:

1. pensate a un numero di tre cifre (ABC). IMPORTANTE: le cifre che compongono il numero devono essere tutte e tre diverse tra loro (esempio 974, non 779);

2. invertite il numero che avete pensato, cioè scrivete il numero al contrario (CBA): nell’esempio precedente 974 diventa 479;

3. fate la seguente sottrazione: numero più grande meno numero più piccolo (974 – 479 = 495);

4. invertite anche il risultato ottenuto per differenza (nell’esempio 594). Se la differenza ha solo due cifre, aggiungete uno zero come prima cifra, (per esempio 32 diventa 032);

5. sommate la differenza (che avete ottenuto nel punto 3) con il suo numero invertito (punto 4). (esempio 495 + 594 = 1089);

6. comunicate il risultato finale.

7. Dov’è la magia? Indipendentemente dal numero iniziale scelto all’inizio, il risultato sarà sempre 1089.

COME È POSSIBILE?

Questo è il momento fondamentale, perché usando la matematica si può capire come mai il trucco funzioni sempre.

ESPRESSIONE “STEP BY STEP”

1. Indichiamo le cifre del numero 974 con le lettere A, B, C. (Nel nostro esempio

A = 9, B = 7, C = 4). A seconda della posizione che occupano, le cifre rappresentano le centinaia, le decine o le unità. Pertanto il numero 974 (novecento-settanta-quattro) lo possiamo scrivere come

974 = 100 × 9 + 10 × 7 + 4

Più in generale, ogni numero di 3 cifre si può rappresentare come

N = 100 × A + 10 × B + C

2. Per lo stesso motivo, il numero invertito sarà 479, cioè

In generale

N' = 100 × 4 + 10 × 7 + 9

N' = 100 × C + 10 × B + A

3. Se calcoliamo la differenza tra numero più grande e numero

più piccolo (D = N – N'), il risultato D ha sempre la forma:

cioè:

dove X + Y = 9.

D = 100 × X + 90 + Y

X 9 Y

S = D + D'

S = 100 × X + 9 × 10 + Y + Y × 100 + 9 × 10 + X

Poiché sappiamo che

S = 100(X + Y) + 180 + (X + Y)

X + Y = 9

S = 100 × 9 + 180 + 9 = 900 + 180 + 9 = 1089

4. La differenza invertita D' sarà della forma Y 9 X; quindi la somma finale sarà:

• la somma tra la differenza e la sua inversa ha una struttura fissa;

• la matematica del sistema decimale fa il resto.

GAMIFICATION

MAGIA PER UN GIORNO

Regole e classifiche: ogni membro della squadra sceglie un numero iniziale diverso (es. 582, 915, 624) ed esegue i calcoli. La squadra deve riconoscere che tutti i risultati sono identici e dichiarare il codice segreto (1089).

Conferimenti di badge: le squadre devono analizzare la spiegazione del trucco presente sulla scheda e provare a illustrarne la dimostrazione. Se agiscono correttamente ottengono un bonus di 50 punti.

Il risultato è 1089 qualunque sia il numero iniziale! Il trucco funziona non per caso, ma perché:

• la sottrazione tra un numero e il suo inverso produce sempre cifre complementari (X e Y che sommano 9);

Come trasformare questo gioco in una sfida in classe? Inseriamo nell’attività didattica, gli elementi propri del Game design (classifiche, conferimenti di badge, giochi a tempo, riconoscimento dei risultati raggiunti, motivazioni aggiuntive).

AZIONE OBIETTIVO

Riproduzione dell’algoritmo/procedimento

Traduzione dal linguaggio naturale al linguaggio algebrico e semplificazione di espressioni

LA SOMMA NASCOSTA 3

Titolo La somma nascosta

Contenuti Somma degli angoli interni di un poligono

Obiettivi

Effettuare calcoli a mente, comprendere come la somma degli angoli interni di un poligono dipende dal numero di lati

Chi gioca Mago o Maga della matematica, Spettatori e Spettatrici

Metodologia Gamification

INTRODUZIONE

Non ci crederai, ma anche la geometria può offrire spunti per creare giochi di magia sorprendenti. Il trucco che scoprirai si basa su una regola geometrica fondamentale e cioè quella per cui la somma degli angoli interni di un qualsiasi poligono può essere calcolata conoscendo solo il numero dei suoi lati (n).

Per la buona riuscita di questo gioco, dovrai semplicemente usare il pensiero inverso e una nota formula della geometria; tutto ciò ti permetterà di indovinare qual è il poligono di partenza.

Per te e la tua classe sarà l’occasione buona per ripetere i nomi dei poligoni e le loro proprietà.

FASE 1

Da questo momento tu sei il Mago o la Maga dei Numeri: rivolgiti a un tuo compagno o a una tua compagna di classe e chiedigli di seguire queste istruzioni:

1. scegli, mentalmente, un poligono tra quelli che conosci: assicurati che abbia un numero di lati maggiore o uguale a 4 (es. un quadrato, un pentagono, un esagono, …);

2. conta il numero di lati del tuo poligono. (Se hai scelto un ottagono, il numero di lati sarà ovviamente n = 8);

3. sottrai 2 dal numero dei lati;

4. moltiplica il risultato per 180;

5. comunica il risultato finale.

FASE 2

Quando il tuo compagno o la tua compagna ti comunica il risultato, esegui mentalmente, o su di un foglio, questi passaggi:

1. aggiungi 360 al risultato che ti hanno comunicato;

2. dividi tutto per 180.

Il risultato finale ti darà il numero dei lati del poligono.

ESEMPIO

Se il risultato finale è “1080”, le operazioni da fare sono le seguenti:

• aggiungi 360 (1080 + 360 = 1440);

• dividi tutto per 180 (1440 : 180 = 8);

In alternativa puoi usare questo trucco:

• dividi il risultato per 180;

• aggiungi 2.

COME È POSSIBILE?

Usare la matematica è il trucco di questo gioco: è sufficiente applicare la formula per calcolare la somma degli angoli interni di un poligono, dato il numero di lati.

ESPRESSIONE “STEP BY STEP”

1. Indicando con n il numero di lati del poligono, la somma (S) degli angoli interni è data dalla formula:

S = (n – 2) × 180

2. Applichiamo la proprietà distributiva, moltiplichiamo per 180 ciascun termine ed effettuiamo alcuni passaggi per ricavare n dalla formula:

S = n × 180 – 2 × 180 S = n × 180 – 360

3. Applichiamo la proprietà del trasporto:

S + 360 = n × 180

n = S + 360 180

Tutto il trucco si basa su una formula di geometria che dice: somma degli angoli interni di un poligono = (n – 2) × 180° dove n è il numero di lati. Il compagno o la compagna usa questa formula al contrario senza accorgersene… e tu la usi per scoprire il suo poligono!

GAMIFICATION

LA BACCHETTA MAGICA

Come trasformare questo gioco in una sfida in classe? Inseriamo nell’attività didattica, gli elementi propri del Game design (classifiche, conferimenti di badge, giochi a tempo, riconoscimento dei risultati raggiunti, motivazioni aggiuntive).

AZIONE

Classifiche, conferimenti di badge: per aver eseguito correttamente la sequenza magica si attribuiscono 10 punti.

Giochi a tempo: per aver identificato correttamente il poligono dell’altra squadra in meno di 2 minuti si attribuiscono 20 punti.

Riconoscimento dei risultati raggiunti: per aver scritto correttamente la formula usata, ovvero

n = (Risultato / 180) + 2 (30 punti)

In premio si riceve la bacchetta magica!

OBIETTIVO

Riproduzione dell’algoritmo/procedimento

Calcolo mentale e applicazione

Spiegazione logica

IL MAGICO TEOREMA DI PICK

Titolo Il magico teorema di Pick

Contenuti Area di un poligono

Obiettivi Effettuare calcoli a mente, riflettere sul concetto di area

Chi gioca Mago o Maga della matematica, Spettatori e Spettatrici

Metodologia Gamification

INTRODUZIONE

Con questo gioco sarai in grado di indovinare l’area senza fare calcoli complessi e “visibili”, ma sfruttando il “segreto” del famoso teorema di Pick. Fare magie nel calcolo delle aree non è mai stato così facile. Per stupire tutti, divertendoti, sarà sufficiente disegnare su carta a quadretti alcune figure e usare un vero e proprio trucco matematico. Il materiale che ti occorre è costituito da una penna (o una matita) e un foglio di carta con un reticolo di punti: puoi usare un foglio a quadretti o un foglio di carta millimetrata, evidenziando i punti del reticolo, come nella seguente figura.

FASE 1

Rivolgiti a un tuo compagno o a una tua compagna di classe e chiedigli di seguire queste istruzioni:

1. scegli un poligono tra quelli che conosci o una figura poligonale qualsiasi e disegnala sul foglio a quadretti: tutti i vertici devono coincidere esattamente con un incrocio della griglia (un punto del reticolo);

2. conta tutti i punti (incroci) della griglia che si trovano sulla linea del perimetro della figura e tieni a mente questo numero (lo indicherai con B);

3. conta tutti i punti interni cioè tutti gli incroci della griglia che si trovano all’interno della figura e tieni a mente questo numero indicandolo con I;

4. comunica questi due numeri: B (punti che si trovano sul bordo) e I (punti interni).

FASE 2

Quando il tuo compagno o la tua compagna ti comunica i risultati, esegui mentalmente, o su di un foglio, questi passaggi:

1. considera il numero dei punti sul bordo (B) e dividilo per due: B/2, 2. aggiungi a quel risultato il numero dei punti interni: B/2 + I, 3. sottrai 1 al totale.

Il risultato che ottieni è esattamente l’area della figura (espressa secondo l’unità di misura rappresentata dai quadrati), eppure sei riuscito a trovarla solo contando i punti!

COME È POSSIBILE?

Il trucco si basa sull’applicazione del teorema di Pick che stabilisce che, per un qualsiasi poligono i cui vertici si trovano sugli incroci della griglia (punti del reticolo), l’area A può essere calcolata con la seguente formula:

A = I + B 2 – 1

dove:

• I è il numero di punti interni al poligono,

• B è il numero di punti sul bordo (inclusi i vertici).

È un teorema magico perché trasforma l’area in un semplice conteggio!

ESEMPIO

Nella figura seguente i punti lungo il perimetro sono B = 12, quelli interni sono I = 27. Per calcolare l’area, applico la formula di Pick e ottengo A = 27 + (12/2) – 1 = 32.

GAMIFICATION

LA BACCHETTA MAGICA

Come trasformare questo gioco in una sfida in classe? Inseriamo nell’attività didattica, gli elementi propri del Game design (classifiche, conferimenti di badge, giochi a tempo, riconoscimento dei risultati raggiunti, motivazioni aggiuntive).

AZIONE

Regole e classifiche: 10 punti bonus per la corretta identificazione dei punti interni I e perimetrali B del poligono.

Conferimenti di badge: 20 punti per la corretta determinazione dell’area A usando la formula.

Giochi a tempo: bonus di 10 punti di tempo/velocità per la squadra che risolve correttamente i primi 3 poligoni.

Motivazioni aggiuntive: iniziate con triangoli semplici (Livello 1), passate a quadrilateri concavi (Livello 2) e finite con poligoni complessi che richiedono di scomporre la figura (l’area può essere calcolata anche per sottrazione, il teorema funziona lo stesso).

OBIETTIVO

Riproduzione dell’algoritmo/procedimento

Calcolo mentale e applicazione

Cooperative learning

Incrementare la motivazione

ALLA SCOPERTA

DELL’INTELLIGENZA ARTIFICIALE

L’Intelligenza Artificiale (IA) non è più una tecnologia del futuro, ma una realtà che è già entrata in molti ambiti della nostra vita quotidiana. La usiamo quando facciamo una ricerca su Google, quando ci vengono suggerite canzoni su Spotify, quando giochiamo a un videogioco o quando usiamo un assistente vocale come Alexa o Siri.

Esistono due tipi principali di IA:

• IA generale, basata su sistemi capaci di replicare il ragionamento umano allo scopo di imparare cose nuove autonomamente e di applicare le conoscenze in contesti diversi. Non abbiamo ancora a disposizione una IA di questo tipo: gli attuali sistemi di IA possono analizzare, per esempio, centinaia di immagini di cellule e imparare a distinguere quelle malate, ma non possono ancora sostituire il medico nella scelta della terapia migliore per curare quelle stesse cellule malate;

• IA ristretta, basata su sistemi estremamente efficaci in ambiti specifici, come riconoscere un’immagine, riassumere o tradurre un testo.

IA non pensa come un essere umano, ma è un insieme di tecnologie che analizza grandi quantità di dati per proporre soluzioni o rispondere alle nostre domande.

COME FUNZIONA IA

IA non impara da sola senza essere guidata e non ha coscienza o emozioni. Anche se può sembrare “intelligente”, in realtà IA si limita a usare un’enorme quantità di dati per capire come rispondere alle domande che le facciamo.

Alla base dei moderni sistemi di apprendimento di IA ci sono le reti neurali artificiali ispirate al funzionamento del cervello umano, ma profondamente diverse. Gli scienziati stimano che il cervello sia composto da circa 87 miliardi di neuroni, uniti da milioni di miliardi di connessioni, che formano una rete tridimensionale in grado svolgere l’equivalente di 38 miliardi di operazioni al secondo.

Le reti neurali artificiali, invece, sono organizzate in strati connessi tra di loro: ogni strato elabora una parte dell’informazione e la trasmette ai successivi, creando una complessa rete di connessioni che, tuttavia, non è paragonabile a quella che esiste tra le cellule del nostro cervello e che caratterizza l’intelligenza naturale.

COS’È UN LARGE LANGUAGE MODEL (LLM)?

Un LLM (modello linguistico di grandi dimensioni) è un tipo speciale di IA che lavora con il linguaggio: sa leggere, scrivere e rispondere in modo molto simile a una persona.

Esempi di LLM sono ChatGPT, Gemini (di Google), Claude, Llama, Copilot… e molti altri. Questi strumenti sono allenati su milioni di testi e possono aiutarti a:

• spiegare concetti difficili;

• correggere errori;

• studiare.

Inoltre, sono in grado di rispondere alle tue domande, creare testi, riassunti, quiz, schemi…

La flessibilità dei diversi LLM nel rispondere alle tue domande su una vastissima quantità di argomenti li rende alleati preziosi per migliorare le tue competenze, organizzare lo studio, risolvere problemi; tuttavia, questi strumenti non sono perfetti. A volte sbagliano, non capiscono bene il contesto o danno informazioni non aggiornate. Per questo è importante verificare sempre quello

che scrivono usando il tuo pensiero critico e le tue conoscenze, mettendo a confronto i dati forniti con quelli provenienti da altre fonti (libri di testo, pubblicazioni, siti specializzati) e consultandoti con adulti esperti.

COME SI PARLA CON L’INTELLIGENZA ARTIFICIALE USANDO I PROMPT!

Nel settore dell’IA e dei Large Language Model (LLM), l’attività più importante è diventata quella di porre domande, che nel linguaggio tecnico prende il nome di prompt engineering

Questa è una buona notizia! Riflettere e chiedere sono state da sempre grandissime competenze umane da stimolare e sviluppare e certamente lo sono ancora di più in questo momento di passaggio all’utilizzo di IA.

Ma che cos’è un prompt? Un prompt è semplicemente ciò che scrivi o chiedi a IA. Più il tuo prompt è chiaro e preciso, migliore sarà la risposta del sistema.

Come si scrive un buon prompt? Ecco uno schema che riassume alcune buone pratiche per formulare domande che funzionano davvero.

Strategia

Chiarisci l’obiettivo

Specifica

Chiedi il livello giusto

Dividi le domande complesse

Chiedi esempi concreti

Specifica il formato della risposta

Modifica il prompt se serve

Adatta la domanda al tuo livello

Crea un dialogo, facendo domande successive

Usalo per risolvere problemi

Cosa fare

Spiega perché fai quella domanda (per un compito, una verifica, una ricerca, …). Per esempio: “Mi serve capire come si semplificano le frazioni per una verifica”.

Non scrivere richieste troppo generiche, scendi nei dettagli!

Per esempio: “Crea una tabella con le differenze tra triangoli equilateri, isosceli e scaleni”.

Vuoi una spiegazione semplice? O qualcosa di più approfondito?

Per esempio: “Spiegami questo contenuto come se dovessi affrontare l’esame di terza media”.

Se l’argomento è difficile, suddividilo e formula più domande.

Per esempio: “Prima spiegami come si calcola una potenza, poi aiutami con le espressioni che le contengono”.

Ti aiutano a capire meglio. Per esempio: “Spiegami come si calcola l’area di un triangolo con un esempio reale”.

Puoi chiedere un elenco, una tabella, un riassunto... Per esempio: “Rispondimi con punti elenco”.

Se la prima risposta non ti convince, puoi migliorare il prompt e riformularlo!

Puoi dire: “Spiegamelo come se avessi 14 anni”. Oppure: “Usa parole semplici, ho qualche difficoltà a capire questo concetto della matematica”.

Puoi continuare a fare domande per approfondire! Per esempio: “Puoi realizzare un quiz di 5 domande su questo argomento, per verificare se ho capito?”.

Con i prompt giusti, IA può aiutarti a capire dove sbagli e come migliorare.

ATTENZIONE ALLA PRIVACY!

L’utilizzo responsabile di un LLM richiede attenzione a questioni come la privacy: è importante evitare di condividere dati personali o sensibili nei prompt!

Quando usi ChatGPT o altri strumenti di IA:

• non scrivere mai dati personali, come nome, indirizzo, scuola e non caricare delle foto personali;

• verifica sempre le informazioni che ottieni;

• usa l’IA come aiuto, ma non come unica fonte.

COME USARE IA A SCUOLA

Secondo l’UNESCO, l’intelligenza artificiale deve aiutare tutti, non solo pochi, rispettare i diritti umani, promuovere l’inclusione, migliorare la scuola e la vita. L’IA non sostituisce gli insegnanti, ma li affianca. Aiuta a imparare meglio, in modo personalizzato e rispettoso dei ritmi di ognuno.

L’IA, pertanto, può diventare un ottimo compagno di studio e può aiutarti a:

• riassumere un testo difficile;

• preparare una verifica;

• capire un concetto complicato;

• fare esercizi;

• trovare idee per un tema o una ricerca.

Ma ricorda: sei sempre tu a controllare l’IA, non il contrario. L’intelligenza vera sei tu!

Per capire meglio in che modo usare IA nello studio, ti suggeriamo alcuni prompt.

Obiettivo

Capire un argomento

Esempio di prompt

“Mi puoi spiegare le potenze in modo semplice, come se fossi in prima media?”

Fare un riassunto “Riassumi questo testo in 5 punti principali: [incolla il testo].”

Fare un confronto “Quali sono le differenze tra un triangolo equilatero, isoscele e scaleno?”

Trovare idee

Studiare meglio

Memorizzare

“Dammi 3 idee originali per esercizi sulle frazioni da usare come allenamento.”

“Aiutami a creare un piano di studio per preparare la verifica di geometria in una settimana.”

“Fammi una mappa mentale per ricordare i passaggi per risolvere un’espressione aritmetica.”

IL PROMPT EFFICACE

OBIETTIVO

Imparare a includere nel prompt l’argomento preciso e chi riceverà la spiegazione.

CHE COSA FARE

• Scegli un argomento di matematica che ti interessa (esempi: frazioni, potenze, triangoli, quadrilateri).

• Decidi chi sarà il destinatario della spiegazione:

– un ragazzo/una ragazza della tua età

– un bambino/una bambina di 9 anni

– un amico/un’amica che non studia scienze.

• Scrivi un prompt che includa l’argomento scelto e il destinatario (età/stile)

• Rileggi il prompt: è abbastanza chiaro? IA capirà cosa vuoi?

ATTIVITÀ

Scegli uno tra questi argomenti: espressioni, poligoni, misure di grandezza

Per ciascuno, scrivi due prompt: uno per un ragazzo/una ragazza di 13 anni; uno per un bambino/ una bambina di 9 anni.

ESEMPI

“Spiegami come funzionano le potenze in modo semplice, come se parlassi con un bambino di 9 anni.”

“Spiegami come funzionano le potenze con dettagli che un ragazzo di 13 anni può capire, usando esempi della vita quotidiana.”

VALUTAZIONE

Prompt scritto

Argomento ben definito? (S/N)

Pubblico ben definito? (S/N)

Pubblico ben definito? (S/N)

Come puoi migliorarlo?

Frazioni

Quadrilateri

Potenze

CONOSCIAMO GEOGEBRA

GeoGebra è la contrazione delle parole “Geometria” e “Algebra”; si tratta infatti di un software free (che puoi scaricare liberamente dal sito www. geogebra.org), molto semplice e intuitivo per studiare geometria, statistica e algebra. In queste pagine imparerai a disegnare semplici figure e a risolvere problemi al computer.

Il vantaggio di usare GeoGebra è che gli oggetti geometrici costruiti sono deformabili mediante lo spostamento dei punti che li formano: basta “prendere” un punto cliccandoci sopra e spostarlo trascinando il mouse o la pennina della LIM. Ogni rappresentazione, inoltre, può essere resa più chiara con una serie di strumenti: l’assegnazione di un nome, la possibilità di differenziare i colori dei vari elementi, effettuare misurazioni, nascondere elementi di costruzione. Insomma, senza abbandonare squadra e compasso, perché il disegno geometrico è importante, grazie a GeoGebra potrai sperimentare il disegno al computer. Buon lavoro!

Informazioni generali

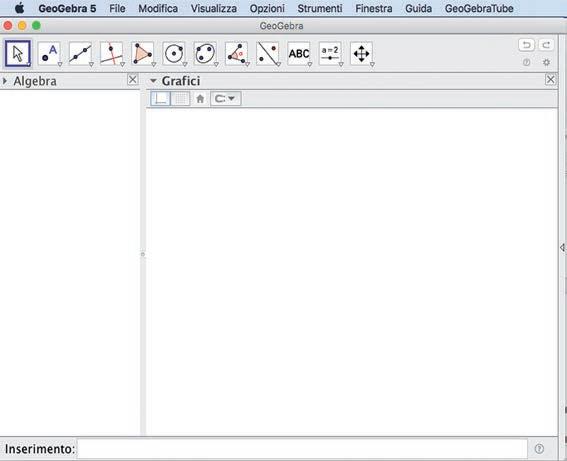
All’apertura di GeoGebra comparirà una finestra predisposta su vista Algebra, con gli assi cartesiani sul piano di lavoro.

Clicca sul triangolino accanto a Grafici per attivare la Barra di stile e

deselezionare il piano cartesiano: il foglio di lavoro è pronto per iniziare.

La ricerca dei comandi da usare è molto semplice. La prima barra è quella dei menu, da cui puoi selezionare i comandi di Windows, come File - Salva con nome …, oppure, ad esempio, Strumenti - Personalizza barra degli strumenti ecc.

La barra degli strumenti di GeoGebra, inserita sotto quella dei menu, contiene 12 icone. Ognuna di esse, cliccando sul suo triangolino in basso a destra (è bianco, ma diventa rosso quando ci passi sopra con il mouse), apre una casella con altri comandi, solitamente simili tra loro e raggruppati sotto un unico nome. Ad esempio, la terza icona apre la casella Segmenti e raggruppa Retta, Segmento, Semiretta e Vettore.

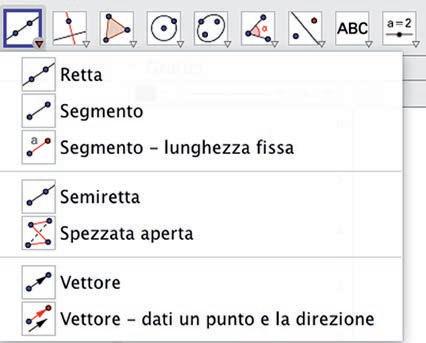
L’uso dei comandi è molto semplice e intuitivo e, se vai con il mouse sopra l’icona, ti appare una finestra che dice che cosa devi fare. Molto spesso lo stesso obiettivo si può raggiungere con modalità diverse. In questa breve guida ne indicheremo sempre una, lasciando a te il piacere di scoprirne altre.

Barra di menu

Movimento Punto

Segmenti

Circonferenza e arco

Poligoni

Retta speciali

Vista Algebra

Oggetti speciali Generali

Misura Trasformazioni

Oggetti azione

Barra degli strumenti

Barra di stile

Vista grafica

Barra di inserimento

ATTENTO: questi software vengono aggiornati spesso e può capitare che il nome di alcuni comandi e le schermate siano leggermente diversi tra una versione e l’altra. Quindi, anche alcuni di quelli che trovi in questo tutorial potranno cambiare in futuro. Le differenze possono dipendere poi dall'uso del sistema operativo Microsoft o Macintosh.

ESERCIZI

Proviamo a usare gli strumenti di GeoGebra per disegnare un punto.

a) Dalla casella Punto della barra degli strumenti seleziona il comando Punto e poi clicca su un punto qualsiasi del piano. Apparirà un punto di colore blu, con la lettera A (i punti si indicano sempre con la lettera maiuscola). Su vista Algebra appariranno le coordinate cartesiane del punto (anche se gli assi sono nascosti, il punto ha sempre delle coordinate).

b) Per modificare le caratteristiche del punto A cliccaci sopra con il tasto destro del mouse e apparirà il Menu contestuale. Da qui potrai: nascondere il punto dal piano, nasconderne l’etichetta (in questo caso la lettera A), rinominarlo con un’altra lettera, eliminarlo o modificarne la grafica. Queste funzioni sono valide per tutte le figure che disegnerai con GeoGebra.

Coniche

Disegnare un punto, rinominarlo e assegnare nuove coordinate

• Disegna un punto a piacere sul piano.

• Con il tasto destro del mouse clicca sul punto: si apre il Menu contestuale

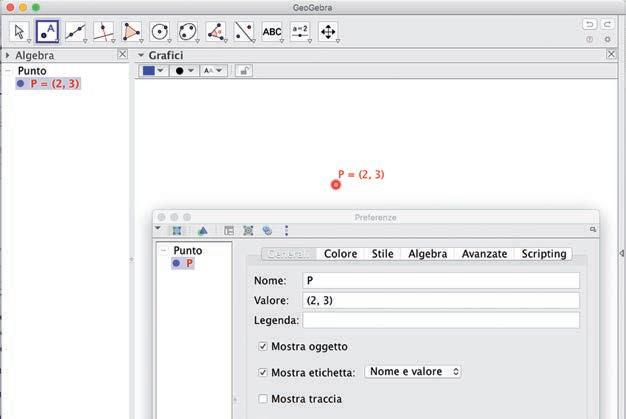
• Seleziona Proprietà… e si apre la finestra Preferenze. Su Generali alla voce Nome rinomina il punto con la lettera P. Scendi su Definizione e assegna le coordinate (2, 3) per ricollocare il punto sul piano. Sposta il mouse su Mostra etichetta e seleziona Nome e valore per rendere visibili le coordinate.

ATTENTO: una volta modificate le coordinate il termine Definizione viene sostituito dal termine Valore.

• Dalla voce Colore (accanto a Generali) seleziona il colore rosso; su Stile scegli il pallino vuoto. Nella figura seguente puoi vedere il risultato finale.

Disegnare un segmento

• Vai alla casella degli strumenti Segmenti; dal triangolino rosso apri la tendina e seleziona il comando Segmento . Trascina il cursore del mouse sul piano e clicca su due punti separati; traccerai un segmento f di estremi AB e di lunghezza casuale.

• Per poter modificare il segmento o spostarlo sul piano devi selezionare Muovi dalla casella Movimento della barra degli strumenti. Per misurare la sua lunghezza vai alla casella degli strumenti Misura e seleziona il comando Distanza o lunghezza : appare una finestra con la misura del segmento.

• Se devi costruire un segmento di una determinata misura, nel menu della casella Segmenti seleziona Segmento - lunghezza fissa . Dopo aver tracciato il primo punto, comparirà una finestra in cui dovrai indicare la lunghezza del segmento.

ESERCIZI

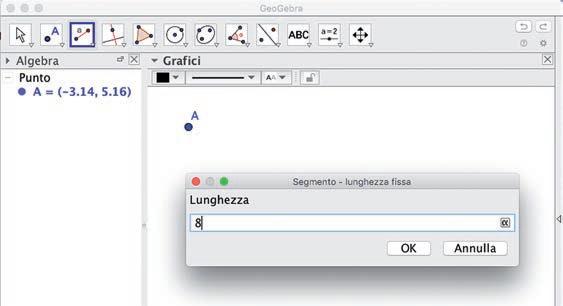
1) Disegna due segmenti consecutivi, entrambi di lunghezza 8; uno di colore rosso e uno verde.

2) Disegna due segmenti adiacenti, uno di colore blu e uno nero, della misura che preferisci.

3) Disegna un segmento di coordinate A (4, 2) e B (9, 2). Quanti centimetri è lungo il segmento?

Individuare il punto medio

Per individuare il punto medio di un segmento, anzitutto segui la procedura per tracciare il segmento.

• Seleziona Punto medio o centro dalla casella degli strumenti Punto.

• Clicca con il puntatore sui punti A e B del segmento e sul piano comparirà il punto medio C, che puoi rinominare M.

ESEMPIO

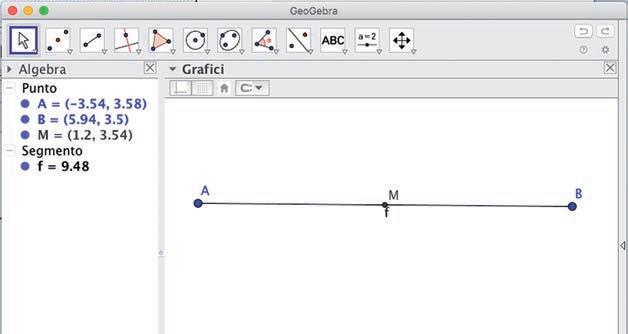
1) Traccia un segmento di coordinate J (2, 9) e K (8, 9). Trova il punto medio M. Quali sono le sue coordinate? Calcola la misura del segmento JM.

2) Disegna due segmenti adiacenti, uno di misura 10 cm e l’altro 8 cm. Trova i punti medi dei due segmenti e calcola la loro distanza, poi verificala con GeoGebra.

3) Disegna il segmento AB e trova il suo punto medio che rinomini M. Trova il punto medio del segmento AM che rinomini M'. Trova infine il punto medio del segmento AM' che rinomini M''. Quanti segmenti AM'' occorrono per formare il segmento AB? Esegui il calcolo aritmetico e verifica il risultato con GeoGebra.

Il piano cartesiano

• Dopo avere aperto GeoGebra, dalla Barra di stile clicca su Mostra/nascondi griglia : appare la griglia con il piano cartesiano. Con la rotellina del mouse puoi ingrandire o ridurre le dimensioni degli assi. Selezionando il tasto Muovi dalla casella Movimento puoi spostarli come vuoi.

• Posizionalo in modo da mettere in evidenza solo il primo quadrante. Seleziona il comando Punto e traccia quattro punti sul piano cartesiano in modo che siano i vertici di un quadrato.

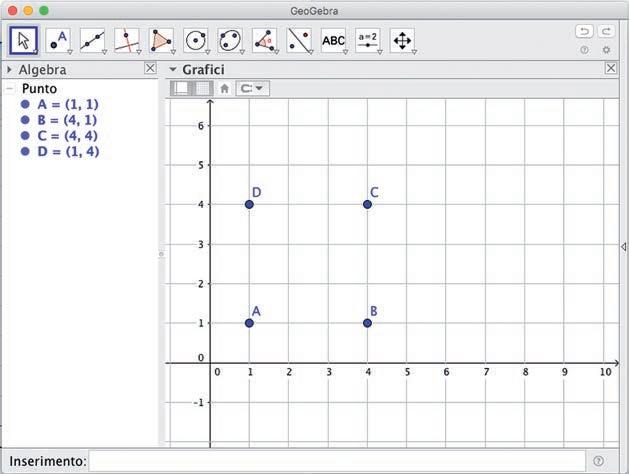
Mostra/nascondi assi Mostra/nascondi griglia

ESEMPIO

1) Traccia sul piano cartesiano quattro punti allineati orizzontalmente, che abbiano come ordinata 3.

2) Traccia sul piano cartesiano quattro punti in modo tale che siano i vertici di un rettangolo.

3) Traccia sul piano due punti di coordinate A (5, 3) e B (1, 2) e poi invertine la posizione con il metodo che ritieni più semplice.

Tracciare un angolo

• Seleziona Angolo dalla casella degli strumenti Misura.

• Traccia sul piano tre punti: delimiteranno i lati e il vertice dell’angolo.

• Per completare la figura bisogna tracciare le due semirette che formano i lati dell’angolo.

Seleziona Semiretta dalla casella Segmenti e clicca su quello che sarà il vertice dell’angolo. Da lì, traccia la semiretta del primo lato dell’angolo.

• Senza cambiare comando, ripeti l’operazione per tracciare la seconda semiretta.

• A questo punto, cliccando con il tasto destro del mouse sull’oggetto interessato, puoi perfezionare la figura rinominando il punto che hai scelto come vertice (in figura, B) in O e nascondere dalla vista gli altri due punti (A e C).

Ricordati che per spostare i punti o le lettere devi selezionare il comando Muovi

Due semirette che hanno la stessa origine determinano sul piano due angoli, uno convesso e l’altro concavo. Se vuoi evidenziare l’angolo concavo devi tracciare i tre punti in senso antiorario, se vuoi evidenziare l’angolo convesso devi tracciarli in senso orario.

= 58.23°

• Se vuoi tracciare un angolo con un’ampiezza prestabilita devi selezionare la funzione Angolo di data misura dalla casella degli strumenti Misura

• Per dividere in due parti congruenti un angolo, dopo aver costruito un angolo generico, seleziona Bisettrice dalla casella degli strumenti Retta speciali, quindi clicca sui tre punti dell’angolo nell’ordine: lato - vertice - lato. L’angolo è individuato da due semirette ma, per praticità, quando lo disegni puoi anche usare due segmenti.

ATTENTO: GeoGebra non usa il sistema sessagesimale, per cui i sottomultipli del grado vengono resi direttamente nel sistema decimale. Ad esempio, l’angolo 40° 30' lo troverai scritto 40.50°.

ESERCIZI

1) Disegna sul piano un angolo di 80°. Traccia la sua bisettrice e poi verifica che i due angoli formati dalla bisettrice siano congruenti.

2) Disegna un angolo di 100° e, usando le bisettrici, ricava un angolo di 25°. Infine, nascondi tutto eccetto l’angolo di 25°.

3) Costruisci due angoli consecutivi di 120° ciascuno.

Tracciare rette parallele e perpendicolari nel piano

• Traccia una retta con il comando Retta , che trovi nella casella Segmenti. Rinominala con la lettera p e nascondi i punti A e B.

• Dall’icona della casella Retta speciali seleziona il comando Retta perpendicolare , clicca sul piano per tracciare un punto esterno alla retta e poi clicca sulla retta p: verrà tracciata la perpendicolare. Rinominala con la lettera s.

• Traccia una retta parallela a p usando il comando Retta parallela della stessa casella Retta speciali e rinominala con la lettera q. Nascondi i punti C e D.

• Per verificare la relazione che intercorre tra le due rette, dalla casella degli strumenti Oggetti speciali seleziona Relazione : clicca su q e poi su s e apparirà la finestra con la scritta “q e s sono perpendicolari”.

• Usando lo stesso piano di lavoro, traccia ora una retta parallela a p e indicala con la lettera r.

Questo ultimo comando ti servirà ogni volta che vuoi verificare l’esattezza di una relazione tra due elementi.

• Traccia un’altra retta perpendicolare a p e rinominala con la lettera t.

• Per ruotare di 45° tutte le rette assegnate, disegna un punto a piacere nel piano. Vai alla casella Trasformazioni e seleziona il comando Rotazione . Clicca su una retta e sul punto comparirà una finestra che ti chiede l’ampiezza dell’angolo: scrivi 45°.

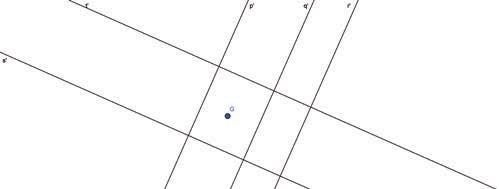
ATTENTO: a ogni rotazione nascondi la retta originaria per non avere troppe rette sul disegno. Quando hai ruotato tutte le rette, controlla che le relazioni tra loro, già verificate precedentemente, non siano cambiate. Per effettuare i controlli usa sempre il comando Relazione .

ESERCIZI

1) Traccia due rette parallele tra loro e misurane la distanza.

2) Traccia due rette perpendicolari e verifica che gli angoli che formano siano retti.

3) Traccia due rette parallele tagliate da una trasversale e gli otto angoli che si formano. Individua le coppie di angoli congruenti e quelle di angoli supplementari.

Disegnare un poligono e analizzarne le caratteristiche

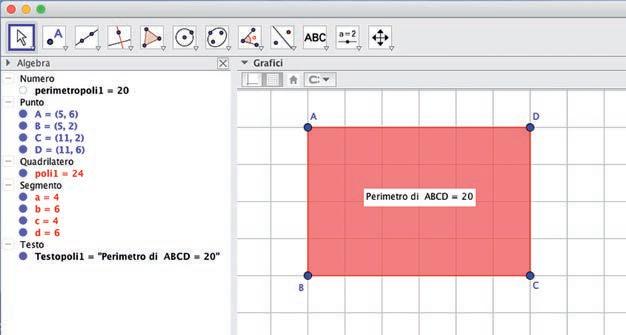
• Seleziona Poligono dalla casella Poligoni. Traccia sul piano una serie di punti non allineati, tanti quanti sono i lati del poligono che vuoi disegnare e chiudi la figura cliccando nuovamente sul primo punto. Si creerà un poligono, con i vertici e i lati in evidenza e la superficie colorata.

• Per conoscere la misura del perimetro vai alla casella degli strumenti Misura e seleziona il comando Distanza o lunghezza che già hai usato per “Disegnare un segmento”. All’interno del poligono comparirà una finestra con la misura del perimetro.

• Se vuoi rendere il disegno più simile a quello del tuo quaderno devi evidenziare la griglia sul piano: clicca su Muovi dalla casella Movimento e nella barra di inserimento comparirà la Griglia . Selezionala e apparirà sul foglio di lavoro.

Disegnare un poligono regolare

• Per disegnare un poligono regolare devi selezionare Poligono regolare dalla casella degli strumenti Poligoni. Il comando ti chiede di tracciare i primi due punti, in modo da determinare tu la lunghezza del lato, quindi una finestra ti chiederà di inserire il numero dei vertici per tracciare il poligono.

• Una volta disegnata la figura, solo i primi due punti rimarranno interattivi e ti permetteranno, cliccandoci sopra con il puntatore, di aumentare o diminuire le dimensioni della figura o di ruotarla. Se la vuoi spostare devi portare il puntatore al suo interno.

ESERCIZI

1) Disegna un rettangolo che abbia i lati di misura doppia rispetto a quello della figura e calcolane il perimetro.

2) Disegna un pentagono regolare con gli angoli interni in evidenza. Calcola la somma degli angoli e verificane l’esattezza con la formula opportuna.

Classificare dei triangoli in base agli angoli

• Costruisci un triangolo acutangolo utilizzando il comando Poligono dalla casella Poligoni Misura l’ampiezza dell’angolo che ha il vertice nel punto A (scegli il comando Angolo nella casella Misura e clicca nei vertici del tuo triangolo, da B a C, in senso orario). Accanto, costruisci un altro triangolo utilizzando lo stesso procedimento.

• Seleziona con il tasto Muovi il vertice F e, tenendo sempre premuto il pulsante del mouse, sposta il punto F in modo che l’ampiezza dell’angolo diventi di 90° per ottenere il triangolo rettangolo DEF (se non riesci, ricorri al comando Angolo di data misura).

• Infine, utilizzando lo stesso procedimento, costruisci il triangolo ottusangolo GHI.

• Con la funzione Testo classifica i tre triangoli in base agli angoli.

ESERCIZI

1) Disegna un triangolo isoscele e poi verifica la congruenza dei lati e degli angoli.

2) Disegna un triangolo qualsiasi e verifica che la somma degli angoli interni è 180°.

Costruire un triangolo equilatero

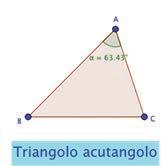
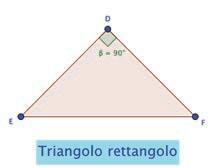
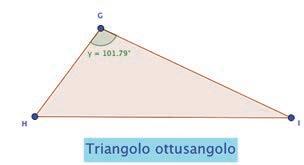
Per disegnare un triangolo equilatero come faresti con righello e compasso, senza utilizzare l’opzione Poligono regolare puoi procedere nel seguente modo.

• Traccia un segmento AB. Con il comando Compasso che trovi nella casella Circonferenza e arco, traccia la circonferenza avente il centro nel punto A e il raggio uguale al segmento AB. Traccia ora la circonferenza avente il centro nel punto B e il raggio uguale al segmento AB.

• Individua uno dei due punti di intersezione delle circonferenze utilizzando il comando Intersezione della casella Punto e indicalo con la lettera C.

• Con il comando Poligono disegna il triangolo equilatero ABC e nascondi le due circonferenze.

ESERCIZIO

Verifica che il triangolo appena disegnato sia equilatero misurando gli angoli e i lati.

Disegnare un quadrato

Ci sono varie modalità per disegnare il quadrato con GeoGebra; la più semplice consiste nel costruire un poligono regolare utilizzando il comando apposito. Qui ti suggeriamo il metodo che somiglia di più a quello che hai imparato in tecnologia usando righello e compasso.

• Disegna un segmento AB; con il comando Retta perpendicolare (che trovi nella casella Retta speciali) traccia due rette perpendicolari passanti per gli estremi A e B del segmento.

• Seleziona il comando Compasso per disegnare una circonferenza avente il centro nel punto A e raggio uguale ad AB. Costruisci un’altra circonferenza con centro nel punto B e raggio uguale ad AB.

• Con il comando Intersezione individua il punto d’intersezione della circonferenza di centro A e la perpendicolare passante per lo stesso punto. Con lo stesso comando individua il punto d’intersezione della circonferenza di centro B e la perpendicolare passante per lo stesso punto. Rinomina i due punti rispettivamente con le lettere D e C.

• Usa il comando Poligono per individuare il quadrato ABCD; usa il comando Mostra/ Nascondi del Menu contestuale (clicca con il tasto destro del mouse per farlo comparire) per nascondere le circonferenze e le rette utilizzate per la costruzione del quadrato.

ESERCIZIO

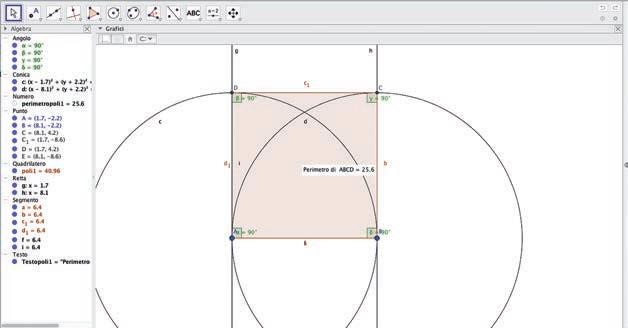
Verifica che il poligono appena disegnato è un quadrato misurando gli angoli e i lati.

Determina il suo perimetro.

Costruzione di un rombo

• Traccia un segmento AB orizzontale, quindi costruisci il suo asse cliccando su Asse di un segmento nella casella Retta speciali

• Individua un punto sull’asse e trova il suo simmetrico rispetto al segmento AB cliccando su Simmetria assiale nella casella Trasformazioni (clicca prima sul punto e poi sul segmento).

• Con il comando Poligono clicca sui quattro punti e traccia il rombo; rinomina i punti in ordine alfabetico e in senso antiorario.

• Nascondi la retta e traccia la diagonale mancante. Trova il punto di intersezione tra le due diagonali e rinominalo con la lettera O.

ESERCIZI

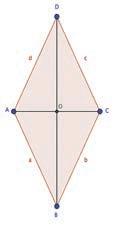
1) Verifica che il disegno appena realizzato sia un rombo misurando la lunghezza dei quattro lati e l’ampiezza degli angoli opposti.

2) Disegna un rettangolo con i comandi che ritieni più opportuni e verifica che abbia i lati opposti congruenti e i quattro angoli retti.

3) Disegna un parallelogramma con i comandi che ritieni più opportuni e verifica che abbia i lati e gli angoli opposti congruenti.

4) Disegna un trapezio isoscele e verifica che i lati obliqui siano congruenti e le basi parallele.

Anche il programma Excel può essere utilizzato come strumento informatico applicato alla matematica. La sua caratteristica principale è la capacità di fare calcoli automaticamente usando delle formule matematiche. Excel può essere utilizzato per ordinare i numeri, fare addizioni, sottrazioni, moltiplicazioni e divisioni, ma anche per creare tabelle e grafici, calcolare potenze e svolgere operazioni con le frazioni. Attraverso il Qrcode e/o l’icona digitale potrai accedere a schede dedicate ed esercizi di matematica da svolgere passo-passo con l’ausilio del programma Excel.

PROGRAMMARE IN MODO SEMPLICE CON SCRATCH 1

Che cos’è Scratch e come si accede

Scratch è un software gratuito attraverso cui è possibile imparare a programmare con un linguaggio completamente grafico creando storie interattive, giochi, progetti multimediali, simulazioni e tanto altro ancora.

Con Scratch si programma senza utilizzare complessi codici di programmazione, ma si usano blocchi di forme e caratteristiche differenti che possono essere incastrati in migliaia di modi, creando quindi tantissime combinazioni diverse. È possibile accedere a Scratch attraverso due modalità:

• online, tramite il link https://scratch.mit.edu

• offline, installando l’app di Scratch (puoi scaricarla dal link https://scratch.mit.edu/download).

Per iniziare, osserva la barra dei menu in alto [Figura 1]. Attraverso questa sezione, puoi creare un nuovo progetto, puoi consultare i progetti condivisi dagli altri utenti e, se sei in difficoltà, puoi accedere alla visione di vari tutorial. Inoltre, puoi registrarti ed entrare gratuitamente a far parte della community di Scratch.

Libreria con progetti condivisi dalla comunità di Scratch

Crea un nuovo progetto

Figura 1: barra dei menu.

Scopri di più sulla piattaforma

Tutorial per iniziare

L’interfaccia di Scratch

Aree per registrarsi o accedere con il proprio account gratuito

Una volta creato un nuovo progetto, osserva che l’ambiente di lavoro è suddiviso in quattro settori principali [Figura 2].

Scelta della lingua e colori

Carica/salva un progetto

Cambia il nome al tuo progetto

Condividi il tuo progetto con la community di Scratch

Consulta materiale e video utile per comprendere l’utilizzo della piattaforma

Categoria dei blocchi

Aggiungi un’estensione per suonare, disegnare, tradurre un testo…

Figura 2: schermata generale del progetto. Le quattro aree principali.

• Nell’ambiente di lavoro, in alto a destra, si trova lo stage, ossia l’area di gioco. In questa area gli sprite, oggetti bidimensionali che rappresentano i personaggi protagonisti del gioco (per esempio, il gatto), interagiscono durante l’esecuzione del programma.

• In basso a destra, invece, si trova l’area delle informazioni, in cui è possibile gestire ogni sprite utilizzato e ogni sfondo selezionato. In un progetto di Scratch si possono inserire uno o più sprite, ai quali viene data una serie di “comandi” per farli muovere, parlare, interagire, calcolare ecc. Oltre al noto gatto di Scratch, si possono scegliere vari sprite nella libreria del sito [Figura 3]; si può anche importare una propria immagine. Inoltre, si possono creare nuovi sprite attraverso un apposito editor grafico.

Cliccando in “Scegli uno Sfondo” si può scegliere quanti e quali sfondi inserire come background all’interno dell’attività.

Cambia il nome allo sprite selezionato

Figura 3: area delle informazioni.

Importa uno sprite personalizzato

Disegna un nuovo sprite

Scegli uno sprite nella libreria di Scratch

Importa uno sfondo

Disegna un nuovo sfondo

Scegli uno sfondo nella libreria di Scratch

• Nell’ambiente di lavoro, a sinistra, si trova l’area dei blocchi [Figura 2]. I blocchi sono i mattoncini che si utilizzano per costruire il programma; sono suddivisi in nove categorie, ognuna caratterizzata da un colore diverso.

• Al centro dell’ambiente, invece, si trova l’area per programmare, chiamata area script [Figura 2]. In questa area è possibile trascinare e sovrapporre i blocchi che servono alla codifica del programma.

NUMERO PRIMO O NUMERO COMPOSTO?

Un numero primo è un numero naturale maggiore di 1 che è divisibile solamente per 1 e per sé stesso. Un numero composto è un numero che ha almeno 3 divisori.

Esempi: 11 è un numero primo, perché divisibile solo per 1 e 11. 4 è un numero composto, perché divisibile per 1, 2 e 4.

Idea del progetto

Per questo esercizio si può scegliere uno sfondo e uno sprite a piacere nell’appostita area delle informazioni in basso a destra.

L’obiettivo di questo esercizio è programmare lo sprite scelto, nel nostro caso il gatto; il codice che verrà programmato consentirà allo sprite di rispondere se il numero inserito è primo o composto. Una procedura per verificare questa richiesta potrebbe essere quella di dividere il numero N scelto per 1, 2, e così via, fino a dividerlo per la metà del numero stesso. Al termine, si chiederà al programma di contare il numero di divisori trovati; se non si trovano divisori al di fuori del numero stesso e di 1, allora il numero è primo.

Attenzione: non si valutano divisori maggiori della metà del numero perché, eccetto il numero stesso, non esistono divisori di un numero che sono maggiori della sua metà.

Crea le variabili

Per questo esercizio sono necessarie tre variabili, da creare nell’apposita area dei blocchi:

• la variabile “N”, ossia il numero scelto;

• la variabile “divisore”;

• la variabile “numero di divisori” [Figura 4].

Queste ultime due vanno deselezionate per non essere visualizzate nello stage

Figura 4: variabili dell’attività.

Crea il codice per lo sprite gatto

Mantieni selezionato lo sprite gatto e, spostando i blocchi nell’area script, crea il codice seguendo i seguenti criteri:

Ø BLOCCHI SITUAZIONE + BLOCCHI VARIABILI + BLOCCO SENSORE

Per impostare la richiesta iniziale, dopo aver stabilito come iniziare il gioco, inserisci un blocco sensore che consente di chiedere un numero qualsiasi da verificare [Figura 5]. In seguito a questa richiesta, imposta i valori iniziali che devono assumere le tre variabili:

• N → deve coincidere con la risposta [Figura 5];

• divisore → deve corrispondere a 2, perché, escludendo 1 che è divisore di tutti i numeri, 2 è il primo divisore che il programma dovrà considerare. Questo eviterà il problema dello 0 e delle situazioni indeterminate o impossibili;

• numero di divisori → deve corrispondere a 2, perché ogni numero ha almeno 2 divisori.

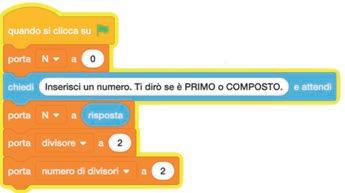
Clicca sulla bandierina verde per iniziare

Questo codice permette di azzerare le richieste precedenti

Figura 5: codice dell’attività (parte 1).

Ø BLOCCHI CONTROLLO + BLOCCHI OPERATORI + BLOCCHI ASPETTO

Per rispondere alla domanda se un numero è primo o composto, bisogna ripetere la divisione del numero stesso per un divisore, fino a quando non sarà più necessario eseguire l’operazione, ossia fino a quando il divisore sarà la metà del numero. Per questo motivo, è fondamentale inserire il blocco “Ripeti fino a quando” con i dati corretti [Figura 6].

Con il primo blocco “se … allora … altrimenti” si chiede al programma, a seconda se la divisione darà resto 0 o meno, di contare il numero dei divisori.

Con l’ultimo blocco “se … allora … altrimenti” si stabilisce se il numero è primo o composto.

Se il numero dei divisori è pari a 2, il numero è primo; se il numero dei divisori è maggiore di 2, il numero è composto.

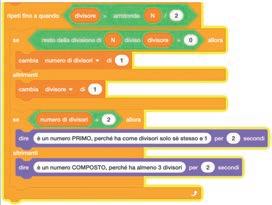
2).

Figura 6: codice dell’attività (parte

CONFRONTIAMO DUE FRAZIONI 3

Confrontare due frazioni significa stabilire quale delle due è maggiore o minore rispetto all’altra, oppure se sono tra loro equivalenti, ossia se rappresentano la stessa quantità. Un metodo per confrontare due frazioni è il metodo del prodotto a croce

Date le frazioni N1 D1 e N2 D2

• si moltiplica il numeratore della frazione 1 per il denominatore della frazione 2;

• si moltiplica il numeratore della frazione 2 per il numeratore della frazione 1. N1 D1 N2 D2

Se N1 × D2 > N2 × D1, allora N1 D1 > N2 D2

Se N1 × D2 < N2 × D1, allora N1 D1 < N2 D2

Se N1 × D2 = N2 × D1, allora N1 D1 = N2 D2 .

Inizia un nuovo progetto e crea le variabili

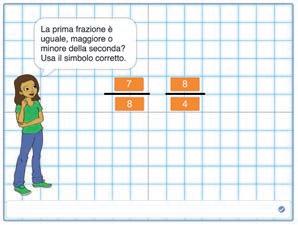
Per questo esercizio è necessario creare cinque variabili nell’apposita area dei blocchi: i quattro termini delle frazioni e la variabile “Risultato” [Figura 7].

Seleziona le prime quattro variabili; in questo modo saranno visibili nello stage.

Deseleziona la variabile “Risultato”: questa variabile deve rimanere nascosta.

Nell’area stage clicca con il tasto destro sulle variabili visualizzate e seleziona “grande”; in questo modo sarà visibile un rettangolo arancione con il valore corrispondente, ma non il nome.

Figura 7: variabili dell’attività.

Crea lo sfondo e scegli uno sprite

Nell’area sfondi seleziona un’immagine a piacere (per esempio, la griglia quadrettata) o colora lo sfondo a piacimento [Figura 8]. Poi, disegna con l’editor di immagini due linee di frazione.

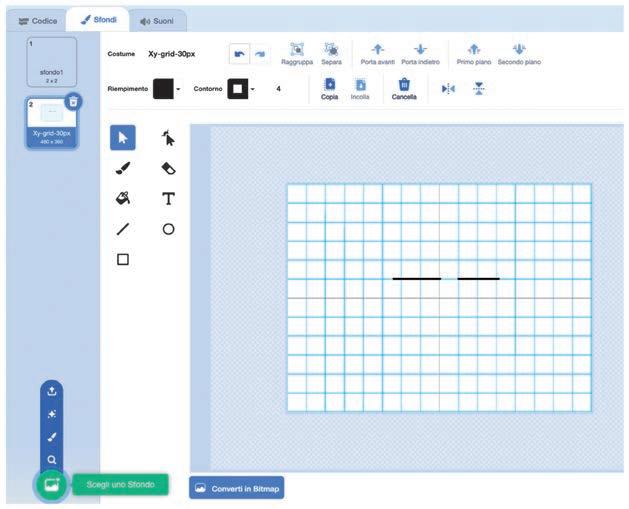
Nello stage sposta le variabili in corrispondenza delle linee appena disegnate, in modo da comporre le due frazioni da confrontare.

Scegli lo sprite principale nell’apposita area delle informazioni in basso a destra. In generale, si può tenere lo sprite preimpostato (il gatto) oppure si può cambiarlo selezionando la funzione “Scegli uno Sprite”. Per questo esercizio scegli lo sprite “Abby” [Figura 9].

Figura 8: editor di sfondi.

Figura 9: area delle informazioni.

Crea il codice per lo sprite Abby

Mantieni selezionato lo sprite Abby e, spostando i blocchi nell’area script, crea il codice seguente:

• BLOCCHI SITUAZIONE → Scegli la modalità di inizio dell’attività. Per esempio, puoi decidere di iniziare quando l’utente clicca sulla bandierina verde.

• BLOCCHI CONTROLLO → Puoi decidere di creare un’attività perpetua. Per fare questo, sposta il blocco “per sempre” all’interno del codice [Figura 10].

• BLOCCHI VARIABILI + BLOCCHI OPERATORI → Inserisci le quattro variabili dentro il codice e assegna loro un numero a caso compreso, per esempio, da 1 a 10; in questo modo, verranno generate frazioni casuali creando un numero considerevole di esercizi [Figura 11].

• Si procede con la programmazione: opera eseguendo le moltiplicazioni tra Numeratore 1 e Denominatore 2 e tra Numeratore 2 e Denominatore 1 e confrontale.

• Con il blocco “se … allora … altrimenti” si associa il risultato del confronto al simbolo corretto.

• BLOCCHI SENSORI + BLOCCHI CONTROLLO + BLOCCHI ASPETTO → Con il comando “chiedi” puoi impostare la domanda da rivolgere all’utente. Riproponendo il blocco “se allora altrimenti” puoi associare la risposta data al risultato e inviare un feedback all’utente attraverso il blocco “dire” [Figura 11].

Figura 10: codice di inizio.

Figura 11: codice dell’attività.

CLASSIFICAZIONE DEI QUADRILATERI

In questo esercizio verrà illustrato come lavorare con differenti sprite a cui verrà associato un codice. L’obiettivo è quello di creare un quiz che richiede una successiva verifica di risposta, non in formato verbale ma grafico.

Attenzione: prima di iniziare, ripassa le caratteristiche dei quadrilateri. L’esercizio è così strutturato:

• ci sono tredici sprite, sei quadrilateri, sei etichette con il nome dei quadrilateri rappresentati e il gatto che illustra come avviare l’esercizio;

• le etichette verranno programmate per essere trascinabili nello spazio. Una volta sovrapposte alla figura piana corrispondente, cambiano aspetto; questo cambio evidenzia la correttezza della risposta.

Crea gli sprite

Il primo passaggio è disegnare gli sprite che rappresentano i quadrilateri. A tal fine, nell’area delle informazioni in basso a destra, è necessario cliccare su “Disegna un nuovo sprite” [Figura 12].

Dopo aver cliccato si apre un editor, all’interno del quale puoi disegnare linee e figure piane, inserire un testo, cambiare colori e spessori ecc. [Figura 13].

Figura 12: area delle informazioni. Strumento per disegnare uno sprite.

Figura 13: editor per disegnare uno sprite.

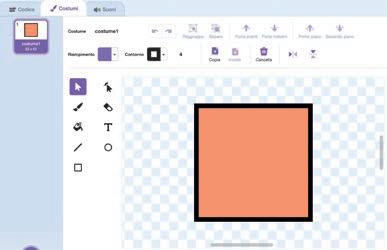
In tal modo puoi creare le figure piane da classificare. In questo caso, sono stati selezionati sei tipi di quadrilateri [Figura 14].

Figura 14: sprite che rappresentano i quadrilateri scelti.

Una volta creati, gli sprite possono essere spostati nello stage nella posizione preferita. Ora procedi creando le etichette. Crea uno sprite per etichetta, disegna un rettangolo e inserisci al suo interno la scritta corrispondente al nome di ogni quadrilatero disegnato [Figura 15].

Parallelogramma

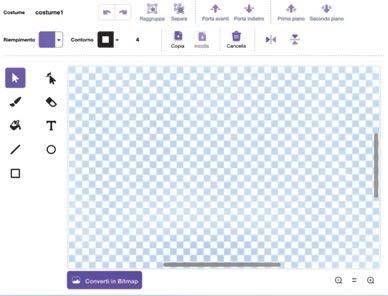
Figura 15: sprite “etichetta”.

Per ogni etichetta è necessario creare un “secondo costume”, ossia la versione di conferma che comparirà nell’esercizio quando si avrà la sovrapposizione tra quadrilatero ed etichetta corretta. È possibile svolgere questa operazione nell’area “Costumi” [Figura 16].

Parallelogramma

Figura 16: area Costumi.

Crea il codice per i vari sprite

Per portare a termine l’esercizio, è necessario creare un codice sia per lo sprite gatto sia per ogni sprite “etichetta” creato.

Codice sprite gatto

Il gatto, in questo caso, ha l’unico ruolo di guidare l’utente e indicare come svolgere l’esercizio.

Per questo motivo, il codice è semplice: dopo aver stabilito come iniziare il gioco, si utilizza il blocco “dire” per comunicare come procedere [Figura 17].

17: codice dello sprite gatto.

Codice sprite “etichette”

Per ogni etichetta è necessario programmare un codice specifico. Ogni etichetta deve essere trascinabile nello spazio; per fare ciò, si utilizza il blocco sensore apposito “rendi lo sprite…” e si attiva l’opzione “trascinabile” [Figura 18].

Per concludere, con gli appositi blocchi “controllo”, si chiede di passare al “secondo costume” ogni volta che avviene la sovrapposizione corretta.

Figura 18: codice di ogni sprite “etichetta”.

Figura