3.3 Review Questions G = 6.67 × 10–11 Nm2/kg2 Me = 5.98 × 1024 kg Re = 6.37 × 106 m 1. What is the force of gravity exerted on a 70.0 kg person on Jupiter (assuming the person could find a place to stand)? Jupiter has a mass of 1.90 × 1027 kg and a radius of 7.18 × 107 m.
2. What is the gravitational field strength of Earth at a distance equal to the Moon’s orbital radius of 3.84 × 108 m? Compare this with the centripetal acceleration of the Moon, calculated earlier in the chapter.
3. Calculate the orbital speed of the Moon around Earth, using the Moon’s orbital radius and the value of Earth’s gravitational field strength at that distance.
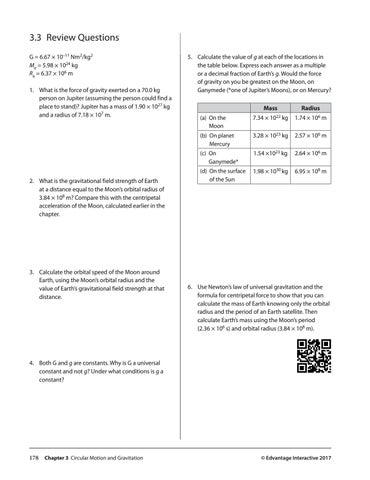
5. Calculate the value of g at each of the locations in the table below. Express each answer as a multiple or a decimal fraction of Earth’s g. Would the force of gravity on you be greatest on the Moon, on Ganymede (*one of Jupiter’s Moons), or on Mercury? Mass
Radius
(a) O n the Moon
7.34 × 1022 kg
1.74 × 106 m
(b) O n planet Mercury
3.28 × 1023 kg
2.57 × 106 m
(c) O n Ganymede*
1.54 ×1023 kg
2.64 × 106 m
(d) O n the surface of the Sun
1.98 × 1030 kg
6.95 × 108 m
6. Use Newton’s law of universal gravitation and the formula for centripetal force to show that you can calculate the mass of Earth knowing only the orbital radius and the period of an Earth satellite. Then calculate Earth’s mass using the Moon’s period (2.36 × 106 s) and orbital radius (3.84 × 108 m).
4. Both G and g are constants. Why is G a universal constant and not g? Under what conditions is g a constant?
178 Chapter 3 Circular Motion and Gravitation
© Edvantage Interactive 2017