Issuu

BC Math 9

BC MATH 9 Author

Laura Epp Numeracy Mentor Support Teacher SD43 Coquitlam, B.C.

COPIES OF THIS BOOK MAY BE OBTAINED BY CONTACTING: Edvantage Interactive E-MAIL: info@edvantageinteractive.com TOLL-FREE CALL: 866.422.7310

BC Math 9 Copyright © 2026, Edvantage Interactive All rights reserved. No part of this publication may be reproduced or transmitted in any form or by any means, or stored in a database or retrieval system, without the prior written permission of Edvantage Interactive.

ISBN: 978-1-77430-539-3

Editorial Development Lead: Lionel Sandner The publisher extends sincere thanks to the pilot teachers and students who tested these materials during the 2025–2026 school year, as well as the following educators for their review and feedback:

About the Cover Cover design and artwork by Ella Quesnel, a Bachelor of Fine Arts graduate from Emily Carr University.

•

Brittany Stockley

•

Carianne Wiebe

•

Gabrielle Szamoskozi

•

Lynda Lewis

•

Nevena Savovic, PhD

•

Terri Galligos

Care has been taken to trace ownership of copyright material contained in this text. The publisher will gladly accept any information that will enable them to rectify any reference or credit in subsequent printings.

Contents

BC Math 9

Welcome to BC Math 9. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . vii 1 Rational Numbers. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1

1.1 What is a Rational Number? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 1.2 Equivalent Rational Numbers. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 1.3 Comparing and Ordering Fractions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 1.4 Operations with Decimals . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 1.1 – 1.4 Check Your Understanding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27 1.5 Adding and Subtracting Fractions. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 1.6 Multiplying and Dividing Fractions. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36 1.7 Order of Operations. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48 1.8 Applications . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53 1 Chapter Review. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58

2 Powers and Roots. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65

2.1 What is a Power? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66 2.2 Exponent Laws – Part 1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74 2.3 Exponent Laws – Part 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80 2.1 – 2.3 Check Your Understanding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86 2.4 Square Roots. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88 2.5 Applications – Scientific Notation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92 2 Chapter Review. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98

3 Polynomials. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105

3.1 What is a Polynomial? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106 3.2 Adding Polynomials . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113 3.3 Subtracting Polynomials . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120 3.1 – 3.3 Check Your Understanding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126 3.4 Multiplying Polynomials . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 129 3.5 Dividing Polynomials . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 138 3.6 Combined Operations and Applications . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 143 3 Chapter Review. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 150

4 Linear Relations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 157

4.1 What is a Linear Relation?. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 158 4.2 Representing Linear Relations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 170 4.3 Graphing Linear Relations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 183 4.1 – 4.3 Check Your Understanding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 196 4.4 Interpreting Graphs of Linear Relations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 201 4.5 Applications . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 208 4 Chapter Review. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 215

5 Linear Equations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 223

5.1 What is a Linear Equation?. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 224 5.2 Solving 1- and 2-Step Equations with Integers. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 232 5.3 Solving 2-Step Equations with Rational Numbers. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 240 5.1 – 5.3 Check Your Understanding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 247 5.4 Solving Multi-step Equations with Brackets. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 249 5.5 Solving Multi-step Equations with Variables on Both Sides. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 253 5.6 How to Solve a Word Problem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 262 5 Chapter Review. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 269

6 Proportional Reasoning . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 279

6.1 What is Proportional Reasoning? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 280 6.2 Scale Diagrams . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 289 6.3 Similar Triangles and Polygons. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 295 6 Chapter Review. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 302

7 Statistics. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 309

7.1 Statistics and the Factors Affecting Data Collection. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 310 7.2 Collecting and Organizing Data. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 320 7.3 Graphing and Interpreting Data. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 324 7 Chapter Review. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 330

8 Financial Literacy Project . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 335

8.1 Financial Basics. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 336 8.2 Project: Creating a Financial Plan . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 341

Introduction iii

Welcome to Edvantage Math: BC Math 9 Before diving into your course, we invite you to read this introduction. It outlines key ideas from modern cognitive science research, ideas that shaped how this textbook was designed to help you learn more effectively and remember for longer.

What Is Learning? Let’s start with a research-based definition from Make It Stick: The Science of Successful Learning: “Learning is acquiring knowledge and skills and having them readily available from memory so you can make sense of future problems and opportunities.” Brown, Roediger, & McDaniel (2014), p. 2 This means that learning isn’t just about reading or listening. It’s about getting ideas and skills into your long-term memory so that you can apply them when you face new challenges. That’s what this course, and this textbook, are designed to help you do.

How Your Brain Learns: A Simplified Model The diagram you’ll see below is a simplified version of the Cognitive Theory of Multimedia Learning (Mayer, 2005), which integrates decades of research on how people learn from words, images, and experiences. The diagram highlights three key memory systems:

Reproduced with permission from Failsafe Strategies for Science and Literacy

•

Sensory memory: Information enters through your senses (especially eyes and ears).

•

Working memory: Where your brain holds and organizes new information.

•

Long-term memory: Where learning is stored and integrated with your prior knowledge.

Understanding how these systems interact is critical for learning effectively.

Attention: The Gatekeeper of Learning You can’t learn what you don’t notice. Your sensory memory only processes what you give attention to. If you're distracted by your phone, for example, you won’t retain what your teacher is saying, no matter how good the explanation. That’s why attention is the first essential skill for learning. This textbook is structured to help you focus on what matters most in each lesson.

Cognitive Load: Why Less Is More Your working memory can only hold about 4 to 7 pieces of new information at once and often fewer when the material is unfamiliar. If too much is thrown at you at once, your brain gets overwhelmed and can’t process it deeply enough to store in long-term memory. That’s called cognitive overload, and it’s a major barrier to learning. To address this, Edvantage Math: BC Math 9 is carefully designed to reduce unnecessary cognitive load so your brain can focus on understanding core ideas. Clear diagrams, structured problem-solving prompts, and scaffolded practice are just a few of the strategies we’ve built in to help.

iv Introduction

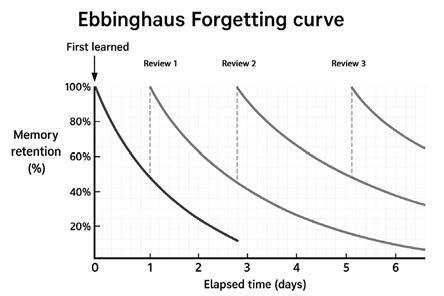
The Importance of Forgetting (and Remembering) Forgetting is normal. It happens to everyone. In fact, it begins as soon as we learn something. This is known as the Ebbinghaus Forgetting Curve and is illustrated in the graph below. But here’s the good news: forgetting can be slowed and even reversed by reviewing information at spaced intervals as shown in the graph. This process is called retrieval practice, and it’s one of the most powerful learning strategies discovered in cognitive science. You’ll find many activities in this book designed to help you remember what you learn when you need it most.

This Book Supports How You Learn Try Together – Partially Worked Solutions Every sample problem is followed by a Try Together problem. This problem is a partially worked solution. This helps you focus on the key aspects of the problem without overloading your working memory with too many steps at once.

How’s it Going? During each chapter, you become the teacher. You'll mark a sample student’s quiz, allowing you to retrieve, evaluate, and apply what you’ve learned. This kind of elaborative practice strengthens long-term memory and makes your learning more durable.

Remembering Ebbinghaus Periodically, you’ll encounter questions that revisit earlier topics even if they’re not part of your current unit. This deliberate spacing and retrieval strengthens memory and prepares you to use math concepts flexibly, not just repeat them on a test.

Final Thoughts If you’ve read this far, congratulations. You’ve already taken the first step in developing strategies that help you learn. This textbook is more than a source of information; it’s a tool to help you become a better learner. Good luck on your journey through BC Math 9.

Introduction v

References and Suggested Reading Ashman, G. (2022). Little Guide for Teachers: Cognitive Load Theory. Brown, P. C., Roediger, H. L., & McDaniel, M. A. (2014). Make It Stick: The Science of Successful Learning. Christodoulou, D. (2014). Seven Myths About Education. Ebbinghaus, H. (1885/1913). Memory: A Contribution to Experimental Psychology. Kirschner, P., & Hendrick, C. (2020). How Learning Happens: Seminal Works in Educational Psychology and What They Mean in Practice. Mayer, R. E. (2005). The Cambridge Handbook of Multimedia Learning. Mirabelli, S., & Sandner, L. (2023) Failsafe Strategies for Science and Literacy

vi Introduction

Welcome to BC Math 9 2026 Challenge Use the four digits (2, 0, 2, 6) exactly once each along with any operations to create expressions equivalent to the numbers from 1 to 20. Can you continue this for the numbers from 1 to 50? Can you find more than one way to express each number from 1 to 20? Examples 0=6×0×2×2 42 = 62 – 20 34 = 62 – 2 + 0 28 = 20 + 2 + 6

11 =

12 =

13 =

14 =

15 =

16 =

17 =

18 =

19 =

10 =

20 =

Introduction vii

viii Introduction

1 Rational Numbers Rational numbers are everywhere. A car travels 15 km and has half a tank of gas. There is a 25% discount on an item that costs $49.95. The temperature outside is –10 °C. All of these numbers are rational. These numbers help us describe, measure, and compare quantities that involve decimals, fractions, percents, and rates.

Big Idea of the Chapter Computational fluency and flexibility with numbers extend to operations with rational numbers. In this chapter you will explore: Rational numbers are numbers that can be represented as a fraction Rational numbers and why they are useful

where m (the numerator) and n (the denominator) are integers and n is not zero.

Add rational numbers

, 0.005 + 0.5 = 0.505

Subtract rational numbers

, 11.19 – 0.076 = 11.114

Multiply rational numbers

, 0.3 × 0.4 = 0.12

Divide rational numbers

, 0.5 divided by 0.25 = 2

Order of operations with rational numbers Apply these concepts

Double a recipe asking for

Model operations to help deepen understanding

Number lines, fraction strips/circles, measuring tools, grids

cup of sugar

Get Started Rational numbers help us manage money ($12.50) and time (12:30 pm). They help us measure things like distance, speed, acceleration, temperature, capacity, area, angles, probability, averages, decibels (sound), lumens (light), pH (acidity) and so much more. In grades 10 to 12, you will study irrational numbers. Together the rational and irrational numbers make up the real numbers used in secondary math. All of the visuals below represent part of something. Specifically, they describe half of something. Identify what each picture is half of.

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

1.1 What is a Rational Number? Warm Up Competency Focus - Model math in contextualized experiences

Pick one of the questions below and solve. •

What fraction of the rectangle above is shaded?

•

How many suns are there compared to the number of moons in the middle picture?

•

How can you share $10 000 evenly with 3 people?

Define Rational Number

Rational numbers are numbers that can be represented as a fraction numerator) and n (the denominator) are integers and n is not zero.

where m (the

Rational numbers help us to accurately represent, describe, compare and understand measurements, probabilities, proportions, and relations. They are everywhere, and there is evidence that they were used by humans for thousands of years, all over the world. “Rational” comes from the Latin word “rationalis” which means reasonable or logical. Here are examples of rational numbers you might see today. Can you add to the list? • 25% tariff. • Overall average for grade 9 courses is 78%. • 10 BC Transit concession tickets for $15.75. • Batting average of 0.300. • Speed limit on the highway is 100 km/h. • 90% chance of rain. • 2 cups of water for every cup of oats. • Minimum wage is $18.25 an hour. • The dimensions of this workbook are 8.5 inches by 11 inches.

2 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

Dividing by Zero

Consider the following division: 6 ÷ 0. Try it on your calculator. Why can’t we divide by zero? Now let's compare it to 6 ÷ 3. How many 3s are in 6? 2 because 3 + 3 = 6. So, how many zeros are there in 6? 0 + 0 + 0 + ... it doesn't work. It doesn't make sense. In math and science, we can use more formal ways to prove something is true or not true. One of them is a proof by contradiction. Let’s assume there is an answer that works, and we will call this answer x. 6 ÷ 0 = x. 1. If 6 ÷ 3 = 2, we know that 2(3) = 6. 2. So, if 6 ÷ 0 = x, then 0(x) = 6. 3. We also know that multiplying by zero gives an answer of zero. 0(x) = 0. 4. 0(x) = 6 and 0(x) = 0 is a contradiction. Our assumption was wrong. That is why 6 ÷ 0 has no answer. In math, we say it is undefined.

Fractions

The word fraction comes from the Latin word meaning “to break”. Fractions help us describe parts of something. They also help us compare quantities and write division clearly. All rational numbers can be written as a fraction. All rational numbers can also be written as either repeating or terminating decimals. • Repeating decimals have a recurring pattern of digits. Example: 0.142 or 0.142142142. • Terminating decimals have a finite number of digits. Example: 0.3 or 0.9876543.

Try This ... 1. With your calculator, convert the following fractions to a decimal number. Divide the numerator by the denominator. Does the decimal terminate or repeat? Write T for terminating and R for repeating beside the fraction. a.

Define Irrational Number

Numbers that are not rational are called irrational. You will study these numbers in grades 10 and 11. Three of the most famous irrational numbers are π, and e. Decimal numbers that are rational must be either repeating or terminating. If they are non-repeating and non-terminating, they are not rational numbers. A set is a collection of objects. In mathematics, sets are often used to group numbers that

Rational Numbers as share similar properties. a Set of Numbers The set of rational numbers is an infinitely large set. It includes numbers that can be written as a fraction of two integers. Some number sets are completely contained within larger sets. For example, every natural number is also a whole number, every whole number is also an integer, and every integer is also a rational number. The set of rational numbers includes these kinds of numbers: • Natural numbers {1, 2, 3 ...} •

Whole numbers {0, 1, 2, 3 ...}

•

Integers {... –3, –2, –1, 0, 1, 2, 3 ... }

•

Fractions like

•

Terminating decimals like 5.25 and 0.07.

•

Repeating decimals like 0.1, 78.658 and 2.33333333

©Edvantage Interactive 2026

RATIONAL NUMBERS Integers

{..., 2, 1,0,1,2,...}

Whole Numbers {0,1,2,3,4,...}

Natural Numbers {1,2,3,4,...}

Chapter 1 Rational Numbers

Try This ... 1a. Circle or highlight the rational numbers in the chart below. Hint: Can you write it as a terminating decimal? Fraction? Repeating decimal? a. 3

b. –2.123

c. 0.8

f. 0.5

g. 0

h. –11

i. 0.2222

j. 1.545454 ...

m. 0.0000001

n. 5678

r. π

s. 3.23467211976

t. –

k. 32 p. –999999

l. q.

–

e. 12.25

1b. How many of the above numbers are natural?_____ Integers? ______Whole numbers?______ terminating decimals?_____ irrational numbers? ____.

2. True or false. If it is true, give an example or reason. If it is false, give a counterexample (an example that contradicts the sentence). a.

All whole numbers are integers.

All integers are natural numbers.

Natural numbers are integers.

All decimal numbers are irrational.

Real numbers can be rational or irrational.

A repeating decimal is irrational.

Terminating decimals are rational.

π is an irrational number.

Extend and Explore

Irrational numbers are numbers that cannot be written as a fraction with integers. Explore the irrational numbers “π” and "e". What do they represent? Why are they useful? Which of the two would you say is the most useful? Explain.

4 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

1.1 Practice 1. Circle the rational numbers in the chart below. a. 0

c. –7.11813519

f. 0.8

g. 13

h. 0.3

i. –2

j. 3.14

k. 3.1415926536 ...

l. –6.789

m. –0.0000008

n. 123456789

s. 1.1111

t. –π

p. –444

–

e. 123.456

2. How many of the numbers in this chart are: Natural _________ Whole numbers _________ Integers _________ Terminating decimals _________ 3. True or false. Is the sentence correct or not? (T or F) Justify your choice. a.

All integers are rational ______ because ____________________________________________________________.

All rational numbers are integers ______. For example _________________________________________________.

Natural numbers are real ______. For example ________________________________________________________.

All decimal numbers are rational ______ because ____________________________________________________.

Real numbers can be rational or irrational ______ because _____________________________________________.

A number can be both an integer and a rational number ______. For example ______________________________.

Terminating decimals are rational ______ because ___________________________________________________.

π is a rational number ______ because ____________________________________________________________.

Rational numbers have been used by humans for almost 100 years. ______ because _______________________.

Dividing by zero always yields a result of zero. ______ because _________________________________________.

4. Fill in the blanks. a. Dividing by zero is ______________. (zero / one / undefined / infinity) b. Decimal numbers that are rational are either _____________ or _____________. c. Rational numbers can be written as fractions with ____________ in the numerator/denominator. d. The top of the fraction is called the __________________. e. 1.23456789 is an example of a _______________ decimal.

1.1 Practice Answer Key 1) Do not circle: k, o, t 2) Natural: 2, Whole: 3, Integer: 4, Terminating decimals: 6 3a) T; an integer can be written as itself over one 3/1 = 3. b) F; one half is not an integer. c) T; example: 2 is a natural number, whole number, integer, rational and real number. d) F; non-terminating, non-repeating decimals cannot be written in the form a/b where a and b are integers. e) T; definition of real number. f) T; for example 2. g) T; they can be written as a fraction with the denominator that is a multiple of 10. h) F; it is non-repeating and non-terminating. i) F; much longer than 100 years (evidence in ancient civilizations). j) F; dividing by zero is undefined. 4a) undefined, b) terminating, repeating, c) integers, d) numerator, e) terminating ©Edvantage Interactive 2026

Chapter 1 Rational Numbers

1.2 Equivalent Rational Numbers Warm Up Competency Focus - Demonstrate mental math strategies with operations using rational numbers. The answer is

. What was the question? How many different questions can you and your class create whose answer is

Equivalent Numbers

We can represent the rational number one half in many different ways and in different realworld contexts. 1:2 ratio of cups of

Half an orange

rice to water

0.5 seconds

Half note in music

Half a tank of gas

notation

Half an inch

2.5 stars out of 5-star rating

une demie (French) un medio (Spanish) 半 (yí bàn) Mandarin

50% battery life remaining

cup

Your share of a pizza if there are 6 people and 3 pizzas

Can you think of another example? (draw or write)

6 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

Equivalent Fractions

Different fractions can represent the same amount. For example, one half of a pizza is the same amount as two quarters of a pizza. The fractions look different, but they represent the same part of the whole. Fractions that represent the same amount are called equivalent fractions.

________

The image above has the left half of each of the circles shaded. Below each circle, write the fraction of the shaded area it represents. What did you notice? Even though the fractions are different, they all represent one half. To create an equivalent fraction, multiply the numerator and denominator by the same number.

Try This ... 1. Write 10 equivalent fractions for

Equivalent Fractions with Negative Numbers

Fractions involving negative numbers can be written in different ways and simplified. As a general rule, if you see one or three negative signs, the fraction is negative. If you see two negative signs, the fraction is positive. Negative two thirds can be written in three ways. • • •

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

Reducing Fractions

In mathematics, we value representing ideas in their simplest form. When it comes to fractions, whenever possible we write them in their simplest equivalent form. All final answers should be simplified. For example,

is a positive number and can be simplified to –

is a negative number and can be simplified to – 5.

Try This ... 1. Reduce the following fractions (simplify). a.

Converting Fractions to Decimals

Every fraction can be written as a decimal number. A fraction represents division. Look closely at the symbol “÷” and you will see a dot in the numerator, a line, and a dot in the denominator. Divide the numerator by the denominator to get the decimal representation. For example:

Try This ... 1. Convert these fractions to decimals. a.

8 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

Mixed Numbers

A mixed number contains a whole number and a fraction ( ). Sometimes it is easier to work with fractions when they are written as a single fraction. A fraction with a numerator greater than or equal to its denominator is called an improper fraction. For example, is an improper fraction. It has a value greater than one. To convert a mixed number to an improper fraction, we do the following: •

Multiply the whole number by the denominator.

•

Add that number to the numerator.

•

Write that sum on top of the original denominator.

Try This ... 1. Convert these mixed numbers to improper fractions. a.

2. Fill in the table. Words one quarter

Fraction

Picture

Equivalent Fraction or

Decimal

Ratio

0.25

1:4

one third

0.375 18:12

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

Writing Decimals as Fractions

Not all decimals can be written as fractions. Terminating and repeating decimals can both be written as fractions. 1.234 is a terminating decimal and can be read as “one and two hundred thirty-four thousandths”. It has 1 unit, 2 tenths, 3 hundredths, and 4 thousandths. Terminating decimals stop. They have a finite (limited) number of digits after the decimal point. To convert terminating decimals to fractions, you can think of place value. 0.5 is a terminating decimal. We can think of it as five tenths, which we can reduce to one half.

0.125 is a terminating decimal. We can think of it as 125 thousandths and reduce.

Try This ... 1. Convert the terminating decimals to fractions. a. 0.77

b. 1.02

c. 21.4

d. 0.9999

Repeating decimals have one or more digits that repeat infinitely. To convert repeating decimals to fractions, you can use patterns or algebra. We will start with patterns. 0.333333… is a repeating decimal. We can also write it as 0.3 or as a fraction . On your calculator, divide the numerators by the denominators in the following fractions. a.

Use this pattern to convert the following fractions to decimals without using a calculator. b.

Discover more patterns. Use your calculator to divide the numerators by the denominators and convert the following fractions to repeating decimals: a.

10 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

Try This ... 1. Convert the fractions to repeating decimals. a.

Now let's try using algebra. To express any repeating decimal as a fraction: 1. 2. 3. 4.

Let x be the number Multiply both sides of the equation by a power of 10 (10, 100, 1000, etc.) to move the repeating part of the decimal to the left of the decimal point. Subtract the original equation when the repeating part starts immediately after the decimal point. If not, multiply by a power of 10 and then subtract. Solve for x.

Sample Problem — Using Algebra to Express a Repeating Decimal as a Fraction Using algebra, express 0.47 as a fraction.

What to Think About

How to Do It

1. Let x be the decimal number. 2. Multiply both sides of the equation by 100. (Move the decimal 2 places to the right.) 3. Subtract step 1 from step 2. 4. Divide both sides by 99.

Learning Tip

Why are the Sample Problem, Try Together and Your Turn grouped together? Before you begin, it helps to understand how the examples in this book work. A Sample Problem introduces a new math skill and shows a complete solution from start to finish. Next, a Try Together question gives you a chance to practise the new skill with some guidance. Parts of the solution are already completed so you can focus on the new idea without having to do every step on your own. Once you feel confident, use what you have learned to complete the Your Turn questions independently.

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

Try Together — Using Algebra to Express a Repeating Decimal as a Fraction Using algebra, express 0.3 as a fraction.

What to Think About

How to Do It

Let x be the number.

Let x = 0.3

Multiply both sides of the equation by 10.

10x = 3. 3

Subtract x.

–x = _____ 9x = _____

Divide both sides by 9.

Simplify.

x = _____

Your Turn — Using Algebra to Express a Repeating Decimal as a Fraction Express each repeating decimal as a fraction. a. 0.123

Extend and Explore

b. 2.12

c. 0.56

A unit fraction is a fraction with a numerator of 1. When written as decimal numbers, which unit fractions are repeating and which are terminating? Why?

Dividing by 7 yields some interesting repeating patterns after the decimal point. Use your calculator to discover them!

12 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

1.2 Practice 1. Match the fraction with its equivalent fraction. a.

____

ii.

____

iii.

____

iv.

2. Fill in the table. Each row should represent the same number in different ways. Words

Fraction

Picture

Equivalent Fractions

Decimal

Ratio

Percent

One Quarter

0.3 40% 3:4 3. Reduce the following fractions. a.

4. Convert the following mixed numbers to improper fractions and vice versa. a.

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

5. Write as an equivalent decimal. a.

6. List 3 rational numbers between each pair of rationals. a.

1.2 Practice Answer Key 1a) iv, b) iii, c) ii, d) i 2)

WORDS

FRACTION

one quarter

1 4

3 PICTURE

EQUIVALENT FRACTIONS

DECIMAL

RATIO

PERCENT

3 2 , 12 8

0.25

1:4

25%

0.2

1:5

20%

0.16

1:6

16.6%

0.125

1:8

12.5%

6) Answers will vary. A sample answer could be:

0.3

1:3

33.3%

4 10

0.4

2:5

40%

6 8

0.75

3:4

75%

5 4 , 20 16

one fifth

1 5

2 3 , 15 10 5 4 , 25 20

one sixth

1 6

2 3 , 18 12

4 24

one eighth

1 8

2 16 3 24

one third

1 3

2 , 39 6 4 12

two fifths

2 5

three quarters

3 4

9 12

Remembering Ebbinghaus – Adding and Subtracting Integers Answer the following: –3 + 3 =

–3 – 3 =

–3 + 2 =

–3 – 2 =

–3 + 1 =

–3 – 1 =

–3 + 0 =

–3 – 0 =

–3 + –1 =

–3 – –1 =

–3 + –2 =

–3 – –2 =

–3 + –3 =

–3 – –3 =

What patterns do you notice when adding and subtracting negative numbers?

14 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

1.3 Comparing and Ordering Fractions Warm Up Competency Focus - Apply strategies to solve problems in context Which is a better deal? Explain your reasoning. 1 dozen for $1.80

16 for $1.95

We can see that

is bigger than

in the pictures below.

Comparing Fractions using Visuals

The symbols >, <, and = are used to compare numbers. The symbol > means greater than, the symbol < means less than, and the symbol = means equal to. Comparing numbers helps you determine which value is larger, smaller, or whether the values are equal. For the image above we can write

. This can seem counterintuitive, because 4 > 3.

Think of fractions as a way to represent division. If we divide the same object into 3 equal pieces or 4 equal pieces, which one will have bigger pieces? Would you rather share a pizza with 3 people or 4 people if you are hungry and want as much pizza as possible? Drawing pictures can help us compare fractions.

Try This ... 1. Compare the fractions using >, < or = a.

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

Comparing Fractions using a Common Denominator

When fractions have different denominators, it can be hard to tell which one is greater. One way to compare them is to rewrite the fractions with the same denominator. Then the fractions are divided into the same-sized parts, making them easier to compare. Which is bigger?

The denominators are different, so we will rewrite the fractions using a common denominator. Both 4 and 3 divide evenly into 12, so we can use 12 as a common denominator. To change into twelfths, multiply both the numerator and denominator by 3. To change into twelfths, multiply both the numerator and denominator by 4.

Now that the fractions have the same denominator, we can compare the numerators. Since 9 > 8, we know that . Therefore, .

Try This ... 1. Which is bigger? a.

Comparing Fractions with the same Numerator or Denominator

If two fractions have the same denominator, the one with the larger numerator is larger. With the same denominator, you're comparing how many pieces of the same size you have. For example, below is a picture of .

•

Five sixths is more than four sixths.

•

Two sixths is more than one sixth.

If two fractions have the same numerator, the one with the smaller denominator is larger. With the same numerator, a smaller denominator means you're dividing into fewer pieces, so each piece is larger. For example, below is a picture of .

16 Chapter 1 Rational Numbers

•

Notice that two halves is more than two thirds.

•

Two thirds is more than two fourths.

©Edvantage Interactive 2026

Comparing Fractions by Converting Fractions to Decimals

Fractions can also be compared by writing them as decimals. To change a fraction to a decimal, divide the numerator by the denominator. Once the fractions are written as decimals, compare the digits from left to right. The first place where the digits are different tells you which number is greater. Which is bigger?

Use a calculator to divide the numerator by the denominator. 0.75 or 0.66666 ... It is easier to compare now. Since 7 > 6, the decimal on the left is bigger. 0.75 > 0.6

Comparing Fractions using a Number Line

When comparing and ordering negative and positive numbers, noticing where they are located on the number line can be helpful, as numbers further to the left on the number line are smaller than ones on the right. Numbers increase in value as we move to the right. For example, consider the number line below. Place the following fractions on the number line and order them from least to greatest. A.

To place the fractions on the number line, write them as mixed numbers with a denominator of 12. A.

After you've placed them on the number line, you can see the order from least to greatest. or

Try This ... 1. Place the numbers on the number line provided. Use the corresponding letters. Use the results to list the numbers from least to greatest. A.

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

Try This ... continued 2. Choose any of the methods discussed in this section to compare the following fractions. Use <, >, or =. a.

3. Arrange from least to greatest. Choose your method. a.

Extend and Explore

Which is bigger?

Why is it important to say x is greater than or equal to zero here?

Remembering Ebbinghaus – Multiplying and Dividing Integers 1. Multiply or divide the integers below. a.

j. 18 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

1.3 Practice 1. Place the numbers on the number line provided. Use the corresponding letters. Then write them in order from least to greatest. B.

−1

− 10 12

8 − 12

6 − 12

4 − 12

2 − 12

2 12

G. –

4 12

6 12

8 12

10 12

2. Place the numbers on the number line provided. Use the corresponding letters. A.

-2.2

-2.1

-2.0

-1.9

-1.8

-1.7

3. Fill in the blanks with one of the following symbols to make a true statement: < , > , = a.

e. i.

f. j.

4. Place the numbers in order from least to greatest. a.

1.3 Practice Answer Key 1)

3a) < b) < c) > d) < e) > f) < g) < h) = i) > j) < k) > l) = 4a)

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

1.4 Operations with Decimals Warm Up Competency Focus - Engage in problem-solving experiences using rational numbers Pick one question and defend your answer. 1. Would you rather have one medium pizza that is $18 for unlimited toppings or $15 plus $1.25 per topping? 2. Which is a better deal: $8.75 for 2 or $12.50 for 3?

Decimal Numbers

Decimal numbers are numbers that contain a decimal point. They are used to represent parts of numbers using place value as shown in the picture below. They are useful when measuring temperature, distance, money, and time.

Decimal Point

Rounding Decimals

How accurate do we need the decimal number to be? It depends on the context. We need to be able to round the decimal to different places depending on what we are doing and what we need the information for. In science, significant figures or significant digits are the digits in the number that are reliable for a given measurement or calculation. When we measure something, we can only be precise to a certain point. Rounding allows us to approximate and to be as accurate as we can. Sometimes an exact decimal is more precise than we need. Rounding lets us replace a number with a nearby value that is easier to read, compare, and use in calculations. The following examples show how to round to different place values.

20 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

1. Round to the nearest unit. No decimal places. Example 1

Example 2

23 456.12 rounds to 23 456

23 456.789 rounds to 23 457

Tenths digit is less than 5

Tenths digit is 5 or greater

2. Round to the nearest tenth. 1 decimal place. Example 1

Example 2

23 456.712 rounds to 23 456.7

23 456.789 rounds to 23 456.8

Hundredths digit is less than 5

Hundredths digit is 5 or greater

3. Round to the nearest hundredth. 2 decimal places. Example 1

Example 2

23 456.712 rounds to 23 456.71

23 456.789 rounds to 23 456.79

Thousandths digit is less than 5

Thousandths digit is 5 or greater

Try This ... 1. Round each number to the indicated accuracy. Unit

Tens

Hundreds

Tenth

Hundredth

427.5968 21 753.893 123 456.789

Adding and Subtracting Decimals

©Edvantage Interactive 2026

When adding and subtracting decimals, it is important to line them up vertically using the decimal points. For example, 55.753 + 3.14

Estimating the answer is around 59 (56 + 3 = 59)

55.753 + 3.14 58.893

Line up the decimal points and add vertically This is close to our estimate of 59

Chapter 1 Rational Numbers

Try This ... 1. Estimate, then calculate. a. 0.005 + 0.5

Multiplying Decimals

b. 11.19 – 0.076

c. 42.8 – 0.49

Multiplying decimals is a lot like multiplying whole numbers. The difference is the placement of the decimal point in the answer. It can help to visualize, estimate, and use the standard algorithm for multiplication. When multiplying decimals, a grid can help you see what the answer means. In the picture below, 3 columns on the left are shaded and 4 rows at the top are shaded. The overlapping region is shaded a different colour. This overlap represents the product of 0.3 and 0.4. Since the overlap covers 12 of the 100 squares in the grid, the product is 0.12.

Try This ... 1a. Show 0.4 × 0.4 on this 10 by 10 blank grid.

22 Chapter 1 Rational Numbers

b. Show 0.5 × 0.3 on this 10 by 10 blank grid.

©Edvantage Interactive 2026

To multiply decimals using the standard algorithm, begin by multiplying as if the numbers were whole numbers. Once the multiplication is complete, count the total number of decimal places in the factors. Place the decimal point in the product so it has the same total number of decimal places. For example, find the product for 0.6 × 0.2. 0.6 × 0.2 If we ignore the decimal points 6 × 2 = 12 There is 1 decimal place in 0.6 and 1 decimal place in 0.2. The product must have 2 decimal places. 12

0.12 and 0.6 × 0.2 = 0.12

Try This ... 1. Multiply the decimals. a. 2.4 × 3.5

b. 0.5 × 30.6

c. 0.03 × 0.02

d. 5 × 0.25

e. 0.1 × 0.1

f. 0.7 × 0.04

Dividing Decimals

Dividing decimals is similar to dividing whole numbers. Rewrite the question so you are dividing whole numbers, then divide as usual. Before calculating, it can help to visualize the problem and estimate the answer to check whether your result is reasonable. 1

0.8 ÷ 0.2 =44 2 3

•

0.8 is the dividend

•

0.2 is the divisor

•

4 is the quotient

The shaded part of the grid represents 0.8, or 8 tenths. Since 0.2 represents 2 tenths, we can divide the shaded region into groups of 2 columns. There are 4 groups, so 0.8 ÷ 0.2 = 4. When dividing decimals, it is often easier to rewrite the question using whole numbers. To do this, multiply both the dividend and divisor by the same power of 10. This does not change the value of the quotient, but it removes the decimal from the divisor. For example, find the quotient for 2.5 ÷ 0.5. 2.5 ÷ 0.5 (2.5 × 10)/(0.5 × 10) Multiplying both the numerator and denominator by 10 gives 25/5 Now divide as usual. 5 Therefore, 2.5 ÷ 0.5 = 5 ©Edvantage Interactive 2026

Chapter 1 Rational Numbers

Try This ... 1. Divide the decimals. a. 10 ÷ 0.25

b. 4.8 ÷ 0.3

c. 6.3 ÷ 0.9

d. 0.036 ÷ 0.006

e. 3.6 ÷ 0.4

f. 0.72 ÷ 0.08

For more complex multiplication and division problems involving decimals, use a calculator. Estimating your answer when using a calculator can help you determine the reasonableness of the answer.

Extend and Explore

Rational numbers can be expressed as decimals, fractions, ratios and percents. How is each of these representations unique? In which real-life situations do we use each of these?

Remembering Ebbinghaus – Finding Factors The factors of 6 are 1, 2, 3 and 6 because 1 × 6 = 6 and 2 × 3 = 6. 1. What are the factors of the following integers? Write them in order from smallest to largest. a. 10 b. 12 c. 18 d. 25 e. 64 f. 100

24 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

1.4 Practice 1. Round each of the decimals to the given place. Unit

Tenths

Hundredths

a. 0.6521 b. 5.93842 c. –16.271 2. Estimate and calculate the following.

a. 2.9 + 3.15

Estimation

Calculation

3+3=6

6.05

b. –10.1 + 9.9 c. 4.7(1.9) d. –7.2 – (– 3.1) e. –9.8(–3.14) f. 15.1 divided by 2.9 g. –24.5 divided by –4.9 3. Given the following decimal numbers: –1.1, 2.9, 3.2, –5.8, 10.3, 4.5, –0.01, –6.4 a. Which two have a sum of –1.11? b. Which two have a difference of 16.1? c. Which have a product of –0.045? d. Which have a quotient of –2? 4. If a = 2.4, b = –1.2 and c = 0.6, what is a + b + c and a – b – c?

5. Calculate the following. a. 0.6 × 0.4

b. 25 ÷ 0.25

c. 1.25 × 0.8

d. 14 ÷ 0.7

e. 0.4 × 1.6

f. 7.5 ÷ 1.5

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

6. Which is a better deal? $21.50 for 3 or $15 for 2. Defend your answer.

7. The table below lists the lowest and highest temperatures in six Canadian cities in 2024. Use this information to answer the questions. City

Low Temperature (°C)

High Temperature (°C)

Calgary

–45.0

36.1

Saskatoon

–39.5

41.1

Vancouver

–17.8

34.4

Victoria

–15.6

35.3

Whitehorse

–52.2

35.6

Winnipeg

–47.8

42.2

a. Write the lowest temperatures in descending order.

b. Write the highest temperatures in ascending order.

c. Which city has the greatest difference between its high and low temperatures? What is the difference?

1.4 Practice Answer Key 1a) 1, 0.7, 0.65 b) 6, 5.9, 5.94 c) –16, –16.3, –16.27 2b) 0; –0.2 c) 10; 8.93 d) –4; –4.1 e) 30; 30.772 f) 5; 5.207 g) 5; 5 3a) –1.1 and –0.01 b) 10.3 and –5.8 c) 4.5 and –0.01 d) –6.4 and 3.2 4) 1.8; 3.0 5a) 0.24 b) 100 c) 1 d) 20 e) 0.64 f) 0.5 6) 7

26 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

1.1 – 1.4 Check Your Understanding 1. Write the definition of a rational number.

2. Rational or Irrational? Circle the rational numbers and star the irrational numbers. a. –23

c. –3.14

d. 5.436436436 ...

e. π

f. –

g. 0

h. 25%

i. –0.1

3. Choose a rational number from the list that is between the pairs of numbers.

0.019, 1.99, –0.1, –3.4558, 0.0015, –0.014

Sample: 0 and 0.002 0.0015

a. 1.5 and 2 ____________

c. –3.456 and –3.455 ____________

and

and –0.09 ____________

e. 0.01 and 0.02 ____________

____________

4. Fill in the table. Words

Fraction

Picture

Equivalent

Decimal

Ratio

Percent

Fraction One third

0.375 75% 5. Insert the correct symbol: <, > or =. a.

_____

d. –0.2 _____ –0.2

_____

6. Label the points on the number line with the corresponding letter or letters.

A. 1.8

B. –2.1

©Edvantage Interactive 2026

C. –0.2

E. –1.5

Chapter 1 Rational Numbers

7. Write the numbers from least to greatest:

8. Convert to fractions in lowest terms. a. 0.125

b. –0.1

c. 12%

d. 0.1

e. –2.5

9. Write the following as simplified fractions. a. 0.12

b. 0.123

10. Round each of the decimals to the given place. Unit

Tenths

Hundredths

0.1234 5.9191 –21.546 11. Calculate the following a. 0.8 × 0.3

b. 7.75 ÷ 0.25

c. 2.5 × 0.8

d. 4.9 ÷ 0.7

e. 0.3 × 1.8

f. 12 ÷ 1.5

Check Your Understanding Answer Key 1) 2) 3) 4)

WORDS

FRACTION

one fifth one eighth one half three eighths three fourths

5) a) > b) > c) > d) <

-3

G E D

-2

-1

EQUIVALENT FRACTIONS

1 3 1 5 1 8 1 2 3 8 3 4

one third

PICTURE

2 3 4 , , 6 9 12 3 4 2 , , 10 15 20 3 4 2 , , 16 24 32 2 3 35 , , 4 6 70 9 12 6 , , 16 24 32 6 9 12 , , 8 12 16

DECIMAL

RATIO

PERCENT

0.3

1:3

1 33 % 3

0.2

1:5

20%

0.125

1:8

12.5%

0.5

1:2

50%

0.375

3:8

37.5%

0.75

3:4

75%

7) 8) 9) 10) 11)

F A

C 0

28 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

1.5 Adding and Subtracting Fractions Warm Up Competency Focus - Connect math concepts to each other and to other areas In the time it takes for you to blink your eye once (

second), light could travel approximately 30 000 kilometres. This is

nearly three-quarters of the way around the Earth. How many kilometres could light travel in two blinks? How many times around the Earth could light travel in that time? How many seconds would that be?

Adding and subtracting fractions involves combining parts of numbers. The denominators of the fractions will determine which process you use. Visualizing the fractions using circles or fraction strips can help with this process. We can also connect these concepts to other subject areas, like rhythmic notation in music.

Visualizing Adding Fractions

©Edvantage Interactive 2026

Fraction strips help us see fractions as parts of the same whole. Because each strip has the same length, we can compare fractions and combine them more easily. By placing strips together, we can see the total amount and build an understanding of how fraction addition works. Using fraction strips and circles can help us make sense of adding and subtracting fractions.

Chapter 1 Rational Numbers

The two pictures below both show that one half plus one half is one.

The image below shows that

. Note that bars are the same length.

Try This ... 1. What fraction addition question could these pictures represent? a.

2. Draw a circle to show that

3. Draw fraction strips to show that

4. In music notation, one whole note represents the same amount of time as two half notes. One whole note also represents the same amount of time as four quarter notes. a. How many quarter notes would have the same amount of time as four eighth notes? (Use the picture to help you answer.)

b. How many half notes would have the same amount of time as eight sixteenth notes?

30 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

Fractions with the Same Denominator

When fractions have the same denominator, they are already divided into equal-sized parts. Because the parts are the same size, we can combine them by adding or subtracting the numerators. The denominator stays the same because the size of the parts has not changed. Think about slices of a pizza. If the pizza is cut into 8 equal slices, each slice is of the whole pizza. If you have 3 slices and get 4 more slices, you now have 7 slices. The pizza is still divided into eighths, so the answer is . Here are three more examples.

After adding or subtracting, check whether the fraction can be simplified. If the numerator is equal to the denominator, the fraction represents one whole.

Try This ... 1. Simplify the following expressions. a.

Fractions with a Different Denominator

When fractions have different denominators, the parts are not the same size. Before we can add or subtract them, we need to rewrite the fractions so they are divided into equal-sized parts. Think about adding and . One fraction is divided into halves and the other is divided into thirds. Since the pieces are different sizes, we cannot combine them directly. Instead, we rewrite both fractions using a common denominator. This creates equivalent fractions with the same-sized parts. Once the denominators match, we can add or subtract the numerators just as we did in the previous section. Visual models can help us see why this works. The models below show how fractions can be rewritten using a common denominator before they are combined.

Steps for Adding and Subtracting Fractions with Different Denominators 1. 2. 3. 4.

©Edvantage Interactive 2026

Find a common denominator (the lowest common multiple, or LCM, of the denominators). Rewrite each fraction as an equivalent fraction with the common denominator. Add or subtract the numerators. Reduce (simplify) if possible.

Chapter 1 Rational Numbers

Sample Problem — Fractions with Different Denominators Simplify

What to Think About

How to Do It

1. Find the common denominator of 5 and 2 which is 10. 2. Rewrite the fractions as equivalent fractions over 10. 3. Add the numerators. You can leave your answer as an improper fraction.

Try Together — Fractions with Different Denominators Fill in the blanks for the following questions. Refer to the steps in the What to Think About in the Sample Problem if needed. a.

Your Turn — Fractions with Different Denominators 1. Simplify the following. Remember to do your work vertically. a.

2. Find the perimeter of this regular pentagon (5 equal sides) by adding the side lengths together.

32 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

1.5 Practice 1. What fraction addition questions do the following pictures represent? a.

2. Solve these expressions by adding or subtracting. a.

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

aa.

3. Add or subtract the fractions. Write your answer in simplest form. b.

4. Evaluate each expression where a. a + b

b. b – a

. c. c + d

d. c – d

e. –c – d

5. Find the perimeter of this regular hexagon (six equal sides) by adding the side lengths together.

1 2

34 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

Remembering Ebbinghaus – Integers

1. Place each set of integers in order from least to greatest. a. –10, 1, –8, 4, –11, –1, 11, –7

b. –3, –4, 0, 34, 4, –34, –43, 3

2. Name three integers between each pair of numbers. a. –12 and –8

b. –100 and –96

Extend and Explore

1.5 Answer Key 1) 2)

3) 4) 5)

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

1.6 Multiplying and Dividing Fractions Warm Up Competency Focus - Reflect on mathematical thinking Here are three possible ways to multiply 12 × 15 using mental mathematics. Method 1

Think of 12 × 10 plus 12 × 5 to give 180

Method 2

Multiply 12 × 3, divide by 2, then multiply by 10

Method 3

Multiply 15 × 2 and then multiply by 6

•

Which do you prefer?

•

Which does most of your class prefer?

•

Can you think of a different way?

Multiplication

We can think of multiplying 2 times –4 in different ways to help us understand 2(−4) = −8. There is often more than one way to represent a mathematical idea. Using models, diagrams, and real-world situations can help us make sense of multiplication with integers. The examples below all show the same calculation from different perspectives.

Repeated addition –4 + (– 4) = –8 Borrowing 4 dollars from 2 friends

2 groups of –4 2 jumps left on the number line

Swimming down 4 metres, then swimming down 4 more metres

Subtracting 4 twice 2 groups of 4 integer chips in an array

2 temperature drops of 4 degrees each

We can visualize multiplying fractions to deepen our understanding. Multiplication with fractions can be interpreted in different ways. Sometimes it represents groups of a fraction, such as two groups of one quarter. Other times it represents taking a fraction of a fraction, such as one half of one quarter. Visual models can help us see what these calculations mean and why they work. Example 1 The two pictures each show one quarter of a pizza left. How much pizza is left altogether? One half.

Two quarters of a pizza equal one half of a pizza. Mathematically, it can be written as a multiplication: 2 ·

Note: the word “of” in a word problem represents a multiplication 36 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

Example 2 What if you wanted to eat half of the pizza shown here?

One half of

Mathematically, this is a multiplication:

Example 3 Here are two different visual representations of ×5=

and can be written as

× 5.

5 bars each representing

5 jumps on the number line each representing

Try This ... 1. What fraction multiplication does this picture represent? One half of __________________ =

× __________________

= __________________

2. Draw a picture or tell a story to prove each statement. You can use words, shapes, pizzas, number lines or another model of your choice. a.

·4=2

©Edvantage Interactive 2026

b. 3 ·

Chapter 1 Rational Numbers

Multiplying fractions can help you find parts of quantities and parts of other fractions. For example, what is one half of one quarter? Once you understand what the fractions represent, the calculation is straightforward. The steps below will help you multiply fractions and write your answers in simplest form. We can follow the four steps listed below to multiply fractions together.

Multiplying Fractions

1. 2. 3. 4.

Reduce (You can also reduce in step 3. Reducing first makes the numbers smaller.) Multiply the numerators together Multiply the denominators together State your answer as a simplified improper fraction (simplify, even if not asked to do so)

Helpful Tips Multiply the numerators and denominators separately. Reduce before multiplying when possible. An integer can be written as a fraction with a denominator of 1. Convert mixed numbers to improper fractions first, before reducing. One negative sign makes the fraction negative. Two negative signs make the fraction positive.

Sample Problem — Multiplying Fractions Multiply

What to Think About

1. Look to see what fractions can be reduced: and

How to Do It 1

2. Multiply.

1×2 2

38 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

Try Together — Multiplying Fractions Multiply

What to Think About

How to Do It

1. Convert mixed numbers to improper fractions.

( ____ ) ( ____ )

2. Reduce. 3. Multiply.

Your Turn — Multiplying Fractions 1. Multiply. Simplify each answer if possible. a.

Multiplying and Negative Signs

When multiplying more than 2 fractions together, it helps to figure out whether the answer will be positive or negative before you start. (–2)(–2)

2 negative signs – answer is positive

(–2)(–2)(–2)

3 negative signs – answer is negative

(–2)(–2)(–2)(–2)

4 negative signs – answer is positive

(–2)(–2)(–2)(–2)(–2)

5 negative signs – answer is negative

In general: Count the number of negative signs. If you count an even number of negative signs, then the answer will be POSITIVE. If you count an odd number of negative signs, the answer will be NEGATIVE. This also works for fractions and decimals.

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

Try This ... 1. Positive or negative? Write + or – if the product is positive or negative. a.

Dividing Fractions

Before learning the rules for dividing fractions, it is helpful to think about what division means. Division can represent sharing something into equal groups or splitting it into equal parts. The examples below show different ways to think about dividing 2 by 4. •

Dividing up two hours evenly to finish 4 short homework assignments

•

Divide 2 into 4 equal-sized parts on a number line

•

Taking

•

Half of half of 2 (dividing by 4 is like taking half of half)

of 2 (a multiplication)

We can visualize dividing fractions to deepen our understanding. In elementary school you learned two ways to divide 6 by 3: the measurement model and the partitive model. Measurement model

Partitive model

We have 6 cookies and 3 plates.

We have 6 cookies and want to put 3 cookies

How many cookies will go on each plate?

on each plate. How many plates are needed?

Each plate gets 2 cookies

There are 2 plates

Now, let's apply these models to dividing fractions. Measurement model

Partitive model

How many thirds are in 2?

If 2 is a third of something, what is all of it?

We have 2 pizzas cut in thirds.

If 2 is one third of something, how much is all

How many thirds do we have?

of it?

We have 6 thirds

2+2+2=6

40 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

Try This ... 1. Model

using the measurement and partitive models.

a. Measurement Model

b. Partitive Model

How many ________________ are in 3 pizzas?

We can also ask: if _________is one half of something, what is all of it?

We can see there are

____

_________

in 3 pizzas.

3+ ______= ______ =

This is the answer we would get from multiplying 3 times 2.

has the same value as 3 · 2.

Dividing by one half is the same as multiplying by 2.

A reciprocal is the inverse of a number. It is the value you get when you divide 1 by the number. This concept will be critical when studying trigonometry and other functions in grades 11 and 12. The reciprocal of . Notice

Reciprocals

If you multiply reciprocals, their product is one. This will always be true with reciprocals.

Hint: For working with decimals: convert decimals to fractions first, then find the reciprocal. Special case: The reciprocal of 0 is undefined. We cannot divide by zero, so we cannot take its reciprocal. This is another important concept for higher levels of mathematics.

Try This ... 1. Find the reciprocals. a.

c. 2

d. –1

f. 0.25

In general: let a, b, c, d be rational numbers and b ≠ 0, c ≠ 0, d ≠ 0.

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

Sample Problem — Reciprocals Calculate 6 divided by one third.

What to Think About

How to Do It

1. Rewrite the question as a multiplication by the

6÷

reciprocal. 2. The reciprocal of

=6·3

is 3.

= 18

3. Simplify.

Try Together — Reciprocals Fill in the blanks.

What to Think About

How to Do It

1. Use the steps above to

help you fill in the blanks for the questions.

Your Turn — Reciprocals 1. Rewrite the following divisions as a multiplication. DO NOT simplify. a.

42 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

Is my answer reasonable? Estimation can help with verifying answers. Estimate (without calculating) the answer to show that the answer provided is NOT correct. This is something you can do to check your work on tests/quizzes. Taking a moment to see if your answer is reasonable is a helpful test-taking skill. For example, a student writes the following on a quiz.

Estimate

How do we know the answer is not correct? The first number is very close to 1 (a little less). The second number is also very close to 1 (a little less). The quotient should be close to dividing one by one, but a little less. 9 is too big.

Try This ... 1. Use estimation to show that these answers are incorrect: a.

Extend and Explore

Multiply 4 different fractions together to get an answer (product) of 1.

Remembering Ebbinghaus – Converting decimals, fractions, ratios, and percents 1. Express as a fraction. a. 0.2

b. 0.3

c. –0.25

d. 0.2

e. 0.123

f. –0.125

g. 0.99

2. Complete the chart with the missing equivalent forms for each number. A percent is a fraction over 100. Ratio

Fraction

Decimal

Percent

3:4

0.33 7%

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

1.6 Practice 1. Fill in the blanks. a. Write two numbers that are their own reciprocal _____ and ____. b. The reciprocal of a very big number is a __________ number. (small or big) c. The reciprocal of a very small number is a _________ number. (small or big) d. The reciprocal of zero is ___________. e. Multiplying any positive number by 2 makes the number. (smaller or larger) f. Multiplying any positive number by one half makes the number. (smaller or larger) g. Dividing a positive number by 2 makes the number. (smaller or larger) h. Dividing a positive number by one half makes the number. (smaller or larger) i. Any whole number can be written as a fraction. 8 = j. The product of a proper fraction and a proper fraction is a(n) ____________ fraction. (choose one - proper or improper) k. 13 times 45 is the same as 15 times ________. l. The product of

is positive or negative. (choose one)

m. The product of

is positive or negative. (choose one)

n. The product of

is positive or negative. (choose one)

o. The product of

is positive or negative. (choose one)

p. The product of

is positive or negative. (choose one)

2. State the reciprocal of each number. a.

c. f. i. l.

3. Draw pictures or tell a story to show why the following is true. b.

44 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

4. How do we know the answer is approximately one without calculating?

5. Multiply (always reduce and do work vertically). a.

6. Divide (hint: write as a multiplication first!). a.

7. Simplify. a.

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

8. Simplify

j. i.

46 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

How’s it Going? 1. Add or subtract the fractions b)

2. Multiply or divide the fractions a)

1.6 Answer Key 1)

2) 3)

4) They are both almost the same value, they are both a little less than 1. 5)

How’s it Going? Answer Key 1a)

b) Correct c)

©Edvantage Interactive 2026

d) Correct

2a) Correct b) Correct c)

Chapter 1 Rational Numbers

1.7 Order of Operations Warm Up Competency Focus - Connect math concepts to other content areas Choose one of the following: •

What is the total cost, including tax, of two T-shirts that cost $21.50 each if there is 5% GST and 7% PST?

•

In a basketball game, how many points is twenty-one 2-point baskets plus twelve 3-point baskets?

When an expression involves several operations, we follow the same order of operations around the world to produce consistent, correct calculations. It is sometimes called BEDMAS or PEDMAS or Please Excuse My Dear Aunt Sara. 1. Brackets or Parentheses

If you see brackets, start there. Simplify what is inside.

2. Exponents

The next thing to look for is exponents – evaluate them.

3. Division/Multiplication

Look for multiplication and division (in any order).

4. Addition/Subtraction

Finally add and subtract in any order.

Consider the expression 2 + 3 · 4. When an expression contains more than one operation, follow the order of operations. In this example, there is both addition and multiplication. Multiplication comes before addition, so calculate 3 × 4 first to get 12. Then add 2 to get the final answer of 14.

Try This ... 1. Simplify the following using the correct order of operations. a.

48 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

Order of Operations with Decimals and Fractions

Decimals and fractions follow the same order of operations as whole numbers. Work through the expression one step at a time using the correct order. Complete operations inside brackets first, then multiplication and division, and finally addition and subtraction. Following the order of operations helps you avoid mistakes and find the correct answer.

Sample Problem — Order of Operations and Fractions Simplify

What to Think About

How to Do It

1. There is addition and multiplication. According to the order of operations, multiply first. 2. Now the expression contains only addition. To add fractions, use a common denominator. 3. The least common denominator of 3 and 8 is 24. Rewrite both fractions using a denominator of 24. 4. Add the numerators and keep the denominator the same.

Try Together — Order of Operations and Fractions Simplify

What to Think About

How to Do It

1. There is division, multiplication, and addition. Complete the division and multiplication first. 2. Divide by multiplying by the reciprocal. Then multiply the fractions. 3. Simplify the products if possible. 4. Find a common denominator. The least common denominator of 4 and 6 is 12. 5. Add the numerators and keep the denominator the same.

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

Your Turn — Order of Operations and Fractions 1. Simplify b.

Extend and Explore

Simplify expressions with fractions.

b. a.

Remembering Ebbinghaus – Rational Numbers 1. Check each column if the number on the left belongs to the set of numbers listed above. Natural numbers: {1, 2, 3...}. Whole numbers: {0, 1, 2, 3…}. Integers: positive and negative whole numbers. Rational numbers: numbers that can be written as a fraction. Number

Natural

Whole Numbers

Integer

Rational

7 –1 0.3 0 –9.9 101 0.5555... π

50 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

1.7 Practice 1. What do the letters of BEDMAS stand for?

2. Simplify. a.

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

1.7 Answer Key 1. Brackets, Exponents, Division, Multiplication, Addition and Subtraction 2. a)

52 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

1.8 Applications When solving a word problem, read the question several times. Focus on what information is known, and what information is wanted. Show your work, explain your thinking, and remember there is often more than one way to solve a problem.

Sample Problem — Fractions and Decimals A baseball player’s batting average is found by dividing the number of hits by the number of times at bat, and rounding to 3 decimal places if needed. a.

What would the batting average be for a player with 206 hits with 816 at bats?

If they have 124 more chances at bat, how many hits would they need to get a 0.300 batting average?

What to Think About

How to Do It

Before we start, we need to know how to calculate the batting average.

a. We want to know the batting average for a player having 206 hits in 816 at bats. 1.

Use a calculator to divide the number of hits by the number of at bats.

Round to 3 decimal places.

= 0.2524509...

The batting average would be 0.252.

= 0.252

b. We want to know how many hits they would need to get a batting average of 0.300 if they can have 124 more at-bats.

The total number of at bats if the player has 816 + 124 at bats is 940. They want a 0.3 batting average. This means 3 hits out of every 10 bats. 1.

Use equivalent fractions.

Rewrite the fraction with a denominator of 940.

The player would need a total of 282 hits.

The player already made 206 hits. They need to make 282. Therefore, they need 76 more hits.

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

Try Together — Applying Rational Numbers a.

If Johoon types at a rate of 60 words per minute, how many minutes will it take for him to type a 1560-word essay?

If he only had 20 minutes, how fast would he need to type?

What to Think About

How to Do It

Part a 1. We know the rate Johoon can type. 2. He needs to type 1560 words. 1560 divided by 60 is ____________. You can also think of it in terms of equivalent fractions. 3. It will take ____________.

Part b 1. If he only had 20 minutes, he will need to type faster, but how fast exactly will he need to type the 1560 words? 2. 3.

Your Turn — Applying Rational Numbers 1. At the movies, Dona ate half the popcorn and Caroline ate a third. Who ate more? How much more?

How much is left?

54 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

Your Turn — continued 2. The value of a house increased by one fifth in one year. a. If the value of the house was one million dollars at the beginning of the year what is the value at the end of the year?

b. If the value was one million dollars at the end of the year what was the value at the beginning of the year?

3. One day the temperature fell from 3.5 °C to –3.3 °C in 3 hours. What was the average temperature change per hour?

Extend and Explore

1. Show that Use this to represent the fraction

. in two different ways.

2. What does x need to be so that the expression is bigger than 1?

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

1.8 Practice 1. If the profit is one third of the sale price before taxes, what is the profit from selling three T-shirts with a sale price of $35.50 each?

2. One day the temperature fell from 4.3 °C to –2.8 °C in 3 hours. What was the average temperature change per hour?

3. An investment loses half of its value. The next day it loses a third of its value. a. What fraction of its original value is the final value?

b. If the initial investment was $1000, how much is left?

4. Alex has 2 hours of homework. She needs

of this time for a science lab. The rest will be evenly split between socials and

math. How much time will Alex spend on math?

5. Research shows that teenagers should get at least 8 hours of sleep a night. What fraction of the day is that? If a person slept one quarter of the day, how many hours is that?

6. If Miguel can paint a wall in half an hour and Ryland can paint a wall in a third of an hour, how long would it take to paint 4 walls together?

56 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

7. Liam has

of one pizza leftover from a party. He gave Jamie

of the leftover pizza for lunch. How much of one pizza did

Jamie get?

8. The table shows 15 days of temperature data for Vancouver. a. Which 3 days were the warmest?

b. How much warmer was April 26 than April 23?

c. What is the difference between the greatest and lowest temperatures listed?

9. Stocks can gain or lose money over time. The following stocks are listed along with the price changes over a one-week period.

Stock A +$2.75 Stock B –$3.75 Stock C +$0.25 Stock D –$2.50 Stock E –$0.49

a. List the stocks in order from the greatest gain to the greatest loss.

b. What is the difference between the value of the greatest gain and the value of the greatest loss listed?

1.8 Practice Answer Key 1)

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

1 Chapter Review 1. Fill in the blanks. a. Subtraction can be modelled by adding the ____________________ of a number. b. Dividing by a number is the same as multiplying by its ____________________. c. A rational number can be written as a quotient of two _______________ as long as the denominator is not ____________. d. Dividing by ____________________ is undefined. e. The bottom of a fraction is called the ____________________. f. Decimal numbers that are rational are either ____________________ or ____________________. 2. Round each number to the indicated accuracy. Unit

Tenths

Hundredths

a. 0.3987 b. 3.14159265 c. –191.191 3. Arrange these numbers from least to greatest without a calculator.

4. Compare each pair of numbers. Fill in the blank with <, > or = . a.

5. Express each decimal as a fraction and each fraction as a decimal. a.

6. Simplify. a.

58 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

aa.

ab.

Chapter 1 Rational Numbers

7. If a = –2, b = 2.4, c = –1.2 and d =

. Calculate.

a. abcd

b. a + b + c + d

c. ab + cd

d. (d – d)/a

e. a(b – c)

f. b/d – a

g. c/b + a/d

h. d(–b + c)

8. Here is the Classic Chocolate Chip Cookies recipe.

List the ingredients you would need to halve this recipe.

60 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

9. One night the temperature fell from 2.9 °C to –3.1 °C in 6 hours. What is the average temperature change per hour?

10. A scientist is mixing solutions for an experiment. She combines:

a. What is the total volume of the mixture?

b. If she needed to divide the mixture evenly into 5 containers, how much would go in each container?

1 Chapter Review Answer Key 1a) opposite b) reciprocal c) integers, zero d) zero e) denominator f) terminating or repeating 2a) 0, 0.4, 0.40 b) 3, 3.1, 3.14 c) –191, –191.2, –191.19 3) 4a) > b) < c) < d) > e) = f) < g) > 5a) 6a)

7a)

10a)

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

How Did It Go? Part 1: Reflecting on Chapter 1 - Check all that apply to you ☐ The content of this chapter is challenging. ☐ I am starting to understand rational numbers. ☐ I can solve problems with fractions. ☐ I find word problems challenging. ☐ I need more time to practice before the test. ☐ I understand and can use decimals. ☐ I feel more confident with fractions than last year. ☐ I can add, subtract, multiply and divide fractions. ☐ I understand how to use BEDMAS. ☐ I have a few questions before the test. ☐ I am confident about the content of this chapter. ☐ I can help others reduce and convert fractions. ☐ I can use many different strategies to model rational numbers. ☐ I feel confident applying skills to word problems. ☐ I am ready to write the test. ☐ My next step is ______________________________________________________.

Part 2: Reflecting on Dividing Fractions Which model do you prefer and why? Measurement model

How many quarters are in a pizza?

Partitive model

If 4 is a quarter of something, what is all of it?

Vocabulary List for Rational Numbers Ascending – Numbers arranged from smallest to largest. BEDMAS – A rule that tells the order in which mathematical operations are performed: Brackets, Exponents, Division and Multiplication, Addition and Subtraction. Calculate – To find an answer by using mathematical operations. Common Denominator – A denominator that is shared by two or more fractions. Decimal – A number written using a decimal point to show place value.

62 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

Denominator – The bottom number in a fraction. It shows how many equal parts make up one whole. Difference – The answer when one number is subtracted from another. Equivalent Fractions – Fractions that represent the same value even though they look different. Estimate – To find an answer that is close to the exact value. Evaluate – To find the value of an expression by performing the required operations. Fraction – A number that represents part of a whole or part of a set. Improper Fraction – A fraction with a numerator that is greater than or equal to its denominator. Integer – A whole number or its opposite. Integers do not include fractions or decimals. Inverse – A number or operation that reverses the effect of another number or operation. Irrational Number – A number that cannot be written as a fraction of two integers. Its decimal form never ends and never repeats. Least Common Multiple (LCM) – The smallest multiple that two or more numbers have in common. Least/Greatest – Least means the smallest value in a set. Greatest means the largest value in a set. Mixed Number – A number made up of a whole number and a fraction. Number Line – A line used to represent numbers in order. Numerator – The top number in a fraction. It shows how many parts are being considered. Opposite – A number that is the same distance from zero as another number but on the opposite side of the number line. Positive/Negative – Positive numbers are greater than zero. Negative numbers are less than zero. Product – The answer when two or more numbers are multiplied. Proper Fraction – A fraction with a numerator that is less than its denominator. Quotient – The answer when one number is divided by another. Rational Number – A number that can be written as a fraction of two integers where the denominator is not zero. Reciprocal – A number that gives a product of 1 when multiplied by the original number. Reduce – To write a fraction in an equivalent form with the smallest possible numerator and denominator. Repeating Decimal – A decimal in which one digit or a group of digits repeats forever. Significant Digits – The digits in a number that contribute to its value and level of precision. Simplify – To rewrite an expression or number in its simplest form without changing its value. Sum – The answer when two or more numbers are added. Terminating Decimal – A decimal that ends after a finite number of digits. Value – The amount or quantity represented by a number or expression. Whole Number – Any of the numbers 0, 1, 2, 3, and so on. Whole numbers do not include negative numbers, fractions, or decimals.

©Edvantage Interactive 2026

Chapter 1 Rational Numbers

Failsafe Vocabulary Check A Venn diagram helps you organize information by showing what is the same and what is different. For Part A, write items that belong only to the first group in the left circle. Write items that belong only to the second group in the right circle. If an item belongs to both groups, write it in the overlapping section. For Part B, the Venn diagrams show groups that fit inside one another. In these diagrams, everything in the smallest circle is also part of the middle circle, and everything in the middle circle is also part of the largest circle. Start by thinking about the relationship between the groups. Then decide where each item belongs. If an item belongs only to the largest group, place it in the outer region. If it belongs to the largest and middle groups, place it in the middle circle. If it belongs to all three groups, place it in the smallest circle. If you are not sure, ask yourself: Is this item part of one group, two groups, or all three groups? Part A: Place the whole numbers from 1 to 12 in the Venn diagram.

Prime Numbers

Factors of 12

Part B: Place the factors of 24, 12 and 6 in the Venn diagram.

64 Chapter 1 Rational Numbers

©Edvantage Interactive 2026

2 Powers and Roots In this chapter, we explore the fundamental concepts of powers and roots, which are essential mathematical tools. Powers allow us to work with very large or very small numbers. Roots, meanwhile, are the inverse operations to powers. Why do we study powers and roots? They help us to break down powers and solve problems involving exponential growth and decay and scientific notation. Together, powers and roots help us to understand, simplify and solve problems in fields such as computer science, engineering, finance, biology, and architecture. They can help us understand and predict the spread of a flu virus, or estimate the age of a dinosaur bone.

Big Idea of the Chapter Computational fluency and flexibility with numbers. In this chapter you will explore: What is a power? exponent? base?

power = baseexponent

Exponent laws

xn · xm = xn+m ; (xn)m = xnm ; x0 = 1 ; x1 = x ; xn/xm = xn−m, x ≠ 0

What is a root?

The nth root of a number a is a number b such that bn = a or example, 33 = 27 so the = 3.

Approximating square roots

We can estimate

Scientific notation

Helps to write very large and very small numbers. For example, 1 200 000 can be written 1.2 × 106.

Applications

Find the length of a side of a square given its area or the length of a side of a cube given its volume.

as 6.5 between

and

= a. For

which are 6 and 7.

Get Started We start with one bacterium that doubles every hour. •

That means 2 bacteria in an hour

•

4 bacteria in two hours

•

8 bacteria in three hours

In 6 hours, how many bacteria will there be?

How many hours will it take until there are at least 1000 bacteria?

©Edvantage Interactive 2026

Chapter 2 Powers and Roots

2.1 What is a Power? Warm Up Competency Focus - Engage in problem-solving experiences that are connected to place and story In the 1990s, chain letters were a widespread phenomenon across Canada. These were typically letters printed on paper that asked recipients to send copies of the letter to a specific number of people (often 5, 10, or 20 people) and included a small amount of money (sometimes $1 – $5) with each copy, with their name added to a list. They promised good luck or fortune if you completed the chain and warned of bad luck if you broke the chain. Imagine you start a chain letter and send it to 5 people. Each of them sends a letter to 5 people, and so on. Complete the chart below with a calculator to determine how many letters would be written if everyone who received a letter sent 5 letters. Generation

Total Letters Sent

What challenges limit the success of chain letters? How does this connect with viral social media content?

What is a Power?

We know we can write 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 as 9 × 3. Multiplication is a shorter way to write a repeated addition. A power is a shorter way to write repeated multiplication. Instead of writing 5 × 5 × 5 × 5 × 5 × 5, we can write: 56 • •

5 is the base. It tells us what we are multiplying 6 is the exponent. It is written as a small number above and to the right of the base. It tells us how many times to multiply the base

Together, they are a power. Powers are found in many formulas. This keeps the formulas as simple as possible to write. For example, to find the volume of a cube, we multiply the length by the width by the height. Since the sides of a cube are all the same, this can be written as s × s × s or s3. Consider 23 = 2 · 2 · 2 = 8. We say the value of this power is 8. When we evaluate a power we get a number. This number could be positive, negative, an integer, a fraction, or even a decimal.

Sample Problem — Repeated Multiplication and Powers Write this repeated multiplication as a power: (–9)(–9)(–9)(–9)(–9)(–9)(–9)

What to Think About

How to Do It

1. What is the base?

–9

2. We are multiplying the base by itself seven times, so the exponent is 7. We use brackets to show that the base is negative.

(–9)7

66 Chapter 2 Powers and Roots

©Edvantage Interactive 2026

Try Together — Repeated Multiplication and Powers Fill in the table. A power has a base and an exponent. Use brackets for negative or fraction bases.

Repeated Multiplication

Base

Exponent

Power

(–3)(–3)(–3)(–3) (0.8)(0.8)(0.8)(0.8)

( )5

Your Turn — Repeated Multiplication and Powers Fill in the table. A power has a base and an exponent. Use brackets for negative or fraction bases. Repeated Multiplication

Base

Exponent

Power

7·7·7·7·7·7·7·7·7·7 (1.2) (1.2) (1.2) (1.2) (–

)(–

)

(–100)(–100)(–100)(–100)(–100)(–100)(–100)(–100)

Exploring the Powers of 2

©Edvantage Interactive 2026

Let’s explore the powers of 2 and their values. In the example below we multiply 2 by itself up to the 10th power of 2. What do you notice about the values? 21 =

22 =

2×2=

23 =

2×2×2=

24 =

2×2×2×2=

25 =

2×2×2×2×2=

26 =

2×2×2×2×2×2=

27 =

2×2×2×2×2×2×2=

128

28 =

2×2×2×2×2×2×2×2=

256

29 =

2×2×2×2×2×2×2×2×2=

512

210 =

2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1024

Chapter 2 Powers and Roots

Have you ever noticed your phone storage size? They always use powers of 2: 32 GB, 64 GB, 128 GB, and 256 GB. Why these numbers? Computers store information in bytes, which are small units of digital memory. Because digital data is binary, using only 0 and 1, these units are always organized in powers of 2. One gigabyte (GB) is close to 230 bytes. Each upgrade doubles the storage, because the amount is multiplying by two again (236 bytes = 64 GB, 237 bytes = 128 GB, 238 bytes = 256 GB).

Powers with Variable Bases

Powers with variable bases follow the same rule as powers with numerical bases. The base will be a variable, such as x, y, or t, that represents unknown numbers. Variables help us to generalize, compare, see patterns, and make predictions. We can multiply variables by numbers called coefficients. For example, we write two times x as 2x. The 2 is the coefficient. Power

Base

Exponent

Coefficient

Repeated Multiplication

x·x·x

(–y)2

–y

(–y)(–y)

5t6

5·t·t·t·t·t·t

–y2

–1

–1 · y · y

Try This ... Fill in the table. Repeated Multiplication

Coefficient

Base

Exponent

Expression (power and coefficient)

a·a·a·a·a·a·a (–b)(–b)(–b)(–b)(–b) 3·c·c·c·c

Multiplying Powers by a Number

We can take a power, like 43 and double it. We would write that as 2 · 43 or 2(43). We call this number 2 a coefficient of the power.

Try This ... Fill in the table. Expression 2 · 43 or 2(43)

Repeated Multiplication 2·4·4·4

Coefficient

Base

Exponent

Value

128

5 · 23 7 · 104 –2 (3)3

68 Chapter 2 Powers and Roots

©Edvantage Interactive 2026

Finding Value of Powers with Negative Numbers

The base of a power can be negative. If this is the case, there will always be brackets around the base. For example: (–2)2 =

(–2)(–2) =

(–2)3 =

(–2)(–2)(–2) =

–8

(–2)4 =

(–2)(–2)(–2)(–2) =

(–2)5 =

(–2)(–2)(–2)(–2)(–2) =

–32

The base for the powers is –2. Notice which values are positive and which are negative. An even exponent gives a positive value. An odd exponent gives a negative value.

Try This ... Fill in the table. Find the base, exponent and value of the following: a. (–1)9

b. (–2)5

c. (–3)3

d. (–10)6

Base =

Exponent =

Value =

The coefficient of a power can be negative. In this case, find the value of the power first and then multiply that by the coefficient. For example: –2 · 32 = –2 · 9

Evaluate the power 32 first.

= –18

Multiply by –2.

Try This ... 1. Evaluate a. –125

b. –4(2)4

c. –24

d. –2(42)

2. Fill in the blanks and notice the differences in the bases and values. a.

b. (–3)2

–32

=3·3

= (–3) · (–3)

= –(3) · (3)

= –9

Base =

Exponent =

Value =

©Edvantage Interactive 2026

Chapter 2 Powers and Roots

Try This ... continued 3. Compare the following powers: 23 and (–2)3 by writing them as repeated multiplications. Are they equal?

4. Explain why (–x)even number is equal to (x)even number.

5. Fill in the table. Expression a. 2 · 43 or 2(4)3

Repeated Multiplication

Coefficient

Base

Exponent

Value

2·4·4·4

128

b. (–2)3 c. 104 d. –2(3)3 e. 11(–1)6 f. – (8)2 g. –52 h. –(–5)2 6. State whether each statement is true or false. If it is false, correct it. a. 52 = –52

b. 52 = (–5)2

c. x2 = (–x)2

d. a4 = –a

e. 53 = (–5)3

f. (–1)3 = –13

Extend and Explore

A googol is defined as 10100 which means it is the number 1 followed by 100 zeros. The term was coined in the 1930s and helps highlight the vastness of numbers that can be formed using exponential notation. 100 A googolplex takes this idea even further. It is defined as 10googol or 1010 . This means a googolplex is a 1 followed by a googol of zeros. The number is so enormous that if you tried to write it out in full, there wouldn’t be enough space in the observable universe to accommodate all its digits. Suppose that when printing a number, each digit occupies exactly one millimetre in width. a. Estimate the physical length (in metres) needed to print all the digits of a googol.

b. Do the same for a googolplex. c. Compare your answers with known distances. For example, compare them with the distance from Earth to the Sun. 70 Chapter 2 Powers and Roots

©Edvantage Interactive 2026

2.1 Practice 1. In the expression 2(10)5 a. 10 is called the _______________.

b. 5 is called a(n) _______________.

c. 2 is called a(n) _______________.

d. 105 is called a(n) _______________.

e. The value of 105 is _______________.

f. The value of 2(10)5 is _______________.

g. A power is a short way to write a _______________ _______________. 2. Write the following repeated multiplications as powers. a. 9 · 9 · 9 · 9 · 9 · 9 · 9 · 9 · 9

d. ( ) ( ) ( )

b. (–3)(–3)(–3)(–3)

c. (0.8) (0.8) (0.8)

e. x · x

f. (–1) (–1) (–1) (–1) (–1) (–1)

3. Fill in the table. Power

Repeated Multiplication

Base

Exponent

Value

7 × 7 or 7 · 7

43 106 44 ( )2 (–5)3 (0.1)3 (

4. Write each value as a power of 3. a. 27

b. 3

c. 81

d. 9

c. 64

d. 16

c. 1000

d. 1 000 000 000

5. Write each value as a power of 2. a. 8

b. 32

6. Write each value as a power of 10. a. 100

©Edvantage Interactive 2026

b. 100 000

Chapter 2 Powers and Roots

7. Fill in the table. Power

Repeated Multiplication

Coefficient

Base

Exponent

Value

3 · 52 11 · 103 –2(42) –62 12(1)7 –(–2)5 –(–10)3 –10(–1)2 8. Arrange these powers from least to greatest value: 62, 25, 43, 34, 52.

9. Write the following as a coefficient times a power. a. 3(2) (2) (2) (2) (2) (2)

b. 9 · 10 · 10 · 10 · 10 · 10 · 10 · 10 · 10

c. 12 · w · w · w

d. 100 · t · t · t · t · t

10. True or false. If false, correct to make true. a. 103 = –103

b. 72 = (–7)2

c. 92 = –92

d. x2 = (–x)2

e. x2 = –x2

f. –x3 = (–x)3

2.1 Practice Answer Key 1a) base b) exponent c) coefficient d) power e) 100 000 f) 200 000 g) repeated multiplication 2a)

72 Chapter 2 Powers and Roots

©Edvantage Interactive 2026

2.1 Practice Answer Key - continued 3)

Power 2

43 106 4

2 1 3 (−5)3

Repeated Mult.

4a)

Base

Exp.

Value

7·7

10 · 10 · 10 · 10 · 10 · 10

1 000 000

256

1 1 · 3 3 (−5)(−5)(−5)

1 3 −5

4·4·4

4·4·4·4

5a)

1 9 −125

2 3

(0.1)3 2 5 − 4

(0.1)(0.1)(0.1) 5 5 − − 4 4

0.1 5 − 4

Power

Repeated Mult.

Coeff.

Base

Exp.

Value

3 · 52

3·5·5

11 000

−2(42 )

−2 · 4 · 4

−2

−32

12 · 1 · 1 · 1 · 1 · 1 · 1 · 1

−2

1000

−1

−10

11 · 103 −62

12(1)7 −(−2)5

−(−10)3

−10(−1)2

11 · 10 · 10 · 10 −(6 · 6)

−1

−[(−2)(−2)(−2)(−2)(−2)]

−1

−10(−1)(−1)

−10

−[(−10)(−10)(−10)]

−1

6a)

0.001 25 16

−10

−36

8) 9a) 10a)

Remembering Ebbinghaus – Ratio, Fractions, Decimals and Percent 1. Fill in the table. Ratio

Fraction

Decimal

Percent

Picture

1:8

0.2

100%

©Edvantage Interactive 2026

Chapter 2 Powers and Roots

2.2 Exponent Laws – Part 1 Warm Up Competency Focus - Apply mathematical understanding through inquiry Would you rather? One penny on the first day, two pennies on the second

$10 000 a day for 30 days

day, four pennies on the third day and so on for 30 days

An Exponent of 1

Any base with an exponent of one equals the base itself. For example, 51 = 5. You can think of it in terms of number of factors when you write a power as a repeated multiplication. x3 means x · x · x. We say x3 has three factors.

Try This ... 1. State how many factors there are in each power. a. x2 __________

b. x9 __________

c. x1 ___________

b. t1 __________

c. (–9)1 __________

2. Evaluate these powers. a. 1211 __________

An Exponent of 0

When using numbers you can sometimes find patterns to help you understand what idea or concept you are investigating. Let's explore how to define the exponent of zero. First, with powers of 10. 103 = 1000

The exponent is the same as the number of zeros

102 = 100

As we move down, the value is divided by 10 each time.

101 = 10 100 = 1

The value we are looking for is 1.

In later math courses you will explore negative exponents. Second, with powers of 2. 23 = 8

As we move down, the value is half of the previous value (divided by 2).

22 = 4 21 = 2 20 = 1

Notice that the value of 20 is 1, which is the same as the value of 100. Based on those two examples, we say x0 = 1 as long as x is not zero.

74 Chapter 2 Powers and Roots

©Edvantage Interactive 2026

Why can't x be zero? On the one hand, when zero is the base with a positive exponent, the power is zero. On the other hand, anything to the power zero is one. This is a contradiction. We say 00 is an indeterminate form. We cannot determine it. In the four examples below, notice the value of the base and the values of the coefficients. This helps evaluate powers accurately. 40

(–4)0

–40

2(40)

Base is 4

Base is –4

Base is 4, coefficient is –1

Base is 4, coefficient is 2

40 = 1

(–4)0 = 1

–40 = –1(40) = –1

2(40) = 2(1) = 2

Try This ... 1. With a partner or two, complete the table. You may use a calculator to check answers. Product

Repeated Multiplication

Rewrite as a Single Power

Evaluate

103 × 104 42 · 43 25 · 24 (–3)4 (–3)6

2. Compare the single power to the product. What do you notice?

Product Law

If we multiply powers with the same base, we can add the exponents. We write: (xm) (xn) = xm + n These three examples show how to apply the product law.

Example 1

Example 2

Example 3

47 · 48

x99 · x

All the powers have a base of a

= 47+8

Notice the bases are the same Add the exponents

= 415

= x99 · x1 = x99+1

Notice the bases are the a4 · a5 · a6 same, and x1 = x Add the exponents

= a4 + 5 + 6

Add the exponents

= a15

= x100

©Edvantage Interactive 2026

Chapter 2 Powers and Roots

Try This ... 1. Write as a single power. a. 85 · 86

b. (–2)3(–2)4

c. x · x7

d. a49 · a50 · a51

Try This ... Discover the Quotient Law 1. With a partner or two, complete the table. You may use a calculator to check answers. Quotient

Repeated Multiplication (Write as a fraction)

Rewrite as a Single Power

Evaluate

75 ÷ 73

2. Compare the single power to the quotient. What do you notice?

If we divide powers with the same base, we can subtract the exponents. We write:

Quotient Law

x cannot be zero as that would create division by zero, examples show how to apply the quotient law.

, which is undefined. These two

Example 1

= x9 – 4 = x5

Example 2

Notice the bases are the same

3100 ÷ 3

Subtract the exponents

= 3100 ÷ 31

Simplify as long as x is not zero

= 3100 – 1

Notice the bases are the same, and 31 = 3

Subtract the exponents

= 399

76 Chapter 2 Powers and Roots

©Edvantage Interactive 2026

Try This ... 1. Write as a single power. a. 78 ÷ 72

Extend and Explore Expression

b. y8 ÷ y

Can you use the product rule, quotient rule, and your understanding of integers to write these expressions as a single power and evaluate? Single Power

Value (if base is a number)

2–3 · 25 =

(0.5)3 (0.5)2 x–2 · x–3 x–5 ÷ x5 x–1 ÷ x–1 62 ÷ 6–3

Remembering Ebbinghaus – Multiplying and Dividing Integers 1. Simplify the following: a. 2 · 5 =

b. (–2)(5) =

c. 2(–5) =

d. (–2)(–5) =

g. –

h. –

©Edvantage Interactive 2026

Chapter 2 Powers and Roots

2.2 Practice 1. Fill in the blanks a. The product law states that xm · xn = __________. b. The quotient law states that as long as x is not zero

__________

c. x1 = __________ d. x0 = __________ when x ≠ 0. 2. Evaluate and explain the difference between 20 and –20.

3. Which of these are examples that could be simplified by the product rule? a. x3 · x4

b. x3 · y4

c. 105 · 102

d. 10x5

4. Fill in the table. Expression with two

Repeated multiplication (write divisions as a

powers

fraction)

Single power

b. x3 · x4

(6 · 6 · 6 · 6 )(6 · 6 · 6)

78 Chapter 2 Powers and Roots

©Edvantage Interactive 2026

5. Evaluate the expressions by using exponent laws. a. 33

b. 121

c. (–3)2

d. 50

e. –50

f. 22 × 23

g. 109 ÷ 106

i. 199 · 121 · 134

k. 9876543210

l. 22 · 23 · 24

c. 109

d. y10

c. 109

d. y10

6. Express the following as a product of two powers. a. 76

b. x4

7. Express the following as a quotient of two powers. a. 76

b. x4

8. Make these statements true. Write exponents in the boxes provided. a.

2.2 Practice Answer Key 1a) 2)

In –20, the base is 2 (not –2) and –1 is the coefficient.

3a) 4a) 5a) 6) 7) 8a)

©Edvantage Interactive 2026

Chapter 2 Powers and Roots

2.3 Exponent Laws – Part 2 Warm Up Competency Focus - Connect mathematical concepts to each other What are the chances of flipping three different coins at the same time and getting 3 tails? Use the flow chart below to help you answer the question. What are all the different possible outcomes of flipping three coins? For example, you could flip HTH – heads on the first coin, tails on the second and heads on the third. How many possible outcomes are there? How is this connected to the value of 23?

Try This ... Discover the Power of a Power Law 1. With a partner or two, complete the table. You may use a calculator to check answers. Power of a Power (102)3

Repeated Multiplication (102) (102) (102) = (10 · 10) (10 · 10) (10 · 10)

Single Power 106

(23)2 5

{(–3)2}

2. Compare the single power to the expression. What do you notice?

Power of a Power Law

To simplify a power raised to an exponent, we can multiply the exponents. Look for a base that is itself a power. (xm)n = xmn This example shows you how to apply the rule. (84)11

The base of the exponent 11 is a power (84)

= 84 · 11

Multiply the exponents and simplify

= 844 We could evaluate this, but often we leave it as a single power, especially if the number is very large. 80 Chapter 2 Powers and Roots

©Edvantage Interactive 2026

Try This ... 1. Write as a single power. Do not evaluate. a. (723)2

c. {(–4)10}

b. (x3)12

Try This ... Discover the Power of a Product 1. With a partner or two, complete the table. You may use a calculator to check answers. Power of a Product (3 · 4)2

Repeated Multiplication

Product of Powers 32 · 42

(3 · 4) (3 · 4) = 3 · 3 · 4 · 4

(5 · 2)3

(xy)2 2. Compare the product of powers to the power of a product. What do you notice?

Power of a Product

From the table we can see that the power of a product is the product of the powers. We write: (xy)m = xm · ym This example shows you how to apply the rule. (3x)2

This is the power of a product

= 32 x2

We can write it as the product of powers

= 9x2

Simplify

32 = 9

Try This ... 1. Write these as a product of powers and simplify when possible. a. (ab)5

©Edvantage Interactive 2026

b. (pq)2

c. (–2x)3

Chapter 2 Powers and Roots

Try This ... Discover the Power of a Quotient 1. With a partner or two, complete the table. You may use a calculator to check answers. Power of a Quotient

Repeated Multiplication

Quotient of Powers

2. Compare the power of a quotient to the quotient of powers. What do you notice?

Power of a Quotient

From the table we can see that the power of a quotient is the quotient of the powers. We write:

This example shows you how to apply the rule. This is the power of a quotient

We can write it as the quotient of powers

Simplify

Try This ... 1. Write as a quotient of powers and simplify where possible. a.

82 Chapter 2 Powers and Roots

©Edvantage Interactive 2026

Order of Operations Review

Exponents have always been a part of BEDMAS (or PEMDAS). 1. Brackets 2. Exponents 3. Division and multiplication from left to right. 4. Addition and subtraction from left to right. Example 1: Simplify the power of a power in the numerator (brackets) Multiply the exponents 2 and 3 to get 6 Add the exponents 6 and 6 (product rule: same base) Subtract the exponents (quotient rule: same base)

Example 2:

Try This ... 1. Simplify where possible. a.

Extend and Explore

You can use the power of a power rule to put these powers in order from smallest to greatest without a calculator. a. 340, 250, 520, 430 b. 36000, 45000, 63000, 54000

©Edvantage Interactive 2026

Chapter 2 Powers and Roots

2.3 Practice 1. Write as a single power. a. (22)2

b. (x13)2

c. (103)3

d. (k12)12

e. (106)2

f. (y12)3

g. (z8)8

h. ((–4)2)3

2. Fill in the table. Power of a power

Single power

Value

a. (103)2 b. (23)2 c. (32)2 d. (104)3 3. Rewrite the following expressions as the product or quotient of powers a. (5y)2

c. (10b)4

e. (bc)2026

4. Rewrite the following expressions as a single power a. x3y3

e. a10b10c10

84 Chapter 2 Powers and Roots

©Edvantage Interactive 2026

5. Combining the exponent laws: Simplify a. 52 · 50 · 51

b. x4 · (x22)3

e. –40x(y10)3 · x2y2

2.3 Practice Answer Key 1a) 2a) 3a) 4a) 5a)

Remembering Ebbinghaus – Adding and Subtracting Integers and Order of Operations 1. Simplify the following: a. 2 – (–3) =

b. 6 – 5 – 4 – 3 – 2 – 1 =

c. –4 – 4 =

d. –4 – (–4) =

e. 3 + –6 – 1 – (–8) =

f. –9 – 3 =

g. 0 – 5 =

h. 10 – (–5) =

2. Simplify a. –3 –2(4)

©Edvantage Interactive 2026

b. 2(5 – (– 5))

Chapter 2 Powers and Roots

2.1 – 2.3 Check Your Understanding 1. In the expression 53 The 5 is called the _______________. The 3 is called an _______________. 53 is called a _______________. The value of the expression is _______________. 2. Fill in the table. Expression

Repeated Multiplication

Single Power

a. x2 · x3 b.

3. Evaluate the powers a. (–4)2

b. –42

c. (23)2

e. (–111)0

f. (–111)1

h. 23 · 22

4. Make these statements true. Write exponents in the boxes provided. a.

86 Chapter 2 Powers and Roots

©Edvantage Interactive 2026

How's it Going? Below is a student’s quiz with 10 questions. Some answers are correct and some are not. Add a check mark if the question is solved correctly. If it is not, circle the error and correct it in the space provided on the right of each question.

1. 32 · 34 = 98

2. 23 · 2 · 22 = 26

3. 62 · 65 = 610

4. 90 = 1

5. –32 = (–3)(–3) = 9

7. (32)5 = 37

8. (122)4 = 128

10.

2.1 – 2.3 Check Your Understanding Answer Key 1a) base, b) exponent, c) power, d) 125 2a)

3a) 4a)

How’s it Going? Answer Key Correct solutions for incorrect answers:

©Edvantage Interactive 2026

Chapter 2 Powers and Roots

2.4 Square Roots Warm Up Competency Focus - Develop mathematical understanding through inquiry

Figure 1

Figure 2 Figure 1

Length

Width

Area (length × width)

Figure 3 Figure 2

Figure 4 Figure 3

Figure 4

1×1=1

How many small squares are in each picture? These numbers are called perfect squares. Why do you think they are called that? Notice the connection to the formula A = lw (in this case the length = width because it is a square). If we call the length x, then the area would be x · x = x2. List the next 15 perfect squares by continuing the above pattern.

What are Square Roots?

A square root is a number that, when multiplied by itself, gives you the original number. Let's unpack that statement. • • • •

The principal square root of a number is denoted by the symbol or . This symbol represents a positive number. The positive square root of 9 ( ) is found by finding two equal factors of the number under the root, in this case 9. Since 3 × 3 = 9, we can say = 3.

88 Chapter 2 Powers and Roots

©Edvantage Interactive 2026

Try This ... 1. Evaluate the following square roots a.

Positive and Negative Roots

If x2 = 100 and we want to know the value(s) of x, we need to consider that there will be a positive root (the principal root) and a negative root. There will be two solutions. For example: (10)(10) = 100 and (–10)(–10) = 100 Therefore, x can equal 10 or –10

Try This ... 1. What values of x make these equations true? Remember there is more than one. a. x2 = 9

b. x2 = 64

c. x2 = 1

d. x2 = 144

Most numbers aren't perfect squares, so their square roots are not whole numbers. You can use

Square Roots of Non- your calculator to find an exact or approximate value using these steps. perfect Squares

1. Locate the square root symbol on your calculator. It may be above the x2 key. 2. Pick one of the following methods. Use the one that gives you the answer 5. 3. If the

is above x2, then you need to press the "2nd" or "shift" button before pressing Method 1

Press

©Edvantage Interactive 2026

and then 25 followed by the = sign

Method 2 Press 25 and then

followed by the = sign

Chapter 2 Powers and Roots

Try This ... 1. Use your calculator to find the square roots. If the value is approximate, round to one decimal (nearest tenth) b.

Estimating the Square Roots of Nonperfect Squares

Without a calculator we can approximate the square root of a non-perfect square. We can do this by using the known perfect squares close to the number and estimating. For example, to find the approximate value of the square roots of 2 and 3 we can say the value for each will be between the perfect squares = 1 and = 2. We can also say that will be closer to and will be closer to . It would be reasonable then to estimate: 1.3 or 1.4 and checking with a calculator the actual value is 1.414213562... 1.6 or 1.7 and checking with a calculator the actual value is 1.7320508...

Try This ... 1. Between which two consecutive integers is the value of the following square roots: b.

2. Estimate the following without a calculator. Use the square roots of perfect squares to help you estimate. b.

Extend and Explore

Create a Root Clock. Instead of writing the numbers 1 to 12, write roots that are equivalent to the numbers 1 to 12. For example: Instead of 2, you could write or or .

90 Chapter 2 Powers and Roots

©Edvantage Interactive 2026

2.4 Practice 1. List the first 10 perfect squares. ________

________

2. Evaluate the following square roots mentally using the list above. a.

3. What values of x make these equations true? There is more than one. a. x2 = 4

b. x2 = 36

c. x2 = 25

4. Use your calculator to find the square roots. If the value is approximate, round to one decimal place, or the nearest tenth. a.

5. Between which two consecutive integers is the value of the following square roots? a.

6. Estimate the following without a calculator, to the nearest tenth. a.

2.4 Practice Answer Key 1) 1, 4, 9, 16, 25, 36, 49, 64, 81, 100

2a) 4 b) 1 c) 3 d) 10 e) 9 f) 7

3a)

4a)

5a) 1 and 2 b) 8 and 9 c) 4 and 5 d) 5 and 6 e) 2 and 3

6a) 3.9 b) 9.9 c) 6.3 d) 4.8 e) 9.1

Remembering Ebbinghaus – Comparing Integers 1. Place these integers in order from smallest to largest: –5, –33, –10, –11, 0, –23, –4, –19 2. Name three integers between –10 and –5. __________, ___________, __________ . 3. Circle which integer is closer to –11. –8, –21, –1, –13

©Edvantage Interactive 2026

Chapter 2 Powers and Roots

2.5 Applications – Scientific Notation Warm Up Competency Focus - Connect mathematical concepts to other content areas (physics, biology, chemistry, computer science,

finance).

Choose one of the following situations and solve. 1.

One trillion is a million million. A stack of $1 trillion in $1 bills would reach more than one-quarter of the way to the moon. If you earned one dollar per second, how long would it take to earn 1 million dollars? 1 billion dollars? 1 trillion dollars?

If a person had 10 billion dollars, how many years would it take to spend it all at the rate of five million dollars per year? How many years would it take to spend it all if the rate changed to spending 1 million dollars per month?

Very Large and Very Small Numbers

In math and science, we often need to describe numbers that are very large or very small. Writing out all the zeros can be difficult and easy to misread, so we use a system that helps organize these numbers in a simpler way. One part of this system uses prefixes, which are short words added to units to show how big or small a quantity is. Large - Positive Powers

Small - Negative Powers

thousand

103

milli (m)

thousandth

10–3

mega (M)

million

106

micro (µ)

millionth

10–6

giga (G)

billion

109

nano (n)

billionth

10–9

tera (T)

trillion

1012

pico (p)

trillionth

10–12

kilo (k)

Scientists use very large and very small numbers in many areas of science. In astronomy, they measure distances between stars. In chemistry, they study the mass of particles like electrons. In physics, they work with values such as the speed of light. In computer science, they deal with large amounts of data. Scientific notation uses powers of 10 and was developed to write these numbers more quickly and clearly. Examples: • A terabyte of data storage is 1 000 000 000 000 bytes or 1012 bytes. • A nanosecond is 0.000 000 001 seconds or 10–9 seconds.

92 Chapter 2 Powers and Roots

©Edvantage Interactive 2026

To express a number in scientific notation, write the number as a product of two numbers: 1. a decimal greater than or equal to 1 but less than 10, 2. a power of 10. Scientific notation always starts with one non-zero digit, then a decimal point. There may be more digits following the decimal point.

Scientific notation with large numbers Scientific Notation 4.56 × 103

Standard Form

What to Think About

4560

Move the decimal 3 places to the right 4.56 × 1000 = 4560

7.65 × 104

76 500

Move the decimal 4 places to the right 7.65 × 10 000 = 76 500

In general: If the exponent is n, a positive whole number, move the decimal to the right n times.

Try This ... 1. Express in scientific notation.

2. Express in standard form

a. 8 500 000

a. 5.3 × 104

b. 13 000 000 000 000

b. 1.23 × 102

c. 2 340 000 000

c. 4.4 × 106

Scientific notation with small numbers Scientific Notation 2.1 × 10–3

Standard Form 0.0021

What to Think About Move the decimal 3 places to the left. Notice there are 2 zeros and a 2

9 × 10–6

0.000 009

Move the decimal 6 places to the left. Notice there are 5 zeros.

In general: If the exponent is negative, move the decimal to the left by the value of the exponent. For example, an exponent of −5 means move the decimal five places to the left.

Try This ... 1. Express in scientific notation.

2. Express in standard form

a. 0.000 3

a. 5.5 × 10–2

b. 0.000 000 007

b. 7.6 × 10–3

c. 0.048

c. 2.34 × 10–6

©Edvantage Interactive 2026

Chapter 2 Powers and Roots

Try This ... continued 3. Write the following using scientific notation a. The internal temperature of the sun is about 15 million °C.

b. A polio virus has a diameter of 0.000 03 mm.

c. Sirius A, the dog star, is over 77 000 000 000 000 km from Earth.

d. One mole of any substance contains approximately 602 000 000 000 000 000 000 000 atoms.

Applications of Powers and Roots

We can use powers and roots to solve problems. When applying these concepts, remember to use accurate units such as cm, cm2, cm3, hours or seconds. Example 1: Volume of a cube ( V = s3) Write the volume of a cube with side length 5 cm as a power, then evaluate. The units should be cubic, which means the exponent is 3. V = s3 V = (5 cm)3

Side length is 5 cm. Replace s with 5 cm

V = 53 cm3

Apply the power of product law

V = 125 cm3

Evaluate 53

Try This ... 1. The area of a circle is given by A = π r2. The diameter of a circle is 18 cm. What is the area of the circle?

94 Chapter 2 Powers and Roots

©Edvantage Interactive 2026

2. Growth Rate – A bacterial population doubles every 3 hours. a. Fill in the table, starting with 200 bacteria. Number of hours passed

Number of bacteria in total

0 (Start) 3 6 9

b. Follow the pattern to predict the number of bacteria after 12 hours.

3. The length of a side of a square can be found using the formula

Extend and Explore

. What is the side length if the area is A = 36 cm2?

1. Use the table below to estimate the population of the world in 2030. The values are approximate and based on United Nations estimates. Year 2000 2010 2020

Population (in billions) ~ 6.1 billion ~ 6.9 billion ~ 7.8 billion

2. What are the largest and smallest numbers that can be displayed on your calculator without scientific notation?

©Edvantage Interactive 2026

Chapter 2 Powers and Roots

2.5 Practice 1. Express in scientific notation. a. 3 400 b. 21 000 000 c. 890 000 2. Express in standard form. a. 3.14 × 102 b. 9.9 × 109 c. 5.432 × 106 3. Express in scientific notation. a. 0.005 b. 0.000 000 31 c. 0.022 4. Express in standard form. a. 1.1 × 10–3 b. 6 × 10–6 c. 3.14 × 10–6 5. Express these measurements in scientific notation. a. The mass of a hydrogen atom is 0.000 000 000 000 000 000 000 00167 grams. b. The distance to the moon is 384 400 km. c. It is estimated that there are 10 quintillion (10 followed by 18 zeros) insects on the Earth. 6. A bacterial population doubles every hour. Fill in the table if we start with 10 bacteria. Number of hours

Number of bacteria in total

0 (Start) 1 2 3 a. How many bacteria are there after 5 hours?

b. How many bacteria are there after 10 hours?

96 Chapter 2 Powers and Roots

©Edvantage Interactive 2026

7. Every person has two birth parents, four birth grandparents, eight birth great-grandparents, and so on. These people are known as direct ancestors. How many direct ancestors does a person have in the 10th generation?

8. Fold a piece of paper in half (giving 2 layers of paper). Fold it in half again (giving 4 layers). Continue folding it in half. How many layers would there be if you could do this 10 times? How many times could you actually do this?

2.5 Practice Answer Key 1a) 2a) 3a) 4a) 5a) 6) Table column values = 7) 1024 ancestors 8) 1024 layers. Actual number of folds will vary. With a regular sheet of paper, about 6 or 7 folds is typical. Try it now!

Remembering Ebbinghaus – Multiplying Fractions 1. Evaluate each product. a.

©Edvantage Interactive 2026

Chapter 2 Powers and Roots

2 Chapter Review 1. Consider the power 34. a. The base is __________

b. The exponent is __________

c. The value is __________

2. Fill in the table. Power

Repeated Multiplication

Base

Exponent

Value

44 5×5×5 25 3. Write each value as a power of 10. a. 1

b. 10 000

c. 10

d. 1 000 000

e. 1 000 000 000 000

f. 100

a. 4

b. 16

c. 1

d. 64

e. 256

f. 4096

4. Write each value as a power of 4.

5. Arrange these powers from least to greatest without a calculator. a. 25, 33, 72, 100, 52, 34

b. –42, (–4)2, 23, (–2)3, (–4)0, (–2)1

6. Write as a single power (xn) a. 85 . 84

b. y2 . y3

c. (74)4

e. x100 ÷ x25

f. 2311 . 2323

g. a . a9

j. (143)3

k. (w10)12

l. 20 . 25 . (23)2

7. Evaluate. Each answer will be a number. a. (–6)2

b. –62

c. (–6)0

d. 660

e. (–1)2026

f. (–1)2025

h. 2 . 52

i. – (–1)0

98 Chapter 2 Powers and Roots

©Edvantage Interactive 2026

8. Evaluate using the exponent laws and the order of operations. a. 34 – 43

b. 7(23) – 2(52)

d. 3 + 2(6)2

e. 2(23)2

g. ((–2)2)2 + (1234567)0

9. Simplify a.

10. True or false. a.

©Edvantage Interactive 2026

Chapter 2 Powers and Roots

11. How many direct ancestors does a person have in the 9th generation?

12. Astronomers estimate that there are about 2 trillion galaxies in the universe. If each galaxy has 100 billion stars, estimate the number of stars in the universe. (Hint: use the product law with powers of 10).

13. A multiple-choice test has four possible answers for each question (a, b, c, d). There are 3 questions. How many different possible ways are there to complete this test? For example, one possible way is to choose 'a' for each answer.

2 Chapter Review Answer Key 1a) 2a) 3a) 4a) 5a) 6a) 7a) 8a) 9a) 10a) 11) 12) 13)

100 Chapter 2 Powers and Roots

©Edvantage Interactive 2026

How Did It Go? Part 1: Reflecting on Chapter 2: Check all that apply to you ☐ The content of this chapter is challenging. ☐ I am starting to understand powers. ☐ I can find the square roots of perfect squares. ☐ I find combining exponent laws challenging. ☐ I need more time to practice before the test. ☐ I understand and can use exponent laws. ☐ I feel more confident solving with exponents than last year. ☐ I can approximate the roots of non-perfect squares. ☐ I understand how to simplify expressions with powers. ☐ I have a few questions before the test. ☐ I am confident about the content of this chapter. ☐ I can help others use exponent laws. ☐ I can use different strategies to simplify expressions with powers and roots. ☐ I feel confident applying skills to word problems. ☐ I am ready to write the test. ☐ My next step is ______________________________________________________.

Part 2: Reflecting on Inverse Operations We know that adding and subtracting are inverse operations. We know this because adding a number and then subtracting the same number brings you back to where you started. Explain how squaring and square roots are inverse operations.

©Edvantage Interactive 2026

Chapter 2 Powers and Roots

101

Vocabulary List for Powers and Roots A Approximate – To find a value that is close to the exact answer.

B Base – The number, variable, or expression that is raised to an exponent in a power.

C Coefficient – The number that multiplies a variable in an expression or equation.

E Evaluate – To find the value of an expression by performing the operations. Exponent – The small number in a power that tells how many times the base is used as a factor. Expression – A mathematical phrase made of numbers, variables, and operations. An expression does not contain an equals sign.

P Power – A way of writing repeated multiplication using a base and an exponent. Product – The result of multiplying two or more numbers.

Q Quotient – The result of dividing one number by another.

R Repeated Multiplication – Multiplying the same number, variable, or expression by itself more than once. Root – A number that, when raised to a given exponent, produces a given value.

S Scientific Notation – A way of writing very large or very small numbers using a number between 1 and 10 multiplied by a power of 10. Simplify – To rewrite an expression in its simplest form without changing its value. Square Root – A number that, when multiplied by itself, equals a given number.

V Value – The numerical result of an expression or calculation.

102 Chapter 2 Powers and Roots

©Edvantage Interactive 2026

Failsafe Vocabulary Check – Chain Notes

A Chain Notes discussion is a way to build ideas together. Read the question and write one response. Then, read what your classmates have written and add a new idea, example, or connection. Try not to repeat ideas that have already been shared. The goal is to build a chain of thinking by connecting your ideas to those of others. Example: How are powers and roots useful? Student 1

They help us describe very big and very small things.

Student 2

They help us understand how bacteria grow.

Student 3

They helped us describe distances to the Sun and Moon.

Student 4

They help us measure things like volume and area.

Student 5

We need powers for scientific notation.

Now use one of these prompts and have a Chain Notes discussion. • Scientific notation is useful because... • One thing I learned about powers is... • One thing I learned about roots is...

Student 1 Student 2 Student 3 Student 4 Student 5 Student 6 Student 7 Student 8 Student 9 Student 10

©Edvantage Interactive 2026

Chapter 2 Powers and Roots

103

104 Chapter 2 Powers and Roots

©Edvantage Interactive 2026

3 Polynomials In math we often solve problems or puzzles. Polynomials are math sentences we use to give us information that we can use to solve the puzzles and problems in a branch of math we call algebra. Let’s look at where some of these words come from. •

Poly means many in Greek and the ending -nomial comes from the Latin nomen, meaning name.

•

Al-jabr means restoration or reunion of broken parts in Arabic.

Polynomials are a fundamental part of algebra. Algebra involves expressions, equations, and functions and is the focus of the next three chapters. Polynomials are a specific type of algebraic expression. They consist of coefficients, variables, exponents that are whole numbers, and operations (+, –, ÷, ×)

Big Idea of the Chapter The principles and processes underlying operations with numbers apply equally to algebraic situations and can be described and analyzed.

In this chapter you will explore: The parts of a polynomial: terms, coefficients, constants, variables, exponents. Degree of a polynomial Add polynomials Subtract polynomials Multiply polynomials Divide polynomials Combine polynomial operations Apply these concepts

Perimeter, area and volume of shapes involving unknown values.

Get Started You are taking an order at a fast food restaurant. The person orders 1 hamburger, 1 large fries and an iced tea, 1 hamburger, 1 medium fries and an iced tea, 2 cheeseburgers, 2 large fries and 2 waters, 1 cheeseburger, medium fries and an iced tea, 3 hamburgers, 1 medium fries and 2 waters. Can you summarize this order in a concise way? How could you abbreviate the words?

©Edvantage Interactive 2026

Chapter 3 Polynomials

105

3.1 What is a Polynomial? Warm Up Competency Focus - Solve problems in context Draw a few rectangles with a perimeter of 16 units. Find the area of each one. What is the largest area you can find?

Polynomials are mathematical expressions used to model, describe, and solve real-world

Polynomials Defined situations across science, engineering, business, and everyday life. They can help us model market trends in business, the concentration of a drug in the bloodstream, the location of planets and comets, and even temperature changes over time. Polynomials are made up of terms separated by addition or subtraction. A term is the product of numbers and variables (letters). For example: the perimeter of a rectangle can be expressed as a polynomial: 2l + 2w, where l is the length and w is the width. It is the sum of 2 terms, 2l and 2w. Let's look at the different parts of this three-term polynomial to see how it is built.

A polynomial can include: •

A coefficient (a number multiplied by a variable): the number 5 in the expression 5xy. And the number 1 in the expression x.

•

One or more variables (letters like a and b that represent an unknown or changeable value): the x and y in 5xy.

•

A constant (a term that is a fixed number that does not contain a variable): the –2 in the expression 3x – 2.

106 Chapter 3 Polynomials

©Edvantage Interactive 2026

The table below gives examples of each of these terms. Expressions

5x + 1

8abcd + 7

Coefficients

Variables

a, b, c, d

Constant

–1

Other important points to remember when using polynomials: •

Write polynomials with descending powers. Instead of 13 + x4 + x2 + x7 + x + x3 + x6 + x5, we write x7 + x6 + x5 + x4 + x3 + x2 + x + 13. This convention makes it easier to compare, combine, graph, and analyze.

•

Remember x = x1 and x0 = 1 when x ≠ 0.

•

3 – x2 + x in standard form would be –x2 + x + 3.

•

A term of a polynomial is the product of numbers and variables (letters and symbols).

•

A term can also be a constant: 3, –0.2.

•

Examples of a term:

•

A polynomial is a sum of terms: y2 – 5y + 1 has 3 terms: y2, – 5y and 1.

•

We have special names for polynomials that have one term, two terms and three

terms. 1 term

monomial

–8, π, 5x, –y, 3.14x2, –1234abcd, h2k2

2 terms

binomial

x + y, a – 3, x2 – 4, t + 10, xy – abc

3 terms

trinomial

a – b – c, x2 + 2x + 1, a3 + b2 – 2

Try This ... 1. Rewrite the following polynomials with descending powers. a. b. 2. Fill in the table 0.5t2 + 5

2x + 1

4x2 – 3x – 2

a2 + 10a – 11

xyz –

Number of Terms Coefficients Variables Constant

©Edvantage Interactive 2026

Chapter 3 Polynomials

107

Try This ... continued 3. Fill in each blank with monomial, binomial, or trinomial. a. _______________

b. _______________

a+b+c

c. _______________

t–4

d. _______________

–3

e. _______________

y2 + 7x + 10

f. _______________

2L + 2W

g. _______________

πr2 The degree of a polynomial tells us important information about the behavior and characteristics of the polynomial. It determines the shape of the graph. It also helps us determine how fast a polynomial will grow and how many roots it has. The degree helps us understand, analyze, and work with polynomials effectively.

Degree

Degree of a term: • If there is one variable, the degree is the value of the exponent. • If there is more than one variable, the degree is the sum of the exponents in the term. • If there is no variable at all, we say the degree is zero. Examples: » 4 can be written as 4 (1) = 4x0, so the degree is zero » 5x can be written as 5x1, so the degree is one » The sum of the exponents in the term ab2c3 is 1 + 2 + 3 = 6, so the degree is 6

Term

Degree

–3x

10y4

–11x2y3

Your Turn — Degree 1. Fill in the table. Term

Degree

7.5y3 –7y9 axy2 3.2

108 Chapter 3 Polynomials

©Edvantage Interactive 2026

The degree of a polynomial is the degree of the term with the highest degree. For example, in the polynomial the degree of each term is written below each term. The highest number is 4, so the degree of the polynomial is 4.

Try This ... 1. Fill in the table below. Polynomial

Degree of Each Term

Degree of Polynomial

y4 – y2 – 1 –3x + 3 abc + ab + c –11x2y3 + abcdxyz + 11 4 – y2 x3 – x7 + 7x – 1.5x2

Modelling Polynomials with Algebra Tiles

Modelling is a powerful process in mathematics that allows us to describe, understand and make predictions. We can model polynomials with algebra tiles to help us understand what they are and how they can be combined. As you work with the tiles, you will see there are limitations. Which polynomials can’t be modelled by algebra tiles? Let’s start with 3 shaded tiles. Notice their length, width and area.

Length: x

Length: 1

Width: x

Width: 1

Area = x (x)

Area = 1 (x)

Area = 1 (1)

= x2 square units Dimensions are x by x

= x square units Dimensions are 1 by x

= 1 square units Dimensions are 1 by 1

Here is an algebra tile model for 2x2 + 2x + 1.

By changing the colour of the tiles, we can represent negative values. This is an algebra tile model for –x2 – x – 1.

©Edvantage Interactive 2026

Chapter 3 Polynomials

109

By changing the colour of the tiles, we can represent negative tiles. Here is an algebra tile model for –2x2 + 5x –1.

Try This — Polynomials and Algebra Tiles 1. Draw an algebra tile representation for each polynomial. a. –2x2 –4x –2

b. x2 –x + 5

2. Match the polynomials with a picture. a. _____ –x2 + 2x – 1

b. _____ x2 –3x – 3

ii.

c. _____ 2x2 + 2

iii.

Extend and Explore

Models in math and science are simplified representations of reality. Every model has limits. Every model has things it shows well and things it cannot show. Identify one limitation of using algebra tiles to represent polynomials.

110 Chapter 3 Polynomials

©Edvantage Interactive 2026

3.1 Practice 1. Fill in the blanks. a. ____________________ is a polynomial with one term. b. The degree of a term with more than one variable is the ____________________ of the exponents of the variables. c. The number that is multiplied by a variable is called a ____________________. d. A ____________________ is a letter that represents an unknown value. e. A trinomial is a polynomial with ____________________ terms. 2. Fill in the chart. Polynomial a.

3t – 9

x2 – 7 + x5y2

2a2 – 6a + 12

–7abc2d3 + 7

1 + y + y4 – y3

Number of Terms

Name

Coefficient

Constant

Variables

Degree

3. Match the polynomials with the descriptions a. _____ One variable, 3 terms, degree of 2

i. ab2 – b2

b. _____ Two variables, 2 terms, degree of 3

ii. – x2 + 6x –9

c. _____ One variable, 2 terms, degree of 1

iii. 7x – 10

d. _____ Two variables, 3 terms, degree of 2

iv. 3x2 – 6xy + y2

4. Create a polynomial that has: a. One variable, 2 terms and a degree of 3

b. Two variables, 3 terms and a degree of 4

c. One variable, 2 terms and a degree of 1

d. A degree of zero

5. Draw an algebra tile representation for the following polynomials. a. –x2 – x + 5 b. 2x2 + 3x – 1

©Edvantage Interactive 2026

Chapter 3 Polynomials

111

6. Match each picture with the polynomial.

a. _____ –x2 + 2x – 3 i.

b. _____ –2x2 – x + 3 ii.

c. _____ x2 – 2x + 3 iii.

d. _____ 2x2 – x – 3 iv.

3.1 Practice Answer Key 1a) 2a) 3a) 4a) b)

5a) 5

−x²

−x 1

−x

x² 1

x x²x

x²

x −1

−1

6a)

Remembering Ebbinghaus – Reducing and Comparing Fractions 1. Reduce the fractions a.

2. Which fraction is greater? a.

112 Chapter 3 Polynomials

©Edvantage Interactive 2026

3.2 Adding Polynomials Warm Up Competency Focus - Demonstrate and apply mental math strategies

quarter: 25 cents

dime: 10 cents

nickel: 5 cents

penny: 1 cent

How many ways can you make change for one dollar using only quarters, dimes, nickels, and pennies? Even though pennies have not been used since 2013, we'll include them here to give more options.

Like Terms

Like terms have the same variables raised to the same exponents. Like terms differ only in their coefficients. These are like terms: x and –5x

–0.1x2 and x2

12 and –1

2ab and 5ab

x2y and xy2

–1 and –x

These are NOT like terms: 2x and x2

4m and 4n

Try This ... 1. Circle the like terms of the given term. Given term a. –11

–11t, 1, –11t2, –12, 19, –t

b. 3b

7, 5b, ab, –b, –1, b3, 3a

c. x2

–2x2, –2x, –2, 0.2x2, –2x2y, 2.2x,

d. 19mn2

mn2, –10m2n, mn, 11n2m, 10mn2, 1.1mn2

e. abc

–abc, ab, 10abc, 2bca, 2ca, –2cba, –a, –2

f. 1

–1.0, –x, –11, x, 11.1, –111t, 29

g. 4x2y

xy2, –x2y, 3xy, 2y2, 2xy2, 11y2x, –1.0

h. 3m3

m3, 3m, –3m3, 2m3, 3m2, –0.3m3,

©Edvantage Interactive 2026

x2, –222x2

Chapter 3 Polynomials

113

Combining Like Terms

Like terms can be combined together by adding or subtracting coefficients. For example, 3 apples and 4 apples is 7 apples. We can use a for “apple”, we can write this as 3a + 4a = 7a. Or we can write 7 apples minus one apple is 6 apples as 7a – a = 6a. Remember that a is the same as 1a in the same way that an apple is one apple. Now using different terms, write 4 teas plus a coffee plus 2 teas plus another coffee. Let t equal tea and c equal coffee. This gives 4t + c +2t + c = 6t + 2c. Algebra tiles can also be used to combine like terms. 2x2 + x + x2 + 2x+ 1 + x2 + 2 can be represented using algebra tiles.

We can also write this more simply as 4x2 + 3x + 3.

Try Together — Combining Like Terms Write an equation to represent:

What to Think About

How to Do It

1. Add the number of shapes starting from the left.

2 circles plus one __________ plus 3 __________ plus 2 __________ .

2. Add the number of circles together and add the

5 circles + __________ or 5c + _________

number of triangles together.

Your Turn — Combining Like Terms 1. Simplify a. A shopper picks two apples plus two bananas and then four apples plus 5 bananas.

b. You're buying a meal for you and your friend. Their order is 2 hamburgers and 1 fries and your order is 1 hamburger and 2 fries.

114 Chapter 3 Polynomials

©Edvantage Interactive 2026

Your Turn — continued c.

2. Simplify by combining like terms: a. xy + 3yx – x2 + 6x2 + 7xy

b. 2d2 + 3d3 – 8d2 – 4 – a + 3a2 –4

c. a2 – 7a + 4 – a + 3a2 – 4

d. –1 – 3t – 9t – 14 – 12 – 2t +1

Adding Polynomials – Vertical Method

We can add three polynomials together by lining them up vertically with their like terms. For example, (2x2 – 3x + 5) + (3x2 + 6x –1) + (x2 + x + 1). Write the three polynomials vertically. Make sure they are written in standard form so that like terms are in a vertical line. Add the like terms.

Try Together — Adding Polynomials Vertically Add the polynomials. (–4x2 – 2x + 1) + (2 + 2x + x2) + (3x2 – 3 – 3x)

What to Think About

How to Do It

1. Arrange polynomials vertically. Make sure they are in standard form. Keep like terms aligned.

2. Add like terms to simplify.

©Edvantage Interactive 2026

Chapter 3 Polynomials

115

Adding Polynomials – Combining Like Terms

We can add polynomials by removing the brackets and combining like terms. For example, the 4 polynomial groups can be rewritten without brackets because they are all being added. (x + 1) + (x + 2) + (x + 3) + (x + 4)

x+1+x+2+x+3+x+4

Now we can look for like terms and add them together. x + x + x + x = 4x and 1 + 2 + 3 + 4 = 10 This gives 4x + 10

Try This ... 1. Add the following polynomials by combining like terms. a. (x + 5) + (x – 2) + (x + 7) + (2x + 1)

b. (x2 + 8x – 4) + (–x2 – 2x + 8)

c. (x - 4) + (2x2 + 5x + 9) + (x + 1) + (–x2 – x + 4)

2. Add the polynomials using the vertical method (5x2 – 2 + 7x) + (4x2 – 7x – 3) + (x2 + x + 5)

Extend and Explore

In a magic square the sum of the rows, columns and diagonals are equal. Use binomials and trinomials to complete the magic square. The sum of the magic square below is 3x2 + 9x – 12.

116 Chapter 3 Polynomials

©Edvantage Interactive 2026

3.2 Practice 1. Circle the like terms in each row. a. 4ab

bc, 8ab, 0, 3ba, 4, ab2, –12ab, 4b

–7x, 1, 7a, –18, π, 7x2, –77

c. x2y

–x2y, xy2, x2, x2y2, 6x2y, –6yx2

d. –x

3x, 1, x, 0.3x, x2,

x, –1

2. Introduce variable(s) where appropriate. a. 4 oranges plus two apples plus 10 oranges plus 5 apples plus an orange.

b. 3 cheeseburgers and 1 order of fries and 1 hamburger and 2 orders of fries and 1 cheeseburger.

3. Simplify by collecting like terms. a. 3x – 4y – x + 8y – 3x – 4y

b. 3x + x2 – 3x – x2 – 3x

c. 4t2 + 4q2 – 3q2 + 6t2 – t2

d. a + ab – a –ab + 3ab – 2a + 3b + 3a – 2b + ab

4. Which of the following expressions simplify to x? a. –11x + 10x

b. x + x

c. x2 – 5x – x2 + 6x

e. x + x + x + x + x – 4x

f. 0.9x – 0.1x – 0.9x – 0.1x

©Edvantage Interactive 2026

Chapter 3 Polynomials

117

5. Add the two polynomials together. a. x2 – 4x + 1; 3x2 –x – 2

b. 5x2 + x – 8; –2x2 + 7x + 1

c. 2y2 + 9y –2; 2y2 – 9y – 2

d. 3x2 – x + 6; –x2 – 1

e. x2 – 4;

f. 0.5a – 1.2; 2.4 – 0.75a

x2 – 4

6. Simplify a. (3x2 + 5x + 7) + (2x2 – 4x + 9)

b. (4a3 – 2a + 6) + (3a3 + 5a – 1)

c. (2p2 +

d. (8z2 + 7.75z – 9.1) + (–5.9z2 – 3.5z + 6.1)

p + 1) + (4p2 – p + 5)

e. (x4 + 2x3 – x + 4) + (–x4 + x2 + 3x – 1)

118 Chapter 3 Polynomials

f. (3b3 + b2 – 5b + 7) + (2b3 – b2 + 4b – 2)

©Edvantage Interactive 2026

7. Create two polynomials that when added together give you x2 + x + 1

8. If a = x2 + x – 2, b = 2x2 – 3x + 4, c = x2 – 5 and d = 3x + 6. What is a + b + c + d?

9. What is the perimeter of a rectangle whose length is 3x2 + 2x + 1 and width is 2x2 – 2x + 1?

10. Find the perimeter of this triangle.

3.2 Practice Answer Key 1a) 2a) 3a)

4a)

5a) 6a) 7) Answers may vary. One possible answer:

and

10)

Remembering Ebbinghaus – Powers of Three 1. Write as a single power. a. 33 × 34 b. 3 × 32

c. 32 × 35 × 37 × 311

2. Write three different products of powers that are equivalent to 310.

©Edvantage Interactive 2026

Chapter 3 Polynomials

119

3.3 Subtracting Polynomials Warm Up Competency Focus - Apply mathematical understanding through problem solving. A rectangular garden with a 1 metre wide path going all around it is shown here. What is the area of the shaded path around the garden?

Subtracting can be thought of as finding the difference or distance between two numbers or quantities. For example: The difference between 7 and 2 is the same as the difference between –3 and 2. It is 5.

Subtracting polynomials means to find the difference or distance between two polynomial expressions. With numbers and polynomials, we can think of subtraction as adding the opposite. This can help us subtract more complex expressions. For example: 3 minus 4 is the same as 3 plus the opposite of 4 3 – 4 = 3 + (–4) a – b = a + (–b)

Opposite of a Polynomial

For a number, the opposite is the additive inverse. A number added to its opposite is zero. For example, the opposite of 5 is –5, because 5 + –5 = 0. Similarly, for a polynomial, when you add it to its opposite you get zero. The opposite of a polynomial can be found by multiplying the entire polynomial by –1. This means positive terms become negative, and negative terms become positive. The opposite of y – 5 is –y + 5 The opposite of –2 – a is 2 + a The opposite of a + b + c is –a – b – c

120 Chapter 3 Polynomials

©Edvantage Interactive 2026

Try This ... 1. Find the opposite for each of the following polynomials. Polynomial

Opposite

a. 100 b. 4 – y c. –x2 – 10 d. 2.5 x2 + 1.25x + 0.5 e. – x3 + x2 – x – f.

Subtracting Polynomials

There are 2 steps to follow when subtracting polynomials. 1. 2.

Rewrite the subtraction as an addition by adding the opposite. Combine like terms.

Sample Problem — Subtracting Polynomials Simplify the following: (3x2 + 5x + 3) – (2x2 – 4x + 1)

What to Think About

How to Do It (3x2 + 5x + 3) – (2x2 – 4x + 1)

1. Add the opposite of the second polynomial.

(3x2 + 5x + 3) + (–2x2 + 4x – 1)

2. Remove brackets.

3x2 + 5x + 3 –2x2 + 4x – 1

3. Combine like terms.

x2 + 9x + 2

©Edvantage Interactive 2026

Chapter 3 Polynomials

121

Try Together — Subtracting Polynomials Simplify the following: (7y – 2y2 + 1) – (3y2 + 5y – 2)

What to Think About

How to Do It (7y – 2y2 + 1) – (3y2 + 5y – 2)

1. Add the __________ of the second polynomial.

(7y – 2y2 + 1) + (__________)

2. Remove brackets.

___________________

3. Combine like terms.

___________________

Your Turn — Subtracting Polynomials 1. Simplify the following a. (3x2 + 2x – 5) – ( x2 – 3x + 4)

Subtracting Polynomials with Algebra Tiles

b. (4x2 – 6x + 8) – (2x2 – 5x – 3)

c. (3x2 + x + 4) – (2x2 + x – 5)

The following pairs of tiles are equivalent to zero. We call these zero pairs.

We can model subtraction with algebra tiles by adding the opposite. Let's take the following algebraic tile model.

(

) ( –

)

Now rewrite with an addition of the opposite.

( 122 Chapter 3 Polynomials

) ( +

) ©Edvantage Interactive 2026

Simplify using zero pairs and like terms.

Try This ... 1. Draw an algebra tile model to represent the following subtraction (2x – 2) – (– x + 3).

2. Create your own subtraction question and model it with algebra tiles.

Extend and Explore

Each letter represents a digit from 0 to 9. Different letters represent different digits. Can you figure out the code? AB + CD = CEA FE + CD = DD GH + JD = HK

©Edvantage Interactive 2026

Chapter 3 Polynomials

123

3.3 Practice 1. Subtracting a number or polynomial is the same as adding its ____________________ . 2. What is the opposite of each polynomial? a. 10

b. –5

c. –10

d. –3

e. x + 1

f. 5 – x

g. –3x – 11.5

h. 4y2 + 2y – 9

i. – x3 – x2 +

j. a – b + c – d

3. Draw an algebra tile representation for each step of subtracting two polynomials. Step 1: (2x2 – 3x + 1) – (x2 –3x – 2)

Step 2: (2x2 – 3x + 1) + (– x2 +3x + 2)

Step 3: x2 + 3

4. If the perimeter of this triangle is 7x – 5, then what is the base?

5. Simplify a. (3x2 + 5x – 2) – (x2 –3x + 4)

b. (5a2 + 3a + 7) – (a2 –2a + 4)

c. (5m2 – 4m – 1) – (2m2 –3m + 2)

d. (7x3 – 3x2 + 2x – 9) – (4x3 + x2 –x + 6)

124 Chapter 3 Polynomials

©Edvantage Interactive 2026

5. continued f. (3.3b2 + 6.6b – 2.2) – (1.1b2 + 2.2b – 5.5)

e. (x3 + x2 – 3x + 5) – (2x3 – x2 + 3x – 5)

3.3 Practice Answer Key 1) opposite 2a) 3) Step 1

Step 2

Step 3

4) 5a)

Remembering Ebbinghaus – Multiplying Fractions

1 2

1 2 1 3

1. Here is an area model for multiplication. The product

can be thought of as half the

length times two thirds of the width. We can see it is 2 of the 6 equal rectangles below. Draw a similar model for

1 3 1 3

· . ·

©Edvantage Interactive 2026

Chapter 3 Polynomials

125

3.1 – 3.3 Check Your Understanding 1. Fill in the blanks. a. A ___________________ is a polynomial with two terms. b. The ___________________ of a term is the sum of the exponents. c. A ___________________ is a letter that represents an unknown value. d. A ___________________ is a polynomial with three terms. e. Subtracting a number is the same as adding its ___________________. f. In the expression 4x – 5 the 4 is called a ___________________ and –5 is called a ___________________. g. ___________________ is a word whose origin is “many terms”. 2. Fill in the chart. Polynomial

Name

Number of Terms

Coefficients

Constant Term

Variables

Degree

3x2y2 + 0.1 6b – 7 a2 – a – 2

0.1t3 + 1 3. Create a polynomial with three terms that has a degree of 2 and 8 as a constant.

4. Circle the terms on the right that are like the term on the left. a. x

5x, –5, 0.5x, x5, 5y,

b. y2

2x2, –y2, 2y, 2y2, –2,

x y2, 2xy,

5. What is the opposite of the following polynomials? a. –3y3 + 4x – a – 1 b. a + b – c +d 6. Draw the opposite polynomial to the one represented here. Write an expression for both.

126 Chapter 3 Polynomials

©Edvantage Interactive 2026

7. What polynomial is represented here (simplify).

8. Add the polynomials using algebra tiles. Use zero pairs and then write the simplified polynomial expression on the blank provided. a. + _________________________________

b. + _________________________________

c. + __________________________________

3.1 – 3.3 Check Your Understanding Answer Key 1a) 2a) 3) 4a)

5a)

6a)

8a)

©Edvantage Interactive 2026

Chapter 3 Polynomials

127

How's it Going? Below is a student’s quiz with four questions. Some answers are correct and some are not. Give a check mark if the question is solved correctly. If it is not, circle the error and correct the error. 1. Simplify the following polynomial a. 2a – b – 2a + 5b – 3a – 4b

b. 3x2 + x – 4 – 5x2 – 4x – 7 – x2 + 2

2a – 2a – 3a – b + 5b – 4b

3x2 – 5x2 – x2 + x – 4x – 4 – 7 + 2

= –3a

= –3x2 – 3x – 9

c. x – y – x – y + x + y – x + y – x =x

2. Write two polynomials that add to x2 – 2x – 1 a. (3x2 + 4x – 5) + (–2x2 – 6x – 4) b. (–x – x – 2) + (2x2 + x – 1) 3. Subtract a. (2x – y – 1) – (x + y +5)

b. (7a – 2a2) – (–7a2 + a)

c. (–12 – b2 + 3b) – ( –8b2 + 1)

= 2x – y – 1 + x – y – 5

= 7a – 2a2 + 7a2 – a

= –12 – b2 + 3b + 8b2 – 1

= 3x – 2y – 6

= 14a2 – 3a

= 7b2 + 3b – 13

4. Find the perimeter of the shape. (Angles are 90°).

How’s it Going? Answer Key 1a) Correct

b) Incorrect

2a) Correct

b) Incorrect

3a) Incorrect

b) Incorrect

c) Correct

4) Correct

128 Chapter 3 Polynomials

©Edvantage Interactive 2026

3.4 Multiplying Polynomials Warm Up Competency Focus - Apply multiple strategies to solve problems in both abstract and contextualized situations Jewel has 9 metres of special fencing to create a rectangular play area for their puppy in the backyard. What should the length and width be so that the puppy has the most room to play?

There are two rules to follow when multiplying monomials: 1. multiply their coefficients (numbers). 2. multiply their variables (add the exponents if they have the same base). These are examples of monomials being multiplied together. 3x2 · 4x3 = 12x5

11a · 11b = 121ab

3y (3y) (3y) = 27y3

Try This ... 1. Simplify the following by multiplying the monomials. a. –2y · 5y2

b. a5 · a5

c. x(–2x)(3x2)(4x3)

d. 0.1x(0.1y)(2z)

©Edvantage Interactive 2026

Chapter 3 Polynomials

129

Monomial Times a Binomial

When you multiply a monomial by a binomial, you can use the distributive property. Multiply each term in brackets separately, then add the results. You "distribute" the multiplication to each term inside the parentheses. Symbolically it can be written as: a(b + c) = ab + ac We can visualize the distributive property. x

3 +

We can write the area of the rectangle on the left as the sum of the two smaller rectangles on the right: 2(x + 3) = 2x + 2(3) 2(x + 3) = 2x + 6

Try This ... 1. Simplify the following by multiplying the polynomials. a. y (y + 1)

b. –x (4 – x)

d. 0.1x (10x – 100)

(4x + 8)

Monomial Times a Polynomial

When we multiply a monomial by a polynomial we multiply the monomial by each term of the polynomial and simplify. For example, 4x (x2 – 4x + 1) We multiply 4x by each of the three terms in brackets.

4x3 – 16x2 + 4x

130 Chapter 3 Polynomials

©Edvantage Interactive 2026

Try This ... 1. Simplify the following by multiplying the polynomials. a. –3a (a2 – 4a + 1)

b. –2 (b2 –10b – 7)

c. y (y3 + y2 + y + 1)

Algebra Tile Connection

(–2x2 + 10x – 12)

The picture below represents multiplying x(x + 2) using algebra tiles.

Width = x

Length = x + 2 Notice the following: • The width is x. • The length is x + 2. • The area is the product of the length and the width x(x + 2). • The area is x2 + 2x. • x(x +2) is the same as x2 + 2x.

Try This ... 1. Draw a picture to represent (2x)(2x).

©Edvantage Interactive 2026

Chapter 3 Polynomials

131

Binomial times Binomial - The Area Model

The area model is another way to visualize multiplying binomials. Instead of multiplying all the terms at once, the rectangle is divided into smaller regions. Each region represents one multiplication. The sum of the four regions gives the final product.

Notice the following: • The top-left rectangle represents a × c. • The top-right rectangle represents a × d. • The bottom-left rectangle represents b × c. • The bottom-right rectangle represents b × d. • Adding the four regions together gives the product of (a + b)(c + d).

Sample Problem — Using the Area Model Use the area model to solve 23 · 48.

What to Think About

1. 23 is 20 + 3. 48 is 40 + 8. 2. The length is 40 +8. The width is 20 + 3. 3. 20 times 40 is the top left area. 20 times 8 is in the top right area. 3 times 40 is the bottom left area. 3 times 8 is the bottom right area.

4. Add the four areas to find total area.

132 Chapter 3 Polynomials

How to Do It

23 · 48 = 1104 (20 + 3) (40 + 8)

800

160

120

= 800 + 160 + 120 + 24 = 1104

©Edvantage Interactive 2026

FOIL Method

When multiplying two binomials, a helpful strategy is the FOIL method. FOIL reminds us to multiply the First, Outer, Inner, and Last terms. This organized approach ensures every pair of terms is multiplied and included in the final expression. (a + b) (c + d) = ac + ad + bc + bd F O I L First: Multiply the first terms in each binomial. ac Outer: Multiply the outer terms (the terms on the left and right outer edges). ad Inner: Multiply the inner terms (the 2 terms in the middle). bc Last: Multiply the last terms in each bracket (the terms immediately to the left of the “)”. bd

Sample Problem — Multiplying Binomials Simplify (x + 2) (x + 5) using the FOIL Method.

What to Think About

How to Do It

1. F for first x times x. O for outer 5 times x. I for inner 2 times x. L for last 2 times 5.

(x + 2) (x + 5) F = x2 O = 5x I = 2x L = 10

2. Simplify the two middle terms (like terms).

= x2 + 5x + 2x + 10 = x2 + 7x + 10

Try Together — Multiplying Binomials Simplify (x + 3) (x – 2) using the FOIL Method.

What to Think About

How to Do It

1. F multiply (x)(x). O multiply (__________)(x). I multiply (__________)(x). L multiply (3)(__________).

(x + 3) (x – 2) F = x2 O = _____ I = 3x L = _____

2. Simplify the two middle terms (like terms)

= x2 + _____ + 3x + _____ = ______________

©Edvantage Interactive 2026

Chapter 3 Polynomials

133

Your Turn — Multiplying Binomials Simplify using the FOIL method. 1. (x – 3) (x + 1)

2. (a – 10) (a – 11)

3. (x + 7) (x + 2)

4. (1 – x) (2 – x)

5. (x – 1) (x – 1)

6. (x + 2) (x + 5)

7. (x + y)2

8. (a + 1)2

Algebra Tiles and the FOIL Method

Algebra tiles provide a visual model for FOIL. Each region of the model represents one of the four products. We can use algebra tiles to multiply (x + 2)(x + 3). In the image below the rectangle has the sides (x + 2) and (x + 3).

The four regions show the four products of FOIL. First: Outer: Inner: Last:

x · x = x2 x · 3 = 3x 2 · x = 2x 2·3=6

Combine the like terms: x2 + 3x + 2x + 6 x2 + 5x + 6

134 Chapter 3 Polynomials

©Edvantage Interactive 2026

Try This ... 1. Draw an algebra tile model for (x + 3)(x + 1). Label the four FOIL products and write the expanded expression.

Extend and Explore

What are the perimeter and area of the following shape?

Remembering Ebbinghaus – Powers 1. Write as a single power. a. x · x =

b. x2 · x3

f. x0 =

x1 =

c. y · y · y · y =

d. (a3)2 =

2. Explain the statement: (–3)2 does not equal –32 ©Edvantage Interactive 2026

Chapter 3 Polynomials

135

3.4 Practice 1a. A polynomial with one term is called a ____________________. b. A polynomial with two terms is called a ____________________. c. a(b + c) = ab + ac is called the ____________________

____________________.

d. FOIL stands for ____________________ ____________________ ____________________

____________________.

2. Multiply the monomials a. 2a × a3

b. (2.5x)(2x)

c. (5x2)(3x2)

d. ( d)( d)

e. (–2b)(–3b)

f. (–q)(–3q)

g. (9x4y)(2x4y3)

h. (1.5t)(–2t)

i. (3x2)2 3. Multiply a monomial by a binomial (distributive property). a. What does this picture represent? 2x 3

4 +

b. Draw a similar picture to represent x(x + 5).

4. What do these pictures made with algebra tile represent?

5. Simplify using the distributive property. a.

136 Chapter 3 Polynomials

©Edvantage Interactive 2026

6. Multiply each monomial by the trinomial. a. 5(a + b + c)

b. –x(x2 – x – 1)

c. 3t(t3 – t2 – 3)

d. –3c(a + b + c)

e. – (6x + 9y – 3)

f. 0.2y(10y2 – 15y + 35)

g. abc(a + b + c)

h. 0.5(0.5k2 – 0.2k – 2)

7. Simplify using the FOIL method. a. (y – 1)(y + 2)

b. (x + 4)(x + 4)

c. (–a – 1)(a + 3)

d. (x – 6)(x + 1)

e. (3m – 2)(3m – 2)

f. (2b + 4)(2b – 4)

g. (a + b)2

h. (x – 3)2

i. (0.1x – 1)(0.1x + 1)

j. (x – y)2

k. ( x – 2)(3x – 9)

l. ( a + b)2

3.4 Practice Answer Key 1a) 2) 3a) 8x + 12 b)

3a) 4)

5) 6a) 7a)

©Edvantage Interactive 2026

Chapter 3 Polynomials

137

3.5 Dividing Polynomials Warm Up Competency Focus - Represent mathematical ideas in pictorial and symbolic forms The area of a rectangle is 4x3 + 6x + 8. The width is 2. What is the length?

Monomial by Monomial

When dividing a monomial by another monomial: 1. Divide the coefficients: 2.

Subtract the exponents of like variables: When the variables are the same, subtract the exponent in the divisor from the exponent in the dividend.

Remember the quotient law: x≠0

Try This ... 1. Divide a.

138 Chapter 3 Polynomials

©Edvantage Interactive 2026

When dividing a polynomial by a monomial, you divide each term of the polynomial separately by the monomial. Then, simplify each resulting term.

Polynomial Divided by a Monomial

Try This ... 1. Divide the following: a.

Using Algebra Tiles

The picture below can help us understand polynomial division. ?

The length of the rectangle can be found by dividing the area by the width. The image above represents • • •

©Edvantage Interactive 2026

The area is –4x2 + 2x. The width is 2x. The length is –2x + 1

Chapter 3 Polynomials

139

Try This ... 1. What division do these pictures represent? What is the missing length for each? a. ? x

b. ?

c. ?

Extend and Explore The volume of a cylinder is given by

. The surface area of a cylinder is given by

twice the radius, write an expression for the ratio of the volume to surface area

140 Chapter 3 Polynomials

. If the height is

©Edvantage Interactive 2026

3.5 Practice 1. Divide the following monomials by a monomial. b. a.

2. Divide the following polynomials by a monomial. a.

3. The length of a rectangle can be found by dividing the area by the width. Find the length of the following rectangles. a. b.

©Edvantage Interactive 2026

Chapter 3 Polynomials

141

4. What division does each algebra tile diagram represent? Find the length (quotient). a. b. ?

3.5 Practice Answer Key 1a) 2a) 3a) 4a)

Remembering Ebbinghaus – Order of Operations with Fractions 1. Simplify a.

142 Chapter 3 Polynomials

©Edvantage Interactive 2026

3.6 Combined Operations and Applications Warm Up

Competency Focus - Visualize to explore mathematical concepts

What is the area of a square with a side length of x + 1? Use this area model to help you find the answer.

Combining Operations

When simplifying more complicated polynomials, remember the order of operations and the strategies you have learned in this chapter.

Sample Problem — Combining Operations Simplify the polynomial 3(x – 4) – 4(x + 3).

What to Think About

How to Do It

1. Brackets are first in BEDMAS.

3(x – 4) – 4(x + 3)

2. Use the distributive property. 3. Combine like terms.

= 3x – 12 – 4x – 12 = –x – 24

Sample Problem — Combining Operations Simplify the expression

What to Think About

How to Do It

1. Simplify the numerator using like terms. 2. Divide each term in the numerator by 2. 3. Subtract numerators (common denominator is 2). –2y – 5

©Edvantage Interactive 2026

Chapter 3 Polynomials

143

Try Together — Combining Operations Simplify.

What to Think About

How to Do It

1. Multiply each terms in brackets by ______________.

2. Write the division as two separate fractions and simplify.

3. Simplify by combining like terms.

Your Turn — Combining Operations 1. Simplify a. 8(x + 30) + 5(2x – 1)

Applications of Polynomial Operations

Use the following formulas to answer the application questions. Area of a square with side length x

A = x · x = x2

Area of a triangle

A= b·h

Area of a rectangle

A=l·w

Volume of a rectangular prism

V =l·w·h

Volume of a cube

V = x3

144 Chapter 3 Polynomials

©Edvantage Interactive 2026

Try This ... 1. Find the area of the shaded region.

2. Find the surface area and volume of a cube with side length 2x.

3. If the area of a rectangle is 9x2 – 3x and the length is 3x, what is the width?

4. Find the volume of the rectangular prism shown.

©Edvantage Interactive 2026

Chapter 3 Polynomials

145

5. Write expressions for the perimeter and area of this L-shaped garden.

6. Find the base of the triangle. Remember A = b · h.

Extend and Explore 1. Use the picture to factor the polynomial x2 + 7x + 10. Hint: Find the length and width.

2. Draw a picture to factor x2 + 5x +4.

146 Chapter 3 Polynomials

©Edvantage Interactive 2026

3.6 Practice 1. Find a partner and simplify these nine questions. Compare answers. If they are not the same, work together to make corrections.

Partner #1 Questions

Partner #2 Questions

a. 4x – 9 + 12 – 7x + y + 5x – y

a. 14 + 3x + 2y – 8x + 7x – 11 – 2y

b. (x2 + 2x) + (3x2 + 2) – (-3x2 + 11x)

b. (5x2 + 8) – (–2x2 + 6x) + (–3x – 6)

c. x – 5(x – 3) – 5

c. –2(3x + 1) + 2x + 12

d. 3x (2x + 4)

d. 6x (x + 2)

f. (3x + 2y) + 4(x – 1) + (6y – 2x – 8)

f. 2(3x + 4y – 6) – x

h. Area of a rectangle with dimensions of (3x) and (4x – 6)

h. Area of a rectangle with dimensions of (6x) and (2x – 3)

i. Perimeter of a square with sides of (2x + 4)

i. Perimeter of a triangle with sides of (x + 9), (2x – 3) and (5x + 10)

©Edvantage Interactive 2026

Chapter 3 Polynomials

147

2. Determine an expression for the perimeter of the following shapes, then simplify. a.

3. The perimeter of a triangle can be represented by 14x2 + 8x. What is the missing side length?

4. Find the area of the rectangle.

5. What is the surface area of this rectangular prism?

148 Chapter 3 Polynomials

©Edvantage Interactive 2026

6. A 1 by 1 square is cut out from each corner of the square with side length x. What is an expression for the area that is left?

7. A rectangle’s length is 2 cm greater than its width. Draw and label the rectangle. What is the perimeter? What is the area? Simplify your expressions.

3.6 Practice Answer Key 1a) 2a) 3) 4) 5) 6) 7)

Remembering Ebbinghaus – Adding and Subtracting Rational Numbers 1. What is one less than

2. What is one more than

a. –3

a. –1

c. 0.1

c. –1.9

d. –2

d. –

e. 0.02

©Edvantage Interactive 2026

Chapter 3 Polynomials

149

3 Chapter Review 1. Vocabulary - Unscramble these words and match them with examples on the right: a. inomalom

i. 3abc

b. barlieva

ii. x, y, a, b

c. kile smert

iii. a(b + c) = ab + ac

d. minolitar

iv. 6y, 12y, –2y

e. fiteccofine

v. a + b + c

f. stannoct

vi. the 5 in 5x

g. vitubirstide yporptre

vii. The 2 in 3x + 2

2. Fill in the chart Polynomial

Number of

Name

Coefficients

Constant Term

Variables

Degree

Terms a. 4x – 1 b. x2 – 6x + 2 c. t + 7 d. abcd – 4 e. 9a3 – 2a + 11 f. 2ab2 – 3bc – 1.5

3. Simplify (use zero pairs) the polynomial represented by the picture below.

4. Draw a model to represent x(x + 2) = x2 + 2x.

150 Chapter 3 Polynomials

©Edvantage Interactive 2026

5. Add or subtract. Then simplify. a. (2a – 3) + (6a – 1)

b. (4n2 – 3n – 1) + (2n2 – 6n – 2)

c. (3x2 + 6x – 8) + (–4x2 – x – 9)

d. ( y2 – y) + (y + y2)

e. (5x3 – x + 7) – (3x3 + 2x – 1)

f. (5x2 + 3x + 7) + (2x2 – x – 3)

g. (–2x2 + 0.75x – 2) – (–3x2 – 1.25x + 2.5)

h. (7x3 + 2x2 – 4x) – (4x3 – 3x2 + 6x)

6. Multiply. Then simplify. a. 2(3x – 4)

b. –6(5x – 10)

c. 2x(8x2 – 9x)

d. –3ab2(4a – 6b + 1)

7. Divide polynomials. a.

©Edvantage Interactive 2026

Chapter 3 Polynomials

151

8. Identify the errors and correct them. a. (–2x2 + 7) – (3x2 + x – 5)

b. –x(2x + 2)

–2x2 + 7 – 3x2 + x – 5

–2x + 2

–2x2 – 3x2 – x + 7 – 5

–5x2 + x + 2

9. Simplify a. 3(3x + 5) – 5(7x – 2)

b. 9x(x – 5) – (x – 2)

c. 2x(–3x + 4) – (6x2 + 11) + 3(x2 – 3x – 1)

d. 3(m – 4) – 2(m – 1) – (m + 1) + 4(m + 2)

10. Find the surface area and volume of a cube with side length 3x.

3 Chapter Review Answer Key 1a) 2a)

4) 5a)

6a) 7a)

8a)

10)

152 Chapter 3 Polynomials

©Edvantage Interactive 2026

How Did It Go? Part 1: Reflecting on Chapter 3 - Check all that apply to you ☐ The content of this chapter is challenging. ☐ I am starting to understand polynomials. ☐ I can simplify polynomials. ☐ I find word problems challenging. ☐ I need more time to practice before the test. ☐ I understand and can combine like terms. ☐ I feel more confident with algebra tiles than last year. ☐ I understand how to add, subtract, multiply and divide polynomials. ☐ I have a few questions before the test. ☐ I am confident about the content of this chapter. ☐ I can help others combine polynomial operations. ☐ I can use many different strategies to simplify polynomials. ☐ I feel confident applying skills to solve word problems. ☐ I am ready to write the test. ☐ My next step is ______________________________________________________.

Part 2: Reflecting on Visual Representations Which representation do you prefer and why?

(x + 3) x

(x + 2) x

x2 + 5x + 6

©Edvantage Interactive 2026

Chapter 3 Polynomials

153

Vocabulary List for Polynomials A Approximate – To find a value that is close to the exact answer.

B Base – The number that is multiplied by itself in a power.

C Coefficient – The number that multiplies a variable in an expression or equation.

E Evaluate – To find the value of an expression by performing the operations. Exponent – The small number in a power that tells how many times the base is used as a factor. Expression – A mathematical statement made of numbers, variables, and operations. An expression does not contain an equals sign.

P Power – A way of writing repeated multiplication using a base and an exponent. Product – The result of multiplying two or more numbers.

Q Quotient – The result of dividing one number by another.

R Repeated Multiplication – Multiplying the same number by itself more than once. Root – A number that can be multiplied by itself a certain number of times to produce a given value.

V Value – The numerical result of an expression or calculation.

154 Chapter 3 Polynomials

©Edvantage Interactive 2026

Failsafe Vocabulary Check Start by writing a definition in your own words. Then add examples and non-examples to help clarify what makes an expression a polynomial. Finally, use the symbols around the organizer to record ways that polynomials can be added, subtracted, multiplied, or divided. Be prepared to explain your thinking to others.

©Edvantage Interactive 2026

Chapter 3 Polynomials

155

156 Chapter 3 Polynomials

©Edvantage Interactive 2026

4 Linear Relations Your earnings from a minimum wage part-time job over time are an example of a linear relation. This chapter is your guide to understanding relations that change at a constant rate. You will represent these relations with words, tables, ordered pairs, graphs, and equations. This will help you understand patterns to make predictions and solve problems.

Big Idea of the Chapter Linear relationships can be represented in many connected ways to identify and generalize patterns. In this chapter you will explore: Represent a linear relation with words, tables of values, ordered pairs, graphs, and equations.

y is the same as x, y = x; (–1, –1), (0, 0), (1, 1).

Interpret graphs of linear relations.

What does the graph tell us? What do the points on the graph tell us?

Distinguish between expression vs equation.

2x + 1 vs 2x + 1 = 5.

Evaluate expressions.

What is the value of 2x + 1 when x = 5? 2(5) + 1 = 11.

Graph straight lines: horizontal, vertical, diagonal.

y = 1, x = 1, y = x.

Distinguish between inputs vs output.

Data you put in vs the result you get after.

Distinguish between independent vs dependent variables.

Input vs output, the dependent variable depends on the independent variable.

Distinguish between discrete vs continuous data.

Separate, specific values vs any value in a range.

Interpolate and extrapolate.

Estimating a value within or inside the data range vs outside the data range.

Use linear relations to solve problems in context.

How much money can I save if I put away 20% of my income over 2 years?

Get Started Canada geese can be seen flying in a "V" shape as shown in the images below.

Picture 1

Picture 2

Picture 3

Picture 4

Picture 5

Look at the three images and consider the following: a. What pattern do you see? b. How many geese would be in picture 4? c. Draw the next two pictures in the space provided. d. Why do Canada geese fly this way?

©Edvantage Interactive 2026

Chapter 4 Linear Relations

157

4.1 What is a Linear Relation? Warm Up Competency Focus - Apply mathematical understanding through inquiry Choose one of the questions below. 1. An Elder starts the day with 4 kg of tsáqwem (Saskatoon berries). After 5 days of picking, she has a total of 49 kg. If she picked the same amount of berries every day, how much did she pick each day? What do you wonder? 2. According to Statistics Canada, the population of Coquitlam, BC was 139 284 in 2016. Five years later, it was 148 625. Estimate the population today. Then compare your estimate with the most recent data. What do you wonder?

Why do we study linear relations?

Defining Linear Relations The hourly outside temperature of Surrey on January 15th

A relation in math occurs when the value of one thing depends on the value of another. • your earnings depend on length of time you work • the litres of gas used by your car depend on how far you drive • the value of your computer or car depends on its age A linear relation is a relation that changes at a constant rate. Studying relations helps us understand how different quantities are connected and how they influence one another. Starting with the study of linear relations is beneficial because they are straightforward; their constant rate of change makes them easy to predict and analyze. They build the foundation to study more complex relations such as quadratic, exponential, logarithmic and trigonometric functions. These complex functions allow us to model a wider range of real-world situations, from the growth of bacteria or the ebb and flow of an ocean tide. You will study more complex relations in Grades 11 and 12. To better understand linear relations, let’s define the two words: relation and linear. A relation in math connects or associates two things together through counting, measuring, matching, or comparing. Here are five examples of relations.

A student receives grades at the end of 8 high school courses.

158 Chapter 4 Linear Relations

The change in cost of French fries in the cafeteria over 10 years

The shoe size of a child from age 1 to 12

The distance a cyclist travels compared with time

©Edvantage Interactive 2026

A linear relation is a special kind of relation. It looks like a straight line when you graph it. When you change one variable, the other changes in a corresponding, constant way. Examples of linear relations: The total cost of a Earnings with an taxi depending on hourly salary the distance travelled

Linear or Not Linear

Comparing temperature in Celsius and Fahrenheit

Distance travelled over time if an object moves at a constant speed

A pattern is a regular or predictable arrangement. We can observe what is happening to a list of numbers and see if there is a pattern, and what kind of pattern it is. We will look at two lists of numbers, one linear and the other non-linear.

Pattern #1: 3, 6, 9, 12 ... starts with three and adds three each time. This is a linear pattern. To find the common difference of a linear pattern: Choose a number in the list and subtract the number on the left. 6–3=3 9–6=3 12 – 9 = 3

The difference between consecutive (in a row) numbers is always the same number. In this case it is 3. Because the difference is the same for all the numbers listed, we call it the common difference (in common means the same).

Linear relations will always have a common difference.

Pattern #2: 3, 9, 27, 81 ... starts with 3 and multiplies by three each time. This is a non-linear pattern. 9–3=6

The differences here are NOT the same, so it is not a linear relation.

27 – 9 = 18 81 – 27 = 54

©Edvantage Interactive 2026

It is, however, an interesting and predictable relation you will study in Grade 11. What do you notice?

Chapter 4 Linear Relations

159

Try This ... 1. Determine if the patterns listed below are linear or non-linear. Hint: Find the common difference by choosing a number in the pattern and subtracting the number on its left. Do the same with a different number from the list. Is the difference the same? Sequence of numbers

If there is a common difference? What is it?

Linear or non-linear (Circle one)

2, 5, 8, 11…

linear or non-linear

10, 0, –10, –20…

linear or non-linear

10, 100, 1000, 10 000…

linear or non-linear linear or non-linear

2, 1, 0.5, 0.25…

linear or non-linear

1.2, 1.1, 1, 0.9…

linear or non-linear

2a. Start with the number 1. Make a list of numbers by adding 4 each time. Is this linear? b. Start with the number 1. Make a list of numbers by multiplying by 4 each time. Is this linear? 3. The common difference is the difference between any two consecutive numbers in a linear pattern. Pick any number and subtract the one on the left. What is the common difference of the following linear patterns? a. 10, 16, 22, 28… b. 10, 4, –2, –8… c. 0.1, 0.2, 0.3, 0.4… d. –100, –90, –80, –70…

160 Chapter 4 Linear Relations

©Edvantage Interactive 2026

When two variables (let’s call them x and y) are related in math, one of them depends on the

Independent vs other. As one of them changes, the other changes. We can say “y depends on x”. If y depends on x, Dependent Variables then y is dependent and x is independent. Your age (a) and your height (h) are two related measurements. How can we decide which of these measurements is dependent and which one is independent? Circle the sentence below that makes the most sense: Your age (a) depends on your height (h)

Your height (h) depends on your age (a)

Questions that can help you choose: • Does your age change when your height changes? • Does your height always change on your birthday? • Does your height change over time? • If your height does not change, can you get older? Therefore, your height (h) depends on your age (a)

Try This ... 1. The table to the right shows wages and sales of a salesperson in dollars. a. Identify the independent and dependent variable.

Sales ($)

Wages ($)

400

500

430

1000

460

1500

490

2000

520

b. Is this a linear relation? How do you know?

2. This table of values shows the height of a baby in the first 12 months of life. Age (months)

Height (cm)

a. Identify the independent and dependent variables.

b. Is this a linear relation? How do you know?

©Edvantage Interactive 2026

Chapter 4 Linear Relations

161

Input/Output

When you add fruit and yogurt (input) to the blender, the blender processes it and gives you a smoothie (output). Imagine you have a magic machine that takes numbers in, does some work on them, and then gives you a new number. The number you put into the machine is called the input and the number you get out of it is called the output. If the machine takes the number 2 and gives 4, what could be happening? It could be adding 2

it could be _______________by 2

To know for sure, we need more information. Let’s try another input. If INPUT of 3 gives an OUTPUT of 5, then you know the machine was _____________. If INPUT of 3 gives an OUTPUT of 6, then you know the machine was _____________. Inputs are independent. Outputs are dependent.

Try This ... 1. Choose the dependent and independent variables (input and output) in each scenario. Hint: Which one depends on the other? Independent variable (input)

Dependent variable (output)

Amount of rainfall and the amount of corn harvested Height of a plant and amount of sunlight The tide and the force of gravity Number of toppings on a pizza and the cost of the pizza Number of pages of a book read and hours spent reading 2. Time is often the independent variable. Why do you think that is?

162 Chapter 4 Linear Relations

©Edvantage Interactive 2026

Expressions vs Equations

In a linear relation, expressions are used to describe parts of the relation. An equation states a relationship. Expression

Equation

Represents a value (number).

States a relationship or condition that can be true or false.

We factor, simplify, expand and evaluate expressions.

We create and solve equations.

Mathematical phrase that combines numbers, Mathematical statement that shows two variables, and operations but does not have expressions are the same using an equal an equals sign. sign (=). Examples:

Examples:

2x – 1, 100, 7x, x2

2x – 1 = 100, 7x = 2x – 1, x2 = 100

Consider the expression 3x – 4. It describes a value. We can take any number, multiply it by 3 and then subtract 4. 3 is the coefficient, x is the variable, and –4 is the constant Coefficient: A number multiplied by the variable Variable: A letter or symbol to represent an unknown value Constant: A number with no variable attached. It is a fixed value.

Try This ... 1. Is this an expression or an equation? Circle the correct answer. a. 5x + 1 = 2

Expression

Equation

b. 2x2 + 2x + 2

Expression

Equation

c. y – 2 = x + 4

Expression

Equation

d. –x – 3

Expression

Equation

2. Fill in the blanks for the following table. Expression 4y + 13

Coefficient

Variable

Constant 13

–2x – 5 2.3

–0.5

–7.5x + 0.1

b+1

r – 3.14

©Edvantage Interactive 2026

Chapter 4 Linear Relations

163

Evaluating an Expression

To evaluate an expression means to find its value by replacing the variable with a number. Expressions may have different values for different variables. The expression 3x has a value of 33 when x = 11 because 3(11) = 33.

Try This ... 1. Fill in the blanks in the chart below for the expression x + 1. Replace x with the number indicated on the left. x

Value of x + 1

How do you know?

1+1=2

–1

9 –11 0.1 2. Evaluate the following expressions. a. 2x + 3 if x = –4

b. 2x + 3 if x = 0.5

c. 2x + 3 if x = ½

= 2(___) + 3

= ___ + 3

= ___

3. Evaluate –4t + 1 when t has the following values: a. t = 0

b. t = 1

c. t = –1

d. t = 2

e. t = –0.25

164 Chapter 4 Linear Relations

©Edvantage Interactive 2026

The Cartesian Coordinate System

Visualizing a pattern or relationship can help us to understand, compare, and solve problems related to the pattern. The Cartesian Coordinate System is used around the world and in many different professions: science, engineering, computer graphics, economics, medicine, geography, robotics, and more. René Descartes, a French mathematician who coined the phrase “I think, therefore I am”, introduced the idea of specifying the location of a point using intersecting lines as measuring guides. The point of intersection of the two lines (or axes) is called the origin. The horizontal axis is labelled x and the vertical axis is labelled y. To specify a point we use an ordered pair of numbers called coordinates. An example of an ordered pair coordinate is (1, 2). The first number is the x-coordinate and tells you the position on the horizontal or x-axis. The second number is the y-coordinate and tells you the position on the vertical or y-axis. There are four quadrants (areas/regions) made by the two lines (x-axis and y-axis). Each point is a certain distance away from the origin. The origin is (0, 0). A point that is 2 units to the left and 5 units up from the origin would be (–2, 5).

Try This ... 1. Write the coordinates (x, y) of the points represented by the letters on the grid. A. (

)

B. (

)

C. (

)

D. (

)

E. (

)

F. (

) Continued on next page ...

©Edvantage Interactive 2026

Chapter 4 Linear Relations

165

2. Plot the following points.

A. (1, 2)

F. (0, –3)

B. (0, 0)

G. (–4, 0)

C. (–3, –3)

H. (2, 2)

D. (5, 4)

I. (–4, 2)

E. (–2, 1)

J. (–1, –4)

Extend and Explore How many regular hexagons can you find in this picture? How did you count? Did you notice any patterns as you counted? Could you use that information to predict the number in a smaller or bigger version of this picture?

Remembering Ebbinghaus – Powers 1. List the perfect squares from 0 to 100.

2. Explain why –32 ≠ (–3)2

166 Chapter 4 Linear Relations

©Edvantage Interactive 2026

4.1 Practice 1. Fill in the Blanks a. Independent variables are ________ (inputs or outputs). They are variables you choose or control. b. Dependent variables are _______(inputs or outputs). These variables measure the effect of the relation. c. 3x + 1 is an example of an _________________ (expression or equation) d. 3x + 1 = 7 is an example of an _______________ (expression or equation) e. In the expression f. The _________________ lines called _________.

the coefficient is ____, the variable is ____, and the constant is ____ coordinate system is a way to locate points on a flat surface using two perpendicular number

g. The ____________ is what we call the point (0, 0) h. The horizontal axis is called the ___________. The vertical axis is called the ______________. 2. Fill in the table. Sequence of numbers

5th term

6th term

Linear or non-linear

a. 4, 7, 10, 13...

linear non-linear

b. 2, 4, 8, 16...

linear non-linear

c. 2, 1, 0, –1...

linear non-linear

, 0, , 1...

Common difference if linear

linear non-linear

e. 1, 0.5, 0.25, 0.125...

linear non-linear

f. 2, 12, 22, 32

linear non-linear

g. 2, –8, –18, –28...

linear non-linear

3. Choose the dependent and independent variables in each scenario. Dependent or Independent?

Dependent or Independent?

a. How many shirts you pack

b. Length of your trip

c. Weight of the ground turkey

d. Cost of the ground turkey

e. Amount of tax you pay when you purchase a calculator

f. Cost of the calculator

g. Time spent playing a video game

h. Level achieved in the video game

©Edvantage Interactive 2026

Chapter 4 Linear Relations

167

4. Fill in the blanks. Expression

Coefficient

Variable

Constant

–5

10x – 2 b + 1.5

y2 5. Evaluate the expressions. a. 5x – 1 if x = 10

b. –2x –1 if x = 1

– 5 if x = 10

d. 0.01x if x = 100

e. 7.2x – 9 if x = 0

h. –0.1x if x = –0.1

if x = 1

if x = 16

6. Find the value of –x – 1 when x has the following values. a. x = 0

b. x = 1

c. x = –1

d. x = 2

e. x = –2

f. x = –100

168 Chapter 4 Linear Relations

©Edvantage Interactive 2026

7. Write the coordinates of the points represented by the letters. A. ( B.(

, ,

) )

C. (

)

D. (

)

E. (

)

F. (

)

8. Plot the following points on the grid provided. A. (0, 0)

F. (0, –4)

B. (–2, –2)

G. (–1, 0)

C. (1, –3)

H. (–3, –1)

D. (3, 4) E. (–2, 5)

4.1 Practice Answer Key 1a) input b) output c) expression d) equation e) –½, x, 3.4 f) Cartesian; axes g)origin h) x-axis; y-axis 2a) 16, 19, linear, 3 b) 32, 64, non-linear c)–2, –3, linear, –1 d) 1½, 2, linear, ½ e) 0.0625, 0.03125, non-linear f) 42, 52, linear, 10 g) –38, –48, linear, –10 3a) dep b) ind c)ind d)dep e)dep f)ind g)ind h)dep

7) A(–2, –2); B(2,4); C(2, –3); D(–1,0); E(–1,2); F(0, 3)

4) row 1: 10, x, –2; row 2: 3y – 5; row 3: 1, b, 1.5; row 4: x; row 5: –½, y, 0,

5a) 49 b) –3 c) 0 d) 1 e) –9 f) 12 g) 1 h) 0.01 6a) –1 b) –2 c) 0 d) –3 e) 1 f) 99

©Edvantage Interactive 2026

Chapter 4 Linear Relations

169

4.2 Representing Linear Relations Warm Up Competency Focus - Use logic and patterns to play games The game Battleship is a great way to practice learning the coordinates on a grid. In this game, the goal is to sink your opponent's ships by searching the grid. Here are the rules. • • • • • • •

2 players: Each player draws one of each ship horizontally or vertically on their grid. Players take turns calling out coordinates, e.g., "Fire at (3, −4)”. The opponent responds with "Hit" if the coordinate hits any part of a ship, or "Miss" if it does not. Players mark hits and misses on the tracking grid. When all coordinates of a ship have been hit, that ship is "sunk." The opponent must announce which ship was sunk. The first player to sink all of the opponent’s ships wins. Your Ships

Tracking Grid

Ship Legend Carrier

5 points

Battleship

4 points

Cruiser

3 points

Submarine

3 points

Destroyer

2 points

170 Chapter 4 Linear Relations

©Edvantage Interactive 2026

Representing Linear Relations

We can represent linear relations in many different ways. We do this to deepen understanding, communicate clearly, generalize, visualize, and solve problems. We can use words, ordered pairs, tables of values, equations, and graphs. Here is an example of a linear relation represented in five different ways:

Words

Equation

Ordered Pairs

For each increase of one in y = –2x + 1 x, y decreases by two. Table of Values x

–1

–3

Connecting Words and Tables of Values

(0, 1), (1, –1) and (2, –3) are points on the graph.

Graph

Words give us context for a relation. They can help us identify the inputs and outputs. By choosing inputs and calculating outputs we can create a table of values.

Sample Problem — Representing Linear Relations Movie tickets are $16 each. The cost of buying tickets depends on the number of tickets. Create a table of values.

What to Think About

Zero tickets cost zero dollars One ticket costs 16 dollars. 2 tickets cost 32 dollars ($16 × 2 = $32) 3 tickets cost 48 dollars ($16 × 3 = $48) 4 tickets cost 64 dollars ($16 × 4 = $64)

©Edvantage Interactive 2026

How to Do It Number of Tickets

Cost ($)

Chapter 4 Linear Relations

171

Try Together — Representing Linear Relations A drone starts at a height of 0.5 metres and rises at a rate of 1 metre per second. Fill in the table of values to show the height of the drone at the time indicated.

What to Think About

How to Do It

The starting height is _______. After one second, the height is _______.

Time (seconds)

After two seconds, the height is _______.

After three seconds, the height is _______.

After four seconds, the height is _______.

After ten seconds, the height is _______.

Height (metres)

4 10

Connecting Equations and Tables of Values

Equations give us a rule to follow to generate outputs for a given input. Pick input values, substitute them into the equation, and then compute the outputs. Place them in a table of values.

Sample Problem — Connecting Equations and Tables of Values Create a table of values from a linear equation: y = 2x + 1.

What to Think About

How to Do It

1. Choose some values for x. We will use the following values for x: –1, 0, 1. 2. Plug each x value into the equation to find y.

y = 2x + 1

when x = –1

when x = 0

when x = 1

y = 2 (–1) + 1

y = 2 (0) + 1

y = 2 (1) + 1

y = –2 + 1

y=0+1

y=2+1

y = –1

y=1

y=3

3. Write the y-values in the table

172 Chapter 4 Linear Relations

–1

©Edvantage Interactive 2026

Try Together — Connecting Equations and Tables of Values Create a table of values from a linear equation: y = –0.5x + 2.5

What to Think About

How to Do It

1. Choose some simple values for x. We will use the following values for x: –1, 0, 1.

y = –0.5x + 2.5

when x = –1

when x = 0

when x = 1

y = –0.5(___) + 2.5

2. Plug each x value into the equation to find y.

3. Calculate y for each x. x

4. Write the values in the table.

–1 0 1

Your Turn — Connecting Equations and Tables of Values 1. Fill in a table of values for each equation. a. y = –x

b. y = x – 4

c. y = 3x + 1

–2

–1

©Edvantage Interactive 2026

Chapter 4 Linear Relations

173

Connecting Words, Equations and Ordered Pairs

Words can give us context for a relation. They help us identify the inputs and outputs which become ordered pairs. Words can also help us to make an equation.

Sample Problem — Connecting Words, Equations and Ordered Pairs Make an equation and list three ordered pairs for the amount of water needed to cook rice if 2 cups of water are needed for every 1 cup of rice.

What to Think About

How to Do It

Cook 1 cup of rice with two cups of water. We double the number of cups of rice to find the cups of water.

y = 2x.

Choose an x value (input), double it, and it becomes the y value (output) to make a list of ordered pairs. To make 1 cup of rice we need 2 cups of water. To make 1.5 cups of rice we need 3 cups of water. To make 2 cups of rice we need 4 cups of water.

The ordered pair is (1, 2). The ordered pair is (1.5, 3). The ordered pair is (2, 4).

Try Together — Connecting Words, Equations and Ordered Pairs Make an equation and a list of 3 ordered pairs that are represented by these words: A student gets $10 per hour to do yard work.

What to Think About 1. If the student works for one hour, they make _______ dollars 2. If the student works for two hours, they make ______ dollars. 3. If the student works for 3 hours, they make _____ dollars

How to Do It The ordered pairs are:

(1, ____) (2 , ____) (3 , ____) y = ____ x

4. If a student works x hours, how much money do they make? Use this pattern to write an equation.

174 Chapter 4 Linear Relations

©Edvantage Interactive 2026

Your Turn — Connecting Words, Equations and Ordered Pairs 1. Make an equation and a list of 3 ordered pairs that are represented by these words: A taxi charges a fee of $2.50 plus an additional $2.50 per km travelled. Let x be the number of km travelled and y be the total cost.

2. A streaming service charges a $10 subscription fee plus $3 per new movie rental.

3. A gym membership charges a monthly fee of $20 plus $5 per group class.

Connecting Tables of Values, Equations and Graphs

We can use a table of values to plot two or more points on a grid, and join them together (if appropriate) to graph a line. An equation can help us fill in the table of values.

Sample Problem — Equations, Table of Values and Graphs Make a table of values and a graph using the equation y = –x.

What to Think About 1. Create a table of values.

2. The table of values gives us 4 points to plot on the grid. Plot them on the grid provided and then draw a line through them.

©Edvantage Interactive 2026

How to Do It x

–1

–2

Chapter 4 Linear Relations

175

Try Together — Equations, Table of Values and Graphs Fill in the table and graph the equation y = 2x – 3.

What to Think About 1. Create a table of values.

2. The table of values gives us 5 points to plot on the grid. Plot them on the grid provided and then draw a line through them.

How to Do It x

–2 –1 0 1 2

Your Turn — Equations, Table of Values and Graphs 1. Fill in the table and graph the equation y = –2x + 4.

–2 –1 0 1 2

176 Chapter 4 Linear Relations

©Edvantage Interactive 2026

Connecting Them All Together

Now let's take words, tables of values, questions and graphs and connect them all together using the following example.

Sample Problem — Connecting it All Together One banquet table seats 8 people, three on each side, and two at the ends. Rectangular tables can be connected end to end, as shown up to a maximum of 6 tables. Make a table of values with 6 ordered pairs, make an equation and a graph.

What to Think About

How to Do It

The equation to represent this is y = 6x + 2 where x is the number of tables and y is the number of people.

Below are three examples of how the tables could be arranged.

Notice how when we add a table in the picture to the right, 6 more people can sit down. Make a table of values and graph to show how many people can be seated. One table seats 8, 2 tables seat 14, up to a maximum of 6 tables seating 38 people.

(6, 38)

(5, 32)

Number of people

We do not join the points on this graph with a line, as it does not make sense to have half a person seated at a table, and we cannot add part of a table. If we extend the line to the left, it touches the y-axis at (0, 2). This point does not make sense, as it means the zero tables provide seating for 2 people.

(4, 26) (3, 20)

(2, 14)

(1, 8) 0

Number of tables

Notice how the number of people is increasing by 6 as we move down the table of values.

©Edvantage Interactive 2026

Chapter 4 Linear Relations

177

Try Together — Connecting it All Together A drone starts at ground level and rises at a rate of 2 metres per second. Use the words in step 1 below to create a table of values, list of ordered pairs, equation, and graph.

What to Think About 1. Words 2. Table of Values

How to Do It x

0 1

3. Ordered Pairs

2 3

4. Equation Questions to consider - Does it make sense to have negative values for x or y here? - In reality, what are some of the limitations of the height of the drone that would impact this relation? - How will these limitations impact the graph?

( 0, ____ ), ( 1, ____ ), ( 2, ____ ), ( 3, ____ ), y=

Your Turn — Connecting it All Together 1. A cell phone plan has a fixed cost of $25 with a local talk rate of 30 cents ($0.30) per minute. The equation representing this is y = 0.3x + 25. a. Create a table of values where x is the number of minutes and y is the cost in dollars. Plot the points on the grid provided and label them.

b. Use the table and graph to answer these questions: i. How much money do you pay if you do not make any phone calls?

ii. Where is that point on the graph?

178 Chapter 4 Linear Relations

©Edvantage Interactive 2026

Extend and Explore 1. What number pattern will the computer print:

2. Rewrite the code so that the computer will print 2, 5, 8 ...

Remembering Ebbinghaus – Evaluate Monomials 1. Find the value of xyz when x = −3, y = −4, and z = −5.

4. Find the value of xyz if x = , y = , z =

2. Find the value of −xyz when x = , y = , and z = .

5. Find the value of – xyz if x = – , y = – , z = –

3. Find the value of x²y²z² when x = −1, y = −2, and z = .

6. Find the value of xyz if x = 0.1, y = 0.2, z = 0.3

©Edvantage Interactive 2026

Chapter 4 Linear Relations

179

4.2 Practice 1. Vocabulary – Fill in the Blanks Linear relations can be represented in different ways. Unscramble the letters a. __________________ drows

b. __________________ letab fo luvase

c. __________________ pragh

d. __________________ questaino

e. __________________ edorred spira 2. Match the equations to the graphs a. y = –2x

b. y = x – 3

ii.

c. y = ½x iii.

d. y = –x + 1 iv.

3. Table of Values and Graphing – A drone starts at a height of 15 metres and falls at a rate of 2 metres per second. Fill in the table of values and plot the points on the grid provided. Time (seconds)

Height (metres)

0 1 2 3 4 5

4. Table of Values and Ordered Pairs – Fill in a table of values for each equation, then list 5 ordered pairs. a. y = –x x

b. y = x + 4

c. y = –2x

d. y = –2x – 1

–2

–1

Ordered pairs:

180 Chapter 4 Linear Relations

Ordered pairs:

©Edvantage Interactive 2026

5. Fill in the blank in each equation using the table of values or list of ordered pairs provided. y = 2x + ____

y = x – ____

y = 3x + ____

y = –x + ____

(1, 4), (2, 7), (3, 10)

(0, 1), (1, 0), (2, –1)

6. Circle the points that are on the graph y = –x – 1. a. (0, –1)

b. (1, 0)

c. (–1, 0)

d. (3, –4)

e. (–10, –11)

f. (–2.5, 1.5)

g. (½, –½)

h. (–½, –½)

7. Fill in the blanks for the ordered pairs for the following linear relation: y = 10x – 3 (1, ____ )

(0, ____ )

(–1, ____ )

(10, ____ )

(½, ____ )

d. (512, 1024)

e. (0.5, 0.25)

8. Circle the ordered pairs that represent ordered pairs for the equation y = 2x. a. (12, 24)

b. (2, 1)

c. (¼, ½)

9. Use the sequence of numbers to answer the following questions: 5, 1, –3, –7… a. Make a table of values for the first five terms of the linear sequence. Term Number

Term Value

b. Using the table can you predict the 6th term? _______ c. Fill in the blank to make an equation for this relation: y = –4x + _______.

©Edvantage Interactive 2026

Chapter 4 Linear Relations

181

10. Count the small circles in each figure. Draw Figure iv. i.

ii.

iii.

iv.

a. Make a table of values with this information

b. Predict the number of small circles in figure v. (x= figure number, y= number of small circles).

c. Describe the relation in words.

d. Draw a graph.

4.2 Practice Answer Key 1a) words b) table of values c) graph d) equations e) ordered pairs 2a) i b) ii c) iv d) iii 3) table: 15, 13, 11, 9, 7, 5 4) table a: 2, 1, 0, –1,–2; table b: 2, 3, 4, 5, 6; table c: 4, 2, 0, –2, –4; table d: 3, 1, –1, –3, –5 5) y=2x + 3, y = x – 1, y = 3x + 1 , y = –x + 1 6) a, c, d, f, h 7) 7, –3, –13, 97, 2 8) a, c, d 9a) (2,1) (3,–3) (4,–7) (5, –11) (6, –15) b) –15, subtract 4 each time c) y = –4x+9 10a) (1,1) (2,5) (3, 9) b) 17 c) add 4 each time d) Graph to the right.

182 Chapter 4 Linear Relations

©Edvantage Interactive 2026

4.3 Graphing Linear Relations Warm Up Competency Focus - Visualize to explore mathematical concepts The four graphs below are similar yet different. What do they have in common? Describe a few characteristics that make them unique. a.

d. c.

Graphing a relation or equation helps us to visualize the relationship. We can see how fast things are changing and how they are changing (increasing or decreasing). We can make predictions and estimations as well as spot outliers and errors. One of the simplest ways to graph a line is to make a table of values to find two or more points on the line. Draw a straight line through the points (a ruler or straightedge can help keep the line straight). There are many other ways we can graph a line and they will be studied in detail next year.

Graphing a Horizontal or Vertical Line

A horizontal line is a straight line that runs left–right, like the horizon. On a coordinate plane it has no vertical change, so every point has the same y‑value. If your thermostat is set for room temperature, the graph of the temperature over time could be a horizontal line. For example, the graph of the table of values is on the grid. The y-value is always 2. The line is horizontal. The equation for this line is y = 2. x

–2

–1

2 • •

©Edvantage Interactive 2026

−5

What is the connection between the table of values and the graph? If the y-axis represented distance and the x-axis represented time, what could be happening here? Can you think of a different scenario to represent this data? Chapter 4 Linear Relations

183

A vertical line is a straight line that runs up–down. On a coordinate plane it has no horizontal change, so every point has the same x‑value. This could represent a fixed date upon which many different events occur. Plot the points on the grid provided. What do you notice about the x-value? What do you notice about the line? The equation for this line is x = 2. x

–2

–1

−5

Can you think of a scenario to represent this data? What is the connection between the table of values and the equation and the graph?

Try Together — Graphing Vertical and Horizontal Lines Graph two lines, one on each grid: x = 1 and y = 5.

What to Think About 1. Plot the points on the grid. 2. Draw a line to join them. 3. Is it vertical or horizontal?

How to Do It x

–1

The equation of the line is _______________.

–1

The equation of the line is _______________.

184 Chapter 4 Linear Relations

©Edvantage Interactive 2026

Your Turn — Graphing Vertical and Horizontal Lines 1. Is the line horizontal or vertical?

–1

–2

The equation of the line is _______________. 2. Is the line horizontal or vertical? x

–3

–1

–3

The equation of the line is _______________. 3. Fill in the blanks in the tables and then graph the following on the grid provided. Label each line with a letter from A to F.

x=8

y=1

–1

x = –6

C. x

y=0

D. y

–6

x=4

E. x

©Edvantage Interactive 2026

y = –7

F. y

Chapter 4 Linear Relations

185

Graphing an Equation in the Form y=x+b

Look at the graphs of y = x and y = x + 2 on the grid provided.

Notice: • The solid line y = x goes through the origin (0, 0). • The dotted line y = x + 2 goes through (0, 2). • These two lines never cross. • If you moved the solid line up 2, you would get the dotted line. • These lines are parallel. Lines that never cross are called parallel.

Try Together — Graphing an Equation in the Form y = x + b Fill in the table of values and plot the points for y = x – 3 and y = x – 5. Draw the two lines on the grid provided.

What to Think About

How to Do It a. y=x–3

1. Fill in the tables

0 2. Plot the points and join them with a line.

1 2 b. y=x–5 x

0 1 2

186 Chapter 4 Linear Relations

©Edvantage Interactive 2026

Your Turn — Graphing an Equation in the Form y = x + b 1. Graph the following lines on the grid provided. Label the lines A-D. y=x–1

A. x

y=x+6

–1

3 2 1

y=x

C. x

y=x–5

D. y

–1

−7 −6 −5 −4 −3 −2 −1 −1

−2 −3 −4 −5 −6 −7

Graphing an Equation in the Form y = –x + b

The linear relations y = x and y = –x are graphed on the grid to the right.

Notice that • y = x is a diagonal line going up and right. • y = –x is a diagonal line going down and right. • The two lines intersect at the origin (0,0). • The lines are perpendicular (90°).

−10

−5

−10

The table of values on the left shows that y increases in value (gets bigger) as x increases. The table of values on the right shows that y decreases in value (gets smaller) as x increases. y=x

©Edvantage Interactive 2026

y = –x

–1

–2

–3

–4

–5

Chapter 4 Linear Relations

187

Try This ... Circle the correct words. 1. If the coefficient of x is positive the line is increasing / decreasing. 2. If the coefficient of x is negative the line is increasing / decreasing. 3. y = 8x – 3 is increasing / decreasing because 8 is positive. 4. y = –3x + 8 is increasing / decreasing because –3 is negative. 5. y = –x – 1 is increasing / decreasing because ____________________________. 6. y =

x–

is increasing / decreasing because ____________________________.

7. y =

is increasing / decreasing.

8. y = 0.1x + 2 is increasing / decreasing.

Try Together — Graphing an Equation in the Form y = –x + b Fill in the table of values and plot the points for y = –x – 3 and y = –x + 5. Draw the two lines on the grid provided.

What to Think About

How to Do It y = –x – 3

A. 1. Fill in tables.

0 2. Plot points

1 2

3. Join them with a line. y = –x + 5

B. 4. Label the line.

0 1 2

188 Chapter 4 Linear Relations

©Edvantage Interactive 2026

Your Turn — Graphing an Equation in the Form y = –x + b 1. Graph the following lines on the grid provided. Label the lines A-D. A. y = –x B. y = –x + 4 C. y = –x – 5 D. y = –x + 1

2. These lines are pa __ __ __ __ __ l.

Graphing an Equation in the Form y = mx + b

Equation Coefficient of x

When you connect the indicated points with horizontal and vertical lines it will look like a staircase.

y=x

y = 2x

y = 3x

What do you notice about these 3 lines? Look at the above graphs. Imagine walking up a hill with the same slant as these 3 lines. • The steeper the hill, the more difficult it would be to climb. • Line y = 2x is twice as steep as y = x. • Line y = 3x is three times as steep as y = x. • All three lines go through the origin (0, 0). • The steepness depends on the coefficient of x. This is the number multiplied by x. • We will use the variable m to represent the steepness, or slope, of the line next year in Math 10.

©Edvantage Interactive 2026

Chapter 4 Linear Relations

189

Try Together— Graphing lines in the form y = mx Fill in the table of values for each equation. Plot the points and draw a line for A. y =

What to Think About

How to Do It

1. Fill in the tables. Even number x values are chosen here to make it easier to divide by 2.

y= x

x and B. y = – x.

x y

2. Plot the points.

2 4

3. Draw the lines.

y=– x

B. x

0 2 4

Your Turn — Graphing lines in the form y = mx 1. Graph the following lines on the grid provided. Label the lines A-D. a. y = 4x

b. y = –4x

c. y =

d. y = –

190 Chapter 4 Linear Relations

©Edvantage Interactive 2026

What Does b do in the Equation y = mx + b

The following lines have been graphed on the grid. y = 3x y = 3x + 1 y = 3x – 3 Notice in this graph, • The three lines are parallel. • They have the same steepness. • They cross the y-axis at points –3, 0, 1. • A y-intercept is a point where a graph crosses the y-axis; in the equation y = mx + b, b is the y-intercept.

Try Together — Graphing linear equations using "b" Graph the following lines on the grid. Notice where they touch the y-axis. These are the y-intercepts. A. y = –2x

What to Think About

B. y = –2x + 2

C. y = –2x + 4

How to Do It y = –2x

A. 1. Make a table of values

B. y = –2x + 2 x

C. y = –2x + 4 x

2. Graph and label the lines

©Edvantage Interactive 2026

Chapter 4 Linear Relations

191

Extend and Explore

Cartoon animators create the illusion of motion by projecting a sequence of drawings called frames. The typical speed of projection in animation is about 24 frames per second (fps). • How many frames would be in a three-minute short film? • Create a one- or two-second animation using a small pack of sticky notes or cut up paper, staple the pages, and create a small booklet.

Remembering Ebbinghaus – Equivalent Fractions 1. Complete each equivalent fraction. a.

2. Fill in the blank with < , > or = a.

3. Which of the following are equal to –

192 Chapter 4 Linear Relations

? Circle them.

©Edvantage Interactive 2026

4.3 Practice 1. Fill in the Blanks a. x = 1 is an example of a ________________________line. (vertical / horizontal) b. y = 1 is an example of a ________________________line. (vertical / horizontal) c. If y = x + 2, the y-intercept of the graph is ________________________. d. The point where the line crosses the y-axis is called a ________________________. e. y = x is an example of a(n) ________________________ line. f. y = –x is an example of a(n) ________________________ line. g. The line y = 4x is _________ times as steep as the line y = x. h. In a decreasing line the value of y gets _________ when the value of x gets bigger. 2. Graph and label with a letter the following lines on the grid provided. a. y = 3 b. x = 7 c. y = –2 d. x = –5 e. y = 0 f. x = 0 g. What do we call the line x = 0? ________________________ h. What do we call the line y = 0? ________________________

3. Graph and label with a letter the following lines on the grid provided. a. y = x b. y = –x c. y = x + 3 d. y = x – 3 e. y = –x + 3 f. y = –x – 3

©Edvantage Interactive 2026

Chapter 4 Linear Relations

193

4. Match the following equations with the graphs on the right a. y = x + 5 b. y = x – 5 c. y = –x + 5 d. y = –x – 5

5. Choose which line corresponds to the following equations a. y = –2x

______

b. y = –2x + 4

______

c. y = –2x – 1

______

d. What do you notice about the 3 lines?

6. Match the two equations to the correct graph. 5

a. y = x + 3

b. y = x + 2

-5

194 Chapter 4 Linear Relations

-5

©Edvantage Interactive 2026

7. Match these 9 equations with the corresponding graphs. Hint: the point where the line touches the y-axis and/or making a table of values can be helpful, along with what you know about increasing, decreasing, horizontal and vertical lines. a. y = –x

b. y = –x – 3

c. y = x – 4

d. x = 3

f. y = ½x

g. y = 2x + 2

h. y = 3x– 3

i. y = –3x

−5

2. ______________________

3. ______________________

−5

4. ______________________

5. ______________________

−5

1. ______________________

−5

e. y = –3

6. ______________________

−5

7. ______________________

−5

8. ______________________

−5

9. ______________________

4.3 Practice Answer Key Please go to Answer Key after the Check Your Understanding questions.

©Edvantage Interactive 2026

Chapter 4 Linear Relations

195

4.1 – 4.3 Check Your Understanding 1. Unscramble the words to fill in the blanks. a. 3x – 2 is an _______________.

ioeersnspx

b. A pattern that changes at a constant rate like y = x and y =–2x + 3 and looks like a straight eilran otlerain line when graphed is called a _______________ _______________. c. An equation that represents how specific quantities like distance, speed and time are related is called a _______________.

malurof

d. A mathematical relationship with two expressions on either side of an equal sign is called an _______________.

qonatuie

e. The letter x in 2x+3 is called a _______________.

abeviral

f. To _______________ –x – 1 when x = –1, we determine the value of this expression when x = –1 letavaue g. A two-column chart that lists inputs and outputs is called a _______________ _______________ _______________.

lebta fo suavle

h. The point (0, 0) is called the _______________.

grioni

i. _______________ lines never intersect.

lelarapel

j. A linear relation is _______________ when the graph of the line goes up and right.

sciengiran

2. Write the coordinates of the points represented by letters. a. (

)

b. (

)

c. (

)

d. (

)

e. (

)

f. (

)

5 c

−5

5 e

a f

−5

3. Each row describes a relation. Which one depends on the other? Relation

Dependent or independent?

a. Number of people in the household

b. Litres of water used in a household

c. Heart rate of a person on an elliptical machine

d. RPM (revolutions per minute) while using the elliptical

e. Number of products sold

f. Revenue from product sales

g. Time of day

h. Number of people in the gym

196 Chapter 4 Linear Relations

©Edvantage Interactive 2026

4. Fill in the blanks Expression

Coefficient

Variable

Constant

a. –3x – 1.5 b. c. c + 1 d. e.

x+ 9

5. Circle the incorrect number in each linear pattern below and correct it. Hint: The common difference should always be the same. a. 2, 6, 11, 14, 18

_____

b. 5, 12, 15, 20, 25

_____

d. –1, –4, –7, –11, –13

_____

e. 0.5, 0.2, –0.1, –0.5, –0.7 _____

c. 37, 34, 31, 27, 25

_____

6. Fill in the blanks a. 2, 5, _____, 11, _____

b. 3, _____, 11, _____, 19

d. 100, 94, _____, _____, 76

e. –2, _____, –18, –26

c. _____, 1, -1, _____, –5

7. For each linear equation create a table of values and a graph. a. y = 5 x

b. x = –2 x

©Edvantage Interactive 2026

Chapter 4 Linear Relations

197

c. y = 2x + 1 x

d. y = 3x – 1 x

8. Which sets of ordered pairs represent linear relations? How do you know? Linear? (Yes / No) Set A

(0, 0) (1, 1)

(2, 4)

(3, 9)

Set B

(0, 0) (1, 1)

(2, 2)

(3, 3)

Set C

(0, 0) (–1, 1) (–2, 2)

(–3, 3)

Set D

(0, 0) (1, –1) (2, –2) (3, –3)

Set E

(0, 0) (1, 1)

(2, 8)

Reason

(3, 27) B

9. If the solid line represents the equation y = –x then what are the equations for lines A, B and C? Hint: look at the y-intercept

−10

−5

−10

198 Chapter 4 Linear Relations

©Edvantage Interactive 2026

How's it Going? Below is a student’s quiz with 9 questions. Some answers are correct and some are not. Give a check mark if the question is solved correctly. If it is not, circle the error and correct the error in the space provided on the right of each question. Evaluate the following expressions for the indicated value of x. a. 5x + 6, x = –4

12 − 3x, x = −2

c. ½ x + 1, x = 2

5(–4) + 6

= 12 − 3(−2)

= ½ (2) + 1

= –20 + 6

= 12 − 6

=1+1

= –26

−2x + 3, x = −1

−4x − 4, x = 1

f. 2x − 5, x = −2

= −2(−1) + 3

= −4(1) − 4

=2(2) − 5

=2+3

=4−5

= −1

g. =

( )+

, x=

0.1x − 0.2, x = 0.2

–3.6x + 2.7, x = 0

= 0.1(0.2) − 0.2

= –3.6 ( 0 ) + 2.7

= 0.02 − 0.2

= 0 + 2.7

= −0.18

= 2.7

2. Graph the following equations on the grid provided. a. x = –3

©Edvantage Interactive 2026

b. y = 1

c. y = – x

Chapter 4 Linear Relations

199

4.3 Practice Answer Key 1a) Vertical b) Horizontal c) 2 d) y-intercept e) Increasing f) decreasing g) 4 h) smaller 2a) y = 3

3a) y = x

b) x = 7

b) y = –x

c) y = –2

c) y = x + 3

d) x = –5

d) y = x – 3

e) y = 0

e) y = –x + 3

f) x = 0

f) y = –x – 3

g) y -axis h) x -axis 4a) A b) B c) D d) C 5a) B b) C c) A these lines are parallel 6a) B b) A 7a) 5 b) 8. c) 6 d) 3 e) 1 f) 4. g) 7 h) 9 i) 2

4.1 – 4.3 Check Your Understanding Answer Key 1a) expression b) linear relation c) formula d) equation e) variable f) evaluate g) table of values h) origin i) parallel j) increasing 2a) (–4, –1) b) (–1, 1) c) (1, 4) d) (3, 1) e) (1, –1) f) (0, –2) 3a) independent b) dependent c) Dependent d) independent e) independent f) dependent g) independent h)dependent 4a) –3, x, –1.5 b) 5x + 5 c) 1, c, 1 d) x –

x, 9

5a) 11 should be 10 b) 12 should be 10 c) 27 should be 28 d) –11 should be –10 e) –0.5 should be –0.4 6a) 8, 14 b) 7, 15 c) 3, –3 d) 88, 82 e) –10 7)

c. y = 2x + 1

−10

−5

−10

d. y = 3x − 1

−1

−10

−5

−10

Note: Table of values may vary 8a) B, C, D because they have a common difference 9a) y = –x – 2 b) y = –x + 2 c) y = –x + 4

How’s it Going? Answer Key a) –14 b) 18 c) Correct d) Correct e) –8

f) –9 g) Correct h) Correct i) Correct

2a) Correct b) Incorrect c) Correct

200 Chapter 4 Linear Relations

©Edvantage Interactive 2026

4.4 Interpreting Graphs of Linear Relations Warm Up Competency Focus - Use reasoning and logic to explore, analyze, and apply mathematical ideas What could these graphs mean? Pick a scenario and tell a story. Share it with a partner or the class.

Discrete vs Continuous

When making a graph using data, it is important to know whether the data is continuous or discrete. Discrete data

Continuous data

Picture

Nature of Values

Specific values

Any value within a range of values

Type of measurement

Counting items

Measuring precisely

Graph

Graph has dots and gaps

Smooth line with no gaps

Examples

Number of cars or number of people

Distance or length of time

©Edvantage Interactive 2026

Chapter 4 Linear Relations

201

Try This ... 1. For each of these examples of data, circle whether each example is discrete or continuous. a. Number of pets in my home

discrete

continuous

b. Number of emails you receive in one day

discrete

continuous

c. Speed of a car driving from home to school and back

discrete

continuous

d. Number of eggs in a carton

discrete

continuous

e. Volume of air in an expanding balloon

discrete

continuous

Interpolation vs Extrapolation

In the graph below we can see that when x = 1, y = 5. When x = 2, y = 10. How can we use the graph below to estimate y when x = 1.5? We use a process called interpolation.

Interpolation is the process of estimating a value within the range of known data points. In the above example, you looked between the values of x = 1 and x = 2 to estimate y when x = 1.5 and we find y = 7.5. Extrapolation is the process of estimating a value outside the range of known data points. In the above example you looked beyond the value of x = 5 and followed the trend to estimate when x = 6. We can estimate y to be 30. Is it reasonable? It is important to make sure that the processes of interpolation and extrapolation make sense and are reasonable. Some numbers won’t make sense in different contexts. It does not always make sense to extrapolate or interpolate.

Try This ... 1. Is each interpolation or extrapolation reasonable? Circle Yes or No a. You track a plant’s height from day 1 to day 10 and see steady growth. You extrapolate this growth linearly to day 100.

Yes

b. You count how many siblings each student has in your class and interpolate to find out who has 2.5 siblings.

Yes

c. You estimate the population of Canada in 2040 by studying the population growth for the last 100 years.

Yes

202 Chapter 4 Linear Relations

©Edvantage Interactive 2026

2. The three points on the graph represent data in a linear relation. Interpolate and extrapolate the following values. Interpolate a. Estimate y when x = 2

______________

b. Estimate y when x = 1

______________

c. Estimate y when x = –2

______________

d. Estimate y when x = –3

______________

Extrapolate e. Estimate y when x = 8

______________

f. Estimate y when x =–8

______________

g. Estimate y when x = 12

______________

h. Estimate y when x = –12 ______________

Interpreting Graphs

Graphs can help us to visualize how things change, and make comparisons and predictions. When you put two lines on the same graph, you can instantly see which one is steeper, which one starts higher, or which one grows faster. If you see a linear pattern on a graph, you can extend that line to see what will happen next.

Sample Problem — Interpreting Graphs Maryam (solid line) and Ada (dotted line) are walking 2 km

to school at different rates. a. How long does it take each person to walk to school?

Distance in km

b. Who is faster? How do you know? c. If they need to arrive at school by 8:45, what time should they leave? d. What is the speed of Maryam in km/min and km/hr?

What to Think About

Time in minutes

How to Do It

Both lines go through the origin (0, 0). This means they both start walking at the same place and time. The solid line goes through (10, 1), (20, 2). The dotted line goes through (20, 1), (40, 2).

a. How long does it take each person to walk to school?

Look at the solid line and find the x-value when y = 2 . The x-value is 20. This means it takes 20 minutes for Maryam to walk 2 km. Look at the dotted line and find the x-value when y =2. The x-value is 40. This means it takes 40 minutes for Ada to walk 2 km.

©Edvantage Interactive 2026

Chapter 4 Linear Relations

203

Sample Problem — Interpreting Graphs – Continued What to Think About b. Who is faster? How do you know? c. If they need to arrive at school by 8:45, what time should they leave? d. What is the speed of Maryam in km/min and km/hr?

How to Do It Maryam is faster because her line is steeper. Maryam needs 20 minutes so she should leave at 8:25. Ada needs 40 minutes so she should leave at 8:05. Maryam takes 10 minutes to walk 1 km, so her speed is or 0.1 km/minute. Maryam takes 10 minutes to walk 1 km. One hour is 60 minutes. In 60 minutes, she can walk 6 km. She can walk which is 6 km/h.

Try This – Interpreting Linear Graphs 1. The graph shows the value (dollars) of a laptop over time (years). Use this graph to answer the following questions: a. What is the y-intercept?

b. What does the y-intercept represent in this situation?

c. Is this relation increasing or decreasing?

Value of laptop ($)

1 000

500

d. When is the computer worth half of its original value?

Time (years)

e. Predict the x-intercept using extrapolation. What does this point represent? f. Each year, the laptop value decreases by _______________.

204 Chapter 4 Linear Relations

©Edvantage Interactive 2026

Try This – Interpreting Linear Graphs - Continued 2. Use the graph below to answer the questions about the pay for a salesperson who works on commission. They are paid a percent of their total sales plus a fixed daily salary. y represents the total pay, x represents the sales in dollars. a. What is the y-intercept? What does it mean here?

b. Is this relation increasing or decreasing?

200

c. What is the total pay on a day when they sell $400 worth of product?

Total Pay ($)

150

d. How much do they need to sell in a day to

100

get paid $200?

Extend and Explore

200

400 600 Total Sales ($)

800

1000

Here is a visual representation of the first 4 centred hexagonal numbers.

Make a table of values to represent the number of dots in figures 1-6. Draw a graph. Write an equation to represent the number of dots. (Hint: it is not linear, it is quadratic and will involve an exponent of 2)

©Edvantage Interactive 2026

Chapter 4 Linear Relations

205

4.4 Practice 1. Which of these examples of data are discrete and which are continuous? a. Number of teachers at your school

discrete

continuous

b. Height of a person over time

discrete

continuous

c. Number of notifications you get on your devices in one day

discrete

continuous

d. Speed of an ambulance

discrete

continuous

e. The number of days of school before a holiday

discrete

continuous

f. Litres of gas in a car

discrete

continuous

2. These 3 points represent data in a linear relation. Interpolate and extrapolate the following points. Interpolate a. Estimate y when x = 1

______________

b. Estimate y when x = ½

______________

c. Estimate y when x = –1

______________

d. Estimate y when x = –½

______________

Extrapolate e. Estimate y when x = 3

______________

f. Estimate y when x =–3

______________

g. Estimate y when x = 4

______________

h. Estimate y when x = –4

______________

3. Isaac (solid line) and Albert (dotted line) are walking 10 km to raise money for cancer research. The y-axis is distance in km and x-axis is time in hours a. How long does it take Isaac to walk 6 km?

b. How long does it take Albert to walk 4 km?

d. If they both started to walk at 11 a.m., what time would they each finish? e. What is the speed of Isaac in km/h?

Distance (km)

c. Which line is steeper? Who is faster? 5

f. What is the speed of Albert in km/h?

Time (hours)

206 Chapter 4 Linear Relations

©Edvantage Interactive 2026

4. Look at the graph representing the value of a car after x years of purchase. a. What is the initial value of the car? b. When is it worth $10 000? c. After one year, what is the value of the car?

d. Can we extrapolate to find out the value of the car after 11 years? e. Each year the car depreciates in value. It decreases by _______________ per year

4.4 Practice Answer Key 1a) discrete b) continuous c) discrete d) continuous e) discrete f) continuous 2a) 3a) 1 hour b) 1 hour c) Isaac d) Isaac: 12:40 pm, Albert 1:30 e) 6 f) 4 4a) $50 000 b) 8 years c) $45 000 d) No. The value of the car cannot go below $0. e) $5000/year

Remembering Ebbinghaus – Comparing Numbers Arrange the following numbers from least to greatest: 1.

©Edvantage Interactive 2026

Chapter 4 Linear Relations

207

4.5 Applications Warm Up Competency Focus - Solve problems connected to financial literacy Maya just started a part‑time job at a café. She earns a fixed weekly salary of $120 plus $8 in tips per hour worked. She plans to save up for a new cell phone that costs $1120. If Maya works 8 hours per week and saves all of her earnings, how many full weeks will it take her to save $1120?

Linear relations describe many real-life scenarios. They can model the cost of a car rental, temperature conversions and problems involving distance, speed, and time. Tips for solving problems with linear relations. • Identify the independent and dependent variables. • Create a table of values and use it to make a graph and/or an equation. • Interpolate and extrapolate where possible. • Check your answer and ask: “Is this reasonable?”

Sample Problem — Running Distance and Time Jamie ran at an average speed of 6 km/h during the Terry Fox Run at GlenEagle Secondary in Coquitlam, BC. He ran for one hour. a. Make a table of values with the time in minutes and distance in km b. Draw a graph c. How far can he run in 20 minutes? d. How long does it take to run 3 km? e. How far does he run in 15 minutes? f. Estimate how long it takes him to run 10 km. g. What other factors might influence your estimation in the previous question? h. Make an equation relating distance in km and time in minutes. i. Can you make an equation relating distance in km and time in hours?

What to Think About a. The distance Jamie runs depends on the time. Distance is the dependent variable. Time is the independent variable. Both of these are positive values d 0 and t 0.

208 Chapter 4 Linear Relations

How to Do It He runs

©Edvantage Interactive 2026

Sample Problem — Running Distance and Time – Continued What to Think About

How to Do It Time (min)

Distance (km)

Zero minutes = zero km

10 minutes = 1 km

20 minutes = 2 km

30 minutes = 3 km

40 minutes = 4 km

50 minutes = 5 km

Let’s use multiples of 10 minutes for the x-values in the table.

60 minutes = 6 km b. Draw a graph. Plot the points from the table. We only need quadrant 1 because both distance and time are positive.

c. How far can he run in 20 minutes?

Look at the table or graph. He can run 2 km in 20 minutes. x = 20, y=2

d. How long does it take to run 3 km?

It takes 30 minutes according to the table x = 30, y = 3

e. How far does he run in 15 minutes?

Interpolation: 15 minutes is halfway between 10 and 20 minutes. He runs halfway between 1 and 2 km, which is 1.5 km

f. Estimate how long it takes him to run 10 km.

Extrapolation: 100 minutes or 1 hour and 40 minutes 10

4 2

©Edvantage Interactive 2026

minutes

100

Chapter 4 Linear Relations

209

Sample Problem — Running Distance and Time – Continued What to Think About

How to Do It

g. What other factors might influence your estimation in the previous question?

This is a reasonable estimate, however Jamie’s pace of running may slow the longer he runs. Also his pace at the beginning, middle and end of the run may differ. We can adjust our estimate. He will likely need 100 to 105 minutes to run 10 km.

h. Make an equation relating the distance he runs and the time in minutes

We can take the number of minutes and divide by 10 to get the number of kilometres. y =

i. Make an equation relating the distance he runs and the time in hours

if x is measured in minutes.

We can take the number of hours and multiply by 6 to get the number of kilometres. y = 6x if x is measured in hours. Check: 30 minutes = 0.5 hours. Does

3 = 3, so yes

Try Together— Distance to Lightning The distance to lightning can be calculated, approximately, using the formula d = 0.34t. t is the time in seconds between seeing the lightning and hearing the thunder. d is the distance, in km.

What to Think About 1a. Make a table of values for t = 0, 1, 2, 3, 5, and 10.

How to Do It Time (sec)

Distance (km)

0 1 2 3 5 10

1b. Graph

210 Chapter 4 Linear Relations

©Edvantage Interactive 2026

Try Together— Distance to Lightning The distance to lightning can be calculated, approximately, using the formula d = 0.34t. t is the time, the number of seconds between seeing the lightning and hearing the sound of thunder. d is the distance, in km.

What to Think About

How to Do It

2. Use the graph to answer the following questions: a. Approximately how many km away is the lightning if the time between lightning and thunder is 4 seconds?

d = 0.34t

b. Approximately how many seconds between lightning and thunder if the lightning is 14 km away?

d = 0.34t

d = 0.34 ( _____ ) d = _____ km

14 = 0.34t t=

seconds

t = _____ seconds c. Are there limitations and factors to consider when using this formula?

Yes, it is important to consider sources of error.

d. Suggest some limitations Limitations include: •

Sound may not travel directly

• •

Your Turn – The Relation between Pay and Number of Hours Worked 1. This graph shows a discrete linear relationship between pay and the number of hours worked. a. Create a table of values for this graph

©Edvantage Interactive 2026

Chapter 4 Linear Relations

211

Your Turn – The Relation between Pay and Number of Hours Worked – Continued b. What is the hourly wage?

c. What is the pay for 10 hours of work?

d. Why do we not join the dots? Write an equation for this relation.

Remembering Ebbinghaus – Equivalent Numbers 1. Fill in the table with equivalent numbers. ratio

fraction

decimal

percent

picture

1:8

0.2

100%

Extend and Explore

Read “Raven Steals the Light”, a traditional Coast Salish story. The Raven often represents a trickster, creator, and transformer and the Eagle often represents power, wisdom, vision, and prestige. What do they represent in this story? Find the average rate of flight speed for each bird in kilometres per hour and metres per second. Which is faster? Compare their average wingspan and lifespan. Make a chart with the information you have gathered. Use credible sources.

212 Chapter 4 Linear Relations

©Edvantage Interactive 2026

4.5 Practice 1. Spain won the World Cup in 2026. They had the most attempts at goal at 140 and the fourth-highest number of goals with 14 goals. If the ratio of goals to attempts at goal was a linear relation, fill in the table below and make a graph.

# of attempts

# of goals

10 40 100 140

200

2. This graph shows a linear relation between pay in dollars and number of hours worked. 40

a. Fill in the table of values for this graph. Hours

0 0.5

1 1.5

b. What is the hourly wage?

Pay ($)

2 20

c. What is the pay for 5 hours of work?

d. What is the pay for 10 hours of work?

0.0

0.5

1.0

1.5

2.0

Hours worked

e. How many hours would need to be worked to buy a pair of headphones that costs $200?

©Edvantage Interactive 2026

Chapter 4 Linear Relations

213

3. The graph represents starting a trip with 55 L of gas in the tank. a. How much fuel remains after driving 100 km?

b. Extrapolate to see if it is possible to drive from Vancouver to Kelowna (389 km) on 55 litres of gas

c. Is it reasonable to interpolate data from this graph? Is it reasonable to extrapolate data from this graph?

4. If a dragonfly eats 50 mosquitoes per day, answer the following questions. a. What is the independent variable? _________________________________________ b. What is the dependent variable? __________________________________________ c. Fill in the table of values Number of Days

1000

Number of Mosquitoes Eaten

900 800

d. Graph the relation

Mosquitoes Eaten

700 600 500 400 300

e. How many mosquitoes can it eat in 5 days?

200 100

f. How many days until it eats 1000 mosquitoes?

Days

4.5 Practice Answer Key 1a) (10,1), (40,4), (100,10), (140,14), (200,20) 2a) 0, 9, 18, 27, 36

b) $18/hr c) $90 d) $180 e) 11.11 hours

3a) 40 L b) no c) yes, yes (if x and y are both positive) 4a) number of days b) number of mosquitoes eaten c) the choices for the independent variable (number of days) may vary in the table: (0,0) (1,50), (2,100), (3,150), (4, 200), (5, 250) d) Ask your teacher for graph e) 250 mosquitoes f) 20 days

214 Chapter 4 Linear Relations

©Edvantage Interactive 2026

4 Chapter Review 1. Find the hidden message by following the instructions: a. Join these 3 horizontal lines (–2, 3) and (–4, 3) (–5, –3) and (–1, –3) (2, –5) and (6, –5) b. Join these 5 vertical lines (2, 1) to (2, 5) (6, 1) to (6, 5) (2, –3) to (2, –7) (6, –3) to (6, –7) (–3, –3) to (–3, –7) c. Join these oblique (slanted) lines (–5,1) to (–3, 5) (–3, 5) to (–1, 1) (2, 5) to (4, 3) (4, 3) to (6, 5) Hint: start in quadrant 1 and go counter-clockwise to find the hidden message. 2. Match the words to their definitions a. _____ Extrapolating

i. A math statement that shows two expressions are the same using an equal sign.

b. _____ y-intercept

ii. Countable values

c. _____ Value of an independent variable iii. The value of a relation when x = 0. d. _____ Discrete data

iv. Estimating within a range of data points.

e. _____ Linear relation

v. A math statement that combines numbers, variables, and operations.

f. _____ Expression

vi. Output

g. _____ Equation

vii. Input

h. _____ Interpolating

viii. Estimating outside a range of known data points.

i. _____ Increasing relation

ix. A relationship where as the input gets larger the output also gets larger.

j. _____ Value of a dependent variable

x. A pattern that is a straight line when graphed.

©Edvantage Interactive 2026

Chapter 4 Linear Relations

215

3. Match the following equations with the graphs on the right. a. _____ y = x + 3 b. _____ y = x – 3 c. _____ y = –x + 3 d. _____ y = –x – 3 e. What do you notice about the four lines?

4. Fill in the blanks for the linear patterns a. 3, –1, ________, –9, ________ b. 3, ________, 9, ________, 15 c. ________, 1, –1, ________, –5 d. 100, 87, ________, ________, 48 e. –15, –10, –5, ________, ________ 5. Match these equations with the corresponding graphs. a. _____ y = –3x + 3

ii.

b. _____ y = x – 2 −3

−2

−1

c. _____ y =2x + 1

−3

−2

−1

−2

−3

f. _____ y = –1

iv.

e. _____ x = 2 −3

−2

−1

−2

−1

216 Chapter 4 Linear Relations

−3

−2

−1

−2

−3

vi.

−3

d. _____ y = –x iii.

−1

−3

−2

−1

−2

−3

6. Which of these examples of data are discrete and which are continuous? a. Number of students in your Math 9 class

discrete

continuous

b. Temperature outside during a 24-hour period

discrete

continuous

c. Number of texts you receive in one day

discrete

continuous

d. Speed of a cyclist riding from home to school and back

discrete

continuous

e. Number of pages in a book

discrete

continuous

f. Volume of water in your water bottle during one school day

discrete

continuous

7. Using the graph of fuel level versus distance in a car, answer the following questions. a. How much fuel is there at the start?

Fuel Level vs Distance

Fuel Level (L)

b. How many km can be driven until this car runs out of fuel? c. How much fuel is used to drive 200 km?

d. Is it possible to drive from North Vancouver to Hope on one tank of gas? e. Is it possible to drive from Victoria to Tofino on one tank of gas?

100

200

Distance (km)

300

400

f. Is it reasonable to interpolate data from this graph to find the amount of fuel needed to drive 20 km? g. Is it reasonable to extrapolate data from this graph to find the fuel needed to drive 400 km? 8. Look at the graph below and tell a story about what could be happening? 6

0 0

Chapter 4 Linear Relations

217

9. Consider the following relations. If they are linear, what is the common difference? Is it increasing or decreasing? a.

c. (1, 1), (2, 2), (3, 3), (4, 4)

Linear: Yes / No

The common difference is: __________ . Increasing / Decreasing

The common difference is: __________. The common difference is: _________ . Increasing / Decreasing Increasing / Decreasing

d. (1, 1), (2, 4), (3, 9), (4, 16)

e. (−3, 8), (−2, 6), (−1, 4), (0, 2)

f. y = –x

Linear: Yes / No

The common difference is: __________ .

The common difference is: __________

The common difference is: _________ .

Increasing / Decreasing

Linear: Yes / No

10. A drone starts at a height of 11 metres and falls at a rate of 1 metre per second. Fill in the missing information for the table of values, ordered pairs, equation, and graph.

0 1 2 (0, ____ ), (1, ____ ), (2, ____ ) Equation: y = ____________ 11. Graph and label with a letter the following lines on the grid provided. a. x = 0 b. y = 0 c. x = 8 d. y = 6 e. x = –3 f. y = –7

218 Chapter 4 Linear Relations

12. Graph the following linear relations on the grid provided. a. y = 3x b. y = 4 c. y = –x – 2 d. y = x – 2

4 Chapter Review Answer Key 1) MATH 2a) viii b) iii c) vii d) ii e) x f) v g) i h) iv i) ix j) vi 3a) A b) C c) B d) D e) A and C, B and D are parallel. A and B, C and D are reflections 4a) –5, –13 b) 6, 12 c) 3, –3 d) 74, 61 e) 0, 5 5a) v b) vi c) iv d) iii e) i f) ii 6a) discrete b) continuous c) discrete d) continuous e) discrete f) continuous 7a) 60 L b) 350 km c) 35 L d) yes, (154 km) e) yes, (317 km) f) yes g) no 8) Answers will vary. One option: The graph is your distance from your house versus time. You are spending some time at the park with a friend. Your friend’s parents drive you to their house which is on the opposite side of the park from your house (your distance from the house is increasing). You hop on a bike there (less steep graph means lower speed) and ride it home. 9a) yes, 5, increasing b) No, n/a , increasing c) yes, 1, increasing d) no, n/a, increasing e) yes, –2, decreasing f) yes, –1, decreasing 10) Table: 11, 10, 9, y = –x + 11 11)

12)

Chapter 4 Linear Relations

219

How Did It Go? Part 1: Reflecting on Chapter 4 - Check all that apply to you ☐ The content of this chapter is challenging. ☐ I am starting to understand linear relations. ☐ I can solve problems with linear relations. ☐ I find word problems challenging. ☐ I need more time to practice before the test. ☐ I understand and can use a table of values. ☐ I feel more confident with graphing than last year. ☐ I know the difference between interpolating and extrapolating. ☐ I understand how to plot ordered pairs. ☐ I have a few questions before the test. ☐ I am confident about the content of this chapter. ☐ I can help others graph straight lines. ☐ I can use many different strategies to represent linear relations. ☐ I feel confident applying skills to word problems. ☐ I am ready to write the test. ☐ My next step is ______________________________________________________.

Part 2: The equation for the x-axis is y = 0 and the equation for the y-axis is x = 0. Fill in the tables of values and use them to draw in the grid provided. Explain in your own words why these are the equations for the axes. y=0 x

x=0 x

220 Chapter 4 Linear Relations

Vocabulary List for Linear Relations C Cartesian coordinate system – The Cartesian system is a two-dimensional coordinate system where each point is defined by an ordered pair (x, y), representing its horizontal and vertical distances from the origin (0, 0). There are four quadrants.

Common difference – The difference between consecutive (in a row) numbers in a linear pattern. The difference is the same for all the consecutive numbers.

Coefficient – A number that is multiplied by a variable in an expression. Example: The 7 in the expression 7x – 6. Constant – A fixed number in an expression that does not change. Example: The –6 in the expression 7x – 6.

D Dependent variable – The effect or outcome. It is the variable that is being measured or evaluated, and its value changes in response to another variable.

E Equation – A mathematical statement representing equality of two expressions. Example: 3x + 1 = 10 or 2x – 1 = 7x – 5. Expression – A combination of numbers, variables and operations that represents a value. Example: –2x + 1 or ½x. Extrapolation – Estimating a value outside of the range of known data points.

H Horizontal line – A straight line that runs left-right. Examples: y = 2, y = 0, or y = –3.

I Independent variable – The cause or input. It is the variable that changes on its own or is manipulated to see how it impacts another value. Input – What you put into a function to get an output. It is the independent variable. Example: In the equation y = 5x, if x = 2 then y = 10. 2 is the input.

Interpolation – Estimating a value within the range of known data points.

L Linear relation – A relation (one thing depends on another) that looks like a straight line when graphed. The rate of change is constant.

O Ordered pairs – Two values written in parentheses and separated by a comma. The first number represents moving left or right on the x-axis. The second number represents moving up or down on the y-axis. Example: An ordered pair (1, 1) means starting at the origin, move one right and one up. In general it looks like (x, y).

Outlier – A data value that is much higher or lower than the rest of the data. Output – What you get out of a function when you input something. It is the dependent variable. Example: In the equation y = 5x, if x = 2 then y = 10. 10 is the output.

S Slope – The steepness and direction of a line. It describes how much the y-value changes for each increase of 1 in the x-value.

T Table of values – A two-column table, or a table with two rows, used to present values of the independent and dependent variables.

V Variable – A symbol, usually a letter, that represents a number or quantity that can vary or may be unknown. Common variables include x, y, a, b and c.

Vertical line – A straight line that runs up-down. Examples: x = 2, x = 0, or x = –3.

Y y-intercept – The point where a graph crosses the y-axis. At the y-intercept, x = 0. In an equation in the form y=mx+b, b is the y-intercept.

Chapter 4 Linear Relations

221

Failsafe Vocabulary Check A "This or That" graphic organizer is a side-by-side comparison tool that helps you contrast two different things. It has two columns—one for each item—so you can see their differences clearly. In the blank This or That chart, pick one of the four pairs of terms and fill it in using the example as a guide. ☐ Input vs output ☐ Expression vs equation ☐ Discrete vs continuous ☐ Interpolate vs extrapolate Term 1

Term 2

Independent Variable

Dependent Variable

Input

Output

Cause

Effect

Often written as x

Often written as y

Plotted on the horizontal axis

Plotted on the vertical axis

First coordinate of a point (x, y)

Second coordinate of a point (x, y)

Term 1

Term 2

Examples: time, age, distance Examples: amount of money earned, test scores, heart rate

222 Chapter 4 Linear Relations

5 Linear Equations This chapter is your guide to understanding and solving linear equations. You will explore a range of strategies to find solutions, both symbolically and pictorially. Hands-on and visual activities are integrated throughout to provide a connection between theory and applications. While most equations will have one clear solution, some might surprise you with no solution at all, or many different answers. You will build foundational skills and confidence to help you solve problems in math and beyond.

Big Idea of the Chapter The principles and processes underlying operations with numbers apply equally to algebraic situations and can be described and analyzed. In this chapter you will explore: Solving equations algebraically and pictorially.

2x + 2 = 12

Preservation of equality Verifying the solution of an equation.

Is x = 5 a solution for 2x + 2 = 12?

Rewrite equations in terms of the variables involved. Distributive property

a(b + c) = ab + ac

Solving linear equations in various forms.

ax = b, ax + b = x, a(x + b) = c, ax + b = cx + d

Strategies to solve equations with fractions.

Multiply by LCM of denominators or cross multiply.

Applications

Distance, speed, and time problems.

Get Started - What do you notice? What do you wonder?

The graph on the right shows that the amount of fuel in the gas tank depends on the distance driven by the vehicle. What do you notice? What do you wonder?

Chapter 5 Linear Equations

223

5.1 What is a Linear Equation? Warm Up Competency Focus - Apply multiple strategies for solving problems, in both abstract and contextual form. 1. Solve the Math Mobile. What number does the circle represent? The triangle? How do you know? Solve each mobile separately.

2. The Magic of Math Step 1: Ask your friend what their favourite number from 1 to 9 is. Multiply it by 3 and remember that number. Step 2: Ask your friend to multiply 37 037 times the product from step 1. Step 3: What happens? Try it with a different number. Explain the pattern.

Linear equations are mathematical equations that represent a straight line when graphed. The simplest example is y = x. When x = 0, y = 0. When x = 1, y = 1. y is the same value as x. Plot three or more points on the blank graph below.

Why do we study linear equations? To help us understand the world around us, we need to understand how things change. The simplest kind of change is a constant change. A linear equation helps us to describe and represent this kind of change, a change that happens at a constant rate. For example, the table on the next page is based on an hourly wage of $20. 224 Chapter 5 Linear Equations

S = 20t Hours

Total Pay

$20 $40

2 100

$2000 $4000

200

The linear equation for this table is S = 20t. We can use this linear equation to: • Make predictions like: How much do you earn after an 8-hour shift? • Solve problems like: How many hours do I need to work to buy headphones that cost $150? Linear equations have a degree of 1, meaning that the largest exponent for the variables x and y is 1. This means you will see terms like y, 3y, x, 2x and , but you will NOT see terms with , x2, x3, y2 in linear equations.

Try This ... Circle the linear equations: Hint: look at the exponents of x and y.

Preservation of Equality

You may have heard a math teacher at school say this: “Whatever you do to one side of an equation, you must do to the other side.” This is the foundation of solving equations and allows us to preserve or keep the equation balanced. The image below illustrates this statement using a balance instead of an equation.

Add a marble on the right

Add a marble on each side

Still balanced

Chapter 5 Linear Equations

225

Verify Your Solution

When solving any equation, it is helpful to check your solution. Double-checking is a useful practice in the real world too. You may have heard of “measure twice, cut once” in carpentry. Pilots also use a variety of double-check procedures to ensure safety and mitigate risks before, during, and after flights. Checking your solution will help you catch and fix your mistakes. It can also help avoid finding a solution that is impossible or unreasonable, a solution that seems right until you put it in context and find out you have divided by zero, gone back in time, or taken the square root of a negative number.

Sample Problem — Checking Your Solution A solution to an equation is a value that makes the equation true. Is x = 2 a solution to 2x – 1 = 3?

What to Think About 1. Check if x = 2 by substituting or replacing x with 2.

How to Do It

2x – 1 = 3 2(2) – 1 = 3

2. Simplify.

4–1=3 3=3

3. Is this a true or false statement? If it is true, it is a solution. If it is false, it is not a solution.

True x = 2 is a solution

Try Together — Checking Your Solution Yichen and Priya are solving the equation 2x + 3 = 5x – 6. Yichen got a solution x = 4 and Priya got x = 3. Who is correct?

Yichen's Solution

Priya’s Solution

1. Check if x = 4.

1. Check if x = 3

2. Replace x with 4.

2. Replace x with 3

2x + 3 = 5x – 6

2( ____ ) + 3 = 5( ___ ) – 6

2(___) + 3 = 5(___) – 6

____ + 3= ____ – 6

___ + 3 = ___ – 6

___ = ___

This is true / false.

This is true / false

Is Yichen correct?

Is Priya correct?

226 Chapter 5 Linear Equations

Your Turn — Checking Your Solution Circle which of the following equations have x = 1 as a solution. a. x + 2 = 3

How Many Solutions?

b. x – 2 = 1

c. 2x = –2

d. –x – 4 = –5

e. 0.75x = 0.75

A linear equation can have one solution, no solution, or infinitely many solutions. After you simplify both sides, compare the variables and constants: • If you get x = a number, there is one solution. • If you get a false statement involving 2 numbers like 4 = 7, there is no solution. • If you get a true statement involving 2 numbers like –3 = –3, then there are an infinite number of solutions.

Sample Problem — How Many Solutions? For the equation 2(x + 3) = 2x + 6, check to see if x = 0, 1, –10 and

are solutions. Don’t forget to use BEDMAS.

x=0

x=1

x = –10

x=½

2 (0 + 3) = 2(0) + 6

2 (1 + 3) = 2(1) + 6

2 (–10 + 3) = 2(–10) + 6

2 ( + 3) = 2( ) + 6

2(3) = 6

2(4) = 8

2(–7) = –20 + 6

2( + ) = 1 + 6

6=6

8=8

–14 = –14

7=7

True

∴x=0

∴x=1

∴ x = –10

∴x=

All four numbers are solutions. In fact, all real numbers will be solutions to this equation. There are infinitely many solutions. In lesson 5.4, you will learn how to prove that these two expressions are equal.

Chapter 5 Linear Equations

227

Try Together — How Many Solutions? When we solve linear equations we often get one solution. Is there always one solution? Consider x+1 = x+1 and x+1=x+2 when x = 0, x = 2 and x = 3. x+1=x+2

x+1=x+1

When x = 0

___ + 1 = ___ + 2

___ + 1 = ___ + 1

___ = ___

This is true / false

When x = 2

___+ 1 = ____+ 2

___ + 1 = ___ + 1

___ = ____

This is true / false

When x = 3

___ + 1 =___ + 2

___ + 1 =___ + 1

___ = ____

This is true / false

What do you notice? Try a few other numbers mentally. Why is this happening?

Your Turn — How Many Solutions? Look at the following equations and determine whether they have no solution or infinite solutions. How do you know? a. 3x – 1 = 3x – 1

b. –x + 4 = –x + 7

c. x = x – 1.5

Learning Tip Sometimes when we solve problems there is one solution, but sometimes there is more than one solution or no solution at all.

228 Chapter 5 Linear Equations

Extend and Explore

Look at the graphs of the 2 straight lines y = x + 1 and y = x + 2. What do you notice about the two lines?

Do they ever cross each other?

How does that relate to solving x + 1 = x + 2?

Remembering Ebbinghaus – Simplifying Expressions 1. Which of these expressions are equal to 3x + 2? Circle all that apply. a.

2. Create 2 expressions that simplify to –x – 1.

3. a. Multiplying by one third is the same as dividing by ____. b. Dividing by one half is the same as multiplying by ___. c. Multiplying by

is the same as dividing by ___.

d. Dividing by

is the same as multiplying by ___.

4. Use the table of values for the linear equation y = x + 1 to plot 3 points on the grid provided. Draw a line through the points.

–1 0

0 1

Chapter 5 Linear Equations

229

5.1 Practice 1. Circle the linear equations: a.

2. Fill in the blank a. You can check your solution to a linear equation by ____________________ your answer into the equation, to see if it makes a

true or false statement.

b. Equations with a degree of one can have no solution, _______________ solution, or infinitely many solutions. c. The degree of a linear equation is always _______________. d. The graph of a linear equation is like a _______________. e. As we solve an equation, we want to make sure we don’t change the equation. This is why we talk about the preservation of _______________.

3. Solve a. b.

4. Simplify the expressions a.

230 Chapter 5 Linear Equations

5. Circle the equation on the right that is equivalent to the one on the left. Hint: Multiply the equations on the left by 2, or –10. Equation

Which is Equivalent?

a. b. c. d. e.

6. Check to see if x=1 is a solution to the following equations. Write yes or no. Show your work. a.

7. How many solutions are there for each equation? How do you know? a.

f. Create a linear equation that has many solutions.

g. Create a linear equation that has no solutions.

5.1 Practice Answer Key 2a)

1a)

3a) 4a) 5a) first 6a)

b) first

c) first

d) first

e) second

7a)

Chapter 5 Linear Equations

231

, –1

5.2 Solving 1- and 2-Step Equations with Integers Warm Up Competency Focus - Apply strategies to solve problems in contextualized situations. Jamie bought 4 bags of dill pickle chips and a chocolate bar for $13.50. The chocolate bar was $1.50. How much did each bag of chips cost?

How did you figure it out?

Equation strips are a visual representation of solving equations. The two strips represent each side of the equal sign. In the image below, the top strip represents an unknown value and 4. The bottom strip represents 15. As an equation this is written ? + 4 = 15.

Equation Strips

4 15

Visually you can determine that to make both strips equal you would make the unknown value 11. In the next example, what is the value of ‘?’? ?

50 To figure out the answer as an equation, we can write the following: Top Strip = Bottom Strip ? + ? +20 = 50 2? + 20 = 50 2? = 30 ? = 15

Try This ... 1. Write an equation to match the pictures below. What are the missing values? How do you know? a. b. c. 5 13

232 Chapter 5 Linear Equations

6 30

6 42

2. Create an equation strip and share it with a partner or the class. Choose a number for the bottom strip, then divide the top strip into sections that include an unknown value. Your equation strip

Your partner’s equation strip

Unknown value = ?

Isolating the Variable

“To isolate” means making a person feel alone or apart from others. In math, it means having the variable, x, by itself on one side of the equation and all other terms on the opposite side. Let’s take the equation x + 1 = 2 as an example where we isolate x. x + 1 = 2 x+1–1=2–1 x = 1

Solving 1-Step Linear Equations

We want to isolate x, so we will do the opposite of adding 1. We subtract 1 from both sides. We simplify and x has been isolated.

A 1-Step linear equation is an equation where you can find the value of the variable by doing just one operation, like adding, subtracting, multiplying, or dividing once. When we use an equation, remember preservation of equality. What you do to one side of the equation, you must do to the other. Your goal is to isolate the variable, x. Your main tool to isolate a variable is to use opposite operations. For example: • If the variable is being multiplied by 2, then DIVIDE both sides by 2. • If the variable is being divided by 2, then MULTIPLY both sides by 2. • If we are adding 4 to the variable, then SUBTRACT 4 from both sides. • If we are subtracting 4 from the variable, then ADD 4 to both sides. •

Remember x = 1x, – x = –1x and x =

Sample Problem — Solving 1-Step Linear Equations (Add and Subtract) x+7=5

What to Think About 1. We want to isolate x. The opposite of adding 7 is subtracting 7. 2. Subtract 7 from both sides. 3. Simplify. 4. Check answer. Is the statement true or false? 5. It is true so the solution is correct. ©Edvantage Interactive 2026

How to Do It x+7=5 x+7–7=5–7 x = –2 –2 + 7 = 5 5 = 5 Answer is true Chapter 5 Linear Equations

233

Sample Problem — Solving 1-Step Linear Equations –3x = 33

What to Think About

How to Do It

1. We want to isolate x. We are multiplying by –3. 2. Do the opposite of multiplying by –3. Divide both sides by –3. 3. Simplify.

x = –11

4. Check answer.

–3 (–11) = 33 33 = 33 (True)

Try Together — Solving 1-Step Linear Equations

1. We want to isolate x. We are dividing x by 2.

2. Do the opposite of dividing by 2. Multiply both sides by 2.

____

3. Simplify.

x = ____

= 12 ( ___ )

= 12

4. Check answer.

_____ = _____ (Is this true? _____)

Your Turn — 1-Step Linear Equations 1. For which equations is the solution x = –2? (Hint: replace x with –2) a.

234 Chapter 5 Linear Equations

Your Turn — 1-Step Linear Equations – continued 2. Solve for x a.

3a. Create a one-step linear equation whose solution is x = 8. (Hint: pick one operation and one number like adding 4, or multiplying by 3).

3b. Share your equation with a partner. Write out their equation and check to see if 8 is a solution.

Chapter 5 Linear Equations

235

Solving 2-Step Linear Equations

A 2-Step linear equation is an equation where you need to do two operations to solve for the variable. 2x + 1 is an example of an expression with 2 operations, multiplying and adding. What does the expression 2x + 1 mean? Start with a number, x. First double it, then add 1. If we want to get back to where we started, we need to undo those two operations. We need to do the opposite of doubling and adding. But in what order? It can help to think of shoes and socks. We start with bare feet and put on socks, then shoes. If we want to get back to bare feet, which should we remove first? Socks or shoes? The shoes, because they were the last thing we put on. In the expression 2x + 1, to isolate x we need to subtract 1 first (opposite to adding 1) and then divide by 2 (opposite of multiplying by 2).

Sample Problem — Solving 2-Step Linear Equations (Opposite is Divide) Solve for x.

What to Think About

How to Do It 3x + 5 = 20

1. Subtract 5 from both sides.

3x + 5 – 5 = 20 – 5

2. Simplify.

3x = 15

3. Divide both sides by 3. 4. Simplify.

x=5

Try Together — Solving 2-Step Linear Equations (Opposite is Multiply) Solve for x.

What to Think About

How to Do It

1. _________ both sides. 2. Simplify. 3. _________ both sides by 5. 4. Simplify.

236 Chapter 5 Linear Equations

Your Turn — Solving 2-Step Linear Equations 1. Solve for x. a.

2a. Create a 2-Step linear equation whose solution is x = 10 and solve it.

2b. Switch with a partner. Write their equation here and check to see if x = 10 is a solution.

Remembering Ebbinghaus – Simplify using the Order of Operations 1. a.

Chapter 5 Linear Equations

237

5.2 Practice 1. Solve for x. a.

k. 0.9x = –99

l. x – 0.75 = –0.25

2. For which equations is the solution x = –1? (Hint: replace x with –1) a.

238 Chapter 5 Linear Equations

3. Solve for x. a.

4. Create two different 2-Step linear equations that have a solution of x = –0.5.

5.2 Practice Answer Key 1a) 2) 3a) 4)

Chapter 5 Linear Equations

239

5.3 Solving 2-Step Equations with Rational Numbers Warm Up Competency Focus - Apply strategies to solve problems in contextualized situations. Choose one of the two questions below. Explain your answer. 1. Would you rather buy a jacket that is 30% off with 5% sales tax OR 25% off with no sales tax? 2. Would you rather buy a gaming console that is 5% off with a $25 rebate after purchase OR 10% off and no tax?

Rational Numbers and Equations

Recall that rational numbers are all the numbers that can be written as a fraction where the numerator and denominator are integers and the denominator is not zero. They include integers, fractions, and terminating or repeating decimals. For example, −3, , 0.75 and –0.3 are all rational numbers. In the last section you learned how to solve 2-Step equations. You can still use those strategies when faced with equations that have rational numbers as coefficients, constants, and solutions. In this section we will introduce new strategies for solving equations involving rational numbers (fractions and decimals). These new strategies offer choice and flexibility, boost understanding and often save time. We will also work with formulas, and use our skills to efficiently find solutions to problems in context, like converting from Fahrenheit to Celsius.

Sample Problem — Solving 2-Step Equations with Rational Numbers Solve for x using one of the strategies covered in the previous section.

What to Think About

How to Do It

We want to isolate x. Add

to both sides.

Simplify (add fractions). Simplify (reduce a fraction). Multiply both sides by 2.

240 Chapter 5 Linear Equations

Try Together — Solving 2-Step Equations with Rational Numbers Solve for x.

What to Think About

How to Do It

Isolate x. Subtract ______ from both sides. Simplify. Multiply both sides by ______. Simplify.

Your Turn — Solving 2-Step Equations with Rational Numbers Solve for x. 1.

4. For which equations is x = a.

a solution? c.

5. Create a 2-Step linear equation whose solution is x=

and solve it.

Chapter 5 Linear Equations

241

Alternate Strategy for Solving 2-Step Equations with Rational Numbers

Solving equations with fractions or decimals can be more challenging. Multiplying every term by the least common multiple (LCM) of the denominators or a suitable multiple of 10 for decimals helps clear these decimals or fractions from the equation. This process results in an equivalent equation with whole numbers, making the steps to solve a 2‑step equation simpler and errors less likely.

Sample Problem — Solving 2-Step Equations with Rational Numbers: Fractions Solve for x.

What to Think About

How to Do It

Find the LCM of the denominators 4 and 2. It is 4. To multiply both sides by 4 (the LCM), we will need to multiply each term by 4. Simplify. Add 4 to both sides. Divide both sides by 3.

Sample Problem — Solving 2-Step Equations with Rational Numbers: Decimals Solve for x. 0.25x + 0.75 = 1.5

What to Think About

How to Do It

What could we multiply everything by to

0.25x + 0.75 = 1.5

eliminate the decimals? Multiply every term by 100.

100(0.25x) + 100(0.75) = 100(1.5)

Simplify.

25x + 75 = 150

Subtract 75.

25x = 75

Divide by 25.

242 Chapter 5 Linear Equations

x=3

Try Together — Solving 2-Step Equations with Rational Numbers Solve for x.

What to Think About

How to Do It

1. Multiply every term by the LCM of 5, 2 and 10: 10.

2. Simplify. 3. Subtract __________ from both sides.

4. Divide both sides by __________.

5. Simplify.

Your Turn — Solving 2-Step Equations with Rational Numbers Solve for x.

3. 0.6x – 1.2 = 3.6

4. –0.3x + 8.5 = 11.5

Chapter 5 Linear Equations

243

Formulas

Formulas are powerful tools in math and science that allow us to quickly find missing information and solve problems. For example, on city streets in British Columbia the speed limit is 50 km/h, unless otherwise posted. The 50 km/h (speed) represents 50 km (distance) in 1 hour (time). As a formula this is written as: speed =

To rewrite this formula in terms of time, we multiply both sides by time (t): st = d And then divide both sides by speed (s):

To rewrite this formula in terms of distance: 1. Multiply both sides by time(t) 2. Simplify 3. This gives distance = speed × time

Try This ... 1. Rewrite the speed formula in terms of time (t).

2. Rewrite the formula Interest (I) = principal (p) × rate (r) × time (t) two different ways.

3. To calculate final velocity, you can use the formula vf = vi + at where vi is initial velocity, a is acceleration and t is time. Rewrite this formula in terms of time.

Extend and Explore

Why is the sum of 3 consecutive integers divisible by 3? Show that the sum of 3 consecutive integers is divisible by 3.

244 Chapter 5 Linear Equations

Remembering Ebbinghaus – Least Common Multiple 1. What is the LCM for the following? a. 10 and 20

b. 2, 4 and 6

c. 3, 6 and 9

d. 20 and 30

e. 2, 3 and 7

f. 3, 6 and 10

5.3 Practice 1. Solve for x

Chapter 5 Linear Equations

245

5.3 Practice – continued 2. Show that

is a solution for a and c. Show that 2.5 is a solution for b and d.

3. Rewrite these statements into formulas, then isolate the indicated variable. a. The area of a rectangle is the length times the width. (width)

b. The perimeter of a rectangle is the sum of the lengths of the four sides. (width)

c. The circumference is 2πr, where r is the radius. (radius)

d. Area of a triangle is half the base times the height. (base)

5.3 Practice Answer Key 1a) 2a) 3a)

246 Chapter 5 Linear Equations

5.1 – 5.3 Check Your Understanding 1. Which equations are equivalent to –x + 8 = –16? a.

2. The perimeter of a regular hexagon is 162 cm (perimeter is the distance around the outside and a regular hexagon is a 6-sided polygon with equal sides). Write an equation to find the length of a side. Then use it to find the length of one side.

3. Make an equation that you will solve where you will add 2 to both sides and then divide by 3 to isolate the variable x.

Chapter 5 Linear Equations

247

4. Create two equations whose solution is –5 and solve them.

5a. Draw a picture to represent 3x – 3 = 6. b. How could you use this picture to find x?

5.1 –5.3 Check Your Understanding Answer Key 2)

1) 3) 4)

5a)

5b) Add three positive unit tiles to both sides, divide the tiles into three equal groups and obtain x = 3.

How's it Going? 1. Below is a student’s quiz with 9 questions. Some answers are correct and some are not. Give a check mark if the question is solved correctly. If it is not, circle the error and correct the error in the space provided on the right of each question.

i. –7 – x = 0 –x = 7 x = –7

248 Chapter 5 Linear Equations

5.4 Solving Multi-step Equations with Brackets Warm Up Competency Focus - Develop, demonstrate and apply mathematical understanding through play, inquiry and problem solving. 1.

Think of a number.

Double the number.

Add 10.

Divide by 2 (take half of it).

Subtract the number you started with in step 1.

What number did you get at the end? Try it with a different number.

What do you notice? What do you wonder?

Think More: Why does it work? Can you make a number trick of your own?

The Distributive Property

Recall the distributive property is a(b + c) = ab + ac Let’s verify the distributive property for a = 3, b = 4 and c = 5. Left Side

Right Side

a(b+c)

ab +ac

3(4+5)

3(4) + 3(5)

3(9)

12 + 15

The values are the same.

Try This ... 1. Rewrite the following expressions using the distributive property. a.

Chapter 5 Linear Equations

249

Sample Problem — Using the Distributive Property to Solve an Equation Solve for x.

What to Think About

How to Do It

1. Use distributive property. 2. Add 3 to both sides. 3. Multiply both sides by 2.

Try Together — Using the Distributive Property to Solve an Equation Solve for x.

How to Do It

What to Think About

0.1(10x – 10) = 11

Use the distributive property.

_________________ = 11

Add ______ to both sides.

x = 12

Your Turn — Using the Distributive Property to Solve an Equation Solve for x. 1.

250 Chapter 5 Linear Equations

Alternate Strategy for Solving Equations with Brackets

Sometimes an equation with brackets can be solved more quickly by dividing first instead of multiplying out the brackets. For example, to solve 2(x +3) = 14: 2(x +3) = 14

Divide both sides by 2.

x+3=7

Then subtract 3.

x=4 This method works because dividing by the number in front of the brackets immediately cancels that factor, leaving a simpler equation. Use this strategy when the number outside the brackets divides evenly into the number on the other side of the equation. Check the relationship between those two numbers first. If the coefficient in front of the brackets is a factor of the constant on the other side, dividing first will usually be the quickest way to the answer.

Try This ... 1. Use the alternate strategy to solve for x. a. –3(x – 4) = 9

b. 5(2x – 1) = 35

Remembering Ebbinghaus – Combining Like Terms 1. Simplify the following expressions a. 2x – 4x + 7x – 9x

b. –x + 5 – x + 8 – x – 13

c. 2(x – 2) + 3(x – 3) + 4(2 – x)

Chapter 5 Linear Equations

251

5.4 Practice 1. Rewrite these expressions without brackets. a.

2. Solve for x.

Extend and Explore

You have 12 identical marbles and a balance scale. One of the marbles is heavier. How many weighings will it take to find the heavier marble? Can you do it in less than 4? What would change if it is not known whether the marble is heavier or lighter?

5.4 Practice Answer Key 1a) 2a)

252 Chapter 5 Linear Equations

5.5 Solving Multi-step Equations with Variables on Both Sides Warm Up Competency Focus - Represent mathematical ideas in concrete, pictorial and symbolic forms. The image below shows 5 bags of marbles on the left with 4 extra marbles and 4 bags on the right with 10 extra marbles. If each bag has the same number of marbles, how many are in each bag if the scale is balanced? Show your thinking.

Solving Equations with Variables on Both Sides

When an equation has variables on both sides, the goal is to gather all the variable terms together so that only one variable remains on one side. Think of it like moving everything of the same kind to the same team. You can use the same opposite-operation strategies you learned for two-step equations: adding to undo subtraction, subtracting to undo addition, multiplying to undo division, or dividing to undo multiplication. The key is to combine like terms so you can simplify and work with fewer pieces.

Sample Problem — Multi-step Equations with Variables on Both Sides Solve for x.

What to Think About

How to Do It 8x − 12 = 6x + 26

Subtract 6x from both sides.

8x − 6x − 12 = 6x − 6x + 26

Add 12 to both sides.

2x−12 + 12 = 26 + 12

Divide by 2.

2x = 38 x = 19

Note: You could also choose to subtract 8x and then subtract 26 from both sides and get the same answer.

Chapter 5 Linear Equations

253

Try Together — Multi-step Equations with Variables on Both Sides Solve for x

What to Think About

How to Do It 3x – 5 = 2x + 6

Move all x terms to one ____.

3x – ____ – 5 = 2x – ____ + 6 x – 5 + ____ = 6 __ ____

Add ____ to both sides.

x = ____

Your Turn — Multi-step Equations with Variables on Both Sides Solve for x. 1. x + 10 = 15 + 6x

Solving Equations with Variables on Both Sides and Brackets

2. 8 – 4x = 5 – 3x

3. 1 – 14x = x – 9

When an equation contains brackets on one or both sides, you will often begin by removing those brackets so you can work with the terms directly. Recall that this is called expanding or using the distributive property. After expansion, you will have an equation with variables on both sides. Then the goal is to gather the x terms together and then isolate the variable by using the opposite operations you already know. Careful expansion makes every other step easier and ensures that the equation stays balanced as you solve it. For example, take the equation 2(x – 3) = x – 7. This can be expanded and solved by: 2x – 6 = x – 7 x = –1 And the answer can be checked by substituting –1 for x. 2(–1 – 3) = –1 – 7 2(–4) = –8 –8 = –8 The statement is true, so the solution is correct.

254 Chapter 5 Linear Equations

Try This ... 1. Solve the equations using the distributive property. a. 5(2x – 3) + 7 = 7x +7

b. 5(x + 7) = 2x – 4

c. 1.5(x + 4) = 3.5 – x

2. Solve and verify:

Solving Equations with Variables on Both Sides Using Fractions and Decimals

When an equation includes fractions or decimals, the first challenge is that these numbers can make each step longer and more complicated. A way to simplify the work is to clear the fractions before you begin solving. To do this, find a number that is a common multiple of all the denominators and multiply every term of the equation by that number. This keeps the equation balanced while turning every fraction into a whole number. In the sample below, multiplying everything by 20, the least common multiple of 5 and 4, removes all fractions in a single step. After that, solving the equation is just like the two-step equations you already know. By clearing fractions or decimals first, you make the rest of the solution faster, clearer, and less prone to mistakes. LCM of 5 and 4 is 20. Multiply by 20 and simplify. Subtract 5x and 60 from both sides. Divide by 3.

Chapter 5 Linear Equations

255

Similarly, with decimals, we can multiply by a power of 10 to eliminate the decimal numbers. In the sample below we multiply everything by 10. This is an optional method. Of the two methods shown here, which do you prefer? Would it depend on whether you had access to a calculator? Method 1 Method 2 0.4x – 3 = –0.4 Multiply everything by 10 to eliminate decimals 4x – 30 = –4 Add 30 4x = 26 Divide by 4 x = 6.5

0.4x – 3 = –0.4 0.4x = 2.6

Add 3 Divide by 0.4

x = 6.5

Try This ... 1. Solve for x. a.

g. 0.5(2x – 3.4) = 1.2x + 0.8 h. –1.3(0.4x + 2.5) = –0.6x – 3.1

256 Chapter 5 Linear Equations

Solving Equations by Cross Multiplying

When two fractions are equal, you can solve for the unknown by cross multiplying. This means you multiply the numerator of one fraction by the denominator of the other and set the two and b and d are not zero, you can rewrite the equation as ad = bc.

products equal. If

Cross multiplying quickly removes the fractions and gives an equation with whole numbers that is easier to solve. This method is especially helpful when working with ratios, proportions, or percent problems.

Sample Problem — Cross Multiplying Solve for x.

What to Think About

How to Do It

Cross multiply. Expand and simplify. Divide both sides by 10.

Sample Problem — Cross Multiply with x in the Denominator Solve for x.

What to Think About

How to Do It

Note that x cannot be zero.

3 is the same as

Cross Multiply. Divide by 3. Check to make sure x is not zero.

Chapter 5 Linear Equations

257

Try Together — Cross Multiplying Solve for x

What to Think About

How to Do It

Cross multiply. Distributive property. Simplify. Divide by 8.

Your Turn — Cross Multiplying 1. Solve for x. b.

, x cannot be ____ .

2. Find x and the perimeter of this triangle. Hint: It is an isosceles triangle with two equal sides.

258 Chapter 5 Linear Equations

Remembering Ebbinghaus – Matching Words to Expressions Match the correct term on the right to the statements on the left. _____ 1. A number plus 5

a. 3x

_____ 2. Triple a number

_____ 3. 4 less than a number

_____ 4. Half of a number

d. x – 4

_____ 5. The total of x and 10

e. 2(x +2)

_____ 6. Twice the sum of x and 2

f. x + 10

_____ 7. Double x and then add 2

g. x + 5

_____ 8. One third of x

h. 2x + 2

5.5 Practice 1. What does this picture represent? Write the equation represented by the picture, then solve it.

2. Solve and check a.

Chapter 5 Linear Equations

259

260 Chapter 5 Linear Equations

3. Solve these equations.

4. Solve these equations. State the value that is not permissible for x. a.

, x ≠ ____.

x ≠ ____.

5. Find x and the perimeter of this triangle.

5.5 Practice Answer Key 1a)

2a)

3a)

4a)

5a)

Chapter 5 Linear Equations

261

5.6 How to Solve a Word Problem Warm Up Competency Focus - Connect math concepts to each other and other areas. A man has to get a fox, chicken and a sack of corn across the river in a boat. The boat can carry him and one other item. If the fox and chicken are left alone, the fox will eat the chicken. If the chicken and the corn are left alone, the chicken will eat the corn. How can he do it?

Working with Words and Expressions

The four operations, addition, subtraction, multiplication and division, can represent a wide variety of words. For example, finding the “total” represents addition. In the table below, write as many words as you can to represent the operations described in each cell. Words for adding

Words for subtracting

Words for multiplying

Words for dividing

Expressions use numbers, variables and operations to represent situations in a compact mathematical form. For example, to represent how much money is made from a job with an hourly wage of $17.85, start with letting x be the number of hours worked. Multiplying 17.85 by x would give the total amount earned. This can be written as 17.85x.

262 Chapter 5 Linear Equations

Try This ... Find the expressions on the right that correspond to the words on the left. 1. _____ Nevena has x pencils and buys 5 more pencils. How many pencils does she have?

a. 4x + 6

2. _____ Tom’s allowance is twice the number of chores he completes in one week. x = number of chores.

b. 15x

3. _____ Total cost of a box of books that sell for 5 dollars each. x is the number of books.

c. 3x + 10

4. _____ Weekly earnings if you work x hours at 15 dollars per hour.

d. x + 5

5. _____ Temperature after x hours, if it drops 1.5 degrees per hour, and starts at 24 degrees.

e. 2x

6. _____ Cost of a cell phone plan which costs 10 dollars plus 3 dollars per gigabyte of data used. x = number of gigabytes.

f. 3x2

7. _____ Perimeter of a rectangle whose length is 3 more than its width. x = width.

g. 24 – 1.5x

8. _____ Area of rectangle whose length is 3 times its width (x = width).

h. 5x

Steps to Solving Word Problems

A variable is a letter that stands for an unknown value. An equation is a statement that two expressions are equal.

Step 1 – What are you trying to find? Read the question twice. • Look at the last sentence. • What is the question being asked? Let x be the answer. Step 2 – Write an equation with x Make an equation that connects the key words in the problem. • For example, Area = length × width, or • Profit = revenue – cost. Step 3 – Solve the equation or make x alone Use strategies learned in this chapter to isolate x. • Preserve equality. What you do to one side, you must do to the other. • Simplify. Step 4 – State the answer • Answer the question with words and use the correct units. Step 5 – Check your solution • Substitute your value of x back into the equation. Is it a true statement? • Does this answer make sense? Is it reasonable? Tip to use all the time: Whenever possible, draw a picture, make a chart, and highlight important numbers and words in the question.

Chapter 5 Linear Equations

263

Sample Problem — Applications Sam has 3 times as much money saved as Taylor. Together they have 100 dollars. How much money does Taylor have saved?

What to Think About

How to Do It

Step 1 – What are you trying to find?

Let x be the amount of money Taylor has saved.

Step 2 – Write an equation with x.

Sam has 3x dollars, Taylor has x dollars, Together they have 100 dollars. The equation is 3x + x = 4x = 100.

Step 3 – Solve the equation or make x alone.

Step 4 – State the answer. Step 5 – Check your solution.

Taylor has saved 25 dollars. If Taylor has 25 dollars, Sam has 3(25) or 75 dollars. Together, they have 25+75 = 100 dollars.

Try Together — Applications On a math test, Tah-leet-sil-mot got two correct answers for every wrong answer. There were 30 questions on the test. How many did she get wrong?

What to Think About

Step 1 – What are you trying to find? Step 2 – Write an equation with x.

How to Do It Let x be the number of _________________________. Tah-leet-sil-mot got ____ answers wrong and ____ answers right. The total number of questions is 30. The equation is __________________ .

Step 3 – Solve the equation or make x alone.

x + ____ = ____ 3x = ____ ____ = 10

Step 4 – State the answer. Step 5 – Check your solution.

Tah-leet-sil-mot got ____ questions __________ on the math test. Questions _________ + questions ________ = total number of questions or 10 +____ = 30

264 Chapter 5 Linear Equations

Your Turn — Applications 1. Jordan scored points in a basketball game by making 2- and 3- point shots. He made 5 more 2-point shots than 3-point shots and scored 45 points in total. How many of each shot did he make?

2. A number is 5 times another number. The sum of the two numbers is 36. What are the two numbers? Hint: let x be the smaller of the two numbers.

3. The sum of two consecutive numbers is 31. Consecutive means “in a row”. For example: 4 and 5 are consecutive numbers. 3 and 4, 7 and 8 are also consecutive. What are the two numbers? Hint: Let x be the smaller number. The larger number will be one more than that because they are consecutive.

Remembering Ebbinghaus – Graphing Linear Equations 1. Match each graph to the correct set of equations. Write A, B or C below each graph.

−1

−2

−3

−4

−3

−2

−1

_______

−4

−3

−2

−1

−4

_______

−4

−3

−2

−1

_______

y=x

y = –2x

y=x+2

y = 2x

y = –2x + 2

y=x–2

y = ½x

y = –2x – 2

Chapter 5 Linear Equations

265

5.6 Practice 1. Match the terms on the left with the statements on the right? a. _____ Carlo has x books and buys 3 more books. How many books does he have?

i. 4x + 10

b. _____ Mohamed's allowance if it is three times the number of chores they complete in one week.

ii. 21.5x

c. _____ Total value of x nickels in dollars.

iii. 2x + 25

d. _____ Weekly earnings if you work x hours at 21.50 dollars per hour.

iv. x + 3

e. _____ Temperature after x hours, if it drops 1.25 degrees per hour, and starts at 23 degrees.

v. 3x

f. _____ Cost of a cell phone plan which costs 25 dollars plus 2 dollars per gigabyte of data used. (x = number of gigabytes).

vi. 2x2

g. _____ Perimeter of a rectangle whose length is 5 more than its width. (x = width).

vii. 23 – 1.25x

h. _____ Area of a rectangle whose length is twice its width. (x = width).

viii. 0.05x

2. Beside each word indicate the operation implied: +, –, ×, ÷ a. total

b. decrease

c. sum

d. loss

e. quotient

f. double

g. difference

h. split evenly

i. increase

j. triple

k. product

l. plus

m. minus

n. less than

o. shared equally

p. reduce

q. gain

r. fewer

s. times

t. more than

3. Which steps are missing in solving a word problem? 1.

What are you trying to find? Let x be the thing you are trying to find. Usually the last sentence has this information.

Write an equation with x using the information from the question.

______________________________________________________________________________________________.

State the answer

______________________________________________________________________________________________.

4. The larger of two positive numbers is seven times the smaller. The difference between the two numbers is 30. Find the numbers.

266 Chapter 5 Linear Equations

5. The length of a rectangle is 3 times its width. The perimeter is 48 cm. What is the width of the rectangle?

6. Find the two consecutive integers which add to 35. Write an equation to represent this situation and then solve it.

7. A taxi ride costs $4.00 plus $2.28 per km. a. How much does a 10 km ride cost?

b. Create an equation for C = cost of the taxi ride, if x is the number of km.

c. Use the equation to find out the cost of a 100 km trip.

d. Use the equation to find out how far you can go for 100 dollars.

8. Michelle and Laura were walking around Perimeter Trail in Mundy Park, Coquitlam, BC. The trail is 4 km long. Estimate the area inside the trail if it is roughly the shape of a rectangle. The ratio of the width to the length is approximately 3:2.

Chapter 5 Linear Equations

267

9. An annual event called the Tribal Journeys or Canoe Journeys is held during the summer months. One community hosts and paddlers from other communities make the canoe journey for 5 days of celebrations. A group from the Haida Nation travelled by canoe to attend a celebration. Another group travelled 5 times as far as the Haida paddlers. The total distance travelled by the two groups was 600 km. How far did the people from Haida Nation travel by canoe?

Extend and Explore

An even number can be represented by 2x, where x is an integer. An odd number can be represented by 2x+1, where x is an integer. Is the sum of 2 odd numbers always even? Show your thinking.

5.6 Practice Answer Key 1a) 2a)

3a) 4) 8)

7a)

268 Chapter 5 Linear Equations

5 Chapter Review 1. Unscramble the words below and write an appropriate symbol next to each word. +, –, ×, ÷, =.

a. mus

b. crudtop

c. friendefec

d. nitoquet

e. laque

f. lotta

g. heards

h. slos

i. dreacese

j. mites

k. scareeni

2. Solve the following

3. Create an equation of each type listed below and solve it.

a. 2-Step Integer

b. 2-Step Brackets

c. 2-Step Variables on Both Sides

d. Combination of brackets, fractions and variables on both sides

4. Rearrange these steps in the correct order. 3x = 9 1. 5x – 2x = 2x – 2x + 9

5x + 3 = 2x + 12 3. x = 3 4. 5x + 3 – 3 = 2x + 12 – 3

Chapter 5 Linear Equations

269

5. Solve these linear equations

270 Chapter 5 Linear Equations

6. Solve 3(x + 4) = 12 in two ways.

Chapter 5 Linear Equations

271

7. The following equations have no solution OR infinitely many solutions. Simplify. Write no solution, or the symbol for infinity below each one. a. 2x + 9 = x + x + 4 + 5

b. 3x + 1 = 4x + 2 – x + 1

c. 5(x – 2) = x + 4(x – 3) + 2

e. 0.5(x + 6) + 2(0.25x + 2)=2x + 7 – x

d. 4(x – 3) + 13 – 2x = 2(x + 1)

8. Rewrite the formulas as indicated in the chart below. a. P = 2(l + w), solve for w, width.

b. V =

d. F=ma, solve for acceleration, a.

e. I=Prt, solve for time, t.

solve for h, height.

c. s =

, solve for time, t.

f. V=lwh, solve for height, h.

9. Find the two consecutive integers which add to 23.

10. Rewrite the formula for the area of trapezoid to isolate the height, h.

272 Chapter 5 Linear Equations

11. Find x and the perimeter of the isosceles triangle.

12. Amir bought a shirt and jeans for 72 dollars. If the cost of the shirt is 12 dollars more than half the price of the jeans, what does each item cost?

13. In a horse race, Heartache is running at 15 m/s and True Love is running at 17 m/s. If Heartache had a 10 m head start, how many seconds will it take for True Love to catch Heartache?

14. A group of university students bought a winning lottery ticket valued at one million dollars. There are 4 students in the group. If the amount is shared evenly, what does each of them receive? If they had agreed that one of them should receive twice the amount each of the three does, how would they split the money?

15. Jen and Soyoung solved this equation: 3(x + 2) = x + 2(x + 3). Jen got x = 8 and Soyoung got x = –1. Check the two solutions and explain the result.

Chapter 5 Linear Equations

273

16. The sum of two consecutive even numbers is 154. What are the two numbers? (Hint: an even number can be represented as 2x, where x is an integer).

17. Three consecutive numbers add to 36. Write an equation to represent this and solve it. Find the 3 numbers.

Extend and Explore 1. On an analog clock, between 1 pm and 2 pm, when does the minute hand overlap the hour hand?

5 Chapter Review Answer Key 1a) 2a) 3)

5a)

6a) 7a) 8a) 9)

10)

11)

14)

12)

13) 15)

16)

17)

274 Chapter 5 Linear Equations

How Did It Go? Part 1: Reflecting on Chapter 5 - Check all that apply to you ☐ The content of this chapter is challenging. ☐ I am starting to understand linear equations. ☐ I can solve simple equations. ☐ I find word problems challenging. ☐ I need more time to practice before the test. ☐ I understand and can use the distributive property. ☐ I feel more confident solving equations than last year. ☐ I can solve 2-step equations. ☐ I understand how to preserve equality in an equation. ☐ I have a few questions before the test. ☐ I am confident about the content of this chapter. ☐ I can help others solve linear equations. ☐ I can use many different strategies to solve linear equations. ☐ I feel confident applying skills to word problems. ☐ I am ready to write the test. ☐ My next step is ______________________________________________________.

Part 2: Reflecting on solving equations In this chapter you learned a variety of ways to solve linear equations, a set of skills you will continue to use in your life in a variety of different ways. Below are three ways to solve the same equation. Which way do you prefer and why?

Here are two ways to solve another equation. Which method do you prefer and why?

3.1(x – 7) = 6.2

Distributive property

3.1(x – 7) = 6.2

Divide by 3.1

3.1x – 21.7 = 6.2

Add 21.7

x–7=2

Add 7

3.1x = 27.9

Divide by 3.1

x=9

Chapter 5 Linear Equations

275

Vocabulary List for Linear Equations B

Balance – Keeping both sides of an equation equal; the idea that what is done to one side must be done to the other.

Check – Substituting the solution back into the original equation to confirm its correctness. Coefficient – The number that multiplies a variable in an expression (for example, 4 in 4x). Constant – A fixed number that does not change, in contrast to a variable. For example, 3 is the constant in 5x + 3. Consecutive – Describes numbers or other items that follow one after another in sequence, such as 4, 5, 6 or 12, 13, 14, 15.

Distributive Property – The property that states a(b + c) = ab + ac, meaning you multiply a number by each term inside the

parentheses.

Equation – A mathematical statement representing the equality of two expressions (for example, 2x + 3 = 11). Evaluate – To calculate the numerical value of an expression. Equality – The relationship between two expressions that have the same value. Equivalent equation – An equation that, while it may look different, has the same solution set as the original equation. 2x = 6 has the

same solution as 3x = 9.

Expression – A combination of numbers, variables, and operations that represents a value (for example, 3x + 5).

Greater than – A comparison symbol (>) showing that one value is larger than another. 4 > 3.

Inverse – A number or operation that reverses the effect of another; for example, the inverse of addition is subtraction. Inequality – A mathematical statement that compares two quantities using symbols such as <, >, ≤, or ≥.

Linear equation – An equation in which each variable has an exponent of 1 and variables are not multiplied together. In two variables, its

graph is a straight line. Example: y = 9x – 2

Less than – A comparison symbol (<) indicating that one value is smaller than another. 3 < 4. Like terms – Terms in an expression that contain the same variable(s) raised to the same power and can be combined.

No solution – Describes an equation that has no value for the variable that makes the equation true.

Preservation of equality – The principle that an equation stays balanced when the same operation is performed on both sides. Prove – To provide logical reasoning or mathematical evidence that confirms a statement is true.

Reciprocal – For any nonzero number a, its reciprocal is

. Examples: 2 and

, –1 and –1, ¾ and

Simplify – To reduce an expression to its simplest form by combining like terms and/or performing operations. Solve – To find the value(s) of the variable(s) that make an equation true. Solution – The value(s) obtained when an equation is solved.

Verify – To check and confirm that a proposed solution satisfies the original equation.

276 Chapter 5 Linear Equations

Failsafe Vocabulary Check The Frayer Model is a graphic organizer that can help you learn and understand vocabulary in a structured way. The example below shows how to fill out the Frayer Model. In the blank Frayer Model, pick one of the three terms and fill it in using the example as a guide. ☐ Preservation of Equality ☐ Distributive Property ☐ Simplify a linear expression

Chapter 5 Linear Equations

277

278 Chapter 5 Linear Equations

6 Proportional Reasoning Proportional reasoning allows us to understand, make predictions and solve problems that involve ratios. This opens the door to a variety of practical applications. For instance, understanding scale diagrams is vital in fields such as architecture, engineering, biology, and design. In these fields, accurate representations of small or large structures or objects are very useful. Similarly, understanding proportional reasoning helps us convert minutes to hours, read a map and predict the length of a road trip, estimate the cost of produce in the grocery store, and double a recipe.

Big Idea of the Chapter Similar shapes have proportional relationships that can be described, measured, and compared. In this chapter you will explore: What is proportional reasoning?

The ability to understand, apply and compare relationships between quantities that are connected by a constant ratio. For example: If you can drive 100 km in one hour, you can drive 200 km in 2 hours.

Linear unit conversion

1 hour = 60 minutes, so 2 hours is 120 minutes.

Scale diagrams

A drawing or representation of an object, place or space that is proportionally smaller or larger than the original. For example: a diagram of an atom in a science textbook.

Enlargement or reduction of a 2D shape

Changing the size of a two-dimensional shape while keeping its proportions the same.

Similar polygons

Polygons that have the same shape but different sizes. Corresponding angles are equal. Corresponding sides are proportional. Examples of polygons are triangles, rectangles and hexagons.

Applications

Proportional reasoning has applications in many fields including mapmaking, photography, engineering, architecture, design, and navigation.

Get Started Compare the left and right sides of the image to the right. If we only use our counting skills, we would say the left and right sides are not equal. We could say the right side is twice as much as the left (double). We could say one side has more or less than the other. We could look at the two sides in a different way. Both sides have something in common. For every heart there are two stars. Instead of counting items we are comparing quantities. This is proportional reasoning. In this chapter, you will explore how ratios, rates, and proportions work together to describe the consistent relationships found in similar figures. Through the analysis of scale diagrams and similar polygons, you will build a strong conceptual understanding of how one quantity changes in relation to another.

Chapter 6 Proportional Reasoning

279

6.1 What is Proportional Reasoning? Warm Up Competency Focus - Use tools to explore objects in our daily lives Metric scavenger hunt: In your classroom, find the lengths indicated in both centimetres and metres using a ruler, metre stick or other measurement tools. Estimation (Choose units)

Object

Centimetres (Round to nearest unit)

Metres (Round to nearest hundredth)

Dimensions of this workbook

Height of your classroom door Distance from one wall of your classroom to the opposite wall Teacher Choice

1. For each of the above measurements, which ones make more sense: centimetres or metres? 2. How close were your estimates to the actual measurement?

If a drawing of a room has a scale of 1 cm representing 1 metre, a room that is 3 metres wide would be drawn as 3 cm on the drawing. Proportional reasoning can be used to scale a recipe, create blueprints of a building, mix substances to obtain a desired concentration, determine discounts, and much more. It is a versatile tool that supports a wide range of real-world applications.

Cross Multiplication

Cross multiplying is a technique that can be used to solve equations in which one rational expression (fraction) is equal to another. This technique is useful in real-world problems involving ratios, scaling and rates. You will use this technique again when studying trigonometry next year. Consider the following proportion: Notice what happens when we multiply the numerator of one fraction by the denominator of the other. Multiplying the numerator of the first fraction by the denominator of the second gives 1 × 10 = 10. Multiplying the numerator of the second fraction by the denominator of the first gives 5 × 2 = 10. Notice how the two products have the same value, 10.

280 Chapter 6 Proportional Reasoning

This will always be true and can be written in general form like this.

where b and d are not zero. ad = bc We can use this to solve many questions involving proportional reasoning. For example, a recipe uses 3 cups of flour for 8 muffins. How much flour is needed for 16 muffins?

Solve for x. Rewrite by cross multiplying. Simplify.

Check solution by substituting x = 6 into the original proportion. Reduce the fraction on the right. Since both sides are equal, the solution is correct.

Try This ... 1. Solve and check your answer. a.

Chapter 6 Proportional Reasoning

281

Here is an alternate strategy to solve cross multiplication equations: remove denominators. We can multiply both sides of the equation by 6.

Simplify.

Try This ... 1. Solve and check your answer with the strategy of your choice. a.

Converting Linear Metric Units

The metric system is an international system of measurement used worldwide for consistency and ease of use. It’s based on units of ten, making conversions simple. It helps people all around the world to communicate clearly and accurately. Key features: • Uses base units like metre (length), gram (mass), and litre (volume). • Prefixes indicate multiples or fractions of units, such as kilo- (1000 times), centi(1/100), and milli- (1/1000). • It’s used in science, medicine, engineering, and everyday life in most countries, including Canada. • Metric units are based on multiples of ten, which makes conversions straightforward. The key conversion factors are: Prefix

Symbol

Value

Example

kilo

1000

1 km = 1000 m

hecto

100

1 hL = 100 L

deca

1 daL = 10 L

(base)

–

1 m, 1 g, 1 L

deci

0.1

1 dm = 0.1 m

centi

0.01

1 cm = 0.01 m

milli

0.001

1 mm = 0.001 m

282 Chapter 6 Proportional Reasoning

Converting Linear Metric Units

When working with measurements, we often need to change from one unit to another, like metres to centimetres. Instead of trying to remember a lot of rules, we can use a simple method based on how units are related to each other. These relationships can be written as fractions that are equal to 1, so multiplying by them does not change the value, only the units. The steps below show an easy and reliable way to convert units correctly. 1. 2. 3. 4.

Identify the starting units and the units you want to convert to. Write down the conversion factor as a fraction. For example, if converting from metres to centimetres, 100 cm = 1 m so we can write that as a fraction that is equivalent to 1. Multiply the original measurement by the conversion fraction (multiplying by 1 does not change the value). Simplify to reach the final answer.

Sample Problem — Converting Units Convert 3.5 metres to centimetres.

What to Think About

How to Do It

3.5 m to cm

Identify the starting units and the units you want to convert to.

Identify the conversion factor.

Multiply by the conversion factor.

Simplify.

350 cm

Try Together — Converting Units Convert 2500 mm to metres.

What to Think About

How to Do It

2500 mm to metres

Identify the starting units and the units you want to convert to.

Identify the conversion factor. How many millimetres are in one metre?

Multiply by the conversion factor.

Simplify.

________ metres

Chapter 6 Proportional Reasoning

283

Your Turn — Converting Units 1. Change 4.2 kilograms into grams.

2. Express 150 cm in metres.

3. Convert 0.75 grams to milligrams.

4. A race track is 3.6 km long. How many metres long is the track?

Converting Time

When converting time, there is often more than one correct way to write the same amount. For example, time can be expressed in hours, minutes, or seconds, and each form represents the same value. Instead of looking for one single answer, the goal is to show that different expressions can be equivalent. The steps you have learned will help you convert between units while keeping the time the same. Here are some common and useful equivalent expressions. •

1 year = 365 days

•

1 year = 12 months •

1 year = 52 weeks

•

1 week = 7 days

•

1 day = 24 hours

1 hour = 60 min

•

1 min = 60 sec

Sample Problem — Converting Time How many minutes are in a day?

What to Think About 1.

There are 7 days in one week, 24 hours in one day, 60 minutes in one hour and 60 seconds in one minute.

We can reduce units that appear in both the numerator and denominator.

We multiply 24 by 60 to get the number of minutes.

284 Chapter 6 Proportional Reasoning

How to Do It

= 1440 minutes

Try Together — Convert Time How many seconds are in a week?

What to Think About 1.

How to Do It

In one week there are 7 days. In one day, there are 24 hours. In one hour there are 60 minutes and in one minute, there are 60 seconds.

We can reduce units that appear in both the numerator and denominator.

Simplify.

Your Turn — Converting Time 1. How many seconds are in an hour?

2. How many minutes are in a 30-day month?

Converting Units in Cooking and Music

Proportional reasoning can help us solve many everyday problems. Whether you are adjusting a recipe or understanding musical notation, the same mathematical ideas can be used in different situations.

Try This ... 1. Use the diagram below to answer the questions. Each row is equivalent to one cup. a. How many ounces in a cup?

b. How many tablespoons in 2 cups?

c. How many mL in

cup?

Chapter 6 Proportional Reasoning

285

Try This ... 2. Use the diagram below to answer the questions. Each row is equivalent. a. How many half notes in a whole note?

b. How many quarter notes in a half note?

c. How many quarter notes in 4 whole notes?

3. A smoothie recipe makes 2 servings. You want to make 4 servings. How much of each ingredient will you need? • cup yogurt •

cup milk

•

cup berries

4. A recipe makes 6 muffins. You want to make 9 muffins. How much of each ingredient will you need? • cups flour •

cup sugar

•

cup milk

Extend and Explore

Other units like speed can also be converted. km/h is kilometres per hour and m/s is metres per second. 1. Convert 108 km/h into m/s

2. The speed of light = 299 792 458 m/s. Convert it to km/h and write it in scientific notation. Use your calculator as needed.

286 Chapter 6 Proportional Reasoning

6.1 Practice 1. Cross multiply. a.

2. Solve for x by cross multiplying. a.

3. Convert the following metric measurements. a. 240 m = _______________ cm

b. 0.4 m = _______________ cm

c. 100 m = _______________ cm

d. 1 km = _______________ cm

e. 49.5 km = _______________ m

f. 1 000 000 000 mm = _______________ km

4. Convert the following measurements of time. a. 3 hours = _______________ minutes

b. 300 minutes = _______________ hours

c. 2 weeks = _______________ hours

d. 2 hours = _______________ seconds

e. 10 years = _______________ weeks

f. 525 600 min = _______________ years

Chapter 6 Proportional Reasoning

287

5. If 1 bumpeda = 6 momos; 1 momo = 4 goombas; and 1 goomba = 3 pips a. How many goombas in a bumpeda? b. How many pips in a momo? c. How many pips in a bumpeda? d. How many momos in 2.5 bumpedas?

6.1 Practice Answer Key 1a) bc b) 2y 2a) 2 b) 10 c) 11 d) 40 e) 36 f) –2 g) –16

h) 3 i) 21 j) 9 k) 50 l) 66

3a) 24 000 b) 40 c) 10 000 d) 100 000 e) 49 500 f) 1000 4a) 180 b) 5 c) 336 d) 7200 e) 520

f) 1

5a) 24 b) 12 c) 72 d) 15

Remembering Ebbinghaus – Representing Proportions in Different Ways 1. Fill in the table. Words

Fraction

Picture

Percent

Decimal

Ratio

One half

20 %

0.3 3:4

288 Chapter 6 Proportional Reasoning

6.2 Scale Diagrams Warm Up Competency Focus - Connect math concepts to other disciplines Copy the diagram onto the larger grid. Make it three times as large as the original.

Map Scales

Scale diagrams allow us to draw very small or large objects while maintaining the shape of the original. A map is a common example of a scale drawing. In this map 1 cm represents 170 km. The distance, in a straight line, from Vancouver to Kamloops is 1.5 cm on the map. Therefore the actual distance can be found by solving a proportion:

Chapter 6 Proportional Reasoning

289

Try This ... 1. Find the actual distance in km for each scale and map distance given. Distance on map (cm)

Scale

a. 1 cm

1:500 000

b. 3.5 cm

1 cm : 5 km

Actual Distance (km)

2. A map has a scale of 1:50 000 (1 cm on the map is 50 000 cm in reality). Two cities are 3.5 cm apart on the map. How far apart are the two cities in reality? Answer in cm and km.

Scale Factor

A scale factor is the constant by which all dimensions of an object are multiplied to create an enlargement or reduction. It is calculated by taking the new size and dividing by the original size. Consider the following scale factor of 3: If we multiply the dimensions of the original figure by 3 we get the dimensions of the enlarged figure. Now consider a scale factor of 0.5 or .

If we multiply the dimensions of the original figure by 0.5 or the reduced figure.

290 Chapter 6 Proportional Reasoning

we get the dimensions of

Enlargement vs Reduction

An enlargement results in an image that is the same shape but proportionally larger than the original. The scale factor will be greater than 1. A reduction results in an image that is the same shape but proportionally smaller than the original. The scale factor will be less than 1. A scale factor of 1 will not change the size of the object.

Try This ... 1. Will this result in an enlargement or a reduction? a. Scale factor is 3.5

b. Scale factor is 0.75

c. Scale factor is 1.1

d. Scale factor is

e. Scale factor is

f. Scale factor is

Calculate Scale Factor

What do you notice about the sizes of the two circles? We can use a matching measurement to determine the scale factor.

New

Original

Try This ... 1. Calculate the scale factor using the information given. Write the answer as a fraction and a ratio. a.

original

new

original

new

Chapter 6 Proportional Reasoning

291

Try This ... continued c.

d. Original rectangle: 4 cm × 6 cm. New rectangle: 8 cm × 12 cm original new

Using Scale Factor to Predict Measurements

Scale factors can help you find real-world measurements from a model. By comparing the model to the actual object, you can calculate unknown lengths. For example, a model car is built to a scale of 1:24. If the model is 15 cm long, how long is the real car?

Try This ... 1. A model airplane has a length of 20 cm. The scale factor used to make the model is 1:75. What is the actual length of the plane in metres?

Extend and Explore

Draw a floor plan of your math classroom or one of the rooms in your home. Use a 1 cm = 1 m scale and draw it on grid paper.

292 Chapter 6 Proportional Reasoning

6.2 Practice 1. Fill in the blanks. a. The scale factor of a new image is

b. A new image with a scale factor larger than one is a(n) ___________________. c. A new image with a scale factor smaller than one is a(n) ___________________. 2. Find the actual distance in km for each scale and map distance given. Scale

Distance on Map (cm)

a. 1 cm : 50 000 cm

2.5 cm

b. 1 cm : 6 km

1.25 cm

Actual Distance (cm)

Actual Distance (km)

3. Will this result in an enlargement or a reduction? a. Scale factor is 1.5

b. Scale factor is 0.99

c. Scale factor is 0.001

4. Calculate the scale factor using the information given. Write the answer as a fraction and as a ratio. a.

new

original

new

Chapter 6 Proportional Reasoning

293

d. Original triangle: sides of 12 cm, 20 cm, 16 cm. New triangle: sides of 3 cm, 5 cm, 4 cm.

5. A living room has the dimensions of 25 mm by 20 mm on a floor plan. The scale factor used to make the model is 1:300. What are the actual dimensions of the living room?

6. A model train set uses a scale of 1:87. The real train is 26 metres long. How long should the model train be?

6.2 Practice Answer Key 1a)

b) enlargement

c) reduction

2a) 125 000 cm, 1.25 km b) 750 000 cm, 7.5 km 3a) E b) R c) R d) R e) E f) Neither – it does not change 4a) 5) 7.5 m × 6 m 6) 0.3 m

Remembering Ebbinghaus – Percents as Fractions Over 100

1. Apply this to prove the following statement. 16% of 25 is the same as 25% of 16.

2. Use this concept to calculate the following mentally (without a calculator). a. 32% of 50 b. 120% of 10 c. 4% of 25

294 Chapter 6 Proportional Reasoning

6.3 Similar Triangles and Polygons Warm Up Competency Focus - Model mathematics in contextualized experiences How can you measure something that is too tall to reach? By comparing shadows, you can use proportional reasoning to determine the height of a tall object. One way to find the height of a tall tree is to measure the length of its shadow. Hold up a ruler (or small stick), perpendicular to the ground, and measure the length of its shadow. If both shadows are measured at the same time, their sides will be proportional.

If a metre stick (1 metre) casts a shadow of 0.25 metres, and a tree casts a shadow of 3 metres, how tall is the tree?

Is there a tree near your school that you can find the height of using this method?

Similar Polygons

A polygon is a closed, flat shape (2D) made up of straight line segments (called sides) that connect at points called vertices (or corners). Polygon

Similar Triangles

Number of Sides

Shape

Triangle

Three-sided

Quadrilateral

Four-sided (squares and rectangles)

Pentagon

Five-sided

Hexagon

Six-sided

Triangles and other polygons with the same shape but different sizes are called similar. If the measurements of two triangles are known, we can determine if they are similar. If BOTH of the following statements are true, the triangles are similar: 1. Corresponding angles are equal. 2. Sides are proportional. D A

Δ ABC ~ ΔDEF

F d

~ means "is similar to"

implies

and

Chapter 6 Proportional Reasoning

295

Consider the following right triangles with corresponding equal angles. Triangle 2

Triangle 1 E

f B

Given: a, b, c, d, e, f are sides A, B, C, D, E, F are angles A = D, B = E, C =

F = 90°

We can see from the grid that side a is 3 and side b is 4. How can we find side c?

Pythagorean Theorem – Review

The Pythagorean Theorem helps you find a missing side in a right triangle. A right triangle has one angle that measures 90 degrees. The longest side is called the hypotenuse. The relationship between the sides is a2+b2=c2. This means you square the two shorter sides, add them together, and the result is equal to the square of the longest side. For example, if one side is 3 cm and another side is 4 cm: a = 3, b = 4, c = ? a2 + b2 = c2 32 + 42 = c2 9 + 16 = c2 25 = c2 5=c

•

Use Pythagorean Theorem.

•

Replace letters with numbers.

•

Evaluate powers.

•

Simplify the left-hand side.

•

Take the square root of both sides.

•

Evaluate the square root.

The hypotenuse is 5 cm. The Pythagorean Theorem only works for right triangles. In Grade 11 you will learn another formula that works for all triangles.

Try This ... 1. Triangle 2 in the image at the top of the page has a height of 6 cm and a base of 8 cm. Calculate the hypotenuse side using a2+b2=c2.

296 Chapter 6 Proportional Reasoning

How do we know the two triangles on the previous page are similar?

How to Prove Two Triangles are Similar

We must show that: 1. Corresponding angles must be equal. 2. Sides must be proportional. 1. Show that the angles are equal. We know this because the information was given to us. 2. Check to see if sides are proportional

These fractions are equivalent. Therefore, the triangles are similar.

Try This ... 1. Are these two triangles similar? Explain your thinking. a.

9 8

8 20

6 5

Chapter 6 Proportional Reasoning

297

Similar Polygons

Two polygons are similar if and only if their corresponding angles are equal and their corresponding sides are proportional. For example, if the polygons are similar, then we know the sides are proportional. This can help us find missing sides. Consider the following similar polygons. x

1.73

We can find the length of side x by using proportional reasoning. • Which side in the second picture corresponds to x in the first picture? • Which side in the second picture corresponds to 6 in the first picture? We can find x using one of the following methods. Method 1: Cross Multiply

Method 2: Scale Factor Multiply both sides by 1.73

Try This ... 1. These trapezoids are similar. Find x.

4 x 6

2. Find a missing side on a different corresponding side.

3. Find a missing side on the larger figure.

298 Chapter 6 Proportional Reasoning

Nested Triangles

Nested triangles are two triangles where one is nested inside the other. A smaller triangle is drawn completely inside a larger triangle, sharing at least one common angle.

Try This ...

x₁

x₂

1. A person is 150 cm tall standing near a small tree. a. Label the 2 separate similar triangles on the right using the nested triangles on the left. b. Then find the height of the tree. The sides will be proportional.

Extend and Explore

Design and draw a two-dimensional floor plan of a building inspired by BC Indigenous architecture with a scale factor of 1 cm : 1 m. a. Choose a traditional Indigenous home (big house, long house, pit house). Write a brief description of the history of the building you chose and the purpose of the elements of the design. b. Design a floor plan for a room of your choice inspired by elements of the design in part a. Important note: Cultural appreciation vs appropriation. Any actual building that is designed with Indigenous inspiration should be designed in consultation or collaboration with an Indigenous knowledge-keeper. This design project is for educational purposes only. More information is available in the teacher guide.

Chapter 6 Proportional Reasoning

299

6.3 Practice 1. Fill in the blanks. a. A closed, flat shape made up of straight line segments is called a ____________________. b. A polygon with 3 sides is called a ____________________. c. A polygon with 4 sides is called a ____________________. d. A polygon with 5 sides is called a ____________________. e. A polygon with 6 sides is called a ____________________. 2. If the measurements of two polygons are known, we can determine whether they are similar. Two polygons are similar if BOTH of the following conditions are true: a. Corresponding angles are ____________________. b. Sides are ____________________. 3. A student is 1.6 m tall and casts a shadow 2 m long. At the same time, a nearby building casts a shadow 25 m long. How tall is the building? Draw a picture.

4. These trapezoids are similar. Find x.

5. Prove that the sides of the following right triangles are proportional. Find the 2 missing sides by using the Pythagorean Theorem.

6. Two similar rectangles are given. Rectangle A: length = 8 cm, width = 5 cm Rectangle B: length = 12 cm, width = ? Find the width of rectangle B.

300 Chapter 6 Proportional Reasoning

7. Δ ABC ~ ΔDEF. Triangle ABC has sides: AB = 6 cm, BC = 8 cm, AC = 10 cm Triangle DEF has sides: DE = 9 cm, DF = 15 cm, EF = ? Find the length of EF.

8. Two triangles have the following measurements. Are these triangles similar? Show your work and explain. Triangle ABC: sides are 3 cm, 4 cm, 5 cm Triangle DEF: sides are 6 cm, 8 cm, 9 cm

6.3 Practice Answer Key 1a) polygon b) triangle c) quadrilateral d) pentagon e) hexagon 2a) equal b) proportional 3) 20 m

4) 1.7

5) 6) 7.5 cm 7) 12 cm 8)

Remembering Ebbinghaus – Combining Like Terms 1. Simplify a. x + y – 5 + x + y – x – y + 5

b. a + a –3 + a2 + 2a + 3a2 – 2 – 3 – 3a

c. 0.6 + 1.4 – 2.4w – 11.4w – 1.4 – 0.2w + 0.4

Chapter 6 Proportional Reasoning

301

6 Chapter Review 1. Solve a.

2. What is the scale factor used to make the new image?

3. If 9 out of 10 smokers would like to quit smoking, how many out of 50 smokers want to quit? How many out of 500? How many out of 1 000 000?

4. Would you rather be paid 45 dollars for 3 hours of work or 80 dollars for 5 hours of the same type of work?

5. If 3 pizzas can feed 8 people, how many pizzas would you need to feed 96 people?

6. You have 10 incandescent light bulbs (power of each one = 60 watts) in your home. You replace them with 10 LED bulbs (power of each one = 10 watts). If you use them for 2 hours per day, how much energy (watt-hours) do you save in one month (30 days)? HINT: Energy = (Power)(Usage time).

302 Chapter 6 Proportional Reasoning

7. One whole note in music is equivalent to 4 quarter notes. 1 quarter note is equivalent to 2 eighth notes. 1 eighth note is equivalent to 2 sixteenth notes. a. How many sixteenth notes in a whole note?

b. How many eighth notes in 2 whole notes?

c. How many sixteenth notes in 3 quarter notes?

8. 1 cup = 16 tablespoons = 48 teaspoons. a. How many teaspoons are in a tablespoon?

b. How many tablespoons are in ½ cup?

c. How many teaspoons are in ¼ cup?

9. The distance between two cities is 150 km. How far apart will they be on a map with a scale of 1 cm : 1 000 000 cm?

10. A baseball player hits a home run once in every 12 games. If they continue at this rate, how many home runs would they get in 84 games?

11. Using the diagram of the insect provided here at a scale of 4:1. a. What is the actual length of the longest wing?

b. What is the actual length of one antenna?

Chapter 6 Proportional Reasoning

303

12. A student can type 40 words per minute. a. How many words can they type per hour?

b. How long would it take to type 3000 words?

13. If one hour of binging on one of your favourite shows has about 8 minutes of commercials, how many hours did you watch if you saw 20 minutes of commercials?

14. The fuel consumption of a car is 8 litres per 100 km. a. How much fuel is needed to travel 175 km?

b. How far can the car travel on 40 litres of gasoline?

15. You are a photographer preparing prints for an exhibition. You have a 4 × 6 digital photo. The gallery wants two different sized prints. a. They request an 80 × 120 print. What scale factor is needed to produce the new image?

b. They also want to print 100 wallet-sized images (2 × 3). What scale factor is needed to produce the new images?

6 Review Answer Key 1a) 2) 1.5 3) 45, 450, 900 000 4) 80 dollars for 5 hours of work (16 dollars per hour) 5) 36 pizzas

6) 30 000 watt-hours

7a) 16 b) 16 c) 12

8a) 3 b) 8 c) 12

9) 15 cm

10) 7

11a) approximately 0.9 cm b) approximately 0.5 cm

12a) 2400 words b) 75 minutes

13) 2.5 hours

14a) 14 litres b) 500 km

15a) 20 b) 0.5

304 Chapter 6 Proportional Reasoning

How Did It Go? Part 1: Reflecting on Chapter 6 - Check all that apply to you ☐ The content of this chapter is challenging. ☐ I am starting to understand proportional reasoning. ☐ I can solve problems involving proportional reasoning. ☐ I find scale diagrams challenging. ☐ I need more time to practice before the test. ☐ I understand and can use proportional reasoning. ☐ I feel more confident using proportional reasoning than last year. ☐ I can cross multiply. ☐ I understand how to calculate scale factor. ☐ I have a few questions before the test. ☐ I am confident about the content of this chapter. ☐ I can help others with proportional reasoning. ☐ I can use many different strategies to apply proportional reasoning. ☐ I feel confident applying skills to word problems. ☐ I am ready to write the test. ☐ My next step is ______________________________________________________.

Part 2: Reflecting on Proportional Reasoning In this chapter, you learned two ways to solve proportions. Compare the solutions below. Which method do you prefer and why?

Method 1

Method 2

Chapter 6 Proportional Reasoning

305

Vocabulary List for Proportional Reasoning C Conversion factor – A conversion factor is a ratio that is equal to 1 and is used to change a measurement from one unit to another. Cross multiply – Cross multiply means multiplying the numerator of each ratio by the denominator of the other ratio to solve a proportion.

E Enlargement – An enlargement is a drawing or figure that has been made larger while keeping the same shape and proportions.

H Hexagon – A hexagon is a polygon with six sides. Hypotenuse – The hypotenuse is the longest side of a right triangle. It is opposite the right angle.

P Pentagon – A pentagon is a polygon with five sides. Proportional reasoning – Proportional reasoning is the process of comparing ratios and using them to solve problems involving quantities that change at the same rate.

Q Quadrilateral – A quadrilateral is a polygon with four sides.

R Ratio – A ratio compares two quantities using division. Reduction – A reduction is a drawing or figure that has been made smaller while keeping the same shape and proportions.

S Scale factor – A scale factor is the number used to enlarge or reduce a figure. Scale diagram – A scale diagram is a drawing in which the size of the original object has been enlarged or reduced by a scale factor. Similar polygons – Similar polygons have the same shape but may have different sizes. Their corresponding angles are equal and their corresponding sides are proportional.

Similar triangles – Similar triangles are triangles that have the same shape but may have different sizes. Their corresponding angles are equal and their corresponding sides are proportional.

306 Chapter 6 Proportional Reasoning

Failsafe Vocabulary Check Use the concept map to review the vocabulary from this chapter. In each blank circle, write a definition, example, diagram, or connection that helps explain the concept.

Chapter 6 Proportional Reasoning

307

308 Chapter 6 Proportional Reasoning

7 Statistics Statistics is the study of collecting, organizing and analyzing numbers and information. We do this to help us understand the world around us, make predictions, and make informed decisions. An athlete who tracks their time to run 5 km can see if they are making progress over time and adjust their training based on these results. When purchasing headphones, a person might gather data about the cost and consumer ratings to help make the best purchase. Checking the weather forecast before a camping trip helps you decide what to pack.

Big Idea of the Chapter Analyzing the validity, reliability and representation of data enables us to compare and interpret data. In this chapter you will explore: What is statistics?

The study of collecting, organizing, and analyzing data (numbers and information) to answer questions and understand patterns in the world around us.

Factors that affect data collection

Bias, use of language, ethics, time and timing, privacy, cultural sensitivity.

Collecting data

Ensures you have relevant, accurate information: valid and reliable, population vs sample; sampling techniques for surveys such as random, convenience, and voluntary response.

Organizing data

Prepares data for analysis. Examples: frequency table, tally chart.

Graphing data

Makes patterns visible. Examples: bar graph, broken line graph.

Interpreting data

Answers questions and supports decisions: mean, median, mode.

Get Started Look at the image of salmon. How many fish are there? You could try to count them, but it will not work. The fish overlap and face different directions. There are too many to keep track of. A direct count is not possible. So we need another way to approach the problem. One option is to focus on a small part of the image. Count the fish in that region, then use that count to estimate the total. Another option is to compare different parts of the image to decide whether the fish are spread evenly. Each method gives an estimate. The value of the answer depends on how well the method is applied and justified. Scientists work in the same way. In British Columbia, salmon return to rivers in large numbers each year. In 2023, about 1.6 million sockeye salmon returned to the Fraser River. In that same year, about 10.5 million pink salmon returned. These values were not obtained by counting each fish. They were estimated using sampling, sonar data, and direct observations. Statistics provides tools for situations like this. When an exact count is not possible, data can be collected and used to produce a reasonable and supported estimate. ©Edvantage Interactive 2026

Chapter 7 Statistics

309

7.1 Statistics and the Factors Affecting Data Collection Warm Up Competency Focus - Use tools to explore relationships and test conjectures 1. Flip a coin 10 times. Write the number of heads ______.

Number of tails ______.

The experimental probability of landing on “heads” is based on what happens during a specific experiment. Use the above numbers to find your experimental probability using this formula:

2. What is your experimental probability?

______.

3. Find a classmate with a different experimental probability and write it here ______. The theoretical probability of the coin landing on “heads” is ½. This means that, in general, we expect heads half the time and tails half the time. Heads and tails are equally likely events. 4. Compare the experimental probabilities to this theoretical probability.

5. If we wanted the experimental probability to be as close as possible to the theoretical probability, what could we do?

Statistics is the study of collecting, organizing and analyzing numbers and information. We do this to help us understand the world around us, make predictions, and make informed decisions. Data is a collection of facts, numbers, observations, or measurements that represent information about people, objects, events, or phenomena. In statistics, data is foundational: everything we do starts with data. The following terminology is key to collecting good data.

Population vs Sample

A population is the entire group of individuals, items, or observations that you want to study or learn about. It's the complete set of all possible members of a group you're interested in. It is often large. Examples: • All Grade 9 students in BC • All voters in the federal election • All the fish in Kootenay Lake If you take a survey that includes every member of a population, it is called a census.

310 Chapter 7 Statistics

A sample is a subset or smaller group selected from the population. It's a portion of the population that you actually study or collect data from. It should represent the population. Examples of subsets of the populations above: • Grade 9 students taking math this term at your school whose last names start with A-L • Randomly selected voters in Kelowna 65 years and over • 100 rainbow trout in Kootenay Lake Why samples are used: • It's often impossible or impractical to study an entire population (too large, too expensive, too time-consuming). • A well-chosen sample can represent the population accurately without studying everyone. • Cost and time are reduced when using a sample instead of studying the whole population. • Sample size is important to consider. - Too small: Results may not be reliable or representative; high margin of error. - Too large: Wasteful of time and resources; diminishing returns.

Try This ... 1. Circle the population and underline the sample in each statement. a. All light bulbs produced by a factory in one year AND 200 light bulbs randomly selected from different production batches throughout the year.

b. All students in a high school AND 100 students randomly selected (25 from each Grade level: 9, 10, 11, 12).

c. 2000 customers who were randomly sent a satisfaction survey AND All customers who shopped at a retail chain in one month.

Characteristics of Data

Data should come from actual observations or measurements. It needs to be factual. Qualitative data describes qualities or characteristics. It is written in words or placed into categories. Examples include favourite ice cream flavours or opinions such as agree, neutral, or disagree. Quantitative data is expressed as numbers. These numbers can be measured or counted. Examples include math test scores, student height, or the number of soccer goals scored. In practice, both types of data are used together. • Quantitative data shows patterns and trends. • Qualitative data helps explain what those patterns mean.

Chapter 7 Statistics

311

Try This ... 1. Identify each of the statements below as qualitative or quantitative data. a. The most popular season of the year, according to a survey_______________________. b. The amount in mm of rain that falls in a day _______________________. c. The quality of a shipment of apples _______________________. d. The value in dollars of a pack of Pokémon cards _______________________. e. Top 10 most popular Pokémon cards _______________________. f. Cost of groceries for a family per week _______________________. g. A person’s heart rate after 10 minutes on the treadmill _______________________.

Valid and Reliable Data

Statisticians want to ensure that their data is both valid and reliable. Understanding the difference is crucial for gathering trustworthy data and drawing accurate conclusions. Reliability Does it give consistent results? If I measure the same thing multiple times, do I get the same answer? Reliable data has four characteristics: • Consistent: Produces the same results across multiple measurements. • Stable: Results don't change arbitrarily. • Repeatable: Different people using the tool get similar results. • Precise: Repeated measurements are close to one another. Unreliable data does not have these four characteristics. For example, a thermometer that gives different readings each time you measure the same temperature. Validity Does it measure what you think it's measuring? Does it measure the right thing? • Accurate: Measures the actual construct or concept you're interested in. • Appropriate: The tool is suitable for what you're trying to measure. • True and correct: Results reflect reality and measure the intended variable. Invalid data does not measure the right thing. For example, using a ruler to measure temperature. Comparing Reliability and Validity The image on the next page shows the same backpack being measured several times using a scale. Each panel represents a different set of results from those measurements. In the first panel, the readings are close to each other and close to the true value. The measurements are consistent and accurate. This is both reliable and valid. In the second panel, the readings are the same each time, but they are not close to the true value. The scale gives consistent results, but it is not measuring correctly. This is reliable, but not valid.

312 Chapter 7 Statistics

In the third panel, the readings change from one measurement to the next, but they are centred around the true value. The measurements are not consistent, but they are still measuring the correct quantity. This is not reliable, but it is valid overall. In the fourth panel, the readings change and are not close to the true value. The measurements are inconsistent and incorrect. This is neither reliable nor valid. Reliability is about consistency. Validity is about measuring the correct value.

Try This ... 1. Identify each of the following statements as being valid or invalid. If invalid, explain why. a. A biology class measures the height of 30 bean plants over 4 weeks using the same ruler, recording measurements weekly. All plants were grown in identical conditions.

b. A student estimates the average height of students in their school by measuring only the basketball team members.

2. Identify each of the following statements as being reliable or unreliable. If unreliable, explain why. a. A weather app predicts next month's temperature based on a single day's observations.

b. Statistics Canada publishes census data collected from all Canadian households every 5 years, with strict quality controls and transparent methodology.

Chapter 7 Statistics

313

Surveys

A survey is a method of collecting data by asking questions to a group of people called a sample. The questions focus on opinions, behaviours, characteristics, or experiences. Surveys can be done verbally or in writing, and the responses can be numerical or descriptive. In this section, you will learn how surveys are used to collect data and what can affect the results. Designing a survey is not just about asking questions. You need to decide who you are collecting data from and how you will collect it. The questions must be clear so that people understand what is being asked. You also need to consider sample size, bias, timing, and how participants are treated. The goal is to collect data that is clear, fair, and useful. Data Collection There is often more than one way to collect data. The method you choose affects the results. To see this, consider the question: How much homework do Grade 9 students do each night? Two different methods are used to collect data. Compare how each method gathers information and how that affects the conclusion. Method 1

Method 2

Sample: Students in advanced classes only.

Sample: Randomly selected Grade 9

This group does not represent all Grade 9

students. This group represents a wider range

students.

of students.

Method: Email survey during the school day.

Method: Paper survey completed during

Not all students will respond. This can affect

class. Most students will respond.

the results. Question: “Don’t you think too much

Question: “On average, how many minutes

homework is assigned?” This question

per night do you spend on homework?” This

suggests an answer.

question is clear and neutral.

Result: Students do too much homework.

Result: A more accurate estimate of time

This conclusion is not reliable because of the

spent on homework. This conclusion is

sample, method, and question.

supported by the way the data was collected.

Factors that Affect Data Collection When data is collected, the results depend on how it is collected. The two methods show that different choices can lead to different conclusions. This is why it is important to consider the factors that affect data collection before drawing any conclusions. Here are some of them: • Design: choose a sample and design a question. • Implementation: choose a sampling method, location, time. • Quality: minimize bias. • Ethics: informed consent, confidentiality, transparency. When these factors are well-managed, you collect data that is more reliable, valid, and useful for drawing accurate conclusions. When they're neglected, data becomes unreliable, biased, or misleading.

314 Chapter 7 Statistics

Writing a Good Survey Question The quality of your data depends on the quality of your questions. If a question is unclear, vague, or biased, the responses will not be useful. Good questions are clear, focused, and easy to answer. They allow people to give accurate responses without confusion. The three examples below show common problems in survey questions and how they can be improved. 1. Vague and Confusing Questions – "Do you like it?" This question is vague and confusing. It uses the pronoun “it” and assumes we know what that is. What does “like” mean? Is it enjoyment, approval, or admiration? It is also a question with only two answers (binary), in this case yes/no. Opinions can be complex and rarely fit into two categories. A question like this loses nuance and misses the middle ground. New and improved question: On a scale of 1 to 10, how much do you enjoy playing first-person video games? 2. Unclear and Undefined Terms – “Do you drink a lot of water?” This question has multiple flaws. “A lot” means different things to different people. For water, does tea count? Does juice count? Does sparkling water count? A yes/no answer loses nuance. There is no time frame. New and improved question: How much plain water, in millilitres, do you drink in a typical day? 3. Leading and Confusing Questions – “You don’t dislike cafeteria food, do you?” This question is a leading question. It implies that one opinion is normal. It is also confusing because of the double negative and can produce inaccurate data. If I like it, do I answer yes or no? New and improved question: Rate your feelings about the new cafeteria specials from 1 to 5. 1 = strongly dislike, 2 = dislike, 3 = neutral, 4 = like, 5 = strongly like.

Try This ... 1. Rewrite these questions to make them clearer. a. Don’t you agree that we should have a school dance in May? b. Do you like pizza and ice cream? c. Do you like online learning? Yes or no, do you like video games? Yes or no d. How do you feel about your phone use? [ ] Very Negative [ ] Negative [ ] Neutral [ ] Positive [ ] Very Positive

Chapter 7 Statistics

315

Bias Bias is when a survey tips the scales in favour of one answer, making the data unfair or misleading. Examples: • The misleading questions above are a form of bias. • Asking people outside a fast-food restaurant whether it is their favourite restaurant. • Asking employees to report how often they exercise when the results will be published in a newsletter. This also raises ethical considerations. A good survey removes bias by asking neutral questions, using fair sampling methods, and creating an environment where respondents feel safe answering honestly.

Try This ... 1. Identify if each of these statements is biased or not. If it is biased, rewrite it to reduce the bias. a. "Don't you think our school's new homework policy is too strict?"

b. How many hours per week do you spend on social media? [ ] 0-5 hours [ ] 6-10 hours [ ] 11-15 hours [ ] 16+ hours

c. How do you rate BC as a province of Canada? [ ] good, [ ] one of the best, [ ] the best, [ ] the GOAT

d. In the last week, how many times did you buy food in the school cafeteria?

Timing The time at which data is collected can affect the results. Responses may change depending on when the survey is given. For example: • Asking high school students after school on Friday to complete a 15-minute in-person survey. • Asking students to rate their classes on September 10th of the school year. • Giving students a 200-question survey to complete between their classes (5-minute break). • Collecting data about ice cream sales in January in Canada.

316 Chapter 7 Statistics

Ethics Data must be collected in a responsible way. Participants should understand what they are being asked and how their information will be used. Privacy must be respected. Ethical factors to consider: • Do the participants consent to the survey? • Do they know what the survey is? • Can they refuse to take the survey with no consequence? • Could this survey cause distress? • Is personal information protected? • Is there a conflict of interest in this survey?

Try This ... 1. Revise each survey to make it more ethical: a. Survey young children at a playground without parental consent.

b. Survey results are sold to a marketing company with personal information without the participants' knowledge.

c. A fast-food restaurant owner surveys their own employees during work hours, asking them to write their names on the form and rate how much they love the restaurant's food.

Extend and Explore Many games are played that involve the sum of two dice. Imagine one of the dice is blue and the other red. • What are the possible outcomes of rolling two 6-sided dice? • If you add the numbers on the two dice, which sums are more likely? Which are least likely? • Which sum is most likely? Which two sums are least likely? Experiment: roll 2 dice 20 times and write the sum of the 2 dice in a chart. What do you notice? Is this consistent with what you thought would happen?

Chapter 7 Statistics

317

7.1 Practice 1. Fill in the blanks. a. The study of collecting, organizing and analyzing numbers and information is called _________________. b. An entire group being studied is a _________________. c. Part of a group being studied is a _________________. d. A collection of facts, numbers, observations, or measurements is called _________________. e. Data that describes characteristics is _________________. f. Data expressed as numbers is called _________________. g. Different readings each time you weigh the same item on the same scale is an example of _________________ data. h. Using a thermometer to measure distance is an example of _________________ data.

2. Would you survey a population or a sample in the following situations: a. You want to find out the favourite pet of the students in your class. _________________ b. You want to find out the favourite role-playing video game for students in your high school. _________________ c. You want to find out which units are the most difficult in Math 10, according to teachers in your school.________________ d. You want to find out how much sleep the average teen in BC gets. _________________

3. For each statement, identify whether the data is qualitative or quantitative. a. Number of followers ________________ b. Before and after photos ________________ c. The amount in mm of snow that falls in a day ________________ d. Top 3 features of a new car ________________ e. Customer satisfaction surveys with a scale (very satisfied, satisfied, not satisfied) ________________ f. Calories per serving ________________ g. Interview transcript ________________

4. Are these examples valid and/or reliable? Example

Is it Valid?

Is it Reliable?

a. An accurate, consistent scale b. A scale that consistently reads 10 kg too high c. A scale that reads slightly different weights for the same object. d. A broken scale that seems to give random weights

318 Chapter 7 Statistics

5. Improve these survey questions: a. "Which is your favourite?”

c. "You don't dislike social media, do you?"

b. "Do you do a lot of homework?"

d. "Do you like PE and science classes?"

7.1 Practice Answer Key 1a) statistics b) population c) sample d) data e) qualitative

f) quantitative g) unreliable h) invalid

2a) Population b) Sample c) Population d) Sample 3a) quantitative b) qualitative c) quantitative d) qualitative e) qualitative f) quantitative g) qualitative 4a) yes, yes b) no, yes c) yes, no d) no, no 5) Answers will vary. a) Rank the following three soft drinks from least to most preferred: Cola; Diet Pop; Cherry Soda b) How many hours of homework do you do on average in one day? less than 1 hour; 1 hour to less than 2 hours; 2 hours to less than 3 hours; 3 hours or more. c) How do you feel about social media? Dislike; Neutral; Like. d) How much do you like PE class? Strongly dislike; dislike; neutral; like; strongly like. How much do you like Science class? Strongly dislike; dislike; neutral; like; strongly like.

Remembering Ebbinghaus – Linear Patterns 1. Fill in the blanks for the linear patterns. a. 3, 5, ____, ____,11, ___ b. 4, ___, 12, ___, 20 c. ______, 1, –4, ___, –14 d. 101, 89, ___, ____, 53

2. For each linear equation, create a table of values and graph them on the grid provided. Label each line. a. y = 7

b. x = 5

c. y=x+5

Chapter 7 Statistics

319

7.2 Collecting and Organizing Data Warm Up Competency Focus - Connect mathematical concepts to personal areas and interests Ask each person in your class how many siblings they have, including step-siblings. Record each response in the chart using tally marks. A tally is a way of counting how many times something occurs. In this case, it shows the number of students. Five is represented as four vertical lines with a fifth line drawn across them. No siblings

One sibling

Two siblings

Three or more siblings

Look at the data. Complete the following statements based on the data and add one of your own. a. Most of the class has… b. Half of the class has… c. Very few students in the class have… d.

Sampling is the process of selecting a smaller group from a larger population to collect data. It is usually not practical to survey every member of a population. Surveying every member of a population is called a census. It takes a great deal of time and resources. Instead, data is collected from a sample and used to make conclusions about the population. The way the sample is chosen matters because it affects how well the results represent the population. Here are several ways to choose a sample.

Sampling Methods

Random sampling: Every member has an equal chance of being selected (reduces bias). Selection is based on chance, which helps reduce selection bias. (like drawing names from a hat or using a random number generator). Example: choose 3 students randomly from your math class. Assign each student a number and use a random number generator. Stratified sampling: Divide the population into groups (strata) based on shared characteristics, then randomly sample from each group to ensure all subgroups are represented fairly. Group characteristics could be age, income level, location, or other relevant information. Example: choose 40 students from a high school by first putting them into grade groups then choosing 10 from each of the grades 9 through 12. Systematic sampling: Start with an ordered list. Choose a random starting point, then select every nth member from the list. Example: To survey every 10th customer, randomly choose a starting number from 1 to 10. If 4 is chosen, survey the 4th, 14th, 24th and 34th customers.

320 Chapter 7 Statistics

Convenience sampling: Select members who are easiest to reach or most available. This is a non-random method based on ease of access. Example: Survey high school students as they enter the main doors between 8:15 and 8:30 a.m. Voluntary sampling: People choose to participate in the survey. Example: Post a survey on the school website; students who want to participate click the link.

Try This ... 1. Which sampling method is used in each situation? a. You ask people in the cafeteria at lunch what their favourite lunch is. _____________________ b. You put all your classmates’ names in a hat to choose 5 students to survey in your class. _____________________ c. You provide an optional questionnaire to fill out to students on the school website. _____________________ d. You ask for a list of students in your school organized alphabetically by last name and ask every 50th person a question. _____________________ e. You split your class according to age, then choose 2 people randomly from each age group. _____________________

Advantages and Disadvantages of each Sampling Method

Different sampling methods can be used to collect data, and each method has strengths and limitations. The method you choose affects how accurate your results are and how well they represent the population. Some methods reduce bias and produce reliable results, but they can take more time and effort. Other methods are faster and easier to use, but they may introduce bias and limit how useful the results are. The tables below compare the advantages and disadvantages of several common sampling methods. Random sampling Advantages Reduces selection bias; can produce

Disadvantages May underrepresent smaller subgroups.

a representative sample and support conclusions about the population. Stratified sampling Advantages

Disadvantages

Can produce a precise, balanced and accurate Can be more difficult, take more time and sample that represents all groups.

money, and require knowledge of the population groups.

Systematic sampling

Advantages

Disadvantages

Simple and quick; can reduce selection bias

Requires an ordered list; a repeating pattern

when a random starting point is used.

in the list may create bias.

Chapter 7 Statistics

321

Convenience sampling Advantages

Disadvantages

Easy, quick and inexpensive; useful for

Can be highly biased, unrepresentative and

testing ideas.

unreliable; results cannot be generalized.

Voluntary sampling Advantages

Disadvantages

Quick, easy and inexpensive; useful for

Can be highly biased, unrepresentative and

exploring ideas.

unreliable; results cannot be generalized.

Try This ... 1. Which sampling methods minimize bias?

2. Which sampling methods are more reliable?

3. Which sampling methods would you use to make an important decision?

4. Which sampling methods would you use to quickly explore or test an idea?

Extend and Explore

Find a real survey, such as a news poll or company survey. Analyze it for bias. What could be improved?

Remembering Ebbinghaus – Solving Equations 1. Solve the following equations. a. 3x + 7 = 13

322 Chapter 7 Statistics

b. 4a + 7 = 3a – 9

7.2 Practice 1. Fill in each blank with the best term for the definition. a. A sample where participants choose to participate. __________________________ b. A sample where every 15th person on an ordered list is chosen. __________________________ c. A sample where every member has the same chance of being selected. __________________________ d. A sample where participants are chosen because they are easily accessible. __________________________ e. A survey where every member of a population participates. __________________________

2. Which sampling methods minimize bias? Explain your answer.

3. Which sampling method would you use to quickly explore or test an idea? Explain your answer.

4. Which of the following factors are issues in each survey description? There may be more than one: bias, cultural sensitivity, privacy, time and timing, use of language, or ethics. a. A survey is given to find the best Valentine’s gift in July.

b. A survey forces participants to answer every question and does not keep answers confidential.

c. A survey question is confusing.

d. A survey about the best sport is given at the entrance to a hockey game.

7.2 Practice Answer Key 1a) voluntary b) systematic c) random d) convenience e) census 2) Random, stratified or systematic because they are random and most likely to accurately represent a population. 3) Convenience or voluntary sampling because these methods are quick and easy to use when initially exploring an idea. 4a) timing b) privacy, ethics c) use of language d) bias

Chapter 7 Statistics

323

7.3 Graphing and Interpreting Data Warm Up Competency Focus - Use reasoning and logic to analyze mathematical ideas Look at the 3 graphs below: they represent the same data. What do you notice?

Graphing Data

Graphs help us organize data so patterns and trends are easier to see. Different types of graphs are useful for different kinds of information. Bar graphs are helpful when comparing separate categories, while broken line graphs show how data changes over time. Choosing the right graph makes it easier to understand and communicate information clearly. Bar graph: a graph that uses rectangular bars to represent and compare quantities. It is useful for comparing categories or groups of discrete data. For example, here is a survey of a group of people and their favourite ice cream flavours: Chocolate: 8 Vanilla: 6 Mint: 3 Strawberry: 4 A bar graph of this data is represented here.

324 Chapter 7 Statistics

Broken line graph: a graph that uses points connected by straight lines to show how data changes over time. It is useful for showing trends, patterns, or changes in continuous data. For example, the table below shows the average temperature for the first five months of the year.

Month

Temperature (°C)

January

February

March

April

May

Choosing the right type of graph helps make data easier to understand, compare, and interpret accurately.

Try This ... 1. Make a bar graph with the following data.

Platform

Percent Teens Using Platform

TikTok

60%

Instagram

69%

Snapchat

54%

YouTube

95%

Discord

38%

Year

Price

2019

$749

2020

$769

2021

$789

2022

$819

2023

$839

2024

$859

2025

$879

Price ($)

2. Create a broken line graph using the following data on the price of smartphone plans over a seven-year period.

2019

2020

2021

2022

Year

2023

2024

2025

Chapter 7 Statistics

325

Measures of Central Tendency

Once numerical data has been collected, it is useful to be able to describe the data in a simple way. One way we can do this is by finding the measures of central tendency: mean, median and mode. The table below defines these three terms. Mean

Median

Mode

Add all the data values

When the data is placed in

The data value that occurs the

together and divide by the

numerical order, it is the

most often is the mode.

number of values.

middle data value.

Sometimes called an average. If there are an even number of data values, take the

It is possible to have no mode, or multiple modes.

average of the two middle values. Now let's find the mean, median, and mode of the following Grade 9 math test marks: 58, 62, 71, 77, 80, 78, 71 The mean is found by adding all the values and dividing by the number of values. A calculator can be helpful for finding the mean.

The mean is 71. The mode is 71 because it occurs most often. The median is found by first placing the data in order and then identifying the middle value. 58, 62, 71, 71, 77, 78, 80 The median is 71 because it is the middle number. In this data set, the mean, median and mode are all 71.

Extend and Explore

The mean (average) is considered the best measure of central tendency. Is it always the best measure? Can you think of situations where the mode or median would be better?

326 Chapter 7 Statistics

Try This ... 1. The average monthly high temperature (°C) in 2025 in Terrace, BC for each month is listed in the chart below. Jan

Feb

Mar

Apr

May

June

July

Aug

Sept

Oct

Nov

Dec

a. What is the mean of the monthly high temperatures?

b. What is the median temperature?

c. What is the mode?

2. Find the mean, median and mode of the following. a. 77, 67, 77, 97

b. 6, 12, 11, 6, 13, 12, 9, 15, 8, 8, 9, 12, 11

Remembering Ebbinghaus – Scale Factor 1. Solve for x. a.

2. On a map, 1 cm represents 50 km. If a distance on the map is x cm, and the real distance is 350 km, what is x?

Chapter 7 Statistics

327

7.3 Practice 1. Create a bar graph using the data below. Month

Website Visits

Jan

1 200

Feb

1 500

Mar

1 400

Apr

1 800

May

2 100

Jun

2 500

2. Create a broken line graph using the data below. Remember to label the axis.

Year

Sales ($)

2018

50 000

2019

65 000

2020

40 000

2021

70 000

2022

85 000

3. Five adult brothers and sisters have the following heights: 192 cm, 165 cm, 189 cm, 165 cm, 195 cm. a. Find the average height of the siblings.

b. One source (ourworldindata.org) indicates that the worldwide average heights are 171 cm for adult males and 161 cm for adult females. Would you consider this a tall family or not?

4. A student training for a track meet recorded the distance she ran each day, in kilometres. Day

Distance (km)

a. Find the mean, mode and median.

b. If on the 6th day she ran 5 km and on the 13th day she ran 10 km (without changes to any other days), what would the new average be?

328 Chapter 7 Statistics

5a. You want to find the current average in math courses for students in your high school. You stand at the entrance in the morning and ask 5 students their marks. Their responses are 95%, 60%, 73%, 88%, 73%. Calculate the mean, median and mode for this sample of students.

b. You continue to ask 15 more students and these are their responses: 75%, 80%, 71%, 63%, 82%, 58%, 71%, 54%, 65%, 90%, 98%, 61%, 70%, 70%, 71%. Calculate the mean, median and mode for the sample of 20 students (include the first 5).

c. Did anything change? Which set of measures of central tendency would be more reliable a) or b)?

6. Find the mean, mode and median for the population of the provinces and territories in Canada Provinces and Territories

Population

Ontario

16.2 million

Quebec

9.1 million

British Columbia

5.7 million

Alberta

5.0 million

Manitoba

1.5 million

Saskatchewan

1.25 million

Nova Scotia

1.08 million

New Brunswick

859 000

Newfoundland and Labrador

545 000

Prince Edward Island

179 000

Yukon

47 000

Northwest Territories

45 000

Nunavut

41 000

Source: Statistics Canada, population estimates as of January 1, 2025.

7.3 Practice Answer Key 1) 2)

3a) 181.2 cm 2, 6 and 8 km

b) yes, the average of 181.2 cm is significantly higher than 171 cm and 161 cm b) 5.79 km

5a) mean: 77.8%, median: 73%, mode: 73%

The values in question b are more reliable because there is more data.

4a) mean: 5.14 km, median: 6 km, mode:

b) mean: 73.4%, median: 71%, mode: 71%

c) all values are lower.

6) Mean: 3 195 846, median: 1 080 000, mode: no mode Chapter 7 Statistics

329

7 Chapter Review 1. Match the following terms to the correct definition. a. _____ Bias

i. The entire group of people or objects being studied.

b. _____ Ethics

ii. A sample created by dividing the population into groups and selecting participants from each group.

c. _____ Population

iii. Data that accurately measures what it is intended to measure.

d. _____ Random Sample

iv. A factor that causes data or results to favour one outcome over another.

e. _____ Stratified Sample

v. A sample in which every member of the population has an equal chance of being selected.

f. _____ Valid Data

vi. Guidelines for conducting research in a fair, respectful, and responsible way.

2. Create a bar graph representing the data provided below from a student’s monthly budget.