Plantar_Matemática_Volume 2

Matemática

Anos Iniciais do Ensino Fundamental

Editora responsável: Jacqueline da Silva Ribeiro Garcia

Organizadora:

EDITORA NOVO RUMO Obra coletiva concebida, desenvolvida e produzida pela Editora Novo Rumo.

Componente curricular: Matemática

Matemática

Organizadora: EDITORA NOVO RUMO

Obra coletiva concebida, desenvolvida e produzida pela Editora Novo Rumo.

Anos Iniciais do Ensino Fundamental

Editora responsável: Jacqueline da Silva Ribeiro Garcia

Especialista em Psicopedagogia pela Universidade Estadual de Londrina (UEL-PR).

Licenciada em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Atuou como professora em escolas do Ensino Básico. Editora e elaboradora de materiais didáticos.

Componente curricular: Matemática 1ª edição Londrina, 2025

Copyright © Editora Novo Rumo, 2025.

Edição Jacqueline da Silva Ribeiro Garcia, Lucília Franco Lemos dos Santos

Assistência editorial Denise Maria Capozzi, Kethelyn Yukari Ogasawara

Revisão técnica Tânia Camila Kochmanscky Goulart

Preparação e revisão Moisés Manzano da Silva (coord.)

Gerência de produção editorial Camila Rumiko Minaki Hoshi

Supervisão de produção editorial Priscilla de Freitas Cornelsen Rosa

Assistência de produção editorial Lorena França Fernandes Pelisson

Coordenação de produção de arte Tamires Rose Azevedo

Edição de arte Keithy Mostachi

Projeto gráfico e design Dayane Barbieri, Keithy Mostachi, Laís Garbelini

Projeto de capa Marcela Pialarissi

Ilustrações de capa Ricardo Gualberto

Coordenação de diagramação Adenilda Alves de França Pucca - Nil

Diagramação AVITS Estúdio Gráfico Ltda., EfeDois Editoração Ltda., Leandro

Júnior Pimenta

Autorização de recursos João Henrique Pedrão Feliciano

Iconografia Alessandra Roberta Arias, Vinícius Costa (trat. imagens)

Objetos digitais

Gerência de produção Erick Lopes de Almeida

Roteiros Camila Vidigal

Edição de imagens Brenda de Oliveira Goes

Desenvolvimento Ohanna Schmitt Bolfe, Tatiana Tissa Kawakami

Dados Internacionais de Catalogação na Publicação (CIP) (Câmara Brasileira do Livro, SP, Brasil)

Plantar matemática : 2º ano : anos iniciais do ensino fundamental / organizadora Editora Novo Rumo ; obra coletiva concebida, desenvolvida e produzida pela Editora Novo Rumo ; editora responsável Jacqueline da Silva Ribeiro Garcia. -- 1. ed. -- Londrina, PR : Editora Novo Rumo, 2025.

Componente curricular: Matemática.

ISBN 978-65-5158-137-3(livro do estudante)

ISBN 978-65-5158-136-6(livro do professor)

ISBN 978-65-5158-141-0(livro do estudante HTML5)

ISBN 978-65-5158-140-3(livro do professor HTML5)

1. Matemática (Ensino fundamental) I. Garcia, Jacqueline da Silva Ribeiro. II. Série.

25-299271.0

CDD-372.7

Índices para catálogo sistemático:

1. Matemática : Ensino fundamental 372.7

Eliete Marques da Silva - Bibliotecária - CRB-8/9380

Reprodução proibida: Art. 184 do Código Penal e Lei 9.610 de 19 de fevereiro de 1998. Todos os direitos reservados à EDITORA NOVO RUMO.

Avenida Doutor Adhemar Pereira de Barros, 1500, sala 804 - Bela Suíça - Londrina-PR CEP 86047-250 - Tel. (43) 3367-2030 contato@editoranovorumo.com.br

Elaboração de originais

Jacqueline da Silva Ribeiro Garcia

Especialista em Psicopedagogia pela Universidade Estadual de Londrina (UEL-PR).

Licenciada em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Atuou como professora em escolas do Ensino Básico. Editora e elaboradora de materiais didáticos.

Fátima Gomes Machado

Especialista em Docência na Educação Superior pela Universidade Estadual de Londrina (UEL-PR).

Licenciada em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Licenciada em Pedagogia pelo Centro Universitário Internacional (Uninter-PR).

Elaboradora e editora de materiais didáticos.

Sandra Aparecida Ferreira Marchi

Especialista em Educação Especial pela Faculdade Catuaí (PR). Especialista em Gestão Escolar, com habilitação em Administração, Supervisão e Orientação Educacional, pela Faculdade Catuaí (PR).

Licenciada em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Professora dos Anos Iniciais do Ensino Fundamental. Elaboradora de materiais didáticos.

Em respeito ao meio ambiente, as folhas deste livro foram produzidas com fibras obtidas de árvores de florestas plantadas, com origem certificada.

Impresso no Parque Gráfico da Editora FTD CNPJ 61.186.490/0016-33

Avenida Antonio Bardella, 300 Guarulhos-SP – CEP 07220-020 Tel. (11) 3545-8600 e Fax (11) 2412-5375

APRESENTAÇÃO

Acreditamos que o aprendizado em Matemática é essencial para que os estudantes se tornem cidadãos ativos e capazes de pensar de forma autônoma e crítica. Esta coleção foi cuidadosamente pensada para ser uma parceira nessa missão, proporcionando uma abordagem integrada e relevante.

Ao longo de cada unidade, o conteúdo se conecta diretamente com a realidade dos estudantes, valorizando o que eles já sabem e incentivando a construção de novos conhecimentos. Nessa dinâmica, o professor não é apenas um detentor do saber, mas um guia e um mediador, orientando os estudantes a serem os protagonistas de sua aprendizagem.

Para apoiar essa jornada, apresentamos este Livro do Professor. Na primeira parte dele, você encontra informações sobre a estrutura da coleção e a Reprodução do Livro do Estudante com as orientações ao professor nas laterais e nos rodapés das páginas reproduzidas, com comentários práticos para auxiliar no dia a dia em sala de aula, como orientações sobre os conteúdos das unidades, atividades extras, momentos sugeridos de avaliação, entre outros subsídios. Na segunda parte, apresentamos o Manual do Professor, onde você encontra desde a estrutura da Base Nacional Comum Curricular (BNCC) e fundamentos teórico-metodológicos da coleção até recursos práticos, como estratégias de avaliação diversificadas, modelos de planejamento de rotina e de sequência didática, quadro de distribuição dos conteúdos e sugestões de cronogramas que contribuem para o desenvolvimento docente.

É importante ressaltar que as sugestões podem ser adequadas de acordo com a realidade da turma e da escola. Esperamos que seja uma ferramenta útil e enriquecedora no processo de ensino-aprendizagem, possibilitando a formação de cidadãos críticos e participativos na sociedade.

Desejamos a você um ótimo ano letivo!

SUMÁRIO

A BASE NACIONAL COMUM CURRICULAR (BNCC) ........................................

AS COMPETÊNCIAS GERAIS DA EDUCAÇÃO BÁSICA ...................................................................... VII

AS COMPETÊNCIAS ESPECÍFICAS........................ VIII

AS UNIDADES TEMÁTICAS, OS OBJETOS DE CONHECIMENTO E AS HABILIDADES ...............IX

OS TEMAS CONTEMPORÂNEOS TRANSVERSAIS .........................................................IX

INTEGRAÇÃO ENTRE OS COMPONENTES CURRICULARES ........................ X A PRÁTICA INTERDISCIPLINAR E O TRABALHO COM PROJETOS INTERDISCIPLINARES ................. X AVALIAÇÃO .......................................................... XI

O PAPEL DO PROFESSOR E A PRÁTICA DOCENTE ....................................... XIV A PRÁTICA PEDAGÓGICA EM AÇÃO .................... XIV O ENSINO DE MATEMÁTICA ............................. XX

FUNDAMENTOS TEÓRICO-METODOLÓGICOS NO ENSINO DE MATEMÁTICA ................................ XX O LETRAMENTO MATEMÁTICO ........................... XXII

ABORDAGENS E PRÁTICAS EM MATEMÁTICA .... XXII

QUADRO DE DISTRIBUIÇÃO DOS CONTEÚDOS ......................................... XXVII

SUGESTÕES DE CRONOGRAMAS .................XXIX

REFERÊNCIAS COMPLEMENTARES PARA A PRÁTICA DOCENTE ........................... XXX

REFERÊNCIAS BIBLIOGRÁFICAS COMENTADAS – LIVRO DO PROFESSOR ...... XXX

MANUAL DO PROFESSOR

CONHEÇA A COLEÇÃO

Esta coleção é composta por dois volumes, sendo 1º e 2º anos destinados aos estudantes e professores dos Anos Iniciais do Ensino Fundamental. Cada volume é organizado em 10 unidades que, por sua vez, são subdivididas em tópicos e seções que desenvolvem as habilidades relacionadas aos objetos de conhecimento e às competências gerais e específicas propostas pela BNCC. Além disso, durante o desenvolvimento dos conteúdos, a coleção aborda os temas contemporâneos transversais, contribuindo para a formação de cidadãos críticos e atuantes na sociedade.

Além dos volumes impressos, a coleção apresenta a versão digital do Livro do Estudante e do Livro do Professor. Esses materiais digitais apresentam recursos acessíveis, favorecendo a utilização por todos os estudantes. Os livros digitais também apresentam como recurso infográficos, que podem ser acessados, na versão digital, por meio do sumário e de ícones indicados nas páginas dos livros.

O LIVRO DO ESTUDANTE

A seguir, apresentamos a estrutura do Livro do Estudante, explicando as características das seções e de outros elementos que compõem a coleção.

VAMOS

INICIAR

Essa seção, presente no início de cada volume, tem o objetivo de avaliar os estudantes com relação aos conhecimentos esperados para o ano de ensino, permitindo a você fazer uma avaliação diagnóstica da turma.

PÁGINAS

DE ABERTURA

Têm como objetivos marcar o início de cada unidade, despertar a atenção dos estudantes para o que será abordado e relacionar os conteúdos aos conhecimentos prévios e à sua realidade próxima.

DESENVOLVIMENTO DOS CONTEÚDOS

Os conteúdos são desenvolvidos por meio de atividades e das seções presentes nas unidades. As atividades relacionadas aos conteúdos são apresentadas ao longo da unidade, de modo integrado e contendo estruturas variadas, a fim de tornar as aulas mais dinâmicas e envolventes e auxiliar no desenvolvimento das habilidades e das competências da BNCC.

VOCABULÁRIO

Apresenta o significado de termos que os estudantes podem desconhecer e que são importantes para a compreensão do texto.

BOXE COMPLEMENTAR

Apresenta textos e imagens com informações complementares ao assunto ou contexto trabalhado na unidade.

COLETIVAMENTE

Explora os temas contemporâneos transversais, contribuindo para a formação cidadã dos estudantes por meio de reflexões e propostas de resoluções de problemas, de modo que eles sejam atuantes na sociedade em que vivem. É subdividida em Conhecendo o problema, Organizando as ideias e Buscando soluções para que, assim, os

estudantes tenham contato com uma situação-problema, reflitam sobre ela e busquem uma solução prática. O tema contemporâneo transversal desenvolvido é identificado nas orientações ao professor

ENTRE TEXTOS

Promove o trabalho com diferentes gêneros textuais, possibilitando o desenvolvimento de habilidades relacionadas à leitura, à escrita, à oralidade e aos processos gerais de compreensão de leitura: localizar e retirar informação explícita de textos; fazer inferências diretas; interpretar e relacionar ideias e informações; analisar e avaliar conteúdos e elementos textuais. A seção apresenta as subdivisões Explorando o texto e Além do texto

DIVIRTA-SE E APRENDA

Aplica o conteúdo estudado na unidade por meio de jogos, brincadeiras e atividades lúdicas.

EXPERIMENTE

O estudante é convidado a realizar atividades práticas que envolvem o assunto estudado na unidade por meio de experimentos ou produções interessantes.

VAMOS AVALIAR O APRENDIZADO

Essa seção propõe uma avaliação formativa com relação aos conteúdos abordados em cada bimestre, possibilitando avaliar a aprendizagem dos estudantes e obter informações para intervenções caso haja defasagens ou dificuldade na assimilação dos conteúdos e conceitos.

SAIBA MAIS

Apresenta sugestões de recursos extras, como livros, filmes e sites. Cada sugestão é acompanhada por uma breve sinopse.

VAMOS CONCLUIR

Presente ao final de cada volume, essa seção contém atividades cujo objetivo é sugerir uma avaliação somativa, de modo que você possa avaliar os estudantes quanto aos conhecimentos adquiridos durante o processo de ensino no ano letivo.

REFERÊNCIAS BIBLIOGRÁFICAS COMENTADAS

Localizada ao final de cada volume, apresenta indicações comentadas de livros, revistas e sites que foram consultados na elaboração do Livro do Estudante

MATERIAL COMPLEMENTAR

Presente no final de cada volume, essas páginas contêm materiais para os estudantes recortarem, manipularem e usarem na resolução de algumas das atividades propostas.

DESAFIO A MAIS

Atividade de caráter desafiador, no final de cada unidade, para instigar o raciocínio lógico matemático do estudante e a busca autônoma por respostas.

ÍCONE DE RESPOSTA ORAL

Indica que os estudantes devem responder oralmente à atividade ou à questão.

ÍCONE DESAFIO

Indica que os estudantes devem registrar as respostas da atividade no caderno.

ÍCONE

CÁLCULO MENTAL

Indica que os estudantes devem realizar as atividades sem o registro escrito de cálculos, incentivando o raciocínio lógico.

OBJETO DIGITAL

Indica que existe na versão digital deste livro um infográfico relacionado ao conteúdo ou ao contexto que está sendo trabalhado.

DESTAQUE DICA

Apresenta dicas que podem auxiliar os estudantes na resolução de algumas atividades.

O

LIVRO DO PROFESSOR

Este Livro do Professor é organizado em duas partes. Esta primeira parte apresenta a estrutura da coleção e a Reprodução do Livro do Estudante, que se refere à reprodução das páginas do Livro do Estudante em tamanho reduzido, com respostas e possíveis comentários para você. Nas laterais e nos rodapés dessas páginas, as orientações ao professor propõem comentários, sugestões de condução para as atividades e respostas de algumas atividades que não foram apresentadas na reprodução da página do Livro do Estudante. Essas orientações colaboram para a prática docente e seu dia a dia em sala de aula e foram elaboradas de modo a explicitar os procedimentos das aulas de forma prática e ao mesmo tempo detalhada, oferecendo suporte à prática docente.

A segunda parte, apresentada após a Reprodução do Livro do Estudante, é intitulada Manual do Professor Ela apresenta a estrutura da BNCC, a fundamentação teórico-metodológica da coleção e aborda diversos assuntos que contribuem para o desenvolvimento docente e para o dia a dia em sala de aula. Além disso, apresenta um quadro de distribuição dos conteúdos com as habilidades e competências da BNCC que estão sendo desenvolvidas em cada unidade, além de sugestões de cronogramas bimestrais, trimestrais e semestrais. Ao final dessa parte, são apresentadas sugestões de referências complementares para a prática docente e as referências bibliográficas comentadas utilizadas como consulta para a produção das orientações ao professor e do Manual do Professor Observe a seguir como as orientações ao professor, que constam na primeira parte deste Livro do Professor, estão estruturadas.

Nas orientações ao professor da seção Vamos iniciar, você encontra os objetivos pedagógicos e as sugestões de intervenção, com base nas respostas dos estudantes, considerando os conhecimentos prévios deles.

OBJETIVOS DA UNIDADE

Destaca os objetivos pedagógicos de cada unidade do Livro do Estudante

SUGESTÃO DE ESTRATÉGIA INICIAL

Fornece dicas para que você possa iniciar as aulas, abordar alguns conteúdos ou realizar uma avaliação diagnóstica de maneira diferente da que foi apresentada no Livro do Estudante

BNCC

Apresenta habilidades, competências e temas contemporâneos transversais da BNCC que estão sendo desenvolvidos em cada conteúdo, destacando as relações entre esses elementos e o conteúdo.

COMENTÁRIOS DIVERSOS

Os comentários e as explicações de caráter prático referentes às atividades do Livro do Estudante e as considerações pedagógicas a respeito de possíveis dificuldades dos estudantes na resolução das atividades, bem como alternativas para consolidar conhecimentos, são inseridos em tópicos ao longo da unidade.

RESPOSTAS

Apresenta as sugestões de respostas de algumas atividades e questões indicadas no Livro do Estudante.

ATIVIDADE EXTRA

Apresenta sugestões de atividades complementares que contribuem para diversificar as estratégias de aprendizagem.

OBJETIVOS

Lista os objetivos pedagógicos de algumas seções do Livro do Estudante.

AVALIANDO

Propõe avaliações formativas para que você possa acompanhar a aprendizagem dos estudantes em diferentes momentos, possibilitando, se for o caso, intervenções no ensino. Para facilitar a avaliação, esse boxe apresenta os objetivos das atividades e as sugestões de intervenção, com foco na recuperação da aprendizagem.

ARTICULANDO CONHECIMENTOS

Destaca momentos em que é possível estabelecer relações entre componentes curriculares de diferentes áreas do conhecimento, além de orientações práticas sobre como realizar as articulações entre os conteúdos.

REFERÊNCIAS COMPLEMENTARES

Fornece ao professor sugestões de livros, sites, artigos, podcasts, entre outros recursos, contribuindo para a sua formação.

SUGESTÃO DE DESAFIO

Ao final de cada unidade, apresentamos uma sugestão de Desafio matemático nas orientações ao professor, que pode ser aplicado em sala de aula, a fim de complementar os conceitos vistos na unidade, instigando o raciocínio lógico dos estudantes.

Nas orientações ao professor, apresentamos comentários e explicações referentes ao Desafio a mais, presente no final do Livro do Estudante, detalhando a resolução desse desafio e indicando possíveis dificuldades encontradas pelos estudantes, bem como alternativas de encaminhamento.

Nas orientações ao professor da seção Coletivamente, apresentamos os objetivos pedagógicos e as orientações sobre o desenvolvimento dos conteúdos e das atividades da seção com os estudantes.

Nas orientações ao professor da seção Entre textos, apresentamos os objetivos pedagógicos e as orientações sobre o desenvolvimento da competência leitora e da competência da escrita por meio do trabalho com essa seção.

Nas orientações ao professor, são apresentados os objetivos pedagógicos das atividades e sugestões de intervenção da seção Vamos avaliar o aprendizado, com base nas possíveis respostas dos estudantes, considerando dificuldades na resolução e dando alternativas para recuperar e consolidar aprendizagens vistas em cada bimestre.

Nas orientações ao professor, são apresentados os objetivos pedagógicos das atividades e sugestões de intervenção da seção Vamos concluir, com base nas possíveis respostas dos estudantes, considerando dificuldades na resolução e dando alternativas para recuperar e consolidar aprendizagens ao final do ano letivo.

LIVRO DO ESTUDANTE

Reprodução do Livro do Estudante

Matemática

Organizadora:

EDITORA NOVO RUMO

Obra coletiva concebida, desenvolvida e produzida pela Editora Novo Rumo.

Editora responsável:

Jacqueline da Silva Ribeiro Garcia

Especialista em Psicopedagogia pela Universidade Estadual de Londrina (UEL-PR).

Licenciada em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Atuou como professora em escolas do Ensino Básico. Editora e elaboradora de materiais didáticos.

Componente curricular: Matemática

1ª edição

Londrina, 2025

11/09/2025 13:57:01

Esta parte do Livro do Professor contém a Reprodução do Livro do Estudante em tamanho reduzido, com respostas das atividades e possíveis comentários para você. Além disso, nas laterais e rodapés há as orientações ao professor que servem como um guia para a prática pedagógica apresentando sugestões sobre como trabalhar as atividades, além de apresentar as respostas que não foram incluídas na reprodução das páginas. Para deixar mais evidente o sentido de leitura, em algumas páginas utilizamos as indicações e .

Anos Iniciais do Ensino Fundamental

Nessa página, estão apresentadas informações técnicas referentes à produção desta coleção.

Copyright © Editora Novo Rumo, 2025.

Edição Jacqueline da Silva Ribeiro Garcia, Lucília Franco Lemos dos Santos

Assistência editorial Denise Maria Capozzi, Kethelyn Yukari Ogasawara

Revisão técnica Tânia Camila Kochmanscky Goulart

Preparação e revisão Moisés Manzano da Silva (coord.)

Gerência de produção editorial Camila Rumiko Minaki Hoshi

Supervisão de produção editorial Priscilla de Freitas Cornelsen Rosa

Assistência de produção editorial Lorena França Fernandes Pelisson

Coordenação de produção de arte Tamires Rose Azevedo

Edição de arte Keithy Mostachi

Projeto gráfico e design Dayane Barbieri, Keithy Mostachi, Laís Garbelini

Projeto de capa Marcela Pialarissi

Ilustrações de capa Ricardo Gualberto

Coordenação de diagramação Adenilda Alves de França Pucca - Nil Diagramação AVITS Estúdio Gráfico Ltda., EfeDois Editoração Ltda., Leandro

Júnior Pimenta

Autorização de recursos João Henrique Pedrão Feliciano

Iconografia Alessandra Roberta Arias, Vinícius Costa (trat. imagens)

Objetos digitais

Gerência de produção Erick Lopes de Almeida

Roteiros Camila Vidigal

Edição de imagens Brenda de Oliveira Goes

Desenvolvimento Ohanna Schmitt Bolfe, Tatiana Tissa Kawakami

Dados Internacionais de Catalogação na Publicação (CIP) (Câmara Brasileira do Livro, SP, Brasil)

Plantar matemática : 2º ano : anos iniciais do ensino fundamental / organizadora Editora Novo Rumo ; obra coletiva concebida, desenvolvida e produzida pela Editora Novo Rumo ; editora responsável Jacqueline da Silva Ribeiro Garcia. -- 1. ed. -- Londrina, PR : Editora Novo Rumo, 2025.

Componente curricular: Matemática.

ISBN 978-65-5158-137-3(livro do estudante)

ISBN 978-65-5158-136-6(livro do professor)

ISBN 978-65-5158-141-0(livro do estudante HTML5)

ISBN 978-65-5158-140-3(livro do professor HTML5)

1. Matemática (Ensino fundamental) I. Garcia, Jacqueline da Silva Ribeiro. II. Série.

25-299271.0

Índices para catálogo sistemático:

1. Matemática : Ensino fundamental 372.7

Eliete Marques da Silva - Bibliotecária - CRB-8/9380

Reprodução proibida: Art. 184 do Código Penal e Lei 9.610 de 19 de fevereiro de 1998. Todos os direitos reservados à EDITORA NOVO RUMO.

Avenida Doutor Adhemar Pereira de Barros, 1500, sala 804 - Bela Suíça - Londrina-PR CEP 86047-250 - Tel. (43) 3367-2030 contato@editoranovorumo.com.br

Elaboração de originais

Jacqueline da Silva Ribeiro Garcia

Especialista em Psicopedagogia pela Universidade Estadual de Londrina (UEL-PR).

Licenciada em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Atuou como professora em escolas do Ensino Básico. Editora e elaboradora de materiais didáticos.

Fátima Gomes Machado

Especialista em Docência na Educação Superior pela Universidade Estadual de Londrina (UEL-PR).

Licenciada em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Licenciada em Pedagogia pelo Centro Universitário Internacional (Uninter-PR).

Elaboradora e editora de materiais didáticos.

Sandra Aparecida Ferreira Marchi

Especialista em Educação Especial pela Faculdade Catuaí (PR).

Especialista em Gestão Escolar, com habilitação em Administração, Supervisão e Orientação Educacional, pela Faculdade Catuaí (PR).

Licenciada em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Professora dos Anos Iniciais do Ensino Fundamental. Elaboradora de materiais didáticos.

Em respeito ao meio ambiente, as folhas deste livro foram produzidas com fibras obtidas de árvores de florestas plantadas, com origem certificada.

Impresso no Parque Gráfico da Editora FTD CNPJ 61.186.490/0016-33 Avenida Antonio Bardella, 300 Guarulhos-SP – CEP 07220-020 Tel. (11) 3545-8600 e Fax (11) 2412-5375

06/10/2025 18:22:23

CDD-372.7

APRESENTAÇÃO

OLÁ, ESTUDANTE!

NA VIDA, A GENTE APRENDE E ENSINA O TEMPO TODO. PROVAVELMENTE VOCÊ JÁ APRENDEU MUITO COM SEUS PROFESSORES, AMIGOS E CONHECIDOS.

NESTE LIVRO, HÁ MOMENTOS TANTO PARA VOCÊ COMPARTILHAR O QUE JÁ VIVEU QUANTO PARA NOVAS DESCOBERTAS. VOCÊ VAI LER E PRODUZIR TEXTOS, RESOLVER PROBLEMAS, ENTENDER COMO FUNCIONAM CERTOS PROCESSOS SOCIAIS E CULTURAIS, ENTRE OUTROS ASSUNTOS.

ESPERAMOS QUE VOCÊ INTERAJA COM SEUS COLEGAS E PARTICIPE DAS ATIVIDADES, DESENVOLVENDO O GOSTO PARTICULAR POR NOVAS DESCOBERTAS. E NÃO SE ESQUEÇA DE QUE SEMPRE PODERÁ TIRAR AS SUAS DÚVIDAS COM O PROFESSOR.

APROVEITE CADA MOMENTO PARA TORNAR ESSE APRENDIZADO MAIS RICO E DIVERTIDO.

BOM ESTUDO!

CONHEÇA SEU LIVRO

A SEGUIR, APRESENTAMOS A ORGANIZAÇÃO DO SEU LIVRO E INDICAMOS COMO ISSO VAI AJUDAR EM SEUS ESTUDOS.

VAMOS INICIAR AS ATIVIDADES DESSA SEÇÃO SERVEM PARA VOCÊ MOSTRAR O QUE JÁ SABE E PERCEBER O QUE PRECISA ESTUDAR UM POUCO MAIS.

3

06/10/2025 19:01:13

O início do ano letivo é um momento importante para os estudantes, pois eles terão o primeiro contato com o livro didático de Matemática e apresentarão suas primeiras expectativas sobre o que vão estudar. Por esse motivo, nesta página, os autores iniciam um diálogo com eles, com o objetivo de sintetizar o que se deve esperar durante o estudo com esse material. Nesse texto, os estudantes são encorajados a participar de modo ativo e cooperativo da aprendizagem, interagindo com a turma e o professor durante as dinâmicas propostas.

Em seguida, a estrutura da coleção é apresentada na seção Conheça seu livro, mostrando as características dos elementos contidos nela, desde as Páginas de abertura até as Referências bibliográficas comentadas e o Material complementar

A seguir, apresentamos as unidades temáticas, os objetos de conhecimento e as habilidades de Matemática da BNCC referentes ao 2º ano do Ensino Fundamental. Eles podem ser consultados sempre que necessário, para nortear os planejamentos de aula ou para esclarecer dúvidas a respeito dos objetos de conhecimento trabalhados nas unidades do volume.

PÁGINAS DE ABERTURA

NESSAS PÁGINAS, VOCÊ VAI ENCONTRAR

UMA IMAGEM E UM TEXTO INICIANDO

A CONVERSA SOBRE O ASSUNTO QUE SERÁ ESTUDADO NA UNIDADE, ALÉM DE ALGUMAS QUESTÕES QUE EXPLORAM O QUE VOCÊ JÁ SABE DO CONTEÚDO.

BASE NACIONAL COMUM CURRICULAR (BNCC) • 2º ano

Unidade temática: Números

Objetos de conhecimento

EXPERIMENTE

PROPOSTAS DE ATIVIDADES PRÁTICAS QUE ENVOLVEM O ASSUNTO DA UNIDADE APLICADO EM EXPERIMENTOS E PRODUÇÕES LEGAIS.

CONTEÚDO

OS CONTEÚDOS DESTE VOLUME SÃO APRESENTADOS POR MEIO DE ATIVIDADES. ALGUMAS SÃO MAIS FÁCEIS, OUTRAS SÃO DESAFIADORAS. MAS NÃO SE PREOCUPE, POIS O APRENDIZADO DA MATEMÁTICA TAMBÉM É CONSTRUÍDO COM TENTATIVAS E ACERTOS.

DIVIRTA-SE E APRENDA VOCÊ PODE APRENDER UM POUCO MAIS OU APLICAR O CONTEÚDO ESTUDADO POR MEIO DE JOGOS, BRINCADEIRAS E ATIVIDADES LÚDICAS.

ENTRE TEXTOS

NESSA SEÇÃO, VOCÊ VAI TRABALHAR COM DIFERENTES GÊNEROS TEXTUAIS, RELACIONANDO O ASSUNTO MATEMÁTICO ESTUDADO A DIVERSOS CONTEXTOS, AO MESMO TEMPO EM QUE DESENVOLVE PRÁTICAS DE LINGUAGEM. 4

• Leitura, escrita, comparação e ordenação de números de até três ordens pela compreensão de características do sistema de numeração decimal (valor posicional e papel do zero)

Habilidades

(EF02MA01) Comparar e ordenar números naturais (até a ordem de centenas) pela compreensão de características do

sistema de numeração decimal (valor posicional e função do zero).

(EF02MA02) Fazer estimativas por meio de estratégias diversas a respeito da quantidade de objetos de coleções e registrar o resultado da contagem desses objetos (até 1 000 unidades).

(EF02MA03) Comparar quantidades de objetos de dois conjuntos, por estimativa e/ou por correspondência (um a um, dois a dois, entre outros), para indicar

“tem mais”, “tem menos” ou “tem a mesma quantidade”, indicando, quando for o caso, quantos a mais e quantos a menos.

06/10/2025 19:01:14

Objetos de conhecimento

• Composição e de decomposição de números naturais (até 1 000)

Habilidades

(EF02MA04) Compor e decompor números naturais de até três ordens, com suporte de material manipulável, por meio de diferentes adições.

COLETIVAMENTE

NESSA SEÇÃO, VOCÊ VAI REFLETIR

SOBRE TEMAS IMPORTANTES QUE CONTRIBUEM PARA A FORMAÇÃO DE CIDADÃOS CRÍTICOS E ATUANTES NA SOCIEDADE, RELACIONADOS A SITUAÇÕES DO COTIDIANO.

VOCABULÁRIO

PARA AJUDAR NA COMPREENSÃO

DESAFIO A MAIS NO FINAL DE CADA UNIDADE, VOCÊ TERÁ UMA ATIVIDADE DESAFIADORA PARA TESTAR SEU RACIOCÍNIO LÓGICO MATEMÁTICO E SUA CAPACIDADE DE OBTER RESPOSTAS.

VAMOS CONCLUIR NO FINAL DO VOLUME, VOCÊ ESTÁ CONVIDADO A RESOLVER AS QUESTÕES DESSA SEÇÃO, PARA AVALIAR SEU PROGRESSO NA APRENDIZAGEM.

VAMOS AVALIAR O APRENDIZADO AO FINAL DE CADA UNIDADE, HÁ UMA SEÇÃO PARA QUE VOCÊ AVALIE SEU AVANÇO NA APRENDIZAGEM ATÉ O MOMENTO.

DOS TEXTOS, ALGUMAS PALAVRAS SÃO DESTACADAS E O SIGNIFICADO DELAS É APRESENTADO. 5

Unidade temática: Números

Objetos de conhecimento

• Construção de fatos fundamentais da adição e da subtração Habilidades

(EF02MA05) Construir fatos básicos da adição e subtração e utilizá-los no cálculo mental ou escrito.

Objetos de conhecimento

• Problemas envolvendo diferentes significados da adição e da subtração (juntar, acrescentar, separar, retirar)

Habilidades

(EF02MA06) Resolver e elaborar problemas de adição e subtração envolvendo números de até três ordens, com os significados de juntar, acrescentar, separar, retirar, utilizando estratégias pessoais.

Objetos de conhecimento

• Problemas envolvendo adição de parcelas iguais (multiplicação) Habilidades

(EF02MA07) Resolver e elaborar problemas de multiplicação (por 2, 3 4 e 5) com

ideia de adição de parcelas iguais por meio de estratégias e formas de registros pessoais, utilizando ou não suporte de imagens e/ou material manipulável.

Objetos de conhecimento

• Problemas envolvendo significados de dobro, metade, triplo e terça parte

Habilidades

(EF02MA08) Resolver e elaborar problemas envolvendo dobro, metade, triplo e terça parte, com o suporte de imagens ou material manipulável, utilizando estratégias pessoais.

Unidade temática: Álgebra

Objetos de conhecimento

SAIBA MAIS APRESENTA SUGESTÕES DE LIVROS, SITES E FILMES QUE ESTÃO RELACIONADOS COM OS CONTEÚDOS ESTUDADOS.

REFERÊNCIAS

BIBLIOGRÁFICAS

COMENTADAS

ESSA SEÇÃO CONTÉM AS REFERÊNCIAS DE LIVROS, REVISTAS E SITES QUE FORAM

UTILIZADOS NA ELABORAÇÃO DO SEU LIVRO.

ÍCONES E DESTAQUES

DESAFIO

INDICA ATIVIDADES DE CARÁTER MAIS DESAFIADOR.

CÁLCULO MENTAL

OBJETOS DIGITAIS REFERÊNCIAS

INDICA ATIVIDADES QUE DEVEM SER REALIZADAS SEM O REGISTRO ESCRITO DE CÁLCULOS, MOTIVANDO O RACIOCÍNIO LÓGICO.

RESPOSTA ORAL

INDICA ATIVIDADES E QUESTÕES QUE VOCÊ PODE RESPONDER ORALMENTE.

DICA

APRESENTA DICAS QUE PODEM FACILITAR A RESOLUÇÃO DE ALGUMAS ATIVIDADES.

INDICA QUE EXISTE, NA VERSÃO DIGITAL DESTE LIVRO, UM INFOGRÁFICO CLICÁVEL RELACIONADO AO CONTEÚDO.

Os sites indicados neste livro podem mostrar imagens e textos diferentes dos que foram pensados para o seu estudo. Isso acontece porque o conteúdo disponível on-line pode ser alterado com o tempo e variar conforme o histórico de pesquisa do usuário. Por isso, não temos como controlar as imagens e textos que aparecem em tais sites

• Construção de sequências repetitivas e de sequências recursivas)

Habilidades

(EF02MA09) Construir sequências de números naturais de ordem crescente ou decrescente a partir de um número qualquer, utilizando uma regularidade estabelecida.

Objetos de conhecimento

• Identificação de regularidade de sequências e determinação de elementos ausentes na sequência Habilidades

(EF02MA10) Descrever um padrão (ou regularidade) de sequências repetitivas e de sequências recursivas, por meio de palavras, símbolos ou desenhos.

(EF02MA11) Descrever os elementos ausentes em sequências repetitivas e em sequências recursivas de números naturais, objetos ou figuras.

Unidade temática: Geometria

Objetos de conhecimento

• Localização e movimentação de pessoas e objetos no espaço, segundo pontos de referência, e indicação de mudanças de direção e sentido

Habilidades

(EF02MA12) Identificar e registrar, em linguagem verbal, ou não verbal, a localização e os deslocamentos de pessoas e de objetos no espaço, considerando mais de um ponto de referência, e indicar as mudanças de direção e de sentido.

NÚMEROS DE 0 A 100 ........................................................................

DE 0 A 19

DE 10 EM 10

DE 0 A 99

E

UNIDADE ADIÇÃO E SUBTRAÇÃO COM NÚMEROS

COM NÚMEROS ATÉ 19

SUBTRAÇÃO COM NÚMEROS ATÉ 99 SEM REAGRUPAMENTO

SUBTRAÇÃO COM REAGRUPAMENTO

UNIDADE

ATÉ 1 000 ........................................................................102 4

Unidade temática: Geometria

Objetos de conhecimento

• Esboço de roteiros e de plantas simples

Habilidades

(EF02MA13) Esboçar roteiros a ser seguidos ou plantas de ambientes familiares, assinalando entradas, saídas e alguns pontos de referência.

Objetos de conhecimento

• Figuras geométricas espaciais (cubo, bloco retangular, pirâmide, cone, cilindro e esfera): reconhecimento e características

Habilidades

(EF02MA14) Reconhecer, nomear e com-

parar figuras geométricas espaciais (cubo, bloco retangular, pirâmide, cone, cilindro e esfera), relacionando-as com objetos do mundo físico.

Objetos de conhecimento

• Figuras geométricas planas (círculo, quadrado, retângulo e triângulo): reconhecimento e características

Habilidades

(EF02MA15) Reconhecer, comparar e nomear figuras planas (círculo, quadrado, retângulo e triângulo), por meio de características comuns. em desenhos apresentados em diferentes disposições ou em sólidos geométricos.

Nesta página, é apresentado o sumário do volume, que foi organizado para facilitar a localização das unidades e das seções. No final do volume, também é possível encontrar a lista dos Objetos digitais que estão indicados nas páginas com ícones correspondentes e que podem ser acessados no material interativo.

Unidade temática: Grandezas e medidas

Objetos de conhecimento

• Medida de comprimento: unidades não padronizadas e padronizadas (metro, centímetro e milímetro)

Habilidades

(EF02MA16) Estimar, medir e comparar comprimentos de lados de salas (incluindo contorno) e de polígonos, utilizando unidades de medida não padronizadas e padronizadas (metro, centímetro e milímetro) e instrumentos adequados

Unidade temática: Grandezas e medidas

Objetos de conhecimento

• Medida de capacidade e de massa: unidades de medida não convencionais e convencionais (litro, mililitro, , grama e quilograma)

Habilidades

(EF02MA17) Estimar, medir e comparar capacidade e massa, utilizando estratégias pessoais e unidades de medida não padronizadas ou padronizadas (litro, mililitro, grama e quilograma).

UNIDADE

Objetos de conhecimento

• Medidas de tempo: intervalo de tempo, uso do calendário, leitura de horas em relógios digitais e ordenação de datas.

Habilidades

(EF02MA18) Indicar a duração de intervalos de tempo entre duas datas, como dias da semana e meses do ano, utilizando calendário, para planejamentos e organização de agenda.

(EF02MA19) Medir a duração de um intervalo de tempo por meio de relógio digital e registrar o horário do início e do fim do intervalo.

Objetos de conhecimento

• Sistema monetário brasileiro: reconhecimento de cédulas e moedas e equivalência de valores Habilidades

(EF02MA20) Estabelecer a equivalência de valores entre moedas e cédulas do sistema monetário brasileiro para resolver situações cotidianas.

UNIDADE

OBJETOS DIGITAIS

UNIDADE 3 • INFOGRÁFICO CLICÁVEL: LEITURA NO DIA A DIA

UNIDADE 5 • INFOGRÁFICO CLICÁVEL: USO SAUDÁVEL DE TELAS

UNIDADE 8 • INFOGRÁFICO CLICÁVEL: GEOMETRIA E O ARTESANATO DOS POVOS INDÍGENAS

UNIDADE 8 • INFOGRÁFICO CLICÁVEL: PLACAS E SINAIS DAS CIDADES

UNIDADE 9 • INFOGRÁFICO CLICÁVEL: A RIQUEZA DO CACAU

UNIDADE 10 • INFOGRÁFICO CLICÁVEL: FEIRAS LIVRES E

Unidade temática: Probabilidade e estatística

Objetos de conhecimento

• Análise da ideia de aleatório em situações do cotidiano

Habilidades

(EF02MA21) Classificar resultados de eventos cotidianos aleatórios como “pouco prováveis”, “muito prováveis”, “improváveis” e “impossíveis”.

Objetos de conhecimento

• Coleta, classificação e representação de dados em tabelas simples e de dupla entrada e em gráficos de colunas

Habilidades

(EF02MA22) Comparar informações de pesquisas apresentadas por meio de tabelas de dupla entrada e em gráficos de colunas simples ou barras, para melhor compreender aspectos da realidade próxima.

(EF02MA23) Realizar pesquisa em universo de até 30 elementos, escolhendo até três variáveis categóricas de seu interesse, organizando os dados coletados em listas, tabelas e gráficos de colunas simples.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Versão final. Brasília: MEC, 2018. p. 282-285. Disponível em: https://www.gov.br/ mec/pt-br/escola-em-tempo-integral/BNCC_EI_ EF_110518_versaofinal.pdf. Acesso em: 14 ago. 2025.

1. Objetivo

Compreender o processo de contagem numérica e resolver adições com até duas parcelas.

Sugestão de intervenção

Caso algum estudante tenha dificuldade em utilizar o processo de contagem, proponha uma conversa a respeito da sequência numérica, usando materiais de contagem para contribuir para esse trabalho. Para a adição, empregue também os materiais de contagem como recurso para a aprendizagem da operação. Proponha outros problemas parecidos, nos quais os estudantes possam utilizar uma estratégia parecida em sua resolução.

2. Objetivo

Empregar o processo de contagem, efetuar subtrações e classificar um número como par ou ímpar.

Sugestão de intervenção

Para remediar possíveis dificuldades acerca do processo de contagem, apresente aos estudantes exemplos de utilização desse processo em situações práticas e utilizando os objetos da sala de aula para esse fim. No caso da subtração, peça a eles que reproduzam a situação apresentada por meio de desenhos, de modo a empregarem a contagem para identificar a resposta. No caso da classificação como números pares e ímpares, explore a formação de duplas na sala de aula para abordar as diferenças entre números pares e ímpares e, assim, empregar esses conceitos na resolução da atividade.

VAMOS INICIAR

1. A COLEÇÃO DE FIGURINHAS DE RUBENS ESTÁ REPRESENTADA

NA IMAGEM.

A ) QUANTAS FIGURINHAS

RUBENS TEM?

FIGURINHAS.

Resposta: 22 FIGURINHAS.

B ) O PAI DE RUBENS O PRESENTEOU COM MAIS

5 FIGURINHAS. QUANTAS

FIGURINHAS ELE PASSOU A TER?

Resposta: 22 + 5 = 27. RUBENS PASSOU A TER 27 FIGURINHAS.

2. VAGNER VENDE FRUTAS NA FEIRA.

A IMAGEM MOSTRA OS ABACATES

QUE ELE TEM NA SUA BARRACA.

A ) QUANTOS ABACATES VAGNER TEM EM SUA BARRACA?

ABACATES.

Resposta: 16 ABACATES.

B ) UM CLIENTE COMPROU 5 ABACATES. QUANTOS AINDA FALTAM SER VENDIDOS?

Resposta: 16 − 5 = 11. FALTAM SER VENDIDOS 11 ABACATES.

C ) O NÚMERO QUE REPRESENTA A QUANTIDADE DE ABACATES QUE AINDA FALTAM SER VENDIDOS É: PAR. ÍMPAR.

Resposta: Os estudantes devem marcar um X na alternativa ÍMPAR.

3. LIGUE CADA OBJETO AO NOME DA FIGURA GEOMÉTRICA ESPACIAL QUE ELE LEMBRA.

IMAGENS SEM PROPORÇÃO ENTRE SI.

CUBO

PARALELEPÍPEDO CILINDRO CONE ESFERA

Resposta: Os estudantes devem ligar o CUBO ao CUBO MÁGICO; o PARALELEPIPEDO à CAIXA DE SAPATOS; o CILINDRO ao BOLO; o CONE à CASQUINHA DE SORVETE; a ESFERA à BOLA.

CASQUINHA DE SORVETE.

4. O PROFESSOR DE CÉLIA COLOCOU APENAS BOLINHAS AZUIS E AMARELAS EM UMA CAIXA.

CONTORNE EM CADA ITEM A

OPÇÃO CORRETA.

A ) SORTEAR UMA BOLINHA AMARELA DESSA CAIXA É:

Resposta: Os estudantes devem contornar a palavra POSSÍVEL.

POSSÍVEL IMPOSSÍVEL

B ) SORTEAR UMA BOLINHA VERMELHA DESSA CAIXA É:

Resposta: Os estudantes devem contornar a palavra IMPOSSÍVEL

POSSÍVEL IMPOSSÍVEL

06/10/2025 17:31:36

3. Objetivo

Reconhecer figuras geométricas espaciais com base em objetos do cotidiano.

Sugestão de intervenção

Para remediação de dúvidas a respeito das figuras geométricas espaciais e suas nomenclaturas, leve para a sala de aula alguns objetos cujos formatos lembrem figuras geométricas espaciais, além de sólidos que simulem essas figuras, para que os estudantes possam manipulá-los e, dessa maneira, estabelecer corretamente as relações entre eles, assim como solicitado na atividade.

4. Objetivo

Classificar eventos como possíveis ou impossíveis.

Sugestão de intervenção

Diante das dificuldades manifestadas a respeito dos principais conceitos envolvendo probabilidade, principalmente quanto à diferenciação entre eventos possíveis e impossíveis, proponha aos estudantes que analisem os resultados possíveis no lançamento de um dado, fazendo perguntas para eles perceberem que, em um dado comum, é um evento possível o sorteio dos números 1, 2, 3, 4, 5 e 6 e um evento impossível o sorteio de qualquer número diferente desses. Com base nesse trabalho, proponha novamente a resolução da atividade, considerando agora o contexto apresentado.

CAIXA DE SAPATOS.

CUBO MÁGICO.

BOLO. BOLA.

5. Objetivo

Empregar corretamente os termos direita e esquerda na localização de objetos.

Sugestão de intervenção

Caso algum estudante tenha dificuldade em resolver a atividade, proponha alguns comandos que envolvam a localização de objetos na sala de aula, de modo que ele possa compreender o uso dos termos direita e esquerda e reconhecer que essas palavras são sempre utilizadas com base em um referencial.

6. Objetivo

Construir trajetos utilizando termos que indicam as direções a serem adotadas.

Sugestão de intervenção

O uso de atividades práticas pode ser um recurso interessante para sanar possíveis dificuldades a respeito de localizações e construção de trajetos. Organize circuitos em sala de aula e peça aos estudantes que descrevam os trajetos utilizando os termos direita, esquerda, para cima e para baixo, de modo a perceberem a importância desses termos na construção de rotas. Outra possibilidade é utilizar mapas para explorar esses conceitos.

7. Objetivo

Reconhecer os dias da semana.

Sugestão de intervenção

Para remediar dificuldades relacionadas ao conhecimento dos dias da semana, desenvolva um trabalho que explore o calendário, de maneira que os estudantes identifiquem atividades que eles realizam durante a semana, como ir à escola, e se familiarizem com os nomes dos dias da semana e a ordem deles.

5. OBSERVE A IMAGEM.

A ) PINTE DE AZUL O LÁPIS NA MÃO DIREITA DO MENINO.

Resposta: Os estudantes devem pintar de azul o lápis 2

B ) PINTE DE VERMELHO O LÁPIS NA MÃO ESQUERDA DO MENINO.

Resposta: Os estudantes devem pintar de vermelho o lápis 1

6. OBSERVE A SEGUIR O SIGNIFICADO DE CADA SETA.

DIREITA ESQUERDA PARA CIMA PARA BAIXO

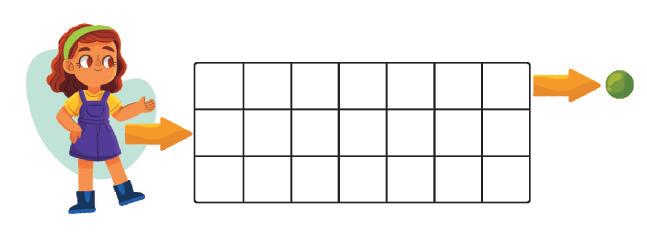
PINTE NA MALHA OS QUADRADINHOS, DE ACORDO COM AS SETAS, PARA INDICAR O CAMINHO QUE LEVA SÍLVIA ATÉ SUA BOLA.

Respostas e comentários nas orientações ao professor

7. NAS FICHAS A SEGUIR, ESTÃO OS NOMES DOS DIAS DA SEMANA.

DOMINGO SEGUNDA-FEIRA TERÇA-FEIRA

QUARTA-FEIRA QUINTA-FEIRA SEXTA-FEIRA SÁBADO

PINTE AS FICHAS COM OS DIAS EM QUE VOCÊ VAI À ESCOLA.

Resposta: Os estudantes devem pintar as fichas com os nomes SEGUNDA-FEIRA, TERÇA-FEIRA, QUARTA-FEIRA, QUINTA-FEIRA e SEXTA-FEIRA.

Resposta 6.

Silvia início

Bola da Silvia Sílvia

Bola da Sílvia

EDITORA

8. OBSERVE A MEDIDA DE MASSA

2 QUILOGRAMAS

3 QUILOGRAMAS

CONTORNE O GATO MAIS PESADO.

Resposta: Os estudantes devem contornar o gato que tem 4 quilogramas

9. AS JARRAS ESTÃO TOTALMENTE CHEIAS DE ÁGUA.

8. Objetivo

Reconhecer e comparar medidas de massa escritas em unidades padronizadas. Sugestão de intervenção

LITRO

LITROS

QUANTOS LITROS DE ÁGUA AS DUAS JARRAS TÊM JUNTAS?

Resposta: 1 + 2 = 3. AS DUAS JARRAS TÊM JUNTAS 3 LITROS DE ÁGUA.

10. PINTE AS FIGURAS DE ACORDO COM AS CORES INDICADAS NA LEGENDA.

CÍRCULO

RETÂNGULO

QUADRADO

TRIÂNGULO

Resposta: Os estudantes devem pintar a figura A de verde, a figura B de azul, a figura C de vermelho e a figura D de amarelo.

10. Objetivo

Reconhecer as figuras geométricas planas e suas nomenclaturas correspondentes.

Sugestão de intervenção

Para sanar possíveis dúvidas acerca do conteúdo da atividade, proponha uma revisão das fi-

guras geométricas planas com base em atividades envolvendo desenhos ou recortes, de modo que os estudantes precisem representar diferentes figuras, identificando suas características, principalmente a quantidade de lados, para que possam relacioná-las às nomenclaturas correspondentes. 4 QUILOGRAMAS

17:31:37

Esta atividade engloba tanto o estudo das medidas de massa quanto a comparação numérica. Nesse sentido, para sanar possíveis dúvidas, proponha um trabalho envolvendo a construção de estimativas para as medidas de massa de alguns animais, de maneira que reconheçam o uso das diferentes unidades de medida de massa, e peça aos estudantes que façam comparações entre elas. Caso a escola disponha de laboratório de informática, avalie a possibilidade de levar a turma para realizar uma pesquisa supervisionada sobre as medidas de massa de alguns animais a fim de compararem os resultados que encontrarem.

9. Objetivo

Resolver problemas envolvendo medidas de capacidade.

Sugestão de intervenção

Como a atividade envolve o reconhecimento de medidas de capacidade e o uso da adição, para evitar possíveis dificuldades sobre esses conceitos, podem ser propostas algumas tarefas práticas em que sejam utilizados instrumentos de medida de capacidade, como jarras e copos medidores, e efetuadas medições e adições envolvendo medidas de capacidade associadas a diferentes objetos, resolvendo, empiricamente, problemas parecidos com o apresentado na atividade.

A. B. C. D.

OBJETIVOS DA UNIDADE

• Estabelecer relação entre a quantidade de elementos e sua representação numérica.

• Reconhecer que 1 dezena corresponde a 10 unidades e que 1 centena corresponde a 10 dezenas.

• Registrar o resultado de contagem ou estimativa de quantidades usando números até 100 com algarismos e por extenso.

• Identificar o sucessor e o antecessor de um número natural.

• Realizar pesquisa e organizar os dados em listas, tabelas ou outros registros.

• Comparar números de uma sequência e reconhecer padrões e regularidades.

• Comparar quantidades utilizando os símbolos > (maior do que), < (menor do que) e = (igual a).

• Analisar acontecimentos aleatórios do dia a dia, identificando se são pouco prováveis, muito prováveis, possíveis ou impossíveis.

• Reconhecer e compreender o significado de números pares e números ímpares.

• Ler e escrever os ordinais do 1º ao 19º

• Identificar a posição de um ordinal em uma sequência de até 19 elementos.

INTRODUÇÃO E

JUSTIFICATIVA

Nesta unidade, é feito um trabalho prolongado com a numeração envolvendo números naturais de 0 a 100. A identificação de unidades, dezenas e centenas é feita por meio de quantificação de objetos e pessoas e com representação em listas, tabelas, quadro de ordens e por extenso, além do apoio do ábaco, de materiais manipuláveis e de representações com cubinhos e barras. São abordadas estratégias de comparação entre números, com o uso dos

UNIDADE1 NÚMEROS DE 0 A 100

DRONE FOTOGRAFANDO UM BOTO-DO-RIO-TUCUXI NA RESERVA DE DESENVOLVIMENTO SUSTENTÁVEL MAMIRAU, NO ESTADO DO AMAZONAS, EM 2018.

símbolos > (maior do que), < (menor do que) e = (igual a), sequência numérica, além de tratar do antecessor e do sucessor de um número. É proposto um trabalho de compreensão e reconhecimento de números pares e números ímpares. A sequência de números ordinais do 1º até o 19º é apresentada aos estudantes por meio de atividades contextualizadas. Também são apresentados alguns procedimentos de contagem que exploram a ideia de acaso, permitindo classificar a chance de resultados possíveis de um evento aleatório.

Habilidades da BNCC trabalhadas na unidade: EF02MA01 , EF02MA02 , EF02MA03 ,

EF02MA04, EF02MA09, EF02MA10, EF02MA11, EF02MA21 e EF02MA23

SUGESTÃO DE ESTRATÉGIA INICIAL

Leve para a sala de aula imagens com diferentes quantidades de pessoas ou objetos. Convide alguns estudantes para registrarem na lousa, da maneira que preferirem, essas quantidades. Caso julgue necessário utilize uma abordagem inclusiva, pedindo aos estudantes que fechem os olhos e, em seguida, bata uma quantidade de palmas de maneira espaçada que represente a quantidade de fotografias da abertura.

O DRONE COM CÂMERA É UM APARELHO

AÉREO DE CONTROLE REMOTO QUE

FACILITA REGISTROS DE IMAGENS CONSIDERADOS DE DIFÍCIL CAPTURA. AS FOTOGRAFIAS E OS VÍDEOS FEITOS POR ESSES EQUIPAMENTOS PODEM SER DESCARREGADOS E SALVOS EM UM COMPUTADOR E ATÉ EDITADOS.

1. Resposta: 15 fotografias.

ALGUMAS FOTOGRAFIAS FORAM TIRADAS POR UM DRONE E ARMAZENADAS NA PASTA DE IMAGENS DE UM COMPUTADOR. QUANTAS FOTOGRAFIAS APARECEM NA TELA NESTE MOMENTO? 1.

2.

EM SUA OPINIÃO, É IMPORTANTE TIRAR FOTOGRAFIAS? POR QUÊ?

2. Respostas pessoais. Comentários nas orientações ao professor

• A questão 2 tem como objetivo avaliar a opinião dos estudantes com relação à importância de fotografar. Verifique se eles têm o hábito de tirar fotografias ou não, incentivando-os a refletir sobre a importância do registro fotográfico, que se dá pelo registro, pela memória, pela emoção e pelo indício visual, por permitir recordar por meio de imagens um momento com mais facilidade. Espera-se que percebam que a fotografia vai além de um simples registro, mas também reconheçam que é um bem precioso quando está relacionado a um fato histórico. A fotografia nos auxilia

FOTOMONTAGEM DE JOHANNES DE PAULO. FOTOS: KITE_RIN/ SHUTTERSTOCK.COM, BEZIKUS/SHUTTERSTOCK.COM, CRISTA WETENKAMP/SHUTTERSTOCK.COM, SNAPASKYLINE/SHUTTERSTOCK.COM, EMMA_GRIFFITHS/SHUTTERSTOCK.COM, ENGEL CHING/SHUTTERSTOCK. COM, EMMANUELLE FIRMAN/SHUTTERSTOCK.COM, LEBID VOLODYMYR/ SHUTTERSTOCK.COM, INGUS KRUKLITIS/ISTOCK/GETTY IMAGES, ULADZIK KRYHIN/SHUTTERSTOCK.COM 15

06/10/2025 17:36:45

a entender o mundo em que vivemos com base em diferentes pontos de vista, uma vez que pode ser usada como registro ou até mesmo como arte, sendo de grande importância, por exemplo, para a publicidade e o jornalismo.

• Aproveite a questão para estabelecer uma aproximação entre os componentes curriculares de Matemática e História, por meio de análise histórica, além da compreensão da imagem e do contexto na qual foi produzida, contribuindo para o pensamento crítico e a compreensão de fontes históricas.

• Explique aos estudantes que, antes das câmeras fotográficas digitais e dos aparelhos similares que registram fotografias, eram usadas câmeras analógicas, que capturavam as imagens em um filme fotográfico. Comente que, para o uso dessas câmeras, as pessoas precisavam adquirir filmes, sendo os mais comuns de 12 a 36 poses, nos quais eram registradas as imagens. Em seguida, era necessário revelar essas fotografias em um ambiente especial, denominado sala escura, que permitia a impressão dessas imagens em papéis próprios para fotografias. Nesse contexto, diga a eles que, por conta da necessidade desses procedimentos e dos custos associados, antigamente muitas pessoas não tiravam tantas fotografias como atualmente. Se possível, leve uma câmera fotográfica desse tipo para a sala de aula e apresente-a aos estudantes.

• No trabalho com a questão 1, proponha aos estudantes que registrem a quantidade de fotografias da maneira como desejarem, mas instigando-os a utilizar os algarismos na representação dessa informação. Durante esse trabalho, motive-os a fazer a contagem para responder à questão, acompanhando-os nesse processo e intervindo sempre que necessário.

• Antes de abordar a atividade 1, pergunte aos estudantes se eles sabem como surgiram os métodos de contagem e os registros de quantidades. Comente com a turma que a humanidade sentiu a necessidade de contar quando começou a plantar e domesticar animais. Para controlar a quantidade de animais, os pastores usavam pedrinhas, cada uma representando um animal do rebanho. Além dessa técnica, surgiram várias maneiras distintas de fazer essa correspondência, como usar ossos, fazer marcas na parede e desenhar nas cavernas.

• No item A da atividade 1, verifique se os estudantes concluem que foi necessária uma quantidade significativa de itens do estojo escolar para representar a quantidade de objetos presentes na imagem. No item B, explique a eles que podem representar as sete garrafas como preferirem, por exemplo, com tracinhos, bolinhas ou estrelas. Caso algum estudante não tenha itens suficientes em seu estojo, proponha a ele que se junte a um colega para realizar a tarefa, cuidando para acolher e dar atenção igualmente a todos, evitando qualquer constrangimento. Para que a atividade atinja seu propósito, é importante que todos se engajem na ação e estejam interessados em resolvê-la.

PASSEANDO PELA HISTÓRIA DOS NÚMEROS

1. ANTES DA CRIAÇÃO DO SISTEMA DE NUMERAÇÃO QUE CONHECEMOS HOJE, AS PESSOAS REPRESENTAVAM QUANTIDADES DE DIVERSAS MANEIRAS, COMO FAZER RISQUINHOS EM OSSOS OU REUNIR PEDRINHAS. VAMOS CONTAR COMO ANTIGAMENTE?

NA CENA, O HOMEM ESTÁ REGISTRANDO EM UM OSSO A QUANTIDADE DE PEIXES QUE PESCOU. PARA CADA PEIXE PESCADO, ELE FEZ UM RISCO NO OSSO.

A ) PARA CADA OBJETO APRESENTADO NA IMAGEM A SEGUIR, COLOQUE SOBRE A SUA CARTEIRA UM ITEM DE SEU ESTOJO ESCOLAR.

Resposta: Os estudantes devem separar 7 itens do estojo escolar.

B ) REPRESENTE, DA MANEIRA QUE PREFERIR, A QUANTIDADE DE GARRAFAS APRESENTADAS NO ITEM A

Resposta pessoal. Espera-se que os estudantes representem, da maneira que preferirem, as 7 garrafas apresentadas no item A

REFERÊNCIAS COMPLEMENTARES

SILVA, Aline Cristina Galindo Almeida; SILVA, Bruno Lopes Oliveira. A origem e evolução dos números: uma breve história. 30 jul 2021. Instituto Federal de Pernambuco. Campus Pesqueira. Disponível em: https://repositorio.ifpe.edu. br/xmlui/bitstream/handle/123456789/990/ AOrigemeaevoluçãodosnúmerosumabrevehis tória.pdf?sequence=1. Acesso em 25 set. 2025. Essa obra tem como objetivo apresentar o surgimento e a origem dos números, com base em civilizações como os babilônios, os gregos, os romanos, entre outras.

2. COM O PASSAR DOS ANOS, OS MÉTODOS DE CONTAGEM E DE REGISTRO DE QUANTIDADES FORAM SE TRANSFORMANDO, E ALGUMAS CIVILIZAÇÕES CRIARAM SÍMBOLOS E SISTEMAS DE NUMERAÇÃO PRÓPRIOS. A SEGUIR, ESTÁ REPRESENTADA A QUANTIDADE DE PEDRINHAS DA IMAGEM, DE ACORDO COM DIFERENTES CIVILIZAÇÕES.

Resposta pessoal. Espera-se que os estudantes relatem suas experiências em relação aos

NUMERAÇÃO MAIA

NUMERAÇÃO GREGA

NUMERAÇÃO BABILÔNICA

NUMERAÇÃO ROMANA

VOCÊ JÁ VERIFICOU ALGUM SÍMBOLO SEMELHANTE NO SEU DIA A DIA? SE SIM, CONVERSE COM OS COLEGAS E DESCREVA EM QUAL SITUAÇÃO ELES APARECERAM.

3. PARA REGISTRAR QUANTIDADES ATUALMENTE, UTILIZAMOS SÍMBOLOS CHAMADOS ALGARISMOS, OS QUAIS ESTÃO REPRESENTADOS A SEGUIR.

0 1 2 3 4

A ) PARA REPRESENTAR A QUANTIDADE DE DEDOS DA SUA

MÃO, QUAL DESSES SÍMBOLOS VOCÊ USARIA?

Resposta: 5

B ) REPRESENTE A QUANTIDADE DE PEDRINHAS MOSTRADAS

USANDO UM ALGARISMO.

Resposta: 8 símbolos apresentados, citando onde os viram e em que situações apareceram.

• Na atividade 3, item A, a proposta é levar os estudantes a associarem a quantidade de dedos da mão ao símbolo 5, que é denominado algarismo. Caso julgue necessário, conte os dedos de uma mão com o auxílio deles, a fim de que identifiquem que a mão tem 5 dedos. No item B, os estudantes devem associar a quantidade de pedrinhas representadas na imagem e representar essa quantidade com os algarismos aprendidos na realização da atividade.

06/10/2025 17:36:47

• Na atividade 2, os estudantes têm a oportunidade de refletir sobre a origem e a diversidade dos sistemas de numeração utilizados por diferentes civilizações ao longo da história. Ao apresentar a eles exemplos de representações numéricas maia, grega, babilônica e romana, o objetivo é compreenderem como a Matemática surgiu da necessidade de contar, organizar e registrar quantidades. Peça aos estudantes que observem os símbolos e comparem com o nosso sistema atual. Pergunte quais são as diferenças que podem notar entre esses sistemas de numeração. Desse modo, eles são motivados a perceber que a Matemática não é uma invenção atual, mas sim um saber construído ao longo de muitos anos, tendo recebido contribuições de vários povos.

• Ao responder à questão proposta na atividade 2, os estudantes vão relacionar os símbolos antigos com situações do cotidiano. Eles podem responder que já viram esses símbolos em relógios com números romanos, livros com capítulos numerados em algarismos romanos, jogos, entre outras situações. Promova um momento de conversa com a turma, solicitando aos estudantes que compartilhem onde já viram esses símbolos e o que sabem sobre eles.

• A atividade 1 relaciona as unidades temáticas de Matemática Números e Probabilidade e estatística ao trabalhar as noções iniciais de Probabilidade e de Estatística. Nesse caso, os estudantes devem analisar as categorias e as quantidades correspondentes a cada um dos pedidos. Se julgar necessário, reproduza as informações na lousa para que façam a análise delas e proponha uma nova estrutura para organização desses dados, conforme solicitado no item D

• Peça a alguns estudantes que indiquem na lousa outras maneiras de organização dessas informações. Uma abordagem que pode complementar o estudo da atividade é propor a eles que estabeleçam um preço para cada produto e calculem os gastos associados ao conjunto de dados presente na atividade. Durante esse trabalho, converse com eles e motive-os a compartilhar suas observações e respostas. Acolha com respeito e atenção as contribuições de todos, dando oportunidade de desenvolverem o raciocínio e exercitarem a comunicação e a argumentação. Essas participações são importantes para evidenciar possíveis defasagens e dificuldades, permitindo a intervenção rápida e precisa do professor por meio de questionamentos e de outras conduções metodológicas. Assim, a recuperação das aprendizagens torna-se mais eficiente e abrangente.

• Motive os estudantes a construírem argumentos e a registrá-los por escrito no caderno, preferencialmente com letra cursiva. Nesse caso, verifique se

NÚMEROS DE 0 A 19

1. C) Resposta pessoal. Os estudantes podem dizer que, ao utilizar esse estilo de marcação, é possível saber a quantidade que foi pedida de cada item, o que facilita a contagem.

1. HELENA E SUA FAMÍLIA FORAM A UMA LANCHONETE.

O ATENDENTE ANOTOU NA COMANDA O QUE SERÁ CONSUMIDO POR ELES.

EU QUERO UMA SALADA DE FRUTAS.

Unidades temáticas integradas

COMANDA: BLOCO DE ANOTAÇÕES IMPRESSO OU PLANILHA VIRTUAL ONDE SÃO ANOTADOS OS PEDIDOS DE CLIENTES.

A ) EXAMINANDO A COMANDA DESSE ATENDENTE, COMO É POSSÍVEL SABER A QUANTIDADE QUE SERÁ CONSUMIDA DE CADA ITEM?

Resposta: É possível saber a quantidade de cada item contando as marcações feitas na comanda.

B ) QUE PRODUTO HELENA E SUA FAMÍLIA VÃO CONSUMIR EM MAIOR QUANTIDADE?

Resposta: Eles vão consumir em maior quantidade o sanduíche.

C ) EM SUA OPINIÃO, COMO ESSE MODO DE MARCAÇÃO PODE AUXILIAR O CÁLCULO DA QUANTIA GASTA PELOS CLIENTES?

JUSTIFIQUE SUA RESPOSTA.

D ) DE QUE OUTRA MANEIRA AS ANOTAÇÕES DOS PEDIDOS PODEM SER FEITAS?

Resposta pessoal. Espera-se que os estudantes respondam que poderiam ser usados tracinhos, números etc.

eles pegam corretamente o lápis, usando o apoio correto dos dedos, e se executam o traçado das letras, palavras e números adequadamente. Ao final, proponha uma roda de conversa para que compartilhem suas percepções, de maneira que todos participem ativamente, sem que haja o predomínio da fala de alguns.

2. RUI, CLÓVIS E INÁCIA REPRESENTARAM EM UM DESENHO TODAS AS PESSOAS QUE MORAM COM ELES.

A ) ESCREVA NOS QUADRINHOS A QUANTIDADE DE PESSOAS

QUE APARECEM EM CADA DESENHO.

RUI CLÓVIS INÁCIA

Resposta: Rui: 4 pessoas; Clóvis: 6 pessoas; Inácia: 7 pessoas.

B ) QUAL DESENHO TEM MAIS PESSOAS?

Resposta: O desenho que representa a família de Inácia.

C ) O DESENHO DE CLÓVIS TEM QUANTAS PESSOAS A MAIS QUE O DESENHO DE RUI?

Resposta: O desenho de Clóvis tem duas pessoas a mais que o desenho de Rui.

D ) EM UMA FOLHA DE PAPEL, DESENHE AS PESSOAS QUE MORAM COM VOCÊ. DEPOIS, ESCREVA A QUANTIDADE DE PESSOAS QUE VOCÊ DESENHOU.

Resposta pessoal. A resposta

depende da quantidade de pessoas que fazem parte do convívio familiar dos estudantes.

E ) ESCREVA O NOME DE CADA PESSOA QUE VOCÊ DESENHOU.

Resposta pessoal. A resposta depende da quantidade de pessoas desenhada no item D. Verifique se os estudantes têm alguma dificuldade no registro dos nomes e, se for o caso, oriente cada um deles soletrando as sílabas e registrando-as na lousa.

ARTICULANDO CONHECIMENTOS

Durante a resolução da atividade 2, é possível estabelecer uma articulação entre os componentes curriculares de Matemática e História, propondo aos estudantes que compartilhem com os colegas as respostas aos itens D e E Solicite a eles que descrevam algumas características de suas famílias, desde fatos agradáveis ocorridos nos últimos meses, e que envolveram essas pessoas, até outras histórias que julguem

06/10/2025 17:36:48

relevantes. Se julgar conveniente e oportuno, converse a respeito das diferentes configurações de famílias e rotinas, ressaltando a importância de valorizar e respeitar cada história de vida familiar. Nesse caso, explique a eles que as famílias podem ter diferentes configurações e que o respeito a essas diferenças enriquece o entendimento sobre inclusão e promove uma sociedade mais tolerante.

• Na resolução da atividade 2, verifique os procedimentos empregados pelos estudantes no reconhecimento das quantidades de pessoas que integram cada grupo e, especificamente nos itens B e C, se estão comparando corretamente essas quantidades.

• Caso julgue necessário, proponha a eles a representação das quantidades utilizando materiais concretos, como tampinhas, e a comparação entre elas. Peça-lhes que, utilizando esses materiais, representem as quantidades de pessoas em cada grupo e façam as comparações solicitadas na atividade.

BNCC

As atividades propostas neste tópico contribuem para o desenvolvimento das habilidades EF02MA01 e EF02MA02 por motivar os estudantes a fazerem estimativas para quantidades de objetos ou pessoas, principalmente por meio da contagem, identificando números naturais correspondentes e fazendo comparações entre eles.

• Na atividade 3, os estudantes farão comparações entre números naturais, partindo da quantificação de objetos. Durante esta atividade, oriente-os a identificar as quantidades de cada tipo de objeto para, na sequência, marcar a resposta correta por meio da comparação com o número 8. Caso algum estudante tenha dificuldade em responder a esta atividade, peça-lhe que analise cada tipo de objeto e identifique se seria necessário acrescentar ou retirar objetos para obter oito itens, relacionando essa ideia de retirar ao fato de haver mais do que oito objetos na situação.

• Durante a resolução da atividade 4, verifique as estratégias aplicadas pelos estudantes para a produção do desenho solicitado das oito frutas. Em caso de dificuldades, peça a eles que façam os desenhos um a um e contem cada desenho elaborado para construir exatamente a quantidade solicitada na atividade. Além disso, diga-lhes que podem desenhar oito frutas diferentes ou repeti-las, desde que a quantidade seja igual a oito.

• A atividade 5 aborda a quantificação de elementos, exigindo dos estudantes a contagem e a associação com o número correspondente. Nesse trabalho, oriente-os a reconhecer as quantidades de cada tipo de elemento por meio de contagens, analisando um tipo de cada vez e estabelecendo as ligações solicitadas.

3. MARQUE UM X NA IMAGEM QUE APRESENTA MAIS DE 8 OBJETOS.

Resposta: Os estudantes devem marcar um X na imagem do item B

IMAGENS SEM PROPORÇÃO ENTRE SI.

4. DESENHE NO QUADRO 8 FRUTAS QUE VOCÊ MAIS GOSTA DE COMER.

Resposta pessoal. Os estudantes devem desenhar 8 frutas que gostem de comer ou que já tenham experimentado, com base em suas vivências.

5. LIGUE OS NÚMEROS REPRESENTADOS NAS FICHAS ÀS QUANTIDADES DE ELEMENTOS CORRESPONDENTES.

IMAGENS SEM PROPORÇÃO ENTRE SI.

4 5 9 1 10

Resposta: Os estudantes devem ligar: 4-C; 5-E; 9-B; 1-A; 10-D.

17:36:49

A. B. C.

D. E.

6. O TEXTO A SEGUIR É TRECHO DE UMA MÚSICA.

PALMA, PALMA, PALMA [...]

PÉ, PÉ, PÉ

RODA, RODA, RODA, CARANGUEJO, PEIXE É

• A atividade 6 aborda o trecho de uma música. No item A , é solicitado aos estudantes que cantem a música com o professor e os colegas. Assim, são explorados os sentidos da fala, ao cantarem a música, e da audição, ao ouvirem a música sendo cantada por eles próprios, os colegas e o professor. Desse modo, é possível promover a inclusão de estudantes com Necessidades Educacionais Especiais (NEE), contribuindo para uma aprendizagem multimodal, pois permite que utilizem os sentidos mais desenvolvidos para construir os conhecimentos matemáticos. Essa proposta favorece a oralidade e o desenvolvimento da memória auditiva e do ritmo corporal. Incentive-os a realizar os movimentos propostos, pois a musicalização corporal pode auxiliar no desenvolvimento da coordenação motora e da concentração. • Nesta atividade, os estudantes devem fazer as contagens das figuras e representar as quantidades usando algarismos e linguagem materna, contribuindo para o reconhecimento da sequência numérica de 1 a 10. Esse momento é oportuno para verificar o traçado das letras e dos algarismos, e garantir que estão pegando o lápis adequadamente, fazendo uso de apoio correto dos dedos. Caso alguns deles apresentem dificuldade na orientação desse traçado, retome o treino do movimento com a mão no ar, mostrando a direção do traçado da escrita do número e das letras. Faça intervenções durante a resolução da atividade, no sentido de auxiliá-los no reconhecimento dos números naturais associados a cada conjunto e na representação por escrito desses números. Ao final, proponha uma conversa com a turma a respeito das diferentes representações para cada número proposto na atividade.

CARANGUEJO NÃO É PEIXE CARANGUEJO, PEIXE É CARANGUEJO SÓ É PEIXE NA ENCHENTE DA MARÉ [...]

6. A) Resposta pessoal. Cante o trecho da música com os estudantes. Caso eles conheçam a letra na íntegra, podem cantá-la também.

A ) CANTE A MÚSICA COM O PROFESSOR E OS COLEGAS.

B ) CONTE OS CARANGUEJOS. DEPOIS, COMPLETE CADA QUADRO COM A QUANTIDADE CORRESPONDENTE DE CARANGUEJOS.

Resposta: A: 1 (UM); B: 2 (DOIS); C: 3 (TRÊS); D: 4 (QUATRO); E: 5 (CINCO); F: 6 (SEIS); G: 7 (SETE); H: 8 (OITO); I: 9 (NOVE); J: 10 (DEZ).

A. 1 (UM)

(TRÊS)

G. 5 ( ) (SEIS)

( ) 7 ( ) ORIGEM POPULAR.

(NOVE) ( ) ( )

ARTICULANDO CONHECIMENTOS

06/10/2025 17:36:49

Aproveite a atividade 6 para estabelecer uma relação entre Matemática e Ciências da Natureza. Comente com os estudantes que existem várias espécies de caranguejo, sendo alguns de água doce ou terrestres, vivendo em manguezais, enquanto outros são de água salgada. Informe também que o caranguejo e o siri têm características semelhantes entre si, como o corpo coberto por uma estrutura rígida, chamada carapaça. Eles também apresentam diferenças entre si. O siri, por exemplo, tem características que favorecem a locomoção no ambiente aquático, como as pernas traseiras adaptadas para nadar.

• Na atividade 7, é apresentado o trecho de um poema sobre diferentes tipos de pingo (de chuva, suor, goteira, chaleira etc.), possibilitando aos estudantes que reconheçam, de modo intuitivo, a presença da água em diversos contextos. Por meio do poema, é abordado o significado de dezena e sua relação com a unidade. Proponha inicialmente a leitura em voz alta e uma conversa a respeito dos pingos de água e em quais situações podemos identificá-los, com base nas situações apresentadas no poema e nas experiências dos estudantes. Em seguida, resolva a atividade, identificando a compreensão deles a respeito das unidades e dezenas. Se julgar conveniente, leve para a sala de aula o material dourado e faça uma comparação entre cubinhos e barras, contribuindo para a diferenciação e a associação entre unidades e dezenas. Aproveite a atividade 7 para alertar sobre os riscos de um recipiente com água aquecida no fogão. Explique aos estudantes que a “fumaça” saindo do recipiente é o vapor de água, e que esse vapor pode provocar queimaduras no contato com a pele. Sendo assim, é preciso tomar cuidado e não colocar as mãos direto no recipiente aquecido, nem na saída do vapor, pois pode provocar acidente com risco sério à saúde e à vida. Oriente-os a sempre pedir auxílio a um adulto nessas situações.

ARTICULANDO CONHECIMENTOS

O trabalho com a atividade 7 oferece oportunidade de articulação com componente curricular de Língua Portuguesa, ao explorar a leitura e a interpretação do poema apresentado. Se julgar conveniente, explore a situação incômoda do poeta com os pingos, pedindo a opinião dos estudantes

7. A) Resposta pessoal. Leia o poema com os estudantes. Professor, professora: Se julgar conveniente, proponha uma leitura alternada

7. O TEXTO A SEGUIR É O TRECHO DE UM POEMA.

entre os estudantes, dividindo o trecho em partes e alternando os grupos leitores.

PINGOS

PINGO DE CHUVA

PINGO DE SUOR

UM PINGO É UM PINGO

A PINGAR... A PINGAR

PINGO DE GOTEIRA

PINGO DE CHALEIRA

UM PINGO É UM PINGO

A PINGAR... A PINGAR

[...]

NÃO CONSIGO DORMIR

ESCUTANDO E CONTANDO

PINGO A PINGO A CAIR

PINGO A PINGO PINGANDO.

25.

A ) LEIA O POEMA COM O PROFESSOR E OS COLEGAS.

B ) CONTE OS PINGOS DE ÁGUA NA IMAGEM A SEGUIR.

Resposta pessoal. Espera-se que os estudantes façam a contagem um a um.

QUANTOS SÃO OS PINGOS DE ÁGUA?

Resposta: 10

1 PINGO REPRESENTA 1 UNIDADE

10 UNIDADES DE PINGOS REPRESENTAM 1 DEZENA.

10 UNIDADES REPRESENTAM 1 DEZENA

PORTANTO, SÃO PINGOS OU 1 DEZENA DE PINGOS.

Resposta: PORTANTO, SÃO 10 PINGOS OU 1 DEZENA DE PINGOS.

8. ALGUNS PINGOS DE ÁGUA ESTÃO REPRESENTADOS A SEGUIR.

A ) DESENHE MAIS UM PINGO DE ÁGUA NESSA CENA.

Resposta: Os estudantes devem desenhar 1 pingo de chuva a mais.

para o fato de a pessoa do poema não conseguir dormir. Verifique se percebem que ela pode estar incomodada com o barulho que os pingos fazem ao cair. Incentive-os a conversar sobre o poema, compartilhando suas percepções e acolhendo a contribuição de todos com respeito e atenção. De modo respeitoso, engaje toda a turma, de modo organizado e respeitoso. Aproveite para perguntar se imaginam que os pingos que estão caindo são poucos ou muitos. Verifique se reparam na repetição da palavra pingo no poema, que pode sugerir que os pingos que caem são muitos.

KALUNGA. PINGOS. IN: KALUNGA. O POETA BRINCALHÃO. CURITIBA: INVERSO, 2018. P.

B ) QUANTOS PINGOS DE ÁGUA HÁ AGORA?

Resposta: 11

C ) COMPLETE O QUE FALTA NAS INFORMAÇÕES.

Resposta: 10 + 1 = 11

10  + = 1 DEZENA MAIS 1 UNIDADE É IGUAL A 11

PODEMOS REPRESENTAR ESSA QUANTIDADE DE PINGOS DE ÁGUA NO QUADRO DE ORDENS.

QUADRO DE ORDENS D U 11

CHUVAS PELO BRASIL

DICA: NO QUADRO DE ORDENS, U SIGNIFICA UNIDADE E D SIGNIFICA DEZENA.

ONDE VOCÊ MORA CHOVE COM FREQUÊNCIA? VOCÊ SABIA

QUE EM ALGUNS MUNICÍPIOS DO BRASIL QUASE NÃO CHOVE

DURANTE O ANO E EM OUTROS CHOVE MUITO?

EM 2024, POR EXEMPLO, O MUNICÍPIO BRASILEIRO

QUE REGISTROU A MENOR OCORRÊNCIA DE CHUVAS FOI

11 ONZE

PINGOS DE ÁGUA DE CHUVA NA JANELA DE UM AUTOMÓVEL, COM A VISTA DE UM ARCO-ÍRIS À FRENTE.

UIBAÍ, NA BAHIA, CAUSANDO PREJUÍZOS À REGIÃO POR CAUSA DA SECA. JÁ O MUNICÍPIO DE CAXIAS DO SUL, NO RIO GRANDE DO SUL, REGISTROU A MAIOR QUANTIDADE DE CHUVAS NESSE MESMO ANO, CAUSANDO VÁRIAS ENCHENTES.

Em seguida, faça a leitura do texto com os estudantes e verifique se compreenderam qual foi a cidade onde mais choveu e em qual menos choveu no Brasil em 2024.

• É importante destacar que nas cidades as chuvas melhoram a qualidade do ar, limpando impurezas e poluentes presentes na atmosfera,

06/10/2025 17:36:51

deixando o ar puro e saudável. Nesse mesmo contexto, nos campos, são fundamentais na agricultura e responsáveis pela irrigação do solo e pelo crescimento das plantações. No entanto, é ideal que ocorram períodos equilibrados entre chuvas e secas, pois toda a qualidade da colheita depende desse equilíbrio.

• Na atividade 8, essa nova gota que os estudantes vão desenhar pode ficar em qualquer lugar da atividade, desde que fique próximo às demais gotas. A atividade aborda o número 11 e sua representação no quadro de ordens. Utilize algum material de contagem, como o material dourado, de modo a demonstrar aos estudantes que, para quantidades a partir de dez unidades, podemos fazer agrupamentos de dez elementos e utilizar a ordem das dezenas. Ressalte que, no caso do número 11, podemos fazer um agrupamento de dez elementos, construindo uma dezena, e que o elemento restante corresponde a uma unidade. Destaque a eles que, na composição do número 11, o primeiro algarismo 1 – à esquerda – denota uma dezena, enquanto o segundo representa uma unidade, associando a estrutura do número com o quadro de ordens. É importante estabelecer uma relação entre o quadro de ordens e o material de contagem, de modo a contribuir para a compreensão da estrutura do sistema de numeração decimal, que é posicional e toma por base agrupamentos na identificação das ordens.

• Antes de ler o texto Chuvas pelo Brasil com os estudantes, pergunte a eles se há muita ou pouca ocorrência de chuvas onde moram e se sabem qual região do Brasil tem a maior ou a menor ocorrência de chuvas.

• Na resolução da atividade 9, aproveite o material de contagem utilizado na atividade 8 e proponha aos estudantes a representação das quantidades de carrinhos de cada item utilizando esse material. Peça a eles que construam agrupamentos com dez elementos, relacionando-os com a dezena, e identifiquem quantos sobraram após essa separação, fazendo uma correspondência com as unidades.

• Aproveite a abordagem para verificar a compreensão dos estudantes a respeito dos números maiores do que dez, bem como da representação desses números por escrito e no quadro de ordens.

Professor, professora: Oriente os estudantes a contornarem, em cada item da atividade 9, grupos de 10 carrinhos para formar uma dezena, contando, em seguida, as unidades não

9. CONTORNE OS CARRINHOS DE CADA ITEM, FORMANDO GRUPOS DE 10. DEPOIS, COMPLETE OS QUADROS ESCREVENDO O NÚMERO QUE REPRESENTA CADA QUANTIDADE.

QUADRO DE ORDENS D U 1 2

12 DOZE

QUADRO DE ORDENS D U TREZE

Resposta: D: 1, U: 3; 13 agrupadas.

QUADRO DE ORDENS D U QUATORZE

Resposta: D: 1, U: 4; 14.

QUADRO DE ORDENS D U QUINZE

Resposta: D: 1, U: 5; 15

10. NOS QUADROS A SEGUIR, DESENHE BOLINHAS DE ACORDO COM A QUANTIDADE INDICADA. DEPOIS, COMPLETE AS INFORMAÇÕES COM O NÚMERO QUE REPRESENTA CADA QUANTIDADE.

A ) DEZESSEIS.

Resposta: Os estudantes devem desenhar

16 bolinhas e completar o quadrinho com o número 16.

B ) DEZESSETE.

Resposta: Os estudantes devem desenhar

17 bolinhas e completar o quadrinho com o número 17.

C ) DEZOITO.

Resposta: Os estudantes devem desenhar

18 bolinhas e completar o quadrinho com o número 18.

D ) DEZENOVE.

Resposta: Os estudantes devem desenhar

• A atividade 10 finaliza a abordagem dos números de 0 a 19 com a representação dos números 16 a 19. Aproveite para avaliar a compreensão dos estudantes a respeito do significado da dezena e sua relação com a unidade. Complemente a atividade propondo que representem esses números no quadro de ordens, assim como na atividade anterior.

AVALIANDO

Objetivo

11. Resposta: Os estudantes devem marcar um X nas alternativas: É POUCO PROVÁVEL QUE BEATRIZ SORTEIE UMA BOLINHA COM UM NÚMERO MAIOR DO QUE 14; É IMPOSSÍVEL QUE BEATRIZ SORTEIE UMA BOLINHA COM UM NÚMERO MAIOR DO QUE 15.

11. BEATRIZ COLOCOU BOLINHAS, DE MESMA MASSA E MESMO MATERIAL, NUMERADAS DE 1 A 15, EM UM GLOBO USADO EM SORTEIO.

19 bolinhas e completar o quadrinho com o número 19.

MARQUE UM X NAS ALTERNATIVAS CORRETAS.

Unidades temáticas integradas

É POUCO PROVÁVEL QUE BEATRIZ SORTEIE UMA BOLINHA COM UM NÚMERO MAIOR DO QUE 1.

É IMPOSSÍVEL QUE BEATRIZ SORTEIE UMA BOLINHA COM UM NÚMERO MAIOR DO QUE 13.

É POUCO PROVÁVEL QUE BEATRIZ SORTEIE UMA BOLINHA COM UM NÚMERO MAIOR DO QUE 14.

É IMPOSSÍVEL QUE BEATRIZ SORTEIE UMA BOLINHA COM UM NÚMERO MAIOR DO QUE 15.

• A atividade 11 integra as unidades temáticas de Matemática Números e Probabilidade e estatística ao trabalhar com bolinhas numeradas de 1 a 15 e a análise dos resultados obtidos na realização de um sorteio, levando os estudantes a classificar esse evento usando os termos pouco provável ou impossível que aconteça

• A atividade 11 visa à compreensão dos estudantes a respeito das chances entre determinados resultados em um sorteio aleatório. Verifique a possibilidade de levar para a sala de aula um globo parecido com o apresentado na atividade,

06/10/2025 17:39:10

contendo bolinhas numeradas de 1 a 15. Deixe os estudantes manipularem o objeto e fazerem simulações. Converse a respeito das respostas apresentadas por eles.

BNCC

A atividade 11 contribui para o desenvolvimento da habilidade EF02MA21 ao propor a classificação de resultados de eventos em pouco provável e impossível de ocorrer.

A atividade 10 permite avaliar os conhecimentos dos estudantes a respeito de números entre 0 e 19, bem como do significado de dezena.

Sugestão de intervenção

Caso algum estudante considere difícil resolver as atividades, proponha a ele que represente as quantidades indicadas em cada item utilizando, por exemplo, bolinhas de gude ou outro material de contagem. Pergunte quantas dezenas estão presentes, desconsiderando as unidades que restam. Observe se ele reconhece que em cada um desses números há uma única dezena, com unidades excedentes. Peça-lhe que relacione essas quantidades de dezenas e unidades com os algarismos que compõem cada um dos números indicados na unidade, na ordem correta, além de tomar como referência essas bolinhas para fazer os desenhos solicitados no enunciado da atividade.

• Para o desenvolvimento desse tópico, espera-se que os estudantes tenham, como pré-requisitos, noções básicas de agrupamentos.

• A atividade 1 aborda os agrupamentos contendo dez elementos, ou seja, as dezenas. Durante a resolução, verifique se compreendem que, se uma dezena contém dez unidades, então duas dezenas devem conter 20 unidades. Eles têm de perceber que a contagem de cada dezena inclui outros dez elementos em um agrupamento, e não apenas um elemento a mais. Se julgar conveniente, faça um comparativo entre o significado de duas dezenas e o do número 11, de modo que percebam que no primeiro caso há vinte elementos no agrupamento, enquanto no segundo há apenas onze, já que esse número indica uma dezena acrescida de uma unidade.

ARTICULANDO CONHECIMENTOS

Durante o trabalho com esta atividade, além da leitura e interpretação do poema, bem como do estudo das dezenas, aproveite para relacionar Matemática e Ciências da Natureza abordando a importância da preservação ambiental. Converse com os estudantes a respeito da contribuição dessas ações para a manutenção da vida das espécies – como o sabiá. Se julgar conveniente, proponha uma pesquisa sobre as características dessa ave, seu hábitat e outras características de interesse da turma.

CONTANDO DE 10 EM 10

1. O TEXTO A SEGUIR É O TRECHO DE UM POEMA.

CANÇÃO DO EXÍLIO

MINHA TERRA TEM PALMEIRAS, ONDE CANTA O SABIÁ;

AS AVES, QUE AQUI GORJEIAM, NÃO GORJEIAM COMO LÁ.

[...]

GONÇALVES DIAS. CANÇÃO DO EXÍLIO. IN: GONÇALVES DIAS. CANÇÃO DO EXÍLIO E OUTROS POEMAS. BARUERI: NOVO SÉCULO, 2023. E-BOOK

EXÍLIO: LOCAL DE MORADIA DE ALGUÉM QUE FOI FORÇADO A MUDAR PARA LONGE DE SUA TERRA DE ORIGEM.

GORJEIAM: CANTAM.

A ) LEIA O TRECHO DO POEMA COM O PROFESSOR E SEUS COLEGAS.

B ) VOCÊ ACHA QUE O AUTOR SENTE SAUDADES DE SUA TERRA? POR QUÊ?

Resposta pessoal. Espera-se que os estudantes percebam que o autor compara elementos da natureza de sua terra com os do lugar

C ) QUANTAS PALMEIRAS APARECEM NA IMAGEM?

NA IMAGEM, APARECEM (DEZ) PALMEIRAS OU UMA DEZENA DE PALMEIRAS.

D ) DESENHE MAIS 10 PALMEIRAS.

Resposta pessoal. Leia o trecho do poema com os estudantes. 10 (DEZ) PALMEIRAS OU UMA DEZENA DE PALMEIRAS.

1. C) Resposta: NA IMAGEM, APARECEM

Resposta: Os estudantes devem desenhar 10 palmeiras, totalizando 20 palmeiras.

E ) CONTORNE AS PALMEIRAS FORMANDO GRUPOS DE 10 UNIDADES

AGORA, APARECEM 20 (VINTE) PALMEIRAS OU DEZENAS DE PALMEIRAS.

Resposta: Os estudantes onde está, mostrando preferência pelos de sua terra natal.

devem contornar as palmeiras formando 2 grupos com 10 unidades cada. AGORA, APARECEM 20 (VINTE) PALMEIRAS OU 2 DEZENAS DE PALMEIRAS.

06/10/2025 17:39:10

2. OS ROBÔS DE BRINQUEDO DE UMA LOJA FORAM ORGANIZADOS EM PRATELEIRAS.

A ) QUANTAS DEZENAS DE ROBÔS APARECEM NAS PRATELEIRAS? DEZENAS DE ROBÔS.

Resposta: 3 DEZENAS DE ROBÔS.

B ) COMPLETE A FRASE. NESSAS PRATELEIRAS, HÁ DEZENAS DE ROBÔS OU (TRINTA) ROBÔS.

Resposta: NESSAS PRATELEIRAS, HÁ 3 DEZENAS DE ROBÔS OU 30 (TRINTA) ROBÔS.

3. RESOLVA O QUE SE PEDE EM CADA ITEM.

A ) DESENHE EM CADA QUADRO 10 RISQUINHOS.

Resposta: Os estudantes devem desenhar 10 risquinhos em cada quadro.

B ) COMPLETE A FRASE A SEGUIR.

AO TODO, DESENHEI DEZENAS DE RISQUINHOS OU (QUARENTA) RISQUINHOS.

Resposta: AO TODO, DESENHEI 4 DEZENAS DE RISQUINHOS OU 40 (QUARENTA) RISQUINHOS.

ATIVIDADE EXTRA

Faça com os estudantes uma atividade de estimativa. Mostre a eles uma fotografia com um grupo de dez pessoas, como se estivessem posando para a fotografia, sem muita organização. Depois, faça os seguintes questionamentos.

• Sem contar um a um, responda: na fotografia aparecem mais de 19 pessoas ou menos?

• Conte e registre a quantidade de pessoas que aparece na fotografia.

27

06/10/2025 17:39:10

• Na imagem, você contou mais, menos ou exatamente uma dezena de pessoas?

Respostas

• Resposta pessoal. A resposta depende da estimativa que os estudantes fizerem e da fotografia apresentada.

• Dez.

• Uma dezena.

• No trabalho com as atividades 2 e 3, verifique se os estudantes estão relacionando a dezena com agrupamentos de dez unidades. Se julgar necessário, recorra ao material de contagem para que possam selecionar as quantidades de itens indicados em cada atividade, agrupá-los de dez em dez e relacionar a quantidade de agrupamentos com a quantidade de dezenas correspondentes.

• Avalie a possibilidade de propor aos estudantes, nesse momento, uma atividade de estimativa, como a sugerida a seguir.

KATHARINE FROTA/ARQUIVO DA EDITORA

• Na atividade 4, os estudantes devem identificar, em cada item, as quantidades de dezenas correspondentes. Destaque a eles que, no momento de separar os alimentos em grupos com dez unidades cada, esses grupos devem conter elementos diferentes para que nenhum seja contado duas vezes.

• Acompanhe-os durante a resolução da atividade, de modo a verificar se compreenderam que a quantidade de grupos formados é o que indica as dezenas correspondentes. Durante a resolução, comente a respeito da importância de manter uma alimentação saudável e balanceada, consumindo frutas e legumes com frequência, hábito que auxilia na prevenção de doenças e no bom funcionamento do organismo.

4. EM CADA QUADRO, CONTORNE OS ALIMENTOS EM GRUPOS DE 10 UNIDADES. DEPOIS, COMPLETE AS FRASES.

Resposta: Os estudantes devem contornar as bananas formando 5 grupos com 10 bananas cada; 5 DEZENAS DE BANANAS OU 50 (CINQUENTA) BANANAS.

DEZENAS DE BANANAS OU (CINQUENTA) BANANAS.

Resposta: Os estudantes devem contornar as laranjas formando 6 grupos com 10 laranjas cada; 6 DEZENAS DE LARANJAS OU 60 (SESSENTA) LARANJAS.

DEZENAS DE LARANJAS OU (SESSENTA) LARANJAS.

DEZENAS DE CENOURAS OU (SETENTA) CENOURAS.

Resposta: Os estudantes devem contornar as cenouras formando 7 grupos com 10 cenouras cada; 7 DEZENAS DE CENOURAS OU 70 (SETENTA) CENOURAS.

C.

5. A IMAGEM A SEGUIR APRESENTA VÁRIOS CUBINHOS.

6. A) Resposta: Regra da sequência: para obter um número dessa sequência, a partir do segundo termo, adicionamos uma dezena ao número anterior.

A ) SEM CONTAR UM A UM, FAÇA UMA ESTIMATIVA E ESCREVA QUANTOS CUBINHOS HÁ AO TODO NA IMAGEM.

CUBINHOS, SEM CONTAR UM A UM.

Resposta pessoal. Espera-se que os

estudantes estimem uma quantidade próxima a 80 cubinhos, sem contar um a um.

B ) CONTORNE OS CUBINHOS FORMANDO GRUPOS DE 10 UNIDADES. DEPOIS, COMPLETE A FRASE.

AO TODO, CONTORNEI DEZENAS DE CUBINHOS,

Resposta: Os estudantes devem contornar os cubinhos formando 8 grupos com

OU SEJA, (OITENTA) CUBINHOS.

AO TODO, CONTORNEI 8 DEZENAS DE CUBINHOS, OU SEJA, 80 (OITENTA) CUBINHOS. 10 cubinhos cada;

6. EM UM PARQUE DE DIVERSÕES, UMA BARRACA OFERECE PRÊMIOS DE ACORDO COM A PONTUAÇÃO DE CADA JOGADOR.

A ) REÚNA-SE COM UM COLEGA E DETERMINEM JUNTOS A REGRA DA SEQUÊNCIA DE PONTOS.

B ) DE ACORDO COM A REGRA DETERMINADA, COMPLETE A SEQUÊNCIA DE PONTOS NA IMAGEM COM OS NÚMEROS QUE FALTAM.

Resposta: 10, 20, 30, 40, 50, 60, 70, 80, 90.

tagem e peça a ele que, inicialmente, represente as duas primeiras pontuações utilizando esses materiais. Em seguida, oriente-o a organizar esses materiais em grupos com dez elementos, identificando quantos desses grupos podem ser formados em relação a cada pontuação. Pergunte como ele representaria o próximo elemento da sequência, de modo a perceber o padrão e reconhecer os números que ocupam cada posição. Nessa atividade, proponha perguntas relacionadas ao conceito de dezena, o que possibilita verificar a compreensão dos estudantes acerca do conteúdo.

BNCC

06/10/2025 17:39:11

A atividade 5 favorece o desenvolvimento da habilidade EF02MA02 ao solicitar aos estudantes a construção de estimativas, sem o uso de contagem, e sua representação empregando algarismos.

Na atividade 6, os estudantes devem reconhecer o padrão de uma sequência numérica, relacionado ao conceito de dezena, e identificar alguns de seus termos, contribuindo para o desenvolvimento das habilidades EF02MA10 e EF02MA11

• Durante o desenvolvimento da atividade 5, verifique se os estudantes estão construindo as estimativas sem utilizar a contagem. Em caso de dificuldade na construção dessa estimativa, pergunte se acham que a quantidade de cubinhos é maior ou menor do que vinte, por exemplo, e prossiga com essas perguntas até que identifiquem uma estimativa que eles acreditem estar suficientemente próxima do resultado correto. Na segunda parte da atividade, observe se os estudantes compreenderam o significado de dezena, orientando-os por meio de questionamentos sempre que julgar necessário.

• Na atividade 6, os estudantes devem associar os termos da sequência com os números analisados nas atividades anteriores. Proponha a eles que indiquem, para cada elemento da sequência, a quantidade de dezenas correspondente.

AVALIANDO

Objetivo

A atividade 6 permite uma investigação a respeito da compreensão das dezenas e dos agrupamentos de dez em dez.

Sugestão de intervenção

Em caso de eventual dificuldade de algum estudante em reconhecer o padrão presente na sequência, distribua materiais de con-

• Na atividade 1, são propostas reflexões envolvendo números discutidos em tópicos anteriores. Analise se os estudantes compreendem que sempre que um conjunto tem dez unidades podemos substituí-lo por uma dezena, mesmo que haja mais dezenas presentes.

• Caso os estudantes tenham dificuldades em compreender essa relação e em resolver a atividade, peça a eles que separem os peixes em grupos contendo dez peixes cada, de tal maneira que percebam que a inclusão de um peixe ocasiona a obtenção de duas dezenas. Reforce a eles que, ao fazer a troca por duas dezenas, não haverá mais qualquer unidade independente, além das que integram as dezenas.

BNCC

Algumas atividades propostas neste tópico contribuem para o desenvolvimento das habilidades EF02MA01, EF02MA02 e EF02MA04, pois propõem aos estudantes o reconhecimento de quantidades, utilizando estimativas e contagem, bem como a comparação entre elas e a composição e decomposição utilizando adições.

NÚMEROS DE 0 A 99

1. NA CASA DE MIGUEL, HAVIA UM AQUÁRIO COM 19 PEIXES.

A ) REPRESENTE A QUANTIDADE DE PEIXES DO AQUÁRIO DA CASA DE MIGUEL.

Resposta: COM ALGARISMOS: 19; POR EXTENSO: DEZENOVE; NO QUADRO DE ORDENS: D: 1, U: 9

• COM ALGARISMOS:

• POR EXTENSO:

• NO QUADRO DE ORDENS:

QUADRO DE ORDENS

D U

B ) MIGUEL GANHOU UM NOVO PEIXE PARA O AQUÁRIO.

AGORA, HÁ PEIXES NO AQUÁRIO.

Resposta: AGORA HÁ 20 PEIXES NO AQUÁRIO.

C ) REPRESENTE A QUANTIDADE DE PEIXES QUE AGORA ESTÃO NO AQUÁRIO:

Resposta: COM ALGARISMOS: 20; POR EXTENSO: VINTE; NO QUADRO DE ORDENS: D: 2, U: 0

• COM ALGARISMOS:

• POR EXTENSO:

• NO QUADRO DE ORDENS:

QUADRO DE ORDENS

D U

2. Resposta: Os estudantes devem completar a 2ª linha com VINTE E UM; a 3ª linha com 22;

2. COMPLETE O QUADRO.

a 5ª linha com VINTE E QUATRO; a 6ª linha com 25; a 8ª linha com VINTE E SETE; e a 9ª linha com 28

NÚMEROS E ESCRITA POR EXTENSO NÚMEROS

ESCRITA POR EXTENSO

20 VINTE

21 VINTE E

23

24 VINTE E

26

27 VINTE E

VINTE E DOIS

VINTE E TRÊS

VINTE E CINCO

VINTE E SEIS

VINTE E OITO

29 VINTE E NOVE

3. NA IMAGEM, ESTÃO APRESENTADAS AS BOLINHAS QUE GUSTAVO TEM.

A ) CONTORNE AS BOLINHAS FORMANDO GRUPOS COM 10 UNIDADES CADA.

B ) QUANTOS GRUPOS COM 10 BOLINHAS VOCÊ FORMOU? GRUPOS.

3. A) Resposta: Os estudantes devem contornar as bolinhas formando 3 grupos com 10 unidades cada, sobrando 4 bolinhas sem contornar. Resposta: 3 GRUPOS. Resposta: 4 BOLINHAS.

C ) SOBRARAM QUANTAS BOLINHAS SEM FORMAR GRUPO? BOLINHAS.

D ) NO TOTAL, HÁ BOLINHAS.

Resposta: NO TOTAL, HÁ 34 BOLINHAS.

• Aproveite a proposta da atividade 2 para conversar com os estudantes a respeito da escrita por extenso dos números. Diga a eles que há nomes especiais para os números de 0 a 20, além dos números 30, 40, e assim por diante. Porém, para os números 21 a 29, 31 a 39, e assim sucessivamente, precisamos juntar palavras na sua representação, assim como na separação entre dezenas e unidades. Comente que na escrita do número 21 precisamos escrever “vinte e um”, sendo o “vinte” referente às dezenas que podem ser formadas e “um”, à quantidade de unidades excedentes. Se julgar conveniente, proponha a eles que escrevam por extenso outros números seguindo essa mesma regra, como 35 e 67.

• Se necessário, escreva cada número na lousa, evidenciando aos estudantes o movimento com a mão e a direção do traçado para a escrita dos algarismos.

• Na atividade 3, comente com os estudantes que as unidades que devemos registrar no quadro de ordens correspondem sempre às unidades que não foram consideradas na identificação das dezenas, ou seja, são as unidades que sobraram após os agrupamentos de dez em dez. Para complementar, proponha uma atividade que envolva o reconhecimento de uma quantidade considerando os agrupamentos de dez em dez e a representação no quadro de ordens, como é mostrado na sugestão a seguir.

ATIVIDADE EXTRA

Leve para a sala de aula caixas contendo diferentes quantidades de objetos, cada caixa contendo um único tipo de objeto. Essas quantidades devem variar de 21 a 39. Leve também fichas contendo ilustrações do quadro de ordens em branco.

06/10/2025 17:39:12

Apresente essas caixas aos estudantes e peça a eles que, inicialmente, estimem quantos objetos há em cada caixa sem fazer contagem um a um. Em seguida, peça-lhes que contem quantos objetos estão presentes em cada caixa e preencham o quadro de ordens.

Ao final, proponha uma conversa com a turma para conferir os resultados obtidos e sanar possíveis dúvidas a respeito do conteúdo.

• A atividade 4 estabelece uma integração entre as unidades temáticas de Matemática Números e Probabilidade e estatística ao trabalhar com dados coletados pelos estudantes e a organização desses dados em uma tabela. Considere a possibilidade de organizar a turma em grupos com 2 ou 3 integrantes, a fim de facilitar o trabalho com a atividade. Nesse caso, cada estudante fica responsável por coletar apenas uma parte da quantidade de dados, de modo que, ao reunir todos os dados, seja possível completar a quantidade de 20 a 30 participantes. Oriente-os a fazer os registros no caderno para, posteriormente, organizá-los e preencher a tabela.

• Proponha aos estudantes que realizem os itens A e B com a ajuda de alguém da família, que os auxiliará nas estratégias que podem adotar no registro dos dados coletados no caderno. Em sala de aula, converse com eles a respeito da possibilidade de registrar essas informações utilizando, por exemplo, risquinhos, bolinhas ou números.

• Durante o preenchimento dos dados, oriente-os a completar o título da tabela de acordo com o ano vigente e a fonte de pesquisa com o nome do estudante ou de cada integrante do grupo.

BNCC

A atividade 4 contribui para o desenvolvimento da habilidade EF02MA23, pois propõe aos estudantes fazer uma pesquisa em um universo de até 30 elementos, organizando os dados coletados em uma tabela.

EXPERIMENTE

4. B) Resposta pessoal. Os registros dependem da quantidade de pessoas que participaram da pesquisa e da maneira como os dados obtidos pelos estudantes foram registrados. Incentive-os a comparar seus registros com os dos colegas.

Unidades temáticas integradas

4. ESCOLHA DE 20 A 30 PESSOAS, ENTRE COLEGAS E FAMILIARES, PARA FAZER UMA PESQUISA.

A ) FAÇA A CADA UMA DELAS A MESMA PERGUNTA QUE ANA ESTÁ FAZENDO.

B ) REGISTRE EM SEU CADERNO OS DADOS OBTIDOS DA MANEIRA QUE PREFERIR.

C ) COM OS DADOS DA PESQUISA, COMPLETE A TABELA A SEGUIR.

QUANTOS IRMÃOS VOCÊ TEM? ANA

AVALIANDO

Objetivo

que completam a tabela dependem dos registros dos estudantes.

QUANTIDADE DE IRMÃOS DOS COLEGAS E FAMILIARES

QUANTIDADE DE IRMÃOS QUANTIDADE DE PESSOAS

NENHUM

MAIS DO QUE 3

FONTE DE PESQUISA: REGISTROS DE

D ) QUANTAS PESSOAS TÊM MAIS DO QUE QUATRO IRMÃOS?

Resposta pessoal. A resposta depende dos dados coletados.

E ) A QUANTIDADE DE PESSOAS QUE NÃO TÊM IRMÃOS É IGUAL, MAIOR OU MENOR DO QUE A QUANTIDADE DE PESSOAS QUE TÊM 1 IRMÃOResposta pessoal.

Resposta pessoal. A resposta depende dos dados coletados. Resposta pessoal. As informações

Compreender dados apresentados em tabelas e identificar seus elementos.

Sugestão de intervenção

Faça aos estudantes algumas perguntas a respeito das tabelas que foram construídas nas atividades deste tópico. Incentive-os a identificar seus elementos e obter conclusões a respeito desses dados. Com antecedência, separe tabe-

las disponíveis na internet para mostrar como é útil esse tipo de representação. Ao selecioná-las, dê preferência a tabelas com valores menores do que 999 e com assuntos pertinentes à faixa etária da turma. Promova uma roda de conversa a respeito das características das tabelas, comparando as simples e de dupla entrada entre si, bem como as vantagens do uso desse tipo de recurso na organização de dados. Aproveite a oportunidade para sanar possíveis dúvidas a respeito das tabelas e sua utilização em diferentes contextos.

5. COMPLETE CADA ITEM COM O QUE FALTA.

A.

DICA: CADA REPRESENTA 10 UNIDADES DE OU UMA DEZENA.

Resposta: 4 DEZENAS E 5 UNIDADES; 40 + 5 = 45; POR EXTENSO: QUARENTA E CINCO; NO QUADRO DE ORDENS: D: 4, U: 5.

QUADRO DE ORDENS

D U

B.

4 DEZENAS E UNIDADES.

+ = POR EXTENSO:

Resposta: 5 DEZENAS E 7 UNIDADES; 50 + 7 = 57; POR EXTENSO: CINQUENTA E SETE; QUADRO DE ORDENS: D: 5, U: 7

QUADRO DE ORDENS D U

C.

5 DEZENAS E UNIDADES.

+ =

POR EXTENSO:

Resposta: 3 DEZENAS E 1 UNIDADE; 30 + 1 = 31; POR EXTENSO: TRINTA E UM; QUADRO DE ORDENS: D: 3, U: 1

QUADRO DE ORDENS D U

3 DEZENAS E UNIDADE.

+ =

POR EXTENSO:

06/10/2025 17:39:13

• Antes de resolver a atividade 5, verifique a possibilidade de levar para a sala de aula o material dourado para que a turma possa, de forma experimental, estabelecer relações entre as peças desse recurso com os conceitos em estudo. Lembre os estudantes de que, nesse caso, o cubinho equivale a 1 unidade e a barra equivale a 1 dezena. Inicialmente, peça a eles que, utilizando esse material, representem os números 5 e 40 e, em seguida, comente que a representação do número 45 pode ser entendida como a adição entre 40 e 5. Estabeleça uma relação entre os agrupamentos de dez em dez e a troca de unidades por barras. Com base na discussão, proponha a resolução da atividade 5 utilizando esse material. Acompanhe o processo, sanando as dúvidas e intervindo sempre que necessário.

• Avalie a possibilidade de levar para a sala de aula um ou mais ábacos para que os estudantes representem neles os números apresentados na atividade 6. Outra possibilidade é construir um ábaco com material reciclável. Para isso, providencie os materiais necessários ou peça aos estudantes que os levem de casa. O ábaco pode ser montado individualmente ou em grupo. Em cada montagem, serão necessários:

• palitos de churrasco sem a ponta;

• uma base para fixação das hastes;

• arruelas, argolas de plástico ou outro material com furo no meio para ser usado como as bolinhas do ábaco;

• caneta colorida para escrever na base a ordem correspondente a cada palito.

centena dezena unidade

• Auxilie os estudantes na montagem do ábaco, a fim de evitar acidentes, principalmente na etapa de fixação das hastes. Se necessário, ofereça ajuda na montagem para evitar que se machuquem nessa etapa. Comente também que a terceira haste será utilizada a partir do próximo tópico.

6. PARA REGISTRAR NÚMEROS E EFETUAR ALGUMAS

OPERAÇÕES, PODEMOS USAR UM INSTRUMENTO CHAMADO ÁBACO. NA IMAGEM DO ÁBACO ESTÃO

REPRESENTADAS 2 DEZENAS E 7 UNIDADES, OU SEJA, O NÚMERO 27.

Resposta: Os estudantes devem ligar os itens da seguinte maneira: A-VINTE E CINCO; B-TRINTA E DOIS; C-QUARENTA E OITO; D-CINQUENTA.

LIGUE CADA ÁBACO A SEGUIR, AO NÚMERO CORRESPONDENTE ESCRITO POR EXTENSO. A. B.

C. D.

7. Resposta: No quadro DECOMPOSIÇÃO DE ALGUNS NÚMEROS, os estudantes devem completar a 3ª linha do quadro com 64 (SESSENTA E QUATRO); a 4ª linha com 60 + 9; 5ª linha com 71 (SETENTA E UM); a 6ª linha com 73 (SETENTA E TRÊS); e a 7ª linha com 70 + 8

7. COMPLETE O QUADRO A SEGUIR. DECOMPOSIÇÃO DE ALGUNS NÚMEROS NÚMERO DECOMPOSIÇÃO

(SESSENTA E DOIS)

( )

(SESSENTA E NOVE) ( )

( )

78 (SETENTA E OITO) VINTE E CINCO TRINTA E DOIS QUARENTA E OITO CINQUENTA

• Para complementar a atividade 6, proponha a representação dos números no quadro de ordens. Depois, peça aos estudantes que escolham um número e o representem no quadro de ordens e no ábaco. Lembre-os de que, ao representarmos um número no ábaco, cada vez que agrupamos 10 contas em uma haste, devemos retirá-las e trocá-las por uma conta que será colocada na haste imediatamente à esquerda.

• Por meio dessa proposta, converse com os estudantes a respeito das relações entre o quadro de ordens e o ábaco, de modo que perce-

bam que a quantidade de contas presente em cada haste do ábaco corresponde ao algarismo que ocupa cada espaço no quadro de ordens.

• Na atividade 7, proponha aos estudantes que representem os números no ábaco. Caso não seja possível distribuir ábacos para a turma, ou não seja possível construir o ábaco indicado no comentário anterior, distribua para cada estudante uma folha impressa contendo a ilustração de ábacos e peça a eles que desenhem as contas do ábaco na representação de cada número da atividade, identificando assim o número de dezenas e unidades correspondentes. SERGIO LIMA/ARQUIVO DA EDITORA

8. NO QUADRO A SEGUIR, LOCALIZE E CONTORNE O NÚMERO CORRESPONDENTE A CADA ITEM.

A ) 5 DEZENAS E 3 UNIDADES.

Resposta: Os estudantes devem contornar o número 53 na 1ª linha do quadro.

B ) 3 DEZENAS E 6 UNIDADES.

Resposta: Os estudantes devem contornar o número 36 na 2ª linha do quadro.

C ) 6 DEZENAS 2 UNIDADES.

Resposta: Os estudantes devem contornar o número 62 na 5ª linha do quadro.

D ) 9 DEZENAS E 1 UNIDADE.

Resposta: Os estudantes devem contornar o número 91 na 6ª linha do quadro.

9. EM CADA SEQUÊNCIA, A REGRA ESTÁ INDICADA SOBRE AS SETAS. DE ACORDO COM A REGRA, COMPLETE A SEQUÊNCIA.

Resposta: 42, 44, 46, 48, 50, 52, 54, 56, 58.

Resposta: 64, 67, 70, 73, 76, 79, 82, 85, 88

Resposta: 90, 89, 88, 87, 86, 85, 84, 83, 82

BNCC

Por envolver o reconhecimento de padrões em sequências numéricas, que podem ser crescentes ou decrescentes, a atividade 9 favorece o desenvolvimento da habilidade EF02MA09 da BNCC.

AVALIANDO

Objetivo

A atividade 9 permite verificar a compreensão dos estudantes a respeito da

representação dos números de 0 a 99, inclusive em relação à presença das ordens unidade e dezena.

Sugestão de intervenção

Diante das dificuldades manifestadas, proponha aos estudantes a representação do primeiro número da sequência do item A em um ábaco. Em seguida, pergunte a eles como podem proceder para representar o segundo termo dessa sequência nesse mesmo ábaco, instigando-os a reconhecer que devem adicionar duas contas na ordem das unidades, ou

• Na atividade 8, os estudantes devem reconhecer os números que representam cada item no quadro. Se houver alguma dificuldade, oriente-os a escrever o número ao lado de cada item para, em seguida, buscá-lo no quadro. Lembre-os de que devem identificar, no quadro, os números com seus algarismos lado a lado e na ordem correta, isto é, não devem procurar cada algarismo do número, mas o número por completo.

• A atividade 9 propõe aos estudantes o reconhecimento do padrão presente em cada uma das três sequências, envolvendo adição ou subtração de um mesmo número. Proponha a eles a resolução da atividade em duplas. Ao final, promova uma discussão a respeito das estratégias que utilizaram para resolver a atividade, sanando as possíveis dúvidas deles.

06/10/2025 17:42:04

seja, adicionar duas unidades. Peça-lhes que repitam esse procedimento com o próximo número da sequência e, com base nesse estudo, completem a sequência, identificando a necessidade de representar dez unidades como uma dezena. Se necessário, oriente-os a repetir esse procedimento para as demais sequências da atividade.

• A atividade 10 estabelece uma integração entre as unidades temáticas de Matemática Números e Probabilidade e estatística ao levar os estudantes a fazer uma pesquisa e organizar os dados coletados em uma tabela. Por meio da coleta e organização das informações, os estudantes estão aprendendo a produzir e disseminar conhecimentos com base em fatos e dados coletados de modo confiável.

• Auxilie os estudantes na organização e construção da tabela. Peça a eles que escrevam também as conclusões a que chegaram com base nesses dados, que serão compartilhadas com a turma posteriormente. Organize um momento de apresentação dos resultados, instigando a participação de todos os integrantes dos grupos tanto na apresentação quanto para comentar os trabalhos dos colegas, fazendo suas contribuições.

• Por fim, converse com eles sobre os resultados obtidos, verificando se percebem que alguns têm preferências iguais e outros, diferentes. Aproveite para salientar a importância de respeitar as diferentes preferências e opiniões.

EXPERIMENTE

10. PARA REALIZAR ESTA ATIVIDADE, A TURMA DEVE SER

ORGANIZADA EM 5 GRUPOS. CONVERSE COM SEU PROFESSOR E OS COLEGAS PARA DECIDIR COMO SERÁ FEITA ESSA DIVISÃO. CADA GRUPO VAI FAZER UMA PESQUISA COM TODOS OS ESTUDANTES DA TURMA. PARA A PESQUISA, DEVEM SER REALIZADAS AS SEGUINTES ETAPAS:

Unidades temáticas integradas

• ESCOLHA DO TEMA DA PESQUISA;

• COLETA DE DADOS;

• ORGANIZAÇÃO DOS DADOS EM UMA TABELA.

O TEMA DE CADA GRUPO SERÁ ESCOLHIDO ENTRE OS APRESENTADOS A SEGUIR POR MEIO DE SORTEIO.

• Brincadeira preferida.

• Fruta preferida.

• Cômodo da casa preferido.

• Quantidade de pessoas que moram na casa.

• Quantidade de irmãos.

DEPOIS QUE OS TEMAS FOREM SORTEADOS, JUNTE-SE AO SEU GRUPO, COLETEM OS DADOS E, POR ÚLTIMO, CONSTRUAM NO CADERNO UMA TABELA PARA ORGANIZAR AS INFORMAÇÕES.

AO TÉRMINO DA ATIVIDADE, CADA GRUPO DEVERÁ APRESENTAR

AOS OUTROS COLEGAS E AO PROFESSOR OS RESULTADOS DA PESQUISA.

BNCC

DICA: CONSTRUAM UMA TABELA SEMELHANTE À APRESENTADA NA SEÇÃO EXPERIMENTE DA PÁGINA 32

Resposta pessoal. A resposta depende do resultado da pesquisa que os estudantes realizarem.

A atividade 10 coloca os estudantes em um papel ativo, solicitando a eles a realização de uma pesquisa, em grupos, envolvendo coleta e organização de dados em uma tabela, o que contribui para o desenvolvimento da habilidade EF02MA23. Ao propor o trabalho com uma situação real e a construção de registros escritos envolvendo os dados e as conclusões obtidas, esta atividade também favorece o desenvolvi-

mento da Competência específica de Matemática 6 da BNCC. Além disso, ao compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática, por meio da integração entre unidades temáticas na atividade 10, os estudantes estão desenvolvendo a Competência específica de Matemática 3 da BNCC.

A CENTENA

POR UMA VIDA MAIS SAUDÁVEL

OS ALIMENTOS DENOMINADOS ORGÂNICOS SÃO

CONSIDERADOS MAIS SAUDÁVEIS PORQUE SÃO CULTIVADOS

SEM O USO DE AGROTÓXICOS, QUE PODEM PREJUDICAR NOSSA SAÚDE.

ESSE TIPO DE PRODUÇÃO NÃO AGRIDE A NATUREZA E NÃO CONTAMINA A ÁGUA, O AR, OS ANIMAIS E AS PLANTAS.

AGROTÓXICOS: PRODUTOS QUE PREVINEM E EXTERMINAM PRAGAS DA AGRICULTURA.

DICA: PARA UMA VIDA MAIS SAUDÁVEL, É PRECISO CUIDAR DA ALIMENTAÇÃO. DÊ PREFERÊNCIA A ALIMENTOS PRODUZIDOS SEM O USO DE AGROTÓXICOS.

O CULTIVO DE ALIMENTOS ORGÂNICOS MANTÉM O SOLO MAIS RICO.

1. O PAI DE MARIANA PLANTA CAQUI ORGÂNICO EM SEU POMAR. ELE EMBALA E VENDE OS CAQUIS EM BANDEJAS COM 10 UNIDADES CADA.

• Antes de abordar a atividade 1, proponha aos estudantes a leitura do texto desta página. Esse texto permite trabalhar a alimentação saudável como tema, além de valorizar a produção de alimentos orgânicos, que em sua maioria é desenvolvida por pequenos agricultores. Também permite abordar assuntos como preservação de rios, florestas e animais. Pergunte aos estudantes se eles conhecem algum agricultor ou uma pessoa que produza alimentos para consumo próprio, explorando as vivências deles acerca do assunto.

• A atividade 1 apresenta aos estudantes a centena, partindo do acréscimo de uma unidade ao número 99. Durante a atividade, caso haja dificuldades, proponha um comparativo entre o que ocorre quando adicionamos uma unidade ao 9 e ao 89 para que possam compreender a obtenção do número 100 a partir do 99.

A ) QUANTOS CAQUIS HÁ AO TODO NA IMAGEM?

CAQUIS.

B ) QUANTOS CAQUIS FALTAM PARA MONTAR MAIS UMA BANDEJA COMPLETA?

CAQUI. Resposta: 99 CAQUIS. Resposta: 1 CAQUI.

06/10/2025 17:42:07

• Na atividade 2, a proposta de representar o número 100 no ábaco e no quadro de ordens possibilita aos estudantes que percebam a organização do sistema de numeração decimal.

• Para a atividade 3, se possível, leve para a sala de aula o material dourado e faça as discussões indicadas na atividade utilizando o cubinho, a barra e a placa. Pergunte aos estudantes a relação que pode ser estabelecida entre unidade e dezena com o material dourado, conforme estudado anteriormente, e estabeleça um comparativo com a relação entre dezena e centena. Complemente a atividade solicitando a eles que representem uma unidade, uma dezena e uma centena no ábaco, de modo a identificarem que em ambos os casos se utiliza apenas uma conta, mas em posições diferentes.

AVALIANDO

Objetivo

Avaliar os conhecimentos dos estudantes a respeito da centena e sua relação com unidade e dezena.

Sugestão de intervenção

Se houver dificuldades na resolução da atividade 3, proponha aos estudantes que separem dez cubinhos e façam a troca por barras, de modo a perceberem que uma barra corresponde a dez cubinhos. Em seguida, peça a eles que separem 100 cubinhos e façam as trocas por barras e depois por uma placa, para favorecer a compreensão das relações entre essas ordens.

2. O PAI DE MARIANA ACRESCENTOU MAIS UM CAQUI PARA MONTAR OUTRA BANDEJA.

VAMOS REPRESENTAR O TOTAL DE CAQUIS EMBALADOS NO ÁBACO E NO QUADRO DE ORDENS.

Resposta: 99 CAQUIS MAIS 1 CAQUI É IGUAL A 100 CAQUIS.

NO ÁBACO

100

NO QUADRO DE ORDENS E NO ÁBACO, A LETRA C REPRESENTA A CENTENA

QUADRO DE ORDENS C D U 1 0 0

99 CAQUIS MAIS 1 CAQUI É IGUAL A CAQUIS.

3. DE ACORDO COM AS REPRESENTAÇÕES, COMPLETE OS ITENS.

10 UNIDADES EQUIVALEM A DEZENA.

Resposta: 10 UNIDADES EQUIVALEM A 1 DEZENA.

10 DEZENAS EQUIVALEM A CENTENA.

Resposta: 10 DEZENAS EQUIVALEM A 1 CENTENA.

C D U

4. B) Resposta: É pouco provável. Porque a quantidade de cartões azuis é muito menor do que a quantidade de cartões vermelhos.

4. TRÊS AMIGOS ESTÃO BRINCANDO DE SORTEAR CARTÕES DE UMA CAIXA. PARA ISSO, ELES GUARDARAM DENTRO DA CAIXA

98 CARTÕES VERMELHOS, 1 VERDE E 1 AZUL, TODOS DE MESMO TAMANHO E MATERIAL. ELES VÃO SORTEAR UM CARTÃO DE CADA VEZ.

Unidades temáticas integradas

A ) QUANTOS CARTÕES ELES GUARDARAM, AO TODO, NA CAIXA?

Resposta: 100 CARTÕES.

99 CARTÕES.

93 CARTÕES.

100 CARTÕES.

95 CARTÕES.

ANTES DE SORTEAR O PRIMEIRO CARTÃO DA CAIXA, OS AMIGOS CONVERSARAM.

É MUITO PROVÁVEL QUE O PRIMEIRO CARTÃO SORTEADO SEJA VERMELHO.

CONCORDO, POIS A QUANTIDADE DE CARTÕES VERMELHOS É MUITO MAIOR DO QUE A QUANTIDADE DE CARTÕES VERDES E AZUIS. É POUCO PROVÁVEL QUE O PRIMEIRO CARTÃO A SER SORTEADO SEJA VERDE.

B ) É MUITO PROVÁVEL OU POUCO PROVÁVEL QUE O PRIMEIRO CARTÃO SORTEADO SEJA AZUL? POR QUÊ? CONVERSE COM SEU PROFESSOR E OS COLEGAS SOBRE ISSO.

C ) AO SORTEAR UM CARTÃO DESSA CAIXA, É MUITO

PROVÁVEL, POUCO PROVÁVEL OU IMPOSSÍVEL QUE ELE SEJA AMARELO? COPIE NA LINHA A SEGUIR SUA RESPOSTA.

Professor, professora: Oriente os estudantes na escrita da palavra que responde ao item C, incentivando o traçado em letra cursiva na pauta apresentada.

pouco provávelmuito provávelimpossível

Resposta: Os estudantes devem copiar na pauta a palavra IMPOSSÍVEL.

Professor, professora: Durante a realização do item C desta atividade, espera-se que os estudantes percebam que não há cartões amarelos na caixa e, consequentemente, não é possível que essa cor de cartão seja sorteada.

BNCC

• A atividade 4 relaciona as unidades temáticas de Matemática Números e Probabilidade e estatística ao trabalhar a interpretação das possíveis cores de cartões a serem sorteados e a análise de uma situação com uma cor que é impossível de ser sorteada.

• A atividade 4 também tem o intuito de favorecer a compreensão dos estudantes com relação ao resultado em um sorteio aleatório, no qual um dos eventos tem mais chances de ocorrer. Avalie a possibilidade de realizar, na prática, a situação descrita, a fim de que compreendam quais são as chances de um evento ocorrer ou não. Para isso, providencie uma caixa ou outro recipiente não transparente e cartões confeccionados com cartolina colorida ou papel-cartão nas quantidades e cores indicadas na atividade, todos com mesmo formato e tamanho. Solicite a cada estudante que sorteie um cartão, anote a cor obtida no caderno e retorne-o à caixa; por fim, verifique qual cor de cartão foi mais sorteada. Após o experimento, converse com os estudantes a respeito das chances de sortear cada cor, validando as respostas para os itens B e C

• Se julgar necessário, após a realização do item C da atividade 4, para reforçar a prática e o direcionamento da escrita das letras, utilize o caderno de caligrafia, de forma que possam desenvolver progressivamente a escrita da letra cursiva.

• Depois de realizar a atividade 4, converse com os estudantes para que identifiquem as características dos assuntos abordados no sorteio realizado na atividade da página 36. Espera-se que eles concluam que as chances nesse sorteio foram iguais, pois foram apresentados 5 temas diferentes e cada um foi disponibilizado apenas uma vez.

06/10/2025 17:42:09

O trabalho com a atividade 4 capacita os estudantes a classificarem resultados de eventos aleatórios como pouco prováveis, muito prováveis, improváveis e impossíveis, conforme orienta a habilidade EF02MA21. Essa classificação é importante para auxiliá-los a discernir situações de possibilidades aplicadas em ocorrências do cotidiano.

• Na atividade 5, comente com os estudantes que estimar uma quantidade não significa acertar o resultado exato, pois estimar é o mesmo que obter um resultado aproximado de uma operação. Havendo dificuldade, proponha uma atividade prática: utilize alguns materiais concretos, como peças de um quebra-cabeça sobre uma mesa, bolinhas de gude em um pote e palitos sobre a mesa, e peça a eles que analisem esses conjuntos e estimem a quantidade de objetos.

• Na atividade 5, a fim de possibilitar a inclusão, leve para a sala de aula fitas de tecido de tamanho suficiente para vendar os olhos dos estudantes. Entregue uma fita para cada um e auxilie-os para que se vendem corretamente e mantenham os olhos fechados durante a proposta. Em seguida, bata cerca de 25 palmas e peça a eles que estimem a quantidade.

• O objetivo da atividade 6 é reforçar com os estudantes a compreensão do sistema de numeração decimal, usando a ideia de agrupamento de unidades e dezenas. Caso tenham dúvidas, use as peças do material dourado para mostrar como realizamos os agrupamentos e as trocas.

5. NAS CENAS A SEGUIR APARECEM ALGUNS ANIMAIS.

PATOS EM UMA LAGOA.

TARTARUGAS RECÉM-NASCIDAS NA AREIA.

IMAGENS SEM PROPORÇÃO ENTRE SI.

FORMIGAS EM UM CAULE.

A ) SEM CONTAR UM A UM, VOCÊ ESTIMA QUE HÁ MENOS DE 100, MAIS DE 100 OU UMA QUANTIDADE PRÓXIMA DE 100:

• PATOS?

Resposta pessoal. Espera-se que os estudantes estimem que há menos de 100 patos, uma quantidade próxima de 100 tartarugas e uma quantidade próxima de 100 formigas.

• TARTARUGAS?

• FORMIGAS?

B ) EM QUAL DAS TRÊS CENAS SERIA POSSÍVEL CONTAR UM A UM OS ANIMAIS PARA CONFERIR SUA ESTIMATIVA?

6. COMPLETE AS SEGUINTES FRASES.

Resposta pessoal. Espera-se que os estudantes digam que é possível contar um a um os animais da primeira cena, pois nas demais cenas há muitos animais ou eles estão agrupados de maneira que não é possível contá-los.

A ) COM 10 UNIDADES, FORMAMOS DEZENA.

Resposta: COM 10 UNIDADES, FORMAMOS 1 DEZENA.

B ) COM 10 DEZENAS, FORMAMOS CENTENA.

Resposta: COM 10 DEZENAS, FORMAMOS 1 CENTENA.

C ) COM 100 UNIDADES, FORMAMOS CENTENA.

Resposta: COM 100 UNIDADES, FORMAMOS 1 CENTENA.

BNCC

Ao realizar estimativas, na atividade 5, os estudantes são motivados a utilizar diferentes estratégias, analisando representações de figuras ou objetos, contribuindo para o desenvolvimento da habilidade EF02MA02

COMPARAÇÃO

1. ALGUNS LÁPIS DE COR FORAM COLOCADOS EM POTES.

BNCC

COMPLETE CADA ITEM COM O NÚMERO QUE REPRESENTA A QUANTIDADE DE LÁPIS DE COR EM CADA POTE.

A ) A QUANTIDADE DE LÁPIS DO POTE VERDE ( ) É MENOR DO

Resposta: A QUANTIDADE DE LÁPIS DO POTE VERDE (5) É MENOR

QUE (< ) A QUANTIDADE DE LÁPIS DO POTE VERMELHO ( ). <

DO QUE (<) A QUANTIDADE DE LÁPIS DO POTE VERMELHO (6). 5 < 6

B ) A QUANTIDADE DE LÁPIS DO POTE AZUL ( ) É MAIOR DO

QUE ( >) A QUANTIDADE DE LÁPIS DO POTE VERMELHO ( ).

Resposta: A QUANTIDADE DE LÁPIS DO POTE AZUL (8) É MAIOR DO QUE

(>) A QUANTIDADE DE LÁPIS DO POTE VERMELHO (6). 8 > 6

C ) A QUANTIDADE DE LÁPIS DO POTE VERDE ( ) É IGUAL (=)

À QUANTIDADE DE LÁPIS DO POTE AMARELO ( ).

Resposta: A QUANTIDADE DE LÁPIS DO POTE VERDE (5) É IGUAL (=) À QUANTIDADE DE LÁPIS DO POTE AMARELO (5). 5 = 5

QUANDO COMPARAMOS QUANTIDADES, PODEMOS USAR OS SÍMBOLOS > (MAIOR DO QUE), < (MENOR DO QUE) OU = (IGUAL A).

Algumas atividades deste tópico propõem a comparação e a ordenação de números naturais com base nas características do sistema de numeração decimal, abordando aspectos da habilidade EF02MA01. Espera-se que os estudantes progridam na capacidade de comparar a quantidade de objetos de dois conjuntos, estabelecendo relação biunívoca de correspondência, contemplando também aspectos da habilidade EF02MA03

06/10/2025 17:42:11

• A proposta da atividade 1 é levar os estudantes a compreenderem o uso dos símbolos > (maior do que), < (menor do que) e = (igual a).

• Se houver dificuldades na resolução da atividade, peça-lhes que reproduzam essa situação utilizando lápis de cor, fazendo os comparativos indicados na atividade com materiais concretos, a fim de perceberem as quantidades de elementos de cada conjunto e como podem compará-las para, na sequência, preencher a atividade corretamente.

• Para a resolução da atividade 2, peça aos estudantes que façam os desenhos solicitados na atividade para, na sequência, compararem as quantidades e utilizarem o símbolo correto. Pergunte a eles qual diferença pode ser destacada em relação à quantidade de maçãs em cada conjunto, reforçando que essa mesma relação pode ser observada ao comparar os números 8 e 7. Se necessário, escreva na lousa o significado de cada símbolo para que possam escolher o mais adequado à situação.

• Na atividade 3, oriente os estudantes a, inicialmente, reconhecerem quais números estão sendo representados em cada ábaco. Em seguida, pergunte a eles quais diferenças e semelhanças observam entre os dois ábacos de cada item. O objetivo é levá-los a reconhecer que a diferença está na quantidade de contas correspondente à ordem das unidades, ou seja, apresentam quantidades diferentes de unidades, com uma dezena cada um.

2. DESENHE NOS QUADROS AS QUANTIDADES DE MAÇÃS INDICADAS. DEPOIS, COMPLETE AS INFORMAÇÕES COM OS SÍMBOLOS > (MAIOR DO QUE), < (MENOR DO QUE) OU = (IGUAL A).

Resposta: Os estudantes devem desenhar oito maçãs no quadro A e sete maçãs no quadro B; 8 > 7.

3. EM CADA ITEM, ESCREVA O NÚMERO REPRESENTADO NOS ÁBACOS. DEPOIS, COMPARE ESSES NÚMEROS E COMPLETE AS INFORMAÇÕES USANDO O SÍMBOLO < (MENOR DO QUE) OU > (MAIOR DO QUE).

Resposta: A. 13 < 15; B. 17 > 14

4. OBSERVE A SEQUÊNCIA DOS NÚMEROS DE 20 A 39.

20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39.

OS NÚMEROS DESSA SEQUÊNCIA FORAM ESCRITOS EM ORDEM CRESCENTE, PORQUE ELES VÃO DO MENOR PARA O MAIOR.

NESSA SEQUÊNCIA, O NÚMERO 21 VEM ANTES DO 27. ASSIM, 21 É MENOR DO QUE 27. 21 < 27

JÁ O NÚMERO 35 VEM DEPOIS DO NÚMERO 27. ASSIM, 35 É MAIOR DO QUE 27. 35 > 27

CONSIDERE A ORDEM DOS NÚMEROS DA SEQUÊNCIA DE 20 A 39

E COMPLETE OS ITENS USANDO O SÍMBOLO < OU >

A ) 20 23

Resposta: 20 < 23

B ) 36 35

Resposta: 36 > 35

C ) 24 38

Resposta: 24 < 38

D ) 33 29

Resposta: 33 > 29

E ) 31 30

Resposta: 31 > 30

F ) 27 25

Resposta: 27 > 25

5. COMPLETE OS ITENS COM OS ALGARISMOS CORRESPONDENTES.

Resposta: A. 71; B. 96; C. 80; D. 43.

A. C. B. D. 7 DEZENAS E 1 UNIDADE 8 DEZENAS

9 DEZENAS E 6 UNIDADES

4 DEZENAS E 3 UNIDADES

ORGANIZE OS NÚMEROS QUE VOCÊ ESCREVEU DO MAIOR PARA O MENOR COMPLETANDO A SEQUÊNCIA. 96 > > > .

Resposta: 96 > 80 > 71 > 43 43

AVALIANDO

Objetivo

Compreender como comparar números entre si utilizando os símbolos adequados.

Sugestão de intervenção

Diante das dificuldades manifestadas, proponha aos estudantes a representação dos números utilizando o ábaco ou o quadro de ordens. Peça a eles que façam comparações envolvendo as dezenas e as unidades para identificar as

06/10/2025 17:42:12

relações que podem ser estabelecidas entre os números. Como complementação, peça-lhes que identifiquem outros números de acordo com a regra, envolvendo as relações maior do que ou menor do que, como um número maior do que 43 e menor do que 71, entre outras possibilidades.

• O objetivo da atividade 4 é levar os estudantes a perceberem as possíveis comparações que podem ser estabelecidas entre os números na sequência numérica. No caso de dificuldade em reconhecer os símbolos adequados em cada item, proponha a eles a utilização de materiais de contagem para representar cada número e identificar a relação correta. Se julgar conveniente, escreva na lousa outros pares de números, entre 20 e 39, para que possam avaliar, conforme a proposta da atividade.

• Na atividade 5 , reforce aos estudantes que a ordem a ser adotada deve ser do maior para o menor, ou seja, ordem decrescente. Oriente-os a iniciar a identificação dos números utilizando algarismos para depois fazer as comparações. Explique a eles que a comparação deve considerar primeiro as quantidades de dezenas, depois as quantidades de unidades.

• Após a resolução das atividades desta página, faça um comparativo entre as ordens que foram adotadas: ressalte que na atividade 4 os números estão escritos em ordem crescente, do menor para o maior, enquanto na atividade 5 a ordem é decrescente, isto é, do maior para o menor.

• As atividades 6 e 7 abordam as definições de antecessor e sucessor. No trabalho com essas atividades, explique aos estudantes que o antecessor pode ser obtido ao retirar uma unidade do número; já o sucessor, adicionando uma unidade a ele.

• Caso algum estudante tenha dificuldade em diferenciar esses conceitos, faça uma abordagem dessas definições envolvendo os números de 1 a 9, para que compreenda essa relação. Em seguida, dê outros exemplos, envolvendo números de dois algarismos. Complemente as discussões com relação a essas duas atividades destacando que um número é sempre maior do que seu antecessor e menor do que seu sucessor.

6. OBSERVE O ESQUEMA A SEGUIR.

ANTECESSORSUCESSOR – 1 + 1

47

49 48

NESSE ESQUEMA, O NÚMERO 47 É CHAMADO ANTECESSOR, PORQUE VEM IMEDIATAMENTE ANTES DO NÚMERO 48. JÁ O NÚMERO 49 É CHAMADO SUCESSOR, PORQUE VEM IMEDIATAMENTE DEPOIS DO NÚMERO 48.

ESCREVA O ANTECESSOR E O SUCESSOR DO NÚMERO

APRESENTADO EM CADA ITEM.

A ) 63

Resposta: ANTECESSOR: 62; SUCESSOR: 64.

ANTECESSOR:

SUCESSOR:

B ) 22

Resposta: ANTECESSOR: 21; SUCESSOR: 23

ANTECESSOR:

SUCESSOR:

C ) 38

Resposta: ANTECESSOR: 37; SUCESSOR: 39.

ANTECESSOR:

SUCESSOR:

D ) 28

Resposta: ANTECESSOR: 27; SUCESSOR: 29

ANTECESSOR:

SUCESSOR:

7. OBSERVE ESTA SEQUÊNCIA DE NÚMEROS.

A ) ESCREVA O ANTECESSOR DE:

• 51.

Resposta: 50

Resposta: 58

B ) ESCREVA O SUCESSOR DE: • 53.

Resposta: 54

Resposta: 61

Resposta: 64

Resposta: 65

DIVIRTA-SE E APRENDA

JOGO DA COMPARAÇÃO DE FICHAS

JUNTE-SE A DOIS OU TRÊS COLEGAS E DESTAQUEM AS FICHAS DA PÁGINA 259 DO MATERIAL COMPLEMENTAR. CADA PARTICIPANTE USA AS FICHAS DE SEU LIVRO.

REGRAS

REGRAS

• SEM MOSTRAR AOS OUTROS PARTICIPANTES, ESCOLHAM NÚMEROS DE 0 A 100 E ESCREVAM UM NÚMERO EM CADA FICHA, SEM REPETIR E SEM USAR NÚMEROS EM SEQUÊNCIA.

• CADA PARTICIPANTE, NA SUA VEZ, DEVE COLOCAR UMA FICHA SOBRE A MESA COM O NÚMERO ESCRITO VIRADO PARA BAIXO.

• QUANDO TODOS TIVEREM AS FICHAS NA MESA, COMBINEM SE O NÚMERO QUE VAI VENCER SERÁ O MENOR, O MAIOR OU SE ELE DEVE ESTAR ENTRE DOIS NÚMEROS (POR EXEMPLO, ENTRE 15 E 25).

• DESVIREM AO MESMO TEMPO AS FICHAS E COMPAREM OS NÚMEROS. QUEM EXPÔS A FICHA COM AS CARACTERÍSTICAS DE ACORDO COM O COMBINADO FICA COM TODAS PARA SI.

• SE OCORRER FICHAS COM NÚMEROS IGUAIS, A RODADA É CANCELADA E RECOMEÇA.

• AO FINAL DAS RODADAS, GANHA QUEM FICOU COM AS FICHAS DE TODOS OS PARTICIPANTES.

• Após destacarem as fichas para o jogo, solicite aos estudantes que escrevam em cada uma números de 0 a 100 como preferirem, mas sem repetição nem números em sequência. Para iniciar o jogo, cada participante deve colocar sobre a mesa uma ficha com o número virado para baixo. Quando todos virarem suas fichas, devem combinar se o número que vai vencer será o maior ou menor ou se deve estar entre dois números, preestabelecidos. Em seguida, todos desviram as fichas, e aquele que tiver o número que atende ao combinado fica com todas. Por fim, vence o participante que ficar com as fichas de todos os outros.

• O jogo é um recurso importante, pois, além de auxiliar no processo de aprendizagem, estabelece a colaboração entre o estudante, os colegas e o professor. Esse recurso permite desenvolver atividades em grupo e levá-los a perceber a importância do respeito às regras.

BNCC

A proposta do jogo visa levar os estudantes a compararem representações numéricas até a ordem das centenas, possibilitando o desenvolvimento da habilidade EF02MA01 da BNCC.

06/10/2025 17:47:00

• Ao resolver a atividade 1, oriente os estudantes a contornarem grupos contendo dois pássaros, independentemente da espécie. Após a resolução da atividade, peça-lhes que desenhem 5 frutas e 10 bolinhas, repetindo o procedimento indicado na atividade e classificando esses números como pares ou ímpares, de modo a verificar a compreensão deles a respeito desses conceitos.

• No item A da atividade 1, solicite aos estudantes que peguem os lápis que tiverem no estojo. Oriente-os a deixar exatamente a quantidade de 13 unidades desse material sobre a mesa. Em seguida, eles devem separar os lápis, compondo de dois em dois sobre a mesa, deixando um espaçamento entre cada grupo. Pergunte, então, se há lápis sem formar grupo de dois. Depois, faça o mesmo processo com 14 lápis. Para concluir, explique a eles que, ao formar grupos de dois em dois objetos, sobrando um objeto, dizemos que a quantidade é ímpar; caso não sobre objeto, dizemos que essa quantidade é par.

PAR E ÍMPAR

1. COM BASE NAS DUAS CENAS, RESOLVA OS ITENS.

CENA 1

A ) NA CENA 1, HÁ 13 PÁSSAROS. CONTORNE OS PÁSSAROS

FORMANDO GRUPOS DE DOIS EM DOIS.

Resposta: Os estudantes devem contornar os pássaros de dois em dois, deixando apenas um pássaro sem grupo.

B ) FICOU ALGUM PÁSSARO SEM FORMAR GRUPO?

Resposta: SIM.

AO FORMAR GRUPOS DE DOIS EM DOIS COM UMA

QUANTIDADE EM QUE SOBRA UM ELEMENTO, TEMOS UM NÚMERO QUE REPRESENTA UMA QUANTIDADE ÍMPAR.

CENA 2

C ) NA CENA 2, HÁ 14 PÁSSAROS. CONTORNE OS PÁSSAROS

FORMANDO GRUPOS DE DOIS EM DOIS.

Resposta: Os estudantes devem contornar os pássaros de dois em dois, não sobrando nenhum pássaro sem grupo.

D ) FICOU ALGUM PÁSSARO SEM FORMAR GRUPO?

Resposta: NÃO.

AO FORMAR GRUPOS DE DOIS EM DOIS COM UMA QUANTIDADE EM QUE NÃO SOBRA ELEMENTO, TEMOS UM NÚMERO QUE REPRESENTA UMA QUANTIDADE PAR

ASSIM, PODEMOS CONCLUIR QUE O NÚMERO É ÍMPAR

E O NÚMERO É PAR.

Resposta: ASSIM, PODEMOS CONCLUIR QUE O NÚMERO 13 É ÍMPAR E O NÚMERO 14 É PAR.

2. UTILIZE 19 PALITOS E AGRUPE-OS DE DOIS EM DOIS.

A ) FICOU ALGUM PALITO SEM FORMAR PAR?

Resposta: SIM, UM PALITO.

B ) ESSA QUANTIDADE DE PALITOS É PAR OU ÍMPAR?

Resposta: ÍMPAR.

3. QUANDO UM NÚMERO TERMINA EM 0, 2, 4, 6 E 8, É PAR. QUANDO TERMINA EM 1, 3, 5, 7 E 9, É ÍMPAR.

A ) ESCREVA 6 NÚMEROS PARES DE 1 A 50.

Resposta pessoal. Sugestão de resposta: 4, 10, 24, 32, 44, 48.

B ) ESCREVA 6 NÚMEROS ÍMPARES DE 1 A 50.

Resposta pessoal. Sugestão de resposta: 7, 15, 21, 33, 45, 49.

4. ALGUNS NÚMEROS FORAM REPRESENTADOS NAS FICHAS A SEGUIR.

• Para o desenvolvimento da atividade 2, separe previamente palitos em quantidade suficiente para todos os estudantes. Distribua o material entre eles para que possam analisar a proposta na atividade e classificar o número como par ou ímpar.

• Ao resolver com os estudantes a atividade 3, verifique se eles identificam e diferenciam corretamente os números pares dos ímpares. Essa compreensão é importante para a construção do repertório numérico e será pré-requisito essencial em conteúdos posteriores que envolvem operações e outros conceitos algébricos.

A ) CONTORNE OS NÚMEROS PARES DE AZUL.

Resposta: Os estudantes devem contornar de azul os números 8, 12, 60, 24 e 36

B ) CONTORNE OS NÚMEROS ÍMPARES DE VERMELHO.

Resposta: Os estudantes devem contornar de vermelho os números 51, 9, 5, 49 e 17

5. RESPONDA ÀS PERGUNTAS A SEGUIR.

A ) QUANTOS ANOS VOCÊ TEM?

Resposta pessoal. A resposta depende da idade de cada estudante. Espera-se que as respostas variem entre 6 e 9 anos, por exemplo.

B ) O NÚMERO QUE REPRESENTA SUA IDADE É PAR OU ÍMPAR? JUSTIFIQUE SUA RESPOSTA.

Resposta pessoal. Espera-se que os estudantes identifiquem se o número que representa a sua idade é par ou ímpar.

sempre têm como algarismo das unidades 0, 2, 4, 6 ou 8.

• Repita o procedimento sugerido para a atividade 4 com os números ímpares para que os estudantes reconheçam que os números terminados em 1, 3, 5, 7 e 9, ou seja, que tenham esses algarismos na ordem das unidades, são sempre ímpares. Esse trabalho também pode ser desenvolvido utilizando como suporte o quadro de ordens ou o ábaco.

• Na atividade 5, cada estudante vai dizer sua idade e responder se o número que representa é par ou ímpar. Assim, po-

dem ocorrer respostas diferentes, sendo importante destacar essa informação durante a correção. Concluída a atividade, proponha uma conversa a respeito das idades, motivando-os a estabelecer uma comparação no sentido de identificar quais são as possibilidades dentro da turma, quais estudantes são mais novos e quais são mais velhos. Aproveite para verificar a compreensão deles a respeito da comparação entre números naturais, pedindo-lhes que registrem essas informações na lousa, utilizando os símbolos aprendidos no tópico anterior.

47

• Os itens A e B da atividade 4 propõem a classificação de números como pares ou ímpares. Durante esse trabalho, proponha aos estudantes que utilizem as estratégias apresentadas ou utilizadas por eles nas atividades anteriores. Se necessário, faça uma retomada a respeito das diferenças entre números pares e ímpares.

• Após a conclusão da atividade 4, peça aos estudantes que observem os números pares que contornaram e procurem identificar qual algarismo ocupa a ordem das unidades, repetindo esse procedimento com os números pares identificados nas atividades anteriores deste tópico. O objetivo é levá-los a compreender que os números pares

06/10/2025 17:47:01

Objetivo

A atividade 4 permite avaliar a compreensão dos estudantes a respeito dos números pares e ímpares.

Sugestão de intervenção

Considerando as dificuldades manifestadas pelos estudantes, proponha a eles que representem alguns dos números indicados na atividade 4 utilizando materiais de contagem, como palitos ou bolinhas de gude, e repitam a estratégia indicada na atividade 1 para responder a esta atividade.

AVALIANDO

• A atividade 1 introduz o trabalho com os números ordinais, considerando os números do 1º ao 19º

• Após a resolução da atividade, peça aos estudantes que façam a leitura em voz alta dos números ordinais. Converse com eles a respeito da relação entre os números ordinais e a sequência de números naturais no sentido cardinal.

ORDINAIS

1. A CLASSIFICAÇÃO DOS ESTUDANTES QUE MAIS PONTUARAM

EM UMA GINCANA DA ESCOLA FOI LISTADA A SEGUIR. PARA

CLASSIFICAR OS ESTUDANTES, PODEMOS USAR ORDINAIS

COMPLETE AS CLASSIFICAÇÕES COM OS ORDINAIS QUE ESTÃO FALTANDO.

CLASSIFICAÇÃO DOS

ESTUDANTES DO 1º AO 10º

NOMECLASSIFICAÇÃO

GABRIELA

CLASSIFICAÇÃO DOS

ESTUDANTES DO 11º AO

NOMECLASSIFICAÇÃO

1. Resposta nas orientações ao professor. 48

DÉCIMO SEXTO VINÍCIUS DÉCIMO SÉTIMO 17º MARIA DÉCIMO OITAVO RODRIGO DÉCIMO NONO

Resposta

1. No quadro CLASSIFICAÇÃO DOS ESTUDANTES DO 1º AO 10º, eles devem completar:

LUCIANO, SEGUNDO, 2º; RICARDO, TERCEIRO, 3º; PEDRO, QUARTO, 4º; ADRIANA, QUINTO, 5º; LUÍS, SEXTO, 6º; HELENA, OITAVO, 8º; PAULA, NONO, 9º; JÚLIO, DÉCIMO, 10º

No quadro CLASSIFICAÇÃO DOS ESTUDANTES DO 11º AO 19º, devem completar: JOÃO, DÉCIMO QUINTO, 15º; CARLA, DÉCIMO SEXTO, 16º; MARIA, DÉCIMO OITAVO, 18º

2. LIGUE CADA ORDINAL À SUA

2º 16º 11º 8º 19º

Resposta: Os estudantes devem ligar: 2º ao SEGUNDO; 16º ao DÉCIMO SEXTO; 11º ao DÉCIMO PRIMEIRO; 8º ao OITAVO; 19º ao DÉCIMO NONO.

DÉCIMO PRIMEIRO

OITAVO

DÉCIMO SEXTO

DÉCIMO NONO

SEGUNDO

3. NA TURMA DE LAURA, O NOME DE CADA ESTUDANTE FOI ORGANIZADO EM ORDEM ALFABÉTICA.

CLASSIFICAÇÃO

DO 1º AO 6º EM

ORDEM ALFABÉTICA

NOMEORDEM

BEATRIZ 1º BENÍCIO 2º DAVI 3º

FÁBIO 4º

GABRIEL 5º GUSTAVO 6º

CLASSIFICAÇÃO

DO 7º AO 12º EM ORDEM ALFABÉTICA

CLASSIFICAÇÃO

DO 13º AO 18º EM ORDEM ALFABÉTICA NOMEORDEM MÁRCIA 13º

14º MURILO 15º PLÍNIO 16º RAQUEL 17º SOFIA 18º

A ) O NOME DE RAQUEL OCUPA QUE ORDEM NO QUADRO?

Resposta: 17º

B ) QUAL É O NOME DO ESTUDANTE QUE ESTÁ NA 5ª ORDEM?

• Para resolver a atividade 2, caso os estudantes tenham alguma dificuldade, retome a sequência dos números ordinais apresentada na atividade 1. Converse com eles a respeito da palavra décimo, que está presente e contribui para a caracterização dos números ordinais do 10º até o 19º

• A atividade 3 envolve a identificação da posição ocupada por estudantes em uma lista construída segundo a ordem alfabética. Antes de resolver a atividade, peça a eles que expliquem quais são as características de uma lista em ordem alfabética e como podemos fazer uma lista segundo essa ordem. Após a correção da atividade, proponha a eles outras perguntas, oralmente, para que reconheçam os números ordinais correspondentes conforme essa lista e digam suas nomenclaturas por extenso.

C ) QUE ORDINAL REPRESENTA A ORDEM DE CADA ESTUDANTE CUJO NOME COMEÇA COM A LETRA B?

Resposta: GABRIEL. Resposta: BEATRIZ: 1º; BENÍCIO: 2º

ATIVIDADE EXTRA

Proponha aos estudantes que escrevam seus nomes na lousa. Se a turma for formada por uma quantidade maior do que 19 estudantes, organize-os em dois grupos, pois eles ainda não estudaram números ordinais maiores do que 19. Em seguida, peça-lhes que construam um quadro, no caderno, com os nomes em ordem

06/10/2025 17:47:01

alfabética, de maneira parecida com a da lista da atividade 3. Em seguida, eles devem associar um número ordinal para cada estudante, conforme a ordem em que seu nome aparece na lista. Ao final, peça a cada estudante que diga em qual posição está na lista, orientando os demais a verificar se as listas estão iguais.

• A atividade 4 integra as unidades temáticas de Matemática Números e Probabilidade e estatística ao trabalhar a análise dos resultados obtidos na realização de um sorteio.

Respostas

4. C) Sim, pois, ao realizar vários sorteios, há maior probabilidade de ser sorteada a ficha de cor amarela e menor probabilidade de ser sorteada a ficha de cor verde.

4. E) Não garante, pois não é possível saber ao certo a cor da ficha que será sorteada, visto que há apenas duas possibilidades de cores que podem ser escolhidas. Se julgar necessário, peça aos estudantes que voltem nos registros realizados no item B e verifiquem se em algum sorteio que fizeram ocorreu de a ficha menos provável ter sido sorteada. Isso os fará refletir e chegar a uma conclusão para o item E

BNCC

O trabalho com a atividade 4 aborda resultados de eventos aleatórios como pouco prováveis, muito prováveis, improváveis e impossíveis, conforme orienta a habilidade EF02MA21

4. D) Resposta: Não. Espera-se que os estudantes percebam que não há fichas azuis no pote e, por isso, não é possível que alguma ficha seja dessa cor.

EXPERIMENTE

4. VOCÊ VAI RECEBER DO PROFESSOR 12 FICHAS, SENDO 10 AMARELAS E 2 VERDES.

Unidades temáticas integradas

A ) SUPONHA QUE TODAS AS FICHAS SEJAM COLOCADAS EM UM POTE ESCURO E, SEM OLHAR, UMA FICHA SEJA SORTEADA.

Resposta: É MUITO PROVÁVEL QUE A COR DA FICHA SEJA AMARELA E POUCO PROVÁVEL QUE SEJA VERDE

É MUITO PROVÁVEL QUE A COR DA FICHA SEJA

E POUCO PROVÁVEL QUE SEJA

B ) COLOQUE EM UM POTE ESCURO TODAS AS FICHAS QUE VOCÊ RECEBEU DO PROFESSOR. SEM OLHAR, SORTEIE

UMA FICHA, ANOTE A COR SORTEADA NA LISTA A SEGUIR E DEVOLVA A FICHA NO POTE. REPITA ESSE PROCESSO 10 VEZES.

Resposta pessoal. A resposta depende do sorteio que os estudantes realizarem.

1º SORTEIO:

2º SORTEIO:

3º SORTEIO:

4º SORTEIO:

5º SORTEIO:

6º SORTEIO:

7º SORTEIO:

8º SORTEIO:

9º SORTEIO:

10º SORTEIO:

4. C) Resposta pessoal. Comentários nas orientações ao professor

C ) DE ACORDO COM OS SEUS REGISTROS, A COR MAIS SORTEADA E A MENOS SORTEADA CORRESPONDEM ÀS CORES INDICADAS NO ITEM A?

D ) AO SORTEAR UMA FICHA, É POSSÍVEL QUE ELA SEJA AZUL? CONVERSE COM COLEGAS.

E ) O FATO DE SER MUITO PROVÁVEL QUE DETERMINADA

COR DE FICHA SEJA SORTEADA GARANTE QUE ELA EFETIVAMENTE SERÁ SORTEADA? CONVERSE COM SEU PROFESSOR E OS COLEGAS.

4. E) Resposta pessoal. Comentários nas orientações ao professor

AVALIANDO

Objetivo

A atividade do Desafio a mais permite verificar a compreensão dos estudantes a respeito da sequência dos números ordinais.

Sugestão de intervenção

Caso algum estudante tenha dificuldade na resolução desta atividade, proponha a ele que a

preencha, inicialmente, apenas com os números ordinais, conforme a ordem de cada atleta na corrida. Se julgar conveniente, retome a sequência discutida na atividade 1. A partir dessa sequência, instigue-o a reconhecer o nome de cada atleta, comparando as posições entre si conforme as descrições.

Resposta: CICLISTA C: HEITOR, 1º; CICLISTA A: RONALDO, 2º; CICLISTA B: CÉSAR, 3º; CICLISTA F: HENRIQUE, 4º; CICLISTA E: CARLOS, 5º; CICLISTA

D: LEVI, 6º; CICLISTA G: JOAQUIM, 7º; CICLISTA

DESAFIO A MAIS

H: OTÁVIO, 8º; CICLISTA I: DANIEL, 9º; CICLISTA

J: MAURÍCIO, 10º

A CENA MOSTRA O MOMENTO DE CHEGADA DOS ATLETAS EM UMA COMPETIÇÃO DE CICLISMO.

SABENDO DAS SEGUINTES INFORMAÇÕES, COMPLETE A IMAGEM COM O NOME E A ORDEM DE CADA CICLISTA.

CÉSAR ESTAVA DUAS POSIÇÕES ATRÁS DE HEITOR.

RONALDO ESTAVA EM SEGUNDO LUGAR.

OTÁVIO ESTAVA UMA POSIÇÃO À FRENTE DE DANIEL.

MAURÍCIO ESTAVA NA ÚLTIMA COLOCAÇÃO.

LEVI ESTAVA ATRÁS DE CARLOS.

HENRIQUE ESTAVA TRÊS POSIÇÕES NA FRENTE DE JOAQUIM.

CONCLUSÃO

Acompanhar o desenvolvimento dos estudantes é fundamental para um ensino bem-sucedido. Ao longo da unidade, foram propostas diversas maneiras de avaliar a aprendizagem da turma. A fim de realizar um monitoramento mais abrangente, registre nos relatórios individuais ou nas fichas de avaliação o desempenho de cada estudante, levando em consideração suas particularidades. Um modelo desse tipo de ficha pode ser

encontrado no tópico Avaliação deste manual. Assim, será possível visualizar de modo individual as trajetórias de aprendizagem, incluindo os avanços e os pontos de dificuldades a serem sanados por meio de atividades que promovam a recuperação dos conteúdos. Esse método de verificar a progressão dos estudos e identificar o que a turma de fato conseguiu aprender é de grande importância para que seja possível repensar estratégias em sala de aula, tor-

• No Desafio a mais , os estudantes trabalham a compreensão e o uso de números ordinais em uma atividade de ordenação. Eles devem observar a posição de cada ciclista na cena e as informações fornecidas, a fim de completar a imagem com o nome e a ordem de chegada de cada um. A atividade exige raciocínio lógico-matemático na interpretação e combinação das pistas, com objetivo de deduzir a colocação de todos os ciclistas. O desafio exige que eles identifiquem relações de posição (“duas posições atrás”, “uma posição à frente”, “três posições à frente”). Caso eles tenham dificuldade ou encontrem uma lógica diferente da esperada, incentive-os a compartilhar com a turma. Faça intervenções pontuais e estratégicas para guiá-los na compreensão da ordem e das relações de posição, como perguntar: “Se o Ronaldo está em 2º, qual é o 1º lugar?” ou “Quem está ocupando a última posição da corrida?”. Sugira que todos anotem a ordem em um rascunho ou numerem os ciclistas na imagem para facilitar a visualização.

Sugestão de Desafio

Descubra o próximo número dessa sequência de números pares: 24, 26, 28, 30,

Resposta

O próximo número da sequência é o 32.

08/10/2025 15:14:04

nando as ações pedagógicas cada vez mais eficazes.

A conclusão da unidade é o momento de avaliar se os objetivos por ela propostos foram alcançados. Para esse diagnóstico, observe no final deste Manual algumas possibilidades de avaliação formativa que permitem realizar o monitoramento da aprendizagem dos estudantes e intervir caso não tenham atingido os resultados.

A.

OBJETIVOS DA UNIDADE

• Reconhecer, comparar e associar figuras geométricas espaciais a objetos do mundo físico.

• Identificar os elementos aresta, face e vértice de uma figura geométrica espacial.

• Reconhecer e nomear o cubo, o bloco retangular ou paralelepípedo retângulo, a esfera, o cilindro, o cone e a pirâmide.

• Classificar as figuras geométricas espaciais de acordo com suas superfícies.

• Identificar e descrever os elementos que faltam em sequências de figuras geométricas espaciais por meio do reconhecimento de regularidades.

INTRODUÇÃO E JUSTIFICATIVA

Nesta unidade, os estudantes são apresentados ao universo das figuras geométricas espaciais, explorando suas formas, características e aplicações no dia a dia. As propostas de atividades favorecem a associação de objetos do cotidiano com figuras espaciais parecidas, por meio de atividades diversificadas e contextualizadas. Ao longo das atividades, os estudantes são levados a reconhecer e diferenciar figuras com apenas superfícies planas daquelas com superfícies arredondadas, desenvolvendo um olhar atento para as formas ao seu redor. Para facilitar a compreensão dos elementos que compõem essas figuras, é utilizado o molde do cubo, auxiliando na visualização e manipulação de suas partes.

Na seção Coletivamente, o intuito é consolidar os conteúdos estudados, levando os estudantes a identificarem formatos parecidos com as figuras geométricas espaciais nas confecções feitas pelos personagens, além de promover reflexões sobre a importân-

UNIDADE FIGURAS GEOMÉTRICAS ESPACIAIS 2

CATEDRAL METROPOLITANA

BASÍLICA MENOR NOSSA SENHORA

DA GLÓRIA, NA CIDADE DE MARINGÁ, NO PARANÁ, EM 2024.

cia do respeito que devemos ter pelas pessoas, integrando o conteúdo matemático a aspectos formativos.

Habilidades da BNCC trabalhadas na unidade: EF02MA10, EF02MA11 e EF02MA14

SUGESTÃO DE ESTRATÉGIA INICIAL

Organize a turma em grupos com quatro ou cinco integrantes e proponha a confecção de uma maquete representando a escola, usando para isso materiais recicláveis que lembrem figuras geométricas espaciais. Providencie, ou reúna durante alguns dias, com a ajuda dos estudan-

tes, embalagens vazias de diferentes formatos. Reserve um lugar na sala de aula para expor os trabalhos realizados. Oriente os estudantes a produzirem etiquetas e fixá-las ao lado das embalagens usadas nas produções, identificando com quais figuras geométricas espaciais essas embalagens são parecidas.

Obtenha mais informações sobre a catedral maringaense acessando o site a seguir. CATEDRAL Metropolitana Basílica Menor Nossa Senhora da Glória. Prefeitura de Maringá. Disponível em: http://www3.maringa.pr.gov.br/ turismo/?cod=atrativos-turisticos/1. Acesso em: 26 jul. 2025.

A CATEDRAL METROPOLITANA BASÍLICA MENOR NOSSA SENHORA DA GLÓRIA, LOCALIZADA NA CIDADE DE MARINGÁ, NO PARANÁ, É PONTO DE VISITAÇÃO DE TURISTAS E MORADORES. ALÉM DA BELEZA DOS SEUS DETALHES INTERNOS, SUA EDIFICAÇÃO IMPRESSIONA PELO FORMATO GEOMÉTRICO E PELA ALTURA.

• Antes de trabalhar com as questões propostas nesta página, leia o texto para os estudantes informações sobre a Catedral Metropolitana Basílica Menor Nossa Senhora da Glória e peça a eles que analisem atentamente a cena apresentada na fotografia. Pergunte o que podem verificar de interessante na cena e deixe que comentem as observações para a turma.

• A questão 1 tem o objetivo de verificar se os estudantes já visitaram algum edifício que tenha o formato parecido com o da catedral apresentada na fotografia de abertura. Caso algum deles tenha visitado alguma construção assim ou mesmo a própria construção, peça que compartilhe a experiência com a turma.

VOCÊ OU ALGUÉM QUE CONHECE JÁ VISITOU UM EDIFÍCIO COM O FORMATO DESSA CATEDRAL?

OBSERVANDO A IMAGEM, A CONSTRUÇÃO DESSA CATEDRAL SE PARECE COM QUAL FIGURA GEOMÉTRICA ESPACIAL?

Resposta: O cone.

CITE O NOME DE UM OBJETO QUE TEM FORMATO PARECIDO COM ESSA CATEDRAL. 1. 2. 3.

1 e 3. Respostas nas orientações ao professor 53

06/10/2025 17:51:58

• As questões 2 e 3 visam identificar o conhecimento prévio dos estudantes a respeito da figura geométrica espacial cone. Mostre uma representação de cone para eles ou leve para a sala de aula alguns objetos com formato parecido, a fim de que analisem suas características.

Respostas

1. Resposta pessoal. Espera-se que os estudantes respondam com base nas próprias vivências e relacionem locais e construções que já visitaram com o formato de figuras geométricas espaciais, em específico, com o cone.

3. Sugestões de resposta: Casquinha de sorvete, chapéu de aniversário, chapéu de fantasia de fada.

• Por meio do trabalho com a atividade 1, são abordados os nomes das figuras geométricas espaciais. Além disso, os estudantes são incentivados a relacionar objetos do cotidiano a essas figuras. Caso tenham dificuldade em realizar o item B, auxilie-os anotando na lousa objetos que lembrem essas figuras ou, se possível, leve alguns desses objetos para a sala de aula.

BNCC

As atividades propostas no tópico A forma dos objetos incentivam os estudantes a reconhecerem, compararem e relacionarem as figuras geométricas espaciais, como cubo, cone, esfera, cilindro, pirâmide e paralelepípedo retângulo ou bloco retangular, a objetos do mundo físico, contemplando, assim, a habilidade EF02MA14 da BNCC.

ATIVIDADE

EXTRA

Peça aos estudantes que verifiquem em suas casas se há objetos que se pareçam com as figuras geométricas espaciais apresentadas no quadro do item B da atividade 1 e anotem em seus cadernos os nomes, tanto dos objetos quanto das figuras geométricas espaciais correspondentes. Depois, faça um quadro na lousa, como o da atividade, e escreva os nomes dos diferentes objetos citados, a fim de aumentar o repertório deles em reconhecer objetos que lembram as figuras geométricas espaciais.

A FORMA DOS OBJETOS

1. O FORMATO DE MUITOS OBJETOS QUE USAMOS NO DIA A DIA SE PARECE COM FIGURAS GEOMÉTRICAS ESPACIAIS. VAMOS

ESTUDAR ALGUMAS DESSAS FIGURAS?

NA COZINHA DE CARLA, HÁ VÁRIOS POTES PARA GUARDAR MANTIMENTOS.

A ) ENTRE AS FIGURAS GEOMÉTRICAS ESPACIAIS A SEGUIR, CONTORNE AQUELA CUJO FORMATO LEMBRA OS POTES DA COZINHA DE CARLA.

Resposta: Os estudantes devem contornar o PARALELEPÍPEDO OU BLOCO RETANGULAR.

B) Resposta pessoal. Sugestão de resposta: Cone: casquinha de sorvete; esfera: bola de futebol; cilindro: latinha de bebida; paralelepípedo ou bloco retangular: caixa de sapato; pirâmide: vela ornamental; cubo: dado.

CUBO. ESFERA. CILINDRO. PARALELEPÍPEDO OU BLOCO RETANGULAR. PIRÂMIDE. CONE.

B ) ESCREVA NO QUADRO O NOME DE UM OBJETO DO SEU DIA A DIA CUJO FORMATO SE PARECE COM CADA FIGURA GEOMÉTRICA ESPACIAL APRESENTADA.

OBJETOS DO DIA A DIA RELACIONADOS À FIGURA GEOMÉTRICA ESPACIAL

FIGURA

GEOMÉTRICA ESPACIAL

OBJETO DO DIA A DIA

AVALIANDO

Objetivo

Associar figuras geométricas espaciais a objetos do dia a dia.

Sugestão de intervenção

Organize os estudantes em duplas e leve-os ao laboratório de informática para que façam uma pesquisa de objetos que lembrem algumas figuras geométricas espaciais. Organize-os de modo que um estudante que já compreendeu o

conteúdo ajude outro que ainda está com dificuldade. Solicite aos estudantes que façam uma lista no caderno para anotarem quatro objetos cujos formatos lembrem cada figura geométrica espacial a seguir.

• Cubo.

• Bloco retangular.

• Pirâmide.

• Esfera.

• Cilindro.

• Cone.

2. ESCREVA OS NOMES DAS FIGURAS GEOMÉTRICAS ESPACIAIS

NO DIAGRAMA A SEGUIR.

Resposta: A: PIRÂMIDE; B: ESFERA; C: PARALELEPÍPEDO; D: CONE; F: CILINDRO.

3. O BASQUETEBOL É UM ESPORTE BASTANTE

POPULAR NO BRASIL. PARA JOGAR UMA PARTIDA DESSE ESPORTE, É UTILIZADA UMA

BOLA COMO A APRESENTADA.

BOLA DE BASQUETEBOL.

O FORMATO DELA LEMBRA QUAL FIGURA GEOMÉTRICA ESPACIAL? MARQUE UM X NA RESPOSTA.

CUBO. ESFERA. CILINDRO.

Resposta: Os estudantes devem marcar um X na ESFERA

4. COM UM COLEGA, PESQUISEM E ESCREVAM, EM SEUS CADERNOS, OS NOMES DE OUTROS CINCO ESPORTES QUE USAM COMO INSTRUMENTO DE JOGO A BOLA, CUJO FORMATO LEMBRA UMA ESFERA.

DICA: PRATICAR ESPORTES E EXERCÍCIOS FÍSICOS FAZ BEM À SAÚDE. SE POSSÍVEL, EXERCITE-SE!

Sugestões de resposta: Futebol, voleibol, beisebol, tênis, tênis de mesa, boliche, bocha, futsal, golfe e polo.

06/10/2025 17:51:58

• A atividade 2 tem por objetivo levar os estudantes a identificarem e nomearem algumas figuras geométricas espaciais, como cone, paralelepípedo retângulo ou bloco retangular, esfera, pirâmide e cilindro. Diga a eles que o nome da figura cubo já foi preenchido e auxilie-os a escrever os outros nomes no diagrama. Comente a respeito do nome do paralelepípedo. Diga-lhes que formalmente falamos paralelepípedo retângulo ou bloco retangular.

• As atividades 3 e 4 têm por objetivo levar os estudantes a reconhecerem e associarem objetos do cotidiano à esfera. Verifique se na escola há bolas de diferentes esportes e leve para a sala de aula. Deixe que os estudantes as analisem e pergunte qual é a figura geométrica espacial que essas bolas lembram. Se possível, peça ao professor do componente curricular de Educação Física que converse com os estudantes sobre o basquetebol e outros esportes que utilizam a bola com formato que lembra uma esfera.

BNCC

A atividade 4 relaciona-se à Competência específica de Matemática 8 da BNCC ao propor aos estudantes que interajam com os colegas a fim de pesquisarem nomes de outros cinco esportes que usam como instrumento a bola, cujo formato lembra uma esfera.

C U B O

A. B.

C.

D.

E.

F.

• Para responderem à atividade 5, peça aos estudantes que observem atentamente a fotografia apresentada, a fim de que reconheçam o rolo compactador, ou rolo compressor de asfalto, e o associem à figura geométrica espacial cilindro.

• Leia com os estudantes o significado de nivelar, apresentado nesta página, e solicite a eles que formem oralmente frases usando essa nova palavra, com o intuito de verificar se compreenderam esse significado.

• A atividade 5 tem por objetivo levar os estudantes a reconhecerem e associarem objetos do cotidiano cujo formato lembra um cilindro. Para um melhor aproveitamento desta atividade, leve para a sala de aula alguns objetos cujos formatos lembram o cilindro. Deixe que os estudantes os manipulem, a fim de que percebam algumas de suas características. A manipulação de objetos contribui para o desenvolvimento do conteúdo e a construção do aprendizado, auxiliando-os no desenvolvimento da visão espacial.

REFERÊNCIAS

COMPLEMENTARES

GONÇALVES, Fernanda Anaia; BASSO, Mila Taunay Perez; LUCERO, Rosemeire Nunes. Materiais manipulativos para o ensino de sólidos geométricos. Organizado por Katia Stocco Smole e Maria Ignez Diniz. Porto Alegre: Penso, 2016. (Coleção Mathemoteca, 5). Essa obra aborda o uso de materiais manipulativos como recursos para favorecer a compreensão dos estudantes sobre os conceitos matemáticos.

5. O ROLO COMPACTADOR É UMA FERRAMENTA USADA PARA NIVELAR TERRENOS, COMPRIMIR O ASFALTO EM CONSTRUÇÃO E DESTRUIR ERVAS DANINHAS QUE CONTAMINAM O SOLO. ESSES ROLOS SÃO MOVIDOS POR TRATORES.

NIVELAR: RETIRAR IRREGULARIDADES DE UMA SUPERFÍCIE PARA QUE

ELA SE TORNE PLANA, ACERTAR O NÍVEL, ALISAR.

ROLO COMPACTADOR, TAMBÉM CONHECIDO COMO ROLO COMPRESSOR DE ASFALTO.

A ) O FORMATO DO ROLO COMPACTADOR LEMBRA QUAL FIGURA GEOMÉTRICA ESPACIAL? MARQUE UM X NA

RESPOSTA CORRETA.

CUBO. CONE.

Resposta: Os estudantes devem marcar um X no CILINDRO.

PARALELEPÍPEDO.

CILINDRO.

B ) DESENHE UM OBJETO DE SEU DIA A DIA QUE TEM O FORMATO DE UM CILINDRO.

Resposta pessoal. Sugestões de resposta: Latinha de bebida, pedaço de cano, caneca e tubo.

6. FERNANDA TOCOU COM AS MÃOS OS OBJETOS A SEGUIR PARA RECONHECER QUAL DELES LEMBRA UM CONE. CONTORNE O OBJETO ESCOLHIDO POR ELA.

Resposta: Os estudantes devem contornar o chapéu de aniversário

IMAGENS SEM PROPORÇÃO ENTRE SI.

Professor, professora: As legendas das imagens da atividade 6 não foram inseridas para não comprometerem a realização da atividade.

EXPERIMENTE

7. Resposta pessoal. Comentários nas orientações ao professor

7. VAMOS CONSTRUIR BRINQUEDOS? PARA ISSO, APROVEITE EMBALAGENS VAZIAS E OUTROS MATERIAIS RECICLÁVEIS CUJOS FORMATOS SE PARECEM COM AS FIGURAS GEOMÉTRICAS ESPACIAIS ESTUDADAS ATÉ O MOMENTO. COM A AJUDA DO PROFESSOR, ESCOLHA O QUE VOCÊ VAI CONSTRUIR E SEPARE AS EMBALAGENS QUE SERVIRÃO PARA A MONTAGEM DO SEU BRINQUEDO. CONFIRA ALGUMAS SUGESTÕES DE BRINQUEDOS QUE PODEM SER CONSTRUÍDOS.

TRENZINHO.

BONECO.

CARRINHO.

ANIMAIS.

ORGANIZEM JUNTOS UMA EXPOSIÇÃO DOS BRINQUEDOS CONSTRUÍDOS E CONVIDEM OS FAMILIARES E OUTROS ESTUDANTES DA ESCOLA PARA PARTICIPAR DESSE MOMENTO.

A atividade proposta no boxe Experimente trabalha com a consciência ambiental dos estudantes ao mostrar que é possível transformar o que seria descartado em algo novo. Por meio desta atividade, é possível discutir, por exemplo,

06/10/2025 17:52:07

a necessidade do cuidado com o meio ambiente e os benefícios da reciclagem para o planeta, incentivando-os a refletir sobre a questão ambiental com base em princípios sustentáveis, contemplando, assim, a Competência específica de Matemática 7 da BNCC.

• A atividade 6, assim como a anterior, visa conduzir os estudantes a reconhecerem figuras geométricas espaciais em objetos do cotidiano, em específico o cone. A atividade indica um contexto em que outro sentido, além da visão, é explorado pela personagem, buscando a inclusão de estudantes com Necessidades Educacionais Específicas (NEE). Se possível, leve para a sala de aula os objetos apresentados na atividade e permita a todos que os manipulem.

• A atividade 7 propõe um trabalho mais lúdico com figuras geométricas espaciais, incentivando a criatividade por meio do processo de construção do objeto pelos estudantes. Ao buscarem por embalagens e outros materiais que possam ser reutilizados para criar os brinquedos, eles podem identificar diferentes formas e explorar suas características na prática. Para a elaboração da exposição das produções, incentive os estudantes a trabalharem em grupo, desenvolvendo o senso de coletividade e cooperação. Além de potencializar o trabalho em equipe durante a elaboração, a exposição dos brinquedos construídos fortalece o vínculo comunitário, valorizando a participação dos familiares e outros membros da comunidade nas atividades escolares.

BNCC

OBJETIVOS

• Compreender que as pessoas são diferentes e aprender a respeitar suas diferenças e opiniões.

• Refletir sobre as atitudes que devemos ter para demonstrar respeito em diversas situações do dia a dia.

• Identificar atitudes adequadas que demonstrem respeito.

• Considerar ações e atitudes que contribuem para vivermos em um mundo melhor.

• Associar os formatos das figuras geométricas espaciais a objetos do dia a dia.

1. CONHECENDO O PROBLEMA

• Leia o texto em voz alta com os estudantes. Depois, oriente-os a observar a cena atentamente e a perceber as diferenças entre os brinquedos construídos pelos personagens. Conduza uma conversa coletiva e deixe que comentem com a turma suas ideias, expressando percepções e opiniões sobre o assunto abordado.

• Propicie um ambiente seguro e acolhedor, para que os estudantes se sintam à vontade para expressarem emoções e aprenderem sobre elas, de maneira a promover o desenvolvimento socioemocional e a autoavaliação deles acerca das próprias emoções.

2. ORGANIZANDO AS IDEIAS

Orientações complementares

• No item A, converse com os estudantes, levando-os a perceber a importância do respeito às diferenças em vários aspectos da vida, pois é assim que as pessoas convivem de maneira saudável com as demais.

• No item B, verifique se eles reconhecem alguns objetos que foram usados na construção do robô, com forma-

COLETIVAMENTE

RESPEITO É SEMPRE BOM!

Professor, professora: O trabalho com esta seção favorece o desenvolvimento do tema contemporâneo transversal Vida familiar e social

CONHECENDO O PROBLEMA 1

PARA UMA BOA CONVIVÊNCIA EM SOCIEDADE, DEVEMOS

RESPEITAR AS PESSOAS, A NATUREZA, OS ANIMAIS E OS BENS MATERIAIS.

EXAMINE NA CENA OS ESTUDANTES DO 2º ANO APRESENTANDO UM TRABALHO DE CONSTRUÇÃO DE BRINQUEDOS FEITOS COM MATERIAIS QUE SE PARECEM COM FIGURAS GEOMÉTRICAS ESPACIAIS.

DURANTE A APRESENTAÇÃO, UM DOS ESTUDANTES FICOU EM DÚVIDA SE O SEU BRINQUEDO SERIA BEM RECEBIDO, POIS PERCEBEU QUE ELE ERA DIFERENTE DOS QUE FORAM APRESENTADOS PELOS COLEGAS.

AO FINAL, A PROFESSORA VALORIZOU O ESFORÇO DE TODOS, DESTACANDO QUE CADA BRINQUEDO TINHA CARACTERÍSTICAS ÚNICAS E QUE AS DIFERENÇAS TORNAM OS TRABALHOS AINDA MAIS INTERESSANTES.

tos parecidos com os das figuras geométricas espaciais estudadas. Depois, conclua essa conversa dizendo que, para sua confecção, foram utilizados objetos que se parecem com o cubo, o cilindro, a esfera, o cone e o bloco retangular ou paralelepípedo retângulo.

• Para trabalhar a questão do item C, auxilie os estudantes perguntando sobre cada brinquedo apresentado pelos personagens da imagem, analisando todos os objetos usados nas confecções, a fim de que percebam que no trem foi utilizado um objeto que se parece com uma pirâmide.

BNCC

As atividades propostas nesta seção favorecem o desenvolvimento das Competências gerais 8 e 9 da BNCC ao fomentar boas ideias sobre as diferenças, levando os estudantes a desenvolverem o exercício da empatia, respeitando a si e ao outro com acolhimento e valorizando a diversidade. Também buscam uma contextualização do que foi estudado nesta unidade, por meio da seção Respeito é sempre bom, desenvolvendo, assim, o tema contemporâneo transversal Vida familiar e social ao proporcionar aos estudantes reflexões sobre atitudes de respeito com o próximo, para que ocorra uma boa convivência em sociedade.

ORGANIZANDO AS IDEIAS 2

A) Resposta pessoal. O objetivo desta questão é levar os estudantes a valorizar todos os trabalhos desenvolvidos.

A ) EM SUA OPINIÃO, POR QUE TODOS OS TRABALHOS DEVEM SER RESPEITADOS APESAR DAS DIFERENÇAS ENTRE ELES?

B ) OS OBJETOS UTILIZADOS PARA CONFECCIONAR O ROBÔ SE PARECEM COM QUAIS FIGURAS GEOMÉTRICAS ESPACIAIS?

C ) EM QUAL DOS BRINQUEDOS APRESENTADOS NA CENA FOI UTILIZADO UM OBJETO QUE SE PARECE COM UMA PIRÂMIDE?

Resposta: No trenzinho.

B) Resposta: Para confeccionar o robô, foram utilizados objetos que se parecem com o cubo, o cilindro, a esfera, o cone e o paralelepípedo.

3

BUSCANDO SOLUÇÕES

A ) CONVERSE COM OS COLEGAS SOBRE ALGUMAS ATITUDES QUE DEVEMOS TER PARA DEMONSTRAR RESPEITO EM SITUAÇÕES DO DIA A DIA.

Resposta pessoal. O objetivo desta questão

é promover a reflexão e o diálogo sobre atitudes respeitosas no cotidiano.

B ) REPRESENTE NO ESPAÇO A SEGUIR, POR MEIO DE UM DESENHO, UMA DESSAS ATITUDES QUE DEMONSTRAM RESPEITO.

Resposta pessoal. Espera-se que os estudantes façam um desenho relacionado com suas reflexões.

C ) COMPARTILHE COM UM COLEGA O DESENHO QUE VOCÊ FEZ E PEÇA A ELE QUE FAÇA UM COMENTÁRIO POSITIVO SOBRE A SUA PRODUÇÃO.

DICA: COLOQUE EM PRÁTICA NO SEU DIA A DIA O QUE APRENDEU SOBRE ATITUDES DE RESPEITO COM O PRÓXIMO PARA UMA BOA CONVIVÊNCIA EM SOCIEDADE.

• Se a proposta da seção Sugestão de estratégia inicial desta unidade foi trabalhada com os estudantes, aproveite o momento para conversar com os estudantes sobre as confecções feitas por eles e as diferenças entre os trabalhos. Nesse momento, valorize os comentários e incentive-os a ressaltar atitudes positivas acerca da experiência. Caso os trabalhos ainda estejam expostos na sala de aula, peça a cada estudante que troque sua produção com a de um colega e faça uma observação positiva do trabalho dele.

06/10/2025 17:52:08

• Se julgar conveniente, proponha uma atividade a fim de complementar o assunto e valorizar o respeito pelos colegas. Para isso, peça a eles que desenhem na lousa um objeto qualquer, como uma casa ou um carro. O importante é que todos desenhem o mesmo elemento a fim de que os desenhos sejam comparados no final. Cada um deve fazer seu desenho à sua maneira. Por fim, pergunte se os desenhos ficaram iguais e deixe que os estudantes citem algumas semelhanças e diferenças.

Orientações complementares

• No item A, se necessário, auxilie os estudantes durante a conversa fazendo alguns questionamentos, como: “Você é gentil com os colegas?”; “Você respeita a opinião dos colegas?”; “Você sabe o que é respeitar as diferenças?”; “Você já presenciou alguma atitude de desrespeito com algum colega?”; “Você sabe que respeito é um direito que todas as pessoas têm?”; “Além de respeitar as pessoas, quais atitudes devemos ter para demonstrar respeito aos animais, às plantas e aos bens materiais?”.

• No item B, incentive os estudantes a apresentarem mensagens positivas por meio do desenho. Além disso, reforce que sempre haverá diferenças entre as pessoas e todas merecem ser respeitadas, pois ser diferente e respeitar as diferenças é o que nos torna pessoas melhores e únicas.

• Incentive os estudantes a colocarem em prática o que aprenderam e a compartilharem as ideias com seus familiares sobre as boas atitudes que contribuem para vivermos em um mundo melhor.

• A atividade 8 propõe aos estudantes que analisem o ambiente em que estão inseridos e onde convivem cotidianamente. Esta atividade pode desenvolver a percepção deles quanto às figuras geométricas espaciais presentes no cotidiano, com ênfase no reconhecimento do paralelepípedo no item A. Para iniciar a resolução, leia o texto do enunciado com os estudantes e contextualize o uso de paralelepípedos no calçamento de ruas, mostrando vídeos de ruas antigas e atuais com esse tipo de pavimentação, se possível. Depois, organize um passeio com a turma pelos arredores da escola ou pontos turísticos da cidade para que possam fazer a pesquisa desse item e identificar as ruas e calçadas revestidas com paralelepípedos no município onde moram, com o objetivo de propiciar a capacidade de observação e reconhecimento de elementos históricos e culturais. Depois, eles podem fazer desenhos no caderno para representar esses lugares e os pontos de referências observados. Para isso, sugira que anotem os nomes das ruas e locais que encontrarem durante o passeio.

• Se julgar oportuno e a escola fornecer condições e tiver instalações físicas para isso, avalie a possibilidade de levar os estudantes ao laboratório de informática para que eles acessem aplicativos de mapas e realizem esse passeio no modo virtual.

• No item B, peça aos estudantes que verifiquem o espaço onde estão e, se julgar pertinente, dê alguns exemplos que podem ser utilizados como inspiração.

• Durante todas as interações, reforce o uso da linguagem matemática mais formal para nomear as figuras geométricas espaciais e

8. ANTES DA INVENÇÃO DO ASFALTO, MUITAS RUAS ERAM CALÇADAS COM BLOCOS DE PEDRAS DE GRANITO, CONHECIDOS COMO PARALELEPÍPEDOS. ELES TÊM ESSE NOME PORQUE SEU FORMATO PARECE COM ESSA FIGURA GEOMÉTRICA ESPACIAL.

BLOCO COM FORMATO DE PARALELEPÍPEDO.

AINDA HOJE, É POSSÍVEL ENCONTRAR CIDADES BRASILEIRAS

QUE MANTÊM ESSE TIPO DE CALÇAMENTO NAS RUAS.

RUA DE PARALELEPÍPEDOS

NA CIDADE DE OURO PRETO, EM MINAS GERAIS, EM 2024.

8. A) Resposta pessoal. Espera-se que os estudantes pesquisem ruas revestidas com paralelepípedos no município onde moram, em cidades próximas ou em outras cidades brasileiras.

CALÇAMENTO DE PARALELEPÍPEDOS EM FORTALEZA, NO CEARÁ, EM 2021.

A ) REALIZE UMA PESQUISA PARA VERIFICAR SE EXISTEM RUAS CALÇADAS COM PARALELEPÍPEDOS NO MUNICÍPIO ONDE VOCÊ MORA OU EM OUTRAS CIDADES BRASILEIRAS.

B ) IDENTIFIQUE E ESCREVA NO CADERNO OS NOMES DE OBJETOS AO SEU REDOR CUJO FORMATO LEMBRE AS FIGURAS GEOMÉTRICAS ESPACIAIS QUE ESTUDAMOS ATÉ O MOMENTO.

Resposta pessoal. Espera-se que os estudantes identifiquem objetos cujo formato lembre figuras geométricas espaciais no ambiente cotidiano.

incentive os estudantes a justificarem as associações com base nas características estudadas.

ATIVIDADE EXTRA

Peça aos estudantes que levem para a sala de aula embalagens de caixas com formato parecido com o paralelepípedo retângulo, como as de creme dental ou de medicamentos, e que possam ser desmontadas facilmente. Oriente-os a desenhar no caderno as embalagens montadas e, depois, desmontadas, para fazerem comparações e observarem as características.

9. LUANA CONSTRUIU UM CUBO UTILIZANDO UM MOLDE QUE A PROFESSORA ENTREGOU A ELA.

NO CUBO MONTADO, DESTACAMOS OS ELEMENTOS FACE, ARESTA E VÉRTICE

AGORA É A SUA VEZ! RECORTE O MOLDE DO CUBO QUE ESTÁ

NA PÁGINA 261 DO MATERIAL COMPLEMENTAR E MONTE-O PARA USÁ-LO NESTA ATIVIDADE.

DEPOIS, CONSIDERANDO O CUBO QUE VOCÊ MONTOU, COMPLETE OS ITENS A SEGUIR COM AS QUANTIDADES CORRETAS.

• FACES: • VÉRTICES: • ARESTAS:

Resposta: 6

• A atividade 9 tem como objetivo apresentar os elementos aresta, face e vértice de uma figura geométrica espacial. Para isso, verifique a possibilidade de levar à sala de aula o molde de um cubo, a fim de que os estudantes possam montar e manipular a figura montada. Se preciso, ajude-os na montagem dos moldes. No entanto, deixe que inicialmente façam tentativas, a fim de desenvolverem a coordenação motora e a noção de perspectiva, além de exercitarem a autonomia na execução de tarefas.

• Leia o texto a seguir, que trata da importância de utilizar materiais manipuláveis para auxiliar na compreensão das figuras geométricas espaciais.

Resposta: 8

Resposta: 12

10. LEIA AS INFORMAÇÕES A SEGUIR. DEPOIS, MARQUE V PARA AS FRASES VERDADEIRAS E F PARA AS FALSAS.

TODO CUBO TEM 6 FACES.

EXISTEM CUBOS COM 10 FACES.

UM CUBO TEM 6 FACES, 8 VÉRTICES E 12 ARESTAS.

Resposta: V. Resposta: F. Resposta: V.

EXISTEM CUBOS COM A MESMA QUANTIDADE DE FACES, VÉRTICES E ARESTAS.

Resposta: F.

• Na atividade 9, como sugestão para promover a inclusão dos estudantes com deficiência visual (cegos e baixa visão), solicite-lhes que se reúnam em grupo e trabalhem de maneira colaborativa, auxiliando uns aos outros. Sugira que troquem suas percepções sobre cada imagem da planificação do cubo, usando a percepção tátil e explorando as características geométricas do cubo com as mãos. Eles podem identificar as seis faces quadradas e compreender como essas partes se conectam para formar o cubo.

06/10/2025 17:52:14

• A atividade 10 visa verificar se os estudantes identificaram as quantidades de arestas, faces e vértices de um cubo. Se julgar conveniente, comente com eles que o tamanho de um cubo não altera a quantidade de seus elementos. É possível levar representações de cubos com tamanhos diferentes e pedir a eles que identifiquem seus elementos, verificando se houve alteração nas quantidades de vértices, arestas e faces.

[...] Enquanto manipula, constrói e representa objetos tridimensionais e a partir das intervenções que o professor faz, problematizando cada atividade, a criança descobre formas, percebe dimensões, observa semelhanças e diferenças, desenvolve noções de perspectiva, nota que alguns sólidos são limitados somente por figuras planas, enquanto outros são arredondados. Posteriormente, tais percepções serão úteis ao aluno na elaboração de relações geométricas mais sofisticadas.

[...]

SMOLE, Kátia Stocco; DINIZ, Maria Ignez; CÂNDIDO, Patrícia. Figuras e formas. Porto Alegre: Artmed, 2003. v. 3. p. 131. (Coleção Matemática de 0 a 6).

• A atividade 11 tem por objetivo apresentar as características que diferenciam as figuras geométricas espaciais que têm apenas superfícies planas das que têm superfícies não planas e arredondadas. Verifique se os estudantes associam as figuras do quadro B com os respectivos nomes ao responderem ao item A, ou seja, cone, cilindro e esfera. Além disso, verifique se identificam as figuras apresentadas no quadro A e as relacionam corretamente com os formatos dos objetos do item B. Questione se os objetos que não contornaram no item B lembram as figuras do quadro B e peça a eles que relacionem cada objeto a uma das figuras de acordo com seus formatos.

• Se necessário, após a atividade 11, para reforçar a prática e o direcionamento da escrita das letras dos nomes das figuras, utilize o caderno de caligrafia, de forma que os estudantes possam desenvolver progressivamente a escrita da letra cursiva.

• Na atividade 12, na próxima página, o intuito é os estudantes identificarem os objetos que têm superfícies não planas e arredondadas.

BNCC

A atividade do boxe Desafio a mais da próxima página, contempla aspectos da habilidade EF02MA10 da BNCC, pois propõe aos estudantes que descrevam o padrão de uma sequência formada por figuras geométricas espaciais e, além disso, identifiquem os próximos elementos dessa sequência, desenvolvendo parcialmente a habilidade EF02MA11 da BNCC.

Sugestão de Desafio

Qual é a figura geométrica espacial que tem 6 faces, 8 vértices e 12 arestas e que todas as suas faces têm o mesmo formato?

11. VAMOS SEPARAR EM DOIS QUADROS AS FIGURAS GEOMÉTRICAS ESPACIAIS QUE ESTUDAMOS.

QUADRO A

QUADRO B

AS FIGURAS GEOMÉTRICAS ESPACIAIS DO QUADRO A TÊM APENAS SUPERFÍCIES PLANAS, E AS DO QUADRO  B TÊM SUPERFÍCIES NÃO PLANAS, OU SEJA, ARREDONDADAS.

A ) AS FICHAS A SEGUIR APRESENTAM O NOME DE FIGURAS GEOMÉTRICAS ESPACIAIS. COPIE NAS LINHAS A SEGUIR O NOME DAS FIGURAS QUE TÊM SUPERFÍCIES NÃO PLANAS.

Resposta: Cone, cilindro, esfera.

B ) CONTORNE, ENTRE OS OBJETOS A SEGUIR, AQUELES QUE LEMBRAM AS FIGURAS DO QUADRO A

Resposta: Os estudantes devem contornar os objetos 1, 3 e 5

IMAGENS SEM PROPORÇÃO ENTRE SI.

11. A) Professor, professora: Oriente os estudantes na escrita das palavras que respondem ao item A, incentivando o traçado em letra cursiva na pauta apresentada.

Resposta Cubo ou paralelepípedo.

12. NA ATIVIDADE ANTERIOR, OS

OBJETOS QUE LEMBRAM AS FIGURAS GEOMÉTRICAS ESPACIAIS DO QUADRO  B

PODEM ROLAR COM FACILIDADE SOBRE

UMA SUPERFÍCIE, DE ACORDO COM

SUA POSIÇÃO. CONTORNE A SEGUIR OS OBJETOS QUE PODEM FAZER ISSO.

Resposta: Os estudantes devem contornar os objetos B e E

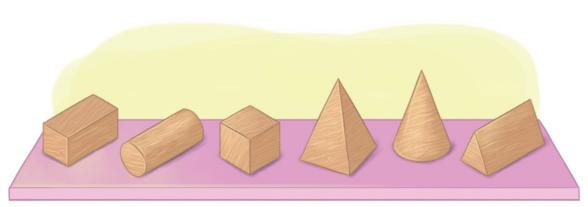
DESAFIO A MAIS

AS FIGURAS GEOMÉTRICAS ESPACIAIS A SEGUIR ESTÃO ORGANIZADAS DE ACORDO COM UMA SEQUÊNCIA.

Unidades temáticas integradas

Início

A ) ESSA SEQUÊNCIA É FORMADA POR QUAIS FIGURAS

GEOMÉTRICAS ESPACIAIS?

Resposta: CILINDRO, CONE E ESFERA.

B ) COM UM COLEGA, DESCREVAM A REGRA UTILIZADA PARA COMPOR ESSA SEQUÊNCIA.

Resposta pessoal. Sugestão de

resposta: O cilindro, o cone e a esfera se repetem nessa ordem.

C ) QUAL FIGURA OCUPA A 8ª POSIÇÃO?

Resposta: CONE.

D ) MARQUE UM X NO QUADRINHO QUE TEM AS TRÊS PRÓXIMAS FIGURAS DESSA SEQUÊNCIA.

Resposta: Os estudantes devem marcar um X no item 2

• A atividade do boxe Desafio a mais estabelece uma integração entre as unidades temáticas de Matemática Geometria e Álgebra ao observar a disposição das figuras em uma sequência, de modo que a turma consiga identificar o padrão, descrevê-lo e determinar os próximos elementos dessa sequência. Para resolver esse desafio, os estudantes devem observar a sequência inicial apresentada e descobrir a lógica da ordem em que as figuras foram organizadas. Como a sequência é formada por cilindro, cone e esfera, a chave para a resolução é a compreensão de que o padrão de repetição se completa a cada três figuras, na ordem “cilindro, cone, esfera”. Se os estudantes tiverem dificuldade ou encontrarem uma lógica diferente da esperada, incentive-os a compartilhar com os colegas como pensaram. Use intervenções pontuais e estratégicas para guiá-los na compreensão da sequência, como perguntar: “Qual é a primeira figura da sequência?”; “E a segunda?”; “E a terceira?”; “O que vem depois da esfera, que é a 3ª figura?”; “A 4ª figura é igual à primeira?”; “Quantas figuras se repetem antes de o padrão recomeçar?”. Perguntas desse tipo ajudam a identificar a regra do padrão e a aplicar o raciocínio para prever as próximas figuras.

CONCLUSÃO

Acompanhar o desenvolvimento dos estudantes é fundamental para um ensino bem-sucedido. Ao longo da unidade, foram propostas diversas maneiras de avaliar a aprendizagem da turma. A fim de realizar um monitoramento mais abrangente e organizado, registre nos relatórios individuais ou nas fichas de avaliação o desempenho de cada estudante, levando em consideração suas particularidades. Um modelo desse tipo de ficha pode ser

encontrado no tópico Avaliação deste manual. Assim, será possível visualizar de modo individual as trajetórias de aprendizagem, incluindo os avanços e os pontos de dificuldades a serem sanados por meio de atividades que promovam a recuperação dos conteúdos.

Esse método de verificar a progressão dos estudos e identificar o que a turma de fato conseguiu aprender e o que ficou com lacunas de absorção é de grande importância para que seja possível re-

06/10/2025 17:52:17

pensar estratégias em sala de aula, tornando as ações pedagógicas cada vez mais eficazes.

A conclusão da unidade é o momento de avaliar se os objetivos por ela propostos foram alcançados. Para esse diagnóstico, observe no final deste Manual algumas possibilidades de avaliação formativa que permitem realizar o monitoramento da aprendizagem dos estudantes e intervir caso não tenham atingido os resultados esperados.

A. B. C. D. E. F.

1. Objetivos

Registrar o resultado da contagem de objetos.

Decompor números naturais de até três ordens por meio da adição.

Sugestão de intervenção

Nesse momento, avalie os progressos e as dificuldades dos estudantes a fim de validar a metodologia usada e, caso seja necessário, propicie uma nova abordagem dos conteúdos estudados. Essa atividade tem por objetivo verificar se eles compreenderam as características do sistema de numeração decimal, realizando contagem de objetos e decompondo o resultado obtido por meio da adição. Caso eles tenham dificuldades, utilize diferentes estratégias de cálculo de contagem e decomposição, aproveitando alguns materiais manipuláveis. Apresente outros exemplos por meio de desenhos na lousa ou separe objetos para que os estudantes digam as quantidades existentes e decomponham os números por meio da adição de dezenas exatas e unidades.

2. Objetivo

Compreender a ideia de maior, menor e igual e comparar números naturais. Sugestão de intervenção

A atividade 2 propõe aos estudantes que completem os itens com as palavras maior, menor ou igual, também usando os símbolos >, < ou =, a fim de verificar se compreenderam a ideia de maior, menor e igual. Caso apresentem dificuldades na realização desta atividade, organize a turma em duplas e entregue a cada uma fichas de papel com números naturais aleatórios. Depois, solicite que conversem entre si e organizem os números das fichas do menor para o maior. Por fim, oriente-os a registrar no caderno os números das fichas usando os símbolos >, < ou =

VAMOS AVALIAR O APRENDIZADO

1. CONTE OS LÁPIS DA IMAGEM A SEGUIR E COMPLETE A FRASE.

NA IMAGEM APARECEM LÁPIS, OU DEZENAS E UNIDADES DE LÁPIS.

Resposta: NA IMAGEM APARECEM 45 LÁPIS, OU 4 DEZENAS E 5 UNIDADES DE LÁPIS.

2. CÁSSIO FEZ AS SEGUINTES ANOTAÇÕES PARA COMPARAR ALGUNS NÚMEROS.

20 É MAIOR DO QUE 10, OU SEJA, 20 > 10.

29 É MENOR DO QUE 31, OU SEJA, 29 < 31

17 É IGUAL A 17, OU SEJA, 17 = 17.

ASSIM COMO CÁSSIO, COMPLETE OS ITENS COM AS PALAVRAS MAIOR DO QUE, MENOR DO QUE OU IGUAL A E OS SÍMBOLOS

>, < OU =

• 55 É 44, OU SEJA, 55 44.

Resposta: 55 É MAIOR DO QUE 44, OU SEJA, 55  > 44

• 73 É 74, OU SEJA, 73 74.

• 35 É 35, OU SEJA, 35 35.

Resposta: 73 É MENOR DO QUE 74, OU SEJA, 73  < 74 Resposta: 35 É IGUAL A 35, OU SEJA, 35  = 35

• 26 É 36, OU SEJA, 26 36.

Resposta: 26 É MENOR DO QUE 36, OU SEJA, 26  < 36.

• 74 É 74, OU SEJA, 74 74.

Resposta: 74 É IGUAL A 74, OU SEJA, 74  = 74

06/10/2025 17:53:51

3. Objetivo

Unidades temáticas integradas

3. DESCUBRA A REGRA DE CADA SEQUÊNCIA. DEPOIS, COMPLETE OS ITENS COM OS NÚMEROS QUE FALTAM.

A ) 10 , 20 , 30 , , 50 , 60 , , , 90

Resposta: Regra: Cada número a partir do segundo é 10 unidades a mais do que o anterior. 10, 20, 30, 40, 50, 60, 70, 80, 90.

B ) 99 , 98 , 97 , , 95 , , , 92 ,

Resposta: Regra: Cada número a partir do segundo é 1 unidade a menos do que o anterior. 99, 98, 97, 96, 95, 94, 93, 92, 91

C ) 5 , 10 , 15 , , , , 35 , , 45

Resposta: Regra: Cada número a partir do segundo é 5 unidades a mais do que o anterior. 5, 10, 15, 20, 25, 30, 35, 40, 45.

D ) 18 , 16 , 14 , , , 8 , , , 2

Resposta: Regra: Cada número a partir do segundo é 2 unidades a menos do que o anterior. 18, 16, 14, 12, 10, 8, 6, 4, 2.

4. UTILIZANDO O SEU MATERIAL ESCOLAR, REPRESENTE PARA O SEU COLEGA UMA QUANTIDADE DE ITENS:

A ) PAR.

Resposta pessoal. Sugestões de resposta: 2 itens, 4 itens, 6 itens.

B ) MENOR DO QUE 10.

Resposta pessoal. Sugestões de resposta: 3 itens, 6 itens, 9 itens.

C ) ÍMPAR QUE SEJA MAIOR DO QUE 6 E MENOR DO QUE 20.

Resposta pessoal. Sugestões de resposta: 7 itens, 9 itens, 19 itens.

DICA: ANOTEM NO CADERNO OS NÚMEROS QUE MOSTRAM AS QUANTIDADES QUE VOCÊS REPRESENTARAM. DEPOIS, CONFIRAM JUNTOS SE AS RESPOSTAS ESTÃO CORRETAS.

5. OBSERVE OS OBJETOS E ESCREVA O NOME DA FIGURA GEOMÉTRICA ESPACIAL QUE ELE LEMBRA.

Resposta: CUBO.

Resposta: CONE.

Resposta: ESFERA.

os números pares e pergunte à turma se a quantidade de colegas em pé representa um número par ou ímpar. Repita o procedimento escolhendo outros estudantes em quantidade que represente um número ímpar e faça questionamentos, verificando a capacidade deles em classificar se uma quantidade representa número par ou número ímpar.

5. Objetivo

Associar figuras geométricas espaciais a objetos do dia a dia.

Sugestão de intervenção

06/10/2025 17:53:52

Caso os estudantes tenham dificuldade em resolver esta atividade, espalhe sobre a sua mesa alguns objetos e algumas embalagens cujos formatos lembrem figuras geométricas espaciais. Posteriormente, peça a algum estudante que escolha um objeto que está sobre a mesa e, depois, pergunte à turma qual é a figura geométrica espacial que esse objeto lembra e leve-os a explicar o porquê, apontando suas características. Repita essa estratégia quantas vezes julgar necessário.

Identificar o padrão das sequências e determinar os elementos ausentes.

Sugestão de intervenção

Essa atividade integra as unidades temáticas de Matemática Números e Álgebra ao propor uma comparação e quatro sequências recursivas entre números naturais.

Inicialmente, peça aos estudantes que descrevam o padrão presente em cada uma das sequências apresentadas e, nesse momento, incentive-os a definir quais são os elementos que faltam em cada uma. Para um melhor aproveitamento desta atividade, peça a um estudante que diga um número e, logo depois, que outro estudante diga outro número de maior valor. Monte a sequência com base na diferença entre os números ditos por eles, deixando alguns espaços em branco para que eles possam dizer quais números estão faltando. Ao final, pergunte qual é a regularidade encontrada.

4. Objetivo

Associar quantidades de itens a números ímpares e pares e compará-los. Sugestão de intervenção

Avalie a necessidade de retomar os conceitos de número par e número ímpar, caso algum estudante tenha dificuldade na resolução dessa atividade. Peça a dois estudantes que se levantem para representar

OBJETIVOS DA UNIDADE

• Efetuar adições e subtrações com resultado até 99.

• Reconhecer o símbolo (+) usado para representar a adição e o símbolo ( ) usado para representar a subtração.

• Resolver situações-problema que envolvam as operações de adição e subtração.

• Desenvolver a capacidade de realizar cálculos mentalmente e estimar resultados de operações, favorecendo a construção do raciocínio lógico.

• Utilizar a régua como ferramenta para resolver adições e subtrações.

• Identificar regularidades e determinar elementos ausentes em sequências.

• Explorar o uso da calculadora como recurso de apoio para realizar cálculos e conferir resultados de operações.

• Ler e interpretar dados expressos em tabelas simples, de dupla entrada e em gráficos de colunas.

INTRODUÇÃO E JUSTIFICATIVA

Nesta unidade, são apresentadas a adição e a subtração com números até 99. São utilizadas diversas estratégias de cálculo, por meio de ábaco, material dourado, régua, calculadora e decomposição de números e algoritmos, com e sem reagrupamento, propondo um trabalho prolongado que pretende auxiliar os estudantes na validação de estratégias e na compreensão das características do sistema de numeração decimal. Também são apresentadas atividades com elaboração e resolução de situações-problema contextualizadas, ligadas ao cotidiano e que envolvem o uso de ferramentas e estratégias de cálculo pessoal. A unidade traz atividades que

ADIÇÃO E SUBTRAÇÃO COM NÚMEROS ATÉ 99

ASSIM COMO CARROS, ÔNIBUS, TRENS, METRÔS E AVIÕES, HÁ EMBARCAÇÕES

QUE SÃO UTILIZADAS NO TRANSPORTE DE PASSAGEIROS E EM PASSEIOS TURÍSTICOS. ALGUMAS SÃO MAIORES, PARA VIAGENS

MAIS LONGAS, E OUTRAS SÃO MENORES, PARA ATRAVESSAR PEQUENOS TRECHOS.

BARCO ELÉTRICO MOVIDO A ENERGIA SOLAR NO RIO MIMOSO, EM BONITO, MATO GROSSO DO SUL, EM 2020.

trabalham sequências numéricas, interpretação de dados em tabelas simples e de dupla entrada, além de gráficos de colunas, entre outras habilidades que permitem desenvolver o pensamento numérico por meio de diferentes perspectivas. Habilidades da BNCC trabalhadas na unidade: EF02MA05 , EF02MA06 , EF02MA09 , EF02MA10, EF02MA11 e EF02MA22

SUGESTÃO DE ESTRATÉGIA INICIAL

Providencie material de contagem, como botões, palitos e pedrinhas. Se possível, também disponibilize material dourado ou ábaco, para

realizar com os estudantes as adições e subtrações, orientando-os a registrar os cálculos e os resultados no caderno. Durante a atividade, escreva na lousa os cálculos que podem ser realizados por eles nesse momento. Apresente-lhes também em flash cards, inserindo as adições em cartões de papel para que os estudantes digam os resultados, encorajando-os a efetuar os cálculos mentalmente ou a registrar as ideias no caderno.

06/10/2025 17:55:53

1. 2. 3.

1 a 3. Respostas nas orientações ao professor

ALÉM DO BARQUEIRO, QUANTOS PASSAGEIROS PODERIAM VIAJAR SENTADOS NA EMBARCAÇÃO QUE APARECE NA IMAGEM?

SE QUATRO PASSAGEIROS ENTRAREM NESSA EMBARCAÇÃO, QUANTOS LUGARES VÃO SOBRAR DESOCUPADOS?

VOCÊ ACHA IMPORTANTE HAVER DIVERSOS MEIOS DE TRANSPORTE? POR QUÊ?

• Peça aos estudantes que analisem a imagem destas páginas e leia com eles o texto apresentado na página 66. Em seguida, pergunte quais meios de transporte coletivo eles conhecem. Ressalte que os meios de transporte podem variar de acordo com a região onde moramos e a embarcação retratada na fotografia é um exemplo dessa situação. Explique que as embarcações podem ter vários tamanhos e que os barcos maiores são utilizados geralmente para travessias cotidianas porque têm mais assentos e são motorizados. Comente também que, além disso, há os navios de pequeno porte, bastante procurados por turistas.

• Pergunte aos estudantes se conhecem ou já utilizaram uma embarcação parecida com a representada na fotografia para fazer a travessia em um rio. Permita-lhes que relatem suas experiências, em caso afirmativo. Acolha com atenção e respeito todos os que quiserem falar, e engaje a turma nos comentários, favorecendo a participação ativa de todos na conversa e dando oportunidade de exercitarem a comunicação e a troca de ideias nesse momento.

• Na questão 1 , comente que, em determinados locais e comunidades, os estudantes usam barcos para chegar à escola. Pergunte-lhes que meio de transporte usam para ir à escola e questione-os sobre qual desses veículos tem capacidade para levar a maior quantidade de passageiros.

• Na questão 2, informe aos estudantes que, em média, um ônibus carrega 48 passageiros sentados. Com base na questão anterior, pergunte-lhes qual é a diferença entre a quantidade de pessoas que um barco elétrico e um ônibus podem carregar.

• Na questão 3, converse com os estudantes sobre a importância e as características dos diferentes meios de transporte usados no deslocamento de pes-

soas, animais, matérias-primas e mercadorias. Espera-se que eles considerem importante haver diferentes meios de transporte, com características apropriadas para cada um deles e para cada região. Por exemplo, um barco é útil em regiões cujo acesso a determinados lugares não pode ocorrer por meio terrestre; já o avião é usado geralmente em longas distâncias; as carretas são usadas para cargas pesadas em viagens mais longas; os caminhões transportam mercadorias urbanas. Mencione também o

06/10/2025 17:55:54

transporte ferroviário, tanto de passageiros quanto de carga.

Respostas 1. 14 pessoas.

2. 10 lugares.

3. Resposta pessoal. Espera-se que os estudantes reconheçam a importância da diversidade de transporte para atender às diferentes necessidades, como exemplificado pelo uso do barco.

• A atividade 1 motiva o desenvolvimento do processo de contagem, de modo mental ou escrito, para trabalhar os fatos básicos da adição. Por meio de ideias pessoais, os estudantes são levados a construir os conceitos de juntar e de acrescentar. Caso tenham dificuldade nesta atividade, disponibilize materiais de contagem, como tampinhas de garrafa, a fim de que façam os procedimentos que Sílvia realizou, ou seja, primeiro representando com tampinhas cada quantidade do cálculo, depois juntando as tampinhas para organizá-las em dois grupos: um com uma dezena de tampinhas e outro com as que sobraram, e, por fim, determinando a quantidade total de tampinhas.

• Para promover a inclusão de estudantes com NEE, é importante oferecer recursos concretos que tornem a aprendizagem mais acessível e significativa. Nesta atividade, uma sugestão é providenciar tampinhas de garrafa, pedrinhas, palitos ou outros objetos de fácil manipulação. Em seguida, peça aos estudantes que representem, inicialmente, a quantidade de tampinhas verdes e, depois, a quantidade de tampinhas azuis. Por fim, proponha que juntem as duas quantidades para obter o total.

ATIVIDADE EXTRA

Para tirar melhor proveito da atividade 1, pergunte aos estudantes se alguma vez já confeccionaram algum brinquedo com materiais reciclados. Em uma roda de conversa, apresente a eles a ideia de sustentabilidade e peça-lhes que, na próxima aula, levem para a sala de aula materiais como papel, garrafa PET, caixa, tampinha de garrafa e copos de plástico para confeccionar um brinquedo da preferência deles.

ADIÇÃO COM RESULTADO ATÉ 19

1. SÍLVIA ESTÁ JUNTANDO TAMPAS DE GARRAFA PET PARA

CONFECCIONAR UM BRINQUEDO.

A ) QUANTAS TAMPAS SÃO:

• VERDES?

Resposta: 8

• AZUIS?

Resposta: 6

B ) AO TODO, QUANTAS TAMPAS SÍLVIA JUNTOU?

TAMPAS VERDES MAIS TAMPAS AZUIS É IGUAL A TAMPAS.

MAIS É IGUAL A .

AO TODO, HÁ TAMPAS.

Resposta: 8 TAMPAS VERDES MAIS 6 TAMPAS AZUIS É IGUAL A 14 TAMPAS; 8 MAIS 6 É IGUAL A 14; AO TODO, HÁ 14 TAMPAS.

C ) NESSA SITUAÇÃO, FOI EFETUADA UMA ADIÇÃO UTILIZANDO SÍMBOLOS, ESCREVEMOS:

8 + 6 = Resposta: 8 + 6 = 14

QUANTIDADE DE TAMPAS VERDES

QUANTIDADE DE TAMPAS AZUIS

QUANTIDADE TOTAL DE TAMPAS

D ) PODEMOS EFETUAR ESSA ADIÇÃO USANDO TAMPAS. ACOMPANHE OS CÁLCULOS E COMPLETE O QUE FALTA.

1º . Resposta: Tampas verdes: 8; tampas azuis: 6.

REPRESENTAMOS COM TAMPAS CADA QUANTIDADE DO CÁLCULO.

BNCC

As atividades desta unidade permitem trabalhar com os estudantes a construção de fatos básicos da adição e da subtração, utilizando procedimentos de cálculo mental ou escrito, bem como o uso da calculadora, contemplando as habilidades EF02MA05 e EF02MA06. Os processos de adição e de subtração são desenvolvidos por meio de situações-problema baseadas em acontecimentos do cotidiano dos estudantes.

06/10/2025 17:55:55

Alguns de seus conhecimentos são retomados e novos procedimentos de cálculo são apresentados, a fim de que possam escolher o melhor procedimento a ser seguido na resolução de uma situação-problema que lhes é determinada. As ideias envolvidas nessas operações propõem o trabalho com o reagrupamento de unidades e a troca por dezena.

2. C) Resposta: Os estudantes devem partir do número 9 na régua e “andar” 4 unidades para a direita. 9 + 4 = 13

2º 8 + 6 10 + 4

JUNTAMOS TODAS AS TAMPAS E, EM SEGUIDA, SEPARAMOS EM DOIS GRUPOS: UM COM UMA DEZENA DE TAMPAS E OUTRO COM AS QUE SOBRARAM.

ASSIM, 8 + 6 = 14 OU 10 + 4 = 14

PORTANTO, SÍLVIA JUNTOU, AO TODO, TAMPAS DE GARRAFA PET.

Resposta: PORTANTO, SÍLVIA JUNTOU, AO TODO, 14 TAMPAS DE GARRAFA PET

2. PODEMOS CALCULAR 8 + 3 USANDO UMA RÉGUA.

8 + 3 = 11

• Na atividade 2 , oriente os estudantes a utilizarem uma régua para efetuarem os cálculos de adição. Caso não haja réguas suficientes para todos, peça-lhes que formem duplas a fim de que possam realizar esta atividade. Explique, na lousa, o passo a passo de como deverão ser efetuados os cálculos de adição com o auxílio desse instrumento. Para facilitar o procedimento, ressalte que é possível marcar no caderno os números a serem adicionados, da mesma maneira que foi feita na figura.

ASSIM COMO APRESENTADO, EFETUE OS CÁLCULOS USANDO UMA RÉGUA.

A ) 6 + 9 =

B ) 3 + 8 =

2. A) Resposta: Os estudantes devem partir do número 6 na régua e “andar” 9 unidades para a direita. 6 + 9 = 15

• Para complementar a atividade 3, proponha aos estudantes que a resolvam no caderno, organizando as parcelas de maneiras diferentes da realizada no Livro do Estudante. Depois, solicite que compartilhem com a turma as estratégias usadas, acolhendo com atenção e respeito a contribuição de todos. É importante que verbalizem o raciocínio a fim de sistematizar o conteúdo e consolidar a aprendizagem. 8 +3

2. B) Resposta: Os estudantes devem partir do número 3 na régua e “andar” 8 unidades para a direita. 3 + 8 = 11

C ) 9 + 4 =

D ) 6 + 6 =

3. RESOLVA OS CÁLCULOS EM SEU CADERNO. DEPOIS, COMPLETE OS ESQUEMAS COM OS RESULTADOS.

Resposta: 10 + 9; 19 Resposta: 9 + 8; 17 Resposta: 8 + 8; 16

NOTE QUE FOI LOCALIZADO, INICIALMENTE, O NÚMERO 8 NA RÉGUA. DEPOIS, “ANDAMOS” 3 UNIDADES PARA A DIREITA E OBTEMOS O RESULTADO. 6 + 4 + 9 10 + 7 + 2 + 8 + 5

2. D) Resposta: Os estudantes devem partir do número 6 na régua e “andar” 6 unidades para a direita. 6 + 6 = 12

06/10/2025 17:55:55

• A atividade 4 estabelece uma integração entre as unidades temáticas de Matemática Números e Probabilidade e estatística ao relacionar dados obtidos de uma pesquisa e a organização desses dados em uma tabela simples.

• A atividade 4 apresenta um contexto próximo da realidade dos estudantes. Oriente-os a observar os registros da professora Carla para completarem a tabela corretamente. Por meio dos questionamentos feitos nos itens B a E, eles podem perceber a importância dos dados organizados em uma tabela, concluindo que essa organização facilita a leitura e a interpretação. Para complementar esta atividade, realize uma pesquisa com a turma sobre os animais de estimação preferidos deles. Registre na lousa os dados coletados e, por fim, em uma tabela.

4. A PROFESSORA CARLA PERGUNTOU

Unidades temáticas integradas

AOS ESTUDANTES DO 2º ANO A QUE ANIMAL DE ESTIMAÇÃO ELES

PREFEREM E ANOTOU AS RESPOSTAS NA LOUSA.

DICA: TODOS OS ESTUDANTES DA TURMA VOTARAM UMA ÚNICA VEZ.

A ) COMPLETE A TABELA COM BASE NOS DADOS QUE A PROFESSORA CARLA ANOTOU NA LOUSA.

Resposta: CACHORRO: 6; GATO: 3; PEIXE: 2; PÁSSARO: 3; OUTROS: 2; NENHUM: 3

ANIMAIS DE ESTIMAÇÃO PREFERIDOS DOS

ESTUDANTES DO 2º ANO A EM AGOSTO DE 2027

ANIMAL CACHORRO GATO PEIXE PÁSSARO OUTROS NENHUM

QUANTIDADE DE ESTUDANTES

FONTE DE PESQUISA: ANOTAÇÕES DA PROFESSORA CARLA.

B ) QUAL ANIMAL TEVE A MAIOR QUANTIDADE DE VOTOS?

Resposta: CACHORRO.

C ) QUANTOS VOTOS O ANIMAL MAIS VOTADO RECEBEU?

Resposta: 6

D ) QUANTOS ESTUDANTES PREFEREM PÁSSARO?

Resposta: 3 ESTUDANTES.

E ) QUANTOS ESTUDANTES DO 2º ANO A RESPONDERAM À PESQUISA?

ESTUDANTES.

Resposta: 6 + 3 + 2 + 3 + 2 + 3 = 19; 19 ESTUDANTES.

5. NESTOR ORGANIZOU ALGUMAS ADIÇÕES NOS QUADROS

A SEGUIR. EFETUE E COMPLETE ESSAS ADIÇÕES COM OS RESULTADOS OBTIDOS.

4 3 2 1

A ) EFETUE E COMPLETE ESSAS ADIÇÕES COM OS RESULTADOS OBTIDOS.

Respostas e comentários nas orientações ao professor

B ) QUAIS REGULARIDADES VOCÊ PODE IDENTIFICAR NAS ADIÇÕES DE CADA QUADRO? CONVERSE COM OS COLEGAS.

Respostas e comentários nas orientações ao professor

C ) NO CADERNO, ESCREVA AS ADIÇÕES DESSES QUADROS CUJO RESULTADO É 9.

Resposta: 1 + 8 = 9; 2 + 7 = 9; 3 + 6 = 9; 4 + 5 = 9

D ) NESTOR ORGANIZOU ADIÇÕES RELACIONADAS AOS NÚMEROS 1, 2, 3 E 4. DE MANEIRA SEMELHANTE, CONSTRUA EM SEU CADERNO QUADROS COM ADIÇÕES RELACIONADAS AOS NÚMEROS DE 5 A 10.

Respostas e comentários nas orientações ao professor

• Na atividade 5, espera-se que os estudantes percebam que há uma regularidade entre as adições efetuadas. Caso não percebam, peça a eles que leiam apenas os resultados para descobrirem a diferença entre um número e o seu sucessor. Caso ainda tenham dúvidas, explique que a regularidade é algo que sempre ocorre e na mesma ordem.

• Verifique, no item C, se os estudantes identificam nos quadros as adições cujos resultados sejam 9. Para um melhor aproveitamento desta atividade, solicite que encontrem nos quadros e registrem no caderno as adições cujos resultados sejam 6 e, depois, as adições cujos resultados sejam 11.

• Para realizar o item D, faça na lousa, com o auxílio dos estudantes, o quadro das adições relacionadas ao número 5 e, depois, permita que façam sozinhos as adições relacionadas aos números de 6 a 10. Em seguida, acompanhe as respostas deles a fim de constatar possíveis dúvidas e intervir, quando necessário.

Respostas

5. A)

1 + 1 = 2

1 + 2 = 3

1 + 3 = 4

1 + 4 = 5

1 + 5 = 6

1 + 6 = 7

1 + 7 = 8

1 + 8 = 9

1 + 9 = 10

1 + 10 = 11

2 + 1 = 3

2 + 2 = 4

2 + 3 = 5

2 + 4 = 6

2 + 5 = 7

2 + 6 = 8

2 + 7 = 9

2 + 8 = 10

2 + 9 = 11

2 + 10 = 12

3 + 1 = 4

3 + 2 = 5

3 + 3 = 6

3 + 4 = 7

3 + 5 = 8

3 + 6 = 9

3 + 7 = 10

3 + 8 = 11

3 + 9 = 12

3 + 10 = 13

4 + 1 = 5

4 + 2 = 6

4 + 3 = 7

4 + 4 = 8

4 + 5 = 9

4 + 6 = 10

4 + 7 = 11

4 + 8 = 12

4 + 9 = 13

4 + 10 = 14

B) Resposta pessoal. Espera-se que os estudantes analisem as operações e apontem algumas regularidades em relação às parcelas e às somas das adições, como o fato de uma das parcelas de todas as adições ser sempre 1 e a outra parcela envolver números naturais consecutivos de 1 a 10. Verifique se eles percebem que as somas são números consecutivos de 2 a 11, na ordem que vão sendo resolvidas.

06/10/2025 17:55:55

D) Espera-se que os estudantes notem que é possível construir os quadros solicitados sem efetuar cálculos, tendo como parâmetro os fatos relevantes. No entanto, é fundamental que eles sejam capazes de efetuar os cálculos, pois as regularidades na organização dos números se repetem em todos os quadros.

• Na atividade 6, ao observarem como Diego resolveu o cálculo 9  + 5 utilizando tracinhos, os estudantes são incentivados a reconhecer uma estratégia simples de contagem para adicionar dois números naturais e visualizarem, de modo concreto, a junção de duas quantidades, compreendendo a operação de adição. Incentive-os a usar outras representações com materiais de contagem, como bolinhas, palitos e tampinhas. Pergunte a eles se conhecem outra maneira de resolver as operações e incentive a comparação das estratégias compartilhadas entre eles.

• A atividade 7 integra as unidades temáticas de Matemática Números e Probabilidade e estatística ao explorar a leitura de informações representadas em um quadro. Verifique se os estudantes leem o quadro corretamente para identificar a quantidade de gols marcados pelas jogadoras. Se necessário, distribua materiais concretos, como tampinhas e palitos, para auxiliá-los na operação de adição.

• Após a realização das operações, explique aos estudantes que essa é uma das principais características de quadros, tabelas e gráficos: eles permitem a leitura e interpretação de informações por meio de elementos visuais, facilitando a análise de dados de maneira mais rápida e intuitiva.

6. DIEGO CALCULOU 9 + 5 USANDO TRACINHOS. PRIMEIRO, ELE DESENHOU

TRACINHOS PARA REPRESENTAR OS NÚMEROS DO CÁLCULO.

DEPOIS, OBTEVE O RESULTADO.

ASSIM COMO APRESENTADO, EFETUE OS CÁLCULOS USANDO TRACINHOS.

A ) 6 + 4 =

Resposta: 6 + 4 = 10

7. NA PARTIDA FINAL DO

Unidades temáticas integradas

CAMPEONATO FEMININO DE FUTSAL, APENAS ALGUMAS

B ) 3 + 9 =

Resposta: 3 + 9 = 12

JOGADORAS MARCARAM GOLS. NO QUADRO, ESTÁ REGISTRADA A QUANTIDADE DE GOLS MARCADOS NESSA PARTIDA.

DICA: CADA EQUIVALE A UM GOL MARCADO.

A ) QUAIS JOGADORAS MARCARAM 3 GOLS?

Resposta: MARCELA E CÍNTIA.

B ) QUAL JOGADORA MARCOU UM GOL?

Resposta: LAURA.

C ) CÍNTIA MARCOU QUANTOS GOLS? GOLS.

Resposta: 3 GOLS.

D ) QUANTOS GOLS AS DUAS JOGADORAS QUE MAIS FIZERAM GOLS MARCARAM JUNTAS? GOLS.

AVALIANDO

Objetivo

Efetuar adições com resultados até 19 utilizando o símbolo da adição.

Efetuar adições e identificar a presença de regularidades nos resultados obtidos.

Sugestão de intervenção

Resposta: 6 + 5 = 11; 11 GOLS.

Caso os estudantes tenham dificuldade no processo de efetuar adição, realize uma atividade com o auxílio das peças do jogo de dominó a fim de retomar o conceito de regularidades nas adições. Organize-os em grupos e distribua três peças de dominó a cada grupo, de modo que todas elas tenham a mesma quantidade de pontos, considerando o total nas duas partes. Depois, pergunte a eles o que as peças têm em comum. O objetivo é levar os estudantes a efetuarem as adições com os pontos das peças do jogo de dominó e compreenderem que a soma dos pontos sempre será a mesma.

ADIÇÃO COM RESULTADO ATÉ 99

SEM REAGRUPAMENTO

1. GIOVANA EFETUOU O CÁLCULO 32 + 53 EM UM ÁBACO.

DEPOIS, ADICIONEI O SEGUNDO NÚMERO, NO CASO 53, ACRESCENTANDO 3 CONTAS NA HASTE DAS UNIDADES E 5 CONTAS NA HASTE DAS DEZENAS. O NÚMERO REPRESENTADO NO ÁBACO CORRESPONDE AO RESULTADO DO CÁLCULO.

PRIMEIRO, COLOQUEI 2 CONTAS NA HASTE DAS UNIDADES E 3 CONTAS NA HASTE DAS DEZENAS, REPRESENTANDO O NÚMERO 32.

ASSIM COMO GIOVANA, DESENHE CONTAS NOS ÁBACOS E OBTENHA A SOMA DE CADA ADIÇÃO.

A ) 41 + 7 =

Resposta: Os estudantes devem desenhar no ábaco 4 contas na haste das dezenas e 8 contas na haste das unidades.

41 + 7 = 48.

B ) 62 + 15 =

Resposta: Os estudantes devem desenhar no ábaco 7 contas na haste das dezenas e 7 contas na haste das unidades.

62 + 15 = 77

ATIVIDADE EXTRA

Para um melhor aproveitamento e como complemento da atividade trabalhada nesta página, peça aos estudantes que resolvam no caderno de duas maneiras diferentes a seguinte situação-problema.

• Luís coleciona carrinhos. Ele tinha 31 carrinhos e ganhou 16 no dia de seu aniversário. Com quantos carrinhos Luís ficou ao todo?

Resposta

• Luís ficou ao todo com 47 carrinhos.

C ) 46 + 11 =

Resposta: Os estudantes devem desenhar no ábaco 5 contas na haste das dezenas e 7 contas na haste das unidades.

46 + 11 = 57.

D ) 53 + 16 =

Resposta: Os estudantes devem desenhar no ábaco 6 contas na haste das dezenas e 9 contas na haste das unidades.

53 + 16 = 69

06/10/2025 17:55:56

• Alguns dos pré-requisitos para este tópico são o reconhecimento e a compreensão do valor posicional das unidades e das dezenas, pois os estudantes devem aplicar esse conhecimento nos procedimentos de cálculo ao efetuar adições.

• O objetivo da atividade 1 é levar os estudantes a efetuarem adições com números de dois algarismos sem reagrupamento, com resultado até 99. Caso haja dificuldade na resolução da atividade, sugira a eles que usem tracinhos para representar as quantidades e que as registrem no caderno.

• Para facilitar a compreensão do uso do ábaco, leve para a sala de aula um ábaco e pergunte aos estudantes se já o conhecem e se sabem a sua função. Faça alguns questionamentos a eles e explique o que for necessário durante a conversa. Algumas sugestões são:

• Para que serve um ábaco?

• O que representa cada haste do ábaco?

• O que representa cada bolinha nas hastes?

• Como podemos identificar o número que está representado no ábaco?

• Quantas contas, ao todo, podemos colocar em cada haste?

• O que significa a ausência de contas em alguma das hastes do ábaco?

• Depois de ter explorado suas características, peça-lhes que desenhem as contas no ábaco em cada item da atividade 1 e, assim como Giovana, obtenham a soma de cada adição.

• A atividade 2 tem como objetivo auxiliar os estudantes na compreensão do valor posicional dos algarismos, utilizando o ábaco de papel. Esse recurso permite visualizar de modo concreto a composição dos números em dezenas e unidades, facilitando a resolução das adições propostas. Verifique como utilizam o ábaco, auxiliando aqueles que tiverem dúvidas.

• Peça aos estudantes que recortem e utilizem o ábaco de papel e as contas disponíveis no Material complementar do final do Livro do Estudante, auxiliando-os, com a sua supervisão, na compreensão desta atividade. Para isso, permita apenas o uso de tesouras com pontas arredondadas e fique atento ao modo como manuseiam esse instrumento, a fim de prevenir acidentes. É importante alertá-los sobre esse cuidado e os riscos do uso inadequado dele. Para alguns estudantes com comprometimento motor ou outra dificuldade física que limite os movimentos de corte, avalie a possibilidade de trazer material já recortado ou de auxiliá-los nessa etapa. Oriente-os também a guardar esse material em um envelope ou saco plástico, pois ele será aproveitado em outras atividades no decorrer do volume, sempre que achar conveniente.

• Na atividade 3, é proposto aos estudantes que façam uma estimativa para determinar quanto custou a compra de Cláudio. Fazer estimativa significa calcular um valor aproximado, o que é muito importante para o desenvolvimento da capacidade de realizarem cálculo mental. Leia o enunciado da atividade e permita-lhes

2. UTILIZANDO O ÁBACO DE PAPEL E AS CONTAS DO MATERIAL

COMPLEMENTAR DAS PÁGINAS 263 E 265, RESOLVA AS ADIÇÕES A SEGUIR.

A ) 24 + 21 =

Resposta: 24 + 21 = 45

B ) 63 + 15 =

Resposta: 63 + 15 = 78

C ) 50 + 36 =

Resposta: 50 + 36 = 86

D ) 49 + 10 =

Resposta: 49 + 10 = 59

3. CLÁUDIO FOI A UMA LOJA E COMPROU UM ESTOJO E UM CADERNO, POIS PRECISAVA DESSES MATERIAIS.

A ) EM SUA OPINIÃO, QUANTOS REAIS CUSTOU A COMPRA DE CLÁUDIO?

MARQUE UM X EM SUA OPÇÃO.

Resposta: Espera-se que os estudantes marquem um X em MENOS DO QUE 50 REAIS

MAIS DO QUE 50 REAIS.

MENOS DO QUE 50 REAIS.

EXATAMENTE 50 REAIS.

B ) PARA OBTER A QUANTIA GASTA POR CLÁUDIO NESSA COMPRA, DEVEMOS CALCULAR 33 + 16 . OBSERVE A SEGUIR, COMO EFETUAR ESSE CÁLCULO E COMPLETE O QUE FALTA.

apresentar suas respostas. Com base nelas, questione quais estratégias foram utilizadas para chegarem a esse resultado. Incentive-os a compartilhar essas estratégias com a turma. Caso alguns estudantes tenham dificuldade em realizar a estimativa, sugira que utilizem o caderno para fazer a adição.

UTILIZANDO CUBINHOS E BARRAS

1º . REPRESENTAMOS OS NÚMEROS 33 E 16 COM CUBINHOS E BARRAS.

33 16

2º . JUNTAMOS OS CUBINHOS (UNIDADES) E AS BARRAS (DEZENAS) E OBTEMOS O RESULTADO DA ADIÇÃO. 33 + 16 = 49

DECOMPONDO OS NÚMEROS

DICA: UM CUBINHO REPRESENTA UMA UNIDADE. CADA BARRA TEM 10 CUBINHOS, REPRESENTANDO UMA DEZENA. 3 3 + 1 6

+ 9 = 49 + +

USANDO O ALGORITMO

PRIMEIRO, ADICIONAMOS AS UNIDADES.

DEPOIS, ADICIONAMOS AS DEZENAS. D U 3 3 + 1 6 9

ATIVIDADE EXTRA

A fim de sanar possíveis dúvidas e para um melhor aproveitamento da atividade desta página, solicite aos estudantes que repitam os mesmos procedimentos para calcular outras adições sem reagrupamento, efetuando os cálculos no caderno, como:

• 41 + 15

• 33 + 13

• 26 + 12

• 24 + 22

• Providencie com antecedência e leve para a sala de aula o material dourado a fim de realizar os procedimentos desenvolvidos no cálculo da adição desta página. Utilize-o para que os estudantes compreendam as composições e trocas necessárias para representar os números. Explique a eles na prática como representar e efetuar o cálculo 33 + 16, seguindo os passos apresentados no Livro do Estudante.

• Caso não haja material dourado suficiente para todos os estudantes, organize-os em duplas para que possam realizar a atividade.

• Alguns estudantes podem ter dificuldade em utilizar o material dourado. Por esse motivo, explique a eles que cada cubinho representa uma unidade e cada barra, uma dezena. Depois, oriente-os a começar a adição juntando as unidades e, em seguida, as dezenas.

• Para trabalhar com a adição pelo método da decomposição, faça alguns exemplos na lousa, que podem ser os mesmos apresentados na Atividade extra, e solicite aos estudantes que os resolvam no caderno. Por fim, utilize o algoritmo efetuando as mesmas adições a fim de que percebam as diferenças entre esses procedimentos de cálculo.

06/10/2025 17:55:57

Respostas

• 41 + 15 = 56

• 33 + 13 = 46

• 26 + 12 = 38

• 24 + 22 = 46

• Se julgar necessário, utilize o ábaco para ajudar os estudantes a compreenderem melhor o algoritmo da adição. Represente cada parcela em um ábaco separado e, em um terceiro ábaco, explique como transportar as unidades e, depois, as dezenas de cada parcela para encontrar o total. Esse recurso é muito útil para que eles entendam, de maneira prática, o processo de reagrupamento, que será estudado posteriormente.

• Na atividade 4, se achar adequado, organize os estudantes em duplas e permita que escolham a estratégia que preferirem para resolver as adições. Caso tenham dificuldade, oriente-os a usar os recursos já trabalhados em sala de aula, como o ábaco ou o algoritmo da adição. Para isso, é importante que alguns ábacos estejam disponíveis para uso durante a atividade.

• O objetivo da atividade 5 é levar os estudantes a desenvolverem o cálculo mental, habilidade essencial para que efetuem cálculos com agilidade, sem recorrer imediatamente ao registro escrito. Incentive-os a pensar em estratégias para realizar as operações de adição apresentadas. Eles podem, por exemplo, usar a estratégia de decomposição:

• 35 + 13 =

= (30 + 10)+ (5 + 3)=

= 40 + 8 = 48

• 35 + 13 = 35 + 10 + 3 =

= 45 + 3 = 48

• Ao final, promova uma discussão com a turma sobre as estratégias utilizadas, incentivando os estudantes a explicarem os raciocínios usados.

3 3 + 1 6 4 9 PARCELAS

SOMA OU TOTAL

Resposta: PORTANTO, CLÁUDIO GASTOU 49 REAIS NESSA COMPRA.

PORTANTO, CLÁUDIO GASTOU REAIS NESSA COMPRA.

4. EFETUE AS ADIÇÕES DA MANEIRA QUE PREFERIR.

A ) 25 + 14 =

Resposta: 25 + 14 = 39

B ) 58 + 31 =

Resposta: 58 + 31 = 89

C ) 64 + 22 =

Resposta: 64 + 22 = 86

D ) 43 + 35 =

Resposta: 43 + 35 = 78

5. SEM EFETUAR OS CÁLCULOS POR ESCRITO, OBTENHA A SOMA EM CADA ITEM. DEPOIS, MARQUE UM X NO RESULTADO CORRETO.

A ) 35 + 13

Resposta: Os estudantes devem marcar um X no quadrinho com o número 48.

+ 16

) 12 + 43

Resposta: Os estudantes devem marcar um X no quadrinho com o número 37.

Resposta: Os estudantes devem marcar um X no quadrinho com o número 55.

6. EFETUE AS ADIÇÕES DA ATIVIDADE ANTERIOR, NO CADERNO, DA MANEIRA QUE PREFERIR E VERIFIQUE SE SUAS RESPOSTAS ESTÃO CORRETAS.

Resposta: Espera-se que os estudantes resolvam as adições da atividade 5 da maneira que preferirem e obtenham o resultado exato. 76

• Na atividade 6, se necessário, incentive os estudantes a utilizarem o ábaco como apoio. Ao final, resolva com a turma as atividades na lousa, utilizando o algoritmo, para que todos possam conferir e comparar os resultados obtidos.

7. CLARICE FOI ATÉ UMA LOJA E ENCONTROU OS PRODUTOS A SEGUIR.

IMAGENS SEM PROPORÇÃO ENTRE SI.

20 REAIS

QUANTOS REAIS CLARICE VAI GASTAR SE COMPRAR: COPO.

A ) UM COPO E UMA CANECA?

REAIS.

Resposta: 20 + 35 = 55; 55 REAIS.

REAIS

B ) UMA CANECA E UMA GARRAFA?

REAIS. + 2 + 2 + 2 + 2

Resposta: 35 + 42 = 77; 77 REAIS.

8. OBSERVE A SEQUÊNCIA E COMPLETE OS ESPAÇOS COM OS NÚMEROS QUE FALTAM.

Resposta: 18, 20, 22, 24, 26, ...

18 , 20 , 22 , , ,

PARA OBTER UM NÚMERO DESSA SEQUÊNCIA, A PARTIR DO SEGUNDO, ADICIONAMOS 2 UNIDADES AO NÚMERO ANTERIOR. DESCUBRA A REGRA E COMPLETE AS PRÓXIMAS SEQUÊNCIAS COM OS NÚMEROS QUE FALTAM.

A.

B.

BNCC

11 , 22 , 33 , , , , 1 , 11 , 21 , , , ,

8. A. Resposta: Para obter um número dessa sequência, a partir do segundo, adicionamos 11 unidades ao número anterior. 11, 22, 33, 44, 55, 66, ...

8. B. Resposta: Para obter um número dessa sequência, a partir do segundo, adicionamos 10 unidades ao número anterior. 1, 11, 21, 31, 41, 51,

A atividade 8 propõe aos estudantes que identifiquem o padrão e usem essa regularidade para completar os números faltantes na sequência, abordando, assim, aspectos da habilidade EF02MA10. Nos itens A e B desta atividade, eles são levados a descobrir suas regras e completá-las com os números naturais que estão faltando. Desse modo, devem descrever os elementos ausentes das sequências, desenvolvendo a habilidade EF02MA11

77

06/10/2025 17:58:12

• Na atividade 7, são exploradas duas possibilidades de compra que podem ser realizadas por Clarice. Leia com os estudantes o enunciado da atividade e oriente-os na resolução dos itens. Para um melhor aproveitamento desta atividade, outras possibilidades de compra podem ser sugeridas. Solicite a eles que escrevam no caderno algumas possibilidades diferentes das apresentadas e que calculem o gasto que Clarice teria. Por exemplo: “Quantos reais Clarice vai gastar se comprar uma caneca e uma garrafa?”; “Quantos reais Clarice vai gastar se comprar duas garrafas?”; “Quantos reais Clarice vai gastar se comprar um copo e uma garrafa?”.

• Para um melhor aproveitamento da atividade 8, organize os estudantes em duplas e solicite a cada um que crie uma regra e escreva uma sequência no caderno. Depois, peça-lhes que troquem os cadernos a fim de que o colega de dupla descubra a regra da sequência e a complete com os próximos cinco elementos. Por fim, eles devem destrocar os cadernos e verificar se a sequência foi completada corretamente.

• Alguns dos pré-requisitos para este tópico são o reconhecimento e a compreensão do valor posicional das unidades e das dezenas, a fim de aplicar esse conhecimento ao realizar adições sem reagrupamento.

• A atividade 1 tem por objetivo levar os estudantes a fazerem uma estimativa para determinar quantas garrafas Beatriz e Débora coletaram juntas. Fazer estimativa significa calcular um valor aproximado, o que é muito importante para o desenvolvimento da capacidade de realizar cálculo mental. Leia o enunciado da atividade e permita a eles que apresentem suas respostas. Com base nelas, questione quais estratégias foram utilizadas para chegarem a esse resultado. Incentive-os a compartilhar com a turma suas estratégias. Caso alguns estudantes tenham dificuldade em realizar a estimativa, sugira que utilizem o caderno para fazer a adição.

• Providencie com antecedência e leve para a sala de aula o material dourado para trabalhar com o tópico Adição com reagrupamento. A primeira estratégia de resolução proposta na atividade 1 tem como objetivo levar os estudantes a resolverem a adição utilizando o material dourado. Para isso, eles devem representar os números 34 e 27 com barras (dezenas) e cubinhos (unidades), e, em seguida, juntar as dezenas e as unidades. Depois, é apresentado a eles o processo de trocar 10 cubinhos por uma barra, ou seja, substituir 10 unidades por uma dezena, o que possibilita compreender o reagrupamento e chegar ao resultado da adição.

ADIÇÃO COM REAGRUPAMENTO

1. PARA REALIZAR UM TRABALHO ESCOLAR, BEATRIZ COLETOU

34 GARRAFAS PET E DÉBORA, 27.

A ) EM SUA OPINIÃO, QUANTAS GARRAFAS PET ELAS COLETARAM JUNTAS?

MARQUE UM X EM SUA OPÇÃO.

MAIS DO QUE 50 GARRAFAS.

MENOS DO QUE 50 GARRAFAS.

EXATAMENTE 50 GARRAFAS.

Resposta: Espera-se que os estudantes marquem um X em MAIS DO QUE 50 GARRAFAS

B ) PARA OBTER A QUANTIDADE DE GARRAFAS PET QUE AS DUAS COLETARAM JUNTAS, PRECISAMOS CALCULAR

34 + 27 . COMPLETE AS INFORMAÇÕES, DE ACORDO COM OS CÁLCULOS APRESENTADOS.

UTILIZANDO CUBINHOS E BARRAS

1º . REPRESENTAMOS OS NÚMEROS 34 E 27 COM CUBINHOS E BARRAS.

34 27

2º . JUNTAMOS OS CUBINHOS (UNIDADES) E AS BARRAS (DEZENAS). EM SEGUIDA, TROCAMOS 10 UNIDADES POR UMA DEZENA E, ASSIM, OBTEMOS O RESULTADO DA ADIÇÃO.

34 + 27 = 61

ATIVIDADE EXTRA

Para um melhor aproveitamento desta atividade, organize os estudantes em duplas e solicite que efetuem outras adições com reagrupamento utilizando o material dourado a fim de consolidar o conteúdo estudado e sanar possíveis dúvidas, caso existam. Algumas sugestões são:

• 33 + 28

• 37 + 37

• 47 + 25

• 56 + 38

Respostas

• 33 + 28 = 61

• 37 + 37 = 74

• 47 + 25 = 72

• 56 + 38 = 94

60 + 1 = 61

DECOMPONDO OS NÚMEROS

Resposta: 50 + 10 + 1 = 60 + 1 = 61

USANDO O ALGORITMO

TROCAMOS 10 U POR 1 D E ADICIONAMOS AS DEZENAS.

BEATRIZ E DÉBORA COLETARAM JUNTAS

Resposta: PORTANTO, BEATRIZ E DÉBORA COLETARAM JUNTAS 61 GARRAFAS PET

2. EFETUE AS ADIÇÕES DA MANEIRA QUE PREFERIR.

Resposta: 45 + 26 = 71

Resposta: 56 + 37 = 93

A ) 45 + 26 = B ) 56 + 37 = C ) 61 + 29 =

Resposta: 61 + 29 = 90

06/10/2025 17:58:12

• Para trabalhar com a adição com reagrupamento pelo método da decomposição apresentado nesta página, faça outros exemplos na lousa, que podem ser os mesmos usados na Atividade extra da página 78, e solicite aos estudantes que resolvam no caderno. Por fim, utilize o algoritmo para efetuar as mesmas adições, levando-os a perceber as diferenças entre esses procedimentos de cálculo. Ao usar o algoritmo da adição com reagrupamento, verifique se compreenderam que o número 1 que “sobe” na ordem das dezenas representa 1 dezena, pois é feita uma troca de 10 unidades por 1 dezena.

• Caso os estudantes tenham dificuldade, solicite que se organizem em duplas e proponha que efetuem as adições com o auxílio do material dourado.

• Relembre os estudantes de que no algoritmo apresentado nesta página, U representa unidade e D representa dezena.

• Na atividade 2, o objetivo é levar os estudantes a efetuarem as adições com reagrupamento da maneira que julgarem mais conveniente. Desse modo, espera-se que recorram aos conhecimentos desenvolvidos no tópico anterior e que comparem os procedimentos de cálculo, validando as estratégias já conhecidas por eles e adquirindo novos conhecimentos de maneira significativa.

• A atividade 3 apresenta aos estudantes uma calculadora e as funções de algumas teclas. Oriente-os a observar a imagem e converse com eles sobre o modo de realizar algumas operações, mostrando-lhes a sequência de teclas necessárias. Use como primeiro exemplo o retratado no livro e, depois, faça outros exemplos antes de resolverem os itens propostos nesta atividade.

• Caso não haja quantidade de calculadoras suficiente para todos os estudantes, organize-os em grupos para realizar esta atividade. Se tiverem dificuldade no uso da calculadora, por ter algumas teclas dispostas de maneira diferente, explique essas diferenças a eles, a fim de que sigam os passos apresentados na atividade, ressaltando que as funções são as mesmas, independentemente da disposição das teclas. Oriente-os durante o desenvolvimento da atividade, de modo a esclarecer possíveis dúvidas.

3. A CALCULADORA É UM INSTRUMENTO USADO PARA FAZER CÁLCULOS. A IMAGEM MOSTRA PARA QUE SERVEM ALGUMAS DE SUAS TECLAS.

LIGAR E ZERAR O VISOR

TECLAS NUMÉRICAS

TECLAS PARA REALIZAR AS OPERAÇÕES

DESLIGAR

ESTA

SEQUÊNCIA DE TECLAS FOI DIGITADA EM UMA CALCULADORA PARA EFETUAR 55 + 36 . QUE RESULTADO APARECEU NO VISOR?

Resposta: 91

DE MANEIRA PARECIDA, REALIZE OS CÁLCULOS A SEGUIR COM UMA CALCULADORA.

Resposta: 38 + 18 = 56

A ) 38 + 18 = B ) 77 + 16

Resposta: 77 + 16 = 93

Resposta: 53 + 27 = 80

C ) 53 + 27 =

Resposta: 65 + 26 = 91

D ) 65 + 26 =

4. RESOLVA, NO CADERNO, AS ADIÇÕES A SEGUIR.

Resposta: 44 + 16 = 60

A ) 44 + 16 =

Resposta: 67 + 24 = 91

B ) 67 + 24 =

Resposta: 55 + 38 = 93

C ) 55 + 38 =

Resposta: 19 + 39 = 58

D ) 19 + 39 =

5. ÁLISSON CALCULOU 37 + 45 MENTALMENTE.

PRIMEIRO, ADICIONO AS UNIDADES:

7  U + 5  U = 12  U DEPOIS, TROCO 10 UNIDADES POR UMA DEZENA: 12  U = 1  D + 2  U

EM SEGUIDA, ADICIONO AS DEZENAS:

1  D + 3  D + 4  D = 8  D PORTANTO, 37 + 45 = 82

ASSIM COMO ÁLISSON, RESOLVA OS CÁLCULOS MENTALMENTE.

Resposta: 17 + 26 = 43

Resposta: 62 + 18 = 80

A ) 17 + 26 = B ) 62 + 18 =

Resposta: 58 + 33 = 91

C ) 58 + 33 =

6. UTILIZE UMA CALCULADORA E VERIFIQUE SE SUAS RESPOSTAS NA ATIVIDADE ANTERIOR ESTÃO CORRETAS.

7. A LOJA PORTO ESTÁ COM AS SEGUINTES OFERTAS.

6. Resposta: Espera-se que os estudantes realizem os cálculos em uma calculadora e obtenham os resultados exatos, confrontando, assim, com os resultados obtidos com o cálculo mental.

COM A AJUDA DO PROFESSOR, ELABORE EM SEU CADERNO UM PROBLEMA DE ADIÇÃO USANDO AS OFERTAS DA LOJA PORTO COMO BASE. DEPOIS, ENTREGUE O PROBLEMA PARA UM COLEGA RESOLVER. POR FIM, CONFIRAM JUNTOS SE A RESPOSTA ESTÁ CORRETA.

7. Resposta pessoal. Espera-se que os estudantes elaborem um problema usando as informações da oferta e consigam resolver o problema elaborado pelo colega.

AVALIANDO

Objetivo

Efetuar adições com resultado até 99 utilizando o material dourado, o método da decomposição e o algoritmo.

Sugestão de intervenção

Organize os estudantes em duplas e entregue a cada uma duas fichas. Solicite que efetuem, em seus cadernos, uma adição com os números das fichas, de três maneiras diferentes: utilizando o material

dourado, o método de decomposição e o algoritmo. As fichas devem conter números que, ao serem adicionados, resultem em um número até 99. Caso os estudantes tenham dificuldade, providencie outras atividades e estratégias com o objetivo de saná-las.

BNCC

Por meio da proposta apresentada na atividade 5, os estudantes são levados a construir fatos básicos da adição e a apli-

• Para a atividade 4, Providencie com antecedência e leve para a sala de aula o material dourado para realizar as adições propostas, a fim de auxiliar na compreensão da atividade.

• Na atividade 5, caso os estudantes tenham dificuldade na realização do cálculo mental, retome a estratégia apresentada por Álisson e escreva na lousa algumas adições envolvendo números menores, solicitando que desenvolvam os cálculos no caderno.

• Oriente os estudantes durante o uso da calculadora na atividade 6, de modo que possam esclarecer dúvidas que surgirem ao manuseá-la.

• Na atividade 7, verifique as dificuldades que os estudantes podem ter na elaboração dos enunciados dos problemas. Ressalte que, ao elaborarem o enunciado de um problema, é muito importante que tenham uma linguagem clara e que apresentem todos os dados necessários para sua resolução.

• Nessa etapa da aprendizagem, é possível que alguns estudantes ainda não se sintam seguros para escrever frases completas sozinhos e precisem de apoio. Por isso, é importante auxiliá-los na atividade 7. Algumas possibilidades são propor a construção coletiva das frases na lousa antes de passarem para o registro individual ou oferecer modelos iniciais para que completem.

06/10/2025 17:58:14

cá-los no cálculo mental, o que orienta a habilidade EF02MA05

A atividade 7 propõe a eles que elaborem um problema envolvendo o cálculo de adição, com os significados de juntar usando estratégias pessoais, o que contempla a habilidade EF02MA06

• Ao relacionar fatos da adição com números representados em quadros e tabelas, a atividade 8 integra as unidades temáticas de Matemática Números e Probabilidade e estatística. Além de explorar a adição, essa atividade apresenta aos estudantes como é realizada a construção de uma tabela simples com informações coletadas em uma pesquisa. Durante a resolução, pergunte aos estudantes quais características eles identificam na tabela do item A. Explique a eles que, ao construir uma tabela, pretende-se organizar as informações visando facilitar a leitura e a interpretação dos dados apresentados. Comente que uma tabela deve conter um título, que indica o assunto principal abordado, e a fonte, com a origem dos dados.

• Para complementar o trabalho com esta atividade, proponha aos estudantes uma coleta de dados a respeito do sabor de suco preferido pelos colegas, organizando os dados em uma tabela, de maneira semelhante à apresentada na atividade. Durante a organização dos dados, estabeleça a indicação de apenas cinco categorias, sendo uma delas a opção “Outros”. Ao final, peça a eles que representem na lousa a tabela que construíram e, com base nela, proponha perguntas à turma, para serem respondidas oralmente visando à interpretação dos dados coletados.

• Ao resolver o item B, verifique se eles identificam a operação de adição como uma maneira de obter o total de entrevistados.

8. B) Resposta pessoal. Espera-se que os estudantes indiquem que podemos utilizar uma adição para obter a quantidade de pessoas entrevistadas.

8. ELISEU FEZ UMA PESQUISA PARA DETERMINAR O SABOR DE SUCO PREFERIDO POR SEUS COLEGAS DAS TURMAS DO 2º ANO DA ESCOLA. OS DADOS OBTIDOS ESTÃO

APRESENTADOS A SEGUIR.

Unidades temáticas integradas

DICA: CADA EQUIVALE A UM VOTO, E TODOS OS ESTUDANTES DE CADA TURMA VOTARAM UMA ÚNICA VEZ.

A ) COMPLETE A TABELA DE ACORDO COM AS ANOTAÇÕES DE ELISEU.

Resposta: UVA: 18; ABACAXI: 10; MORANGO: 12; LARANJA: 11; OUTROS: 13.

SABOR DE SUCO PREFERIDO DOS COLEGAS DE TURMA DE ELISEU EM AGOSTO DE 2027

SABOR DE SUCO QUANTIDADE DE COLEGAS

UVA

ABACAXI

MORANGO

LARANJA

OUTROS

FONTE DE PESQUISA: ANOTAÇÕES DE ELISEU.

NA OPÇÃO “OUTROS”, VOCÊ DEVE INCLUIR OS SABORES MENOS VOTADOS, OU SEJA, LIMÃO, MANGA, CENOURA E CAJU.

B ) DE QUE MANEIRA PODEMOS OBTER O TOTAL DE PESSOAS ENTREVISTADAS? REGISTRE SUA ESTRATÉGIA NO CADERNO. DEPOIS, COMPARTILHE COM OS COLEGAS E O PROFESSOR.

C ) UTILIZANDO UMA CALCULADORA, DETERMINE QUANTOS COLEGAS DE ELISEU PARTICIPARAM DESSA PESQUISA.

Resposta: 64 colegas.

D ) EM SUA OPINIÃO, A ORGANIZAÇÃO DAS INFORMAÇÕES, NA TABELA, FACILITOU A LEITURA? JUSTIFIQUE SUA RESPOSTA.

Resposta pessoal. Espera-se que os estudantes digam que sim, pois a organização dos dados em uma tabela facilita a leitura das informações.

9. O FUNCIONÁRIO DE CERTA LOJA DE SAPATOS REGISTROU

A QUANTIDADE DE QUATRO MODELOS VENDIDOS NOS DOIS ÚLTIMOS DIAS DE ABRIL DE 2027 EM UMA TABELA DE DUPLA

ENTRADA.

QUANTIDADE DE QUATRO MODELOS DE SAPATO VENDIDOS NOS DOIS ÚLTIMOS DIAS DE ABRIL DE 2027

MODELO DE SAPATO QUANTIDADE VENDIDA POR DIA

A ) QUAL FOI O MODELO MAIS VENDIDO NA:

Resposta: MODELO A

• QUINTA-FEIRA?

Resposta: MODELO B

• SEXTA-FEIRA?

B ) QUAL FOI A QUANTIDADE TOTAL DE SAPATOS VENDIDOS NA:

Resposta: 18 + 14 + 11 + 12 = 55; 55 SAPATOS.

• QUINTA-FEIRA? SAPATOS.

Resposta: 10 + 16 + 9 + 14 = 49; 49 SAPATOS.

• SEXTA-FEIRA? SAPATOS.

C ) EM QUAL DIA FOI VENDIDA A MAIOR QUANTIDADE DE SAPATOS?

Resposta: QUINTA-FEIRA.

Unidades temáticas integradas 83

06/10/2025 17:58:16

• Ao relacionar fatos básicos da adição com números representados em uma tabela, a atividade 9 integra as unidades temáticas de Matemática Números e Probabilidade e estatística . Nesta atividade, o objetivo é explorar a adição utilizando dados representados em uma tabela de dupla entrada. Explique aos estudantes que em uma tabela desse tipo podemos fazer várias análises, como comparar os dados entre as linhas para cada coluna fixada, assim como proposto no item A, bem como identificar uma informação específica, fixando uma linha e uma coluna, entre outras possibilidades. Verifique se os estudantes respondem corretamente aos itens ou se têm dificuldade em interpretar a tabela. Faça intervenções sempre que julgar necessário e, se possível, proponha a eles outras comparações diferentes das feitas na atividade para poderem explorar essa tabela com base em outros aspectos.

BNCC

Na atividade 9, os estudantes interpretam e comparam informações apresentadas em uma tabela de dupla entrada, contemplando, assim, aspectos da habilidade EF02MA22

• Antes de propor a atividade 10, providencie calculadoras em quantidade suficiente ou organize a turma em duplas ou trios e distribua uma calculadora para cada grupo.

• A atividade 11 tem por objetivo propor aos estudantes que façam uma estimativa para determinar qual soma resulta em uma quantidade maior do que 65 e qual resulta em uma menor do que 65. Fazer estimativa é muito importante para o desenvolvimento do cálculo mental. Leia o enunciado da atividade e permita a eles que apresentem suas respostas. Com base nelas, questione quais estratégias foram utilizadas para chegarem a esse resultado. Incentive-os a compartilhar com a turma suas estratégias. Caso alguns estudantes tenham dificuldade em realizar a estimativa, sugira que utilizem o caderno para fazer a adição. No item C, sugira que utilizem o ábaco e a calculadora para adicionar os números dois a dois e, em seguida, comparar com as estimativas que fizeram inicialmente.

10. UTILIZANDO UMA CALCULADORA, DETERMINE A QUANTIDADE TOTAL DE CADA MODELO DE SAPATO VENDIDO NESSES DOIS DIAS, DE ACORDO COM AS INFORMAÇÕES DA ATIVIDADE DA PÁGINA ANTERIOR.

Resposta: MODELO A: 28; MODELO B: 30; MODELO C: 20; MODELO D: 26.

11. ALGUNS NÚMEROS ESTÃO REPRESENTADOS NOS ÁBACOS A SEGUIR.

A ) SEM REALIZAR CÁLCULOS POR ESCRITO, FAÇA UMA ESTIMATIVA E INDIQUE DOIS DESSES ÁBACOS CUJA SOMA DOS NÚMEROS REPRESENTADOS SEJA:

Resposta pessoal. Sugestão de resposta: MAIOR DO QUE 65: ábacos 1 e 4; MENOR DO QUE 65: ábacos 2 e 3

• MAIOR DO QUE 65.

• MENOR DO QUE 65.

B ) COMO VOCÊ FEZ PARA ESTIMAR A SOMA SEM EFETUAR CÁLCULOS POR ESCRITO? CONTE PARA OS COLEGAS E O PROFESSOR.

Resposta pessoal. Espera-se que os estudantes compartilhem

C ) UTILIZANDO UMA CALCULADORA, EFETUE AS ADIÇÕES QUE VOCÊ INDICOU NO ITEM A E REGISTRE NOS ESPAÇOS A SEGUIR. DEPOIS, COMPARE COM A SUA ESTIMATIVA.

Resposta pessoal. Espera-se que os estudantes calculem a soma dos números que indicaram e comparem com as suas estimativas do item A com os colegas e o professor as estratégias usadas para fazer as estimativas.

• SOMA MAIOR DO QUE 65.

• SOMA MENOR DO QUE 65.

06/10/2025 18:00:55

SUBTRAÇÃO COM NÚMEROS ATÉ 19

1. NA CESTA DE FRUTAS, HAVIA 8 LARANJAS. PARA FAZER UM SUCO, ELDER RETIROU 2 LARANJAS DA CESTA.

A ) QUANTAS LARANJAS SOBRARAM NA CESTA?

Resposta: 8 LARANJAS MENOS 2 LARANJAS É IGUAL A 6 LARANJAS. 8 MENOS 2 É IGUAL A 6

LARANJAS MENOS LARANJAS É IGUAL A LARANJAS.

MENOS É IGUAL A

B ) NESSA SITUAÇÃO, FOI EFETUADA UMA SUBTRAÇÃO, POIS UMA QUANTIDADE DE LARANJAS FOI RETIRADA DE OUTRA QUANTIDADE. COMPLETE O QUE FALTA NAS INFORMAÇÕES A SEGUIR.

UTILIZANDO SÍMBOLOS, ESCREVEMOS:

Resposta: 8 − 2 = 6

8 − 2 = QUANTIDADE DE LARANJAS QUE HAVIA NA CESTA QUANTIDADE DE LARANJAS RETIRADAS DA CESTA

C ) ACOMPANHE UMA MANEIRA DE EFETUAR ESSA SUBTRAÇÃO E COMPLETE O QUE FALTA.

• DESENHAMOS 8 TRACINHOS PARA REPRESENTAR A QUANTIDADE TOTAL DE LARANJAS DA CESTA.

• DEPOIS, RISCAMOS 2 TRACINHOS, QUE REPRESENTAM AS LARANJAS RETIRADAS. OS 6 TRACINHOS QUE NÃO FORAM RISCADOS REPRESENTAM AS LARANJAS QUE SOBRARAM.

PORTANTO, SOBRARAM LARANJAS.

Resposta: PORTANTO, SOBRARAM 6 LARANJAS.

QUANTIDADE DE LARANJAS QUE SOBRARAM NA CESTA

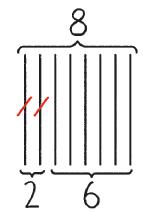
Resposta: 8 − 2 = 6

8 − 2 =

06/10/2025 18:00:55

• A atividade 1 tem por objetivo apresentar o símbolo usado para representar a subtração. Retome e aprimore os conhecimentos prévios dos estudantes com relação a esta operação. Incentive-os a expor suas ideias quanto aos cálculos mentais utilizados durante a resolução da atividade. Faça interferências quando for necessário, visto que a subtração é mais complexa do que a adição para os estudantes.

• Para um melhor aproveitamento desta atividade, apresente a eles outras subtrações para que resolvam em seus cadernos utilizando traços.

• Na atividade 2, as subtrações são realizadas com o auxílio de traços. Essa estratégia é bastante explorada em resoluções de subtrações que envolvem a ideia de tirar. Caso julgue necessário, entregue aos estudantes materiais de contagem, como tampinhas, botões e palitos, para resolverem esta atividade.

• A atividade 3 apresenta a resolução de uma subtração com o auxílio de uma régua. Caso não haja quantidade suficiente de régua para todos os estudantes, peça-lhes que formem duplas a fim de que possam realizar esta atividade. Explique a eles o passo a passo de como deverão ser realizados os cálculos de subtração com o auxílio da régua.

ATIVIDADE EXTRA

Com o objetivo de consolidar as estratégias de cálculos abordadas nesta página, solicite aos estudantes que efetuem no caderno, da maneira que preferirem, as seguintes subtrações:

• 19 5

• 18 3

• 15 14

• 14 3

Respostas

19 5 = 14

18 3

2.

A ) 14 − 3 =

Resposta: Os estudantes devem desenhar 14 tracinhos e riscar 3, restando 11 tracinhos não riscados. 14 − 3 = 11

B ) 18 − 15 =

Resposta: Os estudantes devem desenhar 18 tracinhos e riscar 15, restando 3 tracinhos não riscados. 18 − 15 = 3

3. A) Resposta: Os estudantes devem partir do número 15 na régua e “andar” 4 unidades para a esquerda. 15 − 4 = 11

C ) 17 − 11 =

Resposta: Os estudantes devem desenhar 17 tracinhos e riscar 11, restando 6 tracinhos não riscados. 17 − 11 = 6

D ) 19 − 8 =

Resposta: Os estudantes devem desenhar 19 tracinhos e riscar 8, restando 11 tracinhos não riscados. 19 − 8 = 11

3. VAMOS EFETUAR O CÁLCULO 13 − 6 USANDO UMA RÉGUA. −6 13 13 − 6 = 7

0123456789101112131415

3. B) Resposta: Os estudantes devem partir do número 11 na régua e “andar” 5 unidades

NOTE QUE FOI LOCALIZADO INICIALMENTE O NÚMERO 13 NA RÉGUA. DEPOIS, “ANDAMOS” 6 UNIDADES PARA A ESQUERDA E OBTEMOS O RESULTADO.

ASSIM COMO APRESENTADO, EFETUE OS CÁLCULOS USANDO UMA RÉGUA.

3. D) Resposta: Os estudantes devem partir do número 12 na régua e “andar” 9 unidades para a esquerda. 12 − 9 = 3

A ) 15 − 4 = B ) 11 − 5 = C ) 14 − 12 = D ) 12 − 9 =

3. E) Resposta: Os estudantes devem partir do número 15 na régua e “andar” 8 unidades para a esquerda. 15 − 8 = 7 para a esquerda. 11 − 5 = 6

E ) 15 − 8 =

3. C) Resposta: Os estudantes devem partir do número 14 na régua e “andar” 12 unidades para a esquerda. 14 − 12 = 2

4. NÍVEA EFETUOU O CÁLCULO 15 − 11 DA SEGUINTE MANEIRA.

ASSIM COMO NÍVEA, EFETUE OS CÁLCULOS E ANOTE OS RESULTADOS.

A ) 17 − 15 =

Resposta: 17 − 15 = 2

Resposta: 16 − 11 = 5

Resposta: 19 − 10 = 9

PENSO NO 11 E, DEPOIS, CONTO ATÉ O 15: 12, 13, 14, 15. 4

ASSIM: 15 − 11 = 4

Resposta: 15 − 12 = 3

Resposta: 18 − 12 = 6

5. SEM EFETUAR OS CÁLCULOS POR ESCRITO, RESOLVA MENTALMENTE CADA SITUAÇÃO APRESENTADA E ESCREVA A RESPOSTA.

A ) CRISTIANO PRECISA COSTURAR 15 BOTÕES EM UMA PEÇA DE ROUPA, MAS TEM APENAS 11 DO MESMO MODELO. QUANTAS BOTÕES FALTAM PARA COMPLETAR A QUANTIDADE QUE ELE PRECISA?

Resposta: 15 − 11 = 4; 4 BOTÕES

B ) CELINA PREPAROU 18 BOLINHOS INDIVIDUAIS PARA SERVIR DE SOBREMESA EM UM JANTAR, MAS SOMENTE 11 FORAM CONSUMIDOS. QUANTOS BOLINHOS RESTARAM?

Resposta: 18 − 11 = 7; 7 BOLINHOS

C ) CERTO PRODUTO CUSTA 17 REAIS NA LOJA A E 14 REAIS NA LOJA B. QUAL É A DIFERENÇA DE PREÇO EM REAIS DESSE PRODUTO NESSAS LOJAS?

Resposta: 17 − 14 = 3; 3 REAIS

6. VOLTE À ATIVIDADE ANTERIOR, EFETUE OS CÁLCULOS DE CADA ITEM NO CADERNO DA MANEIRA QUE PREFERIR E VERIFIQUE SE OS RESULTADOS ESTÃO CORRETOS.

Resposta pessoal. A resposta depende da precisão dos cálculos dos estudantes.

• Na atividade 4, uma estratégia que pode auxiliar os estudantes é usar os dedos das mãos para resolverem as subtrações, explorando a ideia de “quanto falta para chegar”, ou seja, eles devem fazer a seguinte pergunta: “Se eu tenho 11 unidades, quanto falta para chegar a 15 unidades?”. Assim, eles devem usar os dedos para contar a partir do número 12 até o número 15, contando (12, 13, 14 e 15) e concluindo que faltam 4 unidades.

• Na atividade 5, os estudantes vão resolver situações-problema por meio do cálculo mental. Caso tenham dificuldade, oriente-os a registrar no caderno os números mencionados no enunciado. Por exemplo, no item A, peça a eles que anotem a quantidade de botões necessária e a quantidade disponível. Com base nisso, eles podem tentar realizar a subtração mentalmente. É importante notar que, em cada item, a subtração é apresentada com uma ideia diferente: completar, retirar e comparar, respectivamente. Por isso, os estudantes podem encontrar mais facilidade em uma situação e mais dificuldade em outra. Esteja atento a essas variações para oferecer o apoio necessário e promover a compreensão dos diferentes significados da subtração.

• Na atividade 6, caso julgue conveniente, organize os estudantes em duplas para verificarem se os resultados da atividade anterior estão corretos.

06/10/2025 18:00:56

• Na atividade 7, ao responderem ao item B, espera-se que os estudantes percebam que há uma regularidade entre as subtrações efetuadas. Caso não percebam, peça-lhes que leiam apenas os resultados para descobrirem a diferença entre um número e o seu sucessor.

• Verifique no item C se os estudantes encontram nos quadros, com facilidade, as subtrações cujos resultados sejam 8. Para um melhor aproveitamento desta atividade, solicite que encontrem nos quadros e registrem no caderno as subtrações cujos resultados sejam 6.

• Para realizar o item D, faça na lousa, com o auxílio dos estudantes, o quadro das subtrações relacionadas ao número 5 e, depois, permita que façam sozinhos as subtrações relacionadas aos números de 6 a 10. Caminhe pela sala de aula a fim de acompanhar o desenvolvimento deles na atividade e sanar possíveis dúvidas, caso necessário. Respostas

7. VIVIANE ORGANIZOU ALGUMAS SUBTRAÇÕES NOS QUADROS A SEGUIR.

A ) EFETUE ESSAS SUBTRAÇÕES E COMPLETE OS CÁLCULOS

COM OS RESULTADOS OBTIDOS.

Respostas e comentários nas orientações ao professor.

B ) QUAIS REGULARIDADES VOCÊ PODE IDENTIFICAR NESSAS SUBTRAÇÕES? CONVERSE COM OS COLEGAS.

7. C) Resposta: 9 − 1 = 8; 10 − 2 = 8; 11 − 3 = 8; 12 − 4 = 8

C ) ENTRE AS SUBTRAÇÕES DESSES QUADROS, ESCREVA

7. B) Resposta pessoal. Espera-se que os estudantes analisem as operações e apontem algumas regularidades em relação ao minuendo, ao subtraendo e à diferença das

AQUELAS CUJO RESULTADO É 8.

Respostas e comentários nas orientações ao professor. subtrações. No quadro 1, por exemplo, o subtraendo de todas as subtrações é sempre 1 e o minuendo são números naturais consecutivos de 2 a 11. Além disso, as diferenças são números consecutivos de 1 a 10, na ordem que vão sendo resolvidas.

D ) VIVIANE ORGANIZOU SUBTRAÇÕES RELACIONADAS AOS

NÚMEROS 1, 2, 3 E 4. DE MANEIRA SEMELHANTE A ELA, CONSTRUA EM SEU CADERNO QUADROS COM SUBTRAÇÕES RELACIONADAS AOS NÚMEROS DE 5 A 10.

06/10/2025 18:00:56

D) Espera-se que os estudantes notem que é possível construir os quadros solicitados sem efetuar cálculos, tendo como parâmetro os fatos relevantes. No entanto, é fundamental que eles sejam capazes de efetuar os cálculos, pois as regularidades na organização dos números se repetem em todos os quadros.

SUBTRAÇÃO COM NÚMEROS ATÉ 99

SEM REAGRUPAMENTO

1. JOAQUIM FEZ ANOTAÇÕES EM CINCO DIAS DE CERTA SEMANA

SOBRE A VENDA DE LIVRETOS DE LITERATURA DE CORDEL EM SUA BANCA.

LIVRETOS VENDIDOS POR DIA, EM CERTA SEMANA

DIA DA SEMANA QUANTIDADE VENDIDA

SEGUNDA-FEIRA35

TERÇA-FEIRA 4 QUARTA-FEIRA32

QUINTA-FEIRA41

SEXTA-FEIRA45

INFOGRÁFICO CLICÁVEL: LEITURA NO DIA A DIA

LITERATURA DE CORDEL: GÊNERO LITERÁRIO POPULAR, COMUM NA REGIÃO NORDESTE DO BRASIL, EM GERAL IMPRESSO EM FOLHETOS DE BAIXO CUSTO E EXPOSTO À VENDA PENDURADO EM CORDÃO OU BARBANTE.

FONTE DE PESQUISA: ANOTAÇÕES DE JOAQUIM, EM 2027.

QUANTOS LIVRETOS JOAQUIM VENDEU NA TERÇA-FEIRA A

MAIS DO QUE NA QUARTA-FEIRA?

PARA DETERMINAR QUANTOS LIVRETOS JOAQUIM VENDEU A

MAIS NA TERÇA-FEIRA DO QUE NA QUARTA-FEIRA, EFETUAMOS 47 − 32 . ACOMPANHE ALGUMAS MANEIRAS DE FAZER ESSE CÁLCULO E COMPLETE O QUE FALTA.

UTILIZANDO CUBINHOS E BARRAS

1º .

REPRESENTAMOS O NÚMERO 47 UTILIZANDO CUBINHOS E BARRAS. EM SEGUIDA, RETIRAMOS 2 CUBINHOS (UNIDADES) E 3 BARRAS (DEZENAS).

06/10/2025 18:00:56

AVALIANDO

Objetivos

Efetuar subtrações que envolvem números até 19 utilizando o símbolo da subtração.

Resolver situações-problema que envolvem as ideias da subtração.

Sugestão de intervenção

Escreva na lousa para que os estudantes copiem e resolvam no caderno as seguintes situações-problema:

• Na festa de Laura, havia 18 convidados. Sabendo que 12 deles foram embora antes das seis ho-

ras da tarde, quantos convidados foram embora depois das seis horas da tarde?

• Henrique tem 16 canetas coloridas. Guardou 12 delas em uma caixa. Quantas canetas ainda faltam ser guardadas?

Respostas

• 18 – 12 = 6; 6 convidados foram embora depois das seis horas da tarde.

• 16 – 12 = 4; Ainda faltam ser guardadas 4 canetas.

• Leia para os estudantes a situação abordada na atividade 1. Explore as informações do quadro perguntando, por exemplo: “Quantos livretos foram vendidos na quinta-feira?”; “E na segunda-feira?”; “Em que dia foi vendida a menor quantidade de livretos?”; “Em que dia foi vendida a maior quantidade de livretos?”.

• Para resolver a situação apresentada, ou seja, determinar quantos livretos Joaquim vendeu a mais na terça-feira do que vendeu na quarta-feira, mostre aos estudantes como se efetua 47 32 na prática utilizando o material dourado com cubinhos e barras, de modo a ilustrar o uso dessa estratégia. Para um melhor aproveitamento desta atividade, explore outros exemplos com eles, utilizando as informações da tabela, como 45 32 , 47 35, 47 32 e 45 35

• Para trabalhar com a subtração pelo método da decomposição, faça alguns exemplos na lousa, a fim de consolidar essa estratégia de cálculo, e solicite aos estudantes que os resolvam no caderno.

• Por fim, utilize o algoritmo efetuando as mesmas subtrações, a fim de que percebam as diferenças existentes entre esses procedimentos de cálculo.

2º . 47 − 32 = 15

OBTEMOS, ASSIM, O RESULTADO DA SUBTRAÇÃO.

DECOMPONDO OS NÚMEROS

Resposta: 10 + 5 = 15

USANDO O ALGORITMO

SUBTRAÍMOS AS UNIDADES.

SUBTRAÍMOS AS DEZENAS.

3

1 5 MINUENDO SUBTRAENDO RESTO OU DIFERENÇA

PORTANTO, NA TERÇA-FEIRA, JOAQUIM VENDEU

LIVRETOS A MAIS DO QUE NA QUARTA-FEIRA. – –

Resposta: PORTANTO, NA TERÇA-FEIRA, JOAQUIM VENDEU 15 LIVRETOS A MAIS DO QUE NA QUARTA-FEIRA.

06/10/2025 18:00:57

LITERATURA DE CORDEL

VOCÊ CONHECE A LITERATURA

DE CORDEL? O NOME CORDEL

TEM ORIGEM NA MANEIRA COMO

ESSES FOLHETOS FICAVAM

TRADICIONALMENTE EXPOSTOS

PARA A VENDA, PENDURADOS EM UMA CORDA. ESSA TRADIÇÃO

VEIO DE PORTUGAL E FICOU MUITO

POPULAR NO NORDESTE DO BRASIL.

LIVRETOS DE CORDEL

EXPOSTOS PARA VENDA, EM OLINDA, NO ESTADO DE PERNAMBUCO, EM 2022.

O CORDEL É UM TIPO DE POEMA COM RIMAS QUE CONTA HISTÓRIAS SOBRE DIVERSOS ASSUNTOS, COMO AVENTURAS, AMOR, HERÓIS E ANIMAIS. AS CAPAS DOS FOLHETOS DE CORDEL, GERALMENTE, SÃO FEITAS COM XILOGRAVURA, UMA TÉCNICA EM QUE UM DESENHO FEITO EM UM PEDAÇO DE MADEIRA É PASSADO PARA O PAPEL, COMO SE FOSSE UM CARIMBO.

2. EFETUE AS SUBTRAÇÕES DA MANEIRA QUE PREFERIR.

B ) 58 − 47 = C ) 75 − 23 = A ) 31 − 11 =

Resposta: 31 − 11 = 20

Resposta: 58 − 47 = 11

Resposta: 75 − 23 = 52

• Pergunte aos estudantes se já viram, ouviram ou leram alguma história de cordel. Caso algum deles conheça, incentive-o a contar a história aos colegas. Se possível, leve alguns folhetos de cordel para serem apreciados pela turma. Informe a eles que, em geral, esses folhetos contêm histórias de seis ou oito páginas, que são populares e apresentam rimas. Comente também que esse tipo de literatura é tradicional em alguns estados da Região Nordeste, mas também podem ser encontrados em outras regiões do país.

• Leia o boxe com informação sobre literatura de cordel e aproveite o assunto abordado para estabelecer uma relação com o componente curricular de Língua Portuguesa, despertando nos estudantes o interesse pela leitura, trabalhando o conceito de rimas como elemento central na estrutura dos poemas de cordel e potencializando a alfabetização. Conversem sobre a importância da leitura para o desenvolvimento e formação das pessoas, exaltando alguns de seus benefícios, como o conhecimento de novos mundos por meio das histórias, o desenvolvimento da imaginação e da criatividade, a melhora na capacidade de comunicação e concentração, entre outros. Pergunte se há algum livro que eles gostariam de ter e, caso não seja possível adquiri-lo, informe-lhes que há outras possibilidades de acesso, como as bibliotecas escolares, municipais ou de bairro.

• O objetivo da atividade 2 é explorar cálculos que envolvam subtrações com números de dois algarismos sem reagrupamento, com resultado até 99. Leve para a sala de aula ábacos e solicite a eles que façam esta atividade na prática, a fim de consolidar a aprendizagem. Caso não haja quantidade suficiente de ábaco para todos, organize a turma em grupos para que possam realizar a atividade.

BNCC

06/10/2025 18:00:59

Nas atividades desta página, os estudantes são levados a construir fatos básicos da subtração e a utilizá-los no cálculo mental ou escrito, além de resolver problemas de subtração envolvendo números de até três ordens, utilizando, para isso, estratégias pessoais, o que contempla aspectos das habilidades EF02MA05 e EF02MA06

• Nas atividades 3 e 4, os estudantes são levados a utilizar as estratégias desenvolvidas anteriormente. Caso tenham dificuldade, verifique a possibilidade de usar material dourado, tracinhos no caderno ou objetos de contagem durante a resolução destas atividades, orientando-os sempre que julgar necessário.

• Na atividade 5, inicialmente, permita que os estudantes resolvam da maneira que acharem mais adequada, utilizando as estratégias que já conhecem. Em seguida, verifique se conseguem identificar que a operação necessária para resolver a situação é a subtração. Caminhe pela sala de aula a fim de acompanhar o desenvolvimento deles na atividade e sanar possíveis dúvidas, caso necessário.

3. ELISA TEM UM BRINQUEDO DE MONTAR E, PARA CONSTRUIR UMA CASINHA, ELA USOU ALGUMAS PEÇAS. A SEGUIR, ESTÃO REPRESENTADAS AS PEÇAS QUE SOBRARAM APÓS

A CONSTRUÇÃO.

A ) QUANTAS PEÇAS SOBRARAM? PEÇAS.

Resposta: 12 PEÇAS.

B ) ELISA TEM AO TODO 36 PEÇAS. QUANTAS PEÇAS ELA USOU

PARA CONSTRUIR A CASINHA? PEÇAS.

Resposta: 36 − 12 = 24; 24 PEÇAS.

4. ALGUNS NÚMEROS ESTÃO REPRESENTADOS NOS ÁBACOS.

A ) QUAL É O NÚMERO REPRESENTADO NO ÁBACO 1?

Resposta: 37

B ) QUAL É O NÚMERO REPRESENTADO NO ÁBACO 2?

Resposta: 14

C ) ESCREVA UMA SUBTRAÇÃO PARA REPRESENTAR A ALTERAÇÃO QUE OCORREU DO ÁBACO 1 PARA O ÁBACO 2

Resposta: 37 − 23 = 14

5. EM UM BARCO DE PASSEIO, EMBARCARAM 43 PASSAGEIROS. SABENDO QUE ELE PODE LEVAR ATÉ 65 PASSAGEIROS POR VEZ, QUANTAS PESSOAS AINDA PODEM EMBARCAR NESSE BARCO?

Resposta: 65 − 43 = 22. Podem embarcar nesse barco 22 PESSOAS.

6. OBSERVE A SEQUÊNCIA DE NÚMEROS.

10 , 8 , 6 , 4 , 2

PARA OBTER UM NÚMERO DESSA SEQUÊNCIA, A PARTIR DO SEGUNDO, SUBTRAÍMOS 2 UNIDADES DO NÚMERO ANTERIOR.

DESCUBRA A REGRA E COMPLETE AS SEQUÊNCIAS COM OS NÚMEROS QUE FALTAM.

88 , 77 , 66 , , , A.

94 , 84 , 74 , , , B.

6. A. Resposta: Para obter um número dessa sequência, a partir do segundo, subtraímos 11 unidades ao número anterior; 88, 77, 66, 55, 44, 33

• A atividade 6 retoma conceitos de regularidade e padrão em sequências numéricas. Faça uma retomada com os estudantes antes de resolverem esta atividade, apresentando alguns exemplos na lousa, a fim de proporcionar uma recuperação de aprendizagem para aqueles que estão com dificuldade e de consolidar os conhecimentos dos estudantes que já dominam esse procedimento.

90 , 80 , 70 , , , C. 6 7 9 9

6. B. Resposta: Para obter um número dessa sequência, a partir do segundo, subtraímos 10 unidades ao número anterior; 94, 84, 74, 64, 54, 44

7. VAMOS EFETUAR 99 − 67 UTILIZANDO UMA CALCULADORA.

COM A CALCULADORA LIGADA, DIGITE A SEQUÊNCIA DE TECLAS A SEGUIR.

6. C. Resposta: Para obter um número dessa sequência, a partir do segundo, subtraímos 10 unidades ao número

Resposta: 32

QUE RESULTADO APARECEU NO VISOR? DE MANEIRA PARECIDA, REALIZE OS CÁLCULOS A SEGUIR COM UMA CALCULADORA.

A ) 38 − 24 =

Resposta: 38 − 24 = 14

B ) 25 − 12 =

Resposta: 25 − 12 = 13

C ) 49 − 40 = D ) 82 − 71 =

Resposta: 49 − 40 = 9

Resposta: 82 − 71 = 11

E ) 63 − 43 = F ) 56 − 22 =

Resposta: 63 − 43 = 20

Resposta: 56 − 22 = 34

DICA: CONFIRA COM UM COLEGA OS RESULTADOS OBTIDOS.

anterior; 90, 80, 70, 60, 50, 40 93

06/10/2025 18:00:59

• Para realizar a atividade 7, providencie calculadoras antecipadamente e leve-as para a sala de aula. Caso não haja quantidade suficiente para todos, organize-os em grupos a fim de resolverem a atividade proposta. Nesta atividade, é sugerido aos estudantes que confiram seus resultados com os colegas, pois esse tipo de interação auxilia no processo de aprendizagem. Incentive-os a investigar o que pode ter acontecido caso um deles apresente algum resultado diferente.

BNCC

Durante a resolução da atividade 6 , os estudantes têm a possibilidade de aprofundar seus conhecimentos sobre sequências numéricas, descrevendo sua regularidade e identificando os elementos ausentes, contemplando, assim, as habilidades EF02MA09, EF02MA10 e EF02MA11

• Ao trabalhar a atividade 1, incentive o cálculo mental e, em seguida, a construção do sistema de registro. Caso algum estudante resolva mentalmente a subtração proposta, aproveite esse momento para promover a colaboração entre eles: um pode explicar oralmente como pensou (seu raciocínio), enquanto o outro registra na lousa a explicação.

• Caso algum estudante resolva mentalmente a subtração proposta, aproveite o momento para promover a colaboração entre todos da turma. Enquanto um colega explica oralmente a construção de seu raciocínio, outro pode registrar na lousa a explicação. Essa prática favorece diferentes maneiras de participação e respeita o tempo e o modo de aprender de cada estudante, permitindo as adaptações necessárias para estudantes com NEE.

• A atividade 1 tem como objetivo apresentar a subtração com reagrupamento com números até 99. Além disso, há em seu contexto dados numéricos expressos em um quadro, permitindo aos estudantes que interpretem esses dados.

• Antes de explicar a estratégia apresentada nesta página para efetuar a subtração com reagrupamento, pergunte aos estudantes como eles resolveriam essa situação. Permita que comentem as próprias estratégias de cálculo e verifique como é possível aproveitar essas ideias, conduzindo uma conversa para estabelecer relações entre as estratégias dos estudantes e as que serão trabalhadas neste tópico.

SUBTRAÇÃO COM REAGRUPAMENTO

1. A ESCOLA CARROSSEL REALIZOU UMA GINCANA COM TRÊS EQUIPES. A PONTUAÇÃO FOI REGISTRADA NO QUADRO A SEGUIR.

PONTUAÇÃO POR EQUIPE EQUIPESPONTUAÇÃO

EQUIPE A 71

EQUIPE B 53

EQUIPE C 62

PARA DETERMINAR QUANTOS PONTOS A EQUIPE A MARCOU A MAIS DO QUE A EQUIPE B, CALCULAMOS 71 − 53 . DE ACORDO COM OS CÁLCULOS APRESENTADOS, COMPLETE O QUE FALTA.

UTILIZANDO CUBINHOS E BARRAS

1

2

REPRESENTAMOS O NÚMERO 71 COM CUBINHOS E BARRAS.

PRECISAMOS RETIRAR 3 UNIDADES DE 1 UNIDADE. COMO 3 É MAIOR DO QUE 1, TROCAMOS 1 BARRA (1 DEZENA) POR 10 CUBINHOS (10 UNIDADES), FICANDO COM 6 DEZENAS E 11 UNIDADES. ENTÃO, RETIRAMOS 3 CUBINHOS (UNIDADES) E 5 BARRAS (DEZENAS) E OBTEMOS O RESULTADO DA SUBTRAÇÃO.

− 53 = 18

DECOMPONDO OS NÚMEROS

Resposta: 10 + 8 = 18

USANDO O ALGORITMO

VAMOS SUBTRAIR 3 UNIDADES DE 1 UNIDADE. COMO 3 É MAIOR DO QUE 1, TROCAMOS 1 DEZENA POR 10 UNIDADES E ADICIONAMOS À 1 UNIDADE EXISTENTE, FICANDO COM 6 DEZENAS E 11 UNIDADES. ASSIM, SUBTRAÍMOS 3 UNIDADES DE 11 UNIDADES. 1º .

PORTANTO, A EQUIPE A MARCOU

PONTOS A MAIS DO QUE A EQUIPE B.

Resposta: PORTANTO, A EQUIPE A MARCOU 18 PONTOS A MAIS DO QUE A EQUIPE B 95

06/10/2025 18:05:49

• Para trabalhar com a subtração com reagrupamento pelo método da decomposição apresentado nesta página, faça outros exemplos na lousa e solicite aos estudantes que os resolvam no caderno. Por fim, utilize o algoritmo efetuando as mesmas subtrações a fim de que percebam as diferenças existentes entre estas estratégias de cálculo. Ao usar o algoritmo da subtração com reagrupamento, enfatize que, ao “riscar” o algarismo 7 e substituí-lo pelo 6, foi feita a troca de 1 dezena por 10 unidades e, por isso, essa dezena passa a ter 11 unidades.

• Para um melhor aproveitamento desta atividade, organize a turma em duplas e solicite que determinem, resolvendo no caderno, quantos pontos a equipe A marcou a mais do que a equipe C e quantos pontos a equipe C marcou a mais do que a equipe B e verifiquem qual foi a maior diferença entre as subtrações efetuadas.

• Na atividade 2, incentive os estudantes a resolverem a situação proposta da maneira que preferirem, usando, para isso, recursos como material dourado, ábaco, reta numérica ou materiais de contagem.

• O objetivo da atividade 3 é levar os estudantes a relacionarem cada enunciado à sua solução. Para isso, auxilie-os a ler e compreender o enunciado da situação-problema, relacionando-o à operação matemática que o representa. Depois, devem escrever a letra no quadro da solução correspondente e, por fim, completar as soluções.

2. EFETUE AS SUBTRAÇÕES DA MANEIRA QUE PREFERIR.

A ) 51 − 34 = B ) 98 − 69 = C ) 76 − 57 =

Resposta: 51 − 34 = 17 Resposta: 98 − 69 = 29 Resposta: 76 − 57 = 19

3. RELACIONE CADA ENUNCIADO À SUA SOLUÇÃO. PARA ISSO, ESCREVA A LETRA NO QUADRO DA SOLUÇÃO CORRESPONDENTE. POR ÚLTIMO, COMPLETE AS SOLUÇÕES.

A.

MARIANE TEM 36 REAIS. CÉSAR TEM 29 REAIS A MAIS DO QUE MARIANE. QUANTOS REAIS CÉSAR TEM?

B.

GABRIELA TINHA 36 REAIS E GASTOU 29 REAIS NA COMPRA DE UM LIVRO. COM QUANTOS REAIS GABRIELA FICOU?

C.

CARMEM TINHA 45 REAIS E GANHOU 18 REAIS DA MÃE DELA. COM QUANTOS REAIS ELA FICOU?

D. 45 − 18 =

ELISA TEM 45 REAIS. MATEUS TEM 18 REAIS A MENOS DO QUE ELISA. QUANTOS REAIS MATEUS TEM?

+ 29 =

− 29 =

+ 18 = Resposta: A. 36 + 29 = 65; B. 36 − 29 = 7; C. 45 + 18 = 63; D. 45 − 18 = 27

06/10/2025 18:05:49

4. UTILIZANDO O ÁBACO DE PAPEL E AS CONTAS RECORTADAS

DAS PÁGINAS 263 E 265 DO MATERIAL COMPLEMENTAR, RESOLVA AS SUBTRAÇÕES A SEGUIR.

A ) 34 − 28 =

Resposta: 34 − 28 = 6

B ) 65 − 56 =

Resposta: 65 − 56 = 9

5. GLÁUCIA TINHA 35 LIVROS EM UMA

CAIXA E GUARDOU 18 DELES EM UMA ESTANTE. QUANTOS LIVROS AINDA FICARAM NA CAIXA?

LIVROS.

6. CARLOS ESTÁ PREPARANDO UM PÃO QUE DEVE FICAR NO FORNO

ASSANDO DURANTE 55 MINUTOS.

JÁ FAZ 16 MINUTOS QUE CARLOS COLOCOU O PÃO PARA ASSAR.

QUANTOS MINUTOS AINDA FALTAM PARA O PÃO TERMINAR DE ASSAR?

C ) 80 − 51 =

Resposta: 80 − 51 = 29

D ) 74 − 17 =

Resposta: 74 − 17 = 57

Resposta: 35 − 18 = 17 17 LIVROS.

Resposta: 55 − 16 = 39. FALTAM 39 MINUTOS PARA O PÃO TERMINAR DE ASSAR.

7. DENILSON PRETENDE COMPRAR UMA CALÇA QUE CUSTA 85 REAIS. PARA ISSO, ELE JÁ ECONOMIZOU 78 REAIS.

Resposta: 78 REAIS.

A ) QUANTOS REAIS DENILSON ECONOMIZOU? REAIS.

B ) ESSA QUANTIA É SUFICIENTE PARA COMPRAR A CALÇA?

Resposta: Não.

C ) CASO A QUANTIA NÃO SEJA SUFICIENTE, QUANTOS REAIS FALTAM PARA DENILSON COMPRAR A CALÇA? REAIS.

Resposta: 85 − 78 = 7 7 REAIS.

97

06/10/2025 18:05:49

• Para a atividade 4, avalie a possibilidade de providenciar cubinhos e barras do material dourado para realizar os cálculos, como recurso complementar na compreensão desta atividade.

• As atividades 5 e 6 abordam situações envolvendo subtração com reagrupamento. Permita aos estudantes que as resolvam da maneira que preferirem. Compartilhe com a turma as diferentes estratégias de resolução e incentive o registro das operações usadas para resolvê-las.

• A atividade 7 aborda uma situação que envolve subtração com ideia de completar. Verifique se os estudantes associam a situação à operação da subtração. Se julgar necessário, faça alguns exemplos na lousa, a fim de consolidar essa estratégia de cálculo, e solicite que os resolvam no caderno.

• A atividade 8 integra as unidades temáticas de Matemática Números e Probabilidade e estatística ao relacionar a quantidade de estudantes por turma e demonstrá-la em um gráfico de barras.

• Na atividade 8, espera-se que os estudantes utilizem os conhecimentos adquiridos sobre os conteúdos trabalhados de adição e subtração por meio da interpretação das informações expressas no gráfico. Para um melhor aproveitamento desta atividade, faça outros questionamentos com relação aos dados do gráfico, por exemplo: “Quantos estudantes estudam no 3º ano?”; “Quantos estudantes estudam no 5º ano?”; “As turmas do 5º ano têm ao todo quantos estudantes a mais do que as turmas do 1º ano juntas?”.

BNCC

A atividade 8 solicita aos estudantes que comparem as informações por meio de um gráfico de barras, abordando, assim, aspectos da habilidade EF02MA22.

8. COM BASE NO GRÁFICO, RESPONDA ÀS QUESTÕES. ESTUDANTES POR TURMA DA ESCOLA ALFA, EM 2027

Unidades temáticas integradas

FONTE DE PESQUISA: SECRETARIA DA ESCOLA ALFA.

A ) QUAL É A TURMA COM A MENOR QUANTIDADE DE

ESTUDANTES?

Resposta: 1º ANO A.

B ) QUAL É O TOTAL DE ESTUDANTES NO 2º ANO?

Resposta: 38 + 35 = 73. NO 2º ANO, ESTUDAM 73 ESTUDANTES.

C ) AS TURMAS DO 2º ANO TÊM AO TODO QUANTOS ESTUDANTES A MAIS DO QUE AS TURMAS DO 3º ANO JUNTAS?

Resposta: 30 + 35 = 65; 73 − 65 = 8. 8 ESTUDANTES A MAIS.

REFERÊNCIAS COMPLEMENTARES

HONORATO, Agda Isabele Gonsalves. Adição e subtração nas séries iniciais: uma abordagem na perspectiva da aprendizagem baseada em jogos. In: CONGRESSO NACIONAL DE EDUCAÇÃO, 8, 2023, João Pessoa. Anais... Disponível em: https://editorarealize.com.br/editora/anais/ conedu/2022/TRABALHO_COMPLETO_EV174_ MD1_ID9325_TB1870_14102022225910.pdf. Acesso em: 2 ago. 2025.

Esse artigo possibilita explorar ideias associadas a jogos envolvendo adição e subtração, abordando esses conteúdos por meio do Jogo dos dados em uma turma do 2º ano do Ensino Fundamental I.

9. ELIANA COMPROU DOIS ÁLBUNS PARA ORGANIZAR SUAS FOTOS. EM UM DELES, É POSSIVEL COLOCAR 42 FOTOS E, NO OUTRO, 16 A MENOS DO QUE NO PRIMEIRO ÁLBUM.

A ) QUANTAS FOTOS É POSSÍVEL ORGANIZAR NO ÁLBUM

MENOR? FOTOS.

B ) QUANTAS FOTOS NO MÁXIMO ELIANA PODE ORGANIZAR NESSES DOIS ÁLBUNS?

FOTOS.

Resposta: 42 − 16 = 26. 26 FOTOS. Resposta: 42 + 26 = 68. 68 FOTOS.

10. COM O PROFESSOR E OS COLEGAS, LEIA O TEXTO A SEGUIR.

Na fila de uma sala de cinema com 80 lugares estão 25 mulheres, 16 crianças e 21 homens.

COM A AJUDA DO PROFESSOR, ELABORE UM PROBLEMA COM ESSES DADOS ENVOLVENDO SUBTRAÇÃO. DEPOIS, DÊ O PROBLEMA QUE VOCÊ FEZ PARA UM COLEGA RESOLVER NO CADERNO. POR ÚLTIMO, VERIFIQUEM SE A RESPOSTA ESTÁ CORRETA.

Resposta pessoal. Espera-se que os estudantes elaborem um problema envolvendo os dados do enunciado e resolvam o problema elaborado pelo colega. Professor, professora: Oriente os estudantes na escrita do problema da atividade 10, incentivando o traçado em letra cursiva na pauta apresentada.

Ao propor a elaboração de um problema envolvendo o cálculo de subtração, com os significados de retirar usando estratégias pessoais em sua resolução, a atividade 11 contempla aspectos da habilidade EF02MA06

06/10/2025 18:05:49

• Na atividade 9, avalie a possibilidade de disponibilizar ábacos aos estudantes para que possam utilizar esse recurso como apoio na realização dos cálculos.

• Na atividade 10, os estudantes devem elaborar um problema com os dados apresentados, envolvendo o cálculo de subtração. Depois, devem entregar o problema para um colega resolver e, por último, verificar se a resposta está correta. Se houver dificuldades ao trabalhar com esta atividade, oriente-os na elaboração dos enunciados dos problemas. Comente que, ao elaborar um enunciado de problema, deve-se considerar algum tema e utilizar informações necessárias para que seja possível obter sua solução. Também é muito importante que o enunciado seja relido e revisado, a fim de aprimorar e verificar se não faltam dados.

• Caso julgue necessário, após a atividade 10, para reforçar a prática e o direcionamento da escrita das frases, utilize o caderno de caligrafia, de modo que eles possam desenvolver progressivamente a escrita da letra cursiva.

BNCC

• A atividade 11 estabelece uma integração entre as unidades temáticas de Matemática Números e Probabilidade e estatística ao relacionar a quantidade de hortaliças colhidas em três semanas, organizada em uma tabela. Na resolução do item B, é possível que alguns estudantes associem a expressão a mais à operação da adição. Caso isso ocorra, oriente-os a comparar a quantidade de pés de alface com a quantidade de pés de rúcula.

BNCC

A atividade 11 solicita aos estudantes que comparem dados apresentados em uma tabela de dupla entrada, abordando, assim, aspectos da habilidade EF02MA22

• No Desafio a mais, os estudantes exercitam o raciocínio lógico-matemático ao completar um quadrado mágico em que cada linha, coluna e diagonal somam 81. Para isso, devem adicionar os dois números já fornecidos e subtrair de 81 para encontrar o número que falta. Exemplo:

• Adicionar os dois números da primeira coluna: 31 + 26 = 57

• Subtrair o resultado da soma mágica: 81 57 = 24 O número 24 preenche o espaço vazio na primeira coluna.

• Aplicar a mesma lógica para outra linha, coluna ou diagonal, preenchendo os demais espaços até completar todo o quadrado.

Resposta

11. HORÁCIO CULTIVA HORTALIÇAS. NA TABELA, ESTÁ APRESENTADA A QUANTIDADE DE ALGUMAS HORTALIÇAS QUE ELE COLHEU DURANTE TRÊS SEMANAS.

HORTALIÇAS COLHIDAS POR HORÁCIO

HORTALIÇA

QUANTIDADE

SEMANA 1SEMANA 2SEMANA 3

PÉ DE ALFACE21 23 18

PÉ DE RÚCULA 18 27 15

CENOURA 21 25 18 BETERRABA14 17 14

HORTALIÇAS: PLANTAS CULTIVADAS EM HORTAS PARA O CONSUMO HUMANO.

FONTE: ANOTAÇÕES DE HORÁCIO. DE ACORDO COM AS INFORMAÇÕES DA TABELA, EFETUE OS CÁLCULOS NO CADERNO E REGISTRE OS RESULTADOS EM CADA ITEM.

A ) DURANTE ESSAS SEMANAS, HORÁCIO COLHEU QUANTOS

PÉS DE ALFACE? PÉS DE ALFACE.

Resposta: 21 + 23 + 18 = 62. 62 PÉS DE ALFACE.

B ) QUANTOS PÉS DE RÚCULA HORÁCIO COLHEU A MAIS NA

SEMANA 2 DO QUE NA SEMANA 1? PÉS DE RÚCULA.

Resposta: 27 − 18 = 9 9 PÉS DE RÚCULA.

C ) DURANTE ESSAS TRÊS SEMANAS, QUANTAS CENOURAS HORÁCIO COLHEU A MAIS DO QUE BETERRABAS?

CENOURAS.

Resposta: 21 + 25 + 18 = 64, 14 + 17 + 14 = 45, 64 − 45 = 19 19 CENOURAS.

DESAFIO A MAIS

DESCUBRA O MISTÉRIO DO QUADRADO MÁGICO! PARA RESOLVER ESTE DESAFIO, VOCÊ PRECISA COMPLETAR OS ESPAÇOS EM BRANCO, GARANTINDO QUE A SOMA DOS NÚMEROS DE CADA LINHA, COLUNA E DIAGONAL SEJA SEMPRE 81.

Resposta nas orientações ao professor 100

AVALIANDO

Objetivo

Identificar as estratégias estudadas para efetuar adições e subtrações com resultado até 99, utilizando cubinhos e barras, decomposição de números, ábaco e algoritmo.

Sugestão de intervenção

Retome os conteúdos, verificando se os estudantes conseguem efetuar adições e subtrações com resultado até 99 usando a decomposição de números, o ábaco e o algoritmo. Proponha

LINHA COLUNA DIAGONAL 28 31 26

06/10/2025 18:05:49

a seguinte atividade coletiva: leve cartolina e canetas, peça que relembrem e comentem as estratégias trabalhadas e registre com eles os exemplos na lousa. Ao final, selecione um exemplo de cada método (cubinhos, barras, ábaco, algoritmo e decomposição), escreva-os na cartolina e fixe-a na sala.

DIVIRTA-SE E APRENDA

JOGO DO CÁLCULO RÁPIDO

PARA BRINCAR COM ESSE JOGO, JUNTE-SE A DOIS

COLEGAS E DESTAQUEM OS CARTÕES DE RESULTADO E DE OPERAÇÕES QUE ESTÃO NAS PÁGINAS 267 E 269 DO MATERIAL

COMPLEMENTAR

NESSE JOGO, O DESAFIO É FAZER O CÁLCULO MAIS RÁPIDO QUE O COLEGA PARA PONTUAR.

REGRAS

• A CADA RODADA, UM DOS PARTICIPANTES DEVE SER O JUIZ, QUE VAI SORTEAR UM CARTÃO COM NÚMERO E COLOCÁ-LO SOBRE A MESA.

• AO SINAL DE INICIAR, OS DOIS PARTICIPANTES DEVEM ENCONTRAR, ENTRE OS CARTÕES QUE TÊM, AQUELE COM A ADIÇÃO OU A SUBTRAÇÃO CUJO RESULTADO SEJA O NÚMERO DO CARTÃO COLOCADO SOBRE A MESA.

• QUEM EFETUAR O CÁLCULO MAIS RÁPIDO E COLOCAR PRIMEIRO O CARTÃO CORRESPONDENTE NA MESA MARCA 2 PONTOS. SE O CARTÃO APRESENTADO NÃO CORRESPONDER AO CÁLCULO CORRETO, O OPONENTE MARCA 1 PONTO.

• QUANDO ACABAREM OS CARTÕES COM NÚMERO, A RODADA TERMINA E VENCE QUEM TIVER MAIS PONTOS.

CONCLUSÃO

Acompanhar o desenvolvimento dos estudantes é fundamental para um ensino bem-sucedido. Ao longo da unidade, foram propostas diversas maneiras de avaliar a aprendizagem da turma. A fim de realizar um monitoramento mais abrangente e organizado, registre nos relatórios individuais ou nas fichas de avaliação o desempenho de cada estudante, levando em consideração suas particularidades. Um modelo desse tipo de ficha pode ser

encontrado no tópico Avaliação deste manual. Assim, será possível visualizar de modo individual as trajetórias de aprendizagem, incluindo os avanços e os pontos de dificuldades a serem sanados por meio de atividades que promovam recuperação dos conteúdos.

Esse método de verificar a progressão dos estudos e identificar o que a turma de fato conseguiu aprender e o que ficou com lacunas de absorção é de grande importância para que seja possível re-

• Para a execução do jogo proposto na seção Divirta-se e aprenda, organize os estudantes em trios e peça a eles que decidam, entre si, quem será o juiz da rodada. Após cada rodada, o jogador vencedor assume o papel de juiz, enquanto os outros dois continuam o jogo.

• Esse jogo incentiva o cálculo mental envolvendo adição e subtração, além de permitir a retomada de conceitos trabalhados de maneira lúdica e significativa.

• Se julgar oportuno, disponibilize uma calculadora ao juiz de cada grupo para que ele verifique os resultados das operações, contribuindo para a autonomia e a conferência coletiva dos cálculos realizados.

Sugestão de Desafio

Quantas vezes podemos subtrair o número 2 do número 22?

Resposta

Podemos subtrair o número 2 do número 22 apenas uma vez.

• Ao propor esta atividade, verifique se os estudantes percebem que é possível subtrair o número 2 do número 22 apenas uma vez, pois, ao efetuar a primeira subtração, o minuendo deixará de ser o 22 e passará a ser o número 20.

06/10/2025 18:05:50

pensar estratégias em sala de aula, tornando as ações pedagógicas cada vez mais eficazes.

A conclusão da unidade é o momento de avaliar se os objetivos por ela propostos foram alcançados. Para esse diagnóstico, observe no final destas orientações algumas possibilidades de avaliação formativa que permitem realizar o monitoramento da aprendizagem dos estudantes e intervir caso eles não tenham atingido os resultados esperados.

OBJETIVOS DA UNIDADE

• Compor e decompor números até 999.

• Ler e escrever os números até 1 000 com algarismos e por extenso.

• Representar os números até 1 000 no quadro de ordens e classes.

• Identificar o antecessor e o sucessor de um número.

• Comparar números e determinar qual é o maior, o menor e quais são iguais.

• Interpretar dados obtidos em pesquisa e organizá-los em tabelas e gráficos.

• Identificar os elementos faltantes em sequências.

• Identificar o Real como unidade do nosso sistema monetário.

• Resolver situações-problema que envolvem o sistema monetário brasileiro.

• Reconhecer cédulas e moedas do sistema monetário brasileiro e equivalência de valores.

INTRODUÇÃO E JUSTIFICATIVA

Nesta unidade, são propostas atividades que trabalham a centena, ampliando o campo numérico até o número 999, de modo que os estudantes reconheçam e escrevam esses números por extenso e com algarismos. As práticas propostas permitem o aprendizado do agrupamento em centenas, da comparação dos números, o uso do ábaco e do quadro de ordens a fim de que eles identifiquem as representações de números até a ordem das centenas. O número 1 000 é apresentado, com o auxílio do material dourado, por meio de agrupamentos e de trocas. São propostas atividades que exploram a interpretação de dados em tabela e gráfico, entre outras habilidades que permitem desenvolver o pensamento numérico. E ainda, a fim de oportunizar a aquisição do conhecimento sobre moedas e cédulas do

UNIDADE4 NÚMEROS ATÉ 1 000

Pipas sendo empinadas em Lancashire, no Reino Unido, durante um festival de pipas à beira-mar, em 14 de setembro de 2024.

Real, são desenvolvidas atividades que envolvem o sistema monetário brasileiro, visando capacitá-los a solucionar situações-problema que envolvam as operações de compra, abrangendo o sistema monetário brasileiro e o reconhecimento de cédulas e moedas e equivalência de valores. Habilidades da BNCC trabalhadas na unidade: EF02MA01 , EF02MA02 , EF02MA03 , EF02MA04, EF02MA09, EF02MA10, EF02MA11 e EF02MA20

SUGESTÃO DE ESTRATÉGIA INICIAL

Organize a turma em equipes com quatro in-

tegrantes cada e providencie palitos de madeira e elásticos em quantidade suficiente para eles. Distribua a cada equipe 90 palitos e 9 elásticos. Oriente-os a reunir os palitos em grupos de 10 e amarrá-los com o elástico, formando o máximo de grupos possível. Ganha a equipe que conseguir formar primeiro os 9 grupos com 10 palitos. Permita às outras equipes que terminem de formar os grupos de palitos, após definir o vencedor. Em seguida, escolha uma das equipes e conte, com a ajuda dos estudantes, os grupos de palitos (10, 20, 30...) para toda a turma. Verifique se eles realizam as contagens, compreendendo, assim, os agrupamentos feitos.

As pipas são brinquedos construídos com varetas de madeira ou de bambu e cobertas por papel de seda, plástico ou tecido. Para empiná-las, amarra-se uma linha em sua armação. Elas podem ter formatos e dimensões variadas, e as mais sofisticadas e criativas podem ser no formato de caixote, pessoa, animal, entre outras.

1 a 3. Respostas nas orientações ao professor

Você já brincou de empinar pipa? Se sim, conte ao professor e aos colegas.

Sem contar uma a uma, estime quantas pipas aparecem na imagem.

Em sua opinião, por que as pessoas retratadas na imagem estão empinando pipas?

cida com as da imagem e se já brincaram ou gostariam de brincar de empinar pipa. Deixe que compartilhem suas experiências com a turma. Engaje todos na troca de informações e acolha com atenção e respeito a contribuição de cada um.

• Após responderem à questão 2 , por meio de uma estimativa, peça aos estudantes que contem as pipas que aparecem na cena. Verifique se as estimativas feitas por eles foram adequadas e próximas da resposta correta. Pergunte qual foi o critério que eles usaram para apresentar uma boa aproximação.

• Após os estudantes responderem à questão 3, pergunte se conhecem algum lugar na cidade onde as pessoas podem se reunir para empinar pipas com segurança.

Respostas

1. Resposta pessoal. Espera-se que os estudantes relatem suas experiências com relação à brincadeira de empinar pipas.

2. Resposta pessoal. Espera-se que os estudantes estimem a quantidade de pipas que há na imagem. Espera-se que eles estimem quantidades entre 100 e 150.

3. Resposta pessoal. Espera-se que os estudantes respondam: para se diverti-

• Leia o texto das páginas de abertura com os estudantes e peça-lhes que analisem a fotografia e seus detalhes. Em seguida, converse com eles sobre a atividade de empinar pipas. Diga-lhes que é uma prática comum, tanto para crianças como para adultos e que em muitos lugares existem competições dessa atividade. No Brasil, empinar pipa é uma prática muito conhecida e, nas diferentes regiões do país, ela pode ser identificada por outros nomes, como arraia, barrilete, papagaio, pandorga e quadrado. Porém, para empinar pipas são necessários alguns cuidados para evitar acidentes. A desatenção e a falta de cuidado são fatores de risco importantes. Os lugares mais seguros para essa prática são praias, parques ou campos abertos, pois nesses locais não há postes nem fios de eletricidade por perto. Enfatize que o contato dos fios com a rede elétrica pode ocasionar choques e queimaduras graves, com perigo à vida. Além disso, o uso de cerol ou qualquer material cortante na linha é proibido, pois pode machucar as pessoas que se enroscarem nela. Finalize informando que a prática de empinar pipas deve ser sempre supervisionada por um adulto, e que é necessário respeitar o espaço de outras pessoas e preservar o meio ambiente.

• Ao abordar a questão 1, pergunte aos estudantes se já viram alguma pipa pare-

06/10/2025 18:08:05

rem, para participarem de um torneio de pipas, para confraternizarem, entre outros motivos.

BNCC

A questão 2 contempla aspectos da habilidade EF02MA02 da BNCC, pois permite que os estudantes desenvolvam estratégias para estimar a quantidade de pipas na fotografia.

JOHN KEENAN/SHUTTERSTOCK.COM

• Para compreender os números até 999, o pré-requisito é o domínio da contagem até 100, a compreensão do conceito de unidades, dezenas e centenas e a relação entre eles.

• Providencie com antecedência e leve para a sala de aula o material dourado para o trabalho com a atividade 1. Utilize-o a fim de que os estudantes compreendam na prática os agrupamentos e as trocas necessárias para representar os números.

• Caso não haja material dourado suficiente para todos os estudantes, organize-os em duplas, para que possam fazer a atividade.

• Leia o enunciado da atividade 1 e pergunte aos estudantes se já viram um arranha-céus e a que cidade ele pertence. Comente que os arranha-céus são considerados símbolos de poder econômico e tornam-se pontos de referência, assim como esculturas, templos ou palácios, em diversos países do mundo, além de atraírem turistas. O objetivo da atividade 1 é introduzir os números até 999. Represente com eles o número 828 utilizando o material dourado e realize tambémsua decomposição por meio de adição. Exponha na lousa esse número no quadro de ordens e sua escrita por extenso.

• Para promover a inclusão de estudantes com NEE, use o material concreto (material dourado) para representar o número 828 com cubinhos, barras e placas, facilitando a manipulação e percepção deles, motivando-os a manipular os materiais, utilizando dessa maneira os sentidos da visão e o tato.

OS NÚMEROS ATÉ 999

1. Arranha-céus são edifícios habitáveis com mais de 40 andares ou com altura de aproximadamente 150 metros de comprimento. No Brasil, existem vários arranha-céus, mas entre os mais altos do mundo está o edifício Burj Khalifa, localizado em Dubai, nos Emirados Árabes Unidos, com altura aproximada de 828 metros de comprimento.

Edifício Burj Khalifa, em Dubai, nos Emirados Árabes Unidos, em 2024.

As imagens mostram a representação do número 828 por meio de cubinhos, barras e placas. Com base nelas, complete corretamente as informações.

centenas. dezenas. unidades.

Resposta: 8 centenas.Resposta: 2 dezenas.

Decomposição: 800 + 20 + 8

Resposta: 8 unidades.

Representação do número 828 no quadro de ordens.

QUADRO DE ORDENS

CENTENA DEZENA UNIDADE

8 2 8

Por extenso: oitocentos e vinte e oito.

BNCC

As atividades deste tópico buscam desenvolver nos estudantes as habilidades EF02MA01 e EF02MA04 da BNCC, ao comparar e ordenar números naturais até a ordem de centenas e apresentar a composição e a decomposição de números naturais de até três ordens, utilizando como suporte o material dourado, o quadro de ordens e o ábaco.

ATIVIDADE EXTRA

A fim de sanar possíveis dúvidas e para um melhor aproveitamento da atividade 1, repita os mesmos processos utilizados, porém com outros números, como 150, 389, 501 ou 998.

2. De acordo com os números representados, complete cada item.

QUADRO DE ORDENS

CENTENA DEZENA UNIDADE

7 2 3

Por extenso:

Dica: Cada algarismo assume um valor de acordo com a posição que ele ocupa no número.

Resposta: 700 + 20 + 3

700 + +

Valor posicional: 3 unidades

Valor posicional: 20 unidades

Valor posicional: 700 unidades

Resposta: Setecentos e vinte e três.

QUADRO DE ORDENS

CENTENA DEZENA UNIDADE

4 5 1

Dica: O número 237, por exemplo, é formado pelos mesmos algarismos que o número 723 indicado anteriormente. No caso do número 237, o valor posicional do algarismo 7 é 7 unidades, do algarismo 3 é 30 unidades e do algarismo 2 é 200 unidades

400 + +

Resposta: 400 + 50 + 1

Valor posicional: unidade

Valor posicional: unidades

Resposta: Unidade: 1 unidade; dezena: 50 unidades; centena: 400 unidades.

Valor posicional: unidades

• A atividade 2 tem por objetivo que os estudantes analisem a composição e decomposição de números, de até três ordens, representados por meio de cubinhos, barras e placas e, posteriormente, que os representem no quadro de ordens, bem como escrevê-los por extenso. Utilize em sala de aula o material dourado, a fim de que eles compreendam na prática os agrupamentos e as trocas necessárias para representar os números.

• Caso não haja material dourado suficiente para todos os estudantes, organize-os em duplas para que possam fazer a atividade.

Por extenso:

Resposta: Quatrocentos e cinquenta e um.

ATIVIDADE EXTRA

Para um melhor aproveitamento da atividade desta página e a fim de sanar possíveis dúvidas, proponha aos estudantes que façam os mesmos procedimentos apresentados na atividade 2 para os números 658, 685, 568, 586, 865 e 856. Pergunte qual é o valor posicional dos algarismos em cada caso e peça-lhes que anotem no caderno a decomposição por adição e a escrita por extenso de cada um.

06/10/2025 18:08:09

• A atividade 3 relaciona as unidades temáticas de Matemática Números e Probabilidade e estatística ao trabalhar com leitura, interpretação e representação, de dados de uma pesquisa, em uma tabela e em um gráfico de colunas.

• A atividade 3 visa possibilitar aos estudantes o preenchimento de uma tabela e a finalização de um gráfico, com dados provenientes de uma pesquisa pronta representada com risquinhos. Proponha-lhes que resolvam esta atividade em duplas, preenchendo cada tipo de representação com os dados indicados na atividade. Peça também a eles que comparem os dois tipos de representações, identificando semelhanças e diferenças, e descrevam suas vantagens com relação à comunicação dos dados. Para concluir a atividade, promova uma discussão a respeito dessas observações, conferindo as construções realizadas pelas duplas.

3. Marlene realizou uma pesquisa em outubro de 2027 para determinar qual é a atividade de lazer preferida de alguns amigos e familiares. A seguir, estão indicados os dados coletados por ela.

Unidades temáticas integradas

Professor, professora: Verifique se os estudantes compreenderam que um tracinho indicado na pesquisa corresponde a um voto. Caso perceba dificuldade, reforce essa informação durante a execução desta atividade.

Qual é o seu lazer preferido? esportes:

Leitura:

Assistir a filmes:

Viajar:

Outros:

Dica: Cada pessoa respondeu apenas uma única vez.

Organize os dados obtidos por Marlene na tabela e no gráfico a seguir.

Lazer preferido de alguns amigos e familiares de Marlene, em 2027

Lazer Quantidade de pessoas

Resposta: Os estudantes devem completar a tabela indicando o nome da atividade de lazer e a quantidade de dados obtidos na pesquisa realizada por Marlene, na ordem indicada, da seguinte maneira: Praticar esportes: 35; Leitura: 20; Assistir a filmes: 45; Viajar: 15; Outros: 5.

Fonte de pesquisa: registros de Marlene.

Resposta: Os estudantes devem utilizar os dados preenchidos na tabela para a composição do gráfico. Confira a resposta desse gráfico nas orientações ao professor

Lazer preferido de alguns amigos e familiares de Marlene, em 2027

Quantidade de pessoas

Fonte de pesquisa: registros de Marlene.

O LAZER NAS COMUNIDADES QUILOMBOLAS

O lazer é diferente para todo mundo! Para muitas crianças, é divertido praticar esportes, ler, assistir a filmes, viajar ou brincar com jogos eletrônicos, por exemplo.

Já em comunidades quilombolas, onde vivem descendentes de pessoas negras que resistiram à escravidão e lutaram por liberdade, o lazer também está presente em atividades como correr ao ar livre, ouvir histórias contadas pelos mais velhos e participar de cantos, danças e brincadeiras tradicionais. Em algumas dessas comunidades, danças como o lundum, a varsa, o carimbó e a mazurca são vividas por crianças e adultos como modo de manter viva a cultura dos seus antepassados.

• Leia o texto apresentado na página com os estudantes e aborde as diferentes maneiras de lazer da cultura dos Quilombolas. Pergunte-lhes se há algum lazer desta cultura que eles também praticam, destacando a importância de respeitar outras culturas. Comente sobre as curiosidades descritas no texto perguntando se eles conhecem os três tipos de danças mencionados. Caso julgue necessário, leve para a sala de aula fotografias, vídeos e músicas que fazem parte da cultura dos quilombolas.

Resposta

Mulheres quilombolas e ribeirinhas dançando o carimbó, na Vila Mangabeira, no Pará, em 2025.

• Para complementar o trabalho da atividade 3, proponha a atividade apresentada a seguir.

ATIVIDADE EXTRA

Materiais

• folha de papel sulfite branca

• folha de papel quadriculado

Passo a passo

a) Peça aos estudantes que escolham um dos temas a seguir e façam uma pesquisa com 10 pessoas, que podem ser seus familiares e amigos.

• Cor preferida (azul, vermelha, verde, outra).

• Animal de estimação preferido (cachorro, gato, outro).

• Filme preferido (comédia, ficção, outro).

b) Oriente os estudantes a coletarem e a organizarem as informações na folha de papel sulfite.

c) Depois, peça a eles que construam, na folha de papel quadriculado, uma tabela e um gráfico com base nos dados coletados. Auxilie-os nessa construção.

d) Por fim, exponha as tabelas e os gráficos feitos pelos estudantes em um cartaz e os deixe expostos na sala de aula.

06/10/2025 18:08:10

Lazer preferido de alguns amigos e familiares de Marlene, em 2027 Quantidade

Fonte de pesquisa: registros de Marlene.

• Caso os estudantes tenham dificuldades na realização da atividade 4, dê o exemplo dos números 15 e 51 e faça o seguinte questionamento: “O algarismo 5 presente nos números citados vale 50 em qual deles?”. Analise as respostas e verifique se todos chegaram à mesma conclusão de que o algarismo 5 vale 50 no número 51, pois ele representa 5 dezenas. Se necessário, retome a atividade 2 e verifique se eles compreendem que os algarismos assumem valores de acordo com a posição que ocupam no número.

• A atividade 5 trabalha o valor posicional do algarismo 8 e do algarismo 2. Explique aos estudantes que o algarismo pode assumir valores diferentes, dependendo da posição que ocupa. Se julgar conveniente, oriente-os a decompor os números que aparecem nas fichas, evidenciando os números 8 e 20.

• Na atividade 6, os estudantes devem identificar o número que está representado no ábaco, fazer sua decomposição e, depois, escrevê-lo por extenso. Após isso, eles devem realizar os mesmos procedimentos nos itens A e B. Assim, são motivados a compor os números com base em suas ordens ou no valor posicional dos algarismos. Se julgar conveniente, organize-os em grupos para resolver as atividades, a fim de que troquem entre si seus conhecimentos.

4. Contorne as fichas com números em que o algarismo 3 vale 30.

303 203 230 330 723 133

Resposta: Os estudantes devem contornar os números 230, 330 e 133.

5. Marque um X nas fichas com números em que o algarismo 8 vale 8 e o algarismo 2 vale 20.

842 128 218 182 483 428

Resposta: Os estudantes devem marcar um X nos números 128 e 428

6. No ábaco a seguir está representado o número 468.

Dica: Nesse ábaco, temos:

U – unidade

D – dezena

C – centena

Decomposição: 400 + 60 + 8

Por extenso: quatrocentos e sessenta e oito. Com base nesse exemplo, complete os itens a seguir de acordo com o número representado em cada ábaco.

Número:

Decomposição: + +

Por extenso:

Respostas: Número: 261; Decomposição:

200 + 60 + 1; Por extenso: duzentos e sessenta e um

Número:

Decomposição: + +

Por extenso:

Respostas: Número: 524; Decomposição:

500 + 20 + 4; Por extenso: quinhentos e vinte e quatro

BNCC

As atividades 4 e 5 têm por objetivo que os estudantes identifiquem os números com valores posicionais específicos. Atividades como essa permitem que eles compreendam as características do sistema de numeração decimal (valor posicional e função do zero), contemplando, assim, a habilidade EF02MA01 da BNCC.

C D U

C D U

C D U

Professor, professora: Confira mais sugestões para complementar esta atividade nas orientações ao professor

7. Represente no ábaco o número indicado em cada item. Para isso, desenhe nas hastes de cada ábaco as contas correspondentes. a ) 324 b ) 432 c ) 234 d ) 925 e ) 290 f ) 806

Resposta: C: 3; D: 2; U: 4.

Resposta: C: 2; D: 3; U: 4.

Resposta: C: 2; D: 9; U: 0.

Resposta: C: 4; D: 3; U: 2.

Resposta: C: 9; D: 2; U: 5.

Resposta: C: 8; D: 0; U: 6.

8. Escreva por extenso o primeiro e o último número representado nos ábacos da atividade anterior.

Resposta: a) Trezentos e vinte e quatro; f) Oitocentos e seis.

9. Com base no quadro, complete corretamente as informações.

Decomposição de alguns números e a escrita por extenso

Número com algarismos Decomposição Por extenso

147 100 + 40 + 7

Resposta: Os estudantes devem completar a 1ª linha com cento e quarenta e sete; a 2ª linha com 300 + 50 + 1 e trezentos e cinquenta e um; e a 3ª linha com 900 + 60 + 0 e novecentos e sessenta

06/10/2025 18:08:11

• A atividade 7 objetiva que os estudantes representem no ábaco o número indicado em cada item. Sendo assim, eles devem ser capazes de identificar o valor posicional dos algarismos representados nos números e representá-los no ábaco.

• Providencie ábacos para a realização da atividade 7 Caso não haja ábacos suficientes para todos os estudantes, organize-os em duplas ou grupos, para que possam fazer as atividades propostas.

• As atividades 7 e 8 se complementam ao solicitar para os estudantes que escrevam por extenso o primeiro número representado no ábaco e também o último. Acompanhe a escrita dos números por extenso e, enquanto eles executam a escrita, verifique se estão realizando o traçado das letras de modo adequado, seguindo a devida orientação e a direção próprias da norma-padrão, a fim de que eles alcancem a fluidez da escrita. Nesse momento, pode ser necessário retomar os procedimentos de escrita escrevendo pausadamente na lousa e propondo que eles copiem. Outra sugestão que pode auxiliar na compreensão do desenvolvimento da escrita é retomar o movimento do traçado com a mão no ar e o recurso da caixa de areia. Caso algum deles continue apresentando dificuldade, pode ser necessário treinar em caderno de caligrafia.

• Caso os estudantes apresentem dificuldades em completar o quadro com o que falta da atividade 9, retome como decompor um número e acompanhe a escrita do número por extenso e, caso necessário, peça a alguns que ditem as sílabas, a fim de auxiliar os que tiverem dúvidas. Se necessário, faça as correções apresentando a escrita na lousa para a turma.

• A atividade 10 estabelece uma integração entre as unidades temáticas de Matemática Números e Grandezas e medidas ao relacionar a comparação de qual dos personagens tem a maior quantia guardada. Por meio de um diálogo entre os amigos Pedro e Bruno, cada um fala a quantia, em reais, que guardou. O objetivo é que os estudantes identifiquem quem guardou a maior quantia e, com o auxílio do ábaco, eles devem representar o número que corresponde à quantia que Pedro e Bruno guardaram.

• Na atividade 11, converse com os estudantes sobre como fazer comparações entre números naturais e leve-os a perceber que devemos sempre começar comparando os algarismos das centenas; se forem iguais, comparamos os algarismos das dezenas; se forem iguais, comparamos os algarismos das unidades. Caso eles apresentem dúvidas, escreva na lousa outros exemplos e analise com eles os algarismos das centenas, das dezenas e das unidades, para que comparem os números identificando qual é o maior e qual é o menor entre eles. Algumas sugestões para fazer as comparações são:

• 168 e 169.

• 201 e 210.

• 879 e 789.

• 330 e 303.

• 233 e 322.

BNCC

10. Acompanhe a conversa de Pedro e Bruno.

Eu já guardei

178 reais este mês. E você?

Eu guardei 165 reais.

Pedro Bruno

a ) Quem tem a maior quantia guardada?

Resposta: Pedro.

b ) Represente, nos ábacos, o número que corresponde à quantia que Pedro e Bruno guardaram.

Resposta: C: 1; D: 7; U: 8. Resposta: C: 1; D: 6; U: 5.

c ) Elabore uma estratégia e determine, entre os números que você representou nos ábacos, qual é o maior.

Resposta: 178

11. Vamos comparar os números 178 e 165 para saber qual é o maior. Primeiro, comparamos os algarismos das centenas.

178 e 165

1 é igual a 1

Portanto, 178 é maior do que 165.

Se os algarismos das centenas forem iguais, comparamos os algarismos das dezenas.

178 e 165

7 é maior do que 6 Unidades

a ) De que maneira podemos comparar números de três algarismos quando os algarismos das centenas e das dezenas forem iguais?

Resposta pessoal. Sugestão de resposta: Comparamos os algarismos das unidades.

b ) Reúna-se com um colega e comparem os números 234 e 239. Qual deles é o menor?

Resposta: 234

A atividade 10 desenvolve aspectos da habilidade EF02MA03 da BNCC ao solicitar que os estudantes comparem quais dos personagens poupou mais dinheiro, dizendo qual é a quantia maior.

C D U C D U

Pedro Bruno

12. a) Resposta pessoal. Espera-se que os estudantes estimem que a malha tem cerca de 140 quadradinhos, que é a quantidade exata de quadradinhos da malha.

12. Para fazer um trabalho, Arthur recortou e coloriu a seguinte malha quadriculada.

a ) Sem contar um a um, estime a quantidade de quadradinhos da malha que Arthur usou. quadradinhos.

b ) Em seu caderno, elabore e indique como obter a quantidade exata de quadradinhos da malha. Em seguida, determine a quantidade de quadradinhos da malha usada por Arthur.

Resposta pessoal. Comentários nas orientações ao professor

c ) A quantidade de quadradinhos que você estimou foi próxima da quantidade de quadradinhos da malha que Arthur usou? Converse com seus colegas sobre os resultados.

Resposta pessoal. A resposta depende das estimativas que os estudantes fizeram.

• Na atividade 12, verifique se as estimativas dos estudantes foram próximas da quantidade de quadrinhos, incentivando-os a comentar suas estratégias para se aproximar da quantidade exata de quadrinhos, realizando cálculos ou contando um a um. Uma opção é adicionar 14 vezes (quantidade de colunas na malha) o número 10 (quantidade de quadradinhos em cada coluna), obtendo, assim, 140, que representa 140 quadradinhos.

13. Na sequência representada, cada número, a partir do segundo, tem 5 unidades a mais do que o anterior.

Unidades temáticas integradas

a ) Complete a sequência com os números que faltam.

420, 425, 430, , 440, , , 455, 460, 465, , , , 485, , 495, 500.

Resposta: 420, 425, 430, 435, 440, 445, 450, 455, 460, 465, 470, 475, 480, 485, 490, 495, 500.

b ) Os números dessa sequência estão organizados em ordem crescente, ou seja, do menor para o maior. O número 485 é maior ou menor do que o número 465?

Resposta: Maior.

c ) Complete corretamente cada item a seguir com o termo é maior do que ou é menor do que

• A atividade 13 estabelece uma integração entre as unidades temáticas de Matemática Números e Álgebra ao relacionar sequências recursivas por meio de observação de regras usadas em seriações numéricas, além dos estudantes serem levados a completar a sequência com os números que estão faltando. De acordo com a regra dada, eles devem comparar, no item c, cada item, escrevendo o termo “maior do que” ou “menor do que” conforme os números apresentados. Atividades como essa contribuem para o raciocínio lógico e capacidade de análise, promovendo a compreensão do sistema de numeração.

Resposta: 440 é maior do que 425.

• 440 425.

BNCC

• 445 455.

Resposta: 445 é menor do que 455.

Resposta: 500 é maior do que 490.

• 500 490.

do resultado da contagem e uma sequência composta de números naturais em ordem crescente, na qual os estudantes devem completar a sequência com os números faltantes, de acordo com o padrão apresentado.

AVALIANDO

Objetivo

Ler e escrever os números até 999 com algarismos e por extenso.

Representar os números até 999 no quadro de ordens.

Compor e decompor números até 999.

Sugestão de intervenção

A fim de obter informações sobre como foi o aprendizado dos estudantes sobre os conteúdos estudados, reproduza na lousa a atividade proposta a seguir e solicite a eles que a copiem e resolvam no caderno.

• Ana e Paulo estavam brincando de adivinhar números. Então, Paulo escreveu três dicas para Ana descobrir o número escolhido:

• O número que escolhi é maior do que 800 e menor do que 823.

• O algarismo das dezenas é 1.

As atividades 12 e 13, desenvolvem aspectos das habilidades EF02MA02 e EF02MA11 da BNCC, ao proporem atividades envolvendo estimativa, o registro

06/10/2025 18:08:11

• O algarismo das unidades é a metade do valor do algarismo das centenas.

Resposta: 814

• Após os estudantes descobrirem qual é esse número, solicite que o representem no quadro de ordens, façam a decomposição desse número por meio de uma adição e, depois, escrevam-no por extenso.

• Observe os estudantes durante o processo de resolução e, caso apresentem dúvidas, proponha outras atividades a fim de saná-las.

• A atividade 14 integra unidades temáticas de Matemática Números e Álgebra ao levar os estudantes a construírem sequências recursivas por meio da observação de regras usadas em seriações numéricas, acompanhando os passos apresentados. Ao final da atividade, proponha uma exposição das sequências criadas por eles. Assim, o trabalho deles será valorizado, contribuindo para a construção da identidade de cada um deles.

• As atividades 15 e 16 utilizam fichas sobrepostas como estratégia para trabalhar a compreensão de características do sistema de numeração decimal, como o valor posicional e a composição dos números naturais de até três ordens. Caso os estudantes apresentem dificuldade, antecipe o uso das fichas na atividade seguinte e proponha na prática essas e outras composições. Alerte para o uso cuidadoso da tesoura ao recortar as peças e inspecione o manuseio dela para que não ocorra acidentes. Enfatize também a importância de usar sempre tesoura com ponta arredondada, minimizando o risco de se machucarem.

• Depois de explorar a composição com as fichas do Material complementar na atividade 17, os estudantes devem organizar os números em ordem crescente na atividade 18, favorecendo a construção do raciocínio lógico e a compreensão de sequência numérica. A proposta de trabalho em dupla, na atividade 17, também permite explorar a interação e a colaboração entre os colegas. Incentive a troca de ideias e de informações entre eles, a fim de enriquecer o aprendizado. Para garantir a inclusão de estudantes cegos ou com baixa visão, é indicado aplicar cola escolar no contorno dos números das fichas, pois o relevo criado pela cola permitirá que eles percebam os números pelo tato, participando ativamente da tarefa proposta.

14. Em seu caderno, escreva uma sequência em ordem decrescente, ou seja, do número maior para o menor. Para isso, acompanhe estes passos:

• O primeiro número da sequência deve ter três algarismos.

• Determine uma regra para a sequência.

• A sequência deve ter 10 números.

Mostre a um colega a sequência que você fez e peça a ele que descubra qual foi a regra que você determinou.

Resposta pessoal. Comentários nas orientações ao professor

15. Usando fichas sobrepostas, Gisele compôs o número 352 da seguinte maneira.

Nesse número, o valor posicional do algarismo 3 é 300 unidades. Qual é o valor posicional do:

a ) algarismo 5?

b ) algarismo 2?

Resposta: 5 dezenas ou 50 unidades.Resposta: 2 unidades.

16. Os números a seguir foram compostos utilizando fichas sobrepostas. Observe e escreva qual foi o número composto em cada item.

a )

b ) c )

Resposta: 295

Resposta: 448

Resposta: 632

17. Junte-se a um colega e recortem do livro de cada um de vocês as fichas sobrepostas que estão nas páginas 271 e 273 do Material complementar. Depois, componha os números a seguir.

605 271 139 410 98 586

Respostas e comentários nas orientações ao professor

18. Escreva, em ordem crescente, os números que aparecem na atividade anterior.

Resposta: 98, 139, 271, 410, 586, 605.

BNCC

A atividade 14 solicita que os estudantes elaborem uma sequência decrescente e, depois, descubram a regra da sequência elaborada por um de seus amigos, e vice-versa. Desse modo, desenvolverão as habilidades EF02MA10 e EF02MA11 da BNCC.

As atividades 15 e 16 têm por objetivo que os estudantes identifiquem os números com valores posicionais específicos e composições de números por meio de adições. Atividades como esta permitem que eles compreendam as características do sistema de numeração decimal (valor posicional e função do zero), contemplando,

assim, as habilidades EF02MA01 e EF02MA04 da BNCC.

Respostas 17. Os estudantes devem usar as fichas para compor os números indicados. Sugestões de respostas:

a) 600 + 5 = 605

b) 200 + 70 + 1 = 271

c) 100 + 30 + 9 = 139

d) 400 + 10 = 410

e) 90 + 8 = 98

f) 500 + 80 + 6 = 586

O NÚMERO 1 000

1. Carlos trabalha no centro de distribuição de uma loja virtual. Ele já organizou 999 caixas dos produtos vendidos e está segurando a última para ser guardada na prateleira.

a ) Ao guardar a última caixa na prateleira, serão armazenadas caixas ao todo.

Resposta: Ao guardar a última caixa na prateleira, serão armazenadas 1 000 caixas ao todo.

b ) A seguir, está a representação desse número no ábaco e no quadro de ordens.

Resposta pessoal. Espera-se que os estudantes sobreponham os pontilhados acompanhando os traçados das letras e dos algarismos apresentados

QUADRO DE ORDENS

UM C D U 1000

C D U UM

Dica: No quadro de ordens e no ábaco, UM representa unidade de milhar.

Copie e escreva o número mil com algarismos e por extenso.

Algarismos:

Por extenso:

Resposta: Assim, 999 caixas mais 1 caixa é igual a 1 000 caixas. para realizar as escritas solicitadas.

1 000 1 000 1 000 1 000

Assim, 999 caixas mais 1 caixa é igual a caixas.

06/10/2025 18:14:16

• A atividade 1 apresenta uma situação real na qual aborda um trabalhador que já organizou 999 caixas de produtos que foram vendidos e está segurando a última caixa para ser guardada na prateleira. Ao guardar a última caixa, é apresentado para os estudantes o número 1 000 e, na sequência, como representar esse número no quadro de ordens, no ábaco e sua escrita por extenso. Nesse contexto, eles terão condições de realizar agrupamentos e trocas a fim de obter o número 1 000.

• Reforçar como é o traçado do número 1 000, auxiliando os que ainda estão em processo de fixação dos numerais. Caso haja algum estudante com baixa visão, entregue-lhe uma folha de papel com a impressão em tamanho ampliado, com alta nitidez e contraste e disponibilize a ele materiais táteis, além de adaptar a iluminação e a posição dele na sala de aula.

• Se necessário, após a atividade 1, para reforçar a prática e o direcionamento da escrita dos números, utilize o caderno de caligrafia, de maneira que eles possam desenvolver progressivamente a escrita da letra cursiva. É importante incentivar a pega de três pontos no lápis, sustentando-o com o indicador e o polegar e apoiando com o dedo médio, pois essa pega favorece a coordenação motora fina, reduz o cansaço das mãos ao escrever e melhora a precisão dos movimentos executados. Desse modo, a escrita ganha fluidez e as letras e os números são desenhados de maneira mais uniforme e com espaçamento adequado.

• Leve para a sala de aula o material dourado para trabalhar a atividade 2 na prática. É muito importante que os estudantes percebam que, ao acrescentar um cubinho à representação de 999, algumas trocas serão necessárias para representar o número 1 000. Para obter o cubo maior, adicionando um cubinho que representa uma unidade, obtêm-se dez cubinhos, que devem ser trocados por uma barrinha para representar a dezena, adicionando, assim, dez barrinhas, ou seja, dez dezenas, que devem ser trocadas por uma placa para representar uma centena. Com isso, obtêm-se dez placas, ou seja, dez centenas, que devem ser trocadas pelo cubo maior, a fim de representar uma unidade de milhar.

• A atividade 3 solicita que os estudantes utilizem os números indicados nas fichas para completar os quadros indicados na reta numérica. O objetivo é trabalhar a representação dos números até 1 000, explorando as centenas exatas na reta numérica.

• A atividade 4 apresenta aos estudantes a sequência dos números naturais de 990 a 1 000. Depois, aborda números antecessores e sucessores por meio das expressões “imediatamente antes” e “imediatamente depois”.

BNCC

A atividade 3 tem por objetivo levar os estudantes a completarem uma sequência de números naturais em ordem crescente com base em uma regularidade estabelecida, assim como previsto na habilidade EF02MA09 da BNCC.

AVALIANDO

Objetivo

Ler e escrever os números até 1 000 com algarismos e por extenso.

Representar os números até 1 000 no quadro de ordens.

2. Com base nas imagens a seguir, complete corretamente as informações.

Resposta: 999 + 1 = 1 000; 1 unidade de milhar ou 1 000 unidades.

= unidade de milhar ou 1 000 unidades.

3. Utilize os números indicados nas fichas para completar os espaços dos quadros indicados na reta numérica.

Resposta: 0; 100; 200; 300; 400; 500; 600; 700; 800; 900; 1000

400 300 600 900

4. Observe a sequência dos números naturais de 990 a 1 000.

990, 991, 992, 993, 994, 995 ,996 ,997, 998, 999, 1 000.

a ) Qual número aparece imediatamente antes de 995?

Resposta: 994

Esse número é chamado de antecessor de 995.

b ) Qual número aparece imediatamente depois de 995?

Resposta: 996

Esse número é chamado de sucessor de 995.

c ) Qual número é o antecessor de 1 000? E qual é o sucessor de 990?

Resposta: 999; 991

Realizar agrupamentos e trocas para obter a unidade de milhar.

Sugestão de intervenção

Verifique a compreensão dos estudantes acerca dos números naturais até 1 000. Observe se eles fazem corretamente as trocas adequadas para obter o número 1 000 ao adicionar uma unidade. Para isso, avalie o desempenho deles durante a resolução das atividades propostas na Unidade e, se necessário, apresente outras atividades para que pratiquem, sobretudo, as que trabalham as representações dos números com o ábaco e com o material dourado, por algarismos

e por extenso. A fim de diagnosticar como está ocorrendo o processo de ensino e aprendizagem e obter informações para sanar possíveis dúvidas, organize os estudantes em grupos e reproduza na lousa a seguinte atividade.

Utilize o material dourado para representar os números 209, 387, 450, 531, 799, 820, 998 e 1 000 e, depois, represente cada número no ábaco e no quadro de ordens. Por fim, escreva por extenso esses números. Diga-lhes que o quadro de ordens e a escrita por extenso devem ser feitos no caderno. Acompanhe todo o processo de resolução e oriente-os conforme julgue necessário.

MOEDAS E CÉDULAS

1. O dinheiro é usado para comprar bens ou serviços. Ao realizarmos uma compra ou contratarmos um serviço, pagamos um valor em dinheiro pela mercadoria ou pelo serviço prestado. Isso acontece na grande maioria dos lugares do mundo, e cada país tem o próprio dinheiro.

Unidades temáticas integradas

O conjunto de cédulas e moedas utilizadas por um país forma o sistema monetário dele. No Brasil, o sistema monetário atual é o Real. Observe as cédulas do Real e complete corretamente as informações.

Imagens sem proporção entre si.

Resposta: 20 reais

Resposta: 5 reaisResposta: 10 reais

Resposta: 100 reais

Do mesmo modo, confira as moedas do Real e complete corretamente as informações.

1 centavo

Resposta: 5 centavos

Resposta: 25 centavosResposta: 50 centavos

Resposta: 1 real

06/10/2025 18:14:18

• A atividade 1 estabelece uma integração entre as unidades temáticas de Matemática Números e Grandezas e medidas ao estabelecer o reconhecimento de cédulas e moedas do sistema monetário brasileiro.

• O objetivo da atividade 1 é propiciar aos estudantes o reconhecimento das cédulas e moedas do sistema monetário brasileiro, bem como seus respectivos valores. Leia com eles o enunciado da atividade e oriente-os em sua resolução.

• Em uma roda de conversa, pergunte aos estudantes se já tiveram experiências de situações de compra e de venda e aproveite a oportunidade para incentivá-los a refletir a respeito da importância do consumo consciente. Diga a eles que sempre devemos fazer pesquisas de preços e comprar somente o que realmente estamos necessitando, a fim de evitarmos o desperdício e conseguirmos poupar dinheiro, atitude essa que nos fornece segurança para o futuro.

BNCC

As atividades deste tópico contemplam a habilidade EF02MA20 da BNCC ao levar os estudantes a estabelecerem equivalência de valores entre cédulas e moedas do sistema monetário brasileiro para resolver situações cotidianas.

• Antes de apresentar a seção Os nomes do nosso dinheiro, pergunte aos estudantes o que sabem sobre a história do dinheiro. Comente que o dinheiro foi inventado pelo ser humano e pergunte se conhecem as razões dessa criação. Informe-lhes que, antes da invenção do dinheiro, era muito comum a prática do escambo, que significa a troca de mercadorias. Com o passar do tempo, as trocas deram lugar às moedas feitas de prata e de ouro e com o surgimento dos bancos houve a invenção das moedas de papel. Cada país desenvolveu sua unidade monetária. Porém a prática do escambo e as moedas comunitárias continuam existindo em algumas partes do mundo.

• Verifique se é possível levar para a sala de aula imagens de notas de sistemas monetários de outros países, a fim de expandir o conhecimento dos estudantes, como o dólar, o euro e o peso.

• Aproveite o assunto explorado nesta página e solicite aos estudantes que façam com seus familiares uma pesquisa sobre como nos dias atuais o dinheiro pode ser substituído. Em seguida, eles devem registrar no caderno por meio de desenhos e frases o que pesquisaram.

• As atividades 2 e 4 solicitam aos estudantes que, usando somente cédulas do nosso sistema monetário brasileiro, representem 450 reais de duas maneiras diferentes e, depois, façam o mesmo com o valor de 2 reais. Sugira a eles que encontrem outras possibilidades de combinação de cédulas e moedas de real para as quantias apresentadas nessas atividades.

• Na atividade 3, se necessário explique a equivalência de forma prática usando materiais concretos.

OS NOMES DO NOSSO DINHEIRO

Antes do Real, outras cédulas e moedas foram utilizadas no Brasil. Alguns exemplos são o Cruzeiro Real, o Cruzeiro, o Cruzado e o Cruzeiro Novo.

2. Usando somente cédulas do sistema monetário brasileiro atual, represente 450 reais de duas maneiras diferentes.

Resposta pessoal. Sugestão de resposta: 2 cédulas de 200 reais e 1 cédula de 50 reais ou 1 cédula de duzentos reais, 2 cédulas de cem reais, 2 cédulas de 20 reais e 1 cédula de 10 reais.

3. Um real equivale a 100 centavos. Escreva por extenso quantos centavos faltam em cada item para completar 1 real.

a ) 38 centavos:

b ) 61 centavos:

c ) 79 centavos:

Resposta: Os estudantes devem escrever que faltam sessenta e dois centavos.

Resposta: Os estudantes devem escrever que faltam trinta e nove centavos.

Resposta: Os estudantes devem escrever que faltam vinte e um centavos.

4. Usando somente moedas do nosso sistema monetário atual, represente 2 reais de duas maneiras diferentes.

Resposta pessoal. Sugestão de resposta: 2 moedas de um real ou 1 moeda de um real e 2 moedas de cinquenta centavos.

AVALIANDO

Objetivo

Reconhecer cédulas e moedas do sistema monetário brasileiro e equivalência de valores.

Sugestão de intervenção

Nesse momento, com o objetivo de sanar possíveis dúvidas com relação ao tópico estudado, solicite que os estudantes façam a seguinte atividade no caderno. Responda às questões.

• Como podemos representar 5 reais utilizando apenas moedas?

• Quantas moedas de 50 centavos são necessárias para obter 6 reais?

• Represente 85 reais usando cédulas e moedas.

• Represente 194 reais usando apenas cédulas.

• Quantas moedas de 10 centavos são necessárias para obter 2 reais?

• Represente 205 reais usando apenas cédulas. Oriente-os durante o desenvolvimento da atividade, de modo que possam esclarecer possíveis dúvidas que surgirem.

Moeda de 1 cruzado. Moeda de 10 cruzeiros reais.

Moeda de 1 cruzado novo. Moeda de 100 cruzeiros.

5. Ligue os itens que têm a mesma quantia representada.

7. Resposta pessoal. Espera-se que os estudantes relatem suas experiências e das pessoas do seu convívio com relação à economia de dinheiro, tendo em vista um objetivo definido Resposta: Os estudantes devem ligar: A-3; B-2; C-1. para o uso do dinheiro guardado.

Imagens sem proporção entre si.

6. Fábio e seus amigos estão guardando dinheiro no banco para fazer uma viagem. Cada um deles já depositou certa quantia em reais.

• Fábio depositou 4 cédulas de 100 reais.

• Márcia depositou uma quantia maior do que a depositada por Fábio.

• Melissa depositou 1 cédula de 50 reais a menos do que a quantia depositada por Fábio.

• Edgar depositou uma quantia maior do que Melissa e menor do que Fábio.

Considerando essas informações, escreva os nomes das pessoas de acordo com as quantias depositadas.

• 350 reais :

• 400 reais :

• 380 reais :

• 450 reais :

7. Você ou as pessoas do seu convívio costumam economizar dinheiro para comprar algo de maior valor ou para fazer uma reserva? Converse com o professor e seus colegas sobre o assunto.

6. Resposta: 350 reais: Melissa; 400 reais: Fábio; 380 reais: Edgar; 450 reais: Márcia

• A atividade 5 tem por objetivo fazer que os estudantes reconheçam valores de cédulas e moedas do Real e estabeleçam a equivalência de valores para formar a mesma quantia com cédulas e moedas diferentes do nosso sistema monetário.

• Aproveite a atividade 6 para desenvolver o raciocínio lógico-matemático dos estudantes, desafiando-os a interpretar informações expressas em linguagem cotidiana para determinar os valores depositados pelos personagens da atividade. Ao relacionarem as pistas às operações com números naturais e valores monetários, os estudantes desenvolvem habilidades importantes ligadas à resolução de problemas e ao sistema monetário.

• Na atividade 7, comente com os estudantes a importância de ter uma reserva de dinheiro para situações inesperadas pois, além de oferecer segurança e tranquilidade, permite lidar com imprevistos sem comprometer o orçamento.

06/10/2025 18:14:22

• A atividade 8 estabelece uma integração entre as unidades temáticas de Matemática Números e Probabilidade e estatística ao utilizar a representação de dados em uma tabela simples, além disso solicita que o estudante faça comparações entre os valores de dois produtos, no item a. Se achar necessário, diga-lhes que, para comparar números de dois algarismos, primeiro compare as dezenas. Caso, as dezenas forem iguais, compare as unidades. No item e, se achar necessário, reforce o conceito de que é possível obter um mesmo valor, utilizando diferentes quantidades de cédulas e moedas.

ATIVIDADE EXTRA

Tendo em vista as atividades que trabalham com as cédulas e moedas do sistema monetário brasileiro, verifique se os estudantes conseguem estabelecer as equivalências entre valores e se têm facilidade de formar as mesmas quantias com cédulas e moedas diferentes. Para um melhor aproveitamento e complemento dessas atividades, peça-lhes que, no caderno, apresentem duas maneiras diferentes de representar as quantias de 120, 270, 355 e 468 reais com cédulas e moedas do nosso sistema monetário brasileiro.

• A atividade 9 estabelece uma integração entre as unidades temáticas de Matemática Números e Probabilidade e estatística ao representar dados em uma tabela simples.

• Ao trabalhar a atividade 10, incentive os estudantes sobre a importância da economia e do planejamento para alcançar seus objetivos. Depois, apresente as estratégias deles na lousa e faça uma pesquisa para saber qual delas seria a melhor a ser adotada.

8. Camila comprou um livro e um estojo. Confira o preço de cada produto.

Preços dos produtos comprados por Camila

Produto Preço

Livro 46 reais

Estojo 25 reais

Fonte de pesquisa: Anotações de Camila.

a ) Qual produto custou mais caro?

Resposta: Livro.

b ) Quantos reais custou esse produto?

Resposta: 46 reais.

c ) Quantos reais custaram os dois produtos?

Resposta: 46 + 25 = 71. Os dois produtos custaram 71 reais.

Unidades temáticas integradas

d ) Para pagar essa compra, Camila deu ao caixa as cédulas a seguir.

Quantos reais Camila recebeu de troco?

Resposta: 50 + 20 + 10 = 80; 80 − 71 = 9. Camila recebeu de troco 9 reais.

e ) Sabendo que Camila recebeu o troco em cédulas e moedas, escreva duas possibilidades de como ela recebeu o dinheiro.

Resposta pessoal. Sugestão de resposta: 1 cédula de 5 reais e 4 moedas de 1 real; 2 cédulas de 2 reais, 4 moedas de 1 real e 2 moedas de 50 centavos.

REFERÊNCIAS COMPLEMENTARES

KITAGAWA, Kate; REVELL Timothy. A vida secreta dos números: uma história global da matemática e seus pioneiros desconhecidos. Tradução de Rafael Rocca dos Santos. São Paulo: Planeta do Brasil, 2025.

Esse livro aborda a história dos números e mostra como a Matemática vai além da perspectiva tradicional, convidando o leitor a compreender melhor o mundo e a história da Matemática. É também uma boa sugestão de consulta para o professor enriquecer as aulas com

informações sobre algumas personalidades responsáveis pela evolução dessa Ciência.

Sugestão de Desafio

Como juntar exatamente 765 reais utilizando apenas cédulas de 100, 50, 20, 10 e moedas de 1 real?

Respostas

Sugestão de resposta: 7 cédulas de 100 reais, 1 cédula de 50 reais, 1 cédula de 10 reais e 5 moedas de 1 real.

9. Em algum momento, durante uma compra, é necessário verificar se a quantia em reais que temos é suficiente para pagar. A seguir, apresentamos o preço de alguns produtos em um supermercado.

Unidades temáticas integradas

Fonte de pesquisa: Anotações de pesquisa de preço de um supermercado.

Preço de alguns produtos em um supermercado

Produto Preço em reais

Pacote de arroz 5 kg 32

Óleo de soja 900 mL 9

Pacote de café 500 g 29

Sabão líquido 3 L 27

a ) Thiago comprou um óleo de soja e um pacote de café e pagou com uma cédula de 50 reais. Efetue os cálculos no caderno e determine quantos reais ele recebeu de troco.

Resposta: 29 + 9 = 38; 50 − 38 = 12. Thiago recebeu de troco 12 reais.

b ) Faça uma estimativa para saber se é possível Joana comprar três desses produtos por 75 reais.

Resposta pessoal. Espera-se que

c ) Calcule, no caderno, o total em reais dos produtos escolhidos no item anterior e verifique se a sua estimativa estava correta.

Resposta: A resposta depende dos produtos escolhidos pelos estudantes no item b

10. Orlando guardou 15 reais em janeiro, 17 reais em fevereiro e 18 reais em março, com o objetivo de comprar uma mochila.

Resposta: 70 reais. os estudantes escolham 3 produtos cujo valor total seja menor do que 75 reais.

Resposta: 15 + 17 + 18 = 50 50 reais.

a ) Efetue os cálculos no caderno e determine quantos reais Orlando guardou durante esses três meses. reais.

b ) Em abril, Orlando guardou mais 20 reais. Juntando com a economia anterior, quantos reais ele conseguiu guardar? reais.

c ) Estime quantos reais Orlando deve guardar por mês, em maio e junho, em média, para que acumule pelo menos 94 reais.

Resposta pessoal. Espera-se que os estudantes estimem uma quantia em reais próxima de 12 reais.

DESAFIO A MAIS

Marina deu 30 reais para cada um dos seus três sobrinhos: Luísa, Pedro e Tiago. Luísa recebeu 2 cédulas, Pedro 3 cédulas e Tiago, 4 cédulas. Escreva os valores das cédulas que cada um recebeu.

• Luíza:

• Pedro:

• Tiago:

Resposta: Luíza: uma cédula de 10 reais e uma de 20 reais; Pedro: três cédulas de 10 reais ou uma cédula de 20 reais e duas de 5 reais; Tiago: duas cédulas de 10 reais e duas de 5 reais. 119

CONCLUSÃO

Acompanhar o desenvolvimento dos estudantes é fundamental para um ensino bem-sucedido. A fim de fazer um monitoramento mais abrangente e organizado, registre nos relatórios individuais ou nas fichas de avaliação o desempenho de cada um, levando em consideração suas particularidades. Um modelo desse tipo de ficha pode ser encontrado no tópico Avaliação deste Manual. Assim, será possível visualizar de modo individual as trajetórias de aprendizagem, incluindo os

avanços e os pontos de dificuldades a serem sanados por meio de atividades que promovam recuperação dos conteúdos. Esse método de verificar a progressão dos estudos e identificar o que a turma de fato conseguiu aprender e o que ficou com lacunas de absorção é de grande importância para que seja possível repensar estratégias em sala de aula, tornando as ações pedagógicas cada vez mais eficazes.

• No Desafio a mais, os estudantes trabalham o raciocínio lógico-matemático com valores monetários. Eles devem interpretar as pistas sobre a quantidade de cédulas a fim de determinar as combinações que somam R$ 30,00 para cada personagem. A proposta exige usar adição e agrupamento de quantias, percebendo que cada sobrinho recebe uma composição específica de cédulas. Se houver dificuldade, sugira o uso de cédulas de papel ou desenhos para simular. Incentive diferentes soluções e promova a troca de ideias entre eles. Faça intervenções estratégicas com perguntas, como: “Se Luíza recebeu R$ 30,00 em duas cédulas, quais seriam?”; “Se Pedro recebeu R$ 30,00 em três cédulas, quais poderiam ser?”.

06/10/2025 18:14:22

A conclusão da unidade é o momento de avaliar se os objetivos por ela propostos foram alcançados. Para esse diagnóstico, observe no final deste Manual algumas possibilidades de avaliação formativa que permitem fazer o monitoramento da aprendizagem dos estudantes e intervir caso eles não tenham atingido os resultados esperados.

OBJETIVOS DA UNIDADE

• Efetuar adições e subtrações com e sem reagrupamento com resultado até 999 utilizando diferentes estratégias.

• Elaborar e resolver situações-problema que envolvam a adição e a subtração.

• Utilizar a adição ou a subtração para descobrir o padrão de uma sequência numérica e determinar os elementos ausentes.

• Resolver situações-problema que envolvem o sistema monetário brasileiro.

• Desenvolver a capacidade de realizar cálculos mentalmente e estimar resultados de operações, por meio do raciocínio lógico.

• Analisar e interpretar o enunciado de uma situação-problema.

INTRODUÇÃO E JUSTIFICATIVA

Nesta unidade, são propostas, de modo contextualizado, atividades que trabalham adições e subtrações, com resultados até 999, com e sem reagrupamento. Ao longo dela, são evidenciados o uso do material dourado, do ábaco, da decomposição e do algoritmo como estratégias de cálculo. São propostas diferentes atividades, algumas delas envolvendo situações do dia a dia dos estudantes, bem como situações de compra, abrangendo o sistema monetário brasileiro. Em certas situações, eles são desafiados a aplicar estratégias de cálculos mentais e a elaborar enunciados de problemas, apropriando-se da linguagem escrita. A unidade propõe atividades com sequências numéricas, permitindo aos estudantes que identifiquem padrões e regularidades por meio das operações de adição e subtração. As propostas envolvem a interpretação de dados apresentados em tabelas, entre outros recursos.

A diversidade de abordagens facilita a compreensão

UNIDADE5

ADIÇÃO E SUBTRAÇÃO

Existem vários tipos de aviões. Alguns são específicos para levar passageiros e outros para transportar cargas.

O interior dos aviões que levam passageiros tem um ou dois corredores, que dão acesso às poltronas. Uma parte desses modelos de avião chega a ter 557 assentos para passageiros na classe econômica e 58 na classe executiva.

das operações básicas, desperta o interesse da turma pela Matemática e respeita os distintos ritmos de aprendizagem.

Habilidades da BNCC trabalhadas na unidade: EF02MA05 , EF02MA06 , EF02MA09 , EF02MA10 e EF02MA11

SUGESTÃO DE ESTRATÉGIA INICIAL

Márcia tem 24 carrinhos e seu primo Mateus tem 5 carrinhos a mais. Quantos carrinhos Mateus tem?

Rafael quer comprar um livro que custa 58 reais. Quantos reais ele precisa poupar para comprar esse livro, se ele tem 43 reais?

Havia 13 crianças em um parque. Chegaram mais 11 crianças para brincar com elas. Quantas crianças há, ao todo, no parque?

Respostas

24 + 5 = 29; Mateus tem 29 carrinhos.

58 43 = 15 ; Rafael precisa poupar 15 reais para comprar o livro.

13 + 11 = 24; No parque, há 24 crianças ao todo.

Você já conheceu um avião? Converse com os colegas sobre o assunto.

Como você faria para determinar quantos passageiros podem viajar no avião citado no texto?

Por que você acha que existem aviões diferentes para passageiros e para carga? Justifique sua resposta.

• Permita aos estudantes que se expressem livremente e decidam que operação matemática ou estratégia pessoal deve ser utilizada, antes de realizarem os cálculos dos problemas propostos na Sugestão de estratégia inicial, justificando cada caso. Os registros dos estudantes podem ser retomados no final da unidade a fim de comparar os procedimentos e os resultados e verificar o progresso da aprendizagem. As situações-problema propostas são importantes, pois envolvem diferentes ideias da adição e da subtração.

• Providencie com antecedência imagens de outros modelos de avião e as apresente aos estudantes. Destaque a relevância desse meio de transporte, pois, além de seguro, ele permite o deslocamento a longas distâncias em intervalos de tempo relativamente curtos.

• Após a leitura do texto inicial, converse com os estudantes sobre a importância do avião para a sociedade, pois esse meio de transporte reduz o tempo das viagens de longas distâncias. Porém, é necessário que haja um aeroporto ou pistas de pouso. Pergunte a eles se já viram um avião de perto ou se conhecem algum aeroporto que fique na cidade onde residem ou próximo a ela.

• Explique aos estudantes que a quantidade de passageiros apresentada por classe é determinada pela companhia aérea e pode variar de um modelo de avião para outro ou até entre os mesmos modelos.

• A questão 1 tem como objetivo levar os estudantes a relatarem as próprias experiências com viagens de avião.

• O objetivo da questão 2 é levar os estudantes a reconhecerem a adição como estratégia para determinar a quantidade total de assentos indicada na situação.

• Ao realizar a questão 3, verifique se os estudantes consideram os aviões importantes, pois proporcionam viagens rápidas, seguras e, em alguns casos, mais

acessíveis e econômicas. Explique a eles que por meio dos aviões de carga é possível transportar bens e mercadorias, como frutas e medicamentos, entre cidades de um mesmo país e entre países.

Respostas

1. Resposta pessoal. Espera-se que os estudantes mencionem que já conheceram um avião, seja por meio de uma viagem, seja por terem visto esse meio de transporte no céu, na televisão ou em livros.

2. Resposta pessoal. Espera-se que os estudantes digam que realizariam uma

06/10/2025 18:16:17

adição, ou seja, adicionariam a quantidade de assentos para passageiros da classe econômica à quantidade da classe executiva.

3. Resposta pessoal. Espera-se que os estudantes reflitam sobre a função dos aviões e compreendam a especificidade do uso de cada tipo, conforme a necessidade do transporte.

Avião na pista do aeroporto de Sinop, estado do Mato Grosso, em 2025.

Interior de um avião de passageiros, em momento de limpeza dos assentos.

1 a 3. Respostas nas orientações ao professor

• Durante o desenvolvimento do trabalho com os conteúdos de adição e de subtração, permita aos estudantes que expressem as próprias estratégias para a resolução das atividades propostas e das situações-problema, pré-requisitos para que eles tenham a oportunidade de construir relações entre a linguagem oral e as diferentes representações matemáticas, além de ampliar o repertório de cálculo.

• A atividade 1 tem como objetivo explorar a adição com significado de juntar, utilizando o material dourado e o algoritmo como estratégia de cálculo. Usando as representações do material dourado, peça aos estudantes que representem os números 105 e 142 e, em seguida, que façam a junção das placas (centenas), das barras (dezenas) e dos cubinhos (unidades), obtendo o resultado da adição. Utilize-o a fim de que a turma compreenda, na prática, os agrupamentos necessários para efetuar a adição.

ADIÇÃO COM RESULTADO ATÉ 999

SEM REAGRUPAMENTO

1. a) Resposta pessoal. Espera-se que os estudantes apresentem a resposta com base em suas estratégias pessoais. Permita que eles conversem livremente, compartilhando seus cálculos e opiniões, antes de iniciar a explicação da resposta.

1. Antônio pretende comprar uma calça e uma jaqueta. Ele encontrou algumas opções em uma loja.

a ) Quantos reais Antônio vai pagar pela compra da calça e da jaqueta nessa loja?

Para determinar a quantia que Antônio vai gastar nessa compra, devemos calcular 105 + 142 . Verifique algumas maneiras de realizar esse cálculo e complete o que falta.

Dica: Cada placa tem 10 barras e representa uma centena

Utilizando o material dourado

Representamos os números 105 e 142 utilizando placas, barras e cubinhos.

Juntando as placas (centenas), as barras (dezenas) e os cubinhos (unidades), obtemos o resultado da adição.

Resposta: 105 + 142 = 247.

105 + 142 =

BNCC

As atividades desta unidade possibilitam aos estudantes construir fatos básicos da adição e da subtração e utilizá-los em procedimentos de cálculo mental ou escrito, contemplando a habilidade EF02MA05. Além disso, incentiva-os a resolver problemas de adição e subtração, com significados de juntar, acrescentar, retirar e separar, por meio de diferentes estratégias pessoais, desenvolvendo, assim, a habilidade EF02MA06

Utilizando algoritmo

1º .

Resposta: 5 U + 2 U = 7 U

5  U + 2  U = U

2º .

3º . Adicionamos as dezenas. Adicionamos as unidades.

Por fim, adicionamos as centenas.

U

Resposta: 1 C + 1 C = 2 C

Resposta: 0 D + 4 D = 4 D

0  D + 4  D = D

1  C + 1  C = C parcelas

soma ou total

Resposta: 105 + 142 = 247

Resposta: Portanto, Antônio vai gastar 247 reais nessa compra.

Portanto, Antônio vai pagar reais nessa compra.

b ) Quantos reais Antônio gastaria nessa loja se tivesse comprado:

• a calça e o tênis?

Resposta: 105 + 132 = 237. Antônio gastaria 237 reais.

• a calça, a jaqueta e o tênis?

Resposta: 105 + 142 + 132 = 379. Antônio gastaria 379 reais.

• Ao apresentar o algoritmo, evidencie o valor posicional dos algarismos, que é uma característica ausente no material dourado. Converse com os estudantes sobre a importância de ter mais de uma estratégia de cálculo para que eles possam escolher a que julgarem mais adequada. Além disso, enfatize que, independentemente da estratégia adotada, a resposta esperada deverá ser a mesma.

• No item b, os estudantes devem calcular quantos reais Antônio teria gastado nessa loja se tivesse comprado a calça e o tênis e, depois, calcular quantos reais ele teria gastado nessa mesma loja se tivesse comprado a calça, a jaqueta e o tênis. No último item, comente que é possível resolver a questão somando a resposta do item anterior ao preço da jaqueta.

123

06/10/2025 18:16:18

• Verifique a possibilidade de utilizar a calculadora como material de apoio, com o intuito de que os estudantes façam a investigação das hipóteses dos cálculos. Incentive e valorize o cálculo mental e, posteriormente, a construção do sistema de registro. No caso de apresentarem a resposta por cálculo mental, incentive-os a descrever os procedimentos usados, a fim de expressarem seu raciocínio lógico e suas estratégias pessoais. Acolha com atenção e respeito as respostas de todos e engaje a turma nos comentários, motivando-os a participar ativamente da conversa. Essa ação participativa promove o desenvolvimento da comunicação e enriquece o vocabulário deles. Com a colaboração dos estudantes, proponha que um deles descreva como pensou (raciocínio) para que um colega registre na lousa a estratégia.

• A atividade 2 tem o objetivo de explorar estratégias de cálculo envolvendo adição. Incentive os estudantes a usarem a estratégia que preferirem.

• Na atividade 3, eles devem completar as adições com os números que estão apresentados nas fichas, utilizando o algoritmo. Para promover a inclusão dos estudantes com NEE, organize os estudantes em duplas e oriente-os a completar cada adição no caderno, testando os números das fichas sem repeti-los. Oriente-os a utilizar a calculadora como ferramenta de validação dos cálculos e a observar se os resultados que escreveram no caderno são os mesmos da calculadora. Caso julgue necessário, auxilie-os a usar a calculadora. Entre as possibilidades, uma sugestão de resposta para essa atividade é: 156 + 522 = 678 e 823 + 112 = 935

2. Efetue as adições a seguir da maneira que preferir.

a ) 148 + 231 =

Resposta: 148 + 231 = 379

b ) 822 + 105 =

Resposta: 822 + 105 = 927

c ) 662 + 132 =

Resposta: 662 + 132 = 794

d ) 503 + 391 =

Resposta: 503 + 391 = 894

3. Complete as adições com os algarismos que estão apresentados nas fichas.

Dica: Cada ficha pode ser utilizada somente uma vez.

Resposta pessoal. Sugestão de respostas: A: 156 + 822 = 978; B: 523 + 112 = 635 Comentários nas orientações ao professor

06/10/2025 18:16:18

A.

B.

4. Virgílio vende pipoca em um parque. No sábado, ele vendeu 120 saquinhos de pipoca e, no domingo, 32 saquinhos a mais do que no sábado.

a ) Quantos saquinhos de pipoca Virgílio vendeu no domingo?

Resposta: 120 + 32 = 152. Virgílio vendeu, no domingo, 152 saquinhos de pipoca.

b ) Quantos saquinhos de pipoca Virgílio vendeu, ao todo, nos dois dias?

Resposta: 120 + 152 = 272. Virgílio vendeu, ao todo, 272 saquinhos de pipoca.

c ) Se Virgílio tivesse vendido 28 saquinhos de pipoca a mais no sábado, quantas centenas de saquinhos ele teria vendido nesses dois dias?

Resposta: 272 + 28 = 300. Virgílio teria vendido 3 centenas de saquinhos de pipoca.

5. Em um aeroporto, embarcaram 124 homens e 225 mulheres durante uma hora. Quantas pessoas, ao todo, embarcaram nessa hora?

Resposta: 124 + 225 = 349. Nessa hora, embarcaram 349 pessoas ao todo.

REFERÊNCIAS COMPLEMENTARES

RODRIGUES, Joana Pereira. A Adição e Subtração no Pré-Escolar e no 1º Ciclo no Ensino Básico. 2017. Dissertação (Mestrado em Educação Pré-Escolar e Ensino do 1º Ciclo do Ensino Básico) – Instituto de Educação da Universidade do Minho, Braga. Disponível em: https://repositorium.sdum.uminho.pt/ handle/1822/57295. Acesso em: 22 ago. 2025.

18:16:18

O trabalho, originalmente de Portugal, investigou como crianças da Educação Infantil e dos anos iniciais do Ensino Fundamental compreendem e utilizam a adição e a subtração, além de identificar possíveis dificuldades para apresentar metodologias e intervenções ao aprendizado dessas operações.

• O objetivo da atividade 4 é incentivar os estudantes a resolverem uma situação-problema que envolve diferentes significados da adição. No item a , aborda-se adição com a ideia de acrescentar. No item b, aborda-se adição com significado de juntar. Não se deve trabalhar a classificação desses significados com os estudantes, pois eles servem para orientar e evidenciar as ideias e estratégias que podem ser exploradas. No item c, eles devem utilizar o resultado do item anterior e adicionar 28 a ele, obtendo 300 como resultado. Verifique se eles estão associando o termo a mais, de modo indevido, à operação de adição, pois o contexto insere um significado de diferença. Caso isso ocorra, retome esse termo no tópico que envolve subtração para associar ao contexto dessa operação.

• A atividade 5, assim como a atividade 6 da próxima página, tem o objetivo de incentivar os estudantes a resolverem situações-problema com significado de juntar. Observe as estratégias usadas por eles e permita-lhes que as compartilhem com a turma. Se necessário, complemente-as.

• A atividade 7 aborda cálculos de adição e representação de seus resultados no ábaco. Assim, os estudantes devem ser capazes de identificar o valor posicional dos algarismos nos resultados das adições e representá-los no ábaco de papel disponível no Material complementar do final do Livro do Estudante. Para um melhor aproveitamento desta atividade, utilize-o a fim de que a turma compreenda, na prática, os agrupamentos necessários para efetuar a adição.

ATIVIDADE EXTRA

Jogo da soma

Providencie ou confeccione dados em formato de tetraedro. Organize a turma em duplas e disponibilize um dado para cada uma. Os estudantes decidirão quem iniciará. Cada participante deve lançar o dado três vezes e registrar os algarismos das faces laterais. Com esses algarismos, ele deve formar um número de três algarismos. Em seguida, o mesmo estudante repete esse procedimento e, depois, passa a vez para o próximo participante. Após cada participante formar os dois números de três algarismos, devem adicioná-los. Vence quem obtiver a maior soma. Uma possível resposta seria: 123 + 423 = 546 Nesse caso, o estudante teria obtido os algarismos 1, 2 e 3 no primeiro lançamento, e os algarismos 2, 3 e 4 no segundo. Essa atividade permite desenvolver a habilidade de efetuar adições, além de favorecer o desenvolvimento do raciocínio lógico, pois os estudantes podem observar que, para formar o maior número possível, é preciso colocar o maior algarismo na casa das centenas e o segundo maior na casa das dezenas.

6. André contou quantos passos tinha de sua casa até a casa de Bianca. Depois, da casa de Bianca até a casa de Carla. Acompanhe, no esquema, a quantidade de passos que ele fez.

Casa de André 132 passosCasa de Bianca 215 passosCasa de Carla

Quantos passos André caminhou, ao todo, para ir da casa dele até a casa de Carla, passando pela casa de Bianca?

Resposta: 132 + 215 = 347.

André caminhou 347 passos.

André caminhou passos.

7. Joana calculou 235 + 152 utilizando um ábaco.

1º .

2º .

Representamos o número 235. C D U

Adicionamos as unidades, as dezenas e as centenas da outra parcela, ou seja, o número 152.

235 + 152 = 387

Usando o ábaco e as contas das páginas 263 e 265 do Material complementar, efetue as adições.

Resposta: 236 + 142 = 378

a ) 236 + 142 =

Resposta: 271 + 315 = 586

b ) 271 + 315 =

Resposta: 259 + 140 = 399

c ) 259 + 140 =

BNCC

Resposta: 365 + 213 = 578

d ) 365 + 213 =

Resposta: 401 + 347 = 748

e ) 401 + 347 =

Resposta: 520 + 408 = 928

f ) 520 + 408 =

Professor, professora: Enfatize aos estudantes que devem guardar esse material após a utilização, pois ele será utilizado em outras unidades no decorrer deste volume.

As atividades desta página incentivam a construção de fatos básicos da adição, utilizando-os em cálculos mentais ou escritos. Também exploram a resolução de problemas de adição, envolvendo número de até três ordens, utilizando estratégias pessoais ou convencionais, o que favorece o desenvolvimento das habilidades EF02MA05 e EF02MA06 da BNCC.

ADIÇÃO COM REAGRUPAMENTO

8. Os moradores do bairro de Júlio se dividiram em dois grupos para arrecadar peças de roupas de frio para doação. O grupo A arrecadou 187 peças e o grupo B arrecadou 234.

Quantas peças de roupa, ao todo, os moradores desse bairro conseguiram arrecadar?

Para determinar a quantidade de peças arrecadadas pelos moradores, precisamos calcular 187 + 234 . Observe algumas maneiras de realizar esse cálculo e complete o que falta nas informações.

Dica: Doar roupas de frio, em bom estado, quando podemos e para quem precisa é um ato de amor e solidariedade.

Utilizando o material dourado

1º .

2º . Representamos os números 187 e 234 utilizando placas, barras e cubinhos.

187 234

Juntamos as placas (centenas), as barras (dezenas) e os cubinhos (unidades). Em seguida, trocamos 10 unidades por 1 dezena e 10 dezenas por 1 centena. Assim, obtemos o resultado da adição.

187 + 234 = 421

Resposta: 400 + 20 + 1 = 421

400 + 20 + 1 =

06/10/2025 18:16:19

• Leia com os estudantes o enunciado da atividade 8 e pergunte a eles quais estratégias de cálculo utilizariam para resolver esta situação-problema. Permita que comentem e compartilhem suas ideias com a turma. Depois, usando o material dourado, represente os números 187 e 234. Mostre a eles o passo a passo de todo o processo, juntando as placas (centenas), as barras (dezenas) e os cubinhos (unidades). Em seguida, realize a troca de 10 unidades por 1 dezena e de 10 dezenas por 1 centena, assim obtemos o resultado da adição. Nesse momento, é importante que os estudantes compreendam todos os procedimentos que envolvem a adição para que não a efetuem de maneira mecânica. Para um melhor aproveitamento desta atividade, verifique se eles compreenderam os conceitos e os procedimentos explorados, solicitando que efetuem outras adições usando o material dourado. • Promova uma reflexão com a turma sobre a cooperação entre as pessoas e a importância de, sempre que possível, contribuir com ações que envolvam doação de alimentos, objetos bem conservados que não utilizamos mais, como cobertores, roupas, brinquedos e outros itens. Esses são gestos que mobilizam solidariedade e empatia.

• Apresente aos estudantes a decomposição dos números 187 e 234 em centenas, dezenas e unidades. Explique a eles os procedimentos em partes das adições, depois de decompor as parcelas, mostrando que 7 + 4 = 11 e 11 = 10 + 1 , ou seja, esse resultado representa uma dezena e uma unidade; de igual modo, devemos adicionar 80 + 30 = = 110 e 110 = 100 + 10 , obtendo uma centena e uma dezena. Assim como o material dourado, essa estratégia de decomposição auxilia a turma a compreender o algoritmo.

• Ao efetuar a adição proposta utilizando o algoritmo, comente que é muito importante sempre organizar unidades abaixo de unidades, dezenas abaixo de dezenas e centenas abaixo de centenas, evidenciando os nomes dos termos da operação de adição (parcelas e soma ou total). Para um melhor aproveitamento desta proposta, utilize o material dourado para retomar as trocas e os reagrupamentos.

• Aproveite a atividade 9 para verificar a aprendizagem dos estudantes com relação à decomposição dos números. Caminhe pela sala de aula, observando os procedimentos que estão sendo utilizados e oriente-os, caso tenham dificuldades.

Decompondo os números

Usando o algoritmo

Adicionamos as unidades.

Resposta: 7 U + 4 U = 11 U

Trocamos 10 dezenas por 1 centena e adicionamos as centenas.

Trocamos 10 unidades por 1 dezena e adicionamos as dezenas.

D + 8  D + 3  D = D

Resposta: 187 + 234 = 421

C + 1  C + 2  C = C

Resposta: 1 C + 1 C + 2 C = 4 C

Portanto, os moradores desse bairro conseguiram arrecadar, ao todo, peças de roupa.

Resposta: Portanto, os moradores desse bairro conseguiram arrecadar, ao todo, 421 peças de roupa.

9. Efetue no seu caderno as adições a seguir, decompondo os números, e complete os itens. a ) 128 + 143 = b ) 265 + 137 =

Resposta: 128 + 143 = 271

Resposta: 265 + 137 = 402

10. Efetue as adições da maneira que preferir.

b ) 347 + 354 = a ) 412 + 309 =

Resposta: 412 + 309 = 721

Resposta: 347 + 354 = 701

11. Mara fez duas viagens com o carro dela. Na primeira viagem, o carro gastou 128 litros de combustível e, na segunda, 142 litros. Quantos litros de combustível o carro de Mara gastou nessas duas viagens?

Resposta: 128 + 142 = 270. O carro de Mara gastou 270 litros de combustível nessas duas viagens.

Unidades temáticas integradas

12. Mateus calculou mentalmente o resultado de 583 + 228 .

Primeiro, vou calcular

580 + 220 . Em seguida, vou adicionar 3 + 8 = 11 ao resultado.

580 + 220 = 800 1º . 3 + 8 = 11 2º .

800 + 11 = 811 3º .

Assim como Mateus, calcule mentalmente as adições a seguir.

a ) 334 + 492 =

Resposta: 334 + 492 = 826

b ) 526 + 295 =

Resposta: 526 + 295 = 821

c ) 673 + 227 =

Resposta: 673 + 227 = 900

d ) 233 + 675 =

Resposta: 233 + 675 = 908

13. Efetue as adições da atividade anterior utilizando uma calculadora e verifique se suas respostas estão corretas.

Resposta: Espera-se que os estudantes utilizem uma calculadora e verifiquem se os resultados obtidos mentalmente na atividade anterior estão corretos.

BNCC

• A atividade 10 tem como objetivo levar os estudantes a escolherem a estratégia de cálculo que preferirem para efetuar adições com reagrupamentos. Aproveite essa atividade para avaliar os procedimentos e o grau de desenvolvimento das resoluções dadas pelos estudantes, observando se têm dúvidas. Se isso acontecer, resolva os itens da atividade usando o material dourado e o método da decomposição.

• A atividade 11 estabelece uma integração entre as unidades temáticas de Matemática Números e Grandezas e medidas ao relacionar a quantidade de combustível que o carro de Mara gastou, usando o litro como unidade de medida para expressar essa quantidade.

• Na atividade 11 solicite aos estudantes que leiam em voz alta o enunciado e pergunte qual operação matemática pode ajudá-los a solucionar o problema. Ao resolverem, verifique se eles estão aplicando a ideia de adição com reagrupamento e, caso tenham dificuldade, disponibilize material dourado ou outro material de contagem para auxiliá-los nos cálculos.

• A atividade 12 tem como objetivo fornecer aos estudantes uma estratégia para ser usada em cálculos mentais, incentivando-os a desenvolver a organização do pensamento e a comunicação matemática. Peça-lhes que verifiquem a estratégia que Mateus aplicou para efetuar a adição e, depois, efetue-a com o auxílio deles, utilizando os mesmos procedimentos que Mateus usou. Dê outros exemplos na lousa. Em seguida, permita que resolvam os itens apresentados na atividade.

• A atividade 13 complementa a atividade 12 por meio da verificação das respostas com uso da calculadora. Oriente a turma sobre o uso da calculadora, que é um instrumento auxiliar de cálculo com a finalidade de verificar se as respostas obtidas estão corretas.

06/10/2025 18:17:56

As atividades desta página possibilitam o desenvolvimento das habilidades EF02MA05 e EF02MA06 ao propiciar aos estudantes que construam fatos básicos da adição, utilizando-os em cálculos mentais ou escritos. Além disso, são incentivados a resolver problemas de adição com números de até três ordens, utilizando estratégias pessoais.

• A atividade 14 estabelece uma integração entre as unidades temáticas de Matemática Números e Grandezas e medidas ao abordar uma situação-problema envolvendo diferentes significados da adição com valor do sistema monetário brasileiro. Além disso, esta atividade envolve um problema de transformação com quantidade inicial desconhecida. É comum que os estudantes associem termos como a mais e ganhou à adição e perdeu e gastou à subtração. Assim, esta atividade busca romper com essa associação ao utilizar o termo pagou em um contexto que envolve adição. No entanto, essa compreensão não é imediata e requer reflexão. Se os estudantes tiverem dificuldade, utilize o mesmo contexto com números menores e, depois, retome o problema proposto.

• Leia com os estudantes o enunciado da atividade 15 e faça alguns questionamentos, levando-os a refletir sobre a resolução de situações-problema, como: “Quais são os dados apresentados neste problema?”; “Quais são as informações necessárias para resolvê-lo?”; “Todas as informações necessárias estão contidas no enunciado ou estão faltando informações?”; “Qual estratégia de cálculo é possível usar?”.

• A atividade 16 solicita a elaboração de um problema com base em uma resposta apresentada. Oriente-os a ler o enunciado da atividade e a identificar contextos que possam ter essa frase como resposta. Ressalte que é importante o enunciado do problema ter uma linguagem simples e todos os dados necessários para a resolução.

Unidades temáticas integradas

14. Sônia pagou 562 reais em dinheiro ao fazer uma compra no supermercado. Sabendo que ainda sobraram 39 reais na carteira, quantos reais Sônia tinha antes de fazer essa compra?

Resposta: 562 + 39 = 601. Sônia tinha 601 reais na carteira antes de fazer as compras no supermercado.

15. Uma confecção produziu 297 blusas na primeira semana de março. Na segunda semana desse mesmo mês, a confecção produziu 158 blusas a mais do que na primeira semana.

a ) Quantas blusas essa confecção produziu na segunda semana?

Resposta: 297 + 158 = 455. Essa confecção produziu 455 blusas na segunda semana.

b ) Quantas blusas essa confecção produziu durante as duas semanas?

Resposta: 297 + 455 = 752. Essa confecção produziu 752 blusas nas duas semanas.

16. Elabore um problema no caderno, em letra cursiva, envolvendo adição que tenha como resposta a frase a seguir. Depois, entregue o problema para um colega resolver. Analisem juntos se o enunciado está coerente com a resposta.

Professor, professora: Oriente os estudantes na escrita do problema da atividade 16, incentivando o traçado em letra cursiva, a fim de que eles treinem esse tipo de escrita.

AVALIANDO

Objetivo

Eles fizeram, ao todo, 972 pontos.

Comentários nas orientações ao professor

Resolver com diferentes estratégias situações-problema envolvendo adição com e sem reagrupamento.

Sugestão de intervenção

Providencie antecipadamente e leve para a sala de aula algumas cópias de diferentes situações-problema envolvendo adição com e sem reagrupamento com resultado até 999. Organize a turma em grupos, entregue uma situação-problema diferente a cada grupo e solicite que a resolvam. Oriente-os a identificar o assunto tratado, os

Resposta pessoal. Espera-se que os estudantes elaborem um problema envolvendo adição com base na informação obtida e, depois, verifiquem com um colega se o problema elaborado por eles corresponde à situação apresentada.

dados apresentados e as estratégias de cálculos que podem usar. Depois, peça a cada grupo que apresente à turma a situação-problema e a estratégia usada para resolvê-la. Por fim, conduza uma conversa com a turma, consolidando e sistematizando os conhecimentos adquiridos. Caso algum estudante tenha dificuldade, retome a atividade 1 das páginas 122 e 123 e a atividade 8 das páginas 127 e 128. Utilize o material dourado para explorar as trocas e os reagrupamentos, que ajudará a dar sentido ao algoritmo, principalmente para o caso de reagrupamento. Depois, sugira alguns problemas envolvendo adição com significado de acrescentar e de juntar.

06/10/2025 18:17:56

17. Complete as sequências apresentadas.

Unidades temáticas integradas

Resposta: 99, 114, 129, 144, 159, 174

Resposta: 156, 207, 258, 309, 360, 411

18. Com um colega, leiam o problema a seguir. Depois, respondam a cada uma das questões.

Ângela tem 280 reais e precisa comprar uma calça que custa 128 reais e um sapato que custa 136 reais. A quantia que Ângela tem é suficiente para fazer essa compra?

a ) Qual é o assunto tratado no enunciado do problema?

Resposta: Os estudantes devem interpretar o enunciado do problema e dizer que ele trata de uma situação de compra envolvendo adição, em que é necessário verificar se o valor disponível é suficiente para realizar uma compra.

b ) Os números que aparecem no enunciado representam qual informação?

Resposta: Os estudantes devem verificar que os números apresentados no problema informam quantias em reais de cada uma das peças.

c ) Com os dados apresentados, é possível resolver o problema? Se a resposta for afirmativa, resolva-o.

Resposta: Sim. 128 + 136 = 264. A quantia que Ângela tem é suficiente para fazer a compra, pois 264 é menor do que 280.

BNCC

A atividade 17 propõe aos estudantes que completem sequências de números naturais em ordem crescente, usando uma regularidade estabelecida. Com isso, é desenvolvida a habilidade EF02MA11. Ao propor a interação com seus pares de forma cooperativa, trabalhando coletivamente na busca de soluções para problemas, a atividade 18 possibilita o de-

06/10/2025 18:17:57

senvolvimento do raciocínio lógico e explora o espírito da investigação, de modo a identificar aspectos consensuais ou não na discussão de determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles, conforme descrito nas Competências específicas de Matemática 2 e 8

• A atividade 17 estabelece uma integração entre as unidades temáticas de Matemática Números e Álgebra ao relacionar sequências recursivas por meio de observação de regras usadas em seriações numéricas, além de levar os estudantes a completarem a sequência com os números que estão faltando, de acordo com a regra dada. Se eles tiverem dificuldade, evidencie a regularidade estabelecida, que é adicionar 15 ao número anterior a partir do segundo termo no item A e adicionar 51 ao número anterior a partir do segundo termo no item B Caso julgue necessário, proponha outras sequências para os estudantes completarem com os números faltantes, com base em uma regra. Atividades como essa contribuem para o raciocínio lógico e a capacidade de análise, promovendo a compreensão do sistema de numeração. • Ao propor a interação com seus pares na busca de solução para o problema, a atividade 18 instiga o desafio e a reflexão para obter soluções, incentivando a criação de critérios dos estudantes em sua capacidade de elaboração de argumentos para solucionar problemas em conjunto, compreendendo os processos matemáticos envolvidos na resolução de problemas.

• A atividade 1 relaciona as unidades temáticas de Matemática Números e Probabilidade e estatística ao trabalhar com leitura e interpretação de dados em uma tabela. Além disso, ela pode ser realizada na prática, representando as quantidades com material dourado, palitos ou outros materiais de contagem.

• A atividade 1 tem o objetivo de incentivar os estudantes a resolverem situações-problema envolvendo a operação de subtração por meio de diferentes estratégias de resolução. O item a desta atividade propõe que façam a comparação de números naturais. O item b aborda uma questão que envolve a operação de subtração com significado de comparar. Observe que o termo a mais nesse contexto implica o cálculo da subtração. Esse é um momento oportuno para evidenciar que a associação de termos a determinada operação pode ocasionar equívocos que conduzem a erros. Se possível, leve para a sala de aula o material dourado para representar os números 256 e 132 e efetuar a operação na prática.

• Ao realizar a decomposição dos números em parcelas de adição, oriente os estudantes a efetuarem a subtração entre as unidades, as dezenas e as centenas de cada número e comente que, depois de efetuadas, serão adicionadas para indicar a resposta.

SUBTRAÇÃO ENVOLVENDO NÚMEROS ATÉ 999 SEM REAGRUPAMENTO

1. Na tabela, está apresentada a quantia que Cleide arrecadou com a venda de sanduíches naturais em três dias de uma semana.

a ) Em quais desses dias

Resposta: Terça-feira. Cleide arrecadou 256 reais. Unidades temáticas integradas

Cleide teve a maior arrecadação com a venda de sanduíches naturais?

Quantos reais ela arrecadou nesse dia?

Quantia em reais arrecadada com a venda de sanduíches naturais

Dia Quantia arrecadada

Segunda-feira 145 reais

Terça-feira 256 reais

Quarta-feira 132 reais

Fonte de pesquisa: Anotações de Cleide em setembro de 2027.

b ) Quantos reais a mais Cleide arrecadou na terça-feira em relação à quarta-feira com a venda dos sanduíches?

Para responder a esta questão, precisamos calcular 256 − 132

Observe algumas maneiras de efetuar esse cálculo e complete o que falta nas informações.

Utilizando o material dourado

1º .

Representamos o número 256 utilizando cubinhos, barras e placas. Em seguida, retiramos 2 cubinhos (unidades), 3 barras (dezenas) e 1 placa (centena).

− 132

Decompondo os números

Resposta: 100 + 20 + 4 = 124

ARTICULANDO CONHECIMENTOS

Aproveite o contexto dessa atividade para realizar um trabalho de integração com Ciências da Natureza, destacando a importância de consumir alimentos saudáveis, por meio de pesquisas de informações nutricionais de diferentes ingredientes na composição do lanche natural, analisando calorias, vitaminas etc. Essa abordagem se articula com a Matemática ao comparar, por meio de gráficos e tabelas, a composição nutricional desse alimento, identificando opções mais saudáveis e nutritivas.

2º .

Obtemos, assim, o resultado da subtração.

Resposta: 256 − 132 = 124

− 132 =

Utilizando o algoritmo

Subtraímos as unidades.

1º . 3º . 2º .

Resposta: 6 U − 2 U = 4 U

Subtraímos as centenas.

Resposta: 2 C − 1 C = 1 C

Subtraímos as dezenas.

Resposta: 5 D − 3 D = 2 D

2 5 6 1 3 2 minuendo subtraendo resto ou diferença

Resposta: 256 − 132 = 124

Portanto, Cleide arrecadou reais a mais na terça-feira em relação à quarta-feira com a venda dos sanduíches naturais.

Resposta: Portanto, Cleide arrecadou 124 reais a mais na terça-feira em relação à quarta-feira com a venda dos sanduíches naturais.

SANDUÍCHES NATURAIS

Uma opção saudável e prática para variar a alimentação é inserir no cardápio diário o consumo de sanduíches naturais, preparados com ingredientes frescos e sem excessos de gordura e sal.

Cada pessoa pode montar seu sanduíche com sua combinação favorita, variando os tipos de recheio, como peito de frango, atum, queijo e vegetais, o que torna essa opção de lanche agradável à maioria das pessoas.

Menina comendo um sanduíche natural.

ARTICULANDO CONHECIMENTOS

Solicite aos estudantes que façam, com seus familiares, uma pesquisa sobre a importância de uma alimentação saudável no nosso dia a dia e seus benefícios. Em seguida, eles devem escrever um bilhete com a conclusão do que pesquisaram, a fim de entregá-lo a você no dia combinado. Essa proposta permite a apropriação da linguagem escrita, favorecendo a integração com o componente curricular de Língua Portuguesa. Aproveite a oportunidade para verificar

06/10/2025 18:17:57

se estão pegando o lápis de maneira adequada e se fazem o traçado das letras seguindo a orientação e a direção da escrita de modo correto. Se julgar conveniente, escreva pausadamente na lousa as palavras e expressões que os estudantes identificarem como complexas e certifique-se de que eles acompanham a maneira como as letras são escritas e as copiam.

• Ao efetuar a subtração usando o algoritmo, converse com os estudantes, destacando o valor posicional dos algarismos, sempre organizando unidades abaixo de unidades, dezenas abaixo de dezenas e centenas abaixo de centenas, pois as estratégias anteriores não usam essa característica. Evidencie os termos da subtração: minuendo, subtraendo e resto ou diferença. Leve-os a perceber que, independentemente da estratégia utilizada, o resultado da subtração proposta será o mesmo.

• A atividade 2 tem o objetivo de explorar a operação de subtração. Utilize o material dourado a fim de que os estudantes compreendam, na prática, o processo que envolve a representação dos números com as peças e a remoção física das peças correspondentes ao subtraendo.

• A atividade 3 aborda o cálculo de subtração e a representação de seu resultado no ábaco. Sendo assim, os estudantes devem ser capazes de identificar o valor posicional dos algarismos para completar o resultado da subtração. Verifique se eles compreenderam que a subtração no ábaco envolve a retirada de contas para representar a diferença entre dois números, conforme mostra a imagem, considerando o valor posicional de cada algarismo. Assim, para realizar uma subtração, posiciona-se no ábaco o número maior, no caso, 258, e, em seguida, retiram-se as contas correspondentes ao número menor, no caso, 146, coluna por coluna, começando pela unidade, depois, pela dezena e, por fim, pelas centenas.

• Assim como na atividade anterior, verifique se os estudantes são capazes de identificar o valor posicional dos algarismos, na atividade 4. Espera-se que eles representem essas quantidades de modo adequado no ábaco de papel disponível no Material complementar do final do Livro do Estudante. Certifique-se de que eles estão compreendendo o procedimento de retirada de contas para representar a diferença entre dois números, considerando o valor posicional de cada algarismo.

2. Efetue as subtrações no caderno e escreva o resultado de cada item.

a ) 259 − 134 =

Resposta: 259 − 134 = 125

b ) 328 − 106 =

Resposta: 328 − 106 = 222

3. Durante uma campanha de vacinação, o posto de saúde do bairro atendeu 258 crianças no período da manhã de sexta-feira. Sabendo que, no período da tarde desse mesmo dia, foram atendidas 146 crianças, calcule a diferença entre as quantidades de crianças atendidas nesse posto entre esses dois períodos do dia.

Para resolver esse problema, precisamos calcular 258  – 146 Vamos efetuar esse cálculo utilizando um ábaco. Complete o que falta nas informações.

Representamos o número 258.

Retiramos as unidades, as dezenas e as centenas correspondentes ao número 146. A quantidade restante de contas no ábaco representa o resultado desse cálculo.

Resposta: 258 − 146 = 112

258 − 146 =

Portanto, a diferença entre a quantidade de crianças atendidas no posto de saúde, entre o período da manhã e o da tarde, foi de crianças.

Resposta: Portanto, a diferença entre a quantidade de crianças atendidas no posto de saúde, entre o período da manhã e o da tarde, foi de 112 crianças.

4. Usando o ábaco e as contas das páginas 263 e 265 do Material complementar, efetue as subtrações.

Professor, professora: Enfatize aos estudantes que eles devem guardar esse material após a utilização, pois ele será utilizado em outras unidades no decorrer deste volume.

a ) 236 − 124 =

Resposta: 236 − 124 = 112

b ) 385 − 275 =

Resposta: 385 − 275 = 110

c ) 576 − 521 =

Resposta: 576 − 521 = 55

d ) 408 − 205 =

Resposta: 408 − 205 = 203

C

5. Complete as subtrações com os algarismos que faltam.

Resposta: A: 689 − 243 = 446; B: 725 − 424 = 301

6. Lia e José estão brincando com um jogo. Eles anotaram a pontuação que fizeram no final da partida. Calcule, no caderno, quantos pontos Lia marcou a mais do que José.

Resposta: 457 − 231 = 226. Lia marcou 226 pontos a mais do que José.

7. Com um colega, leiam o problema a seguir. Depois, respondam a cada uma das questões.

Unidades temáticas integradas

Em uma padaria, havia 178 quilogramas de farinha. Para fazer alguns pães e bolos, o padeiro utilizou 54 quilogramas de farinha. Quantos quilogramas sobraram?

a ) Qual é o assunto tratado no enunciado do problema?

Resposta: Os estudantes devem interpretar o enunciado do problema e dizer que ele trata da diferença entre a quantidade em quilogramas de farinha que havia na padaria e a quantidade de farinha utilizada para fazer os pães e bolos.

b ) Os números que aparecem no enunciado representam qual informação?

Resposta: Os estudantes devem responder que os números apresentados no problema informam a quantidade de farinha em quilogramas.

c ) Com os dados apresentados, é possível resolver o problema? Se a resposta for afirmativa, resolva-o no caderno.

Resposta: Sim. 178 − 54 = 124. Sobraram 124 quilogramas de farinha.

Dica: Resolva o item c desta atividade utilizando o ábaco.

BNCC

Ao propor a interação com seus pares de forma cooperativa, trabalhando coletivamente na busca de soluções para problemas, a atividade 7 possibilita o desenvolvimento do raciocínio lógico e explora o espírito da investigação, de modo a identificar aspectos consensuais ou não na discussão de determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles, conforme descrito nas Competências específicas de Matemática 2 e 8

06/10/2025 18:17:58

• A atividade 5 solicita aos estudantes que completem as subtrações com os algarismos que faltam. Organize a turma em duplas e permita que resolvam a atividade a fim de que reflitam e troquem ideias sobre as estratégias que devem usar para encontrar os algarismos. Depois, converse com os estudantes e observe se as estratégias usadas são válidas, orientando-os e esclarecendo as dúvidas que surgirem.

• A atividade 6 apresenta uma situação-problema em que os estudantes devem efetuar uma subtração com ideia de comparação. Comente que o termo a mais não significa, necessariamente, que a operação a ser feita deve ser uma adição.

• A atividade 7 estabelece uma integração entre as unidades temáticas de Matemática Números e Grandezas e medidas ao abordar uma situação-problema envolvendo medida de massa. Ao propor a interação com seus pares na busca de solução para o problema, a atividade instiga o desafio e a reflexão para obter soluções, incentivando a criação de critérios dos estudantes em sua capacidade de elaboração de argumentos para solucionar problemas em conjunto, compreendendo os processos matemáticos envolvidos na resolução de problemas.

A.

• A atividade 8 estabelece uma integração entre as unidades temáticas de Matemática Números e Grandezas e medidas ao abordar uma situação-problema envolvendo diferentes significados da adição e da subtração com valor do sistema monetário brasileiro.

• A atividade 8 aborda a resolução de problemas envolvendo subtração com significado de retirar. No item a desta atividade, os estudantes devem ler a informação do cartaz para determinar o valor que será economizado por Angélica. O item b, além da subtração, envolve a adição com significado de juntar, a fim de determinar o preço a ser pago pelas duas batedeiras.

• Aproveite o contexto abordado na atividade 8 e converse com os estudantes, levando-os a refletir sobre o ato de realizar compras de objetos de que não precisamos. Muitas vezes, isso ocorre quando somos atraídos por promoções que anunciam preços baixos. Antes de comprar algo, é importante pesquisar os preços do produto, que podem variar muito de uma loja para outra, assim como analisar se essa compra é realmente necessária.

• Para complementar a atividade 9, proponha aos estudantes a seguinte questão: “Na segunda semana, esse comerciante comprou mais 765 garrafas de água para repor o estoque e vendeu 743 unidades. Quantas garrafas ainda sobraram após a venda da segunda semana?”. Verifique se todos chegam à conclusão de que sobraram 134 garrafas de água mineral (112 + 765 = 877).

Por fim, basta calcular 877 743 = 134

8. Angélica está escolhendo batedeiras para comprar, pois precisa substituir as que tinha na cozinha de seu restaurante.

Unidades temáticas integradas

Quero comprar essa batedeira.

a ) Quantos reais Angélica vai economizar na compra da batedeira do cartaz, considerando o preço antes e depois da promoção?

b ) Angélica comprou as batedeiras amarela e verde. Ao pagar essa compra, ela entregou ao caixa 6 cédulas de 100 reais e 1 cédula de 50 reais. Quantos reais Angélica recebeu de troco?

Resposta: 159 − 125 = 34 Angélica vai economizar 34 reais.

Resposta: Total em reais das batedeiras amarela e verde:

335 + 295 = 630. Quantia em reais entregue ao caixa: 100 + 100 + 100 + + 100 + 100 + 100 + 50 = 650 Quantia recebida de troco:

650 − 630 = 20. Portanto, Angélica recebeu 20 reais de troco.

9. Um comerciante tinha 978 garrafas de água mineral para vender. Na primeira semana, ele vendeu 866 unidades. Quantas garrafas sobraram?

DICA: Beber água durante o dia é fundamental para manter o bom funcionamento do corpo.

Resposta: 978 − 866 = 112. Portanto, sobraram 112 garrafas de água mineral.

BNCC

A atividade 8 desta página favorece o desenvolvimento das habilidades EF02MA05 e EF02MA06 ao abordar a construção de fatos básicos da adição e da subtração e utilizá-los no cálculo, bem como na resolução de problemas de adição e de subtração envolvendo números de até três ordens. O tema contemporâneo transversal Educação financeira também é contemplado, pois permite aos estudantes refletirem sobre questões de consumo.

SUBTRAÇÃO COM REAGRUPAMENTO

10. Na cena a seguir, Marcelo e Vanessa estão brincando com um jogo de videogame

a ) No momento da cena, qual é a pontuação de:

b

• Marcelo? pontos.

Resposta: 192 pontos.

INFOGRÁFICO CLICÁVEL: USO SAUDÁVEL DE TELAS

• Vanessa? pontos.

Resposta: 223 pontos.

) Quantos pontos Vanessa fez a mais do que Marcelo?

Para responder a essa pergunta, precisamos calcular 223 − 192 Verifique algumas maneiras de realizar esse cálculo e complete as informações.

Utilizando o material dourado

1º .

Representamos o número 223 com cubinhos, barras e placas. Inicialmente subtraímos as unidades que, nesse caso, correspondem a 2 cubinhos (unidades).

2º .

223 − 2 = 221

Precisamos retirar 9 dezenas de 2 dezenas. Como 9 é maior do que 2, trocamos 1 placa (1 centena) por 10 barras (10 dezenas), ficando com 1 centena e 12 dezenas. Então, retiramos 9 barras (dezenas). Por fim, retiramos 1 placa (centena) e obtemos o resultado da subtração.

223 − 192 =

Resposta: 223 − 192 = 31

09/10/2025 14:55:30

• A atividade 10 apresenta uma situação-problema contextualizando o conteúdo a ser trabalhado e tem como objetivo incentivar os estudantes a explorarem diferentes estratégias a fim de efetuarem subtração com reagrupamento.

• Para um melhor aproveitamento desta atividade, leve o material dourado para a sala de aula e faça, na prática, o cálculo sugerido na página, facilitando o entendimento dos estudantes, pois a utilização desse material permite que eles assimilem os conceitos de maneira concreta, como a composição e a decomposição dos números e a comparação de quantidades.

• A fim de que a turma compreenda de modo significativo e efetivo a subtração com reagrupamento, são propostas várias estratégias para efetuar cálculos.

• Converse com os estudantes sobre a decomposição dos números 223 e 192, proposta na atividade 10, em centenas, dezenas e unidades. Explique a eles que 200 = 100 + 100 e que, para tornar a subtração possível, somaram-se 20 + 100 , ficando com 120 unidades, a fim de subtrair 90 de 120. Assim como o material dourado, essa estratégia auxilia os estudantes a compreenderem o algoritmo por meio da decomposição.

• Ao efetuar a subtração proposta usando o algoritmo, ressalte que é importante organizar unidades abaixo de unidades, dezenas abaixo de dezenas e centenas abaixo de centenas.

Decompondo os números

Resposta: 0 + 30 + 1 = 31

Utilizando o algoritmo

Subtraímos as unidades.

Resposta: 3 U − 2 U = 1 U

Então, subtraímos 9 dezenas de 2 dezenas. Como 9 é maior do que 2, trocamos 1 centena por 10 dezenas e adicionamos às 2 dezenas existentes, ficando com 1 centena e 12 dezenas. Assim, subtraímos 9 dezenas de 12 dezenas.

Resposta: 12 D − 9 D = 3 D

3º .

Por fim, subtraímos as centenas.

Resposta: 223 − 192 = 031

Resposta: 1 C − 1 C = 0 C

Portanto, Vanessa marcou pontos a mais do que Marcelo. minuendo subtraendo resto ou diferença

Resposta: Portanto, Vanessa marcou 31 pontos a mais do que Marcelo. 138

11. Efetue os cálculos usando pelo menos duas estratégias diferentes.

a ) 238 − 146 =

Resposta: 238 − 146 = 92

b ) 873 − 389 =

Resposta: 873 − 389 = 484

12. De acordo com os resultados que você obteve na atividade anterior, efetue em seu caderno os cálculos e complete as informações com os números que faltam.

a ) 238 − 146 = , então 146 + = 238

Resposta: 238 − 146 = 92, então 146 + 92 = 238

b ) 873 − 389 = , então 389 + = 873

Resposta: 873 − 389 = 484, então 389 + 484 = 873

c ) 499 − 198 = , então 198 + = 499

Resposta: 499 − 198 = 301, então 198 + 301 = 499

13. Elza efetuou mentalmente o resultado do cálculo 181 − 29

Subtrair 29 é o mesmo que subtrair 30 e depois adicionar 1 ao resultado.

181 − 29 = = 181 − 30 + 1 = = 151 + 1 = 152

Assim como Elza, calcule mentalmente as subtrações a seguir.

a ) 272 − 19 =

Resposta: 272 − 19 = 253

b ) 481 − 28 =

Resposta: 481 − 28 = 453

c ) 500 − 299 =

Resposta: 500 − 299 = 201

d ) 321 − 298 =

Resposta: 321 − 298 = 23

e ) 702 − 198 =

Resposta: 702 − 198 = 504

f ) 451 − 398 =

Resposta: 451 − 398 = 53

14. Efetue as subtrações da atividade anterior em uma calculadora e verifique se suas respostas estão corretas.

Resposta: Espera-se que os estudantes utilizem uma calculadora e verifiquem se os resultados obtidos mentalmente na atividade anterior estão corretos.

que a calculadora é um instrumento bastante útil mas que não deve substituir o cálculo mental, devendo ser utilizada como uma ferramenta de apoio e investigação. Além disso, devemos sempre conferir os resultados repetindo a operação, pois pode acontecer de digitarmos uma tecla errada durante o processo. Verifique se todos os estudantes possuem calculadora. Se necessário, proponha que façam a atividade em duplas para que todos possam verificar as respostas.

ATIVIDADE EXTRA

Providencie antecipadamente anúncios de jornais ou revistas com preços de produtos que

06/10/2025 18:20:40

estão na promoção, informando o preço antes e depois do desconto. Também é possível disponibilizar, em uma folha de papel, anúncios fictícios, pois é importante que os valores sejam números naturais envolvendo números até 999. Organize a turma em duplas e distribua para cada uma delas dois anúncios. Solicite que calculem o valor economizado em cada situação apresentada, considerando que as compras tenham sido efetuadas com desconto. Depois, solicite a cada dupla que compartilhe suas respostas com a turma.

• A atividade 11 solicita aos estudantes que efetuem as subtrações de pelo menos duas maneiras. Incentive-os a utilizar as estratégias que lhes forem mais convenientes. Desse modo, quanto mais relações são estabelecidas entre as diferentes estratégias usadas, mais eles compreenderão de maneira efetiva a subtração com reagrupamentos. Caso alguns deles tenham dificuldade, retome os métodos estudados, efetuando na lousa outros exemplos de subtrações com reagrupamentos.

• A atividade 12 tem como objetivo levar os estudantes a perceberem que a subtração é a operação inversa da adição. Com isso, essa atividade motiva a observação, a formulação de raciocínios e o reconhecimento de relações entre novas aprendizagens e conhecimentos adquiridos. Pergunte-lhes quais relações eles observam nesta atividade, incentivando, assim, uma conversa sobre as relações entre a adição e a subtração.

• Na atividade 13, é apresentada aos estudantes uma estratégia de cálculo mental para efetuar subtrações. Depois, assim como Elza, eles devem efetuar as subtrações propostas mentalmente.

• Na atividade 14, os estudantes verificarão por meio do uso da calculadora se as respostas do cálculo mental realizado na atividade anterior estão corretas. Ressalte

• Na atividade 15, o objetivo é levar os estudantes a efetuarem os cálculos de adição e subtração no caderno a fim de completarem os esquemas propostos envolvendo fatos básicos da adição e da subtração. Caso eles tenham dificuldade em compreender o esquema, acrescente as explicações necessárias. Observe que nos esquemas do item A, adicionam-se 236 aos números da primeira coluna e subtraem-se 274 do resultado obtido. Já nos esquemas do item B, adicionam-se 347 aos números da primeira coluna e subtraem-se 153 do resultado obtido.

• Organize a turma em duplas para resolverem a atividade 16 a fim de que troquem ideias e experiências entre si, ampliando e consolidando seus repertórios de cálculos. Esta atividade apresenta uma situação-problema que tem por objetivo levar os estudantes a interpretá-la e resolvê-la utilizando os fatos básicos da adição e da subtração com números de até três algarismos. O item a aborda subtração com significado de retirar. O item b envolve, além da subtração, adição com significado de juntar. Caso tenham dificuldade, auxilie-os na interpretação, resolvendo cada item por etapas.

AVALIANDO

Objetivo

Resolver subtrações envolvendo números até 999 com e sem reagrupamento por meio de diferentes estratégias, incluindo as estratégias pessoais.

Sugestão de intervenção

15. Efetue os cálculos no caderno e complete os quadros a seguir com os resultados.

16. Fátima fez 346 salgados para vender em um sábado na feira. Ela conseguiu vender 253 dos salgados que levou.

a ) Quantos salgados não foram vendidos nesse dia?

Resposta: 346 − 253 = 93. Não foram vendidos 93 salgados.

15. Resposta: Os estudantes devem realizar os cálculos no caderno e completar com os seguintes números: Esquema A: 1ª linha: 390; 2ª linha: 917 e 643; 3ª linha: 628 e 354. Esquema B: 1ª linha: 847 e 694; 2ª linha: 450; 3ª linha: 470 e 317

b ) Para vender no domingo, Fátima fez 356 salgados e juntou com aqueles que não foram vendidos no sábado. No final do dia, ela verificou que tinha vendido 32 salgados a mais do que no sábado.

• Quantos salgados Fátima levou para vender no domingo? salgados.

• Quantos salgados Fátima vendeu no domingo? salgados.

• Quantos salgados não foram vendidos no domingo? salgados.

Resposta: 356 + 93 = 449 449 salgados.

Resposta: 253 + 32 = 285 285 salgados.

Resposta: 449 − 285 = 164 164 salgados.

• João está lendo um livro de 685 páginas e já chegou à página 568. Quantas páginas faltam para ele terminar a leitura?

• Ana retirou de sua conta do banco um valor de 365 reais para fazer uma compra. Sabendo que havia 758 reais antes de fazer a retirada, quantos reais sobraram na conta dela?

• Em certo condomínio, foi realizada uma eleição para escolher o novo síndico ou síndica. Romeu obteve 126 votos e Maura, 247. Quantos votos Maura obteve a mais do que Romeu?

Ao término deste tópico, converse com os estudantes sobre algumas situações do cotidiano em que há ideias de subtração. É importante verificar se eles desenvolveram a capacidade de associar as situações propostas às ideias de retirar, comparar ou completar quantidades. Solicite-lhes que resolvam em seus cadernos as seguintes situações-problema.

Durante todo o trabalho pedagógico, a avaliação é um componente muito importante para você e a turma. Por isso, realize a atividade desta seção a fim de detectar possíveis dúvidas dos estudantes e, caso isso aconteça, redirecione o trabalho oferecendo-lhes abordagens mais práticas, por exemplo, utilizando o material dourado.

Respostas

• 117 páginas.

• 393 reais.

• 121 votos.

18:20:40

17. A sequência a seguir foi construída com base em algumas regras. Nela, o primeiro número é 314, e, para determinar o próximo número, a partir do segundo, subtraímos 16 unidades do número anterior.

Efetue os cálculos no caderno e determine os quatro próximos números dessa sequência.

Resposta: 314, 298, 282, 266, 250, 234, 218, ...

314 , 298 , 282 , , , ,

Unidades temáticas integradas

18. No mês passado, 326 pessoas procuraram certo posto de saúde para se vacinarem contra influenza. Desse total, 27 eram gestantes e 81 eram pessoas idosas.

DICA: Para responder aos itens desta atividade, realize e confira os cálculos no caderno.

Influenza: vírus causador da doença conhecida popularmente como gripe.

a ) Ao todo, quantas pessoas gestantes e pessoas idosas procuraram o posto de saúde para se vacinar contra influenza?

Resposta: 81 + 27 = 108. Ao todo, 108 pessoas gestantes e pessoas idosas procuraram o posto de saúde para se vacinarem contra influenza.

b ) Do total de pessoas que procuraram o posto para se vacinar, quantas não eram pessoas idosas nem gestantes?

Resposta: 326 − 108 = 218. Do total de pessoas, 218 não eram idosas nem gestantes.

A IMPORTÂNCIA DAS VACINAS

As vacinas ajudam o sistema de defesa do nosso organismo a produzir respostas para combater doenças que podem ser fatais caso evoluam. Por isso, elas são importantes para pessoas de todas as idades, desde crianças até pessoas idosas.

Momento de vacinação de pessoas idosas da população ribeirinha, nas ilhas de Belém, no Pará, em 2024.

ARTICULANDO CONHECIMENTOS

O assunto tratado no boxe complementar A importância das vacinas favorece a relação entre Ciências da Natureza e Matemática. Aborde a importância da vacinação como modo de prevenção de várias doenças graves que a sociedade enfrenta há muito tempo, evitando que elas se disseminem descontroladamente. Se julgar necessário, compartilhe as experiências da campanha global de vacinação contra a COVID-19, que contribuiu para o combate à doença. Para obter mais informações sobre imunização e compartilhar mais detalhes acerca do assunto, acesse

a página: VACINAÇÃO. Gov.br. Disponível em: https://www.gov.br/saude/pt-br/vacinacao. Acesso em: 26 ago. 2025.

18:20:40

BNCC

A atividade 17 aborda a construção de uma sequência de números naturais em ordem decrescente, usando uma regra estabelecida e solicitando aos estudantes que determinem os próximos quatro números dessa sequência, o que possibilita o desenvolvimento da habilidade EF02MA11 da BNCC.

• A atividade 17 estabelece uma integração entre as unidades temáticas de Matemática Números e Álgebra ao trabalhar a identificação de regularidade de sequências e a determinação de elementos ausentes de uma sequência de números naturais em ordem decrescente a partir de um número dado e uma regra estabelecida.

• Na atividade 18, caso julgue necessário, para contemplar a inclusão, permita que os estudantes a realizarem em grupos, proporcionando um ambiente de discussões acerca dos cálculos de adição e subtração propostos na atividade.

• Na atividade 19, o objetivo é levar os estudantes a efetuarem os cálculos de adição e subtração com números de até três algarismos. O item a aborda a adição por meio do cálculo mental. O item b envolve subtração com significado de tirar. Observe se os estudantes têm dificuldade em compreender os itens. Em caso positivo, auxilie-os na interpretação, resolvendo cada item por etapas.

• A atividade 20 tem como objetivo explorar a elaboração de um problema envolvendo a subtração, baseando-se nas informações de dois panfletos com diferentes anúncios dos mesmos produtos. Observe o contexto, as estratégias e o significado da subtração usados pelos estudantes ao elaborarem e resolverem o problema a fim de detectar possíveis dúvidas. Caso seja necessário, retome esse assunto.

• O trabalho com o Desafio a mais permite estabelecer uma integração entre as unidades temáticas de Matemática Números e Álgebra, na qual os estudantes devem descrever a regra de cada sequência apresentada e usá-la para determinar os números faltantes. Eles devem observar a lógica de cada sequência e, em seguida, efetuar os cálculos para completá-las. Ao reconhecerem as regras, eles poderão preencher os espaços em branco de cada sequência. Caso os estudantes tenham dificuldade, incentive-os a compartilhar com os demais colegas, fazendo intervenções pontuais e estratégicas. Sugira que eles calculem a diferença entre os números para identificar o padrão e, se preciso, que organizem os números em colunas (centena, dezena, unidade) para facilitar a percepção das mudanças.

20. Resposta pessoal. Os estudantes devem elaborar o enunciado de um problema envolvendo subtração com base nas informações contidas no panfleto.

19. Durante três semanas, Alaor fez depósitos no banco com diferentes quantias de dinheiro.

a ) Efetue os cálculos mentalmente e determine quantos reais Alaor depositou durante essas três

semanas. reais.

Resposta: 740 reais.

b ) Na semana 4, Alaor depositou 350 reais a menos do que havia depositado nas outras três semanas juntas. Quantos reais Alaor depositou na semana 4?

Quantia em reais depositada por Alaor durante três semanas

Semana Quantia (em reais)

Semana 1230

Semana 2220

Semana 3290

Fonte de pesquisa: Anotações de Alaor.

Resposta: 740 − 350 = 390. Alaor depositou 390 reais na semana 4.

20. O mesmo produto foi anunciado por duas lojas diferentes. De acordo com esses panfletos, elabore um problema, em seu caderno, envolvendo subtração e usando letra cursiva. Depois, peça a um colega que o resolva e verifique se ele resolveu corretamente.

Professor, professora: Oriente os estudantes na escrita do problema da atividade 20,

incentivando o traçado em letra cursiva, a fim de que eles treinem esse tipo de escrita.

DESAFIO A MAIS

Escreva a regra de cada sequência. Depois, efetue em seu caderno os cálculos e complete-as com os números que estão faltando.

Unidades temáticas integradas

a ) 743, 715, 687, , , ,

Resposta: Regra: Cada número da sequência, a partir do segundo, é obtido

subtraindo 28 unidades do anterior. 743, 715, 687, 659, 631, 603, 575.

b ) 975, 877, 779, , , , .

Resposta: Regra: Cada número da sequência, a partir do segundo, é obtido

subtraindo 98 unidades do anterior. 975, 877, 779, 681, 583, 485, 387.

BNCC

Ao resolver o Desafio a mais, os estudantes são levados a descrever o padrão de cada sequência, além de efetuar os cálculos necessários e completarem com os números que estão faltando, o que possibilita o desenvolvimento das habilidades EF02MA09 e EF02MA10 da BNCC.

LUCAS PALMA/ARQUIVO DA EDITORA

DIVIRTA-SE E APRENDA

Jogo da subtração

Este jogo vai verificar seu conhecimento sobre subtração. Para isso, junte-se a um ou dois colegas e destaquem o molde da trilha, do dado e dos peões das páginas 275 e 277 do Material complementar

REGRAS

• Peguem o material disponibilizado pelo professor. Conversem e decidam quem vai iniciar o jogo.

• Cada jogador posiciona seu peão na casa INICIAR.

• O participante da vez lança o dado para saber quantas casas seu peão vai avançar.

• Na casa em que o peão parar, há um cálculo que o jogador deve resolver. Se ele acertar, ganha o direito de manter o peão nessa casa até a próxima jogada. Se errar, deve voltar com o peão a mesma quantidade de casas que havia avançado.

• Vence o jogo quem atingir primeiro a casa CHEGADA.

DICA: Utilizem uma folha de papel para realizar e conferir os cálculos.

CONCLUSÃO

Acompanhar o desenvolvimento dos estudantes é fundamental para um ensino bem-sucedido. Ao longo da unidade, foram propostas diversas maneiras de avaliar a aprendizagem da turma. A fim de realizar um monitoramento mais abrangente e organizado, registre nos relatórios individuais ou nas fichas de avaliação o desempenho de cada estudante, levando em consideração suas particularidades. Um modelo desse tipo de ficha pode ser

encontrado no tópico Avaliação deste manual. Assim, será possível visualizar de modo individual as trajetórias de aprendizagem, incluindo os avanços e os pontos de dificuldades a serem sanados por meio de atividades que promovam recuperação dos conteúdos. Esse método de verificar a progressão dos estudos e identificar o que a turma de fato conseguiu aprender e o que ficou com lacunas de absorção é de grande importância para que seja possível repensar

• Organize a turma em duplas e auxilie os estudantes na montagem do dado e dos peões para executarem o jogo juntos. Peça-lhes que resolvam as subtrações em uma folha de papel à parte, utilizando cálculo mental ou as estratégias de cálculos que julgarem mais adequadas.

• O jogo, além da ludicidade, desenvolve o trabalho colaborativo e o respeito às regras e promove a inclusão de estudantes com NEE por meio da interação com o tabuleiro e as peças pelo tato e pela visão, o que permite perceber as texturas e as formas dos objetos. Esse trabalho contribui para o desenvolvimento da sensibilidade, utilizando, dessa maneira, os sentidos por meio dos materiais de recurso.

Sugestão de Desafio

O quebra-cabeça de Elisa tem 286 peças. O de Tatiana tem 67 peças a menos que o de Elisa. E o de Rodrigo tem 77 peças a mais que o de Tatiana. Quantas peças de quebra-cabeça eles têm ao todo?

Resposta • 801 peças.

06/10/2025 18:20:41

estratégias em sala de aula, tornando as ações pedagógicas cada vez mais eficazes.

A conclusão da unidade é o momento de avaliar se os objetivos por ela propostos foram alcançados. Para esse diagnóstico, observe no final deste Manual algumas possibilidades de avaliação formativa que permitem realizar o monitoramento da aprendizagem dos estudantes e intervir caso eles não tenham atingido os resultados esperados.

THAIS CASTRO/ARQUIVO DA EDITORA

1. Objetivo

Resolver uma situação-problema que envolva o cálculo da adição com reagrupamento.

Sugestão de intervenção

A fim de sanar possíveis dúvidas e tirar melhor proveito desta atividade, organize os estudantes em grupos e proponha que efetuem a adição que resolve essa situação-problema, com o auxílio do material dourado. Repita essa estratégia explorando outras operações de adição até que as dúvidas sejam sanadas.

2. Objetivo

Resolver situações-problema que envolvam as ideias da subtração.

Sugestão de intervenção

Para superar possíveis dificuldades, retome essa situação-problema e pergunte aos estudantes: “Se Nícolas tivesse feito 17 gols, qual seria a diferença entre a quantidade de gols feitos por ele e Tales?”. Depois, organize a turma em grupos e entregue a cada grupo um cartão com operações de subtração. Peça-lhes que efetuem os cálculos no caderno e, depois, elaborem o enunciado de um problema envolvendo uma dessas subtrações.

3. Objetivo

Resolver uma situação-problema que envolva comparação entre números pares e números ímpares.

Sugestão de intervenção

VAMOS AVALIAR O APRENDIZADO

1. Jairo vai comprar o cinto e a camiseta representados na imagem.

Imagens sem proporção entre si.

49 reais 45 reais

Quantos reais Jairo vai gastar na compra desses dois produtos?

Resposta: 49 + 45 = 94. Jairo vai gastar 94 reais.

2. Em um campeonato de futebol na escola, Nícolas marcou 11 gols, Abel marcou 8 gols, e Tales marcou 4 gols.

a ) Quantos gols Tales marcou a menos do que Nícolas?

Resposta: 11 − 4 = 7. Tales marcou 7 gols a menos do que Nícolas.

b ) Quantos gols Abel marcou a mais do que Tales?

Resposta: 8 − 4 = 4. Abel marcou 4 gols a mais do que Tales.

3. Simone está pensando em um número maior do que 574, menor do que 577 e ímpar. Descubra qual é o número em que ela está pensando e represente-o no ábaco, no quadro de ordens e por extenso.

Resposta: C: 5; D: 7; U: 5.

Por extenso:

Resposta: Quinhentos e setenta e cinco.

Leve para a sala de aula ábacos suficientes para os estudantes e reúna-os em duplas ou grupos caso não tenha a quantidade necessária de material. Represente inicialmente no ábaco um número de até três ordens, diferente dos da atividade, como 550, 676 e 401, e observe se eles conseguem identificar qual número está sendo representado. Repita esse processo quantas vezes achar conveniente. Ajude-os na escrita do número por extenso, passando por suas carteiras e verificando, individualmente, suas dificuldades.

Quadro de ordens C D U

Resposta: C: 5; D: 7; U: 5.

C D U

4. Marcos vai comprar uma televisão e encontrou uma no valor de 923 reais e outra no valor de 1 000 reais.

a ) Escreva no quadro de ordens os números que representam o valor em reais de cada televisão.

Televisão 1

Quadro de ordens

UM C D U

Televisão 2

Quadro de ordens

UM C D U

Resposta: Televisão 1: C: 9, D: 2, U: 3; Televisão 2: UM: 1, C: 0, D: 0, U: 0.

b ) Complete as frases escrevendo por extenso o preço em reais de cada televisão.

• A televisão 1 custa reais.

Resposta: A televisão 1 custa novecentos e vinte e três reais.

• A televisão 2 custa reais.

Resposta: A televisão 2 custa um mil reais.

5. Para uma festa, a padaria de Otaviano recebeu uma encomenda de 850 pães integrais e 570 pães de queijo. Desse total, já foram preparados 685 pães integrais e 398 pães de queijo.

a ) Quantos pães integrais ainda precisam ser preparados?

Resposta: 850 − 685 = 165. Ainda precisam ser preparados 165 pães integrais.

b ) Quantos pães de queijo a mais precisam ser preparados para que a encomenda fique completa?

Resposta: 570 − 398 = 172. Precisam ser preparados 172 pães de queijo a mais para completar a encomenda.

4. Objetivo

Identificar e ordenar no quadro de ordens números até 1 000 e escrevê-los por extenso.

Sugestão de intervenção

Para remediar possíveis dificuldades na representação dos números, desenhe na lousa o quadro de ordens e peça a alguns estudantes que representem um número que será dito. Analise se eles percebem a função do zero no número 1 000. Caso tenham dificuldade na escrita por extenso, decomponha na lousa, da maneira que preferir, os números da atividade para uma melhor visualização de sua escrita.

5. Objetivo

Resolver situações-problema envolvendo o cálculo da subtração com números até 999.

Sugestão de intervenção

Nessa atividade, lembre aos estudantes os conceitos básicos da subtração: “retirar”, “faltar” e “comparar”. Antes de ler os problemas, proponha na lousa algumas subtrações com reagrupamento para que eles pratiquem. Se julgar necessário, peça-lhes que se reúnam em duplas para compartilharem seus conhecimentos. Posteriormente, leia com os estudantes os problemas vagarosamente e analise se conseguem interpretar corretamente.

06/10/2025 18:21:58

OBJETIVOS DA UNIDADE

• Realizar medições utilizando unidades de medida de comprimento não padronizadas.

• Identificar o centímetro e o milímetro como unidades de medida de comprimento padronizadas.

• Reconhecer e usar a régua como um instrumento de medida de comprimento.

• Estimar, medir e comparar comprimentos utilizando o centímetro como unidade de medida.

• Identificar o metro como unidade de medida de comprimento padronizada.

INTRODUÇÃO E JUSTIFICATIVA

Esta unidade desenvolve um trabalho com unidades de medidas padronizadas e não padronizadas para que os estudantes compreendam a diferença entre elas e também meçam e comparem comprimentos usando o metro.

Serão abordadas situações cotidianas que envolvem a comparação entre a medida de comprimento de objetos da sala de aula, utilizando unidades de medida não padronizadas como palmo e pé.

Ao trabalhar com submúltiplos do metro, a unidade abordará medições de comprimentos envolvendo as unidades de medida padronizadas centímetro e milímetro, por meio da régua graduada. Ao longo desse tópico, serão exploradas leituras de medidas de comprimento, bem como situações de medição, comparação e estimativas, sempre com o auxílio da régua. Por fim, será trabalhada a relação entre centímetro e metro. Ao longo desse tópico, serão exploradas leituras de medidas de comprimento, bem como situações de medição, comparação e estimativas.

UNIDADE6 MEDIDAS DE COMPRIMENTO

Habilidade da BNCC trabalhada na unidade: EF02MA16

• Proponha aos estudantes que observem a imagem das páginas de abertura e descrevam a cena. Depois, leia o texto para eles. A fim de complementar as informações apresentadas, explique­ lhes que, além dos cuidados com alimentação, saúde e higiene, um bom crescimento depende, entre outros fatores, de características familiares.

Médica medindo o comprimento da altura de uma menina.

2. Resposta pessoal. O objetivo é que os estudantes relatem, caso saibam, a sua altura no dia da realização da atividade desta questão.

SUGESTÃO DE ESTRATÉGIA INICIAL

Comer bem, cuidar da saúde e manter a higiene são alguns dos fatores que influenciam nosso crescimento. Se medirmos nossa altura hoje e daqui a um ano, podemos determinar quantos centímetros na altura crescemos comparando as duas medidas.

Se a medida do comprimento da altura de uma pessoa era 131 cm no ano passado e hoje é 137 cm, quantos centímetros na altura ela cresceu nesse período?

Resposta: 6 cm

A medida do comprimento de sua altura é maior ou menor do que 100 cm?

Além do centímetro (cm), qual outra unidade de medida de comprimento você conhece? Cite alguns exemplos.

Resposta pessoal. É possível que eles respondam que conhecem o metro (m), o milímetro (mm), o quilômetro (km), entre outras unidades de medida de comprimento.

Régua usada em consultórios pediátricos.

Providencie três fitas com mesma medida de comprimento (pode­se utilizar pedaços de fita adesiva). Organize os estudantes em três grupos e fixe as fitas na lousa. Diga a eles que as fitas têm a mesma medida de comprimento e pergunte: “Como podemos determinar a medida do comprimento dessas fitas sem utilizar instrumentos de medida padronizados?”. Deixe­os conversar e, se necessário, leve­os a perceber que podemos utilizar, por exemplo, partes do corpo para determinar a medida do comprimento solicitado. Entregue uma fita para cada grupo, leve­os a

18:26:44

um local para fazerem as medições necessárias e solicite­lhes que meçam as fitas, sem utilizar um instrumento de medida padronizado, e registrem o resultado obtido, sendo importante que todos realizem as medições. Em seguida, faça os seguintes questionamentos: “Todos obtiveram o mesmo resultado nas medições?”; “O que podemos fazer para que, ao medirmos o comprimento de determinado objeto, os resultados sejam iguais?”. Acolha e ouça com atenção e respeito as ideias e contribuições de toda a turma, deixando que eles se expressem livremente e desenvolvam a oralidade e a capacidade de argumentar.

• A questão 1 permite trabalhar o centímetro em um contexto que envolve subtração. Caso os estudantes apresentem dificuldade em identificar a operação a ser realizada, questione ­os a respeito do quanto o número 137 é maior do que 131.

• Antes de propor a questão 2, questione os estudantes a respeito de alguns objetos que tenham a medida do comprimento maior do que 100 cm, ou seja, maior do que 1 m. Ao propor esta questão, atente a comentários ou brincadeiras que ridicularizem colegas por serem mais baixos ou mais altos do que os demais. Caso perceba esse tipo de comportamento, é importante intervir com delicadeza, destacando que todas as pessoas têm características físicas diferentes e que isso não deve ser motivo de piada ou exclusão. Promova conversas coletivas sobre respeito mútuo, empatia e valorização das diferenças, repudiando qualquer atitude de bullying e fortalecendo um ambiente de acolhimento e diversidade, sem preconceitos de qualquer natureza.

• O objetivo da questão 3 é explorar o conhecimento prévio dos estudantes em relação às unidades de medidas de comprimento. Se necessário, apresente situações em que são utilizadas medidas de comprimento no dia a dia.

• Para o trabalho com o tópico Medindo Comprimento é necessário que os estudantes tenham, como pré­requisito, desenvolvido noções de comparação de tamanhos e comprimentos em situações do cotidiano, reconhecendo quando algo é maior, menor ou do mesmo tamanho que outro. Além disso, é importante que eles compreendam o conceito de medição como uma maneira de quantificar e comparar o espaço ocupado por algo, nesse caso, o comprimento. Usar partes do próprio corpo como referência, como ao comparar a medida da altura dos colegas ou a medida do comprimento de objetos com as mãos ou os pés, é essencial para esta etapa.

• A atividade 1 visa promover o reconhecimento de como fazer medições utilizando unidades de medida não padronizadas e também capacitar os estudantes a perceberem que o uso de unidades de medida não padronizadas nos leva a obter medidas diferentes. Oriente­os a contar quantos palmos cada personagem obteve, sendo 9 palmos de André, 10 de Conceição e 8 de Thaís. Com base nisso, pergunte a eles qual dos personagens tem o maior palmo e qual tem o menor. Com isso, é esperado que eles percebam que, como Conceição obteve a maior medida em palmos, o palmo dela é o menor entre os três. Já no caso de Thaís, como ela obteve a menor medida em palmos, o palmo dela é o maior entre os três. Ao final da atividade, comente que os pés e os polegares, assim como outras partes do corpo, também podem ser usados para medir comprimentos.

MEDINDO COMPRIMENTO

1. André, Conceição e Thaís mediram o comprimento do lado maior da mesa do professor utilizando o palmo como unidade de medida.

palmo

Por que os resultados obtidos foram diferentes?

Resposta pessoal. Espera-se que os estudantes percebam que os resultados obtidos são diferentes porque a medida do palmo de cada pessoa é diferente.

BNCC

As atividades desta unidade visam ao desenvolvimento da habilidade EF02MA16 da BNCC, ao solicitar aos estudantes que estimem, meçam e comparem comprimentos utilizando unidades de medida não padronizadas e padronizadas (metro, centímetro e milímetro). Além disso, eles são levados a estimar e medir o comprimento do contorno de salas, como sugerido nessa habilidade.

André

Conceição

Thaís

ladomaior

EXPERIMENTE

2. Formem grupos com quatro colegas e meçam o comprimento da largura de uma porta utilizando o palmo. Depois, registrem no quadro os resultados obtidos por vocês.

Medida em palmos do comprimento da largura da porta

Nome do colega

Quantidade de palmos

respostas do tipo “quase 5 pés”, “menos de 5 pés” etc.

a ) Marque um X no nome do colega que obteve a maior quantidade de palmos nessa medição.

3. c) Resposta pessoal. Espera-se que os estudantes respondam que os resultados obtidos são diferentes. É possível que, ao medir os comprimentos solicitados, os estudantes não obtenham uma quantidade inteira de pés. Dessa maneira, considere corretas as dos estudantes depende dos registros feitos pelo grupo.

b ) Contorne o nome do colega que obteve a menor quantidade de palmos nessa medição.

Resposta pessoal. A resposta dos

Resposta pessoal. A resposta estudantes depende dos registros feitos pelo grupo.

c ) Pinte de azul o nome do colega que tem o maior palmo.

Resposta pessoal. A resposta dos estudantes depende dos registros feitos pelo grupo.

d ) O colega que tem o maior palmo obteve maior ou menor quantidade de palmos para medir o comprimento da largura da porta, em relação aos demais colegas?

Resposta: Espera-se que os estudantes identifiquem que o colega que tem o palmo com a maior medida de comprimento obteve a menor quantidade de palmos para medir o comprimento da largura da porta.

3. Utilizando seu pé, meça:

a ) o comprimento de uma das paredes de sua sala de aula.

Resposta pessoal. A resposta de cada estudante depende da quantidade de pés usados para medir o comprimento de umas das paredes da sala de aula.

b ) o comprimento da largura da porta da sua sala de aula.

Resposta pessoal. A resposta de cada estudante depende da quantidade de pés usados para medir o comprimento da largura da porta.

c ) Compare os resultados que você obteve nos itens A e B com os resultados de seus colegas. O que você pode observar?

AVALIANDO

Objetivo

• Alerte os estudantes sobre os eventuais riscos na realização dos experimentos propostos nesta página, garantindo a integridade física de si mesmos, dos professores e das demais pessoas envolvidas no processo educacional.

• O objetivo das atividades 2 e 3 é possibilitar aos estudantes fazerem medições de diferentes objetos da sala de aula, utilizando, para isso, unidades de medidas não padronizadas como o palmo e o pé. Na atividade 2, caso eles obtenham medidas não inteiras e apresentem dificuldade na maneira como registrá­las, oriente­os a escrever expressões como “quase 5 palmos” e “menos de 5 palmos”. Se necessário, oriente o posicionamento da mão para realizar medição com o palmo, conforme indicado a seguir.

Palmo

18:26:46

• Ao trabalhar a atividade 3 com os estudantes, oriente­os a não deixar espaços entre um pé e outro, enquanto fazem a medição. Como é esperado que haja divergência entre as respostas obtidas, no momento da comparação dos resultados, verifique se eles compreendem o motivo para isso acontecer, questionando­os a respeito da diferença entre as medidas do comprimento de seus pés.

• A fim de promover a inclusão, permita­lhes realizar as atividades propostas na página juntos, de forma que se socializem e auxiliem uns aos outros, favorecendo o entendimento e a execução das atividades.

Medir o comprimento de objetos utilizando unidades de medida não padronizadas.

Sugestão de intervenção

Solicite aos estudantes que meçam os comprimentos de alguns objetos de dentro da sala de aula, como o da carteira ou o da lousa, utilizando o polegar. Ao final, permita a eles que comparem as suas resoluções e discutam por que os resultados obtidos são diferentes.

RENAN FONSECA/ARQUIVO DA EDITORA

• Na atividade 4, deve ­se ter os devidos cuidados na realização da atividade para evitar possíveis danos físicos a todos os envolvidos. Sendo assim, auxilie os estudantes a cortarem os barbantes com a medida de comprimento sugerido na atividade. No item a, eles devem fazer as comparações entre os barbantes, realizando essa comparação um a um, ou seja, cada estudante faz a comparação com um colega. Peça a eles que coloquem os barbantes sobre a mesa e observem se as medidas são iguais. Caso julgue necessário, leve para a sala de aula uma trena para medir cada barbante e escreva na lousa os resultados. Depois, peça­lhes que observem as medidas na lousa e verifiquem se responderam corretamente. Nos itens b e c, oriente­os a escolher objetos de fácil acesso na escola, para facilitar as medições necessárias. Verifique se eles realizaram as medições corretamente e se os barbantes obtidos foram suficientes para medir os objetos escolhidos. Caso julgue necessário, ajude­os a fazer as medições, auxiliando­os a segurar os barbantes ou os objetos. Peça a eles que compartilhem entre si algumas observações, como se obtiveram os mesmos resultados que os colegas ao realizarem as medições, perguntando a eles o porquê de as medidas serem iguais ou diferentes.

• A atividade 4, favorece a inclusão de estudantes com NEE no ambiente escolar, ao possibilitar o uso dos diferentes sentidos para a realização de medições de objetos.

4. Para esta atividade, você vai precisar de barbante e uma tesoura com pontas arredondadas.

• Segure uma ponta do barbante com os dedos de uma das mãos. Conduzindo o barbante com a outra mão, abra os braços completamente na altura dos ombros e mantenha ele esticado com as pontas dos dedos da outra mão.

• Peça ao seu professor que corte o barbante no ponto que você alcançou com a medida de seus braços abertos.

4. a) Resposta pessoal. Espera-se que os estudantes relatem que obtiveram resultados diferentes ao compararem as medidas de comprimento de seus barbantes.

a ) Compare a medida do comprimento do pedaço do seu barbante com o de seus colegas. As medidas de comprimento obtidas foram iguais ou diferentes? Converse com os colegas e o professor sobre o resultado dessas medidas.

b ) Agora, com a ajuda do professor, escolha dois objetos na escola e faça medições usando o seu pedaço de barbante como unidade de medida. Depois, anote as medidas de comprimento obtidas.

Resposta pessoal. A resposta depende dos objetos escolhidos pelos estudantes. Professor, professora. É possível que, ao medir os comprimentos dos objetos escolhidos, eles não obtenham uma quantidade inteira de “barbantes”. Dessa maneira, considere corretas as respostas do tipo “quase 3 barbantes”, “menos de 6 barbantes” etc. Confira mais informações sobre os itens b e c desta atividade nas orientações ao professor

c ) Compare as medidas de comprimento obtidas por você com as de seus colegas. Caso tenham escolhido o mesmo objeto para medir, verifique se eles obtiveram os mesmos resultados que você.

Resposta pessoal. Espera-se que os estudantes

façam a comparação dos resultados obtidos no item anterior com os resultados encontrados por seus colegas e observem se são os mesmos.

O CENTÍMETRO E O MILÍMETRO

1. A fim de evitar valores diferentes ao fazer uma medição, foram adotadas unidades de medida de comprimento padronizadas, como o centímetro, que abreviamos por cm

Em uma régua com escala em centímetros, a medida da distância entre dois números é igual a 1 centímetro. Assim, a medida da distância entre os números 0 e 1 é igual a 1 centímetro, entre 1 e 2 também é 1 centímetro e assim por diante.

1 cm

Utilizando uma régua, Daniel mediu o comprimento de uma caneta.

• Para o estudo deste tópico é importante que os estudantes tenham, como pré­requisito, desenvolvido noções básicas de comprimento, especialmente por meio das experiências com unidades de medidas não padronizadas, como palmos, passos, pés etc. É importante que eles saibam comparar comprimentos, maior, menor ou igual e tenham familiaridade com a contagem e com os números naturais.

Logo, o comprimento da caneta de Daniel

mede cm

Resposta: Logo, o

comprimento da caneta de Daniel mede 14 cm

Daniel também fez medições em uma fita e observou que a largura dela mede menos do que 1 cm

Nesse caso, para expressar essa medida, podemos utilizar o milímetro (mm), que também é uma unidade padronizada de medida de comprimento.

DICA: Um centímetro está dividido em 10 milímetros. 1 cm = 10 mm

1 mm

Assim, podemos dizer que a largura da fita mede mm. Resposta: Assim, podemos dizer que a largura da fita mede 8 mm

ATIVIDADE EXTRA

Providencie réguas e distribua aos estudantes, em duplas, para que possam fazer esta atividade. Então, solicite a eles que meçam o comprimento de objetos de seu material escolar, como uma borracha, um lápis e o estojo, ou de objetos da sala de aula. Oriente­os a utilizar ambas as unidades de medida estudadas: o centímetro e o milímetro. Ao final, promova um momento em que as duplas possam apresentar seus resultados.

REFERÊNCIAS COMPLEMENTARES

06/10/2025 18:26:46

LIMA, Elon Lages. Medida e forma em geometria. 4. ed. Rio de Janeiro: Sociedade Brasileira de Matemática, 2011.

O livro apresenta a origem histórica da geometria ligada à medição de terras e a volumes. Ele introduz os conceitos de comprimento de área e volume, de maneira acessível ao leitor.

• O objetivo da atividade 1 é que os estudantes, além de compreenderem a utilização da régua para medir comprimentos tanto em centímetros quanto em milímetros, reconheçam a relação entre essas duas unidades de medida padronizadas. Providencie réguas para os estudantes, a fim de que eles possam manipular esse instrumento, realizando a medição de alguns objetos. Converse com eles sobre a importância de utilizar instrumentos padronizados para fazer medições, para perceberem que os resultados obtidos devem ser os mesmos, ao medir algum objeto, utilizando a régua, por exemplo. Para complementar o assunto desenvolvido por meio dela, avalie a possibilidade de trabalhar a Atividade extra sugerida nesta página.

• A atividade 2 tem como objetivo levar os estudantes a desenvolverem a noção de unidade de medida de comprimento, ampliando a compreensão sobre o uso do centímetro e do milímetro. É importante que eles compreendam que nem todas as medidas resultam em um número exato de centímetros. Comente com os estudantes que, ao utilizarem a régua, eles poderão encontrar objetos que medem, por exemplo, 12 milímetros, o que equivale a 1 cm e 2 mm. Aproveite a oportunidade para reforçar a relação entre centímetros e milímetros, explicando que cada centímetro tem 10 mi límetros. Peça ­ lhes que meçam o comprimento de alguns objetos, como estojo, lápis ou caderno, e incentive ­os a registrar a medida completa, utilizando tanto centímetros quanto milímetros. Oriente­os a utilizar a régua corretamente, observando o ponto inicial da medição, no marco zero, e verificando com atenção onde termina o objeto a ser medido. Incentive que façam comparação entre as duas medidas e destaque que, embora o comprimento do objeto seja o mesmo, o modo de expressar a medida de seu comprimento muda conforme a unidade de medida utilizada.

2. Com o auxílio de uma régua, Elisangela mediu o comprimento de seu apontador e verificou que o seu comprimento ficou maior do que 2  cm e menor do que 3  cm

a ) Quanto mede, em milímetros, o comprimento do apontador de Elisangela? mm

Resposta: 28 mm

b ) A medida do comprimento do apontador de Elisangela também pode ser representada da seguinte maneira.

2 centímetros e 8 milímetros ou 2 cm e 8 mm

Represente, em seu caderno, de duas maneiras diferentes, a medida do comprimento dos objetos a seguir.

Resposta: 95 mm ou 9 cm e 5 mm

Resposta: 52 mm ou 5 cm e 2 mm

3. Para confeccionar uma pulseira, Lívia utiliza 30 cm de barbante ao fazer a estrutura e mais 3  cm no acabamento.

a ) Qual é a medida, em milímetros, do comprimento do barbante utilizado por Lívia para fazer o acabamento da pulseira?

b ) Supondo que Lívia faça duas pulseiras como essa, quantos centímetros de barbante no total ela vai usar?

• A atividade 3 é uma boa oportunidade para trabalhar a conversão de unidades de medida, do centímetro para o milímetro. Para complementar esta atividade, pergunte aos estudantes quantos milímetros de barbante Lívia vai usar, ao todo, para fazer a pulseira. Certifique­se de que eles compreendam que é necessário adicionar os 30 cm com 3 cm, ou seja, Lívia precisará de 33 cm. Em seguida, eles devem converter esse valor para milímetros, compreendendo que cada centímetro equivale a 10 milímetros. Assim, 33 centímetros correspondem a 330 milímetros. Peça a eles que compartilhem com a turma as estratégias usadas para realizar essa conversão.

Resposta: Como 1 cm  = 10 mm, então, 3 cm  = 1 cm  + 1 cm  + 1 cm  = 10 mm  + + 10 mm  + 10 mm = 30 mm. Portanto, Lívia utilizou 30 mm de barbante para fazer o acabamento da pulseira.

Resposta: 33 + 33 = 66. Lívia vai usar 66 cm de barbantes para fazer duas pulseiras.

4. Observe alguns instrumentos usados para fazer medições diversas. Imagens sem proporção entre si.

Balança de dois pratos.

Trena.

Relógio digital.

Régua. Termômetro Digital. Paquímetro.

a ) Contorne os instrumentos que podem ser usados para medir o comprimento de objetos.

Resposta: Os estudantes devem contornar a trena, a régua e o paquímetro

b ) Você já utilizou ou conhece algum dos instrumentos de medição apresentados? Converse com o professor e seus colegas.

Resposta pessoal. A resposta depende das vivências que os estudantes relatarem.

5. Meça o comprimento de cada um dos pedaços de barbante a seguir e escreva a medida no espaço adequado.

DICA: Para medir o comprimento de cada pedaço de barbante utilize a régua.

Resposta: 10 cm

Resposta: 7 cm

Resposta: 9 cm

Resposta: 18 mm

Resposta: 12 mm

leve para a sala de aula, como material de apoio, vídeos que mostrem o uso de cada objeto representado, sanando qualquer dúvida que os estudantes possam ter durante a realização deste item.

• O item b da atividade 4 permite a troca de experiências entre os estudantes, levando­os a compartilhar se já utilizaram os instrumentos de medições apresentados na atividade. Caso julgue necessário, comente com eles que alguns desses objetos são pouco utilizados atualmente,

Resposta: 12 cm

• A atividade 4 visa favorecer o reconhecimento dos estudantes com relação a outros instrumentos utilizados para medir comprimento. Pergunte a eles se já usaram os instrumentos de medida que aparecem na atividade. Aproveite o momento para perguntar, ainda, quais medidas esses instrumentos podem indicar. No caso da trena, da régua e do paquímetro analógico, verifique se eles percebem que esses objetos são instrumentos padronizados de unidade de medida. Quanto à balança de dois pratos, ao relógio digital, e ao termômetro digital, avalie o conhecimento prévio deles e, se julgar necessário, comente a respeito de contextos em que utilizamos esses instrumentos.

• Verifique a possibilidade de ampliar o assunto discutido na atividade 4, realizando uma pesquisa, junto aos estudantes, a respeito de outros instrumentos de medida de comprimento, como a trena a laser, que permite uma medição mais precisa. No item a, caso eles não identifiquem a possibilidade do uso do paquímetro para a medição do caderno, comente que o paquímetro é parecido com uma régua e que ele tem extremidades que abrem e fecham encaixando um objeto entre essas extremidades. Em seguida, pergunte a eles se o paquímetro pode ou não ser utilizado para medir um caderno. Se julgar necessário,

06/10/2025 18:26:51

como a balança de dois pratos, e que alguns são bastantes utilizados em indústrias, como o paquímetro universal.

• Na atividade 5, em cada item, o intuito é de promover o uso da régua para medir diferentes comprimentos, em centímetro e milímetro. Providencie antecipadamente réguas em quantidade suficiente para todos os estudantes realizarem as medições, individualmente ou em duplas. Se necessário, auxilie­os no manuseio dessas réguas e no registro da medida obtida.

• Esta atividade integra as unidades temáticas de Matemática Grandezas e medidas, Números e Geometria ao trabalhar unidades de medidas de comprimento padronizadas, relacionando­as à medida de comprimento dos lados de figuras geométricas planas.

• Para a realização das atividades 6 e 7, providencie antecipadamente uma régua para cada estudante para poderem fazer as medições necessárias.

• O objetivo da atividade 6 é possibilitar aos estudantes estimar e medir o comprimento do lado de alguns polígonos, de modo a determinar a medida do comprimento do contorno dessas figuras. Verifique se eles perceberam que os polígonos apresentados têm todos os lados com a mesma medida de comprimento, ou seja, todos são regulares, termo que será estudado em anos posteriores.

• Na atividade 7, o objetivo é levar os estudantes a medirem o comprimento do contorno de cada figura geométrica plana e, ao final, compararem os resultados concluindo que, mesmo sendo figuras diferentes, as medidas do comprimento do contorno delas são iguais.

6. c) Resposta pessoal. Espera-se que os estudantes relatem que as estimativas que fizeram estavam próximas ou exatas das medidas reais.

6. Observe as figuras geométricas planas a seguir.

a ) Estime a medida do comprimento do lado de cada uma dessas figuras.

6. a) Resposta pessoal. A resposta depende da precisão das estimativas feitas pelos estudantes. Espera-se que estimem medidas que se aproximem dos resultados exatos.

b ) Utilizando uma régua, meça o comprimento do lado de cada uma dessas figuras e preencha cada item a seguir.

Resposta: A: 2 cm; B: 1 cm; C: 3 cm

c ) As estimativas que você fez estavam exatas ou próximas da medida real? Converse com o professor e seus colegas.

7. Observe as seguintes figuras geométricas planas.

Unidades temáticas integradas

Utilizando uma régua, meça o comprimento do contorno de cada figura geométrica. Depois, responda aos itens a seguir.

a ) A medida do comprimento do contorno da:

• figura A é cm

Resposta: 12 cm

• figura B é cm

Resposta: 12 cm

• figura C é cm

Resposta: 12 cm

b ) O que você percebeu em relação à medida do comprimento do contorno das três figuras?

Resposta: Espera-se que os estudantes

AVALIANDO

Objetivo

Unidades temáticas integradas percebam que as medidas do comprimento do contorno das três figuras são iguais, mesmo sendo figuras diferentes.

Identificar o centímetro e o milímetro como unidades de medida de comprimento padronizadas, além de utilizar instrumentos de medida para realizar medições com base nessas unidades e estabelecer relações entre elas.

Sugestão de intervenção

Retome alguma das situações de medida feitas por meio de experimentação, como as atividades 2 e 3 da página 149. Providencie algum instrumento de medida, forme grupos com

quatro estudantes e peça a eles que meçam os objetos propostos nessas atividades com esse instrumento e indiquem essas medidas em centímetros e milímetros. Ao final, promova um momento de conversa para que todos os grupos apresentem as medidas obtidas, de modo a verificar a medida correta de cada objeto.

8. Utilizando uma régua, meça o comprimento de seu passo e do passo de dois de seus colegas.

a ) Qual é a medida do comprimento, em centímetros, de seu passo? E a medida do comprimento do passo de seus colegas?

Resposta pessoal. A resposta depende da medida do comprimento do passo de cada estudante.

b ) Se cada um de vocês medir o comprimento do rodapé de uma parede da sala de aula utilizando o próprio passo, quem obterá a menor quantidade de passos? Por quê?

Resposta pessoal. Espera-se que os estudantes respondam que o estudante que tiver o passo com a maior medida de comprimento obterá a menor quantidade de passos, pois quanto maior for a medida do comprimento do passo, menos passos serão necessários para medir o comprimento do rodapé de uma parede da sala de aula.

c ) Estimem em passos a medida do comprimento do contorno de um local na escola escolhido por vocês. Pode ser uma sala, a quadra de esportes ou o pátio do recreio.

Respostas e comentários nas orientações ao professor

d ) Faça a mesma medição em passos e complete a frase. O comprimento do contorno do local escolhido pela turma mede passos.

Respostas e comentários nas orientações ao professor

e ) A medida estimada no item c se aproxima do resultado obtido na sua medição? passo

Respostas e comentários nas orientações ao professor.

eles que validem suas estimativas fazendo cada etapa do item c

• Verifique se a medida estimada pelos estudantes no item d foi próxima da medida obtida no item e. Após fazer todas as atividades com eles, promova um momento em que possam compartilhar os resultados entre si. Durante essa discussão, verifique se eles compreenderam a ideia de comparar relacionada à medição, e que, por conta dessa comparação, a medida obtida pode variar de acordo com a unidade de medida adotada.

Respostas

06/10/2025 18:29:10

8. c) Resposta pessoal. Espera­se que os estudantes escolham um local da escola, como a sala de aula, e estimem o comprimento do contorno, utilizando a unidade de medida de comprimento que preferirem.

d) Resposta pessoal. A resposta depende da medida do comprimento dos passos de cada estudante.

e) Resposta pessoal. Espera ­ se que os estudantes analisem as medidas estimadas e realizadas nos itens c e d, respectivamente, e percebam se as medidas de comprimento se aproximam ou não.

• O intuito da atividade 8 é fazer que os estudantes comparem e estimem medidas, com base na medida do comprimento, em centímetros, de seus passos com o de dois colegas. Organize­os e acompanhe todos os procedimentos para que as ações ocorram sem tumultos, pelo fato de ser uma atividade prática que precisa de movimentação pelos espaços da escola.

• No item a , peça a cada estudante que dê um passo ao lado de sua carteira, faça as marcações do passo de cada um deles no chão com um giz, utilizando como modelo a imagem da página. Depois, peça a eles que façam a medição com a régua e verifiquem se as medidas encontradas coincidem com as de seus colegas.

• No item b, é esperado que os estudantes percebam que, quanto maior a medida de comprimento do passo, menor será a quantidade de passos obtida ao medir o comprimento de uma parede, e vice­versa.

• No item c, peça aos estudantes que estimem quantos passos tem a medida de comprimento do local escolhido na escola. Espera­se que eles estimem uma quantidade grande de passos, pois, geralmente, os locais na escola são grandes em relação à medida do comprimento do passo deles. Em seguida, peça a

• A atividade 9 visa promover o reconhecimento dos estudantes de imagens que configuram ilusões de óptica e levá­los a compreendê­las. Se julgar conveniente, explique a eles que, em algumas situações, o observador pode ver um objeto ou uma figura que “engana o cérebro”, produzindo efeitos inesperados. Esse efeito, conhecido como ilusão de óptica, é um recurso utilizado por muitos artistas para produzir obras criativas e surpreendentes.

• Leve para a sala de aula barbantes suficientes para toda a turma. Auxilie os estudantes na etapa de corte dos barbantes para que fiquem na medida solicitada e ajude ­ os a colar sobre as linhas de cada imagem da atividade. No caso do manuseio com a tesoura, acompanhe os estudantes que executarem os cortes, garantindo que a tesoura seja de pontas arredondadas e que eles tenham cuidado para não se cortarem.

• No caso das imagens que aparecem nessa atividade, a medida do comprimento da linha azul parece ser maior do que a medida do comprimento da linha vermelha, no item A, e o contrário parece ocorrer no item B, por causa da ilusão criada. Apesar disso, espera­se que os estudantes percebam que, na verdade, as medidas do comprimento das duas linhas são iguais, em ambos os itens. Ao final da atividade, solicite a eles que meçam os comprimentos com a régua para verificar que, em cada item, as linhas têm a mesma medida. Se julgar oportuno, aproveite a curiosidade deles e leve outras imagens que utilizam ilusões de óptica para que eles observem e conversem sobre o que elas apresentam.

EXPERIMENTE

9. Em cada item está representada uma figura com um par de linhas, sendo uma vermelha e outra azul.

a ) Com a ajuda de seu professor, e utilizando uma tesoura com pontas arredondadas, corte quatro pedaços de barbante de modo que as medidas do comprimento de cada um deles sejam iguais às medidas de cada linha representada nas imagens. Depois, cole cada pedaço de barbante sobre as linhas vermelha e azul.

Resposta: Os estudantes devem cortar e colar cada pedaço de barbante sobre as linhas vermelha e azul.

b ) Com os olhos fechados, toque em cada linha representada pelos barbantes colados. Depois, estime em cada par de linhas, sem fazer medições, se a medida do comprimento de uma das linhas é igual, maior ou menor do que a medida do comprimento da outra linha. Marque um X na opção que representa a sua resposta à estimativa.

Resposta: Igual.

Maior. Menor. Igual.

A.

B.

C.

O METRO

1. Além do centímetro e do milímetro, outra unidade de medida de comprimento muito utilizada é o metro, que abreviamos como m Observe algumas situações em que o metro é usado como unidade de medida.

Imagens sem proporção entre si.

Dica: Um metro está dividido em 100 partes iguais, e cada uma delas corresponde a 1 cm 1 m = 100 cm

a ) Converse com o professor e os colegas e cite outras situações em que podemos utilizar o metro como unidade de medida de comprimento.

Resposta pessoal. Espera-se que os estudantes citem a medida da altura de uma construção, a medida do comprimento e da largura de um terreno.

b ) Quantos centímetros há em 2 m? 2 m = cm

Resposta: Como 1 m  = 100 cm, temos que:

2 m  = 1 m  + 1 m  = 100 cm  + 100 cm = 200 cm. Portanto, 2 m = 200 cm

c ) Escreva o nome de dois objetos cuja medida do comprimento seja:

• menor do que 1 m.

Resposta pessoal. Sugestão de resposta: Caderno e estojo.

• maior do que 1 m.

Resposta pessoal. Sugestão de resposta: Lousa e carro.

Lembre­os de tomar os cuidados necessários para evitar possíveis acidentes.

AVALIANDO

Objetivo

Identificar o metro como unidade de medida de comprimento padronizada, além de utilizar instrumentos de medida para fazer medições e estabelecer relações entre o metro e o centímetro.

Sugestão de intervenção

157

06/10/2025 18:29:10

Com o auxílio de uma fita métrica, solicite aos estudantes que meçam o comprimento, a largura ou a altura de alguns objetos e façam no caderno uma tabela com essas medidas indicadas em centímetros. Em seguida, questione­os de modo que eles identifiquem quais delas têm mais de um metro de medida de comprimento e quais têm menos. Ao final, verifique quais estratégias eles utilizaram para diferenciar essas medidas.

• Para o trabalho com este tópico, os estudantes devem ter como pré­requisito a compreensão de como se usam as unidades de medidas menores: o milímetro e o centímetro. Pode ser que eles já tenham vivenciado experiências de medições utilizando, por exemplo, a régua ou a fita métrica. Nesse caso, explore esses conhecimentos prévios para auxiliar na compreensão da relação entre essas grandezas.

• A atividade 1 visa apresentar aos estudantes o metro como unidade de medida padronizada, de modo que eles identifiquem algumas situações em que ele é utilizado. Além disso, eles vão identificar quantos centímetros há em um metro. Se necessário, escreva mais relações entre medidas em metros e em centímetros, com a ajuda dos estudantes. Questione ­ os a respeito de quantos centímetros equivalem a 3 m, 4 m, e 5 m, por exemplo, e solicite a eles que, nesse caso, escrevam as relações 3 m = 300 cm, 4 m = 400 cm e 5 m = 500 cm. Para realizarem o item c, leve para a sala de aula pedaços de barbantes com medidas de 1 metro, entregue a cada estudante um pedaço de barbante e sugira ­ lhes que comparem com objetos que estão ao seu redor, como caderno, estojo, cadeira, mesa, lousa, entre outros.

• Ao trabalhar a atividade 2 com os estudantes, alerte ­ os sobre os eventuais riscos na realização dos experimentos propostos, garantindo a integridade física deles próprios, dos professores e das demais pessoas envolvidas no processo educacional. O objetivo des ta atividade é proporcionar aos estudantes que estimem e meçam comprimentos, utilizando o metro como unidade de medida. Providencie um rolo de barbante e entregue a cada estudante um pedaço cuja medida do comprimento seja 1 m. Ao final da atividade, quando eles forem comparar a medida estimada e a medida real, incentive ­os a considerar a medida estimada que registraram sem alterar essa resposta, mesmo que a estimativa seja muito diferente da medida real.

• O objetivo da atividade 3 é que os estudantes façam comparações e desenvolvam noção de proporcionalidade. Auxilie­os a recortar as figuras da página 279 do Material complementar , tomando os devidos cuidados. Oriente­os a deixar todas as figuras sobre a mesa para que possam fazer a comparação das medidas do comprimento de cada objeto. Em seguida, peça­ lhes que reflitam sobre quais objetos podem ser colados em cada quadro, respeitando as devidas medidas. Por fim, auxilie­os na colagem das imagens.

2. Resposta pessoal. Espera-se que os estudantes, utilizando barbantes,

EXPERIMENTE

façam a medição do contorno da medida do comprimento do piso da sala de aula e, por fim, que registrem o resultado obtido e verifiquem se a medida estimada foi próxima da medida real.

2. Formem grupos com quatro colegas e, juntos, estimem a medida, em metros, do comprimento do contorno da sala de aula. Em seguida, com o barbante recebido de seu professor, façam as medições necessárias e verifiquem se a estimativa feita por vocês se aproxima do resultado obtido na medição que fizeram.

Medida estimada:

Dica: Para auxiliar nessa atividade, você vai receber de seu professor um pedaço de barbante cujo comprimento mede 1 m

Medida obtida:

3. Destaque as imagens de objetos que se encontram na página 279 do Material complementar. Depois, cole em cada item um desses objetos de acordo com a medida indicada.

• Objeto cujo comprimento mede menos de 60 cm

Imagens sem proporção entre si.

Resposta: Os estudantes devem colar a imagem do cavaquinho que foi recortado do Material complementar

• Objeto cuja medida do comprimento é maior do que 1 m e menor do que 2 m

Resposta: Os estudantes devem colar a imagem do violoncelo que foi recortado do Material complementar

• Objeto cuja medida do comprimento é maior do que 20 mm e menor do que 150 mm

Resposta: Os estudantes devem colar a imagem da gaita que foi recortada do Material complementar

Experimente. Professor, professora: Esta atividade tem como objetivo que os estudantes comparem a medida que eles estimaram com o resultado obtido na medição com barbante e verifiquem se estão próximas.

BNCC

A atividade 2 está relacionada com a Competência específica de Matemática 8 ao propor aos estudantes que interajam com os colegas a fim de determinar um método para estimar, em metros, a medida do comprimento do contorno da sala de aula. Caso eles apresentem dificuldades no desenvolvimento desta atividade, leve­os

a perceber que, inicialmente, é possível determinar a quantidade aproximada de vezes que o barbante “cabe” na largura e no comprimento da sala de aula e, em seguida, efetuar C + C + L + L, em que C e L indicam, respectivamente, a quantidade aproximada de vezes que o barbante “cabe” no comprimento e na largura da sala de aula, considerando o formato retangular.

4. Em cada item, contorne a unidade de medida mais adequada para expressar quanto mede:

a ) o comprimento de um lápis. m mm cm m mm cm

Resposta: Os estudantes devem contornar a unidade de medida cm

Resposta: Os estudantes devem contornar a unidade de medida m

c ) a espessura de uma moeda.

b ) a largura de uma rua. m mm cm

Resposta: Os estudantes devem contornar a unidade de medida mm.

5. Durante uma atividade na escola, a professora Dirce mediu e anotou a altura dos seguintes estudantes.

Reinaldo

a ) Qual é o nome do estudante cuja medida da altura é exatamente 1 m?

Resposta: Venâncio.

b ) Se um desses estudantes crescer 5  cm, a medida de sua altura

vai atingir 1 m. Qual é o nome desse estudante?

Resposta: Reinaldo.

c ) A diferença entre as medidas da altura de Reinaldo e Sebastião é maior ou menor do que 45 mm?

Resposta: Maior.

d ) Tem algum estudante cuja medida da altura é maior do que 1 m? Se sim, qual é o nome e a medida da altura desse estudante?

Resposta: Sim; Josimar, com 105 cm de altura.

DESAFIO A MAIS

Elena tem três fitas para embrulhar presentes:

• A primeira fita mede 1 m

• A segunda fita é 250 mm menor que a primeira.

• A terceira fita mede 30 cm a mais que a segunda.

• A atividade 4 tem como objetivo levar os estudantes a aprimorarem habilidades de comparação entre objetos com a unidade de medida mais adequada para expressar quanto mede cada um desses objetos. Caso apresentem dúvidas em relação à unidade de medida mais adequada, faça questionamentos a respeito das unidades, a fim de levá­los a compreender que uma unidade de medida pode ser mais adequada do que outra.

Resposta: 105 cm.

Qual é a medida do comprimento, em centímetros, da terceira fita? cm

• O Desafio a mais trabalha a conversão de medidas e a resolução de problemas em etapas. A atividade exige compreender a relação entre metro, centímetro e milímetro e aplicar adição e subtração para resolver. Etapas:

• Converter todas as medidas em centímetros (1 m = 100 cm; 250 mm = 25 cm).

• Calcular a medida da segunda fita: 100 cm   25 cm = 75 cm

• Calcular a medida da terceira fita: 75 cm + 30 cm = 105 cm

159

06/10/2025 18:29:10

Se houver dificuldade, incentive o uso de desenhos ou esquemas e faça perguntas que os ajudem a pensar, como: “Qual é a medida da primeira fita em centímetros?” ou “Se a segunda fita é menor, o que você deve fazer para calcular a medida dela?”.

• A atividade 5 desenvolve um trabalho com unidades de medida de comprimento, especialmente o metro e o centímetro em um contexto que faz parte do dia a dia dos estudantes. No item a, eles são instigados a identificar que 1 metro equivale a 100 centímetros e relacioná­lo à medida da altura de Venâncio. No item b , os estudantes podem usar subtração para verificar quanto falta para Reinaldo e Sebastião atingirem 1 metro, já que Venâncio tem exatamente 1 metro e Josimar tem mais do que 1 metro. No item c, é necessário que os estudantes efetuem uma subtração e, depois, convertam o resultado em milímetros para realizarem a comparação (50 mm > 45 mm). No item d, eles vão fazer a comparação com a medida 100 cm, identificando que Josimar tem a medida da altura maior do que 1 m (105 cm).

OBJETIVOS

• Reconhecer o metro e o centímetro como unidades de medida de comprimento.

• Identificar o que se compra utilizando medidas de comprimento.

• Reconhecer os elementos que caracterizam o gênero textual lista e seus contextos de produção.

• Aperfeiçoar a compreensão de textos e aprimorar a fluência em leitura oral.

• Desenvolver a produção de escrita, além de favorecer o desenvolvimento de vocabulário.

• Solicite aos estudantes que façam a leitura do texto e observem a cena. Converse com eles sobre o tipo de artesanato retratado na imagem e questione se já viram produtos artesanais como esses ou outros tipos de artesanatos. Além disso, verifique se eles conhecem alguém cuja fonte de renda vem dos trabalhos artesanais.

• Comente com os estudantes sobre a importância da valorização desse tipo de trabalho, pois as peças feitas à mão levam mais tempo para serem desenvolvidas, muitas vezes são personalizadas e têm uma riqueza de detalhes que nem sempre máquinas conseguem realizar.

• A questão a tem o objetivo de levar os estudantes a compreenderem a função de uma lista. Caso apresentem dificuldade para responder, peça­lhes que obser vem a quantidade de itens que a mãe solicitou na lista e questione­os sobre a chance de os filhos esquecerem de comprar algum item ou comprarem a quantidade errada.

Professor, professora: O assunto tratado nesta seção possibilita

ENTRE TEXTOS

o trabalho com o tema contemporâneo transversal Trabalho

O artesanato é um trabalho manual produzido por um artesão com materiais variados, como cerâmica, tecelagem, renda, cestaria, madeira e recicláveis. O artesanato brasileiro é um dos mais ricos e criativos do mundo, possibilitando um meio de expressão artística, a preservação das culturas locais e uma alternativa sustentável de renda e de consumo.

a) Resposta pessoal. Espera-se que os estudantes respondam que é para os filhos não se esquecerem de comprar nenhum produto de que ela necessita, além de não errarem na compra da quantidade necessária.

Ana, vamos ao bazar comprar esses itens da lista para a mamãe terminar o trabalho de artesanato?

• 8 m de fita cetim azul

• 2 m de feltro marrom

• 50 cm de feltro branco

• 60 cm de feltro amarelo

• um pacote de olhos de plástico para artesanato (com 10 unidades) Feltro: tecido feito de lã e pelos.

a ) Em sua opinião, por que a mãe de Ana escreveu essa lista?

b) Resposta pessoal. Espera-se que os estudantes digam se já viram algum texto com informação em forma de lista e contem para os colegas e, dessa maneira, relatem seus conhecimentos prévios acerca desse assunto.

EXPLORANDO O TEXTO

b ) Você já leu alguma informação colocada em forma de lista? Conte aos colegas.

c ) A lista é um texto que usamos para organizar itens, como compras ou convidados de uma festa. Cite outros tipos de lista que podem ser feitas.

Resposta pessoal. Espera-se que os estudantes façam correlações com alguns tipos de lista que já tiveram contato, como lista de supermercado, lista de ingredientes para uma receita, entre outros tipos de lista.

EXPLORANDO O TEXTO

Orientações Complementares

b) Esta questão incentiva os estudantes a observarem que a lista é um texto que apresenta uma sequência ou enumeração de nomes de pessoas ou coisas. Explique a eles que listar significa relacionar nomes de pessoas ou coisas para diversos fins, dependendo da necessidade.

c) O intuito desta questão é que os estudantes percebam que há listas com variados itens, a se­

• Esta seção favorece o desenvolvimento de componentes essenciais para a alfabetização, como a compreensão de textos e a fluência em leitura oral, a produção de escrita, além do desenvolvimento de vocabulário, ao apresentar o significado de uma palavra que talvez os estudantes desconheçam.

rem utilizadas com diferentes fins. Sugestão de resposta: lista de materiais escolares, lista dos ajudantes do dia, lista de regras da sala de aula, lista de afazeres de casa.

BNCC

As atividades desta seção favorecem o desenvolvimento da Competência geral 3 da BNCC, bem como o tema contemporâneo transversal Trabalho, pois permite aos estudantes reconhecerem o trabalho artesanal como fonte de renda, além de ser um meio de expressão artística e de preservação das culturas locais.

d) Resposta: Não é importante, pois todos os itens são igualmente necessários

d ) Marque um X na alternativa adequada. Na lista de compras, a ordem dos itens:

não é importante, pois todos os itens listados são igualmente necessários.

é importante para saber que produto comprar primeiro.

ALÉM DO TEXTO

e) Resposta: Os estudantes devem pintar de amarelo os itens feltro amarelo e feltro branco e pintar de azul os itens feltro marrom e fita de cetim azul

e ) A seguir, estão listados os itens que serão comprados com medida de comprimento maior e menor do que 1 m.

Feltro amarelo.

Feltro marrom.

Fita de cetim azul.

Feltro branco.

• Pinte de azul os itens da lista com medida de comprimento maior do que 1 m

• Pinte de amarelo os itens com medida de comprimento menor do que 1 m.

g) Resposta pessoal. A resposta depende das vivências dos

estudantes e das experiências que eles compartilharem com os colegas.

f ) Cite alguns produtos que são vendidos em metros e em centímetros.

g ) Você conhece alguém que faz trabalho artesanal? Se sim, conte aos colegas qual é o tipo de artesanato que essa pessoa produz.

d) Verifique se os estudantes percebem que, no caso da lista apresentada na cena, as ordens dos itens não são importantes, pois sua finalidade é que nenhum item seja esquecido.

ALÉM DO TEXTO Orientações

Complementares

e) Nesta questão, os estudantes devem compreender que 1 m equivale a 100 cm e, assim, concluir que as medidas de comprimento do feltro branco e do feltro amarelo são menores do que 1 m, e as do feltro marrom e da fita de cetim azul são maiores do que 1 m

f) Algumas sugestões de produtos vendidos em metros e em centímetros são: corda, mangueira, arame, cano e fio elétrico.

g) Nesta questão, proponha um momento de interação entre os estudantes, com uma roda de conversa, para que eles troquem informações entre si.

f) Resposta

h ) Além da habilidade com as mãos e o uso da criatividade, outros materiais são usados no trabalho com artesanato. Observe alguns materiais utilizados para fazer artesanato com feltro.

h ) Resposta: Os estudantes devem escrever no caderno uma lista com os seguintes itens: linha, pistola de cola quente, lápis, feltro, fita métrica, agulhas e régua.

pessoal. O objetivo dessa atividade é que os estudantes citem itens que conhecem e que são vendidos em metros e centímetros, como corda, tecido, corrente, mangueira, cano de pvc, entre outros.

Em seu caderno, escreva em letra cursiva uma lista com o nome dos itens que aparecem na imagem, com o seguinte título: “Itens úteis para o artesanato com feltro”.

Professor, professora: Oriente os estudantes na escrita da lista solicitada no item h, incentivando o traçado em letra cursiva, a fim de que eles treinem esse tipo de escrita.

Resposta

Porque uma régua tem o dobro da medida da outra régua. Nesse caso, quanto maior for a régua, menor será a quantidade de unidades de medida (régua) obtida no resultado da medição.

CONCLUSÃO

Ao longo da unidade, foram propostas diversas maneiras de avaliar a aprendizagem da turma, com foco no acompanhamento do desenvolvimento dos estudantes. Aplique um monitoramento mais

abrangente, registrando nos relatórios individuais ou nas fichas de avaliação o desempenho de cada um e considerando suas particularidades. Um modelo desse tipo de ficha pode ser encontrado no tópico Avaliação deste manual. Assim, será possível promover a recuperação dos conteúdos por meio de atividades focadas nas trajetórias individuais de aprendizagem deles, incluindo os avanços e os pontos de dificuldades a serem sanados.

Esse método de verificar a progressão dos estudos e o que a turma de fato con­

06/10/2025 18:29:11

h) A proposta desta questão é desenvolver a produção de escrita.

Sugestão de Desafio

Maria e João mediram o comprimento de uma mesa. Cada um deles usou a régua que tinha na mochila. Os dois obtiveram resultados corretos, porém Maria obteve a medida de 6 réguas e João obteve a medida de 3 réguas. Por que ocorreu essa diferença no resultado deles?

seguiu aprender é de grande importância para que seja possível repensar estratégias em sala de aula, tornando as ações pedagógicas cada vez mais eficazes.

A conclusão da unidade é o momento de avaliar se os objetivos por ela propostos foram alcançados. Para esse diagnóstico, observe no final deste Manual algumas possibilidades de avaliação formativa que permitem fazer o monitoramento da aprendizagem dos estudantes e intervir caso eles não tenham atingido os resultados esperados.

OBJETIVOS DA UNIDADE

• Compreender as ideias da multiplicação.

• Reconhecer o símbolo utilizado para representar a multiplicação.

• Reconhecer a multiplicação como uma adição de parcelas iguais.

• Efetuar multiplicações associadas às ideias de configuração retangular e de possibilidades.

• Efetuar multiplicações de um número de um algarismo por 2, 3, 4 e 5.

• Compreender o significado de dobro e de triplo.

INTRODUÇÃO E JUSTIFICATIVA

Esta unidade trabalha conteúdos que envolvem multiplicações de um número de um algarismo por 2, 3, 4 e 5 e contempla também a ideia de dobro e de triplo. A multiplicação é inserida no contexto da adição de parcelas iguais, na contagem de objetos dispostos em configuração retangular e na contagem de possibilidades. Essas ideias são exploradas por meio de um trabalho prolongado com diferentes atividades envolvendo situações do dia a dia dos estudantes. Essa aprendizagem servirá como pré-requisito para a compreensão das noções multiplicativas presentes em situações-problema.

Habilidades da BNCC trabalhadas na unidade: EF02MA07 e EF02MA08

SUGESTÃO DE ESTRATÉGIA INICIAL

Organize os estudantes em duplas e entregue a eles alguns quebra-cabeças previamente selecionados, que tenham no máximo 30 peças. Após a montagem, eles devem calcular a quantidade de peças, usando a estratégia que julgarem mais interessante durante a conversa na questão A, da página de abertura.

UNIDADE7 MULTIPLICAÇÃO

162

Providencie objetos como tampinhas de garrafa ou palitos. Organize a turma em grupos com três ou quatro integrantes e, em seguida, distribua a cada grupo de 15 a 25 unidades desse material, que possam ser dispostos em configuração retangular. Depois, peça a cada grupo que conte de duas maneiras diferentes a quantidade de objetos recebidos e compartilhem suas estratégias com a turma. Se nenhum dos grupos utilizar a configuração retangular, sugira essa organização e solicite sugestões para obter a quantidade de objetos usando essa estruturação.

• Solicite aos estudantes que leiam as páginas de abertura e respondam às questões como tarefa de casa antes da aula. Oriente-os a anotar as dúvidas para serem discutidas com a turma. Verifique se eles observam ou comentam as imagens nelas apresentadas.

Família reunida para montar um quebra-cabeça.

O quebra-cabeça é um jogo que encanta crianças e adultos. Depois de montado, alguns são colocados em molduras e pendurados nas paredes, já que suas imagens são admiráveis.

Na maioria dos quebra-cabeças, a quantidade de peças de cada coluna é a mesma, assim como a quantidade de peças de cada linha.

Considere o quebra-cabeça a seguir.

Como você calcularia a quantidade de peças desse quebra-cabeça?

Quantas peças há ao todo nesse quebra-cabeça?

Você já montou um quebra-cabeça? Converse com o professor e os colegas sobre esse jogo.

ARTICULANDO CONHECIMENTOS

Aproveite a oportunidade e chame a atenção dos estudantes para a imagem do quebra-cabeça na atividade, perguntando a eles se conhecem o animal representado. Essa abordagem proporcionará uma integração com Ciências da Natureza . Explique a eles que se trata da arara-azul, uma ave da América do Sul que está presente em 11 estados brasileiros. Atualmente, a arara-azul está ameaçada de extinção. Comente também que existem projetos de preservação visando proteger essa espécie. Na página do Instituto Arara Azul, há mais informações acerca do assunto. INSTITUTO Arara Azul. Disponível em: https://www.institutoarara azul.org.br/. Acesso em: 25 jul. 2025.

• Ao responderem às questões 1 e 2, permita aos estudantes que utilizem as próprias estratégias para obter a quantidade total de peças do quebra-cabeça apresentado. Para aqueles que não usarem a multiplicação entre a quantidade de linhas e colunas, ressalte que durante a unidade será estudada uma operação que poderá ajudá-los a calcular de forma ágil a quantidade de peças. Para aqueles que usarem a multiplicação como estratégia, explique que no decorrer da unidade conhecerão melhor essa operação. Verifique se eles perceberam que a quantidade total de 35 peças está representada no destaque da imagem, com o quebra-cabeça completo.

• Na questão 3, caso algum estudante já tenha montado um quebra-cabeça, pergunte-lhe se teve a curiosidade de contar as peças e qual foi a quantidade obtida. Pergunte-lhe também se ele se lembra da imagem montada.

Respostas

1. Resposta pessoal. Cada estudante poderá responder de sua maneira como faria para obter

06/10/2025 18:30:30

a quantidade total de peças do quebra-cabeça. Algumas sugestões de resposta são: contar as peças uma a uma; adicionar a quantidade de linhas à quantidade de peças de cada linha; multiplicar a quantidade de linhas pela quantidade de colunas.

2. Resposta: 35 peças.

3. Resposta pessoal. Espera-se que os estudantes digam se um quebra-cabeça e, em caso afirmativo, relatem suas experiências com esse jogo.

1 a 3. Respostas nas orientações ao professor.

• Para que os estudantes compreendam as diferentes ideias da multiplicação, como a adição de parcelas iguais, a disposição retangular e a representação de possibilidades, é necessário que eles tenham como pré-requisito a compreensão da adição de parcelas iguais, a organização de elementos em linhas e colunas, a leitura e a interpretação de esquemas simples e a noção de combinação de elementos.

• A atividade 1 tem como objetivo explorar agrupamentos com cubinhos como estratégia para ajudar os estudantes a compreenderem as ideias da multiplicação. Ao manipularem a representação dos cubinhos recortados do Material complementar no final da Reprodução do Livro do Estudante e formarem grupos, conforme indicado no item d, eles poderão visualizar a multiplicação como uma adição de parcelas iguais, o que facilita o entendimento do processo. Inicialmente, permita que os estudantes representem de diferentes maneiras os agrupamentos para formar um conjunto com 10 unidades. Depois, peça a eles que façam os reagrupamentos com quantidades iguais. Supervisione o modo como seguram as tesouras com pontas arredondadas, a fim de prevenir acidentes, e oriente-os no posicionamento desse instrumento para o corte adequado e sem riscos à integridade física deles.

• A atividade 1 contribui para a inclusão de estudantes com NEE ao propor a manipulação do material concreto para que observem na prática os agrupamentos, utilizando diferentes sentidos.

IDEIAS DA MULTIPLICAÇÃO

1. José e Bia estão formando agrupamentos com cubinhos.

Para representar 10 unidades, coloquei um a um os cubinhos sobre a mesa.

Eu preferi representar as 10 unidades colocando os cubinhos sobre a mesa de dois em dois.

José Bia

a ) No caderno, escreva uma adição para representar o agrupamento dos 10 cubinhos feito por:

• José.

Resposta: José:

• Bia.

b ) Na representação de José, quantas vezes ele repetiu 1 unidade de cubinho? vezes.

Resposta: 10 vezes.

c ) Na representação de Bia, quantas vezes ela repetiu 2 unidades de cubinho? vezes.

Resposta: 5 vezes.

d ) Além das maneiras que José e Bia representaram, mostre outro jeito de agrupar os cubinhos: coloque 10 unidades sobre a mesa e forme grupos com a mesma quantidade de cubinhos. Para isso, use os cubinhos disponíveis nas páginas 279 e 281 do Material complementar

Resposta: Os estudantes devem compor 10 unidades de cubinhos formando dois grupos com 5 cubinhos cada.

e ) Escreva uma adição para representar o agrupamento de 10 unidades de cubinhos que você fez no item d

Resposta: Os estudantes devem compor a seguinte adição: 5 + 5 = 10

f ) Na representação que você fez no item d, quantas vezes você repetiu a mesma quantidade de cubinhos? vezes.

Resposta: 2 vezes.

BNCC

As atividades deste tópico abordam a resolução de problemas de multiplicação com a ideia de adição de parcelas iguais por meio de estratégias e maneiras pessoais de registro, utilizando ou não suporte de imagens e/ou de material manipulável, possibilitando desenvolver a habilidade EF02MA07 da BNCC.

2. Toda semana, Juliana deposita no cofre a mesma quantia. Ela recebe esse dinheiro de seus pais, mas prefere guardar em vez de gastar.

2. a) Resposta pessoal. Espera-se que os estudantes respondam com base em seus conhecimentos prévios que, neste caso, eles adicionariam 10 vezes a quantia que ela poupou em cada semana. Professor, professora: Esta atividade tem como objetivo levar os estudantes a refletirem, da maneira que preferirem, de quais maneiras eles adicionariam quantias iguais em 10 vezes.

a ) Supondo que Juliana continue poupando a mesma quantia toda semana, qual estratégia você usaria para calcular a quantia total que ela poupou em 10 semanas?

b ) De acordo com as informações ao lado, quantos reais Juliana poupou por semana?

Resposta: 2 reais.

Quantia em reais poupada por Juliana em cada semana

SemanaQuantia poupada

c ) Quantas semanas estão registradas?

Fonte de pesquisa: Anotações de Juliana.

Resposta: 3 semanas.

Para determinar quantos reais Juliana poupou até o momento, podemos efetuar uma adição.

Resposta: 2 + 2 + 2 = 6

2 + 2 + 2 =

três parcelas iguais

Nesse caso, adicionamos 3 vezes 2 reais. Então, podemos indicar essa adição por meio de uma multiplicação.

3 vezes 2 reais é igual a 6 reais3 vezes 2 é igual a 6

06/10/2025 18:30:33

• A atividade 2 estabelece uma integração entre as unidades temáticas de Matemática Números e Probabilidade e estatística ao relacionar a quantia semanal poupada por Juliana e a organização dessa quantia em uma tabela. A atividade 2 tem como objetivo explorar a adição de parcelas iguais para inserir a multiplicação como um modo de representar essa adição. Verifique se os estudantes constroem significativamente a noção de multiplicação com base no conhecimento deles sobre a adição de parcelas iguais. Se julgar conveniente, utilize material concreto, como o material dourado, para simular esse procedimento. • Proponha uma reflexão sobre a finalidade da poupança de Juliana para explorar conceitos da educação financeira. Peça aos estudantes que indiquem possíveis vantagens na atitude de Juliana, pois isso evidenciará seus conhecimentos prévios acerca de educação financeira. Se necessário, complemente as respostas deles sugerindo, por exemplo, que, ao poupar dinheiro quando não precisa gastar, Juliana poderá garantir uma reserva de emergência para um momento de gasto imprevisto, além de ter dinheiro guardado para comprar algo de que precise no futuro. Pergunte também se eles têm o hábito de poupar e como isso pode ser praticado no dia a dia. Comente que evitar o consumo em excesso, refletir sobre nossos gastos e procurar guardar uma parte do que recebemos, dentro das possibilidades de cada um, são atitudes importantes para a formação de um consumidor mais consciente e de uma reserva financeira individual.

Unidades temáticas integradas KLEBER

• Na continuação da atividade 2, evidencie que o símbolo × , usado para indicar uma multiplicação, e a maneira como ele é lido.

• A atividade 3 tem por objetivo explorar a multiplicação com a ideia de adição de parcelas iguais. No item d, verifique se os estudantes reconhecem a multiplicação com base no conhecimento deles sobre a adição de parcelas iguais.

ATIVIDADE EXTRA

Utilize os cubinhos do material dourado para formar 3 agrupamentos com 6 cubinhos em cada um. Em seguida, peça aos estudantes que determinem a quantidade total de cubinhos usando uma adição e uma multiplicação. No primeiro caso, a resposta será 6 + 6 + 6 = 18 e, no segundo, 3 × 6 = 18 . Com relação a esta última, destaque que o número 3 indica a quantidade de agrupamentos e o número 6 indica a quantidade de cubinhos em cada grupo.

Utilizando símbolos, escrevemos:

3 × 2 =

quantidade de semanas quantia em reais poupada por semana

Resposta: 3 × 2 = 6

quantia poupada até o momento

Para representar a multiplicação, utilizamos o símbolo × , que lemos vezes.

Portanto, Juliana poupou até o momento reais.

Resposta: Portanto, Juliana poupou até o momento 6 reais.

3. Um costureiro confeccionou as seguintes camisas de mesmo modelo.

a ) Quantas camisas o costureiro confeccionou?

b ) Quantos botões tem cada camisa?

Resposta: 4

Resposta: 3

c ) Desenhe tracinhos para representar quantos botões o costureiro utilizou ao todo nessas camisas.

Resposta: Os estudantes devem desenhar 12 tracinhos para representar a quantidade total de botões utilizados pelo costureiro.

d ) Complete os espaços a seguir e calcule quantos botões o costureiro utilizou ao todo.

quantidade de botões na 1ª camisa

Resposta: 4 + 4 + 4 = 12

+ + =

quantidade de botões na 2ª camisa

quantidade de botões na 3ª camisa

Resposta: 3 × 4 = 12

× =

quantidade de camisas

quantidade de botões em cada camisa

total de botões

total de botões

4. Joana organizou sua coleção de carrinhos em 3 linhas e 5 colunas. Quantos carrinhos ao todo Joana tem em sua coleção?

linha

quantidade de linhas total de carrinhos ou × = × = coluna

Resposta: 3 × 5 = 15

quantidade de colunas

Resposta: 5 × 3 = 15

quantidade de colunas quantidade de linhas total de carrinhos

Joana tem carrinhos ao todo.

Resposta: Joana tem 15 carrinhos ao todo.

5. Uma lanchonete oferece algumas opções de lanche natural com diferentes tipos de pão, recheio e suco.

a ) Quantas opções de lanche são oferecidas?

b ) Há quantos sabores de suco?

Resposta: 2

Resposta: 3

167

• O objetivo da atividade 4 é explorar a multiplicação com a ideia de configuração retangular, em que os objetos estão dispostos em linhas e colunas. É possível que os estudantes façam a contagem dos carrinhos um a um para obtenção do total. Se isso acontecer, incentive-os a buscar outra maneira de realizar essa contagem. Um exemplo é determinar a quantidade de linhas, a quantidade de carrinhos por linha e depois efetuar a multiplicação desses números. Esta atividade aborda também a propriedade comutativa da multiplicação. Nesse caso, a multiplicação de linhas por coluna ou de colunas por linha não altera o resultado. Sempre que possível, explore essa ideia. No entanto, não é aconselhável nomear a propriedade comutativa nesse momento.

• A atividade 5 tem por objetivo explorar a multiplicação com a ideia de contagem de possibilidades. É possível que os estudantes adicionem a quantidade de lanches naturais à quantidade de sucos. Caso isso aconteça, liste todas as combinações na lousa.

Objetivo

Ao finalizar o estudo deste tópico, espera-se que os estudantes sejam capazes de reconhecer e usar a multiplicação para resolver problemas que envolvam a ideia de adição de parcelas iguais para contar objetos dispostos em configuração retangular e para contar possibilidades.

Sugestão de intervenção

Caso algum estudante não atinja o objetivo proposto, providencie material

concreto, que podem ser tampinhas de garrafa ou cubinhos do material dourado. Retome as atividades 3 e 4 das páginas 166 e 167 e use esse material para representar a quantidade de botões em cada camisa e a quantidade de carrinhos, respectivamente. Com isso, explore no primeiro caso a multiplicação com a ideia de adição de parcelas iguais e, no segundo, de configuração retangular. Providencie também um cardápio com duas opções de sanduíche natural e três opções de suco de fruta e peça aos estudantes que combinem a escolha de

06/10/2025 18:30:33

um sanduíche e um suco. Depois, solicite que indiquem, utilizando uma multiplicação, a quantidade total de possibilidades de escolher, de acordo com esse cardápio, um sanduíche natural e um suco de frutas.

AVALIANDO

cenoura

laranja

• Aproveite o contexto das atividades 5 e 6 para conversar com os estudantes sobre a importância de optar, sempre que possível, por alimentos naturais, como frutas e legumes, ou minimamente processados. Evitar alimentos ultraprocessados, como biscoitos recheados, macarrões instantâneos, refrigerantes e salgadinhos, são hábitos importantes para os cuidados com nossa saúde física.

• A atividade 6 tem como objetivo que os estudantes façam todas as combinações possíveis de um alimento e de um sabor de suco escolhidos por eles.

• Ao elaborar com o colega possibilidades de três alimentos e três sabores de suco, essa atividade favorece a interação com o colega e propicia a autonomia na aprendizagem, promovendo o compartilhamento de conhecimentos aprendendo uns com os outros.

BNCC

A atividade 6, ao propor a interação com seus pares de forma cooperativa, trabalhando coletivamente a ideia de combinações possíveis de três alimentos com três sabores de suco, possibilita o desenvolvimento do raciocínio lógico e explora o espírito da investigação e a busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles, conforme descrito nas Competências específicas de Matemática 2 e 8 da BNCC.

c ) Cada lanche pode ser combinado com um sabor de suco. Complete as combinações.

lanche de atum

Resposta: Laranja; uva.

lanche de cenoura

lanche de frango

Resposta: Laranja; uva.

Resposta: Laranja; uva.

d ) Gislaine vai comprar um lanche e um suco nessa lanchonete. De quantas maneiras diferentes ela pode realizar essa compra?

quantidade de opções de lanches quantidade de sabores de suco quantidade total de maneiras diferentes

Resposta: 3 × 2 = 6

Gislaine pode realizar essa compra de maneiras diferentes.

Resposta: Gislaine pode realizar essa compra de 6 maneiras diferentes.

6. Com um colega, escrevam no caderno 3 alimentos saudáveis e 3 sabores de suco natural de que vocês mais gostam. Depois, escrevam todas as combinações de um alimento e de um sabor de suco que podem ser feitas. Por último, escrevam uma multiplicação para representar o total de combinações possíveis.

Resposta pessoal. Comentários nas orientações ao professor

Resposta 6. Resposta pessoal. Como serão escolhidos 3 alimentos e 3 sabores de suco, espera-se que os estudantes escrevam e efetuem a multiplicação 3 × 3 = 9, obtendo 9 combinações diferentes.

MULTIPLICAÇÃO POR 2

1. Luciano organizou alguns morangos em bandejas.

fileira

a ) Em quantas fileiras as bandejas de morango foram organizadas?

Resposta: 2 fileiras.

b ) Quantas bandejas de morango há em cada fileira?

c ) Quantas bandejas de morango Luciano organizou?

Resposta: 5 bandejas.

Podemos determinar a quantidade de bandejas de morango que Luciano organizou efetuando uma:

• adição.

Resposta: 5 + 5 = 10

+ =

duas parcelas iguais

• multiplicação.

Resposta: 2 × 5 = 10

quantidade de fileiras quantidade de bandejas de morango por fileira quantidade total de bandejas de morango

× = Portanto, Luciano organizou bandejas de morango.

Resposta: Portanto, Luciano organizou 10 bandejas de morango.

2. Com base na disposição das mesas no escritório onde Regina trabalha, complete os cálculos. Quantas mesas há nesse escritório?

Resposta: 6 + 6 = 12

6 + 6 =

Resposta: 2 × 6 = 12

Resposta: 2 + 2 + 2 + 2 + 2 + 2 = 12

2 × = 6 × = 2 + 2 + 2 + 2 + 2 + 2 = ou ou

Resposta: 6 × 2 = 12

Nesse escritório há mesas.

Resposta: Nesse escritório há 12 mesas.

ATIVIDADE EXTRA

Conte antecipadamente a quantidade de estudantes presentes em sala de aula. Se essa quantidade for ímpar, selecione um deles e organize os demais em dois grupos com a mesma quantidade de componentes. Depois, solicite a algum deles que conte a quantidade de colegas em cada grupo e que escreva a soma dessas quantidades na lousa usando uma adição de parcelas iguais e, depois, uma multiplicação. Caso a quantidade de estudantes presentes em sala de aula seja par, escolha dois deles para se dirigirem

06/10/2025 18:21:18

à lousa. Incentive a participação de todos e verifique suas possíveis dificuldades com relação à atividade proposta, para que suas dúvidas sejam sanadas ao fim da atividade.

BNCC

As atividades deste tópico abordam, por meio de estratégias diversas e suporte de imagens, problemas que envolvem multiplicação explorando a ideia de adição de parcelas iguais, contemplando, assim, a habilidade EF02MA07

• Para que os estudantes compreendam as multiplicações por 2, 3, 4 e 5, alguns conhecimentos prévios precisam estar bem desenvolvidos, pois eles são pré-requisitos nesta etapa. Por exemplo, para a compreensão da multiplicação representada pela adição de parcelas iguais, os estudantes precisam entender que, ao multiplicarem por 2, estarão adicionando duas vezes a mesma quantidade. Além disso, a capacidade de representar agrupamentos com objetos de contagem ou desenhos, formando grupos com a mesma quantidade de elementos, também é essencial nessa fase. Esses pré-requisitos auxiliam na construção do sentido da multiplicação como modo mais eficiente de contar quantidades iguais.

• A atividade 1 tem por objetivo apresentar a multiplicação por 2. Os itens a e b remetem à ideia de configuração retangular e o item c, à adição de parcelas iguais, associando-a à multiplicação por 2.

• A atividade 2 tem por objetivo explorar a multiplicação por 2. Nesta atividade, busca-se determinar a quantidade de mesas dispostas em configuração retangular. Explique aos estudantes que nesse contexto é possível ter 2 linhas com 6 mesas por linha (2 × 6) ou 6 linhas com 2 mesas em cada uma (6 × 2). Essa ideia explora a propriedade comutativa da multiplicação.

• A atividade 3 aborda cálculos numéricos relacionando multiplicação por 2 à ideia de adição de parcelas iguais. Nas multiplicações 2 × 4 e 2 × 5 , pergunte aos estudantes o que os números indicam. Espera-se que eles respondam que o algarismo 2 indica a quantidade de agrupamentos em cada item, e os demais algarismos, 4 e 5, a quantidade de objetos por agrupamento

• Proponha a construção do brinquedo utilizando materiais recicláveis como a garrafa PET, aproveitando o contexto do boxe complementar. Você também vai precisar de fita adesiva, bolinha de papel amassado e barbante. Para fazer o bilboquê, primeiramente corte a garrafa PET ao meio e cole a fita adesiva na borda para evitar que os estudantes machuquem os dedos. Use a parte da garrafa com gargalo. Depois, peça a eles que façam uma bolinha de papel amassado e passe fita adesiva em volta dela para deixá-la firme. Prenda uma das pontas do barbante na bolinha e outra dentro da garrafa. Com o bilboquê pronto, eles devem jogar a bolinha para cima, com o objetivo de fazê-la entrar na garrafa.

3. Complete os cálculos de acordo com as imagens a seguir.

Resposta: 4 + 4 = 8

Resposta: 5 + 5 = 10

VOCÊ CONHECE O BILBOQUÊ?

Resposta: 2 × 4 = 8

O bilboquê é um brinquedo composto de duas peças conectadas por um fio, barbante ou cordão que se encaixam. Não se sabe ao certo sua origem, porém alguns estudos sugerem que veio da França. Além da diversão, brincar com o bilboquê ajuda a exercitar a coordenação motora, a concentração e a paciência. Embora seja pouco conhecido em algumas regiões do Brasil, o bilboquê está presente em algumas comunidades, como a comunidade quilombola em Batalha-Piauí, na Região Nordeste. 4 + =

Resposta: 2 × 5 = 10

ARTICULANDO CONHECIMENTOS

Avalie a viabilidade de trabalhar de forma integrada o assunto abordado no boxe complementar com o componente curricular de História ao explorar o fato de que o bilboquê é um brinquedo antigo, que já passou por gerações. Peça aos estudantes que conversem com adultos de sua família e questione se conhecem ou já brincaram com esse brinquedo. Em caso positivo, peça-lhes que comentem como brincavam antigamente com ele.

Um modelo de bilboquê.

4. Felipe comprou 2 borrachas. Cada borracha custa 4 reais. Quantos reais Felipe gastou nessa compra? + = × =

Resposta: 4 + 4 = 8

Resposta: 2 × 4 = 8

Felipe gastou reais nessa compra.

Resposta: Felipe gastou 8 reais nessa compra.

5. Represente as adições de parcelas iguais a seguir por meio de multiplicações.

a ) 0 + 0 = 2 × 0 = 0

b ) 1 + 1 = 2 × 1 = 2

c ) 2 + 2 = 2 × 2 = 4

Resposta: 3 + 3 = 2 × 3 = 6

d ) 3 + 3 = 2 × =

Resposta: 4 + 4 = 2 × 4 = 8

e ) 4 + 4 = 2 × =

Resposta: 5 + 5 = 2 × 5 = 10

f ) 5 + 5 = 2 × =

MULTIPLICAÇÃO POR 3

6. O funcionário de uma empresa está para entregar algumas embalagens de canetas que foram vendidas.

• A atividade 4 utiliza a multiplicação por 2 por meio da ideia de adição com duas parcelas iguais. Com base na atividade anterior, é possível que algum estudante apresente como resposta a multiplicação 4 × 2 = 8. No entanto, o contexto dessa atividade não permite dar sentido à comutatividade.

Dica: Note que os itens a, b e c estão completos.

Resposta: 6 + 6 = 2 × 6 = 12

Resposta: 7 + 7 = 2 × 7 = 14

Resposta: 8 + 8 = 2 × 8 = 16

Resposta: 9 + 9 = 2 × 9 = 18

) 9 + 9 = 2 ×

Resposta: 10 + 10 = 2 × 10 = 20

Resposta: 3 embalagens.

a ) Quantas embalagens foram vendidas? embalagens.

Resposta: 5 canetas.

• adição. • multiplicação.

Resposta: 5 + 5 + 5 = 15

Portanto, foram vendidas canetas. g ) 6 + 6 = 2 × = h ) 7 + 7 = 2 × = i ) 8 + 8 = 2 × =

• A atividade 5 tem como objetivo associar multiplicações por 2 à ideia de adição de duas parcelas iguais. Pergunte aos estudantes se eles observam algum padrão ou regularidade nos resultados das multiplicações. Utilizando essa regularidade, solicite que determinem qual será o resultado da multiplicação 2 × 11, que é 22. Essa proposição motiva a observação, a curiosidade, a criatividade, a formulação de raciocínios e o reconhecimento de relações entre novas aprendizagens e conhecimentos já adquiridos ao relacionar multiplicação por 2 e sequências.

b ) Quantas canetas há em cada embalagem? canetas. Podemos determinar a quantidade de canetas que foram vendidas ao todo efetuando uma:

Resposta: 3 × 5 = 15

k ) 10 + 10 = 2 × = + + = × =

Resposta: Portanto, foram vendidas 15 canetas.

06/10/2025 18:21:18

• A atividade 6 tem por objetivo introduzir a multiplicação por 3 com a ideia de adição de três parcelas iguais.

• A atividade 7 relaciona a multiplicação por 3 com a ideia de contagem de possibilidades. Após a listagem de todas as possibilidades, os estudantes poderão contar as combinações uma a uma ou, de maneira mais rápida, usar a multiplicação para indicar o total de tiaras com laços dispostas em configuração retangular, multiplicando a quantidade de linhas pela quantidade de objetos por linha. Pergunte a eles se seria possível obter o total de combinações sem a necessidade de listá-las. É possível que alguns deles indiquem que, como há 3 opções de laços e 4 modelos de tiara, o total de possibilidades combinadas será determinada pela multiplicação 3 × 4 = 12. Explore também a multiplicação 4 × 3 = 12. A multiplicação nessa ordem indica que a escolha inicial será de uma tiara e depois de um laço.

• A atividade 8 aborda cálculos numéricos envolvendo a multiplicação por 3 associada à ideia de adição de três parcelas iguais. Nas multiplicações 3 × 3 e 3 × 6, pergunte aos estudantes o que os algarismos representam. Espera-se que eles respondam que o algarismo 3 indica a quantidade de agrupamentos em cada item, e os demais algarismos, 3 e 6, a quantidade de objetos por agrupamento.

7. Sabrina tem 3 opções de laço e 4 opções de tiara.

a ) Pinte todos os laços seguindo o padrão e obtenha as diferentes combinações que Sabrina tem para usar as tiaras.

Combinações de cor possíveis para os laços e as tiaras

Cor do laço

Cor da tiara

PretoAmareloAzulVermelho

b ) Complete a multiplicação que representa todas as opções de Sabrina.

7. a) Resposta: Os estudantes devem pintar os laços das tiaras seguindo na linha 2, todos os laços devem ser pintados de azul; e na linha 3, todos os laços devem ser pintados de vermelho. o padrão de cada linha, ou seja, na linha 1, todos os laços devem ser pintados de amarelo;

3 × =

Resposta: 3 × 4 = 12

Sabrina tem opções diferentes de usar todas as tiaras.

Resposta: Sabrina tem 12 opções diferentes de usar todas as tiaras.

8. Escreva e efetue uma adição e uma multiplicação para determinar a quantidade de escovas de dentes em cada item.

+ + =

Resposta: 3 + 3 + 3 = 9; 3 × 3 = 9

ARTICULANDO CONHECIMENTOS

Converse com os estudantes sobre a importância da saúde bucal. Comente que ter uma boca saudável proporciona um sorriso bonito e um hálito puro, além de contribuir para que a mastigação e a digestão dos alimentos sejam eficientes. Pergunte quantas vezes por dia eles

Resposta: 6 + 6 + 6 = 18; 3 × 6 = 18

costumam escovar os dentes. Ressalte que, além da escovação, é importante usar o fio dental, orientando-os sobre higiene pessoal e hábitos regulares que devemos cultivar para garantir a saúde e o bem-estar. Esse diálogo possibilita o trabalho com Ciências da Natureza

Amarelo

Azul

Vermelho

9. Represente as adições de parcelas iguais a seguir por meio de multiplicações.

a ) 0 + 0  +  0 = 3 × 0 = 0

b ) 1 + 1  + 1 = 3 × 1 = 3

c ) 2 + 2  + 2 = 3 × 2 = 6

Resposta: 3 + 3  + 3 = 3 × 3 = 9

d ) 3 + 3  + 3 = 3 × =

Resposta: 4 + 4  + 4 = 3 × 4 = 12

e ) 4 + 4  + 4 = 3 × =

Resposta: 5 + 5  + 5 = 3 × 5 = 15

f ) 5 + 5  + 5 = 3 × =

Resposta: 6 + 6  + 6 = 3 × 6 = 18

g ) 6 + 6  + 6 = 3 × =

DOBRO E TRIPLO

Dica: Note que os itens a, b e c estão completos.

Resposta: 7 + 7  + 7 = 3 × 7 = 21

Resposta: 8 + 8  + 8 = 3 × 8 = 24

Resposta: 9 + 9  + 9 = 3 × 9 = 27

Resposta: 10 + 10  + 10  = 3 × 10 = 30

10. Estas são as garrafas de água que Milena e André vão levar para um acampamento.

a ) Quantas garrafas de água serão levadas para o acampamento?

• Milena:

• André:

Resposta: 2

Resposta: 4

BNCC

b ) Complete o esquema.

Resposta: 2 × 4 = 8

A quantidade de garrafas que André vai levar é equivalente a 2 vezes a quantidade de garrafas de Milena. Nesse caso, podemos dizer que André vai levar o dobro da quantidade de garrafas de Milena.

Dica: Para calcular o dobro de um número, basta multiplicá-lo por 2.

2 × = quantidade de garrafas de Milena quantidade de garrafas de André h ) 7 + 7  + 7 = 3 × = i ) 8 + 8  + 8 = 3 × = j ) 9 + 9  + 9 = 3 × = k ) 10 + 10 + 10 = 3 × =

As atividades deste e do próximo tópico têm como proposta estratégias diversas por meio de suporte de imagens, problemas que envolvem multiplicação explorando a ideia de adição de parcelas iguais e os que envolvem dobro e triplo, contemplando as habilidades EF02MA07 e EF02MA08

173

06/10/2025 18:21:20

• O objetivo da atividade 9 é propor aos estudantes que relacionem a multiplicação por 3 à ideia de adição de três parcelas iguais. Pergunte a eles se observam algum padrão ou regularidade nos resultados das multiplicações. Usando essa regularidade, solicite que determinem qual será o resultado da multiplicação 3 × 11 , que é 33. Essa proposição incentiva a observação, a curiosidade, a criatividade, a formulação de raciocínios e o reconhecimento de relações entre novas aprendizagens e conhecimentos já adquiridos ao relacionar multiplicação por 3 e sequências.

• A atividade 10 tem por objetivo contemplar a ideia de dobro associada à multiplicação por 2. Utilize objetos da sala de aula, como lápis ou borrachas, para explorar outras situações. Por exemplo, separe 3 borrachas e mostre aos estudantes que o dobro dessa quantidade de borrachas equivale a 2 agrupamentos de 3. Em seguida, associe essa situação à multiplicação 2 × 3 = 6

Milena

André

• A atividade 11 tem por objetivo contemplar a ideia de triplo por meio da multiplicação por 3. Também utilizando material concreto, explore outras situações. Faça um agrupamento com 4 objetos e mostre que o triplo dessa quantidade equivale a 3 agrupamentos com 4 objetos, que corresponde à multiplicação 3 × 4 = 12

• O objetivo da atividade 12 é exercitar a ideia de dobro e triplo. Caso alguns estudantes tenham dificuldade, utilize material concreto para representar a quantidade de objetos descritos em cada item. No item a, utilize 2 agrupamentos com 4 objetos em cada um para indicar o dobro de 4. Aproveite essa ideia nos demais itens.

11. Considere os balões em cada quadro.

B.

a ) Quantos balões há:

Resposta: 2

• no quadro A?

Resposta: 6

• no quadro B?

A quantidade de balões do quadro B corresponde a 3 vezes a quantidade de balões do quadro A. Nesse caso, dizemos que no quadro B há o triplo da quantidade de balões do quadro A

b ) Complete o esquema a seguir.

Resposta: 3 × 2 = 6

3 × =

quantidade de balões do quadro A

quantidade de balões do quadro B

Dica: Para calcular o triplo de um número, basta multiplicá-lo por 3.

12. Complete as frases corretamente.

a ) O dobro de 4 prendedores é igual a prendedores.

Resposta: O dobro de 4 prendedores é igual a 8 prendedores.

b ) O dobro de 5 botões é igual a botões.

Resposta: O dobro de 5 botões é igual a 10 botões.

c ) O triplo de 3 copos é igual a copos.

Resposta: O triplo de 3 copos é igual a 9 copos.

d ) O triplo de 4 colheres é igual a colheres.

Resposta: O triplo de 4 colheres é igual a 12 colheres.

MULTIPLICAÇÃO

POR 4

13. Considere a distribuição de carteiras na imagem a seguir.

a ) Quantas são as fileiras de carteiras?

b ) Quantas carteiras há em cada fileira?

Resposta: 4

Resposta: 6

Podemos determinar a quantidade total de carteiras na sala de aula efetuando uma:

• adição.

Resposta: 6 + 6 + 6 + 6 = 24

+ + + =

quatro parcelas iguais

• multiplicação.

Resposta: 4 × 6 = 24

× =

quantidade de fileiras quantidade de carteiras por fileira

quantidade total de carteiras

Resposta: Portanto, na sala de aula há 24 carteiras ao todo.

Portanto, na sala de aula há carteiras ao todo.

06/10/2025 18:18:25

• A atividade 13 tem por objetivo explorar a multiplicação por 4. Nessa atividade, são utilizadas a ideia de adição com parcelas iguais e a configuração retangular.

• Explique aos estudantes que nesse contexto é possível fazer 4 fileiras de 6 carteiras (4 × 6) ou 6 fileiras de 4 carteiras (6 × 4). Com base nisso, mostre a eles que 4 × 6 = 6 × 4 = 24. Essa ideia contribui para a compreensão da propriedade comutativa da multiplicação, sem a necessidade de anunciá-la.

REFERÊNCIAS COMPLEMENTARES

KUHN, Malcus Cassiano; PEREIRA, Jesiane de Freitas. A multiplicação nos anos iniciais do ensino fundamental: da teoria para a prática. Thema , v. 17, n. 2, p. 464-482, jun. 2020. Esse artigo aborda o ensino da multiplicação nos anos iniciais do Ensino Fundamental, com uma abordagem qualitativa, por meio de um estudo bibliográfico, embasado na Teoria da Aprendizagem Significativa, no Campo Conceitual Multiplicativo de Vergnaud e na BNCC.

fileira

• O objetivo da atividade 14 é exercitar a multiplicação por 4 com a ideia de adição de quatro parcelas iguais. Nas multiplicações 4 × 2, item a, 4 × 3, item b, e 4 ×4, item c, pergunte aos estudantes o que os algarismos representam. Espera-se que eles respondam que o algarismo 4 indica a quantidade de agrupamentos em cada item e os demais algarismos, 2, 3 e 4, a quantidade de objetos por agrupamento.

• Para realizar a atividade 15, verifique a possibilidade de levar algumas réguas de 30 cm para a sala de aula ou peça aos estudantes que providenciem esse material. Outra sugestão é reuni-los em grupos e providenciar uma régua para cada grupo. Essa atividade envolve a multiplicação por 4 com a ideia de adição de parcelas iguais. Ao utilizarem a régua, observe se os estudantes partem da marca do zero, pois é possível que alguns iniciem da marca do 1. Após concluírem a atividade, explique-lhes que no item a eles obtiveram 4 intervalos de 4 cm (4 × 4); no item b, 4 intervalos de 5 cm (4 × 5); no item c, 4 intervalos de 6 cm (4 × 6); e no item d, 4 intervalos de 7 cm (4 × 7).

14. Complete os cálculos de acordo com as imagens.

15. Ricardo calculou 4 × 2 utilizando uma régua. Com base nesse cálculo, complete o que falta.

Resposta: 2 + 2 + 2 + 2 = 8

Resposta: 4 × 2 = 8

Agora, utilizando uma régua, resolva os cálculos a seguir de maneira semelhante à de Ricardo.

Resposta: 4 × 4 = 16

Resposta: 4 × 5 = 20

Resposta: 4 × 6 = 24

Resposta: 4 × 7 = 28

a ) 4 × 4 = b ) 4 × 5 = c ) 4 × 6 = d ) 4 × 7 = 2 + 2 + 2 + 2 = 4 × = 0123456789101112131415 + 2

16. Em uma papelaria, um pacote com 3 canetas custa 8 reais.

a ) Quantos reais custam 4 pacotes dessa mesma caneta?

Resposta: 4 × 8 = 32. Quatro pacotes custam 32 reais.

b ) Ao comprar os 4 pacotes, quantas canetas serão adquiridas?

Resposta: 4 × 3 = 12. Serão adquiridas 12 canetas.

17. Represente as adições de parcelas iguais a seguir por meio de multiplicações.

a ) 0 + 0 + 0 + 0 = 4 × 0 = 0

b ) 1 + 1 + 1 + 1 = 4 × 1 = 4

c ) 2 + 2 + 2 + 2 = 4 × 2 = 8

Dica: Note que os itens a, b e c estão completos.

Resposta: 3 + 3 + 3 + 3 = 4 × 3 = 12

d ) 3 + 3 + 3 + 3 = 4 × =

Resposta: 4 + 4 + 4 + 4 = 4 × 4 = 16

e ) 4 + 4 + 4 + 4 = 4 × =

Resposta: 5 + 5 + 5 + 5 = 4 × 5 = 20

f ) 5 + 5 + 5 + 5 = 4 × =

Resposta: 6 + 6 + 6 + 6 = 4 × 6 = 24

g ) 6 + 6 + 6 + 6 = 4 × =

Resposta: 7 + 7 + 7 + 7 = 4 × 7 = 28

h ) 7 + 7 + 7 + 7 = 4 × =

Resposta: 8 + 8 + 8 + 8 = 4 × 8 = 32

i ) 8 + 8 + 8 + 8 = 4 × =

Resposta: 9 + 9 + 9 + 9 = 4 × 9 = 36

j ) 9 + 9 + 9 + 9 = 4 × =

Resposta: 10 + 10 + 10 + 10 = 4 × 10 = 40

k ) 10 + 10 + 10 + 10 = 4 × =

177

06/10/2025 18:18:26

• A atividade 16 tem por objetivo resolver problemas envolvendo multiplicação com a ideia de adição de parcelas iguais por meio de estratégias pessoais. Ao responder aos itens a e b, os estudantes deverão selecionar informações, pois há excesso de dados, uma vez que a quantidade de canetas por pacote não será usada no item a, nem o preço do pacote será usado no item b. Caso eles tenham dificuldade para resolver o primeiro item, use a lousa para escrever a multiplicação com a ideia de adição de parcelas iguais:

8 + 8 + 8 + 8 = 4 × 8 = 32

• O objetivo da atividade 17 é estabelecer relação entre a multiplicação por 4 e a ideia de adição de quatro parcelas iguais. Pergunte aos estudantes se eles observam algum padrão ou regularidade nos resultados das multiplicações. Usando essa regularidade, solicite que determinem qual será o resultado da multiplicação 4 × 11 , que é 44. Essa proposição incentiva a observação, a curiosidade, a criatividade, a formulação de raciocínios e o reconhecimento de relações entre novas aprendizagens e conhecimentos já adquiridos ao relacionar multiplicação por 4 e sequências até a multiplicação por 10.

• O objetivo da atividade 18 é relacionar a multiplicação por 5 com a ideia de adição de parcelas iguais. Avalie a possibilidade de levar alguns materiais como canetas ou tampinhas, faça 5 agrupamentos e indique a quantidade total por meio de uma multiplicação por 5. Por exemplo, com 15 objetos, é possível fazer 5 agrupamentos de 3 objetos em cada um, indicado por 3 + 3 + 3 + 3 + 3 = 5 × 3 = 15

• A atividade 19 aborda cálculo numérico envolvendo multiplicação por 5. Se julgar necessário, use a lousa para escrever cada uma como adição de parcelas iguais. No item A, escreva 3 + 3 + 3 + 3 + 3 = 5 × 3 e, no item B, 7 + 7 + 7 + 7 + 7 = 7 × 5 = 35

Se possível, utilize um ábaco para demonstrar o resultado de cada multiplicação.

AVALIANDO

Objetivo

Ao finalizar o estudo deste conteúdo, espera-se que os estudantes sejam capazes de resolver problemas que envolvam multiplicação por 2, 3, 4 e 5 com a ideia de adição de parcelas iguais e de dobro e triplo.

Sugestão de intervenção

Caso algum estudante não atinja o objetivo proposto, retome algumas atividades deste tópico, como a atividade 18, e faça as representações da situação na lousa ou com materiais manipuláveis. Observe como desenvolver essa estratégia com o exemplo dado, reproduzindo-a também para as situações com multiplicações por 2, 3 e 4.

MULTIPLICAÇÃO

POR 5

18. Leda organizou as mesas para receber os convidados de seu aniversário.

Resposta: 5

a ) Quantas mesas Leda organizou?

Resposta: 4

b ) Quantas cadeiras há em cada mesa?

Podemos determinar a quantidade de cadeiras que Leda organizou efetuando uma:

• adição.

Resposta: 4 + 4 + 4 + 4 + 4 = 20

• multiplicação.

cinco parcelas iguais

Resposta: 5 × 4 = 20

× =

quantidade de mesas

quantidade de cadeiras por mesa

quantidade total de cadeiras

Resposta: Portanto, Leda organizou 20 cadeiras.

Portanto, Leda organizou cadeiras.

19. Em cada item, apenas um dos ábacos apresenta o resultado correto da multiplicação.

Resposta: Os estudantes devem completar cada item fazendo A: 5 × 3 = 15; B: 5 × 7 = 35.

Ábaco 1 Ábaco 2

5 × 3 =

• Complete o cálculo de cada item.

Ábaco 1 Ábaco 2

5 × 7 =

• Contorne o ábaco que representa a resposta correta.

Resposta: No item A, os estudantes devem contornar o ábaco 2; no item B, devem contornar o ábaco 1

Represente na lousa as 5 mesas e, em cada uma, desenhe 4 cadeiras. Faça uma adição de parcelas iguais e, depois, a multiplicação por 5. Altere a quantidade de cadeiras e peça aos estudantes que façam os desenhos e as operações em seus cadernos. Por exemplo, sugira 5 mesas com 3 cadeiras por mesa ou 5 mesas com 2 cadeiras. Outra possibilidade é usar material concreto para representar a quantidade de mesas e de cadeiras, como uma caixinha para a mesa e cubinhos do material dourado para as cadeiras.

Sugestão de Desafio

Se cada um dos meus 5 amigos tem 5 carrinhos, quantos carrinhos eles têm ao todo?

Resposta Eles têm ao todo 25 carrinhos.

• Ao final da unidade, apresente aos estudantes a sugestão de desafio a seguir. Verifique se eles interpretam corretamente o enunciado do desafio e se calculam 5 × 5 = 25 para obter o total de carrinhos.

20. Henrique comprou 5 pacotes de figurinhas para seu álbum. Sabendo que em cada pacote há 8 figurinhas, quantas figurinhas ele comprou?

Resposta: 5 × 8 = 40 Henrique comprou 40 figurinhas.

21. Escreva as seguintes adições de parcelas iguais como multiplicações.

a ) 0 + 0 + 0 + 0 + 0 = 5 × 0 = 0

b ) 1 + 1 + 1 + 1 + 1 = 5 × 1 = 5

c ) 2 + 2 + 2 + 2 + 2  = 5 × 2 = 10

d ) 3 + 3 + 3 + 3 + 3 =

e ) 4 + 4 + 4 + 4 + 4 =

f ) 5 + 5 + 5 + 5 + 5 =

g ) 6 + 6 + 6 + 6 + 6 =

h ) 7 + 7 + 7 + 7 + 7 =

i ) 8 + 8 + 8 + 8 + 8 =

j ) 9 + 9 + 9 + 9 + 9 =

Dica: Note que os itens a, b e c estão completos.

Resposta: 3 + 3 + 3 + 3 + 3 = 5 × 3 = 15

Resposta: 4

Resposta: 5

Resposta:

Resposta: 7

Resposta: 8 + 8 + 8 + 8 + 8  = 5 × 8 = 40

Resposta: 9 + 9 + 9 + 9 + 9  = 5 × 9 = 45

k ) 10 + 10 + 10 + 10 + 10 =

Resposta: 10 + 10 + 10 + 10 + 10 = 5 × 10 = 50

DESAFIO A MAIS

Observe os lápis que Miguel tinha em seu estojo. Seu irmão deu a ele o dobro dessa quantidade. Ele também recebeu de sua mãe o triplo da quantidade que tinha depois de receber os lápis do irmão. Na escola, ele encontrou um amigo que estava sem lápis e doou 5 para ele.

Quantos lápis Miguel tem agora? lápis.

Resposta: 31 lápis.

• Caso os estudantes demonstrem dificuldade, incentive-os a usar representações visuais, como desenhos ou esquemas.

CONCLUSÃO

A fim de realizar um monitoramento mais abrangente, registre nos relatórios individuais ou nas fichas de avaliação o desempenho de cada estudante, considerando suas particularidades. Um modelo desse tipo de ficha pode ser encontrado no tópico Avaliação destas orientações. Assim, será possível promover recuperação dos conteúdos por meio de

atividades com base nas trajetórias de aprendizagem individuais, incluindo os avanços e os pontos de dificuldades a serem sanados. Esse método é de grande importância para que seja possível repensar estratégias em sala de aula, tornando as ações pedagógicas cada vez mais eficazes.

A conclusão da unidade é o momento de avaliar se os objetivos por ela propostos foram alcançados. Para esse diagnóstico, observe no final deste Manual algumas possibilidades de avaliação formativa que permitem realizar o

• Caso os estudantes tenham dificuldade para responder à atividade 20, escreva na lousa uma adição de parcelas iguais e depois utilize a multiplicação.

• Na atividade 21, pergunte a eles se observam algum padrão ou regularidade nos resultados das multiplicações. Usando essa regularidade, solicite que determinem qual será o resultado da multiplicação 5 × 11, que é 55. Deixe que se expressem livremente, acolhendo com atenção e respeito as contribuições de todos. Se algum estudante tiver dificuldade acerca do conteúdo, proponha retomada das explicações para recuperar as defasagens .

• O objetivo do boxe Desafio a mais é que os estudantes pratiquem a resolução de problemas em várias etapas, utilizando operações de multiplicação, adição e subtração para determinar a quantidade final de lápis. Uma possível lógica de resolução é a seguinte:

• Miguel tinha 3 lápis.

• Ele ganhou do irmão o dobro dessa quantidade: 2 × 3 = 6. Assim, ficou com 3 + 6 = 9 lápis.

• Depois, ele recebeu da mãe o triplo dessa nova quantidade: 3 × 9 = 18. Agora ele tem 9 + 18 = 27 lápis.

• Por fim, ele deu 5 lápis para um amigo: 27 5 = 22 lápis. Portanto, Miguel tem agora 22 lápis.

06/10/2025 18:18:27

monitoramento da aprendizagem dos estudantes e intervir caso eles não tenham atingido os resultados esperados.

OBJETIVOS DA UNIDADE

• Identificar objetos do dia a dia que lembram figuras geométricas planas.

• Reconhecer retângulos, triângulos, quadrados e círculos.

• Reconhecer lados e vértices como elementos do quadrado, do retângulo e do triângulo.

• Desenvolver noções espaciais para localizar elementos em relação a um ou mais referenciais.

• Estabelecer relações de posição no espaço.

• Compreender as noções de atrás, ao lado, à frente, em cima, embaixo, à direita e à esquerda.

• Estabelecer pontos de referência para descrever trajetos e deslocar-se no plano e no espaço.

• Identificar e representar caminhos seguindo orientações do trajeto.

• Compreender o significado de: para a direita, para a esquerda, para cima e para baixo.

INTRODUÇÃO E JUSTIFICATIVA

Nesta unidade, os estudantes estudarão conceitos relacionados a figuras geométricas planas, posições e deslocamentos. Essas figuras serão apresentadas como aparecem no cotidiano, muitas vezes como faces de um objeto tridimensional. Ao longo deste tópico, eles farão atividades que os ajudam a enxergar as figuras em objetos como caixas e blocos. Eles também devem relacionar alguns objetos comuns a figuras geométricas planas e identificar essas figuras.

Esta unidade também aborda os conteúdos relacionados ao reconhecimento de localização e deslocamento de pessoas e elementos no plano e no espaço. Os estudantes vão

UNIDADE8 FIGURAS GEOMÉTRICAS PLANAS, LOCALIZAÇÃO E

DESLOCAMENTO

Casa da artista sul-africana Esther Mahlangu, na vila de Mabhoko, Mpumalanga, com fachada e muros pintados no estilo do povo Ndebele, em 2017.

realizar atividades que visam promover a compreensão de termos como atrás, ao lado, à frente, em cima, embaixo, à direita e à esquerda em situações do dia a dia. Por fim, será abordado o reconhecimento de elementos no espaço, nesse sentido eles serão levados a identificar e realizar um determinado caminho, de acordo com indicações em linguagem verbal e não verbal.

Habilidades da BNCC trabalhadas na unidade: EF02MA10, EF02MA11, EF02MA12, EF02MA13 e EF02MA15

SUGESTÃO DE ESTRATÉGIA INICIAL

Organize a turma em grupos com três estudantes cada. Providencie 15 palitos pequenos de madeira com pontas arredondadas, como palitos de sorvete, e uma folha de papel sulfite em branco para cada grupo. Oriente cada grupo a formar e colar na folha o contorno de três figuras geométricas planas usando os palitos. Em seguida, peça a eles que pintem o interior de cada contorno. Espera-se que eles construam um triângulo, um quadrado e um retângulo. Depois, solicite que digam, caso saibam, os nomes das figuras construídas por eles

Na cultura do povo Ndebele, que vive na África do Sul, as mulheres têm o hábito de pintar figuras com cores vibrantes nas fachadas e nos muros das casas. Essa tradição expressa parte da identidade desse povo e da criatividade das mulheres Ndebele.

1. Sugestões de respostas: Quadrados; retângulos; triângulos; círculos.

Identifique, na imagem, pelo menos duas figuras cujo contorno lembra figuras geométricas planas que você conhece. Na região onde você mora, quais figuras geométricas planas você consegue identificar nas construções e nas pinturas feitas nas moradias?

2. Resposta pessoal. A resposta depende das construções e pinturas que os estudantes identificarem na região onde moram.

• Comente com os estudantes que a África do Sul é um país que tem belezas naturais, curiosidades e costumes interessantes, além de uma cultura muito rica. Diga também que é importante para o povo Ndebele preservar a tradição de estampar as casas com muitas cores.

• Se achar conveniente, mostre-lhes a localização da África do Sul em um mapa. Para isso, leve-os ao laboratório de informática, se houver, e peça-lhes que acessem um site de geolocalização por mapas e digitem África do Sul na aba de pesquisa.

• Diga aos estudantes que utilizar figuras planas como adorno é bem comum. Provavelmente eles já viram algo sobre como culturas indígenas utilizam figuras planas em pinturas corporais. Pode-se falar ainda que certas religiões, como as artes islâmicas, usam figuras planas como representação artística.

• Na questão 1 , verifique se os estudantes localizam o contorno de regiões quadradas, retangulares, triangulares e circulares na imagem. Se for necessário, auxilie-os mostrando alguma figura da imagem, como um triângulo. Depois, peça que eles identifiquem outros triângulos.

181

06/10/2025 18:16:18

• Na questão 2, o objetivo é averiguar se os estudantes identificam figuras geométricas planas presentes nas pinturas das construções da região onde moram ou estudam. Se julgar conveniente, fale de figuras que podem ser encontradas pintadas na escola ou próximas dela.

• Como pré-requisito para o estudo das figuras geométricas planas, é necessário que os estudantes tenham desenvolvido noções básicas de contorno, formato e tamanho. Eles também devem reconhecer semelhanças e diferenças entre objetos e devem ser capazes de observar e comparar diferentes formatos em objetos do dia a dia.

• Nesta coleção, utilizaremos o termo “polígono” tanto para nos referirmos à linha poligonal simples e fechada quanto para nos referirmos à região poligonal. A definição de polígonos e o uso detalhado desse termo serão apresentados aos estudantes nos volumes de 4º e de 5º ano desta coleção.

• Na atividade 1, os estudantes devem reconhecer figuras geométricas planas como contornos de faces de figuras geométricas espaciais.

• No item b , eles podem deduzir que o professor Jailton usou o objeto amarelo para desenhar o quadrado e, no item c, verifique se eles perceberam que o objeto verde é o único que tem faces com formato de triângulo. Nesse caso, utilize o erro como caminho de aprendizado, questionando o raciocínio deles e fazendo-os perceber a conclusão correta, sem dar a resposta antecipada. Esse procedimento de resolução por meio de tentativas e erros é uma etapa importante a ser explorada na sistematização dos conteúdos.

• Caso haja dificuldade na resolução dessa atividade, peça aos estudantes que imaginem que estão colocando os objetos apresentados em cima de uma folha de papel e pergunte qual seria a figura obtida por eles ao contornar cada objeto em diferentes posições.

RECONHECENDO FIGURAS GEOMÉTRICAS PLANAS

1. O professor Jailton desenhou e nomeou algumas figuras geométricas planas na lousa.

Para desenhar essas figuras, Jailton apoiou na lousa um objeto cujo formato se parece com uma figura geométrica espacial e, em seguida, contornou uma de suas faces. Confira os objetos que Jailton utilizou e, depois, resolva os itens.

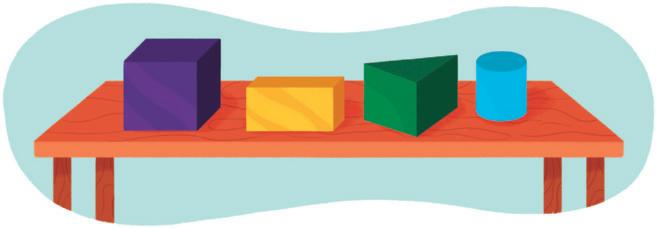
a ) Marque um X no objeto que Jailton utilizou para desenhar o círculo.

Resposta: Os estudantes devem marcar um X no cilindro azul.

b ) Contorne de vermelho o objeto que Jailton utilizou para desenhar o quadrado.

Resposta: Os estudantes devem contornar de vermelho o cubo roxo.

c ) Contorne de azul o objeto que Jailton utilizou para desenhar o triângulo.

Resposta: Os estudantes devem contornar de azul o prisma verde.

BNCC

As atividades apresentadas neste tópico contemplam a habilidade EF02MA15 da BNCC ao trabalhar a capacidade de reconhecer, comparar e nomear as figuras planas, por meio de características comuns, em desenhos apresentados em diferentes disposições ou em sólidos geométricos.

• Se possível, leve para a sala de aula objetos como os apresentados nesta atividade e use-os para desenhar figuras geométricas na lousa, contornando suas faces.

2. Ligue cada objeto a seguir à figura geométrica plana que ele lembra.

Imagens sem proporção entre si.

Professor, professora: As legendas das imagens da atividade 2 não foram inseridas para não comprometerem a realização da atividade.

Resposta: Os estudantes devem ligar as figuras da seguinte maneira: envelope ao retângulo; espelho ao círculo; lajota ao quadrado; bandeirinhas ao triângulo.

3. A seguir, está representado um desenho.

Triângulo

Quadrado

Retângulo

Círculo

Resposta: Os estudantes devem pintar os triângulos de vermelho; o quadrado de verde; o retângulo de azul e o círculo de amarelo.

a ) Pinte o desenho com as cores indicadas na legenda.

b ) Você pintou figuras geométricas diferentes. Quantas de cada tipo há no desenho?

Resposta: Os estudantes devem completar o quadro

da seguinte maneira: Quadrado: 1; Retângulo: 1; Círculo: 1; Triângulo: 7.

Quantidade de figuras

QuadradoRetânguloCírculoTriângulo

06/10/2025 18:16:18

• A atividade 2 solicita que os estudantes associem objetos comuns do dia a dia com figuras geométricas planas. Desta maneira, eles são incentivados a notar a presença de tais formatos em seu entorno.

• É possível que alguns estudantes não reconheçam as imagens e, por isso, não consigam associar as imagens às figuras. Nesse caso, fale um pouco sobre cada objeto e onde ele costuma ser encontrado.

• Após a realização da atividade, avalie se eles ligaram corretamente os objetos à figura geométrica plana que ele lembra e se tiveram dificuldade em distinguir o retângulo do quadrado. Apesar de o quadrado ser um caso particular de retângulo, nessa fase de escolaridade, optou-se por não abordar essa questão.

• A atividade 3 tem por objetivo que os estudantes identifiquem e pintem algumas figuras geométricas planas em um desenho, para depois contar quantas de cada uma delas há.

• Os estudantes podem apresentar dificuldades em localizar as figuras, principalmente o triângulo, uma vez que a junção dos dois triângulos com o quadrado das pernas do gato também forma um triângulo. Nesse caso, explique a eles que devem pintar o quadrado separadamente, mas que esse triângulo (com o quadrado em seu interior) deve ser contado ao completar o quadro.

• Na atividade 4 é esperado que os estudantes identifiquem a quantidade de quadrados nas ilustrações do item a e, no item b, façam um desenho usando quadrados, retângulos, triângulos e círculos.

• Caso haja dificuldade, faça uma breve revisão sobre as características de cada uma dessas figuras geométricas planas. Além disso, desenhe-as na lousa em posições diferentes.

4. Leia os itens a seguir e, depois, faça o que se pede.

a ) Complete os itens escrevendo quantos quadrados você identifica em cada desenho.

Resposta: Os estudantes devem completar

da seguinte maneira: desenho 1: 2; desenho 2: 8; desenho 3: 4.

2

b ) Faça um desenho usando quadrados, retângulos, triângulos e círculos. Você pode usar todas as figuras geométricas planas citadas ou escolher apenas algumas delas. Não se esqueça de dar um nome para seu desenho.

Resposta pessoal. Espera-se que os estudantes façam um desenho de acordo com os modelos do item anterior usando as seguintes figuras geométricas planas: quadrados, retângulos, triângulos e/ou círculos.

ATIVIDADE EXTRA

Solicite aos estudantes que reproduzam o desenho que fizeram no item b da atividade 4, em uma folha de papel A4. Outra possibilidade é disponibilizar círculos, quadrados, triângulos e retângulos feitos de papel colorido e pedir para que colem as figuras de maneira a formar um desenho no papel. Caso opte pela segunda sugestão, providencie com antecedência as figuras, aproximadamente cinco de cada uma delas para cada estudante. Além disso, não se esqueça de variar as cores.

Desenho 1

Desenho 3

Desenho

5. Paloma contornou uma das partes de uma caixa de presente em uma folha de papel e pintou o desenho formado. Para isso, ela segurou a caixa sobre uma folha de papel com uma das mãos e fez o contorno com lápis usando a outra mão.

Momento 1

Momento 2

Momento 3

a ) Qual figura geométrica plana o desenho de Paloma lembra?

Resposta: A figura lembra um triângulo.

b ) Paloma colocou a mesma caixa em outra posição, como indicado na imagem, e repetiu o procedimento. No final, qual figura geométrica plana ficará representada no desenho?

Resposta: A figura lembra um retângulo.

6. José recortou a planificação da superfície do cilindro em três partes.

Planificação do cilindro.

Partes após o recorte.

Cilindro

a ) Após recortar a planificação, quantas partes José obteve?

Resposta: José obteve 3 partes.

b ) Essas partes lembram quais figuras geométricas planas?

Resposta: O círculo e o retângulo.

06/10/2025 18:16:20

• O objetivo da atividade 5 é que os estudantes identifiquem diferentes figuras geométricas planas em um mesmo objeto tridimensional. Para tirar melhor proveito, bem como sanar possíveis dúvidas, leve para a sala de aula uma caixa como a da atividade e, usando-a, faça o desenho de um triângulo e de um retângulo na lousa de modo que eles possam acompanhar. Leve também caixas com outros formatos, organize a turma em grupos e distribua as caixas a eles, pedindo que façam desenhos em folhas de papel usando as faces das caixas como base. Depois, para favorecer a inclusão dos estudantes com NEE nessa atividade, cole um cordão no contorno desenhado e peça para que eles pintem esse cordão utilizando o dedo molhado em tinta.

• A atividade 6 requer que os estudantes identifiquem que, ao recortar a planificação do cilindro, obtêm-se um retângulo e dois círculos. Para isso, eles devem contar quantas partes foram obtidas ao fazer o recorte.

• Para complementar a atividade e auxiliar em dificuldades que possam surgir, leve para a sala de aula moldes do cilindro e distribua aos estudantes, orientando-os a montá-los. Depois, peça que identifiquem no cilindro montado as figuras geométricas respondidas no item b

• Na atividade 7, os estudantes precisam identificar círculos, quadrados, triângulos e retângulos em meio a outras figuras com o intuito de formar um caminho para guiar o pirata ao tesouro. Caso tenham dificuldade, desenhe na lousa as outras figuras (flor, raio, lua e coração) e leve-os a perceber que essas figuras não são figuras geométricas planas.

• Na atividade 8, espera-se que os estudantes identifiquem a quantidade de triângulos da figura no item a considerando, inclusive, o triângulo maior, composto pelos outros quatro. No item b, eles precisam visualizar quantos triângulos sobram na figura depois de se retirar dois palitos do centro. Caso tenham dificuldade na visualização, leve palitos de sorvete para a sala de aula e distribua entre eles depois de organizá-los em grupos, para que manuseiem conforme as orientações do item b. Depois, realize a atividade a seguir.

ATIVIDADE EXTRA

a) Com 15 palitos, construa a figura a seguir. Depois, remova três palitos a fim de obter três quadrados.

CYNTHIA SEKIGUCHI/ ARQUIVO DA EDITORA

b) Com 9 palitos, construa a figura a seguir. Depois, mova quatro palitos a fim de obter cinco triângulos.

7. Para chegar ao baú do tesouro, o pirata deve passar somente por quadrados, triângulos, retângulos e círculos. Trace o caminho que ele deve percorrer para chegar ao baú do tesouro.

Resposta e comentários nas orientações ao professor.

8. A figura foi construída usando palitos de sorvete.

a ) Quantos triângulos estão representados nessa figura?

Resposta: Estão representados 5 triângulos.

b ) Se você tirar dois dos três palitos do meio, quantos triângulos vão continuar representados na figura?

Resposta: Sobrarão 2 triângulos.

FORMAS GEOMÉTRICAS EM CONSTRUÇÕES OU EDIFICAÇÕES

Você já reparou que as figuras geométricas planas estão presentes em construções? Elas podem ser observadas em diferentes edificações, como prédios, casas e pontes. Um exemplo interessante são alguns tipos de pontes.

Nelas, é comum o uso de estruturas com formato triangular, que ajuda a distribuir melhor a massa, tornando a construção mais resistente.

CYNTHIA SEKIGUCHI/ ARQUIVO DA EDITORA CYNTHIA SEKIGUCHI/ ARQUIVO DA EDITORA

c) Com 12 palitos, construa a figura a seguir. Depois, remova dois palitos a fim de obter dois quadrados. Respostas a) Sugestão de resposta:

b) Sugestão de resposta:

SEKIGUCHI/ ARQUIVO DA EDITORA CYNTHIA SEKIGUCHI/ ARQUIVO DA EDITORA

c) Sugestão de resposta: Resposta 7. Pirata

Baú do Tesouro

Ponte Hercílio Luz, em Florianópolis, estado de Santa Catarina, em 2023.

9. Sueli utilizou as mãos para desmontar uma caixa e obteve as seguintes peças.

Momento 1 Momento 2

Momento 3

Momento 4

a ) As peças da caixa que Sueli desmontou lembram quais figuras geométricas planas?

Resposta: O retângulo e o quadrado.

b ) Sueli vai desmontar também a caixa representada a seguir.

INFOGRÁFICO CLICÁVEL: GEOMETRIA E O ARTESANATO DOS POVOS INDÍGENAS

As peças obtidas na desmontagem desta caixa lembram qual figura geométrica plana?

Resposta: Quadrado.

c ) Marque um X na figura a seguir que representa corretamente a resposta ao item anterior.

Resposta: Os estudantes devem marcar um X no quadrado

10. Pinte as peças que faltam de acordo com o padrão da sequência de cores.

Resposta: Os estudantes devem pintar as peças que faltam da seguinte maneira: peças A e C: verde; peça B: vermelho; peças D e G: amarelo; peça E: azul; peça F: marrom.

06/10/2025 18:16:23

• O objetivo da atividade 9 é que os estudantes visualizem a caixa desmontada e identifiquem quais figuras geométricas planas compõem suas partes. No item a, devem escrever quais figuras geométricas planas as peças da caixa desmontada lembram. No item b, é apresentada uma caixa com formato de cubo para que eles percebam que, nesse caso, todas as peças da caixa lembram um quadrado.

• Para tirar melhor proveito do trabalho realizado na atividade 9, avalie a possibilidade de levar para a sala de aula algumas embalagens pequenas e vazias de produtos, com formatos diversificados de poliedros, que possam ser desmontados, como caixas de creme dental. Oriente os estudantes a desmontarem as embalagens e a desenhar no caderno as figuras geométricas planas que as faces das embalagens lembram.

• A atividade 10 tem por objetivo que os estudantes identifiquem o padrão da imagem apresentada. Para aperfeiçoar o trabalho com essa atividade e auxiliar com possíveis dúvidas, organi ze-os em duplas e peça a cada uma que desenhe uma figura utilizando determinada sequência de cores e deixando as partes finais em branco. Em seguida, oriente-os a trocar os desenhos com o colega para pintar as partes em branco de acordo com o padrão identificado. Ao final, eles devem destrocar os desenhos a fim de verificar se foram pintados corretamente.

• A atividade 11 tem o objetivo de levar os estudantes a reconhecer figuras geométricas planas na planificação de uma pirâmide. Oriente-os a observar as partes que compõem a pirâmide montada e peça que as identifiquem em seguida na planificação.

• Na atividade 12, os estudantes precisam, inicialmente, realizar uma estimativa da quantidade de figuras geométricas planas da imagem e, em seguida, contá-las. Além disso, é necessário que verifiquem a quantidade de triângulos, círculos, retângulos e quadrados.

• Nessa atividade, os estudantes podem se confundir e contar todas as figuras de certa cor. Por exemplo, ao verem o triângulo roxo, eles podem contar todas as outras figuras roxas. Para ajudá-los, explique a eles que na imagem há figuras de um mesmo formato, mas com cores diferentes, assim como figuras de mesmas cores, mas com formatos diferentes.

11. Observe a planificação da superfície de uma pirâmide.

Quais figuras geométricas planas podem ser identificadas nessa planificação?

Resposta: Triângulos e quadrado.

12. Observe a imagem a seguir.

a ) Sem contar, estime quantas figuras geométricas planas estão representadas na imagem anterior.

Resposta pessoal. Espera-se que os estudantes estimem que há uma quantidade aproximada de 40 figuras geométricas planas.

b ) Agora, conte quantas figuras geométricas planas estão representadas na imagem anterior.

Resposta: Os estudantes devem contar e obter 40 figuras geométricas planas.

c ) Complete o quadro com a quantidade de figuras geométricas planas da imagem.

Quantidade de figuras geométricas planas

Triângulo Círculo Retângulo Quadrado

Resposta: Os estudantes devem completar o quadro da seguinte maneira: Triângulo: 8; Círculo: 10; Retângulo: 11; Quadrado: 0.

REFERÊNCIAS COMPLEMENTARES

FONSECA, Maria da Conceição F. R. et al O Ensino de geometria na escola fundamental: Três questões para a formação do professor dos ciclos iniciais. São Paulo: Autêntica, 2007. O livro, destinado a professores dos Anos Iniciais do Ensino Fundamental, busca intervir em possíveis questões e problemáticas que podem surgir acerca do ensino da geometria nessa etapa da aprendizagem.

13. Observe o padrão da sequência de figuras geométricas planas representada a seguir.

InÍCIO

13. a) Resposta: Os estudantes devem desenhar as seguintes figuras geométricas planas, nesta ordem: círculo, triângulo, retângulo, círculo e quadrado.

FIM

a ) Desenhe as figuras geométricas planas que faltam na sequência.

b ) Agora, pinte essas figuras geométricas planas de acordo com o padrão da sequência.

Resposta: Os estudantes devem pintar o quadrado na cor vermelha, o triângulo na cor azul, o círculo na cor laranja e o retângulo na verde.

14. Observe as indicações dos lados e dos vértices das figuras geométricas planas a seguir.

vértice vértice vértice lado lado lado

Agora, complete as informações com o que falta.

Resposta: O quadrado tem 4 lados e 4 vértices.

a ) O quadrado tem lados e vértices.

Resposta: O triângulo tem 3 lados e 3 vértices.

b ) O triângulo tem lados e vértices.

Resposta: O retângulo tem 4 lados e 4 vértices.

c ) O retângulo tem lados e vértices.

06/10/2025 18:13:15

• A atividade 13 propõe que os estudantes identifiquem, desenhem e pintem os elementos ausentes em uma sequência de figuras geométricas planas. Caso tenham dificuldades, peça que atentem às figuras que estão antes e depois daquelas que precisam ser desenhadas e que identifiquem essas figuras em outra parte da sequência.

• Avalie a possibilidade de fazer uma adaptação dessa atividade na prática, variando as figuras e as cores apresentadas. Para promover a inclusão, confeccione com antecedência o mesmo esquema do padrão de figuras geométricas em uma folha de papel, colocando no lugar de cada figura, um desenho em papelão da figura representada, deixando um espaçamento entre elas e deixe os espaços onde estão faltando as figuras geométricas.

• A atividade 14 pede que os estudantes determinem a quantidade de lados e de vértices do quadrado, do triângulo e do retângulo. Caso apresentem dificuldade, indique outro lado e outro vértice de cada figura, diferente dos já indicados na atividade, e peça que identifiquem os lados e vértices restantes.

• Para tirar melhor proveito, avalie se é possível organizar os estudantes em duplas durante a realização desta atividade.

BNCC

Ao propor que os estudantes obtenham o padrão de uma sequência repetitiva de figuras geométricas planas, identificando e desenhando os elementos ausentes, desenvolvem-se as habilidades EF02MA10 e EF02MA11 da BNCC.

• A atividade 15 propõe que os estudantes liguem os pontos indicados de uma malha pontilhada e obtenham um retângulo, um triângulo e um quadrado. Depois, é necessário que identifiquem quais figuras têm 4 lados e 4 vértices e, 3 lados e 3 vértices. Para tirar melhor proveito, bem como sanar possíveis dúvidas, providencie antecipadamente malhas quadriculadas com pontos coloridos em posições diferentes dos apresentados nessa atividade e distribua aos estudantes. Avalie a possibilidade de compor mais pontos de modo que haja mais quantidade de uma mesma figura.

• A atividade 16 tem como objetivo que os estudantes identifiquem qual grupo de figuras apresentado contém um triângulo, dois quadrados e dois retângulos. Caso apresentem dificuldades em identificar quem desenhou as figuras solicitadas, peça que eles contem e depois escrevam no caderno quantos quadrados, retângulos e triângulos cada pessoa desenhou. A fim de aprimorar o trabalho realizado, organize-os em duplas e peça que desenhem certa quantidade de retângulos, quadrados e triângulos. Ao final, avalie se desenharam as quantidades corretas.

15. Observe a malha pontilhada representada a seguir.

figura 1

15. a) Resposta: Os estudantes devem ligar os pontos de mesma cor, formando um retângulo, um triângulo e um quadrado.

15. b) Resposta: Os estudantes devem pintar o interior das figuras obtidas no item anterior.

a ) Termine de desenhar as figuras na malha ligando os pontos da mesma cor, assim como foi feito na figura 1.

b ) Agora, pinte o interior das figuras que você desenhou.

c ) Das figuras desenhadas na malha pontilhada, quais delas têm:

• 4 vértices e 4 lados?

• 3 vértices e 3 lados?

Resposta: Os quadrados e o retângulo.Resposta: O triângulo.

16. Observe a seguir os desenhos feitos por Pedro, Henrique, Laura e Camila.

Quem desenhou um triângulo, dois quadrados e dois retângulos?

Resposta: Laura.

AVALIANDO

Objetivo

Reconhecer objetos que lembram as figuras geométricas planas e identificar a quantidade de lados e vértices do quadrado, do retângulo e do triângulo.

Sugestão de intervenção

Leve para a sala de aula imagens de objetos que lembram figuras geométricas planas. Organize a turma em grupos com dois ou três estudantes e peça para que escrevam quais figuras geométricas planas os objetos lembram. Além disso, solicite que escrevam a quantidade de vértices e lados que elas têm.

Pedro Laura Henrique

Camila

DIVIRTA-SE E APRENDA

Jogo das figuras planas

Este jogo vai verificar seu conhecimento sobre figuras geométricas planas. Junte-se a um colega e recortem as peças da página 283 do Material complementar

Regras

REGRAS

• Embaralhem as peças sobre a carteira com as figuras voltadas para baixo e distribuam três para cada participante. As demais peças devem ficar empilhadas e voltadas para baixo sobre a carteira.

• Decidam quem começa a jogar. O primeiro jogador escolhe e apresenta uma de suas peças com a figura voltada para cima sobre a carteira.

• O segundo participante deve verificar se, entre as suas peças, há alguma que se encaixa em um dos lados da peça já colocada, associando sempre o nome à figura ou a figura ao nome. Caso tenha a peça, ele deve encaixá-la ao lado da peça correspondente. Observe um exemplo.

• Disponibilize tempo suficiente para realizar este jogo na sala de aula e verifique se os estudantes têm alguma dificuldade ao jogá-lo. Inicialmente, dê exemplos de como as peças podem ser encaixadas e verifique se eles reconhecem todas as figuras geométricas planas.

• Após finalizarem o jogo, se julgar conveniente, sugira aos estudantes que formem outras duplas e joguem novamente. Uma variação é incluir peças correspondentes às imagens e nomes das figuras geométricas espaciais, aumentando o grau de dificuldade da atividade.

• Como os estudantes poderão levar as peças do jogo para casa, sugira que joguem em casa com os colegas e familiares.

• O jogo proposto nesta seção trabalha o encaixe de figuras geométricas planas, incentivando os sentidos da visão e do tato, que são fundamentais para o desenvolvimento cognitivo, motor e social dos estudantes.

• Se o jogador não tiver uma peça que se encaixe, ele deverá pegar uma das peças empilhadas sobre a carteira. Caso ela também não se encaixe, o jogador deve passar a vez.

Vence o participante que terminar de encaixar todas as peças primeiro.

06/10/2025 18:13:15

RetânguloQuadrado Quadrado

Peça do primeiro jogador

• Para o estudo do tópico Noções de posição é importante que os estudantes tenham como pré-requisito desenvolvido experiências corporais e espaciais no ambiente, deslocando-se e observando a proximidade de objetos que estão ao seu redor.

• A atividade 1 visa desenvolver a capacidade dos estudantes de identificar a localização de pessoas e objetos no espaço, utilizando pontos de referência. Certifique-se de que eles compreenderam o que está apresentado no boxe dica. É importante que eles entendam a necessidade de utilizar um referencial, a fim de auxiliar na localização correta. Para que entendam essa necessidade, indique a posição de um objeto qualquer na sala sem o uso de referencial a dois estudantes diferentes e deixe que eles o localizem.

• Se necessário, peça aos estudantes que descrevam a localização do homem e da mulher que estão sentados no banco do ponto de ônibus. No item d, a fim de auxiliar os estudantes, faça a descrição do local que sua mesa ocupa na sala de aula. Certifique-se de que eles utilizam mais de um ponto de referência ao fazer suas indicações. Se necessário, diga-lhes que ponto de ônibus é o local destinado às paradas dos veículos que realizam o transporte coletivo de pessoas para o embarque e desembarque de passageiros.

Professor, professora: Oriente os estudantes na escrita das respostas da atividade 1. Nos itens b e c, incentive o traçado em letra cursiva nas pautas apresentadas. Se

NOÇÕES DE POSIÇÃO

necessário, escreva os textos na lousa, pausadamente, para que eles os copiem seguindo a ordem correta do traçado.

1. Em muitas situações do dia a dia, precisamos descrever a posição dos objetos ou das pessoas para que sejam localizados. Nesse caso, alguns comandos facilitam essa tarefa.

Observe como Marta descreveu sua posição ao irmão, que combinou de buscá-la depois da aula de inglês.

Estou na frente da escola, ao lado do ponto de ônibus.

a ) Que informações Marta usou para descrever a posição dela ao irmão?

Resposta: Marta informou que estava localizada na frente da escola e ao lado do ponto de ônibus.

b ) Na cena, quem está sentado imediatamente ao lado direito de Marta no ponto de ônibus?

Resposta: Um homem de camisa vermelha.

Dica: Como Marta aparece de costas para a escola e de frente para o leitor desta página, na cena, o lado direito dela não coincide com o lado direito do leitor.

c ) A senhora com o cachorro está segurando a bengala com a mão direita ou a mão esquerda?

Resposta: Está segurando a bengala com a mão esquerda.

d ) Escreva no caderno como você explicaria a um colega a posição da sua carteira na sala de aula.

Resposta pessoal. Espera-se que os

estudantes digam a posição da carteira deles utilizando um ou dois pontos de referência. Professor, professora: Oriente os estudantes na escrita do texto que responde ao item d, incentivando o traçado em letra cursiva.

BNCC

As atividades deste tópico contemplam a habilidade EF02MA12 da BNCC. As noções de posição são abordadas por meio de situações-problema baseadas em circunstâncias do dia a dia. As ideias envolvidas trabalham a capacidade de identificar e registrar, em linguagem verbal e não verbal, a localização e o deslocamento de pessoas e de objetos no espaço, considerando mais de um ponto de referência.

2. Adélia é professora e levou seus estudantes ao cinema. Observe, na ilustração a seguir, como as cadeiras do cinema estão numeradas.

a ) De acordo com a representação, quais são a fileira e o número da cadeira do estudante que está sentado:

• imediatamente à frente da professora?

Resposta: Na fileira B e cadeira número 5

Na fileira e cadeira número .

• imediatamente à direita da professora?

Resposta: Na fileira C e cadeira número 6

Na fileira e cadeira número

• imediatamente à esquerda da professora?

Resposta: Na fileira C e cadeira número 4

Na fileira e cadeira número .

b ) Contorne a cadeira do estudante que está sentado imediatamente atrás da professora.

Resposta: Os estudantes devem contornar a cadeira 5 da fileira D.

BNCC

A atividade 2 promove a relação com a Competência geral 3 da BNCC ao utilizar a sala de cinema como contexto. Converse com os estudantes a respeito do cinema, que faz parte da manifestação artística e cultural de nosso país, e explique que é importante valorizar e desfrutar dessa prática e de outras que fazem parte do cenário artístico-cultural. Avalie, com a Direção da escola e os responsáveis, a possibilidade e a conveniência de providenciar uma saída monitorada da turma para assistir a um filme que esteja em cartaz e que atenda à classificação indicativa adequada para eles.

193

06/10/2025 18:13:16

• O objetivo da atividade 2 é identificar a localização de pessoas com base na observação e na indicação apresentada, a fim de incentivar a compreensão de descrições que fazem uso de termos como à direita, à esquerda, à frente e atrás. • Caso os estudantes apresentem dificuldades na realização desta atividade, indique as fileiras e as carteiras da sala de aula como na atividade e proponha as mesmas questões a eles, só que agora considerando-os como referencial.

• A atividade 3 e o boxe complementar , apresentado nessa página, visa promover a compreensão da localização de pessoas, por meio de descrições que permitam identificar o que está em cima, embaixo, mais perto, mais longe, à direita e à esquerda, considerando um dado referencial.

• Se necessário, complemente as atividades desta página e peça aos estudantes que identifiquem objetos que estão em cima da carteira, embaixo da carteira, e colegas que estão imediatamente à direita e à esquerda.

3. Tiago e Percival são irmãos. Eles dormem no mesmo quarto, em um beliche.

a ) Pinte de vermelho a colcha que está na cama de cima.

3.a) Resposta: Os estudantes devem pintar de vermelho a colcha 1

b ) Pinte de verde a colcha que está na cama de baixo.

3. b) Resposta: Os estudantes devem pintar de verde a colcha 2

c ) Na posição em que os meninos estão na cama, Tiago ficou com a cabeça mais perto da porta, e Percival, com a cabeça mais perto da janela. Quem dorme na cama de cima do beliche?

Resposta: Tiago.

d ) Em relação a você, a janela está à direita ou à esquerda da cena? E a porta?

Resposta: A janela está à esquerda da cena. A porta está à direita da cena.

DESTROS E CANHOTOS

Você já percebeu que temos tendência a usar mais os membros de um lado do corpo para realizar tarefas?

Se os membros do lado direito são os mais usados, a pessoa é destra. Se os membros do lado esquerdo são os mais utilizados, a pessoa é canhota. Normalmente, os destros têm facilidade para escrever com a mão direita, e os canhotos, com a esquerda. Apesar dessas diferenças, a maioria dos objetos e ambientes são adaptados para os destros, o que pode tornar algumas atividades menos práticas e até desconfortáveis para pessoas canhotas. Por isso, é essencial reconhecer essas diferenças e buscar soluções mais inclusivas no cotidiano.

Então, muitas pessoas, por imposição social ou facilidade de adaptação, aprenderam a usar também a mão direita, e algumas usam uma ou outra mão dependendo da necessidade.

Não é raro encontrar canhotos que usam o mouse ou tocam guitarra como destros, possivelmente pelo hábito de usar objetos tradicionais antes de conhecer as versões modificadas e adaptadas para eles. Um exemplo é o cantor e compositor estadunidense James Marchall Hendrix, conhecido como Jimi Hendrix, que era canhoto e tocava com o "braço" da guitarra invertido.

Resposta pessoal. A resposta depende da mão utilizada pelo estudante para escrever.

a ) Qual das mãos você utiliza para escrever?

b ) Além da escrita, que outras habilidades você desempenha mais com os membros de um lado do corpo?

Resposta pessoal. A resposta depende da habilidade do estudante em relação aos membros do corpo dele.

4. Observe a cena em que Joana e Andreia estão disputando uma partida de tênis de mesa.

a ) Em relação à árbitra, na cena, qual das participantes está do lado:

• direito?

Resposta: Joana.

• esquerdo?

Resposta: Andreia.

Árbitra: mulher que comanda, dirige e toma decisões disciplinares durante uma partida esportiva.

b ) Complete as frases com as palavras esquerda, direita, destra e canhota

Resposta: Joana está segurando a raquete com a mão direita, então provavelmente ela é destra

• Joana está segurando a raquete com a mão , então provavelmente ela é .

• Andreia está segurando a raquete com a mão , então provavelmente ela é .

Resposta: Andreia está segurando a raquete com a mão esquerda, então provavelmente ela é canhota.

ATIVIDADE EXTRA

Em um local com bastante espaço, coloque os estudantes enfileirados um ao lado do outro. Eles devem levantar a mão direita ou a mão esquerda, de acordo com os comandos direita, esquerda, destra, canhota dados por você.

AVALIANDO

Objetivo

• A atividade 4 tem o objetivo de promover a compreensão do assunto abordado no boxe complementar. Desse modo, espera-se que os estudantes utilizem os termos destro e canhoto relacionando-os, respectivamente, com direito e esquerdo. Se necessário, a fim de auxiliar a compreensão deles, realize a atividade apresentada no rodapé desta página.

• A atividade 4 promove o desenvolvimento de vocabulário ao abordar o reconhecimento de uma palavra que, possivelmente, os estudantes desconheçam.

15:28:38

Descrever a localização de pessoas no espaço utilizando pelo menos dois pontos de referência.

Sugestão de intervenção

Leve os estudantes para o pátio da escola, diga-lhes para ficarem em lugares diferentes, de maneira que você consiga vê-los. Peça a cada um que descreva a localização de um dos colegas utilizando mais de um ponto de referência.

árbitra

Joana Andreia

James Marshall Hendrix (1942-1970).

• Para desenvolver o trabalho com o tópico Deslocamento é de grande relevância que os estudantes tenham como pré-requisitos ideias básicas de orientação e posição no espaço, como em frente, atrás, ao lado, entre outros. Verifique se eles são capazes de identificar alguns pontos de referência na escola. Pergunte, por exemplo: “O que fica ao lado da biblioteca?”; “O que tem atrás do banco?”; “O que tem em frente a sala dos professores?”.

• A atividade 1 visa desenvolver nos estudantes a capacidade de identificar pontos de referência que permitam se localizar em um determinado lugar. Peça a eles que citem outros pontos de referência, diferentes dos apresentados no item a, indicando o que encontram do caminho da escola até a casa deles. Proponha outros percursos que os estudantes conheçam, a fim de que digam os pontos de referência que eles identificam nesses caminhos.

DESLOCAMENTO

1. Em certas situações, precisamos descrever o deslocamento de um lugar para outro por meio de referências que ajudem uma pessoa a chegar ao destino. Essas referências podem ser uma loja, uma árvore, uma praça ou qualquer outro elemento fixo no trajeto.

a ) Imagine que você precisa explicar o caminho da sua casa até a escola. Cite dois pontos de referência que você indicaria.

Resposta pessoal. Esta atividade tem como objetivo que os estudantes relatem suas experiências pessoais, identificando pontos de referência no deslocamento da casa deles até a escola onde estudam, como monumentos, construções, pontes, rios, lagos, mercados, árvores etc.

b ) Na imagem a seguir, está representado o caminho que Marcos percorre da casa dele até o prédio onde o avô mora.

Imagem com elementos sem proporção entre si. Representação sem escala.

Marque um X nos elementos que aparecem no caminho que Marcos percorre para ir ao prédio do avô.

Farmácia.

Biblioteca.

Escola. Lago. Árvore. Praça.

Resposta: Os estudantes devem marcar um X nos seguintes elementos: biblioteca, árvore, escola e lago.

ATIVIDADE EXTRA

Entregue uma folha em branco para os estudantes e peça que façam um desenho que apresente o caminho que eles realizam de sua casa até a escola, identificando outros pontos de referência, diferentes dos citados no item a da atividade 1.

Prédio onde o avô de Marcos mora

Biblioteca

Escola

Farmácia

Árvore

Chafariz

Casa de Marcos

2. Félix descreveu o caminho que percorreu a pé para chegar a um estabelecimento comercial.

• Félix saiu de casa, atravessou a faixa de segurança e percorreu duas quadras na Rua Tulipas.

• Ele virou à esquerda, atravessou a Rua Tulipas pela faixa de segurança e caminhou uma quadra na Rua das Margaridas.

• Em seguida, ele virou à direita, atravessou a Rua das Margaridas pela faixa de segurança e caminhou três quadras na Rua dos Cravos.

• Por último, ele virou à esquerda e atravessou a Rua dos Cravos pela faixa de segurança e caminhou até o estabelecimento desejado.

a ) Siga a descrição e indique, na imagem, o caminho que Félix percorreu.

Imagem com elementos sem proporção entre si. Representação sem escala. Resposta nas orientações ao professor

RuadasRosas

RuadasPassas

RuaLírio

RuadasMargaridas

Rua Tulipas

Rua das Orquídeas

Rua dos Cravos

RuaGirassol

RuaVioleta

RuaÍris

b ) A que lugar Félix chegou ao final do trajeto?

Resposta: Ele chegou à padaria.

c ) Responda sim ou não. No caminho percorrido, Félix passou por:

• uma biblioteca?

• uma árvore?

Resposta 2. a)

Resposta: Não.

Resposta: Sim.

RuadasRosas

RuadasPassas

RuaLírio

RuadasMargaridas

Rua Tulipas

Rua dos Cravos Rua das Orquídeas

RuaGirassol

RuaVioleta

RuaÍris

• uma escola?

• um teatro?

Resposta: Sim.

Resposta: Não.

• O objetivo da atividade 2 é capacitar os estudantes a compreender, por meio da descrição, o caminho percorrido. Se necessário, a fim de auxiliar na compreensão dos deles, apresente a descrição de outros trajetos para que indiquem na imagem e respondam às perguntas propostas na questão.

ARTICULANDO CONHECIMENTOS

Avalie a possibilidade de trabalhar de forma integrada uma relação com os componentes curriculares de História e de Geografia Propondo aos estudantes que representem o bairro onde moram por meio de desenhos. Oriente-os a fazê-los de maneira que qualquer pessoa entenda a localização da casa onde residem. Uma sugestão para facilitar esse entendimento é pedir a eles que desenhem elementos que caracterizem a região, como praças, farmácias, padarias e supermercados. Avalie a possibilidade de levar alguns mapas ou um atlas geográfico para a sala de aula, a fim de mostrar aos estudantes e deixar que identifiquem a região onde moram. E, depois, peça a eles que contem a história local, por meio de pequenos textos, trazendo informações como a origem do nome do bairro, seus fundadores e marcos históricos.

HELOÍSA PINTARELLI/ARQUIVO DA EDITORA

06/10/2025 18:09:58

Imagem com elementos sem proporção entre si. Representação sem escala.

Casa de Félix

Escola

Igreja

Supermercado

Padaria

Biblioteca

Teatro

• A atividade 3 visa capacitar os estudantes a realizar a leitura da planta de uma casa, de modo que sejam capazes de desenhar um esboço da residência onde moram. Certifique-se de que eles identificam a janela e a porta na planta apresentada na atividade, a fim de que façam essas marcações em seus esboços. Se possível, peça-lhes que façam um desenho da planta da escola, promovendo a compreensão do conteúdo estudado. Se necessário, faça um passeio com eles, para que possam fazer o esboço de maneira mais realista.

ATIVIDADE EXTRA

Providencie antecipadamente uma malha quadriculada 15 × 15. Entregue uma cópia para cada um dos estudantes e peça a eles que representem alguns estabelecimentos e façam a indicação com setas de um trajeto. Em seguida, eles devem trocar a atividade com um colega e traçar o trajeto na malha quadriculada. Por fim, peça que se juntem com o colega e realize a correção.

• O objetivo da atividade 4 é promover a compreensão dos estudantes com relação ao deslocamento no plano seguindo as indicações dadas por meio de linguagem não verbal, ou seja, eles precisam compreender o significado de cada seta para fazer o deslocamento conforme o que está pedido. Lembre-os de realizar as indicações da seta utilizando o cachorro como referencial, considerando os lados direito e esquerdo em relação a ele.

3. Para construir uma casa, primeiro devemos fazer uma planta baixa. A planta baixa é uma representação horizontal dos cômodos da casa e nela são representados quartos, sala, cozinha, banheiro, entre outros. Observe um exemplo de planta baixa.

Corredor

Representação sem escala.

a ) Represente no caderno a planta da residência onde você mora, identificando os cômodos. Depois, observe seu desenho e responda às demais questões.

b ) Em sua residência, o quarto em que você dorme fica mais próximo de qual cômodo?

Resposta pessoal. A resposta depende do desenho da planta da casa dos estudantes.

c ) Nessa residência, qual cômodo fica mais próximo da cozinha?

Resposta pessoal. A resposta depende do desenho da planta da casa dos estudantes.

d ) Nessa residência, ao passar pela porta de entrada principal e virar à direita, a qual cômodo você chega?

Resposta pessoal. A resposta depende do desenho da planta da casa dos estudantes.

4. Siga as setas e pinte na malha quadriculada o caminho que leva o cachorro Rex ao prato de ração.

Dica: Observe no quadro o significado de cada seta.

Resposta nas orientações ao professor

Significado de cada seta

SignificadoSeta

Avance um quadrinho.

Vire à direita.

Vire à esquerda.

3. a) Resposta pessoal. Esta atividade tem como objetivo que os estudantes representem a planta da casa deles, utilizando o modelo apresentado na atividade.

A atividade 3 permite que os estudantes esbocem plantas de ambientes familiares, indicando entradas, saídas e cada um dos cômodos, promovendo o trabalho com a habilidade EF02MA13 da BNCC.

Respostas 4.

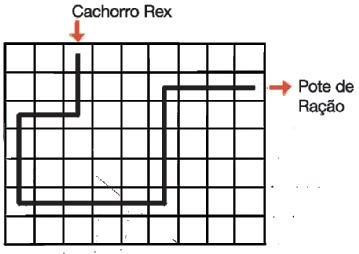
BNCC

Saladeestar

Cozinha

5. A professora Márcia planejou um passeio pela cidade com a turma do 2º ano. Para isso, ela fez um esquema e traçou o roteiro representado a seguir.

Jardim zoológico

Praça

Lanchonete

Prefeitura

Terminal de ônibus

Orientação no esquema

SetaSignificado

Avance um quadrinho.

Vire à direita.

Vire à esquerda.

a ) Desenhe setas para indicar o roteiro traçado em azul nesse esquema, sabendo que os estudantes vão sair do terminal de ônibus e visitar primeiro a prefeitura municipal.

Resposta nas orientações ao professor

b ) Se Márcia quisesse planejar um roteiro mais curto passando apenas por quatro pontos de referência, que local deveria ser eliminado do roteiro anterior?

Resposta: O museu.

c ) Desenhe setas para indicar o caminho sugerido no item b.

Resposta nas orientações ao professor

Respostas

REFERÊNCIAS COMPLEMENTARES

TOUR virtual em 360° graus do Zoo, Secretaria de Estado do Meio Ambiente do Distrito Federal. Disponível em: https:// www.sema.df.gov.br/w/tour-virtual-em -360-graus-do-zoo. Acesso em: 25 jul. 2025.

Esse site permite os visitantes conhecer os espaços destinados a cada animal. O tour virtual é uma iniciativa da Secretaria do Meio Ambiente do Distrito

• A atividade 5 visa capacitar os estudantes a indicar, por meio de linguagem não verbal, um caminho traçado no plano que permita identificar o trajeto percorrido. Para responder aos itens a e c, oriente-os a utilizar as setas conforme a indicação do esquema.

AVALIANDO

Objetivo

Descrever o deslocamento de pessoas no espaço.

Sugestão de intervenção

Usando a imagem apresentada na atividade 2 da página 197, solicite aos estudantes que descrevam o menor trajeto que Felipe pode realizar para ir de sua casa até o supermercado. Certifique-se de que eles utilizam todas as referências necessárias para identificar o trajeto.

06/10/2025 18:09:59

Federal e da Fundação Jardim Zoológico de Brasília, em parceria com o Projeto CITinova, que busca promover cidades sustentáveis no Brasil por meio de investimentos em tecnologias inovadoras e planejamento integrado.

ERA virtual. Disponível em: https:// www.eravirtual.org/. Acesso em: 25 jul. 2025.

Nesse site, é possível visitar museus e exposições temporárias sobre diversos assuntos.

• O assunto abordado na atividade 6 permite uma relação com o componente curricular de Geografia ao abordar a Nova Cartografia Social. Diga aos estudantes que a Cartografia representa o espaço geográfico através de mapas, cartas e outras representações gráficas, geralmente produzidas por especialistas da área. Já a Nova Cartografia Social envolve as comunidades locais na representação de seus territórios, na produção de mapas, destacando seus conhecimentos, vivências e relações com o espaço. Um dos objetivos da Nova Cartografia Social é servir para análises de saúde no território, pois os mapas podem revelar padrões de doenças, acesso a serviços de saúde, condições de saneamento básico entre outros fatores ambientais que afetam a saúde, com intuito de colaborar para formulação de políticas públicas mais adequadas às necessidades de saúde das populações ribeirinhas.

Resposta

6. c) Resposta pessoal. Sugestão de resposta: Os estudantes podem traçar um caminho seguindo em frente pela rua da casa de José, virando à esquerda após passar a padaria, seguir em frente, virar à direita e, por fim, seguir em frente até a igreja.

• Complemente o trabalho com a atividade 6 propondo aos estudantes outras questões, como:

a) O rio fica mais próximo da padaria ou da farmácia?

b) De acordo com a representação, marque um X na opção correta.

( ) A padaria está entre o posto de saúde e a farmácia.

( ) A praça está entre o armazém e o posto de saúde.

6. Muitos povos indígenas brasileiros ainda buscam o direito às terras que ocupam, além do reconhecimento e da preservação de suas culturas, tradições, territórios e modos de vida. Observe a representação que José fez de parte da aldeia onde ele mora.

Fonte: Desenho feito por José.

JOSÉ/ARQUIVO PESSOAL

a ) A casa de José está mais próxima da escola ou da reserva legal?

Resposta: A casa de José está mais próxima da escola.

b ) A escola está mais longe da farmácia ou do armazém?

Resposta: A escola está mais longe da farmácia.

c ) Trace na imagem um caminho da casa de José até a igreja.

6. c) Resposta nas orientações ao professor

DESAFIO A MAIS

No parque, o escorregador fica mais próximo do portão do que o balanço.

A gangorra fica mais longe do portão do que o balanço, porém mais perto do portão do que o gira-gira.

a ) Qual brinquedo é o mais perto do portão?

Resposta: escorregador.

b ) E qual é o brinquedo mais longe do portão?

Resposta: gira-gira.

Respostas 1. O rio fica mais próximo da padaria.

2. Os estudantes devem marcar um X na opção: A praça está entre o armazém e o posto de saúde.

• O Desafio a mais exige que os estudantes interpretem a posição relativa dos brinquedos em relação ao portão, organizando-os do mais próximo ao mais distante. Espera-se que os estudantes percebam que, ao comparar as informações dadas, devem estabelecer uma ordem lógica: primeiro o escorregador, depois o balanço, em seguida a gangorra e, por último, o gira-gira. Para

chegar à resposta, podem usar como estratégia o desenho dos brinquedos em sequência ou a representação da posição de cada brinquedo com ordinais (1º, 2º, 3º e 4º). Caso encontrem uma lógica diferente, incentive-os a compartilhar com a turma.

06/10/2025 18:09:59

Reconhecimento de terras dos povos indígenas

Alguns povos indígenas que habitam o estado de Pernambuco enfrentam grandes desafios para conservar e proteger as terras que ocupam atualmente e garantir o acesso a políticas públicas voltadas para educação escolar, saúde, produção e meio ambiente.

A conservação ambiental e territorial é importante porque beneficia tanto os moradores que retiram recursos dessas terras indígenas para a subsistência quanto as pessoas que adquirem os produtos que esses povos comercializam.

Uma aldeia de Entre Serras, no estado de Pernambuco, habitada pelos povos indígenas da etnia Pankararu, está representada na imagem. Nela, é possível verificar o registro de caminhos de passagem que ligam as moradias e tornam a comunidade integrada.

FUNDAÇÃO NACIONAL DO ÍNDIO. Etnomapeamento da terra indígena Entre Serras de Pankararu Brasília, DF: Funai, 2016. p. 25. Disponível em: https://www.gov.br/funai/pt-br/arquivos/conteudo /cggam/pdf/2017/etnomapeamento-ti-entre-serras-de-pankararu.pdf. Acesso em: 7 jun. 2025.

Subsistência: bens, produtos e outras necessidades considerados meio de sustento; itens que são o mínimo necessário para sobreviver.

Essa representação faz parte de um trabalho de regularização do território dos Pankararu, feito pelos moradores da aldeia para garantir seus direitos territoriais e outros desafios relacionados a eles.

ATIVIDADE EXTRA

Solicite aos estudantes que em duplas reproduzam o mapa da atividade 6, usando um papel transparente em cima do mapa, fazendo contornos de alguns locais indicados do mapa e criem percursos para ir de um ponto a outro, usando comandos tais como: virar à esquerda, à direita, seguir em frente, entre outros. Outra possibilidade é reproduzir uma malha quadriculada em cima do mapa, usando uma régua e localizar alguns lugares usando pontos de referência e comandos envolvendo: em frente, ao lado, acima, abaixo.

06/10/2025 18:10:00

• A articulação com o componente curricular de Geografia no boxe complementar, além de contribuir para a compreensão da necessidade de formular ou adequar políticas públicas voltadas a essas comunidades, possibilita o uso de conhecimentos geométricos para entender a localização e os deslocamentos dentro dos espaços territoriais. Diga aos estudantes que a representação do território dos Pankararu, trata-se de um etnomapa. Os etnomapeamentos e etnozoneamentos são ferramentas de gestão dos territórios, previstas na Política Nacional de Gestão Territorial e Ambiental nas Terras Indígenas, a PNGATI (Decreto nº 7.747 de 05/06/2012). O etnomapeamento é um processo de mapeamento realizado com base nos conhecimentos e saberes dos povos indígenas. Os povos indígenas da etnia Pankararu, fizeram seu etnomapeamento motivados pelo desejo de seus direitos, conservação e proteção de seu território e autonomia cultural e política para melhor desenvolver a gestão ambiental e territorial, entre outros desafios. Para eles, a garantia do direito aos recursos de seu território e o acesso a políticas públicas voltadas para a educação escolar, saúde, produção e meio ambiente são fundamentais. Além disso, a gestão ambiental e territorial das terras indígenas tem impactos positivos não apenas dentro de seus limites, mas também fora dela.

Aldeia Barrocão, em 2014

MARIA

OBJETIVOS

• Reconhecer a importância de uma criança andar acompanhada por um adulto.

• Identificar os perigos nas ruas e em lugares onde há pessoas desconhecidas.

• Refletir sobre a importância de respeitar e obedecer aos pais ou a pessoas responsáveis.

• Identificar a localização de elementos em relação a uma ou mais referências.

• Interpretar as expressões direita e esquerda.

• Discriminar a posição de pessoas e objetos.

1. CONHECENDO O PROBLEMA

• Peça aos estudantes que leiam o texto e analisem a cena apresentada.

• Converse sobre o assunto proposto e pergunte se os estudantes fazem algum trajeto sozinho, quanto tempo costumam demorar e se têm medo de algo durante o percurso. Deixe que falem relatem suas experiências. Depois, solicite que respondam às questões.

2. ORGANIZANDO AS IDEIAS

Orientações

Complementares

a) O objetivo desta questão é que os estudantes reflitam sobre os perigos que estão sujeitos ao andarem sozinhos ou desatentos. Diga-lhes que devemos evitar andar sozinhos, destacando a importância de andar acompanhado por um adulto ao sair de casa. Informe a eles algumas medidas importantes para a segurança de pedestres no trânsito, como olhar para os dois lados antes de atravessar na faixa de pedestre, evitar conversar com pessoas estranhas e nunca entrar em veículos desconhecidos.

b) Caso os estudantes tenham dificuldade em responder a esta questão, oriente-os a observar a cena

COLETIVAMENTE

Sozinho ou acompanhado?

Conhecendo o problema 1

Ao percorrer um trajeto, devemos prestar atenção nos detalhes à nossa volta. É importante prestar atenção se viramos à direita ou à esquerda para andar com segurança e saber como chegar aos lugares rotineiros, como a própria casa ou a escola.

Para que as crianças tenham segurança, é importante que sempre andem acompanhadas por um adulto. Além disso, é importante respeitar os sinais de trânsito, como atravessar vias na faixa de pedestres e caminhar na calçada o mais distante possível da rua.

de maneira que percebam que elas devem seguir em frente até a esquina. Depois disso, questione-os se devem virar para a esquerda ou para a direita. Verifique se todos concluem que elas devem virar à esquerda e, por fim, seguir em frente, atravessando a rua pela faixa de pedestre até chegar à entrada da escola.

c) Nesta questão, espera-se que os estudantes percebam que, assim que abrir o sinal, o motorista deve virar à esquerda para chegar até a farmácia. Se eles tiverem dificuldade em responder, retome os conceitos estudados na unidade, para validar a compreensão deles.

3. BUSCANDO SOLUÇÕES

Orientações Complementares a) Auxilie os estudantes durante a conversa e informe outras medidas de segurança importantes para pedestres, como: nunca atravessar a rua por trás de um ônibus, carro, árvores ou postes, para que o motorista possa vê-los; andar sempre pela calçada e, caso não haja, andar sempre em sentido contrário aos veículos; não brincar em ruas, estacionamentos ou perto de entradas e saídas de garagens.

Organizando as ideias

2. a) e b) Respostas pessoais. Comentários nas orientações ao professor

a ) Em sua opinião, quais são os perigos a que você está sujeito ao andar sozinho ou desatento?

b ) Com base na cena, descreva o trajeto da menina e a mãe dela para concluir o caminho até a escola.

c ) O motorista que está dirigindo o carro vermelho pretende ir até a farmácia. Para isso, ao abrir o sinal, ele deve virar à direita ou à esquerda?

Resposta pessoal. Sugestão de resposta: Os estudantes devem responder que, assim que abrir o sinal, o motorista deve virar à esquerda para chegar até a farmácia.

Buscando soluções

3. a) e b) Respostas

pessoais. Comentários nas orientações ao professor

INFOGRÁFICO CLICÁVEL: PLACAS E SINAIS DAS CIDADES

a ) Com os colegas, citem outras atitudes importantes para a segurança das pessoas no trânsito.

b ) Com a ajuda dos colegas e do professor, confeccionem um cartaz com dicas para ser um bom pedestre.

Dica: Coloque em prática no dia a dia o que aprendeu sobre a importância de respeitar as leis de trânsito.

Sugestão de Desafio

Sou uma figura geométrica plana que não tem vértices e nem lado. Que figura sou?

Resposta

Sou a figura círculo.

CONCLUSÃO

Acompanhar o desenvolvimento dos estudantes é fundamental para um ensino bem-sucedido. Ao longo da unidade, foram propostas diversas maneiras de avaliar a aprendizagem da turma. A fim de

realizar um monitoramento mais abrangente e organizado, registre nos relatórios individuais ou nas fichas de avaliação o desempenho de cada um, levando em consideração suas particularidades. Um modelo desse tipo de ficha pode ser encontrado no tópico Avaliação deste Manual do Professor. Assim, será possível visualizar em nível individual as trajetórias de aprendizagem, incluindo os avanços e os pontos de dificuldades a serem sanados.

Esse método de verificar a progressão dos estudos e identificar o que a turma de fato conseguiu aprender e o que ficou

b) Uma sugestão para realização da atividade é organizar os estudantes em grupos com quatro integrantes e deixe que eles pensem em algumas ideias, pois essa ação é importante para explorar a capacidade de organização do raciocínio deles. Depois, faça uma lista na lousa com as ideias propostas pelos grupos, a fim de registrarem esse raciocínio pensado e discuta com toda a turma, para que escolham as melhores que serão utilizadas para confeccionar os cartazes. Nesse momento, acolha com atenção e respeito a contribuição de todos, fazendo-os sentir que são essenciais para o desenvolvimento da proposta. Se possível, exponha os cartazes no pátio da escola para compartilhar as informações com toda a comunidade escolar. Incentive-os a colocar em prática o que aprenderam e a compartilharem as ideias com os familiares e amigos, motivando-os a fazer o mesmo.

BNCC

O trabalho com esta seção favorece o desenvolvimento da Competência geral 7 da BNCC, bem como o tema contemporâneo transversal Educação para o trânsito , uma vez que orienta os estudantes a ter comportamentos adequados no trânsito e a transitar pelas vias de modo mais atento e seguro.

06/10/2025 18:10:03

com lacunas de absorção é de grande importância para que seja possível repensar estratégias em sala de aula, tornando as ações pedagógicas cada vez mais eficazes.

A conclusão da unidade é o momento de avaliar se os objetivos por ela propostos foram alcançados. Para esse diagnóstico, observe no final deste Manual do Professor algumas possibilidades de avaliação formativa que permitem fazer o monitoramento da aprendizagem dos estudantes e intervir caso eles não tenham atingido os resultados esperados.

1. Objetivo

Identificar o centímetro como unidade de medida de comprimento padronizada e utilizar a régua para realizar medições.

Sugestão de intervenção

Antes de iniciar o trabalho com essa atividade, solicite aos estudantes que listem os instrumentos de medida que conhecem e indiquem quais medem comprimentos, avaliando qual é o mais adequado para realizar a medição descrita no item a Após a realização do item b, se julgar necessário, solicite a eles que meçam o comprimento de outros objetos da sala de aula.

2. Objetivo

Identificar o uso da multiplicação em situações do dia a dia e efetuá-las.

Sugestão de intervenção

A fim de evitar possíveis dificuldades, proponha atividades envolvendo multiplicações por 4 e por 5. Para ampliar a compreensão da propriedade comutativa, providencie e leve para a sala de aula tampinhas e pratos de plástico. Inicie a dinâmica colocando três pratos sobre a mesa e quatro tampinhas dentro de cada prato. Escolha um estudante e pergunte-lhe quantas são as tampinhas no total. Permita-lhe que faça a contagem e responda à questão. Em seguida, coloque quatro pratos e três tampinhas dentro de cada prato. Pergunte a outro estudante quantas são as tampinhas. Verifique se eles percebem que a quantidade de tampinhas é a mesma. Repita o procedimento com outras quantidades.

VAMOS AVALIAR O APRENDIZADO

1. Um pedaço de fita está representado a seguir.

a ) Qual instrumento de medida você utilizaria para medir o comprimento dessa fita?

Resposta: Espera-se que os estudantes respondam que usariam uma régua.

b ) Utilize uma régua e determine a medida do comprimento dessa fita. cm

Resposta: 14 cm

2. As mesas de um salão de festas estão dispostas da seguinte maneira.

a ) As mesas estão separadas em:

Resposta: 4 linhas.

• linhas.

Resposta: 5 colunas.

• colunas.

b ) Escreva uma multiplicação para representar a quantidade total de mesas que há no salão.

Respostas: 5 × 4 = 20 ou 4 × 5 = 20

Nesse salão de festas há mesas ao todo.

Resposta: Nesse salão de festas há 20 mesas ao todo.

3. Com base no formato do contorno de algumas

placas de sinalização de trânsito, escreva os nomes das figuras geométricas planas que elas lembram.

Imagens sem proporção entre si.

Resposta: CírculoResposta: RetânguloResposta: Triângulo

3.

Objetivo

Relacionar figuras geométricas planas a objetos do dia a dia.

Sugestão de intervenção

Caso os estudantes apresentem dificuldade em relacionar os formatos dos objetos a alguma figura geométrica plana, desenhe na lousa a

representação de um retângulo e questione-os se é possível que ele seja a resposta para algum item da atividade. Siga desenhando na lousa outras representações. Depois, peça a algum estudante que vá até a lousa e escreva o nome da figura geométrica desenhada para auxiliar a turma a relacionar os nomes às figuras.

4. Na primeira fase de um jogo, Lucas precisa levar o carro até a chegada. Para isso, ele deve obedecer à seguinte sequência de setas.

Pinte o caminho que Lucas deve percorrer com o carro.

Avance um quadrinho.

Vire à direita.

Vire à esquerda.

Resposta e comentários nas orientações ao professor

5. A imagem a seguir mostra parte do bairro onde Laís mora.

AlagoasRua

Imagem com elementos sem proporção entre si. Representação sem escala.

a ) Trace, na imagem, o caminho mais curto da casa de Laís até a escola.

Resposta e comentários nas orientações ao professor

b ) Escreva os nomes das ruas pelas quais Laís passa para ir à escola de acordo com o caminho que você traçou no item anterior.

Resposta: Rua Paraíba, rua Alagoas e rua Pernambuco.

Respostas 4.

4. Objetivo

Representar caminhos seguindo orientações de um trajeto, além de compreender o significado de direita e esquerda.

Sugestão de intervenção

Caso os estudantes tenham dificuldade em reconhecer os significados das setas apresentadas para indicar o caminho a ser percorrido, oriente-os a se imaginarem na mesma posição em que se encontra o carro da ilustração dessa atividade. É esperado, nesse momento, que eles reconheçam que os comandos “vire à direita” e “vire à esquerda” não representam quadrinhos a serem pintados do caminho, mas a direção para a qual o carro deverá virar para, depois, continuar seguindo a quantidade de setas amarelas indicadas.

5. Objetivo

Estabelecer pontos de referência para descrever trajetos e realizar deslocamentos no plano e no espaço. Sugestão de intervenção

Verifique se os estudantes identificam o caminho mais curto da casa de Laís até a escola. Oriente-os, caso julgue necessário, quanto ao caminho a ser traçado. Espera-se que eles percebam que a primeira rua que Laís vai percorrer é a rua Paraíba, pois é onde ela mora. Depois, verifique se os estudantes identificam que, para percorrer o caminho mais curto, Laís deve passar pela rua Alagoas e, em seguida, pela rua Pernambuco.

06/10/2025 17:53:20

Imagem com elementos sem proporção entre si. Representação sem escala.

RuaPernambuco Farmácia

Escola

Casa

Carro

Banco Supermercado

RuaParaíba

Bahia

RuaPernambuco

Farmácia

Escola

Casa de Laís

OBJETIVOS DA UNIDADE

• Reconhecer a divisão como uma ação de repartir ou distribuir uma quantidade de elementos em partes iguais.

• Reconhecer o símbolo usado para representar a divisão.

• Compreender o significado de metade e de terça parte.

• Efetuar divisões por 2, 3, 4 e 5 com quociente menor do que 10.

INTRODUÇÃO E JUSTIFICATIVA

Nesta unidade, são trabalhadas as ideias de repartir, agrupar e distribuir da divisão por meio de atividades variadas e relacionadas às vivências cotidianas dos estudantes. Esse estudo é fundamental para a compreensão de situações que envolvem partilha de quantidades em partes iguais. Desse modo, enquanto aprendem, eles desenvolvem habilidades essenciais para resolver situações cotidianas. Além disso, a compreensão da divisão contribui para o avanço de outros conceitos matemáticos que serão estudados futuramente.

Primeiramente, são abordadas as ideias da divisão usando materiais de contagem e desenhos, além da noção de “quanto cabe” (por exemplo, quantas vezes o 2 “cabe” no 10) em situações significativas. No início do trabalho com a divisão por 2, é apresentado o símbolo da divisão e feita a associação com as expressões “metade” e “meia dúzia”. Já na divisão por 3, é feita a associação com a expressão “terça parte”. Ao longo da unidade, os estudantes têm a oportunidade de usar a régua como instrumento para auxiliá­los a efetuar a divisão, em um trabalho que busca sistematizar seus conhecimentos e desenvolver diferentes estratégias de cálculos para a obtenção dos resultados.

UNIDADE DIVISÃO 9

Algumas propostas de atividade envolvem elaboração e resolução de situações­problemas e desafios. Essas práticas têm por objetivo contribuir para a construção dos conceitos trabalhados, levando os estudantes a se comunicarem por meio de diferentes linguagens e desenvolver habilidades e competências da BNCC.

Habilidade da BNCC trabalhada na unidade: EF02MA08

SUGESTÃO DE ESTRATÉGIA INICIAL

Convide seis estudantes para irem até a frente da sala de aula, próximo da lousa. Peça­lhes que

se organizem em dois grupos com a mesma quantidade de pessoas, ou seja, dois grupos com três estudantes cada. Depois, solicite que se organizem em três grupos com a mesma quantidade de integrantes, ou seja, três grupos com dois estudantes cada. Para cada ação, motive­os a falar em voz alta a quantidade de grupos e a quantidade de pessoas por grupo, anotando as respostas na lousa. Proceda da mesma maneira com 12 estudantes, pedindo que se organizem em dois, três e quatro grupos com a mesma quantidade de integrantes em cada um. Realize a atividade quantas vezes for necessário, de acordo com o interesse da turma.

Menina executando notas musicais com baquetas no xilofone.

O xilofone é um instrumento musical com teclas feitas de madeira ou metal. Utilizando baquetas, é possível reproduzir notas musicais que se repetem em sequência, do som mais grave para o mais agudo. Ao tocar um xilofone, a coordenação motora e a concentração são trabalhadas de maneira divertida e agradável.

1. 2. 3.

1. Resposta: Dois grupos.

Considerando o xilofone que a menina está tocando, quantos grupos com sete teclas cada é possível formar?

Você conhece as notas musicais ou já ouviu falar sobre esse assunto? Se sim, apresente-as para os colegas e o professor.

Resposta nas orientações ao professor

Além do xilofone, cite outros instrumentos musicais que necessitam de baquetas para serem tocados.

Sugestões de resposta: Bateria, tamborim, taiko e bumbo.

grupos de duas teclas podem ser formados com as teclas do xilofone. Se necessário, incentive­os a representar as teclas em um papel e contornar os grupos formados.

• Ao trabalhar a questão 3 com os estudantes, comente que instrumentos musicais, como o chocalho, o xilofone, a bateria e o pandeiro, são chamados instrumentos de percussão, pois o som deles é obtido por impacto, como raspagem ou agitação, com ou sem o auxílio de baquetas. Incentive­os a comentar se já viram apresentações com instrumentos musicais de percussão, se algum deles toca ou está aprendendo a tocar algum desses instrumentos.

Respostas

207

06/10/2025 17:51:44

2. Resposta pessoal. Espera­se que os estudantes relatem suas experiências pessoais, com base em seus conhecimentos prévios. Caso conheçam as notas musicais, é esperado que citem: dó, ré, mi, fá, sol, lá e si.

• Leia o texto para os estudantes ou solicite a um deles que leia em voz alta para toda a turma. Pergunte se eles já conheciam o xilofone e explique que esse instrumento surgiu há muitos anos. Sua origem, possivelmente, vem do balafon, instrumento originado na África Ocidental. Atualmente, o xilofone está presente em grandes orquestras, além de ser muito apreciado e usado na iniciação dos estudos de música para crianças.

• Ao trabalhar as questões propostas, peça aos estudantes que analisem a fotografia e pergunte a eles quantas teclas (placas) esse instrumento tem.

• Aproveite as questões 1 e 2 para verificar se os estudantes perceberam que, no caso do xilofone apresentado nas páginas de abertura, as teclas (placas) se dividem em duas sequências. A primeira sequência de teclas (placas) tem as mesmas cores da segunda, seguindo um padrão de cores (laranja, amarela, verde, azul­claro, azul­escuro, roxa e vermelha). A sequência em que se ordenam as teclas (placas) de um xilofone é a mesma das teclas do piano, das mais graves às mais agudas. Então, leve­os a perceber que obtemos o som de 7 notas musicais com essas teclas (placas), ou seja, Dó, Ré, Mi, Fá, Sol, Lá e Si. Depois de responderem às questões 1 e 2, pergunte a eles quantos

• Para que os estudantes compreendam as ideias da divisão, é importante que eles tenham desenvolvido alguns pré ­ requisitos, como a contagem e a noção de igualdade entre partes. Também é necessário que tenham sido trabalhadas as ideias da multiplicação, visto que a divisão é a operação inversa da multiplicação. Além disso, devem compreender situações de agrupamento e de repartição em partes iguais, que podem ser exploradas com materiais manipuláveis para facilitar a compreensão desses conceitos.

• O trabalho com este tópico é iniciado por meio da abordagem de uma situação do cotidiano dos estudantes, apresentando atividades que envolvem as ideias presentes na divisão, a fim de que sejam levados a desenvolver esse conceito.

• Para trabalhar a atividade 1, leia o enunciado com os estudantes. Deixe que resolvam essa situação usando as próprias estratégias, com o apoio dos materiais manipuláveis. Essa atividade explora a ideia de separar objetos em grupos com a mesma quantidade em cada um deles. Verifique os procedimentos que os estudantes estão executando e oriente­os, caso tenham dificuldade. Por fim, incentive­os a expor para os colegas essas estratégias, deixando que eles se expressem livremente. Acolha as diferentes ideias com atenção e respeito, permitindo a participação de todos.

• Por se tratar de uma atividade que utiliza material de contagem, os sentidos da visão e do tato são mais utilizados, o que é fundamental para o desenvolvimento cognitivo, motor, emocional e social dos estudantes.

IDEIAS DA DIVISÃO

1. Flávia quer guardar seus livros. Para isso, vai dividi-los igualmente nas caixas que aparecem na imagem.

BNCC

a ) De acordo com a cena, quantos livros Flávia tem?

Resposta: 12 livros.

b ) Quantas caixas ela vai utilizar para guardar todos eles?

Resposta: 3 caixas.

c ) Usando os cubinhos recortados das páginas 279 e 281 do Material complementar como recurso de contagem para representar os livros, determine quantos itens Flávia vai guardar em cada caixa. Depois, marque um X na resposta correta.

Resposta: 4 livros.

3 livros. 4 livros. 5 livros.

livros divididos igualmente em caixas

é igual a livros em cada caixa.

dividido por é igual a .

Resposta: 12 livros divididos igualmente em 3 caixas é igual a 4 livros em cada caixa. 12 dividido por 3 é igual a 4

As atividades desta unidade contemplam a habilidade EF02MA08, citada na BNCC, ao propor a elaboração e a resolução de problemas de divisão envolvendo a metade com suporte de imagens ou material manipulável por meio de estratégias diversas.

2. Faça o que se pede em cada item.

a ) Desenhe 12 estrelas distribuídas igualmente nos dois quadros a seguir.

Resposta: Os estudantes devem desenhar 6 estrelas em cada quadro.

Em cada quadro, será desenhada a mesma quantidade de estrelas. Então, cada um deles terá a metade do total.

b ) Quantas estrelas você desenhou em cada quadro?

Resposta: 6 estrelas.

c ) Complete as frases com o que falta.

Se distribuirmos igualmente 12 estrelas em dois grupos,

Resposta: Se distribuirmos igualmente 12 estrelas em dois grupos, obteremos

obteremos estrelas em cada um.

6 estrelas em cada um. Portanto, foram desenhadas 6 estrelas em cada quadro. 6 estrelas correspondem à metade das 12 estrelas.

Portanto, foram desenhadas estrelas em cada quadro. estrelas correspondem à metade das 12 estrelas.

3. A fita a seguir foi dividida em 15 quadrinhos iguais. Pinte esses quadrinhos formando grupos de 5 e complete a frase.

Resposta: Os estudantes devem formar 3 grupos com 5 quadrinhos cada e pintá-los utilizando cores diferentes.

Foi possível formar grupos com 5 quadrinhos cada.

Resposta: Foi possível formar 3 grupos com 5 quadrinhos cada.

Dica: Pinte cada grupo utilizando uma cor diferente.

• Antes de realizar a atividade 2, providencie e leve para a sala de aula o material dourado, a fim de explorar na prática a ideia de metade com os estudantes. Para isso, coloque 6 cubinhos sobre a mesa, escolha um estudante e solicite que ele os separe em dois grupos com quantidades iguais de cubinhos. Trabalhe a ideia de metade fazendo perguntas como: “Quantos cubinhos tínhamos ao todo?”; “Em quantos grupos eles foram divididos?”; “Quantos cubinhos ficaram em cada grupo?”; “Se dividirmos 10 cubinhos em dois grupos de quantidades iguais, quantos cubinhos cada grupo terá?”. Para um melhor aproveitamento dessa atividade, solicite aos estudantes que dividam outras quantidades de cubinhos em dois grupos com a mesma quantidade, obtendo a metade correspondente. Desse modo, os estudantes se familiarizam com essas divisões e, de maneira progressiva, passam a efetuar mentalmente os cálculos envolvidos em situações que abordam o conceito de “metade”.

• Depois da realização da atividade 2, verifique se os estudantes compreenderam que, para calcular a metade de uma quantidade, basta dividi ­ la por dois, assim, cada quadro terá 6 estrelas.

• Peça aos estudantes que separem três lápis de cores diferentes e, depois, leia o enunciado da atividade 3 com eles. Solicite­lhes que contem 5 quadrinhos e os pintem com uma cor escolhida; em seguida, contem mais 5 quadrinhos, pintando­os com a segunda cor escolhida; e, por fim, repitam esse procedimento usando a terceira cor. Ao final, faça as seguintes perguntas a

06/10/2025 17:51:45

eles: “A fita apresentada foi dividida em quantos quadrinhos?; “Quantos grupos com a mesma quantidade de quadrinhos foi possível formar?”; “Cada grupo ficou com quantos quadrinhos?”.

• Formalize a ideia de divisão escrevendo na lousa, com o auxílio dos estudantes: 15 dividido por 5 é igual a 3.

• Na atividade 4, explique aos estudantes que há várias maneiras de formar grupos com as laranjas, mas que todos os grupos devem ter 4 laranjas. A fim de tirar melhor proveito dessa atividade, desenhe na lousa 12 bolinhas e solicite a um estudante que vá até a lousa e contorne as bolinhas formando grupos com 3 bolinhas cada. Depois, pergunte à turma quantas vezes o 3 “cabe” dentro do 12, levando­os a compreender que a quantidade de grupos formados é a resposta a essa pergunta, ou seja, o 3 “cabe” 4 vezes dentro do 12.

• Após os estudantes contornarem os 4 grupos com 4 laranjas cada, verifique se perceberam que, no item b, cada contorno representa um saquinho nessa situação.

• Aproveite o contexto dessa atividade para comentar com os estudantes sobre a importância da ingestão de frutas para a saúde, dizendo­lhes que a laranja, por exemplo, é rica em vitamina C, além de ter diversos nutrientes que contribuem para o fortalecimento do nosso organismo, evitando que fiquemos doentes.

AVALIANDO

Objetivo

Reconhecer a divisão como uma ação de repartir ou distribuir uma quantidade de elementos em partes iguais.

Sugestão de intervenção

Para acompanhar o desenvolvimento dos estudantes, a fim de detectar possíveis dúvidas, realize a atividade proposta a seguir. Organize a turma em duplas e entregue a cada uma 10 botões e 3 copinhos descartáveis. Peça aos estudantes que:

• dividam 8 botões igualmente em 2 copinhos;

4. A professora apresentou aos estudantes a seguinte situação.

Juliano tem uma laranjeira em casa. Ele colheu 16 laranjas e vai agrupá-las em saquinhos com 4 frutas. Quantas embalagens Juliano vai utilizar?

Para resolver esta atividade, dividimos 16 por 4.

Para isso, precisamos determinar quantas vezes o 4 “cabe” no 16.

a ) Contorne as frutas a seguir formando grupos com 4 laranjas cada.

Resposta: Os estudantes devem contornar as frutas formando 4 grupos com 4 laranjas.

b ) Ao todo, há quantas laranjas? laranjas.

Resposta: 16 laranjas.

c ) A quantidade de grupos formados corresponde ao total de saquinhos que serão utilizados por Juliano.

Resposta: Portanto, Juliano vai usar 4 saquinhos.

Portanto, Juliano vai usar saquinhos.

d ) Juliano vai usar metade das laranjas que colheu para fazer suco para sua família.

Pinte a metade das laranjas.

Resposta: Os estudantes devem pintar 8 laranjas.

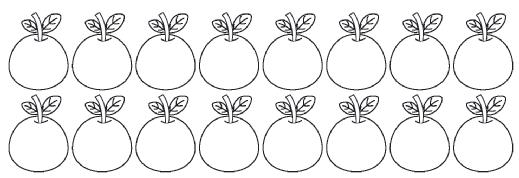
Resposta: Portanto, Juliano vai usar 8 laranjas para fazer suco.

Portanto, Juliano vai usar laranjas para fazer suco.

• dividam 10 botões igualmente em 2 copinhos;

• dividam 6 botões igualmente em 2 copinhos;

• dividam 6 botões igualmente em 3 copinhos;

• dividam 4 botões igualmente em 2 copinhos;

• dividam 9 botões igualmente em 3 copinhos;

• dividam 3 botões igualmente em 3 copinhos.

Ao longo do desenvolvimento da atividade, dê tempo entre um comando e outro para que os estudantes concluam o que lhes foi solicitado. Realize perguntas à turma, como: “Ao dividirmos 8 botões em 2 copinhos, com quantos botões

cada copinho ficou?”; “Ao dividirmos 9 botões em 3 copinhos, com quantos botões cada copinho ficou?”; “Ao dividirmos 10 botões em 2 copinhos, com quantos botões cada copinho ficou?”; entre outras.

Acompanhe a participação dos estudantes, bem como o interesse, a autonomia e o raciocínio, e se apresentam dificuldades. Caso haja, providencie outras atividades e estratégias com o objetivo de saná­las.

ESTUDANDO A DIVISÃO

1. Otávio é um pequeno produtor do município de Petrolina, localizado no estado de Pernambuco. As frutas que produz são vendidas em uma feira popular do bairro. Para comercializá-las, prepara embalagens com quantidades iguais de cada produto.

Produtor colhendo mangas no município de Petrolina, estado de Pernambuco, em 2022.

a ) Determine quantas embalagens serão necessárias para acomodar as frutas apresentadas em cada caso e complete as frases. Se necessário, use material de contagem.

Resposta: Para acomodar 3 cajus em cada embalagem, serão

• Para acomodar 3 cajus em cada embalagem, serão necessárias embalagens.

• Para que os estudantes compreendam os conceitos abordados na atividade 1, é necessário que entendam a ideia de repartir ou agrupar, reconhecendo que, por meio da divisão, obtemos quantidades em partes iguais.

dividido por é igual a

• Para acomodar 4 mangas em cada embalagem, serão necessárias embalagens.

Resposta nas orientações ao professor necessárias 4 embalagens. 12 dividido por 3 é igual a 4

Cajus.

Resposta: Para acomodar 4 mangas em cada embalagem, serão necessárias

2 embalagens. 8 dividido por 4 é igual a 2

dividido por é igual a

• Para acomodar 5 goiabas em cada embalagem, serão necessárias embalagens.

Resposta: Para acomodar 5 goiabas em cada embalagem, serão necessárias

Mangas. Goiabas.

dividido por é igual a . b ) Você costuma consumir frutas? Se sim, quais são as suas frutas preferidas? Converse com o professor e os colegas sobre a importância de incluir esses alimentos no cotidiano.

Imagens sem proporção entre si. 211

• No item b da atividade 1, explique aos estudantes que comer frutas todos os dias ajuda o organismo a funcionar de forma correta e equilibrada, pois as frutas são fontes de vitaminas, minerais, fibras e antioxidantes de extrema importância para o funcionamento do nosso organismo. Além disso, o consumo de frutas auxilia no funcionamento do intestino, contribui para o metabolismo e ajuda na prevenção de doenças.

Respostas

3 embalagens. 15 dividido por 5 é igual a 3

1. b) Resposta pessoal. Espera­se que os estudantes digam que costumam consumir frutas, e que sabem da importância delas para a saúde pessoal. Eles podem citar, como frutas preferidas, aquelas que são típicas da região em que moram, além de frutas sazonais conhecidas em todo o país. As mais comuns são laranja, banana, caqui e maçã, mas podem surgir outros nomes menos comuns, como gabiroba, umbu, manga, carambola, caju, goiaba etc.

06/10/2025 17:51:50

• Para trabalhar a atividade 2, caso os estudantes não tenham 10 lápis de cor, sugira que formem dupla com um colega ou entregue a eles materiais de contagem, como palitos sem extremidades pontiagudas, tampinhas ou objetos do material escolar. Entregue 10 desses materiais para cada um e, na sequência, leia o enunciado para eles. Deixe que resolvam essa situação usando as próprias estratégias, com o apoio dos materiais manipuláveis.

• Essa atividade explora a ideia de separar objetos em grupos com a mesma quantidade. Verifique os procedimentos que os estudantes estão utilizando e oriente­os caso tenham dificuldade. Por fim, solicite que verbalizem o raciocínio para a turma apresentando as estratégias usadas para solucionar essa situação. Nesse momento é importante que eles compreendam o objetivo da atividade e sejam capazes de construir de modo significativo o conceito trabalhado.

2. c) Resposta pessoal. Espera-se que os estudantes relatem as suas estratégias usadas para separar os 10 lápis em dois grupos com a

PRODUÇÃO DE CAJUS NO BRASIL

O caju é uma fruta de sabor marcante que pode ser usada para vários fins. Reconhecida pelos benefícios que propicia à saúde, é amplamente utilizada na culinária para a fabricação de doces e sucos. A castanha é especialmente apreciada. No Brasil, o Nordeste é a principal região de produção de caju em larga escala, com destaque para o Ceará. Porém, o cultivo da fruta também ocorre em outras áreas tropicais, incluindo o Cerrado de Minas Gerais, o que contribui para a diversidade frutífera local. Caju maduro no pé.

2. Junte-se a um colega e coloquem 10 lápis de cor sobre a carteira.

a ) Separe todos esses itens em dois grupos com a mesma quantidade. Quantos lápis há em cada grupo?

Resposta: Em cada grupo há 5 lápis.

b ) Ao fazer essa separação, algum dos lápis ficou fora dos grupos?

Resposta: Não.

c ) Converse com o professor e os colegas sobre a estratégia que você usou para fazer essa separação. Algum colega utilizou o mesmo procedimento?

d ) É possível formar outra quantidade de grupos distribuindo igualmente esses itens sem que sobrem lápis? Desenhe as possibilidades no espaço a seguir.

Resposta: Sim, é possível. Os estudantes podem desenhar 5 grupos com 2 lápis ou 10 grupos com apenas 1 item, ou ainda, 2 grupos com 5 lápis. mesma quantidade.

DIVISÃO POR 2

3. Para uma visita ao museu da cidade, os estudantes do 2º ano A serão divididos igualmente em dois grupos.

a ) De acordo com a imagem, quantos estudantes vão visitar o museu? Marque um X na quantidade correta.

10 estudantes. 16 estudantes.

Resposta: 16 estudantes.

b ) Quantos estudantes ficarão em cada grupo?

Ao dividir igualmente estudantes em grupos, haverá em cada grupo.

Resposta: Ao dividir igualmente 16 estudantes em 2 grupos, haverá 8 em cada grupo. 16 dividido por 2 é igual a 8

dividido por é igual a

Nessa situação, foi realizada uma divisão. Utilizando símbolos, escrevemos: total de estudantes quantidade de grupos quantidade de estudantes em cada grupo : =

Resposta: 16 : 2 = 8

Para representar a divisão, utilizamos o símbolo :, que lemos “dividido por”.

Portanto, em cada grupo haverá estudantes.

Resposta: Portanto, em cada grupo haverá 8 estudantes. Resposta: 9 estudantes.

c ) A turma do 2º ano B, em que há 18 estudantes, também foi dividida igualmente em dois grupos para visitar o museu. Nesse caso, quantos estudantes ficaram em cada grupo? Marque um  X 9 estudantes. 10 estudantes.

• A atividade 3 apresenta uma situação na qual é necessário dividir os estudantes do 2º ano A em grupos com a mesma quantidade de estudantes em cada um. Deixe que a turma exponha suas ideias e estratégias a fim de solucionar essa situação.

• Diga aos estudantes que usamos frequentemente o símbolo : para representar a divisão, mas ele também pode aparecer de outra maneira, como ÷. Nos computadores, celulares e em algumas calculadoras, a barra (/) simboliza divisão, ou seja, “16/2” significa “16 dividido por 2”, assim como “16 : 2”.

• Caso os estudantes apresentem dificuldade na resolução do item c, oriente­os a realizar

213

06/10/2025 17:48:57

procedimentos parecidos com os apresentados anteriormente, utilizando materiais de contagem.

BNCC

O assunto apresentado nesta página possibilita o desenvolvimento de um trabalho que aborde a Competência geral 3, citada na BNCC, valorizando as diversas manifestações artísticas e culturais. A arte é uma construção social capaz de potencializar a percepção das pessoas em relação ao mundo, de acordo com as próprias experiências de vida. Por isso, o contato com o universo artístico é muito importante.

• Antes de trabalhar a atividade 3 com os estudantes, pergunte se algum deles já visitou um museu ou uma exposição de arte. Caso algum tenha tido essa experiência, peça­lhe que compartilhe com os colegas. Comente com eles que museus são instituições onde são reunidos objetos, esculturas, antiguidades e outros elementos que representam patrimônios para a sociedade para fins de pesquisa, coleção, conservação e exposição. Fale sobre a importância de valorizarmos a arte, a cultura e a história de um povo. Atualmente, existem sites de museus e aplicativos para smartphones que disponibilizam um passeio virtual em alguns dos principais museus do mundo. Por meio desses recursos, o visitante virtual simula um passeio no interior dos museus, podendo visualizar todas as salas, corredores e em qualquer direção. Alguns aplicativos disponibilizam as obras em alta resolução, acompanhadas de informações básicas, como título original, ano de criação, dimensões, entre outras. Avalie também com a direção da escola e os responsáveis a possibilidade de levar os estudantes a uma visita presencial a um museu da região onde moram, a fim de enriquecer a experiência cultural deles, promovendo o aprendizado ativo.

• Para realizar a atividade 4, entregue aos estudantes materiais de contagem, como tampinhas, palitos de sorvete, entre outros, a fim de que representem essa situação concretamente, possibilitando um melhor entendimento dos procedimentos de cálculos que devem ser efetuados. Oriente os estudantes a não levarem os objetos à boca, para não correrem o risco de engolir e de se engasgarem com as peças pequenas.

• Pergunte a eles em quais situações do cotidiano usamos a expressão “metade” e deixe que comentem com a turma. Espera­se que citem algumas situações, como “metade de uma fruta”, “metade dos brinquedos” e “metade do dia”.

• Na atividade 5, pergunte aos estudantes qual é o total de figurinhas apresentado. Depois, pergunte como fariam para calcular a metade de 10 figurinhas. Deixe que façam a atividade utilizando seus conhecimentos prévios acerca do assunto e incentive­os a expor suas estratégias de resolução.

• A atividade 6 propõe uma situação­problema na qual os estudantes devem identificar a necessidade de calcular a metade de 18 reais, favorecendo uma integração entre as unidades temáticas Números e Grandezas e Medidas. Explore o conhecimento deles sobre o sistema monetário e, se possível, proponha esse cálculo com fichas que representem as cédulas do Real. Caso apresentem dificuldade e não seja possível usar representações de cédulas, oriente ­os a desenhar no caderno 18 bolinhas e a contornar metade delas, obtendo 9 bolinhas. Em seguida, escreva na lousa a divisão que corresponde a essa situação, ou seja, 18 : 2 = 9, e solicite que identifiquem e contornem o quadro em que está representada a quantia 9 reais.

4. Paulo vai doar algumas das revistas em quadrinhos apresentadas a seguir.

Vou doar metade das revistas em quadrinhos. Para determinar essa quantidade, divido o total de itens por 2.

Quantas revistas em quadrinhos Paulo vai doar?

Resposta: 8 : 2 = 4

: 2 =

total de revistas em quadrinhos

quantidade de revistas em quadrinhos doadas

Portanto, Paulo vai doar revistas em quadrinhos.

Nessa situação, para obtermos a metade de uma quantidade, basta dividi-la por .

5. Contorne metade das figurinhas apresentadas.

Resposta: Os estudantes devem contornar 5 figurinhas.

Resposta: Portanto, Paulo vai doar 4 revistas em quadrinhos. Nessa situação, para obtermos a metade de uma quantidade, basta dividi-la por 2.

6. João pretende comprar um caderno que custa 18 reais. Ele já tem metade dessa quantia. Marque um X no quadro em que está representado o total de dinheiro que João tem.

Unidades temáticas integradas

Imagens sem proporção entre si.

Resposta: Os estudantes devem marcar um X na alternativa A

As atividades desta página trabalham o conceito de metade em situações contextualizadas, com o suporte de imagens ou materiais manipuláveis, utilizando estratégias pessoais, conforme orienta a habilidade EF02MA08 da BNCC.

ATIVIDADE EXTRA

Organize a turma em duplas e entregue 10 peças do jogo de dominó a cada uma. Em seguida, solicite aos estudantes que distribuam as peças entre si. Cada um deverá ficar com a mesma

quantidade de peças, ou seja, a metade do total recebido, que, nesse caso, serão 5 peças. Depois, varie a atividade alterando a quantidade total de peças de cada dupla. Por exemplo, retire 2 peças de cada dupla e oriente­os a distribuí­las novamente. Repita esse procedimento removendo ou acrescentando peças. Outra possibilidade é realizar essa atividade utilizando materiais de contagem, como palitos de sorvete, e que sejam de fácil manuseio.

BNCC

7. Na coleção de Brigite, há uma dúzia de itens, ou seja, ela tem 12 figurinhas. Mateus tem metade dessa quantidade, o que corresponde a meia dúzia

Quantas figurinhas Mateus tem? figurinhas.

Resposta: 12  : 2 = 6 6 figurinhas.

9. Resposta pessoal. A resposta depende da escolha do contexto que os estudantes fizerem. Professor, professora: Oriente a resolução da atividade 9, incentivando a escrita dos textos em letra cursiva, a fim de que treinem essa prática e o uso desse traçado de letra.

8. Leia as informações a respeito da quantidade de morangos que Karina, Luna e Mara colheram do pomar.

De acordo com as dicas, escreva o nome de cada pessoa conforme a quantidade de morangos colhidos.

Luna colheu metade da quantidade colhida por Karina.

Resposta: Mara.

Mara colheu o dobro da quantidade colhida por Karina.

Karina colheu meia dúzia de morangos.

Resposta: Karina. Resposta: Luna.

9. Elabore no caderno, em letra cursiva, um problema envolvendo metade de uma quantidade e peça a um colega que o solucione. Depois, verifique se ele resolveu corretamente.

resolver por meio das próprias estratégias. Depois, retome a atividade, verificando se perceberam que podem iniciar a resolução com base na terceira informação apresentada, registrando que Karina colheu 6 morangos e, em seguida, usem as dicas das duas primeiras informações dadas para determinar os nomes correspondentes.

• Depois de os estudantes terem elaborado o problema solicitado na atividade 9, promova um momento para compartilharem com a turma os seus enunciados e resoluções. Verifique se todas as resoluções apresentam uma divisão por 2. Acolha com atenção e respeito a contribuição de

06/10/2025 17:48:59

cada um e deixe que se expressem livremente, a fim de verbalizarem o raciocínio. Aos estudantes com maior dificuldade, acompanhe dando o suporte adequado, seja com mais explicações, seja com recursos visuais e táteis. Além disso, durante os registros escritos, acompanhe os estudantes verificando como eles pegam o lápis, e se fazem o traçado de letras e números do modo adequado, seguindo a direção e a orientação correta. A pega de três pontos no lápis permite maior fluidez na escrita de letras e de números, além de garantir que o desenvolvimento da escrita ocorra gradualmente e de modo progressivo durante o processo de alfabetização e letramento.

• Leia o enunciado da atividade 7 com os estudantes e certifique­se de que compreenderam que uma dúzia equivale a 12 unidades e meia dúzia, a 6 unidades. Para um melhor aproveitamento desta atividade, solicite aos estudantes que organizem, em suas mesas, uma dúzia de objetos de contagem. Nessa fase do aprendizado, é muito importante que eles trabalhem situações concretas para desenvolver conceitos abstratos, como uma dúzia e meia dúzia. Depois, peça­lhes que dividam esses 12 objetos em dois grupos com a mesma quantidade de objetos. Retome o conceito de metade e explique que, ao dividir 12 por 2, eles obtiveram a metade de 12, ou seja, meia dúzia. Por fim, incentive os estudantes a registrarem no livro suas estratégias de cálculo para resolver a atividade, orientando­os no desenvolvimento de seus conhecimentos prévios acerca do assunto.

• Ao trabalhar a atividade 7 com os estudantes, certifique­se de que eles compreenderam que meia dúzia corresponde à metade de uma dúzia, ou seja, uma dúzia dividida por 2. Por isso, fazemos o cálculo 12 : 2 = 6

• A atividade 8 desafia os estudantes a enfrentarem uma situação diferente, levando­os a pensar de várias maneiras, a fim de resolvê­la. Leia as informações fornecidas no enunciado e dê um tempo para que tentem

A situação proposta na atividade 10 possibilita a integração com Ciências da Natureza, ao tratar do reaproveitamento de materiais, nesse caso, blocos de madeira. Uma possibilidade de trabalhar de forma integrada é discutir os modos como são descartados e como podem ser usados de maneira mais consciente. Diga aos estudantes que, além de materiais que já utilizamos, como garrafas PET ou papel, é possível aproveitar sobras de materiais. É comum, por exemplo, que linhas de produção de algumas fábricas gerem materiais que não são reaproveitados. Por isso, alguns artesãos estabelecem acordos de compra dessas sobras com as fábricas e reaproveitam os materiais de maneira criativa, como o personagem da página em questão.

• Providencie réguas em quantidade suficiente para os estudantes, individualmente ou em dupla, a fim de que tenham oportunidade de manipular esse instrumento e compreender a estratégia demonstrada na atividade 10. Para um melhor aproveitamento da atividade, oriente­os a usar as réguas para efetuar outras divisões, como 12  : 3, 9  : 3, 15  : 3, entre outras. Reforce durante a execução da atividade as perguntas: “Quantas vezes o 3 ‘cabe’ no 12?”; “Quantas vezes o 3 ‘cabe’ no 9?”; “Quantas vezes o 3 ‘cabe’ no 15?”.

ATIVIDADE EXTRA

• 21 : 3

• 15 : 3

• 3 : 3

• 18 : 3

DIVISÃO POR 3

10. Observe a imagem que representa o senhor Josias e leia o que ele está falando.

Utilizando os blocos de madeira que estão sobre a mesa, vou construir outros bonecos como este.

a ) Quantos blocos de madeira estão sobre a mesa?

Resposta: 6 blocos.

b ) Quantos blocos de madeira são utilizados para a construção de cada boneco?

Resposta: 3 blocos.

Para determinar quantos bonecos o senhor Jonas poderá construir, dividimos a quantidade de blocos de madeira que estão sobre a mesa pelo total de materiais utilizados na construção de cada um, ou seja, 6  : 3 Vamos efetuar esse cálculo usando uma régua.

6  : 3 = 2 01234567 3 3

Ao efetuar o cálculo 6  : 3 na régua, verificamos quantas vezes o 3 “cabe” no 6.

Portanto, o senhor Josias poderá construir bonecos com os blocos que estão sobre a mesa.

Resposta: Portanto, o senhor Josias poderá construir 2 bonecos com os blocos que estão sobre a mesa.

Com o objetivo de consolidar as estratégias de cálculos abordadas nesta página, solicite aos estudantes que efetuem, no caderno, da maneira que preferirem, os cálculos a seguir.

Respostas

21 : 3 = 7; 15 : 3 = 5; 3 : 3 = 1; 18 : 3 = 6

11. Efetue as divisões com o auxílio de uma régua.

a ) 3  : 3 =

Resposta: 3  : 3 = 1

b ) 9  : 3 =

Resposta: 9  : 3 = 3

12. A imagem representa a vista de cima de uma sala de aula.

De acordo com a organização dessas cadeiras, responda às questões.

a ) Quantos estudantes há nessa sala de aula?

Resposta: 4 × 6 = 24

quantidade de linhas

c ) 15 : 3 = d ) 18 : 3 =

Resposta: 15  : 3 = 5

Resposta: 18  : 3 = 6

e ) 21 : 3 = f ) 27 : 3 =

Resposta: 21  : 3 = 7

Resposta: 27  : 3 = 9

• Antes de trabalhar a atividade 11 com os estudantes, providencie réguas em quantidade suficiente para todos, individualmente ou em duplas, a fim de que tenham oportunidade de manipular esse instrumento para resolver a atividade, conforme a estratégia sugerida na página anterior.

Resposta: 6 × 4 = 24

total de estudantes × = × = ou

quantidade de colunas

total de estudantes

quantidade de colunas

Nessa sala há estudantes.

quantidade de linhas

Resposta: Nessa sala há 24 estudantes.

b ) A professora organizou grupos com 3 estudantes cada. Quantos grupos foram formados?

Resposta: 24 : 3 = 8

total de estudantes

quantidade de estudantes por grupo

quantidade de grupos : = coluna linha

Resposta: Foram formados 8 grupos.

Foram formados grupos.

• A atividade 12 tem por objetivo que os estudantes estabeleçam relações entre a multiplicação e a divisão, por meio de uma imagem que representa a vista de cima de uma sala de aula. Caso os estudantes apresentem dificuldade em compreender a multiplicação, no item a, oriente ­ os a contar todas as carteiras da ilustração, de maneira que percebam que há 6 colunas com 4 carteiras cada ou 4 grupos de fileiras com 6 carteiras cada. Para auxiliar na resolução do item b, se julgar conveniente, solicite que contornem, na ilustração, grupos com 3 carteiras cada, obtendo 8 grupos, e formalize essa ideia escrevendo na lousa a operação correspondente a essa divisão, ou seja, 24 : 3 = 8

• Por fim, faça o seguinte questionamento aos estudantes: “Se quisermos descobrir por quanto o número foi multiplicado, o que podemos fazer?”. Esse tipo de reflexão os ajudará a compreender a multiplicação como operação inversa da divisão.

06/10/2025 17:49:01

• Para a resolução da ativida de 13 , entregue aos estudantes materiais de contagem para que representarem a situação proposta concretamente, ampliando seus conhecimentos ao realizarem uma divisão por 3, o que possibilita um melhor entendimento do processo de divisão.

• Leia o enunciado da atividade 14 com os estudantes e verifique se eles associam a operação de divisão por 3 à expressão “terça parte”. No caso da operação realizada nessa atividade, comente com eles que 27 : 3 = 9, mostrando que a expressão “a terça parte de 27 é igual a 9” representa essa situação. Para um melhor aproveitamento da atividade, faça outros questionamentos para que eles relacionem a expressão à divisão por 3, como: “Quanto é a terça parte de 12?”; “Quanto é a terça parte de 3?”; “Quanto é a terça parte de 30?”.

• Caso os estudantes demonstrem dificuldade ao resolverem a atividade 15, oriente­os a efetuar inicialmente a operação de divisão correspondente à situação. Espera­se que eles percebam que devem efetuar 6 : 3, obtendo 2 como resultado. Portanto, 2 bolinhas de gude devem ser contornadas, independentemente da posição.

• Para desenvolver a atividade 16, organize os estudantes em duplas e solicite que elaborem e escrevam o enunciado de um problema envolvendo o cálculo de terça parte. Depois, eles deverão trocar os cadernos com o colega da dupla para resolverem o problema elaborado. Por fim, solicite que destroquem os cadernos e verifiquem se as respostas estão corretas.

• A atividade 16 promove o desenvolvimento do componente produção de escrita ao solicitar aos estudantes que elaborem e escrevam o enunciado de um problema associado ao contexto apresentado.

13. Para a realização de uma atividade, o professor Olívio vai distribuir 21 estudantes em equipes com 3 participantes cada. Quantas equipes serão formadas?

Resposta: 21 : 3 = 7

Serão formadas equipes.

Resposta: Serão formadas 7 equipes.

14. Timóteo vai emprestar alguns jogos para Mariana.

15. Contorne a terça parte das bolinhas de gude apresentadas. : = : 3 =

Vou emprestar a terça parte de meus jogos para Mariana. Para determinar essa quantidade, divido o total de itens por 3.

Quantos jogos Timóteo vai emprestar para Mariana?

Resposta: 27 : 3 = 9

Portanto, Timóteo vai emprestar jogos para Mariana.

Resposta: Portanto, Timóteo vai emprestar 9 jogos para Mariana.

Resposta: Os estudantes devem contornar 2 bolinhas de gude.

16. De acordo com a imagem, elabore, no caderno, um problema envolvendo a terça parte dos carros e peça a um colega que o solucione. Depois, verifique se ele resolveu corretamente. Bolinhas de gude.

Resposta pessoal. Esta atividade tem como objetivo propor aos estudantes a elaboração do enunciado de um problema, seguindo a proposta de usar o conceito de terça parte. É esperado que usem a imagem como base para realização dela.

BNCC

As atividades 13, 14 e 15 contemplam aspectos da habilidade EF02MA08 da BNCC ao propor que os estudantes elaborem e resolvam problemas de divisão envolvendo a terça parte com suporte de imagens, por meio de estratégias pessoais.

ATIVIDADE EXTRA

Desenhe na lousa alguns objetos e peça a um estudante que vá até ela e contorne a terça parte da quantidade de objetos desenhados. Faça desenhos de traçado simples, como balões,

flores, estrelas, entre outros. Repita o procedimento com outros desenhos, convidando os demais estudantes a irem até a lousa, a fim de que determinem a terça parte dos desenhos apresentados. Lembre­se de que a quantidade de objetos deve ser representada por um número divisível por 3. Ao final de cada situação, escreva a divisão correspondente na lousa.

DIVISÃO POR 4

17. Raimundo fez uma fornada de biscoitos usando uma receita típica do estado do Rio Grande do Sul. Para armazená-los, eles serão distribuídos em 4 embalagens com quantidades iguais.

a ) De acordo com a cena, quantos biscoitos Raimundo assou?

Resposta: 24 biscoitos.

b ) Quantos biscoitos Raimundo vai armazenar em cada embalagem? Marque um X na resposta correta.

5 biscoitos.

Resposta: 6 biscoitos.

7 biscoitos. 6 biscoitos.

c ) Para determinar a quantidade de biscoitos que Raimundo vai armazenar em cada embalagem, devemos efetuar uma divisão. Complete o esquema e a resposta.

Resposta: 24 : 4 = 6

Portanto, Raimundo vai armazenar biscoitos em cada embalagem.

Resposta: Portanto, Raimundo vai armazenar 6 biscoitos em cada embalagem.

06/10/2025 17:46:21

• Leia o enunciado da atividade 17 com os estudantes e oriente­os durante sua resolução. Caso apresentem dificuldades em identificar a divisão que deve ser escrita no item c, solicite que contornem de 4 em 4 os biscoitos da ilustração, obtendo 6 grupos. Para um melhor aproveitamento da atividade, disponibilize réguas para que efetuem essa divisão, verificando quantas vezes o 4 “cabe” no 24, conforme sugerido anteriormente.

• Se julgar conveniente, mostre na lousa para os estudantes que, nesse caso, temos 24 : 4 = 6 e também 24 : 6 = 4 . Em outras palavras, se o 4 “cabe” 6 vezes no 24, então o 6 “cabe” 4 vezes no 24. Nesta atividade, verifique a possibilidade de utilizar o recurso do material de apoio, como a calculadora, priorizando a investigação das hipóteses dos cálculos. Incentive e valorize o cálculo mental e, posteriormente, a construção do sistema de registro. Se a resposta ocorrer por cálculo mental, incentive o auxílio colaborativo entre os estudantes, no qual um descreve como pensou (raciocínio lógico) e o outro registra na lousa (comunicação) coletivamente ou individualmente. Com isso, espera­se trabalhar de modo cooperativo, promovendo a inclusão dos estudantes com Transtorno do Déficit de Atenção com Hiperatividade (TDAH) e Transtorno do Espectro Autista (TEA). Para favorecer a aprendizagem de estudantes com deficiência visual e que precisem de acompanhamento, ofereça a oportunidade de trabalho em grupos, propondo a um deles que descreva a situação para o colega.

ATIVIDADE EXTRA

Providencie antecipadamente e leve para a sala de aula um jogo de dominó. Coloque as 28 peças sobre a sua mesa e solicite a quatro estudantes que peguem a mesma quantidade de peças. Cada um deverá pegar

7 peças, pois 28 : 4 = 7. Depois, retire algumas peças de dominó da mesa, deixando, por exemplo, 12 peças. Repita o procedimento com outros quatro estudantes, pedindo a cada um que pegue a mesma quantidade de peças. Se julgar necessário, repita o procedimento usando outras quantidades de peças, desde que seja um número divisível por 4. Por fim, oriente os estudantes a registrarem no caderno todas as expressões que representam essas divisões realizadas na prática, como: 4 : 4 = 1; 8 : 4 = 2; 12 : 4 = 3; 16 : 4 = 4; 20 : 4 = 5; 24 : 4 = 6 e 28 : 4 = 7.

• Aproveite o assunto do Boxe complementar e pergunte aos estudantes se, na região em que moram, existe alguma receita de biscoito que faz parte da tradição local. Peça a eles que comentem a respeito, contando a história do biscoito, a fim de valorizar a cultura local, a história e promover a interação social.

• Durante o desenvolvimento das atividades 18 e 19 propostas nesta página, os estudantes têm a oportunidade de ampliar seus conhecimentos, por meio de situações contextualizadas, sobre a operação de divisão por 4.

• A atividade 19 solicita aos estudantes que agrupem 12 bonés, com 4 bonés em cada grupo. Para isso, eles devem contornar os bonés de 4 em 4 e constatar que 3 grupos são formados. Aproveite esse momento para verificar se eles compreendem que, se os 12 bonés forem agrupados de 3 em 3, obtêm­se 4 grupos, ou seja, 12 : 3 = 4

Respostas

18. a) Os estudantes podem desenhar 8 bolinhas e contornar 4 grupos de 2 bolinhas. Se a atividade for efetuada com o auxílio de material de contagem, espera­se que separem 8 objetos e formem com eles 4 grupos com dois objetos cada; 8 : 4 = 2

b) Os estudantes podem desenhar 16 bolinhas e contornar 4 grupos de 4 bolinhas. Se a atividade for efetuada com o auxílio de material de contagem, espera­se que separem 16 objetos e formem com eles 4 grupos com 4 objetos cada; 16 : 4 = 4.

MAIS QUE UM BISCOITO, UMA TRADIÇÃO

A culinária do Rio Grande do Sul foi muito influenciada por pessoas de outros países, especialmente da Alemanha. Quando vieram para a Região Sul do Brasil, esses imigrantes trouxeram tradições e receitas, como os biscoitos, que fazem parte da culinária alemã há muitos anos.

No Brasil, essas receitas foram ajustadas aos ingredientes locais da região. Isso resultou em um biscoito especial, em formato de “V”, conhecido como vovó sentada. O nome foi escolhido porque o formato lembrava, para as pessoas da região, a posição de uma avó sentada observando seus netos brincar.

Biscoito vovó sentada, típico do Rio Grande do Sul.

18. Efetue as divisões com o auxílio de desenhos ou material de contagem. Depois, complete os itens com o resultado de cada uma delas.

Resposta e comentários nas orientações ao professor

a ) 8  : 4 =

b ) 16 : 4 =

19. Contorne os bonés a seguir formando grupos com 4 bonés cada. Depois, complete os itens.

Resposta: Os estudantes devem formar 3 grupos contornando 4 bonés para cada grupo.

Quantos grupos foram formados?

Resposta: 12 : 4 = 3

Portanto, foram formados grupos com bonés cada.

Resposta: Portanto, foram formados 3 grupos com 4 bonés cada.

DIVISÃO POR 5

20. Com base nas embalagens com canetas coloridas, complete o que falta nas frases.

Ao todo, há canetas e embalagens.

Resposta: Ao todo, há 20 canetas e 5 embalagens.

21. Observe a caixa com sabonetes. : = : = : =

Resposta: 20 : 5 = 4

Em cada embalagem há canetas.

Resposta: Em cada embalagem há 4 canetas.

a ) Quantos sabonetes cabem nessa embalagem?

Resposta: 5 sabonetes.

b ) Quantas caixas como essa são necessárias para guardar 15 sabonetes?

São necessárias caixas.

Resposta: São necessárias 3 caixas.

Resposta: 15 : 5 = 3

c ) Marlene comprou 7 dessas caixas. Quantos sabonetes ela adquiriu?

Resposta: 7 × 5 = 35

Marlene adquiriu sabonetes.

Resposta: Marlene adquiriu 35 sabonetes.

AVALIANDO

Objetivo

Calcular a metade e a terça parte de uma quantidade.

Sugestão de intervenção

Escreva na lousa, para que os estudantes copiem e resolvam no caderno, as seguintes situações­problema.

1. Gael tem uma coleção de 9 bonés. Ele resolveu doar aos seus colegas a terça parte dessa quantidade. Quantos bonés ele vai doar?

06/10/2025 17:46:23

2. Maia recebeu de seus pais 18 reais de mesada. Ao ir a uma revistaria, ela gastou metade desse valor. Quantos reais Maia gastou?

Respostas

1. Gael vai doar 3 bonés.

2. Maia gastou 9 reais.

• Na atividade 20, solicite aos estudantes que realizem a contagem de todas as canetas, a fim de determinar o total para poderem expressar a situação apresentada por meio de uma divisão, ou seja, 20 : 5 = 4

• Para tirar melhor proveito da atividade 21, faça alguns questionamentos aos estudantes, por exemplo: “Quantas caixas como esta são necessárias para guardar 20 sabonetes?” ; “Quantas caixas como esta são necessárias para guardar 25 sabonetes?”. Caso demonstrem dificuldades, oriente­os a fazer tracinhos no caderno para agrupá­los e encontrar os resultados das operações propostas.

REFERÊNCIAS COMPLEMENTARES

FREITAS, Leidiane Souza de. Aprendizagem da divisão nos anos iniciais do ensino fundamental: Desafios e possibilidades. 2023. Trabalho de conclusão de curso. Instituto Federal do Espírito Santo. Disponível em: https://repositorio. ifes.edu.br/bitstream/ handle/123456789/4596/ TCCLEIDIANE.pdf? sequence=1. Acesso em 25 set. 2025. Esse trabalho apresenta uma análise a respeito do déficit na operação da divisão de estudantes dos Anos Inicias, propondo intervenções para superar possíveis dificuldades.

• No item a da atividade 22 , verifique se os estudantes percebem que há uma regularidade entre as divisões efetuadas. Caso não percebam, peça a eles que leiam apenas os resultados para descobrirem que, em cada quadro, o resultado das divisões de cima para baixo segue a sequência dos números naturais de 1 a 10.

• No item c, verifique se os estudantes encontram nos quadros as divisões cujos resultados sejam menores do que 4. Para um melhor aproveitamento da atividade, solicite que encontrem nos quadros e registrem no caderno as divisões cujos resultados sejam iguais a 7 e, depois, as divisões cujos resultados sejam maiores do que 8.

• Para realizar o item d, faça na lousa, com o auxílio dos estudantes, o quadro das divisões por 3 e, depois, deixe que façam sozinhos as divisões por 5. Caminhe pela sala de aula, a fim de observar o desenvolvimento deles na atividade e sanar possíveis dúvidas, se necessário.

• No item d, espera­se que os estudantes notem que é possível construir os quadros solicitados sem efetuar cálculos. No entanto, é fundamental que eles sejam capazes de calcular os múltiplos de cada divisor, a fim de construírem a tabuada e obterem os quocientes das divisões, pois as regularidades na organização dos números se repetem em todos os quadros.

Sugestão de Desafio

Juliana comprou 8 elásticos de cabelo e vai dividir com suas 3 amigas. Quantos elásticos de cabelos cada uma vai receber?

Resposta

Cada uma vai receber 2 elásticos de cabelos.

22. Enquanto estudava, Maurício organizou quadros com algumas divisões.

Dividido por 1

Dividido por 2

Dividido por 4

a ) Efetue as divisões e complete os quadros com o resultado de cada uma.

Respostas e comentários nas orientações ao professor

b ) Quais regularidades você identifica em cada um dos quadros apresentados?

Resposta pessoal. Espera-se que os estudantes percebam, por exemplo, que, em cada quadro, o resultado das

divisões, de cima para baixo, é a sequência dos números naturais de 1 a 10.

c ) Entre as divisões desses quadros, escreva aquelas cujo resultado seja menor do que 4.

d ) Maurício organizou divisões relacionadas aos números 1, 2 e 4. De maneira semelhante, construa no caderno quadros com divisões relacionadas aos números 3 e 5.

Respostas e comentários nas orientações ao professor

Respostas 20. a) Dividido por 1: 1:1 = 1; 2:1 = 2; 3:1 = 3; 4:1 = 4; 5 : 1 = 5; 6:1 = 6; 7 : 1 = 7; 8:1 = 8; 9:1 = 9; 10:1 = 10.

Dividido por 2: 2 : 2 = 1; 4 : 2 = 2; 6 : 2 = 3; 8 : 2 = 4; 10 : 2 = 5; 12 : 2 = 6; 14 : 2 = 7; 16 : 2 = 8; 18 : 2 = 9; 20 : 2 = 10

Dividido por 4: 4 : 4 = 1; 8 : 4 = 2; 12 : 4 = 3; 16 : 4 = 4; 20 : 4 = 5; 24 : 4 = 6; 28 : 4 = 7; 32 : 4 = 8; 36 : 4 = 9; 40 : 4 = 10.

20. d) Dividido por 3: 3 : 3 = 1; 6 : 3 = 2; 9 : 3 = 3; 12 : 3 = 4; 15 : 3 = 5; 18 : 3 = 6; 21 : 3 = 7; 24 : 3 = 8; 27 : 3 = 9; 30 : 3 = 10.

Dividido por 5: 5 : 5 = 1; 10 : 5 = 2; 15 : 5 = 3; 20 : 5 = 4; 25 : 5 = 5; 30 : 5 = 6; 35 : 5 = 7; 40 : 5 = 8; 45 : 5 = 9; 50 : 5 = 10.

VINÍCIUS

23. Junto a um colega, leiam o problema a seguir. Depois, respondam às questões.

23. a) Resposta: Os estudantes devem interpretar o enunciado do problema e dizer que se trata de uma situação envolvendo divisão, na qual é necessário repartir uma corda em partes iguais.

Nícolas vai repartir 36 metros de corda em 4 partes iguais. Quantos metros cada parte terá?

a ) Qual é o assunto tratado no enunciado do problema?

b ) Os números que aparecem no enunciado representam qual informação?

Resposta: Os estudantes devem verificar que o número 36 representa uma medida de comprimento, e o número 4, uma quantidade.

c ) Com os dados apresentados é possível solucioná-lo? Se a resposta for afirmativa, resolva-o.

• Na atividade 23, oriente os estudantes a debaterem as estratégias, favorecendo a troca de ideias, a argumentação e o pensamento crítico.

Resposta: Sim. 36  : 4 = 9. Cada parte da corda ficará com 9 metros.

24. Elza guardou seus livros em diferentes caixas, como representado na tabela ao lado.

Quantidade de livros de Elza em 2027

Unidades temáticas integradas

a ) Quantos livros Elza tem ao todo? Efetue os cálculos mentalmente. livros.

Resposta: 10 + 15 + 15 = 40 40 livros.

b ) Ela os distribuirá igualmente em 5 estantes. Quantos livros haverá em cada estante? livros.

DESAFIO A MAIS

CaixaQuantidade de livros

Caixa 1 10

Caixa 2 15

Caixa 3 15

Fonte de pesquisa: Anotações de Elza.

Resposta: 40  : 5 = 8 8 livros.

Jonas tinha 24 carrinhos de brinquedo e resolveu dividir igualmente em 3 caixas. Depois, ele pegou a metade dos carrinhos de cada caixa e colocou em uma quarta caixa. Quantos carrinhos ficaram em cada uma das 4 caixas?

Resposta: Três caixas ficaram com 4 carrinhos cada, e a quarta caixa ficou com 12 carrinhos. 223

4 + 4 + 4 = 12 . A caixa 4 ficará com 12 carrinhos.

• Resposta: As caixas 1, 2 e 3 ficam com 4 carrinhos cada, e a caixa 4 fica com 12 carrinhos. Incentive os estudantes a compartilhar estratégias diferentes.

CONCLUSÃO

Acompanhar o desenvolvimento dos estudantes é fundamental para um ensino bem­sucedido. Ao longo da unidade, foram propostas diversas maneiras de avaliar a aprendizagem da turma. A fim de realizar um monitoramento mais abran­

gente e organizado, registre nos relatórios individuais ou nas fichas de avaliação o desempenho de cada estudante, levando em consideração suas particularidades. Um modelo desse tipo de ficha pode ser encontrado no tópico Avaliação deste Manual do Professor. Assim, será possível visualizar de modo individual as trajetórias de aprendizagem, incluindo os avanços e os pontos de dificuldades a serem sanados por meio de atividades que promovam a recuperação dos conteúdos. Esse método de verificar a progressão dos estudos e identificar o que a turma de fato conseguiu aprender, bem como

• A atividade 24 estabelece uma integração entre as unidades temáticas de Matemática: Números e Probabilidade e estatística , ao relacionar a quantidade de livros de cada caixa e a organização dessa quantidade em uma tabela. Essa atividade propõe uma situação envolvendo adição e divisão, com base em um contexto do dia a dia. No item a, ao solicitar o cálculo mental, eles são motivados a desenvolver estratégias pessoais de adição. No item b, é proposta uma divisão exata, favorecendo a compreensão da ideia de repartir uma quantidade em partes iguais. Promova a troca de conhecimentos coletiva e a valorização de diferentes modos de pensar.

• O objetivo do boxe Desafio a mais é que os estudantes apliquem a divisão e o conceito de metade para determinar a distribuição final dos carrinhos nas caixas. Uma possível lógica de resolução é a seguinte:

• Dividir a quantidade total de carrinhos em 3 caixas: 24:3 = 8. As caixas 1, 2 e 3 ficaram com 8 carrinhos cada.

• Calcular metade dos carrinhos em cada caixa: 8 : 2 = 4 . Agora, as caixas 1, 2 e 3 ficaram com 4 carrinhos cada.

• Calcular quantos carrinhos a quarta caixa recebeu das três caixas:

06/10/2025 17:46:23

os aspectos que ficaram com lacunas de absorção, é de grande importância para repensar estratégias em sala de aula, tornando as ações pedagógicas cada vez mais eficazes.

A conclusão da unidade é o momento de avaliar se os objetivos por ela propostos foram alcançados. Para esse diagnóstico, observe no final deste Manual do Professor. algumas possibilidades de avaliação formativa que permitem realizar o monitoramento da aprendizagem dos estudantes e intervir caso eles não tenham atingido os resultados esperados.

OBJETIVOS DA UNIDADE

• Compreender o significado das expressões “mais leve” e “mais pesado”.

• Comparar massas, com e sem o auxílio de instrumentos de medição.

• Reconhecer o quilograma e o grama como unidades padronizadas de medida de massa.

• Comparar capacidades de recipientes por meio de estratégias pessoais.

• Reconhecer o litro e o mililitro como unidades fundamentais de medida de capacidade.

• Identificar o ano como um período de 12 meses.

• Identificar a semana como um período de 7 dias.

• Reconhecer o relógio de ponteiros e o relógio digital.

• Reconhecer os períodos do dia: manhã, tarde, noite e madrugada.

INTRODUÇÃO E JUSTIFICATIVA

Nesta unidade, os estudantes terão contato com conteúdos sobre medidas de massa, de capacidade e de tempo. Serão abordadas as diferenças entre a medida de massa de objetos, como identificar qual objeto é “mais leve” e “mais pesado”, bem como as unidades padronizadas de medida (quilograma e grama). Será apresentada também a medida de capacidade de diferentes recipientes usados no dia a dia. Serão introduzidas as unidades de medida padronizadas: o litro e o mililitro. E, por fim, serão abordados o calendário, os dias da semana e os meses do ano e apresentados o relógio de ponteiros e o relógio digital como instrumentos usados para medir o tempo. Habilidades da BNCC trabalhadas na unidade: EF02MA17 , EF02MA18 , EF02MA19 e EF02MA22

UNIDADE10

Caranguejo andando na praia.

MEDIDAS DE MASSA, DE CAPACIDADE E DE TEMPO

SUGESTÃO DE ESTRATÉGIA INICIAL

Construa, com a ajuda dos estudantes, uma balança de dois pratos usando dois pratos descartáveis, barbante, tesoura com pontas arredondadas, palitos de churrasco com as pontas cortadas e fita adesiva, conforme a imagem apresentada. Supervisione a construção para evitar acidentes com a tesoura e com os palitos.

• Oriente os estudantes a colocarem pequenos objetos em cada prato da balança, a fim de perceberem quais são mais leves e quais são mais pesados. Compare também objetos com a mesma medida de massa. Para essas medições, providencie e leve para a sala de aula objetos com diferentes medidas de massa.

Em determinadas épocas do ano, as pessoas são proibidas de capturar certos caranguejos. Esses períodos, conhecidos como “andada”, podem ocorrer de novembro a março, com mais frequência em janeiro. A andada é necessária para garantir a reprodução dessas espécies, que saem das tocas e ficam expostas.

1. 2.

3.

2 e 3. Respostas nas orientações ao professor.

De acordo com o texto, em quais meses do ano a andada pode ocorrer?

O que você acha que aconteceria se as pessoas capturassem os caranguejos durante o período da andada?

Em sua opinião, a medida da massa de um caranguejo é maior, menor ou igual a 1 kg? Converse com seus colegas.

Resposta: Novembro, dezembro, janeiro, fevereiro e março. 225

06/10/2025 17:44:09

• Inicie o trabalho solicitando aos estudantes que analisem a fotografia apresentada nas páginas de abertura. Verifique se eles conhecem esse animal e, em caso afirmativo, peça­lhes que comentem suas experiências com os demais colegas.

• Leia com eles o texto da página 225 e conversem sobre a importância de respeitar os períodos do ano em que é proibido capturar caranguejos para assim garantir sua reprodução, mantendo a continuidade da espécie. Diga­lhes que a pesca de peixes também é proibida durante o período de reprodução. Comente que existem várias espécies de caranguejo de água doce, de água salgada ou terrestres que vivem principalmente em manguezais. Explique aos estudantes que o siri é uma espécie de caranguejo com pernas traseiras adaptadas para nadar. Solicite que observem atentamente a cena e que opinem se o animal da imagem tem as características de caranguejo ou de siri. Se julgar necessário, leve a imagem de um siri para que eles percebam a diferença, comparando a imagem com a fotografia da Reprodução do Livro do Estudante

• Ressalte o significado da palavra andada na questão 1 para que seja desenvolvido o vocabulário dos estudantes. Caso eles tenham dificuldade em responder à atividade, repita os meses do ano, a fim de que relembrem a ordem dos meses.

• Na questão 2, relembre o que vocês conversaram sobre a importância de respeitar os períodos do ano para capturar os caranguejos.

• Caso os estudantes não consigam estimar a medida de massa do caranguejo na questão 3, compare­o com outros animais do convívio deles e pergunte a eles se acham que esses animais pesam mais ou menos de 1 kg. Depois, refaça a pergunta, incluindo o caranguejo no questionamento. Esta questão tem como objetivo verificar o conhecimento prévio dos estudantes sobre os caranguejos, estimando a medida de sua massa,

bem como levá­los a comentar se já viram ou não um caranguejo.

Respostas

2. Resposta pessoal. Espera­se que os estudantes respondam que, durante o período da andada, os caranguejos se reproduzem e, se ele não for respeitado, a quantidade de caranguejos pode diminuir, podendo causar a extinção da espécie. 3. Resposta pessoal. Espera­se que os estudantes respondam que a medida da massa de um caranguejo é menor do que 1 kg

• Antes de iniciar o estudo das medidas de massa, é fundamental que os estudantes tenham desenvolvido algumas noções relacionadas à comparação de objetos no cotidiano. Dessa maneira, como pré­requisito, eles devem identificar quais objetos são mais leves e quais são mais pesados. Portanto, é importante que tenham vivenciado situações nas quais precisaram realizar comparações de massas utilizando estratégias como segurar objetos com as mãos, identificando o mais leve e o mais pesado. Esses conhecimentos são necessários para que eles possam compreender, posteriormente, o uso das unidades de medida de massa padronizadas, como o quilograma e o grama, atribuindo sentido ao uso dessas unidades de medida no dia a dia.

• O objetivo da atividade 1 é promover a compreensão do significado de “mais leve” e de “mais pesado” ao levar os estudantes a observarem a situação e a imagem exploradas na página.

• Nos itens a e b da atividade 1, converse com os estudantes pedindo que justifiquem suas respostas, pois assim é possível verificar suas interpretações.

• Aproveite o item c da atividade 1 para explicar que geralmente usamos a palavra “peso” para fazer referência à nossa medida de massa ou à de um objeto ou animal. Como sugestão de ampliação, proponha a atividade extra descrita a seguir.

1. b) Resposta: Aline colocou as compras dela em um carrinho porque são muito pesadas para serem transportadas apenas em sacolas. Já Sofia não

MEDIDAS DE MASSA

1. Sofia e Aline foram fazer compras e se encontraram no supermercado.

Oi, Aline, tudo bem?

Tudo bem! Você veio ao supermercado também?

a ) Em sua opinião, quem está carregando a compra mais leve, Sofia ou Aline?

Resposta pessoal. Espera-se que os estudantes respondam que Sofia está carregando a compra mais leve.

b ) Por que Aline colocou as compras que fez em um carrinho, enquanto Sofia está utilizando uma sacola?

c ) A compra de Aline é mais pesada ou mais leve que a de Sofia?

Resposta: Mais pesada. está utilizando um carrinho porque suas compras são mais leves e podem ser transportadas com facilidade em sacolas.

Quando dizemos que um objeto ou animal é mais leve ou mais pesado que outro, estamos comparando a medida de suas massas. Nesse caso, a medida de massa da compra de Aline é maior do que a da compra de Sofia.

ATIVIDADE EXTRA

Aproveite a atividade 1 e leve para a sala de aula duas sacolas não transparentes com alguns objetos de medidas de massa variadas. A experiência pode ser feita com duas sacolas de mesmos itens em quantidades diferentes (como duas laranjas em uma sacola e 5 laranjas em outra) e depois com itens diferentes que tenham medidas de massa diferentes (como uma sacola com um livro de muitas páginas e outra sacola com um caderno de poucas páginas). Certifique­se de que seja possível perceber essa diferença apenas olhando para as sacolas. Em um primeiro momento, peça aos estudantes que observem as

sacolas e digam qual é a mais leve e qual é a mais pesada. Anote na lousa a opinião dos estudantes e, em seguida, permita a eles que segurem as sacolas e assim verifiquem a resposta correta.

BNCC

As atividades deste tópico contemplam aspectos da habilidade EF02MA17 da BNCC, pois propõem aos estudantes que estimem e comparem a medida de massa de objetos e de pessoas utilizando unidades de medida padronizadas e não padronizadas.

NOÇÕES

2. Contorne:

DE MEDIDAS DE MASSA

a ) O objeto mais pesado.

Resposta: Os estudantes devem contornar o vaso de planta

Tigela de plástico

b ) O objeto mais leve

Ferro de passar roupa

Vaso de planta

Resposta: Os estudantes devem contornar o garfo.

3. A balança é um instrumento de medida utilizado para medir a massa de pessoas, objetos, animais, produtos etc.

Algumas frutas estão apresentadas em balanças de dois pratos em dois momentos.

INFOGRÁFICO CLICÁVEL: FEIRAS LIVRES E UNIDADES DE MEDIDA

De acordo com esses momentos, pinte:

• de amarelo o nome da fruta mais pesada

• de azul o nome da fruta mais leve.

Resposta: Os estudantes devem pintar a palavra Maçã de azul e a palavra Jaca de amarelo.

Abacaxi Maçã Jaca

06/10/2025 17:44:11

• Na atividade 2 , pretende­se que, com base nas imagens, os estudantes retomem os objetos apresentados e suas características, principalmente em relação à medida de massa. Destaque a diferença do enunciado dos itens a e b, em que o primeiro pede o objeto mais pesado e o segundo, o mais leve.

• Na atividade 3, além de conhecerem um tipo de balança, os estudantes são incentivados a fazer comparação entre algumas frutas. Dependendo da comparação feita, uma fruta mais pesada em um momento pode ser mais leve em outro, como no caso do abacaxi. Se os estudantes apresentarem dificuldades para resolver a atividade, relembre a atividade sugerida no início da unidade, em que foi proposta a confecção de uma balança de dois pratos. Recorde o que acontece com o prato da balança que recebe o objeto mais leve (o prato vai subir) e com o prato com o objeto mais pesado (ele vai descer). Em seguida, peça aos estudantes que olhem para o desenho da Reprodução do Livro do Estudante e analisem qual é a fruta mais pesada e qual é a mais leve. Se considerar pertinente, retome a balança de mão confeccionada pelos estudantes e faça o experimento na prática com outras frutas ou objetos.

Garfo

• O objetivo da atividade 4 é apresentar diferentes tipos de balanças para os estudantes e propor a eles que relacionem a medida de massa de cada item indicado nas balanças à unidade de medida de massa apresentada. Confira se eles empregam a unidade ( kg ou g ) corretamente ao responderem à atividade. Fale sobre a importância de especificar a unidade de medida para que o leitor consiga identificar se o objeto é leve ou pesado. Mencione também que elas fazem parte do Sistema Internacional de Unidades (SI), ou seja, não são utilizadas apenas no Brasil. Se considerar pertinente, explique que existe outro sistema de medidas, chamado Sistema Imperial, que usa a libra como unidade de peso e é usado oficialmente apenas nos Estados Unidos, em Mianmar e na Libéria.

• Converse com os estudantes sobre os diferentes tipos de balança, se eles já conheciam e se há na moradia deles alguma dessas balanças. Destaque que todas têm o mesmo objetivo: serem utilizadas como instrumento de medida de massa. Enfatize que, ao subirmos na balança, o que obtemos é a medida de nossa massa, e não nosso peso.

• Na atividade 5, os estudantes precisam relacionar a quantidade apresentada à unidade de medida em estudo. Caso eles apresentem dificuldade para responder, relembre a relação entre quilograma e grama, e depois pergunte a eles a resposta dos itens, se é kg ou g

O QUILOGRAMA E O GRAMA

4. Comparamos anteriormente objetos sem conhecer a medida de suas massas. O quilograma (kg) e o grama (g) são unidades de medida que utilizamos para medir, por exemplo, a massa de objetos, pessoas, animais, alimentos etc. Essa medida pode ser conferida em certos tipos de balança. Confira a seguir alguns exemplos.

Balança digital de cozinha.

Imagens sem proporção entre si.

Balança analógica de cozinha.

Um quilograma equivale a mil gramas, isto é:

1 quilograma = 1 000 gramas

1 kg = 1 000 g

Escreva, em grama ou quilograma, a medida da massa indicada em cada uma das balanças anteriores.

Resposta: 300 g

Resposta: 150 g

5. Complete cada frase com a unidade de medida mais adequada: kg ou g

a ) No açougue de Olavo, foram vendidos 180 de carne em um dia.

Resposta: No açougue de Olavo, foram vendidos 180  kg de carne em um dia.

b ) No mercado, estão à venda bandejas de morango de 500 .

Resposta: No mercado, estão à venda bandejas de morango de 500  g.

c ) Uma bola de futebol tem cerca de 430 .

Resposta: Uma bola de futebol tem cerca de 430  g

d ) O pai de Rúbia tem 75 .

Resposta: O pai de Rúbia tem 75  kg

6. A escola onde Regiane estuda realizou uma gincana com o objetivo de arrecadar material reciclável. Analise a tabela com a medida de massa, em quilogramas, de material reciclável arrecadado pelas turmas de 2º ano.

Unidades temáticas integradas

Quantidade de material reciclável arrecadado pelas turmas de 2º ano, em quilogramas, em 2027

Turma

Medida de massa (em quilogramas) 13 85 12

Fonte de pesquisa: registros da escola onde Regiane estuda. Usando os dados da tabela, foi construído um gráfico de colunas para divulgar o resultado da arrecadação em um mural.

DICA: Cada equivale a um quilograma.

a ) Qual das turmas arrecadou a maior medida de massa, em quilogramas, de material reciclável?

Resposta: 2º ano A

b ) Utilizando uma calculadora, determine quantos quilogramas de material reciclável foram arrecadados pelas quatro turmas de 2º ano nessa gincana.

Resposta: 38 quilogramas.

ARTICULANDO CONHECIMENTOS

A situação proposta na atividade 6 possibilita a integração com Ciências da Natureza ao abordar a questão da reciclagem de materiais. Para promover um trabalho interdisciplinar de forma integrada, proponha aos estudantes uma pesquisa sobre as diferentes características de materiais presentes em objetos de uso cotidiano, discutindo sua origem, como são descartados e como podem ser usados de maneira mais consciente.

BNCC

06/10/2025 17:44:13

As atividades deste tópico contemplam aspectos da habilidade EF02MA22 da BNCC, pois são apresentados gráficos de colunas simples, abordando diferentes contextos, a fim de que os estudantes interpretem e comparem as informações.

• A atividade 6 estabelece uma integração entre as unidades temáticas de Matemática Números e Probabilidade e estatística, ao trabalhar com dados coletados de medida de massa, em quilograma, de material reciclável arrecadado pelas turmas de 2º ano e apresentar esses dados organizados em uma tabela e em um gráfico.

• A atividade 6 incentiva a interpretação de informações apresentadas em gráficos de colunas simples construídos com base em uma tabela. Explique aos estudantes que, assim como as tabelas, os gráficos são utilizados para facilitar a leitura e a interpretação de dados. Diga a eles que os gráficos também devem conter título e fonte de pesquisa.

• Se necessário, auxilie os estudantes a interpretarem quantos quilogramas de material reciclável cada turma arrecadou, identificando as quantidades no eixo vertical ou contando as partes pintadas nas colunas referentes a cada turma. Providencie antecipadamente calculadoras para os estudantes resolverem o item b.

Medida de massa (em quilogramas)

Fonte de pesquisa: Registros da escola em que Regiane estuda.

Quantidade de material reciclável arrecadado pelas turmas de 2º ano, em quilogramas, em 2027

• Atividade 7 tem como objetivo preparar os estudantes para realizarem a próxima atividade, introduzindo as relações entre unidades de medida de massa de maneira contextualizada. Ao perguntar quantos bolos Olga pode fazer com 1 kg ou 2 kg de farinha, os estudantes são motivados a compreenderem que 1 kg equivale a 1 000 g e, portanto, 500 g é a metade de 1 kg . Essa noção é um pré­requisito importante para o trabalho com medidas. Para tornar a atividade mais significativa, leve para a sala de aula algumas embalagens vazias com rótulos de 500 g e de 1 kg, como embalagens de farinha, de feijão ou de açúcar, e permita aos estudantes que manipulem e comparem essas medidas. Durante a discussão, chame a atenção dos estudantes para o seguinte raciocínio: 500 gramas mais 500 gramas equivalem a 1 000 gramas, ou seja, 1 kg , para reforçar com eles a equivalência entre grama e quilograma.

• Na atividade 8, peça aos estudantes que recortem e utilizem a representação dos pesos disponíveis no Material complementar no final da Reprodução do Livro do Estudante, auxiliando­os, com a sua supervisão, para evitar possíveis riscos com a tesoura, na execução dessa atividade.

• O objetivo da atividade 8 é desenvolver o raciocínio lógico­matemático e as noções de equivalência e equilíbrio. Motive os estudantes a adicionarem os valores dos pesos antes de colarem. Incentive o trabalho em duplas ou grupos pequenos, se desejar promover a troca de ideias. Para estudantes que apresentam dificuldades, ofereça pistas visuais e permita o uso de material dourado ou tampinhas para simular os pesos antes de colar. Para estudantes que avançam com mais facilidade, proponha que criem novos desafios de balança para os colegas.

7. Para fazer um bolo, Olga usa 500 g de farinha. Quantos bolos ela pode fazer com:

Resposta: 2 bolos.

a ) 1  kg de farinha? bolos.

Resposta: 4 bolos.

b ) 2  kg de farinha? bolos.

8. Uma balança de dois pratos está em equilíbrio quando as massas em cada um dos pratos têm a mesma medida. Em cada item, cole os pesos necessários para manter a balança em equilíbrio. Para isso, recorte a representação dos pesos que se encontram na página 285 do Material complementar

Dica: Todos os pesos que você recortou deverão ser usados para equilibrar as balanças. Feijão 1 kg

Possível resposta: Os estudantes devem colar, no prato vazio das balanças, os seguintes pesos: Balança A: 3 pesos de 1 kg e 2 pesos de 500 g; Balança B: 1 peso de 5 kg e 5 pesos de 1 kg; Balança C: 4 pesos de 500 g.

9. Juliana verificou a medida da massa de alguns objetos e anotou cada um deles no caderno. Depois, ela realizou outras verificações utilizando os mesmos objetos.

Com base nessas informações, escreva a medida da massa que deve aparecer no visor de cada balança a seguir.

A. B.

Resposta: 990 g

EXPERIMENTE

Resposta: 660 g

Bola de futebol : 420 g

Caderno : 310 g

Tubo de cola : 90 g

Grampeador : 350 g

Livro : 570 g

C.

Resposta: 660 g

10. Forme, no máximo, 4 equipes para brincar de Adivinhe a medida da massa dos objetos

O professor vai mostrar um objeto de cada vez, e as equipes farão estimativas, em gramas ou quilogramas, da medida da massa dos objetos. Todos devem registrar as medidas estimadas em um quadro, no caderno.

Após todas as equipes anotarem seus palpites, o professor colocará o objeto na balança. A equipe que acertar ou registrar a medida mais próxima da massa real do objeto ganha um ponto e registra no caderno.

Qual foi a pontuação de cada equipe? Registre no quadro ao lado.

Pontos por equipe

Equipe 1234

Pontos

Resposta pessoal. Espera-se que os estudantes anotem as suas estimativas em relação à medida da massa dos objetos.

Minha equipe marcou pontos.

AVALIANDO

Objetivos

Comparar medidas de massa com o auxílio de instrumentos de medição (balança).

Reconhecer o quilograma e o grama como unidades padronizadas de medida de massa.

Sugestão de intervenção

Peça aos estudantes que estimem a medida de massa de diferentes objetos do contexto

06/10/2025 17:39:18

escolar, como borracha, caderno, apagador de lousa, apontador e estojo. Solicite que anotem os valores no caderno, usando as unidades de medida estudadas no subtópico O quilograma e o grama. Com o auxílio de uma balança digital, verifiquem a medida de massa real dos objetos e corrijam as respostas, se necessário.

• O objetivo da atividade 9 é que os estudantes percebam que, ao colocar objetos com medidas de massa diferentes na balança, o valor exibido no visor será igual à soma da medida de massa de cada objeto. Explique isso a eles, caso não consigam responder, levantando questionamentos sobre a medida de massa de cada objeto e anotando o valor próximo ao objeto na balança para auxiliá­los nos cálculos.

• Para realizar a atividade 10, providencie, se possível, uma pequena balança digital e objetos com medidas de massa diferentes. Observe se os estudantes estão usando corretamente as unidades de medida para indicar a medida de massa dos objetos. Se o valor estimado estiver muito distante do real, peça a eles que justifiquem suas respostas, para que seja feita a correção adequada.

• A ativi dade 10 também é inclusiva, por utilizar a brincadeira, que motiva o sentido da visão.

• Nas atividades desta página, oportunize a realização em pares, em grupos maiores e/ou menores para incentivar a interação social. Caso haja estudantes que necessitem de auxílio e aceitem ajuda dos colegas, proponha essa interação. Aproveite para propor atividades colaborativas que visem à inclusão dos estudantes com deficiência visual ou auditiva. Caso haja estudantes com deficiência visual, permita a eles que segurem os objetos para estimar sua medida de massa.

• Para que os estudantes compreendam as medidas de capacidade e o uso do litro e do mililitro como unidades de medida padronizadas, é necessário que tenham desenvolvido algumas noções e experiências no cotidiano. Como pré­requisito, é preciso que tenham observado, comparado e estimado situações em que fosse preciso identificar, por exemplo, em qual recipiente cabe mais e em qual cabe menos líquido. Também é preciso que tenham vivenciado ações em que o líquido tenha transbordado do recipiente, percebendo que recipientes de formatos diferentes podem ter capacidades iguais ou diferentes.

• Providencie e leve para a sala de aula recipientes com diferentes dimensões e medidas de capacidade. Utilize esses recipientes para realizar, na prática, algumas comparações com os estudantes, como é feito na atividade 1. Promova questionamentos, de maneira que eles façam suas estimativas antes de cada comparação e consigam entender a diferença entre a medida de capacidade de cada recipiente. Pode ser interessante realizar algumas padronizações em relação à medida, como a quantidade de garrafas necessárias para encher um garrafão ou a quantidade de vezes que a garrafa conseguirá encher o copo.

BNCC

As atividades deste tópico desenvolvem a habilidade EF02MA17 da BNCC, pois propõem aos estudantes que identifiquem e comparem a medida de capacidade de diferentes objetos usando unidades de medida não padronizadas e padronizadas, como litro e mililitro.

MEDIDAS DE CAPACIDADE

1. Em nosso dia a dia, podemos encontrar diferentes recipientes. Confira a seguir alguns deles.

Assim como comparamos medidas de massa e de comprimento, podemos determinar se cabe mais conteúdo em um recipiente ou em outro. Vamos estudar esse assunto?

Garrafão Galão Copo Garrafa

Se a garrafa estiver cheia de água e seu conteúdo for despejado no copo vazio até enchê-lo, vai sobrar água na garrafa. Nesse caso, dizemos que a medida de capacidade da garrafa é maior do que a do copo, ou seja, cabe mais líquido na garrafa que no copo.

a ) Suponha que o galão esteja cheio de água e seu conteúdo seja despejado no garrafão vazio. Nesse caso, o garrafão ficaria completamente cheio? Por quê?

Resposta: Não. Porque a medida de capacidade do garrafão é maior do que a do galão.

b ) Complete as frases com as palavras maior ou menor, de acordo com a medida de capacidade dos recipientes apresentados.

Resposta: O garrafão é o recipiente que tem a maior medida de capacidade.

• O garrafão é o recipiente que tem a medida de capacidade.

Resposta: O copo é o recipiente que tem a menor medida de capacidade.

• O copo é o recipiente que tem a medida de capacidade.

Resposta: A medida de capacidade da garrafa é menor do que a do galão.

• A medida de capacidade da garrafa é do que a do galão.

Resposta: A medida de capacidade do galão é maior do que a da garrafa.

• A medida de capacidade do galão é do que a da garrafa.

2. Alguns recipientes foram colocados sobre a mesa.

Copo Jarra Balde Xícara

a ) Qual desses recipientes tem:

• a maior medida de capacidade?

Copo

Jarra

• a menor medida de capacidade?

Copo

Resposta: Os estudantes devem marcar um X em Balde.

Jarra Balde Balde Xícara Xícara

Resposta: Os estudantes devem marcar um X em Xícara.

b ) Qual recipiente tem medida de capacidade menor do que a do copo?

Resposta: A xícara.

c ) Qual recipiente tem medida de capacidade maior do que a da xícara e menor do que a da jarra?

Resposta: O copo.

3. Para encher o recipiente maior, Joana utiliza 4 copos iguais, todos com a mesma medida de capacidade e totalmente cheios de água. Com base na experiência de Joana, escreva a quantidade de copos de água despejados em cada recipiente nos itens a seguir.

Dica: Os recipientes e os copos em cada item são iguais ao recipiente e aos copos utilizados por Joana.

A. B.

C.

Resposta: 2 copos.

Resposta: 1 copo.

Resposta: 3 copos.

06/10/2025 17:39:19

• O objetivo da atividade 2 é verificar se os estudantes reconhecem a diferença nas medidas de capacidade dos recipientes. Caso haja dúvidas ao resolverem a atividade, lembre­os de que a medida de capacidade do recipiente tem relação com a quantidade de líquido que ele pode armazenar. Para que eles associem a quantidade de líquido nesses recipientes, é conveniente fazer questionamentos como “É mais fácil beber uma jarra de água ou um copo de água?”.

• Caso os estudantes tenham dificuldades para responderem à atividade 3, faça questionamentos que os levem a observar que, no item a, Joana encheu o recipiente até a metade, permitindo que assim façam uma associação e percebam que precisam da metade da quantidade de copos de água, ou seja, 2 copos de água. Essa relação é a proposta da atividade, mas o mesmo pode ser feito para os outros itens.

HELOÍSA

• Leve para a sala de aula alguns recipientes que tenham exatamente a medida de capacidade de 1 L e recipientes com medida de capacidade de 500 mL Apresente­os aos estudantes a fim de que percebam a diferença entre eles. Uma sugestão é utilizar as garrafas de água dos próprios estudantes para medidas, além de copos plásticos para medidas menores do que 500 mL

• Na atividade 4, conduza a conversa, de modo que os estudantes identifiquem a necessidade de usar essas unidades de medida de capacidade no dia a dia. Espera­se que eles digam que costumam comprar ou consumir produtos usando o litro e o mililitro como unidades de medida. Entre esses produtos estão, por exemplo, leite, água, iogurtes e sucos.

• O objetivo da atividade 5 é que os estudantes identifiquem os recipientes com medida de capacidade menor do que 1 L. Caso eles não consigam identificar esses recipientes, mostre que no rótulo de cada embalagem geralmente está especificada a medida de capacidade e relembre a relação entre litro e mililitro.

ATIVIDADE EXTRA

Providencie com antecedência alguns folhetos de supermercados e uma cartolina para a confecção de um cartaz. Peça aos estudantes que recortem imagens de produtos nos folhetos com medidas em litro e em mililitro.

Em seguida, oriente­os a colar essas imagens no cartaz, separando os produtos com medidas em litro dos que têm medidas em mililitro. Após a organização dessas imagens no cartaz, combine com a turma um momento para divulgar aos pais e responsáveis as produções expostas na sala de aula.

O LITRO E O MILILITRO

4. Leia a conversa a seguir entre Elias e a atendente de um supermercado.

Por favor, você tem água em galão de 20 litros?

4. Resposta pessoal. Espera-se que os estudantes citem pelo menos duas situações do dia a dia em que utilizem o litro e o mililitro, como ao comprar água, ao preparar uma receita que líquidos (leite, óleo, água), ao abastecer o carro, ao comprar determinado recipiente, ao ministrar um remédio líquido, entre outras situações. exija usar

Temos água em galões de 20 litros e também em garrafas com 500 mililitros.

Nessa conversa, foram citadas duas unidades de medida de capacidade padronizadas: o litro (L) e o mililitro (mL).

Para medir a capacidade de um recipiente, podemos utilizar diferentes unidades de medida, entre elas o litro e o mililitro. Em geral, usamos o mililitro para representar quantidades menores do que 1 litro.

1 litro = 1 000 mililitros

1 L = 1 000 mL

Converse com seus colegas e com o professor sobre algumas situações do dia a dia em que utilizamos o litro e o mililitro. Cite pelo menos duas delas.

5. Marque um X nas embalagens que têm medida de capacidade menor do que 1 L

500 mL

250 mL

Resposta: Os estudantes devem marcar um X nas alternativas A, B e E

A.

B.

C. D.

E.

6. A medida de capacidade de cada recipiente a seguir é de 1 L Sabendo que cada marcação nesse recipiente corresponde à medida de 200 mL de capacidade, complete os itens a seguir com a quantidade de líquido correspondente.

A. B. C. D.

Resposta: 200 mL

Resposta: 1 000 mL

Resposta: 800 mL

Resposta: 400 mL

7. Complete cada frase com a unidade de medida mais adequada:

L ou mL

a ) Para encher um certo modelo de piscina são necessários

1 000 de água.

Resposta: Para encher um certo modelo de piscina são necessários 1 000  L de água.

b ) Em determinada receita, são utilizados 100 de leite de coco.

Resposta: Em determinada receita, são utilizados 100  mL de leite de coco.

c ) É comum encontrar água de coco em caixinhas de 200

Resposta: É comum encontrar água de coco em caixinhas de 200  mL

8. Isadora foi orientada por uma nutricionista a beber cerca de 2  L de água por dia.

a ) Se Isadora seguir essa orientação, quantos litros de água, aproximadamente, ela deverá beber em

Resposta: 2 × 7 = 14. 14 L de água.

7 dias? L de água.

Nutricionista: profissional da área de saúde que se ocupa da nutrição e da dieta alimentar.

b ) Quantas garrafas de 500 mL de água Isadora deve beber para

atingir a meta de 2 L de água por dia? garrafas de 500 mL.

Resposta: 500 mL + 500 mL + 500 mL + 500 mL = 2 000 mL  = 2 L 4 garrafas de 500 mL

profissionais da saúde. Ao trabalhar a atividade 8, aproveite para conversar com os estudantes sobre a necessidade de ingestão diária e adequada de água para o corpo. Pergunte se costumam beber água com certa frequência ou se esperam sentir sede para fazer isso. Diga­lhes que a sede é um sintoma tardio, ou seja, ao sentirmos sede, a quantidade de líquidos do organismo já se encontra abaixo do desejado. Fale também que a falta de água pode provocar alguns sintomas, como dor de cabeça, tontura, fadiga e fraqueza, e que seu excesso também é prejudicial ao organismo.

AVALIANDO

Objetivos

Reconhecer o litro e o mililitro como unidades fundamentais de medida de capacidade.

Resolver situações­problema que envolvam o litro e o mililitro.

Sugestão de intervenção

Leve para a sala de aula um recipiente transparente com medida de capacidade de 1 L, por exemplo, uma garrafa. Leve também alguns copos com água que

• Se os estudantes apresentarem dificuldades ao respon derem à atividade 6, informe que, em cada item, a quantidade total de líquido do recipiente será igual à soma da quantidade em cada marcação (200 mL). O objetivo da atividade é que eles façam essa associação. Se julgar necessário, eles podem anotar em cada marcação para, posteriormente, realizar a soma. Além disso, verifique se eles observam que o recipiente B está cheio, então a quantidade de líquido neste caso corresponde à sua medida de capacidade total, que está descrita no enunciado da atividade, para que assim desenvolvam a compreensão de textos.

• Na atividade 7, verifique se os estudantes estão completando a frase com a unidade adequada. Pode ser necessário que você relembre a relação entre litro e mililitro, para que fique mais claro.

• A atividade 8 propõe aos estudantes que usem a adição e a multiplicação como instrumentos de resolução, identificando que 2 L é o mesmo que 2 000 mL

BNCC

Ao explorar o assunto de ingestão diária de água, é possível articular o contexto com o tema contemporâneo transversal Saúde, visto que os estudantes devem refletir sobre a importância do consumo diário adequado de água para o bem­estar, como indicam os médicos, nutricionistas e outros

06/10/2025 17:39:20

tenham a medida de capacidade menor do que a do recipiente. Informe aos estudantes a medida de capacidade do recipiente e dos copos.

Faça perguntas aos estudantes, como: “Quantos copos de água são necessários para encher totalmente o recipiente?”; “Quantos copos de água são necessários para encher a metade do recipiente?”. Anote na lousa as perguntas e as respostas e depois verifique com eles, na prática, a resposta correta.

• Para o trabalho com o tópico Medidas de tempo, é importante que os estudantes tenham desenvolvido algumas noções sobre a passagem do tempo no dia a dia. Assim, como pré­requisito, eles devem reconhecer eventos que ocorrem em diferentes momentos do dia (manhã, tarde e noite) e estabelecer uma sequência lógica entre atividades do cotidiano.

• Antes de iniciar este tópico, se julgar conveniente, organize a turma em duplas e providencie um calendário do ano vigente para cada uma delas. Peça aos estudantes que observem o calendário e identifiquem o ano a que se refere, os meses do ano e as semanas. Solicite a cada estudante da dupla que marque, no calendário, uma data que considera importante e justifique sua escolha ao colega. Verifique se eles reconhecem algumas datas comemorativas e peça­lhes que anotem essa informação no calendário. Ao fim, sugira às duplas que troquem informações sobre as datas indicadas por elas.

• Durante a resolução da atividade 1, incentive os estudantes a refletirem sobre a percepção subjetiva do tempo em diferentes situações e reconhecerem instrumentos utilizados para medir o tempo de forma padronizada. No item a, valorize todas as respostas, incentivando a turma a compartilhar exemplos do cotidiano. No item b, os estudantes devem reconhecer os instrumentos utilizados para medir o tempo de maneira objetiva e padronizada.

• Na atividade 2, peça aos estudantes que recortem e utilizem o calendário disponível no Material complementar no final da Reprodução do Livro do Estudante, auxiliando­os, com a sua supervisão, para

MEDIDAS DE TEMPO

1. Acompanhando a rotina de seu dia, Tainá ficou pensativa. Observe o que ela pensou.

Quando estou brincando, o tempo passa tão rápido!

1. a) Resposta pessoal. Espera-se que os estudantes expliquem por que o tempo parece passar de maneira diferente ao realizar algumas tarefas. Verifique se eles percebem que, na verdade, o tempo não muda, ele sempre passa na mesma velocidade, um segundo após o outro. O que muda é a nossa

Menina indígena pensativa.

Quando estou arrumando minhas coisas, parece que demora um tempão!

1. b) Resposta pessoal. Espera-se que os estudantes expliquem quais instrumentos de medida de tempo eles conhecem, como relógio de pulso, relógio de parede, cronômetro, despertador, computadores, calendário, painéis eletrônicos em transportes e temporizadores de eletrodomésticos. percepção sobre ele, ou seja, como o sentimos passar.

a ) ;Em sua opinião, por que o tempo parece passar de maneira diferente para algumas tarefas?

b ) Para mostrar a duração das tarefas, de maneira padronizada para todas as pessoas, foram criados alguns instrumentos de medida de tempo. Escreva em seu caderno alguns desses instrumentos que você conhece e usa em seu dia a dia. Depois, converse com seus colegas e com o professor sobre eles.

REGISTRANDO O TEMPO NO CALENDÁRIO

2. O calendário é um instrumento de medida de tempo. Nele, são registrados os meses, as semanas e os dias do ano. Recorte o calendário da página 287 do Material complementar e cole-o no caderno. No calendário apresentado, os domingos e os feriados estão destacados com uma cor diferente.

Dica: Ao consultar o calendário que você recortou, note que ele tem 12 meses, que é a duração de tempo de um ano

evitar possíveis riscos ao usar a tesoura na execução desta atividade.

• Durante a resolução da atividade 2, diga aos estudantes que os nomes dos dias da semana estão escritos de forma abreviada no calendário. Com a ajuda deles, escreva na lousa cada um desses nomes e suas respectivas abreviações. Para fixar o número referente a cada mês, você pode escrever na lousa algumas datas especiais para os estudantes no formato DD/MM/AAAA.

• Avalie o interesse deles sobre o assunto e, se julgar conveniente, pesquise outros tipos de calendários usados por outros povos atualmente,

como o chinês, o muçulmano, o iorubá, o judaico, o juliano e o kalapalo. Também é possível mostrar calendários usados no passado por outros povos, mas que já não são usados hoje em dia, como o calendário maia e o egípcio.

• Converse com os estudantes sobre a maneira como o calendário é utilizado por eles e pelas pessoas de seu convívio. Pergunte se costumam agendar seus compromissos fazendo marcações no calendário ou se utilizam essa ferramenta somente para se orientarem no tempo.

FABIO COLOMBINI

Usando o calendário que você destacou e colou e conforme a ordem em que os meses ocorrem no ano, complete os quadros a seguir.

Meses 1 ao 6 do ano Número do mêsNome do mês

Janeiro 2 Fevereiro 3 Março 4

Resposta: 4: Abril; 5: Maio; 6: Junho

Meses 7 ao 12 do ano Número do mêsNome do mês

Julho

Resposta: 8: Agosto; 9: Setembro;

10: Outubro; 11: Novembro; 12: Dezembro

3. Consulte o calendário que você destacou e responda às questões.

a ) Quais meses do ano têm 30 dias?

Resposta: Abril, junho, setembro e novembro.

b ) Quais meses do ano têm 31 dias?

Resposta: Janeiro, março, maio, julho, agosto, outubro e dezembro.

c ) Quantos dias o mês de fevereiro tem nesse calendário?

Resposta: 28 dias.

d ) De fevereiro até setembro, quantos meses se passaram?

Resposta: 7 meses.

4. Quantos dias se passaram do dia 3 até o dia contornado de azul no mês de novembro do calendário ao lado?

Resposta: 18 dias.

relação com o evento das Olimpíadas, mostrando a eles que elas ocorrem de 4 em 4 anos, sempre nos anos bissextos.

• A atividade 4 também foi proposta com o intuito de que os estudantes consigam identificar a duração entre duas datas. Caso eles não saibam responder, comente que basta eles contarem o número de dias entre as datas no calendário. Atente a respostas com um dia a mais ou a menos e, se necessário, faça a contagem com os estudantes.

CALENDÁRIO 2027 NOVEMBRO

2-Finados 15-ProclamaçãodaRepública 20-DiaNacionaldeZumbie daConsciênciaNegra

06/10/2025 17:37:15

• O objetivo dos itens a e b da atividade 3 é que os estudantes identifiquem os meses com 30 dias e os meses com 31 dias. Aproveite o momento para ensinar o “truque da mão”, para que os estudantes memorizem a quantidade de dias de cada mês. Nesse truque, os estudantes devem fechar as mãos e contar os meses nas articulações dos dedos. Os meses com 31 dias são indicados nas articulações (ossos) e os que têm 30 dias são indicados nos espaços entre elas, com exceção de fevereiro, que tem 28 ou 29 dias.

• No item c da atividade 3, comente que, de 4 em 4 anos, o mês de fevereiro tem 1 dia a mais do que o comum, isto é, tem 29 dias. Os anos em que isso ocorre são chamados anos bissextos. Cite como exemplo os anos de 2008, 2012, 2016 e 2020. Caso algum estudante questione o motivo, explique a relação dessa variação com o movimento que o planeta Terra faz ao redor do Sol, ressaltando que o assunto será estudado de forma mais aprofundada quando eles estiverem no 4º ano. Para ajudar os estudantes a identificarem os anos bissextos, se julgar oportuno, estabeleça uma

• Na atividade 5, converse com os estudantes sobre as suas atividades durante os dias da semana, se eles seguem uma rotina ou um planejamento. Ressalte a importância de organizar a semana com o objetivo de reservar momentos para estudar (além do período na escola), para cumprir suas responsabilidades em casa, para a prática de atividades física, para ter atividades de lazer com a família e amigos, para descansar etc. Como sugestão de ampliação, pode ser construído um cronograma semanal com os estudantes, indicando o tempo gasto com cada atividade e os dias da semana.

• A atividade 5 trabalha a ordenação dos dias da semana. No dia a dia, é comum a interpretação de que o primeiro dia da semana seja segunda­feira, por ser o primeiro dia útil para a maioria das pessoas. Nesse caso, converse com os estudantes e diga que domingo é considerado o primeiro dia da semana.

ARTICULANDO

CONHECIMENTOS

No boxe complementar, aproveite a relação com o componente curricular de História e converse com os estudantes sobre a rotina de diferentes povos e suas formas distintas de medir o tempo, valorizando o conhecimento tradicional dos povos indígenas e a observação da natureza como forma de organização da vida cotidiana. Para promover um trabalho interdisciplinar de forma integrada, proponha aos estudantes uma pesquisa para identificar diferentes marcadores do tempo presentes na comunidade, como relógio e calendário.

5. Além dos meses do ano, o calendário mostra os dias do mês e os nomes dos dias da semana. Uma semana é composta de 7 dias, e domingo é o primeiro dia da semana.

Complete o esquema a seguir com o nome dos outros dias da semana.

1º dia da semana:

Domingo

Resposta: Domingo, Segunda-feira, Terça-feira, Quarta-feira, Quinta-feira, Sexta-feira, Sábado

2º dia da semana:

5º dia da semana:

3º dia da semana:

4º dia da semana: Quarta-feira

6º dia da semana:

7º dia da semana:

MEDIDAS DE TEMPO E AS TRADIÇÕES POTIGUARAS

Os indígenas potiguaras, que moram na Paraíba, mantêm as tradições de plantio e colheita usando os próprios instrumentos de medida de tempo. Eles se baseiam nas fases da lua, nos movimentos das marés e em outros fenômenos naturais. Usando o conhecimento dos ancestrais e a memória de eventos ou fenômenos passados, exercem regularmente suas atividades tradicionais de agricultura, pesca e extrativismo.

Por exemplo, a colheita do milho é feita nos meses de junho e julho ou em janeiro e fevereiro. A mandioca é plantada e colhida em todos os meses do ano. Já entre os meses de dezembro e fevereiro, eles se dedicam à colheita de caju.

BNCC

As atividades desta página contribuem para o desenvolvimento da habilidade EF02MA18 da BNCC, pois exigem que os estudantes identifiquem a duração de intervalos de tempo entre duas datas e o intervalo entre elas.

6. O gráfico a seguir apresenta a quantidade mensal de filmes a que Marilda assistiu de janeiro a abril de 2027.

Quantidade mensal de filmes a que Marilda assistiu de janeiro a abril de 2027

Quantidade de filmes

JaneiroFevereiroMarço Abril

a ) A quantos filmes Marilda assistiu em fevereiro?

b ) Em que mês ela assistiu a apenas 5 filmes?

Unidades temáticas integradas

Fonte de pesquisa: anotações de Marilda.

Resposta: 12 filmes.

Resposta: Janeiro.

c ) Nos quatro primeiros meses de 2027, Marilda assistiu, ao todo, a quantos filmes? Efetue os cálculos em uma calculadora.

Resposta: 5 + 12 + 3 + 4 = 24. Marilda assistiu a 24 filmes nos quatro primeiros meses de 2027.

7. A cada dois meses, um barco visita as comunidades ribeirinhas da região de Carauari, na Amazônia. O objetivo é coletar produtos locais, como açaí, farinha, borracha, frutas, sementes e pirarucu. Esses produtos são vendidos a preços justos ou enviados para compradores de outros municípios, tudo isso navegando pelas águas do Rio Juruá.

a ) Se a última coleta ocorreu em maio, em que mês o barco havia

passado anteriormente?

Resposta: No mês de março.

b ) A partir de maio, em quais meses ocorrerão as duas próximas visitas do barco coletor?

Resposta: As duas próximas visitas ocorrerão nos meses de julho e setembro.

• A atividade 6 estabelece uma integração entre as unidades temáticas de Matemática Números e Probabilidade e Estatística, ao relacionar a quantidade mensal de filmes a que Marilda assistiu de janeiro a abril de 2027 e ao organizar essas informações em um gráfico de colunas, com o intuito de que os estudantes as interpretem.

• Na atividade 6, confira se os estudantes apresentam dificuldades na interpretação do gráfico e faça explicações para toda a turma, mostrando como podem reconhecer, por exemplo, a quantidade de filmes assistidos em janeiro e em fevereiro por Marilda, ressaltando que as quantidades podem ser obtidas no eixo vertical ou contando as partes pintadas nas colunas referentes a cada mês.

• Aproveite a atividade 7 para reforçar a organização da sequência dos meses e incentive a turma a contá­los de dois em dois, contribuindo para o desenvolvimento do raciocínio. O contexto cultural e geográfico dessa atividade permite valorizar a diversidade regional brasileira, motivando o interesse dos estudantes por outras realidades e estilos de vida, contribuindo para uma aprendizagem com base em situações reais.

BNCC

REFERÊNCIAS COMPLEMENTARES

WALL­E. Direção de Andrew Stanton, 2008. 1 DVD (103 min).

O planeta Terra estava muito poluído, a população deixou robôs para limpar o planeta e foi viver em uma nave. Wall­e é o último desses robôs e sua vida consiste em compactar o lixo existente no planeta. Um dia surge uma nave, que traz um novo e mais moderno robô chamado Eva.

06/10/2025 17:37:16

O contexto desta atividade permite a articulação com os temas contemporâneos transversais Diversidade cultural e Trabalho, pois ressalta como ocorre o processo de comercialização de produtos naturais de uma comunidade ribeirinha do Amazonas, ressaltando a importância da venda a preços justos discutindo as formas de subsistência dessas comunidades.

Mês

• Se os estudantes apresentarem dificuldade para responder à atividade 8 , sugira a eles que escrevam todos os dias da semana e observem de acordo com o enunciado quais são os dias em que Michele trabalha e em quais ela não trabalha. O objetivo é que eles reconheçam 1 semana como um período de 7 dias e identifiquem o intervalo de tempo entre as datas.

• Para a resolução da atividade 9, caso seja necessário, desenhe na lousa o calendário do mês de fevereiro. É importante que os estudantes percebam que a data da consulta de Jussara (26) é a soma da data atual (12) com os 14 dias restantes.

• A atividade 10 tem o objetivo de fazer os estudantes identificarem a diferença de intervalo entre duas datas. Avalie a possibilidade de levar alguns produtos para a sala de aula, a fim de que os estudantes analisem suas datas de validade. Faça questionamentos semelhantes aos da atividade e registre as respostas dos estudantes na lousa. Comente que o leite e a margarina têm prazo de validade menor porque são produtos do gênero alimentício, podendo ocorrer a proliferação de bactérias que fazem mal à saúde e podem causar doenças. Em geral, quanto mais água e gordura os alimentos tiverem em sua composição, mais rapidamente vão se deteriorar.

• Converse com os estudantes a respeito da importância de verificar a validade do produto antes de comprá­lo. Diga que é importante conscientizar também as pessoas da família a desenvolver o hábito de sempre verificar essa data, caso ainda não tenham essa prática. Diga que o lugar em que a data de validade é indicada pode variar conforme o produto e que não devemos consumi­lo com a validade vencida, pois pode ser prejudicial à saúde.

8. Michele é cabeleireira e trabalha em um salão de quinta-feira a sábado.

Resposta: 3

a ) Quantos dias da semana Michele trabalha nesse salão?

b ) Em quais dias da semana Michele não trabalha nesse salão?

Resposta: Domingo, segunda-feira, terça-feira e quarta-feira.

9. Jussara vai fazer uma consulta médica. Sabendo que hoje é dia 12 de fevereiro e a consulta dela será daqui a 14 dias, em que dia será a consulta médica?

Resposta: 26 de fevereiro.

10. A seguir, estão apresentadas a data de fabricação e a data de validade de alguns produtos que compramos no supermercado.

Leite

Fabricação: 12/1/2027. Validade: 12/5/2027.

Margarina

Fabricação: 03/01/2027. Validade: 03/07/2027.

Xampu

Fabricação: Agosto/2025.

Validade: Agosto/2029.

Amaciante de roupas

Fabricação: Mar/2025.

Validade: Mar/2027.

a ) Quais desses produtos têm o prazo de validade maior do que um ano?

Resposta: O xampu e o amaciante de roupas.

b ) Quais desses produtos têm o prazo de validade de seis meses?

Resposta: A margarina.

c ) Suponha que um consumidor comprou o leite no dia 3/5/2027. Esse leite continuou adequado para consumo 5 dias após a compra?

Resposta: Sim.

d ) Se o leite for comprado por outra pessoa no mesmo dia indicado no item c, ele ainda estará adequado para consumir duas semanas depois da compra? Por quê?

Resposta: Não. Porque, após duas semanas (14 dias), o prazo de validade se esgotou.

MEDINDO O TEMPO NO RELÓGIO

11. Um dos instrumentos utilizados para medir o tempo é o relógio

Confira o registro de alguns momentos em um relógio de ponteiros e em um relógio digital.

Relógios marcando 7 horas (7 h)

A.

B. O ponteiro maior indica os minutos

O ponteiro menor indica as horas

Relógio de ponteiros.

Indica as horas

Relógio digital.

a ) No relógio A, o ponteiro maior aponta para qual número?

Indica os minutos Resposta: 12

b ) No relógio B, o que indica que são exatamente 7 horas?

Resposta: 00

INSTRUMENTOS DE MEDIDA DE TEMPO HISTÓRICOS

Atualmente, utilizamos com frequência os relógios de ponteiros e os relógios digitais. Mas nem sempre foi assim. Antigamente, as pessoas utilizavam outros instrumentos para medir o tempo

• Ao iniciar este subtópico com os estudantes, aproveite para verificar o conhecimento prévio deles em relação ao relógio. Pode ser necessário retomar também a leitura das horas nos relógios. Verifique se eles sabem quantas horas tem um dia e que ele pode ser dividido em períodos: manhã, tarde, noite e madrugada. Diga ­ lhes que utilizamos as horas e os minutos, indicados em relógios, para registrar o tempo que passamos dormindo, brincando ou estudando, por exemplo, ou mesmo para saber o momento previsto de realização dessas atividades.

• Se possível, leve para a sala de aula um relógio de ponteiros e/ou um relógio digital para que os estudantes verifiquem esses objetos e identifiquem a hora marcada em cada um deles. Como sugestão de ampliação, eles podem construir um relógio de Sol.

Imagens sem proporção entre si.

Relógio de Sol. Ampulheta.

No relógio de Sol, a hora é estimada pela sombra do pino no mostrador.

Na ampulheta, o tempo é medido pela passagem da areia de um compartimento para o outro, por meio de um orifício.

ARTICULANDO CONHECIMENTOS

No boxe complementar, aproveite a relação com o componente curricular de História e converse com os estudantes sobre a rotina deles nos três grandes períodos do dia: manhã, tarde e noite. Diga­lhes que todos, geralmente, temos rotinas diferentes e que algumas pessoas, para organizarem melhor seus afazeres e compromissos, utilizam uma agenda. Proponha a eles que, no caderno, construam uma agenda para registrar as atividades do dia seguinte. Peça­lhes que escrevam a data e o período do dia de suas principais atividades, identificando e organizando temporalmente fatos da vida cotidiana.

BNCC

06/10/2025 17:37:19

As atividades deste subtópico têm o objetivo de propiciar aos estudantes o desenvolvimento da capacidade de medir a duração de um intervalo de tempo por meio de relógios e registrar os horários do início e do fim desse intervalo, contemplando, assim, a habilidade EF02MA19 da BNCC.

• A atividade 11 apresenta dois tipos de relógio para os estudantes: o relógio de ponteiros e o relógio digital, com o intuito de que eles reconheçam que esses instrumentos são utilizados para medir o tempo. No item b, mostre aos estudantes que, no relógio digital, os dois­pontos (:) separam as horas dos minutos.

• Na atividade 12, é apresentado um novo termo para os estudantes: meio­dia Reforce o significado dessa expressão. Nesse ponto, você também pode falar da expressão meia­noite, cujo uso também é comum.

• Avalie se os estudantes desenham os ponteiros do relógio corretamente. Na atividade 13, o objetivo é que eles consigam ler e representar a hora nos dois tipos de relógio trabalhados na Reprodução do Livro do Estudante. Uma sugestão é levar para a sala de aula um relógio de ponteiros e deixar que eles ajustem a hora do relógio de acordo com o que é pedido na atividade. Você pode também propor outros horários e pedir a eles que os representem no caderno.

• Aproveite a atividade 14 para conversar com os estudantes sobre a importância de dedicar um tempo em casa para os estudos, a fim de que possam resolver as atividades propostas para casa. Incentive também a leitura de livros nesses momentos de estudos em casa. Se eles não tiverem esse hábito, proponha que comecem a praticá­lo com poucos minutos diários, aumentando esse tempo gradativamente. Caso os estudantes estejam em uma escola integral, na qual sugere­se a redução do envio de tarefas para casa, proponha à turma a criação de um “momento da leitura”, separando 15 minutos diários para a prática. Leve­os à biblioteca para que escolham uma obra ou leia com eles um livro, para discuti­lo em um momento oportuno.

12. O relógio a seguir indica o horário em que Aroldo iniciou seu almoço.

a ) Nesse relógio, o ponteiro maior está apontando para o , e o ponteiro menor está apontando para o b ) De acordo com esse relógio, Aroldo iniciou seu almoço às horas ou ao meio-dia

Resposta: Nesse relógio, o ponteiro maior está apontando para o 12, e o ponteiro menor está apontando para o 12

Relógio.

Resposta: De acordo com esse relógio, Aroldo iniciou seu almoço às 12 horas ou ao meio-dia.

13. Desenhe os ponteiros nos relógios a seguir de acordo com a hora indicada no relógio digital.

13. C. Resposta: Os estudantes devem desenhar o ponteiro maior apontando para o 12 e o menor para o 10.

Resposta: Os estudantes devem desenhar o ponteiro maior apontando para o 12 e o menor para o 6.

13. B. Resposta: Os estudantes devem desenhar o ponteiro maior apontando para o 12 e o menor para o 9.

14. Eleonor tem o hábito de estudar em casa. Ela começa às 2 horas da tarde e passa 3 horas estudando.

a ) Registre nos relógios o horário em que Eleonor começa a estudar e o horário em que termina de estudar.

Resposta: 02

Resposta: 05

Começa a estudar Termina de estudar

b ) Qual é o horário em que você começa a estudar em casa? Quanto tempo você costuma passar estudando em casa?

Resposta pessoal. Espera-se que os estudantes respondam qual é a hora em que eles começam a estudar em casa e quanto tempo passam estudando em casa.

A.

B.

C.

15. Para determinar o horário marcado em um relógio de ponteiros, precisamos saber se já passou ou não do meio-dia. Leia o que Antônio disse.

Antes do meio-dia, dizemos 7 horas.

Depois do meio-dia, dizemos 7 horas da noite ou 19 horas, pois: 12 h + 7 h = 19 h.

Complete os espaços de acordo com o horário de cada relógio.

Antes do meio-dia

Resposta: 9 horas. Resposta: 5 horas.

2 horas da tarde ou

Depois do meio-dia

Resposta: 2 h da tarde ou 12 h  + 2 h = 14 h 14 horas.

12 h  + h = h horas.

horas da tarde ou 12 h  + h = h horas.

Resposta: 4 horas da tarde ou 12 h  + 4 h  = 16 h 16 horas.

06/10/2025 17:35:25

• Na atividade 15, são apresentadas aos estudantes duas maneiras de expressar horários após o meio­dia. Se surgirem dúvidas sobre essas representações, forneça outros exemplos e peça­lhes que anotem suas contribuições no caderno. Você pode utilizar como exemplo o horário de alguma programação da TV comumente prestigiada por eles, assim como outras atividades que realizem no período da tarde e da noite.

REFERÊNCIAS COMPLEMENTARES

BIGODE, Antonio José Lopes; FRANT, Janete Bolite. Matemática: soluções para dez desafios do professor. São Paulo: Ática, 2011. Esse livro aborda dez das principais dificuldades do professor de Matemática nos três primeiros anos do Ensino Fundamental. Alguns dos temas são o sentido numérico, o sistema de numeração decimal, operações de adição, subtração, multiplicação e noções de medidas.

ATIVIDADE EXTRA

Organize os estudantes em duplas e desenhe na lousa uma sequência de relógios de ponteiros, de modo que o primeiro marque 4 h, o segundo, 4 h 30 min, o terceiro, 5 h, e assim sucessivamente. Entre eles, desenhe um relógio na posição errada. Entregue a cada dupla uma folha com o desenho de um relógio sem os ponteiros. Em seguida, proponha a eles o seguinte desafio: “Os relógios indicados estão organizados em determinada sequência. Qual deles está fora dessa sequência? Justifique sua resposta.”. Por fim, peça aos estudantes que desenhem na folha o horário que o relógio deveria indicar para não interromper a sequência correta.

• A atividade 16 estabelece integração entre as unidades temáticas de Matemática Números, Grandezas e medidas e Probabilidade e Estatística ao relacionar a quantidade de horas de estudo dos amigos de Francisco e mostrar os dados coletados organizados em uma tabela e em um gráfico.

• A atividade 16, propõe que os estudantes interpretem os dados apresentados na tabela para representá­los no gráfico de colunas simples, que eles deverão terminar de pintar. Desse modo, além da compreensão da estrutura de um gráfico, os estudantes precisarão utilizar seus conhecimentos a respeito de interpretação de tabelas, sendo uma oportunidade interessante para avaliar se algum deles apresenta dificuldade para lidar com esse tipo de representação. Se julgar conveniente, reproduza o gráfico na lousa, indicando as colunas referentes às categorias “menos de 7 horas” e “7 horas”, já presentes na atividade, e construa com a turma a coluna referente à categoria “8 horas”. Ao final, converse com os estudantes sobre as respostas obtidas, observando a compreensão deles acerca desse tipo de representação para os dados.

Unidades temáticas integradas

16. Francisco fez uma pesquisa para saber quantas horas seus amigos dedicaram ao estudo em casa na primeira semana de março de 2027. Em seguida, ele organizou os resultados obtidos em uma tabela.

a ) De acordo com os dados da tabela, pinte no gráfico um para cada hora de estudo dos amigos de Francisco.

Quantidade de horas de estudo dedicadas em casa na primeira semana de março de 2027

Horas de estudo

Quantidade de amigos

Menos de 7 horas 2

7 horas 4 8 horas 10 9 horas 3

Mais de 9 horas 1

Fonte de pesquisa: registros de Francisco.

Resposta: Os estudantes devem pintar 10 quadrinhos para a opção “8 horas”, 3 quadrinhos

Quantidade de horas de estudo dedicadas em casa na primeira semana de março de 2027

Quantidade de amigos

Menos de 7 horas Mais de 9 horas 7 horas8 horas9 horas

Horas de estudo

Dica: As duas primeiras colunas já foram pintadas. para a opção “9 horas” e 1 quadrinho para a opção “Mais de 9 horas”. Comentários nas orientações ao professor

Fonte de pesquisa: registros de Francisco.

b ) Quantos amigos dedicaram entre 7 e 8 horas ao estudo em casa?

Resposta: 14 amigos.

c ) Quantos amigos dedicaram 9 horas ou mais ao estudo em casa?

Resposta: 4 amigos.

d ) Quantos amigos participaram dessa pesquisa?

Resposta: 20 amigos.

AVALIANDO

Objetivos

Reconhecer o relógio de ponteiros e o relógio digital como instrumentos utilizados para medir o tempo.

Ler e representar hora e meia hora em relógio de ponteiros e relógio digital. Expressar horários antes do meio­dia e após o meio­dia.

Sugestão de intervenção

Escreva na lousa diferentes horários, como “7 horas da noite”, “3 horas da tarde” ou “10 horas da manhã”. Peça aos estudantes que desenhem no caderno relógios de ponteiros e relógios digitais com os horários. Lembre­os de que, nos relógios digitais, é possível mostrar o horário após o meio­dia, por exemplo, 19:00

17. Escreva o horário aproximado em que você costuma:

Resposta pessoal. Espera-se que os estudantes escrevam o horário aproximado em que costumam realizar as ações indicadas na atividade 17

• Acordar:

• Ir à escola:

• Tomar banho:

• Almoçar:

• Fazer a tarefa de casa:

• Jantar:

18. Mia começou a assistir a um filme às 18 horas. Sabendo que ele tem duração de 3 horas, a que horas o filme vai terminar?

Resposta: 18 h + 3 h = 21 h. O filme vai terminar às 21 h.

19. Isabela saiu de carro às 9 horas da manhã para uma viagem e chegou às 17 horas do mesmo dia. Quantas horas ela viajou no total? horas.

Resposta: Das 9 h da manhã às 12 h (meio-dia) se passaram 3 h. Das 12 h às 17 h se passaram 5 h. Assim, 3 h + 5 h = 8 h. Isabela viajou 8 horas no total.

20. O médico receitou a Guilherme um medicamento que deve ser ingerido de 6 em 6 horas, durante 7 dias.

Sabendo que Guilherme tomou a primeira dose do medicamento as 14 horas, desenhe os ponteiros no relógio a seguir para indicar o horário em que ele deve tomar a segunda dose do medicamento.

Resposta: Os estudantes devem desenhar o ponteiro maior apontando para o 12 e o menor para o 8.

Guilherme vai tomar a segunda dose do medicamento às horas.

Resposta: Guilherme vai tomar a segunda dose do medicamento às 20 horas.

DESAFIO A MAIS

Entre os relógios a seguir um está marcando o horário correto.

Sabendo que um deles está 1 hora adiantado, outro está 1 hora atrasado e o outro duas horas adiantado, contorne o relógio que marca o horário correto.

ILUSTRAÇÕES: JANAINAOLIVEIRA/ARQUIVO DA EDITORA

Resposta: Os estudantes devem contornar o relógio que está marcando 4 horas. ILUSTRAÇÕES: JANAINA OLIVEIRA/ARQUIVO DA

• No boxe Desafio a mais, os estudantes exercitam o raciocínio lógico­matemático e a compreensão de relações temporais. Eles devem analisar quatro relógios, interpretar as afirmações no texto e deduzir qual marca o horário correto. Uma possível lógica de resolução é a seguinte:

• Do menor para o maior horário, os relógios marcam 3 horas, 4 horas, 5 horas e 6 horas. Apenas um deles marca o horário correto.

• O relógio que marca o menor horário (3 horas) só pode ser o que está mais atrasado, ou seja, 1 hora atrasado

• O relógio que marca o maior horário (6 horas)

06/10/2025 17:35:26

só pode ser o que está mais adiantado, isto é, 2 horas adiantado

• O horário correto é 4 h. O relógio que marca 5 horas está 1 hora adiantado.

• Caso os estudantes encontrem alguma dificuldade ou uma lógica diferente da esperada, sugira que comecem testando uma das horas como a correta e verifiquem se as outras se encaixam nas pistas. Por exemplo, você pode perguntar: “Se a hora correta fosse 5 horas, os outros relógios se encaixariam nas pistas?” Isso os ajuda a organizar o raciocínio de maneira clara e a resolver o problema por eliminação.

• Na atividade 17, incentive os estudantes a escrever o horário das atividades realizadas depois do meio­dia das duas maneiras que foram exploradas anteriormente, para reforçar o conceito.

• A atividade 18 demonstra o uso das horas como referencial de marcação de tempo em tarefas comuns, no caso, assistir a um filme. Durante a resolução, aproveite para perguntar aos estudantes a outra forma de expressar o horário mencionado no enunciado e o horário da resposta (18 h e 21 h).

• A atividade 19 explora a noção de duração de um intervalo de tempo dentro do mesmo dia utilizando horas. Assim, os estudantes são levados a pensar na diferença entre dois horários e a calcular quantas horas se passaram entre eles. Incentive os estudantes a compartilharem as estratégias usadas e acolha com atenção e respeito as contribuições de toda a turma. Permita a eles que expressem verbalmente o raciocínio ao desenvolverem a proposta de resolução. Se necessário, use um relógio analógico como apoio para auxiliar na compreensão da passagem do tempo.

• Na atividade 20, há uma ilustração de um relógio digital marcando 14 h. Comente com os estudantes que nesse tipo de relógio é possível a marcação do horário dessa maneira, o que não acontece no relógio de ponteiros, pois os números vão de 1 a 12. Converse com os estudantes sobre a importância de consultar o médico quando estamos doentes, pois tomar um medicamento sem prescrição médica pode fazer mal à saúde.

OBJETIVOS

• Ler as horas em relógio de ponteiros.

• Utilizar as horas como referencial de marcação de tempo em tarefas diárias.

• Calcular tempo decorrido.

• Reconhecer a importância de organizar o tempo para realizar os afazeres diários.

• Refletir sobre a importância de respeitar o tempo destinado a alguns deveres, como tomar banho ou fazer tarefa escolar.

• Reconhecer os elementos que caracterizam o gênero textual bilhete.

• Ler e interpretar um bilhete.

• Aperfeiçoar a compreensão de textos.

• Aprimorar a fluência em leitura oral.

• Oriente os estudantes a observarem atentamente a cena e a lerem com atenção o texto. Converse com eles a respeito da situação proposta, fazendo­lhes perguntas como “O que aconteceu no primeiro momento da cena? E no segundo?”; “Vocês acham que a atitude de Jean foi correta?”.

• Para motivar a fluência em leitura oral, peça aos estudantes que leiam em voz alta o bilhete escrito por Jean.

• Após a conversa, questione os estudantes para saber se eles se consideram responsáveis em relação às suas tarefas domésticas ou se precisam ser lembrados com frequência para realizá­las. Explique que cumprir suas atividades (como organizar o próprio espaço, arrumar a cama, ajudar a alimentar os animais domésticos) é um exercício de cidadania e de respeito ao convívio familiar. É importante perceberem as vantagens de serem organizados, responsáveis e respeitosos com os espaços compartilhados.

• Esta seção é uma oportunidade para os estudantes aperfeiçoarem a compreensão de textos e a fluência em leitura oral, componentes essenciais para a alfabetização, ao se depararem com o gênero bilhete e terem a oportunidade de interpretá­lo e lê­lo.

ENTRE TEXTOS

Professor professora. O assunto tratado nesta seção possibilita o trabalho com o tema contemporâneo transversal Direitos da criança e do adolescente

Você sabia que as palavras agora, hora, hoje, amanhã, dia e noite estão relacionadas ao tempo?

O tempo é muito valioso. Cada momento do nosso dia é destinado a realizar alguma atividade ou compromisso. Podemos aproveitar nosso dia de diferentes maneiras, como comer, brincar, ir à escola, tomar banho e dormir.

Por isso, é preciso organizar o tempo, distribuindo as atividades do dia a dia e mantendo a disciplina, para que essas ações não gerem consequências desagradáveis, como ficar sem tempo para a diversão.

Jean, arrume sua cama e guarde os brinquedos, depois vá fazer suas tarefas da escola.

Está bem, mãe! Já vou!

Sentindo-se chateado, Jean escreveu o bilhete a seguir.

Mãe, desculpa por não ter arrumado o quarto e não ter feito a tarefa na hora que a senhora pediu. Com carinho, Jean.

BNCC

As atividades propostas nesta seção favorecem o desenvolvimento da Competência geral 7 da BNCC ao abordarem a importância de organizar o tempo para a realização de afazeres diários e respeitar o tempo destinado a eles.

EXPLORANDO O TEXTO

Orientações complementares

a) O objetivo desta questão é que os estudantes identifiquem algumas características de um bilhete. No caso, o bilhete foi escrito por Jean para sua mãe e termina com uma despedida.

06/10/2025 17:35:27

Comente com a turma que a linguagem empregada no texto deve estar de acordo com a pessoa que vai receber o bilhete. Por exemplo, ao escrever um bilhete a um professor, pode­se utilizar “Atenciosamente”, em vez de “Com carinho”. b) Se achar necessário, releia o texto com os estudantes e cite os itens do quadro um a um, pedindo a eles que indiquem se o bilhete tem a característica citada por você.

Jean!

EXPLORANDO O TEXTO

a ) Marque um X na ficha que representa quem escreveu o bilhete e contorne a ficha que representa quem recebeu o bilhete.

Resposta: Os estudantes devem marcar um X em Jean e contornar Mãe de Jean.

Jean

Mãe de Jean

Bilhetes podem terminar com uma despedida. Contorne a despedida no bilhete da página anterior, escrito por Jean.

Resposta: Os estudantes devem contornar no bilhete a frase: Com carinho, Jean

b ) No quadro, estão as principais informações e características de um bilhete.

Conte ao professor quais dessas informações e características o bilhete de Jean tem.

Resposta: Para quem foi escrito, objetividade, quem escreveu e uma despedida.

Composição de um bilhete

Deve ter

Pode ter

Para quem foi escrito Uma expressão carinhosa no início

Objetividade

Quem escreveu

Uma despedida

Data

c ) Qual foi a intenção de Jean ao escrever o bilhete?

Resposta: Pedir desculpas à mãe por não ter feito as tarefas que ela pediu.

ALÉM DO TEXTO

d ) Que hora está indicada no relógio de cada uma das cenas?

Resposta: Primeira cena: 8 horas. Resposta: Segunda cena: 10 horas.

Primeira cena: horas

Segunda cena: horas

e ) Após quantas horas a mãe foi verificar se o filho cumpriu as tarefas solicitadas? horas.

Resposta: 2 horas.

f ) Você tem horário para fazer suas tarefas de casa ou precisa que alguém lembre você desse compromisso todos os dias?

Resposta pessoal. Espera-se que os estudantes listem os horários para fazer as tarefas de casa.

• Beto está carregando as menores frutas e sua cesta é a mais leve.

Resposta

Beto carrega 3 kg de maçã, Caio carrega 5 kg de abacaxi e Ana carrega 4 kg de banana.

CONCLUSÃO

Para acompanhar o desenvolvimento dos estudantes de modo eficiente, foram propostas diversas maneiras de avaliar a aprendizagem da turma. A fim de realizar um monitoramento mais abrangente, registre nos relatórios individuais ou nas

fichas de avaliação o desempenho de cada estudante, levando em consideração suas particularidades. Um modelo desse tipo de ficha pode ser encontrado no tópico Avaliação deste Manual do Professor Assim, será possível promover recuperação dos conteúdos por meio de atividades que contemplem de modo individual as trajetórias de aprendizagem, mapeando os avanços e os pontos de dificuldades a serem sanados.

Esse método de verificar a progressão dos estudos e identificar o que a turma de fato conseguiu aprender é de

c) Pergunte aos estudantes se eles já mandaram bilhetes e qual foi a natureza da mensagem. Destaque a importância de pedir desculpas às pessoas quando fazemos algo errado e como essa atitude ajuda em nossas relações com os amigos.

ALÉM DO TEXTO

Orientações complementares d) Caso apresentem dificuldade na resolução deste item, pergunte aos estudantes qual é a posição de cada ponteiro, incentivando­os a se lembrarem do conteúdo trabalhado. Espera­se que eles façam a contagem do tempo decorrido de uma cena para outra. Se algum deles apresentar dificuldade, sugira uma contagem usando os dedos das mãos. e) Explique aos estudantes a importância de criarem uma rotina para facilitar o cumprimento de compromissos assumidos por eles.

Sugestão de Desafio

Os amigos Ana, Beto e Caio estão carregando cestas com frutas. Uma cesta tem 3 kg de medida de massa, outra tem 5 kg e outra, 4 kg. As frutas que eles carregam são banana, maçã e abacaxi. Cada cesta tem apenas um tipo de fruta. De acordo com as dicas, descubra que fruta está na cesta de cada amigo e qual é a medida de massa desse conteúdo.

247

06/10/2025 17:35:27

• A cesta de frutas mais pesada e com as maiores frutas está com Caio.

grande importância para que seja possível repensar estratégias em sala de aula, tornando as ações pedagógicas cada vez mais eficazes.

A conclusão da unidade é o momento de avaliar se os objetivos por ela propostos foram alcançados. Para esse diagnóstico, confira no final deste Manual do Professor algumas possibilidades de avaliação formativa que permitem realizar o monitoramento da aprendizagem dos estudantes e intervir caso eles não tenham atingido os resultados esperados.

1. Objetivo

Efetuar divisões por 2 com quociente menor do que 10. Sugestão de intervenção

Essa atividade tem por objetivo levar os estudantes a efetuarem as divisões por 2. Questione-os a respeito da expressão que utilizamos (metade) para fazer referência aos resultados das divisões dessa atividade. Proponha aos estudantes que utilizem o método que preferirem para resolvê-la e leve para a sala de aula materiais manipuláveis de contagem, como o material dourado.

2. Objetivo

Compreender os significados de terça parte e dobro

Sugestão de intervenção

Caso os estudantes tenham dificuldade para resolver essa atividade, oriente-os, inicialmente, a contar todos os quadrados que aparecem na ilustração, obtendo 24 quadrados no total. Em seguida, verifique se eles se recordam das operações necessárias para calcular a terça parte (24 : 3 = 8) e para calcular o dobro (2 × 8 = 16).

3. Objetivo

Efetuar multiplicações e divisões por 2 e por 3.

Sugestão de intervenção

Nesse momento, espera-se que os estudantes associem as expressões “dobro e metade” a uma multiplicação e uma divisão por 2, respectivamente; e “triplo e terça parte” a uma multiplicação e uma divisão por 3, respectivamente. Se necessário, oriente-os a fazer desenhos no caderno de maneira a realizar os cálculos correspondentes, de acordo com as estratégias estudadas, ou disponibilize materiais de contagem, a fim de que façam os cálculos na prática.

4. Objetivo

Resolver uma situação-problema envolvendo medidas de massa.

VAMOS AVALIAR O APRENDIZADO

1. Efetue os cálculos.

a ) 6  : 2 =

Resposta: 6  : 2 = 3

b ) 10 : 2 = c ) 16 : 2 =

Resposta: 10  : 2 = 5

2. A seguir estão representados alguns quadrados.

Resposta: 16  : 2 = 8

a ) Contorne a terça parte dos quadrados apresentados.

Resposta: Os estudantes devem contornar, da maneira que preferirem, 8 quadrados.

b ) Qual é o dobro da quantidade de quadrados que você contornou? quadrados.

Resposta: 16 quadrados.

3. Nos itens a seguir, obtenha as quantidades que se pede.

a ) O dobro de 4.

Resposta: 8

b ) A metade de 10.

Resposta: 5

c ) O triplo de 6.

Resposta: 18

Resposta: 4

d ) A terça parte de 12.

4. Com base nas dicas e na medida da massa de Joaquim, Felipe e Vítor registrada em cada balança, escreva o nome de cada um deles.

• A medida da massa de Joaquim é menor do que a medida da massa de Vítor.

Unidades temáticas integradas

• Felipe tem 4 kg a mais de medida de massa do que Vítor.

Resposta: Vítor. Resposta: Joaquim. Resposta: Felipe.

Sugestão de intervenção

Essa atividade integra as unidades temáticas de Matemática Números e Grandezas e medidas ao relacionar, comparar e efetuar cálculos para verificar a medida de massa de três meninos. Se julgar conveniente, proponha uma situação parecida, mas com a medida da massa dos próprios estudantes. Para isso, escolha três deles que conheçam suas medidas de massa e reescreva o problema com os nomes e as medidas de massa desses estudantes. Resolva o problema na lousa para que a turma possa acompanhar e esclarecer as dúvidas que surgirem.

5. Aurora colocou bolinhas coloridas de mesmo tamanho em uma caixa. Depois, ela registrou as quantidades de bolinhas no gráfico a seguir.

Aurora vai sortear uma bolinha dessa caixa. Complete cada frase utilizando uma única vez cada ficha a seguir.

Unidades temáticas integradas

Bolinhas coloridas colocadas na caixa em julho de 2027

Quantidade de bolinhas

a ) É retirar uma bolinha marrom.

Resposta: É impossível retirar uma bolinha marrom.

b ) É retirar uma bolinha amarela.

Resposta: É muito provável retirar uma bolinha amarela.

c ) É retirar uma bolinha verde.

Resposta: É improvável retirar uma bolinha verde.

d ) É retirar uma bolinha vermelha.

Resposta: É pouco provável retirar uma bolinha vermelha.

6. A medida de capacidade do copo é de 300 mL Marque um X na ficha que corresponde à medida de capacidade da jarra.

Copo. Jarra. Xícara.

Resposta: Os estudantes devem marcar X na alternativa 1 L

7. Represente nos relógios digitais as horas marcadas no relógio de ponteiros.

Antes do meio-dia Depois do meio-dia

Resposta: 2:00

Resposta: 14:00

6. Objetivo

Comparar medidas de capacidade de recipientes.

Sugestão de intervenção

Relembre aos estudantes a relação entre as unidades de medida de capacidade litro e mililitro, questionando-os se a medida de capacidade da jarra é maior ou menor do que a do copo. Em seguida, peça a eles que observem as medidas de capacidade indicadas nas fichas a fim de que determinem qual delas é a mais adequada para a jarra.

7. Objetivo

06/10/2025 17:31:48

Identificar horário em relógio de ponteiros e representar em relógios digitais. Sugestão de intervenção

Relembre aos estudantes que o menor ponteiro do relógio indica as horas e o maior indica os minutos. Além disso, explique que os dois pontos (:) separam as horas dos minutos no relógio digital. Com relação ao horário após o meio-dia, recorde que o horário será a soma da hora indicada pelo ponteiro mais 12, já que passou do meio-dia.

5. Objetivo

Compreender as informações apresentadas no gráfico e classificar os resultados dos eventos aleatórios.

Sugestão de intervenção

Essa atividade integra as unidades temáticas de Matemática Números e Probabilidade e estatística ao levar os estudantes a compararem e interpretarem informações apresentadas em gráficos de colunas simples, classificando um evento em “muito provável”, “pouco provável”, “improvável” e “impossível”.

Caso os estudantes tenham dificuldades para interpretar o gráfico, relembre os conceitos desse tipo de representação. Se necessário, faça na lousa um gráfico de barras com a quantidade de meninas e de meninos da turma. Depois, retome o gráfico da atividade e peça a eles que identifiquem a quantidade de bolinhas de cada cor colocadas na caixa por Jurandir, qual é a maior, qual é a menor, quais são as cores das bolinhas etc. Os estudantes também podem colocar um rótulo no topo de cada coluna indicando a quantidade de bolinhas que ela representa. Se houver dificuldades com a probabilidade, faça relações com situações mais simples do cotidiano dos estudantes, como a probabilidade de tomarem banho naquele dia.

Cor da bolinha

Verde Vermelha Amarela Azul

Fonte de pesquisa: Anotações de Aurora.

1. Objetivo

Efetuar adições.

Sugestão de intervenção

Essa atividade integra as unidades temáticas de Matemática Números e Grandezas e medidas ao relacionar o sistema monetário à operação da adição.

Caso os estudantes tenham dificuldade na atividade, proponha uma retomada de conteúdos envolvendo os significados da adição e do algoritmo característico por meio da resolução de outras atividades, construídas com base em outros contextos. Durante esse trabalho, é importante instigá-los também a empregar, além dos algoritmos, estratégias de cálculo mental, explorando os conhecimentos que construíram a respeito deste conteúdo.

2. Objetivo

Ler e interpretar gráficos de colunas simples, efetuar subtrações e reconhecer unidades de medida de massa.

Sugestão de intervenção

Essa atividade integra as unidades temáticas de Matemática Números , Grandezas e medidas e Probabilidade e estatística ao trabalhar a operação da subtração por meio de um gráfico.

Por englobar questões relativas a gráficos, subtrações e medidas de massa, durante a resolução da atividade, é importante observar em qual, ou quais, desses aspectos os estudantes estão manifestando dificuldade. Diante dessa possibilidade, uma abordagem que pode ser proposta é relembrar-lhes a estrutura de um gráfico e como fazer a leitura das informações,

VAMOS CONCLUIR

1. Lúcio comprou os seguintes itens. No total, quantos reais Lúcio gastou nessa compra?

Resposta: 27 + 64 = 91. Lúcio gastou 91 reais.

Lúcio gastou reais.

2. Uma escola promoveu uma gincana para arrecadação de alimentos com três equipes. O gráfico apresenta a quantidade de alimentos arrecadados.

a ) Qual equipe arrecadou a maior quantidade de alimentos, em quilogramas, na gincana?

Resposta: Equipe 2.

b ) Quantos quilogramas de alimentos a equipe 3 arrecadou a mais do que a equipe 1?

Unidades temáticas integradas

Unidades temáticas integradas

27 reais

64 reais

Quantidade de alimentos arrecadados na gincana da escola em maio de 2027

arrecadados (em kg)

Resposta: 155 − 150 = 5. A equipe 3 arrecadou 5 kg a mais do que a equipe 1

apresentando outros exemplos de gráficos para complementar esse trabalho. Além disso, se julgar pertinente, retome unidades de medidas de massa e seu significado propondo outras atividades que envolvam a subtração, aproveitando para retomar o algoritmo correspondente e as estratégias de cálculo mental que também podem ser utilizadas nesses contextos.

Fonte de pesquisa: Registros da secretaria da escola.

3. Escreva os nomes das figuras geométricas espaciais a seguir.

Resposta: Cone. Resposta: Cubo.Resposta: Pirâmide.Resposta: Esfera.

4. A cena a seguir mostra algumas pessoas em uma fila.

B. C.

D.

Escreva o nome de cada pessoa de acordo com as informações das fichas a seguir.

Cíntia está na frente de Lucas.

Resposta: Cíntia.

Sara está atrás de Fabiano.

A. C. B. D.

Resposta: Lucas.

Fabiano é o terceiro da fila.

Resposta: Fabiano.

Resposta: Sara.

5. Siga as setas e pinte na malha a seguir o caminho que leva a criança até o triciclo.

Avance um quadrinho.

Vire à direita.

Vire à esquerda.

Respostas e comentários nas orientações ao professor

5. Objetivo

Interpretar e construir caminhos.

Sugestão de intervenção

Para sanar dúvidas acerca da construção de caminhos, proponha aos estudantes outras atividades em que possam observar o uso dos termos correspondentes, reconhecendo corretamente o trajeto que pode ser construído entre dois pontos com descrições apresentadas oralmente, por figuras ou por escrito.

Resposta 5. Menino

3. Objetivo

Reconhecer figuras geométricas espaciais.

Sugestão de intervenção

Para remediar dificuldades em reconhecer e nomear as figuras geométricas espaciais, pode ser desenvolvido um trabalho voltado a reconhecer os formatos de objetos do cotidiano e associá-los às figuras apresentadas, estabelecendo relação com seus respectivos nomes. Nesse trabalho, é importante motivar os estudantes a reconhecerem semelhanças e diferenças entre essas figuras para que possam estar aptos a reconhecê-las em diferentes atividades e situações.

4. Objetivo

Identificar posições relativas.

Sugestão de intervenção

Caso algum estudante manifeste dúvidas na resolução da atividade, faça uma intervenção no sentido de revisar os conceitos e os termos empregados para a localização de objetos e pessoas por meio de referenciais. Para isso, escreva na lousa as expressões em cima, embaixo, direita, esquerda, em frente e atrás e peça aos estudantes que construam frases utilizando como base as posições dos objetos na sala de aula, observando se compreendem o significado de cada um deles e da importância do referencial para sua utilização.

06/10/2025 17:30:26

Triciclo Criança

Triciclo

A.

6. Objetivo

Ampliar os conhecimentos, por meio de situações contextualizadas, sobre a operação de divisão por 4.

Sugestão de intervenção

Para melhor resolução da atividade 6, peça aos estudantes que efetuem a contagem das flores dentro de cada vaso. Analise se conseguem associar a quantidade total de flores e a quantidade em cada vaso com a operação da divisão. Se necessário, retome os conceitos de divisão.

7. Objetivo

Efetuar multiplicações e reconhecer unidades de medidas de capacidade.

Sugestão de intervenção

Para remediar dificuldades a respeito do cálculo de multiplicações, proponha uma retomada de conteúdos a respeito do algoritmo correspondente, bem como de estratégias de cálculo mental e outros recursos que possam ser empregados na determinação do resultado de uma multiplicação. Faça também uma revisão de conceitos para medidas de capacidade, de modo a retomar, com os estudantes, as principais unidades de medida de capacidade e em quais situações elas podem ser empregadas. Para completar esse trabalho, proponha outras atividades contextualizadas acerca da associação entre multiplicações e medidas de capacidade.

8. Objetivo

Resolver problemas utilizando a divisão.

Sugestão de intervenção

Proponha outras atividades semelhantes para remediar dificuldades manifestadas pelos estudantes durante a resolução dessa atividade. Se julgar conveniente, durante a resolução das atividades, disponibilize

6. A seguir, estão os enfeites que Filomena fez.

a ) Filomena utilizou flores

e vasos para fazer os enfeites.

Resposta: Filomena utilizou 20 flores e 4 vasos para fazer os enfeites.

b ) Em cada vaso, foram

Resposta: 20 : 4 = 5

colocadas flores. : =

Resposta: Em cada vaso, foram colocadas 5 flores.

7. Com a garrafa a seguir, que contém 1 L de água, é possível encher os 4 copos de 250 mL de medida de capacidade que estão ao lado dela. Quantos copos iguais a esse é possível encher com o conteúdo de 3 garrafas?

Resposta: 3 × 4 = 12. É possível encher 12 copos com o conteúdo de 3 garrafas.

8. Adriana tem 12 reais. Sua irmã tem a metade dessa quantia, e seu irmão, a terça parte. Quantos reais têm a irmã e o irmão de Adriana?

Resposta: 12:2 = 6; 12:3 = 4. A irmã de Adriana tem 6 reais, e o irmão tem 4 reais.

9. A imagem a seguir é a representação de um prisma.

a ) Marque um X nas figuras geométricas planas que lembram as faces desse prisma. Resposta: Os estudantes devem marcar um X no triângulo e outro no retângulo.

b ) Escreva os nomes das figuras geométricas planas apresentadas anteriormente.

Resposta: Triângulo, círculo e retângulo.

materiais de contagem que possam contribuir para o estudo da divisão, retomando também o algoritmo e as estratégias de cálculo mental que podem ser empregados nesse contexto.

9. Objetivo

Reconhecer as figuras geométricas planas associadas às faces de prismas.

Sugestão de intervenção

Visando remediar dificuldade em reconhecer as características das figuras geométricas

planas, proponha aos estudantes uma atividade prática para que, utilizando embalagens que lembram o formato de prismas e de outras figuras geométricas espaciais, tracem em uma folha de papel sulfite os formatos de suas faces. Para isso, oriente-os a apoiar a face do objeto a ser desenhada sobre a folha de papel sulfite e traçar ao redor dela com um lápis, a fim de evidenciar seu formato e associar esse desenho às figuras geométricas planas, aproveitando para retomar suas nomenclaturas e principais características.

10. Objetivo

10. Tiago colocou em uma urna cartões numerados de 1 a 100. Marque um X na opção que indica a probabilidade de ele sortear um número:

a ) menor do que 95.

Resposta: Os estudantes devem marcar um X em Muito provável.

Muito provável.

b ) maior do que 100.

Muito provável.

Pouco provável.

Pouco provável. Impossível. Impossível.

Resposta: Os estudantes devem marcar um X em Impossível.

11. Observe as fitas.

a ) Sem medir, estime a medida do comprimento de cada fita.

Resposta pessoal. Espera-se

que os estudantes escrevam a medida de comprimento aproximada para cada fita.

b ) Utilizando uma régua, meça o comprimento de cada fita.

Resposta: 8 cm Resposta: 4 cm Resposta: 3 cm

12. Complete as frases utilizando uma das palavras que aparecem nas fichas.

maio semestre bimestre março domingo sexta-feira

a ) Se hoje é segunda-feira, então ontem foi .

Resposta: Se hoje é segunda-feira, então ontem foi domingo

b ) Se estamos no mês de abril, então o mês anterior foi .

Resposta: Se estamos no mês de abril, então o mês anterior foi março

c ) Um tem 2 meses.

Resposta: Um bimestre tem 2 meses.

12. Objetivo

Compreender e aplicar unidades de medidas de tempo em situações do cotidiano.

Sugestão de intervenção

Para auxiliar com os termos apresentados e remediar dificuldades, proponha outras atividades que envolvam medidas de tempo, como a interpretação de calendários, a fim de que exijam dos estudantes a interpretação e a associação entre as informações coletadas por meio desse instrumento.

06/10/2025 17:30:26

Classificar eventos aleatórios de acordo com as chances de ocorrerem. Sugestão de intervenção

Para remediar as dificuldades apresentadas pelos estudantes, proponha a eles outras situações envolvendo eventos aleatórios para que classifiquem como muito provável, pouco provável ou impossível. Aproveite também as situações apresentadas na Reprodução do Livro do Estudante para retomar os significados de cada um desses termos e discutir com a turma acerca de sua aplicabilidade na classificação de eventos aleatórios.

11. Objetivo

Reconhecer as unidades de medida de comprimento, estimar medidas de comprimento e fazer medições utilizando uma régua. Sugestão de intervenção

No sentido de remediar as dificuldades manifestadas durante a resolução da atividade, proponha aos estudantes uma retomada de conteúdos a respeito das medidas de comprimento abordando as unidades mais utilizadas e ensinando como utilizar uma régua para fazer as medições. Proponha a eles também que estimem medidas de comprimento associadas a objetos da sala de aula, conferindo os resultados por meio de medições com régua.

Fita vermelha

Fita vermelha

Fita azul

Fita azul

Fita verde

Fita verde

• A seção Saiba mais oferece sugestões de leitura para os estudantes, com indicações de livros que podem estar relacionados ao conteúdo ou a contextos trabalhados no volume, além de temas atuais ligados ao convívio social. Verifique se na biblioteca da escola há exemplares dos livros indicados e disponibilize-os para os estudantes manusearem.

SAIBA MAIS

Confira sugestões para ampliar seus conhecimentos sobre alguns temas estudados no volume.

Os passarinhos coloridos de Adel

Acompanhe Adel, uma criança que gosta muito de fazer passarinhos de papel. Quando ele está entretido com sua brincadeira favorita parece não se distrair com nada que surge à sua volta, até que em algum momento do dia, na porta do seu quarto, uma luz vermelha se acende. Descubra o que acontece quando essa luz aparece.

SHARAFEDDINE, Fátima. Os passarinhos coloridos de Adel. Ilustrações de Sara Sanchez. Tradução de Maria Carolina Gonçalves. Rio de Janeiro: Tabla, 2022.

O jogo do vai e vem

Se você fosse um sinal de mais

Nesse livro, são apresentadas algumas situações com o sinal de mais e explicações sobre ele, mostrando sua aplicação prática na operação de adição.

SHASKAN, Trisha Speed. Se você fosse um sinal de mais. Ilustrações de Francesca Carabelli. Tradução de Elisa Zanetti. São Paulo: Editora Gaivota, 2011.

Nesse livro, um passeio de trem é feito por alguns animais. Durante a leitura, enquanto os animais sobem ou descem de cada estação, são propostos desafios de adição e subtração.

MUNIZ, Flávia. O jogo do vai e vem Ilustrações de Fabiana Salomão. São Paulo: FTD, 2012.

Como se fosse dinheiro

Todo recreio, Catapimba levava dinheiro para o lanche da escola, mas sempre recebia seu troco em balas, nada de dinheiro. Até que um dia ele teve uma ideia que mudou essa situação.

ROCHA, Ruth. Como se fosse dinheiro

Ilustrações de Mariana Massarani. São Paulo: Salamandra, 2010.

É o bicho!

O supermetro

Diversas partes do corpo eram usadas para medir o comprimento dos objetos. Porém, essas medidas não eram precisas. De repente, um certo herói surge para solucionar esse problema: o Supermetro!

DANTE, Luiz Roberto. O Supermetro Ilustrações de Luis Paulo Stracioni. São Paulo: Editora do Brasil, 2023.

Nesse livro, cada cena apresenta animais em diversas situações, possibilitando analisar a posição de cada um.

ALPHEN, Jean-Claude R. É o bicho! São Paulo: Companhia das Letrinhas, 2009.

06/10/2025 17:28:01

• Nessa fase em que alguns deles podem não ter se apropriado do processo de leitura, é importante que se incentive a observação das imagens e letras existentes nos livros. Você poderá fazer a leitura em voz alta ou pedir a colaboração de outros estudantes. Converse com eles sobre o enredo e os personagens e peça-lhes que recontem a história para a turma.

• Trabalhe com a leitura da capa do livro que será lido, apresentando-a aos estudantes. Solicite-lhes que relatem oralmente quais os elementos da capa mais chamaram a atenção deles. Ao observarem a capa, esteja atento a quais hipóteses eles têm sobre a história. Nesse momento, é importante que você instigue a curiosidade deles folheando as páginas do livro e mostrando-lhes as principais imagens. No fim da leitura, retome a observação da capa e questione-os sobre as relações entre a capa e a história lida.

A volta ao mundo em labirintos

Viaje o mundo e descubra pontos turísticos dos mais diversos lugares enquanto é desafiado a passar por vários labirintos.

SMITH, Sam. A volta ao mundo em labirintos. Tradução de Luciano Campelo. Londres: Usborne, 2018.

Tem cabimento?

Com poesia, esse livro apresenta noções de quantidade, medidas de tempo e espaço, de maneira criativa e divertida.

Sopa de bruxa

Esse livro narra a história da bruxinha Rafaela em uma disputa culinária. Descubra qual será a receita que ela vai preparar para vencer o desafio e o que acontecerá quando outra bruxa tentar roubá-la.

HAE-WANG, Jeong. Sopa de bruxa Ilustrações de Oh Seung-Min. Tradução de Thais Rimkus. 2. ed. São Paulo: Callis, 2012.

TAUBMAN, Andrea Viviana; PELLEGRINO, Marcelo. Tem cabimento? Ilustrações de Guto Lacaz. São Paulo: Editora do Brasil, 2020.

Marcelo: de hora em hora

Com a ajuda de dona Laura, Marcelo vai descobrindo como contar as horas. Aproveite esse livro para aprender com as descobertas de Marcelo.

Tarsila, menina pintora

ROCHA, Ruth. Marcelo: de hora em hora. Ilustrações de Alberto Llinares. São Paulo: Salamandra, 2013.

Com qual penteado eu vou?

No dia do aniversário de 100 anos do senhor Benedito, seus bisnetos e suas bisnetas preparam belos penteados para irem à festa.

OLIVEIRA, Kiusan de. Com qual penteado eu vou? Ilustrações de Rodrigo Andrade. São Paulo: Editora Melhoramento, 2021.

Conheça a história de uma menina nascida em uma fazenda do interior de São Paulo que se tornou uma artista de importância nacional e internacional.

FIDALGO, Lúcia. Tarsila, menina pintora. Ilustrações de Robson Araújo. São Paulo: Paulus, 2009.

WALL-E

Um robô tem a missão de limpar o planeta Terra depois que os humanos encheram o planeta de resíduos e partiram para um retiro no espaço. Certo dia, chega uma nave com um passageiro a bordo que vai mudar tudo.

WALL-E, de Tim Morris. Estados Unidos, 2008 (98 min).

06/10/2025 17:28:06

• O trabalho com a leitura vai além da alfabetização, pois ela auxilia no desenvolvimento afetivo, físico e intelectual, estabelece relações lógicas, desenvolve o pensamento crítico, a expressão oral e corporal e desperta a criatividade. Por esse motivo, sempre que possível, incentive os estudantes a criar suas próprias histórias e a aplicar o conhecimento adquirido em situações do seu cotidiano.

• As Referências bibliográficas comentadas apresentam os títulos usados como consulta ou embasamento para a construção de unidades do volume. Se julgar conveniente, use essas indicações em consulta e estudos para aprimorar o planejamento das aulas e das propostas de intervenção e de recuperação de aprendizagens.

REFERÊNCIAS BIBLIOGRÁFICAS COMENTADAS

ALVES, Eva Maria Siqueira. A ludicidade e o ensino de matemática: uma prática possível. Campinas: Papirus, 2020.

A autora destaca várias possibilidades de práticas lúdicas em sala de aula, com base nos relatos de suas experiências em sala de aula como professora de Matemática na Educação Básica.

BORBA, Marcelo de Carvalho; PENTEADO, Miriam Godoy. Informática e educação matemática 6. ed. Belo Horizonte: Autêntica, 2019. Nesse livro, os autores discutem temas relacionados à utilização de computadores e de calculadoras gráficas em Educação Matemática.

BRASIL. Decreto nº 11.556, de 12 de junho de 2023. Disponível em: https://www.planalto.gov.br/ccivil_03/_ ato2023-2026/2023/decreto/D11556. htm. Acesso em: 9 jun. 2025. Esse decreto visa implementar políticas, programas e ações para garantir a alfabetização ao final do segundo ano do Ensino Fundamental e recompor o aprendizado para estudantes que não alcançaram os padrões adequados até o final dos Anos Iniciais, garantindo esse direito a todas as crianças brasileiras.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular Versão final. Brasília, DF: MEC, 2018. Disponível em: https:// basenacionalcomum.mec.gov.br/ abase/. Acesso em: 15 jul. 2025. Esse documento indica as aprendizagens mínimas necessárias em cada etapa e para cada área de conhecimento.

CIVARDI, Jaqueline Araújo; SANTOS, Elismar Alves dos. Educação, matemática e inclusão escolar: perspectivas teóricas. Curitiba: Appris, 2018.

Nesse livro, são apresentadas reflexões teóricas sobre a educação matemática inclusiva, aprofundando as discussões sobre Educação, Matemática e inclusão.

DIAS, Marisa da Silva; MORETTI, Vanessa Dias. Números e operações: elementos lógico-históricos para atividades de ensino. Curitiba: InterSaberes, 2012.

As autoras narram o desenvolvimento do conhecimento matemático desde as primeiras civilizações, analisando o papel do professor e da educação na vida em sociedade.

IFRAH, Georges. Os números: a história de uma grande invenção. 4. ed. São Paulo: Globo, 2007.

Essa obra resume a história da Matemática desde a Pré-História, passando por antigas civilizações, como egípcias, babilônias, fenícias, gregas, romanas, hebreias, maias, chinesas, hindus e árabes.

MUNIZ, Cristiano Alberto. Brincar e jogar: enlaces teóricos e metodológicos no campo da educação matemática. Belo Horizonte: Autêntica, 2014.

Esse livro mostra como o jogo e a brincadeira estão ligados com a aprendizagem matemática e oferece subsídios para o ensino de Matemática por meio de atividades lúdicas.

PAIS, Luiz Carlos. Didática da matemática: uma análise da influência francesa. 4. ed. Belo Horizonte: Autêntica, 2019.

Essa obra apresenta aspectos e conceitos fundamentais da Didática Francesa, como transposição didática, contrato didático, obstáculos epistemológicos e engenharia didática.

MATERIAL COMPLEMENTAR

JOGO DA COMPARAÇÃO DE FICHAS

MATERIAL COMPLEMENTAR DA PÁGINA 45

NÚMEROS DE 0 A 100

UNIDADE 1

1. Objetivo

Estabelecer relação entre a quantidade de elementos e sua representação numérica.

Reconhecer que 1 dezena corresponde a 10 unidades e que 1 centena corresponde a 10 dezenas.

Registrar quantidade utilizando números até 100 com algarismos e por extenso.

RECORTAR

• Nesta seção, apresentamos o Material complementar, que contém peças e figuras necessárias para a resolução de algumas atividades do Livro do Estudante . Para usar esse material, é necessário recortar as figuras e as peças apresentadas e, em alguns casos, montar o material recortado.

• A fim de assegurar a integridade física dos estudantes e prevenir acidentes, oriente-os a tomar cuidado no manuseio da tesoura, além de garantir que façam uso apenas de tesouras com pontas arredondadas.

SUGESTÕES DE AVALIAÇÕES COM PROPOSTAS DE INTERVENÇÃO

Nas páginas a seguir deste manual, estão apresentadas sugestões de avaliação formativa com comentários de intervenção, as quais podem ser aplicadas ao final do trabalho de cada tópico ou unidade, conforme o andamento dos conteúdos planejados. Essas avaliações estão organizadas por unidade, com o intuito de auxiliar o acompanhamento educacional e formativo dos estudantes nesse momento, a critério da oportunidade e do planejamento do professor. Porém, se julgar conveniente, reserve algumas delas para serem também utilizadas como avaliação diagnóstica, antes de novos conteúdos.

Atividade

Reconhecendo quantidades por meio de malhas quadriculadas. Sugestão de intervenção

Prepare folhas impressas com malhas quadriculadas nas quais estejam destacados quadradinhos em quantidade entre 1 e 100. Elabore ao menos uma figura que contenha uma quantidade de 1 a 9 quadradinhos, uma contendo 100 quadradinhos e outras duas com quan-

06/10/2025 17:25:00

tidades entre 10 e 99. Distribua cópias dessas folhas entre os estudantes e peça a eles que escrevam, usando algarismos e por extenso, as quantidades de quadradinhos destacadas em cada figura. Além disso, oriente-os a identificar, para cada figura, as quantidades de centenas, dezenas e unidades presentes. Ao final, peça a alguns estudantes que registrem na lousa os dados que obtiveram para que possam comparar os resultados e corrigir a atividade.

2. Objetivos

Representar os números até 100 no quadro de ordens e classes. Ler e escrever números de 0 a 100.

Comparar quantidades utilizando os símbolos > (maior do que), < (menor do que) e = (igual a).

Compreender o significado de par e ímpar. Reconhecer números pares e números ímpares.

Atividade

Escrevendo e classificando números com base em cartões. Sugestão de intervenção

Prepare previamente cartões contendo a representação de números entre 0 e 100 por extenso, com uma mesma quantidade de números pares e ímpares. Distribua um cartão para cada estudante. Peça que, com base nos números representados nos cartões, escrevam a representação em algarismos, preencham um quadro de ordens e classifiquem os números como pares e ímpares. Em seguida, instrua-os a apresentar seus cartões aos colegas com as classificações correspondentes, de modo que confiram as respostas apresentadas. Proponha a eles que se organizem em dois grupos, um com os estudantes que têm cartões com números pares e outro com os que têm números ímpares, e construam uma sequência com os números pares ou ímpares em ordem crescente. Ao final, proponha uma conversa com toda a turma a respeito dos resultados obtidos nessa atividade.

06/10/2025 17:25:00

MOLDE DE CUBO

MATERIAL COMPLEMENTAR DA PÁGINA 61

FIGURAS GEMÉTRICAS ESPACIAIS

3. Objetivo

Comparar números de uma sequência e reconhecer padrões e regularidades.

Atividade

Construindo sequências e reconhecendo padrões.

Sugestão de intervenção

Organize os estudantes em grupos com quatro integrantes cada e proponha a eles

RECORTAR COLAR DOBRAR

• A fim de assegurar a integridade física dos estudantes e prevenir acidentes, oriente-os a tomar cuidado no manuseio da tesoura, além de garantir que façam uso apenas de tesouras com pontas arredondadas.

• Quando os estudantes forem montar o cubo utilizando a planificação, permita que eles realizem essa etapa sozinhos, interferindo somente quando for necessário. Este é um momento importante para os estudantes, pois são desenvolvidas habilidades relacionadas à capacidade e à coordenação motora deles.

que construam uma sequência numérica com dez termos, a qual pode ser crescente ou decrescente, e cuja regularidade envolva a adição ou subtração de uma mesma quantidade. Após essa construção, peça ao grupo que escreva em uma folha de papel sulfite apenas os três primeiros termos dessa sequência. Depois, troque as sequências entre os grupos, garantindo que nenhum tenha recebido a própria

06/10/2025 17:25:00

sequência. No segundo momento, proponha aos grupos que completem a sequência recebida com os outros sete termos que estão faltando, escrevendo abaixo deles o padrão presente nessa sequência. Para concluir a atividade, promova uma roda de conversa com todos, comparando os resultados obtidos entre os grupos, principalmente entre o que elaborou e o que completou cada sequência.

4. Objetivos

Ler e escrever os ordinais do 1º ao 19º

Identificar a posição de um ordinal em uma sequência de até 19 elementos. Atividade

Apostando uma corrida e classificando os competidores conforme a ordem de chegada.

Sugestão de intervenção

Proponha aos estudantes a realização de uma corrida. Peça a eles que decidam

quem vai participar, limitando a quantidade a, no máximo, 19 estudantes. Leve a turma para a quadra ou o pátio da escola e decida com eles qual será o percurso dessa corrida, marcando no chão o ponto de partida e a linha de chegada. Organize os estudantes que vão participar da corrida no ponto de partida e distribua os demais entre os pontos inicial e final da corrida. Os estudantes que ficarem na linha de chegada serão os responsáveis por anotar a ordem de chegada de cada

participante. Realize com eles a corrida na prática. Ao final, em sala de aula, proponha a eles que construam um quadro contendo os nomes de todos os participantes da corrida e a ordem de chegada de cada um utilizando números ordinais. Faça perguntas a eles a respeito das posições de modo que eles explorem a sequência de números ordinais com base nesse contexto.

06/10/2025 17:25:00

ÁBACO DE PAPEL

MATERIAL COMPLEMENTAR DA PÁGINA 74, 97, 126 E 134

ADIÇÃO E SUBTRAÇÃO

UNIDADE 2

1. Objetivos

Associar figuras geométricas espaciais a objetos do dia a dia.

Reconhecer e nomear o cubo, o bloco retangular ou o paralelepípedo retângulo, a esfera, o cilindro, o cone e a pirâmide.

Atividade

Leve para a sala de aula blocos de madeira com formatos que lembram o cubo, a pirâmide, a esfera, o cilindro, o

RECORTAR

cone e o paralelepípedo retângulo ou o bloco retangular. Mostre um a um aos estudantes, pedindo que eles escrevam o nome da figura geométrica representada por aquele bloco de madeira e que desenhem um objeto do dia a dia que o formato lembra. Deixe os nomes das figuras escritos na lousa para os estudantes copiarem caso tenham dificuldade na escrita das palavras.

Sugestão de intervenção

Caso os estudantes tenham dificuldade em nomear as figuras geométricas espa-

• A fim de assegurar a integridade física dos estudantes e prevenir acidentes, oriente-os a tomar cuidado no manuseio da tesoura, além de garantir que façam uso apenas de tesouras com pontas arredondadas.

• Oriente os estudantes a guardarem o ábaco de papel e as contas, pois poderão ser usados em futuras atividades. Para isso, considere providenciar um envelope a cada estudante para que eles possam guardar o material.

08/10/2025 08:29:09

ciais e identificar objetos com formatos parecidos, faça a mesma atividade proposta, mas peça a alguns estudantes que escrevam esses nomes na lousa ou falem para você escrever, além de dizerem qual objeto do dia a dia lembra essa figura. Pergunte à turma se eles concordam ou não, promovendo uma conversa sobre o assunto. Além disso, se necessário, retome com os estudantes as atividades e o assunto abordado nas páginas 40 a 42

2. Objetivos

Identificar o molde do cubo.

Identificar os elementos aresta, face e vértice de uma figura geométrica espacial. Atividade

Apresente aos estudantes alguns moldes de figuras geométricas espaciais, com alguns moldes de cubo entre eles, a fim de que os identifiquem. Depois, com a ajuda dos estudantes, monte os moldes de cubos. Separe eles em grupos e entregue uma representação do cubo montado a cada grupo. Peça-lhes que contem quantos vértices, arestas e faces eles identificam. Por fim, oriente-os a compa-

rar as respostas dos grupos e a conversar para que cheguem a um acordo, caso as respostas dadas sejam diferentes.

Sugestão de intervenção

Caso os estudantes tenham dúvidas, retome com eles a atividade 9 da página 61.

3. Objetivo

Classificar as figuras geométricas espaciais de acordo com suas superfícies. Atividade

Leve para a sala de aula embalagens com formatos que se parecem com o cubo, a pirâmide, a esfera, o cilindro, o cone e o paralelepípedo retângulo ou o

bloco retangular. Promova uma discussão de modo que os estudantes classifiquem essas figuras geométricas espaciais em dois grupos, as que rolam com facilidade dependendo da posição colocada em uma superfície e as que não.

Sugestão de intervenção

Se necessário, providencie uma superfície inclinada e outros objetos que permitam demonstrar que alguns podem rolar com facilidade e outros não, de acordo com suas superfícies e posições, a fim de sanar possíveis dúvidas apresentadas pelos estudantes.

CONTAS DO ÁBACO

MATERIAL COMPLEMENTAR DA PÁGINA 74, 97, 126 E 134

ADIÇÃO E SUBTRAÇÃO

UNIDADE 3

1. Objetivo

Identificar regularidades e determinar elementos ausentes em sequências.

Atividade

Previamente, escreva em uma folha uma sequência numérica com números entre 1 e 99, e guarde-a sem mostrar aos estudantes. Depois, escreva na lousa apenas os três primeiros números da sequência criada. Depois, peça aos

• A fim de assegurar a integridade física dos estudantes e prevenir acidentes, oriente-os a tomar cuidado no manuseio da tesoura, além de garantir que façam uso apenas de tesouras com pontas arredondadas.

RECORTAR

06/10/2025 17:25:01

estudantes que descubram a regularidade da sequência. Permita que eles façam alguns cálculos mentais ou usem o caderno para registrar os cálculos e, depois, apresentar os resultados. Oriente-os, caso necessário.

Sugestão de intervenção

Se os estudantes tiverem dúvidas para identificar a regularidade da sequência e determinar os elementos ausentes, retome a atividade 5 da página 56, abordando novas estratégias.

HELOÍSA

2. Objetivo

Efetuar adições com resultado até 99.

Atividade

Diga aos estudantes que eles vão jogar o Sorteio da adição. Peça a eles que escrevam no caderno um quadro 3 × 3 e insiram nele números aleatórios de 1 a 99, conforme exemplo a seguir.

10 24 55

45 67 37

Na lousa, escreva uma adição e esclareça que quem tiver o valor do resultado no quadro deve marcar esse número com um X. Oriente-os a realizar os cálculos no caderno. Faça esse processo até que algum estudante preencha uma linha, coluna ou diagonal primeiro.

Sugestão de intervenção

Se os estudantes manifestarem dificuldades com relação às operações de adição, proponha o uso de materiais manipuláveis.

JOGO DO CÁLCULO RÁPIDO

MATERIAL COMPLEMENTAR DA PÁGINA 101

ADIÇÃO E SUBTRAÇÃO 1

3. Objetivos

Efetuar adições com resultado até 99. Reconhecer o símbolo usado para representar a adição.

Resolver situações-problema que envolvam adição.

Atividade

Reproduza na lousa a seguinte situação-problema para que os estudantes a resolvam no caderno: “A professora de João pediu que ele comprasse alguns materiais para confeccionar uma máscara”. Observe no quadro o preço de cada produto.

RECORTAR

06/10/2025 17:25:01

Cartolina: 5 reaisCola escolar: 3 reais

Lantejoula: 2 reaisFita colorida: 13 reais

Quantos reais João vai gastar se comprar uma cartolina e uma fita colorida?

Sugestão de intervenção

Caso algum estudante tenha dificuldades na realização da atividade, procure retomar os conteúdos estudados, buscando abordagens diferentes para explicar o assunto, de acordo com as necessidades que forem se tornando evidentes durante a prática.

• A fim de assegurar a integridade física dos estudantes e prevenir acidentes, oriente-os a tomar cuidado no manuseio da tesoura, além de garantir que façam uso apenas de tesouras com pontas arredondadas. Considere disponibilizar um envelope para que guardem as fichas e possam jogar com elas em outros momentos, praticando, assim, cálculos rápidos e mentais.

4. Objetivos

Efetuar subtrações com números até 99. Reconhecer o símbolo usado para representar a subtração.

Resolver situações-problema que envolvam subtração.

Atividade

Reproduza na lousa a seguinte situação-problema para que os estudantes a resolvam no caderno: “Patrícia e Luciano estão jogando video-

game. Patrícia marcou até o momento 75 pontos e Luciano, 68 pontos. Quantos pontos Luciano deve marcar para que haja um empate?”.

Sugestão de intervenção

Caso identifique dificuldades enquanto os estudantes resolvem a situação-problema, proponha o uso de materiais manipuláveis ou retome as estratégias apresentadas no tema Subtração com números até 99

E

1

UNIDADE 4

1. Objetivos

Compor e decompor números até 999. Ler e escrever os números até 1 000 com algarismos e por extenso.

Representar os números até 1 000 no quadro de ordens e classes.

Relacionar a quantidade de 10 centenas à unidade de milhar.

Identificar o antecessor e o sucessor de um número.

Atividade

Leve para a sala de aula, em um saqui-

RECORTAR

nho não transparente, fichas com números de três algarismos até o valor 999. Organize os estudantes em duplas e solicite a cada dupla que sorteie 5 fichas. Depois, oriente os estudantes a representarem os números das fichas sorteadas utilizando:

• o material dourado;

• o ábaco;

• a decomposição em forma de adição;

• o quadro de ordens feito no caderno;

• a escrita por extenso no caderno.

Sugestão de intervenção

Avalie a execução da atividade rea-

• A fim de assegurar a integridade física dos estudantes e prevenir acidentes, oriente-os a tomar cuidado no manuseio da tesoura, além de garantir que façam uso apenas de tesouras com pontas arredondadas.

06/10/2025 17:25:02

lizada pelos estudantes observando a participação de cada um, bem como o interesse, a autonomia e o raciocínio, e se têm dificuldades. Em caso positivo, mude a abordagem, providenciando outras atividades e estratégias com o propósito de saná-las. Proponha também que eles representem o número 1 000 utilizando o material dourado e o ábaco. Depois, peça a eles que escrevam, no caderno, o número 1 000 com algarismos e por extenso, que representem o número 1 000 no quadro de ordens e, por fim, que identifiquem o antecessor e o sucessor desse número.

2. Objetivos

Identificar o Real como unidade do nosso sistema monetário.

Identificar as cédulas e as moedas do Real. Resolver situações-problema que envolvem o sistema monetário brasileiro.

Reconhecer cédulas e moedas do sistema monetário brasileiro e equivalência de valores.

Atividade

Solicite às duplas que devolvam as fichas sorteadas da atividade anterior e façam um novo sorteio de duas fichas. Peça-lhes que representem de duas maneiras diferentes, no caderno, o

valor de cada ficha usando somente cédulas e moedas do nosso sistema monetário brasileiro. Por fim, oriente cada dupla a elaborar uma situação-problema envolvendo o sistema monetário brasileiro com os valores das fichas sorteadas.

Sugestão de intervenção

Caso algum estudante tenha dificuldades na realização das atividades, procure retomar os conteúdos estudados, empregando abordagens diferentes para explicar o assunto, de acordo com as necessidades que forem se tornando evidentes durante a prática.

FICHAS SOBREPOSTAS

MATERIAL COMPLEMENTAR DA PÁGINA 112

NÚMEROS ATÉ 1 000

100 200 300 400 500 600 700 800 900

será 222, que pode ser obtida pela adição dos números 111 + 111. Não é possível obter a soma 999, pois o maior número formado é 444.

Por fim, sugira na lousa uma adição que precise de reagrupamento e peça a eles que resolvam no caderno. Após resolverem, pergunte qual é a diferença que eles perceberam em relação às adições que fizeram antes, ao trabalharem com as fichas.

Sugestão de intervenção

Peça a algumas duplas que compartilhem suas respostas com a turma. Com isso, aprovei-

RECORTAR

06/10/2025 17:25:03

te as respostas apresentadas para destacar os termos da adição e as estratégias utilizadas por elas. Caso haja dificuldades, utilize o material dourado para explicar as trocas e os reagrupamentos. Use também o algoritmo da adição, a fim de que possam comparar as estratégias de resolução. Providencie outras atividades e estratégias com o propósito de sanar as dúvidas. Por exemplo, permita que usem material dourado ou ábaco. Também é possível retomar os exemplos apresentados na unidade.

• A fim de assegurar a integridade física dos estudantes e prevenir acidentes, oriente-os a tomar cuidado no manuseio da tesoura, além de garantir que façam uso apenas de tesouras com pontas arredondadas.

UNIDADE 5

1. Objetivos

Efetuar adições com e sem reagrupamento com resultado até 999 utilizando diferentes estratégias. Resolver situações-problema que envolvam a adição.

Atividade

Confeccione previamente fichas de papel com os algarismos 1, 2, 3 e 4 separadamente, ou seja, cada ficha deve conter apenas um algarismo. Produza fichas de modo que cada estudante receba três fichas de cada um desses algarismos. Organize a turma em duplas e distribua as fichas para cada componente da dupla. Em seguida, diga aos estudantes que deverão usar as fichas para formar o maior número possível de três algarismos. Depois, a dupla deve adicionar os dois números formados. Enriqueça a atividade perguntando: “Qual é a maior soma que pode ser obtida com os algarismos dessas fichas?”; “E qual é a menor?”; “É possível obter a soma 999?”. Respostas: A maior soma é 888, que pode ser obtida pela adição dos números 444 + 444 . A menor soma

2. Objetivos

Efetuar subtrações com e sem reagrupamento envolvendo números até 999 utilizando diferentes estratégias. Resolver situações-problema que envolvam a subtração.

Atividade

Providencie e leve para a sala de aula dois anúncios de jornal ou panfletos que apresentem os preços dos produtos, antes e após a promoção. Lembre-se de que

os preços devem ser menores do que 999 reais. Apresente os anúncios aos estudantes destacando o seu preço normal e o preço promocional. Depois, problematize cada anúncio perguntando a toda a turma o valor do troco recebido pelo cliente, após comprar um dos produtos durante a promoção. Em um primeiro momento, informe a quantia paga pelo cliente; e, no segundo momento, informe aos estudantes o valor do troco recebido pelo cliente após realizar a compra para que eles des-

cubram o valor pago pelo cliente. É importante estar atento aos valores para que os estudantes, ao resolverem os problemas, utilizem a subtração com e sem reagrupamento envolvendo números até 999.

Sugestão de intervenção

Caso alguns estudantes tenham dificuldades, retome com eles as diferentes maneiras de resolver subtrações, abordadas nas páginas 132, 133, 137 e 138, utilizando-as para explorar essa atividade.

FICHAS SOBREPOSTAS

MATERIAL COMPLEMENTAR DA PÁGINA 112

NÚMEROS ATÉ 1 000

RECORTAR

00 10 20 30 40 50 60 70 80 90 0 1 2 3 4 5 6 7 8 9

3. Objetivo

Utilizar a adição ou a subtração para descobrir o padrão de uma sequência numérica.

Atividade

Apresente na lousa quatro sequências numéricas envolvendo números menores do que 500, sendo duas delas construídas a partir do segundo termo com a adição de um mesmo número e duas construídas a partir do segundo termo com a subtração de um mesmo número. Em um primeiro momento, peça aos estudantes que identifiquem em quais é utilizada a adição na regra e em quais é utilizada a subtração. Depois, solicite a eles que digam as regras de cada uma das se-

06/10/2025 17:25:03

quências e, por fim, que escrevam mais dois termos de cada uma.

Sugestão de intervenção

Se os estudantes tiverem dificuldade, inicie com valores menores, por exemplo, as sequências 1, 4, 7, 10, 13, 16 e 12, 10, 8, 6, 4, 2. Além disso, faça questionamentos que os incentivem a pensar em estratégias para descobrir a regra, como: “Os números da primeira sequência estão aumentando ou diminuindo?”; “Se estão aumentando, então é adicionado ou subtraído um valor?”; “Quanto aumentou do primeiro para o segundo termo e do segundo para o terceiro?”.

• A fim de assegurar a integridade física dos estudantes e prevenir acidentes, oriente-os a tomar cuidado no manuseio da tesoura, além de garantir que façam uso apenas de tesouras com pontas arredondadas.

UNIDADE

6

1. Objetivo

Realizar medições utilizando unidades de medida de comprimento não padronizadas.

Atividade

Promova uma atividade em que os estudantes devem medir o comprimento de algum objeto da sala de aula ou do pátio da escola, utilizando as partes do corpo

que preferirem, tomando como referência outra parte do corpo, assim eles podem obter relações entre palmo e polegada, passo e palmo, entre outras. Solicite a eles que façam as medições um de cada vez, respeitando o turno dos colegas e observando a própria medição. Para isso, alerte-os dos eventuais riscos na realização desse experimento, garantindo a integridade física deles próprios, dos professores e das demais pessoas envolvidas no processo educacional.

Sugestão de intervenção

06/10/2025 17:25:03

Auxilie os estudantes no registro das medidas obtidas para que, ao final, elas sejam comparadas. No momento da discussão, incentive-os a falar a respeito das referências adotadas que melhor se adequaram ao experimento. Com isso, verifique se eles percebem que, quanto maior é a medida do comprimento a ser aferido, mais conveniente é a adoção de uma referência cuja medida de comprimento não seja muito pequena; e vice-versa.

DIVIRTA-SE E APRENDA - JOGO DA SUBTRAÇÃO

MATERIAL COMPLEMENTAR DA PÁGINA 143

ADIÇÃO E SUBTRAÇÃO

RECORTAR

2. Objetivos

Identificar o centímetro e o milímetro como unidades de medida de comprimento padronizadas.

Identificar o cm e o mm como a abreviação de centímetro e milímetro, respectivamente.

Reconhecer a régua como um instrumento de medida de comprimento.

Utilizar a régua para realizar medições.

Estimar, medir e comparar comprimentos utilizando o centímetro como unidade de medida.

Atividade

Providencie com antecedência algumas fitas métricas e réguas para que os estudantes, em

08/10/2025 08:30:12

duplas, possam discutir a respeito desses instrumentos e das unidades de medida estudadas, de acordo com os questionamentos propostos a seguir e outros que julgar necessários.

• Quantos centímetros, no total, tem a fita métrica? E a régua?

• A medida da fita métrica é equivalente a quantas medidas da régua? Sugestão de intervenção

Inicialmente, promova um momento em que os estudantes possam compartilhar as resoluções entre si e verificar as respostas dos colegas. Caso surjam dúvidas, permita aos colegas que auxiliem no esclarecimento.

• A fim de assegurar a integridade física dos estudantes e prevenir acidentes, oriente-os a tomar cuidado no manuseio da tesoura, além de garantir que façam uso apenas de tesouras com pontas arredondadas.

3. Objetivos

Identificar o metro como unidade de medida de comprimento padronizada.

Identificar o m como abreviação de metro.

Estimar, medir e comparar comprimentos utilizando o metro como unidade de medida.

Atividade

Realize uma atividade prática com os estudantes, meça a altura deles e anote-as em um quadro, na lousa, indicando-as

apenas em centímetros. Em seguida, promova uma discussão entre eles com base nos seguintes questionamentos:

• Quantos estudantes têm mais do que um metro de altura? E quantos têm menos do que um metro de altura?

• Que estratégia vocês usaram para diferenciar as medidas maiores do que um metro de altura das medidas menores do que um metro de altura?

Sugestão de intervenção

Antes de apresentar os questionamentos aos estudantes, diga-lhes que

uma criança cresce, geralmente, em um ritmo diferente e que diversos fatores influenciam o crescimento, como genética, alimentação e medicação. Esteja atento para evitar comentários vexatórios sobre suas alturas e que possam causar constrangimento aos estudantes. Em seguida, leia os questionamentos, um por vez, para que eles respondam oralmente. Com isso, é esperado que eles percebam que, para nos referirmos à medida de altura 110 cm, por exemplo, podemos dizer “1 m e 10 cm”, pois 110 = 100 + 10

DIVIRTA-SE E APRENDA - JOGO DA SUBTRAÇÃO

MATERIAL COMPLEMENTAR DA PÁGINA 143

ADIÇÃO E SUBTRAÇÃO

COLAR

RECORTAR

DOBRAR

UNIDADE 7

1. Objetivos

Compreender as ideias da multiplicação. Reconhecer o símbolo utilizado para representar a multiplicação.

Reconhecer a multiplicação como uma adição de parcelas iguais.

Efetuar multiplicações associadas às ideias de configuração retangular e de contagem de possibilidades.

Atividade

Elabore um problema semelhante ao da atividade 2 da página 165 com a ideia de adição de parcelas iguais. Utilize o contexto da organização de carteiras de uma sala de aula para elaborar o problema com a ideia de configuração retangular e, por último, utilize um cardápio com 3 opções de sanduíches naturais e 4 opções de suco de frutas para elaborar um problema de contagem de possibilidades. Organize a turma em trios e entregue a cada um os três problemas elaborados

• A fim de assegurar a integridade física dos estudantes e prevenir acidentes, oriente-os a tomar cuidado no manuseio da tesoura, além de garantir que façam uso apenas de tesouras com pontas arredondadas.

06/10/2025 17:25:04

para que resolvam juntos. Acompanhe a realização dos problemas nos grupos e registre as dúvidas e as dificuldades que a turma manifestar.

Sugestão de intervenção

Após a resolução dos problemas, selecione três estudantes, um para cada problema, e peça que compartilhem suas respostas com a turma. Aproveite esse momento para esclarecer as dúvidas observadas durante a resolução, bem como aquelas que surgirem durante a apresentação.

2. Objetivos

Efetuar multiplicações de um número de um algarismo por 2.

Compreender o significado de dobro. Efetuar multiplicações de um número de um algarismo por 3.

Compreender o significado de triplo. Atividade

Providencie material concreto, como tampinhas ou cubinhos do material dourado. Na lousa, desenhe triângulos dispostos em duas linhas, contendo 3, 4 e 5 triângulos por linha. Em seguida, peça aos estudantes que indiquem a quantidade

total de triângulos em cada configuração. É possível que eles contem, um a um, o total de triângulos em cada agrupamento. Se isso acontecer, pergunte a eles se é possível resolver esse problema utilizando uma multiplicação. Depois, utilize o material concreto para explorar o conceito de dobro. Apresente aos estudantes um agrupamento desses objetos com quantidades iguais a 3, 4 e 5 e selecione três objetos para representar o dobro dessas quantidades. Utilize o mesmo contexto para abordar a multiplicação por 3 e a ideia de triplo.

Sugestão de intervenção

Caso algum estudante não tenha atingido os objetivos propostos, revise com ele a multiplicação por 2 utilizando as atividades 1 e 2 da página 169 e a multiplicação por 3 das páginas 171 e 172, com as atividades 6 e 7. Explique que dobrar uma quantidade equivale a multiplicar essa quantidade por 2. Para isso, use o material concreto para formar dois agrupamentos: um com 3 objetos e outro com 6 objetos. Assim, a quantidade de objetos do segundo agrupamento é duas vezes a quantidade do primeiro, ou seja, o dobro, que pode ser indicada por 2 × 3

INSTRUMENTOS MUSICAIS

MATERIAL COMPLEMENTAR DA PÁGINA 158

MEDIDAS DE COMPRIMENTO

RECORTAR

IMAGENS SEM PROPORÇÃO ENTRE SI.

REPRESENTAÇÃO DE CUBINHOS

MATERIAL COMPLEMENTAR DA PÁGINA 164 E 208

MULTIPLICAÇÃO

4. Objetivo

Efetuar multiplicações de um número de um algarismo por 5.

Atividade

Use a lousa para desenhar um plantio de árvores organizado em 5 fileiras horizontais, com 6 árvores por fileira, igualmente espaçadas. Em seguida, peça aos estudantes que indiquem a quantidade de árvores plantadas. Peça a eles que determinem por meio de uma multiplicação qual seria a quantidade de árvores após o plantio de mais duas árvores em cada fileira.

RECORTAR

• A fim de assegurar a integridade física dos estudantes e prevenir acidentes, oriente-os a tomar cuidado no manuseio da tesoura, além de garantir que façam uso apenas de tesouras com pontas arredondadas.

3. Objetivo

Efetuar multiplicações de um número de um algarismo por 4.

Atividade

Em uma folha de papel, providencie com antecedência o desenho de 4 camisas (azul, amarela, rosa e cinza) e 3 bermudas (preta, vermelha e verde). Peça aos estudantes que representem usando uma multiplicação o total de opções na escolha de uma camisa e de uma bermuda. Se preferir, organize um quadro com as camisas na vertical e as bermudas na horizontal, conforme o quadro da atividade 7 da página 137, e sugira que os estudantes pintem as combinações (camisas e bermudas) utilizando as cores indicadas.

Sugestão de intervenção

Caso os estudantes tenham dificuldade em reconhecer a multiplicação 4 × 3 , organize um quadro na lousa e liste todas as combinações das peças. Depois, escreva a multiplicação 4 × 3, que indica a quantidade de camisas combinada com a quantidade de bermudas.

Sugestão de intervenção

06/10/2025 17:25:06

Caso os estudantes tenham dificuldade em reconhecer as multiplicações 5 × 6 e 5 × 8, utilize a ideia de adição de parcelas iguais, 6 + 6 + 6 + 6 + + 6 = 5 × 6 e 8 + 8 + 8 + 8 + 8 = 5 × 8, em que o algarismo 5 indica a quantidade de fileiras e os algarismos 6 e 8 a quantidade de árvores por fileira.

UNIDADE 8

1. Objetivos

Identificar objetos do dia a dia que lembram figuras geométricas planas.

Reconhecer retângulos, triângulos, quadrados e círculos.

Atividade

Providencie, antecipadamente, imagens de alguns objetos do dia a dia que lembram figuras geométricas planas, como a capa de um livro ou uma placa de trânsito com a indicação “dê a preferência”. Peça que, para cada imagem, os

estudantes escrevam em seus cadernos o nome de outro objeto que lembra essa mesma figura geométrica plana e escreva o nome da figura (retângulo, quadrado, triângulo ou círculo) abaixo do objeto.

Sugestão de intervenção

Caso os estudantes não consigam escrever o nome de outro objeto, peça que procurem objetos na sala de aula que lembrem a mesma figura geométrica plana, ou que pensem em algum cômodo da casa onde moram e tentem se lembrar de algum objeto que remeta à mesma figura geométrica plana do objeto da imagem.

REPRESENTAÇÃO DE CUBINHOS

MATERIAL COMPLEMENTAR DA PÁGINA 164 E 208

MULTIPLICAÇÃO

2. Objetivos

Reconhecer os lados e os vértices do quadrado, do retângulo e do triângulo.

Identificar a quantidade de lados e de vértices do quadrado, do retângulo e do triângulo.

Atividade

Organize a turma em grupos com três ou quatro estudantes e entregue uma folha com algumas questões a cada grupo, que deve ser preparada antecipadamente. Algumas sugestões de questões são:

RECORTAR

06/10/2025 17:25:06

• Qual figura geométrica plana tem três vértices e três lados?

• Qual figura geométrica plana tem quatro lados iguais e quatro vértices?

• Qual figura geométrica plana tem quatro vértices e quatro lados?

Sugestão de intervenção

Caso os estudantes tenham dificuldade, retome o trabalho com a atividade 13 da página 171 ou desenhe na lousa um quadrado, um triângulo e um retângulo indicando em cada um deles a quantidade de vértices e de lados.

• A fim de assegurar a integridade física dos estudantes e prevenir acidentes, oriente-os a tomar cuidado no manuseio da tesoura, além de garantir que façam uso apenas de tesouras com pontas arredondadas.

• Oriente os estudantes a guardarem os cubinhos, pois poderão ser usados em futuras atividades. Para isso, considere providenciar um envelope a cada estudante para que eles possam guardar o material.

3. Objetivos

Desenvolver noções espaciais para localizar elementos em relação a um ou mais referenciais.

Estabelecer relações de posição no espaço.

Atividade

Identificando e localizando objetos.

Sugestão de intervenção

Proponha a cada estudante que descreva a toda a turma a posição de determinado objeto na sala de aula. Os demais

estudantes devem validar a indicação feita, apontando erros, acertos e outras possibilidades de descrever o mesmo objeto.

4. Objetivo

Compreender as noções de atrás, ao lado, à frente, em cima, embaixo, à direita e à esquerda.

Atividade

Localizando os colegas na sala de aula.

Sugestão de intervenção

Cada estudante deve descrever em

um pedaço de papel o seu lugar na sala de aula, sem se identificar. Eles devem usar os termos atrás, ao lado, à frente, em cima, embaixo, à direita e à esquerda. Em seguida, recolha os papéis e leia-os com toda a turma a fim de que os estudantes identifiquem o nome do colega, de acordo com a descrição. Certifique-se de que todos estão envolvidos na atividade, apresentando algum palpite. Promova questionamentos para auxiliar os estudantes que tiverem dificuldades.

06/10/2025 17:25:06

JOGO DAS FIGURAS PLANAS

MATERIAL COMPLEMENTAR DA PÁGINA 191

FIGURAS GEOMÉTRICAS PLANAS, LOCALIZAÇÃO E DESLOCAMENTO

RECORTAR

5. Objetivo

RetânguloCírculoTriângulo

• A fim de assegurar a integridade física dos estudantes e prevenir acidentes, oriente-os a tomar cuidado no manuseio da tesoura, além de garantir que façam uso apenas de tesouras com pontas arredondadas. Considere providenciar um envelope a cada estudante para que guardem as fichas e joguem em outros momentos, fixando e reforçando as características e as nomenclaturas das figuras geométricas planas.

CírculoCírculoQuadrado

TriânguloQuadradoRetângulo

TriânguloRetânguloCírculo

TriânguloRetângulo

QuadradoQuadrado

Estabelece pontos de referência para descrever trajetos e deslocar-se no plano e no espaço. Identificar e representar caminhos seguindo orientações do trajeto.

Atividade

Realizando e descrevendo trajetos.

Sugestão de intervenção

Leve os estudantes para um passeio da sala de aula até outro ponto dentro da escola. Em seguida, organize a turma em 5 grupos e peça a eles que descrevam e

façam um desenho que represente o trajeto realizado, indicando alguns pontos de referência. Por fim, deixe que exponham à turma, a fim de identificar semelhanças e diferenças nas indicações feitas por cada grupo. Se necessário, refaça o caminho feito inicialmente para que os estudantes identifiquem possíveis erros.

6. Objetivo

Compreender o significado de “para a direita”, “para a esquerda”, “para cima” e “para baixo”.

06/10/2025 17:25:07

Atividade

Compreendendo e executando comandos.

Sugestão de intervenção

Instrua os estudantes a ficarem enfileirados um ao lado do outro e dê os comandos “para a direita”, “para a esquerda”, “para cima” e “para baixo” para que eles executem. Se necessário, peça aos estudantes com melhor desempenho na atividade que auxiliem os que ainda têm dificuldades.

UNIDADE 9

1. Objetivos

Reconhecer a divisão como uma ação de repartir ou distribuir uma quantidade de elementos em partes iguais.

Reconhecer o símbolo utilizado para representar a divisão.

Atividade

Providencie e leve para a sala de aula algumas representações de cédulas e moedas do sistema monetário brasileiro. Escreva algumas operações de divisão na lousa e questione os estudantes que operações são essas. Organize os estudantes em trios para eles poderem compartilhar ideias e estratégias de resolução e distribua algumas cédulas e moedas a cada grupo.

Sugestão de intervenção

Avalie a execução da atividade realizada pelos estudantes observando a participação de cada um, bem como o interesse, a autonomia e o raciocínio e se apresentam dificuldades. Em caso positivo, mude a abordagem, providenciando outras atividades e estratégias com o propósito de saná-las.

2. Objetivos

Compreender o significado de metade.

Compreender o significado de terça parte.

Atividade

Escreva na lousa os números 6, 12, 18, 24 e 30. Em seguida, solicite aos estudantes que escrevam e representem no caderno por meio de desenhos a metade e a terça parte de cada uma dessas quantidades.

Sugestão de intervenção

Caso algum estudante tenha dificuldades na realização da atividade, retome os conteúdos estudados, buscando abordagens diferentes para explicar o assunto, de acordo com as necessidades que forem se tornando evidentes durante a prática.

PESOS PARA AS BALANÇAS

MATERIAL COMPLEMENTAR DA PÁGINA 230

MEDIDAS DE MASSAS, DE CAPACIDADE E DE TEMPO

3. Objetivo

Efetuar divisões por 2, 3, 4 e 5 com quociente menor do que 10. Atividade

Escreva em pequenos pedaços de papéis 4 divisões cujos divisores podem ser 2, 3, 4 ou 5, aleatoriamente, e coloque-os em uma caixa para a realização de um sorteio. Escreva apenas divisões cujo quociente (resultado) seja menor do que 10. Faça um sorteio para cada estudante e

• A fim de assegurar a integridade física dos estudantes e prevenir acidentes, oriente-os a tomar cuidado no manuseio da tesoura, além de garantir que façam uso apenas de tesouras com pontas arredondadas.

RECORTAR

06/10/2025 17:25:07

solicite a eles que resolvam as divisões sorteadas no caderno. Oriente-os a utilizar as estratégias de cálculos que preferirem. Sugestão de intervenção

Caso eles tenham dificuldades para resolver alguma das divisões, oriente-os a realizar desenhos no caderno ou a utilizar algum material manipulável, conforme as sugestões de estratégias apresentadas durante esta unidade.

• A fim de assegurar a integridade física dos estudantes e prevenir acidentes, oriente-os a tomar cuidado no manuseio da tesoura, além de garantir que façam uso apenas de tesouras com pontas arredondadas.

UNIDADE 10

1. Objetivo

Compreender o significado das expressões mais leve e mais pesado.

Atividade

Leve objetos para a sala de aula e faça comparações com os estudantes, usando dois ou mais objetos. Pergunte qual é o mais leve e qual é o mais pesado. Você também pode, por exemplo, juntar dois objetos e perguntar se juntos são mais pesados do que um terceiro. Faça diversas combinações de modo que eles consigam compreender as expressões.

Sugestão de intervenção

Caso algum estudante tenha dificuldade para responder, permita que ele manuseie os objetos e que, assim, perceba a diferença.

2. Objetivos

Reconhecer alguns tipos de balança.

Identificar a balança como instrumento de medida de massa.

Comparar medidas de massa com e sem o auxílio de instrumentos de medição.

Reconhecer o quilograma e o grama como unidade padronizada de medida de massa.

Identificar o kg como a abreviação de quilograma.

Identificar o g como a abreviação de grama.

Atividade

Leve uma balança digital e diferentes objetos para a sala de aula. Escreva na lousa a medida da massa de

cada objeto e escreva também uma medida de massa equivalente à soma da medida da massa de alguns objetos. Pergunte a eles quais objetos devem ser colocados na balança para se obter essa medida de massa. Em seguida, coloque os objetos na balança digital e confira a resposta.

Sugestão de intervenção

Relembre que a medida da massa exibida no visor da balança deve ser igual à soma das medidas das massas dos objetos que estão nela.

DE 2027

1-Confraternizaçãouniversal

NOVEMBRO

RECORTAR

3. Objetivos

Compreender o significado de medida de capacidade.

Comparar medidas de capacidade de recipientes por meio de estratégias pessoais ou utilizando unidades de medida não padronizadas.

Identificar o uso do litro e do mililitro em situações do dia a dia.

Reconhecer o litro e o mililitro como unidades fundamentais de medida de capacidade.

Identificar o como abreviação de litro.

Identificar o como abreviação de mililitro.

Resolver situações-problema que envolvam o litro e o mililitro.

Atividade

Leve recipientes com diferentes medidas de capacidade para a sala de aula, como copos e garrafas. Para facilitar a visualização, use recipientes transparentes. Faça perguntas aos estudantes, como: “Qual tem a maior medida de capacidade?”; “Qual tem a menor?”. Depois que eles apresentarem suas respostas,

• A fim de assegurar a integridade física dos estudantes e prevenir acidentes, oriente-os a tomar cuidado no manuseio da tesoura, além de garantir que façam uso apenas de tesouras com pontas arredondadas.

• Se achar conveniente, oriente os estudantes a selecionarem um material mais resistente, como cartolina ou papelão, para colarem o calendário, facilitando o manuseio.

pergunte quantos copos são necessários para encher a garrafa, por exemplo, ou adapte as perguntas dos itens de acordo com os objetos que estiver usando. Faça a atividade na prática usando água. Lembre-se de informar aos estudantes a medida de capacidade de cada recipiente usando as unidades de medida estudadas.

Sugestão de intervenção

Caso os estudantes não consigam perceber a diferença, relembre a relação entre mililitro e litro, estudada na página 234

4. Objetivos

Identificar o ano como um período de 12 meses.

Reconhecer os meses do ano.

Reconhecer a utilidade do calendário. Identificar a semana como um período de sete dias. Reconhecer os dias da semana.

Atividade

Pergunte aos estudantes algumas datas importantes, como o aniversário ou o próximo feriado. Peça a eles que escrevam no caderno as datas e quantos dias faltam para cada data.

Sugestão de intervenção

Caso algum estudante tenha dificuldade, leve um calendário para a sala de aula e conte com ele os dias usando o calendário. Outra sugestão é inicialmente usar datas mais próximas da data atual, para que a turma consiga relacioná-las com mais facilidade.

5. Objetivos

Reconhecer o relógio de ponteiros e o relógio digital como instrumentos utilizados para medir o tempo. Expressar horários antes do meio-dia e após o meio-dia.

Atividade

Desenhe na lousa alguns relógios de ponteiros com diferentes horários e registre um intervalo de tempo próximo ao desenho do relógio, como “3 horas depois”. Solicite aos estudantes que desenhem no caderno relógios de ponteiros e relógios digitais com o horário final, ou seja, o horário que está marcando no relógio mais o intervalo de tempo indicado ao lado.

Sugestão de intervenção

Se algum estudante tiver dificuldades para responder à atividade, relembre que o horário final será igual à soma do horário exibido no relógio de ponteiros mais o intervalo de tempo escrito na lousa.

MANUAL DO PROFESSOR

Este Manual do Professor é um complemento à primeira parte do Livro do Professor, oferecendo um suporte para o desenvolvimento docente e para o dia a dia em sala de aula. Neste manual, você encontrará uma série de informações importantes, como a estrutura da BNCC, sugestões para desenvolver um trabalho interdisciplinar, informações sobre conceitos, objetivos e instrumentos de avaliação, reflexões sobre o papel do professor e a prática docente, e a fundamentação teórico-metodológica da coleção. Além disso, encontrará um quadro de distribuição

dos conteúdos com as habilidades, competências gerais e específicas de cada componente curricular e os temas contemporâneos transversais da BNCC que estão sendo desenvolvidas em cada unidade, além de sugestões de cronogramas bimestrais, trimestrais e semestrais. Ao final desta parte, são também apresentadas sugestões de referências complementares para a prática docente e as referências bibliográficas comentadas utilizadas como consulta para a produção das orientações ao professor e deste Manual do Professor

A BASE NACIONAL COMUM CURRICULAR (BNCC)

Desde a publicação da Constituição Federal de 1988, o artigo 210 já previa a necessidade de uma base comum para a educação brasileira. Em 1996, com a aprovação da Lei de Diretrizes e Bases da Educação (LDB), as discussões sobre um documento que orientasse os currículos da Educação Básica em todo o Brasil ganharam ainda mais força. Em 2018, após um amplo processo de debates e contribuições de educadores e da sociedade, a Base Nacional Comum Curricular (BNCC) foi homologada.

A BNCC propõe uma progressão de aprendizagens que visa à formação humana integral dos estudantes e à construção de uma sociedade mais justa, democrática e inclusiva. O documento estabelece um aprendizado mínimo e comum, orientado por competências e habilidades que devem ser desenvolvidas em cada etapa de ensino.

Na BNCC, as áreas de conhecimento são compostas de componentes curriculares. Por meio de unidades temáticas, objetos de conhecimento e habilidades, esses

componentes têm o objetivo de desenvolver as competências gerais e específicas.

AS COMPETÊNCIAS GERAIS DA EDUCAÇÃO BÁSICA

A BNCC orienta que, ao longo da Educação Básica, os estudantes desenvolvam dez competências gerais, que envolvem a mobilização de conhecimentos, habilidades, atitudes e valores. Essas competências são o alicerce, definindo o que se espera que o estudante desenvolva em toda a Educação Básica. Nesta coleção, elas são trabalhadas por meio de temas, discussões e atividades que incentivam a reflexão crítica, com sugestões nas orientações ao professor

A seguir, apresentamos as competências gerais da BNCC.

Competências gerais da Educação Básica

1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.

2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.

4.Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital – bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.

5. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.

6. Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.

7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.

8. Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.

9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Versão final. Brasília: MEC, 2018. p. 9-10. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 14 ago. 2025.

A BNCC propõe que o conteúdo chegue à sala de aula de forma contextualizada, o que exige novas estratégias do professor, como a transposição didática. Isso significa converter o conteúdo científico em uma linguagem acessível e adaptada à realidade dos estudantes. Para isso, o estudo e a reavaliação constante da prática docente são essenciais.

A seguir, apresentamos algumas ações que podem ser aplicadas para desenvolver as competências gerais em sala de aula.

Sugestões de ações docentes para as competências gerais

Competência geral 1: Incentive os estudantes a reconhecerem a importância dos conhecimentos já adquiridos, mostrando como eles servem de base para a compreensão da realidade e para a construção de novos saberes.

Competência geral 2: Exercite a curiosidade intelectual, levando os estudantes a usarem a abordagem científica para investigar, levantar hipóteses, resolver problemas e analisar os resultados por meio de experiências e observações.

Competência geral 3: Proporcione o contato com diferentes manifestações culturais em âmbito local, regional e global e promova atividades artísticas, como grupos de dança, elaboração de roteiros e atuação em peças de teatro, festivais musicais e saraus.

Competência geral 4: Dê subsídios para que os estudantes se comuniquem por meio de diferentes linguagens, ajudando-os a selecionar a mais apropriada para cada situação.

Competência geral 5: Utilize de forma intencional e pedagógica diversas tecnologias em sala de aula, verificando o conhecimento prévio dos estudantes e diversificando os recursos metodológicos.

Competência geral 6: Ajude os estudantes a refletirem sobre o futuro e a importância da liberdade, autonomia e consciência crítica em suas escolhas profissionais e pessoais, valorizando a diversidade de saberes e experiências.

Competência geral 7: Ofereça subsídios para que os estudantes desenvolvam a capacidade de argumentar com base em fatos e dados confiáveis, sabendo selecionar e verificar a origem de diferentes fontes para negociar pontos de vistas e defender ideias.

Competência geral 8: Leve os estudantes a se compreenderem e se valorizarem dentro da diversidade, reconhecendo suas emoções e as dos outros, e exercitando a autocrítica.

Competência geral 9: Promova o exercício da empatia, do diálogo e da cooperação, incentivando os estudantes a resolverem conflitos de forma respeitosa e democrática.

Competência geral 10: Contribua para que os estudantes ajam de modo responsável, guiados por princípios éticos e de cidadania, e conscientes de que suas ações devem estar alinhadas à tomada de decisões inclusivas, sustentáveis e solidárias.

Nesta coleção, as competências gerais que são desenvolvidas em textos, atividades e seções que permeiam os conteúdos são destacadas nas orientações ao professor e são listadas no Quadro de distribuição dos conteúdos

AS COMPETÊNCIAS ESPECÍFICAS

Para que as competências gerais se manifestem em cada componente, a BNCC estabelece as competências específicas. A organização dessas competências no Ensino Fundamental varia: em áreas como Matemática e Ciências da Natureza, competências específicas são as mes-

mas para o componente. Em áreas como Linguagens e Ciências Humanas, há competências específicas por área e também para cada componente curricular que as compõem (Língua Portuguesa, Arte, Educação Física, Língua Inglesa, Geografia e História), reconhecendo as particularidades de cada um. Em todos os casos, as competências específicas colaboram para que os objetivos de aprendizagem sejam claros e coerentes, do nível mais amplo ao mais específico.

A seguir, apresentamos as competências específicas de Matemática.

Competências específicas de Matemática para o Ensino Fundamental

1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.

2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.

6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).

7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.

8. Agir pessoal e coletivamente com respeito, autonomia, responsabilidade, flexibilidade, resiliência e determinação, recorrendo aos conhecimentos das Ciências da Natureza para tomar decisões frente a questões científico-tecnológicas e socioambientais e a respeito da saúde individual e coletiva, com base em princípios éticos, democráticos, sustentáveis e solidários

BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Versão final. Brasília: MEC, 2018. p. 267. Disponível em: https://www.gov.br/mec/pt-br/escola-em-tempo-integral/BNCC_EI_EF_110518_versaofinal.pdf. Acesso em: 14 ago. 2025.

Nesta coleção, as competências específicas que são desenvolvidas em textos, atividades e seções que permeiam os conteúdos são destacadas nas orientações ao professor e listadas no Quadro de distribuição dos conteúdos

AS UNIDADES TEMÁTICAS, OS OBJETOS DE CONHECIMENTO E AS HABILIDADES

Para garantir o desenvolvimento das competências gerais e específicas, a BNCC organiza o currículo em três elementos interligados: unidades temáticas, objetos de conhecimento e habilidades.

As unidades temáticas são os grandes blocos de conhecimento que orientam a organização curricular. Elas funcionam como eixos estruturantes que agrupam temas e conceitos de forma mais ampla, garantindo uma abordagem contextualizada e progressiva ao longo dos anos escolares.

Dentro de cada unidade temática, os objetos de conhecimento são os conteúdos, conceitos e processos que devem ser ensinados.

As habilidades representam o que o estudante deve ser capaz de fazer com o conhecimento. Elas indicam ações, processos e competências a serem desenvolvidos.

Juntos, esses três elementos garantem que o processo de ensino não seja apenas a transmissão de conteúdos. A unidade temática fornece o contexto, o objeto de conhecimento define o tema, e a habilidade define a ação que o estudante precisa executar, garantindo um aprendizado significativo e o desenvolvimento das competências.

Nesta coleção, as habilidades que são desenvolvidas

em textos, atividades e seções que permeiam os conteúdos são destacadas nas orientações ao professor, localizadas na primeira parte deste Manual do professor, mostrando a relação entre os diferentes elementos da BNCC, e são listadas no Quadro de distribuição dos conteúdos.

OS TEMAS CONTEMPORÂNEOS

TRANSVERSAIS

Para enriquecer o trabalho com as habilidades e competências da BNCC e contextualizar o ensino, as propostas pedagógicas devem abordar os temas contemporâneos transversais (TCT). Esses temas são assuntos relevantes para a formação cidadã dos estudantes e para a construção de uma sociedade mais justa, ética e sustentável. São temas com caráter interdisciplinar, que conectam os conteúdos escolares com o cotidiano dos estudantes e com questões importantes em discussão na sociedade. De acordo com o documento Temas Contemporâneos Transversais da BNCC, publicado em 2019, esses temas são de relevância local, regional e global e estão organizados em seis macroáreas.

Educação ambiental

Educação para o consumo

Trabalho

Educação financeira

Educação fiscal

Saúde

Cidadania e civismo

Saúde

Educação alimentar e nutricional

Vida familiar e social

Educação para o trânsito

Educação em direitos humanos

Direitos da criança e do adolescente

Processo de envelhecimento, respeito e valorização do idoso

Multiculturalismo

Ciência e tecnologia

Diversidade cultural

Educação para valorização do multiculturalismo nas matrizes históricas e culturais brasileiras

Ciência e tecnologia

Nesta coleção, esses temas são explorados em diferentes momentos no desenvolvimento dos conteúdos e recebem destaque na seção Coletivamente, contribuindo para a formação cidadã dos estudantes por meio de reflexões e propostas de resoluções para problemas, de modo que eles sejam atuantes na sociedade em que vivem.

INTEGRAÇÃO ENTRE OS COMPONENTES CURRICULARES

Desde a década de 1990, o trabalho interdisciplinar tem ganhado relevância no Brasil, sendo incentivado em todos os níveis da Educação Básica. A interdisciplinaridade é a relação entre dois ou mais componentes curriculares que se unem para obter um conhecimento mais amplo e unificado. Essa abordagem vai além da simples comunicação de ideias; ela integra conceitos, metodologias e terminologias para que o conhecimento se torne mais significativo e conectado à realidade dos estudantes.

Ao integrar os diversos componentes, a interdisciplinaridade amplia a compreensão da realidade e contribui para a formação integral dos estudantes como cidadãos. No ambiente escolar, essa abordagem gera resultados positivos, pois incentiva a colaboração e a contextualização de temas, garantindo que o aprendizado esteja alinhado à vivência dos estudantes.

No desenvolvimento de um trabalho interdisciplinar, tanto o professor quanto os estudantes devem estabelecer conexões entre saberes mais amplos e os conteúdos específicos dos diferentes componentes curriculares. Com base nessa articulação, espera-se que consigam construir uma síntese que amplie sua compreensão, superando o nível de entendimento inicial.

Para que esse processo ocorra de forma efetiva, é imprescindível que o professor assuma um papel mediador nesse percurso, sendo o primeiro a exercitar esse movimento de integração. Nesse contexto, o professor deve mobilizar algumas competências, como: [...]

• diferenciação, comparação e contraste entre diferentes perspectivas disciplinares, profissionais e interdisciplinares;

• identificação de pontos comuns e esclarecimento de como as diferenças se relacionam com a tarefa a ser cumprida;

• delineamento de um entendimento holístico baseado nos pontos comuns, mas que continua suscetível às diferenças.

KLEIN, Julie Thompson. Ensino interdisciplinar: didática e teoria. In: FAZENDA, Ivani Catarina Arantes (org.). Didática e interdisciplinaridade. 17. ed. Campinas: Papirus, 2012. p. 121. (Coleção Práxis).

Além disso, para promover um trabalho interdisciplinar de maneira significativa, é essencial que ele esteja pautado nas experiências, no cotidiano e nos interesses dos estudantes. Isso implica aproveitar as situações que emergem naturalmente em sala de aula, por exemplo, perguntas formuladas por eles, projetos em andamento, investigações e demais práticas pedagógicas, como oportunidades para articular diferentes saberes.

Nas propostas interdisciplinares, é comum que os estudantes atuem em grupo, promovendo a interação entre eles. Essa prática fortalece habilidades importantes como a argumentação, a escuta ativa e a organização de ideias.

Essa abordagem exige metodologias mais dinâmicas e colaborativas, favorecendo a construção coletiva do saber. Ao promover a articulação entre os conteúdos curriculares, ela amplia as possibilidades de leitura e interpretação do mundo, tanto para os professores quanto para os estudantes, permitindo uma compreensão do conhecimento como algo vivo, em constante transformação.

Nesta coleção, você encontrará atividades cujo propósito é integrar diferentes componentes curriculares. As seções Coletivamente e Entre textos, por exemplo, trazem temas e reflexões que possibilitam um trabalho integrado. Além disso, o boxe Articulando conhecimentos detalha algumas integrações nas orientações ao professor, contribuindo para o aumento da criatividade e para a formação crítica e responsável dos estudantes na construção de seu conhecimento.

A PRÁTICA INTERDISCIPLINAR

E O TRABALHO COM PROJETOS

INTERDISCIPLINARES

Para planejar um trabalho interdisciplinar, o ponto de partida é definir os objetivos de aprendizagem. Com base

nisso, se for o caso, é importante dialogar com o professor de outros componentes para planejar estratégias conjuntas, considerando os objetivos previamente levantados, os conhecimentos prévios dos estudantes e como os conteúdos podem ser abordados de forma integrada. Quando não for possível contar com a colaboração do professor de outros componentes curriculares, cabe a você orientar os estudantes nas pesquisas, ensinando-os a buscar fontes confiáveis e adequadas à proposta, a fazer registros relevantes, a organizar as informações obtidas e a planejar como os resultados das pesquisas serão entregues.

PROJETOS INTERDISCIPLINARES

Projetos investigativos e pesquisas também são exemplos de atividades que favorecem o trabalho interdisciplinar em sala de aula, pois envolvem tarefas que integram conhecimentos de diferentes áreas, como planejamento, levantamento de hipóteses, coletas de dados, análises, deduções e conclusões.

Os projetos oferecem aos estudantes oportunidades concretas de participação ativa no processo de construção do conhecimento, contribuindo diretamente para o desenvolvimento de diversas competências, como o pensamento crítico e reflexivo, a argumentação, a valorização do pluralismo de ideias, a criatividade, a cooperação, a autonomia e a comunicação.

Nesse contexto, você continua sendo o mediador, orientando e acompanhando os estudantes para que atuem com autonomia e sejam protagonistas do desenvolvimento do projeto.

É importante ressaltar que a estrutura de um projeto não deve ser encarada como um modelo fixo ou engessado. Os projetos podem assumir diferentes formatos, conforme os objetivos e os contextos de aplicação. Em geral, iniciam-se com uma situação-problema ou uma questão orientadora, que dá origem a um conjunto de etapas organizadas de forma lógica. A seguir, apresentamos um

AVALIAÇÃO

A avaliação tem papel fundamental no processo de ensino-aprendizagem, pois é uma oportunidade de investigar, diagnosticar, refletir e intervir sobre o processo e acompanhar o desenvolvimento dos estudantes e sua atuação enquanto docente.

É fundamental compreender que a avaliação não deve ocorrer apenas em situações isoladas. O acompanhamento do percurso de aprendizagem dos estudantes precisa ser contínuo, tendo como base observações frequentes e diversificadas. Nesse sentido, o processo avaliativo deve fazer parte das práticas pedagógicas do dia a dia, de modo integrado ao planejamento e às atividades desenvolvidas em sala de aula.

A você, a avaliação possibilita observar e refletir sobre sua prática docente e a oportunidade de readequar e reajustar atividades, práticas e estratégias para alcançar determinados objetivos, com a participação ativa dos estudantes nesse processo. Desse modo, é de grande importância a interpretação dos resultados para que,

modelo com etapas fundamentais que podem nortear a construção de um projeto interdisciplinar.

Planejamento

• Definição da situação-problema ou da questão norteadora.

• Conversa sobre o tema e levantamento de hipóteses.

• Elaboração de questões norteadoras com base na situação-problema.

• Formação das equipes, distribuição de tarefas e estabelecimento de metas e prazos.

• Consulta de diversas fontes e coleta de informações.

Execução

• Organização, testes e execução do trabalho.

• Realização de ajustes finais.

• Avaliação durante o processo.

• Definição da participação dos integrantes que conduzirão a apresentação.

Divulgação

• Apresentação dos resultados para a comunidade escolar.

• Publicação do trabalho final.

Avaliação

• Avaliação dos resultados do projeto.

• Realização de autoavaliação.

• Verificação do desempenho e do desenvolvimento das aprendizagens dos estudantes.

Fonte de pesquisa: BENDER, William N. Aprendizagem baseada em projetos: educação diferenciada para o século XXI. Tradução de Fernando de Siqueira Rodrigues. Porto Alegre: Penso, 2014. p. 61.

com base neles, você possa refletir sobre intervenções a serem feitas para sanar possíveis defasagens e, assim, auxiliar no processo de construção do conhecimento, identificando possibilidades de recuperação e progressão do aprendizado.

É essencial que a avaliação seja compreendida como uma ferramenta de inclusão e de apoio ao processo de ensino-aprendizagem, evitando que seja usada apenas como forma de analisar a eficiência e classificar os estudantes. Avaliar não deve ser sinônimo de rotular ou excluir, mas sim de compreender os percursos formativos deles. Para que a avaliação realmente contribua para identificar os progressos, as dificuldades e as possíveis lacunas no desenvolvimento das aprendizagens, é necessário que os critérios sejam previamente compartilhados e discutidos com os estudantes, pois isso favorece a compreensão dos objetivos da avaliação e promove uma participação mais ativa por parte deles.

O planejamento das avaliações deve estar alinhado aos conteúdos e às atividades efetivamente trabalhados em sala de aula, com uma abordagem reflexiva e contextualizada. É essencial considerar os processos de aprendizagem mais adequados à turma e considerar a diversidade de perfis entre os estudantes. Além disso, é recomendável diversificar os instrumentos utilizados, não se restringindo a provas e testes, e incluir diferentes formas de expressão

Avaliação diagnóstica

do conhecimento. Entre as possibilidades, destacam-se atividades em grupo, debates, produções escritas e orais, atividades práticas, questões objetivas e dissertativas, entre outros formatos que respeitem as múltiplas formas de aprender e se comunicar dos estudantes.

Nesta coleção, a ação avaliativa do processo de ensino-aprendizagem propõe três tipos principais: a avaliação diagnóstica, a avaliação formativa e a avaliação de somativa.

A avaliação diagnóstica é o momento de identificar os conhecimentos que os estudantes trazem consigo, além de suas necessidades e dificuldades.

Essa etapa é fundamental para você reajustar as rotas e os objetivos de ensino. É importante ressaltar que a avaliação diagnóstica não precisa de um registro formal; a simples observação de uma atividade em sala de aula, por exemplo, já permite que você identifique as habilidades que precisam ser desenvolvidas ou aperfeiçoadas.

Onde ocorre

Nesta coleção, um exemplo de avaliação diagnóstica está na seção Vamos iniciar, no início de cada volume. Nela, são propostas atividades que possibilitam determinar se será necessário retomar conteúdos, estabelecer objetivos e definir as práticas e as estratégias didáticas. Nas orientações ao professor, você encontra sugestões de intervenção com base na análise das respostas e nas dificuldades dos estudantes.

A avaliação diagnóstica também pode ser feita no início de cada unidade, pois as atividades das páginas de abertura possibilitam diagnosticar os conhecimentos prévios dos estudantes sobre os temas e os conteúdos que serão abordados.

Avaliação formativa

A avaliação formativa acontece ao longo do período letivo. São os processos contínuos pelos quais você obtém indicadores a respeito da aprendizagem dos estudantes.

Desse modo, esse tipo de avaliação possibilita que você realize intervenções, propondo novas estratégias e procedimentos que visam à melhoria e/ou ao aprofundamento dos conhecimentos por parte dos estudantes.

A avaliação formativa pode ter um papel fundamental na melhoria das aprendizagens de todos os alunos. A sua utilização sistemática deve permitir que os alunos conheçam bem: a) o que têm de aprender no final de um dado período de tempo; b) a situação em que se encontram quanto às aprendizagens que têm de desenvolver; e c) os esforços que têm de fazer para aprenderem o que está previsto e descrito nos documentos curriculares. Para tal, a comunicação entre professores e alunos é fundamental, pois é através dela que os alunos podem receber orientações que os ajudam a aprender. [...]

FERNANDES, Domingos. Avaliação formativa: Folha de apoio à formação: Projeto de Monitorização Acompanhamento e Investigação em Avaliação Pedagógica (Maia). Ministério da Educação/Direção-Geral da Educação, 2021. p. 4.

Onde ocorre

Nesta coleção, a avaliação formativa é um processo contínuo e integrado. A seção Vamos avaliar o aprendizado, ao final de cada unidade do Livro do Estudante, oferece atividades que retomam os principais conceitos e noções trabalhados para verificar a aprendizagem com relação aos objetivos estabelecidos. Nas orientações ao professor, o boxe Avaliando complementa essa prática com propostas de atividades avaliativas adicionais. Ele inclui objetivos e estratégias de intervenção, caso seja necessária a retomada de conteúdos e conceitos.

Além disso, é importante o hábito de transitar pela sala de aula e observar os estudantes durante as atividades propostas. Esse acompanhamento mais próximo contribui para que eles se reconheçam como parte do processo de ensino-aprendizagem, desenvolvam sua autonomia e busquem aprimoramento contínuo.

Avaliação somativa

A avaliação somativa é realizada ao final de um período de estudos, em consonância com as práticas pedagógicas da escola. Com base nas respostas a essa avaliação, você poderá refletir sobre ações a serem tomadas para sanar possíveis dificuldades dos estudantes.

Por ser comumente associada a testes e notas que visam classificar o desempenho dos estudantes, é fundamental que ela não seja o único foco do processo avaliativo. A nota é apenas uma das muitas formas de representar os resultados, e essa etapa deve ser considerada como a consequência natural das avaliações diagnóstica e formativa já realizadas.

Ao analisar os resultados, você pode refletir sobre as ações necessárias para sanar possíveis dificuldades, utilizando o de-

sempenho como um indicativo para a retomada de conteúdos e a definição de novas estratégias. Dessa forma, resultados abaixo do esperado não são uma sentença, mas sim um ponto de partida para aprimorar o processo de ensino-aprendizagem.

Onde ocorre

Nesta coleção, a avaliação somativa acontece ao final de cada volume, na seção Vamos concluir. Essa seção oferece atividades que permitem a você verificar os conhecimentos adquiridos pelos estudantes no decorrer do ano letivo. Nas orientações ao professor, você encontra sugestões de intervenção para analisar as respostas e identificar a necessidade de estratégias de remediação, garantindo que os objetivos pedagógicos sejam alcançados.

Para um sistema de avaliação eficiente, é recomendável a combinação das três modalidades, além de usar diferentes instrumentos que auxiliem a obter informações

Provas e testes

Seminários e debates

Portfólios

sobre o desenvolvimento da aprendizagem dos estudantes. Apresentamos a seguir alguns exemplos.

Instrumentos de avaliação

Podem ser elaborados com questões abertas, análise de situações, questões objetivas e quizzes, e realizados de forma regular, abordando conteúdos específicos ou referentes a determinado período.

Possibilitam a você perceber o desenvolvimento de habilidades relacionadas a tarefas como pesquisa, síntese das informações, pensamento crítico e comunicação.

A elaboração de portfólios com base em suas observações e registros em fichas avaliativas contribui não só para analisar o desenvolvimento cognitivo dos estudantes, mas também a maneira como cada um aprende, com atenção especial às habilidades que eles desenvolvem com mais facilidade e as que demandam mais atenção e auxílio para serem desenvolvidas.

Saraus Permite a você verificar o desenvolvimento de habilidades relacionadas a interação social, capacidade de expressão, criatividade, sensibilidade e conhecimento cultural.

Ditados Possibilita que você acompanhe as principais dificuldades dos estudantes com relação à escuta e à escrita.

Autoavaliação

Incentiva o desenvolvimento da autonomia dos estudantes levando-os a refletir sobre sua participação nas atividades, suas dificuldades e aspectos que devem ser melhorados. Com base nessas informações, você pode debater com eles os caminhos para gerar mudanças no planejamento e melhorias para toda a turma.

Para auxiliar o monitoramento das aprendizagens, sugerimos a utilização de uma ficha de avaliação de acompanhamento individual, como a que apresentamos a seguir. Essa ferramenta permite registrar a trajetória de cada estudante, observando seu desenvolvimento com relação aos objetivos e às habilidades trabalhados.

A ficha usa um sistema de marcação simples para identificar o nível de desenvolvimento do estudante.

• S (Sim): o estudante demonstrou ter alcançado o objetivo.

• P (Parcialmente): o estudante atingiu o objetivo de forma incompleta, necessitando de intervenção para avançar.

Escola: preencher com o nome da escola.

Estudante: preencher com o nome do estudante.

• N (Não): o estudante não alcançou o objetivo, sendo necessária uma intervenção imediata. Quando o objetivo é alcançado e marcado com S, você deve incentivar o estudante a aprofundar seus saberes. Se a marcação for P ou N, a ficha serve como um diagnóstico claro, indicando a necessidade de planejar intervenções para que o estudante progrida nos estudos.

Você pode usar esse tipo de ficha para registrar observações feitas durante o trabalho com as seções Vamos iniciar, Vamos avaliar o aprendizado e Vamos concluir do Livro do Estudante, e com o boxe Avaliando das orientações ao professor

Professor(a): preencher com o nome do(a) professor(a).

Turma: preencher com a indicação da turma. Período letivo do registro: preencher com o ano letivo.

Ficha de acompanhamento individual das aprendizagens

Objetivos ou habilidades avaliados S (Sim) P (Parcialmente) N (Não) Observações

Preencher com o objetivo ou a habilidade.

Preencher com o objetivo ou a habilidade.

MODELO

O

No contexto atual da educação, o papel do professor dos Anos Iniciais do Ensino Fundamental vai além da transmissão de conteúdo. Ele deve atuar como mediador do conhecimento, incentivando a autonomia dos estudantes e formando leitores e pensadores críticos. Acima de tudo, o professor é um agente essencial na construção da base educacional e emocional dos estudantes.

Essa etapa da escolarização é marcada por profundas transformações no desenvolvimento cognitivo, afetivo e social dos estudantes. Por isso, a prática pedagógica exige sensibilidade e escuta ativa. Você deve estar atento às necessidades individuais dos estudantes, respeitando seus ritmos de aprendizagem e suas realidades. A construção de vínculos afetivos é fundamental para fortalecer a autoestima e a autonomia, pois são eles que criam um ambiente acolhedor, onde o erro é considerado como parte do processo de aprendizagem e todos os estudantes se sentem seguros para se expressarem.

Sua atuação docente envolve uma reflexão constante sobre os conteúdos, as metodologias e, principalmente, sobre como os estudantes aprendem. Ao aproximar o conteúdo escolar dos conhecimentos prévios deles, você torna o aprendizado mais significativo e prazeroso. Essa abordagem, que valoriza sua bagagem cultural e suas experiências, é fundamental na construção de uma relação positiva deles com o ato de estudar.

O planejamento pedagógico é o ponto de partida, mas a prática em sala de aula é dinâmica, e não linear. É no dia a dia que você conhece os perfis, as necessidades e os ritmos da turma, e que a flexibilidade e a capacidade de adaptação se tornam essenciais. O diálogo constante com a equipe pedagógica e a participação em formações continuadas são atitudes que favorecem o desenvolvimento de uma prática docente mais eficaz e alinhada às reais demandas da turma.

Nessa jornada, você é o principal organizador das ações pedagógicas. É quem acolhe, engaja e dá oportunidade para que os estudantes verbalizem seu raciocínio, escrevam e desenvolvam, no coletivo da turma, a compreensão sobre os motivos das atividades e a formulação das respostas. O livro didático não é apenas um guia, mas um instrumento cultural que serve como mediador entre você e o estudante, auxiliando na construção do conhecimento. Com autonomia, é você quem dá vida a esse material, ajustando-o às necessidades de cada turma para que os estudantes se tornem os protagonistas de sua aprendizagem.

A PRÁTICA PEDAGÓGICA EM AÇÃO

A sala de aula é marcada pela diversidade. Cada estudante traz consigo um conjunto de experiências, saberes e modos de aprender. Essa diversidade se expressa em aspectos comportamentais, cognitivos, afetivos e

socioculturais que influenciam diretamente o modo como cada um constrói o conhecimento. Já as trajetórias individuais são moldadas por fatores como o contexto familiar, as vivências culturais e o ambiente social em que estão inseridos. É seu papel e da equipe escolar acolher essas diferenças.

Nesse sentido, compreender o desenvolvimento dos estudantes exige atenção ao contexto em que vivem, às suas práticas cotidianas e à maneira como atribuem significado às suas experiências. Por isso, uma das grandes questões que se impõe ao trabalho docente é: como planejar intervenções pedagógicas que deem conta da heterogeneidade presente em sala de aula, especialmente em turmas numerosas?

Diante desse desafio, é essencial que você reconheça que não há um único caminho para a aprendizagem. As interações, os ritmos e os interesses variam, e é seu papel estar atento a essas diferenças, promovendo práticas pedagógicas flexíveis e inclusivas. Só assim será possível garantir que todos os estudantes tenham oportunidades reais de desenvolvimento, respeitando suas singularidades sem comprometer a qualidade do processo de ensino-aprendizagem.

A seguir, apresentamos sugestões para auxiliar seu dia a dia, promovendo a adequação de atividades e a progressão do aprendizado, para que os estudantes avancem no próprio ritmo, com o apoio necessário para superar desafios.

A PEGA DO LÁPIS NO PROCESSO DE ALFABETIZAÇÃO

Como os estudantes dos Anos Iniciais do Ensino Fundamental estão no processo de alfabetização, é importante que você os auxilie na apropriação do sistema de escrita. Uma das intervenções relevantes nesse processo é a orientação sobre a pega funcional do lápis. A pega de três pontos, também conhecida como pega tripoide ou trípode, é uma técnica considerada funcional, pois favorece movimentos mais precisos, fluidos e controlados, o que é essencial para o desenvolvimento da escrita e evita fadiga muscular. Para orientar os estudantes, incentive-os a:

• posicionar o lápis de forma relaxada, sem forçar os dedos;

• segurar o lápis entre a ponta do polegar e a lateral do dedo indicador;

• apoiar o lápis no dedo médio para dar suporte e estabilidade;

• deixar os outros dedos (anelar e mínimo) levemente dobrados na palma da mão, servindo de apoio.

É fundamental acompanhar o processo individualmente, observando se a pega está firme, mas não tensa. No entanto, trata-se de um desenvolvimento; desse modo, inicialmente não é recomendada a correção direta da

pega, mas sim uma observação atenta para compreender como cada estudante está se apropriando desses movimentos e o que pode ser feito para progredir.

O desenvolvimento da pega do lápis não se resume apenas a segurar o instrumento. Ele é resultado de uma coordenação motora fina bem desenvolvida. Para auxiliar nesse processo, é importante incluir atividades lúdicas e variadas na rotina da sala de aula que ajudam a fortalecer a musculatura das mãos e dos dedos, como brincar com massinha de modelar ou argila, rasgar papel com as mãos, rasgar papel em pedaços pequenos e fazer bolinhas com as pontas dos dedos, cortar com tesoura de pontas arredondadas e colar pedaços de papel pequenos.

A INCLUSÃO NAS ESCOLAS

Garantir a inclusão de estudantes com deficiência na escola regular não é apenas um dever legal, mas um compromisso ético e pedagógico com a equidade e a justiça social. A legislação brasileira, incluindo a Constituição Federal (1988), a Lei Brasileira de Inclusão (LBI) (2015) e as Diretrizes da Política Nacional de Educação Especial (2008), reforça o papel da escola em assegurar que todos os estudantes tenham acesso a uma educação de qualidade. Contudo, a inclusão vai além de permitir o acesso físico à sala de aula. Ela exige a participação ativa dos estudantes no cotidiano escolar, promovendo aprendizagens significativas e respeitando suas particularidades. Para isso, é essencial o envolvimento de toda a comunidade escolar na construção de um ambiente que valorize as diferenças e que favoreça as interações e o respeito à diversidade. Nesse contexto, o papel do professor é central, como mediador e agente de transformação.

O primeiro passo mais importante é levar ao professor o reconhecimento das diversas dificuldades que deverá encontrar, suas especificidades, suas formas de atuação e como identificá-las em seus alunos. Neste processo, ao professor caberá a autonomia de reconhecer as dificuldades e intervencionar, em sala de aula, para a aplicação de novas metodologias e saberes, para a chegada da cognição.

JOIA, Michele. A inclusão de crianças na escola: o papel do educador diante das dificuldades de aprendizagem. 2. ed. Rio de Janeiro: Wak Editora, 2023. p. 41.

A prática pedagógica inclusiva deve reconhecer que todo estudante tem a capacidade de aprender, desde que seja incentivado por vínculos afetivos e em um ambiente acolhedor. Para isso, as estratégias precisam ser flexíveis e adaptadas às necessidades individuais.

PRÁTICAS PEDAGÓGICAS INCLUSIVAS

A seguir, sugerimos algumas ações que podem ser aplicadas em sala de aula para promover a inclusão.

• Materiais concretos e táteis: utilize materiais com diferentes texturas e relevos para que os estudantes possam explorar o conteúdo de forma sensorial. Ao utilizar recursos visuais, sempre descreva as imagens com clareza, indicando posições e características dos objetos.

• Comunicação clara: apresente os enunciados das atividades de forma clara e direta, evitando ambiguidades, figuras de linguagem ou construções muito complexas. Divida as tarefas em etapas menores e forneça uma instrução por vez. Durante as explicações, posicione-se de frente para os estudantes, facilitando a atenção à sua fala.

• Flexibilização e ritmo: ofereça prazos flexíveis para a entrega de atividades, respeitando o tempo de aprendizagem de cada estudante. Incentive a leitura compartilhada de textos e enunciados para promover a compreensão coletiva e o apoio mútuo.

• Incentivo à expressão: incentive a expressão oral, quando possível, e a organização do pensamento dos estudantes, auxiliando na estruturação das ideias. Ferramentas como alfabeto móvel e banco de palavras são ótimas aliadas para a alfabetização e o fortalecimento da participação dos estudantes no processo de aprendizagem.

• Uso de tecnologia: quando possível, adote recursos tecnológicos que atendem às necessidades específicas dos estudantes, ampliando as possibilidades de acesso ao conteúdo e tornando o aprendizado mais dinâmico e acessível.

• Valorização de estratégias de resolução de problemas: apresente e valorize diferentes estratégias para a resolução de problemas, respeitando a forma única de compreensão e de elaboração de soluções.

O USO DE METODOLOGIAS ATIVAS

O uso de metodologias ativas favorece o engajamento dos estudantes e o desenvolvimento de diversas habilidades. A prática pedagógica exige um planejamento cuidadoso, momentos de discussão em grupo, atividades colaborativas e trocas de saberes, especialmente quando o objetivo é fortalecer competências como leitura, escrita e raciocínio lógico-matemático.

[...]

Metodologias ativas são estratégias de ensino centradas na participação efetiva dos estudantes na construção do processo de aprendizagem, de forma flexível, interligada e híbrida. As metodologias ativas, num mundo conectado e digital, expressam-se por meio de modelos de ensino híbridos, com muitas possíveis combinações. A junção de metodologias ativas com modelos flexíveis e híbridos traz contribuições importantes para o desenho de soluções atuais para os aprendizes de hoje.

MORAN, José. Metodologias ativas para uma aprendizagem mais profunda. In: BACICH, Lilian; MORAN, José (org.). Metodologias ativas para uma educação inovadora: uma abordagem teóricoprática. Porto Alegre: Penso, 2018. p. 4.

A seguir, apresentamos três metodologias ativas que promovem o protagonismo e a autonomia dos estudantes.

Pensar-conversar-compartilhar

É uma estratégia eficaz para aumentar o engajamento dos estudantes, pois promove o pensamento individual e a colaboração, permitindo que todos participem ativamente da aula. A fase individual garante que todos os estudantes tenham oportunidade de organizar suas ideias e de se expressarem. A fase em duplas e a discussão geral mantêm os estudantes ativos e envolvidos no processo de aprendizagem, incentivando o pensamento crítico, a argumentação e a formulação de ideias. Para iniciar, você deve fazer uma pergunta ou lançar um desafio relacionado ao conteúdo da aula e estipular um tempo para os estudantes pensarem sozinhos na resposta. É o momento de organizar as ideias e formular uma primeira hipótese. Depois do tempo de reflexão individual, os estudantes se juntam a um colega. Em duplas, eles devem conversar, compartilhar ideias e chegar a uma conclusão, consolidando o raciocínio e construindo o conhecimento de forma colaborativa. Na etapa final, o professor deve escolher algumas duplas, ou todas, para apresentarem suas ideias, incentivando a participação de todos e levando-os a perceber que há diferentes formas de pensar e de resolver o mesmo problema.

Vire e fale

Essa estratégia é eficaz para aumentar o engajamento e a participação dos estudantes, pois modifica o formato de pergunta e resposta e cria um espaço para que eles possam expressar suas ideias. A conversa em duplas incentiva-os a organizarem suas ideias e a praticarem a escuta ativa. É uma estratégia rápida e simples que pode ser utilizada várias vezes durante a aula para checar a compreensão e manter o ritmo de forma dinâmica e interativa. Para começar, faça uma pergunta clara e direta relacionada ao conteúdo que está sendo trabalhado e que possa ser respondida em cinco minutos. Imediatamente após a pergunta, peça aos estudantes que virem para um dos colegas para conversarem sobre a pergunta, tentando chegar a uma resposta em até cinco minutos. Esse é o momento em que eles devem verbalizar suas ideias uns para os outros, escutando o que o outro tem a dizer e chegando juntos a uma conclusão. Após a conversa em duplas, escolha alguns estudantes, ou todos, para compartilharem as ideias que surgiram nas duplas e faça intervenções quando julgar necessário.

Caminhada na galeria

Essa é uma estratégia colaborativa que envolve a produção de cartazes sobre os conteúdos estudados que devem ser expostos como em uma galeria de arte. A atividade foge da rotina da sala de aula e envolve movimento, o que é indicado para essa faixa etária. Os estudantes aprendem uns com os outros e desenvolvem a capacidade de escutar e argumentar, além de aprimorar a comunicação, o raciocínio e a organização de ideias de forma lúdica e prática, aprofundando os conteúdos que aprenderam. Para trabalhar com essa metodologia, organize a turma em grupos e proponha um tema, uma pergunta ou um problema para ser trabalhado em cada grupo. Oriente os grupos a fazerem pesquisas sobre o assunto e a registrarem as conclusões em cartazes. Depois de prontos, os cartazes devem ser fixados na sala de aula, como se fossem obras de arte, e cada grupo deve escolher um apresentador que ficará ao lado para explicar o trabalho. O restante da turma, em grupos, começa a caminhada pela galeria, observando e analisando as produções dos colegas. Após todos os grupos visitarem as obras da galeria, reúna todos e incentive uma conversa sobre o que foi aprendido. Esse é o momento para discutir as diferentes soluções encontradas, os pontos em comum e o que mais chamou a atenção dos estudantes.

A ORGANIZAÇÃO DO ESPAÇO

Para a organização do trabalho pedagógico em sala de aula, é essencial considerar a disposição do espaço e promover um ambiente pautado pela empatia, pelo respeito mútuo e pela valorização do coletivo, o que contribui para a construção de uma sala de aula acolhedora, na qual o desenvolvimento da autonomia dos estudantes seja incentivado de forma constante.

A fim de promover um ambiente mais dinâmico, inclusivo e colaborativo, você pode alterar a organização tradicional da sala de aula, que tem carteiras enfileiradas e o professor ocupando o papel central como único detentor do saber. Ao repensar a organização da sala de aula como um recurso pedagógico, você amplia as possibilidades de interação, cooperação e construção coletiva do conhecimento, aproximando a prática docente das demandas reais da turma. A seguir, apresentamos algumas sugestões para organizar a sala de aula de diferentes maneiras.

Disposição em grupo: indicada para atividades que exigem colaboração direta e trocas constantes entre os estudantes, como trabalhos em equipe, debates e projetos que precisam de divisão de tarefas, pois a proximidade física facilita a comunicação e o apoio mú-

tuo, incentivando a resolução de problemas de forma coletiva.

Em grupo

Representação de carteiras dispostas em grupo.

Disposição em círculo: indicada para atividades que priorizam a participação de todos, a escuta ativa e a criação de um ambiente de igualdade, como rodas de conversa, discussões sobre temas específicos, contação de histórias e compartilhamento de experiências, permitindo que a construção do conhecimento, a troca de experiências e a comunicação sejam mais diretas e isonômicas entre você e os estudantes.

Representação de carteiras dispostas em círculo.

Disposição em U: indicada para apresentações orais, demonstrações, debates supervisionados ou quando você precisa circular entre as carteiras para dar assistência individual, pois combina sua visibilidade com a possibilidade de interação entre os estudantes, permitindo que todos mantenham o foco na atividade.

Em U

Representação de carteira dispostas em U.

Disposição de frente uns para os outros: parecida com a disposição em grupo, mas pode ser utilizada para trabalhos em duplas, entrevistas ou atividades de reflexão, pois promove uma interação mais focada e próxima, permitindo aos estudantes que se concentrem na troca de informações e ideias entre si, sem a dispersão que um grupo maior poderia causar.

De frente uns para os outros

Representação de carteiras dispostas de frente umas para as outras.

Outra estratégia que ajuda a aproximar o currículo da vida dos estudantes é incentivar a utilização de outros espaços dentro e fora da sala de aula para divulgar o trabalho desenvolvido pela turma, como os murais e as paredes, explorando diferentes recursos e estratégias.

A ORGANIZAÇÃO DO TEMPO E DA ROTINA ESCOLAR

Além da organização do espaço físico, é fundamental atentar à gestão do tempo e da rotina em sala de aula. Estabelecer uma rotina clara e bem estruturada favorece a execução do planejamento pedagógico, garantindo que os horários e as atividades sejam conduzidos de forma sequencial e coerente, sempre respeitando as particularidades e os diferentes ritmos de aprendizagem dos estudantes.

Planejar a prática pedagógica de acordo com a proposta curricular proporciona um ambiente mais estável e acolhedor, no qual os estudantes sabem o que esperar e se sentem mais seguros diante das estratégias utilizadas no dia a dia. Além de facilitar a condução do trabalho docente, essa organização contribui para equilibrar e diversificar as atividades ao longo da semana, ampliando as possibilidades de aprendizagem.

Além das aulas nas quais os conteúdos e as atividades são abordados, é importante que você inclua atividades diversificadas em seu planejamento de rotina, como as sugeridas a seguir.

• Rodas de conversa: podem ser realizadas no começo ou no final da aula para solicitar aos estudantes que relatem alguma vivência pessoal (como forma de explorar os conhecimentos prévios) ou exponham o que aprenderam, quais dificuldades tiveram ou o que gostariam de aprender na próxima aula.

• Momentos de leitura: esses momentos podem ser conduzidos tanto por você, por meio da leitura em voz alta, quanto pelos próprios estudantes, com a leitura compartilhada ou um de cada vez. É importante reservar intervalos de tempo específicos na rotina para a leitura de diferentes textos com a intenção de proporcionar momentos de apreciação e, ao mesmo tempo, ampliar o repertório e os conhecimentos dos estudantes.

• Momentos de registro : essa estratégia consiste em reservar, ao final das aulas, alguns minutos para que os estudantes expressem o que aprenderam. Esse registro pode ser feito por meio da escrita, de esquemas visuais, de desenhos ou até pela oralidade, com gravações em áudio ou vídeo. Essa etapa funciona como uma forma de verificação da aprendizagem, permitindo a você identificar o que foi compreendido e o que ainda precisa ser retomado em aulas futuras ou em atividades de reforço. Os registros podem ser feitos individualmente, em duplas ou em pequenos grupos, de acordo com os objetivos da proposta.

• Visitas guiadas a diferentes espaços de aprendizagem: a sala de aula não é o único ambiente para o aprendizado dos estudantes, por isso é importante sugerir atividades em outros espaços na escola, como laboratórios, bibliotecas, pátio, auditório e jardim, e fora da escola, como teatros, museus, espaços públicos, centros de pesquisas, cinema e centros culturais. Em casos de atividades em espaços fora da escola, é necessário que você solicite, com antecedência, as autorizações para a direção e para os pais ou responsáveis dos estudantes, e as faça com o acompanhamento de outros profissionais

Escola: preencher com o nome da escola.

Professor(a): preencher com o nome do professor.

da escola, bem como a orientação do uso de filtro solar, da ingestão de água e do uso de repelentes e de vestimentas e calçados adequados, visando à segurança, à integridade física e ao bem-estar dos estudantes.

Além dessas atividades, o planejamento de rotina deve incluir atividades lúdicas que incentivem a interação social e momentos que envolvam alimentação e higiene pessoal.

Apresentamos a seguir um exemplo de planejamento de rotina, que pode ser adaptado de acordo com as suas necessidades, as dos estudantes e as da escola.

MODELO

Componente curricular: preencher com o nome do componente curricular. Turma: preencher com a indicação da turma. Data: preencher com o período do planejamento.

Planejamento de rotina

Horário Local Atividade Objetivos

7h30 – 8h Sala de aulaAcolhimento e roda de conversa. Promover a socialização e desenvolver a oralidade.

8h – 9h30 Sala de aula

9h30 – 10h Refeitório, banheiro e pátio

10h – 11h Quadra

Leitura compartilhada de textos e atividades dirigidas de escrita.

Lanche, escovar os dentes, lavar as mãos e recreio.

Brincadeiras tradicionais e jogos cooperativos.

11h – 11h30 Sala de aulaRoda de leitura e fechamento.

Outro recurso pedagógico que pode auxiliar a gestão do tempo e o planejamento de rotina é a sequência didática. Uma sequência didática é um plano de ensino estruturado, composto de um conjunto de atividades ordenadas e interligadas que são desenvolvidas ao longo de várias aulas. A elaboração de sequências didáticas é um recurso pedagógico que pode tornar o planejamento mais eficaz e alinhado às necessidades dos estudantes. Por meio delas, você consegue organizar o processo de ensino de maneira intencional e progressiva, estruturando atividades e estratégias de forma coerente e articulada.

Ao planejar uma sequência didática, você estabelece etapas claras e encadeadas que favorecem a construção do conhecimento ao longo do tempo, seja em alguns dias, semanas ou até meses. Essa organização permite flexibilizar o percurso, ajustando-o conforme o ritmo de aprendizagem da turma e as particularidades do contexto escolar.

Desenvolver habilidades de leitura e de escrita.

Momento de descanso, alimentação, higiene e interação livre.

Desenvolver a expressão corporal e a coordenação motora.

Desenvolver a escuta ativa, retomar as aprendizagens do dia e organizar a sala de aula.

É fundamental que as sequências estejam alinhadas aos objetivos de ensino, considerando também os recursos didáticos disponíveis e a realidade da escola. Outro aspecto essencial é a inclusão de estratégias de avaliação que permitam acompanhar e refletir sobre o avanço dos estudantes ao longo do processo, verificando seu envolvimento e observando as dificuldades que possam surgir. Sempre que julgar necessário, faça intervenções que contribuam para ampliar a compreensão dos conteúdos.

Ao término da sequência didática, registre suas considerações sobre o processo de aprendizagem dos estudantes, destacando avanços e aspectos que ainda precisam ser desenvolvidos.

A seguir, apresentamos uma sugestão de modelo de sequência didática que pode servir como referência. Sinta-se à vontade para adaptá-lo conforme as necessidades da sua turma e os conteúdos que pretende desenvolver.

Escola: preencher com o nome da escola.

Planejamento de Sequência Didática

Professor(a): preencher com o nome do professor.

Componente curricular: preencher com o nome do componente curricular.

Turma: preencher com a indicação da turma.

Data: preencher com o período estimado para o desenvolvimento da sequência didática.

Assunto/conteúdo: preencher com os assuntos ou conteúdos a serem desenvolvidos.

Quantidade de aulas: preencher com a estimativa da quantidade de aulas que será necessária para desenvolver todas as atividades.

1. Objetivos gerais: definir o que se espera que os estudantes sejam capazes de fazer ao fim da sequência didática.

2. Competências e habilidades da BNCC: identificar as habilidades da BNCC que serão trabalhadas.

3. Materiais necessários: fazer uma lista detalhada de todos os materiais que serão necessários para desenvolver as atividades.

4. Etapas da sequência didática: detalhar as etapas de cada aula, organizando as atividades em uma ordem lógica e progressiva.

• Aula 1: descrever o início do trabalho com a sequência didática, que pode ser uma atividade para verificar o que os estudantes já sabem sobre o assunto; pode ser uma roda de conversa, uma dinâmica ou uma pergunta deflagradora para despertar a curiosidade deles.

• Aula 2: em diante: descrever as atividades intermediárias que ajudarão os estudantes a construírem o novo conhecimento; podem ser pesquisas, leituras, discussões, atividades práticas, entre outras dinâmicas.

• Aula final: descrever a última aula, a culminância da sequência didática, e planejar uma atividade final para que os estudantes coloquem em prática tudo o que aprenderam; pode ser a produção de um texto, a apresentação de um trabalho ou a criação de um projeto.

5. Avaliação: definir os critérios (o que será observado) e os instrumentos (como será registrado) que serão utilizados para avaliar a aprendizagem dos estudantes ao longo da sequência didática; a avaliação deve ser contínua, e não apenas ao final.

6. Autoavaliação: após a execução da sequência didática, verificar se ela foi eficaz, se os objetivos foram alcançados, quais desafios surgiram, o que pode ser mudado para a próxima vez e anotar essas reflexões para aprimorar suas práticas pedagógicas.

O USO DE TECNOLOGIAS DIGITAIS

A presença das tecnologias digitais no cotidiano das pessoas é cada vez mais comum, inclusive entre crianças e adolescentes. No entanto, a maneira como esses recursos, especialmente os dispositivos móveis como os celulares, têm sido utilizados dentro das escolas tem gerado muitos debates. O foco dessas discussões recai, principalmente, sobre os efeitos negativos do uso inadequado desses aparelhos no processo de aprendizagem e no desenvolvimento integral dos estudantes.

Estudos recentes reforçam essas preocupações, apontando prejuízos que vão desde a distração em sala de aula até impactos mais sérios, como problemas de saúde física e mental, que incluem aumento da ansiedade, distúrbios do sono, dificuldades de atenção, entre outros. Essas evidências contribuíram para a criação da Lei nº 15.100, de 13 de janeiro de 2025, que estabelece diretrizes para o uso de celulares nas escolas brasileiras.

Os desafios enfrentados com o uso inadequado e desregulado das tecnologias digitais não se restringem ao

ambiente escolar. A Unesco destaca riscos que vão desde o enfraquecimento das relações humanas até ameaças à democracia e aos direitos fundamentais, como a disseminação de discursos de ódio e a violação da privacidade. Tais aspectos mostram que a tecnologia, sem orientação adequada, pode acentuar desigualdades e comprometer valores essenciais.

No contexto escolar, o uso excessivo e sem propósito de recursos digitais tem mostrado efeitos prejudiciais, como o isolamento social, a dependência de redes sociais e a dispersão durante as aulas. Por isso, torna-se indispensável repensar o papel desses recursos na educação.

Por outro lado, quando inserida de maneira planejada e intencional no cotidiano escolar, a tecnologia pode se tornar uma ferramenta poderosa para o processo de ensino-aprendizagem. Recursos como computadores, tablets e celulares, quando utilizados com orientação pedagógica, promovem o acesso à informação, favorecem o desenvolvimento de habilidades críticas e éticas e ampliam o alcance da educação, especialmente em contextos de vulnerabilidade.

A proposta, portanto, não é excluir a tecnologia do ambiente escolar, mas sim incorporá-la com responsabilidade, sempre pautada em objetivos pedagógicos claros e alinhados às competências e aos conteúdos previstos no currículo.

Você tem um papel fundamental nesse processo. Cabe a você planejar atividades que façam uso significativo da tecnologia, promovendo a aprendizagem ativa e a reflexão crítica por parte dos estudantes. A intencionalidade no uso desses recursos deve estar presente desde o momento da escolha da ferramenta até a avaliação dos resultados.

Além disso, é importante lembrar que tecnologias educacionais não se limitam às mais recentes. Televisão, rádio, lousa, projetores e outros dispositivos já fazem parte da rotina escolar há décadas e desempenham papel importante na mediação pedagógica.

BOAS PRÁTICAS NO USO DE TECNOLOGIAS

NA EDUCAÇÃO

Para que a utilização de ferramentas tecnológicas seja eficaz e enriquecedora, é fundamental adotar algumas práticas pedagógicas intencionais. A seguir, apresentamos algumas dicas.

Planejamento pedagógico do uso de recursos tecnológicos

• Definir com clareza os objetivos de aprendizagem.

• Escolher as ferramentas tecnológicas adequadas para alcançar esses objetivos.

• Garantir que o uso dos recursos esteja articulado aos conteúdos e às competências curriculares.

O ENSINO DE MATEMÁTICA

FUNDAMENTOS TEÓRICO-METODOLÓGICOS NO ENSINO DE MATEMÁTICA

As inúmeras demandas e as constantes mudanças do mundo atual requerem uma sociedade composta de indivíduos com conhecimentos e habilidades que lhes permitam interpretar e analisar, de maneira crítica, a grande quantidade de informações veiculadas. Entre as áreas que capacitam os leitores nesse sentido, os conhecimentos matemáticos são um dos que cumprem tal demanda. Assim, é necessário que os cidadãos saibam explorá-los amplamente a fim de se comunicarem e participarem ativamente no mundo em que vivem.

Desse modo, é válido afirmar que o ensino da Matemática, para além do domínio de fórmulas e cálculos, mostra-se uma ferramenta importante na formação integral, social e crítica do cidadão ao desenvolver o raciocínio lógico, a capacidade de reflexão, a argumentação e a resolução de problemas. Nesse sentido, a Matemática pode contribuir para a formação do indivíduo na construção de uma consciência crítica e responsável, a qual, por sua

Desenvolvimento de habilidades críticas

• Propor atividades que incentivem a análise crítica de fontes de informação pelos estudantes.

• Levar os estudantes a refletirem sobre o impacto da tecnologia no cotidiano.

• Incentivar o uso consciente, seguro e responsável da internet.

Integração com outras metodologias

• Combinar o uso de tecnologias com estratégias convencionais, como leitura, escrita e pesquisa de campo.

• Incentivar experiências interativas, como a visita a museus virtuais e o uso de acervos digitais, que ampliam o repertório cultural dos estudantes e fortalecem vínculos com a memória coletiva.

Em resumo, o uso da tecnologia na educação não deve ser encarado como uma solução isolada ou um fim em si mesmo. Ela deve estar a serviço do processo de ensino-aprendizagem e contribuir para a formação crítica, ética e cidadã dos estudantes. Seu olhar pedagógico enquanto docente é essencial para transformar esses recursos em verdadeiros aliados do conhecimento.

Para auxiliar no uso de recursos digitais em consonância com seu planejamento pedagógico, esta coleção apresenta, na sua versão digital, infográficos clicáveis, a fim de complementar e enriquecer o desenvolvimento dos conteúdos.

A lista com os objetos digitais sugeridos em cada volume encontra-se no sumário. Além disso, os momentos de utilização desse recurso foram indicados nas páginas do Livro do Estudante por meio de ícones. Para acessá-los, basta clicar sobre os ícones indicados nas páginas da versão digital do Livro do Estudante

vez, pode se inserir em diversos âmbitos da vida em sociedade, como no consumo consciente, no planejamento da vida financeira, nas questões ambientais e no fortalecimento do respeito à diversidade étnica, cultural e social.

A capacidade de reconhecimento e identificação dos conhecimentos matemáticos como recurso de compreensão e de transformação da realidade, e as habilidades de identificar um problema, compreendê-lo e elaborar uma estratégia para resolvê-lo adequadamente podem ser desenvolvidas nas aulas de Matemática e valorizadas na formação de um profissional.

Nesse processo, espera-se que os estudantes adquiram a competência de resolver problemas e aprendam a validar as estratégias e os resultados obtidos, incentivando diferentes modos de raciocínio, além de utilizar recursos tecnológicos não apenas no ambiente escolar, mas, sobretudo, em seus diferentes contextos do cotidiano. Também é esperado que eles demonstrem segurança e autoconfiança na própria capacidade de se comunicarem matematicamente e de construir conhecimentos matemáticos na busca de soluções.

Ao ensinar Matemática aos estudantes, é necessário

motivar o interesse, a curiosidade e o espírito de investigação deles, desenvolvendo a capacidade do trabalho coletivo e cooperativo. Com isso, eles terão oportunidade de buscar soluções para os problemas propostos, identificando diferentes aspectos ao debaterem sobre determinado assunto, ao mesmo tempo que são constantemente encorajados a defenderem o pluralismo de ideias e o respeito às diferenças, prezando o ritmo e o modo de pensar dos colegas e aprendendo com eles. Este talvez seja um dos mais importantes passos para que se possa construir um ambiente de aprendizagem em que o protagonismo seja a palavra-chave.

Entre outras situações emergentes que envolvem um problema matemático, surge a conveniência de, em determinadas situações, recorrer a ferramentas nos recursos tecnológicos que lhes permitirão desenvolver estratégias na resolução de problemas, enfrentar desafios e comprovar e justificar resultados, além de estabelecer relações entre o conhecimento matemático e outros componentes curriculares. Ainda sob este enfoque, pretende-se articular as diferentes situações de ensino à realidade vivenciada pelos estudantes, na qual os artefatos e recursos da tecnologia estão cada vez mais onipresentes no universo de crianças e jovens. Nesta dimensão, cabe ponderar a relevância de promover a abordagem da matemática crítica, cujo objetivo central é voltado ao desenvolvimento de uma postura reflexiva, questionadora e transformadora, considerando os contextos sociais, culturais, políticos e econômicos nos quais os estudantes estão inseridos.

Entende-se, porém, que a construção do conhecimento matemático deve ser concretizada de modo gradual, em sincronia com o desenvolvimento cognitivo deles. Assim, é sugerida, ao longo dos volumes desta coleção, a utilização de materiais concretos, jogos e situações-problema em contextos significativos, preocupando-se com a inclusão de estudantes de diferentes perfis. Reforçam-se também que as opções metodológicas constantes nesta coleção são apenas sugestões para o professor, o qual deve exercer sua autonomia para a seleção da abordagem que julgar mais conveniente durante o desenvolvimento da sua prática em sala de aula.

Conforme aponta D’Ambrósio (2019), a matemática é uma ciência milenar, construída ao longo da história por diferentes povos, de acordo com suas necessidades, culturas e saberes. Com o passar do tempo e diante da emergência de novas demandas de diferentes gerações, assim como a contínua evolução tecnológica, que impacta os diferentes campos do conhecimento, tornando-se assunto relevante de inúmeros estudos na área educacional, surgiram várias teorias e perspectivas que ajudam na compreensão do processo de aprendizagem matemática. Entre essas teorias, destacam-se:

• a Neurociência, que estuda o desenvolvimento e o funcionamento do cérebro, comprovando que se aprende melhor quando são relacionados novos conceitos às experiências anteriores, fator que justifica a proposição de atividades concretas com o uso de materiais manipuláveis, os quais ajudam a construir representações mentais antes da abstração (COSTA, 2023);

• as epistemologias histórica e genética, que analisam como o conhecimento é construído ao longo da história e no desenvolvimento individual (PALHARES, 2008);

• as abordagens cognitivistas e sociointeracionistas, que valorizam o papel da interação social e dos processos mentais na aprendizagem (VIGOTSKY, 2010);

• o ensino-desenvolvimento, abordagem com influência da psicologia histórico-cultural, cujo expoente maior foi Lev Vygotsky, que considera o ensino um processo dinâmico, interativo e formativo, com vistas a formar sujeitos autônomos, críticos e criativos (VIGOTSKY, 2010).

Com base nessas perspectivas, os professores podem planejar práticas mais significativas e eficazes, respeitando o ritmo e as necessidades de cada estudante e apoiando o desenvolvimento do pensamento matemático desde os primeiros anos escolares. Cabe ao professor ajustar seus procedimentos didático-pedagógicos à perspectiva que considerar mais adequada diante das especificidades de cada estudante, nas mais diversas situações de sua prática docente.

Existem diferentes formas históricas e sociais de matematizar e esse deve ser o ponto de partida para a construção de uma educação matemática crítica. Para D’Ambrosio (2019), “matematizar é uma forma de compreender e explicar o mundo, que varia conforme o contexto histórico, social e cultural”. As diferentes abordagens metodológicas do ensino de matemática trabalhadas de maneira articulada contribuem para que o professor possa aplicar os conceitos e propor atividades utilizando recursos e estratégias de ensino adequados à faixa etária e, sobretudo, à realidade dos estudantes.

Vale destacar que o livro didático é uma importante ferramenta de apoio em sala de aula, no entanto não dever ser o único material de apoio a ser utilizado na condução das aulas. Além disso, ressalta-se a importância de o professor estar atento a teorias, perspectivas e propostas metodológicas apresentadas, como exemplo de algumas ferramentas para a seleção de recursos e apropriação das diferentes abordagens teóricas que propiciam a organização e o planejamento das aulas.

Por esses motivos, esta coleção apresenta, sempre que possível, situações propícias para desenvolver nos estudantes essas capacidades de ler e interpretar o mundo, de expor opiniões e respeitar as dos outros, contribuindo para a sociedade de maneira eficiente e concreta e construindo de modo apropriado os alicerces de uma educação de qualidade. Oferece também algumas sugestões de estratégias e recursos adequados à faixa etária a que se propõe cada categoria, devendo ser destacada a coerência entre a proposta constante na Reprodução do Livro do Estudante e nos materiais destinados aos professores. Aborda ainda algumas sugestões metodológicas que se alinham à proposta e podem auxiliar no trabalho docente, podendo ser adaptável à realidade social e cultural de cada estudante.

A coleção favorece também a compreensão dos pressupostos teórico-metodológicos e os objetivos que fundamentam a proposta didático-pedagógica, de maneira que o professor possa selecionar, entre as diferentes abordagens propostas, as que melhor se adequem à realidade de sua sala de aula. Assim, cabe ao professor a opção pela metodologia que lhe permita desenvolver seu trabalho pedagógico de maneira condizente às diferentes culturas e realidades de seu contexto escolar específico.

Por fim, esta obra busca propiciar a reflexão sobre a prática docente, de modo que o professor amplie sua compreensão sobre seu papel social e a função da escola em potencializar o aprendizado e o real engajamento dos estudantes no seu processo de construção do conhecimento matemático. Ressalta-se, assim, a singularidade desta coleção, uma vez que a utilização e a adequação do professor, a cada vivência em sala de aula, permitem a exploração de múltiplas possibilidades de trabalho docente, propiciando condições para promover a diversidade, a inclusão e a equidade com base na ênfase da experiência cultural dos estudantes como mediadora do conhecimento.

O LETRAMENTO MATEMÁTICO

Com relação ao letramento matemático, é fundamental que ele ocorra de maneira integrada com todos os componentes curriculares. Para isso, ao abordar os conteúdos, proponha situações didáticas contextualizadas que incentivem os estudantes a desenvolverem o raciocínio lógico e a aplicarem o conhecimento matemático na busca de soluções para situações-problema do cotidiano. Essa abordagem facilita a compreensão dos conceitos e reforça sua relevância.

As sugestões de atividades a seguir podem contribuir para o letramento matemático.

• Contagem de objetos usando materiais concretos, como tampinhas e lápis;

• uso e escrita de algarismos por meio de jogos e brincadeiras;

• compreensão do conceito de números;

• realização de operações básicas;

• reconhecimento de formas geométricas na identificação de quantidades e na ordenação de elementos;

• comparação de medidas com o uso de instrumentos não padronizados, como palmos e passos;

• leitura e interpretação de gráficos e tabelas com dados reais sobre a turma e a escola.

ABORDAGENS E PRÁTICAS EM MATEMÁTICA

Ao tomarmos como referência a BNCC, voltamos o olhar para o processo de aprender por meio das capacidades essenciais de formular, empregar, interpretar, avaliar e criar. Sob a perspectiva da Educação Matemática Crítica, é essencial que as situações-problema e as atividades propostas estejam relacionadas a situações e conflitos sociais fundamentais. Os estudantes devem ser considerados produtores de conhecimento, assumindo o protagonismo na apropriação e aquisição do letramento matemático.

Reafirmamos que as abordagens metodológicas aqui sugeridas devem ser contempladas como alternativas, e cada professor também deve ser protagonista de sua prática na escolha da melhor estratégia para auxiliar na construção e no pleno domínio dos conhecimentos matemáticos. Cabe, pois, ao professor, ajustar seus procedimentos didático-pedagógicos com a perspectiva mais adequada para os diferentes perfis estudantis que encontrar no decorrer de sua prática.

Sem nos atrelarmos a uma ou outra abordagem metodológica, por considerarmos que cada uma pode propi-

ciar respostas e/ou alternativas válidas para as demandas educacionais de cada realidade, apresentamos na sequência aportes teóricos sobre a etnomatemática como uma perspectiva coerente com muitas situações no processo de aprendizagem matemática.

Etnomatemática

Em primeiro plano, reconhecemos que a Etnomatemática, perspectiva metodológica proposta por Ubiratan D’Ambrosio, na década de 1980, considera os contextos culturais, sociais e históricos dos estudantes, valorizando os conhecimentos matemáticos de diferentes culturas. Trata-se, assim, de reconhecer as múltiplas matemáticas existentes nos também diversos “brasis” que se estendem pelo país. Nesta obra, consideramos essencial respeitar e valorizar cada contexto social como gerador de cultura. Conforme postula D’Ambrosio (2001), é importante valorizar os saberes matemáticos de modo a superar os mecanismos de exclusão social.

Oliveira (2019) considera que a experimentação educacional se configura como ponto de partida para abordagens investigativas no currículo de matemática com enfoque cultural. As pesquisas na área de educação matemática que utilizam a abordagem etnomatemática têm mostrado as especificidades do conhecimento matemático nas diferentes culturas e grupos sociais.

[...] Cada povo está inserido em realidades próprias, portanto devemos considerar que, ao formular problemas, suas respostas estão intimamente ligadas aos valores de sua cultura. As estratégias na resolução de problemas diferem sobre cada grupo cultural. Cada grupo cultural tem sua forma particular de contar, de desenhar, de se localizar, de medir, pois dependem de um modelo cultural ao qual pertencem. E não há como avaliar habilidades cognitivas fora do contexto cultural.

OLIVEIRA, Morane Almeida de. Matemática básica no sudoeste da Amazônia: uma proposta para escolas indígenas. Curitiba: Appris, 2019. p.28.

Com base no que o autor salienta, denota-se que o processo de aprendizagem da Matemática encontra-se intrinsecamente relacionado à vivência de cada estudante. Assim, não pretendemos apresentar respostas prontas para o ensino do componente, mas estratégias que podem e devem ser adaptadas a cada realidade, sobretudo se considerarmos as dimensões continentais do Brasil.

Nesses termos, entendemos que é urgente superar o método de ensino do componente que tem sido historicamente proposto como padrão.

A Etnomatemática, como uma das muitas abordagens consideradas para a construção dos conhecimentos matemáticos, é explorada em momentos da coleção que permitem traçar os contornos dos diferentes contextos sociais e culturais brasileiros.

Outra abordagem explorada é a resolução de problemas. Retomando os tópicos iniciais, em que confirmamos a importância da Matemática como recurso de compreensão e de transformação da realidade, evidenciamos a presença de resolução dos problemas como uma atividade recorrente no cotidiano das pessoas. Assim, decidir aspectos simples como calcular quantidades de alimentos a serem adquiridos e consumidos, quantias destinadas à

manutenção das despesas diárias e mesmo cálculos mais laborados, como planilhas de gastos, sugerem a presença da Matemática em todas as dimensões da vida humana.

Resolução de problemas

Por sua importância no ensino da Matemática, a resolução de problemas tem recebido destaque em estudos e pesquisas de educadores dessa área.

[...] O aluno deve ser estimulado a realizar um trabalho voltado para a iniciação à “investigação científica”. Nesse sentido, sua atividade intelectual guarda semelhanças com o trabalho do matemático diante da pesquisa, entretanto sem se identificar com ele. Assim, aprender a valorizar o raciocínio lógico e argumentativo torna-se um dos objetivos da educação matemática, ou seja, despertar no aluno o hábito de fazer uso de seu raciocínio e de cultivar o gosto pela resolução de problemas. Não se trata de problemas que exigem o simples exercício da repetição e do automatismo. É preciso buscar problemas que permitam mais de uma solução, que valorizem a criatividade e admitam estratégias pessoais de pesquisa. Essa valorização do uso pedagógico do problema fundamenta-se no pressuposto de que seja possível o aluno [se] sentir motivado pela busca do conhecimento. Seguindo essa ideia, o trabalho com a resolução de problemas amplia os valores educativos do saber matemático e o desenvolvimento dessa competência contribui na capacitação do aluno para melhor enfrentar os desafios do mundo contemporâneo. [...]

PAIS, Luiz Carlos. Didática da matemática: uma análise da influência francesa. 2. ed. Belo Horizonte: Autêntica, 2008. p. 35-36. (Coleção Tendências em Educação Matemática).

A metodologia da resolução de problemas em diferentes níveis de ensino é considerada de grande importância na aprendizagem, pois auxilia na construção de conceitos, além de possibilitar muitas outras competências. Na prática efetiva de ensino, tem-se revelado uma estratégia eficaz no processo de ensino-aprendizagem ao permitir que os estudantes mobilizem os seus conhecimentos prévios para interpretar e gerir informações do seu contexto. Entre as vantagens desta abordagem, apontamos a possibilidade de formação de estudantes mais ativos, despertando a iniciativa, o espírito investigativo e a criatividade. Ademais, a resolução de problemas pode contribuir para o desenvolvimento da autonomia intelectual, preparando-os para enfrentar desafios de forma independente e concretizando as condições de exercerem o protagonismo em sua aprendizagem.

Nesse ponto, cabe questionarmos: O que é um problema? Como vinculá-lo à Matemática? Como se deve trabalhar a resolução de problemas em sala de aula?

Para apontar sugestões como respostas a esses questionamentos, reforçamos a premência em considerar a contextualização de conteúdos como estratégia principal na resolução de problemas. Aqui, reforçamos a necessidade de não propor situações-problema isoladas do contexto de vivência da turma. Um problema adequado às situações vivenciadas por estudantes no Pantanal sul-mato-grossense pode não fazer sentido para os que vivem em uma capital do Sul do país, por exemplo. Os problemas devem estar relacionados a situações e conflitos sociais fundamentais da realidade de cada grupo a que se destinam.

Podemos pensar em problema como uma situação que exige reflexão, análise e resgate de situações similares que já tenhamos solucionado. Assim, um problema pode estar associado a ocasiões que nos levam a obter soluções. São alguns objetivos da resolução de problemas:

• promover o desenvolvimento do letramento matemático;

• mostrar aos estudantes que a Matemática pode ajudar na solução de muitos problemas que surgem no dia a dia;

• propiciar a iniciativa, a criatividade e a independência dos estudantes;

• desenvolver, de modo produtivo, a maneira de pensar dos estudantes por meio da investigação;

• potencializar e aperfeiçoar o raciocínio lógico-matemático dos estudantes;

• utilizar situações já estudadas, trabalhadas ou solucionadas como parâmetro para encontrar soluções para novas situações;

• levar os estudantes a perceberem que muitas situações-problema solucionadas por meio de conteúdos matemáticos são interessantes e desafiadoras.

É oportuno ponderar que o letramento matemático deve ser concebido como o ensino dos conceitos que estão imersos em uma prática social, ou seja, ler e escrever a linguagem matemática que está envolvida em um contexto de práticas sociais. Nos moldes propostos pela OECD (2003), “O letramento matemático implica a compreensão do papel da matemática no mundo, de modo que os indivíduos possam tomar decisões bem fundamentadas e participar como cidadãos reflexivos.”.

Diversas atividades desta coleção permitem que o professor alfabetizador planeje suas aulas para apresentar os conteúdos e as práticas do letramento matemático utilizando a estratégia de resolução de problemas, optando por essa metodologia pedagógica.

Utilização de jogos

É importante valorizar o trabalho com a ludicidade na infância e na adolescência. Estudos comprovam que o trabalho com jogos e brincadeiras colabora para o desenvolvimento de várias habilidades e, assim, para o aprendizado nessas fases da vida. Portanto, é possível inserir tais atividades apropriadas às aulas durante o desenvolvimento dos conteúdos matemáticos, tornando-os mais significativos.

Os jogos favorecem a criatividade, o desenvolvimento da busca de estratégias de resolução, a organização do pensamento e o desenvolvimento da intuição e da crítica. Outro aspecto que merece destaque é a socialização dos estudantes, pois nos jogos surge a necessidade da cooperação de outros indivíduos para estabelecer e seguir regras. O professor precisa se preparar para desenvolver uma atividade com jogos a fim de possibilitar a aprendizagem e a sistematização de conceitos matemáticos explorando ao máximo todo o potencial desse tipo de trabalho. Também deve acompanhar o desempenho dos estudantes, interferir quando for necessário e levantar questões relevantes durante o seu desenvolvimento.

Acreditando nos efeitos positivos para a aprendizagem que essas atividades podem proporcionar, esta coleção apresenta a seção Divirta-se e aprenda, propondo que os jogos e as brincadeiras façam parte das aulas de Matemática, tornando o ensino de conceitos mais des-

contraído. Assim, o professor tem à sua disposição uma ferramenta para promover de maneira lúdica o ensino de fatos aritméticos e conceitos matemáticos.

Recursos tecnológicos

Os constantes avanços tecnológicos observados no mundo atual têm provocado mudanças no modo de vida das pessoas. Os mais diversos segmentos são afetados com essa rápida evolução, inclusive o da educação. Esses avanços, aliados à quantidade de informações veiculadas, desafiam o professor a aliar o ensino e a aprendizagem de Matemática ao uso dos recursos tecnológicos em sua prática.

Os estudantes estão diariamente ligados às tecnologias, que se tornam cada vez mais acessíveis. Esse dinamismo já faz parte da realidade e da cultura da atual geração. Diante desse cenário, cabe à escola proporcionar o contato deles com diferentes mídias e ao professor refletir sobre tais práticas em suas aulas e fornecer aos estudantes ferramentas que os motivem na busca por conhecimento.

Entre os recursos que podem ser disponibilizados está a calculadora. Esse instrumento é importante em diversos momentos, como na verificação de resultados e na correção dos erros. A calculadora também pode ser usada na autoavaliação, na percepção de regularidades, na resolução de situações-problema, como incentivo à descoberta de estratégias e investigação de possíveis soluções para as atividades e na conferência de diversos cálculos no próprio cotidiano dos estudantes.

Durante as atividades com a calculadora, conscientize os estudantes de que, apesar de ser um instrumento que proporciona precisão e agilidade aos resultados, ela não pode decidir por eles. Por esse motivo, é necessário que compreendam antecipadamente as estratégias dos cálculos e sejam capazes de realizá-los sem usar essa ferramenta.

A robótica tem se mostrado uma estratégia inovadora e eficaz, na medida em que pode propiciar experiências práticas que promovem o raciocínio lógico, a criatividade, o trabalho em equipe e a resolução de problemas desde os primeiros anos escolares. Da mesma forma, seus benefícios englobam o desenvolvimento cognitivo, por meio do incentivo à lógica, ao pensamento crítico e à capacidade de resolver problemas. Ademais, promove a aprendizagem significativa e o trabalho cooperativo, ao mesmo tempo que familiariza os estudantes com os conceitos básicos de tecnologia. Não se trata de desenvolver protótipos de robôs, mas é possível criá-los com materiais recicláveis, incentivando a criatividade e a consciência ambiental, ou, ainda, criar narrativas nas quais eles sejam personagens, integrando linguagem oral e tecnologia. Oliveira et al. (2020) esclarecem que a robótica permite a integração de diferentes áreas do conhecimento, como Matemática, Ciências, Tecnologia e Artes, promovendo uma aprendizagem mais rica e significativa.

Reforçam-se, nesse ponto, as concepções trazidas sobre a construção do conhecimento matemático, o qual pode ser concretizado de múltiplas maneiras, mas sempre de modo articulado à vivência de cada estudante. Nesta coleção, não se pretende enfatizar uma única perspectiva, mas apontar opções possíveis para que o professor possa definir estratégias que o auxiliem a traçar caminhos de construção dos conhecimentos matemáticos.

Considerando a agilidade na realização de cálculos e, com isso, mantendo o foco no processo de resolução de problemas e na compreensão dos algoritmos, atividades que promovem o uso de calculadora em sala de aula foram incluídas em alguns momentos desta coleção. Algumas fornecem aos estudantes orientações sobre como utilizá-la, outras solicitam seu uso para conferir resultados de cálculos mentais ou mesmo a exploram como recurso auxiliar na compreensão de procedimentos de cálculo e na percepção de regularidades.

Outro recurso tecnológico em evidência nas últimas décadas é o computador. Essa ferramenta pode ser uma aliada do ensino de Matemática, na medida em que proporciona oportunidades de desenvolver nos estudantes o raciocínio lógico-matemático e abre espaço para pesquisas e busca ágil de informações. Um exemplo de utilidade é aplicar o computador a situações-problema de cunho prático, como em atividades que envolvem a construção de gráficos em estatística ou plotagem de figuras geométricas em geometria. Outro exemplo é nas buscas e consultas orientadas que enriquecem e complementam os conhecimentos prévios e as aulas de modo geral. Além disso, é possível orientar os estudantes quanto ao uso do computador para a finalização de trabalhos e apresentações no formato de seminários e debates.

Cabe a você, professor alfabetizador, escolher os momentos e as oportunidades de potencializar o uso consciente e produtivo dessa ferramenta, trazendo aproveitamento significativo em suas aulas.

Sobre as tecnologias digitais, presença indiscutível no cotidiano do ser humano, entende-se que a escola não pode se esquivar de inseri-las em suas atividades. Nesta coleção, elencamos algumas sugestões para que essa inserção propicie condições de otimizar a aprendizagem dos conceitos matemáticos.

Cálculo mental, aproximação e estimativa

O ensino da Matemática deve levar os estudantes a organizarem o pensamento e analisarem informações e dados de maneira crítica, não podendo, portanto, estar limitado a “fazer contas”. É importante que eles sejam capazes de compreender e estruturar situações, analisá-las, fazer estimativas e ter um raciocínio próprio, explorando diferentes tipos de registros e caminhos de construção.

Diversas situações que necessitam de cálculo mental e cálculo por estimativa ou de aproximação são comuns em nosso dia a dia e vivenciados pelos estudantes desde cedo. Saber a própria idade, quantos pontos obteve em um jogo ou quanto vai pagar por um brinquedo são exemplos da realização do cálculo mental. Imaginar o tempo necessário para chegar a determinado lugar, adivinhar uma quantidade ou medida qualquer ou até mesmo buscar uma estratégia em um jogo são exemplos de cálculo por estimativa ou aproximação. Considerando esses aspectos, o professor deve explorar situações do cotidiano a fim de desenvolver nos estudantes estratégias de cálculos, auxiliando-os, assim, na tomada de decisões e na oralidade.

Nas atividades que exploram o cálculo mental, não importa a rapidez para obter os resultados nem os cálculos decorados, mas sim a agilidade de pensamento e o estabelecimento de relações e regularidades. Por permitir que os estudantes percebam propriedades e regularidades, o cálculo mental contribui para o domínio do cálculo escrito. Desse modo, inserir esse procedimento

nas aulas de Matemática por meio de atividades criativas e flexíveis, que incentivem a estimativa, a formalização e a adaptação progressiva de técnicas de cálculo, auxilia no desenvolvimento da capacidade de resolver problemas e de trabalhar com os números, além de desenvolver habilidades relacionadas à atenção, à memória e à concentração.

A estimativa é um processo rápido e eficaz, cujo objetivo é aproximar um valor por meio de um número, situado dentro de um intervalo plausível, quando não é necessário um valor único e preciso. Porém, o número escolhido não pode ser qualquer um, pois deve ter como base observações anteriores. Várias são as situações cotidianas nas quais a estimativa é empregada como opção de resolução de problemas. Para isso, os valores de referência são importantes. A aproximação, por sua vez, pode ser muito utilizada no trabalho com medidas e grandezas, pois os números que as expressam são, na maioria das vezes, aproximados.

Em razão de as atividades de cálculo mental e de estimativa terem inúmeras características positivas no processo da aprendizagem e serem propostas atuais para o ensino da Matemática, sobretudo no Ensino Fundamental, nesta coleção são apresentadas, em momentos oportunos, atividades que exploram essas características. Elas são destacadas com ícones e incluem cálculos que devem ser resolvidos com base em experiências anteriores ou em estratégias pessoais dos estudantes, sem a utilização de material manipulável, observando padrões e regularidades, algumas vezes sem qualquer registro escrito. Ao trabalhar com essas atividades, é necessário acompanhar o processo dos estudantes e incentivá-los a elaborar estratégias pessoais de resolução. Após realizarem os cálculos, pode ser sugerido a eles que relatem os procedimentos a fim de levá-los a adquirir confiança e a aprimorar diversas habilidades durante o trabalho.

Outros recursos didáticos

Além dos recursos didáticos já citados, como o uso de jogos e brincadeiras, merecem destaque no ensino de Matemática o cálculo mental e aproximado, a estimativa, o uso da calculadora e do computador e o trabalho com materiais manipuláveis. Nos Anos Iniciais do Ensino Fundamental, esses materiais são imprescindíveis para a construção de significados, já que crianças necessitam manipular objetos para compreender determinados conceitos matemáticos. Essa ferramenta motiva os estudantes e auxilia o professor nos processos de ensino e aprendizagem.

O letramento estatístico e probabilístico refere-se à capacidade de interpretar, compreender, comunicar e criticar informações que têm como base dados e em situações que envolvem incertezas. Trata-se de um desdobramento do letramento matemático, voltado especificamente para os campos da Estatística e da Probabilidade, fundamentais na tomada de decisões pessoais, profissionais e sociais.

A cada dia, as crianças têm mais e mais acesso a informações variadas e precocemente entram em contato com conceitos mais complexos. A escola não pode ignorar esse fato e precisa se preparar para discutir esses conceitos, em modos acessíveis às crianças, e, assim, auxiliar no desenvolvimento de raciocínios mais avançados. Com base nas noções intuitivas dos estudantes,

podem-se desenvolver formas de pensar mais complexas por intermédio de ações eficientes promovidas em sala de aula.

BORBA, Rute et al. Levantando Possibilidades para o Desenvolvimento dos Raciocínios Probabilístico e Combinatório de Crianças em Anos Iniciais de Escolarização. In: BORBA, Rute; GUIMARÃES, Gilda (Orgs.). Pesquisa e atividades para o aprendizado matemático na Educação Infantil e nos Anos Iniciais do Ensino Fundamental SBEM, v. 8., 2015, p. 23.

No contexto escolar, desenvolver o letramento estatístico e probabilístico implica permitir que os estudantes compreendam gráficos, tabelas e porcentagens em contextos reais (como notícias, pesquisas e redes sociais), avaliem informações com base em dados estatísticos e probabilidades e tomem decisões informadas frente à incerteza e à variabilidade dos fenômenos.

A BNCC (2019) propõe o trabalho com estatística e probabilidade desde os Anos Iniciais do Ensino Fundamental, ampliando gradualmente a complexidade das análises. A matemática escolar, nesse sentido, ganha uma função social, preparando o estudante para compreender o mundo e atuar sobre ele.

Nesta coleção, esses conceitos são desenvolvidos de forma contínua e integrada ao longo das unidades, permitindo que os estudantes compreendam sua aplicação em diferentes contextos.

Entre os diversos materiais manipuláveis que podem ser usados para auxiliar os estudantes na abstração dos conhecimentos estão o ábaco, o material dourado e as peças ou os objetos que representam as figuras geométricas espaciais, além de embalagens diversas, como palitos de sorvete, tampinhas de garrafa, jornais, revistas, caixas de presente e engrenagens de relógio. O uso desses e de outros materiais pode conduzir os estudantes de maneira criativa no desenvolvimento do raciocínio lógico-matemático e de determinados conceitos.

No que diz respeito ao ábaco de papel, ou ábaco manipulativo, trata-se de uma ferramenta para auxiliar no aprendizado de matemática, especialmente números e operações básicas. Pode ser utilizado para ensinar conceitos como unidades, dezenas, centenas, adição, subtração, comparação de quantidades e valor posicional dos algarismos. Quanto à construção, geralmente é feito com um material que permite escrever e apagar, como papelão ou EVA, e possui colunas que representam unidades, dezenas, centenas etc. Para representar um número, movem-se as peças (contas ou botões, por exemplo) nas colunas correspondentes. Por exemplo, para o número 123, seriam movidas uma peça na coluna das centenas, duas na coluna das dezenas e três na coluna das unidades. Esse ábaco também pode ser utilizado nas operações: na adição, representa-se o primeiro número nele e, em seguida, adiciona-se o segundo número, movendo as peças correspondentes para as colunas corretas. Se necessário, realiza-se a troca de 10 unidades por uma dezena, 10 dezenas por uma centena, e assim por diante. Na subtração, o processo é semelhante: removem-se as peças correspondentes ao número a ser subtraído. Caso necessário, realiza-se a troca de uma dezena por 10 unidades, uma centena por 10 dezenas etc.

O ábaco ainda ajuda a entender o valor posicional dos algarismos em um número. Ao manipular as peças nas diferentes colunas, é possível visualizar como a posição de um algarismo afeta seu valor.

Smole e Diniz (2016) complementam que o uso do ábaco de papel, além de auxiliar na compreensão da organização dos números em unidades, dezenas, centenas etc., permite o desenvolvimento de habilidades de contagem e cálculo, a prática de contagens e a realização de operações matemáticas de forma visual, assim como melhora o raciocínio lógico e a concentração e desenvolve a autonomia e a autoconfiança. Ademais, a possibilidade de visualizar os resultados das operações pode aumentar a confiança dos estudantes em suas habilidades matemáticas.

Outro tipo de material manipulável de fácil acesso são as fichas sobrepostas, utilizadas para ensinar o sistema de numeração decimal, especialmente a composição e a decomposição de números e o valor posicional dos algarismos. Trata-se de um conjunto de fichas que permitem escrever os números de 0 a 99 999. O material consiste em fichas com números de diferentes ordens (unidades, dezenas, centenas etc.) que podem ser sobrepostas para formar e visualizar números maiores, facilitando a compreensão da relação entre eles (SMOLE; DINIZ, 2016). São 40 fichas (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 00, 10, 20, 30, 40, 50, 60, 70, 80, 90, 000, 100, 200, 300, 400, 500, 600, 700, 800, 900, 0000, 1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000) e podem ser produzidas com os estudantes. Os tamanhos de cada ordem devem ser diferentes de modo que eles consigam sobrepor perfeitamente uma sobre a outra. Confira o exemplo.

compor um número. Do mesmo modo, o trabalho com valor posicional é possível, pois as fichas sobrepostas ajudam a entender que o valor de um algarismo muda de acordo com sua posição no número.

Smole e Diniz (2016) ainda mencionam a possibilidade de propor jogos e atividades utilizando as fichas sobrepostas, tais como jogos de adivinhação, desafios de composição e decomposição ou jogos de comparação de números. Assim, entende-se que as fichas sobrepostas são um recurso versátil e eficaz para o ensino de matemática, auxiliando na compreensão do sistema de numeração decimal e no desenvolvimento do raciocínio lógico-matemático.

No entanto, é importante aliá-los a outras abordagens de conhecimento, pois o material por si só não constitui uma fonte única e total de aprendizagem. É necessário que o professor atente às necessidades de cada turma, a fim de adaptar materiais para as competências e habilidades que deseja desenvolver. Alguns benefícios proporcionados com a utilização desses recursos são o aprendizado por meio da manipulação de elementos, a capacidade de abstração, a aproximação dos estudantes à realidade e a fixação da aprendizagem. Esta coleção explora esses aspectos no boxe Experimente. Durante essa abordagem, é possível acompanhar a participação dos estudantes, fornecendo, sempre que possível, as explicações necessárias.

Os gêneros de linguagem também são recursos didáticos úteis em alguns momentos das aulas. Por esse motivo, esta coleção buscou apresentar histórias em quadrinhos, textos extraídos de revistas, jornais, livros e internet, telas de artistas, poemas, músicas, receitas, entre outros gêneros, todos relacionados ao conteúdo estudado.

Aos recursos já citados, podemos acrescentar a introdução à educação financeira. De maneira geral, esse tema tem como objetivo formar cidadãos preparados para lidar com situações desse tipo no dia a dia. Isso não só contribui para o fortalecimento da futura sociedade como apoia os estudantes em iniciativas de tomadas de decisões financeiras mais conscientes. Para abordar esse tema nas atividades, esta coleção utiliza folhetos promocionais de lojas, diferentes faturas e opções de pagamento, situações de compra e venda de produtos e serviços, notas fiscais, extratos bancários, entre outros recursos.

Considerando a necessidade de promover a inclusão de forma efetiva no ambiente escolar, cabe ressaltar a importância de trabalhar as formas multimodais aplicadas ao ensino da Matemática, concebidas como estratégias pedagógicas que utilizam diferentes modos de representação e comunicação, como linguagem visual, tátil, oral, corporal e tecnológica, para favorecer o aprendizado de todos os estudantes, especialmente aqueles com necessidades educacionais especiais. Esta proposta coaduna-se com o pensamento de Vigotsky (2010) quando destaca a importância dos mediadores na construção do processo de aprendizagem. Na mesma direção, situa-se o pensamento de Rojo e Almeida (2012), que defendem o uso de multiletramentos como estratégia para inclusão.

Como sugestão para o uso das fichas sobrepostas, os estudantes podem explorá-las e compará-las, permitindo a identificação dos números e das ordens. Em seguida, pode-se solicitar que formem números específicos sobrepondo as fichas de acordo com a ordem desejada. Para decomposição numérica, as fichas possibilitam demonstrar que um número pode ser decomposto em ordens (unidades, dezenas, centenas etc.), as quais se somam para

Como exemplos de formas multimodais aplicadas à Matemática com foco na inclusão, pode-se mencionar as representações visuais, como gráficos, diagramas, cores e imagens, que auxiliam estudantes com dificuldades de compreensão abstrata. O uso de blocos de Cuisenaire ou de material dourado para representar operações também é uma alternativa válida. Outros materiais concretos, como cubos, peças de encaixe, régua numérica tátil,

ábacos, tangram e geoplano favorecem o aprendizado de estudantes com deficiência visual ou dificuldades cognitivas. Com relação ao atendimento da linguagem oral e auditiva, sugere-se o uso de explicações verbais detalhadas, de histórias matemáticas e de jogos de perguntas e respostas, além de áudios explicativos e recursos com

descrição verbal para estudantes com baixa visão ou dislexia. Da mesma forma, podem ser utilizadas tecnologias assistivas e recursos digitais como softwares educativos com acessibilidade (voz sintetizada, legendas, aumento de contraste), assim como aplicativos que traduzem oralmente símbolos matemáticos.

QUADRO DE DISTRIBUIÇÃO DOS CONTEÚDOS

O quadro apresentado a seguir mostra a progressão dos conteúdos deste volume, destacando as habilidades, as competências e os temas contemporâneos transversais da BNCC trabalhados em cada unidade.

Trata-se de um quadro que pode ser utilizado para ter uma visão geral dos conteúdos das unidades, assim como facilitar a busca por orientações e comentários de práticas pedagógicas sugeridas nas orientações ao professor correspondentes ao Livro do Estudante

Quadro de distribuição dos conteúdos – 2º ano

Unidades

1 - Números de 0 a 100

2 - Figuras geométricas espaciais

• Passeando pela história dos números

• Números de 0 a 19

• Contando de 10 em 10

• Números de 0 a 99

• A centena

• Comparação

• Par e ímpar

• Ordinais

• A forma dos objetos

• História dos números.

• Características do sistema de numeração decimal.

• Dezena.

• Números naturais de 0 a 99.

• Centena.

• Sequências numéricas.

• Noções de probabilidade: pouco provável, muito improvável e impossível.

• Comparação, maior do que (>) e menor do que (<).

• Antecessor e sucessor.

• Números pares e números ímpares.

• Números ordinais.

• Tabelas.

• A forma dos objetos do dia a dia.

• Reconhecimento de figuras geométricas espaciais.

• Relação entre figuras geométricas espaciais e objetos familiares do mundo físico.

• Faces, arestas e vértices de um cubo.

EF02MA01

EF02MA02

EF02MA03

EF02MA04

EF02MA09

EF02MA10

EF02MA11

EF02MA21

EF02MA23

Competências gerais (CG), Competências específicas de Matemática (CEM) e temas contemporâneos transversais

CEM3

CEM6

3 - Adição e subtração com números até 99

• Adição com resultado até 99 sem reagrupamento

• Adição com reagrupamento

• Subtração com números até 99 sem reagrupamento

• Subtração com reagrupamento

• Adição com resultado até 99 sem reagrupamento.

• Adição com resultado até 99 com reagrupamento.

• Sequências numéricas.

• Tabela simples e tabela de dupla entrada.

• Ordem crescente e ordem decrescente.

• Subtração com números até 99 sem reagrupamento.

• Subtração com números até 99 com reagrupamento.

• Situações-problemas envolvendo adição e subtração.

• Gráfico de colunas.

EF02MA10

EF02MA11

EF02MA14

EF02MA05

EF02MA06

EF02MA09

EF02MA10

EF02MA11

EF02MA22

CEM7

CEM8

CG8

CG9

Vida familiar e social.

UnidadesTópicos

4 - Números até 1 000

• Os números até 999

• O número 1 000

• Moedas e cédulas

5 - Adição e subtração

6 - Medidas de comprimento

• Adição com resultado até 999 sem reagrupamento

• Adição com reagrupamento

• Subtração envolvendo números até 999 sem reagrupamento

• Subtração com reagrupamento

• Medindo comprimento O centímetro e o milímetro

• O metro

7 - Multiplicação

• Ideias da multiplicação

Conteúdos Habilidades da BNCC

• Características do sistema de numeração decimal.

• Composição e decomposição de números até 999.

• Valor posicional de números até 999.

• Comparação de números, ordem crescente e decrescente.

• O número 1 000.

• Números até 1 000 na reta numérica.

• Sequências envolvendo números naturais até 1 000.

• Antecessor e sucessor.

• Reconhecimento de moedas e cédulas do real.

• Tabela e gráfico de colunas.

• Adição com resultado até 999 sem reagrupamento.

• Sequências recursivas com números faltantes, obtidos por meio da adição e da subtração.

• Situações-problemas envolvendo a adição e a subtração.

• Situações-problema envolvendo o sistema monetário.

EF02MA01

EF02MA02

EF02MA03

EF02MA04

EF02MA09

EF02MA10

EF02MA11

EF02MA20

Competências gerais (CG), Competências específicas de Matemática (CEM) e temas contemporâneos transversais

8 - Figuras geométricas planas, localização e deslocamento

• Reconhecendo figuras geométricas planas

• Noções de posição

• Deslocamento

• Unidades de medidas de comprimento não padronizadas.

• Centímetro, milímetro e metro.

• Instrumentos de medidas de comprimento.

• Multiplicação associada à ideia de adição de parcelas iguais, de configuração retangular e de possibilidades.

• Multiplicação por 2.

• Multiplicação por 3.

• Dobro e triplo.

• Multiplicação por 4.

• Multiplicação por 5.

• Situações-problema envolvendo multiplicação.

• Triângulos, retângulos, quadrados e círculos.

• Figuras geométricas planas no cotidiano.

• Lados e vértices de algumas figuras geométricas planas.

• Sequências de figuras.

• Noções de posição: à frente, à esquerda, à direita.

• Em cima, embaixo, esquerda, direita, destra, canhota.

• Deslocamento.

• Caminhos.

EF02MA05

EF02MA06

EF02MA09

EF02MA10

EF02MA11 CEM2 CEM8

Educação financeira.

EF02MA16CEM8

CG3

Trabalho.

EF02MA07

EF02MA08 CEM2 CEM8

EF02MA10

EF02MA11

EF02MA12

EF02MA13

EF02MA15

CG3

CG7

Educação para o trânsito.

UnidadesTópicos

9 - Divisão

• Ideias da divisão

• Estudando a divisão

10 - Medidas de massa, de capacidade e de tempo

• Medidas de massa

• Medidas de capacidade

• Medidas de tempo

Conteúdos

• Ideias da divisão: repartir igualmente e medida.

• Divisão por 2.

• Metade, dúzia e meia dúzia.

• Divisão por 3.

• Terça parte.

• Divisão por 4

• Divisão por 5

• Interpretação de dados em tabela.

• Situações-problema envolvendo divisão.

• Mais leve e mais pesado.

• Quilograma e grama.

• Tabela e gráfico.

• Unidades de medida de capacidade não padronizadas.

• Litro e mililitro.

• Medidas de tempo.

• Calendário.

• Relógio de ponteiros e relógio digital.

SUGESTÕES DE CRONOGRAMAS

As propostas de cronogramas apresentadas a seguir têm como objetivo orientar a distribuição das unidades em planejamentos bimestrais, trimestrais e semestrais, respeitando a organização dos volumes anteriormente mencionada.

Cabe destacar que essas sugestões não contemplam outras atividades que possam surgir ao longo do ano letivo, como projetos, eventos escolares ou avaliações ins-

Sugestão de planejamento bimestral

Bimestre

1º

2º

Unidades e tópicos

Unidade 1 – Números de 0 a 100

Unidade 2 – Figuras geométricas espaciais

Unidade 3 – Adição e subtração com números até 99

Unidade 4 – Números até 1 000

Unidade 5 – Adição e subtração

Unidade 6 – Medidas de comprimento

Unidade 7 – Multiplicação

3º

Habilidades da BNCC

Competências gerais (CG), Competências específicas de Matemática (CEM) e temas contemporâneos transversais

EF02MA08CG3

EF02MA17

EF02MA18

EF02MA19

EF02MA22

CG7

Direitos das crianças e do adolescente. Diversidade cultural. Trabalho. Saúde.

titucionais, e que devem ser incorporadas ao planejamento de forma articulada.

Para elaborar essas sugestões, consideramos 200 dias letivos de aula, ou 40 semanas; no entanto, o cronograma deve ser ajustado conforme as especificidades de cada turma, levando em consideração o contexto, o ritmo de aprendizagem dos estudantes e o uso de diferentes recursos e estratégias pedagógicas, que vão além do livro didático.

Sugestão de planejamento trimestral

Trimestre

1º

Unidades e tópicos

Unidade 1 – Números de 0 a 100

Unidade 2 – Figuras geométricas espaciais

Unidade 3 – Adição e subtração com números até 99

Unidade 4 – Números até 1 000

2º

Unidade 5 – Adição e subtração

Unidade 6 – Medidas de comprimento

Unidade 7 – Multiplicação

Sugestão de planejamento semestral

Semestre Unidades e tópicos

Unidade 1 –Números de 0 a 100

Unidade 2 – Figuras geométricas espaciais

1º

Unidade 3 – Adição e subtração com números até 99

Unidade 4 – Números até 1 000

Unidade 5 – Adição e subtração

Unidade 6 – Medidas de comprimento

Unidade 7 – Multiplicação

Unidade 8 – Figuras geométricas planas, localização e deslocamento

Unidade 9 – Divisão

4º

Unidade 10 – Medidas de massa, de capacidade e de tempo

Unidade 8 – Figuras geométricas planas, localização e deslocamento

3º

Unidade 9 – Divisão

Unidade 10 – Medidas de massa, de capacidade e de tempo

2º

Unidade 8 – Figuras geométricas planas, localização e deslocamento

Unidade 9 – Divisão

Unidade 10 – Medidas de massa, de capacidade e de tempo

BACICH, Lilian; HOLANDA, Leandro (org.). STEAM em sala de aula: a aprendizagem baseada em projetos integrando conhecimentos na educação básica. Porto Alegre: Penso, 2020. (Série Desafios da Educação).

A obra aborda o STEAM como uma ferramenta para desenvolver competências, como a criatividade, o pensamento crítico, a comunicação e o trabalho com a colaboração dos estudantes.

BRASIL. Ministério da Saúde. Proteger e cuidar da saúde de adolescentes na atenção básica. 2. ed. Brasília: Ministério da Saúde, 2018. Disponível em: https://bvsms.saude.gov.br/ bvs/publicacoes/proteger_cuidar_adolescentes_atencao_ basica_2ed.pdf. Acesso em: 5 set. 2025.

Documento que visa auxiliar as Equipes de Atenção Básica/Saúde da Família no trabalho com adolescentes nos aspectos relacionados à saúde.

COSTA, Renato Pinheiro da; CASSIMIRO, Élida Estevão; SILVA, Rozinaldo Ribeiro da. Tecnologias no processo de alfabetização nos anos iniciais do ensino fundamental. Docência e Cibercultura, Rio de Janeiro, v. 5, n. 1, p. 97-116, jan./abr. 2021. Disponível em: https://www.e -publicacoes.uerj.br/re-doc/article/view/53068/36747. Acesso em: 16 ago. 2025.

Nesse artigo, os autores abordam a influência da tecnologia no desenvolvimento do processo de alfabetização.

DEHAENE, Stanislas. Os neurônios da leitura: como a ciência explica a nossa capacidade de ler. Tradução de Leonor Scliar-Cabral. Porto Alegre: Penso, 2012.

Nesse livro, o autor francês mostra os progressos da Neurociência e da Psicologia Cognitiva a respeito do ato de ler.

GRISA, Gregório Durlo et al Neurociência e alfabetização: noções fundamentais. Bento Gonçalves: IFRS, 2022.

Nesse livro, os autores se baseiam nos estudos da Neurociência para explicar os processos de alfabetização.

LIMA, Aurilia de Brito et al. (org.). Políticas de inclusão na educação básica. Curitiba: Appris, 2024.

Coletânea de textos que abordam os principais marcos das políticas públicas relacionadas à inclusão, desde as temáticas mais amplas até as mais específicas.

MIRANDA, Elaine (coord.). Educação inclusiva e a parceria da família: uma dimensão terapêutica. São Paulo: Literare Books International, 2021.

Nesse livro, a autora aborda aspectos da inclusão com base em evidências científicas. Além disso, ela busca evidenciar a importância da participação da família na educação inclusiva.

MORAIS, José. Criar leitores: para professores e educadores. Barueri: Manole, 2013.

O livro auxilia professores, pais e profissionais a compreenderem o processo cerebral da criança que está aprendendo a ler considerando seus processos cognitivos e as dificuldades da faixa etária e sugerindo intervenções e estratégias para facilitar a alfabetização.

SANTOS, Maria Lucia dos; PERIN, Conceição Solange Bution. A importância do planejamento de ensino para o bom desempenho do professor em sala de aula.

Cadernos PDE, Curitiba, v. 1, p. 1-24, 2013. (Os Desafios da Escola Pública Paranaense na Perspectiva do Professor PDE).

Nesse artigo, as autoras destacam a importância do planejamento e apresentam propostas que auxiliam o professor a realizar seus planejamentos.

SILVA, Janssen Felipe da; HOFFMANN, Jussara; ESTEBAN, Maria Teresa. Práticas avaliativas e aprendizagens significativas: em diferentes áreas do currículo. Porto Alegre: Mediação, 2012.

Os autores discutem as práticas avaliativas em diferentes áreas do currículo, com destaque para a elaboração de práticas de avaliação articuladas ao fazer pedagógico.

VICKERY, Anitra. Aprendizagem ativa nos anos iniciais do ensino fundamental. Porto Alegre: Penso, 2016.

O livro aborda a importância da aprendizagem ativa e do protagonismo do estudante para a concretização do processo de aprendizagem em sala de aula. Além disso, reúne pesquisas e estudos de casos que vão inspirar os professores a criarem e explorarem estratégias para desenvolver a própria abordagem de ensino.

REFERÊNCIAS BIBLIOGRÁFICAS COMENTADAS –LIVRO DO PROFESSOR

BACICH, Lilian; MORAN, José (org.). Metodologias ativas para uma educação inovadora: uma abordagem teóricoprática. Porto Alegre: Penso, 2018.

Esse livro destaca a importância das estratégias de metodologias ativas para desenvolver a autonomia dos estudantes e a participação efetiva deles no processo de aprendizado.

BENDER, William N. Aprendizagem baseada em projetos: educação diferenciada para o século XXI. Tradução de Fernando de Siqueira Rodrigues. Porto Alegre: Penso, 2014.

Nesse livro, o autor destaca as diretrizes práticas para o trabalho com projetos em sala de aula, fornecendo subsídios para o professor planejar aulas mais eficazes e motivadoras.

BORBA, Rute; BATISTA, Rita; AZEVEDO, Juliana. Levantando possibilidades para o desenvolvimento dos raciocínios probabilístico e combinatório de crianças em anos iniciais de escolarização. In: BORBA, Rute; GUIMARÃES, Gilda (org.). Pesquisa e Atividades para o aprendizado matemático na Educação Infantil e nos Anos Iniciais do Ensino Fundamental. Brasília: SBEM, 2015. v. 8. p. 23-46.

O e-book apresenta contribuições para a sala de aula da Educação Infantil e dos Anos Iniciais do Ensino Fundamental, com resultados de pesquisas referentes à Educação Matemática de início de escolarização e reflexões sobre aplicações da Matemática aos estudantes.

BRASIL. Lei nº 8.069, de 13 de julho de 1990. Disponível em: https://www.planalto.gov.br/ccivil_03/leis/l8069.htm. Acesso em: 5 set. 2025.

Também conhecido como ECA, esse documento visa garantir os direitos fundamentais de crianças e adolescentes, assegurando proteção integral, saúde, educação e dignidade.

BRASIL. Ministério da Educação. Conscientização para o uso de celulares na escola: por que precisamos falar sobre isso? Brasília: MEC, 2025. Disponível em: https:// www.gov.br/mec/pt-br/celular-escola/guia-escolas.pdf. Acesso em: 9 ago. 2025.

Esse documento traz orientações práticas que ajudam o professor na implantação da Lei nº 15.100, que regulamenta o uso de dispositivos eletrônicos portáteis pelos estudantes nas escolas.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Versão final. Brasília: MEC, 2018. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI _EF_110518_versaofinal_site.pdf. Acesso em: 5 set. 2025. Documento que determina as competências gerais e específicas, as habilidades e as aprendizagens que os estudantes brasileiros da Educação Básica precisam desenvolver e colocar em prática ao longo de sua trajetória escolar.

BRASIL. Ministério da Educação. Diretrizes Curriculares Nacionais Gerais da Educação Básica. Brasília: MEC: SEB: Dicei, 2013. Disponível em: https://www.gov.br/mec/ pt-br/media/etnico_racial/pdf/diretrizes_curriculares_ nacionais_para_educacao_basica_diversidade_e_ inclusao_2013.pdf. Acesso em: 3 set. 2025.

Esse documento traz princípios, fundamentos e procedimentos que norteiam as políticas públicas de educação e auxiliam o professor a elaborar, planejar, executar e avaliar práticas pedagógicas na Educação Básica.

BRASIL. Ministério da Educação. Relatório Nacional de Alfabetização Baseada em Evidências. Brasília: MEC: Sealf, 2020. Disponível em: https://www.gov.br/mec/pt -br/media/acesso_informacacao/pdf-arq/RENABE_web. pdf. Acesso em: 3 set. 2025.

Renabe é a abreviação do Relatório Nacional de Alfabetização Baseada em Evidências, uma iniciativa do Brasil em discutir com pesquisadores brasileiros e estrangeiros da área de alfabetização de diferentes campos do conhecimento.

BRASIL. Ministério da Educação. Temas contemporâneos transversais na BNCC: contexto histórico e pressupostos pedagógicos. Brasília, 2019. Disponível em: https://basenacionalcomum.mec.gov. br/images/implementacao/contextualizacao_temas_ contemporaneos.pdf. Acesso em: 3 set. 2025.

O documento apresenta os temas contemporâneos transversais da BNCC e explica a importância de sua utilização no processo de ensino-aprendizagem.

BRITO, Giseli Artioli; FLORES, Maria Marta Lopes. A inclusão de alunos com deficiência intelectual: em foco as práticas pedagógicas. Boletim de Conjuntura, Boa

Vista, ano V, v. 16, n. 48, 2023. Disponível em: https:// revista.ioles.com.br/boca/index.php/revista/article/ view/2879. Acesso em: 18 ago. 2025.

Nesse artigo, as autoras abordam os principais aspectos que influenciaram os resultados de uma pesquisa sobre a inclusão escolar e a qualidade da educação.

CORDEIRO, Claudia Talochinski; OLIVEIRA, Ivanete da Rosa Silva de (org.). Educação e políticas inclusivas: ressignificando a diversidade. Londrina: Syntagma Editores, 2020. Nessa obra, as autoras discutem a inclusão de estudantes com deficiência na escola regular.

COSTA, Raquel Lima Silva. Neurociência e aprendizagem. Revista Brasileira de Educação, Rio de Janeiro, v. 28, 2023. Disponível em: http://educa.fcc.org.br/pdf/rbedu/ v28/1809-449X-rbedu-28-e280010.pdf. Acesso em: 2 set. 2025.

No artigo, a autora apresenta uma revisão de literatura sobre a contribuição da Neurociência para a aprendizagem no contexto escolar.

DEHAENE, Stanislas. Os neurônios da leitura: como a ciência explica a nossa capacidade de ler. Tradução de Leonor Scliar-Cabral. Porto Alegre: Penso, 2012.

O autor francês apresenta os progressos da Neurociência e da Psicologia Cognitiva a respeito do ato de ler.

DINIZ, Margareth; VASCONCELOS, Renata Nunes (org.). Pluralidade cultural e inclusão na formação de professores e professoras. Belo Horizonte: Formato Editorial, 2004.

Nessa obra, as autoras propõem reflexões sobre as práticas educativas e as ações pedagógicas voltadas para uma postura inclusiva.

D’AMBROSIO, Ubiratan. Etnomatemática: elo entre as tradições e a modernidade. 6. ed. Belo Horizonte: Autêntica, 2019. (Coleção Tendências em Educação Matemática).

O autor apresenta nessa obra suas mais recentes concepções acerca da Etnomatemática, uma tendência da qual é um dos fundadores.

FAZENDA, Ivani (coord.). Práticas interdisciplinares na escola. 8. ed. São Paulo: Cortez, 2017.

Nessa obra, os organizadores reúnem diversos textos sobre práticas docentes interdisciplinares no espaço escolar.

FERNANDES, Domingos. Avaliação formativa: folha de apoio à formação: Projeto de Monitorização, Acompanhamento e Investigação em Avaliação Pedagógica (Maia). Ministério da Educação: DireçãoGeral da Educação, 2021. Disponível em: https:// apoioescolas.dge.mec.pt/sites/default/files/2021-02/ folha_avaliacao_formativa.pdf. Acesso em: 6 set. 2025.

Esse material apresenta ações práticas que podem auxiliar o professor no planejamento das estratégias de avaliação.

FERREIRO, Emilia. Alfabetização em processo. 21. ed. São Paulo: Cortez, 2015.

Nesse livro, a autora explica como o processo de alfabetização ocorre no cérebro dos estudantes e sua influência no desenvolvimento dos conhecimentos de outras áreas.

JOIA, Michele. A inclusão de crianças na escola: o papel do educador diante das dificuldades de aprendizagem. 2. ed. Rio de Janeiro: Wak, 2023.

Nesse livro, a autora fornece dicas sobre a inclusão na escola com base em conhecimentos que ela construiu em sua experiência em sala de aula.

KLEIN, Julie Thompson. Ensino interdisciplinar: didática e teoria. 17. ed. Campinas: Papirus, 2012. (Coleção Práxis).

Esse livro traz temas que apresentam resultados de estudos, análises pesquisadas e direcionamentos sob uma perspectiva contextualizada acerca do ensino interdisciplinar, contribuindo para a prática docente.

MELLO, Fabiane de Oliveira; ALLIPRANDINI, Paula Mariza Zedu. Estratégias de aprendizagem de alunos do ensino fundamental em processo de alfabetização. Revista de Psicología, Lima, v. 40, n. 2, 2022. Disponível em: https:// revistas.pucp.edu.pe/index.php/psicologia/article/ view/25503/24038. Acesso em: 16 ago. 2025.

Nesse artigo, as autoras fazem uma análise qualitativa de algumas estratégias de ensino comumente utilizadas no processo de alfabetização.

MORAN, José. Metodologias ativas para uma aprendizagem mais profunda. In: BACICH, Lilian; MORAN, José (org.). Metodologias ativas para uma educação inovadora: uma abordagem teórico-prática. Porto Alegre: Penso, 2018. p. 4.

Essa obra propõe práticas pedagógicas, na Educação Básica e Superior, que valorizam o protagonismo dos estudantes, relacionando com as teorias e auxiliando como suporte.

MOREIRA, Antonio Flávio; CANDAU, Vera Maria (org.). Multiculturalismo: diferenças culturais e práticas pedagógicas. Petrópolis: Vozes, 2008.

O termo multiculturalismo tem sido amplamente usado e envolve distintas instâncias. Na escola, apresenta relação direta com a pluralidade cultural e a realidade cultural contemporânea. A obra tem como objetivo incentivar discussões, estudos e pesquisas que instiguem práticas renovadas em prol de uma sociedade mais justa e solidária.

OLIVEIRA, Morane Almeida de. Matemática básica no sudoeste da Amazônia: uma proposta para escolas indígenas. Curitiba: Appris. 2019.

A obra busca valorizar a etnomatemática mostrando como os povos indígenas aplicam a matemática no seu dia a dia.

ORGANISATION FOR ECONOMIC CO-OPERATION AND DEVELOPMENT (OECD). The PISA 2003 Assessment Framework: Mathematics, Reading, Science and Problem Solving Knowledge and Skills. Paris: OECD Publishing, 2004. Disponível em: https:// www.oecd.org/content/dam/oecd/en/publications/ reports/2003/07/the-pisa-2003-assessment -framework_g1gh34d9/9789264101739-en.pdf. Acesso em: 2 set. 2025.

Define o conteúdo de que os estudantes necessitam para adquirir o que precisam dominar e o contexto em que as habilidades e o conhecimento serão aplicados.

PAIS, Luiz Carlos. Didática da matemática: uma análise da influência francesa. Belo Horizonte: Autêntica, 2019. (Coleção Tendências em Educação Matemática).

Nesse livro, o autor apresenta conceitos fundamentais de uma tendência que ficou conhecida como Didática Francesa. Educadores matemáticos franceses, em sua maioria, desenvolveram uma estratégia particular

de perceber a educação centrada na questão do ensino da Matemática, contribuindo para o desenvolvimento da aprendizagem.

PALHARES, Odana. O ensino e a aprendizagem da matemática na perspectiva piagetiana. Schème –Revista Eletrônica de Psicologia e Epistemologia Genéticas, Marília, v. 1, n. 1, jan./jun. 2008. Disponível em: https://www.marilia.unesp.br/Home/ RevistasEletronicas/Scheme/Vol01Num01-Artigo05.pdf. Acesso em: 2 set. 2025.

No artigo, a autora reflete sobre o objetivo do ensino da Matemática nos primeiros anos, que consiste em ajudar o estudante a construir um raciocínio lógico-matemático.

REIS, Ana Valéria Sampaio de Almeida; DAROS, Thuinie; TOMELIN, Karina Nones. Layouts criativos para aulas inovadoras. Maringá: B42, 2023.

Nesse livro, as autoras sugerem diferentes estratégias de layout das salas de aula a fim de envolver e criar experiências marcantes para os estudantes.

ROJO, Roxane; MOURA, Eduardo (org.). Multiletramentos na escola. São Paulo: Parábola, 2012.

Os autores defendem uma pedagogia dos multiletramentos ao proporem a adoção em sala de aula de práticas situadas, instrução aberta, enquadramento crítico e prática transformadora.

SILVA, Eva Aparecida Gomes da. O desenvolvimento do processo de ensino-aprendizagem do aluno com necessidades educacionais especiais. Revista IberoAmericana de Humanidades, Ciências e Educação, São Paulo, v. 9, n. 3, mar. 2023. Disponível em: https:// periodicorease.pro.br/rease/article/view/8972/3542. Acesso em: 14 ago. 2025.

Nesse artigo, a autora destaca a importância das atividades lúdicas no processo de ensino-aprendizagem dos estudantes com necessidades educacionais especiais.

SMOLE, Katia Stocco; DINIZ, Maria Ignez (org.). Materiais manipulativos para o ensino do sistema de numeração decimal. Porto Alegre: Penso, 2016. (Coleção Mathemoteca).

A obra traz um recorte de alguns conteúdos dos Anos Iniciais do Ensino Fundamental e apresenta uma forma específica de ensino, que inclui o desenvolvimento da leitura e da escrita em Matemática.

SOARES, Magda. Alfabetização e letramento. 5. ed. São Paulo: Contexto, 2018.

Nesse livro, a autora incentiva a releitura de artigos que discutem as práticas escolares de alfabetização e letramento.

UNESCO. VIOLÊNCIA escolar e bullying: relatório sobre a situação mundial. Brasília: Unesco, 2019. Disponível em: https://unesdoc.unesco.org/ark:/48223/pf0000368092/ PDF/368092por.pdf.multi. Acesso em: 5 set. 2025.

Nesse relatório, são apresentados dados sobre a violência escolar e o bullying, além de iniciativas que podem contribuir para a redução dessas ocorrências.

VIGOTSKI, Lev. A formação social da mente. São Paulo: Martins Fontes, 2010.

Esse livro compõe uma seleção cuidadosa dos ensaios mais importantes do autor, editada por um grupo de eminentes estudiosos da obra.