Plantar_Matemática_Volume 1 by FTD Educação

Matemática

Anos Iniciais do Ensino Fundamental

Editora responsável: Jacqueline da Silva Ribeiro Garcia

Organizadora:

EDITORA NOVO RUMO Obra coletiva concebida, desenvolvida e produzida pela Editora Novo Rumo.

Componente curricular: Matemática

Matemática

Organizadora: EDITORA NOVO RUMO

Obra coletiva concebida, desenvolvida e produzida pela Editora Novo Rumo.

Anos Iniciais do Ensino Fundamental

Editora responsável: Jacqueline da Silva Ribeiro Garcia

Especialista em Psicopedagogia pela Universidade Estadual de Londrina (UEL-PR).

Licenciada em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Atuou como professora em escolas do Ensino Básico. Editora e elaboradora de materiais didáticos.

Componente curricular: Matemática 1ª edição Londrina, 2025

Edição Jacqueline da Silva Ribeiro Garcia, Lucília Franco Lemos dos Santos

Assistência editorial Denise Maria Capozzi, Kethelyn Yukari Ogasawara

Revisão técnica Tânia Camila Kochmanscky Goulart

Preparação e revisão Moisés Manzano da Silva (coord.)

Gerência de produção editorial Camila Rumiko Minaki Hoshi

Supervisão de produção editorial Priscilla de Freitas Cornelsen Rosa

Assistência de produção editorial Lorena França Fernandes Pelisson

Coordenação de produção de arte Tamires Rose Azevedo

Edição de arte Keithy Mostachi

Projeto gráfico e design Dayane Barbieri, Keithy Mostachi, Laís Garbelini

Projeto de capa Marcela Pialarissi

Ilustrações de capa Ricardo Gualberto

Coordenação de diagramação Adenilda Alves de França Pucca - Nil

Diagramação AVITS Estúdio Gráfico Ltda., EfeDois Editoração Ltda., Leandro

Júnior Pimenta

Autorização de recursos João Henrique Pedrão Feliciano

Iconografia Alessandra Roberta Arias, Vinícius Costa (trat. imagens)

Objetos digitais

Gerência de produção Erick Lopes de Almeida

Roteiros Camila Vidigal

Edição de imagens Brenda de Oliveira Goes

Desenvolvimento Ohanna Schmitt Bolfe, Tatiana Tissa Kawakami

Dados Internacionais de Catalogação na Publicação (CIP) (Câmara Brasileira do Livro, SP, Brasil)

Plantar matemática : 1º ano : anos iniciais do ensino fundamental / organizadora Editora Novo Rumo ; obra coletiva concebida, desenvolvida e produzida pela Editora Novo Rumo ; editora responsável Jacqueline da Silva Ribeiro Garcia. -- 1. ed. -- Londrina, PR : Editora Novo Rumo, 2025. Componente curricular: Matemática.

ISBN 978-65-5158-123-6(livro do estudante)

ISBN 978-65-5158-122-9(livro do professor)

ISBN 978-65-5158-139-7(livro do estudante HTML5)

ISBN 978-65-5158-138-0(livro do professor HTML5)

1. Matemática (Ensino fundamental) I. Garcia, Jacqueline da Silva Ribeiro. II. Série.

25-299255.0

CDD-372.7

Índices para catálogo sistemático:

1. Matemática : Ensino fundamental 372.7

Eliete Marques da Silva - Bibliotecária - CRB-8/9380

Avenida Doutor Adhemar Pereira de Barros, 1500, sala 804 - Bela Suíça - Londrina-PR CEP 86047-250 - Tel. (43) 3367-2030 contato@editoranovorumo.com.br

Elaboração de originais

Jacqueline da Silva Ribeiro Garcia

Especialista em Psicopedagogia pela Universidade Estadual de Londrina (UEL-PR).

Licenciada em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Atuou como professora em escolas do Ensino Básico. Editora e elaboradora de materiais didáticos.

Fátima Gomes Machado

Especialista em Docência na Educação Superior pela Universidade Estadual de Londrina (UEL-PR).

Licenciada em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Licenciada em Pedagogia pelo Centro Universitário Internacional (Uninter-PR).

Elaboradora e editora de materiais didáticos.

Sandra Aparecida Ferreira Marchi

Especialista em Educação Especial pela Faculdade Catuaí (PR). Especialista em Gestão Escolar, com habilitação em Administração, Supervisão e Orientação Educacional, pela Faculdade Catuaí (PR).

Licenciada em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Professora dos Anos Iniciais do Ensino Fundamental. Elaboradora de materiais didáticos.

Em respeito ao meio ambiente, as folhas deste livro foram produzidas com fibras obtidas de árvores de florestas plantadas, com origem certificada.

Impresso no Parque Gráfico da Editora FTD CNPJ 61.186.490/0016-33

Avenida Antonio Bardella, 300 Guarulhos-SP – CEP 07220-020 Tel. (11) 3545-8600 e Fax (11) 2412-5375

APRESENTAÇÃO

Acreditamos que o aprendizado em Matemática é essencial para que os estudantes se tornem cidadãos ativos e capazes de pensar de forma autônoma e crítica. Esta coleção foi cuidadosamente pensada para ser uma parceira nessa missão, proporcionando uma abordagem integrada e relevante.

Ao longo de cada unidade, o conteúdo se conecta diretamente com a realidade dos estudantes, valorizando o que eles já sabem e incentivando a construção de novos conhecimentos. Nessa dinâmica, o professor não é apenas um detentor do saber, mas um guia e um mediador, orientando os estudantes a serem os protagonistas de sua aprendizagem.

Para apoiar essa jornada, apresentamos este Livro do Professor. Na primeira parte dele, você encontra informações sobre a estrutura da coleção e a Reprodução do Livro do Estudante com as orientações ao professor nas laterais e nos rodapés das páginas reproduzidas, com comentários práticos para auxiliar no dia a dia em sala de aula, como orientações sobre os conteúdos das unidades, atividades extras, momentos sugeridos de avaliação, entre outros subsídios. Na segunda parte, apresentamos o Manual do Professor, onde você encontra desde a estrutura da Base Nacional Comum Curricular (BNCC) e fundamentos teórico-metodológicos da coleção até recursos práticos, como estratégias de avaliação diversificadas, modelos de planejamento de rotina e de sequência didática, quadro de distribuição dos conteúdos e sugestões de cronogramas que contribuem para o desenvolvimento docente.

É importante ressaltar que as sugestões podem ser adequadas de acordo com a realidade da turma e da escola. Esperamos que seja uma ferramenta útil e enriquecedora no processo de ensino-aprendizagem, possibilitando a formação de cidadãos críticos e participativos na sociedade.

Desejamos a você um ótimo ano letivo!

SUMÁRIO

ESPECÍFICAS........................ VIII AS UNIDADES TEMÁTICAS, OS OBJETOS DE CONHECIMENTO E AS HABILIDADES ...............IX OS TEMAS CONTEMPORÂNEOS TRANSVERSAIS .........................................................IX

INTEGRAÇÃO ENTRE OS COMPONENTES CURRICULARES ........................

A PRÁTICA INTERDISCIPLINAR E O TRABALHO COM PROJETOS INTERDISCIPLINARES ................. X AVALIAÇÃO

O PAPEL DO PROFESSOR E

ABORDAGENS E PRÁTICAS EM MATEMÁTICA .... XXII

QUADRO DE DISTRIBUIÇÃO DOS CONTEÚDOS ......................................... XXVII

SUGESTÕES DE CRONOGRAMAS .................XXIX

REFERÊNCIAS COMPLEMENTARES PARA A PRÁTICA DOCENTE ........................... XXX

REFERÊNCIAS BIBLIOGRÁFICAS COMENTADAS – LIVRO DO PROFESSOR ...... XXX

MANUAL DO PROFESSOR

CONHEÇA A COLEÇÃO

Esta coleção é composta por dois volumes, sendo 1º e 2º anos destinados aos estudantes e professores dos Anos Iniciais do Ensino Fundamental. Cada volume é organizado em 10 unidades que, por sua vez, são subdivididas em tópicos e seções que desenvolvem as habilidades relacionadas aos objetos de conhecimento e às competências gerais e específicas propostas pela BNCC. Além disso, durante o desenvolvimento dos conteúdos, a coleção aborda os temas contemporâneos transversais, contribuindo para a formação de cidadãos críticos e atuantes na sociedade.

Além dos volumes impressos, a coleção apresenta a versão digital do Livro do Estudante e do Livro do Professor. Esses materiais digitais apresentam recursos acessíveis, favorecendo a utilização por todos os estudantes. Os livros digitais também apresentam como recurso infográficos, que podem ser acessados, na versão digital, por meio do sumário e de ícones indicados nas páginas dos livros.

O LIVRO DO ESTUDANTE

A seguir, apresentamos a estrutura do Livro do Estudante, explicando as características das seções e de outros elementos que compõem a coleção.

VAMOS

INICIAR

Essa seção, presente no início de cada volume, tem o objetivo de avaliar os estudantes com relação aos conhecimentos esperados para o ano de ensino, permitindo a você fazer uma avaliação diagnóstica da turma.

PÁGINAS

DE ABERTURA

Têm como objetivos marcar o início de cada unidade, despertar a atenção dos estudantes para o que será abordado e relacionar os conteúdos aos conhecimentos prévios e à sua realidade próxima.

DESENVOLVIMENTO DOS CONTEÚDOS

Os conteúdos são desenvolvidos por meio de atividades e das seções presentes nas unidades. As atividades relacionadas aos conteúdos são apresentadas ao longo da unidade, de modo integrado e contendo estruturas variadas, a fim de tornar as aulas mais dinâmicas e envolventes e auxiliar no desenvolvimento das habilidades e das competências da BNCC.

VOCABULÁRIO

Apresenta o significado de termos que os estudantes podem desconhecer e que são importantes para a compreensão do texto.

BOXE COMPLEMENTAR

Apresenta textos e imagens com informações complementares ao assunto ou contexto trabalhado na unidade.

COLETIVAMENTE

Explora os temas contemporâneos transversais, contribuindo para a formação cidadã dos estudantes por meio de reflexões e propostas de resoluções de problemas, de modo que eles sejam atuantes na sociedade em que vivem. É subdividida em Conhecendo o problema, Organizando as ideias e Buscando soluções para que, assim, os

estudantes tenham contato com uma situação-problema, reflitam sobre ela e busquem uma solução prática. O tema contemporâneo transversal desenvolvido é identificado nas orientações ao professor

ENTRE TEXTOS

Promove o trabalho com diferentes gêneros textuais, possibilitando o desenvolvimento de habilidades relacionadas à leitura, à escrita, à oralidade e aos processos gerais de compreensão de leitura: localizar e retirar informação explícita de textos; fazer inferências diretas; interpretar e relacionar ideias e informações; analisar e avaliar conteúdos e elementos textuais. A seção apresenta as subdivisões Explorando o texto e Além do texto

DIVIRTA-SE E APRENDA

Aplica o conteúdo estudado na unidade por meio de jogos, brincadeiras e atividades lúdicas.

EXPERIMENTE

O estudante é convidado a realizar atividades práticas que envolvem o assunto estudado na unidade por meio de experimentos ou produções interessantes.

VAMOS AVALIAR O APRENDIZADO

Essa seção propõe uma avaliação formativa com relação aos conteúdos abordados em cada bimestre, possibilitando avaliar a aprendizagem dos estudantes e obter informações para intervenções caso haja defasagens ou dificuldade na assimilação dos conteúdos e conceitos.

SAIBA MAIS

Apresenta sugestões de recursos extras, como livros, filmes e sites. Cada sugestão é acompanhada por uma breve sinopse.

VAMOS CONCLUIR

Presente ao final de cada volume, essa seção contém atividades cujo objetivo é sugerir uma avaliação somativa, de modo que você possa avaliar os estudantes quanto aos conhecimentos adquiridos durante o processo de ensino no ano letivo.

REFERÊNCIAS BIBLIOGRÁFICAS COMENTADAS

Localizada ao final de cada volume, apresenta indicações comentadas de livros, revistas e sites que foram consultados na elaboração do Livro do Estudante

MATERIAL COMPLEMENTAR

Presente no final de cada volume, essas páginas contêm materiais para os estudantes recortarem, manipularem e usarem na resolução de algumas das atividades propostas.

DESAFIO A MAIS

Atividade de caráter desafiador, no final de cada unidade, para instigar o raciocínio lógico matemático do estudante e a busca autônoma por respostas.

ÍCONE DE RESPOSTA ORAL

Indica que os estudantes devem responder oralmente à atividade ou à questão.

ÍCONE DESAFIO

Indica que os estudantes devem registrar as respostas da atividade no caderno.

ÍCONE

CÁLCULO MENTAL

Indica que os estudantes devem realizar as atividades sem o registro escrito de cálculos, incentivando o raciocínio lógico.

OBJETO DIGITAL

Indica que existe na versão digital deste livro um infográfico relacionado ao conteúdo ou ao contexto que está sendo trabalhado.

DESTAQUE DICA

Apresenta dicas que podem auxiliar os estudantes na resolução de algumas atividades.

LIVRO DO PROFESSOR

Este Livro do Professor é organizado em duas partes. Esta primeira parte apresenta a estrutura da coleção e a Reprodução do Livro do Estudante, que se refere à reprodução das páginas do Livro do Estudante em tamanho reduzido, com respostas e possíveis comentários para você. Nas laterais e nos rodapés dessas páginas, as orientações ao professor propõem comentários, sugestões de condução para as atividades e respostas de algumas atividades que não foram apresentadas na reprodução da página do Livro do Estudante. Essas orientações colaboram para a prática docente e seu dia a dia em sala de aula e foram elaboradas de modo a explicitar os procedimentos das aulas de forma prática e ao mesmo tempo detalhada, oferecendo suporte à prática docente.

A segunda parte, apresentada após a Reprodução do Livro do Estudante, é intitulada Manual do Professor Ela apresenta a estrutura da BNCC, a fundamentação teórico-metodológica da coleção e aborda diversos assuntos que contribuem para o desenvolvimento docente e para o dia a dia em sala de aula. Além disso, apresenta um quadro de distribuição dos conteúdos com as habilidades e competências da BNCC que estão sendo desenvolvidas em cada unidade, além de sugestões de cronogramas bimestrais, trimestrais e semestrais. Ao final dessa parte, são apresentadas sugestões de referências complementares para a prática docente e as referências bibliográficas comentadas utilizadas como consulta para a produção das orientações ao professor e do Manual do Professor Observe a seguir como as orientações ao professor, que constam na primeira parte deste Livro do Professor, estão estruturadas.

Nas orientações ao professor da seção Vamos iniciar, você encontra os objetivos pedagógicos e as sugestões de intervenção, com base nas respostas dos estudantes, considerando os conhecimentos prévios deles.

OBJETIVOS DA UNIDADE

Destaca os objetivos pedagógicos de cada unidade do Livro do Estudante

SUGESTÃO DE ESTRATÉGIA INICIAL

Fornece dicas para que você possa iniciar as aulas, abordar alguns conteúdos ou realizar uma avaliação diagnóstica de maneira diferente da que foi apresentada no Livro do Estudante

BNCC

Apresenta habilidades, competências e temas contemporâneos transversais da BNCC que estão sendo desenvolvidos em cada conteúdo, destacando as relações entre esses elementos e o conteúdo.

COMENTÁRIOS DIVERSOS

Os comentários e as explicações de caráter prático referentes às atividades do Livro do Estudante e as considerações pedagógicas a respeito de possíveis dificuldades dos estudantes na resolução das atividades, bem como alternativas para consolidar conhecimentos, são inseridos em tópicos ao longo da unidade.

RESPOSTAS

Apresenta as sugestões de respostas de algumas atividades e questões indicadas no Livro do Estudante.

ATIVIDADE EXTRA

Apresenta sugestões de atividades complementares que contribuem para diversificar as estratégias de aprendizagem.

OBJETIVOS

Lista os objetivos pedagógicos de algumas seções do Livro do Estudante.

AVALIANDO

Propõe avaliações formativas para que você possa acompanhar a aprendizagem dos estudantes em diferentes momentos, possibilitando, se for o caso, intervenções no ensino. Para facilitar a avaliação, esse boxe apresenta os objetivos das atividades e as sugestões de intervenção, com foco na recuperação da aprendizagem.

ARTICULANDO CONHECIMENTOS

Destaca momentos em que é possível estabelecer relações entre componentes curriculares de diferentes áreas do conhecimento, além de orientações práticas sobre como realizar as articulações entre os conteúdos.

REFERÊNCIAS COMPLEMENTARES

Fornece ao professor sugestões de livros, sites, artigos, podcasts, entre outros recursos, contribuindo para a sua formação.

SUGESTÃO DE DESAFIO

Ao final de cada unidade, apresentamos uma sugestão de Desafio matemático nas orientações ao professor, que pode ser aplicado em sala de aula, a fim de complementar os conceitos vistos na unidade, instigando o raciocínio lógico dos estudantes.

Nas orientações ao professor, apresentamos comentários e explicações referentes ao Desafio a mais, presente no final do Livro do Estudante, detalhando a resolução desse desafio e indicando possíveis dificuldades encontradas pelos estudantes, bem como alternativas de encaminhamento.

Nas orientações ao professor da seção Coletivamente, apresentamos os objetivos pedagógicos e as orientações sobre o desenvolvimento dos conteúdos e das atividades da seção com os estudantes.

Nas orientações ao professor da seção Entre textos, apresentamos os objetivos pedagógicos e as orientações sobre o desenvolvimento da competência leitora e da competência da escrita por meio do trabalho com essa seção.

Nas orientações ao professor, são apresentados os objetivos pedagógicos das atividades e sugestões de intervenção da seção Vamos avaliar o aprendizado, com base nas possíveis respostas dos estudantes, considerando dificuldades na resolução e dando alternativas para recuperar e consolidar aprendizagens vistas em cada bimestre.

Nas orientações ao professor, são apresentados os objetivos pedagógicos das atividades e sugestões de intervenção da seção Vamos concluir, com base nas possíveis respostas dos estudantes, considerando dificuldades na resolução e dando alternativas para recuperar e consolidar aprendizagens ao final do ano letivo.

LIVRO DO ESTUDANTE

Reprodução do Livro do Estudante

Matemática

Organizadora:

EDITORA NOVO RUMO

Obra coletiva concebida, desenvolvida e produzida pela Editora Novo Rumo.

Editora responsável:

Jacqueline da Silva Ribeiro Garcia

Especialista em Psicopedagogia pela Universidade Estadual de Londrina (UEL-PR).

Licenciada em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Atuou como professora em escolas do Ensino Básico. Editora e elaboradora de materiais didáticos.

Componente curricular: Matemática

1ª edição

Londrina, 2025

11/09/2025 13:55:52

Esta parte do Livro do Professor contém a Reprodução do Livro do Estudante em tamanho reduzido, com respostas das atividades e possíveis comentários para você. Além disso, nas laterais e rodapés há as orientações ao professor que servem como um guia para a prática pedagógica apresentando sugestões sobre como trabalhar as atividades, além de apresentar as respostas que não foram incluídas na reprodução das páginas. Para deixar mais evidente o sentido de leitura, em algumas páginas utilizamos as indicações e .

Anos Iniciais do Ensino Fundamental

Nessa página, estão apresentadas informações técnicas referentes à produção desta coleção.

Edição Jacqueline da Silva Ribeiro Garcia, Lucília Franco Lemos dos Santos

Assistência editorial Denise Maria Capozzi, Kethelyn Yukari Ogasawara

Revisão técnica Tânia Camila Kochmanscky Goulart

Preparação e revisão Moisés Manzano da Silva (coord.)

Gerência de produção editorial Camila Rumiko Minaki Hoshi

Supervisão de produção editorial Priscilla de Freitas Cornelsen Rosa

Assistência de produção editorial Lorena França Fernandes Pelisson

Coordenação de produção de arte Tamires Rose Azevedo

Edição de arte Keithy Mostachi

Projeto gráfico e design Dayane Barbieri, Keithy Mostachi, Laís Garbelini

Projeto de capa Marcela Pialarissi

Ilustrações de capa Ricardo Gualberto

Coordenação de diagramação Adenilda Alves de França Pucca - Nil Diagramação AVITS Estúdio Gráfico Ltda., EfeDois Editoração Ltda., Leandro

Júnior Pimenta

Autorização de recursos João Henrique Pedrão Feliciano

Iconografia Alessandra Roberta Arias, Vinícius Costa (trat. imagens)

Objetos digitais

Gerência de produção Erick Lopes de Almeida

Roteiros Camila Vidigal

Edição de imagens Brenda de Oliveira Goes

Desenvolvimento Ohanna Schmitt Bolfe, Tatiana Tissa Kawakami

Dados Internacionais de Catalogação na Publicação (CIP) (Câmara Brasileira do Livro, SP, Brasil)

ISBN 978-65-5158-123-6(livro do estudante)

ISBN 978-65-5158-122-9(livro do professor)

ISBN 978-65-5158-139-7(livro do estudante HTML5)

ISBN 978-65-5158-138-0(livro do professor HTML5)

1. Matemática (Ensino fundamental) I. Garcia, Jacqueline da Silva Ribeiro. II. Série.

CDD-372.7

25-299255.0

Índices para catálogo sistemático:

1. Matemática : Ensino fundamental 372.7

Eliete Marques da Silva - Bibliotecária - CRB-8/9380

Avenida Doutor Adhemar Pereira de Barros, 1500, sala 804 - Bela Suíça - Londrina-PR CEP 86047-250 - Tel. (43) 3367-2030 contato@editoranovorumo.com.br

Elaboração de originais

Jacqueline da Silva Ribeiro Garcia

Especialista em Psicopedagogia pela Universidade Estadual de Londrina (UEL-PR).

Licenciada em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Atuou como professora em escolas do Ensino Básico. Editora e elaboradora de materiais didáticos.

Fátima Gomes Machado

Especialista em Docência na Educação Superior pela Universidade Estadual de Londrina (UEL-PR).

Licenciada em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Licenciada em Pedagogia pelo Centro Universitário Internacional (Uninter-PR).

Elaboradora e editora de materiais didáticos.

Sandra Aparecida Ferreira Marchi

Especialista em Educação Especial pela Faculdade Catuaí (PR).

Especialista em Gestão Escolar, com habilitação em Administração, Supervisão e Orientação Educacional, pela Faculdade Catuaí (PR).

Licenciada em Matemática pela Universidade Estadual de Londrina (UEL-PR).

Professora dos Anos Iniciais do Ensino Fundamental. Elaboradora de materiais didáticos.

Em respeito ao meio ambiente, as folhas deste livro foram produzidas com fibras obtidas de árvores de florestas plantadas, com origem certificada.

Impresso no Parque Gráfico da Editora FTD CNPJ 61.186.490/0016-33 Avenida Antonio Bardella, 300 Guarulhos-SP – CEP 07220-020 Tel. (11) 3545-8600 e Fax (11) 2412-5375

03/10/2025 08:13:34

APRESENTAÇÃO

OLÁ, ESTUDANTE!

NA VIDA, A GENTE APRENDE E ENSINA O TEMPO TODO. PROVAVELMENTE VOCÊ JÁ APRENDEU MUITO COM SEUS PROFESSORES, AMIGOS E CONHECIDOS.

NESTE LIVRO, HÁ MOMENTOS TANTO PARA VOCÊ COMPARTILHAR O QUE JÁ VIVEU QUANTO PARA NOVAS DESCOBERTAS. VOCÊ VAI LER E PRODUZIR TEXTOS, RESOLVER PROBLEMAS, ENTENDER COMO FUNCIONAM CERTOS PROCESSOS SOCIAIS E CULTURAIS, ENTRE OUTROS ASSUNTOS.

ESPERAMOS QUE VOCÊ INTERAJA COM SEUS COLEGAS E PARTICIPE DAS ATIVIDADES, DESENVOLVENDO O GOSTO PARTICULAR POR NOVAS DESCOBERTAS. E NÃO SE ESQUEÇA DE QUE SEMPRE PODERÁ TIRAR AS SUAS DÚVIDAS COM O PROFESSOR.

APROVEITE CADA MOMENTO PARA TORNAR ESSE APRENDIZADO MAIS RICO E DIVERTIDO.

BOM ESTUDO!

CONHEÇA SEU LIVRO

A SEGUIR, APRESENTAMOS A ORGANIZAÇÃO DO SEU LIVRO E INDICAMOS COMO ISSO VAI AJUDAR EM SEUS ESTUDOS.

VAMOS INICIAR AS ATIVIDADES DESSA SEÇÃO SERVEM PARA VOCÊ MOSTRAR O QUE JÁ SABE E PERCEBER O QUE PRECISA ESTUDAR UM POUCO MAIS.

03/10/2025 13:51:33

O início do ano letivo é um momento importante para os estudantes, pois eles terão o primeiro contato com o livro didático de Matemática e apresentarão suas primeiras expectativas sobre o que vão estudar. Por esse motivo, nesta página, os autores iniciam um diálogo com eles, com o objetivo de sintetizar o que se deve esperar durante o estudo com esse material. Nesse texto, os estudantes são encorajados a participar de modo ativo e cooperativo da aprendizagem, interagindo com a turma e o professor durante as dinâmicas propostas.

Em seguida, a estrutura da coleção é apresentada na seção Conheça seu livro, mostrando as características dos elementos contidos nela, desde as Páginas de abertura até as Referências bibliográficas complementares e o Material complementar

A seguir, apresentamos as unidades temáticas, os objetos de conhecimento e as habilidades de Matemática da BNCC referentes ao 1º ano do Ensino Fundamental. Eles podem ser consultados sempre que necessário, para nortear os planejamentos de aula ou para esclarecer dúvidas a respeito dos objetos de conhecimento trabalhados nas unidades do volume.

BASE NACIONAL COMUM CURRICULAR (BNCC) • 1º ano

Unidade temática: Números

Objetos de conhecimento

• Contagem de rotina

PÁGINAS DE ABERTURA

NESSAS PÁGINAS, VOCÊ VAI ENCONTRAR

UMA IMAGEM E UM TEXTO INICIANDO

A CONVERSA SOBRE O ASSUNTO QUE SERÁ ESTUDADO NA UNIDADE, ALÉM DE ALGUMAS QUESTÕES QUE EXPLORAM O QUE VOCÊ JÁ SABE DO CONTEÚDO.

EXPERIMENTE

12. EM DIFERENTES ÉPOCAS E CULTURAS, ERA COMUM USAR PARTES DO PRÓPRIO CORPO PARA MEDIR COMPRIMENTOS. UTILIZE PARTES DO SEU CORPO PARA REALIZAR AS MEDIÇÕES A SEGUIR NA SALA DE AULA.

CONTEÚDO

OS CONTEÚDOS DESTE VOLUME SÃO APRESENTADOS POR MEIO DE ATIVIDADES. ALGUMAS SÃO MAIS FÁCEIS, OUTRAS SÃO DESAFIADORAS. MAS NÃO SE PREOCUPE, POIS O APRENDIZADO DA MATEMÁTICA TAMBÉM É CONSTRUÍDO COM TENTATIVAS E ACERTOS.

PROPOSTAS DE ATIVIDADES PRÁTICAS QUE ENVOLVEM O ASSUNTO DA UNIDADE APLICADO EM EXPERIMENTOS E PRODUÇÕES LEGAIS.

A ) USANDO SEU PÉ, MEÇA A DISTÂNCIA DE SUA CARTEIRA ATÉ A PAREDE MAIS PRÓXIMA.

ENTRE TEXTOS TIRINHAS SÃO PEQUENAS HISTÓRIAS EM QUADRINHOS COM IMAGEM, PODENDO TER TEXTO OU NÃO. A QUANTIDADE DE QUADRINHOS VARIA DE TRÊS A QUATRO, GERALMENTE EM SEQUÊNCIA DE ACONTECIMENTOS. A) VOCÊ JÁ LEU ALGUMA TIRINHA? CONTE AOS COLEGAS. A TIRINHA A SEGUIR TRAZ UMA SITUAÇÃO QUE ENVOLVE A AÇÃO DE COMPARTILHAR. ANALISE A TIRINHA COM O PROFESSOR E OS COLEGAS.

B ) USANDO SEU PALMO, MEÇA A ALTURA DA MESA DO PROFESSOR.

DIVIRTA-SE E APRENDA

C ) USANDO SEU PASSO, MEÇA O COMPRIMENTO DO RODAPÉ DE UMA DAS PAREDES DA SALA DE AULA.

VOCÊ PODE APRENDER

UM POUCO MAIS OU APLICAR O CONTEÚDO

ESTUDADO POR MEIO DE JOGOS, BRINCADEIRAS E ATIVIDADES LÚDICAS.

VOCÊ SABIA

D ) COMPARE COM OS SEUS COLEGAS AS MEDIDAS DE COMPRIMENTO QUE VOCÊ OBTEVE EM CADA SITUAÇÃO. ELAS SÃO IGUAIS OU DIFERENTES? POR QUÊ?

ENTRE TEXTOS NESSA SEÇÃO, VOCÊ VAI TRABALHAR COM DIFERENTES GÊNEROS TEXTUAIS, RELACIONANDO O ASSUNTO MATEMÁTICO ESTUDADO A DIVERSOS CONTEXTOS, AO MESMO TEMPO EM QUE DESENVOLVE PRÁTICAS DE LINGUAGEM.

• Contagem ascendente e descendente

• Reconhecimento de números no contexto diário: indicação de quantidades, indicação de ordem ou indicação de código para a organização de informações Habilidades

(EF01MA01) Utilizar números naturais como indicador de quantidade ou de ordem em diferentes situações cotidianas e

reconhecer situações em que os números não indicam contagem nem ordem, mas sim código de identificação. Objetos de conhecimento

• Quantificação de elementos de uma coleção: estimativas, contagem um a um, pareamento ou outros agrupamentos e comparação Habilidades

(EF01MA02) Contar de maneira exata ou aproximada, utilizando diferentes estraté-

03/10/2025 17:45:33

gias como o pareamento e outros agrupamentos.

(EF01MA03) Estimar e comparar quantidades de objetos de dois conjuntos (em torno de 20 elementos), por estimativa e/ ou por correspondência (um a um, dois a dois) para indicar “tem mais”, “tem menos” ou “tem a mesma quantidade”.

DESAFIO A MAIS NO FINAL DE CADA UNIDADE, VOCÊ TERÁ UMA ATIVIDADE DESAFIADORA PARA TESTAR SEU RACIOCÍNIO LÓGICO MATEMÁTICO E SUA CAPACIDADE DE OBTER RESPOSTAS.

COLETIVAMENTE

NESSA SEÇÃO, VOCÊ VAI REFLETIR SOBRE TEMAS IMPORTANTES QUE CONTRIBUEM PARA A FORMAÇÃO DE CIDADÃOS CRÍTICOS E ATUANTES NA SOCIEDADE, RELACIONADOS A SITUAÇÕES DO COTIDIANO.

VAMOS CONCLUIR NO FINAL DO VOLUME, VOCÊ ESTÁ CONVIDADO A RESOLVER AS QUESTÕES DESSA SEÇÃO, PARA AVALIAR SEU PROGRESSO NA APRENDIZAGEM. 3.

VAMOS AVALIAR O APRENDIZADO AO FINAL DE CADA UNIDADE, HÁ UMA SEÇÃO PARA QUE VOCÊ AVALIE SEU AVANÇO NA APRENDIZAGEM ATÉ O MOMENTO.

Unidade temática: Números

Objetos de conhecimento

• Leitura, escrita e comparação de números naturais (até 100)

• Reta numérica

Habilidades

(EF01MA04) Contar a quantidade de objetos de coleções até 100 unidades e apresentar o resultado por registros verbais e simbólicos, em situações de seu interesse, como jogos, brincadeiras, materiais da sala de aula, entre outros.

(EF01MA05) Comparar números naturais

VOCABULÁRIO PARA AJUDAR NA COMPREENSÃO DOS TEXTOS, ALGUMAS PALAVRAS SÃO DESTACADAS E O SIGNIFICADO DELAS É APRESENTADO. 5 03/10/2025 13:51:36

de até duas ordens em situações cotidianas, com e sem suporte da reta numérica.

Objetos de conhecimento

• Construção de fatos básicos da adição

• Composição e decomposição de números naturais

Habilidades

(EF01MA06) Construir fatos básicos da adição e utilizá-los em procedimentos de cálculo para resolver problemas.

(EF01MA07) Compor e decompor número de até duas ordens, por meio de diferen-

tes adições, com o suporte de material manipulável, contribuindo para a compreensão de características do sistema de numeração decimal e o desenvolvimento de estratégias de cálculo.

Unidade temática: Números

Objetos de conhecimento

SAIBA MAIS APRESENTA SUGESTÕES DE LIVROS, SITES E FILMES QUE ESTÃO RELACIONADOS COM OS CONTEÚDOS ESTUDADOS.

REFERÊNCIAS

BIBLIOGRÁFICAS

COMENTADAS

ESSA SEÇÃO CONTÉM AS REFERÊNCIAS DE LIVROS, REVISTAS E SITES QUE FORAM UTILIZADOS NA ELABORAÇÃO DO SEU LIVRO.

ÍCONES E DESTAQUES

DESAFIO

INDICA ATIVIDADES DE CARÁTER MAIS DESAFIADOR.

CÁLCULO MENTAL

INDICA ATIVIDADES QUE DEVEM SER REALIZADAS SEM O REGISTRO ESCRITO DE CÁLCULOS, MOTIVANDO O RACIOCÍNIO LÓGICO.

RESPOSTA ORAL

INDICA ATIVIDADES E QUESTÕES QUE VOCÊ PODE RESPONDER ORALMENTE.

DICA

MATERIAL COMPLEMENTAR ESSA SEÇÃO CONTÉM MATERIAIS PARA VOCÊ RECORTAR E UTILIZAR NA RESOLUÇÃO DE ALGUMAS ATIVIDADES PROPOSTAS.

APRESENTA DICAS QUE PODEM FACILITAR A RESOLUÇÃO DE ALGUMAS ATIVIDADES.

OBJETOS DIGITAIS

INDICA QUE EXISTE, NA VERSÃO DIGITAL DESTE LIVRO, UM INFOGRÁFICO CLICÁVEL RELACIONADO AO CONTEÚDO.

Os sites indicados neste livro podem mostrar imagens e textos diferentes dos que foram pensados para o seu estudo. Isso acontece porque o conteúdo disponível on-line pode ser alterado com o tempo e variar conforme o histórico de pesquisa do usuário. Por isso, não temos como controlar as imagens e textos que aparecem em tais sites

• Problemas envolvendo diferentes significados da adição e da subtração (juntar, acrescentar, separar, retirar)

Habilidades

(EF01MA08) Resolver e elaborar problemas de adição e de subtração, envolvendo números de até dois algarismos, com os significados de juntar, acrescentar, separar e retirar, com o suporte de imagens e/ ou material manipulável, utilizando estratégias e formas de registro pessoais.

Unidade temática: Álgebra

Objetos de conhecimento

• Padrões figurais e numéricos: investigação de regularidades ou padrões em sequências

Habilidades (EF01MA09) Organizar e ordenar objetos familiares ou representações por figuras, por meio de atributos, tais como cor, forma e medida.

Objetos de conhecimento

• Sequências recursivas: observação de regras usadas utilizadas em seriações numéricas (mais 1, mais 2, menos 1, menos 2, por exemplo)

Habilidades (EF01MA10) Descrever, após o reconhecimento e a explicitação de um padrão (ou regularidade), os elementos ausentes em sequências recursivas de números naturais, objetos ou figuras.

CONHECENDO OS NÚMEROS

DE 0 A 10

DIVIRTA-SE E APRENDA • JOGO DE CARTELAS NUMERADAS

Unidade temática: Geometria

Objetos de conhecimento

• Localização de objetos e de pessoas no espaço, utilizando diversos pontos de referência e vocabulário apropriado

Habilidades

(EF01MA11) Descrever a localização de pessoas e de objetos no espaço em relação à sua própria posição, utilizando termos como à direita, à esquerda, em frente, atrás.

(EF01MA12) Descrever a localização de pessoas e de objetos no espaço segundo

um dado ponto de referência, compreendendo que, para a utilização de termos que se referem à posição, como direita, esquerda, em cima, em baixo, é necessário explicitar-se o referencial.

Objetos de conhecimento

• Figuras geométricas espaciais: reconhecimento e relações com objetos familiares do mundo físico

Habilidades

(EF01MA13) Relacionar figuras geométricas espaciais (cones, cilindros, esferas e

Nesta página, é apresentado o sumário do volume, que foi organizado para facilitar a localização das unidades e das seções. No final do volume, também é possível encontrar a lista dos Objetos digitais que estão indicados nas páginas com ícones correspondentes e que podem ser acessados no material interativo.

blocos retangulares) a objetos familiares do mundo físico.

Objetos de conhecimento

• Figuras geométricas planas: reconhecimento do formato das faces de figuras geométricas espaciais

Habilidades

(EF01MA14) Identificar e nomear figuras planas (círculo, quadrado, retângulo e triângulo) em desenhos apresentados em diferentes disposições ou em contornos de faces de sólidos geométricos.

Unidade temática: Grandezas e medidas

Objetos de conhecimento

• Medidas de comprimento, massa e capacidade: comparações e unidades de medida não convencionais

Habilidades

(EF01MA15) Comparar comprimentos, capacidades ou massas, utilizando termos como mais alto, mais baixo, mais comprido, mais curto, mais grosso, mais fino, mais largo, mais pesado, mais leve, cabe mais, cabe menos, entre outros, para ordenar objetos de uso cotidiano.

Objetos de conhecimento

• Medidas de tempo: unidades de medida de tempo, suas relações e o uso do calendário

Habilidades

(EF01MA16) Relatar em linguagem verbal ou não verbal sequência de acontecimentos relativos a um dia, utilizando, quando possível, os horários dos eventos.

(EF01MA17) Reconhecer e relacionar períodos do dia, dias da semana e meses do ano, utilizando calendário, quando necessário.

(EF01MA18) Produzir a escrita de uma data, apresentando o dia, o mês e o ano, e indicar o dia da semana de uma data, consultando calendários.

OBJETOS DIGITAIS

UNIDADE 1 • INFOGRÁFICO CLICÁVEL: VAMOS CONHECER

UNIDADE 1 • INFOGRÁFICO CLICÁVEL: PRODUÇÃO, COMÉRCIO

UNIDADE 2 • INFOGRÁFICO CLICÁVEL: GEOMETRIA NAS EDIFICAÇÕES

UNIDADE 3 • INFOGRÁFICO CLICÁVEL: A VIDA PASSA NA BEIRA DO RIO 89

UNIDADE 5 • INFOGRÁFICO CLICÁVEL: VAMOS BRINCAR JUNTOS? 147

UNIDADE 9 • INFOGRÁFICO CLICÁVEL: FAZENDO COMPRAS

Unidade temática: Grandezas e medidas

Objetos de conhecimento

• Sistema monetário brasileiro: reconhecimento de cédulas e moedas

Habilidades

(EF01MA19) Reconhecer e relacionar valores de moedas e cédulas do sistema monetário brasileiro para resolver situações simples do cotidiano do estudante. Objetos de conhecimento

• Noção de acaso

Habilidades

(EF01MA20) Classificar eventos envolvendo o acaso, tais como “acontecerá com certeza”, “talvez aconteça” e “é impossível acontecer”, em situações do cotidiano.

Unidade temática:

Probabilidade e estatística

Objetos de conhecimento

• Leitura de tabelas e de gráficos de colunas simples

Habilidades

(EF01MA21) Ler dados expressos em ta-

03/10/2025 13:51:40

belas e em gráficos de colunas simples. Objetos de conhecimento

• Coleta e organização de informações Registros pessoais para comunicação de informações coletadas

Habilidades

(EF01MA22) Realizar pesquisa, envolvendo até duas variáveis categóricas de seu interesse e universo de até 30 elementos, e organizar dados por meio de representações pessoais.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Versão final. Brasília: MEC, 2018. p. 278-281. Disponível em: https://www.gov.br/mec/ pt-br/escola-em-tempo-integral/BNCC_EI_EF_110518_ versaofinal.pdf. Acesso em: 14 ago. 2025.

1. Objetivo

Utilizar as expressões “mais comprido”, “mais baixo” e “mais pesado” para indicar relações de grandeza.

Sugestões de intervenção

Caso os estudantes tenham dificuldade em compreender os itens A e B e as expressões “mais comprido” e “mais baixo”, organize-os em grupos e proponha atividades práticas para que descrevam os atributos de alguns objetos usando expressões como “mais comprido”, “mais curto”, “mais alto” e “mais baixo”. Caso não consigam identificar o cachorro mais leve e o mais pesado no item C, relacione a situação com experiências do cotidiano deles, como segurar um animal de estimação ou identificar um objeto que não são capazes de levantar com as próprias mãos. Após esse trabalho, oriente-os a responder novamente a esse item ou proponha comparações entre os animais apresentados na atividade e outros que eles conheçam.

2. Objetivo

Conhecer os números e a sequência numérica de 1 a 10.

Sugestões de intervenção

Caso os estudantes apresentem dificuldade em relação aos números ou à sequência, oriente-os a contar com o auxílio dos dedos das mãos, riscos no caderno ou outros materiais que possam ser contados. Se necessário, oriente-os também durante o traçado dos números.

VAMOS INICIAR

1. FAÇA O QUE SE PEDE EM CADA ITEM.

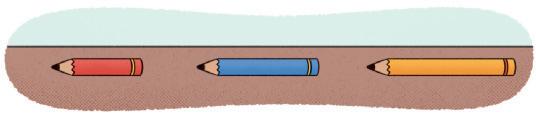
A ) CONTORNE O LÁPIS MAIS COMPRIDO.

Resposta: Os estudantes devem contornar o lápis amarelo.

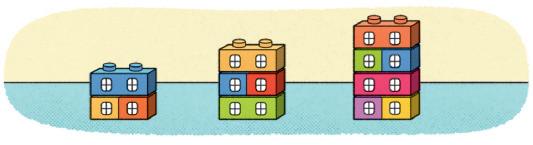
B ) MARQUE UM X NA TORRE MAIS BAIXA

Resposta: Os estudantes devem marcar um X na torre com 2 níveis.

C ) CONTORNE O CACHORRO MAIS PESADO

Resposta: Os estudantes devem contornar o cachorro do meio.

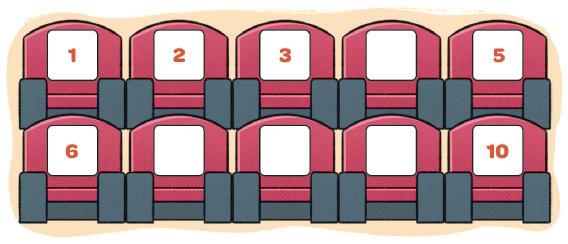
2. AS CADEIRAS DO TEATRO ESTÃO COM ALGUNS NÚMEROS FALTANDO. COMPLETE OS NÚMEROS NA SEQUÊNCIA.

Resposta: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.

3. RUI GANHOU OS LIVROS DE HISTÓRIA REPRESENTADOS NA CENA.

A ) RUI JÁ LEU 4 DESTES LIVROS. QUANTOS AINDA FALTAM SER LIDOS?

LIVROS.

Resposta: 2 LIVROS.

B ) MARQUE UM X NO CÁLCULO QUE EFETUAMOS PARA RESOLVER ESTE PROBLEMA.

6 − 4

Resposta: Os estudantes devem marcar um X no item 6 4.

6 + 4

4. CONTORNE OS LÁPIS DE COR DE GUILHERME AGRUPANDO DE DOIS EM DOIS LÁPIS.

Resposta: Os estudantes devem contornar os lápis, da maneira que preferirem, formando quatro grupos com dois lápis cada.

A ) QUANTOS GRUPOS VOCÊ FORMOU? GRUPOS.

Resposta: 4 GRUPOS.

B ) QUANTOS LÁPIS DE COR GUILHERME TEM? LÁPIS.

Resposta: 8 LÁPIS.

5. DESENHE A CASA DE MARINA NO FINAL DO CAMINHO QUE ESTÁ À DIREITA DELA.

Resposta: Os estudantes devem desenhar uma casa no final do caminho 2

5. Objetivo

Utilizar termos como “à direita” e “à esquerda” para descrever a localização de pessoas e objetos no espaço em relação à própria posição.

Sugestões de intervenção

Caso os estudantes tenham alguma dificuldade na resolução da atividade, organize-os em

03/10/2025 08:19:07

duplas e proponha atividades práticas para que descrevam a localização de objetos explicitando o referencial e utilizando termos como “direita”, “esquerda”, “em cima”, “embaixo” etc. Se a dificuldade for em representar as posições no desenho, oriente-os a se imaginarem no lugar da personagem e apontar para a posição desejada.

3. Objetivo

Resolver subtração envolvendo números de 1 algarismo.

Sugestões de intervenção

No item A, avalie se os estudantes relacionam a situação apresentada à subtração, acompanhando as estratégias usadas por eles. Se necessário, oriente-os a utilizar materiais de contagem e estratégias diversas de cálculo, como o cálculo mental. Para o item B, avalie se eles conhecem os nomes e os significados dos sinais e, caso tenham dificuldade com as noções de adição e subtração, oriente-os a efetuar as operações apresentadas utilizando os dedos ou outras maneiras, para que verifiquem os valores obtidos.

4. Objetivo

Realizar contagem utilizando a ideia de agrupamento.

Sugestões de intervenção

Avalie as estratégias utilizadas pelos estudantes para obter os grupos. Caso necessário, apresente outros conjuntos de desenhos ou objetos, pedindo a eles que formem grupos com dois objetos. Aos poucos, vá aumentando as quantidades. Em seguida, oriente-os a contar os elementos de cada grupo partindo do primeiro elemento.

CAMINHO 1

CAMINHO 2

6. Objetivo

Relacionar objetos do cotidiano a figuras geométricas espaciais.

Sugestões de intervenção

Oriente os estudantes a refletirem sobre as características dos objetos apresentados e o formato das figuras geométricas espaciais. Em seguida, mostre imagens de outros itens para que relacionem com figuras geométricas espaciais. Outra possibilidade é trabalhar com objetos que eles possam manusear e comparar.

7. Objetivo

Identificar e nomear figuras geométricas planas.

Sugestões de intervenção

Caso os estudantes tenham dificuldade, promova uma reflexão sobre as características de cada figura geométrica plana apresentada e peça-lhes que digam as principais diferenças entre elas.

8. Objetivo

Reconhecer padrões em sequências de figuras geométricas planas.

Sugestões de intervenção

Caso surja alguma dificuldade, faça questionamentos à turma, como “Qual figura vem depois do quadrado?”, e apresente diferentes sequências, como as numéricas, para que os estudantes determinem os elementos que faltam.

6. LIGUE CADA OBJETO À FIGURA GEOMÉTRICA

ESPACIAL QUE ELE LEMBRA.

Resposta: Os estudantes devem ligar: A-3; B-1; C-5; D-4; E-2.

IMAGENS SEM PROPORÇÃO ENTRE SI.

A. E. B.

DE SAPATOS.

BOLA DE BASQUETEBOL.

D. C.

COLA ESCOLAR. CHAPÉU DE FESTA.

A ) CONTORNE A FIGURA QUE TEM O MESMO FORMATO DAS OUTRAS DESSA SEQUÊNCIA.

Resposta: Os estudantes devem contornar o retângulo cor-de-rosa.

B ) MARQUE UM X NO NOME DAS FIGURAS QUE APARECEM NESSA SEQUÊNCIA.

Resposta: Os estudantes devem marcar um X na palavra RETÂNGULO.

QUADRADO. RETÂNGULO.

8. DESENHE A FIGURA QUE FALTA PARA COMPLETAR A SEQUÊNCIA.

Resposta: Os estudantes devem desenhar um quadrado vermelho.

7. LUCAS DESENHOU AS FIGURAS A SEGUIR DE ACORDO COM UMA REGRA DE SEQUÊNCIA.

CAIXA

DADO.

9. AS CENAS A SEGUIR ACONTECERAM EM SEQUÊNCIA, MAS ESTÃO FORA DE ORDEM. MARQUE UM X NA CENA QUE ACONTECEU PRIMEIRO.

Resposta: Os estudantes devem marcar um X na cena do meio.

10. DAIANE FEZ UMA PESQUISA COM SEUS AMIGOS E OBTEVE O RESULTADO A SEGUIR. CADA REPRESENTA 1 VOTO.

SABOR DE SUCO NATURAL PREFERIDO, EM 2027

SABOR QUANTIDADE DE AMIGOS

MORANGO

ACEROLA

LARANJA

FONTE DE PESQUISA: REGISTROS DE DAIANE.

A ) MARQUE UM X NA QUANTIDADE DE AMIGOS QUE PREFEREM O SUCO NATURAL SABOR LARANJA. 4 6 7 3

Resposta: Os estudantes devem marcar um X no número 7.

B ) CONTORNE O NOME DO SABOR DE SUCO NATURAL QUE RECEBEU MENOS VOTOS

ACEROLA

Resposta: Os estudantes devem contornar a palavra MORANGO.

LARANJA

MORANGO

03/10/2025 08:19:21

9. Objetivo

Reconhecer, em uma sequência de acontecimentos, a ordem em que eles ocorreram.

Sugestões de intervenção

Caso os estudantes não consigam identificar a ordem dos acontecimentos, faça questionamentos comparando duas cenas, identificando entre cada par qual delas aconteceu primeiro.

10. Objetivo

Compreender informações apresentadas em tabelas.

Sugestões de intervenção

Se os estudantes não conseguirem identificar as informações, trabalhe com eles outras tabelas, explicando os elementos e a relação entre as informações apresentadas em cada linha. Se eles tiverem dificuldade no item A, verifique se perceberam que, nas indicações, cada • corresponde a um voto. Caso tenham dificuldade no item B, peça a eles que determinem todas as quantidades e as comparem entre si. Além disso, verifique se as dificuldades estão relacionadas à contagem e à comparação, e não à interpretação e à leitura da tabela. Se possível, construa uma tabela com a turma, apresentando os dados antes de organizá-los nela. Depois, pode-se refazer a atividade ou avaliar por meio de outras situações que envolvam os dados das tabelas.

OBJETIVOS DA UNIDADE

• Identificar números em situações do cotidiano.

• Ler, escrever e representar números de 0 a 19 com algarismos, por extenso e no quadro de ordens.

• Compreender a ideia de correspondência um a um.

• Quantificar elementos até 19 unidades, representando essas quantidades com algarismos e por extenso.

• Identificar o zero como representação da ausência de elementos.

• Reconhecer que uma dezena corresponde a 10 unidades.

• Identificar os ordinais do 1º ao 10º em situações do dia a dia.

• Reconhecer, em experimentos aleatórios, eventos certos, possíveis ou impossíveis de ocorrer.

• Ler dados expressos em tabelas e em gráficos de colunas simples.

• Coletar, organizar e representar dados de uma pesquisa por meio de gráficos de barras em malha quadriculada.

• Compreender os significados de possível e impossível.

INTRODUÇÃO E JUSTIFICATIVA

Nesta unidade, são trabalhados os números naturais de 0 a 19, com o propósito de despertar nos estudantes a percepção de que os números estão presentes nas mais variadas situações do cotidiano. São introduzidos, um a um, os números de 1 a 9, sendo exploradas suas representações com algarismos e por extenso, bem como suas relações com a quantidade que representam. Apresenta-se o zero como representação da ausência de elementos. Em seguida, propõe-se um trabalho prolongado com números até 19 e o conceito de dezena associado à

UNIDADE

NÚMEROS DE 0 A 19 1

LOCOMOTIVA DE BRINQUEDO E BLOCOS NUMERADOS.

quantidade de 10 elementos, incentivando a representação no quadro de ordens e no ábaco. Esse trabalho tem a justificativa de ser pré-requisito para a construção do repertório numérico dos estudantes e para sistematização do sistema de numeração decimal, importantes no trabalho com números e operações. Também são abordadas estratégias de agrupamentos e trocas, números ordinais, noções entre maior e menor e uso

de números como código de identificação, além de noções iniciais de Estatística e Probabilidade. Habilidades da BNCC trabalhadas na unidade: EF01MA01 , EF01MA02 , EF01MA03 , EF01MA04, EF01MA10, EF01MA20, EF01MA21 e EF01MA22.

03/10/2025 08:26:31

OS NÚMEROS ESTÃO PRESENTES EM QUASE TUDO EM NOSSO COTIDIANO. POR EXEMPLO, UTILIZAMOS NÚMEROS PARA SABER QUANTO CUSTA UM PRODUTO, PARA MEDIR A NOSSA ALTURA, PARA IDENTIFICAR UMA CASA OU PARA CALCULAR A QUANTIDADE DE MEDICAMENTO QUE DEVEMOS TOMAR.

1. 2. 3.

QUAIS NÚMEROS APRESENTADOS NA FOTOGRAFIA VOCÊ CONHECE?

COM OS DEDOS DAS MÃOS, MOSTRE PARA O PROFESSOR QUANTOS BLOCOS NUMERADOS ESTÃO PRESENTES NA IMAGEM.

Resposta: Espera-se que os estudantes levantem nove dedos das mãos.

QUAL DOS NÚMEROS A SEGUIR APARECE NO

BLOCO VERMELHO DA FOTOGRAFIA? CONTORNE-O.

1. Resposta pessoal. Esperase que os estudantes citem os números que conhecem, de acordo com o conhecimento prévio de cada um.

1 2 3 4

Resposta: Os estudantes devem contornar o número 1.

• Na realização da questão 3, pergunte sobre os números que aparecem nos outros blocos. Nessa conversa, avalie o conhecimento prévio deles a respeito dos números apresentados nos blocos numerados da fotografia, com o objetivo de obter melhor aproveitamento do trabalho que será executado na unidade.

SUGESTÃO DE ESTRATÉGIA INICIAL

Escolha 10 estudantes e peça-lhes que se dirijam até a frente da sala de aula. Em seguida,

03/10/2025 08:26:31

solicite aos demais que indiquem quantos estudantes foram à frente, levantando os dedos das mãos. Caso algum deles tenha conhecimento prévio para dizer a quantidade em voz alta, instigue-o a informar.

Após verificar a resposta de todos, peça a um ou dois estudantes que voltem aos seus lugares. Pergunte novamente quantos permanecem à frente. Repita esse procedimento, sempre questionando, até que todos tenham retornado a seus lugares e respondam “nenhum”.

• Leia o texto da página 15 e faça alguns questionamentos aos estudantes a respeito dos números presentes em nosso cotidiano. Pergunte-lhes se costumam notar esses números e em que situações são usados, como citado no texto. Pergunte também se eles conhecem outras situações nas quais são utilizados números. Motive a participação dos estudantes. Eles podem responder, por exemplo, que usam números para a contagem de brinquedos, para dizer a idade deles, para contar a quantidade de lápis de cor, entre outras situações.

• Oriente a resolução das questões propostas na página 15. Incentive-os a falar sobre os números apresentados nos blocos numerados da fotografia.

• A abordagem da questão 1 é essencial para verificar os conhecimentos prévios dos estudantes acerca dos números, pois cada um deles chega ao 1º ano com diferentes experiências matemáticas. Assim, é possível identificar um ponto de partida e adequar estratégias de ensino à realidade da turma.

• Na realização da questão 2, alguns estudantes podem saber como representar a quantidade de blocos numerados usando os dedos das mãos; para os que não conseguem, oriente-os a levantar um dedo para cada bloco que há na imagem.

• A atividade 1 está baseada em uma reflexão histórica, levando os estudantes a compreenderem como antigas civilizações desenvolveram o próprio sistema de contagem, devido à necessidade de controlar o rebanho. O objetivo principal é desenvolver nos estudantes a correspondência um a um, uma habilidade essencial no processo de construção da contagem e noção de quantidade. O pré-requisito necessário nesse tópico é a capacidade de comparação por meio da observação de quantidades para determinar se existe mais, menos ou a mesma quantidade.

• Solicite aos estudantes que observem a imagem e pergunte a eles o que o pastor está usando para representar cada ovelha. Comente com eles que os pastores associavam uma pedra para cada ovelha. Pergunte quantas ovelhas há na imagem e desenhe na lousa uma pedra para cada uma delas. Motive-os a contar em voz alta, à medida que for desenhando as pedras na lousa. Depois, pergunte: “Quantas ovelhas contamos?”; “Quantas pedras desenhamos?”. Isso contribui para a construção do conceito de quantidade e para a noção de que todo objeto pode ser representado por um símbolo.

• Na atividade 2, comente com os estudantes que, além de pedrinhas, os pastores também usavam risquinhos. Complemente a atividade, após os estudantes resolverem o item A , solicitando que o resolvam usando risquinhos, no caderno, para explorar a correspondência um a um. Espera-se que eles façam seis risquinhos. Valorize os pré-requisitos por meio de sondagens, verificando se eles usam seus conhecimentos prévios para expressar as estratégias pessoais na resolução da atividade.

CONHECENDO OS NÚMEROS

1. A NECESSIDADE DE CONTAR

EXISTE DESDE O INÍCIO

DA EXISTÊNCIA DO SER

HUMANO. ANTIGAMENTE, PARA IDENTIFICAR QUANTIDADES, AS PESSOAS USAVAM OS DEDOS DAS MÃOS, DOS PÉS, PEQUENAS PEDRAS, RISCOS EM PEDRAS OU EM OSSOS, GRAVETOS, ENTRE OUTROS MATERIAIS.

PARA CONTAR ANIMAIS, POR EXEMPLO, OS PASTORES ASSOCIAVAM UMA PEDRA PARA CADA OVELHA.

ANALISE A IMAGEM E REPRESENTE A QUANTIDADE DE OVELHAS

DESENHANDO UMA PEDRA PARA CADA ANIMAL DA CENA.

Resposta: Os estudantes devem desenhar 3 pedras.

2. COM BASE NA IMAGEM A SEGUIR, RESOLVA O QUE SE PEDE.

A ) DESENHE PEDRAS

PARA REPRESENTAR A QUANTIDADE DE OVELHAS QUE APARECEM NA IMAGEM.

Resposta: Os estudantes devem desenhar 6 pedras.

B ) ALÉM DE PEDRAS, QUAIS OUTROS MATERIAIS PODEM SER USADOS PARA REPRESENTAR QUANTIDADES?

Resposta pessoal. Espera-se que os estudantes digam exemplos como risquinhos, bolinhas de gude, palitos de sorvete e dedos das mãos.

• Se possível, leve pedrinhas ou tampinhas para a sala de aula e proponha uma atividade prática, por meio da qual os estudantes deverão representar uma quantidade pequena de objetos preestabelecida pelo professor. Assim, eles têm a oportunidade de vivenciar a atividade de modo lúdico antes de realizarem o registro no papel.

BNCC

As atividades 1 e 2 favorecem o desenvolvimento da habilidade EF01MA01, pois motivam os estudantes a identificarem e compararem diferentes estratégias para representar quantidades.

3. OS NÚMEROS ESTÃO SEMPRE PRESENTES EM NOSSO DIA A DIA E APARECEM EM MUITOS LUGARES, COMO EM CASAS, ESCOLAS, RUAS E LOJAS.

MARQUE UM X NAS CENAS EM QUE APARECEM NÚMEROS.

IMAGENS SEM PROPORÇÃO ENTRE SI.

Resposta: Os estudantes devem marcar um X nas cenas A; D; E.

• A atividade 3 busca avaliar se os estudantes já tiveram algum contato prévio com números e se recordam do que já aprenderam sobre eles. É importante auxiliar a turma a identificar os símbolos numéricos, pois este é um dos primeiros contatos com números em ambiente escolar. Além disso, é natural que leve tempo até que todos os estudantes, no próprio tempo, adquiram familiaridade com os símbolos que representam os números. Identifique aqueles que apresentam mais dificuldades, buscando saná-las em atividades posteriores.

• Ao longo da atividade, considere perguntar aos estudantes qual é a representação de cada imagem, exercitando as capacidades de visualização, interpretação e comunicação. Nas imagens em que houver a presença de números, peça a eles que expliquem o que tais números estão representando naquela cena. Caso algum estudante apresente dificuldade, auxilie dizendo, por exemplo, que o número 9, na imagem com a caixa de leite, indica o preço de cada caixa. Mostre que, sem números, não seria possível saber quanto uma pessoa teria de gastar para adquirir o leite.

BNCC

03/10/2025 08:26:34

De maneira introdutória, é apresentada nesse tópico a utilidade dos números em contagens e em códigos de identificação, assim como a presença dos números no cotidiano. Além disso, as atividades trabalham o reconhecimento de números, tanto em algarismos quanto em escrita por extenso. Dessa maneira, são exercitados elementos da habilidade EF01MA01.

• A atividade 4 apresenta uma situação do cotidiano na qual os estudantes devem procurar identificar a presença de números. Essa atividade é propícia para avaliar o conhecimento prévio deles. Verifique se eles já conseguem reconhecer os símbolos numéricos e, principalmente, se são capazes de diferenciá-los das letras. Como as primeiras bases das noções numéricas e verbais mais elementares ainda estão sendo construídas, e como o aprendizado de letras e números é feito em simultaneidade, é comum que haja confusões entre letras e representações numéricas.

• Ao apresentar a atividade 4, pergunte aos estudantes se eles reconhecem o ambiente da imagem: “Vocês já foram a um lugar como esse da imagem?”; “Qual é o nome desse lugar?”; “O que se faz ali?”. Explore as potencialidades das vivências dos estudantes e, pouco a pouco, vá inserindo a percepção de que os números estão em todos os lugares e fazem parte do dia a dia, ajudando-nos nas atividades mais diversas, inclusive em uma feira livre, para fazer compras.

• Quando for trabalhar o item B, forneça pistas de possíveis lugares onde eles tenham visto ou usado números. Utilize exemplos da realidade da turma para ir despertando a percepção da importância dos números em nossa vida, como: a contagem dos brinquedos deles; o número de telefone para contato com pessoas do convívio deles; o número da residência ou do andar do apartamento onde moram; entre outros exemplos.

4. C) Resposta pessoal. Espera-se que os estudantes identifiquem diferentes lugares da escola onde os números aparecem, como em relógios, portas, telefones e cartazes. Além disso,

4. A CENA MOSTRA UM MOMENTO DE TRABALHO DE UM FEIRANTE.

é importante que eles reflitam sobre a utilidade dos números no dia a dia e seu papel na organização e na realização de diversas atividades.

4. A) Resposta: Os estudantes devem contornar: a indicação 12:00 no relógio; o número 2, na balança; os números 5, 9, 7 e 99876-5432 nas plaquetas.

A ) CONTORNE OS NÚMEROS QUE VOCÊ IDENTIFICA NA CENA.

B ) CITE ALGUMAS SITUAÇÕES DO DIA A DIA EM QUE PODEMOS NOTAR A PRESENÇA DE NÚMEROS.

C ) COM A AJUDA DE UM COLEGA, VERIFIQUEM EM QUAIS LUGARES DA SUA ESCOLA VOCÊS PODEM NOTAR A PRESENÇA DE NÚMEROS. COMPARTILHE COM O PROFESSOR E COM OS COLEGAS ESSA EXPERIÊNCIA.

4. B) Resposta pessoal. Espera-se que os estudantes citem contextos próximos da sua realidade, como números em relógios, calendários, placas de carro, dinheiro, embalagens de produtos, jogos, pontuações esportivas ou senhas.

5. OUÇA A PARLENDA QUE O PROFESSOR VAI LER.

UM, DOIS, FEIJÃO COM ARROZ

UM, DOIS

FEIJÃO COM ARROZ

TRÊS, QUATRO

FEIJÃO NO PRATO

CINCO, SEIS

FALAR INGLÊS

SETE, OITO

Resposta: Os estudantes devem citar as palavras

UM, DOIS, TRÊS, QUATRO, CINCO, SEIS, SETE, OITO, NOVE e DEZ.

COMER BISCOITOS

NOVE, DEZ

COMER PASTÉIS. ORIGEM POPULAR.

PARLENDA: RIMA INFANTIL USADA EM BRINCADEIRAS. ELA FAZ PARTE DO FOLCLORE BRASILEIRO.

EM VOZ ALTA, CITE CADA UMA DAS PALAVRAS QUE REPRESENTAM NÚMEROS NESSA PARLENDA.

6. JOSIANE FEZ AS SEGUINTES ATIVIDADES EM CERTO DIA.

Unidades temáticas integradas

• 9 HORAS – ARRUMAR A CASA.

• 10 HORAS – PASSEAR COM O CACHORRO.

• 12 HORAS – ALMOÇAR NA CASA DA VOVÓ.

• 16 HORAS – JOGAR BOLA COM AS AMIGAS.

• 20 HORAS – AJUDAR A COLOCAR A MESA DO JANTAR.

A ) MARQUE UM X NAS ATIVIDADES QUE SERÃO FEITAS ANTES DO ALMOÇO.

Resposta: Os estudantes devem marcar um X nas atividades ARRUMAR A CASA e PASSEAR COM O CACHORRO.

B ) CONTORNE A ATIVIDADE QUE SERÁ FEITA DEPOIS DE JOGAR BOLA COM AS AMIGAS.

Resposta: Os estudantes devem contornar a atividade AJUDAR A COLOCAR A MESA DO JANTAR.

AVALIANDO

Objetivo

Identificar a presença de números em situações do cotidiano, para propiciar a autocompreensão e auxiliar na aprendizagem.

Sugestão de intervenção

Providencie objetos ou figuras com os quais os estudantes estejam acostumados a lidar no cotidiano e que contenham números, como um relógio de parede ou de pulso (analógico ou digital), um calendário mensal ou anual, uma placa de carro ou uma carteira de identidade, e

03/10/2025 08:26:35

os distribua em pontos diversos da sala de aula. Para cada estudante, peça-lhe que encontre, por exemplo, o calendário que está pendurado atrás da porta. Dê as instruções pausadamente, uma de cada vez, a fim de que eles encontrem os objetos espalhados na sala de aula. Após todos encontrarem, explore com eles a leitura dos objetos. Chame a atenção para a importância dos números e seu uso. Verifique se eles reconhecem a presença dos números no cotidiano, com as mais variadas finalidades, classificados de acordo com quatro funções em nosso cotidiano: quantificar, medir, classificar e identificar.

• Ao trabalhar a atividade 5, cante a parlenda e incentive a turma a cantar em conjunto. No momento da leitura, leia pausadamente, auxiliando os estudantes a acompanhar as palavras. Nessa faixa etária, muitos deles ainda podem estar em estágios iniciais de alfabetização, por isso reforce a sonoridade de cada palavra, sílaba a sílaba. Além de reforçar a aprendizagem da leitura, esse procedimento é importante para a própria resolução da atividade. As parlendas fazem parte da tradição cultural brasileira e estão ligadas à literatura oral popular e ao folclore, transmitindo valores e conhecimentos. Em razão do caráter popular e da oralidade da transmissão das parlendas, é comum que haja diferença em alguns versos de região para região. Por isso, levando em consideração as variantes regionais, é possível que os estudantes conheçam a parlenda com outra letra. Se isso ocorrer, acolha as diferenças e aproveite os conhecimentos prévios da turma.

• A atividade 6 estabelece uma integração entre as unidades temáticas de Matemática Números e Grandezas e medidas, ao relacionar medida de tempo com os números que representam as horas exatas. Confira se os estudantes conseguem reconhecer os horários, sabendo identificar os que ocorrem antes do almoço e os que ocorrem depois. Note, ainda, se relacionam os horários com as atividades marcadas na agenda, reconhecendo que eles mesmos ou alguns de seus familiares praticam atividades similares em horários parecidos com os da agenda.

• A atividade 1 apresenta o número 1 com o algarismo e com a escrita por extenso. É importante expressar a quantidade que esse número representa de diferentes maneiras, a fim de que, pouco a pouco, eles sejam capazes de sistematizar o conceito em toda sua abstração. Apresente elementos unitários, mostre o número 1 com os dedos e peça aos estudantes que levantem um dedo para que, eles mesmos, indiquem o que significa 1. Nesse tópico, o pré-requisito necessário é a capacidade de reconhecer os algarismos em sua forma escrita e falada, compreendendo a correspondência entre o número e a quantidade específica de elementos que ele representa.

• Ao realizar o item B da atividade 1 , explique aos estudantes o sentido das setas, mostrando a eles como deve ser executado o traçado desse número. Peça-lhes que passem o dedo indicador sobre o número 1 pontilhado, instruindo-os a seguir as setas. Faça o mesmo para a representação dos números de 2 a 9 e para o 0. Se necessário, escreva cada número na lousa evidenciando aos estudantes o movimento realizado com a mão e a direção do traçado para a escrita dos números.

• Na atividade 2, avalie a possibilidade de levar revistas e jornais à sala de aula e peça aos estudantes que encontrem as ocorrências do número 1. Nesta e em todas as atividades que envolvam o uso de tesouras, certifique-se de que tenham pontas arredondadas e supervisione todas as etapas da atividade, a fim de evitar acidentes. Para realizar a atividade, providencie cola em quantidade suficiente para todos.

NÚMEROS DE 0 A 10

1. NO ESPETÁCULO DO CIRCO MALABARES, HAVIA APENAS UM PALHAÇO SE APRESENTANDO.

A ) MARQUE UM X NA IMAGEM QUE REPRESENTA ESSE ESPETÁCULO.

Resposta: Os estudantes devem marcar um X na imagem B

A. B. C.

BNCC

B ) ESCREVA O NÚMERO UM DE DUAS MANEIRAS.

MÃO COM UM DEDO LEVANTADO. 1 1 1 1 1 1 1

EXPERIMENTE

2. RECORTE DE REVISTAS E JORNAIS SITUAÇÕES QUE

APRESENTAM O NÚMERO 1. DEPOIS, COLE AS IMAGENS NO CADERNO. 1 1 1

Resposta pessoal. Espera-se que os estudantes sobreponham os pontilhados, acompanhando os traçados das letras e do algarismo para escrever o número citado.

Resposta pessoal. Espera-se que os estudantes encontrem e recortem imagens com o número 1 em diferentes contextos, como em datas, manchetes, preços, números de páginas, pontuações ou resultados esportivos.

As atividades desse tópico apresentam aos estudantes, sucessivamente, os números de 1 a 9, destacando a ocorrência de cada uma das unidades em situações cotidianas variadas, nas quais os números naturais são utilizados como indicadores de quantidade. Em muitas das atividades, eles também são levados a reconhecer situações em que os números naturais não indicam contagem ou ordem, mas algum tipo de código de identificação. Dessa maneira, a habilidade EF01MA01 é contemplada em sua integralidade.

As atividades também abordam o que prevê a habilidade EF01MA02, ao proporem a contagem de elementos, incentivando a compreensão de correspondência um a um e o estabelecimento de relações entre a quantidade de elementos e sua representação numérica. Tais contagens são feitas com base em elementos de interesse dos estudantes, e os resultados são apresentados por meio de registros verbais e simbólicos, conforme previsto na habilidade EF01MA04

A ) REPRESENTE, DA MANEIRA QUE PREFERIR, A QUANTIDADE DE GATOS E DE NOVELOS DE LÃ.

Resposta: Os estudantes devem

representar duas unidades em cada quadro, da maneira que preferirem.

B ) ESCREVA O NÚMERO DOIS DE DUAS MANEIRAS. 2 2 GATOS

NOVELOS DE LÃ

MÃO COM DOIS DEDOS LEVANTADOS. 2 2 2 2 2 2

Resposta pessoal. Espera-se que os estudantes sobreponham os pontilhados, acompanhando os traçados das letras e do algarismo para escrever o número citado.

• A atividade 3 , além de apresentar o número 2, é útil para explorar os conhecimentos prévios e a criatividade da turma. A atividade dá plena liberdade para que os estudantes registrem, do modo que preferirem, a quantidade de gatos na imagem. Espera-se que eles utilizem tracinhos, desenhos, algarismos, entre outros tipos de registros, para representar a quantidade de gatos e novelos de lã. Assim, embora os erros de contagem devam ser evitados, o modo de registro da quantidade é pessoal, de maneira que não existe uma única resposta correta. Incentive os estudantes a realizarem representações diversificadas, explorando diferentes maneiras de indicar um número. É possível que alguns deles usem o algarismo “2”, enquanto outros optem por escrever “dois” por extenso, ao passo que outros podem usar bastões de contagem ou mesmo fazer uma bolinha para representar a unidade.

• Escreva na lousa as diversas representações feitas pelos estudantes, inclusive dando sugestões de outros modos de representar o mesmo número, a fim de que a turma compare todas elas e, com isso, sistematize o repertório numérico de modo significativo.

03/10/2025 08:26:36

• Ao trabalhar o item B da atividade 3, escreva o número 2 na lousa, indicando os movimentos que devem ser feitos para desenhar as letras e o algarismo. Enquanto os estudantes preenchem as linhas pontilhadas no Livro do Estudante, verifique se eles seguram o lápis de modo adequado, se têm firmeza nos traços, se não deixam a linha escapar dos caminhos pontilhados e se seguem o sentido correto das setas para traçar os caracteres. Auxilie os que tiverem dificuldade, inclusive segurando em suas mãos, se necessário.

• Antes de apresentar a atividade 4, pergunte se os estudantes já viram alguma joaninha. Apresente a eles algumas questões, como: “Onde é possível encontrá-las?”; “Onde elas gostam de viver?”. Aproveite o contexto da atividade e converse com eles sobre a importância de cuidar bem da natureza e dos animais. Explique que todos os animais, inclusive os insetos pequenos, são importantes para a natureza. Portanto, devemos cuidar deles a fim de garantir ambientes agradáveis para passear e ar puro para respirar.

• Durante a atividade 4 , verifique se os estudantes identificam as três joaninhas sem deixar de contar nenhuma delas. A visualização atenta também faz parte da formação escolar dos estudantes.

• Assim como na atividade 3, ao trabalhar a escrita do número 3, registre-o na lousa, indicando os movimentos que devem ser feitos para desenhar as letras e o algarismo. Enquanto os estudantes preenchem as linhas pontilhadas no livro, caminhe pela sala de aula, verificando se eles seguram o lápis de modo adequado, se têm firmeza nos traços, se não deixam a linha escapar dos caminhos pontilhados e se seguem o sentido correto das setas para representar os caracteres. Auxilie aqueles que apresentarem dificuldades, inclusive segurando em suas mãos, se necessário.

• A atividade 5 retoma a apresentação do número 3 para fazer uma comparação com os outros números estudados até então. Assim, é possível utilizá-la para verificar a aprendizagem até o momento, identificando possíveis falhas e oportunizando outras estratégias para tornar o ensino eficaz a todos os estudantes. Por isso, dê atenção às dificuldades que

4. AS JOANINHAS ESTÃO NO JARDIM.

4. A) Resposta: Os estudantes devem contornar as três joaninhas que estão representadas no jardim.

A ) CONTORNE AS JOANINHAS QUE ESTÃO NO JARDIM.

B ) REPRESENTE, DA SUA MANEIRA, A QUANTIDADE DE JOANINHAS QUE

ESTÃO NO JARDIM.

Resposta: Os estudantes devem representar 3 unidades no quadro, da maneira que preferirem.

3 MÃO COM TRÊS DEDOS LEVANTADOS.

3 3 3 3 3 3 3 3

Resposta pessoal. Espera-se que os estudantes sobreponham os pontilhados, acompanhando os traçados das letras e do algarismo para escrever o número citado.

5. EM CADA NINHO, DESENHE A QUANTIDADE DE OVOS INDICADA.

Resposta: Os estudantes devem desenhar, da esquerda para a direita na página, 1 ovo no primeiro ninho, 2 ovos no segundo ninho e 3 ovos no terceiro ninho.

C ) ESCREVA O NÚMERO TRÊS DE DUAS MANEIRAS. 1 OVO 2 OVOS

possam surgir, identificando quais deles ainda não conseguem associar os números às quantidades correspondentes, bem como os motivos dessas possíveis dificuldades.

6. OBSERVE OS PILOTOS E OS CARROS. DEPOIS, FAÇA O QUE SE PEDE.

A ) LIGUE CADA PILOTO AO CARRO QUE TEM A MESMA COR DO SEU UNIFORME.

Resposta pessoal. Sugestão de resposta: Os estudantes podem ligar o piloto 1 ao carro vermelho; o piloto 2 ao carro verde; o piloto 3 ao carro azul; o piloto 4 ao carro amarelo.

B ) A QUANTIDADE DE CARROS E DE PILOTOS É A MESMA?

Resposta: SIM.

C ) DA FORMA QUE SOUBER, REPRESENTE A QUANTIDADE DE PILOTOS E CARROS.

PILOTOS

Resposta: Os estudantes devem representar 4 unidades em cada quadro, da maneira que preferirem.

CARROS

D ) ESCREVA O NÚMERO QUATRO DE DUAS MANEIRAS.

4 MÃO COM QUATRO DEDOS LEVANTADOS. 4 4 4 4 4 4 4 4

Resposta pessoal. Espera-se que os estudantes sobreponham os pontilhados, acompanhando os traçados das letras e do algarismo para escrever o número citado.

• A atividade 6 induz à percepção de que o pareamento é uma boa maneira para comparar quantidades. Assim, ela oferece as bases, em caráter introdutório, para a compreensão da associação de elementos um a um. É importante mostrar aos estudantes que, quando associamos os pilotos aos respectivos carros, estamos mostrando que a quantidade de pilotos é igual à de carros, pois relacionamos cada piloto a um único carro. Se fosse preciso associar um mesmo piloto a dois carros diferentes, ou se algum dos pilotos ficasse sem carro, então as quantidades de carros e pilotos não seriam as mesmas.

• Verifique ainda se os estudantes percebem intuitivamente que os pilotos e os carros devem ser associados com base em algum elemento em comum que os relacione. Nesse caso, esse elemento é a cor.

• No item C da atividade 6, espera-se que os estudantes utilizem tracinhos, desenhos ou outro tipo de registro para representar a quantidade de pilotos e de carros. Verifique se alguns deles associam corretamente as quantidades à representação com algarismos e, nesse caso, incentive-os a compartilhar seu conhecimento com o restante da turma.

BNCC

03/10/2025 08:26:37

A atividade 6 promove a associação um a um de elementos, incentivando o pareamento como estratégia de contagem, de modo a contemplar o que prevê a habilidade EF01MA02

• Inicie a atividade 7 perguntando se os estudantes conhecem a brincadeira e se costumam praticá-la. O nome da brincadeira pode variar de acordo com as vivências deles e as regiões onde moram. Os nomes mais comuns são Esconde-esconde e Pique-esconde

• Aproveite o contexto da atividade para mostrar a importância dos números, mesmo em momentos de lazer e diversão. Para averiguar os conhecimentos dos estudantes, pergunte até quanto eles contam quando estão brincando de Esconde-esconde . Caso o número seja menor do que 10, pergunte se não seria melhor contar um pouco mais, para dar mais tempo para que os colegas se escondam. Com isso, incentive os estudantes a contarem até o máximo que sabem, verificando quantos números eles já conhecem.

• Avalie a possibilidade de levar os estudantes ao pátio da escola para brincarem de Esconde-esconde. Ao retornar, pergunte-lhes até que número eles contaram enquanto estavam no pique. Ao final da brincadeira, converse com os estudantes sobre a importância de respeitar a vez dos colegas e também em muitas outras situações, como em filas e na sala de aula. Pergunte se durante a brincadeira ocorreu alguma situação em que algum estudante não tenha respeitado a vez do colega e permita-lhes falar sobre como resolveram o problema.

• O item B da atividade 7 explora, por outra abordagem, a ideia de associação um a um. Aqui, cada criança é associada a uma estrela. Com base nisso, verifique se os estudantes percebem que há a mesma quantidade de crianças e de estrelas por eles desenhados.

7. LEILA E SEUS AMIGOS

ESTÃO BRINCANDO NA PRAÇA.

INFOGRÁFICO CLICÁVEL: VAMOS CONHECER O JOGO MANCALA?

UM, DOIS, TRÊS, QUATRO, CINCO...

A ) QUAL É O NOME DA BRINCADEIRA REPRESENTADA NA CENA?

Resposta: As crianças estão brincando de Esconde-esconde ou Pique-esconde.

B ) DESENHE UMA ESTRELA PARA CADA CRIANÇA DA CENA.

Resposta: Os estudantes devem desenhar 5 estrelas para representar cada criança.

C ) ESCREVA O NÚMERO CINCO DE DUAS MANEIRAS.

MÃO COM CINCO DEDOS LEVANTADOS. 5 5 5 5 5 5 5 5

Resposta pessoal. Espera-se que os estudantes sobreponham os pontilhados, acompanhando os traçados das letras e do algarismo para escrever o número citado.

• Para complementar o item C da atividade 7, peça aos estudantes que escrevam o número 5 no caderno, em algarismo e por extenso, sem a presença das linhas pontilhadas. Durante a atividade, verifique possíveis erros, como escrever o algarismo 5 espelhado ou juntar demais a parte curvada do algarismo com a parte reta, fazendo o símbolo se assemelhar a um 6. Nesse caso, proponha a eles praticarem o traçado, usando superfícies diferentes, como areia, ou brincarem com esses formatos usando argila ou massinha de modelar.

8. A) Resposta: Os estudantes devem representar, da maneira que preferirem, as quantidades de carrinhos de cada quadro, sendo: 1 carrinho verde; 2 carrinhos amarelos; 3 carrinhos laranjas; 4 carrinhos azuis; e 5 carrinhos pretos.

A ) COMPLETE OS ESPAÇOS ESCREVENDO, DA MANEIRA QUE PREFERIR, QUANTOS CARRINHOS HÁ DE CADA COR.

B ) HÁ MAIS CARRINHOS AMARELOS OU PRETOS?

Resposta: Há mais carrinhos pretos.

9. A SEGUIR, ESTÃO APRESENTADAS BORBOLETAS E FLORES.

A ) LIGUE CADA BORBOLETA A UMA FLOR.

IMAGENS SEM PROPORÇÃO ENTRE SI.

Resposta pessoal. Espera-se que os estudantes liguem cada uma das 3 borboletas a 3 flores da escolha deles.

B ) QUANTAS FLORES APARECEM NA IMAGEM? FLORES.

Resposta: 5 FLORES.

C ) HÁ MAIS BORBOLETAS OU FLORES?

Resposta: Há mais flores.

• Na atividade 8, incentive os estudantes a fazerem o registro das quantidades de mais de uma maneira, por extenso ou utilizando algarismos, de modo a avaliar se as diversas escritas de um mesmo número já estão se tornando naturais para eles. Ao responderem ao item que questiona se há mais carrinhos amarelos do que pretos, verifique se os estudantes fazem a associação um a um entre os carrinhos pretos e os amarelos ou se estimam a quantidade com base apenas na sensação visual.

• A atividade 9 desenvolve o pareamento entre elementos como modo de comparar quantidades. Em atividades anteriores, a associação um a um indicava que os grupos de elementos tinham, ambos, a mesma quantidade de elementos. Aqui, a associação um a um não se completa, pois algumas flores ficam sem correspondentes. Com base nisso, é esperado que os estudantes percebam que há mais flores do que borboletas.

BNCC

A atividade 9 propõe a comparação de quantidades de objetos de dois conjuntos, por meio da correspondência um a um, a fim de que os estudantes indiquem qual dos conjuntos tem mais elementos. Com isso, contempla-se a habilidade EF01MA03 8.

08:26:39

• A atividade 10 estabelece uma integração entre as unidades temáticas de Matemática Números e Probabilidade e estatística ao determinar a quantidade de frutas de cada tipo e organizar o registro das quantidades em um quadro. Aproveite o contexto dessa atividade e solicite aos estudantes que façam, junto com seus familiares, uma pesquisa sobre a importância e os benefícios do consumo de frutas no dia a dia. Em seguida, eles devem registrar o que pesquisaram no caderno, por meio de desenhos e de frases.

• A atividade 11 explora a contagem, o reconhecimento dos algarismos e a relação entre quantidade e numeral. Acompanhe e oriente o traçado do número 5, auxiliando os que ainda estão em processo de fixação dos numerais. Para complementar, faça a representação dessa quantidade usando os dedos ou objetos concretos para contagem, como tampinhas ou lápis, auxiliando na compreensão. Caso haja algum estudante com baixa visão, entregue-lhe uma folha de papel com a impressão em tamanho ampliado, com alta nitidez e contraste, e disponibilize objetos para servir de apoio tátil.

AVALIANDO

Objetivo

Desenvolver a habilidade de ler e interpretar dados expressos em tabela.

Sugestão de intervenção

Leve para a sala de aula um cartaz confeccionado com cartolina ou uma impressão ampliada, contendo uma tabela com as seguintes informações: Para organizar seus brinquedos, Theo registrou em uma tabela a quantidade de cada um deles. Observe na tabela a quantidade de brinquedos.

10. CONTE E REGISTRE NO QUADRO A SEGUIR A QUANTIDADE DE FRUTAS DE CADA TIPO QUE APARECEM NA MESA.

IMAGENS SEM PROPORÇÃO ENTRE SI.

Professor, professora: Espera-se que os estudantes utilizem tracinhos, desenhos, algarismos, entre outros tipos de registros para completarem o quadro. Sugestão de resposta: Laranja: 3; maçã: 5; banana: 4; pera: 3.

Unidades temáticas integradas

11. FAÇA O QUE SE PEDE EM CADA ITEM.

QUANTIDADE DE FRUTAS, POR TIPO FRUTA QUANTIDADE

A ) MARCELO TEM CINCO CANETAS. CONTORNE A QUANTIDADE DE CANETAS QUE ELE TEM.

Resposta: Os estudantes devem contornar, da maneira que preferirem, cinco canetas

B ) CONTORNE A FICHA COM O NÚMERO QUE REPRESENTA A QUANTIDADE DE CANETAS QUE MARCELO TEM.

Resposta: Os estudantes devem contornar a ficha com o número 5

4 3 2 5 1

Quantidade de brinquedos de Theo, em 2027

Carrinhos

Fonte de pesquisa: Anotações de Theo. Solicite aos estudantes que analisem os dados apresentados na tabela. Em seguida, faça algumas perguntas, como: “Qual é o título dessa tabela?”; “Quantas colunas essa tabela tem? E quantas linhas?”; “Qual brinquedo Theo tem em

maior quantidade?”; “Qual brinquedo Theo tem em menor quantidade?”.

Durante a atividade de leitura e interpretação da tabela, avalie a autonomia e o raciocínio dos estudantes e analise se apresentam dificuldades. Verifique se prestaram atenção nos dados apresentados e analise se contribuíram com respostas coerentes às perguntas. Caso julgue oportuno, faça outras perguntas, de acordo com a necessidade.

Resposta pessoal. Os estudantes devem sobrepor os pontilhados, acompanhando os traçados das letras para escrever o número 1 na forma cursiva minúscula e maiúscula.

Resposta pessoal. Os estudantes devem sobrepor os pontilhados, acompanhando os traçados das letras para escrever o número 2 na forma cursiva minúscula e maiúscula.

dois doisdoisdoisdois 2 Três TrêsTrêsTrêsTrês três trêstrêstrêstrês

Resposta pessoal. Os estudantes devem sobrepor os pontilhados, acompanhando os traçados das letras para escrever o número 3 na forma cursiva minúscula e maiúscula.

3 Quatro QuatroQuatro quatro quatroquatro

Resposta pessoal. Os estudantes devem sobrepor os pontilhados, acompanhando os traçados das letras para escrever o número 4 na forma cursiva minúscula e maiúscula.

Resposta pessoal. Os estudantes devem sobrepor os pontilhados, acompanhando os traçados das letras para escrever o número 5 na forma cursiva minúscula e maiúscula. 27

03/10/2025 08:46:08

• A atividade 12 tem o objetivo de levar os estudantes a completarem os pontilhados para escrever por extenso os números de 1 a 5. Assim, eles terão a oportunidade de desenvolver a coordenação motora fina, o traçado correto e a familiaridade com o formato da letra cursiva desses números. Mostre na lousa como traçar cada número, por extenso, em letra cursiva. Oriente os estudantes a fazerem o movimento com o dedo no ar antes de passarem o lápis nos pontilhados. Nessa etapa, é importante observar como os estudantes estão segurando o lápis e a direção do traçado. Caso seja necessário, corrija-os sempre incentivando o esforço deles.

• Se julgar necessário, após a atividade 12, para reforçar a prática e o direcionamento da escrita dos números, utilize o caderno de caligrafia, com o propósito de desenvolver progressivamente a escrita da letra cursiva.

REFERÊNCIAS COMPLEMENTARES

PINHEIRO, Rafael Marques; LUCCAS, Simone; LUCAS, Lucken Bueno. Sistemas de numeração à luz de uma abordagem histórico-epistemológica Universidad Distrital Francisco Jose de Caldas. Disponível em: https:// revistas.udistrital.edu.co/ index.php/GDLA/article/ view/13030/15036. Acesso em: 23 set. 2025.

O artigo busca investigar o papel da abordagem histórico-epistemológica como fundamentação metodológica, para entender e sintetizar os sistemas de numeração.

• Antes de realizar com os estudantes a atividade 13, verifique se eles demonstram percepções sobre as chances de um evento acontecer, ou seja, as situações em que certamente acontecerá, as situações em que pode ser que aconteça ou não e aquelas em que é impossível de acontecer. Pergunte a eles: “Quando lançamos uma moeda, quais são os resultados possíveis?”; e “É certeza que obteremos cara ou coroa?”. Explique aos estudantes que, no lançamento de uma moeda, sabemos que sairá cara ou coroa. Porém, não temos certeza, por exemplo, ao lançarmos quatro vezes uma moeda, quantas vezes sairá cara ou coroa.

• Essa atividade relaciona as unidades temáticas de Matemática Números e Probabilidade e estatística ao trabalhar a interpretação das possíveis cores de bolinhas a serem sorteadas e a cor de bolinha impossível de ser sorteada, bem como a quantidade de bolinhas. Leia a situação apresentada e instrua os estudantes a analisarem e interpretarem a cena. Analise com eles cada fala dos personagens e, depois, oriente-os a responder aos itens dessa atividade, auxiliando-os em caso de dúvidas.

BNCC

• A atividade 13 aborda a classificação de eventos envolvendo o acaso, como certos, possíveis e impossíveis, em situações do cotidiano, conforme a habilidade EF01MA20 da BNCC.

13. ELAINE COLOCOU AS BOLINHAS REPRESENTADAS A SEGUIR EM UMA CAIXA. DEPOIS, CADA AMIGO DELA SORTEOU UMA BOLINHA E NÃO MOSTROU PARA NINGUÉM. ACOMPANHE O QUE ELES DISSERAM APÓS O SORTEIO.

UMA BOLINHA VERMELHA. 13. A) Resposta: Os estudantes devem marcar um X nas cores AZUL, VERMELHA e AMARELA.

EU PEGUEI

A MINHA BOLINHA É AZUL. JOSÉ

A BOLINHA QUE EU PEGUEI É PRETA.

A ) MARQUE UM X NAS POSSÍVEIS CORES DE BOLINHA QUE PODEM SER SORTEADAS NA SITUAÇÃO APRESENTADA.

AZUL.

VERDE

LETÍCIA GUILHERME VERMELHA. . PRETA. AMARELA. ROSA.

B ) QUANTAS BOLINHAS VERMELHAS HÁ SOBRE A MESA?

Resposta: Há 5 bolinhas vermelhas sobre a mesa.

C ) É POSSÍVEL QUE A AFIRMAÇÃO DE JOSÉ ESTEJA CORRETA? POR QUÊ?

Resposta: SIM. PORQUE DENTRO DA CAIXA HAVIA 5 BOLINHAS VERMELHAS QUE PODIAM SER SORTEADAS.

D ) QUEM DISSE QUE RETIROU UMA COR DE BOLINHA IMPOSSÍVEL DE SER SORTEADA? JUSTIFIQUE SUA RESPOSTA.

Resposta: LETÍCIA, POIS NÃO HÁ BOLINHAS PRETAS DENTRO DA CAIXA.

ATIVIDADE EXTRA

Para complementar o trabalho com a atividade 13, realize esta atividade. Providencie e leve para a sala de aula 10 fichas de cor azul e 4 fichas de cor preta, todas de mesmo formato e dimensões. Mostre-as aos estudantes e, inicialmente, coloque 3 fichas de cada cor dentro de uma caixa não transparente. Diga-lhes que será realizado um sorteio e que eles devem adivinhar qual é a cor da ficha que será retirada da caixa. Repita algumas vezes esse procedimento, permitindo que analisem cada sorteio. Depois, em um segundo momento, coloque as 10 fichas de cor azul e as quatro fichas de cor preta dentro da caixa e

pergunte aos estudantes qual ficha eles acham que pode ser sorteada primeiro.

Verifique se os estudantes percebem, intuitivamente, que é mais provável de ser sorteada uma ficha de cor azul. Por fim, coloque apenas as fichas de cor azul na caixa e pergunte qual cor certamente será sorteada e qual é o motivo de isso acontecer. Faça alguns questionamentos durante todos os sorteios, como: “É possível ou impossível sortear uma ficha de cor amarela?”, “Se a caixa estiver com as 10 fichas de cor azul e as quatro fichas de cor preta, é certeza sortear uma ficha de cor azul?”, entre outras perguntas.

14. SILAS E SEUS AMIGOS ESTÃO ANDANDO DE BICICLETA.

14. A) Resposta: Os estudantes devem representar 6 unidades em cada quadro, da maneira que preferirem.

A ) REPRESENTE, DA SUA MANEIRA, A QUANTIDADE DE CRIANÇAS, BICICLETAS E CAPACETES.

CRIANÇAS

BICICLETAS CAPACETES

B ) ESCREVA O NÚMERO SEIS DE DUAS MANEIRAS.

6666 66 6 6

MÃOS COM SEIS DEDOS LEVANTADOS.

Resposta pessoal. Espera-se que os estudantes sobreponham os pontilhados, acompanhando os traçados das letras e do algarismo para escrever o número citado.

• Para introduzir a atividade 14, pergunte aos estudantes se eles sabem andar de bicicleta ou de outros brinquedos, como skate, patins e patinete, e se gostam de fazer isso. Converse com a turma sobre a importância de brincadeiras que movimentam o corpo e os benefícios de praticar esportes. Enfatize também a importância de realizar essas atividades com segurança, sempre utilizando equipamentos de proteção adequados e sob a supervisão de adultos.

• Verifique se os estudantes expressam adequadamente as quantidades com algarismos, conforme o que estudaram até o momento. Porém, pode ser que alguns estudantes continuem manifestando dificuldade na compreensão dessa correspondência, por falta de apropriação do repertório numérico. Nesse caso, avalie a necessidade e a conveniência de propor mais atividades que explorem materiais de contagem e apresente-as de modo progressivo a eles.

03/10/2025 08:46:13

• Para reforçar o item B da atividade 14, peça aos estudantes que escrevam o número 6 de duas maneiras em seus cadernos. Verifique se eles fazem os símbolos corretamente, sem espelhamento. É muito comum que, em fases iniciais de aprendizagem, eles confundam o algarismo 6 com o algarismo 9, em virtude da semelhança entre os símbolos. Por isso, é importante trabalhar reiteradamente para que sejam evitadas essas confusões. Caso as confusões surjam, e apenas nesse caso, pouco a pouco, vá dando instruções sobre como evitá-las. Uma possibilidade é associar o formato dos algarismos com desenhos, dizendo e mostrando na lousa que o 6 tem uma “barriguinha”, enquanto o 9 se parece com um balão.

LISLLEY

• A atividade 15 relaciona as unidades temáticas de Matemática Números e Probabilidade e estatística ao trabalhar a quantidade de produtos comprados por João em uma papelaria e mostrá-la organizada em um gráfico de colunas. Essa atividade tem o objetivo de desenvolver habilidades de contagem e registro de quantidades em um quadro, além da construção de um gráfico de colunas. Para trabalhar essa atividade, inicialmente apresente a imagem para os estudantes e faça algumas perguntas, como: “Quantas canetas João comprou?”; “E quantas borrachas?”. Depois, ao orientá-los a preencher o quadro, reforce a relação entre cada imagem da tabela (produto) e a quantidade que João comprou de cada produto. Oriente-os a contar os produtos em voz alta, levantando os dedos, se necessário. No item B, explique que um quadrinho no gráfico representa uma unidade de produto que João comprou. Caso os estudantes apresentem dúvidas, mostre na lousa um exemplo de como pintar uma coluna para 3 produtos; por exemplo, se João tivesse comprado três cadernos, teriam que pintar 3 quadrinhos. Converse com eles sobre os elementos importantes do gráfico, como o título, a data, os nomes dos eixos e a fonte de pesquisa. Explore a interpretação do gráfico com a turma fazendo algumas perguntas, identificando se ainda há possíveis dúvidas, a fim de saná-las.

ATIVIDADE EXTRA

15. JOÃO FOI ATÉ A PAPELARIA E COMPROU ALGUNS PRODUTOS.

IMAGENS SEM PROPORÇÃO ENTRE SI.

Unidades temáticas integradas

A ) COMPLETE AS INFORMAÇÕES ESCREVENDO A QUANTIDADE DE PRODUTOS QUE JOÃO COMPROU.

Resposta: Os estudantes devem representar 4 unidades de caneta, 3 unidades de lápis, 2 unidades de borracha e 6 unidades de clipe, da maneira que preferirem.

QUANTIDADES DE PRODUTOS QUE JOÃO COMPROU

PRODUTO

QUANTIDADE

B ) A SEGUIR, PINTE UM QUADRINHO PARA CADA PRODUTO COMPRADO.

Resposta: Os estudantes devem pintar o gráfico da seguinte maneira: 4 quadrinhos na coluna CANETA, 3 quadrinhos na coluna LÁPIS, 2 quadrinhos na coluna BORRACHA e 6 quadrinhos na coluna CLIPE.

PRODUTOS COMPRADOS POR JOÃO EM DEZEMBRO DE 2027

QUANTIDADE

PRODUTO

LÁPIS CANETA

BORRACHACLIPE

Escolha um gráfico de barras que expresse o resultado de uma pesquisa sobre preferências, baseada em um assunto que faça parte do dia a dia dos estudantes, como: o sabor de alimentos (doce ou salgado); o estilo musical; as brincadeiras; as frutas; os animais de estimação. Leve para a sala de aula o gráfico de barras, que deve ser em tamanho grande o suficiente para que toda a turma possa visualizar, e apresente aos estudantes. Solicite a eles que identifiquem o título do gráfico e as informações contidas nos eixos horizontal e vertical. Proponha que, em duplas, cada estudante elabore no caderno quatro perguntas relacionadas ao gráfico, para que seu colega de dupla responda. Por fim, direcione uma conversa com toda a turma para que socializem as perguntas feitas, de modo que todos possam se beneficiar das ideias uns dos outros.

DICA: CADA QUADRINHO REPRESENTA 1 UNIDADE DO PRODUTO QUE JOÃO COMPROU NA PAPELARIA.

FONTE DE PESQUISA: ANOTAÇÕES DE JOÃO.

A ) TERMINE DE COLORIR ESSE ARCO-ÍRIS.

Resposta: Os estudantes devem pintar o arco-íris seguindo as cores iniciais.

B ) DESENHE UM LÁPIS PARA CADA COR QUE VOCÊ USOU AO PINTAR O ARCO-ÍRIS.

Resposta: Os estudantes devem desenhar 7 lápis.

C ) ESCREVA O NÚMERO SETE DE DUAS MANEIRAS.

Resposta pessoal. Espera-se que

os estudantes sobreponham os pontilhados, acompanhando os traçados das letras e do algarismo para escrever o número citado.

• Para apresentar a atividade 16, pergunte aos estudantes se eles já viram um arco-íris: “Alguém já constatou quando é que os arco-íris aparecem?”; “Eles aparecem em dias chuvosos ou ensolarados?”; “Quais são as cores que vocês conseguiram perceber em um arco-íris?”. Aproveite o contexto da atividade para avaliar o conhecimento deles quanto aos nomes das cores. Diga-lhes que as cores do arco-íris são: vermelho, laranja, amarelo, verde, azul, anil e violeta.

• No item B da atividade 16, oriente os estudantes a fazerem desenhos que se pareçam com lápis. Em seguida, permita-lhes pintá-los, de preferência cada um com uma cor do arco-íris e na ordem correta.

• Ao realizar o item C da atividade 16, oriente os estudantes sobre o sentido das setas, mostrando como deve ser feito o traçado desse número. Peça-lhes que passem o dedo indicador sobre o número 7 pontilhado, instruindo-os a seguir as setas.

ATIVIDADE EXTRA

MÃOS COM SETE DEDOS LEVANTADOS. 7

7777 77

03/10/2025 08:46:17

Para complementar a atividade 16 , verifique a possibilidade de levar à sala de aula um aparelho de som com alguma música que trabalhe as cores do arco-íris. Outra possibilidade é promover uma atividade com a produção de cartazes com desenhos de arco-íris, os nomes de suas cores e uma frase com o número que indica a quantidade de cores encontradas no arco-íris.

• A atividade 17 relaciona as unidades temáticas de Matemática Números e Probabilidade e estatística, ao levar os estudantes a identificarem a quantidade de pontos obtidos no lançamento de um dado comum e a interpretação das possibilidades de obter esses pontos. Ao iniciar o trabalho com essa atividade, avalie a possibilidade de cada estudante ter em mãos um dado que possa ser lançado na prática, a fim de analisar suas faces e as possibilidades de resultados em seu lançamento. A inserção de atividades envolvendo esse conteúdo é importante desde as séries iniciais para construir as noções de probabilidade e de estatística.

• A atividade 18 relaciona as unidades temáticas de Matemática Números e Probabilidade e estatística, uma vez que aborda a quantidade de partidas que o time Azul precisa vencer no campeonato de futebol, além de trabalhar com a análise das condições necessárias para que esse time seja o vencedor. A atividade tem por objetivo verificar se os estudantes percebem que, para vencer o campeonato de futebol, o time Azul precisa ganhar as duas próximas partidas e, assim, ser ganhador do campeonato. Porém, se esse time perder a próxima partida, será impossível ser o vencedor e, se ganhar a próxima partida, não é certeza de que seja o vencedor do campeonato sem ter o resultado da partida seguinte. Verifique se os estudantes compreenderam a situação apresentada e a relação das afirmações de cada item com a condição dada para que o time Azul seja vencedor.

AVALIANDO

Objetivo

17. NAS IMAGENS, ESTÃO REPRESENTADOS UM DADO E OS PONTOS

QUE PODEM SER OBTIDOS COM ELE EM UM LANÇAMENTO.

O DADO ESTÁ MARCANDO 2 PONTOS.

17. C) Resposta: Espera-se que os estudantes respondam que é possível sortear 3 pontos em um lançamento, pois entre as opções de sorteio há uma face com 3 pontos. Contudo, não é possível obter 7 pontos em um lançamento, pois entre as opções de sorteio não existe uma face com 7 pontos.

Unidades temáticas integradas

A ) EM UM LANÇAMENTO DESSE DADO, É POSSÍVEL OBTER

3 PONTOS?

Resposta: SIM.

SIM. NÃO.

B ) EM UM LANÇAMENTO DESSE DADO, É POSSÍVEL OBTER

7 PONTOS?

Resposta: NÃO.

SIM. NÃO.

C ) JUSTIFIQUE AS RESPOSTAS DADAS PARA AS QUESTÕES ANTERIORES.

18. PARA VENCER UM CAMPEONATO DE FUTEBOL, O TIME AZUL PRECISA GANHAR AS DUAS PRÓXIMAS PARTIDAS.

Unidades temáticas integradas

A ) É POSSÍVEL QUE O TIME AZUL VENÇA O CAMPEONATO?

Resposta: SIM.

B ) QUANTAS PARTIDAS O TIME AZUL DEVE VENCER PARA GANHAR O CAMPEONATO?

Resposta: DUAS.

C ) SE O TIME AZUL PERDER A PRÓXIMA PARTIDA, É

IMPOSSÍVEL ELE VENCER O CAMPEONATO?

Resposta: SIM.

D ) SE O TIME AZUL VENCER A PRÓXIMA PARTIDA, É CERTO

QUE ELE VAI VENCER O CAMPEONATO?

Resposta: NÃO.

Sugestão de intervenção

Organize os estudantes em duplas e providencie um dado de seis pontos para cada uma delas. Oriente-os a lançar o dado 20 vezes, sendo 10 vezes para cada integrante da dupla, e escrever os resultados obtidos no caderno. Peça a cada integrante que faça oralmente perguntas relacionadas aos eventos obtidos ao colega de dupla. Dê exemplos de perguntas que os estudantes podem fazer:

Reconhecer, em experimentos aleatórios, eventos certos, possíveis ou impossíveis de ocorrerem, com o intuito de propiciar a autocompreensão e auxiliar na aprendizagem.

• Em um lançamento de um dado, é possível que saia um ponto?

• É certeza que, ao lançar um dado, os pontos obtidos sejam maiores do que dois?

• Em um lançamento de um dado, é certo que se obterão cinco pontos?

• O que é impossível de ocorrer ao fazer o lançamento de um dado?

Realize a atividade desta seção a fim de detectar possíveis dúvidas dos estudantes e, caso isso aconteça, redirecione o trabalho oferecendo a eles outras abordagens.

19. OBSERVE A PALAVRA A SEGUIR E FAÇA O QUE SE PEDE.

A ) PINTE A PALAVRA ESCRITA.

Resposta: Os estudantes devem

pintar, com as cores que preferirem, a palavra RESPEITO.

B ) REPRESENTE, DA MANEIRA QUE PREFERIR, A QUANTIDADE DE LETRAS QUE ESSA PALAVRA TEM.

19. B) Resposta: Os estudantes devem representar 8 unidades no quadro, da maneira que preferirem.

19. C) Resposta pessoal. Espera-se que os estudantes citem atitudes como ceder o lugar para as pessoas idosas em transportes públicos, ouvir com atenção suas histórias, ajudá-las em tarefas do dia a dia, tratá-las com paciência e carinho e respeitar suas opiniões e experiências de vida.

C ) CITE UM EXEMPLO DE ATITUDE DE RESPEITO COM AS PESSOAS IDOSAS.

D ) ESCREVA O NÚMERO OITO DE DUAS MANEIRAS.

8888 88

MÃOS COM OITO DEDOS LEVANTADOS.

Resposta pessoal. Espera-se que os estudantes sobreponham

20. DESENHE MAIS CINCO PEDRINHAS.

Resposta: Os estudantes devem desenhar 5 pedrinhas. os pontilhados, acompanhando os traçados das letras e do algarismo para escrever o número citado.

• Na atividade 19, permita aos estudantes que pintem as letras com as cores de sua preferência. Instrua-os a pintar todo o interior das letras, mas sem ultrapassar seus contornos. Em atividades em que devem colorir, é sempre conveniente auxiliá-los a fazer a pintura com esmero, pois isso incentiva a concentração, a disciplina e o senso estético. Durante a atividade, peça-lhes que leiam a palavra. O que ela significa? Deixe-os comentar livremente o que eles entendem por respeito, comparando as opiniões e ajudando-os a construir e solidificar valores morais que enfatizem a importância de respeitarem todas as pessoas. Incentive-os a participar dos comentários, pois é importante engajar toda a turma na atividade. Pergunte à turma: “O que é agir com respeito?”; “Vocês podem dar exemplos de situações em que houve respeito?”; “E quanto a situações em que não houve respeito?”; “Nesses casos, o que é possível fazer para que as pessoas que agem com desrespeito mudem suas atitudes?”.

AGORA TEMOS UM TOTAL DE QUANTAS PEDRINHAS? PEDRINHAS.

Resposta: 8 PEDRINHAS.

ATIVIDADE EXTRA

Para incrementar a atividade 19, peça a cada estudante que escreva o próprio nome no caderno e, em seguida, assim como foi feito com a palavra respeito, contar quantas letras tem o próprio nome. Depois, faça o mesmo com o sobrenome e pergunte quem da turma tem o nome com mais letras e qual é o nome com menos letras. Caso haja na turma estudantes com nomes formados por mais de 10 letras, diga que logo mais estudarão esses números. Outra possibilidade é deixar para trabalhar essa atividade extra mais adiante.

03/10/2025 08:46:18

• No trabalho com a atividade 20, exploram-se as primeiras noções de adição. Os estudantes devem identificar que, havendo três pedrinhas e depois desenhando mais cinco, temos um total de oito. Incentive-os a fazer a mesma relação nos dedos: primeiro eles devem levantar três dedos e, em seguida, acrescentar mais cinco. Quantos dedos ficam levantados ao todo no final?

• A atividade 21 relaciona as unidades temáticas de Matemática Números e Probabilidade e estatística ao utilizar números naturais como indicadores de quantidade de estudantes que gostariam de participar do grupo de estudos da escola e, ainda, ao representar o resultado da pesquisa feita usando uma tabela.

• A atividade 21 apresenta os registros de informações obtidas por uma professora ao realizar uma pesquisa com os estudantes de sua turma, a fim de saber quem gostaria de participar das aulas de reforço da escola. O objetivo é promover a leitura e a interpretação de informações contidas em imagens, nesse caso, organizadas em um quadro. Os quadros são elementos muito importantes, pois representam, de modo ilustrativo e organizado, dados coletados, possibilitando a interpretação do assunto em questão, de maneira simples e objetiva.

• Ao ler essa atividade com os estudantes, e pergunte a eles o que podem perceber ao analisar essa imagem, levando-os a identificar quais são as características do quadro, como a presença das linhas, das colunas e suas divisões, os nomes dos estudantes e o assunto de que esse quadro trata. Pergunte-lhes se já identificaram, em outras situações, quadros parecidos com o apresentado nessa atividade. Permita aos estudantes se manifestarem de modo espontâneo. Eles podem citar quadros de organização de tarefas, de informações nutricionais, de pontuações de um jogo etc. É importante ressaltar que os quadros são considerados ilustrações e são utilizados para apresentar conteúdos, como comparações, classificações e dados numéricos sem a presença de dados estatísticos.

21. A PROFESSORA FEZ UMA PESQUISA COM OS ESTUDANTES PARA SABER QUEM PRETENDIA PARTICIPAR DO GRUPO DE ESTUDO DA ESCOLA. DEPOIS DISSO, ELA REGISTROU AS RESPOSTAS NA LOUSA.

Unidades temáticas integradas

A ) DE ACORDO COM ESSES REGISTROS, COMPLETE AS FRASES A SEGUIR.

• ESTUDANTES PRETENDEM PARTICIPAR DO GRUPO DE ESTUDO.

Resposta: 5 ESTUDANTES PRETENDEM PARTICIPAR DO GRUPO DE ESTUDO.

• ESTUDANTES NÃO PRETENDEM PARTICIPAR DO GRUPO DE ESTUDO.

Resposta: 3 ESTUDANTES NÃO PRETENDEM PARTICIPAR DO GRUPO DE ESTUDO.

• ESTUDANTES RESPONDERAM À PESQUISA.

Resposta: 8 ESTUDANTES RESPONDERAM À PESQUISA.

B ) QUAL SERIA A SUA RESPOSTA PARA ESSA PESQUISA? POR QUÊ?

Resposta pessoal. Espera-se que os estudantes reflitam sobre seu interesse em participar de um grupo de estudo e expressem sua opinião com justificativas simples, como o desejo de aprender mais, estudar com os colegas, ter ajuda com as lições ou até preferir outras atividades.

21. C) Resposta pessoal. Espera-se que os estudantes expressem suas preferências em relação à maneira de estudar, mencionando se gostam mais de estudar sozinhos, por acharem mais tranquilo ou concentrado, ou em grupo, por gostarem da troca de ideias e da ajuda dos colegas.

C ) VOCÊ GOSTA MAIS DE ESTUDAR SOZINHO OU EM GRUPO? CONVERSE COM SEUS COLEGAS SOBRE ESSA QUESTÃO.

A ) PINTE AS FOLHAS QUE AS FORMIGAS ESTÃO CARREGANDO.

Resposta: Os estudantes devem pintar as 9 folhas que aparecem na imagem.

B ) A QUANTIDADE DE FORMIGAS E DE FOLHAS É A MESMA?

Resposta: SIM.

C ) REPRESENTE, DA MANEIRA QUE PREFERIR, QUANTAS FOLHAS VOCÊ PINTOU.

Resposta: Os estudantes devem representar 9 unidades no quadro, da maneira que preferirem.

D ) ESCREVA O NÚMERO NOVE DE DUAS MANEIRAS.

MÃOS COM NOVE DEDOS LEVANTADOS. 9

9999 99 9

Resposta pessoal. Espera-se que os estudantes sobreponham os pontilhados, acompanhando os traçados das letras e do algarismo para escrever o número citado.

03/10/2025 08:46:20

• Recomende aos estudantes que respondam ao item B da atividade 22 sem contar. Incentive-os a perceber que, como cada formiga carrega apenas uma folha e como todas as formigas estão carregando folhas, então a quantidade de formigas e de folhas é a mesma. Assim, exercita-se o princípio da correspondência um a um de agrupamento na contagem.

• Assim como foi feito na atividade 14, peça aos estudantes que também escrevam o número 9 de duas maneiras em seus cadernos. Verifique se eles fazem os símbolos corretamente, sem espelhamentos. É muito comum que estudantes em fases iniciais de aprendizagem confundam o algarismo 9 com o algarismo 6, em virtude da semelhança entre os símbolos. Por isso, é importante trabalhar reiteradamente para que sejam evitadas essas confusões. Nesse caso, pouco a pouco, instrua-os sobre como evitá-las. Uma possibilidade é associar o formato dos algarismos com desenhos, enquanto diz e mostra na lousa que o 6 tem uma “barriguinha”, enquanto o 9 se parece com um balão.

BNCC

O item B da atividade 22 explora a comparação de quantidade de objetos de dois conjuntos (folhas e formigas) com base na correspondência um a um entre seus elementos, evidenciando, assim, aspectos importantes da habilidade EF01MA03

• A atividade 23 mostra que o zero representa a ausência de algum elemento. Apesar de, para fins de contagem, o número zero aparentemente não ter qualquer utilidade, esse conceito é fundamental na construção do sistema de numeração posicional decimal. Isso se torna evidente quando os estudantes passam a estudar os números de dois algarismos, nos quais as dezenas inteiras envolvem um número 0, indicando a ausência de unidades além das dezenas completas.

• Se julgar necessário, após a atividade 23, para reforçar a prática e o direcionamento da escrita do número, utilize o caderno de caligrafia. Com isso, eles desenvolverão progressivamente a escrita da letra cursiva.

• Ao trabalhar a atividade 24 , peça aos estudantes que interpretem as cenas. Explore a compreensão deles sobre o contexto perguntando, por exemplo: “Por que no último quadrinho os gatos não estavam mais no muro?”. Aguarde as respostas e verifique se eles concluem que os animais não estavam mais no muro porque a cena anterior mostra o início de uma chuva, e os gatos provavelmente saíram dali para procurar abrigo.

ARTICULANDO CONHECIMENTOS

Se julgar conveniente, aproveite a relação entre os componentes curriculares de Matemática e Língua Portuguesa e incentive a criatividade dos estudantes sugerindo que elaborem uma continuação para a história. Apresente elementos novos, pedindo que desenhem a próxima cena no caderno com a presença do Sol e de outros animais. Oportunidades como essa são importantes para desenvolver a criatividade e a comunicação da turma.

23. C) Resposta: Espera-se que os estudantes sobreponham os pontilhados acompanhando os traçados das letras e dos algarismos apresentados para escrever o número citado.

23. A FOTOGRAFIA MOSTRA ALGUNS BRINQUEDOS.

A ) QUANTOS PIÕES HÁ NA FOTOGRAFIA?

PIÕES.

Resposta: 2 PIÕES.

B ) QUANTAS BONECAS HÁ NA FOTOGRAFIA?

Resposta: NENHUMA.

PIÕES

C ) ESCREVA O NÚMERO ZERO DE QUATRO MANEIRAS.

MÃO COM NENHUM DEDO LEVANTADO.

24. OBSERVE AS CENAS.

Resposta pessoal. Espera-se que os estudantes sobreponham os pontilhados, acompanhando os traçados das letras para escrever o número zero com algarismo e por extenso, além da forma cursiva minúscula e maiúscula.

A ) QUANTOS GATINHOS HAVIA NO MURO ANTES DA CHUVA?

Resposta: 6 GATINHOS.

B ) QUANTOS GATINHOS FICARAM NO MURO NO FINAL DA HISTÓRIA? REPRESENTE ESSA QUANTIDADE COM UM NÚMERO.

Resposta: NENHUM OU 0.

03/10/2025

25. A) Resposta pessoal. Espera-se que os estudantes estimem que a quantidade de

25. OBSERVE OS QUADROS COM LÁPIS.

QUADRO 1

lápis do quadro 1 é maior do que a do quadro 2

QUADRO 2

A ) SEM CONTAR UM A UM, ESTIME QUAL QUADRO TEM A MAIOR QUANTIDADE DE LÁPIS.

B ) CONTE OS LÁPIS E ESCREVA A QUANTIDADE DELES EM CADA QUADRO.

Resposta: QUADRO 1: 9; QUADRO 2: 8

QUADRO 1.

26. PEDRO E LÍVIA COLECIONAM BOLINHAS.

COLEÇÃO DE BOLINHAS DE PEDRO

QUADRO 2.

COLEÇÃO DE BOLINHAS DE LÍVIA

A ) QUEM TEM MAIS BOLINHAS: PEDRO OU LÍVIA?

Resposta: PEDRO.

B ) DESENHE BOLINHAS NO QUADRO COM A COLEÇÃO DE LÍVIA PARA QUE ELA TENHA A MESMA QUANTIDADE DE BOLINHAS QUE PEDRO.

Resposta: Os estudantes devem desenhar 6 bolinhas na coleção de Lívia.

C ) QUANTAS BOLINHAS VOCÊ DESENHOU? BOLINHAS.

Resposta: 6 BOLINHAS.

AVALIANDO

Objetivo

Ler e escrever números de 0 a 9 com algarismos e por extenso.

Estabelecer a relação entre a quantidade de elementos de 0 a 9, sua representação numérica e sua escrita por extenso.

Compreender a ideia de correspondência um a um.

Sugestão de intervenção

Providencie palitos de sorvete e os distribua aos estudantes para que façam grupos com

03/10/2025 08:51:37

quantidades predeterminadas. Para isso, peça a eles que desenhem quadrados em uma cartolina e colem um palito em um dos quadrados, dois palitos no segundo, três no terceiro, e assim por diante, inclusive mantendo um dos quadrados sem nenhum palito. Embaixo de cada grupo de palitos, os estudantes devem escrever, com algarismos e por extenso, os números que representam a respectiva quantidade de palitos. Durante todo o processo, supervisione as atividades e verifique possíveis dificuldades que eles possam apresentar.

• A atividade 25 exercita a capacidade dos estudantes de realizarem estimativas. É provável que eles, de pronto, comecem a contar os lápis um a um. Por isso, inicie a atividade pedindo-lhes que não contem, apenas digam, sem medo de errar, em qual quadro existe a maior quantidade de lápis. Deixe claro que não há problema em errar. Caso contrário, eles podem contar só para não falar uma resposta errada, o que invalidará o propósito da atividade. Depois que responderem, peça a eles que tentem explicar como chegaram a uma ou outra conclusão. Em seguida, após todos terem emitido suas opiniões, peça-lhes que façam a contagem e confirmem se acertaram ou não no palpite.

• Além de exercitar a habilidade de contagem e a capacidade de fazer comparações entre quantidades de objetos de dois conjuntos, a atividade 26 explora as primeiras noções de subtração. Os estudantes devem identificar que, ao desenharem as bolinhas no quadro com a coleção de Lívia, a fim de que ela tenha a mesma quantidade de bolinhas que Pedro, a quantidade de bolinhas desenhadas será a que falta para que os dois tenham o mesmo total de bolinhas.

BNCC

A atividade 25 exercita a capacidade de realizar estimativas a fim de desenvolver estratégias para identificar qual conjunto tem mais elementos. A atividade 26, com propósito similar, trabalha com contagem para fins de comparação entre a quantidade de elementos de dois conjuntos. Assim, são contempladas as habilidades EF01MA02 e EF01MA03

• Esse tópico introduz o conceito de dezena e apresenta a existência de números maiores do que 9. A transição de unidades para dezenas, isto é, de números com apenas um algarismo para números com dois algarismos, pode ser um grande desafio para alguns estudantes. Essa transição é crucial no desenvolvimento das habilidades de contagem e representação numérica, pois, em certo sentido, as transições futuras, de dezena para centena e de centena para unidade de milhar, seguirão uma lógica análoga. Desse modo, o pré-requisito necessário nesse tópico e nos próximos é a capacidade de reconhecer o sistema de numeração a partir dos agrupamentos em unidades e dezenas e de perceber que o valor de um algarismo muda de acordo com o seu valor posicional.

• A atividade 1 segue o padrão das atividades anteriores da unidade, de modo a dar naturalidade à transição. Ao realizar o item A dessa atividade, dê plena liberdade para os estudantes registrarem, ao modo deles, a quantidade de laranjas que aparecem na imagem. Incentive representações diversificadas, de modo a explorar as variadas maneiras de indicar um número. É possível que alguns estudantes utilizem algarismos, enquanto outros optem por escrever por extenso ou, ainda, por usar bastões de contagem ou mesmo fazer bolinhas que representem as unidades. Escreva na lousa as diversas representações que os estudantes fizeram. No item B, se necessário, proponha outras estratégias antes de solicitar que pratiquem a escrita e o direcionamento dos números, como pedir a eles que façam o traçado do número em caixas de areia.

• Na atividade 2, se julgar conveniente, mencione que, no número 10, o algarismo 1

O NÚMERO 10 10

1. A) Resposta: Os estudantes devem registrar 10 unidades no quadro, da maneira que preferirem.

1. A IMAGEM APRESENTA UM PRATO COM LARANJAS.

A ) REGISTRE, DA MANEIRA QUE PREFERIR, A QUANTIDADE DE LARANJAS QUE APARECEM NA IMAGEM.

1. B) Resposta pessoal. Espera-se que os estudantes sobreponham os pontilhados, acompanhando os traçados das letras e dos algarismos para escrever o número citado.

B ) ESCREVA O NÚMERO DEZ DE DUAS MANEIRAS.

10 10 10 10

MÃOS COM DEZ DEDOS LEVANTADOS.

2. PINTE OS QUADRINHOS DE ACORDO COM A QUANTIDADE DE BOLINHAS DE CADA COR. DEPOIS, ESCREVA O NÚMERO QUE REPRESENTA A QUANTIDADE DE QUADRINHOS QUE VOCÊ PINTOU.

DICA: CADA QUADRINHO CORRESPONDE A UMA BOLINHA.

Resposta: Bolinhas azuis: pintar nove quadrinhos e escrever o número 9; bolinhas amarelas: pintar 10 quadrinhos e escrever o número 10; bolinhas vermelhas: pintar 8 quadrinhos e escrever o número 8.

representa uma dezena e o 0 representa zero unidade (ou seja, nenhuma unidade a mais que a dezena).

Neste tópico, trabalha-se a ideia de dezena e a transição da contagem de unidades para a contagem de números maiores do que 9, incentivando a contagem e a comparação de quantidades de dois conjuntos, em situações com jogos e brincadeiras que despertam o interesse dos estudantes. Exercita-se também a capacidade de realizar estimativas, bem como o registro simbólico dos números. Assim, são contemplados

importantes pontos das habilidades EF01MA02, EF01MA03 e EF01MA04

BNCC

Seis Seis Seis Seis

7 8 9 10

• Se julgar necessário, após a atividade 3, para reforçar a prática e o direcionamento da escrita dos números e, com isso, desenvolver progressivamente a escrita da letra cursiva, utilize o caderno de caligrafia. 3. ESCREVA

Resposta pessoal. Os estudantes devem sobrepor os pontilhados, acompanhando os traçados das letras para escrever o número 6 na forma cursiva minúscula e maiúscula.

SeteSeteSeteSete

Resposta pessoal. Os estudantes devem sobrepor os pontilhados, acompanhando os traçados das letras para escrever o número 7 na forma cursiva minúscula e maiúscula.

Oito Oito Oito Oito

Resposta pessoal. Os estudantes devem sobrepor os pontilhados, acompanhando os traçados das letras para escrever o número 8 na forma cursiva minúscula e maiúscula.

Nove novenovenove NoveNove

Resposta pessoal. Os estudantes devem sobrepor os pontilhados, acompanhando os traçados das letras para escrever o número 9 na forma cursiva minúscula e maiúscula.

Dez seis

Dez Dez Dez

Resposta pessoal. Os estudantes devem sobrepor os pontilhados, acompanhando os traçados das letras para escrever o número 10 na forma cursiva minúscula e maiúscula.

03/10/2025 08:51:40

• A atividade 3 propõe aos estudantes que ampliem a familiaridade com a escrita por extenso dos números usando a letra cursiva. Nessa atividade, é explorado o reconhecimento da sequência numérica, além do treino da escrita para desenvolver a coordenação motora fina. A apresentação do número 10 é significativa, pois marca a transição da contagem de números com apenas um algarismo para a compreensão da dezena, número com dois algarismos. Antes de os estudantes escreverem os números de 6 a 10 em letra cursiva usando o lápis, oriente-os a seguir o pontilhado com o dedo. Relembre os números já trabalhados anteriormente, de 1 a 5, propondo uma contagem oral com a turma de 1 a 10.

• A atividade 4 relaciona as unidades temáticas de Matemática Números e Probabilidade e estatística ao trabalhar com bolinhas numeradas de 1 a 10 e a análise dos resultados obtidos na realização de um sorteio, levando os estudantes a classificarem esse evento usando os termos certeza, talvez aconteça e possível e impossível

• Antes de desenvolver com os estudantes a atividade 4, pergunte a eles se já participaram de algum sorteio. Caso alguém se manifeste, permita que comente com a turma sua experiência.

• Leia o enunciado da atividade 4 e, no item A, verifique se eles respondem corretamente, dizendo que os números de bolinhas que podem ser sorteadas são de 1 a 10. Permita que avaliem cada afirmação do item B, dizendo se é verdadeira ou falsa. Depois, peça a eles que justifiquem cada afirmação falsa, corrigindo-a. Avalie como os estudantes percebem questões que envolvem estudos do acaso e como respondem a elas. Verifique como compreendem os termos é certo, com certeza, é possível e é impossível. Para um melhor aproveitamento desse assunto, realize a atividade a seguir.

4. MARIA ESTÁ PARTICIPANDO DE UM SORTEIO. ELA DEVE RETIRAR UMA BOLINHA DE UMA CAIXA COM 10 BOLINHAS NUMERADAS DE 1 A 10.

Unidades temáticas integradas

A ) QUAIS SÃO OS NÚMEROS POSSÍVEIS DE SEREM SORTEADOS POR MARIA COM ESSAS BOLINHAS?

Resposta: OS POSSÍVEIS NÚMEROS DE SEREM SORTEADOS POR MARIA SÃO: 1, 2, 3, 4, 5, 6, 7, 8, 9 e 10.

B ) DE ACORDO COM AS INFORMAÇÕES ANTERIORES, MARQUE V PARA AS AFIRMAÇÕES VERDADEIRAS E F PARA AS AFIRMAÇÕES FALSAS.

TALVEZ MARIA RETIRE A BOLINHA DE NÚMERO 7.

Resposta: V

É IMPOSSÍVEL QUE MARIA RETIRE A BOLINHA DE NÚMERO 5.

Resposta: F

A BOLINHA DE NÚMERO 1 É UMA DAS QUE MARIA PODE RETIRAR.

Resposta: V

AS BOLINHAS DE NÚMERO 2, 6 E 9 ESTÃO ENTRE AQUELAS QUE MARIA PODE RETIRAR.

Resposta: V

MARIA VAI RETIRAR, COM CERTEZA, A BOLINHA DE NÚMERO 3.

Resposta: F

É POSSÍVEL QUE MARIA RETIRE A BOLINHA DE NÚMERO 11.

Resposta: F

ATIVIDADE EXTRA

Promova com os estudantes, na prática, um sorteio parecido com o de Maria, porém, em vez de bolinhas numeradas de 1 a 10, adapte para fichas numeradas de 1 a 10 e coloque-as em uma caixa. Peça a um estudante que sorteie uma ficha e pergunte aos demais qual número eles acham que será sorteado. Devolva a ficha na caixa e solicite a outro estudante que sorteie uma ficha. Repita esse processo e faça algumas perguntas para a turma, como: “Podemos sortear uma ficha com o número 15?”; “É possível sortear uma ficha com o número 2?”; “É certo sor-

tear uma ficha com um número maior do que 7?”; “É impossível sortear uma ficha com o número 10?”; “O que é impossível de acontecer nesse sorteio?”.

03/10/2025 08:51:41

5. A) Resposta pessoal. A resposta depende do resultado da pesquisa.

EXPERIMENTE

5. VOCÊ VAI FAZER UMA PESQUISA. PARA ISSO, RESOLVA

Unidades temáticas integradas entrevistem 10 colegas e preencham o quadro com as informações obtidas, além de completar o título do quadro com a informação que falta.

O QUE SE PEDE EM CADA ITEM.

A ) ENTREVISTE 10 COLEGAS E PERGUNTE QUAL DAS CORES INDICADAS NO QUADRO ELES PREFEREM. EM SEGUIDA, ANOTE NO QUADRO UM VOTO PARA CADA ENTREVISTADO.

COR PREFERIDA DOS COLEGAS DE COR

QUANTIDADE DE VOTOS

B ) COM BASE NO QUADRO QUE VOCÊ PREENCHEU, COMPLETE E PINTE A SEGUIR UM QUADRINHO PARA CADA VOTO.

COR PREFERIDA DOS COLEGAS DE

FONTE DE PESQUISA: INFORMAÇÕES OBTIDAS POR

C ) A MAIORIA DOS ENTREVISTADOS ESCOLHEU QUAL COR?

Resposta pessoal. A resposta do estudante depende do resultado da pesquisa.

D ) QUANTOS VOTOS A COR MAIS ESCOLHIDA RECEBEU A MAIS DO QUE A COR MENOS ESCOLHIDA?

Resposta pessoal. A resposta de cada estudante depende do resultado da

Resposta pessoal. Espera-se que os estudantes pintem os quadrinhos do gráfico com as informações da pesquisa, ou seja, com os dados anotados no quadro. pesquisa. Professor, professora: Espera-se que os estudantes

• A atividade 5 relaciona as unidades temáticas de Matemática Números e Probabilidade e estatística ao propor uma pesquisa e solicitar o registro dos resultados em um quadro, completando colunas de acordo com a quantidade de votos que as cores receberam.

• A atividade proposta nesta página tem por objetivo verificar a compreensão dos estudantes em relação à coleta e organização de dados obtidos de uma pesquisa em um quadro e analisar se são capazes de expressar e interpretar esses dados em um gráfico de barras, construindo-o na malha quadriculada. Se julgar conveniente, peça aos estudantes que, primeiro, registrem as informações da pesquisa com tracinhos, relacionando, em seguida, essa representação à quantidade de votos de cada cor. Oriente-os na realização dessa atividade, a fim de que eles associem a quantidade de entrevistados indicada na tabela à quantidade de quadrinhos que serão pintados no gráfico.

• Caso julgue necessário, antes de iniciar a atividade, organize a turma em dois grupos, a fim de evitar tumultos na sala de aula e tornar a atividade mais organizada. Dessa maneira, enquanto metade da turma entrevista, a outra metade é entrevistada.

03/10/2025 08:51:41

• O objetivo desse jogo é levar os estudantes a reconhecerem os números por meio da oralidade, da leitura e da escrita com algarismos ou por extenso. Se julgar conveniente, promova várias rodadas do Jogo de cartelas numeradas com toda a turma. Como variação do jogo, organize-os em grupos de quatro ou cinco integrantes e peça a um participante de cada grupo que sorteie as fichas. Caso seja feita essa estratégia de jogo, oriente-os a se revezar para sortear as fichas nas rodadas que se seguirem.

AVALIANDO

Objetivo

Reconhecer que uma dezena corresponde a 10 unidades, para propiciar a autocompreensão e auxiliar na aprendizagem.

Sugestão de intervenção

Ao final desse tópico, procure aplicar atividades com o intuito de avaliar a aprendizagem em relação a uma dezena. Proponha questões de contagem, providenciando materiais apropriados para que eles possam separar elementos em grupos de 10, completando uma dezena. Se possível, apresente novamente aos estudantes o material dourado, a fim de que eles o utilizem nas contagens e montem, usando os cubinhos, uma dezena.

DIVIRTA-SE E APRENDA

JOGO DE CARTELAS NUMERADAS

VAMOS JOGAR COM OS NÚMEROS QUE APRENDEMOS

NESTA UNIDADE? CHAME ALGUNS COLEGAS PARA BRINCAR.

RECORTE AS CARTELAS DA PÁGINA 257 DO MATERIAL

COMPLEMENTAR

REGRAS

• PENSE EM QUATRO NÚMEROS DE 1 A 10 E ANOTE ESSES

NÚMEROS NA CARTELA.

• O PROFESSOR VAI SORTEAR UMA FICHA POR VEZ E DIZER O NÚMERO SORTEADO EM VOZ ALTA.

• VERIFIQUE SE ESSE NÚMERO FOI O QUE VOCÊ ANOTOU NA

CARTELA E MARQUE UM X NELE.

• VENCE A PARTIDA QUEM MARCAR PRIMEIRO TODOS OS NÚMEROS QUE ESTIVEREM NA CARTELA.

A DEZENA

1. NINO CONSTRUIU ALGUNS SAPOS DE PAPEL

FAZENDO DOBRADURAS.

A ) QUANTOS SAPOS DE PAPEL ELE CONSTRUIU?

SAPOS.

Resposta: 6 SAPOS.

B ) NINO CONSTRUIU MAIS UM SAPO. QUANTOS SAPOS SÃO AGORA?

SAPOS.

Resposta: 7 SAPOS.

C ) VAMOS CONTAR SAPOS! CONTE E COMPLETE OS NÚMEROS QUE FALTAM.

Resposta: 4 SAPOS.

1 SAPO. 2 SAPOS. 3 SAPOS. SAPOS.

Resposta: 7 SAPOS.

Resposta: 8 SAPOS.

Resposta: 6 SAPOS.

• A atividade 1 apresenta uma situação em que uma criança brinca com dobraduras de papel. Avalie a possibilidade de entregar folhas de papel sulfite aos estudantes e ensinar algumas dobraduras simples, como barquinhos ou aviõezinhos.

• O propósito do item C da atividade 1 é levar os estudantes a identificarem a sequência dos números naturais de 1 a 9 e, em seguida, incluírem o 10 como extensão natural dessa sequência. Em seguida, é explicitamente apresentado o conceito de dezena, como aquilo que se obtém quando se reúne 10 unidades.

SAPOS. SAPOS. SAPOS. SAPOS. SAPOS. SAPOS.

Resposta: 5 SAPOS.

Resposta: 9 SAPOS.Resposta: 10 SAPOS.

NA SITUAÇÃO APRESENTADA, CONTAMOS 10 SAPOS, OU SEJA, 10 UNIDADES, QUE CHAMAMOS 1 DEZENA

10 UNIDADES OU 1 DEZENA

ATIVIDADE EXTRA

Para complementar a atividade 1, verifique a possibilidade de apresentar à turma o material dourado. Utilize-o para mostrar como 10 quadradinhos reunidos formam uma barra, de maneira que 10 quadradinhos podem ser substituídos por uma barra sem que haja perda ou ganho de quadradinhos. Explique-lhes que os quadradinhos representam as unidades e que a barra representa a dezena.

03/10/2025 08:51:45

• Para ajudar a fixar as ideias exploradas na atividade 1 e para exercitar a compreensão de correspondência um a um, solicite aos estudantes que representem com os dedos a quantidade de sapos em cada conjunto. Ao final da atividade, evidencie que uma dezena é obtida quando estamos com todos os dedos das duas mãos levantados.

• Para estudantes com Necessidades Educacionais Específicas (NEE), sugere-se uma abordagem multimodal, que envolva diferentes sentidos, com o intuito de favorecer a aprendizagem. É possível usar dobraduras de papel, permitindo a manipulação do material. Para facilitar a contagem, os sapos podem ser confeccionados com papéis de texturas diferentes. Se a deficiência for auditiva, use material ilustrado como apoio visual e apresente os números com gestos ou cartões coloridos.

• O propósito da atividade 2 é avaliar se os estudantes absorveram o conceito de dezena. Verifique se todos contornam 10 amendoins. Caso alguém contorne apenas um amendoim, revise o conceito de dezena, buscando novas abordagens para fazê-lo compreender. Caso algum deles contorne uma quantidade próxima de 10, verifique se o que houve foi erro conceitual ou erro na contagem. Em qualquer caso, auxilie o estudante a realizar a contagem novamente e reforce o conceito de dezena.

• Se necessário, ao apresentar a atividade 2, explique que um desenho inteiro corresponde a um amendoim. Não é uma interpretação totalmente descabida algum estudante entender que, em cada casca, há dois amendoins, de modo que queira contornar cinco cascas.

• Se julgar conveniente, compare as respostas da turma e explique que pessoas diferentes podem contornar amendoins diferentes. Cada grupo contornado deve conter exatamente 10 amendoins, não importando quais são esses amendoins em específico.

• A atividade 3 apresenta o quadro de ordens. Esse recurso é de grande importância para articular a aprendizagem acerca dos números maiores do que 10. Visualmente, um estudante em seus primeiros estágios de aprendizagem pode imaginar que 9 é maior do que 10 porque 9 é maior do que 1 e 9 é maior do que 0. Assim, a organização do número em quadro de ordens desfaz esse tipo de equívoco e auxilia no entendimento quanto à maneira correta de comparar números com dois ou mais algarismos.

2. CONTORNE UMA DEZENA DE AMENDOINS.

Resposta: Os estudantes devem contornar, da maneira que preferirem, um total de 10 amendoins, independentemente de suas posições.

3. PODEMOS REPRESENTAR A QUANTIDADE DE BOLINHAS DE GUDE DE LUCAS E GABRIEL EM UM QUADRO DE ORDENS.

LUCAS

QUADRO DE ORDENS DEZENA UNIDADE 0 9

GABRIEL

QUADRO DE ORDENS DEZENA UNIDADE 1 0

A ) LUCAS TEM DEZENA E UNIDADES DE BOLINHAS.

Resposta: LUCAS TEM 0 DEZENA E 9 UNIDADES DE BOLINHAS.

B ) GABRIEL TEM DEZENA E UNIDADE DE BOLINHAS.

Resposta: GABRIEL TEM 1 DEZENA E 0 UNIDADE DE BOLINHAS.

C ) MARQUE UM X NO NOME DE QUEM TEM MAIS BOLINHAS. LUCAS. GABRIEL.

Resposta: Os estudantes devem marcar um X em GABRIEL.

NÚMEROS DE 11 A 19

1. PARA DETERMINAR A QUANTIDADE DE BONÉS A SEGUIR, HENRIQUE OS CONTORNOU FORMANDO GRUPOS DE 10.

QUADRO DE ORDENS

DEZENA UNIDADE

1 1

1 DEZENA E 1 UNIDADE OU 11 UNIDADES

11: ONZE

CONTORNE OS BONÉS FORMANDO GRUPOS DE 10. CONTE TODOS ELES E COMPLETE O QUE FALTA NOS QUADROS.

Resposta: Os estudantes devem contornar, da maneira que preferirem, 10 bonés, sobrando 2 bonés sem contorno.

QUADRO DE ORDENS

DEZENA UNIDADE 1 2

1 DEZENA E 2 UNIDADES OU 12 UNIDADES 12: DOZE

Resposta: Os estudantes devem contornar, da maneira que preferirem, 10 bonés, sobrando 3 bonés sem contorno.

QUADRO DE ORDENS

DEZENA UNIDADE 1 3

Resposta: 13: TREZE.

1 DEZENA E 3 UNIDADES OU 13 UNIDADES : TREZE

QUADRO DE ORDENS

DEZENA UNIDADE 1 4

Resposta: 14: QUATORZE.

Resposta: Os estudantes devem contornar, da maneira que preferirem, 10 bonés, sobrando 4 bonés sem contorno.

1 DEZENA E 4 UNIDADES OU 14 UNIDADES : QUATORZE

• A atividade 1 promove a contagem de objetos do 11 ao 19, incentivando a estratégia de contagem que consiste em separar elementos em grupos de 10, completando uma dezena.

• Instrua os estudantes a perceberem as vantagens da estratégia exercitada na atividade 1, pois ela torna mais rápida e fácil a contagem. Verifique se eles são capazes de perceber nos casos apresentados que, após contornar 10 elementos, a quantidade restante é o algarismo das unidades que será registrado, formando o número que representa a quantidade total de elementos.

03/10/2025 08:51:47

Ao longo desse tópico, expandem-se os trabalhos com dezenas e com números de 10 a 19. Contagens, estimativas e comparações entre a quantidade de elementos em diferentes conjuntos são exploradas nas atividades, sempre em contextos de interesse dos estudantes. É explorado o registro de números de 10 a 19, tanto de modo simbólico quanto verbal e, inclusive, no preenchimento de quadros de ordens. Desse modo, são contempladas as habilidades EF01MA02, EF01MA03 e EF01MA04

D. QUADRO DE ORDENS DEZENA UNIDADE

Resposta: Os estudantes devem contornar, da maneira que preferirem, 10 bonés, sobrando 5 bonés sem contorno.

1 DEZENA E 5 UNIDADES OU 15 UNIDADES 15: QUINZE

Resposta: DEZENA: 1; UNIDADE: 5

E. QUADRO DE ORDENS DEZENA UNIDADE

Resposta: Os estudantes devem contornar, da maneira que preferirem, 10 bonés, sobrando 6 bonés sem contorno.

1 DEZENA E 6 UNIDADES OU 16 UNIDADES 16: DEZESSEIS

Resposta: DEZENA: 1; UNIDADE: 6

F. QUADRO DE ORDENS DEZENA UNIDADE

Resposta: Os estudantes devem contornar, da maneira que preferirem, 10 bonés, sobrando 7 bonés sem contorno.

1 DEZENA E 7 UNIDADES OU 17 UNIDADES 17: DEZESSETE

Resposta: DEZENA: 1; UNIDADE: 7

G. QUADRO DE ORDENS DEZENA UNIDADE

Resposta: Os estudantes devem contornar, da maneira que preferirem, 10 bonés, sobrando 8 bonés sem contorno.

1 DEZENA E 8 UNIDADES OU 18 UNIDADES 18: DEZOITO

Resposta: DEZENA: 1; UNIDADE: 8

H. QUADRO DE ORDENS DEZENA UNIDADE

Resposta: Os estudantes devem contornar, da maneira que preferirem, 10 bonés, sobrando 9 bonés sem contorno.

1 DEZENA E 9 UNIDADES OU 19 UNIDADES 19: DEZENOVE

Resposta: DEZENA: 1; UNIDADE: 9

2. CÉLIA E OS AMIGOS DELA ESTÃO BRINCANDO COM UM JOGO. ELA REGISTROU OS PONTOS FEITOS EM UMA PARTIDA.

Unidades temáticas integradas

CÉLIARENATATIAGOMAURO

DICA: CADA REPRESENTA 1 PONTO.

COM AS INFORMAÇÕES ANOTADAS, CÉLIA CONSTRUIU O GRÁFICO DE BARRAS REPRESENTADO A SEGUIR.

NESTE GRÁFICO, CADA QUADRINHO PINTADO REPRESENTA 1 PONTO.

QUANTIDADE DE PONTOS NA PARTIDA DO JOGO em DEZEMBRO DE 2 2

QUANTIDADE DE PONTOS

FONTE DE PESQUISA: ANOTAÇÕES DE CÉLIA COM BASE NOS PONTOS DO JOGO.

A ) QUANTOS PONTOS RENATA FEZ? PONTOS.

Resposta: 8 PONTOS.

B ) QUEM FEZ MAIS PONTOS NESSA PARTIDA?

Resposta: CÉLIA.

C ) QUANTOS PONTOS? PONTOS.

Resposta: 12 PONTOS.

D ) QUAL PARTICIPANTE FEZ 7 PONTOS?

Resposta: MAURO.

E ) QUANTAS PESSOAS PARTICIPARAM DESSA PARTIDA? PESSOAS.

Resposta: 4 PESSOAS.

de de quadrinhos pintados no gráfico. Depois, auxilie-os a responder aos itens propostos na atividade. Por fim, faça outros questionamentos com base nesse gráfico, como: “Quem fez menos pontos?”; “Quantos pontos Tiago teria que fazer a mais para ter a mesma pontuação que Mauro?”; “Qual foi o total de pontos entre os quatro participantes?”; “Quantos pontos Célia fez a mais que Renata?”.

BNCC

03/10/2025 08:54:28

As atividades desse tópico abordam a leitura de dados expressos em gráficos de colunas simples, além de proporem pesquisas com até duas variáveis categóricas e orientarem a organização dos dados por meio de representações pessoais, conforme as habilidades EF01MA21 e EF01MA22

• A atividade 2 relaciona as unidades temáticas de Matemática Números e Probabilidade e estatística ao levar os estudantes a interpretarem informações expressas em um quadro e em um gráfico de colunas, de acordo com a quantidade de pontos que quatro amigos fizeram em um jogo.

• A atividade 2 explora um gráfico de barras feito com base nos registros do resultado de um jogo entre Célia e seus amigos. Pergunte aos estudantes se eles já se depararam com essa imagem (gráfico de barras) em algum outro lugar. Se algum deles disser que sim, permita que ele verbalize o raciocínio, compartilhando seu conhecimento com a turma, e acolha com atenção a resposta de todos. Depois, motive os estudantes a analisarem e comentarem os elementos do gráfico, como eixo vertical, eixo horizontal, título e fonte de pesquisa. Diga a eles que o eixo horizontal é denominado “Nome” porque foram inseridos nele os nomes dos participantes desse jogo. Já o eixo vertical foi denominado “Quantidade de pontos”, pois nele foi atribuída a pontuação de cada participante.

• Oriente os estudantes a contarem um quadrinho para cada ponto feito pelos participantes do jogo e verifique se há dúvidas na hora de identificarem a quantidade de pontuação registrada e a quantida -

TiagoMauro

Renata Célia

• A atividade 3 é destinada a avaliar a absorção das noções abordadas na atividade 1. Verifique se, para realizar as contagens, os estudantes aplicam a mesma estratégia sugerida na atividade 1, isto é, se eles reúnem parte dos objetos em um grupo de 10 e, em seguida, contam os demais objetos, obtendo a quantidade total.

• Auxilie os estudantes na leitura dos números na coluna da direita, visto que estão escritos por extenso, e não com algarismos.

• Caso os estudantes apresentem dificuldade no reconhecimento da sequência na atividade 4, dê dicas em formato de perguntas ou frases a serem completadas. Por exemplo: “O número que vem depois do 10 é o...?”; “Que número vem depois do 11?”; “Então, depois do 12, que número temos de completar?”.

BNCC

A atividade 4 aborda uma sequência numérica que deve ser reconhecida, interpretada e complementada com elementos ausentes. Esse tipo de atividade é fundamental para desenvolver o raciocínio lógico, o reconhecimento de padrões e a fixação de relações numéricas. Com isso, contempla-se a habilidade EF01MA10

3. LIGUE CADA QUADRO AO NÚMERO QUE REPRESENTA A QUANTIDADE DE OBJETOS QUE ELE CONTÉM.

IMAGENS SEM PROPORÇÃO ENTRE SI.

Resposta: Os estudantes devem ligar: A-DEZESSEIS; B-ONZE; C-QUINZE.

ESCREVA

OS NÚMEROS QUE

FALTAM NA SEQUÊNCIA PARA AJUDAR O COELHO A CHEGAR NA TOCA.

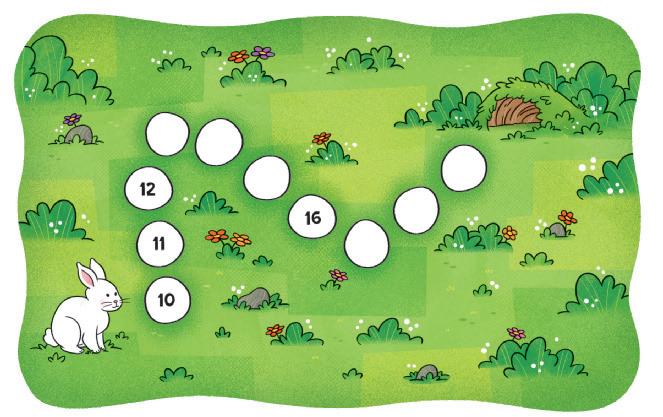
Resposta: 10, 11, 12, 13, 14, 15, 16, 17, 18, 19

C. 4.

5. PODEMOS REPRESENTAR NÚMEROS USANDO CUBINHOS E BARRAS.

UM REPRESENTA 1 UNIDADE.

UMA REPRESENTA 1 DEZENA.

ALGUNS NÚMEROS FORAM REPRESENTADOS A SEGUIR COM CUBINHOS E BARRAS. COMPLETE A SEQUÊNCIA COM OS NÚMEROS QUE FALTAM.

DICA: O PRIMEIRO NÚMERO DESTA SEQUÊNCIA CORRESPONDE AO NÚMERO 11, QUE PODE SER REPRESENTADO POR UM CUBINHO E UMA BARRA.

1 DEZENA E 1 UNIDADE

1 DEZENA E 2 UNIDADES

1 DEZENA E 3 UNIDADES

1 DEZENA E UNIDADES

Resposta: 1 DEZENA E 6 UNIDADES; 16

1 DEZENA E UNIDADES

Resposta: 1 DEZENA E 7 UNIDADES; 17

Resposta: 12

1 DEZENA E 5 UNIDADES

Resposta: 13

1 DEZENA E 4 UNIDADES

Resposta: 15

Resposta: 14

1 DEZENA E 8 UNIDADES

1 DEZENA E 9 UNIDADES

• A atividade 5 tem como objetivo levar os estudantes a observarem uma sequência numérica composta de cubinhos e barra, com o objetivo de reconhecer e completar os números de 11 a 19 usando o material dourado.

• A atividade 5 também pode ser realizada na prática, representando as quantidades com o material dourado, com palitos ou com outros materiais de contagem. Se necessário, auxilie-os na compreensão dessa atividade e oriente-os a utilizar o Material complementar do final do Livro do Estudante e, depois do uso, guardá-lo, pois ele será usado em outras unidades no decorrer deste volume.

• Com o intuito de que todos os estudantes participem da aula, é preciso fazer algumas adaptações e utilizar estratégias inclusivas, de acordo com as necessidades específicas de cada estudante, promovendo a inclusão de estudantes com NEE. Para aqueles com deficiência visual, é recomendado o uso de materiais em relevo, como cubinhos e barras feitos com massinha, facilitando a manipulação e a percepção. Faça a descrição da atividade em voz alta, sempre que possível, e motive os estudantes a manipularem os materiais usando o tato.

Resposta: 18

tendo o rosto visível ao se comunicarem para facilitar a leitura labial. Use cartelas com números, cubinhos e barras ilustradas para facilitar a compreensão da lógica da atividade.

• No caso de estudantes com TEA, TDAH ou síndrome de Down, é recomendado utilizar ilustrações com poucos estímulos por vez. Trabalhe a atividade em tempos curtos e fazendo pequenas pausas. É importante reforçar positivamente cada conquista e, se necessário, possibilitar que a atividade seja realizada em dupla.

Resposta: 19

• No caso de estudantes com deficiência auditiva, é recomendado o uso de recursos visuais e gestos que acompanhem a fala, man-

03/10/2025 08:54:38

• Aproveite o contexto da atividade 6 para comentar com a turma a importância de comer frutas. Elas são fontes de fibras e vitaminas indispensáveis ao crescimento. Para ter uma boa saúde e crescer saudável, é importante ingeri-las regularmente. Pergunte aos estudantes quais são as frutas favoritas deles, de quais eles não gostam e por que não gostam. Essa também pode ser uma oportunidade para demonstrar como as pessoas podem ter gostos e preferências diferentes. A fruta favorita de alguém pode ser a mesma de que o outro não gosta e, ainda assim, eles podem continuar convivendo sem problema algum. Reforce a importância do respeito às diferenças e comente que, se não gostamos de determinada fruta, podemos ingerir outras. As opções são diversas!

• Pergunte quantas frutas os estudantes são capazes de nomear e registre na lousa todas as frutas citadas. Depois, peça-lhes que determinem quantas frutas foram mencionadas ao todo, por meio da contagem.

• Na atividade 7, bem como em outras que os estudantes vão ligar elementos de uma coluna a elementos de outra, oriente-os a traçar as linhas de modo reto e contínuo, deixando evidente qual par de elementos aquela linha está associando. Dê exemplos, na lousa, da maneira adequada de traçar as linhas. Se necessário, auxilie os estudantes na leitura dos números escritos por extenso.

ATIVIDADE EXTRA

6. VILMA COMPROU ALGUMAS FRUTAS NA FEIRA.

LEANDRO LASSMAR/ ARQUIVO DA EDITORA

Resposta: Os estudantes devem contornar o número 15

B ) CONTORNE O NÚMERO QUE REPRESENTA A QUANTIDADE DE LARANJAS.

Resposta: Os estudantes devem contornar o número 18

C ) CONTORNE O NÚMERO QUE REPRESENTA A QUANTIDADE DE BANANAS.

Resposta: Os estudantes devem contornar o número 12

7. LIGUE CADA NÚMERO À ESCRITA POR EXTENSO CORRESPONDENTE.

A ) CONTORNE O NÚMERO QUE REPRESENTA A QUANTIDADE DE MAÇÃS. 13 19 14 15 11 17

Resposta: Os estudantes devem ligar: 13-TREZE; 15-QUINZE; 19-DEZENOVE; 11-ONZE; 14-QUATORZE; 17-DEZESSETE.

A fim de complementar a atividade 6 e fortalecer a capacidade de realizar correspondências um a um, entregue aos estudantes objetos de contagem de diferentes cores e peça-lhes que os agrupem com as mesmas quantidades de bananas, maçãs e laranjas. Uma possibilidade é providenciar tampinhas de garrafa em três cores diferentes, cada uma representando uma fruta, e conferir se eles as organizam adequadamente.

8. DESENHE BOLINHAS DE ACORDO COM A QUANTIDADE INDICADA EM CADA QUADRO. DEPOIS, ESCREVA O NÚMERO QUE REPRESENTA ESSA QUANTIDADE.

DOZE

Resposta: Os estudantes devem desenhar 12 bolinhas e completar com o número 12.

DEZESSEIS

Resposta: Os estudantes devem desenhar 16 bolinhas e completar com o número 16.

QUINZE

Resposta: Os estudantes devem desenhar 15 bolinhas e completar com o número 15.

DEZENOVE

Resposta: Os estudantes devem desenhar 19 bolinhas e completar com o número 19.

9. GIOVANE E MIGUEL ESTÃO PARTICIPANDO DE UM CAMPEONATO DE FUTEBOL.

EU FIZ 14 GOLS NESTE CAMPEONATO.

MIGUEL

EU FIZ 12.

GIOVANE

A ) QUANTOS GOLS GIOVANE FEZ? GOLS.

B ) QUANTOS GOLS MIGUEL FEZ? GOLS.

Resposta: 12 GOLS.

Resposta: 14 GOLS.

C ) MARQUE UM X NO NOME DE QUEM FEZ MAIS GOLS. GIOVANE. MIGUEL.

Resposta: Os estudantes devem marcar um X no nome MIGUEL

• Na atividade 8, verifique se os estudantes desenham a quantidade exata, sem se perderem na contagem. Em caso de erro, confira se o problema se deu na incompreensão do valor ou em falta de atenção para realizarem a contagem enquanto os desenhos eram feitos. • Na atividade 9, os estudantes devem comparar dois valores para dizer qual deles é o maior. No entanto, nesse caso, não há elementos visuais a serem contados e postos em correspondência um a um. Por isso, verifique a estratégia utilizada pelos estudantes para comparar os valores. É possível que alguns já saibam a sequência dos números em ordem crescente e, com base nisso, descubram que 14 é maior do que 12. Outros podem levar em consideração a ideia inspirada pelo quadro de ordens e comparar primeiro o algarismo das dezenas (que é o mesmo em ambos os números) e, em seguida, o algarismo das unidades. Alguns, ainda, podem desenhar 14 bolinhas de um lado e 12 do outro ligando em correspondência uma a uma, a fim de determinar em qual grupo há mais bolinhas. Explore todas essas possibilidades com a turma e mostre que, em todas elas, é possível chegar ao mesmo resultado.

BNCC

A atividade 9 propõe estimativa e comparação de quantidades, mostrando os primeiros passos para compreender relações de “maior” e “menor”, como prevê a habilidade EF01MA03

• A atividade 10 relaciona as unidades temáticas de Matemática Números e Probabilidade e estatística ao trabalhar a construção de um gráfico.

• Aproveite essa atividade para aproximar os estudantes do contexto da agricultura familiar, em que é comum o cultivo e o armazenamento de sementes para diferentes tipos de plantação. Para isso, converse com eles com o intuito de verificar se conhecem o trabalho rural e se apresentam percepção da origem dos alimentos. Valorize a cultura do campo por meio de perguntas como: “Você conhece alguém que planta alimentos ou cuida da terra?”; “Já viu alguém separar sementes para plantar depois?”; “Você sabe de onde vem o milho ou o feijão que comemos?”; “Por que é importante guardar sementes?”; “Já pensou em como uma semente tão pequena pode virar uma planta cheia de frutos?”. Perguntas como essas ajudam a despertar nos estudantes a curiosidade pelos ciclos naturais e pela diversidade presente no mundo rural, promovendo o reconhecimento da importância da agricultura para a vida cotidiana.

10. CLEITON É AGRICULTOR E CULTIVA DIVERSOS TIPOS DE SEMENTES PARA PRODUZIR ALIMENTOS. ELE FEZ AS AMOSTRAS A SEGUIR COM ALGUMAS SEMENTES QUE CULTIVA.

IMAGENS SEM PROPORÇÃO ENTRE SI.

SEMENTES DE FEIJÃO SEMENTES DE MILHO SEMENTES DE ABÓBORA

A ) CONTE AS SEMENTES QUE ELE COLOCOU EM CADA AMOSTRA, ESCREVENDO NOS QUADROS OS NÚMEROS QUE REPRESENTAM AS QUANTIDADES CORRESPONDENTES.

Resposta: SEMENTES DE FEIJÃO: 9; SEMENTES DE MILHO: 15; SEMENTES DE ABÓBORA: 12

BNCC

B ) PINTE OS QUADRINHOS DE ACORDO COM AS QUANTIDADES DE SEMENTES.

Resposta: Os estudantes devem pintar 9 quadrinhos para as sementes de feijão, 15 para as sementes de milho e 12 para as sementes de abóbora.

QUANTIDADES DE SEMENTES DAS AMOSTRAS, EM MAIO DE 2027

SEMENTE

QUANTIDADE 0123456 78910111213 14151617181920

• Para o trabalho com essa atividade, incentive os estudantes a contarem as quantidades de sementes nas ilustrações e a preencherem os quadrinhos antes de iniciar a construção do gráfico de barras. Durante esse processo, promova momentos de conversa que favoreçam a comparação entre as quantidades, fazendo perguntas como: “Qual semente aparece em maior quantidade?”; “Qual aparece em menor quantidade?”; “Quantos grãos de milho a mais há em relação aos grãos de feijão?”; “Se Marcelo quiser guardar a mesma quantidade de cada tipo de semente, quantas precisará juntar ou tirar de cada uma?”. Após a construção do gráfico, verifique se os estudantes percebem que é possível comparar as quantidades representadas pelo tamanho das barras horizontais pintadas por eles.

C ) VOCÊ CONHECE OUTRAS SEMENTES, DIFERENTES DESSAS, QUE TAMBÉM SÃO USADAS POR AGRICULTORES? CONVERSE COM OS COLEGAS SOBRE ISSO. FONTE DE PESQUISA: INFORMAÇÕES OBTIDAS POR CLEITON.

Unidades temáticas integradas estudante. Espera-se que eles citem sementes diferentes das já trabalhadas na atividade, como sementes de girassol, arroz, soja, trigo, cenoura e alface.

Resposta pessoal. A resposta depende das experiências pessoais de cada

Por meio da atividade 10, são mobilizadas habilidades de leitura e interpretação de dados apresentados em gráficos de colunas simples, conforme orienta a habilidade EF02MA20, permitindo aos estudantes explorar informações do cotidiano para desenvolver a capacidade de análise e comparação de dados. Além disso, ao explorar a contagem e o registro de quantida-

des de sementes cultivadas por um agricultor, a atividade também favorece a aproximação com aspectos culturais do campo, contribuindo para que reconheçam a origem dos alimentos e valorizem práticas sustentáveis ligadas à agricultura familiar, contribuindo para o desenvolvimento do tema contemporâneo transversal Educação ambiental

03/10/2025 08:55:23

11. O ÁBACO É UM INSTRUMENTO QUE PERMITE REPRESENTAR QUANTIDADES, REALIZAR CONTAGENS E EFETUAR CÁLCULOS.

A ) O NÚMERO 11 ESTÁ REPRESENTADO NO PRIMEIRO ÁBACO DA SEQUÊNCIA. ESCREVA OS OUTROS NÚMEROS QUE FALTAM.

Professor, professora: Confira mais informações sobre o uso do ábaco nas orientações ao professor.

DICA: NESTE ÁBACO, AS CONTAS SÃO AS PEÇAS DE COR LARANJA. ALÉM DISSO, D SIGNIFICA DEZENA E U SIGNIFICA UNIDADE

1 DEZENA E 1 UNIDADE

1 DEZENA E 2 UNIDADES

1 DEZENA E 3 UNIDADES

• A atividade 11 solicita aos estudantes que façam a representação de números por meio do ábaco de papel disponível no Material complementar do final do Livro do Estudante. Após o uso do material, oriente-os a guardá-lo para ser usado em outras unidades do volume.

1 DEZENA E UNIDADES

Resposta: 1 DEZENA E 6 UNIDADES; 16

Resposta: 12

1 DEZENA E 5 UNIDADES

Resposta: 15

Resposta: 13

1 DEZENA E 4 UNIDADES

Resposta: 14

Professor, professora: Oriente os estudantes a utilizar e guardar o ábaco e as contas utilizadas nesta atividade, pois esse material pode ser utilizado em outras unidades no decorrer deste volume.

1 DEZENA E UNIDADES

1 DEZENA E 9 UNIDADES 11

1 DEZENA E 8 UNIDADES

Resposta: 1 DEZENA E 7 UNIDADES; 17

Resposta: 18

Resposta: 19

B ) RECORTE O ÁBACO E AS CONTAS QUE ESTÃO NAS PÁGINAS

259 E 261 DO MATERIAL COMPLEMENTAR. DEPOIS, ESCOLHA ALGUNS DOS NÚMEROS DESSA SEQUÊNCIA PARA REPRESENTAR NO ÁBACO. POR FIM, PEÇA A UM COLEGA QUE IDENTIFIQUE ESSES NÚMEROS.

Resposta pessoal. A resposta depende dos números que os estudantes escolherem para representar.

AVALIANDO

Objetivo

Ler e escrever números de 11 a 19 com algarismos e por extenso.

03/10/2025 08:55:25

• A atividade 11 explora o sentido do tato, ao levar os estudantes a recortar o ábaco de papel usando as mãos, bem como o da visão, promovendo a inclusão de estudantes com NEE para uma aprendizagem multimodal que pode ser mais eficaz para alguns deles. Para esses estudantes, essa é uma boa oportunidade de promover uma aprendizagem multimodal, ou seja, que envolve diferentes sentidos – visão, tato, audição e movimento. Sempre que possível, incentive o manuseio do ábaco, a fim de que os estudantes percebam a troca de 10 unidades por uma dezena de maneira visual e concreta. Motive-os a verbalizar o que estão fazendo, por exemplo: “Coloquei 10 unidades, agora troco por uma dezena.”, para trabalhar também o sentido da audição.

• Outra possibilidade é construir um ábaco com material reciclável. Para isso, providencie os materiais necessários ou peça aos estudantes que os levem para a sala de aula. O ábaco pode ser montado de modo individual ou coletivo. Para a montagem, serão necessários: palitos de churrasco sem ponta; base de papelão para fixação das hastes; argolas de plástico ou outro material com furo no meio para ser usado como as bolinhas do ábaco; e caneta colorida para escrever na base a ordem correspondente de cada palito.

• Para complementar a atividade, use um ábaco e mostre para os estudantes como ficam alguns valores entre 0 e 19. Peça a eles que digam quais são os valores apresentados.

Estabelecer a relação entre a quantidade de elementos de 11 a 19, sua representação numérica e sua escrita por extenso.

Sugestão de intervenção

Ao final desse tópico, procure aplicar atividades com o intuito de avaliar a aprendizagem dos números de 11 a 19.

Proponha questões de contagem, providenciando materiais manuseáveis. Se possível, apresente aos estudantes o material dourado, para que eles o utilizem para contagens e se familiarizem com esse importante instrumento lúdico.

• A atividade 1 explora situações de agrupamento e organização de objetos, com base na cena em que um grupo de estudantes distribui lápis de cor em porta-lápis. Mesmo estando em processo de construção da contagem, eles podem analisar e comparar a quantidade de objetos por agrupamento, além de refletir sobre isso, identificando relações entre as cenas e estimando quantidades.

• Ao responder aos itens, os estudantes têm a oportunidade de usar diferentes estratégias para refletir sobre quantidades formadas por agrupamentos com quantidades iguais de objetos e sobre a ideia de sobra quando nem todos os recipientes são utilizados. Nesse tópico, o pré-requisito necessário é a capacidade de reconhecer e compreender quantidades, agrupamentos e trocas.

ATIVIDADE EXTRA

• Para complementar a atividade 1, proponha aos estudantes que fiquem em pé e se organizem em duplas com os colegas. Após a formação, questione: “Quantas duplas conseguimos formar?”. Em seguida, peça-lhes que troquem de dupla mais uma vez, agoracom colegas diferentes. Repita o processo novamente, sempre fazendo perguntas relacionadas à contagem das novas duplas formadas. Essa prática ajuda na compreensão dos agrupamentos e das variações que ocorrem com mudanças na quantidade total de participantes.

AGRUPAMENTOS E TROCAS

1. A PROFESSORA SOLICITOU A UM GRUPO DE ESTUDANTES QUE CONTASSE OS LÁPIS DE COR QUE ESTAVAM SOBRE A MESA. PARA AUXILIAR NA CONTAGEM, ELA TAMBÉM DEIXOU ALGUNS PORTA-LÁPIS.

ELES DECIDIRAM CONTAR OS LÁPIS FORMANDO GRUPOS DE LÁPIS NOS PORTA-LÁPIS, COMO INDICADO A SEGUIR.

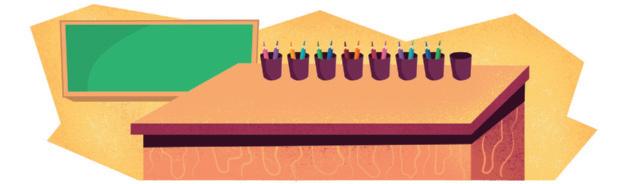
A ) QUANTOS LÁPIS FORAM AGRUPADOS EM CADA PORTA-LÁPIS?

LÁPIS.

Resposta: 2 LÁPIS.

B ) QUANTOS PORTA-LÁPIS ELES UTILIZARAM?

PORTA-LÁPIS.

Resposta: 7 PORTA-LÁPIS.

C ) ALGUM PORTA-LÁPIS NÃO FOI UTILIZADO?

Resposta: SIM.

D ) EM CASO AFIRMATIVO, QUANTOS PORTA-LÁPIS NÃO FORAM

USADOS? PORTA-LÁPIS.

Resposta: 1 PORTA-LÁPIS.

E ) QUANTOS LÁPIS DE COR HÁ AO TODO? LÁPIS.

Resposta: 14 LÁPIS.

AVALIANDO

Objetivo

Estabelecer a relação entre a quantidade de objetos agrupados, sua representação numérica e o uso de agrupamentos de objetos em quantidades iguais, para propiciar a autocompreensão e auxiliar na aprendizagem.

Sugestão de intervenção

Caso os estudantes apresentem dificuldades para compreender a ideia de agrupamentos iguais ou sobras, proponha a eles que manipulem objetos concretos, como lápis ou palitos

de sorvete, para formar agrupamentos desses materiais em recipientes. Incentive a contagem oral e a construção de registros por meio de tracinhos ou desenhos, valorizando essas formas de representação como parte do processo. Ao final, retome a cena com apoio do coletivo, propondo situações parecidas com diferentes materiais da sala de aula.

2. JUNTE-SE A UM COLEGA E RESOLVAM OS ITENS A SEGUIR. PARA ISSO, SEPAREM INICIALMENTE 12 LÁPIS DE COR.

A ) QUANTOS GRUPOS COM 3 LÁPIS CADA É POSSÍVEL FORMAR?

GRUPOS.

Resposta: 4 GRUPOS.

B ) QUANTOS GRUPOS COM 4 LÁPIS CADA É POSSÍVEL FORMAR?

GRUPOS.

Resposta: 3 GRUPOS.

C ) QUANTOS GRUPOS COM 6 LÁPIS CADA É POSSÍVEL FORMAR?

GRUPOS.

Resposta: 2 GRUPOS.

3. JOANA VAI GUARDAR OS SEUS BICHINHOS DE BRINQUEDO A SEGUIR EM CAIXAS COM 5 UNIDADES CADA.

A ) CONTORNE OS BRINQUEDOS FORMANDO GRUPOS DE 5 UNIDADES.

Resposta: Os estudantes devem contornar os brinquedos,

• A atividade 2 tem o objetivo de trabalhar, de modo prático e concreto, a ideia de agrupamento. Ao utilizar 12 lápis de cor, os estudantes são levados a manipular objetos concretos e visualizar a formação de grupos com quantidades diferentes, facilitando a compreensão dos conceitos matemáticos. Ao resolverem os itens A, B e C, eles são levados a perceber que é possível formar quatro grupos de três lápis, três grupos de quatro lápis e dois grupos de seis lápis, respectivamente.

• Além do conteúdo matemático, a atividade 2 também é importante para o desenvolvimento da cooperação e do respeito às ideias do colega de dupla e para a troca de estratégias e soluções.

• Durante a proposta da atividade 2, caminhe pela sala de aula e observe como os estudantes estão interagindo. Busque incentivar o diálogo entre eles e faça as intervenções necessárias.

B ) COM OS BRINQUEDOS APRESENTADOS NA IMAGEM, DE QUANTAS CAIXAS JOANA VAI PRECISAR? CAIXAS.

Resposta: 3 CAIXAS. da maneira que preferirem, formando 3 grupos com 5 unidades cada.

AVALIANDO

Objetivo

Motivar a contagem de objetos organizados em agrupamentos fixos de cinco elementos.

Sugestão de intervenção

Verifique se os estudantes compreendem que as caixas podem conter exatamente cinco brinquedos cada e se conseguem formar os dois grupos corretamente. Caso haja dificuldades, proponha-lhes manusear objetos concretos verbalizando suas estratégias de contagem, dizendo, por exemplo: “Já tenho cinco aqui, agora começo outro grupo...”.

BNCC

03/10/2025 08:55:30

A atividade 2, ao propor a interação entre pares de maneira cooperativa, trabalhando coletivamente a ideia de agrupamentos, favorece o raciocínio lógico e explora o espírito da investigação e a busca de soluções para problemas, de modo a identificar aspectos consensuais ou não em determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles, conforme descrito na Competência específica de Matemática 2 e na Competência específica de Matemática 8 da BNCC.

• A atividade 3 propõe aos estudantes que realizem agrupamentos de 5 em 5 com base no contexto de organização de brinquedos, permitindo o desenvolvimento do raciocínio multiplicativo de modo intuitivo, pois envolve a contagem de grupos com a mesma quantidade.

• A atividade 4 propõe aos estudantes uma situação contextualizada e próxima da realidade deles, ou seja, a participação em uma gincana em duplas. Por meio da observação da cena apresentada e da resolução dos itens propostos, eles são levados a refletir sobre o conceito de formação de duplas e a desenvolver habilidades relacionadas à contagem.

• Inicialmente, pergunte aos estudantes o que é uma gincana e como normalmente eles se organizam para participar. Em seguida, proponha-lhes que respondam ao item B, no qual devem contar o total de estudantes na cena. No item C, ao contornarem a imagem para a formação de duplas, os estudantes são motivados a desenvolver o conceito de pareamento, visualizando a divisão de uma quantidade par em grupos de dois elementos. O item D apresenta uma variação do problema, instigando o raciocínio da turma. Eles deverão concluir que: se dois estudantes não participarem da gincana, então restarão apenas oito, o que permite formar quatro duplas. No item E, organize uma roda de conversa, permitindo aos estudantes compartilharem suas vivências, assim há oportunidade de troca de experiências e desenvolvimento da oralidade.

ATIVIDADE EXTRA

Para complementar a atividade 4, proponha aos estudantes que fiquem em pé e se organizem em duplas com os colegas da sala de aula. Após a formação, questione: “Quantas duplas conseguimos formar?”. Em seguida, peça a eles que troquem de dupla mais uma vez, organizando-se com colegas diferentes. Repita o processo mais uma vez, sempre fazendo perguntas relacionadas à contagem das novas duplas formadas.

4. OS ESTUDANTES DE CERTA ESCOLA VÃO PARTICIPAR DE

UMA

GINCANA EM DUPLAS

DUPLAS: CONJUNTO DE PESSOAS, ANIMAIS OU OBJETOS ORGANIZADOS DE DUAS EM DUAS UNIDADES.

A ) QUANTOS ESTUDANTES APARECEM NA CENA?

Resposta: 10 ESTUDANTES.

ESTUDANTES.

B ) CONTORNE OS ESTUDANTES DA CENA FORMANDO DUPLAS.

Resposta: Os estudantes devem contornar as pessoas da cena, da maneira que preferirem, formando 5 grupos com 2 pessoas cada.

C ) QUANTAS DUPLAS FORAM FORMADAS? DUPLAS.

Resposta: 5 DUPLAS.

D ) SUPONDO QUE DOIS ESTUDANTES NÃO PARTICIPEM DA GINCANA, QUANTAS DUPLAS PODERIAM SER FORMADAS?

Resposta: 4 DUPLAS.

DUPLAS.

E ) VOCÊ JÁ PARTICIPOU DE ALGUMA GINCANA? COMENTE COM OS COLEGAS.

Resposta pessoal. Espera-se que os estudantes conversem entre si com base em suas experiências.

Essa prática ajuda na compreensão dos agrupamentos e das variações que ocorrem na quantidade total de participantes devido a mudanças.

5. NEUZA É COSTUREIRA E COMPROU OS BOTÕES A SEGUIR.

ELA UTILIZA 3 BOTÕES PARA CONFECCIONAR UMA BERMUDA.

A ) CONTORNE OS BOTÕES FORMANDO GRUPOS DE 3 BOTÕES EM CADA UM.

Resposta: Os estudantes devem contornar os botões, da

maneira que preferirem, formando 6 grupos com 3 botões cada.

Resposta: 6 BERMUDAS.

B ) QUANTAS BERMUDAS ELA VAI CONSEGUIR CONFECCIONAR COM ESSA QUANTIDADE DE BOTÕES? BERMUDAS.

6. RICARDO E MARIANA ESTÃO BRINCANDO COM UM JOGO DE FICHAS. NESSE JOGO, A TROCA DAS FICHAS OCORRE:

• TROCANDO 3 FICHAS POR UMA FICHA ;

• TROCANDO 4 FICHAS POR 1 FICHA

A ) MARIANA ESTÁ COM AS SEGUINTES FICHAS.

QUANTAS FICHAS AZUIS E AMARELAS MARIANA VAI RECEBER APÓS FAZER A TROCA?

Resposta: 2 FICHAS AZUIS E 3 FICHAS AMARELAS.

FICHAS AZUIS E FICHAS AMARELAS.

B ) RICARDO OBTEVE AS SEGUINTES FICHAS.

QUANTAS FICHAS AZUIS E AMARELAS RICARDO VAI RECEBER APÓS A TROCA?

Resposta: 3 FICHAS AZUIS E 2 FICHAS AMARELAS.

FICHAS AZUIS E FICHAS AMARELAS.

C ) NESSE JOGO, VENCE QUEM TIVER MAIS FICHAS AMARELAS. QUEM GANHOU ESSA PARTIDA?

Resposta: MARIANA.

03/10/2025 09:00:08

• A atividade 5 tem o objetivo de trabalhar com os estudantes o conceito de agrupamento por meio de uma situação do dia a dia. Primeiramente, leia o enunciado da atividade para a turma e destaque o contexto: Neuza é uma costureira que usa três botões para confeccionar cada bermuda. No item A , comente que eles podem organizar os grupos com três botões da maneira que preferirem. No item B, espera-se que os estudantes concluam que Neuza vai confeccionar seis bermudas, pois 18 dividido por 3 é igual a 6.

• Para complementar essa atividade, leve alguns botões para a sala de aula e proponha aos estudantes que façam os agrupamentos com material concreto. Também é possível realizá-la com outras quantidades de botões, a fim de que os estudantes aprimorem os conceitos estudados.

• A atividade 6 aborda uma situação lúdica que faz parte da realidade dos estudantes, pois envolve um jogo de fichas, no qual é preciso executar agrupamentos e trocas. Leia o enunciado para a turma e certifique-se de que compreenderam a regra do jogo: três fichas verdes são trocadas por uma ficha azul, e quatro fichas vermelhas, por uma ficha amarela. Providencie, antecipadamente, fichas das mesmas cores usadas na atividade e solicite que eles realizem as trocas em sala de aula, antes de resolverem a atividade, promovendo uma vivência da situação. Após efetuarem algumas trocas, oriente-os a resolver a atividade. Por fim, promova uma socialização das estratégias utilizadas, mostrando aos estudantes que há diferentes caminhos para chegar à resposta.

• A atividade 7 propõe contagem e agrupamento em contexto do cotidiano. Converse com os estudantes sobre o trabalho no campo e a comercialização de frutas. Pergunte se eles conhecem alguém que é agricultor, deixe-os compartilhar com os colegas suas experiências e acolha com respeito e atenção as contribuições de todos os que se manifestarem. Oriente-os a contar as maçãs com atenção e a usar estratégias pessoais para a realização dos agrupamentos, de quatro em quatro maçãs, no item A Caso perceba dificuldades, represente na lousa o primeiro agrupamento com eles, como exemplo. No item B, espera-se que os estudantes consigam perceber que Danilo vai precisar de quatro bandejas para embalar as 16 maçãs.

• Para complementar essa atividade, proponha aos estudantes que a realizem utilizando materiais concretos, como tampinhas, botões ou palitos de sorvete. Diga a eles que esses materiais representarão as maçãs. Oriente-os a separar 20 desses materiais em bandejas de quatro unidades cada. Pergunte quantas bandejas seriam necessárias nesse caso. Espera-se que consigam perceber que precisariam de cinco bandejas para embalar as 20 maçãs.

• Motive os estudantes a registrarem as novas situações, que também podem ser feitas por meio de desenhos. Pergunte a eles: “Se vocês tiverem 12 maçãs e precisarem agrupá-las de quatro em quatro, de quantas bandejas vão precisar?”.

7. DANILO É AGRICULTOR E PLANTA MAÇÃS PARA VENDER. VERIFIQUE AS MAÇÃS QUE ELE COLHEU EM CERTO DIA DA SEMANA.

AGRICULTOR: PESSOAS QUE TRABALHAM NO CAMPO CUIDANDO DA TERRA, DAS PLANTAÇÕES E DOS ANIMAIS PARA PRODUZIR OS ALIMENTOS QUE CONSUMIMOS.

A ) DEPOIS DE COLHER AS MAÇÃS, ELE AS ARMAZENA EM BANDEJAS COM 4 MAÇÃS EM CADA UMA. CONTORNE AS MAÇAS FORMADO GRUPOS DE 4 UNIDADES.

B ) QUANTAS BANDEJAS ELE VAI PRECISAR PARA EMBALAR ESSAS MAÇÃS?

Resposta: 4 BANDEJAS.

BANDEJAS.

PRODUÇÃO DE MAÇÃS NO BRASIL

A MAÇÃ É UMA FRUTA MUITO NUTRITIVA E SABOROSA, QUE TRAZ BENEFÍCIOS PARA A SAÚDE. GERALMENTE É CULTIVADA EM REGIÕES EM QUE O CLIMA É MAIS FRIO. NO BRASIL, A REGIÃO COM O CLIMA MAIS FAVORÁVEL PARA PLANTAÇÃO DESSA FRUTA É A REGIÃO SUL.

O ESTADO DE SANTA CATARINA, QUE ATUALMENTE É O MAIOR PRODUTOR BRASILEIRO DE MAÇÃS, ESTÁ LOCALIZADO NESSA REGIÃO.

7. A) Resposta: Os estudantes devem contornar as maçãs, da maneira que preferirem, formando 4 grupos com 4 unidades em cada.

TRABALHADOR REALIZANDO COLHEITA DE MAÇÃS EM MONTE ALEGRE DOS CAMPOS, NO RIO GRANDE DO SUL, EM 2025.

8. VAMOS FAZER BOLINHAS DE PAPEL. PARA ISSO, PEGUE UM PEQUENO PEDAÇO DE PAPEL E AMASSE COM AS MÃOS. DEPOIS, GIRE O PAPEL

NA PALMA DA MÃO PARA DEIXÁ-LO

COM O FORMATO DE UMA BOLINHA. FAÇA ESSE PROCESSO 12 VEZES.

BOLINHAS FEITAS DE PAPEL AMASSADO.

Resposta: 12 BOLINHAS.

A ) QUANTAS BOLINHAS DE PAPEL VOCÊ FEZ? BOLINHAS.

B ) QUANTOS GRUPOS COM 4 BOLINHAS CADA É POSSÍVEL FORMAR?

Resposta: 3 GRUPOS.

GRUPOS.

C ) QUANTOS GRUPOS COM 3 BOLINHAS CADA É POSSÍVEL FORMAR?

Resposta: 4 GRUPOS.

GRUPOS.

9. UM GRUPO COM 3 ESTUDANTES VAI SE REUNIR PARA BRINCAR COM UM JOGO. NA IMAGEM, ESTÃO REPRESENTADOS OS CARTÕES DESSE JOGO.

Professor, professora: Caso os estudantes tenham dificuldade para resolver o item B desta atividade, oriente-os a contornar os cartões que aparecem na imagem, formando grupos com 4 unidades, obtendo, assim, a resposta deste item.

Resposta: 14 CARTÕES.

A ) QUANTOS CARTÕES TEM ESSE JOGO? CARTÕES.

B ) PARA INICIAR A PARTIDA, CADA JOGADOR RECEBE 4 CARTÕES. DE ACORDO COM ESSA REGRA E A QUANTIDADE DE CARTÕES, QUANTOS ESTUDANTES DESSE GRUPO PODERÃO, NO MÁXIMO, JOGAR UMA PARTIDA?

Resposta: 3 ESTUDANTES.

ESTUDANTES.

C ) NO ITEM B, APÓS A DISTRIBUIÇÃO DOS CARTÕES AOS JOGADORES, VÃO SOBRAR CARTÕES SEM DISTRIBUIR?

Resposta: SIM.

Resposta: 2 CARTÕES.

D ) SE SIM, QUANTOS CARTÕES? CARTÕES.

• Após a atividade, proponha aos estudantes que realizem novos agrupamentos, por exemplo: grupos de duas, de seis ou de cinco bolinhas. Essa atividade pode ser desenvolvida em duplas a fim de promover a cooperação e a troca de estratégias entre eles.

• Na atividade 9, converse com os estudantes sobre jogos que utilizam cartões ou fichas e como normalmente esses itens são distribuídos entre os participantes. Depois, pergunte a eles quantos cartões esse jogo usa e deixe-os fazer a contagem, orientando-os a completar o

item A. No item B, os estudantes são motivados a aplicar a regra de distribuição, quatro cartões para cada jogador, a fim de descobrir quantos jogadores, no máximo, podem participar desse jogo. Portanto, farão uma divisão com base em agrupamento, com a ideia de que, para cada grupo de quatro cartões, temos um jogador. Espera-se que os estudantes concluam que três estudantes, no máximo, poderão participar do jogo.

• Nos itens C e D, os estudantes são levados a refletir se sobrarão cartões e, se sobrarem, quantos serão. Esse momento

• A atividade 8 solicita aos estudantes que façam bolinhas de papel. Desse modo, é explorado o sentido do tato na ação de amassar o papel com as mãos para formar as bolinhas, promovendo a inclusão de estudantes com NEE, além de contribuir para uma aprendizagem multimodal, criando uma experiência rica que pode ser mais eficaz para alguns estudantes.

• Para realizar a proposta da atividade 8, providencie, antecipadamente, pedaços de papel em quantidade suficiente para todos os estudantes. Explique a eles que vão trabalhar com bolinhas de papel para resolver a atividade. Oriente-os para que todos consigam fazer as 12 bolinhas. Esse momento é importante para o desenvolvimento da coordenação motora fina e da concentração.

• No item A, instrua-os a contar com atenção e a registrar a quantidade de bolinhas. No item B, eles devem formar grupos de quatro bolinhas. Verifique como farão os grupos e, caso seja necessário, esclareça possíveis dúvidas. Incentive-os a manipular as bolinhas formando os grupos com as próprias mãos, separando cada grupo que tiver quatro bolinhas. No item C, o desafio é conduzi-los a formar grupos de três bolinhas. Verifique se perceberam que com a mesma quantidade de bolinhas eles podem agrupá-las de maneiras diferentes.

03/10/2025 09:00:35

é importante para que percebam que nem sempre uma divisão será exata, podendo haver resto diferente de zero em alguns casos.

• Proponha aos estudantes que façam outras possibilidades de agrupamento, por exemplo, “Se cada participante recebesse dois cartões, sobrariam cartões sem distribuir?”, e peça-lhes que expliquem suas estratégias.

• A atividade 10 relaciona as unidades temáticas de Matemática Números e Probabilidade e estatística, ao levar os estudantes a identificarem a quantidade necessária de selos acumulados em uma campanha para trocarem por alguns produtos e, ainda, interpretarem informações expressas sobre os brindes em uma tabela.

• A atividade 10 apresenta uma boa oportunidade para desenvolver o raciocínio lógico e as habilidades de contagem em uma situação do dia a dia. No item A, os estudantes devem observar a tabela e analisar quais brindes podem ser adquiridos pela mãe de Joana com 8 selos, exigindo deles atenção à correspondência entre a quantidade de selos adquiridos e a quantidade de selos necessários para trocar pelos brindes. No item B, com base em 15 selos acumulados, os estudantes são motivados a calcular quantas taças podem ser trocadas, considerando que, para cada taça, são necessários quatro selos. Já no item C, eles devem calcular a quantidade de selos necessários para duas jarras. Verifique as estratégias usadas por eles. Caso seja necessário, disponibilize materiais concretos para fazerem a representação dessa situação. Comente com os estudantes que os materiais concretos, como tampinhas ou palitos de sorvete, representarão os selos, para que simulem as trocas.

• Para complementar essa atividade, outra sugestão seria fazer uma nova tabela, na lousa, com valores diferentes de quantidades de selos e propor aos estudantes que realizem outras trocas. Essa proposta pode ser feita em duplas ou pequenos grupos.

10. UM MERCADO FEZ UMA

CAMPANHA PARA PRESENTEAR

SEUS CLIENTES COM BRINDES, AO FAZER COMPRAS. A MÃE DE JOANA E O PAI DE MIGUEL

ADERIRAM A ESSA CAMPANHA. NA TABELA, ESTÃO INDICADOS

OS BRINDES OFERECIDOS

AOS CLIENTES CONFORME A QUANTIDADE DE SELOS QUE ELES ACUMULAM AO FAZER

SUAS COMPRAS.

INFOGRÁFICO CLICÁVEL: PRODUÇÃO, COMÉRCIO

E OFERTA DE SABONETES

Unidades temáticas integradas

BRINDES ADQUIRIDOS

NA TROCA DE SELOS

NOME QUANTIDADE DE SELOS

1 TAÇA 4 SELOS

1 TRAVESSA8 SELOS

1 JARRA 9 SELOS

2 PRATOS6 SELOS

FONTE DE PESQUISA:

DEPARTAMENTO DE COMPRAS DO MERCADO EM AGOSTO DE 2027.

2 COPOS5 SELOS

A ) A QUANTIDADE DE SELOS QUE A MÃE DE JOANA

ACUMULOU ESTÁ INDICADA A SEGUIR.

ELA PODE TROCAR ESSES SELOS POR QUAIS DOS BRINDES APRESENTADOS?

Professor, professora: Oriente os estudantes a contarem os selos, agrupando-os de 4 em 4 e verificarem a quantidade de taças que o pai de Miguel pode trocar.

Resposta: 2 copos, 2 pratos, 2 taças ou 1 travessa.

B ) CONTE OS SELOS QUE O PAI DE MIGUEL ACUMULOU E VERIFIQUE POR QUANTAS TAÇAS É POSSÍVEL TROCAR.

Resposta: 3 TAÇAS.

TAÇAS.

C ) QUANTOS SELOS SÃO NECESSÁRIOS ACUMULAR PARA TROCAR POR 2 JARRAS?

Resposta: 18 SELOS.

SELOS.

1. A) Resposta pessoal. Espera-se que os estudantes identifiquem na sala de

NÚMEROS ORDINAIS

aula o colega que está na primeira posição da fila, considerando a ordem do mais baixo para o mais alto, conforme combinado pelo grupo.

1. SORTEIEM, ENTRE VOCÊS, DEZ ESTUDANTES PARA QUE VENHAM À FRENTE DA SALA DE AULA. FORMEM UMA FILA DO MAIS BAIXO PARA O MAIS ALTO.

RESOLVA O QUE SE PEDE, DE ACORDO COM A FILA REPRESENTADA NA CENA.

A ) QUEM É O PRIMEIRO DA FILA?

B ) QUEM É O ÚLTIMO DA FILA?

C ) QUEM É O SEGUNDO DA FILA?

1. B) Resposta pessoal. Espera-se que os estudantes observem na sala de aula e indiquem o colega que ficou na última posição da fila, seguindo o critério de medida de altura estabelecido.

D ) QUE OUTRA REGRA PODE SER USADA PARA ORGANIZAR ESSES ESTUDANTES EM FILA?

EM UMA FILA, CADA ELEMENTO TEM O SEU LUGAR, E A POSIÇÃO DE CADA UM PODE SER INDICADA DA SEGUINTE MANEIRA.

1. C) Resposta pessoal. Espera-se que os estudantes reconheçam quem está logo após o primeiro, respeitando a ordem organizada pela turma.

ESCRITA DOS ORDINAIS ATÉ O 5O PRIMEIROSEGUNDOTERCEIROQUARTOQUINTO 1O 2O 3O 4O 5O

ESCRITA DOS ORDINAIS DO 6O EM DIANTE SEXTOSÉTIMOOITAVONONODÉCIMO...

1. D) Resposta pessoal. Espera-se que os estudantes sugiram outras maneiras de ordenação, como por idade, ordem alfabética dos nomes, mês de nascimento ou medida dos pés.

BNCC

As atividades desse tópico abordam números ordinais utilizando, em diferentes situações cotidianas, números naturais como indicadores de ordem. Assim, importantes aspectos da habilidade EF01MA01 são contemplados.

03/10/2025 09:00:42

• As atividades desse tópico introduzem os números ordinais, que são aqueles que indicam ordem. Se julgar conveniente, para que os estudantes não confundam ordinais com cardinais, destaque a semelhança entre a sonoridade das palavras ordinais e ordem. Nesse tópico o pré-requisito é a capacidade de diferenciar os números cardinais (um, dois, três, ...), que indicam quantidade, dos números ordinais (primeiro, segundo, terceiro, ...), que indicam posição.

• Explique aos estudantes que representamos um ordinal escrevendo a letra o com um traço subscrito na frente do numeral, como “1º” ou “2º”. Nos casos de frases em que as palavras são femininas, podemos trocar a letra o pela letra a, como “1ª vez” ou “3ª etapa”. Exercite essas representações com os estudantes antes de realizar as atividades desse tópico.

• Na atividade 1, ao perguntar qual outra regra pode ser usada para organizar os estudantes em fila, ouça os palpites e dê sugestões à turma, avaliando a compreensão da noção de ordem: “Poderíamos organizá-los de acordo com os nomes, em ordem alfabética?”; “E pela data de nascimento, do mais novo para o mais velho?”; “Nessas situações, as ordens dos estudantes seriam as mesmas ou diferentes?”.

• Utilize o contexto da atividade 1 para conversar com os estudantes sobre a importância das filas. Essa é uma prática comum em escolas, em situações como ao entrar na sala de aula, ao comprar itens na cantina ou no uso do banheiro. Ao respeitar essas normas, a convivência na escola será melhor para todos.

• Ao iniciar a atividade 2, trabalhe de modo que os estudantes não confundam a posição de chegada na corrida com o número que indica a faixa em que o corredor está.

• Ao trabalhar a atividade 3, auxilie os estudantes na escrita correta dos nomes das crianças. Se necessário, oriente-os a copiar as letras com as quais tiverem mais dificuldade.

• Aproveite o contexto da atividade 3 para conversar sobre como as filas facilitam a vida em comunidade, estabelecendo ordem para que todos possam realizar uma atividade sem prejuízo e sem que haja confusão.

2. A CENA MOSTRA A ORDEM DE CHEGADA DE UMA CORRIDA. NENHUM COMPETIDOR PASSA NA FRENTE DO OUTRO.

A ) CONTORNE O 1º COLOCADO DA CORRIDA.

Resposta: Os estudantes devem contornar a competidora RAFAELA

B ) MARQUE UM X NO 2º COLOCADO.

Resposta: Os estudantes devem marcar um X na competidora BRUNA.

C ) PINTE DE AZUL A CAMISETA DO 3º COLOCADO.

Resposta: Os estudantes devem pintar de azul a camiseta do competidor PEDRO

D ) PINTE DE VERDE A CAMISETA DO 4º COLOCADO.

Resposta: Os estudantes devem pintar de verde a camiseta do competidor FELIPE

E ) PINTE DE VERMELHO A CAMISETA DO 5º COLOCADO.

Resposta: Os estudantes devem pintar de vermelho a camiseta do competidor ARTUR

3. A CENA MOSTRA A FILA DA MERENDA ESCOLAR.

A ) QUEM É O 7º NA FILA?

Resposta: JOAQUIM.

B ) QUEM É O 10º NA FILA?

Resposta: CLÉBER.

C ) EM QUE LUGAR DA FILA ESTÁ VIVIANE?

Resposta: 8º

4. ENUMERE AS CENAS COM 2º, 3º E 4º , DE ACORDO COM A ORDEM DOS ACONTECIMENTOS.

Resposta: Os estudantes devem enumerar: B-4º; C-2º; D-3º

DESAFIO A MAIS

DICA: A PRIMEIRA CENA JÁ ESTÁ INDICADA.

ESCREVA NAS BANDEIRINHAS OS NÚMEROS ORDINAIS QUE

ESTÃO FALTANDO. Resposta:

AVALIANDO

Objetivo

• Identificar os ordinais do 1º ao 10º .

• Ler e escrever os ordinais do 1º ao 10º .

• Identificar a posição de um ordinal em uma sequência de até 10 elementos.

Sugestão de intervenção

Solicite aos estudantes que construam um quadro no caderno com a representação dos números ordinais do 1º ao 10º e a escrita deles por extenso, a fim de verificar se eles reconhecem a escrita e a pronúncia desses números. Se julgar

03/10/2025 09:00:50

conveniente, escreva esses números em um cartaz e o exponha na sala de aula.

BNCC

O Desafio a mais aborda uma sequência numérica que deve ser reconhecida, interpretada e complementada com elementos ausentes. Esse tipo de atividade é fundamental para desenvolver o raciocínio lógico, o reconhecimento de padrões e a fixação de relações numéricas. Com isso, contempla-se a habilidade EF01MA10

• A atividade 4 , além de abordar os números ordinais, exercita a capacidade de estruturar uma cena de acordo com sua ocorrência lógica, com começo, meio e fim. Verifique se os estudantes percebem a ordem correta, contando-lhes uma história ou pedindo a eles que comentem como é um passeio ao cinema.

• O Desafio a mais explora a sequência de números ordinais, do primeiro até o décimo, com o intuito de desenvolver nos estudantes a capacidade de reconhecer e ordenar corretamente posições em uma sequência. Oriente-os a observar a sequência formada pelas bandeirinhas e pergunte quais já estão preenchidas com números ordinais. Espera-se que eles digam: 1º , 2º e 3º. Em seguida, pergunte quais números ordinais estão faltando, a fim de verificar se conseguem identificar que, para completar a sequência, são necessários os números: 4º, 5º, 6º, 7º, 8º , 9º e 10º

• Caso os estudantes apresentem dificuldade ao completar a sequência dos números ordinais nesse desafio, faça uma retomada realizando a contagem dos números ordinais oralmente, usando uma fila como apoio visual. Alguns questionamentos também podem auxiliar, como: “Quem é o terceiro da fila?”; “Como é o nome da estudante que está logo após o que ocupa o sexto lugar?”, entre outras perguntas.

OBJETIVOS

• Reconhecer elementos que caracterizam um texto expositivo-argumentativo.

• Interpretar informações contidas no texto com leitura e ajuda do professor.

• Aperfeiçoar a compreensão de textos.

• Aprimorar a fluência em leitura oral.

• Respeitar a ordem de chegada em filas.

Orientações

Complementares

• Comente com os estudantes que o convívio social necessita de regras para evitar injustiças. Pessoas idosas, gestantes ou pessoas com deficiência, por exemplo, têm direito à fila preferencial, pois entende-se que têm menos condições físicas de esperar do que outras pessoas. Embora quem chegue primeiro tenha direito de ser atendido antes, pode haver situações em que outras pessoas precisem passar à frente. Ter a sensibilidade de perceber essas situações e a gentileza de ceder o lugar são exercícios de solidariedade e empatia.

A) Essa questão explora um texto expositivo-argumentativo. Ao ler a questão, reforce as características do texto. Espera-se que eles compreendam que o texto expõe situações que contrariam normas de convívio social.

BNCC

As atividades propostas nessa seção favorecem o desenvolvimento da Competência geral 9 da BNCC, bem como o tema contemporâneo transversal Vida familiar e social, pois enfatizam a importância do respeito às regras e entendimento de seus direitos.

ENTRE TEXTOS

Professor, professora: O assunto tratado nesta seção possibilita o trabalho com o tema contemporâneo transversal Vida familiar e social.

QUANDO PRECISAMOS ESPERAR EM FILA, NÃO DEVEMOS FAZER BAGUNÇA NEM PASSAR NA FRENTE DE OUTRA PESSOA. SE O SEU COLEGA CHEGAR ANTES DE VOCÊ EM UMA FILA, ELE MERECE SER ATENDIDO ANTES. DA MESMA MANEIRA, SE VOCÊ É O PRIMEIRO A CHEGAR, NÃO É JUSTO QUE OUTRA PESSOA PEGUE SEU LUGAR.

LEIA COM O PROFESSOR O TEXTO EXPOSITIVO-ARGUMENTATIVO A SEGUIR, RETIRADO DE UM LIVRO QUE ENSINA BOAS MANEIRAS. LUGARES DE TODOS

[...]

Professor, professora: Confira mais informações sobre esta seção nas orientações ao professor.

AFINAL, NOS LUGARES PÚBLICOS, TODOS TÊM QUE PERCEBER QUE EXISTEM OUTRAS PESSOAS E QUE SUAS AÇÕES VÃO TER INFLUÊNCIA SOBRE ELAS.

SERÁ QUE QUEM CONVERSA ALTO DURANTE UM FILME, JOGA LATA

NA RUA, BAGUNÇA A AULA OU TENTA FURAR FILA PERCEBE QUE ESTÁ PROVOCANDO NOS OUTROS SENTIMENTOS NEGATIVOS?

[...]

CUNHA, BEATRIZ MONTEIRO DA. MODOS E MANEIRAS SÃO PAULO: EVOLUIR, 2000. P. 101.

A ) QUAL É O ASSUNTO ABORDADO NESTA PÁGINA? CONVERSE COM SEUS COLEGAS SOBRE ISSO.

Resposta pessoal. Comentários nas orientações ao professor

EXPLORANDO O TEXTO

Orientações Complementares

B) Nessa questão, verifique se os estudantes reconhecem qual é o título do texto.

C) Verifique se os estudantes compreenderam o que o texto apresenta como atitudes inadequadas e pergunte a eles por que essas atitudes são consideradas assim. Deixe que eles expressem suas opiniões acerca do assunto.

D) Acolha as opiniões dos estudantes. Reforce que é importante manter o respeito e o cuidado ao falar com as pessoas em qualquer situação. Opiniões e direitos devem ser defendidos com argumentos e educação.

ALÉM DO TEXTO

Orientações Complementares

E) Deixe claro que, nessa atividade, apenas as crianças estão na fila esperando pelo brinquedo, e o adulto é um acompanhante.

F) Nesse item, verifique se os estudantes reconhecem os ordinais e a posição em que as crianças estão distribuídas na fila.

G) De modo semelhante ao item F, essa questão avalia a capacidade dos estudantes de nomear a posição de um elemento com base em instruções.

EXPLORANDO O TEXTO ALÉM DO TEXTO

B) Resposta: Os estudantes devem marcar um X na alternativa LUGARES DE TODOS

B ) MARQUE UM X NA ALTERNATIVA QUE APRESENTA O TÍTULO DO TEXTO CITADO.

C) Resposta pessoal. Incentive os estudantes a expressarem suas opiniões e escreva algumas delas na lousa, com ajuda deles.

MODOS E MANEIRAS.

LUGARES DE TODOS.

D) Resposta pessoal. Espera-se que os estudantes comentem que a pessoa que fura a fila desperta nos outros um sentimento de raiva e provocação.

C ) NO TEXTO, A AUTORA QUESTIONA ALGUMAS ATITUDES QUE NÃO SÃO BOAS MANEIRAS DURANTE UM FILME, NA RUA, NA AULA OU EM UMA FILA. COMO DEVEMOS AGIR PARA QUE ESSAS ATITUDES SE TORNEM BOAS? CONVERSE COM O PROFESSOR E OS COLEGAS SOBRE ISSO.

D ) IMAGINE QUE UMA PESSOA TENTA “FURAR” UMA FILA EM QUE VOCÊ ESTÁ. O QUE VOCÊ DIRIA A ESSA PESSOA?

I. Resposta pessoal. Espera-se que os estudantes compreendam que, ao ocupar a última posição da fila, devem manter-se calmos, respeitar os colegas e esperar com paciência.

E ) QUANTAS CRIANÇAS ESTÃO ESPERANDO NA FILA?

Resposta: Oito crianças.

F ) NESTA CENA, QUAL É A COR DO CABELO DA TERCEIRA CRIANÇA DA FILA?

Resposta: Marrom.

G ) QUE POSIÇÃO A CRIANÇA DE ÓCULOS OCUPA NA FILA?

Resposta: 5ª posição.

H ) DESCREVA A CRIANÇA QUE OCUPA A 6ª POSIÇÃO DA FILA.

I ) SE VOCÊ FOR O ÚLTIMO DA FILA, COMO DEVE SE COMPORTAR?

Resposta pessoal. Espera-se que os estudantes observem a imagem da fila e descrevam com atenção as características da criança na 6ª posição, como cor da roupa, expressão e acessórios.

J ) DIGA UMA PALAVRA RELACIONADA AO BOM COMPORTAMENTO EM UMA FILA

DEPOIS, COMPARTILHE ESSA PALAVRA COM UM COLEGA.

Resposta pessoal. Espera-se que os estudantes pensem em palavras relacionadas ao bom comportamento em uma fila, como esperar, ajudar, acolher, cooperar, entre outras.

CONCLUSÃO

Acompanhar o desenvolvimento dos estudantes é fundamental para um ensino bem-sucedido. Ao longo da unidade, foram propostas diversas maneiras de avaliar a aprendizagem da turma. A fim de efetuar um monitoramento mais abrangente e organizado, registre nos relatórios individuais ou nas fichas de avaliação o desempenho de cada estudante, levando em consideração suas particularidades. Um modelo desse tipo de ficha pode ser encontrado na página XIII deste Manual do Professor Assim, é possível acompanhar as trajetórias individuais de aprendizagem, incluindo os avanços e os pontos de dificuldade a

serem sanados.

03/10/2025 09:00:57

Esse método é de grande importância para que seja possível repensar estratégias em sala de aula, tornando as ações pedagógicas cada vez mais eficazes.

A conclusão da unidade é o momento de avaliar se os objetivos por ela propostos foram alcançados. Para esse diagnóstico, apresentamos no final deste Manual do Professor algumas possibilidades de avaliação formativa e intervenção que permitem auxiliar na recomposição da aprendizagem, caso os estudantes não tenham atingido os resultados esperados.

H) O objetivo desse item é desenvolver a capacidade de produção escrita por meio da descrição dos atributos que os estudantes conseguem perceber na imagem.

I) Verifique se os estudantes entendem que, de modo geral, devem obedecer à ordem de chegada, além de aguardar a vez de quem estiver na sua frente. Caso aconteça algo extraordinário que imponha grande necessidade de ser atendido antes, é importante conversar e verificar se as pessoas podem ceder o lugar, respeitando a possibilidade de uma resposta negativa.

J) Ao trabalhar esse item, incentive os estudantes a se expressarem, promovendo um momento de troca de ideias e de desenvolvimento de vocabulário, além de exercitar a autonomia deles e a comunicação.

Sugestão de Desafio

Marina tem cinco brinquedos: elefante, carrinho, boneca, dinossauro e robô.

Descubra a ordem em que ela colocou cada brinquedo, com base nas dicas, e escreva no caderno os nomes de acordo com essa ordem.

Dicas:

• O dinossauro está em 3º lugar.

• O robô está logo depois da boneca.

• A boneca está em 1º lugar.

• O elefante está entre o dinossauro e o carrinho.

• O carrinho está em último lugar.

Resposta

1º: Boneca; 2º: Robô; 3º: Dinossauro; 4º: Elefante; 5º: Carrinho.

OBJETIVOS DA UNIDADE

• Identificar e associar figuras geométricas espaciais a objetos do dia a dia.

• Reconhecer cone, cilindro, esfera, cubo e bloco retangular ou paralelepípedo retângulo.

• Agrupar objetos familiares com base em seus formatos.

INTRODUÇÃO E

JUSTIFICATIVA

Nesta unidade, os estudantes têm um primeiro contato, no volume, com figuras geométricas espaciais, como cubo, bloco retangular ou paralelepípedo retângulo, esfera, cone e cilindro, para que eles reconheçam objetos do cotidiano que lembrem essas figuras geométricas, de modo a ajudá-los a absorver com naturalidade os conceitos abstratos da Geometria. A associação com objetos do cotidiano é fundamental para os estudantes se familiarizarem com as figuras geométricas e estejam preparados para classificações mais rigorosas apresentadas em anos posteriores, o que justifica esse trabalho. Assim, diversas atividades pedem a eles que agrupem objetos em categorias, com base no formato deles e em comparações, o que aguça o reconhecimento de relações e padrões. A unidade incentiva a manipulação de objetos, a comparação de formatos e a construção de cubos e blocos retangulares por meio de moldes adequados, visando desenvolver observação, experimentação e formulação de raciocínios.

Habilidades da BNCC trabalhadas na unidade: EF01MA09 e EF01MA13

UNIDADE2 FIGURAS GEOMÉTRICAS ESPACIAIS

AQUÁRIO COM CORAIS E PEIXES TROPICAIS.

SUGESTÃO DE ESTRATÉGIA INICIAL

Providencie ou peça aos estudantes que levem para a sala de aula um ou dois objetos com diferentes formatos, como blocos lógicos ou embalagens vazias de produtos, a fim de que os apresentem para os colegas. Em seguida, com a ajuda deles, agrupe os objetos com formatos parecidos. Por exemplo, os objetos com formato de pirâmide, os de formato arredondado, os de formato cúbico, entre outros. Explore as características e as semelhanças entre os objetos que foram agrupados. Por fim, organize e mantenha-os na sala de aula, de maneira que seja fácil manuseá-los durante toda a unidade.

• Ao trabalhar as páginas de abertura desta unidade, comente a utilização de aquários como decoração, exposição ou como um recurso para preservação de espécies ameaçadas. Explique-lhes ao observar a redução na quantidade de uma ou mais espécies, os biólogos passam a criar exemplares em aquários, a fim de preservá-los, protegendo-os da poluição, da pesca e de acontecimentos naturais, evitando, assim, sua extinção. Questione se algum estudante possui aquário em casa e se ele sabe quais são os cuidados envolvidos em sua manutenção.

1 e 2. Respostas pessoais. Comentários nas orientações ao professor

O FORMATO DO AQUÁRIO

MENOR LEMBRA QUAIS

OBJETOS QUE VOCÊ CONHECE?

QUE OUTRO FORMATO O AQUÁRIO PODERIA TER?

DESCREVA ESSE FORMATO PARA UM COLEGA E DEPOIS FAÇA UM DESENHO QUE O REPRESENTE NO CADERNO.

ANALISE AS FIGURAS E, EM SEGUIDA, CONTORNE A QUE É PARECIDA COM O AQUÁRIO DA IMAGEM DESTACADA.

3. Resposta: Os estudantes devem contornar a figura E

03/10/2025 09:03:34

• Oriente os estudantes a responderem às questões propostas. Na questão 1, incentive-os a analisar os detalhes do formato do aquário e a pensar em objetos que tenham essas mesmas características, como uma caixa de sapatos ou uma embalagem de gelatina, verbalizando seu raciocínio a fim de mostrar seus conhecimentos prévios.

• Na questão 2, se possível, leve para a sala de aula um aquário pequeno em formato de paralelepípedo, coloque sobre uma mesa e peça aos estudantes que o analisem de diferentes posições, falando de cada uma delas. A atividade fica mais interessante se houver elementos dentro do aquário, pois os estudantes podem descrevê-los com base em diferentes perspectivas. Lembre-se de questioná-los sobre a vista superior, sem mencioná-la formalmente. Para isso, use as expressões “observe de cima” ou “contemple o aquário de cima para baixo”. Oriente-os a falar de quantas maneiras o aquário pode ser apreciado. Acolha com atenção e respeito as respostas de todos que quiserem se manifestar, garantindo que estejam engajados na atividade. Espera-se que eles concluam que é possível apreciar esse objeto pelos lados e de cima. Além disso, se for suspenso acima da altura deles, pode ser apreciado por baixo também.

• Na atividade 3, verifique se os estudantes reconhecem as outras figuras não contornadas e se são capazes de nomear algumas delas. Esse reconhecimento pode apontar os conhecimentos prévios deles, dando pistas a respeito da condução no planejamento das aulas seguintes.

1. 2.

AQUÁRIO COM PEIXES.

A. C. E.

B. D.

• As atividades desta unidade exploram conceitos básicos da Geometria espacial. Procure sempre associá-los com objetos do dia a dia dos estudantes e incentive a manipulação deles, a fim de favorecer a apreciação, a curiosidade, a identificação de padrões e a formulação de raciocínios que levem à compreensão dos conteúdos. A capacidade de associação e de identificar padrões são pré-requisitos necessários para a compreensão desse tópico.

• Ao iniciar a atividade 1 , peça à turma, primeiro, que identifique quais são os objetos no quarto de Pedro. Verifique se os estudantes são capazes de reconhecer e nomear todos os objetos. Peça que citem quais objetos, incluindo brinquedos e móveis, existem no quarto deles. Com isso, envolva-os na recordação de objetos do cotidiano para que as figuras geométricas sejam absorvidas com naturalidade e associadas a esses objetos. Finalize solicitando que eles, com as próprias palavras, expliquem a diferença entre o cubo e a esfera, destacando características de cada uma dessas figuras. O propósito dessa intervenção é incentivar a apreciação e a construção de conceitos, bem como a comunicação verbal, portanto não é necessário que todas as características sejam discutidas. O importante é que os estudantes, por si mesmos, façam verificações e sejam capazes de expressar as próprias constatações. Espera-se que digam que a esfera é redonda, enquanto o cubo não, e que o cubo tem superfícies planas, ao passo que a esfera não.

CONHECENDO FIGURAS GEOMÉTRICAS ESPACIAIS

1. PEDRO ESTÁ BRINCANDO EM SEU QUARTO.

NO QUARTO DE PEDRO, HÁ OBJETOS QUE LEMBRAM FIGURAS

GEOMÉTRICAS ESPACIAIS

ANALISE ALGUMAS DELAS.

A ) CONTORNE OS OBJETOS DO QUARTO DE PEDRO QUE LEMBRAM O CUBO.

Resposta: Os estudantes devem contornar os blocos alfabéticos e o cubo de madeira cúbico.

B ) MARQUE UM X NOS OBJETOS QUE LEMBRAM A ESFERA. CUBO. ESFERA.

Resposta: Os estudantes devem marcar um X na bola de basquetebol e na bola de futebol.

• Com base na imagem e nos conceitos recém-adquiridos de cubo e esfera, peça à turma que cite outros objetos conhecidos e parecidos com cubos e esferas. Caso não se lembrem de objetos com essa característica, cite alguns e peça a eles que digam se esses objetos se assemelham mais com um cubo, uma esfera ou se são completamente diferentes dos dois.

As atividades desta unidade nomeiam figuras geométricas e as associam a objetos do dia a dia, além de incentivar os estudantes a observarem, manipularem e organizarem objetos com base em suas características físicas, com base nas figuras geométricas espaciais estudadas. Assim, contemplam-se importantes aspectos das habilidades EF01MA09 e EF01MA13

BNCC

2. OBSERVE NOVAMENTE O QUARTO DE PEDRO. DEPOIS, RELACIONE OS OBJETOS A SEGUIR LIGANDO OS QUE TÊM FORMATOS PARECIDOS.

Resposta: Os estudantes devem relacionar: A-2; B-4; C-5; D-1; E-3.

A. BLOCO DE MADEIRA CÚBICO.

C. TORRE DE PEÇAS COLORIDAS.

D. BOLA DE FUTEBOL.

E. BLOCO DE MADEIRA RETANGULAR.

A atividade 2 instiga a percepção de que existem similaridades entre atributos de diferentes objetos. Com isso, desenvolve-se nos estudantes a capacidade de organizar e ordenar objetos com base em seus formatos, despertando a abstração necessária para poder compreender as figuras geométricas. Nesse sentido, verifica-se a abordagem da habilidade EF01MA09

DE BASQUETEBOL.

DE MADEIRA CILÍNDRICO.

DE ANIVERSÁRIO.

03/10/2025 09:03:41

• A atividade 2 complementa as ideias trabalhadas na atividade 1, reforçando a associação entre figuras geométricas espaciais e objetos familiares do mundo físico. Contudo, na atividade 2, não se exige um reconhecimento das figuras geométricas em si, e sim uma comparação entre diferentes objetos com base em seus formatos. Para tirar melhor proveito da atividade, providencie objetos com formatos similares aos das imagens para que sejam manipulados pelos estudantes.

• Após realizar a atividade, peça aos estudantes que citem pelo menos mais um objeto que eles conheçam cujo formato lembre cada um dos pares de figuras ligadas entre si.

• A fim de avaliar possíveis conhecimentos prévios dos estudantes, pergunte se eles sabem o nome das figuras geométricas com as quais aqueles objetos se parecem. Nesse momento, ainda não se espera que eles saibam nomear cones e cilindros, por exemplo, mas fazer a pergunta pode ser útil para mensurar o alcance dos conhecimentos da turma.

• Para ajudar a desenvolver o raciocínio lógico matemático e facilitar o acesso dos estudantes com deficiência visual à linguagem matemática, separe alguns objetos concretos com formato das figuras geométricas espaciais e peça que explorem por meio do sentido tátil. Em seguida, por meio de relatos orais, apresente as características desses objetos. A representação concreta de alguns dos formatos sugeridos, que podem ser tocados e apreciados pelos estudantes com dificuldades, possibilita maior contextualização e assimilação do conteúdo.

BNCC

1. BOLA

5. CHAPÉU

3. CAIXA DE PRESENTE.

B. TAMBOR.

2. BLOCO ALFABÉTICO.

4. BLOCO

• Na atividade 3 , mantenha a abordagem sugerida em atividades anteriores, fazendo comparações entre cada uma das figuras geométricas apresentadas com objetos do cotidiano. Tais comparações facilitam a absorção e até mesmo a memorização do conteúdo.

• Verifique se os estudantes percebem, na atividade 3, que o objeto do item A é um paralelepípedo. Essa dificuldade pode surgir devido ao formato das faces dele, que são mais estreitas ou mais largas do que as faces da figura geométrica espacial colocada na atividade como referência. Se os estudantes tiverem dificuldade nessa associação, apresente-lhes outras embalagens em formato de paralelepípedo cujas dimensões sejam diferentes e deixe que façam comparações entre elas para tirarem suas conclusões, verbalizando o raciocínio e trocando ideias com os colegas.

• Ao abordar a atividade 4, pergunte se alguém já brincou com peças similares às da imagem. Se possível, providencie brinquedos parecidos com o da imagem e permita que eles se reúnam em pequenos grupos para brincar. Ao longo da brincadeira, caminhe pela sala de aula, instruindo-os a identificar o formato de cada peça.

• Além das habilidades referentes à Geometria espacial, a atividade 4 explora habilidades de contagem, já trabalhadas na unidade anterior. Caso a turma ainda apresente dificuldade nesse aspecto, retome atividades anteriores, procurando meios alternativos de expor o assunto.

3. OBSERVE AS FIGURAS GEOMÉTRICAS ESPACIAIS A SEGUIR.

ESFERA.

BLOCO RETANGULAR OU PARALELEPÍPEDO RETÂNGULO.

PINTE CADA OBJETO COM A COR DA FIGURA GEOMÉTRICA

ESPACIAL QUE ELE LEMBRA.

Resposta: Os estudantes devem pintar o objeto A de vermelho; o objeto B de azul; o objeto C de amarelo; o objeto D de laranja; o objeto E de verde.

PEGA-VARETAS

4. O TREM FOI CONSTRUÍDO COM

PEÇAS COLORIDAS.

COMPLETE A FRASE COM OS NÚMEROS ADEQUADOS.

NO TREM, HÁ PEÇAS QUE LEMBRAM CUBOS E PEÇAS QUE LEMBRAM CONES.

Resposta: NO TREM, HÁ 4 PEÇAS QUE LEMBRAM CUBOS E 2 PEÇAS QUE LEMBRAM CONES.

• Mantenha a abordagem sugerida em atividades anteriores para ajudar a desenvolver o raciocínio lógico-matemático e facilitar o acesso dos estudantes com deficiência visual à linguagem matemática. Separe alguns objetos concretos com formato das figuras geométricas espaciais e peça que explorem por meio do sentido tátil. Em seguida, por meio de relatos orais, apresente as características desses objetos. A representação concreta de alguns dos formatos sugeridos, sendo os objetos tocados e apreciados pelos estudantes com dificuldades, possibilita maior contextualização e assimilação do conteúdo também por parte de estudantes com alguns transtornos, como TEA e TDAH.

BNCC

A atividade 3 propõe comparação entre objetos que são comuns à realidade dos estudantes e figuras geométricas espaciais. Assim, contemplam-se importantes aspectos da habilidade EF01MA13

09:03:45

B. C.

D. E.

CONE. CILINDRO. CUBO.

5. CONTORNE O NOME DA FIGURA GEOMÉTRICA ESPACIAL QUE LEMBRA O FORMATO DE CADA OBJETO.

Resposta: A. Os estudantes devem contornar a palavra CUBO. B. Os estudantes devem contornar a palavra CILINDRO.

IMAGENS SEM PROPORÇÃO ENTRE SI.

A. B.

DADOS.

CUBO ESFERA

LATA COM MILHO.

CONE CILINDRO

6. ROBERTA CONSTRUIU UMA BONECA. ALGUMAS PEÇAS USADAS POR ELA LEMBRAM FIGURAS GEOMÉTRICAS ESPACIAIS QUE ESTÃO REPRESENTADAS A SEGUIR.

EM CADA ITEM, INDIQUE QUANTAS PEÇAS PARECIDAS COM A FIGURA ELA USOU.

Resposta: A. nenhuma; B. nenhuma; C. 1; D. nenhuma; E. 5.

ATIVIDADE EXTRA

Antes do trabalho com esta página, proponha uma atividade usando imagens impressas e objetos variados, cujo formato lembre figuras geométricas espaciais. Algumas sugestões: cubo: dado, caixa de presente; paralelepípedo retângulo: caixa de sapato, caixa de creme dental; cilindro: latinha de refrigerante, rolha; cone: chapéu de festa de aniversário, funil; esfera: bola de futebol, bolinha de gude. Apresente aos estudantes cada um dos objetos que você levou para a sala de aula. Na sequência, diga o nome de uma figura geométrica espacial e peça a eles

03/10/2025 09:03:46

que verifiquem se algum dos objetos se parece com essa figura geométrica e, se houver, que o separem dos outros objetos e aguardem. Verifique como reagem a essa atividade e, para ajudar, lembre-os das características da figura geométrica em questão. Peça a cada estudante que mostre se encontrou ou não a figura geométrica sugerida. Caso eles não tenham acertado, relembre as características da figura geométrica e ajude-os a identificar o objeto.

• A atividade 5 é destinada a avaliar se os estudantes absorveram os conceitos trabalhados em páginas anteriores. Certifique-se de que eles não confundam o cilindro com outras figuras geométricas similares, como o cone. Caso a turma apresente dificuldade, retome os conceitos buscando abordagens que sejam mais eficazes para as necessidades de cada estudante.

• Verifique a possibilidade de propor à turma a construção, na prática, de um boneco como o da atividade 6. A atividade pode ser feita em grupo ou individualmente, na sala de aula ou como tarefa de casa. Se julgar conveniente, proponha uma organização em roda, diferente das opções tradicionais de agrupamentos, a fim de mudar a rotina dos estudantes e promover interação de modo diferenciado. Atividades práticas que envolvem o manuseio de objetos são importantes para que os estudantes desenvolvam a criatividade e o senso de experimentação.

• Na atividade 7, os estudantes terão a oportunidade de realizar uma atividade investigativa, associando objetos do cotidiano às figuras geométricas espaciais. Para isso, verifique previamente os locais onde há objetos que lembrem as figuras geométricas apresentadas. Conduza o passeio pela escola, pedindo aos estudantes que identifiquem ao redor objetos com os formatos parecidos. Se necessário, auxilie-os no registro dos objetos identificados, sugerindo que façam desenhos e/ou anotem algumas características, como cor e forma.

• Ao constatar que um objeto com formato parecido não foi notado, questione-os sobre as características desse objeto, a fim de que façam a associação desejada.

• Ao final da atividade, converse com os estudantes sobre as dúvidas que surgirem, pois é possível que identifiquem algum objeto de formato ainda não estudado, como a pirâmide.

7. JUNTE-SE A UM COLEGA E FAÇAM UM PASSEIO PELA ESCOLA. DEPOIS, IDENTIFIQUEM OBJETOS QUE SE PARECEM COM AS FIGURAS GEOMÉTRICAS ESPACIAIS APRESENTADAS A SEGUIR.

A ) QUAL DESSAS FIGURAS GEOMÉTRICAS ESPACIAIS NÃO FOI

IDENTIFICADA EM NENHUM FORMATO DOS OBJETOS DA ESCOLA?

Resposta pessoal. A resposta depende dos objetos que serão encontrados na escola.

B ) DOS OBJETOS CITADOS NO ITEM ANTERIOR, QUAIS SE PARECEM COM:

• O CUBO?

Resposta pessoal. Sugestões de resposta: cubo mágico cúbico; caixa de papelão com formato cúbico.

• O PARALELEPÍPEDO?

Resposta pessoal. Sugestões de resposta: caixa de papelão em formato de paralelepípedo; tijolo.

• O CILINDRO?

Resposta pessoal. Sugestões de resposta: pilha comum; lata de tinta.

• O CONE?

Resposta pessoal. Sugestões de resposta: cone de sinalização; chapéu de aniversário.

• A ESFERA?

Resposta pessoal. Sugestões de resposta: bola de basquetebol; bola de voleibol.

C ) TRAGA DE SUA CASA PARA A SALA DE AULA UM OBJETO QUE LEMBRA UMA DAS FIGURAS GEOMÉTRICAS ESPACIAIS APRESENTADAS. QUAL OBJETO VOCÊ ESCOLHEU?

Resposta pessoal. Espera-se que os estudantes relacionem os objetos coletados a algumas das figuras geométricas espaciais apresentadas nesta página.

Ao propor a interação com seus pares de forma cooperativa, trabalhando coletivamente em uma busca no ambiente escolar por objetos do mundo físico que têm formato parecido com as figuras geométricas espaciais, essa atividade possibilita o desenvolvimento do raciocínio lógico, explora o senso de investigação e a busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles, conforme descrito na Competência

específica de Matemática 2 e na Competência específica de Matemática 8 da BNCC.

Ao trabalhar identificação, organização e registro de figuras geométricas espaciais, essa atividade contempla aspectos importantes da habilidade EF01MA09 da BNCC. Ao relacionar figuras geométricas espaciais (cubo, bloco retangular, cilindro, cone e esfera) a objetos familiares do mundo físico, também contempla a habilidade EF01MA13

BNCC

8. ALGUMAS FIGURAS GEOMÉTRICAS ESPACIAIS ESTÃO APRESENTADAS A SEGUIR.

USANDO MASSINHA DE MODELAR, HEITOR CONSTRUIU OS OBJETOS A SEGUIR, QUE LEMBRAM ALGUMAS DESSAS FIGURAS GEOMÉTRICAS ESPACIAIS.

INFOGRÁFICO CLICÁVEL: GEOMETRIA NAS EDIFICAÇÕES

A ) MARQUE UM X NO OBJETO QUE TEM O FORMATO DE CILINDRO.

• A atividade 8 explora as figuras geométricas espaciais por meio de construção e manipulação. Para isso, providencie massinha de modelar suficiente para toda a turma e leve modelos desses formatos geométricos para que eles possam explorar por meio de diferentes sentidos (visão, audição e tato, por exemplo), promovendo a inclusão de estudantes com NEE, além de contribuir para uma aprendizagem multimodal que pode ser mais eficaz para alguns estudantes. Se necessário, faça um relato verbal de algumas características desses sólidos.

• Após realizarem as construções e manipulações, faça questionamentos para a turma sobre o que diferencia um formato do outro. Aproveite para investigar se os estudantes já estão familiarizados com nomenclatura e se não confundem os nomes.

Resposta: Os estudantes devem marcar um X no objeto 2. se que os estudantes construam objetos com formato de cubo, de paralelepípedo, de cilindro, de cone e de esfera.

Resposta: Espera-

B ) JUNTE-SE A UM COLEGA E CONSTRUAM, COM MASSINHA DE MODELAR, OBJETOS QUE LEMBREM AS FIGURAS GEOMÉTRICAS ESPACIAIS APRESENTADAS.

Ao propor a interação com seus pares e a construção, o manuseio e a identificação dos atributos dos objetos com formato de figuras geométricas espaciais, exercitando o raciocínio lógico e o espírito da investigação, essa atividade contempla aspectos importantes da habilidade EF01MA09 da BNCC. Além de contribuir para o desenvolvimento da Competência específica de Matemática 2 e da Competência específica de Matemática 8 da BNCC.

03/10/2025 09:05:48

BNCC

• A atividade 9 promove a construção de um cubo e de um bloco retangular com base em moldes. A familiarização com moldes de figuras espaciais é importante para que os estudantes desde já adquiram noções de planificação, de modo que, em anos posteriores, tenham mais facilidade para entender as relações da Geometria espacial e da Geometria plana. Auxilie-os na montagem dos moldes. Se julgar necessário, proponha que a montagem seja feita como tarefa de casa, a fim de que tenham o auxílio de algum familiar ou responsável na execução do trabalho.

• Apesar de ser essencial o desenvolvimento da motricidade, é importante que o professor esteja atento às dificuldades apresentadas na manipulação de objetos que podem oferecer riscos à integridade física dos estudantes. Por esse motivo, acompanhe com atenção os movimentos com a tesoura e, se necessário, assuma o controle da ação ou oriente devidamente os cortes que eles fizerem, a fim de que o façam em segurança. Garanta também que eles usem tesouras com pontas arredondadas, minimizando, assim, os riscos da atividade. Se houver algum estudante com mobilidade reduzida e que manifeste necessidade de ajuda, ofereça-se para auxiliar.

• Na etapa de fazer desenhos, supervisione as produções da turma, verificando se os objetos escolhidos de fato se assemelham ao cubo e ao bloco retangular. Permita aos estudantes que troquem impressões entre si e auxilie nas dificuldades, instruindo-os para que os desenhos sejam feitos de maneira que seja possível identificar o formato.

• Para facilitar o desenvolvimento da atividade a estudantes com deficiência visual, oferte-lhes um

EXPERIMENTE

9. COM A AJUDA DO PROFESSOR, RECORTE E MONTE OS DOIS MOLDES DAS PÁGINAS 263 E 265 DO MATERIAL

COMPLEMENTAR

VERIFIQUE O AMBIENTE AO SEU REDOR. DEPOIS, DESENHE UM OBJETO QUE LEMBRE CADA FIGURA A SEGUIR.

Resposta pessoal. Espera-se que os estudantes associem o formato do cubo e do paralelepípedo a objetos do dia a dia e façam os desenhos correspondentes.

molde de cada vez, permitindo a apreciação por meio do tato. Explore com eles os objetos que lembram cada uma dessas figuras geométricas espaciais por meio do tato. Passe as mãos dos estudantes no contorno dos objetos, para que percebam o desenho, possibilitando a contextualização e a assimilação da atividade proposta.

REFERÊNCIAS COMPLEMENTARES

BAIRRAL, Marcelo; BRAVO, George; IZAR, Soraya (Org.). Retratos de experiências para visualização em geometria [recurso eletrônico]. Seropédica: EDUR, 2022.

Essa publicação reúne experiências de professores atuantes em laboratórios de práticas e vivências envolvendo a Geometria, que podem auxiliar outros docentes no processo de ensino e aprendizagem e no desenvolvimento da visualização espacial em estudantes.

10. OBSERVE AS FIGURAS GEOMÉTRICAS ESPACIAIS A SEGUIR.

• MARQUE UM X NA SEQUÊNCIA DE FIGURAS GEOMÉTRICAS ESPACIAIS A SEGUIR QUE ESTIVER NA MESMA ORDEM DA SEQUÊNCIA ANTERIOR.

• PINTE ESSAS FIGURAS COM AS CORES CORRESPONDENTES.

Resposta: Os estudantes devem marcar um X na sequência B; os estudantes devem pintar: o cubo de verde; o cone de azul; o paralelepípedo de vermelho; e a esfera de amarelo.

que distinguem uma figura da outra. Após as respostas, promova a montagem a fim de que todos possam conferir as respostas dadas. Caso algum estudante apresente dificuldade na realização das atividades, procure retomar parte dos conteúdos, buscando abordagens diferentes para explicar o assunto, de acordo com as necessidades que forem se tornando evidentes durante a prática.

BNCC

03/10/2025 09:05:49

A atividade 10 promove a comparação de sequências de figuras por meio do formato delas. Assim, é contemplado um importante aspecto da habilidade EF01MA09

• O trabalho com a atividade 10 promove não só a identificação de figuras geométricas espaciais, mas a comparação de elementos em sequência. É importante que os estudantes deem atenção a todas as alternativas, comparando-as entre si, a fim de garantir que haja apenas uma alternativa correta. Portanto, peça a eles que digam o nome das figuras de cada uma das alternativas, na ordem em que aparecem.

• Antes de os estudantes colorirem as figuras por inteiro, peça a eles que indiquem a cor correspondente a cada figura ou que façam pequenos riscos na figura usando a cor determinada, pois, em caso de erro, não será possível corrigir se a figura já estiver completamente pintada. No momento de colorir as figuras, instrua-os a não ultrapassar as margens do contorno.

AVALIANDO

Objetivo

Reconhecer o molde de um cubo e de um bloco retangular.

Sugestão de intervenção

Providencie o molde de um cubo e o molde de um bloco retangular. Sem promover a montagem, peça aos estudantes que identifiquem qual dos moldes é o do cubo e qual é o do bloco retangular. Auxilie-os a identificar, ainda que de modo informal, os elementos

• Para desenvolver a atividade 11, explique aos estudantes que eles devem prestar atenção às sílabas que correspondem a cada figura geométrica espacial mencionada por você, conforme a legenda. Em seguida, devem acompanhar a sequência de figuras de cada item falando a sílaba correspondente a cada uma delas. Avise quando for iniciar a atividade, pedindo silêncio e atenção. Após cada sequência, verifique se eles estão emitindo o som de cada figura geométrica espacial, de acordo com a legenda. Caso considere necessário, escreva a legenda na lousa, evidenciando para os estudantes o som correspondente a cada figura. Esse tipo de atividade favorece o reconhecimento do padrão em uma sequência, associando a linguagem sonora a cada figura geométrica correspondente, tornando a experiência de aprendizado mais envolvente.

• Ao propor a sugestão de Desafio a seguir, como conclusão da Unidade, verifique se os estudantes analisam as informações fornecidas e usam estratégias pessoais para resolver a charada, trabalhando, assim, o raciocínio lógico. Espera-se que eles percebam que a figura geométrica espacial que responde ao desafio é o cone.

Sugestão de Desafio

Sou uma figura geométrica espacial que lembra um chapéu de aniversário. Qual figura geométrica espacial sou eu?

Resposta

A figura geométrica espacial é o cone.

11. O PROFESSOR VAI FALAR AS SÍLABAS QUE CORRESPONDEM A CADA FIGURA GEOMÉTRICA ESPACIAL, CONFORME A LEGENDA.

LEGENDA

FIGURA CUBOPARALELEPÍPEDOCONECILINDROESFERA

SOM DÓ RÉ MI FÁ SOL

A ) ACOMPANHE A SEQUÊNCIA DE FIGURAS DE CADA ITEM, FALANDO A SÍLABA CORRESPONDENTE A CADA UMA DELAS.

Resposta: FÁ, SOL, MI, FÁ, SOL, MI

Resposta: DÓ, RÉ, MI, DÓ, RÉ, MI

Resposta: SOL, RÉ, FÁ, SOL, RÉ, FÁ

B ) SUPONDO QUE ESSAS SEQUÊNCIAS CONTINUEM COM O MESMO PADRÃO, QUAIS SÃO AS DUAS PRÓXIMAS SÍLABAS QUE VOCÊ VAI FALAR:

• NO ITEM 1?

Resposta: FÁ e SOL

• NO ITEM 2? • NO ITEM 3?

Resposta: DÓ e RÉ Resposta: SOL e RÉ

09:05:50

12. AMANDA CONSTRUIU UMA SEQUÊNCIA DE FIGURAS

GEOMÉTRICAS ESPACIAIS SEGUINDO UM PADRÃO.

INÍCIO

A ) A SEQUÊNCIA DE FIGURAS GEOMÉTRICAS ESPACIAIS QUE AMANDA CONSTRUIU É FORMADA POR CUBOS, CONES,

CILINDROS OU ESFERAS?

Resposta: CUBOS.

B ) CONTORNE A PRÓXIMA FIGURA DESSA SEQUÊNCIA.

Resposta: Os estudantes devem contornar o cubo azul.

C ) NESSA SEQUÊNCIA, ESTÁ MUDANDO A COR OU O FORMATO DAS FIGURAS?

Resposta: COR.

DESAFIO

A MAIS

Resposta: Os estudantes devem relacionar: A-3; B-1; C-2.

RELACIONE AS PEÇAS QUE SE ENCAIXAM FORMANDO CUBOS.

• Ao propor a atividade 12, observe se os estudantes reconhecem as figuras geométricas espaciais apresentadas em cada item e se notaram que o padrão utilizado nas sequências é a variação da cor da figura. Após trabalhar essa atividade, se julgar conveniente, oriente-os a construir, no caderno, uma sequência parecida com as apresentadas, desenhando algumas figuras geométricas espaciais. Ao final, promova um momento em que eles possam compartilhar com os colegas suas estratégias pessoais e resoluções.

• Ao identificar o par de figuras geométricas que forma um cubo, no Desafio a mais desta página, exercita-se o raciocínio lógico. Verifique se os estudantes apresentam dificuldade na resolução e interfira apenas se julgar necessário.

• A fim de complementar o trabalho com essa página, avalie a possibilidade de levar para a sala de aula o material dourado e pedir aos estudantes que construam cubos com 8 e 27 cubinhos.

BNCC

A proposta de identificação dos atributos dos objetos com formato de figuras geométricas espaciais exercita o raciocínio lógico e o espírito da investigação. Assim, contemplam-se aspectos relevantes da habilidade EF01MA09 da BNCC e desenvolve-se a Competência específica de Matemática 8 da BNCC.

CONCLUSÃO

Acompanhar o desenvolvimento dos estudantes é fundamental para um ensino bem-sucedido. Ao longo da unidade, foram propostas diversas maneiras de avaliar a aprendizagem da turma, garantindo a progressão do conhecimento. A fim de realizar um monitoramento mais abrangente e organizado, registre nos relatórios individuais ou nas fichas de avaliação o desempenho de cada estudante, levando em consideração suas particularidades. Um modelo desse tipo de ficha pode ser encontrado no tópico

03/10/2025 09:05:51

Avaliação deste Manual do Professor. Assim, será possível visualizar individualmente as trajetórias de aprendizagem, incluindo os avanços e os pontos de dificuldades a serem sanados.

A conclusão da unidade é o momento de avaliar se os objetivos por ela propostos foram alcançados. Para esse diagnóstico, observe no final deste Manual do Professor algumas possibilidades de avaliação formativa que permitem realizar o monitoramento da aprendizagem dos estudantes e intervir para recuperação dos conteúdos, caso eles não tenham atingido os resultados esperados.

1. Objetivos

Contar objetos.

Registrar quantidades.

Sugestão de intervenção

Para identificar se as dificuldades apresentadas pelos estudantes estão relacionadas à contagem ou à escrita dos números, oriente-os a contar a quantidade, por exemplo, de pessoas ou de determinado objeto disponível na sala de aula, a fim de que possam compreender do conteúdo estudado.

2. Objetivo

Comparar quantidades maiores e menores do que uma dezena.

Sugestão de intervenção

Para identificar se os estudantes compreendem que 1 dezena corresponde a 10 unidades, comente a grafia dessa palavra, relacionando-a ao prefixo “dez” e, em seguida, compare-a a quantidades maiores e menores. Explore as respostas oferecidas por eles para os itens B e C, incentivando-os a identificar quantidades que maiores e menores do que uma dezena.

VAMOS AVALIAR O APRENDIZADO

1. A CENA MOSTRA O MOMENTO DE UMA FESTA DE ANIVERSÁRIO.

2. Professor, professora: Existem várias sugestões de resposta para os itens B e C Com a ajuda dos estudantes, escreva algumas delas na lousa.

ESCREVA A QUANTIDADE DE ELEMENTOS DE CADA TIPO QUE APARECEM NA CENA.

• BEXIGAS.

Resposta: 5 BEXIGAS.

• COPOS.

Resposta: 8 COPOS.

• CHAPÉUS DE FESTA.

Resposta: 12 CHAPÉUS DE FESTA.

• VELINHAS.

Resposta: 6 VELINHAS.

2. EM CADA ITEM, FAÇA O QUE SE PEDE.

A ) CONTORNE 1 DEZENA DE ESTRELAS.

Resposta: Os estudantes devem contornar, da maneira que preferirem, 10 estrelas.

B ) CONTORNE MAIS DO QUE 1 DEZENA DE FLORES. Resposta: Os estudantes devem contornar, da maneira que preferirem, 11 flores ou mais.

C ) CONTORNE MENOS DO QUE 1 DEZENA DE BOLINHAS.

Resposta: Os estudantes devem contornar, da maneira que preferirem, 9 bolinhas ou menos.

Resposta: A-5; B-3; C-4; D-1; E-2.

4. PARA CADA SEQUÊNCIA, IDENTIFIQUE E ESCREVA

QUAL

3. Objetivo

Identificar objetos do dia a dia cujos formatos lembram figuras geométricas espaciais.

Sugestão de intervenção

Faça um quadro na lousa e, em seguida, peça aos estudantes que nomeiem as figuras apresentadas na atividade e alguns objetos com formatos que remetam a elas.

No caso de haver estudantes com comprometimento motor manual, é possível realizar essa atividade por meio de apontamento, relacionando as alternativas.

4. Objetivo

Reconhecer o padrão da sequência de cada item das figuras geométricas espaciais.

Sugestão de intervenção

Resposta: Espera-se que o estudante identifique que a figura faltante é um cone azul.

B. INÍCIO

INÍCIO

Resposta: Espera-se que o estudante responda que a figura faltante é uma esfera amarela.

03/10/2025 09:07:05

Questione os estudantes em relação ao padrão de cada item dessa atividade. Espera-se que eles percebam a regularidade na repetição de duas figuras geométricas, alternadamente. Em seguida, solicite aos estudantes que desenhem essas figuras, utilizando as cores adequadas, a fim de que possam resolver a atividade corretamente.

OBJETIVOS DA UNIDADE

• Identificar períodos do dia em situações do cotidiano.

• Estimar a duração do intervalo de tempo.

• Ler e registrar horas exatas em relógio de ponteiros e em relógio digital.

• Identificar e reconhecer a semana como um período de sete dias.

• Reconhecer o calendário como instrumento de marcação de tempo.

• Ler e registrar datas com base em um calendário.

• Ler e interpretar gráfico de barras em malha quadriculada.

• Aprender a interpretar e utilizar expressões como “mais comprido”, “mais curto”, “mais alto”, “mais baixo”, entre outras, para indicar relações de grandeza.

• Reconhecer o centímetro como unidade padronizada de medida de comprimento.

• Realizar medições de comprimento utilizando uma régua graduada em centímetro.

• Comparar e estimar medidas de comprimento.

INTRODUÇÃO E

JUSTIFICATIVA

As atividades desta unidade abordam situações cotidianas, como a identificação de períodos do dia, a ordenação temporal de acontecimentos e as estimativas da duração do intervalo de tempo. Desenvolve se um trabalho de leitura e registro de horas exatas em relógio com ponteiros e digital. Abordase a quantidade de dias de uma semana, propondo leituras e registros de datas com base em um calendário, e a quantidade de meses em um ano e de dias em um mês, com base na leitura desse instrumento. Apresentamse as noções básicas de grandeza e de procedimentos de medições de comprimentos, além do reconhecimento de instrumentos usados para medir essa grandeza.

UNIDADE3

MEDIDAS DE TEMPO E DE COMPRIMENTO

CENA DA ANIMAÇÃO ALICE NO PAÍS DAS MARAVILHAS, EM QUE APARECE O COELHO BRANCO, DE WALT DISNEY, 1951.

Habilidades da BNCC trabalhadas na unidade: EF01MA15, EF01MA16, EF01MA17 e EF01MA18

SUGESTÃO DE ESTRATÉGIA INICIAL

Leve para a sala de aula um relógio de ponteiros grande, um calendário, uma fita métrica ou trena e uma régua, a fim de que todos os estudantes possam manuseálos. Avalie o conhecimento prévio deles sobre leitura e representação das horas no relógio, bem como sobre leitura de datas no calendário. Peça a eles que indiquem no relógio o horário em que costumam executar algumas tarefas, como almoçar, jantar e dormir.

Verifique se conseguem relacionar esses horários com as indicações no instrumento. Peça que indiquem no calendário, por exemplo, o mês das férias escolares e uma data comemorativa. Caso eles não consigam, anote essas dificuldades para retomálas no final da unidade, como verificação de aprendizagem. Mostrelhes as marcações em fita métrica, trena ou régua, e verifique se percebem que os espaçamentos de uma marcação para a outra são iguais. Mantenha o interesse dos estudantes informando que essas questões serão trabalhadas durante o estudo desta unidade.

OS RELÓGIOS SÃO INSTRUMENTOS USADOS PARA MARCAR A PASSAGEM DO TEMPO. REGISTRAR ESSA PASSAGEM É FUNDAMENTAL EM NOSSO DIA A DIA. NA CULINÁRIA, POR EXEMPLO, DETERMINAMOS O TEMPO NECESSÁRIO PARA O PREPARO DE UMA REFEIÇÃO. NA ESCOLA, INDICAMOS O HORÁRIO EM QUE AS AULAS COMEÇAM E TERMINAM.

1. Resposta pessoal. Espera-se que os

estudantes relatem as suas experiências em relação à utilização de relógios ou outro dispositivo para verificar as horas.

1. 2.

NA IMAGEM, O COELHO DE ALICE USA UM RELÓGIO DE BOLSO. VOCÊ TEM ALGUM TIPO DE RELÓGIO OU OUTRO DISPOSITIVO EM QUE SEJA POSSÍVEL VERIFICAR AS HORAS? EM CASO AFIRMATIVO, CONTE PARA O PROFESSOR E OS COLEGAS.

QUAL É O HORÁRIO EM QUE VOCÊ COSTUMA SAIR DE SUA CASA PARA IR ATÉ A ESCOLA?

MARQUE UM X NOS OBJETOS QUE UTILIZAMOS PARA MEDIR A PASSAGEM DO TEMPO.

Resposta: Os estudantes devem marcar um X nas imagens A e D.

IMAGENS SEM PROPORÇÃO ENTRE SI.

2. Resposta pessoal. Esta questão tem como objetivo fazer com que os estudantes se familiarizem com marcadores da

passagem do tempo na rotina do seu dia a dia.

03/10/2025 09:11:19

• Leia o texto para os estudantes e orienteos a observar a imagem. Investigue, por meio de questionamentos, se algum deles sabe ler as horas em um relógio de ponteiros. Peça que identifiquem alguns dos números que aparecem no relógio do coelho.

• Pergunte se alguém da turma conhece o livro ou já assistiu ao filme Alice no País das Maravilhas. Caso alguém conheça o livro ou tenha assistido ao filme, peça que compartilhe com os colegas essas experiências.

• Na questão 1, reforce para os estudantes que o relógio assume uma vasta gama de modelos e formatos, já que é muito integrado na nossa sociedade. Pergunte a eles quais tipos de relógios já viram. Eles podem falar, por exemplo, sobre relógios de pulso, de parede, digitais, smartwatches ou de pêndulo.

• A questão 2 permite aos estudantes falar sobre a rotina diária, situandoa no tempo. Pergunte também a que horas eles voltam da escola.

• O objetivo da questão 3 é que os estudantes reconheçam o relógio como um instrumento utilizado para medir a passagem do tempo. Converse com a turma sobre os dois tipos de relógios apresentados, o de ponteiros ou analógico e o digital. Pergunte a eles qual é a diferença entre os dois relógios representados na questão 3. Verifique se identificam que o relógio de pulso tem ponteiros e o outro não. Aproveite para perguntar se eles conhecem os demais objetos da imagem e sua utilidade.

• A atividade 1 propõe a identificação dos diferentes períodos do dia, compreendendo e usando conceitos de manhã, tarde e noite, com base nas tarefas cotidianas. Solicite a eles que analisem as cenas apresentadas, verificando algumas tarefas realizadas por Maria em um dia. No item A, se houver dificuldades, contextualize as tarefas que ela faz ao longo do dia, destacando os elementos da imagem e, no item B , conduza uma conversa refletindo sobre como são as atividades diárias dos estudantes, situandoas nos períodos de tempo: manhã, tarde ou noite. Converse com eles sobre rotina, que é o hábito de fazer algo sempre da mesma maneira e nos mesmos horários. Pergunte lhes sobre alguns costumes rotineiros, como dormir ao anoitecer, levantarse ao amanhecer, escovar os dentes, tomar café da manhã, ir para a escola, brincar, além de outros afazeres do dia a dia. Complemente dizendo que algumas tarefas sempre terão horários a serem cumpridos, como reuniões e consultas médicas.

MEDIDAS DE TEMPO

1. NA CENA DAS PÁGINAS ANTERIORES, O COELHO DE ALICE USA UM RELÓGIO DE BOLSO PARA SE ORIENTAR NO TEMPO. ALÉM DO RELÓGIO, PODEMOS NOS ORIENTAR USANDO OS PERÍODOS DO DIA.

A ) AS CENAS A SEGUIR MOSTRAM ALGUMAS ATIVIDADES

QUE MARIA FEZ EM UM DIA. IDENTIFIQUE SE AS CENAS

OCORRERAM NO PERÍODO DA MANHÃ, DA TARDE OU DA NOITE

Resposta: CENA 1: MANHÃ; CENA 2: NOITE; CENA 3: TARDE

B ) QUAIS ATIVIDADES VOCÊ REALIZA DURANTE O DIA? O QUE VOCÊ COSTUMA FAZER PELA MANHÃ, À TARDE E À NOITE?

CONVERSE SOBRE ESSE ASSUNTO COM SEUS COLEGAS.

Resposta pessoal. Espera-se que os estudantes falem sobre suas atividades diárias nos diversos ambientes, como o escolar, o familiar, entre outros.

BNCC

As atividades desta seção solicitam aos estudantes que relatem em linguagem verbal e não verbal, a sequência de acontecimentos de um dia, utilizando, quando possível, os horários dos eventos, e abordando, desse modo, o reconhecimento dos períodos do dia, conforme orientam as habilidades EF01MA16 e EF01MA17 da BNCC.

ATIVIDADE EXTRA

Promova uma roda de conversa fazendo alguns questionamentos aos estudantes, como: “Em qual período do dia vocês vão à escola?”; “Em qual período do dia vocês fazem a tarefa de casa?”; “Em qual período do dia vocês almoçam?”; “Vocês brincam de manhã, à tarde ou à noite?”. Após essas reflexões em roda de conversa, entregue uma folha de papel a cada estudante e solicite a eles que desenhem atividades que realizam de manhã, de tarde e de noite. Desse modo, eles identificarão os conceitos de manhã, tarde e noite por meio dos acontecimentos do próprio dia a dia.

CENA 1

CENA 3

CENA 2

2. PAULO PREPAROU UMA DELICIOSA TORTA PARA SUA FAMÍLIA.

A ) NUMERE AS CENAS CONSIDERANDO A ORDEM DAS ETAPAS DE PREPARAÇÃO DA TORTA.

Resposta: Os estudantes devem numerar as cenas da seguinte maneira: A. 3; B. 2; C. 1; D. 4.

A. B. C. D.

B ) EM SUA OPINIÃO, QUANTO TEMPO LEVA PARA PREPARAR UMA TORTA?

PREPARAR O PRÓPRIO ALIMENTO É SAUDÁVEL E, EM MUITOS CASOS, MAIS ECONÔMICO DO QUE COMPRAR ALIMENTOS INDUSTRIALIZADOS. VIVA COM SAÚDE! Resposta pessoal. Espera-se que os estudantes estimem uma média de 3 horas para a preparação de uma torta.

C ) DESENHE UM OBJETO QUE VOCÊ UTILIZARIA PARA MEDIR O TEMPO DE PREPARO DE UMA TORTA.

Resposta pessoal. Espera-se que os estudantes desenhem um relógio de pulso, um telefone celular, um despertador ou um computador, lembrando-se de objetos de casa ou da sala de aula que marcam as horas.

Reconhecer a passagem do tempo por meio da sequenciação de acontecimentos e estimar a duração da realização de uma tarefa.

Sugestão de intervenção

Caso os estudantes não atinjam esses objetivos, retome a imagem da abertura e a questão 1 da página 81 e explique a eles que o relógio possibilita, por exemplo, saber o horário de início e término das aulas. Além disso, orienteos a indicar em qual período do dia eles costumam realizar determinadas atividades, como

brincar, lavar as mãos, arrumar o quarto ou guardar os brinquedos. Peçalhes que estimem a medida do tempo de duração dessas atividades e digam quais delas demoram mais e menos tempo para serem realizadas.

BNCC

Por meio do contexto da atividade 2, converse com os estudantes e destaque a importância de uma alimentação saudável desenvolvendo, dessa maneira, a Competência geral 8 e o tema

• O objetivo da atividade 2 é que os estudantes sejam capazes de reconhecer a sequência temporal e a duração de acontecimentos, identificando a ordem correta das etapas de preparação de uma torta. No item A, converse com eles sobre o intervalo de tempo entre a execução de duas tarefas realizadas por Paulo. No item B, conduza uma reflexão sobre o intervalo de tempo aproximado que é necessário para a execução de algumas atividades. Peça a alguns estudantes que estimem a medida do tempo que levam para executar certas tarefas, como escovar os dentes, tomar banho ou almoçar. No item C, converse com eles sobre os diferentes dispositivos utilizados para medir a duração de intervalos de tempo. Alguns deles podem ser diferentes de um relógio, como o telefone celular e o computador, mas também oferecem essa função.

• Aproveite o contexto da atividade 2 e converse com os estudantes sobre as atividades diárias que eles realizam mais rapidamente e outras que fazem mais devagar. Pergunte também como marcam o tempo gasto nessas atividades.

AVALIANDO

Objetivos

03/10/2025 09:11:21

Reconhecer o relógio e os períodos do dia como recursos para se orientar no tempo.

contemporâneo transversal Educação alimentar e nutricional, no que se refere aos cuidados com a saúde física, proporcionada por uma alimentação com menos produtos industrializados.

ILUSTRAÇÕES: IVY NUNES/ ARQUIVO DA EDITORA

• A atividade 1 solicita que os estudantes analisem o ponteiro maior e o ponteiro menor de um relógio, levandoos a compreender qual é a função de cada um, ou seja, o ponteiro maior tem a finalidade de indicar as horas e o ponteiro menor, os minutos. Depois, eles devem identificar qual horário esse relógio está marcando. Providencie e leve para sala de aula um relógio e faça a leitura das horas inteiras, ajustando para diferentes números e perguntando qual é a hora marcada.

• A atividade 2 tem por objetivo explorar a leitura de horas exatas em um relógio de ponteiros e levar os estudantes a identificarem e registrarem o horário que estão marcando. Caso eles apresentem dificuldades, faça diferentes marcações no relógio levado para a sala de aula, até que o assunto seja compreendido.

• Para indicar a medida de tempo sugerida na atividade 2, no caso de haver estudantes com deficiência visual, verifique a possibilidade de utilizar um relógio com ponteiros e números táteis, de modo que eles possam perceber as medidas indicadas. Para estudantes com níveis de alguns transtornos, como TEA ou TDAH, que os impeçam de realizar a atividade, ou para estudantes com síndrome de Down, relacione os horários descritos a acontecimentos do dia a dia deles. Por exemplo, leveos a refletir, por meio de questionamentos, sobre o que costumam fazer por volta de 9 ou 10 horas da manhã, caso não seja seu horário de estudo. Relacione o horário de 12 horas com a proximidade do momento do almoço, para que os estudantes estabeleçam relação prática com a medida de tempo.

O RELÓGIO E AS HORAS

1. VOCÊ JÁ TEVE CONTATO COM UM RELÓGIO DE PONTEIROS?

NO RELÓGIO A SEGUIR, O PONTEIRO MAIOR INDICA OS MINUTOS E O PONTEIRO MENOR INDICA AS HORAS.

O PONTEIRO MENOR INDICA AS HORAS.

O PONTEIRO MAIOR INDICA OS MINUTOS.

NESSE RELÓGIO, O PONTEIRO MAIOR APONTA PARA O 12 E O PONTEIRO MENOR APONTA PARA O 7. MARQUE UM X NO HORÁRIO QUE ESSE RELÓGIO ESTÁ INDICANDO.

7 HORAS. 12 HORAS. 5 HORAS.

Resposta: Os estudantes devem marcar um X em 7 HORAS

2. ESCREVA O HORÁRIO QUE OS RELÓGIOS A SEGUIR ESTÃO INDICANDO.

Resposta: A: 5 HORAS; B: 9 HORAS; C: 10 HORAS; D: 12 HORAS.

• Aproveite o contexto abordado nesta página e solicite aos estudantes que, em grupos, façam uma pesquisa sobre os tipos de relógios e sua evolução. Após a pesquisa, eles devem registrar no caderno, por meio de desenhos, o que encontraram. Propostas como essa auxiliam no desenvolvimento cognitivo e permitem a interação entre os estudantes.

3. DESENHE NOS RELÓGIOS DE CADA QUADRO OS PONTEIROS QUE INDICAM O HORÁRIO EM QUE VOCÊ GERALMENTE COMEÇA AS SEGUINTES ATIVIDADES.

Resposta pessoal. Espera-se que os estudantes desenhem os horários estimados para a realização de suas atividades cotidianas.

03/10/2025 09:11:22

AVALIANDO

Objetivo

Realizar leituras e registros de horas exatas em relógios de ponteiros.

Sugestão de intervenção

Caso os estudantes apresentem dificuldades no conteúdo estudado, realize a atividade a seguir.

Leve um relógio de parede com ponteiros para a sala de aula e reúna os estudantes em grupos de 3 a 4 participantes. Em seguida, simule, uma a uma, algumas horas nesse relógio, com tempo

suficiente para que os grupos façam os registros no caderno. Depois, solicite que apresentem para a turma ao menos uma de suas respostas, que deve ser comparada com as dos demais grupos. Esse é um momento importante para verificar se os estudantes compreenderam o conteúdo estudado e, caso seja necessário, proponha novas simulações de horas, explicando a função de cada ponteiro, a fim de sanar possíveis dúvidas.

• A atividade 3 propõe que os estudantes registrem os ponteiros em cada relógio indicando o horário em que começam a realizar algumas atividades do cotidiano. É possível que alguns indiquem horários que não são exatos para algumas atividades, como seis e meia. Se isso acontecer, explore esse caso particular e explique que a leitura e o registro de horas como essa serão estudados mais adiante. Para um melhor aproveitamento da atividade, peça a eles que classifiquem as tarefas apresentadas de acordo com o período do dia em que são realizadas – manhã, tarde ou noite – e verifique se reconhecem sequências temporais de acontecimentos cotidianos relatandoas, pré requisito necessário para a compreensão dos períodos do dia.

• Ao iniciar a atividade 4, se necessário, reforce que, em um relógio digital, os algarismos indicados antes dos dois-pontos compõem o número que indica a hora e os que aparecem depois dos doispontos representam a contagem dos minutos. Nos casos apresentados, são horas inteiras e, por esse motivo, aparece o registro 00 depois dos doispontos.

• Ao trabalhar a atividade 5 e as demais atividades desta página, verifique se os estudantes compreendem com facilidade os números representados nos relógios digitais. Avalie a necessidade de escrever na lousa a representação deles, conforme apresentado a seguir, para ajudar na identificação e na leitura de cada algarismo.

4. NO RELÓGIO DIGITAL, OS NÚMEROS APARECEM DIRETAMENTE

NA TELA. NESSE TIPO DE RELÓGIO, OS DOIS PRIMEIROS

NÚMEROS INDICAM AS HORAS E OS DOIS ÚLTIMOS, DEPOIS

DOS DOIS-PONTOS, INDICAM OS MINUTOS.

A ) MARQUE UM X NO HORÁRIO INDICADO NESSE RELÓGIO.

12 HORAS.

Resposta: Os estudantes devem marcar um X em 6 HORAS

B ) COMPLETE AS FRASES COM AS PALAVRAS DAS FICHAS. 6 HORAS. 2 HORAS.

AS HORAS

OS MINUTOS

• O NÚMERO APÓS OS DOIS-PONTOS MARCA .

Resposta: O NÚMERO APÓS OS DOIS-PONTOS MARCA OS MINUTOS

• O NÚMERO ANTES DOS DOIS-PONTOS MARCA .

Resposta: O NÚMERO ANTES DOIS-PONTOS PONTOS MARCA AS HORAS

5. ESCREVA O HORÁRIO INDICADO EM CADA RELÓGIO.

• Ao finalizar a atividade 6, converse com os estudantes sobre alguns horários do dia a dia nos quais eles fazem atividades do interesse deles, como assistir a um programa televisivo ou sair para um passeio diário com um animal de estimação. Se achar conveniente, orienteos a indicar alguns desses horários no relógio digital. Destaque apenas momentos representados com horas inteiras.

HORAS. HORAS. HORAS.

Resposta: 7 HORAS.Resposta: 11 HORAS. Resposta: 2 HORAS.

6. ESCREVA NO RELÓGIO DIGITAL A HORA INDICADA NOS BILHETES.

Resposta: A. 2:00; B. 8:00

DUAS HORAS

OITO HORAS

O CALENDÁRIO

1. LEIA O TEXTO. [...]

O CALENDÁRIO TEM SETE DIAS.

A CADA DIA FAZEMOS COISAS DIFERENTES.

MAS ALGUMAS COISAS SÃO IGUAIS TODOS OS DIAS.

SEGUNDA-FEIRA BRINCAR COM OS AMIGOS

TERÇA-FEIRA LER UM LIVRO

QUARTA-FEIRA VER TELEVISÃO

QUINTA-FEIRA FAZER BAGUNÇA

SEXTA-FEIRA FAZER COMPRAS

SÁBADO SE DIVERTIR

DOMINGO FAZER CARINHO E FICAR COM SEU BICHINHO

JUNTANDO ESSES DIAS TEMOS UMA SEMANA. [...]

DUNBAR, JAMES. TIQUE-TAQUE: O TEMPO NÃO PÁRA. SÃO PAULO: ÁTICA, 2001. P. 16-17. (COLEÇÃO XERETA).

A ) COMPLETE OS QUADRINHOS ESCREVENDO, EM ORDEM, A SEQUÊNCIA DOS NOMES DOS DIAS DA SEMANA.

DOMINGO -FEIRA TERÇA-

Resposta: DOMINGO, SEGUNDA-FEIRA, TERÇA-FEIRA, QUARTA-FEIRA, QUINTA-FEIRA, SEXTA-FEIRA, SÁBADO.

SEXTAQUARTA-FEIRA -FEIRA

SÁBADO

B ) QUANTOS DIAS TEM UMA SEMANA? DIAS.

Resposta: 7 DIAS.

C ) QUAL DIA DA SEMANA FOI ONTEM? E QUAL DIA SERÁ AMANHÃ?

Resposta pessoal. As respostas deste item dependem do dia em que a atividade for realizada pelos estudantes.

D ) QUAL É SEU DIA PREFERIDO DA SEMANA? POR QUÊ?

Resposta pessoal. Espera-se que os estudantes apresentem razões que justifiquem suas preferências. 87

03/10/2025 09:11:22

• Na atividade 1, explore os dias da semana. Enfatize oralmente a organização desses dias e a ordem da disposição deles na semana. No item A, após o preenchimento dos quadrinhos, leia o nome desses dias de maneira ordenada. No item C, aproveite para conversar com a turma sobre o tempo passado (ontem), tempo presente (hoje) e tempo futuro (amanhã).

• O tempo é um dos tópicos estudados no componente curricular de História. A articulação com esse componente está articulada nos momentos da Unidade em que são trabalhados os horários e dias da semana ligados aos afazeres dos estudantes, em cada dia da semana, como ir para a escola, praticar algum esporte, fazer um curso ou qualquer outra atividade rotineira. Explore o item D perguntando a eles por que gostam mais do dia da semana que escolheram. Peça a alguns estudantes que compartilhem sua opinião com os colegas.

BNCC

As atividades desta seção abordam os dias da semana, assim como a indicação do dia da semana referente a uma data, consultando o calendário, conforme orientam as habilidades

EF01MA17 e EF01MA18 da BNCC.

• Durante o desenvolvimento desta atividade, os estudantes realizarão a leitura do texto, bem como a escrita dos dias da semana, ações que desenvolvem a escrita, a fluência em leitura oral, a compreensão de textos e o desenvolvimento de vocabulário. Se julgar conveniente, proponha um trabalho complementar de leitura e produção de texto para ser feito em casa, com o acompanhamento dos familiares ou de outros adultos do convívio deles.

• Na atividade 2 , os estudantes devem identificar qual é o último dia da sequência dos dias da semana, qual é o primeiro dia da sequência e qual é o dia depois de terçafeira. Para um melhor aproveitamento dessa atividade, faça algumas perguntas a eles, como:

• Se hoje é quintafeira, que dia será amanhã?

• Se hoje é domingo, que dia foi ontem?

• Se amanhã será sábado, que dia é hoje?

• Se hoje é quartafeira, que dia será depois de amanhã?

• Para estudantes com deficiência visual, com comprometimento motor e com níveis de transtornos, como TEA e TDAH, que os impeçam de participar, a atividade 2 poderá ser feita por apontamento, relacionando as alternativas.

• Verifique se a turma percebe corretamente a sequência dos dias e os significados de palavras e termos de referência temporal, como ontem, amanhã e depois de amanhã.

• A atividade 3 tem por objetivo abordar o significado da expressão “antes de ontem”. Ao trabalhar com essa atividade, comente com os estudantes que “ontem” significa um dia anterior ao dia de hoje e que a expressão “antes de ontem” significa dois dias anteriores ao dia de hoje. Pergunte a eles se lembram de alguma atividade realizada ontem ou antes de ontem, e orienteos a compartilhar com os colegas suas experiências.

• O objetivo da atividade 4 é levar os estudantes a identificarem o dia imediatamente anterior e o posterior a determinado dia. Essa atividade aborda também a sequenciação dos dias da semana. Para melhor aproveitamento, diga a eles o nome de outros dias, além dos apresentados na atividade, a fim de que citem

2. LIGUE AS FICHAS CORRESPONDENTES, DE ACORDO COM A SEQUÊNCIA DE DIAS DA SEMANA DA ATIVIDADE ANTERIOR.

O ÚLTIMO DIA DA SEQUÊNCIA O PRIMEIRO DIA DA SEQUÊNCIA O DIA DEPOIS DE TERÇA-FEIRA

Resposta: Os estudantes devem ligar as fichas: O ÚLTIMO DIA DA SEQUÊNCIA com SÁBADO; O PRIMEIRO DIA DA SEQUÊNCIA com DOMINGO; O DIA DEPOIS DE TERÇA-FEIRA com QUARTA-FEIRA.

SÁBADO QUARTA-FEIRA DOMINGO

3. COMPLETE A FRASE ESCREVENDO OS DIAS DA SEMANA CORRESPONDENTES.

Resposta pessoal. A resposta depende do dia em que a atividade for realizada.

HOJE É , E ANTES DE ONTEM FOI

4. COMPLETE CADA ITEM COM OS DIAS QUE VÊM ANTES E DEPOIS DO DIA DA SEMANA APRESENTADO.

Resposta: A. TERÇA-FEIRA,

QUARTA-FEIRA, QUINTA-FEIRA; B. QUINTA-FEIRA, SEXTA-FEIRA, SÁBADO; C. DOMINGO, SEGUNDA-FEIRA, TERÇA-FEIRA; D. SEXTA-FEIRA, SÁBADO, DOMINGO

A. B. C.

QUARTA-FEIRA

SEXTA-FEIRA

SEGUNDA-FEIRA

SÁBADO

5. PINTE A FICHA QUE INDICA O DIA DA SEMANA QUE SERÁ DEPOIS DE AMANHÃ.

Resposta pessoal. A resposta desta atividade depende do dia em que ela será realizada pelos estudantes.

SEGUNDA-FEIRA

TERÇA-FEIRA

QUINTA-FEIRA

SEXTA-FEIRA

qual dia vem imediatamente antes e qual dia vem imediatamente depois.

• A atividade 5 explora o significado de dia posterior. Ao resolvêla, retome o significado de “amanhã”, abordado no item C da atividade 1, e explique que o “dia depois de amanhã” significa dois dias posteriores ao dia de hoje.

QUARTA-FEIRA

SÁBADO DOMINGO

6. RESPONDA ÀS QUESTÕES DE ACORDO COM O CALENDÁRIO.

CALENDÁRIO 2027

JANEIRO

FEVEREIRO

MARÇO

1-Confraternizaçãouniversal

6. C) Resposta pessoal. Espera-se que os estudantes identifiquem e escrevam o mês, o dia do mês e o dia da semana que será seu aniversário, utilizando o calendário de 2027.

AGOSTO

A ) QUANTOS MESES HÁ DURANTE O ANO? MESES.

Resposta: 12 MESES.

B ) DE QUE ANO É ESSE CALENDÁRIO?

Resposta: 2027

C ) ESCREVA O DIA DO MÊS, O DIA DA SEMANA E O MÊS DE SEU ANIVERSÁRIO EM 2027.

DIA DO MÊS DIA DA SEMANA MÊS

ATIVIDADE EXTRA

Complemente a atividade 6 realizando a seguinte proposta:

• Confeccione uma ficha em formato retangular para cada mês do ano, totalizando 12 fichas. É importante utilizar papel pouco flexível (cartolina) na confecção das fichas, a fim de tornar mais fácil o manuseio pelos estudantes.

• Confeccione outras fichas e escreva, em cada uma delas, uma dica que permita identificar determinado mês. Por exemplo, em relação ao mês de janeiro, é possível escrever a seguinte dica: “É o primeiro mês do ano”. Já em relação ao

mês de junho, podese escrever, por exemplo: “É o mês em que se comemoram as festas juninas”.

03/10/2025 09:11:23

• Organize os estudantes em trios e distribua para cada grupo fichas com o nome dos meses do ano e outras com as dicas. Em cada grupo, um estudante deverá ler as dicas e os outros dois deverão identificar o nome do mês referente à dica. O estudante que acertar o nome do mês será o leitor das próximas dicas, e assim sucessivamente, até esgotarem todas as dicas. Caso não haja leitores entre eles, pois estão em fase de alfabetização, faça a leitura com o grupo. Ao longo da atividade, intervenha apenas se for necessário, caso existam dúvidas.

• Leia o enunciado proposto na atividade 6 e oriente os estudantes a identificarem os elementos presentes no calendário e a maneira como ele está organizado. Para isso, solicite a eles que analisem com atenção cada elemento.

• O objetivo desta atividade é que os estudantes identifiquem os dias, os meses e o ano no calendário. Promova uma conversa com a turma sobre como os dias, as semanas e os meses são dispostos no calendário, e peça aos estudantes que analisem a variação na quantidade de dias dos meses. Orienteos a responder aos itens propostos na atividade.

BNCC

A atividade 6 solicita aos estudantes que analisem um calendário para responderem a algumas questões, nas quais eles são levados a reconhecer e relacionar os dias da semana e os meses do ano, com o auxílio do calendário, contemplando a habilidade EF01MA17 da BNCC.

• Na atividade 7, os estudantes devem reconhecer o dia do mês e o nome dos dias da semana, além de identificálos no calendário, compreendendo a organiza ção das semanas em um mês. Explique a eles que os dias da semana são indicados de forma abreviada e que as datas de feriados são representadas com destaque.

• O objetivo da atividade 8 é que os estudantes iden tifiquem o dia e o mês em que são comemoradas algu mas datas especiais. Para resolvêla, utilize um calendário para explorar as datas comemorativas que ocorrem durante o ano. Para melhor aproveitamento da atividade, leve para a sala de aula um calendário do ano vigente e solicite aos estudantes que indiquem outras datas comemorativas. Peça que identifiquem o dia da semana e o mês em que elas ocorrerão ou em que já ocorreram.

D ) NO CALENDÁRIO DA PÁGINA ANTERIOR, O MÊS DE DEZEMBRO

TEM QUANTOS DOMINGOS?

Resposta: 4

E ) EM 2027, QUANTOS DIAS TEM O MÊS DE:

• FEVEREIRO? DIAS. • NOVEMBRO? DIAS.

Resposta: 28 DIAS.

Resposta: 30 DIAS.

7. ISADORA FAZ ANIVERSÁRIO NO DIA 6 DE SETEMBRO. NA IMAGEM, ESTÁ APRESENTADO O CALENDÁRIO DO MÊS DE SETEMBRO DE 2027, COM OS DIAS DO MÊS

E DA SEMANA ABREVIADOS. DE ACORDO COM ESSE MÊS, RESOLVA AS QUESTÕES.

A ) CONTORNE O DIA DO ANIVERSÁRIO DA ISADORA.

Resposta: Os estudantes devem contornar o dia 6

B ) EM QUAL DIA DA SEMANA É O ANIVERSÁRIO DE ISADORA EM 2027?

Resposta: SEGUNDA-FEIRA.

CALENDÁRIO 2027

C ) QUANTOS SÁBADOS HÁ EM SETEMBRO DE 2027?

Resposta: 4

D ) EM QUAL DIA DE SETEMBRO OCORRE UM FERIADO?

Resposta: DIA 7.

8. INDIQUE O DIA E O MÊS DE COMEMORAÇÃO DAS DATAS A SEGUIR.

DICA: PARA RESPONDER A ESSES ITENS, USE O CALENDÁRIO DE 2027.

A ) DIA DO TRABALHO.

Resposta: 1 DE MAIO.

B ) NATAL.

Resposta: 25 DE DEZEMBRO.

C ) DIA NACIONAL DE ZUMBI E DA CONSCIÊNCIA NEGRA.

Resposta: 20 DE NOVEMBRO.

AVALIANDO

Objetivo

Identificar os dias, os meses e o ano no calendário.

Sugestão de intervenção

Caso os estudantes apresentem dúvidas sobre o conteúdo abordado nesta seção, organize os estudantes em grupos, apresente alguns

calendários trazidos para a sala de aula e exploreos com a turma, solicitando que identifiquem algumas datas especiais, tais como: data de aniversário deles; Dia das Mães; Dia dos Pais; Natal; Dia Nacional de Zumbi e da Consciência Negra. Pergunte também o nome do dia da semana que antecederá ao Natal e o dia posterior ao Dia das Crianças, e deixe que eles identifiquem esse dia no calendário.

9. O PAI DE DANILO É VENDEDOR DE CARROS. O GRÁFICO A SEGUIR APRESENTA A QUANTIDADE DE CARROS VENDIDOS PELO PAI DE DANILO NOS MESES DE ABRIL, MAIO E JUNHO DE 2027.

QUANTIDADE DE CARROS VENDIDOS EM ALGUNS MESES DE 2027

QUANTIDADE DE CARROS

Unidades temáticas integradas

MÊS

FONTE DE PESQUISA: INFORMAÇÕES DA CONCESSIONÁRIA DE VEÍCULOS.

A ) CONTORNE O MÊS EM QUE O PAI DE DANILO VENDEU A MAIOR QUANTIDADE DE CARROS.

Resposta: Os estudantes devem contornar o mês de ABRIL.

ABRIL MAIO JUNHO

B ) CONTORNE O MÊS EM QUE O PAI DE DANILO VENDEU 7 CARROS.

Resposta: Os estudantes devem contornar o mês de JUNHO.

ABRIL MAIO JUNHO

C ) QUANTOS CARROS, AO TODO, O PAI DE DANILO VENDEU NESSES TRÊS MESES?

Resposta: 21

D ) COMO VOCÊ FEZ PARA RESPONDER À PERGUNTA ANTERIOR?

Sugestão de resposta: Contar os quadrinhos do gráfico referentes aos carros vendidos a cada mês.

AVALIANDO

Objetivos

Ler e interpretar tabelas e gráficos de barras.

Completar gráficos de barras em malha quadriculada com base nas informações apresentadas.

Coletar e organizar dados de uma pesquisa e representálos por meio de gráficos de barras.

Sugestão de intervenção

Verifique se os estudantes reconhecem que os gráficos contêm título, fonte, eixos

vertical e horizontal que representarão quantidades e nomes das variáveis em questão. Caso apresentem dificuldades, auxilieos a chegar a essa percepção, mesmo que de modo informal.

Desenhe, na lousa, uma tabela com duas colunas. Na primeira coluna, coloque o nome de cinco locais interessantes ou bem movimentados de sua cidade, como praça, parque, teatro, comércio, cinema ou algum ponto turístico. Na segunda coluna, registre com tracinhos, de acordo com a votação feita pelos estudantes. Depois, peça a eles que analisem

• A atividade 9 relaciona as unidades temáticas de Matemática Números e Probabilidade e estatística, ao trabalhar a interpretação de gráfico de barras expressando a quantidade de carros vendidos por Danilo em abril, maio e junho de 2027. Faça a leitura dessa atividade com os estudantes e, antes que respondam às questões propostas no Livro do Estudante , peça a eles que apresentem algumas interpretações sobre o gráfico. Deixe que se expressem espontaneamente, realizando intervenções de acordo com as necessidades que surgirem no momento. É importante motivar o interesse de participação pois, desse modo, eles terão oportunidade de desenvolver a oralidade e a comunicação. Por isso, acolha com atenção e respeito as contribuições de todos. Em seguida, conduzaos na resolução das questões propostas e, no item D, incentiveos a compartilhar suas ideias e práticas com a turma, mostrando as estratégias que usaram para responder ao item anterior.

03/10/2025 09:11:23

e votem uma única vez, escolhendo um lugar preferido.

Por fim, entregue a cada estudante uma folha de papel quadriculado e solicite que façam um gráfico de barras para representar essa pesquisa realizada com a turma. Orienteos durante o processo, de modo que possam esclarecer dúvidas que surgirem durante a atividade.

JUNHO MAIO ABRIL

• As atividades desta página envolvem uma cantiga. Pergunte aos estudantes se eles sabem o que são cantigas e, em caso afirmativo, peça que citem suas favoritas. Explique que são pequenos poemas para serem cantados.

• A atividade 1 envolve a noção de medida de comprimento. Em sua resolução, verifique se os estudantes sabem diferenciar objetos curtos de objetos compridos, sem confundir com a noção de largura. Use objetos da sala da aula e indique peças de vestuário para exemplificar a diferença. Faça gestos com as mãos para indicar que objetos mais compridos são mais longos em certa direção. Peça a eles exemplos de outras peças de roupa que sejam compridas (calças são mais compridas do que bermudas, por exemplo).

ARTICULANDO CONHECIMENTOS

O trabalho com a cantiga apresentada favorece a interação entre os componentes curriculares Matemática e Língua Portuguesa. Verifique a possibilidade de levar à sala algum aparelho de som para ouvir a cantiga. Se isso não for possível, cante no ritmo da música e incentive a turma a cantar também. A leitura ritmada é benéfica para a memorização, e isso facilita a identificação dos sons das sílabas no momento da leitura.

Após cantarem, leia a cantiga para os estudantes ou motive uma leitura em grupo, com toda a turma. Nesse caso, a leitura deve ser feita pausadamente e em voz alta para que todos possam acompanhar, pois nessa etapa da aprendizagem é possível que alguns estudantes ainda não estejam alfabetizados.

MEDIDAS DE COMPRIMENTO

1. OUÇA ESTA CANTIGA

A BARATA DIZ QUE TEM

SETE SAIAS DE FILÓ.

É MENTIRA DA BARATA,

ELA TEM É UMA SÓ.

RÁ, RÁ, RÁ, RÓ, RÓ, RÓ, ELA TEM É UMA SÓ. [...]

ORIGEM POPULAR.

CANTIGA: COMPOSIÇÃO POPULAR DESTINADA AO CANTO.

A SAIA DA DONA BARATA, QUE ESTÁ EM UM DOS MANEQUINS, É A MAIS CURTA

A ) MARQUE UM X NA SAIA DA DONA BARATA.

Resposta: Espera-se que os estudantes façam um X na saia azul.

B ) CONTORNE A SAIA MAIS COMPRIDA.

Resposta: Espera-se que os estudantes contornem a saia roxa.

BNCC

As atividades desta unidade promovem a comparação de tamanhos de objetos, animais e pessoas, a fim de contemplar a habilidade EFO1MA15. Nelas, os estudantes vão desenvolver a capacidade de utilizar expressões como mais alto, mais baixo, mais comprido, mais curto, mais estreito, maior e menor para realizar comparações, identificar características e interpretar atributos, adquirindo vocabulário e conceitos para melhor entender a realidade.

2. NAS IMAGENS DOS ANIMAIS A SEGUIR, FAÇA O QUE SE PEDE.

A ) CONTORNE O JACARÉ QUE TEM A CAUDA MAIS CURTA

Resposta: Os estudantes devem contornar o jacaré que está com os olhos abertos.

IMAGENS SEM PROPORÇÃO ENTRE SI.

B ) CONTORNE O TUCANO QUE TEM O BICO MAIS COMPRIDO

Resposta: Os estudantes devem contornar o tucano que está mais perto das folhagens do galho.

C ) CONTORNE O GATO QUE TEM AS ORELHAS MAIS COMPRIDAS E A CAUDA MAIS CURTA

Resposta: Os estudantes devem contornar o gato de coleira vermelha.

uma cauda. Em caso negativo, utilize sinônimos ou indique no desenho onde se localiza a cauda do jacaré. Explique também que a atividade se refere ao comprimento das caudas, e não ao tamanho dos animais como um todo. Utilize gestos com as mãos e faça desenhos na lousa para indicar a diferença entre o comprimento e o tamanho em outras direções.

03/10/2025 09:16:29

• Aproveite a oportunidade para perguntar sobre outros animais e fazer comparações entre diferentes espécies: “Qual animal tem a cauda mais comprida: o gato ou o jacaré?”; “Quem tem o pescoço mais curto: o cavalo ou a girafa?”; “Qual animal tem a perna mais comprida?”; “Qual tem os bigodes mais curtos?”.

• A atividade 2 desta página traz os animais como contexto. Pergunte aos estudantes se eles gostam de animais e se conhecem os representados nos desenhos. Peçalhes que os identifiquem, citando seus nomes, os locais onde habitam e suas características principais.

• Esta atividade exercita, por meio de outro contexto, a habilidade explorada na atividade 1 da página anterior. É importante aplicar um mesmo conceito em situações diferentes, para verificar se os estudantes de fato absorveram a ideia em sua essência, e não apenas decoraram a resposta a ser dada para uma pergunta específica.

• Cada um dos itens da atividade 2 explora o conceito de comprimento de uma forma diferente. No item A , pede se para identificar a cauda mais curta; no item B, o bico mais comprido. Em ambos os casos, a identificação é entre duas imagens, e só um elemento é levado em consideração. Já no item C, a comparação se dá entre três figuras e dois elementos (caudas e orelhas), considerando simultaneamente dois conceitos (comprido e curto). Por isso, certifiquese de que os estudantes compreenderam que apenas um gato deve ser contornado. • Ao falar sobre a cauda dos animais, verifique se os estudantes sabem o que é

• Na atividade 3, caso os estudantes apresentem dúvidas com relação aos termos mais curto e mais comprido, explique lhes que, nesses casos, o curto é o elemento de menor medida de comprimento, enquanto o comprido é o elemento de maior medida de comprimento. Faça uma atividade prática para desenvolver esses conceitos, levando para a sala de aula pedaços de barbante cortados em comprimentos variados e, se for possível, de cores variadas. Distribua os pedaços de barbante aos pares, solicitando que segurem um pedaço em cada mão. Peça aos estudantes que comparem as medidas de comprimento e levantem a mão com o barbante mais curto. Orienteos a trocar de barbante com um colega e peçalhes, dessa vez, que comparem e levantem o barbante mais comprido. Verifique, a cada comando, se eles executam corretamente a ação e se compreenderam o uso dos termos nos comandos executados. Aproveite para tirar qualquer dúvida que eles possam apresentar durante a prática. Essas ações favorecem o raciocínio lógico e a tomada de decisão.

• Para o desenvolvimento da atividade 4 , incentive os estudantes a formarem duplas, para que possam construir um ambiente de discussão, argumentação e troca de pontos de vista, favorecendo o respeito às opiniões dos colegas. A proposta envolve analisar com atenção as informações apresentadas na imagem e, partindo disso, decidir qual trajeto é mais adequado. Em seguida, eles deverão justificar a escolha feita, explicando por que consideram esse o melhor caminho. Incentive o uso de argumentos simples, como distância, facilidade, segurança ou rapidez, de acordo com o contexto da situação.

3. CONSIDERANDO A IMAGEM, FAÇA O QUE SE PEDE.

A ) DESENHE BOLINHAS NO BALÃO QUE TEM O FIO MAIS

COMPRIDO.

Resposta: Os estudantes devem desenhar bolinhas no balão B.

B ) DESENHE TRACINHOS NO BALÃO QUE TEM O FIO MAIS CURTO.

Resposta: Os estudantes devem desenhar tracinhos no balão A

4. WALTER E SUA MÃE VÃO AO PARQUE. IMAGEM COM ELEMENTOS SEM PROPORÇÃO ENTRE SI.

PINTE O CAMINHO MAIS CURTO QUE LEVA WALTER E SUA MÃE AO PARQUE.

Resposta. Os estudantes devem pintar o caminho C

BNCC

Ao realizar a atividade 4 em grupos, os estudantes podem desenvolver a capacidade de produzir argumentos que embasem seus pontos de vista, tornando os convincentes, por meio de conhecimentos matemáticos já estudados, como as noções de comprimento, buscando compreender e atuar no mundo, como orienta a Competência específica de Matemática 2 da BNCC.

5. OBSERVE AS CRIANÇAS A SEGUIR.

A ) MARQUE UM X NA CRIANÇA MAIS ALTA

Resposta: Os estudantes devem marcar um X na criança 1

B ) CONTORNE A CRIANÇA MAIS BAIXA

Resposta: Os estudantes devem contornar a criança 2

6. NA IMAGEM A SEGUIR, ESTÃO REPRESENTADOS ALGUNS

PÁSSAROS NOS GALHOS DE UMA ÁRVORE.

A ) MARQUE UM X NO PÁSSARO QUE ESTÁ NO GALHO MAIS ALTO.

Resposta: Os estudantes devem marcar um X no pássaro 1

B ) CONTORNE O PÁSSARO QUE ESTÁ NO GALHO MAIS BAIXO.

Resposta: Os estudantes devem contornar o pássaro 4

09:16:31

• Tanto quanto possível, apresente exemplos práticos, utilizando elementos da sala de aula e do cotidiano dos estudantes. Explore com eles a percepção de que termos como mais alto e mais baixo sempre são relativos, pois dependem de uma comparação entre dois ou mais elementos.

• A atividade 6 é bastante importante para que os estu dantes aprendam a não confundir as grandezas altura e comprimento. Ao ler o enunciado, verifique se eles compreendem que não se trata de identificar o pássaro que está no galho mais comprido, e sim o que está em uma posição mais alta.

• Ao trabalhar com esta atividade, converse com os estudantes sobre a importância de preservar a natureza. Fazendo a nossa parte, podemos ajudar a cuidar das plantas e dos animais. Aproveite a oportunidade e pergunte quem já plantou uma árvore ou outra planta. Caso tenham plantado, incentive os a contar aos colegas como foi a experiência.

• A atividade 7 , além de avaliar a compreensão do conceito de altura, exercita capacidades básicas de lógica. Nesse sentido, verifique se os estudantes são capazes de realizar as deduções necessárias para identificar cada criança com base nas dicas. Caso eles encontrem dificuldades, instruaos a localizar uma criança de cada vez, começando pelo mais alto e resolvendo até chegar ao mais baixo e percebendo que o nome de cada uma deve ser ligado a apenas uma criança. Para as que têm a mesma altura, pergunte qual dos nomes pode se referir à menina e qual deles pode ser relacionado com o menino.

• Para o desenvolvimento da atividade 7, recomendase oferecer instruções claras e visuais para estudantes com TEA ou TDAH, que tenham dificuldade de realizar a atividade. Por exemplo, use instrumentos concretos de apoio para a comparação das alturas. A leitura das dicas em voz alta, com entonação e destacando as informaçõeschave, também pode auxiliar. Para estudantes com comprometimento motor manual, a atividade pode ser realizada por apontamento ou indicação oral, relacionando as alternativas.

• O objetivo da atividade 8 é reconhecer no cenário o elemento maior, o mais alto e o mais estreito. Na cena, os estudantes precisam identificar os objetos a serem comparados e, então, verificar qual deles segue as condições apresentadas no enunciado. Sugerese a troca de ideias com os estudantes, a fim de auxiliar na identificação de objetos da sala de aula que sirvam para comparação. Aplique nesses comandos e trocas de ideias os termos maior, mais alto e mais estreito.

7.

LEIA AS INFORMAÇÕES. DEPOIS, LIGUE CADA CRIANÇA AO PRÓPRIO NOME.

Resposta: Os estudantes devem ligar: A-RICARDO; B-JULIANO; C-GISELE; D-ROBERTA.

DICA: JULIANO É O MAIS ALTO.

ROBERTA É A MAIS BAIXA. RICARDO E GISELE TÊM A MESMA ALTURA.

8. CONSIDERANDO A IMAGEM, FAÇA O QUE SE PEDE.

A ) MARQUE UM X NO SOFÁ MAIOR

Resposta: Os estudantes devem marcar um X no sofá cor-de-rosa.

B ) CONTORNE O VASO MAIS ALTO.

Resposta: Os estudantes devem contornar o vaso azul.

C ) MARQUE UMA ● NA LISTRA MAIS ESTREITA DA PAREDE.

Resposta: Os estudantes devem marcar uma ● na listra verde acima do sofá roxo.

JULIANO ROBERTA RICARDO GISELE

9. A PROFESSORA ORGANIZOU OS ESTUDANTES EM FILA, DO MAIS BAIXO PARA O MAIS ALTO.

PROFESSORA CÉLIA

RAVI SUELI RUI ANA

A ) CONTORNE O ESTUDANTE MAIS BAIXO.

Resposta: Os estudantes devem contornar o estudante RAVI

B ) MARQUE UM X NO ESTUDANTE MAIS ALTO.

Resposta: Os estudantes devem marcar um X na estudante ANA.

10. PEDRO E LAURA USARAM PEÇAS COLORIDAS PARA REPRESENTAR OS PRÉDIOS ONDE MORAM.

• Nas atividades 9 e 10, verifique se os estudantes fazem a distinção entre os termos mais alto e mais baixo. Se achar conveniente, desenvolva a atividade 9 na prática, solicitando a alguns estudantes que se posicionem diante da sala de aula de acordo com a medida da altura deles. Direcione a ação com respeito e cuidado, levando em conta que alguns deles possam sentir constrangimento ao serem comparados com os colegas da turma. Ao final da atividade, peçalhes que escrevam no caderno o nome de um objeto que consideram mais baixo e outro mais alto do que eles.

PEDRO LAURA

A ) PINTE DE VERDE O QUADRO COM O NOME DE QUEM MONTOU O PRÉDIO MAIS BAIXO.

Resposta: Os estudantes devem pintar de verde o quadro com o nome LAURA

PEDRO LAURA

B ) PINTE DE AZUL O QUADRO COM O NOME DE QUEM MONTOU O PRÉDIO MAIS ALTO.

Resposta: Os estudantes devem pintar de azul o quadro com o nome PEDRO

PEDRO LAURA

C ) O QUE PODE SER FEITO PARA QUE O PRÉDIO MAIS BAIXO SE TORNE O MAIS ALTO?

Sugestão de resposta: Laura deve empilhar na sua construção no mínimo mais três camadas de peças.

• Leve para a sala de aula peças e blocos e, depois de realizar a atividade 10, distribuaos aos estudantes para que montem prédios como os da atividade. Orienteos sobre o assunto em questão e, durante a conversa, faça perguntas para auxiliar na observação e resolução da atividade. Verifique se eles percebem os formatos das peças e se são capazes de identificálos enquanto executam as montagens.

03/10/2025 09:16:32

• A atividade 11 apresenta uma cantiga. Faça a leitura dela com os estudantes e, depois, cantem juntos. Essa atividade tem por objetivo leválos a comparar unidades de medida de comprimento não convencionais. No item A, eles devem observar a imagem e indicar a quantidade de passos dados pelo gigante. É possível que confundam pegadas com passos. Se isso acontecer, selecione um estudante da turma e peça a ele que dê alguns passos na sala de aula. Use essa situação para explicar à turma a diferença entre passos e pegadas. No item B, esperase que os estudantes percebam que precisariam dar mais passos do que o gigante.

• Caso eles apresentem dificuldade, escolha uma medida de distância na sala de aula, por exemplo, a medida de distância entre a mesa do professor e a porta, selecione dois estudantes que aparentam ter passadas com medidas de comprimento diferentes e compare a quantidade de passos de cada um para percorrer esse trajeto. Verifique se eles percebem que, quanto menor for a medida de comprimento do passo, maior será a quantidade de passos necessários para um percurso.

11. LEIA A CANTIGA A SEGUIR. DEPOIS, CANTE-A COM O PROFESSOR E OS COLEGAS.

11. B) Resposta pessoal. Espera-se que os estudantes respondam que deixariam mais pegadas, porque a medida do comprimento

do passo deles é menor do que a medida do passo do gigante, e isso deixaria mais pegadas no chão.

A PISADA DO GIGANTE

LÁ VEM O GRANDE GIGANTE

PISANDO FORTE NO CHÃO

TURURU, TUM, TUM

O SEU PÉ É BEM GRANDÃO

QUANDO BATE

FAZ TREMER O CHÃO

TURURU, TUM, TUM

A ) QUANTAS PEGADAS O GIGANTE DEIXOU AO IR DA PEDRA

ATÉ O LAGO? PEGADAS.

Resposta: 5 PEGADAS.

B ) VOCÊ DEIXARIA MAIS OU MENOS PEGADAS QUE O GIGANTE PARA FAZER O MESMO PERCURSO? POR QUÊ?

EXPERIMENTE

12. EM DIFERENTES ÉPOCAS E CULTURAS, ERA COMUM USAR PARTES DO PRÓPRIO CORPO PARA MEDIR COMPRIMENTOS. UTILIZE PARTES DO SEU CORPO PARA REALIZAR AS MEDIÇÕES A SEGUIR NA SALA DE AULA.

A ) USANDO SEU PÉ, MEÇA A DISTÂNCIA DE SUA CARTEIRA ATÉ A PAREDE MAIS PRÓXIMA.

Resposta pessoal. A resposta depende da medida de comprimento do pé de cada estudante.

B ) USANDO SEU PALMO, MEÇA

A ALTURA DA MESA DO PROFESSOR.

Resposta pessoal. A resposta depende da medida de comprimento do palmo de cada estudante.

C ) USANDO SEU PASSO, MEÇA O COMPRIMENTO DO RODAPÉ DE UMA DAS PAREDES DA SALA DE AULA.

Resposta pessoal. A resposta depende da medida de comprimento do passo de cada estudante.

D ) COMPARE COM OS SEUS COLEGAS AS MEDIDAS DE COMPRIMENTO QUE VOCÊ OBTEVE EM CADA SITUAÇÃO. ELAS SÃO IGUAIS OU DIFERENTES? POR QUÊ? PÉ

PASSO Resposta pessoal. Espera-se que os estudantes percebam que, como a medida do comprimento das partes do corpo varia de uma pessoa para outra, os resultados obtidos podem variar.

BNCC

Na atividade 12, é proposto aos estudantes realizarem medições utilizando partes do próprio corpo. Ao usarem essa estratégia para medir comprimentos, eles experimentam os procedimentos que alguns povos antigos usavam e, com isso, podem perceber que a Matemática é uma ciência humana que resulta das necessidades de diferentes culturas, em diferentes momentos históricos, contribuindo para solucionar problemas, conforme orienta a Competência específica de Matemática 1 da BNCC.

03/10/2025 09:16:40

• Para realizar medições com partes do corpo, na atividade 12, divida a turma em grupos com quatro estudantes. Um grupo por vez deve fazer as medições propostas na atividade, enquanto os demais aguardam. Durante a atividade, oriente cada grupo a responder aos itens da página.

• No item D, os estudantes devem comparar as medidas obtidas em cada situação com as dos colegas. Aproveite esse momento para observar se eles compreenderam que, quando são usadas unidades de medida não padronizadas para expressar a mesma distância (nesse caso, os pés, os palmos e os passos dos estudantes, com medidas de comprimento diferentes), obtêmse resultados diferentes.

• A atividade 12 indica um contexto em que outros sentidos, além da visão, são explorados pelos estudantes: o tato, ao utilizarem o pé; o palmo e o passo para realizarem as medições na sala de aula. O tato é responsável por nos fazer sentir o toque e perceber as características daquilo que entra em contato com nosso corpo, visto que seu órgão principal é a pele, contribuindo para uma aprendizagem multimodal que pode ser eficaz para alguns estudantes, incluindo aqueles com NEE.

PALMO

• Antes de apresentar a atividade 13 do Livro do Estudante, proponha essa dinâmica na prática. Primeiro, organize grupos de três estudantes e proponha a cada equipe que vá até a lousa para medir o comprimento da lousa utilizando o palmo. Depois, os resultados obtidos devem ser registrados em uma tabela. Ao medir com o palmo, os estudantes se familiarizam com o conceito de unidade de medida de maneira prática, visualizando e experimentando o tamanho de um palmo e entendendo que é possível usar medições como essa em diversas situações do dia a dia, por exemplo, para medir o comprimento de uma mesa ou a largura de um livro, aplicando, assim, o conhecimento em situações práticas, além de tornar o aprendizado mais lúdico. Depois de todos os grupos terem realizado as medições e registrado os dados obtidos, faça os questionamentos apresentados no Livro do Estudante a cada grupo, e só então apresente a atividade 13

• Após os estudantes resolverem a atividade proposta, verifique se eles compreenderam que, quanto maior o palmo, menor será a medida de comprimento; e quanto menor o palmo, maior será a medida de comprimento.

13. EM UMA DINÂMICA NA SALA DE AULA, A PROFESSORA CÉLIA PEDIU AOS ESTUDANTES QUE MEDISSEM O COMPRIMENTO DA LOUSA USANDO O PALMO. OS RESULTADOS OBTIDOS POR LÚCIO, VALENTINA E NORBERTO FORAM ANOTADOS EM UMA TABELA.

RESULTADOS DAS MEDIÇÕES DOS ESTUDANTES, EM 2027

NOME

MEDIDA DO COMPRIMENTO (EM PALMOS)

LÚCIO 16

VALENTINA 18

NORBERTO 17

FONTE DE PESQUISA: ANOTAÇÕES DA PROFESSORA CÉLIA.

ESTUDANTE MEDINDO A LOUSA COM AS MÃOS.

A ) OS RESULTADOS OBTIDOS FORAM IGUAIS OU DIFERENTES?

Resposta: DIFERENTES.

B ) QUAL ESTUDANTE TEM O PALMO COM A MAIOR MEDIDA DE

COMPRIMENTO?

Resposta: LÚCIO.

C ) QUAL ESTUDANTE TEM O PALMO COM A MENOR MEDIDA DE

COMPRIMENTO?

Resposta: VALENTINA.

D ) POR QUE OS RESULTADOS OBTIDOS PELOS ESTUDANTES SÃO DIFERENTES?

Resposta pessoal. Espera-se que os estudantes

expliquem que os palmos de cada um têm medidas de comprimentos diferentes.

REFERÊNCIAS COMPLEMENTARES

SILVA, Irineu da. História dos pesos e medidas 2. ed. São Carlos: EdUFSCar, 2023. E-book O livro tem como enfoque a história das grandezas e medidas e sua evolução desde a antiguidade, ressaltando aspectos sociais, culturais e civilizatórios delas.

14. FALE PARA UM COLEGA O NOME DE UMA PESSOA QUE VOCÊ

CONHECE QUE SEJA MAIS ALTA QUE VOCÊ.

Resposta pessoal. A resposta depende da pessoa que o estudante escolher.

15. FALE PARA UM COLEGA O NOME DE UMA PESSOA QUE VOCÊ

CONHECE QUE SEJA MAIS BAIXA QUE VOCÊ.

Resposta pessoal. A resposta depende da pessoa que o estudante escolher.

16. DESENHE UM OBJETO DE SEU DIA A DIA QUE TENHA MEDIDA DE ALTURA MAIOR DO QUE A LIXEIRA DA SALA DE AULA.

Resposta pessoal. A resposta depende do objeto que o estudante vai escolher. Porém, espera-se que ele desenhe um objeto mais alto do que a lixeira da sala de aula, como uma mesa ou uma geladeira.

17. DESENHE UM OBJETO DE SEU DIA A DIA QUE TENHA MEDIDA DE ALTURA MENOR DO QUE O BEBEDOURO DA ESCOLA.

Resposta pessoal. A resposta depende do objeto que o estudante vai escolher. Porém, espera-se que ele desenhe um objeto mais baixo do que o bebedouro da escola, como uma caneca ou uma cadeira.

101

03/10/2025 09:16:41

• As atividades 14, 15, 16 e 17 propiciam aos estudantes trabalharem as noções de medida de comprimento e altura de maneira significativa, utilizando a comparação de tamanhos de pessoas e objetos. Ao aprenderem a comparar tamanhos de pessoas e objetos utilizando os termos “mais alta”, “mais baixa”, “maior” e “menor” de maneira visual, sem precisar de medidas exatas, os estudantes adquirem a capacidade de observar e analisar o mundo ao redor, prérequisitos necessários para progredir em habilidades de linguagem e pensamento lógico.

• Os desenhos realizados pelos estudantes nas atividades 16 e 17 podem ser utiizados como meio de avaliação do processo de aprendizagem, fornecendo informações sobre seus conhecimentos e suas habilidades acerca das noções de medida comprimento e altura.

BNCC

As atividades desta página promovem a comparação de tamanhos de objetos e pessoas, de modo a contemplar a habilidade EF01MA15. Nas atividades, os estudantes vão desenvolver a capacidade de utilizar termos como mais alto, mais baixo, maior e menor para fazerem comparações, identificarem características e interpretarem atributos, adquirindo vocabulário e conceitos para melhor entenderem a realidade.

• Na atividade 18, os estudantes devem identificar, entre vários instrumentos de medidas, quais são aqueles usados para medir comprimentos. Peça a eles que analisem as imagens da atividade e motiveos a expor as informações que têm sobre cada instrumento de medida. Aproveite o contexto da atividade para comentar a função de cada instrumento representado nesta página

• O objetivo da atividade 19 é a cooperação entre os pares, a fim de promover uma aprendizagem contextualizada, por meio da qual busquem situações do dia a dia e escrevam duas em que seja preciso medir comprimentos.

BNCC

Na atividade 19, é proposto aos estudantes interagirem com seus pares de modo cooperativo, trabalhando coletivamente na escrita das situações em que é preciso medir comprimentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles, conforme orienta a Competência específica de Matemática 8 da BNCC.

AVALIANDO

Objetivos

Reconhecer alguns instrumentos utilizados para medir comprimentos.

Identificar o instrumento de medida mais adequado ao objeto a ser medido.

Sugestão de intervenção

Leve para a sala de aula os instrumentos mais usados para medir comprimentos em tarefas cotidianas, como fita métrica, trena e régua. Oriente os estudantes no manuseio deles e na análise de suas diferenças.

18. EM CERTAS SITUAÇÕES DO DIA A DIA, USAMOS INSTRUMENTOS PARA MEDIR COMPRIMENTOS. ALGUNS DELES SÃO ÚTEIS NO TRABALHO DE CERTAS PROFISSÕES. CONTORNE OS INSTRUMENTOS UTILIZADOS PARA MEDIR COMPRIMENTOS.

Resposta: Os estudantes devem contornar os instrumentos B; D; G

IMAGENS

BALANÇA DIGITAL. CALENDÁRIO.

FITA MÉTRICA.

TRENA.

RELÓGIO DE PULSO.

TERMÔMETRO DIGITAL.

RÉGUA.

RECIPIENTE GRADUADO.

19. JUNTE-SE A UM COLEGA E ESCREVAM NO CADERNO DUAS SITUAÇÕES EM QUE É PRECISO MEDIR COMPRIMENTOS.

Resposta pessoal. A resposta depende das vivências dos estudantes. Espera-se que os estudantes deem exemplos de medições do seu dia a dia.

Depois, pergunte qual é o instrumento mais adequado para medir o comprimento:

• da mesa do professor;

• da porta da sala de aula;

• do Livro do Estudante;

• da borracha;

• do lápis;

• do pátio da escola.

Caso os estudantes tenham dificuldade para identificar o instrumento mais adequado para medir os comprimentos propostos, faça as medições na prática com a ajuda deles. Isso garantirá um aprendizado mais eficiente sobre os

instrumentos e permitirá que eles recuperem as defasagens por meio de um trabalho de comparação e de medições.

O CENTÍMETRO

1. A RÉGUA GRADUADA É UM INSTRUMENTO UTILIZADO PARA MEDIR COMPRIMENTOS. A MEDIDA DO COMPRIMENTO DO NÚMERO 0 ATÉ O NÚMERO 1 É DE 1 CENTÍMETRO.

1 CENTÍMETRO

0123456789101112131415

NA RÉGUA, QUANTOS CENTÍMETROS HÁ:

A ) DE 0 ATÉ 2?

Resposta: 2 centímetros.

B ) DE 0 ATÉ 5?

Resposta: 5 centímetros.

C ) DE 3 ATÉ 4?

Resposta: 1 centímetro.

D ) DE 3 ATÉ 7?

Resposta: 4 centímetros.

2. LEONARDO MEDIU O COMPRIMENTO DE SEU LÁPIS USANDO UMA RÉGUA.

0123456789101112131415

ELE POSICIONOU A PARTE DE TRÁS DO LÁPIS NO ZERO, COMO MOSTRA A FIGURA. COM BASE NA IMAGEM, COMPLETE A FRASE.

O LÁPIS DE LEONARDO MEDE CENTÍMETROS DE MEDIDA DE COMPRIMENTO.

Resposta: O LÁPIS DE LEONARDO MEDE 13 CENTÍMETROS DE MEDIDA DE COMPRIMENTO.

qualquer objeto ou segmento, devese sempre posicionála começando no 0, na extremidade inicial do que se pretende medir. Para complementar essa atividade, disponibilize réguas para os estudantes e peça que meçam a imagem do lápis da página. Solicite também que meçam outros objetos, como palitos de sorvete, canudinhos e lápis de cor. Tenha o cuidado de selecionar objetos com medidas de comprimento representadas por números naturais.

ATIVIDADE EXTRA

03/10/2025 09:16:42

Organize a turma em trios e distribua uma régua para cada grupo. Em seguida, solicite a cada estudante que desenhe no caderno: um palito de sorvete medindo 7 centímetros de comprimento; um lápis medindo 10 centímetros de comprimento; e um pedaço de barbante medindo 12 centímetros de comprimento.

• Antes de trabalhar com os estudantes a atividade 1, orienteos a observar atentamente o início e o fim da graduação da régua, comentando que ela não se inicia exatamente em sua extremidade. É importante que eles estejam atentos a esse detalhe para não cometerem erros nas medições que vão realizar.

• O objetivo da atividade 1 é apresentar aos estudantes o centímetro como unidade de medida de comprimento padronizada. Nos itens A a D, é possível que eles indiquem como resultado das medições um centímetro a mais. Nesse caso, eles devem estar considerando as medidas do intervalo, incluindo aquelas que estão nas extremidades. Assim, orienteos a levar em conta somente os intervalos entre as medidas indicadas.

• Para melhor aproveitamento desta atividade e para observar se os estudantes compreenderam a maneira correta de indicar a quantidade de centímetros que há entre os intervalos, faça alguns questionamentos como: “Na régua, quantos centímetros há de 2 a 9?”; “Quantos centímetros há de 0 a 13?”; “Quantos centímetros há de 6 a 12?”; “Quantos centímetros há de 1 a 8?”.

• A atividade 2 trabalha a leitura e o registro da medida do comprimento de um lápis. Diga a eles que, ao utilizar uma régua para medir

• A atividade 3 tem por objetivo levar os estudantes a realizarem medições com a régua. Nesse momento, caso eles apresentem dificuldade ao posicionála, auxilieos no que for necessário. Utilize essa atividade para questionar qual objeto é o mais comprido e qual é o mais curto.

• Na atividade 4, além de medir os comprimentos das fitas com auxílio da régua, os itens B e C abordam a comparação delas, a fim de classificálas em mais curta e mais comprida. É importante que os estudantes sejam capazes de estimar, por meio de comparações, as medidas de comprimento de objetos. Portanto, para melhor aproveitamento dessa atividade, e com o propósito de recuperar a aprendizagem dos estudantes com dificuldade, mostre a eles um par de objetos, como uma caneta e uma borracha, um clipe e um lápis ou um estojo e um caderno, e peça que os comparem e os classifiquem em mais comprido e em mais curto antes de realizar a medição deles.

BNCC

A atividade 4 aborda a comparação de medidas de comprimento utilizando expressões como mais curto e mais comprido, conforme orienta a habilidade EF01MA15 da BNCC.

Aproveite a imagem da escova de dentes da ativida de 3 para destacar a importância da escovação após as principais refeições, como condição para manter a saúde bucal. Com isso, são contemplados aspectos da Competência geral 8 e do tema contemporâneo transversal Saúde da BNCC.

• Conclua o trabalho com a unidade apresentando aos estudantes a sugestão de desafio a seguir. Verifique se eles interpretam as informações desse desafio, identificando que os sete irmãos correspondem aos dias da semana, dos quais cinco têm nomes que são terminados em “feira”.

3. DE ACORDO COM OS OBJETOS A SEGUIR, RESOLVA OS ITENS.

CANETA. ESCOVA DE DENTES.

3. A) Resposta: CANETA: 15 cm; ESCOVA DE DENTES: 10 cm.

IMAGENS SEM PROPORÇÃO ENTRE SI.

A ) UTILIZANDO UMA RÉGUA, MEÇA O COMPRIMENTO DE CADA

UM DESSES OBJETOS.

B ) REGISTRE NO QUADRO A MEDIDA DE CADA UM DELES.

Resposta: CANETA: 15; ESCOVA DE DENTES: 10

MEDIDA DO COMPRIMENTO DOS OBJETOS

OBJETO CANETA ESCOVA DE DENTES

MEDIDA DO COMPRIMENTO (EM CENTÍMETROS)

4. ALGUNS PEDAÇOS DE FITA ESTÃO REPRESENTADOS A SEGUIR.

A ) USANDO UMA RÉGUA, MEÇA O COMPRIMENTO DAS FITAS E REGISTRE NO QUADRO OS RESULTADOS OBTIDOS.

Resposta: VERMELHA: 5; AZUL: 8; VERDE: 11.

MEDIDA DO COMPRIMENTO DAS FITAS

COR DA FITA VERMELHA AZUL VERDE

MEDIDA DO COMPRIMENTO (EM CENTÍMETROS)

B ) QUAL É A COR DA FITA MAIS CURTA?

Resposta: VERMELHA.

C ) QUAL É A COR DA FITA MAIS COMPRIDA?

Sugestão de Desafio

Somos sete irmãos, mas cinco vão à feira, e dois não. Quem somos?

Resposta

Os dias da semana.

AVALIANDO

Objetivos

Reconhecer o centímetro como unidade de medida de comprimento, realizar medições usando uma régua e estimar medidas de comprimento de objetos.

Resposta: VERDE.

Sugestão de intervenção

03/10/2025 09:16:43

Caso algum estudante não atinja os objetivos propostos, retome as atividades 3 e 4 da página 104 Selecione alguns objetos e peça a ele que estime a medida de seus comprimentos. Depois, usando uma régua, meça o comprimento desses itens e escrevaos na lousa comparando com as estimativas feitas por eles. Retome a importância do posicionamento da régua ao medir os objetos, mostrando aos estudantes a posição correta. Selecione antecipadamente os materiais que serão medidos, para que as medidas obtidas sejam números naturais.

5. A IMAGEM MOSTRA UM PEDAÇO DE FITA CUJA

MEDIDA DE COMPRIMENTO É 1 CENTÍMETRO.

1 CENTÍMETRO

A ) ESTIME, EM CENTÍMETROS, A MEDIDA DO COMPRIMENTO DE CADA FITA A SEGUIR.

MEDIDA ESTIMADA DO COMPRIMENTO DA FITA:

• AZUL:

Resposta pessoal. Espera-se que os estudantes estimem

Resposta pessoal. Espera-se que os estudantes estimem que a fita vermelha

• Na atividade 5, após os estudantes estimarem as medidas solicitadas, digalhes que estimar é o mesmo que fazer uma previsão, ou seja, dar uma resposta aproximada antes de ter certeza do resultado. Em seguida, meça o comprimento do apagador e do giz usando uma régua para verificar se as estimativas se aproximaram do resultado obtido.

que a fita azul mede cerca de 11 centímetros. mede cerca de 14 centímetros.

CENTÍMETROS.

• VERMELHA: CENTÍMETROS.

B ) MEÇA O COMPRIMENTO DAS FITAS USANDO UM BARBANTE. PARA ISSO, ESTIQUE O BARBANTE SOBRE ELAS E, DEPOIS, COLOQUE O PEDAÇO DE BARBANTE OBTIDO SOBRE UMA RÉGUA.

MEDIDA DE COMPRIMENTO OBTIDA PARA A FITA:

• AZUL:

• VERMELHA: CENTÍMETROS. Resposta: 11 CENTÍMETROS. Resposta: 14 CENTÍMETROS.

CENTÍMETROS.

C ) A ESTIMATIVA QUE VOCÊ FEZ SE APROXIMOU DA MEDIDA DO COMPRIMENTO OBTIDA COM O BARBANTE? POR QUÊ?

Resposta pessoal. Espera-se que os estudantes percebam que a medida obtida com o barbante é mais precisa do que a estimativa deles.

DESAFIO A MAIS

LEIA AS INFORMAÇÕES E ESCREVA OS NOMES DAS PESSOAS EM ORDEM CRESCENTE DE MEDIDA DE ALTURA.

• LILIAN É MAIS ALTA DO QUE HÉLIO.

• ANA É MAIS BAIXA DO QUE HÉLIO.

• PEDRO É MAIS ALTO DO QUE LILIAN.

PESSOA MAIS BAIXA

PESSOA MAIS ALTA Resposta: ANA, HÉLIO, LILIAN, PEDRO.

CONCLUSÃO

Acompanhar o desenvolvimento dos estudantes é fundamental para um ensino bemsucedido. Ao longo da unidade, foram propostas diversas maneiras de avaliar a aprendizagem da turma. A fim de realizar um monitoramento mais abrangente e organizado, registre nos relatórios individuais ou nas fichas de avaliação o desempenho de cada estudante, levando em consideração suas particularidades e mapeando suas defasagens. Um modelo desse tipo de ficha pode ser encontrado no tópico Avaliação deste Manual do Professor. Assim, será possível visualizar de modo individual as trajetórias de

• No Desafio a mais , os estudantes vão usar as relações de altura entre as pessoas para trabalhar o raciocínio lógico e a organização de informações em sequência. Esperase que eles identifiquem a ordem lógica, justificando a relação de maior que e menor que, combinando as informações para estabelecer uma ordem completa. Para resolver, os estudantes devem analisar cada frase: se Lilian é mais alta que Hélio e Ana é mais baixa que Hélio, então Hélio não é o mais baixo. Se Pedro é mais alto que Lilian, e ela já é mais alta do que Hélio, então a pessoa mais baixa é Ana e a mais alta é Pedro.

• Caso encontrem alguma lógica diferente da esperada, incentiveos a compartilhar com os demais colegas, fazendo intervenções pontuais e estratégicas.

03/10/2025 09:16:43

aprendizagem, incluindo os avanços e os pontos de dificuldades a serem sanados por meio de atividades que promovam recuperação dos conteúdos. Esse método permite repensar estratégias em sala de aula, tornando as ações pedagógicas mais eficazes.

A conclusão da unidade é o momento de avaliar se os objetivos por ela propostos foram alcançados. Para esse diagnóstico, observe no final deste Manual do Professor algumas possibilidades de avaliação formativa que permitem realizar o monitoramento da aprendizagem dos estudantes e intervir caso eles não tenham atingido os resultados esperados.

OBJETIVOS DA UNIDADE

• Compreender as ideias de à direita, à esquerda, mais perto, mais longe, dentro, fora, em cima, embaixo, atrás, entre e em frente.

• Estabelecer pontos de referência para descrever trajetos e deslocar-se no espaço.

• Descrever e registrar deslocamentos por meio de comandos, incluindo a ideia de giro.

Nesta unidade, serão abordadas atividades que envolvem a localização de elementos no espaço por meio de pontos de referência, além daquelas relacionadas aos caminhos que são representados por comandos.

INTRODUÇÃO E JUSTIFICATIVA

Por meio do trabalho realizado com o tópico Noções de localização, os estudantes são incentivados a vivenciar situações relacionadas à localização de objetos, compreendendo as ideias trazidas pelas expressões à direita, à esquerda, mais perto, mais longe, dentro, fora, em cima e embaixo, atrás, entre e em frente. Eles são levados a refletir sobre a importância e a necessidade de estabelecer um ponto de referência e de entender que, em algumas situações, eles mesmos sejam o ponto de referência; em outros, sejam objetos ou pessoas. No tópico Caminhos, são trabalhadas situações que abordam representações caminhos que serão traçados pelos estudantes, com base em comandos apresentados nas atividades.

Habilidades da BNCC trabalhadas na unidade: EF01MA11 e EF01MA12

UNIDADE

LOCALIZAÇÃO E CAMINHOS 4

CRIANÇAS BRINCANDO

NO BALANÇO EM UM PARQUE DE DIVERSÃO.

SUGESTÃO DE ESTRATÉGIA INICIAL

Escolha três estudantes da turma e peça-lhes que se dirijam até a frente da sala de aula a fim de que se organizem em fila. Questione o restante da turma quanto ao posicionamento deles, fazendo perguntas como: “Quem está na frente de João?”; “Quem está atrás de João?”; “Quem está entre Mariana e Otávio?”. Em seguida, eleja outras três pessoas para ficar lado a lado e de costas para os colegas. Amplie os questionamentos, dizendo, por exemplo: “Quem está ao lado de Eduarda?”; “Quem está à esquerda de Miguel?”; “Quem está à direita de Miguel?”. Nes-

se momento, redirecione as respostas incorretas de maneira que possam refletir sobre a análise que fizeram. Anote as dificuldades e retome essa atividade após o estudo do tópico Noções de localização, a fim de verificar a aprendizagem. Os nomes usados nesses exemplos são fictícios.

O BALANÇO É UM BRINQUEDO ENCONTRADO EM MUITOS PARQUES. ELE TEM UM ASSENTO SUSPENSO, AMARRADO POR CORDAS OU CORRENTES EM UMA TRAVE OU NO GALHO DE UMA ÁRVORE. PARA SE DIVERTIR COM ESSE

BRINQUEDO, BASTA SE BALANÇAR SEM COLOCAR OS PÉS NO CHÃO. 1. Resposta pessoal. Espera-se que os estudantes relatem suas experiências com relação ao brinquedo balanço.

VOCÊ JÁ BRINCOU EM UM BALANÇO? SE SIM, CONTE SUA EXPERIÊNCIA AOS COLEGAS.

A MENINA DE TRANÇA ESTÁ À DIREITA OU À ESQUERDA DA MENINA DE CAMISETA BRANCA?

Resposta: À direita.

CONTORNE A FICHA QUE CONTÉM A QUANTIDADE DE PESSOAS SENTADAS NO BALANÇO À ESQUERDA DO MENINO DE CAMISETA VERMELHA.

Resposta: Os estudantes devem contornar o número 2

• Leia o texto para os estudantes e oriente-os a observar a imagem. Investigue, por meio de questionamentos, se algum deles já compreende os significados de direita e esquerda, a partir de determinado ponto de referência.

• Na questão 1, caso haja um parque com balanço na escola, verifique se os estudantes costumam brincar nele e com que frequência. Explique à turma que existem vários tipos de balanço: desde aqueles encontrados em parques até os feitos com um pneu amarrado em uma árvore. Caso algum estudante conheça um tipo diferente de balanço, peça-lhe que compartilhe sua experiência com a turma.

• Antes de responderem às questões 2 e 3, converse com os estudantes sobre os conceitos referentes aos comandos à direita e à esquerda, verificando se eles têm dificuldades em relação a isso. Se necessário, desenhe duas setas na lousa, uma apontando para a esquerda e outra para a direita, rotulando-as devidamente. Nesse momento inicial, considere apenas os casos em que os próprios estudantes são tomados como referencial, para avaliar se um objeto está posicionado à direita ou à esquerda deles.

03/10/2025 09:20:59

• Ao iniciar esta unidade, avalie os conhecimentos prévios dos estudantes, explorando relações de distância e localização a partir do posicionamento deles na sala de aula e dos locais onde se encontram determinados objetos. Faça algumas perguntas, como: “Quem está mais perto da lousa?”; “Quem está mais distante?”; “Quem fica à esquerda da mesa do professor?”; “O que está em cima da mesa?”; “Os lápis estão dentro ou fora do estojo?”; “Quem está sentado na frente da janela?”.

• No decorrer do trabalho com a unidade, busque desenvolver as intuições espaciais dos estudantes, reforçando suas capacidades de localizar elementos considerando algum referencial, bem como de descrever posições relativas entre objetos.

• A atividade 1 desta página introduz noções de localização. Nela, são trabalhados conceitos como mais perto e mais longe, aprimorando a ideia de distância. É importante que os estudantes identifiquem que a distância não deve ser considerada apenas em uma direção (na horizontal ou na vertical, por exemplo). Incentive essa percepção sugerindo atividades complementares que utilizem elementos físicos da sala, aproveitando as conveniências do ambiente.

• Mais do que na teoria, as noções intuitivas dos estudantes devem ser aperfeiçoadas na prática, com ludicidade, por meio de exercícios sensoriais. Nesse sentido, peça-lhes que comentem situações hipotéticas, fazendo perguntas, como: “Caminhando, quem chegaria mais rápido?”; “E se houvesse um som, quem o ouviria mais alto?”.

• Se julgar oportuno, ao abordar o assunto Praia e saúde, mostre, em um relógio de ponteiros ou digital,

NOÇÕES DE LOCALIZAÇÃO

1. A CENA MOSTRA ALGUMAS PESSOAS NA PRAIA.

A ) CONTORNE DE AZUL A CRIANÇA QUE ESTÁ MAIS PERTO DA BOLA.

Resposta: Os estudantes devem contornar de azul a criança 1

B ) CONTORNE DE VERMELHO A PESSOA QUE ESTÁ MAIS LONGE DO VENDEDOR DE ÁGUA DE COCO.

Resposta: Os estudantes devem contornar de vermelho a pessoa 4

C ) CONTORNE DE VERDE A PESSOA QUE ESTÁ MAIS PERTO DA PILHA DE COCOS.

Resposta: Os estudantes devem contornar de verde a pessoa 3

D ) VOCÊ JÁ FOI À PRAIA? SE SIM, CONVERSE COM OS COLEGAS E CONTE COMO FOI ESSE PASSEIO.

Resposta pessoal. A questão tem como objetivo a socialização das respostas dadas pelos estudantes, promovendo um momento de interação e troca de ideias.

PRAIA E SAÚDE

PARA MANTER SUA SAÚDE AO IR À PRAIA, VOCÊ DEVE

SE HIDRATAR, USAR SEMPRE PROTETOR SOLAR, NÃO FICAR MUITAS HORAS EM EXPOSIÇÃO AO SOL E ESTAR SEMPRE ACOMPANHADO DE UM ADULTO, PREFERINDO HORÁRIOS NO INÍCIO DA MANHÃ OU NO FINAL DA TARDE.

os horários preferíveis para exposição ao sol: antes das 10 horas da manhã e depois das 4 horas da tarde.

BNCC

As atividades deste tópico propiciam a descrição de localizações no espaço com base nas posições dos estudantes ou em algum ponto de referência. A atividade 1 aborda conceitos elementares de mais perto e mais longe, evidenciando que essa percepção depende da adoção de um referencial. Dessa maneira, a habilidade EF01MA12 é contemplada.

2. LUCIANA TOCA BERIMBAU NA RODA DE CAPOEIRA.

A ) MARQUE UM X NAS PESSOAS QUE ESTÃO À ESQUERDA DE LUCIANA.

BERIMBAU: INSTRUMENTO MUSICAL DE ORIGEM AFRICANA.

Resposta: Os estudantes devem marcar um X nas pessoas 1, 2 e 3.

B ) CONTORNE AS PESSOAS QUE ESTÃO À DIREITA DE LUCIANA.

Resposta: Os estudantes devem contornar as pessoas 4, 5 e 6

3. OBSERVE A CENA. EM

SEGUIDA, MARQUE

UM X NO QUADRO A SEGUIR, INDICANDO A POSIÇÃO DE CADA

POTE DE TINTA EM RELAÇÃO À CRIANÇA.

Resposta: Os estudantes devem marcar um X no quadro, nas seguintes posições: amarelo: ESQUERDA; azul: DIREITA; verde: DIREITA; vermelho: ESQUERDA.

POSIÇÃO DE CADA POTE DE TINTA, CONFORME A COR

POTE DE TINTA

ESQUERDA

DIREITA

BNCC

As atividades 2 e 3 exercitam a capacidade de descrever a localização de pessoas e de objetos no espaço em relação à própria posição, isto é, tomando a si mesmo como referencial. Assim, a habilidade EF01MA11 é contemplada, incentivando a aprendizagem dos conceitos de direita e esquerda.

03/10/2025 09:21:01

• Ambas as atividades desta página exploram o conceito de lateralidade. No trabalho com elas, sempre posicione seu corpo na mesma orientação que os dos estudantes. Afinal, caso isso não ocorra, a esquerda de um será a direita do outro.

• Na atividade 2, o significado de uma palavra nova é apresentado. O contexto proposto instiga o conhecimento dos estudantes acerca de manifestações culturais. Verifique se é comum haver grupos de capoeira na região onde moram. Caso conheçam algum grupo de capoeiristas, peça-lhes que relatem aos colegas como é a formação dele, se conhecem os instrumentos utilizados, se já assistiram a uma roda de capoeira e como são as músicas.

• Na atividade 3, instrua os estudantes a se colocarem na mesma posição que a criança representada na imagem. Eles podem organizar parte de seus materiais em um lado da carteira e o restante do outro, identificando qual está à esquerda e qual está à direita.

• Para que se lembrem de qual é a esquerda e qual é a direita, é eficiente pensar na esquerda como o lado em que fica o coração. Nesse caso, explique-lhes que, colocando a mão sobre o peito, é possível sentir com mais força os batimentos de um lado do que do outro. Outro recurso útil é associar a direita ou a esquerda a algum acessório de uso constante, como relógio, pulseira ou um desenho no uniforme.

LUCIANA

• Ao trabalhar com a atividade 4 , que propõe a identificação de quem está à direita e à esquerda de uma das meninas da ilustração, verifique se os estudantes percebem que a personagem Isabela está de costas para quem olha a imagem. Assim, a direita de Isabela corresponde à direita do observador. Isso também ocorre em relação à esquerda.

• No desenvolvimento da atividade 5, espera-se que os estudantes considerem a posição de cada uma das personagens para fazerem a leitura da imagem. Verifique se eles percebem, por exemplo, que a direita delas corresponde à esquerda do observador. Caso apresentem dificuldades para isso, auxilie-os nessa análise. Para complementar o trabalho, faça com a turma a correção da frase falsa.

• Na atividade 5 , sugira uma atividade colaborativa, de modo que troquem suas percepções sobre cada imagem, a fim de promover a inclusão dos estudantes. Um grupo pode descrever a primeira imagem; outro, a segunda; e, por fim, o último pode indicar as mudanças que ocorreram, por exemplo.

A ) MARQUE UM X NA MENINA QUE ESTÁ IMEDIATAMENTE À ESQUERDA DE ISABELA.

Resposta: Os estudantes devem marcar um X em MARCELA

B ) CONTORNE A MENINA QUE ESTÁ À DIREITA DE ISABELA.

Resposta: Os estudantes devem contornar AMANDA.

5. BIA E ANA FIZERAM COMPRAS.

MARQUE UM X NA FRASE CORRETA DE ACORDO COM A ILUSTRAÇÃO.

BIA ESTÁ COM O CARRINHO DE COMPRAS NA MÃO DIREITA

ANA ESTÁ COM A SACOLA NA MÃO DIREITA

Resposta: Os estudantes devem marcar um X na frase: ANA ESTÁ COM A SACOLA NA MÃO DIREITA.

ISABELA CHEGOU PARA BRINCAR COM OS AMIGOS DELA.

A ) LIGUE CADA PERSONAGEM À FICHA CORRESPONDENTE.

Resposta: Os estudantes devem ligar a criança da piscina à ficha ESTÁ DENTRO DA PISCINA e a menina de óculos à ficha ESTÁ FORA DA PISCINA

ESTÁ FORA DA PISCINA.

ESTÁ DENTRO DA PISCINA.

B ) DESENHE NA CENA DOIS BRINQUEDOS: UM DENTRO DA PISCINA E O OUTRO FORA. DEPOIS, TERMINE DE PINTAR A IMAGEM.

Resposta pessoal. Comentários nas orientações ao professor.

• Os estudantes possivelmente já vão estar familiarizados com os conceitos de dentro e fora. No entanto, é conveniente comentar que, quando dizemos “dentro”, estamos utilizando algum lugar como referência; portanto, devemos falar “dentro de” algum local. Assim, por exemplo, um lápis sobre a mesa está dentro da sala, mas fora do estojo. Alguém passando no corredor da escola está fora da sala de aula, mas dentro da escola.

• Aproveite essas ideias para complementar a atividade 6. Indique os mais variados objetos e pergunte aos estudantes se estão dentro ou fora de determinado referencial. A cada pergunta, mude o referencial. Complemente a atividade exercitando a imaginação da turma: faça referência a pessoas e objetos que não estão visíveis no momento. Pergunte, por exemplo: “As pessoas esperando o ônibus em uma rodoviária estão dentro ou fora dos veículos?”; “E estão dentro ou fora da rodoviária?”; “Uma tartaruga andando pelo jardim está dentro ou fora de seu casco?”; “Um astronauta indo para a Lua está dentro ou fora do planeta Terra?”; “E está dentro ou fora da nave espacial?”.

BNCC

A atividade 6 evidencia que a utilização de termos que se referem à posição exige que o referencial esteja explícito, em consonância com o que prevê a habilidade EF01MA12

03/10/2025 09:21:04

• Ao trabalhar com o item B, auxilie os estudantes na composição do desenho, acompanhando o controle e a firmeza nos traços. Deixe-os livres para escolher os brinquedos que preferirem e permita que os retratem com plena imaginação. No entanto, tente levá-los a fazer desenhos em escalas proporcionais às reais e a escolher cores adequadas.

• Assim como na atividade da página anterior, é provável que os estudantes já tenham familiaridade com os conceitos de em cima e embaixo. Desse modo, aprofunde a ideia de referencial dando exemplos que estejam próximo deles.

ARTICULANDO

CONHECIMENTOS

Na atividade 7, ao realizarem a leitura do poema, a fluência em leitura oral e a aquisição de vocabulário são desenvolvidas, proporcionando oportunidade de estabelecer relação entre os componentes curriculares de Matemática e de Língua Portuguesa. Explore essa relação ao trabalhar a atividade, pedindo aos estudantes que deem exemplos de animais que conseguem subir em árvores e de outros que não conseguem. Em seguida, solicite que desenhem no caderno algum animal em cima de uma árvore bem alta e outro embaixo. Depois do desenho, eles podem exercitar a criatividade elaborando uma história para a produção deles.

7. LEIA COM O PROFESSOR O TEXTO. DEPOIS, FAÇA O QUE SE

PEDE DE ACORDO COM A CENA.

[...] EU AINDA

ERA UM FILHOTE DE POUCO PELO E SEM

NOME QUANDO SUBI

AQUI PELA PRIMEIRA

VEZ. FUGIA DE UM BANDO DE CÃES QUE

ME VIRAM NA RUA E DECIDIRAM ME PEGAR. MAS NÃO PEGARAM, E

LÁ SE VÃO DOIS ANOS. DESDE ENTÃO NÃO

BOTEI MAIS AS PATAS NO CHÃO. [...]

SARMENTO, TADEU. O GATO DA ÁRVORE DOS DESEJOS BELO HORIZONTE: ABACATE, 2021. P. 8.

A ) MARQUE UM X NO ANIMAL QUE ESTÁ EM CIMA DA ÁRVORE NA CENA.

Resposta: Os estudantes devem marcar um X no gato.

B ) MARQUE UM X NO ANIMAL QUE ESTÁ EMBAIXO DA ÁRVORE NA CENA.

Resposta: Os estudantes devem marcar um X no cachorro.

A ) PINTE O NOME DO BRINQUEDO QUE ESTÁ EM CIMA DA CAMA.

Resposta: Os estudantes devem pintar URSO DE PELÚCIA.

PETECA URSO DE PELÚCIA

B ) MARQUE UM X NO BRINQUEDO QUE ESTÁ EMBAIXO DA CADEIRA.

Resposta: Os estudantes devem marcar um X no macaco de pelúcia.

C ) VOCÊ COSTUMA ORGANIZAR SEU QUARTO OU DEIXA TUDO ESPALHADO? CONVERSE COM OS COLEGAS SOBRE ISSO.

Resposta pessoal. Espera-se que os estudantes dialoguem com os colegas de modo a compreender a importância de ser organizado.

03/10/2025 09:21:06

• Na atividade 8, os estudantes devem identificar, na cena apresentada, o brinquedo que está em cima da cama e o que está embaixo da cadeira. Caso demonstrem dificuldade ao responder aos itens, utilize algum objeto da sala de aula para retomar o assunto. Posicione, por exemplo, um livro em cima de sua mesa e, depois, coloque-o embaixo dela. Faça perguntas sobre a posição do livro nos dois momentos, enfatizando os termos utilizados – em cima, embaixo e outros –, sempre citando o referencial que, nesse exemplo, é a mesa.

• Para melhor aproveitamento da atividade, faça outros questionamentos a respeito da cena, usando objetos que não tiveram a sua localização descrita na atividade como a bola, os patins, a peteca e o caderno.

• Ao trabalhar com a atividade 9, aproveite as experiências da turma para pôr em prática os conhecimentos sobre noções de localização. Faça perguntas relacionadas aos conceitos abordados neste tópico, tomando como referência as brincadeiras que os estudantes fazem nos momentos de lazer.

• Peça que citem algumas de suas brincadeiras favoritas e, com base nelas, deem exemplos de frases com as expressões aprendidas. Por exemplo: “Quando brincamos de Amarelinha, pulamos em cima dos números desenhados no chão”.

• Se julgar conveniente, a fim de motivar a produção escrita, solicite que escrevam os nomes dessas brincadeiras em seus cadernos. Dê-lhes tempo para fazer seus registros e os auxilie se tiverem dificuldades. Alternativamente, peça-lhes que citem os nomes das brincadeiras. Registre-os na lousa, para que copiem no caderno.

9. A CENA A SEGUIR MOSTRA O MOMENTO DE UMA BRINCADEIRA DE ESCONDE-ESCONDE.

A ) CONTORNE DE AZUL A CRIANÇA QUE ESTÁ EMBAIXO DA MESA.

Resposta: Os estudantes devem contornar de azul a criança 2

B ) MARQUE UM X NA CRIANÇA QUE ESTÁ DENTRO DA CASINHA.

Resposta: Os estudantes devem marcar um X na criança 3

C ) CONTORNE DE VERMELHO A CRIANÇA QUE ESTÁ ATRÁS DO BANCO DA PRAÇA.

Resposta: Os estudantes devem contornar de vermelho a criança 4.

VAMOS BRINCAR?

BRINCADEIRAS AO AR LIVRE SÃO MUITO IMPORTANTES PARA O SEU DESENVOLVIMENTO. APROVEITE A OPORTUNIDADE E BRINQUE COM OS AMIGOS SEMPRE QUE PUDER. CONVERSE COM SEUS PAIS OU RESPONSÁVEIS SOBRE AS BRINCADEIRAS DE QUANDO ELES ERAM CRIANÇAS.

A ) CONTORNE A FICHA COM O NOME DA PESSOA QUE ESTÁ ATRÁS DE PEDRO NA FILA.

TIAGO

Resposta: Os estudantes devem contornar a ficha com o nome TIAGO.

B ) CONTORNE A FICHA COM O NOME DA PESSOA QUE ESTÁ ENTRE LUÍZA E TIAGO NA FILA.

TIAGO

Resposta: Os estudantes devem contornar a ficha com o nome PEDRO

C ) CONTORNE A FICHA COM O NOME DA PESSOA QUE ESTÁ IMEDIATAMENTE NA FRENTE DE PEDRO.

TIAGO

Resposta: Os estudantes devem contornar a ficha com o nome LUÍZA

AVALIANDO

Objetivos

• Desenvolver noções espaciais para localizar elementos em relação a um ou mais referenciais.

• Aprender a interpretar e utilizar expressões para localizar objetos no espaço, como perto, longe, esquerda, direita, dentro, fora, em cima, embaixo, atrás, entre e em frente.

Sugestão de intervenção

Providencie cartões com frases de gentileza e amizade e distribua-os em pontos diversos da sala de aula. Peça a cada estudante que encontre um cartão, atendendo a instruções

específicas. Instrua, por exemplo, que um deles busque o cartão que esteja embaixo do caderno, que fica dentro do armário localizado à esquerda da mesa do professor. Forneça os comandos pausadamente, um de cada vez, orientando-o a encontrar o item com base nas expressões exercitadas no tópico. Quando for encontrado, entregue-o como presente. Caso algum deles apresente dificuldade em compreender os comandos, auxilie-o oferecendo novas dicas, até que encontre o cartão que lhe foi destinado. Certifique-se de que haja cartões suficientes para toda a turma e garanta que todos recebam.

• Realize, na prática, uma situação semelhante à apresentada na atividade 10 Para isso, peça a alguns estudantes que fiquem em fila, como costumam fazer na hora do recreio. Em seguida, pergunte à turma quem está atrás e quem está na frente de determinada pessoa. Mostre como essas relações dependem de quem é tomado por referência. Na atividade desta página, por exemplo, Pedro está na frente de Tiago e, ao mesmo tempo, atrás de Luíza.

• Aproveite o contexto para perguntar aos estudantes em quais circunstâncias eles precisam aguardar a vez em uma fila. Pergunte-lhes a importância disso, instruindo-os a perceber as vantagens da organização nas situações que envolvem mais pessoas. Na atividade desta página, leve os estudantes a perceberem que poderia haver discórdia entre as três pessoas se elas não se organizassem em fila. Pergunte-lhes, por exemplo: “Sem estarem organizados em fila, quem receberia o primeiro sorvete?”. Conclua dizendo que, da maneira como se distribuíram, cada um recebeu o que queria de acordo com sua posição.

03/10/2025 09:21:08

• Durante o trabalho com a atividade 11, verifique se os estudantes compreendem que as posições apresentadas envolvem dois elementos e podem variar de acordo com a comparação feita. No caso do cachorro ilustrado no item A , é possível dizer que ele está embaixo da cadeira e em cima da grama. Para melhor aproveitamento, faça outros questionamentos, com o intuito de explorar o uso dos termos que se referem à lateralidade, como: “No item A, existe algum elemento à direita do gato? Se sim, qual?”; “No item B, as crianças estão à frente ou atrás da professora?”; “No item C, o banco está atrás de qual pessoa?”. Enfatize a importância de mencionar o ponto de referência sempre que se indica a localização de um elemento, utilizando termos específicos, como à direita e à esquerda, em cima e embaixo, na frente e atrás.

BNCC

No tópico abordado nesta unidade, desenvolve-se um trabalho no qual os estudantes são incentivados a descrever a localização de pessoas e de objetos no espaço em relação à própria posição ou a determinado ponto de referência. Para isso, devem usar termos, como: à direita, à esquerda, em cima, embaixo, na frente e atrás, entre outros, conforme orientam as habilidades EF01MA11 e EF01MA12 da BNCC.

11. DE ACORDO COM AS IMAGENS, FAÇA O QUE SE PEDE.

A ) MARQUE UM X NO ANIMAL QUE ESTÁ EM CIMA DA CADEIRA E CONTORNE O ANIMAL QUE ESTÁ EMBAIXO DA CADEIRA.

Resposta: Os estudantes devem marcar um X no gato e contornar o cachorro.

B ) MARQUE UM X NA CRIANÇA QUE ESTÁ À ESQUERDA DA PROFESSORA E CONTORNE A CRIANÇA QUE ESTÁ À DIREITA DA PROFESSORA.

Resposta: Os estudantes devem marcar um X em RAVI e contornar OTÁVIO.

C ) MARQUE UM X NA PESSOA QUE ESTÁ ATRÁS DO HIDRANTE E CONTORNE A PESSOA QUE ESTÁ EM FRENTE AO BANCO.

Resposta: Os estudantes devem marcar um X em NICOLAS e contornar BENTO.

RAVI

NICOLAS OTÁVIO

BENTO

12. GUSTAVO ESTÁ SEGURANDO UMA BOLA EM CADA MÃO. PINTE DE VERMELHO A BOLA QUE ESTÁ NA MÃO DIREITA E DE AZUL A BOLA QUE ESTÁ NA MÃO ESQUERDA DE GUSTAVO.

Resposta: Os estudantes devem pintar de azul a BOLA 1 e de vermelho a BOLA 2

13. IMAGINE QUE A CARTEIRA REPRESENTADA A SEGUIR SEJA A QUE VOCÊ OCUPA NA SALA DE AULA.

À FRENTE

À ESQUERDA

Resposta pessoal. Espera-se que os estudantes compreendam os conceitos envolvendo localização e direção.

À DIREITA

ATRÁS

COMPLETE OS ESPAÇOS ESCREVENDO O NOME DO ESTUDANTE OU DO OBJETO QUE OCUPA CADA UMA DAS POSIÇÕES REPRESENTADA NA CENA.

esquerda da carteira de Júlia?”; “Qual é o nome do estudante que está sentado imediatamente atrás da carteira de Laura?”.

• Antes de iniciar a atividade 12, pergunte, sem causar constrangimento, quais estudantes costumam utilizar a mão esquerda para escrever e quais usam a direita. Em seguida, peça-lhes que levantem a mão que utilizam para escrever, verificando se fizeram a associação correta da lateralidade. Retome algumas expressões que envolvem esses conceitos, citando objetos da sala de aula. Verifique se percebem que o personagem Gustavo está de costas para o leitor e, por isso, é possível tomar nosso próprio corpo como referencial para analisar a cena.

• Com o auxílio do professor ou de algum colega, estudantes com deficiência visual poderão realizar a atividade 12 seguindo os comandos orais para levantar os braços ou as mãos, a fim de indicarem as direções direita e esquerda.

• Ao trabalhar com a atividade 13, oriente os estudantes que se sentam na frente, atrás e nas laterais da sala de aula a completarem os espaços escrevendo nomes de objetos que estão nas posições em que não há colegas. Para melhor aproveitamento, faça questionamentos usando localizações e nomes, como: “Quem está sentado imediatamente à direita da carteira de Pedro?”; “Quem está sentado imediatamente à frente da mesa do professor?”; “Quem está sentado imediatamente à

03/10/2025 09:21:10

• Ao realizar a proposta da atividade 13, o estudante percebe o próprio corpo por meio de todos os sentidos, compreendendo que ele ocupa um espaço no ambiente, capta imagens, recebe sons e se movimenta. Para enfatizar isso, refaça a atividade algumas vezes, convidando alguns estudantes a sentarem em uma cadeira à frente da sala e, de olhos vendados, promova experiências sensoriais, tocando uma música, disponibilizando uma fruta cheirosa ou deixando um objeto próximo a eles, de modo que, pelos sentidos de audição, olfato e tato, respondam se esses elementos estão à direita, à esquerda, à frente ou atrás deles. Além de contribuir para uma aprendizagem multimodal que pode ser mais eficaz para alguns estudantes, a atividade possibilita a participação ativa daqueles com NEE.

BOLA 1

BOLA 2

• A atividade 14 propõe aos estudantes o uso dos próprios conhecimentos sobre localização para descrever algumas posições. Leia o enunciado da atividade 14 e oriente-os a responder às questões. Verifique se estão compreendendo as relações de lateralidade e de posicionamento no espaço. Caso apresentem dúvidas, conduza uma conversa com a turma, perguntando: “De acordo com a imagem, quais estudantes se sentam nas laterais da sala de aula?”; “Quem está sentado imediatamente à frente de Patrícia?”; “Quem está sentado imediatamente à direita de Murilo?”; “Quem está sentado imediatamente atrás de Lia?”.

• No item A da atividade, os estudantes devem escrever o nome da personagem correspondente.

• Aproveite o item B para solicitar que descrevam os lugares ocupados por outros estudantes.

• Ao trabalhar com o item D, comente que podemos descrever uma posição de modos diversos. No caso de Robson, por exemplo, seria possível fazer isso das seguintes maneiras: “Robson se senta imediatamente atrás de Antônia”; “Robson se senta imediatamente à direita de Diego”; “Robson se senta imediatamente à esquerda de Lucas”; “Robson se senta imediatamente à frente de Vanessa”.

14. PEDRO FEZ UM DESENHO PARA REPRESENTAR A SALA DE AULA EM QUE ESTUDA.

professora

14. C) Resposta pessoal. Espera-se que os estudantes usem como referência objetos presentes na sala de aula ou os próprios colegas, a fim de fazer a representação por meio de um desenho.

gabriel antônia mariana clara

diego robson lucas patrícia

lia vanessa denise gustavo

pedro josé bruna otávio

murilo keila giovana fernanda

LEIA O QUE UMA ESTUDANTE DESSA TURMA DISSE SOBRE O LUGAR ONDE ELA SENTA.

14. B) Resposta pessoal. A resposta depende dos referenciais que os estudantes escolherem. Eles podem responder, por exemplo, que José se senta imediatamente atrás de Vanessa e imediatamente à esquerda de Bruna.

ESTOU IMEDIATAMENTE À FRENTE DE GUSTAVO, À DIREITA DE LUCAS.

A ) DE ACORDO COM A DESCRIÇÃO DA ESTUDANTE, MARQUE UM X NO LUGAR QUE ELA OCUPA EM SALA DE AULA.

Resposta: Os estudantes devem marcar um X no nome PATRÍCIA. Resposta: O NOME DELA É: PATRÍCIA.

O NOME DELA É:

B ) DESCREVA O LUGAR QUE JOSÉ OCUPA NESSA SALA DE AULA.

C ) FAÇA COMO PEDRO E REPRESENTE EM SEU CADERNO A SALA DE AULA ONDE VOCÊ ESTUDA. INDIQUE SEU LUGAR E O DE SEUS COLEGAS COM OS DEVIDOS NOMES.

D ) DESCREVA O LUGAR QUE VOCÊ OCUPA INDICANDO OS COLEGAS COMO REFERÊNCIA.

Resposta pessoal. Espera-se que os estudantes utilizem objetos e pessoas como referência para descreverem o lugar que eles estão ocupando em sala de aula.

REFERÊNCIAS COMPLEMENTARES

MACEDO, Lino de; BRESSAN, Rodrigo Affonseca. Desafios da aprendizagem: Como as neurociências podem ajudar pais e professores. 3. ed. São Paulo: Papirus 7 Mares, 2019.

Esse livro explica, por meio de um diálogo entre os autores, como as neurociências estão envolvidas e ajudam no processo do desenvolvimento de crianças e adolescentes na escola.

03/10/2025 09:21:11

CAMINHOS

1. REPRESENTE O CAMINHO QUE CARLOS FAZ DO PORTÃO DA ESCOLA ATÉ A SALA DE AULA. PARA ISSO, PINTE OS QUADRINHOS DE ACORDO COM O COMANDO DAS SETAS.

AVANCE UM QUADRINHO

VIRE À DIREITA

VIRE À ESQUERDA

1. A) Resposta pessoal. Espera-se que os estudantes descrevam corretamente o caminho da entrada da escola até a sala de aula.

DICA: CADA SETA INDICA UM QUADRINHO E UMA ORIENTAÇÃO NO ESQUEMA.

1. B) Resposta pessoal. Espera-se que os estudantes descrevam o caminho que percorrem de casa até a escola.

Resposta do diagrama com o caminho pintado nas orientações ao professor

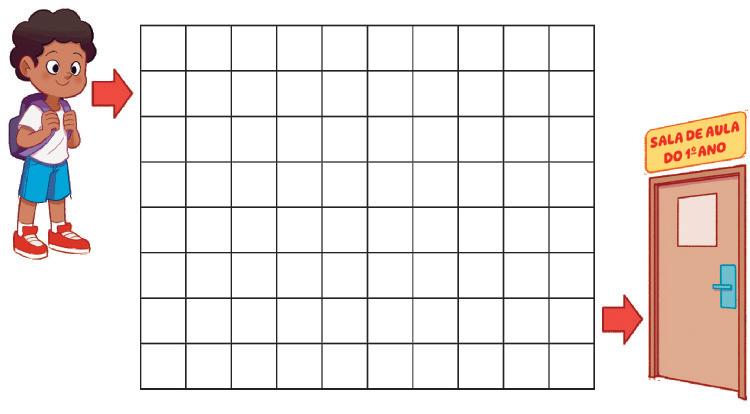
A ) DESCREVA O CAMINHO DA ENTRADA DA ESCOLA ATÉ A SALA DE AULA DE CARLOS.

B ) EXPLIQUE PARA O PROFESSOR E OS COLEGAS O CAMINHO QUE VOCÊ FAZ DE SUA CASA ATÉ A ESCOLA.

Resposta 1.

03/10/2025 09:21:12

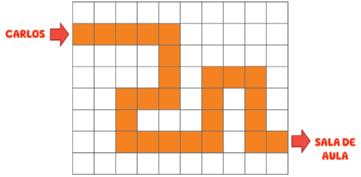
• A atividade 1 trabalha com a orientação do deslocamento, pautando-se no caminho que Carlos faz do portão da escola até a sala de aula. De acordo com os comandos das setas apresentadas, os estudantes devem pintar os quadrinhos. Contextos que envolvem instruções para realizar deslocamentos são importantes para o desenvolvimento da percepção espacial, além do aprimoramento das noções de orientação.

• As rotas que fazem parte do dia a dia são trabalhadas no componente curricular de Geografia . Aproveite para estabelecer uma relação com esse componente e converse com os estudantes sobre os caminhos que costumam percorrer: o trajeto de casa para a escola ou de casa para a padaria, por exemplo. Antes de iniciar a atividade 1, troque ideias com eles a respeito dos comandos e verifique se têm dificuldades em compreendê-los, auxiliando no que for necessário. Eles podem concluir a atividade desenhando no caderno os caminhos que percorrem, indicando pontos de referência conhecidos nesses trajetos.

• Caso demonstrem dificuldade em resolver essa atividade, verifique se percebem que, nesses comandos, o referencial é o personagem Carlos. Cite, por exemplo, que os comandos “vire à direita” e “vire à esquerda” são referentes à direita e à esquerda desse personagem, tomando-o como referencial. Nesse caso, não devemos considerar o próprio corpo ao olhar para a página. Outro ponto importante é o fato de que as instruções “vire” representam um giro, não um caminho a ser percorrido. Assim, no início da resolução da atividade, devem ser pintados cinco quadrinhos e, em seguida, três, correspondentes às setas vermelhas – afinal, as setas azuis e amarelas representam um giro, ou seja, indicam para qual sentido Carlos se virará, não um quadrinho a avançar.

• Antes de trabalhar com a atividade 2, providencie malhas quadriculadas, a fim de que os estudantes resolvam o item B em duplas. Se necessário, apresente a eles outro exemplo antes da resolução. Para isso, desenhe, na lousa, um caminho diferente do apresentado, mas que seja descrito por uma das sequências indicadas, e pergunte-lhes qual delas se refere ao caminho representado por você. Caso demonstrem dificuldades para resolver essa situação, comente que os comandos “vire à direita” e “vire à esquerda”, dados na atividade, correspondem à direita e à esquerda da abelha, tomando-a como referencial.

• Outro ponto é o fato de que os comandos “vire à direita” e “vire à esquerda” representam um giro da abelha, não um quadrinho percorrido. Assim, deve-se considerar um comando de “avance um quadrinho”, pois apenas um está pintado, e, em seguida, “vire à esquerda” e “avance um quadrinho”, pois outro quadrinho à esquerda da posição da abelha naquele momento foi colorido.

ATIVIDADE EXTRA

Leve para a escola um lenço e alguns objetos que devem ser escondidos no pátio ou na quadra. Divida a turma em dois grupos e escolha dois estudantes de cada: um para ficar de olhos vendados – que não verá o objeto sendo escondido – e outro para dar comandos. Disponha alguns obstáculos, de maneira que não seja possível chegar ao item sem desviar deles. Posicione os dois estudantes com olhos vendados em locais distintos, certificando-se de que estejam a uma mesma distância do alvo. Ao seu sinal, cada parceiro deverá orientar aquele que está com os olhos vendados a desviar dos obstáculos. Para isso, pre-

2. PARA CHEGAR ATÉ O FAVO DE MEL, A ABELHA PERCORREU O CAMINHO REPRESENTADO A SEGUIR.

AVANCE UM QUADRINHO

FIM

INÍCIO

VIRE À DIREITA

VIRE À ESQUERDA

A ) MARQUE UM X NA SEQUÊNCIA QUE CORRESPONDE AO

CAMINHO PERCORRIDO PELA ABELHA, DE ACORDO COM O SIGNIFICADO DAS SETAS.

Resposta: Os estudantes devem marcar um X na sequência do item 3

B ) LEIA AS ETAPAS A SEGUIR E FAÇA O QUE SE PEDE.

Professor, professora: Para a realização desta atividade, providencie cópias de malha quadriculada em quantidade suficiente para todos e distribua uma a cada estudante.

• NA MALHA QUADRICULADA FORNECIDA PELO PROFESSOR, MARQUE DOIS QUADRINHOS EM LOCAIS DIFERENTES, UM DE INÍCIO E OUTRO DE FIM

• FAÇA UM TRAÇADO, INDICANDO O CAMINHO DE UM QUADRINHO A OUTRO.

• ENTREGUE A MALHA A UM COLEGA PARA QUE ELE DESENHE UMA SEQUÊNCIA DE SETAS QUE REPRESENTE ESSE CAMINHO.

• POR FIM, CONFIRA SE O COLEGA FEZ A SEQUÊNCIA CORRETA.

Resposta pessoal. Espera-se que os estudantes, de maneira semelhante à apresentada, tracem o caminho na malha quadriculada e desenhem a sequência de setas correspondentes.

cisará usar os seguintes comandos: “vire à direita”, “vire à esquerda”, “avance”. Um exemplo de sequência de comandos: “Avance dois passos, vire à direita e avance um passo. Depois, vire à esquerda e avance três passos”. Combine com a turma que não será permitido utilizar outros comandos e explique que o grupo não deverá ajudar. O primeiro que conseguir levar o colega vendado ao objeto escondido ganha 1 ponto para o grupo. Depois da primeira rodada, outras duplas devem ser escolhidas para repetir a brincadeira, que será refeita até que todos tenham participado. Ao finalizar, ganha o grupo que tiver a maior quantidade de pontos no total.

• Conclua o trabalho com a unidade propondo a sugestão de desafio a seguir. Permita que eles usem o raciocínio lógico para resolver a questão e verifique se usam estratégias pessoais nesse encaminhamento. Verifique se os estudantes percebem que a resposta é 10, porque são as mesmas árvores na ida e na volta do trajeto.

Sugestão de Desafio

Caminhando em uma rua, a professora contou 10 árvores à sua direita. Na volta, na mesma rua, ela contou 10 árvores à sua esquerda. Quantas árvores estão plantadas nessa rua?

Resposta

Estão plantadas 10 árvores.

3. COM BASE NO SIGNIFICADO DAS SETAS, SIGA O COMANDO DELAS E PINTE OS QUADRINHOS DA MALHA PARA TRAÇAR O CAMINHO QUE LEVA BRUNO A UM DOS SEUS BRINQUEDOS.

AVANCE UM QUADRINHO

VIRE À DIREITA

VIRE À ESQUERDA

Resposta do diagrama com o caminho pintado nas orientações ao professor

O CAMINHO LEVOU BRUNO A QUAL BRINQUEDO?

Resposta: BOLA.

• O objetivo da atividade 3 é possibilitar aos estudantes a aplicação dos próprios conhecimentos sobre caminhos e posicionamento com base em dado referencial. Se necessário, relembre os significados dos comandos, como já feito anteriormente.

• No Desafio a mais, os estudantes vão usar as descrições das relações de posição para trabalhar o raciocínio lógico e a organização espacial. A lógica é baseada na combinação das informações para estabelecer uma ordem completa. Os estudantes devem analisar cada frase: “Carla está entre Laura e Tomás.” (A ordem é Tomás-Carla-Laura ou Laura-Carla-Tomás). “Murilo está à esquerda de Tomás.” (Murilo está imediatamente ao lado de Tomás na sequência). Caso encontrem alguma lógica diferente da esperada, incentive-os a compartilhar com os demais colegas, fazendo intervenções pontuais e estratégicas.

DESAFIO A MAIS

QUATRO AMIGOS ESTÃO SENTADOS NO SOFÁ PARA ASSISTIR A UM FILME.

• CARLA ESTÁ ENTRE LAURA E TOMÁS.

• MURILO ESTÁ À ESQUERDA DE TOMÁS.

ESCREVA OS NOMES DOS AMIGOS SENTADOS, DA ESQUERDA PARA A DIREITA.

Resposta: MURILO, TOMÁS, CARLA, LAURA.

CONCLUSÃO

Acompanhar o desenvolvimento dos estudantes é fundamental para um ensino bem-sucedido. Na unidade, foram propostas diversas maneiras de avaliar a aprendizagem da turma. A fim de realizar um monitoramento mais abrangente e organizado, registre, nos relatórios individuais ou nas fichas de avaliação, o desempenho de cada estudante, levando em consideração suas particularidades. Um modelo desse tipo de ficha pode ser encontrado no tópico Avaliação deste

manual. Assim, será possível visualizar de modo individual as trajetórias de aprendizagem, incluindo os avanços e os pontos de dificuldades a serem sanados por meio de atividades que promovam recuperação dos conteúdos. Esse método é de grande importância para repensar estratégias em sala de aula, tornando as ações pedagógicas cada vez mais eficazes.

A conclusão da unidade é o momento de avaliar se os objetivos propostos foram alcançados. No final deste Manual do Professor, apresentamos algumas possibilidades de avaliação formativa para

03/10/2025 09:21:14

realizar o monitoramento da aprendizagem dos estudantes e intervir caso não tenham atingido os resultados esperados.

Resposta 3.

OBJETIVOS DA UNIDADE

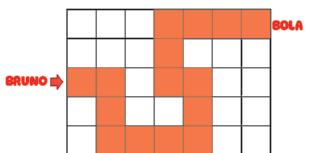
• Estabelecer relação entre a quantidade de elementos e sua representação numérica.

• Ler e escrever números até 100 com algarismos e por extenso.

• Representar números até 100 no quadro de ordens e classes.

• Reconhecer as dezenas exatas.

• Compreender o significado de número par e de número ímpar.

• Estabelecer relação entre números e pontos da reta numérica por meio de comparação.

• Organizar números em ordem decrescente.

INTRODUÇÃO E JUSTIFICATIVA

Nesta unidade, são revisados os números naturais explorados previamente e introduzidos os números naturais até 100, sua representação com algarismos, por extenso e no quadro de ordens e classes. São propostas atividades por meio das quais os estudantes terão a oportunidade de relacionar uma quantidade de elementos à sua representação numérica, compreender o significado de unidade, dezena e centena, conhecer as dezenas exatas, realizar contagens utilizando diferentes estratégias, fazer estimativas, registrar quantidades, compor e decompor números, entre outras habilidades que permitem ampliar o conhecimento de números e compreender características do sistema de numeração decimal.

Também serão abordados os números pares e ímpares e a comparação de números em diversas situações, com e sem o apoio da reta numérica.

5 NÚMEROS DE 0 A 100

EM DIVERSOS LUGARES, EXISTEM ESPAÇOS CONHECIDOS COMO BRINQUEDOTECAS, ONDE AS CRIANÇAS PODEM BRINCAR SOZINHAS OU EM GRUPOS COM DIFERENTES BRINQUEDOS. AS BRINCADEIRAS PODEM OCORRER DE MANEIRA LIVRE OU COM A AJUDA DE UM MONITOR.

Habilidades da BNCC trabalhadas na unidade: EF01MA01 , EF01MA02 , EF01MA03 , EF01MA04, EF01MA05, EF01MA07, EF01MA10 e EF01MA22.

SUGESTÃO DE ESTRATÉGIA INICIAL

Peça aos estudantes que levem para a sala de aula materiais de contagem, como pedrinhas, tampinhas e lápis usados, dentro de potes vazios ou de saquinhos plásticos. Nesse primeiro momento, é recomendado que não sejam apresentados mais do que dez elementos de cada tipo. Inicialmente, peça a eles que estimem

a quantidade de cada elemento. Depois, com a ajuda da turma, conte os elementos e verifique quem respondeu corretamente ou deu a resposta mais próxima da correta. Incentive o registro das quantidades de elementos com algarismos, por extenso ou da maneira que os estudantes preferirem.

MOMENTO DE DIVERSÃO EM UMA BRINQUEDOTECA.

O QUE A CRIANÇA RETRATADA NA FOTOGRAFIA ESTÁ

FAZENDO NA BRINQUEDOTECA?

SEM CONTAR UM A UM, RESPONDA: NESSA FOTOGRAFIA, APARECEM MAIS OU MENOS DE VINTE DINOSSAUROS?

CONTE OS DINOSSAUROS DE BRINQUEDO. DEPOIS, PINTE O QUADRINHO COM O NÚMERO QUE REPRESENTA

A QUANTIDADE TOTAL DE DINOSSAUROS QUE VOCÊ CONTOU.

Resposta: Os estudantes devem pintar o quadrinho com o número 18.

3. 8 11 15 5 18 13

1. Resposta: Espera-se que os estudantes respondam que a criança está brincando com dinossauros de brinquedo.

2. Resposta pessoal. Espera-se que os estudantes respondam que há menos de vinte dinossauros.

• Durante o desenvolvimento desta unidade, os estudantes vão realizar atividades nas quais devem escrever palavras ao responderem às questões, ações que os auxiliam a desenvolver a escrita. Além disso, eles também vão fazer a leitura e a interpretação de enunciados de atividades, ampliando, assim, a fluência em leitura oral, a compreensão de textos e o desenvolvimento de vocabulário. Durante essas ações, acompanhe com atenção a maneira como os estudantes pegam o lápis e como registram as palavras. Caso considere necessário, escreva cada letra na lousa evidenciando o movimento com a mão e a direção do traçado para a escrita das letras. Para o traçado dos algarismos, proceda de maneira semelhante.

• Em uma brinquedoteca, o objetivo principal é incentivar a criança por meio do lúdico, oferecendo brinquedos e brincadeiras variadas que promovem o interesse e a atenção com atividades que podem ser dirigidas ou espontâneas. Um espaço como esse conta com brinquedos variados e jogos, favorecendo o desenvolvimento do raciocínio lógico, da criatividade, da sociabilidade, além de proporcionar acesso a experiências e descobertas. Caso a escola não disponha de uma brinquedoteca, avalie com a direção e os responsáveis a possibilidade de levar os estudantes para fazerem uma visita a um desses locais que estejam disponíveis na cidade em que moram.

03/10/2025 09:24:53

• Caso eles apresentem dificuldades ao responderem à questão 3, relembreos das estratégias utilizadas para contar até 19.

• Leia o texto para os estudantes ou motive uma leitura em grupo. Nesse caso, leia pausadamente e em voz alta para que eles possam acompanhar, pois nesta etapa da aprendizagem é possível que alguns deles ainda não estejam alfabetizados.

• Ao responderem à questão 1, pergunte se eles conhecem uma brinquedoteca e como ela é.

• Na questão 2, esperase que eles já estejam familiarizados com quantidades até 19 e consigam constatar um valor próximo do real.

• Ao iniciar esse tópico, avalie a possibilidade de expor em uma parede da sala de aula um cartaz com os números de 0 a 100, escritos com algarismos.

• Na resolução da atividade 1, dê atenção à maneira que os estudantes realizam a contagem. Observe se eles contam os gibis com algum tipo de organização ou se a contagem é feita a esmo. Outras ativida des desta unidade vão explorar a habilidade de realizar contagens de modo organi zado, pré requisito necessário para dar ao estudante familiaridade com a noção de quantidade e a relação entre números e objetos, mas é importante já notar quais estudantes apresentam dificuldades.

• Nos casos em que os estudantes já conheçam bem os números de 0 a 20, mas ainda assim errem por um ou dois o valor correto da contagem, verifique se o erro se deu por falta de concentração ou por falta de organização. Sugiralhes que façam de novo a contagem, instruindoos a contar os gibis primeiro da esquerda para direita e, depois, de cima para baixo, ou então a organizálos em blocos menores. Eles também podem fazer pequenas marcações com o lápis nos gibis que já foram contados, sem deixar nenhum de fora da contagem nem contálo em duplicidade.

• Na resolução do item A da atividade 1, se necessário, disponibilize materiais de contagem para que os estudantes possam realizar essa atividade na prática, representando as quantidades com tampinhas, lápis, palitos ou com outros materiais. Depois, verifique como eles registraram a quantidade de gibis. Avalie a possibilidade de escreverem na lousa as diferentes maneiras como a registraram. A utilização da lousa pode promover a

REPRESENTANDO NÚMEROS ATÉ 99

1. ESTES SÃO OS GIBIS DE AUGUSTO.

A ) QUANTOS GIBIS AUGUSTO TEM? REPRESENTE, DA MANEIRA QUE PREFERIR, ESSA QUANTIDADE.

Resposta pessoal. Espera-se que os estudantes representem preferencialmente com algarismos o número 19.

B ) COM A AJUDA DO PROFESSOR, LEIA E COMPLETE A FRASE COM OS NÚMEROS ADEQUADOS.

Resposta: 10 + 9 EQUIVALE A 1 DEZENA E 9 UNIDADES, QUE

10 + 9 EQUIVALEM A DEZENA E UNIDADES, QUE TAMBÉM

EQUIVALEM A UNIDADES.

Resposta: DEZENA: 1; UNIDADE: 9 TAMBÉM EQUIVALEM A 19 UNIDADES.

QUADRO DE ORDENS DEZENA UNIDADE

AUGUSTO GANHOU DE PRESENTE MAIS UM GIBI.

AGORA, ELE TEM AO TODO 20 GIBIS.

20 UNIDADES EQUIVALEM A 2 DEZENAS.

20 (VINTE)

QUADRO DE ORDENS DEZENA UNIDADE 2 0

Professor, professora: Durante a realização do item A desta atividade, os estudantes podem representar a quantidade de gibis da maneira que preferirem fazendo 19 risquinhos ou 19 bolinhas, por exemplo.

interatividade e o engajamento dos estudantes, além de propiciar acesso aos diferentes tipos de registro dos colegas.

• Aproveite o item B da atividade 1 e verifique a compreensão do conceito de unidades e de dezenas, mostrando aos estudantes a importância da posição de cada algarismo na composição de um número. Assim, eles estarão desenvolvendo o pensamento lógico, a noção de quantidade e a compreensão do sistema de numeração decimal.

BNCC

A atividade 1 permite aos estudantes desenvolverem métodos para realizar a contagem da quantidade de itens de uma coleção de até 100 objetos, expressando o resultado em linguagem verbal e simbólica. Desse modo, as habilidades EF01MA01, EF01MA02 e EF01MA04 são contempladas.

2. COM A AJUDA DO PROFESSOR, ESCREVA OS NÚMEROS QUE

REPRESENTAM A QUANTIDADE DE CUBINHOS

EM CADA ITEM.

Resposta: B: 22; C: 23; D: 24; E: 25; F: 26; G: 27; H: 28; I: 29.

ATIVIDADE EXTRA

Aproveite a atividade 2 e peça aos estudantes que desenhem no caderno uma sequência de figuras de até 30 unidades em ordem decrescente. Eles podem representar as quantidades com quadrinhos, bolinhas ou outro desenho da escolha deles. Lembreos de finalizar os registros escrevendo os números que representam as quantidades.

UMREPRESENTA 1 UNIDADE.

UMAFORMADA POR 10 CUBINHOS REPRESENTA 1 DEZENA.

03/10/2025 09:24:54

Na atividade 2, ao contarem a quantidade de cubinhos e escreverem os números que a representam, os estudantes têm a oportunidade de desenvolver as habilidades EF01MA04 e EF01MA07

• A atividade 2 pode ser realizada na prática, representando as quantidades com os cubinhos e as barras disponíveis nas páginas 267 e 269 do Material complementar do final do Livro do Estudante, auxiliandoos, com a sua supervisão, na compreensão desta atividade. Orienteos a guardar esse material, pois ele será utilizado em outras atividades no decorrer do volume, sempre que achar conveniente.

• Explore o máximo possível a associação entre números e suas representações por meio das barras e dos cubinhos. O material dourado é uma excelente ferramenta para o aprendizado dos números, pois promove de modo intuitivo a absorção das relações numéricas fundamentais. Portanto, se esse material estiver disponível na escola, utilizeo sempre que julgar adequado.

• Se a atividade for feita na prática, verifique a possibilidade de permitir aos estudantes manusearem o material. Nesse caso, certifiquese de que a atividade seja feita de maneira segura. Como os cubinhos das unidades são pequenos, o ideal é que um de cada vez manuseie o material, sempre com sua supervisão.

BNCC

• Na atividade 3, se necessário, auxilie os estudantes na leitura dos números escritos por extenso. Leia os dois primeiros e observe se eles são capazes de ler os demais sozinhos. Em caso negativo, prossiga a leitura, no tempo adequado, auxiliando os a reconhecer as sílabas. Verifique também se eles conseguem fazer corretamente a conversão para algarismos, visto que podem representar os números da maneira que preferirem. Nesta atividade, ao fazer a leitura dos números escritos por extenso, os estudantes desenvolvem a fluência em leitura oral e o desenvolvimento de vocabulário.

• A atividade 4 avalia e exercita a capacidade dos estudantes de realizarem estimativas. É provável que, de pronto, eles comecem a contar as bolinhas uma a uma. Por isso, inicie a atividade pedindo às duplas que não façam a contagem, apenas registrem, sem medo de errar, a quantidade de bolinhas de cada quadro. Deixe claro que não há problema em errar, pois, caso contrário, eles podem tentar contar só para não dar uma resposta errada, o que invalidará o propósito da atividade.

• Após cada dupla dar sua resposta, peça que tentem explicar por que chegaram a uma ou outra conclusão. Na sequência, depois de todos terem emitido suas opiniões, peçalhes que façam a contagem das bolinhas uma a uma e confirmem se acertaram ou não o valor que estimaram.

BNCC

3. ESCREVA OS NÚMEROS CORRESPONDENTES A CADA ESCRITA POR EXTENSO.

Resposta: 24

A ) VINTE E QUATRO:

Resposta: 25

B ) VINTE E CINCO:

Resposta: 26

C ) VINTE E SEIS:

Resposta: 27

D ) VINTE E SETE:

4. JUNTE-SE A UM COLEGA E RESOLVAM O QUE SE PEDE.

A ) SEM CONTAR, ESTIMEM A QUANTIDADE DE BOLINHAS QUE HÁ EM CADA QUADRO. DEPOIS, ESCREVAM O NÚMERO QUE REPRESENTA CADA ESTIMATIVA.

Resposta pessoal. Espera-se que

os estudantes estimem e escrevam a quantidade de bolinhas que há em cada quadro.

B ) CONTEM AS BOLINHAS E ESCREVAM O NÚMERO QUE REPRESENTA A QUANTIDADE EXATA DE BOLINHAS QUE HÁ EM CADA QUADRO.

Resposta: 20 BOLINHAS.

QUADRO A: BOLINHAS.

Resposta: 24 BOLINHAS.

QUADRO B: BOLINHAS.

Resposta: 26 BOLINHAS.

QUADRO C: BOLINHAS.

Resposta: 22 BOLINHAS.

QUADRO D: BOLINHAS.

C ) O QUE VOCÊS PUDERAM PERCEBER AO COMPARAR O NÚMERO

QUE REPRESENTA A QUANTIDADE EXATA DE BOLINHAS DE CADA QUADRO E A QUANTIDADE DE BOLINHAS ESTIMADA? CONVERSEM COM O PROFESSOR E OS COLEGAS.

Resposta pessoal. Espera-se que os estudantes comparem se acertaram ou não as estimativas feitas por eles com a quantidade de bolinhas que há em cada quadro.

Nas atividades 3 e 4, os estudantes leem os números escritos por extenso, fazem estimativas, realizam contagem e apresentam o resultado da contagem com o registro numérico. Dessa maneira, eles desenvolvem as habilidades EF01MA01 , EF01MA02 , EF01MA03 e EF01MA04. Também desenvolvem aspectos da Competência específica de Matemática 8 da BNCC ao interagirem com seus pares, de maneira cooperativa, a fim de identificarem aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.

03/10/2025 09:24:55

5. JUNTE-SE A UM COLEGA E RESOLVAM OS ITENS.

A ) SEM CONTAR UM A UM, ESTIMEM SE NA IMAGEM A SEGUIR APARECEM MAIS OU MENOS DE 20 FLORES.

Resposta pessoal.

Espera-se que os estudantes estimem que há mais de 20 flores no jardim.

B ) CONTEM E REGISTREM A QUANTIDADE DE FLORES QUE APARECEM NA IMAGEM.

Unidades temáticas integradas

Resposta: 24

6. ISABEL FEZ UMA PESQUISA PARA SABER QUAL É O ANIMAL PREFERIDO DOS COLEGAS DA TURMA. ELA REGISTROU OS VOTOS OBTIDOS DA SEGUINTE MANEIRA.

ANIMAL PREFERIDO DOS COLEGAS DE ISABEL ANIMAL QUANTIDADE DE VOTOS CACHORRO GATO CAVALO PÁSSARO OUTROS

A ) QUAL FOI O ANIMAL MAIS VOTADO?

Resposta: PÁSSARO.

DICA: CADA REPRESENTA 1 VOTO.

FONTE DE PESQUISA: ANOTAÇÕES DE ISABEL.

6. C) Resposta pessoal. Espera-se que os estudantes compreendam que “OUTROS” significa que alguns animais não citados na tabela também receberam votos.

QUANTAS PESSOAS VOTARAM NESSE ANIMAL?

Resposta: 9

B ) QUANTAS PESSOAS PARTICIPARAM DA PESQUISA?

Resposta: 24

C ) EM SUA OPINIÃO, O QUE SIGNIFICA A OPÇÃO “OUTROS” NO QUADRO? CONVERSE COM OS COLEGAS.

D ) QUAL É O SEU ANIMAL PREFERIDO? CONTE PARA OS COLEGAS.

Resposta pessoal. Espera-se que os estudantes conversem entre si sobre seus animais preferidos, compartilhando essas preferências.

03/10/2025 09:24:55

• A atividade 5 avalia a capacidade dos estudantes de fazerem estimativas. Por isso, inicie a atividade pedindo que não contem, mas que apenas digam, sem medo de errar, se há mais ou menos de 20 flores. Reforce que não há problema em errar, pois, caso contrário, eles podem invalidar o propósito da atividade. Após cada dupla dar sua resposta, peçalhes que façam a contagem das flores uma a uma e confirmem se acertaram ou não a quantidade estimada.

• A atividade 6 promove uma integração entre as unidades temáticas Probabilidade e Estatística e Números, ao relacionar a contagem e a comparação de quantidades de votos com o registro, a leitura e a interpretação de uma tabela. Ao resolver o item C, verifique se os estudantes compreendem que “outros”, na tabela, representa o nome dos animais não citados e que também receberam votos.

BNCC

Os itens C e D da atividade 6 permitem desenvolver aspectos da Competência específica de Matemática 8 da BNCC ao propor a interação entre os estudantes e a troca de ideias em relação a determinados pontos de vista, com o intuito de identificar aspectos consensuais ou não na discussão de um determinado assunto, respeitando o modo de pensar dos colegas e aprendendo uns com os outros.

• A atividade 7 permite estabelecer uma integração entre a unidades temáticas de Matemática Números e Álgebra, ao apresentar aos estudantes uma sequência de números naturais e leválos a reconhecer os elementos faltantes ou ausentes dessa sequência. Durante a resolução desta atividade, oriente os estudantes a analisarem a sequência inicialmente e, depois, escreverem os números que faltam na imagem. Confira se eles completaram corretamente a sequência e verifique a possível ocorrência de números escritos de maneira incorreta. Nessa faixa etária, é comum que os estudantes façam números espelhados ou que troquem o 6 pelo 9, por exemplo.

• Ao trabalhar com a atividade 8, leia com os estudantes o texto do quadro Dica e reforce que não há mais bolinhas nos saquinhos, além daquelas que conseguimos ver. Dê ênfase ao fato de que todos os saquinhos têm a mesma quantidade de bolinhas. Desse modo, eles poderão responder ao item B com mais facilidade, sem precisar contar as 30 bolinhas. Se eles não identificarem com facilidade a quantidade total, instruaos a perceber que há uma dezena de bolinhas em cada saquinho. Pensando em 10 bolinhas como uma dezena, os estudantes vão perceber com mais facilidade que, ao todo, os três saquinhos contêm 3 dezenas. Como 3 dezenas é igual a 30 unidades, a quantidade total de bolinhas é 30.

• Para que os estudantes com deficiência visual realizem a atividade 8, separe 30 bolinhas ou quaisquer 30 objetos iguais. Ao realizar a leitura para esse estudante, entreguelhe os objetos para que possam ser sentidos pelo tato e contados conforme a ordem e as quantidades indicadas na

7. ESCREVA OS NÚMEROS QUE FALTAM NA SEQUÊNCIA.

Resposta: 1, 2,

3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29

Unidades temáticas integradas

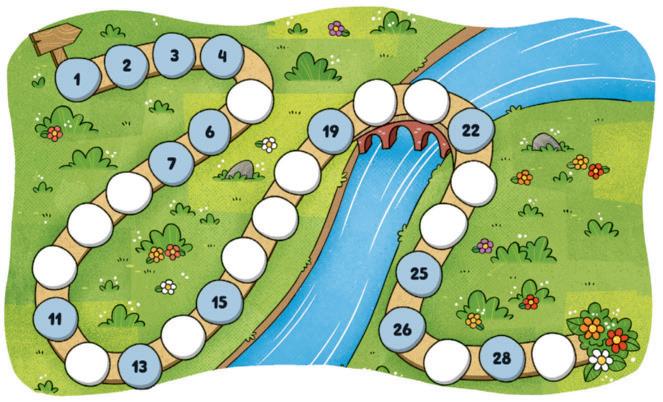
8. SAMARA SEPAROU ALGUMAS BOLINHAS EM GRUPOS DE MESMA QUANTIDADE. DEPOIS, ELA GUARDOU CADA GRUPO DE BOLINHAS EM UM SAQUINHO.

DICA: TODAS AS BOLINHAS GUARDADAS NOS SAQUINHOS ESTÃO VISÍVEIS.

A ) QUANTAS BOLINHAS HÁ EM CADA SAQUINHO?

Resposta: 10

B ) QUANTOS SAQUINHOS DE BOLINHAS SAMARA FORMOU?

Resposta: 3

C ) A QUANTIDADE DE BOLINHAS EM SAQUINHOS É IGUAL A 30 BOLINHAS.

30 (TRINTA)

proposta, favorecendo a construção do raciocínio da atividade.

BNCC

Na atividade 7 , os estudantes são levados a reconhecer os elementos ausentes em uma sequência recursiva de números naturais, conforme orienta a habilidade EF01MA10, para, em seguida, completar a sequência com esses elementos.

Na atividade 8, eles são incentivados a realizar a contagem da quantidade de objetos de uma coleção fazendo agrupamentos de 10 para, em

QUADRO DE ORDENS DEZENA UNIDADE

Resposta: A QUANTIDADE DE BOLINHAS EM 3 SAQUINHOS É IGUAL A 30 BOLINHAS.

3 0

seguida, expressar o resultado em linguagem verbal e simbólica. Dessa maneira, são contempladas as habilidades EF01MA01, EF01MA02 e EF01MA04.

03/10/2025 09:24:56

EXPERIMENTE

9. Resposta pessoal. A resposta depende do esporte preferido dos colegas do estudante.

9. VOCÊ VAI PESQUISAR O ESPORTE FAVORITO DOS SEUS AMIGOS

OU DE PESSOAS CONHECIDAS E CADA ENTREVISTADO DEVE ESCOLHER SOMENTE UM ESPORTE. ENTREVISTE AO MENOS 30 PESSOAS. PARA FACILITAR, SIGA OS PASSOS 1 E 2.

Unidades temáticas integradas

PASSO 1

USE O CARTÃO DE RASCUNHO

DA PÁGINA 271 DO MATERIAL

COMPLEMENTAR PARA COLETAR A

RESPOSTA DOS SEUS COLEGAS. ANOTE UM TRACINHO PARA CADA RESPOSTA.

PASSO 2

CONTE NO CARTÃO DE RASCUNHO QUANTAS PESSOAS ESCOLHERAM CADA ESPORTE. PREENCHA A TABELA A SEGUIR COM OS NÚMEROS QUE REPRESENTAM AS QUANTIDADES ANOTADAS NO CARTÃO DE RASCUNHO.

ESPORTE PREFERIDO DOS COLEGAS DE ESPORTE QUANTIDADE DE PESSOAS

FUTEBOL

VOLEIBOL

BASQUETEBOL

TÊNIS

NATAÇÃO

OUTROS

FONTE DE PESQUISA:

AO FINAL, APRESENTE O RESULTADO DE SUA PESQUISA AOS COLEGAS E COMPAREM OS REGISTROS FEITOS.

BNCC

Ao executar a atividade 9, os estudantes realizarão uma pesquisa com até 30 elementos, envolvendo duas variáveis categóricas, organizando dados por meio de representações pessoais, o que contempla a habilidade EF01MA22 da BNCC.

ARTICULANDO CONHECIMENTOS

03/10/2025 09:24:56

• O assunto trabalhado nesta página permite estabelecer relação com o componente curricular de Educação Física, ao propor uma pesquisa sobre a preferência nos esportes. Converse com os estudantes sobre o esporte mais votado na turma. Pergunte se eles praticam algum esporte e se essa opção aparece na pesquisa deles. Aproveite essa oportunidade para dizer que os esportes e as atividades físicas fortalecem os músculos, proporcionam bemestar e deixam o indivíduo mais disposto, além de oferecerem oferecerem outros benefícios.

• A atividade 9 promove uma integração entre as unidades temáticas Números e Probabilidade e estatística ao relacionar números com pesquisa, coleta e organização dos dados obtidos. Nesta atividade, são trabalhadas noções de Estatística e Probabilidade. Para os estudantes, o desafio é descobrir maneiras de organizar e de registrar dados obtidos em uma pesquisa, por meio de atividades práticas. Para o trabalho com essa atividade, inicialmente, oriente os estudantes a usarem o cartão de rascunho, disponível na página 271, na seção Material complementar, que se encontra no final do Livro do Estudante, auxiliandoos, com a sua supervisão, na compreensão desta atividade. Para controlar a amostra e não tornar cansativa a atividade, orienteos também a estipular a quantidade mínima e máxima de entrevistados, nesse caso, no mínimo 20 e no máximo 30 pessoas, e dê um prazo para a coleta das informações, combinando o dia em que eles deverão levar para a sala de aula o resultado da pesquisa. Eles podem envolver os adultos do convívio deles para a realização da atividade. Cada estudante deve completar o título da tabela com seu próprio nome e indicar, na fonte de pesquisa, a origem da coleta de informações, como “Colegas da sala de aula” ou “Colegas do bairro”.

• Ao trabalhar com a atividade 9, outro sentido, além da visão, é explorado pelos estudantes, pois a pesquisa ativa a audição e a linguagem, uma vez que eles precisam perguntar e registrar a resposta ouvida. A construção da tabela, por sua vez, exige atenção visual, organização espacial e utilização da linguagem para descrever os resultados.

• Leve os estudantes a perceberem que, na atividade 10, a contagem pode ser feita com mais rapidez e facilidade ao observar que os palitos estão agrupados de 10 em 10. Para complementar a atividade, verifique a possibilidade de entregar a eles uma quantidade de palitos de sorvete e pedirlhes que determinem quantos há no total, por meio de agrupamentos de 10 em 10. Como em toda atividade que envolve manuseio de materiais diferentes dos usuais, certifiquese de que eles não oferecem risco aos estudantes. Atividades desse tipo sempre devem ser supervisionadas por você.

• Caso não haja palitos na escola, para realizar a atividade 10, oriente os estudantes a recortarem as imagens dos palitos, disponíveis na página 273, na seção Material complementar do final do Livro do Estudante, auxiliandoos no recorte e uso desse material. Orienteos a guardar os palitos em envelope, pote ou saco plástico, a fim de usálos em outras atividades no decorrer do volume, sempre que achar conveniente.

BNCC

Na atividade desta página, os estudantes são incentivados a realizar a contagem da quantidade de objetos de uma coleção fazendo agrupamentos de 10 para, em seguida, expressar o resultado em linguagem simbólica. Dessa maneira, são contempladas as habilidades EF01MA01, EF01MA02 e EF01MA04

10. ESCREVA O NÚMERO QUE REPRESENTA A QUANTIDADE DE PALITOS EM CADA QUADRO.

Professor, professora: Esta atividade pode ser

realizada na prática com os estudantes. Para isso, eles devem recortar e utilizar os palitos disponíveis na página 273 do Material complementar

Resposta: 32 PALITOS.

Resposta: 34 PALITOS.

Resposta: 36 PALITOS.

Resposta: 39 PALITOS.

11. OS NÚMEROS ESTÃO PRESENTES EM ALGUMAS BRINCADEIRAS. NA IMAGEM A SEGUIR, ALGUMAS CRIANÇAS ESTÃO BRINCANDO DE ESCONDE-ESCONDE.

... 22, 23, 24, 25, ...

A ) NA CENA, APARECEM VÁRIAS CRIANÇAS SE ESCONDENDO, ENQUANTO OUTRA CONTA ATÉ 40. COM O PROFESSOR E OS COLEGAS, CONTINUE CONTANDO OS PRÓXIMOS NÚMEROS A PARTIR DO ÚLTIMO QUE APARECE NO BALÃO DE FALA.

Resposta: 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40.

B ) ESCREVA A SEQUÊNCIA DOS NÚMEROS QUE VOCÊ, O PROFESSOR E SEUS COLEGAS DISSERAM.

Resposta: 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40.

C ) CITE OUTRAS BRINCADEIRAS QUE UTILIZAM NÚMEROS.

Resposta pessoal. Espera-se que os estudantes citem, por exemplo, amarelinha, pular corda etc.

03/10/2025 09:24:57

• Ao trabalhar com a atividade 11, converse com os estudantes para saber se eles já conhecem a brincadeira e se costumam brincar de Esconde-esconde com os amigos. Pergunte se preferem se esconder ou procurar os amigos e questione até que número contam quando brincam disso. Perguntas assim, ao envolverem os estudantes em clima de descontração e leválos, desde cedo, a enxergar aplicações da Matemática em seu cotidiano, até mesmo em momentos de lazer, proporcionam uma aprendizagem mais significativa.

• No item A, o ideal é que os estudantes continuem a contagem partindo do último número presente no balão de fala do garoto. Contudo, caso sintam dificuldade, eles podem contar iniciando do 20, seguindo até o 25, e daí em diante. É importante, ainda assim, que percebam que os números da sequência são do 26 em diante.

• No item B, verifique se os estudantes fazem adequadamente a organização dos números em ordem crescente. Uma possibilidade de trabalho é pedir lhes que escrevam, um a um, os números na lousa. Também pode ser divertido e produtivo que alguém (um estudante ou mesmo você) se disponha a fingir que está contando em meio a uma brincadeira de Esconde-esconde, enquanto os demais observam a contagem e registram os números com algarismos.

• No desenvolvimento da atividade 12, bem como em todas as atividades que envolvam estimativas feitas sem contagem, é importante enfatizar que não é preciso ter medo de errar. Incentive os a emitir sua opinião sobre qual quadro contém mais palitos, sem os censurar em caso de erro. Aliás, caso a opinião deles se revele equivocada, aproveite a oportunidade para evidenciar como os números são importantes na nossa vida: sem eles, podemos nos confundir ao comparar quantidades. Ao longo da atividade, verifique se fizeram corretamente as comparações e estimativas e se perceberam que, ao agruparmos os elementos, a estimativa se torna mais fácil.

• Ao fim da atividade, peça a eles que comentem quais são as vantagens de separar objetos em grupos na hora de contálos.

BNCC

A atividade desta página permite aos estudantes estimar e comparar a quantidade de objetos de dois conjuntos para indicar qual tem mais, além de realizar contagem fazendo agrupamentos de 10. Desse modo, são contempladas as habilidades EF01MA02 e EF01MA03

Esta atividade favorece o desenvolvimento do raciocínio lógico e do espírito de investigação, conforme descrito na Competência específica de Matemática 2 da BNCC.

12. RESOLVA OS ITENS A SEGUIR.

A ) SEM CONTAR UM A UM, RESPONDA: QUAL DOS DOIS

QUADROS APRESENTADOS NESSE ITEM TEM MAIS PALITOS?

QUADRO 1

QUADRO 2

Resposta pessoal. Espera-se que os estudantes respondam que o quadro 2 é o que tem mais palitos.

B ) CONTORNE OS PALITOS A SEGUIR FORMANDO GRUPOS DE 10.

QUADRO 1

QUADRO 2

Resposta: No quadro 1, os estudantes devem formar 4 grupos com 10 palitos, sobrando 1 palito sem contornar; no quadro 2, devem formar 4 grupos com 10 palitos, sobrando 5 palitos sem contornar.

NO ITEM B, QUAL DOS DOIS QUADROS TEM MAIS PALITOS?

Resposta pessoal. Espera-se que os estudantes respondam que o quadro 2 é o que tem mais palitos.

C ) COMPARE AS DUAS SITUAÇÕES E VERIFIQUE SE A SUA

RESPOSTA FOI A MESMA NOS ITENS A E B

estudantes comparem os itens e verifiquem se as estimativas feitas foram iguais ou não.

D ) EM ALGUM DOS ITENS FOI MAIS FÁCIL OBTER A RESPOSTA?

SE SIM, EM QUAL DELES?

Resposta pessoal. Espera-se que os estudantes percebam que, agrupando os elementos de 10 em 10, a estimativa se torna mais fácil. Resposta pessoal. Espera-se que os

Resposta: Os estudantes devem ligar os pontos com a sequência numérica do 1 ao 50 para formar a figura de um cachorro.

A ) QUAL FIGURA SE FORMOU AO LIGAR OS PONTOS?

Resposta: Ao ligar os pontos, formou-se a figura de um cachorro.

B ) PINTE A IMAGEM.

Resposta pessoal. Os estudantes devem pintar a imagem do cachorro.

14. LEIA, COM A AJUDA DO PROFESSOR, OS NÚMEROS A SEGUIR. DEPOIS, LIGUE CADA NÚMERO À SUA ESCRITA POR EXTENSO.

50 52 54 56 58

Resposta: Os estudantes devem ligar cada número à respectiva escrita por extenso, ou seja, 50 ao CINQUENTA; 52 ao CINQUENTA E DOIS; 54 ao CINQUENTA E QUATRO; 56 ao CINQUENTA E SEIS; 58 ao CINQUENTA E OITO.

ATIVIDADE EXTRA

Providencie cinco folhas de papel sulfite e caneta hidrográfica ou giz de cera. Divida cada folha em quatro partes para confeccionar fichas e numereas de 0 a 20.

Organize a turma em dois grupos. Posicione as fichas em sequência na lousa e faça a contagem oral com os estudantes. Em seguida, peça a eles que fiquem de costas para a lousa, retire dela

CINQUENTA E SEIS

CINQUENTA E DOIS

CINQUENTA E OITO

CINQUENTA E QUATRO

CINQUENTA

03/10/2025 09:24:57

uma ficha qualquer e reordene as que ficaram, de maneira que não seja possível identificar o espaço de onde ela foi retirada.

Peça aos estudantes que olhem para a lousa novamente e desafieos a descobrir qual foi o número retirado da sequência. O estudante que acertar marca ponto para a sua equipe. Realize quantas rodadas desejar ou continue enquanto houver interesse da turma.

• Na atividade 13, alguns estudantes podem perceber de imediato que a imagem formada será a de um cachorro, podendo, assim, traçar o contorno sem seguir a ordem numérica. Como não é essa a proposta da atividade, orienteos a começar a linha pelo número 1 e seguir em ordem crescente até o 50. Em seguida, peçalhes que pintem a imagem, cuidando para não ultrapassar as margens do contorno.

• Para os estudantes com pouca habilidade de coordenação motora fina, a atividade 13 poderá ser realizada com auxílio nos traçados, para dar forma ao desenho da atividade. Nesse caso, devese fornecer suporte individualizado, favorecendo a compreensão e a inclusão dos estudantes com síndrome de Down e deficiências físicas.

• Na atividade 14, bem como em outras, os estudantes vão associar elementos de uma coluna a elementos de outra, traçando as linhas de modo reto e contínuo e deixando evidente qual par de elementos aquela linha está associando. Se necessário, auxilieos na leitura dos números escritos por extenso e verifique se estão fazendo corretamente a conversão para algarismos. Atividades de associar elementos de uma coluna a elementos de outra são ótimos recursos para promover o desenvolvimento da identificação e compreensão dos números com sua escrita por extenso, além de incentivar o raciocínio lógico.

• A atividade 15 pode ser realizada na prática, representando as quantidades com material dourado. Para isso, solicite que eles usem as peças recortadas do Material complementar e usadas no início desta Unidade.

• Procure deixar bem claro para os estudantes a relação entre a unidade e a dezena. Se julgar conveniente, promova a atividade em duplas, incentivandoos a compartilhar ideias e trabalhar em equipe.

BNCC

Na atividade desta página, ao contarem as quantidades de cubinhos e escreverem os números que as representam, os estudantes têm a oportunidade de desenvolver as habilidades EF01MA04 e EF01MA07

15. ESCREVA OS NÚMEROS QUE REPRESENTAM A QUANTIDADE DE CUBINHOS DE

CADA ITEM.

Resposta: A: 60; B: 61; C: 62; D: 63; E: 64; F: 65; G: 66; H: 67; I: 68; J: 69.

16. AJUDE GABRIELA A ENCONTRAR SEU GATO. PARA ISSO, PINTE UM CAMINHO QUE PASSE PELA SEQUÊNCIA DOS NÚMEROS DE 1 ATÉ 70.

Resposta: Os estudantes devem passar pelo caminho cuja sequência numérica seja composta pelos números de 1 a 70.

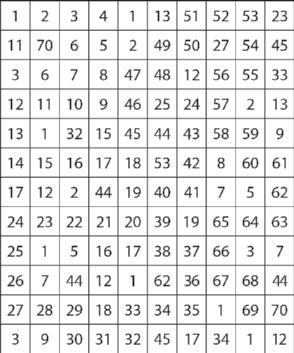
17. NO QUADRO DE ORDENS DE CADA ITEM, ESCREVA O NÚMERO REPRESENTADO NO ÁBACO.

17. Resposta: A) Dezena: 7, Unidade: 5; B) Dezena: 7, Unidade: 2

QUADRO DE ORDENS

D U

U D U

QUADRO DE ORDENS

D U

SERGIO LIMA/ ARQUIVO

18. COMPLETE OS ITENS COM OS NÚMEROS QUE FALTAM.

A ) OITENTA: 80

B ) OITENTA E UM:

Resposta: OITENTA E UM: 81

C ) OITENTA E QUATRO:

Resposta: OITENTA E QUATRO: 84

D ) OITENTA E SEIS:

Resposta: OITENTA E SEIS: 86

E ) OITENTA E OITO:

Resposta: OITENTA E OITO: 88

F ) OITENTA E NOVE:

Resposta: OITENTA E NOVE: 89

BNCC

• Na atividade 16, diga aos estudantes que, antes de pintar o caminho, o ideal é fazer um traço leve com o lápis de escrever, para que seja possível apagar e fazer de novo caso eles errem. Quando tiverem certeza de que o caminho indicado está correto, permitalhes que pintem com a cor que escolherem.

• A atividade 17 pode ser realizada na prática, explorando os benefícios da representação dos números no ábaco. Assim como o material dourado, o ábaco fornece uma experiência sensorial de grande utilidade na apreensão dos números, sobretudo no que diz respeito à organização de unidades e dezenas. Caso não haja ábacos disponíveis para todos os estudantes, ou ao menos para grupos de 3 ou 4, utilize apenas um, mas deixe o bem visível e manuseie o lentamente, de maneira que todos consigam enxergálo e interpretar o significado de suas peças. Aproveite para trabalhar a composição e a decomposição de alguns números. Para isso, peça a um estudante que vá até a frente da sala e represente, no ábaco, o número 70. Nesse momento, escreva o número 70 na lousa. Peça ao mesmo estudante que acrescente uma conta à vareta das unidades e pergunte para a turma qual número está representado no ábaco agora. Depois de responderem, escreva na lousa “70 mais 1 é igual a 71”. Repita esse procedimento para os números de 72 a 79, chamando outros estudantes para fazerem a representação no ábaco.

• Na atividade 18, pode ser necessário auxiliar os estudantes na leitura dos números escritos por extenso. Leia os dois primeiros e observe se eles são capazes de ler os demais sozinhos. Acompanhe as tentativas de leitura daqueles que apresentarem mais dificuldade e observe se eles fazem corretamente a representação por meio de algarismos.

03/10/2025 09:28:33

Na atividade 17, ao trabalhar com o ábaco, os estudantes terão que compor números de até duas ordens com o suporte de material manipulável, o que contribui para a compreensão de características do sistema de numeração e desenvolve aspectos da habilidade EF01MA07

• Ao trabalhar com a atividade 19, verifique se os estudantes percebem que a forma de organização das bolinhas em grupos de 10 é equivalente a contar as bolinhas de dezena em dezena. Confira se compreenderam a ideia e se eles se recordam de atividades anteriores, em que outros elementos (palitos e material dourado) foram agrupados da mesma maneira.

• Comente com os estudantes que organizar objetos em grupos de 10 é uma estratégia que facilita a contagem. Perguntelhes se já fizeram isso antes ou se já viram alguém fazendo, como ao separar em grupos menores uma grande quantidade de moedas para contar.

• Caso os estudantes apresentem dificuldades em reconhecer os números escritos por extenso, explore o máximo possível as semelhanças de sonoridade entre os nomes das dezenas e os algarismos que os representam (por exemplo, ajudandoos a associar o trinta ao três e o noventa ao nove).

• Ao lerem os números escritos por extenso, na atividade desta página, os estudantes desenvolvem a fluência em leitura oral e adquirem vocabulário.

BNCC

Na atividade desta página, os estudantes são incentivados a realizar a contagem da quantidade de objetos de uma coleção agrupados de 10 em 10, para, em seguida, expressar o resultado em linguagem verbal e relacionálo com sua escrita com algarismos e por extenso. Dessa maneira, são contemplados aspectos das habilidades EF01MA02 e EF01MA04

19. PODEMOS CONTAR FORMANDO GRUPOS DE 10. AS BOLINHAS APRESENTADAS FORAM ORGANIZADAS EM SAQUINHOS FORMANDO GRUPOS COM 10 UNIDADES CADA.

20: VINTE

10: DEZ 30: TRINTA

40: QUARENTA 60: SESSENTA

70: SETENTA

50: CINQUENTA

80: OITENTA

90: NOVENTA

LEIA, COM A AJUDA DO PROFESSOR, OS NÚMEROS A SEGUIR. DEPOIS, LIGUE A ESCRITA POR EXTENSO AO NÚMERO CORRESPONDENTE.

Resposta: Espera-se que os estudantes liguem cada escrita por extenso ao respectivo número escrito com algarismos, ou seja, SETENTA ao 70; VINTE ao 20; NOVENTA ao 90; DEZ ao 10; CINQUENTA ao 50.

20. DESENHE PALITOS PARA COMPLETAR 99 PALITOS.

Resposta: Os estudantes devem desenhar 8 palitos no último quadro.

21. LIGUE CADA QUANTIDADE DE CUBINHOS AO NÚMERO CORRESPONDENTE ESCRITO POR EXTENSO.

NOVENTA E CINCO NOVENTA

Resposta: Os estudantes devem ligar: A-NOVENTA; B-NOVENTA E DOIS; C-NOVENTA E CINCO.

AVALIANDO

Objetivos

Relacionar a quantidade de elementos com sua representação numérica.

Reconhecer as dezenas exatas.

Sugestão de intervenção

Escolha uma dezena exata e escrevaa na lousa com algarismos e por extenso. Em seguida, pergunte aos estudantes quantos grupos com

03/10/2025 09:28:36

10 palitos são necessários para representar esse número. Usando palitos e elásticos, deixe que representem os números formando os grupos para comprovarem a resposta que deram. Repita a atividade com outras dezenas exatas. Caso eles apresentem dificuldades ao indicar a quantidade de grupos com os 10 palitos necessários para representar um número, proponha atividades que auxiliem no esclarecimento das dúvidas.

• Na atividade 20, verifique se os estudantes percebem que, em cada quadro, há uma dezena de palitos e que, portanto, não é necessário contálos um por um. Auxilieos a perceber que os 9 grupos já completos correspondem a 9 dezenas de palitos que, por sua vez, correspondem a 90 palitos. Assim, o último grupo deve conter 9 unidades. É importante ressaltar que um dos palitos já está desenhado e confirmar se os estudantes entendem que devem desenhar apenas 8 palitos para completar 99. Aproveite a oportunidade para sondar os conhecimentos deles sobre o conceito de centena, perguntando quantos palitos haveria ao todo se fosse desenhado mais um palito junto aos 99 que estão na página.

• Inicie a atividade 21 pedindo aos estudantes que observem as figuras e, então, pergunte se eles lembram que uma barrinha representa dez cubinhos, de modo que a quantidade de barras corresponde às dezenas e a quantidade de cubinhos isolados corresponde às unidades. Em seguida, orienteos a contar a quantidade de barrinhas e cubinhos isolados em cada representação e associar cada quantidade ao número escrito por extenso que a representa. Ao fazer a leitura dos números escritos por extenso, os estudantes desenvolvem a fluência em leitura oral e o desenvolvimento de vocabulário.

BNCC

Nas atividades desta página, os estudantes vão realizar a contagem da quantidade de objetos de uma coleção agrupados de 10 em 10 e apresentar o resultado por meio de registros verbais ou simbólicos, contemplando aspectos das habilidades EF01MA02 e EF01MA04

• A atividade 22 avalia e exercita a capacidade dos estudantes de realizarem estimativas. É provável que eles iniciem a atividade contando os cajus um a um. Por isso, peça às duplas que não contem, mas que apenas digam, sem medo de errar, a quantidade de cajus que o feirante vai levar para a feira. Deixe claro que não há problema em errar, pois, caso contrário, eles podem invalidar o propósito da atividade.

• Após cada dupla dar sua resposta, peça a eles que expliquem como chegaram a uma ou outra conclusão. Na sequência, depois de todos terem emitido suas opiniões, peçalhes que façam a contagem dos cajus e confirmem se acertaram ou não o valor dado no palpite.

• Aproveite o contexto da atividade 22 para comentar com os estudantes sobre a profissão de feirante e a fruta apresentada. Se algum estudante for parente ou conhecido de um adulto que exerça essa profissão, incentiveo a comentar sobre esse assunto. Questione também se eles já experimentaram caju, o suco dele ou a castanha dessa fruta. Deixe que se expressem e contem suas experiências para a turma.

• Na atividade 23, se necessário, auxilie os estudantes na leitura dos números escritos por extenso. Para isso, leia os dois primeiros e observe se eles são capazes de ler os demais sozinhos. Em caso negativo, prossiga a leitura, no tempo adequado, auxiliandoos a reconhecer as sílabas. Verifique também se eles conseguem fazer corretamente a conversão para algarismos. Ao fazerem a leitura dos números escritos por extenso, os estudantes desenvolvem a fluência em leitura oral e o vocabulário.

22. FÁBIO É UM FEIRANTE. ELE ORGANIZOU UMA PORÇÃO DE CAJUS

EM BANDEJAS PARA VENDER NA FEIRA.

A ) JUNTE-SE A UM COLEGA E, SEM CONTAR, RESPONDAM: FÁBIO ORGANIZOU MAIS OU MENOS DE 80 CAJUS PARA VENDER NA FEIRA?

Sugestão de resposta: Espera-se que os estudantes respondam que Fábio organizou mais de 80 cajus.

B ) ESTIMEM QUANTOS CAJUS FÁBIO ORGANIZOU.

C ) CONTEM E ESCREVAM A QUANTIDADE TOTAL DE CAJUS.

Resposta: 99

22. B) Resposta pessoal. Espera-se que os estudantes estimem e escrevam no caderno a quantidade de cajus que o feirante organizou.

23. COMPLETE OS ITENS COM OS NÚMEROS QUE FALTAM.

A ) NOVENTA: 90

B ) NOVENTA E UM:

Resposta: NOVENTA E UM: 91

C ) NOVENTA E TRÊS:

Resposta: NOVENTA E TRÊS: 93

BNCC

Na atividade 22, os estudantes fazem estimativa, realizam contagem e apresentam o resultado da contagem por meio de registro numérico. Dessa maneira, eles desenvolvem as habilidades EF01MA01, EF01MA02, EF01MA03 e EF01MA04. Ao explorar o contexto de um feirante que vende cajus, a atividade 22 valoriza a diversidade de saberes e vivências culturais e apropriase de conhecimentos e experiências que aproximam os estudantes de algumas

D ) NOVENTA E CINCO:

Resposta: NOVENTA E CINCO: 95

E ) NOVENTA E OITO:

Resposta: NOVENTA E OITO: 98

F ) NOVENTA E NOVE:

Resposta: NOVENTA E NOVE: 99

relações próprias do mundo do trabalho, conforme aspectos da Competência geral 6 da BNCC. Além disso, desenvolvem aspectos da Competência específica de Matemática 8 da BNCC ao interagirem com seus pares, de maneira cooperativa, a fim de identificarem aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.

O NÚMERO 100

1. AS CRIANÇAS ESTÃO BRINCANDO DE PULAR CORDA.

BNCC

A ) QUAL É O PRÓXIMO NÚMERO QUE AS CRIANÇAS VÃO FALAR?

Resposta: 100

B ) COM A AJUDA DO PROFESSOR, LEIA E COMPLETE O QUADRO COM O NÚMERO ADEQUADO.

99 MAIS 1 É IGUAL A .

C ) ESCREVA O NÚMERO CEM DE DUAS MANEIRAS. ... 98, 99, ...

Resposta: 99 MAIS 1 É IGUAL A 100. letras e dos algarismos apresentados para realizar as escritas solicitadas.

6. C) Resposta pessoal. Espera-se que os estudantes sobreponham os pontilhados acompanhando os traçados das

D ) VOCÊ JÁ BRINCOU DE PULAR CORDA? SE SIM, CONTE AOS COLEGAS COMO FOI. 100100100100100

Resposta pessoal. A resposta depende das vivências de cada estudante, se brincou ou não de pular corda.

Na atividade 1, é apresentado aos estudantes o número 100. Com isso, a contagem de quantidades correspondentes a objetos de coleções com até 100 unidades é abordada, utilizando registros verbais e simbólicos para a representação dos resultados. Assim, a habilidade EF01MA04 é contemplada.

03/10/2025 09:28:38

• O objetivo do item A da atividade 1 é verificar se os estudantes já sabem que o sucessor de 99 é 100. Caso eles não saibam responder de imediato, peçalhes que contem juntos, em voz alta, os números de 90 em diante, a fim de que se recordem do número 100. Outra possibilidade é você contar os números em voz alta, simulando a contagem das crianças da cena, mas fazendo uma pausa interrogativa depois do 99. Mesmo que os estudantes já saibam que após o 99 vem o número 100, confira, no item B, se eles já sabem representar esse número usando algarismos. Depois que todos fizerem seus registros, escreva o número 100 na lousa para eles verificarem se escreveram corretamente.

• Ao trabalhar com o item C, certifiquese de que os estudantes de fato são capazes de registrar o número 100 tanto por extenso quanto com algarismos, e não apenas de copiar o número escrito em outras ocorrências na mesma página. Se necessário, peça a eles que fechem o livro por alguns minutos e escrevam ambas as representações no caderno. Se necessário, escreva o número na lousa tanto por extenso quanto com algarismos, evidenciando para eles o movimento com a mão e a direção do traçado para a escrita do número.

• Aproveitando a descontração no item D, pergunte até quanto eles contam quando pulam corda e se já chegaram até 100 ou mesmo se foram além. Caso tenham ido além, pergunte quais números vêm depois do 100. Desse modo, é possível explorar o potencial que a atividade fornece para misturar diversão com aprendizagem.

• Ao escrever o número 100 por extenso e com algarismos, na atividade desta página, os estudantes desenvolvem a produção de escrita.

• Durante as explicações do item E da atividade 1, aproveite ao máximo as vantagens visuais da utilização do ábaco e do material dourado. Se possível, leve esses materiais para a sala de aula e utilizeos reiteradamente, permitindo o uso a todos os estudantes, fazendo as associações entre um e outro e notando as equivalências de significados em diferentes representações. Caso não seja possível utilizálos em sala de aula, faça desenhos na lousa em tamanho grande, permitindo à turma acompanhar o passo a passo da construção dos desenhos, de modo que os reproduzam no caderno. Ao desenhar o material dourado, tente manter a escala correta, retratando fidedignamente que dez barras equivalem a uma placa. Além disso, dê tempo suficiente para que os estudantes se convençam (seja contando linhas e colunas, seja contando um a um os cubinhos) de que a placa de fato contém 100 cubinhos.

• Ao trocar 10 unidades por uma dezena e 10 dezenas por uma centena, mostre aos estudantes a importância do algarismo 0. Façaos perceber que o acréscimo de um 0 à direita torna o número maior, enfatizando que a posição dos algarismos em um número é de extrema importância. Esse é um prérequisito necessário para que se compreenda que o sistema de numeração decimal é posicional, significando que os algarismos têm valor diferente dependendo de sua posição.

E ) PODEMOS REPRESENTAR O NÚMERO CEM NO ÁBACO E NO QUADRO DE ORDENS. NO ÁBACO, C SIGNIFICA CENTENA.

QUADRO DE ORDENS CENTENA DEZENA UNIDADE

1 0 0

C D U

APRENDEMOS ANTERIORMENTE QUE, AO AGRUPAR DEZ CUBINHOS, OBTEMOS UMA DEZENA, QUE É REPRESENTADA POR UMA BARRA.

CORRESPONDEM A 10 UNIDADES 1 DEZENA

QUANDO AGRUPAMOS DEZ BARRAS, OBTEMOS UMA CENTENA, QUE É REPRESENTADA POR UMA PLACA.

CORRESPONDEM A 10 DEZENAS 1 CENTENA ÁBACO.

RESPONDA ÀS QUESTÕES.

• QUANTAS UNIDADES CORRESPONDEM A 1 DEZENA?

UNIDADES.

Resposta: 10 UNIDADES.

• QUANTAS UNIDADES CORRESPONDEM A 1 CENTENA? UNIDADES.

Resposta: 100 UNIDADES.

2. LIGUE A QUANTIDADE DE CUBINHOS AO ÁBACO CORRESPONDENTE.

Resposta: Os estudantes devem ligar: A-3; B-1; C-2; D-5; E-7; F-4; G-6.

• A atividade 2 exercita a capacidade de interpretar diferentes representações de um mesmo número. É importante que os estudantes sejam capazes de fazer conversões mentalmente, tornando se capazes de identificar números em diferentes notações (por extenso, com algarismos ou por meio de algum recurso visual). Caso eles se esqueçam, reforce o significado de U, D e C no ábaco, fazendoos perceber que são, respectivamente, as iniciais de unidade, dezena e centena

• Se julgar oportuno, realize essa atividade em duplas, incentivando a colaboração e a interação entre os estudantes.

AVALIANDO

Objetivo

Ler e escrever números até 100 com algarismos e por extenso.

Sugestão de intervenção

Faça um ditado com alguns números de 0 a 100. Explique aos estudantes que os números ditados deverão ser escritos no caderno com algarismos e por extenso. Enquanto ditar, caminhe pela sala a fim de perceber as possíveis dificuldades na grafia dos números. Para finalizar, peçalhes que, um de cada vez, escrevam na lousa um dos números ditados e façam as correções necessárias.

BNCC

Na atividade 2, os estudantes vão realizar a contagem da quantidade de objetos de uma coleção agrupados de 10 em 10 e associar o resultado ao número representado em um ábaco, contemplando, assim, aspectos das habilidades EF01MA02 e EF01MA04

• A atividade 3 exercita a capacidade de interpretar a sequência dos números de 1 até 100. É importante que os estudantes sejam capazes de representar os números que estão faltando no quadro. Confira se eles completaram corretamente a sequência e verifique a possível ocorrência de números escritos de maneira incorreta. Nesse caso, procure identificar as dificuldades deles no registro gráfico dos números. Se julgar necessário, escreva pausadamente na lousa os números, cuidando para que eles acompanhem o traçado e aprendam com a prática. Conclua pedindo a eles que expliquem o que puderam observar em relação a sequência dos números no quadro. Depois das explicações dadas, observe se todos chegaram à mesma conclusão de que a regularidade dos elementos ausentes sempre ocorre acrescentando uma unidade para obter o próximo número.

• Para complementar a atividade 4, apresente desafios extras aos estudantes. Escreva na lousa sequências com números faltantes e oriente os estudantes a copiálas no caderno para completá las. Contudo, desta vez não dê dicas de imediato; dê dicas apenas se tiverem dificuldade para identificar os padrões das sequências. Algumas possibilidades de sequências são:

90, 92, 94, ■, 98, ■ 100, 99, 98, ■, 96, ■, ■, 93, ■, 91. 15, 25, ■, 45, 55, ■ , 75, ■

3. ESCREVA OS NÚMEROS QUE ESTÃO FALTANDO A SEGUIR.

BNCC

Resposta: 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92,

4. ESCREVA OS NÚMEROS QUE ESTÃO FALTANDO NAS SEQUÊNCIAS, DE ACORDO COM AS DICAS.

93, 94, 95, 96, 97, 98, 99, 100

DICA: NO ITEM A, ACRESCENTE 1 UNIDADE PARA OBTER O PRÓXIMO NÚMERO.

A ) 92, 93, 94, , , 97, 98, ,

Resposta: 92, 93, 94, 95, 96, 97, 98, 99, 100

DICA: NO ITEM B, ACRESCENTE 1 DEZENA PARA OBTER O NÚMERO SEGUINTE.

B ) 40, 50, 60, , 80, , .

Resposta: 40, 50, 60, 70, 80, 90, 100

DICA: NO ITEM C, DIMINUA 3 UNIDADES PARA OBTER O PRÓXIMO NÚMERO.

C ) 100, 97, 94, , 88, , , .

Resposta: 100, 97, 94, 91, 88, 85, 82, 79

DICA: NO ITEM D, DIMINUA 1 DEZENA PARA OBTER O PRÓXIMO NÚMERO.

D ) 95, 85, 75, , 55, , .

Resposta: 95, 85, 75, 65, 55, 45, 35

• Essa atividade é desafiadora para a faixa etária dos estudantes, de modo que deve ser proposta tomando os devidos cuidados para não frustrar algum deles. Se os estudantes conseguirem completar essas sequências sem usar dicas, solicite a eles que expliquem como descobriram o padrão de cada uma. Na primeira sequência, por exemplo, eles devem concluir que foram acrescentadas duas unidades ao número anterior (94) para obter o próximo número (96); na segunda, devem ter retirado uma unidade ao número anterior (98) para obter o próximo número (97); já na terceira, eles devem concluir que foi acrescentada uma dezena ao número anterior (25) para obter o próximo número (35).

seguida, completar a sequência com esses elementos.

03/10/2025 09:28:39

Já na atividade 4, eles são incentivados a descrever, após a explicitação de um padrão de regularidade, os elementos ausentes em sequências recursivas de números naturais, conforme orienta a habilidade EF01MA10

Na atividade 3, os estudantes são levados a reconhecer os elementos ausentes em uma sequência recursiva de números naturais, conforme orienta a habilidade EF01MA10, para, em

PAR E ÍMPAR

1. CÁTIA PLANTOU FLORES EM SEU JARDIM.

A ) OBSERVE A IMAGEM E CONTORNE AS FLORES DE DUAS EM DUAS.

Resposta: Os estudantes devem contornar as flores formando três grupos com duas flores cada, ficando uma flor sem ser contornada.

B ) QUANTAS FLORES CÁTIA PLANTOU?

C ) FICOU ALGUMA FLOR SEM CONTORNAR?

Resposta: 7

Resposta: SIM.

AO CONTORNAR AS FLORES DE DUAS EM DUAS, SOBROU UMA FLOR.

QUANDO FORMAMOS GRUPOS DE DOIS EM DOIS COM UMA QUANTIDADE E SOBRA UM ELEMENTO, DIZEMOS QUE O NÚMERO QUE REPRESENTA ESSA QUANTIDADE É ÍMPAR.

NESSE CASO, DIZEMOS QUE O NÚMERO 7 É: PAR. ÍMPAR.

Resposta: Os estudantes devem marcar um X na palavra ÍMPAR.

• O objetivo da atividade 1 é iniciar o desenvolvimento do trabalho com a noção de paridade. Ela apresenta o caso de uma quantidade ímpar, ao passo que a atividade 2, da página 144, apresenta uma situação similar, indicando, porém, uma quantidade par, a fim de que os estudantes captem a essência da distinção entre números pares e ímpares. A noção de paridade é mais facilmente compreendida por meio de exemplos, agrupando elementos dois a dois e verificando se, ao final todos eles foram agrupados ou se ficou um sobrando.

• Verifique se os estudantes compreenderam o que é um número ímpar e se marcaram corretamente que o número 7 é ímpar. Se julgar necessário, faça desenhos na lousa e peçalhes que os agrupem dois a dois e, em seguida, digam se o número que representa a quantidade de elementos é par ou é ímpar. O mesmo exercício pode ser reproduzido com o manuseio de objetos: peça aos estudantes que separem 7 lápis em grupos de dois, a fim de verificar se 7 é um número ímpar.

BNCC

A atividade 1 da página 143 e a atividade 2 da página 144 permitem aos estudantes contarem, de maneira exata ou aproximada usando diferentes estratégias, como o agrupamento de dois em dois, contemplando a habilidade EF01MA02

03/10/2025 09:28:39

• A atividade 2 complementa a atividade 1 no sentido de apresentar a noção de paridade aos estudantes. Em contraste à atividade 1, a atividade 2 ilustra uma situação envolvendo um número par.

• O mesmo exercício prático pode ser proposto aqui: peça aos estudantes que separem 8 lápis em grupos de dois, a fim de determinar se 8 é um número par ou ímpar.

• Depois de realizadas as atividades 1 e 2, solicite a eles que deem exemplos de outros números pares e de ímpares. Peçalhes, ainda, que expliquem como descobriram que os números escolhidos como exemplos são pares ou ímpares.

• Na atividade 3, verifique se os estudantes percebem que os dedos podem ser agrupados aos pares, para descobrir se o número é par ou ímpar. Caso alguém fique sem par, é conveniente que um deles pratique a brincadeira com o professor ou com algum convidado de outra turma que estiver disponível no momento.

• A atividade 3 indica um contexto em que os sentidos da visão, do tato e da audição são explorados pelos estudantes, pois eles utilizam: a visualização das mãos e dos dedos para contar e identificar os números; e a sensação do toque na pele ao fechar a mão e a audição no som da voz ao falar “par” ou “ímpar”. Essas ações favorecem a inclusão de estudantes com NEE, além de propiciar a coordenação motora fina, a atenção, o raciocínio lógico, a linguagem e a compreensão de conceitos matemáticos.

2. CÁTIA PLANTOU MAIS UMA FLOR EM SEU JARDIM.

A ) CONTORNE AS FLORES DE DUAS EM DUAS.

Resposta: Os estudantes devem contornar as flores formando quatro grupos com duas flores cada.

B ) QUANTAS FLORES ESTÃO PLANTADAS AGORA?

Resposta: 8

C ) FICOU ALGUMA FLOR SEM CONTORNAR?

Resposta: NÃO.

AO CONTORNAR AS FLORES DE DUAS EM DUAS, NÃO SOBROU NENHUMA FLOR.

QUANDO FORMAMOS GRUPOS DE DOIS EM DOIS COM UMA QUANTIDADE E NÃO SOBRA QUALQUER ELEMENTO, DIZEMOS QUE O NÚMERO QUE REPRESENTA ESSA QUANTIDADE É PAR

NESSE CASO, DIZEMOS QUE O NÚMERO 8 É:

PAR. ÍMPAR.

Resposta: Os estudantes devem marcar um X na palavra PAR.

EXPERIMENTE

3. JUNTE-SE A UM COLEGA PARA BRINCAR!

CADA UM, NA SUA VEZ, DEVE MOSTRAR UMA QUANTIDADE DE DEDOS PARA O COLEGA, PODENDO USAR AS DUAS MÃOS. O COLEGA DEVE IDENTIFICAR SE A QUANTIDADE DE DEDOS MOSTRADOS REPRESENTA UM NÚMERO PAR OU ÍMPAR.

Resposta pessoal. Espera-se que os estudantes tenham compreendido o significado de números pares e ímpares e identifiquem se o colega acertou ou não a quantidade de dedos que ele mostrar.

AVALIANDO

Objetivo

Compreender o significado de número par e de número ímpar.

Sugestão de intervenção

Como a brincadeira sugerida na atividade 3 é realizada com pares, aproveite a oportunidade para que a turma descubra se a quantidade de estudantes na sala é par ou ímpar: se todos participarem da brincadeira, a quantidade é par; se um ficar sem dupla na organização das equipes, a quantidade é ímpar.

4. RITA ESTÁ BRINCANDO COM DADOS. AO LANÇAR UM DADO QUALQUER, O NÚMERO QUE REPRESENTA A QUANTIDADE DE PONTOS OBTIDOS POR ELA PODE SER PAR OU ÍMPAR.

COMPLETE O QUADRO COM O NÚMERO QUE REPRESENTA O LANÇAMENTO DE UM DADO. DEPOIS, VERIFIQUE SE ESSE NÚMERO É PAR OU ÍMPAR.

DICA: A PRIMEIRA LINHA DO QUADRO JÁ ESTÁ PREENCHIDA.

LANÇAMENTOS DE UM DADO

LANÇAMENTO NÚMERO QUE REPRESENTA O LANÇAMENTO PAR OU ÍMPAR? 1 ÍMPAR

Resposta: B. 3-ÍMPAR; C. 2-PAR; D. 4-PAR; E. 6-PAR; F. 5-ÍMPAR.

03/10/2025 09:30:54

• Na atividade 4, auxilie os estudantes a perceberem que as bolinhas dos dados representam um número e esse número pode ser par ou ímpar.

• Caso algum estudante fique com dúvidas, promova essa atividade na prática. É conveniente que eles pratiquem o jogo com o professor ou então em pares. Para isso, providencie dados suficientes para que todos os estudantes participem do jogo.

MENINA BRINCANDO COM DADOS.

• Na atividade 5, antes de os estudantes começarem a contagem dos carrinhos, pergunte a eles se sabem dizer se a quantidade é par ou ímpar apenas com base nos contornos que fizeram. No item B , caso tenham dificuldade para escrever a palavra “par”, orienteos a observar sua escrita no enunciado da atividade ou escrevaa na lousa para que a copiem.

• O objetivo da atividade 6 é incentivar diferentes estratégias desenvolvidas por eles com intuito de verificar o trabalho com a noção de paridade. A atividade apresenta uma situação similar à da atividade 4, mas indicando quantidade par e quantidade ímpar, a fim de que os estudantes captem a essência da distinção entre pares e ímpares. A noção de paridade é mais facilmente compreendida por meio de agrupamentos de elementos dois a dois, verificando se ao final todos eles foram agrupados ou se ficou um sobrando. Verifique se os estudantes compreenderam essa estratégia ou se utilizaram outra. Se julgar necessário, apresente as estratégias das duplas na lousa, validando com os demais colegas.

BNCC

5. CONTORNE OS CARRINHOS FORMANDO GRUPOS DE DOIS EM DOIS.

Resposta: Os estudantes devem contornar os carrinhos formando quinze grupos com dois carrinhos cada.

A ) QUANTOS CARRINHOS APARECEM NA IMAGEM?

Resposta: 30

B ) O NÚMERO QUE REPRESENTA A QUANTIDADE DE

CARRINHOS É PAR OU ÍMPAR?

Resposta: PAR.

6. JUNTE-SE A UM COLEGA E UTILIZEM UMA ESTRATÉGIA PARA VERIFICAR SE O NÚMERO QUE REPRESENTA A QUANTIDADE DE BOLINHAS É PAR OU ÍMPAR.

Resposta: Os estudantes devem marcar um X na palavra ÍMPAR.

Resposta pessoal. A resposta depende das estratégias escolhidas pelos estudantes. Espera-se que eles contornem as quantidades de bolinhas formando grupos de dois em dois. No entanto, eles podem obter a resposta de diferentes maneiras.

PAR. ÍMPAR.

QUAL ESTRATÉGIA VOCÊS USARAM PARA VERIFICAR SE O NÚMERO QUE REPRESENTA A QUANTIDADE DE BOLINHAS É PAR OU ÍMPAR? COMENTE COM OS COLEGAS E O PROFESSOR.

As atividades 5 e 6 permitem aos estudantes fazerem a contagem de maneira exata ou aproximada, com diferentes estratégias, como o agrupamento de dois em dois, a fim de contemplar a habilidade EF01MA02. Já a atividade 6 permite desenvolver aspectos da Competência específica de Matemática 8 da BNCC, ao propor aos estudantes a interação com seus pares, de maneira cooperativa, a fim de identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.

Resposta pessoal. A resposta depende das estratégias escolhidas pelos estudantes.

7. OS NÚMEROS TERMINADOS EM 0, 2, 4, 6 E 8 SÃO PARES. E OS NÚMEROS TERMINADOS EM 1, 3, 5, 7 E 9 SÃO ÍMPARES

A ) COMPLETE AS SEQUÊNCIAS DE NÚMEROS PARES.

Resposta: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20

• 2, 4, 6, , 10, , 14, 16, ,

Resposta: 74, 76, 78, 80, 82, 84, 86, 88

• 74, 76, 78, 80, , , , .

B ) COMPLETE AS SEQUÊNCIAS DE NÚMEROS ÍMPARES.

Resposta: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19

• 1, 3, 5, , , , , 15, 17, .

Resposta: 73, 75, 77, 79, 81, 83, 85, 87, 89.

• 73, 75, 77, , , , , , 89.

8. PAOLA E DÉBORA ESTÃO BRINCANDO DE AMARELINHA NO PÁTIO DA ESCOLA.

ESCREVA OS NÚMEROS ÍMPARES QUE APARECEM NA CENA.

Resposta: 1, 3, 5, 7 e 9.

EXPERIMENTE

INFOGRÁFICO CLICÁVEL: VAMOS BRINCAR JUNTOS?

9. JUNTE-SE A UM COLEGA PARA BRINCAR DE AMARELINHA!

O PROFESSOR VAI APRESENTAR AS REGRAS DESSA BRINCADEIRA PARA VOCÊS. DEPOIS, CONVERSE SOBRE ELAS COM O COLEGA E COMECEM A BRINCAR.

REFERÊNCIAS COMPLEMENTARES

RIPOLL, Cydara; RANGEL, Leticia; GIRALDO, Victor. Livro do Professor de Matemática na Educação Básica: Números Naturais. Rio de Janeiro: Sociedade Brasileira de Matemática, 2016.

A obra explora a base conceitual e o percurso histórico dos números naturais e examina como aparecem no Ensino Fundamental, destacando os marcos teóricos, as operações básicas, seus significados e contextos.

03/10/2025 09:31:12

• Na atividade 7, se necessário, dê alguns exemplos a fim de que os estudantes percebam, na prática, que os números terminados em 0, 2, 4, 6 ou 8 são pares e que os números terminados em 1, 3, 5, 7 ou 9 são ímpares. Utilize material de contagem ou desenhos na lousa para representar na prática as quantidades dos números. A cada quantidade representada, forme grupos de dois para verificar se sobram ou não elementos.

• Nas atividades 8 e 9, verifique se os estudantes percebem e identificam os números pares e ímpares. Pratique a brincadeira e verifique se algum dos estudantes ficou com alguma dúvida, dando as explicações necessárias. A brincadeira Amarelinha, além de trabalhar as noções de números pares e ímpares, desenvolve o raciocínio lógico e a avaliação de distância e força necessárias para lançar a pedra, além de promover a comunicação entre os pares.

BNCC

A atividade 7 permite que eles descrevam, após a explicitação de um padrão de regularidade, os elementos ausentes em sequências recursivas de números naturais, conforme orienta a habilidade EF01MA10

• A atividade 1 tem como objetivo introduzir as noções de maior e menor, com base na comparação entre as quantidades de elementos de dois conjuntos. Antes de iniciar o trabalho com os estudantes, organize dois grupos com quantidades diferentes de lápis ou outro material de contagem e peça a eles que digam, sem contar, qual dos dois contém mais lápis. Em seguida, coloque os lápis do primeiro grupo ao lado dos lápis do segundo, juntando os um a um. Após essa introdução, faça a contagem da quantidade de lápis, registre os números na lousa e verifique se eles compreendem que, se um número representa uma quantidade maior de elementos do que outro, dizemos que ele é maior do que o outro número e, se ele representa uma quantidade menor de elementos, dizemos que ele é menor do que o outro número. Esses prérequisitos são necessários para desenvolver e compreender os termos maior do que e menor do que em relação à quantidade de elementos de dois conjuntos. Além disso, é fundamental o conhecimento de contagem e reconhecimento de números.

• Nesse momento, ainda não é adequado utilizar as notações matemáticas > (maior) e < (menor). O ideal, nessa faixa etária, é usar as expressões escritas por extenso. Para tanto, caso os estudantes apresentem dificuldade na escrita, instruaos a copiar do enunciado as expressões que desejam utilizar.

COMPARANDO NÚMEROS

1. JOSIAS, FABIANA E REGINA COLECIONAM FIGURINHAS.

JOSIAS

FABIANA

REGINA

COMPLETE AS INFORMAÇÕES COM A QUANTIDADE DE FIGURINHAS DE CADA UM. DEPOIS, COMPARE AS QUANTIDADES ESCREVENDO OS NÚMEROS CORRESPONDENTES.

Resposta: QUANTIDADE DE FIGURINHAS DE JOSIAS: 24.

QUANTIDADE DE FIGURINHAS DE JOSIAS:

Resposta: QUANTIDADE DE FIGURINHAS DE FABIANA: 19

QUANTIDADE DE FIGURINHAS DE FABIANA: .

Resposta: A QUANTIDADE DE FIGURINHAS DE JOSIAS É MAIOR DO QUE A QUANTIDADE DE FIGURINHAS DE FABIANA.

A QUANTIDADE DE FIGURINHAS DE É MAIOR

DO QUE A QUANTIDADE DE FIGURINHAS DE FABIANA.

É MAIOR DO QUE

Resposta: QUANTIDADE DE FIGURINHAS DE JOSIAS: 24

Resposta: 24 É MAIOR DO QUE 19

QUANTIDADE DE FIGURINHAS DE JOSIAS: .

Resposta: QUANTIDADE DE FIGURINHAS DE REGINA: 28

QUANTIDADE DE FIGURINHAS DE REGINA: .

A QUANTIDADE DE FIGURINHAS DE JOSIAS É MENOR DO

Resposta: A QUANTIDADE DE FIGURINHAS DE JOSIAS É MENOR DO QUE A QUANTIDADE DE FIGURINHAS DE REGINA

QUE A QUANTIDADE DE FIGURINHAS DE

É MENOR DO QUE

BNCC

Na atividade desta página, os estudantes terão que comparar a quantidade de elementos de dois conjuntos para indicar qual tem mais e qual tem menos, desenvolvendo, assim, as habilidades EF01MA03 e EF01MA05

Resposta: 24 É MENOR DO QUE 28

2. RUI É PADEIRO E REGISTROU EM UMA TABELA A QUANTIDADE DE FORNADAS DE PÃES QUE ELE ASSOU DURANTE 4 SEMANAS.

PÃES ASSADOS DURANTE

4 SEMANAS DE JULHO DE 2026

SEMANAQUANTIDADE DE FORNADAS

1ª SEMANA 8

2ª SEMANA 9

3ª SEMANA 5

4ª SEMANA 7

FONTE DE PESQUISA: ANOTAÇÕES DE RUI.

Unidades temáticas integradas

FORNADAS: QUANTIDADE DE PÃES ASSADOS DE UMA SÓ VEZ NO MESMO FORNO.

A ) EM QUAL SEMANA RUI ASSOU A MAIOR QUANTIDADE DE FORNADAS DE PÃES?

Resposta: 2ª SEMANA.

B ) EM QUAL SEMANA ELE ASSOU A MENOR QUANTIDADE DE FORNADAS DE PÃES?

Resposta: 3ª SEMANA.

3. JOSIANE FEZ UMA PESQUISA NO BAIRRO ONDE MORA. ELA QUERIA SABER QUANTAS PESSOAS SEPARAM OS RESÍDUOS SÓLIDOS PARA RECICLAR.

Unidades temáticas integradas

• 18 PESSOAS RESPONDERAM QUE SEPARAM OS RESÍDUOS.

• 12 PESSOAS RESPONDERAM QUE NÃO SEPARAM OS RESÍDUOS.

A ) COMPLETE A TABELA COM OS DADOS OBTIDOS POR JOSIANE.

QUANTIDADE DE PESSOAS DO BAIRRO QUE SEPARAM OU NÃO SEPARAM OS RESÍDUOS SÓLIDOS DE 2027

SEPARAM OS RESÍDUOS QUANTIDADE DE PESSOAS

SIM NÃO

Resposta: SIM: 18; NÃO: 12.

FONTE DE PESQUISA: ANOTAÇÕES DE JOSIANE.

B ) VOCÊ E AS PESSOAS DE SUA FAMÍLIA TÊM O HÁBITO DE SEPARAR OS RESÍDUOS SÓLIDOS PARA RECICLAR?

Resposta pessoal. A resposta depende dos hábitos familiares de cada estudante.

AVALIANDO

Objetivos

Identificar os elementos de uma tabela. Ler e interpretar dados expressos em tabelas. Completar tabelas para registrar informações.

Sugestão de intervenção

A avaliação é uma intervenção muito importante, que fornece ao professor informações sobre como está ocorrendo a aprendizagem dos estudantes. Por isso, nesse momento, providencie antecipadamente e leve para a sala de aula algumas cópias, em quantidade suficiente,

149

03/10/2025 09:31:13

de tabelas que apresentem dados numéricos conhecidos por eles, como de revistas, jornais, internet ou rótulos de alimentos. Organize a turma em duplas e entregue três tabelas diferentes a cada uma. Orienteos a identificar o assunto tratado em cada tabela, os dados numéricos apresentados, o título, sua estrutura, entre outros dados. Depois, peça a cada dupla que apresente para a turma suas tabelas, comentando seus elementos. Por fim, conduza uma conversa sistematizando os conhecimentos desenvolvidos.

• As atividades 2 e 3 relacionam as unidades temáticas Números e Probabilidade e estatística ao trabalhar a interpretação de tabela. Comente com os estudantes que tabela é uma estrutura que usamos para organizar e expressar dados, de maneira simples, a fim de identificar informações sobre determinado assunto.

• Na atividade 3, são informadas as quantidades de pessoas que Josiane entrevistou e que responderam se separam ou não separam o resíduo sólido orgânico dos recicláveis. Com base nessas informações os estudantes devem completar a tabela. Para que aproveitem bem essas atividades, sugira que os estudantes as resolvam em duplas ou grupos. Em relação ao item B da atividade 3, se julgar oportuno, peça a eles que realizem uma pesquisa para entender o motivo de algumas pessoas não estarem habituadas a separar o resíduo sólido orgânico do material reciclável. Alguns motivos são: falta de informação, falta de tempo e falta de acesso à coleta seletiva. A falta de saneamento básico pode trazer sérias consequências ao meio ambiente, como contaminação do solo com chorume, emissão de gases poluentes e proliferação de doenças.

• O objetivo da atividade 4 é explorar a comparação de dois conjuntos com a mesma quantidade de elementos, de maneira que os estudantes compreendam o significado da expressão é igual a e a utilizem ao fazer comparações. Se possível, realize uma atividade prática semelhante à que foi sugerida para a atividade 1, porém organizando grupos com quantidades iguais de elementos.

• Na atividade 5, a comparação dos números é feita com o suporte da reta numérica, cuja utilização é importante para tornar mais significativa a aprendizagem, ao tornar imediata a identificação visual da relação de ordem, facilitando a comparação entre dois números. No trabalho com a reta numérica, peça aos estudantes que passem o dedo sobre os números, a fim de facilitar a localização e favorecer a concentração. Aos poucos, a tendência é que a identificação seja mais imediata e que essa estratégia não seja mais necessária. Além disso, evidencie que, na reta numérica, o espaçamento entre dois números consecutivos é sempre o mesmo (a distância entre 1 e 2 é a mesma que entre 2 e 3, e assim por diante). Peça aos estudantes que, se possível, mantenham essa proporção nos desenhos que fizerem no caderno. Note que há várias opções de resposta para os itens A e B. Com a ajuda da turma, escreva algumas delas na lousa.

BNCC

Na atividade 5, é abordada a comparação de números naturais de até duas ordens usando a reta numérica como suporte, a fim de auxiliar na compreensão dos estudantes, conforme orienta a habilidade EF01MA05

4. CADA QUADRO CONTÉM A MESMA QUANTIDADE DE GIZ DE CERA. ESCREVA EM CADA QUADRO O NÚMERO QUE REPRESENTA A QUANTIDADE CORRESPONDENTE, COMPLETANDO A SENTENÇA.

Resposta: 8 É IGUAL A 8

É IGUAL A

5. PODEMOS COMPARAR ALGUNS NÚMEROS UTILIZANDO A RETA NUMÉRICA.

OS NÚMEROS QUE APARECEM NA RETA ESTÃO ORGANIZADOS DO MENOR PARA O MAIOR, DA ESQUERDA PARA A DIREITA. NESSE CASO, DIZEMOS QUE OS NÚMEROS ESTÃO EM ORDEM CRESCENTE

O NÚMERO 17, POR EXEMPLO, ESTÁ DEPOIS DO NÚMERO 15. LOGO, 17 É MAIOR DO QUE 15.

A ) COM BASE NOS NÚMEROS NA RETA NUMÉRICA, COMPLETE AS FRASES.

Respostas pessoais. Comentários nas orientações ao professor

• 15 É MAIOR DO QUE

• 8 É MAIOR DO QUE

O NÚMERO 8, POR EXEMPLO, ESTÁ ANTES DO NÚMERO 10. LOGO, 8 É MENOR DO QUE 10.

B ) VERIFIQUE OS NÚMEROS NA RETA NUMÉRICA E COMPLETE AS FRASES.

Respostas pessoais. Comentários nas orientações ao professor.

• 11 É MENOR DO QUE . 012345678910111213141516171819

• 1 É MENOR DO QUE .

6. COMPLETE OS ESPAÇOS INDICADOS NA RETA NUMÉRICA COM OS NÚMEROS QUE APARECEM NAS FICHAS.

Resposta: 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100

100 92 87 95

858688899091939496979899

CONSULTE A RETA NUMÉRICA E COMPLETE CADA ITEM COM É MENOR DO QUE, É MAIOR DO QUE OU É IGUAL A.

Resposta: 89 É MAIOR DO QUE 86.

A ) 89 86.

• Ao trabalhar com a atividade 6, explique aos estudantes que o trecho da reta numérica apresentado na página é apenas uma parte dela, pois eles podem estranhar o fato de que ela não começa no número 1, e sim no número 85. Explique, ilustrando na lousa, que a reta pode ser estendida para a esquerda ou para a direita, com o acréscimo dos números adequados, mas, nesse momento, vamos estudar até o 100. Em todas as etapas, represente as explicações por meio de desenhos na lousa.

Resposta: 93 É IGUAL A 93.

B ) 93 93.

Resposta: 95 É MENOR DO QUE 99.

C ) 95 99.

Resposta: 90 É MAIOR DO QUE 87.

D ) 90 87.

Resposta: 94 É MAIOR DO QUE 92.

E ) 94 92.

Resposta: 97 É MENOR DO QUE 100.

F ) 97 100.

DESAFIO A MAIS

AJUDE RUTE A ORGANIZAR FICHAS NUMERADAS EM ORDEM DECRESCENTE. PARA ISSO, ESCREVA A SEQUÊNCIA FORMADA PELOS NÚMEROS DAS FICHAS.

Resposta: 95, 93, 88, 86, 75, 72, 70, 54, 50, 49.

, , , , , , , , ,

AVALIANDO

Objetivo

Comparar números, usando termos como é maior do que, é menor do que e é igual a

Sugestão de intervenção

Entregue a cada estudante 20 palitos de sorvete. Peça a eles que coloquem 8 palitos sobre a carteira, do lado esquerdo, e 12 do lado direito. Pergunte: “Qual dos lados tem a maior quantidade de palitos?”;

“Qual dos lados tem a menor quantidade de palitos?”. Depois, peça a eles que coloquem 10 palitos de sorvete de cada lado da carteira e pergunte: “A quantidade de palitos do lado direito é maior, menor ou igual à quantidade de palitos do lado esquerdo?”. Repita a atividade com outras quantidades de palitos até perceber que os estudantes estão utilizando corretamente as palavras maior, menor e igual para fazer comparações entre quantidades de elementos de dois grupos.

03/10/2025 09:31:13

BNCC

• Oriente os estudantes a consultarem a reta numérica que está na mesma página, no Desafio a mais, para organizar os primeiros números, tomando o cuidado de observar que, nesta atividade, a reta deve ser enxergada da direita para a esquerda, já que os números devem ser dispostos em ordem decrescente. Para os demais números, eles podem comparar, nesta ordem, o algarismo da dezena e, depois, o algarismo das unidades, a fim de descobrirem qual número é maior do que o outro. Outra estratégia seria pensar nos números em ordem crescente, preenchendo os espaços em branco da direita para a esquerda, e não da esquerda para a direita. Por isso, confira as resoluções dos estudantes e as compare, conversando com a turma sobre as diferentes maneiras de resolver uma mesma atividade.

Nas atividades desta página, ao compararem números naturais com e sem o suporte da reta numérica, os estudantes desenvolvem a habilidade EF01MA05

OBJETIVOS

• Compreender a importância de competir, não focando apenas na vitória.

• Desenvolver relações amigáveis com os colegas.

• Aprender a respeitar e compreender as diferenças.

• Incentivar a fluência em leitura oral e o desenvolvimento de vocabulário.

• Reconhecer números pares e números ímpares.

1. CONHECENDO O PROBLEMA

• Leia com os estudantes o texto, orientandoos a observar a ilustração.

• Comente com eles que as brincadeiras são momentos agradáveis de diversão e descontração e que eles devem evitar focar apenas na vitória, pois essa atitude gera um clima de rivalidade, mal estar no grupo e inimizades.

• Se julgar conveniente, realize uma brincadeira competitiva, como Carrinho de mão. Se considerar viável, faça essa atividade em parceria com o professor do componente curricular de Educação Física, em um espaço adequado, como uma quadra.

• Explore os conceitos de par e ímpar no momento da organização de equipes. Converse com os estudantes sobre a importância da diversão, independentemente de ganharem ou não, pois as brincadeiras e competições são ótimas oportunidades de convivência, autoconhecimento e troca de ideias.

• Em caso de atitudes inadequadas que possam levar a um acidente, mostre com bons exemplos que aquela não é uma atitude aceitável. Também não se deve oferecer prêmios aos vencedores da brincadeira, reforçando, assim, o objetivo da seção.

2. ORGANIZANDO AS IDEIAS

Orientações complementares

A) O objetivo dessa questão é conhecer o histórico dos

COLETIVAMENTE

COMPETIR É DIVERTIDO!

CONHECENDO O PROBLEMA 1

Professor, professora: O assunto tratado nesta seção possibilita o trabalho com o tema contemporâneo transversal Vida familiar e social

EM BRINCADEIRAS E JOGOS, ALGUMAS VEZES VENCEMOS E EM OUTRAS, PERDEMOS. ISSO É NATURAL! O IMPORTANTE É A COMPETIÇÃO, A DIVERSÃO E O APRENDIZADO DURANTE A BRINCADEIRA. ALÉM DISSO, PODEMOS FAZER NOVOS AMIGOS E APRENDER A RESPEITAR AS SUAS DIFERENÇAS, LIMITAÇÕES E DIFICULDADES.

AS CRIANÇAS DA CENA A SEGUIR ESTÃO SE DIVERTINDO, MESMO SABENDO QUE APENAS UMA DUPLA VAI VENCER.

ORGANIZANDO AS IDEIAS 2

A ) VOCÊ JÁ PARTICIPOU DE ALGUMA COMPETIÇÃO? NESSE CASO, CONTE AOS COLEGAS COMO FOI.

Resposta pessoal. Comentários nas orientações ao professor

B ) VOCÊ PREFERE PARTICIPAR DE UM JOGO MESMO SABENDO QUE EXISTE POSSIBILIDADE DE NÃO VENCER OU PREFERE FICAR SEM JOGAR?

Resposta pessoal. Comentários nas orientações ao professor

estudantes em relação à participação ou não de competições. Incentiveos a relatar suas experiências. Cada um deve esperar a vez para falar.

B) Nesta questão, esperase que os estudantes manifestem preferência por brincar. Digalhes que não devem ter medo de perder e que, ao deixar de fazer uma atividade por achar que não vão ganhar, estão deixando passar a oportunidade de se divertirem.

C) Caso haja dificuldade para responder a esta questão, oriente os estudantes a contarem os colegas que estão esperando, formando grupos de dois em dois, verificando se vai sobrar alguém sem par.

BNCC

As questões propostas nesta seção favorecem o desenvolvimento das Competências gerais 8 e 10 da BNCC e o tema contemporâneo transversal Vida familiar e social, pois permitem aos estudantes aprender a lidar com as próprias emoções e as dos outros, além de favorecer a reflexão sobre respeito ao participar de brincadeiras buscando diversão mesmo sem ganhar. Também destacam princípios éticos ao propor que eles interajam coletivamente respeitando a vez dos colegas antes da deles.

C ) NA CENA, HÁ UMA QUANTIDADE DE CRIANÇAS QUE ESTÃO AGUARDANDO PARA BRINCAR NAS PRÓXIMAS RODADAS. O NÚMERO QUE REPRESENTA ESSA QUANTIDADE É PAR OU ÍMPAR?

Resposta: Par. Comentários nas orientações ao professor

D ) AO TODO, QUANTOS PARES DE CRIANÇAS VÃO PARTICIPAR

NAS PRÓXIMAS RODADAS DA BRINCADEIRA?

Resposta: Quatro. Comentários nas orientações ao professor

BUSCANDO SOLUÇÕES

A ) COM OS COLEGAS E COM O PROFESSOR, LEIA A FRASE.

Resposta pessoal. Comentários nas orientações ao professor

EM UMA BRINCADEIRA OU COMPETIÇÃO, O IMPORTANTE É SE EMPENHAR E SE DIVERTIR, MESMO NÃO SENDO O VENCEDOR.

FAÇA UM DESENHO NO ESPAÇO A SEGUIR PARA ILUSTRAR A MENSAGEM DESSA FRASE.

B ) COLOQUE EM PRÁTICA NO SEU DIA A DIA AS IDEIAS DA MENSAGEM APRESENTADA NA FRASE.

Resposta pessoal. Comentários nas orientações ao professor 153

D) Caso os estudantes tenham dificuldade em responder a essa questão, use uma estratégia parecida com a da questão C. Esperase que eles respondam que vão participar quatro pares de estudantes nas próximas rodadas da brincadeira.

3. BUSCANDO SOLUÇÕES

Orientações

Complementares

A) Nesta questão, ajude os estudantes a compreenderem a importância do empenho e da diversão em uma brincadeira. Diga que é fundamental respeitar os colegas, suas diferenças e limitações. Ao final, incentiveos a mostrar a produção para os demais. Peça a eles que leiam em voz alta a frase, auxiliando a leitura quando necessário.

B) Esta questão os incentiva a colocar em prática o que aprenderam. Orienteos a compartilhar as ideias levantadas com os familiares e amigos.

• Conclua o trabalho com a unidade propondo a sugestão de desafio a seguir. Deixe que eles usem o raciocínio lógico para resolver a questão. Verifique se os estudantes analisam as informações e identificam que existem 5 algarismos 9 de 0 a 50, que estão nos números: 9, 19, 29, 39 e 49

Sugestão de Desafio

Quantos 9 existem de 0 a 50?

Resposta

Existem 5 algarismos 9 de 0 a 50

CONCLUSÃO

em consideração suas particularidades. Um modelo desse tipo de ficha pode ser encontrado no tópico Avaliação deste Manual do Professor. Assim, será possível visualizar de modo individual as trajetórias de aprendizagem, incluindo os avanços e os pontos de dificuldades a serem sanados por meio de atividades que promovam recuperação dos conteúdos. Esse método de verificar a progressão dos estudos e identificar o que a turma de fato conseguiu aprender e o que ficou com lacunas de absorção é de grande importância para que seja possível re

03/10/2025 09:31:14

pensar estratégias em sala de aula, tornando as ações pedagógicas cada vez mais eficazes.

A conclusão da unidade é o momento de avaliar se os objetivos por ela propostos foram alcançados. Para esse diagnóstico, observe no final deste Manual do Professor algumas possibilidades de avaliação formativa que permitem realizar o monitoramento da aprendizagem dos estudantes e intervir caso eles não tenham atingido os resultados esperados.

1. Objetivos

Efetuar medição de comprimento usando régua. Comparar medidas de comprimento por meio da subtração.

Sugestão de intervenção

Para superar possíveis dificuldades, retome as estimativas feitas pelos estudantes no item A e, após medirem o comprimento dos objetos no item B, confronte-as com a medida obtida. Essa constatação é importante para que percebam se fizeram ou não uma boa estimativa. Durante o processo de medição, é esperado que alguns deles posicionem a régua partindo de 1, e não do zero. Caso isso ocorra, verifique se eles contam a quantidade de centímetros de maneira correta, independentemente do posicionamento inicial ou se desconsideram o centímetro que vai do zero ao 1. Para isso, o posicionamento correto é importante.

Em relação à comparação das medidas de comprimento apresentadas, organize os estudantes em duplas e proponha a eles que, usando a régua, tracem duas linhas: a primeira de mesmo comprimento que o do lápis e a segunda de mesmo comprimento que o do apontador, sobrepondo-as. Para isso, eles devem utilizar lápis de cores diferentes. A extensão da linha não sobreposta é a diferença procurada. Com base na atividade anterior, é possível também que alguns estudantes reconheçam a operação de subtração. Caso isso aconteça, é importante abordá-la.

1. A) Resposta pessoal. Espera-se que os estudantes, sem usar instrumento de medida de comprimento, marquem um X no lápis.

VAMOS AVALIAR O APRENDIZADO

1. OBSERVE AS IMAGENS.

IMAGENS SEM PROPORÇÃO ENTRE SI.

A ) SEM USAR INSTRUMENTO DE MEDIÇÃO, MARQUE UM X NO OBJETO QUE VOCÊ ACHA QUE TEM A MAIOR MEDIDA DE COMPRIMENTO.

B ) USE UMA RÉGUA PARA MEDIR O COMPRIMENTO DOS OBJETOS. CONTORNE O NOME DO OBJETO QUE TEM A MAIOR MEDIDA DE COMPRIMENTO.

Resposta: Os estudantes devem contornar a palavra LÁPIS.

LÁPIS APONTADOR

QUANTOS CENTÍMETROS DE COMPRIMENTO O OBJETO MAIS COMPRIDO TEM A MAIS QUE O OBJETO MAIS CURTO?

CENTÍMETROS A MAIS.

Resposta: 4 CENTÍMETROS A MAIS.

2. ANA E SEUS AMIGOS ESTÃO PARTICIPANDO DE UM MOMENTO DE LEITURA COM A PROFESSORA.

A ) CONTORNE DE AZUL A CRIANÇA QUE ESTÁ MAIS DISTANTE DE RUI.

Resposta: Os estudantes devem contornar de azul a IARA.

B ) MARQUE UM X NA CRIANÇA QUE ESTÁ IMEDIATAMENTE À DIREITA DE ANA.

Resposta: Os estudantes devem marcar um X em RUI.

C ) CONTORNE DE VERDE A CRIANÇA QUE ESTÁ IMEDIATAMENTE À ESQUERDA DE IARA.

Resposta: Os estudantes devem contornar de verde o JOÃO.

2. Objetivo

Desenvolver conceitos envolvendo noções de localização.

Sugestão de intervenção

Verifique se os estudantes compreendem as noções de mais distante, imediatamente à direita e imediatamente à esquerda, pois são impor-

tantes para a resolução dessa atividade. Em caso de dificuldade, proponha situações práticas na sala de aula, questionando a localização dos próprios estudantes em relação a seus colegas. Essa situação também pode ser executada em ambiente aberto, no pátio da escola, com a turma em roda e observando os colegas ao lado e os objetos próximos ou distantes deles.

ANA JOÃO RUI IARA

3. OBSERVE OS SIGNIFICADOS DAS SETAS.

AVANCE UM QUADRINHO

VIRE À DIREITA VIRE À ESQUERDA

PARA IR ATÉ A CASA DE SEU AMIGO, CARLOS PRECISA SEGUIR OS SEGUINTES PASSOS.

PINTE O CAMINHO CORRESPONDENTE A ESTES PASSOS NA MALHA.

Resposta nas orientações ao professor.

4. ESCREVA OS NÚMEROS REPRESENTADOS NOS ÁBACOS. O PRIMEIRO NÚMERO JÁ FOI ESCRITO.

Resposta: B: 34; C: 39; D: 73; E: 28; F: 42; G: 61; H: 80

03/10/2025 09:32:33

3. Objetivo

Identificar as noções de localização e deslocamento. Sugestão de intervenção Espera-se que os estudantes tenham progredido na capacidade de seguir instruções e possam desenhar o caminho correto sem maiores dificuldades. No entanto, caso algum deles não consiga resolver a atividade, proponha a seguinte dinâmica: leve-os ao pátio da escola e posicione-os de maneira que todos possam executar os mesmos movimentos com base nos comandos que forem dados pelo professor, como dar dois passos para frente, virar para esquerda e, em seguida, dar um passo em alguma direção indicada.

4. Objetivo

• Promover a compreensão de valor posicional.

Sugestão de intervenção

• Leve um ábaco para sala de aula e solicite aos estudantes que, individualmente, indiquem o número representado nele. Caso tenha mais de um ábaco disponível, é possível realizar essa atividade em grupo.

Resposta

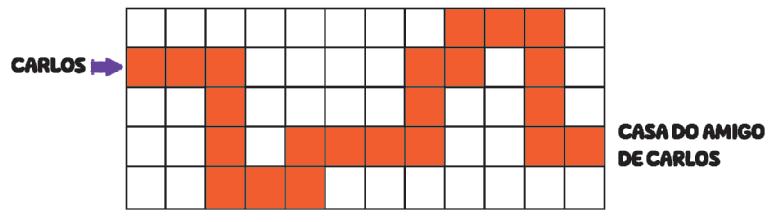
• Para estudantes com deficiências visuais ou auditivas, apresente-lhes o ábaco a fim de que possam compreender sua estrutura e, em seguida, proponha à turma a realização dessa atividade em pares ou em grupos, incentivando, assim, a interação social. Nesse caso, eles devem usar o tato para identificar as quantidades representadas ou um dos colegas pode fazer a descrição oralmente para os demais.

OBJETIVOS DA UNIDADE

• Reconhecer o Real como unidade monetária brasileira.

• Identificar e relacionar as cédulas e moedas utilizadas no sistema monetário brasileiro.

• Resolver problemas do cotidiano que envolvam valores do sistema monetário expressos em cédulas e moedas.

• Relacionar situações de compra com troco para efetuar um pagamento, envolvendo as operações de adição e subtração.

• Representar preços de produtos, mostrados em cédulas e moedas, em um gráfico.

INTRODUÇÃO E JUSTIFICATIVA

Nesta unidade, são apresentadas atividades que envolvem o sistema monetário brasileiro por meio de diferentes atividades, buscando identificar os conhecimentos prévios dos estudantes relacionados a esse conteúdo. Propõe-se o reconhecimento de cédulas e moedas do sistema monetário, bem como a equivalência entre elas. Nesse sentido, diferentes atividades envolvem situações de compra em diferentes locais, como supermercado e papelaria, além de situações que envolvem troco, contemplando algumas ideias da adição e subtração. É enfatizada também a importância de poupar dinheiro para a aquisição de um bem, levando os estudantes a refletirem e avaliarem atitudes relacionadas ao uso do dinheiro.

Habilidades da BNCC trabalhadas nesta unidade: EF01MA19 e EF01MA21

UNIDADE6 SISTEMA MONETÁRIO

SUGESTÃO DE ESTRATÉGIA INICIAL

Para iniciar esta unidade, avalie a conveniência de ler para os estudantes o texto a seguir.

POR QUE EXISTE?

Nem sempre existiu dinheiro, antigamente não existiam cidades, as comunidades eram menores, os deslocamentos eram mais difíceis, não existiam carros e aviões, as pessoas tinham sua produção no campo e, quando precisavam de coisas ou alimentos que não produziam, trocavam as sobras da própria produção por coisas ou alimentos com outras pessoas.

À medida que as comunidades iam crescendo e aumentando as trocas, ficava complicado carregar

CRIANÇA

GUARDANDO MOEDA EM UM COFRINHO.

as mercadorias que seriam trocadas de um lado para outro. Você já imaginou ter que levar três vacas para buscar tijolos para construir sua casa? Foi por isso que o dinheiro foi inventado, para facilitar as trocas.

Vários objetos como peles de animais, conchas, chá e metais preciosos foram usados como dinheiro, eles eram escolhidos pelo valor que tinham para cada comunidade.

Coisas que existiam em menor quantidade normalmente eram consideradas como valiosas.

LIGOCKI, Carolina Simões Lopes; IUNES, Silvana Maria Silva. Educação financeira na escola: com empreendedorismo, ética, sustentabilidade e cidadania. Brasília: Oficina, 2014. v. 5. p. 6.

GUARDAR DINHEIRO, QUANDO POSSÍVEL, É UMA ATITUDE QUE TODOS DEVERIAM TER. É SEMPRE

ACONSELHÁVEL GUARDAR UMA PARTE DO DINHEIRO ADQUIRIDO PARA O CASO DE UM IMPREVISTO OU PARA COMPRAR ALGO DE MAIOR VALOR.

1 a 3. Respostas pessoais. Comentários nas orientações ao professor

VOCÊ JÁ GUARDOU

DINHEIRO EM UM COFRINHO OU CONHECE ALGUÉM DA SUA CASA

QUE GUARDA DINHEIRO?

QUAIS CÉDULAS DE REAL

VOCÊ CONHECE? CITE

PELO MENOS DUAS DELAS. HEITOR GUARDOU 9 REAIS EM SEU COFRINHO. CONTORNE, ENTRE AS CÉDULAS E MOEDAS A SEGUIR, A QUANTIA QUE ELE GUARDOU.

IMAGENS SEM PROPORÇÃO ENTRE SI.

• As questões de 1 a 3 exploram os conhecimentos prévios dos estudantes em relação ao sistema monetário brasileiro e ao uso do dinheiro. Durante a resolução da questão 1, pergunte a eles se já compraram algo com o dinheiro que pouparam e como conseguiram economizar.

• Ao responderem à questão 2, fale sobre as cédulas e as moedas do Real. Ao citarem as cédulas que conhecem, questione-os com relação às que têm maior valor, comparando-as duas a duas, como 2 reais e 20 reais, 5 reais e 50 reais.

• Em relação à questão 3, como há diferentes possibilidades de obter essa quantidade, incentive os estudantes a calcularem a quantia usando

03/10/2025 09:36:44

composições diferentes da apresentada, como 1 + 1 + 2 + 5 ou 2 + 2 + 5. Aproveite a atividade para explorar a equivalência entre cédulas e moedas. Questione-os se eles têm ou já tiveram um cofrinho e aproveite para destacar a importância desse objeto para a formação do hábito de poupar.

BNCC

Na questão 3, o estudante precisa reconhecer e relacionar valores de cédulas e moedas para resolvê-la, conforme orienta a habilidade EF01MA19 da BNCC.

• Após a leitura do texto, peça aos estudantes que exponham sua opinião sobre as trocas que eram feitas antes do surgimento do dinheiro. É provável que eles já tenham experimentado a troca de objetos com os colegas, como figurinhas de uma coleção ou bolinhas de um jogo. Esse assunto abre espaço para uma larga discussão sobre a necessidade do dinheiro.

• Em seguida, converse com eles sobre a importância de controlar os gastos e de criar uma reserva de dinheiro para emergências, como comprar um medicamento, ou para investimento, como adquirir uma casa. Explique também a importância do consumo consciente, que envolve atitudes como usar sacolas retornáveis, evitar o uso de sacolas plásticas e materiais descartáveis, reaproveitar embalagens, evitar o desperdício de alimentos, economizar água e manter as luzes de cada cômodo da casa apagadas quando não estiverem em uso. Converse com eles também sobre a importância de evitar compras intempestivas de produtos de que não precisam, como um brinquedo ou um calçado que já possuem. Essas compras quase sempre são motivadas por propagandas ou modismo.

• Ao trabalhar a atividade 1, oriente os estudantes a recortarem e usarem as representações das cédulas e moedas do Real disponíveis no Material complementar do final do Livro do Estudante, auxiliando-os e supervisionando-os no recorte das cédulas e moedas durante o uso deste material. Essas representações favorecem a análise e percepção das características do Real por meio de diferentes sentidos, como o visual e o tátil. A manipulação de representações concretas do Real favorece a compreensão e a inclusão dos estudantes com NEE, como o TEA e o TDAH.

• Aproveite a oportunidade de escrever os números por extenso para treinar a escrita. Se necessário, proponha outras estratégias antes de solicitar que os estudantes pratiquem a escrita e o direcionamento das letras, como pedir que façam o traçado em caixas de areia. Para estudantes com maior dificuldade, pode ser necessário reforçar a prática e o direcionamento da escrita das letras usando o caderno de caligrafia, a fim de que desenvolvam progressivamente a escrita da letra cursiva.

• Na página do Banco Central, é possível obter informações sobre o sistema monetário brasileiro, incluindo as famílias de moedas e cédulas do Real e suas características. Disponível em: https://www.bcb. gov.br/cedulasemoedas/ cedulas. Acesso em: 7 ago. 2025.

• Converse com os estudantes sobre a cédula de 200 reais, que passou a fazer parte do nosso sistema monetário em 2020. Nesse momento, eles ainda não trabalharam com números maiores do que 100, mas é interessante conhecer essa cédula. Explique a eles que a cédula de 200 reais

UNIDADE MONETÁRIA BRASILEIRA: REAL

1. USAMOS O DINHEIRO PARA MEDIR E COMPARAR O VALOR DE BENS E SERVIÇOS. O REAL É A MOEDA OFICIAL DO SISTEMA

MONETÁRIO BRASILEIRO. VAMOS CONHECER AS MOEDAS E ALGUMAS CÉDULAS DO NOSSO SISTEMA.

RECORTE AS IMAGENS DAS CÉDULAS E MOEDAS, DISPONÍVEIS

NO MATERIAL COMPLEMENTAR NAS PÁGINAS 275, 277 E 279

COM ELAS, COMPLETE O QUE FALTA NAS INFORMAÇÕES.

2 (DOIS) REAIS. A.

5 ( ) REAIS.

10 (DEZ) REAIS. C.

20 ( ) REAIS.

(CINQUENTA) REAIS.

100 (CEM) REAIS. F.

Resposta:

I. ( ) CENTAVOS.

5 (CINCO) CENTAVOS. G. (VINTE E CINCO) CENTAVOS.

1 (UM) REAL. K. (CINQUENTA) CENTAVOS.

B: 5 (CINCO) REAIS; D: 20 (VINTE) REAIS; E: 50 (CINQUENTA) REAIS; H: 10 (DEZ) CENTAVOS; I: 25 (VINTE E CINCO) CENTAVOS; J: 50 (CINQUENTA) CENTAVOS.

é equivalente a duas de 100 reais ou a quatro de 50 reais. Fale também sobre a moeda de 1 centavo, que, embora tenha parado de ser emitida em 2004, continua em circulação.

BNCC

As atividades abordadas nesta unidade favorecem aspectos da habilidade EF01MA19, ao apresentar diversas situações contextualizadas que motivam os estudantes a reconhecerem e relacionarem valores de moedas e cédulas do sistema monetário brasileiro.

IMAGENS SEM PROPORÇÃO ENTRE SI.

ARTICULANDO CONHECIMENTOS

03/10/2025 09:36:45

No reverso das cédulas de Real, há animais da fauna brasileira. Explore a menção desses animais estabelecendo relação com Ciências da Natureza. Cite algumas características desses animais para os estudantes, pois muitos deles associam o valor comercial da cédula ao animal nela representado antes de reconhecê-la pelo seu valor. Verifique se alguns deles já ouviram falar desses animais ou se os reconhecem de alguma experiência pessoal, tendo visto exemplares deles em filmes ou em parques florestais, na natureza. Em caso afirmativo, incentive-os a comentar suas experiências.

2. PEDRO FEZ COMPRAS NO MERCADO. ASSOCIE CADA ALIMENTO AO VALOR REPRESENTADO PELAS CÉDULAS E MOEDAS.

Resposta: Os estudantes devem associar: A-2; B-3; C-1.

IMAGENS SEM PROPORÇÃO ENTRE SI.

12 REAIS

31 REAIS

Unidades temáticas integradas

6 REAIS

3. A) Resposta pessoal. Espera-se que os estudantes respondam que a menina comprou o que queria no mercado com o seu dinheiro, mas pensando em poupar o troco para comprar um produto de maior valor, no caso, uma bicicleta.

VOCÊ COSTUMA FAZER COMPRAS DE ALIMENTOS COM SEUS FAMILIARES? EM CASO AFIRMATIVO, CONTE ESSA EXPERIÊNCIA PARA SEUS COLEGAS.

Resposta pessoal. Espera-se que os estudantes relatem suas experiências com seus familiares em tarefas que envolvem a realização de compras de alimentos.

3. COM UM COLEGA, RESPONDAM AOS ITENS DE ACORDO COM AS CENAS.

A ) O QUE VOCÊS ENTENDERAM AO ANALISAR AS CENAS?

B ) VOCÊS COSTUMAM POUPAR DINHEIRO? NA OPINIÃO DE VOCÊS, QUAL É A IMPORTÂNCIA DE POUPAR?

Resposta pessoal.

Espera-se que os estudantes respondam que poupar dinheiro é importante para situações inesperadas ou para adquirir um bem ou serviço de maior valor.

159

• A atividade 2 estabelece integração entre as unidades temáticas de Matemática Grandezas e medidas e Números ao associar os valores monetários dos produtos, representados com cédulas e moedas, a um número natural. Além disso, para associar o preço de cada produto, será necessário recorrer ao conceito de adição com a ideia de juntar, adicionando os valores das cédulas e moedas que compõem o preço de cada produto. Evidencie também a correlação entre os produtos mostrados na atividade e seus respectivos preços, para que os estudantes comecem a desenvolver um parâmetro de preços para determinados itens, a fim de que, em momentos futuros, desenvolvam as noções de caro e barato. Aproveite o contexto para orientar os estudantes, quando forem ao mercado com seus familiares, a evitarem a compra de itens desnecessários, bem como produtos industrializados, optando, sempre que possível, por alimentos saudáveis, como frutas.

• A atividade 3 tem por objetivo fazer com que os estudantes reconheçam a importância de poupar para comprar algo. Aproveite o contexto da atividade e pergunte se eles sabem o que é troco. Se necessário, explique a eles o significado desse termo. Ao trabalhar o item B dessa atividade, converse com os estudantes sobre o hábito de poupar e os benefícios dessa atitude.

Caso algum estudante já tenha poupado dinheiro para comprar algo, peça que conte para os colegas sua experiência. Explique aos estudantes o que seria comprar o necessário e como evitar o consumo excessivo. Cite exemplos do que é necessário, como comprar alimentos, medicamentos, roupas e calçados em quantidade suficiente para o consumo. Uma sugestão para esse momento é propor a eles que façam uma lista do que consideram necessário. Depois, peça que comparem com a lista de um colega e reflitam sobre os motivos das diferenças entre elas. Nesse momento, verifique se eles percebem que o que é considerado necessário para um estudante pode ser supérfluo para o outro.

BNCC

03/10/2025 09:36:46

A atividade 3, ao propor a interação cooperativa dos estudantes com seus pares, recorrendo aos conhecimentos matemáticos para compreenderem e atuarem no mundo, respeitando o modo de pensar dos colegas e aprendendo com eles, contempla as Competências específicas de Matemática 2 e 8 da BNCC.

2. 3.

B. A. C.

• A atividade 4 estabelece uma integração entre as unidades temáticas de Matemática Grandeza e medidas, Probabilidade e estatística e Números ao levar os estudantes a representarem os preços dos produtos, mostrados em cédulas e moedas, em um gráfico. Além disso, para determinar o preço de cada produto, será necessário recorrer ao conceito de adição com a ideia de juntar. Explique a eles que o eixo horizontal do gráfico representa os produtos e o eixo vertical, o preço em reais. Use o exemplo da tesoura para orientá-los a realizar a atividade. Aproveite esse contexto para enriquecer a atividade, propondo novas situações, como: “Qual é o produto mais caro?”; “Quantos reais o caderno é mais caro do que a borracha?”; “Dispondo da quantia de 5 reais, quais produtos poderiam ser comprados?”. Ao final, mostre aos estudantes que o gráfico ajuda a visualizar melhor o produto mais barato e o produto mais caro, pela medida da altura das barras. Em se tratando de educação financeira, destaque a importância de pesquisar o preço dos produtos antes de realizar a compra. Essa é uma maneira de economizar dinheiro.

ATIVIDADE EXTRA

Providencie antecipadamente cola branca, folha de papel A4 e modelos de cédulas de 2 reais, de 5 reais, de 10 reais e de moedas de 1 real. Organize a turma em duplas. Em seguida, distribua para cada dupla cola, folhas, cédulas e moedas confeccionadas em quantidade suficiente. Depois, solicite aos integrantes de cada dupla que componham os valores a seguir usando essas cédulas e moedas de duas maneiras diferentes:

a) 6 reais;

b) 9 reais;

c) 13 reais.

4. DAVI FOI À PAPELARIA PESQUISAR O PREÇO DE ALGUNS PRODUTOS. VERIFIQUE O PREÇO DE CADA UM DELES.

Unidades temáticas integradas PASSAKORN

TESOURA COM PONTAS ARREDONDADAS.

BORRACHA.

CADERNO.

COLA. CAIXA DE LÁPIS DE COR.

IMAGENS SEM PROPORÇÃO ENTRE SI.

RÉGUA.

NAS COLUNAS DO GRÁFICO A SEGUIR, CADA QUADRINHO EQUIVALE A 1 REAL. PINTE NAS COLUNAS CORRESPONDENTES A QUANTIDADE DE QUADRINHOS QUE REPRESENTA O PREÇO DE CADA PRODUTO.

PREÇO DOS PRODUTOS PESQUISADOS POR DAVI EM 2027

PREÇO (EM REAIS)

11 REAIS

10 REAIS

9 REAIS

8 REAIS

FONTE DE PESQUISA: PAPELARIA DO BAIRRO.

Resposta: Os estudantes devem pintar 8 quadrinhos da coluna do caderno; 10 quadrinhos da coluna da caixa de lápis de cor; 2 quadrinhos da coluna da borracha; 3 quadrinhos na coluna da régua; e 6 quadrinhos na coluna da cola.

Oriente-os a fazer a colagem das composições na folha. Caso não seja possível confeccionar as cédulas e moedas, a resposta pode ser elaborada com desenhos, que devem ser registrados no caderno.

Sugestões de respostas

a) Três cédulas de 2 reais ou uma moeda de 1 real e uma cédula de 5 reais.

b) Duas cédulas de 2 reais e uma cédula de 5 reais ou três moedas de 1 real e três cédulas de 2 reais.

c) Três moedas de 1 real e uma cédula de 10 reais ou três moedas de 1 real e duas cédulas de 5 reais.

BNCC

A atividade 4 explora a leitura de dados expressos em um gráfico, aspecto indicado na habilidade EF01MA21 da BNCC. Verifique se os estudantes percebem que a organização dos dados facilita a compreensão e a análise de cada informação.

5. COM 8 MOEDAS DE 1 REAL E UMA CÉDULA DE 10 REAIS, OBTEMOS 18 REAIS. CONTORNE AS CÉDULAS E MOEDAS A SEGUIR PARA OBTER UMA QUANTIA DE 18 REAIS.

IMAGENS SEM PROPORÇÃO ENTRE SI.

Resposta pessoal. Sugestão de resposta: Os estudantes devem contornar 2 cédulas de 2 reais, 2 cédulas de 5 reais e 4 moedas de 1 real.

6. ODAIR TEM 45 REAIS PARA LEVAR OS DOIS FILHOS AO CIRCO.

A ) COM O VALOR EM REAIS QUE ODAIR TEM, É POSSÍVEL COMPRAR AS ENTRADAS?

Resposta: Os estudantes devem marcar um X no SIM.

SIM NÃO

B ) EXPLIQUE ORALMENTE SUA RESPOSTA.

Resposta pessoal: Espera-se que os estudantes digam que o valor que Odair tem é maior do que o preço dos ingressos.

161

03/10/2025 09:36:57

• O objetivo da atividade 5 é compor um valor monetário usando cédulas e moedas. Outras possibilidades de respostas são: 2 + 2 + 2 + + 2 + 5 + 5; 1 + 1 + 2 + 2 + 2 + + 5 + 5. Essa atividade possibilita relacionar cédulas e moedas. Por exemplo, uma cédula de 2 reais equivale a duas moedas de 1 real. Como há várias respostas para esta atividade, com a ajuda dos estudantes, escreva algumas na lousa. Incentive-os a obter respostas distintas e oriente-os a copiar no caderno para treinar a escrita.

• Na atividade 6, peça aos estudantes que façam uma estimativa para responder ao item A, conferindo depois se a resposta está correta. Verifique se eles compreenderam que, nessa situação, Odair precisará comprar uma entrada para adultos, de 20 reais, e duas entradas para crianças, de 10 reais cada. Com isso, o resultado será 40 reais. Incentive a participação ativa de toda a turma, acolhendo com atenção e respeito as respostas e contribuições de todos. Deixe que se expressem livremente, pois dessa maneira vão exercitar a comunicação e a argumentação.

• O objetivo da atividade 7 é abordar a ideia de troco associada de modo intuitivo ao conceito de subtração por meio da ideia de retirar. Aproveite a oportunidade para promover a inclusão dos estudantes de modo que troquem suas percepções sobre cada item. Sugira a eles que resolvam os itens A e B em dupla, em que um deles extrai os dados do problema e o outro faz a representação usando os dedos. Essa estratégia serve para construir e consolidar a compreensão do repertório numérico e das operações, ao usar partes do corpo como recurso de suporte na ação de “tirar um a um” até obter o resultado. Além disso, é uma oportunidade para auxiliar a compreensão de contagem dos estudantes com defasagens na aprendizagem relacionadas a quantidades.

• Na atividade 7, reafirme com os estudantes a importância de consumir alimentos saudáveis pensando na saúde física. Evidencie também o preço dos produtos. Os estudantes que costumam ir ao mercado com os familiares podem comentar se esses preços são caros, baratos ou justos. Pergunte se eles sabem o preço de uma garrafinha de água e peça que comparem com o preço mostrado na atividade.

7. FÁBIO FOI A UMA PADARIA E USOU UMA CÉDULA DE 5 REAIS E DUAS CÉDULAS DE 2 REAIS PARA COMPRAR UM SANDUÍCHE NATURAL QUE CUSTA 8 REAIS. USANDO OS DEDOS DA MÃO, ELE CALCULOU SEU TROCO.

MOSTRO 9 DEDOS. DEPOIS, ESCONDO 8 DEDOS E VERIFICO QUE SOBROU APENAS 1 DEDO. ASSIM, VOU RECEBER 1 REAL DE TROCO.

IMAGENS SEM PROPORÇÃO ENTRE SI.

CONTANDO NOS DEDOS COMO FÁBIO, DETERMINE O TROCO NA COMPRA DE CADA ALIMENTO.

PÃO DE QUEIJO.

TROCO: REAIS.

GARRAFA DE ÁGUA.

TROCO: REAL.

Resposta: A: TROCO: 2 REAIS; B: TROCO: 1 REAL.

8. BIA VAI AO CINEMA NO DIA DO SEU ANIVERSÁRIO.

A ) APÓS PAGAR O INGRESSO COM UMA CÉDULA DE

INGRESSOSINGRESSOS

INGRESSO MEIA-ENTRADA 16 REAIS

20 REAIS, BIA RECEBEU TROCO? MARQUE UM X NA OPÇÃO CORRETA.

SIM. NÃO.

Resposta: Os estudantes devem marcar um X no quadrinho SIM.

COMPLETE: BIA RECEBEU DE TROCO.

Resposta: BIA RECEBEU 4 REAIS DE TROCO.

B ) VOCÊ JÁ FOI AO CINEMA? SE SIM, RELATE SUA EXPERIÊNCIA COM OS COLEGAS.

Resposta pessoal. Espera-se que os estudantes que já foram ao cinema compartilhem sua experiência com a turma, relatando a que filme assistiram e algumas características do ambiente, como iluminação, som e tamanho da tela, por exemplo.

• No item A, da atividade 8 , verifique se os estudantes conhecem a palavra ingresso. Em seguida, questione-os sobre outras possibilidades de realizar o pagamento. Espera-se que eles percebam que era possível, por exemplo, usar uma cédula de 10 reais, uma de 5 e uma de 2 reais. Aproveite o contexto dessa atividade para conversar com os estudantes sobre a importância de poupar dinheiro, seja para adquirir um item que se deseja, como um brinquedo, seja para realizar passeios e viagens, seja, simplesmente, para ter uma reserva de emergência.

• O item B propicia um momento oportuno para conversar com os estudantes sobre suas experiências com atividades culturais, como cinema, teatro e museus. Peça que relatem suas experiências com esses lugares e, ao final, acrescente que os parques públicos, disponíveis em muitas cidades, são espaços que oferecem diversas oportunidades de lazer. Se julgar oportuno e a escola dispuser de condições e permissões dos responsáveis, combine um passeio cultural escolhido com a ajuda dos estudantes.

FÁBIO

A. B.

REAIS 4 REAIS

Unidades temáticas integradas

IMAGENS SEM PROPORÇÃO ENTRE SI.

ELE CALCULOU QUANTOS REAIS VAI RECEBER DE TROCO USANDO OS DEDOS DAS MÃOS.

CONTEI A QUANTIA QUE EU TINHA E MOSTREI 7 DEDOS. DEPOIS, ESCONDI 6 DEDOS E VERIFIQUEI QUE SOBROU APENAS 1 DEDO. ASSIM, COMPREENDI QUE VOU RECEBER 1 REAL DE TROCO.

FAÇA COMO NÍCOLAS E DETERMINE O TROCO NA COMPRA DE UMA UNIDADE DE CADA ITEM A SEGUIR.

• A atividade 9 promove uma integração entre as unidades temáticas de Matemática Grandezas e medidas e Números, ao relacionar situações de compra com troco para efetuar um pagamento, envolvendo intuitivamente as operações de adição e subtração. Verifique se os estudantes percebem que apenas uma das cédulas seria suficiente para efetuar o pagamento. A contagem de acréscimo ou de retirada com suporte dos dedos é uma estratégia útil para construir significativamente o repertório numérico e as operações.

• Na situação apresentada na atividade 9, verifique se eles notaram que o personagem comprou duas borrachas de 3 reais cada uma. Nesse caso, ele gastou 6 reais nessa compra e o troco corresponde ao que falta para 7 reais, ou seja, a quantia que ele tinha menos o que gastou. Verifique se eles aplicam a mesma estratégia para resolver os itens propostos. Para resolver essa atividade na prática, oriente os estudantes a usarem as cédulas e moedas recortadas do Material Complementar. Complemente a atividade apresentando outras situações em que o troco seja igual ao valor de uma das cédulas, com quantias menores do que 20. 9. NÍCOLAS USOU

TROCO: REAIS. TROCO: REAIS.

Resposta: TROCO: 3 REAIS. Resposta: TROCO: 2 REAIS.

03/10/2025 09:37:02

3 REAIS

BORRACHA.

7 REAIS

3 REAIS

ESTOJO. CANETA.

• A atividade 10 retrata uma situação possivelmente já vivenciada por algum estudante, ainda que em um contexto diferente, como em uma feira ou em uma padaria. Antes de iniciá-la, pergunte a eles se costumam acompanhar alguém da família ao supermercado ou à feira livre e, em caso afirmativo, peça que compartilhem em quais locais eles já foram.

• No item A , verifique se fazem a leitura e a adição correta para identificarem a quantia disponível para compra. No item B, enfatize que se deseja saber qual produto não pode ser comprado, pois o valor dele é superior à quantia disponível. No item C, pergunte a eles se seria possível comprar duas garrafas de iogurte. Sobraria troco? Essa atividade integra as unidades temáticas de Matemática Grandezas e medidas e Números, ao relacionar valores em reais com situações de compra envolvendo a noção intuitiva de adição e subtração. Para superar as dificuldades de alguns estudantes, recorra a material de contagem e simule as situações com exemplos práticos.

• Ao final da atividade, fale com os estudantes sobre a importância de elaborar uma lista antes de ir ao supermercado ou à feira, pois isso economiza tempo e evita a compra de itens supérfluos.

REFERÊNCIAS COMPLEMENTARES

BELINTANE, Maria. Educação para o consumo consciente Ilustrações de Valéria Cantelli. Americana: Adonis, 2019.

Esse livro aborda ações voltadas à qualidade de vida de crianças, jovens e adultos, bem como ao exercício do consumo consciente.

10. LIA E SUA MÃE FORAM AO MERCADO COM A QUANTIA A SEGUIR.

Unidades temáticas integradas

IMAGENS SEM PROPORÇÃO ENTRE SI.

A ) QUANTOS REAIS LIA E SUA MÃE TÊM? REAIS.

Resposta: 38 REAIS.

B ) CONTORNE OS PRODUTOS QUE ELAS NÃO CONSEGUEM COMPRAR COM ESSA QUANTIA.

Resposta: Os estudantes devem contornar o sabão em pó e o leite em pó.

C ) COM O DINHEIRO QUE ELAS TÊM, É POSSÍVEL COMPRAR DOIS PACOTES DE CAFÉ?

Resposta: NÃO.

D ) COM A QUANTIA QUE ELAS TÊM, É POSSÍVEL COMPRAR UM PACOTE DE ARROZ?

Resposta: SIM.

11. JOANA GUARDOU A QUANTIA A SEGUIR EM SEU COFRINHO.

11. B) Resposta pessoal. Espera-se que os estudantes relatem as suas experiências com relação ao hábito de guardar dinheiro para o futuro, a fim de comprar algo de maior valor.

IMAGENS SEM PROPORÇÃO ENTRE SI.

A ) QUANTOS REAIS JOANA ECONOMIZOU? REAIS.

Resposta: 21 REAIS.

B ) VOCÊ JÁ GUARDOU DINHEIRO PARA COMPRAR ALGO QUE GOSTARIA DE TER? CONVERSE COM SEUS COLEGAS SOBRE ESSA EXPERIÊNCIA.

C ) NO QUADRO A SEGUIR, DESENHE ALGO QUE VOCÊ PODERIA COMPRAR COM A MESMA QUANTIA QUE JOANA ECONOMIZOU.

Resposta pessoal. Comentários nas orientações ao professor

DESAFIO A MAIS

MIRIAM E ANDRÉ TÊM

JUNTOS A QUANTIA INDICADA PELAS CÉDULAS E A MOEDA. MIRIAM TEM 2 REAIS A MAIS QUE ANDRÉ.

QUANTOS REAIS ANDRÉ TEM? REAIS.

Resposta: 4 REAIS.

AVALIANDO

Objetivo

Ao final desta unidade, espera-se que os estudantes compreendam o Real como unidade monetária brasileira, além de conhecer suas cédulas e moedas e a relação entre elas. Também é esperado que percebam a importância de poupar dinheiro e outros recursos, com vistas ao consumo consciente e sustentável.

Sugestão de intervenção

Caso os estudantes não atinjam os objetivos propostos, use as cédulas e moedas recortadas

03/10/2025 09:37:05

anteriormente da seção Material complementar do final do Livro do Estudante e peça que componham, de duas maneiras diferentes, os seguintes valores monetários: 7 reais; 12 reais. Em seguida, solicite a dois estudantes que compartilhem suas respostas com a turma. Aproveite esse momento para esclarecer as dúvidas que surgirem. Com relação ao hábito de poupar, se necessário, retome a atividade 3 da página 159 e evidencie a atitude da criança. Acrescente que é importante poupar não apenas para comprar um bem ou serviço, mas também para estar preparado para situações inesperadas.

• O objetivo da atividade 11 é enfatizar a importância de poupar para realizar sonhos e metas. Diga aos estudantes que poupar também é planejar e controlar os gastos para realizar algo no futuro.

• No item A , verifique se os estudantes notam que, além de moedas, é possível guardar cédulas de dinheiro em um cofrinho. Porém, é importante considerar que, se o cofrinho não for ventilado, a umidade pode danificar as cédulas. Nesse caso, é recomendado que as cédulas sejam guardadas em um cofrinho com boa ventilação ou em um local seco e livre de umidade. No item B, pode ocorrer de algum estudante não relatar nada a respeito do hábito de guardar dinheiro. Para evitar constrangimentos, considere que há diferentes realidades e contextos e, dentro do possível, apresente aos estudantes os benefícios de poupar dinheiro. Aproveite o item C para reforçar essa ideia de poupar, pois o estudante vai desenhar algo que poderia comprar com a mesma quantia que Joana economizou.

• No Desafio a mais , os estudantes devem usar as cédulas e moedas para trabalhar o raciocínio lógico-matemático e a compreensão de proporção. Para resolver o desafio, eles devem, primeiramente, adicionar os valores das cédulas e moedas para obter o total (5 + 2 + 2 + 1 = 10). Depois, eles podem retirar a diferença de 2 reais que Miriam tem a mais, ficando com 8 reais e, por meio de tentativa e erro, descobrir quais duas quantias iguais resulta em 8. Caso encontrem alguma lógica diferente da esperada, incentive-os a compartilhar com os demais colegas, fazendo intervenções pontuais e estratégicas.

OBJETIVOS

• Compreender que o hábito de poupar pode beneficiar as pessoas quando querem comprar algo e não têm a quantia suficiente.

• Refletir sobre a importância do dinheiro e de não gastar sem necessidade.

• Resolver situação-problema envolvendo comparação e equivalência de valores monetários.

• Incentivar a fluência em leitura oral e a produção de escrita.

1. CONHECENDO O PROBLEMA

• Leia o texto com os estudantes. Oriente-os a identificar nas cenas os diferentes hábitos de Clara e Jasmim ao receberem o dinheiro de seus pais e de seus avós. Verifique se eles percebem que Clara escolheu usar seu dinheiro e, depois, percebeu que também gostaria de ter comprado um chinelo. Já Jasmim decidiu guardar o dinheiro até juntar a quantia necessária para comprar um tênis. Ambas fizeram escolhas válidas, de acordo com seus desejos e suas prioridades no momento.

• Incentive uma conversa sobre o destino do dinheiro que recebemos, como presente ou para uma necessidade específica, considerando as diferentes realidades familiares dos estudantes. Auxilie-os a pensar sobre planejamento, prioridades e desejos, entendendo que nem sempre conseguimos tudo o que gostaríamos de uma só vez.

• Esta seção desenvolve fluência em leitura oral, ao solicitar que os estudantes leiam uma quadrinha, assim como a produção de escrita, ao solicitar que eles completem a quadrinha escrevendo uma palavra que represente algo que gostariam de adquirir.

COLETIVAMENTE

APRENDENDO A POUPAR

CONHECENDO O PROBLEMA 1

Professor, professora: O assunto tratado nesta seção possibilita o trabalho com o tema contemporâneo transversal Educação para o consumo

CLARA E JASMIM SÃO IRMÃS GÊMEAS. NO DIA DO ANIVERSÁRIO

DELAS, SEUS PAIS DERAM 50 REAIS A CADA UMA DE PRESENTE. SEUS AVÓS TAMBÉM DERAM 30 REAIS A CADA UMA, PARA QUE

ELAS PUDESSEM COMPRAR O QUE DESEJASSEM. OBSERVE NAS

CENAS O QUE ELAS FIZERAM COM O DINHEIRO QUE RECEBERAM NESSE MÊS.

EBA! VOU COM MEUS PAIS NA LOJA DE BRINQUEDOS

GASTAR O MEU DINHEIRO!

VOU GUARDAR

MEU DINHEIRO POR ENQUANTO PARA, DEPOIS, CONSEGUIR COMPRAR UM TÊNIS NOVO.

CLARA

EU GOSTARIA DE UM CHINELO NOVO, MAS JÁ

GASTEI TODO MEU DINHEIRO.

BNCC

As atividades propostas nesta seção favorecem o desenvolvimento da Competência geral 7 da BNCC, bem como o tema contemporâneo transversal Educação para o consumo, pois permitem a reflexão sobre a importância de poupar dinheiro e de não gastar sem necessidade.

2. ORGANIZANDO AS IDEIAS

A) O objetivo desta questão é que os estudantes reflitam sobre a maneira como a menina gastou seu dinheiro e analisem a consequência das escolhas de cada uma delas.

JASMIM

COMO É BOM POUPAR, POIS JÁ TENHO O DINHEIRO PARA COMPRAR UM TÊNIS!

B) Nesta questão, espera-se que os estudantes percebam que o hábito de poupar dinheiro pode ser benéfico, quando se quer comprar algo e não se tem a quantia suficiente ou quando se pretende adquirir algo de melhor qualidade e durabilidade.

C) Espera-se que os estudantes compreendam que, se Clara escolhesse comprar o chinelo de 60 reais, sobrariam 20 reais para ela poupar. Se necessário, sistematize a situação na lousa para que eles compreendam esse raciocínio.

ORGANIZANDO AS IDEIAS

2. B) Resposta pessoal. Espera-se que os estudantes reconheçam que o fato de Clara e Jasmim terem escolhas diferentes não configura um erro, mas sim uma experiência natural de lidar com prioridades e limites.

Professor, professora: Informações complementares nas orientações ao professor

A ) CONVERSE COM SEUS COLEGAS SOBRE AS ATITUDES DE CLARA E JASMIM AO RECEBEREM O DINHEIRO DE PRESENTE DOS PAIS E DOS AVÓS.

B ) O QUE VOCÊ ACHOU DAS ESCOLHAS DE CLARA E JASMIM? VOCÊ JÁ PASSOU POR UMA SITUAÇÃO DESSA?

C ) O CHINELO QUE CLARA QUER CUSTA 60 REAIS. O DINHEIRO QUE RECEBEU DOS PAIS E DOS AVÓS É SUFICIENTE PARA ESSA COMPRA OU ELA PRECISARIA POUPAR E COMPRAR DEPOIS? SE FOR SUFICIENTE, SOBRARIA TROCO?

Resposta: Sim, será suficiente. Espera-se que os estudantes efetuem os cálculos e verifiquem que, se ela optasse em comprar o chinelo, sobraria 20 reais de troco.

BUSCANDO SOLUÇÕES 3

Professor, professora: Informações complementares nas orientações ao professor

A ) OUÇA A QUADRINHA QUE O PROFESSOR VAI LER.

RECEBI UM DINHEIRINHO E GUARDEI,

JUNTEI COM OUTRO QUE GANHEI... A BOLA QUE TANTO QUERIA

FINALMENTE POSSO COMPRAR.

VIU COMO VALE A PENA POUPAR?

PRODUZIDO ESPECIALMENTE PARA ESTA OBRA. NESSA QUADRINHA, QUAL É O BRINQUEDO QUE O AUTOR FALA QUE POUPOU DINHEIRO PARA COMPRAR?

Resposta: UMA BOLA.

2. A) Resposta pessoal. Espera-se que os estudantes percebam, com base nas atitudes de Clara e Jasmim, a importância de guardar dinheiro pensando em situações inesperadas ou para adquirir algo que se deseja.

B ) O TÊNIS DE JASMIM CUSTOU 98 REAIS. QUANTOS REAIS ELA PRECISOU POUPAR PARA COMPRÁ-LO?

Resposta: 18 REAIS.

C ) FAÇA UM DESENHO EM SEU CADERNO PARA ILUSTRAR CLARA COM SEU CHINELO E JASMIM COM SEU TÊNIS. DEPOIS, MOSTRE AOS COLEGAS.

DICA: COLOQUE EM PRÁTICA NO SEU DIA A DIA O QUE APRENDEU SOBRE A IMPORTÂNCIA DE POUPAR.

Resposta pessoal. Espera-se que os estudantes ilustrem no caderno o desenho informado no item C

CONCLUSÃO

Acompanhar o desenvolvimento dos estudantes é fundamental para um ensino bem-sucedido. Ao longo da unidade, foram propostas diversas maneiras de avaliar a aprendizagem da turma. A fim de realizar um monitoramento mais abrangente e organizado, registre nos relatórios individuais ou nas fichas de avaliação o desempenho de cada estudante, levando em consideração suas particularidades. Um modelo desse tipo de ficha pode ser

encontrado no tópico Avaliação deste Manual do Professor. Assim, será possível visualizar de modo individual as trajetórias de aprendizagem, incluindo os avanços e os pontos de dificuldades a serem sanados por meio de atividades que promovam recuperação dos conteúdos. Esse método de verificar a progressão dos estudos e identificar o que a turma de fato conseguiu aprender e o que ficou com lacunas de absorção é muito importante para repensar estratégias em sala

Leia a quadrinha com os estudantes, pausadamente, interpretando as informações com a participação deles. Repita a leitura várias vezes até que a memorizem e, em seguida, incentive-os a ler para os colegas. Essa prática possibilita desenvolver a fluência em leitura oral.

• Enfatize que nesse pagamento não houve troco. Sendo assim, eles não podem usar a cédula de 10 reais. É possível que os estudantes usem 4 cédulas de 2 reais ou 4 moedas de um real e duas cédulas de dois reais. Nesse caso, questione-os se essa é a menor quantidade de cédulas e de moedas e incentive-os a perceber que devem, inicialmente, usar as cédulas de maior valor sem ultrapassar o preço do produto e, em seguida, complementar com a moeda.

Sugestão

de Desafio

José comprou um brinquedo que custa 8 reais e pagou o valor exato, usando a menor quantidade de cédulas e moedas possível. Quantas cédulas e moedas ele usou?

Resposta

Ele usou uma cédula de 5 reais, uma cédula de 2 reais e uma moeda de 1 real.

03/10/2025 09:37:06

de aula, tornando as ações pedagógicas cada vez mais eficazes.

A conclusão da unidade é o momento de avaliar se os objetivos por ela propostos foram alcançados. Para esse diagnóstico, observe no final deste Manual do Professor algumas possibilidades de avaliação formativa que permitem realizar o monitoramento da aprendizagem dos estudantes e intervir caso eles não tenham atingido os resultados esperados.

OBJETIVOS DA UNIDADE

• Efetuar adições com total até 99.

• Reconhecer o símbolo usado para representar a adição.

• Utilizar o algoritmo da adição sem reagrupamento.

• Resolver situações-problema que envolvam as ideias de juntar ou acrescentar da adição.

• Desenvolver a capacidade de realizar cálculo mental e estimativas.

• Identificar os elementos faltantes em sequências recursivas de números naturais por meio da adição.

• Comparar quantidades por meio de observação e contagem.

• Compreender a ideia de dobro e de metade.

• Explorar o uso da calculadora como recurso de apoio para realizar cálculos simples, favorecendo a construção do pensamento matemático.

• Ler e interpretar dados expressos em tabelas.

• Utilizar a régua como ferramenta para resolver adições.

INTRODUÇÃO E JUSTIFICATIVA

Nesta unidade, é apresentada a adição associada às ideias de juntar e acrescentar. Espera-se que os estudantes construam significativamente as primeiras noções dessa operação. São utilizadas diversas estratégias, como contagem, uso do ábaco, material dourado, calculadora, régua e algoritmos, a fim de que os estudantes resolvam atividades e situações-problema contextualizadas e ligadas ao cotidiano, envolvendo o cálculo de adições, com números de até dois algarismos sem reagrupamento.

As atividades propostas favorecem o desenvolvimento do cálculo mental,

UNIDADE7 ADIÇÃO

a agilidade de pensamento e a autonomia, propondo um trabalho prolongado que parte do repertório numérico e da diversidade de estratégias dos estudantes. É incentivada a busca por soluções eficientes na resolução de situações do dia a dia, apresentando noções importantes, como o dobro e a metade, relacionando-as com a adição. Também é proposto que eles elaborem problemas envolvendo adição, reconheçam que duas adições diferentes podem ter o mesmo resultado e usem a adição no reconhecimento de padrões em sequências numéricas. Essa abordagem diversificada fortalece a compreensão da adição, além de contribuir para o prazer

em aprender Matemática, respeitando as diferentes particularidades de aprendizagem da turma.

03/10/2025 09:40:03

Habilidades da BNCC trabalhadas na unidade: EF01MA03 , EF01MA06 , EF01MA07 , EF01MA08, EF01MA10 e EF01MA21.

MAÇÃS, PERAS E BANANAS.

O CONSUMO DE FRUTAS FAZ BEM À SAÚDE. ALÉM DE SEREM SABOROSAS, ELAS PODEM AJUDAR A COMBATER A OBESIDADE E ALGUMAS OUTRAS DOENÇAS QUANDO INGERIDAS REGULARMENTE.

1. Resposta pessoal. Espera-se que os estudantes relatem as suas experiências em relação ao consumo regular de frutas, além de incentivar a escrita do nome de cada uma delas.

VOCÊ TEM O COSTUME DE CONSUMIR FRUTAS REGULARMENTE?

SE SIM, ESCREVA EM SEU CADERNO O NOME DE UMA DELAS.

QUANTAS FRUTAS APARECEM NA FOTOGRAFIA?

MAÇÃS. PERAS. BANANAS.

Resposta: 2 MAÇÃS; 3 PERAS; 2 BANANAS.

MARQUE UM X NO NÚMERO QUE REPRESENTA O TOTAL DE FRUTAS QUE APARECE NA FOTOGRAFIA.

Resposta: Os estudantes devem marcar um X no número 7

SUGESTÃO DE ESTRATÉGIA INICIAL

Leve para a sala de aula palitos de sorvete coloridos ou utilize os lápis de cor dos estudantes. Forme grupos de até cinco palitos ou lápis de mesma cor. Depois, realize questionamentos, como: “Quantos palitos vermelhos foram agrupados?”; “Quantos palitos azuis?”; “Juntando os palitos vermelhos com os azuis, quantos serão ao todo?”. Incentive-os a fazer o cálculo mentalmente e, somente depois, a contar os palitos agrupados para conferir a resposta.

03/10/2025 09:40:05

• Leia o texto e as questões das páginas de abertura para os estudantes, verificando se eles compreendem o conteúdo.

• Ao responder à questão 1, verifique se eles identificam quais frutas consomem no dia a dia. Se julgar conveniente, peça a eles que escrevam os nomes das frutas que seus colegas indicaram.

• Para a questão 2, é esperado que os estudantes sejam capazes de identificar as cores de cada fruta e realizar as respectivas contagens.

• Na questão 3, é possível verificar a capacidade dos estudantes de explicar o raciocínio que utilizaram e compartilhar as estratégias usadas para obter o total de frutas que aparecem na fotografia. Incentive-os a apresentar suas ideias, a fim de compartilhar com os colegas o que já sabem. Ao verbalizar o que estão pensando, os estudantes têm a oportunidade de compreender melhor o objetivo da atividade e de progredir na sistematização do conteúdo. Por isso, eles devem ser ouvidos com atenção e respeito.

• Nos relatos sobre a resposta à questão 3, os estudantes podem informar diferentes estratégias. Valo rize cada uma delas e aproveite para avaliar a compreensão deles e a capacidade de usarem o conhecimento prévio em suas ideias de resolução.

• Antes de iniciar o trabalho com este tópico, verifique a possibilidade de levar para a sala de aula alguns objetos de contagem, como palitos de sorvete, tampinhas de garrafa e clipes, a fim de usá-los durante o desenvolvimento das atividades propostas, auxiliando os estudantes nas estratégias de cálculos.

• Durante o trabalho com a atividade 1, pergunte aos estudantes qual estratégia foi usada por eles para responder ao item C. Se julgar conveniente, sugira que representem no caderno, utilizando tracinhos, a quantidade de jogadores que aparecem de pé e, depois, a quantidade de jogadores que aparecem agachados na fotografia. Peça a eles que contem todos os tracinhos feitos para obterem a quantidade total de jogadores. Diga que a ideia proposta nesta questão é a de juntar uma quantidade à outra.

IDEIAS DA ADIÇÃO

1. OS JOGADORES DO TIME DE FUTSAL DA ESCOLA DOM PEDRO

POSARAM PARA UMA FOTOGRAFIA ANTES DO JOGO.

A ) QUANTOS JOGADORES ESTÃO DE PÉ?

Resposta: 5

B ) QUANTOS JOGADORES ESTÃO AGACHADOS?

Resposta: 3

C ) AO TODO, QUANTOS JOGADORES HÁ NA IMAGEM?

JOGADORES MAIS JOGADORES É IGUAL A JOGADORES.

Resposta: 5 JOGADORES MAIS 3 JOGADORES É IGUAL A 8 JOGADORES. 5 MAIS 3 É IGUAL A 8 AO TODO HÁ 8 JOGADORES.

MAIS É IGUAL A . AO TODO HÁ JOGADORES.

D ) UTILIZANDO SÍMBOLOS, ESCREVEMOS:

DICA: SÍMBOLO DE MAIS: + SÍMBOLO DE IGUAL: =

QUANTIDADE DE JOGADORES DE PÉ + QUANTIDADE DE JOGADORES AGACHADOS = QUANTIDADE TOTAL DE JOGADORES

Resposta: 5 + 3 = 8

A ADIÇÃO É UMA OPERAÇÃO MATEMÁTICA USADA PARA JUNTAR OU ACRESCENTAR QUANTIDADES.

ARTICULANDO CONHECIMENTOS

É possível realizar atividade 1 propondo uma integração com o componente curricular de Educação Física. Solicite a eles que busquem informações sobre a quantidade de jogadores de algum esporte, como basquetebol, futebol, futsal ou handebol. Também é possível fazer uma pesquisa com a turma, a fim de verificar se praticam algum esporte, e registrar a quantidade de estudantes que preferem cada um para, depois, adicioná-las, a fim de obter a quantidade total de cada preferência.

BNCC

03/10/2025 09:40:05

A atividade 1 tem como objetivo levar os estudantes a construírem fatos básicos da adição, além de usá-los em procedimentos de cálculos na resolução de problemas, desenvolvendo, assim, a habilidade EF01MA06 da BNCC.

2. CLÁUDIA ESTÁ BRINCANDO DE PESCARIA.

A ) QUANTOS PEIXES VERDES ELA PESCOU?

B ) QUANTOS PEIXES

VERMELHOS ELA PESCOU?

PEIXES.

C ) QUANTOS PEIXES CLÁUDIA

PESCOU AO TODO?

PEIXES.

D ) COMPLETE A FRASE E O CÁLCULO CONFORME OS ELEMENTOS QUE APARECEM NA CENA.

MAIS 3 PEIXES VERMELHOS É IGUAL A 7 PEIXES. 4 MAIS 3 É IGUAL A 7 4 + 3 = 7

MAIS É IGUAL A . Resposta: 4 PEIXES. Resposta: 3 PEIXES. Resposta: 7 PEIXES.

Professor, professora: Oriente os estudantes na escrita da frase que

PEIXES. + =

Resposta: 4 PEIXES VERDES responde ao item E, incentivando o traçado em letra cursiva na pauta apresentada.

PEIXES VERDES MAIS PEIXES VERMELHOS É IGUAL A PEIXES.

E ) DE ACORDO COM A IMAGEM ANTERIOR, ELABORE UMA QUESTÃO ENVOLVENDO ADIÇÃO E ESCREVA NAS LINHAS A SEGUIR. DEPOIS, PEÇA A UM COLEGA QUE A RESPONDA.

2. E) Resposta pessoal. A resposta depende da criatividade dos estudantes e das informações que eles retirarem da cena para elaborar a questão.

• Ao trabalhar com a atividade 2, verifique se os estudantes conhecem a brincadeira de pescaria apresentada na cena e explique-a aos que não conhecem. Caso necessário, diga-lhes que os peixes pescados por Cláudia são os que estão em cima do balcão.

• No item E, oriente-os a elaborar uma questão que envolva adição. Para um melhor aproveitamento desta atividade, peça a eles que, de modo espontâneo e organizado, apresentem a questão elaborada para os colegas. Ao propor aos estudantes que produzam uma questão envolvendo uma adição, eles são motivados a desenvolver habilidades e atitudes relacionadas à leitura e à escrita, favorecendo o desenvolvimento da produção de escrita.

• Priorize o uso do material concreto ao trabalhar com a atividade 2, a fim de favorecer a inclusão dos estudantes com dificuldades de aprendizagem ou necessidades especiais específicas, como o TEA e o TDAH. As contribuições do material concreto servem para a aprendizagem de todos os estudantes. Outra estratégia é separar igualmente a quantidade representada no Livro do Estudante. Se possível, providencie objetos com o mesmo formato entre si para não fugir da proposta da atividade.

03/10/2025 09:40:05

• Durante o trabalho com a atividade 3, oriente os estudantes, no item A, a realizarem a contagem das cores usadas por Ivo para pintar o carro.

• No item B, da mesma maneira, oriente-os a realizar a contagem das cores usadas por Ivo para pintar a casa. Já no item C, deixe que usem suas estratégias pessoais para determinar quantas cores ao todo Ivo usou no desenho, e verifique se estão avançando em relação à ideia de juntar quantidades, que é o objetivo das atividades que trabalham adição nessa página.

3. A IMAGEM A SEGUIR APRESENTA O DESENHO DE IVO EM TRÊS MOMENTOS DIFERENTES.

CORES DO CARRO MAIS CORES DA CASA É IGUAL A CORES. IVO USOU CORES DIFERENTES. + = 1º . 2º .

3º . A ) QUANTAS CORES IVO USOU PARA PINTAR O CARRO? CORES.

Resposta: 2 CORES. Resposta: 3 CORES.

B ) QUANTAS CORES IVO USOU PARA PINTAR A CASA? CORES.

C ) AO TODO, QUANTAS CORES DIFERENTES ELE USOU PARA COLORIR O DESENHO?

Resposta: 2 CORES DO CARRO MAIS 3 CORES DA CASA É IGUAL A 5 CORES.

Resposta: 2 + 3 = 5

Resposta: IVO USOU 5 CORES DIFERENTES.

03/10/2025 09:40:06

4. COMPLETE O QUE FALTA PARA REPRESENTAR A QUANTIDADE DE PEIXES DE CADA ITEM.

• Na atividade 4, os estudantes devem completar com o que falta para representar a quantidade de peixes em cada item. Oriente-os a completar e efetuar as adições contando as figuras em cada item. Relacione as quantidades que eles contaram com os algarismos que completaram nas expressões de adições.

Resposta: 8 + 4 = 12 + 6 =

C. 8 + =

• Na atividade 5, após identificar o item em que há a maior quantidade de peixes, auxilie-os na escrita da resposta.

Resposta: 10 + 5 = 15

Resposta: 11 + 6 = 17 + =

5. NA ATIVIDADE ANTERIOR, EM QUE ITEM HÁ, AO TODO, A MAIOR QUANTIDADE DE PEIXES?

Resposta: ITEM B

BNCC

A atividade 5 propõe que os estudantes comparem a quantidade de peixes, sem ultrapassar 19, a fim de identificar em qual item há maior quantidade de peixes, desenvolvendo, assim, a habilidade EF01MA03 da BNCC.

03/10/2025 09:40:06

• Acompanhe os estudantes durante a resolução da atividade 6 e auxilie-os em caso de possíveis dúvidas. Ao completar a quantidade de lápis por meio do desenho, os estudantes elaboram como adicionar mais objetos para chegar à quantidade desejada, desenvolvendo, desse modo, seu raciocínio lógico e reforçando a habilidade de contar e relacionar o número com a quantidade.

• Na atividade 7, é abordada uma situação em que os estudantes devem interpretar as informações apresentadas para calcular quantos pontos Fernanda tem ao todo, depois de ganhar mais 6 pontos. Leia o enunciado com eles, auxilie-os em possíveis dúvidas e, se necessário, faça questionamentos, como: “O que devemos fazer para resolver esse problema?”; “Devemos resolver por adição, para saber quantos pontos Fernanda tem agora?”.

• Durante o trabalho com a atividade 8, oriente os estudantes a identificarem as adições e efetuá-las. Nesse momento, eles podem apresentar dificuldades em desenhar a quantidade correta de estrelas. Caso isso ocorra, oriente-os a contar as estrelas que desenharam para verificar se o resultado que obtiveram está certo.

6. NA IMAGEM A SEGUIR, ESTÃO REPRESENTADOS OS LÁPIS DE COR QUE EDGAR TEM.

A ) QUANTOS LÁPIS DE COR EDGAR TEM? LÁPIS.

Resposta: 12 LÁPIS.

B ) DESENHE E PINTE MAIS 4 LÁPIS NO QUADRO. AGORA, HÁ

QUANTOS LÁPIS NO TOTAL? LÁPIS.

Resposta: 16 LÁPIS. 12 + 4 = 16

7. PEDRO E FERNANDA ESTÃO BRINCANDO COM UM JOGO.

FERNANDA TINHA 12 PONTOS E GANHOU MAIS 7. QUANTOS PONTOS FERNANDA TEM AGORA?

Resposta: 12 + 7 = 19. FERNANDA TEM AGORA 19 PONTOS.

FERNANDA TEM AGORA PONTOS.

8. DESENHE ESTRELAS DE ACORDO COM AS INDICAÇÕES. DEPOIS, COMPLETE OS NÚMEROS QUE FALTAM NO ESQUEMA.

A. B. C. 5 +3 +3

Os estudantes devem desenhar 8 estrelas no quadro B e 11 estrelas no quadro C 5 + 3 = 8; 8 + 3 = 11

9. GUSTAVO OBTEVE O RESULTADO DE 9 + 3 DESENHANDO BOLINHAS.

10 + 2 = 12

ASSIM COMO GUSTAVO, DESENHE BOLINHAS E DETERMINE O RESULTADO DOS SEGUINTES CÁLCULOS.

8 + 3 = A.

Resposta: 8 + 3 = 10 + 1 = 11. Os estudantes devem desenhar 8 bolinhas e depois mais 3. Em seguida, devem contornar as 10 primeiras bolinhas, sobrando 1 bolinha sem contornar, obtendo 10 + 1 = 11

9 + 5 = B.

Resposta: 9 + 5 = 10 + 4 = 14. Os estudantes devem desenhar 9 bolinhas e depois mais 5. Em seguida, devem contornar as 10 primeiras bolinhas, sobrando 4 bolinhas sem contornar, obtendo 10 + 4 = 14

7 + 6 = C.

Resposta: 7 + 6 = 10 + 3 = 13. Os estudantes devem desenhar 7 bolinhas e depois mais 6. Em seguida, devem contornar as 10 primeiras bolinhas, sobrando 3 bolinhas sem contornar, obtendo 10 + 3 = 13

D. 9 + 9 =

Resposta: 9 + 9 = 10 + 8 = 18. Os estudantes devem desenhar 9 bolinhas e depois mais 9. Em seguida, devem contornar as 10 primeiras bolinhas, sobrando 8 bolinhas sem contornar, obtendo 10 + 8 = 18

• Na atividade 9, explique aos estudantes que, nesse exemplo, foram agrupadas 10 bolinhas como estratégia de cálculo. Se eles apresentarem dificuldades, providencie o material dourado e demonstre as parcelas de cada adição com os cubinhos, trocando dez cubinhos por uma barra e perguntando a eles quantos cubinhos e barras são necessários para representar essa soma. Explique, em seguida, que essa quantidade é referente ao resultado da operação. Ao final, verifique como assimilaram essa estratégia.

• Caso haja na sala de aula estudantes com síndrome de Down ou com deficiências físicas, pode ser proposto que a atividade 9 seja realizada em pares ou em grupos, para incentivar a interação social e favorecer a cooperação entre os colegas.

03/10/2025 09:40:07

• Na atividade 10, auxilie os estudantes a efetuarem as adições dos itens A e B de um modo diferente, sendo esse o objetivo da atividade. Oriente-os a realizar os cálculos de adição de maneira parecida com o exemplo apresentado, com o auxílio de uma régua. Verifique se eles têm dificuldade nessas adições e, se julgar necessário, desenhe a régua na lousa para auxiliá-los nas resoluções. No item A, mostre a eles que é preciso adicionar 6 unidades ao 2 e, no item B, 9 unidades ao 5.

• A atividade 10 indica um contexto em que os sentidos da visão e tato são explorados pelos estudantes, pois utilizam a visão para localizar os números da régua ao efetuar os cálculos de adição e as mãos e os dedos, que se movem para traçar as setas por meio da sensação de pressão ao usar a régua e o lápis, promovendo o desenvolvimento da coordenação motora fina, a atenção, o raciocínio lógico e a compreensão de conceitos matemáticos.

• Para estudantes NEE, principalmente aqueles com deficiência visual, a régua pode ser adaptada com marcações em relevo, fitas adesivas táteis ou, se possível, é interessante usar régua braile, permitindo que os estudantes “sintam” os números e as unidades de medida. Dessa maneira, eles podem acompanhar os movimentos e “andar” na régua por meio do tato, facilitando a compreensão do cálculo.

• A atividade 11 apresenta a ideia de dobro por meio das adições. Leia com os estudantes a frase de cada item, reforçando a ideia de cada uma, e oriente-os a preencher as adições. Esse conceito será utilizado nas próximas atividades deste tópico.

10. VERIFIQUE COMO LEILA CALCULOU 8 + 7 USANDO UMA RÉGUA. INICIALMENTE ELA LOCALIZOU O NÚMERO 8 NA RÉGUA. DEPOIS, “ANDOU” 7 UNIDADES PARA A DIREITA E OBTEVE O RESULTADO.

10. A) Resposta: Os estudantes devem partir do número 2 na régua e “andar” 6 unidades para a direita. 2 + 6 = 8

DE MANEIRA PARECIDA, EFETUE OS CÁLCULOS USANDO UMA RÉGUA.

10. B) Resposta: Os estudantes devem partir do número 5 na régua e “andar” 9 unidades para a direita. 5 + 9 = 14

A ) 2 + 6 = B ) 5 + 9 = 0123456789101112131415

11. LEIA AS INFORMAÇÕES COM O PROFESSOR. DEPOIS, COMPLETE AS FRASES COM OS NÚMEROS QUE FALTAM.

A ) O DOBRO DE 1 É IGUAL A 2.

Resposta: 1 + 1 = 2

B ) O DOBRO DE 2 É IGUAL A 4.

Resposta: 2 + 2 = 4

C ) O DOBRO DE 3 É IGUAL A

Resposta: O DOBRO DE 3 É IGUAL A 6 3 + 3 = 6

D ) O DOBRO DE 4 É IGUAL A .

Resposta: O DOBRO DE 4 É IGUAL A 8 4 + 4 = 8

12. ANA TEM 5 LÁPIS E MARCOS TEM O DOBRO DA QUANTIDADE DE LÁPIS DE ANA.

MARQUE UM X NO NÚMERO QUE REPRESENTA A QUANTIDADE DE LÁPIS QUE MARCOS TEM. 8 12 10 9

Resposta: Os estudantes devem marcar um X no número 10

• Na atividade 12, é abordada uma situação em que os estudantes são levados a interpretar as informações apresentadas para calcular o dobro de 5. Leia o enunciado com eles e auxilie-os na interpretação. Depois, pergunte-lhes qual é a adição que deve ser efetuada para resolver o problema. Para um melhor aproveitamento desta atividade, pergunte aos estudantes: “Quantos lápis Marcos teria se Ana tivesse 7 lápis? E se ela tivesse 9 lápis?”.

13. ACOMPANHE O QUE RAFAEL ESTÁ DIZENDO.

TENHO 8 FIGURINHAS E MÁRCIA TEM A METADE, OU SEJA, 4 FIGURINHAS. 8 É O DOBRO DE 4, ASSIM, 4 É A METADE DE 8.

AGORA, COMPLETE AS FRASES COM OS NÚMEROS QUE FALTAM.

A ) A METADE DE 6 É IGUAL A

Resposta: A METADE DE 6 É IGUAL A 3

B ) A METADE DE 10 É IGUAL A .

Resposta: A METADE DE 10 É IGUAL A 5

14. CONTORNE A METADE DOS DADOS.

Resposta: Os estudantes devem contornar, da maneira que preferirem, 5 dados.

15. CONSIDERE A QUANTIDADE DE CLIPES QUE BIA, JUSSARA E SILAS TÊM.

SILAS JUSSARA

CONTORNE EM CADA ITEM A PALAVRA QUE COMPLETA A FRASE.

Professor, professora: Oriente os estudantes no registro das respostas da atividade 15, incentivando o traçado em letra cursiva, a fim de treinar esse tipo de escrita.

A ) SILAS TEM DE CLIPS DE BIA.

Resposta: Os estudantes devem contornar O DOBRO.

• A atividade 13 tem por objetivo trabalhar a ideia de metade relacionada à ideia de dobro, apresentada na página anterior. Para um melhor aproveitamento desta atividade, solicite aos estudantes que façam no caderno outros itens parecidos com os que foram propostos no Livro do Estudante, como: “Quanto é a metade de 12?”; “Quanto é a metade de 4?”; “Quanto é a metade de 14?”. Caso eles apresentem dificuldades, utilize material de contagem e realize na prática a atividade proposta.

• O objetivo da atividade 14 é que os estudantes identifiquem qual é a metade da quantidade de dados apresentados na imagem, ou seja, a metade de 10. Sendo assim, eles devem contornar 5 dados. Verifique se eles apresentam dificuldades na resolução desta atividade e, se necessário, desenhe na lousa algumas quantidades de objetos, como bolinhas, e oriente-os a identificar e contornar a metade da quantidade desenhada.

B ) JUSSARA TEM DE CLIPS DE BIA.

Resposta: Os estudantes devem contornar A METADE.

C ) BIA TEM DE CLIPS DE JUSSARA. o dobro o dobro o dobro a metade a metade a metade

Resposta: Os estudantes devem contornar O DOBRO.

AVALIANDO

Objetivos

Conhecer os fatos básicos e as ideias da adição.

Efetuar adição com duas parcelas de números naturais com total até 19.

Sugestão de intervenção

Providencie botões ou outros materiais de contagem e proponha adições utilizando-os, como 5 botões + 3 botões = 8 botões. Após os estudantes efetuarem a adição sugerida, pergunte a eles: “Se forem acrescentados 2 bo-

03/10/2025 09:42:25

tões, quantos haverá no total?”. Nesse momento, enfatize que acrescentar significa adicionar considerando o último resultado. Logo, não há necessidade de adicionar tudo novamente. Se eles apresentarem dificuldades durante a realização desta atividade, faça o passo a passo com eles, utilizando objetos iguais, tracinhos na lousa ou dedos. Depois, apresente outras situações e peça a eles que repitam os passos e obtenham os resultados.

• Durante o trabalho com a atividade 15, cujo objetivo é identificar quantidades que são metade e dobro de outras, oriente os estudantes a contarem os clipes de cada pessoa e registrarem em seus cadernos. Caso eles apresentem dificuldades com a estrutura da atividade, conduza-a perguntando a eles qual opção de cada frase está correta: “Silas tem o dobro dos clipes de Bia?”; “Silas tem a metade dos clipes de Bia?”; “Jussara tem o dobro dos clipes de Bia?”; “Jussara tem a metade dos clipes de Bia?”; “Bia tem o dobro dos clipes de Jussara?”; “Bia tem a metade dos clipes de Silas?”.

BIA

• O trabalho com o tópico Adição com números até 99 sugere aos estudantes que utilizem o material dourado ou outros tipos de materiais manipuláveis como recurso para a realização dos cálculos, a fim de facilitar o entendimento deles em relação às operações que envolvem duas ordens.

• A atividade 1 tem como objetivo apresentar uma adição envolvendo números de dois algarismos e relembrar o símbolo que indica a operação de adição (+) e o sinal de igual (=).

• O contexto abordado na atividade 1 possibilita o desenvolvimento de vocabulário, pois apresenta aos estudantes uma nova palavra (pomar), permitindo que ampliem e desenvolvam a habilidade de produzir e compreender a linguagem oral.

• Em um primeiro momento, avalie se os estudantes compreendem as informações apresentadas e se fi zeram a contagem da quantidade de laranjas corretamente. Em seguida, pergunte a eles se conhecem alguma estratégia para obter o total de laranjas colhidas. Uma estratégia que pode ser apresentada a eles antes de prosseguir com a atividade é a contagem, fazendo uma pausa entre a contagem das laranjas da cesta de Alice e a das laranjas da cesta de José, a fim de que percebam a quantidade colhida por eles como uma parcela da adição, e não como uma única quantidade.

ADIÇÃO COM NÚMEROS ATÉ 99

1. ALICE E JOSÉ FORAM AO POMAR COLHER LARANJAS.

LARANJAS COLHIDAS POR ALICE.

LARANJAS COLHIDAS POR JOSÉ.

Resposta: 13 LARANJAS

A ) QUANTAS LARANJAS ALICE COLHEU? LARANJAS.

Resposta: 12 LARANJAS

B ) QUANTAS LARANJAS JOSÉ COLHEU? LARANJAS.

PODEMOS DETERMINAR O TOTAL DE LARANJAS COLHIDAS POR MEIO DE UMA ADIÇÃO

POMAR: CONJUNTO DE ÁRVORES FRUTÍFERAS.

13 LARANJAS MAIS 12 LARANJAS É IGUAL A 25 LARANJAS.

UTILIZANDO SÍMBOLOS, ESCREVEMOS: 13 + 12 = 25

BNCC

PODEMOS EFETUAR ESSA ADIÇÃO DE OUTRAS MANEIRAS. COMPLETE O CÁLCULO A SEGUIR COM OS NÚMEROS QUE FALTAM.

UTILIZANDO CUBINHOS E BARRAS

1º .

2º .

REPRESENTAMOS OS NÚMEROS 13 E 12 COM CUBINHOS E BARRAS.

NESSA REPRESENTAÇÃO, CADA BARRA É FORMADA POR 10 CUBINHOS.

JUNTAMOS OS CUBINHOS (UNIDADES) E AS BARRAS (DEZENAS).

Resposta: 13 + 12 = 25

+ =

DECOMPONDO OS NÚMEROS

Resposta: 20 + 5 = 25

Resposta: PORTANTO, ALICE E JOSÉ COLHERAM AO TODO 25 LARANJAS.

PORTANTO, ALICE E JOSÉ COLHERAM AO TODO _______________ LARANJAS.

Para efetuar a adição apresentada nesta página, sugere-se o uso de materiais manipuláveis como recurso para a realização dos cálculos, contemplando, assim, a habilidade EF01MA08 da BNCC. Além disso, nas atividades 1 e 2 do tópico Adição com números até 99, os estudantes desenvolvem em parte a habilidade EF01MA07 da BNCC, ao decompor e compor alguns números em unidades e dezenas com material manipulável e ao usar o algoritmo da adição.

• Nesta página, são apresentadas outras maneiras de efetuar a adição proposta na atividade 1 da página anterior, primeiro por meio de cubinhos e barras e, depois, usando a decomposição dos números.

• Providencie com antecedência e leve para a sala de aula o material dourado. Utilize-o a fim de que os estudantes compreendam na prática a representação dos números e a junção dos cubinhos e das barras para efetuarem a adição proposta.

• Caso não haja material dourado em quantidade suficiente para todos os estudantes, organize-os em duplas para que possam realizar a atividade.

• Oriente-os durante todo o processo, fazendo as explicações necessárias e também indicando o que precisam completar nos respectivos espaços.

ATIVIDADE EXTRA

Para melhor aproveitamento das estratégias de resolução estudadas, solicite aos estudantes que efetuem as adições utilizando cada maneira apresentada nesta página. Algumas sugestões de operações são:

• 15 + 11 = ■

• 32 + 16 = ■

• 43 + 21 = ■

• 52 + 34 = ■

Respostas

• 15 + 11 = 26

• 32 + 16 = 48

• 43 + 21 = 64

• 52 + 34 = 86

03/10/2025 09:42:26

• Durante o trabalho com a atividade 2, cuja finalidade é a de que os estudantes efetuem adições com o auxílio do material dourado, verifique se eles identificam corretamente os números correspondentes aos cubinhos e às barras em cada item. No quadro em que é apresentado o total em cada item, observe se eles preenchem as parcelas da adição com os números indicados, e não com outros valores, como as dezenas e as unidades. Caso eles estejam apenas contando as dezenas e as unidades no quadro em que é apresentado o total, apresente outras adições em que são mostradas as parcelas, e não o valor total. Isso pode ser executado com material dourado, por meio de desenhos na lousa ou com outra estratégia prática que seja conveniente.

• O objetivo da atividade 3 é levar os estudantes a interpretarem o enunciado e usarem uma adição para obter a resposta. Eles podem apresentar dificuldade para interpretar a soma de elementos diferentes, sendo assim, diga que laranjas e bananas são frutas e, se necessário, leia novamente o enunciado, substituindo o nome das frutas pela palavra frutas, fortalecendo o sentido de que estão sendo adicionadas duas quantidades de um mesmo elemento. Caso os estudantes apresentem dificuldades na adição, oriente-os a desenhar em seus cadernos as frutas ou usar um tracinho para representar cada uma e, depois, efetuar a adição. Em seguida, oriente-os a usar o algoritmo para efetuar a adição novamente e validar os resultados obtidos.

ATIVIDADE EXTRA

A fim de sanar possíveis dúvidas e também para um melhor aproveitamento da atividade 3, proponha aos estudantes que resolvam no caderno as seguintes operações:

2. DETERMINE

O RESULTADO DA ADIÇÃO DE ACORDO COM OS CUBINHOS E AS BARRAS APRESENTADOS E COMPLETE O QUE FALTA NAS INFORMAÇÕES.

REPRESENTAMOS OS NÚMEROS 13 E 11 COM CUBINHOS E BARRAS.

Resposta: 11; 13 + 11 = 24

REPRESENTAMOS OS NÚMEROS 18 E 10 COM CUBINHOS E BARRAS.

Resposta: 18; 18 + 10 = 28

REPRESENTAMOS OS NÚMEROS 23 E 16 COM CUBINHOS E BARRAS.

Resposta: 16; 23 + 16 = 39

3. PAULO USOU 15 LARANJAS E 12 BANANAS PARA FAZER UMA SALADA DE FRUTAS. AO TODO, QUANTAS FRUTAS ELE USOU?

Resposta: 15 + 12 = 27. PAULO USOU AO TODO 27 FRUTAS.

15 + =

PAULO USOU AO TODO FRUTAS.

• 13 + 14 = ■

• 20 + 6 = ■

• 43 + 15 = ■

• 31 + 12 = ■

Respostas

• 13 + 14 = 27

• 20 + 6 = 26

• 43 + 15 = 58

• 31 + 12 = 43

Disponibilize o material dourado para o trabalho com esta atividade. Caso não haja o suficiente para todos os estudantes, organize-os em duplas para que possam realizá-la.

DIVIRTA-SE E APRENDA

ROLETA DA ADIÇÃO

VAMOS BRINCAR DE ADICIONAR?

COM ESSE JOGO, VOCÊ VAI TESTAR SEUS CONHECIMENTOS SOBRE A ADIÇÃO. PARA ISSO, JUNTE-SE A UM COLEGA. VOCÊ VAI PRECISAR DE UM LÁPIS, DE UM CLIPE E DA ROLETA DA ADIÇÃO DA PÁGINA 281 DO MATERIAL COMPLEMENTAR

REGRAS

• COLOQUE O CLIPE NO CENTRO DA ROLETA E FIRME O LÁPIS

SOBRE ELE PARA SEGURÁ-LO.

• GIRE O CLIPE UMA VEZ E ANOTE EM UMA FOLHA DE PAPEL O NÚMERO EM QUE ELE PAROU. REPITA O GIRO, ANOTANDO O SEGUNDO NÚMERO OBTIDO.

• ADICIONE OS DOIS NÚMEROS QUE VOCÊ SORTEOU NA ROLETA.

• CONFIRA A SUA SOMA COM A DO COLEGA. GANHA UM PONTO QUEM OBTIVER A MAIOR SOMA E VENCE A PARTIDA QUEM FIZER MAIS PONTOS EM 10 RODADAS.

DICA: CADA PARTICIPANTE GANHARÁ UM PONTO SE A SOMA FOR A MESMA PARA OS DOIS.

• Outra possibilidade é orientar os estudantes a estimarem quem vai obter a maior soma, antes de adicionarem os números obtidos, permitindo que formulem estratégias próprias de cálculo mental.

• Apresentamos a seguir um exemplo dos valores obtidos em uma partida e sua suposta pontuação.

• Segunda rodada:

• Bruno: 4 + 1 = 5

• Camila: 1 + 4 = 5

Portanto, cada um recebe um ponto.

• Terceira rodada:

• Bruno: 7 + 2 = 9

• A seção Divirta-se e aprenda desta página propõe um jogo no qual os participantes devem realizar o cálculo de adição com os resultados obtidos ao girar a roleta duas vezes. Nesse jogo, ganha um ponto o que obtiver a maior soma ou aqueles que obtiverem uma soma igual.

• O objetivo deste jogo é motivar o desenvolvimento da habilidade do cálculo mental da adição com números até nove.

03/10/2025 09:42:27

• Com antecedência, providencie lápis, papel e clipes em quantidade suficiente para todos os estudantes. Verifique se eles compreenderam como jogar. Se julgar conveniente, proponha uma competição, realizando no mínimo cinco rodadas, considerando como vencedor o que obtiver a maior pontuação no total.

• Caso os estudantes apresentem dificuldades relacionadas à adição dos números, solicite a eles que anotem no caderno os números em que o clipe parou e, depois, efetuem a adição com material de contagem.

• Para um melhor aproveitamento desta atividade, sugira aos estudantes que adicionem sempre um mesmo número ao resultado obtido após girarem o clipe. Por exemplo, fixando o 3, cada vez que eles girarem a roleta, devem adicionar 3 ao resultado obtido nela. Depois de cinco rodadas, vence quem obtiver a maior pontuação.

• Quinta rodada:

• Bruno: 2 + 5 = 7

• Camila: 3 + 5 = 8

Portanto, Camila recebe um ponto. Então, nessa partida, Camila ganhou 4 pontos ao todo e Bruno ganhou 2 pontos. Assim, Camila é a vencedora. REGRAS

• Primeira rodada:

• Bruno: 3 + 1 = 4

• Camila: 4 + 3 = 7

Portanto, Camila recebe um ponto.

• Camila: 2 + 4 = 6

Portanto, Bruno recebe um ponto.

• Quarta rodada:

• Bruno: 3 + 2 = 5

• Camila: 2 + 4 = 6

Portanto, Camila recebe um ponto.

• A atividade 4 apresenta como Felipe efetuou 32 + 21 usando o algoritmo, uma estratégia diferente para efetuar adições. Caso julgue necessário, antes de propor a atividade da página, apresente outros exemplos a eles. Depois, oriente-os a resolver o item B no Livro do Estudante, usando a mesma estratégia de Felipe.

• É apresentado aos estudantes o significado de uma nova palavra (algoritmo), contribuindo para o desenvolvimento de vocabulário e da habilidade de produzir e compreender a linguagem oral.

• Para os estudantes com TEA, com TDAH e com síndrome de Down, a atividade 4 poderá ser realizada com o uso do recurso do material de apoio, como a calculadora, para priorizar a investigação das hipóteses dos cálculos. Incentive e valorize o cálculo mental e, posteriormente, a construção do sistema de registro. Se a resposta acontecer por cálculo mental, poderá utilizar o auxílio colaborativo entre os estudantes, em que um descreve como pensou e o outro registra na lousa a proposta. Esse acompanhamento analítico por parte do professor é importante para verificar como os estudantes estão progredindo no raciocínio lógico e na compreensão do conteúdo.

INICIALMENTE, FELIPE REPRESENTOU OS NÚMEROS 32 E 21 COMO INDICADO.

DEPOIS, ADICIONOU AS UNIDADES.

ALGORITMO: SEQUÊNCIA DE PASSOS PARA CHEGAR A UM RESULTADO.

DICA: NESSA REPRESENTAÇÃO, D SIGNIFICA DEZENA E U SIGNIFICA UNIDADE

EM SEGUIDA, ADICIONOU AS DEZENAS.

2 UNIDADES MAIS 1 UNIDADE É IGUAL A 3 UNIDADES.

3 DEZENAS MAIS 2 DEZENAS É IGUAL A 5 DEZENAS.

A ) QUAL FOI O RESULTADO DO CÁLCULO OBTIDO POR FELIPE?

Resposta: 53

B ) ASSIM COMO FELIPE, EFETUE AS ADIÇÕES A SEGUIR USANDO O ALGORITMO.

Resposta: 46 + 23 = 69 Resposta: 25 + 10 = 35 Resposta: 14 + 31 = 45

46 + 23 = • 25 + 10 = • 14 + 31 =

5. ISADORA FEZ UMA PESQUISA

PARA SABER QUAL MEIO DE LOCOMOÇÃO CADA ESTUDANTE

DA SALA DE AULA DELA UTILIZA PARA IR À ESCOLA. CADA UM

VOTOU APENAS UMA VEZ.

EM SEGUIDA, ISADORA

REGISTROU AS INFORMAÇÕES DE SUA PESQUISA EM UMA TABELA

LOCOMOÇÃO: AÇÃO DE IR DE UM LUGAR A OUTRO.

MEIO DE LOCOMOÇÃO

UTILIZADO PELOS ESTUDANTES DO 1º ANO A PARA IR À ESCOLA, EM 202 7

TIPO DE TRANSPORTE QUANTIDADE DE ESTUDANTES

CARRO DE PASSEIO12

ÔNIBUS 10

BICICLETA 11

A PÉ 14

FONTE DE PESQUISA: ANOTAÇÕES DE ISADORA.

RESPONDA ÀS QUESTÕES COM BASE NAS INFORMAÇÕES DA TABELA.

A ) A MAIORIA DOS ESTUDANTES QUE ISADORA ENTREVISTOU

USA QUAL MEIO DE LOCOMOÇÃO?

Resposta: A PÉ.

B ) QUANTOS ESTUDANTES UTILIZAM OS MEIOS DE LOCOMOÇÃO:

• CARRO DE PASSEIO E ÔNIBUS?

ESTUDANTES.

Resposta: 12 + 10 = 22 22 ESTUDANTES.

Resposta: 22 + 25 = 47; 47 ESTUDANTES.

C ) ISADORA ENTREVISTOU

QUANTOS ESTUDANTES

AO TODO?

ESTUDANTES.

• BICICLETA E A PÉ?

ESTUDANTES.

Resposta: 11 + 14 = 25 25 ESTUDANTES.

BNCC

D ) QUAL MEIO DE LOCOMOÇÃO VOCÊ USA PARA IR À ESCOLA?

Resposta pessoal. Espera-se que os estudantes respondam quais meios de locomoção utilizam para ir à escola.

E ) ALÉM DOS MEIOS DE LOCOMOÇÃO CITADOS, QUAIS OUTROS VOCÊ CONHECE?

Resposta pessoal. Espera-se que os estudantes explicitem quais meios de locomoção conhecem.

A atividade 5 aborda a leitura de dados expressos em tabelas, conforme a habilidade EF01MA21 da BNCC.

03/10/2025 09:42:28

• Antes de solicitar aos estudantes que respondam aos itens da atividade 5 , faça perguntas que os incentivem a interpretar os dados expostos nessa tabela, como: “Qual é o título dessa tabela?”; “Quantas colunas têm essa tabela?”; “Por que na fonte de pesquisa está escrito ‘Anotações de Isadora’?”; “Quais meios de locomoção foram inseridos na tabela?”; “Qual meio de locomoção é o mais usado pelos estudantes que foram entrevistados?”; “Quantos estudantes não utilizam a bicicleta nem o carro de passeio para irem à escola?”. Depois, oriente os estudantes a responderem às questões propostas.

• O objetivo do item C é que os estudantes percebam que, para saber o total de colegas que Isadora entrevistou, eles deverão adicionar a quantidade de cada tipo de locomoção apresentado na tabela. O objetivo das questões D e E é que os estudantes conversem sobre o meio de transporte que utilizam para irem à escola. Durante a realização do item D, caso os estudantes tenham alguma dificuldade, oriente-os a adicionar os resultados obtidos no item anterior para obter a resposta. Aproveite o assunto e converse sobre as soluções de mobilidade urbana que visam tornar o trânsito mais fluido e livre de congestionamentos.

• No item E, espera-se que eles citem, por exemplo, van, trem, motocicleta, metrô, barco, táxi etc.

• É apresentada uma nova palavra aos estudantes (locomoção), o que contribui para a aquisição das habilidades fundamentais à alfabetização, como o desenvolvimento de vocabulário.

• Antes de trabalhar com a atividade 6, verifique a possibilidade de levar um tabuleiro de xadrez para a sala de aula. Pergunte aos estudantes se eles conhecem o xadrez e, se julgar conveniente, peça que o expliquem aos colegas. Uma possível explicação é dizer que o xadrez é um jogo para dois competidores, jogado no mundo todo, e que envolve um tabuleiro com 64 casas, no qual cada jogador tem 16 peças e busca dar xeque-mate no rei adversário. Se julgar conveniente, mostre as peças para eles e explique o movimento de cada uma delas.

• Na atividade 7, leia o enunciado com os estudantes e verifique se eles compreendem o significado de juntar, proposto pelo problema, relacionado com o conceito de adição. Converse sobre o que eles entenderam do enunciado e sobre as estratégias que podem ser usadas para efetuar essa adição. Para um melhor aproveitamento desta atividade, proponha o uso do algoritmo para efetuar essa adição, solicitando a eles que avaliem qual das estratégias foi mais fácil nesse caso: o uso da contagem ou do algoritmo.

6. AO TÉRMINO DE UMA PARTIDA DE XADREZ, O JOGADOR COM AS PEÇAS CLARAS TINHA CAPTURADO 10 PEÇAS, ENQUANTO O JOGADOR COM AS PEÇAS ESCURAS TINHA CAPTURADO 13 PEÇAS.

MOMENTO DE UMA PARTIDA DO JOGO DE XADREZ.

A ) QUANTAS PEÇAS FORAM CAPTURADAS AO TODO?

Resposta: 10 + 13 = 23. FORAM CAPTURADAS AO TODO 23 PEÇAS.

FORAM CAPTURADAS AO TODO PEÇAS.

B ) ELABORE UMA QUESTÃO USANDO QUANTIDADES DE PEÇAS CLARAS E ESCURAS DE UM JOGO DE XADREZ. DEPOIS, PEÇA A UM COLEGA QUE RESPONDA A ESSA QUESTÃO.

7. RODRIGO TEM 23 GIBIS E PEDRO, SEU IRMÃO, 34 GIBIS. AO TODO, QUANTOS GIBIS OS IRMÃOS TÊM JUNTOS?

Resposta: 23 + 34 = 57. RODRIGO E SEU IRMÃO TÊM JUNTOS 57 GIBIS.

RODRIGO E SEU IRMÃO TÊM JUNTOS GIBIS.

6. B) Resposta pessoal. Neste item, espera-se que os estudantes elaborem uma questão envolvendo a adição. Uma sugestão de questão é: Em um jogo de xadrez, Ana capturou 14 peças claras e Heitor capturou 12 peças escuras. Quantas peças foram capturadas ao todo?

ARTICULANDO CONHECIMENTOS

Uma possibilidade de trabalho com a atividade 6 é desenvolver uma integração com o componente curricular de Educação Física. Com a ajuda dos estudantes, promova uma busca pelas regras do jogo e incentive-os a disputar entre si. O jogo de xadrez auxilia o desenvolvimento do raciocínio lógico e sua prática promove o respeito pelos parceiros de competição.

Aproveite o contexto abordado nesta atividade e solicite aos estudantes que façam com seus colegas uma pesquisa sobre a história do

jogo de xadrez. Em seguida, eles devem registrar no caderno, com desenhos e frases, o que pesquisaram.

03/10/2025 09:44:45

BNCC

O item B da atividade 6 solicita aos estudantes que elaborem uma questão envolvendo adição com números de até dois algarismos, com os significados de juntar e acrescentar, utilizando estratégias pessoais, abordando, assim, aspectos da habilidade EF01MA08 da BNCC.

8. NEUZA EFETUOU MENTALMENTE O SEGUINTE CÁLCULO.

AO ADICIONAR 4 DEZENAS COM 2 DEZENAS, OBTENHO 6 DEZENAS, OU SEJA, 60 UNIDADES.

ASSIM: 40 + 20 = 60

ASSIM COMO NEUZA, EFETUE OS CÁLCULOS A SEGUIR MENTALMENTE.

A ) 30 + 50 =

Resposta: 30 + 50 = 80

B ) 10 + 20 =

Resposta: 10 + 20 = 30

C ) 70 + 20 =

Resposta: 70 + 20 = 90

D ) 30 + 30 =

Resposta: 30 + 30 = 60

9. CAROLINA TINHA 14 REAIS E GANHOU MAIS 12 REAIS DE SEU PAI. QUANTOS REAIS CAROLINA TEM AGORA?

REAIS.

Resposta: 14 + 12 = 26 26 REAIS.

10. ALGUMAS FIGURAS GEOMÉTRICAS ESPACIAIS ESTÃO REPRESENTADAS A SEGUIR.

A ) QUANTOS SÃO OS CILINDROS AZUIS? CILINDROS.

Resposta: 12 CILINDROS.

B ) QUAL É A QUANTIDADE DE CILINDROS VERDES?

CILINDROS.

Resposta: 13 CILINDROS.

C ) QUANTOS CILINTROS TEM NO TOTAL? CILINDROS.

Resposta: 25 CILINDROS.

185

03/10/2025 09:44:47

• Para realizar a atividade 8, que propõe uma estratégia de cálculo mental com dezenas, leia com os estudantes a fala de Neuza e, se julgar conveniente, represente a operação citada com o material dourado ou desenhos na lousa. Oriente-os a usar a mesma estratégia de Neuza para efetuar os cálculos. Se for necessário, efetue o cálculo do item A em voz alta, antes de eles resolverem os outros itens.

• Na atividade 9, leia o enunciado com os estudantes e verifique se eles compreendem o significado de acrescentar, proposto pelo problema, relacionado com o conceito de adição. Converse sobre o que eles entenderam do enunciado e sobre as estratégias que podem ser usadas para efetuar essa adição.

• Durante o trabalho com a atividade 10, oriente os estudantes a identificarem as figuras geométricas espaciais para, depois, realizarem a contagem e responderem às questões. Após a resolução, verifique se algum estudante, ao realizar a contagem dos cilindros azuis, proposto no item A, acabou contando também os cones azuis, considerando a cor, e não o formato da figura. Da mesma maneira, no item B, verifique se esse estudante acabou contando também os cubos verdes considerando a cor, e não o formato da figura. Caso isso ocorra, explique as diferenças entre as figuras geométricas espaciais apresentadas e proponha que façam a contagem novamente dos cilindros azuis e verdes.

• Oriente os estudantes durante o desenvolvimento das atividades desta página e, caso apresentem dúvidas, proponha outras atividades com novas abordagens, objetivando esclarecê-las.

• A atividade 11 apresenta como Andréia efetuou 14 + 23 usando o ábaco, uma estratégia diferente para efetuar adições. Leve para a sala de aula um ábaco e explique na prática essa adição para os estudantes. Caso julgue necessário, antes de propor as atividades dessa página, apresente outros exemplos a eles. Depois, oriente-os a resolver o item B, usando a mesma estratégia de Andréia. Caso eles apresentem dificuldade na realização da atividade, oriente-os a recortar e utilizar a representação do ábaco de papel e as contas disponíveis no Material complementar do Livro do Estudante. Ao recortarem o ábaco e as contas, acompanhe e supervisione principalmente os estudantes com limitações motoras ou que ainda não tenham habilidade com a tesoura, prevenindo acidentes e cuidando da integridade física de toda a turma.

• Espera-se que os estudantes desenhem nos ábacos, inicialmente, as contas que representam as unidades e as dezenas da primeira parcela, nessa ordem, nas varetas correspondentes; depois, acrescentem as contas que representam as unidades e as dezenas da segunda parcela, também nessa ordem, nas varetas correspondentes. Desse modo, estarão representando o passo a passo da adição na ordem em que ocorre no algoritmo.

11. VERIFIQUE COMO ANDRÉIA EFETUOU 14 + 23

USANDO UM ÁBACO

INICIALMENTE, ELA REPRESENTOU O NÚMERO

14 COLOCANDO 4 CONTAS NA VARETA DAS UNIDADES E 1 CONTA NA VARETA DAS DEZENAS.

COMO ELA VAI ACRESCENTAR 23 UNIDADES AO 14, COLOCOU 3 CONTAS NA VARETA DAS UNIDADES E 2 CONTAS NA VARETA DAS DEZENAS. O RESULTADO DO CÁLCULO É O NÚMERO REPRESENTADO NO ÁBACO.

A ) QUAL FOI O RESULTADO DO CÁLCULO OBTIDO POR ANDRÉIA?

Resposta: 14 + 23 = 37

B ) DESENHE BOLINHAS NOS ÁBACOS E, ASSIM COMO ANDRÉIA, EFETUE AS ADIÇÕES. 14 + 23 37

Resposta: 22 + 21 = 43

Resposta: 27 + 30 = 57

22 + 21 = 31 + 43 = 27 + 30 = 56 + 13 = 14 + 23 =

Resposta: 31 + 43 = 74

Resposta: 56 + 13 = 69

REFERÊNCIAS COMPLEMENTARES

DIAS, Marisa da Silva; MORETT, Vanessa Dias. Número e operações: elementos lógico-históricos para atividade de ensino. Curitiba: InterSaberes, 2012.

Esse livro aborda uma viagem pela história, ajudando a compreender o conhecimento matemático e seu desenvolvimento desde as primeiras civilizações. Apresenta também curiosidades, explicações didáticas e análises sobre o papel do professor e da educação na vida em sociedade.

ATIVIDADE EXTRA

A fim de sanar possíveis dúvidas e também para melhor aproveitamento da atividade 11, solicite aos estudantes que repitam os mesmos processos utilizados por Andréia, porém efetuando outras adições no caderno, como 23 + 34; 15 + 32; 45 + 13 e 27 + 11. Caso algum estudante apresente dificuldade, proponha que utilize material de contagem. A prática com esses recursos pode ajudar a superar defasagens e contribuir para recuperação do conteúdo.

12. VERIFIQUE COMO EFETUAR 32 + 27 NA CALCULADORA.

1º . COM A CALCULADORA LIGADA, REGISTRE O NÚMERO 32 DIGITANDO AS TECLAS 3 E 2

2º .

DIGITE A TECLA E NA SEQUÊNCIA, REGISTRE O NÚMERO 27 DIGITANDO AS TECLAS 2 E 7 .

3º . POR ÚLTIMO, DIGITE A TECLA E OBTENHA O RESULTADO NO VISOR DA CALCULADORA.

A ) QUAL FOI O RESULTADO OBTIDO?

Resposta: 59

B ) FAÇA ESTIMATIVAS E DETERMINE O RESULTADO DE CADA UMA DAS ADIÇÕES. DEPOIS, UTILIZANDO UMA CALCULADORA, VERIFIQUE SE SUAS ESTIMATIVAS SÃO PRÓXIMAS OU IGUAIS AOS RESULTADOS EXATOS.

Resposta: 16 + 22 = 38

• 16 + 22 =

Resposta: 53 + 21 = 74

• 53 + 21 =

Resposta: 67 + 32 = 99

• 67 + 32 =

Resposta: 74 + 12 = 86

• 74 + 12 =

13. DUAS TURMAS DO 1º ANO SAÍRAM EM UMA VIAGEM. UMA

TURMA TEM 26 ESTUDANTES E A OUTRA TEM 32 ESTUDANTES. QUANTOS ESTUDANTES SAÍRAM NESSA VIAGEM?

Resposta: 26 + 32 = 58

NESSA VIAGEM SAÍRAM ESTUDANTES.

Resposta: NESSA VIAGEM SAÍRAM 58 ESTUDANTES.

03/10/2025 09:44:50

• Verifique as estratégias dos estudantes para estimar os resultados das adições no item B, da atividade 12, pedindo a alguns que compartilhem as ideias com os colegas da sala. Verifique se todos compreendem que o motivo dessa atividade é desenvolver a capacidade de realizar estimativas e trabalhar com aproximação de resultados. Dê oportunidade a toda a turma para verbalizar o raciocínio, acolhendo com atenção e respeito todas as ideias. Uma das dificuldades durante a atividade pode se referir ao repertório numérico, caso os estudantes ainda não o tenham consolidado. Sendo assim, as contagens coletivas e a representação sistemática de quantidades com material de contagem são estratégias com bons resultados.

• Ao utilizar a calculadora, a atividade 12 explora os sentidos da visão, ao observar os números no visor; do tato, ao apertar os botões da calculadora; e da audição, visto que algumas calculadoras produzem sons ao apertar os botões, promovendo a inclusão de estudantes com NEE, além de contribuir para uma aprendizagem multimodal que pode ser mais eficaz para alguns estudantes.

• Leia o enunciado da atividade 13 com os estudantes e auxilie-os na interpretação da situação-problema. Além de identificar as informações apresentadas, eles devem determinar a quantidade total de estudantes na viagem, e é esperado que utilizem a adição como ferramenta para obterem essa quantidade.

• A atividade 14 apresenta uma sequência de números que deve ser obtida por meio de adições. Os estudantes devem completar a sequência com os números que representam a quantidade de figurinhas que Beatriz terá após abrir cada um dos pacotes que ganhou, sabendo que, em cada um deles, há 11 figurinhas. Caso eles apresentem dificuldades com as adições, faça na lousa alguns exemplos de sequências nas quais os números aumentem de duas em duas unidades, partindo do 12; de três em três unidades, partindo do 12; e, por fim, de dez em dez unidades, partindo do 12, com o objetivo de levá-los a perceber os procedimentos que deverão realizar nesta atividade.

• Para a atividade 15, diga aos estudantes que eles podem usar a estratégia que preferirem para efetuar as adições. O objetivo desta atividade é levá-los a perceber que parcelas diferentes podem gerar um mesmo resultado em uma adição. Para um melhor aproveitamento, pergunte a eles se existem outras adições com esse mesmo resultado e proponha-lhes que determinem algumas delas.

14. BEATRIZ JÁ TEM 12 FIGURINHAS E GANHOU DO SEU PAI OS

4 PACOTES A SEGUIR.

CADA NÚMERO DA SEQUÊNCIA A SEGUIR REPRESENTA A QUANTIDADE DE FIGURINHAS QUE BEATRIZ TERÁ APÓS ABRIR CADA PACOTE. COMPLETE OS ESPAÇOS COM OS NÚMEROS QUE FALTAM.

Resposta: Os estudantes devem completar a sequência: 12, 23, 34, 45 e 56, correspondendo à quantidade total de figurinhas após a abertura de cada pacote de figurinhas. 12 + 11 = 23; 23 + 11 = 34; 34 + 11 = 45; 45 + 11 = 56.

FIGURINHAS QUE BEATRIZ JÁ TINHA

12 +11 +11 +11 +11

TOTAL APÓS ABRIR O 1º PACOTE

TOTAL APÓS ABRIR O 2º PACOTE

15. OBSERVE A ADIÇÃO A SEGUIR.

10 + 18 = 28

Resposta: 12 + 16 = 28

Resposta: 13 + 11 = 24

AVALIANDO

Objetivo

TOTAL APÓS ABRIR O 4º PACOTE

TOTAL APÓS ABRIR O 3º PACOTE

MARQUE UM X NAS ADIÇÕES COM O MESMO RESULTADO DA ADIÇÃO EM DESTAQUE. 12 + 16 = 13 + 11 = 17 + 11 = 15 + 12 =

Resposta: 17 + 11 = 28

Resposta: 15 + 12 = 27

Resposta: Os estudantes devem marcar um X nos cálculos 12 + 16 e 17 + 11

Efetuar adições com duas parcelas de números naturais com resultado até 99.

Sugestão de intervenção

Após a resolução da atividade 14, solicite aos estudantes que continuem completando a sequência proposta, de modo que a quantidade total de figurinhas que Beatriz conseguiu juntar seja 89, e questione-os com a seguinte pergunta: “Se cada pacote contém 11 figurinhas, quantos pacotes ela deverá abrir a fim de obter um total

de 89 figurinhas?”. Oriente os estudantes durante o desenvolvimento da atividade, de modo a esclarecer possíveis dúvidas que surgirem.

03/10/2025 09:44:52

BNCC

O trabalho da atividade 14 contempla aspectos da habilidade EF01MA10 da BNCC, ao solicitar aos estudantes que completem uma sequência com os números faltantes, com base em um padrão estabelecido.

Resposta: Cálculos: 15 + 5 = 20; 20 + 5 = 25; 25 + 5 = 30; 30 + 5 = 35

Sequência: 15, 20, 25, 30, 35

Resposta: Cálculos: 12 + 4 = 16; 16 + 4 = 20; 20 + 4 = 24; 24 + 4 = 28.

Sequência: 12, 16, 20, 24, 28

DESAFIO A MAIS

• Gabriel nasceu 10 dias depois de Lucas. 16 12 15 20 25

• Martina nasceu no dia 11.

• Na atividade 16, os estudantes devem identificar a quantidade que está sendo adicionada a cada número, o que os auxiliará a obterem os dois números seguintes.

• A atividade 1 do boxe Desafio a mais integra as unidades temáticas Números e Grandezas e medidas, ao explorar uma atividade que envolve raciocínio lógico em um contexto de datas de nascimento. Para auxiliar a resolução, faça questionamentos, como: “Sabemos o dia em que Martina nasceu?”; “Devemos usar a adição para saber o dia em que Lucas e Gabriel nasceram?”.

TRÊS AMIGOS FAZEM ANIVERSÁRIO NO MÊS DE ABRIL. EFETUE OS CÁLCULOS EM SEU CADERNO E DESCUBRA EM QUAIS DIAS CADA UM DELES FAZ ANIVERSÁRIO.

• Lucas nasceu 5 dias depois de Martina.

A ) QUE DIA MARTINA NASCEU?

B ) QUE DIA LUCAS NASCEU?

C ) QUE DIA GABRIEL NASCEU? 16. EFETUE OS CÁLCULOS E ESCREVA OS PRÓXIMOS NÚMEROS DA SEQUÊNCIA.

BNCC

A atividade 16 contempla aspectos da habilidade EF01MA10 da BNCC, ao solicitar aos estudantes que completem uma sequência com os números faltantes, com base em um padrão estabelecido.

CONCLUSÃO

Acompanhar o desenvolvimento dos estudantes é fundamental para um ensino bem-sucedido. Ao longo da unidade, foram propostas diversas maneiras de avaliar a aprendizagem da turma. A fim de

Unidades temáticas integradas

Resposta: MARTINA NASCEU NO DIA 11

Resposta: 11 + 5 = 16. LUCAS NASCEU DIA 16

Resposta: 16 + 10 = 26

GABRIEL NASCEU DIA 26.

189

• Para finalizar o trabalho com essa unidade, proponha o desafio a seguir. Incentive os estudantes a analisarem e interpretarem as informações apresentadas. Comente que esse desafio explora o arredondamento e a estratégia de aproximação para incentivar o cálculo mental. Ao final, verifique se todos chegaram ao resultado 50. Depois, peça a eles que efetuem os cálculos para determinarem o valor exato.

Sugestão de Desafio

Qual é o número terminado em zero mais próximo do resultado de 30 + 19?

Resposta

O número terminado em zero mais próximo dessa adição é o 50.

realizar um monitoramento mais abrangente e organizado, registre nos relatórios individuais ou nas fichas de avaliação o desempenho de cada estudante, levando em consideração suas particularidades. Um modelo desse tipo de ficha pode ser encontrado no tópico Avaliação deste Manual do Professor. Assim, será possível visualizar de modo individual as trajetórias de aprendizagem, incluindo os avanços e os pontos de dificuldades a serem sanados por meio de atividades que promovam recuperação dos conteúdos. Esse

03/10/2025 09:44:53

método é de grande importância para que seja possível repensar estratégias em sala de aula, tornando as ações pedagógicas cada vez mais eficazes.

A conclusão da unidade é o momento de avaliar se os objetivos por ela propostos foram alcançados. Para esse diagnóstico, observe no final deste Manual do Professor algumas possibilidades de avaliação formativa que permitem realizar o monitoramento da aprendizagem dos estudantes e intervir caso eles não tenham atingido os resultados esperados.

KEITHY MOSTACHI/ ARQUIVO DA EDITORA

OBJETIVOS DA UNIDADE

• Identificar figuras geométricas planas em objetos presentes no dia a dia.

• Reconhecer, nomear e comparar triângulos, retângulos, quadrados e círculos.

• Identificar figuras geométricas planas em diferentes posições e no contorno de peças com formato de figuras geométricas espaciais.

• Identificar e descrever os elementos que faltam em sequências de figuras geométricas planas por meio do reconhecimento de padrões ou regularidades.

INTRODUÇÃO E JUSTIFICATIVA

Nesta unidade, são apresentadas aos estudantes as figuras geométricas planas: triângulo, quadrado, retângulo e círculo. Esse estudo é necessário para que os estudantes desenvolvam, posteriormente, a capacidade de investigar propriedades, fazer conjecturas e produzir argumentos geométricos convincentes. Por meio de atividades variadas e significativas, eles devem reconhecer esses formatos em objetos do cotidiano, favorecendo a conexão entre o conhecimento matemá tico e a realidade ao re dor deles, explorando propostas que envolvem a observação de sequências e incentivandoos a identificar regularidades ou padrões por meio delas. Além disso, há atividades que desafiam os estudantes a localizarem figuras geométricas planas em uma composição e a reconhecêlas em obras de arte, como uma oportunidade de ampliar o repertório visual e cultural de cada um deles. Por fim, a unidade trabalha o reconhecimento das figuras planas presentes nas faces ou nos contornos de peças com formato de

UNIDADE

FIGURAS GEOMÉTRICAS PLANAS 8

INDÍGENAS DA ETNIA TUPINAMBÁ DE OLIVENÇA, DURANTE CELEBRAÇÃO NO PARQUE QUINTA DA BOA VISTA, RIO DE JANEIRO, EM 2024.

figuras geométricas espaciais, promovendo a compreensão espacial e o desenvolvimento da percepção das relações entre as formas bidimensionais e tridimensionais.

Habilidades da BNCC trabalhadas na unidade: EF01MA09 e EF01MA14

SUGESTÃO DE ESTRATÉGIA INICIAL

Leve blocos lógicos e/ou materiais equivalentes para a sala de aula e organize os estudantes em grupos de até 3 integrantes para manusear os blocos por algum tempo. Depois, orienteos a classificar as peças de acordo com um ou mais

atributos geométricos, como cores, espessura e formato. Perceba as dificuldades deles e acolha com atenção e respeito os comentários de todos, buscando identificar os momentos coerentes de intervenção para superar os obstáculos de aprendizagem. Em seguida, deixe que explorem o material, empilhando ou usando as peças em algumas representações, como casinha, carrinho ou robô. Verifique a troca de informações entre eles e intervenha apenas se considerar necessário. Por fim, peçalhes que desenhem no caderno as representações ou os empilhamentos que fizeram. Eles podem, inclusive, usar as peças como apoio para representar seus contornos.

03/10/2025

2. A FOTOGRAFIA APRESENTADA REGISTRA UMA REUNIÃO DE INDÍGENAS TUPINAMBÁ PARA CELEBRAR A CHEGADA AO BRASIL DE UM MANTO SAGRADO DE SEU POVO. ESSE MANTO HAVIA SIDO ROUBADO DOS TUPINAMBÁ POR COLONIZADORES EUROPEUS HÁ MAIS DE 300 ANOS E ESTAVA EXPOSTO EM UM MUSEU DA DINAMARCA. ALÉM DE SEREM EXPRESSÕES CULTURAIS, ALGUNS OBJETOS SÃO SAGRADOS PARA OS POVOS INDÍGENAS POR SEREM USADOS EM CELEBRAÇÕES OU CARREGAREM ELEMENTOS DE SUAS CRENÇAS. OS POVOS INDÍGENAS SENTEM ORGULHO DE SUA CULTURA. A PINTURA CORPORAL, FORMADA POR DIVERSAS FIGURAS, É UM EXEMPLO DESSA TRADIÇÃO CULTURAL, COMO É POSSÍVEL VERIFICAR NA IMAGEM.

2. Resposta: Espera-se que os estudantes marquem um X no quadrado, no retângulo e no triângulo relatarem os seus conhecimentos sobre a cultura indígena.

1. Resposta pessoal. Esta questão tem como objetivo fazer os estudantes

VOCÊ CONHECE ALGO MAIS DA CULTURA INDÍGENA? CONTE PARA O PROFESSOR E OS COLEGAS. DE ACORDO COM O TEXTO, UM ELEMENTO CULTURAL MARCANTE DOS POVOS INDÍGENAS SÃO AS PINTURAS CORPORAIS. EM ALGUNS POVOS, COMO OS TUPINAMBÁ, ESSAS PINTURAS LEMBRAM FIGURAS GEOMÉTRICAS PLANAS. MARQUE UM X NAS FIGURAS GEOMÉTRICAS PLANAS QUE SE ASSEMELHAM

AOS GRAFISMOS PINTADOS NOS CORPOS DAS PESSOAS PRESENTES NA FOTOGRAFIA.

• O trabalho com as páginas 190 e 191 permite estabelecer relação com o componente curricular de História. Diga aos estudantes que podemos observar a influência de vários povos, como indígenas, europeus e africanos, nas características culturais das comunidades que vivem no nosso país. O resultado dessa influência pode ser visto, por exemplo, no artesanato típico da Região Norte, nos produtos feitos de algodão na Região CentroOeste e nas bolsas e carteiras feitas de fibra na Região Sudeste. Ao trabalhar a questão 1, se julgar conveniente, pergunte aos estudantes se há artesanato produzido por indígenas na região em que moram e se há algum desses artesanatos nas casas deles. Aproveite a curiosidade dos estudantes para orientálos a pesquisar com os adultos de seu convívio sobre a composição da família de cada um e se algum deles tem ascendência indígena. Eles podem compartilhar essas informações com os colegas e comparar características e costumes que acharem interessantes. • Caso julgue necessário, ao resolver a questão 2, complemente perguntando aos estudantes que figuras geométricas planas eles identificaram na imagem. Para cada resposta que eles derem, escreva o nome da figura e esboce o desenho na lousa. Por fim, questioneos se essas figuras estão todas na imagem ou se faltou alguma delas.

• Ao iniciar esse tópico, é possível realizar um trabalho em conjunto com a turma, reproduzindo as figuras geométricas planas na lousa ou em papel, e solicitando aos estudantes que falem os nomes de cada uma delas. Nesse momento, orienteos a identificar algumas características das figuras e expor suas observações para os colegas.

• Durante o trabalho com a atividade 1, leia com os estudantes o nome das figuras geométricas planas apresentadas, desenhando na lousa cada uma delas. Verifique a possibilidade de levar para a sala de aula imagens de artesanatos que envolvem figuras geométricas planas para a identificação dos estudantes.

• Na atividade 1, é apresentado o significado de uma palavra nova, contribuindo para o desenvolvimento de vocabulário.

• Aproveite essa atividade para solicitar aos estudantes que pesquisem, com os adultos de seu convívio, informações sobre a cultura indígena e compartilhem os dados coletados com os colegas. Outra possibilidade é pedirlhes que pesquisem personalidades indígenas que contribuíram e contribuem com as áreas social, econômica, política e científica no Brasil e também com a divulgação da causa indígena.

• Ao finalizar a atividade 2, solicite aos estudantes que desenhem padrões semelhantes aos observados e que, depois, troquem com o de um colega, nomeando as figuras geométricas utilizadas para compor o desenho, reforçando os conceitos apresentados na abertura.

• Caso os estudantes apresentem dificuldade na atividade 2, desenhe na lousa a sequência de figuras geométricas planas e completea com as duas próximas figuras de cada item, para que eles identifiquem qual é a sequência correta.

FIGURAS GEOMÉTRICAS PLANAS NO COTIDIANO

1. UMA DAS MANEIRAS DE ENFEITAR UM VASO É UTILIZANDO UM PADRÃO DE FIGURAS GEOMÉTRICAS. ESSE TRABALHO MUITAS VEZES É FEITO POR ARTESÃOS. ANALISE OS VASOS A SEGUIR.

Resposta: Os estudantes devem ligar : o vaso A ao TRIÂNGULO; o vaso B ao QUADRADO; o vaso C ao CÍRCULO e ao RETÂNGULO.

ARTESÃOS: INDIVÍDUOS QUE PRODUZEM ARTE OU OFÍCIO QUE DEPENDE DE TRABALHOS MANUAIS.

LIGUE AS PARTES DO PADRÃO DE CADA VASO ÀS FIGURAS GEOMÉTRICAS PLANAS QUE ESSAS PARTES LEMBRAM.

2. ANALISE O PADRÃO DE FIGURAS GEOMÉTRICAS PLANAS QUE COMPÕE A SEQUÊNCIA.

INÍCIO

MARQUE UM X NO ITEM COM AS DUAS PRÓXIMAS FIGURAS GEOMÉTRICAS PLANAS QUE MANTÊM O PADRÃO DESSA SEQUÊNCIA.

Resposta: Os estudantes devem marcar um X no item B

As atividades desse tópico propiciam o desenvolvimento da habilidade EF01MA14, ao apresentar figuras geométricas planas para reconhecimento e nomeação em diferentes desenhos.

A atividade 2 permite o desenvolvimento da habilidade EF01MA09 ao solicitar que o estudante aponte e organize os objetos pelos atributos, para determinar o padrão da sequência.

BNCC

A. B. C.

QUADRADO. CÍRCULO. TRIÂNGULO. RETÂNGULO.

3. ISABELA FEZ ALGUNS CARIMBOS USANDO ESPUMA. ELA UTILIZOU UM DELES PARA CARIMBAR A FIGURA A SEGUIR.

CÍRCULO.

A ) CONTORNE O CARIMBO QUE ISABELA UTILIZOU PARA FAZER ESSE CÍRCULO.

Resposta: Os estudantes devem contornar o carimbo 3.

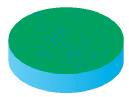
B ) MARQUE UM X NO CARIMBO USADO PARA FAZER CADA FIGURA.

TRIÂNGULO

QUADRADO

RETÂNGULO

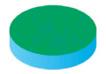
Resposta: Os estudantes devem marcar um X: no carimbo 1 para a linha do TRIÂNGULO; no carimbo 2, para a linha do QUADRADO; no carimbo 4 para a linha do RETÂNGULO.

03/10/2025 09:47:33

• Para o trabalho com a atividade 3, verifique a possibilidade de levar para a sala de aula alguns carimbos de espuma para os estudantes manusearem ou forneça tinta para desenharem as figuras em uma folha de papel. Esses carimbos podem ser feitos recortando uma esponja ou usando outros materiais, como o papel.

• Realizar a atividade na prática é uma forma de tirar possíveis dúvidas dos estudantes, incentivar a criatividade e a reflexão no processo de ensino e aprendizagem.

• Para reforçar a ideia da figura geométrica plana trabalhada na atividade 4, providencie canudos e barbante em quantidade suficiente para todos os estudantes e proponha uma situação prática. Orienteos na passagem do barbante por dentro dos canudos e finalize a montagem com um nó, como mostra a imagem a seguir, para representar um triângulo.

• Ao ler o poema da atividade 4 com os estudantes e depois que eles apresentarem a resposta escrita, é incentivada a fluidez em leitura oral e a produção de escrita. Orienteos sobre a direção e o sentido que devem seguir para escrever. Verifique também como eles pegam no lápis e se o apoiam corretamente nos dedos, a fim de desenvolverem a escrita das letras e dos algarismos. Acompanhe os que apresentarem maior dificuldade e, se julgar conveniente, peça a algum deles que explique os movimentos realizados para executar os traçados desses registros.

• O ato de pintar apenas as partes da imagem com formato de triângulo, no item A da atividade 4, envolve principalmente a visão e o tato. A primeira para percepção da cor, do formato do desenho e da composição final, enquanto o segundo é essencial para o controle do lápis e a pressão exercida no papel, promovendo a inclusão de estudantes com NEE e contribuindo para uma aprendizagem multimodal que pode ser mais eficaz para alguns.

4. LEIA O POEMA A SEGUIR.

UM POEMA PARA OS TRIÂNGULOS

UM, DOIS, TRÊS!

TRÊS LADOS ELE TEM. UMA PONTA É PONTUDA, AS OUTRAS DUAS

SÃO TAMBÉM. [...]

SERGIO LIMA/ARQUIVO DA EDITORA HELOÍSA PINTARELLI/ARQUIVO DA EDITORA

i6207_1p012m_g27_e002 RESGATE resgatar ilustração de triângulo veio de: g23_ftd_mp_1bam_p108 código antigo i2487zz_1bam_g23_ftd

LALAU. UM POEMA PARA OS TRIÂNGULOS. EM: LALAU. HIPOPÓTAMO, BATATA FRITA, NARIZ: TUDO DEIXA UM POETA FELIZ! SÃO PAULO: DCL, 2009.

A ) PINTE APENAS AS PARTES DA IMAGEM COM FORMATO DE TRIÂNGULO.

Resposta nas orientações ao professor

Resposta

B ) A SILHUETA DE QUAL ANIMAL APARECEU APÓS A PINTURA?

Resposta: A SILHUETA DE UM PÁSSARO.

SILHUETA: DESENHO COM POUCOS DETALHES QUE REPRODUZ O FORMATO DE ALGO, COMO SOMBRA.

ATIVIDADE EXTRA

Desenhe, na lousa, a figura a seguir. Em seguida, desafie os estudantes a identificarem quantos triângulos estão representados nela.

Resposta Esperase que os estudantes identifiquem 5 triângulos.

5. UTILIZANDO PAPEL COLORIDO, CARLOS RECORTOU ALGUMAS FIGURAS QUE LEMBRAM QUADRADOS E RETÂNGULOS. DEPOIS, ELE COLOU ESSAS FIGURAS E OBTEVE O DESENHO DE UM ÔNIBUS.

PEDAÇOS DE PAPEL RECORTADOS.

Resposta: A: 3 QUADRADOS; B: 4 RETÂNGULOS.

MONTAGEM PRONTA.

COMPLETE O QUADRO COM A QUANTIDADE DE QUADRADOS E RETÂNGULOS UTILIZADOS NO DESENHO DO ÔNIBUS.

B. A. QUADRADOS.

6. O ARTISTA VICTOR VASARELY É FAMOSO PELO USO DE FIGURAS GEOMÉTRICAS EM VÁRIAS DE SUAS OBRAS. CONTORNE AS IMAGENS COM OS NOMES DAS FIGURAS GEOMÉTRICAS PLANAS QUE VOCÊ

CONSEGUE IDENTIFICAR NESTA OBRA DE ARTE.

RETÂNGULOS.

PARTICIPAÇÕES DE FOLCLORE PLANETÁRIO Nº 1, DE VICTOR VASARELY. RESINA, ÍMÃ, POLIESTIROL, ESPUMA DE POLIURETANO, ESPUMA DE POLIESTIRENO EXPANDIDO. 1969. UNIVERSIDADE DE EAST ANGLIA, NORFOLK, REINO UNIDO.

SERGIO LIMA/ARQUIVO DA EDITORA ILUSTRAÇÕES: SERGIOLIMA/ARQUIVO DA EDITORA

QUADRADO. CÍRCULO. TRIÂNGULO.

Resposta: Os estudantes devem contornar CÍRCULO e QUADRADO.

195

03/10/2025 09:47:36

• Caso os estudantes apresentem dúvidas na realização da atividade 5, mostre outras imagens compostas de figuras geométricas planas. Desenhe as figuras na lousa ou reproduzaas em uma folha e entregue a eles para que identifiquem a quantidade das figuras geométricas planas presentes. Observe um exemplo da imagem de um cachorro formado por figuras geométricas planas.

• A obra de arte apresentada na atividade 6 possui dimensões 52,8 cm × 52,8 cm. No entanto, essa informação foi omitida no Livro do Estudante pelo fato de eles ainda não conhecerem números decimais. Verifique a possibilidade de pesquisar e apresentar outras obras desse artista durante a resolução dessa e da próxima atividade, observando quais figuras geométricas planas eles conseguem identificar. Ao ler os nomes das figuras geométricas planas escritas por extenso, os estudantes desenvolvem a fluência em leitura oral e vocabulário.

• Para trabalhar com a atividade 7, organize os estudantes em duplas ou trios e entregue uma folha de papel por grupo. Auxilieos a dividir os trabalhos entre eles e a desenhar as figuras geométricas planas. Organize com eles a maneira de expor os trabalhos, que pode ser dentro da sala de aula, em algum espaço na escola ou em outros lugares. Orienteos a observar e respeitar o trabalho dos colegas.

• Para garantir maior inclusão na proposta da atividade 7 para estudantes com deficiência auditiva ou síndrome de Down, uma possibilidade é oferecer uma oportunidade concreta, uma vez que eles tendem a ter dificuldades com propostas abstratas. Para isso, reproduza e entregue a eles imagens de figuras geométricas planas e solicite que criem alguma composição por meio de colagens no caderno, facilitando a compreensão do enunciado em relação à imagem.

• Verifique se os estudantes identificam os nomes das figuras geométricas planas que aparecem na atividade 8. Caso apresentem dificuldade com a escrita, escreva na lousa os nomes, evidenciando o movimento com a mão e a direção do traçado para a escrita, e solicitelhes que preencham o diagrama com esses nomes.

EXPERIMENTE

7. JUNTE-SE A UM COLEGA E FAÇAM UM DESENHO EM UMA FOLHA DE PAPEL, COM FIGURAS QUE LEMBREM AS FIGURAS

GEOMÉTRICAS PLANAS QUE ESTAMOS ESTUDANDO. O DESENHO PODE SER INSPIRADO NA OBRA DO ARTISTA VICTOR VASARELY.

DEPOIS, COM A TURMA, REALIZEM UMA EXPOSIÇÃO COM OS TRABALHOS QUE FIZERAM.

Resposta pessoal. Comentários nas orientações ao professor

8. COMPLETE O DIAGRAMA ESCREVENDO O NOME DE CADA FIGURA

GEOMÉTRICA PLANA.

B. C.

Resposta: Os estudantes devem escrever o nome das seguintes figuras geométricas planas, A: TRIÂNGULO; B: QUADRADO; C: CÍRCULO; D: RETÂNGULO.

9. NA ESCOLA DE ISAQUE, FOI REALIZADA UMA FEIRA CULTURAL DOS ESTADOS BRASILEIROS. ELE É BAIANO E APRESENTOU NA FEIRA UM MURAL COM ALGUMAS INFORMAÇÕES, FOTOGRAFIAS E A BANDEIRA DO ESTADO ONDE NASCEU.

A ) EM QUAL ESTADO ISAQUE NASCEU?

Resposta: BAHIA.

B ) QUAIS FIGURAS GEOMÉTRICAS PLANAS PODEMOS IDENTIFICAR NA BANDEIRA DO ESTADO ONDE ELE NASCEU?

Resposta: Os estudantes podem identificar as seguintes figuras: quadrado, triângulo e retângulo.

EXPERIMENTE

Resposta pessoal. Espera-se que os estudantes façam o desenho das bandeiras tendo como referências as figuras geométricas planas estudadas até o momento. Confira instruções acerca desta atividade nas orientações ao professor

10. JUNTE-SE A UM COLEGA E FAÇAM UM DESENHO EM UMA FOLHA DE PAPEL REPRODUZINDO A BANDEIRA DOS OUTROS ESTADOS BRASILEIROS. DEPOIS, COM A TURMA, REALIZEM UMA EXPOSIÇÃO COM OS TRABALHOS.

AVALIANDO

Objetivo

Identificar e nomear figuras geométricas planas.

Sugestão de intervenção

Solicite aos estudantes que representem, por meio de um desenho, quatro objetos do seu cotidiano que se pareçam com as figuras geométricas planas que acabamos de estudar. Em seguida, digalhes para nomear os objetos desenhados com o nome da figura geométrica plana com que se parecem. Caso os estudantes

03/10/2025 09:48:53

apresentem dificuldades ao realizar esta atividade, escreva na lousa o nome das figuras planas e auxilie no esclarecimento de possíveis dúvidas.

• Amplie a atividade 9 apresentando as bandeiras dos estados brasileiros para que os estudantes possam encontrar a imagem da bandeira do estado em que nasceram. Proponha a eles que pesquisem, por exemplo, os principais pontos turísticos desse estado e, depois, façam um cartaz destacandoos. Aproveite e orienteos a identificar as figuras geométricas planas nas imagens das bandeiras.

• Na atividade 10, verifique se os estudantes utilizam as figuras geométricas planas que aparecem em bandeiras dos estados brasileiros. Dê algumas instruções para as duplas, como: inicie fazendo uma pesquisa para saber as cores e os formatos de cada bandeira. Se a escola tiver laboratório de informática, verifique a possibilidade de ir até lá com os estudantes para pesquisarem on-line, mas caso não tenha, é possível buscar as informações em livros na biblioteca da escola. Após a pesquisa, comece o desenho das bandeiras pelo seu formato geral, para só depois inserir os detalhes e, por fim, as cores. Cada dupla pode optar por utilizar régua, lápis, canetas ou pincéis. Depois de pronto, para expor os trabalhos das duplas, proponha aos estudantes a organização das bandeiras em ordem alfabética ou por região. Aproveite para perguntar a eles: “Quais figuras geométricas aparecem nas bandeiras?”; “Qual mais se repetiu?”; “E qual figura geométrica menos apareceu nas bandeiras?”.

• Um possível trabalho com este tópico é levar para a sala de aula alguns objetos que os estudantes possam contornar, como Tiago fez na atividade 1, e identificar as figuras geométricas planas. Outra possibilidade é reproduzir moldes desses objetos em folhas de papel e montar para eles contornarem enquanto observam os exemplos do tópico. Se julgar conveniente, conduza a escrita do nome da figura geométrica plana que observaram no papel em que foi feito o contorno.

• Ao resolver a atividade 1, pergunte aos estudantes o que aconteceria caso Tiago utilizasse outra face da caixa. Verifique se eles observam que, em qualquer face da caixa que lembra um cubo, o contorno resulta em um desenho que lembra o quadrado.

BNCC

O trabalho com este tópico desenvolve a habilidade EF01MA14, ao solicitar que os estudantes identifiquem as figuras planas nos contornos das faces de figuras geométricas planas.

RECONHECENDO FIGURAS GEOMÉTRICAS PLANAS

1. VERIFIQUE COMO TIAGO USOU UMA CAIXA EM FORMATO DE CUBO PARA DESENHAR UM QUADRADO.

QUADRADO SENDO DESENHADO.

DESENHO DO QUADRADO CONCLUÍDO.

A ) MARQUE UM X NO OBJETO QUE TIAGO TAMBÉM PODE USAR PARA DESENHAR UM QUADRADO.

Resposta: Os estudantes devem marcar um X no CUBO MÁGICO.

CAIXA DE SAPATOS.

CONE DE SINALIZAÇÃO.

IMAGENS SEM PROPORÇÃO ENTRE SI.

CUBO MÁGICO. PASTA.

COPO.

BOLA.

B ) QUAL OBJETO DO SEU DIA A DIA VOCÊ ESCOLHERIA PARA DESENHAR UM QUADRADO?

Resposta pessoal. Sugestões de resposta: Dado; caixa com formato de cubo.

C ) EM SEU CADERNO, DESENHE UM QUADRADO USANDO O OBJETO QUE ESCOLHEU NO ITEM B.

Resposta pessoal. Espera-se que os estudantes providenciem e contornem o objeto escolhido e desenhem um quadrado.

2. USANDO OUTRA CAIXA QUE LEMBRA UM BLOCO RETANGULAR, TIAGO DESENHOU UM RETÂNGULO

RETÂNGULO SENDO DESENHADO.

A ) MARQUE UM X NOS OBJETOS QUE

DESENHO DO RETÂNGULO CONCLUÍDO.

TIAGO PODE USAR PARA DESENHAR UM RETÂNGULO.

IMAGENS SEM PROPORÇÃO ENTRE SI. Resposta: Os estudantes devem marcar

CAIXA DE PRESENTE.

BOLA.

CHAPÉU DE ANIVERSÁRIO.

LATA.

EMBALAGEM DE CREME DENTAL.

Resposta pessoal. Sugestões de resposta: Caixa com formato de bloco retangular; livro com formato de bloco retangular.

GARRAFA TÉRMICA.

B ) QUAL OBJETO DO SEU DIA A DIA VOCÊ ESCOLHERIA PARA DESENHAR UM RETÂNGULO?

C ) EM SEU CADERNO, DESENHE UM RETÂNGULO USANDO O OBJETO QUE ESCOLHEU NO ITEM B.

Resposta pessoal. Espera-se que os estudantes providenciem e contornem o objeto escolhido e desenhem um retângulo. um X na CAIXA DE PRESENTE e na EMBALAGEM DE CREME DENTAL.

REFERÊNCIAS COMPLEMENTARES

STOCCO, Kátia; DINIZ, Maria Ignez; CÂNDIDO, Patrícia. Figuras e Formas. São Paulo: Penso, 2014.

O livro aborda a Matemática de maneira lúdica e prazerosa, apresentando diferentes modos de perceber a realidade e as relações entre as figuras geométricas.

03/10/2025 09:49:02

• Para a atividade 2, desenhe o contorno de um objeto com uma das faces retangular para os estudantes observarem ou deixe que eles desenhem. Nesse caso, use objetos em que a face lembra um retângulo, tomando cuidado para que as medidas dos comprimentos dos lados desse objeto não sejam tão próximas, a fim de que eles não confundam com o quadrado. Verifique se perceberam a diferença entre a face quadrada e a face retangular não quadrada.

• Caso eles apresentem dúvidas, proponha a realização prática desta atividade. Para isso, providencie com antecedência objetos com formato de um bloco retangular para todos os estudantes.

• Para trabalhar com a atividade 3, desenhe o contorno de um objeto com uma das faces triangular e outro com uma das faces circular para os estudantes observarem ou deixe que eles desenhem. Caso os estudantes tenham dificuldades em identificar as figuras geométricas planas nas imagens apresentadas, uma opção é desenhar um retângulo, um quadrado e um círculo em seus cadernos e comparálos com as imagens da atividade.

• Durante o trabalho com a atividade do boxe Desafio a mais, verifique se os estudantes identificam que o triângulo e o quadrado foram contornados ao usar uma caixa que lembra uma pirâmide, e que apenas uma das caixas foi utilizada para obter os dois contornos. Uma maneira de reforçar esse entendimento é explicar que, da caixa que lembra uma pirâmide de base quadrada, é possível obter contornos parecidos com o triângulo e o quadrado. Pergunte se é possível obter um contorno semelhante a um triângulo de uma caixa que remete a um cubo. No item B desse desafio, ao solicitar que os estudantes es crevam os nomes das figuras geométricas planas, desenvolvese a produção de escrita.

ATIVIDADE EXTRA

Após trabalhar com as atividades deste tópico, faça o levantamento de exemplos, citados pelos estudantes, de outros objetos cujos contornos lembram um quadrado, um triângulo, um círculo e um retângulo. É esperado que eles citem objetos do seu cotidiano. Caso algum estudante mencione um objeto que os colegas não conheçam, motiveo a explicar seu formato para os colegas, explicando onde fica a face cujo contorno parece a figura geométrica indicada.

3. A PARTE DESTACADA DE VERDE NA FIGURA GEOMÉTRICA ESPACIAL LEMBRA UM TRIÂNGULO.

LIGUE CADA FIGURA GEOMÉTRICA ESPACIAL A SEGUIR À FICHA COM O NOME DA FIGURA GEOMÉTRICA PLANA DESTACADA DE VERDE.

CILINDRO.

CUBO. PARALELEPÍPEDO RETÂNGULO OU BLOCO RETANGULAR.

Resposta: Os estudantes devem ligar: CILINDRO ao CÍRCULO; CUBO ao QUADRADO; PARALELEPÍPEDO RETÂNGULO ou BLOCO RETANGULAR ao RETÂNGULO.

DESAFIO A MAIS

RAÍSSA UTILIZOU UMA EMBALAGEM E FEZ

DOIS DESENHOS EM UMA FOLHA DE PAPEL.

A ) CONTORNE A EMBALAGEM QUE RAÍSSA USOU.

Resposta: Os estudantes devem contornar a embalagem 1

1. 2. 3. 4.

B ) ESCREVA A SEGUIR OS NOMES DAS FIGURAS GEOMÉTRICAS PLANAS QUE OS DESENHOS OBTIDOS POR ELA LEMBRAM.

Resposta: Os estudantes devem escrever nos quadros, em letra cursiva, os nomes: Triângulo; Quadrado.

Professor, professora: Oriente os estudantes na escrita das palavras que respondem ao item B do desafio, incentivando o traçado em letra cursiva na pauta apresentada.

AVALIANDO

Objetivo

Relacionar figuras geométricas planas com o contorno de faces de peças com formatos de figuras geométricas espaciais.

Sugestão de intervenção

Leve blocos de madeira que tenham formato de figuras geométricas espaciais ou materiais equivalentes para a sala de aula e organize os estudantes em grupos de até três integrantes. Deixeos manusear as peças por algum tempo. Perceba as dificuldades deles e acolha com

atenção e respeito os comentários de todos, buscando identificar os momentos coerentes de intervenção para superar os obstáculos de aprendizagem. Depois, orienteos a contornar cada peça e identificar quais figuras geométricas planas surgiram do contorno. Em seguida, solicite que nomeiem esses contornos desenhados com o nome da figura geométrica plana. Caso apresentem dificuldade, escreva na lousa os nomes das figuras planas e auxilie no esclarecimento de possíveis dúvidas.

DIVIRTA-SE E APRENDA

TRILHA DAS FIGURAS GEOMÉTRICAS

VAMOS FAZER UMA TRILHA?

PLANAS

COM ESTE JOGO, VOCÊ VAI TESTAR SEUS CONHECIMENTOS SOBRE AS FIGURAS GEOMÉTRICAS PLANAS. PARA ISSO, JUNTE-SE A TRÊS COLEGAS. VOCÊS VÃO PRECISAR DOS PEÕES, DO TABULEIRO E DO DADO DAS PÁGINAS 283 A 287 DO MATERIAL COMPLEMENTAR

REGRAS

• DECIDAM QUAL PEÃO CADA JOGADOR VAI REPRESENTAR E QUEM DEVE INICIAR A PARTIDA. DEPOIS, POSICIONEM OS PEÕES NA CASA SAÍDA DO TABULEIRO.

• O JOGADOR, NA SUA VEZ, LANÇA O DADO. O NÚMERO SORTEADO REPRESENTARÁ A QUANTIDADE DE CASAS QUE ELE VAI AVANÇAR COM O SEU PEÃO NO TABULEIRO.

• A CASA EM QUE O PEÃO DO JOGADOR PARAR ESTARÁ REPRESENTADA POR UMA FIGURA GEOMÉTRICA PLANA. SE O JOGADOR DISSER O NOME CORRETO DA FIGURA, PERMANECE NESSA CASA. CASO CONTRÁRIO, DEVE RETORNAR PARA SUA POSIÇÃO ANTERIOR NO TABULEIRO.

• VENCE A PARTIDA QUEM ATINGIR PRIMEIRO A LINHA DE CHEGADA

CONCLUSÃO

Acompanhar o desenvolvimento dos estudantes é fundamental para um ensino bemsucedido. Ao longo da unidade, foram propostas diversas maneiras de avaliar a aprendizagem da turma e a fim de realizar um monitoramento mais abrangente e organizado, registre nos relatórios individuais ou nas fichas de avaliação o desempenho de cada estudante, levando em consideração suas particularidades. Um modelo desse tipo de ficha pode ser encontrado no tópico Avaliação

deste Manual do Professor. Assim, será possível visualizar de modo individual as trajetórias de aprendizagem, incluindo os avanços e os pontos de dificuldades a serem sanados por meio de atividades que promovam recuperação dos conteúdos. Esse método de verificar a progressão dos estudos e identificar o que a turma de fato conseguiu aprender e o que ficou com lacunas de absorção é de grande importância para que seja possível repensar estratégias em sala de aula, tornando as ações pedagógicas cada vez mais eficazes.

• A seção Divirta-se e aprenda desta página propõe um jogo no qual os participantes devem identificar e nomear as figuras geométricas presentes nas casas do tabuleiro.

• O objetivo do jogo é motivar o desenvolvimento do raciocínio lógico, da observação e da capacidade de identificar, nomear e diferenciar figuras geométricas planas, de maneira lúdica e significativa.

• Oriente os a recortar e montar os moldes das peças que serão utilizadas como marcadores, assim como o tabuleiro e o dado disponíveis na seção Material complementar do final do Livro do Estudante, auxiliandoos na montagem do jogo. Verifique se eles compreenderam como jogar, sanando as possíveis dúvidas.

• Complemente o estudo da unidade propondo aos estudantes o desafio a seguir. Verifique se eles analisam atentamente as informações fornecidas e se interpretam o que está sendo solicitado. Esperase que eles percebam que a figura geométrica plana em questão é o triângulo, reconhecendo suas características.

Sugestão de Desafio

Sou uma figura geométrica plana que tem três lados. Quem sou eu?

Resposta

A figura geométrica plana é o triângulo.

03/10/2025 09:49:02

A conclusão da unidade é o momento de avaliar se os objetivos por ela propostos foram alcançados. Para esse diagnóstico, observe no final deste Manual do Professor algumas possibilidades de avaliação formativa que permitem realizar o monitoramento da aprendizagem dos estudantes e intervir caso eles não tenham atingido os resultados esperados.

1. Objetivos

Compor valores monetários usando cédulas e moedas do Real.

Comparar valores monetários a partir da noção de adição.

Reconhecer e relacionar valores de cédulas e moedas para resolver problemas em contextos simples. Sugestão de intervenção

Para realizar essa atividade, organize os estudantes em duplas e incentive-os a trocar estratégias de resolução. Se julgar conveniente, oriente-os a usar as cédulas e moedas do Real, recortadas do Material complementar e usadas na unidade 6. Enfatize a necessidade de guardar esse material, a fim de aproveitá-lo em outras unidades deste volume.

2. Objetivo

Reconhecer figuras geométricas planas. Sugestão de intervenção

Identifique se os estudantes são capazes de reconhecer as figuras que formam o corpo do palhaço e avalie a necessidade de apresentar objetos nos quais seja possível reconhecer as figuras geométricas planas no contorno de sua superfície, a fim de consolidar essa ação de reconhecimento. Uma possibilidade é providenciar peças do tangram, de blocos lógicos e de outros jogos com esses formatos, para que eles possam identificar as figuras geométricas planas estudadas. Permita-lhes brincar com as peças cujos formatos eles reconhecem, formando alguns desenhos. Conforme o reconhecimento, incentive-os a fazer associação com a nomenclatura dessas figuras para posterior correspondência.

VAMOS AVALIAR O APRENDIZADO

1. ROBERTO E VANESSA ECONOMIZARAM PARTE DO DINHEIRO QUE RECEBERAM DOS PAIS.

A ) COMPLETE O QUADRO COM A QUANTIA EM REAIS QUE ELES TÊM NO MOMENTO.

IMAGENS SEM PROPORÇÃO ENTRE SI. QUANTIDADE DE CÉDULAS E MOEDAS

NOME

ROBERTO VANESSA

QUANTIA TOTAL EM REAIS

B ) AO TODO, QUANTOS REAIS ROBERTO E VANESSA TÊM NO MOMENTO? REAIS.

QUANTIDADE DE CÉDULAS DE 10 REAIS

QUANTIDADE DE MOEDAS DE 1 REAL

Resposta: 13 + 5 = 18 18 REAIS.

2. ESCREVA OS NOMES DE TODAS AS FIGURAS GEOMÉTRICAS PLANAS QUE ESTÃO REPRESENTADAS NO DESENHO DO PALHAÇO.

Resposta: Retângulo, quadrado, círculo, triângulo.

1. A) Resposta: Roberto: quantidade de cédula de 10 reais: 1; quantidade de moedas de 1 real: 3. Vanessa: quantidade de cédulas de 10 reais: 0; quantidade de moedas de 1 real: 5

3. COMPLETE AS ADIÇÕES COM OS NÚMEROS QUE FALTAM DE ACORDO COM AS QUANTIDADES DE OBJETOS DE CADA ITEM. DEPOIS, RESPONDA ÀS QUESTÕES.

A. 10

Resposta: 10; 6; 10 + 6 = 16

• OS NÚMEROS QUE REPRESENTAM AS QUANTIDADES DE BONÉS SÃO PARES OU ÍMPARES?

Resposta: PARES.

• O RESULTADO DA ADIÇÃO DESSES NÚMEROS É UM NÚMERO

PAR OU ÍMPAR?

Resposta: PAR.

B. 10 + = 15 + =

Resposta: 15; 3; 15 + 3 = 18

• OS NÚMEROS QUE REPRESENTAM AS QUANTIDADES DE

CANECAS SÃO PARES OU ÍMPARES?

Resposta: ÍMPARES.

• O RESULTADO DA ADIÇÃO DESSES NÚMEROS É UM NÚMERO PAR OU ÍMPAR?

Resposta: PAR.

3. Objetivo

Desenvolver as habilidades de contar, adicionar e classificar números em par ou ímpar.

03/10/2025 09:49:57

Sugestão de intervenção

Retome os conceitos abordados nessa atividade e, para reforçá-los, apresente aos estudantes situações-problema que sejam pautadas na realidade deles. Em seguida, desenhe um quadro na lousa, a fim de que eles possam identificar em outras adições a generalização abordada. Essa atividade permite também avaliar se os estudantes compreendem que a soma de dois números ímpares resulta em um número par, e a organização a seguir pode contribuir para isso.

CLASSIFICAÇÃO DA SOMA DE DUAS PARCELAS EM PAR OU ÍMPAR

PARCELA PARCELA SOMA PAR OU ÍMPAR

ILUSTRAÇÕES:

OBJETIVOS DA UNIDADE

• Resolver situações-problema que envolvam as ideias de retirar, separar, comparar e completar da subtração.

• Reconhecer o símbolo que representa a subtração.

• Efetuar subtrações sem reagrupamento com resultado até 99.

• Efetuar cálculo mental e estimativas em cálculos de subtrações simples.

• Identificar os elementos faltantes em sequências recursivas de números naturais por meio da subtração.

• Reconhecer e diferenciar números pares e ímpares.

• Ler e interpretar dados expressos em tabelas e transferi-los para gráficos de colunas.

• Resolver situações-problema envolvendo subtração.

INTRODUÇÃO E

JUSTIFICATIVA

Nesta unidade, os estudantes são convidados a explorar as ideias associadas à subtração, que são: retirar, separar, comparar e completar quantidades.

As propostas de atividades favorecem a compreensão dos conceitos da subtração, permitem que os estudantes realizem cálculos sem reagrupamento, elaborem e resolvam problemas contextualizados, com suporte de imagens, material manipulável, utilizando estratégias e modos de registros pessoais.

São apresentadas algumas atividades que envolvem o trabalho com sequências numéricas, nas quais é possível reconhecer os padrões e as regularidades por meio de cálculos subtrativos. Além disso, são propostas situações de compra com troco para efetuar um pagamento, envolvendo valores do sistema monetário expressos em cédulas e moedas, além de

UNIDADE9 SUBTRAÇÃO

explorar a interpretação de dados em tabela e gráfico, entre outras habilidades que permitem desenvolver o pensamento numérico, sob diferentes perspectivas, buscando compreensão e organização, bem como o desenvolvimento de aprendizagens significativas.

Habilidades da BNCC trabalhadas na unidade:

EF01MA06 , EF01MA08 , EF01MA10 , EF01MA19 e EF01MA21

SUGESTÃO DE ESTRATÉGIA INICIAL

Reúna os estudantes em duplas e oriente cada um deles a escrever o primeiro nome em uma

folha de papel. Em seguida, oriente-os a contar quantas letras tem cada nome e depois a comparar quantas letras um nome tem a mais ou a menos do que o outro. Caso haja duplas com a mesma quantidade de letras nos nomes, mostre-lhes que apresentam a mesma quantidade. Por fim, escreva na lousa os nomes com a maior e com a menor quantidade de letras. Com a ajuda deles, faça questionamentos para comparar as quantidades, trabalhando os conceitos de “tem mais” e “tem menos”.

CRIANÇAS JOGANDO DAMAS.

DAMAS É UM JOGO DE TABULEIRO MUITO CONHECIDO. PARA JOGAR, SÃO NECESSÁRIOS

DOIS PARTICIPANTES E CADA

UM DELES INICIA O JOGO COM 12 PEÇAS. VENCE QUEM CAPTURAR TODAS AS PEÇAS DO OUTRO JOGADOR.

quantas peças claras e quantas escuras há no tabuleiro e a descobrir quantas faltam. Registre as dificuldades que eles tiverem para retornar a essa questão após o estudo da unidade.

• Uma das propostas dessas questões é que os estudantes comparem as quantidades. É importante que eles notem que a expressão “a mais” não está necessariamente ligada à adição, mas sim à comparação de quantia. Use o momento para discutir sobre a importância do raciocínio matemático em jogos como damas e xadrez.

• Ao final da questão 3, se for possível, promova um momento para os estudantes jogarem damas. Não havendo tabuleiros e peças disponí-

NO MOMENTO DA CENA, QUEM ESTÁ COM MAIS

PEÇAS NO TABULEIRO: O JOGADOR COM AS PEÇAS

CLARAS OU O JOGADOR

COM AS ESCURAS?

Resposta:

NO MOMENTO EM QUE ESSE JOGO FOI

FOTOGRAFADO, QUANTAS

PEÇAS ESCURAS

JÁ HAVIAM SIDO CAPTURADAS?

Resposta: Duas.

VOCÊ JÁ JOGOU DAMAS?

SE SIM, CONTE ESSA

EXPERIÊNCIA PARA OS COLEGAS E O PROFESSOR.

Resposta pessoal. Comentários nas orientações ao professor.

O jogador com as peças claras. 205

03/10/2025 09:51:26

veis para o jogo, construa com eles tabuleiros de 64 casas, intercalando escuras e claras, usando cartolina e canetinhas coloridas. As peças do jogo poderão ser substituídas por 24 tampinhas de garrafa, sendo 12 escuras e 12 claras ou outras peças de sua preferência.

• O professor pode levar até a sala de aula um jogo de damas para que os estudantes manuseiem o tabuleiro e façam a contagem das peças e sua distribuição nele.

• Após ler o texto para os estudantes, fale sobre as regras do Jogo de damas. Inicialmente, é importante que eles mencionem o que já sabem sobre ele. Explique que o jogo é praticado por dois jogadores e são utilizadas 12 peças claras e 12 peças escuras. Cada peça se movimenta em diagonal, sobre as casas escuras, para a frente e uma casa por vez. Isso só não acontece quando uma peça é tomada do adversário, quando a peça de um jogador “salta” sobre a do adversário e ocupa a casa vazia imediatamente depois dela, movimento que pode ser sequencial. Nesse caso, o jogador coloca a sua peça na casa vazia e recolhe a peça do adversário. Toda peça que chega à oitava linha do tabuleiro é promovida a “dama”, podendo mover-se pelo tabuleiro por quantas casas escuras quiser, para a frente ou para trás. Ganha o jogo aquele que capturar todas as peças do adversário ou impedi-las de se movimentar.

• Ao responderem à questão 1, verifique se os estudantes percebem que o jogador com mais peças está em vantagem, pois capturou mais peças do que seu oponente.

• Na questão 2, o objetivo é avaliar o conhecimento prévio dos estudantes a respeito do conteúdo que será estudado na unidade: a subtração. Como no início do jogo são 12 peças por jogador, oriente-os a contar

• Ao trabalhar com a atividade 1 , objetivando promover a inclusão dos estudantes com NEE, sugere-se uma abordagem multimodal, que envolva diferentes sentidos e favoreça a aprendizagem. No caso de estudantes com deficiência visual, cegos ou com baixa visão, por exemplo, é possível usar material concreto para representar as maçãs, sendo possível a manipulação.

• Durante a resolução desta atividade, dê atenção à maneira como os estudantes realizam a contagem. Verifique se eles contam as maçãs com algum tipo de organização. Outras atividades desta unidade vão explorar a habilidade de realizar contagens de modo organizado, mas é importante perceber quais estudantes apresentam dificuldades e que defasagens eles precisam superar. Pode ser interessante realizar a contagem das linhas e depois das colunas, mostrando maneiras de organizar os cálculos. Nos itens B e C da atividade 1, verifique como os estudantes compreendem o conceito de subtração, pois ela é uma das operações matemáticas que usamos com frequência, dentro e fora das salas de aula. Desse modo, para exercitar a compreensão do conceito de subtração, é importante que os estudantes consigam identificar situações nas quais deverão usar a subtração e entender o seu significado.

BNCC

A atividade 1 permite aos estudantes resolverem problemas de subtração associando a operação à ideia de retirar quantidades, expressando o resultado da subtração por meio de registro numérico, de modo a contemplar a habilidade EF01MA08

IDEIAS DA SUBTRAÇÃO

1. NA FRUTEIRA FORAM COLOCADAS ALGUMAS MAÇÃS.

A ) QUANTAS MAÇÃS HÁ NA FRUTEIRA?

Resposta: 8 MAÇÃS.

MAÇÃS.

B ) RÚBIA VAI RETIRAR DUAS MAÇÃS DESSA FRUTEIRA PARA FAZER UMA RECEITA. RISQUE NA IMAGEM A QUANTIDADE DE MAÇÃS QUE RÚBIA VAI RETIRAR.

Resposta: Os estudantes devem riscar 2 maçãs.

C ) PARA SABER A QUANTIDADE QUE VAI SOBRAR NA FRUTEIRA, EFETUAMOS UMA SUBTRAÇÃO, POIS UMA QUANTIDADE DE MAÇÃS SERÁ RETIRADA DO TOTAL DE MAÇÃS. OBSERVE E COMPLETE A FRASE A SEGUIR.

MAÇÃS MENOS MAÇÃS É IGUAL A MAÇÃS.

MENOS É IGUAL A

DICA: SÍMBOLO DE MENOS: SÍMBOLO DE IGUAL: =

Resposta: 8 MAÇÃS MENOS 2 MAÇÃS É IGUAL A 6 MAÇÃS; 8 MENOS 2 É IGUAL A 6 8 MENOS 2 É IGUAL A 6. VÃO SOBRAR 6 MAÇÃS NA FRUTEIRA.

QUANTIDADE DE MAÇÃS NA FRUTEIRA

QUANTIDADE DE MAÇÃS QUE RÚBIA VAI RETIRAR

VÃO SOBRAR MAÇÃS NA FRUTEIRA.

QUANTIDADE DE MAÇÃS QUE VAI SOBRAR NA FRUTEIRA MENOSÉ IGUAL A A SUBTRAÇÃO É UMA OPERAÇÃO MATEMÁTICA USADA PARA RETIRAR, COMPARAR E COMPLETAR QUANTIDADES.

2. JOSÉ TEM 6 LIVROS E O PRIMO DELE TEM 9 LIVROS.

PARA SABER QUANTOS LIVROS JOSÉ TEM A MENOS DO QUE SEU PRIMO, COMPARAMOS QUANTIDADES.

PARA COMPARAR QUANTIDADES, EFETUAMOS UMA SUBTRAÇÃO. OBSERVE E COMPLETE A FRASE A SEGUIR.

9 LIVROS MENOS 6 LIVROS É IGUAL A LIVROS.

MENOS É IGUAL A .

Resposta: 9 LIVROS MENOS 6 LIVROS É IGUAL A 3 LIVROS. 9 MENOS 6 É IGUAL A 3. 9 − 6 = 3. PORTANTO, JOSÉ TEM 3 LIVROS A MENOS DO QUE SEU PRIMO.

PORTANTO, JOSÉ TEM LIVROS A MENOS DO QUE SEU PRIMO.

3. DE ACORDO COM OS ANIMAIS APRESENTADOS, FAÇA O QUE SE PEDE.

A ) COMPLETE O NOME DE CADA UM DOS ANIMAIS COM AS LETRAS QUE FALTAM.

Resposta: GALINHA; GATO.

B ) COMPLETE AS FRASES COM AS QUANTIDADES CORRETAS.

• A PALAVRA GALINHA TEM LETRAS.

Resposta: A PALAVRA GALINHA TEM 7 LETRAS.

• A PALAVRA GATO TEM LETRAS.

Resposta: A PALAVRA GATO TEM 4 LETRAS.

• 7 LETRAS MENOS 4 LETRAS É IGUAL A LETRAS.

Resposta: 7 LETRAS MENOS 4 LETRAS É IGUAL A 3 LETRAS.

• A PALAVRA GALINHA TEM LETRAS A MAIS DO QUE A PALAVRA GATO

Resposta: A PALAVRA GALINHA TEM 3 LETRAS A MAIS DO QUE A PALAVRA GATO.

• A PALAVRA GATO TEM LETRAS A MENOS DO QUE A PALAVRA GALINHA

Resposta: A PALAVRA GATO TEM 3 LETRAS A MENOS DO QUE A PALAVRA GALINHA.

ATIVIDADE EXTRA

Aproveite a atividade 3 e oriente os estudantes a compararem as palavras “professor” e “professora” e dizerem qual delas tem mais letras. Então, usando o mesmo procedimento, solicite que indiquem quantas letras a menos tem a palavra “ensino” comparada com a palavra “dedicação”. Por fim, oriente-os a citar uma palavra com duas letras a menos do que o primeiro nome deles e a registrar as quantidades escrevendo os números que as representam.

BNCC

03/10/2025 09:51:26

Ao abordarem comparação de quantidades, efetuando uma subtração, e a escrita do resultado por meio de registro numérico, as atividades 2 e 3 possibilitam o desenvolvimento da habilidade EF01MA08

• A atividade 2 pode ser realizada na prática, representando as quantidades com palitos, tampinhas ou com outros materiais de contagem. Como a ideia da atividade não é de retirar, utilize a comparação das quantidades para efetuar o cálculo. Caso os estudantes apresentem dificuldade, proponha que um deles segure nove objetos de contagem enquanto outro segura seis. Depois, pergunte quem tem mais objetos e como poderíamos descobrir a quantidade a mais.

• A atividade 3 convida os estudantes a completarem os nomes dos animais com as letras que faltam, trabalhando não apenas a ortografia, como também a ideia de comparar quantidades. Desse modo, eles deverão refletir sobre a grafia de palavras, relacionando com a operação matemática para comparar quantidades e incluindo novos conhecimentos aos que já apresentam. Se necessário, auxilie-os na leitura dos nomes dos animais. Leia o nome do primeiro animal e verifique se eles são capazes de ler sozinhos o nome do segundo animal. Em caso negativo, prossiga a leitura, no tempo adequado, auxiliando-os a reconhecer as palavras. Verifique também se conseguem efetuar corretamente a subtração e ofereça o apoio do material de contagem, se necessário.

ILUSTRAÇÕES:

• Na atividade 4, foi apresentada a ideia de retirar utilizando figuras, propiciando aos estudantes sentido e significado ao objeto matemático para construir sua autonomia. Verifique se eles compreenderam a ideia associada, como a de retirar quantidades. Para exercitar a compreensão do conceito de subtração, pode ser interessante que eles representem as situações utilizando material de contagem, como palitos.

• Ao trabalhar com a atividade 5, oriente os estudantes a utilizarem a régua para efetuar as subtrações, chamando a atenção para o fato de que ela deve ser considerada da direita para a esquerda, já que os números são dispostos em ordem crescente. Por isso, confira as resoluções feitas por eles, conversando com a turma sobre as diferentes maneiras de resolver um mesmo exercício. Antes de propor a atividade, forneça outros exemplos de subtração utilizando a régua como recurso, para verificar a compreensão da estrutura do raciocínio.

BNCC

Na atividade 4 , os estudantes utilizam figuras para efetuar a subtração e apresentam o resultado por meio de registro numérico. Dessa maneira, eles desenvolvem a habilidade EF01MA08

Na atividade 5, eles realizam as subtrações utilizando a régua, após reconhecerem a maneira como os números estão dispostos, ou seja, da direita para a esquerda e em ordem crescente. Então, eles apresentam o resultado da subtração por meio de registro numérico. Dessa maneira, desenvolvem as habilidades EF01MA08 e EF01MA10.

5. A) Resposta: Os estudantes devem partir do número 7 na régua e “andar” 2 unidades para a esquerda. 7 − 2 = 5

DESENHEI 7 FIGURAS E, DEPOIS, RISQUEI 4. AS FIGURAS QUE SOBRARAM SEM RISCAR SÃO O RESULTADO DA SUBTRAÇÃO.

7 − 4 = 3

ASSIM COMO MARA, EFETUE AS SUBTRAÇÕES A SEGUIR.

5. B) Resposta: Os estudantes devem partir do número 4 na régua e “andar” 3 unidades para a esquerda. 4 − 3 = 1 5. C) Resposta: Os estudantes devem partir do número 8 na régua e “andar” 4 unidades para a esquerda; 8 − 4 = 4

Professor, professora: Espera-se que os estudantes utilizem o mesmo método de subtração efetuado por Mara. Oriente-os a desenhar as figuras e a riscá-las para a obtenção do resultado

A ) 5 − 2 =

Resposta: Os estudantes devem desenhar cinco estrelas e riscar duas; 5 − 2 = 3

B ) 6 − 3 =

Resposta: Os estudantes devem desenhar seis estrelas e riscar três; 6 − 3 = 3

5. A PROFESSORA PEDIU A ROGER QUE CALCULASSE 8 − 3 UTILIZANDO UMA RÉGUA. PARA ISSO, ELE LOCALIZOU INICIALMENTE O NÚMERO 8 NA RÉGUA. DEPOIS, “ANDOU” 3 UNIDADES PARA A ESQUERDA E OBTEVE O RESULTADO.

4. VERIFIQUE COMO MARA EFETUOU 7 − 4 UTILIZANDO FIGURAS. −3

8 − 3 = 5

ASSIM COMO ROGER, JUNTE-SE A UM COLEGA E, UTILIZANDO UMA RÉGUA, EFETUE AS SUBTRAÇÕES.

A ) 7 − 2 =

B ) 4 − 3 =

C ) 8 − 4 =

5. D) Resposta: Os estudantes devem partir do número 5 na régua e “andar” 4 unidades para a esquerda; 5 − 4 = 1

E ) 10 − 8 =

F ) 9 − 5 =

5. F) Resposta: Os estudantes devem partir do número 9 na régua e “andar” 5 unidades para a esquerda; 9 − 5 = 4 das operações.

D ) 5 − 4 = 123456789101112131415 0 8

5. E) Resposta: Os estudantes devem partir do número 10 na régua e “andar” 8 unidades para a esquerda; 10 − 8 = 2

6. EM CADA QUADRO, FAÇA OS RISQUINHOS QUE FALTAM PARA COMPLETAR 10 UNIDADES. DEPOIS, COMPLETE AS FRASES E AS SUBTRAÇÕES.

PARA COMPLETAR 10 RISQUINHOS, FALTAM UNIDADES. A.

Resposta: Os estudantes devem desenhar 4 risquinhos.

Resposta: PARA COMPLETAR 10 RISQUINHOS, FALTAM 4 UNIDADES.

− 4 =

Resposta: 10 − 4 = 6

Resposta: Os estudantes devem desenhar 7 risquinhos.

PARA COMPLETAR 10 RISQUINHOS, FALTAM UNIDADES.

Resposta: PARA COMPLETAR 10 RISQUINHOS, FALTAM 7 UNIDADES.

Resposta: 10 − 7 = 3

7. JEAN VAI FAZER UM BOLO PARA SUA IRMÃ. PARA ISSO, ELE VAI USAR 3 OVOS DA CAIXA REPRESENTADA NA IMAGEM.

A ) QUANTOS OVOS HÁ NA CAIXA?

Resposta: 9 OVOS.

OVOS.

B ) QUANTOS OVOS JEAN VAI PRECISAR PARA FAZER O BOLO? OVOS.

Resposta: 3 OVOS.

C ) QUANTOS OVOS VÃO SOBRAR NA CAIXA APÓS O PREPARO DO BOLO?

SOBRARÃO OVOS NA CAIXA.

Resposta: 9 − 3 = 6; SOBRARÃO 6 OVOS NA CAIXA.

BNCC

A atividade 6 dessa página permite aos estudantes utilizarem desenhos para completar e descobrir a parte que falta para chegar ao todo e, então, apresentar o resultado da subtração por meio de registro numérico. Dessa maneira, eles desenvolvem a habilidade EF01MA08.

A atividade 7 permite que eles resolvam problemas de subtração associados à ideia de retirar quantidades, expressando o resultado da subtração por meio de registro numérico, contemplando, assim, a habilidade EF01MA08

03/10/2025 09:51:27

• No desenvolvimento da atividade 6 , incentive os estudantes a comentarem, com as próprias palavras, quais são as vantagens de desenhar para completar, na resolução de uma atividade de subtração. Verifique se eles compreendem a ideia de completar, ou seja, situações nas quais é necessário descobrir qual é a parte que falta para chegar ao todo. Novamente, pode ser interessante utilizar materiais manipulativos para a contagem nesses casos e, em seguida, efetuar o registro.

• Na atividade 7, proponha que os estudantes formem duplas e verifique que estratégia de resolução eles usaram. Caso apresentem dificuldades ao apresentarem suas respostas, relembre-os das estratégias utilizadas até aqui, a fim de construir um caminho de recuperação de conteúdo. Em caso de dificuldades, sugira que risquem a quantidade de ovos necessária para o preparo do bolo e, em seguida, analisem a quantidade de ovos que sobrou.

AVALIANDO

Objetivos

Compreender as ideias da subtração.

Efetuar subtrações com números até 10.

Sugestão de intervenção

Faça simulações usando os dedos das mãos com quantidades de 1 até 10. Apresente situações aos estudantes nas quais eles possam fazer os cálculos pensando primeiro no todo e depois tirando uma parte dele. Para finalizar, solicite que um de cada vez apresente uma situação na qual faz os cálculos utilizando os dedos das mãos pensando no todo e depois abaixando uma parte deles.

• Ao trabalhar a atividade 1, pergunte quais estudantes da turma gostam de jogar bola e se costumam acompanhar jogos de futebol. Incentive-os a contar quais regras do jogo de futebol eles conhecem.

• O objetivo do item A da atividade 1 é verificar se os estudantes sabem contar. Caso eles não saibam responder de imediato, convide-os a contar juntos, em voz alta, a quantidade de jogadores que aparecem na imagem. Caso note que a contagem ocorre sem ordem, proponha-a em fileiras, primeiro os que estão em pé e depois os que estão ajoelhados.

• Ao trabalhar com os itens B, C e D, certifique-se de que os estudantes conseguem determinar a quantidade de jogadores que ficaram em campo por meio da subtração e do registro do resultado.

BNCC

A atividade 1 permite aos estudantes resolverem problemas de subtração associados à ideia de retirar quantidades, expressando o resultado da subtração por meio de registro numérico, contemplando, assim, a habilidade EF01MA08

UM POUCO MAIS DE SUBTRAÇÃO

1. A EQUIPE DE FUTEBOL DE SAULO SE REUNIU PARA TIRAR UMA FOTOGRAFIA ANTES DA PARTIDA.

A ) QUANTOS JOGADORES APARECEM NA IMAGEM?

Resposta: 13

B ) NA IMAGEM A SEGUIR, APENAS ALGUNS JOGADORES NÃO ENTRARAM EM CAMPO.

BANCO DE RESERVAS

QUANTOS JOGADORES ESTÃO EM CAMPO?

Resposta: 11

C ) QUANTOS JOGADORES ESTÃO NO BANCO DE RESERVAS?

Resposta: 2

D ) PODEMOS DETERMINAR A QUANTIDADE DE JOGADORES QUE FICARAM EM CAMPO POR MEIO DE UMA SUBTRAÇÃO. COMPLETE AS FRASES COM OS NÚMEROS QUE FALTAM.

13 JOGADORES MENOS JOGADORES É IGUAL A JOGADORES.

Resposta: 13 JOGADORES MENOS 2 JOGADORES É IGUAL A 11 JOGADORES.

MENOS É IGUAL A

Resposta: 13 MENOS 2 É IGUAL A 11

UTILIZANDO SÍMBOLOS, ESCREVEMOS:

Resposta: 13 − 2 = 11. PORTANTO, 11 JOGADORES FICARAM EM CAMPO.

2. CELINA DETERMINOU O RESULTADO DO CÁLCULO 15 − 5 DA SEGUINTE MANEIRA.

A ) 16 − 4 = B ) 19 − 6 = 15 5 = 10

Resposta: 16 − 4 = 12. Os estudantes devem desenhar 16 tracinhos e riscar 4

DE MANEIRA SEMELHANTE, DETERMINE O RESULTADO DAS SUBTRAÇÕES A SEGUIR.

A. PORTANTO, JOGADORES FICARAM EM CAMPO.

Resposta: 19 − 6 = 13. Os estudantes devem desenhar 19 tracinhos e riscar 6

3. NAS SUBTRAÇÕES A SEGUIR, FORAM UTILIZADOS CUBINHOS E BARRAS PARA REPRESENTAR QUANTIDADES. DE ACORDO COM A QUANTIDADE DE CUBINHOS QUE NÃO FORAM RISCADOS EM CADA ITEM, COMPLETE AS SUBTRAÇÕES.

Resposta: 13 − 1 = 12

Resposta: 18 − 5 = 13

13 − = 13 − 1 = 17 − = 11 18 − = 13

ATIVIDADE EXTRA

Aproveite a atividade 2 e conduza os estudantes na resolução dos cálculos no caderno utilizando risquinhos para subtrair os itens a seguir.

• 17 3 =

• 12 0 =

•

• Na atividade 2, espera-se que os estudantes resolvam as subtrações representando as quantidades com traços e riscando a quantidade subtraída para obter o resultado. Ao final, eles deverão contar quantos traços não foram riscados para indicar o resultado da operação. Caso eles apresentem dificuldade na resolução, escreva na lousa os cálculos, determinando o resultado de 15 5, conforme a atividade. Uma opção também é utilizar material de contagem, como pedrinhas, tampinhas, botões ou palitos, para auxiliá-los na compreensão do cálculo.

• Para realizar a atividade 3, é possível usar os cubinhos e as barras que foram recortados anteriormente do Material complementar . Com eles, os estudantes podem conferir, na prática, os cálculos de subtração propostos, percebendo que a diferença é representada pela quantidade de cubos que não foram riscados em cada item da atividade. Oriente-os a retomar e usar esse material sempre que julgar conveniente.

BNCC

Resposta: 17 − 6 = 11

Nas atividades 2 e 3, os estudantes comparam quantidades efetuando uma subtração e apresentam o resultado por meio de registro numérico. Dessa maneira, eles desenvolvem a habilidade EF01MA08

03/10/2025 09:51:28

Respostas: 17 3 = 14

12 0 = 12

19 6 = 13

15 4 = 11

18 8 = 10

• A atividade 4 convida os estudantes a completarem cada uma das frases por meio de uma subtração. Assim, verifique se eles são capazes de ler sozinhos. Em caso negativo, prossiga a leitura, no tempo adequado, auxiliando-os a reconhecer as frases, e verifique se conseguem efetuar corretamente a subtração. Nesta atividade, o objetivo é utilizar a ideia de retirar. Dessa maneira, opte por usar um vocabulário que possibilite enfatizar que os animais saíram da cena ou se retiraram dela.

• Na atividade 4, com o intuito de que todos os estudantes participem da aula, é preciso realizar algumas adaptações e estratégias inclusivas, promovendo a inclusão de estudantes com NEE. Por exemplo, para os estudantes com deficiência visual, tanto os cegos quanto os de baixa visão, é necessário descrever as imagens, sempre tomando cuidado para que a fala seja pausada e tenha os detalhes essenciais à compreensão do que se pede.

• A atividade 5 trabalha a subtração com a ideia de separar. Incentive os estudantes a organizarem as informações do enunciado no boxe e, depois, a completarem o texto. Verifique se eles efetuam corretamente a subtração e compreendem o contexto proposto. Caso perceba dificuldades, retome brevemente o conteúdo e relembre os métodos vistos anteriormente para o cálculo da subtração, de maneira paciente e encorajadora, a fim de engajar a todos na atividade.

4. DE ACORDO COM AS CENAS EM CADA ITEM, COMPLETE AS FRASES E REPRESENTE CADA UMA DELAS POR MEIO DE UMA SUBTRAÇÃO.

CENA 1

CENA 2

A ) HAVIA CACHORROS NO GRUPO, MAS 2 DELES FORAM EMBORA.

Resposta: HAVIA 12 CACHORROS NO GRUPO, MAS 2 DELES FORAM EMBORA. 12 − 2 = 10. RESTARAM 10 CACHORROS.

= RESTARAM CACHORROS.

CENA 1

CENA 2

B ) HAVIA GATOS NO GRUPO, MAS DELES FORAM EMBORA.

Resposta: HAVIA 10 GATOS NO GRUPO, MAS 3 DELES FORAM EMBORA. 10 − 3 = 7. RESTARAM 7 GATOS.

RESTARAM GATOS.

5. PATRÍCIA COMPROU 18 ADESIVOS PARA COLAR EM SUA AGENDA. ELA SEPAROU 3 REPETIDOS E OS DEU PARA SUA IRMÃ. COM QUANTOS ADESIVOS PATRÍCIA FICOU? PATRÍCIA FICOU COM ADESIVOS.

Resposta: 18 − 3 = 15. PATRÍCIA FICOU COM 15 ADESIVOS.

AVALIANDO

Objetivos

Compreender as ideias da subtração. Efetuar subtrações com números até 19.

Sugestão de intervenção

A atividade 4 convida os estudantes a completarem as frases por meio de uma subtração utilizando abordagem comparativa entre as cenas para que, assim, reconheçam a quantidade retirada nos casos. Aproveite a oportunidade e trabalhe de modo que os estudantes participem da cena. Para isso, alguns deles podem ficar em pé e os que estiverem sentados devem contar a

quantidade de estudantes que estão em pé; depois, alguns que estão de pé sentam-se também, para que todos que estão sentados respondam quantos restaram em pé.

BNCC

Nas atividades 4 e 5, os estudantes realizam contagem e comparam quantidades, por meio de subtração, e apresentam o resultado em registro numérico. Dessa maneira, eles desenvolvem a habilidade EF01MA08

6. HOUVE UMA ELEIÇÃO PARA ESCOLHER O REPRESENTANTE DE TURMA DO 1º ANO. A QUANTIDADE DE VOTOS QUE CADA UM DOS CANDIDATOS RECEBEU FOI ANOTADA NA TABELA.

Unidades temáticas integradas

VOTOS RECEBIDOS PELOS CANDIDATOS A REPRESENTANTE DA TURMA DO 1º ANO

CANDIDATO JULIANALÚCIOOTÁVIOMÁRCIADANIELA

QUANTIDADE DE VOTOS 56 10 37

FONTE DE PESQUISA: ANOTAÇÕES DA PROFESSORA DO 1º ANO EM MARÇO DE 2027.

A ) QUEM GANHOU A ELEIÇÃO?

Resposta: OTÁVIO.

DICA: CADA ESTUDANTE VOTOU UMA ÚNICA VEZ.

B ) QUAL FOI A DIFERENÇA DE VOTOS ENTRE O CANDITADO MAIS VOTADO E O MENOS VOTADO? VOTOS.

Resposta: 10 − 3 = 7 7 VOTOS.

C ) COMPLETE O GRÁFICO A SEGUIR COM AS INFORMAÇÕES DA TABELA, PINTANDO UM QUADRINHO PARA CADA VOTO QUE OS CANDIDATOS RECEBERAM.

DICA: A COLUNA CORRESPONDENTE AOS VOTOS QUE JULIANA RECEBEU JÁ ESTÁ PINTADA.

Resposta: Os estudantes devem pintar, de baixo para cima, 6 quadrinhos para Lúcio, 10 quadrinhos para Otávio, 3 quadrinhos para Márcia e 7 quadrinhos para Daniela.

FONTE DE PESQUISA: ANOTAÇÕES DA PROFESSORA DO 1º ANO EM 2027.

RECEBIDOS POR

Quantidade

03/10/2025 09:53:17

• A atividade 6 promove uma integração entre as unidades temáticas de Matemática Números e Probabilidade e estatística, ao relacionar a contagem e a comparação de quantidades de votos com o registro, a leitura e a interpretação de uma tabela. Essa integração também é favorecida no item C, ao trabalhar a construção de um gráfico de barras.

• Se necessário, disponibilize materiais de contagem para auxiliar os estudantes na resolução dessa atividade. Por meio de questionamentos, confira se ainda apresentam dúvidas acerca das estratégias de cálculo de subtrações.

BNCC

Na atividade 6, os estudantes fazem a leitura e a interpretação da tabela. Dessa maneira, eles desenvolvem a habilidade EF01MA21

Candidato

MárciaDaniela

Otávio

Lúcio Juliana

• Ao trabalhar a atividade 7, verifique se os estudantes perceberam que o personagem tinha duas cédulas de 5 reais, totalizando 10 reais. Nesse caso, ele gastou 6 reais nessa compra e o troco corresponde à diferença entre a quantia que Fábio tinha e o que ele gastou. Eles devem aplicar a mesma estratégia nos demais itens. Amplie essa atividade propondo outras quantias e itens a comprar, envolvendo valores menores do que 20. Se necessário, utilize a representação das cédulas do Real que foram recortadas do Material complementar, a fim de auxiliar os estudantes a conferirem, na prática, situações de compra envolvendo troco como a desta página.

BNCC

Na atividade 7, os estudantes relacionam situações de compra e troco, envolvendo a operação de subtração, contemplando, dessa maneira, a habilidade EF01MA19

7. FÁBIO USOU DUAS CÉDULAS DE 5 REAIS PARA COMPRAR UM CADERNO EM UMA PAPELARIA.

IMAGENS SEM PROPORÇÃO ENTRE SI.

6 REAIS

FÁBIO CALCULOU QUANTOS REAIS VAI RECEBER DE TROCO.

CONTEI E MOSTREI 10 DEDOS. DEPOIS ESCONDI 6 DEDOS E VERIFIQUEI QUE SOBRARAM 4 DEDOS. ASSIM, VOU RECEBER 4 REAIS DE TROCO.

Resposta: 10 − 6 = 4

10 − =

ASSIM COMO FÁBIO, DETERMINE O TROCO NA COMPRA DE CADA ITEM A SEGUIR.

5 REAIS

Resposta: TROCO: 5 REAIS.

TROCO: REAIS.

6 REAIS

Resposta: TROCO: 1 REAL.

TROCO: REAL.

Professor, professora: Ao trabalhar com esta atividade, enfatize para os estudantes o cuidado que devemos ter ao manusear objetos como a tesoura, que precisam de atenção e supervisão de um adulto para evitar acidentes.

CADERNO.

COLA BASTÃO.

BORRACHA ESCOLAR.

8. ALICE E HEITOR UTILIZARAM ESTRATÉGIAS DIFERENTES PARA CALCULAR A SUBTRAÇÃO 9 − 6 COM OS DEDOS DAS MÃOS.

COM 6 DEDOS LEVANTADOS, COMPLETO ATÉ CHEGAR A 9.

NESSE CASO, PRECISEI LEVANTAR MAIS 3 DEDOS. ASSIM, 9 − 6 = 3.

9. C) Resposta: A operação de subtração depende dos números par e ímpar que os estudantes escolherem. Porém, independentemente dos números escolhidos pelos estudantes, espera-se que eles percebam, com base em experimentações, que o resultado de subtrações com essa característica terá sempre como resultado um número ímpar.

INICIALMENTE, LEVANTO 9 DEDOS. DEPOIS, ABAIXO 6 DEDOS, FICAM 3 DEDOS LEVANTADOS. PORTANTO, 9 − 6 = 3

FAÇA COMO ALICE OU HEITOR E RESOLVA AS SUBTRAÇÕES A SEGUIR.

• A atividade 8 aborda duas diferentes estratégias de cálculo usando os dedos das mãos. Resolva com a turma algumas subtrações por meio das duas estratégias apresentadas. Depois, pergunte qual eles preferem e permita que compartilhem com a turma.

Resposta: 9 − 4 = 5

B ) 10 − 3 = A ) 9 − 4 =

Resposta: 10 3 = 7

9. JUNTE-SE A UM COLEGA E FAÇAM O QUE SE PEDE.

A ) EFETUEM A SUBTRAÇÃO A SEGUIR.

Resposta: 16 5 = 11

16 − 5 =

B ) NO CÁLCULO DO ITEM A, O NÚMERO 16 É PAR E O NÚMERO 5 É ÍMPAR. O RESULTADO DESSA SUBTRAÇÃO É UM

NÚMERO PAR OU ÍMPAR?

Resposta: ÍMPAR.

C ) ESCREVAM E RESOLVAM, NO CADERNO, OUTRA SUBTRAÇÃO ENVOLVENDO UM NÚMERO PAR E OUTRO ÍMPAR. DEPOIS, VERIFIQUEM SE A RESPOSTA OBTIDA POR VOCÊS É IGUAL À DO ITEM ANTERIOR.

BNCC

• Ao exercitarem o senso crítico e analítico na resolução da atividade 9, testando para constatar padrões e regularidades, os estudantes estão desenvolvendo a capacidade de investigar, organizar e comunicar informações relevantes, a fim de produzir argumentos convincentes, conforme orienta a Competência específica de Matemática 4 da BNCC.

03/10/2025 09:53:22

• A atividade 9 explora a capacidade dos estudantes de obterem conclusões com base em experimentações. Nesse caso, não é possível sistematizar uma conclusão apenas com os itens apresentados. Porém, a situação permite levantar questionamentos para motivá-los a testar outras subtrações, a fim de verificar e constatar padrões e regularidades. Com isso, eles desenvolverão a observação, além do senso crítico e analítico. Se os estudantes apresentarem dificuldades em aplicar o conceito de par e ímpar, escreva alguns números na lousa e distribua material de contagem, como palitos ou tampinhas de garrafas. Em seguida, instrua-os a separar esse material conforme a quantidade dos números apresentados, um por vez. Explique que eles devem agrupar o material dois a dois, conferindo, ao final, se todos os objetos ficaram agrupados ou se sobrou algum. Nos casos em que sobrar um elemento, o número representado é ímpar. Se necessário, mostre outras operações de subtração com números pares e ímpares, a fim de verificar se eles compreendem que, nesse tipo de operação, o resultado sempre resulta em um número ímpar.

• A atividade 10 propõe uma situação envolvendo a subtração com significado de retirar. No item A, os estudantes devem perceber que deverão calcular quantas caixinhas de leite sobraram na prateleira após a retirada feita pelo primeiro cliente. No item B, certifique-se de que eles compreenderam que devem efetuar uma segunda subtração considerando o resultado da primeira ( 17 6 = 11 ). Caso alguns estudantes apresentem dificuldades, entregue-lhes materiais de contagem, como tampinhas, palitos ou cubinhos do material dourado, a fim de que representem essa situação na prática.

• A atividade 11 trabalha uma situação que envolve o sistema monetário. Nesse sentido, os estudantes são levados a analisar, em um contexto do dia a dia, quantos reais faltam para Heitor comprar o brinquedo. Para tanto, é necessário que os estudantes realizem uma contagem para determinar a quantia, em reais, que Osmar já tem. Verifique as estratégias usadas pelos estudantes e incentive-os a resolver a atividade empregando duas estratégias diferentes. Ao final, mostre para a turma quais são elas.

BNCC

Na atividade 11, os estudantes reconhecem e relacionam valores de moedas e cédulas do sistema monetário brasileiro para resolver situações simples do cotidiano, contemplando, desse modo, a habilidade EF01MA19

10. NA PRATELEIRA DE UM MERCADO, HAVIA 17 CAIXINHAS DE LEITE E UM CLIENTE COMPROU 6 DESSAS CAIXINHAS. DEPOIS, OUTRO CLIENTE COMPROU MAIS 4 CAIXINHAS.

A ) QUANTAS CAIXINHAS DE LEITE FICARAM NA PRATELEIRA APÓS A COMPRA FEITA PELO PRIMEIRO CLIENTE?

CAIXINHAS.

Resposta: 17 − 6 = 11. 11 CAIXINHAS.

B ) E APÓS A SEGUNDA COMPRA? CAIXINHAS.

Resposta: 11 − 4 = 7 7 CAIXINHAS.

11. OSMAR ESTÁ ECONOMIZANDO PARA COMPRAR UM BRINQUEDO QUE CUSTA 18 REAIS. OBSERVE A SEGUIR O DINHEIRO QUE ELE JÁ TEM.

INFOGRÁFICO CLICÁVEL: FAZENDO COMPRAS NO SUPERMERCADO

QUANTOS REAIS FALTAM PARA OSMAR COMPRAR O BRINQUEDO? REAIS.

Resposta: 18 − 7 = 11. 11 REAIS.

SUBTRAÇÃO COM NÚMEROS ATÉ 99

1. PODEMOS EFETUAR 38 15 USANDO UM ÁBACO.

INICIALMENTE, REPRESENTAMOS O NÚMERO 38 COLOCANDO 8 CONTAS NA VARETA DAS UNIDADES E 3 CONTAS NA VARETA DAS DEZENAS.

COMO VAMOS SUBTRAIR 15 UNIDADES DE 38, RETIRAMOS 5 CONTAS DA VARETA DAS UNIDADES E 1 CONTA DA VARETA DAS DEZENAS. O NÚMERO REPRESENTADO NO ÁBACO CORRESPONDE AO RESULTADO DA SUBTRAÇÃO.

A ) QUAL FOI O RESULTADO OBTIDO?

D U

B ) EFETUE AS SUBTRAÇÕES A SEGUIR. PARA ISSO, DESENHE NO ÁBACO AS CONTAS CORRESPONDENTES. DEPOIS, RISQUE AS QUE FOREM RETIRADAS.

Resposta: Em cada ábaco, os estudantes devem desenhar, inicialmente, as contas correspondentes ao minuendo e, depois, riscar as contas que representam a quantidade indicada no subtraendo. 45 12 = 33; 16 11 = 5; 91 80 = 11; 63 22 = 41

• A atividade 1 visa reforçar a compreensão da subtração por meio do ábaco. Se possível, leve alguns ábacos para a sala de aula a fim de que os estudantes possam efetuar as subtrações na prática. O ábaco pode ser considerado uma das calculadoras mais antigas utilizadas pelo ser humano, visto que permite fazer operações de adição e de subtração de maneira parecida com a prática do cálculo mental.

• Para a realização dessa atividade, utilize o ábaco de papel e as contas que foram recortados anteriormente do Material complementar, a fim de auxiliar os estudantes a conferir, na prática, como efetuar os cálculos de subtração utilizando esse recurso.

• No item B da atividade 1, verifique como os estudantes compreendem o conceito de subtração e a ideia de retirar quantidades. Desse modo, para exercitar a compreensão do conceito de subtração, é importante que eles consigam identificar situações nas quais deverão usar a subtração e entender o significado dessa operação.

BNCC

• A atividade 2 apresenta duas maneiras de efetuar a mesma subtração. Diante disso, incentive os estudantes a comentarem, com as próprias palavras, quais são as vantagens de usar cubinhos e barras ou o quadro de ordens. Verifique qual das estratégias é mais comum aos estudantes e se eles compreendem a ideia de completar, ou seja, quando é necessário descobrir a parte que falta para chegar ao todo. Se necessário, utilize as representações de cubinhos e barras recortados anteriormente do Material complementar, com o objetivo de auxiliar os estudantes a verificar, na prática, os agrupamentos e as trocas ao efetuarem cálculos envolvendo a operação de subtração.

• Caso eles apresentem dificuldades ao responderem quais são as vantagens das estratégias utilizadas na atividade, relembre-os do que foi aprendido até aqui e reforce a importância dos cubinhos, das barras e do quadro de ordens. Para isso, oriente o estabelecimento de comparações entre esses recursos, fazendo perguntas como: “Com quantos cubinhos formamos uma dezena?” e “Uma barra é formada por quantas dezenas?”. O objetivo é compreender a ideia de classificar os números quanto à sua ordem ou classe.

BNCC

A atividade 2 desta página permite o uso de estratégias para completar e descobrir a parte que falta para chegar ao todo, além de apresentar o resultado da subtração por meio de registro numérico. Dessa maneira, é desenvolvida a habilidade EF01MA08.

2. RAVI TEM 24 FOTOGRAFIAS E JÁ ORGANIZOU 13 DELAS EM UM ÁLBUM.

QUANTAS FOTOGRAFIAS AINDA FALTAM SER ORGANIZADAS?

PODEMOS DETERMINAR A QUANTIDADE DE FOTOGRAFIAS

EFETUANDO 24 − 13 .

OBSERVE DUAS MANEIRAS DE EFETUAR ESSA SUBTRAÇÃO E COMPLETE O QUE FALTA.

UTILIZANDO CUBINHOS E BARRAS

REPRESENTAMOS O NÚMERO 24 COM CUBINHOS E BARRAS.

DICA: OS CUBINHOS E AS BARRAS RISCADAS SIGNIFICAM QUE FORAM RETIRADOS.

RETIRAMOS 3 DAS 4 UNIDADES. DEPOIS, RETIRAMOS 1 DAS 2 DEZENAS. ASSIM, OBTEMOS O RESULTADO DO CÁLCULO.

UTILIZANDO O QUADRO DE ORDENS

SUBTRAÍMOS AS UNIDADES.

4 UNIDADES MENOS 3 UNIDADES

É IGUAL A UNIDADE.

Resposta: 24 − 13 = 11 1 DEZENA É IGUAL A 1 DEZENA. PORTANTO, AINDA FALTAM SER ORGANIZADAS 11 FOTOGRAFIAS.

DEPOIS, SUBTRAÍMOS AS DEZENAS.

2 4 – 1 3 U 24 − 13 =

2 DEZENAS MENOS 1 DEZENA

É IGUAL A DEZENA.

PORTANTO, AINDA FALTAM SER ORGANIZADAS FOTOGRAFIAS.

Resposta: 4 UNIDADES MENOS 3 UNIDADES É IGUAL A 1 UNIDADE; 2 DEZENAS MENOS

A ) REGISTRE NO QUADRO A QUANTIDADE DE INSETOS QUE APARECEM NA IMAGEM.

Resposta: BORBOLETA: 5; FORMIGA: 10; ABELHA: 4; TOTAL: 19

QUANTIDADE DE INSETOS

INSETO BORBOLETAFORMIGAABELHA TOTAL QUANTIDADE

Resposta: 19 INSETOS.

B ) QUANTOS INSETOS HÁ NA IMAGEM? INSETOS.

Resposta: 9 INSETOS.

C ) QUANTOS INSETOS ESTÃO VOANDO? INSETOS.

D ) COMPLETE A SUBTRAÇÃO PARA

DETERMINAR A QUANTIDADE DE INSETOS QUE NÃO ESTÃO VOANDO.

NÃO ESTÃO VOANDO INSETOS.

Resposta: 19 − 9 = 10. NÃO ESTÃO VOANDO 10 INSETOS.

1 9 – 9 U

03/10/2025 09:53:23

• Na resolução da atividade 3 , os estudantes têm contato com diferentes tipos de representações, como a organização de informações em quadros. • É possível que eles apresentem dificuldades para preencher o quadro. Nesse caso, auxilie-os como julgar conveniente. Se necessário, utilize material ou uma estratégia diferenciada de contagem, como riscar ou contornar os animais com cores diferentes.

BNCC

A atividade desta página propõe contagem e comparação de quantidades para completar a subtração. Desse modo, são contempladas as habilidades EF01MA06 e EF01MA08 Essa atividade também desenvolve o raciocínio lógico e o espírito de investigação, conforme descrito na Competência específica de Matemática 2 da BNCC.

• Durante a realização da atividade 4 , por meio de questionamentos, leve os estudantes a comentarem suas ações. Pergunte: “Que quantidade total está representada com o material dourado no item A?”; “Que quantidade foi riscada nessa imagem?”; “Que quantidade ficou sem riscar?”; O que essa quantidade sem riscar representa?”. Repita as perguntas para os outros itens, até compreenderem que os cubinhos não riscados em cada item representam o resto da subtração e obterem os demais resultados sem ajuda. Se possível, disponibilize material dourado ou a representação do material dourado disponível no Material complementar ao final do Livro do Estudante , explicando que, após separarem o material referente ao total da quantidade, é preciso retirar a quantidade de material riscado em cada item. O que sobrar representa o resto da subtração.

• Ao trabalhar com a atividade 4, faça algumas adaptações para incluir os estudantes com NEE. Caso haja estudantes com deficiência visual, tanto com baixa visão quanto cegos, sugere-se o uso de materiais em relevo, sendo possível uma adaptação na qual os cubinhos e as barras sejam feitos com EVA ou com massinha, facilitando a manipulação e a percepção. Faça a descrição da atividade em voz alta, sempre que possível, e motive os estudantes a manipularem os materiais usando o tato. Se houver estudantes com deficiência auditiva, sugere-se o uso de recursos visuais e gestos que acompanhem a fala, mantendo o rosto visível ao se comunicar para facilitar que os estudantes façam a leitura labial.

4.

NAS SUBTRAÇÕES A SEGUIR, FORAM UTILIZADOS CUBINHOS E BARRAS PARA REPRESENTAR QUANTIDADES. ANALISE A QUANTIDADE DE CUBINHOS E BARRAS QUE FORAM RISCADOS EM CADA QUADRO E COMPLETE AS SUBTRAÇÕES.

Resposta: 34 − 21 = 13

5.

Resposta: 65 − 41 = 24

5. Professor, professora:

Na atividade 5, incentive os estudantes a utilizarem diferentes métodos para efetuar os cálculos. Se julgar conveniente, proponha que eles compartilhem as estratégias de cálculo deles.

Resposta: 84 − 52 = 32

Resposta: 79 − 63 = 16

Resposta: 94 − 31 = 63

Resposta: 83 − 42 = 41

Resposta: 95, 85, 75, 65, 55, 45, 35, 25, 15, 5...

, 28 , 26 , 24 , , ,

Resposta: 30, 28, 26, 24, 22, 20, 18, 16, 14, 12...

Resposta: 94 − 54 = 40

Unidades temáticas integradas 221

03/10/2025 09:56:32

• Na atividade 5, os estudantes têm a oportunidade de efetuar as subtrações da maneira que preferirem. Diante disso, verifique qual estratégia é a mais utilizada por eles. Certifique-se de que todos estão compreendendo os procedimentos básicos da subtração. Incentive-os a usar diferentes métodos para efetuar os cálculos. Se julgar conveniente, proponha que as estratégias de cálculos sejam compartilhadas entre os colegas. Aproveite para observar se surgem dúvidas e verifique a necessidade de relembrar brevemente as maneiras de efetuar a operação proposta.

• A atividade 6 visa reforçar o reconhecimento de um padrão dos elementos ausentes em sequências recursivas de números naturais. Verifique a possível ocorrência de números escritos incorretamente e se os estudantes completaram adequadamente a sequência.

• A atividade 6 promove uma integração entre as unidades temáticas de Matemática Números e Álgebra, ao relacionar a contagem subtraindo de 10 em 10 unidades e a observação da regra usada em uma sequência recursiva de números naturais. A mesma recorrência é trabalhada no item B, com a subtração sucessiva de 2 em 2 unidades.

BNCC

A atividade 6 permite explorar o reconhecimento de um padrão dos elementos ausentes em uma sequência de números naturais. Dessa maneira, é desenvolvida a habilidade EF01MA10

• A atividade 7 visa potencializar a compreensão da subtração, por meio de cálculo mental. Oriente os estudantes a utilizarem o cálculo mental, valorizando o conhecimento matemático cotidiano deles. Considere a espontaneidade das estratégias e a agilidade de pensamento, assim como o estabelecimento de relações e regularidades, pois cada um tem seu jeito e tempo para aprender. Verifique possíveis dificuldades apresentadas pelos estudantes e auxilie-os na compreensão do cálculo mental para que percebam propriedades e regularidades. Encoraje-os a refletir sobre suas ações, ousando aprender a pensar, explorar e descobrir. Desse modo, poderão desenvolver o raciocínio lógico e progredir na capacidade de análise e síntese de situações.

• Na atividade 8, a ideia é que os estudantes comparem quantidades. É importante que eles notem que a expressão “a menos” não está necessariamente ligada à subtração, mas à comparação de quantidades.

• A atividade 9 amplia as estratégias de cálculo mental, em que os estudantes são motivados a fazer aproximações para mais e, ao final, retirar o excedente. Ao resolver esta atividade, é possível que algum estudante utilize outras estratégias apresentadas. É importante deixá-los livres para recorrerem à estratégia de cálculo mental que julgarem mais adequada.

BNCC

A atividade 8 permite comparar quantidades para completar a subtração e apresentar o resultado por meio de registro numérico. Desse modo, é contemplada a habilidade EF01MA08.

7. CONFIRA COMO ISRAEL

EFETUOU 50 − 20 MENTALMENTE.

ASSIM COMO ELE, CALCULE MENTALMENTE AS SUBTRAÇÕES A SEGUIR.

A ) 40 − 10 =

Resposta: 40 − 10 = 30

B ) 50 − 10 =

Resposta: 50 − 10 = 40

C ) 80 − 30 =

Resposta: 80 − 30 = 50

D ) 70 − 40 =

Resposta: 70 − 40 = 30

EFETUAR 50 − 20 É O MESMO QUE CONSIDERAR 5 DEZENAS MENOS 2 DEZENAS, QUE DÁ 3 DEZENAS, OU SEJA, 30. ASSIM, 50 − 20 = 30

8. IARA E IAGO FORAM A UMA LOJA DE ARTIGOS DE FESTA. ELA

COMPROU 60 BEXIGAS E ELE COMPROU 20. QUANTAS BEXIGAS IAGO COMPROU A MENOS DO QUE IARA?

DICA: RESOLVA ESTA ATIVIDADE MENTALMENTE, USANDO A ESTRATÉGIA DA ATIVIDADE ANTERIOR. − =

Resposta: 60 − 20 = 40. IAGO COMPROU 40 BEXIGAS A MENOS DO QUE IARA.

IAGO COMPROU BEXIGAS A MENOS DO QUE IARA.

9. RAQUEL USOU A SEGUINTE ESTRATÉGIA PARA CALCULAR 27 − 19

19 EQUIVALE A UMA UNIDADE A MENOS QUE 20. ASSIM, EU CALCULO 27 − 20 = 7

PARA COMPENSAR, ADICIONO 1 AO RESULTADO E OBTENHO 8. ASSIM, 27 − 19 = 8

FAÇA COMO RAQUEL E RESOLVA AS SUBTRAÇÕES A SEGUIR.

A ) 16 − 9 =

Resposta: 16 − 9 = 7

B ) 34 − 29 =

Resposta: 34 − 29 = 5

C ) 70 − 59 = D ) 73 − 69 =

Resposta: 70 − 59 = 11

Resposta: 73 − 69 = 4

10. VALÉRIA GANHOU ALGUNS BONÉS PARA JUNTAR À SUA COLEÇÃO. COM ISSO, ELA PASSOU A TER 16 BONÉS.

QUANTOS BONÉS VALÉRIA TINHA NA SUA COLEÇÃO ANTES DE GANHAR OS 4 BONÉS?

BONÉS.

Resposta: 16 − 4 = 12 12 BONÉS.

11. JUNTE-SE A UM COLEGA E, COM BASE EM CADA SITUAÇÃO, ELABOREM UMA PERGUNTA. DEPOIS, TROQUEM A ATIVIDADE COM OUTRA DUPLA DE COLEGAS PARA UMA DUPLA RESPONDER À PERGUNTA DA OUTRA. POR ÚLTIMO, CONFIRAM SE AS RESPOSTAS OBTIDAS ESTÃO CORRETAS.

A.

Professor, professora: Oriente os estudantes na escrita das frases que respondem aos itens da atividade 11, incentivando o traçado em letra cursiva na pauta apresentada.

Certo estacionamento tem 28 �eículos estacionados. Desses �eículos, 16 são carros e o restante são motos.

PERGUNTA:

Resposta pessoal. Comentários nas orientações ao professor

Elias e Gisele foram ao restaurante. Ele pagou 37 reais em sua refeição e ela, 11 reais a menos.

PERGUNTA:

Resposta pessoal. Comentários nas orientações ao professor

A atividade 11, ao propor a interação com seus pares de maneira cooperativa, trabalhando coletivamente na elaboração de uma pergunta em relação à situação proposta, possibilita o desenvolvimento do raciocínio lógico, a exploração do espírito da investigação e a busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles, conforme descrito na Competência específica de Matemática 2 e na Competência específica de Matemática 8 da BNCC.

03/10/2025 09:56:34

• Na atividade 10, incentive os estudantes a efetuarem as subtrações da maneira que preferirem. Diante disso, verifique qual estratégia é a mais utilizada por eles, bem como se compreendem os algoritmos básicos da subtração. Aproveite para verificar se surgem dúvidas e avalie a necessidade de relembrar brevemente as maneiras de efetuar a operação proposta.

• A atividade 11 motiva os estudantes a elaborarem perguntas em situações-problema. Dessa maneira, eles são levados a desenvolver o pensamento matemático e a autonomia. A realização da atividade em duplas contribui para a troca de ideias, facilitando o processo de aprendizagem. Leia os enunciados dos itens A e B para os estudantes e oriente-os a identificar as principais informações de cada situação. Explique a eles que é importante elaborarem perguntas coerentes com os textos a que se referem. Ao final, solicite que as duplas compartilhem perguntas e respostas.

• Caso julgue necessário, após a atividade 11, para reforçar a prática e o direcionamento da escrita, utilize o caderno de caligrafia, de modo que seja possível desenvolver progressivamente a escrita da letra cursiva.

BNCC

• Ao trabalhar as atividades 12 e 13, disponibilize calculadoras para todos os estudantes da turma. Se não houver material suficiente, organize-os em duplas. Explore o uso desse recurso para desenvolver a habilidade de fazer estimativas e aproximações.

• Essas estratégias favorecem a capacidade de efetuar cálculos mentais e de aplicar com êxito os conceitos referentes às operações de adição e de subtração.

12. OBSERVE COMO EFETUAR 86 – 32 NA CALCULADORA.

1º . 2º . 3º .

COM A CALCULADORA

LIGADA, REGISTRE O NÚMERO 86

DIGITANDO AS TECLAS 8 E 6 .

DIGITE A TECLA E, NA SEQUÊNCIA, REGISTRE O NÚMERO 32

DIGITANDO AS TECLAS 3 E 2

A ) QUAL FOI O RESULTADO OBTIDO?

POR ÚLTIMO, DIGITE A TECLA E OBTENHA O RESULTADO NO VISOR DA CALCULADORA.

Resposta: 54

B ) FAÇA ESTIMATIVAS E RESOLVA CADA SUBTRAÇÃO.

DEPOIS, USE A CALCULADORA PARA CONFERIR SE SUAS ESTIMATIVAS FICARAM PRÓXIMAS OU IGUAIS AOS RESULTADOS EXATOS.

• 56 − 15 =

Resposta: 56 − 15 = 41

• 89 − 64 =

Resposta: 89 − 64 = 25

• 75 − 42 =

Resposta: 75 − 42 = 33

68 − 34 =

Resposta: 68 − 34 = 34

98 − 77 =

Resposta: 98 − 77 = 21

51 − 40 =

Resposta: 51 − 40 = 11

13. ESCREVA DUAS SUBTRAÇÕES DIFERENTES DAS APRESENTADAS

NA ATIVIDADE ANTERIOR. DEPOIS, SOLICITE A UM COLEGA QUE ESTIME O RESULTADO.

UTILIZANDO UMA CALCULADORA, CONFIRA AS ESTIMATIVAS DO SEU COLEGA.

Resposta pessoal. Espera-se que os estudantes estimem resultados próximos ou iguais à resposta exata.

REFERÊNCIAS COMPLEMENTARES

FORMAÇÃO de Professores de Matemática: Contribuições para o Desenvolvimento Profissional e Equidade de Ensino. IFEcast: Minha Comunidade. 22 jun. 2021. Disponível em: https://open.spotify.com/episode/53zGKR Z0bB1G7iyQ2fqsGC. Acesso em: 24 set. 2025. Nesse podcast, o professor Edicarlos Pereira comenta sobre o ensino da Matemática, apresentando contribuições para a formação continuada dos professores vinculada com aspectos da equidade no ensino.

14. NA CAIXA DE LÁPIS DE COR DE TAMARA CABEM 48 LÁPIS.

ALGUNS DELES FORAM RETIRADOS DA CAIXA.

A IMAGEM MOSTRA A CAIXA NESSE MOMENTO.

A ) NO MOMENTO, QUANTOS LÁPIS HÁ NA CAIXA? LÁPIS.

Resposta: 12 LÁPIS

B ) QUANTOS LÁPIS DE COR FORAM RETIRADOS DA CAIXA?

FORAM RETIRADOS LÁPIS DA CAIXA.

Resposta: 48 − 12 = 36 FORAM RETIRADOS 36 LÁPIS DA CAIXA.

15. COM BASE NA CENA APRESENTADA, ELABORE EM SEU CADERNO UM PROBLEMA DE SUBTRAÇÃO. DEPOIS, FORME DUPLA COM UM COLEGA PARA UM RESOLVER O PROBLEMA ELABORADO PELO OUTRO.

Resposta pessoal. Espera-se que os estudantes, ao analisarem a cena, consigam elaborar um problema envolvendo uma operação de subtração, com base na imagem representada na cena.

DESAFIO A MAIS

SÉRGIO TINHA 26 FIGURINHAS. ELE GUARDOU 11 E DEU 3 PARA SEU IRMÃO. O RESTANTE FOI COLADO POR ELE NO SEU ÁLBUM.

QUANTAS FIGURINHAS SÉRGIO COLOU NO SEU ÁLBUM?

FIGURINHAS.

Resposta: 26 − 11 = 15; 15 − 3 = 12 12 FIGURINHAS.

03/10/2025 09:56:34

BNCC

As atividades desta página propõem contagem e comparação de quantidades, para completar a subtração e apresentar o resultado da subtração por meio de registro numérico. Dessa maneira, eles desenvolvem a habilidade EF01MA08

• Na atividade 14, foi apresentada a ideia de retirar usando imagem como suporte, propiciando aos estudantes sentido e significado do objeto matemático para construir sua autonomia. Dessa maneira, verifique se eles compreenderam a ideia associada, como a de retirar quantidades, e sugira que contem, por exemplo, os espaços vazios para obter a quantidade de lápis que está faltando.

• A elaboração de um problema na atividade 15 possibilita estabelecer lógicas próprias e consolidar conceitos matemáticos, atribuindo significado à operação aritmética envolvida. Auxilie-os na elaboração do problema. Instigue-os a analisar a quantidade de copos cheios e vazios representados na cena, a fim de que percebam como podem associar tais quantidades com a operação de subtração. Após a elaboração do problema, proponha uma organização em duplas, a fim de que troquem com o colega os problemas elaborados por eles e resolvam o que outro elaborou. • O Desafio a mais propõe uma situação-problema para trabalhar o raciocínio lógico-matemático e a resolução de problemas de duas ou mais etapas. Espera-se que eles identifiquem a informação principal do problema e compreendam a sequência de operações para chegar à resposta correta. Para resolver, eles devem, primeiro, calcular a quantidade de figurinhas que foram guardadas e dadas ao irmão (11 + 3 = 14). Em seguida, devem subtrair esse total da quantidade inicial para descobrir quantas figurinhas foram coladas no álbum (26 14 = 12). Outra estratégia é fazer as subtrações em sequência, ou seja, efetuar 26 11 = 15 e 15 3 = 12 Caso encontrem alguma lógica diferente da esperada, incentive-os a compartilhar com os demais colegas, fazendo intervenções pontuais e estratégicas.

A atividade 16, ao propor a interação com seus pares de maneira cooperativa, possibilita o desenvolvimento do racio-

cínio lógico, explora o espírito da investigação e a busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, conforme descrito nas Competências específicas de Matemática 2 e 8 da BNCC. Ao trabalhar coletivamente na situação proposta, eles estarão desenvolvendo o respeito pelo modo de pensar dos colegas e aprendendo com eles.

OBJETIVOS

• Relacionar o elemento apresentado às características de uma tirinha.

• Interpretar e relacionar ideias e informações contidas na tirinha.

• Contribuir para o desenvolvimento de vocabulário e a fluência em leitura oral.

• Aperfeiçoar a compreensão de textos e desenvolver a produção escrita.

• Reconhecer a importância de compartilhar.

Orientações

Complementares

A) Ao ler essa questão para os estudantes, reforce as características de uma tirinha com a intenção de eles lembrarem se já viram uma ou se alguém já leu esse gênero para eles.

BNCC

As atividades propostas nessa seção favorecem o desenvolvimento da Competência geral 8 da BNCC, bem como o tema contemporâneo transversal Vida familiar e social, pois permitem a compreensão da importância de compartilhar o que se tem com os outros, além de possibilitar a reflexão sobre a sensação de bem-estar que esse ato pode trazer.

EXPLORANDO O TEXTO

Orientações

Complementares

B) Esta questão objetiva levar os estudantes a observarem com mais cuidado a tirinha e a identificarem a quantidade de personagens que compõem a pequena história. Caso apresentem dificuldade, faça questionamentos, como: “Se houvesse somente uma criança nessa tirinha?”; “Qual número representaria essa quantidade”; “E se houvesse duas crianças?” e assim por diante.

ENTRE TEXTOS

Professor, professora: O assunto tratado nesta seção possibilita o trabalho com o tema contemporâneo transversal Vida familiar e social.

TIRINHAS SÃO PEQUENAS HISTÓRIAS EM QUADRINHOS COM IMAGEM, PODENDO TER TEXTO OU NÃO. A QUANTIDADE DE QUADRINHOS VARIA DE TRÊS A QUATRO, GERALMENTE EM SEQUÊNCIA DE ACONTECIMENTOS.

A ) VOCÊ JÁ LEU ALGUMA TIRINHA? CONTE AOS COLEGAS.

A TIRINHA A SEGUIR TRAZ UMA SITUAÇÃO QUE ENVOLVE A AÇÃO DE COMPARTILHAR. ANALISE A TIRINHA COM O PROFESSOR E OS COLEGAS.

A) Resposta pessoal. Espera-se que os estudantes comentem com os colegas se já leram alguma tirinha. Nesse caso, incentive-os a relatar

suas experiências e preferências em relação a esse gênero textual.

VOCÊ SABIA QUE COMPARTILHAR VAI ALÉM DE REPARTIR, DAR OU EMPRESTAR ALGO MATERIAL A ALGUÉM? PODEMOS COMPARTILHAR TEMPO, SABEDORIA, EXPERIÊNCIAS, ATENÇÃO E AMOR.

EXPLORANDO O TEXTO

Comentários nas orientações ao professor.

B ) MARQUE UM X NO NÚMERO QUE REPRESENTA A QUANTIDADE DE PERSONAGENS QUE PARTICIPAM DESSA SITUAÇÃO. 4 2 1 3

Resposta: Os estudantes devem marcar um X no número 4

C ) ESCREVA COMO SE LÊ O NÚMERO MARCADO NO ITEM B

Resposta: Quatro.

Professor, professora: Oriente os estudantes na escrita da palavra que responde à questão C, incentivando o traçado em letra cursiva na pauta apresentada.

C) Antes da realização desta questão, se necessário, escreva como se lê o número na lousa, evidenciando o movimento com a mão e a direção do traçado em letra cursiva. Caso haja estudantes canhotos na turma, repita a operação, indicando o movimento e a direção do traçado para esse grupo.

D) Nesta questão, espera-se que os estudantes identifiquem o que foi compartilhado entre os personagens. Comente a importância de compartilhar com os colegas algo que no momento só nós temos. Na tirinha apenas Armandinho tinha o guarda-chuva, porém ele foi generoso e

compartilhou com os amigos que não tinham guarda-chuva. Assim, ele cuidou de quem estava ao seu redor fazendo o bem.

BECK, ALEXANDRE. ARMANDINHO CINCO. FLORIANÓPOLIS: A. C. BECK, 2015. P. 93.

G) Resposta pessoal. O objetivo desta questão é fazer os estudantes relatarem suas experiências relacionadas ao compartilhamento.

D ) CONTE AO PROFESSOR E AOS COLEGAS O QUE FOI COMPARTILHADO ENTRE OS PERSONAGENS DA TIRINHA. DEPOIS JUSTIFIQUE SUA RESPOSTA.

ALÉM DO TEXTO

Resposta: O objeto

compartilhado foi o guarda-chuva. Espera-se que os estudantes justifiquem que Armandinho compartilhou o guarda-chuva para os outros meninos não se molharem, pois, naquele momento, somente um deles tinha guarda-chuva.

NA TIRINHA A SEGUIR, ANA E EDUARDO ESTÃO

COMPARTILHANDO BRINQUEDOS.

ANA, COMPARTILHE ESSES BRINQUEDOS COM O EDUARDO.

Comentários nas orientações ao professor.

EDUARDO, VOU COMPARTILHAR MAIS BRINQUEDOS COM VOCÊ PARA FICARMOS COM A MESMA QUANTIDADE.

E ) COM QUANTOS BRINQUEDOS CADA CRIANÇA FICOU NO SEGUNDO QUADRINHO?

Resposta: ANA: 4 BRINQUEDOS. EDUARDO: 2 BRINQUEDOS.

EDUARDO

ANA BRINQUEDOS.

BRINQUEDOS.

F ) QUANTOS BRINQUEDOS EDUARDO AINDA PRECISA RECEBER DE ANA PARA QUE OS DOIS FIQUEM COM A MESMA

QUANTIDADE? BRINQUEDO.

Resposta: 1 BRINQUEDO.

G ) VOCÊ JÁ COMPARTILHOU OBJETOS OU BRINQUEDOS COM ALGUÉM? CONVERSE COM OS COLEGAS SOBRE A IMPORTÂNCIA DE COMPARTILHAR O QUE TEMOS.

H ) CRIE UMA HISTÓRIA RELACIONADA AO COMPARTILHAMENTO E DESENHE ESSA HISTÓRIA NO CADERNO EM FORMATO DE TIRINHA. DEPOIS, MOSTRE O QUE VOCÊ FEZ PARA UM COLEGA.

Resposta pessoal. Espera-se que os estudantes elaborem

uma história em formato de tirinha, tendo como base as informações apresentadas nesta seção.

CONCLUSÃO

03/10/2025 09:56:35

Orientações

Complementares

E) Essa questão incentiva os estudantes a realizarem a contagem das quantidades de brinquedos apresentados na cena. Caso alguém apresente dificuldade em responder, conte com ele, marcando cada brinquedo já contado com um lápis. F) Essa pergunta leva os estudantes a analisarem como devem compartilhar para ficarem com a mesma quantidade. Se tiverem dificuldade, represente na lousa as quantidades de brinquedos e faça uma simulação.

G) Essa questão conscientiza os estudantes sobre a importância de compartilhar e de dialogar.

H) Essa proposta desenvolve alguns dos aspectos da alfabetização, como aquisição de vocabulário e produção escrita, ao solicitar que os estudantes produzam a própria história em formato de tirinha.

• Incentive os estudantes a colocarem em prática, no dia a dia, o que aprenderam. Solicite que leiam as tirinhas com seus familiares e conversem com eles sobre uma maneira de realizarem um momento solidário, compartilhando algo.

• Conclua o trabalho da unidade propondo o desafio a seguir. Verifique se os estudantes percebem que o termo inicial é desconhecido, e que eles podem usar a ideia de completar para resolver essa questão, usando material de contagem ou fazendo desenhos no caderno. Para obter o resultado (8), eles podem usar o raciocínio de adicionar 5 unidades ao número 3.

Sugestão

de Desafio

Bento levou morangos para comer em um piquenique. Durante o lanche, ele comeu 5 morangos e sobraram 3. Quantos morangos ele levou ao piquenique?

Resposta Ele levou 8 morangos.

Acompanhar a aprendizagem dos estudantes é fundamental para um ensino bem-sucedido. A fim de realizar monitoramento mais abrangente e organizado, registre nos relatórios individuais ou nas fichas de avaliação o desempenho deles, levando em consideração suas particularidades. Um modelo desse tipo de ficha pode ser encontrado no tópico Avaliação deste Manual do Professor. Assim, será possível visualizar de modo individual as trajetórias de aprendizagem, incluindo os avanços e os pontos de dificuldades a serem sanados por meio de atividades que

promovam recuperação dos conteúdos. Esse método fornece pistas para repensar estratégias em sala de aula, tornando as ações pedagógicas cada vez mais eficazes.

A conclusão da unidade é o momento de avaliar se os objetivos por ela propostos foram alcançados. Para esse diagnóstico, temos no final deste Manual do Professor algumas possibilidades de avaliação formativa que permitem realizar o monitoramento da aprendizagem e intervir caso os resultados esperados não sejam atingidos.

OBJETIVOS

• Compreender o significado das expressões mais leve e mais pesado

• Reconhecer a balança como instrumento de medida de massa.

• Resolver situações-problema que envolvem comparação entre medidas de massa.

• Reconhecer o quilograma como unidade-padrão para medida de massa.

• Diferenciar recipientes que contêm mais líquido dos que contêm menos líquido.

• Identificar se um recipiente está cheio ou vazio.

• Perceber a presença do litro no dia a dia.

• Reconhecer o litro como unidade-padrão para medida de capacidade.

• Ler e interpretar dados apresentados em tabelas e gráficos de colunas simples.

• Elaborar problema envolvendo medida de massa.

INTRODUÇÃO E JUSTIFICATIVA

Nesta unidade, são trabalhados conteúdos relacionados a medidas de massa e de capacidade, com ênfase em sua aplicação no dia a dia.

Inicialmente, são explorados os termos leve e pesado, bem como o uso da balança de dois pratos para comparar objetos, de modo a favorecer a compreensão desses termos.

No tópico O quilograma, utilizando a balança digital, os estudantes são incentivados a identificar a massa de pessoas e produtos diversos, além de analisar e interpretar tabelas e gráficos com base em dados relacionados a essa unidade de medida de massa.

Já o tópico Medidas de capacidade promove a reflexão sobre a capacidade de armazenamento de

UNIDADE10

MEDIDAS DE MASSA E MEDIDAS DE CAPACIDADE

MÃE SERVINDO LEITE NO COPO PARA A FILHA.

recipientes, como copos, jarras e garrafas. Para tanto, são propostas atividades práticas, a fim de que eles possam construir conhecimento de maneira significativa.

Por fim, no tópico O litro, os estudantes são levados a reconhecer o uso dessa unidade-padrão em produtos que fazem parte do cotidiano deles. As atividades desse tópico visam ao desenvolvimento da competência para identificar objetos com capacidade maior, menor ou igual a 1 litro.

Habilidades da BNCC trabalhadas na unidade: EF01MA15 e EF01MA21

SUGESTÃO DE ESTRATÉGIA INICIAL

Escreva na lousa “Produtos medidos em litros” e “Produtos medidos em quilogramas”. Em seguida, peça aos estudantes que citem exemplos desses produtos e anote-os. Ao realizar essa atividade, verifique a noção dos estudantes em relação a essas unidades de medida, observando a capacidade deles para distingui-las. Em um momento oportuno, ao final da unidade, retome essas anotações a fim de verificar a evolução do aprendizado da turma.

retratada, de modo a favorecer a resposta correta a essa questão. Ao longo do trabalho com a unidade, o uso de recipientes como jarras e copos com medidas de capacidade diferentes torna a aprendizagem significativa, além de contextualizar os conteúdos estudados.

ARTICULANDO CONHECIMENTOS

Em parceria com o professor de Ciências da Natureza, o conteúdo relacionado a mamíferos pode ser abordado apresentando aos estudantes os animais que produzem leite, quais destes leites são

O LEITE É UM ALIMENTO PRESENTE EM NOSSO DIA A DIA. ELE PODE CONTRIBUIR PARA A SAÚDE DO CORPO E A BOA FORMAÇÃO DOS OSSOS E DOS DENTES.

ALÉM DE SER CONSUMIDO PURO, O LEITE É INDISPENSÁVEL PARA A PRODUÇÃO DE ALGUNS ALIMENTOS, COMO QUEIJO, IOGURTE E MANTEIGA.

Professor, professora: Mais informações sobre o assunto abordado na abertura desta unidade nas orientações ao professor.

1 a 3. Respostas nas orientações ao professor.

1. 2. 3.

VOCÊ CONSOME LEITE COM FREQUÊNCIA EM SEU COTIDIANO? EM SUA OPINIÃO, O QUE ACONTECERIA SE DESPEJÁSSEMOS TODO O CONTEÚDO DA JARRA NO COPO?

CITE ALGUNS PRODUTOS USADOS EM SEU DIA A DIA QUE LEVAM LEITE EM SUA FABRICAÇÃO.

próprios para o consumo humano e qual é a importância da ingestão desse alimento como fonte de cálcio, proteínas e vitaminas. Além disso, é possível comentar com eles que, apesar de ser uma importante fonte de vitaminas, os seres humanos são os únicos mamíferos a consumir leite na fase adulta. Há, no entanto, muitas pessoas que consomem “leites” vegetais, que são produzidos usando alimentos como soja, arroz, aveia e coco. Em geral, esse consumo é feito por pessoas que apresentam intolerância à lactose ou alergia à proteína do leite de vaca, bem como por

• Antes de ler o texto com os estudantes, converse com eles sobre a imagem apresentada e peça-lhes que descrevam com as próprias palavras o que está acontecendo na cena.

• Aproveite o contexto para conversar com os estudantes sobre o consumo de leite e seus derivados em nosso dia a dia. Além de ser consumido como bebida em algumas refeições, esse produto é utilizado como matéria-prima na produção de queijo, manteiga e iogurte, entre outros alimentos.

• As questões 1 e 3 abordam o consumo de leite e seus derivados no dia a dia. Levando em consideração a realidade dos estudantes, converse com eles sobre como ocorre o consumo de leite e seus derivados e em quais refeições. Verifique com a escola e os responsáveis a possibilidade de preparar com eles uma bebida à base desse alimento ou de levá-los para visitar uma indústria de processamento de laticínios, a fim de apresentar-lhes o processo de produção de leite e seus derivados.

• Na questão 2, espera-se que os estudantes percebam que a jarra tem capacidade maior do que o copo e, portanto, ela vai transbordar. Avalie a possibilidade de levar para a sala de aula uma jarra com algum líquido que possa ser reaproveitado (para evitar o desperdício). Assim, é possível reproduzir na prática a cena

03/10/2025 09:59:33

indivíduos que optam pela não ingestão de alimentos de origem animal.

2. Resposta pessoal. Espera-se que os estudantes respondam que o leite transbordaria do copo, pois a capacidade dele é menor do que a capacidade da jarra.

1. Resposta pessoal. Espera-se que os estudantes relatem as próprias experiências em relação ao consumo ou não de leite como alimento no cotidiano.

3. Sugestões de resposta: Leite condensado; doce de leite; bebidas lácteas; leites fermentados; leite em pó; sorvetes; creme chantili; requeijão; creme de leite.

• Antes de iniciar o trabalho com a atividade desta página, converse com os estudantes sobre os termos massa e peso . Comente que é comum nos referirmos às medidas de massa como “peso”, por exemplo, “O ‘peso’ de uma pessoa é 78 kg” ou “O ‘peso’ do pacote de arroz é 5 kg”. Se julgar conveniente, informe a eles que a distinção entre esses dois conceitos será estudada em anos posteriores e não será trabalhada nos anos iniciais do Ensino Fundamental.

• A atividade 1 tem como objetivo a comparação de medidas de massa, possibilitando aos estudantes inferirem, por meio da observação, qual objeto é o mais pesado e, por oposição, qual é o mais leve. Se necessário, após a realização do item B, apresente-lhes pares de objetos da sala de aula ou que eles conheçam e, em seguida, peça que identifiquem qual é o mais leve e qual é o mais pesado, por meio da visão e do tato. A comparação empírica do “peso” de dois objetos usando o tato promove a inclusão de estudantes com deficiência visual.

• Aproveite o assunto abordado no item C para conversar com os estudantes sobre a importância de tratar bem os animais. Por dependerem dos seres humanos para ter uma rotina adequada e uma vida saudável e feliz, os animais de estimação precisam de ambiente protegido do sol e da chuva, água limpa e comida adequada. Enfatize também a importância de que sejam vacinados para prevenir doenças graves que possam levá-los à morte, bem como doenças que possam ser transmitidas para os seres humanos (zoonoses), a fim de garantir mais saúde e bem-estar a todos. Além desses cuidados, os animais de estimação precisam de afeto. O tratamento gentil

MEDIDAS DE MASSA

1. NO DIA A DIA, USAMOS AS PALAVRAS LEVE E PESADO PARA

COMPARAR A MEDIDA DA MASSA DE OBJETOS OU DE SERES VIVOS. VAMOS ESTUDAR ESSE ASSUNTO?

Professor, professora: Ao abordar essa conversa, aplique um exemplo prático com os estudantes. Para isso, solicite a eles que utilizem

objetos presentes na sala de aula e verifiquem na prática, por meio de comparação, qual objeto é o mais pesado e qual é considerado mais leve.

Resposta pessoal. Esperase que os estudantes citem momentos em que levantaram objetos com medidas de massa distintas e perceberam, por meio de comparação, que um era mais pesado que outro, assim como um era mais leve que outro.

EM QUAIS SITUAÇÕES VOCÊ JÁ PERCEBEU QUE A MEDIDA DA MASSA DE UM OBJETO ERA MAIOR DO QUE A DE OUTRO?

FÁTIMA E MILENA ESTÃO PASSEANDO COM SEUS ANIMAIS DE ESTIMAÇÃO.

OLÁ, QUE BOM TE ENCONTRAR POR AQUI!

1. A) Resposta pessoal. Espera-se que os estudantes relatem suas experiências com relação a terem ou não animais de estimação nas residências onde moram.

QUE LINDO O SEU CACHORRO!

FÁTIMA

A ) VOCÊ OU ALGUM FAMILIAR TEM ANIMAL DE ESTIMAÇÃO? SE SIM, DIGA QUAL.

B ) QUAL CACHORRO VOCÊ ACHA QUE É MAIS PESADO: O DE FÁTIMA OU O DE MILENA?

Resposta pessoal. Espera-se que

C ) EM SUA OPINIÃO, POR QUE É IMPORTANTE CUIDAR BEM DOS ANIMAIS DE ESTIMAÇÃO? CONVERSE COM OS COLEGAS SOBRE ISSO.

Resposta pessoal. Comentários nas orientações ao professor os estudantes respondam que o cachorro de Fátima é mais pesado.

dado aos animais faz bem a eles e ao cuidador.

Mencione aos estudantes que essas ações levam ao desenvolvimento de valores como respeito, responsabilidade, empatia e compromisso.

BNCC

Nesta unidade, os estudantes são levados a comparar medidas de capacidade e de massa ao fazerem uso de termos como mais pesado, mais leve, cabe mais e cabe menos. As atividades promovem a ordenação de objetos do cotidiano com base nas medidas de massa ou de capacidade, conforme orienta a habilidade EF01MA15 da BNCC.

REFERÊNCIAS COMPLEMENTARES

03/10/2025 09:59:35

MOURA, Ellen Michelle Barbosa de; FRAZ, Joeanne Neves; SANTOS, Karla Vanessa Gomes dos; MOREIRA, Geraldo Eustáquio. Grandezas e Medidas no contexto da inclusão: a Educação Matemática na formação do professor. Educação Matemática Debate, Montes Claros, v. 5, n. 11, p. 1–25, 2021. Disponível em: https:// www.periodicos.unimontes.br/index.php/emd/ article/view/3778. Acesso em: 24 set. 2025. O artigo propõe-se a analisar práticas de ensino em Educação Matemática, fundamentadas nos princípios da educação inclusiva, a partir da realização de uma oficina pedagógica voltada ao estudo de Grandezas e Medidas.

MILENA

ILUSTRAÇÕES:

2. O INSTRUMENTO USADO PARA MEDIR A MASSA DE OBJETOS, ANIMAIS, PESSOAS E ALIMENTOS, POR EXEMPLO, É A BALANÇA ENTRE OS VÁRIOS TIPOS, TEMOS A BALANÇA DE DOIS PRATOS, COMO A REPRESENTADA A SEGUIR.

BOLA

MELANCIA

DE ACORDO COM OS PRATOS DESSA BALANÇA, MARQUE UM X NA RESPOSTA CORRETA EM CADA ITEM.

A ) O QUE É MAIS PESADO?

Resposta: Os estudantes devem marcar um X em MELANCIA.

BOLA. MELANCIA.

B ) O QUE É MAIS LEVE?

Resposta: Os estudantes devem marcar um X em BOLA.

BOLA. MELANCIA.

3. O OBJETO A SEGUIR FOI COLOCADO NA BALANÇA DE DOIS PRATOS.

3. B) Resposta: O objeto desenhado deve ser mais leve porque as balanças precisam se manter em desequilíbrio.

3. A) Resposta: Os estudantes devem desenhar um objeto que seja mais leve do que o tubo de cola, como um clipe, um palito de fósforo ou uma pena.

A ) DESENHE UM OBJETO NO PRATO VAZIO PARA QUE O PRATO COM A COLA AINDA CONTINUE MAIS BAIXO QUE O OUTRO. B ) O OBJETO DESENHADO POR VOCÊ DEVE SER MAIS PESADO OU MAIS LEVE DO QUE O TUBO DE COLA? POR QUÊ?

AVALIANDO

Objetivo

Empregar as expressões mais leve e mais pesado para ordenar diferentes tipos de objetos.

Sugestão de intervenção

Entregue para cada estudante um quarto de folha de papel sulfite tamanho A4 com o nome de um objeto. Em seguida, peça que, acima desse nome, eles escrevam o nome de um objeto que seja mais leve e abaixo dele, o nome de um objeto que seja mais pesado. Ao final dessa etapa, recolha os pedaços de papel e faça a leitura

03/10/2025 09:59:35

de cada um deles com toda a turma, promovendo um momento de conversa para auxiliar os estudantes que ainda demonstram dificuldade na comparação entre o que é mais leve e o que é mais pesado.

BNCC

As atividades desta página abordam a comparação de medidas de massa por meio da classificação de objetos do dia a dia dos estudantes em mais leve e mais pesado, conforme orienta a habilidade EF01MA15 da BNCC.

• Ao trabalhar as atividades desta página, avalie a possibilidade de levar para a sala de aula uma balança de dois pratos, a fim de que os estudantes possam usá-la para comparar as medidas de massa de alguns objetos e verificar qual deles é o mais leve ou mais pesado.

• Ao realizar as atividades desta página, comente que, em uma balança de dois pratos, a diferença de altura entre eles está relacionada à diferença entre as medidas de massa dos objetos colocados sobre cada um deles; portanto, o objeto mais pesado estará no prato que estiver mais baixo, enquanto o objeto mais leve estará no prato que ficar mais alto.

• Por meio da observação, a atividade 2 visa ao desenvolvimento da habilidade de identificar o objeto mais leve e o mais pesado. A fim de facilitar essa compreensão, é utilizada a balança de dois pratos.

• O objetivo da atividade 3 é levar os estudantes a fazerem uma estimativa em relação à medida de massa de um determinado objeto, de modo que possam pensar em outro objeto que seja mais pesado. Se possível, peça aos estudantes que segurem um tubo de cola em uma mão e outro objeto mais pesado na outra, a fim de auxiliar na compreensão da atividade. Verifique se eles percebem que o prato com a cola continua mais baixo do que o outro, é necessário que o objeto que eles representarem seja mais leve do que ela.

• A atividade 1 visa desenvolver nos estudantes a compreensão do que é quilograma e de que tipo de produto é vendido usando essa unidade de medida. Após os estudantes responderem à atividade, escreva o nome de alguns produtos na lousa e pergunte quais deles são ou não vendidos por quilograma.

• O objetivo da atividade 2 é apresentar medidas de massa específicas, de modo que eles se apropriem da representação do quilograma (kg) em uma balança digital.

• Após os estudantes responderem ao item B da atividade 2, peça que calculem a diferença da medida de massa de Maurício e de Célia, ou seja, 22 kg 17 kg = 5 kg

ATIVIDADE EXTRA

Com base na atividade 2, solicite aos estudantes que realizem a atividade extra a seguir. Se achar conveniente, após realizarem essa atividade, faça alguns questionamentos a fim de verificar se eles recorreram à adição ou à subtração para responderem qual é a medida de massa desses animais.

Pedro mediu a massa de alguns animais de seu sítio: um cachorro, um coelho, um gato e uma galinha. De acordo com as informações, verifique qual das fichas a seguir indica a medida de massa de cada animal.

10 kg

4 kg 3 kg 6 kg

a) A medida de massa do gato é um número par maior do que 5.

b) A medida de massa da galinha é um número ímpar.

c) O coelho tem medida de massa maior do que a da galinha.

d) A medida de massa do cachorro é um número formado por dois algarismos.

O QUILOGRAMA

1. UMA UNIDADE DE MEDIDA UTILIZADA PARA INDICAR A MEDIDA DA MASSA DE OBJETOS, PESSOAS, ENTRE OUTROS CASOS, É O QUILOGRAMA

NO AÇOUGUE, POR EXEMPLO, ALGUMAS CARNES SÃO VENDIDAS DE ACORDO COM A MEDIDA DE MASSA DELAS EM QUILOGRAMA. MARQUE UM X NOS PRODUTOS VENDIDOS EM QUILOGRAMA.

Resposta: Os estudantes devem marcar um X nos produtos A e C.

2. NO VISOR DE CADA

BALANÇA ESTÁ INDICADA

A MEDIDA DE MASSA, EM QUILOGRAMA, DE CADA CRIANÇA.

DICA: USAMOS kg PARA ABREVIAR A PALAVRA QUILOGRAMA

A ) CONTORNE A CRIANÇA QUE TEM A MAIOR MEDIDA DE MASSA.

Resposta: Os estudantes devem contornar o personagem MAURÍCIO.

B ) SE MAURÍCIO E CÉLIA

SUBIREM EM UMA ÚNICA

BALANÇA, AO MESMO TEMPO, QUAL SERÁ

A MEDIDA DE MASSA

INDICADA NO VISOR?

Resposta: 22 + 17 = 39 ou 17 + 22 = 39.

A MEDIDA DE MASSA INDICADA SERÁ QUILOGRAMAS.

Resposta: A MEDIDA DE MASSA INDICADA SERÁ 39 QUILOGRAMAS.

Respostas

a) Medida da massa do gato: 6 kg.

b) Medida da massa da galinha: 3 kg

c) Medida da massa do coelho: 4 kg

d) Medida da massa do cachorro: 10 kg

MAURÍCIO

CÉLIA

3. O GRÁFICO APRESENTA DADOS QUE OS ESTUDANTES

DO 1º ANO COLETARAM SOBRE A MEDIDA DE MASSA DE ALGUNS PRODUTOS VENDIDOS EM MERCADOS.

MEDIDA DE MASSA, EM QUILOGRAMA, DE ALGUNS PRODUTOS, EM 2027

MEDIDA DE MASSA (EM QUILOGRAMA)

A ) NO GRÁFICO:

Unidades temáticas integradas

• A atividade 3 promove uma integração com as unidades temáticas de Matemática Números e Probabilidade e estatística , ao trabalhar com o registro, a leitura e a interpretação de um gráfico visando ao reconhecimento de alguns produtos vendidos por quilograma, de modo que os estudantes identifiquem a medida de massa exata de cada um deles. Se necessário, explique que cada quadrinho representa um 1 quilograma; assim, basta contar a quantidade de quadrinhos pintados com a cor verde, para identificar a medida de massa de cada um dos produtos apresentados.

• Explique que algumas lojas vendem esse tipo de produto a granel, ou seja, de acordo com a quantidade desejada pelo cliente.

• CONTORNE A IMAGEM DO PRODUTO QUE TEM A MAIOR MEDIDA DE MASSA.

Resposta: Os estudantes devem contornar a

imagem que representa a ração com 10 kg

• MARQUE UM X NA IMAGEM DO PRODUTO QUE TEM A MENOR MEDIDA DE MASSA.

Resposta: Os estudantes devem marcar

um X na imagem que representa o açúcar com 1 kg

B ) ESCREVA, EM QUILOGRAMA, A MEDIDA DE MASSA DE CADA PRODUTO INDICADO NO GRÁFICO.

Resposta: AÇÚCAR: 1 QUILOGRAMA.

• AÇÚCAR: QUILOGRAMA.

Resposta: ARROZ: 5 QUILOGRAMAS.

• ARROZ: QUILOGRAMAS.

Resposta: FEIJÃO: 2 QUILOGRAMAS.

• FEIJÃO: QUILOGRAMAS.

Resposta: RAÇÃO PARA CACHORRO: 10 QUILOGRAMAS.

• RAÇÃO PARA CACHORRO: QUILOGRAMAS.

03/10/2025 09:59:36

• Se julgar conveniente, leve para sala de aula panfletos de mercados e peça aos estudantes que recortem e colem no caderno as imagens e os preços dos produtos vendidos por quilograma.

BNCC

A atividade 3 propõe um trabalho que explora a habilidade EF01MA21, pois é solicitado que os estudantes façam a leitura e a interpretação de um gráfico.

REFERÊNCIAS

COMPLEMENTARES

Bueno, Renata. A balança. São Paulo: FTD, 2019. De maneira lúdica, as crianças são levadas a compreender que a balança se movimenta conforme o peso dos elementos dispostos sobre ela.

• O objetivo da atividade 4 é apresentar aos estudantes outros produtos, a fim de que eles identifiquem, com base nas informações da embalagem ou do tipo de produto, se são ou não vendidos por quilograma. Se necessário, explique que, na caixa de leite, está indicado que contém 1 L, isto é, 1 litro, unidade de medida de capacidade que será estudada posteriormente.

• A atividade 5 promove uma integração com as unidades temáticas de Matemática Números e Probabilidade e estatística, ao trabalhar com o registro, a leitura e a interpretação de uma tabela. Essa atividade visa ampliar o trabalho com quilogramas por meio da leitura de tabela e do uso das operações de adição e subtração. Assim, é possível retomar conteúdos abordados em unidades anteriores e verificar a aprendizagem dos estudantes. Analise como eles estão efetuando os cálculos e se compreenderam como são calculadas as operações de adição e subtração sugeridas na atividade, respondendo às possíveis dúvidas.

• O enunciado dessa atividade apresenta uma nova palavra aos estudantes (nutricionista), o que contribui para a aquisição de habilidades fundamentais à alfabetização, como o desenvolvimento de vocabulário.

BNCC

Na atividade 5, os estudantes são convidados a fazer leitura e a interpretação de uma tabela. Dessa maneira, eles desenvolvem a habilidade EF01MA21

4. GREGÓRIO COMPROU OS PRODUTOS REPRESENTADOS A SEGUIR.

IMAGEM COM ELEMENTOS SEM PROPORÇÃO ENTRE SI.

FARINHA DE TRIGO SAL LEITE

A ) MARQUE UM X NOS PRODUTOS QUE GREGÓRIO COMPROU EM QUILOGRAMA.

Resposta: Os estudantes devem marcar um X nas

B ) DE ACORDO COM A RESPOSTA DO ITEM A, CONTORNE O PRODUTO QUE TEM A MAIOR MASSA.

Resposta: Os estudantes devem contornar a imagem que representa a FARINHA DE TRIGO. imagens que representam a FARINHA DE TRIGO e o SAL.

5. UM NUTRICIONISTA ORGANIZOU EM UMA TABELA A MEDIDA DE MASSA EM QUILOGRAMAS DOS MEMBROS DE UMA FAMÍLIA.

MEDIDA DE MASSA DOS MEMBROS DA FAMÍLIA EM MAIO DE 2027 MEMBRO DA FAMÍLIA

MEDIDA DE MASSA (EM QUILOGRAMAS)

JOAQUIM (PAI) 87

ISAURA (MÃE) 64

YURI (FILHO) 53

TAINARA (FILHA) 34

HUGO (FILHO) 22

FONTE DE PESQUISA: INFORMAÇÕES DO NUTRICIONISTA.

A ) QUANTOS QUILOGRAMAS TÊM OS TRÊS FILHOS JUNTOS?

QUILOGRAMAS.

B ) QUANTOS QUILOGRAMAS É A DIFERENÇA ENTRE AS MEDIDAS DE MASSA DO PAI E DA MÃE?

QUILOGRAMAS.

Unidades temáticas integradas

NUTRICIONISTA: PROFISSIONAL DE SAÚDE DEDICADO AO ESTUDO DA NUTRIÇÃO E DA ALIMENTAÇÃO.

Resposta: 53 + 34 = 87; 87 + 22 = 109 109 QUILOGRAMAS.

Resposta: 87 − 64 = 23 23 QUILOGRAMAS.

DE CAFÉ DA MANHÃ.

1 QUILOGRAMA 2 QUILOGRAMAS 3 QUILOGRAMAS

CONFEITARIA: ESTABELECIMENTO ONDE SÃO FABRICADOS E/OU COMERCIALIZADOS DOCES, BISCOITOS, BOLOS, TORTAS, SALGADOS ETC.

AKIRA DECIDIU COMPRAR A CESTA COM

A MAIOR MEDIDA DE MASSA PARA LEVAR AO CAFÉ DA MANHÃ DA FAMÍLIA. COMO A FAMÍLIA DE AKIRA É MUITO GRANDE, ELE DECIDIU ADICIONAR MAIS ALGUNS ITENS DA LOJA. OBSERVE COMO FICOU A CESTA.

A ) DE QUANTOS QUILOGRAMAS É A DIFERENÇA DA CESTA DEPOIS DE AKIRA ADICIONAR OS ITENS?

QUILOGRAMAS.

B ) SE A CONFEITARIA COBRAR 40 REAIS POR QUILOGRAMA

ADICIONADO, QUANTOS REAIS A MAIS AKIRA PAGARÁ PELA

CESTA? REAIS.

5 QUILOGRAMAS

Resposta: 5 − 3 = 2 2 QUILOGRAMAS.

Resposta: 40 + 40 = 80 80 REAIS.

C ) COM BASE NAS INFORMAÇÕES APRESENTADAS, ELABORE EM SEU CADERNO UM PROBLEMA ENVOLVENDO MEDIDAS DE MASSA. DEPOIS, FORME DUPLA COM UM COLEGA PARA UM RESOLVER O PROBLEMA ELABORADO PELO OUTRO.

Resposta pessoal. Espera-se que os estudantes elaborem um problema tendo como base as informações apresentadas no enunciado.

03/10/2025 09:59:38

• O objetivo da atividade 6 é fazer com que os estudantes compreendam como é feito o pagamento de alimentos vendidos por quilograma. Nesse caso, as cestas com determinadas quantidades têm preço fixo. Como Akira adicionou mais 2 kg à cesta, precisou pagar por esse adicional. Explique aos estudantes que outros alimentos, como frutas e legumes, são vendidos a um determinado preço por quilograma.

• O enunciado dessa atividade apresenta uma nova palavra aos estudantes ( confeitaria ), o que contribui para a aquisição de habilidades fundamentais à alfabetização, como o desenvolvimento de vocabulário.

AVALIANDO

Objetivo

Reconhecer o quilograma como unidade-padrão de medida de massa.

Sugestão de intervenção

Divida a turma em duplas e escreva o nome de algumas frutas e legumes na lousa, com etiquetas informando o preço do quilograma de cada um deles. Em seguida, peça aos estudantes que calculem o valor a ser pago por 2, 3 e 4 quilogramas de alguns desses produtos. Observe como as duplas estão efetuando os cálculos e como estão se ajudando. Ao final, faça uma sistematização a fim de verificar se os estudantes compreenderam como é calculado o valor a ser pago por produtos comprados por quilograma. 6.

• Para resolver as atividades 7, 8, 9 e 10, os estudantes devem efetuar operações de adição e subtração, conteúdos abordados em unidades anteriores, conforme a situação-problema, identificando as informações relevantes e encontrando a operação correta para resolver cada uma delas.

• As atividades dessa página promovem o raciocínio lógico, o desenvolvimento do pensamento crítico e a percepção de que a Matemática é útil para resolver problemas reais, como os apresentados nas atividades. Verifique quais estratégias os estudantes usaram e quais dificuldades eles encontraram, a fim de sanar possíveis dúvidas. Incentive-os a compartilhar com os colegas as estratégias pessoais de resolução, mostrando como fizeram para compreender o objetivo da atividade e as ações deles para resolvê-la.

7. PARA PREPARAR UMA RECEITA, JOANA FOI AO SUPERMERCADO E COMPROU 3 QUILOGRAMAS DE FARINHA DE TRIGO E 5 QUILOGRAMAS DE FUBÁ. QUANTOS QUILOGRAMAS DE ALIMENTOS ELA COMPROU?

QUILOGRAMAS.

Resposta: 3 + 5 = 8 ou 5 + 3 = 8. 8 QUILOGRAMAS.

8. FELIPE FOI À FEIRA E COMPROU 4 QUILOGRAMAS DE LARANJA, 2 QUILOGRAMAS DE MAÇÃ E 3 QUILOGRAMAS DE BANANA. AO TODO, QUANTOS QUILOGRAMAS DE FRUTAS ELE COMPROU?

QUILOGRAMAS.

Resposta: 4 + 2 = 6; 6 + 3 = 9. 9 QUILOGRAMAS.

9. EM UM PACOTE HAVIA 8 QUILOGRAMAS DE RAÇÃO DE GATO. PARA ALIMENTAR SEUS GATOS, NILDA USOU, EM CERTO MÊS, 2 QUILOGRAMAS DESSA RAÇÃO.

QUANTOS QUILOGRAMAS DE RAÇÃO SOBRARAM NO PACOTE?

QUILOGRAMAS.

Resposta: 8 − 2 = 6 6 QUILOGRAMAS.

10. O CACHORRO DE WALTER TEM 7 QUILOGRAMAS E O DE SAMARA TEM 4 QUILOGRAMAS.

QUANTOS QUILOGRAMAS O CACHORRO DE SAMARA TEM A MENOS QUE O CACHORRO DE WALTER?

QUILOGRAMAS.

Resposta: 7 − 4 = 3 3 QUILOGRAMAS.

MEDIDAS DE CAPACIDADE

1. OBSERVE A IMAGEM.

A ) MARQUE UM X NO COPO EM QUE CABE MAIS LÍQUIDO.

Resposta: Os estudantes devem marcar um X no copo 2.

B ) CONTORNE O COPO EM QUE CABE MENOS LÍQUIDO.

Resposta: Os estudantes devem contornar o copo 4

2. A QUANTIDADE DE LÍQUIDO QUE UM RECIPIENTE PODE CONTER INDICA SUA CAPACIDADE.

A ) CONTORNE A JARRA QUE TEM A MAIOR CAPACIDADE.

Resposta: Os estudantes devem contornar a jarra 2

B ) AS GARRAFAS A SEGUIR TÊM A MESMA CAPACIDADE, MAS CADA UMA DELAS TEM QUANTIDADES DIFERENTES DE ÁGUA.

SABENDO QUE ESSAS GARRAFAS SÃO IGUAIS, FAÇA O QUE SE PEDE.

• CONTORNE A GARRAFA QUE TEM MAIS ÁGUA.

Resposta: Os estudantes devem contornar a garrafa 4

• MARQUE UM X NA GARRAFA QUE ESTÁ COM MENOS ÁGUA.

Resposta: Os estudantes devem marcar um X na garrafa 6

03/10/2025 10:03:13

• Se possível, leve para a sala de aula uma jarra e quatro recipientes transparentes, com diferentes tamanhos, como os apresentados na atividade 1 desta página. Com a jarra cheia de líquido, mostre aos estudantes que a quantidade de líquido diminui ao encher cada um dos recipientes. Essa ação auxiliará na compreensão de qual dos recipientes pode armazenar mais líquido e qual pode armazenar menos.

• O objetivo da atividade 2 é fazer com que os estudantes verifiquem que a capacidade de um determinado recipiente se altera de acordo com o tamanho dele e, assim, diferenciem capacidade de quantidade. Se necessário, explique que a garrafa com maior quantidade de água atingiu sua capacidade pois, geralmente, a capacidade desses recipientes não ultrapassa a base onde é colocada a tampa.

BNCC

Ao abordar a comparação de medidas de capacidade, a atividade 1 promove o desenvolvimento da habilidade EF01MA15 da BNCC por meio do uso de termos como cabe mais e cabe menos

• A atividade 3 visa levar os estudantes a estabelecerem relação entre a quantidade de líquido que há em determinando recipiente e sua capacidade, de modo a identificarem a quantidade necessária para ocupar a capacidade total desse recipiente. Se possível, leve para a sala de aula quatro garrafas transparentes de mesmo tamanho. Primeiro, coloque nelas quantidades de líquido que não sejam suficientes para encher totalmente uma garrafa ao transferir o líquido delas para apenas uma delas. Em seguida, coloque quantidades que, ao transferir para apenas uma, atinja a capacidade e haja sobra.

• O objetivo da atividade 4 é desenvolver a noção de divisão em partes iguais. Nesse sentido, verifique se os estudantes entenderam que a quantidade de água de coco é maior do que a capacidade de cada um dos copos. Portanto, é necessário mais de um copo para esvaziar todo o conteúdo da caixa.

AVALIANDO

Objetivo

Comparar a medida de capacidade de diferentes recipientes por meio da observação e da experimentação.

Sugestão de intervenção

Providencie recipientes com medidas de capacidade e formatos diferentes e algum líquido que possa ser reaproveitado. Coloque esses recipientes sobre uma mesa, de modo que todos os estudantes possam visualizá-los. Em seguida, encha alguns deles e faça perguntas aos estudantes, de modo que sejam capazes de distinguir, por exemplo, se o líquido de determinado recipiente cabe em outro ou, ainda, quantas vezes é preciso usar o conteúdo de determinado recipiente para encher outro.

3. C) Resposta pessoal. Espera-se que os estudantes respondam que não, pois a capacidade de um frasco é insuficiente para caber o azeite de todos os frascos juntos. Nesse caso, seria necessário um frasco com capacidade maior.

3. NA IMAGEM, OS FRASCOS APRESENTADOS TÊM O MESMO FORMATO E O MESMO TAMANHO.

A ) CONTORNE O FRASCO QUE ESTÁ COM MAIS AZEITE.

Resposta: Os estudantes devem contornar o frasco 4

B ) MARQUE UM X NO FRASCO QUE ESTÁ COM MENOS AZEITE.

Resposta: Os estudantes devem marcar um X no frasco 3

C ) EM SUA OPINIÃO, É POSSÍVEL COLOCAR O AZEITE DE TODOS OS FRASCOS EM APENAS UM FRASCO, IGUAL AO REPRESENTADO, SEM QUE TRANSBORDE? POR QUÊ?

4. ROBERTO VAI DESPEJAR UMA CAIXA DE ÁGUA DE COCO EM ALGUNS COPOS DE MESMA CAPACIDADE.

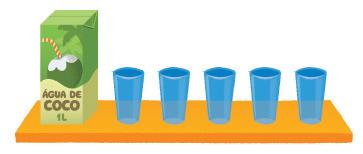
A ) EM SUA OPINIÃO, QUANTOS DESSES COPOS ROBERTO VAI CONSEGUIR ENCHER COMPLETAMENTE? CONVERSE COM OS COLEGAS SOBRE ISSO.

Resposta e comentários nas orientações ao professor.

B ) ROBERTO ENCHEU EXATAMENTE 4 COPOS COM UMA CAIXA DE ÁGUA DE COCO. PARA ENCHER 5 COPOS IGUAIS A ESSES, É NECESSÁRIO MAIS OU MENOS DE UMA CAIXA DE ÁGUA DE COCO? MARQUE UM X NA RESPOSTA. MENOS DE UMA CAIXA. MAIS DE UMA CAIXA.

Resposta: Os estudantes devem marcar um X na alternativa MAIS DE UMA CAIXA.

C ) QUANTAS CAIXAS DE ÁGUA DE COCO SÃO NECESSÁRIAS PARA ENCHER 8 COPOS IGUAIS AOS DE ROBERTO?

SÃO NECESSÁRIAS CAIXAS DE ÁGUA DE COCO. 1. 2. 3. 4.

Resposta: 4 + 4 = 8. SÃO NECESSÁRIAS 2 CAIXAS DE ÁGUA DE COCO.

Resposta 4. A) Resposta pessoal. Espera-se que os estudantes digam que depende da quantidade de líquido que cabe em cada copo, pois, embora tenham mesma capacidade, não há informações sobre qual é essa medida de capacidade.

5. Professor, professora. Ao realizarem esta atividade, é possível que os estudantes invertam a ordem das respostas dos itens, sendo outra

EXPERIMENTE

possibilidade de resposta: QUANTO MAIS VAZIO ESTÁ O RECIPIENTE, MAIS AGUDO É O SOM; QUANTO MAIS CHEIO ESTÁ O RECIPIENTE, MAIS GRAVE É O SOM.

5. VOCÊ SABIA QUE PODEMOS PRODUZIR SONS COM RECIPIENTES QUE CONTENHAM QUANTIDADES DIFERENTES DE LÍQUIDO?

PARA REALIZAR ESTE EXPERIMENTO, VOCÊ VAI PRECISAR DE:

• CINCO OU MAIS RECIPIENTES DE VIDRO DE MESMO TAMANHO E MESMO FORMATO;

• CORANTE PARA ALIMENTOS;

• ÁGUA;

• UMA COLHER.

SIGA AS ETAPAS A SEGUIR PARA REALIZAR O EXPERIMENTO.

A ) COLOQUE DIFERENTES QUANTIDADES DE ÁGUA NOS RECIPIENTES E ORGANIZE TODOS DO MAIS CHEIO PARA O MAIS VAZIO.

B ) MISTURE O LÍQUIDO DE CADA RECIPIENTE COM UM CORANTE DIFERENTE.

C ) AGORA, VOCÊ VAI PRODUZIR SONS: TOQUE OS RECIPIENTES COM A COLHER.

D ) COMPLETE AS FRASES COM AS PALAVRAS DAS FICHAS. AO PRODUZIR SOM COM OS RECIPIENTES, VOCÊ NOTOU QUE:

• QUANTO MAIS

ESTÁ O RECIPIENTE, MAIS

GRAVE VAZIO

CHEIO AGUDO

É O SOM.

Resposta: QUANTO MAIS CHEIO ESTÁ O RECIPIENTE, MAIS GRAVE É O SOM. QUANTO MAIS VAZIO ESTÁ O RECIPIENTE, MAIS AGUDO É O SOM.

• QUANTO MAIS

ESTÁ O RECIPIENTE, MAIS

É O SOM.

ARTICULANDO CONHECIMENTOS

• A atividade 5 proposta nesta página permite um trabalho integrado com o componente curricular de Arte, ao explorar a música e os sons produzidos por recipientes em circunstâncias previamente estabelecidas. Escolha antecipadamente os recipientes que serão usados no experimento, prevendo o som que o objeto vai emitir de acordo

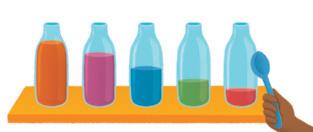
• Para o bom desenvolvimento dessa atividade, providencie antecipadamente os materiais necessários e leve para a sala de aula a quantidade de cores necessária para tingir o líquido, de acordo com a quantidade de recipientes. Cores diferentes possibilitam aos estudantes visualizarem com mais facilidade a quantidade de água em cada recipiente. Primeiramente, mostre aos estudantes como tocar os recipientes com a colher; em seguida, permita que todos façam esse processo. O objetivo dessa atividade é promover a curiosidade, a criatividade e a experimentação. Verifique se os estudantes identificam que um som agudo está associado a um som “fino”, enquanto um som grave, a um som “grosso” –se necessário, comente isso com eles.

• Ao trabalhar com o sentido tátil, essa atividade promove a inclusão de estudantes com deficiência visual. Além disso, o uso de materiais concretos facilita a interação e a inclusão de estudantes com algum transtorno, como TEA e TDAH. Verifique se há algum estudante com deficiência auditiva. Se necessário, adapte a atividade utilizando algum recurso que transforme o som em vibração ou recorra a um intérprete.

03/10/2025 10:03:14

com a quantidade de líquido. Para a segurança de todos, é recomendado usar recipientes que não quebrem com facilidade. Sendo assim, procure escolher preferencialmente recipientes que não sejam feitos com vidro, mas, se forem, que ele seja espesso e resistente, a fim de prevenir acidentes.

• A atividade 1 apresenta o litro com uma unidade-padrão de medida de capacidade, além de verificar se os estudantes reconhecem alguns produtos vendidos com base nessa unidade de medida.

• Aproveite esse momento e escreva na lousa o nome de outros produtos vendidos por litro e por quilograma. Peça aos estudantes que identifiquem quais são vendidos por litro e, se julgar necessário, diga-lhes para verificar quais são vendidos por quilograma, a fim de retomar o conteúdo já estudado e responder a possíveis dúvidas.

O LITRO

1.

IMAGENS SEM PROPORÇÃO ENTRE SI.

O LITRO É UMA UNIDADE DE MEDIDA DE CAPACIDADE QUE

INDICA A QUANTIDADE DE LÍQUIDO QUE UM RECIPIENTE PODE

CONTER. VÁRIOS PRODUTOS SÃO VENDIDOS EM LITRO NO DIA A DIA.

CONTORNE OS PRODUTOS A SEGUIR QUE SÃO VENDIDOS EM LITRO.

Resposta: Os estudantes devem contornar as imagens da caixa de leite, do detergente e do galão de água.

TELEVISOR. DETERGENTE.

ARROZ. ÁGUA.

LEITE. BISCOITO.

2. NA IMAGEM, A GARRAFA 3 TEM CAPACIDADE PARA 1 LITRO DE ÁGUA.

2. B) Resposta pessoal. Espera-se que os estudantes digam que compararam as dimensões das garrafas 1, 2, 4 e 5 com a dimensão da garrafa 3, que tem capacidade de 1 litro.

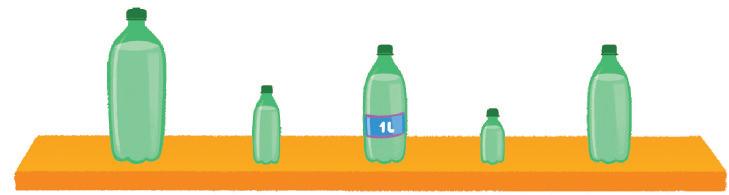
A ) COMPARE AS DEMAIS GARRAFAS COM A GARRAFA 3 E MARQUE UM X NA MEDIDA DE CAPACIDADE ADEQUADA PARA CADA UMA DELAS.

GARRAFA 1

MAIS DO QUE 1 LITRO.

GARRAFA 2

MAIS DO QUE 1 LITRO.

GARRAFA 4

MAIS DO QUE 1 LITRO.

GARRAFA 5

MAIS DO QUE 1 LITRO.

DICA: USAMOS L PARA ABREVIAR A PALAVRA LITRO

Resposta: Os estudantes devem marcar um X em MAIS DO QUE 1 LITRO.

1 LITRO.

Resposta: Os estudantes devem marcar um X em MENOS DO QUE 1 LITRO.

1 LITRO.

MENOS DO QUE 1 LITRO. MENOS DO QUE 1 LITRO.

Resposta: Os estudantes devem marcar um X em MENOS DO QUE 1 LITRO.

1 LITRO.

MENOS DO QUE 1 LITRO.

Resposta: Os estudantes devem marcar um X em 1 LITRO.

1 LITRO.

MENOS DO QUE 1 LITRO.

B ) COMO VOCÊ OBTEVE AS RESPOSTAS DO ITEM ANTERIOR?

ATIVIDADE EXTRA

Reproduza o quadro a seguir para os estudantes ou peça que o copiem no caderno.

Objetos sem marcação de

03/10/2025 10:03:20

Oriente os estudantes a selecionarem quatro objetos que não apresentam marcação de capacidade, como panelas, potes, jarras e copos, e solicite que escrevam no quadro o nome desses objetos na coluna dos recipientes. Peça a eles que façam uma estimativa da capacidade deles, indicando se eles têm capacidade igual, maior ou menor do que 1 litro. Em seguida, solicite que encham um recipiente com 1 litro de capacidade com água e verifiquem se suas estimativas estão corretas colocando água nos recipientes que eles selecionaram. MODELO

• A atividade 2 visa desenvolver a compreensão da quantidade de líquido que cabe em um recipiente por meio da comparação de um determinado recipiente com outro que comporta exatamente 1 litro. Avalie a possibilidade de levar para a sala de aula embalagens vazias de alguns produtos com capacidade de 1 litro, 2 litros e menos de 1 litro, como caixa de leite, embalagem de 2 ou 5 litros de amaciante e caixinha de suco, respectivamente. Assim, os estudantes poderão fazer as comparações necessárias. Outra possibilidade é escolher embalagens de um mesmo produto com capacidades diferentes.

• Avalie a possibilidade de pedir aos estudantes que façam em casa a atividade extra a seguir.

• A atividade 3 tem como objetivo desenvolver nos estudantes a ideia de divisão em partes iguais. Se necessário, represente a quantidade de 7 xícaras na lousa usando palitos e, com a ajuda dos estudantes, risque a quantidade de palitos que representa quantas xícaras Fernanda encheu utilizando 1 litro de leite, a fim de que eles percebam que sobrarão 2 palitos sem riscar.

• A atividade 4 visa à comparação entre recipientes com medidas de capacidade distintas, de modo que os estudantes sejam capazes de identificar qual tem a maior capacidade e qual tem a menor. Além disso, aborda a adição e a subtração, conteúdos estudados anteriormente. Se necessário, apresente outros questionamentos, como: “Quantos litros de água Alice precisa usar para encher completamente dois baldes iguais ao balde 1?”; “Quantos litros de água Alice, precisa usar para encher completamente dois baldes iguais ao balde 2?”. Dê oportunidade a todos para responderem e participarem da intervenção, e acolha com respeito e atenção todas as ideias e contribuições. Durante essa troca de informações, verifique a maneira como constroem as frases para responderem e as estratégias pessoais que estão usando. Percebendo dificuldades e não sendo possível saná-las nesse momento, elabore um plano de recuperação para trabalhar com eles as defasagens.

• Ao final da unidade, proponha o desafio apresentado a seguir. Nele, os estudantes devem obter a medida de massa de um objeto por comparação indireta. Verifique se eles percebem que, ao substituir o mamão pelo objeto e mantendo a balança em equilíbrio, é possível concluir que o mamão tem 1 kg de medida de massa.

3. COM O PROFESSOR, LEIA O QUE FERNANDA DISSE.

COM 1 LITRO DE LEITE, É POSSÍVEL ENCHER EXATAMENTE 5 XÍCARAS COMO ESTA.

A ) PARA ENCHER 7 XÍCARAS IGUAIS A ESSA, É NECESSÁRIO MAIS DE 1 LITRO OU MENOS DE 1 LITRO DE LEITE? MARQUE UM X NA RESPOSTA CORRETA.

Resposta: Os estudantes devem marcar um X em MAIS DE UM LITRO.

MENOS DE UM LITRO.

B ) DE ACORDO COM A CENA, QUANTOS LITROS DE LEITE

SERIAM NECESSÁRIOS PARA ENCHER 15 XÍCARAS IGUAIS A ESSA? MARQUE UM X NA RESPOSTA CORRETA.

1 LITRO.

MAIS DE UM LITRO. 2 LITROS. 3 LITROS.

Resposta: Os estudantes devem marcar um X em 3 LITROS.

4. ALICE TEM DOIS BALDES. A MEDIDA DE CAPACIDADE DE CADA UM DELES ESTÁ INDICADA NA IMAGEM.

A ) QUAL DESSES BALDES TEM MAIOR MEDIDA DE CAPACIDADE? .

Resposta: BALDE 2

B ) QUAL É A DIFERENÇA, EM LITROS, ENTRE AS MEDIDAS DE CAPACIDADE DOS BALDES 1 E 2?

LITROS.

C ) QUANTOS LITROS DE ÁGUA ALICE PRECISA UTILIZAR PARA ENCHER COMPLETAMENTE OS DOIS BALDES?

LITROS.

Resposta: 16 − 10 = 6 6 LITROS.

Resposta: 16 + 10 = 26 26 LITROS.

Sugestão de Desafio

Em uma balança de dois pratos, estavam equilibrados um mamão e uma manga. Retirando o mamão, colocando um objeto com massa de um quilograma, a balança continuou em equilíbrio. Qual é a medida da massa do mamão?

Resposta

A medida da massa do mamão é 1 kg

AVALIANDO

Objetivo

Identificar o uso do litro como unidade de medida de capacidade.

Sugestão de intervenção

Peça aos estudantes que digam o nome de alguns produtos vendidos em recipientes com menos de 1 litro, 1 litro e mais de 1 litro. Provavelmente, eles vão citar produtos como suco, achocolatado, refrigerante, leite, água, água de coco e produtos de limpeza.

Professor, professora: Oriente os estudantes na escrita das palavras que respondem aos itens B e C da atividade 5, incentivando o traçado em letra cursiva na pauta apresentada.

5. A TABELA APRESENTA A QUANTIDADE DE GASOLINA QUE BRUNO COLOCOU EM SUA MOTO DURANTE CINCO DIAS DE UMA SEMANA.

QUANTIDADE DE GASOLINA ABASTECIDA EM CINCO DIAS DE UMA SEMANA DIA MEDIDA DA CAPACIDADE (EM LITROS)

SEGUNDA-FEIRA 3

TERÇA-FEIRA 4

QUARTA-FEIRA 5

QUINTA-FEIRA 3

SEXTA-FEIRA 6

FONTE DE PESQUISA: ANOTAÇÕES DE BRUNO.

A ) NA QUARTA-FEIRA, QUANTOS LITROS DE GASOLINA BRUNO

Resposta: 5 LITROS.

COLOCOU? LITROS.

B ) EM QUAL DIA ELE COLOCOU MAIOR QUANTIDADE DE GASOLINA?

Resposta: Sexta-feira.

C ) EM QUAIS DIAS ELE COLOCOU A MESMA QUANTIDADE DE GASOLINA? Resposta: Segunda-feira e quinta-feira.

D ) CALCULE MENTALMENTE QUANTOS LITROS DE GASOLINA

FORAM COLOCADOS A MAIS NA SEXTA-FEIRA DO QUE NA

Resposta: 2 LITROS.

TERÇA-FEIRA. LITROS.

DESAFIO A MAIS

PARA PREPARAR OS PRATOS DE CERTO RESTAURANTE, FORAM COMPRADOS 11 LITROS DE ÓLEO DE SOJA, 12 LITROS DE ÓLEO DE MILHO E 14 LITROS DE ÓLEO DE GIRASSOL. NO PRIMEIRO

Resposta: 11 + 12 = 23; 23 + 14 = 37; 37 – 20 = 17 17 LITROS.

MÊS, 20 LITROS DE ÓLEO FORAM USADOS. QUANTOS LITROS DE ÓLEO AINDA RESTAM NO RESTAURANTE? LITROS.

Unidades temáticas integradas 243

CONCLUSÃO

Acompanhar a aprendizagem dos estudantes é fundamental para um ensino bem-sucedido. A fim de realizar um monitoramento mais abrangente e organizado, registre nos relatórios individuais ou nas fichas de avaliação o desempenho de cada estudante, levando em consideração suas particularidades. Um modelo desse tipo de ficha pode ser encontrado no tópico Avaliação deste Manual do professor. Assim, será possível visualizar de modo individual as trajetórias de aprendizagem, incluindo os avanços e os pontos de dificuldades a serem sanados por meio de atividades que promovam recuperação dos conteúdos.

03/10/2025 10:03:20

Esse método de verificar a progressão dos estudos e identificar o que a turma de fato conseguiu aprender e o que ficou com lacunas de absorção é de grande importância para que seja possível repensar estratégias em sala de aula, tornando as ações pedagógicas cada vez mais eficazes.

A conclusão da unidade é o momento de avaliar se os objetivos por ela propostos foram alcançados. Para esse diagnóstico, observe no final deste Manual do professor. algumas possibilidades de avaliação formativa que permitem realizar o monitoramento da aprendizagem dos estudantes e intervir caso eles não tenham atingido os resultados esperados.

• A atividade 5 promove uma integração com as unidades temáticas Números e Probabilidade e estatística, ao trabalhar com o registro, a leitura e a interpretação de uma tabela. Esteja atento à maneira como pegam o lápis, se usam corretamente o apoio dos dedos formando pega de três pontos e se executam os traçados orientados pelo sentido e direção corretos das letras e dos números. Podem ser necessárias outras estratégias, usando recursos como a caixa de areia, a escrita com tinta e a escrita no ar, para treinarem o movimento e a direção do traçado.

• No Desafio a mais, os estudantes devem usar uma situação-problema do cotidiano para trabalhar o raciocínio lógico-matemático e a resolução de problemas de duas ou mais etapas, além aplicarem as operações de adição e subtração, conteúdo já abordado em unidades anteriores. Espera-se que eles identifiquem a informação principal do problema e compreendam a sequência de operações para chegar à resposta correta. Para resolver, eles devem, primeiramente, juntar as quantidades de todos os óleos comprados (11 + 12 + 14 = 37). Em seguida, devem subtrair a quantidade usada para descobrir o que resta no restaurante (37 − 20 = 17). Caso encontrem alguma lógica diferente da esperada, incentive-os a compartilhar com os demais colegas, fazendo intervenções pontuais e estratégicas.

1. Objetivos

Identificar quantias compostas de cédulas e moedas do Real.

Comparar quantias por meio da noção de subtração. Sugestão de intervenção

No item A, observe se os estudantes reconhecem as cédulas e moedas presentes na atividade. Caso surja alguma dificuldade, destaque o número que indica o valor da cédula e da moeda. Para compor as quantias, eles devem aplicar seus conhecimentos sobre a ideia de juntar quantidades. Apesar de ser um conhecimento abordado em outros momentos, pode ocorrer dificuldade nessa ação. Nesse caso, oriente-os a fazer contagem completando as quantidades, com ou sem auxílio de material de contagem. No item B, havendo dificuldades, proponha aos estudantes que façam correspondência entre as cédulas e moedas de cada personagem. Por exemplo, ambos têm uma cédula de 5 reais, e as duas cédulas de 2 reais que Débora tem equivalem às quatro moedas de 1 real de Ivo. Logo, ela tem uma moeda de 1 real a mais do que ele. Essa correspondência auxilia na resposta do item C, que também pode ser obtida por meio da subtração. Essa atividade envolve o reconhecimento e a capacidade de relacionar valores de cédulas e moedas para resolver problemas em contextos simples do cotidiano.

VAMOS AVALIAR O APRENDIZADO

1. DÉBORA E IVO TÊM AS QUANTIAS REPRESENTADAS A SEGUIR.

DÉBORA IVO

A ) COMPLETE A FRASE.

IMAGENS SEM PROPORÇÃO ENTRE SI.

DÉBORA TEM REAIS E IVO TEM REAIS.

Resposta: DÉBORA TEM 10 REAIS E IVO TEM 9 REAIS.

B ) MARQUE UM X NO NOME DA PESSOA QUE TEM A MAIOR QUANTIA.

Resposta: Espera-se que os estudantes marquem um X em DÉBORA

DÉBORA IVO

C ) CONTORNE A QUANTIA EM REAIS QUE REPRESENTA A DIFERENÇA ENTRE AS QUANTIAS QUE DÉBORA E IVO TÊM.

Resposta: Espera-se que os estudantes contornem 1 REAL

3 REAIS 1 REAL 0 REAL

2. EM UMA RUA, O NÚMERO DE CADA CASA É 3 UNIDADES MAIOR DO QUE O DA CASA ANTERIOR. ESCREVA A NUMERAÇÃO DE CADA CASA, SABENDO QUE EM DUAS DELAS O NÚMERO JÁ ESTÁ INDICADO.

Resposta: 7; 10; 13; 16; 19.

2. Objetivos

Reconhecer regularidade em uma sequência. Descrever os elementos ausentes em uma sequência.

Sugestão de intervenção

Para auxiliar na dificuldade dos estudantes, escreva na lousa diferentes tipos de sequências, começando pelas mais simples, como a sequência de adição ou subtração de 1 unidade, progre-

dindo para adição ou subtração de 2 unidades. Verifique se os estudantes percebem que, para continuar a sequência pode ser efetuada uma adição e, para regredir nela, deve ser feita uma subtração. Depois disso, retome a atividade e incentive-os a verificar que as 3 unidades devem ser adicionadas à quantidade anterior ou já identificada para obter a quantidade seguinte, que vai representar a próxima numeração.

3. MARIA REGISTROU AS MEDIDAS DE CAPACIDADE DE TRÊS RECIPIENTES

QUE HÁ NA CASA DELA.

A ) NO RECIPIENTE A CABEM

QUANTOS LITROS A MAIS DO QUE NO RECIPIENTE B?

LITROS.

Resposta: 10 5 = 5 5 LITROS.

MEDIDAS DE CAPACIDADE DE TRÊS RECIPIENTES

RECIPIENTE

MEDIDA DE CAPACIDADE

A 10 LITROS

B 5 LITROS

C 2 LITROS

B ) QUAL É A MEDIDA DE CAPACIDADE DOS TRÊS RECIPIENTES JUNTOS? LITROS.

Resposta: 10 + 5 + 2 = 17 ou 10 + 5 = 15 e 15 + 2 = 17; 17 LITROS.

4. IGOR ESCREVEU A MEDIDA DA MASSA DE QUATRO AMIGOS EM FICHAS E AS COLOCOU EM UMA URNA.

27 QUILOGRAMAS

31 QUILOGRAMAS

28 QUILOGRAMAS

34 QUILOGRAMAS

A ) AO SORTEAR UMA DESSAS FICHAS, É CERTO, POSSÍVEL OU IMPOSSÍVEL QUE A MEDIDA OBTIDA SEJA MENOR DO QUE

25 QUILOGRAMAS? MARQUE UM X NA RESPOSTA CORRETA.

Resposta: Os estudantes devem marcar X em IMPOSSÍVEL.

CERTO

POSSÍVEL

IMPOSSÍVEL

B ) SORTEANDO UMA DESSAS FICHAS, É CERTO, POSSÍVEL OU IMPOSSÍVEL QUE A MEDIDA OBTIDA SEJA MAIOR DO QUE

30 QUILOGRAMAS? MARQUE UM X NA RESPOSTA CORRETA.

Resposta: Os estudantes devem marcar X em POSSÍVEL

CERTO

POSSÍVEL

IMPOSSÍVEL

245

03/10/2025 10:04:10

3. Objetivos

Comparar medidas de capacidade.

Efetuar cálculos usando medidas de capacidade. Sugestão de intervenção

Apresente imagens de produtos com as capacidades indicadas na tabela ou, se possível, leve para a sala de aula embalagens vazias desses produtos, para que os estudantes possam manipular.

Essa atividade envolve a comparação de medidas de capacidade para resolver problemas em contextos simples do cotidiano.

4. Objetivo

Determinar se um evento é certo, possível ou impossível de ocorrer em um sorteio.

Sugestão de intervenção

Para sanar dúvidas relacionadas ao significado dos termos utilizados, peça aos estudantes que indiquem as possibilidades de retirada da urna. Se possível, realize o experimento com eles. Para tanto, produza fichas com as medidas apresentadas e providencie uma sacola ou caixa de onde seja possível retirar uma ficha sem que se leia o que está escrito. Promova um debate com os estudantes a fim de identificar os contextos de uso dos termos certo, possível e impossível

1. Objetivos

Reconhecer as figuras geométricas espaciais.

Identificar figuras geométricas espaciais na imagem.

Sugestão de intervenção

A fim de remediar eventuais dificuldades no reconhecimento das figuras geométricas espaciais, faça questionamentos utilizando objetos disponíveis na escola, como móveis, caixas, cesto de lixo, entre outros. Outra possibilidade é levar para a sala de aula caixas, dados, brinquedos, entre outros objetos que lembrem figuras geométricas espaciais, e solicitar aos estudantes que identifiquem a que figuras geométricas espaciais cada um desses objetos se assemelha.

2. Objetivos

Realizar medição de comprimentos.

Efetuar uma subtração. Sugestão de intervenção

Leve para a sala de aula vários barbantes cortados em diversos tamanhos. Organize os estudantes em duplas e, em seguida, distribua dois barbantes de maneira que as duplas tenham a oportunidade de medi-los. Peça a cada dupla que indique a medida, em centímetros, do comprimento dos dois barbantes, bem como a diferença da medida de comprimento entre eles. Se necessário, auxilie-os nas medições e na comparação entre as medidas obtidas.

1. Resposta: Os estudantes devem pintar no boneco os cubos de azul, os blocos retangulares de verde, os cones de vermelho, as esferas de

VAMOS CONCLUIR

1. PINTE AS PARTES DO BONECO CONFORME AS CORES DAS FIGURAS GEOMÉTRICAS ESPACIAIS NA LEGENDA.

LEGENDA

MARQUE UM X NA FIGURA GEOMÉTRICA ESPACIAL DA LEGENDA QUE NÃO FAZ PARTE DO BONECO.

Resposta: Os amarelo e os cilindros de laranja. estudantes devem marcar um X na pirâmide.

2. UTILIZANDO UMA RÉGUA, MEÇA O COMPRIMENTO DAS FITAS A SEGUIR.

A MEDIDA DO COMPRIMENTO DA FITA VERDE TEM QUANTOS CENTÍMETROS A MAIS DO QUE A MEDIDA DA FITA AMARELA?

Resposta: 8 − 3 = 5

Resposta: A MEDIDA DO COMPRIMENTO DA FITA VERDE TEM 5 CENTÍMETROS A MAIS DO QUE A MEDIDA DA FITA AMARELA.

A MEDIDA DO COMPRIMENTO DA FITA VERDE TEM CENTÍMETROS A MAIS DO QUE A MEDIDA DA FITA AMARELA.

03/10/2025 10:05:18

3. OS HORÁRIOS EM QUE OTÁVIO E REBECA SAÍRAM DE SUAS CASAS PARA TRABALHAR NO PERÍODO DA MANHÃ ESTÃO INDICADOS NOS RELÓGIOS.

OTÁVIO SAIU DE SUA CASA QUANTAS HORAS DEPOIS DE REBECA?

Resposta: 9 − 7 = 2

OTÁVIO REBECA

OTÁVIO SAIU DE SUA CASA HORAS DEPOIS DE REBECA.

Resposta: OTÁVIO SAIU DE SUA CASA 2 HORAS DEPOIS DE REBECA.

4. NÍCOLAS, RENAN E LUANA FORAM A UM ESTÁDIO DE FUTEBOL ASSISTIR A UM JOGO ACOMPANHADOS DE SEUS PAIS.

DICA: PARA RESOLVER ESTA ATIVIDADE, IDENTIFIQUE INICIALMENTE QUAL É A DIREITA DE NÍCOLAS. NÍCOLAS

A ) RENAN VAI SE SENTAR À DIREITA DE NÍCOLAS. CONTORNE DE VERMELHO A CADEIRA EM QUE RENAN VAI SE SENTAR.

Resposta: Os estudantes devem contornar de vermelho a cadeira 1

B ) LUANA VAI SE SENTAR IMEDIATAMENTE À ESQUERDA DE NÍCOLAS. CONTORNE DE AMARELO A CADEIRA EM QUE LUANA VAI SE SENTAR.

Resposta: Os estudantes devem contornar de amarelo a cadeira 3

03/10/2025 10:05:18

3. Objetivos

Ler as horas em um relógio de ponteiros.

Efetuar uma subtração. Sugestão de intervenção

Auxilie os estudantes na leitura das horas em um relógio de ponteiros e a resolver subtrações. Se possível, leve para a sala de aula um relógio com ponteiros grandes, a fim de que todos possam manuseá-los. Em seguida, proponha atividades do cotidiano deles, de modo que, além de fazer a leitura do relógio, eles resolvam uma subtração. Avalie a conve ni ência de propor que, em duplas, eles indiquem a hora em que realizam determinadas tarefas, como acordar, almoçar, jantar, dormir, brincar e fazer o dever escolar. Caso haja diferenças entre os horários indicados pelos integrantes da dupla, elas deverão ser anotadas.

Objetivo

Identificar direita e esquerda em relação ao personagem da atividade. Sugestão de intervenção

Propor atividades práticas no pátio da escola ou na sala de aula, para que os estudantes possam reconhecer direita e esquerda em relação a eles mesmos e em relação aos personagens da atividade.

5. Objetivo

Contar quantidades.

Sugestão de intervenção

Acompanhe as dificuldades dos estudantes em realizar a contagem, observando como eles utilizam diferentes estratégias para resolver o item B. Esclareça possíveis dúvidas, de modo que todos possam compre ender os procedimentos. Comente as estratégias usadas pelos estudantes e, se julgar conveniente, incentive a turma a compartilhar estratégias pessoais, enriquecendo o aprendizado e promovendo novas descobertas àqueles que ainda não sistematizaram o conhecimento sobre o assunto.

6. Objetivo

Elaborar adições e resolvê-las.

Sugestão de intervenção

Com base nas respostas dos estudantes, identifique possíveis dificuldades na elaboração das quatro adições possíveis cujo resultado seja o proposto na atividade. Caso apresentem dúvidas, proponha outras atividades para auxiliar na compreensão da noção de adição. Para tanto, escreva em cada item uma ou duas adições possíveis cujo resultado seja 10, aumentando gradativamente conforme as respostas dadas por eles.

5. ARTUR FOI À PRAIA COM SEUS AMIGOS E TIROU UMA FOTOGRAFIA DOS PÉS DA TURMA.

A ) QUANTOS PÉS ESTÃO APARECENDO

NESSA FOTOGRAFIA?

Resposta: 12

B ) QUANTOS DEDOS APARECEM NA

FOTOGRAFIA?

Resposta: 60

PÉS NA AREIA.

6. UTILIZANDO OS NÚMEROS QUE VOCÊ JÁ ESTUDOU, ESCREVA EM CADA ITEM QUATRO ADIÇÕES POSSÍVEIS CUJO RESULTADO SEJA:

Sugestões de resposta:

A: 10 + 8 = 18; 15 + 3 = 18; 11 + 7 = 18; 9 + 9 = 18.

B: 13 + 13 = 26; 20 + 6 = 26; 23 + 3 = 26; 21 + 5 = 26

7. LIGUE CADA FIGURA GEOMÉTRICA PLANA À FICHA COM O NOME DELA.

Resposta: Os estudantes devem ligar: A-QUADRADO; B-TRIÂNGULO; C-CÍRCULO.

CÍRCULO

7. Objetivos

Reconhecer figuras geométricas planas. Nomear as figuras geométricas planas identificadas.

Sugestão de intervenção

Para sanar dúvidas quanto ao reconhecimento e à capacidade de relacionar figuras geométri-

TRIÂNGULO

QUADRADO

cas planas às nomenclaturas correspondentes, levante hipóteses acerca da existência de objetos disponíveis na sala de aula que se assemelham a elas. Além disso, proponha aos estudantes que identifiquem objetos e móveis que lembram figuras geométricas planas, nomeando-os. Para finalizar, pergunte quais outros objetos eles conhecem que se assemelham a essas figuras.

8. ANA, DANIELA E RUI ESTÃO BRINCANDO COM UM JOGO DE TABULEIRO. NESSE JOGO, A CADA RODADA, O JOGADOR DEVE AVANÇAR COM SUA FICHA A QUANTIDADE DE CASAS SORTEADA NO DADO.

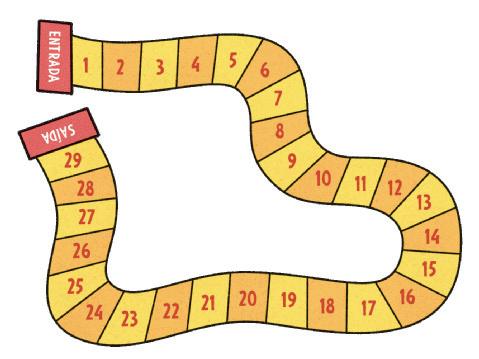
A ) ANA ESTAVA COM SUA FICHA NA CASA DE NÚMERO 12. ELA LANÇOU O DADO E SORTEOU O NÚMERO 4. PARA QUAL NÚMERO DESSE TABULEIRO ELA DEVERÁ MOVER SUA FICHA?

Resposta: 12 + 4 = 16. Para o número 16.

B ) DANIELA ESTAVA COM SUA FICHA NA CASA DE NÚMERO 8. PARA QUAL NÚMERO DO TABULEIRO ELA DEVERÁ MOVER SUA FICHA SE, AO LANÇAR O DADO, O NÚMERO SORTEADO FOI 6?

Resposta: 8 + 6 = 14. Para o número 14.

C ) RUI ESTAVA COM A FICHA NA CASA DE NÚMERO 15. SE ELE LANÇOU O DADO E SORTEOU O NÚMERO 5, PARA QUAL NÚMERO DO TABULEIRO DEVERÁ MOVER SUA FICHA?

Resposta: 15 + 5 = 20. Para o número 20.

D ) APÓS AS JOGADAS DE ANA, DANIELA E RUI DESCRITAS ANTERIORMENTE, ESCREVA O NOME DO JOGADOR QUE ESTÁ MAIS PRÓXIMO DA SAÍDA.

Resposta: Os estudantes deverão comparar as jogadas de cada jogador e verificar que Rui está mais perto da saída.

03/10/2025 10:05:20

8. Objetivos

Resolver situações-problema que envolvem adição. Comparar números naturais.

Sugestão de intervenção Leia pausadamente a atividade para melhor interpretação das perguntas. Nos itens A, B e C, evidencie para os estudantes que o número sorteado no dado é a quantidade de casas que o jogador deve mover a ficha. Caso apresentem dificuldades em reconhecer a adição como meio de solucionar o problema, oriente-os a marcar a posição inicial de cada jogador no tabuleiro e contar a quantidade referente ao número sorteado, até chegar à casa esperada. Verifique se eles associaram essa ação a operação da adição, bem como se observaram que o jogador que está na casa de maior número é o que está mais próximo da saída. Para melhor aproveitamento dessa atividade, monte tabuleiros semelhantes a esse usando materiais recicláveis. Organize os estudantes em grupos e distribua os tabuleiros. Explique as regras e, em seguida, permita-lhes jogar por conta própria, a fim de que identifiquem e compreendam como o jogo funciona na prática.

RUI

ANA

DANIELA

9. Objetivo

Resolver operações de subtração utilizando o algoritmo.

Sugestão de intervenção

A fim de remediar possíveis dificuldades, recorde com eles os procedimentos de cálculo da subtração usando o algoritmo. Antes de iniciar a atividade, proponha aos estudantes outros cálculos em que seja possível praticar mentalmente subtrações com números menores. Auxilie na leitura dos itens da atividade e, se necessário, leve para a sala de aula materiais de contagem, como palitos, tampinhas e material dourado, para que eles possam compreender a noção de retirar, que é proposta nos itens. Comente a importância do uso do algoritmo como recurso de cálculo em operações de subtração e a facilidade que ele oferece aos procedimentos.

9. LEIA CADA SITUAÇÃO COM A AJUDA DO PROFESSOR. DEPOIS, RESOLVA AS OPERAÇÕES COM O ALGORITMO PARA DETERMINAR O QUE SOBROU EM CADA CAIXA.

WALTER TINHA DUAS BANDEJAS COM 12 OVOS CADA. ELE USOU 11 OVOS AO PREPARAR UMA RECEITA. COMPLETE A SUBTRAÇÃO PARA DETERMINAR A QUANTIDADE DE OVOS QUE

SOBRARAM NAS BANDEJAS.

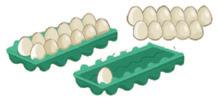
Resposta: Os estudantes devem preencher, no algoritmo, o minuendo 24 e o subtraendo 11. 24 − 11 = 13

SOBRARAM OVOS NAS BANDEJAS.

Resposta: SOBRARAM 13 OVOS BAS BANDEJAS.

JOANA TEM UMA CAIXA COM 36 LÁPIS DE COR. PARA FAZER UM TRABALHO, ELA RETIROU 15 LÁPIS DESSA CAIXA. COMPLETE A SUBTRAÇÃO PARA DETERMINAR A QUANTIDADE DE LÁPIS QUE

SOBRARAM NA CAIXA.

Resposta: Os estudantes devem preencher, no algoritmo, o

Resposta: SOBRARAM 21 LÁPIS DE COR NA CAIXA.

SOBRARAM LÁPIS DE COR NA CAIXA.

RAUL É PROFESSOR E TEM UMA CAIXA COM 48 UNIDADES DE GIZ. PARA DAR AULA, ELE RETIROU 14 UNIDADES DE GIZ DO TOTAL QUE HAVIA NA EMBALAGEM. COMPLETE A SUBTRAÇÃO PARA DETERMINAR QUANTAS UNIDADES DE GIZ SOBRARAM NA EMBALAGEM.

Resposta: Os estudantes

devem preencher, no

algoritmo, o minuendo 48 e o subtraendo 14. 48 14 = 34

Resposta: SOBRARAM 34 UNIDADES DE GIZ NA EMBALAGEM. minuendo 26 e o subtraendo 15. 36 − 15 = 21

SOBRARAM UNIDADES DE GIZ NA EMBALAGEM.

10. O GRÁFICO APRESENTA A MEDIDA

DA MASSA APROXIMADA DE ALGUNS ANIMAIS AMEAÇADOS DE EXTINÇÃO.

DICA: NESTE GRÁFICO, CADA QUADRINHO PINTADO REPRESENTA 1 QUILOGRAMA.

MEDIDA DA MASSA APROXIMADA DE ALGUNS ANIMAIS AMEAÇADOS DE EXTINÇÃO EM 2025

MEDIDA DA MASSA (EM QUILOGRAMAS)

JAGUATIRICA

FONTE DE PESQUISA: ADW. DISPONÍVEL EM: https://animaldiversity.org/about/. ACESSO EM: 4 ABR. 2025.

A ) QUAL É A MEDIDA DA MASSA APROXIMADA, EM QUILOGRAMAS, DO GATO-PALHEIRO?

QUILOGRAMAS.

Resposta: 6 QUILOGRAMAS.

B ) QUAL ANIMAL TEM, APROXIMADAMENTE, 9 QUILOGRAMAS DE MEDIDA DE MASSA? MARQUE UM X NO NOME DELE.

Resposta: Os estudantes devem marcar um X em MACACO-ARANHA.

JAGUATIRICA

MACACO-ARANHA

GATO-PALHEIRO

CACHORRO-DO-MATO-VINAGRE

11. JANE COMPROU 3 GARRAFAS

DE SUCO PARA A FESTA DE SEU ANIVERSÁRIO. CADA GARRAFA

CONTÉM 3 LITROS DE SUCO. QUANTOS LITROS DE SUCO ELA COMPROU NO TOTAL?

Resposta: 3 + 3 + 3 = 9. JANE COMPROU NO TOTAL 9 LITROS DE SUCO.

10. Objetivos

Realizar a leitura de informações dispostas em um gráfico.

Reconhecer o quilograma como uma unidade de medida de massa.

Sugestão de intervenção

Avalie a necessidade de remediar possíveis dificuldades relacionadas à interpretação de gráficos e ao reconhecimento das medidas de massa por meio da comparação. Se julgar conveniente, complemente a atividade elaborando um gráfico de barras utilizando os dados coletados sobre a medida da massa dos estudantes da turma, de maneira semelhante ao proposto na atividade. Em seguida, faça questionamentos como: “Quantos estudantes apresentam medida da massa na faixa entre 18 kg e 25 kg?”; “Qual é a faixa de medida de massa mais comum entre os estudantes?”. Ouça as falas dos estudantes, a fim de conduzir de modo respeitoso a conversa e coibir situações desagradáveis e de bullying em relação ao assunto medida de massa.

JANE COMPROU NO TOTAL LITROS DE SUCO.

11. Objetivos

Reconhecer o litro como uma unidade de medida de capacidade.

Resolver uma adição. Sugestão de intervenção

Durante a resolução da atividade, identifique se algum estudante manifesta dificuldade para interpretar as medidas apresentadas, propondo questionamentos como: “A quantidade de garrafas de suco que Jane comprou não foi suficiente e ela teve que sair para comprar mais 2 garrafas de 3 litros. Desse modo, quantos litros de suco ela comprou no total?”. Verifique se eles calculam 9 + 3 + 3 = 15, concluindo corretamen-

03/10/2025 10:05:21

te que Jane comprou no total 15 litros de suco. Outras variações dessa situação podem ser apresentadas, como dizer que Jane comprou uma garrafa de suco de 5 litros ou, ainda, 5 garrafas de 1 litro de suco.

BNCC

A atividade 10 propõe situações-problema em contexto hipotético, não diretamente relacionado ao aspecto prático-utilitário, de modo a permitir aos estudantes expressarem as próprias respostas e conclusões, recorrendo, para isso, a diferentes registros e variadas linguagens, além do texto escrito em língua materna, conforme orienta a Competência específica de Matemática 6

GATO-PALHEIRO

MACACO-ARANHA

CACHORRO-DO-MATO-VINAGRE

• A seção Saiba mais oferece sugestões de leitura para os estudantes, com indicações de livros que podem estar relacionados ao conteúdo ou a contextos trabalhados no volume, além de temas atuais ligados ao convívio social. Verifique se na biblioteca da escola há exemplares dos livros indicados e disponibilize-os para os estudantes manusearem.

SAIBA MAIS

CONFIRA SUGESTÕES PARA AMPLIAR SEUS CONHECIMENTOS SOBRE ALGUNS TEMAS ESTUDADOS NESTE VOLUME.

QUEM VAI FICAR COM O PÊSSEGO?

OS ANIMAIS DA FLORESTA ENCONTRARAM UM PÊSSEGO GRANDE E MADURO. LOGO COMEÇARAM A DISCUTIR SOBRE QUEM FICARIA COM ELE.

AH-HAE, YOON. QUEM VAI FICAR COM O PÊSSEGO? ILUSTRAÇÕES DE YANG HYE-WON. TRADUÇÃO DE THAIS RIMKUS. 2. ED. SÃO PAULO: CALLIS, 2010.

O LIVRO DE NÚMEROS DO MARCELO

MARCELO VAI APRENDER SOBRE OS NÚMEROS DE MODO CURIOSO E INTERESSANTE, POR MEIO DE DITADOS E CANTIGAS POPULARES.

ROCHA, RUTH. O LIVRO DE NÚMEROS DO MARCELO ILUSTRAÇÕES DE ALBERTO LLINARES. SÃO PAULO: SALAMANDRA, 2013.

NÚMEROS

OS NÚMEROS DE 0 A 10, SEUS VALORES E CONCEITOS SÃO APRESENTADOS NESSE LIVRO POR MEIO DE UMA DIVERTIDA PARTIDA DE FUTEBOL.

ANDRADE, RODRIGO. NÚMEROS. SÃO PAULO: COMPANHIA DAS LETRINHAS, 2025.

SÁBADO

AOS SÁBADOS, MÃE E FILHA SEMPRE SE DIVERTEM JUNTAS. MAS, EM UM DESSES DIAS, ACONTECE ALGO DIFERENTE: UMA APRESENTAÇÃO ÚNICA E IMPERDÍVEL. VAMOS DESCOBRIR O QUE TORNA ESSE SÁBADO TÃO ESPECIAL?

MORA, OGE. SÁBADO SÃO PAULO: VR EDITORA, 2021.

CACHINHOS DE OURO A FAMÍLIA URSO SAIU PARA DAR UM PASSEIO. MAS, AO RETORNAR PARA CASA E ENTRAR NO QUARTO, FOI SURPREENDIDA POR UMA CENA INESPERADA. QUEM SERÁ A MENINA QUE ESTÁ DEITADA NA CAMA?

MACHADO, ANA MARIA. CACHINHOS DE OURO. ILUSTRAÇÕES DE ELLEN PESTILI. SÃO PAULO: FTD, 2004.

TODAS AS PESSOAS CONTAM

CADA UMA TEM SEU JEITO DE VIVER, BRINCAR E SONHAR. JUNTAS, ESSAS PESSOAS MOSTRAM QUE OS NÚMEROS FAZEM PARTE DA NOSSA VIDA, E CADA PESSOA É IMPORTANTE, INCLUSIVE VOCÊ! VAMOS CONHECER A HISTÓRIA CONTADA NESSE LIVRO?

ROSKIFTE, KRISTIN. TODAS AS PESSOAS CONTAM TRADUÇÃO DE KRISTIN LIE GARRUBO. SÃO PAULO: COMPANHIA DAS LETRINHAS, 2020.

• Nessa fase em que alguns deles podem não ter se apropriado do processo de leitura, é importante que se incentive a observação das imagens e letras existentes nos livros. Você poderá fazer a leitura em voz alta ou pedir a colaboração de outros estudantes. Converse com eles sobre o enredo e os personagens e peça-lhes que recontem a história para a turma.

03/10/2025 10:06:28

• Trabalhe com a leitura da capa do livro que será lido, apresentando-a aos estudantes. Solicite-lhes que relatem oralmente quais os elementos da capa mais chamaram a atenção deles. Ao observarem a capa, esteja atento a quais hipóteses eles têm sobre a história. Nesse momento, é importante que você instigue a curiosidade deles folheando as páginas do livro e mostrando-lhes as principais imagens. No fim da leitura, retome a observação da capa e questione-os sobre as relações entre a capa e a história lida.

O MENINO E O DINHEIRO

GUARDAR DINHEIRO PODE SER COMO PLANTAR UMA SEMENTE: É PRECISO CUIDAR, ESPERAR E TER PACIÊNCIA. NESSA HISTÓRIA, UM MENINO

DESCOBRE QUE POUPAR AJUDA A REALIZAR SONHOS. ALÉM DISSO, SÃO APRESENTADAS ALGUMAS ESTRATÉGIAS QUE NOS AUXILIAM A ADQUIRIR OBJETOS MATERIAIS POR MEIO DA COMPRA.

DOMINGOS, REINALDO. O MENINO E O DINHEIRO. 5. ED. SÃO PAULO: DSOP, 2017.

UM REDONDO PODE SER QUADRADO?

NESSE LIVRO, O REDONDO CONSEGUE SER VÁRIAS COISAS, ATÉ MESMO UMA GIRAFA. SEU PROBLEMA É CONSEGUIR VIRAR UM QUADRADO. SERÁ QUE ELE VAI CONSEGUIR?

CANINI, RENATO. UM REDONDO PODE SER QUADRADO? SÃO PAULO: FORMATO EDITORIAL, 2007.

FORMAS

DUAS IRMÃS GÊMEAS FARÃO SUA FESTA DE ANIVERSÁRIO NO PARQUE DAS FORMAS. VAMOS DESCOBRIR O QUE ELAS VÃO ENCONTRAR POR LÁ?

ANDRADE, RODRIGO. FORMAS. SÃO PAULO: COMPANHIA DAS LETRINHAS, 2025.

FLORISVALDO

FLORISVALDO É UM SENHORZINHO MUITO APEGADO A SUA ROTINA, ATÉ QUE ALGO INESPERADO ACONTECE E, NESSE MOMENTO, SURGE UMA NOVA AMIZADE EM SUA VIDA.

BIANCA, DÉBORA. FLORISVALDO ILUSTRAÇÕES DE PAULA KRANZ. SÃO PAULO: CIRANDA CULTURAL, 2022.

MEU NOME É MALALA

ESSE LIVRO CONTA A HISTÓRIA DE MALALA, UMA MENINA QUE LUTOU PELO DIREITO DE ESTUDAR E FOI A PESSOA MAIS JOVEM A RECEBER O PRÊMIO NOBEL DA PAZ. SUAS AÇÕES

INSPIRAM CRIANÇAS E DEMAIS LEITORES A APRENDER E SONHAR COM UM MUNDO MELHOR.

YOUSAFZAI, MALALA. MEU NOME É MALALA. ILUSTRAÇÕES DE MARIAM QURAISHI. SÃO PAULO: COMPANHIA DAS LETRINHAS, 2024.

UM DIA DE NEVE

BASEADO NO FAMOSO LIVRO DE EZRA JACK KEATS, O FILME UM DIA DE NEVE CONTA A HISTÓRIA DE UM MENINO CHAMADO PETER, QUE ACORDA EM UMA MANHÃ DE INVERNO E DESCOBRE QUE NEVOU. ACOMPANHE O DIA DESSE PERSONAGEM, EM UMA MÁGICA CAMINHADA PELA NEVE ATÉ A CASA DE SUA AVÓ.

UM DIA DE NEVE, DE JAMIE BADMINTON E RUFUS BLACKLOCK. ESTADOS UNIDOS/REINO UNIDO, 2016 (38 MIN).

MUSEU DE ARTE INDÍGENA (MAI)

PARA CONHECER UM MUSEU, NEM SEMPRE É PRECISO SAIR DE CASA. O MAI, SITUADO EM CURITIBA, NO PARANÁ, APRESENTA UM GRANDE ACERVO DE ARTIGOS DA CULTURA INDÍGENA QUE PODE SER VISTO POR MEIO DE UM TOUR VIRTUAL.

MUSEU DE ARTE INDÍGENA (MAI). TOUR VIRTUAL 360. DISPONÍVEL EM: https://www.tourvirtual360.com.br/mai/mai.html. ACESSO EM: 7 AGO. 2025.

• O trabalho com a leitura vai além da alfabetização, pois ela auxilia no desenvolvimento afetivo, físico e intelectual, estabelece relações lógicas, desenvolve o pensamento crítico, a expressão oral e corporal e desperta a criatividade. Por esse motivo, sempre que possível, incentive os estudantes a criar suas próprias histórias e a aplicar o conhecimento adquirido em situações do seu cotidiano.

03/10/2025 10:06:29

• As Referências bibliográficas comentadas apresentam os títulos usados como consulta ou embasamento para a construção de unidades do volume. Se julgar conveniente, use essas indicações em consulta e estudos para aprimorar o planejamento das aulas e das propostas de intervenção e de recuperação de aprendizagens.

REFERÊNCIAS BIBLIOGRÁFICAS COMENTADAS

ALVES, Eva Maria Siqueira. A ludicidade e o ensino de matemática: uma prática possível. Campinas: Papirus, 2020.

A autora destaca várias possibilidades de práticas lúdicas em sala de aula, com base nos relatos de suas experiências em sala de aula como professora de Matemática na Educação Básica.

BORBA, Marcelo de Carvalho; PENTEADO, Miriam Godoy. Informática e educação matemática 6. ed. Belo Horizonte: Autêntica, 2019. Nesse livro, os autores discutem temas relacionados à utilização de computadores e de calculadoras gráficas em Educação Matemática.

BRASIL. Decreto nº 11.556, de 12 de junho de 2023. Disponível em: https://www.planalto.gov.br/ccivil_03/_ ato2023-2026/2023/decreto/D11556. htm. Acesso em: 9 jun. 2025. Esse decreto visa implementar políticas, programas e ações para garantir a alfabetização ao final do segundo ano do Ensino Fundamental e recompor o aprendizado para estudantes que não alcançaram os padrões adequados até o final dos Anos Iniciais, garantindo esse direito a todas as crianças brasileiras.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular Versão final. Brasília, DF: MEC, 2018. Disponível em: https:// basenacionalcomum.mec.gov.br/ abase/. Acesso em: 15 jul. 2025. Esse documento indica as aprendizagens mínimas necessárias em cada etapa e para cada área de conhecimento.

CIVARDI, Jaqueline Araújo; SANTOS, Elismar Alves dos. Educação, matemática e inclusão escolar: perspectivas teóricas. Curitiba: Appris, 2018.

Nesse livro, são apresentadas reflexões teóricas sobre a educação matemática inclusiva, aprofundando as discussões sobre Educação, Matemática e inclusão.

DIAS, Marisa da Silva; MORETTI, Vanessa Dias. Números e operações: elementos lógico-históricos para atividades de ensino. Curitiba: InterSaberes, 2012.

As autoras narram o desenvolvimento do conhecimento matemático desde as primeiras civilizações, analisando o papel do professor e da educação na vida em sociedade.

IFRAH, Georges. Os números: a história de uma grande invenção. 4. ed. São Paulo: Globo, 2007.

Essa obra resume a história da Matemática desde a Pré-História, passando por antigas civilizações, como egípcias, babilônias, fenícias, gregas, romanas, hebreias, maias, chinesas, hindus e árabes.

MUNIZ, Cristiano Alberto. Brincar e jogar: enlaces teóricos e metodológicos no campo da educação matemática. Belo Horizonte: Autêntica, 2014.

Esse livro mostra como o jogo e a brincadeira estão ligados com a aprendizagem matemática e oferece subsídios para o ensino de Matemática por meio de atividades lúdicas.

PAIS, Luiz Carlos. Didática da matemática: uma análise da influência francesa. 4. ed. Belo Horizonte: Autêntica, 2019.

Essa obra apresenta aspectos e conceitos fundamentais da Didática Francesa, como transposição didática, contrato didático, obstáculos epistemológicos e engenharia didática.

MATERIAL COMPLEMENTAR

JOGO DE CARTELAS NUMERADAS

MATERIAL COMPLEMENTAR DA PÁGINA 53

NÚMEROS DE 0 A 19

SUGESTÕES DE AVALIAÇÃO COM PROPOSTAS DE INTERVENÇÃO

Nas páginas a seguir deste manual, estão apresentadas sugestões de avaliação formativa com comentários de intervenção, as quais podem ser aplicadas ao final do trabalho dos tópicos ou unidades, conforme o andamento dos conteúdos planejados. Essas avaliações estão organizadas por unidade, com o intuito de auxiliar o acompanhamento educacional e formativo dos estudantes nesse mo-

RECORTAR

mento, a critério da oportunidade e do planejamento do professor. Porém, se julgar conveniente, reserve algumas delas para serem utilizadas como avaliação diagnóstica, antes de novos conteúdos.

UNIDADE 1

1. Objetivo

Identificar a presença de números em situações do cotidiano.

Nesta seção, apresentamos o Material complementar, que contém peças e figuras necessárias para a resolução de algumas atividades do Livro do Estudante. Para usar esse material, é necessário recortar as figuras e as peças apresentadas e, em alguns casos, montar o material recortado. A fim de assegurar a integridade física dos estudantes e prevenir acidentes, oriente-os a tomar cuidado no manuseio da tesoura, além de garantir que façam uso apenas de tesouras com pontas arredondadas.

Atividade

03/10/2025 10:07:52

Peça aos estudantes que consultem, em casa, em jornais, revistas ou outros meios que algum adulto fornecer a eles, situações em que são utilizados números de 1 a 19.

Sugestão de intervenção

Os estudantes devem levar pelo menos três exemplos para a sala de aula, dizer quais são os números e em que ocasião eles foram utilizados.

UNIDADE

2. Objetivos

Ler e escrever números de 0 a 19 com algarismos e por extenso.

Atividade

Providencie fichas com números de 0 a 19 e entregue uma para cada estudante (pode haver repetição de números).

Sugestão de intervenção

Assim que o estudante receber uma ficha, ele deve dizer qual número é aquele

e escrevê-lo no caderno com algarismo e por extenso.

3. Objetivo

Estabelecer a relação entre a quantidade de elementos, sua representação numérica e sua escrita por extenso de números de 0 a 10.

Atividade

Sugestão de intervenção

Um deles deve estar em quantidade igual ao número da ficha do estudante, outro deve estar em quantidade inferior e o outro em quantidade maior. O objetivo é de que o estudante identifique os grupos. A atividade também pode ser realizada em grupos pequenos, de modo que a cada grupo é atribuído um número diferente.

Use a mesmas fichas da sugestão anterior, mas mantenha apenas os números de 0 a 10. Além das fichas, entregue a cada estudante três grupos de objetos de contagem (um de cada cor, por exemplo).

ÁBACO DE PAPEL

MATERIAL COMPLEMENTAR DA PÁGINA 53

NÚMEROS DE 0 A 19

4. Objetivo

Compreender a ideia de correspondência um a um. Identificar o número zero como representação da ausência de elementos.

Atividade

Desenhe na lousa quadros e em cada um represente bolinhas em quantidades de 0 a 10.

Sugestão de intervenção

Peça aos estudantes que representem com os dedos a quantidade do primeiro quadro, ou seja, para cada bolinha desenhada

RECORTAR

eles devem levantar um dedo. Ajude-os a fazer essa correspondência. Caso tenham dificuldade de usar as mãos, peça que correspondam essas quantidades com materiais de contagem, como palitos. Dê uma atenção maior quando forem representar o número zero, para que percebam a ausência de elementos nesse caso.

5. Objetivos

Reconhecer que uma dezena corresponde a 10 unidades. Representar números no quadro de ordens.

• A fim de assegurar a integridade física dos estudantes e prevenir acidentes, oriente-os a tomar cuidado no manuseio da tesoura, além de garantir que façam uso apenas de tesouras com pontas arredondadas. Oriente os estudantes a guardarem o ábaco de papel e as contas, pois poderão ser usados em futuras atividades. Para isso, considere providenciar um envelope para cada estudante, para que eles possam guardar o material.

Atividade

03/10/2025 10:07:52

Providencie materiais de contagem para que eles possam separar elementos em grupos de 10, completando uma dezena.

Sugestão de intervenção

Assim que os estudantes receberem o material de contagem e o separarem em grupos de 10, deverão escrever no caderno sua representação numérica e por extenso e indicar no quadro de ordens.

6. Objetivo

Identificar os ordinais do 1º ao 10º em situações do dia a dia.

Atividade

Desenvolva, com a turma, atividades contendo brincadeiras, como disputar corrida. Para cada brincadeira, escolha de três a cinco competidores.

Sugestão de intervenção

Ao fim dos desafios, pergunte quem foi o primeiro colocado, o segundo, e assim sucessivamente. Em outras brincadeiras, em vez de dizer a colocação e perguntar o nome do estudante,

diga o nome e pergunte sua colocação. Varie as equipes, a fim de que não haja muitas repetições de ganhadores, e propicie a participação de todos, sem permitir constrangimentos. Ao longo da dinâmica, desmotive competitividades excessivas e enfatize que a diversão está em brincar e em aprender. Incentive o espírito de solidariedade e companheirismo nas brincadeiras. Caso algum estudante apresente dificuldade na realização das atividades, procure retomar parte dos conteúdos, buscando abordagens diferentes para explicar o assunto, de acordo com as necessidades que forem se tornando evidentes na prática.

03/10/2025 10:07:52

CONTAS DO ÁBACO

MATERIAL COMPLEMENTAR DA PÁGINA 53

NÚMEROS DE 0 A 19

UNIDADE 2

1. Objetivos

Identificar objetos do cotidiano que lembrem figuras geométricas espaciais.

Agrupar objetos familiares com base no formato.

Atividade

Providencie com antecedência diferentes objetos e embalagens de produtos, como caixas

RECORTAR

03/10/2025 10:07:52

de creme dental, rolo de papel higiênico e caixas de sapato. Em sala, embaralhe os objetos e peça aos estudantes que, em grupos, organizem os objetos com base no formato. Sugestão de intervenção

Depois de organizados os objetos, os estudantes devem dizer o nome das figuras geométricas que esses objetos lembram. Em seguida, registre por escrito na lousa os nomes dessas figuras geométricas e peça-lhes que copiem.

UNIDADE 3

1. Objetivos

Reconhecer a hora como unidade de medida de tempo.

Ler e registrar horas exatas em relógios digitais.

Atividade

Providencie uma folha de papel que tenha a ilustração de três relógios digitais, um marcando 10 horas, um 12 horas e o outro 5 horas. Peça aos estudantes que contornem o relógio que indica o horário de início da tarde. Em seguida, entregue

um desenho de relógio digital que não tenha horário marcado e peça a eles que representem o horário de início do período da noite.

03/10/2025 10:07:52

Sugestão de intervenção

Caso os estudantes não saibam definir que o período da tarde se inicia às 12 horas, exemplifique com atividades como a hora de almoçar. Solicite também a eles que leiam as horas dos demais relógios. Caso surjam dificuldades na marcação das horas, peça que consultem a unidade para relembrar o uso desse dispositivo.

EXPERIMENTE

MATERIAL COMPLEMENTAR DA PÁGINA 74

FIGURAS GEOMÉTRICAS ESPACIAIS

2. Objetivos

Identificar a semana como um período de sete dias.

Reconhecer e nomear os dias da semana.

Reconhecer o calendário como instrumento de marcação de tempo.

Ler e registrar datas com base em um calendário.

Atividade

Em uma folha de papel, reproduza o calendário da atividade 6 da página 89

RECORTAR COLAR

Distribua esse calendário aos estudantes e solicite que contornem o mês que tem dois feriados e os dias em que eles ocorrerão. Verifique se eles identificam o dia de ocorrência de alguns feriados, como o dia 2 de novembro (feriado de Finados), que será em uma terça-feira, e o dia 20 de novembro (Dia Nacional de Zumbi e da Consciência Negra), que será em um sábado.

Sugestão de intervenção

Peça aos estudantes que marquem um X no mês de outubro desse calendário. Pergunte a eles quantos dias tem esse

• Quando os estudantes forem montar o cubo utilizando a planificação, deixe que eles realizem essa etapa sozinhos, e interfira somente quando for necessário.

Este é um momento importante para os estudantes, pois são desenvolvidas habilidades relacionadas a capacidade e coordenação motora deles.

03/10/2025 10:07:52

mês e em que dia da semana será comemorado o Dia das Crianças. Verifique se eles identificam o mês de outubro com facilidade e se indicam o dia 12, que será em uma terça-feira. Caso eles apresentem dificuldades, mude a abordagem, usando diferentes estratégias com o propósito de saná-las.

3. Objetivo

Realizar medições utilizando as unidades de medida de comprimento não padronizadas passo, pé e palmo.

Atividade

Providencie um pedaço de barbante com medida de comprimento entre 50 e 60 centímetros. Selecione três estudantes e peça que determinem, usando o próprio palmo, a medida do com-

primento desse barbante. Em seguida, pergunte à turma se as medidas obtidas pelos colegas foram iguais. Depois, questione-os por que isso acontece.

Sugestão de intervenção

Explique a eles que as medidas foram diferentes porque a medida do comprimento do palmo deles é diferente.

EXPERIMENTE

MATERIAL COMPLEMENTAR DA PÁGINA 74

FIGURAS GEOMÉTRICAS ESPACIAIS

4. Objetivos

Reconhecer o centímetro como unidade padronizada de medida de comprimento.

Comparar e realizar medições de comprimento utilizando uma régua graduada em centímetro.

Atividade

Providencie palitos de picolé, canudos e fitas de papel com medidas de comprimento variadas, cujas medidas sejam números naturais. Registre a medida de comprimento do palito, do canudo e da fita em cartões retangulares. Organize a turma em trios e, em seguida, distribua os objetos, os cartões e uma régua. Peça aos

RECORTAR COLAR

03/10/2025 10:07:52

estudantes que indiquem qual dos objetos é o mais comprido e estimem a medida do comprimento. Depois, solicite ao grupo que, com o uso da régua, relacione os objetos à suas medidas de comprimento, indicados nos cartões.

Sugestão de intervenção

Retome essa atividade e meça os objetos com toda a turma, destacando o posicionamento da régua. Na lousa, faça duas colunas: uma para desenhar os objetos e outra para registrar as medidas dos comprimentos. Depois, ligue os objetos à medida de comprimento correspondente.

• Oriente os estudantes a guardarem os cubinhos e as barras, pois poderão ser usados em futuras atividades. Para isso, considere providenciar um envelope para cada estudante, para que eles possam guardar o material.

5. Objetivo

Reconhecer a régua, a trena e a fita métrica como instrumentos de medida de comprimento.

Atividade

Providencie uma folha com a imagem dos seguintes objetos: fita métrica, relógio, calendário, termômetro, recipiente graduado, régua e trena. Peça aos estudantes que contornem os objetos que são usados para medir comprimentos.

Sugestão de intervenção

03/10/2025 10:07:52

Leve esses objetos ou alguns deles para a sala de aula. Converse com os estudantes sobre em que situações e por quais motivos a fita métrica, a trena e a régua são utilizadas.

CUBINHOS E BARRAS

MATERIAL COMPLEMENTAR DA PÁGINA 125

NÚMEROS DE 0 A 100

UNIDADE 4

1. Objetivo

Compreender as ideias de perto, longe, à direita, à esquerda, dentro, fora, em frente, atrás, em cima, entre e embaixo.

Atividade

Proponha que os estudantes descrevam algumas posições, dentro da sala de aula, com base em uma expressão dada previamente, como “atrás”. Explique a ideia da atividade, e deixe um tempo para

RECORTAR

que, sentados nas carteiras, observem as posições uns dos outros, além das posições dos objetos na sala de aula. Em seguida, escolha um deles e solicite que descreva a posição de dois estudantes por meio da expressão “atrás”. Espera-se que ele diga algo como “Ricardo está sentado atrás de Eduarda”. Continue a atividade escolhendo outros estudantes e solicitando que formulem outras frases com base nas demais expressões que foram estudadas nesta unidade, incentivando-os a citar dois estudantes, dois objetos,

um estudante e um objeto, entre outros.

03/10/2025 10:07:52

Sugestão de intervenção

Caso os estudantes apresentem dificuldade em formular uma frase com base na expressão citada, apresente um exemplo para orientar a resposta, escolhendo outros dois elementos. Expera-se que eles percebam que há várias possibilidades de respostas, dependendo da quantidade de elementos na sala de aula.

2. Objetivos

Estabelecer pontos de referência para descrever trajetos e deslocar-se no espaço. Descrever e registrar deslocamentos por meio de comandos, incluindo a ideia de giro.

Atividade

No pátio da escola, desenhe um quadriculado e posicione dois estudantes em dois locais desse quadriculado. Peça que, a cada assovio seu, um deles se movimente para a frente ou para trás, ou gire para a direita ou para a esquerda, com a intenção de ir até a posição do outro. Após ele se movimentar, pergunte aos estudantes que estão observando: “Qual foi o movimento feito pelo

estudante considerando-o um ponto de referência?”. Observe se eles conseguem responder corretamente. Faça essa atividade com vários deles sendo usados como peças do jogo, até que todos tenham participado.

Sugestão de intervenção

03/10/2025 10:07:52

Caso eles permaneçam com dificuldade, apresente uma atividade parecida, porém apresentada na lousa, na qual os comandos dados por você, com o giz, para movimentar representações de objetos se deslocando, devem ser ditos por eles. Varie a atividade pedindo a eles que deem os comandos em vez de dizerem qual comando você indicou.

CUBINHOS E BARRAS

MATERIAL COMPLEMENTAR DA PÁGINA 125

NÚMEROS DE 0 A 100

UNIDADE 5

1. Objetivos

Ler e escrever números até 100 com algarismos e por extenso.

Reconhecer as dezenas exatas.

Atividade

Represente na lousa os números 1 a 15, dispondo os dez primeiros em uma linha e os cinco restantes na linha de baixo, tomando o cuidado de manter em uma mesma

RECORTAR

coluna os números cujo algarismo das unidades seja o mesmo.

03/10/2025 10:07:52

Sugestão de intervenção

Peça aos estudantes que copiem os números no caderno e completem a sequência até o 100, instruindo-os a seguir o padrão adequado. Solicite, ainda, que circulem as dezenas exatas. Depois, indique alguns dos números da lista para eles escreverem por extenso.

Outra possibilidade é pedir que registrem, com algarismos e por extenso, núme-

ros como: idade dos colegas e de si mesmo, idade dos pais, quantidade de pessoas que vivem com eles em casa, quantidade de estudantes na sala de aula. Para cada um desses números, solicite-lhes que indiquem as dezenas e as unidades. Além disso, escolha alguma dezena exata e pergunte quantos grupos de dez palitos seriam necessários para representar esse número.

2. Objetivos

Estabelecer relação entre a quantidade de elementos e sua representação numérica.

Compreender o significado de número par e de número ímpar.

Atividade

Leve para a sala de aula objetos ou utilize o material dourado para fazer grupos e peça aos estudantes que contem a quantidade de elementos e a registrem com algarismos, dizendo se ela é par ou ímpar.

Sugestão de intervenção

Verifique se, para descobrir a paridade, os estudantes agrupam os elementos dois a dois ou se primeiro fazem a contagem e, depois, com base no algarismo das unidades, determinam se o número é par ou é ímpar. A atividade também pode ser realizada pedindo a eles que levem à escola materiais de contagem, como pedrinhas, tampinhas e lápis usados.

EXPERIMENTE

MATERIAL COMPLEMENTAR DA PÁGINA 129

NÚMEROS DE 0 A 100

RECORTAR

• Oriente os estudantes a guardarem as cédulas e moedas do Real, pois poderão ser usadas em futuras atividades. Para isso, considere providenciar um envelope para cada estudante, para que eles possam guardar o material.

UNIDADE 5

3. Objetivos

Representar os números até 100 no quadro de ordens e classes.

Comparar números, utilizando termos como é maior do que, é menor do que e é igual a

Estabelecer relação entre números e pontos da reta numérica.

FUTEBOL VOLEIBOL

BASQUETEBOL

TÊNIS NATAÇÃO OUTROS

Organizar números em ordem crescente e em ordem decrescente.

Atividade

Peça aos estudantes que digam alguns números, como a própria idade ou a de um familiar, o número do sapato, quantos lápis há em determinada caixa, o número que vem imediatamente depois do 84 e o número que vem imediatamente antes do 97. Com essa lista de números registrada na lousa, solicite a eles que os organizem em ordem crescente e em ordem decrescente.

Sugestão de intervenção

Escolha alguns dos números que estejam mais próximos entre si e solicite aos estudantes que os representem em uma reta numérica. Para auxiliá-los na construção da reta, escolha números de dois em dois e faça perguntas como: “Esse número é menor do que este outro, maior do que este outro ou igual a este outro?”. Com base nas respostas, pergunte qual número deve ficar à esquerda e qual deve ficar à direita na reta numérica.

A atividade pode ser incrementada com a utilização de fichas numeradas de 1 a 100, podendo haver repetição, acomodadas em uma caixa. Trace uma reta numérica bem comprida na lousa, com marcações ao alcance dos estudantes e apenas nas dezenas exatas. Forme grupos pequenos e peça a cada grupo que retire pares de fichas e comparem os números, dizendo qual é o maior deles ou se são iguais entre si. Se acertarem a resposta, eles devem colocar as fichas

03/10/2025 10:07:53

sob a reta desenhada na lousa, na posição correta ocupada pelo número. Caso errem a resposta, eles devem devolver as fichas na caixa. Se algum estudante apresentar dificuldade, retome a explicação do conteúdo, buscando abordagem diferente para explicar, de acordo com as necessidades que se apresentarem na prática.

UNIDADE 6

1. Objetivos

Reconhecer o Real como unidade monetária brasileira.

Identificar as cédulas e as moedas utilizadas no sistema monetário brasileiro.

Atividade

Providencie imagens ou modelos das cédulas e moedas de nosso sistema monetário, apresentando-as aos estudantes, em sala de aula. Em seguida, solicite a eles que as identifiquem, destacando algumas de suas características como cor e animal que as estampam. Observe se eles

fazem referência ao tamanho das cédulas, que também é uma característica importante.

Sugestão de intervenção

É possível que algum estudante tenha dificuldade em reconhecer alguma cédula ou moeda. Caso isso aconteça, retome a atividade 1 da página 158 e destaque as cédulas e a escrita dos nomes. Complemente essa intervenção pedindo a eles que indiquem objetos que podem ser comprados utilizando, por exemplo, uma moeda de 1 real ou uma cédula de 2 reais. Com isso, eles poderão estabelecer uma relação entre a cédula ou moeda e o preço do produto.

PALITOS DE PAPEL

MATERIAL COMPLEMENTAR DA PÁGINA 130

NÚMEROS DE 0 A 100

2. Objetivo

Relacionar cédulas e moedas do sistema monetário brasileiro.

Atividade

Providencie uma folha com imagens de dois produtos de mercado descaracterizados com a indicação dos seguintes preços: 10 reais; 17 reais. Providencie também modelos da moeda de 1 real e das cédulas de 2 reais, 5 reais e 10 reais. Organize a turma em duplas e, em seguida, distribua para cada uma a folha, três moedas de 1 real, duas cédulas de 2 reais, duas cédulas de 5 reais e uma cédula de 10 reais. Depois, solicite a cada

RECORTAR

03/10/2025 10:07:53

dupla que represente de duas maneiras diferentes o preço de cada produto usando as cédulas e moedas que receberam.

Sugestão de intervenção

Acompanhe a realização da atividade entre as duplas e registre as dificuldades observadas. Depois, peça a algumas duplas que compartilhem as respostas com a turma. Nesse momento, aproveite para explicar as dúvidas observadas. Essa atividade tem mais de uma resposta. Explore as diferentes possibilidades para que os estudantes percebam a relação entre as cédulas e moedas.

UNIDADE 7

1. Objetivos

Efetuar adições com total até 19. Reconhecer o símbolo usado para representar a adição.

Atividade

Escreva na lousa dois números de um algarismo e peça aos estudantes que obtenham a soma. Solicite que façam a contagem da quantidade referente ao primeiro número e continuem a contagem a partir desse valor, para a quantida-

de referente ao segundo número. Depois, peça que representem essa adição usando os símbolos, + e =. Inicie com um número pequeno, cuja soma seja menor do que 10, e aumente os valores cujas somas sejam até 19.

Sugestão de intervenção

03/10/2025 10:07:53

Caso eles apresentem dificuldades, faça alguns exemplos usando objetos iguais, tracinhos na lousa ou os dedos. Apresente um exemplo e faça outros solicitando a eles que digam os próximos passos. Depois, peça que repitam os passos e obtenham o resultado.

CÉDULAS DO REAL

MATERIAL COMPLEMENTAR DA PÁGINA 158

SISTEMA MONETÁRIO

2. Objetivo

RECORTAR

Efetuar adições com total até 99. Utilizar o algoritmo da adição sem reagrupamento.

Atividade

Proponha a adição de dois números de dois algarismos, com resultado até 99 e sem reagrupamento. Apresente alguns exemplos que respeitem essas condições e com dificuldade progressiva. Use diferentes estratégias como cubi-

03/10/2025 10:07:55

nhos e barras, algoritmo, ábaco, cálculo mental ou estimativas.

Sugestão de intervenção

Com base nessas estratégias, avalie se os estudantes compreendem os conceitos da adição e conseguem aplicá-los corretamente. Se necessário, faça uma retomada de cada estratégia em que eles apresentarem dificuldades e reforce trabalhando com novos exemplos.

3. Objetivos

Associar adição às ideias de juntar e acrescentar.

Resolver situações-problema que envolvam as ideias de juntar e acrescentar da adição.

Atividade

Use problemas com os significados de juntar e acrescentar, de maneira direta ou explícita, para avaliar se os estudantes reconhecem a adição como ferramenta, exigindo que a situação seja interpretada

corretamente. Use situações do dia a dia deles, como as que envolvem brinquedos, objetos e frutas. Avalie também se as dificuldades apresentadas se referem à interpretação da situação ou ao reconhecimento da adição como ferramenta, fazendo perguntas como: “O que queremos obter?” e “O que podemos usar para chegar ao resultado?”.

Sugestão de intervenção

Caso algum estudante apresente dificuldades, comece com situações mais

simples, lendo lentamente o enunciado e indicando as informações necessárias para chegar ao resultado. Outra possibilidade é relacionar os problemas propostos com situações em que as informações são apresentadas diretamente, permitindo que os estudantes relacionem esses dois tipos de atividade, podendo ser usados os mesmos números ou números diferentes na comparação.

03/10/2025 10:07:55

CÉDULAS DO REAL

MATERIAL COMPLEMENTAR DA PÁGINA 158

SISTEMA MONETÁRIO

RECORTAR

4. Objetivo

Compreender a ideia de dobro e de metade. Atividade

Leve materiais de contagem aos estudantes e entregue quantidades pares a cada um. Peça a eles que separem metade da quantidade. Depois, disponibilize uma quantidade desse material e solicite que busquem mais materiais de contagem, na sua mesa ou em um local da sala, de modo que eles fiquem com o dobro da quantidade inicial.

Sugestão de intervenção

10:07:58

Caso os estudantes apresentem dificuldades, demonstre com pequenas quantidades; por exemplo, para demonstrar a quantidade 4, separe a metade e diga que metade de 4 é 2. Faça o inverso também, separe 2 e diga que, para obter o dobro, precisa juntar mais 2 e, assim, obter 4. Faça com outas quantidades conforme necessário.

5. Objetivo

Identificar os elementos faltantes em sequências recursivas de números naturais, após o reconhecimento de seu padrão.

Atividade

Apresente diferentes sequências com números naturais, nas quais o padrão seja obtido por uma adição. Comece apresentando na lousa uma sequência em que o padrão seja adicionar uma unidade a cada termo e peça aos estudantes que determinem os outros termos. Em seguida, apresente sequências em que o valor adicio-

nado a cada termo seja maior, tomando cuidado para não exigir adições que precisem de reagrupamento. Nesses casos, escolha como elemento ausente os que permitem uma adição adequada e com resultado até 99.

Sugestão de intervenção

Avalie o desenvolvimento da atividade proposta, observando a participação de cada um, bem como o interesse, a autonomia e o raciocínio e se apresentam dificuldades. Caso haja dificuldades, mude a abordagem, providenciando outras atividades e estratégias com o objetivo de saná-las.

MOEDAS DO REAL

MATERIAL COMPLEMENTAR DA PÁGINA 158

SISTEMA MONETÁRIO

UNIDADE 8

1. Objetivo

Identificar figuras geométricas planas no dia a dia.

Atividade

Utilize atividades para reforçar e avaliar o conhecimento dos estudantes sobre as figuras geométricas planas no dia a dia.

Sugestão de intervenção

Uma sugestão é apresentar objetos de nosso entorno e que se pareçam com figuras geomé-

RECORTAR

03/10/2025 10:08:00

tricas planas, pedindo a eles que digam em voz alta os nomes das figuras geométricas planas que esses objetos lembram. Outra abordagem é apresentar uma imagem que contenha triângulos, quadrados, retângulos e círculos, e pedir aos estudantes que identifiquem essas figuras. Essa imagem pode ser feita desenhando em uma folha de papel e reproduzindo para os estudantes pintarem com a cor indicada, ou desenhando na lousa e pedindo a eles que indiquem onde estão as figuras.

2. Objetivos

Reconhecer triângulos, retângulos, quadrados e círculos.

Identificar os elementos que completam a sequência.

Atividade

Construa uma sequência de figuras geométricas planas na lousa e determine com os estudantes as figuras seguintes.

Sugestão de intervenção

Apresente sequências em que faltam elementos no meio e peça aos estudantes que indiquem

quais são eles. Caso apresentem dificuldades em identificar os elementos da sequência, apresente sequências com dois tipos de figuras e aumente a quantidade de elementos progressivamente. Outra possibilidade é pedir aos estudantes que elaborem uma sequência com as figuras geométricas planas que eles conhecem e, depois, solicitar aos colegas que a continuem. Assim, é possível verificar o entendimento deles sobre o assunto e a capacidade de elaboração de padrões em sequências.

03/10/2025 10:08:00

ROLETA DA ADIÇÃO

MATERIAL COMPLEMENTAR DA PÁGINA 181

ADIÇÃO

RECORTAR

3. Objetivo

Identificar figuras geométricas planas no contorno de sólidos geométricos.

Atividade

Apresente objetos que lembram sólidos geométricos na sala de aula, escolhendo alguns que possuam faces cujo contorno lembra um triângulo, um quadrado, um retângulo e um círculo.

Sugestão de intervenção

figura geométrica plana se parece o contorno obtido. Outra opção para avaliar e aprofundar o conhecimento é apresentar alguns sólidos geométricos diferentes e pedir-lhes que indiquem quais deles podem ser contornados para obter a figura geométrica plana indicada. Dificuldades podem ser remediadas por meio de revisão e exemplos mais detalhados, avaliando caso a caso as necessidades específicas dos estudantes. 1 2 3 4 5 6 7 8 9

Se possível, faça os exemplos contornando um dos objetos e pergunte aos estudantes com qual

03/10/2025 10:08:00

UNIDADE 9

1. Objetivos

Compreender as ideias da subtração. Efetuar subtrações com números até 10. Resolver situações-problema que envolvem subtrações.

Atividade

Represente na lousa situações nas quais os estudantes possam realizar os cálculos pensando primeiro no todo e depois tirando uma parte dele.

Sugestão de intervenção

03/10/2025 10:08:00

Algumas situações possíveis são: “Tenho 10 bolas, serão retiradas 5 bolas. Quantas bolas vão sobrar?”; “Em uma fruteira havia 10 bananas. Leandro possui cinco amigos e cada um deles comeu uma banana. Quantas bananas restaram na fruteira?”. Na sequência, peça aos estudantes que copiem as situações apresentadas no caderno e completem a subtração, instruindo-os caso necessário.

TABULEIRO GEOMÉTRICO

MATERIAL COMPLEMENTAR DA PÁGINA 201

FIGURAS GEOMÉTRICAS PLANAS

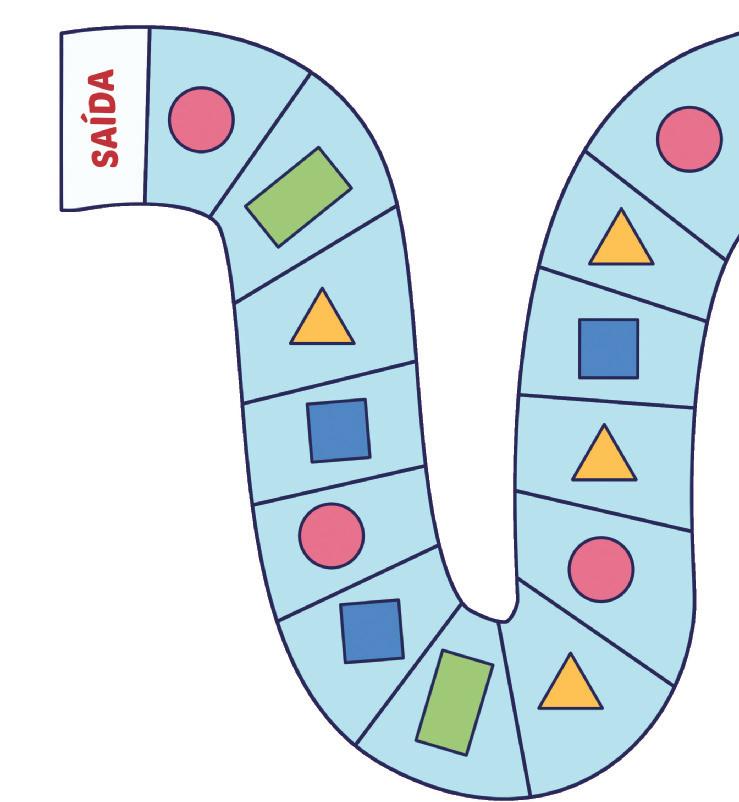
RECORTAR COLAR 283

2. Objetivos

Efetuar subtrações com números até 19.

Reconhecer o símbolo ( ) utilizado para representar a subtração.

Resolver situações-problema que envolvem subtrações com números até 19.

Atividade

Leve objetos para a sala de aula ou utilize o material de contagem, de modo que cada estudante tenha 19 elementos.

Sugestão de intervenção

Peça aos estudantes que contem a quantidade de elementos e registrem no caderno essa

03/10/2025 10:08:00

quantidade com algarismo. Depois, solicite a eles que retirem certa quantidade e registrem quantos elementos restaram. Verifique se, para descobrir o resultado da subtração, os estudantes agrupam os elementos ou se primeiro fazem a contagem e, depois, com base no algarismo das unidades, determinam o resultado. Para essa atividade também pode ser solicitado que os próprios estudantes levem à escola materiais de contagem, como pedrinhas, tampinhas ou lápis. Peça a eles que registrem no caderno a subtração utilizando os símbolos matemáticos. Depois, verifique se o uso do sinal de subtração e da estrutura da sentença matemática está correto.

3. Objetivo

Efetuar subtrações sem reagrupamento com resultado até 99 utilizando diferentes estratégias.

Atividade

Leve material dourado para a sala de aula ou utilize o material de contagem, de modo que cada estudante tenha 29 elementos.

Sugestão de intervenção

Peça aos estudantes que retirem uma quantidade de elementos e pergunte a eles quan-

tos restaram. Depois, solicite que registrem, no caderno, a operação que fizeram. Repita esse processo quantas vezes achar necessário ou de acordo com a interação da turma.

Caso algum estudante apresente dificuldade na realização da atividade, retome o tema Subtração com números até 99 nas páginas 123 a 127, buscando abordagens diferentes para explicar o assunto, de acordo com a necessidade dele.

TABULEIRO GEOMÉTRICO

MATERIAL COMPLEMENTAR DA PÁGINA 201

FIGURAS GEOMÉTRICAS PLANAS

RECORTAR

UNIDADE 10

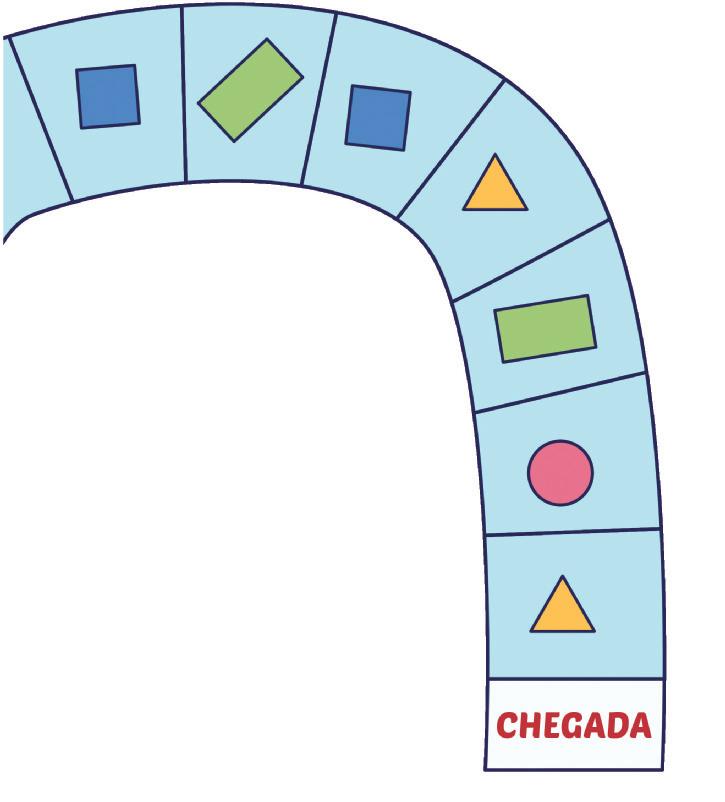
1. Objetivo

Compreender o significado das expressões mais leve e mais pesado

Atividade

Peça aos estudantes que escolham dois objetos da sala de aula, como lápis, apagador, livro,

03/10/2025 10:08:01

estojo ou mochila. Eles devem segurar os objetos, um em cada mão ao mesmo tempo, e verificar qual é o mais leve e qual é o mais pesado.

Sugestão de intervenção

Se necessário, providencie antecipadamente outros objetos de fácil manipulação para auxiliar os estudantes nessa verificação.

2. Objetivos

Reconhecer a balança como instrumento de medida de massa.

Resolver situações-problema que envolvam comparação entre medidas de massa.

Reconhecer o quilograma como unidade-padrão para a medida de massa.

Atividade

Proponha o seguinte problema aos estudantes.

Juliana colocou dois objetos juntos sobre uma balança e verificou que a medida da massa era 45 kg. Ao retirar o objeto A, a balança indicou 13 kg. Determine a medida da massa do objeto B.

Sugestão de intervenção

Se necessário, retome a atividade 2 da página 232 a fim de auxiliar os estudantes. Certifique-se de que eles compreendem o uso de kg para indicar quilograma e questione-os sobre onde eles costumam ver algum tipo de balança.

MOLDE DO DADO E PEÕES

MATERIAL COMPLEMENTAR DA PÁGINA 201

FIGURAS GEOMÉTRICAS PLANAS

14 5 2 3 6

RECORTAR COLAR

3. Objetivos

Diferenciar recipientes que contêm mais líquido daqueles que contêm menos líquido. Identificar se um recipiente está cheio ou vazio.

Atividade

Verifique a possibilidade de levar para a sala de aula recipientes com diferentes medidas de capacidade. Promova discussões e experimentações com os formatos e as medidas de capa-

03/10/2025 10:08:01

cidade dos recipientes. Peça aos estudantes que ordenem os recipientes em ordem decrescente de acordo com a medida de capacidade, ou seja, do que tem maior medida de capacidade para o que tem menor medida de capacidade.

Sugestão de intervenção

A fim de auxiliar no processo de aprendizagem, deixe os estudantes manipularem os materiais. Se necessário, retome as atividades das páginas 237 e 238

4. Objetivos

Perceber a presença do litro em situações do dia a dia.

Reconhecer o litro como unidade-padrão para a medida de capacidade.

Atividade

Leve para a sala de aula embalagens vazias de alguns produtos com diferentes medidas de

capacidade, para que os estudantes possam estimar quais produtos são vendidos em embalagens com menos de 1 litro, exatamente 1 litro e mais de 1 litro.

03/10/2025 10:08:01

Sugestão de intervenção

Se necessário, deixe os estudantes manipularem esses produtos para determinar quais são vendidos em embalagens com menos de 1 litro, exatamente 1 litro e mais de 1 litro.

MANUAL DO PROFESSOR

Este Manual do Professor é um complemento à primeira parte do Livro do Professor, oferecendo um suporte para o desenvolvimento docente e para o dia a dia em sala de aula. Neste manual, você encontrará uma série de informações importantes, como a estrutura da BNCC, sugestões para desenvolver um trabalho interdisciplinar, informações sobre conceitos, objetivos e instrumentos de avaliação, reflexões sobre o papel do professor e a prática docente, e a fundamentação teórico-metodológica da coleção. Além disso, encontrará um quadro de distribuição

dos conteúdos com as habilidades, competências gerais e específicas de cada componente curricular e os temas contemporâneos transversais da BNCC que estão sendo desenvolvidas em cada unidade, além de sugestões de cronogramas bimestrais, trimestrais e semestrais. Ao final desta parte, são também apresentadas sugestões de referências complementares para a prática docente e as referências bibliográficas comentadas utilizadas como consulta para a produção das orientações ao professor e deste Manual do Professor

A BASE NACIONAL COMUM CURRICULAR (BNCC)

Desde a publicação da Constituição Federal de 1988, o artigo 210 já previa a necessidade de uma base comum para a educação brasileira. Em 1996, com a aprovação da Lei de Diretrizes e Bases da Educação (LDB), as discussões sobre um documento que orientasse os currículos da Educação Básica em todo o Brasil ganharam ainda mais força. Em 2018, após um amplo processo de debates e contribuições de educadores e da sociedade, a Base Nacional Comum Curricular (BNCC) foi homologada.

A BNCC propõe uma progressão de aprendizagens que visa à formação humana integral dos estudantes e à construção de uma sociedade mais justa, democrática e inclusiva. O documento estabelece um aprendizado mínimo e comum, orientado por competências e habilidades que devem ser desenvolvidas em cada etapa de ensino.

Na BNCC, as áreas de conhecimento são compostas de componentes curriculares. Por meio de unidades temáticas, objetos de conhecimento e habilidades, esses

componentes têm o objetivo de desenvolver as competências gerais e específicas.

AS COMPETÊNCIAS GERAIS DA EDUCAÇÃO BÁSICA

A BNCC orienta que, ao longo da Educação Básica, os estudantes desenvolvam dez competências gerais, que envolvem a mobilização de conhecimentos, habilidades, atitudes e valores. Essas competências são o alicerce, definindo o que se espera que o estudante desenvolva em toda a Educação Básica. Nesta coleção, elas são trabalhadas por meio de temas, discussões e atividades que incentivam a reflexão crítica, com sugestões nas orientações ao professor

A seguir, apresentamos as competências gerais da BNCC.

Competências gerais da Educação Básica

1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.

2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.

4.Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital – bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.

5. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.

6. Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.

7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.

8. Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.

9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Versão final. Brasília: MEC, 2018. p. 9-10. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 14 ago. 2025.

A BNCC propõe que o conteúdo chegue à sala de aula de forma contextualizada, o que exige novas estratégias do professor, como a transposição didática. Isso significa converter o conteúdo científico em uma linguagem acessível e adaptada à realidade dos estudantes. Para isso, o estudo e a reavaliação constante da prática docente são essenciais.

A seguir, apresentamos algumas ações que podem ser aplicadas para desenvolver as competências gerais em sala de aula.

Sugestões de ações docentes para as competências gerais

Competência geral 1: Incentive os estudantes a reconhecerem a importância dos conhecimentos já adquiridos, mostrando como eles servem de base para a compreensão da realidade e para a construção de novos saberes.

Competência geral 2: Exercite a curiosidade intelectual, levando os estudantes a usarem a abordagem científica para investigar, levantar hipóteses, resolver problemas e analisar os resultados por meio de experiências e observações.

Competência geral 3: Proporcione o contato com diferentes manifestações culturais em âmbito local, regional e global e promova atividades artísticas, como grupos de dança, elaboração de roteiros e atuação em peças de teatro, festivais musicais e saraus.

Competência geral 4: Dê subsídios para que os estudantes se comuniquem por meio de diferentes linguagens, ajudando-os a selecionar a mais apropriada para cada situação.

Competência geral 5: Utilize de forma intencional e pedagógica diversas tecnologias em sala de aula, verificando o conhecimento prévio dos estudantes e diversificando os recursos metodológicos.

Competência geral 6: Ajude os estudantes a refletirem sobre o futuro e a importância da liberdade, autonomia e consciência crítica em suas escolhas profissionais e pessoais, valorizando a diversidade de saberes e experiências.

Competência geral 7: Ofereça subsídios para que os estudantes desenvolvam a capacidade de argumentar com base em fatos e dados confiáveis, sabendo selecionar e verificar a origem de diferentes fontes para negociar pontos de vistas e defender ideias.

Competência geral 8: Leve os estudantes a se compreenderem e se valorizarem dentro da diversidade, reconhecendo suas emoções e as dos outros, e exercitando a autocrítica.

Competência geral 9: Promova o exercício da empatia, do diálogo e da cooperação, incentivando os estudantes a resolverem conflitos de forma respeitosa e democrática.

Competência geral 10: Contribua para que os estudantes ajam de modo responsável, guiados por princípios éticos e de cidadania, e conscientes de que suas ações devem estar alinhadas à tomada de decisões inclusivas, sustentáveis e solidárias.

Nesta coleção, as competências gerais que são desenvolvidas em textos, atividades e seções que permeiam os conteúdos são destacadas nas orientações ao professor e são listadas no Quadro de distribuição dos conteúdos

AS COMPETÊNCIAS ESPECÍFICAS

Para que as competências gerais se manifestem em cada componente, a BNCC estabelece as competências específicas. A organização dessas competências no Ensino Fundamental varia: em áreas como Matemática e Ciências da Natureza, competências específicas são as mes-

mas para o componente. Em áreas como Linguagens e Ciências Humanas, há competências específicas por área e também para cada componente curricular que as compõem (Língua Portuguesa, Arte, Educação Física, Língua Inglesa, Geografia e História), reconhecendo as particularidades de cada um. Em todos os casos, as competências específicas colaboram para que os objetivos de aprendizagem sejam claros e coerentes, do nível mais amplo ao mais específico.

A seguir, apresentamos as competências específicas de Matemática.

1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.

2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.

6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).

7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.

8. Agir pessoal e coletivamente com respeito, autonomia, responsabilidade, flexibilidade, resiliência e determinação, recorrendo aos conhecimentos das Ciências da Natureza para tomar decisões frente a questões científico-tecnológicas e socioambientais e a respeito da saúde individual e coletiva, com base em princípios éticos, democráticos, sustentáveis e solidários

BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Versão final. Brasília: MEC, 2018. p. 267. Disponível em: https://www.gov.br/mec/pt-br/escola-em-tempo-integral/BNCC_EI_EF_110518_versaofinal.pdf. Acesso em: 14 ago. 2025.

Nesta coleção, as competências específicas que são desenvolvidas em textos, atividades e seções que permeiam os conteúdos são destacadas nas orientações ao professor e listadas no Quadro de distribuição dos conteúdos

AS UNIDADES TEMÁTICAS, OS OBJETOS DE CONHECIMENTO E AS HABILIDADES

Para garantir o desenvolvimento das competências gerais e específicas, a BNCC organiza o currículo em três elementos interligados: unidades temáticas, objetos de conhecimento e habilidades.

As unidades temáticas são os grandes blocos de conhecimento que orientam a organização curricular. Elas funcionam como eixos estruturantes que agrupam temas e conceitos de forma mais ampla, garantindo uma abordagem contextualizada e progressiva ao longo dos anos escolares.

Dentro de cada unidade temática, os objetos de conhecimento são os conteúdos, conceitos e processos que devem ser ensinados.

As habilidades representam o que o estudante deve ser capaz de fazer com o conhecimento. Elas indicam ações, processos e competências a serem desenvolvidos.

Juntos, esses três elementos garantem que o processo de ensino não seja apenas a transmissão de conteúdos. A unidade temática fornece o contexto, o objeto de conhecimento define o tema, e a habilidade define a ação que o estudante precisa executar, garantindo um aprendizado significativo e o desenvolvimento das competências.

Nesta coleção, as habilidades que são desenvolvidas

em textos, atividades e seções que permeiam os conteúdos são destacadas nas orientações ao professor, localizadas na primeira parte deste Manual do professor, e são listadas no Quadro de distribuição dos conteúdos, mostrando a relação entre os diferentes elementos da BNCC.

OS TEMAS CONTEMPORÂNEOS TRANSVERSAIS

Para enriquecer o trabalho com as habilidades e competências da BNCC e contextualizar o ensino, as propostas pedagógicas devem abordar os temas contemporâneos transversais (TCT). Esses temas são assuntos relevantes para a formação cidadã dos estudantes e para a construção de uma sociedade mais justa, ética e sustentável. São temas com caráter interdisciplinar, que conectam os conteúdos escolares com o cotidiano dos estudantes e com questões importantes em discussão na sociedade. De acordo com o documento Temas Contemporâneos Transversais da BNCC, publicado em 2019, esses temas são de relevância local, regional e global e estão organizados em seis macroáreas.

Educação ambiental

Educação para o consumo

Trabalho

Educação financeira

Educação fiscal

Saúde

Cidadania e civismo

Saúde

Educação alimentar e nutricional

Vida familiar e social

Educação para o trânsito

Educação em direitos humanos

Direitos da criança e do adolescente

Processo de envelhecimento, respeito e valorização do idoso

Multiculturalismo

Ciência e tecnologia

Diversidade cultural

Educação para valorização do multiculturalismo nas matrizes históricas e culturais brasileiras

Ciência e tecnologia

Nesta coleção, esses temas são explorados em diferentes momentos no desenvolvimento dos conteúdos e recebem destaque na seção Coletivamente, contribuindo para a formação cidadã dos estudantes por meio de reflexões e propostas de resoluções para problemas, de modo que eles sejam atuantes na sociedade em que vivem.

INTEGRAÇÃO ENTRE OS COMPONENTES CURRICULARES

Desde a década de 1990, o trabalho interdisciplinar tem ganhado relevância no Brasil, sendo incentivado em todos os níveis da Educação Básica. A interdisciplinaridade é a relação entre dois ou mais componentes curriculares que se unem para obter um conhecimento mais amplo e unificado. Essa abordagem vai além da simples comunicação de ideias; ela integra conceitos, metodologias e terminologias para que o conhecimento se torne mais significativo e conectado à realidade dos estudantes.

Ao integrar os diversos componentes, a interdisciplinaridade amplia a compreensão da realidade e contribui para a formação integral dos estudantes como cidadãos. No ambiente escolar, essa abordagem gera resultados positivos, pois incentiva a colaboração e a contextualização de temas, garantindo que o aprendizado esteja alinhado à vivência dos estudantes.

No desenvolvimento de um trabalho interdisciplinar, tanto o professor quanto os estudantes devem estabelecer conexões entre saberes mais amplos e os conteúdos específicos dos diferentes componentes curriculares. Com base nessa articulação, espera-se que consigam construir uma síntese que amplie sua compreensão, superando o nível de entendimento inicial.

Para que esse processo ocorra de forma efetiva, é imprescindível que o professor assuma um papel mediador nesse percurso, sendo o primeiro a exercitar esse movimento de integração. Nesse contexto, o professor deve mobilizar algumas competências, como: [...]

• diferenciação, comparação e contraste entre diferentes perspectivas disciplinares, profissionais e interdisciplinares;

• identificação de pontos comuns e esclarecimento de como as diferenças se relacionam com a tarefa a ser cumprida;

• delineamento de um entendimento holístico baseado nos pontos comuns, mas que continua suscetível às diferenças.

KLEIN, Julie Thompson. Ensino interdisciplinar: didática e teoria. In: FAZENDA, Ivani Catarina Arantes (org.). Didática e interdisciplinaridade. 17. ed. Campinas: Papirus, 2012. p. 121. (Coleção Práxis).

Além disso, para promover um trabalho interdisciplinar de maneira significativa, é essencial que ele esteja pautado nas experiências, no cotidiano e nos interesses dos estudantes. Isso implica aproveitar as situações que emergem naturalmente em sala de aula, por exemplo, perguntas formuladas por eles, projetos em andamento, investigações e demais práticas pedagógicas, como oportunidades para articular diferentes saberes.

Nas propostas interdisciplinares, é comum que os estudantes atuem em grupo, promovendo a interação entre eles. Essa prática fortalece habilidades importantes como a argumentação, a escuta ativa e a organização de ideias.

Essa abordagem exige metodologias mais dinâmicas e colaborativas, favorecendo a construção coletiva do saber. Ao promover a articulação entre os conteúdos curriculares, ela amplia as possibilidades de leitura e interpretação do mundo, tanto para os professores quanto para os estudantes, permitindo uma compreensão do conhecimento como algo vivo, em constante transformação.

Nesta coleção, você encontrará atividades cujo propósito é integrar diferentes componentes curriculares. As seções Coletivamente e Entre textos, por exemplo, trazem temas e reflexões que possibilitam um trabalho integrado. Além disso, o boxe Articulando conhecimentos detalha algumas integrações nas orientações ao professor, contribuindo para o aumento da criatividade e para a formação crítica e responsável dos estudantes na construção de seu conhecimento.

A PRÁTICA INTERDISCIPLINAR

E O TRABALHO COM PROJETOS

INTERDISCIPLINARES

Para planejar um trabalho interdisciplinar, o ponto de partida é definir os objetivos de aprendizagem. Com base

nisso, se for o caso, é importante dialogar com o professor de outros componentes para planejar estratégias conjuntas, considerando os objetivos previamente levantados, os conhecimentos prévios dos estudantes e como os conteúdos podem ser abordados de forma integrada. Quando não for possível contar com a colaboração do professor de outros componentes curriculares, cabe a você orientar os estudantes nas pesquisas, ensinando-os a buscar fontes confiáveis e adequadas à proposta, a fazer registros relevantes, a organizar as informações obtidas e a planejar como os resultados das pesquisas serão entregues.

PROJETOS INTERDISCIPLINARES

Projetos investigativos e pesquisas também são exemplos de atividades que favorecem o trabalho interdisciplinar em sala de aula, pois envolvem tarefas que integram conhecimentos de diferentes áreas, como planejamento, levantamento de hipóteses, coletas de dados, análises, deduções e conclusões.

Os projetos oferecem aos estudantes oportunidades concretas de participação ativa no processo de construção do conhecimento, contribuindo diretamente para o desenvolvimento de diversas competências, como o pensamento crítico e reflexivo, a argumentação, a valorização do pluralismo de ideias, a criatividade, a cooperação, a autonomia e a comunicação.

Nesse contexto, você continua sendo o mediador, orientando e acompanhando os estudantes para que atuem com autonomia e sejam protagonistas do desenvolvimento do projeto.

É importante ressaltar que a estrutura de um projeto não deve ser encarada como um modelo fixo ou engessado. Os projetos podem assumir diferentes formatos, conforme os objetivos e os contextos de aplicação. Em geral, iniciam-se com uma situação-problema ou uma questão orientadora, que dá origem a um conjunto de etapas organizadas de forma lógica. A seguir, apresentamos um

AVALIAÇÃO

A avaliação tem papel fundamental no processo de ensino-aprendizagem, pois é uma oportunidade de investigar, diagnosticar, refletir e intervir sobre o processo e acompanhar o desenvolvimento dos estudantes e sua atuação enquanto docente.

É fundamental compreender que a avaliação não deve ocorrer apenas em situações isoladas. O acompanhamento do percurso de aprendizagem dos estudantes precisa ser contínuo, tendo como base observações frequentes e diversificadas. Nesse sentido, o processo avaliativo deve fazer parte das práticas pedagógicas do dia a dia, de modo integrado ao planejamento e às atividades desenvolvidas em sala de aula.

A você, a avaliação possibilita observar e refletir sobre sua prática docente e a oportunidade de readequar e reajustar atividades, práticas e estratégias para alcançar determinados objetivos, com a participação ativa dos estudantes nesse processo. Desse modo, é de grande importância a interpretação dos resultados para que,

modelo com etapas fundamentais que podem nortear a construção de um projeto interdisciplinar.

Planejamento

• Definição da situação-problema ou da questão norteadora.

• Conversa sobre o tema e levantamento de hipóteses.

• Elaboração de questões norteadoras com base na situação-problema.

• Formação das equipes, distribuição de tarefas e estabelecimento de metas e prazos.

• Consulta de diversas fontes e coleta de informações.

Execução

• Organização, testes e execução do trabalho.

• Realização de ajustes finais.

• Avaliação durante o processo.

• Definição da participação dos integrantes que conduzirão a apresentação.

Divulgação

• Apresentação dos resultados para a comunidade escolar.

• Publicação do trabalho final.

Avaliação

• Avaliação dos resultados do projeto.

• Realização de autoavaliação.

• Verificação do desempenho e do desenvolvimento das aprendizagens dos estudantes.

Fonte de pesquisa: BENDER, William N. Aprendizagem baseada em projetos: educação diferenciada para o século XXI. Tradução de Fernando de Siqueira Rodrigues. Porto Alegre: Penso, 2014. p. 61.

com base neles, você possa refletir sobre intervenções a serem feitas para sanar possíveis defasagens e, assim, auxiliar no processo de construção do conhecimento, identificando possibilidades de recuperação e progressão do aprendizado.

É essencial que a avaliação seja compreendida como uma ferramenta de inclusão e de apoio ao processo de ensino-aprendizagem, evitando que seja usada apenas como forma de analisar a eficiência e classificar os estudantes. Avaliar não deve ser sinônimo de rotular ou excluir, mas sim de compreender os percursos formativos deles. Para que a avaliação realmente contribua para identificar os progressos, as dificuldades e as possíveis lacunas no desenvolvimento das aprendizagens, é necessário que os critérios sejam previamente compartilhados e discutidos com os estudantes, pois isso favorece a compreensão dos objetivos da avaliação e promove uma participação mais ativa por parte deles.

O planejamento das avaliações deve estar alinhado aos conteúdos e às atividades efetivamente trabalhados em sala de aula, com uma abordagem reflexiva e contextualizada. É essencial considerar os processos de aprendizagem mais adequados à turma e considerar a diversidade de perfis entre os estudantes. Além disso, é recomendável diversificar os instrumentos utilizados, não se restringindo a provas e testes, e incluir diferentes formas de expressão

Avaliação diagnóstica

do conhecimento. Entre as possibilidades, destacam-se atividades em grupo, debates, produções escritas e orais, atividades práticas, questões objetivas e dissertativas, entre outros formatos que respeitem as múltiplas formas de aprender e se comunicar dos estudantes.

Nesta coleção, a ação avaliativa do processo de ensino-aprendizagem propõe três tipos principais: a avaliação diagnóstica, a avaliação formativa e a avaliação de somativa.

A avaliação diagnóstica é o momento de identificar os conhecimentos que os estudantes trazem consigo, além de suas necessidades e dificuldades.

Essa etapa é fundamental para você reajustar as rotas e os objetivos de ensino. É importante ressaltar que a avaliação diagnóstica não precisa de um registro formal; a simples observação de uma atividade em sala de aula, por exemplo, já permite que você identifique as habilidades que precisam ser desenvolvidas ou aperfeiçoadas.

Onde ocorre

Nesta coleção, um exemplo de avaliação diagnóstica está na seção Vamos iniciar, no início de cada volume. Nela, são propostas atividades que possibilitam determinar se será necessário retomar conteúdos, estabelecer objetivos e definir as práticas e as estratégias didáticas. Nas orientações ao professor, você encontra sugestões de intervenção com base na análise das respostas e nas dificuldades dos estudantes.

A avaliação diagnóstica também pode ser feita no início de cada unidade, pois as atividades das páginas de abertura possibilitam diagnosticar os conhecimentos prévios dos estudantes sobre os temas e os conteúdos que serão abordados.

Avaliação formativa

A avaliação formativa acontece ao longo do período letivo. São os processos contínuos pelos quais você obtém indicadores a respeito da aprendizagem dos estudantes.

Desse modo, esse tipo de avaliação possibilita que você realize intervenções, propondo novas estratégias e procedimentos que visam à melhoria e/ou ao aprofundamento dos conhecimentos por parte dos estudantes.

A avaliação formativa pode ter um papel fundamental na melhoria das aprendizagens de todos os alunos. A sua utilização sistemática deve permitir que os alunos conheçam bem: a) o que têm de aprender no final de um dado período de tempo; b) a situação em que se encontram quanto às aprendizagens que têm de desenvolver; e c) os esforços que têm de fazer para aprenderem o que está previsto e descrito nos documentos curriculares. Para tal, a comunicação entre professores e alunos é fundamental, pois é através dela que os alunos podem receber orientações que os ajudam a aprender. [...]

FERNANDES, Domingos. Avaliação formativa: Folha de apoio à formação: Projeto de Monitorização Acompanhamento e Investigação em Avaliação Pedagógica (Maia). Ministério da Educação/Direção-Geral da Educação, 2021. p. 4.

Onde ocorre

Nesta coleção, a avaliação formativa é um processo contínuo e integrado. A seção Vamos avaliar o aprendizado, ao final de cada unidade do Livro do Estudante, oferece atividades que retomam os principais conceitos e noções trabalhados para verificar a aprendizagem com relação aos objetivos estabelecidos. Nas orientações ao professor, o boxe Avaliando complementa essa prática com propostas de atividades avaliativas adicionais. Ele inclui objetivos e estratégias de intervenção, caso seja necessária a retomada de conteúdos e conceitos.

Além disso, é importante o hábito de transitar pela sala de aula e observar os estudantes durante as atividades propostas. Esse acompanhamento mais próximo contribui para que eles se reconheçam como parte do processo de ensino-aprendizagem, desenvolvam sua autonomia e busquem aprimoramento contínuo.

Avaliação somativa

A avaliação somativa é realizada ao final de um período de estudos, em consonância com as práticas pedagógicas da escola. Com base nas respostas a essa avaliação, você poderá refletir sobre ações a serem tomadas para sanar possíveis dificuldades dos estudantes.

Por ser comumente associada a testes e notas que visam classificar o desempenho dos estudantes, é fundamental que ela não seja o único foco do processo avaliativo. A nota é apenas uma das muitas formas de representar os resultados, e essa etapa deve ser considerada como a consequência natural das avaliações diagnóstica e formativa já realizadas.

Ao analisar os resultados, você pode refletir sobre as ações necessárias para sanar possíveis dificuldades, utilizando o de-

sempenho como um indicativo para a retomada de conteúdos e a definição de novas estratégias. Dessa forma, resultados abaixo do esperado não são uma sentença, mas sim um ponto de partida para aprimorar o processo de ensino-aprendizagem.

Onde ocorre

Nesta coleção, a avaliação somativa acontece ao final de cada volume, na seção Vamos concluir. Essa seção oferece atividades que permitem a você verificar os conhecimentos adquiridos pelos estudantes no decorrer do ano letivo. Nas orientações ao professor, você encontra sugestões de intervenção para analisar as respostas e identificar a necessidade de estratégias de remediação, garantindo que os objetivos pedagógicos sejam alcançados.

Para um sistema de avaliação eficiente, é recomendável a combinação das três modalidades, além de usar diferentes instrumentos que auxiliem a obter informações

Provas e testes

Seminários e debates

Portfólios

sobre o desenvolvimento da aprendizagem dos estudantes. Apresentamos a seguir alguns exemplos.

Instrumentos de avaliação

Podem ser elaborados com questões abertas, análise de situações, questões objetivas e quizzes, e realizados de forma regular, abordando conteúdos específicos ou referentes a determinado período.

Possibilitam a você perceber o desenvolvimento de habilidades relacionadas a tarefas como pesquisa, síntese das informações, pensamento crítico e comunicação.

A elaboração de portfólios com base em suas observações e registros em fichas avaliativas contribui não só para analisar o desenvolvimento cognitivo dos estudantes, mas também a maneira como cada um aprende, com atenção especial às habilidades que eles desenvolvem com mais facilidade e as que demandam mais atenção e auxílio para serem desenvolvidas.

Saraus Permite a você verificar o desenvolvimento de habilidades relacionadas a interação social, capacidade de expressão, criatividade, sensibilidade e conhecimento cultural.

Ditados Possibilita que você acompanhe as principais dificuldades dos estudantes com relação à escuta e à escrita.

Autoavaliação

Incentiva o desenvolvimento da autonomia dos estudantes levando-os a refletir sobre sua participação nas atividades, suas dificuldades e aspectos que devem ser melhorados. Com base nessas informações, você pode debater com eles os caminhos para gerar mudanças no planejamento e melhorias para toda a turma.

Para auxiliar o monitoramento das aprendizagens, sugerimos a utilização de uma ficha de avaliação de acompanhamento individual, como a que apresentamos a seguir. Essa ferramenta permite registrar a trajetória de cada estudante, observando seu desenvolvimento com relação aos objetivos e às habilidades trabalhados.

A ficha usa um sistema de marcação simples para identificar o nível de desenvolvimento do estudante.

• S (Sim): o estudante demonstrou ter alcançado o objetivo.

• P (Parcialmente): o estudante atingiu o objetivo de forma incompleta, necessitando de intervenção para avançar.

Escola: preencher com o nome da escola.

Estudante: preencher com o nome do estudante.

• N (Não): o estudante não alcançou o objetivo, sendo necessária uma intervenção imediata. Quando o objetivo é alcançado e marcado com S, você deve incentivar o estudante a aprofundar seus saberes. Se a marcação for P ou N, a ficha serve como um diagnóstico claro, indicando a necessidade de planejar intervenções para que o estudante progrida nos estudos.

Você pode usar esse tipo de ficha para registrar observações feitas durante o trabalho com as seções Vamos iniciar, Vamos avaliar o aprendizado e Vamos concluir do Livro do Estudante, e com o boxe Avaliando das orientações ao professor

Professor(a): preencher com o nome do(a) professor(a).

Turma: preencher com a indicação da turma. Período letivo do registro: preencher com o ano letivo.

Ficha de acompanhamento individual das aprendizagens

Objetivos ou habilidades avaliados S (Sim) P (Parcialmente) N (Não) Observações

Preencher com o objetivo ou a habilidade.

MODELO

O

No contexto atual da educação, o papel do professor dos Anos Iniciais do Ensino Fundamental vai além da transmissão de conteúdo. Ele deve atuar como mediador do conhecimento, incentivando a autonomia dos estudantes e formando leitores e pensadores críticos. Acima de tudo, o professor é um agente essencial na construção da base educacional e emocional dos estudantes.

Essa etapa da escolarização é marcada por profundas transformações no desenvolvimento cognitivo, afetivo e social dos estudantes. Por isso, a prática pedagógica exige sensibilidade e escuta ativa. Você deve estar atento às necessidades individuais dos estudantes, respeitando seus ritmos de aprendizagem e suas realidades. A construção de vínculos afetivos é fundamental para fortalecer a autoestima e a autonomia, pois são eles que criam um ambiente acolhedor, onde o erro é considerado como parte do processo de aprendizagem e todos os estudantes se sentem seguros para se expressarem.

Sua atuação docente envolve uma reflexão constante sobre os conteúdos, as metodologias e, principalmente, sobre como os estudantes aprendem. Ao aproximar o conteúdo escolar dos conhecimentos prévios deles, você torna o aprendizado mais significativo e prazeroso. Essa abordagem, que valoriza sua bagagem cultural e suas experiências, é fundamental na construção de uma relação positiva deles com o ato de estudar.

O planejamento pedagógico é o ponto de partida, mas a prática em sala de aula é dinâmica, e não linear. É no dia a dia que você conhece os perfis, as necessidades e os ritmos da turma, e que a flexibilidade e a capacidade de adaptação se tornam essenciais. O diálogo constante com a equipe pedagógica e a participação em formações continuadas são atitudes que favorecem o desenvolvimento de uma prática docente mais eficaz e alinhada às reais demandas da turma.

Nessa jornada, você é o principal organizador das ações pedagógicas. É quem acolhe, engaja e dá oportunidade para que os estudantes verbalizem seu raciocínio, escrevam e desenvolvam, no coletivo da turma, a compreensão sobre os motivos das atividades e a formulação das respostas. O livro didático não é apenas um guia, mas um instrumento cultural que serve como mediador entre você e o estudante, auxiliando na construção do conhecimento. Com autonomia, é você quem dá vida a esse material, ajustando-o às necessidades de cada turma para que os estudantes se tornem os protagonistas de sua aprendizagem.

A PRÁTICA PEDAGÓGICA EM AÇÃO

A sala de aula é marcada pela diversidade. Cada estudante traz consigo um conjunto de experiências, saberes e modos de aprender. Essa diversidade se expressa em aspectos comportamentais, cognitivos, afetivos e

socioculturais que influenciam diretamente o modo como cada um constrói o conhecimento. Já as trajetórias individuais são moldadas por fatores como o contexto familiar, as vivências culturais e o ambiente social em que estão inseridos. É seu papel e da equipe escolar acolher essas diferenças.

Nesse sentido, compreender o desenvolvimento dos estudantes exige atenção ao contexto em que vivem, às suas práticas cotidianas e à maneira como atribuem significado às suas experiências. Por isso, uma das grandes questões que se impõe ao trabalho docente é: como planejar intervenções pedagógicas que deem conta da heterogeneidade presente em sala de aula, especialmente em turmas numerosas?

Diante desse desafio, é essencial que você reconheça que não há um único caminho para a aprendizagem. As interações, os ritmos e os interesses variam, e é seu papel estar atento a essas diferenças, promovendo práticas pedagógicas flexíveis e inclusivas. Só assim será possível garantir que todos os estudantes tenham oportunidades reais de desenvolvimento, respeitando suas singularidades sem comprometer a qualidade do processo de ensino-aprendizagem.

A seguir, apresentamos sugestões para auxiliar seu dia a dia, promovendo a adequação de atividades e a progressão do aprendizado, para que os estudantes avancem no próprio ritmo, com o apoio necessário para superar desafios.

A PEGA DO LÁPIS NO PROCESSO DE ALFABETIZAÇÃO

Como os estudantes dos Anos Iniciais do Ensino Fundamental estão no processo de alfabetização, é importante que você os auxilie na apropriação do sistema de escrita. Uma das intervenções relevantes nesse processo é a orientação sobre a pega funcional do lápis. A pega de três pontos, também conhecida como pega tripoide ou trípode, é uma técnica considerada funcional, pois favorece movimentos mais precisos, fluidos e controlados, o que é essencial para o desenvolvimento da escrita e evita fadiga muscular. Para orientar os estudantes, incentive-os a:

• posicionar o lápis de forma relaxada, sem forçar os dedos;

• segurar o lápis entre a ponta do polegar e a lateral do dedo indicador;

• apoiar o lápis no dedo médio para dar suporte e estabilidade;

• deixar os outros dedos (anelar e mínimo) levemente dobrados na palma da mão, servindo de apoio.

É fundamental acompanhar o processo individualmente, observando se a pega está firme, mas não tensa. No entanto, trata-se de um desenvolvimento; desse modo, inicialmente não é recomendada a correção direta da

pega, mas sim uma observação atenta para compreender como cada estudante está se apropriando desses movimentos e o que pode ser feito para progredir.

O desenvolvimento da pega do lápis não se resume apenas a segurar o instrumento. Ele é resultado de uma coordenação motora fina bem desenvolvida. Para auxiliar nesse processo, é importante incluir atividades lúdicas e variadas na rotina da sala de aula que ajudam a fortalecer a musculatura das mãos e dos dedos, como brincar com massinha de modelar ou argila, rasgar papel com as mãos, rasgar papel em pedaços pequenos e fazer bolinhas com as pontas dos dedos, cortar com tesoura de pontas arredondadas e colar pedaços de papel pequenos.

A INCLUSÃO NAS ESCOLAS

Garantir a inclusão de estudantes com deficiência na escola regular não é apenas um dever legal, mas um compromisso ético e pedagógico com a equidade e a justiça social. A legislação brasileira, incluindo a Constituição Federal (1988), a Lei Brasileira de Inclusão (LBI) (2015) e as Diretrizes da Política Nacional de Educação Especial (2008), reforça o papel da escola em assegurar que todos os estudantes tenham acesso a uma educação de qualidade. Contudo, a inclusão vai além de permitir o acesso físico à sala de aula. Ela exige a participação ativa dos estudantes no cotidiano escolar, promovendo aprendizagens significativas e respeitando suas particularidades. Para isso, é essencial o envolvimento de toda a comunidade escolar na construção de um ambiente que valorize as diferenças e que favoreça as interações e o respeito à diversidade. Nesse contexto, o papel do professor é central, como mediador e agente de transformação.

O primeiro passo mais importante é levar ao professor o reconhecimento das diversas dificuldades que deverá encontrar, suas especificidades, suas formas de atuação e como identificá-las em seus alunos. Neste processo, ao professor caberá a autonomia de reconhecer as dificuldades e intervencionar, em sala de aula, para a aplicação de novas metodologias e saberes, para a chegada da cognição.

JOIA, Michele. A inclusão de crianças na escola: o papel do educador diante das dificuldades de aprendizagem. 2. ed. Rio de Janeiro: Wak Editora, 2023. p. 41.

A prática pedagógica inclusiva deve reconhecer que todo estudante tem a capacidade de aprender, desde que seja incentivado por vínculos afetivos e em um ambiente acolhedor. Para isso, as estratégias precisam ser flexíveis e adaptadas às necessidades individuais.

PRÁTICAS PEDAGÓGICAS INCLUSIVAS

A seguir, sugerimos algumas ações que podem ser aplicadas em sala de aula para promover a inclusão.

• Materiais concretos e táteis: utilize materiais com diferentes texturas e relevos para que os estudantes possam explorar o conteúdo de forma sensorial. Ao utilizar recursos visuais, sempre descreva as imagens com clareza, indicando posições e características dos objetos.

• Comunicação clara: apresente os enunciados das atividades de forma clara e direta, evitando ambiguidades, figuras de linguagem ou construções muito complexas. Divida as tarefas em etapas menores e forneça uma instrução por vez. Durante as explicações, posicione-se de frente para os estudantes, facilitando a atenção à sua fala.

• Flexibilização e ritmo: ofereça prazos flexíveis para a entrega de atividades, respeitando o tempo de aprendizagem de cada estudante. Incentive a leitura compartilhada de textos e enunciados para promover a compreensão coletiva e o apoio mútuo.

• Incentivo à expressão: incentive a expressão oral, quando possível, e a organização do pensamento dos estudantes, auxiliando na estruturação das ideias. Ferramentas como alfabeto móvel e banco de palavras são ótimas aliadas para a alfabetização e o fortalecimento da participação dos estudantes no processo de aprendizagem.

• Uso de tecnologia: quando possível, adote recursos tecnológicos que atendem às necessidades específicas dos estudantes, ampliando as possibilidades de acesso ao conteúdo e tornando o aprendizado mais dinâmico e acessível.

• Valorização de estratégias de resolução de problemas: apresente e valorize diferentes estratégias para a resolução de problemas, respeitando a forma única de compreensão e de elaboração de soluções.

O USO DE METODOLOGIAS ATIVAS

O uso de metodologias ativas favorece o engajamento dos estudantes e o desenvolvimento de diversas habilidades. A prática pedagógica exige um planejamento cuidadoso, momentos de discussão em grupo, atividades colaborativas e trocas de saberes, especialmente quando o objetivo é fortalecer competências como leitura, escrita e raciocínio lógico-matemático.

[...]

Metodologias ativas são estratégias de ensino centradas na participação efetiva dos estudantes na construção do processo de aprendizagem, de forma flexível, interligada e híbrida. As metodologias ativas, num mundo conectado e digital, expressam-se por meio de modelos de ensino híbridos, com muitas possíveis combinações. A junção de metodologias ativas com modelos flexíveis e híbridos traz contribuições importantes para o desenho de soluções atuais para os aprendizes de hoje.

MORAN, José. Metodologias ativas para uma aprendizagem mais profunda. In: BACICH, Lilian; MORAN, José (org.). Metodologias ativas para uma educação inovadora: uma abordagem teóricoprática. Porto Alegre: Penso, 2018. p. 4.

A seguir, apresentamos três metodologias ativas que promovem o protagonismo e a autonomia dos estudantes.

Pensar-conversar-compartilhar

É uma estratégia eficaz para aumentar o engajamento dos estudantes, pois promove o pensamento individual e a colaboração, permitindo que todos participem ativamente da aula. A fase individual garante que todos os estudantes tenham oportunidade de organizar suas ideias e de se expressarem. A fase em duplas e a discussão geral mantêm os estudantes ativos e envolvidos no processo de aprendizagem, incentivando o pensamento crítico, a argumentação e a formulação de ideias. Para iniciar, você deve fazer uma pergunta ou lançar um desafio relacionado ao conteúdo da aula e estipular um tempo para os estudantes pensarem sozinhos na resposta. É o momento de organizar as ideias e formular uma primeira hipótese. Depois do tempo de reflexão individual, os estudantes se juntam a um colega. Em duplas, eles devem conversar, compartilhar ideias e chegar a uma conclusão, consolidando o raciocínio e construindo o conhecimento de forma colaborativa. Na etapa final, o professor deve escolher algumas duplas, ou todas, para apresentarem suas ideias, incentivando a participação de todos e levando-os a perceber que há diferentes formas de pensar e de resolver o mesmo problema.

Vire e fale

Essa estratégia é eficaz para aumentar o engajamento e a participação dos estudantes, pois modifica o formato de pergunta e resposta e cria um espaço para que eles possam expressar suas ideias. A conversa em duplas incentiva-os a organizarem suas ideias e a praticarem a escuta ativa. É uma estratégia rápida e simples que pode ser utilizada várias vezes durante a aula para checar a compreensão e manter o ritmo de forma dinâmica e interativa. Para começar, faça uma pergunta clara e direta relacionada ao conteúdo que está sendo trabalhado e que possa ser respondida em cinco minutos. Imediatamente após a pergunta, peça aos estudantes que virem para um dos colegas para conversarem sobre a pergunta, tentando chegar a uma resposta em até cinco minutos. Esse é o momento em que eles devem verbalizar suas ideias uns para os outros, escutando o que o outro tem a dizer e chegando juntos a uma conclusão. Após a conversa em duplas, escolha alguns estudantes, ou todos, para compartilharem as ideias que surgiram nas duplas e faça intervenções quando julgar necessário.

Caminhada na galeria

Essa é uma estratégia colaborativa que envolve a produção de cartazes sobre os conteúdos estudados que devem ser expostos como em uma galeria de arte. A atividade foge da rotina da sala de aula e envolve movimento, o que é indicado para essa faixa etária. Os estudantes aprendem uns com os outros e desenvolvem a capacidade de escutar e argumentar, além de aprimorar a comunicação, o raciocínio e a organização de ideias de forma lúdica e prática, aprofundando os conteúdos que aprenderam. Para trabalhar com essa metodologia, organize a turma em grupos e proponha um tema, uma pergunta ou um problema para ser trabalhado em cada grupo. Oriente os grupos a fazerem pesquisas sobre o assunto e a registrarem as conclusões em cartazes. Depois de prontos, os cartazes devem ser fixados na sala de aula, como se fossem obras de arte, e cada grupo deve escolher um apresentador que ficará ao lado para explicar o trabalho. O restante da turma, em grupos, começa a caminhada pela galeria, observando e analisando as produções dos colegas. Após todos os grupos visitarem as obras da galeria, reúna todos e incentive uma conversa sobre o que foi aprendido. Esse é o momento para discutir as diferentes soluções encontradas, os pontos em comum e o que mais chamou a atenção dos estudantes.

A ORGANIZAÇÃO DO ESPAÇO

Para a organização do trabalho pedagógico em sala de aula, é essencial considerar a disposição do espaço e promover um ambiente pautado pela empatia, pelo respeito mútuo e pela valorização do coletivo, o que contribui para a construção de uma sala de aula acolhedora, na qual o desenvolvimento da autonomia dos estudantes seja incentivado de forma constante.

A fim de promover um ambiente mais dinâmico, inclusivo e colaborativo, você pode alterar a organização tradicional da sala de aula, que tem carteiras enfileiradas e o professor ocupando o papel central como único detentor do saber. Ao repensar a organização da sala de aula como um recurso pedagógico, você amplia as possibilidades de interação, cooperação e construção coletiva do conhecimento, aproximando a prática docente das demandas reais da turma. A seguir, apresentamos algumas sugestões para organizar a sala de aula de diferentes maneiras.

Disposição em grupo: indicada para atividades que exigem colaboração direta e trocas constantes entre os estudantes, como trabalhos em equipe, debates e projetos que precisam de divisão de tarefas, pois a proximidade física facilita a comunicação e o apoio mú-

tuo, incentivando a resolução de problemas de forma coletiva.

Em grupo

Representação de carteiras dispostas em grupo.

Disposição em círculo: indicada para atividades que priorizam a participação de todos, a escuta ativa e a criação de um ambiente de igualdade, como rodas de conversa, discussões sobre temas específicos, contação de histórias e compartilhamento de experiências, permitindo que a construção do conhecimento, a troca de experiências e a comunicação sejam mais diretas e isonômicas entre você e os estudantes.

Representação de carteiras dispostas em círculo.

Disposição em U: indicada para apresentações orais, demonstrações, debates supervisionados ou quando você precisa circular entre as carteiras para dar assistência individual, pois combina sua visibilidade com a possibilidade de interação entre os estudantes, permitindo que todos mantenham o foco na atividade.

Em U

Representação de carteira dispostas em U.

Disposição de frente uns para os outros: parecida com a disposição em grupo, mas pode ser utilizada para trabalhos em duplas, entrevistas ou atividades de reflexão, pois promove uma interação mais focada e próxima, permitindo aos estudantes que se concentrem na troca de informações e ideias entre si, sem a dispersão que um grupo maior poderia causar.

De frente uns para os outros

Representação de carteiras dispostas de frente umas para as outras.

Outra estratégia que ajuda a aproximar o currículo da vida dos estudantes é incentivar a utilização de outros espaços dentro e fora da sala de aula para divulgar o trabalho desenvolvido pela turma, como os murais e as paredes, explorando diferentes recursos e estratégias.

A ORGANIZAÇÃO DO TEMPO E DA ROTINA ESCOLAR

Além da organização do espaço físico, é fundamental atentar à gestão do tempo e da rotina em sala de aula. Estabelecer uma rotina clara e bem estruturada favorece a execução do planejamento pedagógico, garantindo que os horários e as atividades sejam conduzidos de forma sequencial e coerente, sempre respeitando as particularidades e os diferentes ritmos de aprendizagem dos estudantes.

Planejar a prática pedagógica de acordo com a proposta curricular proporciona um ambiente mais estável e acolhedor, no qual os estudantes sabem o que esperar e se sentem mais seguros diante das estratégias utilizadas no dia a dia. Além de facilitar a condução do trabalho docente, essa organização contribui para equilibrar e diversificar as atividades ao longo da semana, ampliando as possibilidades de aprendizagem.

Além das aulas nas quais os conteúdos e as atividades são abordados, é importante que você inclua atividades diversificadas em seu planejamento de rotina, como as sugeridas a seguir.

• Rodas de conversa: podem ser realizadas no começo ou no final da aula para solicitar aos estudantes que relatem alguma vivência pessoal (como forma de explorar os conhecimentos prévios) ou exponham o que aprenderam, quais dificuldades tiveram ou o que gostariam de aprender na próxima aula.

• Momentos de leitura: esses momentos podem ser conduzidos tanto por você, por meio da leitura em voz alta, quanto pelos próprios estudantes, com a leitura compartilhada ou um de cada vez. É importante reservar intervalos de tempo específicos na rotina para a leitura de diferentes textos com a intenção de proporcionar momentos de apreciação e, ao mesmo tempo, ampliar o repertório e os conhecimentos dos estudantes.

• Momentos de registro : essa estratégia consiste em reservar, ao final das aulas, alguns minutos para que os estudantes expressem o que aprenderam. Esse registro pode ser feito por meio da escrita, de esquemas visuais, de desenhos ou até pela oralidade, com gravações em áudio ou vídeo. Essa etapa funciona como uma forma de verificação da aprendizagem, permitindo a você identificar o que foi compreendido e o que ainda precisa ser retomado em aulas futuras ou em atividades de reforço. Os registros podem ser feitos individualmente, em duplas ou em pequenos grupos, de acordo com os objetivos da proposta.

• Visitas guiadas a diferentes espaços de aprendizagem: a sala de aula não é o único ambiente para o aprendizado dos estudantes, por isso é importante sugerir atividades em outros espaços na escola, como laboratórios, bibliotecas, pátio, auditório e jardim, e fora da escola, como teatros, museus, espaços públicos, centros de pesquisas, cinema e centros culturais. Em casos de atividades em espaços fora da escola, é necessário que você solicite, com antecedência, as autorizações para a direção e para os pais ou responsáveis dos estudantes, e as faça com o acompanhamento de outros profissionais

Escola: preencher com o nome da escola.

Professor(a): preencher com o nome do professor.

da escola, bem como a orientação do uso de filtro solar, da ingestão de água e do uso de repelentes e de vestimentas e calçados adequados, visando à segurança, à integridade física e ao bem-estar dos estudantes.

Além dessas atividades, o planejamento de rotina deve incluir atividades lúdicas que incentivem a interação social e momentos que envolvam alimentação e higiene pessoal.

Apresentamos a seguir um exemplo de planejamento de rotina, que pode ser adaptado de acordo com as suas necessidades, as dos estudantes e as da escola.

MODELO

Componente curricular: preencher com o nome do componente curricular. Turma: preencher com a indicação da turma. Data: preencher com o período do planejamento.

Planejamento de rotina

Horário Local Atividade Objetivos

7h30 – 8h Sala de aulaAcolhimento e roda de conversa. Promover a socialização e desenvolver a oralidade.

8h – 9h30 Sala de aula

9h30 – 10h Refeitório, banheiro e pátio

10h – 11h Quadra

Leitura compartilhada de textos e atividades dirigidas de escrita.

Lanche, escovar os dentes, lavar as mãos e recreio.

Brincadeiras tradicionais e jogos cooperativos.

11h – 11h30 Sala de aulaRoda de leitura e fechamento.

Outro recurso pedagógico que pode auxiliar a gestão do tempo e o planejamento de rotina é a sequência didática. Uma sequência didática é um plano de ensino estruturado, composto de um conjunto de atividades ordenadas e interligadas que são desenvolvidas ao longo de várias aulas. A elaboração de sequências didáticas é um recurso pedagógico que pode tornar o planejamento mais eficaz e alinhado às necessidades dos estudantes. Por meio delas, você consegue organizar o processo de ensino de maneira intencional e progressiva, estruturando atividades e estratégias de forma coerente e articulada.

Ao planejar uma sequência didática, você estabelece etapas claras e encadeadas que favorecem a construção do conhecimento ao longo do tempo, seja em alguns dias, semanas ou até meses. Essa organização permite flexibilizar o percurso, ajustando-o conforme o ritmo de aprendizagem da turma e as particularidades do contexto escolar.

Desenvolver habilidades de leitura e de escrita.

Momento de descanso, alimentação, higiene e interação livre.

Desenvolver a expressão corporal e a coordenação motora.

Desenvolver a escuta ativa, retomar as aprendizagens do dia e organizar a sala de aula.

É fundamental que as sequências estejam alinhadas aos objetivos de ensino, considerando também os recursos didáticos disponíveis e a realidade da escola. Outro aspecto essencial é a inclusão de estratégias de avaliação que permitam acompanhar e refletir sobre o avanço dos estudantes ao longo do processo, verificando seu envolvimento e observando as dificuldades que possam surgir. Sempre que julgar necessário, faça intervenções que contribuam para ampliar a compreensão dos conteúdos.

Ao término da sequência didática, registre suas considerações sobre o processo de aprendizagem dos estudantes, destacando avanços e aspectos que ainda precisam ser desenvolvidos.

A seguir, apresentamos uma sugestão de modelo de sequência didática que pode servir como referência. Sinta-se à vontade para adaptá-lo conforme as necessidades da sua turma e os conteúdos que pretende desenvolver.

Escola: preencher com o nome da escola.

Planejamento de Sequência Didática

Professor(a): preencher com o nome do professor.

Componente curricular: preencher com o nome do componente curricular.

Turma: preencher com a indicação da turma.

Data: preencher com o período estimado para o desenvolvimento da sequência didática.

Assunto/conteúdo: preencher com os assuntos ou conteúdos a serem desenvolvidos.

Quantidade de aulas: preencher com a estimativa da quantidade de aulas que será necessária para desenvolver todas as atividades.

1. Objetivos gerais: definir o que se espera que os estudantes sejam capazes de fazer ao fim da sequência didática.

2. Competências e habilidades da BNCC: identificar as habilidades da BNCC que serão trabalhadas.

3. Materiais necessários: fazer uma lista detalhada de todos os materiais que serão necessários para desenvolver as atividades.

4. Etapas da sequência didática: detalhar as etapas de cada aula, organizando as atividades em uma ordem lógica e progressiva.

• Aula 1: descrever o início do trabalho com a sequência didática, que pode ser uma atividade para verificar o que os estudantes já sabem sobre o assunto; pode ser uma roda de conversa, uma dinâmica ou uma pergunta deflagradora para despertar a curiosidade deles.

• Aula 2: em diante: descrever as atividades intermediárias que ajudarão os estudantes a construírem o novo conhecimento; podem ser pesquisas, leituras, discussões, atividades práticas, entre outras dinâmicas.

• Aula final: descrever a última aula, a culminância da sequência didática, e planejar uma atividade final para que os estudantes coloquem em prática tudo o que aprenderam; pode ser a produção de um texto, a apresentação de um trabalho ou a criação de um projeto.

5. Avaliação: definir os critérios (o que será observado) e os instrumentos (como será registrado) que serão utilizados para avaliar a aprendizagem dos estudantes ao longo da sequência didática; a avaliação deve ser contínua, e não apenas ao final.

6. Autoavaliação: após a execução da sequência didática, verificar se ela foi eficaz, se os objetivos foram alcançados, quais desafios surgiram, o que pode ser mudado para a próxima vez e anotar essas reflexões para aprimorar suas práticas pedagógicas.

O USO DE TECNOLOGIAS DIGITAIS

A presença das tecnologias digitais no cotidiano das pessoas é cada vez mais comum, inclusive entre crianças e adolescentes. No entanto, a maneira como esses recursos, especialmente os dispositivos móveis como os celulares, têm sido utilizados dentro das escolas tem gerado muitos debates. O foco dessas discussões recai, principalmente, sobre os efeitos negativos do uso inadequado desses aparelhos no processo de aprendizagem e no desenvolvimento integral dos estudantes.

Estudos recentes reforçam essas preocupações, apontando prejuízos que vão desde a distração em sala de aula até impactos mais sérios, como problemas de saúde física e mental, que incluem aumento da ansiedade, distúrbios do sono, dificuldades de atenção, entre outros. Essas evidências contribuíram para a criação da Lei nº 15.100, de 13 de janeiro de 2025, que estabelece diretrizes para o uso de celulares nas escolas brasileiras.

Os desafios enfrentados com o uso inadequado e desregulado das tecnologias digitais não se restringem ao

ambiente escolar. A Unesco destaca riscos que vão desde o enfraquecimento das relações humanas até ameaças à democracia e aos direitos fundamentais, como a disseminação de discursos de ódio e a violação da privacidade. Tais aspectos mostram que a tecnologia, sem orientação adequada, pode acentuar desigualdades e comprometer valores essenciais.

No contexto escolar, o uso excessivo e sem propósito de recursos digitais tem mostrado efeitos prejudiciais, como o isolamento social, a dependência de redes sociais e a dispersão durante as aulas. Por isso, torna-se indispensável repensar o papel desses recursos na educação.

Por outro lado, quando inserida de maneira planejada e intencional no cotidiano escolar, a tecnologia pode se tornar uma ferramenta poderosa para o processo de ensino-aprendizagem. Recursos como computadores, tablets e celulares, quando utilizados com orientação pedagógica, promovem o acesso à informação, favorecem o desenvolvimento de habilidades críticas e éticas e ampliam o alcance da educação, especialmente em contextos de vulnerabilidade.

A proposta, portanto, não é excluir a tecnologia do ambiente escolar, mas sim incorporá-la com responsabilidade, sempre pautada em objetivos pedagógicos claros e alinhados às competências e aos conteúdos previstos no currículo.

Você tem um papel fundamental nesse processo. Cabe a você planejar atividades que façam uso significativo da tecnologia, promovendo a aprendizagem ativa e a reflexão crítica por parte dos estudantes. A intencionalidade no uso desses recursos deve estar presente desde o momento da escolha da ferramenta até a avaliação dos resultados.

Além disso, é importante lembrar que tecnologias educacionais não se limitam às mais recentes. Televisão, rádio, lousa, projetores e outros dispositivos já fazem parte da rotina escolar há décadas e desempenham papel importante na mediação pedagógica.

BOAS PRÁTICAS NO USO DE TECNOLOGIAS

NA EDUCAÇÃO

Para que a utilização de ferramentas tecnológicas seja eficaz e enriquecedora, é fundamental adotar algumas práticas pedagógicas intencionais. A seguir, apresentamos algumas dicas.

Planejamento pedagógico do uso de recursos tecnológicos

• Definir com clareza os objetivos de aprendizagem.

• Escolher as ferramentas tecnológicas adequadas para alcançar esses objetivos.

• Garantir que o uso dos recursos esteja articulado aos conteúdos e às competências curriculares.

O ENSINO DE MATEMÁTICA

FUNDAMENTOS TEÓRICO-METODOLÓGICOS NO ENSINO DE MATEMÁTICA

As inúmeras demandas e as constantes mudanças do mundo atual requerem uma sociedade composta de indivíduos com conhecimentos e habilidades que lhes permitam interpretar e analisar, de maneira crítica, a grande quantidade de informações veiculadas. Entre as áreas que capacitam os leitores nesse sentido, os conhecimentos matemáticos são um dos que cumprem tal demanda. Assim, é necessário que os cidadãos saibam explorá-los amplamente a fim de se comunicarem e participarem ativamente no mundo em que vivem.

Desse modo, é válido afirmar que o ensino da Matemática, para além do domínio de fórmulas e cálculos, mostra-se uma ferramenta importante na formação integral, social e crítica do cidadão ao desenvolver o raciocínio lógico, a capacidade de reflexão, a argumentação e a resolução de problemas. Nesse sentido, a Matemática pode contribuir para a formação do indivíduo na construção de uma consciência crítica e responsável, a qual, por sua

Desenvolvimento de habilidades críticas

• Propor atividades que incentivem a análise crítica de fontes de informação pelos estudantes.

• Levar os estudantes a refletirem sobre o impacto da tecnologia no cotidiano.

• Incentivar o uso consciente, seguro e responsável da internet.

Integração com outras metodologias

• Combinar o uso de tecnologias com estratégias convencionais, como leitura, escrita e pesquisa de campo.

• Incentivar experiências interativas, como a visita a museus virtuais e o uso de acervos digitais, que ampliam o repertório cultural dos estudantes e fortalecem vínculos com a memória coletiva.

Em resumo, o uso da tecnologia na educação não deve ser encarado como uma solução isolada ou um fim em si mesmo. Ela deve estar a serviço do processo de ensino-aprendizagem e contribuir para a formação crítica, ética e cidadã dos estudantes. Seu olhar pedagógico enquanto docente é essencial para transformar esses recursos em verdadeiros aliados do conhecimento.

Para auxiliar no uso de recursos digitais em consonância com seu planejamento pedagógico, esta coleção apresenta, na sua versão digital, infográficos clicáveis, a fim de complementar e enriquecer o desenvolvimento dos conteúdos.

A lista com os objetos digitais sugeridos em cada volume encontra-se no sumário. Além disso, os momentos de utilização desse recurso foram indicados nas páginas do Livro do Estudante por meio de ícones. Para acessá-los, basta clicar sobre os ícones indicados nas páginas da versão digital do Livro do Estudante

vez, pode se inserir em diversos âmbitos da vida em sociedade, como no consumo consciente, no planejamento da vida financeira, nas questões ambientais e no fortalecimento do respeito à diversidade étnica, cultural e social.

A capacidade de reconhecimento e identificação dos conhecimentos matemáticos como recurso de compreensão e de transformação da realidade, e as habilidades de identificar um problema, compreendê-lo e elaborar uma estratégia para resolvê-lo adequadamente podem ser desenvolvidas nas aulas de Matemática e valorizadas na formação de um profissional.

Nesse processo, espera-se que os estudantes adquiram a competência de resolver problemas e aprendam a validar as estratégias e os resultados obtidos, incentivando diferentes modos de raciocínio, além de utilizar recursos tecnológicos não apenas no ambiente escolar, mas, sobretudo, em seus diferentes contextos do cotidiano. Também é esperado que eles demonstrem segurança e autoconfiança na própria capacidade de se comunicarem matematicamente e de construir conhecimentos matemáticos na busca de soluções.

Ao ensinar Matemática aos estudantes, é necessário

motivar o interesse, a curiosidade e o espírito de investigação deles, desenvolvendo a capacidade do trabalho coletivo e cooperativo. Com isso, eles terão oportunidade de buscar soluções para os problemas propostos, identificando diferentes aspectos ao debaterem sobre determinado assunto, ao mesmo tempo que são constantemente encorajados a defenderem o pluralismo de ideias e o respeito às diferenças, prezando o ritmo e o modo de pensar dos colegas e aprendendo com eles. Este talvez seja um dos mais importantes passos para que se possa construir um ambiente de aprendizagem em que o protagonismo seja a palavra-chave.

Entre outras situações emergentes que envolvem um problema matemático, surge a conveniência de, em determinadas situações, recorrer a ferramentas nos recursos tecnológicos que lhes permitirão desenvolver estratégias na resolução de problemas, enfrentar desafios e comprovar e justificar resultados, além de estabelecer relações entre o conhecimento matemático e outros componentes curriculares. Ainda sob este enfoque, pretende-se articular as diferentes situações de ensino à realidade vivenciada pelos estudantes, na qual os artefatos e recursos da tecnologia estão cada vez mais onipresentes no universo de crianças e jovens. Nesta dimensão, cabe ponderar a relevância de promover a abordagem da matemática crítica, cujo objetivo central é voltado ao desenvolvimento de uma postura reflexiva, questionadora e transformadora, considerando os contextos sociais, culturais, políticos e econômicos nos quais os estudantes estão inseridos.

Entende-se, porém, que a construção do conhecimento matemático deve ser concretizada de modo gradual, em sincronia com o desenvolvimento cognitivo deles. Assim, é sugerida, ao longo dos volumes desta coleção, a utilização de materiais concretos, jogos e situações-problema em contextos significativos, preocupando-se com a inclusão de estudantes de diferentes perfis. Reforçam-se também que as opções metodológicas constantes nesta coleção são apenas sugestões para o professor, o qual deve exercer sua autonomia para a seleção da abordagem que julgar mais conveniente durante o desenvolvimento da sua prática em sala de aula.

Conforme aponta D’Ambrósio (2019), a matemática é uma ciência milenar, construída ao longo da história por diferentes povos, de acordo com suas necessidades, culturas e saberes. Com o passar do tempo e diante da emergência de novas demandas de diferentes gerações, assim como a contínua evolução tecnológica, que impacta os diferentes campos do conhecimento, tornando-se assunto relevante de inúmeros estudos na área educacional, surgiram várias teorias e perspectivas que ajudam na compreensão do processo de aprendizagem matemática. Entre essas teorias, destacam-se:

• a Neurociência, que estuda o desenvolvimento e o funcionamento do cérebro, comprovando que se aprende melhor quando são relacionados novos conceitos às experiências anteriores, fator que justifica a proposição de atividades concretas com o uso de materiais manipuláveis, os quais ajudam a construir representações mentais antes da abstração (COSTA, 2023);

• as epistemologias histórica e genética, que analisam como o conhecimento é construído ao longo da história e no desenvolvimento individual (PALHARES, 2008);

• as abordagens cognitivistas e sociointeracionistas, que valorizam o papel da interação social e dos processos mentais na aprendizagem (VIGOTSKY, 2010);

• o ensino-desenvolvimento, abordagem com influência da psicologia histórico-cultural, cujo expoente maior foi Lev Vygotsky, que considera o ensino um processo dinâmico, interativo e formativo, com vistas a formar sujeitos autônomos, críticos e criativos (VIGOTSKY, 2010).

Com base nessas perspectivas, os professores podem planejar práticas mais significativas e eficazes, respeitando o ritmo e as necessidades de cada estudante e apoiando o desenvolvimento do pensamento matemático desde os primeiros anos escolares. Cabe ao professor ajustar seus procedimentos didático-pedagógicos à perspectiva que considerar mais adequada diante das especificidades de cada estudante, nas mais diversas situações de sua prática docente.

Existem diferentes formas históricas e sociais de matematizar e esse deve ser o ponto de partida para a construção de uma educação matemática crítica. Para D’Ambrosio (2019), “matematizar é uma forma de compreender e explicar o mundo, que varia conforme o contexto histórico, social e cultural”. As diferentes abordagens metodológicas do ensino de matemática trabalhadas de maneira articulada contribuem para que o professor possa aplicar os conceitos e propor atividades utilizando recursos e estratégias de ensino adequados à faixa etária e, sobretudo, à realidade dos estudantes.

Vale destacar que o livro didático é uma importante ferramenta de apoio em sala de aula, no entanto não dever ser o único material de apoio a ser utilizado na condução das aulas. Além disso, ressalta-se a importância de o professor estar atento a teorias, perspectivas e propostas metodológicas apresentadas, como exemplo de algumas ferramentas para a seleção de recursos e apropriação das diferentes abordagens teóricas que propiciam a organização e o planejamento das aulas.

Por esses motivos, esta coleção apresenta, sempre que possível, situações propícias para desenvolver nos estudantes essas capacidades de ler e interpretar o mundo, de expor opiniões e respeitar as dos outros, contribuindo para a sociedade de maneira eficiente e concreta e construindo de modo apropriado os alicerces de uma educação de qualidade. Oferece também algumas sugestões de estratégias e recursos adequados à faixa etária a que se propõe cada categoria, devendo ser destacada a coerência entre a proposta constante na Reprodução do Livro do Estudante e nos materiais destinados aos professores. Aborda ainda algumas sugestões metodológicas que se alinham à proposta e podem auxiliar no trabalho docente, podendo ser adaptável à realidade social e cultural de cada estudante.

A coleção favorece também a compreensão dos pressupostos teórico-metodológicos e os objetivos que fundamentam a proposta didático-pedagógica, de maneira que o professor possa selecionar, entre as diferentes abordagens propostas, as que melhor se adequem à realidade de sua sala de aula. Assim, cabe ao professor a opção pela metodologia que lhe permita desenvolver seu trabalho pedagógico de maneira condizente às diferentes culturas e realidades de seu contexto escolar específico.

Por fim, esta obra busca propiciar a reflexão sobre a prática docente, de modo que o professor amplie sua compreensão sobre seu papel social e a função da escola em potencializar o aprendizado e o real engajamento dos estudantes no seu processo de construção do conhecimento matemático. Ressalta-se, assim, a singularidade desta coleção, uma vez que a utilização e a adequação do professor, a cada vivência em sala de aula, permitem a exploração de múltiplas possibilidades de trabalho docente, propiciando condições para promover a diversidade, a inclusão e a equidade com base na ênfase da experiência cultural dos estudantes como mediadora do conhecimento.

O LETRAMENTO MATEMÁTICO

Com relação ao letramento matemático, é fundamental que ele ocorra de maneira integrada com todos os componentes curriculares. Para isso, ao abordar os conteúdos, proponha situações didáticas contextualizadas que incentivem os estudantes a desenvolverem o raciocínio lógico e a aplicarem o conhecimento matemático na busca de soluções para situações-problema do cotidiano. Essa abordagem facilita a compreensão dos conceitos e reforça sua relevância.

As sugestões de atividades a seguir podem contribuir para o letramento matemático.

• Contagem de objetos usando materiais concretos, como tampinhas e lápis;

• uso e escrita de algarismos por meio de jogos e brincadeiras;

• compreensão do conceito de números;

• realização de operações básicas;

• reconhecimento de formas geométricas na identificação de quantidades e na ordenação de elementos;

• comparação de medidas com o uso de instrumentos não padronizados, como palmos e passos;

• leitura e interpretação de gráficos e tabelas com dados reais sobre a turma e a escola.

ABORDAGENS E PRÁTICAS EM MATEMÁTICA

Ao tomarmos como referência a BNCC, voltamos o olhar para o processo de aprender por meio das capacidades essenciais de formular, empregar, interpretar, avaliar e criar. Sob a perspectiva da Educação Matemática Crítica, é essencial que as situações-problema e as atividades propostas estejam relacionadas a situações e conflitos sociais fundamentais. Os estudantes devem ser considerados produtores de conhecimento, assumindo o protagonismo na apropriação e aquisição do letramento matemático.

Reafirmamos que as abordagens metodológicas aqui sugeridas devem ser contempladas como alternativas, e cada professor também deve ser protagonista de sua prática na escolha da melhor estratégia para auxiliar na construção e no pleno domínio dos conhecimentos matemáticos. Cabe, pois, ao professor, ajustar seus procedimentos didático-pedagógicos com a perspectiva mais adequada para os diferentes perfis estudantis que encontrar no decorrer de sua prática.

Sem nos atrelarmos a uma ou outra abordagem metodológica, por considerarmos que cada uma pode propi-

ciar respostas e/ou alternativas válidas para as demandas educacionais de cada realidade, apresentamos na sequência aportes teóricos sobre a etnomatemática como uma perspectiva coerente com muitas situações no processo de aprendizagem matemática.

Etnomatemática

Em primeiro plano, reconhecemos que a Etnomatemática, perspectiva metodológica proposta por Ubiratan D’Ambrosio, na década de 1980, considera os contextos culturais, sociais e históricos dos estudantes, valorizando os conhecimentos matemáticos de diferentes culturas. Trata-se, assim, de reconhecer as múltiplas matemáticas existentes nos também diversos “brasis” que se estendem pelo país. Nesta obra, consideramos essencial respeitar e valorizar cada contexto social como gerador de cultura. Conforme postula D’Ambrosio (2001), é importante valorizar os saberes matemáticos de modo a superar os mecanismos de exclusão social.

Oliveira (2019) considera que a experimentação educacional se configura como ponto de partida para abordagens investigativas no currículo de matemática com enfoque cultural. As pesquisas na área de educação matemática que utilizam a abordagem etnomatemática têm mostrado as especificidades do conhecimento matemático nas diferentes culturas e grupos sociais.

[...] Cada povo está inserido em realidades próprias, portanto devemos considerar que, ao formular problemas, suas respostas estão intimamente ligadas aos valores de sua cultura. As estratégias na resolução de problemas diferem sobre cada grupo cultural. Cada grupo cultural tem sua forma particular de contar, de desenhar, de se localizar, de medir, pois dependem de um modelo cultural ao qual pertencem. E não há como avaliar habilidades cognitivas fora do contexto cultural.

OLIVEIRA, Morane Almeida de. Matemática básica no sudoeste da Amazônia: uma proposta para escolas indígenas. Curitiba: Appris, 2019. p.28.

Com base no que o autor salienta, denota-se que o processo de aprendizagem da Matemática encontra-se intrinsecamente relacionado à vivência de cada estudante. Assim, não pretendemos apresentar respostas prontas para o ensino do componente, mas estratégias que podem e devem ser adaptadas a cada realidade, sobretudo se considerarmos as dimensões continentais do Brasil.

Nesses termos, entendemos que é urgente superar o método de ensino do componente que tem sido historicamente proposto como padrão.

A Etnomatemática, como uma das muitas abordagens consideradas para a construção dos conhecimentos matemáticos, é explorada em momentos da coleção que permitem traçar os contornos dos diferentes contextos sociais e culturais brasileiros.

Outra abordagem explorada é a resolução de problemas. Retomando os tópicos iniciais, em que confirmamos a importância da Matemática como recurso de compreensão e de transformação da realidade, evidenciamos a presença de resolução dos problemas como uma atividade recorrente no cotidiano das pessoas. Assim, decidir aspectos simples como calcular quantidades de alimentos a serem adquiridos e consumidos, quantias destinadas à

manutenção das despesas diárias e mesmo cálculos mais laborados, como planilhas de gastos, sugerem a presença da Matemática em todas as dimensões da vida humana.

Resolução de problemas

Por sua importância no ensino da Matemática, a resolução de problemas tem recebido destaque em estudos e pesquisas de educadores dessa área.

[...] O aluno deve ser estimulado a realizar um trabalho voltado para a iniciação à “investigação científica”. Nesse sentido, sua atividade intelectual guarda semelhanças com o trabalho do matemático diante da pesquisa, entretanto sem se identificar com ele. Assim, aprender a valorizar o raciocínio lógico e argumentativo torna-se um dos objetivos da educação matemática, ou seja, despertar no aluno o hábito de fazer uso de seu raciocínio e de cultivar o gosto pela resolução de problemas. Não se trata de problemas que exigem o simples exercício da repetição e do automatismo. É preciso buscar problemas que permitam mais de uma solução, que valorizem a criatividade e admitam estratégias pessoais de pesquisa. Essa valorização do uso pedagógico do problema fundamenta-se no pressuposto de que seja possível o aluno [se] sentir motivado pela busca do conhecimento. Seguindo essa ideia, o trabalho com a resolução de problemas amplia os valores educativos do saber matemático e o desenvolvimento dessa competência contribui na capacitação do aluno para melhor enfrentar os desafios do mundo contemporâneo. [...]

PAIS, Luiz Carlos. Didática da matemática: uma análise da influência francesa. 2. ed. Belo Horizonte: Autêntica, 2008. p. 35-36. (Coleção Tendências em Educação Matemática).

A metodologia da resolução de problemas em diferentes níveis de ensino é considerada de grande importância na aprendizagem, pois auxilia na construção de conceitos, além de possibilitar muitas outras competências. Na prática efetiva de ensino, tem-se revelado uma estratégia eficaz no processo de ensino-aprendizagem ao permitir que os estudantes mobilizem os seus conhecimentos prévios para interpretar e gerir informações do seu contexto. Entre as vantagens desta abordagem, apontamos a possibilidade de formação de estudantes mais ativos, despertando a iniciativa, o espírito investigativo e a criatividade. Ademais, a resolução de problemas pode contribuir para o desenvolvimento da autonomia intelectual, preparando-os para enfrentar desafios de forma independente e concretizando as condições de exercerem o protagonismo em sua aprendizagem.

Nesse ponto, cabe questionarmos: O que é um problema? Como vinculá-lo à Matemática? Como se deve trabalhar a resolução de problemas em sala de aula?

Para apontar sugestões como respostas a esses questionamentos, reforçamos a premência em considerar a contextualização de conteúdos como estratégia principal na resolução de problemas. Aqui, reforçamos a necessidade de não propor situações-problema isoladas do contexto de vivência da turma. Um problema adequado às situações vivenciadas por estudantes no Pantanal sul-mato-grossense pode não fazer sentido para os que vivem em uma capital do Sul do país, por exemplo. Os problemas devem estar relacionados a situações e conflitos sociais fundamentais da realidade de cada grupo a que se destinam.

Podemos pensar em problema como uma situação que exige reflexão, análise e resgate de situações similares que já tenhamos solucionado. Assim, um problema pode estar associado a ocasiões que nos levam a obter soluções. São alguns objetivos da resolução de problemas:

• promover o desenvolvimento do letramento matemático;

• mostrar aos estudantes que a Matemática pode ajudar na solução de muitos problemas que surgem no dia a dia;

• propiciar a iniciativa, a criatividade e a independência dos estudantes;

• desenvolver, de modo produtivo, a maneira de pensar dos estudantes por meio da investigação;

• potencializar e aperfeiçoar o raciocínio lógico-matemático dos estudantes;

• utilizar situações já estudadas, trabalhadas ou solucionadas como parâmetro para encontrar soluções para novas situações;

• levar os estudantes a perceberem que muitas situações-problema solucionadas por meio de conteúdos matemáticos são interessantes e desafiadoras.

É oportuno ponderar que o letramento matemático deve ser concebido como o ensino dos conceitos que estão imersos em uma prática social, ou seja, ler e escrever a linguagem matemática que está envolvida em um contexto de práticas sociais. Nos moldes propostos pela OECD (2003), “O letramento matemático implica a compreensão do papel da matemática no mundo, de modo que os indivíduos possam tomar decisões bem fundamentadas e participar como cidadãos reflexivos.”.

Diversas atividades desta coleção permitem que o professor alfabetizador planeje suas aulas para apresentar os conteúdos e as práticas do letramento matemático utilizando a estratégia de resolução de problemas, optando por essa metodologia pedagógica.

Utilização de jogos

É importante valorizar o trabalho com a ludicidade na infância e na adolescência. Estudos comprovam que o trabalho com jogos e brincadeiras colabora para o desenvolvimento de várias habilidades e, assim, para o aprendizado nessas fases da vida. Portanto, é possível inserir tais atividades apropriadas às aulas durante o desenvolvimento dos conteúdos matemáticos, tornando-os mais significativos.

Os jogos favorecem a criatividade, o desenvolvimento da busca de estratégias de resolução, a organização do pensamento e o desenvolvimento da intuição e da crítica. Outro aspecto que merece destaque é a socialização dos estudantes, pois nos jogos surge a necessidade da cooperação de outros indivíduos para estabelecer e seguir regras. O professor precisa se preparar para desenvolver uma atividade com jogos a fim de possibilitar a aprendizagem e a sistematização de conceitos matemáticos explorando ao máximo todo o potencial desse tipo de trabalho. Também deve acompanhar o desempenho dos estudantes, interferir quando for necessário e levantar questões relevantes durante o seu desenvolvimento.

Acreditando nos efeitos positivos para a aprendizagem que essas atividades podem proporcionar, esta coleção apresenta a seção Divirta-se e aprenda, propondo que os jogos e as brincadeiras façam parte das aulas de Matemática, tornando o ensino de conceitos mais des-

contraído. Assim, o professor tem à sua disposição uma ferramenta para promover de maneira lúdica o ensino de fatos aritméticos e conceitos matemáticos.

Recursos tecnológicos

Os constantes avanços tecnológicos observados no mundo atual têm provocado mudanças no modo de vida das pessoas. Os mais diversos segmentos são afetados com essa rápida evolução, inclusive o da educação. Esses avanços, aliados à quantidade de informações veiculadas, desafiam o professor a aliar o ensino e a aprendizagem de Matemática ao uso dos recursos tecnológicos em sua prática.

Os estudantes estão diariamente ligados às tecnologias, que se tornam cada vez mais acessíveis. Esse dinamismo já faz parte da realidade e da cultura da atual geração. Diante desse cenário, cabe à escola proporcionar o contato deles com diferentes mídias e ao professor refletir sobre tais práticas em suas aulas e fornecer aos estudantes ferramentas que os motivem na busca por conhecimento.

Entre os recursos que podem ser disponibilizados está a calculadora. Esse instrumento é importante em diversos momentos, como na verificação de resultados e na correção dos erros. A calculadora também pode ser usada na autoavaliação, na percepção de regularidades, na resolução de situações-problema, como incentivo à descoberta de estratégias e investigação de possíveis soluções para as atividades e na conferência de diversos cálculos no próprio cotidiano dos estudantes.

Durante as atividades com a calculadora, conscientize os estudantes de que, apesar de ser um instrumento que proporciona precisão e agilidade aos resultados, ela não pode decidir por eles. Por esse motivo, é necessário que compreendam antecipadamente as estratégias dos cálculos e sejam capazes de realizá-los sem usar essa ferramenta.

A robótica tem se mostrado uma estratégia inovadora e eficaz, na medida em que pode propiciar experiências práticas que promovem o raciocínio lógico, a criatividade, o trabalho em equipe e a resolução de problemas desde os primeiros anos escolares. Da mesma forma, seus benefícios englobam o desenvolvimento cognitivo, por meio do incentivo à lógica, ao pensamento crítico e à capacidade de resolver problemas. Ademais, promove a aprendizagem significativa e o trabalho cooperativo, ao mesmo tempo que familiariza os estudantes com os conceitos básicos de tecnologia. Não se trata de desenvolver protótipos de robôs, mas é possível criá-los com materiais recicláveis, incentivando a criatividade e a consciência ambiental, ou, ainda, criar narrativas nas quais eles sejam personagens, integrando linguagem oral e tecnologia. Oliveira et al. (2020) esclarecem que a robótica permite a integração de diferentes áreas do conhecimento, como Matemática, Ciências, Tecnologia e Artes, promovendo uma aprendizagem mais rica e significativa.

Reforçam-se, nesse ponto, as concepções trazidas sobre a construção do conhecimento matemático, o qual pode ser concretizado de múltiplas maneiras, mas sempre de modo articulado à vivência de cada estudante. Nesta coleção, não se pretende enfatizar uma única perspectiva, mas apontar opções possíveis para que o professor possa definir estratégias que o auxiliem a traçar caminhos de construção dos conhecimentos matemáticos.

Considerando a agilidade na realização de cálculos e, com isso, mantendo o foco no processo de resolução de problemas e na compreensão dos algoritmos, atividades que promovem o uso de calculadora em sala de aula foram incluídas em alguns momentos desta coleção. Algumas fornecem aos estudantes orientações sobre como utilizá-la, outras solicitam seu uso para conferir resultados de cálculos mentais ou mesmo a exploram como recurso auxiliar na compreensão de procedimentos de cálculo e na percepção de regularidades.

Outro recurso tecnológico em evidência nas últimas décadas é o computador. Essa ferramenta pode ser uma aliada do ensino de Matemática, na medida em que proporciona oportunidades de desenvolver nos estudantes o raciocínio lógico-matemático e abre espaço para pesquisas e busca ágil de informações. Um exemplo de utilidade é aplicar o computador a situações-problema de cunho prático, como em atividades que envolvem a construção de gráficos em estatística ou plotagem de figuras geométricas em geometria. Outro exemplo é nas buscas e consultas orientadas que enriquecem e complementam os conhecimentos prévios e as aulas de modo geral. Além disso, é possível orientar os estudantes quanto ao uso do computador para a finalização de trabalhos e apresentações no formato de seminários e debates.

Cabe a você, professor alfabetizador, escolher os momentos e as oportunidades de potencializar o uso consciente e produtivo dessa ferramenta, trazendo aproveitamento significativo em suas aulas.

Sobre as tecnologias digitais, presença indiscutível no cotidiano do ser humano, entende-se que a escola não pode se esquivar de inseri-las em suas atividades. Nesta coleção, elencamos algumas sugestões para que essa inserção propicie condições de otimizar a aprendizagem dos conceitos matemáticos.

Cálculo mental, aproximação e estimativa

O ensino da Matemática deve levar os estudantes a organizarem o pensamento e analisarem informações e dados de maneira crítica, não podendo, portanto, estar limitado a “fazer contas”. É importante que eles sejam capazes de compreender e estruturar situações, analisá-las, fazer estimativas e ter um raciocínio próprio, explorando diferentes tipos de registros e caminhos de construção.

Diversas situações que necessitam de cálculo mental e cálculo por estimativa ou de aproximação são comuns em nosso dia a dia e vivenciados pelos estudantes desde cedo. Saber a própria idade, quantos pontos obteve em um jogo ou quanto vai pagar por um brinquedo são exemplos da realização do cálculo mental. Imaginar o tempo necessário para chegar a determinado lugar, adivinhar uma quantidade ou medida qualquer ou até mesmo buscar uma estratégia em um jogo são exemplos de cálculo por estimativa ou aproximação. Considerando esses aspectos, o professor deve explorar situações do cotidiano a fim de desenvolver nos estudantes estratégias de cálculos, auxiliando-os, assim, na tomada de decisões e na oralidade.

Nas atividades que exploram o cálculo mental, não importa a rapidez para obter os resultados nem os cálculos decorados, mas sim a agilidade de pensamento e o estabelecimento de relações e regularidades. Por permitir que os estudantes percebam propriedades e regularidades, o cálculo mental contribui para o domínio do cálculo escrito. Desse modo, inserir esse procedimento

nas aulas de Matemática por meio de atividades criativas e flexíveis, que incentivem a estimativa, a formalização e a adaptação progressiva de técnicas de cálculo, auxilia no desenvolvimento da capacidade de resolver problemas e de trabalhar com os números, além de desenvolver habilidades relacionadas à atenção, à memória e à concentração.

A estimativa é um processo rápido e eficaz, cujo objetivo é aproximar um valor por meio de um número, situado dentro de um intervalo plausível, quando não é necessário um valor único e preciso. Porém, o número escolhido não pode ser qualquer um, pois deve ter como base observações anteriores. Várias são as situações cotidianas nas quais a estimativa é empregada como opção de resolução de problemas. Para isso, os valores de referência são importantes. A aproximação, por sua vez, pode ser muito utilizada no trabalho com medidas e grandezas, pois os números que as expressam são, na maioria das vezes, aproximados.

Em razão de as atividades de cálculo mental e de estimativa terem inúmeras características positivas no processo da aprendizagem e serem propostas atuais para o ensino da Matemática, sobretudo no Ensino Fundamental, nesta coleção são apresentadas, em momentos oportunos, atividades que exploram essas características. Elas são destacadas com ícones e incluem cálculos que devem ser resolvidos com base em experiências anteriores ou em estratégias pessoais dos estudantes, sem a utilização de material manipulável, observando padrões e regularidades, algumas vezes sem qualquer registro escrito. Ao trabalhar com essas atividades, é necessário acompanhar o processo dos estudantes e incentivá-los a elaborar estratégias pessoais de resolução. Após realizarem os cálculos, pode ser sugerido a eles que relatem os procedimentos a fim de levá-los a adquirir confiança e a aprimorar diversas habilidades durante o trabalho.

Outros recursos didáticos

Além dos recursos didáticos já citados, como o uso de jogos e brincadeiras, merecem destaque no ensino de Matemática o cálculo mental e aproximado, a estimativa, o uso da calculadora e do computador e o trabalho com materiais manipuláveis. Nos Anos Iniciais do Ensino Fundamental, esses materiais são imprescindíveis para a construção de significados, já que crianças necessitam manipular objetos para compreender determinados conceitos matemáticos. Essa ferramenta motiva os estudantes e auxilia o professor nos processos de ensino e aprendizagem.

O letramento estatístico e probabilístico refere-se à capacidade de interpretar, compreender, comunicar e criticar informações que têm como base dados e em situações que envolvem incertezas. Trata-se de um desdobramento do letramento matemático, voltado especificamente para os campos da Estatística e da Probabilidade, fundamentais na tomada de decisões pessoais, profissionais e sociais.

A cada dia, as crianças têm mais e mais acesso a informações variadas e precocemente entram em contato com conceitos mais complexos. A escola não pode ignorar esse fato e precisa se preparar para discutir esses conceitos, em modos acessíveis às crianças, e, assim, auxiliar no desenvolvimento de raciocínios mais avançados. Com base nas noções intuitivas dos estudantes,

podem-se desenvolver formas de pensar mais complexas por intermédio de ações eficientes promovidas em sala de aula.

BORBA, Rute et al. Levantando Possibilidades para o Desenvolvimento dos Raciocínios Probabilístico e Combinatório de Crianças em Anos Iniciais de Escolarização. In: BORBA, Rute; GUIMARÃES, Gilda (Orgs.). Pesquisa e atividades para o aprendizado matemático na Educação Infantil e nos Anos Iniciais do Ensino Fundamental SBEM, v. 8., 2015, p. 23.

No contexto escolar, desenvolver o letramento estatístico e probabilístico implica permitir que os estudantes compreendam gráficos, tabelas e porcentagens em contextos reais (como notícias, pesquisas e redes sociais), avaliem informações com base em dados estatísticos e probabilidades e tomem decisões informadas frente à incerteza e à variabilidade dos fenômenos.

A BNCC (2019) propõe o trabalho com estatística e probabilidade desde os Anos Iniciais do Ensino Fundamental, ampliando gradualmente a complexidade das análises. A matemática escolar, nesse sentido, ganha uma função social, preparando o estudante para compreender o mundo e atuar sobre ele.

Nesta coleção, esses conceitos são desenvolvidos de forma contínua e integrada ao longo das unidades, permitindo que os estudantes compreendam sua aplicação em diferentes contextos.

Entre os diversos materiais manipuláveis que podem ser usados para auxiliar os estudantes na abstração dos conhecimentos estão o ábaco, o material dourado e as peças ou os objetos que representam as figuras geométricas espaciais, além de embalagens diversas, como palitos de sorvete, tampinhas de garrafa, jornais, revistas, caixas de presente e engrenagens de relógio. O uso desses e de outros materiais pode conduzir os estudantes de maneira criativa no desenvolvimento do raciocínio lógico-matemático e de determinados conceitos.

No que diz respeito ao ábaco de papel, ou ábaco manipulativo, trata-se de uma ferramenta para auxiliar no aprendizado de matemática, especialmente números e operações básicas. Pode ser utilizado para ensinar conceitos como unidades, dezenas, centenas, adição, subtração, comparação de quantidades e valor posicional dos algarismos. Quanto à construção, geralmente é feito com um material que permite escrever e apagar, como papelão ou EVA, e possui colunas que representam unidades, dezenas, centenas etc. Para representar um número, movem-se as peças (contas ou botões, por exemplo) nas colunas correspondentes. Por exemplo, para o número 123, seriam movidas uma peça na coluna das centenas, duas na coluna das dezenas e três na coluna das unidades. Esse ábaco também pode ser utilizado nas operações: na adição, representa-se o primeiro número nele e, em seguida, adiciona-se o segundo número, movendo as peças correspondentes para as colunas corretas. Se necessário, realiza-se a troca de 10 unidades por uma dezena, 10 dezenas por uma centena, e assim por diante. Na subtração, o processo é semelhante: removem-se as peças correspondentes ao número a ser subtraído. Caso necessário, realiza-se a troca de uma dezena por 10 unidades, uma centena por 10 dezenas etc.

O ábaco ainda ajuda a entender o valor posicional dos algarismos em um número. Ao manipular as peças nas diferentes colunas, é possível visualizar como a posição de um algarismo afeta seu valor.

Smole e Diniz (2016) complementam que o uso do ábaco de papel, além de auxiliar na compreensão da organização dos números em unidades, dezenas, centenas etc., permite o desenvolvimento de habilidades de contagem e cálculo, a prática de contagens e a realização de operações matemáticas de forma visual, assim como melhora o raciocínio lógico e a concentração e desenvolve a autonomia e a autoconfiança. Ademais, a possibilidade de visualizar os resultados das operações pode aumentar a confiança dos estudantes em suas habilidades matemáticas.

Outro tipo de material manipulável de fácil acesso são as fichas sobrepostas, utilizadas para ensinar o sistema de numeração decimal, especialmente a composição e a decomposição de números e o valor posicional dos algarismos. Trata-se de um conjunto de fichas que permitem escrever os números de 0 a 99 999. O material consiste em fichas com números de diferentes ordens (unidades, dezenas, centenas etc.) que podem ser sobrepostas para formar e visualizar números maiores, facilitando a compreensão da relação entre eles (SMOLE; DINIZ, 2016). São 40 fichas (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 00, 10, 20, 30, 40, 50, 60, 70, 80, 90, 000, 100, 200, 300, 400, 500, 600, 700, 800, 900, 0000, 1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000) e podem ser produzidas com os estudantes. Os tamanhos de cada ordem devem ser diferentes de modo que eles consigam sobrepor perfeitamente uma sobre a outra. Confira o exemplo.

valor posicional é possível, pois as fichas sobrepostas ajudam a entender que o valor de um algarismo muda de acordo com sua posição no número.

Smole e Diniz (2016) ainda mencionam a possibilidade de propor jogos e atividades utilizando as fichas sobrepostas, tais como jogos de adivinhação, desafios de composição e decomposição ou jogos de comparação de números. Assim, entende-se que as fichas sobrepostas são um recurso versátil e eficaz para o ensino de matemática, auxiliando na compreensão do sistema de numeração decimal e no desenvolvimento do raciocínio lógico-matemático.

No entanto, é importante aliá-los a outras abordagens de conhecimento, pois o material por si só não constitui uma fonte única e total de aprendizagem. É necessário que o professor atente às necessidades de cada turma, a fim de adaptar materiais para as competências e habilidades que deseja desenvolver. Alguns benefícios proporcionados com a utilização desses recursos são o aprendizado por meio da manipulação de elementos, a capacidade de abstração, a aproximação dos estudantes à realidade e a fixação da aprendizagem. Esta coleção explora esses aspectos no boxe Experimente. Durante essa abordagem, é possível acompanhar a participação dos estudantes, fornecendo, sempre que possível, as explicações necessárias.

Os gêneros de linguagem também são recursos didáticos úteis em alguns momentos das aulas. Por esse motivo, esta coleção buscou apresentar histórias em quadrinhos, textos extraídos de revistas, jornais, livros e internet, telas de artistas, poemas, músicas, receitas, entre outros gêneros, todos relacionados ao conteúdo estudado.

Aos recursos já citados, podemos acrescentar a introdução à educação financeira. De maneira geral, esse tema tem como objetivo formar cidadãos preparados para lidar com situações desse tipo no dia a dia. Isso não só contribui para o fortalecimento da futura sociedade como apoia os estudantes em iniciativas de tomadas de decisões financeiras mais conscientes. Para abordar esse tema nas atividades, esta coleção utiliza folhetos promocionais de lojas, diferentes faturas e opções de pagamento, situações de compra e venda de produtos e serviços, notas fiscais, extratos bancários, entre outros recursos.

Como sugestão para o uso das fichas sobrepostas, os estudantes podem explorá-las e compará-las, permitindo a identificação dos números e das ordens. Em seguida, pode-se solicitar que formem números específicos sobrepondo as fichas de acordo com a ordem desejada. Para decomposição numérica, as fichas possibilitam demonstrar que um número pode ser decomposto em ordens (unidades, dezenas, centenas etc.), as quais se somam para compor um número. Do mesmo modo, o trabalho com

Considerando a necessidade de promover a inclusão de forma efetiva no ambiente escolar, cabe ressaltar a importância de trabalhar as formas multimodais aplicadas ao ensino da Matemática, concebidas como estratégias pedagógicas que utilizam diferentes modos de representação e comunicação, como linguagem visual, tátil, oral, corporal e tecnológica, para favorecer o aprendizado de todos os estudantes, especialmente aqueles com necessidades educacionais especiais. Esta proposta coaduna-se com o pensamento de Vigotsky (2010) quando destaca a importância dos mediadores na construção do processo de aprendizagem. Na mesma direção, situa-se o pensamento de Rojo e Almeida (2012), que defendem o uso de multiletramentos como estratégia para inclusão.

Como exemplos de formas multimodais aplicadas à Matemática com foco na inclusão, pode-se mencionar as representações visuais, como gráficos, diagramas, cores e imagens, que auxiliam estudantes com dificuldades de compreensão abstrata. O uso de blocos de Cuisenaire ou de material dourado para representar operações também é uma alternativa válida. Outros materiais concretos, como cubos, peças de encaixe, régua numérica tátil,

ábacos, tangram e geoplano favorecem o aprendizado de estudantes com deficiência visual ou dificuldades cognitivas. Com relação ao atendimento da linguagem oral e auditiva, sugere-se o uso de explicações verbais detalhadas, de histórias matemáticas e de jogos de perguntas e respostas, além de áudios explicativos e recursos com

descrição verbal para estudantes com baixa visão ou dislexia. Da mesma forma, podem ser utilizadas tecnologias assistivas e recursos digitais como softwares educativos com acessibilidade (voz sintetizada, legendas, aumento de contraste), assim como aplicativos que traduzem oralmente símbolos matemáticos.

QUADRO DE DISTRIBUIÇÃO DOS CONTEÚDOS

O quadro apresentado a seguir mostra a progressão dos conteúdos deste volume, destacando as habilidades, as competências e os temas contemporâneos transversais da BNCC trabalhados em cada unidade.

1 – Números de 0 a 19

• Conhecendo os números

• Números de 0 a 10

• O número 10

• A dezena

• Números de 11 a 19

• Agrupamentos e trocas

• Números ordinais

Trata-se de um quadro que pode ser utilizado para ter uma visão geral dos conteúdos das unidades, assim como facilitar a busca por orientações e comentários de práticas pedagógicas sugeridas nas orientações ao professor correspondentes ao Livro do Estudante

Quadro de distribuição dos conteúdos – 1º ano

2 – Figuras geométricas espaciais

• Conhecendo figuras geométricas espaciais

• História da contagem.

• Números no cotidiano.

• Correspondência um a um.

• Associação da quantidade à representação numérica.

• O número 1.

• O número 2.

• O número 3.

• O número 4.

• O número 5.

• O número 6.

• O número 7.

• O número 8.

• O número 9.

• Noções de probabilidade: certos, possíveis e impossíveis.

• O número zero.

• Dezena.

• Leitura e escrita de números de 0 a 19 com algarismos e por extenso.

• Sequência numérica até 19.

• Maior e menor.

• Interpretação de tabelas e gráficos de colunas.

• Registro de informações em tabelas e gráficos de colunas.

• Agrupamentos de objetos em quantidades iguais.

• Ordinais do 1º ao 10º

• Associação de figuras geométricas espaciais no cotidiano.

• Reconhecimento de cubo, paralelepípedo retângulo, esfera, cone, cilindro.

• Sequências de figuras.

EF01MA01

EF01MA02

EF01MA03

EF01MA04

EF01MA10

EF01MA20

EF01MA21

EF01MA22

Competências gerais (CG), Competências específicas de Matemática (CEM) e temas contemporâneos transversais

CG9

Vida familiar e social

EF01MA09

EF01MA13

CEM2 CEM8

UnidadesTópicos

3 – Medidas de tempo e de comprimento

• Medidas de tempo

• O relógio e as horas

• O calendário

• Medidas de comprimento

• O centímetro

4 – Localização e caminho

5 – Números de 0 a 100

• Noções de localização

• Caminhos

• Representando números até 99

• O número 100

• Par e ímpar

• Comparando números

6 – Sistema monetário

• Unidade monetária brasileira

• O Real

7 – Adição

• Ideias da adição

• Adição com total até 99

8 – Figuras geométricas planas

Conteúdos

• Períodos do dia: manhã, tarde e noite.

• Leitura de horas inteiras em relógios de ponteiros e em relógios digitais.

• Dias da semana.

• O calendário: meses do ano.

• Interpretação de gráfico.

• Mais comprido e mais curto.

• Mais alto e mais baixo.

• Unidades de medida de comprimento não padronizadas.

• Instrumentos de medida de comprimento.

• O centímetro.

• Noções de localização: mais perto e mais longe, esquerda e direita, dentro e fora, em cima e embaixo, atrás, entre e à frente.

• Caminhos.

• Representação de caminhos na malha quadriculada.

• Números naturais de 0 a 100.

• Formação de grupos de 10.

• O número 100.

• Par e ímpar.

• Sequências numéricas com números naturais até 100.

• Números pares.

• Números ímpares.

• Comparação de números naturais até 100 na reta numérica.

• Reta numérica.

• Igual e diferente.

• Maior e menor.

• Ordem crescente e ordem decrescente dos números naturais até 100.

• Pesquisa estatística.

• Tabelas.

• Sistema monetário.

• Cédulas e moedas do Real.

• Relação entre quantias de cédulas e moedas de mesmo valor.

• Gráfico de colunas.

• Adição com total até 99.

• Reconhecimento do símbolo utilizado para representar uma adição.

• Adição com mais de duas parcelas.

• Ideias da adição: juntar ou acrescentar.

• Diferentes estratégias de cálculo para resolver uma adição.

• Algoritmo da adição sem reagrupamento.

• Dobro e metade.

• Leitura e interpretação de tabela.

• Sequências recursivas com números faltantes, obtidos por meio da adição.

Habilidades da BNCC

EF01MA15

EF01MA16

EF01MA17

EF01MA18

Competências gerais (CG), Competências específicas de Matemática (CEM) e temas contemporâneos transversais

EF01MA21 CG8 CEM1 CEM2 CEM8

EF01MA11

EF01MA12

EF01MA01

EF01MA02

EF01MA03

EF01MA04

EF01MA05

EF01MA07

EF01MA10

EF01MA22

CEM2

CEM8

CG6

CG8

CG10

Vida familiar e social

EF01MA19

EF01MA21 CEM2 CEM8

Educação para o consumo

EF01MA03

EF01MA06

EF01MA07

EF01MA08

EF01MA10

EF01MA21 CG7 CEM2 CEM8

• Figuras geométricas planas no cotidiano

• Reconhecendo figuras geométricas planas

• Identificação de figuras planas no dia a dia.

• Reconhecimento de figuras geométricas planas: triângulos, retângulos, quadrados e círculos.

• Sequência de figuras.

EF01MA09

EF01MA14 CEM2

UnidadesTópicos

– Subtração

• Ideias da subtração

• Um pouco mais de subtração

• Subtração com números até 99

– Medidas de massa e medidas de capacidade

• Medidas de massa

• O quilograma

• Medidas de capacidade

• O litro

Conteúdos

• Subtração com números até 99.

• Reconhecimento do símbolo utilizado para representar uma subtração.

• Ideias da subtração.

• Diferentes estratégias de cálculo para resolver uma subtração.

• Leitura e interpretação de tabela e gráfico de colunas.

• Representação de gráfico de colunas.

• Subtração com números até 99.

• Algoritmo da subtração sem reagrupamento.

• Sequências recursivas com números faltantes, obtidos por meio da subtração.

• Noções de grandeza: mais leve e mais pesado.

• Instrumento de medida utilizado para medir massa.

• O quilograma.

• Noções de grandeza: mais líquido e menos líquido, cheio e vazio, cabe mais e cabe menos.

• O litro.

• Mais de um litro e menos de um litro.

• Leitura e interpretação de tabela e gráfico de colunas.

SUGESTÕES DE CRONOGRAMAS

As propostas de cronogramas apresentadas a seguir têm como objetivo orientar a distribuição das unidades em planejamentos bimestrais, trimestrais e semestrais, respeitando a organização dos volumes anteriormente mencionada.

Cabe destacar que essas sugestões não contemplam outras atividades que possam surgir ao longo do ano letivo, como projetos, eventos escolares ou avaliações ins-

Sugestão de planejamento bimestral

Bimestre

1º

2º

Habilidades da BNCC

EF01MA08

EF01MA10

EF01MA19

EF01MA21

Competências gerais (CG), Competências específicas de Matemática (CEM) e temas contemporâneos transversais

CEM2

CEM4

CG8

Vida familiar e social

EF01MA15

EF01MA21

3º

Unidades e tópicos

Unidade 1 – Números de 0 a 19

Unidade 2 – Figuras geométricas espaciais

Unidade 3 – Medidas de tempo e de comprimento

Unidade 4 – Localização e caminhos

Unidade 5 – Números de 0 a 100

Unidade 6 – Sistema monetário

Unidade 7 – Adição

Unidade 8 – Figuras geométricas planas

Unidade 9 – Subtração

4º

Unidade 10 – Medidas de massa e de capacidade

CG8

titucionais, e que devem ser incorporadas ao planejamento de forma articulada.

Para elaborar essas sugestões, consideramos 200 dias letivos de aula, ou 40 semanas; no entanto, o cronograma deve ser ajustado conforme as especificidades de cada turma, levando em consideração o contexto, o ritmo de aprendizagem dos estudantes e o uso de diferentes recursos e estratégias pedagógicas, que vão além do livro didático.

Sugestão de planejamento trimestral

Trimestre Unidades e tópicos

Unidade 1 – Números de 0 a 19

1º

Unidade 2 – Figuras geométricas espaciais

Unidade 3 – Medidas de tempo e de comprimento

Unidade 4 – Localização e caminhos

2º

Unidade 5 – Números de 0 a 100

Unidade 6 – Sistema monetário

Unidade 7 – Adição

Unidade 8 – Figuras geométricas planas

3º

Unidade 9 – Subtração

Unidade 10 – Medidas de massa e de capacidade

Sugestão de planejamento semestral

Semestre

Unidades e tópicos

Unidade 1 – Números de 0 a 19

Unidade 2 – Figuras geométricas espaciais

1º

Unidade 3 – Medidas de tempo e de comprimento

Unidade 4 – Localização e caminhos

Unidade 5 – Números de 0 a 100

Unidade 6 – Sistema monetário

Unidade 7 – Adição

2º

Unidade 8 – Figuras geométricas planas

Unidade 9 – Subtração

Unidade 10 – Medidas de massa e de capacidade

BACICH, Lilian; HOLANDA, Leandro (org.). STEAM em sala de aula: a aprendizagem baseada em projetos integrando conhecimentos na educação básica. Porto Alegre: Penso, 2020. (Série Desafios da Educação).

A obra aborda o STEAM como uma ferramenta para desenvolver competências, como a criatividade, o pensamento crítico, a comunicação e o trabalho com a colaboração dos estudantes.

BRASIL. Ministério da Saúde. Proteger e cuidar da saúde de adolescentes na atenção básica. 2. ed. Brasília: Ministério da Saúde, 2018. Disponível em: https://bvsms.saude.gov.br/ bvs/publicacoes/proteger_cuidar_adolescentes_atencao_ basica_2ed.pdf. Acesso em: 5 set. 2025.

Documento que visa auxiliar as Equipes de Atenção Básica/Saúde da Família no trabalho com adolescentes nos aspectos relacionados à saúde.

COSTA, Renato Pinheiro da; CASSIMIRO, Élida Estevão; SILVA, Rozinaldo Ribeiro da. Tecnologias no processo de alfabetização nos anos iniciais do ensino fundamental. Docência e Cibercultura, Rio de Janeiro, v. 5, n. 1, p. 97-116, jan./abr. 2021. Disponível em: https://www.e -publicacoes.uerj.br/re-doc/article/view/53068/36747. Acesso em: 16 ago. 2025.

Nesse artigo, os autores abordam a influência da tecnologia no desenvolvimento do processo de alfabetização.

DEHAENE, Stanislas. Os neurônios da leitura: como a ciência explica a nossa capacidade de ler. Tradução de Leonor Scliar-Cabral. Porto Alegre: Penso, 2012.

Nesse livro, o autor francês mostra os progressos da Neurociência e da Psicologia Cognitiva a respeito do ato de ler.

GRISA, Gregório Durlo et al Neurociência e alfabetização: noções fundamentais. Bento Gonçalves: IFRS, 2022.

Nesse livro, os autores se baseiam nos estudos da Neurociência para explicar os processos de alfabetização.

LIMA, Aurilia de Brito et al. (org.). Políticas de inclusão na educação básica. Curitiba: Appris, 2024.

Coletânea de textos que abordam os principais marcos das políticas públicas relacionadas à inclusão, desde as temáticas mais amplas até as mais específicas.

MIRANDA, Elaine (coord.). Educação inclusiva e a parceria da família: uma dimensão terapêutica. São Paulo: Literare Books International, 2021.

Nesse livro, a autora aborda aspectos da inclusão com base em evidências científicas. Além disso, ela busca evidenciar a importância da participação da família na educação inclusiva.

MORAIS, José. Criar leitores: para professores e educadores. Barueri: Manole, 2013.

O livro auxilia professores, pais e profissionais a compreenderem o processo cerebral da criança que está aprendendo a ler considerando seus processos cognitivos e as dificuldades da faixa etária e sugerindo intervenções e estratégias para facilitar a alfabetização.

SANTOS, Maria Lucia dos; PERIN, Conceição Solange Bution. A importância do planejamento de ensino para o bom desempenho do professor em sala de aula.

Cadernos PDE, Curitiba, v. 1, p. 1-24, 2013. (Os Desafios da Escola Pública Paranaense na Perspectiva do Professor PDE).

Nesse artigo, as autoras destacam a importância do planejamento e apresentam propostas que auxiliam o professor a realizar seus planejamentos.

SILVA, Janssen Felipe da; HOFFMANN, Jussara; ESTEBAN, Maria Teresa. Práticas avaliativas e aprendizagens significativas: em diferentes áreas do currículo. Porto Alegre: Mediação, 2012.

Os autores discutem as práticas avaliativas em diferentes áreas do currículo, com destaque para a elaboração de práticas de avaliação articuladas ao fazer pedagógico.

VICKERY, Anitra. Aprendizagem ativa nos anos iniciais do ensino fundamental. Porto Alegre: Penso, 2016.

O livro aborda a importância da aprendizagem ativa e do protagonismo do estudante para a concretização do processo de aprendizagem em sala de aula. Além disso, reúne pesquisas e estudos de casos que vão inspirar os professores a criarem e explorarem estratégias para desenvolver a própria abordagem de ensino.

REFERÊNCIAS BIBLIOGRÁFICAS COMENTADAS –LIVRO DO PROFESSOR

BACICH, Lilian; MORAN, José (org.). Metodologias ativas para uma educação inovadora: uma abordagem teóricoprática. Porto Alegre: Penso, 2018.

Esse livro destaca a importância das estratégias de metodologias ativas para desenvolver a autonomia dos estudantes e a participação efetiva deles no processo de aprendizado.

BENDER, William N. Aprendizagem baseada em projetos: educação diferenciada para o século XXI. Tradução de Fernando de Siqueira Rodrigues. Porto Alegre: Penso, 2014.

Nesse livro, o autor destaca as diretrizes práticas para o trabalho com projetos em sala de aula, fornecendo subsídios para o professor planejar aulas mais eficazes e motivadoras.

BORBA, Rute; BATISTA, Rita; AZEVEDO, Juliana. Levantando possibilidades para o desenvolvimento dos raciocínios probabilístico e combinatório de crianças em anos iniciais de escolarização. In: BORBA, Rute; GUIMARÃES, Gilda (org.). Pesquisa e Atividades para o aprendizado matemático na Educação Infantil e nos Anos Iniciais do Ensino Fundamental. Brasília: SBEM, 2015. v. 8. p. 23-46.

O e-book apresenta contribuições para a sala de aula da Educação Infantil e dos Anos Iniciais do Ensino Fundamental, com resultados de pesquisas referentes à Educação Matemática de início de escolarização e reflexões sobre aplicações da Matemática aos estudantes.

BRASIL. Lei nº 8.069, de 13 de julho de 1990. Disponível em: https://www.planalto.gov.br/ccivil_03/leis/l8069.htm. Acesso em: 5 set. 2025.

Também conhecido como ECA, esse documento visa garantir os direitos fundamentais de crianças e adolescentes, assegurando proteção integral, saúde, educação e dignidade.

BRASIL. Ministério da Educação. Conscientização para o uso de celulares na escola: por que precisamos falar sobre isso? Brasília: MEC, 2025. Disponível em: https:// www.gov.br/mec/pt-br/celular-escola/guia-escolas.pdf. Acesso em: 9 ago. 2025.

Esse documento traz orientações práticas que ajudam o professor na implantação da Lei nº 15.100, que regulamenta o uso de dispositivos eletrônicos portáteis pelos estudantes nas escolas.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Versão final. Brasília: MEC, 2018. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI _EF_110518_versaofinal_site.pdf. Acesso em: 5 set. 2025. Documento que determina as competências gerais e específicas, as habilidades e as aprendizagens que os estudantes brasileiros da Educação Básica precisam desenvolver e colocar em prática ao longo de sua trajetória escolar.

BRASIL. Ministério da Educação. Diretrizes Curriculares Nacionais Gerais da Educação Básica. Brasília: MEC: SEB: Dicei, 2013. Disponível em: https://www.gov.br/mec/ pt-br/media/etnico_racial/pdf/diretrizes_curriculares_ nacionais_para_educacao_basica_diversidade_e_ inclusao_2013.pdf. Acesso em: 3 set. 2025.

Esse documento traz princípios, fundamentos e procedimentos que norteiam as políticas públicas de educação e auxiliam o professor a elaborar, planejar, executar e avaliar práticas pedagógicas na Educação Básica.

BRASIL. Ministério da Educação. Relatório Nacional de Alfabetização Baseada em Evidências. Brasília: MEC: Sealf, 2020. Disponível em: https://www.gov.br/mec/pt -br/media/acesso_informacacao/pdf-arq/RENABE_web. pdf. Acesso em: 3 set. 2025.

Renabe é a abreviação do Relatório Nacional de Alfabetização Baseada em Evidências, uma iniciativa do Brasil em discutir com pesquisadores brasileiros e estrangeiros da área de alfabetização de diferentes campos do conhecimento.

BRASIL. Ministério da Educação. Temas contemporâneos transversais na BNCC: contexto histórico e pressupostos pedagógicos. Brasília, 2019. Disponível em: https://basenacionalcomum.mec.gov. br/images/implementacao/contextualizacao_temas_ contemporaneos.pdf. Acesso em: 3 set. 2025.

O documento apresenta os temas contemporâneos transversais da BNCC e explica a importância de sua utilização no processo de ensino-aprendizagem.

BRITO, Giseli Artioli; FLORES, Maria Marta Lopes. A inclusão de alunos com deficiência intelectual: em foco as práticas pedagógicas. Boletim de Conjuntura, Boa

Vista, ano V, v. 16, n. 48, 2023. Disponível em: https:// revista.ioles.com.br/boca/index.php/revista/article/ view/2879. Acesso em: 18 ago. 2025.

Nesse artigo, as autoras abordam os principais aspectos que influenciaram os resultados de uma pesquisa sobre a inclusão escolar e a qualidade da educação.

CORDEIRO, Claudia Talochinski; OLIVEIRA, Ivanete da Rosa Silva de (org.). Educação e políticas inclusivas: ressignificando a diversidade. Londrina: Syntagma Editores, 2020. Nessa obra, as autoras discutem a inclusão de estudantes com deficiência na escola regular.

COSTA, Raquel Lima Silva. Neurociência e aprendizagem. Revista Brasileira de Educação, Rio de Janeiro, v. 28, 2023. Disponível em: http://educa.fcc.org.br/pdf/rbedu/ v28/1809-449X-rbedu-28-e280010.pdf. Acesso em: 2 set. 2025.

No artigo, a autora apresenta uma revisão de literatura sobre a contribuição da Neurociência para a aprendizagem no contexto escolar.

DEHAENE, Stanislas. Os neurônios da leitura: como a ciência explica a nossa capacidade de ler. Tradução de Leonor Scliar-Cabral. Porto Alegre: Penso, 2012.

O autor francês apresenta os progressos da Neurociência e da Psicologia Cognitiva a respeito do ato de ler.

DINIZ, Margareth; VASCONCELOS, Renata Nunes (org.). Pluralidade cultural e inclusão na formação de professores e professoras. Belo Horizonte: Formato Editorial, 2004.

Nessa obra, as autoras propõem reflexões sobre as práticas educativas e as ações pedagógicas voltadas para uma postura inclusiva.

D’AMBROSIO, Ubiratan. Etnomatemática: elo entre as tradições e a modernidade. 6. ed. Belo Horizonte: Autêntica, 2019. (Coleção Tendências em Educação Matemática).

O autor apresenta nessa obra suas mais recentes concepções acerca da Etnomatemática, uma tendência da qual é um dos fundadores.

FAZENDA, Ivani (coord.). Práticas interdisciplinares na escola. 8. ed. São Paulo: Cortez, 2017.

Nessa obra, os organizadores reúnem diversos textos sobre práticas docentes interdisciplinares no espaço escolar.

FERNANDES, Domingos. Avaliação formativa: folha de apoio à formação: Projeto de Monitorização, Acompanhamento e Investigação em Avaliação Pedagógica (Maia). Ministério da Educação: DireçãoGeral da Educação, 2021. Disponível em: https:// apoioescolas.dge.mec.pt/sites/default/files/2021-02/ folha_avaliacao_formativa.pdf. Acesso em: 6 set. 2025.

Esse material apresenta ações práticas que podem auxiliar o professor no planejamento das estratégias de avaliação.

FERREIRO, Emilia. Alfabetização em processo. 21. ed. São Paulo: Cortez, 2015.

Nesse livro, a autora explica como o processo de alfabetização ocorre no cérebro dos estudantes e sua influência no desenvolvimento dos conhecimentos de outras áreas.

JOIA, Michele. A inclusão de crianças na escola: o papel do educador diante das dificuldades de aprendizagem. 2. ed. Rio de Janeiro: Wak, 2023.

Nesse livro, a autora fornece dicas sobre a inclusão na escola com base em conhecimentos que ela construiu em sua experiência em sala de aula.

KLEIN, Julie Thompson. Ensino interdisciplinar: didática e teoria. 17. ed. Campinas: Papirus, 2012. (Coleção Práxis).

Esse livro traz temas que apresentam resultados de estudos, análises pesquisadas e direcionamentos sob uma perspectiva contextualizada acerca do ensino interdisciplinar, contribuindo para a prática docente.

MELLO, Fabiane de Oliveira; ALLIPRANDINI, Paula Mariza Zedu. Estratégias de aprendizagem de alunos do ensino fundamental em processo de alfabetização. Revista de Psicología, Lima, v. 40, n. 2, 2022. Disponível em: https:// revistas.pucp.edu.pe/index.php/psicologia/article/ view/25503/24038. Acesso em: 16 ago. 2025.

Nesse artigo, as autoras fazem uma análise qualitativa de algumas estratégias de ensino comumente utilizadas no processo de alfabetização.

Essa obra propõe práticas pedagógicas, na Educação Básica e Superior, que valorizam o protagonismo dos estudantes, relacionando com as teorias e auxiliando como suporte.

MOREIRA, Antonio Flávio; CANDAU, Vera Maria (org.). Multiculturalismo: diferenças culturais e práticas pedagógicas. Petrópolis: Vozes, 2008.

O termo multiculturalismo tem sido amplamente usado e envolve distintas instâncias. Na escola, apresenta relação direta com a pluralidade cultural e a realidade cultural contemporânea. A obra tem como objetivo incentivar discussões, estudos e pesquisas que instiguem práticas renovadas em prol de uma sociedade mais justa e solidária.

OLIVEIRA, Morane Almeida de. Matemática básica no sudoeste da Amazônia: uma proposta para escolas indígenas. Curitiba: Appris. 2019.

A obra busca valorizar a etnomatemática mostrando como os povos indígenas aplicam a matemática no seu dia a dia.

ORGANISATION FOR ECONOMIC CO-OPERATION AND DEVELOPMENT (OECD). The PISA 2003 Assessment Framework: Mathematics, Reading, Science and Problem Solving Knowledge and Skills. Paris: OECD Publishing, 2004. Disponível em: https:// www.oecd.org/content/dam/oecd/en/publications/ reports/2003/07/the-pisa-2003-assessment -framework_g1gh34d9/9789264101739-en.pdf. Acesso em: 2 set. 2025.

Define o conteúdo de que os estudantes necessitam para adquirir o que precisam dominar e o contexto em que as habilidades e o conhecimento serão aplicados.

PAIS, Luiz Carlos. Didática da matemática: uma análise da influência francesa. Belo Horizonte: Autêntica, 2019. (Coleção Tendências em Educação Matemática).

Nesse livro, o autor apresenta conceitos fundamentais de uma tendência que ficou conhecida como Didática Francesa. Educadores matemáticos franceses, em sua maioria, desenvolveram uma estratégia particular

de perceber a educação centrada na questão do ensino da Matemática, contribuindo para o desenvolvimento da aprendizagem.

PALHARES, Odana. O ensino e a aprendizagem da matemática na perspectiva piagetiana. Schème –Revista Eletrônica de Psicologia e Epistemologia Genéticas, Marília, v. 1, n. 1, jan./jun. 2008. Disponível em: https://www.marilia.unesp.br/Home/ RevistasEletronicas/Scheme/Vol01Num01-Artigo05.pdf. Acesso em: 2 set. 2025.

No artigo, a autora reflete sobre o objetivo do ensino da Matemática nos primeiros anos, que consiste em ajudar o estudante a construir um raciocínio lógico-matemático.

REIS, Ana Valéria Sampaio de Almeida; DAROS, Thuinie; TOMELIN, Karina Nones. Layouts criativos para aulas inovadoras. Maringá: B42, 2023.

Nesse livro, as autoras sugerem diferentes estratégias de layout das salas de aula a fim de envolver e criar experiências marcantes para os estudantes.

ROJO, Roxane; MOURA, Eduardo (org.). Multiletramentos na escola. São Paulo: Parábola, 2012.

Os autores defendem uma pedagogia dos multiletramentos ao proporem a adoção em sala de aula de práticas situadas, instrução aberta, enquadramento crítico e prática transformadora.

SILVA, Eva Aparecida Gomes da. O desenvolvimento do processo de ensino-aprendizagem do aluno com necessidades educacionais especiais. Revista IberoAmericana de Humanidades, Ciências e Educação, São Paulo, v. 9, n. 3, mar. 2023. Disponível em: https:// periodicorease.pro.br/rease/article/view/8972/3542. Acesso em: 14 ago. 2025.

Nesse artigo, a autora destaca a importância das atividades lúdicas no processo de ensino-aprendizagem dos estudantes com necessidades educacionais especiais.

SMOLE, Katia Stocco; DINIZ, Maria Ignez (org.). Materiais manipulativos para o ensino do sistema de numeração decimal. Porto Alegre: Penso, 2016. (Coleção Mathemoteca).

A obra traz um recorte de alguns conteúdos dos Anos Iniciais do Ensino Fundamental e apresenta uma forma específica de ensino, que inclui o desenvolvimento da leitura e da escrita em Matemática.

SOARES, Magda. Alfabetização e letramento. 5. ed. São Paulo: Contexto, 2018.

Nesse livro, a autora incentiva a releitura de artigos que discutem as práticas escolares de alfabetização e letramento.

UNESCO. VIOLÊNCIA escolar e bullying: relatório sobre a situação mundial. Brasília: Unesco, 2019. Disponível em: https://unesdoc.unesco.org/ark:/48223/pf0000368092/ PDF/368092por.pdf.multi. Acesso em: 5 set. 2025.

Nesse relatório, são apresentados dados sobre a violência escolar e o bullying, além de iniciativas que podem contribuir para a redução dessas ocorrências.

VIGOTSKI, Lev. A formação social da mente. São Paulo: Martins Fontes, 2010.

Esse livro compõe uma seleção cuidadosa dos ensaios mais importantes do autor, editada por um grupo de eminentes estudiosos da obra.