Linguagens formais

MARCUS VINICIUS MIDENA RAMOS

JOÃO JOSÉ NETO

ITALO SANTIAGO VEGA

LINGUAGENS FORMAIS

Teoria e conceitos

LINGUAGENSFORMAIS Teoriaeconceitos

MarcusViniciusMidenaRamos

JoãoJoséNeto

ItaloSantiagoVega

Linguagensformais:teoriaeconceitos

©2023MarcusViniciusMidenaRamos,JoãoJoséNetoeItaloSantiagoVega

EditoraEdgardBlücherLtda.

Publisher EdgardBlücher

Editores EduardoBlüchereJonatasEliakim

Coordenaçãoeditorial AndressaLira

Produçãoeditorial ArianaCorrêa

Diagramação MarcusViniciusMidenaRamos

Revisãodetexto MaurícioKatayama

Capa LaércioFlenic

Imagemdacapa iStockphoto

EditoraBlucher

RuaPedrosoAlvarenga,1245,4ºandar

CEP04531-934–SãoPaulo–SP–Brasil

Tel.:55113078-5366

contato@blucher.com.br

www.blucher.com.br

SegundooNovoAcordoOrtográfico,conforme6.ed.do VocabulárioOrtográficodaLíngua Portuguesa,AcademiaBrasileiradeLetras,julhode2021.Éproibidaareproduçãototalou parcialporquaisquermeiossemautorizaçãoescritadaeditora.Todososdireitosreservados pelaEditoraEdgardBlücherLtda.

Capítulo1

Elementosdematemáticadiscreta

As linguagensformais (oulinguagensestruturadasemfrases)podemservistascomoconjuntos.Consequentemente,muitodateoriaedosprincipais resultadosdaáreadelinguagens formaisestábaseadonaaindamaisfundamentalteoriadosconjuntosdamatemáticadiscreta. Ateoriadosconjuntosérelativamenteextensa,edelaserão apresentadosnestecapítuloapenasostópicos,conceitosedefiniçõesquesemostrammaisimportantesparaafundamentação eoestudodoscapítulosseguintes.

Alémdisso,relaçõesefunçõessãodeespecialimportânciaparadescreverasrelações entreosobjetosdeestudo,eporissosãoassuntoscontempladosnestecapítulo.

Damesmaforma,éprecisoconhecerumpoucodelógicaedeprovadeteoremaspara podercompreenderosignificadodosenunciadoseasestratégiasdeprovasusadasnotexto.

Completamarelaçãodetópicosdamatemáticadiscretaquesãorelevantesparalinguagensformaiseautômatosconceitosbásicosdegrafoseárvores.

1.1Conjuntos

Um conjunto éumacoleçãodeelementosemquenãosãoconsideradasocorrênciasmúltiplas delesnemhárelaçãodeordementreeles.

Exemplo1.1 Ainclusãodoelemento ♦ noconjunto {♣, ♦, ♥, ♠} resultanopróprioconjunto {♣, ♦, ♥, ♠},poiselejáfazpartedoconjuntoe,portanto,nãodeveserconsideradonovamente.Poroutro lado,oconjunto {♣, ♦, ♥, ♠} éigualaoconjunto {♦, ♣, ♠, ♥},umavezquenãoexisterelaçãode ordementreoselementosqueoscompõem. ⋆

Algunsconjuntospodemserespecificadosatravésdasimples enumeração detodosos seuselementos,denotadosentrechaveseseparadosporvírgulas.

Exemplo1.2 Oconjuntoformadopeloselementos0, 1, 2, 3érepresentadopor {0, 1, 2, 3}.Oconjunto {a, b, c, d, e, f } éformadopelasseisprimeirasletrasdoalfabetoromano.Oconjunto {01, 231, 33, 21323} contémoselementos01, 231, 33e21323. ⋆

Conjuntospodemserreferenciadosatravésdenomes,arbitrariamenteescolhidos.

Exemplo1.3 X = {0, 1, 2, 3}, Y = {a, b, c, d, e, f }.Assim,osnomes X e Y passamadenotarosconjuntoscorrespondentes. ⋆

Onúmerodeelementoscontidoemumconjunto A édenotadopor |A|.

Exemplo1.4 NoExemplo1.3, |X | = 4, |Y | = 6. ⋆

Ossímbolos ∈ e / ∈ servemparadenotarseumdeterminadoelemento pertence ou não pertence aumconjunto,respectivamente.

Elementosdematemáticadiscreta

Exemplo1.5 NoExemplo1.3,0

Conjuntospodemconterumnúmerofinitoouinfinitodeelementos.Noprimeirocaso, oconjuntopodeserdenotadoenumerando-se(relacionando-seexplicitamente)todososelementosqueocompõem,comofoifeitoparaosconjuntos X e Y doExemplo1.3,quesão conjuntosfinitos.

Conjuntosinfinitos podemserdenotadosatravésdaespecificação(formalouinformal) deregrasoupropriedadesquedevemsersatisfeitasportodososseuselementos,possibilitandoassimasuaidentificaçãoprecisaecompletaapartirde umaespecificaçãofinita.

Exemplo1.6 P ={x | x éumnúmeroprimo}, Q ={y |∃n inteirotalque y = n2}.Oprimeiroexemplodeveserlidodaseguinteforma:“P éoconjuntoformadopeloselementos x,talque x éumnúmeroprimo”.Emoutraspalavras, P éoconjunto,infinito,formadoportodososnúmerosprimos: {2, 3, 5, 7, 11, 13, 17 }.Oconjunto Q,tambéminfinito,éformadoportodososnúmerosquecorrespondemaoquadradodealgumnúmerointeiro: {0, 1, 4, 9, 16...}. ⋆

Quandoumconjuntoéespecificadoapartirderegras,osímbolo“|”deveserlidocomo “talque”,eserveparaintroduzirascondiçõesquedevemser satisfeitaspelosmembrosdo conjunto,queassimtornam-seconhecidos.

Oconjuntoquenãocontémnenhumelementorecebeonomede conjuntovazio.O conjuntovazioédenotadopor/0ouaindapor {}.Assim, {} =/0.Pordefinição, |/0 | = 0. Doisconjuntossãoditos idênticos,ousimplesmente iguais,seelescontêmexatamente osmesmoselementos.Aigualdadededoisconjuntosédenotadaatravésdosímbolo“=”.

Exemplo1.7 Considere Z = {a, b} e W = {b, a}.Então, Z = W ⋆

AteoriadeconjuntosapresentadanestaseçãoéumresumodachamadaTeoriaIngênua deConjuntos(doinglês NaïveSetTheory)elaboradaporGeorgCantornofinaldoséculo XIX.Talteoria,apesardesimples,permiteenunciaralguns paradoxos,entreosquaisomais famosoéoParadoxodeRussell,propostoporBertrandRussellem1901,equeenvolve apenasosconceitosdeformaçãodeconjuntoedepertencimento:

Seja S oconjuntoformadoportodososconjuntosquenãosãoelementosdesi mesmos,econsidereapergunta:“S éelementodesimesmo?”

Paratentarresponderaessapergunta,pode-seconsiderarduassituaçõesdistintas.Na primeira,supõe-seque S sejaumelementodesimesmo.Então,deacordocomadefinição, S nãodeveriafazerpartede S,umavezque S contémapenasconjuntosquenãosãoelementos desimesmos.Poroutrolado,pode-sesuporocasocontrário, ouseja,que S nãosejaum elementodesimesmo.Então,peladefinição, S sequalificacomoumelementodesimesmo. Portanto,qualquerquesejaocasoqueseconsidere,temosumacontradição.Logo,ahipótese éfalsaenãoexisteumconjunto S comtalcaracterística.

Afimdeevitaraformulaçãodeparadoxoscomoesse,foramdesenvolvidasteoriasde conjuntosalternativas,comoéocasodaTeoriadeTiposdopróprioRusselletambéma TeoriaAxiomáticadeZermelo,queposteriormenteserviude baseparaaTeoriaAxiomática deZermelo-FraenkelcomoAxiomadaEscolha(ZFC).Essaúltimaéconsideradaumdos principaisfundamentosdamatemáticamoderna.

Umconjunto A édito“contido emumconjunto B”,condiçãoestadenotadaatravésdo símbolo“⊆”,setodoelementode A fortambémelementode B.Nestecasodiz-se,equivalentemente,que“A éum subconjunto de B”ou,ainda,que“B contém A”.Osconjuntos/0e A são,pordefinição,subconjuntosdequalquerconjunto A.Noteque/0 ⊆ /0.

Exemplo1.8 Paraosconjuntos A = {b, c, d}, B = {a, b, c, d, e} e C = {e, a, d, b, c} tem-seque A ⊆ B e B ⊆ C.Portanto,pode-sedizerque A estácontidoem B eem C,que A ésubconjuntode B ede C,que C contém A e B e,ainda,que B e C sãosubconjuntosumdooutroouqueestãocontidosumnooutro B e C,poroutrolado,nãoestãocontidosem A. ⋆

Doisconjuntos M e N sãoiguaisseesomentese M ⊆ N e N ⊆ M,etaligualdadeé denotadapor M = N.A desigualdade dedoisconjuntoséexpressaatravésdosímbolo“=”, ocorrendo,portanto,quandonomáximoapenasumadasduascondições M ⊆ N e N ⊆ M for verdadeira.

Exemplo1.9 NoExemplo1.8, A ⊆ B,porém A = B.Como B ⊆ C e C ⊆ B,então B = C ⋆

Se M ⊆ N e M = N,diz-seque M éum subconjuntopróprio de N.Osímbolo ⊂ denotaessacondição: M ⊂ N.Oconjunto/0ésubconjuntoprópriodequalquerconjunto, excetodopróprioconjunto/0.

Exemplo1.10 NoExemplo1.8, A ésubconjuntoprópriode B,porém B nãoésubconjuntoprópriode C.Logo, A ⊂ B.

Algumasoperaçõesimportantessobreconjuntossãoapresentadasaseguir.

Conjuntopotênciaou“powerset”

Denotadopor2A,onde A éumconjunto.Essaoperaçãoéutilizadaparadesignaroconjunto formadoportodosospossíveissubconjuntosde A:

União

Auniãodedoisconjuntos A e B correspondeaoconjuntoformadoportodososelementos contidosemcadaumdosdoisconjuntos A e B.Elementosrepetidosemambososconjuntos sãoconsideradosumaúnicaveznoconjuntounião:

Trata-sedeumaoperaçãoassociativa,ouseja,umaoperação paraaqualvaleapropriedade:

Ageneralizaçãodaoperaçãodeuniãoédenotadadaseguinteforma:

Aoperaçãodeuniãoétambémcomutativa,ouseja:

Elementosdematemáticadiscreta

paraquaisquerconjuntos A e B

Oconjuntovazio/0éo elementoneutro daoperaçãodeunião.Paratodoconjunto A, A

Intersecção

Define-seaintersecçãodedoisconjuntos A e B comosendoacoleçãodetodososelementos comunsaosdoisconjuntos:

Tambémemdecorrênciadaassociatividadedessaoperação,a suageneralizaçãoédenotadadeformasimilaraocasodaunião:

Damesmaformaqueaunião,aoperaçãodeintersecçãoétambém comutativa:

paraquaisquerconjuntos A e B

Aintersecçãodequalquerconjuntocomoconjuntovazioproduzcomoresultadoo próprioconjuntovazio,ouseja, A ∩ /0 = /0.Oconjuntovazio,nessecaso,édenominado aniquilador daoperaçãodeintersecção.

Exemplo1.13 {a, b, c}∩{c, d} =

{c, d} {a, b}∩{c, d} = /0. {a, b, c, d}∩ /0 = /0. ⋆

Doisconjuntos A e B sãoditos disjuntos se A ∩ B = /0.

Exemplo1.14 Osconjuntos {a, b, c} e {c, d} nãosãodisjuntos,pois {a, b, c}∩{c, d} = {c} = {}.Os conjuntos {a, b} e {c, d} sãodisjuntos,pois {a, b}∩{c, d} = /0. ⋆

Diferença

Define-seadiferençaentredoisconjuntos A e B (nestaordem)comosendooconjuntoformadoportodososelementosde A nãopertencentesaoconjunto B.Denota-seesseconjunto como:

A B = {x | x ∈ A e x / ∈ B}

Exemplo1.15 {a, b, c}−{c, d} = {a, b} {a, b}−{a, b, c} = /0. {a, b, c}−{d, e} = {a, b, c} {c, d}− {a, b, c} = {d}. {a, b, c}−{a, b} = {c}. {d, e}−{a, b, c} = {d, e}. ⋆

Essaoperaçãonãoéassociativa(nocasogeral, A (B C) =(A B) C)nemcomutativa(nocasogeral, A B = B A).

Exemplo1.16

Note,noentanto,quese A = B = C,entãoaoperaçãosetornacomutativa(produzindo sempre/0comoresultado),mascontinuasendonãoassociativa.

Complementação

Define-seacomplementaçãodeumconjunto A emrelaçãoaoconjunto B, A ⊆ B,comosendo oconjuntodetodososelementosde B quenãopertencema A.Denota-seesseconjuntocomo:

AB = B A

Muitasvezesessaoperaçãoédefinidaparaumconjunto A emrelaçãoaumoutroconjunto B subentendidoe,nessecaso,escreve-sesimplesmente:

A = B A

Diz-se,nessecaso,queoconjuntosubentendidoéoconjunto universodaoperação.O resultadodaoperaçãoéconhecidosimplesmentecomo complemento de A

Produtocartesiano

Oprodutocartesianodedoisconjuntoséoconjuntoformadoportodososparesordenados (a, b),emque a éumelementode A,e b umelementode B:

Um parordenado éumarepresentaçãodedoiselementosseparadosporvírgula e delimitadosporparênteses,comoem (a, b).Talrepresentaçãoimplicaumarelaçãodeordem emqueoelemento a éanterioraoelemento b.Consequentemente,se a = b,então (a, b) = (b, a)

Se A e B sãoconjuntosfinitos,então

Exemplo1.19 ConsiderenovamenteoExemplo1.18esuponha C = {♦}.Estruturalmente,éfácil perceberque

Finalmente,observeque,se A = B = C,entãoaoperaçãosetornacomutativamas continuanãoassociativa.Defato, A × (A

.

Partição

Define-se partição deumconjunto A comosendoqualquercoleçãoformadapor n subconjuntosnãovaziosde A, n 1,talque:

ouseja,auniãodaspartes(osconjuntos Ai)deveformarotodo(oconjunto A)e,alémdisso, aintersecçãoentrequaisquerduaspartesconsideradas(Ai e A j)ésemprevazia.

Exemplo1.20 Seja A = {a, b, c, d}.Então, {{a, b}, {c, d}} éumapartiçãode A.Damesmaforma,o conjunto {{a}, {b}, {c}, {d}},bemcomo {{a, b, c, d}},entreváriosoutros. ⋆

Aseguirserãoapresentadosquatroimportantesresultados acercadeconjuntos,osdois primeirosconhecidoscomo LeisdeDeMorgan,osquaisserãoúteisnademonstraçãode outrosteoremasmaisadiantenotexto.

Teorema1.1(LeisdeDeMorgan) “Sejam A e B doisconjuntosquaisquer.Então A ∩ B =

A ∪ B e A ∪ B = A ∩ B.”

Aprovaalgébricadaprimeiralei(A ∩ B = A ∪ B,ourepresentaçãodaintersecçãopormeio dacomplementaçãoedaunião)procededaseguinteforma:

• Deve-seprovarque x ∈ A ∩ B ⇒ x ∈ A ∪ B;etambém

• Deve-seprovarque x ∈ A ∪ B ⇒ x ∈ A ∩ B.

Paraoprimeirocaso,temosquese x ∈ A ∩ B,então x ∈ A e x ∈ B.Logo, x ∈ A e x ∈ B

Portanto, x ∈ A ∪ B.Consequentemente, x ∈ A ∪ B.Paraosegundocaso,temosquese x ∈ A ∪ B,então x ∈ A ∪ B.Portanto,(i) x ∈ A e(ii) x ∈ B.Então, x ∈ A e x ∈ B.Logo, x ∈ A ∩ B

Parafacilitaroentendimentodestaprova,bastaanalisaro DiagramadeVenndaFigura 1.1.Daesquerdaparaadireita,asáreashachuradasdosdiagramasrepresentam,respectivamente, A, B, A ∪ B e A ∪ B

Aprovaalgébricadasegundalei(A ∪ B = A ∩ B,ourepresentaçãodauniãopormeioda complementaçãoedaintersecção)procededaseguinteforma:

• Deve-seprovarque x ∈ A ∪ B ⇒ x ∈ A ∩ B;etambém

• Deve-seprovarque x ∈ A ∩ B ⇒ x ∈ A ∪ B

Paraoprimeirocaso,temosquese x ∈ A ∪ B,então(i) x ∈ A e x ∈ B,ou(ii) x ∈ A e x ∈ B, ou(iii) x ∈ A e x ∈ B.Emoutraspalavras,(i) x ∈ A e x / ∈ B,ou(ii) x ∈ A e x ∈ B,ou(iii) x ∈ A e x / ∈ B

Emqualquercaso, x ∈ A ∩ B.Logo, x ∈ A ∩ B.Paraosegundocaso,temosquese x ∈ A ∩ B, então x ∈ A ∩ B.Portanto,(i) x ∈ A,ou(ii) x ∈ B,ou(iii)osdoiscasosanterioresacontecem simultaneamente.Se(i)forverdade,entãoconclui-seque x ∈ A.Se(ii)forverdade,conclui-se que x ∈ B.Se(iii)forverdade,conclui-sequeosdoiscasosanterioressãoverdadeiros.Em qualquersituação,temosque x ∈ A ∪ B

Parafacilitaroentendimentodestaprova,bastaanalisaro DiagramadeVenndaFigura 1.2.Daesquerdaparaadireita,asáreashachuradasdosdiagramasrepresentam,respectivamente, A, B, A ∩ B e A ∩ B

Exemplo1.21

Capítulo2

Conceitosbásicosdelinguagens

Estecapítuloapresentaediscuteosprincipaisconceitosbásicosassociadosaoestudode linguagens,comoéocasodossímbolos,dascadeiasedaslinguagenspropriamenteditas, assimcomodosmétodosempregadosparaaformalizaçãodaslinguagens,comoéocasodas gramáticasedosreconhecedores(pormeiodosautômatos).

Anoçãodeconjunto,introduzidanocapítuloanterior,éutilizadaparadefinirduas novasnoçõesfundamentais:alfabetos(conjuntosfinitosenãovazioscujoselementossão símbolos)elinguagens(conjuntosfinitosouinfinitoscujos elementossãocadeiasconstruídas comossímbolosdeumalfabeto).

Símbolospodemseragrupadosnaformadeumconjunto,casoem queelerecebeo nomedealfabeto.Conjuntos,poroutrolado,podemserformadosporelementosdeoutra natureza,enãoapenasporsímbolos.Éocaso,porexemplo,de conjuntoscujoselementos sãocadeias(sequênciasfinitasdesímbolos),quenestecaso recebemonomedelinguagem, econjuntoscujoselementostambémsãoconjuntos,equepodemrepresentar,porexemplo, conjuntos(tambémchamadosdeclasses)delinguagens.

Asgramáticaspossuemgrandeimportâncianaanáliseenaespecificaçãoformaldasintaxedelinguagens,principalmentedaslinguagensdeprogramação,aopassoqueosreconhecedoresdefinemmodelosqueservemcomobaseparaaconstruçãodeanalisadoresléxicos esintáticosnoscompiladoreseinterpretadoresdetaislinguagens.Naprática,oestudosistemáticodaslinguagensformaisedosautômatosviabilizou odesenvolvimentodetécnicas eficientesparaautilizaçãoeconômicadaslinguagensdeprogramação,originando-seemseu estudograndepartedointeressequerecaisobreosassuntos ligadosaessetema.

OcapítuloseencerracomaapresentaçãodaHierarquiadeChomsky,usualmenteempregadanaclassificaçãohierárquicadaslinguagensconformeseugraudecomplexidade,e emtornodaqualsecostumadesenvolverboapartedateoriadaslinguagensformaiseautômatos.Tomando-secomobaseessahierarquia,sãoefetuadas consideraçõespreliminares sobreaspropriedadesesobreacaracterizaçãoformaldecadaumadasclassesdelinguagens poreladefinidas.

2.1Símbolosecadeias

Os símbolos, 1 tambémdenominados palavras ou átomos,sãorepresentaçõesgráficas,indivisíveis,empregadasnaconstruçãode cadeias.Estassãoformadasatravésdajustaposição deumnúmerofinitodesímbolos,obtidosdealgumconjuntofinitonãovazio,denominado alfabeto.Umalfabetoé,portanto,umconjuntocujoselementossãosímbolosusadosna construçãodecadeias.

1Naliteraturaeminglêssãoconhecidoscomo tokens.

Conceitosbásicosdelinguagens

Cadasímboloéconsideradocomoumaunidadeatômica,nãoimportandoasuaparticularrepresentaçãovisual.Sãoexemplosdesímbolos: a, abc, begin, if , 5, 1024, 2.017e4. Perceba-sequenãoháumadefiniçãoformalpara“símbolo”.Deve-seintuiroseusignificado comoentidadeabstrata,edessaformaaceitá-locomobaseparaateoriaqueserádesenvolvida.Pode-sedizerquesetratadeumconceitoprimitivo.

Exemplo2.1 Suponhaque a e b sejamsímbolos.Então, {a, b} éumalfabetoe aaabbb e babab são exemplosdecadeiassobreessealfabeto.

Aolongodestetextoseráadotadaaseguinteconvençãoparadenotarsímbolos,cadeias ealfabetos:

•Símbolos:letrasminúsculasdoiníciodoalfabetoromano: (a, b, c...).

•Cadeias:letrasminúsculasdofinaldoalfabetoromano (r, s, x, w ),ouletrasminúsculasdoalfabetogrego (α,β,γ )

•Alfabetos:letrasmaiúsculasdoalfabetogrego (Σ, Γ, ∆...).

Exemplo2.2 Comoexemplodealfabetopodemosmencionaroconjunto Σ dosdígitoshexadecimais, emquecadaelemento(dígito)desseconjuntocorrespondeaumdeterminadosímbolo:

Naturalmente,ascadeiasquepodemserconstruídasapartir dossímbolosdessealfabetocorrespondemaosnumeraishexadecimais:123, a0b56, fe5dc, b, abc, 55efff ...

O comprimento deumacadeiaéumnúmeronaturalquedesignaaquantidadedesímbolosqueacompõem.Ocomprimentodeumacadeia α édenotadopor |α|.

Exemplo2.3 Considerem-seascadeias α = 1,β = 469, χ = ble60,φ = df .Então, |α| = 1, |β| = 3, |χ| = 5e |φ| = 2,tambémconstruídassobreoalfabeto Σ doExemplo2.2.

Dá-seonomede cadeiaelementar (ou unitária)aqualquercadeiaformadaporum únicosímbolo,comoéocasodacadeia α doExemplo2.3.Naturalmente,todacadeiaunitária temcomprimento1.

Umoutroimportanteexemplodealfabetocorrespondeaoconjuntodossímbolosdefinidosemalgumdicionáriodalínguaportuguesa.Noteque,diferentementedoalfabeto Σ anteriormenteconsiderado,emquetodosossímboloseramcompostosdeumúnicocaractere,ossímbolosdestenovoalfabetosãoconstruídosapartirdaconcatenaçãodeumnúmero variáveldecaracteres(nocaso,asletrasdoalfabetoromano).Paraopresenteestudo,embora representadoscomdiversoscaracteres,taissímbolossãoconsideradosindivisíveis,eascorrespondentescadeiaselementaresapresentam,poressarazão,comprimentounitárioquando consideradasnocontextodalínguaportuguesa.

Considerando-seaindaquetalalfabetoésuficientementeextensoparaconterasconjugaçõesdetodososverbos,asformasflexionadasdetodosos adjetivos,substantivosetc., enfim,todasaspalavraspossíveisdeseremempregadasemnossoidioma,entãoacadeia “Exemplodeumacadeianonovoalfabeto” deveráserconsideradaumacadeiaválida,construídaapartirdossímbolosdessealfabeto,eoseucomprimentoéiguala7.Notequeesse alfabetodalínguaportuguesa,apesardeextenso,éfinito,e tambémqueépossívelconstruir umaquantidadeinfinitadecadeiasdecomprimentofinitocomossímbolosdele.Observe-se que,entreestas,hácadeiasquenalínguaportuguesanãofazemsentido.Porexemplo, “cadeiaumaexemploerradoo”.Asdemaissãoempregadasnasdiversasformasdecomunicação humana.

Oconceitode cadeiavazia éespecialmenteimportantenateoriadaslinguagensformais.Denota-sepor ε acadeiaformadaporumaquantidadenuladesímbolos,istoé, a cadeiaquenãocontémnenhumsímbolo.Formalmente,|ε| = 0. Duascadeias,sejamelaselementaresounão,podemseranexadas,formandoumasó cadeia,atravésdaoperaçãode concatenação.Essaoperaçãofornececomoresultadouma novacadeia,formadapelajustaposiçãoordenadadossímbolosquecompõemosseusoperandosseparadamente.Observe-sequeaoperaçãodeconcatenaçãoentreumacadeiaeum símboloérealizadaatravésdaconcatenaçãodacadeiaemquestãocomacadeiaelementar correspondenteaosímbolo.Denota-seaconcatenaçãodeduascadeias α e β como α β ou, simplesmente, αβ.

Exemplo2.4 Considereoalfabeto Σ = {a, b, c, d},eascadeias α = abc, β = dbaca e σ = a.A concatenaçãodacadeia α comacadeia β éassimobtida: α ·β = αβ = abcdbaca,e |αβ| = |α| + |β| = 3 + 5 = 8.Damesmaforma,obtém-seaconcatenaçãode β com α: β · α = βα = dbacaabc,e, |βα| = |β| + |α| = 5 + 3 = 8.Note-seque,nesteexemplo, αβ = βα.Aconcatenaçãodacadeia α com acadeiaelementar σ édadapor: α σ = ασ = abca,e |ασ| = |α| + |σ| = 3 + 1 = 4.Finalmente,a concatenaçãodacadeiaelementar σ comacadeia β éobtidacomo: σ β = σβ = adbaca,e |σβ| = |σ

|β| = 1 + 5 = 6. ⋆

Comosepodeperceber,aoperaçãodeconcatenação,emboraassociativa,nãoécomutativa.Dadastrêscadeias α,β,γ quaisquer,pode-sesempreafirmarque (αβ)γ = α(βγ)

Poroutrolado,dependendodosparticulares α e β considerados,podeserqueou αβ = βα ou αβ = βα (porexemplo,se α e/ou β foremcadeiasvaziasou,ainda,se α = β).

Nocasodacadeiavazia ε (elementoneutroemrelaçãoaooperadordeconcatenação) sãoválidasasseguintesrelações:

1. αε = εα = α

2. |αε| = |εα| = |α|

Diz-sequeumacadeia α éum prefixo deoutracadeia β seforpossívelescrever β como αγ.Acadeia α édita sufixo de β se β puderserescritacomo γα.Emambosos casos,admite-seapossibilidadede γ = ε.Noscasosemque γ = ε,diz-seque α é,respectivamente, prefixopróprio ou sufixopróprio dacadeia β.Notequeacadeiavazia ε pode serconsideradasimultaneamenteprefixoousufixodequalquercadeia.

Exemplo2.5 Considereacadeia abc.Ascadeias ε, a, ab e abc sãoprefixosdela.Ascadeias ε, a, ab sãoprefixosprópriosdela,masacadeia abc não.Ascadeias ε, c, bc e abc sãosufixosdela.Ascadeias ε, c, bc sãosufixosprópriosdela,masacadeia abc não. ⋆

Dadasquatrocadeias α,β,γ e δ,umacadeia α échamada subcadeia deumacadeia β sempreque β = γαδ.Note-seque,se γ ou δ ouambosforemvazios,adefiniçãotambémse aplica.Note-setambémqueprefixosesufixossãocasosparticularesdesubcadeias.

Exemplo2.6 Considereacadeia abc.Ascadeias ε, a, b, c, ab, bc e abc sãosubcadeiasdela.Acadeia ac nãoésubcadeiade abc ⋆

Umacadeia α éditao reverso deumacadeia β,denotando-seofatopor α = βR,se α contiverosmesmossímbolosque β,porémjustapostosnosentidoinverso,ouseja:

Pordefinição,

Conceitosbásicosdelinguagens

Exemplo2.7 Considerem-seascadeias α = 123abc e β = d.Então, αR = cba321e βR = d ⋆

Finalmente,convenciona-seque σi representaacadeiaformadapor“i”símbolos σ concatenados.Pordefinição, σ0 = ε

Exemplo2.8 Considere-seosímbolo a.Então: a0 = ε; a

2.2Linguagens

Uma linguagemformal éumconjunto,finitoouinfinito,decadeiasdecomprimentofinito, formadaspelaconcatenaçãodesímbolosdeumalfabetofinito enãovazio.Umalinguagem formalé,portanto,umconjuntoondeoselementosdelesãocadeiasconstruídassobreum alfabeto.Notequeumalinguagempodeservazia(ouseja,podenãoconternenhumacadeia) ouaindapodeconteracadeiavaziacomoumdosseuselementos.

Alémdasoperaçõespreviamentedefinidasparaconjuntos,comounião,diferença,intersecçãoetc.,outrasoperações,comoaconcatenaçãoeosfechamentos,tambémsãofundamentaisparaadefiniçãoeoestudodaslinguagensformais.Essasnovasoperações,definidas aseguir,derivamdiretamentedaoperaçãodeconcatenaçãodecadeiasintroduzidanaseção anterior.

Antesdeapresentá-las,convémnotaradistinçãoqueháentreosseguintesconceitos:

•cadeiavazia ε;

•conjuntovazio/0;

•conjuntoquecontémapenasacadeiavazia {ε};

•conjuntoquecontémapenasoconjuntovazio {/0 }

Oprimeirodeles, ε,denotaacadeiavazia,ouseja,umacadeiadecomprimentozero, aopassoqueosdemaissãocasosparticularesdeconjuntos:/0denotaumalinguagemvazia, ouseja,umalinguagemquenãocontémnenhumacadeia, {ε} denotaumalinguagemque contémumaúnicacadeia(acadeiavazia),e {/0 } denotaumconjuntoquecontémumúnico elemento,oconjuntovazio.Observe-seque |ε| = |/0 | = 0e |{ε}| = |{/0 }| = 1.

Note-seadiferençaconceitualqueháentrealfabetos,linguagensecadeias.Alfabetos sãoconjuntos,finitosenãovazios,desímbolos,atravésdecujaconcatenaçãosãoobtidasas cadeias.Linguagens,porsuavez,sãoconjuntos,finitos(eventualmentevazios)ouinfinitos, decadeias.Umacadeiaétambémdenominada sentença deumalinguagem,ousimplesmentesentença,nocasodeelapertenceràlinguagememquestão.Linguagenssão,portanto, coleçõesdesentençassobreumdadoalfabeto.

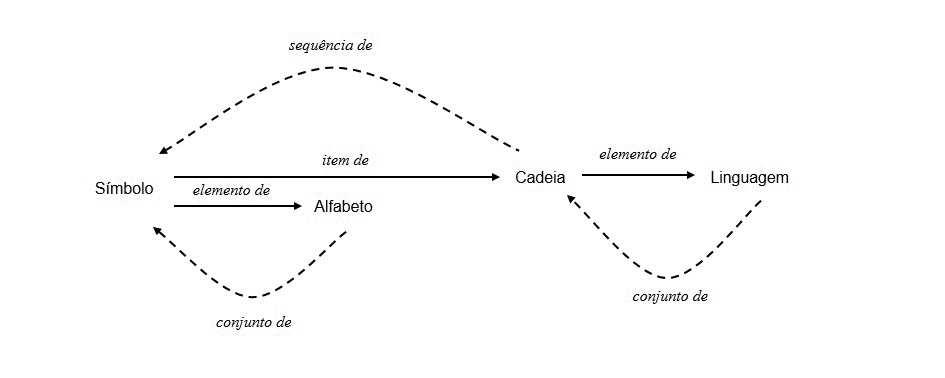
AFigura2.1ilustraarelaçãoentreosconceitosdesímbolo, alfabeto,cadeiaelinguagem.

AsváriasleiturascontidasnaFigura2.1são:“símboloéelementodealfabeto”;“alfabetoéconjuntodesímbolos”;“símboloéitemdecadeia”;“cadeiaésequênciadesímbolos”; “cadeiaéelementodelinguagem”e“linguageméconjuntodecadeias”.

Outramaneiradeassociarsignificadosaostermos“símbolo”,“alfabeto”,“cadeia”e “linguagem”éapresentadanaFigura2.2,quetambémilustra oconceitode“sentença”.

AFigura2.2facilitaoentendimentodasrelaçõesentreosconceitos:(i)umconjunto desímbolosformaumalfabeto,(ii)apartirdeumalfabeto(finito)formam-se(infinitas) cadeias;(iii)determinadascadeiassãoescolhidasparafazerpartedeumalinguagem;(iv) umalinguageméumconjuntodecadeias,queporissosãotambémdenominadassentenças.

Exemplo2.9 Osímbolo a éelementodoalfabeto {a} etambémumitemdacadeia aaa,queporsua vezéelementodalinguagem {aaa}.Poroutrolado,alinguagem {aaa} éumconjuntoquecontéma cadeia aaa,acadeia aaa éumasequênciadesímbolos a eoalfabeto {a} contémosímbolo a.AFigura 2.3ilustraessesconceitos,conformeaFigura2.1.

Exemplo2.10 AFigura2.4ilustraumaaplicaçãodosconceitosdaFigura2.2aoalfabeto {a, b}.A linguagemapresentadaé,naturalmente,apenasumadasinúmerasquepodemsercriadasapartirdesse alfabeto.

Diz-sequeumalinguagem L,definidasobreumalfabeto Σ,simplesmente observa uma propriedade p setodasassentençasde L exibem p.Diz-seque L,definidasobre Σ, satisfaz apropriedade p setodasassentençasde L exibem p e,alémdisso, L foramaiorlinguagem quesepodedefinirsobre Σ comtalpropriedade.Emoutraspalavras,se L contiver todas as cadeiassobre Σ quepossuemapropriedade p.Ointeressemaior,naturalmente,recaisobre aslinguagensquesatisfazemumacertapropriedade(ouconjuntodepropriedades)aoinvés daquelasqueapenasobservamapropriedade.

Exemplo2.11 Considereoalfabeto Σ = {a, b, c} eapropriedade p “iniciarcomosímbolo a”.Então:

•Alinguagem L0 = {ab, abc, accbb} observa p;

•Alinguagem L1 = cadeiassobre Σ queiniciamcom a eterminamcom a observa p;

•Alinguagem L2 = cadeiassobre Σ queiniciamcom a epossuemcomprimentopar observa p;

•Alinguagem L3 = cadeiassobre Σ queiniciamcom a econtémasubcadeia abc observa p;

•Alinguagem L4 = cadeiassobre Σ queiniciamcom a satisfaz p.

AlémdasoperaçõessobreconjuntosdefinidasnaSeção1.1,apresentamosaseguir maisalgumasoperaçõesqueserãoúteisaolongodorestantedotexto.Taisoperaçõessão definidasapartir(i)danoçãobásicadelinguagemenquantoconjuntodecadeiasetambém (ii)daoperaçãodeconcatenaçãodecadeias.

Figura2.1 Símbolo,alfabeto,cadeiaelinguagem.

Concatenação

A concatenação deduaslinguagens X e Y ,denotadapor X Y ousimplesmente XY ,correspondeaumconjunto Z formadopelacoleçãodetodasascadeiasquepossamserobtidaspela concatenaçãodecadeias x ∈ X comcadeias y ∈ Y ,nessaordem.Formalmente,

Z = X Y = XY = {xy | x ∈ X e y ∈ Y }

Notarqueessaoperaçãoéassociativa,pois X (Y Z)=(X Y ) Z,masnãoécomutativa, umavezquenemsempre X Y = Y X.Alémdisso, {ε} éoelementoneutrodaoperaçãode concatenação,pois X ·{ε} = {ε}· X = X,e/0éoaniquiladordessaoperação,pois X · /0 = /0 X = /0.

Exemplo2.12 Seja X = {aa, bbb, ccc} e Y = {00, 11}.Então, Z = X ·Y = {aa00, bbb00, ccc00, aa11, bbb11, ccc11}.Observar,nestecaso,que X Y = Y Z. ⋆

Aconcatenação ΣΣ,quegeracadeiasdecomprimento2formadassobreumalfabeto Σ,étambémrepresentadapor Σ2.Analogamente,aconcatenação ΣΣΣ,quegeracadeias decomprimento3sobreoalfabeto Σ,érepresentadacomo Σ3,eassimsucessivamente.

Generalizando-se: Σi = ΣΣi 1 , i > 0

Pordefinição, Σ0 = {ε}

Exemplo2.13 Considere-se Σ = {a, b, c}.Então,

• Σ0 = {ε}

• Σ1 = {a, b, c}

• Σ2 = {aa, ab, ac, ba, bb, bc, ca, cb, cc}

• Σ3 = {aaa, aab, aac, aba, abb, abc,..., ccc}

Figura2.2 Símbolo,alfabeto,cadeia,sentençaelinguagem.

Capítulo3

Linguagensregulares

Nestecapítuloserãoestudadasaslinguagensregulareseas diversasformasatravésdasquais elaspodemsergeradasoureconhecidas:

•Gramáticasregulares.

•Conjuntosregulares(maisusualmenterepresentadosatravésdasexpressõesregulares).

•Autômatosfinitos.

Emprimeirolugar,serãoapresentadoscadaumdessesformalismos.Depois,serámostradaaequivalênciaentreelesquantoàclassedelinguagensquesãocapazesderepresentar —aslinguagensregulares—,eserãoapresentadostambémalgoritmosquepermitemefetuar aobtençãodeumarepresentaçãoapartirdecadaumadasoutras.

Especialênfaseserádedicadaaoestudodosautômatosfinitos:serãointroduzidasas notaçõeseosconceitos,semprerelacionandoessetipodereconhecedoraomodelogeral, apresentadonocapítuloanterior.Tambémseráapresentada umaintroduçãoaostransdutores finitos.

Posteriormente,serãoconsideradasaspropriedadesexibidaspelaslinguagensdotipo3 emsuasdiversasrepresentações.Emparticular,o“Pumping Lemma”daslinguagensregulares,muitoútilnademonstraçãodequecertaslinguagensnãosãoregulares,etambémpara demonstrardiversosoutrosimportantesteoremasrelativosàslinguagensdessaclasse.Outra fundamentalpropriedaderefere-seàexistênciadeumautômatomínimo(eúnico)paracada linguagemregularconsiderada,oqualpodeserobtidoconformeométodopráticoapresentado.

Emseguida,serãoanalisadasalgumasvaliosasoperaçõesquepreservamaregularidade daslinguagensdotipo3,eque,poressemotivo,tambémsãoúteisparadeterminaracategoria deChomskyaqueumalinguagempossapertencer.

Finalmente,serãoapresentadasedemonstradas,noúltimoitemdestecapítulo,algumas questõesdecidíveisreferentesàclassedaslinguagensregulares.

3.1Gramáticasregulares

As gramáticaslinearesàdireita foramapresentadasanteriormente,naSeção2.7.Trata-se degramáticascujasregras α → β atendemexclusivamenteàsseguintescondições:

Exemplo3.1 AgramáticadoExemplo2.41élinearàdireita.Damesmaforma,agramáticaapresentadaaseguirtambémélinearàdireita.

V = {S, X ,Y, a, b}

Σ = {a, b}

P = {S → aS, S → bS, S → bX , X → bY,Y → b}

Notequetodasasregrascontêmexatamenteumsímbolonãoterminaldoladoesquerdoe,alémdisso, queoladodireitodetodasasregraséumacadeiadoconjunto (Σ ∪{ε})(N ∪{ε}) Alinguagemgerada poressagramáticacompreendetodasascadeiassobreoalfabeto {a, b} queterminamcom bbb. ⋆

As gramáticaslinearesàesquerda,porsuavez,possuemregras α → β emqueas seguintescondiçõessãoobservadasemtodaselas:

• α ∈ N;

• β ∈ (N ∪{ε})(Σ ∪{ε})

Exemplo3.2 AgramáticadoExemplo2.42élinearàesquerda.Damesmaforma,agramáticaapresentadaaseguirtambémélinearàesquerda.

V = {S, X ,Y, Z, a, b}

Σ = {a, b}

P = {S → Xb, X → Yb,Y → Zb, Z → Za, Z → Zb, Z → ε}

Notequetodasasregrascontêmexatamenteumsímbolonãoterminaldoladoesquerdoe,alémdisso, queoladodireitodetodasasregraséumacadeiadoconjunto (N ∪{ε})(Σ ∪{ε}) Alinguagemgerada porestagramáticaéamesmadoexemploanterior,ouseja,compreendetodasascadeiassobreoalfabeto {a, b} queterminamcom bbb

Sejamlinearesàdireitaoulinearesàesquerda,oladoesquerdodasregrasdasgramáticasregularesésempreumúnicosímbolonãoterminal.Já oladodireitodasregrasde taisgramáticasésempreformadopornomáximodoissímbolos (terminalenãoterminal,se direita,ounãoterminalterminal,seesquerda).Oladodireitopodeaindaserformadopor apenasumúnicosímboloterminal,umúnicosímbolonãoterminalouaindaacadeiavazia.

Exemplo3.3 Agramáticaapresentadaaseguirnãoélinearàdireitanemlinearàesquerda:

V = {S, X ,Y, Z, a, b}

Σ = {a, b}

P = {S → Xb, X → Yb,Y → Zb, Z → aZ, Z → bZ, Z → ε}

Notequetodasasregrascontêmexatamenteumsímbolonãoterminaldoladoesquerdo.Noentanto,as trêsprimeirasregrascolocamosímbolonãoterminaldolado esquerdo,aopassoqueasduasseguintes ocolocamdoladodireito.Aúltimaregraéválidatantonumtipodegramáticaquantonooutro.A linguagemgeradaporessagramáticaéamesmadoexemploanterior,ouseja,compreendetodasas cadeiassobreoalfabeto {a, b} queterminamcom bbb ⋆

Algunsautoresconsideramasseguintesextensõesnadefiniçãodasregras α → β de gramáticaslinearesàdireitaeàesquerda:

Nessasextensões,admite-seumaquantidadequalquerdesímbolosterminaisnolado direitodasproduçõesgramaticais,enãonomáximoum,comofoiestabelecidonadefinição original.Taisextensõesemnadaalteramaclassedelinguagensrepresentáveisporessestipos degramáticas,constituindooseuusomeraconveniência.OTeorema3.1trazademonstração dessaequivalência.

Demonstra-sequeasgramáticaslinearesàesquerdaouàdireitageramexatamentea mesmaclassedelinguagens.Portanto,éindiferenteoempregodeumaououtradessas duasvariantesdegramática,jáqueambaspossuemamesmacapacidadederepresentaçãode linguagens.

Poressemotivo,asgramáticaslinearesàdireitaouàesquerdasãotambémdenominadas gramáticasregulares.Essetermoserveparadesignarambosostiposdegramáticalinear. Aslinguagensgeradasporgramáticasregularesrecebemonomede linguagensregulares. OTeorema3.2estabeleceaequivalênciaentregramáticaslineares,àdireitaeàesquerda.

Quandoumagramáticalinearàdireitapossuinomáximoumúnicosímboloterminal doladodireitodassuasregras,elarecebeadenominaçãode gramáticalinearàdireitaunitária.Independentementedaquantidadedesímbolosterminaisdo ladodireito,agramática recebeadenominaçãode gramáticalinearàdireitanãounitária.Dessamaneira,toda gramáticalinearàdireitaunitáriaétambémumagramáticalinearàdireitanãounitária,mas ocontrárionemsempreéverdadeiro.Omesmovalepara gramáticalinearàesquerda unitária e gramáticalinearàesquerdanãounitária.

Otermo gramáticalinearàdireita (ou gramáticalinearàesquerda)denotagramáticasdequalquerumdosdoistipos(unitáriaounãounitária).Uma gramáticaregular é,portanto,uma gramáticalinearàdireita(GLD) ouuma gramáticalinearàesquerda (GLE).

Uma gramáticalinear (nãonecessariamenteàesquerdaouàdireita)éumagramática quepossuinomáximoumúnicosímbolonãoterminaldoladodireitodassuasregras.Assim, gramáticaslinearesàesquerdaouàdireitasãocasosparticularesdegramáticaslineares:toda gramáticalinearàesquerdaouàdireitaétambémumagramáticalinear,porémoinverso nemsempreéverdadeiro.Alinguagemgeradaporumagramáticalinearéchamadade linguagemlinear,eestanãoénecessariamenteumalinguagemregular.

Exemplo3.4 Agramáticalinearapresentadaaseguirgeraumalinguagemlinearqueélivredecontexto enãoregular(ak bk com k ≥ 0),conformeserávistomaisadiante:

S → aSb

S → ε

Logo,todalinguagemregularétambémlinear,porémnemtoda linguagemlinearé regular.Passamosagoraaoteoremaqueestabeleceaequivalênciaentreasgramáticaslineares àdireitaeasgramáticaslinearesàesquerda.

Teorema3.1(GLDnãounitária ⇒ unitária) “Se G1 éumagramáticacompostaapenasde produçõesdotipo α →

Algoritmo3.1(GLDnãounitária ⇒ unitária) “Substituiçãodasproduçõesdeumagramáticalinearàdireita,naforma α → β, β ∈ Σ∗(N ∪{ε}),porconjuntosdeproduçõesequivalentes,naforma α → β, β ∈ (Σ ∪{ε})(N ∪{ε}).”

• Entrada:umagramáticalinearàdireitaG1 =(V1, Σ, P1, S1),cujasproduçõessão daforma α → β,β ∈ Σ∗(N ∪{ε})

• Saída:umagramáticalinearàdireitaG2 =(V2, Σ, P2, S2),talqueL(G2)= L(G1) e cujasproduçõessãotodasdaforma α → β,β ∈ (Σ ∪{ε})(N ∪{ε}).

• Método:

1.N2 ← N1;

2.P2 ← /0 ;

3.Paracada α → β ∈ P1,

Algoritmosemelhantepodeserfacilmentedesenvolvidoparaocasodasgramáticas linearesàesquerdanãounitárias,deformaaobterumagramáticaequivalentecujasregras

Exemplo3.5 Considere-seagramática G1:

AaplicaçãodoAlgoritmo3.1resultanagramática

Atítulodeilustração,considerem-seasderivaçõesdasentença abcdefg,respectivamente,em G1 e G2:

Teorema3.2(GLD ⇔ GLE) “Se G1 éumagramáticalinearàdireitaunitária,entãoexiste umagramáticalinearàesquerdaunitária G2 talque L(G1)= L(G2),evice-versa.”

OAlgoritmo3.2mostracomosepodemapearasregrasdeumaGLD G1 nasregrasde umaGLE G2,detalformaque L(G2)= L(G1).Omesmoalgoritmopodeserusado,nosentido inverso,paramapearasregrasdeumaGLE G2 nasregrasdeumaGLD G1,detalformaque

L(G1)= L(G2)

Algoritmo3.2(GLD ⇒ GLE) “ObtençãodeumaGLEquegeraamesmalinguagemque umaGLD”

• Entrada:umaGLDunitáriaG1 =(V, Σ, P, S);éimportantequeSnãocompareça doladodireitodenenhumaregradoconjuntoP(vejaobservaçãovaseguir).1

• Saída:umaGLEunitáriaG2 =(V, Σ, P′ , S) talqueL(G2)= L(G1).

• Método:oconjuntoderegrasdeG2 (P′)éobtidoapartirdoconjuntoderegrasde G1 (P),conformeomapeamentodaTabela3.1.

GLD GLE Observação

S → µ S → µ i)

S → µA A → µ ii)

A → µ S → Aµ iii)

A → µB B → Aµ iv)

Qualquerquesejaocaso,Séaraizdagramática, µ ∈ Σ∗,A ∈ N −{S} eB ∈ N {S},ondeNéoconjuntodesímbolosnãoterminaise Σ éoconjuntodeterminais.

Observações:

i)SearaizdaGLDgeraumasentença(µ)diretamentepormeiodeuma regra,amesmaregradeveexistirnaGLEcorrespondente.

ii)OsprimeirossímbolosgeradospelaGLD(µ)precisamserosúltimos aseremgeradospelaGLEcorrespondente.

iii)OsúltimossímbolosgeradospelaGLD(µ)precisamserosprimeiros aseremgeradospelaGLEcorrespondente.

iv)Geraçãodossímbolosintermediários.

v)Casocontrário,nãoseriapossívelgerarosdemaissímbolosdasentença(pelocasoii,S → µAdaGLDsetransformarianaregraS → µS damesmaGLDeproduziriaaregraS → µ naGLEcorrespondente).

vi)Conformemostradoaseguir,ossímbolosnãoterminaissãousadosna ordeminversanaGLDenaGLE.

Se,naGLD,assentençassãoconstruídasdaesquerdaparaadireita,naGLEelas serãoconstruídasnosentidooposto,ouseja,dadireitaparaaesquerda.Sómuda,portanto,

Tabela3.1 MapeamentodeGLDemGLEpara L evice-versa

1Seesseforocaso,pode-secriarumnovosímbolonãoterminal Z,paraserusadocomonovaraizdagramática,e adicionararegra Z → S aela.

osentidoemqueassentençassãogeradas.Vejamoscomosãogeradasassentençasem

G1:

AconstataçãodequeasregrasdaGLD G1 usadasacimasãomapeadasemregrasdeuma GLE G2 (conformeaTabela3.1)mostraque

Emseguida,énecessárioprovarquetodasentençageradapelaGLE G2 (obtidaapartirde umaGLD G1 conformeaTabela3.1)étambémgeradapor G1.Issogaranteque L(G2) ⊆

(G1)

e,portanto,que L(G1)= L(G2).Defato,todaderivaçãonaGLE G2 temoseguinteformato:

Capítulo4

Linguagenslivresdecontexto

Aslinguagenseasgramáticaslivresdecontextoforaminicialmenteconcebidascomaintençãodepermitiraformalizaçãosintáticadaslinguagens naturais([13],[16]).Logose percebeu,noentanto,queaslinguagensnaturais(inglês,portuguêsetc.)sãosignificativamentemaiscomplexasdoqueaclassedelinguagensrepresentáveisatravésdasgramáticas livresdecontexto,diminuindoemmuito,emconsequência,o interessedosestudiososdas linguagensnaturaispelasgramáticasdessetipo.

Poroutrolado,aslinguagenslivresdecontextodespertaramuminteressemuitogrande nacomunidadecientíficaligadaàáreadecomputação,quevia grandespossibilidadesde aplicaçãodessaclassedelinguagensnaanáliseenaformalizaçãodelinguagensartificiais, emparticularaslinguagensdeprogramação.

Valelembrarque,àépocaemqueissoaconteceu,emmeadosdadécadade1950,a linguagemFORTRANjáhaviasidodefinida,ealgumasimplementaçõesexperimentaisestavamsendoutilizadasnodesenvolvimentodeaplicações.Comoateoriadelinguagensainda principiavaoseudesenvolvimento,nãosurpreendeofatode quealinguagemFORTRAN tenhasidooriginalmenteespecificada—eimplementada—demaneiraquasequetotalmenteempírica,semquehouvesse,comoháhoje,umsólidolastroteóricoeconceitualpara fundamentarseuprojeto.

Poressemotivo,inúmerasdificuldadesforamenfrentadasno iníciodoprojetoFORTRAN,asquaistiveramcomoconsequênciaosseguintes“registrosdeépoca”:

1.Elevada“complexidadeaparente”dosproblemasdeformalizaçãosintáticaede construçãodosaceitadoressintáticosdaslinguagensdeprogramação.

2.Arbitrariedadenaimposiçãoderestriçõesnosprojetosdelinguagensdealtonível, tornandomaisdifícilsuautilizaçãoporpartedosusuários.

Comoconsequênciadaslimitaçõesteóricasverificadasnaépoca,praticamenteinexistiammétodosparaaformalizaçãosintáticadaslinguagensdeprogramaçãoeparaaconstruçãosistemáticadeseusreconhecedores.Oadventodateoria daslinguagenseseuposterior relacionamentocomateoriadosautômatosocorreramjustamentenomomentoemqueanecessidadedemétodosetécnicashaviasetornadobastanteclara,emfunçãodessaprimeira experiência,afimdepossibilitaraevoluçãodasnovasáreas deconhecimentoemergentes dentrodacomputação:adaslinguagensdeprogramaçãoeados compiladores.

Nessesentido,opapeldasgramáticaslivresdecontextofoi extremamenteimportante, umavezque,sedeumladopermitiuodesenvolvimentodenotaçõesbastanteadequadaspara aformalizaçãodasintaxedaslinguagensartificiais,poroutroensejouodesenvolvimentode técnicasmuitoeficientesdeconstruçãodereconhecedoressintáticos,algumasdelasinclusiveatravésdemapeamentosefetuadosdiretamenteapartir dasgramáticasdasrespectivas linguagens.

Assim,asgramáticaslivresdecontextocontribuíramsignificativamenteparadesmitificaracomplexidadedosentãonovosproblemasqueseapresentavam,simplificando-os consideravelmente.UmexemplodissofoiadefiniçãodanotaçãoBNF([17]),logoapósa definiçãodasgramáticaslivresdecontextoporChomsky([9]).AnotaçãoBNF(siglade Backus-NaurForm)eratambémdestinadaàrepresentaçãodegramáticaslivres decontexto efoiconcebidaespecificamenteparausoemlinguagensartificiais,emparticularemlinguagensdeprogramação.Elafoiutilizadapelaprimeiraveznaespecificaçãodalinguagemde programaçãoAlgol60([18],[19]),tendoseuusosedifundidobastanteatéosdiasdehoje.

Atualmente,graçasaograndedesenvolvimentoteóricoverificadonasúltimasdécadas, taisproblemas,longedeteremsetornadotriviais,tiveram bemdeterminadososlimitesde suacomplexidade,e,comoconsequência,adiversificaçãode métodoseresultadosteóricos conhecidospermitequeelespossamsertratadosdeformarotineiraesistemáticanodiaadia doprofissionaldecomputação.

Nestecapítuloserámostradaaimportânciadasgramáticaslivresdecontextonaformalizaçãodaslinguagensdeprogramaçãodealtoníveleserãodefinidososconceitosdeárvores dederivação,ambiguidadeeanálisesintática,entreoutros.Aseguir,serãoapresentadose demonstradosalgunsimportantesresultadosreferentesàsimplificaçãodasgramáticaslivres decontexto,àsuarepresentaçãoemformasnormaiseaanálisedeterminísticadescendente.

4.1Gramáticaslivresdecontexto

Asgramáticaslivresdecontextopodemserutilizadas,entreoutrasaplicações,pararepresentarsubconjuntos(bastantelimitados)delinguagensnaturais.Considereoseguinteexemplo:

<frase> → <sujeito><verbo><complemento>

<sujeito> → Ohomem

<sujeito> → Amulher

<verbo> → leu

<verbo> → escreveu

<complemento> → um <adjetivo> livro

<adjetivo> → ótimo

<adjetivo> → péssimo

<adjetivo> → ε

Comosepodeperceber,ossímbolosnãoterminaisemgramáticaslivresdecontextopodem serutilizadospararepresentarclassessintáticasbemdefinidas,permitindoumelevadograu deintuiçãoedeclarezanainterpretaçãoenaestruturaçãodassentençaspertencentesàlinguagem.

Quandoutilizadaspararepresentarsubconjuntosdelinguagensnaturais,oumesmolinguagens“pseudonaturais”,porexemplo,aslinguagensempregadasemsistemasdeconsulta abancosdedadoseemdiversosoutrostiposdeinterfaceshomem-máquina,especialmente nosaplicativosvoltadosparausuáriosleigosemcomputação,asgramáticaslivresdecontexto desempenhamumpapelmuitoimportanteparaosprojetistasdetaissistemas,poispermitem aformalizaçãodalinguagemdeinterface,facilitandoaconstruçãodeseurespectivoreconhecedor.

Noentanto,amaioraplicaçãodasgramáticaslivresdecontextoocorrenaformalização sintáticadaslinguagensdeprogramaçãodealtonível.Rigorosamente,nãosepodedizerque taislinguagenssejampropriamentelivresdecontexto.Naverdade,aformalizaçãocompleta desuasintaxeexigiriadispositivosmaiscomplexos,comoé ocasodasgramáticasdotipo1, umavezqueagrandemaioriadetaislinguagensapresentadependênciasdecontextoquenão podemserrepresentadasporgramáticasdotipo2,oulivresdecontexto.

Nãoobstante,asimplicidadedasgramáticaslivresdecontextoastornamuitoatraentes paraarepresentaçãoformal,aindaqueparcial,dasintaxedetaislinguagens.Asgramáticas livresdecontextoconstituem,pois,umasoluçãodecompromissoemqueorigordadefinição sintáticaéligeiramentesacrificadoemfavordousodeumanotaçãomuitomaisintuitivae fácildesermanipuladadoqueasgramáticasdotipo1.Dessemodo,asdependênciasde contextocostumamserrepresentadasàparte,emalgumaoutranotação—eventualmenteem linguagemnatural—quesirvadecomplementaçãoàgramática dotipo2paraarepresentaçãodasdependênciasdecontexto.Asgramáticasformaisdotipo1,devidoàsuaelevada complexidadedemanipulação,nãocostumamserutilizadasnapráticapararepresentardependênciasdecontextoemlinguagensdeprogramação,nemmesmodeformaparcial.

Acaracterísticaquetornaasgramáticaslivresdecontexto especialmenteadequadasà formalizaçãosintáticadaslinguagensdeprogramaçãoéasuacapacidadederepresentaçãode construçõesaninhadas,quesãofrequentementeencontradasemlinguagensdessacategoria. Construçõesaninhadascostumamocorreremlinguagensdeprogramação,porexemplo,na construçãodeexpressõesaritméticas,emquesubexpressõessãodelimitadas,atravésdouso deparênteses;naestruturaçãodofluxodecontrole,emquecomandosinternossãoinseridoscomoparteintegrantedeoutrosexternos;naestruturaçãodoprograma,emqueblocos, módulos,procedimentosefunçõessãoempregadosparacriar diferentesescoposetc.

O balanceamentodetermos éumaconsequênciadaexistênciadeconstruçõesaninhadas.Todaconstruçãoaninhada,sejaporrecursãodireta ourecursãoindireta,provoca algumtipodebalanceamentodetermos,emqueostermosemquestãosãoosímbolos(ou termos)quedelimitamaconstruçãoaninhada.Umexemplotípicodissosãoosparênteses quedelimitamnovasocorrênciasdeexpressõesdentrodeoutrasexpressões.

ConformedefinidonoCapítulo2,uma gramáticalivredecontexto éumaquádrupla (V , Σ, P, S) comosseguintescomponentes:

• V :conjunto(finitoenãovazio)dossímbolosterminaisenãoterminais;corresponde ao vocabulário dagramática;

• Σ:conjunto(finitoenãovazio)dossímbolosterminais;correspondeao alfabeto da linguagemdefinidapelagramática;

• P:conjunto(finitoenãovazio)das regras (ou produções),todasnoformato α → β, com α ∈ (V Σ) e β ∈ V ∗;

• S: raiz (ou símboloinicial)dagramática, S ∈ (V Σ).

Exemplo4.1 Alinguagem L = {akbk | k 0} doExemplo3.4énãoregular,conformeprovadono Exemplo3.65.Poroutrolado,trata-sedeumalinguagemlivredecontexto,umavezqueelaégerada pelagramáticalivredecontextoapresentadanopróprioExemplo3.4.Defato,épossívelprovarque alinguagemgeradaporaquelagramáticacoincidecom L.Aprovaéfeitaporinduçãoem i usandoa

propriedade P(i): ∀i ≥ 1, P(i)=(S ⇒i w) ⇔ (w = ai 1bi 1)

Aprovadacondiçãonecessária PN (i)=(S ⇒i w) ⇒ (w = ai 1bi 1) éapresentadaaseguir.

•Basedaindução:

– i = 1.

Linguagenslivresdecontexto

– PN (1)=(S ⇒ ε) pelaaplicaçãodiretadaregra S → ε

– w = a0b0 = ε

•Hipóteseindutiva:

– PN (i)=(S ⇒i w) ⇒ (w = ai 1bi 1) éválidapara i ≥ 1.

•Passodeindução:

– PN (i) implica PN (i + 1)

– Prova:

* S ⇒i+1 aSb ⇒i w.

* Pelahipóteseindutiva, S ⇒i ai 1bi 1 .

* Logo, S ⇒i+1 aSb ⇒i aai 1bi 1b,ouseja, S ⇒i+1 aibi Aprovadacondiçãosuficiente PS(i)=(w = ai 1bi 1) ⇒ (S ⇒i w) éapresentadaaseguir.

•Basedaindução:

– i = 1.

– w = a0b0 = ε.

– PS(1)=(S ⇒ ε) pelaaplicaçãodiretadaregra S → ε.

•Hipóteseindutiva:

– PS(i)=(w = ai 1bi 1) ⇒ (S ⇒i w) éválidapara i ≥ 1.

•Passodeindução:

– PS(i) implica PS(i + 1).

– Prova:

* Pelahipóteseindutiva, (w = ai 1bi 1) ⇒ (S ⇒i w)

* aibi = aa i 1bi 1 w

b

* Épossívelfazer S ⇒ aSb pelousodaregra S → aSb.

* Portanto, S ⇒ aSb ⇒i aai 1bi 1 w

b.

* Logo, S ⇒ aSb ⇒i aibi,ouseja, S ⇒i+1 aibi

Destamaneira,ficaclaroque L eagramáticadoExemplo3.4sãoexatamenteamesmalinguagem ⋆

Exemplo4.2 Seja P oconjuntoderegrasaseguireconsiderem-se Σ, V e S subentendidos.

Considere-seasentença a + a.Elapodeserobtidaatravésdaseguintesequênciadederivações:

Notequeaderivaçãodaprimeiraexpressão(

a + a)comparecenaderivaçãodasegundaexpressão (E ⇒∗ a ∗ (a + a)),porémentreparênteses.Issocaracterizaumaninhamento combalanceamentode termos.

Observe-sequealinguagemgeradapelagramáticadesseexemplocompreendeassentençasque representamexpressõesaritméticascorretamenteformadassobreooperando a comosoperadores“∗” e“+”.Subexpressõesdelimitadasatravésdeparêntesestambém sãoadmitidas,epodemsercompostas combasenasmesmasregrasutilizadasparaconstruiraexpressãoinicial.Nãofazempartedalinguagem definidaporessagramática,porexemplo,cadeiasemquenãohajaplenacorrespondênciadosímbolo “(”comseupar“)”.Porexemplo,nãofazempartedessalinguagemcadeiasnasquaisaquantidade de“(”édiferentedaquantidadede“)”,ouqueiniciamcom“)”.Emoutraspalavras,trata-sedeuma linguagemqueadmiteoaninhamentodeexpressõesatravésdo usodeparêntesescomodelimitadores, equecontémapenasexpressõesválidasdopontodevistadousodosparênteses.

O aninhamento deconstruções(ou balanceamento determos)éacaracterísticaque distingueaslinguagensestritamentedotipo2daslinguagensdotipo3:pertencemaumalinguagemestritamentedotipo2apenasetãosomenteassentençasemque,paracadaocorrênciadeumdadodelimitador(porexemplo,um“abre-parênteses”),hajaemcorrespondênciaa ocorrênciadeumoutro,atravésdoqualseformaopar(porexemplo,um“fecha-parênteses”). Alémdisso,asubcadeiasituadaentreessepardedelimitadorespodesergeradaatravésdas mesmasregrasdeformaçãoválidasparaasentençacompleta, caracterizandodessamaneira oaninhamentodesuasconstruções.

Exemplo4.3 NoExemplo4.2,oconjuntoderegras:

→ (E)

mostraqueexisteumarecursãoindiretacomonãoterminal E queprovocaoaninhamentodeexpressões: E ⇒∗ (E).Ouseja,agramáticapermitequeumaexpressãosejausadadentrodeoutraexpressão. Nestecaso,oaninhamentodeexpressõescausaobalanceamentodosparênteses:cada“(”dolado esquerdo(antesdeumaexpressão)ésempreacompanhadoporum“)”doladodireito(depoisdaexpressão).

Note-seque,atravésderegrasdeproduçãolivresdecontexto,épossívelespecificar construçõesmaisrestritasdoqueasobteníveismedianteousodeproduçõesdegramáticaslineares.Assim,comregraslivresdecontextoépossívelcaracterizaraninhamentossintáticos, osquaisnãopodemserdescritosapenascomproduçõeslinearesàdireitaouàesquerda(ou qualquercombinaçãodelas).Emoutraspalavras,asgramáticaslivresdecontextopermitem imporrestriçõesadicionaisàquelasquesepodemconstruir emgramáticasregulares,podendo assimcaracterizarsubconjuntosdaslinguagensregulares quegozemdapropriedadedeterminadapelosaninhamentossintáticos.Dessaforma,asgramáticaslivresdecontextotornam-se muitoúteisparaaespecificaçãodelinguagensdeprogramação,amaioriadasquaisexibe aninhamentossintáticos.

Arepresentaçãodeaninhamentosemgramáticasdotipo2decorredeumapropriedade característicadasgramáticasdestetipo,denominada self-embeddingproperty.Umnãoterminal Y édito self-embedded,ou autorrecursivocentral,se,apartirdele,forpossívelderivar

algumaformasentencialemqueonãoterminal Y ressurja,delimitadoporcadeiasnãovazias determinaisàsuaesquerdaeàsuadireita:

Y ⇒∗ αY β, com α,β ∈ Σ+

UmnãoterminalZéditosimplesmente autorrecursivo se,apartirdele,forpossível derivaralgumaformasentencialemque Z ressurja,acompanhadodepelomenosumacadeia nãovaziadeterminaisàsuaesquerdaouàsuadireita:

Z ⇒ αZβ, com α,β ∈ Σ∗ ,αβ = ε

Naturalmente,todonãoterminalautorrecursivocentralétambémumnãoterminalautorrecursivo,masocontrárionãoénecessariamenteverdadeiro.Seumagramáticalivrede contexto G possuipelomenosumnãoterminalautorrecursivocentral,diz-seque G é autoembutida (doinglês self-embedded).

Umsímbolonãoterminal essencial éaquelequenãopodeserremovidodagramática(ousubstituído)sobpenadeprovocarmodificaçõesnalinguagemsendodefinida.Caso contrário,eleédito nãoessencial

Umalinguagem L édita estritamentelivredecontexto,oulivredecontextonãoregular,seelaforlivredecontextoenãoforregular.Existem váriasmaneirasdecaracterizar linguagensestritamentelivresdecontexto.Umadelasépor meiodaapresentaçãodeuma gramáticalivredecontextoquegera L e,aomesmotempo,deumaprova(porexemplopor meiodaaplicaçãodo“PumpingLemma”paraaslinguagensregulares)deque L nãoéregular.

Umamaneiraalternativasedáquandotodasasgramáticasque geram L sãoautoembutidas,ouseja,quandotodaselaspossuempelomenosumnão terminal autorrecursivo central.Issoéomesmoqueafirmarque L égeradaapenasporgramáticasquepossuem, necessariamente,pelomenosumsímbolonãoterminalautorrecursivocentralessencial.Ou seja,setodasasgramáticasquegeram L sãoautoembutidas,entãoqualquergramáticaque gera L possuiumsímbolonãoterminalautorrecursivocentralessencial.Emoutraspalavras, L éumalinguagemcomcaracterísticadeaninhamentoqueadistinguedeumalinguagem regular(eé,portanto,estritamentelivredecontexto)eque,porisso,precisaserrepresentada pormeiodeumsímbolonãoterminalautorrecursivocentralessencial.

Provarqueumalinguageméestritamentelivredecontextodestasegundamaneiranão é,noentanto,trivial,eaprimeiramaneiraaindaéamaisusada.Asegundamaneiraserve, principalmente,paranosajudaraentendercomoofatodealinguagemserlivredecontexto enãoregularsemanifestanasgramáticasqueageram(especificamente,pelapresençadeum símbolonãoterminalautorrecursivocentralessencialemtodaselas).

Poroutrolado,osimplesfatodeumagramáticaserautoembutidanãogaranteanão regularidadedalinguagemdefinidaporestagramática:épossívelidentificarlinguagensregularesgeradasporgramáticascomnãoterminaisautorrecursivoscentraisque,nessescasos, nãosãoessenciais.OExemplo4.4ilustraessasituação.

Exemplo4.4 Agramáticacujasregrasconstituemoconjuntoabaixoédotipo2epossuiumnão terminalautorrecursivocentral(S,emdecorrênciadaprodução S → aSa),podendo,portanto,sercaracterizadacomoumagramáticaautoembutida:

Capítulo5

Linguagenssensíveisaocontexto

Linguagenssensíveisaocontextosãoaquelascujassentençasexibemcaracterísticasdedependência—ouvinculação—entretrechosdistintosdelas.Ouseja,determinadaspartesde umasentençasóserãoconsideradasválidasseocorreremsimultaneamenteatrechosrelacionados,presentesemoutrasregiõesdamesmasentença.Daíaorigemdonome“sensibilidade aocontexto”.

Deve-se,noentanto,entendercorretamenteosignificadodo termo“sensibilidadeao contexto”,tambémconhecidocomo“dependênciadecontexto”,poisnãoéqualquertipode vinculaçãoquecaracterizaessapropriedadedaslinguagens.

Emparticular,nãoseestáinteressadoemquaisquerdasdependênciasquepossamser representadasporgramáticaslivresdecontexto,comosequênciassimplesdesímbolosou mesmoobalanceamentodesímbolos,típicodaslinguagenslivresdecontexto.

Exemplo5.1 Sejaalinguagemdassentençasquerepresentamexpressõesaritméticascomatéquatro operaçõessobreoalfabeto {a, b},geradapelagramática:

Umexemplodesentençapertencenteaessalinguagemé a (b +(a/b) ∗ a).Éclaroque,nestecaso, épossívelverificaralgumasdependênciasdecontexto,nosentidoliteraldapalavra.Porexemplo,as ocorrênciasdosparênteses.Nãoseriapossívelfecharosegundoparênteseseoprimeironãotivesse sidoaberto.Outroexemploéque,decadaladodosímbolodedivisão,deveexistirumaletra“a”ou “b”,representandocadaumdosoperandosdessaoperação.

Taistiposde“dependênciadecontexto”podemserfacilmenterepresentadosporgramáticaslivresdecontextoe,porisso,nãoserãoconsideradoscomotalnesteestudo.

Aqui,poroutrolado,ointeresseémaioremoutrostiposdedependênciascontextuais,quenãopossamserrepresentadasatravésdasgramáticaslivresdecontexto.Taisdependênciascaracterizamlinguagensmaiscomplexasqueaslinguagenslivresdecontexto,e constituemoobjetodestecapítulo.

Épreciso,portanto,analisaressetipodedependências,referidasnestaintrodução.Um bomexemploparaoseuentendimentosãoasdependênciasdecontextoquesãoencontradas naslinguagensdeprogramaçãodealtonívelmaiscomuns.

Taislinguagenscostumamoferecerdeclaraçõesdiversas,porexemplo,declaraçõesde tipos,deconstantes,devariáveis,deprocedimentos,defunçõesetc.Taisdeclaraçõescumpremopropósitoduplodeacrescentarnovosnomesaoespaçodenomescriadopeloprogramador,edeassociar-lhesatributos(porexemplo,nocasodasvariáveis,seustipos;nocaso dasfunções,aquantidadeeotipodeseusparâmetros,bemcomootipodovalorretornado).

Umavezdeclarados,osnovosnomespodemserempregadosnocorpodoprograma. Normalmente,taislinguagensexigemqueapenasnomesdeclaradospossamserreferenciados emcomandoseexpressões;alémdisso,queautilizaçãodeles sejafeitadeformacoerente comosatributosquelhesforamassociados.

Éocaso,porexemplo,deseutilizar,noladoesquerdodeumcomandodeatribuição, apenasvariáveisdeclaradasevisíveisnolocaldareferência.Éocasotambémdeseutilizar, naexpressãodoladodireitodeumcomandodeatribuição,apenasosnomeseliteraiscujos atributossejamcompatíveiscomasoperaçõesqueestejamsendoempregadas.

Dessaforma,acorreçãosintáticadeumasentença,nocasoum programaescritoem umalinguagemdealtonível,sósecompletaseascondiçõesanterioresforemverificadas. Estácriada,portanto,umadependênciadecontextoentreos atributosdosnomesconstantes nasrespectivasdeclaraçõeseaformacomoelessãomanipuladosaolongodoprograma.

Exemplo5.2 Considere-se,porexemplo,oseguintetrechodeprogramaescritonalinguagemC:

voidmain(){intx;scanf(“%d”,&x);printf(“%d”,x);}

Existeumaclaravinculaçãoentreadeclaraçãodavariável“x”eareferênciaaelanoscomandos deleituraeimpressão.Seelanãotivessesidodeclarada,ou seosseusatributosnãofossemcompatíveis comamaneiracomoelaéutilizadanessescomandos,nãoseria possívelconsiderartalsentençacomo válidadopontodevistasintático. ⋆

Dependênciasdecontextosão,portanto,umacaracterísticafundamentaldaslinguagens deprogramaçãoemgeral.Dopontodevistamaisteórico,aslinguagensformaiscomtais característicasconstituemumaclassedelinguagenssobre aqualrecaeminteressesequestões similaresàsestudadasnoscapítulosanteriores,entreasquaismaneirasdeformalizá-lasdo pontodevistagramatical,modelosdereconhecimento,propriedadesmaisimportanteseseu relacionamentocomasdemaisclassesdelinguagens.

5.1Gramáticassensíveisaocontexto

Cabe,nesteponto,justificaraincapacidadedasgramáticas livresdecontextopararepresentarlinguagenssensíveisaocontexto.Rigorosamente,o“PumpingLemma”paralinguagens livresdecontexto,apresentadonoCapítulo4(Teorema4.21),cumpreopapeldedemonstrar aexistênciadelinguagensquenãosejamlivresdecontexto, ouseja,delinguagensquenão podemserrepresentadasatravésdegramáticaslivresdecontexto.Umaanáliseumpouco maisdetalhadadanaturezadasgramáticaslivresdecontextorevelaaorigemdassuaslimitaçõeseservecomoelementomotivadorparaaconceituaçãodeumanovaclassedegramáticas —adasgramáticassensíveisaocontexto.

Aorestringiroladoesquerdodasregrasgramaticaisaumúnicosímbolonãoterminal,asgramáticaslivresdecontextoestabelecemquetodasasderivaçõessejamfeitas considerando-seapenasonãoterminalselecionadoparaasubstituição,nãoimportandoos símbolos(terminaisenãoterminais)queorodeiamàesquerdaeàdireita—ouseja,oseu contexto.Daíaorigemdotermo“livredecontexto”,poisaestruturasintáticadostrechosjá

desenvolvidosdacadeianuncaélevadaemconsideraçãoquandodasubstituiçãodeumnão terminalpeloladodireitodaregraescolhida.

Issotornaimpossívelrepresentarcasoscomoodadeclaraçãodevariáveis,umavez queasubstituiçãodossímbolosnãoterminaisquerepresentam,porexemplo,adeclaraçãode variáveleocomandodeatribuiçãonãopodeservinculadaduranteoprocessodederivaçãoda cadeia,paraevitar,porexemplo,ageraçãodesentençasque contenhamreferênciasanomes inválidosoudetiposincompatíveiscomaoperaçãoaplicada.

Parasuperartallimitação,empregam-seasgramáticassensíveisaocontexto.Formalmente,uma gramáticasensívelaocontexto G =(V, Σ, P, S) éaquelacujasregrasdoconjunto P obedecemaoformato α → β,onde:

Gramáticassensíveisaocontextoeliminamarestriçãodequeoladoesquerdodasregrassejaformadoporumúnicosímbolo,edequeestesejaumsímbolonãoterminal.Tais gramáticasadmitemqualquerquantidadedesímbolosdolado esquerdo,sejamelesterminaisounãoterminais.Exigemapenasquedoladoesquerdoexistapelomenosumsímbolo nãoterminale,também,queoladodireitopossuaumaquantidadedesímbolosnãoinferior àquelaencontradanoladoesquerdodamesmaregra.

Define-seinicialmente linguagemsensívelaocontexto comosendoaquelaquepossa serdefinidaatravésdeumagramáticasensívelaocontexto.Conformeconvencionadona Seção2.7,essadefiniçãoéestendidaparaqualquerlinguagem L quecontenhaacadeiavazia, desdeque L −{ε} possasergeradaporumagramáticasensívelaocontexto.

Define-se linguagemestritamentesensívelaocontexto comosendoumalinguagem sensívelaocontextomasnãolivredecontexto.

Exemplo5.3

B,C}, {a, b, c}, P, S),com

P = {S → aSBC, S → abC, CB → BC, bB → bb, bC → bc, cC → cc}

Todasasregrasdessagramáticasatisfazemàcondiçãodepossuirpelomenosumnãoterminaldolado esquerdoeumasequênciaarbitráriadesímbolosdoladodireito,porémdecomprimentonuncainferior aocomprimentoverificadonoladoesquerdodamesmaregra.

Algumasderivaçõespossíveissão:

• S ⇒ abC ⇒ abc;

• S ⇒ aSBC ⇒ aabCBC ⇒ aabBCC ⇒ aabbCC ⇒ aabbcC ⇒ aabbcc;

• S ⇒ aSBC ⇒ aaSBCBC ⇒ aaabCBCBC ⇒ aaabBCCBC ⇒ aaabBCBCC ⇒ aaabBBCCC ⇒ aaabbBCCC ⇒ aaabbbCCC ⇒ aaabbbcCC ⇒ aaabbbccC ⇒ aaabbbccc

Éfácildemonstrarque L(G1)= {anbncn | n 1} (vejaExemplo2.34).Étambémpossível demonstrar,pelaaplicaçãodo“PumpingLemma”paralinguagenslivresdecontexto,que L(G1) não éumalinguagemlivredecontexto(vejaExemplo4.82).Logo, nãoexistequalquergramáticalivre

434 Linguagenssensíveisaocontexto

decontextoquesejacapazdegerar L(G1),e,portanto, L éumalinguagemestritamentesensívelao contexto.

Umarápidaanálisedasproduçõesde G1 possibilitaacompreensãodalógicaqueexisteem suaconcepção:asduasregrasiniciaisgeramformassentenciaisnasquaisumacertaquantidadede símbolos“a”éseguidaporpares“bC”(inicial)ou“BC”(seguintes),detalformaqueasquantidadesde

“ a”,“B”(ou“b”)e“C”sejamidênticas—comoem aaabCBCBC.Aregra CB → BC permitequeos

“B”seos“C”ssejamagrupados—gerando,nesteexemplo, aaabBBCCC.Asdemaisregrasefetuam assubstituiçõesdosnãoterminaispelosterminaiscorrespondentes,comocuidadodeevitarquetais substituiçõespossamserutilizadasparagerarsentençasdistintasdasqueestãorelacionadasacima. ⋆

Asgramáticassensíveisaocontextosãoditas monotônicas,poisocomprimentodas formassentenciaisobtidasduranteoprocessodederivação deumasentençanuncasofre redução.EssacaracterísticaseráexploradanaSeção5.5,parafinsdeassociaçãodessaclasse delinguagenscomoseurespectivomodelodereconhecimento maissimples.

Exemplo5.4 Considere-seagramática G2 =({a, b, c, S, A, B,C}, {a, b, c}, P, S),com

P = {S → ABC,

S → ABCS,

AB → BA, AC → CA, BA → AB, BC → CB, CA → AC, CB → BC, A → a, B → b, C → c}

Analise-seagoraaderivaçãodealgumassentenças:

• S ⇒ ABC ⇒ aBC ⇒ abC ⇒ abc;

• S ⇒ ABC ⇒ ACB ⇒ CAB ⇒ CBA ⇒ cBA ⇒ cbA ⇒ cba;

• S ⇒ ABCS ⇒ ABCABC ⇒ BACABC ⇒ BACBAC ⇒ BACBCA ⇒ bACBCA ⇒ baCBCA ⇒ bacBCA ⇒ bacbCA ⇒ bacbcA ⇒ bacbca.

Asduasregrasiniciaisinseremquantidadesidênticasdesímbolos A, B e C naformasentencial. Asregrasseguintessãoutilizadaspara“embaralhar”esses símbolosdemaneiraarbitrária.Astrês últimassubstituemcadasímbolonãoterminalpelorespectivosímboloterminal.

Alinguagemgeradapor G2 consisteemtodasassentençassobre {a, b, c} —comcomprimento mínimo3—,detalformaqueasquantidadesdessessímbolossejamsempreidênticas.Formalmente:

ComonoExemplo5.3,pode-sedemonstrarqueessalinguagemé estritamentesensívelaocontexto.Paraissoésuficienteprovar,atravésdo“PumpingLemma”,queelanãoélivredecontexto.

Gramáticasdessetipogeramlinguagensdenominadassensíveisaocontexto,ousimplesmentedotipo1.Ainspeçãorigorosadosformatosadmitidosparaasproduçõesdas gramáticasdotipo1nãopermiteacaracterizaçãoimediatadetodaequalquergramática(e,

consequentemente,dascorrespondenteslinguagens)dotipo2comosendotambémdotipo 1.Issodecorredofatodequeasgramáticasdotipo2admitema cadeiavazia ε comoalternativadesubstituiçãoparaoladoesquerdodequalquerprodução,oquenãoépermitidoem gramáticasdotipo1emfunçãodarestrição |α| |β| Rigorosamente,umalinguagemédita sensívelaocontexto seesomentese:

• ε / ∈ L e L = L(G),onde G éumagramáticasensívelaocontexto,ou

• ε ∈ L e L −{ε} podesergeradaporumagramáticasensívelaocontexto.

Nesteúltimocaso,aceita-sequearegra S → ε sejaincluídanagramática,porémdesde que S (araizdagramática)nãocompareçadoladodireitodenenhumaoutraregra.Dessa formaevita-seageraçãodeformassentenciaisquepossamsofrercontraçãoduranteoprocessodederivação.Aúnicapossibilidadedeissoocorrercorrespondeàderivaçãoinicial, quandoosímboloasersubstituídoéaprópriaraizdagramática.

Cumpre,nesteponto,estabelecerumaimportanterelaçãoentrelinguagenslivresde contextoelinguagenssensíveisaocontexto.Suponha-se,inicialmente,que L = L(G),onde G éumagramáticalivredecontexto,e,adicionalmente,que ε / ∈ L.Éfácilperceber,neste caso,que G satisfazatodasasespecificaçõesdeumagramáticasensível aocontexto,poisnão haveránenhumaregracom ε àdireita.Logo, L(G) serátambémumalinguagemsensívelao contexto.Ouseja:linguagenslivresdecontextoquenãocontêmacadeiavaziasãotambém linguagenssensíveisaocontexto.

Caso ε ∈ L(G),e G sejaumagramáticalivredecontexto,seránecessárioaplicartransformaçõesem G obtendo-se G′,demodoque:

• S → ε sejaaúnicaregravaziaem G′;

• S nãocompareçanoladodireitodenenhumaoutraregrade G′;

• L(G)= L(G′).

ComofoidemonstradonoTeorema4.7,taltransformaçãoésemprepossível.Todae qualquergramáticalivredecontextopodesertransformada,semprejuízodalinguagemque estiversendodefinida,emumaoutragramáticaemqueacadeia vaziacompareceapenasna produção S → ε,sendo S araizdagramática.Alémdisso, S garantidamentenãofigurano ladodireitodenenhumaoutraprodução.Issosignificaqueoúnicoefeitopráticodapresença deproduçõesdotipo A → ε, A ∈ N,emgramáticaslivresdecontextoquaisquer,énaeventual incorporaçãodacadeiavaziacomosentençanalinguagemdefinida.

Portanto,comexceçãodaprodução S → ε,asgramáticasdotipo2podemsersempre convertidasparaumformatoqueastorneumcasoparticulardasgramáticasdotipo1.Em outraspalavras,tem-sequequalquergramáticadotipo2,desdequedevidamenteconvertidaparaesseformatopadronizado,eamenosdaprodução S → ε,torna-setambémuma gramáticadotipo1.

Assim,éfatoque G′,excetopelaregravazia,éumagramáticasensívelaocontextoe, consequentemente, L(G′) −{ε} éumalinguagemsensívelaocontexto.Logo, L(G)= L(G′) é,deacordocomadefinição,umalinguagemsensívelaocontexto.

Comoconsequência,pode-seconcluirquetodalinguagemlivredecontextoétambém umalinguagemsensívelaocontexto.Ficaclaro,também,que aslinguagenslivresdecontextoconstituemumsubconjuntoprópriodaslinguagenssensíveisaocontexto.

Parafinalizar,algumasobservaçõesdeordemprática.Émuitocomum,quandoseespecificamlinguagensdeprogramação,fazerusodegramáticaslivresdecontexto.Talartifício mascara,noentanto,aexistênciadasdependênciasdecontexto,asquaisacabamsendoex-

cluídasdaformalizaçãogramatical.Essaestratégiapossuipelomenosumaimportanterazão desereumaimportanteconsequência:

•Arazãodeserconsistenofatodequeformalismosdistintos,adequadosparaarepresentaçãodelinguagenssensíveisaocontexto(porexemplo, asgramáticassensíveis aocontexto),sãorelativamentecomplexosedifíceisdeseremtrabalhadosquando setratadeespecificarasdependênciasdecontextotípicasdaslinguagensdeprogramação.Opta-se,assim,porumaquestãodepraticidade,pelo usodeformalismos maissimples,emparticularoslivresdecontexto.

•Aconsequênciadessapráticaéquealinguagemresultanteseráumsuperconjunto dalinguagempretendida.Alémdassentençasqueobservamestritamenteasregrasdedependênciasdecontextodalinguagem,outrascadeias,indesejadas,que nãoobservamtaisdependências,acabamsendoincorporadas àlinguagemdefinida. Edissoresultaanecessidadedeseacrescentaremfiltrosparaeliminá-lasdalinguagem,preservando-seapenasascadeiasefetivamenteaderentesàespecificação original.

Trata-se,portanto,deumaestratégiaoriginadaapartirde umanecessidadedesimplificarasoluçãodoproblema,masqueresulta,emmomentoposterior,nanecessidadede incorporaçãodefiltrosquedescartemascadeiasinválidas.

Exemplo5.5 Considere-seagramáticadefinidapeloconjuntodeproduçõesaseguir,representativa deumalinguagemdeprogramaçãoquepossibilitadeclaraçõesdevariáveisseguidasdecomandosde atribuiçãoeexpressões.

{Programa → DeclaracoesComandos, Declaracoes → DeclaracoesDeclaracao

ε, Declaracao → “%”Identificador, Comandos → ComandosComando

ε, Comando → “#”Identificador“ = ”Expressao, Expressao → Expressao“ + ”Expressao

Expressao“ ∗ ”Expressao

Talsentençapodeserentendidacomoumprogramacontendoadeclaraçãodeduasvariáveis(“a”e“b”, nasduaslinhasiniciais)eousodeambasemdoiscomandosdeatribuição(nasduaslinhasfinais).

Capítulo6

Linguagensrecursivas

Linguagensrecursivassãoaquelasquesãoaceitasporumtipomuitogeraldereconhecedor:a MáquinadeTuringsemlimitaçãodememória,tambémconhecidacomoMáquinadeTuring comfitainfinitaou,simplesmente,MáquinadeTuring.

Comoopróprionomesugere,asMáquinasdeTuringcomfitainfinitadiferemdas apresentadasnocapítuloanterior—asMáquinasdeTuringcomfitalimitada—justamente pelofatodenãoapresentaremrestriçõesquantoaocomprimentodafitadetrabalho.Noque serefereaosdemaisaspectos,elassãodefinidasdeformamuitosimilar.

Apesardesetratardeumadiferençaaparentementepoucosignificativa,ofatodeafita detrabalhocomportarinfinitasposiçõespossibilita,conformeestádemonstradonoTeorema 6.4,oreconhecimentodeumacategoriadelinguagensmaisabrangentedoqueaslinguagens sensíveisaocontexto.Estas,porsuavez,conformeveremos maisadiante,constituemum subconjuntoprópriodaslinguagensrecursivas.

Diferentementedaslinguagenssensíveisaocontexto,noentanto,nãohácaracterização conhecidaparaaslinguagensrecursivasemtermosgramaticais.Ouseja,nãoépossível caracterizaressaclassedelinguagensapartirdaformulaçãoderestriçõesaoformatodas produçõesgramaticaisgerais—procedimentoadotadoparadefinirasclassesdaslinguagens regulares,daslivresdecontextoetambémdassensíveisaocontexto.

Damesmaforma,nãosãoconhecidaseventuaispropriedadesestruturaisquepossamser consideradasparaefeitodecaracterizaçãodeumalinguagemcomosendorecursiva.Se,por outrolado,aslinguagensregulares,aslivresdecontextoe assensíveisaocontextopodemser facilmenteidentificadasapartirdetaispropriedades—concatenação,uniãoefechamentode termosnocasodasregulares,balanceamentodetermosnaslivresdecontextoevinculaçãode termosnassensíveisaocontexto—,aslinguagensrecursivasnãoexibemcaracterísticasde naturezaequivalente,quepoderiamservirparaidentificar umadeterminadalinguagemcomo sendoestritamentedessaclasse.

Aúnicacaracterizaçãoqueresta,portanto,ébaseadanomodelodereconhecimento.O restantedestecapítuloserádedicadoàformalizaçãoeàdiscussãodasMáquinasdeTuring esuaspropriedades.Nasequência,aslinguagensrecursivasserãodefinidascomosendo umaclasseparticulardelinguagensaceitaporessetipodedispositivo(poisaslinguagens recursivasnãosãoaúnicaclassedelinguagensporeleaceita).Finalmente,serádemonstrado quetodalinguagemsensívelaocontextoétambémrecursivae,alémdisso,queexistepelo menosumalinguagemrecursivaquenãoésensívelaocontexto.Emresumo,demonstrarse-áqueaclassedaslinguagenssensíveisaocontextoconstituiumsubconjuntopróprioda classedaslinguagensrecursivas.Linguagensquesãorecursivasporémnãosãosensíveisao contextosãodenominadaslinguagens estritamenterecursivas.

6.1MáquinasdeTuring

MáquinasdeTuring (comfitailimitadaouinfinita)sãodispositivosdereconhecimentode cadeiasquepossuemasseguintesdiferençasemrelaçãoàsMáquinasdeTuringcomfita limitada,discutidasnoCapítulo5:

1.Afitadetrabalhopossuicomprimentoinfinito,sendolimitadaàesquerdaesem limitaçãoàdireita.1

2.Acadeiadeentradaédelimitadaapenasàesquerda,pormeiodeumsímboloespecial,representadopor“<”,quenãofazpartedoalfabetodeentrada.Juntamente comessesímbolo,acadeiaaserprocessadaéposicionadadeformatalquefique ajustadaàesquerdasobreafita.Ocursordeacessoinicialmenteapontaosímbolo maisàesquerdadacadeiadeentrada,ouseja,osímboloimediatamenteàdireita domarcador“<”.2

3.Asposiçõesdafitaàdireitadoúltimosímbolodacadeiadeentradasãoinicialmentepreenchidascomumsímboloespecial—representadopor B,queindicaque aquelasposiçõesestãovagas.Osímbolo B tambémnãofazpartedoalfabetode entrada.3

4.Ocursordeacessopodesedeslocarlivrementesobreafitadetrabalho,excetopara aesquerdadaprimeiraposiçãodafita.Casoissoocorra,acomputaçãoencerra-se anormalmente.

AFigura6.1ilustraaconfiguraçãoinicialdeumaMáquinadeTuringcomcadeiade entradaiguala σ1σ2σ3...σn.Formalmente,umaMáquinadeTuringédefinidacomo:

M =(Q, Σ, Γ, δ, q0,<, B, F )

onde:

• Q éoconjuntofinitonãovaziodeestados.

• Σ éoalfabetodeentrada,formadoporumconjuntofinitonãovaziodesímbolos.

• Γ éumconjunto,tambémfinitoenãovazio,desímbolosquepodem serlidose/ou escritosnafitadetrabalho. Γ ⊇ Σ

• δ éafunçãoparcialdetransição, δ : Q × Γ → 2Q×Γ×{E,D} .

• q0 éoestadoinicial, q0 ∈ Q.

1Dependendodoautor,nãohálimitaçãotampoucoàesquerda.

2Algunsautoresdesconsideramousodomarcador“<”esupõemqueaprimeiraposiçãodafitadetrabalhoseja ocupadapeloprimeirosímbolodacadeiaaseranalisada.

3Dependendodoautor,outrossímbolossãousadospararepresentarposiçõesvagasdafitadetrabalho.

Figura6.1 MáquinadeTuring.

•“<” ∈ Γ,“<” / ∈ Σ,éosímboloqueindicaaprimeiraposiçãodafitadetrabalho. Durantetodaaoperaçãodamáquina,osímbolo“<”nãopodesergravadoemnenhuma outraposiçãodafita.

• B ∈ Γ, B / ∈ Σ,éosímboloutilizadoparapreencherinicialmentetodasas posições àdiretadacadeiadeentradanafita.Duranteaoperaçãodamáquina,osímbolo B podesergravadoemqualquerposiçãodafita.

• F ⊆ Q éoconjuntodeestadosfinais.

A configuração deumaMáquinadeTuringéindicadaporumatripla

(α, qk,β) ∈ Γ∗ × Q × Γ∗

onde qk éoestadocorrente, α ∈ Γ∗ éaporçãodoconteúdodafitadetrabalhoqueseencontra àesquerdadocursordeacesso,e β ∈ Γ∗ éaporçãodoconteúdodafitadetrabalhoquese encontraàdireitadocursordeacesso,incluindoaposiçãocorrentementeapontadaporele.

A configuraçãoinicial é (<, q0,γ),onde q0 éoestadoiniciale γ ∈ Σ∗ éacadeiade entradaaseranalisada.Ocursordeacessoaponta,portanto,exatamenteoprimeirosímbolo dacadeiadeentrada γ.Aporção α darepresentação (α, qk,β) corresponde,nestecaso, àcadeiaunitária <.Uma configuraçãofinal édefinidacomo (λ, q f , µ),com q f ∈ F e λ, µ ∈ Γ∗

Astransiçõescontidasnafunção δ especificampossibilidadesnãodeterminísticasde movimentação,queconduzemodispositivodeumaconfiguraçãoparaaconfiguraçãoseguinte.Diz-sequeodispositivo para quandoafunção δ nãofordefinidaparaopar (estado, símbolodeentrada) corrente.

Osímbolo“⊢”denotaumarelaçãosobreasconfiguraçõesdeumaMáquinadeTuring:

Portanto,amovimentaçãodeumaconfiguraçãoparaaseguinte érepresentadapor:

Emcasodetentativadedeslocamentodocursordeacessopara aesquerdadaprimeira posiçãodafita,acomputaçãoencerra-seanormalmente.Nestecaso,acadeiadeentradaé rejeitada,nãoimportandoseoestadoemqueamáquinaseencontraéfinalounão.

Arigor,oempregodosímbolo“<”parasinalizaroiníciodafitadetrabalhoédesnecessário.Diversostextosconsideramqueaprimeiraposiçãoda fitasejaocupadapeloprimeiro símbolodacadeiadeentrada,semperdadegeneralidade.Aincorporaçãodeleaomodelo,no entanto,contribuiparaaconstruçãodemáquinasmaissimples,namedidaemqueocontrole dosdeslocamentosdocursordeacesso,afimdeevitarotérminoanormaldacomputação, tambémpodesersimplificado.

Adefiniçãodafunçãodetransição δ deixaclaroquesetratadeumdispositivo não determinístico.Noentanto,tambémépossíveldefinirMáquinasdeTuringcom fitailimitada determinísticas,bastandoparaissomodificarafunçãodetransiçãopara:

ConformeaSeção6.3,MáquinasdeTuringcomfitailimitada nãodeterminísticas podemsempresertransformadasemMáquinasdeTuringcomfita ilimitadaequivalentes porém determinísticas,assimcomoocorrenocasodosautômatosfinitos.Portanto,pode-

510 Linguagensrecursivas

setrabalharindistintamentecomMáquinasdeTuringcomfita ilimitadanãodeterminísticas oudeterminísticas,semqueissoacarretequalquermodificaçãonaclassedelinguagensque taisdispositivossãocapazesdeaceitar.Talcaracterísticadifere,poroutrolado,daquelaque éexibidapelosautômatosdepilha,que,emsuaversãonãodeterminística,sãocapazesde reconhecerumaclassemaisampladelinguagensdoqueasversõesdeterminísticas.Difere, também,docasodasMáquinasdeTuringcomfitalimitada,pois atéomomentoaindanãose sabeseexisteounãoessaequivalência.

AlinguagemaceitaporumaMáquinadeTuringcomfitainfinitaé oconjuntodas cadeiasquesãocapazesdeconduzirodispositivodesdeasua configuraçãoinicial(única paraumadeterminadacadeiadeentrada)atéumaconfiguração finalqualquernaqualele estejaparado—sempossibilidadedemovimentação.Formalmente,

admitindo-se,comocondiçãodeparada,que

nãosejadefinida para (q f , σ).Estecritériodeaceitaçãoédenominado estadofinal paradiferenciardeoutros doiscritériosalternativos(porémequivalentes)quesãoapresentadosnaSeção6.2.

NocasodasMáquinasdeTuringdeterminísticas(comcritériodeaceitação“estado final”),bastaanalisaraconfiguraçãodeparada(sehouver)parasaberseacadeiafoiaceita ourejeitada.Éclaroqueacadeiapodeprovocarum“loop”infinito,masofatoéquepara cadacadeiadeentradaháumaúnicasequênciademovimentações.

NocasodasMáquinasdeTuringnãodeterminísticas(comcritériodeaceitação“estado final”),épossívelqueexistamváriassequênciasdemovimentaçõesparaumamesmacadeia deentrada.Paradeterminarseumacadeiadeentradaéaceita,rejeitadaouprovoca“loop”de processamentoinfinito,deve-seconsiderarasregrasapresentadasnaSeção5.4.

UmaMáquinadeTuring M,determinísticaounãodeterminística,particionaoconjunto Σ∗ (onde Σ éoseualfabetodeentrada),portanto,emtrêslinguagensdistintas: ACEITA(M), REJEITA(M) e LOOP(M).

Seja L alinguagemaceitaporumaMáquinadeTuring M.Se w1 ∈ L,então M para eaceita w1.Considere-se,porém,acadeia w2 ∈ Σ∗ L.Nestecaso, M podetantoparar, rejeitandoaentrada,quantoentraremloopinfinito,semnuncaatingirumacondiçãode parada.

Umalinguagem L édita recursiva seexistirpelomenosumaMáquinadeTuring M tal que:

1.Paratodacadeia w ∈ L, M paraeaceita w

2.Paratodacadeia z ∈ Σ∗ L, M paraerejeita z.

Ouseja, M atingeacondiçãodeparadaparatodaequalquercadeiaquelheésubmetida, nãoimportandoseestapertenceounãoa L.Emoutraspalavras, L érecursivaseexistir pelomenosumaMáquinadeTuringtalque L(M)= ACEITA(M), REJEITA(M)= Σ∗

ACEITA(M) e LOOP(M)= /0.EssaMáquinadeTuringpodeterfitalimitada(casoemque L,alémdeserrecursiva,étambémsensívelaocontexto)ouilimitada(casoemque L é recursiva,porémnãoésensívelaocontexto).

Umalinguagemrecursivaétambémdita linguagemdecidível.Essetermodenotaofato deque,paraessaclassedelinguagens,sempreexistepelomenosumaMáquinadeTuringque aceitaareferidalinguagem,qualquerquesejaacadeiausadacomoentrada(nãoimportase elapertenceounãoàlinguagem),equesemprepara.Aparadapodeocorrercomaceitação ourejeiçãodacadeia.

ConformeserádiscutidonoCapítulo7,aslinguagensrecursivasnãosãoaúnicaclasse delinguagensaceitaspelasMáquinasdeTuring.Naverdade, orelaxamentodacondiçãode paradaparacadeiasnãopertencentesàlinguagemfazcomque omodelopossaserusado paradefinirumaclassemaisampladelinguagens,denominadaslinguagensrecursivamente enumeráveis.

Exemplo6.1 Amáquina M apresentadanaFigura6.2étalque L(M)= abc(a |

.

Figura6.2 MáquinadeTuringqueaceita abc(a | b | c)∗ paraoExemplo6.1.

Osmovimentosque M executanaaceitaçãodealgumassentençaspertencentesa L,desdea configuraçãoinicialatéaconfiguraçãofinal,sãomostradosa seguir:

• (<, q0, abcB) ⊢ (< a, q1, bcB) ⊢ (< ab, q2, cB) ⊢ (< abc, q3, B) ⊢ (< abcB, q4,β)

• (<, q0, abcaB) ⊢ (< a, q1, bcaB) ⊢ (< ab, q2, caB) ⊢ (< abc, q3, aB) ⊢

(< abca, q3, B) ⊢ (< abcaB, q4,β)

• (<, q0, abccbaB) ⊢ (< a, q1, bccbaB) ⊢ (< ab, q2, ccbaB) ⊢ (< abc, q3, cbaB) ⊢

(< abcc, q3, baB) ⊢ (< abccbB, q3, aB) ⊢ (< abccbaB, q3, B) ⊢ (< abccbaB, q4,β)

Osímbolo B éusado,nestescasos,paragarantirqueacadeiadeentradanãocontenhasímbolos estranhosaoalfabeto {a, b, c}.Acadeia β,usadanaconfiguraçãofinaldostrêscasos,éformadapor umasequênciainfinitadesímbolos B

Arejeiçãodealgumascadeiaspertencentesa Σ∗,porémnãopertencentesa L,podeserilustrada atravésdosseguintesexemplos:

• (<, q0, b)

• (<, q0, aB) ⊢ (< a, q1, B)

• (<, q0, abb) ⊢ (< a, q1, bb) ⊢ (< ab, q2, b)

Note-seque,noscasosacima, M parasempreemconfiguraçõesnãofinais,umavezque,respectivamente, q0, q1 e q2 sãoestadosnãofinais.

L éumalinguagemrecursiva,umavezque M semprepara,qualquerquesejaacadeiadeentrada w ∈ Σ∗ quelhesejaapresentada.

Exemplo6.2 AMáquinadeTuring M ilustradanaFigura6.3aceitaalinguagem L = {wwR | w ∈ {a, b}∗ }.Sãoexemplosdecadeiasaceitaspor M:

• (<, q0, aaB) ⊢ (< X , q1, aB) ⊢ (< Xa, q1, B) ⊢ (< X , q2, aB) ⊢

(<, q3, XXB) ⊢ (< X , q0, XB)

• (<, q0, baabB) ⊢ (< Y, q4, aabB) ⊢ (< Ya, q4, abB) ⊢ (< Yaa, q4, bB) ⊢

(< Yaab, q4, B) ⊢ (< Yaa, q5, bB) ⊢ (< Ya, q6, aYB) ⊢ (< Y, q6, aaYB) ⊢

(<, q6,YaaYB) ⊢ (< Y, q0, aaYB) ⊢ (< YX , q1, aYB) ⊢ (< YXa, q1,YB) ⊢

(< YX , q2, aYB) ⊢ (< Y, q3, XXYB) ⊢ (< YX , q0, XYB)

• (<, q0, bbbbbbB) ⊢ (< Y, q4, bbbbbB) ⊢ (< Yb, q4, bbbbB) ⊢

(< Ybb, q4, bbbB) ⊢ (< Ybbb, q4, bbB) ⊢ (< Ybbbb, q4, bB) ⊢

(< Ybbbbb, q4, B) ⊢ (< Ybbbb, q5 , bB) ⊢ (< Ybbb, q6, bYB) ⊢

(< Ybb, q6, bbYB) ⊢ (< Yb, q6, bbbYB) ⊢ (< Y, q6, bbbbYB) ⊢

(<, q6,YbbbbYB) ⊢ (< Y, q0, bbbbYB) ⊢ (< YY, q4, bbbYB) ⊢

(< YYb, q4, bbYB) ⊢ (< YYbb, q4, bYB) ⊢ (< YYbbb, q4,YB) ⊢

Figura6.3 MáquinadeTuringqueaceita {wwR | w ∈{a, b}∗ } paraoExemplo6.2.

(< YYbb, q5, bYB) ⊢ (< YYb, q6, bYYB) ⊢ (< YY, q6, bbYYB) ⊢

(< Y, q6,YbbYYB) ⊢ (< YY, q0, bbYYB) ⊢ (< YYY, q4, bYYB) ⊢

(< YYYb, q4,YYB) ⊢ (< YYY, q5, bYYB) ⊢ (< YY, q6,YYYYB) ⊢

(< YYY, q0,YYYB)

Sãoexemplosdecadeiasrejeitadaspor M:

• (<, q0, bB) ⊢ (< Y, q4, B) ⊢ (<, q5,YB)

• (<, q0, abB) ⊢ (< X , q1, bB) ⊢ (< Xb, q1, B) ⊢ (< X , q2, bB)

• (<, q0, bbaaaaB) ⊢ (< Y, q4, baaaaB) ⊢ (< Yb, q4, aaaaB) ⊢ (< Yba, q4, aaaB) ⊢

(< Ybaa, q4, aaB) ⊢ (< Ybaaa, q4 , aB) ⊢ (< Ybaaaa, q4 , B) ⊢ (< Ybaaa, q5, aB)

Seja L ⊆ Σ∗ umalinguageme M umaMáquinadeTuring.Diz-seque M aceita (ou define) L se M écapazdeatingirumaconfiguraçãofinalparatodasascadeias quepertencem a L,nãoimportandooqueacontecequandoumacadeiapertencentea Σ∗ L ésubmetida a M.Poroutrolado,diz-seque M decide L se,paraqualquercadeiapertencentea Σ∗ , M semprepara,aceitandoassentençasde L erejeitandoasdemais.Finalmente, M reconhece L se M gerasaídasdistintasindicando,paracadacadeiapertencentea Σ∗,seelapertenceou nãoa L.Naturalmente,se M reconhece L,então M decideL.Se M decide L,normalmenteé simplesfazer M reconhecer L.Finalmente,se M decideoureconhece L,éclaroque M aceita L.Ameraaceitação,poroutrolado,nãoimplicaquesejapossíveldecidiroureconheceruma linguagem.

6.2Critériosdeaceitação

Ocritériodeaceitação“estadofinal”,definidonaSeção6.1e utilizadonosExemplos6.1e 6.2,podesersubstituído,semprejuízodalinguagemdefinidaporumaparticularMáquinade Turing,pelocritério“parada”,conformeexplicadoaseguir.

Capítulo7

Linguagensrecursivamente enumeráveis

Umalinguagem L édita recursivamenteenumerável (ousimplesmente irrestrita)sefor aceitaporpelomenosumaMáquinadeTuring M.Ouseja:

1.Paratodacadeia w ∈ L, M paraeaceita w.

2.Paratodacadeia z ∈ Σ∗ L, M paraerejeita z ouexecutaumasequênciainfinitade movimentações.

Emoutraspalavras, L érecursivamenteenumerávelseexistiralgumaMáquinadeTuringtalque L(M)= ACEITA(M),com REJEITA(M) ∪ LOOP(M)= Σ∗ ACEITA(M)

Taldefiniçãoinduzaumapartiçãodaclassedaslinguagensrecursivamenteenumeráveis,compostapelasseguintessubclasses(Figura7.1).

•Asubclassedaslinguagens L aceitasporMáquinasdeTuringqueparamparatodas ascadeiasdeentrada z ∈ Σ∗ L;talsubclassecorrespondeàclassedaslinguagens recursivas,apresentadaanteriormentenaSeção6.1.

•Asubclassedasdemaislinguagens L,asquaissãoaceitasporMáquinasdeTuring queiniciamumasequênciainfinitademovimentaçõesparapelomenosumacadeia deentrada z ∈ Σ∗ L.

Damesmaformaqueaslinguagensrecursivas,ediferentementedaslinguagensregulares,livresdecontextoesensíveisaocontexto,nãoseconhecequalquertipodeestrutura quepermitaidentificaraslinguagensrecursivamenteenumeráveisapenaspelainspeçãodas propriedadessintáticasdesuassentenças.

Aslinguagensrecursivamenteenumeráveissão,portanto,inicialmentecaracterizadasa partirdasMáquinasdeTuring.Conformeseráestudadoadiante,elastambémpodemsercaracterizadaspormeiodomodelomaisgeraldegramáticas,as chamadasgramáticasirrestritas (verSeção7.1).

Figura7.1 Subclassesdaclassedaslinguagensrecursivamenteenumeráveis.

536 Linguagensrecursivamenteenumeráveis

Amaiorimportânciadessaclassedelinguagensresideemsua aplicaçãoaodesenvolvimentoteóricodacomputação.

ConformeestudadonoCapítulo6,aslinguagensrecursivassãotambémconhecidas comolinguagensdecidíveis.Issoocorreporque,paratalclassedelinguagens,ésempre possívelobterumaMáquinadeTuringquesempreparaemrespostaaqualquerentradaque lhesejasubmetida,nãoimportaseaceitandoourejeitandotalentrada.Cadeiasquepertencem àlinguagemsãoaceitasecadeiasquenãolhepertencemsãorejeitadas.Essacaracterística éparticularmenteútilquandosedesejaestudaracomputabilidadededeterminadostiposde problema,emparticulardoschamadosproblemasdedecisão.

Umalinguagemédita estritamenterecursivamenteenumerável seelaforrecursivamenteenumerávelenãoforrecursiva.Ouseja,seelaforaceitaapenasporMáquinas deTuringquenecessariamenteentramem“loop”comalgumacadeiaquenãopertenceà linguagem.

7.1Gramáticasirrestritas

Umagramática G =(V, Σ, P, S) édita irrestrita senenhumarestriçãoadicionalforaplicada àssuasregrasdeprodução,quedevemseguiraformageral α → β, α ∈ V ∗NV ∗ ,β ∈ V ∗ Observarqueasgramáticasregulares,aslivresdecontexto eassensíveisaocontextosão casosparticularesdasgramáticasirrestritas.

Note-seque,diferentementedoqueocorrecomasgramáticas sensíveisaocontexto, asgramáticasirrestritasadmitemqueoladodireitodasregras(β)possuaumnúmerode símbolosmenorqueoladoesquerdocorrespondente(α).Issofazcomquepossahaver reduçãonotamanhodasformassentenciaisduranteoprocessodederivaçãodesentenças.

Algunsautoresconsideramumformatoaindamaisgeralparaasregrasdasgramáticasirrestritas: α ∈ V + ,β ∈ V ∗.Esseformatopermitequeoladoesquerdodasregrasseja formadoporqualquercombinaçãodesímbolosterminaisenão terminais,incluindocadeias formadasexclusivamenteporsímbolosterminais,oquenãoé permitidonoformatoaqui adotado.

Naverdade,ambasasdefiniçõessãoequivalentes,podendoserusadasindistintamente. Aconversãoderegrasdoformatomaisgeral(α ∈ V + ,β ∈ V ∗)paraoformatomenosgeral (α ∈ V ∗NV ∗ ,β ∈ V ∗)podeserfeitaaplicando-seatécnicautilizadanademonstraçãodoTeorema5.1,emquenovossímbolosnãoterminaissãocriadosesubstituemtodasasocorrências desímbolosterminais,eagramáticaéacrescidadeproduçõesunitáriasqueconvertemcada umdessesnovossímbolosnãoterminaisnossímbolosterminaiscorrespondentes.

Asconvençõeseaterminologiaadotadasnaapresentaçãoediscussãodosdemaistipos degramáticatambémsãoaplicáveisaocasodasgramáticasirrestritas.Derivações,formas sentenciaisealinguagemgeradapelagramáticasãodenotadasdeformaidênticaàqueles casos.

Exemplo7.2 Agramática G =({S, A,C, a, b, c}, {a, b, c}, P, S),com P:

{S → aAbc

A → aAbC | ε Cb → bC Cc → cc}

geraalinguagem aibici , i 1.EssamesmalinguagemfoianteriormenteformuladanoCapítulo5atravésdeumagramáticasensívelaocontexto(verExemplo5.14).Nopresenteexemplo,elaéformalizada atravésdeumagramáticairrestrita(porcausadaprodução A → ε,emque |A| > |ε|).Exemplosde derivação:

• S ⇒ aAbc ⇒ abc

• S ⇒ aAbc ⇒ aaAbCbc ⇒ aaaAbCbCbc ⇒ aaabCbCbc ⇒ aaabCbbCc ⇒ aaabbCbCc ⇒ aaabbbCCc ⇒ aaabbbCcc ⇒ aaabbbccc

Aaplicaçãodaprodução S → aAbc,seguidade n aplicaçõesdaprodução A → aAbC e,finalmente, daaplicaçãodaprodução A → ε,geraumaformasentencialdotipo an+1(bC)nbc.Atransposição dossímbolos“b”paraoladoesquerdo,juntoaossímbolos“a”,éfeitacomoauxíliodaprodução Cb → bC.Apósaaplicaçãodessaprodução n + 1vezes,chega-seàformasentencial an+1bn+1Cnc Finalmente,aaplicaçãodaprodução Cc → cc por n vezessubstituiosnãoterminais“C”pelosterminais “ c”correspondentes,conduzindoàgeraçãodasentença an+1bn+1cn+1 . ⋆

Exemplo7.3 Agramática G =({S, B, X , a, b}, {a, b}, P, S),com P:

{S → aBSa | aBXa

Ba → aB

BX → Xb aX → a}

geraalinguagem aibiai , i 1.Aprodução aX → a caracterizaestagramáticacomosendoirrestrita, umavezque |aX | > |a|

Asduasproduçõesiniciaisgeramformassentenciaisdotipo (aB)nXan.Apartirdesseponto, aaplicaçãorepetidadaprodução Ba → aB permiteobterformassentenciaisdotipo anBnXan.Resta, portanto,substituirossímbolosnãoterminais“B”porterminais“b”paragerarassentençaspretendidas, tarefaestaqueécumpridapelastrêsúltimasproduções.Onãoterminal“X”servecomodelimitador, separandoascadeiasàsuaesquerdaeàsuadireita.Eleéusado,inicialmente,comoreferênciapara substituirossímbolos“B”por“b”e,finalmente,paraseautorremoverdaformasentencial,gerando anbnan.Exemplosdederivação:

• S ⇒ aBXa ⇒ aXba ⇒ aba

• S ⇒ aBSa ⇒ aBaBSaa ⇒ aBaBaBXaaa ⇒ aaBBaBXaaa ⇒ aaBaBBXaaa ⇒ aaaBBBXaaa ⇒ aaaBBXbaaa ⇒ aaaBXbbaaa ⇒ aaaXbbbaaa ⇒ aaabbbaaa

7.2Formanormalparagramáticasirrestritas

Devidoaofatodeasgramáticasregulares,livresdecontextoesensíveisaocontextoconstituíremcasosparticularesdasgramáticasirrestritas,a formanormalqueseráapresentada aseguirpodeseraplicadaindistintamenteemqualquertipo degramáticaexaminadaatéo momento.

Ademonstraçãodoteoremaseguintebaseia-senademonstraçãode[46],que,porsua vez,éumageneralizaçãodaformaconhecidacomoFormaNormaldeKurodaparagramáticassensíveisaocontexto(verSeção5.3).

Teorema7.1(Formanormalparagramáticasirrestritas) “Todagramáticairrestrita G1 = (V1, Σ, P1, S) defineumalinguagem L quetambémpodesergeradaporumaoutragramática G2 =(V2, Σ, P2, S),equivalente,cujasproduçõessãotodasdasseguintesformas:(1) S → ε; (2) A → σ;(3) A → B;(4) A → BC;(5) AB → AC;(6) AB → CB;(7) AB → C,onde S, A, B,C ∈ N2 e σ ∈ Σ

ConformeoAlgoritmo7.1,descritoaseguir,oqualincorporaasseguintesetapas:

i.Eliminaçãodasproduçõesvazias.

ii.Incorporaçãodaprodução(1),casoacadeiavaziafaçapartedalinguagem.

iii.Substituiçãodossímbolosterminaispornovossímbolosnãoterminaiseincorporaçãodenovasproduçõesdaforma(2),umaparacadasímboloterminalde G1

iv.Substituiçãodasproduções α → β,emque |α| |β|,porumnovoconjuntode produçõesdasformas(3),(4),(5),(6)e(7).

v.Substituiçãodasproduções α → β,emque |α| > |β|,porumnovoconjuntode produçõesdasformas(3),(4),(5),(6)e(7).

Algoritmo7.1(Formanormalparagramáticasirrestritas) “Obtençãodeumagramática irrestritanaformanormal.”

• Entrada:umagramáticairrestritaG1 =(V1, Σ, P1, S).

• Saída:umagramáticairrestritaG2 =(V2, Σ, P2, S),naformanormal,etalque L(G2)= L(G1)

• Método:

1.Início:

2.Etapa(i):

Eliminam-seasproduçõesdaformaA → ε contidasemP1:

3.Etapa(ii):

Incorporaçãodacadeiavazia,seforocaso:

4.Etapa(iii):

Eliminaçãodosterminaisoriginaisesuasubstituiçãopornãoterminais correspondentes:

V

5.Etapa(iv):

1 }

Eliminaçãodasproduções α → β, |α| |β|: – Paracadaprodução α → β emP1,com |α| |β|,tem-se:

α = A1A2 Am

β = B1B2...Bn = B1B2...BmBm+1...Bn, comAi, B j ∈ N1, n m

1. –

Fazer:

N2 ← N2 ∪{Xi, 1 i n 1}

P2 ← P2∪

{A1 → B1X1

X1A2 → B2X2

X2A3 → B3X3

Xm 2Am 1 → Bm 1Xm 1

Xm 1Am → BmXm

Xm → Bm+1Xm+1

Xm+1 → Bm+2Xm+2

Xn 2 → Bn 1Xn 1

Xn 1 → Bn}

6.Etapa(v):Eliminaçãodasproduções α → β, |α| > |β|: – Paracadaprodução α → β,com |α| > |β|,tem-se:

β

7.Término:

AsproduçõesdotipoAB → CDgeradasnasetapas(iv)e(v)devemainda sersubstituídasporumconjuntodeproduçõesequivalente, porémem conformidadecomasformas(3),(4),(5),(6)e(7):

Todasasproduçõesde G2 estãoemalgumdosformatospermitidosnaformanormal desejada,completandoaprova.

Exemplo7.4 Deacordocomaetapa(iv

Paracompletar,aprodução(7.2)deveaindasersubstituída peloconjunto:

Transformaçãosemelhantedeveseraplicadanaprodução(7.3),poisasdemaisjáseencontramenquadradasnosformatosoriginalmentepropostos.

Capítulo8

Conclusões

Oestudodasclassesdelinguagensdiscutidasnestelivro,apresentadasemordemcrescente decomplexidade,econfiguradascomoconjuntossucessivamentemaisabrangentes,permite queseobtenhaumavisãoestruturadadoassunto,comespecialênfasenosaspectosquediferenciamcadaclasseestudadadarespectivaclasseantecessora.

Opresentecapítuloapresentaumresumodosprincipaisresultadosregistradosnoscapítulosanteriores,oferecendo,assim,umavisãopanorâmicadaessênciacontidaemcada umdessescapítulos,etambémdositensquefazemcomquecertasclassesdelinguagensse assemelhemousediferenciem.

Poroutrolado,aaplicabilidadedelinguagensformaiseautômatos,noscamposprático eteórico,nãoseencerraemsimesma,apresentandogranderelevânciaparaáreasqueserão destacadasmaisadiantenestecapítulo.

8.1Umahierarquiadeclassesdelinguagens

Estetextoapresentouosprincipaisresultadosdateoriade linguagensformaiseautômatos, seguindoestritamenteumasequênciaqueseinicioucomaclassedelinguagensmaisrestrita conhecida(adaslinguagensregulares),eseencerroucomaclassedelinguagensmaisamplaconhecida(adaslinguagensrecursivamenteenumeráveis),passandogradativamentede umaclassemaisrestritaparaamaisgeralseguinte,dentrodeumaescaladecomplexidade crescente,baseadanaHierarquiadeChomsky,eprocurandosempreampliarohorizontedo leitor,semanteciparmodelos,conceitosouteoriasrelativosàsclassesdelinguagensmais avançadas.

Aresumealgunsdosprincipaisresultadoscolhidosaolongo desteestudo,1 paracada classedelinguagensconsiderada,equeserãobrevementerevistosnasequência.

ApartirdaHierarquiadeChomskyoriginal(definidaem[9]e[10]),foramidentificadas,caracterizadasesituadasimportantessubclassesadicionaisdelinguagens:adaslinguagenslivresdecontextodeterminísticas,adaslinguagenslivresdecontextonãoambíguas,a daslinguagensrecursivaseadaslinguagensnãogramaticais.

Excluindo,naturalmente,aclassedaslinguagensnãogramaticais,todasasdemaisclassespodemsercaracterizadasemtermosgramaticais,exceto aclassedaslinguagensrecursivas,cujadefiniçãoébaseadaunicamentenoconceitodeumaMáquinadeTuringquesempre para,enãoemgramáticas.

Dopontodevistadoreconhecimento,trêsmodelosdistintos,comseisvariantesimportantes,foramapresentados:osautômatosfinitos,osautômatosdepilha(nasversõesdeterminísticaenãodeterminística)easMáquinasdeTuring(nasversõescomfitalimitada,

1Nestaseção,aindicação“N.A.”significa“nãoseaplica”,e“?”simbolizaqueoresultadonãoédoconhecimento dosautoresatéomomentodapublicaçãodestelivro.

Tabela8.1 Classesdelinguagensesuascaracterísticasprincipais

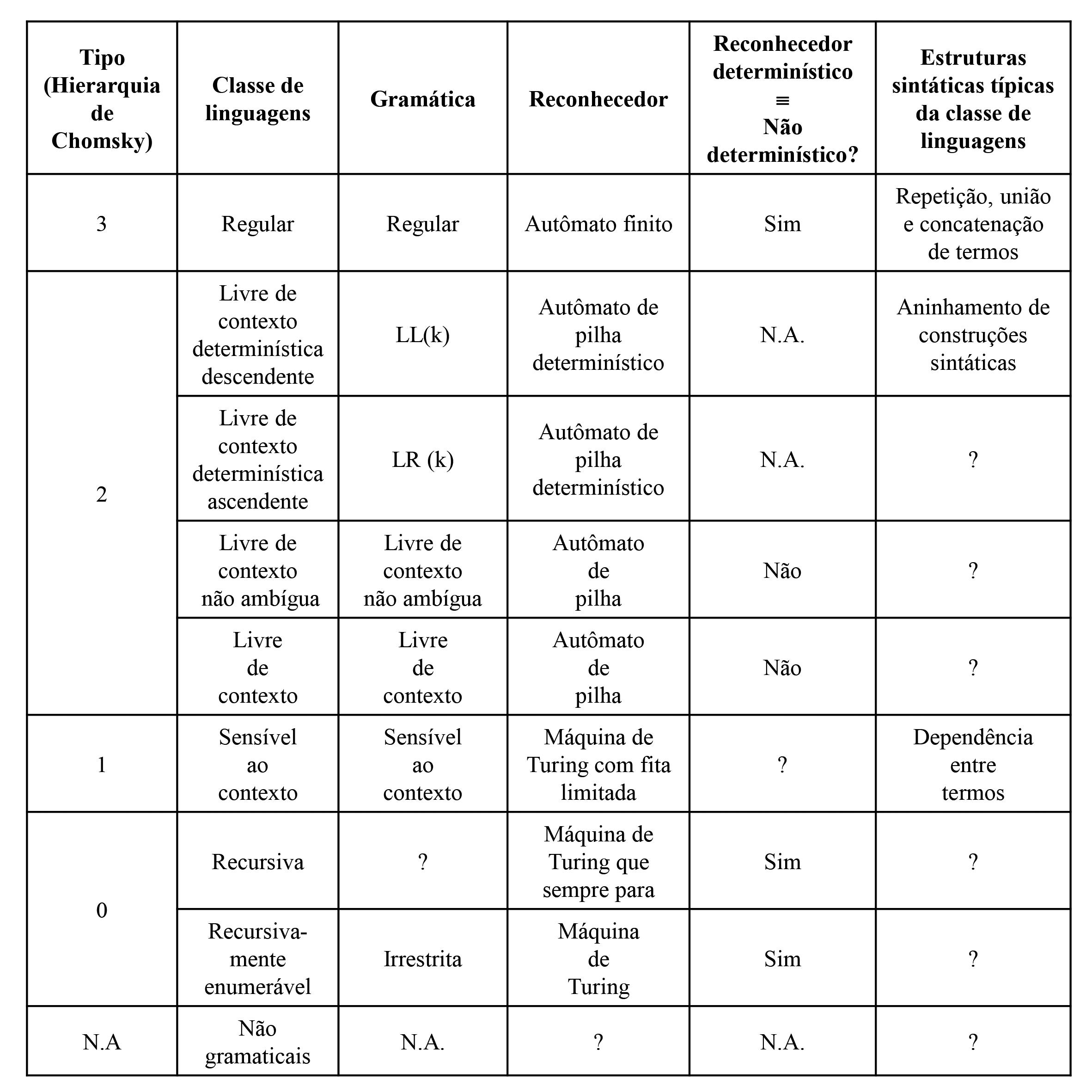
semlimitaçãodefitaequesempreparam,esemlimitaçãodefita,quepodemounãoparar). Cadaumdessesseistiposdedispositivoestáassociadoaoreconhecimentodeumasubclasse específicadelinguagens.

Quandoaquestãodaequivalênciaentreasversõesdeterminísticaenãodeterminística deummesmomodelodereconhecedoréconsiderada,sabe-secomcertezaqueapenasos autômatosdepilhapossuemversõesqueaceitamsubclassesdiferentesdelinguagens.ExcetoaMáquinadeTuringcomfitalimitada,paraaqualosautoresnãotêmconhecimentode quesetenhaconseguidodemonstraratéhojeseexisteounãoequivalênciaentreasversões determinísticaenãodeterminística([47]),todosasdemaisformulaçõesetiposdereconhecedorpossuemversõesquesãocomprovadamenteequivalentesquantoaessequesito.

Dequalquerforma,osfatoscomrelaçãoàsversõesdeterminísticaenãodeterminística decadaumdosmodelosdereconhecedorconsideradossãoosseguintes:

•Autômatofinito:asversõessãoequivalentes,existeumalgoritmodeconversãoe eleéusadonaprática(paraaumentaraeficiênciadaanálise).

•Autômatodepilha:asversõesnãosãoequivalentes.

•MáquinadeTuringcomfitalimitada:nãosesabeseasversões sãoequivalentesou não.

•MáquinadeTuringcomfitailimitada:asversõessãoequivalentes,existeumalgoritmodeconversão,porémelenãoéusadonaprática(porqueaumentamuitoo tempodeexecução).

Adicionalmente,épossíveldeterminarapossibilidadedeobtençãodeumreconhecedorquenuncaentraem“loop”infinitoparacadaumadasprincipaisclassesdelinguagens consideradas:

•Linguagemregular:sim,épossível;existeumalgoritmoquemanipulaoautômato finitocorrespondentediretamente(bastaeliminarastransiçõesemvaziodele).

•Linguagemlivredecontexto:sim,épossível;porém,nãoexisteumalgoritmoque manipuleoautômatodepilhacorrespondentediretamente(nestecaso,ésuficiente construirumautômatodepilhacombasenaFormaNormaldeChomskyouForma NormaldeGreibachdagramáticaquegeraarespectivalinguagem).

•Linguagemsensívelaocontexto:sim,épossivel;porém,nãoexisteumalgoritmo quemanipuleaMáquinadeTuringcomfitalimitadadiretamente.

•Linguagemrecursivamenteenumerável:sóépossívelsealinguagemfortambém recursiva;nestecaso,porém,nãoexisteumalgoritmoqueconsigatransformara correspondenteMáquinadeTuring;sealinguagemnãoforrecursiva,entãonãoé possível.

Finalmente,éconvenienteconsiderarasdiferentesclassesdelinguagensdopontode vistaexclusivodaspropriedadessintáticasqueasdistinguemumasdasoutras—independentementedotipodegramáticasoureconhecedoresempregadosparaasuaespecificação. Dessaforma,pelomenostrêsclassesdelinguagenspodemser facilmenteidentificadas:adas linguagensregulares,adaslinguagenslivresdecontextodeterminísticaseadaslinguagens sensíveisaocontexto.Asdemaisclassesdelinguagens,noquesejadoconhecimentodos autoresdestelivro,nãoexibempropriedadessintáticasconhecidasquesepossaconsiderar como“típicas”detodasaslinguagensdamesmaclasse.

Conformeresultadosapresentadosaolongodotexto,todasasclassesdelinguagens consideradasconstituemumahierarquiadeinclusãoprópria,queiniciacomaclassedas linguagensregulareseterminacomaclassedaslinguagensnãogramaticais.AFigura8.1 ilustraareferidahierarquiaeincluireferênciasparaexemplosdelinguagensquetornama relaçãodeinclusãoprópriaemcadanível.Aslinguagens(erespectivasclasses)consideradas

580 Conclusões

• L6 = {anbncn | n 1} (Sensíveisaocontexto)

• L7 = {αi | αi / ∈ L(Gi), ∀i 1}

(Recursivas)

• L8 = {C(M)w ∈ Σ∗ | w ∈ L(M)} (Recursivamenteenumeráveis)

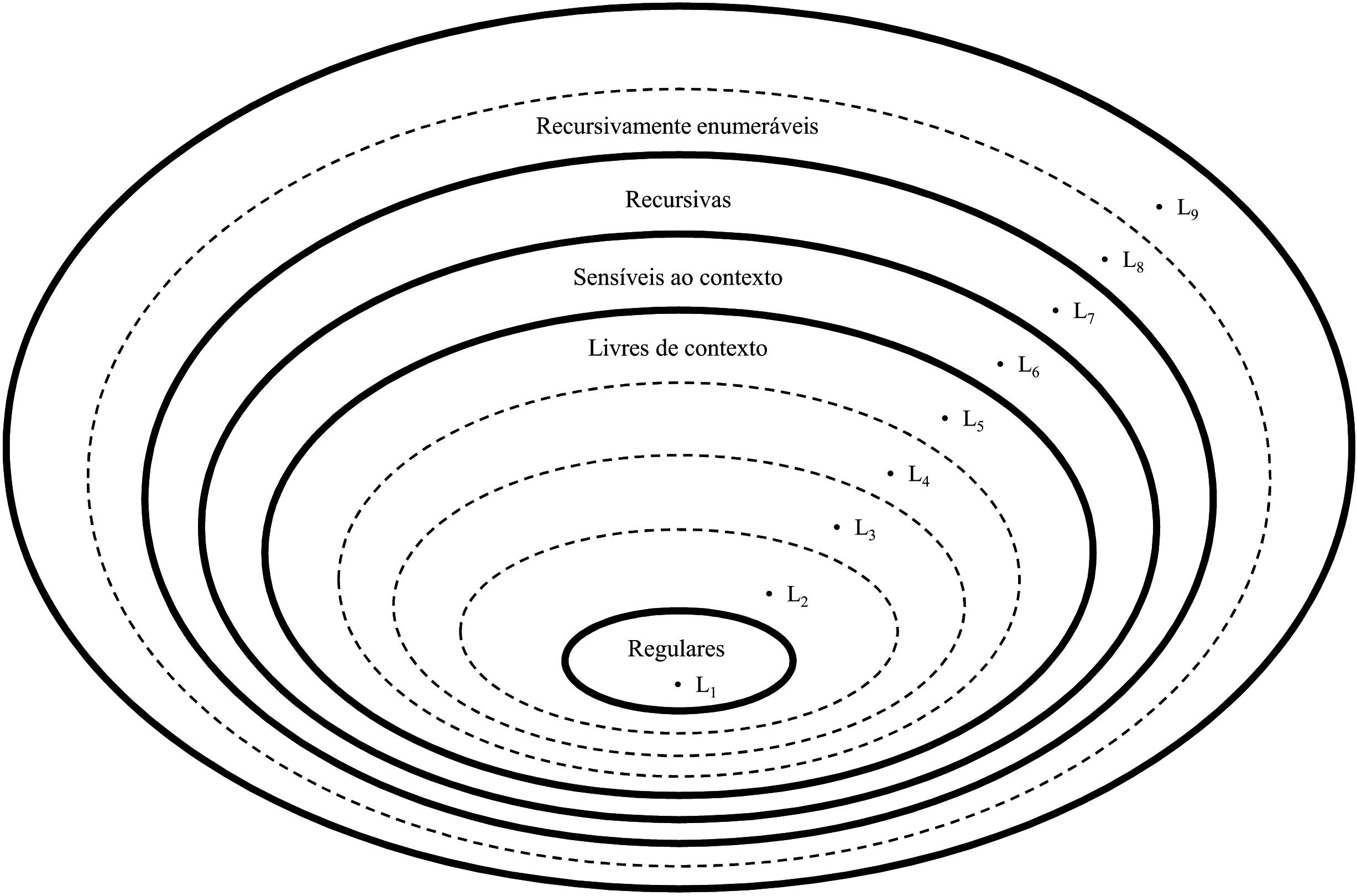
• L9 = {C(M)w ∈ Σ∗ | w / ∈ L(M)} (Estruturadasemfrases)

Asrelaçõesdeinclusãoeinclusãoprópriaentreasprincipaisclassesdelinguagens relacionadasnaFigura8.1foramjustificadasaolongodoscapítulosanteriores,deacordo comaestratégiadescritaaseguir.Asclassesdelinguagens sãoconsideradasaospares,com Cint denotandoaclassemaisinternae Cext ,aclassemaisexterna.

1. Cext :Linguagenslivresdecontexto. Cint :Linguagensregulares.

•Linguagemanalisada: {anbn | n 1}

• Cint ⊂ Cext :Linguagensregularessãogeradasporgramáticaslivresde contexto(Teorema4.17).

• Cint = Cext :

– {anbn | n 1} nãoélivredecontexto,pelo“PumpingLemma” paraaslinguagensregulares(Teorema3.22);

– {anbn | n 1} élivredecontextopoiségeradaporumagramáticalivredecontexto(Exemplo5.20).

Figura8.1 Hierarquiadeinclusãoprópriadasclassesdelinguagens.

2. Cext :Linguagenssensíveisaocontexto. Cint :Linguagenslivresdecontexto.

•Linguagemanalisada: {anbncn | n 1}

• Cint ⊂ Cext :Linguagenslivresdecontextosãogeradasporgramáticas sensíveisaocontexto(Teorema5.5).

• Cint = Cext :

– {anbncn | n 1} nãoélivredecontexto,pelo“PumpingLemma” paraaslinguagenslivresdecontexto(Teorema4.21);

– {anbncn | n 1} ésensívelaocontextopoiségeradaporuma gramáticasensívelaocontexto(Exemplo5.19).

3. Cext :Linguagensrecursivas. Cint :Linguagenssensíveisaocontexto.

•Linguagemanalisada: LR = {αi | αi / ∈ L(Gi), ∀i 1}

• Cint ⊂ Cext :LinguagenssensíveisaocontextosãoreconhecidasporMáquinasdeTuringcomfitalimitada(Teorema6.3).

• Cint = Cext :

– LR = {αi | αi / ∈ L(Gi), ∀i 1} nãoésensívelaocontexto,por contradição(Teorema5.8);

– LR = {αi | αi / ∈ L(Gi), ∀i 1} érecursiva,porconstrução(Teorema6.4).

4. Cext :Linguagensrecursivamenteenumeráveis.

Cint :Linguagensrecursivas.

•Linguagemanalisada: LU = {C(M)w | w ∈ L(M)}.

• Cint ⊂ Cext :LinguagensrecursivassãoreconhecidasporMáquinasdeTuring(Teorema7.6).

• Cint = Cext :

– LU = {C(M)w | w ∈ L(M)} nãoérecursiva,porcontradição(Teorema6.5);

– LU = {C(M)w | w ∈ L(M)} érecursivamenteenumerável,por construção(Teorema7.7).

AsTabelas8.2e8.3apresentamumresumodasprincipaispropriedadesdefechamento edasprincipaisquestõesdedecisãoconsideradasparacada classedelinguagens.Onde empregada,aletra“N”indicaqueaclassenãoéfechadaemrelaçãoaumadeterminada propriedadeou,ainda,queaquestãonãoédecidívelparaaquelaclassedelinguagens.

8.2Próximospassos

Oestudodaslinguagensformaiseautômatoséfundamentalparaoentendimentoeodomínio deváriasoutrasáreasdacomputação,mastrêssedestacamperanteasdemais:

•Construçãodeprocessadoresparalinguagensdeprogramação.

•Estudodadecidibilidadedelinguagens(econjuntos).

•Estudodacomplexidadedealgoritmos.

Aslinguagensregulareseaslinguagenslivresdecontextosãoabaseparaaespecificaçãodelinguagensdeprogramaçãodealtonível,etambémpara oprojetoeaimplementação deseusrespectivosanalisadoressintáticos.Estes,porsuavez,sãoabaseparaaestruturaçãodecompiladoreseinterpretadoresparaasinúmeraslinguagensusadasnodiaadiado profissionaledoleigoemcomputação,queasempregamextensivamente,deformadireta ouindireta,conscienteouinconsciente.Pode-sedizer,portanto,queessaáreaconstituiuma importanteaplicaçãopráticadateoriadelinguagensformaiseautômatos.

Outrasáreasdeaplicaçãoincluemaespecificaçãoeaimplementaçãodeprotocolosde comunicaçãoedelinguagensdescript,dedescriçãodedados,deprojetodecircuitosdigitais edemodelagemdesistemasbiológicos.Anoapósano,asaplicaçõespráticasdateoriadas linguagensregularesetambémdaslinguagenslivresdecontextonãoparadeaumentar,tanto dentroquantoforadacomputação.

Poroutrolado,nocampoteórico,provavelmenteamaioraplicaçãodateoriadelinguagenseautômatosrecaisobreoestudodadecidibilidadedelinguagensedacomplexidadede algoritmos.ConformediscutidonosCapítulos6e7,aconstataçãodadecibilidadedelinguagensconfereacertezadaexistênciadealgoritmosquepossamserusadospararesolvera classedeproblemasrepresentadaportaislinguagens.Aconstataçãodaindecidibilidadede umalinguagem,porsuavez,garanteainexistênciadeumasoluçãogeralparaoproblema, quandoseconsideramtodasassuaspossíveisinstâncias.

Aquestão,noentanto,nãoseresumeàmeraexistênciaouinexistênciadealgoritmos paraseresolverdeterminadosproblemas.

Alémda decidibilidade deumproblema(representadopormeiodeumalinguagem), deseja-seestabelecerosparâmetrosqueindiquemograudedificuldadenaexecuçãodesoluçõesparaumcertoproblema.Assim,nãobastaumproblemaserdecidível.Éimportante

Tabela8.2 Resumodasprincipaispropriedadesdefechamento

Tabela8.3 Resumodasprincipaispropriedadesdedecisão

Concebido como referência para cursos superiores da área de computação, este livro explora tópicos sobre as linguagens definidas pela Hierarquia de Chomsky. Contudo, seu alcance foi expressivamente ampliado pela inclusão de introduções à matemática discreta, aos conceitos básicos de linguagens, à classe das linguagens recursivas, à análise sintática descendente, à decidibilidade e à complexidade.

Fruto de diversos anos da experiência docente e dedicação dos autores, em diversas instituições de ensino, à disciplina Linguagens Formais e Autômatos, esta obra, repleta de exemplos e exercícios, mitiga a aridez intrínseca dos muitos assuntos estudados, tornando-os mais acessíveis a um público-alvo amplo e diversificado.