Mathematics with Applications In the Management Natural and Social Sciences 11th Edition Lial Soluti by edithiw64

Chapter 2 Graphs, Lines, and Inequalities

Section 2.1 Graphs, Lines, and Inequalities

1. (1, –2) lies in quadrant IV

(–2, 1)lies in quadrant II

(3, 4) lies in quadrant I

(–5, –6) lies in quadrant III

2. (,2)  lies in quadrant I

  3,2 lies in quadrant IV

(4,0) lies in no quadrant (3,3) lies in quadrant II

3. (1, –3) is a solution to 3x – y – 6 = 0 because 3(1) – (–3) – 6 = 0 is a true statement.

4. (2, –1) is a solution to 22 6815xyxy because 22 (2)(–1)6(2)8(1)15  is a true statement.

5. (3, 4) is not a solution to  22 226xy because 22 (32)(42)37,  not 6.

6. (1, –1) is not a solution to 22 4 23 xy because 22 1(1)5 236  , not 4 .

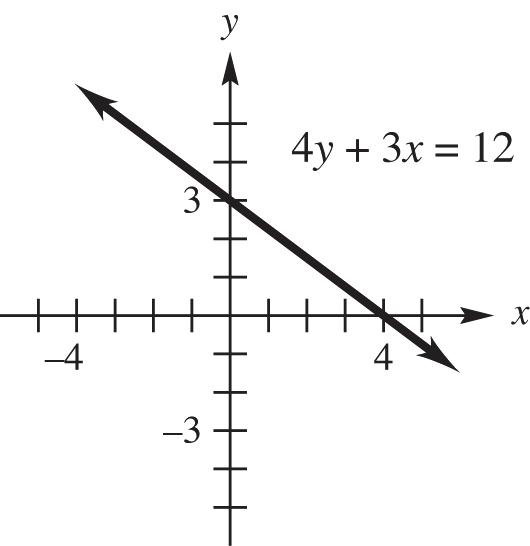
7. 4y + 3x = 12

Find the y-intercept. If x = 0, 43(0)124123 yyy 

The y-intercept is 3. Next find the x-intercept. If y = 0,   403123124 xxx 

The x-intercept is 4. Using these intercepts, graph the line.

8. 2x + 7y = 14

Find the y-intercept. If x = 0, 2(0)7147142 yyy 

The y-intercept is 2. Next find the x-intercept. If y = 0,

  270142147 xxx 

The x-intercept is 7. Using these intercepts, graph the line.

9. 8x + 3y = 12

Find the y-intercept. If x = 0, 3124 yy

The y-intercept is 4.

Next, find the x-intercept. If y = 0, 123 812 82 xx

The x-intercept is 3 2

Using these intercepts, graph the line.

10. 9y – 4x = 12

Find the y-intercept. If x = 0, 124 94(0)12912 93 yyy 

The y-intercept is 4 3

Next find the x-intercept. If y = 0, 9(0)4124123 xxx 

The x-intercept is –3.

(continuedonnextpage)

Mathematics with Applications In the Management Natural and Social Sciences 11th Edition Lial Solutions Manual Full Download: http://testbanktip.com/download/mathematics-with-applications-in-the-management-natural-and-social-sciences-11th-edition-lial-solutions-manual/ Download all pages and all chapters at: TestBankTip.com

Using these intercepts, graph the line.

15. The x-intercepts are –1 and 2. The y-intercept is –2.

16. The x-intercept is 1. There is no y-intercept.

17. 3x + 4y = 12

To find the x-intercept, let y = 0: 34(0)123124 xxx 

The x-intercept is 4.

11. x = 2y + 3

Find the y-intercept. If x = 0, 3 02323 2 yyy 

The y-intercept is 3 2

Next, find the x-intercept. If y = 0, 2(0)33xx

The x-intercept is 3. Using these intercepts, graph the line.

To find the y-intercept, let x = 0:   304124123 yyy 

The y-intercept is 3.

18. x – 2y = 5

To find the x-intercept, let y = 0: 2(0)55xx 

The x-intercept is 5.

To find the y-intercept, let x = 0. 5 02525 2 yyy 

The y-intercept is 5 2

19. 2x – 3y = 24

To find the x-intercept, let y = 0: 23(0)2422412 xxx 

The x-intercept is 12.

To find the y-intercept, let x = 0: 2(0)3243248 yyy 

12. x – 3y = 0

Find the y-intercept. If x = 0, 300 y 

The y-intercept is 0. Since the line passes through the origin, the x-intercept is also 0. Find another point on the line by arbitrarily choosing a value for x. Let x = 3. Then, 331 yy 

The point with coordinates (3, 1) is on the line. Using this point and the origin, graph the line.

The y-intercept is –8.

20. 3x + y = 4

To find the x-intercept, let y = 0: 4 30434 3 xxx 

The x-intercept is 4 3

To find the y-intercept, let x = 0: 3(0)44 yy 

The y-intercept is 4.

21. 2 9 yx

To find the x-intercepts, let y = 0: 22 09993 xxx 

The x-intercepts are 3 and –3.

To find the y-intercept, let x = 0: 099 y 

The y-intercept is –9.

13. The x-intercepts are where the rays cross the x-axis, –2.5 and 3. The y-intercept is where the ray crosses the y-axis, 3.

14. The x-intercept is 3; the y-intercept is 1.

CHAPTER2GRAPHS,LINES,ANDINEQUALITIES

22. 2 4 yx

To find the x-intercepts, let y = 0:

To find the y-intercept, let x = 0: 2 3(0)4(0)44 y 

The y-intercept is –4.



22 044 4 not a real number xx x



There is no x-intercept.

To find the y-intercept, let x = 0:

2 044 y 

The y-intercept is 4.

23. 2 20 yxx

To find the x-intercepts, let y = 0:

2 0200(5)(4) 505 or 404 xxxx xxxx  

The x-intercepts are –5 and 4.

To find the y-intercept, let x = 0:

2 002020 y 

The y-intercept is –20.

24. 2 561yxx

To find the x-intercepts, let y = 0:

2 05610(51)(1)



xxxx xxxx

27. 2 yx

x-intercept: 2 00 xx 

-intercept: y = 0



1 510 or 101 5

The x-intercepts are 1 5 and –1.

To find the y-intercept, let x = 0:

2 5(0)6(0)11 y 

The y-intercept is 1.

25. 2 257yxx

To find the x-intercepts, let y = 0:

2 0257 xx 

This equation does not have real solutions, so there are no x-intercepts.

To find the y-intercept, let x = 0:

2 2(0)5(0)77 y 

The y-intercept is 7.

26. 2 344yxx

To find the x-intercepts, let y = 0:

2 033 y

 

xxxx xxxx

2 03440(32)(2) 2 320 or 202 3

The x-intercepts are 2 and 2 3

SECTION2.1GRAPHS,LINES,ANDINEQUALITIES 49

xy –2 4 –1 1 0 0 1 1 2 4

2 2 yx x-intercept:

real

  y-intercept:

yy xy –2 6 –1 3 0 2 1 3 2 6 29. 2 3 yx x-intercepts:

 y-intercepts:

 xy –3 6 –1 –2 0 –3 1 –2 3 6



28.

22 022 2 not a

number

2 022

22 0333 xxx

30. 2 2 yx

x-intercept: 2 020 xx 

-intercept: 2(0)0 y 

33. 3 yx 

x-intercept: 3 00 xx 

y-intercept: 3 00yy

34. 3 3 yx

x-intercept: 33 3 0333 xxx 

y-intercept: 3 033yy

32. 2 23yxx

-intercept: 2 0230(3)(1) 303 or 101 xxxx xxxx

-intercept: 2 (0)2(0)33 y 

35. 3 1 yx

x-intercept: 33 3 01111 xxx 

y-intercept: 3 011 y  xy –2 –7

CHAPTER2GRAPHS,LINES,ANDINEQUALITIES



xy –2 8 –1 2 0 0 1 2 –2 8

 x

  y

xy –2

–1 12 0 5 1 0 2 –3

31. 2 65yxx

-intercept: 2 0650(1)(5) 101 or 505 xxxx xxxx

-intercept: 2 (0)6(0)55 y 

  y

xy –3 0 –2 –3 –1 –4 0 –3 1 0

xy –2 –8 –1 –1 0 0 1 1 2 8

0 –3 1 –2 2 5

–2 –11 –1 –4

–1 0 0 1 1 2 2 9

x-intercept:

y-intercept:

41. 2008; 20 million pounds

42. 2009; approximately 11 million pounds

43. 2011

44. No years

45. (a) about $1,250,000

(b) $1,750,000

46. (a) about $1,000,000

(b) about $2,250,000.

47. (a) about $500,000

(b) about $1,000,000.

SECTION2.1GRAPHS,LINES,ANDINEQUALITIES 51

36. 3 2 x y  x-intercept: 3 00 2 x x  y-intercept: 0 0 2 y  xy –2 –4 –1 –1/2 0 0 1 1/2 2 4 37. 4 yx x-intercept: 04044 xxx  y-intercept: 0442 y  xy –2 21.4  –1 31.7  0 2 2 62.4  5 3 38. 2 yx x-intercept: 02022 xxx  y-intercept: 022, y  not a real number xy 2 0 3 1 6 2 11 3 39. 2 4 yx  x-intercept: 222 04044 42 xxx x   y-intercept: 42 y  xy –2 0 –1 31.7  0 2 2 31.7  5 0

2 9



40.

222 09099 93 xxx x  

2 9093 y  xy –3 0 –1 222.8  0 3 1 222.8  3 0

48. (a) about $250,000

(b) about $1,250,000

49. beef, about 59 pounds; chicken, about 83 pounds; pork, about 47.5 pounds

50. 2002

51. 2001

52. In 2001, annual per person beef consumption was about 66 pounds, while in 2010, annual per person beef consumption was about 59 pounds, so beef consumption decreased about 7 pounds between 2001 and 2010.

53. about $512 billion

54. in 2005–2010

55. in 2008–2015

56. In 2015, sales are projected to be about $590 billion, while in 2010, sales were about $523 billion, so sales are projected to increase about $67 billion.

57. H–P, about $16.50; Intel, about $21

58. H–P, about $17.00; Intel, about $22

59. About $17.25 on Day 14

60. About $22.60 on Day 12

61. No

62. On day 1, the H–P share price was about $15.00, while the H–P share price was about $16.50 on day 21. So, the H–P share price increased by about $1.50 for the month.

CHAPTER2GRAPHS,LINES,ANDINEQUALITIES

63. 2 1 yxx 64. 2 2 yxx  65. 3 (3)yx 66. 3222yxx 67. 3231yxxx 68. 4252yxx

69. 4322 yxxx 

The “flat” part of the graph near 1 x  looks like a horizontal line segment, but it is not. The y values increase slightly as you trace along the segment from left to right.

70. (a) 4322 yxxx 

74. x ≈ .7555

[–3, 3] by [–5, 5]

75. x ≈ –1.7521

[–3, 3] by [–2, 12]

76. x ≈ 2.7693

(b) The lowest point on the graph is approximately at (–.5, –.6875). Answers vary.

71. 1.1038 x 

[–3, 3] by [–2, 6]

72. .6823 x 

[–1, 53] by [–5, 5]

77. 32 .05561.2869.7617.4yxxx 

[4, 9] by [0, 10]

The maximum value of the total assets between 2005 and 2008 was approximately $6.99 trillion.

78. 32 .05561.2869.7617.4yxxx 

[–3, 3] by [–3, 3]

73. 2.1017 x 

[7, 12] by [0, 10]

The minimum value of the total assets between 2008 and 2011 was approximately $6.79 trillion.

[–3, 3] by [–5, 5]

SECTION2.1GRAPHS,LINES,ANDINEQUALITIES 53

79. Plot 32 y.3287.7559.0397.1 xxx  on [6, 12] by [40, 50], then find the minimum of the curve.

6. Through the origin, (0, 0), and (8, –2) slope 2021 8084 

7. Through (–1, 4) and (–1, 6) 642 slope ,not defined 1(1)0

The slope is undefined.

The minimum value of the household assets between 2007 and 2011 was approximately $45.41 trillion.

80. Plot 32 y.3287.7559.0397.1 xxx  on [4, 9] by [45, 55], then find the maximum of the curve.

8. Through (–3, 5) and (2, 5) slope 550 0 2(3)5

9. b = 5, m = 4 y = mx + b y = 4x + 5

10. b = –3, m = –7 y = mx + b

y = –7x – 3

11. b = 1.5, m = –2.3

y = mx + b

y = –2.3x + 1.5

12. b = –4.5, m =2.5

The maximum value of the household assets between 2005 and 2008 was approximately $49.24 trillion.

Section 2.2 Equations of Lines

1. Through (2, 5) and (0, 8) 8533 slope 0222

2. Through (9, 0) and (12, 12) slope 12012 4 1293

3. Through (–4, 14) and (3, 0) slope 14014 2 437

4. Through (–5, –2) and (–4, 11) slope 21113 13 5(4)1

5. Through the origin and (–4, 10); the origin has coordinate (0, 0). 100105 slope 4042

54 CHAPTER2GRAPHS,LINES,ANDINEQUALITIES

x   













4.5 13. b = 4, 3 4 m  y = mx + b 3 4 4 yx 14. b = –3, 4 3 m  y = mx + b 4 3 3 yx 15. 2x – y = 9 Rewrite in slope-intercept form. 29 29 yx yx   m = 2, b = –9.

= mx + b

= 2.5x –

16. x + 2y = 7

Rewrite in slope-intercept form.

17. 6x = 2y + 4

Rewrite in slope-intercept form.

24. There are many correct answers, including:

Rewrite in slope-intercept form.

25. (a) Largest value of slope is at C.

(b) Smallest value of slope is at B.

(d) Closest to 0 is at D

26. (a) y = 3x + 2

The slope is positive, and the y-intercept is positive. This is line D.

(b) y = –3x + 2

The slope is negative, and the y-intercept is positive. This is line B.

The slope is positive, and the y-intercept is negative. This is line A.

(d) y = –3x – 2

The slope is negative, and the y-intercept is negative. This is line C.

Rewrite in slope-intercept form.

21. 2x – 3y = 0

Rewrite in slope-intercept form.

22. y = 7 can be written as

23. x = y – 5

Rewrite in slope-intercept form.

27. 2x – y = –2

Find the x-intercept by setting y = 0 and solving for x: 202221 xxx 

Find the y-intercept by setting x = 0 and solving for y: 2(0)222 yyy 

Use the points (–1, 0) and (0, 2) to sketch the graph:

SECTION2.2EQUATIONSOFLINES 55

27 17 22 yx yx   17 22,.mb

26432 yxyx  m = 3, b = –2.

18. 4x + 3y = 24

3424 4 8 3 yx yx   4 ,8. 3 mb

9616 9616 216 39 yx yx yx    216 39,.mb

19. 6x – 9y = 16 Write in slope-intercept form.

20. 4x + 2y = 0

242 yxyx  m = –2, b

= 0.

2 32 3 yxyx  2 ,0. 3 mb

y = 0

m = 0, b

x + 7

= 7.

y = x

m = 1, b

+ 5

= 5

28. 2y + x = 4

Find the x-intercept by setting y = 0 and solving for x: 2(0)44 xx 

Find the y-intercept by setting x = 0 and solving for y: 204242 yyy 

Use the points (4, 0) and (0, 2) to sketch the graph:

31. 4x – 5y = 2

Find the x-intercept, by setting y = 0 and solving for x: 1

45(0)242 2 xxx 

Find the y-intercept by setting x = 0 and solving for y:

29. 2x + 3y = 4

Find the x-intercept by setting y = 0 and solving for x: 23(0)4242 xxx 

Find the y-intercept by setting x = 0 and solving for y: 4 2(0)3434 3 yyy 

Use the points (2, 0) and 4 0, 3  

to sketch the graph:

Use the points 1 ,0 2 

and 2 0, 5

to sketch the graph:

30. –5x + 4y = 3

Find the x-intercept by setting y = 0 and solving for x: 3

54(0)353 5 xxx 

Find the y-intercept by setting x = 0 and solving for y: 3 5(0)4343 4 yyy 

Use the points 3 ,0 5    and 3 0, 4    to sketch the graph:

32. 3x + 2y = 8

Find the x-intercept by setting y = 0 and solving for x:

Find the y-intercept by setting x = 0 and solving for y:

Use the points 8 ,0 3     and (0, 4) to sketch the graph:

CHAPTER2GRAPHS,LINES,ANDINEQUALITIES



2 4(0)5252 5 yyy 



  

 

32(0)838 3 xxx 

3(0)28284

yyy 

33. For 4x – 3y = 6, solve for y

For 3x + 4y = 8, solve for y.

38. 2x – y = 6 and x – 2y = 4

Solve each equation for y to find the slope.

The two slopes are 4 3 and 3 4 . Since

, the lines are perpendicular.

34. 2x – 5y = 7 and 15y – 5 = 6x Solve each equation for y to find the slope.

The slopes are not equal, and their product is

, not –1, so the lines are neither parallel nor perpendicular.

39. Triangle with vertices (9, 6), (–1, 2) and (1, –3).

a. Slope of side between vertices (9, 6) and (–1, 2):

Slope of side between vertices (–1, 2) and (1, –3):

The slope of each line is 2 , 5 so the lines are parallel.

35. For 3x + 2y = 8, solve for y.

For 6y = 5 – 9x, solve for y

Since the slopes are both 3 2 , the lines are parallel.

36. x – 3y = 4 and y = 1 – 3x Solve each equation for y to find the slope.

Slope of side between vertices (1, –3) and (9, 6):

b. The sides with slopes 2 5 and 5 2 are perpendicular, because 25 1 52

. Thus, the triangle is a right triangle.

40. Quadrilateral with vertices (–5, –2), (–3, 1), (3, 0), and (1, –3):

a. Slope of side between vertices (–5, –2) and (–3, 1):

The product of the slopes is 1 (3)1 3  

, so the lines are perpendicular.

37. For 4x = 2y + 3, solve for y

2y = 2x + 3, solve for y.

Since the two slopes are 2 and 1, the lines are neither parallel nor perpendicular.

Slope of side between vertices (–3, 1) and (3, 0):

Slope of side between vertices (3, 0) and (1, –3):

Slope of side between vertices (1, –3) and (–5, –2):

SECTION2.2EQUATIONSOFLINES 57



2 3 yx

2 4 yx  

43 1 34   

27 257527 55 15561565 6521 151553 xyyxyx

yxx   

yxyx



2 yx

yx

3434

1331 xyyxyx yxx

 





3 2 2 yx

3 2 yx

For

262626 1 24242 2 xyyxyx xyyxyx  

1 21 2     

6242 9(1)105 m 

2(3)55 1122 m 

3699 1988 m 

  

2133 5(3)22 m 

3366



1011

0(3)3 312



3(2)321 1(5)156 m   

b. Yes, the quadrilateral is a parallelogram because opposite sides have the same slope and are therefore parallel.

41. Use point-slope form with 11 2 (,)(3,2), 3 xym

45. 11 (,)(10,1),0 xym

46. 11 (,)(3,9),0 xym

47. Since the slope is undefined, the equation is that of a vertical line through (–2, 12).

48. Since the slope is undefined, the equation is that of a vertical line through (1, 1).

49. Through (–1, 1) and (2, 7) Find

50. Through (2, 5) and (0, 6)

11 (,)(2,3),3

CHAPTER2GRAPHS,LINES,ANDINEQUALITIES

 11() 2 2((3)) 3 2 2(3) 3 2 22 3 2 3 yymxx yx yx yx yx      42.

xym 11() 4 (2)((5)) 5 4 2(5) 5 4 24 5 4 2 5 yymxx yx yx yx yx     

11 4 (,)(5,2), 5

yx     44. 11 1 (,)(3,4), 4 xym 11() 1 (4)(3) 4 1 4(3) 4 4163 413 113 44 yymxx yx yx yx yx yx      

43.

xym 11() 33(2) 336 33 yymxx yx yx

 11() 10(10) 101 yymxx yx yy   

 11() (9)0((3)) 909 yymxx yx yy   

x = –2

x = 1

slope. 716 2 2(1)3 m  Use the point-slope form with   (2,7),11 xy    11 72(2) 724 23 yymxx yx yx yx    

the

Find the slope. 561 202 m  Use the point-slope form with   (0,6),11 xy    11 1 6(0) 2 yymxx yx   1 6 2 1 6 2 yx yx  

51. Through (1, 2) and (3, 9) Find the slope.



yymxx yx yy

11 90(7) 909

 

11,(3,4)xy

52. Through (–1, –2) and (2, –1) Find the

425 245 5 22 2

53. Through the origin with slope 5.

11,(6,8)xy

54. Through the origin and horizontal. A horizontal line has slope 0.

1 606

55. Through (6, 8) and vertical. A vertical line has undefined slope.

SECTION2.2EQUATIONSOFLINES 59

927 312 m 

the point-slope form with   (1,2),11 xy  .   11 7 2(1) 2 77 2 22 73 22 273 yymxx yx yx yx yx     

Use

2(1)11 1233 m 

the point-slope form with   (1,2),11 xy    11 1 (2)((1)) 3 1 2(1) 3 361 35 yymxx yx yx yx yx     

slope.

Use

 



  11 05(0)5 yymxx yxyx  

11,(0,0)xy

; m = 5

  11,(0,0)xy    11 00(0) 0 yymxx ym y   

 



11,(6,8)xy

x = 6

 

56. Through (7, 9) and parallel to y = 6. The line y = 6 has slope 0.   

 11,(7,9)xy 



xy yx yxm     

42(3)

yx yx yx    

57. Through (3, 4) and parallel to 4x – 2y = 5. Find the slope of the given line because a line parallel to the line has the same slope.

426 22 yymxx

1 . 2 m   

  

2166 222 yymxx yx yx yx    

58. Through (6, 8) and perpendicular to y = 2x – 3. The slope of the given line is 2, so the slope of a line perpendicular to the given line has the slope

11 1 8(6) 2

0(6)6

m   

   11 01(6)6 yymxx yxyx  

59. x-intercept 6; y-intercept –6 Through the points (6, 0) and (0, –6).

11,(6,0)xy

60. Through (–5, 2) and parallel to the line through (1, 2) and (4, 3).

The slope of the given line is

so the slope of a line

parallel to the line is also 1 . 3

61. Through (–1, 3) and perpendicular to the line through (0, 1) and (2, 3).

The slope of the given line is 1 132 1, 022 m

so the slope of a line

perpendicular to the line is 2 1 1. 1 m 

62. y-intercept 3 and perpendicular to 2x – y + 6 = 0.

The slope of this line is 2, so the slope of a line

perpendicular to the line is 1 . 2

63. Let cost x = 15,965 and life: 12 years. Find D

11 15,9651330.42 12

The depreciation is $1330.42 per year.

64. Cost: $41,762; life: 15 years

11 41,7622784.13 15

The depreciation is $2784.13 per year.

65. Let cost x = $201,457; life: 30 years  11 201,4576715.23

The depreciation is $6715.23 per year.

66. Let x = the amount of the bonus. The manager received as a bonus .10(165,000 – x),so x = .10(165,000 – x). Solve this equation. 16,500.10 1.1016,500 16,500

The bonus amounted to $15,000, so the correct choice is (b).

67. a. x = 5

13.695133.6202.05

There were about $202.05 billion or $202,050,000,000 in sales from drug prescriptions in 2005.

b. x = 10.   13.6910133.6270.5 y

There were about $270.5 billion or $270,500,000,000 in sales from drug prescriptions in 2010.

x x

68. a. x = 10 40.89(10)405.3814.2 y





The total revenue generated from hospital care will be $1 trillion in the year 2014.

CHAPTER2GRAPHS,LINES,ANDINEQUALITIES



2311 , 1433 m



  

3 365 311 yymxx yx yx yx    



11,(5,2)xy

11 1 2((5))



 

  

yymxx yx

   

11,(1,3)xy

11 31((1)) 31 2

yx yx

26026

xyyx 

 

3(0)

26 26 yymxx yx yx yx    

11,(0,3)xy 

11 1



Dx n    



Dx n    

1.10 xx x x   

15,000

y 

 



c. y = 340 34013.69133.6 206.413.69 15.1   

Sales from drug prescriptions will be about $340 billion in the year 2015.

The total revenue generated from hospital care in 2010 was about $814.2 billion or $814,200,000,000.

b. y = 1000 100040.89405.3 594.740.8914.5 x xx 

69. a. x = 0

1.8(0)384.6384.6 y 

There were approximately 384.6 thousand or 384,600 employees working in the motion picture and sound industries in 2000.

b. x = 10

1.8(10)384.6366.6 y 

There were approximately 366.6 thousand or 366,600 employees working in the motion picture and sound industries in 2010.

c. y = 350 3501.8384.6 34.61.819.2 x xx  

This corresponds to the year 2019. There will be approximately 350,000 employees working in the motion picture and sound industries in 2019.

70. a. x = 10. 42.1(10)16,28815,867 y 

There were 15,687 golf facilities in 2010.

b. y = 15,500. 15,50042.116,288 78842.118.7 x xx  

This corresponds to the year 2018. There will be 15,500 golf facilities in 2018.

71. a. The given data is represented by the points (5, 35.1) and (11, 29.7).

b. Find the slope.

72. a.     11 , 0,16.3 xy  and     22 , 10,14.9 xy 

Find the slope. 14.916.31.4 .14 10010 m 

Use the slope-intercept form with (0, 16.3). .1416.3yx

b. Let x = 15.   .141516.314.2 y 

According to the model, there will be 14.2 million union workers in 2015.

73. a.     11 , 0,.4 xy  and     22 , 10,.75 xy 

Find the slope. .75.4.35 0.035 10010

The y-intercept is .4, so the equation of the line is y = 0.035x + 0.4.

b. The year 2014 corresponds to x = 2014 – 2002 = 14. 0.035(12)0.40.82 y

In 2014, the price for chicken legs will be about $0.82 per pound.

11 , 0,.6 xy  and

22 , 10,1.25 xy 

Find the slope. 1.25.6.65 0.065

The y-intercept is .6, so the equation of the line is y = 0.065x + 0.6.

b. The year 2010 corresponds to x = 2010 – 2002 = 8. 0.065(8)0.61.12 y

In 2010, the price for chicken thighs was about $1.12 per pound

c. The year 2009 corresponds to x = 9. 0.9(9)39.631.5 y

Total sales associated with lawn care were about $31.5 billion in 2009.

d. y = 25. 250.939.6 14.60.916.2 x xx 

This corresponds to the year 2016. Total sales associated with lawn care will reach $25 billion in 2016.

75. a.     11 , 0,36845 xy  and     22 , 10,27200 xy 

Find the slope. 27,20036845 964.5 100 m 

The y-intercept is 36,845, so the equation is 964.536,845.yx

SECTION2.2EQUATIONSOFLINES 61

29.735.15.4 0.9 1156 m  11() 29.70.9(11) 29.70.99.9 0.939.6 yymxx yx yx yx    





m 





 

74.

  

 

10010 m 



b. The year 2006 corresponds to x = 2006 – 2000 = 6. 964.5(6)36,84531058 y 

In 2006, there were about 31,058 federal drug arrests.

76. a.     11 , 0,1.5 xy  and     22 , 10,4.5 xy  Find the slope. 4.51.5 .3 100 m 

The y-intercept is 1.5, so the equation is .31.5.yx

b. The year 2007 corresponds to x = 2007 – 2000 = 7. .3(7)1.53.6 y 

In 2007, the total amount of drugs seized was about 3.6 million pounds.

c. 5.7.31.54.2.314 xxx  This corresponds to the year 2014. There will be 5.7 million pounds of drugs seized in 2014.

77. a. The slope of –.01723 indicates that on average, the 5000-meter run is being run .01723 seconds faster every year. It is negative because the times are generally decreasing as time progresses.

b. .01723(2012)47.6112.94 y 

The model predicts that the time for the 5000-m run will be about 12.94 minutes in the 2012 Olympics.

78. a. Using data points (1980, 106.9) and (2010, 153.9), the slope is:

153.9106.9 1.57 20101980 m 

Each year there is an average increase of about 1.57 million civilians.

Section 2.3 Linear Models

1. a. Let (,11 ) xy be (32, 0) and (,22 ) xy be (68, 20). Find the slope. 200205 6832369 m

Use the point-slope form with (32, 0). 55 0(32)(32) 99 yxyx

b. Let x = 50. 55(5032)(18)10C 99 y

Let x = 75. 55(7532)(43)23.89C 99 y 

2.   55 3232 99 yxCF 

a. F = 58°F 55(5832)(26)14.4 99 CC

b. C = 50°C

153.91.572010

153.91.5720152010

153.97.85161.75

There will be about 161.75 million civilians in the labor force in 2015.

5 1032 9 905160 70514

F F



55(86732)(835)463.89 99 CC 

5 3295160 9 416040

CHAPTER2GRAPHS,LINES,ANDINEQUALITIES







  

yx y yy











  

5 5032 9 4505160 6105122 F F FF



c. C = –10°C   

d. F = –20°F 55(2032)(52)28.9 99 CC

3. F = 867°



CFFFF

 

4. When are Celsius and Fahrenheit temperatures numerically equal? Set F = C:

The temperatures are numerically equal at –40°.

5. Let     11 , 6,201.6 xy  and     22 , 11,224.9. xy  Find the slope.

224.9201.6 4.66 116

201.64.66(6)

201.64.6627.96

4.66173.64.

To estimate the CPI in 2008, let x = 8.

 4.668173.64210.92 y 

To estimate the CPI in 2015, let x = 15.

 4.6615173.64243.54 y 

6. Let     11 , 1,127.1 xy  and

8. Let     11 , 0,14.1 xy  and     22 , 8,17.2. xy 

Find the slope. 17.214.1 0.3875 80 m 

The y-intercept is 14.1, so the equation is 0.387514.1.yx

To estimate the number of employees working in the health care and social assistance industries in 2014, let x = 2014 – 2000 = 14.

  0.38751414.119.525 y 

The number of employees will be about 19.525 million in 2014.



 22 , 11,140.8. xy  Find the slope.

140.8127.113.7 1.37 11110

127.11.37(1)

127.11.371.37

1.37125.73.

To estimate the number of filed returns in 2005, let x = 2005 – 2000 = 5.   1.375125.73132.58 y 

There were about 132.58 million examined returns in 2005.

To estimate the examined returns in 2012, let x = 2012 – 2000 = 12   1.3712125.73142.17 y 

There were about 142.17 million examined returns in 2012

7. Let     11 , 0,6.0 xy  and     22 , 8,6.5. xy 

Find the slope. 6.56.0 0.0625 80 m 

The y-intercept is 6.0, so the equation is 0.06256.0.yx

To estimate the number of employees working in the finance and insurance industries in 2010, let x = 2010 – 2000 = 10.

  0.0625106.06.625 y 

The number of employees was estimated to be 6.625 million in 2010.

11 22   21 21

,(50,320) 440320120 4 805030 yy m xx 

Each mile per hour increase in the speed of the bat will make the ball travel 4 more feet.

806,400

minhrday yxx 



Data Point (x, y) Model Point   ˆ , xy Residu al ˆ yy Squared Residual  2 ˆ yy (7, 5036) (7,5013.8) 22.2 492.84 (8, 4847) (8, 4870.2) –23.2 538.24 (9, 4714) (9, 4726.6) –12.6 158.76 (10,4589)(10, 4583) 6 36 (11,4447)(11,4439.4) 7.6 57.76

SECTION2.3LINEARMODELS 63

m 

yx yx yx   



m 

yx yx yx  



  

,(80,440)

9. Find the slope of the line. xy

10. 1120 gal60 min12 hr

After 30 days, y = 806,400(30) = 24,192,000 gallons

11. a. 143.66019yx

(continuednextpage)

Sum of the residuals for model 1 = 0

Sum of the residuals for model 2 = 42

b. Sum of the squares of the residuals for model 1 = 1283.6

Sum of the squares of the residuals for model 2 = 8712

c. Model 1 is the better fit.

b. Sum of the squares of the residuals for model 1= 40.55.

Sum of the squares of the residuals for model 2= 241.6.

c. Model 1 is the better fit.

13. Plot the points. [5, 12] by [150, 220]

Visually, a straight line looks to be a good model for the data.

The coefficient of correlation is r ≈ .956, which indicates that the regression line is a good fit for the data.

14. Plot the points.

[0, 15] by [400, 2000]

Visually, a straight line looks to be a poor model for the data because it shows a great deal of curvature.

The coefficient of correlation is r ≈ –.906, which indicates that the regression line is a good fit for the data, but the plot shows otherwise.

CHAPTER2GRAPHS,LINES,ANDINEQUALITIES

yx Data Point (x, y) Model Point   ˆ , xy Residu al ˆ yy Squared Residual  2 ˆ yy (7, 5036) (7,5058.6) –22.6 510.76 (8, 4847) (8, 4888.4) –41.4 1713.96 (9, 4714) (9, 4718.2) –4.2 17.64 (10,4589) (10, 4548) 41 1681 (11,4447) (11,4377.8) 69.2 4788.64

170.26250

a. 2.147yx Data Point (x, y) Model Point   ˆ , xy Residual ˆ yy Squared Residual  2 ˆ yy (5, 53) (5,57.5) –4.5 20.25 (8, 67) (8,63.8) 3.2 10.24 (11, 71) (11,70.1) 0.9 0.81 (14, 75) (14,76.4) –1.4 1.96 (17, 80) (17,82.7) –2.7 7.29 2.844yx Data Point (x, y) Model Point   ˆ , xy Residual ˆ yy Squared Residual  2 ˆ yy (5, 53) (5,58) –5 25 (8, 67) (8,66.4) 0.6 0.36 (11, 71) (11,74.8) –3.8 14.44 (14, 75) (14,83.2) –8.2 67.24 (17, 80) (17,91.6) –11.6 134.56 Sum of the residuals for model 1 = –4.5 Sum of the residuals for model 2 = –28

12.

15. a. Using a graphing calculator, the regressionline model is 5.90146.59.yx

b. The year 2015 corresponds to x = 15. Using the regression-line model generated by a graphing calculator, we have   5.9015146.59235.09, y  or about $235 billion in sales.

16. a. Using a graphing calculator, we find that the linear model is 7.72407.94yx

b. The year 2015 corresponds to x = 35. Using the regression-line model generated by a graphing calculator, we have   7.7235407.94137.74, y  or about 137 deaths per 100,000 people from heart disease.

17. a. Using a graphing calculator, the regressionline model is y = –3.96x + 73.98.

b. The year 2016 corresponds to x = 16. Using the regression-line model generated by a graphing calculator, we have   3.961673.9810.62, y  or about $10.62 billion in revenue.

18. a. Using a graphing calculator, the regressionline model is

y = 14.9x + 2822.

b. Using the regression-line model:

Let x = 150 feet squared.

y = 14.9(150) + 2822 = 5057

Let x = 280 feet squared.

y = 14.9(280) + 2822 = 6994

Let x = 420 feet squared.

y = 14.9(420) + 2822 = 9080

The predicted values are very close to the actual data values.

c. Using the regression-line model:

Let x = 235 feet squared.

y = 14.9(235) + 2822 = 6323.5

Adam should choose the closest value above the requirement. therefore, Adam should choose the 6500 BTU air conditioner.

19. a. Using a graphing calculator, the regression line model for estimated operating revenue (in billions of dollars) from internet publishing and broadcasting is given by 2.372.02.

b. Let x = 12 (2012).

2.37122.0226.42 billion

Let x = 14 (2014).

2.37142.0231.16 billion y 

The operating revenue was about $26.42 billion in 2012 and will be about $31.16 billion in 2014.

20. a. Using a graphing calculator, the regression-line model is 0.6268.28.

b. 0.62(9)68.2862.7. y  There were about 62.7 million subscribers in 2009.

c. Let y = 55. 550.6268.28

13.280.62

x x x

There will be 55 million subscribers in the year 2021.

d. Using a graphing calculator, the coefficient of correlation is about –.915.

yx

b. 2.318(6)55.8841.972. y  There were about 41,972 traffic fatalities in 2006.

c. Let y = 28. 282.31855.88



27.882.318



12.03

There were 28,000 traffic fatalities in the year 2012.

22. a. Using a graphing calculator, the regression-line model for men is .21552.6.

yx

b. Using a graphing calculator, the regression-line model for women is .14465.4.

SECTION2.3LINEARMODELS 65

yx



y 

 



yx

21.4   

21. a. Using a graphing calculator, the regression-line model is 2.31855.88.

x x x 

d. Using a graphing calculator, the coefficient of correlation is about –.972.

yx

xx xx x

  

c. .21552.6.14465.4 .07112.8 180.3

According to the models, the life expectancy of men will be the same as women in the year 2080.

Section 2.4 Linear Inequalities

1. Use brackets if you want to include the endpoint, and parentheses if you want to exclude it.

2. (c). –7 > –10

3. –8k ≤ 32

Multiply both sides of the inequality by 1 8 Since this is a negative number, change the direction of the inequality symbol.

88(8)(32)4 kk 

The solution is [–4, ∞).

4. –4a ≤ 36

Multiply both sides by 1 4 Change the direction of the inequality symbol.

44(4)(36)9 aa 

The solution is [– 9, ∞).

5. 20 b 

Multiply both sides by 1 2

20(2)(0)0 22 bbb 

The solution is (–∞, 0). To graph this solution, put a parenthesis at 0 and draw an arrow extending to the left.

6. 6 – 6z < 0 Add 6z to both sides. 6660666 zzzz

Multiply both sides by 1 6

11 (6)(6)1 or 1 66 zzz 

The solution is (1, ∞).

7. 3414 x  Subtract 4 from both sides. 344144310

Multiply each side by 1 3

The solution is 10 , 3

8. 2y – 7 < 9 Add 7 to both sides. 27797216 yy

Multiply both sides by 1 2

For exercises 9–26, we give the solutions without additional explanation.

9. 53 5535 8 (1)()(1)(8)

The

66 CHAPTER2GRAPHS,LINES,ANDINEQUALITIES



  1110 310 333 xx

      



22(2)(16)8 yy

Solution is (–∞, 8).

8 p p p p p     

solution

∞, –8].

39 11 (3)9 33 3 r r r r       

The

is (–

10. 53(5)4(5)

with Applications In the Management Natural and Social Sciences 11th Edition Lial Solutions Manual

Download: http://testbanktip.com/download/mathematics-with-applications-in-the-management-natural-and-social-sciences-11th-edition-lial-solutions-manual/ Download all pages and all chapters at: TestBankTip.com

solution is [3, ∞). Mathematics

Full