SOCIALE

SOCIALE RECHTVAARDIGHEID, WISKUNDIG BEKEKEN

IK HERINNER ME NOG GOED MIJN EERSTE REACTIE TOEN IK ENKELE JAREN GELEDEN LAS DAT HET VAK WERELDORIËNTATIE – MET DE BESTE BEDOELINGEN –OPGESPLITST ZOU WORDEN IN EEN STUK “MENS EN MAATSCHAPPIJ” EN EEN STUK “WETENSCHAP EN TECHNIEK”. IK DACHT METEEN: WAAROM NIET “MENS EN WETENSCHAP” OF “TECHNIEK EN MAATSCHAPPIJ”? TECHNOLOGISCHE VOORUITGANG STAAT TOCH NIET LOS VAN DE MAATSCHAPPIJ? EN WAT IS WETENSCHAP ANDERS DAN MENSELIJK INZICHT IN DE NATUUR?

GIOVANNI SAMAEY, NUMERIEKE ANALYSE EN TOEGEPASTE WISKUNDE, DEPARTEMENT COMPUTERWETENSCHAPPEN, KU LEUVEN

Die gedachte kwam onlangs terug bij me op toen ik de aankondiging kreeg dat er een workshop georganiseerd zou worden over “computationele en wiskundige aanpakken voor sociale rechtvaardigheid” 1 . Van 8 tot 10 maart – nog steeds helaas virtueel – aan het Institute for Computational and Experimental Research in Mathematics (ICERM) van Brown University (VS). Op die workshop komen wiskundigen vanuit verschillende instellingen samen om lezingen te geven en te debatteren over de rol van wiskunde bij het begrijpen van mechanismen die leiden tot sociale onrechtvaardigheid.

Sociale rechtvaardigheid heeft betrekking op eerlijke relaties tussen individuen en de samenleving. De term omvat kwesties als gelijkheid, diversiteit en inclusie en is historisch gezien geworteld in de sociale en geesteswetenschappen. Toch maakt de wiskunde een complementaire en krachtige aanpak mogelijk, dankzij de inzichten die ontstaan zijn in domeinen als dynamische systemen, de studie van complexe netwerken, toegepaste topologie, stochastische processen (waarin toeval een rol speelt), data-analyse en meer. Dit soort wiskundige technieken is aan een opmars bezig binnen de sociale wetenschappen, en er zijn intussen wiskundig onderbouwde studies uitgevoerd op een heel scala aan sociale kwesties, zoals verkiezingen, haatzaaierij, gezondheidszorg en gendergelijkheid. Van het voorspellen van rellen tot het effect van fooien op restaurants: noem een sociaal thema en er zijn wiskundigen mee bezig.

Een mooi voorbeeld van een onverwachte wiskundige aanpak van een sociaal fenomeen is een studie van de grootschalige rellen van 2005 in Frankrijk2. Op 27 oktober 2005 stierven twee jongeren bij het binnendringen in een onderstation van de elektriciteit, terwijl ze probeerden te ontsnappen aan een politiepatrouille. Woedende bewoners verzamelden zich spontaan op straat. Er braken rellen uit, die zich voornamelijk uitten door de vernieling van auto’s en confrontaties met de politie. In de weken daarop breidden de rellen zich uit, zonder centrale organisatie of politieke eisen, tot in meer dan 800 Franse gemeenten. In de studie worden de dagelijkse gegevens van de nationale Franse politie gebruikt om de dynamiek van de verspreiding van de rellen te onderzoeken. Het doel was om een minimaal wiskundig model te vinden dat de realiteit kwantitatief kan reproduceren. Dat is ook gelukt: een model dat vaak gebruikt wordt om de verspreiding van epidemieën te beschrijven, blijkt kwantitatief de volledige dynamiek van de rellen te verklaren, zowel in ruimte als in tijd. De verspreiding van deze rellen blijkt niet uitgelokt door reizende relschoppers: het lijkt eerder zo dat rellen in de nabijheid bepaalde mensen aanzetten om zelf gewelddadig te worden. De enige sociologische variabele die nodig was in het model was de mate van ontbering in de buurt waar de mensen woonden. Het is opmerkelijk dat geografische nabijheid zo’n grote rol speelde, want via de media was overal dezelfde informatie beschikbaar.

Het voornaamste voordeel van een wiskundige benadering van dit soort problemen (en tegelijk ook de grootste moeilijkheid) is dat ze een kwantitatieve analyse mogelijk maakt (in tegenstelling tot een louter kwalitatieve analyse). Toch is het belangrijk even stil te staan bij de vraag hoe betrouwbaar die resultaten zijn, en wat ze precies betekenen. Het is niet omdat berekeningen overeenkomen met de realiteit, dat de aannames correct zijn die in het wiskundige model gemaakt worden. Zeker als je de vrijheid hebt om je model wat te kneden tot het de beschikbare data zo goed mogelijk reproduceert.

Alles staat of valt met de beschikbaarheid van een goed wiskundig model. Zo’n model is in wezen niets meer dan een beschrijving in formules van de fenomenen die belangrijk zijn in het proces dat we willen bestuderen. Hiervoor zijn twee zaken cruciaal: een correcte beschrijving in formules (waarvoor wiskundige kennis nodig is) en een goede kennis van het fenomeen dat je wil bestuderen. Dat laatste is belangrijk om expliciet te benadrukken: de aannames van de sociale wetenschappers dienen als invoer bij het opstellen van een model. Dat betekent dat je niet kan nagaan

1 “https://icerm.brown.edu/events/htw-21-mcasj/#workshopoverview 2 “https://www.nature.com/articles/s41598-017-18093-4

of die aannames correct zijn, enkel of ze plausibel zijn. Met “plausibel” bedoelen we dan dat de aannames aanleiding geven tot berekeningen die overeenkomen met de werkelijke gebeurtenissen.

In het geval van de Franse rellen was de aanname dat het ontstaan van rellen “een beetje lijkt” op het uitbreken van een epidemie: er zijn “besmette” mensen – die zijn aan het vechten. Er zijn “vatbare” mensen – die hebben een kans om te beginnen vechten als ze in de buurt van rellen komen. En er zijn “immune” mensen. Die zijn klaar met vechten. Het model in de studie maakte twee aannames: mensen worden “vatbaarder” om te beginnen vechten als ze in een armere buurt wonen, en als er rellen zijn in buurten in de omgeving. Die aannames waren voldoende om een simulatie uit te voeren die heel goed overeenkwam met de reële gebeurtenissen. Het moet wel gezegd dat het model nog wat vrijheid toelaat: zo kan je kiezen hoeveel vatbaarder mensen worden in functie van de armoede in hun buurt, en hoe sterk de aantrekkingskracht is van naburige rellen om zelf in actie te schieten. Die vrijheid wordt gebruikt om ervoor te zorgen dat de simulaties zo sterk mogelijk bij de beschikbare politiegegevens aansluiten. Over hoe dat gebeurt (en zelfs over wat we bedoelen met “zo sterk mogelijk aansluiten bij de gegevens”) kunnen we ook nog een stevig wiskundig boompje opzetten. Wil dit alles nu zeggen dat het verspreiden van massale rellen echt enkel veroorzaakt wordt door armoede? Niet noodzakelijk! Dit soort simulaties biedt enkel argumenten voor de stelling dat armoede voldoende is om de verspreiding van de rellen te verklaren. Het omgekeerde is niet noodzakelijk waar. Als we de armoede wegwerken, zullen rellen in het wiskundige model geen kans krijgen, maar dat betekent niet veel voor het “echte leven”. Als we erin zouden slagen de armoede weg te werken, kan het nog altijd zo zijn dat in het echte leven rellen ontstaan op basis van een andere drijvende kracht – die op dit moment nog niet in het model zit. Het zou in elk geval al een bijzonder groot succes zijn als we ooit in een situatie komen waarin we dit kunnen testen.

Het wiskundig bestuderen van sociale rechtvaardigheid biedt tal van opportuniteiten, zowel voor wiskundigen als voor sociale wetenschappers. Voor sociale wetenschappers biedt het een kans om hun kwalitatieve ideeën in berekeningen te proppen om te zien of de mechanismes die zij bedenken plausibel zijn. Voor wiskundigen zijn deze toepassingen een goudmijn om het maatschappelijke belang van wiskunde te vergroten en om vanuit hun interesse en expertise mee te helpen aan een betere wereld.

OEFENING 4

KANGOEROE - SPRINGMUIS 2020, VRAAG 3

Welke tegel ontbreekt er?

A

B

C

D

E

HET STAPELEN VAN CIRKELS

WAARSCHUWING VOORAF: DEZE TEKST GAAT NIET OVER PANNENKOEKEN, HOEWEL DIT HET EERSTE IS WAARAAN DE VLAAMSE LEZER DENKT WANNEER HIJ IETS HOORT OVER “GESTAPELDE CIRKELS”. HET IS NOCHTANS WEL WAAR DAT EEN WISKUNDIGE BEST WAT KAN BETEKENEN IN DE KEUKEN WANNEER ER PANNENKOEKEN GEBAKKEN WORDEN. VOORAL ALS ALLE PANNENKOEKEN EEN VERSCHILLENDE DIAMETER HEBBEN EN VAN GROOT NAAR KLEIN GESTAPELD MOETEN WORDEN. OMDAT DE DIAMETERS VAN GEBAKKEN PANNENKOEKEN ZICH ZELDEN IN MONOTOON DALENDE VOLGORDE AANDIENEN, MOETEN WE DE STAPEL ACHTERAF FATSOENLIJK RANGSCHIKKEN. OM NIET TE KLIEDEREN MET ETEN IS DE ENIGE TECHNIEK DIE HIERVOOR TOELAATBAAR IS, DE SPATELFLIPPING:

Figuur 1 De eerste flipping keert de volgorde om van de bovenste drie pannenkoeken, terwijl de tweede flipping de volledige stapel omkeert.

RUDI PENNE EN PAUL LEVRIE, UANTWERPEN

Om dit efficiënt te laten verlopen, roep je er het best een wiskundige pannenkoekenflipper bij. Deze expert weet hoe je bijvoorbeeld een stapel van 19 tot een propere toren van steeds kleinere pannenkoeken kan ordenen met maximaal 22 flippingen. Maar hij weet ook dat op dit moment (januari 2021) het gegarandeerde flipmaximum nog niet gekend is voor een stapel van 20 pannenkoeken.

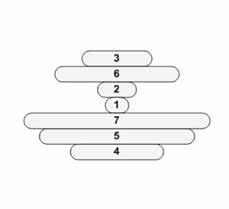
Figuur 2 Met hoeveel spatelflippingen kan je deze stapel correct ordenen?

Jacob Goodman was de eerste om zich als pannenkoekenflipper te outen door in 1975 in de American Mathematical Monthly de vraag te stellen, ietwat schroomvallig onder het pseudoniem Harry Dweighter (= harried waiter): wat is het minimale aantal spatelflippingen om de pannenkoekenstapel mooi geordend te krijgen? Hoe zou jij trouwens deze vraag oplossen voor de stapel hierboven met 7 pannenkoeken? Zelfs Bill Gates ontdekte de pannenkoekenflipper in zich en schreef er ooit een wetenschappelijk artikel over. Deze tekst gaat dus niet over pannenkoeken, maar zeker ook niet over corona, blij dat we zijn om eindelijk over iets anders te kunnen praten. Al willen we toch even opmerken dat het sluiten van alle landsgrenzen en het kiezen voor een totaal isolement soms heilzaam kan zijn voor een volk. Neem nu Japan bijvoorbeeld. Het leefde tijdens de zogenaamde Edoperiode van 1603 tot 1867 vrijwillig geïsoleerd van het westen en kende hierdoor boeiende economische, filosofische en culturele ontwikkelingen. Een groot deel van de Japanse eigenheid zoals we die nu kennen, is toen ontstaan of tot bloei gekomen. In deze context gaan we onze gedachten echter niet richten op geisha’s of haiku’s, maar eerder op de fameuze sangaku’s. Deze gekleurde houten tabletten werden in de Edo-periode opgehangen in shinto-heiligdommen of boeddhistische tempels, waarschijnlijk als geschenk voor goden of heiligen. (zie figuur 3)

Met weinig of geen tekst illustreren sangaku’s een zelf bedachte meetkundige eigenschap over driehoeken, vierkanten, ellipsen en vooral cirkels. Zeg nu zelf, veel ontroeren der en edeler kan een geschenk niet zijn. Omdat een sangaku bovendien zichtbaar was voor de andere tempelbezoekers, streefde de maker meestal naar een esthetische geometrie en imponerende complexiteit. Een YouTube battle avant la lettre dus. De ideale sangaku is een mystiek verbond tussen zijn artistieke schepper, een zuivere meetkundige eigenschap (god) en de uitgedaagde toeschouwer. Vele sangaku’s zijn ons bekend dankzij het missionariswerk van de Japanse wiskundige Hidetoshi Fukagawa in Amerika. Lees bijvoorbeeld: - H. Fukagawa, D. Pedoe, Japanese

Temple Geometry Problems, 1989; - of H. Fukagawa, A. Rothman,

Sacred Mathematics: Japanese

Temple Geometry, 2008.

Hieruit tonen we de volgende vijf-cirkels-sangaku (zie figuur 4).

Als u zich afvraagt hoe men erin geslaagd is om vijf identieke cirkelschijven op deze manier in een vierkant te klemmen, dan kunnen we u geruststellen. Die vraag is namelijk exact de bedoeling van deze sangaku. Een goede student met meetkundige bagage kan uitrekenen

Figuur 3 Mooie cirkelconfiguraties in een Japanse boeddhistische tempel

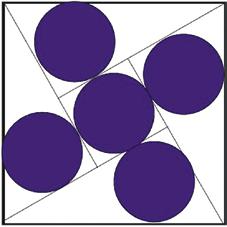
Figuur 4 De 5-cirkel-sangaku

dat bovenstaande configuratie enkel lukt indien de straal R van de cirkels zich verhoudt t.o.v. de zijde Z van het vierkant als:

Al moet gezegd dat afhankelijk van het culturele kader of de context van het vraagstuk, het niet altijd de numerieke oplossing is die gezocht wordt. Zo werden in de Griekse oudheid meetkundige problemen gekraakt met zuivere passer-enliniaalconstructies, terwijl in het Edo-tijdperk de meetkunde wel eens met behulp van origami bedreven werd. Probeer dit laatste eens zelf met de volgende (bescheiden) uitdaging. Leg een rond bierviltje (bijvoorbeeld) in de hoek van een vierkant tafelkleedje of kaartmatje. Als we het vierkant plooien zoals aangegeven in figuur 5, totdat een zijde de cirkel raakt, dan heb je de straal van de cirkel “bepaald” als de uitstekende lengte x. Net zoals vele andere sangaku’s is de vijf-cirkels-sangaku een voorbeeld van een wiskundige stapeling. De objecten die gestapeld worden, mogen van willekeurige vorm, omvang of dimensie zijn, zolang ze elkaar maar niet overlappen. Een mooie illustratie is de stapeling van 19 identieke cirkels in een gelijkzijdige driehoek zoals bedacht door de Hongaarse wiskundige Farkas Bolyai.

Deze was bedoeld als optimaal plantschema voor bomen. Al zien wij eerder toepassingen in onze wijnkelder. Hongaren blijken toevallig erg bekwaam in deze discipline. Zo zoekt en vindt Zsófia Ruttkay ook inspiratie in de natuur voor “dichtbegroeide” cirkelstapelingen, meer bepaald bij de uitzetting van waterlelies (in de tuin van Monet, of als we in het thema willen blijven, in de vijver van een boeddhistische tempel):

Figuur 5 (uit het tijdschrift Pythagoras, 38.5)

Figuur 6 De meest compacte manier om 19 cirkels in een gelijkzijdige driehoek te stapelen Figuur 7 De leliemetafoor van Ruttkay voor een stapeling met 5 cirkels

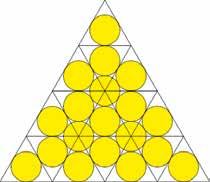
Figuur 8 Hoe 5 cirkels organisch evolueren tot een starre stapeling in een vierkant

In de loop van de 20ste eeuw is het stapelen een aparte wiskundige discipline geworden. Wereldwijd zijn er mensen die professioneel hun echte dagen en denkbeeldige containers vullen met cirkels of bollen of met wat dan ook hun pad kruist. Meestal is de uitdaging van deze rekkenvullers van de wiskunde het maximaliseren van de stapeldichtheid, of anders gezegd, het minimaliseren van de verspilde (lege) ruimte. De vakkennis van een meetkundige expert in het stapelen van cirkels kan soms goed van pas komen. Hij weet hoeveel flessen wijn in een doos raken, en hij heeft het inzicht hoe zoveel mogelijk ronde bierkaartjes uit een rechthoekig vel te snijden. Bovendien, als hij graag moeilijke woorden gebruikt, en niet lijdt aan hippopotomonstrosesquippedaliofobie, weet hij waar hij de constellatiepunten moet plaatsen voor een optimale kwadratuuramplitudemodulatie.

Maar een wiskundige cirkelinpakker weet ook hoeveel stoelen je in een aula of theaterzaal kan opstellen (en hoe), met de garantie op een minimale afstand tussen de toeschouwers. Wie de kunst beheerst om 5 cirkels optimaal te stapelen in een (blauw) vierkant, weet ook waar vijf mensen te plaatsen in een (rood) vierkant zodat de afstand tot de dichtste buur zo groot mogelijk is. En dat is exact zoals getoond wordt in figuur 9. (Hierbij verontschuldigen we ons voor de veelvoorkomende academische misvatting om mensen te verwarren met oneindig kleine punten.) In figuren 10, 11 en 12 zie je hoe onze professionele cirkelstapelaar uit een (groen) papieren vierkant N cirkels knipt om zo weinig mogelijk aan tussenliggende ruimte te verkwisten. Of hoe hij N puntmensen plaatst in een (rode) vierkante kamer om de kleinste afstand tussen twee personen te maximaliseren.

Figuur 9

Figuur 10 N=16: volgens een vierkant rooster.

Figuur 11 N=17: verrassend patroon.

Figuur 12 N=20: volgens een hexagonaal patroon. Thue (1890) geeft dit hexagonaal patroon de optimale stapeling van identieke cirkels in een onbegrensd vlak, waarbij een maximale dichtheid van ongeveer 91% ( om exact te zijn) behaald wordt.

Het maakt ons in ieder geval nederig om te merken dat bijen geen wiskunde nodig hebben om hun honingdruppels in dit optimale patroon van regelmatige zeshoeken te laten opdrogen.

Mogelijke (onderling gelinkte) verklaringen waarom honingraten zeshoekig zijn: 1. Bijen passen het Theorema van

Thue toe wanneer ze hun cirkelvormige honingdruppels efficiënt stapelen op een beschikbaar oppervlak. 2. Bijen willen cellen met maximale oppervlakte (= honingvoorraad) begrenzen met minimale omtrek (= kost), en weten dat de cirkel hiervoor de optimale geometri-

sche vorm is. Maar helaas, cirkels betegelen het vlak niet (verspilde ruimte), dus gaan ze voor een convexe veelhoektegel met zoveel mogelijk hoekpunten. De oud-Griekse bijen wisten al dat dit een zeshoek is. 3. Bijen hebben nooit getwijfeld over het honingraatvermoeden:

“Het hexagonaal rooster is de meest zuinige manier om het vlak in gelijke cellen te verdelen met maximale oppervlakte” (pas formeel bewezen door Thomas

Hales in 1999).

Anderzijds, zodra er wanden zijn aan de beschikbare ruimte of het gegeven papier begrensd is, wat wel eens voorvalt in de wereld die we aantreffen, dreigt dit optimale hexagonale patroon zich inefficiënt te gedragen aan de randen. Eigenlijk is de honingraatoplossing voor 20 cirkels eerder een uitzondering. Meestal wordt een optimale oplossing verkregen door de schijven hier en daar uit elkaar te schuiven, soms meer naar de rand toe, zoals bij de 17 cirkels. Wanneer je 16 flessen zo goed mogelijk wil stapelen in een vierkante doos zal dan weer (toevallig?) een loodrecht rooster de beste ingeving blijken. Beginnende cirkelstapelaars menen hier een eigenschap te ontwaren, want ook 4, 9, 25 of 36 cirkels worden in een vierkante container optimaal geschikt via een vierkant rooster. Maar hun meer ervaren collega’s weten dat dit dan weer niet geldt voor !

Ieder verschillend aantal cirkels lijkt wel om een ad-hocoplossing

Figuur 13

Deze voorbeelden suggereren dat optimale cirkelpatronen zich niet door een vaste formule laten bepalen. Eigenlijk is het patroon met de 20 cirkels nog het minst verrassend, want dit is de oplossing die iedere wijnverzamelaar of transporteur van soepblikken al bedacht heeft. Het is de bekende hexagonale schikking, waarbij iedere cirkel exact zes andere zou raken indien de container zich in alle richtingen oneindig uitstrekte. Volgens het Theorema van

te vragen, maar er komt echt wel wat wiskundig vakmanschap bij kijken. En natuurlijk ook computerrekentijd. Anderzijds is het zo dat origamiwiskundigen (ja, die zijn er ook) zoals Erik Demaine en Robert Lang hebben aangetoond dat er nooit een efficiënt algoritme zal gevonden worden om een optimale stapel van cirkels te berekenen voor een rechthoekig stuk papier, wat zij betreuren want dit had handig geweest bij het tekenen van bepaalde vouwpatronen. Maar eigenlijk wilden we het niet hebben over origami, en al helemaal niet over haiku’s, pannenkoeken of bijtjes, laat staan over corona.

Maar als kleine toegift of dienstverlening voor de organisatoren onder jullie hebben we laten uitrekenen hoeveel toeschouwers we op een coronaveilige wijze kunnen plaatsen bij een ceremonie of podiumact in een ruimte van 10 op 10 meter, hiernaast weergegeven door een rood vierkant. In de eerste oplossing kunnen we 59 stoelen zetten, in evenveel middelpunten van cirkels waarvoor een diameter van 1,5 m genomen werd. Laat ons toe jullie nog eens te waarschuwen voor de veelvoorkomende academische misvatting om mensen te verwarren met oneindig kleine punten. Dan is de tweede oplossing met 43 stoelen en een diameter van 1,8 m meer realistisch (schouderbreedte van 30 cm). Wie een nog grotere marge verkiest, kunnen we cirkels met een diameter van 2 m aanbevelen, waarvoor de computer onverwachts een vierkant raster van 36 stippen als oplossing heeft. Mooier hoeft het niet te worden voor ons.

(http://www.packomania.com/)

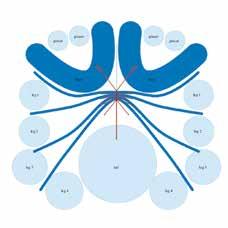
Figuur 14 Hoe het origamipatroon voor een schorpioen bepaald wordt door een stapeling van cirkels (en rivieren)

Figuur 15

Problemen oplossen kan je leren. Er bestaan zoekstrategieën die je kunnen helpen om een coole probleemoplosser te worden. Eén van die zoekstrategieën is: GISSEN EN MISSEN Bij ‘gissen en missen’ los je het probleem op door het antwoord (of een stukje van het antwoord) op goed geluk te raden en uit te proberen. Lukt dat: des te beter! Lukt dat niet: geen probleem, doe een nieuwe poging! Probeer eens te ‘gissen en missen’ bij de volgende Kangoeroevragen.

Op een tak zitten 5 vogels. Elke vogel fluit zoveel keer als het aantal vogels dat hij ziet. Bijvoorbeeld: Anna fluit 4 keer want ze ziet 4 vogels. Plots draait er 1 vogel zich om. Opnieuw fluiten de vogels zoveel keer als het aantal vogels dat ze zien. Deze keer wordt er in totaal meer gefloten dan de eerste keer. Welke vogel heeft zich omgedraaid?

Anna Bill Charlie Donia Egon

A Anna B Bill C Charlie D Donia E Egon

Springmuis 2016,vraag22

Timon legt met lucifers een gesloten pad op het rooster. Timon legt met lucifers een gesloten pad op hetEen stuk van het pad heeft hij al gelegd. De getallen rooster. Een stuk van het pad heeft hij al gelegd.geven aan hoeveel lucifers op elk vierkant liggen. Hoeveel lucifers gebruikt Timon voor dat pad?Degetallengevenaanhoeveellucifersopelkvierkant liggen.HoeveellucifersgebruiktTimonvoordatpad?

1 2 2 2 2 1 0 3 3 0 2 2 2 3 2 0 Eva zet 6 stuks speelgoed in de kast.

A 12 B 14 C 16 D 18 E 20A 12 B 14 C 16 D 18 E 20 Wallabie2019,vraag20 Wallabie 2019,vraag20

In de Kleurstraat staan 5 huizen:In de Kleurstraat staan 5 huizen: een blauw, een geel, een groen,een blauw, een geel, een groen,een paars en een rood huis. eenpaarseneenroodhuis.DehuizenDe huizen zijn genummerd van 1 tot 5.zijngenummerdvan1tot5. • • Naast het rode huis staat maar Naast het rode huis staat maar 1 huis en dat is het groene.1huisendatishetgroene. • Het groene huis staat tussen • het rode en het blauwe huis.Het groene huis staat tussen

Welke kleur heeft huis nummer 3?hetrodeenhetblauwehuis. Welkekleurheefthuisnummer3? A blauw B geel C groen D paars E rood

1 2 3 4 5

A blauw B geel C groen D paars E roodWallaroe 2019,vraag11 Wallaroe2019,vraag11

staat juist onder en rechts van

staat juist boven en links van

Welk stuk speelgoed komt rechts bovenaan in de kast?

A B C D E

Wombat 2017,vraag15

18 maart 2021

Ellie loopt door de doolhof. De getallen Ellie loopt door dedoolhof. De getallen die ze die ze tegenkomt, gaan van klein naar tegenkomt, gaan van klein naar groot. Langs groot. Langs welke uitgang verlaat ze welkeuitgangverlaatzededoolhof? de doolhof? 4

6 INGANG

3

5 1

9 2 4

10 6

(uitwijkperiode tot 22 april 2021) 5 6 7 8 9 9 5 8 9 12 Internationale wedstrijd in 5 edities 12 14 6 10 9 met prijzen voor alle deelnemers: A B C D E A A A AB B B B C C C C D D D DE E E E Wombat 1ste en 2de leerjaar Koala 2018,vraag12Koala2018,vraag12 Springmuis 3de en 4de leerjaar Koala 5de en 6de leerjaar Wallabie/Wallaroe 1ste en 2de leerjaar secundair onderwijs A- en B-stroom kangoeroe.org instagram.com/kangoeroewedstrijd facebook.com/kangoeroewedstrijd

V.U.: VWO vzw, E. Sabbelaan 53 8500 Kortrijk