EEN HARTJE

EEN HARTJE OP DE MUUR

UITWISKELING

EIND JUNI 2014 STOOTTE IK IN DE STANDAARD WEEKBLAD (DS 25 JUNI 2014) OP EEN MERKWAARDIGE FOTO. DE FOTO WAS GENOMEN OP DE BEGRAAFPLAATS VAN LAKEN WAAR ELK JAAR OP 21 JUNI ROND HET MIDDAGUUR IN HET GRAFMONUMENT VAN HET ECHTPAAR EVRARD-FLIGNOT EEN PRACHTIG FENOMEEN WAAR TE NEMEN IS. DE ZON SCHIJNT DAN DOOR EEN CIRKELVORMIG GAT IN HET DAK VAN EEN TEMPELTJE EN WERPT OP DE MUREN EEN LICHTVLEK AF IN DE VORM VAN EEN HARTJE (ZIE FIGUUR 1). DE MAN HEEFT HET GRAFMONUMENT LATEN ONTWERPEN VOOR ZIJN VROUW ALS TEKEN VOOR HUN EEUWIGE LIEFDE.

HILDE EGGERMONT

(REDACTIE UITWISKELING)

Dit fenomeen wilde ik wel eens met eigen ogen zien. Helaas moest ik daar een jaar voor wachten en op 21 juni 2015 was het dan zo ver. Ik trok ’s morgens onder een grijze hemel naar Laken en als bij wonder trokken de wolken rond kwart voor twaalf open en het prachtige hart werd zichtbaar op de muur. Mede dank zij de perfecte timing van de wolken had het iets magisch. Je krijgt een prachtig samenspel van kunst (in de achterwand heb je een half ingewerkt beeldhouwwerk van een treurende vrouw, een ‘pleurante’), architectuur (de constructie van het tempeltje) en natuur (het jaarlijks

Figuur 1 Eeuwige liefde

(bron: laekendecouverte.be)

weerkerende invallende zonlicht bij de zomerzonnewende). Het feit dat de hand van de pleurante reikt tot net aan het hartje, maakt deze verwevenheid nog sterker. De moeite om het eens live te gaan aanschouwen, maar bedenk dat je niet alleen bent!

Ik vroeg me af hoe de architect dit voor elkaar kreeg. Hoewel er in de bouwaanvraag van het grafmonument geen verwijzing gemaakt wordt naar het verschijnsel, staat het toch vast dat het geen toeval is. Maar hoe kon de architect dit berekenen?

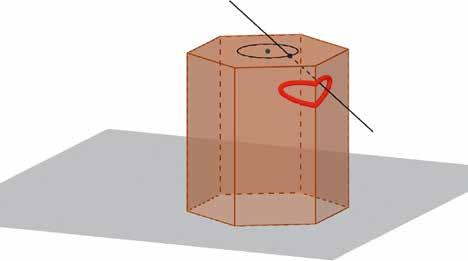
Het tempeltje (zie figuur 2) zelf is zeshoekig van vorm. In het midden van het dak zit een cirkelvormig gat (zie figuur 3). Op een vlakke muur is de lichtvlek een ellips. De lichtstralen door het gat vormen immers een scheve cilinder. Een vlakke doorsnede van deze cilinder is een ellips.

Het hartje wordt gevormd in een hoek waar twee muren samenkomen en wordt dus gevormd door twee stukken ellips. Op het hoogtepunt van het fenomeen zijn deze twee stukken symmetrisch t.o.v. de hoeklijn. Een half uur later is deze symmetrie al duidelijk doorbroken (zie figuur 4).

OP ZOEK NAAR DE WISKUNDE ACHTER HET HARTJE Het is duidelijk dat hier heel wat wiskunde achter schuilgaat. Ik hoopte dat hier een interessante (grote) opdracht voor mijn leerlingen in zat. Maar toen ik alles zelf begon

Figuur 2 Het tempeltje

Figuur 3 Het cirkelvormige gat in het dak

uit te werken, bleek het toch wel wat ingewikkelder dan ik op het eerste gezicht dacht en bleef ik met heel wat vragen zitten. Mijn bewondering voor de architect nam wel toe!

DE SCHEVE CILINDER Omwille van de symmetrie van het resultaat nemen we aan dat de zonnestralen invallen evenwijdig met het verticaal diagonaalvlak van het zeshoekig prisma dat het tempeltje voorstelt.

De hoek die de zonnestralen maken met het horizontale vlak wordt bepaald door de hoogte van de zon. Laken ligt op 51°NB en op 21 juni staat op de (zonne-)middag de zon precies boven de Kreeftskeerkring (23,5°NB). Dat maakt dat de zon op haar hoogste punt op 62,5° (=90°-(51°-23,5°)) staat. Blijkbaar is het tempeltje niet helemaal naar het zuiden gericht, want je moet het fenomeen om 11.50 uur bewonderen en niet om 14u (de zonnemiddag tijdens het zomeruur). De hoek zal dus minder zijn dan deze maximale hoek van 62,5°. Op de site www.timeanddate.com/sun/belgium/brussels?month=6&year=2015 kun je de richting en de hoogte van de zon op elk moment van een willekeurige dag van het jaar berekenen. Hieruit blijkt dat de zonnehoogte op 21 juni om 11:50 uur 55° is in de richting 49° ZO. Ik had helaas geen kompas bij om de oriëntatie van het tempeltje te controleren.

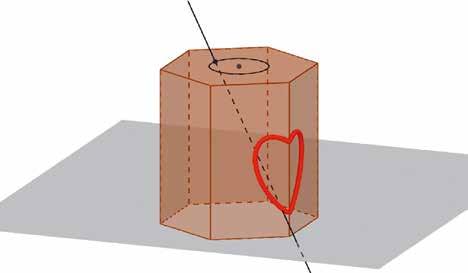
Figuur 5

De invallende zonnestralen vormen een cilinder waarvan de doorsnede met een horizontaal vlak een cirkel is. De doorsnede met een vlak loodrecht op de as van de cilinder is bijgevolg een ellips. Wat ons het meest interesseert zijn de doorsneden van die cilinder met verticale vlakken.

DE ELLIPSEN Omdat er op twee muren geprojecteerd wordt, krijgen we twee ellipsen. We krijgen die echter niet helemaal te zien omdat er slechts op een halfvlak geprojecteerd wordt.

De afbeelding hierboven (figuur 6) is een vlakke voorstelling van de projectie op twee vlakken die een hoek van 120° vormen. De snijlijn van de vlakken is de symmetrieas van de figuur. Het is niet erg dat er nog ‘wangetjes’ van de ene ellips onder de andere uitkomen. Het wangetje aan de linkerkant maakt immers deel uit van de ellips aan de rechterkant. De twee ellipsen worden op verschillende vlakken geprojecteerd. De ellips met grote as van linksboven naar rechtsonder is de projectie op de muur die aan de linkerkant het dichtst bij de waarnemer staat. De ellips met grote as van rechtsboven naar linksonder ligt links van de symmetrielijn in het denkbeeldige verlengde van de muur aan de rechterkant en dus achter het vlak waarop de linkerkant van het hartje te zien is.

Als we de precieze vorm en grootte van het hartje willen achterhalen, moeten we bv. de grote en de kleine as van de ellips(en) bepalen. Dit is o.a. nodig om de hand van de pleurante precies te positioneren.

Dit brengt ons bij het wiskundig probleem hoe je de lengte en de richting van de assen van de ellips kunt berekenen. Het vlak (of de muur) waarmee we de cilinder snijden, maakt een hoek van 30° met het verticale vlak γ loodrecht op het

Figuur 6 Een hartje uit twee ellipsen

verticale vlak van de zonnestraal (figuur 7). Bij de projectie op het vlak heeft de horizontale as lengte en de verticale met de straal van de cirkelvormig opening. Deze assen zijn echter assen van een fictieve ellips, maar misschien kunnen ze helpen om de assen van de echte ellipsen te berekenen (figuur 8).

Uit de lengte van de assen blijkt dat de ellips op het vlak maar een staande ellips is op voorwaarde dat > 45°. Als de zon niet hoog genoeg staat, hebben we dus een liggende ellips. Dit heeft ook gevolgen voor het hartje. Door verschillende hoeken uit te proberen, zien we bij kleinere hoeken inderdaad een platgedrukt hartje (zie figuur 9).

HET MIDDELPUNT Het middelpunt van de ellipsen op de muren kunnen we gemakkelijker bepalen. Omdat de evenwijdige projectie het midden van een lijnstuk bewaart, is het beeld van

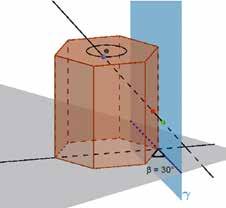
Figuur 7 Het hulpvlak Figuur 8 Een hulpellips in het vlak

Figuur 9 Het hartje bij =20°

het middelpunt van de cirkel het middelpunt van de ellips. Dit heeft als gevolg dat het middelpunt van de ellips op de snijlijn van de muren ligt. De hoogte van dat middelpunt is te berekenen met wat elementaire driehoeksmeting. Het bevindt zich op afstand onder het plafond van het tempeltje. De parameter d stelt de straal van de omgeschreven cirkel van de zeshoek voor. Waar ik echter geen vat op krijg, is de helling en de lengte van de assen van de ellipsen. Wie hier een tipje van de sluier kan oplichten, mag zeker een mailtje sturen naar de redactie van Uitwiskeling (redactie@uitwiskeling.be)!

Dit artikel verscheen in Uitwiskeling 32/1. In Uitwiskeling 32/3 verscheen een vervolgartikel waarin de wiskunde uit het eerste artikel verder is uitgewerkt. Op www.uitwiskeling.be vind je alle info.

OEFENING 2

KANGOEROE - KOALA 2020, VRAAG 10

In de eerste mand ligt 1 appel, in de tweede mand liggen 4 appels, in de derde 6 en in de laatste 9. Louis wil evenveel appels in elke mand. Hoeveel appels moet hij minstens verplaatsen?

A 3

B 4

C 5

D 6

E 7