VBTL 2 - Leerwerkboek Getallen, algebra, data & onzekerheid by die Keure

LEERWERKBOEK

Getallenleer i Algebra Data en onzekerheid

Björn Carreyn

Filip Geeurickx

Roger Van Nieuwenhuyze

CARTOONS

Dave Vanroye

Hoe gebruik je VBTL?

Dit boek bevat zes hoofdstukken vol getallen, algebra, data en onzekerheid. Elk hoofdstuk is opgebouwd uit verschillende paragrafen met aan het einde een handige samenvatting. Bij de inhoudstafel van elk hoofdstuk kun je ook een QR-code vinden. Via die codes kun je extra ﬁlmpjes met uitleg bekijken.

Deﬁnities vind je op een rode achtergrond. Eigenschappen vind je op een groene achtergrond. Methodes, rekenregels en formules vind je op een zachtblauwe achtergrond.

Wiskunde is een eeuwenoude wetenschap. De geschiedenis van de wiskunde en de herkomst van bepaalde begrippen worden zachtpaars afgedrukt. Wiskunde kent veel links met andere vakken We tonen zo’n link in een paarsgekleurd kadertje.

1 2 * Na de samenvatting vind je een reeks oefeningen. Bij oefeningen die extra uitdagend zijn, zie je een sterretje naast het nummer. Bij sommige oefeningen moet je verder denken dan de net geziene leerstof. Je maakt dan gebruik van heuristieken. Deze oefeningen herken je aan de wiskunderugzak.

ICT is een ideaal hulpmiddel. Bij dit boek hoort een webpagina van GeoGebra, gevuld met heel wat digitale oefeningen en applets. Die vind je terug via www.polpo.be.

Vaardigheden

Na elk hoofdstuk wordt een wiskundige vaardigheid in de kijker gezet. Ook in het portfolioschriftje, dat bij dit boek hoort, kun je vaardigheden inoefenen.

Wat moet je kennen en kunnen?

Na de vaardigheden zie je een handig overzicht van wat je moet kennen en kunnen na het geziene hoofdstuk. Kleur rechts de eerste kolom smileys als je de leerstof herhaalde voor een grote toets. Kleur de laatste kolom als je de leerstof beheerst voor je examen.

Herhalingsoefeningen

Wanneer je wiskunde studeert, maak je uiteraard heel wat oefeningen opnieuw en maak je oefeningen die je in de klas niet maakte. Elk hoofdstuk sluit af met drie pagina’s herhalingsoefeningen

Een ideale test voor jezelf om te zien of je de leerstof beheerst.

Welkom in de wetenschappelijke wereld van de wiskunde !

De basis van de getallenleer heb je vorig schooljaar geleerd. We bouwen verder met nog meer regelmaat en patronen en belanden zo bij algebra.

Een balansmethode om een vergelijking op te lossen ? Verschillende methodes om realistische vraagstukken uit te werken ? Je leert het allemaal in het tweede jaar.

Zoals je merkt aan het versnellingsapparaat van deze fiets is elk onderdeeltje belangrijk om vlot te kunnen schakelen. Gewoon de juiste versnelling kiezen en trappen maar !

Inhoud

Getallenleer I Algebra I Data en onzekerheid

Rekenen met rationale getallen

1.1 Wat voorafging 9

1.2 Oplossingsmethodes voor vraagstukken 34

Extra’s 46

Machten

2.1 Machten met gehele exponenten 53

2.2 Wetenschappelijke schrijfwijze 82

Extra’s 93

Rekenen met algebraïsche uitdrukkingen

3.1 Eentermen en veeltermen 101

3.2 Som en verschil van algebraïsche uitdrukkingen 116

3.3 Product van algebraïsche uitdrukkingen 128

3.4 Merkwaardige producten 145

Extra’s 160

Data en onzekerheid

4.1 Gegevens voorstellen in een absolute frequentietabel 167

4.2 Data verwerken in tabellen en diagrammen 169

4.3 Centrummaten en spreidingsmaat 176

4.4 Een eigen onderzoek uitvoeren 180

200

Oplossingsmethodes voor vraagstukken

5.1 Vergelijkingen oplossen in q 207

5.2 Vraagstukken oplossen 230 Extra’s 245

Evenredigheden

6.1 Evenredigheden 253

6.2 Recht en omgekeerd evenredig 272

Rekenen met rationale getallen 1

Wiskunde is een heel oude wetenschap. Eerst dachten we dat ze ontstond in het Mesopotamië van 5000 jaar geleden, maar we moeten nog 15000 jaar verder in de tijd.

Dit beentje van Ishango werd in 1960 in toenmalig Belgisch-Kongo opgegraven. Het is 10 centimeter lang, licht gebogen en heeft drie reeksen inkervingen. Wetenschappers zoeken nog naar de juiste betekenis ervan.

Was het een kalender, een toverstokje, een instrument om de visvangst te verdelen of gewoon het eerste wiskundige spelletje?

Meer dan 22000 jaar later is het aan jou om al je kennis van het eerste jaar even op te frissen.

© Koninklijk Belgisch Instituut voor Natuurwetenschappen

Rekenen met rationale getallen

1.1 Wat voorafging

1 Getalverzamelingen 9

2 Symbolen in de wiskunde 10

3 De optelling en de aftrekking 12

4 De vermenigvuldiging 13

5 De deling 14

6 De machtsverheffing 15

7 De vierkantsworteltrekking 16

8 De volgorde van de bewerkingen 17

9 Samenvatting 18

10 Oefeningen 19

1.2 Oplossingsmethodes voor vraagstukken

1 Hoofdbewerkingen 34

2 De regel van drie & de verhoudingstabel 35

3 Het gebruik van letters bij regelmaat 36

4 Vergelijkingen 37

5 Vraagstukken

6 Procentrekenen

7 Samenvatting

Extra’s Vaardigheden :

Bekijk de instructievideo’s

1.1 Wat voorafging

1Getalverzamelingen

Vorig schooljaar leerde je rekenen met natuurlijke, gehele en rationale getallen. Je maakte ook kennis met getallen die niet tot Q behoren.

N is de verzameling van de natuurlijke getallen.

N = { 0, 1, 2, 3, 4, 5, …}

Z is de verzameling van de gehele getallen

Z = { 0, 1, –1, 2, –2, 3, –3, 4, –4, …}

Q is de verzameling van de rationale getallen

In deze verzameling zitten : – alle gehele getallen ; – alle breuken ;

– alle decimale getallen ; – alle onbegrensde decimale vormen met een periode.

Irrationale getallen (getallen die niet in Q zitten) hebben een onbegrensde decimale schrijfwijze zonder periode.

We stellen ze hiernaast voor in een handig overzicht.

2 Symbolen in de wiskunde

∈∉⊂⊄⟹⟺

Voorbeelden :

8 ∈ N

Voorbeelden :

N ⊂ Z

Voorbeelden :

5 6 ∈ Q

Betekenis :

8 is een element van de verzameling van de natuurlijke getallen.

π/ ∈ Q

Lees :

8 is een natuurlijk getal.

8 ∈ N

5 6 ∈ Q

Betekenis :

π/ ∈ Q

5 6 is een element van de verzameling van de rationale getallen.

Lees :

8 ∈ N

Betekenis :

Z ⊂ Q

Z ⊂ / N

De verzameling van de natuurlijke getallen is een deelverzameling van de verzameling van de gehele getallen.

Lees :

Alle natuurlijke getallen zijn gehele getallen.

a is een natuurlijk getal ⟹

a is een geheel getal

Betekenis : Als a een natuurlijk getal is, dan is a ook een geheel getal. (implicatie)

Z ⊂ Q

5 6 ∈ Q

π/ ∈ Q

Betekenis : p is geen element van de verzameling van de rationale getallen.

Lees : p is geen rationaal getal.

Taak :

Lees : Elk natuurlijk getal is ook een geheel getal.

Z ⊂ / N

5 6 is een rationaal getal. N ⊂ Z

Betekenis :

De verzameling van de gehele getallen is een deelverzameling van de verzameling van de rationale getallen.

Lees :

N ⊂ Z

Z ⊂ Q

Alle gehele getallen zijn rationale getallen.

Z ⊂ / N

Betekenis :

De verzameling van de gehele getallen is geen deelverzameling van de verzameling van de natuurlijke getallen.

Lees :

Niet alle gehele getallen zijn natuurlijke getallen.

a is een veelvoud van 2 ⟺ 2 is een deler van a

Betekenis : a is een veelvoud van 2 als en slechts als 2 een deler is van a (equivalentie)

Lees :

a is een veelvoud van 2 en 2 is een deler van a zijn gelijkwaardige uitspraken.

Vul telkens het correcte symbool in of geef het resultaat. Kies uit de symbolen die hierboven uitgelegd zijn. a –7 Z e N Q

15 5 N

Rekenen met rationale getallen

Symbolen in de wiskunde worden gebruikt om bepaalde relaties kort en makkelijk weer te geven. We herhalen enkele symbolen waarmee je vorig jaar kennismaakte.

∩∪\

Voorbeelden :

del 8 = { 1, 2, 4, 8}

del 10 = { 1, 2, 5, 10}

del 8 ∩ del 10 = { 1, 2}

Voorstelling : 1 . 2 5 . 10 4 8

del 8 del 10

del 8 ∩ del 10

Betekenis :

In de doorsnede zitten de getallen die een deler zijn van 8 en die ook een deler zijn van 10.

Algemeen :

Je bekomt de verzameling met hierin de elementen die behoren tot de ene en de andere verzameling.

Voorbeelden :

del 8 = { 1, 2, 4, 8}

del 10 = { 1, 2, 5, 10}

del 8 ∪ del 10 = { 1, 2, 4, 5, 8, 10}

Voorstelling : 1 2 5 10 . 4 . 8 . del 8 ∪ del 10 del 8 del 10

Betekenis :

In de unie zitten de getallen die een deler zijn van 8 of die een deler zijn van 10

Algemeen :

Je bekomt de verzameling met hierin de elementen die behoren tot de ene of de andere verzameling.

Voorbeelden :

del 8 = { 1, 2, 4, 8}

del 10 = { 1, 2, 5, 10}

del 8 \ del 10 = { 4, 8}

Voorstelling : 1 2 5 10 4 . 8 .

del

Betekenis :

In het verschil zitten de getallen die een deler zijn van 8, maar niet van 10.

Lees : Je bekomt de verzameling met hierin de elementen die behoren tot de eerste, maar niet tot de tweede verzameling.

We kunnen ook bewerkingen met meerdere verzamelingen uitvoeren. In het uitvoeren vullen we een klaverbladdiagram met de elementen van volgende verzamelingen.

Voorbeeld:

A = { x | x is een letter van het woord WISKUNDE}

B = { x | x is een letter van het woord NIET}

C = { x | x is een letter van het woord SAAI}

Merk op :

Eén van deze gebieden is leeg en wordt daarom gearceerd.

De lege verzameling noteer je als {} of ∅

Taak :

Noteer onderstaande verzamelingen door opsomming :

a A ∩ B ∩ C =

b A ⧵ ( B ∪ C) =

c ( B ∩ C) ⧵ A =

3 De optelling en de aftrekking

Gehele en decimale getallen

Gehele en decimale getallen optellen

Als de twee getallen hetzelfde teken hebben :

1 Behoud het teken.

2 Tel de absolute waarden op.

Als de twee getallen een verschillend teken hebben :

1 Neem het teken van het getal met de grootste absolute waarde

2 Trek de absolute waarden van elkaar af (grootste – kleinste).

Voorbeelden :

15 + 39 = 54 –104 + ( –41) =–145 17 + ( –38,15) =–21,15 –85,02 + 27,19 =–57,83

Om het verschil te zoeken van twee getallen tel je bij het eerste getal het tegengestelde van het tweede getal op en pas je de rekenregel toe.

Voorbeelden : 18 ( 3)= 18 + 3 = 21 3,26 4,83 = 3,26 +( 4,83) = 8,09

5 ( 21)= 5 + 21 = 16

Breuken

Om verschillende breuken met elkaar op te tellen (of af te trekken), ga je als volgt te werk :

Breuken optellen en aftrekken

1 Vereenvoudig – indien mogelijk – elke breuk.

2 Maak de breuken gelijknamig.

3 Tel de tellers op (of trek de tellers van elkaar af) en behoud de noemer.

4 Vereenvoudig – indien mogelijk – het resultaat.

Voorbeelden : 8 14 + 12 36 = 4 7 + 1 3 = 12 21 + 7 21 = 19 21

Terminologie : term 2 7 + 1 7 = 3 7

4 De vermenigvuldiging

Gehele en decimale getallen

Gehele en decimale getallen vermenigvuldigen

1 Bepaal eerst het teken : – bij een oneven aantal mintekens in de opgave ; + bij een even aantal mintekens in de opgave.

2 Vermenigvuldig de absolute waarden.

Voorbeelden :

Breuken

Om breuken met elkaar te vermenigvuldigen, ga je als volgt te werk :

Breuken vermenigvuldigen

1 Bepaal het teken : – bij een oneven aantal mintekens in de opgave ; + bij een even aantal mintekens in de opgave.

2 Noteer een grote breukstreep.

3 Vermenigvuldig de tellers met elkaar zonder dit product uit te werken.

4 Vermenigvuldig de noemers met elkaar zonder dit product uit te werken.

5 Vereenvoudig.

6 Vermenigvuldig de resterende tellers met elkaar en de resterende noemers met elkaar. Voorbeeld

Terminologie : 2 5 1 3 = 2 15 factor factor product maalteken

5 De deling

Gehele en decimale getallen

Gehele en decimale getallen delen

1 Bepaal eerst het teken : – bij een oneven aantal mintekens in de opgave ; + bij een even aantal mintekens in de opgave.

2 Deel de absolute waarden.

Voorbeelden :

48 : ( –3) =–16 –18,75 : ( –7,5) = 2,5 –100 : ( –10) = 10

: ( –2) =–1800 1,44 : ( –1,2) =–1,2 –0,5 : 2,5 =–0,2

Breuken

Om breuken door elkaar te delen ga je als volgt te werk :

Breuken delen

1 Bepaal vooraf het teken : – bij een oneven aantal mintekens in de opgave ; + bij een even aantal mintekens in de opgave.

2 Vermenigvuldig de eerste breuk met het omgekeerde van de tweede breuk.

3 Pas de regel voor het vermenigvuldigen van breuken toe.

Voorbeeld : 24 14 : 6 5 = 24 14 · 5 6 = 2 ✄ 4 ✚✚ 24 5 ✚✚ 14 7 ✁ 6 1 = 2 5 7 · 1 = 10 7

Terminologie :

31,64:0,4 = 79,1

deeltaldelerquotiënt deelteken

6 De machtsverhefﬁng

Vorig jaar leerde je al machten berekenen zoals 23 = 8.

Moeilijkere opgaven kon je met behulp van je rekenmachine berekenen.

machten

∀ a ∈ Q, ∀ n ∈ N \ { 0, 1} : a n = a a ·…· a (n factoren)

∀ a ∈ Q : a 1 = a

∀ a ∈ Q0 : a 0 = 1

Voorbeelden :

32 = 3 3 = 9 43 = 4 4 4 = 64

25 = 2 · 2 · 2 · 2 · 2 = 32 106 = 1000000

Machten berekenen van een negatief getal

1 Bepaal het teken : – als de exponent een oneven getal is; het resultaat heeft dus het teken van het grondtal ; + als de exponent een even getal is.

2 Zoek de macht van de absolute waarde van dit getal.

Voorbeelden : ( –10)2 = 100 ( –2)3 =–8

Terminologie :

Bij 46 noemen we 4 het grondtal 6 de exponent 46 de macht

Opmerkingen : –

Je moet goed opletten voor de mintekens in de opgaven. Onthoud dat de exponent slaat op datgene wat er net voor staat. Als dat een haakje is, dan slaat de exponent op alles wat tussen de haakjes staat.

Voorbeelden :

–( –5)3 =–( –125) = 125 –( –2)4 =–( 16) =–16 –8 2 =–64 –

De eerste macht van een getal is altijd dat getal zelf.

Voorbeelden :

( 5,26)1 = 5,26

( –27,5)1 =–27,5

– De nulde macht van een getal verschillend van 0 is altijd 1.

Voorbeelden :

70 = 1

( –18)0 = 1

Het grondtal van een macht kan ook een breuk zijn. Let goed op waar de exponent bij hoort.

Voorbeelden :

3 4 2 = 3 4 3 4 = 9 16

32 4 = 3 3 4 = 9 4

3 4 2 = 3 4 3 4 = 9 16

3 4 1 = 3 4

3 4 0 = 1

Verderop in dit boek leer je heel wat rekenregels zodat je veel meer zult kunnen uitrekenen zonder rekenmachine.

7 De vierkantsworteltrekking

Voorbeelden :

√25 = 5omdat52 = 25 enomdathetresultaatpositiefmoetzijn.

9 16 = 3 4 omdat 3 4 2 = 9 16 enomdathetresultaatpositiefmoetzijn.

√0,36 = 0,6omdat (0,6)2 = 0,36 enomdathetresultaatpositiefmoetzijn.

Om de vierkantswortel van een niet-volkomen kwadraat, breuk of decimaal getal te berekenen, kun je je rekenmachine gebruiken. Om vlot uit het hoofd te kunnen rekenen is het zinvol om de eerste zestien volkomen kwadraten te herkennen. Leer ze daarom van boven naar onderen en van onderen naar boven uit het hoofd.

x 0123456789 101112131415

x 2 0149 162536496481100121144169196225

8 De volgorde van de bewerkingen

De volgorde van de bewerkingen.

1 Als er haakjes in de opgave staan, werk je die eerst uit. Komen er binnen deze haakjes opnieuw haakjes voor, dan start je in de binnenste haakjes.

2 Daarna bereken je alle machtsverheffingen en worteltrekkingen.

3 Dan bereken je de vermenigvuldigingen en delingen van links naar rechts.

4 Ten slotte reken je de optellingen en aftrekkingen uit, ook van links naar rechts.

Voorbeelden :

25:52 23 · √16

= 25:25 8 · 4

Taak : Controleer met de CAS van GeoGebra.

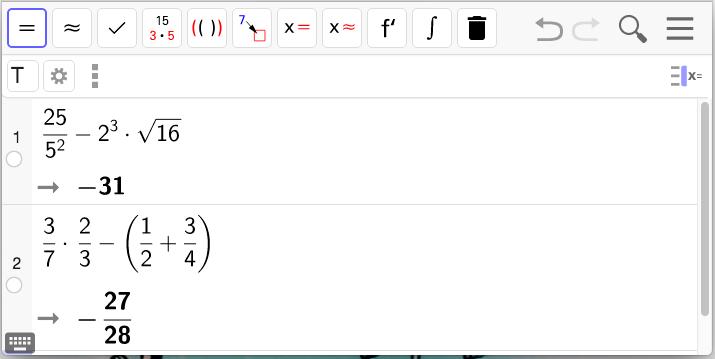
Volgorde van de bewerkingen

1 Werk de haakjes uit. Staan er in de opgaven verschillende soorten haakjes, dan werk je eerst de binnenste haakjes uit.

2 Bereken alle machtsverheffingen en worteltrekkingen.

3 Bereken de vermenigvuldigingen en delingen van links naar rechts.

4 Reken de optellingen en aftrekkingen van links naar rechts uit.

9Samenvatting

• Je kent de betekenis van natuurlijke, gehele en rationale getallen.

• Je kent de betekenis van de symbolen ∈, ∉, ⊂, ⊄, ⟹ en ⟺.

∈ … is een element van …

∉ … is geen element van …

⊂ … is een deelverzameling van …

⊄ … is geen deelverzameling van …

⟹ als … dan …

⟺ … als en slechts als …

• Je kunt volgende symbolen gebruiken: ∪, ∩ en \.

A ∩ B(doorsnede) : de verzameling van de elementen die behoren tot A en tot B.

A ∪ B(unie) : de verzameling van de elementen die behoren tot A of tot B.

A \ B (verschil) : de verzameling van de elementen die behoren tot A en niet tot B.

• Je weet dat de lege verzameling voorgesteld wordt als {} of ∅.

• Je kunt rationale getallen optellen, aftrekken, vermenigvuldigen en delen.

• Je kent de definitie van machten.

a n = a a ·…· a n factoren met n > 1

a 1 = a

a 0 = 1 a ≠ 0

• Je kunt een macht van een rationaal getal berekenen (ook met ICT).

• Je kunt de vierkantswortel van een rationaal getal berekenen (ook met ICT).

• Je kunt de volgorde van bewerkingen toepassen.

1 Haakjes.

2 Machtsverheffingen en worteltrekkingen van links naar rechts.

3 Vermenigvuldigingen en delingen van links naar rechts.

4 Optellingen en aftrekkingen van links naar rechts.

Staan er in de opgave verschillende soorten haakjes, dan werk je eerst de binnenste haakjes uit.

10Oefeningen

Plaats deze getallen in de juiste verzameling. 04 –4 4 3 4 3 √9 √5 p 3,63,66 … 2,184 … 4 2 Q Z N … … .. . . . . . .

Vul aan met de symbolen ∈, ∉, ⊂ of ⊄

a3,5 Z g7 del28

b3,5 Q h7 7N c Z Q i3N 6N

del12 l N0 Z +

Plaats ⟹, ⟸ of ⟺ indien mogelijk.

a x ∈ del 16 x ∈ del 48 e a > 5 a > 2

b 3x + 2 = 5 x = 1 f a is een deler van b b is een veelvoud van a

c x ∈ Q x ∈ Z g a 2 = 100 a = 10

Vul aan.

a N ∪ Z = g del 8 ∩ del 4 =

b Z–∪ Z+= h del 8 \ del 4 =

c N ∩ Z = i del 8 ∪ del 4 =

d N ∪ Z+= j Z+0∩ Z–0=

e del 24 \ del 6 = k2N ∩ 4N = f Z+∩ Z–= l4N \ 2N = 1 2 3 4

Noteer steeds een punt en een 6 in het gebied waar het getal 6 thuishoort.

Noteer steeds een punt en een 1 in het gebied waar het getal 1 thuishoort.

a X is de verzameling van even natuurlijke getallen

Y is de verzameling van delers van 12

b X is de verzameling van even veelvouden van 5

Y is de verzameling van delers van 30

c X = { 1, 4, 7, 10}

Y = { 0, 6, 12, 18,…}

d X = del 30

Y = del 20

e X = 3N

Y = 2N

f X = { x ∈ N : x < 10}

Y = { x ∈ N : x > 5}

g X is de verzameling van het aantal ogen dat je kunt gooien met een dobbelsteen

Y is de verzameling van het aantal ogen dat je kunt gooien met twee dobbelstenen

h X = { x ∈ Z : | x | = 6}

Y = N

Aan acht leerlingen werd gevraagd of ze met de fiets naar school komen, deelnemen aan de Kangoeroewedstrijd en lang haar hebben. Hun antwoorden werden in een klaverbladdiagram genoteerd.

Rekenen met rationale

Miel . Roos . Fay. Gerard . Liv

Lore Achraf .

A is de verzameling van leerlingen die met de fiets naar school komen

B is de verzameling van leerlingen die deelnemen aan de Kangoeroewedstrijd

C is de verzameling van leerlingen met lang haar

Waar of vals? Zet een kruisje in de correcte kolom.

a Gerard, die lange haren heeft, komt niet met de fiets naar school.

b Miel neemt deel aan de Kangoeroewedstrijd, maar komt niet met de fiets naar school.

c Achraf neemt deel aan de Kangoeroewedstrijd, maar heeft geen lange haren en komt niet met de fiets naar school.

d Esraa komt met de fiets naar school en neemt niet deel aan de Kangoeroewedstrijd.

e Liv, die lange haren heeft, doet mee aan de Kangoeroewedstrijd.

f Fay, die lange haren heeft, komt met de fiets naar school en doet mee aan de Kangoeroewedstrijd.

g Fay en Liv hebben allebei lange haren en komen allebei met de fiets naar school.

WAARVALS

Zoek de uitvinder. In welk gebied zit elk gegeven? Noteer de letter die bij dit gebied hoort. De laatste letter krijg je alvast cadeau…

A = { x | x is een Belgische stripfiguur} X = { x | x is de naam van een Belgische provincie}

B = { x | x is een figuur die er niet menselijk uitziet} Y = { x | x is de naam van een Belgische stad}

C = { x | x is een is een figuur die een eigen museum heeft} Z = { x | x vind je terug in Wallonië}

a Kuifje

b Dinant

c Antwerpen

d Luik

e Madame Tussaud

f Marsupilami

g Namen

Omschrijf telkens wat er thuishoort in het groen ingekleurde gebied.

a A is de verzameling van rode figuren

B is de verzameling van kubussen

C is de verzameling van ruimtefiguren met als volume 1m3

b A is de verzameling van alle even natuurlijke getallen

B is de verzameling van natuurlijke getallen groter dan –20

C is de verzameling van natuurlijke getallen kleiner dan 10

c A is de verzameling van alle inwoners van Gent

B is de verzameling van alle liefhebbers van geschiedenis

C is de verzameling van alle leerkrachten

d A is de verzameling van HORECA Vlaanderen

B is de verzameling van bedrijven uit West-Vlaanderen

C is de verzameling van alle vestigingen van Starbucks

e A is de verzameling van meisjesnamen die starten met L

B is de verzameling van meisjesnamen die eindigen met E

C is de verzameling van meisjesnamen met vier letters

Plaats bij de klaverbladdiagrammen van vorige oefening een sterretje in het gebied waar onderstaande elementen thuishoren.

a een rode bol met volume 1 m3

b 17

c leraar geschiedenis uit Aalst

d Hawaiian Poké Bowl Antwerpen

e LIESELORE

Werk uit.

a 7 (+5) = j 13 + 4 =

b4 +( 9) = k13 +( 6) =

c6 3 = l13 29 =

d 5 + 7 = m 2 8 =

e3 ( 4) = n24 37 = f 13 ( 3) = o17 ( 4) = g 10 ( 20) = p 425 + 125 = h189 +( 19) =

Werk uit.

a5 +( 7) ( 3) (+5)+( 3) =

b 5 ( 7)+( 9) =

c25 +( 14) (+7) (+7) ( 9) = d 4 +( 3)+(+5)+(+7)+( 2) = e 4 +( 16) ( 2)+(+5)+( 1) =

7 + 3 +( 9) 4 + 6 =

Werk uit.

Arthur schrijft in elke cirkel een getal zodat elk getal gelijk is aan de som van de 2 getallen in de aangrenzende cirkels. Hij vulde al 2 getallen in. Welk getal komt in de groene cirkel ?

(A) –5 (B) –3 (C) –2 (D) –1 (E) 2

WALLABIE 2025 probleem 15© Vlaamse Wiskunde Olympiade vzw

Rekenen met rationale getallen

Magische vierkanten.

Een magisch vierkant is een vierkant waarbij de som van elke rij, kolom en diagonaal gelijk is.

Vul volgende magische vierkanten aan.

magische som 102

Een beetje magie…

Een magisch vierkant (of een tovervierkant) is een vierkant waarin de som van de getallen van elke horizontale rij, elke verticale rij en elke diagonale rij dezelfde is. Vijf eeuwen geleden was er een magisch vierkant te zien in een ets van de Duitse kunstenaar Dürer. De som is telkens 34. Hij verwerkte er meteen ook het jaartal 1514 in en zorgde voor enkele extra’s: de vier hoeken samen of de vier middelste vakken vormen 34 en als je het vierkant verdeelt in vier kleinere vierkanten, is ook daar de som steeds 34.

Bereken volgende gedurige producten.

a 3 · 4 · ( 2) · 1 · ( 3) =

b1 · ( 1) · ( 2) · ( 2) · 3 · ( 3) =

c8 · ( 5) · ( 3) · 2 · ( 1) =

d7 ( 5) ( 3) 4 0 ( 6) =

e2 ( 4) ( 2) 4 1 =

f 3 ( 2) ( 1) 5 ( 25) =

Werk uit.

a 36: ( 4) = h 22: ( 11) =

b 25: ( 25) = i 1:1 =

c 6:2 = j96: ( 16) =

d2: ( 2) = k 144:12 =

e0: ( 4) = l1000: ( 8) =

f 36: ( 12) = m 1000: ( 25) =

g36: ( 1) = n360: ( 12) =

Werk uit en herken door een regelmaat te ontdekken welk getal in het vijfde vakje komt.

Werk uit.

Vul aan en ontdek de verborgen boodschap door de oplossingen te vervangen door de corresponderende letter van het alfabet (1 = A, 2 = B, …).

Bereik de eindmeet zonder fouten.

AANKOMST

100

Werk uit.

a5 · (7 2) 8e [15: ( 3) ( 7)] : ( 1)

b32 5 · 3 + √16

f40 · 2 +( 14:7)

c8 (5 3 + 6) 22

g ( 21:3) 32 2: ( 6)

d (18 5) : (7 20)

h ( 14 + √25) :3 2 1

Werk uit.

a 3 2 : 5 4 + 3 8 3 · 1 3 1 2

d (0,2 + 0,8 · 1,25) :0,4 2,75

b 2 3 2 : 4 3 1 16 + 1 3 1 2

e1,6:6,4 (0,5 + 0,125 4)

c4 6 5 : 4 14 3 4 1 2

f7,2:6 · 5 (2,74 2,34)

Rekenen met rationale getallen

Ingewikkelde berekeningen maak of controleer je het best met ICT.

Voorbeeld : 3 4 + 1 2 · 3 2 2 + 1 5 · 21 4 + 9 4

Methode 1 :

Controle met Photomath.

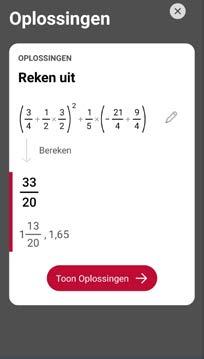
Met deze gratis app controleer je in eerste instantie je oplossing. Open de app. Trek een foto van deopgave. Controleer jouw oplossing. Foutje gemaakt? Tik dan op Toon oplossingen en je krijgt de tussenstappen tezien.

Methode 3 :

Controle met de CAS van GeoGebra 6.

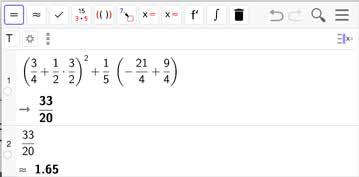
Methode 2 :

Controle met Microsoft Math Solver.

Waaraanisdebreuk 77772 5555 2222 gelijk,alsjedezevereenvoudigt?

van ICT

WIZEXPERT 2023 probleem 1© Stichting Wiskunde Kangoeroe

”Ik ben een getal. Ik ben kleiner dan mijn helft en groter dan mijn dubbele. Als je me optelt bij mijn kwadraat, dan is de som 0. Welk getal ben ik?”

–2

–1

WIZPROF 2022 probleem 7© Stichting Wiskunde Kangoeroe

1.2 Oplossingsmethodes voor vraagstukken

In deze paragraaf herhalen we de oplossingsmethodes die je vorig jaar aangeleerd kreeg.

1Hoofdbewerkingen

Yes, je mag op jeugdkamp! Net voor je vertrek gaf je moeder je nog wat zakgeld mee. De helft hiervan ging naar de drankjes ’s avonds. Bij de dropping kocht je ook nog twee appelkoeken en een flesje water in een winkeltje. Je betaalde hiervoor 3,10 euro. Voor de kaartjes die je opstuurde naar het thuisfront moest je 4,40 euro betalen.

Na het kamp had je nog 5 euro over, maar die mocht je van je moeder in je spaarpot stoppen. Hoeveel gaf ze jou als zakgeld mee ?

Oplossing :

Dit probleem kun je oplossen met hoofdbewerkingen. Als je weet dat de helft van je zakgeld naar drankjes ging, dan heb je nog steeds de andere helft over. Die wordt als volgt verdeeld :

€ 3,10 winkeltje

€ 4,40 kaartjes

€ 5,00 overschot

€ 12,50 totaal

Om het oorspronkelijke bedrag te kennen, moet je dit totaal verdubbelen.

Antwoord :

Je moeder gaf je € 25 zakgeld mee voor het kamp.

Taak :

Als drie wafels en twee pannenkoeken samen 6,60 euro kosten en vijf wafels en twee pannenkoeken samen 9 euro kosten, hoeveel kost dan één pannenkoek ?

2De regel van drie & de verhoudingstabel

WISKUNDE & WETENSCHAPPEN

Apollo 11 was de eerste ruimtemissie waarbij de mens voet op de maan zette. De missie werd gelanceerd in 1969. De Apollo 11 deed in totaal dertig omwentelingen rond onze maan.

Het duurde wel even voor die maan werd bereikt. De beginsnelheid was fenomenaal: 25000 km/h.

Zodra de raket in de ruimte was,deed ze iets meer dan 78 uur over een afstand van 384400 km. Wat was de gemiddelde snelheid van de Apollo 11 in de ruimte ?

Oplossing :

Met de regel van drie : In een verhoudingstabel :

Antwoord:

De gemiddelde snelheid in de ruimte was ongeveer 4928 km/h.

Taak :

a In elke verhoudingstabel is een fout geslopen. Verbeter die.

b Een schaalmodel van onze maan (straal 1737 km) heeft als straal 1 cm. Hoe groot is het schaalmodel van de aarde (6371 km) en onze zon (straal 696340 km) ?

3Het gebruik van letters bij regelmaat

De eigenaar van een feestzaal overweegt nieuwe tafels te kopen die naast elkaar opgesteld moeten worden. Hij twijfelt tussen vierkante en achthoekige tafels.

Hoeveel zitplaatsen bekom je als je van elk 10 tafels voorziet ?

Noteer ook de formule die het aantal zitplaatsen weergeeft in functie van het aantal tafels.

OPSTELLING 1

Je merkt op de voorstelling dat elke tafel bovenaan en onderaan één stoel heeft. Helemaal links en helemaal rechts komt er telkens één stoel bij.

Woordformule : het aantal stoelen is gelijk aan het aantal tafels maal twee plus twee

Letterformule : s = 2 · t + 2

Oplossing : Bij 10 tafels wordt het aantal stoelen : 2 10 +

OPSTELLING 2

Je merkt op de voorstelling dat elke tafel zes stoelen heeft (drie boven en drie onder). Helemaal links en helemaal rechts komt er telkens één stoel bij.

Woordformule : het aantal stoelen is gelijk aan het aantal tafels maal zes plus twee

Letterformule : s = 6 t + 2

Oplossing : Bij 10 tafels wordt het aantal stoelen: 6 10 + 2 = 60 + 2 = 62

Taak :

Deze tafels kunnen zowel in de lengte als in de breedte tegen elkaar geschoven worden. Bepaal voor elke mogelijkheid de letterformule en het aantal stoelen bij tien tafels.

Rekenen met rationale getallen

4Vergelijkingen

Zodra in een gelijkheid als 2 + ( –5) =–3 een of meerdere getallen vervangen worden door een onbekende, spreken we van een vergelijking. Vorig schooljaar leerde je deze eenvoudige vergelijkingen op te lossen.

x + a = b

inbeideleden a aftrekken

x = b a

Merk op :

x a = b

inbeideleden a optellen

x = b + a

x a = b

beideleden delendoor a (= 0)

x = b a

Bij a x = b mag het getal a nooit 0 zijn. Kun je verklaren waarom ?

Voorbeelden :

x +( 5)= 13 x

x : a = b

beideleden vermenigvuldigen met a x = b a

Doordat je de distributieve eigenschap kent, kun je al een stap verder gaan. Je moet dan eerst de haakjes wegwerken en daarna de termen met x samenbrengen in één lid.

Voorbeelden :

2 · ( x + 4)= 6

2 x + 8 = 6

2 x = 6 8

2 x = 14 x =( 14) :2 x = 7 ( x 5)= 3 · (2 x + 4)

Merk op :

Je kunt steeds je resultaat controleren met ICT of door de onbekende in de opgave te vervangen door de oplossing.

2 ( 7 + 4) ? = 6

2 ( 3) ! = 6 ( 1 5) ? = 3 (2 ( 1)+ 4) ( 6) ? = 3 ( 2 + 4) 6 ! = 3 2

Taak : Los volgende vergelijkingen op : x + 2 3 = 1

5Vraagstukken

Bij sommige vraagstukken kun je het te zoeken getal vervangen door x . Je ‘vertaalt’ dan het vraagstuk naar een vergelijking. Dat noemen we mathematiseren. Het vraagstuk beantwoorden en controleren noemen we demathematiseren

Methode :

Het vraagstuk begrijpen :

1 Lees grondig het vraagstuk.

2 Wat je zoekt, stel je voor door x

Oplossing :

3 Vertaal het vraagstuk naar een vergelijking.

4 Los de vergelijking op.

Antwoord :

5 Formuleer het antwoord en controleer.

Voorbeeld :

Het hoofdkwartier van Apple in San Francisco is een groot cirkelvormig gebouw. Je kunt er als bezoeker niet zomaar binnen, maar je kunt wel rond het gebouw wandelen. Dat is een wandeling van 1,458 km. Bepaal de straal van de buitencirkel.

Keuze van de onbekende x : x is de straal van de buitencirkel.

Oplossing :

Antwoord : De straal van de buitencirkel van het gebouw is ongeveer 232 meter.

Taak : Los dit vraagstuk op door het om te vormen naar een vergelijking.

Een lieveheersbeestje besluit om te wandelen over alle ribben van een balk en legt 46 cm af. Hoe hoog is de balk als l = 5 cm en b = 2,5 cm ?

6Procentrekenen

Veel vraagstukken in verband met procentrekenen kun je terugbrengen tot een vergelijking. 17 % van 400 is gelijk aan 68

In een opgave met procenten is (zoals in bovenstaande zin) een van de gekleurde getallen het te zoeken getal. We stellen het te zoeken getal voor door x en zetten dan de opgave om in een vergelijking.

Hoeveel procent van 400 is gelijk aan 68 ?

x % van 400 is 68

x 100 · 400 = 68

x 400 = 68 100

x 400 = 6800

= 6800:400

= 17

17% van een bepaald getal is 68. Zoek dat getal.

17% van x is 68

7Samenvatting

• Je kunt een probleem oplossen door gebruik te maken van : – hoofdbewerkingen ; – de regel van drie; – een verhoudingstabel.

• Je kunt vergelijkingen oplossen van de volgende vormen.

Hoeveel is 17% van 400 ?

17% van 400 is x

• Je kunt eenvoudige vraagstukken oplossen met behulp van een vergelijking.

Methode :

Het vraagstuk begrijpen :

1 Lees grondig het vraagstuk.

2 Wat je zoekt, stel je voor door x

Oplossing :

3 Vertaal het vraagstuk naar een vergelijking.

4 Los de vergelijking op.

Antwoord :

5 Formuleer het antwoord en controleer.

8 Oefeningen

Het boekenpakket van Jack bestaat uit huurboeken, werkboeken en schriften.

Het pakket bestaat uit 1 2 huurboeken en 2 7 werkboeken.

Druk met een breuk uit hoeveel schriften er in het boekenpakket van Jack zitten.

Anke en Robbe zitten in het tweede secundair en plannen hun kerstvakantie. Ze willen graag op winterkamp in Oostenrijk. Om de skiliften te mogen gebruiken gedurende een week betaalt een volwassene 135 euro. Hoeveel moeten Anke en Robbe voor het gebruik van de skiliften betalen als zij maar 7 9 van het bedrag van een volwassene moeten betalen ?

Kwik is het enige metaal dat bij kamertemperatuur vloeibaar is. Al in 1500 voor Christus waren ze op de hoogte van de gevaren van dit giftige metaal. Eén liter kwik weegt 13,6 kg. Hoeveel weegt het potje kwik dat je leerkracht in de kast staan heeft? De inhoud van het potje is 20 cl. Het gewicht van het potje is te verwaarlozen.

Een kunstenaar heeft 500 cm3 koper nodig om een beeld te gieten. Het soortelijk gewicht van koper is 8,96 gram per cm3. Hoeveel zal het beeldje van de kunstenaar wegen ? 1 2 3 4

Rekenen met rationale getallen

Regelmaat bij lucifers. Vul telkens de tabel aan door figuur 4 te schetsen en alle gebruikte aantallen lucifers te noteren in de onderste rij. Noteer ook de formule die het aantal lucifers l weergeeft in functie van de figuur met nummer n .

LUCIFERS

AANTAL GEBRUIKTE LUCIFERS l

letterformule:

LUCIFERS AANTAL GEBRUIKTE LUCIFERS l

letterformule:

LUCIFERS AANTAL GEBRUIKTE LUCIFERS l

letterformule:

Los volgende vergelijkingen op.

a x +( 25)= 175

e x : ( 11)= 11

b 4 x = 60

f ( 3)+ x = 7

c 2 3 x = 3 2

g x 24,75 = 4,75

d x 1 3 = 5 12 h x : ( 2)= 14

Los volgende vergelijkingen op.

a5 · ( x 3)= 20

e2 · (2 x 3)= x + 6

b2 x + 6 = 4 x 2f ( x + 2)= 8

c x = 3 x 16 g 3 · ( x + 5)= 24

d 1 2 (4 x 6)= 5h

(10 x 2)= 9

Los volgende vraagstukken op met behulp van een vergelijking.

aAlsjeeengetalvermenigvuldigtmet 3 7 ,danbekomje 2 3 .Bepaalditgetal.

b De eigenaar van een manege kocht drie nieuwe paarden om op te leiden. De prijs van het tweede paard is 5 6 van de prijs van het eerste, maar evengoed 1 2 van de prijs van het derde paard. Voor het derde paard betaalde hij 2500 euro.

Bepaal de prijs van de andere paarden.

c Welk getal moet je van –6 aftrekken om –20 te krijgen ?

d Van de 328000 bezoekers aan het Natuurhistorisch Museum in Brussel waren er 3 keer meer bezoekers die individueel het museum bezochten dan in groep. Hoeveel museumbezoekers kwamen in groep naar dit museum ?

Rekenen met rationale getallen

Vul aan.

a 45% van 180 is d % van 500 is 80.

b 12,5% van 640 is e % van 200 is 300.

c 60% van is 300. f 25% van is 450.

WISKUNDE & AARDRIJKSKUNDE

De grootte van het aardoppervlak is ongeveer 510 miljoen km2

70,9% van dit aardoppervlak bestaat uit water.

97,2% van dit water wordt gevormd door zeeën en oceanen.

a Hoeveel km2 van het aardoppervlak bestaat uit water ?

b Hoeveel km2 wordt ingenomen door zeeën en oceanen ?

Iemand koopt op een veiling een schilderij van 3000 euro. Hierbij moeten nog 18% veilingkosten en 4% volgrecht betaald worden. Hoeveel betaalt de koper van het schilderij ?

Mikeheefthonden,katten,koeienenkangoeroesalshuisdier.Hijheeft24huisdieren, 1 8 deeldaarvanishond, 3 4 deelisgeenkoeen 2 3 deelisgeenkat.

Hoeveel kangoeroes heeft Mike ?

(A) 4 (B) 5 (C) 6 (D) 7 (E) 8

WIZPROF 2019 vraag 17© Stichting Wiskunde Kangoeroe

Tabita wil zes paprika’s kopen. Een paprika kost 1 euro. Vijf winkels hebben een uitzonderlijke aanbieding.

– winkel 1 : ‘Eén paprika kopen, de tweede tegen halve prijs.’

– winkel 2 : ‘Twee paprika’s kopen, de derde gratis.’

winkel 3 : ‘Vijf paprika’s kopen, de zesde gratis.’

– winkel 4 : ‘Op alle paprika’s 25% korting.’

– winkel 5 : ‘Bij aankoop van minstens 3 paprika’s, 30% korting!’

In welke winkel bespaart Tabita het meest op de aankoop van zes paprika’s ?

(A)winkel 1(B)winkel 2(C)winkel 3(D)winkel 4(E)winkel 5

JWO 2020 eerste ronde, vraag 5© Vlaamse Wiskunde Olympiade vzw

Vaardigheden | Wiskundetaal bewerkingen

HORIZONTAAL

1 als het product van twee factoren het dubbel is van de eerste factor, dan is de andere factor

4 bij 23 = 8 noem je 2 het …

5 bij 5 6 = 30 noem je 5 een

8 bij 23 = 8 noem je 3 de …

10 resultaat van een optelling

11 als het aftrektal gelijk is aan de aftrekker, dan bekom je …

VERTICAAL

2 de nulde macht van een van nul verschillend getal is steeds

3 ander woord voor tweede macht

6 bij 3 + 5 = 8 noem je 3 een

7 resultaat van een aftrekking

9 resultaat van een vermenigvuldiging

H oofdstuk 2 wordt …

Rekenen met rationale getallen 1

moet ik leren

dit

❒ Ik weet wat natuurlijke, gehele, rationale en irrationale getallen zijn.

❒ Ik ken de betekenis van de symbolen ∈, ∉, ⊂ en ⊄.

❒ Ik ken de betekenis van de symbolen ⟹ en ⟺

❒ Ik ken de betekenis van de symbolen ∪, ∩ en \ en kan de doorsnede, unie en verschil van twee verzamelingen bepalen.

❒ Ik kan rationale getallen optellen en aftrekken.

❒ Ik kan rationale getallen vermenigvuldigen.

❒ Ik kan een rationaal getal delen door een (van nul verschillend) rationaal getal.

❒ Ik ken de definitie van machten en kan een macht berekenen van een rationaal getal.

❒ Ik kan de vierkantswortel berekenen van een rationaal getal.

❒ Ik ken de volgorde van de bewerkingen en kan ze toepassen in oefeningen.

❒ Ik kan vraagstukken oplossen met hoofdbewerkingen.

❒ Ik kan vraagstukken oplossen met de regel van drie of met een verhoudingstabel.

❒ Ik kan regelmaat herkennen in een reeks gegevens.

❒ Ik kan regelmaat herkennen en omzetten naar een woorden letterformule

❒ Ik ken de vier eigenschappen om een vergelijking op te lossen.

❒ Ik kan een vraagstuk oplossen met behulp van een vergelijking.

❒ Ik kan vraagstukken over procenten oplossen. 39

Rekenen met rationale getallen

Werk uit.

a –7 + ( –16) =

i 3,25 – ( –1,75) = j 5 3 2 = = k 4 3 9 24 5 11 = = l 2 3 : 12 18 = = m 7 21 11 14 = = n 52 3 = 1 / 7

b –12 – 5 =

c9 + ( –13) =

d 14 + ( –3) – ( –5) – ( –6) =

e ( –1,25) 6,5 4 2 =

f 8 12 + 8 10 = = g 2: 2 5 = = h 144 25 =

A = de verzameling van leerlingen met blauwe ogen.

B = de verzameling van leerlingen die groter zijn dan 1,60 m.

Zet een kruisje in de juiste kolom.

Kwinten heeft blauwe ogen en is niet groter dan 1,60 m.

Lise heeft blauwe ogen en is groter dan 1,60 m.

a In welk vlinderdiagram werd ( A ⧵ B) ∪ ( B ⧵ A) aangeduid ?

b In welk vlinderdiagram werd ( A ⧵ B) ∪ B aangeduid ?

Werk uit. Denk aan de volgorde van de bewerkingen.

Kwinten . Marie . Lise .

Voor een actie voor een goed doel heeft een klas besloten om bij het eerstvolgende oudercontact zelfgemaakte icetea te verkopen. Per liter water is hiervoor 8 gram thee nodig, 250 g frambozen en 30 ml honing. Er worden 200 ouders verwacht. Hoeveel thee, frambozen en honing moeten ze voorzien als we ervan uitgaan dat de helft van de ouders een glas icetea (25 cl) zal kopen ?

6 / 4

Los volgende vergelijkingen op.

a c x 2 3 = 1 x : 5 4 = 1 3

b d 3 x = 27 10 · ( x 50)= 240

7 / 2

In een klein symfonisch orkest bespeelt 35 % van de 60 muzikanten een blaasinstrument.

Hoeveel muzikanten zijn dat ?

Los dit vraagstuk op met behulp van een vergelijking.

/ 2

James Cameron is een beroemde filmregisseur (van o.a. Titanic en Avatar) die ook een passie heeft voor de diepzee. In 2012 daalde hij in zijn eentje in deze kleine capsule (een bathyscaaf) naar de diepste plek op onze planeet : de Marianentrog. Toen op zijn instrumentenbord stond af te lezen dat hij zich op –6711 meter bevond, was er nog een bepaalde weg af te leggen. Hoeveel moest hij nog afdalen als je weet dat deze Marianentrog zich bevindt op –10 911 meter ?

Mark Thiessen, NG Image Collection

Machten 2

Hoodstuktitel

Met machten gaat het serieus snel vooruit.

Stel dat je in een raket wordt weggeschoten en dat we de afstand tot de aarde uitdrukken in kilometer. Dan is een van de verste foto’s die we kunnen bekijken, genomen op 1017 km hoogte.

Je ziet dan de sterren van ons melkwegstelsel.

Doordringen in de kleinste deeltjes van de kernfysica levert ons quarks op.

Die quarks zijn heel veel kleine, elementaire deeltjes die nog kleiner zijn dan een atoom of een elektron. Grootte: ongeveer 10–23 m.

Machten

2.1 Machten met gehele exponenten

1 Machten met een gehele exponent 53

2 Product van machten met hetzelfde grondtal 55

3 Quotiënt van machten met hetzelfde grondtal 56

4 Macht van een macht 57

5 Macht van een product 58

6 Macht van een quotiënt 59

7 Samenvatting 63

8 Oefeningen 64

2.2 Wetenschappelijke schrijfwijze

1 Machten van 10 82

2 De wetenschappelijke schrijfwijze 83

3 Omzetten naar de wetenschappelijke schrijfwijze 84

4 De wetenschappelijke schrijfwijze wegwerken 85

5 Rekenen met getallen in de wetenschappelijke schrijfwijze 86

6 Samenvatting 86

7 Oefeningen 87

Extra’s

Vaardigheden : maten omzetten 93

Wat moet je kennen en kunnen ? 95

Herhalingsoefeningen 96

Bekijk de instructievideo’s

2.1 Machten met gehele exponenten

1Machten met een gehele exponent

Vorig schooljaar leerde je machten berekenen van rationale getallen waarbij de exponent een natuurlijk (met andere woorden een positief geheel) getal was.

74 = 7 · 7 · 7 · 7 = 2401 (een product van 4 factoren 7)

We vragen ons af wat er zou gebeuren mocht de exponent een negatief geheel getal zijn. Volg nu eens de onderstaande redenering, waarbij we de exponent telkens één geheel kleiner maken.

24 = 2 2 2 2 = 16

23 = 2 · 2 · 2 = 8 22 = 2 · 2 = 4 21 = 2 = 2 20 = 2 2 = 1

Vaststelling :

Telkens als je de exponent met één geheel vermindert, wordt het resultaat gedeeld door twee. Telkens als je de exponent met één geheel vermeerdert, wordt het resultaat vermenigvuldigd met twee.

Merk op :

• Je ziet dus dat 2–3 het omgekeerde is van 23

• Deze redenering is ook geldig voor andere grondtallen. Zo is 5–3 het omgekeerde van 53.

• De nulde macht van een getal is steeds 1, behalve als het getal nul is. De macht 00 wordt niet gedefinieerd.

Voorbeelden :

Omdat het grondtal elk rationaal getal verschillend van 0 mag voorstellen, kunnen we die vervangen door een letter. Om te komen tot een definitie in symbolen vervangen we ook de exponent door een letter :

macht met negatieve exponent ∀a ∈ Q0 , ∀n ∈ N :

= 1

∀a , b ∈ Q0 , ∀n ∈ N : a b n = b n a n In bovenstaande definitie mag je a ook vervangen door een breuk. Volg mee wat er gebeurt :

De breuk wordt omgedraaid en de exponent verandert van teken.

Als het grondtal een breuk is, kun je de definitie in symbolen als volgt noteren : macht met negatieve exponent

Om het jou gemakkelijker te maken, kun je bij het rekenen met machten de oefeningen sneller oplossen door gebruik te maken van enkele rekenregels :

• product van machten met hetzelfde grondtal

• quotiënt van machten met hetzelfde grondtal

• macht van een macht

• macht van een product

• macht van een quotiënt

( 4)

2 Product van machten met hetzelfde grondtal

Voorbeelden : 24 23 =(2 2 2 2) (2 2 2)

Vanuit die getallenvoorbeelden kunnen we onderstaande rekenregel afleiden : rekenregel in woorden:

=( 4)5 1 ( 4)2 =( 4) ( 4) ( 4) ( 4) ( 4) ( 4) 1 ( 4) ( 4) =( 4) ( 4) ( 4) =( 4)2 =( 4)5+( 2) 7 74 = 7 (7 7 7

Om machten met hetzelfde grondtal te vermenigvuldigen, behoud je het grondtal en tel je de exponenten bij elkaar op. in symbolen:

Voorbeelden

We kunnen de rekenregel ook toepassen als het grondtal van de macht een letter is. De letter is dan de plaatsvervanger van een willekeurig grondtal verschillend van 0.

Voorbeelden :

Merk op :

• Let op bij exponent 1: die wordt meestal niet geschreven.

x 3 x = x 4

• De rekenregel geldt ook voor een product van meerdere machten.

x 4 · x 3 · x 2 · x = x 4 + 3 + 2 + 1 = x 10

a 2 · a 5 · a –4 = a 2 + 5 + ( –4) = a 3

3 Quotiënt van machten met hetzelfde grondtal

Voorbeelden : 28 :25 = 28 25

Vanuit die getallenvoorbeelden kunnen we onderstaande rekenregel afleiden: rekenregel in woorden:

Om machten met hetzelfde grondtal door elkaar te delen, behoud je het grondtal en trek je de exponenten van elkaar af. in symbolen:

Voorbeelden :

We kunnen deze rekenregel ook toepassen als het grondtal van de macht een letter is. De letter is dan plaatsvervanger van een willekeurig grondtal verschillend van 0.

Voorbeelden :

b 5 : b 2 = b 5 ( 2) = b 5+2

Merk op :

• Let op bij exponent 1: die wordt meestal niet geschreven.

b 4 : b = b 4–1 = b 3

• De rekenregel geldt ook bij meerdere machten en in combinatie met de vorige rekenregel.

a 4 a 5 : a 6 = a 4 + 5 – 6 = a 3

x 3 : x ⋅ x 4 : x 5 = x 3 – 1 + 4 – 5 = x 1 = x

4 Macht van een macht

Voorbeelden :

Vanuit die getallenvoorbeelden kunnen we onderstaande rekenregel afleiden : rekenregel in woorden: Om een macht tot een macht te verheffen, behoud je het grondtal en vermenigvuldig je de exponenten. in symbolen:

Voorbeelden :

We kunnen deze rekenregel ook toepassen als het grondtal van de macht een letter is. De letter is dan plaatsvervanger van een willekeurig grondtal verschillend van 0.

Voorbeelden :

5 Macht van een product

Voorbeelden :

(2 10)4 =(2 10) (2 10) (2 10) (2 10)

= 2 10 2 10 2 10 2 10

= 24 · 104

= 160000

(3 · 4)3 =(3 · 4) · (3 · 4) · (3 · 4)

= 3 4 3 4 3 4

= 33 43 = 1728

Zokunjeopeenanderemanier204 berekenen.

Zokunjeopeenanderemanier123 berekenen.

Vanuit die getallenvoorbeelden kunnen we onderstaande rekenregel afleiden : rekenregel in woorden in woorden: Om een product tot een macht te verheffen, verhef je elke factor tot die macht. in symbolen:

Voorbeelden :

We kunnen deze rekenregel ook toepassen als de factoren van het product letters zijn. De letter is dan plaatsvervanger van een willekeurig getal verschillend van 0.

Voorbeelden :

Merk op :

We kunnen de rekenregel ook van rechts naar links toepassen. Dat kan je soms wat rekenvoordeel opleveren.

25 55 = ( 2 5)5

105

6 Macht van een quotiënt

Voorbeelden : (1:2)4 = 1 2 4

Vanuit deze getallenvoorbeelden kunnen we onderstaande rekenregel afleiden : rekenregel in woorden in woorden:

Om een quotiënt tot een macht te verheffen, verhef je deeltal en deler tot die macht. of

Om een breuk tot een macht te verheffen, verhef je teller en noemer tot die macht. in symbolen:

Grote en kleine getallen: stel je voor …

10 22 m (of 1 miljoen lichtjaren) is de doorsnede van ons melkwegstelsel.

1016 m (of 1 lichtjaar) is de afstand die het licht in 1 jaar aﬂegt.

107 m (of tienduizend kilometer) is de diameter van de aarde.

10 0 m (of 1 meter) is de lengte van de veer van een pauw.

10 – 5 m (of 10 micrometer) is de diameter van een cel van ons DNA.

10 –14 m (of 10 femtometer) is de diameter van een atoom.

Voorbeelden

We kunnen deze rekenregel ook toepassen als deeltal en deler (of teller en noemer) letters bevatten.

De letters zijn dan plaatsvervanger van een willekeurig getal verschillend van 0.

Voorbeelden

Taak : Controleer met ICT.

Een handig hulpblad

➀ Knip de volgende pagina uit op de stippellijn in de rug.

Op die bladzijde zie je nu twee soorten lijnen:

➁ dikke stippellijn: hier plooi je over de volle breedte; ➂ dunne stippellijn: die knip je met een schaar door.

Correct uitgevoerd?

Dan heb je een handig hulpblad bij het studeren van deze belangrijke rekenregels.

)

a ∈ Q 0 , ∀ n , p

Z : ( a n ) p = a n · p

Q 0 , ∀ n ∈ Z : ( a : b ) n = a n : b n

a , b

Q 0 , ∀ n ∈ Z : a b n = a n b n

QUOTIËNT VAN MACHTEN MET HETZELFDE GRONDTAL grondtal behouden exponenten aftrekken

Q 0 , ∀ n , p ∈ Z : a n : a p = a n a p = a n p

a ∈ Q 0 , ∀ n , p

Z : ( a n ) p = a n · p

Q 0 ,

Z : ( a · b ) n = a n · b n ∀ a , b ∈ Q 0 , ∀ n ∈ Z : ( a : b ) n = a n : b n ∀ a , b ∈ Q 0 , ∀ n ∈ Z : a b n = a n b n ∀ a ∈ Q 0 , ∀ n , p ∈ Z :

n ∈ Z : ( a : b ) n = a n : b n

n , p ∈ Z : ( a n ) p = a n · p ∀ a , b ∈ Q 0 , ∀ n ∈ Z : ( a · b ) n = a n · b n

Z : a n : a p = a n a p = a n p

Q 0 ,

PRODUCT VAN MACHTEN MET HETZELFDE GRONDTAL grondtal behouden exponenten optellen

a , b ∈ Q 0 , ∀ n ∈ Z : ( a : b ) n = a n : b n ∀ a , b ∈ Q 0 , ∀ n ∈ Z : a b n = a n b n ∀ a ∈ Q 0 , ∀ n , p ∈ Z : a n · a p = a n + p ∀ a ∈ Q 0 , ∀ n , p ∈ Z : a n : a p = a n a p = a n p ∀ a ∈ Q 0 , ∀ n , p ∈ Z : ( a n ) p = a n · p ∀ a , b ∈ Q 0 , ∀ n ∈ Z : ( a · b ) n = a n · b n ∀ a , b ∈ Q 0 , ∀ n ∈ Z : ( a : b ) n = a n : b n ∀ a , b ∈ Q 0 , ∀ n ∈ Z : a b n = a n b n ∀ a ∈ Q 0 , ∀ n , p ∈ Z : a n · a p = a n + p ∀ a ∈ Q 0 , ∀ n , p ∈ Z : a n : a p = a n a p = a n p ∀ a ∈ Q 0 , ∀ n , p ∈ Z : ( a n ) p = a n · p

MACHT MET NEGATIEVE EXPONENT grondtal omkeren exponent van teken veranderen

a , b

Q 0 , ∀ n

QUOTIËNT verhef deler en deeltal tot de macht

a , b ∈ Q 0 , ∀ n ∈ Z : ( a · b ) n = a n · b n ∀ a , b ∈ Q 0 , ∀ n ∈ Z : ( a : b ) n = a n : b n ∀ a , b ∈ Q 0 , ∀ n ∈ Z : a b n = a n b n

Q 0 ,

n , p

MACHT VAN EEN

Z : ( a n ) p = a n · p

a ∈ Q 0 , ∀ n , p ∈ Z : a n : a p = a n a p = a n p

a ∈ Q 0 , ∀ n , p ∈ Z : a n · a p = a n + p

Q 0 , ∀ n ∈ Z : ( a : b ) n = a n : b n ∀ a , b

a , b

Q 0 , ∀ n ∈ Z : ( a · b ) n = a n · b n

Q 0 , ∀ n , p

Z :

PRODUCT verhef elke factor tot de macht

MACHT VAN EEN

a ∈ Q 0 , ∀ n , p ∈ Z : ( a n ) p = a n · p ∀ a , b ∈ Q 0 , ∀ n ∈ Z : ( a · b ) n = a n · b n ∀ a , b ∈ Q 0 , ∀ n ∈ Z : ( a : b ) n = a n : b n ∀ a , b ∈ Q 0 , ∀ n ∈ Z : a b n = a n b n

MACHT VAN EEN

MACHT grondtal behouden exponenten vermenigvuldigen

n : a p = a n a p = a n p

MACHT MET NEGATIEVE EXPONENT MACHT

HETZELFDE GRONDTAL

MACHT VAN EEN MACHT

QUOTIËNT VAN MACHTEN MET HETZELFDE GRONDTAL

7Samenvatting

• Je kunt de definitie van een macht met gehele exponenten noteren.

∀a ∈ Q0 , ∀n ∈ N : a n = 1 a n

∀a , b ∈ Q0 , ∀n ∈ N : a b n = b a n

• Je kunt de rekenregels voor machten formuleren en toepassen.

Om machten met hetzelfde grondtal met elkaar te vermenigvuldigen, behoud je het grondtal en tel je de exponenten bij elkaar op.

∀a ∈ Q0, ∀n , p ∈ Z : a n a p = a n +p

Om machten met hetzelfde grondtal door elkaar te delen, behoud je het grondtal en trek je de exponenten van elkaar af.

∀a ∈ Q0, ∀n , p ∈ Z : a n : a p = a n –p

Om machten tot een macht te verheffen, behoud je het grondtal en vermenigvuldig je de exponenten.

∀a ∈ Q0, ∀n , p ∈ Z : ( a n ) p = a n p

Om een product tot een macht te verheffen, verhef je elke factor tot die macht.

∀a , b ∈ Q0, ∀n ∈ Z : ( a b) n = a n b n

Om een quotiënt tot een macht te verheffen, verhef je deeltal en deler tot die macht.

∀a , b ∈ Q0, ∀n ∈ Z : ( a : b) n = a n : b n

Om een breuk tot een macht te verheffen, verhef je teller en noemer tot die macht.

∀a , b ∈ Q0, ∀n ∈ Z : a b n = a n b n

Machten van 10: de voorvoegsels

De voorvoegsels die je in de wetenschappen gebruikt, duiden eigenlijk op een vermenigvuldiging van een macht van 10. De voorvoegsels voor grotere getallen ken je wellicht van de grootte van de harde schijf van een computer. De voorvoegsels van kleinere getallen zul je later in wetenschappelijke vakken bestuderen.

machtvan10voorvoegselsymboolmachtvan10voorvoegselsymbool

10 24 yotta Y 10 –1 deci d

10 21 zetta Z 10 – 2 centi c 1018 exa E 10 – 3 milli m 1015 peta P 10 – 6 micro μ 1012 tera T 10 – 9 nano n

10 9 giga G 10 –12 pico p

10 6 mega M 10 –15 femto f

10 3 kilo k 10 –18 atto a

10 2 hecto h 10 – 21 zepto z

101 deca da 10 – 24 yocto y

8Oefeningen

Schrijf de volgende producten als een macht.

Bereken de volgende machten met negatieve exponenten.

Kleur het vakje groen als de macht een positief resultaat oplevert.

Werk uit door de rekenregel ‘product van machten met hetzelfde grondtal’ toe te passen. a22 23 = e0,32 0,3 2 = b2 4 22 = f 3 7 2 3 7

= c 2 3 2 2 3 2 =

Werk uit door de rekenregel ‘product van machten met hetzelfde grondtal’ toe te passen. De letters in de grondtallen stellen een rationaal getal voor verschillend van nul.

Werk uit. De letters in de grondtallen stellen een rationaal getal voor verschillend van nul.

Werk uit door de rekenregel ‘quotiënt van machten met hetzelfde grondtal’ toe te passen. a24 :22 = f75 :7 1 = b 102 103 = g 23 2 2 =

Werk uit door de rekenregel ‘quotiënt van machten met hetzelfde grondtal’ toe te passen. De letters in de grondtallen stellen een rationaal getal voor verschillend van nul.

Werk uit. Opgelet! Zowel het grondtal als de exponent kunnen letters zijn. De letters in de grondtallen stellen een rationaal getal voor verschillend van nul.

Werk uit door de rekenregel ‘macht van een macht’ toe te passen.

Werk uit door de rekenregel ‘macht van een macht’ toe te passen. De letters in de grondtallen stellen een rationaal getal voor verschillend van nul.

Werk uit. Opgelet! Zowel het grondtal als de exponent kunnen letters zijn. De letters in de grondtallen stellen eenrationaal getal voor verschillend van nul.

WISKUNDE & AARDRIJKSKUNDE

Een van de laatste stukjes ‘onontgonnen gebied’ van Noord-Amerika is Alaska. Het telt anderhalf miljoen vierkante kilometer en die werden allemaal in 1867 voor slechts 7000000 dollar overgekocht van Rusland. De hoofdstad is Juneau en de gemiddelde temperatuur in het noorden van deze staat is –12 °C. In het zuiden wordt het echter warmer, tot 35 °C.

Alaska telt heel wat ‘National Parks’, waar je geniet van de ongerepte natuur en de wildernis. Maar je kunt er ook nog oog in oog komen te staan met kariboes, elanden, zwarte beren en grizzly’s. En dat is niet zonder gevaar !

De plaatselijke gidsen zullen je dan ook uitgebreid inlichten over wat je moet doen als je zo’n kanjer plots voor je ziet staan.

De natuur krijgt in Alaska dus de hoofdrol. Je vindt er de hoogste berg uit Noord-Amerika, de Mount McKinley, 6194 m hoog, en er zijn 70 vulkanen. Ongeveer 5% van Alaska is gletsjergebied. Er zijn meer dan 5000 gletsjers (waarvan sommige zelfs 8km lang!) en je vindt er ook ontzettend veel meren. Het aantal meren in Alaska vind je door onderstaande puzzel op te lossen. De letters in de grondtallen stellen een rationaal getal voor verschillend van nul.

Verbind de opgave met de correcte oplossing en noteer dan onderaan bij de letter van de oefening het cijfer dat je boven de oplossing vindt. Het getal dat je zo vormt, is het aantal meren in Alaska. Je kunt het steeds ter plaatse gaan natellen !

Werk uit door de rekenregel ‘macht van een product’ toe te passen.

a (2a )2 = f ( 2ab )2 = b (4 c )3 = g (2ac )3 = c ( ab )2 = h 1 2 ac 2 = d ( 3 c )2 = i ( ab )3 =

Werk uit door de rekenregel ‘macht van een product’ toe te passen. De letters in de grondtallen stellen een rationaal getal voor verschillend van nul. a 2a 2 b 2 = f 0,5 x 2 y 3 2 =

Werk uit. Opgelet! Zowel het grondtal als de exponent kunnen letters zijn. De letters in de grondtallen stellen eenrationaal getal voor verschillend van nul. a x y k = f a 2 b 3 c m =

Werk uit door de rekenregel ‘macht van een quotiënt’ toe te passen.

Werk uit door de rekenregel ‘macht van een quotiënt’ toe te passen. De letters in de grondtallen stellen een rationaal getal voor verschillend van nul.

Werk uit. Opgelet! Zowel het grondtal als de exponent kunnen letters zijn. De letters in de grondtallen stellen eenrationaal getal voor verschillend van nul.

Bewijzen maar …

Je hoeft niet alles in de wiskunde zomaar aan te nemen. Daarom zul je geregeld een verklaring of bewijs terugvinden van rekenregels of eigenschappen.

We kunnen zo’n bewijs opbouwen dankzij de gekende leerstof van dit en van het vorige schooljaar. Bij elke stap van een bewijs hoort een verantwoording. Eigenlijk een beetje het antwoord op de vraag: “Waarom mag je dat uit de vorige stap afleiden?”

Er bestaan in de wiskunde verschillende soorten bewijzen.

Dit bewijs steunt op een hele reeks gelijkheden. We vertrekken bij het linkerlid en proberen (via definities en eigenschappen) bij het rechterlid uit te komen. Volg je mee ?

Voorbeeld : bewijs de eerste rekenregel ∀a ∈ Q0, ∀n ,p ∈ N : a n a p = a n +p

Gegeven : a ∈ Q0 n , p ∈ N voorwaardeletters

Te bewijzen : a n · a p = a n +p

Bewijs : a n a p =(a a a ) n factoren (a a a ) p factoren

= a a ... a n +p factoren

= a n +p

deﬁnitiemacht

hetvermenigvuldigenin Q isassociatief

deﬁnitiemacht

Ook voor gehele exponenten is de uitspraak waar.

Bewijs op een analoge manier een andere rekenregel.

Werk uit door rekenregels van machten toe te passen. De letters in de grondtallen stellen een rationaal getal voor verschillend van nul.

Werk uit. De letters in de grondtallen stellen een rationaal getal voor verschillend van nul.

a ( a )2 a 5 3 = b a 2 4 : a 4 = c a 3 · b 2 4 · c 5 a 2 · b 10 · ( c 2 )3 = d a 3 · a 4 (a 2 )3 =

Werk uit door rekenregels van machten toe te passen. De letters in de grondtallen stellen een rationaal getal voor verschillend van nul.

a 2 a 2 b 2 2 =

b a 2 3 · b 2 · a 2

b 4 · a 3 =

c k 2 · k 4 · n 3 k 3 n 2 3 = d

a 2 bc 3 3 (2ab ) 2 = e 1 2 a 2 b 2 a 3 · b · a 2 =

b a 2 3 b 3 2 a 5 2 · b 4 = d (1,5) 3 · 6,22 43 = 25 * 26 *

Bereken met ICT. De letters in de grondtallen stellen een rationaal getal voor verschillend van nul.

a 8 7 2 7 25 42 2 3 = c 2,53 82 : 16 4 ( 2,5) 2 =

Werk uit. Gebruik zo veel mogelijk rekenregels om de opgave te vereenvoudigen. Bestudeer vooraf grondig het voorbeeld.

Voorbeeld : 8 + 32:4 + 1 2 3 22 2 =

= 23 + 25 :22 + 23 22 · 2

= 23 + 23 + 23 23

= 2 · 23

= 24

= 16

Vul aan. De letters in de grondtallen stellen een rationaal getal voor verschillend van nul.

Bepaal telkens x . De letters in de grondtallen stellen een rationaal getal voor verschillend van nul.

Werk uit zoals in het voorbeeld.

Werk

( –164)4 : 824

: ( 0,5)2

Boven de poolcirkel

Op expeditie naar het noorden van Scandinavië ?

Alvast geen slecht idee. Als je echt bijna in het meest noordelijke punt van Noorwegen, Zweden of Finland (je mag zelf kiezen) bent, passeer je de poolcirkel. Boven deze magische grens gaat de zon in de zomer gedurende zestig dagen niet onder! Je ziet dan ’s nachts de middernachtzon. De plaatselijke bevolking moet echter in de winter een even lange poolnacht doormaken! Ter plaatse kun je kennismaken met een ijskathedraal, een ijshotel, het noorderlichtmuseum, prehistorische rotstekeningen (zelfs tot 8000 jaar oud) en in één dorpje vind je nog een attractie: de enige echte …

Om te weten te komen over wie of wat we het hier hebben, los je elke oefening op. Zoek de letter die bij het antwoord staat en vorm hiermee het antwoord. De letters in de grondtallen stellen een rationaal getal voor verschillend van nul.

b 1

2 a 2 bc ab 3

15 · ( 1) 2 ( 1)

5 1 54 5 2 a 1 b 2 2 c ac 3 ( 4) 2 · ( 4) 3 ( 4) 4 ( 9) 1 ( )2 ( )3 9 5 2 1 a 2 1 2 b 1 b 2 a 2 bc 3 2 15 ( 1) ( 1)

5 1 54 5 2 1 b 2 2 ( ) 4 ( 9)

) 1 ( 9)2 · ( 9)3 ( 9)4 5 2 1 a 2 b 1 2 7 b 1 b 2 a 2 bc ab 3 2 15 ( 1) 2 ( 1) 52 · 5 1 · 54 5 2 a 1 b 2 2 c ac 3 ( 4) 2 ( 4) 3 ( 4) 4 ( 9) 1 ( 9)2 ( 9)3 ( 9)4 5 2 1 a 2 b 1 2 7 b 1 b 2 a 2 bc ab 3 2 15 ( 1) 2 ( 1)

52 5 1 54 5 2 a 1 b 2 2 c ac 3 ( 4) 2 ( 4) 3 ( 4) 4 ( 9) 1 9 · 9 ( )4 2 2 b 1 7 b b 2 a ab 2 15 ( 1) 2 ( 1) · · a 1 b 2 c ac 3 ( 4) 2 ( 4) 3 ( 4)

Welke macht van 2 bekom je als je

a 16 acht keer vermenigvuldigt met 2 ?

c210 halveert ?

b44 optelt met 44 ?

d84 deelt door 44 ?

Welke van de volgende getallen is geen kwadraat én ook geen derde macht ?

(A) 29 (B) 310 (C) 411 (D) 512 (E) 613

WIZPROF 2015 vraag 8© Stichting Wiskunde Kangoeroe

Hetgetal 88 44 + 44 isgelijkaan

(A) 2 (B) 28 (C) 212 (D) 214 (E) 215

JWO 2024 eerste ronde, vraag 21© Stichting Wiskunde Kangoeroe

2.2 Wetenschappelijke schrijfwijze

1Machten van 10

WISKUNDE & WETENSCHAPPEN

Machten van tien worden in de wetenschap veel gebruikt.

1 = 100

= 101

= 102

= 103

= 104

= 105

De exponent is gelijk aan het aantal nullen achter de 1.

De exponent zonder het minteken geeft het aantal nullen weer voor de 1.

Maak een reis mee van 1000000000000000000000000000000000000 m of (iets makkelijker) 1036 m.

Eén miljoen lichtjaren van ons verwijderd: het melkwegstelsel.

Ons zonnestelsel. De blauwe lijn volgt onze planeet.

De kern van een koolstofatoom = 10 femtometer.

Spiraalgedraaide strengen DNA.

Ziehier onze planeet met enkele miljarden passagiers.

Je ziet de individuele cellen van het eikenblad.

2De wetenschappelijke schrijfwijze

Machten van 10 zijn belangrijk om heel grote getallen (zoals 100 biljoen) en heel kleine getallen (zoals –10 miljard) makkelijk weer te geven. Maar ze zijn ook erg handig om getalletjes tussen –1 en 1 (zoals 0,000000000125) weer te geven.

De wetenschappelijke schrijfwijze steunt in grote mate op machten van 10.

wetenschappelijke schrijfwijze

De wetenschappelijke schrijfwijze van een getal verschillend van nul is dit getal geschreven als een product van twee factoren.

–De eerste factor is een decimaal getal met één beduidend cijfer (een cijfer verschillend van nul) voor de komma.

–De tweede factor is een macht van 10.

Voorbeelden :

7,2 103 –8,34 10–5

3 1017 6 100

10000 km boven een deel van Amerika.

10 km verwijderd van een park in Florida.

100 meter boven het dak van een labo en een bosje.

Hier zie je het blad van een eik honderd keer vergroot.

1 dm boven het oppervlak van een blad van een eik.

10 m boven een eikenboom.

3 Omzetten naar de wetenschappelijke schrijfwijze

De absolute waarde is groter dan 1 – Plaats de komma na het eerste beduidende cijfer. Tel hoeveel plaatsen je de komma naar links verschoven hebt.

– Vermenigvuldig met een macht van 10. De exponent is het aantal plaatsen dat je de komma naar links verschoof.

150000000 = 1,5 · ……

150000000 = 1,5 · 108

8 cijfers naar links

Voorbeelden :

5730 = 5,73 · 103 –1012,53 =–1,01253 · 103 –273,45 =–2,7345 · 102 2 = 2 · 100

De absolute waarde is kleiner dan 1 – Plaats de komma na het eerste beduidende cijfer. Tel hoeveel plaatsen je de komma naar rechts verschoven hebt.

– Vermenigvuldig met een macht van 10. De exponent is het aantal plaatsen dat je de komma naar rechts verschoof, voorafgegaan door een minteken.

0,000015 = 1,5 · ……

0,000015 = 1,5 · 10–5

5 cijfers naar rechts

Voorbeelden :

0,4 = 4 · 10–1

0,00000321 = 3,21 ·10–6 –0,0003 = –3 · 10–4 –0,000503 =–5,03 ·10–4

Als je rekenmachine in wetenschappelijke schrijfwijze staat (zie volgende bladzijde), zul je onmiddellijk de wetenschappelijke schrijfwijze kunnen aflezen. Tik je getal in en druk op enter .

De ingenieursnotatie

Een speciale vorm van de wetenschappelijke schrijfwijze is de ingenieursnotatie (of technische notatie). Hierbij is de exponent van tien steeds een drievoud. De absolute waarde van de eerste factor is een getal tussen 0 en 1000. Zo zal 1,2 10 4 in de ingenieursnotatie genoteerd worden als 12 10 3

4 De wetenschappelijke schrijfwijze wegwerken

De exponent bij de macht van tien is positief – Schuif de komma zoveel plaatsen op naar rechts als de exponent aangeeft. Voeg indien nodig nullen toe.

1,5 · 108 = 150000000

8 cijfers naar rechts

Voorbeelden :

2 · 107 = 2 · 10000000 2,1 · 104 = 2,1 · 10000 = 20000000 = 21000

4,3210987 106 = 4,3210987 1000000 6 101 = 6 10 = 4321098,7 = 60

1,90872374 · 107 = 1,90872374 · 10000000 3,1418 · 100 = 3,1418 = 19087237,4

De exponent bij de macht van 10 is negatief – Schuif de komma zoveel plaatsen naar links als (de absolute waarde van) de exponent aangeeft. Noteer een nul voor de komma. 1,5 · 10–5 = 0,000015

5 cijfers naar links

Voorbeelden : 9,42 · 10 4 = 9,42 · 0,0001 4 · 10 5 = 0,00004 = 0,000942

2,5 · 10 6 = 0,0000025 1,237 · 10 2 = 0,01237

Ook deze omzetting gebeurt (meestal) heel makkelijk met je rekenmachine. Maak gebruik van de toets ×10n en zorg ervoor dat de wetenschappelijke schrijfwijze (sci) is uitgeschakeld. Wegens de beperktheid van het schermpje zal je rekenmachine getallen zoals 3,5 · 1013 niet kunnen omzetten.

5 Rekenen met getallen in de wetenschappelijke schrijfwijze

Hiervoor gebruik je de eigenschappen van het vermenigvuldigen in Q. Volg je even mee ?

( 2,3 · 10–1) · ( 5 · 103) = 2,3 · 10–1 · 5 · 103

het vermenigvuldigen in Q is associatief = 2,3 · 5 · 10–1 · 103 het vermenigvuldigen in Q is commutatief

= 11,5 · 102 uitwerken en rekenregel van machten = 1,15 · 103 omzetten naar wetenschappelijke schrijfwijze

Je zet dus de machten van 10 achteraan samen. Het product van die machten van 10 vind je door de rekenregels toe te passen.

Je zoekt ook het product van de twee decimale getallen. Indien nodig moet je het eindresultaat nog omzetten in de wetenschappelijke schrijfwijze.

Voorbeelden :

3,6 · 102

9 · 10 3 = 3,6 9 102 ( 3) = 0,4 105 = 4 10 1 105 = 4 · 104

1,2 10 2 2 = (1,2)2 10 2 2 = 1,44 10 4

6Samenvatting

• Je weet dat de wetenschappelijke schrijfwijze van een getal verschillend van nul een product is van twee factoren : – een decimaal getal met één beduidend cijfer voor de komma – een macht van 10

• Je kunt elk rationaal getal omzetten naar de wetenschappelijke schrijfwijze.

• Je kunt elke wetenschappelijke schrijfwijze omzetten naar een rationaal getal.

• Je kunt rekenen met getallen in de wetenschappelijke schrijfwijze.

7Oefeningen

Zet volgende getallen om in de wetenschappelijke schrijfwijze.

a In Japan haalde de JR-Maglev, een magneetzweeftrein, een snelheidsrecord van 603 km/h.

b De afstand van de aarde tot de zon bedraagt ongeveer 149500000000 m.

c De diameter van een elektron is 0,000000000000014 m.

d Een zeer gevoelige stroomsterktemeter meet tot op 0,0001 ampère nauwkeurig.

e De snelheid van het geluid bedraagt 1188 km/h.

f De snelheid van het licht bedraagt 1 079244000 km/h.

g De aarde weegt 5 976000000000000000000000 kg.

h De afstand van de aarde tot de maan is ongeveer 380000 km.

i Eén potje yoghurt bevat 350000000 bacteriën.

j Een kernfysicus werkt met erg kleine oppervlakten. Zo is één barn gelijk aan 0,000000000000000000000000 1 mm2

k Een virus heeft een diameter van 0,000000009 m.

De massa van de zon is ongeveer 300000 keer die van de aarde.

Zoek de massa van de aarde in vraag 1 en bepaal de massa van de zon. Schrijf je getal in de wetenschappelijke schrijfwijze.

5 *

Schrijf deze getallen zonder macht van 10.

a 7,45 104 = g 4,3 10 –4 =

b –9,3 · 106 = h –2 · 10 –5 =

c 2 108 = i 7,21 10 –3 =

d –4,362 102 = j –3,4934 10 –1 = e 2,0085 103 = k 2,571 10 –4 = f 6,842 · 105 =

Rangschik de getallen van klein naar groot. a –3 1023 5 1023 1,2 1023 –1,8 1023 3 1023

b 6,2 · 1048 –6,2 · 10 –47 6,2 · 10 –48 6,2 · 1046 –6,2 · 1047

Zet volgende getallen om in de wetenschappelijke schrijfwijze.

a –310,5 102 =

b 25000 · 10 –4 =

c 100 =

d –1835,5 105 =

e 0,01 10 –2 =

f –0,1 =

g 0,12 102 =

h –0,0004 10 –4 =

i 0,0004 104 = 3 4

De Dagelijkse Spiegel – 5 januari 2026

Het hoogste gebouw ter wereld

Ooit al eens voor het Atomium gestaan in Brussel? Vond je dat een imposant gebouw?

Met zijn 103 m hoogte is dit echter niet het hoogste gebouw van België. Daarvoor moeten we naar het Pajottenland, waar we in Sint-PietersLeeuw de VRT-zendmast vinden, goed voor een hoogte van 302 m.

Kan het hoger? Uiteraard! Een flatgebouw is officieel een ‘wolkenkrabber’ als het hoger is dan 35 m. De stad met de meeste wolkenkrabbers is Hongkong, waar er ongeveer 6800 te vinden zijn.

Waar is de hoogste ter wereld? Niet inKuala Lumpur, waar de Petronas Towers als een mooie identieke tweeling tot 452 m geraken. Ook niet de Willis Tower in Chicago (443 m hoog) of de Taipei 101 in de hoofdstad van Taiwan, die met zijn 508 m hoogte verschillende jaren de eerste plaats bekleedde in deze hitlijst. Voor het hoogste gebouw moeten we naar de Verenigde Arabische Emiraten, waar in2010 de laatste steen (en zendmast) geplaatst is op de Burj Khalifa, mede dankzij de Belgische firma Besix!

Er werd voor dit bouwwerk 142000 m2 speciaal glas gebruikt, dat bestand is tegen de warme temperaturen van Dubai. Om het hele gebouw te koelen is 10000000 l water nodig. In het gebouw vind je ook de snelste liften ter wereld: ze gaan omhoog en omlaag met een snelheid van 64,8 km/h.

Reportage Dubai – 14

van 950000 liter. Het prijskaartje?

Goedkoop zal het wel niet geweest zijn, maar met 5000000000 euro zul je aardig in de buurt komen. Een hoog bedrag als je weet dat sommige van de 5000 arbeiders werkten voor 5 euro per dag.

Wat brengt de toekomst?

Er wordt gewerkt aan de Jeddah Tower, een megabuilding hoger dan 1000 m!

De eerste 37 verdiepingen zijn voor het Armanihotel. Op verdieping 78 is er een zwembad en daarna zijn er een heleboel appartementen. Per dag wordt gerekend op een waterverbruik

Maar hoeveel meter hoog is die wolkenkrabber eigenlijk ?

Zet elk getal dat in de tekst vetgedrukt is om naar de wetenschappelijke schrijfwijze. Zoek de oplossing in dit rooster en kleur het mooi in. Je vindt de hoogte terug, uitgedrukt in meter.

Bereken met behulp van machten van 10 en noteer het resultaat in de wetenschappelijke schrijfwijze.

a ( 7 10 –1) ( 1,2 10 –2) f 4,5 102 9 · 10 3

b ( 2 10 –4) ( 5 10 6) ( 3,2 10) g ( 1,2 10 –3)2

c ( –1 10 3) ( 1,25 10 –4) ( 8 102) h ( –1,5 10 12)2

d 9,33 · 104 3,11 · 103 i ( 2 10 5)–2

e 6 103 3 104 9 · 105 j 6,8 105 4,2 103 2,1 105 3,4 10 2

Bereken met behulp van ICT.

WISKUNDE & WETENSCHAPPEN

a Kleine, maar dan ook echt kleine afstanden …

De Zweedse natuurkundige Ångström studeerde en werkte aan de universiteit van Uppsala in de 19e eeuw. Naar hem is de eenheid 1 ångström (1Å, lees als ongstreum [ˈ ŋstrøm] ) genoemd.

Die komt overeen met 10 –10 m. De eenheid wordt onder meer gebruikt om de afmetingen van een atoom uit te drukken.

Het kleinste atoom is dat van helium. Het heeft een straal van 0,3Å.

Hoeveel m is dat? Noteer in de wetenschappelijke schrijfwijze.

b Grote, maar dan ook echt heel grote afstanden !

De gemiddelde afstand van de aarde tot de zon wordt 1 AE (astronomische eenheid) genoemd. Die afstand bedraagt ongeveer 150miljoen km.

Afstanden tussen de sterren drukken we niet uit in AE wegens te klein. Daarvoor gebruik je een lichtjaar. Dat is de afstand die het licht aflegt in één jaar. Dat is toch nog een hele afstand als je weet dat het licht zich voortbeweegt met een snelheid van 300000km/s.

Noteer de snelheid van het licht in km/h.

Als de gemiddelde omtrek van de aarde ongeveer 40000km is, na hoeveel seconden is het licht dan rond deaarde gegaan ?

Hoeveel km legt het licht af tijdens één jaar (365,24 dagen) ?

Noteer dit wetenschappelijk en rond af op twee cijfers na de komma.

De dichtstbijzijnde ster bij onze planeet (naast de zon) is de Proxima Centauri. Die bevindt zich op een afstand van 268000AE van de zon. Hoeveel km is dat ?

Noteer dit wetenschappelijk en rond af op twee cijfers na de komma.

WISKUNDE & WETENSCHAPPEN

In technische vakken wordt vaak gebruikgemaakt van de ingenieursnotatie (op je rekenmachine mode ENG) of technische notatie. Die lijkt sterk op de wetenschappelijke schrijfwijze. Ook hier heb je een product van tweefactoren :

– eerste factor : een getal verschillend van nul met 1, 2 of 3 cijfers voor de komma – tweede factor : een macht van 10 waarbij de exponent een drievoud is

Zet volgende getallen om in de ingenieursnotatie.

a 12000 = e –0,000072 =

b 0,000005 = f 85000000000 =

c 6,7 · 10 4 = g 7,5 · 10 26 =

d –5 840000 = h –3,8 10 –5 =

In een van deze boxen zit een slang. Maar een van de stickers heeft een opschrift dat FOUT is. Waar zit de slang ?

In deze box zit GEEN slang

= 42

In deze box zit een slang

Bij het spelletje Candy Crush is het de bedoeling om drie snoepjes in dezelfde kleur naast elkaar te krijgen. Er zijn snoepjes in zes kleuren. Hiernaast zie je een mogelijke start van het eerste level.

In het eerste vakje staat een oranje snoepje, maar dat had evengoed een van de andere vijf kleuren kunnen zijn. In totaal tel je 40 vakjes. Hoeveel verschillende combinaties zijner mogelijk ?

Vaardigheden | Maten omzetten

WISKUNDE & BIOLOGIE

Eén miljardste van een meter is een nanometer (1 nm).

Of ook: één miljoenste van een millimeter.

Niet echt zichtbaar dus.

Links zie je een aantal foto’s van groot naar klein.

De lengtes zijn telkens uitgedrukt in meter.

Vul in de vakjes de begrippen in. Kies uit : DNA – MIER – HAAR – ROODBORSTJE –MOLECULEN – BACTERIE – RODE BLOEDCELLEN – VLO – VIRUS –NANO ABACUS

Deze tips zullen zeker helpen.

– Een NANO ABACUS is een telraam met allemaal balletjes die 1nm (nanometer) groot zijn.

– MOLECULEN zijn kleiner dan VIRUSSEN.

– Een BACTERIE is tien keer groter dan een VIRUS.

Vergelijk even een tennisbal met onze grote aardbol. Dan is die wel klein, niet ?

Dezelfde vergelijking geldt voor een mininanoballetje tegenover de tennisbal van zonet.

Bij de productie van Legoblokjes wordt een foutenmarge toegestaan van 0,0001mm.

Hoeveel nm is dit ? 1 2

Druk dit uit met een macht van 10.

a Eén nanogram is dus 10 –9 gram.

Met hoeveel kilogram komt dat overeen ?

b Je leerkracht weegt 90kg.

Met hoeveel ng komt dit overeen ?

Nano is afgeleid van het Grieks en Latijn en betekent ‘dwerg’.

Het voorzetsel wordt ook gebruikt bij gewicht en massa. Zo is één nanogram één miljardste van een gram.

1 ng = 0,000000001 g

c Eén zandkorreltje weegt 10 –3 gram.

Hoeveel nanogram weegt één zandkorreltje ?

d Hoeveel zandkorrels zitten er in deze ‘fitness sandbag’ ?

Nog kleiner? Jawel! Duizend keer kleiner dan nano is pico (afgeleid van het Italiaanse piccolo, ‘klein’) en één miljoen keer kleiner dan nano is femto (afgeleid van het Deense femten, ‘vijftien’). Weet je waarom ‘femto’ werd gekozen? Na femto stopt de naamgeving

Bacteriën kunnen zich (in ideale omstandigheden) erg snel voortplanten. Zo ontstaan er uit één bacterie elke 20minuten twee dochtercellen. Als je vandaag om 12.00 uur start met één bacterie, uit hoeveel bacteriën bestaat een kolonie morgenmiddag om 12.00 uur ?

Machten 2

moet ik leren

dit

❒ Ik ken de definitie van een macht met een gehele exponent.

❒ Ik ken de rekenregel om het product van machten met hetzelfde grondtal te bepalen (in woorden en in symbolen).

❒ Ik kan de rekenregel toepassen om het product van machten met hetzelfde grondtal te bepalen.

❒ Ik ken de rekenregel om het quotiënt van machten met hetzelfde grondtal te bepalen (in woorden en in symbolen).

❒ Ik kan de rekenregel toepassen om het quotiënt van machten met hetzelfde grondtal te bepalen.

❒ Ik ken de rekenregel om een macht van een macht te bepalen (in woorden en in symbolen).

❒ Ik kan de rekenregel toepassen om een macht van een macht te bepalen.

❒ Ik ken de rekenregel om een macht van een product te bepalen (in woorden en in symbolen).

❒ Ik kan de rekenregel toepassen om een macht van een product te bepalen.

❒ Ik ken de rekenregel om een macht van een quotiënt te bepalen (in woorden en in symbolen).

❒ Ik kan de rekenregel toepassen om een macht van een quotiënt te bepalen.

❒ Ik kan één of meerdere rekenregels bewijzen.

❒ Ik ken de definitie van de wetenschappelijke schrijfwijze van een getal.

❒ Ik kan een rationaal getal omzetten naar de wetenschappelijke schrijfwijze.

❒ Ik kan elke wetenschappelijke schrijfwijze omzetten naar een rationaal getal.

❒ Ik kan rekenen met getallen die genoteerd zijn in de wetenschappelijke schrijfwijze.

pagina ik ken het ! oké voor examen

54 

55 

56 

59 

72 

85 

86 

Machten 2

1 / 3

Plooi plooi plooi …

Stel dat je een erg groot blad papier hebt.

Dat ene grote blad plooi je in twee. Dan heb je één keer geplooid en liggen er netjes twee bladen op elkaar. Als je deze dan nog een keer plooit, dan heb je vier bladen op elkaar liggen.

a Vul de tabel verder aan.

AANTAL KEER PLOOIEN

AANTAL BLADEN OP ELKAAR

GENOTEERD ALS MACHT VAN 2 1 2 21

b Als je het oorspronkelijke blad n keer zou plooien, hoeveel bladen liggen dan op elkaar ?

c Hoe hoog is je ‘propje’ papier als je het blad 64 keer zou kunnen plooien ?

Ga ervan uit dat 100 bladen op elkaar overeenkomt met 1 cm.

d Als je weet dat de afstand van de aarde tot de zon gelijk is aan 1AE (één astronomische eenheid is ongeveer 150 miljoen km), druk dan de hoogte van je propje uit in AE.

Nu even andersom. Als je na je laatste plooi één vierkante cm zou willen overhouden als papieroppervlak, hoe groot was je blad dan bij de start van deze originele plooiactiviteit ?

Verbind op een passende wijze.

/ 2 3 / 2

Ken je de rekenregels? Verbind elk bolletje met het overeenkomende vierkantje.

Om machten met hetzelfde grondtal te vermenigvuldigen, …

Om machten met hetzelfde grondtal door elkaar te delen,

Om een macht tot een macht te verheffen, … ◯

Om een product tot een macht te verheffen, ◯

verhef je elke factor tot die macht.

… behoud je het grondtal en trek je de exponenten van elkaar af.

behoud je het grondtal en vermenigvuldig je de exponenten.

… behoud je het grondtal en tel je de exponenten bij elkaar op.

4 / 6

Pas eerst een rekenregel toe en werk (indien mogelijk) verder uit. De letters in de grondtallen stellen een rationaal getal voor verschillend van nul.

a 3 a 2 a =

( –2)3 ( –2)–5 =

2ab 3 4

( –1)6 ( –1)–3 ( –1)2

Zet volgende getallen om naar de wetenschappelijke schrijfwijze.

a De landing op de maan werd in 1969 door 650000000 mensen live bekeken op televisie.

b De kleinste inscriptie ooit geschreven had een hoogte van 0,00000015 cm.

c De clip van Despacito (van Luis Fonsi) werd op YouTube al meer dan 8 600000000 keer bekeken.

d Het kleinste wagentje ooit gebouwd bestaat uit koolstofatomen en is 0,000000001 m groot.

Zet om naar de gewone schrijfwijze.

a –6,125 1012 =

b 200 · 10 –9 =

Werk uit door te rekenen met machten van 10. Noteer je eindantwoord in de wetenschappelijke schrijfwijze.

Klopt de gelijkheid? Kleur dan het vakje groen.

3 Rekenen met algebraïsche uitdrukkingen

Hoodstuktitel 0

Simon Stevin was een Vlaamse wiskundige. Als jongeman hield hij van reizen en zo verzamelde hij een schat aan wiskundekennis.

Hij was ook een tijd raadsman van prins Maurits van Oranje, voor wie hij in 1601 een zeilwagen ontwierp.

Hij schreef heel wat boeken, waarvan De Thiende (1586) het belangrijkste was. Dat boekje telde 36 bladzijden en was in een eenvoudige taal geschreven. Hij leverde heel wat bijdragen over algebra, meetkunde en intresttabellen, en voerde breuken in met als noemer een macht van tien. Zo noteerde hij 4,58 als 4(0)5(1)8(2).

Ook voor de wiskundige woordenschat was deze Bruggeling belangrijk.

Hij voerde woorden in zoals wiskunde, driehoek, delen, omtrek, middellijn en wortel. Woorden die de huidige wiskunde niet hebben gehaald, waren uytbreng (voor product) en teerlincxwortel (voor derdemachtswortel).

Zijn standbeeld pronkt nog steeds op het Simon Stevinplein in Brugge.

Rekenen met algebraïsche uitdrukkingen

3.1 Eentermen en veeltermen

1 Letterformules : eentermen 101

2 Eentermen 102

3 Gelijksoortige eentermen 103

4 Getalwaarde van een eenterm 103

5 Letterformules 104

6 Veeltermen 105

7 Getalwaarde van een veelterm 106

8 Samenvatting 107

9 Oefeningen 108

3.2 Som en verschil van algebraïsche uitdrukkingen

1 Som en verschil van eentermen 116

2 Veeltermen herleiden en rangschikken 117

3 Som van veeltermen 118

4 Verschil van veeltermen 118

5 Samenvatting 119

6 Oefeningen 120

3.3 Product van algebraïsche uitdrukkingen

1 Product van eentermen 128

2 Macht van een eenterm 129

3 Product van een veelterm met een eenterm 130

4 Product van veeltermen 131

5 Samenvatting 132

6 Oefeningen 133

3.4 Merkwaardige producten

1 Kwadraat van een tweeterm 145

2 Product van twee toegevoegde tweetermen 146

3 Merkwaardige producten in een vierkant 147

4 Samenvatting 147

5 Oefeningen 148

Extra’s

Vaardigheden : computationeel denken 160

Wat moet je kennen en kunnen ? 161

Herhalingsoefeningen 162

Bekijk de instructievideo’s

3.1

Eentermen en veeltermen

1Letterformules: eentermen

Voorbeeld 1 : in de wei

In het eerste jaar leerde je hoe je regelmaat kunt herkennen en veralgemenen. Een landbouwer wil een afsluiting bouwen in de vorm van een vierkant.

FIGUUR

Vul nu volgende tabel aan.

4n wordt een eenterm genoemd. Een eenterm bestaat uit een getalgedeelte en een lettergedeelte. 4 n ↑↑ getal-lettergedeeltegedeelte

Voorbeeld 2 : omtrek driehoek

Driehoek ABC is een gelijkzijdige driehoek.

De omtrek van DABC is 3a . Ook 3a is een eenterm.

Vul nu volgende tabel aan.

2Eentermen

4n , 3a , 5xy , 9a 2 en 1 4 c worden eentermen genoemd omdat ze een product zijn van getallen en letters.

Het getalgedeelte wordt steeds vooraan genoteerd en noemen we de coëfficiënt

eenterm

Een eenterm is een product van een coëfficiënt en letterfactoren met positieve exponenten.

EENTERMCOËFFICIËNTLETTERGEDEELTE

1 2 n 2 1 2 n 2 5xy 5 xy –ab –1 ab

We maken volgende afspraken :

De coëfficiënt schrijf je steeds vooraan.

– Tussen de coëfficiënt en het lettergedeelte hoef je geen maalteken te noteren.

–

De letterfactoren rangschik je alfabetisch.

De letterfactoren schrijf je zo compact mogelijk: gebruik hiervoor exponenten.

– De coëfficiënten 1 en –1 schrijf je niet.

Voorbeelden : 1ab = ab –1x 2y =–x 2y

graad van de eenterm

De graad van een eenterm in een letter is de exponent van die letter in de eenterm.

De graad van een eenterm in alle letters is de som van de exponenten van alle letters die in de eenterm voorkomen.

Voorbeelden :

4n is van de eerste graad in n .

1 2 n 2 is van de tweede graad in n

5xy is van de eerste graad in x , van de eerste graad in y en van de tweede graad in x en y

8a 2b 3 is van de tweede graad in a , van de derde graad in b en van de vijfde graad in a en b

4 x n , 1 5 x p + 2 en3 x 2 y n + 3 zijn eentermen waarvan de exponenten die in de letters voorkomen, zelf letters zijn.

3Gelijksoortige eentermen

De eentermen 7a en –41a hebben hetzelfde lettergedeelte: a

De eentermen –b 2 en 1,7b 2 hebben hetzelfde lettergedeelte: b 2

De eentermen 9ab 2 en 11ab 2 hebben hetzelfde lettergedeelte: ab 2

De eentermen 3x 2y en 5xy 2 hebben niet hetzelfde lettergedeelte.

gelijksoortige eentermen

Gelijksoortige eentermen zijn eentermen die hetzelfde lettergedeelte hebben.

1 2 ab , –9ab, ab en 0,25ab zijn gelijksoortige eentermen.

3x, 4y, 7x 2 zijn niet-gelijksoortige eentermen.

4Getalwaarde van een eenterm

Om de getalwaarde van een eenterm te bepalen, vervang je de letters door de gegeven getallen en werk je daarna de rekenoefening uit.

Voorbeeld : Degetalwaardevan4a 2 bals a = 1 2 en b = 3 5 wordt: 4 · 1 2 2 · 3 5

Taak : Bereken telkens de getalwaarde.

5Letterformules

Voorbeeld 1 : de chocoladeautomaat

Een producent van automaten heeft volgende modellen op de markt. De koper kan een keuze maken uit een miniautomaatje (waarin 10 repen passen) tot heel grote automaten. Om aan het aantal repen te komen moet je ook rekening houden met de schuifjes waar telkens al een reep op jou ligt te wachten.

Vul nu volgende tabel aan.

n 2 + n 2 + n of ook 2n 2 + n wordt een veelterm genoemd. Een veelterm is een som van eentermen. 2n 2 + n ↑ ↑ eenterm eenterm

Voorbeeld 2 : huisje tekenen

De omtrek van deze figuur is a + 2b + 2c .

Ook dit noemen we een veelterm.

Vul nu volgende tabel aan.

6Veeltermen

Voorbeelden :

a 2 + 4a iseen veelterm

1 5 y 3 + 2 y 1 5 iseenveelterm

2,5a + 3,5 b iseenveelterm

veelterm

Een veelterm is een som van eentermen.

Een veelterm met precies twee termen noemen we een tweeterm.

Voorbeelden :

a 2 – a

0,12x 2 + 0,8x 6b – 9

Een veelterm met precies drie termen noemen we een drieterm.

Voorbeelden :

2a 2 5a + 8

2 x 2 6 x + 7

3 2 x 2 1 3 y + 4

graad in een letter van een veelterm

De graad van een veelterm in een letter is de grootste exponent waarmee die letter in de veelterm voorkomt.

Voorbeelden :

3a 3 + 2a 2 1 4 a isvandederdegraadin a

2 5 x 2 y 5 + 2 x 3 y 2 isvandederdegraadin x isvandevijfdegraadin y isvande7egraadin x en y (deeerstetermheeftalsgraad2 + 5 = 7endetweedetermheeft alsgraad3 + 2 = 5;degrootstegraadvanbeidetermenis7)

Herkomst van de algebra:Nicholas Saunderson

Nicholas Saunderson (1682–1739) was professor aan de universiteit van Cambridge, waar hij door King George was aangesteld om les te geven en zelfs toe te treden tot de koninklijke familie. Toen Richard een jaar oud was, werd hij blind door de waterpokken. Hij leerde zichzelf lezen en schrijven door de inscripties te betasten op de graven van het kerkhof. Hij schreef voor zijn leerlingen twee boeken: ‘Elements of Algebra’ en ‘Method of Fluxions’. Bovendien ontwierp hij een ‘rekenmachine’ waarmee hij algebraïsche oefeningen door tastzin kon oplossen. In zijn geboortedorp Penistone (Groot-Brittannië) kun je een korte wiskundewandeling maken en over zijn leven is zelfs een musical gemaakt: ‘No Horizon’.

7Getalwaarde van een veelterm

Voorbeeld 1 : papegaaiduikers

De grootte van een populatie papegaaiduikers laat zich voor een tiental jaren beschrijven door de formule

2t 2 + t + 40 met t : het aantal jaren

Vul nu volgende tabel aan.

waarde van de letter die voorkomt in de veelterm getalwaarde van de veelterm

Om de getalwaarde van een veelterm te bepalen, vervang je de letters door de gegeven getallen en werk je daarna de rekenoefening verder uit.

Voorbeeld 2 : priemgetallen

Wellicht ken je nog de betekenis van een priemgetal : een natuurlijk getal dat precies twee verschillende delers heeft, namelijk 1 en zichzelf. Al eeuwenlang zijn mensen op zoek naar een formule die alleen maar priemgetallen weergeeft. Misschien is het deze formule wel, ooit bestudeerd door Euler

n 2 + n + 41 met n : een natuurlijk getal

Vul nu volgende tabel aan.

Zet je onderzoek voort voor volgende waarden van n : 12, 14, 22, 39 en 40. Wat kun je besluiten ?

Voorbeeld 3 : Bereken de getalwaarde van

8Samenvatting

• Je weet wat een eenterm is.

Een eenterm is een product van een coëfficiënt en letterfactoren met positieve exponenten.

• Je kunt de graad van een eenterm in een letter bepalen.

De graad van een eenterm in een letter is de exponent van die letter in de eenterm.

• Je kunt de graad van een eenterm (in alle letters) bepalen.

De graad van een eenterm is de som van de exponenten van alle letters die in de eenterm voorkomen.

• Je weet wat gelijksoortige eentermen zijn.

Gelijksoortige eentermen zijn eentermen die hetzelfde lettergedeelte hebben.

• Je kunt de getalwaarde berekenen van een eenterm.

Om de getalwaarde te berekenen van een eenterm vervang je de letters door de gegeven getallen en werk je daarna de rekenoefening uit.

• Je weet wat een veelterm is.

Een veelterm is een som van eentermen.

• Je kunt de graad van een veelterm in een letter bepalen.

De graad van een veelterm in een letter is de grootste exponent waarmee die letter in de veelterm voorkomt.

• Je kunt de getalwaarde berekenen van een veelterm.

Om de getalwaarde te berekenen van een veelterm, vervang je de letters door de gegeven getallen en werk je daarna de rekenoefening uit.

9Oefeningen

Door welke eenterm kun je …

a… de omtrek van een ruit met zijde z weergeven ?

b… de oppervlakte van een vierkant met zijde z weergeven ?

c… een willekeurig even getal voorstellen ?

d… een willekeurig zevenvoud voorstellen ?

e… de omtrek van een cirkel met straal r voorstellen ?

f… de oppervlakte van een parallellogram met basis b en hoogte h weergeven ?

g… de oppervlakte van een ruit met grote diagonaal D en kleine diagonaal d weergeven ?

Vul de tabel aan.

Zet gelijksoortige eentermen in dezelfde kleur.

–

b3x 2 7x 8 12x 13x 2 24

Schets telkens de vierde figuur. Bepaal daarna de eenterm waarmee je het aantal streepjes in de n -de figuur weergeeft.

In het pretpark staat een achtbaan met kevertjes.

Alle keverwagentjes hebben als lengte a

a Druk met een eenterm de lengte uit van de totale keversliert.

b Hoe lang is de keversliert als de lengte a gelijk is aan 150cm ?

De totale oppervlakte van een kubus wordt gegeven door A = 6z 2

Bereken de totale oppervlakte van een kubus als

a z = 4 cm

b z = 8 cm

c z = 12,5 cm

Bereken de getalwaarde van de volgende eentermen. a2ab voor a = 5en b =–4

Vul in met de gepaste graad.

GEGEVEN GEVRAAGD

a3x 4y

graad in x

graad in y

graad in x en y

b x 4 – 2x 3 + 8x – 5 graad in x

c 6 – 7a + a 2 + 2a 4 graad in a

graad in x

d x 3 + x 2y 5 – y 4

graad in y

e 4t 3 – 5t + t 7 – 16t 4 graad in t

graad in x

f x 4 + 3x 3y + 2x 2y 5 + 6y 2

graad in y

a Noteer een eenterm van de derde graad, waarbij de graad in x drie is.

b Noteer een eenterm van de vierde graad, waarbij de graad in x drie is.

c Noteer een tweeterm met twee onbekenden waarbij de graad in x twee is en de graad in y ook twee is.

ANTWOORD

Schets telkens de vierde figuur. Bepaal daarna de veelterm waarmee je het aantal stippen in de n -de figuur weergeeft.

STIPPEN 35 7

Vul in de tabel de getalwaarde van de veelterm in. Je kunt gebruikmaken van een rekenblad.

a 3x + 4

b 3x 2 + 4

c 5x – 3

d 2x 2 – 3x + 4

e x 3 + 2x – 8

Bereken de getalwaarde van de volgende veeltermen.

Jill doet in de maand augustus een vakantiejob in Disneyland

Parijs in een snoepkraam. In haar arbeidscontract staat dat ze een eenmalige verplaatsingsvergoeding krijgt van 50euro. Per uur zal Jill 11,50euro verdienen.

a Druk met een veelterm uit hoeveel Jill zal verdienen in de maand augustus als je het aantal uren voorstelt door de letter u

b Elke dag moet Jill 8 uur werken. Hoeveel euro verdient Jill als ze in de maand augustus 25 dagen gewerkt heeft? Maak gebruik van de veelterm die je hierboven opstelde.

Oppervlakte bij meetkundige lichamen.

a De manteloppervlakte van een cilinder bereken je met de formule :

Am = 2pr h h r

Bereken de manteloppervlakte op 0,01cm2 nauwkeurig als r = 4cm en h = 12cm.

b De totale oppervlakte van een kegel bereken je met de formule :

At = p r ( r + a ) r a

Bereken de totale oppervlakte op 0,01cm2 nauwkeurig als r = 6cm en a = 20cm.

c De totale oppervlakte van een balk bereken je met de formule :

At = 2 (l h + l b + b h ) l b h

Bereken de totale oppervlakte nauwkeurig als l = 5cm, b = 4,5cm en h = 3cm.

d De totale oppervlakte van een bol bereken je met de formule :

A = 4pr 2 r

Bereken de totale oppervlakte op 0,01 cm2 nauwkeurig als r = 4 cm.

De getalwaarde van de veelterm ax 3 + 3x – 7voor x = 1is –2.

Zoek de waarde van a

De getalwaarde van de veelterm ax 2 + x + b voor x = 0is0.

De getalwaarde voor dezelfde veelterm voor x = 2is3.

Zoek a en b .

De getalwaarde van de veelterm ax 2 – 4x – b voor x = 0is2.

De getalwaarde voor dezelfde veelterm voor x = 2is –8.

Bepaal a en b .

Hoeveel gehele getallen n bestaan er zodat 12 n + 5 een geheel getal is ?

2 (B) 4 (C) 6 (D) 7 (E)12

3.2 Som en verschil van algebraïsche uitdrukkingen

1Som en verschil van eentermen

Voorbeelden :

2a + 5a = ( 2 + 5) a het vermenigvuldigen is distributief t.o.v. het optellen in Q = 7a

1 2 b 3 b = 1 2 3 · b = 1 2 6 2 b = 5 2 b het vermenigvuldigen is distributief t.o.v. het aftrekken in Q

We spreken af dat we tussenstappen (zo veel mogelijk) weglaten :

7 x + 18 x = 25 x

9 y 5 y = 14 y

2 x 2 + x 2 6 x 2 = 3 x 2 6 x 2 = 3 x 2

3 4 ab 2 1 3 ab 2 = 9 12 ab 2 4 12 ab 2 = 5 12 ab 2

Merk op :

Alle eentermen hebben hetzelfde lettergedeelte.

Een vorm zoals 2a + 3b kun je niet korter noteren (herleiden) omdat de eentermen niet-gelijksoortig zijn.

Gelijksoortige eentermen optellen en aftrekken

Om gelijksoortige eentermen op te tellen of af te trekken : – Bereken de som of het verschil van de coëfficiënten. – Behoud het lettergedeelte.

Als de eentermen letters in de exponenten hebben, gebruik je dezelfde werkwijze.

Voorbeelden :

2 x n + 5 x n = 7 x n −→ lettergedeelteis x n

5 y q + 12 y q = 7 y q −→ lettergedeelteis y q

3 x m +1 1 3 x m +1 = 8 3 x m +1 −→ lettergedeelteis x m +1

Maar xm + xn kun je niet korter noteren of herleiden omdat de eentermen niet hetzelfde lettergedeelte hebben.

2Veeltermen herleiden en rangschikken

Onderzoeksopdracht 1 :

Bereken de omtrek van de ruit.

Noteer deze omtrek zo bondig mogelijk.

De veelterm a + a + a + a kun je eenvoudiger (= met minder termen) schrijven : a + a + a + a = 4a

Onderzoeksopdracht 2 :

Bereken de lengte van [FE] en van [AF].

Bereken nadien de omtrek van de veelhoek ABCDEF. Noteer ook deze omtrek zo eenvoudig mogelijk.

De veelterm 4x + 2y + 2x + y + 2x + 3y kun je nog herleiden. Je zult dan alle gelijksoortige eentermen optellen of aftrekken.

Tip : onderstreep alle gelijksoortige termen op dezelfde manier. Vergeet niet om het bewerkingsteken voor elke term mee te onderstrepen.

4x + 2y + 2x + y + 2x + 3y = 4x + 2x + 2x + 2y + y + 3y = 8x + 6y

Herleiden

Om een veelterm te herleiden, maak je de som of het verschil van de gelijksoortige eentermen.

Voorbeeld : a 3 + a – 2a 2 + 6

Om in een veelterm wat orde te scheppen, kunnen we de veelterm rangschikken

Rangschikken

Om een veelterm te rangschikken, zul je de veelterm noteren naar dalende of stijgende machten van een bepaalde letter.

Voorbeelden :

5 x 5 + 12 x 4 3 x 3 + 8 x 2 17 x isgerangschiktnaardalendemachtenvan x

5 6 y + 8 y 2 7 y 4 isgerangschiktnaarstijgendemachtenvan y

1 4 a 2 6 5 ab + b 2 isgerangschiktnaardalendemachtenvan a ,maarooknaarstijgende machtenvan b .

3Som van veeltermen

Voorbeelden :

( 2a 2 + 3a ) + ( 5a 2 – 2a )

= 2a 2 + 3a + 5a 2 – 2a het optellen van rationale getallen is associatief

= 2a 2 + 5a 2 + 3a – 2a het optellen van rationale getallen is commutatief

= 7a 2 + a

= x 2 + 2x + 3 + 3x 2 – 4x + 5

= x 2 + 3x 2 + 2x – 4x + 3 + 5

Som van veeltermen

Om een som van veeltermen te berekenen: – Werk de haakjes weg. – Tel de gelijksoortige termen op.

4Verschil van veeltermen

Herinner je je de a – (

regels om haakjes

weg te werken

Voorbeelden

Verschil van veeltermen

Om een verschil van twee veeltermen te berekenen:

– Werk de haakjes weg : laat het minteken en de haakjes voor de tweede veelterm weg en vervang elke term van de veelterm door zijn tegengestelde.

– Tel de gelijksoortige termen op.

Je kunt jezelf controleren door van de opgave een foto te trekken met de app Photomath of Mathsolver. Ook met de CAS van GeoGebra kun je rekenen met veeltermen.

Voorbeeld :

5Samenvatting

• Je kunt gelijksoortige eentermen optellen en aftrekken.

– Bereken de som of het verschil van de coëfficiënten.

– Behoud het lettergedeelte.

• Je kunt een veelterm herleiden en rangschikken.

– Om een veelterm te herleiden, maak je de som of het verschil van de gelijksoortige eentermen.

– Om een veelterm te rangschikken, zul je de veelterm noteren naar dalende of stijgende machten van een bepaalde letter.

• Je kunt de som bepalen van veeltermen.

– Werk de haakjes weg.

– Tel de gelijksoortige termen op.

• Je kunt het verschil bepalen van veeltermen.

– Werk de haakjes weg: laat het minteken en de haakjes voor de tweede veelterm weg en vervang elke term van die veelterm door zijn tegengestelde.

– Tel de gelijksoortige termen op.

6Oefeningen

Maak de som of het verschil van volgende eentermen.

a2p + 3p =

b4 x + x =

c7m 4m =

e s 3 s =

f4 x 2 y + 6 x 2 y =

g3a m + 2a m =

d 1 2 y + 1 3 y = h 4 5 x + 1 2 x =

Herleid volgende veeltermen.

a 2 y + y 2 6 y =

b3 x 6 + 5 x 2 =

c4 x 2 + 6 x 8 11 x + 2 x 2 11 =

d5 x 2 5 x 3 + 8 3 x 2 + 12 x 3 4 =

e3 x 2 + 5 x 2 + 8 x 3 x 2 =

f 1 4 x 2 2 3 x + 1 5 + 5 8 1 3 x + 3 10 x 2 =

g0,4 x 0,2 x 2 0,01 x 2 + 2,1 x = h 2 5 x 2 2 3 x + 1 2 3 4 x 2 + 6 5 + 4 x =

i1,5 x 3 2,5 x 2 + 5 2,5 x 3 + 3,5 x 2 =

Drie op een rij Kleur in onderstaande tabel telkens drie opeenvolgende vakjes fluogeel als de som van de eerste twee vakjes gelijk is aan het derde vakje. De vakjes kunnen zowel horizontaal, verticaal als schuin op elkaar volgen.

Voorbeelden :

Rangschik deze veeltermen naar dalende machten van x . Bepaal ook de graad van de veelterm.

a8 – 4x 3 + 17x 2 – 3x 4 + 17x = Graad =

b x 4 – x + 7 – x 2 – 3x 3 = Graad =

c –5 – 2x 3 + 8x – 2x 4 = Graad =

Rangschik deze veelterm naar dalende machten van y . Bepaal ook de graad van de veelterm.

– y + 2y 4 – y 2 – y 5 = Graad =

Herleid, indien mogelijk, volgende veeltermen.

a2 x n 7 x n + x n =

b 1 5 x n + 1 2 x n =

c2 x 2 + x n 3 x 2 5 x n =

d x m +1 3 x m + 2 x m 1 5 x m +1 + x m =

e4 x m +2 2 x m + x m +2 3 x m =

Heel wat schaatsers draaien het liefst rondjes aan de buitenkant van de ijsbaan en laten de middenruimte van de ijspiste links liggen. Op deze ovaalvormige ijspiste wordt het daarom aangenamer schaatsen dan op een rechthoekige ijsbaan.

Hoe groot is de omtrek van deze ijspiste als a = 8 m en b = 2,5 m?

Schrijf de omtrek van volgende veelhoeken zo eenvoudig mogelijk.

Bereken de som van volgende veeltermen.

a (5 x ) + (8 3 x ) =

b x 2 x + 2 x 2 3 x =

c 2 x 2 + 3 x 4 + 7 x 2 4 x + 6 =

d 3 8 x 2 5 x 1 5 + 1 4 x 2 3 x 4 5 = e 0,7 x 3 + 2,5 x 1,3 + 2,5 3,6 x + 3 x 3 =

= h 12,1 x 3 1,21 x + (2,11 x + 2,11) =

Bereken het verschil van volgende veeltermen.

a (2a + 3) (5a + 18) =

b 15 x 2 10 2 x 2 10 =

c 8 x 2 + 5 x 20 2 x 2 3 x + 15 =

d 1,25 x 2 + 6 x 2,4 0,5 x 2 + 2,5 x 1,2 =

e 5 9 x 2 5 x 1 5 1 3 x 2 3 x 1 3 =

f x 2,5 0,5 x 2 + x 3 3 x 3 2,5 + 1,5 x 2 3 x =

g 2 11 x 2 + 3 x 3 x 2 + 5 2 x =

h 4 3 x 2 1 2 x + 5 6 4 2 x 2 + 1 2 x 1 9 =

Bereken. Controleer met ICT.

a (4a + 5 b ) + (6a 4 b ) =

b (2a 6 b ) (3a + 4 b ) =

c 5 x + 4 y + 2 2 y 6 x 3 =

d (4 x + 2) [(2 x + 3) (5 x 6)] =

Bij een magisch vierkant is de som van elke kolom, elke rij en elke diagonaal hetzelfde. Vul nu de volgende magische vierkanten in.

Bereken.

Vul aan zodat de gelijkheid klopt.

Gevraagd:

3.3 Product van algebraïsche uitdrukkingen

1Product van eentermen

De vloer van een garage is bedekt met vierkante tegels waarvan de zijde x cm is.

De lengte van deze garage kan worden uitgedrukt met de eenterm 6x .

De breedte kan worden uitgedrukt met de eenterm 5x

We willen graag de oppervlakte kennen van de vloer van deze garage.

Om dit te kunnen berekenen moet je een beroep doen op een aantal zaken uit jouw wiskunderugzak.

De formule voor de oppervlakte van een rechthoek: A = l · b .

De eigenschappen van de vermenigvuldiging.

‘Het vermenigvuldigen van rationale getallen is commutatief en associatief.’

–

De rekenregel voor machten met eenzelfde grondtal.

‘Om machten met eenzelfde grondtal te vermenigvuldigen, behoud je het grondtal en tel je de exponenten metelkaar op.’

De oppervlakte van de vloer van de garage wordt dus :

6x 5x = 6 5 x x = 30x 2

Controleer op de figuur en je zult 30 vierkante tegels tellen, elk met een oppervlakte van x 2 cm2

Eentermen vermenigvuldigen

Om eentermen met elkaar te vermenigvuldigen :

– Bereken het product van de coëfficiënten.

– Bereken het product van de letterfactoren (pas de regel toe om machten met eenzelfde grondtal met elkaar te vermenigvuldigen). x x

Voorbeelden : Met letterexponenten :

2 ( –4a ) =–8a

7x 3 ( x 5) = 7x 8

0,4c 3d = 1,2cd 2 3 xy · 3 7 y = 2 7 xy 2

2Macht van een eenterm

Voorbeeld : 2

Macht van een eenterm

Om een macht van een eenterm te berekenen : – Bereken de macht van de coëfficiënt. – Bereken de macht van het lettergedeelte (pas de regel toe om een macht van een macht te berekenen).

Nog meer voorbeelden :

Taak : Controleer met ICT.

3Product van een veelterm met een eenterm

De oppervlakte A van de grote groene rechthoek kun je op verschillende manieren weergeven.

A groterechthoek = (2a + 4) a ←−➊

A groterechthoek = A rechthoek1 + A rechthoek2 = 2a a + 4 a = 2a 2 + 4a ←−

Omdat ➊=➋, is dus ook ( 2

Inderdaad, volg even mee en herken de distributiviteit van het vermenigvuldigen ten opzichte van het optellen (de haakjesregel): ( 2a + 4) a = 2a a + 4 a = 2a 2 + 4a

Voorbeelden :

Product van een eenterm met een veelterm

Om een eenterm met een veelterm te vermenigvuldigen :

– Vermenigvuldig elke term van de veelterm met de eenterm.

– Werk de verkregen producten uit.

Herleid, indien mogelijk, de verkregen veelterm.

De werkwijze is ook geldig voor eentermen en veeltermen met verschillende letters.

Voorbeelden : –3xy ( x 2 – 5xy + 2y 2)

=–3xy x 2 – 3xy ( –5xy ) – 3xy 2y 2

=–3x 3y + 15x 2y 2 – 6xy 3

4Product van veeltermen

Bij het vermenigvuldigen van veeltermen zullen we ook gebruikmaken van de distributieve eigenschap van devermenigvuldiging ten opzichte van de optelling.

Bovendien weten we ook dat we gelijksoortige eentermen kunnen herleiden.

( a + 2) ( a + 3) = a ( a + 3) + 2 ( a + 3)

= a 2 + 3a + 2a + 6

= a 2 + 5a + 6

( 2a + 3) · ( 4a – 5) = 2a · ( 4a – 5) + 3 · ( 4a – 5) = 8a 2 – 10a + 12a – 15 = 8a 2 + 2a – 15

Product van twee veeltermen

Om twee veeltermen met elkaar te vermenigvuldigen :

– Vermenigvuldig elke term van de eerste veelterm met elke term van de tweede veelterm. – Werk de verkregen producten uit.

Herleid, indien mogelijk, de verkregen veelterm.

Opmerking : Let op voor de (min)tekens !

Voorbeelden :

( 2x – 3) · ( 2x 2 – 4x + 7) = 2x · 2x 2 + 2x · ( –4x ) + 2x · 7 – 3 · 2x 2 –

= 4x 3 – 8x 2 + 14x – 6x 2 + 12x – 21

= 4x 3 – 14x 2 + 26x – 21

( 3a – 2b ) ( a – 3b ) = 3a a + 3a ( –3b ) – 2b a – 2b ( –3b )

= 3a 2 – 9ab – 2ab + 6b 2

=3a 2 – 11ab + 6b 2 a 3 a 2 a 2 2a 3a 6

Als je al veel geoefend hebt, mag je ook bepaalde tussenstappen weglaten.

5Samenvatting

• Je kunt eentermen met elkaar vermenigvuldigen.

– Bereken het product van de coëfficiënten.

– Bereken het product van de letterfactoren. Pas de rekenregel toe om machten met hetzelfde grondtal te vermenigvuldigen.

• Je kunt een macht van een eenterm berekenen.

– Bereken de macht van de coëfficiënt.

– Bereken de macht van het lettergedeelte. Pas de rekenregel toe om een macht van een macht te berekenen.

• Je kunt een eenterm met een veelterm vermenigvuldigen.

– Vermenigvuldig elke term van de veelterm met de eenterm.

– Werk de verkregen producten uit.

Herleid, indien mogelijk, de verkregen veelterm.

• Je kunt twee veeltermen met elkaar vermenigvuldigen.

Vermenigvuldig elke term van de eerste veelterm met elke term van de tweede veelterm.

– Werk de verkregen producten uit.

Herleid, indien mogelijk, de verkregen veelterm.

Herkomst van de algebra: Evariste Galois Het leven van Evariste Galois (1811–1832) leest als een roman, gevuld met revolutionaire praktijken, een onbeantwoorde liefde, twee gevangenisbezoeken en een duel. Maar hij had ook een onmiskenbaar wiskundetalent, dat pas na zijn dood werd erkend. Hij werd ‘de tienerwiskundige’ genoemd en heeft de basis gelegd voor het al dan niet vinden van oplossingsmethodes voor algebraïsche vergelijkingen van hogere graad. Ook al was Evariste een van de knapste wiskundestudenten van zijn school, hij haalde altijd tekorten op examens en discussieerde uren met zijn leerkrachten, die zijn genie niet erkenden. Hij deed ook tweemaal mee aan het toelatingsexamen van de prestigieuze École Polytechnique, maar ving ook daar bot. De omstandigheden van zijn dood zijn vrij mysterieus, maar we weten wel dat hij in een duel is gestorven. Hij was er vrij zeker van dat hij het niet zou overleven en pende daarom de nacht voor het duel al zijn wiskundige theorieën neer in een brief. Hij werd geraakt in de buik en overleed de dag erna aan zijn verwondingen.

6Oefeningen

Bereken.

a 103 104 = f –4 ( –4t ) = b24 23 = g 10 103 =

c 2 5x = h 102 10 22 =

d 1000 · 102 = i 0 · 18m = e25 22 = j 102 101 10 =

Bereken de producten van de volgende eentermen.

a x 3 x 2 = g3a ( –4a ) =

b a 4 a 5 = h2t 4 ( 3t 2) =

c x 2 a 2 x 3 a 3 = i –3b 3 ( –8b ) =

d ( 2x 2) ( –3x 3) = j ( –7x 2y 3) ( –3x ) =

e ( –2y 4) ( –4y 2) = k9a 3b 2c 4ab 3c 2 =

f –2a 5a 3 = l4x 2yz 8 ( –6x 6yz 5) =

Vervolledig onderstaande tabel.

Bereken de producten van de volgende eentermen.

a 2 3 xy 2 3 4 x 3 y =

b 6a 3 b 2 2 3 a 2 b 4 =

c ax 3 5 3 a 2 x 2 =

d 3 5 x 4 y 5 3 x 2 y =

e1,5a 3 b · 2ab · 4a 2 b =

f 2,5 x 4 2 x 3 6 x 2 0,1 x =

g 4 7 x 4 3 x 2 =

h 2 5 a 3 10 9 b 5 =

i0,17 x 3 0,2 y 4 =

j4a 2 bc 8 · 6a 6 b 3 c =

k 4 7 x 6 y 5 8 xy 5 z 3 10 xy 3 =

l 2,3 x 4 5 x 9 y 2 = Werk uit.

a y 2x y x =

b a x a x –1 a x +2 =

c d x · d 2x –4 =

d a x –2 a 2x +1 =

e d x d =

f y a x y x a =

g a 2 · d 3 · a 1–x · d x –5 =

h2a x +1 4a 2x –4 = 4 * 5

Vul aan zodat de gelijkheid klopt.

11x 2 = 77x 5

2 x =–4x 3 b5a =–25ab

Bepaal de gevraagde machten.

Bepaal in een lettervorm de oppervlakte van de rechthoeken en de inhoud van de kubus en de balk.

Bij een bepaalde oefening is de oplossing 64a 4b 16. Vind zelf drie opgaven uit met drie verschillende bewerkingen die dit als resultaat geven.

Een mengelmoes. Werk uit.

= b 1 2 a 3 + 1 2 a 3 =

Een mengelmoes met letterexponenten. Werk uit.

= Volg de pijlen en vul aan.

Wat hoort op de plaats van het vraagteken ?

Bereken het product van de eenterm met de veelterm.

a2 x · (3 x + 4) = b 3 (a 2 6a + 5) =

c0,5 (4 x 2 + 6 x 2) =

d0,25 ( 12 z 3 + 8 z 2 16) = e 5 x 2 (4 x 9) =

f3 x · (4 x 2 + 2 x 3) = g 2a (a 2 2a + 4) = h 1 5 (3 x 2 6) = i 1 2 (18 y 4 + y 2 + 2) =

j0,5 x · (4 x 2 + 2 x 8) = k 2 3 · 3 2 x 2 + 1 2 x 2 3 =

l 5a 3 b 2 3a 2 + 4 b 3 3a 2 =

Bereken volgende producten van een eenterm met een veelterm.

a4 b 2 · (8 b 2 2 b ) =

b5 y 2 (10 y 3 + 15 y 2 ) =

c (5a 3 3a 2 + 4) 3a =

d (6 x 2 2 x + 7) 2 x 3 = e 1 5 (50 x 3 + 25 x 2 ) = f 2 3 x 9 4 x 75 x 2 = g 1 2 x 3 ( x 5 1) = h (8 y 2 + 4 y 6) 1 4 y =

i ( 4,2 x 2 + 6,3 x 1,2) · 0,5 x 3 = j 1 3 a · 3 4 a 5 1 2 a = k (2 y 4 8 y 2 24) · 1 4 y =

l0,25a 2 ( 40a 2 + 80a 16) =

Carl Friedrich Gauss.

Er doet een verhaal de ronde dat de jonge Johann Carl Friedrich Gauss op school als strafwerk eens de eerste 100 getallen bij elkaar moest optellen. Binnen enkele seconden had Gauss al het antwoord gevonden. Hij ging als volgt te werk : 12345...9899100 10099989796321 101101101101101101101101

Er staat nu 100 keer de uitkomst 101. Aangezien hij alle getallen twee keer had, deelde hij het product door twee.

De som van de eerste 100 getallen = 100 101 2 = 5050

Door die redenering te veralgemenen voor n natuurlijke getallen krijg je volgende formule : de som van de eerste n natuurlijke getallen is gelijk aan: n (n + 1) 2

Toon aan dat de formule ook te schrijven is als 1 2

Geef voor de totale oppervlakte van volgende figuren een passende lettervorm.

Welke oplossing hoort bij de vier vragen ?

a de oppervlakte van het rechterzijvlak

b het volume van deze balk

c de hoeveelheid draad die je nodig hebt om een draadmodel van deze balk te maken

d de manteloppervlakte van deze balk

Bereken de volgende producten van veeltermen.

a ( x + 5) · (2 x 3) =

b ( x + 3) ( x + 4) =

c (2 x + 7) (3 x 4) =

d a 1 2 · a + 1 3 =

e ( x 2 7) ( x 2 + 4) =

f (1,2 x 1) (1,2 x + 1) =

g 2 3 x 2 + 3 4 x 5 6 4 3 x 3 2 =

h (4 x 2 + 3) · (6 x 2 2 x + 4) =

Werk uit. Een mengelmoes.

a ( x 2 + 3 x 4) (2 x 2 6 x + 5) =

b (4 x 2 + 6 x ) (3 x 5) =

c (2 x 3 3 x 2 4)+(2 x 2 3 x + 6) =

d (4 x 3 + 2 x 2 + 5) 3 x 4 =

e 1 5 x 2 3 x + 2 3 2 5 x 2 + 1 3 x 5 6 =

f (0,5 x 2 4 x + 2,5) ( 3 x 2 ) =

g (0,5 x 4 4 x 3 ) (3 x 2 2,1) =

h (a + 5) ( a 2 a + 1) =

i ( y 2 y 1) ( y + 2) =

j 1 2 m 2 m (2m 4) =

k 1 2 a + 1 3 · 1 2 a + 1 3 =

Kraak de code !

De bekende boekenreeks is

Werk uit en herleid. Controleer je antwoorden met ICT.

Voorbeeld : 2x · ( x – 2) – 2( x 2 + 2x – 1) opsplitsen in deelproblemen uitwerken

= ✟✟ 2 x 2 4 x ✟✟ 2 x 2 4 x + 2

= 8 x + 2 herleiden

a –x ( 5 – x ) – 2x ( x – 1)

b –( 5 – 2x – x 2) – 3x ( 6 – 2x )

c – 3 – ( 6x – x 2) – ( –x 2 – 3x + 17)

d ( x – 2) ( 3 – 2x ) ( –2x + 10)

23 24 * 25 *

De juf van deze klas schrijft voor de verandering geen opgave op het bord, maar wel een resultaat: 18x 3y 2

Bedenk per leerling een opgave zodat 18x 3y 2 het resultaat is. Hou voor de gebruikte bewerkingen rekening met wat op het T-shirt staat van de leerlingen.

Werk uit en herleid.

a a n (a + 3) =

b x n ( x 2 x + 1) =

c x n 1 · ( x + 1) =

d (a n 3) · (5 + 2a n ) =

Werk uit en herleid.

a 3 2 x m +1 (4 x m 6 x ) = b 1 3 a m b m · 3 4 a 2m +1 b 1 2 ab 2m 1

c (4 x n )(4 + x n )

3.4 Merkwaardige producten

Sommige producten van veeltermen zijn zo speciaal dat je ze veel sneller kunt uitwerken. We noemen die producten merkwaardige producten. Dit schooljaar zul je twee formules leren zodat je ze gebruiksklaar in je wiskunderugzak hebt zitten.

1 Kwadraat van een tweeterm

Hoe kom je aan de eerste formule? Volg even mee …

Algemeen :

kwadraat

(a + b )2 =(a + b ) (a + b )

tweeterm

= a · a + a · b + b · a + b · b

= a 2 + ab + ab + b 2

Voorbeeld :

= a 2 + 2ab + b 2 ( x + 4)2 =( x + 4) ( x + 4)

x 2 + 4 x + 4 x + 16

x 2 + 8 x + 16

In het resultaat heb je naast het kwadraat van de eerste term en het kwadraat van de andere term nog het dubbel product van beide termen.

Kwadraat van een tweeterm in symbolen : ( a + b )2 = a 2 + 2ab + b 2 in woorden : Het kwadraat van een tweeterm is gelijk aan de som van het kwadraat van de eerste term ; het dubbel product van de twee termen ; het kwadraat van de tweede term.

Merk op :

• De twee kwadraattermen zijn steeds positief.

• Het dubbel product is positief als beide termen in de opgave hetzelfde toestandsteken hebben. Is een van beide termen negatief, dan is het dubbel product negatief.

Voorbeelden :

(a + 3)2 = a 2 + 2 3 a + 32 = a 2 + 6a + 9

Als je voldoende geoefend hebt, zul je de tussenstap weglaten en onmiddellijk het eindresultaat noteren.

2 Product van twee toegevoegde tweetermen

Toegevoegde tweetermen zijn tweetermen waarbij één term dezelfde is gebleven en de andere term van teken isveranderd.

Voorbeelden :

x + 5en x – 5

2 – 3x en –3x – 2

a + b en a – b

Hoe kom je aan de tweede formule? Volg even mee

Algemeen : Voorbeeld :

(a + b ) (a b )= a a a b + b a b b

= a 2 ab + ab b 2

= a 2 b 2 ( x 8) · ( x + 8)= x · x + 8 · x 8 · x 8 · 8

= x 2 + 8 x 8 x 64

= x 2 64

Merk op :

In de tussenstap staan steeds twee tegengestelde termen die verdwijnen. Het eindresultaat is het verschil van het kwadraat van de gelijke term met het kwadraat van een van de tegengestelde termen.

Product van toegevoegde tweetermen in symbolen : ( a + b ) · ( a – b )= a 2 – b 2 in woorden : Het product van twee toegevoegde tweetermen is gelijk aan het verschil van : het kwadraat van de gelijke term met het kwadraat van een van de tegengestelde termen.

Tip : – Onderstreep in de opgave de term die gelijk gebleven is. – Kijk ook na of de andere term wel degelijk van teken veranderde. Is dat niet het geval, dan heb je hier te maken met de eerste formule.

Voorbeelden : (a + 3) (a 3)= a 2 32 = a 2 9

Als je voldoende geoefend hebt, zul je de tussenstap weglaten en onmiddellijk het eindresultaat noteren.

3 Merkwaardige producten in een vierkant

Beide formules kun je ook voorstellen in een vierkant.

Kwadraat van een tweeterm a b a b

A grootvierkant =(a + b ) (a + b ) =(a + b )2 A grootvierkant = a 2 + ab + ba + b 2 = a 2 + 2ab + b 2

Besluit : ( a + b ) 2 = a 2 + 2ab + b 2

Product van twee toegevoegde tweetermen

Besluit : ( a + b ) ( a – b ) = a 2 – b 2

4Samenvatting

• Je kent volgende formules voor merkwaardige producten en kunt ze verklaren en toepassen.

KWADRAAT VAN EEN TWEETERM

( a + b )2 = a 2 + 2ab + b 2

Het kwadraat van een tweeterm is gelijk aan de som van het kwadraat van de eerste term ; het dubbel product van de twee termen ; het kwadraat van de tweede term.

PRODUCT VAN TOEGEVOEGDE TWEETERMEN

( a + b ) · ( a – b ) = a 2 – b 2

Het product van twee toegevoegde tweetermen is gelijk aan het verschil van : het kwadraat van de gelijke term met het kwadraat van een van de tegengestelde termen.

5 Oefeningen

Werk uit met behulp van het merkwaardig product

Werk uit met behulp van het merkwaardig

Werk uit met behulp van het merkwaardig product (a + b )2 = a 2 + 2ab + b 2

a (a m + 5)2 =

b a m +2 + 3 2 =

c (a n b ab n )2 =

d a m +1 a 2m 1 2 = e 3 4 a 2m 4 3 a m +2 2 =

Wat hoort niet thuis in het rijtje ?

Vul de ontbrekende termen aan.

Noteer een toegevoegde tweeterm.

a x + 3 →

b a 1 →

c6 b →

d10 + x 2 →

e0,5 + m →

f 1 5 + 10a →

Werk uit met behulp van het merkwaardig product (a + b ) (a – b ) = a 2 – b 2 .

a (a 3) · (a + 3) =

b ( x 5) (5 + x ) =

c (0,5 + a ) ( 0,5 + a ) =

d ( b + 10) · ( b 10) =

e (a 3 2) ( 2 a 3 ) =

f ( x + 1) ( x 1) =

g ( 0,1 + a ) · (0,1 + a ) =

h 1 3 + x 1 3 + x =

i (a 2 10) · ( 10 a 2 ) =

j ( y + 2) (2 y ) =

k 2 5 x · x 2 5 =

l 1 3 + a 1 3 + a =

m (2a 1) · (2a + 1) =

n y + 3 2 y 3 2 =

o ( x + 8) · ( x 8) =

Werk uit met behulp van het merkwaardig product (a + b ) (a – b ) = a 2 – b 2

a (2a + 3) (2a 3) =

b ( a 2 + 11 b ) (a 2 + 11 b ) =

c ( y 3 z 7 ) ( z 7 y 3 ) =

d (3 x 2 1) ( 3 x 2 1) =

e ( b + c ) ( b + c ) = f 10 3 a + b · b 10 3 a =

g ( x 2 y ) ( x 2 y ) =

h ( x 2 y ) ( x 2 + y ) =

i 5 7 x 2 + y 3 5 7 x 2 y 3 =

j (0,3a 2 b ) · (0,3a 2 + b ) =

k ( x 6 y 2 ) · ( y 2 + x 6 ) =

l 5 2 y 4 1 5 2 y 4 + 1 =

m (5a c ) (5a + c ) =

n ( 1,5a 2 + b 2 ) (1,5a 2 + b 2 ) =

Werk uit met behulp van het merkwaardig product (a + b ) (a – b ) = a 2 – b 2

a (a n + 3) · (a n 3) =

b x 2m +1 3 x 2m +1 + 3 =

c 1 3 x n 3 8 y n 3 8 y n 1 3 x n =

d ((a + b ) 1) ((a + b ) + 1) =

e ( x 2) y ( x 2) + y =

Wat hoort niet thuis in het rijtje ? ( a + 4)( 4 – a )( –a + 4)( 4 + a ) a 2 – 16 ( –a – 4)( –4 + a ) 16 – a 2

Vul de ontbrekende termen aan. a + 3 3 = 36a 2 b 5 x + = 49 y 16 c x 3 + x 3 = 1

Werk uit met behulp van een merkwaardig product.

a ( x 2 y ) · ( x + 2 y ) =

b (3a + 1)2 = c x 1 3 y 2 =

d (a 4 b ) · (a + 4 b ) = e 2 3 a 1 2 1 2 2 3 a =

f ( x + 5 y )2 = g 2 3 x 3 2 y 2 =

h (a 6) · ( 6 + a ) =

i ( x + 0,5 y ) · ( x + 0,5 y ) =

j 0,1a 2 + b 2 2 = k 5 x 3 + 1 5 x 2 =

l (0,4 x 0,2) (0,2 + 0,4 x ) =

m ( b 2 + 5) ( b 2 + 5) =

Het hoeft niet altijd een kruiswoordraadsel te zijn. In het onderstaande kruistermenraadsel vul je per vakje niet één letter maar één term van je uitkomst in. Kijk even mee naar het voorbeeld en je zult begrijpen hoe het werkt. Als een term een minteken voor zich heeft, moet je dit minteken ook in het vakje noteren. Los alle oefeningen op en controleer jezelf op die manier.

Voorbeeld :

A ( a 2b – 2)( a 2b + 2) = a 4b 2 – 4 1 2 3 4 5 6

a 4b 2 –4

HORIZONTAAL

VERTICAAL A ab 2 1 ab 2 + 1

4 + 2 b 2 2

8 + + 4 b 4 B 3 4ab 2 (3 + ) = 9 16a 2 b 4 1 2 a 4 b 2 2 C 2 + a 2 2 6ab 3 b 2 ( ) = 36a 2 b 6 b 4

D 8 b 2 1 2 = 64 b 4 (3ab 9a ) (3ab + 9a ) 1 ab 2 + 2 2

Werk uit met behulp van merkwaardige producten en herleid. Controleer je antwoorden met ICT.

a (a + b )2 + (a b )2

(3 a ) · (3 + a ) (a 3)2

x 3 + 3 x 3 3 x 6 + 9

3 + 3 x 3 3 x 6 9

d x

e x 2 y 2 + 2 y x 2

f x 2 + 1 ( x 1) x 4 1 ( x + 1)

g (a + 2) (a 2) 2 (a 2)

h 1 3 x 1 5 y 2 1 3 x + 1 5 y 2

Werk uit met behulp van merkwaardige producten en herleid.

( x n 1)( x n + 1) ( x n 1)2 = = = =

Bereken de oppervlakte van het grote vierkant.

9 cm2

Newton en Pascal

Er bestaan formules om ( x + y)n te berekenen voor elk natuurlijk getal n. De formule om deze merkwaardige producten te berekenen draagt de naam ‘binomium van Newton’, genoemd naar de Britse wetenschapper uit de 17e eeuw, sir Isaac Newton (die van de appel en de zwaartekracht). Zo is

Om aan de coëfﬁciënten te raken die in deze producten moeten worden gebruikt, kun je gebruikmaken van de ‘driehoek van Pascal’, genoemd naar de Franse wiskundige uit de 17e eeuw, Blaise Pascal, de schepper van de eerste mechanische rekenmachine.

In deze driehoek is elk getal gelijk aan de som van de twee getallen die erboven staan (links en rechts).

De getallen in deze driehoek spelen ook een rol bij kansberekening. Per rij geeft de som van de getallen een macht van 2 weer en zo zijn er nog wel wat gebieden in de wiskunde waar deze driehoek gebruikt kan worden (bv. in de verzamelingenleer). Zelfs de eerste vier machten van 11 zijn in deze driehoek terug te vinden. Kun je zien waar? De driehoek van Pascal ziet er als volgt uit:

Als (x + 1)(x – 1) = 6, dan is (x 2 + 1)(x 2 – 1) gelijk aan

(A)12 (B)24 (C)36 (D)48 (E)60

JWO 2015 eerste ronde, vraag 16© Vlaamse Wiskunde Olympiade vzw

Als x – y = x 2 – y 2 = 25, dan is x gelijk aan

(A) 5

JWO 2010 eerste ronde, vraag 9© Vlaamse Wiskunde Olympiade vzw

Welke van onderstaande bewerkingen hoort op de plaats van het vraagteken zodat het hele rooster correct kan worden aangevuld voor alle waarden van x ?

x + 3 + 1 – 1 ( x + 1) ?

JWO 2015 eerste ronde, vraag 6 © Vlaamse Wiskunde Olympiade vzw

(A)vermenigvuldigen met x

(B)vermenigvuldigen met x – 2

(C)vermeerderen met x 2 + 2x

(D) verdubbelen

(E)kwadrateren

Op een erg zonnige dag wil je aan de kust een ijsje kopen. Maar heel veel mensen hadden datzelfde idee.

In de lange rij wachtenden staat 70% van de kopers voor jou in de rij en 20% van de kopers achter jou.

Hoeveel mensen staan te wachten in de rij ?

Welke rationale getallen stellen x , y en z voor als je weet dat

x y = 4

y · z = 16

x z = 1

Vaardigheden | Computationeel denken

De bever is een dier dat bekend is door zijn ijver, samenwerkingsvermogen en probleemoplossend denken. Daarom koos Bebrasoprichtster professor Dagiene (universiteit Vilnius) voor de naam Bebras, wat Litouws is voor bever. Ondertussen is Bebras uitgegroeid tot een internationale wedstrijd dat het computationeel denken bij studenten bevordert. Breng je deze twee opgaven tot een goed eind ?

Berukone

Een Berukone-puzzel bestaat uit een rooster met (hier en daar) getallen in de vakjes. Elk getal komt twee keer voor. Om de puzzel op te lossen, moet je elk van deze getallenparen verbinden met een lijn. Deze verbindingslijn moet horizontaal of verticaal van vakje naar vakje lopen, maar mag op elk vakje 90 graden draaien. Een lijn mag niet door een getal lopen en mag een andere lijn niet kruisen. Er zijn Berukone-puzzels die je niet kunt oplossen :

Deze Berukone-puzzel kan opgelost worden.Deze Berukone-puzzel kan niet opgelost worden.

12 2

21 2 1

Slechts één van de Berukone-puzzels hieronder kan niet opgelost worden. Welke ?

Auteur tekst en afbeeldingen: Wolfgang Pohl (Duitsland) / Vertaling: Kris Coolsaet (België)

Videoklas

Lerares Ava geeft online les. Op haar computerscherm ziet Ava dat er zich 9 leerlingen bij haar klas hebben aangesloten: Emma, Maya, Bella, Lee, Raul, Hannah, Diana, Alice en James. Elk van de 9 leerlingen gebruikt een andere computer in de schoolbibliotheek. De 9 kinderen zitten naast elkaar aan één lange tafel en Ava kan op haar scherm zien naast wie elke leerling zit. Wie zit er precies in het midden van die tafel ?

A Emma B Maya C Bella D Lee E Raul F Hannah G Diana H Alice I James

Auteur tekst en afbeeldingen: Khairul Anwar M. Zaki (Maleisië) / Vertaling: Kris Coolsaet (België)

Rekenen met algebraïsche uitdrukkingen 3

moet ik leren

dit

❒ Ik ken de definitie van een eenterm.

❒ Ik kan de graad bepalen van een eenterm in een letter.

❒ Ik kan de graad bepalen van een eenterm (in alle letters).

❒ Ik ken de definitie van gelijksoortige eentermen.

❒ Ik kan de getalwaarde van een eenterm berekenen.

❒ Ik ken de definitie van een veelterm.

❒ Ik kan de graad bepalen van een veelterm in een letter.

❒ Ik kan de getalwaarde van een veelterm berekenen.

❒ Ik kan gelijksoortige eentermen optellen of aftrekken.

❒ Ik kan een veelterm herleiden en rangschikken.

❒ Ik kan veeltermen optellen en aftrekken.

❒ Ik kan eentermen vermenigvuldigen.

❒ Ik kan een macht berekenen van een eenterm.

❒ Ik kan het product bepalen van een veelterm met een eenterm.

❒ Ik kan het product bepalen van twee veeltermen.

❒

Ik ken de formule voor het kwadraat van een tweeterm in woorden en in symbolen en kan ze toepassen.

❒ Ik weet wat toegevoegde tweetermen zijn.

❒

Ik ken de formule voor het product van twee toegevoegde tweetermen in woorden en in symbolen en kan ze toepassen.

Rekenen met algebraïsche uitdrukkingen 3

Naam

Bepaal de getalwaarde van

a –2ab als a = 5en b =–2 b5x 2 –y als x =–3 en y = 50

Wat is bij de veelterm 2x 3 – 3x 2y – 9y 4

a de graad in x ?

b de graad in y ?

c de graad in z ?

Werk uit, herleid en rangschik naar dalende macht in x . a 5 x + 2 x 3 + 3 x 2 6 x 2 + 2,5 x 3 5 x

Schrijf de omtrek zo eenvoudig mogelijk.

Vul aan zodat de gelijkheid klopt.

a 1 4 a 3 b + = 1 4 a 3 b b2 x 2 + = 10 x 2

Bereken.

a4a + 8a =

b4a · 8a = c 2 3 x · 9 4 x 2 =

Vul aan met = of ≠ a x 3 · x 3 · x 3 x 27 c4x 4 · 4x 4 ………16x 8

b ( x 4 – 4)( x 4 + 4) x 8 – 16

Hoe groot is de oppervlakte van deze tuin ?

a Druk uit met een veelterm.

d4x 4 + 4x 4 8x 8

b Als a = 5 m en b = 8 m, hoe groot is dan de oppervlakte ?

Bereken.

a2 x · ( 3 x + 8) = b 1 4 16 x 2 8 3 =

c (3a + 1)(2a 4) =

/ 3

Werk uit met de formule ( a + b ) ( a – b ) = a 2 – b 2

(a + 5) (a 5)=

/ 3 11 / 3 12 / 1

( 3 b + 2) (3 b + 2)= 1 2 b 3 5 5 + 1 2 b 3 =

Werk uit met de formule (a + b )2 = a 2 + 2ab + b 2

( b + 3)2 =

(4 x 3)2 = 2 3 b 2 1 2 = Wat hoort niet in het rijtje ?

( 2x + 3) ( 2x – 3)( –2x – 3)2 ( 2x + 3) ( 2x + 3)( 2x + 3)2 ( –2x – 3) ( –2x – 3)

Hoodstuktitel

Data en onzekerheid 4

In alle media krijg je ze voorgeschoteld : cijfertabellen, graﬁeken en diagrammen.

Ze stellen allerhande gegevens voor die snel en handig in beeld worden gebracht. Maak in dit hoofdstuk kennis met een mooie inleiding van de statistiek. Laat Excel en GeoGebra je ICT-tools zijn om alles te verwerken.

Eindig je statistische kennistocht met het uitwerken van een eigen onderzoek. Dat kan individueel of in groep. Dat kan puur wiskundig, maar ook in samenwerking met een ander vak.

Data en onzekerheid

4.1 Gegevens voorstellen in een absolute frequentietabel

1 Absolute frequentie 167

2 Numerieke en categorische data 168

4.2 Data verwerken in tabellen en diagrammen

1 De vier seizoenen 169

2 Misleidende grafieken 173

3 De inwoners van het Vlaamse Gewest 175

4.3 Centrummaten en spreidingsmaat

1 Gemiddelde, mediaan en modus 176

2 Variatiebreedte 177

3 Het gemiddelde, de mediaan, de modus en de variatiebreedte berekenen met ICT als de ruwe gegevens gekend zijn 178

4 Het gemiddelde, de mediaan, de modus en de variatiebreedte berekenen met ICT als een frequentietabel gegeven is 179

4.4 Een eigen onderzoek uitvoeren

1 Twee dobbelstenen gooien 180

2 Simulatie met ICT 181

3 Verkeersgedrag bij jongeren (de quiz) 182

4 Samenvatting 184

5 Oefeningen 185

Extra’s

Vaardigheden : taalvaardigheid : een bingo van statistiekwoordenschat 200

Wat moet je kennen en kunnen ? 201

Herhalingsoefeningen 202

Bekijk de instructievideo’s

4.1 Gegevens voorstellen in een absolute frequentietabel

1 Absolute frequentie

Voorbeeld :

In een klas met 24 leerlingen zijn dit de resultaten van de jongste wiskundetest op tien punten.

We zullen nu deze resultaten weergeven in een overzichtelijke frequentietabel

– In een eerste kolom komen alle mogelijke waarnemingsgetallen.

In een tweede kolom noteer je de (enkelvoudige) absolute frequentie : dit is het aantal keer dat dit waarnemingsgetal voorkomt in de gegevensset.

Je kunt ook een kolom toevoegen met hierin de cumulatieve absolute frequentie. Dit is het aantal keer dat dit waarnemingsgetal voorkomt, samengesteld met de frequenties van de kleinere waarnemingsgetallen.

We kunnen volgende uitspraken doen :

– Er waren 2 leerlingen die 8/10 behaalden op deze test.

– Vier leerlingen scoorden minder dan de helft.

Er waren 14 leerlingen die lager scoorden dan 7/10.

(enkelvoudige en cumulatieve) absolute frequentie

De (enkelvoudige) absolute frequentie van een waarnemingsgetal is het aantal keer dat dit waarnemingsgetal voorkomt.

De cumulatieve absolute frequentie van een waarde is de som van de absolute frequenties van deze waarde met alle voorgaande absolute frequenties.

2Numerieke en categorische data

De data in het voorbeeld van vorige bladzijde zijn numerieke data. Met numerieke data kun je rekenen. Je kunt uitmaken wat het grootste en het kleinste gegeven is en het is nuttig om er een gemiddelde van te berekenen.

Voorbeelden van numerieke data : – het aantal huisdieren in een gezin – de massa van de boekentas – de oppervlakte van bouwgronden – de lengte van personen – de tijd die je nodig hebt om rond de piste te lopen

Als het niet mogelijk is (of niet nuttig is) om een gemiddelde te berekenen, dan zijn de data categorische data

Voorbeelden van categorische data : – kruis of munt opgooien van een muntstuk – geboortemaand – bloedgroep – favoriete radiozender – postnummer van je gemeente

Statistiek

Statistiek is de wetenschap die data verzamelt, bewerkt en interpreteert. Het eerste statistisch materiaal vinden we terug in Engeland. Dankzij de zakenmannen John Graunt (1620–1674) en Thomas Malthus (1766–1834) werden de eerste analyses gepubliceerd in verband met sterftevallen in en rond London. Vanaf de 17e eeuw werd kansrekening gebruikt om de statistische gegevens te ontleden en hypothesen te formuleren. Het waren de Zwitserse wiskundige Bernouilli (1654–1705) en zijn Franse collega Laplace (1749–1827) die de statistiek in de wiskunde opnamen. De eerste zinvolle doelgerichte bewerking van statistisch materiaal gebeurde door onze landgenoot Adolphe Quetelet (1796–1874). Hij legde het verband tussen misdadigheid en leeftijd, geslacht, opvoeding, seizoen enz. Hij riep ook het eerste statistisch congres bij elkaar in Brussel in 1855. Hij wordt dan ook de stichter van de moderne statistiek genoemd.

4.2 Data verwerken in tabellen en diagrammen

1De vier seizoenen

Aan 30 personen werd gevraagd wat hun favoriete seizoen is. Dit waren de antwoorden : ZomerHerfstZomerWinterZomerWinterHerfstZomerWinterLente LenteLenteZomerZomerZomerHerfstHerfstHerfstWinterLente WinterWinterZomerZomerHerfstZomerWinterZomerZomerLente

We gaan het volgende uitvoeren :

a een frequentietabel opstellen met GeoGebra ;

b een dotplot tekenen met GeoGebra ;

c een staafdiagram en een cirkeldiagram tekenen met Excel ; d de middelpuntshoeken uit het getekende cirkeldiagram berekenen.

a Een frequentietabel opstellen met GeoGebra

Lente 5

Zomer12

Herfst 6

Winter 7 30

Hiervoor brengen we in GeoGebra 6 de gegevens in het rekenblad in.

We selecteren ze en maken er een lijst l1 van (rechtermuisknop gebruiken en kiezen voor creëer).

In het algebravenster brengen we het volgende in :

D7 = TelAls(x == C7,l1)

Daarna trekken we de vulgreep door naar beneden.

Om het totale aantal ondervraagde personen te krijgen (30), typen we in het algebravenster nog het volgende in :

D12 = som(D7 : D10)

Uit deze frequentietabel kunnen we het volgende afleiden :

– Aan 30 personen werd gevraagd wat hun favoriete seizoen was.

De data die werden opgetekend zijn categorische data.

– 12 van de 30 ondervraagde personen kozen de zomer als favoriete seizoen.

– De herfst was het minst favoriete seizoen van de ondervraagde personen.

7 van de 30 ondervraagde personen hadden een voorkeur voor de winter.

b Een grafische voorstelling tekenen met GeoGebra

We tekenen met GeoGebra 6 ook een dotplot van de gegevens.

– De gegevens zijn al geselecteerd en in een lijst gebracht met de naam l1.

– Geef in het algebravenster het commando dotplot(l1) in.

Pas de labels op de assen aan. Daarvoor druk je eerst op de selecteerknop en klik je vervolgens met de rechtermuisknop in het tekenvenster. Kies daarna onderaan voor tekenvenster en pas dan zowel op de x-as als de y-as de labels aan.

– Via Tekst typ je de verschillende seizoenen in.

Ook andere grafische voorstellingen zijn mogelijk met GeoGebra.

– Staafdiagram: typ staafdiagram(l1, 0.5) in. Het laatste getal tussen de haakjes geeft de breedte weer van de staafjes.

c Een staafdiagram en een cirkeldiagram tekenen met Excel

– Kopieer de gegevens vanuit GeoGebra in Excel of voer ze opnieuw in Excel in.

– Selecteer de gegevens in Excel en geef ze een naam door te klikken op A1 (zie pijl).

Klik daarop en typ het woord ‘seizoenen’.

We maken dan deze tabel.

In cel D7 typen we in : = aantal.als(seizoenen;C7) (klik op C7)

Nadien trekken we alles met de vulgreep naar beneden door.

In cel D12 typen we in : = som(…) selecteer het gebied D7 tot D10.

Je krijgt dit resultaat.

We tekenen dan een staafdiagram en een cirkeldiagram met de geziene methodes van vorig jaar.

Selecteer de 2 kolommen uit de opgestelde frequentietabel en klik op invoegen. Klik nu op aanbevolen grafieken, kies het passende type en werk verder af door een titel in te vullen, de gegevenslabels aan te brengen …

12 6 7 Fa voriete seizoen

12 6 7

LenteZomerHerfstWinter

d De middelpuntshoeken uit het getekende cirkeldiagram berekenen We berekenen nu met het rekenblad van Excel ook de groottes van de getekende middelpuntshoeken.

Een eenvoudige methode is: met de muisaanwijzer op de getekende gebieden staan, de percentages aflezen en noteren. Nadien vermenigvuldig je dan die percentages met 360.

Een andere methode is in de cel E7 het volgende intypen : = D7/D$12*360 Eerst klikken we uiteraard op de nodige cellen. We typen de naam van de cellen zelf niet in en gebruiken ook de toets F4 om dollartekens bij te voegen. In dit geval klikken we tweemaal op F4. De rij 12 mag immers niet wijzigen, daarom plaatsen we er een $-teken voor. Nadien trekken we met de vulgreep alles door naar onderen.

De middelpuntshoek die hoort bij Zomer meet 144°. De middelpuntshoek die hoort bij Winter meet 84°.

2Misleidende graﬁeken

a Gegevens vergelijken die niet zinvol te vergelijken zijn

Volgende gegevens worden weergegeven in een staafdiagram.

Dit staafdiagram is correct weergegeven maar het kan de indruk geven naar de buitenwereld dat school B een betere school is dan de twee andere. Dat komt omdat het diagram het aantal geslaagde leerlingen per school weergeeft en geen rekening houdt met het feit dat er op school B veel meer leerlingen zijn dan op de andere scholen !

Een eerlijker beeld krijgen we als we de percentages geslaagde leerlingen weergeven.

Hieruit blijkt nu dat het percentage geslaagde leerlingen in de drie scholen vrij dicht bij elkaar ligt en ongeveer 70% is !

b Gebruik van een niet-aangepaste schaal op de y-as

Ook deze grafiek is misleidend. De reden is dat de as links niet begint bij 0 maar bij 66. Dat kan de indruk wekken dat het percentage geslaagde leerlingen in school B beduidend hoger ligt dan in school A.

c Niet alle data weergeven

Je gebruikt enkel de data die je nodig hebt om je eigen waarheid te vertellen. Je neemt maar een deel van de gegevens. We noemen dit cherry picking. Zo ging het aandeel van Apple tussen januari en april er inderdaad op achteruit. Maar bekijk je de aandelenkoers over een veel langere periode, dan concludeer je iets anders

d Verkeerd gebruik van tekeningen

De gemiddelde grootte van mannen uit verschillende landen wordt weergegeven in deze voorstelling.

Je zou haast denken dat de Nederlander dubbel zo groot is als de persoon uit India.

Daar waar de voeten de grond raken, zou eigenlijk de horizontale as moeten starten vanaf 0 (en niet vanaf 1,5 m).

NEERKIJKEN OP DE REST VAN DE WERELD (gemiddelde hoogte van de man in m)

Doordat in deze 3D-versie van een cirkeldiagram erg de nadruk wordt gelegd op het uitspringende groene cirkelsegment, lijkt de indruk te ontstaan dat jongeren in hun vrije tijd veel lezen.

Nederland USA CanadaEngelandIndia Filipijnen

LEZEN

GAMEN

SPORT

SOCIALE MEDIA

ONTSPANNING NA SCHOOLTIJD

3De inwoners van het Vlaamse Gewest

Volgende frequentietabel geeft een overzicht van het aantal inwoners van het Vlaams Gewest. 2000200420082012201620202024

De opgetekende data zijn numerieke data. Het aantal inwoners van het Vlaamse Gewest op 1 januari 2000 bedroeg 5940251. In de onderste rij van de tabel zie je de evolutie ten opzichte van het jaar 2000. We verklaren hoe we aan 114,8 komen in die onderste rij voor het jaar 2024. 5940251komtovereenmet100

1komtovereenmet

100 5940251

6821770komtovereenmet

100 · 6821770 5940251 = 114,839760... ≈ 114,8

We brengen de jaartallen en de evolutie in het rekenblad en tekenen een lijndiagram. Als je niet naar de getallen op de verticale as kijkt, zou je kunnen concluderen dat de groei op twintig jaar meer dan verdubbelde, wat uiteraard niet zo is.

Je krijgt een eerlijke grafiek als je het minimum van de verticale as op nul zet.

Het Vlaamse Gewest

Evolutie aantal inwoners Vlaams Gewest

België heeft een ingewikkelde staatsstructuur. Naast de federale overheid zijn er immers drie gemeenschappen en drie gewesten die elk kunnen kiezen hoe ze besturen. Toen er in 1970 een staatshervorming plaatsvond, werden drie ‘cultuurgemeenschappen’ opgericht, met elk een eigen parlement. Bij een volgende staatshervorming werd het voorzetsel ‘cultuur’ geschrapt. Naast de Vlaamse Gemeenschap zijn er ook een Franstalige Gemeenschap en een Duitstalige Gemeenschap. Deze zijn o.a. bevoegd over het onderwijs.

Naast de cultuur- en taalgebonden gemeenschappen heeft ons land ook drie gewesten : het Vlaamse Gewest, het Waalse Gewest en het Brusselse Hoofdstedelijke Gewest. Deze zijn bevoegd voor economie, werkgelegenheid, landbouw, openbare werken, energie, ruimtelijke ordening, vervoer (behalve de NMBS) alsook het wetenschappelijk onderzoek in de vermelde domeinen.

4.3 Centrummaten en spreidingsmaat

1Gemiddelde, mediaan en modus

Het gemiddelde, de mediaan en de modus zijn kengetallen die het ‘midden’ van een reeks gegevens beschrijven. Ze geven aan waar het ‘midden’ van een reeks gegevens zich situeert. We noemen ze centrummaten.

gemiddelde

Het gemiddelde van enkele getallen is gelijk aan de som van die getallen, gedeeld door het aantal getallen.

Voorbeeld :

Bereken het gemiddelde van 12, 8, 14, 22 en 16.

– Tel de getallen op: 12 + 8 + 14 + 22 + 16 = 72.

Delen door het aantal getallen: 72 : 5 = 14,4

– Het gemiddelde is 14,4.

mediaan

De mediaan van enkele getallen verkrijg je door eerst de getallen te rangschikken van klein naar groot. Is het aantal getallen… … oneven, dan is de mediaan het middelste getal; … even, dan is de mediaan het gemiddelde van de twee middelste getallen.

Voorbeeld 1 :

Bereken de mediaan van 12, 8, 14, 22 en 16.

– Ordenen : 8 12 14 16 22

Voorbeeld 2 :

Bereken de mediaan van 23, 14, 38, 12, 28 en 8.

– Ordenen : 8 12 14 23 28 38

Het middelste getal is 14, dus de mediaan is 14. – Het gemiddelde van 14 en 23 is 18,5.

– De mediaan is 18,5.

modus

De modus van een reeks gegevens is het gegeven dat het vaakst voorkomt in die reeks gegevens.

Voorbeeld :

Zo is van de waarnemingen 10, 7, 8, 7, 13, 22, 24, 15 de modus 7.

Welke van deze kengetallen je kiest om het ‘centrum’ weer te geven, is afhankelijk van het onderzoek.

– Als de gegevens dicht bij elkaar liggen en dus niet veel van elkaar afwijken, zal je vaak kiezen voor het gemiddelde.

– Als er sprake is van uitschieters (gegevens die sterk afwijken van de rest van de waarnemingen), dan zal je eerder kiezen voor de mediaan om het midden van de gegevens te beschrijven.

– Om de modus te bepalen, is er weinig rekenwerk nodig. Maar de modus zelf kan veel minder ‘in het centrum liggen’ dan de andere centrummaten.

2Variatiebreedte

Op twee verschillende dagen in de herfst werd de temperatuur bijgehouden.

De gemiddelde temperatuur op dag 1 is 6°C.

De gemiddelde temperatuur op dag 2 is ook 6°C.

De spreiding van de waarnemingen op dag 2 lijkt groter te zijn dan op dag 1.

Het gemiddelde geeft dus niet alle kenmerken weer van de gegevens.

Het is vaak nodig om ook een idee te hebben wat de spreiding van de gegevens of waarnemingen betreft.

Een eenvoudige maat om de spreiding van gegevens weer te geven is de variatiebreedte

De variatiebreedte = grootste gegeven – kleinste gegeven.

De variatiebreedte van dag 1 is 8 °C – 4°C = 4 °C

De variatiebreedte van dag 2 is 11°C – 1°C = 10°C

Op de tweede dag waren de waarnemingen dus meer verspreid dan op de eerste dag.

variatiebreedte

De variatiebreedte is het verschil tussen de maximale en minimale waarde.

Merk op :

• Deze drie dotplots geven de resultaten weer van eenzelfde wiskundetest in drie verschillende klassen. Waar is de variatiebreedte het grootst ?

• Later zal je nog andere spreidingsmaten leren, zoals de standaardafwijking, om een betere maat voor de spreiding van de gegevens weer te geven.

3 Het gemiddelde, de mediaan, de modus en de variatiebreedte berekenen met ICT als de ruwe gegevens gekend zijn

Charlie heeft gedurende 15 dagen het aantal mails bijgehouden dat hij per dag krijgt.

We berekenen van die gegevens met GeoGebra het gemiddelde, de mediaan, de modus en de variatiebreedte :

Breng hiervoor de gegevens in het rekenblad van GeoGebra in.

– Selecteer de gegevens en maak er een lijst l1 van.

– De commando’s die je daarna moet gebruiken, zijn :

gemiddelde(l1) mediaan(l1) modus(l1) max(l1) - min(l1)

In Excel gelden dezelfde commando’s:

– Geef eerst een naam aan de gegevens, bijvoorbeeld opgave

Geef dan de commando’s gemiddelde(opgave), mediaan(opgave) en modus(opgave) in.

– Geef ten slotte het commando max(opgave) - min(opgave) in.

In kolom D werden de producten berekend van de getallen die in kolom B en C staan en nadien opgeteld. De variatiebreedte kunnen we ook uit de tabel halen

4.4 Een eigen onderzoek uitvoeren

1Twee dobbelstenen gooien

Tijd om een eigen onderzoek uit te voeren met de opgedane kennis. Hieronder zie je een voorbeeld dat je per twee leerlingen kunt uitvoeren. Twee dobbelstenen moeten 50 maal opgegooid worden en telkens moet je viaturven het aantal gegooide ogen bijhouden.

a Stel de volgende frequentietabel op en breng alles in het rekenblad in.

b Teken dan zowel een staafdiagram als een dotplot van de gegevens.

c Bereken nadien het gemiddelde aantal ogen dat gegooid werd en de mediaan.

d Bereken de variatiebreedte.

e Hoeveel keer gooide je 8 ogen ?

f Is er een aantal ogen dat je geen enkele keer gooide? Kan dat wel ?

g Wat is de modus ?

h Wat is de kans dat als je eenmaal 2 dobbelstenen opgooit, je 6 ogen gooit ? Is de kans om 8 ogen te gooien (2 dobbelstenen eenmaal opgooien) dezelfde als de hierboven gevonden kans? Bereken ook die kans.

Taak :

– Werk per twee.

– Stel nadien jullie bevindingen en getekende diagrammen voor aan de klasgroep.

– Hebben andere klasgenoten dezelfde resultaten gevonden? Verklaar !

2Simulatie met ICT

Het is mogelijk om dit alles te simuleren met de computer door gebruik te maken van GeoGebra 6.

– Open het rekenblad en het algebravenster.

– Breng volgend commando in het algebravenster in :

A1 = toevalsgetaltussen(1,6) + toevalsgetaltussen(1,6)

– Trek nadien de cel door naar beneden met de vulgreep tot 50.

– Selecteer deze gegevens en maak er een lijst l1 van. –

Geef dan in het algebravenster het commando staafdiagram(l1,0.5) in.

– Druk nadien op Ctrl + R en er wordt voortdurend 50 keer opnieuw opgegooid met de 2 dobbelstenen.

Het aangepaste staafdiagram verschijnt in het tekenvenster.

Als je nu het gemiddelde aantal ogen, de mediaan, de modus en de variatiebreedte berekent in het rekenblad met de gekende commando’s, dan zullen die ook steeds wijzigen als je op Ctrl + R drukt.

3 Verkeersgedrag bij jongeren (de quiz)

Jongeren verplaatsen zich erg vaak met de fiets. Hoe zo’n jongere zich gedraagt in het verkeer wordt vaak beïnvloed door

– leeftijd:hoe ouder de jongere, hoe vaker er risicogedrag is – moeite: het dragen van een helm kost echt wel erg veel moeite – vrienden: één op twee jongeren geeft aan dat hun vrienden op de fiets hun gsm vastnemen

Tijd voor een onderzoek in je klas. Het onderzoek bestaat uit een quiz en een enquête. De enquête vind je terug als voorlaatste oefening.

SCOREAANTAL

Ken je het verkeersreglement? Doe de quiz op de volgende bladzijde. Bespreek de oplossingen. Wat was jouw score? En de scores van je klasgenoten ?

a Vul de frequentietabel aan.

b Stel deze gegevens voor met een staafdiagram. Gebruik ICT.

c Bereken het rekenkundig gemiddelde.

d Bepaal de mediaan.

e Bepaal de modus.

f Wat is de variatiebreedte ?

g Hoeveel leerlingen van jouw klas behaalde minder dan de helft ?

h Hoeveel procent van de leerlingen van jouw klas slaagde op de quiz ?

De ﬁetser wil rechts afslaan. Mag dat ?

A Ja, want een ﬁets is geen gemotoriseerd verkeer.

B Ja, op voorwaarde dat hij of zij geen tegemoetkomend verkeer hindert.

C Nee, de verboden rijrichting geldt voor alle bestuurders.

Geldt hier de voorrang van rechts ?

Deze auto’s rijden stapvoets. Er is geen ﬁetspad. Langs welke kant mag de ﬁetser de auto’s inhalen ?

A Langs rechts en links.

B Langs links.

C Langs rechts.

Waar moet ik rijden met een elektrische step ?

Mag ik op dit ﬁetspad tegen de rijrichting ﬁetsen ?

A Ja.

B Ja, maar enkel binnen de bebouwde kom.

C Nee.

Wie heeft voorrang ?

Nee, want de ﬁetser volgt een doorlopend ﬁetspad.

Nee, want er staan verkeersborden die de voorrang regelen.

C Ja, de ﬁetser moet voorrang verlenen aan de auto.

Je gebruikt als voetganger het zebrapad als er één aanwezig is binnen een bepaalde afstand. Welk is die afstand ?

A Op het voetpad.

B Op het ﬁetspad.

C Ik mag kiezen, maar op het voetpad mag het enkel stapvoets.

Wie heeft voorrang ?

A De tram.

B De voetganger, maar enkel binnen de bebouwde kom.

C De voetganger.

De slagbomen zijn open. Mag ik deze overweg overrijden ?

A De ﬁetser als hij naast de ﬁets stapt.

B De automobilist.

C De ﬁetser als hij ﬁetst.

A Ja.

B Ja, tenzij je een belsignaal hoort.

C Neen.

4Samenvatting

• Je kunt een frequentietabel opstellen.

De absolute frequentie is het aantal keer dat een bepaalde waarneming voorkomt.

• Je kent het verschil tussen numerieke en categorische data.

Met numerieke data kun je rekenen. Je kunt uitmaken wat het grootste en het kleinste gegeven is en je kunt er het gemiddelde van berekenen.

Voorbeelden :

aantal huisdieren

– massa van de boekentas

– oppervlakte van bouwgronden

Met categorische data kun je niet rekenen.

Voorbeelden :

– geboortemaand

– bloedgroep

– kennis van Excel

• Je kunt data met ICT verwerken in tabellen en diagrammen.

lijndiagram staafdiagram cirkeldiagram dotplot

• Je kent de definities van deze centrummaten: gemiddelde, mediaan en modus.

Het gemiddelde van enkele getallen is gelijk aan de som van die getallen gedeeld door het aantal getallen.

De mediaan van enkele getallen verkrijg je door eerst de getallen te rangschikken van klein naar groot. Is het aantal getallen

… oneven, dan is de mediaan het middelste getal ; even, dan is de mediaan het gemiddelde van de twee middelste getallen.

De modus van een reeks gegevens is het gegeven dat het vaakst voorkomt in die reeks gegevens. Als er meerdere gegevens het vaakst voorkomen, dan is er geen modus.

• Je weet dat de variatiebreedte het verschil is tussen de maximale en minimale waarde.

• Je kunt het gemiddelde, de mediaan, de modus en de variatiebreedte berekenen met ICT.

• Je kunt voorstellingen en centrummaten interpreteren bij een statistisch onderzoek.

5 Oefeningen

Zijn volgende data numeriek of categorisch? Zet een kruisje in de correcte kolom.

NUMERIEK CATEGORISCH

a favoriete frisdrank

b afstand school – thuis

c merk van je smartphone

d lengte van een baby’tje

e postnummer

f tijd om 100 m af te leggen

g kennis van GeoGebra

h aantal sneeuwdagen per jaar

i bloedgroep

j geboortemaand

Wim noteerde van 18 voorbijrijdende personenwagens het merk.

RENAULTFORDCITROENRENAULTAUDI PORSCHE VOLVO RENAULTAUDI VOLKSWAGEN OPELAUDIFORD VOLVO BMWBMWAUDI HYUNDAI

a Stel een frequentietabel op die dit alles weergeeft.

b Hoeveel keer heeft Wim een personenwagen van het merk FORD zien voorbijrijden tijdens deze periode ?

Hoeveel mensen doen aan carpoolen? Hiervoor werd een onderzoek gedaan waarbij het aantal inzittenden van 30 passerende wagens werd geteld. Dit zijn de resultaten. 1422111133 1114532113 5421121211

a Stel een frequentietabel op.

b Teken een staafdiagram van deze gegevens.

Via de app Fever Tracker ziet Simon zijn lichaamstemperatuur. Dit zijn de gegevens van de laatste 10 uur.

Teken een lijndiagram dat dit verloop van de temperatuur van Simon weergeeft.

Hiernaast vind je het aantal gevallen van bewezen internetfraude in België.

a Zijn deze data numeriek of categorisch ?

b De voornaamste bron van internetfraude is phishing. Wat betekent phishing ?

bron: Federale Politie

c Teken met ICT een passend diagram dat dit cijfermateriaal weergeeft.

d Bereken de procentuele toename van 2019 naar 2023.

In een klas van 24 leerlingen wordt gevraagd hoeveel uren ze per week sporten. In deze frequentietabel zijn de resultaten weergegeven.

Bereken hoeveel uren per week gemiddeld wordt gesport door de leerlingen in deze klas.

Vul in.

a De mediaan van de eerste 7 priemgetallen is

b Het gemiddelde van x , x + 2, x + 4 en x + 6 is 10. Dan is x =

c Het gemiddelde van de eerste n getallen is 3. De waarde van n is _________________________________________

Bij de jongste editie van de sponsorloop werden door de leerlingen van klassen 2A, 2B, 2C, 2D en 2E volgende afstanden gelopen. 2A2B2C2D2E

aantal leerlingen 2425221923

totaal aantal km gelopen door de leerlingen van de klas 170200158158166 gemiddelde per leerling

a Vul in de tabel voor elke klas de gemiddeld gelopen afstand per leerling aan.

b Bereken het gemiddelde aantal gelopen kilometers per leerling voor de vijf klassen.

Een firma houdt bij hoelang het duurt vooraleer een pakje bij de consument wordt geleverd. De resultaten van 112 verzonden pakjes staan in de frequentietabel.

AANTAL DAGEN

a Vul de laatste kolom aan.

b Hoeveel pakjes zijn maximaal twee dagen onderweg?

c De firma maakt reclame met de slogan ‘meer dan 90% van onze pakjes worden de volgende dag geleverd’. Klopt deze slogan ?

Bereken van de volgende getallenreeksen telkens het gemiddelde, de mediaan, de modus en de variatiebreedte.

GETALLENREEKSGEMIDDELDEMEDIAANMODUS VARIATIEBREEDTE

a 284815 9 54 9 28 9

b 1113 7 23 21 7 12

c –9 –22 –1 –45 –22

d 10510885 108 9048

e 17 7 11 9 7 12 79 20172813

f –40 –50 –7 –45 –18 –7 –12 –7

g 100582071050 85820 8050

a Noteer 9 getallen waarvan de mediaan gelijk is aan 18.

b Noteer 10 getallen waarvan de mediaan gelijk is aan 18.

Gemiddelde :

Bereken van volgende reeksen gegevens met ICT het gemiddelde, de mediaan, de modus en de variatiebreedte. a

Mediaan :

Modus :

Variatiebreedte :

Gemiddelde :

Mediaan :

Modus :

Variatiebreedte :

Gemiddelde :

Mediaan :

Modus :

Variatiebreedte :

Gemiddelde :

Mediaan :

Modus :

Variatiebreedte :

Noteer tien getallen waarvan de mediaan gelijk is aan 8,5 en het gemiddelde gelijk is aan 10,5. Het gemiddelde van 15 getallen is 28. Hoe groot wordt het gemiddelde als je bij een van de getallen 12 optelt ?

In deze dotplot wordt weergegeven hoeveel stukken fruit jij de afgelopen twee weken dagelijks hebt opgegeten.

a Bepaal de mediaan.

b Bereken het gemiddelde aantal stukken fruit dat je de afgelopen twee weken dagelijks opat.

Het gemiddelde van de getallen 14, 12, 18, 22, x , 36, 9 en 14 is 16. Bereken x .

Het gemiddelde van de laatste test wiskunde was 7,4/10. De meisjes van de klas behaalden een gemiddelde van 8/10. De twaalf jongens van de klas behaalden een gemiddelde van 7/10. Hoeveel meisjes zitten er in deze klas ?

Het gemiddelde van zes getallen is 4. We voegen een zevende getal toe, zodat het gemiddelde 5 wordt.

Bepaal dit zevende getal.

Bij 30 voetbalwedstrijden heeft de assistent van de trainer het aantal doelpunten opgetekend.

a Bereken het gemiddelde aantal gescoorde doelpunten per wedstrijd.

b Bereken de mediaan.

c Bepaal de modus en de variatiebreedte.

Van 30 kinderen werd de lengte gemeten in cm. De resultaten werden verwerkt in een stengelbladdiagram Bij deze voorstelling zie je links (de stengel) het aantal tientallen. Rechts (de bladeren) staan de eenheden netjes geordend. De kleinste kinderen in dit onderzoek meten dus 120 cm en 122 cm. 12

a Bereken de gemiddelde lengte.

b Bepaal de mediaan en de modus.

c Hoeveel kinderen zijn groter dan 150 cm ?

d Hoeveel procent van de kinderen zijn groter dan 140 cm ?

e Zet de gegevens om in een dotplot. Welke centrummaat is nu onmiddellijk af te lezen ?

Onderzoeksopdrachten.

Onderzoek proefondervindelijk (met getallenvoorbeelden) wat in onderstaande situaties gebeurt. Formuleer het resultaat in een mooie zin.

a Onderzoek wat er gebeurt met het gemiddelde van enkele getallen als je alle getallen met eenzelfde getal vermeerdert.

b Onderzoek wat er gebeurt met het gemiddelde van enkele getallen als je alle getallen met eenzelfde getal vermenigvuldigt

c Beschouw deze elf getallen: 9 164822 96 31 34 28 52 20 Bereken het gemiddelde en de mediaan. Verander het grootste getal door een nog groter getal. Welke invloed heeft dit op het gemiddelde en de mediaan ?

Welke centrummaat beschrijft het best het midden bij :

a 111210 9 12,511,5

b aantal minuten vertraging van de trein

c 1224 9 23 3 15

d gegevensset met enkele uitschieters

e een onderzoek naar kennis van Excel (slecht, voldoende, goed)

f resultaten van een toets wiskunde

Stel twee rijen van telkens 10 waarnemingen op die dezelfde variatiebreedte hebben, maar die toch een duidelijk verschil in spreiding vertonen.

In de klas van Korneel werd aan de leerlingen gevraagd hoeveel huisdieren ze hebben. Dit zijn de antwoorden.

a Zijn de opgetekende data numeriek of categorisch ?

b Teken met ICT een staafdiagram van de gegevens.

c Bepaal het gemiddelde aantal dieren dat de leerlingen thuis hebben.

d Bepaal de mediaan.

Bij het medisch onderzoek van het CLB werd van 20 kleuters de lengte (in cm) genoteerd. Dit zijn de resultaten.

a Zijn de opgetekende data numeriek of categorisch ?

b Teken met ICT een dotplot.

c Bepaal met ICT de gemiddelde lengte, de mediaan en de modus.

d Bepaal de variatiebreedte.

e Hoeveel van de 20 kleuters meten 83 cm ?

f Hoe kun je makkelijk aan de hand van de dotplot de mediaan bepalen ?

Gegeven is deze dotplot : a Stel een frequentietabel op.

b Bepaal het gemiddelde en de mediaan.

Timo en co leveren pokébowls aan huis.

Van de laatste 30 leveringen aan huis noteerden ze de tijd die nodig was om de pokébowls rond te brengen. 15′ betekent dat Timo 15 minuten onderweg was. Je vindt de resultaten terug in de tabel hiernaast.

a Teken een dotplot van de gegevens.

b Hoeveel keer had Timo meer dan 15′ nodig om de pokébowls ergens te bezorgen ?

c Bereken de gemiddelde tijd die Timo nodig had om pokébowls aan huis te leveren.

d Bereken de mediaan en de variatiebreedte.

Simuleer met de computer 50 worpen met drie dobbelstenen. Teken met ICT een passend staafdiagram. Bereken het gemiddelde, de mediaan, de modus en de variatiebreedte.

Een tehuis vangt een aantal weeskinderen op. Het frequentiediagram geeft weer hoeveel kinderen er van elke leeftijd zijn. Wat is de gemiddelde leeftijd van deze kinderen ?

(A) 4 (B)4,5 (C) 5 (D)5,5 (E)17,5

JWO 2019 eerste ronde, vraag 15 © Vlaamse Wiskunde Olympiade vzw

Vier broers zijn verschillend van lengte; van klein naar groot zijn de achtereenvolgende lengteverschillen telkens hetzelfde. Sietse is kleiner dan Adam, maar groter dan Hielke. Benjamin is kleiner dan Hielke. Sietse is 184 cm groot. De gemiddelde lengte is 178 cm.

Hoeveel cm is Benjamin groot ?

(A)160 (B)166 (C)172 (D)184 (E)190

WIZPROF 2017 vraag 17 © Stichting Wiskunde Kangoeroe

De gemiddelde lengte van de inwoners van Rievendelf is 1,78 m. In Kazzatoem is dat 1,58 m. Arwin verhuist van Rievendelf naar Kazzatoem. Onder welke voorwaarde is het zeker dat de gemiddelde lengte in beide plaatsen toeneemt ? (A)

als Arwin groter is dan 1,58 m (B) als Arwin groter is dan 1,78 m (C) als Arwin kleiner is dan 1,58 m (D) als Arwin kleiner is dan 1,78 m (E) als Arwin tussen 1,58 m en 1,78 m groot is

JWO 2025 tweede ronde, probleem 1 © Vlaamse Wiskunde Olympiade vzw

De verzamelingen X en Y bevatten getallen: X = { 1, 2} en Y = { 3, 4, 5}. Sanja wil het gemiddelde van de getallen in X en het gemiddelde van de getallen in Y verhogen door 1 getal van de ene naar de andere verzameling te verplaatsen. Welk getal verplaatst ze ?

(A) 1 (B) 2 (C) 3 (D) 4 (E) 5

WALLABIE 2025 probleem 20 © Vlaamse Wiskunde Olympiade vzw

Een eigen onderzoek: verkeersgedrag bij jongeren (de enquête).

MIJN ENQUÊTE

A Als ik ﬁets, luister ik naar muziek met beide oortjes of een koptelefoon.

Ik draag reﬂecterende kledij in het donker. Zo ben ik tot meer dan 100 meter ver zichtbaar.

C Als het voetgangerslicht op rood staat, zal ik nooit de straat oversteken.

D Als ik ﬁets, zal ik nooit een helm dragen.

E Een vrachtwagen wacht voor het rode licht. Ik rijd op de ﬁetssuggestiestrook tot aan het stoplicht, naast de vrachtwagen.

F Met de ﬁets zal ik in het donker zeker met werkende ﬁetslichten rijden.

a Beoordeel deze stellingen door in de voor jou toepasbare kolom een kruisje te plaatsen.

Je kiest voor JA als je helemaal met de stelling akkoord gaat.

We illustreren de vier aankruismogelijkheden aan de hand van de eerste stelling.

A JA Als ik fiets, luister ik steeds naar muziek met beide oortjes of een koptelefoon.

EERDER WEL Als ik fiets, luister ik meestal naar muziek met beide oortjes of een koptelefoon.

EERDER NIET Als ik fiets, luister ik af en toe naar muziek met beide oortjes of een koptelefoon.

NEEN Als ik fiets, luister ik nooit naar muziek met beide oortjes of een koptelefoon.

b Verzamel alle resultaten van je klasgenoten en zet de data om in percentages.

KLASENQUÊTE

A Als ik ﬁets, luister ik naar muziek met beide oortjes of een koptelefoon.

BIk draag reﬂecterende kledij in het donker. Zo ben ik tot meer dan 100 meter ver zichtbaar.

C Als het voetgangerslicht op rood staat, zal ik nooit de straat oversteken.

D Als ik ﬁets, zal ik nooit een helm dragen.

E Een vrachtwagen wacht voor het rode licht. Ik rijd op de ﬁetssuggestiestrook tot aan het stoplicht, naast de vrachtwagen.

F Met de ﬁets zal ik in het donker zeker met werkende ﬁetslichten rijden.

c Verdeel de klas in zes groepjes. Elke groep stelt de gegevens voor van één stelling met behulp van een cirkeldiagram. Welke stelling bespreekt jouw groep?

d Als je aan de hand van je resultaten een krantenartikel zou schrijven, wat zou dan een gepaste titel kunnen zijn ?

e Bedenk een gefundeerd idee dat jij als minister van verkeer zou kunnen voorstellen.

Een statistisch onderzoek.

Maak individueel of in groep een van onderstaande onderzoeken.

BASISVRAGEN : dit doe je voor elk onderzoek.

a Verwerk de gegevens in een frequentietabel.

b Zijn de opgetekende data numeriek of categorisch ?

c Zet de gegevens om in een staafdiagram, dotplot, cirkeldiagram of lijndiagram.

d Bepaal (indien nuttig) het gemiddelde, de mediaan, de modus en de variatiebreedte.

EXTRA VRAGEN : bij elk onderzoek staan nog enkele extra vragen.

WISKUNDE & WETENSCHAPPEN

MEISJES ZIJN BETERE WETENSCHAPPERS

Welke wetenschappelijke vakken hebben jullie ?

Vraag de resultaten op van het laatste proefwerk.

EXTRA’S :

Maak ook een parallel stengelblad waarbij je de resultaten van jongens en meisjes apart weergeeft.

Klopt de titel van het onderzoek? Verklaar grondig je antwoord. Vergelijk eventueel ook met de resultaten van andere klassen.

LET’S GAME

Hoeveel tijd (in minuten) spendeer je op een schooldag aan gamen ?

EXTRA’S :

Hoeveel procent van de leerlingen gamet? Zet de gegevens ook om in een cirkeldiagram. Bereken ook de grootte van de getekende middelpuntshoeken. Stel dezelfde vraag maar verander een schooldag in een weekend. Beantwoord de basisvragen en vergelijk ze met de antwoorden van je eerste onderzoek.

FIETSEN

Vraag aan de leerlingen van je klas hoeveel fietsen ze thuis hebben.

EXTRA’S :

Hoeveel procent van de leerlingen heeft meer dan drie fietsen thuis ?

SPORTEN IS GEZOND

Dit is de top 10 van het aantal sportclubs in het Vlaamse Gewest.

VOETBAL 6745

WIELRENNEN 4426

WANDELEN 1539

DANSEN 1404

VOLLEYBAL 1172

PAARDRIJDEN 1121

GYMNASTIEK 1043

PETANQUE 1015

TENNIS 936

FITNESS 774

Vraag aan de leerlingen van je klas wie lid is van een sportclub.

EXTRA’S : Zet de gegevens van het Vlaamse Gewest in een passend diagram. Vergelijk de gegevens van je klas met die van het Vlaamse Gewest.

WISKUNDE & LO

DOE EEN SPRINTJE

Bij dit vakoverschrijdend onderzoek verwerk je de resultaten van een les lichamelijke opvoeding. Elke leerling sprint over een bepaalde afstand (bv. 100 m). Iemand noteert de tijd die elke leerling hiervoor nodig heeft. Noteer enkel volledige seconden (bv. 15 seconden).

EXTRA’S :

Welke centrummaat gebruik je om te weten : – of je bij de snelste 50% van de leerlingen bent ? – welk resultaat het vaakst werd opgetekend ? Vergelijk de resultaten van jouw klas met andere klassen die ook voor dit onderzoek kozen.

WISKUNDE & ECONOMIE

WE KOPEN ONLINE …

Stel volgende twee vragen aan je klasgenoten :

Wat koop je het vaakst online ?

Welke online shop bezoek je het vaakst ?

– Hoeveel euro besteed je per maand online ?

EXTRA’S :

Hoeveel procent van de leerlingen in je klas koopt nooit online?

Geef een aantal voor- en nadelen van online kopen.

HOOGSPRINGEN

Tijdens de turnles noteren we de maximale hoogte die elke leerling van de klas springt. Gebruik de centimeter als eenheid.

EXTRA’S : – Is er een relatie tussen de lengte van de leerling en de gesprongen hoogte ? – Hoeveel % van de leerlingen sprong hoger dan jij ?

WAAR GAAN WE OP VAKANTIE

Vraag aan de leerlingen van je klas in welk land ze het afgelopen jaar op vakantie zijn geweest. Als er meerdere keren op vakantie werd gegaan, kiest de leerling enkel de verste vakantiebestemming. Wat is het reisbudget per persoon ?

EXTRA’S :

Hoeveel procent van de klas ging op vakantie in eigen land? Vraag je ook met welk vervoermiddel ze op vakantie gingen? Dan kun je de basisvragen ook beantwoorden bij deze onderzoeksvraag.

Vaardigheden | Taalvaardigheid: een bingo van statistiekwoordenschat

Op Polpo vindt de leerkracht al het nodige om deze bingo in goede banen te leiden.

1 Noteer deze begrippen willekeurig op de bingokaart. frequentietabel – numerieke data – categorische data – GeoGebra – middelpuntshoek – dotplot –cirkeldiagram – lijndiagram – gemiddelde – modus – mediaan – variatiebreedte – uitschieter

2 Luister aandachtig (of kijk goed) naar de omschrijvingen die je leerkracht geeft of projecteert. Herken je een van de begrippen? Kleur dan het vakje van je bingokaart in.

3 Is je bingokaart volledig ingekleurd? Mooi zo! Roep nu BINGO ! Laat je buur of je leerkracht je kaart controleren. Speel daarna verder door je buur te helpen.

Data en onzekerheid 4

moet ik leren

dit

❒ Ik kan gegevens in een frequentietabel weergeven en interpreteren. 167

❒ Ik ken de betekenis van (cumulatieve) absolute frequentie. 167

❒ Ik ken het onderscheid tussen numerieke en categorische data.

168

❒ Ik kan (met behulp van ICT) gegevens voorstellen. Ik maak hiervoor gebruik van een frequentietabel, een dotplot, een staafdiagram, een lijndiagram en een cirkeldiagram. 169

❒ Ik weet wanneer een grafiek misleidend is. 173

❒ Ik ken de betekenis van het gemiddelde en kan dit berekenen (ook met ICT). 176

❒ Ik ken de betekenis van de mediaan en kan die berekenen (ook met ICT). 176

❒ Ik ken de betekenis van de modus en kan die berekenen (ook met ICT). 176

❒ Ik weet wanneer welke centrummaat zinvol is om te gebruiken.

❒ Ik ken de betekenis van de variatiebreedte en kan die berekenen (ook met ICT).

176

177

❒ Ik kan data verzamelen en een eigen statistisch onderzoek uitvoeren. 180

Data en onzekerheid 4

1 / 10

De rugzakken in een klas van 20 leerlingen worden gewogen op 0,5 kg nauwkeurig. Dit zijn de resultaten. 8,59,07,54,09,011,010,59,59,510,0 7,57,09,510,011,510,07,57,07,58,0

a Vul de frequentietabel aan. AANTAL

b Zijn deze data numeriek of categorisch ?

c Teken een staafdiagram.

d Bereken de centrummaten.

gemiddelde

mediaan modus

e Bereken de variatiebreedte.

f Stel dat de rugzak maximaal 8 kg mag wegen. Bij hoeveel leerlingen is dat het geval? Hoeveel procent is dat ?

g Hoeveel weegt jouw boekentas/rugzak? Bespreek enkele tips die je gebruikt om deze lichter te maken.

Naam Totaal

2 / 5

In deze dotplot vind je de schoenmaten terug van de leerlingen van klas 2A.

a Hoeveel leerlingen telt klas 2A ?

b Welke centrummaat valt onmiddellijk af te lezen van de dotplot ?

c Vul aan : gemiddelde = mediaan = modus =

3 / 4

In de volgende tabel wordt een voorspelling gedaan van de groei van het aantal inwoners van het Vlaamse Gewest van 2023 tot 2050, telkens op 1 januari van het desbetreffende jaar.

a Teken met ICT een lijndiagram dat dit cijfermateriaal weergeeft.

b Bereken de procentuele stijging die men verwacht van 2023 naar 2050.

c Als die procentuele stijging dezelfde is van 2050 naar 2077, hoeveel inwoners telt het Vlaamse Gewest dan in 2077 ?

JAARAANTAL INWONERS

2023 6 774807

2030 7 004580

2040 7 287292

2050 7 519198

We spreken van een sneeuwdag als er in de loop van deze dag sneeuw is waargenomen. In deze tabel vind je het aantal sneeuwdagen in Ukkel tussen 2017 en 2024. Het betreft steeds de winter die in dat jaar eindigt.

JAARAANTAL SNEEUWDAGEN

Zet deze gegevens om in een lijndiagram.

Op de sportdag konden de leerlingen kiezen uit vier programma’s. Zet deze gegevens met ICT om in een cirkeldiagram.

KEUZE AANTAL

wildwateravontuur 134 zaalsporten 85 mountainbikeparcours69 muurklimmen 107

/ 4

/ 3

a Het gemiddelde van 12, 14, 15, 17, 19, 21, 22, 23, 28 en x is 19. Bepaal x

b De mediaan van 12, 14, 15, 17, 19, 21, 22, 23, 28 en x is 20. Bepaal x

c De modus van 12, 14, 15, 17, 19, 21, 22, 23, 28 en x is 21. Bepaal x .

d De variatiebreedte van 12, 14, 15, 17, 19, 21, 22, 23, 28 en x is 22. Bepaal x .

/ 4

Oplossingsmethodes voor vraagstukken 5

Hoodstuktitel 0

De Griekse wiskundige Eratosthenes leefde rond 200 voor Christus en werd bekend door de eerste grondige schatting van de omtrek van de aarde. Hij deed een beroep op alle oplossingsmethodes die toen gekend waren.

Die omtrek hebben we ondertussen al veel nauwkeuriger berekend. Bovendien kan de omtrek van een cirkel berekend worden door de eenterm 2πr. Met de zeef van Eratosthenes haalt hij wel nog de Vlaamse wiskundeboeken. Wellicht herinner je je die zeef nog van vorig schooljaar.

Herinner je je ook nog procenten, vergelijkingen en vraagstukken?

We frissen het allemaal voor jou op.

Oplossingsmethodes voor vraagstukken

5.1 Vergelijkingen oplossen in q

1 Gelijkheden 207

2 Vergelijkingen van de vorm x + a = b en ax = b 209

3 De balansmethode 210

4 Vergelijkingen oplossen 211

5 Vergelijkingen met haakjes oplossen 212

6 Samenvatting 214

7 Oefeningen 215

5.2 Vraagstukken oplossen

1 Betekenis van x 230

2 Oplossen van een vraagstuk 231

3 Samenvatting 233

4 Oefeningen 234

Extra’s

Vaardigheden : kritisch denken 245

Wat moet je kennen en kunnen ? 247

Herhalingsoefeningen 248

Bekijk de instructievideo’s

5.1 Vergelijkingen oplossen in q

1Gelijkheden

Voorbeelden : 11 2 = 5,5 20% = 1 5

7 · 3 = 21 3 + 1

Al die uitspraken zijn voorbeelden van een gelijkheid. Wat links van het gelijkheidsteken staat, noemen we het linkerlid, wat rechts van het gelijkheidsteken staat, noemen we het rechterlid.

Onderzoek 1 :

Wat zou er gebeuren als je in beide leden van een gelijkheid een getal optelt ? Hieronder zien we twee gelijke hoeveelheden taart.

Wat gebeurt er als we bij elke hoeveelheid taart 1 8 van een taart toevoegen ?

De gelijkheid blijft behouden !

eigenschap in woorden in woorden:

Je mag in beide leden van een gelijkheid hetzelfde getal optellen (of aftrekken). in symbolen: ∀a , b , m ∈ Q : a = b ⇐⇒ a + m = b + m ⇐⇒ a m = b m

Voorbeeld : 3 + 1 = 4

3 + 1 + 2 = 4 + 2(ditklopt,want6 = 6)

Onderzoek 2 :

Wat zou er gebeuren als je beide leden met een (van nul verschillend) getal vermenigvuldigt ?

Hieronder zien we twee gelijke hoeveelheden taart.

Wat gebeurt er als we de hoeveelheden verdubbelen ?

De gelijkheid blijft behouden !

eigenschap in woorden:

Je mag beide leden van een gelijkheid vermenigvuldigen (of delen) met eenzelfde getal verschillend van 0. in symbolen:

∀a , b ∈ Q, ∀m ∈ Q0 : a = b ⇐⇒ a m = b m ⇐⇒ a m = b m

Voorbeelden

2Vergelijkingen van de vorm x + a = b en ax = b

Vorig jaar leerde je deze vergelijkingen oplossen. We herhalen hier even de aangeleerde techniek. De eigenschappen van de gelijkheden dienen als argumentatie voor de tussenstappen. VERGELIJKING

Je mag in beide leden van een gelijkheid eenzelfde getal optellen of aftrekken. In de praktijk zul je deze tussenstap niet noteren.

Je mag beide leden van een gelijkheid vermenigvuldigen of delen door eenzelfde getal verschillend van 0.

In de praktijk zul je deze tussenstap niet noteren.

Voorbeelden :

3De balansmethode

De balans is in evenwicht en je moet ervoor zorgen dat dat steeds zo blijft ! Bekijk deze twee voorbeelden. Onderaan zie je hoe je het moet noteren.

Voorbeeld 1 : =

Neem in beide schalen 5 weg.

Je noteert : 2 x + 5 = 11 2 x + 5 5 = 11 5 2 x = 6

Houd in beide schalen de helft over.

x 4 = 24 4 x = 6 = x kg = 1 kg

Voorbeeld 2 :

13x + 19 9 x + 43

Neem in beide schalen 19 weg.

13x 9x + 24

Neem in beide schalen 9x weg.

Houd in beide schalen één vierde over.

Je noteert : 13 x + 19 = 9 x + 43 13 x + 19 19 = 9 x + 43 19 13 x = 9 x + 24 13 x 9 x = 9 x + 24 9 x 4 x = 24

4Vergelijkingen oplossen

Vergelijkingen oplossen

1 Werk de haakjes weg.

2 Breng alle termen in x samen in één lid

Alle andere termen breng je samen in het andere lid.

Je maakt gebruik van de eerste eigenschap van gelijkheden.

3 Maak de som in beide leden.

4 Deel door de coëfficiënt van x (of breng de vergelijking in de vorm x = ...).

Je maakt gebruik van de tweede eigenschap van gelijkheden.

5 Je kunt jezelf controleren door een proef uit te voeren.

Voorbeelden :

Het is nuttig om ook een proef te maken.

Dit kan makkelijk met ICT. Controleren kan ook door x in de opgave te vervangen door jouw oplossing.

Je controleert of het linkerlid gelijk is aan het rechterlid.

Voorbeeld : Proef :

De proef klopt

5Vergelijkingen met haakjes oplossen

In een vergelijking kunnen er ook haakjes voorkomen. Als we zulke vergelijkingen hebben, moet je eerst de haakjes wegwerken. We kunnen dit doen door gebruik te maken van de distributiviteit van de vermenigvuldiging ten opzichte van de optelling.

Voorbeeld : Proef :

3 (2 x 3)= 7

Voorbeeld : Proef

Heb je in een vergelijking veel breuken, dan kun je soms de vergelijking vereenvoudigen door de noemers weg tewerken. Dat kan door elk lid te vermenigvuldigen met het kleinste gemeenschappelijk veelvoud van deverschillende noemers die in de vergelijking voorkomen. Uiteraard zul je altijd voorrang verlenen aan hetuitwerken van de haakjes!

Voorbeelden :

4 x + 1 = 1 3 x + 1 2

(2,3,4)= 12

12 x + 12 12 = 4 12 x + 6 12

· 9 12 x + 12 12 = 12 · 4 12 x + 6 12 9 x + 12 = 4 x + 6 9 x 4 x = 6 12

Je kunt ook hier de proef uitvoeren door elke x in de vergelijking te vervangen door de verkregen oplossing.

Controleer jezelf met ICT

Typ de vergelijking in de CAS van GeoGebra in, klik daarna op het icoontje x = en de oplossing van de vergelijking verschijnt op het scherm.

6Samenvatting

• Je kent de eigenschappen van gelijkheden die het oplossen van vergelijkingen makkelijker maken.

– Je mag in beide leden van een gelijkheid hetzelfde getal optellen (of aftrekken).

∀a , b , m ∈ Q : a = b ⇐⇒ a + m = b + m

⇐⇒ a m = b m

– Je mag beide leden van een gelijkheid vermenigvuldigen (of delen) met eenzelfde getal, verschillend van 0.

∀a , b ∈ Q, ∀m ∈ Q0 : a = b ⇐⇒ a · m = b · m ⇐⇒ a m = b m

• Je kunt vergelijkingen oplossen met haakjes.

1 Werk de haakjes weg.

2 Breng alle termen in x samen in één lid.

Alle andere termen breng je samen in het andere lid.

Je maakt gebruik van de eerste eigenschap van gelijkheden.

3 Maak de som in beide delen.

4 Deel door de coëfficiënt van x (of breng de vergelijking in de vorm x = …).

Je maakt gebruik van de tweede eigenschap van gelijkheden.

5 Je kunt jezelf controleren door een proef uit te voeren.

Vergelijkingen 3000 jaar geleden ‘Aha, zijn geheel, zijn zevende, het is 19.’

Die korte vreemde zin werd gevonden in een meer dan 3000 jaar oude Egyptische papyrusrol. In 1858 kocht de Schotse antiquair Henry Rhind die papyrus in een winkeltje in het Nijldorp Luxor. Het stuk werd te zijner ere Rhind-papyrus genoemd. Het blijkt een van de oudste wiskundige documenten te zijn die nog bestaan. Het werd opgetekend door een Egyptische klerk die Ahmes heette. Het zinnetje dat hierboven staat, is een vraagstukje dat we in de vorm van een vergelijking kunnen gieten. Het betekent eigenlijk: van een onbekend getal (Aha) is de som van het getal (zijn geheel) en het zevende deel van dat getal (zijn zevende) gelijk aan 19 (het is 19).

of: x + 1 7 x = 19

Deze eenvoudige vergelijking kun je ongetwijfeld zelf oplossen.

7Oefeningen

de volgende vergelijkingen op in Q

Los de volgende vergelijkingen op in Q

In de babykamer van Adil hangen speeltjes die perfect in evenwicht zijn. Op de stukjes staat het gewicht in gram. Bepaal het gewicht van het stukje met een letter op.

Los de volgende vergelijkingen op in Q

x 3 = 2 + 2 x

4 + 4 x = 4 + x

2 x 48 = 13 x + 12

Los de volgende vergelijkingen op in Q

Stel telkens de vergelijking op en los ze nadien op.

Zoek x met behulp van volgende pijlvoorstelling.

Los de volgende vergelijkingen op in Q

a 7 (p 2)= 14

d (4 x 2) 5 = 27

b 18 = 3 ( x 5)

e 4 (3 x )+ 5 x = 15

c 3 · (2k 1)= 5 · (k 4) f 3 · (m + 0,5)= 5 · (m 0,3)

Welke vergelijking heeft dezelfde oplossing als 2x + 3 =–9?

Welke vergelijkingen hebben als oplossing 3 ?

Werk uit en zet de vergelijkingen die 3 als oplossing hebben in een fluokleurtje. Bij elke vergelijking staat een woord. Met de fluowoorden maak je een mooi spreekwoord.

Met de gevonden woorden kan ik dit spreekwoord maken :

Los de volgende vergelijkingen op in Q

Controleer met ICT of de getallen 1, 2 of 3 een oplossing zijn voor de vergelijkingen.

Verbind telkens de opgave met de oplossing.

Daan en Merel rijden, elk van bij hen thuis, met de fiets naar school. Ze wonen op dezelfde weg, maar Daan woont op 7 km van de school en Merel woont op 5,5 km van de school. Daan fietst met zo’n snelheid dat hij elke minuut 350 m aflegt. Merel is iets trager en rijdt met een snelheid van 200 m/min.

Om te achterhalen wanneer en op welke afstand van de school ze elkaar zullen treffen, moeten we volgende vergelijking oplossen (alle afstanden zijn omgezet in m).

7000 – 350x = 5500 – 200x

a Los de vergelijking op. Welke informatie heb je nu gekregen ?

b Hoeveel meter zijn Daan en Merel op dat moment van school verwijderd ?

Bekijk onderstaande schema’s. Welke vergelijking hoort hierbij? Los de vergelijking op.

Vul dit kruisgetallenraadsel in door de vergelijkingen op te lossen. In elk vakje noteer je één cijfer.

HORIZONTAAL VERTICAAL A 4a 7 = 157 • 3a 5 = 2a + 6

6 x 500 = 4 ( x + 31)

C 2 ( x + 2) 7 = x • 3 x = x 150

3 5 1 20 x 45 24 = 0 D 0,5 x 15 = 2 (0,2 x + 7) • x + 2 2 x = 0

0,5 x 2,5 = 0,4 x + 10 • x 3 = 3 x

Los de volgende vergelijkingen op in Q door de haakjes en noemers weg te werken.

6 x 2 = x 4

Los de volgende vergelijkingen op in Q

Om moeilijke vergelijkingen op te lossen, gebruik je het best ICT.

Voorbeeld : 3 ( x 2) 8 + 5 3 = 4 x 9 3 7 x 9 4

Methode 1 : stap voor stap oplossen met Photomath

Methode2 : controle met Microsoft Math Solver

Los nu deze vergelijkingen op met ICT.

a x 6 2 x 1 6 1 3 2 5 x 3 = 0

b 3 (2 x + 1) 5 + x 1 2 1 = 5 x 3 c 5 · (2 x 1) 4 + 3 · ( x 5) 2 = 1 4 d 1 5 1 3 (10 x 9) 5 6 2 5 x 4 = 7 30

Methode 3 : controle met de CAS van GeoGebra 6

Je merkt dat GeoGebra de oplossing noteert als een verzameling.

Omgekeerd redeneren. Vervolledig de tabel om de onderstaande vergelijking op te lossen.

2 ( x + 6) 3 4 = 2

WISKUNDETAAL

VERGELIJKING

REDENEREN

een getal x ⟵ oplossing vergelijking

tel er 6 bij op

vermenigvuldig met 2

deel door 3

trek er 4 van af 2 · ( x + 6) 3 4 = 2

We spreken af dat a ♥ b betekent: ab + a + b . Bijvoorbeeld 5 ♥ 8 = 5 · 8 + 5 + 8 = 53.

Er is een getal x waarvoor geldt: 3 ♥ 5 = 2 ♥ x

Welk getal is x ?

(A) 3 (B) 6 (C) 7 (D)10 (E)12

(A) 2 (B) 3 (C) 4 (D) 5 (E) 6

5.2 Vraagstukken oplossen

1Betekenis van x

Hoe je een vraagstuk oplost met behulp van een vergelijking, leerde je al vorig jaar. Belangrijk hierbij is dat je werkt met (en op zoek gaat naar) een onbekende. Die stel je meestal voor door x . Omdat de omzetting van de tekst naar een wiskundige vergelijking de moeilijkste stap is bij het oplossen van het vraagstuk, geven we een opwarmertje.

Bedek met een blad de rechterhelft en zoek zelf de wiskundige uitdrukking in functie van x .

• dehelftvaneengetal

hetviervoudvaneengetal

driemeerdaneengetal

tweeopeenvolgendegetallen

tweeopeenvolgendeevengetallen

eenonevengetal

viermeerdanhetdubbelvaneengetal

+ 4 • hetverschilvan x en7

• tweegetallendiealssom10geven

drievierdevaneengetal

tweegetallendiealsproduct10geven

hetdrievoudvandesomvan2en

tweegetallenwaarvanhetverschil10is

2Oplossen van een vraagstuk

Hoe een vraagstuk oplossen met een vergelijking :

STAP 1 : Lees en herlees het vraagstuk. Je weet waarover het gaat en wat er gezocht wordt.

STAP 2 : Geef een betekenis aan de onbekende x. Als er meerdere dingen gevraagd zijn, kan de keuze van x het je een stuk makkelijker maken. Dit noemen we mathematiseren

STAP 3 : Zet het vraagstuk om in een vergelijking. Zoek in de tekst naar een gelijkheid. Meestal is dit weergegeven door ‘is’ of ‘is gelijk aan’.

STAP 4 : Los de vergelijking op. Dit is meestal geen probleem, omdat je al moeilijkere vergelijkingen opgelost hebt.

STAP 5 : Geef een antwoord op de vraag. Controleer. Dit noemen we demathematiseren.

De proef maken via de vergelijking is geen garantie, want je kunt een foute vergelijking opgesteld hebben. Maak daarom ook een proef op het vraagstuk zelf.

Wees ook kritisch over je antwoord. Is je antwoord wel realistisch? Een vader die 3,6 jaar jong is; een persoon die per maand € 2,00 verdient; mijn broers die –6 euro moeten verdelen of 11,24 personen die aanwezig zijn op een toneelvoorstelling …

Het zijn allemaal antwoorden die erg onwaarschijnlijk zijn.

Voorbeeld 1 : een geheim getal

Ismaël heeft op een papiertje een getal neergeschreven. Zijn vriend Tom moet dat getal achterhalen.

Hij krijgt van Ismaël volgende informatie …

Als je het neergeschreven getal met 2 vermenigvuldigt en het resultaat nadien met 18 vermindert, dan krijg je 12.

STAP 1 : Tom leest en herleest het vraagstuk.

Hij weet dat hij een getal moet vinden.

STAP 2 : Tom geeft aan de onbekende x een betekenis: x is het neergeschreven getal.

STAP 3 : Tom stelt de vergelijking op : Het neergeschreven getal vermenigvuldigen met 2. → 2x

Dat resultaat verminderen met 18. → 2x – 18

Dan krijg je 12. → 2x – 18 = 12

STAP 4 : Hij lost de vergelijking op :

2 x 18 = 12

= 12 + 18

STAP 5 : Tom formuleert een antwoord.

Het getal dat Ismaël neergeschreven heeft, is 15.

Controle: 2 15 – 18 = 30 – 18 = 12

De proef klopt.

Voorbeeld 2 : in de toneelzaal Bij een toneelvoorstelling zijn er toegangskaarten van 4 euro (voor kinderen) en van 7 euro (voor volwassenen). In totaal zijn er 400 mensen in de zaal, die allen samen aan de kassa 2110 euro betaalden. Hoeveel volwassenen en hoeveel kinderen zitten er in de zaal ?

STAP 1 : Je leest een vraagstuk en merkt dat dit vraagstuk moeilijker is dan het vorige omdat hier twee dingen worden gevraagd. Ook het opstellen van de vergelijking vraagt wat meer werk. Daarom zul je eerst proberen te schatten.

SCHATTEN EN REDENEREN

Stel: er zijn 250 kinderen. Dan zijn er 150 ( = 400 – 250) volwassenen.

4 · 250 + 7 · 150 = bedrag in de kassa

STAP 2 : x is het aantal kinderen in de zaal.

400 – x is het aantal volwassenen in de zaal.

OPSTELLEN EN VERGELIJKEN

Om de vergelijking op te stellen zul je het blauwe en rode getal vervangen door een uitdrukking in x Er zijn geen 250 kinderen maar x kinderen. Er zijn geen 150 volwassenen maar 400 – x volwassenen. Het bedrag in de kassa moet 2110 euro zijn.

STAP 3 : De vergelijking wordt dan : 4 · x + 7 · ( 400 – x ) = 2110

STAP 4 :

4 x + 7 (400 x )= 2110

4 x + 2800

7 x = 2110

4 x 7 x = 2110 2800

3 x = 690

x = 230

STAP 5 : Er waren 230 kinderen en 170 volwassenen op de voorstelling.

Controle : 4 · 230 + 7 · 170 = 2110

Voorbeeld 3 : WISKUNDE & CULTUUR

Het Parthenon in Griekenland was oorspronkelijk detempel van de godin Athena. De tempel werd voor het eerst gebouwd in de zesde eeuw voor Christus. In het begin van vorige eeuw was er een grondige renovatie. Heel wat stukken van het Parthenon werden weggehaald, gerestaureerd en teruggeplaatst.

Als de stukken per 5 op een pallet gelegd werden, waren er 5 palletten meer nodig dan als de stukken per 6 op een pallet gelegd werden. Hoeveel stukken van het Parthenon werden gerestaureerd ?

STAP 1 : Je leest en herleest het vraagstuk. Als je verdeelt per 5, dan moet je het aantal stukken delen door 5. Als je verdeelt per 6, dan moet je het aantal delen door 6.

STAP 2 : x is het aantal stukken dat gerestaureerd werd.

STAP 3 : De vergelijking wordt : x 5 = x 6 + 5

STAP 4 :

30 · x 5 = 30 · x 6 + 30 · 5

6 x = 5 x + 150

6 x 5 x = 150 x = 150

STAP 5 : Er werden 150 stukken van het Parthenon gerestaureerd.

Controle : Als je 150 deelt door 6, dan bekom je 25. Als je 150 deelt door 5, dan bekom je 30, dat is 5 meer dan 25.

3Samenvatting

• Je kunt een vraagstuk oplossen dat leidt tot een vergelijking van de eerste graad met één onbekende.

Stap 1 : Lees en herlees grondig het vraagstuk.

Stap 2 : Geef een betekenis aan de onbekende x

Stap 3 : Zet het vraagstuk om in een vergelijking.

Stap 4 : Los de vergelijking op.

Stap 5 : Geef een duidelijk antwoord op de vraag. Controleer. x 5 = x 6 + 5

4Oefeningen

Noteer in symbolen :

a het zesvoud van x

b de helft van x

c 8 maal x

d het verschil van x en 5

e het quotiënt van x en 3

f het verschil van 5 en x

g het omgekeerde van x

h het tegengestelde van x

i het dubbel van x + 1

j 1 meer dan het dubbel van x

k 6 minder dan het drievoud van x

l de helft van x vermeerderd met 5

Noteer in symbolen :

a twee opeenvolgende even getallen

b twee opeenvolgende oneven getallen

c 5 minder dan de helft van x

d de som van de kwadraten van x en y

e het kwadraat van de som van x en y

f twee opeenvolgende oneven getallen, waarvan 2x + 1 het grootste is

g het tegengestelde van het omgekeerde van x

h het omgekeerde van het tegengestelde van x

i de helft van het verschil van x en 8

j twee opeenvolgende drievouden

k twee opeenvolgende drievouden

waarvan het grootste ook een zesvoud is

l 3 meer dan het dubbel van x

Vul in met de gepaste lettervorm.

a Saartje is nu x jaar oud. Hoe oud is ze binnen 5 jaar ?

b Alistair heeft 65 euro in zijn spaarpot. Hij geeft er x euro van uit. Hoeveel euro heeft hij nog ?

c Samen hebben Miel en Tuur 1700 postzegels. Als Miel er x heeft, hoeveel heeft Tuur er dan ?

d Als de lengte van een rechthoek zes keer zo groot is als de breedte x , hoe noteer je dan die lengte ?

e Mathis en Hannes maakten samen 15 doelpunten. Mathis maakte er x . Hoeveel keer scoorde Hannes ?

f Jutta en Liah hebben samen 100 stripalbums. Jutta heeft x strips. Als ze met elkaar 25 strips ruilen, hoeveel strips heeft Jutta dan ?

g In onze klas zitten 23 leerlingen, waarvan x jongens. Hoeveel meisjes zitten er in onze klas ?

h Ik heb x briefjes van 10 euro in mijn portefeuille. Met hoeveel euro komt dit overeen ?

i Victor en Staf zijn samen x jaar oud. Wat was twee jaar geleden hun gezamenlijke leeftijd ?

Los deze vraagstukken op door middel van een vergelijking.

a Tel je bij een getal 7 op, dan bekom je –11. Wat is dat getal ?

b Tien minder dan het dubbel van een getal is 36. Wat is dat getal ?

Oma verdeelt 30 euro onder Fie, Lola en Mats. Fie krijgt de helft van het bedrag dat Lola krijgt en Mats krijgt evenveel als de twee anderen samen. Hoeveel krijgt elk ?

Een man at 124 druiven op in 4 dagen. Elke dag at hij 6 druiven meer op dan de dag ervoor. Hoeveel druiven at de man de eerste dag ?

In een paardenstal zijn een aantal paarden en vrouwen aanwezig.

Tel ik het aantal hoofden (een paard is een edel dier en heeft dus ook een hoofd), dan krijg ik 41.

Tel ik het aantal benen (inderdaad, een paard heeft geen poten, maar benen), dan krijg ik 116.

Hoeveel paarden en hoeveel vrouwen zijn er in de stal ?

Enkele zoek-de-leeftijd-probleempjes.

a Julie en Aurélie zijn tweelingen van 4 jaar. Wanneer zullen ze samen zo oud zijn als hun vader op dat moment ? De vader is nu 32 jaar.

b Bart is 2 jaar ouder dan Lisa en de kleine Maggie is 1 jaar. Over 5 jaar zijn de drie kinderen samen even oud als mama Marge nu is, namelijk 34. Hoe oud zijn Bart en Lisa nu ?

c Moeder is momenteel 32 jaar. Haar kinderen zijn 10 jaar, 5 jaar en 3 jaar. Over hoeveel jaar zal moeder net zo oud zijn als alle kinderen samen ?

d Samen zijn Kuifje en Zonnebloem 70 jaar jong. Vijf jaar geleden was Zonnebloem vier keer zo oud als Kuifje op dat moment.Hoe oud is Kuifje nu ?

e Lars is drie jaar ouder dan Guus. Hun vader is 32 jaar. Over 5 jaar zullen beide kinderen samen zo oud zijn alshun vader op dat moment.Hoe oud zijn ze nu ?

Wendy eet met haar broer en haar ouders eenzelfde menu in een restaurant. Ronald kiest samen met zijn ouders in hetzelfde restaurant voor een ander menu dat 9 euro (per persoon) duurder is. Beide gezinnen betalen evenveel. Hoeveel kost het menu van Wendy ?

Boer Vandevelde heeft een aantal kippen en schapen. Als hij alle pootjes en poten optelt, komt hij aan 134. Telt hij het aantal koppen samen, dan krijgt hij 50. Hoeveel kippen en schapen heeft boer Vandevelde ?

Professor Arachne verzamelt allerlei soorten spinnen en bijen. In totaal heeft hij nu al 320 diertjes. Als hij alle pootjes zou tellen (een spin heeft 8 pootjes, een bij heeft er 6), dan zou hij er 2272 tellen. Hoeveel spinnen en hoeveel bijen heeft professor Arachne ?

De speelgoedmaker Gepetto wil weten hoeveel keer zijn houten pop Pinocchio in het komende uur liegt. Als Pinocchio liegt, dan wordt zijn neus 2 cm langer, spreekt hij de waarheid, dan wordt zijn neus 1,5 cm korter. Bij de start van het onderzoek meet de neus van Pinocchio 5 cm. Na één uur heeft Pinocchio 22 keer een uitspraak gedaan, zijn neus is nu 14 cm lang. Hoeveel keer heeft Pinocchio gelogen ?

Op de Kangoeroewedstrijd worden er 24 meerkeuzevragen gesteld. Per juist antwoord krijg je 5 punten en per fout antwoord krijg je 0 punten. Vul je niets in, dan krijg je 1 punt. Van de 24 vragen had Sienna er 2 fout. Hoeveel juiste antwoorden gaf Sienna als je weet dat zij een score had van 70 punten ?

Een erfenis van 50 000 euro wordt onder vier zonen verdeeld. De eerste zoon krijgt de helft van het deel van de tweede. De derde krijgt 2500 euro meer dan de eerste en de vierde krijgt zoveel als de drie andere zonen samen. Hoeveel krijgt elke zoon ?

De rit van Grenoble naar Courchevel in de Tour de France was 195 km lang. Het aantal kilometer dat geklommen moest worden, was 10 km minder lang dan het aantal kilometer dat er afgedaald moest worden. Het vlakke gedeelte was 5 km minder lang dan de beklimmingen en afdalingen samen. Hoeveel kilometer hebben de renners moeten klimmen ?

Wat is er aan de hand ?

Deze vraagstukken moet je niet oplossen. Bespreek wat er bijzonder aan is.

a Onze school maakt voor een project eigen chocoladerepen die verkocht worden tegen 3 euro per reep. De gemiddelde verkoop per leerling bedraagt 35,5 repen. Hoeveel repen werden er door alle leerlingen samen verkocht ?

b Nelle laat een terras aanleggen met een oppervlakte van 90 m2. De lengte van dat terras is 10 m. Bovendien voorziet ze een houten omheining die 25 euro per m2 kost.

c Eén liter benzine wordt vandaag verkocht tegen 1,204 euro per liter. In het journaal hoor je dat morgen de prijs met 4 eurocent per liter zal stijgen. Je besluit nog snel je wagen vol te tanken. Hoeveel zal je tankbeurt kosten ?

WISKUNDE & MILIEU

Oude kranten, oude proefwerken, reclamefolders, posters… Het wordt allemaal keurig selectief opgehaald en het krijgt een tweede leven als toiletpapier.

a Hoeveel toiletrolletjes worden er jaarlijks verbruikt? Bepaal het aantal door middel van een vergelijking enmet volgende gegevens.

Als we 10 miljoen minder dan de helft van het aantal zouden nemen, hebben we 1 21 van het aantal toiletrolletjes na 10 jaar.

b Een rolletje bevat 25 m papier. Hoeveel km toiletpapier verbruikt België in 1 jaar ?

c Hoeveel keer kunnen we hiermee de wereld (omtrek ongeveer 40000km) rond ?

Na een voorstelling van Nerdland wordt heel wat promomateriaal verkocht, waaronder boeken. Het team legt vanavond alle boeken in rijen van 6 stuks en heeft er dan nog 3 over. Als ze ze leggen in rijen van 8stuks, dan hebben ze twee rijen minder, maar zijn er 3 boeken tekort. Hoeveel boeken liggen er die avond op de merch-stand ?

Geldproblemen.

a Nadat je papa geld afhaalde aan de automaat heeft hij 270 euro in zijn portefeuille, verdeeld over briefjes van 10 euro en briefjes van 20 euro. Hoeveel briefjes van 10 euro heeft hij als je weet dat er 22 briefjes uit de automaat kwamen ?

b Hoe kun je 2,15 euro betalen in stukken van 5 cent en 20 cent als je in totaal 22 geldstukken hebt ?

c Esther heeft surfen als nieuwe hobby en koopt een surfpak en een surfplank, samen voor 190 euro. De plank kost 10 euro meer dan het drievoud van de prijs van het surfpak. Hoeveel kost de surfplank ?

In een plaatselijke supermarkt is er koffie van 12 euro en van 16,50 euro per kg. Een caféhouder koopt beide soorten en betaalt in totaal voor 10 kg koffie 133,50 euro. Hoeveel kilogram kocht hij van elke soort ?

In een koffiebranderij worden drie soorten koffie gemengd. De eerste soort kost 7 euro per kg, de tweede soort kost 3,20euro per kg en de derde soort kost 8,20 euro per kg. Van de eerste soort werdtweemaal zoveel gebruikt als van detweede soort. Van de derde soort koffie werd maar een derde gebruikt van de hoeveelheid van de tweede soort. Bereken de kostprijs voor 1 kg gemengde koffie als je weet dater in totaal 900 kg koffie werd gemalen.

In een klas van 33 leerlingen volgt iedereen biologie en/of informatica. Drie van de leerlingen volgen beide vakken. Het aantal leerlingen dat alleen informatica volgt, is het dubbele van het aantal dat alleen biologie volgt. Hoeveel leerlingen volgen informatica ?

Een vader, een moeder en hun drie kinderen zijn samen 80 jaar. De twee jongste kinderen zijn 6 en 8 jaar. Hoe oud waren de ouders en kinderen 7 jaar geleden samen ? (A)35 (B)36

Een balkvormige doos heeft een volume van 4800 cm3. Hoeveel kleine balkvormige doosjes met afmetingen l = 4 cm, b = 2 cm en h = 2 cm kunnen in die doos als je weet dat de grote doos een vierkant als grondvlak heeft ener geen lege ruimte overblijft ? Kun je met zekerheid de afmetingen van de grote doos bepalen ?

De breuken 5 3 en 5 x hebben als product en als som hetzelfde rationaal getal.Bepaal x

Vaardigheden | Kritisch denken

Kritisch denken is noodzakelijk om problemen te analyseren, fouten terug te vinden en antwoorden te interpreteren. We bekijken enkele voorbeelden.

VOORBEELD

De koffiebranderij maakt voor een speciale ‘paasblend’ een mix van twee soorten koffiebonen. De eerste wordt normaal verkocht aan 14 euro per kg, de andere aan 19 euro per kg. De verhouding van de eerste soort tot de tweede soort is 3 : 2. Wat zal de uiteindelijke prijs voor één kg zijn ?

Zet de breuk 5 8 om naar zijn decimale vorm.

FOUT ANTWOORD

DENK KRITISCH NA

21 euroAls een mix gemaakt wordt van twee soorten koffie (een goedkopere en een duurdere soort), dan zal de verkoopprijs steeds liggen tussen de twee gegeven prijzen. In dit geval is het juiste antwoord 16 euro per kg.

99 euroEen promotie die je niet wil? Je zou denken dat de oorspronkelijke prijs niet 49 euro was, maar 149 euro. Maar dan klopt het gegeven kortingspercentage niet meer.

1,6

ENERGIEFACTUUR

2021 + 6%

2022 + 6%

2023 + 6%

2024 + 6%

2025 + 6%

Een Japans bad is kleiner dan onze baden. Ze hebben bvb. als afmetingen 1 m op 1 m en een diepte van 70 cm. Als je zo’n bad voor 60% vult, hoeveel water heb je dan in je bad ?

+ 30 % prijsstijging na vijf jaar

Dit antwoord kan niet correct zijn, vermits in de opgave een breuk staat waar teller kleiner is dan de noemer.

Bij verdere analyse merk je dat verkeerdelijk de noemer door de teller werd gedeeld.

Als de prijs elk jaar met 6 % stijgt, dan is die prijs na vijf jaar gestegen met bijna 34 %.

Je moet immers telkens ook de bijgetelde 6 % in rekening brengen.

42 literOpletten met eenheden. De diepte van het bad staat in centimeter, de andere gegevens in meter. Kies een eenheid uit. Vermits er naar liter gevraagd wordt (en je weet dat 1 liter overeenkomt met 1 dm3) kun je alles omzetten naar decimeter.

Zo kom je aan 0,7 ⋅ 10 ⋅ 10 ⋅ 7 = 420 liter

De som is 4663.Die som klopt helemaal. Reken maar na. Maar is het wel nuttig om die som uit te rekenen ?

Ook grafische voorstellingen kunnen misleidend zijn. Wat kan er beter bij onderstaande voorstellingen ?

Roos vergelijkt haar punten van de laatste vier schooljaren in het lager onderwijs.

Ze giet het eindpercentage in een mooi staafdiagram.

derde jaarvierde jaarvijfde jaarzesde jaar

1/3 van onze operationele begroting gaat naar financiële bijstand 20 miljoen 60 miljoen 2

Van het fonds STARFINANCE werd de evolutie (in euro) gedurende een aantal jaren bijgehouden.

Dit zijn de resultaten :

De bank wil reclame maken en publiceert deze grafiek : 605 515 485 390 STARFINANCE

20212022202320242025 jaar bedrag (in euro)

Tijdens de laatste verkiezingscampagne werd in een stad een folder verspreid met volgend staafdiagram.

Oplossingsmethodes voor vraagstukken

dit moet ik leren

❒ Ik ken de eigenschappen van gelijkheden die het oplossen van vergelijkingen makkelijker maken.

❒ Ik kan een vergelijking van de vorm x + a = b , ax = b en ax + b = c oplossen.

❒ Ik kan vergelijkingen oplossen waarin haakjes en/of breuken voorkomen.

❒ Ik kan een vraagstuk oplossen met behulp van vergelijkingen.

pagina ik ken het ! oké voor examen

207

209

212

231

Oplossingsmethodes voor vraagstukken

Los volgende vergelijkingen op.

Los volgende vergelijking op in Q

2 / 2

3 / 3

Welke van de volgende vergelijkingen heeft als oplossing 3 ?

4 / 2

Noteer in wiskundige symbolen :

a het drievoud van x

b vijf meer dan het dubbel van x

c drie opeenvolgende natuurlijke getallen waarbij n de kleinste is

d Oona en Ivana waren twee jaar terug samen x jaar, dit jaar zijn ze samen …

5 / 3

Vader is nu 51 jaar en zijn zoon is 11 jaar. Ooit zal de vader kunnen zeggen dat hij dubbel zou oud is als zijn zoon. Binnen hoeveel jaar zal dat gebeuren ?

Los volgende vraagstukken op met behulp van een vergelijking.

a Bij een filmvoorstelling zijn 240 betalende toeschouwers aanwezig. Een aantal van hen betaalde 14,10 euro. De anderen betaalden het verminderde tarief van 10,55 euro. Hoeveel toeschouwers betaalden dit verminderde tarief als je weet dat de ticketopbrengst voor deze zaal 2950,90 euro bedroeg ?

6 / 3 / 3

b Op Christmas Island in de Indische Oceaan valt niet echt veel te beleven. Een kleine duizend inwoners, enkele tientallen toeristen en dat zal het zijn. Maar elk jaar speelt er zich iets merkwaardigs af. In de maand november, na de eerste regenbui, verlaten enkele krabbetjes het regenwoud, kruipen door en over alles heen en storten zich dan massaal in de oceaan. De mannetjes nemen er een frisse duik en graven zich in het zand in, wachtend op een vrouwtje om de krabbensoort voort te planten. Zodra deze taak erop zit, keren ze terug naar het regenwoud. De vrouwtjes blijven achter en keren een tweetal weken later terug. Als ik hun aantal met zeven zou vermenigvuldigen, heb ik 850 miljoen meer dan een derde van het oorspronkelijke aantal. Bereken het aantal krabben.

Evenredigheden

Hoodstuktitel

De mens Vitruvius is een tekening van Leonardo da Vinci, waarop dit kunstwerk aan de universiteit van Milaan is gebaseerd.

Op de tekening vind je een mens terug met ‘ideale verhoudingen’: de afstand van de navel tot aan de tenen verhoudt zich tot de afstand van hoofd tot tenen zoals de afstand van hoofd tot navel zich verhoudt tot de afstand van navel tot tenen.

Die verhouding wordt ook wel de gulden snede genoemd en is gelijk aan 1 + √ of ongeveer 1,62.

Maar er zitten nog meer dergelijke ideale verhoudingen in het lichaam, zoek maar even op…

Vitruvius in Quarantine

Evenredigheden

6.1 Evenredigheden

1 Verhoudingen 253

2 Evenredigheid 254

3 Kenmerk van een evenredigheid 255

4 Vierde evenredige 257

5 Middelevenredig 257

6 Omvormen van formules 258

7 Samenvatting 259

8 Oefeningen 260

6.2 Recht en omgekeerd evenredig

1 Recht evenredige grootheden 272

2 Grafieken van recht evenredige grootheden tekenen met ICT 274

3 Omgekeerd evenredige grootheden 275

4 Grafieken van omgekeerd evenredige grootheden tekenen met ICT 277

5 Niet-evenredige grootheden 278

6 Modelvraagstukken 279

7 Samenvatting 280

8 Oefeningen 281

Extra’s

Syntheseoefeningen 292

Wat moet je kennen en kunnen ? 294

Herhalingsoefeningen 295

Bekijk de instructievideo’s

6.1

Evenredigheden

1Verhoudingen

Verhoudingen kom je overal tegen. Je maakte eerder al kennis met een verhoudingstabel, de regel van drie, schaalberekening, gelijkvormigheid

Voorbeeld 1: wafelbak

Oom Leo en tante Suzy gaan wafels bakken. Hiervoor hebben ze onder andere 900 gram zelfrijzende bloem en 9 eieren nodig. Als Leo in de kast kijkt, vindt hij maar 600 gram bloem. Hoeveel eieren zal Suzy erin mengen ?

Oplossing :

We stellen een verhoudingstabel op. : 3 2

Deverhoudingenzijntelkensgelijk:

Antwoord :

Tante Suzy zal 6 eieren in 600 gram bloem mengen.

Controle : 900 : 9 = 600 : 6

Voorbeeld 2: van Parijs naar Gent

Een auto rijdt lange tijd op de autosnelweg met een gemiddelde snelheid van 90 km/h. Op basis van deze gegevens kunnen we een tabel opstellen.

2Evenredigheid

evenredigheid

Een evenredigheid is een gelijkheid van twee verhoudingen. in symbolen : a b = c d met b = 0en d = 0

Voorbeelden :

5 = 6 10 Lees:3staattot5zoals6staattot10. of:3verhoudtzichtot5zoals6tot10.

Terminologie

3Kenmerk van een evenredigheid

Voorbeelden : Tegenvoorbeelden : 14 4 = 7 2 en14 · 2 = 4 · 7 8 32 = 4 16 en8 16 = 32 4 300 3 = 400 4 en300 · 4 = 3 · 400 3 8 = 1 4 want3 · 4 = 8 · 1 4 5 = 16 25 want4 25 = 5 16

eigenschap in woorden: In een evenredigheid is het product van de uiterste termen gelijk aan het product van de middelste termen. in symbolen:

We kunnen die eigenschap ook bewijzen. Eerst kijken we goed naar wat we moeten bewijzen. Een gelijkheid wordt herschreven tot een andere gelijkheid zonder noemers.

Bewijs :

Gegeven :

b = 0, d = 0

Te bewijzen : a · d = b · c

Bewijs : a b = c d

beideledenvermenigvuldigenmet b d (= 0) a b b d = c d b d

vereenvoudigen a ✓ b · ✓ b · d = c ✓ d · b · ✓ d a d = c b a b = c d

omgekeerde van de eigenschap in woorden:

Als twee producten aan elkaar gelijk zijn, dan kun je met de factoren een evenredigheid vormen. in symbolen: ∀a , c ∈ Q, ∀ b , d ∈ Q0 : a d = b c =⇒ a b = c d

Ook die eigenschap kunnen we bewijzen. Eerst kijken we eens goed wat we moeten bewijzen. Een gelijkheid wordt herschreven tot een andere gelijkheid met noemers.

Bewijs :

Gegeven : Te bewijzen : a b = c d

a · d = b · c

b = 0, d = 0

Bewijs :

a d = b c

beideledendelendoor b endoor d ( b d = 0)

a · d

b d = b · c b d vereenvoudigen

a ✓ d b ✓ d = ✓ b c ✓ b d

a b = c d

De eigenschap en de omgekeerde eigenschap kunnen we samenvoegen tot een kenmerk.

kenmerk van een evenredigheid

∀a , c ∈ Q, ∀ b , d ∈ Q0 : a b = c d ⇐⇒ a d = b c

Merk op :

Het product van de middelste termen en het product van de uiterste termen worden samen soms de kruisproducten genoemd. Zo kun je het kenmerk van een evenredigheid ook een gelijkheid van kruisproducten noemen. a b = c d a ⋅ d = b ⋅ c

4Vierde evenredige

vierde evenredige

x is de vierde evenredige van de getallen a , b en c ⇐⇒ a b = c x

Voorbeeld : bepaal de vierde evenredige tussen 2, 7 en 8

Dit probleem is makkelijk op te lossen met behulp van het kenmerk van een evenredigheid.

2 7 = 8 x kenmerkvaneenevenredigheid

2 · x = 7 · 8

2 x = 56 x = 28

Antwoord :

De vierde evenredige tussen 2, 7 en 8 is 28.

5 Middelevenredig

middelevenredig

x is middelevenredig tussen de getallen a en b ⇐⇒ a x = x b

Voorbeeld : bepaal de middelevenredigen tussen 2 en 8

Dit probleem is gemakkelijk op te lossen met behulp van het kenmerk van een evenredigheid.

2 x = x 8

kenmerkvaneenevenredigheid

2 8 = x x

x 2 = 16

∗ x = 4 of x = 4

Antwoord :

4 en –4 zijn middelevenredig tussen 2 en 8.

Opmerking :

* We moeten ons afvragen voor welke waarde(n) van x het kwadraat 16 is. Met behulp van je rekenmachine of door jouw kennis van de volkomen kwadraten zie je al vlug dat x gelijk kan zijn aan 4.

Let op! Ook het kwadraat van een negatief getal is positief. Welk negatief getal heeft als kwadraat 16? Na wat denkwerk vind je dat x ook gelijk kan zijn aan –4.

Bepaal de middelevenredigen van a en b : a x = x b ⇐⇒ x 2 = a b

Dat wil zeggen dat a · b strikt positief moet zijn, anders is er geen middelevenredige van a en b

6Omvormen van formules

Voorbeeld 1 : de wet van Ohm WISKUNDE & WETENSCHAPPEN

De wet van Ohm beschrijft de relatie tussen spanning (U ), stroomsterkte (I ) en weerstand (R ) van een object.

R = U I met R : weerstand in ohm ( W)

U : spanning in volt ( V)

I : stroomsterkte in ampère ( A)

Een batterij met een weerstand van 10 ohm wordt in een circuit gebracht, waar een stroom gemeten wordt van 2 ampère. Welke spanning levert die batterij ?

Oplossing : R = U I

U = R I

In die formule vullen we de gegeven waarden in.

U = 10 W · 2 A = 20 V

Antwoord :

De spanning van deze batterij is 20 V.

Voorbeeld 2: oppervlakte trapezium

De oppervlakte van een trapezium wordt bepaald door de formule : A = ( B + b ) h 2

2 A =( B + b ) h

2 · A h B = b met A : oppervlakte

B : lengte grote basis

b : lengte kleine basis

h : hoogte

Bepaal de lengte van de kleine basis van dit trapezium als je weet dat de oppervlakte 12,75 cm2 is.

2 A h = B + b

Oplossing : A = ( B + b ) · h 2

2 · A =( B + b ) · h

2 · A h = B + b

2 A h B = b

Antwoord :

In de omgevormde formule vullen we de gegeven waarden in. b = 2 · 12,75 3 5 = 8,5 5 = 3,5

De kleine basis heeft een lengte van 3,5 cm.

Controle : (5 + 3,5) 3 2 = 12,75

7Samenvatting

• Je kunt eenvoudige problemen oplossen met een verhoudingstabel.

• Je weet dat een evenredigheid een gelijkheid is van twee (of meer) verhoudingen.

a b = c d b = 0, d = 0

• Je kent de terminologie bij evenredigheden.

a b = c d a : de eerste term

b : de tweede term

c : de derde term

d : de vierde term

a en d : de uiterste termen

b en c : de middelste termen

• Je kunt het kenmerk van een evenredigheid formuleren in woorden en symbolen. Je kunt de twee eigenschappen bewijzen waaruit het kenmerk is opgebouwd.

• Je kunt de vierde evenredige berekenen in een evenredigheid als de eerste drie termen in de evenredigheid gegeven zijn.

• Je kunt formules omvormen. x isdevierdeevenredigevandegetallen a , b en c ⇐⇒ a b = c x

• Je kunt de middelevenredigen berekenen als de uiterste termen in de evenredigheid gegeven zijn.

x is middelevenredig tussen de getallen a en b ⇐⇒ a x = x b

8Oefeningen

Noteer als een verhouding.

a één seconde ten opzichte van één minuut

b het aantal meisjes in de klas ten opzichte van het aantal jongens in de klas

c het aantal lesuren wiskunde deze week t.o.v. het aantal lessen per week

d één seizoen t.o.v. één jaar

e één centiliter t.o.v. één liter

f de omtrek van een vierkant met zijde 1 t.o.v. de omtrek van een vierkant met zijde 3

g de oppervlakte van een vierkant met zijde 1 t.o.v. de oppervlakte van een vierkant met zijde 3

h de inhoud van een kubus met zijde 1 t.o.v. de inhoud van een kubus met zijde 3

Waar koop je het voordeligst 30 eieren? Werk met een verhoudingstabel.

In de middeleeuwen werd kaas in Brugge verhandeld met als eenheid de wage. Eén wage van toen komt overeen met 60,6kg.

Als een handelaar na één dag drie wagen kaas had verkocht, met hoeveel kg komt dit dan overeen ?

WISKUNDE & TECHNIEK

Vul de tabel aan als je weet dat de lengte van deze hoofdluis 0,25cm is. Werk op 0,01cm nauwkeurig.

WISKUNDE & AARDRIJKSKUNDE

De schaal onderaan een kaart geeft aan in welke mate eenbepaalde afstand werd weergegeven.

De E40 ligt voor 4,8 km in de gemeente Ternat.

Op welke schaal werd bovenstaande kaart weergegeven ? 4 5 *

Het oculair van een microscoop geeft aan hoeveel keer er vergroot wordt als je erdoor kijkt. Zo zal een speelgoedmicroscoop met oculair 5 :1 alles vijf keer vergroten.

a Hoe lang wordt dit weergegeven op een kaart met onderstaande schaal ?

b Op de kaart hierboven ligt de E40 over 4,8cm in Ternat.

Kaartgegevens

Als je België in een boek zou weergeven gevuld met topografische kaarten op schaal 1 : 50000, dan zou dat boek 204bladzijden dik zijn. Maar het NGI (Nationaal Geografisch Instituut) drukt ook topografische kaarten op schaal 1 : 10000. Waarom is het een slecht idee om ook die kaarten te bundelen in één boek ?

Vorm met de gegeven getallen telkens een evenredigheid. Kijk uit voor de volgorde: als de vier getallen niet in de juiste volgorde staan, moet je ze zelf eerst correct ordenen.

a4 ; 8; 16 en 32 c 36; 18; 40 en 20 e 16; 1; –2 en – 8

b9 ; 6; 24 en 36 d3 ; 5; 15 en 9 f 0,25; 0,4; 0,5 en 0,8

Vervolledig volgende evenredigheden.

Bepaal x in de volgende evenredigheden met behulp van de hoofdeigenschap.

Bepaal x in de volgende evenredigheden met behulp van het kenmerk van een evenredigheid.

Bepaal de vierde evenredige tot :

a5;7en11 c 6;21en 24

e1,8;2,4en30

b8;4en64 d 11;3en 7

f8; 2 3 en 4 5

Bepaal telkens de middelevenredigen tussen de twee gegeven getallen.

a4en16 c 4en 64 e9en0,36

b3en75 d5en2000 f5000en 1 2

Bepaal x in de volgende evenredigheden.

Los volgende problemen op.

a Zoek twee getallen die zich verhouden als 2 en 5 en waarvan de som 28 is.

b De zijden van een driehoek verhouden zich als 4, 5 en 7. De omtrek van de driehoek is 128 cm. Hoe lang zijn de zijden ?

c Een breedbeeldtelevisie heeft als verhouding 16 : 9. Wat is de lengte als de breedte van het toestel 63cm is ?

d De oppervlakte van een rechthoek is 300 cm2. De lengte en de breedte verhouden zich als 4: 3. Bepaal de lengte van deze rechthoek.

e Bepaal de vierde evenredige tot 3a , 2b en 4a

f Bepaal de middelevenredigen van 2a en 8a

g Bereken x in x 7 x 1 = x + 4 x 2

In een rechthoekige driehoek is de hoogte op de schuine zijde middelevenredig tussen de stukken waarin zij de schuine zijde verdeelt.

Noteer deze uitspraak in symbolen met behulp van de tekening en bepaal de hoogte als je weet dat de schuine zijde 7,24 cm is en | CD | = 3,24 cm.

WISKUNDE & WETENSCHAPPEN

De massadichtheid r van een materiaal drukt de verhouding uit tussen de massa m van het materiaal en zijn volume V .

ρ = m V

met r : massadichtheid

m : massa

V : volume

a Vorm de formule om naar V

b Bereken het volume van een massief gouden beeldje als je weet dat de massadichtheid van goud 19,3g/cm3 is en het beeldje een massa heeft van 200gram.

Vorm de volgende formules om naar de gevraagde letter.

a OPPERVLAKTE VAN EEN RECHTHOEK

b OMTREK VAN EEN RECHTHOEK

c OMTREK VAN EEN VIERKANT

d OPPERVLAKTE VAN EEN TRAPEZIUM

e OPPERVLAKTE VAN EEN RUIT

f OMTREK VAN EEN CIRKEL

g TWEEDE WET VAN NEWTON

h FORMULE VOOR DE MASSADICHTHEID

i WET VAN OHM

j FORMULE VOOR DRUK

k OPPERVLAKTE VAN EEN CIRKEL

WISKUNDE & AARDRIJKSKUNDE

De gemiddelde afstand van de aarde tot de zon wordt 1 AE (astronomische eenheid) genoemd enis ongeveer gelijk aan 150 miljoen km. De omwentelingstijd van de aarde om de zon bedraagt één jaar. Volgende tabel geeft een overzicht van de afstand en de omwentelingstijd van bepaalde planeten ten opzichte van de zon.

a Bereken telkens de verhouding t d . Werk op 0,01 nauwkeurig.

Wat stel je vast ?

t d

b Bereken nu telkens de verhouding t 2 d 3 . Werk op 0,01 nauwkeurig.

Wat stel je vast ?

t 2 d 3

c Wat is de omwentelingstijd van Jupiter als de afstand van Jupiter tot de zon ongeveer gelijk is aan 5,20 AE?

Toon aan en probeer, indien mogelijk, de uitspraak ook in woorden te noteren.

a a b = c d ⇐⇒ a c = b d

d a b = c d ⇐⇒ d b = c a

b a b = c d ⇐⇒ d c = b a e a b = c d ⇐⇒ a + c a = b + d b

c a b = c d ⇐⇒ a + c a c = b + d b d

f a b = c d ⇐⇒ 2a 3 c 6a c = 2 b 3d 6 b d

6.2 Recht en omgekeerd evenredig

1Recht evenredige grootheden

Voorbeeld 1 : afgelegde weg

Tabel :

TIJD (IN UREN)

AFGELEGDE WEG (IN KM)

De tijd en de afgelegde weg zijn afhankelijke grootheden.

Als je tweemaal langer rijdt, bij constante snelheid, dan zul je ook tweemaal meer kilometers afleggen.

Grafiek :

We kunnen dit voorbeeld in een grafiek weergeven. Op de x -as plaatsen we de tijd (in uren) en op de y -as noteren we de afgelegde weg (in km). We plaatsen de punten (1, 100), (2, 200), (4, 400) en (6, 600) in het rooster. We stellen vast dat alle roosterpunten op een halfrechte liggen die start in de oorsprong.

afgelegde weg (in km) tijd (in uren)

Formule :

Het quotiënt van de overeenkomstige maatgetallen is constant : 1 100 = 2 200 = 4 400 = 6 600

Zo kunnen we een formule opstellen die het lineair verband weergeeft tussen de tijd ( t ) in uren en de afgelegde weg ( s ) in km. De verhouding van de overeenkomstige maatgetallen is constant : t s = 1 100 ⇐⇒ s = 100 t

Hierbij noemen we 100 de evenredigheidsfactor

Voorbeeld 2 : koffie & espresso

Tabel :

Als de hoeveelheid koffie vijfmaal groter wordt, dan kunnen er vijfmaal meer espresso’s gemaakt worden.

Als de hoeveelheid koffie tweemaal kleiner wordt, dan kunnen er tweemaal minder koppen koffie gemaakt worden.

Grafiek :

We kunnen dit voorbeeld in een grafiek weergeven. Op de x -as plaatsen we de hoeveelheid koffie (in gram) en op de y -as noteren we het aantal espresso’s. We plaatsen de punten (100, 12), (500, 60), (250, 30) en (1000, 120) in het rooster.

aantal espresso’s hoeveelheid koffie (in gram)

We stellen opnieuw vast dat alle roosterpunten op een halfrechte liggen die start in de oorsprong.

Formule :

De verhouding van de overeenkomstige maatgetallen is constant: 100 12 = 500 60 = 250 30 = 1000 120

Zo kunnen we nu een formule opstellen die het verband weergeeft tussen het aantal espresso’s ( e ) en de gebruikte hoeveelheid koffie ( k ). k e = 100 12 ⇐⇒ 100e = 12k ⇐⇒ e = 12 100 k ⇐⇒ e = 0,12k

Hierbij is 0,12 de evenredigheidsfactor.

recht evenredig

Twee grootheden zijn recht evenredig als het quotiënt van hun overeenkomstige maatgetallen constant is.

Tabel : De verhouding van overeenkomstige maatgetallen is constant.

Grafiek : Een rechte door de oorsprong.

Verklaar waarom dit bij de voorbeelden beperkt bleef tot een halfrechte die start in (0, 0).

Formule: y x = c met c de evenredigheidsfactor

2Graﬁeken van recht evenredige grootheden tekenen met ICT

Voorbeeld 1 :

Methode : –

Breng de koppels in het rekenblad in.

– Versleep de y -as tot de getekende punten mooi in beeld komen. –

Zorg ervoor dat de getekende punten enkel de waarde weergeven en niet de naam. –

–

Geef in het algebravenster volgend commando in : functie(100x,0,10)

Breng de gepaste labels aan op de x -as en op de y -as. Klik daarvoor op de selecteerknop, klik nadien met derechtermuisknop in het tekenvenster en ga naar tekenvenster ; klik op de x -as en pas het label aan.

Doe dan hetzelfde voor de y -as.

Voorbeeld 2 :

3 Omgekeerd evenredige grootheden

Voorbeeld 1 :

Een auto moet een afstand van 120km afleggen. De tijd die hiervoor nodig is, is afhankelijk van de snelheid van de auto.

Tabel : SNELHEID (IN KM/H) 6030120

TIJD (IN UREN) 241

De snelheid en de tijd zijn afhankelijke grootheden.

Als de snelheid tweemaal groter wordt, zal de tijd om dezelfde weg af te leggen tweemaal kleiner worden.

Als de snelheid tweemaal kleiner wordt, zal de tijd om dezelfde weg af te leggen tweemaal groter worden.

We stellen vast dat het product van de overeenkomstige maatgetallen steeds hetzelfde is.

Grafiek :

We kunnen ook dit voorbeeld in een grafiek weergeven. We plaatsen de punten (60, 2), (30, 4) en (120, 1) in het rooster en zoeken nog enkele andere punten. Zo vinden we (15, 8) en 90, 4 3

tijd (in uren)

0 1 2 3 4 5 6 7 8 102030405060708090100110120130 0

snelheid (in km/h)

Als je alle punten met een vloeiende lijn verbindt, krijg je de grafiek die hoort bij deze situatie. Deze kromme noemen we ook wel een hyperbooltak

Formule :

Het is duidelijk dat het product van de overeenkomstige maatgetallen gelijk is aan 120 : 60 · 2 = 30 · 4 = 120 · 1

Woordformule : snelheid maal tijd = 120

Formule in symbolen : v · t = 120 of t = 120 v

Voorbeeld 2 :

De oppervlakte van een parallellogram is 20 dm2. Hoe kunnen de basis en de hoogte variëren ?

Tabel :

De lengte van de basis en de lengte van de hoogte zijn afhankelijke grootheden.

Als de basis tweemaal groter wordt, zal de hoogte tweemaal kleiner worden.

Als de basis tweemaal kleiner wordt, zal de hoogte tweemaal groter worden.

We stellen vast dat het product van de overeenkomstige maatgetallen steeds hetzelfde is.

Grafiek :

Ook op basis van deze gegevens kan er een grafiek getekend worden.

We plaatsen de punten (2, 10), (4, 5), (5, 4), (10, 2), (16; 1,25) en (20, 1) in het rooster.

We herkennen opnieuw een hyperbooltak.

Formule :

Het is duidelijk dat het product van de overeenkomstige maatgetallen gelijk is aan 20.

1 · 20 = 2 · 10 = 4 · 5

Woordformule : basis maal hoogte = 20

Formule in symbolen : b · h = 20 of h = 20 b

omgekeerd evenredig

Twee grootheden zijn omgekeerd evenredig als het product van hun overeenkomstige maatgetallen constant is.

Tabel : Het product van overeenkomstige maatgetallen is constant.

Grafiek : Een hyperbool.

Verklaar waarom dit bij de voorbeelden beperkt bleef tot een hyperbooltak.

Formule: x y = c met c de evenredigheidsfactor

4 Graﬁeken van omgekeerd evenredige grootheden tekenen met ICT

Voorbeeld 1 :

Methode : –

Breng de koppels in het rekenblad in.

– Versleep de x -as tot de getekende punten mooi in beeld komen.

– Zorg ervoor dat de getekende punten enkel de waarde weergeven en niet de naam. –

Geef in het algebravenster volgend commando in : functie 120 x 1,200

– Breng de gepaste labels aan op de x -as en op de y -as.

Voorbeeld 2 :

5 Niet-evenredige grootheden

Voorbeeld :

Hiernaast zie je de aanbieding van de week bij Slagerij Schellekes.

Tabel :

Als iemand drie hamburgers wil, dan krijgt hij er vier en betaalt hij 5,10 euro. Als iemand vier hamburgers wil, dan bestelt hij er drie en betaalt hij 5,10 euro. Als iemand zes hamburgers wil, dan krijgt hij een pakket van vier hamburgers voor 5,10 euro en betaalt hij apart nog twee hamburgers.

Vaststelling :

3 5,10 = 4 5,10 De verhouding van de overeenkomstige maatgetallen is niet constant.

3 · 5,10 ≠ 4 · 5,10 Het product van de overeenkomstige maatgetallen is niet constant.

Besluit : het aantal hamburgers is niet evenredig met de prijs in euro in deze situatie.

Merk op :

Deze vaststelling blijkt ook duidelijk uit de grafiek. De punten liggen niet op één rechte door de oorsprong en ook niet op een hyperbooltak.

6 Modelvraagstukken

Voorbeeld 1 : wateroverlast

Een kelder wordt na een overstroming leeggepompt door vier identieke pompen in drie uur. In hoeveel tijd doen zes identieke pompen dit ?

Het probleem begrijpen :

Ik moet de tijd berekenen. Hoe meer pompen ingezet worden, hoe sneller dekelder leeg is.

Tabel :

AANTAL POMPEN 46

TIJD (IN UREN) 3 x

Formule :

Het verband is omgekeerd evenredig; het product van de overeenkomstige maatgetallen is constant :

4 3 = 6 x

12 = 6 · x x = 2

Antwoord :

Zes pompen halen de kelder leeg in twee uur.

Controle : ik heb minder tijd nodig: dat klopt al en 4 · 3 = 6 · 2

Voorbeeld 2 : stof voor een trouwkleed

Daphné is op zoek naar stof voor haar trouwkleed. In de winkel ziet ze een soort die ze heel erg mooi vindt : 4 m stof die 210 euro kost. Hoeveel zal Daphné betalen voor 7 m van die stof ?

Het probleem begrijpen :

Hoe meer stof ze koopt, hoe meer ze zal betalen. Er is geen promotie.

Tabel :

LENGTE (IN METER) 47

PRIJS (IN EURO) 210 x

Formule :

Het verband is recht evenredig; het quotiënt van de overeenkomstige maatgetallen is constant, de evenredigheidsfactor is 52,50 :

4 210 = 7 x

4 x = 7 210

4 x = 1470

x = 367,50

Antwoord : Voor zeven meter stof zal Daphné 367,50 euro betalen.

Controle : ze zal meer betalen en 4 120 = 7 367,50

WISKUNDE & WETENSCHAPPEN

Voorbeeld 3: massadichtheid goud

De massadichtheid van een stof geeft weer wat de massa is van een bepaald volume van deze stof.

Het wordt weergegeven met de Griekse letter rho en is dus het quotiënt van massa en volume.

ρ = m V

Meestal wordt massadichtheid uitgedrukt in kg/m3 of in g/cm3

Zo is bijvoorbeeld de massadichthied van water ongeveer 1000 kg/m3 of 1 g/cm3

Eén cm3 goud heeft een massa van 19,3 gram. De dichtheid van goud is dus 19,3 g/cm3

ρ = 19,3 g/cm3

Bepaal het volume van een goudstaaf die 1 kg weegt.

Oplossing :

19,3 1 = 1000 x 19,3 x = 1000 x = 1000 19,3 x ≈ 52

Antwoord :

1 kg goud heeft een volume van ongeveer 52 cm3.

7 Samenvatting

• Je weet dat een verband tussen twee grootheden recht evenredig, omgekeerd evenredig of niet-evenredig kan zijn. – Twee grootheden zijn recht evenredig als het quotiënt van hun overeenkomstige maatgetallen constant is. – Twee grootheden zijn omgekeerd evenredig als het product van hun overeenkomstige maatgetallen constant is.

• Je kunt de evenredigheidsfactor c bepalen bij evenredige grootheden. – recht evenredige grootheden : y x = c – omgekeerd evenredige grootheden : x y = c

• Je weet dat de grafische voorstelling van twee recht evenredige grootheden een rechte door de oorsprong is.

• Je weet dat de grafische voorstelling van twee omgekeerd evenredige grootheden een hyperbooltak is.

• Je kunt een formule opstellen die hoort bij twee recht (of omgekeerd) evenredige grootheden.

8 Oefeningen

Kruis aan of het verband recht evenredig (RE), omgekeerd evenredig (OE) of niet evenredig (NE) is.

REOENE

a De prijs van het waterverbruik is met het aantal m3 water.

b De hoeveelheid snoep die je met 5 euro kunt kopen, is met de prijs voor 100 gram snoep.

c Het aantal uren dat ik leer voor mijn proefwerk wiskunde is met het percentage dat ik behaal.

d Het aantal tegels om een garage te vloeren is met de grootte van de tegels.

e Het aantal liter verf dat je nodig hebt, is met de oppervlakte die geverfd moet worden.

f De bouwtijd is met het aantal bouwvakkers die meehelpen.

g Mijn gewicht is met mijn lengte.

h Het deel van de winst van een bedrijf dat één persoon krijgt, is met het aantal aandeelhouders.

i Het brandstofverbruik van een wagen is met de afstand die hij aflegt.

j Het aantal gelijke stukken waarin ik een taart verdeel, is met de grootte van de stukken.

k Het zakgeld dat ik wekelijks krijg, is met mijn leeftijd.

l Het bedrag dat elke erfgenaam krijgt, is met het aantal erfgenamen.

m De afstand tot het onweer is met de tijd tussen bliksem en donderslag.

Kruis aan of het verband recht evenredig (RE), omgekeerd evenredig (OE) of niet evenredig (NE) is.

a De straal van een cirkel is met de omtrek van de cirkel.

b De hoogte van een prisma is met de oppervlakte van het grondvlak bij een constant volume.

c Een zijde van een ruit is met de lengte van de grote diagonaal van de ruit.

d De basis van een driehoek is met de oppervlakte van de driehoek.

e De lengte van de zijde van een kubus is met de inhoud van de kubus.

REOENE

Bij de onderstaande voorbeelden zijn de grootheden steeds recht evenredig. Bepaal telkens de evenredigheidsfactor.

opgehaald sponsorgeld in €

d b e woordformule : loon van de loodgieter = 30 keer het aantal uur dathij heeft gewerkt letterformule : l = 30 u

CINEMATICKETS ( t )

formule : r = 11,20 · t

f woordformule : duikersdiepte in meter = 12 keer het aantal minuten dat je daalt letterformule : d =–12 ⋅ t

Bij de onderstaande voorbeelden zijn de grootheden steeds omgekeerd evenredig. Bepaal telkens de evenredigheidsfactor.

aantaldagenomdeoogstbinnentehalen

b oppervlakte rechthoek = 36 cm2

e woordformule : tijd t (in dagen) om een boek te lezen = 3600 gedeeld door het aantal bladzijden b dat je per dag leest letterformule : t ⋅ b = 3600

f woordformule : tijd t (in minuten) om een babbeltje te doen met elke vriend = 120 gedeeld door het aantal vrienden v letterformule : t v = 120

Een tandwiel met 27 tanden grijpt in op een tandwiel met 48 tanden. Het eerste doet 96 toeren per minuut. Hoeveel omwentelingen doet het tweede in dezelfde tijd ?

Een waterkraan met een debiet van 180 liter per minuut vult een vergaarbak in 3 uur. In hoeveel tijd zal een kraan met een debiet van 120 liter per minuut die bak vullen ?

In Amerika wordt de snelheid in het wegverkeer uitgedrukt in mijl per uur (mph). Op de foto hiernaast zie je borden van snelheidsbeperkingen in Amerika. Welkesnelheid zou er in België op staan, mochten die 2 borden hier staan, als je weet dat 5 mijl ongeveer overeenkomt met 8 km ?

Een wandelaar legt 22 km af in 4 uur. Hoeveel km zal hij afleggen in 5 uur als zijn snelheid constant blijft ?

Een boom is 8 m hoog en heeft een schaduw van 4,4 m. Op hetzelfde tijdstip heeft een andere boom een schaduw van 9,35 m. Hoe hoog is die andere boom ?

Voor 5 m3 eikenhout betaalde een meubelmaker 4500 euro. Hoeveel zou hij voor 8 m3 van gelijkwaardige kwaliteit moeten betalen ?

Een boer heeft genoeg voer in voorraad om 60 koeien 10 weken te kunnen voeren. Hoelang komt hij met dezelfde hoeveelheid toe als hij 10 koeien verkoopt ?

Frank zal in de zomer een vloer leggen. Hij heeft hiervoor 200 tegels nodig van 9 dm2. Maar in de doe-het-zelfzaak valt zijn oog op mooie tegels van 4 dm2. Hoeveel tegels van 4 dm2 heeft hij nodig om deze vloer te leggen ?

Om een wand te schilderen van 10 m breed en 4 m hoog gebruikt een schilder 5 liter verf. Hoeveel liter verf heeft hij nodig om een wand van 7 m op 4 m te schilderen ?

Kijk bij elke grafiek of de grootheden recht evenredig, omgekeerd evenredig of niet evenredig zijn.

Verbind dus telkens een zwart bolletje met een groen bolletje.

Remafstand van een wagen.

Leid uit dit krantenartikel af of de remafstand en snelheid recht evenredige grootheden, omgekeerd evenredige grootheden of niet-evenredige grootheden zijn.

STOPAFSTAND IN METER

Afstand houden bij mist

GENT – Rij niet te snel bij beperkte zichtbaarheid en hou afstand. Zo vermijdt u aanrijdingen bij dichte mist. Maar hoe snel is een aangepaste snelheid bij een beperkte zichtbaarheid ?

De rijkswacht heeft daarvoor enkele tips:

- op de autoweg is er een afstand van ongeveer veertig meter tussen twee verlichtingspalen;

- ziet u slechts één verlichtingspaal, dan mag u maximaal 50 km per uur rijden;

- ziet u twee verlichtingspalen, dan mag u 80 km per uur rijden; - ziet u vijf verlichtingspalen, dan mag u 100 km per uur rijden.

Vergeet niet het mistlicht achteraan aan te steken. Het mistlicht brandt uitsluitend als de koplampen zijn aangestoken. Blijf met de kruislichten aan rijden, ook als de mist minder dicht is. Enkele kilometers verder kan er opnieuw een dicht mistgordijn hangen.

’s Winters kan de mist vastvriezen en wordt het wegdek plots spekglad. Wees daarom bijzonder voorzichtig op ijzelgevoelige plaatsen zoals bruggen en opritten.

— J.M.B

Lynthe doet een vakantiejob en verdient 15 euro per uur.

a Maak een tabel met het aantal gewerkte uren (1, 2, 4, 8, 10 en 20) en het verdiende bedrag in euro.

b Vul aan: De twee grootheden zijn evenredig.

c Maak een lijngrafiek die het loon weergeeft in functie van het aantal gewerkte uren.

d Bepaal de formule en de evenredigheidfactor.

Het bedrijfje van Josse en Julie maakt winst. Er wordt besloten om 3600 euro van deze winst uit te keren aan de aandeelhouders. Hoeveel zou elke aandeelhouder ontvangen ?

a Maak een passende tabel bij deze situatie.

b Vul aan: De twee grootheden zijn evenredig.

c Maak een lijngrafiek die het ontvangen bedrag weergeeft in functie van het aantal aandeelhouders.

d Bepaal de formule en de evenredigheidfactor.

Mare kent een truucje: als je de tijd telt tussen bliksem en donder, dan weet je ongeveer hoever het onweer verwijderd is. Drie seconden tellen wil zeggen dat het onweer op één kilometer van ons verwijderd is.

a Maak een passende tabel bij deze situatie.

b Vul aan: De twee grootheden zijn evenredig.

c Maak een lijngrafiek die de afstand weergeeft in functie van het aantal getelde seconden.

d Bepaal de formule en de evenredigheidfactor.

De wet van Ohm (genoemd naar de Duitse natuurkundige Georg Ohm) geeft het verband weer tussen elektrische spanning U , stroomsterkte I en weerstand R . Ada bestudeert de stroomsterkte en de weerstand bij een constante spanning.

a Ada noteert haar bevindingen in deze tabel.

b Vul aan: De twee grootheden zijn evenredig.

c Maak een lijngrafiek die de stroomsterkte weergeeft in functie van de weerstand.

d Bepaal de formule en de evenredigheidfactor.

Alain zou met een team van twaalf personen op expeditie gaan naar de Noordpool. Hij voorziet voldoende water en voedsel voor tien dagen.

a AANTAL EXPEDITIELEDENAANTAL DAGEN VOEDSEL

b Het aantal expeditieleden is evenredig met het aantal dagen voedsel.

c Net voor het vertrek zeggen vier expeditieleden af. Hoeveel dagen kan het team langer op de Noordpool verblijven met het voorziene voedsel?

d Maak met ICT de grafiek die het aantal dagen voedsel weergeeft in functie van het aantal expeditieleden.

Om je weg te vinden naar pakweg Amsterdam of Utrecht, kun een beroep doen op deze wegenkaart van ANWB. De kaart is weergegeven op een schaal van 1 : 200000.

a Als je op de kaart een afstand meet van 5 cm, hoe lang is dit dan in werkelijkheid ?

b Vul de tabel verder aan en teken met ICT de bijbehorende grafiek.

AFMETING (IN CM) OP KAART k 5

WERKELIJKE AFMETING (IN KM) w

c Geef de formule die de werkelijke afstand weergeeft in functie van de gemeten afstand op de kaart.

d Wat is de evenredigheidsfactor ? ____________________________________________________________________

a Als x en y recht evenredig zijn (met evenredigheidsfactor c 1) en y en z zijn ook recht evenredig (met evenredigheidsfactor c 2), dan zijn x en z

A recht evenredig met evenredigheidsfactor c 1 c 2

B recht evenredig met evenredigheidsfactor c 1 c 2

C omgekeerd evenredig met evenredigheidsfactor c 1 c 2

D omgekeerd evenredig met evenredigheidsfactor c 1 c 2

b Als x en y recht evenredig zijn (met evenredigheidsfactor c ) dan zijn x + x en y + y ...

A recht evenredig met evenredigheidsfactor c

B recht evenredig met evenredigheidsfactor 2

C recht evenredig met evenredigheidsfactor 2c

D niet evenredig

De vergelijking a 5 = 7 b moet kloppend gemaakt worden door voor a en b positieve gehele getallen in te vullen.

Hoeveel verschillende combinaties van a en b zijn er mogelijk ?

(A) 0 (B) 1 (C) 2 (D) 3 (E) 4

Syntheseoefeningen

TRUC 1

SNELREKENEN

Dit laat je zien :

Merkwaardig

Je zegt dat je heel snel bepaalde vermenigvuldigingen uit het hoofd kunt uitrekenen.

Voorbeeld : 297 · 303

Na enkele seconden heb je het antwoord: 89 991.

Dit zul je doen :

Beide getallen hebben hetzelfde verschil met 300.

297 · 303 = ( 300 – 3) · ( 300 + 3) = 3002 – 32 = 90 000 – 9 = 89 991

Dit is de uitleg :

Je steunt volledig op het merkwaardig product

( a + b ) · ( a – b ) = a 2 – b 2

Ben je hier goed in? Dan kun je ook het andere merkwaardig product gebruiken. Laat iemand een getal kiezen en zeg dat jij het kwadraat uit het hoofd zult uitrekenen.

Voorbeeld : 6112

In je hoofd doe je dit: 6112 = ( 600 + 11)2

= 6002 + 2 · 600 · 11 + 112

= 360 000 + 13 200 + 121

= 373 321

TRUC 2

Deelbaarheid door 9

HET MAGISCHE EUROBILJET

Dit laat je zien :

– Je neemt een willekeurig eurobiljet uit je portefeuille en vraagt dat iemand het nummer ervan noteert op een blad papier.

– Laat dit (grote) getal vermenigvuldigen met een getal naar keuze. Leen je rekenmachine hiervoor uit.

– Vraag nu om één cijfer van deze reeks te omcirkelen en daarna dit gigantische getal op het bord te noteren. De cijfers mogen zelfs in een andere volgorde staan, maar het omcirkelde getal moet hij/zij geheimhouden.

– Bekijk het getal vanop een afstand en zeg dan het geheime getal.

Dit zul je doen :

Het eurobiljet is niet zo willekeurig gekozen. Vooraf heb je immers nagekeken of het nummer een veelvoud is van 9 !

Dit getal blijft na vermenigvuldiging een veelvoud van 9.

Als het grote product op het bord staat, zul je in gedachten alle cijfers schrappen die samen 9 geven. Het geheime getal is dan het verschil van 9 met het resterende cijfer. L INK MET WISKUND E

Dit is de uitleg :

TOVEREN MET WISKUNDE

Je kent ze wel: goochelaars en illusionisten die allerhande toverkunstjes met getallen uitvoeren en daarmee even een wowgevoel creëren. Met de getallenkennis van dit jaar kun je al heel wat van die goochelacts begrijpen en misschien zelfs verklaren. We geven hier zes voorbeelden.

Tip : leer eerst het trucje goed uit het hoofd. Oefen enkele keren met je buur in de klas en trek er dan de wijde wereld mee in.

TRUC 3

IK KEN JE LEEFTIJD

Dit laat je zien : – Je vraagt iemand om de maand waarin hij/zij geboren is als een getal op te schrijven. Januari is 1, februari 2 enzovoort.

– Tel bij dat getal 2 op.

Vermenigvuldig met 100. – Tel je leeftijd hierbij op.

– Trek er 365 van af.

– Nu vraag je welk getal de persoon uitkomt.

– Nu zeg jij in welke maand de persoon geboren is en hoe oud hij/zij is.

Dit zul je doen :

Als de persoon het eindgetal zegt, tel jij in gedachten 165 (te onthouden!) bij dat getal op.

De twee cijfers die rechts in het getal staan, wijzen op de leeftijd. Het andere cijfer (of: de andere cijfers) wijst (of : wijzen) op de geboortemaand. Volgorde van de bewerkingen

Dit is de uitleg :

Je steunt op algebra, de distributieve eigenschap en het rekenen met letters om deze truc te verklaren. Probeer het enkele keren.

Je leerde dat een getal deelbaar is door 9 als de som van de cijfers deelbaar is door 9.

TRUC 4

KWADRATEREN

Dit laat je zien :

Titel van de vaardigheden

TRUC 6

ABSURDE TRUC

Dit laat je zien :

Deelbaarheid door 9 L INK MET WISKUND E

Je vraagt iemand een getal te geven dat eindigt op een 5. Je belooft snel het kwadraat van dit getal te geven.

Voorbeeld : 652

Na enkele seconden heb je het antwoord : 4225.

Dit zul je doen :

Omdat het getal moet eindigen op een 5, zal je antwoord steeds eindigen op 25. Maar er komen nog enkele cijfers voor !

Vermenigvuldig datgene wat voor de 5 staat in de opgave met één meer dan zichzelf. Dat getal plaats je voor de 25.

Voorbeeld : 652

6 · 7 = 4225

Dit is de uitleg :

Stel, x is het cijfer dat voor de 5 komt. Dan is het getal dat je als opgave krijgt x 5 ook te noteren als 10 · x + 5. Hierin mag x zelfs een getal van meerdere cijfers vormen.

Als je het kwadrateert, heb je dus :

( 10 · x + 5)2

Wat doe je in gedachten ?

Je gaat x vermenigvuldigen met ( x + 1).

Omdat je de uitkomst voor het getal 25 zal plaatsen, heb je dit eigenlijk met 100 vermenigvuldigd.

100 · x · ( x + 1)

Niet vergeten dat je ook de 25 moet bijtellen.

100 · x · ( x + 1) + 25

Uitgewerkt wordt dit : 100x 2 + 100x + 25

En beide resultaten zijn natuurlijk gelijk !

( 10x + 5)2 = 100x 2 + 100x + 25

TRUC 5

Veeltermen vermenigvuldigen

SNEL VERMENIGVULDIGEN

Dit laat je zien :

Vraag iemand naar de twee laatste cijfers van zijn gsm-nummer en laat hem het volgende berekenen op zijn rekenmachine:

– Deze twee cijfers vormen een getal, vermenigvuldig ze met 2.

– Tel hier 50 bij op.

– Trek er je schoenmaat van af.

– Tel je huisnummer erbij op.

– Vermenigvuldig met 27.

– Trek hier 90 van af.

– Maak de som van de cijfers.

– Heeft het resultaat meer dan één cijfer? Maak dan opnieuw de som van de cijfers.

– Doe dit tot je maar één cijfer overhoudt

– Draai dan het bord om waar je een grote 9 hebt genoteerd.

Dit zul je doen :

Vooraf noteer je een grote 9 op de achterkant van het bord. Daarna geef je de instructies waarvan het lijkt dat ze erg willekeurig zijn gekozen. Wat ook zo is, behalve deze twee: vermenigvuldigen met 27 en er 90 van aftrekken zorgt ervoor dat je resultaat een veelvoud is van 9.

Dit is de uitleg :

Je leerde dat een getal deelbaar is door 9 als de som van de cijfers deelbaar is door 9.

Als vervolg op truc drie kun je dit proberen. Vraag twee getallen van telkens twee cijfers. Jij zult zeer snel deze getallen vermenigvuldigen. Je mag zelfs op het bord deze bewerkingen uitvoeren !

Voorbeeld : 53 · 84 = ?

Dit zul je doen :

Start met de eenheden :

3 · 4 = 12 > eenheden (dus straks maal 1)

Vermenigvuldig het eerste cijfer van het eerste getal met het tweede cijfer van het andere getal.

Doe hetzelfde met de twee andere cijfers en tel op.

5 · 4 + 3 · 8 = 20 + 24 = 44 > tientallen (dus straks maal 10)

Vermenigvuldig de tientallen.

5 · 8 = 40 > honderdtallen (dus straks maal 100)

Alles optellen :

40 · 100 + 44 · 10 + 12 = 4000 + 440 + 12 = 4452

Dit is de uitleg :

Dit is de wiskundige verklaring. Probeer dit te verklaren (redeneer met de gebruikte kleurcodes). ( 50 + 3) · ( 80 + 4) = 50 ·

3 · 4

Evenredigheden 6

moet ik leren

dit

❒ Ik ken de definitie van een evenredigheid.

❒ Ik weet wat bedoeld wordt met eerste, tweede, derde en vierde term.

❒ Ik weet wat bedoeld wordt met uiterste en middelste termen.

❒ Ik ken het kenmerk van een evenredigheid.

❒ Ik kan het kenmerk van een evenredigheid bewijzen.

❒ Ik ken de definitie van de vierde evenredige tot drie getallen.

❒ Ik ken de definitie van de middelevenredige van twee getallen.

❒ Ik kan een formule omvormen naar een gevraagde letter.

❒ Ik ken de definitie van recht evenredige grootheden.

❒ Ik kan de evenredigheidsfactor bepalen.

❒ Ik ken de definitie van omgekeerd evenredige grootheden.

❒ Ik kan vraagstukken oplossen in verband met evenredigheden.

Evenredigheden

1 / 2

Kruis aan of het verband recht evenredig, omgekeerd evenredig of niet evenredig is.

De prijs (in euro) van verse kersen en het gewicht (in gram) per aankoop.

Het aantal koekjes per persoon en het aantal personen in de groep, bij een vast aantal koekjes.

Het gewicht en de leeftijd van een jongere.

Het debiet van een kraan en de tijd waarin een volledige emmer wordt gevuld.

De lengte van een zijde van een ruit en de omtrek van die ruit.

2 / 2

Als ik chocolademousse maak voor de 18 leerlingen van het tweede jaar, gebruik ik 9 eieren.

Hoeveel eieren heb ik nodig als ik chocolademousse wil maken voor 30 leerlingen?

3 / 2

20 leerlingen van de klas betalen elk 2,20 euro voor een cadeautje voor een zieke klasgenoot.

De klastitularis en de directeur beslissen om mee te doen aan dit mooie idee.

Hoeveel zal elke persoon nu moeten betalen ?

Naam

Totaal

Orde / Stiptheid

4 / 4

Op de speelplaats van een school hangen een aantal nestkastjes. Daarin verblijven gierzwaluwen. Gierzwaluwen zijn uitstekende zwevers. In pure glijvlucht – dus zonder vleugelslagen en zonder steun van stijgende luchtstromen – kan een gierzwaluw 11 meter horizontaal glijden op slechts een meter daling. Bij een daling van 3meter is de glijafstand dus33 meter.

a Vul de tabel hiernaast aan.

b Maak een grafiek in onderstaand rooster van deze situatie.

glijafstand (in m) daling (in m)

0 10 20 30 40 50

c Maak een formule in symbolen voor dit verband. Noteer ook de evenredigheidsfactor.

d Hoe noemen we de grafische voorstelling ?

5 / 2

Vul aan.

De vierde evenredige tot 6, 9 en 18 is

De middelevenredigen van 2 en 72 zijn

6 / 2

Vorm een evenredigheid

a… met volgende getallen : 45, 21, 15 en 7. b… waarvan 4 en 20 de middelste termen zijn.

7 / 3

Bereken de waarde van x door het kenmerk van een evenredigheid toe te passen.

24 = 11 8

8 / 3

Een garage meet 9 m bij 4 m. Thomas zal de garage betegelen en bestudeert vier verschillende tegelgroottes: 10 cm op 10 cm, 20 cm op 20 cm, 30 cm op 30 cm en 40 cm op 40 cm.

a Vul deze tabel aan.

OPPERVLAKTE GARAGEOPPERVLAKTE TEGELS AANTAL TEGELS

b Bij een constante oppervlakte (hier 36 m2) is het aantal gebruikte tegels met de oppervlakte van één tegel.

c Maak met ICT een passende lijngrafiek die het aantal tegels weergeeft in functie van de oppervlakte van één tegel. Noteer de formule en de evenredigheidsfactor.

Trefwoordenregister

A absolute frequentie 167

B balansmethode 210

C categorische data 168 centrummaten 176 coëfficiënt 102 computationeel denken 160 cumulatieve absolute frequentie 167

D deelverzameling 10 demathematiseren 38 doorsnede 11

E eenterm 101, 102 element 10 enkelvoudige absolute frequentie 167 equivalentie 10 evenredigheid 254 evenredigheidsfactor 273, 276 exponent 15

F formules omvormen 258 frequentietabel 167

G gehele getallen 9 gelijkheid 207 gelijksoortige eentermen 103 gemiddelde 176 getalwaarde 103 graad 102 grondtal 15

H hyperbooltak 275

I implicatie 10 ingenieursnotatie 84, 92 irrationale getallen 9

K kenmerk van een evenredigheid 256 kruisproduct 256 kwadraat van een tweeterm 145

L lege verzameling 11

M macht 15, 54 mathematiseren 38 mediaan 176 merkwaardige producten 145 middelevenredig 257 middelste termen 254 misleidende grafieken 173 modus 176

N natuurlijke getallen 9 numerieke data 168

O omgekeerd evenredig 276

P priemgetal 106

R rationale getallen 9 recht evenredig 273 regel van drie 35 regelmaat 101

S spreidingsmaat 176 stengelbladdiagram 191

T technische notatie 84, 92 toegevoegde tweetermen 146

U uiterste termen 254 unie 11

V variatiebreedte 177 veelterm 104, 105 vergelijking 37, 209 verhoudingen 253 verhoudingstabel 35 verschil 11 vierde evenredige 257 vierkantswortel 16 volgorde van bewerkingen 17 vraagstuk 38, 230

W wetenschappelijke schrijfwijze 83