John e freunds mathematical statistics with applications 8th edition miller solutions manual by debra.spigner849

John E Freunds Mathematical Statistics With Applications 8th Edition Miller Solutions Manual Visit to Download in Full: https://testbankdeal.com/download/john-e-freunds-mathema tical-statistics-with-applications-8th-edition-miller-solutions-manual/

3.1 (a) No, because f(4) is negative; (b) Yes; (c) No, because f(1) + f(2) + f(3) + f(4) = 18 19 is less than 1.

3.2 (a) No, because f(1) is negative; (b) Yes; (c) No, because f(0) + f(1) + f(2) + f(3) + f(4) + f(5) is greater than 1.

3.3 ()0fx  for each value of x and

thus

From Theorem A.1 we obtain 1 (,2)(1)(21) 6 Skkkk

Thus, for ()fx to be a distribution function, 6 , 0 (1)(21) ck kkk



1 () 4  

x xx fxc    

1 1 1/41 4 1 3/43 1 4 n Sn     as n  . Therefore, 3 c  .

3.6 For c > 0, f(x) diverges. For c = 0, f(x) = 0 for all x, and it cannot be a density function

3.9 (a) No, because (4)1; F  (b) No, because (2)(1);FF  (c) Yes.

John E Freunds Mathematical Statistics With Applications 8th Edition Miller Solutions Manual Visit TestBankDeal.com to get complete for all chapters

Chapter3

k x kk fxkkkkk      

 

C 

c    ;

, 12 137 c 

22(1) ()(12)1 (1)(1)2

3.4 (a) (1235)1; c

1 15

(b) 555 511 234

thus

 

kk xx fxcxcSk



 

(d) 11

The right-hand sum is a geometric progression with a = 1 and r = 1/4. For x = 1 to n, this sum equals

3.5 For ()(1) fxkkx  to converge to 1, 0 < k < 1.

24 MathematicalStatistics,8E Copyright © 2014 Pearson Education, Inc. 3.10 41 (0); 205 f  26123 (1), 20205 f   41 (2) 205 F  ()Fx  0 1/5 4/5 1        0 01 12 2 x x x x     3.11 (a) 511 632  ; (b) 111 236  ; (c) 1 (1) 3 f  , 1 (4) 6 f  , 1 (6) 3 f  and 1 (10), 6 f  0 elsewhere. 3.12 ()Fx  0 1/15 3/15 6/15 10/15 1          1 12 23 34 45 5 x x x x x x       3.13 (a) 3 4 (b) 311 424  (c) 1 2 (d) 13 1 44  (e) 311 442  (f) 31 1 44  3.14 3 (1) 25 f  , 4 (2), 25 f  5 (3) 25 f  , 6 (4) 25 f  , 7 (5) 25 f  ()Fx  0 3/25 7/25 12/25 18/25 1          1 12 23 34 45 5 x x x x x x       63 (1) 5025 F  , 147 (2) 5025 F  , 2412 (3) 5025 F  , 3618 (4) 5025 F  , 50 (5)1 50 F  , checks 3.15 (a) 111 ()1()1() PxxPxxFx  for i = 1, 2, …, n (b) 11 ()1()1() ii PxxPxxFx  for i = 2, …, n and 1 ()1Pxx

Chapter3 25 Copyright © 2014 Pearson Education, Inc. 3.16 0 1 ()(2) 5 1 Fxx         2 27 7 x x x    3.17 (a) 7 2 7 111 ()(72)1 2 555fxdxdxx    (b) 5 3 112 (53) 555 dx   3.18 (a) ()0,fx  0, x  and 0 00 ()1 x fxdxedxe   (c) 1 1 (1) x Pxedxe    3.19 (a) ()0,fx  01 x  and 1 0 ()1fxdx   (c) 0.5 2 0.1 (0.10.5)30.124 Pxxdx   3.20 (a) 3.2 2 3.2 111 (1)(8.324)0.54 2 8828 yz ydyy     (b) 3.2 2.9 3.2 111 (1)(8.327.105)0.1519 2.9 8828 x y ydyy     3.21 222 2 11111 (1)44 2 88282882 y y tyy tdtyyy         2 0 2 1 ()4 24 82 1 4 y y Fyyy y              (a) 13.22 (3.2)3.240.54 82 F    

26 MathematicalStatistics,8E Copyright © 2014 Pearson Education, Inc. (b) 12.92 (3.2)(2.9)0.542.940.540.38810.1519 82 FF     3.22 (a) 44 1/2 1/2 00 4 14 0 1/2 cxdxcxdxcc x   1 4 c  (b) 1/4 1/2 0 1/4 1111111 0 4441/2224 4 x Pxdxxdx x     1 0 1 111 (1)11 0 22 4 Pxdxx x   3.23 1 () 2 Fxx  0 1 () 2 1 Fxx         0 04 4 x x x    1111 4224 F     and 1 = 11 (1)1 22 F  3.24 00 1 ()[1](1) 222 z z zz zuuz kk Fzkzedzkeduee   k = 2 3.25 0 0 () 1 0 zz z Fz ez         3.26 23 1/4 1315 (32) 0 4163232 Pxxx    1 23 1/2 1 1311 6(1)(32)1 1/2 2442 Pxxxdxxx      3.27 23 0 ()6(1)32 x Fxxxdxxx   23 0 ()32 1 Fxxx       0 01 1 x x x    1325 4166432 Px   and 1321 1 2482 Px   

Chapter3 27 Copyright © 2014 Pearson Education, Inc. 3.28 2 0 () 2 x x Fxxdx  0 to 1 22 1 2 1113 ()(2)22 1 222222 21 2 x x Fxxdxxxxx x x       2 2 0 0 01 2 () 21 12 2 1 2 x x x Fx x xx x               3.29 0 11 () 33 x Fxdxx   0 to 1 1 () 3 Fx  1 to 2 1 ()(2) 2 to 4 3 1 (1 3 Fxx x   0 0 1 01 3 1 () 12 3 1 (1) 24 3 1 4 x xx Fxx xx x                   3.30 (a) 11.2 22 0.81 11.2 11 (2)20.32)2.40.7220.36 0.81 2222 xdxxdxxxx        (b) 22 (1.2)(0.8)2(1.2)1(1.2)(0.8) 22 2.40.7210.320.36 FF         3.31 0 x  ()0Fx  01 x  2 () 4 x Fx  1 (1) 4 F  12 x  11 () 24 Fxx 3 (2) 4 F  23 x  2 35 () 244 x Fxx (3) F = 1 3 x  ()1Fx 

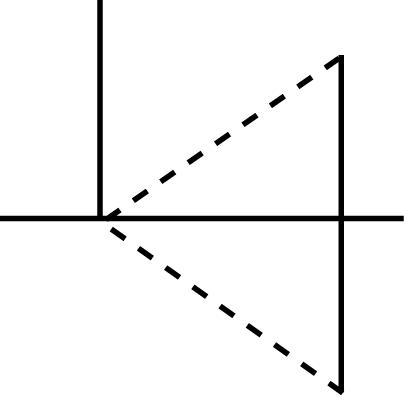
28 MathematicalStatistics,8E Copyright © 2014 Pearson Education, Inc. 3.32 (a) 11311 ; 22442 FF   (3)(2)110FF 3.33 dF1 dx2  , 1 () 2 fx  for 11 x  ; 0 elsewhere 1111 1 2222 Px    ; (23)Px = 0 3.34 (a) 916 (5)1 2525 F  (b) 99 1(8)11 6464 F  3.35 2 dF18 dy y  for 0; y  elsewhere (a) 5 22 3 5 189916 1 3 2525 dy yy   ; (b) 22 8 18999 0 8 6464 dy yy     3.37 2 (2)(2)1313(0.1353)10.40740.5926 PxFe (13)(3)(1)14124212 =2(0.3679)4(0.0498)0.73580.19920.5366 PxFFeee   4 (4)1(4)55(0.0183)0.0915 PxFe 3.38 x dF xe dx  for > 0; 0 elsewhere 3.39 (a) for 0 x  ()0Fx  (b) for 00.5 x  1 () 2 Fxx  (c) for 0.51 x    1131 ()1 2242 Fxxx     (d) for 1 x  ()0fx  3.40 (a) ()0;fx  (b) 1 (); 2 fx  (c) 1 (); 2 fx  (d) ()0fx  3.41 2411513 (2),(2),(21)844848 PZPZPZ   and 11 (02)1 22 Pz

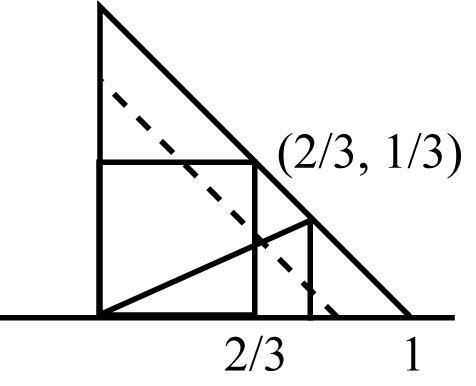
Chapter3 29 Copyright © 2014 Pearson Education, Inc. 3.42 (a) 1 ; 20 (b) 113 ; 488  (c) 1111 ; 64122  (d) 111287 6244012030  3.43 (a) 111 6124  ; (b) 0 ; (c) 1117 1262424  ; (d) 1119 1 120120  3.44 (25101492510101318)1 c  1 89 c  3.45 (a) 129 (10910) 8989  ; (b) 15 (14) 8989  (c) 155 (95101318) 8989  3.46 (a) (028012)1 k  f(3, 1) differs in sign from all other terms 3.47 x y 0 1 2 3 0 1 2 3 0 0 1 30 1 15 1 10 0 0 1 30 1 10 1 5 y 1 1 30 1 15 1 10 2 15 1 1 30 2 15 3 10 8 15 2 1 15 1 10 2 15 1 6 2 1 10 3 10 3 5 1 density joint distribution function 3.48 (a) (,)0Pxy (b) (,)1Pxy (c) (,)(,) three probabilities FbcFac (,)(,) FbcFac  3.49 11 2 2 00 () 2 x x x xy kxxydydxkxydx x     11 33 333 00 2 1 222 xxk kxxdxkxdx     k = 2

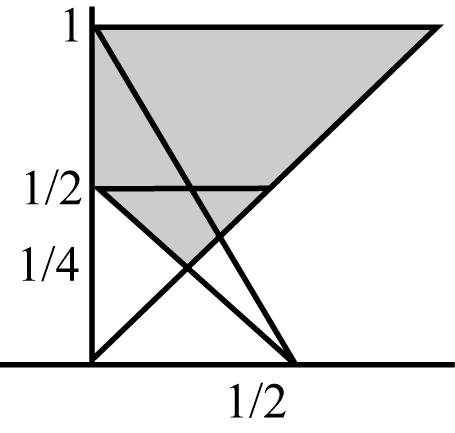
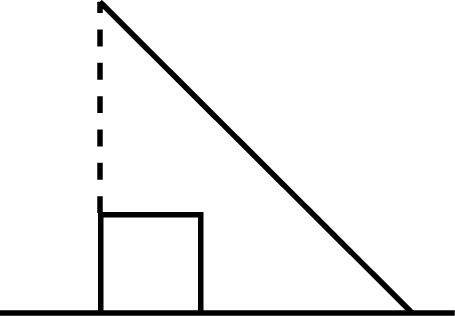
30 MathematicalStatistics,8E Copyright © 2014 Pearson Education, Inc. 3.50 1/21/21/21/2 2 2 0000 1/2 224 23 0 1/2 1 24 2412 0 22 1/2 111 121212 0 4834322464 12121 (683) 64336416 x x xy xydydxdxxxdx xxxx xxdx                   3.51 (a) 1 2 (b) 12245 121 23399  (c) 12111131 2 23323393    (,)2 Fxyxy  for 0,0,1xyxy 3.52 (a) 111 2 222  3.53 1/21 1/41/21/20 11 yy y dxdydxdy yy   1 1ln 2=1-0.3466=0.6534 2  3.54 2244222222() xyxyxy F xeyexyexye yx     0,0xy and (,)0fxy  elsewhere 3.55 22 2 2 224 142 111 4 22() 1 xyuu xedxyedyedueee         3.56 2 FFxxyxy eee xxy    0,0xy = 0 elsewhere 3.57 2 33 232 22 3 () 2 Xyx edxedyeee      3.58 (,)(,)(,)(,) FbdFadFbcFac 

Chapter3 31 Copyright © 2014 Pearson Education, Inc. 3.59 a = 1, b = 3, c = 1, d = 2 32123111 231121 2131 1213 (3,2)(1,2)(3,1)(1,1) (1)(1)(1)(1)(1)(1)(1)(1) (1)(1)(1)(1)(1)(1) (1)(1)(1)(1) ()()0 FFFF eeeeeeee eeeeee eeee eeee         .074 3.60 44141411 441141 414114 14141 (2,2)(1,2)(2,1)(1,1) (1)(1)(1)(1)(1)(1)(1)(1) (1)(1)(1)(1)(1)(1) (1)()(1)() ()()( FFFF eeeeeeee eeeeee eeeeee eeeee       42 ) e 3.61 336 235225224 456232 (3,3)(2,3)(3,2)(2,2) (1) (1)(1(1) 2() QED FFFF eee eeeeeeeee eeeee     3.62 x = 1, 2 y = 1, 2, 3 z = 1, 2 (1224362448612)1 1 54 k k   3.63 (a) 11 (12) 5418  (b) 1147 (86) 545427  3.64 (a) 191 (1224) 54546  ; (b) 0; (c) 1 3.65 1 11 000 (1) yz z xyzdxdydz  11 2 00 1 (1)(1) 2 z yzyzdydz  1 11 000 (1)1 yz z kxyzdxdydz  k = 144

32 MathematicalStatistics,8E Copyright © 2014 Pearson Education, Inc. 3.66 1 1/21/2 000 144 (1)0.15625 xy x xyzdzdydx  3.68 (a) 1/21/21/2 000 1 (23) 3 xyzdzdydx   1/21/2 2 00 1/21/2 00 1/21/2 2 00 1/2 1 (23) 0 32 131 328 1/2 1311131 0 348321616 1131161 316323233216 z xyzdydx xydydx xyyydxxdx                  3.69 (a) 13 (1),(1)44gg (b) 511 (1),(0), (1) 848 hhh  (c) 1/81 (11) 1/81/25 f   ; 1/24 (11) 1/81/25 f   3.70 (a) 11117 (0) 124812015 g  ; 1117 (1) 642015 g  111 (2) 244015 g  (b) 1117 (0) 1262424 h  ; 11121 (1) 444040 h  117 (2) 82040 h  ; 1 (3) 120 h  (c) 1/410 (01) 21/4021 f  ; 10 (11) 21 f  ; 1/401 (21) 21/2021 f  (d) 1/125 (00) 56/12028 w  ; 1/415 (10) 56/12028 w  ; 1/815 (20) 56/12056 w  1/1201 (30) 56/12056 w 

Chapter3 33 Copyright © 2014 Pearson Education, Inc. 3.71 (a) (,)(12) for 1,2,3 10836 xyxy mxyx  ; 1,2,3 y  (b) (,)(123) for 1,2,3 10818 xzxz nxzx  ; 1,2 z  (c) ()(123) for 1,2,3 366 xx gxx  (d) /64 (1,2) 2/363 zz z φ  for 1,2 z  (e) /36 (,3) 1/218 yzyz yz ψ  for 1,2,3 y  ; 1,2 z  3.72 (a) 5 (0) 12 g  , 1 (1) 2 g  ; 1 (2) 12 g  0 5/12 () 11/12 1 Gx         0 01 12 2 x x x x     (b) 2/94 (01) 7/187 1/63 (11) 7/187 f f   0 (1)4/7 1 Fx       0 01 1 x x x    3.73 (a) 1 () 2 fx  for 1, 1 x  ; 1 () 2 gy  for 1, 1 y  ; 111 224  , independent (b) 2 (0) 3 f  , 1 (1) 3 f  , 1 (0), 3 g  2 (1) 3 g  1212 (0,0) 3339 f  not independent 3.74 (a) 2 2 0 2 1111 (2) 2(42)(21) 0 44242 y xydyxyxx      for 01 x  = 0 elsewhere (b) 11 11 42 (21) 13 46 22 y fyy          for 02 y  = 0 elsewhere

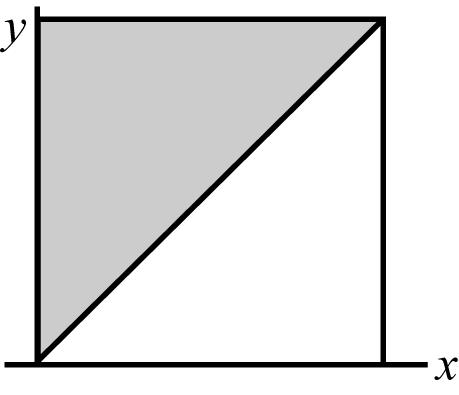
34 MathematicalStatistics,8E Copyright © 2014 Pearson Education, Inc. 3.75 (a) 1 2 0 1 111 (2) ()(1) 0 444xydxxxyy   for 02 y  = 0 elsewhere (b) 1 (21) 1 4 (1)(21) 1 2 (2) 4 x fxx   for 01 x  = 0 elsewhere 3.76 (a) 1 23 2 0 223 333 1 ()24()24 0 223 12(1)12(1)8(1) 12(1)8(1)4(1) x x yxyy fxyxyydy xxxx xxx       4(1)3 01 () 0 elsewhere xx fx      (b) 1 222 0 1 ()24()24(1)(1)(1) 2 11 24(1)1(1)24(1) 222 y gyyxyydyyyyyyy y yyyyy               12(1)2 01 0 elsewhere yyy      (,)()() fxyfxgy  not independent 3.77 (a) 1 1ln01 1 ()lnln1ln 0elsewhere x xx gxdyyx x y       (b) 0 1 01 11 ()(0) 0 elsewhere y x hydxy yy       1 1(ln) independent xnot y 

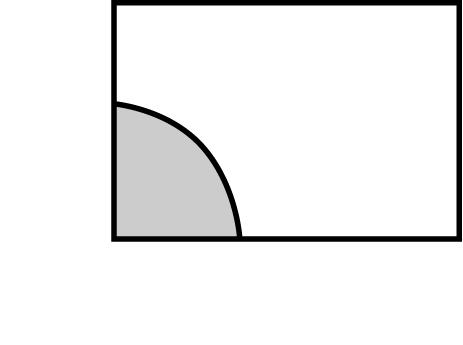
Chapter3 35 Copyright © 2014 Pearson Education, Inc. 3.78 (a) 3 2 1212 213 1 2 () (,) 1 1 2 2 x x xxexx fxxx x xe        2 2 2 2 1 26 1 01 3 ,2 5 11 3 0 elsewhere 32 x x x fx              (b) 3 3 223 12 231 2 1 01,0 () (,) 2 1 0 elsewhere 2 x x xexx xxe gxxx x            3.79()(,) gxfxydy     0 ()(,) (,) x GxfxydyFx     2 1 0 ()(,) 0 elsewhere x ex GxFx        3.80 13123213 (,)(,,) (,,)MxxfxxxdxFxx     1123231 ()(,,) (,,)GxfxxxdxdxFx     (a) 3 3 13 231113 13 0 0 or 0 1 (,)(1)(1) 01,0 2 1 x1,0 x x xx Mxxxxexx ex           (b) 1 1111 1 0 0 1 ()(1) 01 2 1 1 x Gxxxx x          

36 MathematicalStatistics,8E Copyright © 2014 Pearson Education, Inc. 3.81 11 1 1 01 () 2 0 elsewhere xx gx        22 2 1 01 () 2 0 elsewhere xx hx        3 3 3 1 () 0elsewhere x ex x φ        1,23123 (,)()()() fxxxgxhxx φ  not independent 1313 (,)()() mxxgxx φ  independent 2323 (,)()() nxxhxx φ  independent 3.82 (a) 1 02, 03 (,) 6 0elsewhere xy gxy        (b) /4 11 624 ππ  (a) 5 (0) 14 g  , 5 (1) 28 g  , 3 (2) 28 g  (b) 3.283 (00) 10/2810 φ  , 6/286 (10) 10/2810 φ  , 1/281 (20) 10/2810 φ  3.83 Heads Tails Probability H-T 0 4 1/16 4 1 3 4/16 2 2 2 6/16 0 3 1 4/16 2 4 0 1/16 4 3.84 1 2 3 1 3 4 1 4 5 2 3 5 2 4 6 3 4 7 (a) x 3 4 5 6 7 ()fx 1/6 1/6 2/6 1/6 1/6 0 3 1/634 2/645 () 4/656 5/667 17 x x x Fx x x x                

Chapter3 37 Copyright © 2014 Pearson Education, Inc. 3.85 2 () 3 PH  (a) 1 (0) 27 P  , 6 (1) 27 P  , 12212 (2)3,,,33327 P  , 8 (3) 27 P  (b) 161219 27272727  3.86 0 1/27 () 7/27 19/27 1 Fx           0 01 12 23 3 x x x x x      720 1 2727 198 1 2727   (a) (b) 3.87 0 0.40 ()0.70 0.90 1 FV           0 01 12 23 3 V V V V V      3.88 (a) 0.200.100.30  (b) 10.700.30  3.89 Yes; ()0fx  for 2,3,12 x  and 12 2 ()1 x fx    3.90 S 2 3 4 5 6 7 8 9 10 11 12 1/36 3/36 6/36 10/36 15/36 21/36 26/36 30/36 33/36 35/36 1 3.91 (a) 1 (228.65227.5)0.23 5  ; (b) 1 (231.66229.34)0.464 5  ; (c) 1 (232.5229.85)0.53 5  3.92 3 2 111 ()(36)3628828832 x Fxxdxcx     so that F( 6) = 0 and F(6) = 1. (a) 181120817 (2)(72)288322883227 F  (b) 111110717571325 (6)(1)1(36)128832288328642854FF (c) (3)(1)(1089)3611199110719095 288288328828832883432 FF      (d) 0

38 MathematicalStatistics,8E Copyright © 2014 Pearson Education, Inc. 3.93 /30 ()111/30/30/30 30301/30 x xxx e Fxedxcccee   (a) 18/300.6 (18)1110.54880.4512 Fee (b) 27/3036/300.91.2 (36)(27)0.40660.30120.1054 FFeeee (c) 48/301.6 1(48)0.2019 Fee  3.94 322 20,00020,00010,000 ()11 (100)2(100)(100) Fxdxc xxx    (a) 2 10,0001 1(200) 9 300 F  (b) 10,0003 (100)1 40,0004 f  3.95 (a) 2 251 1(10)0.25 4 10 F  (b) 2 2539 (8)1 64 8 F  (c) 222 252525(2516)1 (15)(12) 16 12151516 FF 3.96 /3 /3/3 0 1111 () 991/93311 x x xx e Fxxedxcxccex     c =1 (a) 22 (6)131313(0.1353)0.5491 Fee (b) 3 1(9)44(0.0498)0.1992 Fe  3.97 323 (0,0,2)3 002     3 (0,0) 28 f  , 6 (0,1) 28 f  , 1 (0,2) 28 f  323 (1,0,1)9 101     9 (1,0) 28 f  , 3 (2,0) 28 f  , 6 (1,1) 28 f  323 (0,1,1)6 011     323 (2,0,0)3 200     323 (1,1,0)6 110     323 (0,2,0)1 020    

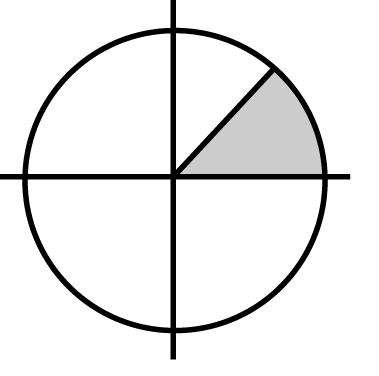
Chapter3 39 Copyright © 2014 Pearson Education, Inc. 3.98 (b) 3.99 1 (0,3) 8 f  , 3 (1,2) 8 f  , 3 (2,1) 8 f  , 1 (3,0) 8 f  1 (0,3) 8 g  , 3 (1,1) 8 g  , 3 (2,1) 8 g  , 1 (3,3) 8 g  3.100 (a) Probability = 1/8 (b) 111 44 π π  3.101 (a)  0.30.3 0.220.2 0.3 2 20.40.6 0.2 5 5 2 0.3 55 50.3038 0.2 22 psps p p pedsdpedp e edpee        (b) 0.3010.300.30 0.2500.250.25 0.300.300.25 1 5 55(1) 0 5[]5(0.300.25]0.01202 pspsp p pedsdpedpedp peee    3.102 (a) 0.40.40.4 2 000 0.4 22 (23) (3) 0 55xydxdyxxydy   0.4 0 2 (0.161.2 5 21.2(0.16)(0.16)(0.4)0.064 52 ydy       x 0 1 2 0 1 9 1 9 1 36 y 1 1 3 1 6 2 1 4

40 MathematicalStatistics,8E Copyright © 2014 Pearson Education, Inc. (b) 0.510.5 2 00.80 1 22 (23) (3) 0.8 55xydxdyxxydy  0.50.5 00 2 22 (13)(0.642.4) (0.60.36) 55 22 0.5 (0.30.36)(0.0750.18)0.102 0 55 yydyydy yy    3.103 (a) 5 (0) 14 g  , 15 (1) 28 g  and 3 (2) 28 g  (b) 3 (00) 10 φ  , 6 (10) 10 φ  , and 1 (20) 10 φ  3.104 (a) 1111 2 0.300.30.3 2 1 222 (4) (2)(2) 0 555 1 2 2 0.3 52 210.092 522520.6(1.855)0.742 xydydxxyydxxdx x x          (b) 1 0 22 ()(4) (2) 55 gxxydyx   (2/5)(4) () (2/5)(2) xy gyx x    , 40.2 (0.2) 2.2 y gy   0.5 0 110.6 (40.2) 2.22.22.2(0.50.1)0.273 ydy  3.105 (a) 4847188 (0,0) 5251221 f  , 48416 (0,1) 5251221 f  44816 (1,0) 5251221 f  , 48416 (1,1) 5251221 f  , 431 (1,2) 5251221 f  (b) 18816204 (0) 221221 g   , 16117 (1) 221221 g   (c) 16/22116 (01), 17/22117 φ  1/2211 (11) 17/22117 φ 

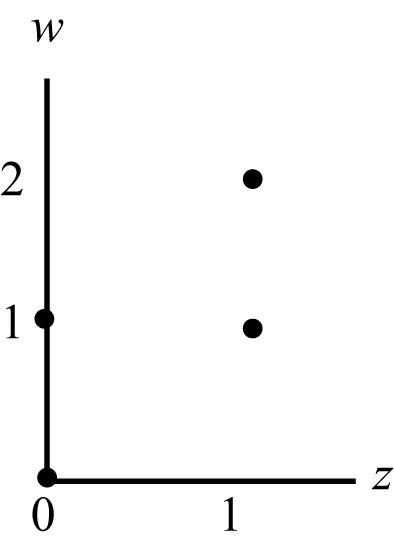
Chapter3 41 Copyright © 2014 Pearson Education, Inc. 3.106 (,)5 ps fpspe  0.20.4 p  0 s  (a) 0 50.20.4 5 55 0 0elsewhere ps psps p e pedspe p        (b) for 0 (,)5 ()5 0elsewhere ps ps pes fpspe gs      (c) 3 (1/4)/40.75 0 3 1 1 0 4 ss edsee     3.107 (a) /2 20 1020 120 50 25 0 elsewhere x x x x x dy x         (b) 120 2 25 (), 20 50 x x yx x x φ     1/6612 (12) 0elsewhere y y φ      (c) 112 (128)4 663  3.108 2 (,)(23) 5 fxyxy  2 1 2323 ()22 0 5252 43 01 55 0 elsewhere y gxxyx xx              2 1 2 ()(3) 0 5 (2/5)(13)01 0elsewhere hyxxy yy       (,)()() fxygxhy 

42 MathematicalStatistics,8E Copyright © 2014 Pearson Education, Inc. 3.109 (a) 3 123 333 123 223 (20,000) 0, 0, 0 (,,) (100)(100)(100) 0 elsewhere xxx fxxx xxx         (b) 100100 333123 123 00200 20,00020,00020,000 (100)(100)(100) 3311 44916 dxdxdx xxx     3.110 (a) 5 9 4 5 7 9 9 8 6 1 3 5 0 2 1 7 0 8 4 5 2 0 2 1 3 1 (b) 5f 4 5s 9 5 7 9 9 8 6f 1 3 0 2 0 1 0 4 2 0 2 1 3 1 6s 5 7 8 5 (c) The double-stem display is more informative. 3.111 *=Station 105 o = Station 107 o o o o o o * * o o o * * o o * * * * * o * * * 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 3.112 *=Lathe A o = Lathe B * * o o o o * * * * * * * o o o o 1.28 1.30 1.32 1.34 1.36 1.38 1.40 1.42 1.44 1.46 1.48 1.50 1.52 1.54 1.56 3.115 Class Limits Frequency 40.0 44.9 5 45.0 49.9 7 50.0 54.9 15 55.0 59.9 23 60.0 64.9 29 65.0 69.9 12 70.0 74.9 8 75.0 79.9 1 100

Chapter3 43 Copyright © 2014 Pearson Education, Inc. 3.117 The class boundaries are: 39.95, 44.95, 49.95, 54.95, 59.95, 64.95, 69.95, 79.95; the class interval is 5; the class marks are: 42.45, 47.45, 52.45, 57.45, 62.45, 67.45, 72.45, 77.45. 3.118 The class boundaries are: 2.95, 4.95, 6.95, 8.95, 10.95, 12.95, 14.95; the class interval is 2; the class marks are: 3.95, 5.95, 7.95, 9.95, 9.95, 11.95, 13.95. 3.116 Class Limits Frequency 3.0 4.9 15 5.0 6.9 25 7.0 8.9 17 9.0 10.9 11 11.0 12.9 8 13.0 14.9 4 80 3.119 Class Limits Frequency Class Boundary Class Mark 0 1 12 0.5 1.5 0.5 2 3 7 1.5 3.5 2.5 4 5 4 3.5 5.5 4.5 6 7 5 5.5 7.5 6.5 8 9 1 7.5 9.5 8.5 10 11 0 9.5 11.5 10.5 12 13 1 11.5 13.5 12.5 30 3.120 Class Limits Frequency Percentage 3.0 4.9 15 18.75% 5.0 6.9 25 31.25 7.0 8.9 17 21.25 9.0 10.9 11 13.75 11.0 12.9 8 10.00 13.0 14.9 4 5.00 80 100.00 3.121 Class Limits Frequency Percentage 40.0 44.9 5 5.0% 45.0 49.9 7 7.0 50.0 54.9 15 15.0 55.0 59.9 23 23.0 60.0 64.9 29 29.0 65.0 69.9 12 12.0 70.0 74.9 8 8.0 75.0 79.9 1 1.0 100 100.0

44 MathematicalStatistics,8E Copyright © 2014 Pearson Education, Inc. 3.122 Percentage Class Limits Shipping Department Security Department 0 1 43.3% 45.0% 2 3 30.0 27.5 4 5 16.7 17.5 6 7 6.7 7.5 8 9 3.3 2.5 100.0 100.0 The patterns seem comparable for the two departments. 3.125 Cumulative Percentage Class Limits Shipping Department Security Department 1.5 43.3% 45.0% 3.5 73.3 72.5 5.5 90.0 90.0 7.5 96.7 97.5 9.5 100.0 100.0 3.123 Upper Class Boundary Frequency Cumulative Frequency 44.95 5 5 49.95 7 12 54.95 15 27 59.95 23 50 64.95 29 79 69.95 12 91 74.95 8 99 79.95 1 100 100 3.124 Upper Class Boundary Frequency Cumulative Frequency 4.95 15 15 6.95 25 40 8.95 17 57 10.95 11 68 12.95 8 76 14.95 4 80 100

others.

3.130 The class marks are found from the class boundaries by averaging them; thus, the first class mark is (2.95 + 4.95)/2 = 3.95, and so forth.

3.135 The MINITAB output is: 3.136 The MINITAB output is:

last class

greater than that of the

2 3 7 4 5 4 6 7 5 8 13 2 30 3.127 (a) Class Limits Frequency Class Marks 0 99 4 49.5 (b) Yes, [see

(a).. 100 199 3 149.5 200 299 4 249.5 300 324 7 312.0 325 349 14 337.0 350 399 6 374.5 38

the

part

MIDDLE OF INTERVAL NUMBER OF OBSERVATIONS 6.0 2 ** 6.5 5 ***** 7.0 4 **** 7.5 5 ***** 8.0 5 ***** 8.5 3 *** 9.0 2 ** 9.5 2 ** 10.02 2 ** MIDDLE OF INTERVAL NUMBER OF OBSERVATIONS 40 1 * 45 7 ******* 50 11 *********** 55 21 ********************* 60 21 ********************* 65 23 *********************** 70 10 ********** 75 6 ****** John E Freunds Mathematical Statistics With Applications 8th Edition Miller Solutions Visit TestBankDeal.com to get complete for all chapters