

ĐỀ THI HỌC KỲ MÔN TOÁN NĂM HỌC 2022 – 2023 Ths Nguyễn Thanh Tú eBook Collection MA TRẬN, ĐỀ THI HỌC KỲ I – NĂM HỌC 2022 2023 THEO SÁCH CHÂN TRỜI SÁNG TẠO, CÁNH DIỀU, KẾT NỐI TRI THỨC MÔN TOÁN 10 CÓ GIẢI CHI TIẾT WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405


ĐỀ THI HỌC KỲ MÔN TOÁN NĂM HỌC 2022 – 2023 Ths Nguyễn Thanh Tú eBook Collection MA TRẬN, ĐỀ THI HỌC KỲ I – NĂM HỌC 2022 2023 THEO SÁCH CHÂN TRỜI SÁNG TẠO MÔN TOÁN 10 CÓ GIẢI CHI TIẾT WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL.COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405
Môn: Toán 10 1. TRẮC NGHIỆM ( 7 điểm) 35 câu 4 CÂU TỰ LUẬN Chủ đề Nội dung Mức độ NB TH VD VDC CHƯƠNG 1 (5 câu)
Mệnh đề 1 1 0 0 Tập hợp các phép toán trên tập hợp 2 1 0 0 CHƯƠNG 2 (5 câu)
Bất phương trình bậc nhất hai ẩn 1 1 0 0 Hệ bất phương trình bậc nhất hai ẩn 2 1 0 TL1 CHƯƠNG 3 (4 câu)
CHƯƠNG 4 (8 câu)
Hàm số và đồ thị 1 1 0 0
Hàm số bậc hai 1 1 Tl 1 0
Giá trị lượng giác của góc từ 0o đến 1800 2 1 0 0 Hệ thức lượng trong tam giác 2 1 0 0 Giải tam giác 0 2 TL1 0
Định nghĩa vectơ 1 0 0 0
CHƯƠNG 5 (8 câu)
Tổng hiệu vectơ (Lực) 1 1 0 0
Tích của một số với một vectơ 1 1 0 0
Tích vô hướng của hai vec tơ 1 2 TL1 0
Số gần đúng Sai số 2 0 0 0
CHƯƠNG 6 (5 câu)
Các số đặc trưng đo xu thế trung tâm 1 1 0 0 Các số đặc trưng đo độ phân tán 1 0 0 Tổng số câu 20 15 3 1
DẠYKÈMQUYNHƠN OFFICIAL MA TRẬN ĐỀ THI HỌC KỲ I NĂM HỌC 2022 2023 THEO SÁCH CTST
1. Trắc nghiệm
Câu 1: Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Hà Nội là một thành phố của Việt Nam.
b) Được sống thật là hạnh phúc!
c) 68125 += . d) Bạn thấy học Toán thú vị không?
A. 1. B. 2. C. 3. D. 4.
Câu 2: Mệnh đề phủ định của P : "Tam giác ABC là tam giác cân" là:
A. Tam giác ABC không phải là tam giác cân
B. Tam giác ABC là tam giác vuông
C. Tam giác ABC là tam giác đều D. ABC không phải là một tam giác
Câu 3: Cho ba tập hợp: {0;1;2;3},{4}MNxx == và {1;2;3;4;5}. Khẳng định nào sau đây là đúng? A. NP . B. MP = . C. MN = D. NP = .
Câu 4: Cho tập hợp {13}Mxx=− . Mệnh đề nào sau đây đúng?
A. [1;3) M =− B. (1;3] M =− C. (1;3) M =− . D. {1;0;1} M =− .

Câu 5: Cho tập hợp [2;3] A =− và (0;) B =+ . Tập hợp AB là
A. [2;) −+ . B. (0;3]. C. [0;3] D. (0;3). Câu 6: Phần không bị gạch (kể cả d) ở Hình 5 là miền nghiệm của bất phương trình: A. 1 2 yx . B. 2 yx . C. 2. yx D. 1 2 yx .
DẠYKÈMQUYNHƠN
ĐỀ SỐ 1
OFFICIAL
Câu 7: Bạn Phúc muốn dùng 500000 đồng để mua x gói kẹo và y cái bánh pizza. Biết rằng mỗi gói kẹo có giá là 40000 đồng, mỗi cái bánh pizza có giá là 75000 đồng. Mối liên hệ giữa x và y để Phúc không mua hết số tiền ban đầu là:
A. 4000075000500000 +xy
B. 4000075000500000 +xy C. 4000075000500000 +xy D. 4000075000500000 +xy
Câu 8: Phần không bị gạch chéo ở hình bên biểu diễn miền nghiệm của hệ bất phương trình nào sau đây?
A. 0 236 y xy +

B. 0 3260 y xy +− C. 0 3260 x xy +−
D. 0 326 x xy +
Câu 9: Mẹ đi chợ mua x kg thịt và y kg cá. Biết rằng mỗi kilôgam thịt có giá 120 nghìn đồng, mỗi kilôgam cá có giá 80 nghìn đồng. Hệ bất phương trình biểu thị mối liên hệ giữa x và y để số tiền mẹ đi chợ không hết quá 500 nghìn đồng và được tổng nhiều hơn 4kg thịt, cá là:
DẠYKÈMQUYNHƠN
OFFICIAL
80120500 4 + + xy xy B. 12080500 4 + + xy xy C. 12080500 4 + + xy xy D. 12080500 4 + + xy xy Câu 10: Cho hệ bất phương trình 2 3 yxa yxb −+ + với a và b là các hằng số. Trong mặt phẳng Oxy , nếu (0;1) là một nghiệm của hệ bất phương trình thì điều kiện nào sau đây là đúng? A. ab . B. ab = C. ab . D. ab =−
A.
Câu 11: Cho góc ,0;90 thoả mãn tan2tan2 =− . Mối liên hệ của hai góc đó là
A. và bù nhau.
B. và phụ nhau.
C. và bằng nhau.
D. và không có mối liên hệ.
Câu 12: Cho góc với 3 tan 4 = . Giá trị của cos là
A. 4 5 . B. 4 5 . C. 5 4 D. 5 4
Câu 13: Rút gọn biểu thức sin cot 1cos x Px x =+ + , ta được
A. sin x . B. 1 sin x . C. cos x . D. 1 cos x
Câu 14: Cho tam giác ABC có 2,1ABAC== và 0 60. A = Tính độ dài cạnh .BC
A. 2. BC = B. 1. BC = C. 3. BC = D. 2. BC =
Câu 15: Cho tam giác ABC có 222 0 abc+− . Khi đó:
A. Góc 090 C B. Góc 090 C C. Góc 090 C = D. Không thể kết luận được gì về góc .C
Câu 16: Tam giác ABC có 0 6812' A = , 0 3444' B = , 117. AB = Tính AC ? A. 68. B. 168. C. 118. D. 200. Câu 17: Cho ABC có 0 4,5,150.acB=== Diện tích của tam giác ABC là A. 53. B. 103. C. 10. D. 5.
Câu 18: Cho tam giác ABC có 20,10ab== , 0 30. B = Số đo góc A là A. 090 A = B. 060 A = C. 045 A = D. 0120 A =
Câu 19: Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Hỏi cặp vec tơ nào sau đây cùng hướng? A. AB và MB B. MN và CB C. MA và MB D. AN và CA Câu 20: Cho ba điểm ,, ABC phân biệt. Đẳng thức nào sau đây là đúng?
DẠYKÈMQUYNHƠN
OFFICIAL
A. ABACBC +=
B. CABABC −= .
C. ABCACB += .
D. ABBCCA −=
Câu 21: Trong các công thức sau, công thức nào không biểu diễn y là hàm số của x ?
A. 23+=xy
B. 2 2 =− yxx C. 1 = y x .

D. 22 4 +=xy .
Câu 22: Cho đồ thị hàm số () = yfx ở Hình 4. Phát biểu nào sau đây là đúng?
OFFICIAL
A. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 1.
B. Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 1
C. Hàm số đồng biến trên khoảng (1;) −+ , nghịch biến trên khoảng (;1) −−
D. Hàm số đồng biến trên .
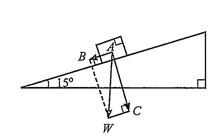
Câu 23: Một ô tô có trọng lượng 15000N đứng trên một con dốc nghiêng 15 so với phương ngang. Lực có khả năng kéo ô tô xuống dốc có độ lớn là A. 14489,89 N . B. 3882,29 N C. 4019,24 N . D. 7500N
Câu 24: Cho hình thang ,//,2 = MNPQMNPQMNPQ . Phát biểu nào sau đây là đúng? A. 2
Câu 25: Trên đường thẳng MN lấy điểm P sao cho 3 MNMP =− . Điểm P được xác định đúng trong hình vẽ nào sau đây:
DẠYKÈMQUYNHƠN
=
=−
= MNPQ B. 2
MQNP C. 2
MNPQ D. 2=− MQNP .
A. Hình 3 B. Hình 4 C. Hình 1 D. Hình 2
Câu 26: Trong các hàm số sau, hàm số nào không là hàm số bậc hai?
A. 2 42=−++yxx
B. ( ) 2 251=+−yxxx
C. 3(68)=−−yxx

D. 2 6 =+ yxx
Câu 27: Cho hàm số 2 ()288 =++fxxx . Phát biểu nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng (4;) −+ , nghịch biến trên khoảng (;4) −− .
B. Hàm số đồng biến trên khoảng (2;) −+ , nghịch biến trên khoảng (;2) −− .
OFFICIAL
C. Hàm số đồng biến trên khoảng (;2) −− , nghịch biến trên khoảng (2;) −+
D. Hàm số đồng biến trên khoảng (;4) −− , nghịch biến trên khoảng (4;) −+ .
Câu 28: Nếu hai điểm , MN thoả mãn 4=−MNNM thì độ dài đoạn thẳng MN bằng bao nhiêu?
A. 4 = MN B. 2 = MN C. 16= MN ; D. 256 = MN .
Câu 29: Cho hình vuông ABCD cạnh .a Đẳng thức nào sau đây đúng?
A. 2 . ABACa = B. 2 .2ABACa = C. 2 2 . 2 ABACa = D. 2 1 2 ABACa =
Câu 30: Cho hình vuông ABCD cạnh a . Gọi E là điểm đối xứng của D qua .C Đẳng thức nào sau đây đúng?
A. 2 .2.AEABa = B. 2 .3.AEABa = C. 2 .5.AEABa = D. 2 .5.AEABa =
Câu 31: Số quy tròn của 219,46 đến hàng chục là:
A. 210. B. 219,4. C. 219,5. D.
DẠYKÈMQUYNHƠN
220. Câu 32: Biết số gần đúng 37975421 a = có độ chính xác 150 d = . Hãy xác định các chữ số đáng tin của a. A. 3, 7, 9 B. 3, 7, 9, 7 C. 3, 7, 9, 7, 5 D. 3, 7, 9, 7, 5, 4 Câu 33: Số áo bán được trong một quý ở cửa hàng bán áo sơ mi nam được thống
như
Cỡ áo 36 37 38 39 40 41 42
kê
sau:
(Số áo bán được)
Giá trị mốt của bảng phân bố tần số trên bằng
A. 38 B. 126 C. 42 D. 12
Câu 34: Tiền lương hàng tháng của 7 nhân viên trong một công ty du lịch lần lượt là:6,5; 8,4; 6,9; 7,2; 2,5; 6,7; 3,0 (đơn vị: triệu đồng). Số trung vị của dãy số liệu thống kê trên bằng
A. 6,7 triệu đồng. B. 7,2 triệu đồng. C. 6,8 triệu đồng. D. 6,9 triệu đồng.
Câu 35: Năng suất lúa hè thu (tạ/ha) năm 1998 của 31 tỉnh ở Việt Nam được thống kê trong bảng sau:
OFFICIAL
Giá trị 3 35 x = có tần số bằng A. 6 B. 4 C. 7 D. 9 2. Tự luận
Câu 36: Hai bạn An và Bình trao đổi với nhau: An nói: Tớ đọc ở một tài liệu thấy nói rằng cổng Trường Đại học Bách khoa Hà Nội có dạng một parabol, khoảng cách giữa hai chân cổng là 8m và chiều cao của cổng tính từ một điểm trên mặt đất cách chân cổng là 0,5m là 2,93m. Từ đó tớ tính ra được chiều cao của cổng parabol đó là 12m .


Sau một hồi suy nghĩ, Bình nói: Nếu dữ kiện như bạn nói, thì chiều cao của cổng parabol mà bạn tính ra ở trên là không chính xác. Dựa vào thông tin mà An đọc được, em hãy tính chiều cao của cổng Trường Đại học Bách Khoa Hà Nội để xem kết quả bạn An tính được có chính xác không nhé.
Câu 37: Một học sinh dự định vẽ các tấm thiệp xuân làm bằng tay để bán trong một hội chợ Tết. Cần 2 giờ để vẽ một tấm thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ để vẽ một tấm thiệp loại lớn có
DẠYKÈMQUYNHƠN
Tầ
ố
n s
13 45 126 125 110 40 12
giá 20 nghìn đồng. Học sinh này chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải vẽ ít nhất 12 tấm. Hãy cho biết bạn ấy cần vẽ bao nhiêu tấm thiệp mồi loại để có được nhiều tiền nhất.
Câu 38: Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A ) đến trường (điểm B ) phải leo lên và xuống một con dốc (Hình 24). Cho biết đoạn thẳng AB dài 762m , ˆ ˆ 6,4 ==AB .
a) Tính chiều cao h của con dốc theo đơn vị mét (làm tròn kết quả đến hàng đơn vị).
b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ trung bình lên dốc là 4 / kmh và tốc độ trung bình khi xuống dốc là 19 / kmh .
Câu 39: Chất điểm A chịu tác động của ba lực 123 ,, FFF như hình và ở trạng thái cân bằng (tức là 123 0 FFF++= ). Tính độ lớn của các lực 23 , FF biết 1F có độ lớn là 20 N .

OFFICIAL
DẠYKÈMQUYNHƠN
Lời giải tham khảo BẢNG
1B 2A 3C 4A 5B 6D 7A 8A 9D 10C 11B 12A 13B 14C 15B 16A 17D 18A 19A 20C 21D 22D 23B 24C 25A 26B 27B 28A 29A 30A 31D 32C 33A 34A 35D 1. Trắc nghiệm Câu 40: Trong các câu sau, có bao nhiêu câu là mệnh đề? a) Hà Nội là một thành phố của Việt Nam. b) Được sống thật là hạnh phúc! c) 68125 += d) Bạn thấy học Toán thú vị không? A. 1. B. 2. C. 3. D. 4. Lời giải Theo định nghĩa mệnh đề thì các câu: a), c) là mệnh đề. Đáp án là B Câu 41: Mệnh đề phủ định của P : "Tam giác ABC là tam giác cân" là: A. Tam giác ABC không phải là tam giác cân B. Tam giác ABC là tam giác vuông C. Tam giác ABC là tam giác đều D. ABC không phải là một tam giác
ĐÁP ÁN TRẮC NGHIỆM
Câu 42: Cho ba tập hợp: {0;1;2;3},{4}MNxx == và {1;2;3;4;5}. Khẳng định nào sau đây là đúng?
A. NP . B. MP = . C. MN = . D. NP = .
Câu 43: Cho tập hợp {13}Mxx=− . Mệnh đề nào sau đây đúng?
A. [1;3) M =− . B. (1;3] M =− C. (1;3) M =− . D. {1;0;1} M =− .

Câu 44: Cho tập hợp [2;3] A =− và (0;) B =+ . Tập hợp AB là

A. [2;) −+ . B. (0;3]. C. [0;3] D. (0;3).
OFFICIAL
Câu 45: Phần không bị gạch (kể cả d) ở Hình 5 là miền nghiệm của bất phương trình: A. 1 2 yx . B. 2 yx . C. 2. yx D. 1 2 yx . Câu 46: Bạn Phúc muốn
DẠYKÈMQUYNHƠN
dùng 500000 đồng để mua x gói kẹo và y cái bánh pizza. Biết rằng mỗi gói kẹo có giá là 40000 đồng, mỗi cái bánh pizza có giá là 75000 đồng. Mối liên hệ giữa x và y để Phúc không mua hết số tiền ban đầu là: A. 4000075000500000 +xy B. 4000075000500000 +xy C. 4000075000500000 +xy D. 4000075000500000 +xy Câu 47: Phần không bị gạch chéo ở hình bên biểu diễn miền nghiệm của hệ bất phương trình nào sau đây?
A. 0 236 y xy + B. 0 3260 y xy +− C. 0 3260 x xy +− D. 0 326 x xy +
Câu 48: Mẹ đi chợ mua x kg thịt và y kg cá. Biết rằng mỗi kilôgam thịt có giá 120 nghìn đồng, mỗi kilôgam cá có giá 80 nghìn đồng. Hệ bất phương trình biểu thị mối liên hệ giữa x và y để số tiền mẹ đi chợ không hết quá 500 nghìn đồng và được tổng nhiều hơn 4kg thịt, cá là:
A. 80120500 4 + + xy xy B. 12080500 4 + + xy xy C. 12080500 4 + + xy xy D. 12080500 4 + + xy xy
Câu 49: Cho hệ bất phương trình 2 3 yxa yxb −+ + với a và b là các hằng số. Trong mặt phẳng Oxy , nếu (0;1) là một nghiệm c
DẠYKÈMQUYNHƠN OFFICIAL
.
,0;90 thoả
=− .
ệ
ủa
A. và bù nhau. B. và phụ nhau. C. và
nhau. D. và không có
liên
. Câu
Cho góc với 3 tan 4 = . Giá trị của cos là A. 4 5 B. 4 5 C. 5 4
ủa hệ bất phương trình thì điều kiện nào sau đây là đúng? A. ab
B. ab = C. ab . D. ab =− . Câu 50: Cho góc
mãn tan2tan2
Mối liên h
c
hai góc đó là
bằng
mối
hệ
51:
Câu 52: Rút gọn biểu thức sin cot 1cos x Px x =+ + , ta được
A. sin x . B. 1 sin x . C. cos x . D. 1 cos x Lời giải sincos1cos1 1cossin(1cos)sinsin xxx P xxxxx + =+== ++ . Vậy đáp án là B
Câu 53: Cho tam giác ABC có 2,1ABAC== và 0 60. A = Tính độ dài cạnh .BC A. 2. BC = B. 1. BC = C. 3. BC = D. 2. BC = Lời giải Chọn C Theo định lý cosin ta có: 220 2..cos60BCABACABAC =+− 22 1 212.2.1. 2 =+− 3. =
Câu 54: Cho tam giác ABC có 222 0 abc+− . Khi đó: A. Góc 090 C B. Góc 090 C C. Góc 090 C = D. Không thể kết luận được gì về góc .C Lời giải Chọn B. Ta có: 222 cos 2 abc C ab +− = . Mà: 222 0 abc+− suy ra: 0cos090 CC
Câu 55: Tam giác
DẠYKÈMQUYNHƠN OFFICIAL D.
5 4
0
ọ
Ta
00000
ABCC ++==−−=
ặt
sinsinsinsinsinsin
ABCBCC =====
ABC có
6812' A = , 0 3444' B = , 117. AB = Tính AC ? A. 68. B. 168. C. 118. D. 200. Lời giải Câu 56: Ch
nA.
có: Trong tam giác ABC :
1801806812'3444'774'
. M
khác 0 0 .sin117.sin3444' 68.
sin774' abcACABABB AC
Câu 57: Cho ABC có 0 4,5,150.acB=== Diện tích của tam giác ABC là
A. 53. B. 103. C. 10. D. 5.
Lời giải
Chọn D
Ta có 0 111 ..sin.4.5sin15010.5. 222 SacB====
Câu 58: Cho tam giác ABC có 20,10ab== , 0 30. B = Số đo góc A là
A. 090 A = B. 060 A = C. 045 A = D. 0120 A = Lời giải Chọn A Tacó 0 0 2010201020 20sin190 1 sinsinsinsin30sinsin 2
ab AA ABAAA ======
Câu 59: Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Hỏi cặp vec tơ nào sau đây cùng hướng?
A. AB và MB B. MN và CB C. MA và MB D. AN và CA Lời giải Chọn A
Ta có AB và MB cùng hướng
Câu 60: Cho ba điểm ,, ABC phân biệt. Đẳng thức nào sau đây là đúng?
A. ABACBC += . B. CABABC −= C. ABCACB += D. ABBCCA −= .
Câu 61: Trong các công thức sau, công thức nào không biểu diễn y là hàm số của x ?
A. 23+=xy . B. 2 2 =− yxx . C. 1 = y x D. 22 4 +=xy Lời giải Chọn D
Câu 62: Cho đồ thị hàm số () = yfx ở Hình 4. Phát biểu nào sau đây là đúng?

DẠYKÈMQUYNHƠN
OFFICIAL
A. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 1.
B. Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 1.
C. Hàm số đồng biến trên khoảng (1;) −+ , nghịch biến trên khoảng (;1) −− .
D. Hàm số đồng biến trên
Chọn D
Lời giải
Câu 63: Một ô tô có trọng lượng 15000N đứng trên một con dốc nghiêng 15 so với phương ngang. Lực có khả năng kéo ô tô xuống dốc có độ lớn là
A. 14489,89 N . B. 3882,29 N C. 4019,24 N D. 7500N

có khả năng kéo ô tô xuống dốc là lực
giải
OFFICIAL
DẠYKÈMQUYNHƠN
Lời
Lực
AB . Xét tam giác ACW vuông tại C , có 15 CAW = . Ta có sin CWAB A AWAW == Suy ra 15000sin153882,29 ABN = . Câu 64: Cho hình thang ,//,2 = MNPQMNPQMNPQ . Phát biểu nào sau đây là đúng? A. 2 = MNPQ B. 2 = MQNP C. 2=− MNPQ D. 2=− MQNP . Lời giải Ta có 222 MNMIQPPQ ===− Chọn C Câu 65: Trên đường thẳng MN lấy điểm P sao cho 3 MNMP =− . Điểm P được xác định đúng trong hình vẽ nào sau đây:
A. Hình 3 B. Hình 4 C. Hình 1 D. Hình 2 Lời giải Chọn A 3 MNMPMN =− ngược hướng với MP và 3 MNMP =
Câu 66: Trong các hàm số sau, hàm số nào không là hàm số bậc hai?
A. 2 42=−++yxx .
B. ( ) 2 251=+−yxxx . C. 3(68)=−−yxx .

D. 2 6 =+ yxx . Lời giải Chọn B
OFFICIAL
Câu 67: Cho hàm số 2 ()288 =++fxxx . Phát biểu nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng (4;) −+ , nghịch biến trên khoảng (;4) −−
B. Hàm số đồng biến trên khoảng (2;) −+ , nghịch biến trên khoảng (;2) −− .
C. Hàm số đồng biến trên khoảng (;2) −− , nghịch biến trên khoảng (2;) −+
D. Hàm số đồng biến trên khoảng (;4) −− , nghịch biến trên khoảng (4;) −+ Lời giải Chọn B
DẠYKÈMQUYNHƠN
Câu
Nếu hai điểm , MN thoả mãn 4=−MNNM thì độ dài đoạn thẳng MN bằng bao nhiêu? A. 4 = MN B. 2 = MN C. 16= MN ; D. 256 = MN Lời giải 2 4..cos180442 =−==−== MNNMMNNMMNMN . Chọn A Câu 69: Cho hình vuông ABCD cạnh a Đẳng thức nào sau đây đúng? A. 2ABACa = B. 2 .2ABACa = C. 2 2 2 ABACa = D. 2 1 . 2 ABACa = Lời giải Chọn A Ta có ( ) 0,45ABACBAC== nên 02 2 ...cos45.2. 2 ABACABACaaa === Câu 70: Cho hình vuông ABCD cạnh a . Gọi E là điểm đối xứng của D qua .C Đẳng thức nào sau đây đúng?
68:
A. 2 .2.AEABa = B. 2 .3.AEABa = C. 2 .5.AEABa = D. 2 .5.AEABa =
Lời giải Chọn A
Ta có C là trung điểm của DE nên 2.DEa = Khi đó ( ) 0 .... AEABADDEABADABDEAB =+=+ ( ) 02 ..cos,..cos02. DEABDEABDEABa ===
Câu 71: Số quy tròn của 219,46 đến hàng chục là: A. 210. B. 219,4. C. 219,5. D. 220.
Lời giải Chọn D
A B
E D C
13 45 126 125 110 40 12 Giá trị mốt của bảng phân bố tần số trên bằng A. 38 B. 126 C. 42 D. 12 Lời giải Chọn A Vì giá trị 3 38 x = có
trong m
DẠYKÈMQUYNHƠN
OFFICIAL
tần số 3 126 n = lớn nhất. Câu 74: Tiền lương hàng tháng của 7 nhân viên
ột
ty
lịch lần
6,5; 8,4; 6,9; 7,2; 2,5; 6,7; 3,0 (đơn vị
ệ
ọ
Sắp xếp
ứ
Câu 72: Biết số gần đúng 37975421 a = có độ chính xác 150 d = . Hãy xác định các chữ số đáng tin của a. A. 3, 7, 9 B. 3, 7, 9, 7 C. 3, 7, 9, 7, 5 D. 3, 7, 9, 7, 5, 4 Lời giải Vì sai số tuyệt đối đến hàng trăm nên các chữ số hàng nghìn trở lên của a là đáng tin. Vậy các chữ số đáng tin của a là 3, 7, 9, 7, 5. Đáp án C. Câu 73: Số áo bán được trong một quý ở cửa hàng bán áo sơ mi nam được thống kê như sau: Cỡ áo 36 37 38 39 40 41 42 Tần số (Số áo bán được) ự
công
du
lượt là:
: triệu đồng). Số trung vị của dãy số li
u thống kê trên bằng A. 6,7 triệu đồng. B. 7,2 triệu đồng. C. 6,8 triệu đồng. D. 6,9 triệu đồng. Lời giải Ch
n A
th
t
các số liệu thống kê, ta thu dược dãy tăng các số liệu sau:2,5;3,0;6,5;6,7;6,9;7,2; 8,4 (đơn vị: triệu đồng). Số trung vị 6,7 e M = triệu đồng.
Số các số liệu thống kê quá ít ( 710 n = ), do đó không nên chọn số trung bình cộng làm đại diện cho các số liệu đã cho. Trong trường hợp này ta chọn số trung vị 6,7 e M = triệu đồng làm đại diện cho tiền lương hàng tháng của 7 nhân viên.
Câu 75: Năng suất lúa hè thu (tạ/ha) năm 1998 của 31 tỉnh ở Việt Nam được thống kê trong bảng sau: Giá trị 3 35 x = có tần số bằng A. 6. B. 4. C. 7. D. 9. Lời giải Chọn D
2. Tự
luận
Câu 76: Hai bạn An và Bình trao đổi với nhau: An nói: Tớ đọc ở một tài liệu thấy nói rằng cổng Trường Đại học Bách khoa Hà Nội có dạng một parabol, khoảng cách giữa hai chân cổng là 8m và chiều cao của cổng tính từ một điểm trên mặt đất cách chân cổng là 0,5m là 2,93m. Từ đó tớ tính ra được chiều cao của cổng parabol đó là 12m


OFFICIAL
Sau một hồi suy nghĩ, Bình nói: Nếu dữ kiện như bạn nói, thì chiều cao của cổng parabol mà bạn tính ra ở trên là không chính xác. Dựa vào thông tin mà An đọc được, em hãy tính chiều cao của cổng Trường Đại học Bách Khoa Hà Nội để xem kết quả bạn An tính được có chính xác không nhé.
Lời giải Chọn hệ trục tọa độ Oxy sao cho một chân cổng đặt tại gốc tọa độ, chân còn lại đặt trên tia Ox . Khi đó cổng parabol là một phần của đồ thị hàm số dạng 2 =+ yaxbx (do parabol đi qua gốc tọa độ nên hệ số tự do bằng 0).
DẠYKÈMQUYNHƠN
Parabol đi qua các điểm có tọa độ (8;0)A và (0,5;2,93)B
Thay tọa độ của , AB vào hàm số ta có: 2 2
= =+ =+ =

293 0.8.8 375 2344 2,93.0,5.0,5 375
a ab ab b
Suy ra có hàm số 2 2932344 375375 =+ yxx Hàm số có đỉnh 4688 4; 375 I
Suy ra chiều cao của cổng là 4688 12,5 375 m Kết quả của An gần chính xác.
Câu 77: Một học sinh dự định vẽ các tấm thiệp xuân làm bằng tay để bán trong một hội chợ Tết. Cần 2 giờ để vẽ một tấm thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ để vẽ một tấm thiệp loại lớn có giá 20 nghìn đồng. Học sinh này chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải vẽ ít nhất 12 tấm. Hãy cho biết bạn ấy cần vẽ bao nhiêu tấm thiệp mồi loại để có được nhiều tiền nhất.
Lời giải Ta có các điều kiện ràng buộc đối với x, y như sau:
Hiển nhiên 0,0xy
Tổng số giờ vẽ không quá 30 giờ nên 2330 +xy
Số tấm thiệp tối thiểu là 12 tấm nên 12 +xy
DẠYKÈMQUYNHƠN
OFFICIAL
Từ đó ta có hệ bất phương trình:
+ +
2330 12 (,) 0 0
Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy , ta được như hình dưới.
Miền không tô màu (miền tam giác ABC , bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phươnng trình.
Với các đỉnh (6;6),(15;0),(12;0) ABC
Gọi F là số tiền (đơn vị: nghìn đồng) thu được, ta có: 1020=+ Fxy
Tính giá trị của F tại các đỉnh của tam giác:
Tại (6;6):10.620.6180 =+= AF

Tại (15;0):10.1520.0150 =+= BF
Tại (12;0):10.1220.0120 =+= CF
F đạt giá trị lớn nhất bằng 180 tại (6;6)A . Vậy bạn học sinh đó cần vẽ 6 tấm thiệp loại nhỏ và 6 tấm thiệp loại to để có được nhiều tiền nhất.
Câu 78: Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A ) đến trường (điểm B ) phải leo lên và xuống một con dốc (Hình 24). Cho biết đoạn thẳng AB dài 762m , ˆ ˆ 6,4 ==AB . a) Tính chiều cao h của con dốc theo đơn vị mét (làm tròn kết quả đến hàng đơn vị). b) Hỏi bạn An đến trường lúc mấy
DẠYKÈMQUYNHƠN
OFFICIAL
xy xy xy x y
giờ? Biết rằng tốc độ trung bình lên dốc là 4 / kmh và tốc độ trung bình khi xuống dốc là 19 / kmh . Lời giải a) Xét tam giác ABC ta có: 18064170 =−−= ACB . Áp dụng định lí sin ta có: sin762sin4306( sinsinsinsin170) === ABACABB ACm CBC . Xét tam giác vuông AHC ta có sin306sin632( ) == hCHACAm Vậy chiều cao con dốc là khoảng 32m b) Áp dụng định lí sin ta có: 762sin6459( sinsinsin170) == BCAB BCm AC Ta có: 306 0,306 ;459 0,459 == ACmkmCBmkm Như vậy, thời gian bạn An đi từ nhà đến trường là: =++= 0,3060,459 0,1(giôø) 6(phuùt). 419419 ACCB t


DẠYKÈMQUYNHƠN OFFICIAL
Dễ
hình bình hành ABCD. Do đó vecto u chính là vecto AC Vì chất điểm A ở trang thái cân bằng nên 123 0 FFF++= hay 33 0 vaø uFuF += là hai vecto đối nhau. A là trung điểm của EC Bước 2: Ta có: 123 20,, FADFABFAC ==== Do ,, ACE thẳng hàng nên 18060CABEAB =−= 403 906030cos303 sin30203 3 AD AC CAD ABDCAC == =−= === Vậy 23 203403 , 33 FF==
Vậy bạn An đến trường lúc khoảng 6 giờ 6 phút. Câu 79: Chất điểm A chịu tác động của ba lực 123 ,, FFF như hình và ở trạng thái cân bằng (tức là 123 0 FFF++= ). Tính độ lớn của các lực 23 , FF biết 1F có độ lớn là 20 N Lời giải Bước 1: Đặt 12 uFF =+ . Ta xác định các điểm như hình dưới.
dàng xác định điểm C , là điểm thứ tư của
1. Trắc nghiệm
Câu 1: Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Hãy mở cửa ra! b) Số 25 chia hết cho 8. c) Số 17 là số nguyên tố. d) Bạn thích ăn phở không? A. 1. B. 2. C. 3. D. 4. Câu 2: Cho mệnh đề chứa biến ()Px : " 2 15 xx + " (với x là số thực). Mệnh đề nào sau đây là đúng?
A. (0)P . B. (3)P . C. (4)P . D. (5)P .
Câu 3: Cho tập hợp 2 9 =Axx . Tập hợp A là: A. {0;1;2;3} = A . B. [0;3]. = A C. {0;3} = A . D. {3;2;1;0;1;2;3}=−−− A . Câu 4: Viết tập hợp ( )( ) 22240=−−= Bxxxx bằng cách liệt kê các phần tử của tập hợp thì ta được: A. {2;0;2;2}=− B B. {2;0;2}=− B C. {2} = B D. {2;2}=− B Câu 5: Trong các tập hợp sau, tập hợp nào là tập hợp rỗng? A. {(1)(21)0} =++= Axxx B. {(1)(21)0} =++=Bxxx C. {(1)(21)0} =++=Cxxx D. {(1)(21)0} =++=Dxxx
Câu 6: Miền nghiệm của bất phương trình bậc nhất hai ẩn 578 −xy là:
A. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy chứa gốc tọa độ (0;0)O (kể cả bờ).
B. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy không chứa gốc tọa độ (0;0)O (kể cả bờ).
C. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy chứa gốc tọa độ (0;0)O (không kể bờ).
D. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy không chứa gốc tọa độ (0;0)O (không kể bờ).
DẠYKÈMQUYNHƠN
ĐỀ SỐ 2
OFFICIAL
Câu 7: Bất phương trình nào sau đây KHÔNG là bất phương trình bậc nhất hai ẩn? A. 290 xy−+ . B. 3(1)2xy + C. 22 3(1)xyx+− D. 2(3)3(22)2 xyxy +++ . Câu 8: Cho hệ bất phương trình 1 1 1 1 xy xy xy xy + +− − −− . Diện tích miền nghiệm () H của hệ bất phương trình đã cho là A. 1. B. 2. C. 2 .
Câu 9: Cho hệ bất phương trình 235 (1) 35(2) 2
+ + . Gọi 12 , SS lần lượt là tập nghiệm của các bất phương trình (1) và (2). Mệnh đề nào sau đây đúng?
A. 12SS . B. 21SS . C. 12SS = . D. 12SS
xy xy
Câu 10: Anh Tuấn là du học sinh tại Mỹ và có hai công việc làm thêm vào mùa hè. Anh ấy làm gia sư được trả 12 USD mỗi giờ và làm nhân viên thu ngân ở siêu thị được trả 9,5 USD mỗi giờ. Gọi x là số giờ anh ấy làm gia sư và y là số giờ anh ấy làm nhân viên thu ngân. Anh ầy có thể làm việc không quá 20 giờ mỗi tuần. Hỏi cặp số (;) xy nào sau đây thể hiện anh ấy kiếm được ít nhất 220 USD mỗi tuần? A. (10;10). B. (12;8). C. (11;10) D. (9;9) Câu 11: Giá trị của biểu thức 0000 sin30cos60sin60cos30 P =+ bằng A. 3 P =− B. 0 P = C. 3 P = D. 1 P = Câu 12: Cho là góc nhọn và 1 sincos 2 = . Giá trị của sincos M =+ là A. 1. B. 2. C. 2 D. 2
DẠYKÈMQUYNHƠN
D. 4.
OFFICIAL
( ) (
tan180 1
xx
−
x
2
cos x
x .
2tan x
Câu 13: Rút gọn biểu thức
)
sinsin90 x P
=+
với ( ) 0;90 x
ta được A. 2 1 cos
. B.
1
. C. tan
D.
. Câu 14: Tam giác ABC có 0 8,3,60.acB=== Độ dài cạnh b bằng bao nhiêu? A. 49. B. 97 C. 7. D. 61. Câu 15: Cho tam giác ABC thoả mãn: 222 3 bcabc +−= . Khi đó: A. 0 30. A = B. 0 45. A = C. 0 60. A = D. 075 A = . Câu 16: Cho tam giác ABC , biết 13,14,15.abc=== Tính góc B?
A. 0 5949'. B. 0 537'. C. 0 5929'. D. 0 6222'.
Câu 17: Cho tam giác ABC có 110;46;6ACb=== . Khẳng định nào sau đây đúng?
A. 24;13,9;10,6Bac=
C. 24;12,7;10,1Bac= .

B. 24;13,8;10,7Bac=
D. 24;12,6;10,2Bac= .
Câu 18: Cho tam giác ABC có 6;7;12abc=== . Khẳng định nào sau đây đúng?
A. ABC có 1 góc tù. B. ABC có 3 góc nhọn.
C. ABC là tam giác vuông. D. 20 A .
Câu 19: Hai vectơ có cùng độ dài và cùng hướng gọi là
A. Hai vectơ cùng hướng. B. Hai vectơ cùng phương. C. Hai vectơ đối nhau. D. Hai vectơ bằng nhau.
Câu 20: Cho ABC và điểm M thoả mãn điều kiện MAMCMB += . Khẳng định nào sau đây là SAI?
A. ABAMAC += .
B. BABCBM += C. Tứ giác ABCM là hình bình hành. D. MABC =
Câu 21: Tập xác định của hàm số 4220182019yxx=−− là A. ( ) 1; −+ . B. ( );0− . C. ( ) 0;+ . D. ( ) ; −+ .
Câu 22: Cho hàm số 5 yfxx . Khẳng định nào sau đây là sai?
A. 15 f . B. 210 f . C. 1 1 5 f . D. 210 f .
Câu 23: Một giá đỡ có dạng tam giác ABC vuông cân tại đỉnh A được gắn vào tường như hình bên. Người ta treo vào vị trí C một vật nặng 10N . Cường độ lực tác động vào tường tại điểm A và B là
A. (5 N;10 N). B. (10 ;10 )NN . C. (10;102 )NN D. (10;103 )NN
Câu 24: Cho đoạn thẳng AB và O là trung điểm của AB . Khẳng định nào sau đây là đúng?
A. 2 = ABOA. B. 2 = ABOB .
DẠYKÈMQUYNHƠN
OFFICIAL
C. 2=− ABOB .
D. 2 = AOAB .
Câu 25: Cho ba điểm phân biệt ,, ABC . Nếu 3 ABAC =− thì đẳng thức nào dưới đây đúng?
A. 4 BCAC =− B. 2 BCAC =− C. 2 BCAC = D. 4 BCAC =
Câu 26: Hàm số 2 yaxbxc =++ , (0) a đồng biến trong khoảng nào sau đậy?
A. ;. 2 b a −− B. ;. 2 b a −+ C. ;. 4a −+ D. ;. 4a −−
Câu 27: Cho parabol ( ) 2 :321Pyxx=−+ . Điểm nào sau đây là đỉnh của ( )P ?
A. ( )0;1 I B. 12 ; 33 I C. 12 ; 33 I D. 12 ; 33 I
Câu 28: Phát biểu nào sau đây là đúng?
A. Nếu , ab khác 0 và (,)90 ab thì 0 ab ; B. Nếu , ab khác 0 và (,)90 ab thì 0 ab ; C. Nếu , ab khác 0 và (,)90 ab thì 0 ab ; D. Nếu , ab khác 0 và (,)90 ab thì 0 ab .
Câu 29: Cho tam giác ABC . Tập hợp các điểm M thỏa mãn .0MABC = là: A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Câu 30: Cho tam giác đều ABC cạnh 2 = a . Hỏi mệnh đề nào sau đây sai?
A. ( ) .2 = ABACBCBC B. .2 =− BCCA C. ( ).4+=−ABBCAC D. ( ).2−=BCACBA
Câu 31: Số quy tròn của số gần đúng 673582 với độ chính xác 500 = d là: A. 673500. B. 674000. C. 673000. D. 673600.
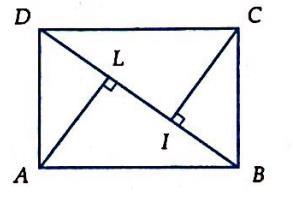
Câu 32: Cho hình chữ nhật ABCD. Gọi AL và CI tương ứng là đường cao của các tam giác ADB và BCD. Cho biết 1 DLLIIB=== . Diện tích của hình chữ nhật ABCD (chính xác đến hàng phần trăm) là: A. 4,24 B. 2,242 C. 4,2 D. 4,2426
Câu 33: Điểm kiểm tra môn Toán cuối năm của một nhóm gồm 9 học sinh lớp 6 lần lượt là 1; 1; 3; 6; 7; 8; 8; 9; 10. Điểm trung bình của cả nhóm gần nhất với số nào dưới đây?
A. 7,5 B. 7 C. 6,5 D. 5,9
Câu 34: Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là
A.
A. Phương sai luôn là một số không âm.
B. Phương sai là bình phương của độ lệch chuẩn.
C. Phương sai càng lớn thì độ phân tán quanh số trung bình càng lớn.
DẠYKÈMQUYNHƠN
OFFICIAL
Mốt. B.
Số trung bình. C. Số trung vị. D. Độ lệch chuẩn. Câu 35: Chọn khẳng định sai trong các khẳng định sau:
D. Phương sai luôn lớn hơn độ lệch chuẩn.
2. Tự luận
Câu 36: Giả sử độ cao h (đơn vị: mét) của một quả bóng golf tính theo thời gian t (đơn vị: giây) trong một lần đánh của vận động viên được xác định bằng một hàm số bậc hai và giá trị tương ứng tại một số thời điểm được cho bởi bảng dưới đây: Thời gian (s) 0 0,5 1 2 3 Độ cao (m) 0 28 48 64 48

a) Xác định hàm số bậc hai biểu thị độ cao ( )hm của quả bóng golf tính theo thời gian ()ts .
b) Sau bao lâu kể từ khi vận động viên đánh bóng thì bóng lại chạm đất?
Câu 37: Bác Năm dự định trồng khoai lang và khoai mì trên mảnh đất có diện tích 8 ha. Nếu trồng 1 ha khoai lang thì cần 10 ngày công và thu được 20 triệu đồng. Nếu trồng 1 ha khoai mì thì cần 15 ngày công và thu được 25 triệu đồng. Bác Năm cần trồng bao nhiêu hecta cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng được không quá 90 ngày công cho việc trồng khoai lang và khoai mì.
Câu 38: Quan sát cây cầu dây văng minh hoạ ở Hình 25.
OFFICIAL
Tại trụ cao nhất, khoảng cách từ đỉnh trụ (vị trí A ) tới chân trụ trên mặt cầu (vị trí H ) là 150m , độ dài dây văng dài nhất nối từ đỉnh trụ xuống mặt cầu (vị trí B ) là 300m, khoảng cách từ chân dây văng dài nhất tới chân trụ trên mặt cầu là 250m (Hình 26). Tính độ dốc của cầu qua trụ nói trên (làm tròn kết quả đến hàng phần mười theo đơn vị độ).
Câu 39: Một vật đồng chất được thả vào một cốc chất lỏng. Ở trạng thái cân bằng, vật chìm một nửa thể tích trong chất lỏng. Tìm mối liên hệ giữa trọng lực P của vật và lực đẩy Archimedes F mà chất lỏng tác động lên vật. Tính tỉ số giữa trọng lượng riêng của vật và của chất lỏng.

DẠYKÈMQUYNHƠN
Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM 1B 2D 3A 4B 5D 6D 7D 8B 9A 10B 11D 12D 13D 14C 15A 16C 17A 18A 19D 20D 21D 22C 23C 24B 25D 26B 27B 28C 29B 30C 31B 32A 33D 34A 35D 1. Trắc nghiệm Câu 40: Trong các câu sau, có bao nhiêu câu là mệnh đề? a) Hãy mở cửa ra! b) Số 25 chia hết cho 8. c) Số 17 là số nguyên tố. d) Bạn thích ăn phở không?
A. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy chứa gốc tọa độ (0;0)O (kể cả bờ).
B. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy không chứa gốc tọa độ (0;0)O (kể cả bờ).
C. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy chứa gốc tọa độ (0;0)O (không kể bờ).
D. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy không chứa gốc tọa độ (0;0)O (không kể bờ).
Câu 46: Bất phương trình nào sau đây KHÔNG là bất phương trình bậc nhất hai ẩn? A. 290 xy−+ . B. 3(1)2xy + C. 22 3(1)xyx+− D. 2(3)3(22)2 xyxy +++
DẠYKÈMQUYNHƠN OFFICIAL
của tập hợp thì ta được: A. {2;0;2;2}=− B B. {2;0;2}=− B C. {2} = B D. {2;2}=− B Câu 44: Trong các tập hợp sau, tập hợp nào là tập hợp rỗng? A. {(1)(21)0} =++= Axxx B. {(1)(21)0} =++=Bxxx C. {(1)(21)0} =++=Cxxx . D. {(1)(21)0} =++=Dxxx . Câu 45: Miền nghiệm của bất phương trình bậc nhất hai ẩ
A. 1. B. 2. C. 3. D. 4. Câu 41: Cho mệnh đề chứa biến ()Px : " 2 15 xx + " (với x là số thực). Mệnh đề nào sau đây là đúng? A. (0)P . B. (3)P . C. (4)P . D. (5)P . Câu 42: Cho tập hợp 2 9 =Axx . Tập hợp A là: A. {0;1;2;3} = A . B. [0;3]. = A C. {0;3} = A . D. {3;2;1;0;1;2;3}=−−− A . Câu 43: Viết tập hợp ( )( ) 22240=−−= Bxxxx bằng cách liệt kê các phần tử
n 578 −xy là:
Cho hệ bất phương trình 1 1 1 1 xy xy xy xy + +− − −− . Diện tích miền nghiệm () H của hệ bất phương trình đã cho là A. 1. B. 2. C. 2 D. 4. Câu 48: Cho hệ bất phương trình 235 (1) 35(2) 2 xy xy + + . Gọi 12 , SS lần lượt là tập nghiệm của các bất phương trình (1) và (2). Mệnh đề nào sau đây đúng? A. 12SS B. 21SS
Câu 47:
C. 12SS = D. 12SS .
Câu 49: Anh Tuấn là du học sinh tại Mỹ và có hai công việc làm thêm vào mùa hè. Anh ấy làm gia sư được trả 12 USD mỗi giờ và làm nhân viên thu ngân ở siêu thị được trả 9,5 USD mỗi giờ. Gọi x là số giờ anh ấy làm gia sư và y là số giờ anh ấy làm nhân viên thu ngân. Anh ầy có thể làm việc không quá 20 giờ mỗi tuần. Hỏi cặp số (;) xy nào sau đây thể hiện anh ấy kiếm được ít nhất 220 USD mỗi tuần? A. (10;10) B. (12;8) C. (11;10). D. (9;9). Lời giải Số tiền mà anh Tuấn kiếm được là 129,5
OFFICIAL
DẠYKÈMQUYNHƠN
129,5220 20 0;0 xy xy xy + + Thay lần lượt các đáp án ta
B
Câu 50: Giá trị của biểu thức 0000 sin30cos60sin60cos30 P =+ bằng A. 3 P =− B. 0 P = C. 3 P = D. 1 P = Lời giải Chọn D 00002020 sin30sin30cos30cos30sin30cos301 P =+=+= . Câu 51: Cho là góc nhọn và 1 sincos 2 = . Giá trị của sincos M =+ là A. 1. B. 2. C. 2 . D. 2 . Lời giải 22(sincos)12sincos2 M =+=+= . Suy ra 2 M = (vì )0 M Câu 52: Rút gọn biểu thức ( ) ( ) tan180 1 sinsin90 x P xx =+ − với ( ) 0;90 x ta được A. 2 1 cos x B. 2 1 cos x C. tan x D. 2tan x Câu 53: Tam giác ABC có 0 8,3,60.acB=== Độ dài cạnh b bằng bao nhiêu? A. 49. B. 97 C. 7. D. 61.
xy + (USD). Theo đề bài ta có hệ bất phương trình
có đáp án
thoả mãn.
Chọn C.
Ta có: 2222202cos832.8.3.cos60497 bacacBb =+−=+−==
Câu 54: Cho tam giác ABC thoả mãn: 222 3 bcabc +−= . Khi đó: A. 0 30. A = B. 0 45. A = C. 0 60. A = D. 075 A = . Lời giải
Câu 55: ChọnA.
Ta có: 222 0 33 cos30. 222 bcabc AA bcbc +− ====
Câu 56: Cho tam giác ABC , biết 13,14,15.abc=== Tính góc B? A. 0 5949'. B. 0 537'. C. 0 5929'. D. 0 6222'. Lời giải Chọn C. Ta có: 222222 0 13151433 cos5929'. 22.13.1565 acb BB ac +−+− ===
Câu 57: Cho tam giác ABC có 110;46;6ACb=== . Khẳng định nào sau đây đúng?
A. 24;13,9;10,6Bac= B. 24;13,8;10,7Bac= C. 24;12,7;10,1Bac= . D. 24;12,6;10,2Bac= .
giải
DẠYKÈMQUYNHƠN
OFFICIAL Lời giải
ABC có 1 góc tù. B. ABC có 3 góc nhọn. C. ABC là tam giác vuông.
20 A . Lời giải Góc lớn nhất trong tam giác ABC là C 222 157 cos21 2168 bca AA bc +− == . 222 59 cos135 284 abc CC ab +− ==− . Vậy ABC có 1 góc tù. Câu 59: Hai vectơ có cùng độ dài và cùng hướng gọi là A. Hai vectơ cùng hướng. B. Hai vectơ cùng phương. C. Hai vectơ đối nhau. D. Hai vectơ bằng nhau. Lời giải Chọn D
Lời
Ta có ( ) 18024BAC=−+= Áp dụng định lý sin, ta được: .sin.sin 13,9;10,6sinsin bAbC ac BB == . Câu 58: Cho tam giác ABC có 6;7;12abc=== . Khẳng định nào sau đây đúng? A.
D.
Hai vectơ bằng nhau là hai vectơ có cùng độ dài và cùng hướng.
Câu 60: Cho ABC và điểm M thoả mãn điều kiện MAMCMB += . Khẳng định nào sau đây là SAI? A. ABAMAC += . B. BABCBM += . C. Tứ giác ABCM là hình bình hành. D. MABC = .
Lời giải MAMCMBMCMBMAMCAB +==−= . Khi đó tứ giác ABCM là hình bình hành. Do đó phương án C là đúng. Với phương án , AB , ta áp dụng quy tắc hình bình hành suy ra A và B là đúng. Vì ABCM là hình bình hành nên MABC =−
Câu 61: Tập xác định của hàm số 4220182019yxx=−− là A. ( ) 1; −+ . B. ( );0− . C. ( ) 0;+ . D. ( ) ; −+ .
Lời giải
Chọn D Hàm số là hàm đa thức nên xác định với mọi số thực x .
Câu 62: Cho hàm số 5 yfxx . Khẳng định nào sau đây là sai? A. 15 f . B. 210 f . C. 1 1 5 f . D. 210 f .
Lời giải Chọn C
Ta có 50 yfxxx nên 1 1 5 f là mệnh đề sai.
Câu 63: Một giá đỡ có dạng tam giác ABC vuông cân tại đỉnh A được gắn vào tường như hình bên. Người ta treo vào vị trí C một vật nặng 10N . Cường độ lực tác động vào tường tại điểm A và B là
Lời giải

DẠYKÈMQUYNHƠN
OFFICIAL
(5 N;10 N). B. (10 ;10 )NN .
(10;102
NN .
(10;103
A.
C.
)
D.
)NN
Tại điểm C , lực kéo F có phương thẳng đứng hướng xuống dưới. Ta thấy F là hợp của hai lực 1F và 2F có giá lần lượt là hai đường thẳng AC và BC . Do đó hai lực tác động vào điểm A và B khi treo vật vào vị trí điểm C lần lượt là 1F và 2F . vi tam giác ABC vuông cân tại C . Do đó 1 ||10 FFN == và 2 ||2||102sin45 F FFN === . Câu 64: Cho đoạn thẳng AB và O là trung điểm của AB


DẠYKÈMQUYNHƠN
OFFICIAL
.
A. 2 =
.
2 =
.
=−
.
=
. Lời
Câu
ba
,, ABC . Nếu 3 ABAC =− thì
nào dưới đây đúng? A. 4 BCAC =− B. 2 BCAC =− C. 2 BCAC = D. 4 BCAC = Lời giải Chọn D Câu 66: Hàm số 2 yaxbxc =++ , (0) a đồng biến trong khoảng nào sau đậy? A. ;. 2 b a −− B. ;. 2 b a −+ C. ;. 4a −+ D. ;. 4a −− Lời giải Chọn B 0. a Bảng biến thiên
Khẳng định nào sau đây là đúng?
ABOA
B.
ABOB
C. 2
ABOB
D. 2
AOAB
giải Chọn B
65: Cho
điểm phân biệt
đẳng thức
Câu 67: Cho parabol ( ) 2 :321Pyxx=−+ . Điểm nào sau đây là đỉnh của ( )P ?
A. ( )0;1 I B. 12 ; 33 I C. 12 ; 33 I
Lời giải Chọn B
D. 12 ; 33 I
Hoành độ đỉnh của ( ) 2 :321Pyxx=−+ là 1 23 b x a =−= 2 112 32.1 333 y =−+= .
Vậy 12 ; 33 I .
Câu 68: Phát biểu nào sau đây là đúng?
A. Nếu , ab khác 0 và (,)90 ab thì 0 ab ;
B. Nếu , ab khác 0 và (,)90 ab thì 0 ab ;
C. Nếu , ab khác 0 và (,)90 ab thì 0 ab ; D. Nếu , ab khác 0 và (,)90 ab thì 0 ab . Lời giải Chọn C
Câu 69: Cho tam giác ABC . Tập hợp các điểm M thỏa mãn .0MABC = là: A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn. Lời giải Chọn B. Ta có .0. MABCMABC =⊥ Vậy tập hợp các điểm M là đường thẳng đi qua A và vuông góc với BC
70:
tam giác đề
ABC
ạnh 2
DẠYKÈMQUYNHƠN
OFFICIAL
( ) .2 = ABACBCBC B. .2 =− BCCA C. ( ).4+=−ABBCAC
)
−=
tích vô hướng ở
vế trái với vế phải. Câu 71: Phương án A: ( ) o ..cos602.2 === ABACABACxABACBCBC nên loạiA. Phương án B: o ..cos1202 ==−BCCABCAC nên loại B. Phương án C:( )..4+== ABBCACACAC , o .2.2.cos1202 ==− BCCA nên chọn C. Câu 72: Số quy tròn của số gần đúng 673582 với độ chính xác 500 = d là: A. 673500. B. 674000. C. 673000. D. 673600. Lời giải
Câu
Cho
u
c
= a . Hỏi mệnh đề nào sau đây sai? A.
D. (
.2
BCACBA Lời giải Chọn C Ta đi tính
các phương án. So sánh
Chọn B
Câu 73: Cho hình chữ nhật ABCD. Gọi AL và CI tương ứng là đường cao của các tam giác ADB và BCD. Cho biết 1 DLLIIB=== . Diện tích của hình chữ nhật ABCD (chính xác đến hàng phần trăm) là: A. 4,24 B. 2,242 C. 4,2 D. 4,2426 Lời giải
Câu 74: Đáp ánA.
Ta có: 2 .2ALBLLD== do đó 2 AL = . Lại có 3 BD = Suy ra diện tích của hình chữ nhật là: 323.1,41421356...4,24264...4,24 =
OFFICIAL
Câu 75: Điểm kiểm tra môn Toán cuối năm của một nhóm gồm 9 học sinh lớp 6 lần lượt là 1; 1; 3; 6; 7; 8; 8; 9; 10. Điểm trung bình của cả nhóm gần nhất với số nào dưới đây? A. 7,5. B. 7 . C. 6,5. D. 5,9. Lời giải Chọn D Điểm trung bình của cả nhóm là 91136788910535,(8)5, 99 == +++++ +++ .
Câu 76: Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là
A. Mốt. B. Số trung bình. C. Số trung vị. D. Độ lệch chuẩn. Lời giải Chọn A
Câu 77:
DẠYKÈMQUYNHƠN
Chọn khẳng định sai trong các khẳng đị
A. Phương sai luôn là một
B. Phương sai là bình phương
C. Phương sai càng lớn
D. Phương sai luôn
Chọn D Phương sai 2 x S còn độ lệch chuẩn 2 xx SS = nhưng không thể khẳng
phương sai
lớn hơn độ lệch chuẩn.
nh sau:
số không âm.
của độ lệch chuẩn.
thì độ phân tán quanh số trung bình càng lớn.
lớn hơn độ lệch chuẩn. Lời giải
định
luôn
2. Tự luận
Câu 78: Giả sử độ cao h (đơn vị: mét) của một quả bóng golf tính theo thời gian t (đơn vị: giây) trong một lần đánh của vận động viên được xác định bằng một hàm số bậc hai và giá trị tương ứng tại một số thời điểm được cho bởi bảng dưới đây: Thời gian (s) 0 0,5 1 2 3 Độ cao (m) 0 28 48 64 48
a) Xác định hàm số bậc hai biểu thị độ cao ( )hm của quả bóng golf tính theo thời gian ()ts
b) Sau bao lâu kể từ khi vận động viên đánh bóng thì bóng lại chạm đất? Lời giải
a) Xét hàm số bậc hai biểu thị độ cao h phụ thuộc t có dạng 2 () =++ htatbtc , trong đó a khác 0. Theo đề bài:
Với 0,0==th , ta có: 0 = c nên 2 () =+ htatbt . Khi đó:
+ Với 1,48==th , ta có: 2 114848 +=+= abab
+ Với 2,64==th , ta có: 2 22644264 +=+= abab
Giải hệ phương trình 4816 426464 +==− +== aba abb . Suy ra 2 ()1664 =−+ httt
OFFICIAL
Thay các giá trị tương ứng còn lại của bảng vào công thức trên, ta thấy phù hợp. Vậy hàm số bậc hai cần tìm là 2 ()1664 =−+ httt
b) Bóng chạm đất khi 2 ()1664 =−+ httt . Suy ra ta có: 0 = t hoặc 4 = t Vậy sau 4 giây kể từ khi vận động viên đánh bóng thì bóng lại chạm đất.
Câu 79: Bác Năm dự định trồng khoai lang và khoai mì trên mảnh đất có diện tích 8 ha. Nếu trồng 1 ha khoai lang thì cần 10 ngày công và thu được 20 triệu đồng. Nếu trồng 1 ha khoai mì thì cần 15 ngày công và thu được 25 triệu đồng. Bác Năm cần trồng bao nhiêu hecta cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng được không quá 90 ngày công cho việc trồng khoai lang và khoai mì.
giải Gọi x là số hecta trồng khoai lang và y là số hecta trồng khoai mì.
DẠYKÈMQUYNHƠN
Ta có hệ bất phương trình mô tả các điều kiện ràng buộc: 8 101590 0 0. xy xy x y + + Biểu diễn miền nghiệm của hệ bất phương trình trên hệ trục toạ độ Oxy ta được miền đa giác OABC. Toạ độ các đỉnh của đa giác đó là: (0;0);(0;6);(6;2);(8;0) OABC
Lời
Gọi F là số tiền (đơn vị: triệu đồng) bác Năm thu được, ta có: 2025=+ Fxy .
Ta phải tìm , xy thoả mãn hệ bất phương trình sao cho F lớn nhất, nghĩa là tìm giá trị lớn nhất của 2025=+ Fxy trên miền đa giác OABC
Tính các giá trị của biểu thức F tại các đỉnh của đa giác, ta có:
Tại (0;0):20.025.00 =+= OF ;


Tại (0;6):20.025.6150 =+= AF ;
Tại (6;2):20.625.2170 =+= BF ;
Tại (8;0):20.825.0160 =+= CF .
Ta thấy F đạt giá trị lớn nhất bằng 170 tại (6;2)B

Vậy để thu được nhiều tiền nhất, bác Năm cần trồng 6 ha khoai lang và 2 ha khoai mì.
Câu 80: Quan sát cây cầu dây văng minh hoạ ở Hình 25.
Tại trụ cao nhất, khoảng cách từ đỉnh trụ (vị trí A ) tới chân trụ trên mặt cầu (vị trí H ) là 150m , độ dài dây văng dài nhất nối từ đỉnh trụ xuống mặt cầu (vị trí B ) là 300m, khoảng cách từ chân dây văng dài nhất tới chân trụ trên mặt cầu là 250m (Hình 26). Tính độ dốc của cầu qua trụ nói trên (làm tròn kết quả đến hàng phần mười theo đơn vị độ). Lời giải
DẠYKÈMQUYNHƠN
OFFICIAL
KBH Xét tam giác ABH , áp dụng định lí côsin ta có: 2222222501503001 cos93,8. 2.2.250.15015 +−+− ===− BHAHAB AHBAHB BHAH Xét tam giác BHK ta có: 93,8903,8 −= HBK (tính chất góc ngoài tam giác). Vậy
của cầu qua trụ
.
Độ dốc của cầu là góc nghiêng giữa đường cầu qua trụ và phương nằm ngang, tức là góc
độ dốc
theo đề bài là khoảng 3,8
tích trong chất lỏng. Tìm mối liên hệ giữa trọng lực P của vật và lực đẩy Archimedes F mà chất lỏng tác động lên vật. Tính tỉ số giữa trọng lượng riêng của vật và của chất lỏng.
Lời giải
Lực đẩy Archimedes AF và trọng lực P đều tác động lên vật theo phương thẳng đứng, hai lực này ngược hướng. Do ở trạng thái cân bằng vật nổi (chìm một nửa), nên hai lực này có cường đọ bằng nhau.
Gọi d , d' tương ứng là trọng lượng riêng của vật và trọng lượng riêng của chất lỏng: gọi V là thể tích của vật. Khi đó trọng lượng của vật bằng || == PPdV . (1)
Lực đẩy Archimedes tác động lên vật có cường độ bằng 2 == Aa V FFd . (2)
Từ (1) và (2), để ý rằng = APF , suy ra 2 = d d
DẠYKÈMQUYNHƠN
OFFICIAL Câu 81: Một vật đồng chất được thả vào một cốc chất lỏng. Ở trạng thái cân bằng, vật chìm một nửa thể
1. Trắc nghiệm
Câu 1: Trong các phát biểu sau, phát biểu nào là mệnh đề toán học?
A. Nước là hợp chất tạo bởi hai nguyên tố là hydrogen và oxygen.
B. Sông Hương là con sông chảy qua thành phố Huế.
C. Ngày 30 tháng 4 năm 1975 là ngày Giải phóng miền Nam.
D. Số 2022 chia hết cho 4.
Câu 2: Mệnh đề phủ định của P : "Tam giác ABC là tam giác cân" là:
A. Tam giác ABC không phải là tam giác cân
B. Tam giác ABC là tam giác vuông
C. Tam giác ABC là tam giác đều
D. ABC không phải là một tam giác
Câu 3: Kí hiệu , lần lượt là tập số hữu tỉ, tập số thực. Kết luận nào sau đây là đúng?
A. B. C. D.
Câu 4: Cho hai tập hợp {2;5},{(5)()()0} ==−−−= ABxxxaxb với , ab là các số thực cho trước. Tất cả các cặp số (;) ab đề = AB là: A. (2;2),(5;5),(5;2). B. (2;2),(2;5),(5;2). C. (2;5),(2;2),(5;5) D. (2;2),(2;5),(5;2),(5;5)

Câu 5: Cho hai tập hợp , AB phân biệt và khác rỗng thoả mãn = ABA. Kết luận nào sau đây là đúng?
A. BA B. AB C. =AB D. \ = ABA
Câu 6: Tập nghiệm của bất phương trình 350 xy−+ là
A. Nửa mặt phẳng chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (không bao gồm đường thẳng).
B. Nửa mặt phẳng không chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (bao gồm đường thẳng).
C. Nửa mặt phẳng không chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (không bao gồm đường thẳng).
D. Nửa mặt phẳng chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (không bao gồm đường thẳng).
Câu 7: Miền nghiệm của bất phương trình 236 xy+ (miền không bị gạch) được biểu diễn bởi hình vẽ nào dưới đây? A.
DẠYKÈMQUYNHƠN
ĐỀ SỐ 3
OFFICIAL
B. C. D. Câu 8: Có bao nhiêu hệ bất phương trình bậc nhất hai ẩn trong ba hệ bất phương trình sau đây?
A. 0. B. 1. C. 2. D. 3. Câu 9: Miền nghiệm của hệ bất phương trình 2021 2022 xy xy
KHÔNG chứa điểm nào sau đây? A. (1001;1021). B. (2021;0). C. (2021;2022) D. (2021;2022).
Câu 10: Công ty trách nhiệm hữu hạn ĐỨC MẠNH trong một đợt quảng cáo và bán khuyến mãi hàng hoá (một sản phẩm mới của công ty) cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B . Trong đó xe loại A có 10 chiếc, xe loại B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, loại B giá 3 triệu đồng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất? Biết rằng xe loại A chỉ chở tối đa 20 người và 0,6 tấn hàng. Xe loại B chỉ chở tối đa 10 người và 1,5 tấn hàng. A. 4 xe loại A và 5 xe loại B
B. 5 xe loại A và 6 xe loại B . C. 5 xe loại A và 4 xe loại B D. 6 xe loại A và 4 xe loại B . Câu 11: Cho là góc tù và 1 sincos 2 += . Giá trị của 33 sincos M =− là



DẠYKÈMQUYNHƠN OFFICIAL
2
3(1)3(1)211. 345 xyxyyx xy yxxy xy −++ − ++− +
234(3)(5) ;2(5)và
−
+
A. 37 16 B. 117 16 .
C. 57 16 . D. 57 16 .
Câu 12: Cho 1 sin 3 = với 090 . Giá trị của cos là A. 2 3 . B. 2 3 C. 22 3 D. 22 3 .
Câu 13: Cho tan3 =− . Giá trị của cos là A. 1 2 . B. 1 2 . C. 1 4 D. 1 4
Câu 14: Tam giác ABC có 0 150,3,2. === CBCAC Tính cạnh AB ? A. 13 B. 3. C. 10 D. 1
Câu 15: Cho tam giác ABC , biết 24,13,15.abc=== Tính góc A? A. 0 3334'. B. 0 11749'. C. 0 2837'. D. 0 5824'.
Câu 16: Cho tam giác ABC có 3,5ABBC== và độ dài đường trung tuyến 13 BM = . Tính độ dài AC A. 11. B. 4. C. 9 2 . D. 10 .
Câu 17: Cho tam giác ABC vuông tại A có ABa = , 2 ACa = . Diện tích tam giác ABC là A. 2 2a B. 2 4a C. 2 3 2 a D. 2 a .
Câu 18: Cho tam giác ABC có góc ABC bằng 060 , = ACa . Tính bán kính đường tròn ngoại tiếp tam giác ABC ?
A. a . B. 3 3 a . C. 43 3 a . D. 3 a .
Câu 19: Hai vectơ được gọi là bằng nhau khi và chỉ khi
DẠYKÈMQUYNHƠN
OFFICIAL
A. Giá của chúng trùng nhau và độ dài của chúng bằng nhau
B. Chúng trùng với một trong các cặp cạnh đối của một hình bình hành
C. Chúng trùng với một trong các cặp cạnh của một tam giác đều.
D. Chúng cùng hướng và độ dài của chúng bằng nhau.
Câu 20: Cho hình bình hành ABCD. Khẳng định nào sau đây là đúng.
A. ABACAD += B. ABACDA −= C. ABACCB += D. ABACBC −=
Câu 21: Cho hàm số ( ) 2
x x fx x xx
223khi2 1 2khi2
+
. Tính ( ) ( )22Pff=+− . A. 3 P = . B. 2 P = . C. 7 3 P = . D. 6 P = .
Câu 22: Trong các hàm số sau, hàm số nào là hàm đồng biến trên ? A. 12 yx =− B. 32yx=+ C. 2 21yxx=+− D. ( )223yx=−− .
Câu 23: Một vật có khối lượng m được treo cố định trên trần nhà bằng hai sợi dây không dãn có độ dài như nhau. Biết rằng lực căng dây 1T và 2T có độ lớn như nhau bằng 600N và hợp với nhau một góc 60 (hình bên). Trọng lượng của vật là

DẠYKÈMQUYNHƠN
OFFICIAL
=
tam giác ABC
là đúng? A. 3=− AMGM B. 3 2 = AMGM . C. 3 2 = AMGM .
3 = AMGM .
Cho tam
A. 600N B. 6003 N C. 1200N . D. 12003 N Câu 24: Cho
và M là trung điểm của , BCG là trọng tâm của tam giác. Khẳng định nào sau đây
D.
Câu 25:
giác ABC . Gọi I là trung điểm của BC .Khẳng định nào sau đây đúng A. BIIC B. 32BIIC C. 2 BIIC D. 2BIIC Câu 26: Giao điểm của parabol 2 ():32 Pyxx=−+ với đường thẳng 1 yx=− là:
A. ( ) ( )1;0;3;2 . B. ( ) ( )0;1;2;3 .
C. ( ) ( )1;2;2;1 . D. ( ) ( )2;1;0;1 .
Câu 27: Một chiếc ăng ten chảo parabol có chiều cao 0,5 hm = và đường kính miệng 4 dm = . Mặt cắt
qua trục là một parabol dạng 2 yax = . Biết m a n = , trong đó m, n là các số nguyên dương nguyên tố cùng nhau. Tính mn
A. 7 mn−= B. 7 mn−=− C. 31 mn−= D. 31 mn−=−
Câu 28: Cho tam giác ABC . Giá trị của biểu thức BACA bằng:
A. cos ABACBAC . B. cos −ABACBAC . C. cos ABACABC . D. cos ABACACB .
Câu 29: Cho tam giác ABC cân tại A , o ˆ 120 A = và ABa = . Tính . BACA
A. 2 2 a . B. 2 2 a . C. 2 3 2 a . D. 2 3 2 a .
Câu 30: Cho hình vuông ABCD tâm O . Hỏi mệnh đề nào sau đây sai? A. .0 = OAOB B. 1 2 = OAOCOAAC C. .. = ABACABCD . D. .. = ABACACAD .
Câu 31: Biết số gần đúng 7975421 a = có độ chính xác 150 d = . Hãy ước lượng sai số tương đối của a A. 0,0000099 a B. 0,000039 a C. 0,0000039 a D. 0,000039 a Câu 32: Biết số gần đúng 173,4592 a = có sai số tương đối không vượt quá 1 10000 , hãy ước lượng sai số tuyệt đối của a và viết a dưới dạng chuẩn. A. 0,17;173,4 a a = B. 0,017;173,5 a a = C. 0,4592;173,5 a a = D. 0,017;173,4 a a =
Câu 33: Thời gian chạy 50m của 20 học sinh được ghi lại trong bảng dưới đây: Thời gian (giây) 8,3 8,4 8,5 8,7 8,8 Tần số 2 3 9 5 1 Hỏi trung bình mỗi học sinh chạy 50m hết bao lâu ? A. 8,54. B. 4. C. 8,50. D. 8,53.
Câu 34: Một tổ học sinh gồm 10 học sinh có điểm kiểm tra giữa học kì 2 môn toán như sau: 5;6;7;5;8;8;10;9;7;8. Tính điểm trung bình của tổ học sinh đó. A. 7 . B. 8. C. 7,3. D. 7,5.
Câu 35: Để đánh giá mức độ phân tán của các số liệu thống kê so với số trung bình, ta dùng đại lượng nào sau đây? A. Số trung bình. B. Số trung vị C. Mốt. D. Phương sai.
DẠYKÈMQUYNHƠN
OFFICIAL
2. Tự luận
Câu 36: Để mua được một chiếc xe đạp thể thao trị giá 15 triệu đồng, bạn Nam hàng ngày bỏ vào lợn đất tiết kiệm 50000 đồng từ tiền tiêu vặt mẹ cho.
a) Thiết lập hàm số biểu thị số tiền y (nghìn đồng) bạn Nam tiết kiệm được theo thời gian t (ngày) và số tiền ban đầu a (nghìn đồng) mà bạn Nam có.
b) Nếu ban đầu bạn Nam có 5000000 đồng thì sau bao lâu bạn Nam mới có thể mua được chiếc xe đạp đó (giả sử giá chiếc xe đó không đổi)?
Câu 37: Tìm giá tri lớn nhất và giá tri nhỏ nhất của biểu thức (;)2 =+ Fxyxy với (;) xy thuộc miền nghiệm của hệ bất phương trình

Câu 38: Một người đứng ở vị trí A trên nóc một ngôi nhà cao 4m đang quan sát một cây cao cách ngôi nhà 20m và đo được 45 = BAC (Hình 27). Tính chiều cao của cây đó (làm tròn kết quả đến hàng phần mười theo đơn vị mét).
OFFICIAL
Câu 39: Máy bay A đang bay về hướng Đông Bắc với tốc độ 600 / kmh. Cùng lúc đó, máy bay B đang bay về hướng Tây Nam với tốc độ 800 / kmh . Biểu diễn vectơ vận tốc b của máy bay B theo vectơ vận tốc a của máy bay A
DẠYKÈMQUYNHƠN
xy x y
4 0 0 +
Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM 1D 2A 3C 4B 5A 6C 7C 8C 9D 10C 11D 12D 13A 14A 15B 16B 17D 18B 19D 20B 21A 22B 23B 24D 25A 26A 27B 28A 29B 30C 31B 32B 33D 34C 35D 1. Trắc nghiệm Câu 40: Trong các phát biểu sau, phát biểu nào là mệnh đề toán học? A. Nước là hợp chất tạo bởi hai nguyên tố là hydrogen và oxygen. B. Sông Hương là con sông chảy qua thành phố Huế.
C. Ngày 30 tháng 4 năm 1975 là ngày Giải phóng miền Nam. D. Số 2022 chia hết cho 4.
Câu 41: Mệnh đề phủ định của P : "Tam giác ABC là tam giác cân" là:
A. Tam giác ABC không phải là tam giác cân
B. Tam giác ABC là tam giác vuông C. Tam giác ABC là tam giác đều D. ABC không phải là một tam giác Câu 42: Kí hiệu , lần lượt là tập số hữu tỉ, tập số thực. Kết luận nào sau đây là đúng? A. . B. . C. . D. . Câu 43: Cho hai tập hợp {2;5},{(5)()()0}
ABxxxaxb với , ab là các số thực cho trước. Tất cả các cặp số (;) ab đề = AB là: A. (2;2),(5;5),(5;2) B. (2;2),(2;5),(5;2) C. (2;5),(2;2),(5;5) D. (2;2),(2;5),(5;2),(5;5) Lời giải (5)()()05;; −−−==== xxaxbxxaxb Để = AB thì trong hai số , ab chắc chắn phải có một số bằng 2, số còn lại bằng 2 hoặc 5. Vậy ta có: (;)(2;2),(2;5),(5;2) = ab Chọn B


Câu 44: Cho hai tập hợp , AB phân biệt và khác rỗng thoả mãn = ABA. Kết luận nào sau đây là đúng? A. BA. B. AB . C. =AB . D. \ = ABA . Câu 45: Tập nghiệm của bất phương trình 350 xy−+ là
A. Nửa mặt phẳng chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (không bao gồm đường thẳng).
B. Nửa mặt phẳng không chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (bao gồm đường thẳng).
C. Nửa mặt phẳng không chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (không bao gồm đường thẳng).
D. Nửa mặt phẳng chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (không bao gồm đường thẳng).
Câu 46: Miền nghiệm của bất phương trình 236 xy+ (miền không bị gạch) được biểu diễn bởi hình vẽ nào dưới đây? A. B.
DẠYKÈMQUYNHƠN
OFFICIAL
==−−−=
chứa điểm nào sau đây? A. (1001;1021). B. (2021;0). C. (2021;2022) D. (2021;2022).


Câu 49: Công ty trách nhiệm hữu hạn ĐỨC MẠNH trong một đợt quảng cáo và bán khuyến mãi hàng hoá (một sản phẩm mới của công ty) cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B . Trong đó xe loại A có 10 chiếc, xe loại B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, loại B giá 3 triệu đồng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất? Biết rằng xe loại A chỉ chở tối đa 20 người và 0,6 tấn hàng. Xe loại B chỉ chở tối đa 10 người và 1,5 tấn hàng.
A. 4 xe loại A và 5 xe loại B
B. 5 xe loại A và 6 xe loại B .
C. 5 xe loại A và 4 xe loại B
D. 6 xe loại A và 4 xe loại B .
Lời giải Gọi x và y lần lượt là số xe loại A và (010;09;,) Bxyxy . Khi đó tổng chi phí thuê
DẠYKÈMQUYNHƠN OFFICIAL
2 234(3)(5) ;2(5)và 3(1)3(1)211. 345 xyxyyx xy yxxy xy −++ − ++− + A.
2021
xy − +
C. D. Câu 47: Có bao nhiêu hệ bất phương trình bậc nhất hai ẩn trong ba hệ bất phương trình sau đây?
0. B. 1. C. 2. D. 3. Câu 48: Miền nghiệm của hệ bất phương trình
2022 xy
KHÔNG
xe là 43 Txy =+ (triệu đồng). Xe A chở tối đa 20 người, xe B chở tối đa 10 người nên tổng số người 2 xe chở tối đa được là 2010xy + (người). Xe A chở được 0,6 tấn hàng, xe B chở được 1,5 tấn hàng nên tổng lượng hàng 2 xe chở được là 0,61,5xy + (tấn).
các
phí thấp
công
bỏ
,
thấy
DẠYKÈMQUYNHƠN OFFICIAL
A. 37 16
16 .
. Lời
=−+ . Từ 113
244 ra +==−=− Mặt khác 2 (sincos)12sincos −=− Suy ra 7 sincos 2 −= (vì là góc
= . Câu 51: Cho 1 sin 3 = với 090 . Giá trị của cos là A. 2 3 . B. 2 3 . C. 22 3 D. 22 3 . Lời giải Ta có 2 2 122 cos1sin1 33 =−=−= Câu 52: Cho tan3 =− . Giá trị của cos là A. 1 2 .
Theo giả thiết, ta có 010 09 2010140(*) 0,61,59 x y xy xy + + tứ giác với 5 (10;2),(10;9),;9,(5;4) 2 ABCD Biểu thức 43 Txy =+ đạt giá trị nhỏ nhất tại một trong
đỉnh của tứ giác ABCD
ta
T đạt giá trị nhỏ nhất tại 5 x = và 4 y = . Khi đó, chi
nhất mà
ty
ra là 32 triệu đồng. Câu 50: Cho là góc tù và 1 sincos 2 += . Giá trị của 33 sincos M =− là
B. 117
C. 57 16 D. 57 16
giải (sincos)(1sincos) M
sincossuysincos1
tù). Do đó, 57 16 M
B. 1 2 C. 1 4 D. 1 4
Lời giải Ta có 2 2 1 1tan cos += . Suy ra 2 1 cos 4 = . Vì tan30 =− nên 1 cos 2 =− .
Câu 53: Tam giác ABC có 0 150,3,2. === CBCAC Tính cạnh AB ?
A. 13 . B. 3. C. 10. D. 1. Lời giải Chọn A Theo định lí cosin trong ABC ta có: Câu 54: 222 2..cos =+− ABCACBCACBC 13= 13 = AB . ChọnA.
Câu 55: Cho tam giác ABC , biết 24,13,15.abc=== Tính góc A? A. 0 3334'. B. 0 11749'. C. 0 2837'. D. 0 5824'. Lời giải Chọn B. Ta có: 222222 0 1315247 cos11749'. 22.13.1515 bca AA bc +−+− ===−
A
3 M C B
13 5
Câu 56: Cho tam giác ABC có 3,5ABBC== và độ dài đường trung tuyến 13 BM = . Tính độ dài AC . A. 11 B. 4 C. 9 2 D. 10 Lời giải Chọn B Theo công thức tính độ dài đường trung tuyến;ta có: ( ) 222222 2 2 35 134 2424 BABCACAC BMAC ++ =−=−=
Câu 57: Cho tam giác ABC vuông tại A có ABa = , 2 ACa = . Diện tích tam giác ABC là
DẠYKÈMQUYNHƠN
OFFICIAL
A. 2 2a B. 2 4a C. 2 3 2 a D. 2 a .
Lời giải
Tam giác ABC vuông tại A có ABa = , 2 ACa = . Khi đó 2 1 2 ABC SABACa ==
Câu 58: Cho tam giác ABC có góc ABC bằng 060 , = ACa . Tính bán kính đường tròn ngoại tiếp tam giác ABC ?
A. a . B. 3 3 a . C. 43 3 a . D. 3 a . Lời giải
Theo Định lí Sin ta có: ==== 0 3 2 sin2.sin3 2sin60 ACACaa RR BB
Câu 59: Hai vectơ được gọi là bằng nhau khi và chỉ khi
A. Giá của chúng trùng nhau và độ dài của chúng bằng nhau
B. Chúng trùng với một trong các cặp cạnh đối của một hình bình hành
C. Chúng trùng với một trong các cặp cạnh của một tam giác đều.
D. Chúng cùng hướng và độ dài của chúng bằng nhau.
Lời giải
Chọn D
Hai véc tơ được gọi là bằng nhau khi và chỉ khi chúng cùng hướng và độ dài của chúng bằng nhau.
Câu 60: Cho hình bình hành ABCD. Khẳng định nào sau đây là đúng.
A. ABACAD += . B. ABACDA −= . C. ABACCB += . D. ABACBC −= . Lời giải Chọn B
DẠYKÈMQUYNHƠN
OFFICIAL
Ta có ABACCB −= . Do ABCD là hình bình hành nên D C A B = nên ABACDA −= . Câu 61: Cho hàm số ( ) 2 223khi2 1 2khi2 x x fx x xx = + . Tính ( ) ( )22Pff=+− A. 3 P = B. 2 P = C. 7 3 P = D. 6 P = Lời giải Chọn A Ta có: ( ) ( ) ( )2 2223 2222 21 ff+−=+−+ 3 P = . O D A B C
Câu 62: Trong các hàm số sau, hàm số nào là hàm đồng biến trên ? A. 12 yx =− B. 32yx=+ C. 2 21yxx=+− D. ( )223yx=−− . Lời giải Chọn B. 32yx=+ đồng biến trên vì có hệ số góc 30 a = Câu 63: Một vật có khối lượng m được treo cố định trên trần nhà bằng hai sợi dây không dãn có độ dài như nhau. Biết rằng lực căng dây 1T và 2T có độ lớn như nhau bằng 600N và hợp với nhau một góc 60 (hình bên). Trọng lượng của vật là A. 600N B. 6003 N . C. 1200N . D. 12003 N


DẠYKÈMQUYNHƠN
OFFICIAL
Lời
Ta có 12222cos302cos30TOHOAT === 3 26006003(). 2 N == Vậy trọng lượng của vật là 6003
. Đáp án
Câu 64: Cho tam giác ABC và M là trung điểm của , BCG là trọng tâm của tam giác. Khẳng
nào sau đây là đúng? A. 3=− AMGM B. 3 2 = AMGM .
giải Xét tam giác OAH như hình vẽ.
N
là B
định
C. 3 2 = AMGM . D. 3 = AMGM . Lời giải Chọn D

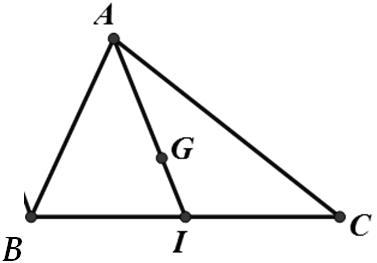
Câu 65: Cho tam giác ABC . Gọi I là trung điểm của BC .Khẳng định nào sau đây đúng A. BIIC B. 32BIIC C. 2 BIIC D. 2BIIC Lời giải
Chọn A Vì I là trung điểm của BC nên BICI và BI cùng hướng với IC do đó hai vectơ BI , IC bằng nhau hay BIIC . Câu 66: Giao điểm của parabol 2 ():32 Pyxx=−+ với đường thẳng 1 yx=− là: A. ( ) ( )1;0;3;2 B. ( ) ( )0;1;2;3 C. ( ) ( )1;2;2;1 D. ( ) ( )2;1;0;1 Lờigiải Chọn A Phương trình hoành độ giao điểm: 2 321xxx−+=− 2 430xx −+= 1 3 x x =
DẠYKÈMQUYNHƠN
OFFICIAL
. Câu 67: Một chiếc ăng ten chảo parabol có chiều cao 0,5 hm = và đường kính miệng 4 dm = . Mặt cắt qua trục là một parabol dạng 2 yax = . Biết m a n = , trong đó m, n là các số nguyên dương nguyên tố cùng nhau. Tính mn A. 7 mn−= B. 7 mn−=− C. 31 mn−= D. 31 mn−=− Lời giải Đáp án B. Từ giả thiết suy ra parabol 2 yax = đi qua điểm 1 2; 2 I
= . 110xyx==−= 312xyx==−= Hai giao điểm là: ( ) ( )1;0;3;2
Từ đó ta có 2 11 .2 28 aa == Vậy 187 mn−=−=− .
Câu 68: Cho tam giác ABC . Giá trị của biểu thức BACA bằng:
A. cos ABACBAC . B. cos −ABACBAC . C. cos ABACABC . D. cos ABACACB . Lời giải Chọn A
Câu 69: Cho tam giác ABC cân tại A , o ˆ 120 A = và ABa = . Tính . BACA A. 2 2 a . B. 2 2 a . C. 2 3 2 a . D. 2 3 2 a . Lời giải Chọn B Ta có o2 1 ...cos120 2 ==− BACABACAa
Câu 70: Cho hình vuông ABCD tâm O . Hỏi mệnh đề nào sau đây sai? A. .0 = OAOB . B. 1 .. 2 = OAOCOAAC . C. = ABACABCD D. = ABACACAD Lời giải Chọn C
Câu 71: Phương án A: ⊥ OAOB suy ra .0 = OAOB nên loạiA. Phương án B: .0 = OAOC và 1 .0 2 = OAAC suy ra 1 ..0 2 ==OAOCOAAC nên loại B. Phương án C: o2 2 ...cos45.2. 2 === ABACABACABABAB . 02...cos180==− ABCDABDCAB ..ABACABCD nên chọn C. Câu 72: Biết số gần đúng 7975421 a = có độ chính xác 150 d =
DẠYKÈMQUYNHƠN
OFFICIAL
. Hãy ước lượng sai số tương đối của a. A. 0,0000099 a B. 0,000039 a C. 0,0000039 a D. 0,000039 a Lời giải Theo Ví dụ 1 ta có các chữ số đáng tin của a là 3, 7, 9, 7, 5 Cách viết chuẩn của 337975.10 a = Sai số tương đối thỏa mãn: 150 0,0000039 37975421 a = (tức là không vượt quá 0,0000039 ). Câu 73: Biết số gần đúng 173,4592 a = có sai số tương đối không vượt quá 1 10000 , hãy ước lượng sai số tuyệt đối của a và viết a dưới dạng chuẩn. A. 0,17;173,4 a a = B. 0,017;173,5 a a = C. 0,4592;173,5 a a = D. 0,017;173,4 a a = Lời giải
Từ công thức a a a = , ta có 1 173,4592.0,017 10000 a =
Vậy chữ số đáng tin là 1, 7, 3, 4. Dạng chuẩn của a là 173,5 a = . Đáp án B.
Câu 74: Thời gian chạy 50m của 20 học sinh được ghi lại trong bảng dưới đây: Thời gian (giây) 8,3 8,4 8,5 8,7 8,8 Tần số 2 3 9 5 1
Hỏi trung bình mỗi học sinh chạy 50m hết bao lâu ? A. 8,54. B. 4. C. 8,50. D. 8,53. Lời giải
Chọn D Thời gian trung bình để mỗi học sinh chạy được 50m là 8,3.28,4.38,5.98,7.58,8 8,53 20 x ++++ == .
Câu 75: Một tổ học sinh gồm 10 học sinh có điểm kiểm tra giữa học kì 2 môn toán như sau: 5;6;7;5;8;8;10;9;7;8. Tính điểm trung bình của tổ học sinh đó. A. 7 . B. 8. C. 7,3. D. 7,5. Lời giải Chọn C Điểm trung bình của tổ học sinh đó là: 5.267.28.3910 7,3 10 x +++++ ==
Câu 76: Để đánh giá mức độ phân tán của các số liệu thống kê so với số trung bình, ta dùng đại lượng nào sau đây?
A. Số trung bình. B. Số trung vị C. Mốt. D. Phương sai. Lời giải Chọn D Dựa vào ý nghĩa của phương sai và độ lệch chuẩn để đo mức độ phân tán của các số liệu trong mẫu quanh số trung bình.
2. Tự luận
Câu 77: Để mua được một chiếc xe đạp thể thao trị giá 15 triệu đồng, bạn Nam hàng ngày bỏ vào lợn đất tiết kiệm 50000 đồng từ tiền tiêu vặt mẹ cho. a) Thiết lập hàm số biểu thị số tiền y (nghìn đồng) bạn Nam tiết kiệm được theo thời gian t (ngày) và số tiền ban đầu a (nghìn đồng) mà bạn Nam có. b) Nếu ban đầu bạn Nam có 5000000 đồng thì sau bao lâu bạn Nam mới có thể mua được chiếc xe đạp đó (giả sử giá chiếc xe đó không đổi)? Lời giải a) Hàm số biểu thị số tiền bạn Nam tiết kiệm được theo thời gian t là: 50 =+ yta
DẠYKÈMQUYNHƠN
OFFICIAL
b) Ta có: 5000 = a nên 505000=+yt Bạn Nam đủ tiền mua xe đạp khi 1500050500015000200 =+== ytt . Vậy sau 200 ngày thì bạn Nam đủ tiền mua xe đạp thể thao.
nghiệm của hệ bất phương trình 4 0 0
+
xy x y Lời giải
+
xy x y
Bước 1. Xác định miền nghiệm của hệ bất phương trình 4 0 0
Miền nghiệm của hệ bất phương trình trên là miền tam giác OAB với các đỉnh (0;0),(0;4),(4;0)OAB .
Bước 2. Tính giá trị của F tại các đỉnh của tam giác: ( ) ( ) ( ) 0;00,4;04,0;48 . FFF===
Bước 3. So sánh các giá trị thu được của F ở Bước 2, ta được giá trị nhỏ nhất là 0 và giá trị lớn nhất là 8.
Vậy giá trị nhỏ nhất cần tìm của F là (0;0)0 = F và giá trị lớn nhất cần tìm là (0;4)8 = F . Câu 79: Một người đứng ở vị trí A trên nóc một ngôi nhà cao 4m đang quan sát một cây cao cách ngôi nhà


DẠYKÈMQUYNHƠN OFFICIAL
ấ
ủa biểu
ức
ộc miền
Câu 78: Tìm giá tri lớn nhất và giá tri nhỏ nh
t c
th
(;)2 =+ Fxyxy với (;) xy thu
Lời giải Xét tam giác vuông ABH ta có: 22 420426()=+= ABm (định lí Pythagore) và 4 tan0,211,3 20 ==ABHABH . Do đó, 9011,378,7 −= ABC . Suy ra 1804578,756,3 −−= ACB . Áp dụng định lí sin cho tam giác ABC ta có: sinsin = BCAB AC sin426sin45 17,3() sinsin56,3 = ABA BCm C Vậy cây cao khoảng 17,3m
20m và đo được 45
= BAC (Hình 27). Tính chiều cao của cây đó (làm tròn kết quả đến hàng phần mười theo đơn vị mét).
Câu 80: Máy bay A đang bay về hướng Đông Bắc với tốc độ 600 / kmh. Cùng lúc đó, máy bay B đang bay về hướng Tây Nam với tốc độ 800 / kmh . Biểu diễn vectơ vận tốc b của máy bay B theo vectơ vận tốc a của máy bay A
Lời giải
Vecto , ab là vecto vận tốc của máy bay A và máy bay b.
Do đó ||,|| ab lần lượt là độ lớn của vecto vận tốc tương ứng.
Ta có: ||600,||800 ==ab ||8004 ||6003 b a ==
Hai hướng Đông Bắc và Tây Nam là ngược nhau, do đó 4 3 ba =−

DẠYKÈMQUYNHƠN OFFICIAL
1. Trắc nghiệm
Câu 1. Cho mệnh đề A: "8 không chia hết cho 2 " và mệnh đề :B " 31 ". Xét các mệnh đề sau:
a) Mệnh đề AB . b) Mệnh đề BA . c) Mệnh đề AB d) Mệnh đề AB . Số mệnh đề đúng trong các mệnh đề trên là A. 1. B. 2. C. 3. D. 4. Câu 2. Mệnh đề phủ định của mệnh đề :",230"Txx−+ là A. " ,230xx −+ ". B. " ,230"xx −+ C. " ,230"xx −+ . D. " ,230"xx −+ . Câu 3. Cho hai tập hợp {;} = Aab và {;;;;} = Babcde . Có bao nhiêu tập hợp X mà AXB ? A. 6. B. 7. C. 8. D. 11. Câu 4. Cho tập hợp {20} =−Axx . Tập hợp A là: A. {2;1;0}=−− A B. [2;0]=− A C. (2;0)=− A D. {2;0}=− A Câu 5. Cho hai tập hợp [5;0],[0;) =−=+AB . Khi đó: A. {0} =AB B. =AB C. [5;)=−+AB D. (5;)=−+AB Câu 6. Miền nghiệm của bất phương trình 35xy−− là nửa mặt phẳng chứa điểm A. (3;0). B. (3;1). C. (1;3). D. (0;0)
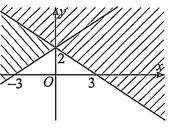
Câu 7. Phần không bị gạch (không kể d) ở Hình 4 là miền nghiệm của bất phương trình: A. 326 +xy B. 236 +xy C. 236 +xy D. 326 +xy Câu 8. Miền không bị gạch (tính cả biên) trong hình vẽ dưới đây là miền nghiệm của hệ bất phương trình bậc nhất hai ẩn nào sau đây?

DẠYKÈMQUYNHƠN
ĐỀ SỐ 4
OFFICIAL
A. 236 236 xy xy + −− B. 236 236 xy xy + −−
D. 236 236 xy xy +
−
. Câu 9. Miền nghiệm của hệ bất phương trình bậc nhất hai ẩn 20112022 0 xy y +
nằm trong góc phần tư nào? A. I. B. II. C. III. D. IV. Câu 10. Một xưởng có một máy cắt và một máy tiện dùng để sản xuất trục sắt và đinh ốc. Để sản xuất 1 tấn trục sắt thì lần lượt máy cắt chạy trong 3 giờ và máy tiện chạy trong 1 giờ, tiền lãi là 2 triệu đồng. Để sản xuất 1 tấn đinh ốc thì lần lượt máy cắt và máy tiện chạy trong 1 giờ, tiền lãi là 1 triệu đồng. Một máy không thể đồng thời sản xuất cả hai loại. Máy cắt làm không quá 6 giờ/ngày, máy tiện làm không quá 4 giờ/ngày. Hỏi một ngày xưởng nên sản xuất bao nhiêu tấn mối loại để tiền lãi là cao nhất?
A. 2 tấn trục sắt và 2 tấn đinh ốc.
B. 3 tấn trục sắt và 1 tấn đinh ốc.
C. 2 tấn trục sắt và 3 tấn đinh ốc. D. 1 tấn trục sắt và 3 tấn đinh ốc.
Câu 11. Rút
DẠYKÈMQUYNHƠN OFFICIAL
C. 236 236 xy xy +−
−−
là A. 2.
2.
2 .
2 Câu 13. Trên nửa đường tròn đơn vị, cho điểm M sao cho 120 = MOx . Toạ độ điểm M là: A. 31 ; 22 . B. 31 ; 22 C. 13 ; 22 D. 13 ; 22 . Câu 14. Cho ;;cab là độ dài 3 cạnh của tam giác ABC . Biết 7 = b ; 5 = c ; 4 cos 5 A = . Tính độ dài của a . A. 32 . B. 72 2 . C. 23 8 . D. 6.
gọn biểu thức tansin sincot xx M xx =− với ( ) 0;90 x
ta được A. sin x B. cos x C. 1 sin x D. 1 cos x . Câu 12. Cho là góc tù và tancot2 +=− . Giá trị của sincos M =−
B.
C.
D.
Câu 15. Tam giác ABC có 6,42,2.abc=== M là điểm trên cạnh BC sao cho 3 BM = . Độ dài đoạn AM bằng bao nhiêu?
A. 9. B. 9. C. 3. D. 1 108. 2
Câu 16. Cho tam giác ABC có góc 60 BAC = và cạnh 3 BC = . Tính bán kính của đường tròn ngoại tiếp tam giác ABC
A. 4 R = B. 1 R = C. 2 R = D. 3 R =
Câu 17. Tam giác ABC có 6812'= A , 3444'= B , 117. = AB Khi đó độ dài AC xấp xỉ bằng ?
A. 68. B. 168. C. 118. D.200.
Câu 18. Tam giác ABC có 6cm = AB , 30 = BAC , 75 = ACB . Tính diện tích của tam giác ABC . A. 2183cm B. 2 93 cm C. 218cm D. 29cm

Câu 19. Mệnh đề nào sau đây sai ?
A. 0 AA B. 0 cùng phương với mọi vectơ C. 0 AB D. 0 cùng hướng với mọi vectơ
Câu 20. Cho hình chữ nhật ABCD tâm O . Trong các mệnh đề sau, mệnh đề nào sai?
OFFICIAL
A. 0 ABBCBD+−= B. 0 OAOC+= C. 0 ABBCCA++= D. 0 ADBC−=
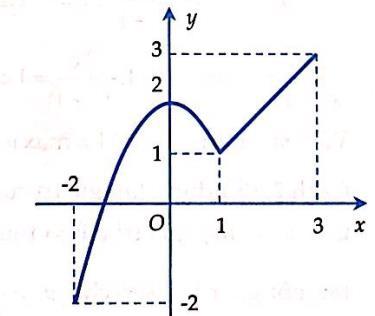
Câu 21. Cho hàm số ( )yfx = xác định trên đoạn 2;3 có đồ thị được cho như trong hình dưới đây: Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của ( )fx trên đoạn 2;3 . Tính Mm + . A. 0 Mm+= B. 1 Mm+= C. 2 Mm+= D. 3 Mm+= Câu 22. Trong các điểm sau đây điểm nào thuộc đồ thị của hàm số? A. ( ) 1 . 2;3 M B. ( ) 2 0; 1. M C. 3 11 ; . 22 M D. ( ) 4 . 1;0 M Câu 23. Một máy bay có vectơ vận tốc chỉ theo hướng bắc, vận tốc gió là một vectơ theo hướng đông như Hình 7. Tính độ dài vectơ tổng của hai vectơ nói trên (chọn giá trị gần đúng). A. 209 B. 208 C. 210 D. 211 Câu 24. Cho 0 a . Khẳng định nào sau đây là sai? A. a và 4a cùng phương. B. a và 4a cùng phương.
DẠYKÈMQUYNHƠN
C. a và 4a không cùng hướng. D. a và 4a ngược hướng.
Câu 25. Cho tam giác ABC . Gọi M và N lần lượt là trung điểm của AB và AC . Trong các mệnh đề sau, tìm mệnh đề sai? A. 2 ABAM = B. 2 ACCN = C. 2 BCNM =− D. 1 2 CNAC =−
Câu 26. Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống. Biết rằng quỹ đạo của quả bóng là một cung parabol trong mặt phẳng với hệ tọa độ Oth, trong đó t là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên; h là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2m. Sau đó 1 giây, nó đạt độ cao 8,5m và 2 giây sau khi đá lên, nó đạt độ cao 6m. Hỏi sau bao lâu thì quả bóng sẽ chạm đất kể từ khi được đá lên (tính chính xác đến hàng phần trăm? A. 2,56 giây B. 2,57 giây C. 2,58 giây D. 2,59 giây Câu 27. Cho hàm số 2 41yxx=−++ . Khẳng định nào sau đây sai? A. Trên khoảng ( );1− hàm số đồng biến. B. Hàm số nghịch biến trên khoảng ( ) 2;+ và đồng biến trên khoảng ( );2− . C. Trên khoảng ( ) 3;+ hàm số nghịch biến. D. Hàm số nghịch biến trên khoảng ( ) 4;+ và đồng biến trên khoảng ( );4−
OFFICIAL
Câu 28. Cho tam giác ABC . Giá trị của biểu thức ABBC bằng:
A. cos ABBCABC . B. cos ABACABC . C. cos ABBCABC . D. cos ABBCBAC .
Câu 29. Cho hình thang vuông ABCDcó đáy lớn 4 ABa = , đáy nhỏ 2 CDa = , đường cao 3 ADa = ; I là trung điểm của AD Khi đó ( ) + IAIBID bằng : A. 2 9 2 a . B. 2 9 2 a . C. 0 . D. 2 9a . Câu 30. Tam giác ABC vuông ở A và có góc o50 = B . Hệ thức nào sau đây là sai? A. ( ) o , 130= ABBC B. ( ) o , 40 = BCAC C. ( ) o , 50 = ABCB D. ( ) o , 120= ACCB Câu 31. Tính chu vi của hình chữ nhật có các cạnh là 3,4560,01 x = (m) và 12,7320,015 y = (m) và ước lượng sai số
10 học sinh có điểm kiểm tra giữa học kì 2 môn toán như sau: 5;6;7;5;8;8;10;9;7;8. Tính điểm trung bình của tổ học sinh đó. A. 7 B. 8 C. 7,3 D. 7,5 Câu 35. Chọn câu đúng trong các câu trả lời sau đây: Phương sai bằng: A. Một nửa của độ lệch chuẩn B. Căn bậc hai của độ lệch chuẩn. C. Hai lần của độ lệch chuẩn D. Bình phương của độ lệch chuẩn
DẠYKÈMQUYNHƠN
32. Tính diện tích S của hình chữ nhật có các
(m) và ước lượng sai số tuyệt đối mắc phải. A. 44,002 S = ( 2 m ); 0,176 S B. 44,002
= ( 2 m ); 0,0015 S C. 44,002 S = ( 2 m ); 0,025 S D. 44,002 S = ( 2 m ); 0,0025 S Câu 33. Một tổ học sinh gồm 10 học sinh có điểm kiểm tra cuối học kì 1 môn toán như sau: 7;5;6;6;6;8;7;5;6;9 . Tìm mốt của dãy trên. A. 0 6 M = . B. 0 7 M = . C. 0 5 M = . D. 0 8 M = . Câu 34. Một tổ học sinh gồm
tuyệt đối mắc phải. A. 32,3760,025;0,05 L L = B. 32,3760,05;0,025 L L = C. 32,3760,5;0,5 L L = D. 32,3760,05;0,05 L L = Câu
cạnh là 3,4560,01 x = (m) và 12,7320,015 y =
S
2. Tự luận
Câu 1. Năm 2003, nhiệt độ ngày tại Death Valley (Thung Lũng Chết), California, được xác định qua hàm số: 2 ()0,00180,65750,95 =−++ tddd , trong đó t là nhiệt độ tính theo độ đo Fahrenheit ( ) F và d là ngày trong năm tính từ 1/1/2003. Nhiệt độ cao nhất trong năm đó là bao nhiêu độ
F ? Vào ngày nào?
Câu 2. Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 280kg chất A và 18kg chất
B . Với một tấn nguyên liệu loại I, người ta có thể chiết xuất được 40kg chất A và 1,2kg chất
B . Với một tấn nguyên liệu loại II, người ta có thể chiết xuất được 20kg chất A và 3kg chất
B . Giá mỗi tấn nguyên liệu loại I là 4 triệu đồng và loại II là 3 triệu đồng. Hỏi người ta phài dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất mà vẫn đạt được mục tiêu đề ra? Biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp tối đa 10 tấn nguyên liệu loại I và 9 tấn nguyên liệu loại II.
OFFICIAL
DẠYKÈMQUYNHƠN
Câu
Cho tam giác ABC
333 2
c
+− = +− .
C = . Câu 4. Cho hai hình bình hành ABCD và ABCD có chung đỉnh A . Chứng minh rằng hai tam giác BCD và BCD có cùng trọng tâm Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM 1A 2C 3C 4B 5A 6C 7D 8A 9D 10D 11B 12C 13C 14A 15C 16B 17A 18D 19C 20A 21B 22B 23A 24C 25B 26C 27D 28A 29B 30D 31D 32A 33A 34C 35D 1. Trắc nghiệm Câu 1. Cho mệnh đề A: "8 không chia hết cho 2 " và mệnh đề :B " 31 ". Xét các mệnh đề sau: a) Mệnh đề AB . b) Mệnh đề BA c) Mệnh đề AB d) Mệnh đề AB . Số mệnh đề đúng trong các mệnh đề trên là A. 1. B. 2. C. 3. D. 4. Lời giải Ta có mệnh đề A sai, mệnh đề A đúng; mệnh đề B đúng, mệnh đề B sai. Khi đó, mệnh đề đúng là: a ). Đáp án là A Câu 2. Mệnh đề phủ định của mệnh đề :",230"Txx−+ là A. " ,230xx −+ ". B. " ,230"xx −+ C. " ,230"xx −+ . D. " ,230"xx −+ . Lời giải Mệnh đề phủ định của mệnh đề T là " ,230"xx −+ . Câu 3. Cho hai tập hợp {;} = Aab và {;;;;} = Babcde . Có bao nhiêu tập hợp X mà AXB ? A. 6. B. 7. C. 8. D. 11. Câu 4. Cho tập hợp {20} =−Axx . Tập hợp A là: A. {2;1;0}=−− A B. [2;0]=− A C. (2;0)=− A D. {2;0}=− A Câu 5. Cho hai tập hợp [5;0],[0;) =−=+AB . Khi đó: A. {0} =AB B. =AB C. [5;)=−+AB D. (5;)=−+AB Câu 6. Miền nghiệm của bất phương trình 35xy−− là nửa mặt phẳng chứa điểm A. (3;0).
3.
thoả mãn
abc
abc
Chứng minh góc 60
B. (3;1) C. (1;3). D. (0;0). Câu 7. Phần không bị gạch (không kể d) ở Hình 4 là miền nghiệm của bất phương trình:


A. 326 +xy B. 236 +xy C. 236 +xy D. 326 +xy Câu 8. Miền không bị gạch (tính cả biên) trong hình vẽ dưới đây là miền nghiệm của hệ bất phương trình bậc nhất hai ẩn nào sau đây?
A. 236 236 xy xy + −− B. 236 236 xy xy + −− C. 236 236 xy xy +− −− D. 236 236 xy xy + − Câu 9. Miền nghiệm của hệ bất phương trình bậc nhất hai ẩn 20112022 0 xy y + nằm trong góc phần tư nào? A. I. B. II. C. III. D. IV. Câu 10. Một xưởng có một máy cắt và một máy tiện dùng để sản xuất trục sắt và đinh ốc. Để sản xuất 1 tấn trục sắt thì lần lượt máy cắt chạy trong 3 giờ và máy tiện chạy trong 1 giờ, tiền lãi là 2 triệu đồng. Để sản xuất 1 tấn đinh ốc thì lần lượt máy cắt và máy tiện chạy trong 1 giờ, tiền lãi là 1 triệu đồng. Một máy không thể đồng thời sản xuất cả hai loại. Máy cắt làm không quá 6 giờ/ngày, máy tiện làm không quá 4 giờ/ngày. Hỏi một ngày xưởng nên sản xuất bao nhiêu tấn mối loại để tiền lãi là cao nhất?
A. 2 tấn trục sắt và 2 tấn đinh ốc.
B. 3 tấn trục sắt và 1 tấn đinh ốc.
C. 2 tấn trục sắt và 3 tấn đinh ốc.
D. 1 tấn trục sắt và 3 tấn đinh ốc. Lời giải
Gọi ,(0,0) xyxy là số tấn trục sắt và đinh ốc sản xuất trong ngày.
Số tiền lãi mỗi ngày: (;)2 Lxyxy =+ .
DẠYKÈMQUYNHƠN
OFFICIAL
Số giờ làm việc mỗi ngày của máy cắt: 36 xy+
Số giờ làm việc mỗi ngày của máy tiện: 4 xy+ .
Ta có bài toán tìm giá trị lớn nhất của (,)Lxy biết 36 4 0,0
+ + (*).
xy xy xy
Miền nghiệm của (*) là miền tứ giác OABC với (0;0),(2;0),(1;3),(0;4) OABC
Ta có: (0;0)0,(2;0)4,(0;4)4,(1;3)5 LLLL==== . Vậy mỗi ngày cần sản
DẠYKÈMQUYNHƠN
OFFICIAL
gọn biểu thức
xx M xx =− với
x ta được A. sin x B. cos x . C. 1 sin x . D. 1 cos x Lời giải 22 tansin1sincos cos sincotcoscoscos xxxx Mx xxxxx =−=−== Câu 12. Cho là góc tù và tancot2 +=− . Giá trị của sincos M =− là A. 2. B. 2 C. 2 D. 2 . Lời giải Từ sincos 2 cossin +=− suy ra 1 sincos 2 =− . 2 (sincos)12sincos2 −=−= . Suy ra sincos2 −= Vì là góc tù nên sincos0sincos2 M −=−= Câu 13. Trên nửa đường tròn đơn vị, cho điểm M sao cho 120 = MOx . Toạ độ điểm M là: A. 31 ; 22 . B. 31 ; 22 . C. 13 ; 22 D. 13 ; 22 . Lời giải Điểm M có toạ độ là (;) ab . Ta có: cos120,sin12013 22 ==−== ab Chọn C Câu 14. Cho ;;cab là độ dài 3 cạnh của tam giác ABC . Biết 7 = b ; 5 = c ; 4 cos 5 A = . Tính độ dài của a A. 32 B. 72 2 C. 23 8 D. 6 Lời giải
xuất 1 tấn trục sắt và 3 tấn đinh ốc thì thu được tiền lãi cao nhất là 5 triệu đồng. Câu 11. Rút
tansin sincot
( ) 0;90
Chọn A Áp dụng định lí cosin cho tam giác ABC ta có: 22222 4 2.cos752.7.5.18 5 abcbcA=+−=+−= .
Suy ra: 1832 a == .
Câu 15. Tam giác ABC có 6,42,2.abc=== M là điểm trên cạnh BC sao cho 3 BM = . Độ dài đoạn AM bằng bao nhiêu?
A. 9. B. 9. C. 3. D. 1 108. 2
Lời giải Chọn C.
Ta có: Trong tam giác ABC có 66aBC== mà 3 BM = suy ra M là trung điểm BC
Suy ra: 222 22 93 24 a bca AMmAM + ==−==
OFFICIAL
BCBC RR AA ==== . Câu 17. Tam giác ABC có 6812'= A , 3444'= B , 117. = AB Khi đó độ
dài AC xấp xỉ b
DẠYKÈMQUYNHƠN
ằ
Lời
Ta
:
++==−−=
. Mặt khác
Câu 16. Cho tam giác ABC có góc 60 BAC = và cạnh 3 BC = . Tính bán kính của đường tròn ngoại tiếp tam giác ABC A. 4 R = B. 1 R = C. 2 R = D. 3 R = Lời giải Chọn B Ta có: 3 21 sin2sin 3 2. 2 sinsinsinsinsinsinsin774' ===== abcACABABB AC ABCBCC Câu 18. Tam giác ABC có 6cm = AB , 30 = BAC , 75 = ACB . Tính diện tích của tam giác ABC A. 2183cm . B. 2 93 cm . C. 218cm . D. 29cm . Lời giải Chọn D Ta có ( ) 18075 =−+== ABCBACACBACB Suy ra tam giác ABC cân tại A nên 6cm ==ABAC . Vậy diện tích tam giác ABC là: 2 1 ..sin9 cm 2 == ABC SABACBAC . Câu 19. Mệnh đề nào sau đây sai ? A. 0 AA B. 0 cùng phương với mọi vectơ C. 0 AB D. 0 cùng hướng với mọi vectơ Lời giải Chọn C
ng ? A. 68. B. 168. C. 118. D.200.
giải Chọn A
có: Trong tam giác ABC
1801806812'3444'774'
ABCC
.sin117.sin3444' 68.


DẠYKÈMQUYNHƠN OFFICIAL Đáp án C sai vì có thể xảy ra trường hợp 0. ABAB Câu 20. Cho hình chữ nhật ABCD tâm O . Trong các mệnh đề sau, mệnh đề nào sai? A. 0 ABBCBD+−= B. 0 OAOC+= C. 0 ABBCCA++= D. 0 ADBC−= Lời giải Chọn A ( ) 00200 ABBCBDACBDOCODDC +−=−=−== ( Không thỏa mãn) 0 OAOC+= ( thỏa mãn vì O là trung điểm của AC ) 00ABBCCAACCA ++=+= ( thỏa mãn) 0 ADBC−= ( thỏa mãn). Câu 21. Cho hàm số ( )yfx = xác định trên đoạn 2;3 có đồ thị được cho như trong hình dưới đây: Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của ( )fx trên đoạn 2;3 . Tính Mm + . A. 0 Mm+= B. 1 Mm+= C. 2 Mm+= D. 3 Mm+= Lời giải Quan sát trên đồ thị ta thấy 3 M = (ứng với 3 x = ), 2 m =− (ứng với 2 x =− ). Vậy 1 Mm+= Đáp án B. Câu 22. Trong các điểm sau đây điểm nào thuộc đồ thị của hàm số? A. ( ) 1 . 2;3 M B. ( ) 2 0; 1. M C. 3 11 ; . 22 M
D. ( ) 4 . 1;0 M Lời giải Chọn B Thay 0 x = vào hàm số ta thấy 1 y =− . Vậy ( ) 2 0;1 M thuộc đồ thị hàm số. Câu 23. Một máy bay có vectơ vận tốc chỉ theo hướng bắc, vận tốc gió là một vectơ theo hướng đông như Hình 7. Tính độ dài vectơ tổng của hai vectơ nói trên (chọn giá trị gần đúng).
A. 209 B. 208 C. 210 D. 211
Lời giải
Gọi AB và BC lần lượt là vecto vận tốc của máy bay và vận tốc của gió. Ta có: += ABBCAC Suy ra 222220060209( /) =+=+ ACABBCkmh . Vậy độ dài vectơ tổng của hai vectơ nói trên là khoảng 209 / kmh.

Câu 24. Cho 0 a . Khẳng định nào sau đây là sai?
A. a và 4a cùng phương.
B. a và 4a cùng phương.
C. a và 4a không cùng hướng. D. a và 4a ngược hướng.
Lời giải Chọn C
Câu 25. Cho tam giác ABC . Gọi M và N lần lượt là trung điểm của AB và AC . Trong các mệnh đề sau, tìm mệnh đề sai?
A. 2 ABAM = B. 2 ACCN = C. 2 BCNM =− D. 1 2 CNAC =−
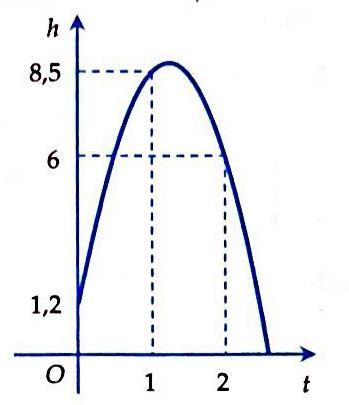
Lời giải
Chọn B
Câu 26. Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống. Biết rằng quỹ đạo của quả bóng là một cung parabol trong mặt phẳng với hệ tọa độ Oth, trong đó t là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên; h là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2m. Sau đó 1 giây, nó đạt độ cao 8,5m và 2 giây sau khi đá lên, nó đạt độ cao 6m. Hỏi sau bao lâu thì quả bóng sẽ chạm đất kể từ khi được đá lên (tính chính xác đến hàng phần trăm? A. 2,56 giây B. 2,57 giây C. 2,58 giây D. 2,59 giây Lời giải
DẠYKÈMQUYNHƠN
OFFICIAL
)0;1;2 , ( )1;8;5 và ( )2;6 Từ đó ta có 1,24,9 8,512,2 4261,2 ca abcb abcc ==− ++== ++== .
Đáp án C. Gọi phương trình của parabol quỹ đạo là 2 hatbtc =++ . Từ giả thiết suy ra parabol đi qua các điểm (
Vậy phương trình của parabol quỹ đạo là 2 4,912,21,2htt=−++ .
Giải phương trình 2 04,912,21,20htt =−++= ta tìm được một nghiệm dương là 2,58 t .
Câu 27. Cho hàm số 2 41yxx=−++ . Khẳng định nào sau đây sai?

A. Trên khoảng ( );1− hàm số đồng biến.
B. Hàm số nghịch biến trên khoảng ( ) 2;+ và đồng biến trên khoảng ( );2− .
C. Trên khoảng ( ) 3;+ hàm số nghịch biến.
D. Hàm số nghịch biến trên khoảng ( ) 4;+ và đồng biến trên khoảng ( );4−
Lời giải
Chọn D
Đỉnh của parabol: 2 2 I b x a =−=
Bảng biến thiên của hàm số: Dựa vào bảng biến thiên suy ra khẳng định D sai.
OFFICIAL
Câu 28. Cho tam giác ABC . Giá trị của biểu thức ABBC bằng: A. cos ABBCABC . B. cos ABACABC . C. cos ABBCABC . D. cos ABBCBAC . Lời giải Chọn A Câu 29. Cho hình thang vuông ABCDcó đáy lớn 4 ABa = , đáy nhỏ 2 CDa = , đường cao 3 ADa = ; I là trung điểm của AD. Khi đó ( ) + IAIBID bằng : A. 2 9 2 a
DẠYKÈMQUYNHƠN
+=++==−
nào sau đây là sai? A. ( ) o , 130= ABBC . B. ( ) o , 40 = BCAC . C. ( ) o , 50 = ABCB . D. ( ) o , 120= ACCB . Lời giải Chọn D Phương án A:( ) ( ) 0o , 180, 130 =−=ABBCABCB nên loại#A. Phương án B:( ) ( ) o , , 40 ==BCACCBCA nên loại B. Phương án C:( ) ( ) o , , 50 ==ABCBBABC nên loại C. Phương án D:( ) ( ) 0o , 180, 140 =−=ACCBCACB nên chọn D. Câu 31. Tính chu vi của hình chữ nhật có các cạnh là 3,4560,01 x = (m) và 12,7320,015 y = (m) và ước lượng sai số tuyệt đối mắc phải.
. B. 2 9 2 a . C. 0 . D. 2 9a . Lời giải Chọn B Ta có ( ) ( ) 2 9 ..2. 2
a IAIBIDIAIAABIDIAID nên chọn B. Câu 30. Tam giác ABC vuông ở A và có góc o50 = B . Hệ thức
A. 32,3760,025;0,05 L L =
B. 32,3760,05;0,025 L L = C. 32,3760,5;0,5 L L = D. 32,3760,05;0,05 L L =
Lời giải Chu vi ( ) ( ) 223,45612,73232,376Lxy=+=+= (m) Sai số tuyệt đối ( ) 20,010,0150,05 L += Vậy 32,3760,05 L = (m). Đáp án D. Câu 32. Tính diện tích S của hình chữ nhật có các cạnh là 3,4560,01 x = (m) và 12,7320,015 y = (m) và ước lượng sai số tuyệt đối mắc phải.
A. 44,002 S = ( 2 m ); 0,176 S B. 44,002 S = ( 2 m ); 0,0015 S C. 44,002 S = ( 2 m ); 0,025 S D. 44,002 S = ( 2 m ); 0,0025 S Lời giải
Diện tích 3,456.12,73244,002 Sxy=== ( 2 m ) Sai số tương đối S không vượt quá: 0,010,0150,004 3,45612,732 += Sai số tuyệt đối S không vượt quá: .44,002.0,0040,176 S S = . Đáp án#A. Câu 33. Một tổ học sinh gồm 10 học sinh có điểm kiểm tra cuối học kì 1 môn toán như sau: 7;5;6;6;6;8;7;5;6;9 . Tìm mốt của dãy trên. A. 0 6 M = . B. 0 7 M = . C. 0 5 M = D. 0 8 M = Lời giải Chọn C Giá trị 6 x = là giá trị có tần số lớn nhất 4 n = . Vậy mốt của điều tra trên là: 0 6 M = Câu 34. Một tổ học sinh gồm 10 học sinh có điểm kiểm tra giữa học kì 2 môn toán như sau: 5;6;7;5;8;8;10;9;7;8. Tính điểm trung bình của tổ học sinh đó. A. 7 . B. 8. C. 7,3. D. 7,5. Lời giải Chọn C Điểm trung bình của tổ học sinh đó là: 5.267.28.3910 7,3 10 x +++++ == .
Câu 35. Chọn câu đúng trong các câu trả lời sau đây: Phương sai bằng: A. Một nửa của độ lệch chuẩn B. Căn bậc hai của độ lệch chuẩn. C. Hai lần của độ lệch chuẩn. D. Bình phương của độ lệch chuẩn. Lời giải
DẠYKÈMQUYNHƠN
OFFICIAL
luận Câu 1. Năm 2003, nhiệt độ ngày tại Death Valley (Thung Lũng Chết), California, được xác định qua hàm số: 2 ()0,00180,65750,95 =−++ tddd , trong đó t là nhiệt độ tính theo độ đo Fahrenheit ( ) F và d là ngày trong năm tính từ 1/1/2003. Nhiệt độ cao nhất trong năm đó là bao nhiêu độ F ? Vào ngày nào? Lời giải Ta có: 2 2 365 ()0,00180,65750,950,0018110,90125 2 =−++=−−+ tdddd 110,90125
Chọn D Ta có phương sai là: 2 x s Độ lệch chuẩn: 2 xx ss = Suy ra phương sai bằng bình phương của độ lệch chuẩn 2. Tự
Vậy nhiệt độ cao nhất của năm đó là ( ) 110,90125 F sau 182,5 ngày kể từ ngày 1/1/2003.
Nhiệt độ cao nhất vào giữa ngày 2/7/2003
Câu 2. Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 280kg chất A và 18kg chất
B . Với một tấn nguyên liệu loại I, người ta có thể chiết xuất được 40kg chất A và 1,2kg chất B . Với một tấn nguyên liệu loại II, người ta có thể chiết xuất được 20kg chất A và 3kg chất B . Giá mỗi tấn nguyên liệu loại I là 4 triệu đồng và loại II là 3 triệu đồng. Hỏi người ta phài dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất mà vẫn đạt được mục tiêu đề ra? Biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp tối đa 10 tấn nguyên liệu loại I và 9 tấn nguyên liệu lo
là (;)43 =+ Fxyxy (triệu đồng). Vậy bài toán trở thành tìm giá trị nhỏ nhất của (;)Fxy với (;) xy thoả mãn hệ bất phương trình bậc nhất hai ẩn ở trên.
Bước 1. Xác định miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên. Miền nghiệm là miền tứ giác ABCD với (5;4),(10;2),(10;9),(2,5;9) ABCD . Bước 2. Tinh giá trị của F tại các đỉnh của tứ giác ABCD.
Ta có: (5;4)32,(10;2)46,(10;9)67,(2,5;9)37 ====FFFF
So sánh các giá trị này ta thấy (5;4)F là nhỏ nhất. Do đó, giá trị nhỏ nhất của (;)Fxy với (;) xy thoả mãn hệ bất phương trình trên là (5;4)32 = F Vậy người ta cần mua 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II đễ chi phí là nhỏ nhất.

DẠYKÈMQUYNHƠN
và chỉ khi 365365 0 22 −==dd
OFFICIAL Dấu bằng xảy ra khi
ại II. Lời giải Gọi x và y lần lượt là số tấn nguyên liệu loại I và loại II mà người ta cần dùng. Khi đó khối lượng chất A chiết xuất
1,23( ) + xykg . Từ giả thiết
4020280214 1,23181,2318 hay 1010 99. xyxy xyxy xx yy ++ ++ Hơn nữa, số tiền người
mua
được là 4020( ) + xykg . Khối lượng chất B chiết xuất được là
ta có hệ bất phương trình sau:
ta phải trả để
nguyên liệu

DẠYKÈMQUYNHƠN OFFICIAL Câu 3. Cho tam giác ABC thoả mãn 333 2 abc c abc +− = +− . Chứng minh góc 60 C = Lời giải Ta có 333 233323 () abc cabcabcc abc +− =+−=+− +− Suy ra 332222 () ababcaabbc +=+−+= 2222 1 2coscos60 2 aabbababCCC −+=+−== Từ đó ta có điều phải chứng minh. Câu 4. Cho hai hình bình hành ABCD và ABCD có chung đỉnh A . Chứng minh rằng hai tam giác BCD và BCD có cùng trọng tâm Lời giải Gọi G là trọng tâm tam giác BCD suy ra 0 GBGCGD ++= 0 GBGCGDBBCCDD +++++= . (1) Mặt khác theo quy tắc phép trừ và hình bình hành ta có ( ) ( ) ( ) BBCCDDABABACACADAD ++=−+−+− ( ) ( ) ABADACABADAC =+−+++ ACACACAC =−−+ 0 = (2) Từ (1) và (2) ta có 0 GBGCGD ++= hay G là trọng tâm tam giác BCD
1. Trắc nghiệm
Câu 1: Phủ định của mệnh đề: "Tổng ba góc trong một tam giác bằng 180 " là mệnh đề
A. "Tổng ba góc trong một tam giác lớn hơn 180 ".
B. "Tổng ba góc trong một tam giác nhỏ hơn180".
C. "Tổng ba góc trong một tam giác không bằng 180 ". D. "Tổng ba góc trong một tam giác không vượt quá 180 ". Câu 2: Trong các mệnh đề sau, mệnh đề nào là đúng? A. " 2 ,42"
{1;2;3;4;5} = A . Tập hợp X thoả mãn \{1;3;5} = AX và \{6;7} = XA là A. {2;4} B. {6;7} C. {2;4;6;7} D. {1;3;5;6;7}
Câu 4: Cho hai tập hợp (1;2),[;2] =−=+ ABmm . Tìm m để AB khác tập rỗng.
A. 32− m . B. 32− m . C. 2 m hoặc 3− m D. 2 m hoặc 3− m
Câu 5: Cho tập hợp {32}Mxx=− . Mệnh đề nào sau đây đúng?
A. (3;2) M =− B. [3;2) M =− . C. (3;2] M =− . D. {3;2;1} M =−−−

Câu 6: Miền nghiệm của bất phương trình 44 xy+− KHÔNG chứa điểm nào sau đây?
A. (1;1). B. (1;2). C. (2021;2022) D. (1;1)
Câu 7: Miền không bị gạch (tính cả biên) trong hình vẽ bên là miền nghiệm của bất phương trình bậc nhất hai ẩn nào? A.
Câu 8: Cặp số nào sau đây là nghiệm của hệ bất phương trình
A. (2;0) B. (0;2). C. (4;2).
?
DẠYKÈMQUYNHƠN OFFICIAL ĐỀ 04
xxx .
xxx hoặc
− x . C. " 2 ,42 xxx ".
− xxx ”.
Cho
B. " 2 ,42
2"
D. " 2 ,422
Câu 3:
tập hợp
44xy+
44xy+
41 xy
44
−−
. B.
C.
+ D.
xy
.
36
24 xy xy + −
+ −− −



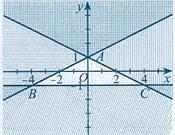
xy xy y
Câu 9: Miền nghiệm của hệ bất phương trình 22 22 1
được xác định bởi miền đa giác nào sau đây? A. B. C. D. Câu 10: Một đơn vị bộ đội cần mua ít nhất 300 kg gạo. Có hai loại gạo, loại I có giá là 30000 đồng/ kg, loại II có giá 20000 đồng/ kg. Gọi , xy lân lượt là số gạo loại I, II đơn vị mua. Hệ bất phương trình biểu thị mối liên hệ của x và y để số tiền đơn vị mua gạo không hết quá 7000000 đồng là: A. 8 32700 + + xy xy B. 300 33700 + + xy xy C. 300 32700 + + xy xy
DẠYKÈMQUYNHƠN
D. (3;3)
OFFICIAL
Câu 11: Cho góc thoả mãn 90180 và sin3 5 = . Giá trị của cos là: A. 4 5 . B. 4 5 C. 2 5 . D. 2 5 Câu 12: Cho góc thoả mãn 0180 và 2 cos 3 =− . Giá trị của tan là: A. 5 2 .
D. 300 32700 + + xy xy
B. 5 2 . C. 2 5 . D. 2 5
Câu 13: Cho tam giác ABC vuông tại A. Chọn khẳng định sai trong các khẳng định sau:
A. cossin = BC. B. sincos = BC. C. tancot = BC . D. tancot =− CB.
Câu 14: Cho các điểm (1;1),(2;4),(10;2). ABC Góc BAC bằng bao nhiêu?
A. 090 . B. 0 60. C. 0 45. D. 0 30.
Câu 15: Tam giác ABC có 9 AB = cm, 15 BC = cm, 12 AC = cm. Khi đó đường trung tuyến AM của tam giác có độ dài là
A. 10cm. B. 9cm. C. 7,5cm. D. 8cm.
Câu 16: Cho tam giác ABC có ,, ABcACbBCa === . Chọn khẳng định đúng
A. 222 cos 2 bca A bc +− = . B. 222 cos bca A bc +− = C. 222 cos 2 bca A bc ++ = . D. 222 cos 2 abc A bc = .
Câu 17: Bộ ba số nào sau đây là độ dài 3 cạnh của một tam giác tù?
A. 2;3;4. B. 3;4;5. C. 4;5;6. D. 5;6;7.
Câu 18: Cho tam giác ABC có , = BCa , = CAb = ABc thỏa 222 3. +=+ bcabc Tìm số đo của góc
A của tam giác ABC A. 120 B. 60 C. 150 D. 30
Câu 19: Cho hình vuông ABCD . Khẳng định nào sau đây đúng? A. ACBD B. ABCD C. ABBC D. Hai vectơ , ABAC cùng hướng.
Câu 20: Gọi O là tâm hình bình hành .ABCD Đẳng thức nào sau đây sai? A. OAOBCD B. OBOCODOA C. ABADDB D. BCBADCDA Câu 21: Cho hàm số 3 32yxx=−+ . Điểm nào sau đây thuộc đồ thị hàm số đã cho? A. ( )2;0 . B. ( )1;1 . C. ( )2;12 . D. ( )1;1 .
Câu 22:
DẠYKÈMQUYNHƠN
OFFICIAL
Tập xác định của hàm số 3 22 x y x = là A. \1 . B. \3 . C. \2 . D. ( ) 1;+ . Câu 23: Cho ba lực 123 ,, FFF cùng tác động vào một vật tại một điểm làm vật đứng yên (Hình). Xét 423 =+ FFF . Phát biểu nào sau đây là đúng?
A. 41 = FF . B. 41 2 = FF . C. 41 2=− FF . D. 41 =− FF

Câu 24: Cho đoạn thẳng AB và điểm C nằm giữa hai điểm , AB . Khẳng định nào sau đây là đúng?
A. = AC ACAB AB B. =− AC ACAB AB C. = AB ACAB AC . D. =− AB ACAB AC . Câu 25: Cho 0 a và điểm O . Gọi , MN lần lượt là hai điểm thỏa mãn 3 OMa = và 4 ONa =− . Khi đó: A. 7 MNa = B. 5 MNa =− C. 7 MNa =− D. 5 MNa =−
Câu 26: Trục đối xứng của đồ thị hàm số 2 yaxbxc =++ , (0) a là đường thẳng nào dưới đây? A. . 2 b x a =− B. . 2 c x a =− C. . 4 x a =− D. Không có.
Câu 27: Tọa độ giao điểm của ( ) 2 :4 Pyxx =− với đường thẳng :2dyx=−− là A. ( )0;2 M , ( )2;4 N B. ( )1;1 M , ( )2;0 N C. ( )3;1 M , ( )3;5 N D. ( )1;3 M , ( )2;4 N
Câu 28: Cho đoạn thẳng AB . Tập hợp các điểm M nằm trong mặt phẳng thoả mãn 0 =MAMB là: A. Đường tròn tâm A bán kính AB . B. Đường tròn tâm B bán kính AB . C. Đường trung trực của đoạn thẳng AB D. Đường tròn đường kính AB
DẠYKÈMQUYNHƠN
OFFICIAL
. Câu 29: Cho hình vuông ABCD, tính ( ) cos,ABCA A. 1 2 B. 1 2 C. 2 2 D. 2 2 Câu 30: Cho tam giác ABC vuông cân tại A có 2 BCa = .Tính CACB A. 2 = CACBa B. = CACBa C. 2 . 2 = a CACB D. .2 = CACBa Câu 31: Xấp xỉ số π bởi số 355 113 . Hãy đánh giá sai số tuyệt đối biết: 3,141592653,14159266
A. 7 2,8.10 a B. 7 28.10 a C. 7 1.10 a D. 6 2,8.10 a
Câu 32: Độ cao của một ngọn núi đo được là 1372,5 h = m. Với sai số tương đối mắc phải là 0,5‰. Hãy xác định sai số tuyệt đối của kết quả đo trên và viết h dưới dạng chuẩn.
A. ( ) 0,68625;1373 h hm== B. ( ) 0,68626;1372 h hm== C. ( ) 0,68625;1372 h hm== D. ( ) 0,68626;1373 h hm==
Câu 33: Cân nặng của 40 học sinh lớp 10 trường THPT A được cho bởi bảng sau .
Tính số trung bình cộng của mẫu số liệu trên
A. 38,26 x = . B. 40,25 x = . C. 39,65 x = . D. 40,83 x = .
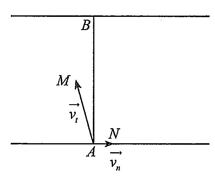

Câu 34: Kết quả điểm kiểm tra 15’ môn Toán của 100 em học sinh được trình bày ở bảng sau: Điểm 3 4 5 6 7 8 9 10 Cộng Tần số 3 5 11 17 30 19 10 5 100
Số trung bình cộng của bảng phân bố tần số nói trên là
A. 6,88 . B. 7,12. C. 6,5. D. 7,22 .
Câu 35: Cho phương sai của các số liệu bằng 4. Tìm độ lệch chuẩn. A. 4. B. 2. C. 16. D. 8. 2. Tự luận
Câu 36: Lập bảng biến thiên và vẽ đồ thị của hàm số 2 23=−−+yxx
Câu 37: Một người bán nước giải khát đang có 25g bột nho và 100 g đường để pha chế hai loại nước nho A và B . Để pha chế 1l nước nho loại A cần 10 g đường và 1g bột nho; để pha chế 1l nước nho loại B cần 10 g đường và 4g bột nho. Mỗi lít nước nho loại A khi bán lãi được 30 nghìn đồng, mỗi lít nước nho loại B khi bán lãi được 40 nghìn đồng. Hỏi người đó nên pha chế bao nhiêu lít nước nho mỗi loại để có lợi nhuận cao nhất?
Câu 38: Ta giả sử hai bờ sông là hai đường thẳng song song cách nhau 2km. Một chiếc tàu nhỏ đi từ điểm A ở bờ bên này sang điểm B ở bờ bên kia với vận tốc riêng của tàu (tức là vận tốc của tàu so với dòng nước) là 20 / kmh. Giả sử AB vuông góc với bờ sông (như hình vẽ). Cho biết vận tốc của dòng nước so với bờ là không đổi 5 / kmh (giả sử phương dòng nước chảy song song với bờ sông).
a) Cần giữ lái cho tàu tạo với bờ sông một góc nhọn bằng bao nhiêu độ để tàu sang bờ bên kia theo phương AB ? b) Tính vận tốc của tàu so với bờ. Hỏi sau bao lâu thì tàu sẽ tới bờ bên kia? (Các kết quả tính toán ở câu a) và câu b) ở trên được làm tròn đến hàng phần trăm).
DẠYKÈMQUYNHƠN
OFFICIAL
Câu 39: Cho tam giác ABC cố định và điểm M di động. Chứng minh rằng 45 vMAMBMC =+− không phụ thuộc vào vị trí của điểm M

Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM
1C 2B 3C 4A 5B 6D 7B 8C 9C 10D 11B 12A 13C 14A 15C 16A 17A 18D 19C 20B 21C 22A 23D 24A 25C 26A 27D 28D 29D 30A 31A 32A 33C 34A 35B
1. Trắc nghiệm
Câu 40: Phủ định của mệnh đề: "Tổng ba góc trong một tam giác bằng 180 " là mệnh đề
không
DẠYKÈMQUYNHƠN
OFFICIAL
A.
2 ,42" xxx B. " 2 ,42 xxx hoặc
−
Lời
tập hợp (1;2),[;2] =−=+ ABmm . Tìm m để AB khác tập rỗng. A. 32− m . B. 32− m . C. 2 m hoặc 3− m . D. 2 m hoặc 3− m . Câu 44: Cho tập hợp {32}Mxx=− . Mệnh đề nào sau đây đúng? A. (3;2) M =− . B. [3;2) M =− . C. (3;2] M =− D. {3;2;1} M =−−− Câu 45: Miền nghiệm của bất phương trình 44 xy+− KHÔNG chứa điểm nào sau đây? A. (1;1). B. (1;2) C. (2021;2022) D. (1;1) . Câu 46: Miền không bị gạch (tính cả biên) trong hình vẽ bên là miền nghiệm của bất phương trình bậc nhất hai ẩn nào?
A. "Tổng ba góc trong một tam giác lớn hơn 180 ". B. "Tổng ba góc trong một tam giác nhỏ hơn180". C. "Tổng ba góc trong một tam giác không bằng 180 ". D. "Tổng ba góc trong một tam giác
vượt quá 180 ". Câu 41: Trong các mệnh đề sau, mệnh đề nào là đúng?
"
2"
x C. " 2 ,42 xxx ". D. " 2 ,422 − xxx ”. Câu 42: Cho tập hợp {1;2;3;4;5} = A . Tập hợp X thoả mãn \{1;3;5} = AX và \{6;7} = XA là: A. {2;4}. B. {6;7}. C. {2;4;6;7}. D. {1;3;5;6;7}.
giải Dùng biểu đồ Ven như Hình 3 để minh họa hai tập hợp A, X. Chọn C Câu 43: Cho hai
+ −−





xy xy y
− được xác
định bởi miền đa giác nào sau đây? A. B. C. D. Câu 49: Một đơn vị bộ đội cần mua ít nhất 300 kg gạo. Có hai loại gạo, loại I có giá là 30000 đồng/ kg, loại II có giá 20000 đồng/ kg. Gọi , xy lân lượt là số gạo loại I, II đơn vị mua. Hệ bất phương trình biểu thị mối liên hệ của x và y để số tiền đơn vị mua gạo không hết quá 7000000 đồng là: A. 8 32700 + + xy xy B. 300 33700 + + xy xy
DẠYKÈMQUYNHƠN OFFICIAL
A. 44xy+ . B. 44xy+ . C. 41 xy+ D. 44xy−− Câu 47: Cặp số nào sau đây là nghiệm của hệ bất phương trình 36 ? 24 xy xy + −
A. (2;0) B. (0;2) C. (4;2). D. (3;3) . Lời giải. Với 4,2==−xy ta có: 43 + . (2)26 −=− và 2.4(2)104 −−= . Chọn C . Câu 48: Miền nghiệm của hệ bất phương trình 22 22 1
DẠYKÈMQUYNHƠN OFFICIAL
+ + xy
xy xy
ả
và sin3 5 = . Giá trị của cos
5 .
4 5
5 .
5 Lời giải Ta
22
+= . Do đó 22 cos1sin1916 2525 =−=−= . Do
nên cos0 . Suy ra 4 cos 5 =− .
B Câu
ả
và 2 cos 3 =− . Giá trị của tan
5 2 . B. 5 2 . C. 2 5 . D. 2 5 Giải Ta có: 22 sincos1 += . Do đó 22 sin1cos145 99 =−=−= Do 0180 nên sin0 . Suy ra 5 sin 3 = . Vậy sin5 tan cos2 ==− . Chọn A Câu 52: Cho tam giác ABC vuông tại A. Chọn khẳng định sai trong các khẳng định sau: A. cossin = BC. B. sincos = BC. C. tancot = BC D. tancot =− CB Câu 53: Cho các điểm (1;1),(2;4),(10;2). ABC Góc BAC bằng bao nhiêu? A. 090 . B. 0 60. C. 0 45. D. 0 30. Lời giải Câu 54: ChọnA. Ta có: (1;3) AB = , (9;3) AC =− .
C. 300 32700
xy D. 300 32700 +
+
Câu 50: Cho góc
tho
mãn 90180
là: A. 4
B.
C. 2
D. 2
có:
sincos1
90180
Chọn
51: Cho góc
tho
mãn 0180
là: A.
Suy ra: 0 cos090. ABAC BACBAC ABAC ===
Câu 55: Tam giác ABC có 9 AB = cm, 15 BC = cm, 12 AC = cm. Khi đó đường trung tuyến AM của tam giác có độ dài là A. 10cm. B. 9cm. C. 7,5cm. D. 8cm. Lời giải Chọn C Ta có 222 2 24 ABACBC AM + =− 222 91215225 244 + =−= 15 2 AM = .
Câu 56: Cho tam giác ABC có ,, ABcACbBCa === . Chọn khẳng định đúng
A. 222 cos 2 bca A bc +− = . B. 222 cos bca A bc +− = C. 222 cos 2 bca A bc ++ = . D. 222 cos 2 abc A bc = Lời giải Chọn A
Câu 57: Bộ ba số nào sau đây là độ dài 3 cạnh của một tam giác tù? A. 2;3;4. B. 3;4;5. C. 4;5;6. D. 5;6;7. Lời giải Chọn A Dễ thấy phương án B là độ dài 3 cạnh của một tam giác vuông. Một tam giác là tam giác tù khi góc lớn nhất là góc tù. Ngoài ra góc lớn nhất là góc đối diện với cạnh lớn nhất. Gọi góc lớn nhất của các tam giác trong các phương án B, C, D là góc A và cạnh lớn nhất là cạnh có độ dài a . Áp dụng hệ quả của định lí Côsin với góc đối diện với cạnh lớn nhất 222 cos 2 +− = bca A bc cho từng phương án.
Với phướng án C, ta có: 222 4561 cos0 2.4.58 +− == A , nên góc A nhọn (loại).
Với phướng án D, ta có: 222 5671 cos0 2.5.65 +− == A nên góc A nhọn (loại).
DẠYKÈMQUYNHƠN
OFFICIAL
Câu 58: Cho tam giác ABC có , = BCa , = CAb = ABc thỏa 222 3. +=+ bcabc Tìm số đo của góc A của tam giác ABC . A. 120 B. 60 C. 150 D. 30 Lời giải Chọn D Ta có 222 3 +=+ bcabc 222 3 +−=bcabc 222 3 +− = bca bc 222 3 22 +− = bca bc 3 cos 2 = A 30 = A . Vậy số đo của góc A của tam giác ABC là 30 Câu 59: Cho hình vuông ABCD . Khẳng định nào sau đây đúng?
Với phướng án A, ta có: 222 2341 cos0 2.2.34 +− ==− A nên góc A tù (chọn).
A. ACBD B. ABCD

C. . ABBC D. Hai vectơ , ABAC cùng hướng. Lời giải
Chọn C
Vì ABBCABBC
Câu 60: Gọi O là tâm hình bình hành .ABCD Đẳng thức nào sau đây sai?
A. OAOBCD . B. OBOCODOA. C. ABADDB D. BCBADCDA Lời giải Chọn B
Câu 61: +) Đáp ánA. Ta có OAOBBACD Vậy A đúng.
+) Đáp án B. Ta có . OBOCCBAD ODOAAD Vậy B sai.
OFFICIAL
+) Đáp án C. Ta có ABADDB Vậy C đúng.
+) Đáp án D. Ta có BCBAAC DCDAAC Vậy D đúng.
Câu 62: Cho hàm số 3 32yxx=−+ . Điểm nào sau đây thuộc đồ thị hàm số đã cho? A. ( )2;0 . B. ( )1;1 . C. ( )2;12 . D. ( )1;1 . Lời giải Chọn C Thay tọa độ điểm vào hàm số ta thấy chỉ có điểm ( )2;0 thỏa mãn. Câu 63: Tập xác định của hàm số 3 22 x y x = là A. \1 B. \3 C. \2 D. ( ) 1;+ Lời giải Chọn
DẠYKÈMQUYNHƠN
A Điều kiện xác định : 2201 xx− Nên tập xác định của hàm số là : \1 D = . Câu 64: Cho ba lực 123 ,, FFF cùng tác động vào một vật tại một điểm làm vật đứng yên (Hình). Xét 423 =+ FFF . Phát biểu nào sau đây là đúng? A. 41 = FF . B. 41 2 = FF
C. 41 2=− FF . D. 41 =− FF .
Lời giải Vì vật đứng yên nên 1231441 00 ++=+==− FFFFFFF . Chọn D
Câu 65: Cho đoạn thẳng AB và điểm C nằm giữa hai điểm , AB . Khẳng định nào sau đây là đúng?
A. = AC ACAB AB B. =− AC ACAB AB C. = AB ACAB AC . D. =− AB ACAB AC . Lời giải Chọn A
Câu 66: Cho 0 a và điểm O . Gọi , MN lần lượt là hai điểm thỏa mãn 3 OMa = và 4 ONa =− . Khi đó: A. 7 MNa = B. 5 MNa =− C. 7 MNa =− D. 5 MNa =− Lời giải Chọn C Ta có: 437 MNONOMaaa =−=−−=− Câu 67: Trục đối xứng của đồ thị hàm số 2 yaxbxc =++ , (0) a là đường thẳng nào dưới đây? A. . 2 b x a =− B. . 2 c x a =− C. . 4 x a =− D. Không có. Lời giải Chọn A Câu 68: Tọa độ giao điểm của ( ) 2 :4 Pyxx =− với đường thẳng :2dyx=−− là A. ( )0;2 M , ( )
OFFICIAL
DẠYKÈMQUYNHƠN
ọ
Hoành độ giao điểm của ( )P và d là nghiệm
ủa
22 1 42320 2 x xxxxx x = −=−−−+= = . Vậy tọa độ giao điểm của ( )P và d là ( )1;3 M , ( )2;4 N Câu 69: Cho đoạn thẳng AB . Tập hợp các điểm M nằm trong mặt phẳng thoả mãn 0 =MAMB là: A. Đường tròn tâm A bán kính AB . B. Đường tròn tâm B bán kính AB C. Đường trung trực của đoạn thẳng AB . D. Đường tròn đường kính AB . Lời giải Chọn D
2;4 N B. ( )1;1 M , ( )2;0 N C. ( )3;1 M , ( )3;5 N D. ( )1;3 M , ( )2;4 N Lời giải Ch
n D
c
phương trình:
Câu 70: Cho hình vuông ABCD, tính ( ) cos,ABCA
A. 1 2 B. 1 2 C. 2 2 D. 2 2 Lời giải Chọn D Đầu tiên ta đi tìm số đo của góc ( ) , ABCA sau đó mới tính ( ) cos,ABCA Vì ( ) ( ) ( ) oo 2 ,180,135cos, 2 =−==−ABCAABCAABCA .
Câu 71: Cho tam giác ABC vuông cân tại A có 2 BCa = .Tính CACB A. 2 . = CACBa . B. . = CACBa . C. 2 2 = a CACB . D. .2 = CACBa . Lời giải Chọn A Ta có 2 2 .2. 2 ==aaa CACB Câu 72: Xấp xỉ số π bởi số 355 113 . Hãy đánh giá sai số tuyệt đối biết: 3,141592653,14159266 . A. 7 2,8.10 a B. 7 28.10 a C. 7 1.10 a D. 6 2,8.10 a Lời giải Câu 73: Đáp ánA. Ta có (sử dụng máy tính bỏ túi) 355 3,14159292...3,1415929293 113 Do vậy 355 03,141592933,14159265 113 −− 0,00000028 Vậy sai số tuyệt đối nhỏ hơn 7 2,8.10 . Câu 74: Độ

DẠYKÈMQUYNHƠN OFFICIAL
ố
ệt đối của
ế
ả đo trên và viết h dưới dạng chuẩn. A. ( ) 0,68625;1373 h hm== B. ( ) 0,68626;1372 h hm== C. ( ) 0,68625;1372 h hm== D. ( ) 0,68626;1373 h hm== Lời giải Câu 75: Đáp ánA. Theo công thức h h h = ta có: 0,5 .1372.5.0,68625 1000 hh h === Và h viết dưới dạng chuẩn là 1373 h = (m) Câu 76: Cân nặng của 40 học sinh lớp 10 trường THPT A được cho bởi bảng sau
cao của một ngọn núi đo được là 1372,5 h = m. Với sai số tương đối mắc phải là 0,5‰ Hãy xác định sai s
tuy
k
t qu
Tính số trung bình cộng của mẫu số liệu trên.
A. 38,26 x = . B. 40,25 x = . C. 39,65 x = . D. 40,83 x = .

Lời giải
Chọn C
Giá trị đại diện của từng lớp cân nặng là: 36, 38, 40, 42. Khi đó số trung bình cộng của mẫu số liệu trên là: 36.638.940.1142.14 39,65 40 x +++ == .
Câu 77: Kết quả điểm kiểm tra 15’ môn Toán của 100 em học sinh được trình bày ở bảng sau: Điểm 3 4 5 6 7 8 9 10 Cộng Tần số 3 5 11 17 30 19 10 5 100 Số trung bình cộng của bảng phân bố tần số nói trên là
A. 6,88 . B. 7,12. C. 6,5. D. 7,22 . Lời giải
Số trung bình cộng của bảng phân bố tần số nói trên là: 3.34.55.116.177.308.199.1010.5 6,88 100 +++++++ =
Câu 78: Cho phương sai của các số liệu bằng 4. Tìm độ lệch chuẩn. A. 4. B. 2. C. 16. D. 8.
Lời giải Ta có độ lệch chuẩn là căn bậc hai của phương sai Nên 2 42 xx ss=== . 2. Tự luận
Câu 79: Lập bảng biến thiên và vẽ đồ thị của hàm số 2 23=−−+yxx Lời giải 10;1 2 =−−=− b a a . Đỉnh: (1;4)I , trục đối xứng: 1=− x Hàm số đồng biến trên khoảng (;1) −− , nghịch biến trên khoảng (1;) −+ . Bảng biến thiên: Bảng một số giá trị Đồ thị.


DẠYKÈMQUYNHƠN
OFFICIAL
Câu 80: Một người bán nước giải khát đang có 25g bột nho và 100 g đường để pha chế hai loại nước nho A và B . Để pha chế 1l nước nho loại A cần 10 g đường và 1g bột nho; để pha chế 1l nước nho loại B cần 10 g đường và 4g bột nho. Mỗi lít nước nho loại A khi bán lãi được 30 nghìn đồng, mỗi lít nước nho loại B khi bán lãi được 40 nghìn đồng. Hỏi người đó nên pha chế bao nhiêu lít nước nho mỗi loại để có lợi nhuận cao nhất? Lời giải Gọi x và y lần lượt là số lít nước nho loại A và B người đó có thể pha chế. Ta có hệ bất phương trình: 425 10 0 0.
+ +
xy xy x y
Miền nghiệm của hệ bất phương trình là miền tứ giác OABC, trong đó (0;0)O ; (10;0);(5;5);(0;6,25) ABC

OFFICIAL
Gọi F là số tiền lãi (đơn vị: nghìn đồng) thu được, ta có: 3040=+ Fxy . Ta có: Tại (0;0):30.040.00 =+= OF ; Tại (10;0):30.1040.0300 =+= AF ; Tại (5;5):30.540.5350 =+= BF ; Tại (0;6,25):30.040.6,25250 =+= CF Ta thấy F đạt GTLN bằng 350 tại (5;5)B Vậy người đó nên pha chế 5l nước nho mỗi loại để có lợi nhuận cao nhất.

Câu 81: Ta giả sử hai bờ sông là hai đường thẳng song song cách nhau 2km. Một chiếc tàu nhỏ đi từ điểm A ở bờ bên này sang điểm B ở bờ bên kia với vận tốc riêng của tàu (tức là vận tốc của tàu so với dòng nước) là 20 / kmh. Giả sử AB vuông góc với bờ sông (như hình vẽ). Cho biết vận tốc của dòng nước so với bờ là không đổi 5 / kmh (giả sử phương dòng nước chảy song song với bờ sông).
a) Cần giữ lái cho tàu tạo với bờ sông một góc nhọn bằng bao nhiêu độ để tàu sang bờ bên kia theo phương AB ?
b) Tính vận tốc của tàu so với bờ. Hỏi sau bao lâu thì tàu sẽ tới bờ bên kia?
DẠYKÈMQUYNHƠN
(Các kết quả tính toán ở câu a) và câu b) ở trên được làm tròn đến hàng phần trăm).
Lời giải
a) Vận tốc thực của tàu so với bờ là , tntn vvv =+ .
Để cho tàu luôn chạy theo phương AB thì phương của , tnv phải có phương là AB và chiều là hướng từ A đến B (như hình vẽ).
Ta có sin51 204 MCAN MAC AMAM ====
Suy ra 14,48 MAC Vậy góc nhọn của tàu tạo với bờ sông là 9014,4875,52 −= .
b) Do tam giác ANC vuông tại A nên 22 515 ACCNAN=−= .
Vậy vận tốc của tàu so với bờ là 19,36 / kmh . Thời gian để tàu qua sông là 2 0,1 515 giờ.
Câu 82: Cho tam giác ABC cố định và điểm M di động. Chứng minh rằng 45 vMAMBMC =+− không phụ thuộc vào vị trí của điểm M Lời giải ( ) ( ) 45454 vMAMBMCMCCAMCCBMCCACB =+−=+++−=+
Vì A, B, C cố định nên v không đổi Vậy v không phụ thuộc vào vị trí của điểm M
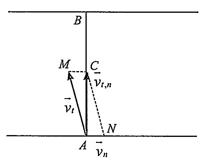
DẠYKÈMQUYNHƠN
OFFICIAL
1. Trắc nghiệm
Câu 1. Cho mệnh đề : P "6 là số hoàn hảo" và mệnh đề Q : "Hà Nội là thủ đô của Việt Nam". Phát
biểu của mệnh đề PQ là
A. Nếu 6 là số hoàn hảo thì Hà Nội là thủ đô của Việt Nam.
B. Nếu Hà Nội là thủ đô của Việt Nam thì 6 là số hoàn hảo.
C. 6 là số hoàn hảo nếu Hà Nội là thủ đô của Việt Nam.
D. Nếu 6 là số hoàn hảo thì Hà Nội không là thủ đô của Việt Nam.
Câu 2. Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Đại dịch Covid 19 thật đáng sợ!
b) Hà Nam là một tỉnh của Việt Nam. c) 37 là một số nguyên tố. d) Cậu có thích học môn Lịch sử và Địa lí không?
OFFICIAL
A. 4. B. 3. C. 2. D. 1. Câu 3. Cho tập hợp {34}Axx=− và {1;3;9} B = . Tập hợp ()\ CABB = là A. {3;2;1;0;2} C =−−− . B. {3;2;1;0;2;4} C =−−− . C. {3;1;2} C =−− D. {3;2;1;0;1;2;3} C =−−− Câu 4. Cho tập ( ) ( ) 2249 0 .13 3 xxx Xx −−++ == Số tập con của X là A. 4. B. 0. C. 6. D. 8. Câu 5. Cho biểu đồ Ven sau đây. Phần được gạch sọc biểu diễn tập hợp nào? A. \ AB B. \ BA C. AB D. AB Câu 6. Miền nghiệm của bất phương trình 31 +xy là nửa mặt phẳng tạo bởi đường thẳng :31( +=dxy kể cả d ) chứa điểm có toạ độ nào sau đây? A. (0;0). B. (3;1) C. (1;1) D. (2;9)


DẠYKÈMQUYNHƠN
ĐỀ SỐ 7
. Câu 7. Phần không bị gạch (kể cả d ) ở Hình 3 là miền nghiệm của bất phương trình: A. 1 x B. 1 x C. 1 y D. 1 y Câu 8. Cặp số nào sau đây là nghiệm của hệ bất phương trình: 3515 ? 236 xy xy +− − A. (0;3).
B. (1;1)
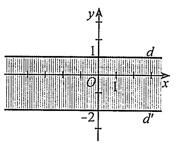
C. (5;2). D. (2;3).
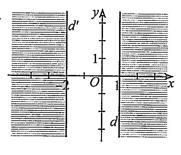

Câu 9. Miền nghiệm của hệ bất phương trình 1 2 − y y được xác định bởi phần không bị gạch và không kể hai đường thẳng , dd ' nào sau đây?
A. B. C. D.
Câu 10. Chủ cửa hàng điện thoại mang 200 triệu đồng hoặc mua điện thoại loại 10 triệu đồng hoặc máy tính bảng loại 9 triệu đồng ở đại lí cấp một. Gọi , xy lần lượt là số chiếc điện thoại và máy tính mà chủ cửa hàng mua. Cặp số (;) xy nào sau đây biểu thị số chiếc điện thoại và máy tính mà chủ cửa hàng có thể mua? A. (10;12) B. (11;10)
C. (9;13)
D. (11;11)

DẠYKÈMQUYNHƠN
OFFICIAL
Câu 11. Cho góc thoả mãn 0180 và 3 cos 5 =− . Giá trị của sin là: A. 3 5 . B. 4 5 . C. 4 5 D. 2 5 . Câu 12. Cho góc thoả mãn 0180 và tan2 =− . Giá trị của cot là: A. 2. B. 1 2 C. 1 2 . D. 3. Câu 13. Giá trị biểu thức tan0tan10tan20tan30 = T bằng: A. 0. B. 1. C. 1
.
.
D. 2.
Câu 14. Cho tam giác ABC có 04,3,30ABACBAC=== . Khi đó diện tích tam giác ABC bằng A. 3 B. 43 C. 63 D. 6

Câu 15. Cho tam giác ABC có 02,3,60ABACBAC=== . Khi đó bán kính đường tròn ngoại tiếp tam giác ABC bằng:
A. 621 7 . B. 7 . C. 21 3 . D. 321 7 .
Câu 16. Cho tam giác ABC nhọn có 3 BCa = và bán kính đường tròn ngoại tiếp tam giác ABC là 3 Ra = . Tính số đo góc A .
A. 120 = A B. 45 = A C. 30 = A D. 60 = A
Câu 17. Cho tam giác ABC có 4 c = , 6 b = , 60 = A . Chiều cao a h của tam giác ABC là: A. 321 7 a h = . B. 621 7 a h = . C. 1221 7 a h = . D. 221 7 a h = .
Câu 18. Cho tam giác ABC có 2 a = , 6 b = , 31 c =+ . Tính bán kính R của đường tròn ngoại tiếp. A. 2 . B. 2 2 . C. 2 . 3 D. 3.
Câu 19. Cho hình bình hành ABCD tâm O. Vectơ đối của BO là
A. CO B. AO C. DO D. OC Câu 20. Cho hình vuông ABCD cạnh a , độ dài vectơ ABACBD −+ bằng: A. a . B. 3a . C. 2 a . D. 22a . Câu 21. Cho hàm số 21 khi1 1khi 01 12 khi x0
xx yx x
− = − . Giá trị lớn nhất của hàm số trên 2;2 là: A. 2. B. 4. C. 5. D. 7. Câu 22. Điểm nào sau đây thuộc đồ thị của hàm số ( ) 2 1 x y xx = ? A. ( )0;1 M B. ( )2;1 M C. ( )2;0 M D. ( )1;1 M Câu 23. Trên Hình biểu diễn ba lực 123 ,, FFF cùng tác động vào một vật ở vị trí cân bằng A . Cho biết 1230,40== FNFN . Tính cường độ của lực 3F A. 50. B. 40. C. 30. D. 20.
DẠYKÈMQUYNHƠN
OFFICIAL
Câu 24. Cho đoạn thẳng AB . Gọi M là một điểm trên AB sao cho 1 4 = AMAB . Khẳng định nào sau đây sai? A. 1 3 = MAMB B. 1 4 = AMAB C. 3 4 = BMBA D. 3=− MBMA
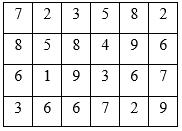
Câu 25. Cho tam giác ABC . Gọi I là trung điểm của AB . Tìm điểm M thỏa mãn hệ thức 20MAMBMC++= .
A. M là trung điểm của BC
B. M là trung điểm của IC
C. M là trung điểm của IA
D. M là điểm trên cạnh IC sao cho 2 IMMC =
Câu 26. Hàm số 2 411yxx=−+ đồng biến trên khoảng nào trong các khoảng sau đây? A. (2;) −+ B. (;) −+ C. (2;) + D. (;2) −
Câu 27. Một quả bóng cầu thủ sút lên rồi rơi xuống theo quỹ đạo là parabol. Biết rằng ban đầu quả bóng được sút lên từ độ cao 1m sau đó 1 giây nó đạt độ cao 10m và 3,5 giây nó ở độ cao 6,25m Hỏi độ cao cao nhất mà quả bóng đạt được là bao nhiêu mét? A. 11m . B. 12m. C. 13m. D. 14m.
Câu 28. Cho a và b là hai vectơ cùng hướng và đều khác vectơ 0 . Mệnh đề nào sau đây đúng? A. .. abab = . B. .0ab = . C. .1ab =− . D. .. abab =− .
Câu 29. Cho tam giác đều ABC cạnh bằng a và H là trung điểm BC . Tính . AHCA A. 2 3 4 a . B. 2 3 4 a . C. 2 3 2 a . D. 2 3 2 a .
Câu 30. Biết a , b 0 và .. abab =− . Câu nào sau đây đúng
A. a và b cùng hướng. B. a và b nằm trên hai dường thẳng hợp với nhau một góc o120 . C. a và b ngược hướng. D. A, B, C đều sai.
Câu 31. Độ cao của một ngọn núi đo được là 2373,5 hm = với sai số tương đối mắc phải là 0,5‰. Hãy viết h dưới dạng chuẩn. A. 2373 m B. 2370 m C. 2373,5 m D. 2374 m
Câu 32. Trong một phòng thí nghiệm, hằng số c được xác định gần đúng là 3,54965 với độ chính xác 0,00321 d = Dựa vào d, hãy xác định chữ số chắc chắn của c A. 3; 5; 4 B. 3; 5; 4; 9 C. 3; 5; 4; 9; 6 D. 3; 5; 4; 9; 6; 5
Câu 33. Cho mẫu số liệu thống kê 2;4;6;8;10 . Số trung bình của mẫu số liệu trên là: A. 7 . B. 12. C. 6.5. D. 6 . Câu 34. Điểm kiểm tra của 24 học sinh được ghi lại trong bảng sau: Tìm mốt của điểm điều tra. A. 2 B. 7 C. 6 D. 9 Câu 35. Nếu đơn vị đo của số liệu là kg thì đơn vị của độ lệch chuẩn là
DẠYKÈMQUYNHƠN
OFFICIAL
2. Tự luận
Câu 1. Một cây cầu treo có trọng lượng phân bố đều dọc theo chiều dài của nó. Cây cầu có trụ tháp đôi
cao 75m so với mặt của cây cầu và cách nhau 400m . Các dây cáp có hình dạng đường parabol và được treo trên các đỉnh tháp. Các dây cáp chạm mặt cầu ở tâm của cây cầu. Tìm chiều cao của dây cáp tại điểm cách tâm của cây cầu 100 m (giả sử mặt của cây cầu là bằng phẳng).

Câu 2. Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 12 g hương liệu, 9 lịt nước và 315 g đường đề pha chế hai loại nước A và B . Để pha chế 1 lít nước A cần 45g đường, 1 lít nước và 0,5 g hương liệu; để pha chế 1 lít nước B cần 15 g đường, 1 lít nước và 2g hương liệu. Mỗi lít nước A nhận được 60 điểm thưởng, mỗi lít nước B nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước mỗi loại để đội chơi được số điểm thưởng là lớn nhất?
Câu 3. Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 45 và 75 . Biết khoảng cách giữa hai vị trí A, B là 30m (Hình). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
DẠYKÈMQUYNHƠN
A. kg. B. kg 2
đơn vị D. kg 2
OFFICIAL
C. Không có
Câu 4. Cho hình vuông ABCD cạnh a. Chứng minh rằng 232 vMAMBMCMD =−+− không phụ thuộc vào vị trí của điểm M Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM 1A 2C 3A 4D 5A 6A 7B 8B 9B 10B 11B 12C 13A 14A 15C 16D 17B 18A 19C 20A 21C 22C 23A 24A 25B 26C 27C 28A 29B 30C 31B 32A 33D 34C 35A 1. Trắc nghiệm Câu 1. Cho mệnh đề : P "6 là số hoàn hảo" và mệnh đề Q : "Hà Nội là thủ đô của Việt Nam". Phát biểu của mệnh đề PQ là A. Nếu 6 là số hoàn hảo thì Hà Nội là thủ đô của Việt Nam.
B. Nếu Hà Nội là thủ đô của Việt Nam thì 6 là số hoàn hảo.
C. 6 là số hoàn hảo nếu Hà Nội là thủ đô của Việt Nam.
D. Nếu 6 là số hoàn hảo thì Hà Nội không là thủ đô của Việt Nam.
Câu 2. Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Đại dịch Covid 19 thật đáng sợ!
b) Hà Nam là một tỉnh của Việt Nam. c) 37 là một số nguyên tố.
d) Cậu có thích học môn Lịch sử và Địa lí không? A. 4. B. 3. C. 2. D. 1. Câu 3. Cho tập hợp {34}Axx=− và {1;3;9} B = . Tập hợp ()\ CABB = là A. {3;2;1;0;2} C =−−− B. {3;2;1;0;2;4}

OFFICIAL
DẠYKÈMQUYNHƠN
C =−−− . C. {3;1;2} C =−− . D.
C =−−− . Câu 4. Cho tập ( ) ( ) 2249 0 .13 . 3 xxx Xx −−++ == Số tập con của X là A. 4. B. 0. C. 6. D. 8. Lời giải Chọn D Xét phương trình ( ) ( ) 22 491330 xxx −−++= ( ) 2 2 490 1330 x xx −= −++= 3 2 1 3 x x x = = = 3 2() 1 x doxQ x = = Khi đó tập 3 ,1 2 X = vậy số tập con của X là 3 28 = Câu 5. Cho biểu đồ Ven sau đây. Phần được gạch sọc biểu diễn tập hợp nào? A. \ AB B. \ BA C. AB D. AB Câu 6. Miền nghiệm của bất phương trình 31 +xy là nửa mặt phẳng tạo bởi đường thẳng :31( +=dxy kể cả d ) chứa điểm có toạ độ nào sau đây? A. (0;0). B. (3;1). C. (1;1) D. (2;9) Lời giải. Với 0,0==xy ta có: 3.0001 += . Chọn A. Câu 7. Phần không bị gạch (kể cả d ) ở Hình 3 là miền nghiệm của bất phương trình:
{3;2;1;0;1;2;3}





DẠYKÈMQUYNHƠN OFFICIAL
i , xy lần
t là số chiếc điện thoạ
mà chủ cửa hàng mua. Cặp số (;) xy nào
u
ị
ố chiếc
n
ạ
chủ cửa hàng có thể mua? A. (10;12). B. (11;10). C. (9;13) D. (11;11) Câu 11. Cho góc thoả mãn 0180 và 3 cos 5 =− . Giá trị của sin là: A. 3 5 B. 4 5 . C. 4 5
A. 1 x . B. 1 x . C. 1 y . D. 1 y . Câu 8. Cặp số nào sau đây là nghiệm của hệ bất phương trình: 3515 ? 236 xy xy +− − A. (0;3) B. (1;1). C. (5;2). D. (2;3) Câu 9. Miền nghiệm của hệ bất phương trình 1 2 − y y được xác định bởi phần không bị gạch và không kể hai đường thẳng , dd ' nào sau đây? A. B. C. D. Câu 10. Chủ cửa hàng điện thoại mang 200 triệu đồng hoặc mua điện thoại loại 10 triệu đồng hoặc máy tính bảng loại 9 triệu đồng ở đại lí cấp một. Gọ
lượ
i và máy tính
sau đây biể
th
s
điệ
tho
i và máy tính mà
DẠYKÈMQUYNHƠN OFFICIAL D. 2
số đo góc A . A. 120 = A . B. 45 = A . C. 30 = A . D. 60 = A . Lời giải Chọn D Áp dụng định lý sin trong tam giác ABC , ta có 33 2sin sin22 23 ==== BCBCa RA AR a Suy ra 60 = A (do tam giác ABC nhọn). Câu 17. Cho tam giác ABC có 4 c = , 6 b = , 60 = A . Chiều cao a h của tam giác ABC là: A. 321 7 a h = . B. 621 7 a h = . C. 1221 7 a h = . D. 221 7 a h = . Lời giải Chọn B Ta có: 222 2.cos abcbcA =+− 2 28 a = 27 a =
5 Câu 12. Cho góc thoả mãn 0180 và tan2 =− . Giá trị của cot là: A. 2. B. 1 2 C. 1 2 . D. 3. Câu 13. Giá trị biểu thức tan0tan10tan20tan30 = T bằng: A. 0. B. 1. C. 1 D. 2. Lời giải Vì tan00 = nên 0 = T Chọn A Câu 14. Cho tam giác ABC có 04,3,30ABACBAC=== . Khi đó diện tích tam giác ABC bằng A. 3. B. 43. C. 63 . D. 6 . Lời giải Chọn A 0 11 ..sin.4.3.sin303. 22 ABC SABACBAC === Câu 15. Cho tam giác ABC có 02,3,60ABACBAC=== . Khi đó bán kính đường tròn ngoại tiếp tam giác ABC bằng: A. 621 7 B. 7 C. 21 3 D. 321 7 Lời giải Chọn C 22222 1 2...cos232.2.3.7 2 BCABACABACBAC=+−=+−= Bán kính đường tròn ngoại tiếp tam giác ABC bằng: 0 721 2sin2.sin603 BC R BAC === Câu 16. Cho tam giác ABC nhọn có 3 BCa = và bán kính đường tròn ngoại tiếp tam giác ABC là 3 Ra = . Tính
Diện tích tam giác: 11 ..sin. 22 a SbcAha == ..sin621 7 a bcA h a ==
Câu 18. Cho tam giác ABC có 2 a = , 6 b = , 31 c =+ . Tính bán kính R của đường tròn ngoại tiếp. A. 2 B. 2 2 C. 2 . 3 D. 3. Lời giải Chọn A Ta có : 222 cos 2 bca A bc +− = 2 2 = 45 A = . Do đó : 2sin a R A = 2 2.sin45 = 2 = .
Câu 19. Cho hình bình hành ABCD tâm O. Vectơ đối của BO là A. CO B. AO C. DO D. OC Lời giải Chọn C Từ hình vẽ suy ra BODO
Câu 20. Cho hình vuông ABCD cạ
DẠYKÈMQUYNHƠN OFFICIAL
nh a , độ dài vectơ ABACBD −+ bằng: A. a . B. 3a .
.
. Lời giải Vì ABCD là hình vuông nên: CACBCD =+ và BDBCBA =+ Ta có: ABACBDABCABDABCDCBBABC −+=++=++++ ABCDCBABCBCD =++−−= Mà CDa = . Từ đó độ dài ABACBDa −+= Câu 21. Cho hàm số 21 khi1 1khi 01 12 khi x0 xx yx x − = − . Giá trị lớn nhất của hàm số trên 2;2 là: A. 2. B. 4. C. 5. D. 7. Lời giải Chọn C Trên 1;2 hàm số 21yx=− đồng biến nên giá trị lớn nhất bằng ( ) 23 y = Trên ( )0;1 hàm số 1 y = nên giá trị lớn nhất bằng 1 y = . Trên 2;0 hàm số 12 yx =− nghịch biến nên giá trị lớn nhất bằng ( ) 25 y −= . Vậy giá trị lớn nhất của hàm số trên 2;2 là ( ) 25 y −= Câu 22. Điểm nào sau đây thuộc đồ thị của hàm số ( ) 2 1 x y xx = ? O C A B D
C. 2 a
D. 22a


DẠYKÈMQUYNHƠN OFFICIAL A.
cho các lực 123 ,, FFF và vectơ AE
thi cho hợp lực F của 12 , FF . Khi đó, do 90 = BAC , nên tứ giác ABEC là hình chữ nhật. Từ đó, do 30() = ABN , 40( ) = ACN , suy ra 22 ||304050( ). FAEN ==+= Do vật ở vị trí cân bằng, nên hai lực F và 3F có cùng cường độ và ngược hướng, tức là các vectơ AE và AD là các vectơ có cùng độ dài và ngược hướng. Bởi vậy, cường độ của lực 3F bằng 3 ||50()=== FFAEN . Câu 24. Cho đoạn thẳng AB . Gọi M là một điểm trên AB sao cho 1 4 = AMAB . Khẳng định nào sau đây sai?
( )0;1 M B. ( )2;1 M C. ( )2;0 M D. ( )1;1 M Lời giải Với 2 x = thì 0 y = . Vậy điểm ( )2;0 M thuộc đồ thị hàm số đã cho. Đáp án C. Câu 23. Trên Hình biểu diễn ba lực 123 ,, FFF cùng tác động vào một vật ở vị trí cân bằng A . Cho biết 1230,40== FNFN . Tính cường độ của lực 3F A. 50. B. 40. C. 30. D. 20. Lời giải Ta sử dụng các vectơ ,, ABACAD lần lượt biều thị
biểu
Câu 25. Cho tam giác ABC . Gọi I là trung điểm của AB . Tìm điểm M thỏa mãn hệ thức 20MAMBMC++=
A. M là trung điểm của BC B. M là trung điểm của IC C. M là trung điểm của IA D. M là điểm trên cạnh IC sao cho 2 IMMC =
Lời giải Chọn B 202200 MAMBMCMIMCMIMC ++=+=+= M là trung điểm của IC
Câu 26. Hàm số 2 411yxx=−+ đồng biến trên khoảng nào trong các khoảng sau đây? A. (2;) −+ B. (;) −+ C. (2;) + D. (;2) − Lời giải Chọn C Ta có bảng biến thiên: Từ bảng biến thiên ta thấy, hàm số đồng biến trên khoảng (2;) +
Câu 27. Một quả bóng cầu thủ sút lên rồi rơi xuống theo quỹ đạo là parabol. Biết rằng ban đầu quả bóng được sút lên từ độ cao 1m sau đó 1 giây nó đạt độ cao 10m và 3,5 giây nó ở độ cao 6,25m Hỏi độ cao cao nhất mà quả bóng đạt được là bao nhiêu mét? A. 11m . B. 12m. C. 13m. D. 14m . Lời giải Chọn C

DẠYKÈMQUYNHƠN
1
=
1
= AMAB C. 3
= BMBA D. 3=− MBMA
OFFICIAL A.
3
MAMB B.
4
4
Biết rằng quỹ đạo của quả bóng là một cung parabol nên phương trình có dạng 2 yaxbxc =++ Theo bài ra gắn vào hệ tọa độ và sẽ tương ứng các điểm A , B , C nên ta có 1 10 12,253,56,25 c abc abc = ++= ++= 3 12 1 a b c =− = = . Suy ra phương trình parabol là 2 3121yxx=−++ Parabol có đỉnh (2;13)I . Khi đó quả bóng đạt vị trí cao nhất tại đỉnh tức 13m h = Câu 28. Cho a và b là hai vectơ cùng hướng và đều khác vectơ 0 . Mệnh đề nào sau đây đúng? A. .. abab = . B. .0ab = . C. .1ab =− . D. .. abab =− . Lời giải 12 10 8 6 4 2 5 y x O A B C
Do a và b là hai vectơ cùng hướng nên ( ) ( ) 0 ,0cos,1 abab=⎯⎯→= .
Vậy .. abab = .
Câu 29. Cho tam giác đều ABC cạnh bằng a và H là trung điểm BC . Tính . AHCA
A. 2 3 4 a B. 2 3 4 a C. 2 3 2 a D. 2 3 2 a Lời giải Chọn B
Ta có ( ) 2 o 33 ...cos,..cos150 24 ===− AHCAAHCAAHCAaaa .
Câu 30. Biết a , b 0 và .. abab =− . Câu nào sau đây đúng
A. a và b cùng hướng. B. a và b nằm trên hai dường thẳng hợp với nhau một góc o120 .
C. a và b ngược hướng. D. A, B, C đều sai. Lời giải Chọn C Ta có ( ) ( ) ...cos,.cos,1 =−=−=− abababababab nên a và b ngược hướng Câu 31. Độ cao của một ngọn núi đo được là 2373,5 hm = với sai số tương đối mắc phải là 0,5‰. Hãy viết h dưới dạng chuẩn. A. 2373 m B. 2370 m C. 2373,5 m D. 2374 m Lời giải Đáp án B. h h h = , ta có: 0,5 .2373,5.1,18675 1000 h hh === h viết dưới dạng chuẩn là 2370 h = m. Câu 32. Trong một phòng thí nghiệm, hằng số c được xác
DẠYKÈMQUYNHƠN
Chọn
OFFICIAL
A
đị
ần
0,00321 d = . Dựa vào d, hãy xác định chữ số chắc chắn của c.
5; 4 B. 3; 5; 4; 9
Ta
0,003210,005 nên chữ số
chắn là 3; 5; 4.
33. Cho mẫu số liệu thống kê 2;4;6;8;10 . Số trung bình của mẫu số liệu trên là: A. 7 B. 12 C. 6.5 D. 6 Lời giải Số trung bình của mẫu số liệu trên là: 246810 6 5 x ++++ == . Câu 34. Điểm kiểm tra của 24 học sinh được ghi lại trong bảng sau:
nh g
đúng là 3,54965 với độ chính xác
A. 3;
C. 3; 5; 4; 9; 6 D. 3; 5; 4; 9; 6; 5 Lời giải Đáp án#A.
có:
4 (hàng phần trăm) là chữ số chắc chắn, do đó c có 3 chữ số chắc
Câu
Tìm mốt của điểm điều tra.
A. 2. B. 7 . C. 6 . D. 9.

Lời giải
Ta có bảng thống kê sau:
Ta thấy điểm 6 có tần số lớn nhất nên mốt của điểm điều tra là: 0 6 M = .
Câu 35. Nếu đơn vị đo của số liệu là kg thì đơn vị của độ lệch chuẩn là
A. kg. B. kg 2
C. Không có đơn vị D. kg 2
OFFICIAL
Lời giải Chọn A
2. Tự luận
Câu 1. Một cây cầu treo có trọng lượng phân bố đều dọc theo chiều dài của nó. Cây cầu có trụ tháp đôi cao 75m so với mặt của cây cầu và cách nhau 400m . Các dây cáp có hình dạng đường parabol và được treo trên các đỉnh tháp. Các dây cáp chạm mặt cầu ở tâm của cây cầu. Tìm chiều cao của dây cáp tại điểm cách tâm của cây cầu 100 m (giả sử mặt của cây cầu là bằng phẳng).

Lời giải Chọn hệ trục toạ độ Oxy như Hình 6.13: Trục Ox dọc theo mặt của cây cầu, trục Oy vuông góc với trục Ox tại tâm của cây cầu. Khi đó các dây cáp có hình dạng đường parabol có bề lõm hướng lên trên và đỉnh của parabol là gốc (0;0)O . Vì thế ta giả sử công thức của parabol là 2,0=yaxa .
Theo giả thiết, cây cầu có trụ tháp đôi cao 75 m so với mặt của cây cầu và cách nhau 400 m nên ta có các điểm (200;75)A và (200;75)B thuộc parabol. Khi đó ta có: 2 3 75200. 1600 aa == Do đó, phương trình của parabol là: 2 3 1600 = yx
DẠYKÈMQUYNHƠN
1600
Vậy chiều cao của dây cáp tại điểm cách tâm của cây cầu 100 m là 18,75 m.
Fxyxy (điểm). Ta cần tìm giá trị lớn nhất của (;)Fxy với (;) xy thoả mãn hệ trên. Miền nghiệm của hệ là miền ngũ giác OABCD với (0;6),(4;5),(6;3) ABC , (7;0)D và (0;0)O .


DẠYKÈMQUYNHƠN
Với 100= x ta có 2 3 10018,75
== y
OFFICIAL
+ + + x y xy xy xy Số điểm thưởng đội chơi nhận được là (;)6080 =+
Tính giá trị của F tại các đỉnh của ngũ giác: (0;6)480,(4;5)640 ==FF
(6;3)600,(7;0)420 ==FF và (0;0)0 = F . So sánh các giá trị đó ta được giá trị lớn nhất
Câu 2. Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 12 g hương liệu, 9 lịt nước và 315 g đường đề pha chế hai loại nước A và B . Để pha chế 1 lít nước A cần 45g đường, 1 lít nước và 0,5 g hương liệu; để pha chế 1 lít nước B cần 15 g đường, 1 lít nước và 2g hương liệu. Mỗi lít nước A nhận được 60 điểm thưởng, mỗi lít nước B nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước mỗi loại để đội chơi được số điểm thưởng là lớn nhất? Lời giải Gọi x và y lần lượt là số lít nước loại A và B cần pha chế. Khi đó, theo đề bài ta có hệ bất phương trình tìm là (4;5)640 = F . Vậy cần pha chế 4 lít nước loại A và 5 lít nước loại
0 0 9 4515315 0,5212. là lớn
,
cần
B đề số điểm thưởng nhận được
nhất.


DẠYKÈMQUYNHƠN OFFICIAL Câu
ột
ờ
ể
từ vị
đế
vị
)? Lời giải Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB . Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển. Ta có: 18018075115 =−=−=ABCCBH ( ) ˆ 180()1804511520 =−+=−+= ACBAACB Áp dụng định lí sin trong tam giác ABC ta có: sinsin = ABAC CB 30 sinsin11579,5 sinsin20 == AB ACB C Tam giác ACH vuông tại H nên ta có: sin.sin45.79,556 ==CHAAC Vậy ngọn hải đăng cách bờ biển 56m Câu 4. Cho hình vuông ABCD cạnh a. Chứng minh rằng 232 vMAMBMCMD =−+− không phụ thuộc vào vị trí của điểm M Lời giải Gọi O là tâm hình vuông Theo quy tắc ba điểm ta có ( ) ( ) ( ) ( ) 232 vMOOAMOOBMOOCMOOD =+−+++−+ 232 OAOBOCOD =−+− Mà ,2 ODOBOCOAvOA =−=−=− Suy ra 232 vMAMBMCMD =−+− không phụ thuộc vào vị trí của điểm M
3. M
người đi dọc b
bi
n
trí A
n
trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 45 và 75 . Biết khoảng cách giữa hai vị trí A, B là 30m (Hình). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị
DẠYKÈMQUYNHƠN OFFICIAL
1. Trắc nghiệm
Câu 1: Mệnh đề nào sau đây là mệnh đề tương đương?
A. 10 chia hết cho 5 là điều kiện cần để 10 chia hết cho 2.
B. Hình vuông là hình chữ nhật.
C. Hình thang nội tiếp đường tròn khi và chỉ khi nó là hình thang cân.
D. Nếu 63 chia hết cho 7 thì hình thoi có hai đường chéo vuông góc nhau.
Câu 2: Mệnh đề: " 2 ,33xx " khẳng định là
A. Bình phương của mỗi số thực lớn hơn 33.
B. Có ít nhất một số thực mà bình phương của nó lớn hơn 33.
C. Chỉ có một số thực có bình phương lớn hơn 33.
D. Nếu x là số thực thì 2 33 x .
Câu 3: Cho A là tập hợp các số tự nhiên chẵn không lớn hơn 12,{6} Bnn= , {412}Cnn= . Mệnh đề nào sau đây là đúng? A. () ABCB = . B. () ABCA = . C. () ABCC = D. ()ABC= .
Câu 4: Cho tập hợp (3;]Am =− và {3}Bxx= . Giá trị nguyên dương của m để tập hợp (\) AB có đúng 10 phần tử là A. 10. B. 11. C. 12. D. 13. Câu 5: Cho (;2)[6;) CA =−+ và [5;9) CB = . Tập hợp XAB = là A. [2;5) B. (2;5) C. [2;5]. D. [6;9).
Câu 6: Cặp số nào sau đây là nghiệm của bất phương trình 55−+ xy ? A. (1;9) B. (2;1). C. (2;2). D. (0;5)
Câu 7: Miền nghiệm của bất phương trình 2 −+ xy được xác định bởi miền nào (nửa mặt phẳng không bị gạch và không kể d) sau đây?
DẠYKÈMQUYNHƠN
ĐỀ SỐ 8
OFFICIAL
A. B. C. D.
Câu 8: Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình 0 33 5?
xy xy xy
− −− + A. (3;2)A B. (6;3)B . C. (6;4)C . D. (5;4)D




Câu 9: Cho điểm (3;3)A và điểm M thuộc miền nghiệm của hệ bất phương trình 20 20 20 20
xy xy xy xy
+− ++ −++ −+ Độ dài AM lớn nhất là A. 22 B. 52 C. 10 . D. 34 .
Câu 10: Một cửa hàng bán hai loại mặt hàng A và B . Biết rằng cứ bán một mặt hàng loại A cửa hàng lãi 5 nghìn đồng, bán một mặt hàng loại B cửa hàng lãi 7 nghìn đồng. Gọi , xy lần lượt là số mặt hàng loại A và mặt hàng loại B mà cửa hàng đó bán ra trong một tháng. Cặp số (;) xy nào sau đây biểu thị số mặt hàng bán ra mỗi loại của cửa hàng trong một tháng mà tổng số tiền lãi không ít hơn 30 triệu đồng? A. (1000;2000) B. (3000;1000) . C. (2000;3000).
DẠYKÈMQUYNHƠN
OFFICIAL
D. (3000;2000)
Câu 11: Cho góc thoả mãn 0180 và cot2 =− . Giá trị của sin là: A. 1 2 B. 1 5 C. 5 5 . D. 5 5 Câu 12: Giá trị biểu thức tan1tan2.tan89 = T bằng: A. 0. B. 1. C. 1. D. 2. Câu 13: Cho 1 sin 4 = , với 090 . Giá trị cos bằng A. 15 4 . B. 15 4 . C. 15 16 . D. 15 16 .
Câu 14: Cho tam giác ABC có 4cm = AB ; 12cm= AC và góc 120 BAC = . Tính diện tích tam giác ABC . A. 123 ( 2 cm ) B. 243( 2 cm ) C. 12( 2 cm ) D. 24( 2 cm ) Câu 15: Cho tam giác ABC thỏa mãn 222 2.0BCACABBCAC +−−= . Khi đó, góc C có số đo là A. 150 C = B. 60 C = . C. 45 C = D. 30 C = Câu 16: Tam giác ABC có 60,45BC và 5 AB . Tính độ dài cạnh AC . A. 56 2 AC B. 53. AC C. 56 3 AC D. 56 4 AC Câu 17: Một tam giác có ba cạnh là 52, 56, 60. Bán kính đường tròn ngoại tiếp tam giác đó là A. 65 4 B. 40 C. 32,5 D. 65,8
Câu 18: Cho tam giác ABC có 12 AB = , 13 AC = , 5 BC = . Diện tích S của tam giác ABC là: A. 30 S = B. 40 = S C. 50 = S D. 60 = S Câu 19: Cho tam giác ABC , có thể xác định được bao nhiêu véc tơ khác véc tơ không có điểm đầu và điểm cuối là các đỉnh của tam giác đã cho? A. 4 B. 5 C. 7 D. 6. Câu 20: Tổng MNPQRNNPQR ++++ bằng vectơ nào sau đây? A. MR B. MN C. PR D. MP Câu 21: Cho hàm số ( ) 326116yfxxxx ==−+− . Kết quả sai là
DẠYKÈMQUYNHƠN
OFFICIAL
A. ( ) 10 f = . B. ( ) 20 f = . C. ( ) 30 f = . D. ( ) 424 f −=− .
Câu 22: Tập xác định của hàm số 2 5 1 = y x là
A. \1 . B. \1;1 . C. \1 . D. .
Câu 23: Cho tam giác ABC đều có cạnh là 6. Tính ABAC +
A. 62 . B. 18. C. 12. D. 63 .
Câu 24: Cho đoạn thẳng AB và M là một điểm trên đoạn AB sao cho 1 5 MAAB = . Trong các khẳng định sau, khẳng định nào sai ?
A. 1 5 AMAB = B. 1 4 MAMB =− C. 4 MBMA =− D. 4 5 MBAB =−
Câu 25: Cho hình bình hành ABCD, điểm M thõa mãn 4AMABADAC =++ . Khi đó điểm M là:
A. Trung điểm của AC B. Điểm C C. Trung điểm của AB D. Trung điểm của AD
Câu 26: Cho hàm số 2 (0)yaxbxca =++ có đồ thị (P). Biết đồ thị của hàm số có đỉnh (1;1)I và đi qua điểm (2;3)A . Tính tổng 222 Sabc =++
A. 3 B. 4 C. 29 D. 1
Câu 27: Cho hàm số 2 43.yxx=−++ Chọn khẳng định đúng.
A. Hàm số đồng biến trên . B. Hàm số nghịch biến trên . C. Hàm số đồng biến trên ( ) 2;+ D. Hàm số nghịch biến trên ( ) 2;+
Câu 28: Cho hai vectơ a và b khác 0 . Xác định góc giữa hai vectơ a và b khi ...abab =− A. o180 = . B. o0 = . C. o90 = . D. o45 = .
Câu 29: Cho 2 vectơ a và b có 4 a = , 5 b = và ( ) o,120ab = .Tính ab + A. 21. B. 61. C. 21. D. 61. Câu 30: Cho tam giác ABC vuông tại A có o ˆ 60 B = , ABa = . Tính ACCB A. 2 3a . B. 2 3a . C. 3a . D. 0 . Câu 31: Cho giá trị gần đúng của
DẠYKÈMQUYNHƠN
OFFICIAL
8 17 là 0,47. Sai số tuyệt đối của số 0,47 là: A. 0,001. B. 0,002.
.
. Câu 32: Cho giá trị gần đúng của 3 7 là 0,429. Sai số tuyệt đối của số 0,429 là: A. 0,0001. B. 0,0002. C. 0,0004. D. 0,0005. Câu 33: Kết quả điểm kiểm tra 45 phút môn Hóa Học của 100 em học sinh được trình bày ở bảng sau: Điểm 3 4 5 6 7 8 9 10 Cộng Tần số 3 5 14 14 30 22 7 5 100 Số trung bình cộng của bảng phân bố tần số nói trên là
C. 0,003
D. 0,004
A. 6,82 . B. 4. C. 6,5. D. 7,22 .

Câu 34: Điều tra tiền lương một tháng của 100 người lao động trên địa bàn một xã ta có bảng phân bố tần số sau:
Tiền lương (VND) 5.000.000 6.000.000 7.000.000 8.000.000 9.000.000 9.500.000 Tần số 26 34 20 10 5 5
Tìm mốt của bảng phân bố tần số trên.
A. 5.000.000. B. 6.000.000. C. 7.500.000. D. 9.500.000.
Câu 35: Tìm phát biểu đúng về phương sai của một mẫu số liệu.
A. Phương sai được sử dụng làm đại diện cho các số liệu của mẫu.
B. Phương sai được sử dụng để đánh giá mức độ phân tán của các số liệu thống kê (so với số trung bình).
C. Phương sai được tính bằng tổng số phần tử của một mẫu số liệu.
D. Phương sai là số liệu xuất hiện nhiều nhất (số liệu có tần số lớn nhất) trong bảng các số liệu thống kê
2. Tự luận
Câu 36: Bác Hùng dùng 200m hàng rào dây thép gai để rào miếng đất đủ rộng thành một mảnh vườn hình chữ nhật.
a) Tìm công thức tính diện tích ()Sx của mảnh vườn hình chữ nhật rào được theo chiều rộng ( )xm của mảnh vườn đó. b) Tìm kích thước của mảnh vườn hình chữ nhật có diện tích lớn nhất có thể rào được.
Câu 37: Bác Năm dự định trồng ngô và đậu xanh trên một mảnh đất có diện tích 8 ha. Nếu trồng 1 ha ngô thì cần 20 ngày công và thu được 40 triệu đồng. Nếu trồng 1 ha đậu xanh thì cần 30 ngày công và thu được 50 triệu đồng. Bác Năm cần trồng bao nhiêu hecta cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng không quá 180 ngày công cho việc trồng ngô và đậu xanh.
Câu 38: Gia đình bạn An sở hữu một mảnh đất hình tam giác. Chiều dài của hàng rào MN là 150m , chiều dài của hàng rào MP là 230m . Góc giữa hai hàng rào MN và MP là 110 (Hình 21)
a) Diện tích mảnh đất mà gia đình bạn An sở hữu là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)? b) Chiều dài hàng rào NP là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)? Câu 39:
DẠYKÈMQUYNHƠN
OFFICIAL
Cho tam giác ABC. Gọi A’, B’, C’ là các điểm xác định bởi 2011'2012'0 ABAC+= , 2011'2012'0 BCBA+= ; 2011'2012'0 CACB+= . Chứng minh hai tam giác ABC và A’B’C’ có cùng trọng tâm. Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM
1C 2B 3B 4D 5A 6D 7D 8A 9D 10C 11D 12B 13A 14A 15C
16A 17C 18A 19D 20A 21D 22B 23D 24D 25A 26C 27D 28A 29A 30B 31A 32D 33A 34B 35B
1. Trắc nghiệm
Câu 40: Mệnh đề nào sau đây là mệnh đề tương đương?
A. 10 chia hết cho 5 là điều kiện cần để 10 chia hết cho 2.
B. Hình vuông là hình chữ nhật.
C. Hình thang nội tiếp đường tròn khi và chỉ khi nó là hình thang cân.
D. Nếu 63 chia hết cho 7 thì hình thoi có hai đường chéo vuông góc nhau.
Câu 41: Mệnh đề: " 2 ,33xx " khẳng định là
A. Bình phương của mỗi số thực lớn hơn 33.
B. Có ít nhất một số thực mà bình phương của nó lớn hơn 33.
C. Chỉ có một số thực có bình phương lớn hơn 33.
D. Nếu x là số thực thì 2 33 x
Câu 42: Cho A là tập hợp các số tự nhiên chẵn không lớn hơn 12,{6} Bnn= , {412}Cnn= . Mệnh đề nào sau đây là đúng?
A. () ABCB = . B. () ABCA = . C. () ABCC = D. ()ABC= . Câu 43: Cho tập hợp (3;]Am =− và {3}Bxx= . Giá trị nguyên dương của m để tập hợp (\) AB có đúng 10 phần tử là A. 10.
DẠYKÈMQUYNHƠN
OFFICIAL
B. 11. C. 12. D. 13. Lời giải Ta có [3;3] B =− . Theo giả thiết thì \ AB nên 3 m và \(3;] ABm = . Như vậy, để tập hợp (\) AB có 10 phần tử thì (\){4;5;;13} AB = do đó 13 m = Câu 44: Cho (;2)[6;) CA =−+ và [5;9) CB = . Tập hợp XAB = là A. [2;5). B. (2;5). C. [2;5] D. [6;9) Lời giải [2;6),(;5)[9;)AB==−+ . Suy ra [2;5) XAB== . Câu 45: Cặp số nào sau đây là nghiệm của bất phương trình 55−+ xy ? A. (1;9) B. (2;1).
C. (2;2) D. (0;5). Câu 46: Miền nghiệm của bất phương trình 2 −+ xy được xác định bởi miền nào (nửa mặt phẳng không bị gạch và không kể d) sau đây? A. B. C. D. Câu 47: Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình




DẠYKÈMQUYNHƠN OFFICIAL
20 20 20 20 xy xy xy xy +− ++ −++ −+ Độ dài
A.
0 33 5? xy xy xy − −− + A. (3;2)A B. (6;3)B C. (6;4)C . D. (5;4)D . Câu 48: Cho điểm (3;3)A và điểm M thuộc miền nghiệm của hệ bất phương trình
AM lớn nhất là
22 B. 52 C. 10 . D. 34 . Lời giải Miền nghiệm của hệ bất phương trình là miền không bị gạch trong hình bên. Suy ra độ dài AM lớn nhất khi và chỉ khi M trùng với đỉnh nào đó của đa giác nghiệm.
Câu 49: Một cửa hàng bán hai loại mặt hàng A và B . Biết rằng cứ bán một mặt hàng loại A cửa hàng lãi 5 nghìn đồng, bán một mặt hàng loại B cửa hàng lãi 7 nghìn đồng. Gọi , xy lần lượt là số mặt hàng loại A và mặt hàng loại B mà cửa hàng đó bán ra trong một tháng. Cặp số (;) xy nào sau đây biểu thị số mặt hàng bán ra mỗi loại của cửa hàng trong một tháng mà tổng số tiền lãi không ít hơn 30 triệu đồ
A. (1000;2000). B. (3000;1000) C. (2000;3000) D. (3000;2000).

DẠYKÈMQUYNHƠN
OFFICIAL
Câu
Cho góc thoả mãn 0180 và cot2 =− . Giá trị của sin là: A. 1 2 . B. 1 5 . C. 5 5 D. 5 5 Lời giải Ta có: 22 22 222 coscos1sin1 cotcot1cot sinsinsinsin ===+= . Do đó 2 22 111 sin 1cot1(2)5 === ++− . Vì 0180 nên 5 sin 5 = . Chọn D Câu 51: Giá trị biểu thức tan1tan2.tan89 = T bằng: A. 0. B. 1. C. 1. D. 2. Lời giải Ta có: ( )( ) ( ) tan1tan89tan2tan88tan44tan46tan45 = T ( )( ) ( ) tan1cot1tan2cot2tan44cot44tan45 = 1.1.111.== Chọn B Câu 52: Cho 1 sin 4 = , với 090 . Giá trị cos bằng
ng?
50:
A. 15 4 . B. 15 4 . C. 15 16 . D. 15 16 . Lời giải Chọn A Ta có 2 22 115 cos1sin1 416 =−=−= 15 cos 4 = (do 090 ) Vậy 15 cos 4 = .
Câu 53: Cho tam giác ABC có 4cm = AB ; 12cm= AC và góc 120 BAC = . Tính diện tích tam giác ABC . A. 123 ( 2 cm ) B. 243( 2 cm ) C. 12( 2 cm ) D. 24( 2 cm ) Lời giải
Chọn A
Diện tích tam giác ABC là 1 ..sin 2 SABACBAC = 1 .4.12.sin120 2 = 123 = ( 2 cm )
Câu 54: Cho tam giác ABC thỏa mãn 222 2.0BCACABBCAC +−−= . Khi đó, góc C có số đo là A. 150 C = . B. 60 C = . C. 45 C = . D. 30 C = . Lời giải Chọn C Theo đề ra ta có: 222 2.0BCACABBCAC +−−= 222 2. BCACABBCAC+−= 222 2 BCACAB BCAC +− =
DẠYKÈMQUYNHƠN OFFICIAL
2cos20 C −= 2 cos 2 C = 45 C = Câu 55: Tam giác ABC có 60,45BC và 5 AB . Tính độ dài cạnh AC . A. 56 . 2 AC B. 53. AC C. 56 3 AC D. 56 . 4 AC Lời giải Chọn A Theo định lí sin ta có: 0 0 556 sinsin2 sin45 sin60 ABACAC AC CB Câu 56: Một tam giác có ba cạnh là 52, 56, 60. Bán kính đường tròn ngoại tiếp tam giác đó là A. 65 4 . B. 40. C. 32,5. D. 65,8. Lời giải Chọn C Ta có: 525660 84 2 p ++ == Áp dụng hệ thức Hê rông ta có: ( ) ( ) ( ) 84.8452.8456.84601344 S =−−−= Mặt khác 52.56.60 32,5 444.1344 abcabc SR RS ==== Câu 57: Cho tam giác ABC có 12 AB = , 13 AC = , 5 BC = . Diện tích S của tam giác ABC là:
A. 30 S = B. 40 = S C. 50 = S D. 60 = S
Lời giải
Chọn A
Ta có: 222 BABCAC += nên tam giác ABC vuông tại B.
Diện tích tam giác là: 1 .30 2 SBABC== .
Câu 58: Cho tam giác ABC , có thể xác định được bao nhiêu véc tơ khác véc tơ không có điểm đầu và điểm cuối là các đỉnh của tam giác đã cho?
A. 4 B. 5 C. 7 D. 6.
Lời giải Các véc tơ khác véc tơ không có điểm đầu và điểm cuối là các đỉnh của tam giác đã cho gồm ,,,,,. ABBAACCABCCB Vậy có 6 véc tơ.
Câu 59: Tổng MNPQRNNPQR ++++ bằng vectơ nào sau đây?
.MR B. .MN C. .PR D. .MP
giải
A
có MNPQRNNPQRMNNPPQQRRNMN
DẠYKÈMQUYNHƠN
OFFICIAL
số 2 5 1 = y x là A. \1 B. \1;1
số đã cho xác định khi 2 1 10 1 − − x x x . Vậy tập xác định của hàm số là \1;1=− D .
Cho tam giác ABC đều có
ạnh là
62 B. 18
A.
Lời
Chọn
Ta
++++=++++= . Câu 60: Cho hàm số ( ) 326116yfxxxx ==−+− . Kết quả sai là A. ( ) 10 f = B. ( ) 20 f = C. ( ) 30 f = D. ( ) 424 f −=− Lời giải Chọn D ( ) 4210 f −=− . Câu 61: Tập xác định của hàm
C. \1 D. Lời giải Chọn B Hàm
Câu 62:
c
6. Tính ABAC + A.
C. 12 D. 63 Lời giải Chọn D
M
t khác ta có: 222263ABACAIABACAIAIAI
Câu 63: Cho đoạn thẳng AB và M là một điểm trên đoạn AB sao cho 1 5 MAAB = . Trong các khẳng định sau, khẳng định nào sai ? A. 1 5 AMAB = B. 1 4 MAMB =− C. 4 MBMA =− D. 4 5 MBAB =− Lời giải Chọn D


Ta thấy MB và AB cùng hướng nên 4 5 MBAB =− là sai.
Câu 64: Cho hình bình hành ABCD, điểm M thõa mãn 4AMABADAC =++ . Khi đó điểm M là: A. Trung điểm của AC B. Điểm C C. Trung điểm của AB D. Trung điểm của AD Lời giải Chọn A
Theo quy tắc hình bình hành, ta có:
Câu 65: Cho hàm số 2 (0)yaxbxca =++ có đồ thị (P). Biết đồ thị của hàm số có đỉnh (1;1)I và đi qua điểm (2;3)A . Tính tổng 222 Sabc =++ A. 3 B. 4 C. 29 D. 1 Lời giải Chọn C Vì đồ thị hàm số 2 (0)yaxbxca =++ có đỉnh (1;1)I và đi qua điểm (2;3)A nên ta có hệ:

DẠYKÈMQUYNHƠN OFFICIAL
ọ
G
i I là trung điểm của BC. Vì tam giác ABC đều có cạnh là 6, nên ta có AIBC ⊥ .
Xét tam giác AIB vuông tại I , có 222222226327 ABAIIBAIABIB=+=−=−= . Suy ra 2733 AI ==
ặ
+=+====
;2− nghịch biến trên ( ) 2;+ .
Câu 67: Cho hai vectơ a và b khác 0 . Xác định góc giữa hai vectơ a và b khi abab =−
o180
0
90
o45
DẠYKÈMQUYNHƠN OFFICIAL 112 4234234 203 1 2 abcabca abcabcb babc a ++=++== ++=++==− +== −=
Nên 222 Sabc =++ =29 Câu 66: Cho hàm số 2 43.yxx=−++ Chọn khẳng định đúng. A. Hàm số đồng biến trên . B. Hàm số nghịch biến trên . C. Hàm số đồng biến trên ( ) 2;+ . D. Hàm số nghịch biến trên ( ) 2;+ . Lời giải Chọn D Do 1 a =− nên hàm số đồng biến trên ( )
61. Lời giải Chọn A Ta có ( ) ( ) 2 22 22 2.2cos,21+=+=++=++= ababababababab . Câu 69: Cho tam giác ABC vuông tại A có o ˆ 60 B = , ABa = . Tính . ACCB A. 2 3a . B. 2 3a . C. 3a . D. 0 . Lời giải Chọn B Ta có o2 3 ...cos1503.2.3 2 ==−=− ACCBACBCaaa . Câu 70: Cho giá trị gần đúng của 8 17 là 0,47. Sai số tuyệt đối của số 0,47 là: A. 0,001. B. 0,002. C. 0,003. D. 0,004. Lời giải Câu 71: ChọnA. Ta có 8 0,470588235294... 17 = nên sai số tuyệt đối của 0,47 là 8 0,470,474,4710,001 17 =−−= .
A.
= . B. o
= . C. o
= . D.
= . Lời giải Chọn A Ta có ( ) ...cos, ababab = Mà theo giả thiết abab =− , suy ra ( ) ( ) 0cos,1,180 abab=−⎯⎯→= Câu 68: Cho 2 vectơ a và b có 4 a = , 5 b = và ( ) o,120ab = .Tính ab + A. 21. B. 61. C. 21. D.
Câu 72: Cho giá trị gần đúng của 3 7 là 0,429. Sai số tuyệt đối của số 0,429 là: A. 0,0001. B. 0,0002. C. 0,0004. D. 0,0005. Lời giải Chọn D. Ta có 3 0,428571... 7 = nên sai số tuyệt đối của 0,429 là 3 0,4290,4294,42850,0005 7 =−−= .
Câu 73: Kết quả điểm kiểm tra 45 phút môn Hóa Học của 100 em học sinh được trình bày ở bảng sau: Điểm 3 4 5 6 7 8 9 10 Cộng Tần số 3 5 14 14 30 22 7 5 100 Số trung bình cộng của bảng phân bố tần số nói trên là A. 6,82 . B. 4. C. 6,5. D. 7,22 . Lời giải Số trung bình cộng của bảng phân bố tần số nói trên là 3.34.55.146.147.308.229.710.5 6,82 100 x +++++++ ==
Câu 74: Điều tra tiền lương một tháng của 100 người lao động trên địa bàn một xã ta có bảng phân bố tần số sau: Tiền lương (VND) 5.000.000 6.000.000 7.000.000 8.000.000 9.000.000 9.500.000 Tần số 26 34 20 10 5 5
Tìm mốt của bảng phân bố tần số trên.
A. 5.000.000. B. 6.000.000. C. 7.500.000. D. 9.500.000. Lời giải Ta có giá trị 6.000.000 có tần số lớn nhất nên là mốt của bảng phân bố tần số trên.
Câu 75: Tìm phát biểu đúng về phương sai của một mẫu số liệu.
A. Phương sai được sử dụng làm đại diện cho các số liệu của mẫu
B. Phương sai được sử dụng để đánh giá mức độ phân tán của các số liệu thống kê (so với số trung bình).
C. Phương sai được tính bằng tổng số phần tử của một mẫu số liệu.
D. Phương sai là số liệu xuất hiện nhiều nhất (số liệu có tần số lớn nhất) trong bảng các số liệu thống kê.
Lời giải Ý nghĩa của phương sai: Phương sai được sử dụng để đánh giá mức độ phân tán của các số liệu thống kê (so với số trung bình). (SGK)
2. Tự luận
DẠYKÈMQUYNHƠN OFFICIAL
Bác
Câu 76:
Hùng dùng 200m hàng rào dây thép gai để rào miếng đất đủ rộng thành một mảnh vườn hình chữ nhật. a) Tìm công thức tính diện tích ()Sx của mảnh vườn hình chữ nhật rào được theo chiều rộng ( )xm của mảnh vườn đó. b) Tìm kích thước của mảnh vườn hình chữ nhật có diện tích lớn nhất có thể rào được. Lời giải a) Chiều dài của mảnh vườn là: 100( )xm .
Do đó, ta có công thức diện tích ( ) 22()(100)100 =−=−+ Sxxxxxm
b) Mảnh vườn hình chữ nhật có diện tích lớn nhất khi hàm số 2 ()100 =−+ Sxxx đạt giá trị lớn nhất. Vì 10=− a nên hàm số bậc hai này đạt giá trị lớn nhất tại 50 2 =−= b x a Vậy mảnh vườn có diện tích lớn nhất khi nó có kích thước là 50 50 mm (tức là khi nó trở thành hình vuông).
Câu 77: Bác Năm dự định trồng ngô và đậu xanh trên một mảnh đất có diện tích 8 ha. Nếu trồng 1 ha ngô thì cần 20 ngày công và thu được 40 triệu đồng. Nếu trồng 1 ha đậu xanh thì cần 30 ngày công và thu được 50 triệu đồng. Bác Năm cần trồng bao nhiêu hecta cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng không quá 180 ngày công cho việc trồng ngô và đậu xanh.
Lời giải Gọi x là số hecta đất trồng ngô và y là số hecta đất trồng đậu xanh.
Ta có các điều kiện ràng buộc đối với , xy như sau:
Hiển nhiên 0,0xy .
OFFICIAL
Diện tích canh tác không vượt quá 8 ha nên 8 xy+ . Số ngày công sử dụng không vượt quá 180 nên 2030180 xy+ .
Từ đó, ta có hệ bất phương trình mô tả các điều kiện ràng buộc:
+ +
xy xy x y
8 2030180 0 0
Biểu diễn miền nghiệm của hệ bất phương trình này trên hệ trục toạ độ Oxy , ta được miền tứ giác OABC (Hình).
Toạ độ các đỉnh của tứ giác đó là: (0;0);(0;6)OA ; (6;2);(8;0)BC . Gọi F là số tiền (đơn vị: triệu đồng) bác Năm thu được, ta có: 4050 Fxy =+ Ta phải tìm , xy thoả mãn hệ bất phương trình sao cho F đạt giá trị lớn nhất, nghĩa là tìm giá trị lớn nhất của biểu thức 4050 Fxy =+ trên miền tứ giác OABC

Tính các giá trị của biểu thức F tại các đỉnh của đa giác, ta có: Tại (0;0):40.050.00OF =+= ;
Tại (0;6):40.050.6300AF =+=
Tại (6;2):40.650.2340BF =+= ;
Tại (8;0):40.850.0320CF =+= .
F đạt giá trị lớn nhất bằng 340 tại (6;2)B .
Vậy để thu được nhiều tiền nhất, bác Năm cần trồng 6 ha ngô và 2 ha đậu xanh.
DẠYKÈMQUYNHƠN
a) Diện tích mảnh đất mà gia đình bạn An sở hữu là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)? b) Chiều dài hàng rào NP là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)? Lời giải a) Diện tích mảnh đất của gia đình bạn An (tam giác MNP ) là: ( ) 2 11 sin150230sin11016209,7 22

DẠYKÈMQUYNHƠN OFFICIAL
m ,
Câu 78: Gia đình bạn An sở hữu một mảnh đất hình tam giác. Chiều dài của hàng rào MN là 150
chiều dài của hàng rào MP là 230m . Góc giữa hai hàng rào MN và MP là 110 (Hình 21) .
Lời
AAABAC ++= Tương tự ta có 4023'201120120 BBBCBA ++= 4023'201120120 CCCACB ++= Cộng về với vế lại ta được ( ) 4023'''0'''0 AABBCCBAACCBAABBCC +++++=++= Suy ra ''''''0GAGBGCGAGBGCGAGBGC ++=++++= Do đó G là trọng tâm của
giác
== SMNMPMm . b) Áp dụng định lí côsin ta có: =+−=+−
222222cos1502302150230cos110 98999,39. NPMNMPMNMPM Suy ra 98999,39314,6( ) NPm Vậy chiều dài hàng rào NP là khoảng 314,6m Câu 79: Cho tam giác ABC. Gọi A’, B’, C’ là các điểm xác định bởi 2011'2012'0 ABAC+= , 2011'2012'0 BCBA+= ; 2011'2012'0 CACB+= . Chứng minh hai tam giác ABC và A’B’C’ có cùng trọng tâm.
giải. Gọi G là trọng tâm tam giác ABC 0 GAGBGC ++= Ta có ( ) ( ) 2011'2012'02011'2012'0 ABACAAABAAAC +=+++= 4023'201120120
tam
A’B’C’
1. Trắc nghiệm
Câu 1. Mệnh đề: " 2 ,21 n n + là số nguyên tố" khẳng định là
A. Tồn tại số tự nhiên n để 2 21 n + là số nguyên tố.
B. Tồn tại duy nhất số tự nhiên n để 2 21 n + là số nguyên tố.
C. Với mọi số tự nhiên n thì 2 21 n + là hợp số.
D. Với mọi số tự nhiên n thì 2 21 n + là số nguyên tố.
Câu 2. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
a) Nếu tam giác có hai trung tuyến bằng nhau thì tam giác đó là tam giác cân.
b) Tam giác ABC vuông tại C nếu và chỉ nếu 222 ABCACB =+
OFFICIAL
c) 2 ,210xxx −+ d) 22 ,(1)nnn ++ là số chẵn. A. 1. B. 2. C. 3. D. 4. Câu 3. Cho ,, ABC là ba tập hợp bất kì khác rỗng, được biểu diễn bằng biểu đồ Ven như hình bên. Phần gạch sọc trong hình biểu diễn tập hợp nào sau đây?
A. ()\ABC . B. ()ABC . C. ABC D. ()\BCA



Câu 4. Số các số nguyên dương lẻ nhỏ hơn 1000 và chia hết cho 3 là A. 166. B. 167. C. 333. D. 499.
Câu 5. Hình nào sau đây là biểu diễn theo biểu đồ Ven của tập hợp B là con của tập hợp A ? A. B. C. D.
Câu 6. Cặp số nào sau đây không là nghiệm của bất phương trình 42 +xy ?
A. (1;0) B. (1;2) . C. (5;2).


DẠYKÈMQUYNHƠN
ĐỀ 09
tấm là 250 tấn/giờ, công suất sản xuất thép cuộn là 150 tấn/giờ. Mỗi tấn thép tấm có giá 250 USD, mỗi tấn thép cuộn có giá 300 USD. Biết rằng mỗi tuần thị trường chỉ tiêu thụ tối đa 5000 tấn thép tấm và 3500 tấn thép cuộn. Hỏi cần sản xuất bao nhiêu tấn thép mỗi loại trong một tuần để lợi nhuận thu được là cao nhất? Câu 11. Cho góc thoả mãn 0180 và tan2 =− . Giá trị của cos là:








DẠYKÈMQUYNHƠN OFFICIAL D. (1;0) Câu 7. Miền nghiệm của bất phương trình 3 −+yx được xác định bởi miền nào (nửa mặt phẳng không bị gạch và kể cả d ) sau đây? A. C. B. D. Câu 8. Miền nghiệm của hệ bất phương trình: 0 0 1 x y xy − được xác định bởi miền đa giác nào sau đây? A. B. C. D. Câu 9. Diện tích miền nghiệm () H của hệ bất phương trình 1 0 2 26 x y y xy + là A. 1. B. 3. C. 4. D. 9. Câu 10. Nhà máy A chỉ có một máy cán thép có thể sản xuất hai sản phẩm là thép tấm và thép cuộn (máy không thể sản xuất hai loại thép cùng lúc và có thể làm việc 40 giờ một tuần). Công suất sản xuất thép
A. 3 3 .
B. 2 2 . C. 3 3 D. 1 3 .
Câu 12. Biết 2 sin 5 = ,(90180) oo . Hỏi giá trị của tan bằng bao nhiêu?
A. 21 2 B. 221 21 C. 221 21 D. 21 2
Câu 13. Với 0180 giá trị lượng giác nào dưới đây luôn không âm? A. sin. B. tan. C. cos. D. cot.
Câu 14. Trong tam giác ABCvới ,, ABcBCaCAb === . Tìm mệnh đề đúng
A. 222 2cos. abcbcA =++ B. 222 2cos. abcbcA =+− C. 222 cos. abcbcA =+− D. 222 2sin. abcbcA =+−
Câu 15. Tam giác ABC có ,, ABcBCaCAb === và có diện tích là S . Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn góc C . Khi đó diện tích tam giác mới tạo nên bằng. A. 3S . B. 4S . C. 2S . D. 6S .
Câu 16. Cho tam giác ABC có 5,4ABAC== , trung tuyến 33 BM = . Tính diện tích tam giác ABC A. 36 B. 46 C. 213 D. 2433
Câu 17. Cho tam giác ABC với BCa = , ACb = , ABc = . Diện tích của ABC là A. 1 sin 2 ABC SacC = B. 1 sin 2 ABC SbcB = C. 1 sin 2 ABC SacB = . D. 1 sin 2 ABC SbcC = .
Câu 18. Cho tam giác ABC với BCa = , 120 BAC = . Bán kính đường tròn ngoại tiếp ABC là A. 3 2 a R = B. 2 a R = C. 3 3 a R = D. = Ra
Câu 19. Cho hai véctơ a và b là các véctơ khác 0 . Biết véctơ a là véctơ đối của véctơ b . Khẳng định nào sau đây sai?
A. Hai véctơ a
DẠYKÈMQUYNHƠN
OFFICIAL
, b cùng phương B.
a , b
độ dài C. Hai véctơ a , b chung điểm đầu. D. Hai
a , b ngược hướng. Câu 20. Cho tam giác ABC xác định vị trí điểm D sao cho ADACAB =− A. D là đỉnh thứ tư của hình bình hành ADBC B. D trùng điểm B . C. D trùng điểm C D. D là đỉnh thứ tư của hình bình hành ABCD. Câu 21. Tìm tập xác định D của hàm số ( )( ) 2 1 14 x y xx + = +− A. \2 D = B. \2 D = C. \1;2 D =− D. \1;2 D =− Câu 22. Tìm giá trị nhỏ nhất của hàm số ( ) ( )2 2 3 fxxx=+−
Hai véctơ
cùng
véctơ
A. 0 B. 9 2 C. 9 2 D. 3 2
Câu 23. Trên Hình biểu diên ba lực 1F , 23 , FF cùng tác động vào một vật ở vị trí cân bằng 0. Cho biết cường độ của 12 , FF đều bằng 100N và góc tạo bởi 1F và 2F bằng 120 . Tính cường độ của lực 3F . A. 190 B. 200 C. 100 D. 80 Câu 24. Cho ABC . Đặt , aBCbAC == . Các cặp vectơ nào sau đây cùng phương? A. 2,2abab ++ B. 2,2 abab C. 5,102 abab +−− D. , abab +− Câu 25. Cho tam giác ABC có điểm O thỏa mãn: 2 OAOBOCOAOB +−=− . Khẳng định nào sau đây là đúng? A. Tam giác ABC đều B. Tam giác ABC cân tại C C. Tam giác ABC vuông tại C D. Tam giác ABC cân tại B Câu 26. Cho Parabol (P): 2 yaxbxc =++ có đỉnh (2;0)I và () P cắt trục Oy tại điểm (0;1) M . Khi đó Parabol (P) có hàm số là A. B. C. . D. Câu 27. Giá trị nào của m thì đồ thị hàm số 2 3 yxxm =++ cắt trục hoành tại hai điểm phân biệt? A. 9 4 m

DẠYKÈMQUYNHƠN
OFFICIAL
ab =− Xác định góc giữa hai vectơ a và .b A. o30 = . B. o45 = . C. o60 = . D. o120 = . Câu 29. Cho 2 vectơ đơn vị a và b thỏa 2 ab+= . Hãy xác định ( )( ) 3425 abab −+ A. 7 B. 5 C. 7 D. 5 Câu 30. Cho hình thang vuông ABCDcó đáy lớn 4 ABa = , đáy nhỏ 2 CDa = , đường cao 3 ADa = .Tính . DABC A. 2 9a B. 2 15a C. 0 D. 2 9a Câu 31. Qua điều tra dân số kết quả thu được số đân ở tỉnh B là 2.731.425 người với sai số ước lượng không quá 200 người. Các chữ số không đáng tin ở các hàng là: A. Hàng đơn vị. B. Hàng chục. C. Hàng trăm. D. Cả A, B, C. Câu 32. Nếu lấy 3,14 làm giá trị gần đúng của thì sai số là: A. 0,001. B. 0,002. C. 0,003. D. 0,004. Câu 33. Cho bảng phân bố tần số sau: khối lượng 20 học sinh lớp 10A ( ) 2 1 :31 4 Pyxx=−−− ( ) 2 1 :1 4 Pyxx=−−− ( ) 2 1 :1 4 Pyxx=−+− ( ) 2 1 :21 4 Pyxx
− . B. 9 4 m − . C. 9 4 m . D. 9 4 m Câu 28. Cho hai vectơ a và b thỏa mãn 3, a = 2 b = và .3.
=−+−
Số trung bình cộng x của bảng số liệu đã cho là A. 53 x = . B. 52,8 x = . C. 52,2 x = . D. 52 x = . Câu 34. Kết quả thi môn Toán giữa kì 11 của lớp 3 10A trường THPT Ba Vì được thống kê như sau: Giá trị mốt 0 M của bảng phân bố tần số trên bằng A.5. B.7. C.8. D.12. Câu 35. Theo kết quả thống kê điểm thi giữa kỳ 2 môn toán khối 11 của một trường THPT, người ta tính được phương sai của bảng thống kê đó là 2 0,573 x s = . Độ lệch chuẩn của bảng thống kê đó bằng A. 0,812 B. 0,757 C. 0,936 D. 0,657

2. Tự luận
Câu 1. Một quả bóng được ném lên trên theo phương thẳng đứng từ mặt đất với vận tốc ban đầu 14,7 / ms . Khi bỏ qua sức cản của không khí, độ cao của quả bóng so với mặt đất (tính bằng mét) có thể mô tả bởi phương trình 2 ()4,914,7. httt =−+
a) Sau khi ném bao nhiêu giây thì quả bóng đạt độ cao lớn nhất? b) Tìm độ cao lớn nhất của quả bóng. c) Sau khi ném bao nhiêu giây thì quả bóng rơi chạm đất?
Câu 2. Một người dùng ba loại nguyên liệu ,, ABC để sản xuất ra hai loại sản phẩm P và Q . Để sản xuất 1 kg mỗi loại sản phẩm P hoặc Q phải dùng một số kilôgam nguyên liệu khác nhau. Tổng số kilôgam nguyên liệu mỗi loại mà người đó có và số kilôgam từng loại nguyên liệu cần thiết để sản xuất ra 1kg sản phẩm mỗi loại được cho trong bảng sau:

Biết 1kg sản phẩm P có lợi nhuận 3 triệu đồng và 1 kg sản phẩm Q có lợi nhuận 5 triệu đồng. Hãy lập phương án sản xuất hai loại sản phẩm trên sao cho có lãi cao nhất.
Câu 3. Hai người A và B cùng quan sát một con tàu đang neo đậu ngoài khơi tại vị trí C . Người A đứng trên bờ biển, người B đứng trên một hòn đảo cách bờ một khoảng 100= ABm. Hai người tiến hành đo đạc và thu được kết quả: 54,74 ==CABCBA (Hình 22). Hỏi con tàu cách hòn đảo bao xa (làm tròn kết quả đến hàng phần mười theo đơn vị mét)?
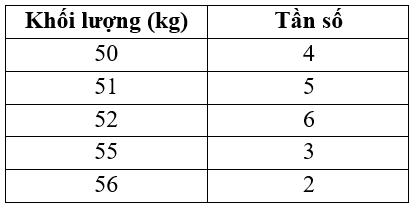
DẠYKÈMQUYNHƠN
OFFICIAL
Câu 4. Hai tam giác ABC và A’B’C’ lần lượt có trọng tâm là G, G’. Chứng minh rằng '''3' AABBCCGG ++= . Từ đó suy ra “ Điều kiện cần và đủ để hai tam giác ABC và A’B’C’ có cùng trọng tâm là '''0AABBCC++= Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM
A. Tồn tại số tự nhiên n để 2 21 n + là số nguyên tố.
B. Tồn tại duy nhất số tự nhiên n để 2 21 n + là số nguyên tố.
C. Với mọi số tự nhiên n thì 2 21 n + là hợp số.
D. Với mọi số tự nhiên n thì 2 21 n + là số nguyên tố.
Câu 2. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
a) Nếu tam giác có hai trung tuyến bằng nhau thì tam giác đó là tam giác cân. b) Tam giác ABC vuông tại C nếu và chỉ nếu 222 ABCACB =+ . c) 2 ,210xxx −+ . d) 22 ,(1)nnn ++ là số chẵn. A. 1. B. 2. C. 3. D. 4. Câu 3. Cho ,, ABC là ba tập hợp bất kì khác rỗng, được biểu diễn b


DẠYKÈMQUYNHƠN OFFICIAL
11C 12C 13A
1D 2C 3B 4B 5B 6B 7B 8D 9B 10D
14B 15D 16B 17C 18C 19C 20D 21D 22B 23C 24C 25C 26C 27D 28D 29C 30A 31D 32A 33C 34C 35B 1. Trắc nghiệm Câu 1. Mệnh đề: " 2 ,21 n n + là số nguyên tố" khẳng định là
A. ()\ABC B. ()ABC . C. ABC . D. ()\BCA . Câu
Số các số nguyên dương
ỏ
A. 166. B. 167. C. 333. D. 499.
Gọi
ằng biểu đồ Ven như hình bên. Phần gạch sọc trong hình biểu diễn tập hợp nào sau đây?
4.
lẻ nh
hơn 1000 và chia hết cho 3 là
Lời giải
A là tập các số nguyên dương chia hết cho 3 và nhỏ hơn 1000.
Gọi B là tập số nguyên dương chẵn chia hết cho 3 nhỏ hơn 1000, tức B là tập các số nguyên dương chia hết cho 6 và nhỏ hơn 1000.
Gọi C là tập số nguyên dương lẻ chia hết cho 3 nhỏ hơn 1000. Như vậy ABC = và BC= , suy ra ()()() nAnBnC =+ . Do đó ()()()333166167 nCnAnB=−=−= .
Câu 5. Hình nào sau đây là biểu diễn theo biểu đồ Ven của tập hợp B là con của tập hợp A ?
A. B. C. D.
OFFICIAL
Câu 6. Cặp số nào sau đây không là nghiệm của bất phương trình 42 +xy ? A. (1;0). B. (1;2) . C. (5;2). D. (1;0)








Câu 7. Miền nghiệm của bất phương trình 3 −+yx được xác định bởi miền nào (nửa mặt phẳng không bị gạch và kể cả d ) sau đây? A. C. B. D.
Câu 8. Miền nghiệm của hệ bất phương trình: 0 0 1
− được xác định bởi miền đa giác nào sau đây?
x y xy
DẠYKÈMQUYNHƠN
H là hình thang
nữa ABCD là hình thang vuông tại A và D . Suy ra diện tích hình () H là (12)23()


dvdt
10. Nhà máy A chỉ có một máy cán thép có thể sản xuất hai sản phẩm là thép tấm và thép cuộn (máy không thể sản xuất hai loại thép cùng lúc và có thể làm việc 40 giờ một tuần). Công suất sản xuất thép tấm là 250 tấn/giờ, công suất sản xuất thép cuộn là 150 tấn/giờ. Mỗi tấn thép tấm có giá 250 USD, mỗi tấn thép cuộn có giá 300 USD. Biết rằng mỗi tuần thị trường chỉ tiêu thụ tối đa 5000 tấn thép tấm và 3500 tấn thép cuộn. Hỏi cần sản xuất bao nhiêu tấn thép mỗi loại trong một tuần để lợi nhuận thu được là cao nhất?
A. 5000 tấn thép tấm và 3500 tấn thép cuộn.
B. 4166,66 tấn thép tấm và 3500 tấn thép cuộn.
C. 5000 tấn thép tấm và 0 tấn thép cuộn.
D. 5000 tấn thép tấm và 3000 tấn thép cuộn. Lời giải
Gọi , xy là số tấn thép cuộn và thép tấm nhà máy đó sản suất trong một tuần. Số giờ máy sử dụng để sản xuất trong tuần là 250150 xy + (giờ).


Số tiền thu được là (;)250300 Fxyxy =+ với , xy thoả mãn hệ bất phương trình

DẠYKÈMQUYNHƠN OFFICIAL
Câu
1
x
y
+ là
Lời
A. B. C. D.
9. Diện tích miền nghiệm () H của hệ bất phương trình
0 2 26
y
xy
A. 1. B. 3. C. 4. D. 9.
giải Miền ()
ABCD với (1;0),(3;0),(2;2),(1;2) ABCD Hơn
2
+ = . Câu
DẠYKÈMQUYNHƠN OFFICIAL 40 250150 5000;3500. xy xy + Thử các phương án vào ta có phương án D thoả mãn yêu cầu. Câu 11. Cho góc thoả mãn 0180 và tan2 =− . Giá trị của cos là: A. 3 3 . B. 2 2 . C. 3 3 D. 1 3 . Lời giải Ta có: 22 22 222 sinsin1cos1 tantan1tan coscoscoscos ===+= . Do đó 2 2 2 111 cos 1tan3 1(2) === + +− . Vì 0180 mà tan0 và sin0 nên cos0 suy ra 3 cos 3 =− . Chọn C Câu 12. Biết 2 sin 5 = ,(90180) oo . Hỏi giá trị của tan bằng bao nhiêu? A. 21 2 B. 221 21 C. 221 21 D. 21 2 Lời giải Chọn C Ta có: 2 222 21 cos sincos1cos125 521 cos 5 = +==− =− Theo đề bài: 21 90180cos 5 oo =− Vậy 2 sin221 5 tan cos21 21 5 ===− . Câu 13. Với 0180 giá trị lượng giác nào dưới đây luôn không âm? A. sin. B. tan. C. cos. D. cot. Lời giải Chọn A Nhìn vào bảng xét dấu của các giá trị lượng giác của một góc bất kỳ ta thấy sin luôn không âm. Câu 14. Trong tam giác ABCvới ,, ABcBCaCAb === . Tìm mệnh đề đúng. A. 222 2cos. abcbcA =++ B. 222 2cos. abcbcA =+− C. 222 cos. abcbcA =+− D. 222 2sin. abcbcA =+− Lời giải Chọn B
Câu 15. Tam giác ABC có ,, ABcBCaCAb === và có diện tích là S . Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn góc C . Khi đó diện tích tam giác mới tạo nên bằng. A. 3S B. 4S C. 2S D. 6S Lời giải Chọn D
Diện tích tam giác ABC là: 1 ...sin 2 = SBCCAC Diện tích tam giác mới bằng: 11 .2.3.sin6...sin6. 22 BCCACBCCACS ==
16. Cho tam giác ABC có
DẠYKÈMQUYNHƠN
OFFICIAL
( ) ( )2 2
22 222 24334 4 57 422 BABCAC BMAC BMBCBA + +− + ==−=−= .
ABC , ta có: 547 8 22 ABACBC p ++++ === Áp dụng công thức Heron cho tam giác ABC ta có: ( )( )( ) ( )( )( ) 885848746 ABC SppABpACpBC =−−−=−−−= Câu 17. Cho tam giác ABC với BCa = , ACb = , ABc = . Diện tích của ABC là A. 1 sin 2 ABC SacC = B. 1 sin 2 ABC SbcB = C. 1 sin 2 ABC SacB = . D. 1 sin 2 ABC SbcC = . Lời giải Chọn C Ta
1 sin 2 ABC SacB = . Câu 18. Cho tam giác ABC với BCa = , 120 BAC = . Bán kính đường tròn ngoại tiếp ABC là A. 3 2 a R = B. 2 a R = C. 3 3 a R = D. = Ra Lời giải Chọn C Theo định lý trong tam giác ta có 13 2. 2sin1203 sin === BCaa RR BAC Câu 19. Cho hai véctơ a và b là các véctơ khác 0 . Biết véctơ a là véctơ đối của véctơ b . Khẳng định nào sau đây sai? A. Hai véctơ a , b cùng phương. B. Hai véctơ a , b cùng độ dài. C. Hai véctơ a , b chung điểm đầu D. Hai véctơ a , b ngược hướng Lời giải Chọn
Ta có hai véctơ đối nhau là hai véctơ ngược hướng và cùng độ dài nên các phương án A, B, D đều đúng Câu 20. Cho tam giác ABC xác định vị trí điểm D sao cho ADACAB =− sin
Câu
5,4ABAC== , trung tuyến 33 BM = . Tính diện tích tam giác ABC . A. 36 . B. 46 . C. 213. D. 2433 Lời giải Chọn B Ta có:
222
Gọi p là nửa chu vi của tam giác
có:
C
A. D là đỉnh thứ tư của hình bình hành ADBC .
B. D trùng điểm B C. D trùng điểm C . D. D là đỉnh thứ tư của hình bình hành ABCD Lời giải
DẠYKÈMQUYNHƠN OFFICIAL
+ − − .
Đáp án D. Lưu ý: Nếu rút gọn 2 1 4 y x = rồi khẳng định \2 D = là sai. Vì với 1 x =− thì biểu thức ban đầu ( )( ) 2 1 14 x xx + +− không xác định. Câu 22. Tìm giá trị nhỏ nhất của hàm số ( ) ( )2 2 3 fxxx=+− A. 0 B. 9 2 C. 9 2 D. 3 2 Lời giải Tập xác định D = . + ( ) 2 22 99399 :269232 42222xfxxxxxx =−+=−++=−+ . + ( ) 93 22fxx== . Vậy ( ) min9 2 fx = Đáp án B. Câu 23. Trên Hình biểu diên ba lực 1F , 23 , FF cùng tác động vào một vật ở vị trí cân bằng 0. Cho biết cường độ của 12 , FF đều bằng 100N và góc tạo bởi 1F và 2F bằng 120 C B D A
Chọn D Ta có ADACABBC =−= AD cùng hướng và cùng độ dài với BC ABCD là hình bình hành ( quan sát thêm hình vẽ) Câu 21. Tìm tập xác định D của hàm số ( )( ) 2 1 14 x y xx + = +− . A. \2 D = B. \2 D = C. \1;2 D =− D. \1;2 D =− Lời giải Điều kiện xác định: 2 101 402 x x x x
Vậy \1;2 D =−
Tính cường độ của lực 3F A. 190. B. 200. C. 100. D. 80. Lời giải Ta sử dụng các vectơ ,, OAOBOC và OD lần lượt biểu diễn cho các lực 123 ,, FFF và hợp lực F của 12 , FF Khi đó, do 12=+ FFF và 12 100 ==FF , nên tứ giác AOBD là hình thoi. Từ đó, do 120 = AOB , suy ra 60 = OAD , do đó tam giác AOD đều. Bởi vậy ||100 ===FODOA . Do vật ở vị trí cân bằng nên hai lực F và 3F ngược hướng và có cường độ bằng nhau, tức là hai vectơ OD và OC là hai vectơ đối nhau. Suy ra cường độ của lực 3F bằng


DẠYKÈMQUYNHƠN
OFFICIAL
.
== .
vectơ nào sau đây cùng phương? A. 2,2abab ++ B. 2,2 abab C. 5,102 abab +−− D. , abab +− Lời giải Chọn C Ta có: 1022.(5)5 ababab −−=−++ và 102ab cùng phương. Câu 25. Cho tam giác ABC có điểm O thỏa mãn: 2 OAOBOCOAOB +−=− . Khẳng định nào sau đây là đúng? A. Tam giác ABC đều B. Tam giác ABC cân tại C C. Tam giác ABC vuông tại C D. Tam giác ABC cân tại B Lời giải Chọn C
3 ||100( ).FFN == Câu 24. Cho ABC
Đặt , aBCbAC
Các cặp

DẠYKÈMQUYNHƠN OFFICIAL Gọi I là trung điểm của AB . Ta có: 2 OAOBOCOAOBOAOCOBOCBACACBAB +−=−−+−=+= 1 2.2 2 CIABCIABCIAB === Tam giác ABC vuông tại C . Câu 26. Cho Parabol (P): 2 yaxbxc =++ có đỉnh (2;0)I và () P cắt trục Oy tại điểm (0;1) M . Khi đó Parabol (P) có hàm số là A. . B. . C. D. Lời giải Chọn C Parabol ( ) 2 : Pyaxbxc=++⎯⎯→ đỉnh 2 ; 24 bb Ic aa Theo bài ra, ta có (P) có đỉnh ( ) ( ) 22 224 2;01 4 0 4 b ba a I bbac c a −= =− = −= Lại có (P) cắt Oy tại điểm ( )0;1 M suy ra ( ) ( )0112yc=−=− Từ (1), (2) suy ra 22 44 1 4 1;1 11 baba a babb bc cc =−=− =− =−= ==− =−=− (vì 00ba== loại) Câu 27. Giá trị nào của m thì đồ thị hàm số 2 3 yxxm =++ cắt trục hoành tại hai điểm phân biệt? A. 9 4 m − . B. 9 4 m − . C. 9 4 m . D. 9 4 m Lời giải Chọn D Cho 2 30xxm++= (1) Để đồ thị cắt trục hoành tại hai điểm phân biệt khi phương trình (1) có hai nghiệm phân biệt 2 9 0340940 4 mmm −− . Câu 28. Cho hai vectơ a và b thỏa mãn 3, a = 2 b = và .3.ab =− Xác định góc giữa hai vectơ a và b A. o30 = . B. o45 = . C. o60 = . D. o120 = . Lời giải Chọn D Ta có ( ) ( ) ( ) 0 .31 ...cos,cos,,120 3.22 ab ababababab ab =⎯⎯→===−⎯⎯→= Câu 29. Cho 2 vectơ đơn vị a và b thỏa 2 ab+= . Hãy xác định ( )( ) 3425 abab −+ A. 7 B. 5 C. 7 D. 5 Lời giải ( ) 2 1 :31 4 Pyxx=−−− ( ) 2 1 :1 4 Pyxx=−−− ( ) 2 1 :1 4 Pyxx=−+− ( ) 2 1 :21 4 Pyxx=−+−
1 ==ab , ( )2 24.1 +=+== ababab , ( )( ) 22 34256207.7 −+=−+=− abababab
Câu 30. Cho hình thang vuông ABCDcó đáy lớn 4 ABa = , đáy nhỏ 2 CDa = , đường cao 3 ADa = .Tính . DABC A. 2 9a . B. 2 15a . C. 0. D. 2 9a Lời giải Chọn A Vì ( ) 2 ...9 =++==− DABCDABAADDCDAADa nên chọn#A.

Câu 31. Qua điều tra dân số kết quả thu được số đân ở tỉnh B là 2.731.425 người với sai số ước lượng không quá 200 người. Các chữ số không đáng tin ở các hàng là: A. Hàng đơn vị. B. Hàng chục. C. Hàng trăm. D. Cả A, B, C. Lời giải Chọn D. Ta có 1001000 50200500 22 d === các chữ số đáng tin là các chữ số hàng nghìn trở đi. Câu 32. N

DẠYKÈMQUYNHƠN
Chọn C
OFFICIAL
=
=−−=
7. C.8.
12. Lời
Mốt của bảng phân bố tần suất là giá trị có tần số lớn nhất nên ta có 0 8 M = . Câu 35. Theo kết quả thống kê điểm thi giữa kỳ 2 môn toán khối 11 của một trường
ngườ
ta tính được phương sai của bảng thống kê đó
2
= . Độ lệch chuẩn của bảng thống
đó bằng A.
B.
ếu lấy 3,14 làm giá trị gần đúng của thì sai số là: A. 0,001. B. 0,002. C. 0,003. D. 0,004. Lời giải Chọn#A. Ta có 3,141592654...
nên sai số tuyệt đối của 3,14 là 3,143,143,1410,001
. Câu 33. Cho bảng phân bố tần số sau: khối lượng 20 học sinh lớp 10A Số trung bình cộng x của bảng số liệu đã cho là A. 53 x = B. 52,8 x = C. 52,2 x = D. 52 x = Lời giải Giá trị trung bình 50.451.552.655.356.2 52,2 20 x ++++ == . Câu 34. Kết quả thi môn Toán giữa kì 11 của lớp 3 10A trường THPT Ba Vì được thống kê như sau: Giá trị mốt 0 M của bảng phân bố tần số trên bằng A.5. B.
D.
giải
THPT,
i
là
0,573 x s
kê
0,812
0,757 C. 0,936 D. 0,657 Lời giải
2. Tự luận
Câu 1. Một quả bóng được ném lên trên theo phương thẳng đứng từ mặt đất với vận tốc ban đầu 14,7 / ms . Khi bỏ qua sức cản của không khí, độ cao của quả bóng so với mặt đất (tính bằng mét) có thể mô tả bởi phương trình 2 ()4,914,7. httt =−+
a) Sau khi ném bao nhiêu giây thì quả bóng đạt độ cao lớn nhất?
b) Tìm độ cao lớn nhất của quả bóng.
c) Sau khi ném bao nhiêu giây thì quả bóng rơi chạm đất? Lời giải
a) Quả bóng đạt độ cao lớn nhất khi ()ht đạt giá trị lớn nhất, tức là khi 1,5= t (giây).
Vậy sau khi ném 1,5 giây thì quả bóng đạt độ cao lớn nhất. b) Ta có 2 (1,5)4,9(1,5)14,71,511,025 =−+= h . Độ cao lớn nhất của quả bóng là 11,025m c) Quả bóng chạm đất tức là 2 ()04,914,700 =−+== htttt (loại) hoặc 3 = t Vậy sau khi ném 3 giây thì quả bóng chạm đất.
Câu 2. Một người dùng ba loại nguyên liệu ,, ABC để sản xuất ra hai loại sản phẩm P và Q . Để sản xuất 1 kg mỗi loại sản phẩm P hoặc Q phải dùng một số kilôgam nguyên liệu khác nhau. Tổng số kilôgam nguyên liệu mỗi loại mà người đó có và số kilôgam từng loại nguyên liệu cần thiết để sản xuất ra 1kg sản phẩm mỗi loại được cho trong bảng sau:
Biết 1kg sản phẩm P có lợi nhuận 3 triệu đồng và 1 kg sản phẩm Q có lợi nhuận 5 triệu đồng. Hãy lập phương án sản xuất hai loại sản phẩm trên sao cho có lãi cao nhất. Lời

DẠYKÈMQUYNHƠN
xx ss==
OFFICIAL Ta có công thức tính độ lệch chuẩn là 2 0,5730,757
.
Gọi x là số kilôgam sản phẩm , Py là số kilôgam sản phẩm Q cần sản xuất.
phương trình: 2210 24 2412 0 0 xy y xy x y + + Biểu diễn miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy , ta được như
giải
Ta có hệ bất
Hình.
Miền nghiệm là miền ngũ giác OCBAD (Hình) với các đỉnh: (0;0);(0;2);(2;2)OCB ; (4;1);(5;0)AD

Gọi F là số tiền lãi (đơn vị: triệu đồng) thu được, ta có: 35 Fxy =+ .
Tính giá trị của F tại các đỉnh của ngũ giác:
Tại (0;0):3.05.00OF =+= ;
Tại (0;2):3.05.210CF =+= ;
Tại (2;2):3.25.216BF =+= ;
Tại (4;1):3.45.117AF =+=
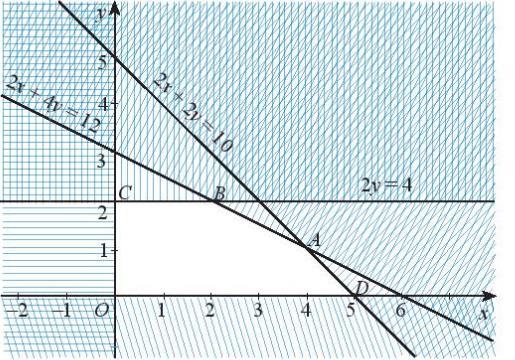
Tại (5;0):3.55.015DF =+= .
F đạt giá trị lớn nhất bằng 17 tại (4;1)A Vậy người đó cần sản xuất 4kg sản phẩm P và 1kg sản phẩm Q để có lãi cao nhất là 17 triệu đồng.
Câu 3. Hai người A và B cùng quan sát một con tàu đang neo đậu ngoài khơi tại vị trí C . Người A đứng trên bờ biển, người B đứng trên một hòn đảo cách bờ một khoảng 100= ABm. Hai người tiến hành đo đạc và thu được kết quả: 54,74
DẠYKÈMQUYNHƠN
OFFICIAL
n
Lời giải Xét tam giác ABC . Ta có: ˆ 180547452 =−−= C . Áp dụng định lí sin ta có: sinsin = BABC CA . Suy ra sin100sin54102,7( sinsin52) == BAA BCm C . Vậy con tàu cách hòn đảo khoảng 102,7 m. Câu 4. Hai tam giác ABC và A’B’C’ lần lượt có trọng tâm là G, G’. Chứng minh rằng '''3' AABBCCGG ++= . Từ đó suy ra “ Điều kiện cần và đủ để hai tam giác ABC và A’B’C’ có cùng trọng tâm là '''0AABBCC++= Lời giải.
==CABCBA (Hình 22). Hỏi con tàu cách hòn đảo bao xa (làm tròn kết quả đế
hàng phần mười theo đơn vị mét)?
DẠYKÈMQUYNHƠN OFFICIAL Ta có ( )''''1AAAGGGGA =++ ( )''''2BBBGGGGB =++ ( )''''3CCCGGGGC =++ Cộng vế với vế ta được ( ) ( ) '''3'''''''3' AABBCCAGBGCGGGGAGBGCGG ++=++++++= Vì G , G là trọng tâm của tam giác ABC , ABC nên 0 0 AGBGCG AGBGCG ++= ++= . Từ đẳng thức trên ta thấy G trùng G khi và chỉ khi 0 GG = tức là 0 AABBCC ++=
1. Trắc nghiệm
Câu 1. Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Hãy bỏ rác đúng nơi quy định!
b) Hoàng Sa, Trường Sa là quần đảo thuộc chủ quyền của Việt Nam.
c) 2021 là số nguyên tố.
d) Bạn có biết nấu cơm không? A. 4. B. 3. C. 2. D. 1.
Câu 2. Mệnh đề: “ ( ) *,1234:5 nnn n +++ ” khẳng định là
A. Tồn tại số nguyên dương n để 1234 nnn+++ chia hết cho 5. B. Tồn tại duy nhất số nguyên dương n để 1234 nnn+++ chia hết cho 5.
C. Với mọi số tự nhiên n thì 1234 nnn+++ chia hết cho 5. D. Với mọi số nguyên dương n thì 1234 nnn+++ chia hết cho 5.
Câu 3. Cho tập hợp {2180}Axx=− và 1 0 10 Bx x = . Tập hợp AB là
A. [9;10]. B. [9;10). C. (9;10) D. (9;10] Câu 4. Cho tập hợp (;5)Amm=+ và (10;) B =+ . Số các giá trị nguyên dương của tham số m để \ ABA = là A. 5. B. 4. C. 3. D. 6. Câu 5. Trong các tập hợp sau, tập hợp nào là tập hợp rỗng?
A. {(1)(21)0} =++= Axxx . B. {(1)(21)0} =++=Bxxx . C. {(1)(21)0} =++=Cxxx . D. {(1)(21)0} =++=Dxxx .

Câu 6. Miền nghiệm của bất phương trình 5312 −xy là nửa mặt phẳng tạo bởi đường thẳng :5312 −=dxy (không kể d ) chứa điểm có toạ độ nào sau đây? A. (2;1) B. (0;0) C. (1;2) . D. (3;4). Câu 7. Miền nghiệm của bất phương trình 1 2 2 −yx được xác định bởi miền nào (nửa mặt phẳng không bị gạch và không kể d) sau đây? A. B.

DẠYKÈMQUYNHƠN
ĐỀ 10
OFFICIAL



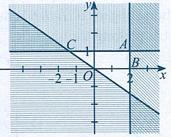

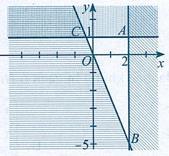

DẠYKÈMQUYNHƠN OFFICIAL C.
Câu 8. Miền nghiệm
1 2 0 20 x y y xy + được
đây? A.
C.
Câu 9. Miền đa giác không
gạch ở
là
A. 0 0 22 + x y xy B. 0 0 22 x y xy + C. 0 0 22. + x y xy D. 0 0 22. + x y xy Câu 10. Miền nghiệm của hệ bất phương trình 1 1 4 x y xy + là miền ( ) H . Gọi M là một điểm thuộc ( ) H . Độ dài OM ngắn nhất là A. 2 . B. 10 .
D.
của hệ bất phương trình:
xác định bởi miền đa giác nào sau
B.
D.
bị
Hình
miền nghiệm của hệ bất phương trình:
C. 22 D. 1.
Câu 11. Cho là góc tù. Khẳng định nào sau đây là đúng? A. tan0 B. cos0 C. sin0 D. cot0
Câu 12. Cho sin3 5 x = . Tính 22 4sin3cos Pxx =+ ?
A. 91 25 P = B. 84 25 P = C. 19 25 P = D. 109 25 P =
Câu 13. Cho 1 sin 3 = với 00 90180 . Giá trị của cos bằng
A. 2 3 . B. 2 3 . C. 22 3 . D. 22 3 .
Câu 14. Cho ABC có 0 60,8,5.===Bac Độ dài cạnh b bằng:
A. 7. B. 129. C. 49. D. 129 .
Câu 15. Cho ;;cab là độ dài 3cạnh của một tam giác. Mệnh đề nào sau đây không đúng? A. 2 aabac + B. 222 2 acbac ++ C. 222 2 bcabc ++ D. 2abbcb + Câu 16. Trong mặt phẳng, cho tam giác ABC có 4cm AC = , góc 60 A = , 45 B = . Độ dài cạnh BC là
A. 26 B. 223 + C. 232 D. 6
Câu 17. Cho tam giác ABC có 60 = B và 45 = C , = BCa . Độ dài cạnh AB bằng
A. 632 2 −+ a B. ( )13−+ a C. ( )13 + a D. 632 2 + a
Câu 18. Cho tam giác ABC có 47 = a , 6 = b và 8 = c . Diện tích S của tam giác ABC là A. 97 . B. 79 . C. 9. D. 7 .
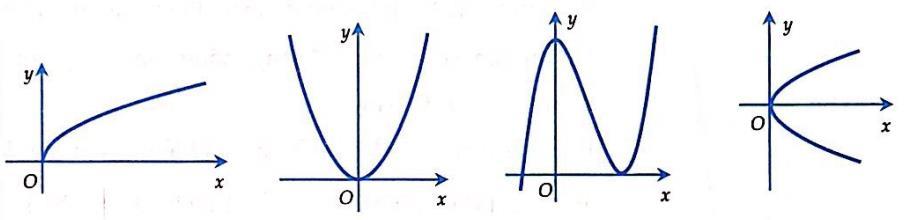
Câu 19. Mệnh đề nào sau đây sai?
A. Hai véctơ cùng phương là hai véctơ có giá song song hoặc trùng nhau
B. Véctơ không cùng phương với mọi véctơ
C. Hai véctơ cùng phương thì cùng hướng.
D. Hai véctơ bằng nhau là hai véctơ có cùng hướng và cùng độ dài.
Câu 20. Cho hai điểm , AB phân biệt. Xác định điểm M sao cho 0 MAMB+= . A. Không tìm được điể
DẠYKÈMQUYNHƠN
OFFICIAL
ằm trên
cong
số dạng ( )yfx = ? A. B. C. D. Câu 22. Cho hàm số ( ) 2 2211 11 xx y xx −−− = − neáu neáu . Tính ( )1 f .
m M B. M ở vị trí bất kì. C. M n
đường trung trực của AB D. M là trung điểm của AB Câu 21. Đường
trong hình nào dưới đây không phải là đồ thị của một hàm
A. 6. B. 6. C. 5. D. 5.

Câu 23. Hình 4.19 biểu diễn hai lực 12 , FF cùng tác động lên một vật, cho 123,2 FNFN == . Tính độ lớn của hợp lực 12 FF + A. 20 B. 19 C. 19 D. 23 Câu 24. Biết rằng hai vec tơ a và b không cùng phương nhưng hai vec tơ 32ab và (1)4 xab ++ cùng phương. Khi đó giá trị của x là: A. 7 B. 7 C. 5 D. 6 Câu 25. Cho ngũ giác ABCDE . Gọi ,,, MNPQ lần lượt là trung điểm các cạnh ,,, ABBCCDDE . Gọi I và J lần lượt là trung điểm các đoạn MP và NQ . Khẳng định nào sau đây đúng? A. 1 2 IJAE = B. 1 3 IJAE = C. 1 4 IJAE = D. 1 5 IJAE = Câu 26. Cho hàm số 2 61yxx=−+− . Hàm số đồng biến trên khoảng nào dưới đây? A. ( );3− B. ( ) 3;+ C. ( );6− D. ( ) 6;+ Câu 27. Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4m còn kích thước cửa ở giữa là 3m x 4m. Hãy tính khoảng cách giữa hai điểm A và B . (xem hình vẽ bên dưới) A. 5m. B. 8,5m. C. 7,5m. D. 8m. Câu 28. Cho tam giác đều ABC có cạnh bằng a Tính tích vô hướng ABAC A.
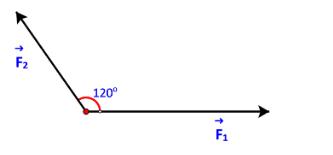
DẠYKÈMQUYNHƠN
OFFICIAL
2 .2.ABACa = B. 2 3 . 2 a ABAC =− C. 2 . 2 a ABAC =− D. 2 . 2 a ABAC = Câu 29. Cho hai vectơ a và b . Biết a =2, b = 3 và ( ) o,120ab = .Tính ab + A. 73 + . B. 73 . C. 723 . D. 723 + . Câu 30. Cho hai điểm , BC phân biệt. Tập hợp những điểm M thỏa mãn 2 . = CMCBCM là : A. Đường tròn đường kính BC . B. Đường tròn( ) ; BBC C. Đường tròn ( ) ; CCB D. Một đường khác. Câu 31. Nếu lấy 3,1416 làm giá trị gần đúng của thì có số chữ số chắc là: A. 5. B. 4. C. 3. D. 2. Câu 32. Số gần đúng của 2,57656 a = có ba chữ số
đáng tin viết dưới dạng chuẩn là: A. 2,57. B. 2,576. C. 2,58. D. 2,577. Câu 33. Điểm thi toán cuối năm của một nhóm gồm 7 học sinh lớp 11 là 1; 3; 4; 5; 7; 8; 9. Số trung vị của dãy số liệu đã cho là A. 6. B. 4. C. 7. D. 5. Câu 34. Điểm thi toán cuối năm của một nhóm gồm 7 học sinh lớp 11 là
1; 3; 4; 5; 7; 8; 9. Số trung vị trên của dãy số liệu đã cho là A. 8. B. 3. C. 7. D. 5. Câu 35. Cho mẫu số liệu 1x , 2x ,…, Nx có số trung bình là x . Phương sai được tính theo công thức nào trong các công thức sau A. 1
1 N i i x N = . B. ( ) 1


1 N i i xx N = . C. ( ) 2 1
1 N i i xx N = . D. ( ) 2 1
1 N i i xx N = .
2. Tự luận
Câu 1. Tại một buổi khai trương, người ta làm một cổng chào có đường viền trong của mặt cắt là đường parabol. Người ta đo khoảng cách giữa hai chân cổng là 4,5m . Từ một điểm trên thân cổng người ta đo được khoảng cách tới mặt đât (điêm H ) là 1,8m và khoảng cách từ điểm H tới chân cồng gần nhất là 1m . Hãy tính chiều cao của cồng chào đó (tính theo đường viền trong) theo đơn vị mét và làm tròn kết quả đến hàng phần mười.
Câu 2. Bạn Lan thu xếp được không quá 10 giờ để làm hai loại đèn trung thu tặng cho các trẻ em khuyết tật. Loại đèn hình con cá cần 2 giờ để làm xong 1 cái, còn loại đèn ông sao chỉ cần 1 giờ để làm xong 1 cái. Gọi x, y lần lượt là số đèn hình con cá và đèn ông sao bạn Lan sẽ làm. Hãy lập hệ bất phương trình mô tả điều kiện của x, y và biểu diễn miền nghiệm của hệ bất phương trình đó.
Câu 3. Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một con tàu C đang neo đậu ngoài khơi. Người đó tiến hành đo đạc và thu được kết quả: 30 ,60,50
ABmCABCBA (Hình 23). Tính khoảng cách từ vị trí A đến con tàu C (làm tròn kết quả đến hàng phần mười theo đơn vị mét).
DẠYKÈMQUYNHƠN
OFFICIAL
4. Cho tam giác ABC . Trên các cạnh AB , BC , CA ta lấy lần lượt các điểm M , N , P sao cho AMBNCP ABBCCA == . Chứng minh rằng hai tâm giác ABC và MNP có cùng trọng tâm. Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM 1C 2D 3B 4A 5D 6A 7C 8A 9C 10A 11A 12B 13C 14A 15C 16A 17B 18A 19C 20D 21D 22A 23C 24A 25C 26A 27D 28D 29C 30A 31B 32A 33D 34A 35D 1. Trắc nghiệm Câu 1. Trong các câu sau, có bao nhiêu câu là mệnh đề? a) Hãy bỏ rác đúng nơi quy định! b) Hoàng Sa, Trường Sa là quần đảo thuộc chủ quyền của Việt Nam. c) 2021 là số nguyên tố. d) Bạn có biết nấu cơm không?
===
Câu
A. 4. B. 3. C. 2. D. 1.
Câu 2. Mệnh đề: “ ( ) *,1234:5 nnn n +++ ” khẳng định là
A. Tồn tại số nguyên dương n để 1234 nnn+++ chia hết cho 5.
B. Tồn tại duy nhất số nguyên dương n để 1234 nnn+++ chia hết cho 5.
C. Với mọi số tự nhiên n thì 1234 nnn+++ chia hết cho 5.
D. Với mọi số nguyên dương n thì 1234 nnn+++ chia hết cho 5.
Câu 3. Cho tập hợp {2180}Axx=− và 1 0 10 Bx x = . Tập hợp AB là
A. [9;10] B. [9;10). C. (9;10) . D. (9;10].

Lời
giải
Ta có [9;) A =+ và (;10) B =− . Suy ra [9;10) AB= . Câu 4. Cho tập hợp (;5)Amm=+ và (10;) B =+ . Số các giá trị nguyên dương của tham số m để \ ABA = là A. 5. B. 4. C. 3. D. 6.


Lời giải
Ta có \5105 ABAABmm ==+ .
Câu 5. Trong các tập hợp sau, tập hợp nào là tập hợp rỗng? A. {(1)(21)0} =++= Axxx B. {(1)(21)0} =++=Bxxx C. {(1)(21)0} =++=Cxxx . D. {(1)(21)0} =++=Dxxx .
Câu 6. Miền nghiệm của bất phương trình 5312 −xy là nửa mặt phẳng tạo bởi đường thẳng :5312 −=dxy (không kể d ) chứa điểm có toạ độ nào sau đây? A. (2;1). B. (0;0). C. (1;2) . D. (3;4) Câu 7. Miền nghiệm của bất phương trình 1 2 2 −yx được xác định bởi miền nào (nửa mặt phẳng không bị gạch và không kể d) sau đây? A. B. C. D.

DẠYKÈMQUYNHƠN
OFFICIAL





DẠYKÈMQUYNHƠN OFFICIAL Câu 8. Miền nghiệm của hệ bất phương trình: 1 2 0 20 x y y xy + được xác định bởi miền đa giác nào sau đây? A. B. C. D. Câu 9. Miền đa giác không bị gạch ở Hình là miền nghiệm của hệ bất phương trình: A. 0 0 22 + x y xy B. 0 0 22 x y xy + C. 0 0 22. + x y xy D. 0 0 22. + x y xy Câu 10. Miền nghiệm của hệ bất phương trình 1 1 4 x y xy + là miền ( ) H . Gọi M là một điểm thuộc ( ) H . Độ dài OM ngắn nhất là A. 2 .
DẠYKÈMQUYNHƠN OFFICIAL B. 10 .
Lời
Câu
5 x = .
22
=+ ?
= .
= .
=
=
Lời giải Chọn B Ta có 222 9844sin3cossin33 2525 Pxxx =+=+=+= Câu 13. Cho 1 sin 3 = với 00 90180 . Giá trị của cos bằng A. 2 3 . B. 2 3 . C. 22 3 . D. 22 3 . Lời giải Chọn C Có 1 sin 3 = 2 18 cos1 99 =−= mà 00 90180 22 cos0cos 3 =− Câu 14. Cho ABC có 0 60,8,5.===Bac Độ dài cạnh b bằng: A. 7. B. 129. C. 49. D. 129 . Lời giải Chọn#A. Ta có: 2222202cos852.8.5.cos60497 bacacBb =+−=+−== . Câu 15. Cho ;;cab là độ dài 3cạnh của một tam giác. Mệnh đề nào sau đây không đúng? A. 2 aabac + . B. 222 2 acbac ++ . C. 222 2 bcabc ++ . D. 2abbcb + . Lời giải Chọn C Do 222 2.cos2 bcabcAbc +−= 222 2 bcabc ++ nên mệnh đề C sai. Áp dụng bất đẳng thức tam giác ta có 2 abcaabac ++ ;đáp án A đúng. Tương tự 2acbabbcb ++ ;mệnh đề D đúng. Ta có: 222 2.cos2 acbacBac +−= 222 2 acbac++ ;mệnh đề B đúng. Câu 16. Trong mặt phẳng, cho tam giác ABC có 4cm AC = , góc 60 A = , 45 B = . Độ dài cạnh BC là A. 26 B. 223 + C. 232 D. 6 Lời giải Chọn A
C. 22 . D. 1. Lời giải Ta có hình (H) là tam giác ABC với (1;1),(1;3),(3;1) ABC Suy ra độ dài nhỏ nhất của OM là 112 += Câu 11. Cho
là góc tù. Khẳng định nào sau đây là đúng? A. tan0
B. cos0 C. sin0 D. cot0
giải Chọn A
Ta có
là góc tù nên sin0,cos0 suy ra tan0
12. Cho sin3
Tính
4sin3cos Pxx
A. 91 25 P
B. 84 25 P
C. 19 25 P
. D. 109 25 P
.
Câu 17. Cho tam giác ABC có 60 = B và 45 = C , = BCa . Độ dài cạnh AB bằng A. 632 2 −+ a B. ( )13−+ a C. ( )13 + a D. 632 2 + a Lời giải Áp dụng định lý hàm sin vào tam giác ABC ta có: ( ) sin .13 sinsinsinsin ====−+ BCABACC ABBCa ACBA
Câu 18. Cho tam giác ABC có 47 = a , 6 = b và 8 = c . Diện tích S của tam giác ABC là A. 97 B. 79 C. 9 D. 7 Lời giải Áp dụng định lý hàm số cosin vào tam giác ABC ta có: ( )2 222 476436 57

A. Hai véctơ cùng phương là hai véctơ có giá song song hoặc trùng nhau.
B. Véctơ không cùng phương với mọi véctơ
C. Hai véctơ cùng phương thì cùng hướng
D. Hai véctơ bằng nhau là hai véctơ có cùng hướng và cùng độ dài.
Lời giải Chọn C
Mệnh đề sai là mệnh đề “Hai véctơ cùng phương thì cùng hướng”.
Câu 20.
DẠYKÈMQUYNHƠN OFFICIAL
Ta có sinsin BCAC AB = 4.3 2 26 2 2 BC ==
cos 216 2.47.8 +− +− === acb B ac 2 819 sin1cos 25616 =−==BB Diện tích tam giác ABC là 119sin.47.8.97 2216 ===SacB Câu 19. Mệnh đề nào sau đây sai?
Cho hai điểm , AB phân biệt. Xác định điểm M sao cho 0 MAMB+= . A. Không tìm được điểm M B. M ở vị trí bất kì. C. M nằm trên đường trung trực của AB D. M là trung điểm của AB Lời giải Chọn D Ta có 0 MAMBMAMB +==− . Do đó M là trung điểm của AB . Câu 21. Đường cong trong hình nào dưới đây không phải là đồ thị của một hàm số dạng ( )yfx = ? A. B. C. D. Lời giải


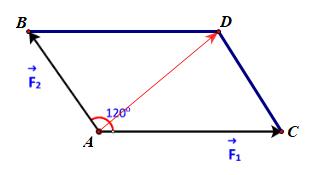
DẠYKÈMQUYNHƠN OFFICIAL Đường cong trong hình D không phải là đồ thị của một hàm số dạng ( )yfx = vì mỗi giá trị 0 x ứng với hai giá trị phân biệt của y. Đáp án D. Câu 22. Cho hàm số ( ) 2 2211 11 xx y xx −−− = − neáu neáu . Tính ( )1 f . A. 6. B. 6. C. 5. D. 5. Lời giải Chọn A Vì ( ) ( ) 12126 f −=−−−=− nên chọn#A. Câu 23. Hình 4.19 biểu diễn hai lực 12 , FF cùng tác động lên một vật, cho 123,2 FNFN == . Tính độ lớn của hợp lực 12 FF + A. 20 B. 19 C. 19 D. 23 Lời giải Dựng hình bình hành ABDC với hai cạnh là hai vectơ 12 , FF như hình vẽ Ta có: 1212 || FFACABADFFADAD +=+=+== Xét ABD ta có: 123,2.BDACFABF===== 18018012060ABDBAC =−=−= Theo định lí cosin ta có:


DẠYKÈMQUYNHƠN OFFICIAL 222 2222 12 2cos 23223cos12019 1919 V?y ADABBDABBDABD ADAD ADFF =+− =+−= =+=
,,, ABBCCDDE . Gọi I và J lần lượt là trung điểm các đoạn MP và NQ . Khẳng định nào sau đây đúng? A. 1 2 IJAE = B. 1 3 IJAE = C. 1 4 IJAE = D. 1 5 IJAE = Lời giải Chọn C Ta có: 2IJIQINIMMQIPPNMQPN =+=+++=+ ( ) 1 2 2 MQMAAEEQ MQAEBDMQAEBD MQMBBDDQ =++ =+=+ =++ , 1 2 PNBD =− Suy ra: ( ) 1111 2 2224 IJAEBDBDAEIJAE =+−== . Câu 26. Cho hàm số 2 61yxx=−+− . Hàm số đồng biến trên khoảng nào dưới đây? A. ( );3− B. ( ) 3;+ C. ( );6− D. ( ) 6;+ Lời giải Ta có ( ) 6 10,3 22.1 b a a =−== . Suy ra hàm số đồng biến trên khoảng ( );3− . Đáp án#A. Câu 27. Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4m còn kích thước cửa ở giữa là 3m x 4m. Hãy tính khoảng cách giữa hai điểm A và B . (xem hình vẽ bên dưới) A. 5m. B. 8,5m. C. 7,5m. D. 8m. Lời giải Chọn D
Câu 24. Biết rằng hai vec tơ a và b không cùng phương nhưng hai vec tơ 32ab và (1)4 xab ++ cùng phương. Khi đó giá trị của x là: A. 7 B. 7 C. 5 D. 6 Lời giải Chọn A Điều kiện để hai vec tơ 32ab và (1)4 xab ++ cùng phương là: 14 7 32 x x + ==− . Câu 25. Cho ngũ giác ABCDE . Gọi ,,, MNPQ lần lượt là trung điểm các cạnh
hình

DẠYKÈMQUYNHƠN OFFICIAL
.
ế
ab + A. 73 + . B. 73 . C. 723 . D. 723 + . Lời giải Chọn C Ta có ( ) ( ) 2 22 22 2.2,723 +=+=++=++=− ababababababcosab Câu 30. Cho hai điểm , BC phân biệt. Tập hợp những điểm M thỏa mãn 2 . = CMCBCM là : A. Đường tròn đường kính BC . B. Đường tròn( ) ; BBC . C. Đường tròn ( ) ; CCB . D. Một đường khác. Lời giải Chọn A 22 ..0.0 =−== CMCBCMCMCBCMCMMB . Tập hợp điểm M là đường tròn đường kính BC . Câu 31. Nếu lấy 3,1416 làm giá trị gần đúng của thì có số chữ số chắc là: A. 5. B. 4. C. 3. D. 2. Lời giải
Gắn hệ trục tọa độ Oxy như
vẽ, chiếc cổng là 1 phần của parabol ( )P : 2 yaxbxc =++ với 0 a . Do parabol ( )P đối xứng qua trục tung nên có trục đối xứng 000 2 b xb a =−== Chiều cao của cổng parabol là 4m nên ( )0;4 G 4 c = . ( )P : 2 4 yax=+ Lại có, kích thước cửa ở giữa là 3m x 4m nên ( ) ( )2;3,2;3EF 1 344 4 aa ===− . Vậy ( )P : 2 1 4 4 yx=−+ Ta có 2 4 1 40 4 4 x x x = −+= =− nên ( )4;0 A , ( )4;0 B hay 8 AB = (m). Câu 28. Cho tam giác đều ABC có cạnh bằng .a Tính tích vô hướng ABAC A. 2 .2.ABACa = B. 2 3 2 a ABAC =− C. 2 2 a ABAC =− D. 2 2 a ABAC = Lời giải Chọn D Xác định được góc ( ) , ABAC là góc A nên ( ) 0 ,60.ABAC = Do đó ( ) 2 0 ...cos,..cos60. 2 a ABACABACABACaa=== Câu 29. Cho hai vectơ a và b
Bi
t a =2, b = 3 và ( ) o,120ab = .Tính
Chọn B. Ta có 3,141592654... = nên sai số tuyệt đối của 3,1416 là 3,14163,14163,14150,0001 =−−= . Mà 0,00010,00050,001 2 d == nên có 4 chữ số chắc.
Câu 32. Số gần đúng của 2,57656 a = có ba chữ số đáng tin viết dưới dạng chuẩn là: A. 2,57. B. 2,576. C. 2,58. D. 2,577. Lời giải Chọn#A. Vì a có 3 chữ số đáng tin nên dạng chuẩn là 2,57.

Câu 33. Điểm thi toán cuối năm của một nhóm gồm 7 học sinh lớp 11 là 1; 3; 4; 5; 7; 8; 9. Số trung vị của dãy số liệu đã cho là A. 6. B. 4. C. 7. D. 5. Lời giải Mẫu số liệu đã cho có 7 phần tử, đã sắp theo thứ tự không giảm. Nên số trung vị là số đứng giữa dãy. Vậy số trung vị là 5.
Câu 34. Điểm thi toán cuối năm của một nhóm gồm 7 học sinh lớp 11 là 1; 3; 4; 5; 7; 8; 9. Số trung vị trên của dãy số liệu đã cho là A. 8. B. 3. C. 7. D. 5. Lời giải Chọn A Câu 35. Cho mẫu số liệu 1x , 2x ,…, Nx có số trung bình là x . Phương sai được tính theo công thức nào trong các công thức sau A. 1
1 N i i x N = B. ( ) 1
1 N i i xx N = C. ( ) 2 1
1 N i i xx N = D. ( ) 2 1
1 N i i sxx N =
2. Tự luận
1 N i i xx N = Lời giải Phương sai được tính theo công thức ( ) 2 2 1
11NN ii ii sxx NN==
=−
=− hoặc 2 22 2 11
Câu 1. Tại một buổi khai trương, người ta làm một cổng chào có đường viền trong của mặt cắt là đường parabol. Người ta đo khoảng cách giữa hai chân cổng là 4,5m . Từ một điểm trên thân cổng người ta đo được khoảng cách tới mặt đât (điêm H ) là 1,8m và khoảng cách từ điểm H tới chân cồng gần nhất là 1m . Hãy tính chiều cao của cồng chào đó (tính theo đường viền trong) theo đơn vị mét và làm tròn kết quả đến hàng phần mười.
Lời giải Chọn hệ trục tọ độ sao cho gốc toạ độ O trùng một chân của cổng, trục hoành nằm trên đường nối hai chân cổng (đơn vị trên các trục tính theo mét) (Hinh 10). Gọi hàm số bậc hai có đồ thị chứa đường viền trong của cổng chào trên là 2 =++ yaxbxc . Từ giả thiết bài toán ta có đồ thị hàm số đi qua các điểm (0;0),(4,5;0),(1;1,8) OAB
DẠYKÈMQUYNHƠN
OFFICIAL
không quá 10 giờ để làm hai loại đèn trung thu tặng cho các trẻ em khuyết tật. Loại đèn hình con cá cần 2 giờ để làm xong 1 cái, còn loại đèn ông sao chỉ cần 1 giờ để làm xong 1 cái. Gọi x, y lần lượt là số đèn hình con cá và đèn ông sao bạn Lan sẽ làm. Hãy lập hệ bất phương trình mô tả điều kiện của x, y và biểu diễn miền nghiệm của hệ bất phương trình đó.
Lời giải Ta có các điều kiện ràng buộc đối với x, y như sau: - Hiển nhiên 0,0xy

Tổng số giờ làm không quá 10 giờ nên 210 +xy
+

xy xxy y Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy, ta được như hình dưới.
Từ đó ta có hệ bất phương trình: 210 0(,) 0
Miền không tô màu (miền tam giác OAB , bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình. Câu 3. Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một con tàu C đang neo đậu ngoài khơi. Người đó tiến hành đo đạc và thu được kết quả: 30 ,60,50 === ABmCABCBA (Hình 23). Tính khoảng cách từ vị trí A đến con tàu C (làm tròn kết quả đến hàng phần mười theo đơn vị mét).
DẠYKÈMQUYNHƠN OFFICIAL Thay toạ độ các điểm trên
2 2 18 4,54,50 35 81 111,8 35 = += += = a ab ab b Suy ra
=+
hàm số trên có tung độ là 2
+ .
ạn Lan thu xếp đượ
vào hàm số, ta được 0 = c và hệ phương trình:
ta có hàm sô: 2 1881 3535
yxx . Từ đó, đỉnh của đồ thị
189819 2,6 354354
Vậy chiều cao của cổng là khoảng 2,6 m. Câu 2. B
c
Lời giải
Xét tam giác ABC . Ta có: ˆ 180605070 =−−= C Áp dụng định lí sin ta có: sinsin = BAAC CB . Suy ra sin30sin5024,5( sinsin70) == BAB ACm C Vậy khoảng cách từ vị trí A đến con tàu C là khoảng 24,5m . Câu 4. Cho tam giác ABC . Trên các cạnh AB , BC , CA ta lấy lần lượt các điểm M , N , P sao cho AMBNCP ABBCCA == . Chứng minh rằng hai tâm giác ABC và MNP có cùng trọng tâm. Lời giải Giả sử AM k AB = suy ra AMkAB = , BNkBC = , CPkCA = .
Cách 1. Gọi G , G lần lượt là trọng tâm của ABC và MNP . Suy ra 0 AGBGCG++= và 0 MGNGPG ++= ( )* Ta có AMkAB = AGGGGMkAB ++= Tương tự BGGGGNkBC ++= và CGGGGMkBC ++= Cộng vế theo vế từng đẳng thức trên ta được ( ) ( ) ( ) 3 AGBGCGGGGMGNGPkABBCCA

Kết hợp với ( )* ta được 0 GG = . Suy ra điều phải chứng minh. Cách 2. Gọi G là trọng tâm của ABC suy ra 0 GAGBGC++= Ta có ( ) 0

GMGNGPGAAMGBBNGCCP AMBNCP kABkBCkCA kABBCCA
++=+++++ =++ =++ =++
Vậy hai tam giác ABC và NMP có cùng trọn tâm.
DẠYKÈMQUYNHƠN OFFICIAL
++++++=++ .
=


ĐỀ THI HỌC KỲ MÔN TOÁN NĂM HỌC 2022 – 2023 Ths Nguyễn Thanh Tú eBook Collection MA TRẬN, ĐỀ THI HỌC KỲ I – NĂM HỌC 2022 2023 THEO SÁCH CÁNH DIỀU MÔN TOÁN 10 CÓ GIẢI CHI TIẾT WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL.COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405
MA TRẬN ĐỀ THI HỌC KỲ I NĂM HỌC 2022 2023-THEO SÁCH CÁNH DIỀU
Môn: Toán 10
1. TRẮC NGHIỆM ( 7 điểm) 35 câu 4 CÂU TỰ LUẬN
Chủ đề
CHƯƠNG 1 (5 câu)
CHƯƠNG 2 (5 câu)
CHƯƠNG 3 (9 câu)
CHƯƠNG 4 (16 câu)
Nội dung
Mức độ
NB TH VD VDC
Mệnh đề 1 1 0 0 Tập hợp 2 1 0 0
Bất phương trình bậc nhất hai ẩn 1 1 0 0
Hệ bất phương trình bậc nhất hai ẩn 2 1 0 TL1
Hàm số và đồ thị 1 1 0 0
Hàm số bậc hai 1 1 0 0
Dấu tam thức bậc hai 2 0 0 0
Bất phương trình bậc hai một ẩn 1 0 0 0
Hai dạng phương trình chứa căn 1 1 0 TL1
Giá trị lượng giác của góc từ 0o đến 1800 2 1 0 0
Hệ thức lượng trong tam giác Giải tam giác 2 3 TL 1 0 Định nghĩa vectơ 1 0 0 0
Tổng hiệu vectơ (Lực) 1 1 TL 1* 0
Tích của một số với một vectơ 1 1 0 0
Tích vô hướng của hai vectơ 1 2 TL1* 0
Tổng số câu 20 15 3 1
DẠYKÈMQUYNHƠNOFFICIAL
1. Trắc nghiệm
Câu 1. Trong các câu sau, có bao nhiêu câu là mệnh đề toán học?
a) Hà Nội là một thành phố của Việt Nam. b) Được sống thật là hạnh phúc! c) 68125 += d) Bạn thấy học Toán thú vị không? A. 1. B. 2. C. 3. D. 4. Câu 2. Mệnh đề phủ định của P : "Tam giác ABC là tam giác cân" là:
A. Tam giác ABC không phải là tam giác cân B. Tam giác ABC là tam giác vuông C. Tam giác ABC là tam giác đều D. ABC không phải là một tam giác Câu 3. Cho ba tập hợp: {0;1;2;3},{4}MNxx == và {1;2;3;4;5}. Khẳng định nào sau đây là đúng?
A. NP B. MP = . C. MN = D. NP = Câu 4. Cho tập hợp {13}Mxx=− . Mệnh đề nào sau đây đúng?
A. [1;3) M =− B. (1;3] M =− C. (1;3) M =− . D. {1;0;1} M =− .

Câu 5. Cho tập hợp [2;3] A =− và (0;) B =+ . Tập hợp AB là
A. [2;) −+ . B. (0;3]. C. [0;3] D. (0;3) Câu 6. Phần không bị gạch (kể cả d) ở Hình 5 là miền nghiệm của bất phương trình:
DẠYKÈMQUYNHƠN
ĐỀ 01
OFFICIAL
A. 1 2 yx . B. 2 yx . C. 2. yx D. 1 2 yx . Câu 7. Bạn Phúc muốn dùng 500000 đồng để mua x gói kẹo và y cái
pizza.
gói kẹo có giá là 40000 đồng, mỗi cái bánh pizza có giá là 75000 đồng. Mối liên hệ giữa x và y để Phúc không mua hết số tiền ban đầu là: A. 4000075000500000 +xy B. 4000075000500000 +xy C. 4000075000500000 +xy D. 4000075000500000 +xy Câu 8. Phần không bị gạch chéo ở hình bên biểu diễn miền nghiệm của hệ bất phương trình nào sau đây?
bánh
Biết rằng mỗi
A. 0 236 y xy +
B. 0 3260 y xy +− C. 0 3260 x xy +− D. 0 326 x xy + Câu 9. Mẹ đi chợ mua x kg thịt và y kg cá. Biết rằng mỗi kilôgam thịt có giá 120 nghìn đồng, mỗi kilôgam cá có giá 80 nghìn đồng. Hệ bất phương trình biểu thị mối liên hệ giữa x và y để số tiền mẹ đi chợ không hết quá 500 nghìn đồng và được tổng nhiều hơn 4kg thịt, cá là:
A. 80120500 4 + + xy xy B. 12080500 4 + + xy xy C. 12080500 4 + + xy xy D. 12080500 4 + + xy xy
Câu 10. Cho hệ bất phương trình 2 3 yxa yxb −+ + với a và b là các hằng số. Trong mặt phẳng Oxy , nếu (0;1) là một nghiệm

DẠYKÈMQUYNHƠN
OFFICIAL
của hệ bất phương trình thì điều kiện nào sau
A. ab . B.
= . C.
. D.
=− . Câu 11. Cho góc ,0;90 thoả mãn tan2tan2 =− . Mối liên hệ của hai góc đó là A. và bù nhau. B. và phụ nhau. C. và bằng nhau. D. và không có mối liên hệ. Câu 12. Cho góc với 3 tan 4 = . Giá trị của cos là A. 4 5 . B. 4 5 C. 5 4 . D. 5 4
đây là đúng?
ab
ab
ab
Câu 13. Rút gọn biểu thức sin cot 1cos x Px x =+ + , ta được
A. sin x B. 1 sin x . C. cos x . D. 1 cos x
Câu 14. Cho tam giác ABC có 2,1ABAC== và 0 60. A = Tính độ dài cạnh .BC A. 2. BC = B. 1. BC = C. 3. BC = D. 2. BC =
Câu 15. Cho tam giác ABC có 222 0 abc+− . Khi đó: A. Góc 090 C B. Góc 090 C C. Góc 090 C = D. Không thể kết luận được gì về góc C
Câu 16. Tam giác ABC có 0 6812' A = , 0 3444' B = , 117. AB = Tính AC ? A. 68. B. 168. C. 118. D. 200.

Câu 17. Cho ABC có 0 4,5,150.acB=== Diện tích của tam giác ABC là A.53. B. 103. C. 10. D.5.
Câu 18. Cho tam giác ABC có 20,10ab== , 0 30. B = Số đo góc A là A. 090 A = . B. 060 A = . C. 045 A = . D. 0120 A = .
Câu 19. Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Hỏi cặp vec tơ nào sau đây cùng hướng?
A. AB và MB B. MN và CB C. MA và MB D. AN và CA Câu 20. Cho ba điểm ,, ABC phân biệt. Đẳng thức nào sau đây là đúng? A. ABACBC += B. CABABC −= . C. ABCACB += D. ABBCCA −= . Câu 21. Trong các công thức sau, công thức nào không biểu diễn y là hàm số của x ? A. 23+=xy B. 2 2 =− yxx C. 1 = y x D. 22 4 +=xy Câu 22. Cho đồ thị hàm số () = yfx ở Hình 4. Phát biểu nào sau đây là đúng?
DẠYKÈMQUYNHƠN
OFFICIAL
A. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 1.
B. Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 1
C. Hàm số đồng biến trên khoảng (1;) −+ , nghịch biến trên khoảng (;1) −− .
D. Hàm số đồng biến trên .
Câu 23. Một ô tô có trọng lượng 15000N đứng trên một con dốc nghiêng 15 so với phương ngang. Lực có khả năng kéo ô tô xuống dốc có độ lớn là
A. 14489,89 N B. 3882,29 N C. 4019,24 N . D. 7500N .
Câu 24. Cho hình thang ,//,2 = MNPQMNPQMNPQ . Phát biểu nào sau đây là đúng?
OFFICIAL
A. 2 = MNPQ B. 2 = MQNP C. 2=− MNPQ D. 2=− MQNP Câu 25. Trên đường thẳng MN lấy điểm P sao cho 3 MNMP =− . Điểm P được xác định đúng trong hình vẽ nào sau đây: A. Hình 3 B. Hình 4 C. Hình 1 D. Hình 2 Câu 26. Trong các hàm số sau, hàm số nào không là hàm số bậc hai?

A. 2 42=−++yxx . B. ( ) 2 251=+−yxxx . C. 3(68)=−−yxx . D. 2 6 =+ yxx
Câu 27. Cho hàm số 2 ()288 =++fxxx . Phát biểu nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng (4;) −+ , nghịch biến trên khoảng (;4) −− .
B. Hàm số đồng biến trên khoảng (2;) −+ , nghịch biến trên khoảng (;2) −− .
C. Hàm số đồng biến trên khoảng (;2) −− , nghịch biến trên khoảng (2;) −+
D. Hàm số đồng biến trên khoảng (;4) −− , nghịch biến trên khoảng (4;) −+
DẠYKÈMQUYNHƠN
Câu 28. Nếu hai điểm , MN thoả mãn 4=−MNNM thì độ dài đoạn thẳng MN bằng bao nhiêu? A. 4 = MN B. 2 = MN C. 16= MN ; D. 256 = MN Câu 29. Cho hình vuông ABCD cạnh .a Đẳng thức nào sau
đúng? A. 2ABACa = B. 2 .2ABACa = C. 2 2 2 ABACa = D. 2 1 . 2 ABACa = Câu 30. Cho hình vuông ABCD cạnh a . Gọi E là
xứng của D
C Đẳng
đúng? A. 2 .2.AEABa =
2
=
2
=
=
Cho
.
đây
điểm đối
qua
thức nào sau đây
B.
.3.AEABa
C.
.5.AEABa
D. 2 .5.AEABa
Câu 31.
tam thức bậc hai 2 ()(0) =++fxaxbxca . Trong các phát biểu sau, phát biểu nào đúng? A. ()0
fx với mọi x khi và chỉ khi 0 a và 0 B. ()0 fx với mọi x khi và chỉ khi 0 a và 0
C. ()0 fx với mọi x khi và chỉ khi 0 a và 0 . D. ()0 fx với mọi x khi và chỉ khi 0 a và 0 .
bất phương
nào
bậc hai một

Câu 34. Trong các phát biểu sau, phát biểu nào đúng?
A. Tập nghiệm của phương trình ()() = fxgx là tập nghiệm của phương trình 2()[()] = fxgx
B. Tập nghiệm của phương trình ()() = fxgx là tập hợp các nghiệm của phương trình 2()[()] = fxgx thoả mãn bất phương trình ()0 gx
C. Mọi nghiệm của phương trình 2()[()] = fxgx đều là nghiệm của phương trình ()() = fxgx .
D. Tập nghiệm của phương trình ()() = fxgx là tập hợp các nghiệm của phương trình 2()[()] = fxgx thoả mãn bất phương trình ()0 fx
Câu 35. Một ngọn hải đăng đặt tại vị trí A cách bờ biển một khoảng 4 = ABkm. Giả sử bờ biển là đường thẳng, trên bờ biển có một cái kho ở vị trí C cách B một khoảng là 5km . Người canh hải đăng có thể chèo thuyền từ A đến điểm M trên bờ biển với vận tốc 3 / kmh rồi đi bộ đến C với vận tốc 5 / kmh (như hình vẽ). Khoảng cách giữa B và M là bao nhiêu để thời gian người đó đến kho là 124
DẠYKÈMQUYNHƠN OFFICIAL
−−+ . C. ( ) ( ) ;33;\7 4 −−+ D.
7 ;33;
−−
Câu 32. Trong các bất phương trình sau,
trình
không là bất phương trình
ẩn? A. 2 230−+ xx . B. 2 0,53(2)0 −−yy . C. 2 230−−xxy . D. 2 230 − x . Câu 33. Hàm số 2 2 32 x y xx = −+− có tập xác định là A. ( ) ( ) ;33; −−+ . B. ( ) ;33;\7 4
( )
4
A. 3km. B. 3,5km C. 5km D. 2,5km . 2. Tự luận Câu 1. Tìm tất cả các giá trị của tham số m để phương trình 2 2(2)2−++= xmxmx (1) có hai nghiệm phân biệt. Câu 2. Một học sinh dự định vẽ các tấm thiệp
để vẽ một tấm
20
phút?
xuân làm bằng tay để bán trong một hội chợ Tết. Cần 2 giờ
thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ để vẽ một tấm thiệp loại lớn có giá
nghìn đồng. Học sinh này chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải vẽ ít
nhất 12 tấm. Hãy cho biết bạn ấy cần vẽ bao nhiêu tấm thiệp mồi loại để có được nhiều tiền nhất.
Câu 3. Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A ) đến trường (điểm B ) phải leo lên và xuống một con dốc (Hình 24). Cho biết đoạn thẳng AB dài 762m , ˆ
6,4 ==AB a) Tính chiều cao h của con dốc theo đơn vị mét (làm tròn kết quả đến hàng đơn vị).

b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ trung bình lên dốc là 4 / kmh và tốc độ trung bình khi xuống dốc là 19 / kmh .
Câu 4. Chất điểm A chịu tác động của ba lực 123 ,, FFF như hình và ở trạng thái cân bằng (tức là 123 0 FFF++= ). Tính độ lớn của các lực 23 , FF biết 1F có độ lớn là 20 N .
OFFICIAL
DẠYKÈMQUYNHƠN
ˆ
1A
3C 4A 5B 6D 7A 8A
23B 24C 25A 26B 27B 28A 29A 30A 31B 32C 33B 34B 35A 1. Trắc nghiệm Câu 1. Trong
sau, có
mệnh đề toán học? a)
phố
b)
là mệnh đề toán học. Câu 2. Mệnh đề phủ định của P : "Tam giác ABC là tam giác cân" là: A. Tam giác ABC không phải là tam giác cân B. Tam giác ABC là tam giác vuông C. Tam giác ABC là tam giác đều D. ABC không phải là một tam giác Câu 3. Cho ba tập hợp: {0;1;2;3},{4}MNxx == và {1;2;3;4;5}. Khẳng định nào sau đây là đúng? A. NP . B. MP = C. MN = . D. NP = . Câu 4. Cho tập hợp {13}Mxx=− . Mệnh đề nào sau đây đúng?
Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM
2A
9D 10C 11B 12A 13B 14C 15B 16A 17D 18A 19A 20C 21D 22D
các câu
bao nhiêu câu là
Hà Nội là một thành
của Việt Nam.
Được sống thật là hạnh phúc! c) 68125 += . d) Bạn thấy học Toán thú vị không? A. 1. B. 2. C. 3. D. 4. Lời giải Theo định nghĩa mệnh đề thì câu: c)
A. [1;3) M =− B. (1;3] M =− . C. (1;3) M =− . D. {1;0;1} M =−

Câu 5. Cho tập hợp [2;3] A =− và (0;) B =+ . Tập hợp AB là

A. [2;) −+ B. (0;3] C. [0;3]. D. (0;3).
Câu 6. Phần không bị gạch (kể cả d) ở Hình 5 là miền nghiệm của bất phương trình:
A. 1 2 yx B. 2 yx C. 2. yx D. 1 2 yx
Câu 7. Bạn Phúc muốn dùng 500000 đồng để mua x gói kẹo và y cái bánh pizza. Biết rằng mỗi gói kẹo có giá là 40000 đồng, mỗi cái bánh pizza có giá là 75000 đồng. Mối liên hệ giữa x và y để Phúc không mua hết số tiền ban đầu là:
A. 4000075000500000 +xy B. 4000075000500000 +xy C. 4000075000500000 +xy D. 4000075000500000 +xy
Câu 8. Phần không bị gạch chéo ở hình bên biểu diễn miền nghiệm của hệ bất phương trình nào sau đây?
DẠYKÈMQUYNHƠN
OFFICIAL
A. 0 236 y xy + B. 0 3260 y xy +− C. 0 3260 x xy +− D. 0 326 x xy +
Mẹ đi chợ mua x kg thịt và y kg cá. Biết rằng mỗi kilôgam thịt có giá 120 nghìn đồng, mỗi kilôgam cá có giá 80 nghìn đồng. Hệ bất phương trình biểu thị mối liên hệ giữa x và y để số tiền mẹ đi chợ không hết quá 500 nghìn đồng và được tổng nhiều hơn 4kg thịt, cá là: A. 80120500 4 + + xy xy
Câu 9.
B. 12080500 4 + + xy xy
C. 12080500 4 + + xy xy
D. 12080500 4 + + xy xy
Câu 10. Cho hệ bất phương trình 2 3 yxa yxb −+ + với a và b là các hằng số. Trong mặt phẳng Oxy , nếu
(0;1) là một nghiệm của hệ bất phương trình thì điều kiện nào sau đây là đúng?
A. ab . B. ab = . C. ab . D. ab =− .
11. Cho góc ,0;90
DẠYKÈMQUYNHƠN
OFFICIAL
Câu 12. Cho góc với 3 tan 4 = . Giá trị của cos là A. 4 5 . B. 4 5 C. 5 4 . D. 5 4 . Câu 13. Rút gọn biểu thức sin cot 1cos x Px x =+ + , ta được A. sin x . B. 1 sin x C. cos x D. 1 cos x . Lời giải sincos1cos1 1cossin(1cos)sinsin xxx P xxxxx + =+== ++ . Vậy đáp án là B Câu 14. Cho tam giác ABC có 2,1ABAC== và 0 60. A = Tính độ dài cạnh .BC A. 2. BC = B. 1. BC = C. 3. BC = D. 2. BC = Lời giải Chọn C Theo định lý cosin ta có: 220 2..cos60BCABACABAC =+− 22 1 212.2.1. 2 =+− 3. = Câu 15. Cho tam giác ABC có 222 0 abc+− . Khi đó:
Câu
thoả mãn tan2tan2 =− . Mối liên hệ của hai góc đó là A. và bù nhau. B. và phụ nhau. C. và bằng nhau. D. và không có mối liên hệ.
A. Góc 090 C B. Góc 090 C C. Góc 090 C = D. Không thể kết luận được gì về góc .C Lời giải
Chọn B. Ta có: 222 cos 2 abc C ab +− = . Mà: 222 0 abc+− suy ra: 0cos090 CC .
Câu 16. Tam giác ABC có 0 6812' A = , 0 3444' B = , 117. AB = Tính AC ? A. 68. B. 168. C. 118. D. 200. Lời giải Chọn#A. Ta có: Trong tam giác ABC : 00000 1801806812'3444'774'ABCC ++==−−= Mặt khác 0 0 .sin117.sin3444' 68. sinsinsinsinsinsin sin774' abcACABABB AC ABCBCC =====
Câu 17. Cho ABC có
DẠYKÈMQUYNHƠN
OFFICIAL
90 A = . B. 060 A = . C. 045 A = . D. 0120 A = . Lời giải Chọn A Tacó 0 0 2010201020 20sin190 1 sinsinsinsin30sinsin 2 ab AA ABAAA ====== Câu 19. Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Hỏi cặp vec tơ nào sau đây cùng hướng? A. AB và MB B. MN và CB C. MA và MB D. AN và CA Lời giải Chọn A Ta có AB và MB cùng hướng Câu 20. Cho ba điểm ,, ABC phân biệt. Đẳng thức nào sau đây là đúng? A. ABACBC += . B. CABABC −= C. ABCACB += D. ABBCCA −= .
0 4,5,150.acB=== Diện tích của tam giác ABC là A.53. B. 103. C. 10. D.5. Lời giải Chọn D Ta có 0 111 ..sin.4.5sin15010.5. 222 SacB==== Câu 18. Cho tam giác ABC có 20,10ab== , 0 30. B = Số đo góc A là A. 0
Câu 21. Trong các công thức sau, công thức nào không biểu diễn y là hàm số của x ?
A. 23+=xy
B. 2 2 =− yxx
C. 1 = y x


D. 22 4 +=xy .
Chọn D
Lời giải
Câu 22. Cho đồ thị hàm số () = yfx ở Hình 4. Phát biểu nào sau đây là đúng?
A. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 1.
B. Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 1
C. Hàm số đồng biến trên khoảng (1;) −+ , nghịch biến trên khoảng (;1) −− .
D. Hàm số đồng biến trên
Lời giải Chọn D
Câu 23. Một ô tô có trọng lượng 15000N đứng trên một con dốc nghiêng 15 so với phương ngang. Lực có khả năng kéo ô tô xuống dốc có độ lớn là A. 14489,89 N . B. 3882,29 N . C. 4019,24 N D. 7500N .
Lời giải Lực có khả năng kéo ô tô xuống dốc là lực AB . Xét tam giác ACW vuông tại C , có 15 CAW = . Ta có sin CWAB A AWAW == Suy ra 15000sin153882,29 ABN
DẠYKÈMQUYNHƠN
OFFICIAL
2 = MNPQ
2 =
=−
=−
= . Câu 24. Cho hình thang ,//,2 = MNPQMNPQMNPQ . Phát biểu nào sau đây là đúng? A.
B.
MQNP C. 2
MNPQ D. 2
MQNP . Lời giải
Ta có 222 MNMIQPPQ ===− Chọn C
Câu 25. Trên đường thẳng MN lấy điểm P sao cho 3 MNMP =− . Điểm P được xác định đúng trong hình vẽ nào sau đây:
A. Hình 3 B. Hình 4 C. Hình 1 D. Hình 2 Lời giải Chọn A 3 MNMPMN =− ngược hướng với MP và 3 MNMP = .
Câu 26. Trong các hàm số sau, hàm số nào không là hàm số bậc hai?
A. 2 42=−++yxx
B. ( ) 2 251=+−yxxx . C. 3(68)=−−yxx . D. 2 6 =+ yxx .


Lời giải Chọn B
Câu 27. Cho hàm số 2 ()288 =++fxxx . Phát biểu nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng (4;) −+ , nghịch biến trên khoảng (;4) −− .
B. Hàm số đồng biến trên khoảng (2;) −+ , nghịch biến trên khoảng (;2) −− C. Hàm số đồng biến trên khoảng (;2) −− , nghịch biến trên khoảng (2;) −+ .
D. Hàm số đồng biến trên khoảng (;4) −− , nghịch biến trên khoảng (4;) −+ . Lời giải Chọn B
DẠYKÈMQUYNHƠN
OFFICIAL
Câu 28. Nếu hai điểm , MN thoả mãn 4=−MNNM thì độ dài đoạn thẳng MN bằng bao nhiêu? A. 4 = MN B. 2 = MN C. 16= MN ; D. 256 = MN Lời giải 2 4..cos180442 =−==−== MNNMMNNMMNMN Chọn A Câu 29. Cho hình vuông ABCD cạnh .a Đẳng thức nào sau đây đúng? A. 2ABACa = B. 2 .2ABACa = C. 2 2 2 ABACa = D. 2 1 . 2 ABACa = Lời giải Chọn A
Câu 30. Cho hình vuông ABCD cạnh a . Gọi E là điểm đối xứng của D qua .C Đẳng thức nào sau đây đúng?
A. 2 .2.AEABa = B. 2 .3.AEABa = C. 2 .5.AEABa = D. 2 .5.AEABa = Lời giải
Chọn A
Ta có C là trung điểm của DE nên 2.DEa = Khi đó ( ) 0 .... AEABADDEABADABDEAB =+=+ ( ) 02 ..cos,..cos02. DEABDEABDEABa ===
A B
E D C
Câu 31. Cho tam thức bậc hai 2 ()(0) =++fxaxbxca Trong các phát biểu sau, phát biểu nào đúng?
A. ()0 fx với mọi x khi và chỉ khi 0 a và 0 .
B. ()0 fx với mọi x khi và chỉ khi 0 a và 0
C. ()0 fx với mọi x khi và chỉ khi 0 a và 0
D. ()0 fx với mọi x khi và chỉ khi 0 a và 0 .
Lời giải Chọn B
Câu 32. Trong các bất phương trình sau, bất phương trình nào không là bất phương trình bậc hai một ẩn?
2 32 x y 320 30 xx x
xx = −+− −+− − Ta có 2 3 30 3 x x x
− − Xét 2 320xx−+−= 2 32 xx−=− ( )2 2
− −=−
20 32 x xx
x x
=
2 7 4
7 4 x = Do đó tập xác định của hàm số đã cho là ( ) ;33;\7 4 D =−−+ . Câu 34. Trong các phát biểu sau, phát biểu nào đúng?
DẠYKÈMQUYNHƠN
OFFICIAL
Ta có ( ) 0,45ABACBAC== nên 02 2 ...cos45.2. 2 ABACABACaaa ===
A. 2 230−+ xx B. 2 0,53(2)0 −−yy C. 2 230−−xxy D. 2 230 − x Lời giải Chọn C Câu 33. Hàm số 2 có tập xác định là A. ( ) ( ) ;33; −−+ B. ( ) ;33;\7 4 −−+ C. ( ) ( ) ;33;\7 4 −−+ . D. ( ) 7 ;33; 4 −− . Lời giải Chọn B Hàm số đã cho xác định khi 2 2
A. Tập nghiệm của phương trình ()() = fxgx là tập nghiệm của phương trình 2()[()] = fxgx .
B. Tập nghiệm của phương trình ()() = fxgx là tập hợp các nghiệm của phương trình 2()[()] = fxgx thoả mãn bất phương trình ()0 gx .

C. Mọi nghiệm của phương trình 2()[()] = fxgx đều là nghiệm của phương trình ()() = fxgx
D. Tập nghiệm của phương trình ()() = fxgx là tập hợp các nghiệm của phương trình 2()[()] = fxgx thoả mãn bất phương trình ()0 fx .
Chọn B
Lời giải
OFFICIAL
Câu 35. Một ngọn hải đăng đặt tại vị trí A cách bờ biển một khoảng 4 = ABkm. Giả sử bờ biển là đường thẳng, trên bờ biển có một cái kho ở vị trí C cách B một khoảng là 5km . Người canh hải đăng có thể chèo thuyền từ A đến điểm M trên bờ biển với vận tốc 3 / kmh rồi đi bộ đến C với vận tốc 5 / kmh (như hình vẽ). Khoảng cách giữa B và M là bao nhiêu để thời gian người đó đến kho là 124 phút? A. 3km B. 3,5km C. 5km . D. 2,5km .
DẠYKÈMQUYNHƠN
124 phút 31 15 = giờ. Đặt ( ) = BMxkm , điều kiện: 05 x . Ta có: 2 16( ),5( ) =+=− AMxkmMCxkm Thời gian để người canh hải đăng di chuyển từ A đến C là: 2 165 35 +− + xx (giờ). Ta có phưong trình: 2 16531 3515 +− += xx hay 2 516163 +=+xx. Giải phương trình này ta được nghiệm 3 = x Vậy 3 = BMkm. 2. Tự luận Câu 1. Tìm tất cả các giá trị của tham số m để phương trình 2 2(2)2−++= xmxmx (1) có hai nghiệm phân biệt. Lời giải Điều kiện 0 x . Bình phương hai vế của phương trình (1) ta được: 2222(2)2 hay (2)20(2)xmxmxxmxm −++=−++= Để phương trình (1) có hai nghiệm phân biệt thì phương trình (2) có hai nghiệm phân biệt thoả mãn điều kiện 0 x
Lời giải. Chọn A Đổi:
nên nhận thấy phương trình (2) có hai nghiệm 2; == xxm.
+
+

xy xy xy
bao gồm cả các cạnh) trong hình trên là phần giao của các
biểu diễn nghiệm của
chiều cao h của con dốc theo đơn vị mét (làm tròn kết quả đến hàng đơn vị).
DẠYKÈMQUYNHƠN
Ta có 12
+=+ = xxm xxm
OFFICIAL
12 2 2
Để phương trình (2) có hai nghiệm phân biệt thoả mãn điều kiện 0 x thì 0 m và 2 m Vậy để phương trình (1) có hai nghiệm phân biệt thì 0 m và 2 m Câu 2. Một học sinh dự định vẽ các tấm thiệp xuân làm bằng tay để bán trong một hội chợ Tết. Cần 2 giờ để vẽ một tấm thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ để vẽ một tấm thiệp loại lớn có giá 20 nghìn đồng. Học sinh này chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải vẽ ít nhất 12 tấm. Hãy cho biết bạn ấy cần vẽ bao nhiêu tấm thiệp mồi loại để có được nhiều tiền nhất. Lời giải Ta có các điều kiện ràng buộc đối với x, y như sau: Hiển nhiên 0,0xy Tổng số giờ vẽ không quá 30 giờ nên 2330 +xy Số tấm thiệp tối thiểu là 12 tấm nên 12 +xy Từ đó ta có hệ bất phương trình:
2330 12 (,) 0 0 x y
ˆ 6,4 ==AB . a) Tính
b) Hỏi bạn
độ trung
Lời
a) Xét tam giác ABC ta có: 18064170 =−−= ACB . Áp dụng định lí sin ta có: sin762sin4306( sinsinsinsin170) === ABACABB ACm CBC
Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy , ta được như hình dưới.
Miền không tô màu (miền tam giác ABC ,
miền nghiệm và cũng là phần
hệ bất phươnng trình. Với các đỉnh (6;6),(15;0),(12;0) ABC Gọi F là số tiền (đơn vị: nghìn đồng) thu được, ta có: 1020=+ Fxy Tính giá trị của F tại các đỉnh của tam giác: Tại (6;6):10.620.6180 =+= AF Tại (15;0):10.1520.0150 =+= BF Tại (12;0):10.1220.0120 =+= CF F đạt giá trị lớn nhất bằng 180 tại (6;6)A . Vậy bạn học sinh đó cần vẽ 6 tấm thiệp loại nhỏ và 6 tấm thiệp loại to để có được nhiều tiền nhất. Câu 3. Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A ) đến trường (điểm B ) phải leo lên và xuống một con dốc (Hình 24). Cho biết đoạn thẳng AB dài 762m , ˆ
An đến trường lúc mấy giờ? Biết rằng tốc độ trung bình lên dốc là 4 / kmh và tốc
bình khi xuống dốc là 19 / kmh
giải
Xét tam giác vuông AHC ta có sin306sin632( ) == hCHACAm .
Vậy chiều cao con dốc là khoảng 32m. b) Áp dụng định lí sin ta có: 762sin6459( sinsinsin170) == BCAB BCm AC .
Ta có: 306 0,306 ;459 0,459 == ACmkmCBmkm Như vậy, thời gian bạn An đi từ nhà đến trường là: =++= 0,3060,459 0,1(giôø) 6(phuùt). 419419 ACCB t


Vậy bạn An đến trường lúc khoảng 6 giờ 6 phút. Câu 4. Chất điểm A chịu tác động của ba lực 123 ,, FFF như hình và ở trạng thái cân bằng (tức là 123 0 FFF++= ). Tính độ lớn của các lực 23 , FF biết 1F có độ lớn là 20 N .
Lời
DẠYKÈMQUYNHƠN
OFFICIAL
giải Bước 1: Đặt 12 uFF =+ . Ta xác định các điểm như hình dưới. Dễ dàng xác định điểm C , là điểm thứ tư của hình bình hành ABCD. Do đó vecto u chính là vecto AC Vì chất điểm A ở trang thái cân bằng nên 123 0 FFF++= hay 33 0 vaø uFuF += là hai vecto đối nhau. A là trung điểm của EC . Bước 2: Ta có: 123 20,, FADFABFAC ==== Do ,, ACE thẳng hàng nên 18060CABEAB =−= 403 906030cos303 sin30203 3 AD AC CAD ABDCAC == =−= === Vậy 23 203403 , 33 FF== .
DẠYKÈMQUYNHƠN OFFICIAL
1. Trắc nghiệm Câu 1. Trong các câu sau, có bao nhiêu câu là mệnh đề toán học?
a) Hãy mở cửa ra! b) Số 25 chia hết cho 8. c) Số 17 là số nguyên tố. d) Bạn thích ăn phở không? A. 1. B. 2. C. 3. D. 4. Câu 2. Cho mệnh đề chứa biến ()Px : " 2 15 xx + " (với x là số thực). Mệnh đề nào sau đây là đúng? A. (0)P B. (3)P C. (4)P D. (5)P Câu 3. Cho tập hợp 2 9 =Axx . Tập hợp A là: A. {0;1;2;3} = A . B. [0;3]. = A C. {0;3} = A D. {3;2;1;0;1;2;3}=−−− A Câu 4. Viết tập hợp ( )( ) 22240=−−= Bxxxx bằng cách liệt kê các phần tử của tập hợp thì ta được: A. {2;0;2;2}=− B . B. {2;0;2}=− B . C. {2} = B . D. {2;2}=− B . Câu 5. Trong các tập hợp sau, tập hợp nào là tập hợp rỗng?
bậc nhất hai ẩn 578 −xy là:
A. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy chứa gốc tọa độ (0;0)O (kể cả bờ).
B. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy không chứa gốc tọa độ (0;0)O (kể cả bờ).
C. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy chứa gốc tọa độ (0;0)O (không kể bờ).
D. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy không chứa gốc tọa độ (0;0)O (không kể bờ).
Câu 7. Bất phương trình nào sau đây KHÔNG là bất phương trình bậc nhất hai ẩn? A. 290
DẠYKÈMQUYNHƠN
ĐỀ 02
OFFICIAL
A. {(1)(21)0} =++= Axxx . B. {(1)(21)0} =++=Bxxx . C. {(1)(21)0} =++=Cxxx D. {(1)(21)0} =++=Dxxx Câu 6. Miền nghiệm của bất phương trình
−+
+
+−
xyxy +++ Câu 8. Cho hệ bất phương trình 1 1 1 1 xy xy xy xy + +− − −− . Diện tích miền nghiệm () H của hệ bất phương
đã cho là A. 1. B. 2. C. 2 D. 4. Câu 9. Cho hệ bất phương trình 235 (1) 35(2) 2 xy xy + + . Gọi 12 , SS lần lượt là tập nghiệm của
phương trình (1) và (2). Mệnh đề nào sau
A. 12SS . B. 21SS . C. 12SS =
xy
B. 3(1)2xy
. C. 22 3(1)xyx
. D. 2(3)3(22)2
trình
các bất
đây đúng?
Câu 10. Anh Tuấn là du học sinh tại Mỹ và có hai công việc làm thêm vào mùa hè. Anh ấy làm gia sư được trả 12 USD mỗi giờ và làm nhân viên thu ngân ở siêu thị được trả 9,5 USD mỗi giờ. Gọi x là số giờ anh ấy làm gia sư và y là số giờ anh ấy làm nhân viên thu ngân. Anh ầy có thể làm việc không quá 20 giờ mỗi tuần. Hỏi cặp số (;) xy nào sau đây thể hiện anh ấy kiếm được ít nhất 220 USD mỗi tuần? A. (10;10). B. (12;8). C. (11;10). D. (9;9) Câu 11. Giá trị của biểu thức 0000 sin30cos60sin60cos30 P =+ bằng A. 3 P =− B. 0 P = C. 3 P = D. 1 P = Câu 12. Cho là góc nhọn và 1 sincos 2 = . Giá trị của sincos M =+ là A. 1. B. 2. C. 2 . D. 2 Câu 13. Rút gọn biểu thức ( ) ( ) tan180 1 sinsin90 x P xx
OFFICIAL
=+ − với ( ) 0;90 x
ta được A. 2 1 cos x B. 2 1 cos x . C. tan x D. 2tan x Câu 14. Tam giác ABC có 0 8,3,60.acB=== Độ dài cạnh b bằng bao nhiêu? A. 49. B. 97 C. 7. D. 61. Câu 15. Cho tam giác ABC thoả mãn: 222 3 bcabc +−= . Khi đó: A. 0 30. A = B. 0 45. A = C. 0 60. A = D. 075 A = . Câu 16. Cho tam giác ABC , biết 13,14,15.abc=== Tính góc B? A. 0 5949'. B. 0 537'. C. 0 5929'. D. 0 6222'. Câu 17. Cho tam giác ABC có 110;46;6ACb=== . Khẳng định nào sau đây đúng?
DẠYKÈMQUYNHƠN
D. 12SS
24;13,9;10,6Bac=
Bac= .
Bac= . Câu 18. Cho tam giác ABC có 6;7;12abc=== . Khẳng định nào sau đây đúng? A. ABC có 1 góc tù. B. ABC có 3 góc nhọn. C. ABC là tam giác vuông. D. 20 A Câu 19. Hai vectơ có cùng độ dài và cùng hướng gọi là A. Hai vectơ cùng hướng. B. Hai vectơ cùng phương. C. Hai vectơ đối nhau. D. Hai vectơ bằng nhau Câu 20. Cho ABC và điểm M thoả mãn điều kiện MAMCMB += . Khẳng định nào sau đây là SAI? A. ABAMAC += . B. BABCBM +=
A.
B. 24;13,8;10,7Bac= C. 24;12,7;10,1
D. 24;12,6;10,2
C. Tứ giác ABCM là hình bình hành.
D. MABC =
Câu 21. Tập xác định của hàm số 4220182019yxx=−− là
A. ( ) 1; −+ . B. ( );0− . C. ( ) 0;+ . D. ( ) ; −+ .
Câu 22. Cho hàm số 5 yfxx . Khẳng định nào sau đây là sai?
A. 15 f B. 210 f C. 1 1 5 f D. 210 f
OFFICIAL
Câu 23. Một giá đỡ có dạng tam giác ABC vuông cân tại đỉnh A được gắn vào tường như hình bên. Người ta treo vào vị trí C một vật nặng 10N . Cường độ lực tác động vào tường tại điểm A và B là
A. (5 N;10 N).
B. (10 ;10 )NN
C. (10;102 )NN D. (10;103 )NN .
Câu 24. Cho đoạn thẳng AB và O là trung điểm của AB . Khẳng định nào sau đây là đúng? A. 2 = ABOA. B. 2 = ABOB . C. 2=− ABOB . D. 2 = AOAB . Câu 25. Cho ba điểm phân biệt ,, ABC . Nếu 3 ABAC =− thì đẳng thức nào dưới đây đúng? A. 4 BCAC

DẠYKÈMQUYNHƠN
số 2 yaxbxc =++ , (0) a
A. ;. 2 b a −− B. ;. 2 b a −+ C. ;. 4a −+ D. ;. 4a −− Câu 27. Cho parabol ( ) 2 :321Pyxx=−+ . Điểm nào sau đây là đỉnh của ( )P ? A. ( )0;1 I B. 12 ; 33 I C. 12 ; 33 I D. 12 ; 33 I Câu 28. Phát biểu nào sau đây là đúng? A. Nếu , ab khác 0 và (,)90 ab thì 0 ab ; B. Nếu , ab khác 0 và (,)90 ab thì 0 ab ; C. Nếu , ab khác 0 và (,)90 ab thì 0 ab ; D. Nếu , ab khác 0 và (,)90 ab thì 0 ab Câu 29. Cho tam giác ABC . Tập hợp các điểm M thỏa mãn .0MABC = là: A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn. Câu 30. Cho tam giác đều ABC cạnh 2 = a .
mệnh đề nào sau đây sai? A. ( ) .2 = ABACBCBC B. .2 =− BCCA
=− B. 2 BCAC =− C. 2 BCAC = D. 4 BCAC = Câu 26. Hàm
đồng biến trong khoảng nào sau đậy?
Hỏi
y 4 4 1
O x
các phát biểu sau, phát biểu nào đúng?
A. Tập nghiệm của phương trình ()() = fxgx là tập nghiệm của phương trình ()() = fxgx .
B. Tập nghiệm của phương trình ()() = fxgx là tập nghiệm của phương trình 22 [()][()] fxgx =
C. Mọi nghiệm của phương trình ()() = fxgx đều là nghiệm của phương trình ()() = fxgx
D. Tập nghiệm của phương trình ()() = fxgx là tập hợp các nghiệm của phương trình ()() = fxgx thoả mãn bất phương trình ()0 fx (hoặc ()0 gx ).
Câu 35. Số nghiệm của phương trình 2 331.xx+=− là A. 0. B. 1. C. 2. D. 3.
2. Tự luận
Câu 1. Giả sử độ cao h (đơn vị: mét) của một quả bóng golf tính theo thời gian t (đơn vị: giây) trong một lần đánh của vận động viên được xác định bằng một hàm số bậc hai và giá trị tương ứng tại một số thời điểm được cho bởi bảng dưới đây: Thời gian (s) 0 0,5 1 2 3 Độ cao (m) 0 28 48 64 48 a) Xác định hàm số bậc hai biểu thị độ cao ( )hm của quả bóng golf tính theo thời gian ()ts . b) Sau bao lâu kể từ khi vận động viên đánh bóng thì bóng lại chạm đất?
Câu 2. Bác Năm dự định trồng khoai lang và khoai mì trên mảnh đất có diện tích 8 ha. Nếu trồng 1 ha khoai lang thì cần 10 ngày công và thu được 20 triệu đồng. Nếu trồng 1 ha khoai mì thì cần 15 ngày công và thu được 25 triệu đồng. Bác Năm cần trồng bao nhiêu hecta cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng được không quá 90 ngày công cho việc trồng khoai lang và khoai mì.
Câu 3. Quan sát cây cầu dây văng minh hoạ ở Hình 25.
DẠYKÈMQUYNHƠN OFFICIAL C. ( ).4+=−ABBCAC D. ( ).2−=BCACBA
.
Câu 31. Tập nghiệm của bất phương trình 2 3180−++ xx là: A. [3;6] B. (3;6). C. (;3)(6;) −−+ . D. (;3][6;) −−+ Câu 32. Cho tam thức ( ) ( ) 2 0, fxaxbxca =++ 2 4 bac=− . Ta có ( ) 0 fx với x khi và chỉ khi: A. 0 0 a
. B. 0 0 a
C. 0 0 a . D. 0 0 a . Câu 33. Cho hàm số ( ) 2 yfxaxbxc ==++ có đồ thị như hình vẽ. Đặt 2 4 bac=− , tìm dấu của a và . A. 0 a , 0 B. 0 a , 0 C. 0 a , 0 = D. 0 a , , 0 = Câu 34. Trong
( )yfx =
OFFICIAL
Tại trụ cao nhất, khoảng cách từ đỉnh trụ (vị trí A ) tới chân trụ trên mặt cầu (vị trí H ) là 150m , độ dài dây văng dài nhất nối từ đỉnh trụ xuống mặt cầu (vị trí B ) là 300m, khoảng cách từ chân dây văng dài nhất tới chân trụ trên mặt cầu là 250m (Hình 26). Tính độ dốc của cầu qua trụ nói trên (làm tròn kết quả đến hàng phần mười theo đơn vị độ).

Câu 4. Một vật đồng chất được thả vào một cốc chất lỏng. Ở trạng thái cân bằng, vật chìm một nửa thể tích trong chất lỏng. Tìm mối liên hệ giữa trọng lực P của vật và lực đẩy Archimedes F mà chất lỏng tác động lên vật. Tính tỉ số giữa trọng lượng riêng của vật và của chất lỏng. Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM

DẠYKÈMQUYNHƠN
1B 2D 3A 4B
7D 8B 9A 10B 11D 12D 13D 14C
16C
22C 23C 24B 25D 26B 27B 28C 29B 30C 31A 32A 33A 34D 35B 1. Trắc nghiệm Câu 1. Trong các câu sau, có bao nhiêu câu là mệnh đề toán học? a) Hãy mở cửa ra! b) Số 25 chia hết cho 8. c) Số 17 là số nguyên tố. d) Bạn thích ăn phở không? A. 1. B. 2. C. 3. D. 4. Câu 2. Cho mệnh đề chứa biến ()Px : " 2 15 xx + " (với x là số thực). Mệnh đề nào sau đây là đúng? A. (0)P . B. (3)P . C. (4)P . D. (5)P . Câu 3. Cho tập hợp 2 9 =Axx . Tập hợp A là: A. {0;1;2;3} = A B. [0;3]. = A C. {0;3} = A . D. {3;2;1;0;1;2;3}=−−− A . Câu 4. Viết tập hợp ( )( ) 22240=−−= Bxxxx bằng cách liệt kê các phần tử của tập hợp thì ta được: A. {2;0;2;2}=− B B. {2;0;2}=− B C. {2} = B D. {2;2}=− B Câu 5. Trong các tập hợp sau, tập hợp nào là tập hợp rỗng? A. {(1)(21)0} =++= Axxx B. {(1)(21)0} =++=Bxxx C. {(1)(21)0} =++=Cxxx . D. {(1)(21)0} =++=Dxxx . Câu 6. Miền nghiệm của bất phương trình bậc nhất hai ẩn 578 −xy là: A. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy chứa gốc tọa độ (0;0)O (kể cả bờ). B. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy không chứa gốc tọa độ (0;0)O (kể cả bờ).
5D 6D
15A
17A 18A 19D 20D 21D
C. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy chứa gốc tọa độ (0;0)O (không kể bờ).
D. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy không chứa gốc tọa độ (0;0)O (không kể bờ).
Câu 7. Bất phương trình nào sau đây KHÔNG là bất phương trình bậc nhất hai ẩn?
A. 290 xy−+
B. 3(1)2xy + . C. 22 3(1)xyx+− D. 2(3)3(22)2 xyxy +++
trình (1) và (2). Mệnh đề nào sau đây đúng?
A. 12SS . B. 21SS C. 12SS = . D. 12SS . Câu 10. Anh Tuấn là du học sinh tại Mỹ và có hai công việc làm thêm vào mùa hè. Anh ấy làm gia sư được trả 12 USD mỗi giờ và làm nhân viên thu ngân ở siêu thị được trả 9,5 USD mỗi giờ. Gọi x là số giờ anh ấy làm gia sư và y là số giờ anh ấy làm nhân viên thu ngân. Anh ầy có thể làm việc không quá 20 giờ mỗi tuần. Hỏi cặp số (;) xy nào sau đây thể hiện anh ấy kiếm được ít nhất 220 USD mỗi tuần?
(10;10). B. (12;8) C. (11;10) D. (9;9).
DẠYKÈMQUYNHƠN
OFFICIAL
1 1 1 1 xy xy xy xy + +− − −− . Diện
ề
ủ
ệ
Câu 8. Cho hệ bất phương trình
tích mi
n nghiệm () H c
a h
bất phương trình đã cho là A. 1. B. 2. C. 2 . D. 4. Câu 9. Cho hệ bất phương trình 235 (1) 35(2) 2 xy xy + + . Gọi 12 , SS lần lượt là tập nghiệm của các bất phương
Lời
Số tiền mà anh Tuấn kiếm được là 129,5xy + (USD). Theo đề bài ta có hệ bất phương trình 129,5220 20 0;0 xy xy xy + + Thay lần lượt các đáp án ta có đáp án B thoả mãn. Câu 11. Giá trị của biểu thức 0000 sin30cos60sin60cos30 P =+ bằng A. 3 P =− B. 0 P = C. 3 P = D. 1 P = Lời giải Chọn D 00002020 sin30sin30cos30cos30sin30cos301 P =+=+= Câu 12. Cho là góc nhọn và 1 sincos 2 = . Giá trị của sincos M =+ là
A.
giải
A. 1. B. 2. C. 2 . D. 2
Lời giải 22(sincos)12sincos2 M =+=+= . Suy ra 2 M = (vì )0 M
Câu 13. Rút gọn biểu thức ( ) ( ) tan180 1 sinsin90 x P xx
=+ − với ( ) 0;90 x ta được A. 2 1 cos x B. 2 1 cos x . C. tan x D. 2tan x
Câu 14. Tam giác ABC có 0 8,3,60.acB=== Độ dài cạnh b bằng bao nhiêu? A. 49. B. 97 C. 7. D. 61. Lời giải Chọn C. Ta có: 2222202cos832.8.3.cos60497 bacacBb =+−=+−==
Câu 15. Cho tam giác ABC thoả
DẠYKÈMQUYNHƠN OFFICIAL
5949'. B. 0 537'. C. 0 5929'. D. 0 6222'. Lời giải Chọn C. Ta có: 222222 0 13151433 cos5929'. 22.13.1565 acb BB ac +−+− === Câu 17. Cho tam giác ABC có 110;46;6ACb=== . Khẳng định nào sau đây đúng? A. 24;13,9;10,6Bac= . B. 24;13,8;10,7Bac= . C. 24;12,7;10,1Bac= D. 24;12,6;10,2Bac= Lời giải Ta có ( ) 18024BAC=−+= Áp dụng định lý sin, ta được: .sin.sin 13,9;10,6sinsin bAbC ac BB == .
mãn: 222 3 bcabc +−= . Khi đó: A. 0 30. A = B. 0 45. A = C. 0 60. A = D. 075 A = . Lời giải Chọn#A. Ta có: 222 0 33 cos30. 222 bcabc AA bcbc +− ==== Câu 16. Cho tam giác ABC , biết 13,14,15.abc=== Tính góc B? A. 0
Câu 18. Cho tam giác ABC có 6;7;12abc=== . Khẳng định nào sau đây đúng?
A. ABC có 1 góc tù. B. ABC có 3 góc nhọn.
C. ABC là tam giác vuông. D. 20 A . Lời giải Góc lớn nhất trong tam giác ABC là C 222 157 cos21 2168 bca AA bc +− == . 222 59 cos135 284 abc CC ab +− ==− .

Vậy ABC có 1 góc tù.
Câu 19. Hai vectơ có cùng độ dài và cùng hướng gọi là
A. Hai vectơ cùng hướng. B. Hai vectơ cùng phương. C. Hai vectơ đối nhau. D. Hai vectơ bằng nhau Lời giải Chọn D Hai vectơ bằng nhau là hai vectơ có cùng độ dài và cùng hướng. Câu 20. Cho ABC và điểm M thoả mãn điều kiện MAMCMB += . Khẳng định nào sau đây là SAI? A. ABAMAC += . B. BABCBM += C. Tứ giác ABCM là hình bình hành. D. MABC = . Lời giải MAMCMBMCMBMAMCAB +==−= . Khi đó tứ giác ABCM là hình bình hành. Do đó phương án C là đúng. Với phương án , AB , ta áp dụng quy tắc hình bình hành suy ra A và B là đúng. Vì ABCM là hình bình hành nên MABC =− . Câu 21. Tập xác định của hàm số 4220182019yxx=−− là A. ( ) 1; −+ B. ( );0− C. ( ) 0;+ D. ( ) ; −+ Lời giải Chọn D Hàm số là hàm đa thức nên xác định với mọi số thực x . Câu 22. Cho hàm số 5 yfxx . Khẳng định nào sau đây là sai? A. 15 f B. 210 f C. 1 1 5 f D. 210 f Lời giải Chọn C Ta có 50 yfxxx nên
DẠYKÈMQUYNHƠN
OFFICIAL
1 1 5 f là mệnh đề sai. Câu 23. Một giá đỡ có dạng tam giác ABC vuông cân tại đỉnh A được gắn vào tường như hình bên. Người ta treo vào vị trí C một vật nặng 10N . Cường độ lực tác động vào tường tại điểm A và B là
A. (5 N;10 N).
B. (10 ;10 )NN .
C. (10;102 )NN D. (10;103 )NN .
Lời giải Tại điểm C , lực kéo F có phương thẳng đứng hướng xuống dưới. Ta thấy F là hợp của hai lực 1F và 2F có giá lần lượt là hai đường thẳng AC và BC . Do đó hai lực tác động vào điểm
A và B khi treo vật vào vị trí điểm C lần lượt là 1F và 2F . vi tam giác ABC vuông cân tại C .
Do đó 1 ||10 FFN == và 2 ||2||102


DẠYKÈMQUYNHƠN
OFFICIAL
===
B Câu 25. Cho ba điểm phân biệt ,, ABC . Nếu 3 ABAC =− thì đẳng thức nào dưới đây đúng? A. 4 BCAC =− B. 2 BCAC =− C. 2 BCAC = D. 4 BCAC = Lời giải Chọn D Câu 26. Hàm số 2 yaxbxc =++ , (0) a đồng biến trong khoảng nào sau đậy? A. ;. 2 b a −− B. ;. 2 b a −+ C. ;. 4a −+ D. ;. 4a −− Lời giải Chọn B 0. a Bảng biến thiên
sin45 F FFN
Câu 24. Cho đoạn thẳng AB và O là trung điểm của AB . Khẳng định nào sau đây là đúng? A. 2 = ABOA. B. 2 = ABOB . C. 2=− ABOB . D. 2 = AOAB . Lời giải Chọn
Câu 27. Cho parabol ( ) 2 :321Pyxx=−+ . Điểm nào sau đây là đỉnh của ( )P ?
A. ( )0;1 I B. 12 ; 33 I C. 12 ; 33 I
Lời giải Chọn B
D. 12 ; 33 I
Hoành độ đỉnh của ( ) 2 :321Pyxx=−+ là 1 23 b x a =−= 2 112 32.1 333 y =−+= .
Vậy 12 ; 33 I
Câu 28. Phát biểu nào sau đây là đúng?
A. Nếu , ab khác 0 và (,)90 ab thì 0 ab ; B. Nếu , ab khác 0 và (,)90 ab thì 0 ab ; C. Nếu , ab khác 0 và (,)90 ab thì 0 ab ; D. Nếu , ab khác 0 và (,)90 ab thì 0 ab . Lời giải Chọn C
Câu 29. Cho tam giác ABC . Tập hợp các điểm M thỏa mãn .0MABC = là: A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn. Lời giải Chọn B. Ta có .0. MABCMABC =⊥ Vậy tập hợp các điểm M là đường thẳng đi qua A và vuông góc với BC Câu 30. Cho tam giác đều ABC cạnh 2 = a . Hỏi mệnh đề nào sau đây sai? A. ( ) .2 = ABACBCBC . B. .2 =− BCCA . C. ( ).4+=−ABBCAC . D. ( ).2−=BCACBA . Lời giải Chọn C Ta đi tính tích vô hướng ở các phương án.
DẠYKÈMQUYNHƠN
OFFICIAL
So sánh vế trái với vế phải. Phương án A: ( ) o ..cos602.2 === ABACABACxABACBCBC nên loại#A. Phương án B: o ..cos1202 ==−BCCABCAC nên loại B. Phương án C:( )..4+== ABBCACACAC , o .2.2.cos1202 ==− BCCA nên chọn C. Câu 31. Tập nghiệm của bất phương trình 2 3180−++ xx là: A. [3;6]. B. (3;6). C. (;3)(6;) −−+ D. (;3][6;) −−+ Lời giải Chọn A Câu 32. Cho tam thức ( ) ( ) 2 0, fxaxbxca =++ 2 4 bac=− . Ta có ( ) 0 fx với x khi và chỉ khi:
biệt nên 0 Câu 34. Trong các phát biểu sau, phát biểu nào đúng?
A. Tập nghiệm của phương trình ()() = fxgx là tập nghiệm của phương trình ()() = fxgx
B. Tập nghiệm của phương trình ()() = fxgx là tập nghiệm của phương trình 22 [()][()] fxgx = .
C. Mọi nghiệm của phương trình ()() = fxgx đều là nghiệm của phương trình ()() = fxgx
D. Tập nghiệm của phương trình ()() = fxgx là tập hợp các nghiệm của phương trình ()() = fxgx thoả mãn bất phương trình ()0 fx (hoặc ()0 gx ). Lời giải
DẠYKÈMQUYNHƠN OFFICIAL A. 0 0 a B. 0 0 a C. 0 0 a D. 0 0 a Lời
0
giải Chọn A Áp dụng định lý về dấu của tam thức bậc hai ta có: ( ) 0 fx với x khi và chỉ khi
0 a Câu 33. Cho hàm số ( ) 2 yfxaxbxc ==++ có đồ thị như hình vẽ. Đặt 2 4 bac=− , tìm dấu của a và A. 0 a , 0 B. 0 a , 0 C. 0 a , 0 = D. 0 a , , 0 = Lời giải Chọn#A. * Đồ thị hàm số là một Parabol quay lên nên 0 a và đồ thị hàm số cắt trục Ox tại hai điểm phân
D Câu 35. Số nghiệm của phương trình 2 331.xx+=− là A. 0. B. 1. C. 2. D. 3. Lời giải Chọn B Điều kiện xác định: x ( ) 2 2 2 310 331 331 x xx xx − +=− +=− 2 1 13 31 1 86201 4 x x x x xx x = = −−= =− O x y 4 4 1 ( )yfx =
Chọn
Câu 1. Giả sử độ cao h (đơn vị: mét) của một quả bóng golf tính theo thời gian t (đơn vị: giây) trong một lần đánh của vận động viên được xác định bằng một hàm số bậc hai và giá trị tương ứng tại một số thời điểm được cho bởi bảng dưới đây: Thời gian (s) 0 0,5 1 2 3 Độ cao (m) 0 28 48 64 48
a) Xác định hàm số bậc hai biểu thị độ cao ( )hm của quả bóng golf tính theo thời gian ()ts .
b) Sau bao lâu kể từ khi vận động viên đánh bóng thì bóng lại chạm đất? Lời giải
a) Xét hàm số bậc hai biểu thị độ cao h phụ thuộc t có dạng 2 () =++ htatbtc , trong đó a khác 0. Theo đề bài: Với 0,0==th , ta có: 0 = c nên 2 () =+ htatbt . Khi đó: + Với 1,48==th , ta có: 2 114848 +=+= abab . + Với 2,64==th , ta có: 2 22644264 +=+= abab . Giải hệ phương trình 4816 426464 +==− +== aba abb . Suy ra 2 ()1664 =−+ httt Thay các giá trị tương ứng còn lại của bảng vào công thức trên, ta thấy phù hợp. Vậy hàm số bậc hai cần tìm là 2 ()1664 =−+ httt . b) Bóng chạm đất khi 2 ()1664 =−+ httt . Suy ra ta có: 0 = t hoặc 4 = t Vậy sau 4 giây kể từ khi vận động viên đánh bóng thì bóng lại chạm đất. Câu 2. Bác Năm dự định trồng khoai lang và khoai mì trên mảnh đất có diện tích 8 ha. Nếu trồng 1 ha khoai lang thì cần 10 ngày công và thu được 20 triệu đồng. Nếu trồng 1 ha khoai mì thì cần 15 ngày công và thu được 25 triệu đồng. Bác Năm cần trồng bao nhiêu hecta cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng được không quá 90 ngày công cho việc trồng khoai lang và khoai mì.

Lời giải Gọi x là số hecta trồng khoai lang và y là số hecta trồng khoai mì.
Ta có hệ bất phương trình mô tả các điều kiện ràng buộc:
8 101590 0 0.
+ + Biểu diễn miền nghiệm của hệ bất phương trình trên hệ trục toạ độ Oxy ta được miền đa giác OABC. Toạ độ các đỉnh của đa giác đó là: (0;0);(0;6);(6;2);(8;0) OABC .
xy xy x y
Gọi F là số tiền (đơn vị: triệu đồng) bác Năm thu được, ta có: 2025=+ Fxy . Ta phải tìm , xy thoả mãn hệ bất phương trình sao cho F lớn nhất, nghĩa là tìm giá trị lớn nhất của 2025=+ Fxy trên miền đa giác OABC Tính các giá trị của biểu thức F tại các đỉnh của đa giác, ta có: Tại (0;0):20.025.00 =+= OF ;
DẠYKÈMQUYNHƠN
2. Tự luận
OFFICIAL
Tại (0;6):20.025.6150 =+= AF ;

Tại (6;2):20.625.2170 =+= BF ;
Tại (8;0):20.825.0160 =+= CF
Ta thấy F đạt giá trị lớn nhất bằng 170 tại (6;2)B .
Vậy để thu được nhiều tiền nhất, bác Năm cần trồng 6 ha khoai lang và 2 ha khoai mì. Câu 3. Quan sát cây cầu dây văng minh hoạ ở Hình 25.
Tại trụ cao nhất, khoảng cách từ đỉnh trụ (vị trí A ) tới chân trụ trên mặt cầu (vị trí H ) là 150m , độ dài dây văng dài nhất nối từ đỉnh trụ xuống mặt cầu (vị trí B ) là 300m, khoảng cách từ chân dây văng dài nhất tới chân trụ trên mặt cầu là 250m (Hình 26). Tính độ dốc của cầu qua trụ nói trên (làm tròn kết quả đến hàng phần mười theo đơn vị độ). Lời giải Độ dốc của cầu là góc nghiêng giữa đường cầu qua trụ và phương nằm ngang, tức là góc KBH Xét tam giác ABH , áp dụng định lí côsin ta có: 2222222501503001 cos93,8. 2.2.250.15015
BHAHAB AHBAHB BHAH Xét tam giác BHK ta có: 93,8903,8
+−+−
HBK (tính chất góc ngoài tam giác). Vậy độ dốc của cầu qua trụ theo đề bài là khoảng 3,8
Câu 4. Một vật đồng chất được thả vào một cốc chất lỏng. Ở trạng thái cân bằng, vật chìm một nửa thể tích trong chất lỏng. Tìm mối liên hệ giữa trọng lực P của vật và lực đẩy Archimedes F mà chất lỏng tác động lên vật. Tính tỉ số giữa trọng lượng riêng của vật và của chất lỏng. Lời giải
Lực đẩy Archimedes AF và trọng lực P đều tác động lên vật theo phương thẳng đứng, hai lực này ngược hướng. Do ở trạng thái cân bằng vật nổi (chìm một nửa), nên hai lực này có cường đọ bằng nhau. Gọi d , d' tương ứng là trọng lượng riêng của vật và trọng lượng riêng của chất lỏng: gọi V là thể tích của vật. Khi đó trọng lượng của vật bằng || == PPdV . (1)
Lực đẩy Archimedes tác động lên vật có cường độ bằng 2 == Aa V FFd . (2) Từ (1) và (2), để ý rằng = APF , suy ra 2 = d d .

DẠYKÈMQUYNHƠN
OFFICIAL
−=
===−
1. Trắc nghiệm
Câu 1. Trong các phát biểu sau, phát biểu nào là mệnh đề toán học?
A. Nước là hợp chất tạo bởi hai nguyên tố là hydrogen và oxygen.
B. Sông Hương là con sông chảy qua thành phố Huế.
C. Ngày 30 tháng 4 năm 1975 là ngày Giải phóng miền Nam.
D. Số 2022 chia hết cho 4.
Câu 2. Mệnh đề phủ định của P : "Tam giác ABC là tam giác cân" là:
A. Tam giác ABC không phải là tam giác cân
B. Tam giác ABC là tam giác vuông C. Tam giác ABC là tam giác đều D. ABC không phải là một tam giác
Câu 3. Kí hiệu , lần lượt là tập số hữu tỉ, tập số thực. Kết luận nào sau đây là đúng?
A. B. C. D.
Câu 4. Cho hai tập hợp {2;5},{(5)()()0} ==−−−= ABxxxaxb với , ab là các số thực cho trước. Tất cả các cặp số (;) ab đề = AB là: A. (2;2),(5;5),(5;2). B. (2;2),(2;5),(5;2). C. (2;5),(2;2),(5;5) D. (2;2),(2;5),(5;2),(5;5)



Câu 5. Cho hai tập hợp , AB phân biệt và khác rỗng thoả mãn = ABA. Kết luận nào sau đây là đúng?
A. BA. B. AB . C. =AB . D. \ = ABA .
Câu 6. Tập nghiệm của bất phương trình 350 xy−+ là
A. Nửa mặt phẳng chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (không bao gồm đường thẳng).
B. Nửa mặt phẳng không chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (bao gồm đường thẳng).
C. Nửa mặt phẳng không chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (không bao gồm đường thẳng).
D. Nửa mặt phẳng chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (không bao gồm đường thẳng).
Câu 7. Miền nghiệm của bất phương trình 236 xy+ (miền không bị gạch) được biểu diễn bởi hình vẽ nào dưới đây?
A. B. C.
DẠYKÈMQUYNHƠN
ĐỀ SỐ 3
OFFICIAL
D. Câu 8. Có bao nhiêu hệ bất phương trình bậc nhất hai ẩn trong ba hệ bất phương trình sau đây?
234(3)(5) ;2(5)và 3(1)3(1)211. 345

A. 0. B. 1. C. 2. D. 3. Câu 9. Miền nghiệm của hệ bất phương trình 2021 2022 xy xy − + KHÔNG chứa điểm nào sau đây? A. (1001;1021). B. (2021;0). C. (2021;2022) D. (2021;2022) Câu 10. Công ty trách nhiệm hữu hạn ĐỨC MẠNH trong một đợt quảng cáo và bán khuyến mãi hàng hoá (một sản phẩm mới của công ty) cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B . Trong đó xe loại A có 10 chiếc, xe loại B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, loại B giá 3 triệu đồng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất? Biết rằng xe loại A chỉ chở tối đa 20 người và 0,6 tấn hàng. Xe loại B chỉ chở tối đa 10 người và 1,5 tấn hàng.
A. 4 xe loại A và 5 xe loại B . B. 5 xe loại A và 6 xe loại B . C. 5 xe loại A và 4 xe loại B D. 6 xe loại A và 4 xe loại B . Câu
DẠYKÈMQUYNHƠN OFFICIAL
2
xyxyyx xy yxxy xy −++ − ++− +
Cho
1
2 += . Giá
A. 37 16 B. 117 16 C. 57 16 . D. 57 16 . Câu 12. Cho 1 sin 3 = với 090 . Giá trị của cos là A. 2 3 . B. 2 3 C. 22 3 D. 22 3 Câu 13. Cho tan3 =− . Giá trị của cos là
11.
là góc tù và
sincos
trị của 33 sincos M =− là
A. 1 2
B. 1 2 C. 1 4 . D. 1 4
Câu 14. Tam giác ABC có 0 150,3,2. === CBCAC Tính cạnh AB ?
A. 13 B. 3. C. 10 D. 1
Câu 15. Cho tam giác ABC , biết 24,13,15.abc=== Tính góc A? A. 0 3334'. B. 0 11749'. C. 0 2837'. D. 0 5824'.
Câu 16. Cho tam giác ABC có 3,5ABBC== và độ dài đường trung tuyến 13 BM = . Tính độ dài AC .
A. 11. B. 4. C. 9 2 . D. 10 .
Câu 17. Cho tam giác ABC vuông tại A có ABa = , 2 ACa = . Diện tích tam giác ABC là
A. 2 2a . B. 2 4a . C. 2 3 2 a . D. 2 a .
Câu 18. Cho tam giác ABC có góc ABC bằng 060 , = ACa . Tính bán kính đường tròn ngoại tiếp tam giác ABC ?
A. a . B. 3 3 a . C. 43 3 a . D. 3 a .
Câu 19. Hai vectơ được gọi là bằng nhau khi và chỉ khi
A. Giá của chúng trùng nhau và độ dài của chúng bằng nhau
B. Chúng trùng với một trong các cặp cạnh đối của một hình bình hành
C. Chúng trùng với một trong các cặp cạnh của một tam giác đều.
D. Chúng cùng hướng và độ dài của chúng bằng nhau.
Câu 20. Cho hình bình hành ABCD. Khẳng định nào sau đây là đúng.
DẠYKÈMQUYNHƠN
OFFICIAL
B.
−= C. ABACCB += D. ABACBC −= Câu 21. Cho hàm số ( ) 2 223khi2 1 2khi2 x x fx x xx = + . Tính ( ) ( )22Pff=+− A. 3 P = . B. 2 P = . C. 7 3 P = . D. 6 P = . Câu 22. Trong các hàm số sau, hàm số nào là hàm đồng biến trên ? A. 12 yx =− B. 32yx=+ C. 2 21yxx=+− D. ( )223yx=−− . Câu 23. Một vật có khối lượng m được treo cố định trên trần nhà bằng hai sợi dây không dãn có độ dài như nhau. Biết rằng lực căng dây 1T và 2T có độ lớn như nhau bằng 600N và hợp với nhau một góc 60 (hình bên). Trọng lượng của vật là
A. ABACAD +=
ABACDA
A. 600N B. 6003 N C. 1200N . D. 12003 N .
Câu 24. Cho tam giác ABC và M là trung điểm của , BCG là trọng tâm của tam giác. Khẳng định nào sau đây là đúng?
A. 3=− AMGM B. 3 2 = AMGM . C. 3 2 = AMGM . D. 3 = AMGM .

OFFICIAL
Câu 25. Cho tam giác ABC . Gọi I là trung điểm của BC .Khẳng định nào sau đây đúng A. BIIC B. 32BIIC C. 2 BIIC D. 2BIIC Câu 26. Giao điểm của parabol 2 ():32 Pyxx=−+ với đường thẳng 1 yx=− là: A. ( ) ( )1;0;3;2 . B. ( ) ( )0;1;2;3 . C. ( ) ( )1;2;2;1 D. ( ) ( )2;1;0;1
Câu 27. Một chiếc ăng ten chảo parabol có chiều cao 0,5 hm = và đường kính miệng 4 dm = . Mặt cắt qua trục là một parabol dạng 2 yax = . Biết m a n = , trong đó m, n là các số nguyên dương nguyên tố cùng nhau. Tính mn
DẠYKÈMQUYNHƠN
Cho
giác ABC . Giá trị của
A. cos ABACBAC . B. cos ABACBAC . C. cos ABACABC . D. cos ABACACB . Câu 29. Cho tam giác ABC cân tại A , o ˆ 120 A = và ABa = . Tính . BACA A. 2 2 a . B. 2 2 a . C. 2 3 2 a . D. 2 3 2 a . Câu 30. Cho hình vuông ABCD tâm O . Hỏi mệnh đề nào sau đây sai? A. .0 = OAOB B. 1 .. 2 = OAOCOAAC C. = ABACABCD D. = ABACACAD Câu 31. Cho tam thức bậc hai 2 ()288 fxxx=−+− . Trong các mệnh đề sau, mệnh đề nào đúng? A. ()0fx với mọi x B. ()0fx với mọi x
. A. 7 mn−= B. 7 mn−=− C. 31 mn−= D. 31 mn−=− Câu 28.
tam
biểu thức
BACA bằng:
C. ()0fx với mọi x . D. ()0fx với mọi x .
Câu 32. Tam thức nào dưới đây luôn dương với mọi giá trị của x ?
A. 2 102xx−+ B. 2 210xx C. 2 210xx−+ D. 2 210xx −++
Câu 33. Tập nghiệm của bất phương trình 2 214200 xx−+ là A. ( ) ;25; S =−+ . B. ( ) ( ) ;25; S =−+ . C. ( )2;5 S = D. 2;5 S =


Câu 34. Tập nghiệm của phương trình 2 215 xx−=−− là
A. 1;5. S = B. 1. S = C. 5. S = D. . S =
Câu 35. Số nghiệm của phương trình 2 4321 xx −=− là: A. 0. B. 1. C. 2. D. 3.
2. Tự luận
Câu 1. Để mua được một chiếc xe đạp thể thao trị giá 15 triệu đồng, bạn Nam hàng ngày bỏ vào lợn đất tiết kiệm 50000 đồng từ tiền tiêu vặt mẹ cho.
a) Thiết lập hàm số biểu thị số tiền y (nghìn đồng) bạn Nam tiết kiệm được theo thời gian t (ngày) và số tiền ban đầu a (nghìn đồng) mà bạn Nam có. b) Nếu ban đầu bạn Nam có 5000000 đồng thì sau bao lâu bạn Nam mới có thể mua được chiếc xe đạp đó (giả sử giá chiếc xe đó không đổi)?
Câu 2. Tìm giá tri lớn nhất và giá tri nhỏ nhất của biểu thức (;)2 =+ Fxyxy với (;) xy thuộc miền nghiệm của hệ bất phương trình
Câu 3. Một người đứng ở vị trí A trên nóc một ngôi nhà cao 4m đang quan sát một cây cao cách ngôi nhà 20m và đo được 45 = BAC (Hình 27). Tính chiều cao của cây đó (làm tròn kết quả đến hàng phần mười theo đơn vị mét).
Câu 4. Máy bay A đang bay về hướng Đông Bắc với tốc độ 600 / kmh. Cùng lúc đó, máy bay B đang bay về hướng Tây Nam với tốc độ 800 / kmh . Biểu diễn vectơ vận tốc b của máy bay B theo vectơ vận tốc a của máy bay A
Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM
DẠYKÈMQUYNHƠN
OFFICIAL
x y
4 0 0 +
xy
1D 2A 3C 4B 5A 6C 7C 8C 9D 10C 11D 12D 13A 14A 15B 16B 17D 18B 19D 20B 21A 22B 23B 24D 25A 26A 27B 28A 29B 30C 31C 32C 33C 34D 35B

1. Trắc nghiệm
Câu 1. Trong các phát biểu sau, phát biểu nào là mệnh đề toán học?
A. Nước là hợp chất tạo bởi hai nguyên tố là hydrogen và oxygen.
B. Sông Hương là con sông chảy qua thành phố Huế.
C. Ngày 30 tháng 4 năm 1975 là ngày Giải phóng miền Nam.
D. Số 2022 chia hết cho 4.
Câu 2. Mệnh đề phủ định của P : "Tam giác ABC là tam giác cân" là:
OFFICIAL
A. Tam giác ABC không phải là tam giác cân B. Tam giác ABC là tam giác vuông C. Tam giác ABC là tam giác đều D. ABC không phải là một tam giác Câu 3. Kí hiệu , lần lượt là tập số hữu tỉ, tập số thực. Kết luận nào sau đây là đúng? A. . B. . C. . D. . Câu 4. Cho hai tập hợp {2;5},{(5)()()0} ==−−−= ABxxxaxb với , ab là các số thực cho trước. Tất cả các cặp số (;) ab đề = AB là: A. (2;2),(5;5),(5;2). B. (2;2),(2;5),(5;2). C. (2;5),(2;2),(5;5). D. (2;2),(2;5),(5;2),(5;5). Lời giải (5)()()05;; −−−==== xxaxbxxaxb Để = AB thì trong hai số , ab chắc chắn phải có một số bằng 2, số còn lại bằng 2 hoặc 5. Vậy ta có: (;)(2;2),(2;5),(5;2) = ab . Chọn B Câu 5. Cho hai tập hợp , AB phân biệt và khác rỗng thoả mãn = ABA. Kết luận nào sau đây là đúng? A. BA B. AB C. =AB D. \ = ABA Câu 6. Tập nghiệm của bất phương trình 350 xy−+ là
A. Nửa mặt phẳng chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (không bao gồm đường thẳng).
B. Nửa mặt phẳng không chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (bao gồm đường thẳng).
C. Nửa mặt phẳng không chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (không bao gồm đường thẳng).
D. Nửa mặt phẳng chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (không bao gồm đường thẳng).
Câu 7. Miền nghiệm của bất phương trình 236 xy+ (miền không bị gạch) được biểu diễn bởi hình vẽ nào dưới đây? A.
DẠYKÈMQUYNHƠN
chứa điểm nào sau đây? A. (1001;1021) B. (2021;0). C. (2021;2022). D. (2021;2022)
Câu 10. Công ty trách nhiệm hữu hạn ĐỨC MẠNH trong một đợt quảng cáo và bán khuyến mãi hàng hoá (một sản phẩm mới của công ty) cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B . Trong đó xe loại A có 10 chiếc, xe loại B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, loại B giá 3 triệu đồng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất? Biết rằng xe loại A chỉ chở tối đa 20 người và 0,6 tấn hàng. Xe loại B chỉ chở tối đa 10 người và 1,5 tấn hàng.
A. 4 xe loại A và 5 xe loại B .
B. 5 xe loại A và 6 xe loại B C. 5 xe loại A và 4 xe loại B D. 6 xe loại A và 4 xe loại B .


Lời giải Gọi x và y lần lượt là số xe loại A và (010;09;,) Bxyxy .

DẠYKÈMQUYNHƠN OFFICIAL
2
3(1)3(1)211. 345 xyxyyx xy yxxy xy −++ − ++− +
2021
xy xy − +
B. C. D. Câu 8. Có bao nhiêu hệ bất phương trình bậc nhất hai ẩn trong ba hệ bất phương trình sau đây?
234(3)(5) ;2(5)và
A. 0. B. 1. C. 2. D. 3. Câu 9. Miền nghiệm của hệ bất phương trình
2022
KHÔNG
Khi đó tổng chi phí thuê xe là 43 Txy =+ (triệu đồng). Xe A chở tối đa 20 người, xe B chở tối đa 10 người nên tổng số người 2 xe chở tối đa được là 2010xy + (người). Xe A chở được 0,6 tấn hàng, xe B chở được 1,5 tấn hàng nên tổng lượng hàng 2 xe chở được là 0,61,5xy + (tấn). Theo giả thiết, ta có 010 09 2010140(*) 0,61,59 x y xy xy + + tứ giác với 5 (10;2),(10;9),;9,(5;4) 2 ABCD
DẠYKÈMQUYNHƠN OFFICIAL Biểu thức 43 Txy =+ đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác ABCD, ta thấy T đạt giá trị nhỏ nhất tại 5 x = và 4 y = . Khi đó, chi phí thấp nhất mà công ty bỏ ra là 32 triệu đồng. Câu 11. Cho là góc tù và 1 sincos 2 += . Giá trị của 33 sincos M =− là A. 37 16 . B. 117 16 . C. 57 16 D. 57 16 Lời giải (sincos)(1sincos) M =−+ Từ 113sincossuysincos1244 ra +==−=− Mặt khác 2 (sincos)12sincos −=− . Suy ra 7 sincos 2 −= (vì là góc tù). Do đó, 57 16 M = . Câu 12. Cho 1 sin 3 = với 090 . Giá trị của cos là A. 2 3 . B. 2 3 C. 22 3 . D. 22 3 . Lời giải Ta có 2 2 122 cos1sin1 33 =−=−= . Câu 13. Cho tan3 =− . Giá trị của cos là A. 1 2 . B. 1 2 . C. 1 4 D. 1 4 . Lời giải Ta có 2 2 1 1tan cos += . Suy ra 2 1 cos 4 = . Vì tan30 =− nên 1 cos 2 =− . Câu 14. Tam giác ABC có 0 150,3,2. === CBCAC Tính cạnh AB ? A. 13 . B. 3. C. 10. D. 1. Lời giải
Chọn A Theo định lí cosin trong ABC ta có: 222 2..cos =+− ABCACBCACBC 13= 13 = AB . Chọn#A.
Câu 15. Cho tam giác ABC , biết 24,13,15.abc=== Tính góc A? A. 0 3334'. B. 0 11749'. C. 0 2837'. D. 0 5824'. Lời giải Chọn B. Ta có: 222222 0 1315247 cos11749'. 22.13.1515 bca AA bc +−+− ===−
Câu 16. Cho tam giác ABC có 3,5ABBC== và độ dài đường trung tuyến 13 BM = . Tính độ dài AC . A. 11 B. 4 C. 9 2 D. 10 Lời giải Chọn B
công thức tính độ dài đường trung tuyến;ta có:
DẠYKÈMQUYNHƠN
OFFICIAL
=
=
ABC
== . Câu
Cho tam giác ABC có góc ABC
0
=
ABC ? A.
Lời
Theo
( ) 222222 2 2 35 134 2424 BABCACAC BMAC ++ =−=−= Câu 17. Cho tam giác ABC vuông tại A có ABa = , 2 ACa = . Diện tích tam giác ABC là A. 2 2a . B. 2 4a . C. 2 3 2 a . D. 2 a Lời giải Tam giác ABC vuông tại A có ABa
, 2 ACa
. Khi đó 2 1 2
SABACa
18.
bằng
60 ,
ACa . Tính bán kính đường tròn ngoại tiếp tam giác
a B. 3 3 a C. 43 3 a D. 3 a
giải Theo Định lí Sin ta có: ==== 0 3 2 sin2.sin3 2sin60 ACACaa RR BB . Câu 19. Hai vectơ được gọi là bằng nhau khi và chỉ khi A. Giá của chúng trùng nhau và độ dài của chúng bằng nhau. B. Chúng trùng với một trong các cặp cạnh đối của một hình bình hành. C. Chúng trùng với một trong các cặp cạnh của một tam giác đều. D. Chúng cùng hướng và độ dài của chúng bằng nhau. 13 5 3 M C B A
Chọn D
Hai véc-tơ được gọi là bằng nhau khi và chỉ khi chúng cùng hướng và độ dài của chúng bằng nhau.
Câu 20. Cho hình bình hành ABCD. Khẳng định nào sau đây là đúng. A. ABACAD += . B. ABACDA −= . C. ABACCB += . D. ABACBC −= . Lời giải Chọn B

B C
O D A
Ta có ABACCB −= . Do ABCD là hình bình hành nên D C A B = nên ABACDA −= .
Câu 21. Cho hàm số ( ) 2
x x fx x xx
223khi2 1 2khi2
=
+
. Tính ( ) ( )22Pff=+− . A. 3 P = B. 2 P = C. 7 3 P = D. 6 P = Lời giải Chọn A Ta có: ( ) ( ) ( )2 2223 2222 21 ff+−=+−+ 3 P = . Câu 22. Trong các hàm số sau, hàm số nào là hàm đồng biến trên ? A. 12 yx =− B. 32yx=+ C. 2 21yxx=+− D. ( )223yx=−− . Lời giải Chọn B. 32yx=+ đồng biến trên vì có hệ số góc 30 a = Câu 23. Một vật có khối lượng m được treo cố định trên trần nhà bằng hai sợi dây không dãn có độ dài như nhau. Biết rằng lực căng dây 1T và 2T có độ lớn như nhau bằng 600N và hợp với nhau một góc 60 (hình bên). Trọng lượng của vật là A. 600N B. 6003 N C. 1200N D. 12003 N .
DẠYKÈMQUYNHƠN OFFICIAL
Lời giải
Vậy trọng lượng của vật là 6003 N . Đáp án là B .
Câu 24. Cho tam giác ABC và M là trung điểm của , BCG là trọng tâm của tam giác. Khẳng định nào sau đây là đúng?
A. 3=− AMGM B. 3 2 = AMGM . C. 3 2 = AMGM . D. 3 = AMGM . Lời giải Chọn D

Câu 25. Cho tam giác ABC . Gọi I là trung điểm của BC .Khẳng định nào sau đây đúng A. BIIC B. 32BIIC C. 2 BIIC D. 2BIIC Lời giải Chọn

DẠYKÈMQUYNHƠN OFFICIAL Lời
giải Xét tam giác OAH như hình vẽ. Ta có 12222cos302cos30TOHOAT === 3 26006003(). 2 N ==
. Câu 26. Giao điểm của parabol 2 ():32 Pyxx=−+ với đường thẳng 1 yx=− là: A. ( ) ( )1;0;3;2 B. ( ) ( )0;1;2;3 C. ( ) ( )1;2;2;1 . D. ( ) ( )2;1;0;1 . Lờigiải Chọn A Phương trình hoành độ giao điểm: 2 321xxx−+=− 2 430xx −+= 1 3 x x = = . 110xyx==−=
A Vì I là trung điểm của BC nên BICI và BI cùng hướng với IC do đó hai vectơ BI , IC bằng nhau hay BIIC
Hai giao điểm là: ( ) ( )1;0;3;2 .

Câu 27. Một chiếc ăng - ten chảo parabol có chiều cao 0,5 hm = và đường kính miệng 4 dm = . Mặt cắt qua trục là một parabol dạng 2 yax = . Biết m a n = , trong đó m, n là các số nguyên dương nguyên tố cùng nhau. Tính mn A. 7 mn−= B. 7 mn−=− C. 31 mn−= D. 31 mn−=−
Lời giải Đáp án B. Từ giả thiết suy ra parabol 2 yax = đi qua điểm 1 2; 2 I
DẠYKÈMQUYNHƠN
OFFICIAL 312xyx==−=
2 11 .2 28
==
−=−=−
Cho
ABC . Giá trị của biểu thức BACA bằng:
cos
.
−
.
.
. Lời giải Chọn A Câu 29. Cho tam giác ABC cân tại A , o ˆ 120 A = và ABa = . Tính BACA A. 2 2 a . B. 2 2 a . C. 2 3 2 a . D. 2 3 2 a . Lời giải Chọn B Ta có o2 1 ...cos120 2 ==− BACABACAa Câu 30. Cho hình vuông ABCD tâm O . Hỏi mệnh đề nào sau đây sai? A. .0 = OAOB B. 1 2 = OAOCOAAC C. .. = ABACABCD . D. .. = ABACACAD . Lời giải Chọn C Phương án A: ⊥ OAOB suy ra .0 = OAOB nên loại#A. Phương án B: .0 = OAOC và 1 .0 2 = OAAC suy ra 1 ..0 2 ==OAOCOAAC nên loại B. Phương án C: o2 2 ...cos45.2. 2 === ABACABACABABAB . 02...cos180==− ABCDABDCAB ABACABCD nên chọn C. Câu 31. Cho tam thức bậc hai 2 ()288 fxxx=−+− . Trong các mệnh đề sau, mệnh đề nào đúng? A. ()0fx với mọi x B. ()0fx với mọi x
. Từ đó ta có
aa
Vậy 187 mn
Câu 28.
tam giác
A.
ABACBAC
B. cos
ABACBAC
C. cos ABACABC
D. cos
ABACACB
C. ()0fx với mọi x . D. ()0fx với mọi x .
Lời giải
Chọn C Ta có ( )2 2 ()2(44)220 fxxxx=−−+=−− với mọi x .
Vậy: ()0fx với mọi x .
Câu 32. Tam thức nào dưới đây luôn dương với mọi giá trị của x ?
A. 2 102xx−+ B. 2 210xx C. 2 210xx−+ D. 2 210xx −++ Lời giải Chọn C. Tam thức luôn dương với mọi giá trị của x phải có 0 0 a nên Chọn C.
Câu 33. Tập nghiệm của bất phương trình 2 214200 xx−+ là A. ( ) ;25; S =−+ . B. ( ) ( ) ;25; S =−+ . C. ( )2;5 S = D.
thời gian t (ngày) và số tiền ban đầu a (nghìn đồng) mà bạn Nam có. b) Nếu ban đầu bạn Nam có 5000000 đồng thì sau bao lâu bạn Nam mới có thể mua được chiếc xe đạp đó (giả sử giá chiếc xe đó không đổi)? Lời giải a) Hàm số biểu thị số tiền bạn Nam tiết kiệm được theo thời gian t là: 50 =+ yta
DẠYKÈMQUYNHƠN
OFFICIAL
= Lời
Chọn
Bất
Vậy
= .
2
−=−− là
= B. 1. S = C. 5. S = D. S = Lời giải Chọn D Vì 2 50 x −− vậy
vô
m Câu 35. Số nghiệm của phương trình 2 4321 xx −=− là: A. 0. B. 1. C. 2.
Lời giải Chọn B 2 22 1 2 210 4321 1 43441 3 7 1 x x xx x xxx x x − −=− = −=−+ = = Vậy phương trình có 1 nghiệm 2. Tự luận Câu 1. Để mua được một chiếc xe đạp thể thao trị giá 15 triệu đồng, bạn Nam hàng ngày bỏ vào lợn đất tiết kiệm 50000 đồng từ tiền tiêu vặt mẹ cho. a) Thiết lập hàm số biểu thị số tiền y (nghìn đồng) bạn Nam tiết kiệm được
2;5 S
giải
C
phương trình 010 x 25 x
( )2;5 S
Câu 34. Tập nghiệm của phương trình
215 xx
A.
1;5. S
phương trình
nghiệ
D. 3.
theo
b) Ta có: 5000 = a nên 505000=+yt . Bạn Nam đủ tiền mua xe đạp khi 1500050500015000200 =+== ytt . Vậy sau 200 ngày thì bạn Nam đủ tiền mua xe đạp thể thao.
+
Câu 2. Tìm giá tri lớn nhất và giá tri nhỏ nhất của biểu thức (;)2 =+ Fxyxy với (;) xy thuộc miền nghiệm của hệ bất phương trình 4 0 0
giải
+
Bước 1. Xác định miền nghiệm của hệ bất phương trình 4 0 0
xy x y Miền nghiệm của hệ bất phương trình trên là miền tam giác OAB với các đỉnh (0;0),(0;4),(4;0)OAB . Bước 2. Tính giá trị của F tại các đỉnh của tam giác: ( ) ( ) ( ) 0;00,4;04,0;48 . FFF===
Bước 3. So sánh các giá trị thu được của F ở Bước 2, ta được giá trị nhỏ nhất là 0 và giá trị lớn nhất là 8.
Vậy giá trị nhỏ nhất cần tìm của F là (0;0)0 = F và giá trị lớn nhất cần tìm là (0;4)8 = F . Câu 3. Một người đứng ở vị trí A trên nóc một ngôi nhà cao 4m đang quan sát một cây cao cách ngôi nhà 20m và đo được 45


DẠYKÈMQUYNHƠN OFFICIAL
xy x y Lời
Lời giải Xét tam giác vuông ABH ta có: 22 420426()=+= ABm (định lí Pythagore) và 4 tan0,211,3 20 ==ABHABH . Do đó, 9011,378,7 −= ABC . Suy ra 1804578,756,3 −−= ACB Áp dụng định lí sin cho tam giác ABC ta có: sinsin = BCAB AC sin426sin45 17,3() sinsin56,3 = ABA BCm C . Vậy cây cao khoảng 17,3m . Câu 4. Máy bay A đang bay về hướng Đông Bắc với tốc độ 600 / kmh. Cùng lúc đó, máy bay B đang bay về hướng Tây Nam với tốc độ 800 / kmh . Biểu diễn vectơ vận tốc b của máy bay B theo vectơ vận tốc a của máy bay A
= BAC (Hình 27). Tính chiều cao của cây đó (làm tròn kết quả đến hàng phần mười theo đơn vị mét).
Lời giải
Vecto , ab là vecto vận tốc của máy bay A và máy bay b.
Do đó ||,|| ab lần lượt là độ lớn của vecto vận tốc tương ứng.
Ta có: ||600,||800 ==ab ||8004 ||6003 b a ==
Hai hướng Đông Bắc và Tây Nam là ngược nhau, do đó 4 3 ba =−

DẠYKÈMQUYNHƠN OFFICIAL
1. Trắc nghiệm
Câu 1. Cho mệnh đề A : "8 không chia hết cho 2 " và mệnh đề : B " 31 ". Xét các mệnh đề sau:
a) Mệnh đề AB b) Mệnh đề BA c) Mệnh đề AB d) Mệnh đề AB Số mệnh đề đúng trong các mệnh đề trên là A. 1. B. 2. C. 3. D. 4. Câu 2. Mệnh đề phủ định của mệnh đề :",230"Txx−+ là A. " ,230xx −+ ". B. " ,230"xx −+ . C. " ,230"xx −+ D. " ,230"xx −+ Câu 3. Cho hai tập hợp {;} = Aab và {;;;;} = Babcde . Có bao nhiêu tập hợp X mà AXB ? A. 6. B. 7. C. 8. D. 11. Câu 4. Cho tập hợp {20} =−Axx . Tập hợp A là: A. {2;1;0}=−− A . B. [2;0]=− A . C. (2;0)=− A . D. {2;0}=− A . Câu 5. Cho hai tập hợp [5;0],[0;) =−=+AB . Khi đó: A. {0} =AB B. =AB C. [5;)=−+AB D. (5;)=−+AB Câu 6. Miền nghiệm của bất phương trình 35xy−− là nửa mặt phẳng chứa điểm A. (3;0). B. (3;1). C. (1;3). D. (0;0) Câu 7. Phần không bị gạch (không kể d) ở Hình 4 là miền nghiệm của bất phương trình: A. 326 +xy B. 236 +xy C. 236 +xy D. 326 +xy Câu 8. Miền không bị gạch (tính cả biên) trong hình vẽ dưới đây là miền nghiệm của hệ bất phương trình bậc nhất hai ẩn nào sau đây?


DẠYKÈMQUYNHƠN
ĐỀ SỐ 4
OFFICIAL
A. 236 236 xy xy + −− B. 236 236 xy xy + −−
D. 236 236 xy xy + −
. Câu 9. Miền nghiệm của hệ bất phương trình bậc nhất hai ẩn 20112022 0 xy y + nằm trong góc phần tư nào? A. I. B. II. C. III. D. IV. Câu 10. Một xưởng có một máy cắt và một máy tiện dùng để sản xuất trục sắt và đinh ốc. Để sản xuất 1 tấn trục sắt thì lần lượt máy cắt chạy trong 3 giờ và máy tiện chạy trong 1 giờ, tiền lãi là 2 triệu đồng. Để sản xuất 1 tấn đinh ốc thì lần lượt máy cắt và máy tiện chạy trong 1 giờ, tiền lãi là 1 triệu đồng. Một máy không thể đồng thời sản xuất cả hai loại. Máy cắt làm không quá 6 giờ/ngày, máy tiện làm không quá 4 giờ/ngày. Hỏi một ngày xưởng nên sản xuất bao nhiêu tấn mối loại để tiền lãi là cao nhất?
A. 2 tấn trục sắt và 2 tấn đinh ốc.
B. 3 tấn trục sắt và 1 tấn đinh ốc.
C. 2 tấn trục sắt và 3 tấn đinh ốc. D. 1 tấn trục sắt và 3 tấn đinh ốc.
Câu 11. Rút
DẠYKÈMQUYNHƠN OFFICIAL
C. 236 236 xy xy +−
−−
là A. 2.
2
2 D. 2 . Câu 13. Trên nửa đường tròn đơn vị, cho điểm M sao cho 120 = MOx . Toạ độ điểm M là: A. 31 ; 22 . B. 31 ; 22 . C. 13 ; 22 D. 13 ; 22 Câu 14. Cho ;;cab là độ dài 3 cạnh của tam giác ABC . Biết 7 = b ; 5 = c ; 4 cos 5 A = . Tính độ dài của a A. 32 B. 72 2 C. 23 8 D. 6
gọn biểu thức tansin sincot xx M xx =− với ( ) 0;90 x
ta được A. sin x B. cos x C. 1 sin x D. 1 cos x . Câu 12. Cho là góc tù và tancot2 +=− . Giá trị của sincos M =−
B.
C.
Câu 15. Tam giác ABC có 6,42,2.abc=== M là điểm trên cạnh BC sao cho 3 BM = . Độ dài đoạn AM bằng bao nhiêu?
A. 9. B. 9. C. 3. D. 1 108. 2
Câu 16. Cho tam giác ABC có góc 60 BAC = và cạnh 3 BC = . Tính bán kính của đường tròn ngoại tiếp tam giác ABC .
A. 4 R = . B. 1 R = . C. 2 R = . D. 3 R = .

Câu 17. Tam giác ABC có 6812'= A , 3444'= B , 117. = AB Khi đó độ dài AC xấp xỉ bằng ? A. 68. B. 168. C. 118. D.200.
Câu 18. Tam giác ABC có 6cm = AB , 30 = BAC , 75 = ACB . Tính diện tích của tam giác ABC .
A. 2183cm B. 2 93 cm C. 218cm D. 29cm

Câu 19. Mệnh đề nào sau đây sai ?
A. 0 AA . B. 0 cùng phương với mọi vectơ. C. 0 AB D. 0 cùng hướng với mọi vectơ
OFFICIAL
Câu 20. Cho hình chữ nhật ABCD tâm O . Trong các mệnh đề sau, mệnh đề nào sai?
A. 0 ABBCBD+−= . B. 0 OAOC+= . C. 0 ABBCCA++= . D. 0 ADBC−= .
Câu 21. Cho hàm số ( )yfx = xác định trên đoạn 2;3 có đồ thị được cho như trong hình dưới đây:
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của ( )fx trên đoạn 2;3 . Tính Mm + . A. 0 Mm+= B. 1 Mm+= C. 2 Mm+= D. 3 Mm+= Câu 22. Trong các điểm sau đây điểm nào thuộc đồ thị
DẠYKÈMQUYNHƠN
A. ( ) 1 . 2;3 M B.
2
22
D.
.
Câu
Một máy bay có vectơ
Hình 7. Tính
của hàm số?
( )
0; 1. M C. 3 11 ; .
M
( ) 4
1;0 M
23.
vận tốc chỉ theo hướng bắc, vận tốc gió là một vectơ theo hướng đông như
độ dài vectơ tổng của hai vectơ nói trên (chọn giá trị gần đúng). A. 209 B. 208 C. 210 D. 211 Câu 24. Cho 0 a . Khẳng định nào sau đây là sai?
A. a và 4a cùng phương.
B. a và 4a cùng phương.
C. a và 4a không cùng hướng. D. a và 4a ngược hướng.
Câu 25. Cho tam giác ABC . Gọi M và N lần lượt là trung điểm của AB và AC . Trong các mệnh đề sau, tìm mệnh đề sai?
A. 2 ABAM = B. 2 ACCN = C. 2 BCNM =− D. 1 2 CNAC =−
Câu 26. Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống. Biết rằng quỹ đạo của quả bóng là một cung parabol trong mặt phẳng với hệ tọa độ Oth, trong đó t là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên; h là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2m. Sau đó 1 giây, nó đạt độ cao 8,5m và 2 giây sau khi đá lên, nó đạt độ cao 6m. Hỏi sau bao lâu thì quả bóng sẽ chạm đất kể từ khi được đá lên (tính chính xác đến hàng phần trăm? A. 2,56 giây B. 2,57 giây C. 2,58 giây D. 2,59 giây
Câu 27. Cho hàm số 2 41yxx=−++ . Khẳng định nào sau đây sai? A. Trên khoảng ( );1− hàm số đồng biến. B. Hàm số nghịch biến trên khoảng ( ) 2;+ và đồng biến trên khoảng ( );2−
OFFICIAL
C. Trên khoảng ( ) 3;+ hàm số nghịch biến. D. Hàm số nghịch biến trên khoảng ( ) 4;+ và đồng biến trên khoảng ( );4−
Câu 28. Cho tam giác ABC . Giá trị của biểu thức ABBC bằng:
A. cos ABBCABC . B. cos ABACABC . C. cos −ABBCABC . D. cos ABBCBAC . Câu 29. Cho hình thang vuông ABCDcó đáy lớn 4 ABa = , đáy nhỏ 2 CDa = , đường cao 3 ADa = ; I là trung điểm của AD Khi đó ( ) + IAIBID bằng : A. 2 9 2 a . B. 2 9 2 a . C. 0 . D. 2 9a . Câu 30. Tam giác ABC vuông ở A và có góc o50 = B . Hệ thức nào sau đây là sai? A. ( ) o , 130= ABBC B. ( ) o , 40 = BCAC C. ( ) o , 50 = ABCB D. ( ) o , 120= ACCB Câu 31. Tìm khẳng định đúng trong các khẳng định sau? A. ( ) 2 325
DẠYKÈMQUYNHƠN
fxxx=+− là tam thức bậc hai. B. ( ) 24fxx=− là tam thức bậc hai. C. ( ) 3 321fxxx=+− là tam thức bậc hai. D. ( ) 42 1 fxxx=−+ là tam thức bậc hai. Câu 32. Cho ( ) 2 fxaxbxc =++ , ( )0 a và 2 4 bac=− . Cho biết dấu của khi ( )fx luôn cùng dấu với hệ số a với mọi x . A. 0 . B. 0 = . C. 0 . D. 0 . Câu 33. Tập nghiệm của bất phương trình 2 250 x − là A. ( )5;5 S =− B. 5 x C. 55 x − D. ( ) ( ) ;55; S =−−+ Câu 34. Số nghiệm của phương trình ( ) 22 3443xxxx −−=−+ là: A. 0. B. 1. C. 2. D. 3. Câu 35. Tổng các nghiệm của phương trình ( ) 22 11032xxxx −−=−+ là: A. 4. B. 1. C. 2. D. 3.
2. Tự luận
Câu 1. Năm 2003, nhiệt độ ngày tại Death Valley (Thung Lũng Chết), California, được xác định qua hàm số: 2 ()0,00180,65750,95 =−++ tddd , trong đó t là nhiệt độ tính theo độ đo Fahrenheit ( ) F và d là ngày trong năm tính từ 1/1/2003. Nhiệt độ cao nhất trong năm đó là bao nhiêu độ
F ? Vào ngày nào?
Câu 2. Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 280kg chất A và 18kg chất
B . Với một tấn nguyên liệu loại I, người ta có thể chiết xuất được 40kg chất A và 1,2kg chất
B . Với một tấn nguyên liệu loại II, người ta có thể chiết xuất được 20kg chất A và 3kg chất
B . Giá mỗi tấn nguyên liệu loại I là 4 triệu đồng và loại II là 3 triệu đồng. Hỏi người ta phài dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất mà vẫn đạt được mục tiêu đề ra? Biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp tối đa 10 tấn nguyên liệu loại I và 9 tấn nguyên liệu loại II.
OFFICIAL
DẠYKÈMQUYNHƠN
Câu
Cho
333 2
c
+− = +− .
C = . Câu 4. Cho hai hình bình hành ABCD và ABCD có chung đỉnh A . Chứng minh rằng hai tam giác BCD và BCD có cùng trọng tâm Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM 1A 2C 3C 4B 5A 6C 7D 8A 9D 10D 11B 12C 13C 14A 15C 16B 17A 18D 19C 20A 21B 22B 23A 24C 25B 26C 27D 28A 29B 30D 31A 32A 33A 34B 35A 1. Trắc nghiệm Câu 1. Cho mệnh đề A : "8 không chia hết cho 2 " và mệnh đề : B " 31 ". Xét các mệnh đề sau: a) Mệnh đề AB . b) Mệnh đề BA . c) Mệnh đề AB . d) Mệnh đề AB . Số mệnh đề đúng trong các mệnh đề trên là A. 1. B. 2. C. 3. D. 4. Lời giải Ta có mệnh đề A sai, mệnh đề A đúng; mệnh đề B đúng, mệnh đề B sai. Khi đó, mệnh đề đúng là: a ). Đáp án là A Câu 2. Mệnh đề phủ định của mệnh đề :",230"Txx−+ là A. " ,230xx −+ ". B. " ,230"xx −+ C. " ,230"xx −+ D. " ,230"xx −+ Lời giải Mệnh đề phủ định của mệnh đề T là " ,230"xx −+ Câu 3. Cho hai tập hợp {;} = Aab và {;;;;} = Babcde . Có bao nhiêu tập hợp X mà AXB ? A. 6. B. 7. C. 8. D. 11. Câu 4. Cho tập hợp {20} =−Axx . Tập hợp A là: A. {2;1;0}=−− A B. [2;0]=− A C. (2;0)=− A D. {2;0}=− A Câu 5. Cho hai tập hợp [5;0],[0;) =−=+AB . Khi đó:
3.
tam giác ABC thoả mãn
abc
abc
Chứng minh góc 60
A. {0} =AB . B. =AB . C. [5;)=−+AB D. (5;)=−+AB . Câu 6. Miền nghiệm của bất phương trình 35xy−− là nửa mặt phẳng chứa điểm


A. (3;0) B. (3;1). C. (1;3). D. (0;0) Câu 7. Phần không bị gạch (không kể d) ở Hình 4 là miền nghiệm của bất phương trình:
A. 326 +xy B. 236 +xy C. 236 +xy D. 326 +xy Câu 8. Miền không bị gạch (tính cả biên) trong hình vẽ dưới đây là miền nghiệm của hệ bất phương trình bậc nhất hai ẩn nào sau đây?
A. 236 236 xy xy + −− B. 236 236 xy xy + −− C. 236 236 xy xy +− −− D. 236 236 xy xy + − . Câu 9. Miền nghiệm của hệ bất phương trình bậc nhất hai
M
t máy không thể đồng thời sản xuất cả hai loại. Máy cắt làm không quá 6 giờ/ngày, máy tiện làm không quá 4 giờ/ngày. Hỏi một ngày xưởng nên sản xuất bao nhiêu tấn mối loại để tiền lãi là cao nhất?
A. 2 tấn trục sắt và 2 tấn đinh ốc.
B. 3 tấn trục sắt và 1 tấn đinh ốc.
C. 2 tấn trục sắt và 3 tấn đinh ốc.
D. 1 tấn trục sắt và 3 tấn đinh ốc.
DẠYKÈMQUYNHƠN
OFFICIAL
ẩn 20112022
+
nằ
ần tư
D. IV. Câu 10. Một xưởng có một máy cắt và một máy tiện dùng để sản xuất trục sắt và đinh ốc. Để sản xuất 1 tấn trục sắt thì lần lượt máy cắt chạy trong 3 giờ và máy tiện chạy trong 1 giờ, tiền lãi
Để sản
ệu đồng.
0 xy y
m trong góc ph
nào? A. I. B. II. C. III.
là 2 triệu đồng.
xuất 1 tấn đinh ốc thì lần lượt máy cắt và máy tiện chạy trong 1 giờ, tiền lãi là 1 tri
ộ
Lời giải
Gọi ,(0,0) xyxy là số tấn trục sắt và đinh ốc sản xuất trong ngày.
Số tiền lãi mỗi ngày: (;)2 Lxyxy =+
Số giờ làm việc mỗi ngày của máy cắt: 36 xy+
Số giờ làm việc mỗi ngày của máy tiện: 4 xy+ .
Ta có bài toán tìm giá trị lớn nhất của (,)Lxy biết 36 4 0,0
+ + (*).
xy xy xy
Miền nghiệm của (*) là miền tứ giác OABC với (0;0),(2;0),(1;3),(0;4) OABC . Ta có: (0;0)0,(2;0)4,(0;4)4,(1;3)5 LLLL==== . Vậy mỗi ngày cần sản xuất 1 tấn trục
OFFICIAL
DẠYKÈMQUYNHƠN
sắt và 3 tấn đinh ốc thì thu được tiền lãi cao nhất là 5 triệu đồng. Câu 11. Rút gọn biểu thức tansin sincot xx M xx =− với ( ) 0;90 x ta được A. sin x B. cos x C. 1 sin x D. 1 cos x . Lời giải 22 tansin1sincos cos sincotcoscoscos xxxx Mx xxxxx =−=−== Câu 12. Cho là góc tù và tancot2 +=− . Giá trị của sincos M =− là A. 2. B. 2 C. 2 D. 2 . Lời giải Từ sincos 2 cossin +=− suy ra 1 sincos 2 =− . 2 (sincos)12sincos2 −=−= . Suy ra sincos2 −= . Vì là góc tù nên sincos0sincos2 M −=−= . Câu 13. Trên nửa đường tròn đơn vị, cho điểm M sao cho 120 = MOx . Toạ độ điểm M là: A. 31 ; 22 B. 31 ; 22 C. 13 ; 22 . D. 13 ; 22 . Lời giải Điểm M có toạ độ là (;) ab . Ta có: cos120,sin12013 22 ==−== ab Chọn C Câu 14. Cho ;;cab là độ dài 3 cạnh của tam giác ABC . Biết 7 = b ; 5 = c ; 4 cos 5 A = . Tính độ dài của a
A. 32 . B. 72 2 . C. 23 8 . D. 6. Lời giải Chọn A Áp dụng định lí cosin cho tam giác ABC ta có: 22222 4 2.cos752.7.5.18 5 abcbcA=+−=+−=
Suy ra: 1832 a == Câu 15. Tam giác ABC có 6,42,2.abc=== M là điểm trên cạnh BC sao cho 3 BM = . Độ dài đoạn AM bằng bao nhiêu? A. 9. B. 9. C. 3. D. 1 108. 2 Lời giải Chọn C. Ta có: Trong tam giác ABC có 66aBC== mà 3 BM = suy ra M là trung điểm BC Suy ra: 222 22 93 24 a bca AMmAM + ==−==
16. Cho tam giác ABC có góc 60 BAC = và
DẠYKÈMQUYNHƠN
OFFICIAL
ABC có 6812'= A , 3444'= B , 117. = AB Khi đó độ dài AC xấp xỉ bằng ? A. 68. B. 168. C. 118. D.200. Lời giải Chọn A Ta có: Trong tam giác ABC : 1801806812'3444'774' ++==−−= ABCC Mặt khác .sin117.sin3444' 68. sinsinsinsinsinsinsin774' ===== abcACABABB AC ABCBCC Câu 18. Tam giác ABC có 6cm = AB , 30 = BAC , 75 = ACB . Tính diện tích của tam giác ABC A. 2183cm . B. 2 93 cm . C. 218cm . D. 29cm . Lời giải Chọn D Ta có ( ) 18075 =−+== ABCBACACBACB Suy ra tam giác ABC cân tại A nên 6cm ==ABAC . Vậy diện tích tam giác ABC là: 2 1 ..sin9 cm 2 == ABC SABACBAC . Câu 19. Mệnh đề nào sau đây sai ?
Câu
cạnh 3 BC = . Tính bán kính của đường tròn ngoại tiếp tam giác ABC . A. 4 R = . B. 1 R = . C. 2 R = . D. 3 R = . Lời giải Chọn B Ta có: 3 21 sin2sin 3 2. 2 BCBC RR AA ==== Câu 17. Tam giác


DẠYKÈMQUYNHƠN OFFICIAL
(
O
điểm của AC ) 00
++=+=
0
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của ( )fx trên đoạn 2;3 .
+
A. 0 Mm
A. 0 AA B. 0 cùng phương với mọi vectơ C. 0 AB D. 0 cùng hướng với mọi vectơ Lời giải Chọn C Đáp án C sai vì có thể xảy ra trường hợp 0. ABAB Câu 20. Cho hình chữ nhật ABCD tâm O . Trong các mệnh đề sau, mệnh đề nào sai? A. 0 ABBCBD+−= . B. 0 OAOC+= . C. 0 ABBCCA++= . D. 0 ADBC−= . Lời giải Chọn A
) 00200 ABBCBDACBDOCODDC +−=−=−== ( Không thỏa mãn)
0 OAOC+= ( thỏa mãn vì
là trung
ABBCCAACCA
( thỏa mãn)
ADBC−= ( thỏa mãn). Câu 21. Cho hàm số ( )yfx = xác định trên đoạn 2;3 có đồ thị được cho như trong hình dưới đây:
Tính Mm
.
+= B. 1 Mm+= C. 2 Mm+= D. 3 Mm+= Lời giải Quan sát trên đồ thị ta thấy 3 M = (ứng với 3 x = ), 2 m =− (ứng với 2 x =− ). Vậy 1 Mm+= . Đáp án B. Câu 22. Trong các điểm sau đây điểm nào thuộc đồ thị của hàm số? A. ( ) 1 . 2;3 M B. ( ) 2 0; 1. M C. 3 11 ; . 22 M D. ( ) 4 . 1;0 M Lời giải
Chọn B
Thay 0 x = vào hàm số ta thấy 1 y =− . Vậy ( ) 2 0;1 M thuộc đồ thị hàm số.
Câu 23. Một máy bay có vectơ vận tốc chỉ theo hướng bắc, vận tốc gió là một vectơ theo hướng đông như Hình 7. Tính độ dài vectơ tổng của hai vectơ nói trên (chọn giá trị gần đúng).
A. 209 B. 208 C. 210 D. 211 Lời giải Gọi AB và BC lần lượt là vecto vận tốc của máy bay và vận tốc của gió. Ta có: += ABBCAC

Suy ra 222220060209( /) =+=+ ACABBCkmh . Vậy độ dài vectơ tổng của hai vectơ nói trên là khoảng 209 / kmh
Câu 24. Cho 0 a . Khẳng định nào sau đây là sai?
A. a và 4a cùng phương.
B. a và 4a cùng phương.
C. a và 4a không cùng hướng. D. a và 4a ngược hướng.
Lời giải Chọn C
Câu 25. Cho tam giác ABC . Gọi M và N lần lượt là trung điểm của AB và AC . Trong các mệnh đề sau, tìm mệnh đề sai?
A. 2 ABAM = B. 2 ACCN = C. 2 BCNM =− D. 1 2 CNAC =−
Lời giải Chọn B
Câu 26. Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống. Biết rằng quỹ đạo của quả bóng là một cung parabol trong mặt phẳng với hệ tọa độ Oth, trong đó t là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên; h là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2m. Sau đó 1 giây, nó đạt độ cao 8,5m và 2 giây sau khi đá lên, nó đạt độ cao 6m. Hỏi sau bao lâu thì quả bóng sẽ chạm đất kể từ khi được đá lên (tính chính xác đến hàng phần trăm? A. 2,56 giây B. 2,57 giây C. 2,58 giây D. 2,59 giây Lời giải Đáp án C. Gọi phương trình của parabol quỹ đạo là 2 hatbtc =++ . Từ giả thiết suy ra parabol đi qua các điểm ( )0;1;2 , ( )1;8;5 và ( )2;6
DẠYKÈMQUYNHƠN
OFFICIAL
==−


ca abcb abcc
đó ta có 1,24,9 8,512,2 4261,2
phương trình của parabol quỹ đạo là 2 4,912,21,2htt=−++ . Giải phương trình 2 04,912,21,20htt =−++= ta tìm được một nghiệm dương là 2,58 t . Câu 27. Cho hàm số 2 41yxx=−++ . Khẳng định nào sau đây sai? A. Trên khoảng ( );1− hàm số đồng biến. B. Hàm số nghịch biến trên khoảng ( ) 2;+ và đồng biến trên khoảng ( );2− .
C. Trên khoảng ( ) 3;+ hàm số nghịch biến. D. Hàm số nghịch biến trên khoảng ( ) 4;+ và đồng biế
DẠYKÈMQUYNHƠN OFFICIAL
Từ
++== ++== Vậy
. Lời giải Chọn D Đỉnh của parabol: 2 2 I b x a =−= Bảng biến thiên của hàm số: Dựa vào bảng biến thiên suy ra khẳng định D sai. Câu 28. Cho tam giác ABC . Giá trị của biểu thức ABBC bằng: A. cos ABBCABC . B. cos ABACABC . C. cos ABBCABC . D. cos ABBCBAC . Lời giải Chọn A Câu 29. Cho hình thang vuông ABCDcó đáy lớn 4 ABa = , đáy nhỏ 2 CDa = , đường cao 3 ADa = ; I là trung điểm của AD. Khi đó ( ). + IAIBID bằng : A. 2 9 2 a B. 2 9 2 a C. 0 D. 2 9a Lời giải
n trên khoảng ( );4−
Ta có ( ) ( ) 2 9 ..2. 2 +=++==− a IAIBIDIAIAABIDIAID nên chọn B.
Câu 30. Tam giác ABC vuông ở A và có góc o50 = B . Hệ thức nào sau đây là sai?
A. ( ) o , 130= ABBC . B. ( ) o , 40 = BCAC . C. ( ) o , 50 = ABCB . D. ( ) o , 120= ACCB .
Lời giải
Chọn D
Phương án A:( ) ( ) 0o , 180, 130 =−=ABBCABCB nên loại#A.
Phương án B:( ) ( ) o , , 40 ==BCACCBCA nên loại B.
Phương án C:( ) ( ) o , , 50 ==ABCBBABC nên loại C.
Phương án D:( ) ( ) 0o , 180, 140 =−=ACCBCACB nên chọn D.
Câu 31. Tìm khẳng định đúng trong các khẳng định sau? A. ( ) 2 325fxxx=+− là tam thức bậc hai B. ( ) 24fxx=− là tam thức bậc hai C. ( ) 3 321fxxx=+− là tam thức bậc hai D. ( ) 42 1 fxxx=−+ là tam thức bậc hai Lời giải Chọn#A.
* Theo định nghĩa tam thức bậc hai thì ( ) 2 325fxxx=+− là tam thức bậc hai Câu 32. Cho ( ) 2 fxaxbxc =++ , ( )0 a và 2 4 bac=− . Cho biết dấu của khi ( )fx luôn cùng dấu với hệ số a với mọi x . A. 0 . B. 0 = . C. 0 . D. 0 .
Lời giải Chọn#A. * Theo định lý về dấu của tam thức bậc hai thì ( )fx luôn cùng dấu với hệ số a với mọi x khi 0 Câu 33. Tập nghiệm của bất
DẠYKÈMQUYNHƠN
Chọn B
OFFICIAL
phương trình 2 250 x − là A. ( )5;5 S =− . B. 5 x . C. 55 x − D. ( ) ( ) ;55; S =−−+ Lời giải Chọn A Bất phương trình 2 250 x − 55 x − . Vậy ( )5;5 S =− . Câu 34. Số nghiệm của phương trình ( ) 22 3443xxxx −−=−+ là: A. 0. B. 1. C. 2. D. 3. Lời giải Chọn B Điều kiện xác định 22 x − ( ) ( ) ( )( ) 22 2 2 3443 3431 3() 41(*) xxxx xxxx xL xx −−=−+ −−=−− = −=−
ít nhất 280kg chất A và 18kg chất
B . Với một tấn nguyên liệu loại I, người ta có thể chiết xuất được 40kg chất A và 1,2kg chất
B . Với một tấn nguyên liệu loại II, người ta có thể chiết xuất được 20kg chất A và 3kg chất
DẠYKÈMQUYNHƠN OFFICIAL Giải (*) 2 2 1 41117(TM) 22302 17(L) 2 x x x xx xx x + = −=− −−= = Vậy phương trình có 1 nghiệm Câu 35. Tổng các nghiệm của phương trình ( ) 22 11032xxxx −−=−+ là: A. 4. B. 1. C. 2. D. 3. Lời giải Chọn A Điều kiện xác định 1010 x − ( ) ( ) ( )( ) 22 2 2 11032 11021 1() 102(*) xxxx xxxx xTM xx −−=−+ −−=−− = −=− Giải (*) ( ) 2 2 2 2 2 102 3() 102 1() x x xx xTM xx xL −=− = −=− =− Vậy tổng các nghiệm của phương trình bằng 4 2. Tự luận Câu 1. Năm 2003, nhiệt độ ngày tại Death Valley (Thung Lũng Chết), California, được xác định qua hàm số: 2 ()0,00180,65750,95 =−++ tddd , trong đó t là nhiệt độ tính theo độ đo Fahrenheit ( ) F và d là ngày trong năm tính từ 1/1/2003. Nhiệt độ cao nhất trong năm đó là bao nhiêu độ F ? Vào ngày nào? Lời giải Ta có: 2 2 365 ()0,00180,65750,950,0018110,90125 2 =−++=−−+ tdddd 110,90125 . Dấu bằng xảy ra khi và chỉ khi 365365 0 22 −==dd . Vậy nhiệt độ cao nhất của năm đó là ( ) 110,90125 F sau 182,5 ngày kể từ ngày 1/1/2003. Nhiệt độ cao nhất vào giữa ngày 2/7/2003 Câu 2. Người ta dự định dùng hai loại nguyên liệu để chiết xuất
B . Giá mỗi tấn nguyên liệu loại I là 4 triệu đồng và loại II là 3 triệu đồng. Hỏi người ta phài dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất mà vẫn đạt được mục tiêu đề ra? Biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp tối đa 10 tấn nguyên liệu loại I và 9 tấn nguyên liệu loại II. Lời giải Gọi x
OFFICIAL
đồng). Vậy bài toán trở thành tìm giá trị nhỏ nhất của (;)Fxy với (;) xy thoả mãn hệ bất phương trình bậc nhất hai ẩn ở trên. Bước 1. Xác định miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên. Miền nghiệm là miền tứ giác ABCD với (5;4),(10;2),(10;9),(2,5;9) ABCD Bước 2. Tinh giá trị của F tại các đỉnh của tứ giác ABCD.
Fxyxy
Ta có: (5;4)32,(10;2)46,(10;9)67,(2,5;9)37 ====FFFF . So sánh các giá trị này ta thấy (5;4)F là nhỏ

DẠYKÈMQUYNHƠN
và y lần lượt là số tấn nguyên liệu loại I và loại II mà người ta cần dùng. Khi đó khối lượng chất A chiết xuất được là 4020( ) + xykg . Khối
1,23( ) + xykg . Từ giả
4020280214 1,23181,2318 hay 1010 99. xyxy xyxy xx yy ++ ++ Hơn nữa, số tiền người ta phải trả để mua nguyên liệu là (;)43 =+
lượng chất B chiết xuất được là
thiết ta có hệ bất phương trình sau:
(triệu
nhất. Do đó, giá trị nhỏ nhất của (;)Fxy với (;) xy thoả mãn hệ bất phương trình trên là (5;4)32 = F . Vậy người ta cần mua 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II đễ chi phí là nhỏ nhất. Câu 3. Cho tam giác ABC thoả mãn 333 2 abc c abc +− = +− . Chứng minh góc 60 C = . Lời giải Ta có 333 233323 () abc cabcabcc abc +− =+−=+− +− Suy ra 332222 () ababcaabbc +=+−+=

DẠYKÈMQUYNHƠN OFFICIAL 2222 1 2coscos60 2 aabbababCCC −+=+−== T
Câu
Lời
Gọi G
BCD suy ra 0 GBGCGD ++= 0 GBGCGDBBCCDD +++++= . (1) Mặt
( ) ( ) ( ) BBCCDDABABACACADAD ++=−+−+− ( ) ( ) ABADACABADAC =+−+++ ACACACAC =−−+ 0 = (2) Từ (1) và (2) ta có 0 GBGCGD ++= hay
ừ đó ta có điều phải chứng minh.
4. Cho hai hình bình hành ABCD và ABCD
có chung đỉnh A . Chứng minh rằng hai tam giác BCD
và BCD
có cùng trọng tâm
giải
là trọng tâm tam giác
khác theo quy tắc phép trừ và hình bình hành ta có
G là trọng tâm tam giác BCD
1. Trắc nghiệm
Câu 1. Phủ định của mệnh đề: "Tổng ba góc trong một tam giác bằng 180 " là mệnh đề
A. "Tổng ba góc trong một tam giác lớn hơn 180 ".
B. "Tổng ba góc trong một tam giác nhỏ hơn180".
C. "Tổng ba góc trong một tam giác không bằng 180 ".
D. "Tổng ba góc trong một tam giác không vượt quá 180 ".
Câu 2. Trong các mệnh đề sau, mệnh đề nào là đúng?
đề nào sau đây đúng?
A. (3;2) M =− . B. [3;2) M =− . C. (3;2] M =− D. {3;2;1} M =−−− .

Câu 6. Miền nghiệm của bất phương trình 44 xy+− KHÔNG chứa điểm nào sau đây? A. (1;1). B. (1;2) C. (2021;2022) D. (1;1) .
Câu 7. Miền không bị gạch (tính cả biên) trong hình vẽ bên là miền nghiệm của bất phương trình bậc nhất hai ẩn nào?
DẠYKÈMQUYNHƠN OFFICIAL ĐỀ SỐ 5
,42" xxx B. " 2 ,42 xxx hoặc 2"− x C. " 2 ,42 xxx ". D. " 2 ,422 − xxx ”. Câu 3. Cho tập hợp {1;2;3;4;5} = A . Tập hợp X thoả mãn \{1;3;5} = AX và \{6;7} = XA là: A. {2;4}. B. {6;7}. C.
. D.
. Câu 4. Cho hai tập hợp (1;2),[;2]
A. " 2
{2;4;6;7}
{1;3;5;6;7}
=−=+ ABmm . Tìm m để AB khác tập rỗng. A. 32− m . B. 32− m . C. 2 m hoặc 3− m . D. 2 m hoặc 3− m . Câu 5. Cho tập hợp {32}Mxx=− . Mệnh
A. 44xy+ . B. 44xy+ C. 41 xy+ D. 44xy−− .
Cặp số nào sau đây là
của hệ bất phương trình 36 ? 24 xy xy + − A.
.
22 22 1 xy xy y + −− −
Câu 8.
nghiệm
(2;0) B. (0;2)
C. (4;2). D. (3;3) Câu 9. Miền nghiệm của hệ bất phương trình
được xác định bởi miền đa giác nào sau đây?
A. B. C. D. Câu 10. Một đơn vị bộ đội cần mua ít nhất 300 kg gạo. Có hai loại gạo, loại I có giá là 30000 đồng/ kg, loại II có giá 20000 đồng/ kg. Gọi , xy lân lượt là số gạo loại I, II đơn vị mua. Hệ bất phương trình biểu thị mối liên hệ của x và y để số tiền đơn vị mua gạo không hết quá 7000000 đồng là: A. 8 32700




DẠYKÈMQUYNHƠN OFFICIAL
+
Câu
thoả mãn 90180 và sin3 5 = . Giá trị của cos là: A. 4 5 . B. 4 5 C. 2 5 . D. 2 5 Câu 12. Cho góc thoả mãn 0180 và 2 cos 3 =− . Giá trị của tan là: A. 5 2 . B. 5 2 . C. 2 5 . D. 2 5 . Câu 13. Cho tam giác ABC vuông tại A .
khẳng định
+
xy xy B. 300 33700 + + xy xy C. 300 32700 + + xy xy D. 300 32700 + + xy xy
11. Cho góc
Chọn
sai trong các khẳng định sau:
A. cossin = BC B. sincos = BC C. tancot = BC D. tancot =− CB
Câu 14. Cho các điểm (1;1),(2;4),(10;2). ABC Góc BAC bằng bao nhiêu?
A. 090 . B. 0 60. C. 0 45. D. 0 30.
Câu 15. Tam giác ABC có 9 AB = cm, 15 BC = cm, 12 AC = cm. Khi đó đường trung tuyến AM của tam giác có độ dài là A. 10cm. B. 9cm. C. 7,5cm. D. 8cm.
Câu 16. Cho tam giác ABC có ,, ABcACbBCa === . Chọn khẳng định đúng
A. 222 cos 2 bca A bc +− = . B. 222 cos bca A bc +− = C. 222 cos 2 bca A bc ++ = . D. 222 cos 2 abc A bc =
Câu 17. Bộ ba số nào sau đây là độ dài 3 cạnh của một tam giác tù?
A. 2;3;4 B. 3;4;5 C. 4;5;6 D. 5;6;7
Câu 18. Cho tam giác ABC có , = BCa , = CAb = ABc thỏa 222 3. +=+ bcabc Tìm số đo của góc
A của tam giác ABC . A. 120 . B. 60 . C. 150 . D. 30 .
Câu 19. Cho hình vuông ABCD . Khẳng định nào sau đây đúng?
A. .ACBD B. .ABCD
C. ABBC D. Hai vectơ , ABAC cùng hướng.
Câu 20. Gọi O là tâm hình bình hành .ABCD Đẳng thức nào sau đây sai ?
A. OAOBCD . B. OBOCODOA. C. ABADDB . D. BCBADCDA.
Câu 21. Cho hàm số 3 32yxx=−+ . Điểm nào sau đây thuộc đồ thị hàm số đã cho? A. ( )2;0 B. ( )1;1 C. ( )2;12 D. ( )1;1
Câu 22. Tập xác định của hàm số 3 22 x y x = là A. \1 . B. \3 . C. \2 . D. ( ) 1;+ .
Câu 23. Cho ba lực 123 ,, FFF cùng tác động vào một vật tại một điểm làm vật đứng yên (Hình). Xét 423 =+ FFF . Phát biểu nào sau đây là đúng?
A. 41 = FF B. 41 2 = FF . C. 41 2=− FF D. 41 =− FF
Câu 24. Cho đoạn thẳng AB và điểm C nằm giữa hai điểm , AB . Khẳng định nào sau đây là đúng?

DẠYKÈMQUYNHƠN
OFFICIAL
A. = AC ACAB AB B. =− AC ACAB AB C. = AB ACAB AC . D. =− AB ACAB AC . Câu 25. Cho 0 a và điểm O . Gọi , MN lần lượt là hai điểm thỏa mãn 3 OMa = và 4 ONa =− . Khi đó: A. 7 MNa = B. 5 MNa =− C. 7 MNa =− D. 5 MNa =− Câu 26. Trục đối xứng của đồ thị hàm số 2 yaxbxc =++ , (0) a là đường thẳng nào dưới đây? A. 2 b x a =− B. 2 c x a =− C. 4 x a =− D. Không có. Câu 27. Tọa độ giao điểm của ( ) 2 :4 Pyxx =− với đường thẳng :2dyx=−− là A. ( )0;2 M , ( )2;4 N . B. ( )1;1 M , ( )2;0 N . C. ( )3;1 M , ( )3;5 N D. ( )1;3 M , ( )2;4 N
Câu 28. Cho đoạn thẳng AB . Tập hợp các điểm M nằm trong mặt phẳng thoả mãn 0 =MAMB là:
A. Đường tròn tâm A bán kính AB .
B. Đường tròn tâm B bán kính AB . C. Đường trung trực của đoạn thẳng AB D. Đường tròn đường kính AB .
Câu 29. Cho hình vuông ABCD, tính ( ) cos,ABCA
A. 1 2 B. 1 2 C. 2 2 D. 2 2 Câu 30. Cho tam giác ABC vuông cân tại A có 2 BCa = .Tính CACB A. 2 . = CACBa . B. . = CACBa . C. 2 . 2 = a CACB . D. .2 = CACBa . Câu 31. Cho tam thức ( ) 2 8x16 fxx=−+ . Khẳng định nào sau đây là đúng? A. phương trình ( ) 0 fx = vô nghiệm. B. ( ) 0 fx với mọi x C. ( ) 0 fx
DẠYKÈMQUYNHƠN OFFICIAL
với mọi x D. ( ) 0 fx khi 4 x Câu 32. Cho tam thức bậc hai ( ) 2 1 fxx=+ . Mệnh đề nào sau đây đúng? A. ( ) ( ) 0;fxx−+ . B. ( ) 01fxx==− . C. ( ) ( )0;1fxx− . D. ( ) ( )00;1fxx . Câu 33. Tập nghiệm S của bất phương trình 2 60 xx−− A. ( ) ( ) ;32: S =−−+ . B. 2;3 . C. 3;2 D. ( ) ;32; −−+ Câu 34. Tập nghiệm S của phương trình 233 xx−=− là A. S = B. 2 S = C. 6;2 S = D. 6 S = Câu 35. Tìm số giao điểm giữa đồ thị hàm số 34yx=− và đường thẳng 3 yx=− A. 2 giao điểm. B. 4 giao điểm. C. 3 giao điểm. D. 1 giao điểm.
2. Tự luận
Câu 1. Lập bảng biến thiên và vẽ đồ thị của hàm số 2 23=−−+yxx

Câu 2. Một người bán nước giải khát đang có 25g bột nho và 100 g đường để pha chế hai loại nước nho A và B . Để pha chế 1l nước nho loại A cần 10 g đường và 1g bột nho; để pha chế 1l nước nho loại B cần 10 g đường và 4g bột nho. Mỗi lít nước nho loại A khi bán lãi được 30 nghìn đồng, mỗi lít nước nho loại B khi bán lãi được 40 nghìn đồng. Hỏi người đó nên pha chế bao nhiêu lít nước nho mỗi loại để có lợi nhuận cao nhất?
Câu 3. Ta giả sử hai bờ sông là hai đường thẳng song song cách nhau 2km. Một chiếc tàu nhỏ đi từ điểm A ở bờ bên này sang điểm B ở bờ bên kia với vận tốc riêng của tàu (tức là vận tốc của tàu so với dòng nước) là 20 / kmh. Giả sử AB vuông góc với bờ sông (như hình vẽ). Cho biết vận tốc của dòng nước so với bờ là không đổi 5 / kmh (giả sử phương dòng nước chảy song song với bờ sông).
OFFICIAL
a) Cần giữ lái cho tàu tạo với bờ sông một góc nhọn bằng bao nhiêu độ để tàu sang bờ bên kia theo phương AB ? b) Tính vận tốc của tàu so với bờ. Hỏi sau bao lâu thì tàu sẽ tới bờ bên kia? (Các kết quả tính toán ở câu a) và câu b) ở trên được làm tròn đến hàng phần trăm). Câu 4. Cho tam giác ABC cố định và điểm M di động. Chứng minh rằng 45 vMAMBMC =+− không phụ thuộc vào vị trí của điểm M
DẠYKÈMQUYNHƠN
Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM 1C 2B 3C 4A 5B 6D 7B 8C 9C 10D 11B 12A 13C 14A 15C 16A 17A 18D 19C 20B 21C 22A 23D 24A 25C 26A 27D 28D 29D 30A 31C 32A 33B 34D 35D 1. Trắc nghiệm Câu 1. Phủ định của mệnh đề: "Tổng ba góc trong một tam giác bằng 180 " là mệnh đề A. "Tổng ba góc trong một tam giác lớn hơn 180 ". B. "Tổng ba góc trong một tam giác nhỏ hơn180". C. "Tổng ba góc trong một tam giác không bằng 180 ". D. "Tổng ba góc trong một tam giác không vượt quá 180 ". Câu 2. Trong các mệnh đề sau, mệnh đề nào là đúng? A. " 2 ,42" xxx . B. " 2 ,42 xxx hoặc 2"− x . C. " 2 ,42 xxx ". D. " 2 ,422 − xxx ”. Câu 3. Cho tập hợp {1;2;3;4;5} = A . Tập hợp X thoả mãn \{1;3;5} = AX và \{6;7} = XA là: A. {2;4}. B. {6;7}. C. {2;4;6;7}. D. {1;3;5;6;7}. Lời giải
Dùng biểu đồ Ven như Hình 3 để minh họa hai tập hợp A, X. Chọn C
Câu 4. Cho hai tập hợp (1;2),[;2] =−=+ ABmm . Tìm m để AB khác tập rỗng. A. 32− m B. 32− m C. 2 m hoặc 3− m D. 2 m hoặc 3− m

Câu 5. Cho tập hợp {32}Mxx=− . Mệnh đề nào sau đây đúng?
A. (3;2) M =− B. [3;2) M =− . C. (3;2] M =− . D. {3;2;1} M =−−−

Câu 6. Miền nghiệm của bất phương trình 44 xy+− KHÔNG chứa điểm nào sau đây?
A. (1;1). B. (1;2). C. (2021;2022) D. (1;1)
Câu 7. Miền không bị gạch (tính cả biên) trong hình vẽ bên là miền nghiệm của bất phương trình bậc nhất hai ẩn nào?
A. 44xy+ . B. 44xy+ . C. 41 xy+ D. 44xy−−
8. Cặp số nào sau đây là
DẠYKÈMQUYNHƠN
OFFICIAL
−
==−
ủ
22 22
−− −
Câu
nghiệm của hệ bất phương trình 36 ? 24 xy xy +
A. (2;0) B. (0;2) C. (4;2). D. (3;3) . Lời giải. Với 4,2
xy ta có: 43 + . (2)26 −=− và 2.4(2)104 −−= . Chọn C . Câu 9. Miền nghiệm c
a hệ bất phương trình
1 xy xy y +
được xác định bởi miền đa giác nào sau đây?
A. B. C. D. Câu 10. Một đơn vị bộ đội cần mua ít nhất 300 kg gạo. Có hai loại gạo, loại I có giá là 30000 đồng/ kg, loại II có giá 20000 đồng/ kg. Gọi , xy lân lượt là số gạo loại I, II đơn vị mua. Hệ bất phương trình biểu thị mối liên hệ của x và y để số tiền đơn vị mua gạo không hết quá 7000000 đồng là: A. 8 32700 + + xy xy B. 300 33700




DẠYKÈMQUYNHƠN OFFICIAL
+ + xy xy C. 300
+ + xy xy D.
+ +
Câu 11. Cho góc thoả mãn 90180 và sin3 5 = . Giá trị của cos là: A. 4 5 B. 4 5 . C. 2 5 D. 2 5 . Lời giải Ta có: 22 sincos1 += . Do đó 22 cos1sin1916 2525 =−=−= . Do 90180 nên cos0 . Suy ra 4 cos 5 =− Chọn B Câu 12. Cho góc thoả mãn 0180 và 2 cos 3 =− . Giá trị của tan là: A. 5 2 . B. 5 2 .
32700
300 32700
xy xy
D. 2 5 . Giải Ta có: 22 sincos1 += . Do đó 22 sin1cos145 99 =−=−= Do 0180 nên sin0 . Suy ra 5 sin 3 = . Vậy sin5 tan cos2 ==− Chọn A
Câu 13. Cho tam giác ABC vuông tại A . Chọn khẳng định sai trong các khẳng định sau: A. cossin = BC B. sincos = BC. C. tancot = BC . D. tancot =− CB. Câu 14. Cho các điểm (1;1),(2;4),(10;2). ABC Góc BAC bằng bao nhiêu? A. 090 . B. 0 60. C. 0 45. D. 0 30. Lời giải Chọn#A. Ta có: (1;3) AB = , (9;3) AC =− . Suy ra: 0 cos090. ABAC BACBAC ABAC === Câu 15. Tam giác ABC có 9 AB = cm, 15 BC = cm, 12 AC = cm. Khi đó đường trung tuyến AM của tam giác có độ dài là A. 10cm. B. 9cm. C. 7,5cm. D. 8cm
DẠYKÈMQUYNHƠN OFFICIAL C.
2 5 .
C Ta
222 2 24 ABACBC AM + =− 222 91215225 244 + =−= 15 2
Câu 16. Cho tam giác ABC có ,, ABcACbBCa === . Chọn khẳng
đúng A. 222 cos 2 bca A bc +− = . B. 222 cos bca A bc +− = C. 222 cos 2 bca A bc ++ = . D. 222 cos 2 abc A bc = . Lời giải Chọn A Câu 17. Bộ ba số nào sau đây là độ dài 3 cạnh của một tam giác tù? A. 2;3;4 B. 3;4;5 C. 4;5;6 D. 5;6;7 Lời giải Chọn A Dễ thấy phương án B là độ dài 3 cạnh của một tam giác vuông. Một tam giác là tam giác tù khi góc lớn nhất là góc tù. Ngoài ra góc lớn nhất là góc đối diện với cạnh lớn nhất. Gọi góc lớn nhất của các tam giác trong các phương án B, C, D là góc A và cạnh lớn nhất là cạnh có độ dài a .
. Lời giải Chọn
có
AM = .
định
từng phương án.
Với phướng án C, ta có: 222 4561 cos0 2.4.58 +− == A , nên góc A nhọn (loại).
Với phướng án D, ta có: 222 5671 cos0 2.5.65 +− == A nên góc A nhọn (loại).
Với phướng án A, ta có: 222 2341 cos0 2.2.34 +− ==− A nên góc A tù (chọn).
DẠYKÈMQUYNHƠN OFFICIAL Áp dụ
ệ quả của đị
lí
đố
diệ
v
ất 222 cos 2 +− = bca A bc cho
ng h
nh
Côsin với góc
i
n
ới cạnh lớn nh
ọ
Ta có 222
+=+
222
=
bc 222 3 22 +− = bca bc
cos
=
Vậ
ố
+)
+)
ODOAAD
+)
án
+) Đáp
Chọn C
Câu 18. Cho tam giác ABC có , = BCa , = CAb = ABc thỏa 222 3. +=+ bcabc Tìm số đo của góc A của tam giác ABC A. 120
B. 60
C. 150
D. 30
Lời giải Ch
n D
3
bcabc 222 3 +−=bcabc
3 +−
bca
3
2
A 30 = A .
y s
đo của góc A của tam giác ABC là 30 Câu 19. Cho hình vuông ABCD . Khẳng định nào sau đây đúng? A. ACBD B. ABCD C. ABBC D. Hai vectơ , ABAC cùng hướng. Lời giải Chọn C Vì ABBCABBC Câu 20. Gọi O là tâm hình bình hành .ABCD Đẳng thức nào sau đây sai ? A. OAOBCD . B. OBOCODOA. C. ABADDB . D. BCBADCDA. Lời giải Chọn B
Đáp án#A. Ta có OAOBBACD Vậy A đúng.
Đáp án B. Ta có OBOCCBAD
Vậy B sai.
Đáp
C. Ta có .ABADDB Vậy C đúng.
án D. Ta có . BCBAAC DCDAAC Vậy D đúng. Câu 21. Cho hàm số 3 32yxx=−+ . Điểm nào sau đây thuộc đồ thị hàm số đã cho? A. ( )2;0 B. ( )1;1 C. ( )2;12 D. ( )1;1 Lời giải
giải

DẠYKÈMQUYNHƠN OFFICIAL
Thay tọa độ điểm vào hàm số ta thấy chỉ có điểm ( )2;0 thỏa mãn. Câu 22. Tập xác định của hàm số 3 22 x y x = là A. \1 . B. \3 . C. \2 . D. ( ) 1;+ . Lời giải Chọn A Điều kiện xác định : 2201 xx− Nên tập xác định của hàm số là : \1 D = Câu 23. Cho ba lực 123 ,, FFF cùng tác động vào một vật tại một điểm làm vật đứng yên (Hình). Xét 423 =+ FFF . Phát biểu nào sau đây là đúng? A. 41 = FF B. 41 2 = FF C. 41 2=− FF D. 41 =− FF .
giải Chọn A Câu 25. Cho 0 a và điểm O . Gọi , MN lần lượt là hai điểm thỏa mãn 3 OMa = và 4 ONa =− . Khi đó: A. 7 MNa = B. 5 MNa =− C. 7 MNa =− D. 5 MNa =− Lời giải Chọn C Ta có: 437 MNONOMaaa =−=−−=− Câu 26. Trục đối xứng của đồ thị hàm số 2 yaxbxc =++ , (0) a là đường thẳng nào dưới đây? A. . 2 b x a =− B. . 2 c x a =− C. . 4 x a =− D. Không có. Lời giải Chọn A Câu 27. Tọa độ giao điểm của ( ) 2 :4 Pyxx =− với đường thẳng :2dyx=−− là
Lời
Vì vật đứng yên nên 1231441 00 ++=+==− FFFFFFF Chọn D Câu 24. Cho đoạn thẳng AB và điểm C nằm giữa hai điểm , AB . Khẳng định nào sau đây là đúng? A. = AC ACAB AB B. =− AC ACAB AB C. = AB ACAB AC . D. =− AB ACAB AC . Lời
A. ( )0;2 M , ( )2;4 N B. ( )1;1 M , ( )2;0 N
C. ( )3;1 M , ( )3;5 N . D. ( )1;3 M , ( )2;4 N . Lời giải
Chọn D
Hoành độ giao điểm của ( )P và d là nghiệm của phương trình: 22 1 42320 2 x xxxxx x
= −=−−−+=
. Vậy tọa độ giao điểm của ( )P và d là ( )1;3 M , ( )2;4 N
Câu 28. Cho đoạn thẳng AB . Tập hợp các điểm M nằm trong mặt phẳng thoả mãn 0 =MAMB là:
A. Đường tròn tâm A bán kính AB . B. Đường tròn tâm B bán kính AB C. Đường trung trực của đoạn thẳng AB D. Đường tròn đường kính AB . Lời giải Chọn D
Câu 29. Cho hình vuông ABCD, tính ( ) cos,ABCA
A. 1 2 B. 1 2 C. 2 2 D. 2 2 Lời giải
Chọn D Đầu tiên ta đi tìm số đo của góc ( ) , ABCA sau đó mới tính ( ) cos,ABCA Vì ( ) ( ) ( ) oo 2 ,180,135cos, 2 =−==−ABCAABCAABCA .
Câu 30. Cho tam giác ABC vuông cân tại A có 2 BCa = .Tính CACB
A. 2 . = CACBa . B. . = CACBa . C. 2 . 2 = a CACB . D. .2 = CACBa . Lời giải Chọn A Ta có 2 2 .2. 2 . ==aaa CACB
Câu
DẠYKÈMQUYNHƠN OFFICIAL
=
31. Cho tam thức ( ) 2 8x16 fxx=−+ . Khẳng định nào sau đây là đúng? A. phương trình ( ) 0 fx = vô nghiệm. B. ( ) 0 fx với mọi x . C. ( ) 0 fx với mọi x . D. ( ) 0 fx khi 4 x . Lời giải Chọn C Ta có ( ) ( )2 2 8x164fxxx =−+=− . Suy ra ( ) 0 fx với mọi x . Câu 32. Cho tam thức bậc hai ( ) 2 1 fxx=+ . Mệnh đề nào sau đây đúng? A. ( ) ( ) 0;fxx−+ B. ( ) 01fxx==− C. ( ) ( )0;1fxx− . D. ( ) ( )00;1fxx . Lời giải Chọn A
DẠYKÈMQUYNHƠN OFFICIAL Ta
2
, x
ậ
ệ
ủ
−− .
=−
−=−
B.
=
=
6 S = Lời giải Chọn D 233 xx−=− ( )2 30 233 x xx − −=− 2 3 2369 x xxx −=−+ 2 3 8120 x xx −+= 3 66 2 x x x x = = = Câu 35. Tìm số giao điểm giữa đồ thị hàm số 34yx=− và đường thẳng 3 yx=− . A. 2 giao
B.
Lời giải
D Số
=−
343 xx−=− ( ) ( ) 2 2 30 343 x xx − −=− 2 3 3469 x xxx −=−+ 2 3 9130 x xx −+= 3 929 2 929 2 x x x = + = 929 2 x + = . Vậy đồ thị hàm số 34yx=− và đường thẳng 3 yx=− có 1 giao điểm chung. 2. Tự luận Câu 1. Lập bảng biến thiên và vẽ đồ thị của hàm số 2 23=−−+yxx . Lời giải 10;1 2 =−−=− b a a Đỉnh: (1;4)I , trục đối xứng: 1=− x Hàm số đồng biến trên khoảng (;1) −− , nghịch biến trên khoảng (1;) −+ Bảng biến thiên:
có ( )
110 fxx=+
Câu 33. T
p nghi
m S c
a bất phương trình 2 60 xx
A. ( ) ( ) ;32: S =−−+ B. 2;3 C.
3;2 D. (
) ;32; −−+ Lời giải Chọn B Ta có: 2 6023xxx −−− Tập nghiệm bất phương trình là: 2;3 S
Câu 34. Tập nghiệm S của phương trình 233 xx
là A. S =
2 S
C.
6;2 S
D.
điểm.
4 giao điểm. C. 3 giao điểm. D. 1 giao điểm.
Chọn
giao điểm giữa đồ thị hàm số 34yx
và đường thẳng 3 yx=− là số nghiệm của phương trình hoành độ giao điểm:
Bảng một số giá trị Đồ thị.
Câu 2. Một người bán nước giải khát đang có 25g bột nho và 100 g đường để pha chế hai loại nước nho A và B . Để pha chế 1l nước nho loại A cần 10 g đường và 1g bột nho; để pha chế 1l nước nho loại B cần 10 g đường và 4g bột nho. Mỗi lít nước nho loại A khi bán lãi được 30 nghìn đồng, mỗi lít nước nho loại B khi bán lãi được 40 nghìn đồng. Hỏi người đó nên pha chế bao nhiêu lít nước nho mỗi loại để có lợi nhuận cao nhất?
Lời giải Gọi x và y lần lượt là số lít nước nho loại A và B người đó có thể pha chế. Ta có hệ bất phương trình: 425 10 0 0.
+ + Miền nghiệm của hệ bất phương trình là miền tứ giác OABC, trong đó (0;0)O ; (10;0);(5;5);(0;6,25) ABC .
xy xy x y
Gọi F là số tiền lãi (đơn vị: nghìn đồng) thu được, ta có: 3040=+ Fxy
Ta có: Tại (0;0):30.040.00 =+= OF ;

Tại (10;0):30.1040.0300 =+= AF ;


Tại (5;5):30.540.5350 =+= BF ;
Tại (0;6,25):30.040.6,25250 =+= CF .

Ta thấy F đạt GTLN bằng 350 tại (5;5)B
Vậy người đó nên pha chế 5l nước nho mỗi loại để có lợi nhuận cao nhất.
DẠYKÈMQUYNHƠN
OFFICIAL
m A ở bờ bên này sang điểm B ở bờ bên kia với vận tốc riêng của tàu (tức là vận tốc của tàu so với dòng nước) là 20 / kmh. Giả sử AB vuông góc với bờ sông (như hình vẽ). Cho biết vận tốc của dòng nước so với bờ là không đổi 5 / kmh (giả sử phương dòng nước chảy song song với bờ sông).
a) Cần giữ lái cho tàu tạo với bờ sông một góc nhọn bằng bao nhiêu độ để tàu sang bờ bên kia theo phương AB ? b) Tính vận tốc của tàu so với bờ. Hỏi sau bao lâu thì tàu sẽ tới bờ bên kia? (Các kết quả tính toán ở câu a) và câu b) ở trên được làm tròn đến hàng phần trăm). Lời giải a) Vận tốc thực của tàu so với bờ là , tntn vvv =+
Để cho tàu luôn chạy theo phương AB thì phương của , tnv phải có phương là AB và chiều là hướng từ A đến B (như hình vẽ). Ta có sin51 204 MCAN MAC AMAM ==== . Suy ra 14,48 MAC Vậy góc nhọn của tàu tạo với bờ sông là 9014,4875,52 −= b) Do tam giác ANC vuông tại A nên 22 515 ACCNAN=−= . Vậy vận tốc của tàu so với bờ là 19,36 / kmh . Thời gian để tàu qua sông là 2 0,1 515


DẠYKÈMQUYNHƠN
Câu
đi từ điể
OFFICIAL
3. Ta giả sử hai bờ sông là hai đường thẳng song song cách nhau 2km. Một chiếc tàu nhỏ
giờ. Câu 4. Cho tam giác ABC cố định và điểm M di động. Chứng minh rằng 45 vMAMBMC =+− không phụ thuộc vào vị trí của điểm M Lời giải ( ) ( ) 45454 vMAMBMCMCCAMCCBMCCACB =+−=+++−=+ Vì A, B, C cố định nên v không đổi Vậy v không phụ thuộc vào vị trí của điểm M
1. Trắc nghiệm
Câu 1. Chọn mệnh đề đúng trong các mệnh đề sau:
A. " 2 ,11 1 + x xx x ". B. " 2 ,11" 1 + x xx x C. 2 ",11" 1 + x xx x D. 2 ",12" 1 + x xx x
Câu 2. Cách viết nào sau đây để viết đúng mệnh đề: “ 2 không phải là số hữu tỉ”? A. 2 B. 2 C. 2 D. 2
Câu 3. Cho hai tập hợp {1;2;3;4} = A và {1;3;5} = B . Có bao nhiêu tập hợp
2. B. 3. C. 4. D. 6.
4. Trong đợt hội diễn văn nghệ chào mừng 20/11, lóp 10C đăng kí tham gia ba tiết mục là hát tốp ca, múa và diễn kịch. Trong danh sách đăng kí, có 12 học sinh đăng kí hát tốp ca, 10 học sinh đăng kí múa, 8 học sinh đăng kí diễn kịch, trong đó có 3 học sinh đăng kí hai tiết mục là hát tốp ca và tiết mục múa, 4 học sinh đăng kí hai tiết mục là hát tốp ca và diễn kịch, 2 học sinh đăng kí hai tiết mục múa và diễn kịch, 1 học sinh đăng kí cả ba tiết mục. Hỏi lớp 10 A có tất cả bao nhiêu học sinh đăng kí tham gia hội diễn văn nghệ? A. 22. B. 23. C. 25. D. 30. Câu 5. Cho ba tập hợp: ( )( ) 22140,{ AxxxBnn =−−== là ước của 12} và {1;2;3} C = . Gọi ()nX là số phần tử của tập X . Mệnh đề nào sau đây là đúng? A. ()()() nBnAnC B. ()()() nBnCnA C. ()()() nCnAnB . D. ()()() nCnBnA . Câu 6. Cửa hàng A bán hai loại đồ uống từ cafe: bán một cốc cafe trứng lãi 20 nghìn đồng và bán một cốc cafe nâu đá lãi 15 nghìn đồng. Gọi , xy lần lượt là số cốc cafe trứng và nâu đá được cửa hàng bán trong một ngày nào đó. Cặp số (;) xy nào sau đây biểu thị số cốc cafe mỗi loại mà cửa hàng bán được để tiền lãi trong ngày đó không ít hơn 1 triệu đồng?
A. (25;25). B. (30;20). C. (41;11) D. (40;15) Câu 7. Cặp số nào sau đây là nghiệm của bất phương trình 21 −xy ? A. (1;1). B. (1;2)
DẠYKÈMQUYNHƠN
ĐỀ SỐ 6
OFFICIAL
X mà XA và XB ? A.
Câu
.
Cặp số nào sau
2 43? xy xy −+− +− A.
39 28 6 xy xy y + + là
C. (1;1) D. (0;0)
Câu 8.
đây không là nghiệm của hệ bất phương trình:
(4;1) B. (1;4). C. (0;5). D. (1;8) Câu 9. Miền nghiệm của hệ bất phương trình:
phần mặt phẳng chứa điểm có toạ độ:
A. (1;2) B. (0;0). C. (3;0). D. (8;4)
Câu 10. Biết , xy thoả mãn hệ phương trình 2 36 2312
A. 4047,2 B. 4043,2 C. 4043 D. 4047
+− −+ −
xy xy xy Giá trị nhỏ nhất của hàm số
Câu 11. Cho tam giác ABC không phải là tam giác vuông. Chọn khẳng định sai trong các khẳng định sau:
A. sinsin()0 ++=ABC B. coscos()0 ++=ABC . C. tantan()0 ++=ABC D. cotcot()0 ++=ABC . Câu 12. Cho góc nhọn . Biểu thức 22 (sincot)(costan) + bằng: A. 0. B. 1. C. 2. D. 22 tancot + Câu 13. Cho góc nhọn . Biểu thức ( ) tantan90 − bằng: A. 1. B. 1 C. 2tan D. 2cot .
Câu 14. Cho tam giác ABC có o4,6,120ABACBAC=== . Độ dài cạnh BC là A. 219 B. 19 C. 319 D. 27 Câu 15. Cho tam giác ABC có 3,4,6ABACBC=== . Khi đó độ dài đường trung tuyến của tam giác ABC kẻ từ A bằng A. 9 2 B. 7 2 C. 14 2 D. 18 2 Câu 16. Cho tam giác ABC có 2,3,4ABACBC=== . Khi đó độ dài đường cao của tam giác ABC kẻ từ A bằng A. 315 2 . B. 315 4 . C. 315 8 . D. 315 . Câu 17. Trong tam giác
DẠYKÈMQUYNHƠN
OFFICIAL
ABC bất kì có ,, === BCaCAbABc . Bán kính đường tròn ngoại tiếp tam giác ABC là: A. sin = a R A . B. sin = b R A . C. 2sin = a R A . D. 2sin = c R A . Câu 18. Tam giác ABC có 30 = A ; 20 b = ; 5 = c . Diện tích của tam giác ABC bằng: A. 25. B. 253 . C. 252 . D. 255 . Câu 19. Cho ba điểm , , ABC phân biệt. Khi đó: A. Điều kiện cần và đủ để , , ABC thẳng hàng là AB cùng phương với .AC
B. Điều kiện đủ để , , ABC thẳng hàng là với mọi ,M MA cùng phương với AB
C. Điều kiện cần để , , ABC thẳng hàng là với mọi ,M MA cùng phương với .AB
D. Điều kiện cần để , , ABC thẳng hàng là .ABAC =
Câu 20. Nếu MNPQ là một hình bình hành thì ta có
A. MNPQ = B. MNMQMP −= C. MPNQ = D. MNMQMP +=
Câu 21. Tập xác định của hàm số ( )2 2 3 x y x + = là
A. ( );3− . B. ( ) 3;+ . C. \3 . D. .
Câu 22. Xét sự biến thiên của hàm số ( ) 3 = fx x trên khoảng ( ) 0;+ . Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng ( ) 0;+
B. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng ( ) 0;+ .
C. Hàm số đồng biến trên khoảng ( ) 0;+ .
D. Hàm số không đồng biến, không nghịch biến trên khoảng ( ) 0;+ .
OFFICIAL
Câu 23. Trên mặt phẳng, chất điểm A chịu tác dụng của ba lực 123 ,, FFF và ở trạng thái cân bằng. Góc giữa hai vectơ 12 , FF bằng 60 . Tính độ lớn của 3F , biết 11 23 == FFN A. 6 B. 7 C. 8 D. 9
Câu 24. Cho đoạn thẳng BC và điểm A nằm giữa hai điểm , BC . Khẳng định nào sau đây là đúng?
A. = AC ACAB AB B. =− AC ACAB AB C. = AB ACAB AC . D. =− AB ACAB AC .
Câu 25. Tìm giá trị của m sao cho amb = , biết rằng , ab ngược hướng và 5,15ab== A. 3 m = B. 1 3 m =− C. 1 3 m = D. 3 m =−
Câu 26. Khi một quả bóng được đá lên nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết quỹ đạo của quả bóng là một cung parabol trong mặt phẳng tọa độ Oth có phương trình 2 hatbtc 0 a , trong đó t là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên, h là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2 m và sau 1 giây
DẠYKÈMQUYNHƠN
thì nó đạt
abc. A. 18,3 abc . B. 6,1 abc . C. 8,5 abc . D.
. Câu 27. Xác định các hệ số a và b để Parabol ( ) 2 :4 Pyaxxb =+− có đỉnh ( )1;5 I . A. 3 2 a b = =− B. 3 2 a b = = C. 2 3 a b = = D. 2 3 a b = =− Câu 28. Nếu hai điểm , MN thoả mãn 9=−MNNM thì: A. 9 = MN . B. 3 = MN . C. 81 = MN . D. 6 = MN .
độ cao 8,5m , sau 2 giây nó đạt độ cao 6m . Tính tổng
15,9 abc
Câu 29. Cho hình vuông ABCD có cạnh a . Tính ABAD

A. 0 B. a C. 2 2 a D. 2 a
Câu 30. Cho M là trung điểm AB , tìm biểu thức sai:
A. =− MAABMAAB B. =− MAMBMAMB C. .. = AMABAMAB . D. .. = MAMBMAMB .
Câu 31. Cho tam thức bậc hai 2 ()(0) fxaxbxca=++ . Mệnh đề nào sau đây đúng?
A. Nếu 0 thì ( )fx luôn cùng dấu với hệ số a , với mọi x .
B. Nếu 0 thì ( )fx luôn trái dấu với hệ số a , với mọi x . C. Nếu 0 = thì ( )fx luôn cùng dấu với hệ số a , với mọi \ 2 b x a − . D. Nếu 0 thì ( )fx luôn cùng dấu
1 ;2 2
Câu 34. Tổng các nghiệm (nếu có) của phương trình: 212 xx
bằng: A. 6. B. 1. C. 5. D. 2. Câu 35. Phương trình 2 422xxx −+=− có bao nhiêu nghiệm? A. 3 B. 0 C. 2 D. 1
2. Tự luận
Câu 1. Hai ô tô xuất phát tại cùng một thời điểm từ hai vị trí A và O với vận tốc trung bình lần lượt là 50 / kmh và 40 / kmh trên hai con đường vuông góc với nhau và giao tại O . Hướng đi của hai xe thể hiện ở Hình 19. Biết 8 = AOkm . Gọi x (giờ) là thời gian hai xe bắt đầu chạy cho tới khi cách nhau 5km (tính theo đường chim bay) trước khi ô tô đi từ A đến vị trí O . Tìm x .
DẠYKÈMQUYNHƠN
OFFICIAL
với hệ số b , với mọi x Câu 32. Cho tam thức bậc hai ( ) 2 45fxxx=−−+ . Tìm tất cả giá trị của x để ( ) 0 fx A. ( ) ;15; x−−+ B. 1;5 x − C. 5;1 x− . D. ( )5;1 x − . Câu 33. Tìm tập xác định của hàm số 2 252yxx=−+ . A. ) 1 ;2; 2 −+
−
B. ) 2;+ C. 1 ; 2
D.
−=−
Câu 2. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức (;)43 =− Fxyxy trên miền nghiệm của hệ bất phương trình 4 5 5 4 +− + − −− xy xy xy xy Câu 3. Một người đứng trên mũi tàu thả neo giữa biển và phát hiện trên bờ biển (giả sử
thẳng) có hai ngọn
các góc tạo
góc
là 15
bờ biển là một đường
hải đăng cách nhau 5km (theo bản đồ hàng hải). Người đó xác định được
thành giữa các đường ngắm của hai ngọn hải đăng và đường thẳng từ tàu vuông
với bờ
và 35
(hình bên).
văn nghệ chào mừng 20/11, lóp 10C đăng kí tham gia ba tiết mục là hát tốp ca, múa và diễn kịch. Trong danh sách đăng kí, có 12 học sinh đăng kí hát tốp ca, 10 học sinh đăng kí múa, 8 học sinh đăng kí diễn kịch, trong đó có 3 học sinh đăng kí hai tiết mục là hát tốp ca và tiết mục múa, 4 học sinh đăng kí hai tiết mục là hát tốp ca và diễn kịch, 2 học sinh đăng kí hai tiết mục múa và diễn kịch, 1 học sinh đăng kí cả ba tiết mục. Hỏi lớp 10 A có tất cả bao nhiêu học sinh đăng kí tham gia hội diễn văn nghệ? A. 22. B. 23. C. 25. D. 30.
Lời giải
Gọi ,, ABC lần lượt là tập hợp các học sinh tham gia các tiết mục hát tốp ca, múa và diễn kịch và được minh họa bởi Hình 4. Khi đó, ABC là tập hợp tất cả các học sinh đăng kí tham gia hội diễn văn nghệ, ABC là tập hợp tất cả các học sinh tham gia cả ba tiết mục.

DẠYKÈMQUYNHƠN OFFICIAL
Lời
BẢNG
NGHIỆM 1C 2B 3C 4A 5B 6D 7C 8A 9D 10A 11A 12B 13A 14A 15C 16C 17C 18A 19A 20D 21C 22A 23A 24B 25B 26C 27C 28B 29A 30D 31C 32C 33A 34C 35D 1. Trắc nghiệm Câu 1. Chọn mệnh đề đúng trong các mệnh đề sau: A. " 2 ,11 1 + x xx x ". B. " 2 ,11" 1 + x xx x . C. 2 ",11" 1 + x xx x D. 2 ",12" 1 + x xx x Câu 2. Cách viết nào sau đây để viết đúng mệnh đề: “ 2 không phải là số hữu tỉ”? A. 2 . B. 2 . C. 2 . D. 2 . Câu 3. Cho hai tập hợp {1;2;3;4} = A và {1;3;5} = B . Có bao nhiêu tập hợp X mà XA và XB ? A. 2. B. 3. C.
D.
Do XA và XB nên () XAB .
AB
Chọn C Câu
Hãy tính khoảng cách theo đơn vị kilômét giữa con tàu và bờ biển nối hai ngọn hải đăng (kết quả làm tròn đến hàng phần trăm). Câu 4. Cho tam giác ABC và một điểm M bất kì. Chứng minh rằng 2 vMAMBMC =+− không phụ thuộc vào vị trí của điểm M. Dựng điểm D sao cho CDv =
giải tham khảo
ĐÁP ÁN TRẮC
4.
6. Lời giải
Mà
nên tập hợp X có thể là: {1},{3},{1;3}, .
4. Trong đợt hội diễn
Cách 1: Tập ABC là phần chung của ba tập hợp ,, ABC . Ta điền số phần tử vào tập hợp trong cùng (phần giao của ba tập hợp) rồi lần lượt ra đến ngoài. Sau đó, cộng tất cả các giá trị trên mỗi phần, ta được số phần tử của tập ABC . Vậy số học sinh đăng kí tham gia hội diễn văn nghệ là 22 học sinh. Cách 2: Ta có thể tính số học

nCnBnA
6. Cửa hàng A bán hai loại đồ uống từ cafe: bán một c
c cafe trứng lãi 20 nghìn đồng và bán một cốc cafe nâu đá lãi 15 nghìn đồng. Gọi , xy lần lượt là số cốc cafe trứng và nâu đá được cửa hàng bán trong một ngày nào đó. Cặp số (;) xy nào sau đây biểu thị số cốc cafe mỗi loại mà cửa hàng bán được để tiền lãi trong ngày đó không ít hơn 1 triệu đồng? A. (25;25) B. (30;20) C. (41;11). D. (40;15). Lời giải Ta cần điều kiện là: 2015100043200 xyxy ++ Câu 7. Cặp số nào sau đây là nghiệm của bất phương trình 21 −xy ? A. (1;1). B. (1;2) C. (1;1) D. (0;0). Lời giải. Với 1,1==−xy ta có: 2.1(1)31 −−= . Chọn C Câu 8. Cặp số nào sau đây không là nghiệm của hệ bất phương
DẠYKÈMQUYNHƠN OFFICIAL
văn nghệ như sau: ()()()()()()()() 12108342122 . nABCnAnBnCnBCnABnACnABC =++−−−+ =++−−−+= Câu 5. Cho ba tập hợp: ( )( ) 22140,{ AxxxBnn =−−== là ước của 12} và {1;2;3} C = . Gọi ()nX là số phần tử của tập X . Mệnh đề nào sau đây là đúng? A. ()()() nBnAnC B.
. C.
.
trình: 2 43? xy xy −+− +− A. (4;1). B. (1;4) C. (0;5) D.
. Câu 9. Miền nghiệm của hệ bất phương trình: 39 28 6 xy xy y + + là phần mặt phẳng chứa điểm có toạ độ: A.
.
sinh đăng kí tham gia hội diễn
()()() nBnCnA
()()() nCnAnB
D. ()()()
Câu
ố
(1;8)
(1;2)
DẠYKÈMQUYNHƠN OFFICIAL
B. (0;0) C. (3;0). D. (8;4). Câu 10. Biết , xy thoả mãn hệ phương trình 2 36 2312 +− −+ − xy xy xy Giá trị nhỏ nhất của hàm số
2tan . D. 2cot Câu 14. Cho tam giác ABC có o4,6,120ABACBAC=== . Độ dài cạnh BC là A. 219 . B. 19 . C. 319 . D. 27 . Lời giải Chọn A Theo định lí cosin, ta có 222 2..cos76219BCABACABACABC =+−== Câu 15. Cho tam giác ABC có 3,4,6ABACBC=== . Khi đó độ dài đường trung tuyến của tam giác ABC kẻ từ A bằng A. 9 2 . B. 7 2 . C. 14 2 . D. 18 2 . Lời giải Chọn C Giả sử AM là đường trung tuyến của tam giác ABC kẻ từ A Ta có 222222 2 346714 242422 ABACBC AMAM ++ =−=−== . Câu 16. Cho tam giác ABC có 2,3,4ABACBC=== . Khi đó độ dài đường cao của tam giác ABC kẻ từ A bằng
A. 4047,2 B. 4043,2 C. 4043 D. 4047 Câu 11. Cho tam giác ABC không phải là tam giác vuông. Chọn khẳng định sai trong các khẳng định sau: A. sinsin()0 ++=ABC . B. coscos()0 ++=ABC C. tantan()0 ++=ABC . D. cotcot()0 ++=ABC . Lời giải Ta có: 180 ++=ABC . Suy ra: 180 +=− BCA. Do đó sinsin()0 ++ABC . Chọn A Câu 12. Cho góc nhọn . Biểu thức 22 (sincot)(costan) + bằng: A. 0. B. 1. C. 2. D. 22 tancot + Lời giải Ta có: sincos tan,cotcossin == . Do đó 2222 (sincot)(costan)cossin1 +=+= Chọn B Câu 13. Cho góc nhọn . Biểu thức ( ) tantan90 bằng: A. 1. B. 1. C.
S SAHBCAH BC
2 1315 28 ABC
. Câu 17. Trong tam giác ABC bất kì có ,, === BCaCAbABc . Bán kính đường tròn ngoại tiếp tam giác ABC là: A. sin = a R A . B. sin = b R A . C. 2sin = a R A . D. 2sin = c R A . Lời giải Chọn C Theo định lí sin ta có: 2 sinsinsin2sin ==== abca RR ABCA Câu 18. Tam giác ABC có 30 = A ; 20 b = ; 5 = c . Diện tích của tam giác ABC bằng: A. 25 B. 253 C. 252 D. 255 Lời giải Chọn A
Ta có 1 .sin25 2 ==SbcA .
Câu 19. Cho ba điểm , , ABC phân biệt. Khi đó:
A. Điều kiện cần và đủ để , , ABC thẳng hàng là AB cùng phương với .AC B. Điều kiện đủ để , , ABC thẳng hàng là với mọi ,M MA cùng phương với .AB C. Điều kiện cần để , , ABC thẳng hàng là với mọi ,M MA cùng phương với .AB D. Điều kiện cần để , , ABC thẳng hàng là .ABAC = Lời giải Chọn A Câu 20.
DẠYKÈMQUYNHƠN OFFICIAL
A. 315 2 . B. 315 4 . C. 315 8 . D. 315 . Lời giải Chọn C Ta có: 9 22 ABACBC p ++ ==
( )( )( ) 315 234 4 ABC Spppp
=−−−=
Mà
ABC
===
ếu MNPQ là
ột
thì ta có A. MNPQ = B. MNMQMP −= C. MPNQ = D. MNMQMP += Lời giải Chọn D Theo quy tắc hình bình hành. Câu 21. Tập xác định của hàm số ( )2 2 3 x y x + = là A. ( );3− B. ( ) 3;+ C. \3 D. Lời giải Chọn C Điều kiện: 303.xx− TXĐ: \3. Câu 22. Xét sự biến thiên của hàm số ( ) 3 = fx x trên khoảng ( ) 0;+ . Khẳng định nào sau đây đúng?
N
m
hình bình hành
A. Hàm số nghịch biến trên khoảng ( ) 0;+
B. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng ( ) 0;+
C. Hàm số đồng biến trên khoảng ( ) 0;+ D. Hàm số không đồng biến, không nghịch biến trên khoảng ( ) 0;+
lớn của 3F , biết 11 23 == FFN A. 6 B. 7 C. 8 D. 9 Lời giải Ta sử dụng các vectơ ,, ABACAD lần lượt biểu thị cho các lực 123 ,, FFF và vectơ AE để biểu thị cho hợp lực F của hai lực 12 , FF . Khi đó, tứ giác BACE là một hình bình hành. Từ đó, do 23 ==ABAC và 60 = BAC nên BACE là một hình thoi và tam giác ABC là một tam giác đều.

DẠYKÈMQUYNHƠN OFFICIAL
A ( ) ( ) ( ) ( ) ( ) ( ) 1212 2121 21 21212121 ,0;: 3 333 0 + −=−==− xxxx xxfxfx fxfx xxxxxxxx Vậy hàm số nghịch biến
0;+ . Câu 23. Trên mặt phẳng, chất điểm A chịu tác dụng của ba lực 123 ,, FFF
ở trạ
ữa hai vectơ 12 , FF bằng 60 .
Do đó 3 26 2 == AB AE Do A ở vị trí cân bằng nên hai lực F và 3F có củng cường độ và ngược hướng, tức là các vectơ AD và AE đối nhau. Bởi vậy, cường độ của lực 3F bẳng 3 ||6()=== FFAEN Câu 24. Cho đoạn thẳng BC và điểm A nằm giữa hai điểm , BC . Khẳng định nào sau đây là đúng? A. = AC ACAB AB B. =− AC ACAB AB C. = AB ACAB AC . D. =− AB ACAB AC . Lời giải Chọn B Câu 25. Tìm giá trị của m sao cho amb = , biết rằng , ab ngược hướng và 5,15ab==
Lời giải Chọn
trên khoảng ( )
và
ng thái cân bằng. Góc gi
Tính độ
Lời giải Chọn B
Do , ab ngược hướng nên 51 153 a m b =−=−=− .
Câu 26. Khi một quả bóng được đá lên nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết quỹ đạo của quả bóng là một cung parabol trong mặt phẳng tọa độ Oth có phương trình 2 hatbtc
0 a , trong đó t là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên, h là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2 m và sau 1 giây thì nó đạt độ cao 8,5m , sau 2 giây nó đạt độ cao 6m . Tính tổng abc A. 18,3 abc . B. 6,1 abc . C. 8,5 abc . D. 15,9 abc . Lời giải Chọn C
DẠYKÈMQUYNHƠN
A. 3 m = B. 1 3 m =− C. 1 3 m = D. 3 m =−
OFFICIAL
Từ giả thiết của bài toán ta có hệ phương trình 49 10 1,2 61 8,5 5 426 1,2 a c abcb abc c =− = ++== ++= = 17 2 abc ++= Câu 27. Xác định các hệ số a và b để Parabol ( ) 2 :4 Pyaxxb =+− có đỉnh ( )1;5 I A. 3 . 2 a b = =− B. 3 . 2 a b = = C. 2 . 3 a b = = D. 2 . 3 a b = =− Lời giải Chọn C Ta có: 4 112. 2 I xa a =−−=−= Hơn nữa ( )IP nên 543. abb −=−−= Câu 28. Nếu hai điểm , MN thoả mãn 9=−MNNM thì: A. 9 = MN . B. 3 = MN . C. 81 = MN . D. 6 = MN . Lời giải Chọn B Câu 29. Cho hình vuông ABCD có cạnh a . Tính ABAD A. 0 B. a C. 2 2 a D. 2 a Lời giải Chọn A Ta có o ...cos900 ==ABADaa . Câu 30. Cho M là trung điểm AB , tìm biểu thức sai: A. =− MAABMAAB B. =− MAMBMAMB C. .. = AMABAMAB . D. .. = MAMBMAMB . Lời giải
Phương án A: , MAAB ngược hướng suy ra o ...cos180. ==− MAABMAABMAAB nên loại#A.
Phương án B: , MAMB ngược hướng suy ra o ...cos180. ==− MAMBMAMBMAMB nên loại B.
Phương án C: , AMAB cùng hướng suy ra o ...cos0. == AMABAMABAMAB nên loại C.
Phương án D: , MAMB ngược hướng suy ra o ...cos180. ==− MAMBMAMBMAMB nên chọn D.
Câu 31. Cho tam thức bậc hai 2 ()(0) fxaxbxca=++ . Mệnh đề nào sau đây đúng?
A. Nếu 0 thì ( )fx luôn cùng dấu với hệ số a , với mọi x
B. Nếu 0 thì ( )fx luôn trái dấu với hệ số a , với mọi x .
C. Nếu 0 = thì ( )fx luôn cùng dấu với hệ số a , với mọi \ 2 b x a − D. Nếu 0 thì ( )fx luôn cùng dấu với hệ số b , với mọi x . Lời giải Chọn C
thức
fxxx
tất
giá
0 fx
OFFICIAL
DẠYKÈMQUYNHƠN
Chọn D
. D. 1 ;2 2 . Lời giải Chọn#A. Hàm số xác định 2 2520 xx −+ 1 2 2 x x . Câu 34. Tổng các nghiệm (nếu có) của phương trình: 212 xx−=− bằng: A. 6. B. 1. C. 5. D. 2. Lời giải Chọn C +) Với điều kiện 202xx− ta có phương trình đã cho tương đương với phương trình: 22 1() 21(2)650 5(/) xL xxxx xtm = −=−−+= = . Vậy phương trình có nghiệm duy nhất 5 x = Câu 35. Phương trình 2 422xxx −+=− có bao nhiêu nghiệm? A. 3 B. 0 C. 2 D. 1 Lời giải Chọn D 2 422xxx −+=− ( )2 2 220 422 x xxx − −+=− 2 1 51240 x xx −+= ( ) ( ) 1 2 2 5 x xn xl = = .
Câu 32. Cho tam
bậc hai ( ) 2 45
=−−+ . Tìm
cả
trị của x để ( )
. A. ( ) ;15; x−−+ . B. 1;5 x − . C. 5;1 x− D. ( )5;1 x − Lời giải Chọn C. Ta có ( ) 0 fx = 2 450xx −−+= 1 x = , 5 x =− Mà hệ số 10 a =− nên: ( ) 0 fx 5;1 x− Câu 33. Tìm tập xác định của hàm số 2 252yxx=−+ . A. ) 1 ;2; 2 −+ . B. ) 2;+ . C. 1 ; 2 −
2. Tự luận
Câu 1. Hai ô tô xuất phát tại cùng một thời điểm từ hai vị trí A và O với vận tốc trung bình lần lượt là 50 / kmh và 40 / kmh trên hai con đường vuông góc với nhau và giao tại O . Hướng đi của hai xe thể hiện ở Hình 19. Biết 8 = AOkm . Gọi x (giờ) là thời gian hai xe bắt đầu chạy cho tới khi cách nhau 5km (tính theo đường chim bay) trước khi ô tô đi từ A đến vị trí O . Tìm x
Lời giải
Quãng đường ô tô xuất phát từ , AO đi được sau x giờ lần lượt là 50( )xkm và 40( )xkm . Sau x giờ, ô tô xuất phát từ vị trí A đến C cách O một khoảng 850( ) =− OCxkm Sau x giờ, ô tô xuất phát từ vị trí O đến D cách O một khoảng Hình 20 40( ) = ODxkm . Để 8500 − x thì 00,16 x . Do tam giác OCD là tam giác vuông nên ta có: =+=−+2222 (850)(40).CDOCODxx Ta có phương trình: 22 (850)(40)5 −+= xx . Bình phương hai vế ta có: −+=−++=−+= 22222 (850)(40)252500800641600254100800390. xxxxxxx
Phương trình có hai nghiệm là 0,1 = x và 39 410 = x . Đối chiếu với điều kiện 00,16 x , ta nhận cả hai giá trị trên của x Vậy thời gian hai xe bắt đầu chạy cho tới khi cách nhau 5km (tính theo đường chim bay) trước khi ô tô đi từ A đến vị trí O là 39 410 giờ và 0,1 giờ.


DẠYKÈMQUYNHƠN
Vậy
OFFICIAL
2 x = là nghiệm của phương trình.
ị lớn nhất và giá trị nhỏ nhấ
ủ
ể
hệ bất phương trình 4 5 5 4 +− + − −− xy xy xy xy Lời giải Miền nghiệm của hệ bất phương trình bậc nhất hai ẩn là hình vuông ABCD với (5;0),(0,5;4,5),(4;0) ABC và (0,5;4,5)D .
Câu 2. Tìm giá tr
t c
a bi
u thức (;)43 =− Fxyxy trên miền nghiệm của
Tính giá trị của F tại các đỉnh của tứ giác: (5;0)20,(0,5;4,5)31 2 =−=FF , (4;0)16 −=− F và (0,5;4,5)23 2


F . So sánh các giá trị đó ta được giá trị lớn nhất cần tìm là (5;0)20 = F và giá trị nhỏ nhất cần tìm là (4;0)16 −=− F . Câu 3. Một người đứng trên mũi tàu thả neo giữa biển và phát hiện trên bờ biển (giả sử bờ biển là một đường thẳng) có hai ngọn hải đăng cách nhau 5km (theo bản đồ hàng hải). Người đó xác định được các góc tạo thành giữa các đường ngắm của hai ngọn hải đăng và đường thẳng từ tàu vuông góc với bờ là 15 và 35 (hình bên).
Hãy tính khoảng cách theo đơn vị kilômét giữa con tàu và bờ biển nối hai ngọn hải đăng (kết quả làm tròn đến hàng phần trăm). Lời giải Gọi , BC lần lượt là chân ngọn hải đăng thứ nhất và thứ hai. Gọi A là điểm người đứng trên tàu và H là hình chiếu của A lên BC .
DẠYKÈMQUYNHƠN OFFICIAL
=−
Theo giả thiết ta có 75,55,50.
===== Áp dụng Định lí sin cho tam giác ABC ta có sinsin ACBC ABCBAC = . Suy ra sin5sin75 6,30 sin50 sin BCABC AC BAC == Trong tam giác vuông AHC ta có cos6,30cos355,16( ).AHACHACkm =
HBAABCHCAACBBAC
Câu 4. Cho tam giác ABC và một điểm M bất kì. Chứng minh rằng 2 vMAMBMC =+− không phụ thuộc vào vị trí của điểm M. Dựng điểm D sao cho CDv = Lời giải

Ta có ( ) ( ) 22 vMAMBMCMAMCMBMCCACBCO =+−=−+−=+=
( Với O là trung điểm của AB)
Vậy 2 vCO = không phụ thuộc vào vị trí của điểm M
Vì 2 CDvCO == nên D là điểm đối xứng của C qua O
DẠYKÈMQUYNHƠN OFFICIAL
1. Trắc nghiệm
Câu 1. Cho mệnh đề : P "6 là số hoàn hảo" và mệnh đề Q : "Hà Nội là thủ đô của Việt Nam". Phát
biểu của mệnh đề PQ là
A. Nếu 6 là số hoàn hảo thì Hà Nội là thủ đô của Việt Nam.
B. Nếu Hà Nội là thủ đô của Việt Nam thì 6 là số hoàn hảo.
C. 6 là số hoàn hảo nếu Hà Nội là thủ đô của Việt Nam.
D. Nếu 6 là số hoàn hảo thì Hà Nội không là thủ đô của Việt Nam.
Câu 2. Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Đại dịch Covid 19 thật đáng sợ!
b) Hà Nam là một tỉnh của Việt Nam. c) 37 là một số nguyên tố. d) Cậu có thích học môn Lịch sử và Địa lí không?
OFFICIAL
A. 4. B. 3. C. 2. D. 1. Câu 3. Cho tập hợp {34}Axx=− và {1;3;9} B = . Tập hợp ()\ CABB = là A. {3;2;1;0;2} C =−−− . B. {3;2;1;0;2;4} C =−−− . C. {3;1;2} C =−− D. {3;2;1;0;1;2;3} C =−−− Câu 4. Cho tập ( ) ( ) 2249 0 .13 3 xxx Xx −−++ == Số tập con của X là A. 4. B. 0. C. 6. D. 8. Câu 5. Cho biểu đồ Ven sau đây. Phần được gạch sọc biểu diễn tập hợp nào? A. \ AB B. \ BA C. AB D. AB Câu 6. Miền nghiệm của bất phương trình 31 +xy là nửa mặt phẳng tạo bởi đường thẳng :31( +=dxy kể cả d ) chứa điểm có toạ độ nào sau đây? A. (0;0)


DẠYKÈMQUYNHƠN
ĐỀ SỐ 7
. B. (3;1) C. (1;1) D. (2;9). Câu 7. Phần không bị gạch (kể cả d ) ở Hình 3 là miền nghiệm của bất phương trình: A. 1 x B. 1 x C. 1 y D. 1 y Câu 8. Cặp số nào sau đây là nghiệm của hệ bất phương trình: 3515 ? 236 xy xy +− − A. (0;3).
B. (1;1)

C. (5;2). D. (2;3).


Câu 9. Miền nghiệm của hệ bất phương trình 1 2 − y y được xác định bởi phần không bị gạch và không kể hai đường thẳng , dd ' nào sau đây?
A. B. C. D.
Câu 10. Chủ cửa hàng điện thoại mang 200 triệu đồng hoặc mua điện thoại loại 10 triệu đồng hoặc máy tính bảng loại 9 triệu đồng ở đại lí cấp một. Gọi , xy lần lượt là số chiếc điện thoại và máy tính mà chủ cửa hàng mua. Cặp số (;) xy nào sau đây biểu thị số chiếc điện thoại và máy tính mà chủ cửa hàng có thể mua? A. (10;12) B. (11;10)
C. (9;13)
D. (11;11)

DẠYKÈMQUYNHƠN
OFFICIAL
Câu 11. Cho góc thoả mãn 0180 và 3 cos 5 =− . Giá trị của sin là: A. 3 5 . B. 4 5 . C. 4 5 D. 2 5 . Câu 12. Cho góc thoả mãn 0180 và tan2 =− . Giá trị của cot là: A. 2. B. 1 2 C. 1 2 . D. 3. Câu 13. Giá trị biểu thức tan0tan10tan20tan30 = T bằng: A. 0. B. 1. C. 1
.
.
D. 2.
Câu 14. Cho tam giác ABC có 04,3,30ABACBAC=== . Khi đó diện tích tam giác ABC bằng A. 3 B. 43 C. 63 D. 6

Câu 15. Cho tam giác ABC có 02,3,60ABACBAC=== . Khi đó bán kính đường tròn ngoại tiếp tam giác ABC bằng:
A. 621 7 . B. 7 . C. 21 3 . D. 321 7 .
Câu 16. Cho tam giác ABC nhọn có 3 BCa = và bán kính đường tròn ngoại tiếp tam giác ABC là 3 Ra = . Tính số đo góc A .
A. 120 = A B. 45 = A C. 30 = A D. 60 = A
Câu 17. Cho tam giác ABC có 4 c = , 6 b = , 60 = A . Chiều cao a h của tam giác ABC là: A. 321 7 a h = . B. 621 7 a h = . C. 1221 7 a h = . D. 221 7 a h = .
Câu 18. Cho tam giác ABC có 2 a = , 6 b = , 31 c =+ . Tính bán kính R của đường tròn ngoại tiếp. A. 2 . B. 2 2 . C. 2 . 3 D. 3.
Câu 19. Cho hình bình hành ABCD tâm O. Vectơ đối của BO là
A. CO B. AO C. DO D. OC Câu 20. Cho hình vuông ABCD cạnh a , độ dài vectơ ABACBD −+ bằng: A. a . B. 3a . C. 2 a . D. 22a . Câu 21. Cho hàm số 21 khi1 1khi 01 12 khi x0
xx yx x
− = − . Giá trị lớn nhất của hàm số trên 2;2 là: A. 2. B. 4. C. 5. D. 7. Câu 22. Điểm nào sau đây thuộc đồ thị của hàm số ( ) 2 1 x y xx = ? A. ( )0;1 M B. ( )2;1 M C. ( )2;0 M D. ( )1;1 M Câu 23. Trên Hình biểu diễn ba lực 123 ,, FFF cùng tác động vào một vật ở vị trí cân bằng A . Cho biết 1230,40== FNFN . Tính cường độ của lực 3F A. 50. B. 40. C. 30. D. 20.
DẠYKÈMQUYNHƠN
OFFICIAL
Câu 24. Cho đoạn thẳng AB . Gọi M là một điểm trên AB sao cho 1 4 = AMAB . Khẳng định nào sau đây sai? A. 1 3 = MAMB B. 1 4 = AMAB C. 3 4 = BMBA D. 3=− MBMA
Câu 25. Cho tam giác ABC . Gọi I là trung điểm của AB . Tìm điểm M thỏa mãn hệ thức 20MAMBMC++= .
A. M là trung điểm của BC
B. M là trung điểm của IC
C. M là trung điểm của IA
D. M là điểm trên cạnh IC sao cho 2 IMMC =
Câu 26. Hàm số 2 411yxx=−+ đồng biến trên khoảng nào trong các khoảng sau đây? A. (2;) −+ B. (;) −+ C. (2;) + D. (;2) −
Câu 27. Một quả bóng cầu thủ sút lên rồi rơi xuống theo quỹ đạo là parabol. Biết rằng ban đầu quả bóng được sút lên từ độ cao 1m sau đó 1 giây nó đạt độ cao 10m và 3,5 giây nó ở độ cao 6,25m Hỏi độ cao cao nhất mà quả bóng đạt được là bao nhiêu mét? A. 11m . B. 12m. C. 13m. D. 14m.
Câu 28. Cho a và b là hai vectơ cùng hướng và đều khác vectơ 0 . Mệnh đề nào sau đây đúng?
A. .. abab = . B. .0ab = . C. .1ab =− . D. .. abab =− .
Câu 29. Cho tam giác đều ABC cạnh bằng a và H là trung điểm BC . Tính . AHCA A. 2 3 4 a . B. 2 3 4 a . C. 2 3 2 a . D. 2 3 2 a .
Câu 30. Biết a , b 0 và .. abab =− . Câu nào sau đây đúng A. a và b cùng hướng. B. a và b nằm trên hai dường thẳng hợp với nhau một góc o120 . C. a và b ngược hướng. D. A, B, C đều sai. Câu 31. Gọi S là tập nghiệm của bất phương trình 2 870xx−+ . Trong các tập hợp sau, tập nào không là tập con của S ? A. ( ;0− . B.
2. Tự luận
Câu 1. Một người đi bộ xuất phát từ B trên một bờ sông (coi là đường thẳng) với vận tốc 6 / kmh để gặp một người chèo thuyền xuất phát cùng lúc từ vị trí A với vận tốc 3 / kmh. Nếu người chèo thuyền di chuyển theo đường vuông góc với bờ thì phải đi một khoảng cách 300 = AHm và gặp người đi bộ tại địa điểm cách B một khoảng 1400= BHm . Tuy nhiên, nếu di chuyển theo cách đó thì hai người không tới cùng lúc. Để hai người đến cùng lúc thì mỗi người cùng di chuyển về vị trí C (Hình 22).
DẠYKÈMQUYNHƠN
OFFICIAL
.
Tập
−+
−
( ) 2;+ Câu 33. Số nghiệm nguyên của bất phương trình 2 23150 xx−− là A. 6. B. 5. C. 8. D. 7 . Câu 34. Số nghiệm của phương trình 32xx −= là A. 2. B. 1. C. 3.
) 6;+
C. ) 8;+ . D. ( ;1−− . Câu 32.
nghiệm của bất phương trình 2 320 x x −+ là A. ( )1;2 B. ( ) ( ) ;12;
C. ( );1
D.
D. 0 . Câu 35. Số nghiệm của phương trình 222523xxxx −+=−+ là A. 2 B. 3 C. 1 D. 0
Câu 2.


a) Tính khoảng cách CB .
b) Tính thời gian từ khi hai người xuất phát cho đến khi gặp nhau cùng lúc.
Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 12 g hương liệu, 9 lịt nước và 315 g đường đề pha chế hai loại nước A và B . Để pha chế 1 lít nước A cần 45g đường, 1 lít nước và 0,5 g hương liệu; để pha chế 1 lít nước B cần 15 g đường, 1 lít nước và 2g hương liệu. Mỗi lít nước A nhận được 60 điểm thưởng, mỗi lít nước B nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước mỗi loại để đội chơi được số điểm thưởng là lớn nhất?
Câu 3. Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 45 và 75 . Biết khoảng cách giữa hai vị trí A, B là 30m (Hình). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm
OFFICIAL
DẠYKÈMQUYNHƠN
Câu 4. Cho hình vuông ABCD cạnh a. Chứng minh rằng 232 vMAMBMCMD =−+− không phụ thuộc vào vị trí của điểm M Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM 1A 2C 3A 4D 5A 6A 7B 8B 9B 10B 11B 12C 13A 14A 15C 16D 17B 18A 19C 20A 21C 22C 23A 24A 25B 26C 27C 28A 29B 30C 31B 32A 33A 34A 35C 1. Trắc nghiệm Câu 1. Cho mệnh đề : P "6 là số hoàn hảo" và mệnh đề Q : "Hà Nội là thủ đô của Việt Nam". Phát biểu của mệnh đề PQ là A. Nếu 6 là số hoàn hảo thì Hà Nội là thủ đô của Việt Nam. B. Nếu Hà Nội là thủ đô của Việt Nam thì 6 là số hoàn hảo. C. 6 là số hoàn hảo nếu Hà Nội là thủ đô của Việt Nam. D. Nếu 6 là số hoàn hảo thì Hà Nội không là thủ đô của Việt Nam. Câu 2. Trong các câu sau, có bao nhiêu câu là mệnh đề? a) Đại dịch Covid 19 thật đáng sợ! b) Hà Nam là một tỉnh của Việt Nam. c) 37 là một số nguyên tố.
tròn kết quả đến hàng đơn vị)?
ng :31( +=dxy kể cả d ) chứa điểm có toạ độ nào sau đây? A. (0;0). B. (3;1) C. (1;1) D. (2;9). Lời giải. Với 0,0==xy ta có: 3.0001 += . Chọn A. Câu 7. Phần không bị gạch (kể cả d ) ở Hình 3 là miền nghiệm của bất phương trình: A. 1 x B. 1 x C. 1 y D. 1 y Câu 8. Cặp số nào sau đây là nghiệm của hệ bất phương trình: 3515 ? 236 xy xy +− − A. (0;3).


DẠYKÈMQUYNHƠN OFFICIAL d) Cậu có thích học môn Lịch sử và Địa lí không? A. 4. B. 3. C. 2. D. 1. Câu 3. Cho tập hợp {34}Axx=− và {1;3;9} B = . Tập hợp ()\ CABB = là A. {3;2;1;0;2} C =−−− . B.
C =−−− . C.
C =−− . D.
C =−−− Câu 4. Cho tập ( ) ( ) 2249 0 .13 3 xxx Xx −−++ == Số tập con của X là A. 4. B. 0. C. 6. D. 8. Lời giải Chọn D Xét phương trình ( ) ( ) 22 491330 xxx −−++= ( ) 2 2 490 1330 x xx −= −++= 3 2 1 3 x x x = = = 3 2() 1 x doxQ x = = Khi đó tập 3 ,1 2 X = vậy số tập con của X là 3 28 = Câu 5. Cho biểu đồ Ven sau đây. Phần được gạch sọc biểu diễn tập hợp nào? A. \ AB B. \ BA C. AB D. AB Câu 6. Miền nghiệm của bất phương
31 +xy
nử
mặt
ẳng tạ
ởi đường
ẳ
{3;2;1;0;2;4}
{3;1;2}
{3;2;1;0;1;2;3}
trình
là
a
ph
o b
th
B. (1;1) C. (5;2). D. (2;3).




Câu 9. Miền nghiệm của hệ bất phương trình 1 2 − y y được xác định bởi phần không bị gạch và không
kể hai đường thẳng , dd ' nào sau đây?
A. B. C. D.
OFFICIAL
Câu 10. Chủ cửa hàng điện thoại mang 200 triệu đồng hoặc mua điện thoại loại 10 triệu đồng hoặc máy tính bảng loại 9 triệu đồng ở đại lí cấp một. Gọi , xy lần lượt là số chiếc điện thoại và máy tính mà chủ cửa hàng mua. Cặp số (;) xy nào sau đây biểu thị số chiếc điện thoại và máy tính mà chủ cửa hàng có thể mua? A. (10;12) B. (11;10). C. (9;13). D. (11;11)
DẠYKÈMQUYNHƠN
Câu 11. Cho góc thoả mãn 0180 và 3 cos 5 =− . Giá trị của sin là: A. 3 5 . B. 4 5 . C. 4 5 D. 2 5 . Câu 12. Cho góc thoả mãn 0180 và tan2 =− . Giá trị của cot là: A. 2. B. 1 2 C. 1 2 . D. 3. Câu 13. Giá trị biểu thức tan0tan10tan20tan30 = T bằng: A. 0. B. 1. C. 1
Lời giải Vì tan00 = nên 0 = T . Chọn A
Câu 14. Cho tam giác ABC có 04,3,30ABACBAC=== . Khi đó diện tích tam giác ABC bằng A. 3 B. 43 C. 63 D. 6 Lời giải Chọn A 0 11 ..sin.4.3.sin303. 22 ABC SABACBAC === Câu 15. Cho tam giác ABC có 02,3,60ABACBAC=== . Khi đó bán kính đường tròn ngoại tiếp tam giác ABC bằng: A. 621 7 B. 7 C. 21 3 D. 321 7 Lời giải Chọn C 22222 1 2...cos232.2.3.7 2 BCABACABACBAC=+−=+−= Bán kính đường tròn ngoại tiếp tam giác ABC bằng: 0 721 2sin2.sin603 BC R BAC === Câu 16. Cho tam giác ABC nhọn có 3 BCa = và bán kính đường tròn ngoại tiếp tam giác ABC là 3 Ra = . Tính số đo góc A A. 120 = A . B. 45 = A . C. 30 = A . D. 60 = A . Lời giải Chọn D Áp dụng định lý sin trong tam giác ABC , ta có 33 2sin sin22 23 ==== BCBCa RA AR a Suy ra 60 = A (do tam giác ABC nhọn). Câu 17. Cho tam giác ABC có 4 c = , 6 b =
DẠYKÈMQUYNHƠN OFFICIAL
D. 2.
, 60 = A . Chiều cao a h của tam giác ABC là: A. 321 7 a h = B. 621 7 a h = C. 1221 7 a h = D. 221 7 a h = Lời giải Chọn B Ta có: 222 2.cos abcbcA =+− 2 28 a = 27 a = . Diện tích tam giác: 11 ..sin. 22 a SbcAha == ..sin621 7 a bcA h a == Câu 18. Cho tam giác ABC có 2 a = , 6 b = , 31 c =+ . Tính bán kính R của đường tròn ngoại tiếp. A. 2 . B. 2 2 . C. 2 . 3 D. 3. Lời giải Chọn A Ta có : 222 cos 2 bca A bc +− = 2 2 = 45 A =
Trên 1;2 hàm số 21yx=− đồng biến nên giá trị lớn nhất bằng ( ) 23 y = Trên ( )0;1 hàm số 1 y = nên giá trị lớn nhất bằng 1 y = Trên 2;0 hàm số 12 yx =− nghịch biến nên giá trị lớn nhất bằng ( ) 25 y −= Vậy giá trị lớn nhất của hàm số trên 2;2 là ( ) 25 y −= .
Câu 22. Điểm nào sau đây
DẠYKÈMQUYNHƠN OFFICIAL Do đó :
a R
= 2
= 2 =
.
2sin
A
2.sin45
Câu 19. Cho hình bình hành ABCD tâm O. Vectơ đối của BO là A. CO . B. AO . C. DO . D. OC . Lời giải Chọn C Từ hình vẽ suy ra BODO Câu 20. Cho hình vuông ABCD cạnh a , độ dài vectơ ABACBD −+ bằng: A. a B. 3a C. 2 a D. 22a Lời giải Vì ABCD là hình vuông nên: CACBCD =+ và BDBCBA =+ Ta có: ABACBDABCABDABCDCBBABC −+=++=++++ ABCDCBABCBCD =++−−= Mà CDa = . Từ đó độ dài ABACBDa −+= . Câu 21. Cho hàm số 21 khi1 1khi 01 12 khi x0 xx yx x − = −
Giá trị lớn nhất của hàm số trên 2;2 là: A. 2. B. 4. C. 5. D. 7. Lời giải Chọn C
thuộc đồ thị của hàm số ( ) 2 1 x y xx = ? A. ( )0;1 M B. ( )2;1 M C. ( )2;0 M D. ( )1;1 M Lời giải Với 2 x = thì 0 y = . Vậy điểm ( )2;0 M thuộc đồ thị hàm số đã cho. Đáp án C. Câu 23. Trên Hình biểu diễn ba lực 123 ,, FFF cùng tác động vào một vật ở vị trí cân bằng A . Cho biết 1230,40== FNFN . Tính cường độ của lực 3F . O C A B D


DẠYKÈMQUYNHƠN OFFICIAL A. 50. B. 40. C. 30. D. 20. Lời giải Ta sử dụng các vectơ ,, ABACAD lần lượt biều thị cho các lực 123 ,, FFF và vectơ AE biểu thi cho hợp lực F của 12 , FF Khi đó, do 90 = BAC , nên tứ giác ABEC là hình chữ nhật. Từ đó, do 30() = ABN , 40( ) = ACN , suy ra 22 ||304050( ). FAEN ==+= Do vật ở vị trí cân bằng, nên hai lực F và 3F có cùng cường độ và ngược hướng, tức là các vectơ AE và AD là các vectơ có cùng độ dài và ngược hướng. Bởi vậy, cường độ của lực 3F bằng 3 ||50()=== FFAEN Câu 24. Cho đoạn thẳng AB . Gọi M là một điểm trên AB sao cho 1 4 = AMAB . Khẳng định nào sau đây sai? A. 1 3 = MAMB B. 1 4 = AMAB C. 3 4 = BMBA D. 3=− MBMA Câu 25. Cho tam giác ABC . Gọi I là trung điểm của AB . Tìm điểm M thỏa mãn hệ thức 20MAMBMC++= . A. M là trung điểm của BC B. M là trung điểm của IC C. M là trung điểm của IA
D. M là điểm trên cạnh IC sao cho 2 IMMC =
Lời giải
Chọn B 202200 MAMBMCMIMCMIMC ++=+=+= M là trung điểm của IC .
Câu 26. Hàm số 2 411yxx=−+ đồng biến trên khoảng nào trong các khoảng sau đây?
A. (2;) −+ B. (;) −+ C. (2;) + D. (;2) −

Lời giải
Chọn C
Ta có bảng biến thiên:
Từ bảng biến thiên ta thấy, hàm số đồng biến trên khoảng (2;) +
Câu 27. Một quả bóng cầu thủ sút lên rồi rơi xuống theo quỹ đạo là parabol. Biết rằng ban đầu quả bóng được sút lên từ độ cao 1m sau đó 1 giây nó đạt độ cao 10m và 3,5 giây nó ở độ cao 6,25m. Hỏi độ cao cao nhất mà quả bóng đạt được là bao nhiêu mét? A. 11m . B. 12m. C. 13m. D. 14m .
Lời giải Chọn C
DẠYKÈMQUYNHƠN
OFFICIAL
Biết rằng quỹ đạo của quả bóng là một cung parabol nên phương trình có dạng
Theo bài ra gắn vào hệ tọa độ và sẽ tương ứng các điểm A , B , C nên ta có 1 10 12,253,56,25 c abc abc = ++= ++= 3 12 1 a b c =− = = . Suy ra phương trình parabol là 2 3121yxx=−++ Parabol có đỉnh (2;13)I . Khi đó quả bóng đạt vị trí cao nhất tại đỉnh tức 13m h = Câu 28. Cho a và b là hai vectơ cùng hướng và đều khác vectơ 0 . Mệnh đề nào sau đây đúng? A. .. abab = . B. .0ab = . C. .1ab =− . D. .. abab =− . Lời giải Chọn A Do a và b là hai vectơ cùng hướng nên ( ) ( ) 0 ,0cos,1 abab=⎯⎯→= . Vậy abab = . Câu 29. Cho tam giác đều ABC cạnh bằng a và H là trung điểm BC . Tính . AHCA 12 10 8 6 4 2 5 y x O A B C
2 yaxbxc =++
Lời giải
Chọn B
Ta có ( ) 2 o 33 ...cos,..cos150 24 ===− AHCAAHCAAHCAaaa
Câu 30. Biết a , b 0 và .. abab =− . Câu nào sau đây đúng
A. a và b cùng hướng. B. a và b nằm trên hai dường thẳng hợp với nhau một góc o120 . C. a và b ngược hướng. D. A, B, C đều sai.
Lời giải
Chọn C
Ta có ( ) ( ) ...cos,.cos,1 =−=−=− abababababab nên a và b ngược hướng
DẠYKÈMQUYNHƠN OFFICIAL A. 2 3 4 a
2 3
a
2 3
a
2 3
a
B.
4
C.
2
D.
2
A Ta có 2 32012. x xx −+ Vậy tập nghiệm của bất phương trình 2 320 x x −+ là ( )1;2 . Chọn đáp án#A. Câu 33. Số nghiệm nguyên của bất phương trình 2 23150 xx−− là A. 6 B. 5 C. 8 D. 7 Lời giải Chọn#A. Xét ( ) 2 2315fxxx=−− . ( ) 0 fx = 3129 4 x = Ta có bảng xét dấu: x 3129 4 3129 4 + ( )fx + 0 0 + Tập nghiệm của bất phương trình là 31293129 ; 44 S −+ =
Câu 31. Gọi S là tập nghiệm của bất phương trình 2 870xx−+ . Trong các tập hợp sau, tập nào không là tập con của S ? A. ( ;0− . B. ) 6;+ . C. ) 8;+ . D. ( ;1−− . Lời giải Chọn B Ta có 2 1 870 7 x xx x −+ . Suy ra tập nghiệm của bất phương trình là ( ) ;17; S =−+ Do đó ) 6; S + . Câu 32. Tập nghiệm của bất phương trình 2 320 x x −+ là A. ( )1;2 B. ( ) ( ) ;12; −+ C. ( );1− D. ( ) 2;+ Lời giải Chọn
2. Tự luận
Câu 1. Một người đi bộ xuất phát từ B trên một bờ sông (coi là đường thẳng) với vận tốc 6 / kmh để gặp một người chèo thuyền xuất phát cùng lúc từ vị trí A với vận tốc 3 / kmh. Nếu người chèo thuyền di chuyển theo đường vuông góc với bờ thì phải đi một khoảng cách 300 = AHm và gặp người đi bộ tại địa điểm cách B một khoảng 1400= BHm . Tuy nhiên, nếu di chuyển theo cách đó thì hai người không tới cùng lúc. Để hai người đến cùng lúc thì mỗi người cùng di chuyển về vị trí C (Hình 22). a) Tính khoảng cách CB . b) Tính thời gian từ khi hai người xuất phát cho đến khi gặp nhau cùng lúc.

DẠYKÈMQUYNHƠN OFFICIAL Do đó bất phương trình có 6 nghiệm nguyên là 2, 1, 0 , 1, 2, 3. Câu 34. Số nghiệm của phương trình 32xx −= là A. 2. B. 1. C. 3. D. 0 . Lời giải Chọn A Ta có 32xx −= 2 0 32 x xx −= 2 0 320 x xx −+= 0 1 2 2 1 x x x x x = = = = Vậy phương trình đã cho có 2 nghiệm. Câu 35. Số nghiệm của phương trình 222523xxxx −+=−+ là A. 2 B. 3 C. 1 D. 0 Lời giải Chọn C Ta có: 2 250, xxx−+ Đặt 2 25txx=−+ , ta có phương trình trở thành 2 tt=− ( )2 2 2 22 24 1 2540 4 t t t ttt t tt tt t =−= = −+= =− = . Khi đó ( )2 2 425101 xxxx =−+−== . Thử lại ta thấy 1 x = thỏa mãn. Suy ra phương
trình đã cho có một nghiệm.
Lời giải a)
CHxmx
Ta
22 300,1400 =+=− ACxCBx
Vì
C nên +− =+=− 22 22 3001400 23001400. 30006000 xx xx Giải
) = xm với 0 x Vậy
) =−= CBm b)
cho đến khi tới C là 10 phút. Câu 2. Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 12 g hương liệu, 9 lịt nước và 315 g đường đề pha chế hai loại nước A và B . Để pha chế 1 lít nước A cần 45g đường, 1 lít
Đặt ( )(0)=
.
có:
.
hai người gặp nhau cùng lúc tại
phương trình trên ta có: 400(
khoảng cách 14004001000(
Thời gian hai người bắt đầu di chuyển
nước và 0,5 g hương liệu; để pha chế 1 lít nước B cần 15 g đường, 1 lít nước và 2g hương liệu. Mỗi lít nước A nhận được 60 điểm thưởng, mỗi lít nước B nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước mỗi loại để đội chơi được số điểm thưởng là lớn nhất? Lời giải Gọi x và y lần lượt là số lít nước loại A và B cần pha chế. Khi đó, theo đề bài ta có hệ bất phương trình
ờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 45 và 75 . Biết khoảng cách giữa hai vị trí A, B là 30m (Hình). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

DẠYKÈMQUYNHƠN OFFICIAL
+ + + x
của
==FF và
=
= F . Vậy
Câu
Một người đi dọc b
0 0 9 4515315 0,5212.
y xy xy xy Số điểm thưởng đội chơi nhận được là (;)6080 =+ Fxyxy (điểm). Ta cần tìm giá trị lớn nhất của (;)Fxy với (;) xy thoả mãn hệ trên. Miền nghiệm của hệ là miền ngũ giác OABCD với (0;6),(4;5),(6;3) ABC , (7;0)D và (0;0)O . Tính giá trị
F tại các đỉnh của ngũ giác: (0;6)480,(4;5)640 ==FF , (6;3)600,(7;0)420
(0;0)0
F . So sánh các giá trị đó ta được giá trị lớn nhất cần tìm là (4;5)640
cần pha chế 4 lít nước loại A và 5 lít nước loại B đề số điểm thưởng nhận được là lớn nhất.
3.


DẠYKÈMQUYNHƠN OFFICIAL
Gọi
Ta
=−=−=ABCCBH ( ) ˆ 180()1804511520 =−+=−+= ACBAACB
ABC
==
Tam
==
Vậy
hải đăng cách bờ biển 56m Câu 4. Cho hình vuông ABCD cạnh a. Chứng minh rằng 232 vMAMBMCMD =−+− không phụ thuộc vào vị trí của điểm M Lời giải. Gọi O là tâm hình vuông Theo quy tắc ba điểm ta có ( ) ( ) ( ) ( ) 232 vMOOAMOOBMOOCMOOD =+−+++−+ 232 OAOBOCOD =−+− Mà ,2 ODOBOCOAvOA =−=−=− Suy ra 232 vMAMBMCMD =−+− không phụ thuộc vào vị trí của điểm M
Lời giải
C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB . Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.
có: 18018075115
Áp dụng định lí sin trong tam giác
ta có: sinsin = ABAC CB 30 sinsin11579,5 sinsin20
AB ACB C
giác ACH vuông tại H nên ta có: sin.sin45.79,556
CHAAC
ngọn
1. Trắc nghiệm
Câu 1. Mệnh đề nào sau đây là mệnh đề tương đương?
A. 10 chia hết cho 5 là điều kiện cần để 10 chia hết cho 2.
B. Hình vuông là hình chữ nhật.
C. Hình thang nội tiếp đường tròn khi và chỉ khi nó là hình thang cân.
D. Nếu 63 chia hết cho 7 thì hình thoi có hai đường chéo vuông góc nhau.
Câu 2. Mệnh đề: " 2 ,33xx " khẳng định là
A. Bình phương của mỗi số thực lớn hơn 33.
B. Có ít nhất một số thực mà bình phương của nó lớn hơn 33.
C. Chỉ có một số thực
bình phương lớn hơn
. Giá trị nguyên dương của m để tập hợp (\) AB có đúng 10 phần tử là A. 10. B. 11. C. 12. D. 13. Câu 5. Cho (;2)[6;) CA =−+ và [5;9) CB = . Tập hợp XAB = là A. [2;5). B. (2;5). C. [2;5] D. [6;9)


Câu 6. Cặp số nào sau đây là nghiệm của bất phương trình 55−+ xy ? A. (1;9) . B. (2;1) C. (2;2) D. (0;5).
Câu 7. Miền nghiệm của bất phương trình 2 −+ xy được xác định bởi miền nào (nửa mặt phẳng không bị gạch và không kể d) sau đây? A. B.
DẠYKÈMQUYNHƠN
ĐỀ SỐ 8
OFFICIAL
{412}Cnn= . Mệnh
sau
đúng? A. () ABCB = B. () ABCA = C. () ABCC = . D. ()ABC= . Câu 4. Cho tập hợp (3;]Am =− và {3}Bxx=
có
33. D. Nếu x là số thực thì 2 33 x . Câu 3. Cho A là tập hợp các số tự nhiên chẵn không lớn hơn 12,{6} Bnn= ,
đề nào
đây là
C. D.
Câu 8. Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình
A. (3;2)A . B. (6;3)B C. (6;4)C D. (5;4)D . Câu 9. Cho điểm (3;3)A và điểm M thuộc miền nghiệm của hệ bất phương trình


Độ dài AM lớn nhất là A. 22 B. 52 . C. 10 D. 34 .
Câu 10. Một cửa hàng bán hai loại mặt hàng A và B . Biết rằng cứ bán một mặt hàng loại A cửa hàng lãi 5 nghìn đồng, bán một mặt hàng loại B cửa hàng lãi 7 nghìn đồng. Gọi , xy lần lượt là số mặt hàng loại A và mặt hàng loại B mà cửa hàng đó bán ra trong một tháng. Cặp số (;) xy nào sau đây biểu thị số mặt hàng bán ra mỗi loại của cửa hàng trong một tháng mà tổng số tiền lãi không ít hơn 30 triệu đồng?
DẠYKÈMQUYNHƠN OFFICIAL
0
5? xy
xy − −− +
xy xy xy +− ++ −++ −+
33
xy
20 20 20 20 xy
A.
. D.
. Câu 11. Cho góc thoả mãn 0180 và cot2 =− . Giá trị của sin là: A. 1 2 . B. 1 5 C. 5 5 . D. 5 5 . Câu 12. Giá trị biểu thức tan1tan2.tan89 = T bằng: A. 0. B. 1. C. 1.
(1000;2000) B. (3000;1000) C. (2000;3000)
(3000;2000)
D. 2.
Câu 13. Cho 1 sin 4 = , với 090 . Giá trị cos bằng
A. 15 4 . B. 15 4 . C. 15 16 . D. 15 16 .
Câu 14. Cho tam giác ABC có 4cm = AB ; 12cm= AC và góc 120 BAC = . Tính diện tích tam giác ABC .
A. 123 ( 2 cm ). B. 243( 2 cm ). C. 12( 2 cm ). D. 24( 2 cm ).
Câu 15. Cho tam giác ABC thỏa mãn 222 2.0BCACABBCAC +−−= . Khi đó, góc C có số đo là A. 150 C = . B. 60 C = . C. 45 C = . D. 30 C = .
Câu 16. Tam giác ABC có 60,45BC và 5 AB . Tính độ dài cạnh AC .
A. 56 2 AC B. 53. AC C. 56 . 3 AC D. 56 4 AC
Câu 17. Một tam giác có ba cạnh là 52, 56, 60. Bán kính đường tròn ngoại tiếp tam giác đó là
A. 65 4 . B. 40. C. 32,5. D.65,8.
Câu 18. Cho tam giác ABC có 12 AB = , 13 AC = , 5 BC = . Diện tích S của tam giác ABC là: A. 30 S = B. 40 = S C. 50 = S D. 60 = S
Câu 19. Cho tam giác ABC , có thể xác định được bao nhiêu véc tơ khác véc tơ không có điểm đầu và điểm cuối là các đỉnh của tam giác đã cho?
A. 4. B. 5 C. 7. D. 6.
Câu 20. Tổng MNPQRNNPQR ++++ bằng vectơ nào sau đây?
A. .MR B. .MN C. .PR D. .MP
Câu 21. Cho hàm số ( ) 326116yfxxxx ==−+− . Kết quả sai là A. ( ) 10 f = B. ( ) 20 f = C. ( ) 30 f = D. ( ) 424 f −=− Câu 22. Tập xác định của hàm số 2 5 1 = y x là A. \1 . B. \1;1 . C. \1 . D. . Câu
DẠYKÈMQUYNHƠN
OFFICIAL
ABC
có cạnh
6.
18
Cho
thẳng AB và
AB
5
=
khẳng định nào sai ? A. 1 5 AMAB = B. 1 4 MAMB =− C. 4 MBMA =− D. 4 5 MBAB =− Câu 25. Cho hình bình hành ABCD, điểm M thõa mãn 4AMABADAC =++ . Khi đó điểm M là: A. Trung điểm của AC B. Điểm C C. Trung điểm của AB D. Trung điểm của AD Câu 26. Cho hàm số 2 (0)yaxbxca =++ có đồ thị (P). Biết đồ thị của hàm số có đỉnh (1;1)I và đi qua điểm (2;3)A . Tính tổng 222 Sabc =++ A. 3. B. 4. C. 29. D. 1. Câu 27. Cho hàm số 2 43.yxx=−++ Chọn khẳng định đúng. A. Hàm số đồng biến trên B. Hàm số nghịch biến trên C. Hàm số đồng biến trên ( ) 2;+ D. Hàm số nghịch biến trên ( ) 2;+ Câu 28. Cho hai vectơ a và b khác 0 . Xác định góc giữa hai vectơ a và b khi abab =−
23. Cho tam giác
đều
là
Tính ABAC + . A. 62 B.
C. 12 D. 63 Câu 24.
đoạn
M là một điểm trên đoạn
sao cho 1
MAAB
. Trong các khẳng định sau,
A. o180 = . B. o0 = . C. o90 = . D. o45 = . Câu 29. Cho 2 vectơ a và b có 4 a = , 5 b = và ( ) o,120ab = .Tính ab + A. 21. B. 61. C. 21. D. 61. Câu 30. Cho tam giác ABC vuông tại A có o ˆ 60 B = , ABa = . Tính . ACCB A. 2 3a . B. 2 3a . C. 3a . D. 0 . Câu 31. Bất phương trình 2 230xx −++ có tập nghiệm là A. ( ) ( ) ;13; −−+ B. ( )1;3 C. 1;3 D. ( )3;1 Câu 32. Tập nghiệm của bất phương trình 2 120 xx −++ là A. ( ) ;34; −−+ B. C. ( ) ;43; −−+ D. 3;4 Câu 33. Biểu thức ( )( ) 2 310345 xxx−+− âm khi và chỉ khi A. 5 ;. 4 x − B. 15 ;;3. 34 x − C. ( ) 15 ;3;. 34 x + D. 1 ;3. 3 x

Câu 34. Nghiệm của phương trình 566 xx+=− bằng A. 15 B. 6 C. 2 và 15 D. 2 Câu 35. Tích các nghiệm của phương trình 2211xxxx++=+− là A. 3 B. 3 C. 1 D. 0
2. Tự luận
Câu 1. Người ta muốn thiết kế một vườn hoa hình chữ nhật nội tiếp trong một miếng đất hình tròn có đường kính bằng 50m (Hình 23). Xác định kích thước vườn hoa hình chữ nhật để tổng quãng đường đi xung quanh vườn hoa đó là 140m . Câu 2. Bác Năm dự định trồng ngô và đậu xanh trên một mảnh đất có diện tích 8 ha. Nếu trồng 1 ha ngô thì cần 20 ngày công và thu được 40 triệu đồng. Nếu trồng 1 ha đậu xanh thì cần 30 ngày công và thu được 50 triệu đồng. Bác Năm cần trồng bao nhiêu hecta cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng không quá 180 ngày công cho việc trồng ngô và đậu xanh.
Câu 3. Gia đình bạn An sở hữu một mảnh đất hình tam giác. Chiều dài của hàng rào MN là 150m , chiều dài của hàng rào MP là 230m . Góc giữa hai hàng rào MN và MP là 110 (Hình 21) .
a) Diện tích mảnh đất mà gia đình bạn An sở hữu là bao nhiêu mét vuông (làm tròn kết
DẠYKÈMQUYNHƠN OFFICIAL
b) Chiều
Câu 4. Cho tam giác ABC. Gọi A’, B’, C’
xác
bởi 2011'2012'0 ABAC+= , 2011'2012'0 BCBA+= ; 2011'2012'0 CACB+= . Chứng minh hai tam giác ABC và
có cùng trọng tâm. Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM
quả đến hàng phần mười)?
dài hàng rào NP là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
là các điểm
định
A’B’C’
1C 2B 3B 4D 5A 6D 7D 8A 9D 10C 11D 12B 13A 14A 15C 16A 17C 18A 19D 20A 21D 22B 23D 24D 25A 26C 27D 28A 29A 30B 31B 32D 33B 34A 35B
1. Trắc nghiệm
Câu 1. Mệnh đề nào sau đây là mệnh đề tương đương?
A. 10 chia hết cho 5 là điều kiện cần để 10 chia hết cho 2.
B. Hình vuông là hình chữ nhật.
C. Hình thang nội tiếp đường tròn khi và chỉ khi nó là hình thang cân.
D. Nếu 63 chia hết cho 7 thì hình thoi có hai đường chéo vuông góc nhau.
Câu 2. Mệnh đề: " 2 ,33xx " khẳng định là
A. Bình phương của mỗi số thực lớn hơn 33.
B. Có ít nhất một số thực mà bình phương của nó lớn hơn 33.
C. Chỉ có một số thực có bình phương lớn hơn 33. D. Nếu x là số thực thì 2 33 x .
3. Cho A là tậ
DẠYKÈMQUYNHƠN
OFFICIAL
AB = do đó 13 m = . Câu 5. Cho (;2)[6;) CA =−+ và [5;9) CB = . Tập hợp XAB = là A. [2;5) B. (2;5). C. [2;5]. D. [6;9) Lời giải [2;6),(;5)[9;)AB==−+ . Suy ra [2;5) XAB== . Câu 6. Cặp số nào sau đây là nghiệm của bất phương trình 55−+ xy ? A. (1;9) B. (2;1). C. (2;2). D. (0;5). Câu 7. Miền nghiệm của bất phương trình 2 −+ xy được xác định bởi miền nào (nửa mặt phẳng không bị gạch và không kể d) sau đây?
Câu
p hợp các số tự nhiên chẵn không lớn hơn 12,{6} Bnn= , {412}Cnn= . Mệnh đề nào sau đây là đúng? A. () ABCB = . B. () ABCA = C. () ABCC = D. ()ABC= . Câu 4. Cho tập hợp (3;]Am =− và {3}Bxx= . Giá trị nguyên dương của m để tập hợp (\) AB có đúng 10 phần tử là A. 10. B. 11. C. 12. D. 13. Lời giải Ta có [3;3] B =− . Theo giả thiết thì \ AB nên 3 m và \(3;] ABm = . Như vậy, để tập hợp (\) AB có 10 phần tử thì (\){4;5;;13}
A. B. C. D. Câu 8. Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình 0 33 5?
xy xy xy
− −− + A. (3;2)A . B. (6;3)B C. (6;4)C D. (5;4)D . Câu 9. Cho điểm (3;3)A và điểm M thuộc miền nghiệm của hệ bất phương trình 20 20 20 20





xy xy xy xy
+− ++ −++ −+ Độ dài AM lớn nhất là A. 22 B. 52 . C. 10 D. 34 . Lời giải Miền nghiệm của hệ bất phương trình là miền không bị gạch trong hình bên. Suy ra độ dài AM lớn nhất khi và chỉ khi M trùng với đỉnh nào đó của đa giác nghiệm. Câu 10. Một cửa hàng bán hai loại mặt hàng A và B . Biết rằng cứ bán một mặt hàng loại A cửa hàng lãi 5 nghìn đồng, bán một mặt hàng loại B cửa hàng lãi 7 nghìn đồng. Gọi , xy lần lượt là số mặt hàng loại A và mặt hàng loại B mà cửa hàng đó bán ra trong một tháng. Cặp số (;) xy
DẠYKÈMQUYNHƠN OFFICIAL
DẠYKÈMQUYNHƠN OFFICIAL nào
đây biểu thị số mặt hàng bán ra mỗi loại của cửa hàng trong một tháng mà tổng số tiền lãi
30 triệu đồng?
.
.
. Câu 11. Cho góc thoả mãn 0180 và cot2 =− . Giá trị của sin là:
1 2 . B. 1 5 . C. 5 5 . D. 5 5 . Lời giải Ta có: 22 22 222 coscos1sin1 cotcot1cot sinsinsinsin ===+= . Do đó 2 22 111 sin 1cot1(2)5 === ++− . Vì 0180 nên 5 sin 5 = Chọn D Câu 12. Giá trị biểu thức tan1tan2.tan89 = T bằng: A. 0. B. 1. C. 1 D. 2. Lời giải Ta có: ( )( ) ( ) tan1tan89tan2tan88tan44tan46tan45 = T ( )( ) ( ) tan1cot1tan2cot2tan44cot44tan45 = 1.1.111.== Chọn B Câu 13. Cho 1 sin 4 = , với 090 . Giá trị cos bằng A. 15 4 . B. 15 4 . C. 15 16 . D. 15 16 . Lời giải Chọn A Ta có 2 22 115 cos1sin1 416 =−=−= 15 cos 4 = (do 090 ) Vậy 15 cos 4 = . Câu 14. Cho tam giác ABC có 4cm = AB ; 12cm= AC và góc 120 BAC = . Tính diện tích tam giác ABC . A. 123 ( 2 cm ). B. 243( 2 cm ). C. 12( 2 cm ). D. 24( 2 cm ). Lời giải Chọn A Diện tích tam giác ABC là 1 ..sin 2 SABACBAC = 1 .4.12.sin120 2 = 123 = ( 2 cm ) Câu 15. Cho tam giác ABC thỏa mãn 222 2.0BCACABBCAC +−−= . Khi đó, góc C có số đo là
sau
không ít hơn
A. (1000;2000) B. (3000;1000)
C. (2000;3000)
D. (3000;2000)
A.
A. 150 C = . B. 60 C = . C. 45 C = . D. 30 C = . Lời giải
Chọn C Theo đề ra ta có: 222 2.0BCACABBCAC +−−= 222 2. BCACABBCAC+−= 222 2 BCACAB BCAC +− = 2cos20 C −= 2 cos 2 C = 45 C = .
Câu 16. Tam giác ABC có 60,45BC và 5 AB . Tính độ dài cạnh AC A. 56 2 AC B. 53. AC C. 56 3 AC D. 56 4 AC Lời giải
Chọn A Theo định lí sin ta có: 0 0 556 sinsin2 sin45 sin60 ABACAC AC CB . Câu 17. Một tam giác có ba cạnh là 52, 56, 60. Bán kính đường tròn ngoại tiếp tam giác đó là A. 65 4 . B. 40. C. 32,5. D.65,8. Lời giải Chọn C Ta có: 525660 84 2 p ++ == Áp dụng hệ thức Hê rông ta có: ( ) ( ) ( ) 84.8452.8456.84601344 S =−−−= . Mặt khác 52.56.60 32,5 444.1344 abcabc SR RS ====
Câu 18. Cho tam giác ABC có 12 AB = , 13 AC = , 5 BC = . Diện tích S của tam giác ABC là: A. 30 S = B. 40 = S C. 50 = S D. 60 = S Lời giải Chọn A Ta có: 222 BABCAC += nên tam giác ABC vuông tại B. Diện tích tam giác là: 1 .30 2 SBABC== .
Câu 19. Cho tam giác ABC , có thể xác định được bao nhiêu véc tơ khác véc tơ không có điểm đầu và điểm cuối là các đỉnh của tam giác đã cho? A. 4. B. 5 C. 7 . D. 6. Lời giải Các véc tơ khác véc tơ không có điểm đầu và điểm cuối là các đỉnh của tam giác đã cho gồm ,,,,,.
DẠYKÈMQUYNHƠN OFFICIAL
ABBAACCABCCB Vậy có 6 véc tơ. Câu 20. Tổng MNPQRNNPQR ++++ bằng vectơ nào sau đây? A. MR B. MN C. PR D. MP Lời giải Chọn A Ta có MNPQRNNPQRMNNPPQQRRNMN ++++=++++= Câu 21. Cho hàm số ( ) 326116yfxxxx ==−+− . Kết quả sai là A. ( ) 10 f = B. ( ) 20 f = C. ( ) 30 f = D. ( ) 424 f −=− Lời giải Chọn D ( ) 4210 f −=− . Câu 22. Tập xác định của hàm số 2 5 1 = y x là



DẠYKÈMQUYNHƠN OFFICIAL A. \1 B. \1;1
\1
Lời
Chọn B Hàm
2
− − x x x Vậy
=− D . Câu
Cho
u
ạ
.
+ . A.
Lời
Gọi I là trung điểm của BC. Vì tam giác ABC đều có cạnh là 6, nên ta có AIBC ⊥ . Xét tam giác AIB vuông tại I , có 222222226327 ABAIIBAIABIB=+=−=−= Suy ra 2733 AI == Mặt khác ta có: 222263ABACAIABACAIAIAI +=+==== . Câu
Cho
1 5
=
A.
= B.
4
=− C.
=− D.
=− Lời
Chọn
Ta
Câu
Cho
.
A. Trung
C. Trung
Lời
A. 3. B. 4. C. 29. D. 1.
C.
D.
giải
số đã cho xác định khi
1 10 1
tập xác định của hàm số là
\1;1
23.
tam giác ABC đề
có c
nh là 6
Tính ABAC
62 B. 18 C. 12 D. 63
giải Chọn D
24.
đoạn thẳng AB và M là một điểm trên đoạn AB sao cho
MAAB
. Trong các khẳng định sau, khẳng định nào sai ?
1 5 AMAB
1
MAMB
4 MBMA
4 5 MBAB
giải
D
thấy MB và AB cùng hướng nên 4 5 MBAB =− là sai.
25.
hình bình hành ABCD, điểm M thõa mãn 4AMABADAC =++
Khi đó điểm M là:
điểm của AC B. Điểm C
điểm của AB D. Trung điểm của AD
giải Chọn A Theo quy tắc hình bình hành, ta có: Câu 26. Cho hàm số 2 (0)yaxbxca =++ có đồ thị (P). Biết đồ thị của hàm số có đỉnh (1;1)I và đi qua điểm (2;3)A . Tính tổng 222 Sabc =++
Nên 222 Sabc =++ =29 Câu 27. Cho hàm số
yxx=−++ Chọn khẳng định đúng. A. Hàm số đồng biến trên . B. Hàm số nghịch biến trên . C. Hàm số đồng biến trên ( ) 2;+ . D. Hàm số nghịch biến trên ( ) 2;+ . Lời giải Chọn D Do 1 a =− nên hàm số đồng biến trên ( );2− nghịch biến trên ( ) 2;+ . Câu 28. Cho hai vectơ a và b khác 0 . Xác định góc giữa hai vectơ a và b khi ...abab =− A. o180 = . B. o0 = . C. o90 = . D. o45 = . Lời giải
Chọn A Ta có ( ) ...cos, ababab = . Mà theo giả thiết abab =− , suy ra ( ) ( ) 0cos,1,180 abab=−⎯⎯→= Câu 29. Cho 2 vectơ a và b có 4 a = , 5 b = và ( ) o,120ab = .Tính ab + A. 21. B. 61. C. 21. D. 61. Lời giải Chọn A Ta có ( ) ( ) 2 22
DẠYKÈMQUYNHƠN OFFICIAL Lời giải
đồ
112 4234234 203 1 2 abcabca abcabcb babc a ++=++== ++=++==− +== −=
Chọn C Vì
thị hàm số 2 (0)yaxbxca =++ có đỉnh (1;1)I và đi qua điểm (2;3)A nên ta có hệ:
2 43.
22 2.2cos,21+=+=++=++= ababababababab Câu 30. Cho tam giác ABC vuông tại A có o ˆ 60 B = , ABa = . Tính . ACCB A. 2 3a . B. 2 3a . C. 3a . D. 0 . Lời giải Chọn B Ta có o2 3 ...cos1503.2.3 2 ==−=− ACCBACBCaaa Câu 31. Bất phương trình 2 230xx −++ có tập nghiệm là A. ( ) ( ) ;13; −−+ . B. ( )1;3 . C. 1;3 . D. ( )3;1 . Lời giải Chọn B Ta có: 2 23013xxx −++− Câu 32. Tập nghiệm của bất phương trình 2 120 xx −++ là A. ( ) ;34; −−+ . B. . C. ( ) ;43; −−+ D. 3;4 Lời giải Chọn D Ta có 2 12034xxx −++− Vậy tập nghiệm của bất phương trình là 3;4 .
DẠYKÈMQUYNHƠN OFFICIAL Câu 33. Biểu thức ( )( ) 2 310345 xxx−+− âm khi và chỉ khi
x −
x − C.
x +
x Lời giải Đặt ( ) ( )( ) 2 310345fxxxx =−+− Phương trình 2 3 310301 3 x xx x = −+= = và 5 450. 4 xx−== Lập bảng xét dấu x − 1 3 5 4 3 + 2 3103 xx−+ + 0 0 + 45 x 0 + + ( )fx 0 + 0 0 + Dựa vào bảng xét dấu, ta thấy ( ) 15 0;;3. 34 fxx − ChọnB. Câu 34. Nghiệm của phương trình 566 xx+=− bằng A. 15. B. 6. C. 2 và 15. D. 2. Lời giải Chọn A 22 6 606 56615 2 56123617300 15 x xx xxx x xxxxx x − +=−= = +=−+−+= = . Vây phương trình đã cho có nghiệm duy nhất là 15 x = . Câu 35. Tích các nghiệm của phương trình 2211xxxx++=+− là A. 3. B. 3. C. 1. D. 0 . Lời giải Chọn B Ta có: 2 10, xxx++ ( )2 222222 1111201120 xxxxxxxxxxxx ++=+−++−++−=++−++−= ( ) 2 2 11 12(1) xxvn xx ++=− ++= 22 (1)1230 xxxx ++=+−= Do đó: 12 3 .3 1 xx ==− . 2. Tự luận Câu 1. Người ta muốn thiết kế một vườn hoa hình chữ nhật nội tiếp trong một miếng đất hình tròn có đường kính bằng 50m (Hình 23). Xác định kích thước vườn hoa hình chữ nhật để tổng quãng đường đi xung quanh vườn hoa đó là 140m Lời giải
A. 5 ;. 4
B. 15 ;;3. 34
( ) 15 ;3;. 34
D. 1 ;3. 3
Đặt độ dài một cạnh của hình chữ nhật là ( )(050) xmx . Vì độ dài đường chéo hình chữ nhật bằng đường kính hình tròn nên độ dài cạnh còn lại của hình chữ nhật đó là 2 2500() xm . Khi đó, tổng quãng đường đi xung quanh vườn hoa bằng chu vi hình chữ nhật là: ( ) 2 22500140( ) −+=xxm . Giải phương trình trên ta có: 40( ) = xm hoặc 30( ) = xm . Nếu 40( ) = xm thì độ dài cạnh còn lại là 30m và ngược lại. Vậy kích thước vườn hoa là 3040 m .
Câu 2. Bác Năm dự định trồng ngô và đậu xanh trên một mảnh đất có diện tích 8 ha. Nếu trồng 1 ha ngô thì cần 20 ngày công và thu được 40 triệu đồng. Nếu trồng 1 ha đậu xanh thì cần 30 ngày công và thu được 50 triệu đồng. Bác Năm cần trồng bao nhiêu hecta cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng không quá 180 ngày công cho việc trồng ngô và đậu xanh.
Lời giải Gọi x là số hecta đất trồng ngô và y là số hecta đất trồng đậu xanh. Ta có các điều kiện ràng buộc đối với , xy như sau:
Hiển nhiên 0,0xy .
Diện tích canh tác không vượt quá 8 ha nên 8 xy+ Số ngày công sử dụng không vượt quá 180 nên 2030180 xy+
OFFICIAL
Từ đó, ta có hệ bất phương trình mô tả các điều kiện ràng buộc:
+ +
xy xy x y
8 2030180 0 0
Biểu diễn miền nghiệm của hệ bất phương trình này trên hệ trục toạ độ Oxy , ta được miền tứ giác OABC (Hình).
Toạ độ các đỉnh của tứ giác đó là: (0;0);(0;6)OA ; (6;2);(8;0)BC Gọi F là số tiền (đơn vị: triệu đồng) bác Năm thu được, ta có: 4050 Fxy =+ . Ta phải tìm , xy thoả mãn hệ bất phương trình sao cho F đạt giá trị lớn nhất, nghĩa là tìm giá trị lớn nhất của biểu thức 4050 Fxy =+ trên miền tứ giác OABC. Tính các giá trị của biểu thức F tại các đỉnh của đa giác, ta có: Tại (0;0):40.050.00OF =+= ;

DẠYKÈMQUYNHƠN
F đạt giá trị lớn nhất bằng 340 tại (6;2)B . Vậy để thu được nhiều tiền nhất, bác Năm cần trồng 6 ha ngô và 2 ha đậu xanh. Câu 3. Gia đình bạn An sở hữu một mảnh đất hình tam giác. Chiều dài của hàng rào MN là 150m , chiều dài của hàng rào MP là 230m . Góc giữa hai hàng rào MN và MP là 110 (Hình 21) .
Tại (0;6):40.050.6300AF =+= Tại (6;2):40.650.2340BF =+= ; Tại (8;0):40.850.0320CF =+=
a) Diện tích mảnh đất mà gia đình bạn An sở hữu là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)? b) Chiều dài hàng rào NP là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)? Lời giải a) Diện tích mảnh đất của gia đình bạn An (tam giác MNP ) là: ( ) 2 11 sin150230sin11016209,7 22
G là trọng tâm tam giác ABC 0 GAGBGC ++= Ta có ( ) ( ) 2011'2012'02011'2012'0 ABACAAABAAAC +=+++= 4023'201120120 AAABAC ++= Tương tự ta có 4023'201120120 BBBCBA ++= 4023'201120120 CCCACB ++= Cộng về với vế lại ta được ( ) 4023'''0'''0 AABBCCBAACCBAABBCC +++++=++= Suy ra ''''''0GAGBGCGAGBGCGAGBGC ++=++++= Do đó G là trọng tâm của tam giác A’B’C’

DẠYKÈMQUYNHƠN OFFICIAL
Lời
== SMNMPMm b) Áp dụng định lí côsin ta có: =+−=+−
222222cos1502302150230cos110 98999,39. NPMNMPMNMPM Suy ra 98999,39314,6( )
NPm Vậy chiều dài hàng rào NP là khoảng 314,6m . Câu 4. Cho tam giác ABC. Gọi A’, B’, C’ là các điểm xác định bởi 2011'2012'0 ABAC+= , 2011'2012'0 BCBA+= ; 2011'2012'0 CACB+= . Chứng minh hai tam giác ABC và A’B’C’ có cùng trọng tâm.
giải. Gọi
1. Trắc nghiệm
Câu 1. Mệnh đề: " 2 ,21 n n + là số nguyên tố" khẳng định là
A. Tồn tại số tự nhiên n để 2 21 n + là số nguyên tố.
B. Tồn tại duy nhất số tự nhiên n để 2 21 n + là số nguyên tố.
C. Với mọi số tự nhiên n thì 2 21 n + là hợp số.
D. Với mọi số tự nhiên n thì 2 21 n + là số nguyên tố.
Câu 2. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
a) Nếu tam giác có hai trung tuyến bằng nhau thì tam giác đó là tam giác cân.
b) Tam giác ABC vuông tại C nếu và chỉ nếu 222 ABCACB =+
c) 2 ,210xxx −+ d) 22 ,(1)nnn ++ là số chẵn. A. 1. B. 2. C. 3. D. 4. Câu 3. Cho ,, ABC là ba tập hợp bất kì khác rỗng, được biểu diễn bằng biểu đồ Ven như hình bên. Phần gạch sọc trong hình biểu diễn tập hợp nào sau đây?
A. ()\ABC . B. ()ABC . C. ABC D. ()\BCA



Câu 4. Số các số nguyên dương lẻ nhỏ hơn 1000 và chia hết cho 3 là
A. 166. B. 167. C. 333. D. 499.
Câu 5. Hình nào sau đây là biểu diễn theo biểu đồ Ven của tập hợp B là con của tập hợp A ? A. B. C. D.
Câu 6. Cặp số nào sau đây không là nghiệm của bất phương trình 42 +xy ?
A. (1;0) B. (1;2) . C. (5;2).


DẠYKÈMQUYNHƠN
ĐỀ SỐ 9
OFFICIAL
thép tấm là 250 tấn/giờ, công suất sản xuất thép cuộn là 150 tấn/giờ. Mỗi tấn thép tấm có giá 250 USD, mỗi tấn thép cuộn có giá 300 USD. Biết rằng mỗi tuần thị trường chỉ tiêu thụ tối đa 5000 tấn thép tấm và 3500 tấn thép cuộn. Hỏi cần sản xuất bao nhiêu tấn thép mỗi loại trong một tuần để lợi nhuận thu được là cao nhất?
A. 5000 tấn thép tấm và 3500 tấn thép cuộn.
B. 4166,66 tấn thép tấm và 3500 tấn thép cuộn.







C. 5000 tấn thép tấm và 0 tấn thép cuộn.

DẠYKÈMQUYNHƠN OFFICIAL D.
được
Câu
0 0 1 x y xy − được
Câu
bất phương trình 1 0 2 26 x y y xy + là A. 1. B. 3. C. 4. D. 9. Câu 10. Nhà máy A chỉ có một
(máy không
xuất
(1;0) Câu 7. Miền nghiệm của bất phương trình 3 −+yx
xác định bởi miền nào (nửa mặt phẳng không bị gạch và kể cả d ) sau đây? A. C. B. D.
8. Miền nghiệm của hệ bất phương trình:
xác định bởi miền đa giác nào sau đây? A. B. C. D.
9. Diện tích miền nghiệm () H của hệ
máy cán thép có thể sản xuất hai sản phẩm là thép tấm và thép cuộn
thể sản xuất hai loại thép cùng lúc và có thể làm việc 40 giờ một tuần). Công suất sản
D. 5000 tấn thép tấm và 3000 tấn thép cuộn.
Câu 11. Cho góc thoả mãn 0180 và tan2 =− . Giá trị của cos là:
A. 3 3 B. 2 2 C. 3 3 D. 1 3 .
Câu 12. Biết 2 sin 5 = ,(90180) oo . Hỏi giá trị của tan bằng bao nhiêu?
A. 21 2 B. 221 21 C. 221 21 D. 21 2
Câu 13. Với 0180 giá trị lượng giác nào dưới đây luôn không âm? A. sin. B. tan. C. cos. D. cot.
Câu 14. Trong tam giác ABCvới ,, ABcBCaCAb === . Tìm mệnh đề đúng.
A. 222 2cos. abcbcA =++ B. 222 2cos. abcbcA =+− C. 222 cos. abcbcA =+− D. 222 2sin. abcbcA =+−
Câu 15. Tam giác ABC có ,, ABcBCaCAb === và có diện tích là S . Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn góc C . Khi đó diện tích tam giác mới tạo nên bằng.
A. 3S . B. 4S . C. 2S . D. 6S .
Câu 16. Cho tam giác ABC có 5,4ABAC== , trung tuyến 33 BM = . Tính diện tích tam giác ABC A. 36 B. 46 C. 213 D. 2433 Câu 17. Cho tam giác ABC với BCa = , ACb = , ABc = . Diện tích của ABC là A. 1 sin 2 ABC SacC = B. 1 sin 2 ABC SbcB = C. 1 sin 2 ABC SacB = . D. 1 sin 2 ABC SbcC = . Câu 18. Cho tam giác ABC với BCa = , 120 BAC = . Bán kính đường tròn ngoại tiếp ABC là
A. 3 2 a R = B. 2 a R = C. 3 3 a R = D. = Ra
DẠYKÈMQUYNHƠN
OFFICIAL
Cho hai véctơ a và b là
a
sai? A. Hai véctơ a , b cùng
. B. Hai
độ dài. C. Hai véctơ a , b chung điểm đầu. D. Hai véctơ a , b ngược hướng. Câu 20. Cho tam giác ABC xác định vị trí điểm D sao cho ADACAB =− A. D là đỉnh thứ tư của hình bình hành ADBC B. D trùng điểm B . C. D trùng điểm C . D. D là đỉnh thứ tư của hình bình hành ABCD. Câu 21. Tìm tập xác định D của hàm số ( )( ) 2 1 14 x y xx + = +−
Câu 19.
các véctơ khác 0 . Biết véctơ
là véctơ đối của véctơ b . Khẳng định nào sau đây
phương
véctơ a , b cùng
A. \2 D = B. \2 D = C. \1;2 D =− D. \1;2 D =−

Câu 22. Tìm giá trị nhỏ nhất của hàm số ( ) ( )2 2 3 fxxx=+− .
A. 0 B. 9 2 C. 9 2 D. 3 2
Câu 23. Trên Hình biểu diên ba lực 1F , 23 , FF cùng tác động vào một vật ở vị trí cân bằng 0. Cho biết cường độ của 12 , FF đều bằng 100N và góc tạo bởi 1F và 2F bằng 120 . Tính cường độ của lực 3F . A. 190 B. 200 C. 100 D. 80 Câu 24. Cho ABC . Đặt , aBCbAC == . Các cặp vectơ nào sau đây cùng phương? A. 2,2abab ++ B. 2,2 abab C. 5,102 abab +−− D. , abab +− Câu 25. Cho tam giác ABC có điểm O thỏa mãn: 2 OAOBOCOAOB +−=− . Khẳng định nào sau đây là đúng? A. Tam giác ABC đều B. Tam giác ABC cân tại C C. Tam giác ABC vuông tại C D. Tam giác ABC cân tại B Câu 26. Cho Parabol (P): 2 yaxbxc =++ có đỉnh (2;0)I và () P cắt trục Oy tại điểm (0;1) M . Khi đó Parabol (P) có hàm số là A. B. C. . D. Câu 27. Giá trị nào của m thì đồ thị hàm số 2 3 yxxm
DẠYKÈMQUYNHƠN
OFFICIAL
=++ cắt trục hoành tại hai điểm phân biệt? A. 9 4 m − . B. 9 4 m − . C. 9 4 m . D. 9 4 m Câu 28. Cho hai vectơ a và b thỏa mãn 3, a = 2 b = và .3.ab =− Xác định góc giữa hai vectơ a và .b A. o30 = . B. o45 = . C. o60 = . D. o120 = . Câu 29. Cho 2 vectơ đơn vị a và b thỏa 2 ab+= . Hãy xác định ( )( ) 3425 abab −+ A. 7 B. 5 C. 7 D. 5 Câu 30. Cho hình thang vuông ABCDcó đáy lớn 4 ABa = , đáy nhỏ 2 CDa = , đường cao 3 ADa = .Tính . DABC A. 2 9a B. 2 15a C. 0 D. 2 9a Câu 31. Cho biểu thức ( ) 2 412 4 x fx xx = . Tập hợp tất cả các giá trị của x thỏa mãn ( )fx không dương là A. ( ( ) 0;34; x+ . B. ( );03;4 x− . ( ) 2 1 :31 4 Pyxx=−−− ( ) 2 1 :1 4 Pyxx=−−− ( ) 2 1 :1 4 Pyxx=−+− ( ) 2 1 :21 4 Pyxx=−+−
tường đó 2m . Ban đầu, bác Dũng đặt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng vào
mép trên của bức tường (Hình 21a). Sau đó, bác Dũng dịch chuyển chân thang vào gần chân bức tường thêm 1m thì bác Dũng nhận thấy thang tạo với mặt đất một góc 45 (Hình 21b). Bức tường cao bao nhiêu mét?
Câu 2. Một người dùng ba loại nguyên liệu ,, ABC để sản xuất ra hai loại sản phẩm P và Q . Để sản xuất 1 kg mỗi loại sản phẩm P hoặc Q phải dùng một số kilôgam nguyên liệu khác nhau. Tổng số kilôgam nguyên liệu mỗi loại mà người đó có và số kilôgam từng loại nguyên liệu cần thiết để sản xuất ra 1kg sản phẩm mỗi loại được cho trong bảng sau:

Biết 1kg sản phẩm P có lợi nhuận 3 triệu đồng và 1 kg sản phẩm Q có lợi nhuận 5 triệu đồng. Hãy lập phương án sản xuất hai loại sản phẩm trên sao cho có lãi cao nhất.
Câu 3. Hai người A và B cùng quan sát một con tàu đang neo đậu ngoài khơi tại vị trí C . Người A đứng trên bờ biển, người B đứng trên một hòn đảo cách bờ một khoảng 100= ABm. Hai người tiến hành đo đạc và thu được kết quả: 54,74
==CABCBA (Hình 22). Hỏi con tàu cách hòn đảo bao xa (làm tròn kết quả đến hàng phần mười theo đơn vị mét)?

DẠYKÈMQUYNHƠN OFFICIAL C. ( ) );03;4 x− D. ( ) ( );03;4 x− Câu 32. Tìm tập nghiệm S của bất phương trình 2 440xx−+ A. \2 S = . B. S = . C. ( ) 2; S =+ . D. \2 S =− . Câu 33. Biểu thức ( )( )( ) 222 42359 xxxxx −+−++ âm khi A. ( )1;2 x . B. ( ) ( )3;21;2 x−− . C. 4. x D. ( ) ( ) ( )
x−−−+ . Câu 34. Tập nghiệm của phương trình 4721 xx+=− là A. 210210 ; 22 −+ . B. 210 2 + . C. 210 2 . D. Một phương án khác. Câu 35. Phương trình 2 2351 xxx+−=+ có nghiệm: A. 1 x = B. 2 x = C. 3 x = D. 4 x = 2. Tự luận Câu 1. Để leo lên một bức tường, bác Dũng dùng một chiếc thang cao hơn bức
;32;12;
Câu 4. Hai tam giác ABC và A’B’C’ lần lượt có trọng tâm là G, G’. Chứng minh rằng '''3' AABBCCGG ++= . Từ đó suy ra “ Điều kiện cần và đủ để hai tam giác ABC và A’B’C’ có cùng trọng tâm là '''0AABBCC++= Lời giải tham khảo

Câu 1. Mệnh đề: " 2 ,21 n n + là số nguyên tố" khẳng định là
A. Tồn tại số tự nhiên n để 2 21 n + là số nguyên tố.
B. Tồn tại duy nhất số tự nhiên n để 2 21 n + là số nguyên tố.
C. Với mọi số tự nhiên n thì 2 21 n + là hợp số.
D. Với mọi số tự nhiên n thì 2 21 n + là số nguyên tố.
Câu 2. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
a) Nếu tam giác có hai trung tuyến bằng nhau thì tam giác đó là tam giác cân. b) Tam giác ABC vuông tại C nếu và chỉ nếu 222 ABCACB =+ c) 2 ,210xxx −+ d) 22 ,(1)nnn ++ là số chẵn. A. 1. B. 2. C. 3. D. 4. Câu 3. Cho ,, ABC là ba tập hợp bất kì khác rỗng, được biểu diễn b

DẠYKÈMQUYNHƠN OFFICIAL
1D 2C 3B 4B 5B 6B 7B 8D 9B 10D 11C 12C 13A 14B 15D 16B 17C 18C 19C 20D 21D 22B 23C 24C 25C 26C 27D 28D 29C 30A 31C 32A
BẢNG ĐÁP ÁN TRẮC NGHIỆM
33D 34B 35B 1. Trắc nghiệm
ằng
ểu
Ven
Phần gạch sọc trong hình biểu diễn tập hợp
A. ()\ABC . B. ()ABC . C. ABC D. ()\BCA Câu 4. Số các số nguyên dương lẻ nhỏ hơn 1000 và chia hết cho 3 là A. 166. B. 167. C. 333. D. 499. Lời
Gọi A là tập các số nguyên dương chia
cho
và
bi
đồ
như hình bên.
nào sau đây?
giải
hết
3
nhỏ hơn 1000.
Gọi B là tập số nguyên dương chẵn chia hết cho 3 nhỏ hơn 1000, tức B là tập các số nguyên dương chia hết cho 6 và nhỏ hơn 1000.
Gọi C là tập số nguyên dương lẻ chia hết cho 3 nhỏ hơn 1000. Như vậy ABC = và BC= , suy ra ()()() nAnBnC =+ . Do đó ()()()333166167 nCnAnB=−=−= .
Câu 5. Hình nào sau đây là biểu diễn theo biểu đồ Ven của tập hợp B là con của tập hợp A ?
A. B. C. D.
OFFICIAL
Câu 6. Cặp số nào sau đây không là nghiệm của bất phương trình 42 +xy ? A. (1;0). B. (1;2) . C. (5;2). D. (1;0)








Câu 7. Miền nghiệm của bất phương trình 3 −+yx được xác định bởi miền nào (nửa mặt phẳng không bị gạch và kể cả d ) sau đây? A. C. B. D.
Câu 8. Miền nghiệm của hệ bất phương trình: 0 0 1
− được xác định bởi miền đa giác nào sau đây?
x y xy
DẠYKÈMQUYNHƠN
H là hình thang
nữa ABCD là hình thang vuông tại A và D . Suy ra diện tích hình () H là (12)23()


dvdt
10. Nhà máy A chỉ có một máy cán thép có thể sản xuất hai sản phẩm là thép tấm và thép cuộn (máy không thể sản xuất hai loại thép cùng lúc và có thể làm việc 40 giờ một tuần). Công suất sản xuất thép tấm là 250 tấn/giờ, công suất sản xuất thép cuộn là 150 tấn/giờ. Mỗi tấn thép tấm có giá 250 USD, mỗi tấn thép cuộn có giá 300 USD. Biết rằng mỗi tuần thị trường chỉ tiêu thụ tối đa 5000 tấn thép tấm và 3500 tấn thép cuộn. Hỏi cần sản xuất bao nhiêu tấn thép mỗi loại trong một tuần để lợi nhuận thu được là cao nhất?
A. 5000 tấn thép tấm và 3500 tấn thép cuộn.
B. 4166,66 tấn thép tấm và 3500 tấn thép cuộn.
C. 5000 tấn thép tấm và 0 tấn thép cuộn.
D. 5000 tấn thép tấm và 3000 tấn thép cuộn. Lời giải
Gọi , xy là số tấn thép cuộn và thép tấm nhà máy đó sản suất trong một tuần. Số giờ máy sử dụng để sản xuất trong tuần là 250150 xy + (giờ).


Số tiền thu được là (;)250300 Fxyxy =+ với , xy thoả mãn hệ bất phương trình

DẠYKÈMQUYNHƠN OFFICIAL
Câu
1
x
y
+ là
Lời
A. B. C. D.
9. Diện tích miền nghiệm () H của hệ bất phương trình
0 2 26
y
xy
A. 1. B. 3. C. 4. D. 9.
giải Miền ()
ABCD với (1;0),(3;0),(2;2),(1;2) ABCD Hơn
2
+ = . Câu
DẠYKÈMQUYNHƠN OFFICIAL 40 250150 5000;3500. xy xy + Thử các phương án vào ta có phương án D thoả mãn yêu cầu. Câu 11. Cho góc thoả mãn 0180 và tan2 =− . Giá trị của cos là: A. 3 3 . B. 2 2 . C. 3 3 D. 1 3 . Lời giải Ta có: 22 22 222 sinsin1cos1 tantan1tan coscoscoscos ===+= . Do đó 2 2 2 111 cos 1tan3 1(2) === + +− . Vì 0180 mà tan0 và sin0 nên cos0 suy ra 3 cos 3 =− . Chọn C Câu 12. Biết 2 sin 5 = ,(90180) oo . Hỏi giá trị của tan bằng bao nhiêu? A. 21 2 B. 221 21 C. 221 21 D. 21 2 Lời giải Chọn C Ta có: 2 222 21 cos sincos1cos125 521 cos 5 = +==− =− Theo đề bài: 21 90180cos 5 oo =− Vậy 2 sin221 5 tan cos21 21 5 ===− . Câu 13. Với 0180 giá trị lượng giác nào dưới đây luôn không âm? A. sin. B. tan. C. cos. D. cot. Lời giải Chọn A Nhìn vào bảng xét dấu của các giá trị lượng giác của một góc bất kỳ ta thấy sin luôn không âm. Câu 14. Trong tam giác ABCvới ,, ABcBCaCAb === . Tìm mệnh đề đúng. A. 222 2cos. abcbcA =++ B. 222 2cos. abcbcA =+− C. 222 cos. abcbcA =+− D. 222 2sin. abcbcA =+− Lời giải Chọn B
Câu 15. Tam giác ABC có ,, ABcBCaCAb === và có diện tích là S . Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn góc C . Khi đó diện tích tam giác mới tạo nên bằng. A. 3S B. 4S C. 2S D. 6S Lời giải Chọn D
Diện tích tam giác ABC là: 1 ...sin 2 = SBCCAC Diện tích tam giác mới bằng: 11 .2.3.sin6...sin6. 22 BCCACBCCACS ==
16. Cho tam giác ABC có
DẠYKÈMQUYNHƠN
OFFICIAL
( ) ( )2 2
22 222 24334 4 57 422 BABCAC BMAC BMBCBA + +− + ==−=−= .
ABC , ta có: 547 8 22 ABACBC p ++++ === Áp dụng công thức Heron cho tam giác ABC ta có: ( )( )( ) ( )( )( ) 885848746 ABC SppABpACpBC =−−−=−−−= Câu 17. Cho tam giác ABC với BCa = , ACb = , ABc = . Diện tích của ABC là A. 1 sin 2 ABC SacC = B. 1 sin 2 ABC SbcB = C. 1 sin 2 ABC SacB = . D. 1 sin 2 ABC SbcC = . Lời giải Chọn C Ta
1 sin 2 ABC SacB = . Câu 18. Cho tam giác ABC với BCa = , 120 BAC = . Bán kính đường tròn ngoại tiếp ABC là A. 3 2 a R = B. 2 a R = C. 3 3 a R = D. = Ra Lời giải Chọn C Theo định lý trong tam giác ta có 13 2. 2sin1203 sin === BCaa RR BAC Câu 19. Cho hai véctơ a và b là các véctơ khác 0 . Biết véctơ a là véctơ đối của véctơ b . Khẳng định nào sau đây sai? A. Hai véctơ a , b cùng phương. B. Hai véctơ a , b cùng độ dài. C. Hai véctơ a , b chung điểm đầu D. Hai véctơ a , b ngược hướng Lời giải Chọn
Ta có hai véctơ đối nhau là hai véctơ ngược hướng và cùng độ dài nên các phương án A, B, D đều đúng Câu 20. Cho tam giác ABC xác định vị trí điểm D sao cho ADACAB =− sin
Câu
5,4ABAC== , trung tuyến 33 BM = . Tính diện tích tam giác ABC . A. 36 . B. 46 . C. 213. D. 2433 Lời giải Chọn B Ta có:
222
Gọi p là nửa chu vi của tam giác
có:
C
A. D là đỉnh thứ tư của hình bình hành ADBC .
B. D trùng điểm B C. D trùng điểm C . D. D là đỉnh thứ tư của hình bình hành ABCD Lời giải
DẠYKÈMQUYNHƠN OFFICIAL
+ − − .
Đáp án D. Lưu ý: Nếu rút gọn 2 1 4 y x = rồi khẳng định \2 D = là sai. Vì với 1 x =− thì biểu thức ban đầu ( )( ) 2 1 14 x xx + +− không xác định. Câu 22. Tìm giá trị nhỏ nhất của hàm số ( ) ( )2 2 3 fxxx=+− A. 0 B. 9 2 C. 9 2 D. 3 2 Lời giải Tập xác định D = . + ( ) 2 22 99399 :269232 42222xfxxxxxx =−+=−++=−+ . + ( ) 93 22fxx== . Vậy ( ) min9 2 fx = Đáp án B. Câu 23. Trên Hình biểu diên ba lực 1F , 23 , FF cùng tác động vào một vật ở vị trí cân bằng 0. Cho biết cường độ của 12 , FF đều bằng 100N và góc tạo bởi 1F và 2F bằng 120 C B D A
Chọn D Ta có ADACABBC =−= AD cùng hướng và cùng độ dài với BC ABCD là hình bình hành ( quan sát thêm hình vẽ) Câu 21. Tìm tập xác định D của hàm số ( )( ) 2 1 14 x y xx + = +− . A. \2 D = B. \2 D = C. \1;2 D =− D. \1;2 D =− Lời giải Điều kiện xác định: 2 101 402 x x x x
Vậy \1;2 D =−
Tính cường độ của lực 3F A. 190. B. 200. C. 100. D. 80. Lời giải Ta sử dụng các vectơ ,, OAOBOC và OD lần lượt biểu diễn cho các lực 123 ,, FFF và hợp lực F của 12 , FF Khi đó, do 12=+ FFF và 12 100 ==FF , nên tứ giác AOBD là hình thoi. Từ đó, do 120 = AOB , suy ra 60 = OAD , do đó tam giác AOD đều. Bởi vậy ||100 ===FODOA . Do vật ở vị trí cân bằng nên hai lực F và 3F ngược hướng và có cường độ bằng nhau, tức là hai vectơ OD và OC là hai vectơ đối nhau. Suy ra cường độ của lực 3F bằng


DẠYKÈMQUYNHƠN
OFFICIAL
.
== .
vectơ nào sau đây cùng phương? A. 2,2abab ++ B. 2,2 abab C. 5,102 abab +−− D. , abab +− Lời giải Chọn C Ta có: 1022.(5)5 ababab −−=−++ và 102ab cùng phương. Câu 25. Cho tam giác ABC có điểm O thỏa mãn: 2 OAOBOCOAOB +−=− . Khẳng định nào sau đây là đúng? A. Tam giác ABC đều B. Tam giác ABC cân tại C C. Tam giác ABC vuông tại C D. Tam giác ABC cân tại B Lời giải Chọn C
3 ||100( ).FFN == Câu 24. Cho ABC
Đặt , aBCbAC
Các cặp

DẠYKÈMQUYNHƠN OFFICIAL Gọi I là trung điểm của AB . Ta có: 2 OAOBOCOAOBOAOCOBOCBACACBAB +−=−−+−=+= 1 2.2 2 CIABCIABCIAB === Tam giác ABC vuông tại C . Câu 26. Cho Parabol (P): 2 yaxbxc =++ có đỉnh (2;0)I và () P cắt trục Oy tại điểm (0;1) M . Khi đó Parabol (P) có hàm số là A. . B. . C. D. Lời giải Chọn C Parabol ( ) 2 : Pyaxbxc=++⎯⎯→ đỉnh 2 ; 24 bb Ic aa Theo bài ra, ta có (P) có đỉnh ( ) ( ) 22 224 2;01 4 0 4 b ba a I bbac c a −= =− = −= Lại có (P) cắt Oy tại điểm ( )0;1 M suy ra ( ) ( )0112yc=−=− Từ (1), (2) suy ra 22 44 1 4 1;1 11 baba a babb bc cc =−=− =− =−= ==− =−=− (vì 00ba== loại) Câu 27. Giá trị nào của m thì đồ thị hàm số 2 3 yxxm =++ cắt trục hoành tại hai điểm phân biệt? A. 9 4 m − . B. 9 4 m − . C. 9 4 m . D. 9 4 m Lời giải Chọn D Cho 2 30xxm++= (1) Để đồ thị cắt trục hoành tại hai điểm phân biệt khi phương trình (1) có hai nghiệm phân biệt 2 9 0340940 4 mmm −− . Câu 28. Cho hai vectơ a và b thỏa mãn 3, a = 2 b = và .3.ab =− Xác định góc giữa hai vectơ a và b A. o30 = . B. o45 = . C. o60 = . D. o120 = . Lời giải Chọn D Ta có ( ) ( ) ( ) 0 .31 ...cos,cos,,120 3.22 ab ababababab ab =⎯⎯→===−⎯⎯→= Câu 29. Cho 2 vectơ đơn vị a và b thỏa 2 ab+= . Hãy xác định ( )( ) 3425 abab −+ A. 7 B. 5 C. 7 D. 5 Lời giải ( ) 2 1 :31 4 Pyxx=−−− ( ) 2 1 :1 4 Pyxx=−−− ( ) 2 1 :1 4 Pyxx=−+− ( ) 2 1 :21 4 Pyxx=−+−
DẠYKÈMQUYNHƠN OFFICIAL Chọn C 1 ==ab , ( )2 24.1 +=+== ababab , ( )( ) 22 34256207.7 −+=−+=− abababab
= .Tính .
.
.
Vì ( )
...9 =++==−
Câu
Cho biểu thức ( ) 2 412 4 x fx xx = . Tập hợp tất cả các
trị của x thỏa
A. ( ( ) 0;34; x+ B. ( );03;4 x− C. ( ) );03;4 x− . D. ( ) ( );03;4 x− . Lời giải Chọn C. Ta có: 2 412 0 4 x xx 0 34 x x hay ( ) );03;4 x− . Câu 32. Tìm tập nghiệm S của bất phương trình 2 440xx−+ A. \2 S = . B. S = . C. ( ) 2; S =+ . D. \2 S =− . Lời giải Chọn#A. * Bảng xét dấu: x − 2 + 2 44xx−+ + 0 + * Tập nghiệm của bất phương trình là \2 S = . Câu 33. Biểu thức ( )( )( ) 222 42359 xxxxx −+−++ âm khi A. ( )1;2 x . B. ( ) ( )3;21;2 x−− . C. 4. x D. ( ) ( ) ( ) ;32;12; x−−−+ . Lời giải Đặt ( ) ( )( )( ) 222 42359fxxxxxx =−+−++ Phương trình 2 2 40. 2 x x x = −= =− Phương trình 2 1 230. 3 x xx x = +−= =− Ta có 2 22 511 590590. 24 xxxxxx ++=++++= Lập bảng xét dấu: x − 3 2 1 2 + 2 4 x 0 + 0 + 0 2 23xx+− + 0 0 + + 2 59xx++ + + + + + ( )fx 0 + 0 0 + 0
Câu 30. Cho hình thang vuông ABCDcó đáy lớn 4 ABa = , đáy nhỏ 2 CDa = , đường cao 3 ADa
DABC A. 2 9a
B. 2 15a
C. 0. D. 2 9a Lời giải Chọn A
2
DABCDABAADDCDAADa nên chọn#A.
31.
giá
mãn ( )fx không dương là
2. Tự luận

Câu 1. Để leo lên một bức tường, bác Dũng dùng một chiếc thang cao hơn bức tường đó 2m . Ban đầu, bác Dũng đặt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng vào mép trên của bức tường (Hình 21a). Sau đó, bác Dũng dịch chuyển chân thang vào gần chân bức tường thêm 1m thì bác Dũng nhận thấy thang tạo với mặt đất một góc 45 (Hình 21b). Bức tường cao bao nhiêu mét?
Lời giải Gọi chiều cao bức tường là ( )(0) xmx . Khi đặt chiếc thang mà đầu trên của chiếc thang đó chạm đúng vào mép trên của bức tường thì khoảng cách chân thang đến chân tường là 22 (2)( ) +− xxm . Khi thang tạo với mặt đất một góc 45 thì khoảng cách từ chân thang đến chân tường là ( )xm . Theo đề bài ta có phương trình: 22 (2)1 +−=+xxx .
DẠYKÈMQUYNHƠN OFFICIAL Dựa vào bảng xét dấu ta thấy ( )( )( ) 222 3 42359021 2 x xxxxxx x − −+−++− ( ) ( ) ( ) ;32;12;. x −−−+ Chọn D. Câu 34. Tập nghiệm của phương trình 4721 xx+=− là A. 210210 ; 22 −+ . B. 210 2 + . C. 210 2 D. Một phương án khác. Lời giải Chọn B Ta có ( )2 2 2101 47212 47214860 x x xx xx xx − +=− +=− = 1 2 210 2 x x = 210 2 x + = . Vậy 210 2 x + = Câu 35. Phương trình 2 2351 xxx+−=+ có nghiệm: A. 1 x = B. 2 x = C. 3 x = D. 4 x = Lời giải Chọn B Ta có : 2 2351 xxx+−=+ ( )2 2 10 2351 x xxx + +−=+ 2
+−=
= .
1 60 x xx −
2 x
Giải phương trình trên ta có: 3( ) = xm với 0 x . Vậy chiều cao bức tường là 3m. Câu 2. Một người dùng ba loại nguyên liệu ,, ABC để sản xuất ra hai loại sản phẩm P và Q . Để sản xuất 1 kg mỗi loại sản phẩm P hoặc Q phải dùng một số kilôgam nguyên liệu khác nhau. Tổng số kilôgam nguyên liệu mỗi loại mà người đó có và số kilôgam từng loại nguyên liệu cần thiết để sản xuất ra 1kg sản phẩm mỗi loại được cho trong bảng sau:
OFFICIAL
Biết 1kg sản phẩm P có lợi nhuận 3 triệu đồng và 1 kg sản phẩm Q có lợi nhuận 5 triệu đồng. Hãy lập phương án sản xuất hai loại sản phẩm trên sao cho có lãi cao nhất. Lời giải Gọi x là số kilôgam sản phẩm , Py là số kilôgam sản phẩm Q cần sản xuất. Ta có hệ bất phương trình: 2210

Biểu diễn miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy , ta được như Hình.
Miền nghiệm là miền ngũ giác OCBAD (Hình) với các đỉnh: (0;0);(0;2);(2;2)OCB ; (4;1);(5;0)AD .
Gọi F là số tiền lãi (đơn vị: triệu đồng) thu được, ta có: 35 Fxy =+ . Tính giá trị của F tại các đỉnh của ngũ giác: Tại (0;0):3.05.00OF =+= ;

DẠYKÈMQUYNHƠN
x
+
24 2412 0 0 xy y xy
y +
Tại (0;2):3.05.210CF =+= ;
Tại (2;2):3.25.216BF =+= ;
Tại (4;1):3.45.117AF =+=

Tại (5;0):3.55.015DF =+= .
F đạt giá trị lớn nhất bằng 17 tại (4;1)A Vậy người đó cần sản xuất 4kg sản phẩm P và 1kg sản phẩm Q để có lãi cao nhất là 17 triệu đồng.
Câu 3. Hai người A và B cùng quan sát một con tàu đang neo đậu ngoài khơi tại vị trí C . Người A đứng trên bờ biển, người B đứng trên một hòn đảo cách bờ một khoảng 100= ABm. Hai người tiến hành đo đạc và thu được kết quả: 54,74 ==CABCBA (Hình 22). Hỏi con tàu cách hòn đảo bao xa (làm tròn kết quả đến hàng phần mười theo đơn vị mét)?
Lời giải Xét tam giác ABC . Ta có: ˆ 180547452
OFFICIAL
=−−= C . Áp dụng định lí sin ta có: sinsin = BABC CA . Suy ra sin100sin54102,7( sinsin52) == BAA BCm C Vậy con tàu cách hòn đảo khoảng 102,7 m. Câu 4. Hai tam giác ABC và A’B’C’ lần lượt có trọng tâm là G, G’. Chứng minh rằng '''3' AABBCCGG ++= . Từ đó suy ra “ Điều kiện cần và đủ để hai tam giác ABC và A’B’C’ có cùng trọng tâm là '''0AABBCC
DẠYKÈMQUYNHƠN
++=
Ta
( )
=++ ( )''''2BBBGGGGB =++ ( )''''3CCCGGGGC =++ Cộng vế với vế ta được ( ) ( ) '''3'''''''3' AABBCCAGBGCGGGGAGBGCGG ++=++++++= Vì G , G là trọng tâm của tam giác ABC , ABC nên 0 0 AGBGCG AGBGCG ++= ++= Từ đẳng thức trên ta thấy G trùng G khi và chỉ khi 0 GG = tức là 0 AABBCC ++= .
Lời giải.
có
''''1AAAGGGGA
1. Trắc nghiệm
Câu 1. Trong các câu sau, có bao nhiêu câu là mệnh đề toán học?
a) Hãy bỏ rác đúng nơi quy định!
b) Hoàng Sa, Trường Sa là quần đảo thuộc chủ quyền của Việt Nam.
c) 2021 là số nguyên tố.
d) Bạn có biết nấu cơm không? A. 4. B. 3. C. 2. D. 1.
Câu 2. Mệnh đề: “ ( ) *,1234:5 nnn n +++ ” khẳng định là
A. Tồn tại số nguyên dương n để 1234 nnn+++ chia hết cho 5.
B. Tồn tại duy nhất số nguyên dương n để 1234 nnn+++ chia hết cho 5.
C. Với mọi số tự nhiên n thì 1234 nnn+++ chia hết cho 5.
D. Với mọi số nguyên dương n thì 1234 nnn+++ chia hết cho 5.
Câu 3. Cho tập hợp {2180}Axx=− và 1 0 10 Bx x = . Tập hợp AB là
A. [9;10]. B. [9;10) C. (9;10) D. (9;10]. Câu 4. Cho tập hợp (;5)Amm=+ và (10;) B =+ . Số các giá trị nguyên dương của tham số m để \ ABA = là A. 5. B. 4. C. 3. D. 6. Câu 5. Trong các tập hợp sau, tập hợp nào là tập hợp rỗng?
A. {(1)(21)0} =++= Axxx . B. {(1)(21)0} =++=Bxxx . C. {(1)(21)0} =++=Cxxx D. {(1)(21)0} =++=Dxxx

Câu 6. Miền nghiệm của bất phương trình 5312 −xy là nửa mặt phẳng tạo bởi đường thẳng :5312 −=dxy (không kể d ) chứa điểm có toạ độ nào sau đây? A. (2;1) B. (0;0) C. (1;2) . D. (3;4). Câu 7. Miền nghiệm của bất phương trình 1 2 2 −yx được xác định bởi miền nào (nửa mặt phẳng không bị gạch và không kể d) sau đây? A. B.

DẠYKÈMQUYNHƠN
ĐỀ SỐ 10
OFFICIAL







DẠYKÈMQUYNHƠN OFFICIAL
1 2 0 20 x y y xy + được
A. 0 0 22 + x y xy B. 0 0 22 x y xy + C. 0 0 22. + x y xy D. 0 0 22. + x y xy
C. D. Câu 8. Miền nghiệm của hệ bất phương trình:
xác định bởi miền đa giác nào sau đây? A. B. C. D. Câu 9. Miền đa giác không bị gạch ở Hình là miền nghiệm của hệ bất phương trình:
Câu 10. Miền nghiệm của hệ bất phương trình 1 1 4
+ là miền ( ) H . Gọi M là một điểm thuộc
x y xy
( ) H . Độ dài OM ngắn nhất là A. 2 B. 10 C. 22 D. 1. Câu 11. Cho là góc tù. Khẳng định nào sau đây là đúng? A. tan0 B. cos0 C. sin0 D. cot0
Câu 12. Cho sin3 5 x = . Tính 22 4sin3cos Pxx =+ ? A. 91 25 P = . B. 84 25 P = . C. 19 25 P = . D. 109 25 P = .
Câu 13. Cho 1 sin 3 = với 00 90180 . Giá trị của cos bằng
A. 2 3 . B. 2 3 . C. 22 3 . D. 22 3 .
Câu 14. Cho ABC có 0 60,8,5.===Bac Độ dài cạnh b bằng: A. 7. B. 129. C. 49. D. 129 .
Câu 15. Cho ;;cab là độ dài 3cạnh của một tam giác. Mệnh đề nào sau đây không đúng?
A. 2 aabac + B. 222 2 acbac ++ C. 222 2 bcabc ++ D. 2abbcb +
Câu 16. Trong mặt phẳng, cho tam giác ABC có 4cm AC = , góc 60 A = , 45 B = . Độ dài cạnh BC là
A. 26 . B. 223 + . C. 232. D. 6 .
Câu 17. Cho tam giác ABC có 60 = B và 45 = C , = BCa . Độ dài cạnh AB bằng A. 632 2 −+ a B. ( )13−+ a C. ( )13 + a D. 632 2 + a
Câu 18. Cho tam giác ABC có 47 = a , 6 = b và 8 = c . Diện tích S của tam giác ABC là A. 97 B. 79 C. 9 D. 7 Câu 19. Mệnh đề nào sau đây sai?
véctơ cùng phương là hai véctơ có giá song song hoặc trùng nhau.
không cùng phương với mọi véctơ
véctơ cùng phương thì cùng hướng D. Hai véctơ bằng nhau là hai véctơ có cùng hướng và cùng độ dài. Câu 20. Cho hai điểm , AB phân biệt. Xác định điểm M sao cho 0 MAMB+= A. Không tìm được điểm M . B. M ở vị trí bất kì. C. M nằm trên đường trung trực của AB D. M là trung điểm của AB Câu 21. Đường cong trong hình nào dưới đây không phải là đồ thị của một hàm số dạng
DẠYKÈMQUYNHƠN OFFICIAL
A. Hai
B. Véctơ
C. Hai
( )yfx = ?
A. B. C. D. Câu 22. Cho hàm số ( ) 2
xx y xx
−−− = −
2211 11
neáu neáu . Tính ( )1 f A. 6 B. 6 C. 5 D. 5 Câu 23. Hình 4.19 biểu diễn hai lực 12 , FF cùng tác động lên một vật, cho 123,2 FNFN == . Tính độ lớn của hợp lực 12 FF + A. 20 B. 19 C. 19 D. 23 Câu 24. Biết rằng hai vec tơ a và b không cùng phương nhưng hai vec tơ 32ab và (1)4 xab ++ cùng phương. Khi đó giá trị của x là: A. 7 B. 7 C. 5 D. 6
Câu 25. Cho ngũ giác ABCDE . Gọi ,,, MNPQ lần lượt là trung điểm các cạnh ,,, ABBCCDDE . Gọi I và J lần lượt là trung điểm các đoạn MP và NQ . Khẳng định nào sau đây đúng? A. 1 2 IJAE = B. 1 3 IJAE = C. 1 4 IJAE = D. 1 5 IJAE =
Câu 26. Cho hàm số 2 61yxx=−+− . Hàm số đồng biến trên khoảng nào dưới đây? A. ( );3− B. ( ) 3;+ C. ( );6− D. ( ) 6;+ Câu 27. Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4m còn kích thước cửa ở giữa là 3m x 4m. Hãy tính khoảng cách giữa hai điểm A và B . (xem hình vẽ bên dưới) A. 5m. B. 8,5m. C. 7,5m. D. 8m. Câu 28.



DẠYKÈMQUYNHƠN
OFFICIAL
2
=
Cho tam giác đều ABC có cạnh bằng a Tính tích vô hướng ABAC A. 2 .2.ABACa = B. 2 3 . 2 a ABAC =− C. 2 . 2 a ABAC =− D. 2 . 2 a ABAC = Câu 29. Cho hai vectơ a và b . Biết a =2, b = 3 và ( ) o,120ab = .Tính ab + A. 73 + B. 73 C. 723 D. 723 + Câu 30. Cho hai điểm , BC phân biệt. Tập hợp những điểm M thỏa mãn
.
CMCBCM là :
A. Đường tròn đường kính BC . B. Đường tròn( ) ; BBC
C. Đường tròn ( ) ; CCB . D. Một đường khác.
Câu 31. Trong các phát biểu sau, phát biểu nào sai?
A. 2 20−−xx khi và chỉ khi (;1)(2;) −−+ x
B. 2 20−−xx khi và chỉ khi [1;2]− x .
C. 2 20−−xx khi và chỉ khi (1;2)− x
D. 2 20−−xx khi và chỉ khi (;1)(2;) −−+ x
Câu 32. Cho hàm số () = yfx có đồ thị ở Hình 15.
OFFICIAL
Trong các phát biểu sau, phát biểu nào sai?
A. ()0 fx khi và chỉ khi (1;3) x . B. ()0 fx khi và chỉ khi (;1][3;) −+ x

C. ()0 fx khi và chỉ khi (1;3) x D. ()0 fx khi và chỉ khi [1;3] x .
Câu 33. Tập xác định của hàm số 2 23yxx=−++ là: A. ( )1;3 . B. ( ) ( ) ;13; −−+ . C. 1;3 D. ( ) ;13; −−+

Câu 34. Tập nghiệm của phương trình 212xx −=− là: A. 1;5. S = B. 1. S = C. 5. S = D. 2;3. S =
Câu 35. Số nghiệm của phương trình 2 3972 xxx−+=− là A. 3. B. 1. C. 0 . D. 2.
2. Tự luận
Câu 1. Hằng ngày bạn Hùng đều đón bạn Minh đi học tại một vị trí trên lề đường thẳng đến trường. Minh đứng tại vị trí A cách lề đường một khoảng 50m để chờ Hùng. Khi nhìn thấy Hùng đạp xe đến địa điểm B , cách mình một đoạn 200m thì Minh bắt đầu đi bộ ra lề đường để bắt kịp xe. Vận tốc đi bộ Minh là 5 / kmh , vận tốc xe đạp của Hùng là 15 / kmh . Hãy xác định vị trí C trên lề đường để hai bạn gặp nhau mà không bạn nào phải chờ người kia (làm tròn kết quả đến hàng phần mười).
Câu 2. Bạn Lan thu xếp được không quá 10 giờ để làm hai loại đèn trung thu tặng cho các trẻ em khuyết tật. Loại đèn hình con cá cần 2 giờ để làm xong 1 cái, còn loại đèn ông sao chỉ cần 1 giờ
DẠYKÈMQUYNHƠN
để
làm xong 1 cái. Gọi x, y lần lượt là số đèn hình con cá và đèn ông sao bạn Lan sẽ làm. Hãy lập hệ bất phương trình mô tả điều kiện của x, y và biểu diễn miền nghiệm của hệ bất phương trình đó.
Câu 3. Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một con tàu C đang neo đậu ngoài khơi. Người đó tiến hành đo đạc và thu được kết quả: 30 ,60,50 === ABmCABCBA (Hình 23). Tính khoảng cách từ vị trí A đến con tàu C (làm tròn kết quả đến hàng phần mười theo đơn vị mét).
Câu 4. Cho tam giác ABC . Trên các cạnh AB , BC , CA ta lấy lần lượt các điểm M , N , P sao cho AMBNCP ABBCCA == . Chứng minh rằng hai tâm giác ABC và MNP có cùng trọng tâm.


Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM
OFFICIAL
1. Trắc nghiệm
Câu 1. Trong các câu sau, có bao nhiêu câu là mệnh đề toán học? a) Hãy bỏ rác đúng nơi quy định! b) Hoàng Sa, Trường Sa là quần đảo thuộc chủ quyền của Việt Nam. c) 2021 là số nguyên tố. d) Bạn có biết nấu cơm không? A. 4. B. 3. C. 2. D. 1. Câu 2. Mệnh đề: “ ( ) *,1234:5 nnn n +++ ” khẳng định là
A. Tồn tại số nguyên dương n để 1234 nnn+++ chia hết cho 5. B. Tồn tại duy nhất số nguyên dương n để 1234 nnn+++ chia hết cho 5. C. Với mọi số tự nhiên n thì 1234 nnn+++ chia hết cho 5.
DẠYKÈMQUYNHƠN
1D 2D 3B 4A 5D 6A 7C 8A 9C 10A 11A 12B 13C 14A 15C 16A 17B 18A 19C 20D 21D 22A 23C 24A 25C 26A 27D 28D 29C 30A
32A 33C
31D
34B 35C
Câu 3. Cho tập hợp {2180}Axx=− và 1 0 10 Bx x = . Tập hợp AB là A. [9;10] B. [9;10). C. (9;10) . D. (9;10]. Lời giải Ta có [9;) A =+ và (;10) B =− . Suy ra [9;10) AB= . Câu 4. Cho tập hợp (;5)Amm=+ và (10;) B =+ . Số các giá trị nguyên dương của tham số m để \ ABA = là A. 5. B. 4. C. 3. D. 6.
D. Với mọi số nguyên dương n thì 1234 nnn+++ chia hết cho 5.
Ta có \5105 ABAABmm ==+ .
Câu 5. Trong các tập hợp sau, tập hợp nào là tập hợp rỗng?
A. {(1)(21)0} =++= Axxx . B. {(1)(21)0} =++=Bxxx . C. {(1)(21)0} =++=Cxxx . D. {(1)(21)0} =++=Dxxx .








Câu 6. Miền nghiệm của bất phương trình 5312 −xy là nửa mặt phẳng tạo bởi đường thẳng :5312 −=dxy (không kể d ) chứa điểm có toạ độ nào sau đây? A. (2;1). B. (0;0) C. (1;2) D. (3;4).
Câu 7. Miền nghiệm của bất phương trình 1 2 2 −yx được xác định bởi miền nào (nửa mặt phẳng không bị gạch và không kể d) sau đây? A. B. C. D. Câu 8. Miền nghiệm của hệ bất phương trình:
+
x y y xy
1 2 0 20
được xác định bởi miền đa giác nào sau đây? A. B. C. D. Câu 9. Miền đa giác không bị gạch ở Hình là miền nghiệm của hệ bất phương trình:
DẠYKÈMQUYNHƠN
Lời
OFFICIAL
giải

DẠYKÈMQUYNHƠN OFFICIAL
+ x
x
+
+ x
x
ệ
ủ
ệ
ất
1
4 x
+ là
ề
ọ
ột
(
. Độ dài
ắn nhất
.
.
Lời giải Ta có hình (H) là tam giác ABC với (1;1),(1;3),(3;1) ABC Suy ra độ dài nhỏ nhất của OM là 112 += Câu 11. Cho là góc tù. Khẳng định nào sau đây là đúng? A. tan0 . B. cos0 . C. sin0 . D. cot0 . Lời giải Chọn A Ta có là góc tù nên sin0,cos0 suy ra tan0 . Câu 12. Cho sin3 5 x = . Tính 22 4sin3cos Pxx =+ ? A. 91 25 P = . B. 84 25 P = . C. 19 25 P = . D. 109 25 P = . Lời giải Chọn B Ta có 222 9844sin3cossin33 2525 Pxxx =+=+=+=
A. 0 0 22
y xy B. 0 0 22
y xy
C. 0 0 22.
y xy D. 0 0 22.
+
y xy Câu 10. Miền nghi
m c
a h
b
phương trình
1
y xy
mi
n ( ) H . G
i M là m
điểm thuộc
) H
OM ng
là A. 2
B. 10 . C. 22
D. 1.
90180
.
ng A. 2 3 . B. 2 3 . C. 22 3 . D. 22 3 . Lời giải Chọn C Có 1 sin 3 = 2 18 cos1 99 =−= mà 00 90180 22 cos0cos 3 =− Câu 14. Cho ABC có 0 60,8,5.===Bac Độ dài cạnh b bằng: A. 7. B. 129. C. 49. D. 129 . Lời giải Chọn#A. Ta có: 2222202cos852.8.5.cos60497 bacacBb =+−=+−== . Câu 15. Cho ;;cab là độ dài 3cạnh của một tam giác. Mệnh đề nào sau đây không đúng? A. 2 aabac + B. 222 2 acbac ++ C. 222 2 bcabc ++ D. 2abbcb + Lời giải Chọn C Do 222 2.cos2 bcabcAbc +−= 222 2 bcabc ++ nên mệnh đề C sai. Áp dụng bất đẳng thức tam giác ta có 2 abcaabac ++ ;đáp án A đúng. Tương tự 2acbabbcb ++ ;mệnh đề D đúng. Ta có: 222 2.cos2 acbacBac
DẠYKÈMQUYNHƠN OFFICIAL Câu
+−= 222 2 acbac++ ;mệnh đề
Câu 16. Trong mặt phẳng, cho tam giác ABC có 4cm AC = , góc 60 A = , 45 B = . Độ dài cạnh BC là A. 26 B. 223 + C. 232 D. 6 Lời giải Chọn A Ta có sinsin BCAC AB = 4.3 2 26 2 2 BC == Câu 17. Cho tam giác ABC có 60 = B và 45 = C , = BCa . Độ dài cạnh AB bằng A. 632 2 −+ a . B. ( )13−+ a . C. ( )13 + a . D. 632 2 + a . Lời giải Áp dụng định lý hàm sin vào tam giác ABC ta có: ( ) sin .13 sinsinsinsin ====−+ BCABACC ABBCa ACBA Câu 18. Cho tam giác ABC có 47 = a , 6 = b và 8 = c . Diện tích S của tam giác ABC là A. 97 . B. 79 . C. 9. D. 7 . Lời giải Áp dụng định lý hàm số cosin vào tam giác ABC ta có:
13. Cho 1 sin 3 = với 00
Giá trị của cos bằ
B đúng.
ac 2 819 sin1cos 25616 =−==BB


216 2.47.8
Diện tích tam giác ABC là 119sin.47.8.97 2216 ===SacB
Câu 19. Mệnh đề nào sau đây sai?
A. Hai véctơ cùng phương là hai véctơ có giá song song hoặc trùng nhau.
B. Véctơ không cùng phương với mọi véctơ.
C. Hai véctơ cùng phương thì cùng hướng
D. Hai véctơ bằng nhau là hai véctơ có cùng hướng và cùng độ dài Lời giải Chọn C Mệnh đề sai là mệnh đề “Hai véctơ cùng phương thì cùng hướng”.
Câu 20. Cho hai điểm , AB phân biệt. Xác định điểm M sao cho 0 MAMB+= A. Không tìm được điểm M .
B. M ở vị trí bất kì. C. M nằm trên đường trung trực của AB . D. M là trung điểm của AB . Lời giải Chọn D Ta có 0 MAMBMAMB +==− Do đó M là trung điểm của AB
DẠYKÈMQUYNHƠN
( )2 222 476436 57 cos
+− +− === acb B
OFFICIAL
Đáp án
Câu 21. Đường cong trong hình nào dưới đây không phải là đồ thị của một hàm số dạng ( )yfx = ? A. B. C. D. Lời giải Đường cong trong hình D không phải là đồ thị của một hàm số dạng ( )yfx = vì mỗi giá trị 0 x ứng với hai giá trị phân biệt của y.
D.


DẠYKÈMQUYNHƠN OFFICIAL Câu 22. Cho hàm số ( ) 2 2211 11 xx y xx −−− = − neáu neáu . Tính ( )1 f A. 6 B. 6 C. 5 D. 5 Lời giải Chọn A Vì ( ) ( ) 12126 f −=−−−=− nên chọn#A. Câu 23. Hình 4.19 biểu diễn hai lực 12 , FF cùng tác động lên một vật, cho 123,2 FNFN == . Tính độ lớn của hợp lực 12 FF + A. 20 B. 19
19
23 Lời giải Dựng hình bình hành ABDC với hai cạnh là hai vectơ 12 , FF như hình vẽ Ta có: 1212 || FFACABADFFADAD +=+=+== Xét ABD ta có: 123,2.BDACFABF===== 18018012060ABDBAC =−=−= Theo định lí cosin ta có: 222 2222 12 2cos 23223cos12019 1919 V?y ADABBDABBDABD ADAD ADFF =+− =+−= =+= Câu 24. Biết rằng hai vec tơ a và b không cùng phương nhưng hai vec tơ 32ab và (1)4 xab ++ cùng phương. Khi đó giá trị của x là: A. 7 B. 7 C. 5 D. 6 Lời giải Chọn A Điều kiện để hai vec tơ 32ab và (1)4 xab ++ cùng phương là: 14 7 32 x x + ==− . Câu 25. Cho ngũ giác ABCDE . Gọi ,,, MNPQ lần lượt là trung điểm các cạnh ,,, ABBCCDDE . Gọi I và J lần lượt là trung điểm các đoạn MP và NQ . Khẳng định nào sau đây đúng?
C.
D.
ra: ( ) 1111
26. Cho hàm số
2224
61yxx=−+− . Hàm số đồng biến trên khoảng nào dưới đây? A. ( );3
B. ( ) 3;+ C. ( );6− D. ( ) 6;+ Lời giải Ta có ( ) 6 10,3 22.1 b a a =−== . Suy ra hàm số đồng biến trên khoảng ( );3− . Đáp án#A. Câu 27. Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4m còn kích thước cửa ở giữa là 3m x 4m. Hãy tính khoảng cách giữa hai điểm A và B . (xem hình vẽ bên dưới) A. 5m. B. 8,5m. C. 7,5m. D. 8m. Lời giải Chọn D


Gắn hệ trục tọa độ Oxy như hình vẽ, chiếc cổng là 1 phần của parabol ( )P : 2 yaxbxc =++ với 0 a

DẠYKÈMQUYNHƠN OFFICIAL A. 1 2 IJAE = B. 1 3 IJAE = C. 1 4 IJAE = D. 1 5 IJAE =
MQMAAEEQ
=++ =+=+ =++
Lời giải Chọn C Ta có: 2IJIQINIMMQIPPNMQPN =+=+++=+ ( ) 1 2 2
MQAEBDMQAEBD MQMBBDDQ
, 1 2 PNBD =− Suy
2
IJAEBDBDAEIJAE =+−== Câu
2
−
Do parabol ( )P đối xứng qua trục tung nên có trục đối xứng 000 2 b xb a =−==
Chiều cao của cổng parabol là 4m nên ( )0;4 G 4 c = . ( )P : 2 4 yax=+
Lại có, kích thước cửa ở giữa là 3m x 4m nên ( ) ( )2;3,2;3EF 1 344 4 aa ===− Vậy ( )P : 2 1 4 4 yx=−+ Ta có 2 4 1 40 4 4 x x x
= −+= =− nên ( )4;0 A , ( )4;0 B hay 8 AB = (m).
Câu 28. Cho tam giác đều ABC có cạnh bằng .a Tính tích vô hướng ..ABAC A. 2 .2.ABACa = B. 2 3 2 a ABAC =− C. 2 2 a ABAC =− D. 2 2 a ABAC = Lời giải Chọn D Xác định được góc ( ) , ABAC là góc A nên ( ) 0 ,60.ABAC = Do đó ( ) 2 0 ...cos,..cos60. 2 a ABACABACABACaa===
DẠYKÈMQUYNHƠN OFFICIAL
m , BC phân biệt. Tập hợp những điểm M thỏa mãn 2 = CMCBCM
: A. Đường tròn đường kính BC . B. Đường tròn( ) ; BBC . C. Đường tròn ( ) ; CCB D. Một đường khác. Lời giải Chọn A 22 ..0.0 =−== CMCBCMCMCBCMCMMB Tập hợp điểm M là đường tròn đường kính BC Câu 31. Trong các phát biểu sau, phát biểu nào sai? A. 2 20−−xx khi và chỉ khi (;1)(2;) −−+ x . B. 2 20−−xx khi và chỉ khi [1;2]− x . C. 2 20−−xx khi và chỉ khi (1;2)− x . D. 2 20−−xx khi và chỉ khi (;1)(2;) −−+ x . Lời giải Chọn D Câu 32. Cho hàm số () = yfx có đồ thị ở Hình 15.
Câu 29. Cho hai vectơ a và b . Biết a =2, b = 3 và ( ) o,120ab = .Tính ab + A. 73 + . B. 73 . C. 723 . D. 723 + . Lời giải Chọn C Ta có ( ) ( ) 2 22 22 2.2,723 +=+=++=++=− ababababababcosab . Câu 30. Cho hai điể
là
Trong các phát biểu sau, phát biểu nào sai?
A. ()0 fx khi và chỉ khi (1;3) x . B. ()0 fx khi và chỉ khi (;1][3;) −+ x . C. ()0 fx khi và chỉ khi (1;3) x D. ()0 fx khi và chỉ khi [1;3] x

Lời giải
Chọn A
Câu 33. Tập xác định của hàm số 2 23yxx=−++ là: A. ( )1;3 B. ( ) ( ) ;13; −−+ C. 1;3 . D. ( ) ;13; −−+ .
Lời giải Chọn C Hàm số 2 23yxx=−++ xác định khi 2 23013xxx −++− Vậy tập xác định của hàm số là 1;3 D =− .
Câu 34. Tập nghiệm của phương trình 212xx −=−
t khoảng 50m để chờ Hùng. Khi nhìn thấy Hùng đạp xe đến địa điểm B , cách mình một đoạn 200m thì Minh bắt đầu đi bộ ra lề đường để bắt kịp xe. Vận tốc đi bộ Minh là 5 / kmh , vận tốc xe đạp của Hùng là 15 / kmh . Hãy xác định vị trí C
DẠYKÈMQUYNHƠN
OFFICIAL
là: A. 1;5. S = B. 1. S = C. 5. S = D. 2;3. S = Lời giải Chọn B Thay các giá trị vào phương trình có 1 x = vào thỏa mãn phương trình. Câu 35. Số nghiệm của phương trình 2 3972 xxx−+=− là A. 3. B. 1. C. 0 . D. 2. Lời giải Chọn C ( ) 2 2 2 20 3972 3972 x xxx xxx − −+=− −+=− 2 20 2530 x xx − −+= 2 1 3 2 x x x x = = Vậy phương trình vô nghiệm. PHẦN 2. TỰ LUẬN Câu 1. Hằng ngày bạn Hùng đều đón bạn Minh đi học tại một vị trí trên lề đường thẳng đến trường. Minh đứng tại vị trí A cách lề đường mộ
200505015 5015
BCBHCHx
hai bạn gặp nhau tại C , nên thời gian đi từ A đến C bằng thời gian đi từ B đến C, nên ta có phương trình: 2 2
xx xx
−+ = −=+
Bình phương hai vế được: ( ) 22 2
xxx xx xx
−+=+
+−= −
Thử lại phương trình và điều kiện 0 x thì 25,4 = x thỏa mãn. Vậy vị trí điểm C là cách H 1 khoảng 25,4 m. Câu 2. Bạn Lan thu xếp được không quá 10 giờ để làm hai loại đèn trung thu tặng cho các trẻ em khuyết tật. Loại đèn hình con cá cần 2 giờ để làm xong 1 cái, còn loại đèn ông sao chỉ cần 1 giờ để làm xong 1 cái. Gọi x, y lần lượt là số đèn hình con cá và đèn ông sao bạn Lan sẽ làm. Hãy lập hệ bất phương trình mô tả điều kiện của x, y và biểu diễn miền nghiệm của hệ bất phương trình đó. Lời giải
có: 222502500=+=+ACxx Từ đó ta có hệ bất
phương trình:

DẠYKÈMQUYNHƠN OFFICIAL
ả đến
trên lề đường để hai bạn gặp nhau mà không bạn nào phải chờ người kia (làm tròn kết qu
hàng phần mười). Lời giải Đặt (0)
=CHxx Ta
22 210 0(,) 0 + xy xxy y Biểu
BH
=−= =−=− Vì
50152500 155 501532500
375001001592500 810015150000 25,4ho?c 73,8
Ta có các điều kiện ràng buộc đối với x, y như sau: Hiển nhiên 0,0xy Tổng số giờ làm không quá 10 giờ nên 210 +xy
diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy, ta được như hình dưới.
Miền không tô màu (miền tam giác OAB , bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình. Câu 3. Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một con tàu C đang neo đậu ngoài khơi. Người đó tiến hành đo đạc và thu được kết quả: 30 ,60,50 === ABmCABCBA (Hình 23). Tính khoảng cách từ vị trí A đến con tàu C (làm tròn kết quả đến hàng phần mười theo đơn vị mét). Lời giải Xét tam giác ABC . Ta có: ˆ 180605070



DẠYKÈMQUYNHƠN
OFFICIAL
4. Cho tam giác ABC . Trên các cạnh AB , BC , CA ta lấy lần lượt các điểm M , N , P sao cho AMBNCP ABBCCA == . Chứng minh rằng hai tâm giác ABC và MNP có cùng trọng tâm. Lời giải Giả sử AM k AB = suy ra AMkAB = , BNkBC = , CPkCA = . Cách 1. Gọi G , G lần lượt là trọng tâm của ABC và MNP Suy ra 0 AGBGCG++= và 0 MGNGPG ++= ( )* . Ta có AMkAB = AGGGGMkAB ++= Tương tự BGGGGNkBC ++= và CGGGGMkBC ++= Cộng vế theo vế từng đẳng thức trên ta được ( ) ( ) ( ) 3 AGBGCGGGGMGNGPkABBCCA ++++++=++ Kết hợp với ( )* ta được 0 GG = Suy ra điều phải chứng minh. Cách 2. Gọi G là trọng tâm của ABC suy ra 0 GAGBGC++=
=−−= C Áp dụng định lí sin ta có: sinsin = BAAC CB Suy ra sin30sin5024,5( sinsin70)
== BAB ACm C Vậy khoảng cách từ vị trí A đến con tàu C là khoảng 24,5m . Câu
Ta có ( ) 0
Vậy hai tam giác ABC và NMP có cùng trọn tâm.
DẠYKÈMQUYNHƠN OFFICIAL
GMGNGPGAAMGBBNGCCP
++=+++++
AMBNCP kABkBCkCA kABBCCA
=++ =++ =++ =


ĐỀ THI HỌC KỲ MÔN TOÁN NĂM HỌC 2022 – 2023 Ths Nguyễn Thanh Tú eBook Collection MA TRẬN, ĐỀ THI HỌC KỲ I – NĂM HỌC 2022 2023 THEO KẾT NỐI TRI THỨC MÔN TOÁN 10 CÓ GIẢI CHI TIẾT WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL.COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405
MA TRẬN ĐỀ THI HỌC KỲ I NĂM HỌC 2022 2023 THEO SÁCH KNTT
Môn: Toán 10
1. TRẮC NGHIỆM ( 7 điểm) 35 câu 4 CÂU TỰ LUẬN ( 3 ĐIỂM) Chủ đề Nội dung Mức độ NB TH VD VDC
CHƯƠNG 1 (5 câu)
Mệnh đề 1 1 0 0 Tập hợp 2 1 TL1 0 CHƯƠNG 2 (5 câu)
CHƯƠNG 3 (8 câu)
Bất phương trình bậc nhất hai ẩn 1 1 0 0 Hệ bất phương trình bậc nhất hai ẩn 2 1 0 TL1
Giá trị lượng giác của góc từ 0o đến 1800 2 1 0 0 Hệ thức lượng trong tam giác 2 1 0 0 Giải tam giác 0 2 TL1 0
Định nghĩa vectơ 1 0 0 0 Tổng hiệu vectơ (Lực) 2 2 0 0
CHƯƠNG 4 (12 câu)
Tích của một số với một vectơ 1 1 TL1 0 Vecto trong mặt phẳng tọa độ 1 1
Tích vô hướng của hai vectơ 1 2 0 0
CHƯƠNG 5 (5 câu)
Số gần đúng Sai số 2 0 0 0
Các số đặc trưng đo xu thế trung tâm 1 1 0 0 Các số đặc trưng đo độ phân tán 1 0 0 Tổng số câu 20 15 3 1
DẠYKÈMQUYNHƠNOFFICIAL
1. Trắc nghiệm
Câu 1. Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Hà Nội là một thành phố của Việt Nam. b) Được sống thật là hạnh phúc! c) 68125 += . d) Bạn thấy học Toán thú vị không? A. 1. B. 2. C. 3. D. 4. Câu 2. Mệnh đề phủ định của P : "Tam giác ABC là tam giác cân" là:
A. Tam giác ABC không phải là tam giác cân B. Tam giác ABC là tam giác vuông C. Tam giác ABC là tam giác đều D. ABC không phải là một tam giác Câu 3. Cho ba tập hợp: {0;1;2;3},{4}MNxx == và {1;2;3;4;5}. Khẳng định nào sau đây là đúng?

A. NP . B. MP = . C. MN = . D. NP = . Câu 4. Cho tập hợp {13}Mxx=− . Mệnh đề nào sau đây đúng? A. [1;3) M =− B. (1;3] M =− C. (1;3) M =− D. {1;0;1} M =− Câu 5. Cho tập hợp [2;3] A =− và (0;) B =+ . Tập hợp AB là A. [2;) −+ . B. (0;3]. C. [0;3]. D. (0;3). Câu 6. Phần không bị gạch (kể cả d) ở Hình 5 là miền nghiệm của

DẠYKÈMQUYNHƠN
ĐỀ SỐ 1
OFFICIAL
A. 1 2 yx B. 2 yx C. 2. yx D. 1 2 yx Câu 7. Bạn Phúc muốn dùng 500000 đồng để mua x gói
kẹo có giá là 40000 đồng, mỗi cái bánh pizza có giá là 75000 đồng. Mối liên hệ giữa x và y để Phúc không mua hết số tiền ban đầu là: A. 4000075000500000 +xy B. 4000075000500000 +xy C. 4000075000500000 +xy D. 4000075000500000 +xy Câu 8. Phần không bị gạch chéo ở hình bên biểu diễn miền nghiệm của hệ bất phương trình nào sau đây? A. 0 236 y xy + B. 0 3260 y xy +− C. 0 3260 x xy +− D. 0 326 x xy +
bất phương trình:
kẹo và y cái bánh pizza. Biết rằng mỗi gói
Câu 9. Mẹ đi chợ mua x kg thịt và y kg cá. Biết rằng mỗi kilôgam thịt có giá 120 nghìn đồng, mỗi kilôgam cá có giá 80 nghìn đồng. Hệ bất phương trình biểu thị mối liên hệ giữa x và y để số tiền mẹ đi chợ không hết quá 500 nghìn đồng và được tổng nhiều hơn 4kg thịt, cá là: A. 80120500 4 + + xy xy B. 12080500 4 + + xy xy C. 12080500 4 +
thoả mãn tan2tan2 =− . Mối liên hệ của hai góc đó là A. và bù nhau. B. và phụ nhau. C. và bằng nhau. D. và không có mối liên hệ. Câu 12. Cho góc với 3 tan 4 = . Giá trị của cos là A. 4 5 B. 4 5 C. 5 4 D. 5 4 Câu 13. Rút gọn biểu thức sin cot 1cos x Px x =+ + , ta được A. sin x B. 1 sin x C. cos x D. 1 cos x Câu 14. Cho tam giác ABC có 2,1ABAC== và 0 60. A = Tính độ dài cạnh .BC A. 2. BC = B. 1. BC = C. 3. BC = D. 2. BC = Câu 15. Cho tam giác ABC có 222 0 abc+− . Khi đó: A. Góc 090 C B. Góc 090 C C. Góc 090 C = D. Không thể kết luận được gì về góc C Câu 16. Tam giác ABC có 0 6812' A = , 0 3444' B = , 117. AB = Tính AC ? A. 68. B. 168. C. 118. D. 200.
Câu 17. Cho ABC có 0 4,5,150.acB=== Diện tích của tam giác ABC là A.53. B. 103. C. 10. D.5. Câu 18. Cho tam giác ABC có 20,10ab== , 0 30. B = Số đo góc A là A. 090 A = . B. 060 A = . C. 045 A = . D. 0120 A = . Câu 19. Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Hỏi cặp vec tơ nào sau đây
DẠYKÈMQUYNHƠN
OFFICIAL
+ xy xy D. 12080500 4 + + xy xy Câu 10. Cho hệ bất phương trình 2 3 yxa yxb −+ + với a và b là các hằng số. Trong mặt phẳng Oxy , nếu (0;1) là một nghiệm của hệ bất phương trình thì điều kiện nào sau đây là đúng? A. ab . B. ab = . C. ab . D. ab =− . Câu 11. Cho góc ,0;90
ABC phân biệt. Đẳng thức nào sau đây là đúng? A. ABACBC += B. CABABC −= C. ABCACB += D. ABBCCA −= Câu 21. Cho hình bình hành ABCD. Đẳng thức nào sau đây là SAI ? A. ADBC = . B. ABBCAC += . C. ABADCA +=− D. BABCAC += . Câu 22. Cho hình vuông DABC có cạnh bằng 2 Tính DTABACA =++ A. 22 T = . B. 42 T = . C. 4 T = . D. 2 T = . Câu 23. Một ô tô có trọng lượng 15000N đứng trên một con dốc nghiêng 15 so với phương ngang. Lực có khả năng kéo ô tô xuống dốc có độ lớn là
cùng hướng? A. AB và MB B. MN và CB C. MA và MB D. AN và CA Câu 20. Cho ba điểm ,,
A. 14489,89 N . B. 3882,29 N . C. 4019,24 N . D. 7500N .
Câu 24. Cho hình thang ,//,2 = MNPQMNPQMNPQ . Phát biểu nào sau đây là đúng?
A. 2 = MNPQ B. 2 = MQNP C. 2=− MNPQ D. 2=− MQNP

Câu 25. Trên đường thẳng MN lấy điểm P sao cho 3 MNMP =− . Điểm P được xác định đúng trong hình vẽ nào sau đây:
A. Hình 3 B. Hình 4 C. Hình 1 D. Hình 2
Câu 26. Toạ độ của vectơ 32=−+ uij là: A. (3;2) B. (2;3) C. (3;2) ij D. (3;2)
Câu 27. Trên trục ' xOx cho tọa độ các điểm B, C lần lượt là 2 m và 2 32mm++ . Tìm m để đoạn thẳng BC có độ dài nhỏ nhất. A. 2 m = B. 1 m = C. 1 m =− D. 2 m =−

Câu 28. Nếu hai điểm , MN thoả mãn 4=−MNNM thì độ dài đoạn thẳng MN bằng bao nhiêu?
A. 4 = MN B. 2 = MN C. 16= MN ; D. 256 = MN
Câu 29. Cho hình vuông ABCD cạnh .a Đẳng thức nào sau đây đúng?
A. 2 . ABACa = B. 2 .2ABACa = C. 2 2 . 2 ABACa = D. 2 1 2 ABACa =
Câu 30. Cho hình vuông ABCD cạnh a . Gọi E là điểm đối xứng của D qua C Đẳng thức nào sau đây đúng?
A. 2 .2.AEABa = B. 2 .3.AEABa = C. 2 .5.AEABa = D. 2 .5.AEABa =
Câu 31. Số quy tròn của 219,46 đến hàng chục là:
A. 210. B. 219,4. C. 219,5. D. 220.
13 45 126 125 110 40 12 Giá trị mốt của
bảng phân bố tần số trên bằng A. 38 B. 126 C. 42 D. 12 Câu 34. Tiền lương hàng tháng của 7 nhân viên trong một công ty du lịch lần lượt là:6,5; 8,4; 6,9; 7,2; 2,5
DẠYKÈMQUYNHƠN
OFFICIAL
Câu 32. Biết số gần đúng 37975421 a = có độ chính xác 150 d = . Hãy xác định các chữ số đáng tin của a. A. 3, 7, 9 B. 3, 7, 9, 7 C. 3, 7, 9, 7, 5 D. 3, 7, 9, 7, 5, 4 Câu 33. Số áo bán được trong một quý ở cửa hàng bán áo sơ mi nam được thống kê như sau: Cỡ áo 36 37 38 39 40 41 42 Tần số (Số áo bán được) ; 6,7; 3,0 (đơn vị: triệu đồng). Số trung vị của dãy số liệu thống kê trên bằng A. 6,7 triệu đồng. B. 7,2 triệu đồng. C. 6,8 triệu đồng. D. 6,9 triệu đồng. Câu 35. Năng suất lúa hè thu (tạ/ha) năm 1998 của 31 tỉnh ở Việt Nam được thống kê trong bảng sau: Giá trị 3 35 x = có tần số bằng A. 6 B. 4 C. 7 D. 9
2. Tự luận
Câu 1. Trong một trường THPT, khối 10 có 160 em học sinh tham gia câu lạc bộ Toán, 140 em tham gia câu lạc bộ Tin, 100 em học sinh tham gia cả hai câu lạc bộ. Hỏi khối 10 có bao nhiêu học sinh?.

Câu 2. Một học sinh dự định vẽ các tấm thiệp xuân làm bằng tay để bán trong một hội chợ Tết. Cần 2 giờ để vẽ một tấm thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ để vẽ một tấm thiệp loại lớn có giá 20 nghìn đồng. Học sinh này chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải vẽ ít nhất 12 tấm. Hãy cho biết bạn ấy cần vẽ bao nhiêu tấm thiệp mồi loại để có được nhiều tiền nhất.
Câu 3. Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A ) đến trường (điểm B ) phải leo lên và xuống một con dốc (Hình 24). Cho biết đoạn thẳng AB dài 762m , ˆ ˆ 6,4 ==AB .
a) Tính chiều cao h của con dốc theo đơn vị mét (làm tròn kết quả đến hàng đơn vị). b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ trung bình lên dốc là 4 / kmh và tốc độ trung bình khi xuống dốc là 19 / kmh Câu 4. Chất điểm A chịu tác động của ba lực 123 ,, FFF như hình và ở trạng thái cân bằng (tức là
OFFICIAL
DẠYKÈMQUYNHƠN
Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM 1B 2A 3C 4A 5B 6D 7A 8A 9D 10C 11B 12A 13B 14C 15B 16A 17D 18A 19A 20C 21D 22C 23B 24C 25A 26A 27C 28A 29A 30A 31D 32C 33A 34A 35D 1. Trắc nghiệm Câu 1. Trong các câu sau, có bao nhiêu câu là mệnh đề? a) Hà Nội là một thành phố của Việt Nam. b) Được sống thật là hạnh phúc! c) 68125 += . d) Bạn thấy học Toán thú vị không? A. 1. B. 2. C. 3. D. 4. Lời giải Theo định nghĩa mệnh đề thì các câu: a), c) là mệnh đề. Đáp án là B Câu 2. Mệnh đề phủ định của P : "Tam giác ABC là tam giác cân" là: A. Tam giác ABC không phải là tam giác cân B. Tam giác ABC là tam giác vuông C. Tam giác ABC là tam giác đều D. ABC không phải là một tam giác
123 0 FFF++= ). Tính độ lớn của các lực 23 , FF biết 1F có độ lớn là 20 N .
Câu 3. Cho ba tập hợp: {0;1;2;3},{4}MNxx == và {1;2;3;4;5}. Khẳng định nào sau đây

đúng?
A. NP B. MP = C. MN = . D. NP = .
Câu 4. Cho tập hợp {13}Mxx=− . Mệnh đề nào sau đây đúng?
A. [1;3) M =− . B. (1;3] M =− . C. (1;3) M =− D. {1;0;1} M =− .

Câu 5. Cho tập hợp [2;3] A =− và (0;) B =+ . Tập hợp AB là
A. [2;) −+ B. (0;3]. C. [0;3]. D. (0;3)
Câu 6. Phần không bị gạch (kể cả d) ở Hình 5 là miền nghiệm của bất phương trình: A. 1 2 yx . B. 2 yx . C. 2. yx D. 1 2 yx .
Câu 7. Bạn Phúc muốn dùng 500000 đồng để mua x gói kẹo và y cái bánh pizza. Biết rằng mỗi gói kẹo có giá là 40000 đồng, mỗi cái bánh pizza có giá là 75000 đồng. Mối liên hệ giữa x và y để
DẠYKÈMQUYNHƠN
OFFICIAL
là
Phúc không mua hết số tiền ban đầu là: A. 4000075000500000 +xy B. 4000075000500000 +xy C. 4000075000500000 +xy D. 4000075000500000 +xy Câu 8. Phần không bị gạch chéo ở hình bên biểu diễn miền nghiệm của hệ bất phương trình nào sau đây? A. 0 236 y xy + B. 0 3260 y xy +− C. 0 3260 x xy +−
Câu 9. Mẹ đi chợ mua x kg thịt và y kg cá. Biết rằng mỗi kilôgam thịt có giá 120 nghìn đồng, mỗi kilôgam cá có giá 80 nghìn đồng. Hệ bất phương trình biểu thị mối liên hệ giữa x và y để số tiền mẹ đi chợ không hết quá 500 nghìn đồng và được tổng nhiều hơn 4kg thịt, cá là: A. 80120500 4 + + xy xy B. 12080500 4 + + xy xy C. 12080500 4 + + xy xy D. 12080500 4 + + xy xy Câu 10. Cho hệ bất phương trình 2 3 yxa yxb −+ + với a và b là các hằng số. Trong mặt phẳng Oxy , nếu (0;1) là một nghiệm của hệ bất phương trình thì điều kiện nào sau đây là đúng? A. ab . B. ab = C. ab D. ab =− Câu 11. Cho góc ,0;90 thoả mãn tan2tan2 =− . Mối liên hệ của hai góc đó là A. và bù nhau. B. và phụ nhau. C. và bằng nhau. D. và không có mối liên hệ.
DẠYKÈMQUYNHƠN OFFICIAL
D. 0 326 x xy +
4 5 .
4 5
5 4 .
5 4 Câu 13. Rút gọn biểu thức sin cot 1cos x Px x =+ + , ta
c A. sin x B. 1 sin x C. cos x . D. 1 cos x Lời
sincos1cos1 1cossin(1cos)sinsin xxx P xxxxx + =+== ++ .
Câu 14.
tam
ABC có 2,1
== và 0
A. 2. BC = B. 1. BC = C.
BC = D. 2. BC =
Câu 12. Cho góc với 3 tan 4 = . Giá trị của cos là A.
B.
C.
D.
đượ
giải
Vậy đáp án là B .
Cho
giác
ABAC
60. A = Tính độ dài cạnh .BC
3.
Lời giải
Chọn C Theo định lý cosin ta có: 220 2..cos60BCABACABAC =+− 22 1 212.2.1. 2 =+− 3. =
Câu 15. Cho tam giác ABC có 222 0 abc+− . Khi đó: A. Góc 090 C B. Góc 090 C C. Góc 090 C = D. Không thể kết luận được gì về góc .C Lời giải Chọn B. Ta có: 222 cos 2 abc C ab +− = . Mà: 222 0 abc+− suy ra: 0cos090 CC
Câu 16. Tam giác ABC có 0 6812' A = , 0 3444' B = , 117. AB = Tính AC ? A. 68. B. 168. C. 118. D. 200. Lời giải Chọn#A. Ta có: Trong tam giác ABC : 00000 1801806812'3444'774'ABCC ++==−−= Mặt khác 0 0 .sin117.sin3444' 68. sinsinsinsinsinsin sin774' abcACABABB AC ABCBCC
DẠYKÈMQUYNHƠN
OFFICIAL
222
==== Câu
Cho
==
090 A =
=
= Lời
Chọn A Tacó 0 0 2010201020 20sin190 1 sinsinsinsin30sinsin 2 ab AA ABAAA ====== Câu 19. Cho
===== Câu 17. Cho ABC có 0 4,5,150.acB=== Diện tích của tam giác ABC là A.53. B. 103. C. 10. D.5. Lời giải Chọn D Ta có 0 111 ..sin.4.5sin15010.5.
SacB
18.
tam giác ABC có 20,10ab
, 0 30. B = Số đo góc A là A.
B. 060 A
C. 045 A = D. 0120 A
giải
tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Hỏi cặp vec tơ nào sau đây cùng hướng? A. AB và MB B. MN và CB C. MA và MB D. AN và CA Lời giải Chọn A
Ta có AB và MB cùng hướng Câu 20. Cho ba điểm ,, ABC phân biệt. Đẳng thức nào sau đây là đúng? A. ABACBC += B. CABABC −= . C. ABCACB += D. ABBCCA −= . Câu 21. Cho hình bình hành ABCD. Đẳng thức nào sau đây là SAI ? A. ADBC = B. ABBCAC += . C. ABADCA +=− D. BABCAC += . Câu 22. Cho hình vuông DABC có cạnh bằng 2 . Tính DTABACA =++ . A. 22 T = . B. 42 T = . C. 4 T = . D. 2 T = . Lời giải Chọn C D22 TABACAACACACAC =++=+== Xét tam giác vuông ABC có ( ) ( ) 22 222 2242ACABBCAC =+=+== . Vậy D4TABACA=++= . Câu 23. Một ô tô có trọng lượng 15000N đứng trên một con dốc nghiêng 15 so với phương ngang. Lực có khả năng kéo ô tô xuống dốc có độ lớn là A. 14489,89 N . B. 3882,29 N . C. 4019,24 N . D. 7500N Lời giải Lực có khả năng kéo ô tô xuống dốc là lực AB . Xét tam giác ACW vuông tại C , có


DẠYKÈMQUYNHƠN
OFFICIAL
15 CAW = . Ta có sin CWAB A AWAW == Suy ra 15000sin153882,29 ABN = . Câu 24. Cho hình thang ,//,2 = MNPQMNPQMNPQ . Phát biểu nào sau đây là đúng? A. 2 = MNPQ
B. 2 = MQNP C. 2=− MNPQ D. 2=− MQNP Lời giải Ta có 222 MNMIQPPQ ===− Chọn C


Câu 25. Trên đường thẳng MN lấy điểm P sao cho 3 MNMP =− . Điểm P được xác định đúng trong hình vẽ nào sau đây: A. Hình 3 B. Hình 4 C. Hình 1 D. Hình 2 Lời giải Chọn A 3 MNMPMN =− ngược hướng với MP và 3 MNMP = .
Câu 26. Toạ độ của vectơ 32=−+ uij là: A. (3;2). B. (2;3). C. (3;2) ij D. (3;2) Lời giải
DẠYKÈMQUYNHƠN OFFICIAL
Câu
Trên trục ' xOx cho tọa độ các điểm B,
lần
m
2
++
thẳng BC có độ dài nhỏ nhất. A. 2 m = B. 1 m = C. 1 m =− D. 2 m =− Lời giải Đáp án C ( )2 2 24133mBCBCmmm==++=++ . BC nhỏ nhất khi 101mm+==− Câu 28. Nếu hai điểm , MN thoả mãn 4=−MNNM thì độ dài đoạn thẳng MN bằng bao nhiêu? A. 4 = MN B. 2 = MN C. 16= MN ; D. 256 = MN . Lời giải 2 4..cos180442 =−==−== MNNMMNNMMNMN . Chọn A Câu 29. Cho hình vuông ABCD cạnh a Đẳng thức nào sau đây đúng?
Chọn A
27.
C
lượt là 2
và
32mm
. Tìm m để đoạn
A. 2 . ABACa = B. 2 .2ABACa = C. 2 2 2 ABACa = D. 2 1 2 ABACa =
Lời giải
Chọn A
Ta có ( ) 0,45ABACBAC== nên 02 2 ...cos45.2. 2 ABACABACaaa ===
Câu 30. Cho hình vuông ABCD cạnh a . Gọi E là điểm đối xứng của D qua C Đẳng thức nào sau đây đúng?
A. 2 .2.AEABa = B. 2 .3.AEABa = C. 2 .5.AEABa = D. 2 .5.AEABa =
Lời giải
Chọn A
Ta có C là trung điểm của DE nên 2.DEa = Khi đó ( ) 0 AEABADDEABADABDEAB =+=+ ( ) 02 ..cos,..cos02. DEABDEABDEABa ===
Câu 31. Số quy tròn của 219,46 đến hàng chục là: A. 210. B. 219,4. C. 219,5. D. 220. Lời giải Chọn D
A B
E D C
Câu 32. Biết số gần đúng 37975421 a = có độ chính xác 150 d = . Hãy xác định các chữ số đáng tin của a A. 3, 7, 9 B. 3, 7, 9, 7 C. 3, 7, 9, 7, 5 D. 3, 7, 9, 7, 5, 4 Lời giải Vì sai số tuyệt đối đến hàng trăm nên các chữ số hàng nghìn trở lên của a là đáng tin. Vậy các chữ số đáng tin của a là 3, 7, 9, 7, 5. Đáp án C. Câu 33. Số áo bán được trong một quý ở cửa hàng bán áo sơ mi nam được thống kê như sau: Cỡ áo 36 37 38 39 40 41 42
DẠYKÈMQUYNHƠN
OFFICIAL
126 C. 42 D. 12 Lời giải Chọn A Vì giá trị 3 38 x = có tần số 3 126 n = lớn nhất. Câu 34. Tiền lương hàng tháng của 7 nhân viên trong một công ty du lịch lần lượt là:6,5; 8,4; 6,9; 7,2; 2,5; 6,7; 3,0 (đơn vị: triệu đồng). Số trung vị của dãy số liệu thống kê trên bằng A. 6,7 triệu đồng. B. 7,2 triệu đồng. C. 6,8 triệu đồng. D. 6,9 triệu đồng. Lời giải Chọn A
Tần số (Số áo bán được) 13 45 126 125 110 40 12 Giá trị mốt của bảng phân bố tần số trên bằng A. 38 B.
Sắp xếp thứ tự các số liệu thống kê, ta thu dược dãy tăng các số liệ
sau:2,5;3,0;6,5;6,7;6,9;7,2; 8,4 (đơn vị: triệu đồng).
Số trung vị 6,7 e M = triệu đồng. Số các số liệu thống kê quá ít ( 710 n = ), do đó không nên chọn số trung bình cộng làm đại diện cho các số liệu đã cho. Trong trường hợp này ta chọn số trung vị 6,7 e M = triệu đồng làm đại diện cho tiền lương hàng tháng của 7 nhân viên.

Câu 35. Năng suất lúa hè thu (tạ/ha) năm 1998 của 31 tỉnh ở Việt Nam được thống kê trong bảng sau:
Giá trị 3 35 x = có tần số bằng A. 6 B. 4 C. 7 D. 9
Lời giải Chọn D
2. Tự luận
Câu 1. Trong một trường THPT, khối 10 có 160 em học sinh tham gia câu lạc bộ Toán, 140 em tham gia câu lạc bộ Tin, 100 em học sinh tham gia cả hai câu lạc bộ. Hỏi khối 10 có bao nhiêu học sinh?.
Lời giải Gọi A là tập hợp các bạn tham gia câu lạc bộ Toán. B là tập hợp các bạn tham gia câu lạc bộ Tin như vậy số học sinh của khối 10 là số phần tử của tập hợp \ ABABB = vậy có: 160140–100200 += học sinh khối 10.
Câu 2. Một học sinh dự định vẽ các tấm thiệp xuân làm bằng tay để bán trong một hội chợ Tết. Cần 2 giờ để vẽ một tấm thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ để vẽ một tấm thiệp loại lớn có giá 20 nghìn đồng. Học sinh này chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải vẽ ít nhất 12 tấm. Hãy cho biết bạn ấy cần vẽ bao nhiêu tấm thiệp mồi loại để có được nhiều tiền nhất. Lời giải
DẠYKÈMQUYNHƠN
OFFICIAL
u
Tổng
vẽ
30 giờ nên 2330 +xy Số tấm thiệp tối thiểu là 12 tấm nên 12 +xy Từ đó ta có hệ bất phương trình: 2330 12 (,) 0 0 + + xy xy xy x y Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy , ta được như hình dưới.
Ta có các điều kiện ràng buộc đối với x, y như sau: Hiển nhiên 0,0xy
số giờ
không quá
Miền không tô màu (miền tam giác ABC , bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phươnng trình.
Với các đỉnh (6;6),(15;0),(12;0) ABC
Gọi F là số tiền (đơn vị: nghìn đồng) thu được, ta có: 1020=+ Fxy
Tính giá trị của F tại các đỉnh của tam giác:
Tại (6;6):10.620.6180 =+= AF

Tại (15;0):10.1520.0150 =+= BF
Tại (12;0):10.1220.0120 =+= CF
F đạt giá trị lớn nhất bằng 180 tại (6;6)A .
OFFICIAL
Vậy bạn học sinh đó cần vẽ 6 tấm thiệp loại nhỏ và 6 tấm thiệp loại to để có được nhiều tiền nhất. Câu 3. Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A ) đến trường (điểm B ) phải leo lên và xuống một con dốc (Hình 24). Cho biết đoạn thẳng AB dài 762m , ˆ ˆ 6,4 ==AB . a) Tính chiều cao h của con dốc theo đơn vị mét (làm tròn kết quả đến hàng đơn vị). b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ trung bình lên dốc là 4 / kmh và tốc độ trung bình khi xuống dốc là 19 / kmh Lời giải a) Xét tam giác ABC ta có: 18064170
DẠYKÈMQUYNHƠN
CBC . Xét tam giác vuông AHC ta có sin306sin632( ) == hCHACAm Vậy chiều cao con dốc là khoảng 32m b) Áp dụng định lí sin ta có: 762sin6459( sinsinsin170) == BCAB BCm AC . Ta có: 306 0,306 ;459 0,459 == ACmkmCBmkm Như vậy, thời gian bạn An đi từ nhà đến trường là: =++= 0,3060,459 0,1(giôø) 6(phuùt). 419419 ACCB t Vậy bạn An đến trường lúc khoảng 6 giờ 6 phút. Câu 4. Chất điểm A chịu tác động của ba lực 123 ,, FFF như hình và ở trạng thái cân bằng (tức là 123 0 FFF++= ). Tính độ lớn của các lực 23 , FF biết 1F có độ lớn là 20 N
=−−= ACB . Áp dụng định lí sin ta có: sin762sin4306( sinsinsinsin170)
=== ABACABB ACm
Lời giải Bước 1: Đặt 12 uFF =+ . Ta xác định các điểm như hình dưới.

Dễ dàng xác định điểm C , là điểm thứ tư của hình bình hành ABCD. Do đó vecto u chính là vecto AC Vì chất điểm A ở trang thái cân bằng nên 123 0 FFF++= hay 33 0 vaø uFuF += là hai vecto đối nhau. A là trung điểm của EC Bước 2: Ta có: 123 20,, FADFABFAC ==== Do ,, ACE thẳng hàng nên 18060CABEAB =−=

OFFICIAL
DẠYKÈMQUYNHƠN
403 906030cos303 sin30203 3 AD AC CAD ABDCAC == =−= === Vậy 23 203403 , 33 FF==
1. Trắc nghiệm Câu 1. Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Hãy mở cửa ra! b) Số 25 chia hết cho 8. c) Số 17 là số nguyên tố. d) Bạn thích ăn phở không? A. 1. B. 2. C. 3. D. 4. Câu 2. Cho mệnh đề chứa biến ()Px : " 2 15 xx + " (với x là số thực). Mệnh đề nào sau đây là đúng? A. (0)P . B. (3)P . C. (4)P . D. (5)P . Câu 3. Cho tập hợp 2 9 =Axx . Tập hợp A là: A. {0;1;2;3} = A B. [0;3]. = A C. {0;3} = A . D. {3;2;1;0;1;2;3}=−−− A . Câu 4. Viết tập hợp ( )( ) 22240=−−= Bxxxx bằng cách liệt kê các phần tử của tập hợp thì ta được: A. {2;0;2;2}
A. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy chứa gốc tọa độ (0;0)O (kể cả bờ).
B. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy không chứa gốc tọa độ (0;0)O (kể cả bờ).
C. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy chứa gốc tọa độ (0;0)O (không kể bờ).
D. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy không chứa gốc tọa độ (0;0)O (không kể bờ).
nào
được trả 12 USD mỗi giờ và làm nhân viên thu ngân ở siêu thị được trả 9,5 USD mỗi giờ. Gọi x là số giờ anh ấy làm gia sư và y là số giờ anh ấy làm nhân viên thu ngân. Anh ầy có thể làm việc không quá 20 giờ mỗi tuần. Hỏi cặp số (;) xy nào sau đây thể hiện anh ấy kiếm được ít nhất 220 USD mỗi tuần?
DẠYKÈMQUYNHƠN
ĐỀ 02
OFFICIAL
rỗng? A.
=++=
B.
=++=
D.
Câu
=− B B. {2;0;2}=− B C. {2} = B D. {2;2}=− B Câu 5. Trong các tập hợp sau, tập hợp nào là tập hợp
{(1)(21)0}
Axxx
{(1)(21)0} =++=Bxxx C. {(1)(21)0}
Cxxx
{(1)(21)0} =++=Dxxx
6. Miền nghiệm của bất phương trình bậc nhất hai ẩn 578 −xy là:
xy−+ . B.
xy + .
22 3(1)xyx+− D. 2(3)3(22)2 xyxy +++ . Câu 8. Cho hệ bất phương trình 1 1 1 1 xy xy xy xy + +− − −− . Diện tích miền nghiệm () H của hệ bất phương trình đã cho là A. 1. B. 2. C. 2 D. 4. Câu 9. Cho hệ bất phương trình 235 (1) 35(2) 2 xy xy + + . Gọi 12 , SS lần lượt là tập nghiệm của các bất phương trình (1) và (2). Mệnh đề nào sau đây đúng? A. 12SS B. 21SS C. 12SS = D. 12SS Câu 10. Anh Tuấn là du học sinh tại Mỹ và có hai công việc làm thêm vào mùa hè.
ấy
Câu 7. Bất phương trình
sau đây KHÔNG là bất phương trình bậc nhất hai ẩn? A. 290
3(1)2
C.
Anh
làm gia sư
A. (10;10) B. (12;8) C. (11;10) D. (9;9)
Câu 11. Giá trị của biểu thức 0000 sin30cos60sin60cos30 P =+ bằng A. 3 P =− . B. 0 P = . C. 3 P = . D. 1 P = .
Câu 12. Cho là góc nhọn và 1 sincos 2 = . Giá trị của sincos M =+ là A. 1. B. 2. C. 2 D. 2 Câu 13. Rút gọn biểu thức ( ) ( ) tan180 1 sinsin90 x P xx
=+ − với ( ) 0;90 x ta được A. 2 1 cos x B. 2 1 cos x C. tan x D. 2tan x Câu 14. Tam giác ABC có 0 8,3,60.acB=== Độ dài cạnh b bằng bao nhiêu? A. 49. B. 97 C. 7. D. 61. Câu 15. Cho tam giác ABC thoả mãn: 222 3 bcabc +−= . Khi đó: A. 0 30. A = B. 0 45. A = C. 0 60. A = D. 075 A = . Câu 16. Cho tam giác ABC , biết 13,14,15.abc=== Tính góc B? A. 0 5949'. B. 0 537'. C. 0 5929'. D. 0 6222'. Câu 17. Cho tam giác ABC có 110;46;6ACb=== . Khẳng định nào sau đây đúng?
A. 24;13,9;10,6Bac= B. 24;13,8;10,7Bac= C. 24;12,7;10,1Bac= . D. 24;12,6;10,2Bac= .
Câu 18. Cho tam giác ABC có 6;7;12abc=== . Khẳng định nào sau đây đúng?
A. ABC có 1 góc tù. B. ABC có 3 góc nhọn. C. ABC là tam giác vuông. D. 20 A .
Câu 19. Hai vectơ có cùng độ dài và cùng hướng gọi là
A. Hai vectơ cùng hướng. B. Hai vectơ cùng phương. C. Hai vectơ đối nhau. D. Hai vectơ bằng nhau. Câu 20. Cho ABC và điểm M thoả mãn điều kiện MAMCMB += . Khẳng định nào sau đây là SAI? A. ABAMAC += B. BABCBM += C. Tứ giác ABCM là hình bình hành. D. MABC = . Câu 21. Cho tam giác ABC đều cạnh bằng a . Độ dài vectơ ABAC bằng A. 0. B. a C. 2a D. 2 a Câu 22. Cho hình bình hành ABCD có tâm O . Đẳng thức nào sau đây
DẠYKÈMQUYNHƠN
OFFICIAL
? A. OBOCODOA −=− B.
−= C. ABADDB −= . D.
−=− . Câu 23. Một giá đỡ có dạng tam giác ABC vuông cân tại đỉnh A được gắn vào tường như hình
Người ta treo vào vị trí C một vật nặng 10N . Cường độ lực tác động vào tường tại điểm A và B là
là SAI
OAOBCD
BCBADCDA
bên.
A. (5 N;10 N). B. (10 ;10 )NN . C. (10;102 )NN . D. (10;103 )NN .
Câu 24. Cho đoạn thẳng AB và O là trung điểm của AB . Khẳng định nào sau đây là đúng?
A. 2 = ABOA. B. 2 = ABOB . C. 2=− ABOB . D. 2 = AOAB . Câu 25. Cho ba điểm phân biệt ,, ABC . Nếu 3 ABAC =− thì đẳng thức nào dưới đây đúng?
A. 4 BCAC =− B. 2 BCAC =− C. 2 BCAC = D. 4 BCAC =
Câu 26. Tọa độ của vectơ 5 = uj là: A. (5;0). B. (5;) j . C. (0;5) j . D. (0;5).
Câu 27. Trong hệ trục tọa độ Oxy , cho hai điểm ( )1;1 M , ( )4;1 N . Tính độ dài véctơ MN A. 13 MN = B. 5 MN = C. 29 MN = D. 3 MN =

Câu 28. Phát biểu nào sau đây là đúng?
A. Nếu , ab khác 0 và (,)90 ab thì 0 ab ; B. Nếu , ab khác 0 và (,)90 ab thì 0 ab ; C. Nếu , ab khác 0 và (,)90 ab thì 0 ab ; D. Nếu , ab khác 0 và (,)90 ab thì 0 ab
Câu 29. Cho tam giác ABC . Tập hợp các điểm M thỏa mãn .0MABC = là: A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn. Câu 30. Cho tam giác đều ABC cạnh 2 = a . Hỏi mệnh đề nào sau đây sai? A. ( ) .2 = ABACBCBC . B. .2 =− BCCA . C. ( ).4+=−ABBCAC . D. ( ).2−=BCACBA .
Câu 31. Số quy tròn của số gần đúng 673582 với độ chính xác 500 = d là: A. 673500. B. 674000. C. 673000. D. 673600. Câu 32. Cho hình chữ nhật ABCD. Gọi AL và CI tương ứng là đường cao của các tam giác ADB và BCD. Cho biết 1 DLLIIB=== . Diện tích của hình chữ nhật ABCD (chính xác đến hàng phần trăm) là: A. 4,24 B. 2,242 C. 4,2 D. 4,2426
Câu 33. Điểm kiểm tra môn Toán cuối năm của một nhóm gồm 9 học sinh lớp 6 lần lượt là 1; 1; 3; 6; 7; 8; 8; 9; 10. Điểm trung bình của cả nhóm gần nhất với số nào dưới đây?
A. 7,5. B. 7 . C. 6,5. D. 5,9.
Câu 34. Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là
A. Mốt. B. Số trung bình. C. Số trung
DẠYKÈMQUYNHƠN
OFFICIAL
vị. D. Độ lệch chuẩn. Câu 35. Chọn khẳng định sai trong các khẳng định sau: A. Phương sai luôn là một số không âm. B. Phương sai là bình phương của độ lệch chuẩn. C. Phương sai càng lớn thì độ phân tán quanh số trung bình càng lớn. D. Phương sai luôn lớn hơn độ lệch chuẩn.
Câu 1. Một lớp có 45 hs, đăng kí chơi ít nhất một trong hai môn thể thao là bóng đá và cầu lông. Có 30 em đăng kí môn bóng đá, 25 em đăng kí môn cầu lông. Hỏi có bao nhiêu em đăng kí cả hai môn thể thao?.
Câu 2. Bác Năm dự định trồng khoai lang và khoai mì trên mảnh đất có diện tích 8 ha. Nếu trồng 1 ha khoai lang thì cần 10 ngày công và thu được 20 triệu đồng. Nếu trồng 1 ha khoai mì thì cần 15 ngày công và thu được 25 triệu đồng. Bác Năm cần trồng bao nhiêu hecta cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng được không quá 90 ngày công cho việc trồng khoai lang và khoai mì.
Câu 3. Quan sát cây cầu dây văng minh hoạ ở Hình 25.
Tại trụ cao nhất, khoảng cách từ đỉnh trụ (vị trí A ) tới chân trụ trên mặt cầu (vị trí H ) là 150m , độ dài dây văng dài nhất nối từ đỉnh trụ xuống mặt cầu (vị trí B ) là 300m, khoảng cách từ chân dây văng dài nhất tới chân trụ trên mặt cầu là 250m (Hình 26). Tính độ dốc của cầu qua trụ nói trên (làm tròn kết quả đến hàng phần mười theo đơn vị độ).

Câu 4. Một vật đồng chất được thả vào một cốc chất lỏng. Ở trạng thái cân bằng, vật chìm một nửa thể tích trong chất lỏng. Tìm mối liên hệ giữa trọng lực P của vật và lực đẩy Archimedes F mà chất lỏng tác động lên vật. Tính tỉ số giữa trọng lượng riêng của vật và của chất lỏng. Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM

DẠYKÈMQUYNHƠN
OFFICIAL 2. Tự luận
1B 2D 3A 4B 5D 6D 7D 8B 9A 10B 11D 12D 13D 14C 15A 16C 17A 18A 19D 20D 21B 22A 23C 24B 25D 26D 27A 28C 29B 30C 31B 32A 33D 34A 35D 1. Trắc nghiệm Câu 1. Trong các câu sau, có bao nhiêu câu là mệnh đề? a) Hãy mở cửa ra! b) Số 25 chia hết cho 8. c) Số 17 là số nguyên tố. d) Bạn thích ăn phở không? A. 1. B. 2. C. 3. D. 4. Câu 2. Cho mệnh đề chứa biến ()Px : " 2 15 xx + " (với x là số thực). Mệnh đề nào sau đây là đúng? A. (0)P B. (3)P C. (4)P D. (5)P Câu 3. Cho tập hợp 2 9 =Axx . Tập hợp A là: A. {0;1;2;3} = A . B. [0;3]. = A C. {0;3} = A D. {3;2;1;0;1;2;3}=−−− A Câu 4. Viết tập hợp ( )( ) 22240=−−= Bxxxx bằng cách liệt kê các phần tử của tập hợp thì ta được: A. {2;0;2;2}=− B . B. {2;0;2}=− B . C. {2} = B . D. {2;2}=− B . Câu 5. Trong các tập hợp sau, tập hợp nào là tập hợp rỗng? A. {(1)(21)0} =++= Axxx . B. {(1)(21)0} =++=Bxxx .
Câu
A. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy chứa gốc tọa độ (0;0)O (kể cả bờ).
B. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy không chứa gốc tọa độ (0;0)O (kể cả bờ).
C. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy chứa gốc tọa độ (0;0)O (không kể bờ).
D. Nửa mặt phẳng bờ là đường thẳng :578 −=dxy không chứa gốc tọa độ (0;0)O (không kể bờ).
i
SS lần lượt là tập nghiệm của các bất phương trình (1) và (2). Mệnh đề nào sau đây đúng? A. 12SS . B. 21SS . C. 12SS = D. 12SS . Câu 10. Anh Tuấn là du học sinh tại Mỹ và có hai công việc làm thêm vào mùa hè. Anh ấy làm gia sư được trả 12 USD mỗi giờ và làm nhân viên thu ngân ở siêu thị được trả 9,5 USD mỗi giờ. Gọi x là số giờ anh ấy làm gia sư và y là số giờ anh ấy làm nhân viên thu ngân. Anh ầy có thể làm việc không quá 20 giờ mỗi tuần. Hỏi cặp số (;) xy nào sau đây thể
DẠYKÈMQUYNHƠN
OFFICIAL C. {(1)(21)0} =++=Cxxx D. {(1)(21)0} =++=Dxxx
Câu 6. Miền nghiệm của bất phương trình bậc nhất hai ẩn 578 −xy là:
1 1 1 1 xy xy xy xy + +− − −− . Diện
ệm
ủ
ệ
.
hiện anh ấy kiếm được ít nhất 220 USD mỗi tuần? A. (10;10). B. (12;8). C. (11;10) D. (9;9). Lời giải Số tiền mà anh Tuấn kiếm được là 129,5xy + (USD). Theo đề bài ta có hệ bất phương trình 129,5220 20 0;0 xy xy xy + + Thay lần lượt các đáp án ta có đáp án B thoả mãn. Câu 11. Giá trị của biểu thức 0000 sin30cos60sin60cos30 P =+ bằng A. 3 P =− . B. 0 P = . C. 3 P = . D. 1 P = . Lời giải
7. Bất phương trình nào sau đây KHÔNG là bất phương trình bậc nhất hai ẩn? A. 290 xy−+ B. 3(1)2xy + . C. 22 3(1)xyx+− . D. 2(3)3(22)2 xyxy +++ Câu 8. Cho hệ bất phương trình
tích miền nghi
() H c
a h
bất phương trình đã cho là A. 1. B. 2. C. 2 D. 4. Câu 9. Cho hệ bất phương trình 235 (1) 35(2) 2 xy xy +
+
Gọ
12 ,
DẠYKÈMQUYNHƠN OFFICIAL Chọn D
Lời giải Chọn
Ta
Câu
=
=
L
Ta
222
33 cos30. 222 bcabc AA bcbc +− ====
ABC
biết
abc===
Lờ
ả
Chọn
Ta
222222
cos5929'. 22.13.1565 acb BB ac +−+− ===
00002020 sin30sin30cos30cos30sin30cos301 P =+=+= Câu 12. Cho là góc nhọn và 1 sincos 2 = . Giá trị của sincos M =+ là A. 1. B. 2. C. 2 D. 2 . Lời giải 22(sincos)12sincos2 M =+=+= . Suy ra 2 M = (vì )0 M . Câu 13. Rút gọn biểu thức ( ) ( ) tan180 1 sinsin90 x P xx =+ với ( ) 0;90 x ta được A. 2 1 cos x . B. 2 1 cos x C. tan x . D. 2tan x Câu 14. Tam giác ABC có 0 8,3,60.acB=== Độ dài cạnh b bằng bao nhiêu? A. 49. B. 97 C. 7. D. 61.
C.
có: 2222202cos832.8.3.cos60497 bacacBb =+−=+−== .
15. Cho tam giác ABC thoả mãn: 222 3 bcabc +−= . Khi đó: A. 0 30. A
B. 0 45. A
C. 0 60. A = D. 075 A = .
ời giải Chọn#A.
có:
0
Câu 16. Cho tam giác
,
13,14,15.
Tính góc B? A. 0 5949'. B. 0 537'. C. 0 5929'. D. 0 6222'.
i gi
i
C.
có:
0 13151433
Câu 17. Cho tam giác ABC có 110;46;6ACb=== . Khẳng định nào sau đây đúng? A. 24;13,9;10,6Bac= B. 24;13,8;10,7Bac= C. 24;12,7;10,1Bac= . D. 24;12,6;10,2Bac= .
Ta có ( ) 18024BAC=−+=
Áp dụng định lý sin, ta được: .sin.sin 13,9;10,6sinsin bAbC ac BB ==
Câu 18. Cho tam giác ABC có 6;7;12abc=== . Khẳng định nào sau đây đúng?
A. ABC có 1 góc tù. B. ABC có 3 góc nhọn. C. ABC là tam giác vuông. D. 20 A Lời giải Góc lớn nhất trong tam giác ABC là C . 222 157 cos21 2168 bca AA bc +− == 222 59 cos135 284 abc CC ab +− ==−
Vậy ABC có 1 góc tù.
Câu 19. Hai vectơ có cùng độ dài và cùng hướng gọi là
A. Hai vectơ cùng hướng. B. Hai vectơ cùng phương. C. Hai vectơ đối nhau. D. Hai vectơ bằng nhau
Lời giải Chọn D Hai vectơ bằng nhau là hai vectơ có cùng độ dài và cùng hướng. Câu 20. Cho ABC và điểm M thoả mãn điều kiện MAMCMB += . Khẳng định nào sau đây là SAI?
A. ABAMAC += B. BABCBM += . C. Tứ giác ABCM là hình bình hành. D. MABC = Lời giải MAMCMBMCMBMAMCAB +==−= . Khi đó tứ giác ABCM là hình bình hành. Do đó phương án C là đúng. Với phương án , AB , ta áp dụng quy tắc hình bình hành suy ra A và B là đúng. Vì ABCM là hình bình hành nên MABC =− . Câu 21. Cho tam giác ABC đều cạnh bằng a . Độ dài
DẠYKÈMQUYNHƠN
OFFICIAL Lời giải
ằng A. 0. B. a . C. 2a D. 2 a . Câu 22. Cho
ABCD có
O . Đẳng
SAI ? A. OBOCODOA −=− B. OAOBCD −= . C. ABADDB −= . D. BCBADCDA −=− . Câu 23. Một giá đỡ có dạng tam giác ABC vuông cân tại đỉnh A được gắn vào tường như hình bên. Người ta treo vào vị trí C một vật nặng 10N . Cường độ lực tác động vào tường tại điểm A và B là
vectơ ABAC b
hình bình hành
tâm
thức nào sau đây là
A. (5 N;10 N). B. (10 ;10 )NN C. (10;102 )NN D. (10;103 )NN .

Lời giải Tại điểm C , lực kéo F có phương thẳng đứng hướng xuống dưới. Ta thấy F là hợp của hai lực 1F và 2F có giá lần lượt là hai đường thẳng AC và BC . Do đó hai lực tác động vào điểm A và B khi treo vật vào vị trí điểm C lần lượt là 1F và 2F . vi tam giác ABC vuông cân tại C Do đó 1 ||10 FFN

DẠYKÈMQUYNHƠN OFFICIAL
F FFN === Câu 24. Cho đoạn thẳng AB và O là trung điểm của AB . Khẳng định nào sau đây là đúng? A. 2 = ABOA. B. 2 = ABOB . C. 2=− ABOB . D. 2 = AOAB . Lời giải Chọn B Câu 25. Cho ba điểm phân biệt ,, ABC . Nếu 3 ABAC =− thì đẳng thức nào dưới đây đúng? A. 4 BCAC =− B. 2 BCAC =− C. 2 BCAC = D. 4 BCAC = Lời giải Chọn D Câu 26. Tọa độ của vectơ 5 = uj là: A. (5;0). B. (5;) j C. (0;5) j .
== và 2 ||2||102sin45
D. (0;5)
Chọn D
Lời giải
Câu 27. Trong hệ trục tọa độ Oxy , cho hai điểm ( )1;1 M , ( )4;1 N . Tính độ dài véctơ MN .
A. 13 MN = . B. 5 MN = . C. 29 MN = . D. 3 MN = .
Lời giải Chọn A ( )3;2 MN =− ( )2 2 3213 MN =+−= .
Câu 28. Phát biểu nào sau đây là đúng?
A. Nếu , ab khác 0 và (,)90 ab thì 0 ab ; B. Nếu , ab khác 0 và (,)90 ab thì 0 ab ; C. Nếu , ab khác 0 và (,)90 ab thì 0 ab ; D. Nếu , ab khác 0 và (,)90 ab thì 0 ab Lời giải Chọn C
OFFICIAL
Câu 29. Cho tam giác ABC . Tập hợp các điểm M thỏa mãn .0MABC = là: A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Lời giải
Chọn B. Ta có .0. MABCMABC =⊥ Vậy tập hợp các điểm M là đường thẳng đi qua A và vuông góc với BC
Câu 30. Cho tam giác đều ABC cạnh 2 = a . Hỏi mệnh đề nào sau đây sai? A. ( ) .2 = ABACBCBC . B. .2 =− BCCA . C. ( ).4+=−ABBCAC . D. ( ).2−=BCACBA .
Lời giải
Chọn C Ta đi tính tích vô hướng ở các phương án. So sánh vế trái với vế phải. Phương án A: ( ) o ..cos602.2 === ABACABACxABACBCBC nên loại#A. Phương án B: o ..cos1202 ==−BCCABCAC
DẠYKÈMQUYNHƠN
án C:
Câu 31. Số quy tròn của số gần đúng 673582 với độ chính xác 500 = d là: A. 673500. B. 674000. C. 673000. D. 673600. Lời giải Chọn B Câu 32. Cho hình chữ nhật ABCD. Gọi AL và CI tương ứng là đường cao của các tam giác ADB và BCD. Cho biết 1 DLLIIB=== . Diện tích của hình chữ nhật ABCD (chính xác đến hàng phần trăm) là: A. 4,24 B. 2,242 C. 4,2 D. 4,2426 Lời giải Đáp án#A.
nên loại B. Phương
( )..4+== ABBCACACAC , o .2.2.cos1202 ==− BCCA nên chọn C.
Ta có: 2 .2ALBLLD== do đó 2 AL = . Lại có 3 BD = Suy ra diện tích của hình chữ nhật là: 323.1,41421356...4,24264...4,24 = Câu 33. Điểm kiểm tra môn Toán cuối năm của một nhóm gồm 9 học sinh lớp 6 lần lượt là 1; 1; 3; 6; 7; 8; 8; 9; 10. Điểm trung bình của cả nhóm gần nhất với số nào dưới đây? A. 7,5. B. 7 . C. 6,5. D. 5,9. Lời giải Chọn D Điểm trung bình của cả nhóm là 91136788910535,(8)5, 99 == +++++ +++ .

Câu 34. Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là A. Mốt. B. Số trung bình. C. Số trung vị D. Độ lệch chuẩn. Lời giải Chọn A
Câu 35. Chọn khẳng định sai trong các khẳng định sau:
A. Phương sai luôn là một số không âm.
B. Phương sai là bình phương của độ lệch chuẩn.
C. Phương sai càng lớn thì độ phân tán quanh số trung bình càng lớn. D. Phương sai luôn lớn hơn độ lệch chuẩn. Lời giải Chọn D
Phương sai 2 x S còn độ lệch chuẩn 2 xx SS = nhưng không thể khẳng định phương sai luôn lớn hơn độ lệch chuẩn.
2. Tự luận Câu 1. Một lớp có 45 hs, đăng kí chơi ít nhất một trong hai môn thể thao là bóng đá và cầu lông. Có 30 em đăng kí môn bóng đá, 25 em đăng kí môn cầu lông. Hỏi có bao nhiêu em đăng kí cả hai môn thể thao?. Lời giải +) Gọi A là tập hợp các bạn đăng ký môn bong đá, B là tập hợp các bạn đăng kí cầu lông, gọi x là số bạn đăng ký cả hai môn. +) Tập hợp số học sinh của lớn là: \ ABABB = : Ta có: 25304510. xx +−== Vậy có 10 bạn đăng ký cả hai môn. Câu 2. Bác Năm dự định trồng khoai lang và khoai mì trên mảnh đất có diện tích 8 ha. Nếu trồng 1 ha khoai lang thì cần 10 ngày công và thu được 20 triệu đồng. Nếu trồng 1 ha khoai mì thì cần 15 ngày công và thu được 25 triệu đồng. Bác Năm cần trồng bao nhiêu hecta cho mỗi loại cây để
DẠYKÈMQUYNHƠN OFFICIAL
thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng được không quá 90 ngày công cho việc trồng khoai lang và khoai mì.
Lời giải
Gọi x là số hecta trồng khoai lang và y là số hecta trồng khoai mì.
Ta có hệ bất phương trình mô tả các điều kiện ràng buộc:
+ +
xy xy x y
8 101590 0 0.
Biểu diễn miền nghiệm của hệ bất phương trình trên hệ trục toạ độ Oxy ta được miền đa giác OABC. Toạ độ các đỉnh của đa giác đó là: (0;0);(0;6);(6;2);(8;0) OABC
Gọi F là số tiền (đơn vị: triệu đồng) bác Năm thu được, ta có: 2025=+ Fxy
Ta phải tìm , xy thoả mãn hệ bất phương trình sao cho F lớn nhất, nghĩa là tìm giá trị lớn nhất của 2025=+ Fxy trên miền đa giác OABC
Tính các giá trị của biểu thức F tại các đỉnh của đa giác, ta có:
Tại (0;0):20.025.00 =+= OF ;


Tại (0;6):20.025.6150 =+= AF ;
Tại (6;2):20.625.2170 =+= BF ;
Tại (8;0):20.825.0160 =+= CF
Ta thấy F đạt giá trị lớn nhất bằng 170 tại (6;2)B

Vậy để thu được nhiều tiền nhất, bác Năm cần trồng 6 ha khoai lang và 2 ha khoai mì. Câu 3. Quan sát cây cầu dây văng minh hoạ ở Hình 25.
Tại trụ cao nhất, khoảng cách từ đỉnh trụ (vị trí A ) tới chân trụ trên mặt cầu (vị trí H ) là 150m , độ dài dây văng dài nhất nối từ đỉnh trụ xuống mặt cầu (vị trí B ) là 300m, khoảng cách từ chân dây văng dài nhất tới chân trụ trên mặt cầu là 250m (Hình 26). Tính độ dốc của cầu qua trụ nói trên (làm tròn kết quả đến hàng phần mười theo đơn vị độ). Lời giải Độ dốc của cầu là góc nghiêng giữa đường cầu qua trụ và phương nằm ngang, tức là góc KBH . Xét tam giác ABH , áp dụng định lí côsin ta có: 2222222501503001 cos93,8. 2.2.250.15015
DẠYKÈMQUYNHƠN
OFFICIAL
===− BHAHAB
+−+−
AHBAHB BHAH
Xét tam giác BHK ta có: 93,8903,8
HBK (tính chất góc ngoài tam giác). Vậy độ dốc của cầu qua trụ theo đề bài là khoảng 3,8 .
Câu 4. Một vật đồng chất được thả vào một cốc chất lỏng. Ở trạng thái cân bằng, vật chìm một nửa thể tích trong chất lỏng. Tìm mối liên hệ giữa trọng lực P của vật và lực đẩy Archimedes F mà chất lỏng tác động lên vật. Tính tỉ số giữa trọng lượng riêng của vật và của chất lỏng.
Lời giải
Lực đẩy Archimedes AF và trọng lực P đều tác động lên vật theo phương thẳng đứng, hai lực này ngược hướng. Do ở trạng thái cân bằng vật nổi (chìm một nửa), nên hai lực này có cường đọ bằng nhau.
Gọi d , d' tương ứng là trọng lượng riêng của vật và trọng lượng riêng của chất lỏng: gọi V là thể tích của vật. Khi đó trọng lượng của vật bằng || == PPdV . (1)
Lực đẩy Archimedes tác động lên vật có cường độ bằng 2 == Aa V FFd . (2)
Từ (1) và (2), để ý rằng = APF , suy ra 2 = d d .
OFFICIAL
DẠYKÈMQUYNHƠN
−=
1. Trắc nghiệm
Câu 1. Trong các phát biểu sau, phát biểu nào là mệnh đề toán học?
A. Nước là hợp chất tạo bởi hai nguyên tố là hydrogen và oxygen.
B. Sông Hương là con sông chảy qua thành phố Huế.
C. Ngày 30 tháng 4 năm 1975 là ngày Giải phóng miền Nam.
D. Số 2022 chia hết cho 4.
Câu 2. Mệnh đề phủ định của P : "Tam giác ABC là tam giác cân" là:
A. Tam giác ABC không phải là tam giác cân
B. Tam giác ABC là tam giác vuông C. Tam giác ABC là tam giác đều
D. ABC không phải là một tam giác
Câu 3. Kí hiệu , lần lượt là tập số hữu tỉ, tập số thực. Kết luận nào sau đây là đúng?
A. B. C. D.
Câu 4. Cho hai tập hợp {2;5},{(5)()()0} ==−−−= ABxxxaxb với , ab là các số thực cho trước. Tất cả các cặp số (;) ab đề = AB là: A. (2;2),(5;5),(5;2). B. (2;2),(2;5),(5;2). C. (2;5),(2;2),(5;5) D. (2;2),(2;5),(5;2),(5;5)




Câu 5. Cho hai tập hợp , AB phân biệt và khác rỗng thoả mãn = ABA. Kết luận nào sau đây là đúng?
A. BA. B. AB . C. =AB . D. \ = ABA .
Câu 6. Tập nghiệm của bất phương trình 350 xy−+ là
A. Nửa mặt phẳng chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (không bao gồm đường thẳng).
B. Nửa mặt phẳng không chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (bao gồm đường thẳng).
C. Nửa mặt phẳng không chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (không bao gồm đường thẳng).
D. Nửa mặt phẳng chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (không bao gồm đường thẳng).
Câu 7. Miền nghiệm của bất phương trình 236 xy+ (miền không bị gạch) được biểu diễn bởi hình vẽ nào dưới đây?
DẠYKÈMQUYNHƠN
ĐỀ SỐ 3
OFFICIAL
A. B. C. D. Câu 8. Có bao nhiêu hệ bất phương trình bậc nhất hai ẩn trong ba hệ bất phương trình sau đây? 2 234(3)(5) ;2(5)và 3(1)3(1)211. 345 xyxyyx xy yxxy xy −++ − ++− + A. 0. B. 1. C. 2. D. 3. Câu 9. Miền nghiệm của hệ bất phương trình 2021 2022 xy xy − + KHÔNG chứa điểm nào sau đây? A. (1001;1021) B. (2021;0) C. (2021;2022) D.
(2021;2022)
Câu 10. Công ty trách nhiệm hữu hạn ĐỨC MẠNH trong một đợt quảng cáo và bán khuyến mãi hàng hoá (một sản phẩm mới của công ty) cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B . Trong đó xe loại A có 10 chiếc, xe loại B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, loại B giá 3 triệu đồng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất? Biết rằng xe loại A chỉ chở tối đa 20 người và 0,6 tấn hàng. Xe loại B chỉ chở tối đa 10 người và 1,5 tấn hàng. A. 4 xe loại A và 5 xe loại B . B. 5 xe loại A và 6 xe loại B C. 5 xe loại A và 4 xe loại B D. 6 xe loại A và 4 xe loại B
OFFICIAL
là A. 2 3 . B. 2 3 . C. 22 3 . D. 22 3 . Câu 13. Cho tan3 =− . Giá trị của cos là A. 1 2 . B. 1 2 . C. 1 4 . D. 1 4 . Câu 14. Tam giác ABC có 0 150,3,2. === CBCAC Tính cạnh AB ? A. 13 . B. 3. C. 10. D. 1. Câu 15. Cho tam giác ABC , biết 24,13,15.abc=== Tính góc A? A. 0 3334'. B. 0 11749'. C. 0 2837'. D. 0 5824'.
Giá trị của cos
Câu 16. Cho tam giác ABC có 3,5ABBC== và độ dài đường trung tuyến 13 BM = . Tính độ dài AC A. 11 B. 4 C. 9 2 D. 10
Câu 17. Cho tam giác ABC vuông tại A có ABa = , 2 ACa = . Diện tích tam giác ABC là
A. 2 2a . B. 2 4a . C. 2 3 2 a . D. 2 a
Câu 18. Cho tam giác ABC có góc ABC bằng 060 , = ACa . Tính bán kính đường tròn ngoại tiếp tam giác ABC ?
A. a . B. 3 3 a . C. 43 3 a . D. 3 a .
Câu 19. Hai vectơ được gọi là bằng nhau khi và chỉ khi
A. Giá của chúng trùng nhau và độ dài của chúng bằng nhau.
B. Chúng trùng với một trong các cặp cạnh đối của một hình bình hành. C. Chúng trùng với một trong các cặp cạnh của một tam giác đều. D. Chúng cùng hướng và độ dài của chúng bằng nhau. Câu 20. Cho hình bình hành ABCD. Khẳng định nào sau đây là đúng. A. ABACAD += . B. ABACDA −= . C. ABACCB += . D. ABACBC −= . Câu 21. Cho tam giác ABC vuông tại A có 3,4.ABAC Tính CAAB A. 2 CAAB . B. 213 CAAB .
DẠYKÈMQUYNHƠN
Câu
Cho là góc tù và
.
11.
1 sincos 2 += . Giá trị của 33 sincos M =− là A. 37 16 B. 117 16 C. 57 16 D. 57 16 Câu 12. Cho 1 sin 3 = với 090
.
C. 5 CAAB . D. 13 CAAB .
Câu 22. Cho hình bình hành ABCD. Hãy chỉ ra mệnh đề SAI trong các mệnh đề sau:
A. Không tồn tại điểm M thoả mãn đẳng thức: MAMBAB −=
B. Nếu M là trọng tâm của tam giác ABC thì: 0 MAMBMC++=
C. 0 MAMBMCM −−= trùng với D .

D. Với mọi điểm M tuỳ ý, ta luôn có: MAMCMBMD +=+
Câu 23. Một vật có khối lượng m được treo cố định trên trần nhà bằng hai sợi dây không dãn có độ dài như nhau. Biết rằng lực căng dây 1T và 2T có độ lớn như nhau bằng 600N và hợp với nhau một góc 60 (hình bên). Trọng lượng của vật là
OFFICIAL
A. 600N B. 6003 N . C. 1200N . D. 12003 N .
Câu 24. Cho tam giác ABC và M là trung điểm của , BCG là trọng tâm của tam giác. Khẳng định nào sau đây là đúng?
A. 3=− AMGM B. 3 2 = AMGM . C. 3 2 = AMGM . D. 3 = AMGM .
Câu 25. Cho tam giác ABC . Gọi I là trung điểm của BC .Khẳng định nào sau đây đúng
A. BIIC B. 32BIIC C. 2 BIIC D. 2BIIC
Câu 26. Trong hệ tọa độ Oxy cho 1 5. 2 uij =− Tọa độ của vecto u là A. 1 ;5. 2 u = B. 1 ;5. 2 u =− C. ( ) 1;10. u =− D. ( ) 1;10. u =−
Câu 27. Trong mặt phẳng
DẠYKÈMQUYNHƠN
cos ABACBAC . C. cos ABACABC . D. cos ABACACB . Câu 29. Cho tam giác ABC cân tại A , o ˆ 120 A = và ABa = . Tính BACA A. 2 2 a . B. 2 2 a . C. 2 3 2 a . D. 2 3 2 a . Câu 30. Cho hình vuông ABCD tâm O . Hỏi mệnh đề nào sau đây sai? A. .0 = OAOB B. 1 2 = OAOCOAAC C. .. = ABACABCD . D. .. = ABACACAD . Câu 31. Biết số gần đúng 7975421 a = có độ chính xác 150 d = . Hãy ước lượng sai số tương đối của a. A. 0,0000099 a B. 0,000039 a C. 0,0000039 a D. 0,000039 a
toạ độ Oxy , cho (2;5)A . Toạ độ của vecto OA là: A. (2;5) B. (2;5) C. (2;5) D. (2;5) Câu 28. Cho tam giác ABC . Giá trị của biểu thức BACA bằng: A. cos ABACBAC . B.
Câu 32. Biết số gần đúng 173,4592 a = có sai số tương đối không vượt quá 1 10000 , hãy ước lượng sai
số tuyệt đối của a và viết a dưới dạng chuẩn. A. 0,17;173,4 a a = B. 0,017;173,5 a a = C. 0,4592;173,5 a a = D. 0,017;173,4 a a =


Câu 33. Thời gian chạy 50m của 20 học sinh được ghi lại trong bảng dưới đây: Thời gian (giây) 8,3 8,4 8,5 8,7 8,8 Tần số 2 3 9 5 1
Hỏi trung bình mỗi học sinh chạy 50m hết bao lâu ?
A. 8,54. B. 4. C. 8,50. D. 8,53.
Câu 34. Một tổ học sinh gồm 10 học sinh có điểm kiểm tra giữa học kì 2 môn toán như sau: 5;6;7;5;8;8;10;9;7;8. Tính điểm trung bình của tổ học sinh đó. A. 7 . B. 8. C. 7,3. D. 7,5.
Câu 35. Để đánh giá mức độ phân tán của các số liệu thống kê so với số trung bình, ta dùng đại lượng nào sau đây? A. Số trung bình. B. Số trung vị C. Mốt. D. Phương sai.
OFFICIAL
2. Tự luận
Câu 1. Trong 100 học sinh lớp 10 có 70 học sinh nói được tiếng Anh, 45 học sinh nói được tiếng Pháp và 23 học sinh nói được cả hai tiếng Anh và Pháp. Hỏi có bao nhiêu học sinh không nói được hai thứ tiếng?.
Câu 2. Tìm giá tri lớn nhất và giá tri nhỏ nhất của biểu thức (;)2 =+ Fxyxy với (;) xy thuộc miền nghiệm của hệ bất phương trình 4 0 0
Câu 3. Một người đứng ở vị trí A trên nóc một ngôi nhà cao 4m đang quan sát một cây cao cách ngôi nhà 20m và đo được 45 = BAC (Hình 27). Tính chiều cao của cây đó (làm tròn kết quả đến hàng phần mười theo đơn vị mét).
Câu 4. Máy bay A đang bay về hướng Đông Bắc với tốc độ 600 / kmh. Cùng lúc đó, máy bay B đang bay về hướng Tây Nam với tốc độ 800 / kmh . Biểu diễn vectơ vận tốc b của máy bay B theo vectơ vận tốc a của máy bay A
DẠYKÈMQUYNHƠN
x y
+
xy
Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM
1D 2A 3C 4B 5A 6C 7C 8C 9D 10C 11D 12D 13A 14A 15B
16B 17D 18B 19D 20B 21C 22C 23B 24D 25A 26B 27B 28A 29B 30C
31B 32B 33D 34C 35D
1. Trắc nghiệm
Câu 1. Trong các phát biểu sau, phát biểu nào là mệnh đề toán học?
A. Nước là hợp chất tạo bởi hai nguyên tố là hydrogen và oxygen.
B. Sông Hương là con sông chảy qua thành phố Huế.
C. Ngày 30 tháng 4 năm 1975 là ngày Giải phóng miền Nam.
D. Số 2022 chia hết cho 4.
Câu 2. Mệnh đề phủ định của P : "Tam giác ABC là tam giác cân" là:
A. Tam giác ABC không phải là tam giác cân
B. Tam giác ABC là tam giác vuông
C. Tam giác ABC là tam giác đều D. ABC không phải là một tam giác Câu 3. Kí hiệu , lần lượt là tập số hữu tỉ, tập số thực. Kết luận nào sau đây là đúng? A. . B. . C.
. D. . Câu 4. Cho hai tập hợp {2;5},{(5)()()0}
i , ab là các số thực
c. Tất cả các cặp số (;) ab đề = AB là: A. (2;2),(5;5),(5;2). B. (2;2),(2;5),(5;2). C. (2;5),(2;2),(5;5). D. (2;2),(2;5),(5;2),(5;5). Lời giải (5)()()05;; −−−==== xxaxbxxaxb . Để = AB thì trong hai số , ab chắc chắn phải có một số bằng 2, số còn lại bằng 2 hoặc 5. Vậy ta có: (;)(2;2),(2;5),(5;2) = ab . Chọn B Câu 5. Cho hai tập hợp , AB phân biệt và khác rỗng thoả mãn = ABA. Kết luận nào sau đây là đúng? A. BA B. AB C. =AB D. \ = ABA Câu 6. Tập nghiệm của bất phương trình 350 xy−+ là

A. Nửa mặt phẳng chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (không bao gồm đường thẳng).
B. Nửa mặt phẳng không chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (bao gồm đường thẳng).
C. Nửa mặt phẳng không chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (không bao gồm đường thẳng).
D. Nửa mặt phẳng chứa gốc toạ độ, bờ là đường thẳng 35yx=+ (không bao gồm đường thẳng).
DẠYKÈMQUYNHƠN
OFFICIAL
==−−−= ABxxxaxb vớ
cho trướ
vẽ
Câu 7. Miền nghiệm của bất phương trình 236 xy+ (miền không bị gạch) được biểu diễn bởi hình
nào dưới đây? A.
chứa điểm nào sau đây? A. (1001;1021) B. (2021;0). C. (2021;2022). D. (2021;2022) Câu 10. Công ty trách nhiệm hữu hạn ĐỨC MẠNH trong một đợt quảng cáo và bán khuyến mãi hàng hoá (một sản phẩm mới của công ty) cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B . Trong đó xe loại A có 10 chiếc, xe loại B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, loại B giá 3 triệu đồng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất? Biết rằng xe loại A chỉ chở tối đa 20 người và 0,6 tấn hàng. Xe loại B chỉ chở tối đa 10 người và 1,5 tấn hàng.

A. 4 xe loại A và 5 xe loại B .
B. 5 xe loại A và 6 xe loại B C. 5 xe loại A và 4 xe loại B D. 6 xe loại A và 4 xe loại B .

Lời giải Gọi x và y lần lượt là số xe loại A và (010;09;,) Bxyxy . Khi

DẠYKÈMQUYNHƠN OFFICIAL
2
3(1)3(1)211. 345 xyxyyx xy yxxy xy −++ − ++− +
2021 2022
xy − +
B. C. D. Câu 8. Có bao nhiêu hệ bất phương trình bậc nhất hai ẩn trong ba hệ bất phương trình sau đây?
234(3)(5) ;2(5)và
A. 0. B. 1. C. 2. D. 3. Câu 9. Miền nghiệm của hệ bất phương trình
xy
KHÔNG
đó tổng chi phí thuê xe là 43 Txy =+ (triệu đồng). Xe A chở tối đa 20 người, xe B chở tối đa 10 người nên tổng số người 2 xe chở tối đa được là 2010xy + (người). Xe A chở được 0,6 tấn hàng, xe B chở được 1,5 tấn hàng nên tổng lượng hàng 2 xe chở được là 0,61,5xy + (tấn). Theo giả thiết, ta có 010 09 2010140(*) 0,61,59 x y xy xy + + tứ giác với 5 (10;2),(10;9),;9,(5;4) 2 ABCD
DẠYKÈMQUYNHƠN OFFICIAL
T
=
u
ra +==−=− Mặt khác 2 (sincos)12sincos −=− . Suy ra 7 sincos 2 −= (vì là góc tù). Do đó, 57 16 M = . Câu 12. Cho 1 sin 3 = với 090 . Giá trị của cos là A. 2 3 . B. 2 3 C. 22 3 . D. 22 3 . Lời giải Ta có 2 2 122 cos1sin1 33 =−=−= . Câu 13. Cho tan3 =− . Giá trị của cos là A. 1 2 . B. 1 2 . C. 1 4 D. 1 4 . Lời giải Ta có 2 2 1 1tan cos += . Suy ra 2 1 cos 4 = . Vì tan30 =− nên 1 cos 2 =− . Câu 14. Tam giác ABC có 0 150,3,2. === CBCAC Tính cạnh AB ? A. 13 . B. 3. C. 10. D. 1. Lời giải
Biểu thức 43 Txy =+ đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác ABCD, ta thấy
đạt giá trị nhỏ nhất tại 5 x = và 4 y
. Khi đó, chi phí thấp nhất mà công ty bỏ ra là 32 triệ
đồng. Câu 11. Cho là góc tù và 1 sincos 2 += . Giá trị của 33 sincos M =− là A. 37 16 . B. 117 16 . C. 57 16 D. 57 16 Lời giải (sincos)(1sincos) M =−+ Từ 113sincossuysincos1244
Chọn A Theo định lí cosin trong ABC ta có: 222 2..cos =+− ABCACBCACBC 13= 13 = AB . Chọn#A.
Câu 15. Cho tam giác ABC , biết 24,13,15.abc=== Tính góc A? A. 0 3334'. B. 0 11749'. C. 0 2837'. D. 0 5824'. Lời giải Chọn B. Ta có: 222222 0 1315247 cos11749'. 22.13.1515 bca AA bc +−+− ===−
Câu 16. Cho tam giác ABC có 3,5ABBC== và độ dài đường trung tuyến 13 BM = . Tính độ dài AC . A. 11 B. 4 C. 9 2 D. 10 Lời giải Chọn B
Theo công thức tính độ dài đường trung tuyến;ta có: (
DẠYKÈMQUYNHƠN
OFFICIAL
) 222222 2 2 35 134 2424 BABCACAC BMAC ++ =−=−= Câu 17. Cho tam giác ABC vuông tại A có ABa = , 2 ACa = . Diện tích tam giác ABC là A. 2 2a . B. 2 4a . C. 2 3 2 a . D. 2 a Lời giải Tam giác ABC vuông tại A có ABa = , 2 ACa = . Khi đó 2 1 2 ABC SABACa == . Câu 18. Cho tam giác ABC có góc ABC bằng 060 , = ACa . Tính bán kính đường tròn ngoại tiếp tam giác ABC ? A. a B. 3 3 a C. 43 3 a D. 3 a Lời giải Theo Định lí Sin ta
==== 0 3 2 sin2.sin3 2sin60 ACACaa RR BB . Câu
Hai vectơ
ọ
có:
19.
được g
i là bằng nhau khi và chỉ khi A. Giá của chúng trùng nhau và độ dài của chúng bằng nhau. B. Chúng trùng với một trong các cặp cạnh đối của một hình bình hành. C. Chúng trùng với một trong các cặp cạnh của một tam giác đều. D. Chúng cùng hướng và độ dài của chúng bằng nhau. 13 5 3 M C B A
Lời giải
Chọn D
Hai véc-tơ được gọi là bằng nhau khi và chỉ khi chúng cùng hướng và độ dài của chúng bằng nhau.
Câu 20. Cho hình bình hành ABCD. Khẳng định nào sau đây là đúng.
A. ABACAD += . B. ABACDA −= . C. ABACCB += . D. ABACBC −= . Lời giải Chọn B

Ta có ABACCB −= . Do ABCD là hình bình hành nên D C A B = nên ABACDA −= .
Câu 21. Cho tam giác ABC vuông tại A có 3,4.ABAC Tính CAAB
OFFICIAL
A. 2 CAAB . B. 213 CAAB .
C. 5 CAAB D. 13 CAAB Lời giải Chọn C
Ta có 2222345. CAABCBBCABAC
Câu 22. Cho hình bình hành ABCD. Hãy chỉ ra mệnh đề SAI trong các mệnh đề sau:
A. Không tồn tại điểm M thoả mãn đẳng thức: MAMBAB −= . B. Nếu M là trọng tâm của tam giác ABC thì: 0 MAMBMC++= C. 0 MAMBMCM −−= trùng với D .
D. Với mọi điểm M tuỳ ý, ta luôn có: MAMCMBMD +=+ . Câu 23. Một vật có khối lượng m được treo cố định trên trần nhà bằng hai sợi dây không dãn có độ dài như nhau. Biết rằng lực căng dây 1T và 2T có độ lớn như nhau bằng 600N và hợp với nhau một góc 60 (hình bên). Trọng lượng của vật là
A. 600N B. 6003 N . C. 1200N . D. 12003 N .
DẠYKÈMQUYNHƠN
Lời
giải O D A B C
Ta có 12222cos302cos30TOHOAT
3 26006003(). 2 N

Vậy trọng lượng của vật là 6003 N . Đáp án là B . Câu 24. Cho tam giác ABC và M là trung điểm của , BCG là trọng tâm của tam giác. Khẳng định nào sau đây là đúng? A. 3=− AMGM B. 3 2 = AMGM . C. 3 2 = AMGM . D. 3 = AMGM . Lời giải Chọn D Câu 25. Cho tam giác ABC . Gọi I là trung điểm của BC .Khẳng định nào sau đây đúng

DẠYKÈMQUYNHƠN OFFICIAL Xét tam giác OAH như hình vẽ.
Vì I là trung điểm của BC nên BICI và BI
với
nhau hay BIIC Câu 26. Trong hệ tọa độ Oxy cho 1 5. 2 uij =− Tọa độ của vecto u là A. 1 ;5. 2 u = B. 1 ;5. 2 u =− C. ( ) 1;10. u =− D. ( ) 1;10. u =− Lời giải Chọn B Có 11 5;5 22uiju =−=− . Câu 27. Trong mặt phẳng toạ độ Oxy , cho (2;5)A . Toạ độ của vecto OA là: A. (2;5). B. (2;5).
===
==
A. BIIC B. 32BIIC C. 2 BIIC D. 2BIIC Lời giải Chọn A
cùng hướng
IC do đó hai vectơ BI , IC bằng
C. (2;5) D. (2;5).
Lời giải Chọn B
Câu 28. Cho tam giác ABC . Giá trị của biểu thức BACA bằng:
A. cos ABACBAC . B. cos −ABACBAC . C. cos ABACABC . D. cos ABACACB .
Lời giải Chọn A
Câu 29. Cho tam giác ABC cân tại A , o ˆ 120 A = và ABa = . Tính BACA
A. 2 2 a . B. 2 2 a . C. 2 3 2 a . D. 2 3 2 a .
Lời giải Chọn B
Ta có o2 1 ...cos120 2 ==− BACABACAa .
Câu 30. Cho hình vuông ABCD tâm O . Hỏi mệnh đề nào sau đây sai?
A. .0 = OAOB . B. 1 .. 2 = OAOCOAAC . C. = ABACABCD D. = ABACACAD Lời giải Chọn C Phương án A: ⊥ OAOB suy ra .0 = OAOB nên loại#A. Phương án B: .0 = OAOC và 1 .0 2 = OAAC suy ra 1 ..0 2 ==OAOCOAAC nên loại B. Phương án C: o2 2 ...cos45.2. 2 === ABACABACABABAB .
DẠYKÈMQUYNHƠN
OFFICIAL
Biết số gần đúng 7975421 a = có độ chính xác 150 d =
Hãy ước lượng sai số tương đối của a. A. 0,0000099 a B. 0,000039 a C. 0,0000039 a D. 0,000039 a Lời giải Theo Ví dụ 1 ta có các chữ số đáng tin của a là 3, 7, 9, 7, 5 Cách viết chuẩn của 337975.10 a = Sai số tương đối thỏa mãn: 150 0,0000039 37975421 a = (tức là không vượt quá 0,0000039 ). Câu 32. Biết số gần đúng 173,4592 a = có sai số tương đối không vượt quá 1 10000 , hãy ước lượng sai số tuyệt đối của a và viết a dưới dạng chuẩn. A. 0,17;173,4 a a = B. 0,017;173,5 a a = C. 0,4592;173,5 a a = D. 0,017;173,4 a a = Lời giải Từ công thức a a a = , ta có 1 173,4592.0,017 10000 a = Vậy chữ số đáng tin là 1, 7, 3, 4.
02...cos180==− ABCDABDCAB ..ABACABCD nên chọn C. Câu 31.
.
Dạng chuẩn của a là 173,5 a = . Đáp án B. Câu 33. Thời gian chạy 50m của 20 học sinh được ghi lại trong bảng dưới đây: Thời gian (giây) 8,3 8,4 8,5 8,7 8,8 Tần số 2 3 9 5 1 Hỏi trung bình mỗi học sinh chạy 50m hết bao lâu ? A. 8,54. B. 4. C. 8,50. D. 8,53.
Lời giải
Chọn D
Thời gian trung bình để mỗi học sinh chạy được 50m là 8,3.28,4.38,5.98,7.58,8 8,53 20 x ++++ ==
Câu 34. Một tổ học sinh gồm 10 học sinh có điểm kiểm tra giữa học kì 2 môn toán như sau: 5;6;7;5;8;8;10;9;7;8. Tính điểm trung bình của tổ học sinh đó. A. 7 . B. 8. C. 7,3. D. 7,5. Lời giải
Chọn C Điểm trung bình của tổ học sinh đó là: 5.267.28.3910 7,3 10 x +++++ == .
Câu 35. Để đánh giá mức độ phân tán của các số liệu thống kê so với số trung bình, ta dùng đại lượng nào sau đây?
A. Số trung bình. B. Số trung vị C. Mốt. D. Phương sai.
Lời giải Chọn D Dựa vào ý nghĩa của phương sai và độ lệch chuẩn để đo mức độ phân tán của các số liệu trong mẫu quanh số trung bình.
2. Tự luận
Câu 1. Trong 100 học sinh lớp 10 có 70 học sinh nói được tiếng Anh, 45 học sinh nói được tiếng Pháp và 23 học sinh nói được cả hai tiếng Anh và Pháp. Hỏi có bao nhiêu học sinh không nói được hai thứ tiếng?. Lời giải
+) Gọi A là tập hợp số học sinh nói được tiếng Anh, B là tập hợp số học sinh nói được tiếp Pháp Tập hợp số học sinh nói được cả 2 tiếng là: AB và có 23 học sinh Vậy có 1002377 −= học sinh không nói được cả hai thứ tiếng. +) Tập hợp số học sinh nói được ít nhất 1 thứ tiếng là: \ ABB và có: 40452392 +−= học sinh Vậy số học sinh không nói được tiếng gì là: 100928
DẠYKÈMQUYNHƠN
OFFICIAL
−= học sinh không nói được
hai thứ tiếng. Câu 2. Tìm giá tri lớn nhất và giá tri nhỏ nhất của biểu thức (;)2 =+ Fxyxy với (;) xy thuộc miền nghiệm của hệ bất phương trình 4 0 0 + xy x y Lời giải
một trong
+
xy x y
Bước 1. Xác định miền nghiệm của hệ bất phương trình 4 0 0
Miền nghiệm của hệ bất phương trình trên là miền tam giác OAB với các đỉnh (0;0),(0;4),(4;0)OAB .
Bước 2. Tính giá trị của F tại các đỉnh của tam giác: ( ) ( ) ( ) 0;00,4;04,0;48 . FFF===
Bước 3. So sánh các giá trị thu được của F ở Bước 2, ta được giá trị nhỏ nhất là 0 và giá trị lớn nhất là 8.
OFFICIAL
Vậy giá trị nhỏ nhất cần tìm của F là (0;0)0 = F và giá trị lớn nhất cần tìm là (0;4)8 = F Câu 3. Một người đứng ở vị trí A trên nóc một ngôi nhà cao 4m đang quan sát một cây cao cách ngôi nhà 20m và đo được 45 = BAC (Hình 27). Tính chi



DẠYKÈMQUYNHƠN
ều cao
ủa
phần mười theo
Lời giải Xét tam giác vuông ABH ta có: 22 420426()=+= ABm (định lí Pythagore) và 4 tan0,211,3 20 ==ABHABH . Do đó, 9011,378,7 −= ABC . Suy ra 1804578,756,3 −−= ACB . Áp dụng định lí sin cho tam giác ABC ta có: sinsin = BCAB AC sin426sin45 17,3() sinsin56,3 = ABA BCm C Vậy cây cao khoảng 17,3m Câu 4. Máy bay A đang bay về hướng Đông Bắc với tốc độ 600 / kmh. Cùng lúc đó, máy bay B đang bay về hướng Tây Nam với tốc độ 800 / kmh . Biểu diễn vectơ vận tốc b của máy bay B theo vectơ vận tốc a của máy bay A Lời giải
c
cây đó (làm tròn kết quả đến hàng
đơn vị mét).
Vecto , ab là vecto vận tốc của máy bay A và máy bay b.
Do đó ||,|| ab lần lượt là độ lớn của vecto vận tốc tương ứng.
Ta có: ||600,||800 ==ab ||8004 ||6003 b a ==
Hai hướng Đông Bắc và Tây Nam là ngược nhau, do đó 4 3 ba =−
DẠYKÈMQUYNHƠN OFFICIAL
1. Trắc nghiệm
Câu 1. Cho mệnh đề A : "8 không chia hết cho 2 " và mệnh đề : B " 31 ". Xét các mệnh đề sau:
a) Mệnh đề AB . b) Mệnh đề BA . c) Mệnh đề AB d) Mệnh đề AB Số mệnh đề đúng trong các mệnh đề trên là A. 1. B. 2. C. 3. D. 4. Câu 2. Mệnh đề phủ định của mệnh đề :",230"Txx−+ là A. " ,230xx −+ ". B. " ,230"xx −+ C. " ,230"xx −+ D. " ,230"xx −+ Câu 3. Cho hai tập hợp {;} = Aab và {;;;;} = Babcde . Có bao nhiêu tập hợp X mà AXB ? A. 6. B. 7. C. 8. D. 11. Câu 4. Cho tập hợp {20} =−Axx . Tập hợp A là: A. {2;1;0}=−− A . B. [2;0]=− A . C. (2;0)=− A . D. {2;0}=− A . Câu 5. Cho hai tập hợp [5;0],[0;) =−=+AB . Khi đó: A. {0} =AB B. =AB C. [5;)=−+AB D. (5;)=−+AB Câu 6. Miền nghiệm của bất phương trình 35xy−− là nửa mặt phẳng chứa điểm A. (3;0). B. (3;1). C. (1;3). D. (0;0)

Câu 7. Phần không bị gạch (không kể d) ở Hình 4 là miền nghiệm của bất phương trình: A. 326 +xy B. 236 +xy C. 236 +xy D. 326 +xy Câu 8. Miền không bị gạch (tính cả biên) trong hình vẽ dưới đây là miền nghiệm của hệ bất phương trình bậc nhất hai ẩn nào sau đây?

DẠYKÈMQUYNHƠN
ĐỀ SỐ 4
OFFICIAL
A. 236 236 xy xy + −− B. 236 236 xy xy + −−
D. 236 236 xy xy + −
. Câu 9. Miền nghiệm của hệ bất phương trình bậc nhất hai ẩn 20112022 0 xy y + nằm trong góc phần tư nào? A. I. B. II. C. III. D. IV. Câu 10. Một xưởng có một máy cắt và một máy tiện dùng để sản xuất trục sắt và đinh ốc. Để sản xuất 1 tấn trục sắt thì lần lượt máy cắt chạy trong 3 giờ và máy tiện chạy trong 1 giờ, tiền lãi là 2 triệu đồng. Để sản xuất 1 tấn đinh ốc thì lần lượt máy cắt và máy tiện chạy trong 1 giờ, tiền lãi là 1 triệu đồng. Một máy không thể đồng thời sản xuất cả hai loại. Máy cắt làm không quá 6 giờ/ngày, máy tiện làm không quá 4 giờ/ngày. Hỏi một ngày xưởng nên sản xuất bao nhiêu tấn mối loại để tiền lãi là cao nhất?
A. 2 tấn trục sắt và 2 tấn đinh ốc.
B. 3 tấn trục sắt và 1 tấn đinh ốc.
C. 2 tấn trục sắt và 3 tấn đinh ốc. D. 1 tấn trục sắt và 3 tấn đinh ốc.
Câu 11. Rút
DẠYKÈMQUYNHƠN OFFICIAL
C. 236 236 xy xy +−
−−
là A. 2.
2
2 D. 2 . Câu 13. Trên nửa đường tròn đơn vị, cho điểm M sao cho 120 = MOx . Toạ độ điểm M là: A. 31 ; 22 . B. 31 ; 22 . C. 13 ; 22 D. 13 ; 22 Câu 14. Cho ;;cab là độ dài 3 cạnh của tam giác ABC . Biết 7 = b ; 5 = c ; 4 cos 5 A = . Tính độ dài của a A. 32 B. 72 2 C. 23 8 D. 6
gọn biểu thức tansin sincot xx M xx =− với ( ) 0;90 x
ta được A. sin x B. cos x C. 1 sin x D. 1 cos x . Câu 12. Cho là góc tù và tancot2 +=− . Giá trị của sincos M =−
B.
C.
Câu 15. Tam giác ABC có 6,42,2.abc=== M là điểm trên cạnh BC sao cho 3 BM = . Độ dài đoạn AM bằng bao nhiêu?
A. 9. B. 9. C. 3. D. 1 108. 2
Câu 16. Cho tam giác ABC có góc 60 BAC = và cạnh 3 BC = . Tính bán kính của đường tròn ngoại tiếp tam giác ABC .
A. 4 R = B. 1 R = C. 2 R = D. 3 R =
Câu 17. Tam giác ABC có 6812'= A , 3444'= B , 117. = AB Khi đó độ dài AC xấp xỉ bằng ?
A. 68. B. 168. C. 118. D.200.
Câu 18. Tam giác ABC có 6cm = AB , 30 = BAC , 75 = ACB . Tính diện tích của tam giác ABC
A. 2183cm . B. 2 93 cm . C. 218cm . D. 29cm .

Câu 19. Mệnh đề nào sau đây sai ?
A. 0 AA B. 0 cùng phương với mọi vectơ
C. 0 AB . D. 0 cùng hướng với mọi vectơ.
Câu 20. Cho hình chữ nhật ABCD tâm O . Trong các mệnh đề sau, mệnh đề nào sai?
OFFICIAL
A. 0 ABBCBD+−= . B. 0 OAOC+= . C. 0 ABBCCA++= . D. 0 ADBC−= .
Câu 21. Cho bốn điểm ,,, ABCD . Đẳng thức nào sau đây đúng
A. ABCDADBD +=+ . B. ABCDADCB +=+ . C. ABCDADAC +=+ D. ABCDADBC +=+
Câu 22. Cho hình bình hành ABCD. Chọn khẳng định đúng
A. CACBBA =− . B. ACBABC =+ . C. BADC = . D. BABCBD += .
Câu 23. Một máy bay có vectơ vận tốc chỉ theo hướng bắc, vận tốc gió là một vectơ theo hướng đông như Hình 7. Tính độ dài vectơ tổng của hai vectơ nói trên (chọn giá trị gần đúng).
A. 209 B. 208 C. 210 D. 211
Câu 24. Cho 0 a . Khẳng định nào sau đây là sai?
A. a và 4a cùng phương.
B. a và
DẠYKÈMQUYNHƠN
4a cùng phương. C. a và 4a không cùng
D. a và 4a ngược
Câu 25. Cho tam giác ABC . Gọi M và N lần lượt là trung điểm của AB và AC . Trong các mệnh đề sau, tìm mệnh đề sai? A. 2 ABAM = B. 2 ACCN = C. 2 BCNM =− D. 1 2 CNAC =− Câu 26. Trong mặt phẳng toạ độ Oxy , cho (1;3),(2;1)AB . Tọa độ của vectơ AB là: A. (1;4) B. (3;4) C. (3;4).
hướng.
hướng.
D. (1;2)
Câu 27. Trong mặt phẳng toạ độ Oxy , cho (2;4),(2;) =−−=− uvxyy . Hai vectơ u và v bằng nhau nếu: A. 1 4 = =− x y B. 3 4 =− =− x y C. 1 4. = = x y D. 3 4 =− = x y Câu 28. Cho tam giác ABC . Giá trị của biểu thức ABBC bằng: A. cos ABBCABC . B. cos ABACABC . C. cos ABBCABC . D. cos ABBCBAC . Câu 29. Cho hình thang vuông ABCDcó đáy lớn 4 ABa = , đáy nhỏ 2 CDa = , đường cao 3 ADa = ; I là trung điểm của AD Khi đó ( ). + IAIBID bằng : A. 2 9 2 a . B. 2 9 2 a . C. 0 . D. 2 9a .
Câu 30. Tam giác ABC vuông ở A và có góc o50 = B . Hệ thức nào sau đây là sai? A. ( ) o , 130= ABBC . B. ( ) o , 40 = BCAC . C. ( ) o , 50 = ABCB . D. ( ) o , 120= ACCB .
Câu 31. Tính chu vi của hình chữ nhật có các cạnh là 3,4560,01 x = (m) và 12,7320,015 y = (m) và ước lượng sai số tuyệt đối mắc phải. A. 32,3760,025;0,05 L L = B. 32,3760,05;0,025 L L = C. 32,3760,5;0,5 L L = D. 32,3760,05;0,05 L L =
Câu 32. Tính diện tích S của hình chữ nhật có các cạnh là 3,4560,01 x = (m) và 12,7320,015 y = (m) và ước lượng sai số tuyệt đối mắc phải.
A. 44,002 S = ( 2 m ); 0,176 S B. 44,002 S = ( 2 m ); 0,0015 S C. 44,002 S = ( 2 m ); 0,025 S D. 44,002 S = ( 2 m ); 0,0025 S
Câu 33. Một tổ học sinh gồm 10 học sinh có điểm kiểm tra cuối học kì 1 môn toán như sau: 7;5;6;6;6;8;7;5;6;9 . Tìm mốt của dãy trên. A. 0 6 M = . B. 0 7 M = . C. 0 5 M = . D. 0 8 M = .
Câu 34. Một tổ học sinh gồm 10 học sinh có điểm kiểm tra giữa học kì 2 môn toán như sau: 5;6;7;5;8;8;10;9;7;8. Tính điểm trung bình của tổ học sinh đó. A. 7 . B. 8. C. 7,3. D. 7,5.
35. Chọn
2. Tự luận
Câu 1. Cho hai tập hợp [;2],[;1] =+=+ AaaBbb . Tìm điều kiện của , ab để AB .
Câu 2. Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 280kg chất A và 18kg chất
B . Với một tấn nguyên liệu loại I, người ta có thể chiết xuất được 40kg chất A và 1,2kg chất
B . Với một tấn nguyên liệu loại II, người ta có thể chiết xuất được 20kg chất A và 3kg chất
DẠYKÈMQUYNHƠN
OFFICIAL
Câu
câu đúng trong các câu trả lời sau đây: Phương sai bằng: A. Một nửa của độ lệch chuẩn B. Căn bậc hai của độ lệch chuẩn C. Hai lần của độ lệch chuẩn. D. Bình phương của độ lệch chuẩn.
B . Giá mỗi tấn nguyên liệu loại I là 4 triệu đồng và loại II là 3 triệu đồng. Hỏi người ta phài dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất mà vẫn đạt được mục tiêu đề ra? Biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp tối đa 10 tấn nguyên liệu loại I và 9 tấn nguyên liệu loại II.
Câu 3. Cho tam giác ABC thoả mãn 333 2 abc c abc +− = +− . Chứng minh góc 60 C = Câu 4. Cho hai hình bình hành ABCD và ABCD
có chung đỉnh A . Chứng minh rằng hai tam giác BCD
Mệnh
AB . d) Mệnh đề AB Số mệnh đề đúng trong các mệnh đề trên là A. 1. B. 2. C. 3. D. 4. Lời giải Ta có mệnh đề A sai, mệnh đề A đúng; mệnh đề B đúng, mệnh đề B sai. Khi đó, mệnh đề đúng là: a ). Đáp án là A Câu 2. Mệnh đề phủ định của mệnh đề :",230"Txx−+ là A. " ,230xx −+ ". B. " ,230"xx −+ . C. " ,230"xx −+ D. " ,230"xx −+ Lời giải Mệnh đề phủ định của mệnh đề
DẠYKÈMQUYNHƠN
OFFICIAL
Lời
1A 2C 3C 4B 5A 6C 7D 8A 9D 10D 11B 12C 13C 14A 15C_ 16B 17A 18D 19C 20A 21B 22D 23A 24C 25B 26C 27B 28A 29B 30D 31D 32A 33A 34C 35D 1. Trắ
ệm Câu 1. Cho mệnh đề A : "8 không chia hết cho 2 " và mệnh đề : B " 31 ". Xét các mệnh đề sau: a)
AB . b)
. c)
T là " ,230"xx −+ Câu 3. Cho hai tập hợp {;} = Aab và {;;;;} = Babcde . Có bao nhiêu tập hợp X mà AXB ? A. 6. B. 7. C. 8. D. 11. Câu 4. Cho tập hợp {20} =−Axx . Tập hợp A là: A. {2;1;0}=−− A . B. [2;0]=− A . C. (2;0)=− A . D. {2;0}=− A . Câu 5. Cho hai tập hợp [5;0],[0;) =−=+AB . Khi đó: A. {0} =AB . B. =AB . C. [5;)=−+AB D. (5;)=−+AB . Câu 6. Miền nghiệm của bất phương trình 35xy−− là nửa mặt phẳng chứa điểm A. (3;0). B. (3;1). C. (1;3). D. (0;0) Câu 7. Phần không bị gạch (không kể d) ở Hình 4 là miền nghiệm của bất phương trình:
và BCD
có cùng trọng tâm
giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM
c nghi
Mệnh đề
Mệnh đề BA
đề
A. 326 +xy . B. 236 +xy . C. 236 +xy . D. 326 +xy

Câu 8. Miền không bị gạch (tính cả biên) trong hình vẽ dưới đây là miền nghiệm của hệ bất phương trình bậc nhất hai ẩn nào sau đây?
OFFICIAL
A. 236 236 xy xy + −−
B. 236 236 xy xy + −− C. 236 236 xy xy +− −−
D. 236 236 xy xy + − .
Câu 9. Miền nghiệm của hệ bất phương trình bậc nhất hai ẩn 20112022 0 xy y + nằm trong góc phần tư nào? A. I. B. II. C. III. D. IV.

Câu 10. Một xưởng có một máy cắt và một máy tiện dùng để sản xuất trục sắt và đinh ốc. Để sản xuất 1 tấn trục sắt thì lần lượt máy cắt chạy trong 3 giờ và máy tiện chạy trong 1 giờ, tiền lãi là 2 triệu đồng. Để sản xuất 1 tấn đinh ốc thì lần lượt máy cắt và máy tiện chạy trong 1 giờ, tiền lãi là 1 triệu đồng. Một máy không thể đồng thời sản xuất cả hai loại. Máy cắt làm không quá 6 giờ/ngày, máy tiện làm không quá 4 giờ/ngày. Hỏi một ngày xưởng nên sản xuất bao nhiêu tấn mối loại để tiền lãi là cao nhất?
A. 2 tấn trục sắt và 2 tấn đinh ốc.
B. 3 tấn trục sắt và 1 tấn đinh ốc.
C. 2 tấn trục sắt và 3 tấn đinh ốc.
D. 1 tấn trục sắt và 3 tấn đinh ốc.
Lời giải
Gọi ,(0,0) xyxy là số tấn trục sắt và đinh ốc sản xuất trong ngày.
Số tiền lãi mỗi ngày: (;)2 Lxyxy =+ .
Số giờ làm việc mỗi ngày của máy cắt: 36 xy+
Số giờ làm việc mỗi ngày của máy tiện: 4 xy+
DẠYKÈMQUYNHƠN
+ +
(*). Miền nghiệm của (*) là miền tứ giác OABC với (0;0),(2;0),(1;3),(0;4) OABC . Ta có: (0;0)0,(2;0)4,(0;4)4,(1;3)5 LLLL==== . Vậy mỗi ngày cần sản xuất 1 tấn trục sắt và 3 tấn đinh ốc thì thu được tiền lãi cao nhất là 5 triệu đồng. Câu 11. Rút gọ
c tansin sincot xx M
DẠYKÈMQUYNHƠN OFFICIAL
n
ểu thứ
xx =− với (
Ta có bài toán tìm giá trị lớn nhất của (,)Lxy biết 36 4 0,0 0;90 x ta
xy xy xy c A. sin x . B. cos x . C. 1 sin x . D. 1 cos x Lời giải 22 tansin1sincos cos sincotcoscoscos xxxx Mx xxxxx =−=−== . Câu 12. Cho là góc tù và tancot2 +=− . Giá trị của sincos M =− là A. 2. B. 2. C. 2 . D. 2 Lời giải Từ sincos 2 cossin +=− suy ra 1 sincos 2 =− 2 (sincos)12sincos2 −=−= . Suy ra sincos2 −= . Vì là góc tù nên sincos0sincos2 M −=−= . Câu 13. Trên nửa đường tròn đơn vị, cho điểm M sao cho 120 = MOx . Toạ độ điểm M là: A. 31 ; 22 . B. 31 ; 22 C. 13 ; 22 D. 13 ; 22 Lời giải Điểm M có toạ độ là (;) ab . Ta có: cos120,sin12013 22 ==−== ab . Chọn C Câu 14. Cho ;;cab là độ dài 3 cạnh của tam giác ABC . Biết 7 = b ; 5 = c ; 4 cos 5 A = . Tính độ dài của a . A. 32 . B. 72 2 . C. 23 8 . D. 6. Lời giải Chọn A Áp dụng định lí cosin cho tam giác ABC ta có:
bi
)
đượ
Suy ra: 1832 a ==
Câu 15. Tam giác ABC có 6,42,2.abc=== M là điểm trên cạnh BC sao cho 3 BM = . Độ dài đoạn AM bằng bao nhiêu?
A. 9. B. 9. C. 3. D. 1 108. 2 Lời giải Chọn C.
Ta có: Trong tam giác ABC có 66aBC== mà 3 BM = suy ra M là trung điểm .BC
Suy ra: 222 22 93 24 a bca AMmAM + ==−== .
Câu 16. Cho tam giác ABC có góc 60 BAC = và cạnh 3 BC = . Tính bán kính của đường tròn ngoại tiếp tam giác ABC . A. 4 R = . B. 1 R = . C. 2 R = . D. 3 R = . Lời giải Chọn B Ta có: 3 21 sin2sin 3 2. 2
BCBC RR AA ====
Câu 17. Tam giác ABC có 6812'= A , 3444'= B , 117. = AB Khi đó độ dài AC xấp xỉ bằng ? A. 68. B. 168. C. 118. D.200.
DẠYKÈMQUYNHƠN
22222 4 2.cos752.7.5.18 5 abcbcA=+−=+−=
OFFICIAL
Ta
1801806812'3444'774' ++==−−=
Mặt
.sin117.sin3444'
sinsinsinsinsinsinsin774' ===== abcACABABB
ABCBCC Câu 18. Tam giác ABC có 6cm = AB , 30 = BAC , 75 = ACB . Tính diện tích của tam giác ABC A. 2183cm . B. 2 93 cm . C. 218cm . D. 29cm . Lời giải Chọn D Ta có ( ) 18075 =−+== ABCBACACBACB Suy ra tam giác ABC cân tại A nên 6cm ==ABAC . Vậy diện tích tam giác ABC là: 2 1 ..sin9 cm 2 == ABC SABACBAC Câu 19. Mệnh đề nào sau đây sai ? A. 0 AA . B. 0 cùng phương với mọi vectơ. C. 0 AB . D. 0 cùng hướng với mọi vectơ. Lời giải Chọn C Đáp án C sai vì có thể xảy ra trường hợp 0. ABAB
Lời giải Chọn A
có: Trong tam giác ABC :
ABCC
khác
68.
AC
D A B
C
D. BABCBD += Lời giải Chọn D Theo quy tắc hình bình hành ta có: BABCBD += . Câu 23. Một máy bay có vectơ vận tốc chỉ theo hướng bắc, vận tốc gió là một vectơ theo hướng đông như Hình 7. Tính độ dài vectơ tổng của hai vectơ nói trên (chọn giá trị gần đúng). A. 209 B. 208 C. 210 D. 211 Lời giải


DẠYKÈMQUYNHƠN OFFICIAL Câu 20. Cho hình chữ nhật ABCD tâm O . Trong các mệnh đề sau, mệnh đề nào sai? A. 0 ABBCBD+−= B. 0 OAOC+= C. 0 ABBCCA++= D. 0 ADBC−= Lời giải Chọn A ( ) 00200 ABBCBDACBDOCODDC +−=−=−== ( Không thỏa mãn) 0 OAOC+= ( thỏa mãn vì O là trung điểm của AC ) 00ABBCCAACCA ++=+= ( thỏa mãn) 0 ADBC−= ( thỏa mãn). Câu 21. Cho bốn điểm ,,, ABCD . Đẳng thức nào sau đây đúng A. ABCDADBD +=+ . B. ABCDADCB +=+ . C. ABCDADAC +=+ D. ABCDADBC +=+ Lời giải Chọn B ( ) ( ) 0 ABCDADDBCBBDADCBDBBDADCBADCB +=+++=+++=++=+ Câu 22. Cho hình bình hành ABCD. Chọn khẳng định đúng A.
=− B.
=+ C.
=
CACBBA
ACBABC
BADC
Gọi AB và BC lần lượt là vecto vận tốc của máy bay và vận tốc của gió. Ta có: += ABBCAC .
Suy ra 222220060209( /) =+=+ ACABBCkmh .
Vậy độ dài vectơ tổng của hai vectơ nói trên là khoảng 209 / kmh.
Câu 24. Cho 0 a . Khẳng định nào sau đây là sai?
A. a và 4a cùng phương.
B. a và 4a cùng phương.
C. a và 4a không cùng hướng. D. a và 4a ngược hướng.
Chọn C
Lời giải
Câu 25. Cho tam giác ABC . Gọi M và N lần lượt là trung điểm của AB và AC . Trong các mệnh đề sau, tìm mệnh đề sai? A. 2 ABAM = B. 2 ACCN = C. 2 BCNM =− D. 1 2 CNAC =− Lời giải
Chọn B
Câu 26. Trong mặt phẳng toạ độ Oxy , cho (1;3),(2;1)AB . Tọa độ của vectơ AB là: A. (1;4) B. (3;4). C. (3;4). D. (1;2) Lời giải Chọn C
Câu 27. Trong mặt phẳng toạ
DẠYKÈMQUYNHƠN
OFFICIAL
độ Oxy , cho (2;4),(2;) =−−=− uvxyy . Hai vectơ u và v bằng
nếu: A. 1 4 = =− x y B. 3 4 =− =− x y C. 1 4. = = x y D. 3 4 =− = x y Lời giải Chọn B Câu 28. Cho tam giác ABC . Giá trị của biểu thức ABBC bằng: A. cos ABBCABC . B. cos ABACABC . C. cos ABBCABC . D. cos ABBCBAC . Lời giải Chọn A Câu 29. Cho hình thang vuông ABCDcó đáy lớn 4 ABa = , đáy nhỏ 2 CDa = , đường cao 3 ADa = ; I là trung điểm của AD Khi đó ( ). + IAIBID bằng : A. 2 9 2 a . B. 2 9 2 a . C. 0 . D. 2 9a . Lời giải
nhau
Ch
Ta có ( ) ( ) 2 9 ..2. 2 +=++==− a IAIBIDIAIAABIDIAID nên chọn B.
Câu 30. Tam giác ABC vuông ở A và có góc o50 = B . Hệ thức nào sau đây là sai?
A. ( ) o , 130= ABBC . B. ( ) o , 40 = BCAC . C. ( ) o , 50 = ABCB . D. ( ) o , 120= ACCB .
Lời giải
Chọn D
Phương án A:( ) ( ) 0o , 180, 130 =−=ABBCABCB nên loại#A.
Phương án B:( ) ( ) o , , 40 ==BCACCBCA nên loại B.
Phương án C:( ) ( ) o , , 50 ==ABCBBABC nên loại C.
Phương án D:( ) ( ) 0o , 180, 140 =−=ACCBCACB nên chọn D. Câu 31. Tính chu vi của hình chữ nhật có các cạnh là 3,4560,01 x = (m) và 12,7320,015 y = (m) và ước lượng sai số tuyệt đối mắc phải. A. 32,3760,025;0,05 L L = B. 32,3760,05;0,025 L L = C. 32,3760,5;0,5 L L = D. 32,3760,05;0,05 L L =
Lời giải Chu vi ( ) ( ) 223,45612,73232,376Lxy=+=+= (m) Sai số tuyệt đối ( ) 20,010,0150,05 L += Vậy 32,3760,05 L = (m). Đáp án D. Câu 32. Tính diện tích S của hình chữ nhật có các cạnh là 3,4560,01 x = (m) và 12,7320,015 y = (m) và ước lượng sai số tuyệt đối mắc phải.
A. 44,002 S = ( 2 m ); 0,176 S B. 44,002 S = ( 2 m ); 0,0015 S C. 44,002 S = ( 2 m ); 0,025 S D. 44,002 S = ( 2 m ); 0,0025 S Lời giải Diện tích 3,456.12,73244,002 Sxy=== ( 2 m ) Sai số tương đối S không vượt quá: 0,010,0150,004 3,45612,732 += Sai số tuyệt đối S không vượt quá: .44,002.0,0040,176 S S = Đáp án#A. Câu 33.
DẠYKÈMQUYNHƠN
OFFICIAL
ọn B
ổ
ọ
sinh g
. Tìm mốt của dãy trên. A. 0 6 M = . B. 0 7 M = . C. 0 5 M = . D. 0 8 M = . Lời giải Chọn C Giá trị 6 x = là giá trị có tần số lớn nhất 4 n = . Vậy mốt của điều tra trên là: 0 6 M = . Câu 34. Một tổ học sinh gồm 10 học sinh có điểm kiểm tra giữa học kì 2 môn toán như sau: 5;6;7;5;8;8;10;9;7;8. Tính điểm trung bình của tổ học sinh đó. A. 7 B. 8 C. 7,3 D. 7,5 Lời giải Chọn C Điểm trung bình của tổ học sinh đó là: 5.267.28.3910 7,3 10 x +++++ == Câu 35. Chọn câu đúng trong các câu trả lời sau đây: Phương sai bằng: A. Một nửa của độ lệch chuẩn
Căn bậc hai của độ lệch chuẩn C. Hai lần của độ lệch chuẩn.
Bình phương của độ lệch chuẩn.
Một t
h
c
ồm 10 học sinh có điểm kiểm tra cuối học kì 1 môn toán như sau: 7;5;6;6;6;8;7;5;6;9
B.
D.
hai lo
i nguyên
ệu
nh
t
chất A và 18kg chấ
i một tấn nguyên liệu loại I, người ta có thể chiết xuất được 40kg chất A và 1,2kg chất B . Với một tấn nguyên liệu loại II, người ta có thể chiết xuất được 20kg chất A và 3kg chất
B . V
B . Giá mỗi tấn nguyên liệu loại I là 4 triệu đồng và loại II là 3 triệu đồng. Hỏi người ta phài dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất mà vẫn đạt được mục tiêu đề ra? Biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp tối đa 10 tấn nguyên liệu loại I và 9 tấn nguyên liệu loại II. Lời giải Gọi x và y lần lượt là số tấn nguyên liệu loại I và loại II mà người ta cần dùng. Khi đó khối lượng chất A chiết xuất được là 4020( ) + xykg . Khối lượng chất B chiết xuất được là 1,23( ) + xykg . Từ giả thiết ta có hệ bất phương trình sau:
Hơn nữa, số tiền người ta phải trả để mua nguyên liệu là (;)43 =+ Fxyxy (triệu đồng). Vậy bài toán trở thành tìm giá trị nhỏ nhất của (;)Fxy với (;) xy thoả mãn hệ bất phương trình bậc nhất hai ẩn ở trên. Bước 1. Xác định miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên. Miền nghiệm là miền tứ giác ABCD với (5;4),(10;2),(10;9),(2,5;9) ABCD . Bước 2. Tinh giá trị của F tại các đỉnh của tứ giác ABCD
DẠYKÈMQUYNHƠN OFFICIAL Lời giải
D Ta
x s
xx
=
2. Tự
Câu
Cho hai tập hợp [;2],[;1] =+=+ AaaBbb . Tìm điều kiện của , ab để AB Lời
Ta
=AB Để =AB khi và chỉ khi 22 11 +−− +− abab baab Từ đó suy ra điều kiện để AB là 21−− ab .
Chọn
có phương sai là: 2
Độ lệch chuẩn: 2
ss
Suy ra phương sai bằng bình phương của độ lệch chuẩn
luận
1.
giải
xét trường hợp
Câu 2. Người ta dự định dùng
ạ
li
để chiết xuất ít
ấ
280kg
t
ớ
1,23181,2318 hay
99. xyxy xyxy xx yy ++ ++
4020280214
1010

DẠYKÈMQUYNHƠN OFFICIAL Ta có: (5;4)32,(10;2)46,(10;9)67,(2,5;9)37 ====FFFF . So sánh các giá trị này ta thấy (5;4)F là nhỏ nhất. Do đó, giá trị nhỏ nhất của (;)Fxy với (;) xy thoả mãn hệ bất phương trình trên là (5;4)32 = F . Vậy người ta cần mua 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II đễ chi phí là nhỏ nhất. Câu 3. Cho tam giác ABC thoả mãn 333 2 abc c abc +− = +− . Chứng minh góc 60 C = . Lời giải Ta có 333 233323 () abc cabcabcc abc +− =+−=+− +− Suy ra 332222 () ababcaabbc +=+−+= 2222 1 2coscos60 2 aabbababCCC −+=+−== Từ đó ta có điều phải chứng minh. Câu 4. Cho hai hình bình hành ABCD và ABCD có chung đỉnh A . Chứng minh rằng hai tam giác BCD và BCD có cùng trọng tâm Lời giải

DẠYKÈMQUYNHƠN OFFICIAL Gọi G là trọng tâm tam giác BCD suy ra 0 GBGCGD ++= 0 GBGCGDBBCCDD +++++= . (1) Mặt khác theo quy tắc phép trừ và hình bình hành ta có ( ) ( ) ( ) BBCCDDABABACACADAD ++=−+−+− ( ) ( ) ABADACABADAC =+−+++ ACACACAC =−−+ 0 = (2) Từ (1) và (2) ta có 0 GBGCGD ++= hay G là trọng tâm tam giác BCD
1. Trắc nghiệm
Câu 1. Phủ định của mệnh đề: "Tổng ba góc trong một tam giác bằng 180 " là mệnh đề
A. "Tổng ba góc trong một tam giác lớn hơn 180 ".
B. "Tổng ba góc trong một tam giác nhỏ hơn180".
C. "Tổng ba góc trong một tam giác không bằng 180 ".
D. "Tổng ba góc trong một tam giác không vượt quá 180 ".
Câu 2. Trong các mệnh đề sau, mệnh đề nào là đúng?
đề nào sau đây đúng?
A. (3;2) M =− . B. [3;2) M =− . C. (3;2] M =− D. {3;2;1} M =−−− .

Câu 6. Miền nghiệm của bất phương trình 44 xy+− KHÔNG chứa điểm nào sau đây? A. (1;1). B. (1;2) C. (2021;2022) D. (1;1) .
Câu 7. Miền không bị gạch (tính cả biên) trong hình vẽ bên là miền nghiệm của bất phương trình bậc nhất hai ẩn nào?
DẠYKÈMQUYNHƠN OFFICIAL ĐỀ SỐ 5
,42" xxx B. " 2 ,42 xxx hoặc 2"− x C. " 2 ,42 xxx ". D. " 2 ,422 − xxx ”. Câu 3. Cho tập hợp {1;2;3;4;5} = A . Tập hợp X thoả mãn \{1;3;5} = AX và \{6;7} = XA là: A. {2;4}. B. {6;7}. C.
. D.
. Câu 4. Cho hai tập hợp (1;2),[;2]
A. " 2
{2;4;6;7}
{1;3;5;6;7}
=−=+ ABmm . Tìm m để AB khác tập rỗng. A. 32− m . B. 32− m . C. 2 m hoặc 3− m . D. 2 m hoặc 3− m . Câu 5. Cho tập hợp {32}Mxx=− . Mệnh
A. 44xy+ . B. 44xy+ C. 41 xy+ D. 44xy−− .
Cặp số nào sau đây là
của hệ bất phương trình 36 ? 24 xy xy + − A.
.
22 22 1 xy xy y + −− −
Câu 8.
nghiệm
(2;0) B. (0;2)
C. (4;2). D. (3;3) Câu 9. Miền nghiệm của hệ bất phương trình
được xác định bởi miền đa giác nào sau đây?
A. B. C. D. Câu 10. Một đơn vị bộ đội cần mua ít nhất 300 kg gạo. Có hai loại gạo, loại I có giá là 30000 đồng/ kg, loại II có giá 20000 đồng/ kg. Gọi , xy lân lượt là số gạo loại I, II đơn vị mua. Hệ bất phương trình biểu thị mối liên hệ của x và y để số tiền đơn vị mua gạo không hết quá 7000000 đồng là: A. 8 32700




DẠYKÈMQUYNHƠN OFFICIAL
+
Câu
thoả mãn 90180 và sin3 5 = . Giá trị của cos là: A. 4 5 . B. 4 5 C. 2 5 . D. 2 5 Câu 12. Cho góc thoả mãn 0180 và 2 cos 3 =− . Giá trị của tan là: A. 5 2 . B. 5 2 . C. 2 5 . D. 2 5 . Câu 13. Cho tam giác ABC vuông tại A .
khẳng định
+
xy xy B. 300 33700 + + xy xy C. 300 32700 + + xy xy D. 300 32700 + + xy xy
11. Cho góc
Chọn
sai trong các khẳng định sau:
A. cossin = BC B. sincos = BC C. tancot = BC D. tancot =− CB
Câu 14. Cho các điểm (1;1),(2;4),(10;2). ABC Góc BAC bằng bao nhiêu?
A. 090 . B. 0 60. C. 0 45. D. 0 30.
Câu 15. Tam giác ABC có 9 AB = cm, 15 BC = cm, 12 AC = cm. Khi đó đường trung tuyến AM của tam giác có độ dài là A. 10cm. B. 9cm. C. 7,5cm. D. 8cm.
Câu 16. Cho tam giác ABC có ,, ABcACbBCa === . Chọn khẳng định đúng
A. 222 cos 2 bca A bc +− = . B. 222 cos bca A bc +− = C. 222 cos 2 bca A bc ++ = . D. 222 cos 2 abc A bc =

Câu 17. Bộ ba số nào sau đây là độ dài 3 cạnh của một tam giác tù?
A. 2;3;4 B. 3;4;5 C. 4;5;6 D. 5;6;7
Câu 18. Cho tam giác ABC có , = BCa , = CAb = ABc thỏa 222 3. +=+ bcabc Tìm số đo của góc A của tam giác ABC . A. 120 . B. 60 . C. 150 . D. 30 .
Câu 19. Cho hình vuông ABCD . Khẳng định nào sau đây đúng?
A. .ACBD B. .ABCD C. ABBC D. Hai vectơ , ABAC cùng hướng.
Câu 20. Gọi O là tâm hình bình hành .ABCD Đẳng thức nào sau đây sai ?
A. OAOBCD . B. OBOCODOA. C. ABADDB . D. BCBADCDA.
Câu 21. Tính tổng MNPQRNNPQR . A. MR B. MN C. PR D. MP Câu 22. Cho 6 điểm ,,,,, ABCDEF . Tổng véc tơ: ++ ABCDEF bằng A. ++ AFCEDB B. ++ AECBDF C. ++ ADCFEB D. AEBCDF ++ Câu 23. Cho ba lực 123 ,, FFF cùng tác động vào một vật tại một điểm làm vật đứng yên (Hình). Xét 423 =+ FFF . Phát biểu nào sau đây là đúng? A. 41
DẠYKÈMQUYNHƠN
OFFICIAL
= FF B. 41 2 = FF C. 41 2=− FF D. 41 =− FF Câu 24. Cho đoạn thẳng AB và điểm C nằm giữa hai điểm , AB . Khẳng định nào sau đây là đúng?
A. = AC ACAB AB
B. =− AC ACAB AB C. = AB ACAB AC . D. =− AB ACAB AC .
Câu 25. Cho 0 a và điểm O . Gọi , MN lần lượt là hai điểm thỏa mãn 3 OMa = và 4 ONa =− . Khi đó: A. 7 MNa = B. 5 MNa =− C. 7 MNa =− D. 5 MNa =− Câu 26. Cho hình bình hành ABCD có (1;2)A , (3;2),(4;1)BC . Toạ độ của đỉnh D là: A. (8;3). B. (3;8) C. (5;0) D. (0;5).

Câu 27. Cho hai vectơ (1;3)=− u và (2;5)=− v . Tọa độ của vectơ + uv là:
A. (1;2) B. (2;1) C. (3;8) . D. (3;8).
Câu 28. Cho đoạn thẳng AB . Tập hợp các điểm M nằm trong mặt phẳng thoả mãn 0 =MAMB là:
A. Đường tròn tâm A bán kính AB . B. Đường tròn tâm B bán kính AB C. Đường trung trực của đoạn thẳng AB . D. Đường tròn đường kính AB . Câu 29. Cho hình vuông ABCD, tính ( ) cos,ABCA A. 1 2 . B. 1 2 . C. 2 2 . D. 2 2 . Câu 30. Cho tam giác ABC vuông cân tại A có 2 BCa = .Tính CACB A. 2 .
DẠYKÈMQUYNHƠN
OFFICIAL
Xấp xỉ số π bởi số 355 113 .
giá
số
đối biết: 3,141592653,14159266 . A. 7 2,8.10 a B. 7 28.10 a C. 7 1.10 a D. 6 2,8.10 a Câu 32. Độ cao của một ngọn núi đo được là 1372,5 h = m. Với sai số tương đối mắc phải là 0,5‰ Hãy xác định sai số tuyệt đối của kết quả đo trên và viết h dưới dạng chuẩn. A. ( ) 0,68625;1373 h hm== B. ( ) 0,68626;1372 h hm== C. ( ) 0,68625;1372 h hm== D. ( ) 0,68626;1373 h hm== Câu 33. Cân nặng của 40 học sinh lớp 10 trường THPT A được cho bởi bảng sau Tính số trung bình cộng của mẫu số liệu trên. A. 38,26 x = . B. 40,25 x = . C. 39,65 x = . D. 40,83 x = .
= CACBa . B. . = CACBa . C. 2 . 2 = a CACB . D. .2 = CACBa . Câu 31.
Hãy đánh
sai
tuyệt
Câu 34. Kết quả điểm kiểm tra 15’ môn Toán của 100 em học sinh được trình bày ở bảng sau: Điểm 3 4 5 6 7 8 9 10 Cộng
Tần số 3 5 11 17 30 19 10 5 100
Số trung bình cộng của bảng phân bố tần số nói trên là
A. 6,88 . B. 7,12. C. 6,5. D. 7,22 .

Câu 35. Cho phương sai của các số liệu bằng 4. Tìm độ lệch chuẩn. A. 4. B. 2. C. 16. D. 8.
2. Tự luận
Câu 1. Trong lớp 10 A có 45 học sinh trong đó có 25 em thích môn văn, 20 em thích môn toán, 18 em thích môn sử, 6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên:
Câu 2. Một người bán nước giải khát đang có 25g bột nho và 100 g đường để pha chế hai loại nước nho A và B . Để pha chế 1l nước nho loại A cần 10 g đường và 1g bột nho; để pha chế 1l nước nho loại B cần 10 g đường và 4g bột nho. Mỗi lít nước nho loại A khi bán lãi được 30 nghìn đồng, mỗi lít nước nho loại B khi bán lãi được 40 nghìn đồng. Hỏi người đó nên pha chế bao nhiêu lít nước nho mỗi loại để có lợi nhuận cao nhất?
Câu 3. Ta giả sử hai bờ sông là hai đường thẳng song song cách nhau 2km. Một chiếc tàu nhỏ đi từ điểm A ở bờ bên này sang điểm B ở bờ bên kia với vận tốc riêng của tàu (tức là vận tốc của tàu so với dòng nước) là 20 / kmh. Giả sử AB vuông góc với bờ sông (như hình vẽ). Cho biết vận tốc của dòng nước so với bờ là không đổi 5 / kmh (giả sử phương dòng nước chảy song song với bờ sông).
a) Cần giữ lái cho tàu tạo với bờ sông một góc nhọn bằng bao nhiêu độ để tàu sang bờ bên kia theo phương AB ? b) Tính vận tốc của tàu so với bờ. Hỏi sau bao lâu thì tàu sẽ tới bờ bên kia? (Các kết quả tính toán ở câu a) và câu b) ở trên được làm tròn đến hàng phần trăm). Câu 4. Cho tam giác ABC cố định và điểm M di động. Chứng minh rằng 45 vMAMBMC =+− không phụ thuộc vào vị trí của điểm M
DẠYKÈMQUYNHƠN
OFFICIAL
BẢNG
NGHIỆM 1C 2B 3C 4A 5B 6D 7B 8C 9C 10 D 11 B 12 A 13 C 14 A 15 C 16 A 17 A 18 D 19 C 20 B 21 B 22 C 23 D 24 A 25 C 26 D 27 A 28 D 29 D 30 A 31 A 32 A 33 C 34 A 35 B
Lời giải tham khảo
ĐÁP ÁN TRẮC
1. Trắc nghiệm Câu 1. Phủ định của mệnh đề: "Tổng ba góc trong một tam giác bằng 180 " là mệnh đề
A. "Tổng ba góc trong một tam giác lớn hơn 180 ".
B. "Tổng ba góc trong một tam giác nhỏ hơn180".
C. "Tổng ba góc trong một tam giác không bằng 180 ".
D. "Tổng ba góc trong một tam giác không vượt quá 180 ". Câu 2. Trong các mệnh đề sau, mệnh đề nào là đúng?
A. " 2 ,42"
minh họa hai tập hợp A, X. Chọn C
Câu 4. Cho hai tập hợp (1;2),[;2] =−=+ ABmm . Tìm m để AB khác tập rỗng. A. 32− m . B. 32− m . C. 2 m hoặc 3− m . D. 2 m hoặc 3− m . Câu 5. Cho tập hợp {32}Mxx=− . Mệnh đề nào sau đây đúng? A. (3;2) M =− B. [3;2) M =− . C. (3;2] M =− . D. {3;2;1} M =−−− Câu 6. Miền nghiệm của bất phương trình 44 xy+− KHÔNG chứa điểm nào sau đây?


A. (1;1). B. (1;2). C. (2021;2022) D. (1;1) . Câu 7. Miền không bị gạch (tính cả biên) trong hình vẽ bên là miền nghiệm của bất phương trình bậc nhất hai ẩn nào?
A. 44xy+ . B. 44xy+ . C. 41 xy+ D. 44xy−−
Câu 8. Cặp số nào sau đây là nghiệm của hệ bất phương trình 36 ? 24 xy xy + −
DẠYKÈMQUYNHƠN
OFFICIAL
xxx B.
xxx hoặc 2"− x C. " 2 ,42 xxx ".
− xxx ”. Câu
Cho
ập hợp {1;2;3;4;5} =
.
ậ
ợ
ả
= AX
\{6;7} = XA
" 2 ,42
D. " 2 ,422
3.
t
A
T
p h
p X tho
mãn \{1;3;5}
và
là: A. {2;4} B. {6;7} C. {2;4;6;7} D. {1;3;5;6;7} Lời giải Dùng biểu đồ Ven như Hình 3 để
A. (2;0) B. (0;2). C. (4;2). D. (3;3)




Lời giải. Với 4,2==−xy ta có: 43 + . (2)26 −=− và 2.4(2)104 −−= . Chọn C .
Câu 9. Miền nghiệm của hệ bất phương trình 22 22 1
xy xy y
+ −− − được xác định bởi miền đa giác nào sau đây?
A. B. C. D. Câu 10. Một đơn vị bộ đội cần mua ít nhất 300 kg gạo. Có hai loại gạo, loại I có giá
của x và y để số tiền đơn vị mua gạo không hết quá 7000000 đồng
DẠYKÈMQUYNHƠN
OFFICIAL
loại II có giá 20000 đồng/ kg. Gọi , xy lân lượt là số gạo loại
trình biểu thị mối liên hệ
là: A. 8 32700 + + xy xy B. 300 33700 + + xy xy C. 300 32700 + + xy xy D. 300 32700 + + xy xy Câu 11. Cho góc thoả mãn 90180 và sin3 5 = . Giá trị của cos là: A. 4 5 . B. 4 5 C. 2 5 . D. 2 5 Lời giải
là 30000 đồng/ kg,
I, II đơn vị mua. Hệ bất phương
DẠYKÈMQUYNHƠN OFFICIAL
ABAC
Câu 15. Tam
ABC có 9 AB = cm, 15 BC = cm, 12 AC = cm. Khi đó đường trung tuyến AM của tam giác có độ dài là A. 10cm B. 9cm C. 7,5cm D. 8cm Lời giải Chọn C Ta có 222 2 24 ABACBC AM + =− 222 91215225 244 + =−= 15 2 AM = Câu 16. Cho tam giác ABC có ,, ABcACbBCa === . Chọn khẳng định đúng A. 222 cos 2 bca A bc +− = . B. 222 cos bca A bc +− = C. 222 cos 2 bca A bc ++ = . D. 222 cos 2 abc A bc = Lời giải
Ta có: 22 sincos1 += . Do đó 22 cos1sin1916 2525 =−=−= . Do 90180
nên cos0 . Suy ra 4 cos 5 =− Chọn B Câu 12. Cho góc thoả mãn 0180 và 2 cos 3 =− . Giá trị của tan là: A. 5 2 . B. 5 2 . C. 2 5 . D. 2 5 . Giải Ta có: 22 sincos1 += . Do đó 22 sin1cos145 99 =−=−= Do 0180 nên sin0 . Suy ra 5 sin 3 = . Vậy sin5 tan cos2 ==− Chọn A Câu 13. Cho tam giác ABC vuông tại A . Chọn khẳng định sai trong các khẳng định sau: A. cossin = BC. B. sincos = BC. C. tancot = BC . D. tancot =− CB. Câu 14. Cho các điểm (1;1),(2;4),(10;2). ABC Góc BAC bằng bao nhiêu? A. 090 . B. 0 60. C. 0 45. D. 0 30. Lời giải Chọn#A. Ta có: (1;3) AB = , (9;3) AC =− . Suy ra: 0 cos090. . ABAC BACBAC
===
giác
Chọn A
Câu 17. Bộ ba số nào sau đây là độ dài 3 cạnh của một tam giác tù? A. 2;3;4. B. 3;4;5. C. 4;5;6. D. 5;6;7. Lời giải
Chọn A
Dễ thấy phương án B là độ dài 3 cạnh của một tam giác vuông. Một tam giác là tam giác tù khi góc lớn nhất là góc tù. Ngoài ra góc lớn nhất là góc đối diện với cạnh lớn nhất. Gọi góc lớn nhất của các tam giác trong các phương án B, C, D là góc A và cạnh lớn nhất là cạnh có độ dài a .
Áp dụng hệ quả của định lí Côsin với góc đối diện với cạnh lớn nhất 222 cos 2 +− = bca A bc cho từng phương án.
Với phướng án C, ta có: 222 4561 cos0 2.4.58 +− == A , nên góc A nhọn (loại).
Với phướng án D, ta có: 222 5671 cos0 2.5.65 +− == A nên góc A nhọn (loại).
Với phướng án A, ta có: 222 2341 cos0 2.2.34 +− ==− A nên góc A tù (chọn).
Câu 18. Cho tam giác ABC có , = BCa , = CAb = ABc thỏa 222 3. +=+ bcabc Tìm số đo của góc A của tam giác ABC A. 120 B. 60 C. 150 D. 30 Lời giải Chọn D Ta có 222 3 +=+ bcabc 222 3 +−=bcabc 222 3 +− = bca bc 222 3 22 +− = bca bc 3 cos 2 = A 30 =
DẠYKÈMQUYNHƠN
OFFICIAL
. Vậy số đo
A
Câu
Cho
A. ACBD B. ABCD C. ABBC D. Hai
Lời giải Chọn C Vì ABBCABBC Câu 20. Gọi O là tâm hình bình hành .ABCD Đẳng thức nào sau đây sai ? A. OAOBCD . B. OBOCODOA. C. ABADDB D. BCBADCDA Lời giải Chọn B +) Đáp án#A. Ta có OAOBBACD Vậy A đúng. +) Đáp án B. Ta có OBOCCBAD ODOAAD Vậy B sai. +) Đáp án C. Ta có .ABADDB Vậy C đúng.
A
của góc
của tam giác ABC là 30
19.
hình vuông ABCD . Khẳng định nào sau đây đúng?
vectơ , ABAC cùng hướng.

DẠYKÈMQUYNHƠN OFFICIAL +) Đáp án D. Ta có BCBAAC DCDAAC Vậy D đúng. Câu 21. Tính tổng MNPQRNNPQR . A. MR B. .MN C. PR D. MP Lời giải Chọn B Ta có MNPQRNNPQRMNNPPQQRRNMN . Câu 22. Cho 6 điểm ,,,,, ABCDEF . Tổng véc tơ: ++ ABCDEF bằng A. ++ AFCEDB B. ++ AECBDF C. ++ ADCFEB D. AEBCDF ++ Lời giải Chọn C ( ) ( ) ( ) ABCDEFADDBCFFDEBBFADCFEB ++=+++++=++ Câu 23. Cho ba lực 123 ,, FFF cùng tác động vào một vật tại một điểm làm vật đứng yên (Hình). Xét 423 =+ FFF . Phát biểu nào sau đây là đúng? A. 41 = FF . B. 41 2 = FF . C. 41 2=− FF . D. 41 =− FF . Lời giải Vì vật đứng yên nên 1231441 00 ++=+==− FFFFFFF Chọn D Câu 24. Cho đoạn thẳng AB và điểm C nằm giữa hai điểm , AB . Khẳng định nào sau đây là đúng? A. = AC ACAB AB B. =− AC ACAB AB C. = AB ACAB AC . D. =− AB ACAB AC . Lời giải Chọn A Câu 25. Cho 0 a và điểm O . Gọi , MN lần lượt là hai điểm thỏa mãn 3 OMa = và 4 ONa =− . Khi đó: A. 7 MNa = B. 5 MNa =− C. 7 MNa =− D. 5 MNa =− Lời giải
Chọn C
Ta có: 437 MNONOMaaa =−=−−=−
Câu 26. Cho hình bình hành ABCD có (1;2)A , (3;2),(4;1)BC . Toạ độ của đỉnh D là:
A. (8;3). B. (3;8) C. (5;0) D. (0;5).
Lời giải Chọn D
Câu 27. Cho hai vectơ (1;3)=− u và (2;5)=− v . Tọa độ của vectơ + uv là:
A. (1;2) . B. (2;1) . C. (3;8) D. (3;8).
Lời giải Chọn A
Câu 28. Cho đoạn thẳng AB . Tập hợp các điểm M nằm trong mặt phẳng thoả mãn 0 =MAMB là:
A. Đường tròn tâm A bán kính AB B. Đường tròn tâm B bán kính AB C. Đường trung trực của đoạn thẳng AB . D. Đường tròn đường kính AB Lời giải Chọn D
Câu 29. Cho hình vuông ABCD, tính ( ) cos,ABCA
OFFICIAL
ọ
tiên
đi tìm
của góc (
giải
đó mớ
DẠYKÈMQUYNHƠN
n A Ta có 2 2 .2. 2 ==aaa CACB . Câu 31. Xấp xỉ số π bởi số 355 113 . Hãy đánh giá sai số tuyệt đối biết: 3,141592653,14159266 A. 7 2,8.10 a B. 7 28.10 a C. 7 1.10 a D. 6 2,8.10 a Lời giải Đáp án#A. Ta có (sử dụng máy tính bỏ túi) 355 3,14159292...3,1415929293 113 Do vậy
A. 1 2 . B. 1 2 . C. 2 2 . D. 2 2 . Lời
Ch
n D Đầu
ta
số đo
) , ABCA sau
i tính ( ) cos,ABCA Vì ( ) ( ) ( ) oo 2 ,180,135cos, 2 =−==−ABCAABCAABCA Câu 30. Cho tam giác ABC vuông cân tại A có 2 BCa = .Tính . CACB A. 2 = CACBa B. = CACBa C. 2 2 = a CACB D. .2 = CACBa Lời giải Chọ
0,00000028 Vậy sai số tuyệt đối nhỏ hơn 7 2,8.10 . Câu 32. Độ cao của một ngọn núi đo được là 1372,5 h = m. Với sai số tương đối mắc phải là 0,5‰. Hãy xác định sai số tuyệt đối của kết quả đo trên và viết h dưới dạng chuẩn. A. ( ) 0,68625;1373 h hm== B. ( ) 0,68626;1372 h hm== C. ( ) 0,68625;1372 h hm== D. ( ) 0,68626;1373 h hm== Lời giải Đáp án#A. Theo công thức h h h = ta có: 0,5 .1372.5.0,68625 1000 hh h === Và h viết dưới dạng chuẩn là 1373 h = (m) Câu 33. Cân nặng của 40 học sinh lớp 10 trường THPT A được cho bởi bảng sau Tính số trung bình cộng của mẫu số liệu trên. A. 38,26 x = B. 40,25 x = C. 39,65 x = D. 40,83 x = Lời giải Chọn C Giá trị đại diện của từng lớp cân nặng là: 36, 38, 40, 42 Khi đó số trung bình cộng của mẫu số liệu trên là: 36.638.940.1142.14 39,65 40 x +++ == Câu 34. Kết quả điểm kiểm tra 15’ môn Toán của 100 em học sinh được trình bày ở bảng sau: Điểm 3 4 5 6 7 8 9 10 Cộng Tần số 3 5 11 17 30 19 10 5 100 Số trung bình cộng của

DẠYKÈMQUYNHƠN
−−
OFFICIAL 355 03,141592933,14159265 113
bảng phân bố tần số nói trên là A. 6,88 B. 7,12 C. 6,5 D. 7,22 Lời giải Số trung bình cộng của bảng phân bố tần số nói trên là: 3.34.55.116.177.308.199.1010.5 6,88 100 +++++++ = Câu 35. Cho phương sai của các số liệu bằng 4. Tìm độ lệch chuẩn. A. 4 B. 2 C. 16 D. 8 Lời giải Ta có độ lệch chuẩn là căn bậc hai của phương sai Nên 2 42 xx ss=== .
Câu 1. Trong lớp 10 A có 45 học sinh trong đó có 25 em thích môn văn, 20 em thích môn toán, 18 em thích môn sử, 6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên:
Lời giải Gọi ,, abc theo thứ tự là số học sinh chỉ thích môn Văn, Sử, Toán: x là số học sinh chỉ thích hai môn Văn và Toán; y là số học sinh chỉ thích hai môn Sử và Toán; z là số học sinh chỉ thích hai môn là Văn và Sử. Ta có số em thích ít nhất một môn là 45639 −=
Dựa vào biều đồ ven ta có hệ phương trình
Cộng vế với vế (1),(2),(3) ta có
abcxyz (5) Từ (4) và (5), ta có 2(395)156320

abcabcabc Vậy chỉ có 20 em thích chỉ một trong ba môn trên. Câu 2. Một người bán nước giải khát đang có 25g bột nho và 100 g đường để pha chế hai loại nước nho A và B . Để pha chế 1l nước nho loại A cần 10 g đường và 1g bột nho; để pha chế 1l nước nho loại B cần 10 g đường và 4g bột nho. Mỗi lít nước nho loại A khi bán lãi được 30 nghìn đồng, mỗi lít nước nho loại B khi bán lãi được 40 nghìn đồng. Hỏi người đó nên pha chế bao nhiêu lít nước nho mỗi loại để có lợi nhuận cao nhất? Lời giải
DẠYKÈMQUYNHƠN OFFICIAL
2. Tự luận
(
(
5251 5182 5203
+++= +++= +++= ++++++= axz byz cxy xyzabc
2()1563+++++==
phương trình: 425 10 0 0. xy xy x y + + Miền nghiệm của hệ bất phương trình là miền tứ giác OABC, trong đó (0;0)O ; (10;0);(5;5);(0;6,25) ABC . Gọi F là số tiền lãi (đơn vị: nghìn đồng) thu được, ta có: 3040=+ Fxy .
) ( ) ( )
)
5394
+++−−−−+=++=
Gọi x và y lần lượt là số lít nước nho loại A và B người đó có thể pha chế. Ta có hệ bất
Ta có: Tại (0;0):30.040.00 =+= OF ;


Tại (10;0):30.1040.0300 =+= AF ;
Tại (5;5):30.540.5350 =+= BF ;
Tại (0;6,25):30.040.6,25250 =+= CF .
Ta thấy F đạt GTLN bằng 350 tại (5;5)B Vậy người đó nên pha chế 5l nước nho mỗi loại để có lợi nhuận cao nhất.
Câu 3. Ta giả sử hai bờ sông là hai đường thẳng song song cách nhau 2km. Một chiếc tàu nhỏ đi từ điểm A ở bờ bên này sang điểm B ở bờ bên kia với vận tốc riêng của tàu (tức là vận tốc của tàu so với dòng nước) là 20 / kmh. Giả sử AB vuông góc với bờ sông (như hình vẽ). Cho biết vận tốc của dòng nước so với bờ là không đổi 5 / kmh (giả sử phương dòng nước chảy song song với bờ sông).
OFFICIAL
a) Cần giữ lái cho tàu tạo với bờ sông một góc nhọn bằng bao nhiêu độ để tàu sang bờ bên kia theo phương AB ? b) Tính vận tốc của tàu so với bờ. Hỏi sau bao lâu thì tàu sẽ tới bờ bên kia? (Các kết quả tính toán ở câu a) và câu b) ở trên được làm tròn đến hàng phần trăm). Lời giải a) Vận tốc thực của tàu so với bờ là , tntn vvv =+ Để cho tàu luôn chạy theo phương AB thì phương của , tnv phải có phương là AB và chiều là hướng từ A đến B (như hình vẽ).
DẠYKÈMQUYNHƠN
MAC AMAM ==== . Suy
14,48 MAC .
−= b) Do tam giác ANC vuông
A nên 22 515 ACCNAN=−= .
vận tốc của tàu so với bờ là 19,36 / kmh . Thời gian để tàu qua sông là 2 0,1 515 giờ. Câu 4. Cho tam giác ABC cố định và điểm M di động. Chứng minh rằng 45 vMAMBMC =+− không phụ thuộc vào vị trí của điểm M Lời giải ( ) ( ) 45454 vMAMBMCMCCAMCCBMCCACB =+−=+++−=+ Vì A, B, C cố định nên v không đổi
Ta có sin51 204 MCAN
ra
Vậy góc nhọn của tàu tạo với bờ sông là 9014,4875,52
tại
Vậy
Vậy v không phụ thuộc vào vị trí của điểm M
DẠYKÈMQUYNHƠN OFFICIAL
1. Trắc nghiệm
Câu 1. Cho mệnh đề : P "6 là số hoàn hảo" và mệnh đề Q : "Hà Nội là thủ đô của Việt Nam". Phát
biểu của mệnh đề PQ là
A. Nếu 6 là số hoàn hảo thì Hà Nội là thủ đô của Việt Nam.
B. Nếu Hà Nội là thủ đô của Việt Nam thì 6 là số hoàn hảo.
C. 6 là số hoàn hảo nếu Hà Nội là thủ đô của Việt Nam.
D. Nếu 6 là số hoàn hảo thì Hà Nội không là thủ đô của Việt Nam.
Câu 2. Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Đại dịch Covid-19 thật đáng sợ!
b) Hà Nam là một tỉnh của Việt Nam. c) 37 là một số nguyên tố. d) Cậu có thích học môn Lịch sử và Địa lí không?
OFFICIAL
A. 4. B. 3. C. 2. D. 1. Câu 3. Cho tập hợp {34}Axx=− và {1;3;9} B = . Tập hợp ()\ CABB = là A. {3;2;1;0;2} C =−−− . B. {3;2;1;0;2;4} C =−−− C. {3;1;2} C =−− . D. {3;2;1;0;1;2;3} C =−−− . Câu 4. Cho tập ( ) ( ) 2249 0 .13 . 3 xxx Xx −−++ == Số tập con của X là A. 4. B. 0. C. 6. D. 8. Câu 5. Cho biểu đồ Ven sau đây. Phần được gạch sọc biểu diễn tập hợp nào? A. \ AB B. \ BA C. AB D. AB Câu 6. Miền nghiệm của bất phương trình 31 +xy là nửa mặt phẳng tạo bởi đường thẳng :31( +=dxy kể cả d ) chứa điểm có toạ độ nào sau đây? A. (0;0). B. (3;1) C. (1;1) D. (2;9). Câu 7. Phần không bị gạch (kể cả d ) ở Hình 3 là miền nghiệm của bất phương trình: A. 1 x . B. 1 x . C. 1 y . D. 1 y . Câu 8. Cặp số nào sau đây là nghiệm của hệ bất phương trình: 3515 ? 236 xy xy +− − A. (0;3).


DẠYKÈMQUYNHƠN
ĐỀ SỐ 7
B. (1;1)


C. (5;2). D. (2;3).


Câu 9. Miền nghiệm của hệ bất phương trình 1 2 − y y được xác định bởi phần không bị gạch và không kể hai đường thẳng , dd ' nào sau đây?
A. B. C. D.
Câu 10. Chủ cửa hàng điện thoại mang 200 triệu đồng hoặc mua điện thoại loại 10 triệu đồng hoặc máy tính bảng loại 9 triệu đồng ở đại lí cấp một. Gọi , xy lần lượt là số chiếc điện thoại và máy tính mà chủ cửa hàng mua. Cặp số (;) xy nào sau đây biểu thị số chiếc điện thoại và máy tính mà chủ cửa hàng có thể mua? A. (10;12) B. (11;10) C. (9;13). D. (11;11).
DẠYKÈMQUYNHƠN
OFFICIAL
Câu 11. Cho góc thoả mãn 0180 và 3 cos 5 =− . Giá trị của sin là: A. 3 5 B. 4 5 C. 4 5 D. 2 5 Câu 12. Cho góc thoả mãn 0180 và tan2 =− . Giá trị của cot là: A. 2. B. 1 2 . C. 1 2 D. 3. Câu 13. Giá trị biểu thức tan0tan10tan20tan30 = T bằng: A. 0. B. 1. C. 1.
D. 2.
Câu 14. Cho tam giác ABC có 04,3,30ABACBAC=== . Khi đó diện tích tam giác ABC bằng A. 3. B. 43. C. 63 . D. 6.

Câu 15. Cho tam giác ABC có 02,3,60ABACBAC=== . Khi đó bán kính đường tròn ngoại tiếp tam giác ABC bằng: A. 621 7 B. 7 C. 21 3 D. 321 7
Câu 16. Cho tam giác ABC nhọn có 3 BCa = và bán kính đường tròn ngoại tiếp tam giác ABC là 3 Ra = . Tính số đo góc A
A. 120 = A B. 45 = A C. 30 = A D. 60 = A
Câu 17. Cho tam giác ABC có 4 c = , 6 b = , 60 = A . Chiều cao a h của tam giác ABC là: A. 321 7 a h = . B. 621 7 a h = . C. 1221 7 a h = . D. 221 7 a h = .
Câu 18. Cho tam giác ABC có 2 a = , 6 b = , 31 c =+ . Tính bán kính R của đường tròn ngoại tiếp.
A. 2 . B. 2 2 . C. 2 . 3 D. 3.
Câu 19. Cho hình bình hành ABCD tâm O. Vectơ đối của BO là
A. CO . B. AO . C. DO . D. OC .
Câu 20. Cho hình vuông ABCD cạnh a , độ dài vectơ ABACBD −+ bằng:
A. a B. 3a C. 2 a D. 22a Câu 21. Cho ABC gọi ,, MNP lần lượt là trung điểm các cạnh ,, ABACBC . Hỏi + MPNP bằng vec tơ nào?
A. AM . B. PB . C. AP . D. MN . Câu 22. Cho lục giác đều ABCDEF có tâm O . Đẳng thức nào dưới đây là đẳng thức sai? A. 0 OAOBEO+−= B. BCFEAD −= C.OAOBEBOC −=− D. 0 ABCDFE+−= Câu 23. Trên Hình biểu diễn ba lực 123 ,, FFF cùng tác động vào một vật ở vị trí cân bằng A . Cho biết 1230,40== FNFN . Tính cường độ của lực 3F . A. 50 B. 40 C. 30 D. 20
DẠYKÈMQUYNHƠN
OFFICIAL
Câu 24. Cho đoạn thẳng AB . Gọi M là một điểm trên AB sao cho 1 4 = AMAB . Khẳng định nào sau
đây sai? A. 1 3 = MAMB B. 1 4 = AMAB C. 3 4 = BMBA D. 3=− MBMA
Câu 25. Cho tam giác ABC . Gọi I là trung điểm của AB . Tìm điểm M thỏa mãn hệ thức 20MAMBMC++=
A. M là trung điểm của BC
B. M là trung điểm của IC
C. M là trung điểm của IA
D. M là điểm trên cạnh IC sao cho 2 IMMC =
Câu 26. Cho tam giác ABC có (4;6),(1;2),(7;2) ABC . Toạ độ trọng tâm G của tam giác ABC là: A. 10 4; 3 B. (8;4) C. (2;4) D. (4;2).
Câu 27. Cho hai điểm (2;4) M và (1;2)N . Khoảng cách giữa hai điểm M và N là: A. 13 B. 5 C. 13. D. 37 .
Câu 28. Cho a và b là hai vectơ cùng hướng và đều khác vectơ 0 . Mệnh đề nào sau đây đúng?
A. .. abab = . B. .0ab = . C. .1ab =− . D. .. abab =− .
Câu 29. Cho tam giác đều ABC cạnh bằng a và H là trung điểm BC . Tính AHCA A. 2 3 4 a B. 2 3 4 a C. 2 3 2 a D. 2 3 2 a
Câu 30. Biết a , b 0 và abab =− . Câu nào sau đây đúng
A. a và b cùng hướng. B. a và b nằm trên hai dường thẳng hợp với nhau một góc o120 C. a và b ngược hướng. D. A, B, C đều sai
Câu 31. Độ cao của một ngọn núi đo được là 2373,5 hm = với sai số tương đối mắc phải là 0,5‰. Hãy viết h dưới dạng chuẩn.
A. 2373 m B. 2370 m C. 2373,5 m D. 2374 m
Câu 32. Trong một phòng thí nghiệm, hằng số c được xác định gần đúng là 3,54965 với độ chính xác 0,00321 d = . Dựa vào d, hãy xác định chữ số chắc chắn của c. A. 3; 5; 4 B. 3; 5; 4; 9 C. 3; 5; 4; 9; 6 D. 3; 5; 4; 9; 6; 5 Câu 33. Cho mẫu số liệu thống kê 2;4;6;8;10 . Số trung bình của mẫu số liệu trên là: A. 7 B. 12 C. 6.5 D. 6 Câu 34. Điểm kiểm tra của 24 học sinh được ghi lại trong bảng sau:
DẠYKÈMQUYNHƠN
OFFICIAL
Tìm mốt của điểm điều tra. A. 2 B. 7 C. 6 D. 9
Câu 35. Nếu đơn vị đo của số liệu là kg thì đơn vị của độ lệch chuẩn là A. kg. B. kg 2 C. Không có đơn vị D. kg 2
2. Tự luận
Câu 1. Cho hai tập hợp [4;2]=− A và [8;2]=−+Ba . Tìm a để AB có vô số phần tử.


OFFICIAL
Câu 2. Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 12 g hương liệu, 9 lịt nước và 315 g đường đề pha chế hai loại nước A và B . Để pha chế 1 lít nước A cần 45g đường, 1 lít nước và 0,5 g hương liệu; để pha chế 1 lít nước B cần 15 g đường, 1 lít nước và 2g hương liệu. Mỗi lít nước A nhận được 60 điểm thưởng, mỗi lít nước B nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước mỗi loại để đội chơi được số điểm thưởng là lớn nhất?
Câu 3. Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 45 và 75 . Biết khoảng cách giữa hai vị trí A, B là 30m (Hình). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
DẠYKÈMQUYNHƠN
Câu 4. Cho hình vuông ABCD cạnh a. Chứng minh rằng 232 vMAMBMCMD =−+− không phụ thuộc vào vị trí của điểm M Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM 1A 2C 3A 4D 5A 6A 7B 8B 9B 10B 11B 12C 13A 14A 15C 16D 17B 18A 19C 20A 21C 22D 23A 24A 25B 26D 27A 28A 29B 30C 31B 32A 33D 34C 35A
1. Trắc nghiệm
Câu 1. Cho mệnh đề : P "6 là số hoàn hảo" và mệnh đề Q : "Hà Nội là thủ đô của Việt Nam". Phát biểu của mệnh đề PQ là
A. Nếu 6 là số hoàn hảo thì Hà Nội là thủ đô của Việt Nam.
B. Nếu Hà Nội là thủ đô của Việt Nam thì 6 là số hoàn hảo.
C. 6 là số hoàn hảo nếu Hà Nội là thủ đô của Việt Nam.
D. Nếu 6 là số hoàn hảo thì Hà Nội không là thủ đô của Việt Nam.
Câu 2. Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Đại dịch Covid 19 thật đáng sợ!
b) Hà Nam là một tỉnh của Việt Nam. c) 37 là một số nguyên tố. d) Cậu có thích học môn Lịch sử và Địa lí không? A. 4. B. 3. C. 2. D. 1. Câu 3. Cho tập hợp {34}Axx=− và

OFFICIAL
DẠYKÈMQUYNHƠN
()\
=−−− .
Câu
ậ
( ) ( ) 2249 0 .13 . 3 xxx Xx −−++ == Số tập con của X là A.
C. 6.
Lời giải Chọn D Xét phương trình ( ) ( ) 22 491330 xxx −−++= ( ) 2 2 490 1330 x xx −= −++= 3 2 1 3 x x x = = = 3 2() 1 x doxQ x = = Khi đó tập 3 ,1 2 X = vậy số tập con của X là 3 28 = Câu 5. Cho biểu đồ Ven sau đây. Phần được gạch sọc biểu diễn tập hợp nào? A. \ AB B. \ BA C. AB D. AB Câu 6. Miền nghiệm của bất phương trình 31 +xy là nửa mặt phẳng tạo bởi đường thẳng :31( +=dxy kể cả d ) chứa điểm có toạ độ nào sau đây? A. (0;0). B. (3;1). C. (1;1) D. (2;9) Lời giải. Với 0,0==xy ta có: 3.0001 += . Chọn A. Câu 7. Phần không bị gạch (kể cả d ) ở Hình 3 là miền nghiệm của bất phương trình:
{1;3;9} B = . Tập hợp
CABB = là A. {3;2;1;0;2} C
B. {3;2;1;0;2;4} C =−−− . C. {3;1;2} C =−− D. {3;2;1;0;1;2;3} C =−−−
4. Cho t
p
4. B. 0.
D. 8.





DẠYKÈMQUYNHƠN OFFICIAL
i , xy lần lượt là số chiếc điện thoạ
và
mà chủ cửa hàng mua. Cặp số (;) xy nào sau
u thị
ố chiếc điện thoạ
chủ cửa hàng có thể mua? A. (10;12) B. (11;10). C. (9;13). D. (11;11) Câu 11. Cho góc thoả mãn 0180 và 3 cos 5 =− . Giá trị của sin là: A. 3 5 . B. 4 5 . C. 4 5
A. 1 x . B. 1 x . C. 1 y . D. 1 y . Câu 8. Cặp số nào sau đây là nghiệm của hệ bất phương trình: 3515 ? 236 xy xy +− − A. (0;3). B. (1;1). C. (5;2) D. (2;3) Câu 9. Miền nghiệm của hệ bất phương trình 1 2 − y y được xác định bởi phần không bị gạch và không kể hai đường thẳng , dd ' nào sau đây? A. B. C. D. Câu 10. Chủ cửa hàng điện thoại mang 200 triệu đồng hoặc mua điện thoại loại 10 triệu đồng hoặc máy tính bảng loại 9 triệu đồng ở đại lí cấp một. Gọ
i
máy tính
đây biể
s
i và máy tính mà
DẠYKÈMQUYNHƠN OFFICIAL D.
số đo góc A . A. 120 = A . B. 45 = A . C. 30 = A . D. 60 = A . Lời giải Chọn D Áp dụng định lý sin trong tam giác ABC , ta có 33 2sin sin22 23 ==== BCBCa RA AR a . Suy ra 60 = A (do tam giác ABC nhọn). Câu 17. Cho tam giác ABC có 4 c = , 6 b = , 60 = A . Chiều cao a h của tam giác ABC là: A. 321 7 a h = . B. 621 7 a h = . C. 1221 7 a h = . D. 221 7 a h = . Lời giải Chọn B Ta có: 222 2.cos abcbcA =+− 2 28 a = 27 a =
2 5 . Câu 12. Cho góc thoả mãn 0180 và tan2 =− . Giá trị của cot là: A. 2. B. 1 2 C. 1 2 D. 3. Câu 13. Giá trị biểu thức tan0tan10tan20tan30 = T bằng: A. 0. B. 1. C. 1. D. 2. Lời giải Vì tan00 = nên 0 = T Chọn A Câu 14. Cho tam giác ABC có 04,3,30ABACBAC=== . Khi đó diện tích tam giác ABC bằng A. 3. B. 43. C. 63 . D. 6. Lời giải Chọn A 0 11 ..sin.4.3.sin303. 22 ABC SABACBAC === Câu 15. Cho tam giác ABC có 02,3,60ABACBAC=== . Khi đó bán kính đường tròn ngoại tiếp tam giác ABC bằng: A. 621 7 B. 7 C. 21 3 D. 321 7 Lời giải Chọn C 22222 1 2...cos232.2.3.7 2 BCABACABACBAC=+−=+−= Bán kính đường tròn ngoại tiếp tam giác ABC bằng: 0 721 2sin2.sin603 BC R BAC === Câu 16. Cho tam giác ABC nhọn có 3 BCa = và bán kính đường tròn ngoại tiếp tam giác ABC là 3 Ra = . Tính
Diện tích tam giác: 11 ..sin. 22 a SbcAha == ..sin621 7 a bcA h a ==
Câu 18. Cho tam giác ABC có 2 a = , 6 b = , 31 c =+ . Tính bán kính R của đường tròn ngoại tiếp.
A. 2 . B. 2 2 . C. 2 . 3 D. 3. Lời giải Chọn A Ta có : 222 cos 2 bca A bc +− = 2 2 = 45 A = . Do đó : 2sin a R A = 2 2.sin45 = 2 = .
Câu 19. Cho hình bình hành ABCD tâm O. Vectơ đối của BO là A. CO . B. AO . C. DO . D. OC . Lời giải Chọn C
Từ hình vẽ suy ra BODO
Câu 20. Cho hình vuông ABCD cạnh a , độ dài vectơ ABACBD −+ bằng: A. a B. 3a C. 2 a D. 22a Lời giải Vì ABCD là hình vuông nên: CACBCD =+ và BDBCBA =+ . Ta có: ABACBDABCABDABCDCBBABC −+=++=++++ ABCDCBABCBCD =++−−= Mà
DẠYKÈMQUYNHƠN
OFFICIAL
= . Từ đó
gọi ,, MNP
Vì ,, MNP lần lượt là trung điểm các cạnh ,, ABACBC nên MP là đường trung bình của ABC 1 //; 2 MPACMPACNA== Từ đó tứ giác ABCD là hình bình hành. Hay ; NPAMMPANMPNPANAMAP ==+=+= Câu 22. Cho lục giác đều ABCDEF có tâm O . Đẳng thức nào dưới đây là đẳng thức sai? A. 0 OAOBEO+−= B. BCFEAD −= C.OAOBEBOC −=− D. 0 ABCDFE+−= Lời giải O C A B D
CDa
độ dài ABACBDa −+= . Câu 21. Cho ABC
lần lượt là trung điểm các cạnh ,, ABACBC . Hỏi + MPNP bằng vec tơ nào? A. AM B. PB C. AP D. MN Lời giải
Theo hình vẽ, ta có: ABCDFE +− ABBOEF=++ ABBOOA=++ 0 AA == . Câu 23. Trên Hình biểu diễn ba lực 123 ,, FFF cùng tác động vào một vật ở vị trí cân bằng A . Cho biết 1230,40== FNFN . Tính cường độ của lực 3F . A. 50 B. 40 C. 30 D. 20


Lời giải Ta sử dụng các vectơ ,, ABACAD lần lượt biều thị cho các lực 123 ,, FFF và vectơ AE biểu thi cho hợp lực F của 12 , FF

DẠYKÈMQUYNHƠN OFFICIAL Chọn D
Khi đó, do 90 = BAC , nên tứ giác ABEC là hình chữ nhật. Từ đó, do 30()
ABN
40( ) = ACN , suy ra 22 ||304050( ). FAEN ==+= Do vật ở vị trí cân bằng, nên hai lực F và 3F có cùng cường độ và ngược hướng, tức là các vectơ AE và AD là các vectơ có cùng độ dài và ngược hướng. Bởi vậy, cường độ của lực 3F bằng 3 ||50()=== FFAEN . Câu 24. Cho đoạn thẳng AB . Gọi M là một điểm trên AB sao cho 1 4 = AMAB . Khẳng định nào sau đây sai? A. 1 3 = MAMB B. 1 4
AMAB C. 3 4
BMBA D. 3
MBMA Câu 25. Cho tam giác ABC . Gọi I là trung điểm của AB . Tìm điểm M thỏa mãn hệ thức 20MAMBMC++= A. M là trung điểm của BC B. M là trung điểm của IC C. M là trung điểm của IA D. M là điểm trên cạnh IC sao cho 2 IMMC = Lời giải Chọn B 202200 MAMBMCMIMCMIMC ++=+=+= M là trung điểm của IC
Câu 26. Cho tam giác ABC có (4;6),(1;2),(7;2) ABC . Toạ độ trọng tâm G của tam giác ABC là: A. 10 4; 3 . B. (8;4). C. (2;4). D. (4;2)
Lời giải Chọn D
Câu 27. Cho hai điểm (2;4) M và (1;2)N . Khoảng cách giữa hai điểm M và N là: A. 13 . B. 5 . C. 13. D. 37
giải
DẠYKÈMQUYNHƠN OFFICIAL
=
,
=
=
=−
Cho a và b là
=
Lời
Chọn A Do a và b là
)
=⎯⎯→= Vậy abab = Câu
Cho
A.
4
2
2
Lời
Chọn A Câu 28.
hai vectơ cùng hướng và đều khác vectơ 0 . Mệnh đề nào sau đây đúng? A. .. abab
. B. .0ab = . C. .1ab =− . D. .. abab =− .
giải
hai vectơ cùng hướng nên (
( ) 0 ,0cos,1 abab
29.
tam giác đều ABC cạnh bằng a và H là trung điểm BC . Tính . AHCA
2 3 4 a B. 2 3
a C. 2 3 2 a D.
3
a
Lời giải Chọn B
Ta có ( ) 2 o 33 ...cos,..cos150 24 ===− AHCAAHCAAHCAaaa .
Câu 30. Biết a , b 0 và .. abab =− . Câu nào sau đây đúng

A. a và b cùng hướng. B. a và b nằm trên hai dường thẳng hợp với nhau một góc o120 C. a và b ngược hướng. D. A, B, C đều sai Lời giải Chọn C
Ta có ( ) ( ) ...cos,.cos,1 =−=−=− abababababab nên a và b ngược hướng Câu 31. Độ cao của một ngọn núi đo được là 2373,5 hm = với sai số tương đối mắc phải là 0,5‰. Hãy viết h dưới dạng chuẩn. A. 2373 m B. 2370 m C. 2373,5 m D. 2374 m Lời giải Đáp án B. h h h = , ta có: 0,5 .2373,5.1,18675 1000 h hh === h viết dưới dạng chuẩn là 2370 h = m. Câu 32. Trong một phòng thí nghiệm, hằng số c được xác định gần đúng là 3,54965 với độ chính xác 0,00321 d = . Dựa vào d, hãy xác định chữ số chắc chắn của c A. 3; 5; 4 B. 3; 5; 4; 9 C. 3; 5; 4; 9; 6 D. 3; 5; 4; 9; 6; 5 Lời giải Đáp án#A. Ta có: 0,003210,005 nên chữ số 4 (hàng phần trăm) là chữ số chắc chắn, do đó c có 3 chữ số chắc chắn là 3; 5; 4. Câu 33. Cho mẫu số liệu th
DẠYKÈMQUYNHƠN
OFFICIAL
ống kê 2;4;6;8;10 . Số trung bình của mẫu số liệu trên
A. 7 B. 12
Lời
Số trung bình của mẫu số liệu trên là: 246810 6 5 x ++++ == Câu 34. Điểm kiểm tra của 24 học sinh được ghi lại trong bảng sau: Tìm mốt của điểm điều tra. A. 2 B. 7 C. 6
9 Lời
Ta
bảng thống kê sau:
là:
C. 6.5 D. 6
giải
D.
giải
có
2. Trong m
mãn yêu cầu bài toán.
c thi pha chế, mỗi đội chơi được sử dụng tối đa 12 g hương liệu, 9 lịt nước và 315 g đường đề pha chế hai loại nước A và B . Để pha chế 1 lít nước A cần 45g đường, 1 lít nước và 0,5 g hương liệu; để pha chế 1 lít nước B cần 15 g đường, 1 lít nước và 2g hương liệu. Mỗi lít nước A nhận được 60 điểm thưởng, mỗi lít nước B nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước mỗi loại để đội chơi được số điểm thưởng là lớn nhất? Lời giải Gọi x và y lần lượt là số lít nước loại A và B cần pha chế. Khi đó, theo đề bài
DẠYKÈMQUYNHƠN OFFICIAL Ta thấy điểm 6 có tần số lớn nhất nên mốt của điểm điều tra là: 0 6 M = . Câu 35. Nếu đơn vị đo của số liệu là kg thì đơn vị của độ lệch chuẩn là A. kg. B. kg 2 C. Không
đơn
2 Lời giải Chọn A 2. Tự luận Câu 1. Cho hai tập hợp [4;2]=− A và [8;2]=−+Ba . Tìm a để AB có vô số phần tử. Lời giải Điều kiện: 2810+−−aa Để AB có vô số phần tử khi và chỉ khi AB có nhiều hơn 1 phần tử, tức là 246 +−−aa . Khi đó [4;2]khi 22 [4;2]khi 22 =−++ =−+ ABaa
[4;2]khi
=−+− =−
Vậy
− a
ta có hệ bất phương trình 0 0 9 4515315 0,5212. + + + x y xy xy xy Số điểm thưởng đội chơi nhận được
có
vị D. kg
ABa hay
60 [4;2] khi 0
ABaa ABa
6
thỏa
Câu
ột cuộ
là (;)6080 =+ Fxyxy (điểm). Ta cần tìm giá trị lớn nhất của (;)Fxy với (;) xy thoả mãn hệ trên. Miền nghiệm của hệ là miền ngũ giác OABCD với (0;6),(4;5),(6;3) ABC , (7;0)D và (0;0)O .
Tính giá trị của F tại các đỉnh của ngũ giác: (0;6)480,(4;5)640 ==FF , (6;3)600,(7;0)420 ==FF và (0;0)0 = F . So sánh các giá trị đó ta được giá trị lớn nhất cần tìm là (4;5)640 = F . Vậy cần pha chế 4 lít nước loại A và 5 lít nước loại B đề số điểm thưởng nhận được là lớn nhất. Câu 3. Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 45 và 75 . Biết khoảng cách giữa hai vị trí A, B là 30m (Hình). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

Lời giải Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB . Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.

DẠYKÈMQUYNHƠN
OFFICIAL
ACBAACB
dụng định lí sin trong tam giác ABC ta có: sinsin = ABAC CB 30 sinsin11579,5 sinsin20
ACB C Tam giác ACH vuông tại H nên ta có: sin.sin45.79,556 ==CHAAC Vậy ngọn hải đăng cách bờ biển 56m. Câu 4. Cho hình vuông ABCD cạnh a. Chứng minh rằng 232 vMAMBMCMD =−+− không phụ thuộc vào vị trí của điểm M Lời giải Gọi O là tâm hình vuông Theo quy tắc ba điểm ta có ( ) ( ) ( ) ( ) 232 vMOOAMOOBMOOCMOOD =+−+++−+ 232 OAOBOCOD =−+− Mà ,2 ODOBOCOAvOA =−=−=− Suy ra 232 vMAMBMCMD =−+− không phụ thuộc vào vị trí của điểm M

DẠYKÈMQUYNHƠN OFFICIAL
=−+=−+=
Ta có: 18018075115 =−=−=ABCCBH ( ) ˆ 180()1804511520
Áp
== AB
1. Trắc nghiệm
Câu 1. Mệnh đề nào sau đây là mệnh đề tương đương?
A. 10 chia hết cho 5 là điều kiện cần để 10 chia hết cho 2.
B. Hình vuông là hình chữ nhật.
C. Hình thang nội tiếp đường tròn khi và chỉ khi nó là hình thang cân.
D. Nếu 63 chia hết cho 7 thì hình thoi có hai đường chéo vuông góc nhau.
Câu 2. Mệnh đề: " 2 ,33xx " khẳng định là
A. Bình phương của mỗi số thực lớn hơn 33.
B. Có ít nhất một số thực mà bình phương của nó lớn hơn 33.
C. Chỉ có một số thực
bình phương lớn hơn
. Giá trị nguyên dương của m để tập hợp (\) AB có đúng 10 phần tử là A. 10. B. 11. C. 12. D. 13. Câu 5. Cho (;2)[6;) CA =−+ và [5;9) CB = . Tập hợp XAB = là A. [2;5). B. (2;5). C. [2;5] D. [6;9)


Câu 6. Cặp số nào sau đây là nghiệm của bất phương trình 55−+ xy ? A. (1;9) . B. (2;1) C. (2;2) D. (0;5).
Câu 7. Miền nghiệm của bất phương trình 2 −+ xy được xác định bởi miền nào (nửa mặt phẳng không bị gạch và không kể d) sau đây? A. B.
DẠYKÈMQUYNHƠN
ĐỀ SỐ 8
OFFICIAL
{412}Cnn= .
A. () ABCB = B. () ABCA = C. () ABCC = . D. ()ABC= .
(3;]
=− và
có
33. D. Nếu x là số thực thì 2 33 x . Câu 3. Cho A là tập hợp các số tự nhiên chẵn không lớn hơn 12,{6} Bnn= ,
Mệnh đề nào sau đây là đúng?
Câu 4. Cho tập hợp
Am
{3}Bxx=
C. D.
Câu 8. Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình
A. (3;2)A . B. (6;3)B . C. (6;4)C D. (5;4)D Câu 9. Cho điểm (3;3)A và điểm M thuộc miền nghiệm của hệ bất phương trình


dài AM lớn nhất là A. 22 . B. 52 . C. 10 D. 34 .
Câu 10. Một cửa hàng bán hai loại mặt hàng A và B . Biết rằng cứ bán một mặt hàng loại A cửa hàng lãi 5 nghìn đồng, bán một mặt hàng loại B cửa hàng lãi 7 nghìn đồng. Gọi , xy lần lượt là số mặt hàng loại A và mặt hàng loại B mà cửa hàng đó bán ra trong một tháng. Cặp số (;) xy nào sau đây biểu thị số mặt hàng bán ra mỗi loại của cửa hàng trong một tháng mà tổng số tiền lãi không ít hơn 30 triệu đồng?
(1000;2000)
DẠYKÈMQUYNHƠN OFFICIAL
0
5? xy
xy − −− +
xy xy xy +− ++ −++ −+
33
xy
20 20 20 20 xy
Độ
A.
.
.
D.
Câu 11. Cho góc thoả mãn 0180 và cot2 =− . Giá trị của sin là: A. 1 2 B. 1 5 C. 5 5 D. 5 5 . Câu 12. Giá trị biểu thức tan1tan2.tan89 = T bằng: A. 0. B. 1. C. 1.
B. (3000;1000)
C. (2000;3000)
(3000;2000)
D. 2.
Câu 13. Cho 1 sin 4 = , với 090 . Giá trị cos bằng
A. 15 4 . B. 15 4 . C. 15 16 . D. 15 16 .
Câu 14. Cho tam giác ABC có 4cm = AB ; 12cm= AC và góc 120 BAC = . Tính diện tích tam giác ABC
A. 123 ( 2 cm ). B. 243( 2 cm ). C. 12( 2 cm ). D. 24( 2 cm ).
Câu 15. Cho tam giác ABC thỏa mãn 222 2.0BCACABBCAC +−−= . Khi đó, góc C có số đo là A. 150 C = B. 60 C = . C. 45 C = D. 30 C =
Câu 16. Tam giác ABC có 60,45BC và 5 AB . Tính độ dài cạnh AC .
A. 56 2 AC B. 53. AC C. 56 3 AC D. 56 4 AC
Câu 17. Một tam giác có ba cạnh là 52, 56, 60. Bán kính đường tròn ngoại tiếp tam giác đó là
A. 65 4 B. 40 C. 32,5 D.65,8
Câu 18. Cho tam giác ABC có 12 AB = , 13 AC = , 5 BC = . Diện tích S của tam giác ABC là:
A. 30 S = . B. 40 = S . C. 50 = S . D. 60 = S .
Câu 19. Cho tam giác ABC , có thể xác định được bao nhiêu véc tơ khác véc tơ không có điểm đầu và điểm cuối là các đỉnh của tam giác đã cho?
A. 4. B. 5 C. 7. D. 6.
Câu 20. Tổng MNPQRNNPQR ++++ bằng vectơ nào sau đây?
A. .MR B. .MN C. .PR D. .MP
Câu 21. Cho hình vuông ABCD cạnh bằng a . Tính độ dài véc tơ BABC + . A. 3 a . B. 2 a . C. a . D. 2a .
Câu 22. Cho hình bình hành ABCD tâm O . Khẳng định nào sau đây sai? A. 0 AOBOCODO+++= . B. AODAOB += . C. OABOAB −= . D. ABDC = .
Câu 23. Cho tam giác ABC đều có cạnh là 6. Tính ABAC + . A. 62 . B. 18. C. 12. D. 63 .
Câu 24. Cho đoạn thẳng AB và M là một điểm trên đoạn AB sao cho 1 5 MAAB = . Trong các khẳng định
DẠYKÈMQUYNHƠN
OFFICIAL
sau, khẳng định nào sai ? A. 1 5 AMAB = B. 1 4 MAMB =− C. 4 MBMA =− D. 4 5 MBAB =− Câu 25. Cho hình bình hành ABCD, điểm M thõa mãn 4AMABADAC =++ . Khi đó điểm M là: A. Trung điểm của AC B. Điểm C C. Trung điểm của AB D. Trung điểm của AD Câu 26. Cho hai vectơ (4;3)=−− u và (1;7)=−− v . Góc giữa hai vectơ u và v là: A. 90 . B. 60 . C. 45 D. 30
Câu 27. Trong hệ trục tọa độ Oxy , cho hai điểm ( ) ( )2;1,4;3AB . Tọa độ của véctơ AB bằng A. ( )8;3 AB =− B. ( )2;4 AB =−− C. ( )2;4 AB = D. ( )6;2 AB =
Câu 28. Cho hai vectơ a và b khác 0 . Xác định góc giữa hai vectơ a và b khi abab =− A. o180 = . B. o0 = . C. o90 = . D. o45 = .
Câu 29. Cho 2 vectơ a và b có 4 a = , 5 b = và ( ) o,120ab = .Tính ab + A. 21. B. 61 . C. 21. D. 61.
Câu 30. Cho tam giác ABC vuông tại A có o ˆ 60 B = , ABa = . Tính . ACCB A. 2 3a . B. 2 3a . C. 3a . D. 0 .
Câu 31. Cho giá trị gần đúng của 8 17 là 0,47. Sai số tuyệt đối của số 0,47 là: A. 0,001. B. 0,002. C. 0,003. D. 0,004.
Câu 32. Cho giá trị gần đúng của 3 7 là 0,429. Sai số tuyệt đối của số 0,429 là:
A. 0,0001. B. 0,0002. C. 0,0004. D. 0,0005.
OFFICIAL
Câu 33. Kết quả điểm kiểm tra 45 phút môn Hóa Học của 100 em học sinh được trình bày ở bảng sau: Điểm 3 4 5 6 7 8 9 10 Cộng Tần số 3 5 14 14 30 22 7 5 100 Số trung bình cộng của bảng phân bố tần số nói trên là
A. 6,82 . B. 4. C. 6,5. D. 7,22 .
Câu 34. Điều tra tiền lương một tháng của 100 người lao động trên địa bàn một xã ta có bảng phân bố tần số sau: Tiền lương (VND) 5.000.000 6.000.000 7.000.000 8.000.000 9.000.000 9.500.000 Tần số 26 34 20 10 5 5
Tìm mốt của bảng phân bố tần số trên.
A.5.000.000. B. 6.000.000. C.7.500.000. D.9.500.000.
Câu 35. Tìm phát biểu đúng về phương sai của một mẫu số liệu.
A. Phương sai được sử dụng làm đại diện cho các số liệu của mẫu
B. Phương sai được sử dụng để đánh giá mức độ phân tán của các số liệu thống kê (so với số trung bình).
C. Phương sai được tính bằng tổng số phần tử của một mẫu số liệu.
D. Phương sai là số liệu xuất hiện nhiều nhất (số liệu có tần số lớn nhất) trong bảng các số liệu thống kê
1 ha đậu xanh thì cần 30 ngày công và thu được 50 triệu đồng. Bác Năm cần trồng bao nhiêu hecta cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng không quá 180 ngày công cho việc trồng ngô và đậu xanh.
Câu 3. Gia đình bạn An sở hữu một mảnh đất hình tam giác. Chiều dài của hàng rào MN là 150m , chiều dài của hàng rào MP là 230m . Góc giữa hai hàng rào MN và MP là 110 (Hình 21) .
DẠYKÈMQUYNHƠN
2. Tự luận Câu 1. Cho hai tập họp (3;5],[;) =−=+ABa . Tìm a để a) [2;5]=−AB b) AB có đúng một phần tử. Câu 2. Bác Năm dự định trồng ngô và đậu xanh trên một mảnh đất có diện tích 8 ha. Nếu trồng 1 ha ngô thì cần 20 ngày công và thu được 40 triệu đồng. Nếu trồng
a) Diện tích mảnh đất mà gia đình bạn An sở hữu là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)? b) Chiều dài hàng rào NP là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Câu 4. Cho tam giác ABC. Gọi A’, B’, C’ là các điểm xác định bởi 2011'2012'0 ABAC+= , 2011'2012'0 BCBA+= ; 2011'2012'0 CACB+= . Chứng minh hai tam giác ABC và A’B’C’ có cùng trọng tâm.
1. Trắc nghiệm
Câu 1. Mệnh đề nào sau đây là mệnh đề tương đương?
A. 10 chia hết cho 5 là điều kiện cần để 10 chia hết cho 2.
B. Hình vuông là hình chữ nhật.
C. Hình thang nội tiếp đường tròn khi và chỉ khi nó là hình thang cân.
D. Nếu 63 chia hết cho 7 thì hình thoi có hai đường chéo vuông góc nhau.
Câu 2. Mệnh đề: " 2 ,33xx " khẳng định là

A. Bình phương của mỗi số thực lớn hơn 33.
B. Có ít nhất một số thực mà bình phương của nó lớn hơn 33.
Chỉ
DẠYKÈMQUYNHƠN
OFFICIAL
Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM 1C 2B 3B 4D 5A 6D 7D 8A 9D 10C 11D 12B 13A 14A 15C 16A 17C 18A 19D 20A 21B 22C 23D 24D 25A 26C 27C 28A 29A 30B 31A 32D 33A 34B 35B
số
D. Nếu x là số thực thì 2 33 x Câu 3. Cho A là tập hợp các số tự nhiên chẵn không lớn hơn 12,{6} Bnn= , {412}Cnn= . Mệnh đề nào sau đây là đúng? A. () ABCB = B. () ABCA = C. () ABCC = . D. ()ABC= . Câu 4. Cho tập hợp (3;]Am =− và {3}Bxx= . Giá trị nguyên dương của m để tập hợp (\) AB có đúng 10 phần tử là A. 10. B. 11. C. 12. D. 13. Lời giải Ta có [3;3] B =− . Theo giả thiết thì \ AB nên 3 m và \(3;] ABm = . Như vậy, để tập hợp (\) AB có 10 phần tử thì (\){4;5;;13} AB = do đó 13 m =
C.
có một
thực có bình phương lớn hơn 33.
5. Cho (;2)[6;) CA =−+ và [5;9) CB = . Tập hợp XAB = là



A. [2;5). B. (2;5). C. [2;5] D. [6;9) Lời giải [2;6),(;5)[9;)AB==−+ . Suy ra [2;5) XAB== Câu 6. Cặp số nào sau đây là nghiệm của bất phương trình 55−+ xy ? A. (1;9) . B. (2;1). C. (2;2) D. (0;5) Câu 7. Miền nghiệm của bất phương trình 2 −+ xy được xác định bởi miền

DẠYKÈMQUYNHƠN OFFICIAL
Câu
nào (nửa mặt phẳng không bị gạch và không kể d) sau đây? A. B. C. D. Câu 8. Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình 0 33 5? xy xy xy − −− + A. (3;2)A B. (6;3)B . C. (6;4)C . D. (5;4)D Câu 9. Cho điểm (3;3)A và điểm M thuộc miền nghiệm của hệ bất phương trình 20 20 20 20 xy xy xy xy +− ++ −++ −+ Độ dài AM lớn nhất là A. 22 B. 52 C. 10
Lời giải Miền nghiệm của hệ bất phương trình là miền không bị gạch trong hình bên. Suy ra độ dài AM lớn nhất khi và chỉ khi M trùng với đỉnh nào đó của đa giác nghiệm.
OFFICIAL
Câu 10. Một cửa hàng bán hai loại mặt hàng A và B . Biết rằng cứ bán một mặt hàng loại A cửa hàng lãi 5 nghìn đồng, bán một mặt hàng loại B cửa hàng lãi 7 nghìn đồng. Gọi , xy lần lượt là số mặt hàng loại A và mặt hàng loại B mà cửa hàng đó bán ra trong một tháng. Cặp số (;) xy nào sau đây biểu thị số mặt hàng bán ra mỗi loại của cửa hàng trong một tháng mà tổng số tiền lãi không ít hơn 30 triệu đồng? A. (1000;2000). B. (3000;1000) C. (2000;3000) D. (3000;2000). Câu 11. Cho góc

DẠYKÈMQUYNHƠN
D. 34 .
0180 và cot2 =− . Giá trị của sin là: A. 1 2 B. 1 5 C. 5 5 D. 5 5 . Lời giải Ta có: 22 22 222 coscos1sin1 cotcot1cot sinsinsinsin ===+= . Do đó 2 22 111 sin 1cot1(2)5 === ++− . Vì 0180 nên 5 sin 5 = . Chọn D Câu 12. Giá trị biểu thức tan1tan2.tan89 = T bằng: A. 0. B. 1. C. 1 D. 2. Lời giải Ta có: ( )( ) ( ) tan1tan89tan2tan88tan44tan46tan45 = T ( )( ) ( ) tan1cot1tan2cot2tan44cot44tan45 = 1.1.111.== Chọn B Câu 13. Cho 1 sin 4 = , với 090 . Giá trị cos bằng A. 15 4 B. 15 4 C. 15 16 D. 15 16 Lời giải
thoả mãn
Câu 14. Cho tam giác ABC có 4cm = AB ; 12cm= AC và góc 120 BAC = . Tính diện tích tam giác ABC . A. 123 ( 2 cm ). B. 243( 2 cm ). C. 12( 2 cm ). D. 24( 2 cm ). Lời giải
A
DẠYKÈMQUYNHƠN OFFICIAL
Chọn A Ta có 2 22 115 cos1sin1 416 =−=−= 15 cos 4 = (do 090 ). Vậy 15 cos 4 = .
16. Tam giác ABC có 60,45BC và 5 AB . Tính độ dài cạnh AC . A. 56 2 AC B. 53. AC C. 56 . 3 AC D. 56 4 AC Lời giải Chọn A Theo định lí sin ta có: 0 0 556 sinsin2 sin45 sin60 ABACAC AC CB . Câu 17. Một tam giác có ba cạnh là 52, 56, 60. Bán kính đường tròn ngoại tiếp tam giác đó là A. 65 4 B. 40 C. 32,5 D.65,8 Lời giải Chọn C Ta có: 525660 84 2 p ++ == Áp dụng hệ thức Hê rông ta có: ( )
S =−−−=
52.56.60
444.1344 abcabc SR RS ==== Câu
Cho tam giác ABC có 12 AB = , 13 AC =
=
Diện
S =
giải Chọn A Ta có: 222 BABCAC += nên tam giác ABC vuông tại B. Diện tích tam giác là: 1 .30 2 SBABC== . Câu 19. Cho tam giác ABC , có thể xác định được bao nhiêu véc tơ khác véc tơ không có điểm đầu và điểm cuối là các đỉnh của tam giác đã cho? A. 4. B. 5 C. 7. D. 6.
Chọn
Diện tích tam giác ABC là 1 ..sin 2 SABACBAC = 1 .4.12.sin120 2 = 123 = ( 2 cm ) Câu 15. Cho tam giác ABC thỏa mãn 222 2.0BCACABBCAC +−−= . Khi đó, góc C có số đo là A. 150 C = . B. 60 C = . C. 45 C = . D. 30 C = . Lời giải Chọn C Theo đề ra ta có: 222 2.0BCACABBCAC +−−= 222 2. BCACABBCAC+−= 222 2 . BCACAB BCAC +− = 2cos20 C −= 2 cos 2 C = 45 C = Câu
( ) ( ) 84.8452.8456.84601344
Mặt khác
32,5
18.
, 5 BC
.
tích S của tam giác ABC là: A. 30
B. 40 = S C. 50 = S D. 60 = S Lời
Lời giải
Các véc tơ khác véc tơ không có điểm đầu và điểm cuối là các đỉnh của tam giác đã cho gồm ,,,,,. ABBAACCABCCB Vậy có 6 véc tơ.
Câu 20. Tổng MNPQRNNPQR ++++ bằng vectơ nào sau đây?
A. .MR B. .MN C. .PR D. .MP Lời giải Chọn A
Ta có MNPQRNNPQRMNNPPQQRRNMN ++++=++++= .
OFFICIAL
Câu 21. Cho hình vuông ABCD cạnh bằng a . Tính độ dài véc tơ BABC + A. 3 a B. 2 a C. a D. 2a Lời giải Chọn B 2 BABCBDa +== .
Câu 22. Cho hình bình hành ABCD tâm O . Khẳng định nào sau đây sai?
A. 0 AOBOCODO+++= . B. AODAOB += . C. OABOAB −= . D. ABDC = . Lời giải Chọn C
C
O
D A B
Ta có: 0 AOBOCODOAOCOBODO +++=+++= . Suy ra A đúng.
Ta có: AODAOCCBOB +=+= . Suy ra B đúng. Ta có: OABOOAOBAB −=+ . Suy ra C sai.
Ta có: ABDC = đúng.
Câu 23. Cho tam giác ABC đều có cạnh là 6. Tính ABAC +
A. 62 B. 18 C. 12 D. 63 Lời giải Chọn D
DẠYKÈMQUYNHƠN
24. Cho đoạn thẳng AB và M là một điểm trên đoạn AB sao cho 1 5 MAAB = . Trong các khẳng định sau, khẳng định nào sai ? A. 1 5 AMAB = B. 1 4 MAMB =− C. 4 MBMA =− D. 4 5 MBAB =− Lời giải Chọn D Ta thấy MB và AB cùng hướng nên 4 5 MBAB =− là sai. Câu 25. Cho hình bình hành ABCD, điểm M thõa mãn 4AMABADAC =++ . Khi đó điểm M là: A. Trung điểm của AC B. Điểm C C. Trung điểm của AB D. Trung điểm của AD Lời giải Chọn A

Theo quy tắc hình bình hành, ta có: Câu 26. Cho hai vectơ (4;3)=−− u và (1;7)=−− v . Góc giữa hai vectơ u và v là: A.


DẠYKÈMQUYNHƠN OFFICIAL Gọi I là trung điểm của BC. Vì tam giác ABC đều có cạnh là 6,
ta có
⊥ . Xét tam giác AIB vuông tại I , có 222222226327 ABAIIBAIABIB=+=−=−= . Suy
2733 AI == Mặt khác
+=+====
nên
AIBC
ra
ta có: 222263ABACAIABACAIAIAI
Câu
90 B. 60 C. 45 D. 30 . Lời giải Chọn C Câu 27. Trong hệ trục tọa độ Oxy , cho hai điểm ( ) ( )2;1,4;3AB . Tọa độ của véctơ AB bằng A. ( )8;3 AB =− . B. ( )2;4 AB =−− . C. ( )2;4 AB = . D. ( )6;2 AB = . Lời giải Chọn C ( ) ( ) ;2;4.BABA ABxxyyAB =−−=
DẠYKÈMQUYNHƠN OFFICIAL
Câu 28. Cho hai vectơ a và b khác 0 . Xác định góc giữa hai vectơ a và b khi ...abab =− A. o180 = . B. o0 = . C. o90 = . D. o45 = . Lời giải
8 0,470,474,4710,001 17 =−−= .
trị gần đúng
3 7
D. Ta có 3 0,428571... 7 = nên sai số tuyệt đối của
là 3 0,4290,4294,42850,0005 7 =−−= . Câu 33. Kết quả điểm kiểm tra 45 phút môn Hóa Học của 100 em học sinh được trình bày ở bảng sau: Điểm 3 4 5 6 7 8 9 10 Cộng Tần số 3 5 14 14 30 22 7 5 100 Số trung bình cộng của bảng phân bố tần số nói trên là A. 6,82 . B. 4. C. 6,5. D. 7,22 . Lời giải Số trung bình cộng của bảng phân bố tần số nói trên là
Chọn A Ta có ( ) ...cos, ababab = Mà theo giả thiết .. abab =− , suy ra ( ) ( ) 0cos,1,180 abab=−⎯⎯→= Câu 29. Cho 2 vectơ a và b có 4 a = , 5 b = và ( ) o,120ab = .Tính ab + A. 21. B. 61. C. 21. D. 61. Lời giải Chọn A Ta có ( ) ( ) 2 22 22 2.2cos,21+=+=++=++= ababababababab Câu 30. Cho tam giác ABC vuông tại A có o ˆ 60 B = , ABa = . Tính ACCB A. 2 3a . B. 2 3a . C. 3a . D. 0 . Lời giải Chọn B Ta có o2 3 ...cos1503.2.3 2 ==−=−
ACCBACBCaaa . Câu 31. Cho giá trị gần đúng của 8 17 là 0,47. Sai số tuyệt đối của số 0,47 là: A. 0,001. B. 0,002. C. 0,003. D. 0,004. Lời giải Chọn#A. Ta có 8 0,470588235294... 17 = nên sai số tuyệt đối của 0,47 là
Câu 32. Cho giá
của
là 0,429. Sai số tuyệt đối của số 0,429 là: A. 0,0001. B. 0,0002. C. 0,0004. D. 0,0005. Lời giải Chọn
0,429
100
Câu 34. Điều tra tiền lương một tháng của 100 người lao động trên địa bàn một xã ta có bảng phân bố tần số sau:
Tiền lương (VND) 5.000.000 6.000.000 7.000.000 8.000.000 9.000.000 9.500.000 Tần số 26 34 20 10 5 5
Tìm mốt của bảng phân bố tần số trên.
A.5.000.000 B. 6.000.000 C.7.500.000 D.9.500.000
Lời giải
Ta có giá trị 6.000.000 có tần số lớn nhất nên là mốt của bảng phân bố tần số trên.
Câu 35. Tìm phát biểu đúng về phương sai của một mẫu số liệu.
A. Phương sai được sử dụng làm đại diện cho các số liệu của mẫu
B. Phương sai được sử dụng để đánh giá mức độ phân tán của các số liệu thống kê (so với số trung bình).
C. Phương sai được tính bằng tổng số phần tử của một mẫu số liệu.
D. Phương sai là số liệu xuất hiện nhiều nhất (số liệu có tần số lớn nhất) trong bảng các số liệu thống kê.
Lời giải Ý nghĩa của phương sai: Phương sai được sử dụng để đánh giá mức độ phân tán của các số liệu thống kê (so với số trung bình). (SGK)
2. Tự luận
Câu 1. Cho hai tập họp (3;5],[;) =−=+ABa . Tìm a để
a) [2;5]=−AB b) AB có đúng một phần tử. Lời giải a) Để [2;5]=−AB khi và chỉ khi 3 2 2 − =− =− a a a .
Vậy 2=− a là giá trị cần tìm. b) Để AB có đúng một phần tử khi và chỉ khi 5 = a . Khi đó {5} =AB . Vậy 5 = a là giá trị cần tìm. Câu 2. Bác Năm dự định trồng ngô và đậu xanh trên một mảnh đất có diện tích 8 ha. Nếu trồng 1 ha ngô thì cần 20 ngày công và thu được 40 triệu đồng. Nếu trồng 1 ha đậu xanh thì cần 30 ngày công và thu được 50 triệu đồng. Bác Năm cần trồng bao nhiêu hecta cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng không quá 180 ngày công cho việc trồng ngô và đậu xanh. Lời giải Gọi x là số hecta đất trồng ngô và y là số hecta đất trồng đậu xanh. Ta có các điều kiện
DẠYKÈMQUYNHƠN
OFFICIAL 3.34.55.146.147.308.229.710.5 6,82
x +++++++ == .
ràng buộc đối với , xy như sau: Hiển nhiên 0,0xy . Diện tích canh tác không vượt quá 8 ha nên 8 xy+ . Số ngày công sử dụng không vượt quá 180 nên
Từ đó, ta có hệ bất
8
0 0 xy xy x y + +
2030180 xy+
phương trình mô tả các điều kiện ràng buộc:
2030180
Biểu diễn miền nghiệm của hệ bất phương trình này trên hệ trục toạ độ Oxy , ta được miền tứ giác OABC (Hình).
Toạ độ các đỉnh của tứ giác đó là: (0;0);(0;6)OA ; (6;2);(8;0)BC .


Gọi F là số tiền (đơn vị: triệu đồng) bác Năm thu được, ta có: 4050 Fxy =+ .
Ta phải tìm , xy thoả mãn hệ bất phương trình sao cho F đạt giá trị lớn nhất, nghĩa là tìm giá trị lớn nhất của biểu thức 4050 Fxy =+ trên miền tứ giác OABC.
Tính các giá trị của biểu thức F tại các đỉnh của đa giác, ta có:
Tại (0;0):40.050.00OF =+= ;
Tại (0;6):40.050.6300AF =+=
Tại (6;2):40.650.2340BF =+= ;
Tại (8;0):40.850.0320CF =+= .
OFFICIAL
F đạt giá trị lớn nhất bằng 340 tại (6;2)B Vậy để thu được nhiều tiền nhất, bác Năm cần trồng 6 ha ngô và 2 ha đậu xanh. Câu 3. Gia đình bạn An sở hữu một mảnh đất hình tam giác. Chiều dài của hàng rào MN là 150m , chiều dài của hàng rào MP là 230m . Góc giữa hai hàng rào MN và MP là 110 (Hình 21)
a) Diện tích mảnh đất mà gia đình bạn An sở hữu là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)? b) Chiều dài hàng rào NP là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
DẠYKÈMQUYNHƠN
2 11 sin150230sin11016209,7 22 == SMNMPMm b) Áp dụng định lí côsin ta có: =+−=+− 222222cos1502302150230cos110 98999,39. NPMNMPMNMPM Suy ra 98999,39314,6( ) NPm Vậy chiều dài hàng rào NP là khoảng 314,6m . Câu 4. Cho tam giác ABC. Gọi A’, B’, C’ là các điểm xác định bởi 2011'2012'0 ABAC+= , 2011'2012'0 BCBA+= ; 2011'2012'0 CACB+= . Chứng minh hai tam giác ABC và A’B’C’ có cùng trọng tâm. Lời giải. Gọi G là trọng tâm tam giác ABC 0 GAGBGC ++= Ta có ( ) ( ) 2011'2012'02011'2012'0 ABACAAABAAAC +=+++= 4023'201120120 AAABAC ++= Tương tự ta có 4023'201120120 BBBCBA ++=
Lời giải a) Diện tích mảnh đất của gia đình bạn An (tam giác MNP ) là: ( )
Suy ra ''''''0GAGBGCGAGBGCGAGBGC ++=++++= Do đó G là trọng tâm của tam giác A’B’C’
OFFICIAL
CCCACB ++=
DẠYKÈMQUYNHƠN
4023'201120120
Cộng về với vế lại ta được ( ) 4023'''0'''0 AABBCCBAACCBAABBCC +++++=++=
1. Trắc nghiệm
Câu 1. Mệnh đề: " 2 ,21 n n + là số nguyên tố" khẳng định là
A. Tồn tại số tự nhiên n để 2 21 n + là số nguyên tố.
B. Tồn tại duy nhất số tự nhiên n để 2 21 n + là số nguyên tố.
C. Với mọi số tự nhiên n thì 2 21 n + là hợp số.
D. Với mọi số tự nhiên n thì 2 21 n + là số nguyên tố.
Câu 2. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
a) Nếu tam giác có hai trung tuyến bằng nhau thì tam giác đó là tam giác cân.
b) Tam giác ABC vuông tại C nếu và chỉ nếu 222 ABCACB =+ .
c) 2 ,210xxx −+ d) 22 ,(1)nnn ++ là số chẵn. A. 1. B. 2. C. 3. D. 4.
Câu 3. Cho ,, ABC là ba tập hợp bất kì khác rỗng, được biểu diễn bằng biểu đồ Ven như hình bên. Phần gạch sọc trong hình biểu diễn tập hợp nào sau đây?
A. ()\ABC B. ()ABC . C. ABC . D. ()\BCA .


Câu 4. Số các số nguyên dương lẻ nhỏ hơn 1000 và chia hết cho 3 là
A. 166. B. 167. C. 333. D. 499.
Câu 5. Hình nào sau đây là biểu diễn theo biểu đồ Ven của tập hợp B là con của tập hợp A ? A. B. C. D.
Câu 6. Cặp số nào sau đây không là nghiệm của bất phương trình 42 +xy ?
A. (1;0) B. (1;2)



DẠYKÈMQUYNHƠN
ĐỀ SỐ 9
OFFICIAL
A chỉ có một máy cán thép có thể sản xuất hai sản phẩm là thép tấm và thép cuộn (máy không thể sản xuất hai loại thép cùng lúc và có thể làm việc 40 giờ một tuần). Công suất sản xuất thép tấm là 250 tấn/giờ, công suất sản xuất thép cuộn là 150 tấn/giờ. Mỗi tấn thép tấm có giá 250 USD, mỗi tấn thép cuộn có giá 300 USD. Biết rằng mỗi tuần thị trường chỉ tiêu thụ tối đa 5000 tấn thép tấm và 3500 tấn thép cuộn. Hỏi cần sản xuất bao nhiêu tấn thép mỗi loại trong một tuần để lợi nhuận thu được là cao nhất?
A. 5000 tấn thép tấm và 3500 tấn thép cuộn. B. 4166,66 tấn thép tấm và 3500 tấn thép cuộn.








DẠYKÈMQUYNHƠN OFFICIAL C.
.
Câu
0 0 1 x y xy − được
Câu
1 0 2 26 x y y xy + là A. 1. B. 3. C. 4. D. 9.
(5;2) D. (1;0)
Câu 7. Miền nghiệm của bất phương trình 3 −+yx được xác định bởi miền nào (nửa mặt phẳng không bị gạch và kể cả d ) sau đây? A. C. B. D.
8. Miền nghiệm của hệ bất phương trình:
xác định bởi miền đa giác nào sau đây? A. B. C. D.
9. Diện tích miền nghiệm () H của hệ bất phương trình
Câu 10. Nhà máy
C. 5000 tấn thép tấm và 0 tấn thép cuộn. D. 5000 tấn thép tấm và 3000 tấn thép cuộn.
Câu 11. Cho góc thoả mãn 0180 và tan2 =− . Giá trị của cos là:
A. 3 3 . B. 2 2 . C. 3 3 D. 1 3 Câu 12. Biết 2 sin 5 = ,(90180) oo . Hỏi giá trị của tan bằng bao nhiêu?
A. 21 2 B. 221 21 C. 221 21 D. 21 2
Câu 13. Với 0180 giá trị lượng giác nào dưới đây luôn không âm?
A. sin B. tan C. cos D. cot
Câu 14. Trong tam giác ABCvới ,, ABcBCaCAb === . Tìm mệnh đề đúng.
A. 222 2cos. abcbcA =++ B. 222 2cos. abcbcA =+− C. 222 cos. abcbcA =+− D. 222 2sin. abcbcA =+−
Câu 15. Tam giác ABC có ,, ABcBCaCAb === và có diện tích là S . Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn góc C . Khi đó diện tích tam giác mới tạo nên bằng. A. 3S B. 4S C. 2S D. 6S
Câu 16. Cho tam giác ABC có 5,4ABAC== , trung tuyến 33 BM = . Tính diện tích tam giác ABC A. 36 B. 46 C. 213 D. 2433
Câu 17. Cho tam giác ABC với BCa = , ACb = , ABc = . Diện tích của ABC là A. 1 sin 2 ABC SacC
DẠYKÈMQUYNHƠN OFFICIAL
là A. 3 2 a R = B. 2 a R = C. 3 3 a R = D. = Ra Câu 19. Cho hai véctơ a và b là các véctơ khác 0 . Biết véctơ a là véctơ đối của véctơ b . Khẳng định nào sau đây sai? A. Hai véctơ a , b cùng phương B. Hai véctơ a , b cùng độ dài C. Hai véctơ a , b chung điểm đầu D. Hai véctơ a , b ngược hướng Câu 20. Cho tam giác ABC xác định vị trí điểm D sao cho ADACAB =− A. D là đỉnh thứ tư của hình bình hành ADBC B. D trùng điểm B C. D trùng điểm C D. D là đỉnh thứ tư của hình bình hành ABCD
= . B. 1 sin 2 ABC SbcB = . C. 1 sin 2 ABC SacB = . D. 1 sin 2 ABC SbcC = . Câu 18. Cho tam giác ABC với BCa = , 120 BAC = . Bán kính đường tròn ngoại tiếp ABC
Câu 21. Cho 4 điểm phân biệt A , B , C , D . Đẳng thức nào sau đây đúng?
A. ABDADCCB +=+ B. ACBDBCDA +−= C. ACADCBBD −=− .D. ABADCDBC −=+ .

Câu 22. Cho tam giác ABC có I là trung điểm của cạnh BC và G là trọng tâm. Đẳng thức nào sau đây sai?
A. GAGBGC += B. CBBACA += C. 0 GAGBGC++= D. 0 IBIC+=
OFFICIAL
Câu 23. Trên Hình biểu diên ba lực 1F , 23 , FF cùng tác động vào một vật ở vị trí cân bằng 0. Cho biết cường độ của 12 , FF đều bằng 100N và góc tạo bởi 1F và 2F bằng 120 . Tính cường độ của lực 3F . A. 190 B. 200 C. 100 D. 80
Câu 24. Cho ABC . Đặt , aBCbAC == . Các cặp vectơ nào sau đây cùng phương? A. 2,2abab ++ B. 2,2 abab C. 5,102 abab +−− D. , abab +−
Câu 25. Cho tam giác ABC có điểm O thỏa mãn: 2 OAOBOCOAOB +−=− . Khẳng định nào sau đây là đúng? A. Tam giác ABC đều B. Tam giác ABC cân tại C C. Tam giác ABC vuông tại C D. Tam giác ABC cân tại B
Câu 26. Côsin của góc giữa hai vectơ (1;1) = u và (2;1)=− v là: A. 1 10 B. 10 10 C. 10 10 . D. 3 10 .
Câu 27. Cho tam giác ABC có (2;6),(2;2),(8;0) ABC . Khi đó, tam giác ABC là: A. Tam giác đều. B. Tam giác vuông tại A. C. Tam giác có góc tù tại A D. Tam giác cân tại A.
Câu 28. Cho hai vectơ a và b thỏa mãn 3, a = 2 b = và .3.ab =− Xác định góc giữa hai vectơ a và b A. o30 = . B. o45 = . C. o60 = . D. o120 = . Câu 29. Cho 2 vectơ đơn vị a và b thỏa 2 ab+= . Hãy xác định ( )( ) 3425 abab −+ A. 7 . B. 5. C. 7. D. 5.
DẠYKÈMQUYNHƠN
Câu 30. Cho hình thang vuông ABCDcó đáy lớn 4 ABa = , đáy nhỏ 2 CDa = , đường cao 3 ADa = .Tính DABC
A. 2 9a . B. 2 15a . C. 0. D. 2 9a
Câu 31. Qua điều tra dân số kết quả thu được số đân ở tỉnh B là 2.731.425 người với sai số ước lượng không quá 200 người. Các chữ số không đáng tin ở các hàng là: A. Hàng đơn vị. B. Hàng chục. C. Hàng trăm. D. Cả A, B, C.

Câu 32. Nếu lấy 3,14 làm giá trị gần đúng của thì sai số là:
A. 0,001. B. 0,002. C. 0,003. D. 0,004.
Câu 33. Cho bảng phân bố tần số sau: khối lượng 20 học sinh lớp 10A
Số trung bình cộng x của bảng số liệu đã cho là
OFFICIAL
A. 53 x = B. 52,8 x = C. 52,2 x = D. 52 x =

Câu 34. Kết quả thi môn Toán giữa kì 11 của lớp 3 10A trường THPT Ba Vì được thống kê như sau: Giá trị mốt 0 M của bảng phân bố tần số trên bằng
A.5. B.7. C.8. D.12.
Câu 35. Theo kết quả thống kê điểm thi giữa kỳ 2 môn toán khối 11 của một trường THPT, người ta tính được phương sai của bảng thống kê đó là 2 0,573 x s = . Độ lệch chuẩn của bảng thống kê đó bằng A. 0,812 B. 0,757 C. 0,936 D. 0,657 2.

DẠYKÈMQUYNHƠN
1. Cho hai tập họp [2;1]=+Am và 1 ; 2 =+ B Tìm m để AB chỉ có đúng một 1 phần tử.
2. Một người dùng ba loại nguyên liệu ,, ABC để sản xuất ra hai loại sản phẩm P và Q . Để sản xuất 1 kg mỗi loại sản phẩm P hoặc Q phải dùng một số kilôgam nguyên liệu
Tổng số kilôgam nguyên liệu mỗi loại mà người đó có và số kilôgam từng loại nguyên liệu
thiết để sản xuất ra 1kg sản phẩm mỗi loại
Tự luận Câu
Câu
khác nhau.
cần
được cho trong bảng sau:
Biết 1kg sản phẩm P có lợi nhuận 3 triệu đồng và 1 kg sản phẩm Q có lợi nhuận 5 triệu đồng. Hãy lập phương án sản xuất hai loại sản phẩm trên sao cho có lãi cao nhất.
Câu 3. Hai người A và B cùng quan sát một con tàu đang neo đậu ngoài khơi tại vị trí C . Người A đứng trên bờ biển, người B đứng trên một hòn đảo cách bờ một khoảng 100= ABm. Hai người tiến hành đo đạc và thu được kết quả: 54,74 ==CABCBA (Hình 22). Hỏi con tàu cách hòn đảo bao xa (làm tròn kết quả đến hàng phần mười theo đơn vị mét)?
OFFICIAL
Câu 4. Hai tam giác ABC và A’B’C’ lần lượt có trọng tâm là G, G’. Chứng minh rằng '''3' AABBCCGG ++= . Từ đó suy ra “ Điều kiện cần và đủ để hai tam giác ABC và A’B’C’ có cùng trọng tâm là '''0AABBCC++= Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM 1D 2C 3B 4B 5B 6B 7B 8D 9B 10D 11C 12C 13A 14B 15D 16B


1. Trắc nghiệm
Câu 1. Mệnh đề: " 2 ,21 n n + là số nguyên tố" khẳng định là
A. Tồn tại số tự nhiên n để 2 21 n + là số nguyên tố.
B. Tồn tại duy nhất số tự nhiên n để 2 21 n + là số nguyên tố.
C. Với mọi số tự nhiên n thì 2 21 n + là hợp số. D. Với mọi số tự nhiên n thì 2 21 n + là số nguyên tố. Câu 2. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau? a) Nếu tam giác có hai trung tuyến
DẠYKÈMQUYNHƠN
17C 18C 19C 20D 21A 22A 23C 24C 25C 26C 27B 28D 29C 30A 31D 32A 33C 34C 35B
b) Tam giác ABC vuông tại C
222 ABCACB =+ . c) 2 ,210xxx −+ d) 22 ,(1)nnn ++ là số chẵn. A. 1. B. 2. C. 3. D. 4. Câu 3. Cho ,, ABC là ba tập hợp bất kì khác rỗng, được biểu diễn bằng biểu đồ Ven
Phần gạch sọc trong hình biểu diễn tập
A. ()\ABC B. ()ABC C. ABC . D. ()\BCA .
bằng nhau thì tam giác đó là tam giác cân.
nếu và chỉ nếu
như hình bên.
hợp nào sau đây?
Câu 4. Số các số nguyên dương lẻ nhỏ hơn 1000 và chia hết cho 3 là
A. 166. B. 167. C. 333. D. 499.







Lời giải
Gọi A là tập các số nguyên dương chia hết cho 3 và nhỏ hơn 1000.
Gọi B là tập số nguyên dương chẵn chia hết cho 3 nhỏ hơn 1000, tức B là tập các số nguyên dương chia hết cho 6 và nhỏ hơn 1000.
Gọi C là tập số nguyên dương lẻ chia hết cho 3 nhỏ hơn 1000. Như vậy ABC = và BC= , suy ra ()()() nAnBnC =+ Do đó ()()()333166167 nCnAnB=−=−= .
Câu 5. Hình nào sau đây là biểu diễn theo biểu đồ Ven của tập hợp B là con của tập hợp A ?
A. B. C. D.
OFFICIAL
Câu 6. Cặp số nào sau đây không là nghiệm của bất phương trình 42 +xy ? A. (1;0). B. (1;2) . C. (5;2) D. (1;0)

Câu 7. Miền nghiệm của bất phương trình 3 −+yx được xác định bởi miền nào (nửa mặt phẳng không bị gạch và kể cả d ) sau đây?
A. C. B. D.
x y xy
Câu 8. Miền nghiệm của hệ bất phương trình: 0 0 1
−
được xác định bởi miền đa giác nào sau đây?
DẠYKÈMQUYNHƠN
() H là hình thang
nữa ABCD là hình thang vuông tại A và D . Suy ra diện tích hình () H là (12)23() 2 dvdt


10. Nhà máy A chỉ có một máy cán thép có thể sản xuất hai sản phẩm là thép tấm và thép cuộn (máy không thể sản xuất hai loại thép cùng lúc và có thể làm việc 40 giờ một tuần). Công suất sản xuất thép tấm là 250 tấn/giờ, công suất sản xuất thép cuộn là 150 tấn/giờ. Mỗi tấn thép tấm có giá 250 USD, mỗi tấn thép cuộn có giá 300 USD. Biết rằng mỗi tuần thị trường chỉ tiêu thụ tối đa 5000 tấn thép tấm và 3500 tấn thép cuộn. Hỏi cần sản xuất bao nhiêu tấn thép mỗi loại trong một tuần để lợi nhuận thu được là cao nhất?
A. 5000 tấn thép tấm và 3500 tấn thép cuộn.
B. 4166,66 tấn thép tấm và 3500 tấn thép cuộn.
C. 5000 tấn thép tấm và 0 tấn thép cuộn.
D. 5000 tấn thép tấm và 3000 tấn thép cuộn. Lời giải
Gọi , xy là số tấn thép cuộn và thép tấm nhà máy đó sản suất trong một tuần. Số giờ máy sử dụng để sản xuất trong tuần là 250150 xy + (giờ).


Số tiền thu được là (;)250300 Fxyxy =+ với , xy thoả mãn hệ bất phương trình

DẠYKÈMQUYNHƠN OFFICIAL
1
+ là
Lời
A. B. C. D. Câu 9. Diện tích miền nghiệm () H của hệ bất phương trình
0 2 26 x y y xy
A. 1. B. 3. C. 4. D. 9.
giải Miền
ABCD với (1;0),(3;0),(2;2),(1;2) ABCD Hơn
+ = Câu
DẠYKÈMQUYNHƠN OFFICIAL 40 250150 5000;3500. xy xy + Thử các phương án vào ta có phương án D thoả mãn yêu cầu. Câu 11. Cho góc thoả mãn 0180 và tan2 =− . Giá trị của cos là: A. 3 3 . B. 2 2 . C. 3 3 D. 1 3 Lời giải Ta có: 22 22 222 sinsin1cos1 tantan1tan coscoscoscos ===+= . Do đó 2 2 2 111 cos 1tan3 1(2) === + +− . Vì 0180 mà tan0 và sin0 nên cos0 suy ra 3 cos 3 =− Chọn C Câu 12. Biết 2 sin 5 = ,(90180) oo . Hỏi giá trị của tan bằng bao nhiêu? A. 21 2 B. 221 21 C. 221 21 D. 21 2 Lời giải Chọn C Ta có: 2 222 21 cos sincos1cos125 521 cos 5 = +==− =− Theo đề bài: 21 90180cos 5 oo =− Vậy 2 sin221 5 tan cos21 21 5 ===− Câu 13. Với 0180 giá trị lượng giác nào dưới đây luôn không âm? A. sin. B. tan. C. cos. D. cot. Lời giải Chọn A Nhìn vào bảng xét dấu của các giá trị lượng giác của một góc bất kỳ ta thấy sin luôn không âm. Câu 14. Trong tam giác ABCvới ,, ABcBCaCAb === . Tìm mệnh đề đúng A. 222 2cos. abcbcA =++ B. 222 2cos. abcbcA =+− C. 222 cos. abcbcA =+− D. 222 2sin. abcbcA =+−
Lời giải
Chọn B
Câu 15. Tam giác ABC có ,, ABcBCaCAb === và có diện tích là S . Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn góc C . Khi đó diện tích tam giác mới tạo nên bằng. A. 3S B. 4S C. 2S D. 6S Lời giải
Chọn D
Diện tích tam giác ABC là: 1 ...sin 2 = SBCCAC
Diện tích tam giác mới bằng: 11 .2.3.sin6...sin6. 22 BCCACBCCACS ==
Câu 16.
DẠYKÈMQUYNHƠN
OFFICIAL
5,4
== ,
n 33 BM = .
Ta
( ) ( )2 2 222 22 222 24334 4 57 422 BABCAC BMAC BMBCBA + +− + ==−=−= .
chu vi của tam giác ABC , ta có: 547 8 22 ABACBC p ++++ === . Áp dụng công thức Heron cho tam giác ABC ta có: ( )( )( ) ( )( )( ) 885848746 ABC SppABpACpBC =−−−=−−−= Câu 17. Cho tam giác ABC với BCa = , ACb = , ABc = . Diện tích của ABC là A. 1 sin 2 ABC SacC = . B. 1 sin 2 ABC SbcB = . C. 1 sin 2 ABC SacB = D. 1 sin 2 ABC SbcC = Lời giải Chọn C Ta có: 1 sin 2 ABC SacB = Câu 18. Cho tam giác ABC với BCa = , 120 BAC = . Bán kính đường tròn ngoại tiếp ABC là A. 3 2 a R = . B. 2 a R = . C. 3 3 a R = . D. = Ra . Lời giải Chọn C Theo định lý trong tam giác ta có 13 2. 2sin1203 sin === BCaa RR BAC . Câu 19. Cho hai véctơ a và b là các véctơ khác 0 . Biết véctơ a là véctơ đối của véctơ b . Khẳng định nào sau đây sai? A. Hai véctơ a , b cùng phương. B. Hai véctơ a , b cùng độ dài. C. Hai véctơ a , b chung điểm đầu D. Hai véctơ a , b ngược hướng Lời giải Chọn C sin
Cho tam giác ABC có
ABAC
trung tuyế
Tính diện tích tam giác ABC A. 36 B. 46 C. 213 D. 2433 Lời giải Chọn B
có:
Gọi p là nửa
Ta có hai véctơ đối nhau là hai véctơ ngược hướng và cùng độ dài nên các phương án A, B, D đều đúng
Câu 20. Cho tam giác ABC xác định vị trí điểm D sao cho ADACAB =−
A. D là đỉnh thứ tư của hình bình hành ADBC .
B. D trùng điểm B .
C. D trùng điểm C
D. D là đỉnh thứ tư của hình bình hành ABCD.
Lời giải
Chọn D
Ta có ADACABBC =−= AD cùng hướng và cùng độ dài với BC ABCD là hình bình hành ( quan sát thêm hình vẽ)
Câu 21. Cho 4 điểm phân biệt A , B , C , D . Đẳng thức nào sau đây đúng?
A. ABDADCCB +=+ . B. ACBDBCDA +−= . C. ACADCBBD −=− D. ABADCDBC −=+ Lời giải Chọn A
Ta có ABDADCCBDAABDCCBDBDB +=++=+= (luôn đúng). Câu 22. Cho tam giác ABC có I là trung điểm của cạnh BC và G là trọng tâm. Đẳng thức nào sau đây sai?

DẠYKÈMQUYNHƠN
OFFICIAL
Ta
Suy ra đẳ
A. GAGBGC += B. CBBACA += C. 0 GAGBGC++= D. 0 IBIC+= Lời giải Chọn A
có 0 GAGBGCGAGBGCGABC +=+−==
ng thức trên là sai vì hai vectơ , GABC không cùng hướng. Câu 23. Trên Hình biểu diên ba lực 1F , 23 , FF cùng tác động vào một vật ở vị trí cân bằng 0. Cho biết cường độ của 12 , FF đều bằng 100N và góc tạo bởi 1F và 2F bằng 120 . C B D A
Tính cường độ của lực 3F . A. 190 B. 200 C. 100 D. 80 Lời giải Ta sử dụng các vectơ ,, OAOBOC và OD lần lượt biểu diễn cho các lực 123 ,, FFF và hợp lực F của 12 , FF Khi đó, do 12=+ FFF và 12 100 ==FF , nên tứ giác AOBD là hình thoi. Từ đó, do 120 = AOB , suy ra 60 = OAD , do đó tam giác AOD đều. Bởi vậy ||100 ===FODOA Do vật ở vị trí cân bằng nên hai lực F và 3F ngược hướng và có cường độ bằng nhau, tức là hai vectơ OD và OC là hai vectơ đối nhau. Suy ra cường độ của lực 3F bằng


DẠYKÈMQUYNHƠN
OFFICIAL
.
==
nào sau đây cùng phương? A. 2,2abab ++ B. 2,2 abab C. 5,102 abab +−− D. , abab +− Lời giải Chọn C Ta có: 1022.(5)5 ababab −−=−++ và 102ab cùng phương. Câu 25. Cho tam giác ABC có điểm O thỏa mãn: 2 OAOBOCOAOB +−=− . Khẳng định nào sau đây là đúng? A. Tam giác ABC đều B. Tam giác ABC cân tại C C. Tam giác ABC vuông tại C D. Tam giác ABC cân tại B Lời giải Chọn C
3 ||100( ).FFN == Câu 24. Cho ABC
Đặt , aBCbAC
. Các cặp vectơ
Gọi I là trung điểm của AB . Ta có: 2 OAOBOCOAOBOAOCOBOCBACACBAB +−=−−+−=+= 1 2.2 2 CIABCIABCIAB === Tam giác ABC vuông tại C .
Câu 26. Côsin của góc giữa hai vectơ (1;1) = u và (2;1)=− v là: A. 1 10 . B. 10 10 C. 10 10 D. 3 10 Lời giải Chọn C
Câu 27. Cho tam giác ABC có (2;6),(2;2),(8;0) ABC . Khi đó, tam giác ABC là: A. Tam giác đều. B. Tam giác vuông tại A. C. Tam giác có góc tù tại A D. Tam giác cân tại A. Lời giải Chọn B Câu 28. Cho hai vectơ a và b thỏa mãn 3, a = 2 b = và .3.ab =− Xác định góc giữa hai vectơ a và b A. o30

DẠYKÈMQUYNHƠN
OFFICIAL
giải Chọn D Ta có ( ) ( ) ( ) 0 .31 ...cos,cos,,120 3.22 . ab ababababab ab =⎯⎯→===−⎯⎯→= Câu 29. Cho 2 vectơ đơn vị a và b thỏa 2 ab+= . Hãy xác định ( )( ) 3425 abab −+ A. 7 . B. 5. C. 7. D. 5. Lời giải Chọn C 1 ==ab , ( )2 24.1 +=+== ababab , ( )( ) 22 34256207.7 −+=−+=− abababab Câu 30. Cho hình thang vuông ABCDcó đáy lớn 4 ABa = , đáy nhỏ 2 CDa = , đường cao 3 ADa = .Tính DABC A. 2 9a . B. 2 15a . C. 0. D. 2 9a Lời giải Chọn A Vì ( ) 2 ...9 =++==− DABCDABAADDCDAADa nên chọn#A.
= . B. o45 = . C. o60 = . D. o120 = . Lời
Câu 31. Qua điều tra dân số kết quả thu được số đân ở tỉnh B là 2.731.425 người với sai số ước lượng không quá 200 người. Các chữ số không đáng tin ở các hàng là: A. Hàng đơn vị. B. Hàng chục. C. Hàng trăm. D. Cả A, B, C. Lời giải Chọn D. Ta có 1001000 50200500 22 d === các chữ số đáng tin là các chữ số hàng nghìn trở đi. Câu 32. Nếu lấy 3,14 làm giá trị gần đúng của thì sai số là: A. 0,001. B. 0,002. C. 0,003. D. 0,004. Lời giải Chọn#A. Ta có 3,141592654... = nên sai số tuyệt đối của 3,14 là 3,143,143,1410,001
ống kê như sau: Giá trị mốt 0 M của bảng phân bố tần số trên bằng A.5. B.7. C.8. D.12. Lời giải Mốt của bảng phân bố tần suất là giá trị


DẠYKÈMQUYNHƠN
OFFICIAL
có tần số lớn nhất nên ta có 0 8 M = . Câu 35. Theo kết quả thống kê điểm thi giữa kỳ 2 môn toán khối 11 của một trường THPT, người ta tính được phương sai của bảng thống kê đó là 2 0,573 x s = . Độ lệch chuẩn của bảng thống kê đó bằng A. 0,812 B. 0,757 C. 0,936 D. 0,657 Lời giải Ta có công thức tính độ lệch chuẩn là 2 0,5730,757 xx ss== . 2. Tự luận Câu 1. Cho hai tập họp [2;1]=+Am và 1 ; 2 =+ B Tìm m để AB chỉ có đúng một 1 phần tử. Lời giải
=−−= . Câu 33. Cho bảng phân bố tần số sau: khối lượng 20 học sinh lớp 10A Số trung bình cộng x của bảng số liệu đã cho là A. 53 x = . B. 52,8 x = . C. 52,2 x = . D. 52 x = . Lời giải Giá trị trung bình 50.451.552.655.356.2 52,2 20 x ++++ == Câu 34. Kết quả thi môn Toán giữa kì 11 của lớp 3 10A trường THPT Ba Vì được th
Điều kiện: 211 + mm Để AB chỉ có đúng 1 phần tử khi và chỉ khi 11 1 22 +==−mm không thỏa mãn điều kiện. Vậy không tồn tại giá trị m để thỏa mãn yêu cầu bài toán. Câu 2. Một người dùng ba loại nguyên liệu ,, ABC để sản xuất ra hai loại sản phẩm P và Q . Để sản xuất 1 kg mỗi loại sản phẩm P hoặc Q phải dùng một số kilôgam nguyên liệu khác nhau. Tổng số kilôgam nguyên liệu mỗi loại mà người đó có và số kilôgam từng loại nguyên liệu cần thiết để sản xuất ra 1kg sản phẩm mỗi loại được cho trong bảng sau:


OFFICIAL
Biết 1kg sản phẩm P có lợi nhuận 3 triệu đồng và 1 kg sản phẩm Q có lợi nhuận 5 triệu đồng. Hãy lập phương án sản xuất hai loại sản phẩm trên sao cho có lãi cao nhất. Lời giải Gọi x là số kilôgam sản phẩm , Py là số kilôgam sản phẩm Q cần sản xuất. Ta có hệ bất phương trình:
Biểu diễn miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy , ta được như Hình.
DẠYKÈMQUYNHƠN
2210 24 2412 0 0 xy y xy x y + +
Miền nghiệm là miền ngũ giác OCBAD (Hình) với các đỉnh: (0;0);(0;2);(2;2)OCB ; (4;1);(5;0)AD .

Gọi F là số tiền lãi (đơn vị: triệu đồng) thu được, ta có: 35 Fxy =+ .
Tính giá trị của F tại các đỉnh của ngũ giác:
Tại (0;0):3.05.00OF =+= ;
Tại (0;2):3.05.210CF =+= ;
Tại (2;2):3.25.216BF =+= ;
Tại (4;1):3.45.117AF =+=
Tại (5;0):3.55.015DF =+= .
F đạt giá trị lớn nhất bằng 17 tại (4;1)A .
Vậy người đó cần sản xuất 4kg sản phẩm P và 1kg sản phẩm Q để có lãi cao nhất là 17 triệu đồng.
OFFICIAL
Câu 3. Hai người A và B cùng quan sát một con tàu đang neo đậu ngoài khơi tại vị trí C . Người A đứng trên bờ biển, người B đứng trên một hòn đảo cách bờ một khoảng 100= ABm. Hai người tiến hành đo đạc và thu được kết quả: 54,74 ==CABCBA (Hình 22). Hỏi con tàu cách hòn đảo bao xa (làm tròn kết quả đến hàng phần mười theo đơn vị mét)? Lời giải Xét tam giác ABC . Ta có: ˆ 180547452
=−−= C . Áp dụng định lí sin ta có: sinsin = BABC CA Suy ra sin100sin54102,7( sinsin52)
DẠYKÈMQUYNHƠN
Từ đó suy ra “ Điều kiện cần và
để hai
có cùng trọng
là '''0AABBCC++= Lời giải. Ta có ( )''''1AAAGGGGA =++ ( )''''2BBBGGGGB =++ ( )''''3CCCGGGGC =++ Cộng vế với vế ta được ( ) ( ) '''3'''''''3' AABBCCAGBGCGGGGAGBGCGG ++=++++++= Vì G , G là trọng tâm của tam giác ABC , ABC nên 0 0 AGBGCG AGBGCG ++= ++= Từ đẳng thức trên ta thấy G trùng G khi và chỉ khi 0 GG = tức là 0 AABBCC ++= .
== BAA BCm C . Vậy con tàu cách hòn đảo khoảng 102,7 m. Câu 4. Hai tam giác ABC và A’B’C’ lần lượt có trọng tâm là G, G’. Chứng minh rằng '''3' AABBCCGG ++= .
đủ
tam giác ABC và A’B’C’
tâm
1. Trắc nghiệm
Câu 1. Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Hãy bỏ rác đúng nơi quy định!
b) Hoàng Sa, Trường Sa là quần đảo thuộc chủ quyền của Việt Nam.
c) 2021 là số nguyên tố.
d) Bạn có biết nấu cơm không? A. 4. B. 3. C. 2. D. 1.
Câu 2. Mệnh đề: “ ( ) *,1234:5 nnn n +++ ” khẳng định là
A. Tồn tại số nguyên dương n để 1234 nnn+++ chia hết cho 5. B. Tồn tại duy nhất số nguyên dương n để 1234 nnn+++ chia hết cho 5.
C. Với mọi số tự nhiên n thì 1234 nnn+++ chia hết cho 5. D. Với mọi số nguyên dương n thì 1234 nnn+++ chia hết cho 5.
Câu 3. Cho tập hợp {2180}Axx=− và 1 0 10 Bx x = . Tập hợp AB là


A. [9;10]. B. [9;10) C. (9;10) D. (9;10]. Câu 4. Cho tập hợp (;5)Amm=+ và (10;) B =+ . Số các giá trị nguyên dương của tham số m để \ ABA = là A. 5. B. 4. C. 3. D. 6. Câu 5. Trong các tập hợp sau, tập hợp nào là tập hợp rỗng? A. {(1)(21)0} =++= Axxx . B. {(1)(21)0} =++=Bxxx . C. {(1)(21)0} =++=Cxxx D. {(1)(21)0} =++=Dxxx
Câu 6. Miền nghiệm của bất phương trình 5312 −xy là nửa mặt phẳng tạo bởi đường thẳng :5312 −=dxy (không kể d ) chứa điểm có toạ độ nào sau đây? A. (2;1) B. (0;0) C. (1;2) . D. (3;4). Câu 7. Miền nghiệm của bất phương trình 1 2 2 −yx được xác định bởi miền nào (nửa mặt phẳng không bị gạch và không kể d) sau đây? A. B.
DẠYKÈMQUYNHƠN
ĐỀ SỐ 10
OFFICIAL
C. D. Câu 8. Miền nghiệm của hệ bất phương trình:


xác định bởi miền đa giác nào sau đây? A. B. C. D. Câu 9. Miền đa giác không bị gạch ở Hình là miền nghiệm của hệ bất phương trình:





DẠYKÈMQUYNHƠN OFFICIAL
1
x
+
A. 0 0 22 + x y xy B. 0 0 22 x y xy + C. 0 0 22. + x y xy
2 0 20
y y xy
được
D. 0 0 22.
Câu 10. Miền nghiệm của hệ bất phương trình 1 1 4
x y xy
+ là miền ( ) H . Gọi M là một điểm thuộc ( ) H . Độ dài OM ngắn nhất là A. 2 . B. 10 . C. 22 D. 1. Câu 11. Cho là góc tù. Khẳng định nào sau đây là đúng? A. tan0 . B. cos0 . C. sin0 . D. cot0 .
Câu 12. Cho sin3 5 x = . Tính 22 4sin3cos Pxx =+ ? A. 91 25 P = . B. 84 25 P = . C. 19 25 P = . D. 109 25 P = . Câu 13. Cho 1 sin 3 = với 00 90180 . Giá trị của cos bằng A. 2 3 . B. 2 3 . C. 22 3 . D. 22 3 .
Câu 14. Cho ABC có 0 60,8,5.===Bac Độ dài cạnh b bằng: A. 7. B. 129. C. 49. D. 129 . Câu 15. Cho ;;cab là độ dài 3cạnh của một tam giác. Mệnh đề nào sau đây không đúng? A. 2 aabac + . B. 222 2 acbac ++ . C. 222 2 bcabc ++ . D. 2abbcb + . Câu 16. Trong mặt phẳng, cho tam giác ABC có 4cm AC = , góc 60 A = , 45 B = . Độ dài cạnh BC là A. 26 . B. 223 + . C. 232. D. 6 . Câu 17. Cho tam giác ABC có 60 =
DẠYKÈMQUYNHƠN OFFICIAL
+ x y xy
B và 45 = C , = BCa . Độ dài cạnh AB bằng A. 632 2 −+ a B. ( )13−+ a C. ( )13 + a D. 632 2 + a Câu 18. Cho tam giác ABC có 47 = a , 6 = b và 8 = c . Diện tích S của tam giác ABC là A. 97 . B. 79 . C. 9. D. 7 . Câu 19. Mệnh đề nào sau đây sai? A. Hai véctơ cùng phương là hai véctơ có giá song song hoặc trùng nhau B. Véctơ không cùng phương với mọi véctơ C. Hai véctơ cùng phương thì cùng hướng. D. Hai véctơ bằng nhau là hai véctơ có cùng hướng và cùng độ dài. Câu 20. Cho hai điểm , AB phân biệt. Xác định điểm M sao cho 0 MAMB+= . A. Không tìm được điểm M B. M ở vị trí bất kì. C. M nằm trên đường trung trực của AB . D. M là trung điểm của AB .
Câu 21. Cho hình bình hành ABCDtâm O . Kết quả nào sau đây là đúng A. ABADAC −= . B. ABOAAB =− . C. COOBBA −= . D. AOODCB += .

Câu 22. Cho sáu điểm ,,,,, ABCDEF bất kì trên mặt phẳng. Tìm đẳng thức sai trong các đẳng thức sau: A. 0 BACBDCBD . B. ABCDEFCACBEDCF . C. ABCDADCB D. ABCDEAEDCB
OFFICIAL
Câu 23. Hình 4.19 biểu diễn hai lực 12 , FF cùng tác động lên một vật, cho 123,2 FNFN == . Tính độ lớn của hợp lực 12 FF + A. 20 B. 19 C. 19 D. 23
Câu 24. Biết rằng hai vec tơ a và b không cùng phương nhưng hai vec tơ 32ab và (1)4 xab ++ cùng phương. Khi đó giá trị của x là: A. 7 B. 7 C. 5 D. 6
Câu 25. Cho ngũ giác ABCDE . Gọi ,,, MNPQ lần lượt là trung điểm các cạnh ,,, ABBCCDDE . Gọi I và J lần lượt là trung điểm các đoạn MP và NQ . Khẳng định nào sau đây đúng? A. 1 2 IJAE = B. 1 3 IJAE = C. 1 4 IJAE = D. 1 5 IJAE = Câu 26. Trong hệ trục toạ độ Oxy , toạ độ của vectơ 83 aji =− bằng A. ( )3;8 a =− . B. ( )3;8 a =− . C. ( )8;3 a = . D. ( )8;3 a =− . Câu 27. Trong mặt phẳng Oxy , cho hai điểm ( )1;3 B và ( )3;1 C . Độ dài vectơ BC bằng A. 6 B. 25 C. 2 D. 5 Câu 28. Cho tam giác đều ABC có cạnh bằng a Tính tích vô hướng ABAC A. 2 .2.ABACa = B. 2 3 . 2 a ABAC =− C. 2 2 a ABAC =− D. 2 2 a ABAC = Câu 29. Cho hai vectơ a và b . Biết a =2, b = 3 và ( ) o,120ab = .Tính ab + A. 73 + B. 73 C. 723 D. 723 + Câu 30. Cho hai điểm , BC phân biệt. Tập
DẠYKÈMQUYNHƠN
hợp những điểm M thỏa mãn 2 . = CMCBCM là : A. Đường tròn đường kính BC . B. Đường tròn( ) ; BBC C. Đường tròn ( ) ; CCB D. Một đường khác. Câu
Nếu lấy 3,1416 làm giá trị gần đúng của thì có số chữ số chắc là: A. 5. B. 4. C. 3. D. 2. Câu 32. Số gần đúng của 2,57656 a = có ba chữ số đáng tin viết dưới
A. 2,57. B.
. C.
. D.
. Câu 33. Điểm thi toán cuối năm của
nhóm gồm 7
sinh
11 là 1; 3; 4; 5; 7; 8; 9. Số trung vị của
liệu đã cho là
31.
dạng chuẩn là:
2,576
2,58
2,577
một
học
lớp
dãy số
A. 6. B. 4. C. 7. D. 5.
Câu 34. Điểm thi toán cuối năm của một nhóm gồm 7 học sinh lớp 11 là 1; 3; 4; 5; 7; 8; 9. Số trung vị trên của dãy số liệu đã cho là
A. 8. B. 3. C. 7. D. 5. Câu 35. Cho mẫu số liệu 1x , 2x ,…, Nx có số trung bình là x . Phương sai được tính theo công thức nào trong các công thức sau
A. 1
2. Tự luận
1 N i i x N B. ( ) 1
1 N i i xx N = C. ( ) 2 1
1 N i i xx N = D. ( ) 2 1


1 N i i xx N =
Câu 1. Trong lớp 11A có 16 học sinh giỏi môn Toán, 15 học sinh giỏi môn Lý và 11 học sinh giỏi môn Hóa. Biết rằng có 9 học sinh vừa giỏi Toán và Lý (có thể giỏi thêm môn Hóa), 6 học sinh vừa giỏi Lý và Hóa (có thể giỏi thêm môn Toán), 8 học sinh vừa giỏi Hóa và Toán (có thể giỏi thêm môn Lý) và trong đó chỉ có đúng 11 học sinh giỏi đúng hai môn. Hỏi có bao nhiêu học sinh của lóp.
a) Giỏi cả ba môn Toán, Lý, Hóa. b) Giỏi đúng một môn Toán, Lý hoặc Hóa.
Câu 2. Bạn Lan thu xếp được không quá 10 giờ để làm hai loại đèn trung thu tặng cho các trẻ em khuyết tật. Loại đèn hình con cá cần 2 giờ để làm xong 1 cái, còn loại đèn ông sao chỉ cần 1 giờ để làm xong 1 cái. Gọi x, y lần lượt là số đèn hình con cá và đèn ông sao bạn Lan sẽ làm. Hãy lập hệ bất phương trình mô tả điều kiện của x, y và biểu diễn miền nghiệm của hệ bất phương trình đó.
Câu 3. Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một con tàu C đang neo đậu ngoài khơi. Người đó tiến hành đo đạc và thu được kết quả: 30 ,60,50 === ABmCABCBA (Hình 23). Tính khoảng cách từ vị trí A đến con tàu C (làm tròn kết quả đến hàng phần mười theo đơn vị mét). Câu 4.
DẠYKÈMQUYNHƠN
OFFICIAL
Cho tam giác ABC . Trên các cạnh AB
BC
CA ta lấy lần lượt các điểm
AMBNCP ABBCCA == . Chứng minh rằng hai tâm giác ABC
Lời giải tham khảo BẢNG ĐÁP ÁN TRẮC NGHIỆM 1C 2D 3B 4A 5D 6A 7C 8A 9C 10A 11A 12B 13C 14A 15C 16A 17B 18A 19C 20D 21C 22A 23C 24A 25C 26A 27B 28D 29C 30A 31B 32A 33D 34A 35D 1. Trắc nghiệm Câu 1. Trong các câu sau, có bao nhiêu câu là mệnh đề? a) Hãy bỏ rác đúng nơi quy định! b) Hoàng Sa, Trường Sa là quần đảo thuộc chủ quyền của Việt Nam. c) 2021 là số nguyên tố.
,
,
M , N , P sao cho
và MNP có cùng trọng tâm.
d) Bạn có biết nấu cơm không?
A. 4. B. 3. C. 2. D. 1.
Câu 2. Mệnh đề: “ ( ) *,1234:5 nnn n +++ ” khẳng định là
A. Tồn tại số nguyên dương n để 1234 nnn+++ chia hết cho 5.
B. Tồn tại duy nhất số nguyên dương n để 1234 nnn+++ chia hết cho 5.
C. Với mọi số tự nhiên n thì 1234 nnn+++ chia hết cho 5.
D. Với mọi số nguyên dương n thì 1234 nnn+++ chia hết cho 5.
Câu 3. Cho tập hợp {2180}Axx=− và 1 0 10 Bx x = . Tập hợp AB là

A. [9;10]. B. [9;10) C. (9;10) D. (9;10]. Lời giải Ta có [9;) A =+ và (;10) B =− . Suy ra [9;10) AB= Câu 4. Cho tập hợp (;5)Amm=+ và (10;) B =+ . Số các giá trị nguyên dương của tham số m để \ ABA = là A. 5. B. 4. C. 3. D. 6.
Lời giải Ta có \5105 ABAABmm ==+ Câu 5. Trong các tập hợp sau, tập hợp nào là tập hợp rỗng? A. {(1)(21)0} =++= Axxx B. {(1)(21)0} =++=Bxxx C. {(1)(21)0} =++=Cxxx . D. {(1)(21)0} =++=Dxxx .



Câu 6. Miền nghiệm của bất phương trình 5312 −xy là nửa mặt phẳng tạo bởi đường thẳng :5312 −=dxy (không kể d ) chứa điểm có toạ độ nào sau đây? A. (2;1). B. (0;0) C. (1;2) D. (3;4).
Câu 7. Miền nghiệm của bất phương trình 1 2 2 −yx được xác định bởi miền nào (nửa mặt phẳng không bị gạch và không kể d) sau đây? A. B. C. D.
DẠYKÈMQUYNHƠN
OFFICIAL





DẠYKÈMQUYNHƠN OFFICIAL Câu 8. Miền nghiệm của hệ bất phương trình: 1 2 0 20 x y y xy + được xác định bởi miền đa giác nào sau đây? A. B. C. D. Câu 9. Miền đa giác không bị gạch ở Hình là miền nghiệm của hệ bất phương trình: A. 0 0 22 + x y xy B. 0 0 22 x y xy + C. 0 0 22. + x y xy D. 0 0 22. + x y xy Câu 10. Miền nghiệm của hệ bất phương trình 1 1 4 x y xy + là miền ( ) H . Gọi M là một điểm thuộc ( ) H . Độ dài OM ngắn nhất là A. 2
DẠYKÈMQUYNHƠN OFFICIAL B. 10 . C. 22 D. 1. Lời giải Ta
hình (H) là tam giác ABC với
ABC Suy ra độ dài nhỏ nhất
OM là 112 += Câu 11. Cho là góc tù. Khẳng định nào sau đây là đúng? A. tan0 . B. cos0 . C. sin0 . D.
. Lời giải Chọn A Ta có là góc tù nên sin0,cos0 suy ra tan0 . Câu 12. Cho sin3 5 x = . Tính 22 4sin3cos Pxx =+ ? A. 91 25 P = . B. 84 25 P = . C. 19 25 P = . D. 109 25 P = . Lời giải Chọn B Ta có 222 9844sin3cossin33 2525 Pxxx =+=+=+= . Câu 13. Cho 1 sin 3 = với 00 90180 . Giá trị của cos bằng A. 2 3 B. 2 3 C. 22 3 D. 22 3 Lời giải Chọn C Có 1 sin 3 = 2 18 cos1 99 =−= mà 00 90180 22 cos0cos 3 =− . Câu 14. Cho ABC có 0 60,8,5.===Bac Độ dài cạnh b bằng: A. 7. B. 129. C. 49. D. 129 . Lời giải Chọn#A. Ta có: 2222202cos852.8.5.cos60497 bacacBb =+−=+−== Câu 15. Cho ;;cab là độ dài 3cạnh của một tam giác. Mệnh đề nào sau đây không đúng? A. 2 aabac + B. 222 2 acbac ++ C. 222 2 bcabc ++ D. 2abbcb + Lời giải Chọn C Do 222 2.cos2 bcabcAbc +−= 222 2 bcabc ++ nên mệnh đề C sai. Áp dụng bất đẳng thức tam giác ta có 2 abcaabac ++ ;đáp án A đúng. Tương tự 2acbabbcb ++ ;mệnh đề D đúng. Ta có: 222 2.cos2 acbacBac +−= 222 2 acbac++ ;mệnh đề B đúng. Câu 16. Trong mặt phẳng, cho tam giác ABC có 4cm AC = , góc 60 A = , 45 B = . Độ dài cạnh BC là
có
(1;1),(1;3),(3;1)
của
cot0
A. 26 . B. 223 + . C. 232. D. 6 . Lời giải Chọn A Ta có sinsin BCAC AB = 4.3 2 26 2 2
BC == . Câu 17. Cho tam giác ABC có 60 = B và 45 = C , = BCa . Độ dài cạnh AB bằng A. 632 2 −+ a B. ( )13−+ a C. ( )13 + a D. 632 2 + a Lời giải Áp dụng định lý hàm sin vào tam giác ABC ta có: ( ) sin .13 sinsinsinsin ====−+ BCABACC ABBCa ACBA Câu 18. Cho tam giác ABC có 47 = a , 6 = b và 8 = c . Diện tích S của tam giác ABC là A. 97 B. 79 C. 9 D. 7 Lời giải Áp dụng định lý hàm số cosin vào tam giác ABC ta có: ( )2 222 476436 57 cos 216 2.47.8 +− +− === acb B ac 2 819 sin1cos 25616 =−==BB Diện tích tam giác ABC là 119sin.47.8.97 2216 ===SacB .
Câu 19. Mệnh đề nào sau đây sai?
A. Hai véctơ cùng phương là hai véctơ có giá song song hoặc trùng nhau.
B. Véctơ không cùng phương với mọi véctơ
C. Hai véctơ cùng phương thì cùng hướng. D. Hai véctơ bằng nhau là hai véctơ có cùng hướng và cùng độ dài. Lời giải Chọn C Mệnh đề sai là mệnh đề “Hai
DẠYKÈMQUYNHƠN OFFICIAL
véctơ cùng phương thì cùng hướng” Câu 20. Cho hai điểm , AB phân biệt. Xác định điểm M sao cho 0 MAMB+= A. Không tìm được điểm M B. M ở vị trí bất kì. C. M nằm trên đường trung trực của AB D. M là trung điểm của AB Lời giải Chọn D Ta có 0 MAMBMAMB +==− Do đó M là trung điểm của AB Câu 21. Cho hình bình hành ABCDtâm O . Kết quả nào sau đây là đúng A. ABADAC −= B. ABOAAB =− C. COOBBA −= D. AOODCB += Lời giải
Chọn C Xét hình bình hành ABCD tâmO : COOBCODOCOODCDBA −=−=+== Câu 22. Cho sáu điểm ,,,,, ABCDEF bất kì trên mặt phẳng. Tìm đẳng thức sai trong các đẳng thức sau: A. 0 BACBDCBD B. ABCDEFCACBEDCF C. ABCDADCB . D. ABCDEAEDCB . Lời giải Chọn A

0 BACBDCBDCBBABDDCCABCBCCABA . Vô lí. Vậy A sai. Có thể giải thích thêm.
0 ABCDADDBCBBDADCBDBBDADCBADCB . Vậy C đúng.
ABCDEFCACBEDCF CAABCDEFCBEDCF CBCDEFCBEDCFCDEFEDCF B đúng bằng cách chứng minh tương tự C.
DẠYKÈMQUYNHƠN OFFICIAL
ABCDEAEDCBEAABCDEDCB EBCDEDCB D đúng bằng cách chứng minh tương tự C. Câu 23. Hình 4.19 biểu diễn hai lực 12 , FF cùng tác động lên một vật, cho 123,2 FNFN == . Tính độ lớn của hợp lực 12 FF + A. 20 B. 19 C. 19 D. 23 Lời giải Dựng hình bình hành ABDC với hai cạnh là hai vectơ 12 , FF như hình vẽ
Câu 24. Biết rằng hai vec tơ a và b không cùng phương nhưng hai vec tơ 32ab và (1)4 xab ++ cùng phương. Khi đó giá trị của x là: A. 7 B. 7 C. 5 D. 6 Lời giải Chọn A Điều kiện để hai vec tơ 32ab và (1)4 xab ++ cùng phương là: 14 7 32 x x + ==− Câu 25. Cho ngũ giác ABCDE . Gọi ,,, MNPQ lần lượt là trung điểm các cạnh ,,, ABBCCDDE . Gọi I và J lần lượt là trung điểm các


DẠYKÈMQUYNHƠN OFFICIAL
ADABBDABBDABD
=+− =+−= =+=
đoạn MP và NQ . Khẳng định nào sau
A. 1 2 IJAE = B. 1 3 IJAE = C. 1 4 IJAE = D. 1 5 IJAE = Lời giải Chọn C Ta có: 2IJIQINIMMQIPPNMQPN =+=+++=+ ( ) 1 2 2 MQMAAEEQ MQAEBDMQAEBD MQMBBDDQ =++ =+=+ =++ , 1 2 PNBD =− Suy ra: ( ) 1111 2 2224 IJAEBDBDAEIJAE =+−== . Câu 26. Trong hệ trục toạ độ Oxy , toạ độ của vectơ 83 aji =− bằng A. ( )3;8 a =− B. ( )3;8 a =− C. ( )8;3 a = D. ( )8;3 a =−
Ta có: 1212 || FFACABADFFADAD +=+=+== Xét ABD ta có: 123,2.BDACFABF===== 18018012060ABDBAC =−=−= Theo định lí cosin ta có: 222 2222 12 2cos 23223cos12019 1919 V?y
ADAD ADFF
đây đúng?
Lời giải
Chọn A
Ta có ( )83383;8ajiija =−=−+=− .
Câu 27. Trong mặt phẳng Oxy , cho hai điểm ( )1;3 B và ( )3;1 C . Độ dài vectơ BC bằng
A. 6 B. 25 C. 2 D. 5 Lời giải Chọn B
Tính độ dài vectơ BC ( ) ( )2 2 4;2422025BCBCBC=−==+−== . Vậy 25 BC =
Câu 28. Cho tam giác đều ABC có cạnh bằng .a Tính tích vô hướng ABAC A. 2 .2.ABACa = B. 2 3 2 a ABAC =− C. 2 . 2 a ABAC =− D. 2 . 2 a ABAC = Lời giải
Chọn D
Xác định được góc ( ) , ABAC là góc A nên ( ) 0 ,60.ABAC = Do đó ( ) 2 0 ...cos,..cos60. 2 a ABACABACABACaa===
hai vectơ
và b
Biế
a =2, b
73 + . B. 73
3
giải
ab
723
D. 723 +
DẠYKÈMQUYNHƠN
OFFICIAL
ng kính BC . B. Đường tròn( ) ; BBC . C. Đường tròn ( ) ; CCB . D. Một đường khác. Lời giải Chọn A 22 ..0.0 =−== CMCBCMCMCBCMCMMB . Tập hợp điểm M là đường tròn đường kính BC Câu 31. Nếu lấy 3,1416 làm giá trị gần đúng của thì có số chữ số chắc là: A. 5. B. 4. C. 3. D. 2. Lời giải Chọn B. Ta có 3,141592654... = nên sai số tuyệt đối của 3,1416 là 3,14163,14163,14150,0001 =−−= Mà 0,00010,00050,001 2 d == nên có 4 chữ số chắc. Câu 32. Số gần đúng của 2,57656 a = có ba chữ số đáng tin viết dưới dạng chuẩn là: A. 2,57. B. 2,576. C. 2,58. D. 2,577. Lời giải
Câu 29. Cho
a
.
t
=
và ( ) o,120ab = .Tính
+ A.
. C.
.
. Lời
Chọn C Ta có ( ) ( ) 2 22 22 2.2,723 +=+=++=++=− ababababababcosab . Câu 30. Cho hai điểm , BC phân biệt. Tập hợp những điểm M thỏa mãn 2 . = CMCBCM là : A. Đường tròn đườ
Chọn#A. Vì a có 3 chữ số đáng tin nên dạng chuẩn là 2,57
Câu 33. Điểm thi toán cuối năm của một nhóm gồm 7 học sinh lớp 11 là 1; 3; 4; 5; 7; 8; 9. Số trung vị của dãy số liệu đã cho là A. 6. B. 4. C. 7. D. 5. Lời giải Mẫu số liệu đã cho có 7 phần tử, đã sắp theo thứ tự không giảm. Nên số trung vị là số đứng giữa dãy. Vậy số trung vị là 5.
Câu 34. Điểm thi toán cuối năm của một nhóm gồm 7 học sinh lớp 11 là 1; 3; 4; 5; 7; 8; 9. Số trung vị trên của dãy số liệu đã cho là A. 8. B. 3. C. 7. D. 5. Lời giải Chọn A
OFFICIAL
2. Tự luận
Câu 1. Trong lớp 11A có 16 học sinh giỏi môn Toán, 15 học sinh giỏi môn Lý và 11 học sinh giỏi môn Hóa. Biết rằng có 9 học sinh vừa giỏi Toán và Lý (có thể giỏi thêm môn Hóa), 6 học sinh vừa giỏi Lý và Hóa (có thể giỏi thêm môn Toán), 8 học sinh vừa giỏi Hóa và Toán (có thể giỏi thêm môn Lý) và trong đó chỉ có đúng 11 học sinh giỏi đúng hai môn. Hỏi có bao nhiêu học sinh của lóp.
a) Giỏi cả ba môn Toán, Lý, Hóa.
b) Giỏi đúng một môn Toán, Lý hoặc Hóa. Lời giải Gọi ,, TLH lần lượt là tập hợp các học sinh giỏi Toán, Lý, Hóa; B là tập hợp học sinh giỏi đúng hai môn. Theo giả thiết ta có ()9,()6,()8
DẠYKÈMQUYNHƠN
u
ố liệu 1x
2
N i i x
.
) 1
N i i xx
2
1
i
Câu 35. Cho mẫ
s
,
x ,…, Nx có số trung bình là x . Phương sai được tính theo công thức nào trong các công thức sau A. 1 1
N
B. (
1
N = . C. ( ) 2 1 1 N i i xx N = . D. ( ) 2 1 1 N i i xx N = . Lời giải Phương sai được tính theo công thức ( )
2
1 N
i sxx N = =− hoặc 2 22 2 11 11NN ii ii sxx NN== =−
++
TLH
ta có: ()()()3()() ++−= nTLnLHnHTnTLHnB Hay 1 ()[()()()()]4 3 =++−= nTLHnTLnLHnHTnB Vậy có 4 học sinh giỏi cả ba môn Toán,
===nTnLHnHT a) Xét tổng ( )()()
nTLnLHnHT thì mỗi phần tử của tập hợp
được tính ba lần do đó
Lý, Hóa.
b) Xét ()() + nTLnLT thì mỗi phần tử của tập hợp TLH được tính hai lần do đó số học sinh chỉ giỏi đúng môn Toán là: ()[()()()]16(984)3 −+−=−+−=nTnTLnHTnTLH


Tương tự, ta có số học sinh chỉ giỏi đúng môn Lý ()[()()()]15(964)4 −+−=−+−=nLnTLnLHnTLH
Tương tự, ta có số học sinh chỉ giỏi đúng môn Hóa ()[()()()]11(864)1 −+−=−+−=nHnHTnLHnTLH
Suy ra số học sinh giỏi đúng một môn Toán, Lý hoặc Hóa là 3418 ++= Câu 2. Bạn Lan thu xếp được không quá 10 giờ để làm hai loại đèn trung thu tặng cho các trẻ em khuyết tật. Loại đèn hình con cá cần 2 giờ để làm xong 1 cái, còn loại đèn ông sao chỉ cần 1 giờ để làm xong 1 cái. Gọi x, y lần lượt là số đèn hình con cá và đèn ông sao bạn Lan sẽ làm. Hãy lập hệ bất phương trình mô tả điều kiện của x, y và biểu diễn miền nghiệm của hệ bất phương trình đó.
Lời giải
Ta có các điều kiện ràng buộc đối với x, y như sau: Hiển nhiên 0,0xy Tổng số giờ làm không quá 10 giờ nên 210 +xy
+
xy xxy y
Từ đó ta có hệ bất phương trình: 210 0(,) 0
Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy, ta được như hình dưới.
Miền không tô màu (miền tam giác OAB , bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình.
DẠYKÈMQUYNHƠN
OFFICIAL
Câu 3. Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một con tàu C đang neo
ngoài khơi. Người đó tiến hành đo đạc và thu được kết quả: 30 ,60,50 === ABmCABCBA (Hình 23). Tính khoảng cách từ vị trí A đến con tàu C (làm tròn kết quả đến hàng phần mười theo đơn vị mét). Lời giải Xét tam giác ABC . Ta có: ˆ 180605070

=−−= C . Áp dụng định lí sin ta có: sinsin = BAAC CB Suy ra sin30sin5024,5( sinsin70)
== BAB ACm C . Vậy khoảng cách từ vị trí A đến con tàu C là khoảng 24,5m Câu 4. Cho tam giác ABC . Trên các cạnh AB , BC , CA ta lấy lần lượt các điểm M , N , P sao cho AMBNCP ABBCCA == . Chứng minh rằng hai tâm giác ABC và MNP có cùng trọng tâm. Lời giải Giả sử AM k AB = suy ra AMkAB = , BNkBC = , CPkCA = . Cách 1. Gọi G , G lần lượt là trọng tâm của ABC và MNP . Suy ra 0 AGBGCG++= và 0 MGNGPG ++= ( )* . Ta có AMkAB = AGGGGMkAB

DẠYKÈMQUYNHƠN OFFICIAL
đậu
++=
(
++++++=++
= .
Ta
( ) 0 GMGNGPGAAMGBBNGCCP AMBNCP kABkBCkCA kABBCCA ++=+++++ =++ =++ =++ =
++= . Tương tự BGGGGNkBC
++= và CGGGGMkBC
. Cộng vế theo vế từng đẳng thức trên ta được
) ( ) ( ) 3 AGBGCGGGGMGNGPkABBCCA
. Kết hợp với ( )* ta được 0 GG
Suy ra điều phải chứng minh. Cách 2. Gọi G là trọng tâm của ABC suy ra 0 GAGBGC++= .
có
Vậy hai tam giác ABC và NMP có cùng trọn tâm.














































































































































