GIẢI PHÁP ĐỂ CHINH PHỤC BÀI TOÁN TÌM MÔ ĐUN LỚN NHẤT, MÔ ĐUN NHỎ NHẤT TRONG SỐ PHỨC

Ths

1. Đặtvấn đề

1.1. Lý do chọn đề tài: lý luận, thực tiễn Trong chương trình Toán THPT, phần đại số ở chương trình lớp 12, học sinh được hoàn thiện hiểu biết của mình về các tập hợp số thông qua việc cung cấp một tập hợp số, gọi là Số phức. Trong chương này, học sinh đã bước đầu làm quen với các phép toán cộng, trừ, nhân, chia, khai căn, lấy môđun, ... các số phức. Bằng cách đặt tương ứng mỗi số phức ( ) 2 ,,1zxyixyi =+∈=− ℝ với mỗi

điểm ( ) ; Mxy trên mặt phẳng tọa độ Oxy , ta thấy giữa đại số và hình học có mối liên hệ khá “gần gũi”. Hơn nữa, nhiều bài toán Đại số bên Số phức, khi chuyển sang hình học, từ những con số khá trừu tượng, bài toán đã được minh họa một cách rấ trực quan, sinh động và cũng giải được bằng Hình học với phương pháp rất đẹp. Đặc biệt, trong các kì thi THPT Quốc gia trong những năm gần đây, việc sử dụng phương pháp hình học để giải quyết các bài toán về

số phức là một trong những phương pháp khá hay và hiệu quả. Đặc biệt là bài toán tìm môđun lớn nhất, môđun nhỏ nhất của số phức. Hơn nữa nếu ta biểu diễn bằng phương pháp hình học được trên giấy đối với những bài toán môđun

số phức thì ta có thể lựa chọn đáp án một cách dễ dàng.

Mặt khác, tìm giá trị nhỏ nhất, giá trị lớn nhất - cụm từ ấy hàm chứa một mảng kiến thức rất rộng, trọng tâm trong chương trình toán học ở phổ thông mà phần lớn thí sinh rất “e ngại” khi đối diện với nó. Đặc biệt việc áp dụng phương

pháp hình học vào bài toán số phức giúp người học có cái nhìn mới lạ, hấp dẫn, thú vị và lôi cuốn khơi tạo sự đam mê, hang say Toán học, giúp bạn học và bạn

đọc thấy sự đa dạng của phương pháp hình học trong các mảng Toán hơn, thấy

được việc giải quyết các bài toán cực trị trong số phức trở nên đơn giản, nhẹ

nhàng hơn.

Sáng kiến được trình bày theo hướng giải quyết những câu hỏi:

- Phải bắt đầu từ đâu?

- Khai thác, khám phá, phát hiện và kiến tạo vấn đề ra sao?

- Thực hiện giải pháp như thế nào? ...

Từ đó hình thành ý tưởng giúp tìm ra phương pháp xử lí hiệu quả cho bài toán.

1.2. Xác định mục đích nghiên cứu

Trong đề tài này, tác giả sẽ tìm hiểu cực trị hình học và áp dụng nó trong

việc giải bài toán cực trị trong số phức: Tìm mô đun lớn nhất, mô đun nhỏ nhất

của một số phức hay xuất hiện trong chương trình toán ở phổ thông.

Nhà toán học nổi tiếng Polia cho rằng: ‘ Ví như dòng sông nào cũng bắt nguồn

từ những con suối nhỏ, mỗi bài toán dù khó đến đâu cũng có nguồn gốc từ

những bài toán đơn giản...”. Viết đề tài này tác giả mong ước bản thân tiến bộ

hơn, góp một chút suy nghĩ, một chút ý tưởng, một chút đề xuất giải pháp chinh

phục đến với những dòng suối nhỏ kia.

1.3. Đối tượng nghiên cứu

Đối tượng nghiên cứu của tác giả trong đề tài này chủ yếu là bài toán tìm mô đun, mô đun lớn nhất, mô đun nhỏ nhất của một số phức thường hay xuất hiện trong các đề thi học kì, thi THPT Quốc gia.

1.4. Đối tượng khảo sát, thực nghiệm

Đề tài này được triển khai nghiên cứu, thực hiện cho các lớp ban khoa học tự nhiên và học sinh khá, giỏi bộ môn toán thuộc trường trung học phổ thông Ngô Lê Tân; các thầy cô giáo trong nhóm Toán của trường.

1.5. Phương pháp nghiên cứu

Tác giả coi mình là thí sinh đi thi kì thi học kì, thi trung học phổ thông

Quốc gia, đối diện trực tiếp với bài toán, tác giả tự mình giải quyết những câu hỏi: Phải bắt đầu như thế nào? Khai thác vấn đề ra sao? Làm thế nào để tìm ra giải pháp? Giải pháp nào mới khả thi, dễ áp dụng?... Từ đó, tác gải làm rõ những

đặc điểm, tính chất đặc trưng của các đại lượng ẩn dấu trong bài toán, bắt được nhịp cầu gắn kết giữa điều đã biết và điều cần tìm, nhìn được bài toán từ phía bên trong, lột tả bản chất của bài toán, tạo ra ý tưởng khác lạ có tính đột phá. Từ những phát hiện mới, tác giả chọn lọc, hình thành phương pháp, biểu đạt ngôn ngữ và tường minh nội dung.

1.6. Phạm vi và thời gian nghiên cứu Đề tài được tác giả nghiên cứu và áp dụng giảng dạy trong các tiết dạy tự chọn ở lớp 12 trong phạm vi toán trung học phổ thông, thời gian nghiên cứu bốn năm học: 2015- 2016, 2016-2017, 2017-2018,2018-2019.

Đề tài chắc chắn còn nhiều thiếu sót, vì vậy mong quý thầy cô, các bạn đóng góp ý kiến để đề tài hoàn thiện hơn.

Xin chân thành cảm ơn!

2.Nộidung

2.1.Nhữngnộidunglýluậncóliênquantrựctiếp đếnvấn đề nghiên

cứu.

Bài toán tìm mô đun lớn nhất, mô đun nhỏ nhất trong số phức có một vị trí xứng đáng trong phần toán học số phức nói riêng và trong chương trình toán phổ thông nói chung. Hầu hết các bài toán này rất phông phú, đa dạng, yêu cầu cao về tư duy, kỹ năng và thường không thể giải quyết bằng phương pháp cơ

bản trực tiếp. Chính vì thế việc tìm tòi những ý tưởng có lý, có căn cứ nhằm tiếp

cận và giải quyết được bài toán là vô cùng cần thiết. Những ý tưởng tự tìm tòi

được sẽ giúp người học nâng cao khả năng quan sát, linh cảm, trực giác toán học ngày càng tinh tế. Với cách tự nghiên cứu sẽ chỉ ra cho học sinh cách giải toán chứ không đơn thuần chỉ là giải toán cho học sinh. Điều này mang đậm tính đổi mới về phương pháp.

Ngoài ra, những ý tưởng đó còn tạo được tâm lý tự tin, lòng đam mê cho người học khi đối diện với bài toán khó.

2.2. Thực trạng vấn đề nghiên cứu.

Thực tế dạy và học cho thấy rằng hầu hết thí sinh đều thiếu tự tin khi đối diện với bài toán tìm giá trị lớn nhất, giá trị nhỏ nhất của mô đun số phức. Bên

cạnh đó có rất ít tài liệu về số phức để giáo viên và học sinh tham khảo, lượng bài tập về số phức trong sách giáo khoa còn nhiều hạn chế. Chính vì vậy mà việc giảng dạy và học tập của giáo viên và học sinh gặp không ít khó khăn. Bài toán

tìm tập hợp các điểm trong mặt phẳng biểu diễn số phức z có mô đun lớn nhất, nhỏ nhất có quan hệ mật thiết với nhau. Trong quá trình giảng dạy phần nội dung này, tôi nhận thấy vẫn còn một số học sinh chưa giải quyết được bài toán

tìm tập hợp các điểm biểu diễn số phức dù tập hợp các điệm cần tìm thông thường là đường thẳng, đường tròn, đường elip, ... Nhiều học sinh lại gặp rất nhiều khó khăn khi giải quyết bài toán tìm giá trị lớn nhất, nhỏ nhất của mô đun của một số phức. Để làm tốt được bài toán này trước hết học sinh phải tìm được tập hợp các điểm biểu diễn số phức sau đó áp dụng kiến thức về bất đẳng thức, lượng giác, hình học phẳng, ... để từ đó tìm ra được giá trị lớn nhất, nhỏ nhất cần tìm.

Hơn nữa, tìm giá trị lớn nhất, giá trị nhỏ nhất của một biểu thức mô đun trong số phức là các bài toán hay và khó thường xuất hiện trong các kì thi học kì, kì thi THPT Quốc gia. Bài toán này rất được sự quan tâm của các bạn học sinh yêu toán, các thầy cô giáo dạy bộ môn toán. Trong quá trình dạy học cho học sinh, tôi thường hướng dẫn học sinh tập phát triển, mở rộng, đào sâu từ những bài toán cơ bản, quen thuộc để tạo ra những bài toán mới lạ, cũng chính

từ đó mà hình thành cho các em kỹ năng quy từ các bài toán lạ về vận dụng các

bài toán quen thuộc. Với kinh nghiệm giảng dạy của mình cũng như qua trao đổi

học tập, nghiên cứu cùng với các đồng nghiệp tôi đã mạnh dạn đưa ra một số kỹ

năng nhằm hình thành và phát triển, nâng cao khả năng giải quyết các bài toán

về giá trị lớn nhất, giá trị nhỏ nhất của mô đun trong số phức. Từ đó, tôi đã viết

chuyên đề sáng kiến “Đề xuất giải pháp chinh phục bài toán tìm mô đun lớn

nhất, mô đun nhỏ nhất trong số phức” nhằm giúp học sinh có thể chủ động, tự tin hơn khi đứng trước các bài toán về giá trị lớn nhất - giá trị nhỏ nhất của mô

đun trong số phức.

Một vấn đề nữa không kém phần quan trọng là sự trải nghiệm, va chạm qua cả một quấ trình để tích lũy, đúc kết kinh nghiệm. Từ đó, tạo ra những ý

nghĩ mới mang tính bước ngoặt, độc lập và hữu dụng.

2.3. Mô tả, phân tích các giải pháp

Việc hình thành, mô tả, phân tích các giải pháp được tác giả trình bày tường minh, chi tiết thông qua nghiên cứu từng bài toán từ các đề thi học kì, các đề thi thử THPT Quốc gia và đề thi THPT Quốc gia.

2.3.1. Kiến thức cơ bản, thiết yếu

*Mộtsố địnhnghĩavàkíhiệucầnthiết.

• Số i : Ta thừa nhận có một số mà bình phương của nó bằng 1, kí hiệu:

i . Như vậy: 2 1 i =− .

•Số phức: Mỗi biểu thức dạng zxyi =+ trong đó , xy ∈ ℝ được gọi là

mộtsố phức. x :phầnthực; y :phần ảo.

•Mô đun của số phức: Với mỗi số phức zxyi =+ , giá trị biểu thức 22 xy + gọilàmô đuncủa z .Kíhiệulà z .Như vậy: 22 zxy =+ .

•Cho số phức zxyi =+ . Ta gọi xyi là số phức liên hợp của z và kí hiệulà zxyi =− .

•Với mỗi số phức zxyi =+ , xác định điểm ( ) ; Mxy trên mặtphẳngtọa

độ Oxy . Điểm M gọilàbiểudiễnhìnhhọccủasố phức z .

•Chohaisố phức zxyi =+ , ''' zxyi =+ , ( ) ,,',' xyxy ∈ ℝ

+Phépcộng: ( ) ( )''' zzxxyyi +=+++

+Phéptrừ: ( ) ( )''' zzxxyyi −=−+−

+Phépnhân: ( ) ( ) .''''' zzxxyyxyxyi =−++

+Phépchia: .' ' '.' zzz z zz = với '00 zi ≠+

*Mộtsố kíhiệuchuyểntừ số phứcsangtọa độ Oxy .

•Với ( ) ; Mxy là điểmbiểudiễnsố phức zxyi =+ thì zOM = .

•Với ( ) ; Mxy và ( )'';'Mxy lần lượt là điểm biểu diễn các số phức zxyi =+ , ''' zxyi =+ thì ''zzMM −= .

•Chohaisố phức , ABzz có điểmbiểudiễnlà , AB .Tậphợpcác điểm M

biểudiễncủasố phức z thỏamãnhệ thức AB zzzz −=− là đườngtrungtrực

của đoạn AB .

• 0 M là điểmbiểudiễncủasố phức 0z , 0 R > , tập hợp các điểm M biểu

diễn của số phức z thỏa mãn hệ thức 0 zzR −= là đường tròn tâm 0 M , bán

kính R .

2.3.2. Phương pháp hình học trong một số bài toán tìm mô đun, mô đun

lớn nhất, mô đun nhỏ nhất trong số phức.

Bàitoán1.Xét các số phức , zw thỏa mãn 224 zizi +−=− và 1 wiz=+ .

Tìm giá trị nhỏ nhất của Pw =

Cách1.(Dùngphươngpháphìnhhọc)

Phântíchvà tìmlờigiải.

Quansátbiểuthức1 Pwiz==+ tathấycó thể biến đổi

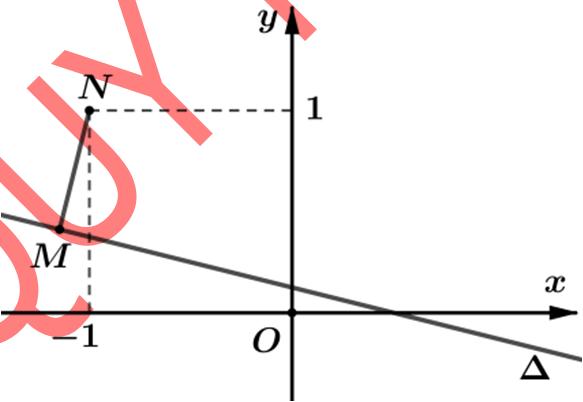
() 1 iziziziMN +=−=−= với () 0;1 N , M là điểm biểu diễn của số phức z

Vậy việc tìm giá trị nhỏ nhất củabiểu thức đưa về tìm điểm vị trí điểm M để MN ngắn nhất với tập hợp điểm M thỏa điều kiện cho trước là một đường thẳng có phương trình:2 xy ∆+= .

Lờigiải. Đặt zxyi =+ () , xy ∈ ℝ và () ; Mxy là điểm biểu diễn số phức. z

Từ ()()() 222 2 2242242 zizixyxyxy +−=−  ++−=+−⇔+=  tập hợp điểm M là đường thẳng:2. xy ∆+=

Ta có () 1 PwiziziziMN = +−− == == với ()0;1. N

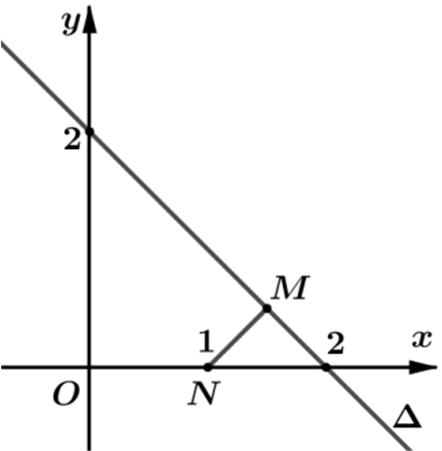
Dựa vào hình vẽ ta thấy () minmin 012 2 ,. 2 2 PMNdN +− ==∆==

Cách2(Dùngbất đẳngthứcBunhiacopxki).

Đặt zxyi =+ () , xy ∈ ℝ và () ; Mxy là điểm biểu diễn số phức. z

tr

Lấy ý tưởng từ bài toán trên ta có bài toán tương tự sau

Bàitoán2.Xét các số phức z thỏa mãn 12.zzi =−+ Tìm giá trị nhỏ nhất

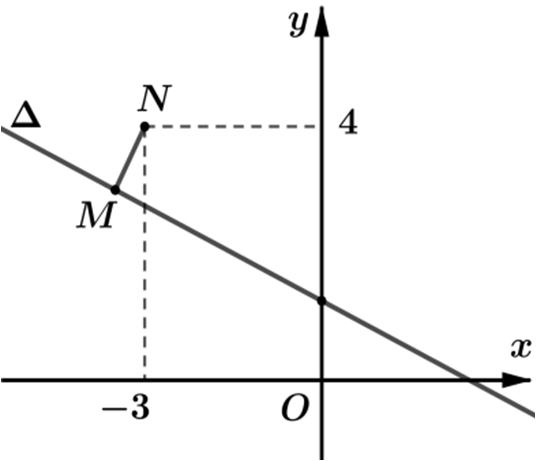
của biểu thức ()12112 Pizi =+++

Lờigiải.

Cách1(Dùngphươngpháphìnhhọc)

Đặt zxyi =+ () , xy ∈ ℝ và () ; Mxy là điểm biểu diễn số phức. z

Từ ()() 22 22 1212245 zzixyxyxy =−+  +=−+−+⇔+=  tập hợp điểm M là đường thẳng:245. xy ∆+=

Tacó () 112 12112125345 12 i PiziizziMN i + =+++=++=+−= + với ()3;4. N

Dựa vào hình vẽ ta thấy () () minminmin 2.34.455 5.,5. 202 PMNPdN −+− ⇔→=∆==

Cách2(Dùngtínhchấthàmsố bậchai).

Từ 5 2452 2 xyxy +=  =− . Khi đó,

2 2222 2 11185343424530 24 zixyyyyyfy

là hàm số bậc hai có 50 a => nên đạt giá trị nhỏ nhất bằng 5 4 . Vậy 2 2 min 255 534 42 PziP =+−≥

Bàitoán3. Xét các số phức z thỏa mãn 13. zizi +−=− Tìm giá trị lớn

nhất của biểu thức Pw = , với 1 w z = .

Phântíchvà tìmlờigiải.

Đây là bài toán biến thể từ hai bài toán trên khi 1 z lớn nhất khi và chỉ khi

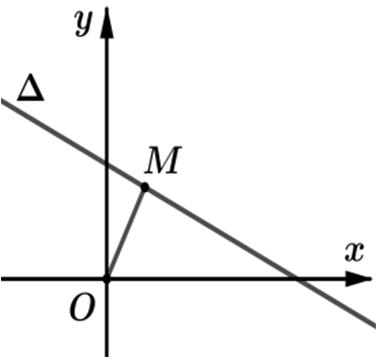
z nhỏ nhất khi và chỉ khi OM nhỏ nhất, M là điểm biểu diễn của số phức z

với tâp hợp điểm M thỏa điều kiện cho trước là một đường thẳng có phương

trình:247 xy ∆+=

Lờigiải.

Cách1.(Dùngphươngpháphìnhhọc)

Đặt zxyi =+ () , xy ∈ ℝ và () ; Mxy là điểm biểu diễn số phức. z

Từ

()()() 222 2 13113247 zizixyxyxy +−=−  ++−=+−⇔+= 

tập hợp điểm M là đường thẳng:247. xy ∆+=

2 13213253 wiwicdcdcd ++≤− 

tậ

hợp điểm N biểu diễn số phức w là phần tô đậm như trên đồ thị có tính biên

2 :53 xy ∆+=− .

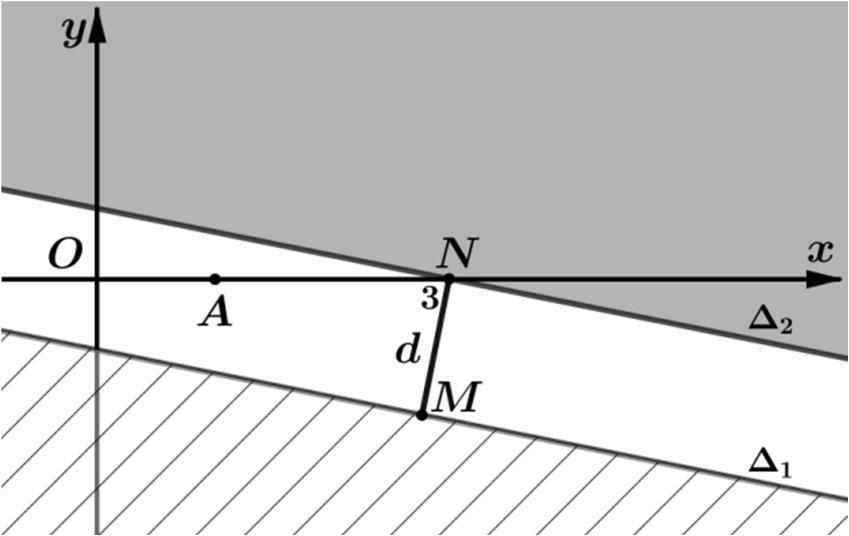
Dựavàohìnhvẽ tathấy Dấu "" = xảyrakhivàchỉ khi 1 M ∈∆ , 2 N ∈∆ và 2 MN ⊥∆ .

Nhậnxét: Bài toán này phức tạp hơn, khiến học sinh cảm thấy lúng túng hơn các bài toán trên ở chỗ xuất hiện bất đẳng thức 132 zizi −−≤+ và 132 wiwi ++≤− và điều khác biệt nữa là xuất hiện tới hai số phức z và w

Nhưngnếu để ý mộtchútthì ở biểu thức zw chínhlà độ dài MN với , MN là điểmbiểudiễncủa z và w .Vậy P nhỏ nhấtkhivà chỉ khi MN nhỏ nhấtkhi và chỉ khi () 12 , MNd=∆∆

Bàitoán7.Xét các số phức z thỏa mãn 11 iz −+= . Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức . Pz =

Phântíchvà tìmlờigiải.

Biến đổi đẳngthức 11 iz −+= như sau 1111izizizi −+=⇔−+=⇔+=

.Vậytậphợp điểmbiểudiễncủasố phức z là một đườngtrònnên bàitoántrên

đượcgiảiquyết đơngiảnnhư sau.

Lờigiải.

Cách1.(Dùngphươngpháphìnhhọc)

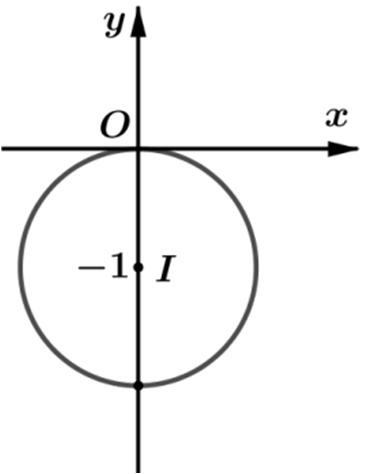
Tacó 11.11izizizi −+=⇔−+=⇔+=  tậphợpcác điểmbiểudiễn

số phức z thuộc đườngtròncótâm () 0;1 I ,bánkính 1 R = .

Cách2.(Dùngphươngpháplượnggiác)

Từ () 22 2

11111zizxy +=⇔+=⇔++= suy ra luôn tồn tại số

[] 0;2 απ ∈ saocho: sin;1cosxyαα==−+ .

Khi đó, () 2 2 2 sin1cos22cos z ααα=+−+=−

Do cos1 α ≤ nên 2 0402 zz≤≤  ≤≤

Vậy minmax0,2PP== .

Cách3.(Dùngbất đẳngthứctamgiác).

Ápdụngbất đẳngthứctamgiác,tacó

11102zizizizzz −≤+≤+⇔−≤≤+⇔≤≤

Vậy minmax0,2PP== .

Bàitoán8.Xét các số phức z thỏa mãn 231zi−−= . Tìm giá trị lớn nhất

và giá trị nhỏ nhất của biểu thức 1 Pzi =++ .

Phântíchvà tìmlờigiải.

Điểm khác biệt với bài toán 11 là ở biểu thức 1 Pzi =++ chứa z , ta có

thể biến đổivà đưavề dạngquenthuộcnhư sau: 11 zizi ++=+− .Khi đó,bài

toándễ dàng đượcgiảiquyếtnhư sau.

Lờigiải.

Cách1.(Dùngphươngpháphìnhhọc)

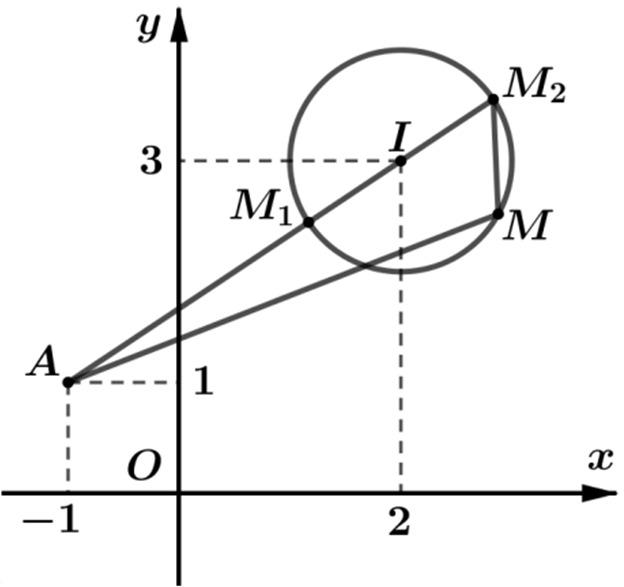
Ta có 231zi−−=  tập hợp các điểm M biểu diễn số phức z thuộc

đườngtròncótâm () 2;3 I ,bánkính 1. R = s

Tacó 11 PziziMA =++=+−= với ()1;1. A

Cách2(Dùngphươngpháplượnggiác).

Từ ()() 22 231231zixy −−=⇔−+−= nên tồn tại số [] 0;2 απ ∈ sao cho:2sin;3cos xyαα=+=+

Khi đó

()()()() 22222 1113sin2cos146sin4coszixy αααα+−=++−=+++=++

Do 2 2136sin4cos21314213114213 zi αα −≤+≤  −≤+−≤+

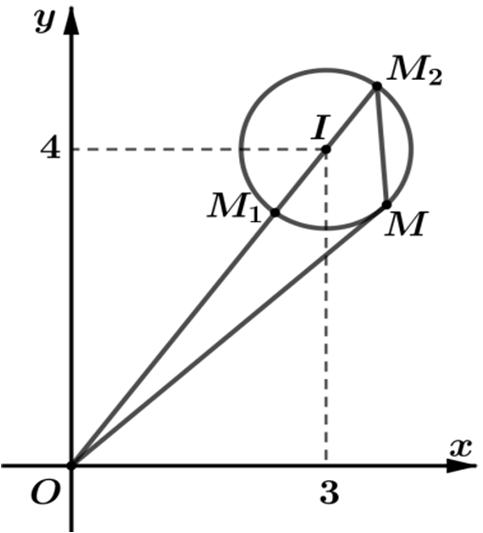
1311131 zi  −≤+−≤+

Vậy minmax131,131PP=−=+ .

Cách3(Dùngbất đẳngthứctamgiác).

Tacó ()()

+−−−≤++−−≤++−−

⇔−≤+−≤+

322332233223 1311131 iziiziizi zi

Vậy minmax131,131PP=−=+ .

Tươngtự bàitoántrên,tacó bàitoánsau.

Bài toán 9.Xét các số phức z thỏa mãn ()1172. izi ++−= Tìm giá trị

nhỏ nhất và giá trị lớn nhất của . Pz =

Lờigiải.

Cách1.(Dùngphươngpháphìnhhọc)

Ta có () () 172 1172341 11 i izizzi ii ++−=⇔+=⇔−+=  ++ tập

hợpcác điểm M biểudiễnsố phức z thuộc đườngtròncótâm () 3;4 I ,bánkính

1 R = .

514 516 POMOIR POMOIR  ==−=−=

==+=+=

Từ () ()() 22 341341zixy −+=⇔−+−= suy ra luôn tồn tại số

[] 0;2 απ ∈ saocho: 3sin;4cosxyαα=+=+ .

Khi đó, ()() 2223sin4cos266sin8cos z αααα=+++=++

Do 106sin8cos10 αα −≤+≤ nên 2 163646 zz≤≤  ≤≤

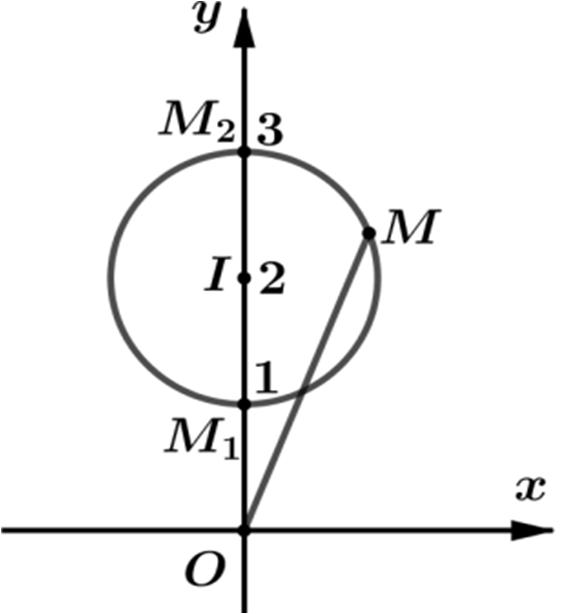
Vậy minmax4,6PP== .

Cách3.(Dùngbất đẳngthứctamgiác).

Ápdụngbất đẳngthứctamgiác,tacó

() 34343451546 zizizizzz −+≤−+≤++⇔−≤≤+⇔≤≤ .

Vậy minmax4,6PP== .

Bàitoán10.Xét các số phức , zw thỏa mãn () 1 21 1 iz i + += và wiz = Tìm

giá trị lớn nhất của biểu thức Pzw =−

Phântíchvà tìmlờigiải.

Từ biểu thức zw với wiz = nên 12 zwzizziz −=−=−= đưa về yêu

cầuquenthuộc.

Lờigiải.

Cách1.(Dùngphươngpháphìnhhọc).

Từ () ()121 1 2121 111 izi i zzi iii +− +=⇔+=⇔−=  −++ tập hợp các

điểm M biểudiễnsố phức z thuộc đườngtròncótâm ()0;2, I bánkính 1. R =

Theo giả thiết 122 wiz PzwzizzizOM = =−=−=−== với ()0;0. O

Dựavàohìnhvẽ tathấy max22222132.POMOIR==+=+=

Cách2.(Dùngphươngpháplượnggiác)

Từ ()2 2 2121zixy −=⇔+−= suyraluôntồntạisố [] 0;2 απ ∈ saocho: sin;2cosxyαα==+ .

Khi đó, () 22 2 sin2cos54cos z ααα=++=+

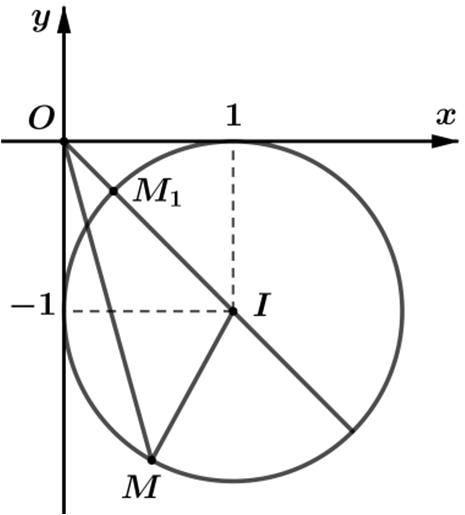
Do cos1 α ≤ nên 2 1913 zz≤≤  ≤≤

Vậy max 32 P = .

Cách3.(Dùngbất đẳngthứctamgiác).

Ápdụngbất đẳngthứctamgiác,tacó 223232zizizz −≤−⇔≤⇔≤ .

Vậy max 32 P = .

Cùng ý tưởngnhư bàitoán14,tacó bàitoán15sau đây.

Bàitoán11.Xét các số phức 12 , zz thỏa mãn 1 11zi−+= và 212.ziz = Tìm

giá trị nhỏ nhất của biểu thức 12 2 Pzz =− .

Lờigiải.

Cách1.(Dùngphươngpháphìnhhọc).

Từ 1 11zi−+=  tập hợp các điểm M biểu diễn số phức 1z thuộc đường

tròncótâm ()1;1, I bánkính 1. R =

Theo giả thiết ta có 21 2

12111 2222122 ziz PzzzizizOM = =−=−=−= với ()0;0. O

Dựavàohìnhvẽ tathấy

min122222221422.POMOIR==−=−=−

Cách2.(Dùngphươngpháplượnggiác)

Từ ()() 22 1 11111zixy −+=⇔−++= suy ra luôn tồn tại số [] 0;2 απ ∈

saocho: 1sin;1cosxyαα=+=−+

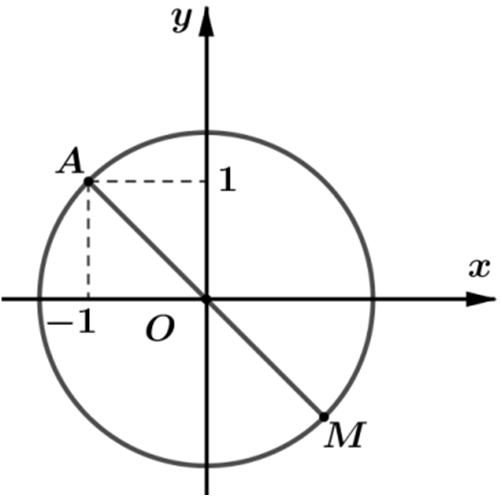
Khi đó, ()() 222 1 1sin1cos32sin2cos z αααα=++−+=+−

Do 2sin2cos22 αα−≤

nên 2 1 1 3223222121 zz−≤≤+  −≤≤+

Vậy min 422 P =− .

Cách3.(Dùngbất đẳngthứctamgiác).

Ápdụngbất đẳngthứctamgiác,tacó () 111 1 11211212 zizizz −−≤−−⇔−≤⇔−+≤≤+ .

Vậy min 422 P =− .

Bài toán 12.Xét các số phức z thỏ

Tacó 1 PziMA =+−= với ()1;1. A Vậy max 2222. PAOR=+=+=

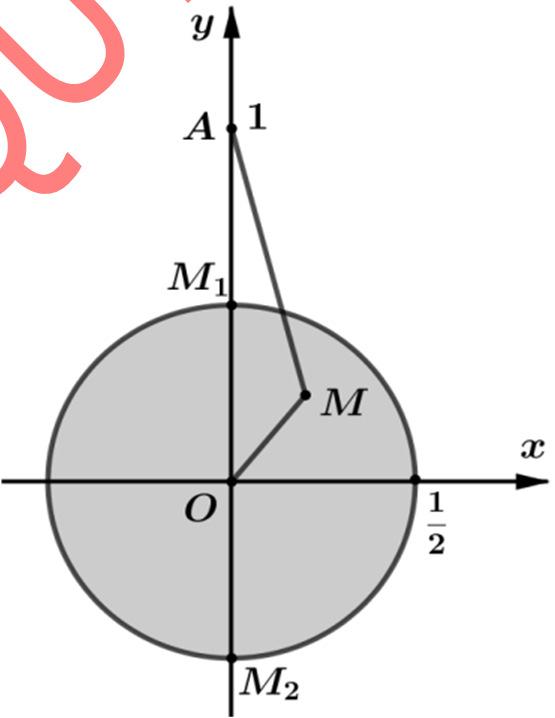
Nhậnxét.

Tư duy bài này cũng giống như những bài trên nhưng khá phức tạp hơn mộtchút ở giả thiết.

Bàitoán13.Xét các số phức z thỏa mãn 2 z ≥ . Biểu thức Pzi z + = đạt giá trị nhỏ nhất và giá trị lớn nhất lần lượt tại 1z và 2z . Tìm phần ảo của số phức 12. wzz =+

Lờigiải.

Biến đổi 11 1 zii Pii zzzz + ==+=−=− .

Nhậnxét.

Bàitoán nàythoạt đầu đễ đánhlừangười làmlẩn quẩn đitìm phần ảo của số phức w theo phương pháp đại số thông thường. Điều này sẽ vô cùng khó

khăn và có thể đi vào ngõ cụt nhưng nếu để ý kĩ thì biểu thức Pzi z + = phân

tích đượcthànhnhư sau 11 1' i iizi zzz +=−=−=− với 1 ' z z =

Bàitoán14.Xét các số phức z thỏa mãn 1. z = Tìm giá trị lớn nhất và nhỏ

nhất của 2 . 2 Pzi z + =

Phântíchvàtìmlờigiải.

Điều kiện 1 z = → tập hợp điểm biểu diễn của z là đường tròn tâm O ,

bánkính 1 R = .Khókhăncủabàitoánnàylàviệcbiến đổibiểuthức P .Dễ đưa người độc nhầm lẫn và cứ bám víu vào 1 z = là đường tròn và sẽ phụ thuộc

đường tròn này sẽ đi đến ngõ cụt. Để ý biểu thức 2 2 zi z + là phép chia hai số

phức,nếu dùngsố phức phụ 2 2 zi w z + = thì khi đó 2 2 wi z w + = và dựavào 1 z =

nên 2 1 2 wi w + = .Từ đâytìmra đượctập điểmbiểudiễnsố phức w là đườngtròn

và bài toán trở nên dễ dàng hơn khi đánh giá đượ

Bài toán 15.Xéthaisố phức 12 , zz thay đổithỏamãn

1212 422.zzzzi −=++−= Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu

thức 22 12 . zz +

Phântíchvà tìmlờigiải.

Bài toán này lạ hơn các bài toán trên là có tới hai số phức 12 , zz . Quan sát

biểuthức 12 2 zz−= đó chínhlà đoạn 2 MN = ,với , MN là các điểmbiể

á trị nhỏ nhấtcủa P đưavề tìmgiá trị lớnnhất,giá trị nhỏ nhấtcủa OK ,nghĩalà tìm điểm K saocho 2 2 2 2 MN OK + đạtgiá trị lớnnhấtvà

giá trị nhỏ nhất.

Từ biểu thức 12 422zzi++−= biến đổi thành 12 21 2 zzi + +−= cho thấy

tập hợp K là đường tròn tâm () 2;1 A , bán kính bằng 1. Đến đây bài toán trở nêndễ dànghơnvà đượctrìnhbàygiảichitiếtnhư sau.

Lờigiải.

Gọi , MN lầnlượtlà điểmbiểudiễncủahaisố phức 12 , . zz

Gọi K làtrung điểmcủa MNK  là điểmbiểudiễncủasố phức 12 . 2 zz +

 12 22.zzMN −=  =

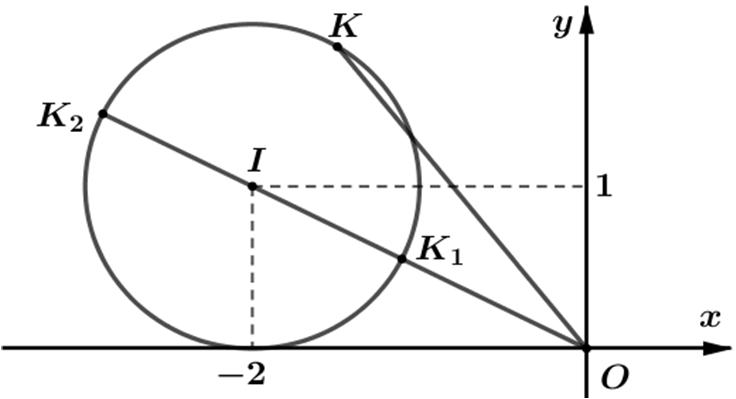
 12 12 42221 2 zz zzii + ++−=⇔+−=  tập hợp các điểm K thuộc đường

tròncótâm ()2;1, I bánkính 1. R =

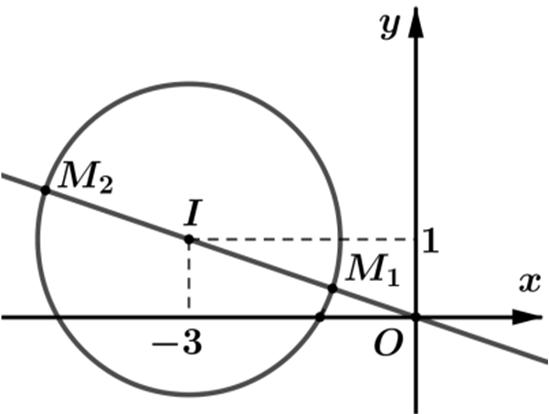
Bài toán 16.Cho số phức z thỏa mãn đồng thời 125zi−+= và 1 zi ω=++ có môđun lớn nhất. Tính z.

Phântíchvà tìmlờigiải.

Dữ kiệnlà số phức ω có môđunlớnnhấtnêntasẽ đitìmtậphợpbiểudiễn của ω.

Từ 1 zi ω=++ biến đổilàmsao để vế phảixuấthiện 12 zi −+ thì bàitoán xemnhư đã đượcgiảiquyết.Cụ thể bàitoán đượcgiảinhư sau.

Lờigiải.

Tacó ()() 1122212. ziziiiziωωω =++⇔=−++−⇔−+=−+

Suy ra 2125 izi ω−+=−+=  tập hợp các điểm M biểu diễn số

phức ω thuộc đườngtròncótâm ()2;1, I bánkính 5. R =

Dựavàohìnhvẽ tathấysố phức ω cómôđunlớnnhấtcó điểmbiểudiễnlà

() 1 4;2. M

Với () 1 1 4;2423332. zi Miziz ω ω =++  =−→=−  =

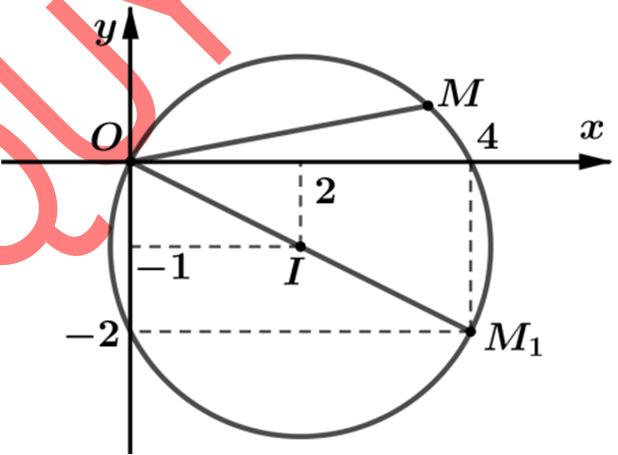
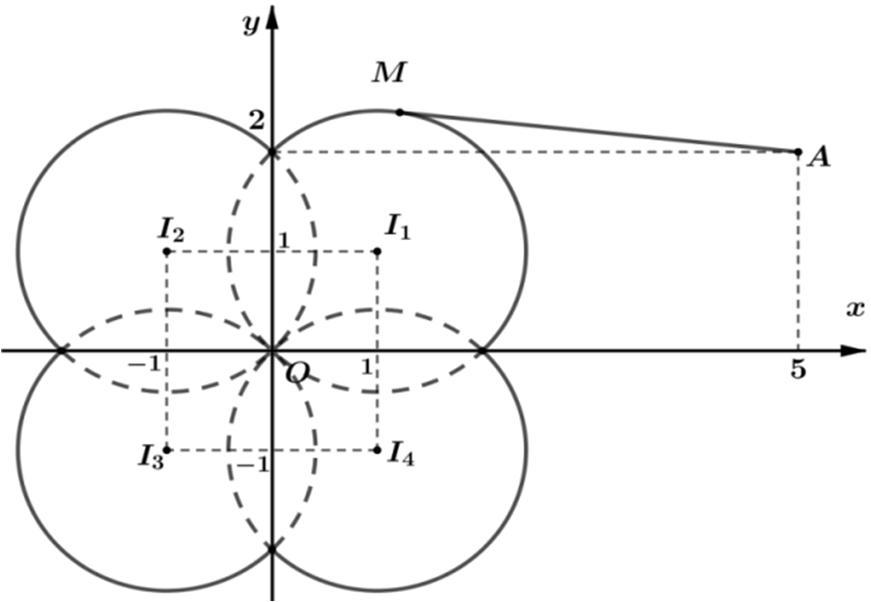
Bài toán 17.Xét các số phức z thỏa mãn 2422.zi−−= Trong các số phức w thỏa mãn ()1,wzi =+ g

i

w

w lần lượt là số phức có môđun nhỏ nhất và môđun lớn nhất. Tính 12ww + .

Phântíchvà tìmlờigiải.

Từ biểu thức ()21 wi =+ ta suy ra được 12 wziz =+= mà tập hợp

biểudiễncủa z là một đườngtrònnênbàitoán đượcgiảiquyếtdễ dàngnhư sau.

Lờigiải.

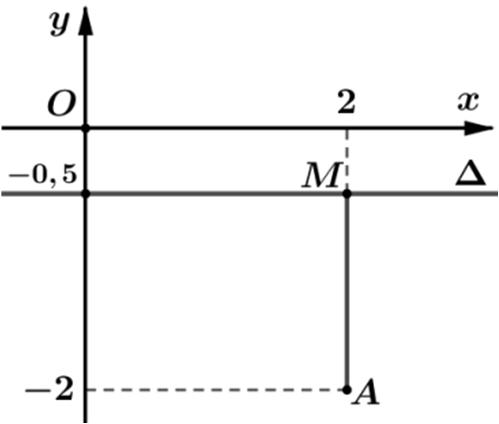
Từ 2422zi−−=  tập hợp các điểm M biểu diễn số phức z thuộc

đườngtròncótâm ()2;4, I bánkính 22. R =

Tacó ()1.122 PwzizizOM ==+=+== với ()0;0. O

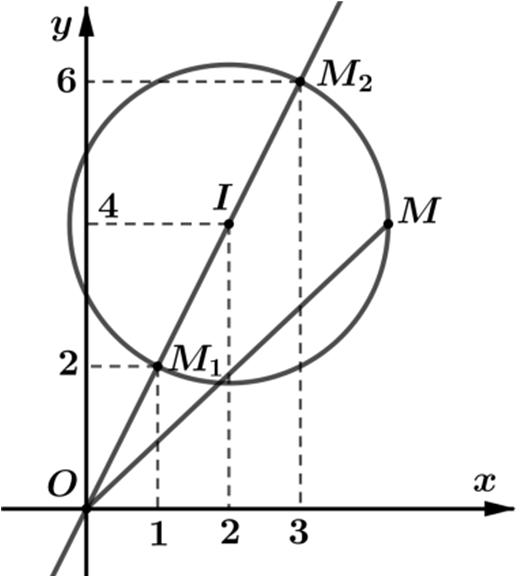
Dựavàohìnhvẽ tathấy

 min1 2.POM =

Dấu '''' = xảyra

()() 111212113. MMziwiii⇔≡⇔=+  =++=−+

 max22.POM =

Dấu '''' = xảyra

()() 223636139. MMziwiii⇔≡⇔=+  =++=−+

Vậy 12 412. wwi +=−+

Bài toán 18.Xét các số phức z thỏa 1225zi−+= và số phức ω thỏa () () 5103425. iizi ω +=−− Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P ω = .

Lờigiải.

Tacó

() () 5103425 iizi ω +=−−

() ()() 5103412535 iizii ω ⇔+=−−+−− (mục đích để tạora 12 zi −+ )

() ()() 5105353412 iiizi ω ⇔+++=−−+ (chuyểnvế).

Suyra () ()() 51053534125.25105. iiizi ω +++=−−+==

535105 3232 510510 i ii ii ωωω + ⇔+=⇔++=⇔+−=  ++ tập hợp các điểm

M biểudiễnsố phức ω thuộc đườngtròncótâm ()3;1, I bánkính 2. R =

Bài toán 19.Xét các số phức z thỏa mãn 2 . zzzzz ++−= Tìm giá trị

lớn nhất của biểu thức 52 Pzi =−− .

Phântíchvà tìmlờigiải.

Bài toán này dữ kiện có vẻ khó khăn howncacs bài toán trên nhưng nếu

bình tĩnh phân tích kĩ ta cảm thấy nó cũng khá dễ chịu khi khai thác dữ kiện 222 22 zzzzzxyxy ++−=⇔+=+ với () , zxyixy=+∈ ℝ . đến đây

dáng dấp của đường tròn hiện ra. Vậy bài toán trở nên dễ dàng và được giải

quyếtnhư sau.

 +=

2 2. zzx zxyizzyi zzxy

222   =−  −=   ==+  

Từ giả thiết 222 22. zzzzzxyxy ++−=  +=+ () *

  TH 1. 0 0, x y ≥   ≥  khi đó () * trở thành ()() 22 112xy−+−= có hình biểu diễnlàcungtrònnétliền ở gócphầntư thứ ()I.

  Tươngtự chocáctrườnghợpcònlại(thamkhảohìnhvẽ)

Gọi () 5;2 A và () ; Mxy là điểm biểu diễn số phức ,z khi đó

52. PziMA =−−=

Vì A nằm ở gócphầntư thứ () I nên MA lớnnhấtkhi M phảinằm ở góc phầntư thứ ()III.

Suyra max33 352. MAAIR=+=+ Vậy max352. P =+

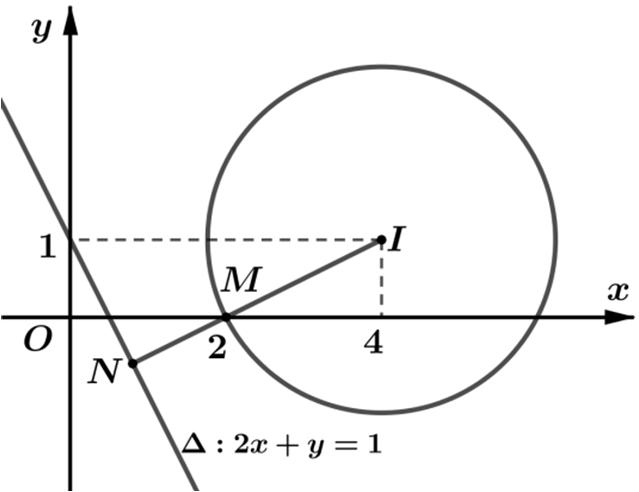
Bàitoán20. Xét các số phức 1z thỏa mãn 22 1121zzi−−+= và các số

phức 2z thỏa mãn 2 45zi−−= . Tìm giá trị nhỏ nhất của 12Pzz =−

Phântíchvà tìmlờigiải.

Tachú ý biểuthứccầntìm 12Pzz =− đó chínhlà độ dài đoạnthẳng NM , với , NM là điểmbiểudiễnsố phức 12 , zz .Vậyyêucầubàitoáncó thể đưavề

bàitoán“Tìmgiá trị ngắnnhấtcủa đoạnthẳng MN ”.Bâygiờ taxemtậphợp , MN là gì?

Từ giả thiết 22 1121zzi−−+= chotatậphợp N là một đườngthẳng

:210 xy ∆+−= và 2 45zi−−= thì tậphợp M là một đườngtròn () C tâm ()4;1,bánkính 5 R =

Vậybàitoántrở thànhtìm điểm N ∈∆ và ()MC ∈ saocho MN ngắnnhất.

Lờigiải.

G

Từ đósuyra [] min 835 ,5. 5 5 PMNdIR==∆−=−=

Bài toán 21.Gọi() 1 Clàtậphợpcácsố phứcwthỏamãn

2332. wiwi +−≤−+ Gọi () 2 Clà tập hợp các số phức z thỏa mãn

241.zi−+≤ Tìm giá trị nhỏ nhất của biểu thức Pwz =−

Lờigiải.

Đặt () ; ,,,.zxyiwabixyab =+=+∈ ℝ Tacó

 2332 wiwi +−≤−+

()()()() 2222 23320 ayabab  ++−≤−++⇔−≤  tập hợp điểm M biểu diễnsố phức w thuộcnửamặtphẳngbờ :0 xy ∆−= vàkể cả bờ (miềntô đậm như hìnhvẽ).Gọimiềnnàylà () 1 . C

 ()()

1. R =

()()

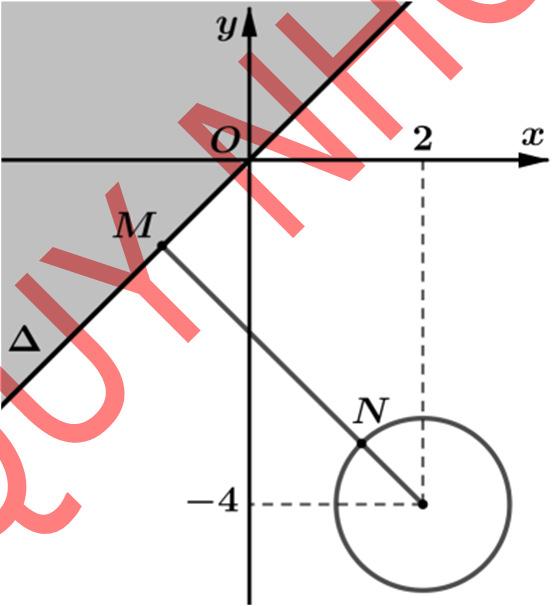
22 241241241 zixyixy −+≤  −++≤⇔−++≤  tập hợp điểm N biểu diễn số phức z là hình tròn () 2C có tâm ()2;4, I bán kính

Khi đóbiểuthức PzwMN =−= làkhoảng cách từ một điểmthuộc () 1C

đếnmột điểmthuộc () 2C .

Từ đósuyra [] min ,321.PdIR=∆−=−

Nhậnxét.Tư duybàitoántrêncũnggiốngnhư bàitoán24.

Bài toán 22.Xét các số thức z thỏa mãn 24 zizi −≤− và 331zi−−=

.Tìm giá trị lớn nhất của biểu thức 21 Pz=−+ .

Phântíchvà tìmlờigiải.

Từ biểuthức 211PzMB=−+=+ ,với () 2;0 B và M làtậphợp điểmbiểu

diễncủa z .Vậyyêucâubàitoántrở thành“Tìmvị trí điểm M saocho 1 MB +

lớnnhất”.

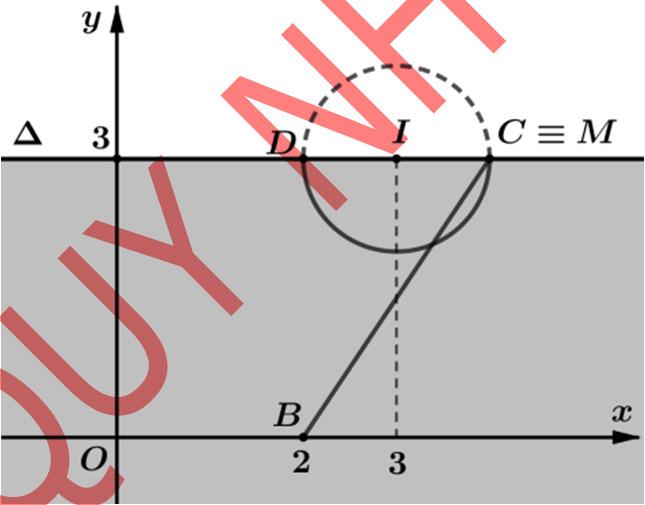
Ta đitìm điểm M .Với điềukiệnbàitoánnàythì z thỏamãnhai điềukiện 24 zizi −≤− và 331zi−−= cho nên tập hợp điểm biểu diễn M của z vừa thuộc nửa mặt phẳng bờ :3 y ∆= và thuộc đường tròn tâm () 3;3 I , bán kính 1 R = nên tập hợp điểm M thuộc cung tròn CD nằm phía mặt phẳng. Vậy bài toántrêncó lờigiảinhư sau.

Lờigiải.

Gọi () , zxyixy=+∈ ℝ .Tacó



()() 2222 24243 zizixyxyy −≤−  +−≤+−⇔≤  tập hợp điểm

biểu diễnsố phức z thuộcnửamặtphẳngbờ :3 y ∆= ,kể cả bờ (miền tô đậm).

Gọimiềnnàylà () 1C



()() ()() 22 331331331 zixyixy −−=  −+−=⇔−+−=  tập hợp

điểmbiểudiễnsố phức z là đườngtròn () 2C cótâm ()3;3, I bánkính 1. R =

Như vậy tập hợp điểm M biểu diễn số phức z là giao của () 1C và () 2C .

Đó chính là phần cung tròn nét liền như trên hình vẽ (có tính 2 điểm đầu mút ()() 2;3, 4;3 DC củacung).

Khi đó 211PzMB=−+=+ với () 2;0 B và MB là khoảng cách từ điểm

B đếnmột điểmthuộccungtròn CD .

Từ đósuyra max 1131. PBC=+=+

Bài toán 23.Xét các số phức , zw thỏa mãn 221iziz−−≤− và

{} max22,2. wiw+−≤ Tìm giá trị nhỏ nhất của biểu thức Pzw =− .

Lờigiải.

Gọi ();, MxyN lầnlượtlà điểmbiểudiễncủahaisố phức ,.zw

 221221 izizziz −−≤−⇔−+≤−

()()() 222 2 2212470 xyxyxy ⇔−++≤−+⇔−++≤  tập hợp điểm M biểudiễnsố phức z thuộcnửamặtphẳngbờ :2470 xy ∆−++= khôngchứa O (kể cả bờ).

 {} max22,2, wiw+−≤ suyra () () 222 2,2;2 22, 0;0 wiNII wNOO

N  thuộcphầnchungcủahaihìnhtròn () ;2I và () ;2O .Màhaihìnhtròn

nàytiếpxúcngoàitại điểm ()1;1. E Do đó ()1;1. NE≡−

Ta có PzwMN =−= nên P nhỏ nhất khi MN ngắn nhất, khi đó M là

hìnhchiếucủa N trên ∆ và () () () min 2 2

214.17 13 ,. 25 24 PdN −−++ =∆== −+

Nhậnxét. Bàitoántrênkế thừa ý tưởngtừ cácbàitoán25,26và 27nhưng

có điểmmới ở dữ kiên {} max22,2 wiw+−≤ .

Bài toán 24.Xét các số phức , zw thỏa mãn {} max;11 . 122 zzi wiwi  −−≤   ++≤−−   Tìm

giá trị nhỏ nhất của biểu thức Pzw =−

Lờigiải.

Gọi (),; MNxy lầnlượtlà điểmbiểudiễncủahaisố phức ,.zw



()()()() 2222 1221221 wiwixyxy ++≤−−  +++≤−+− 0 xy ⇔+≤  tập hợp điểm N biểu diễn số phức w thuộc nửa mặt phẳng

bờ :0 xy ∆+= vàkể cả bờ (miềntô đậmnhư hìnhvẽ).

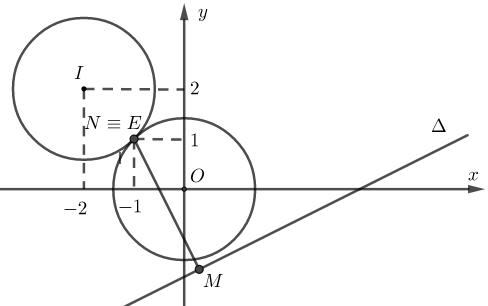
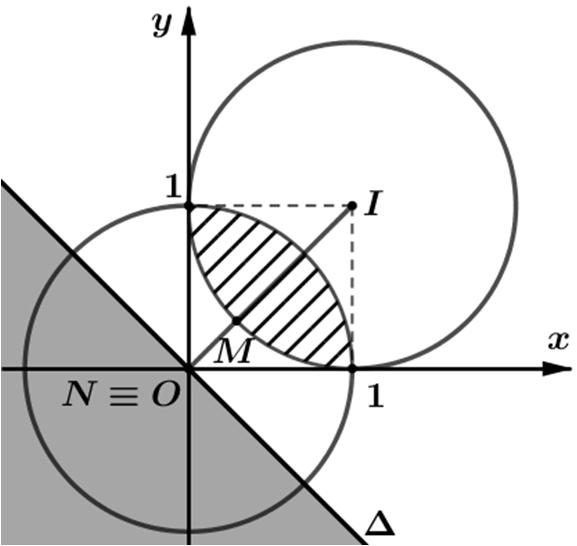
 {} max;11, zzi−−≤ suyra () () 111,1;1 1, 0;0 1 ziMII MOO z  −−≤≤  

M  thuộc phần chung của hai hình tròn () ;1 I và () ;1O (phần gạch sọc như hìnhvẽ).

Ta có PzwMN =−= nên P nhỏ nhấtkhi MN ngắn nhất.Dựa vào hình

vẽ tathấy MN ngắnnhấtkhi NO ≡ và min 121. MNOI=−=−

Bàitoán25.Kí hiệu S là tập hợp các số phức z thỏa mãn 134 z −= và 12 zmizmi ++=++ (trong đó m ∈ℝ ). Gọi 12 , zz là hai số phức thuộc tập

hợp Ssao cho 12 zzlà lớn nhất. Khi đó, hãy tính giá trị của biểu thức

12 . zz +

Phântíchvà tìmlờigiải.

Mới đầu,tâmlí họcsinhthấysự có mặtcủathamsố m là cảmthấylolắng

và muốnné tránhnhưngchúngtanêncố gắngbìnhtĩnh để giảiquyếtvấn đề.

Nếu gọi , AB lần lượt là các điểm biểu diễn của số phức 12 , zz thì yêu cầu bài

toántrở thành“Tính độ dàicủa OAOB + ”.

Từ 134 z −= và 12 zmizmi ++=+= suy ra tập hợp biểu diễn của z

vừathuộc đườngtròn () C tâm () 1;0 I ,bánkính 34 R = và thuộc đườngthẳng

()() 224230 mxmy ∆−+−+= . Đường thẳng ∆ này sẽ cắt đường tròn tại hai

điểm đó chínhlà , AB

Hơn nữa 12zz đạt giá trị lớn nhất nên AB lớn nhất suy ra AB chính là

đường kính của đường tròn () C khi đó I sẽ là trung điểm của đoạn AB . Vậy

2 OAOBOI += .Vậy đến đâycoinhư bàitoán đã đượchoàntoàngiảiquyêt.

Lờigiải.

Đặ

Từ () 1 và ()2, suy ra tập các điểmbiểu diễn số phức z củatập S làgiao

điểmcủa ∆ và (). C

Gọi , AB lần lượt là các điểm biểu diễn của hai số phức 12 , . zz Suy ra

12 .zzAB −=

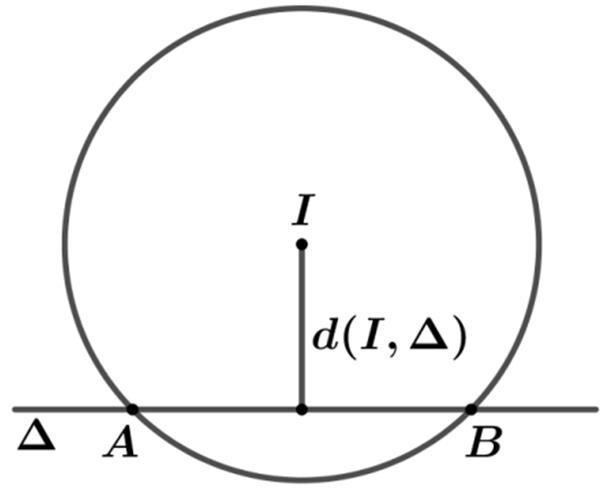
Để AB lớnnhất () , dI ⇔∆ nhỏ nhất ⇔∆ điqua điểm .I

Khi đó I làtrung điểmcủa AB nên 12 222.zzOAOBOIOI

Bài toán 26.Biết số phức () ; zxyixy=+∈ ℝ thỏamãn đồngthời

()345zi−+= và biểu thức 22 2 Pzzi =+−− đạt giá trị lớn nhất. Tính z.

Phântíchvà tìmlờigiải.

Bài toán nàyyêu cầutìm môđun của z trong đó z thỏa mãn hai điều kiện đã cho.

Điềukiệnthứ nhấtlà ()345zi−+= suyratậphợpcác điểmbiểudiễnsố

phức z là đườngtròn () C cótâm () 3;4 I vàbánkính 5 R =

Điều kiện thứ hai 22 2 Pzzi =+−− suy ra tập hợp điểm biểu diễn của z thuộc đườngthẳng :4230 xyP ∆++−= .

Vậy để bàitoánnàytính đượcthì phảitồntạisố phức z có nghĩalà đường thẳng ∆ và đườngtròn () C phảicó điểmchungkhuvà chỉ khi () , dIR ∆≤ .Từ

đâysẽ tìm được max P và bàitoánsẽ đượcgiảiquyếtdễ dàng.

Lờigiải. Vì ()345zi−+=  tập hợp các điểm biểu diễn số phức z là đường

tròn () C cótâm () 3;4 I vàbánkính 5 R = .

Tacó

4230. xyP  ++−=

Tatìm P saocho đườngthẳng :4230 xyP ∆++−= và đườngtròn () C có

điểmchung

1283 ,523101333. 20 P dIRPP ++−

xy

Do đó max 33 P = .Dấu "" = xảyra

Vậy 22 5552 z =+= .

Với ý tưởngnhư bàitrên,cácbàitoán31,32tươngtự.

Bài toán27.Xét các số phức z thỏa mãn 1313.zi−−= Tìm giá trị nhỏ

t và lớ

điểm biểu diễn số phức z là đường tròn () C có tâm ()1;3, I bán kính

13. R =

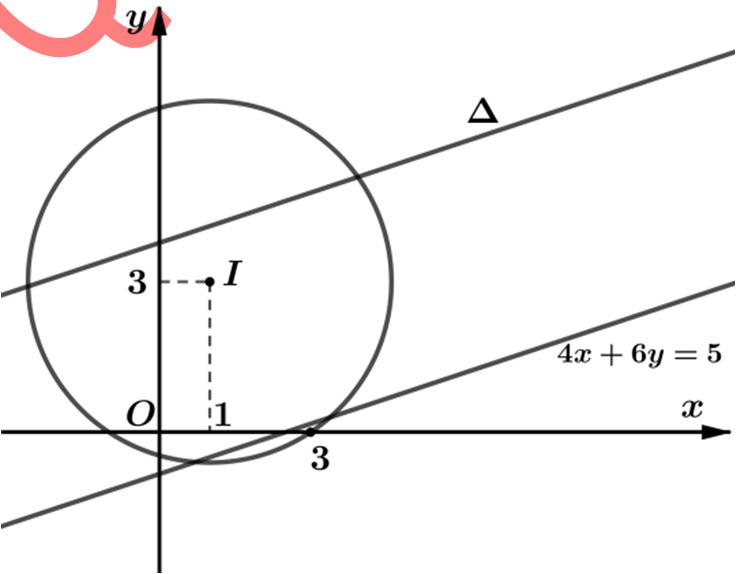
 Lại có 22 234654650. PzzixyxyP =+−−=+−  +−−= Suy ra tậphợpcácsố phức z thuộc đườngthẳng :4650. xyP ∆+−−= Để tồntại z thì ∆ và () C phảicó điểmchung [] 4.16.35 ,13 1636 P dIR +−− ⇔∆≤⇔≤ + 1726943 PP⇔−≤⇔ −≤≤

Dấu '''' = xảyrakhi

 thay 43 max :464. 40 38 P Pxy = =→∆+−= Tọa độ điểm z thỏa

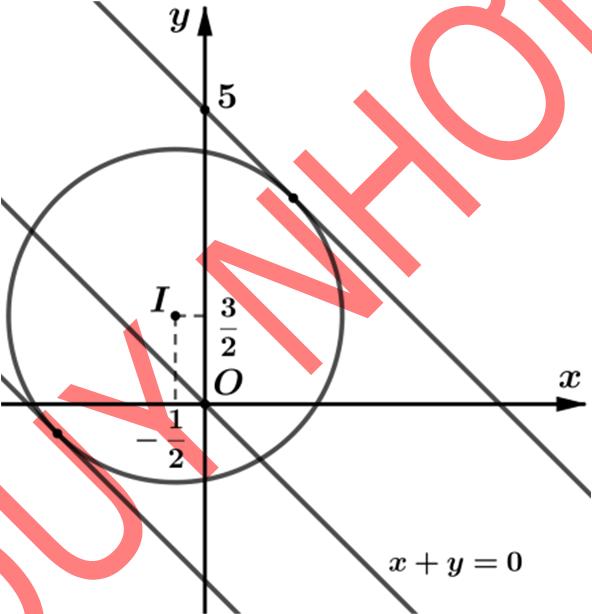
Bài toán 29.Xét các số phức z thỏa mãn 212.zi +=+ Tìm giá trị nhỏ

nhất của biểu thức |12||34||56| Pzizizi =−−+−−+−−

Phântíchvà tìmlờigiải.

Phân tích biểu thức P ta thấy có thể viết biểu thức P chính bằng tổng

MAMBMC ++ với M là điểm biểu diễn của số phức z còn

()()() 1;2,3;4,5;6ABC và đặc biệt là ba điểm ,, ABC thẳng hàng và cùng nằm

trên đường thẳng :10dxy−+= Đến đây dựa vào hình vẽ thì đáp án bài toán

đã hiệnradễ dàng.

Lờigiải. Đặt () ,.zxyixy=+∈ ℝ

Khi đó ()22 21225zixy +=+  ++=  tập hợp điểm M biểu diễn số

phức z thuộc đườngtròn () C cótâm ()2;0, I bánkính 5. R =

Ta có 123456 PziziziMAMBMC =−−+−−+−−=++ với ()()() 1;2,3;4,5;6ABC .

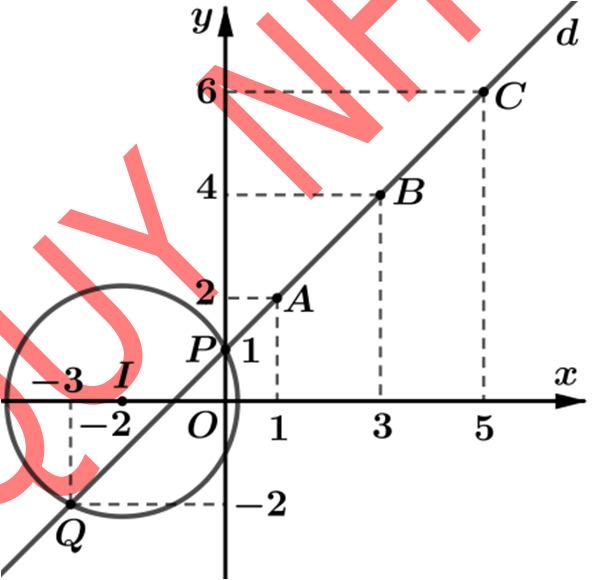
Nhận thấy các điểm , , ABC cùng thuộc đường thẳng :1.dyx=+

Đườngthẳng d cắt đườngtròn () C tạihai điểm () 0;1 P và ()3;2. Q

Vậy min PMP ⇔≡ và min 92. PPAPBPC=++=

2.4. Kết quả thực hiện

2.4.1. Hiệu quả trong công tác giảng dạy.

* Đốivớigiáoviên

Tài liệu viết về số phức cụ thể là về bài toán tìm giá trị lớn nhất, giá trị nhỏ nhất của mô đun trong số phức vẫn còn hạn chế. Vì vậy đối với giáo viên (kể cả học sinh) thì sáng kiến này là một tài liệu chuyên khảo hữu ích cho mỗi giáoviên,giúpchogiáoviêntiếtkiệm đượcnhiềuthờigian để nghiêncứu

Tàiliệu để giáoviênbồidưỡngônluyệncuốicấp ở cáctrườngTHPT.

* Đốivớihọcsinh

Tác giả đã vận dụng phương pháp trên và những phương pháp khác nữa trongviệcbồidưỡngônluyệnhọcsinhônthiTHPTQuốcgiacủatrườngTHPT

Ngô Lê Tân. Tương lai, tác giả cố gắng cùng đồng nghiệp bồi dưỡng thêm để

cùngnângcaokiếnthứcgiúpcácemvượtquakìthiTHPTQuốcgia.

Trong năm học 2018-2019 tôi đã thực hiện đề tài này trên lớp 12A2 và

kiểmnghiệmkếtquả saumộtthờigian ứngdụng đêtàinhư sau:

2.4.2. Lợi ích kinh tế - Nâng cao hiệu quả giảng dạy của giáo viên, đặc biệt là dạy học theo hướng nghiên cứu bài học và tiết kiệm được thời gian soạn giảng nghiên cứu, nghĩalàcóthêmthờigianlàmviệckhác để tăngthunhập, ổn định đờisốngkinh tế củagia đình.

-Nângcaochấtlượnghọctậpcủahọcsinh,giúphọcsinhcóthêmnguồn tài liệu học tập chuyên sâu bổ ích, hiệu quả, nghĩa là giuso cho các em và gia

đình đỡ phảitốnmộtkhoảngtiền đề muasáchthamkhảocholĩnhvựcnày.

2.4.3. Lợi ích xã hội

- Đề tàicóthể nóilàmón ăntinhthần,củngcố niềmtingiúpcácemvững

bước hơn trên con đường chinh phục tri thức của mình, giúp các em tránh xa

được các tệ nạn xãhội, tránh xa được những cám dỗ vật chất đời thường, cũng

như các trò chơi điện tử, la cà quán xá phổ biến hiện nay, ... góp phần làm cho diện mạo xã hội ngày càng tích cực hơn, khởi sắc hơn. Một xã hội mà ở đó có

nhữngconngườinhiềulòng đammêtronghọctập,hứngthútronglao động.

- Đề tài góp phần giảm thiểu học sinh bỏ học và tạo ra được môi trường học tập thật sự thân thiện. Một môi trường học tập mà ở đó giáo viên cởi mở, gầngũi,nhiệttìnhtronggiảngdạy,họcsinhtíchcựctronghọctậpvàphụ huynh họcsinhthìhàilòng,tintưởngvàosự giáodụcvàphốihợptốtvớinhàtrường.

3.Kếtluậnvàkhuyếnnghị

3.1. Những kết luận đánh giá cơ bản về sáng kiến

Chínhtừ nhữngthựctrạngvàtồntại đãnêu ở phần đầubàiviết,bằngtâm huyếtvàsự nỗ lựchếtmình củabảnthân,tôi đãhoànthiện được đề tàinày với hyvọngsẽ manglạimộtsố kếtquả:

Thứ nhất, có thể nói đây là một đề tài sáng kiến tương đối mới. Mới ở phương pháp, mới ở cách nhìn nhận, ở cách tiếp xúc và phân tích bài toán tìm giátrị lớnnhất,nhỏ nhấtcủamô đuntrongsố phức.

Thứ hai, qua đề tài này tác giả đã cung cấp them được một phương pháp giải toán “mới”. Một cách tiếp cận mới giúp bài toán tìm giá trị lớn nhất, nhỏ nhấtcủamô đuntrongsố phứcbớt điphầnnào“khôkhan”vàkhócủanó,tạora tính đadạngvàphongphúhơnchobàitoánnày.Qua đó,giúpngườihọctoánvà làmtoántự tinhơnkhitiếpcậnmộtbàitoánmới.

Đặc biệt, điều mà tácgiả hy vọng cuối cùng đó là đề tài này có thể được sử dụng trong thực tiễn bồi dưỡng, ôn luyện cho học sinh cuối cấp thi THPT Quốcgiavànângcaonănglựcchuyênmônchogiáoviên.

Tómlại,khithựchiệndạyvàhọctheosángkiếnnày,giaoasviênsẽ kích thích đượcsự nghiêncứucủahọcsinh,tínhtự họccủahọcsinh,sự đammêcủa họcsinh.Từ đó,nângcao hứngthú,tính tựugiáctrong họctập,pháttriểnnăng

lựccủahọcsinh,chấnchỉnh đượccáchhọctheolề lốicũ đãkhôngcònphùhợp

với chương trình giáo dục hiện nay của Việt Nam, cũng như theo kịp nền giáo dụctiêntiếntrênthế giới.Giúphọcsinhtừngbướckhắcphục đượctínhlườivề

tư duy, về rèn luyện kỹ năng, kỹ xảo trong giải toán, tiếp thu bài một cách thụ

động để tiến tới ham thích tìm tòi, phát hiện và sáng tạo, tự rèn luyện kỹ năng sống. Từ đó, sẽ đào tạo ra những con người mới, năng động, sáng tạo, độc lập trong công việc và có một khối óc phát triển toàn diện, dáp ứng được mọi nhu cầukhắtkhevề conngườitrongthời đạimới.

3.1.2. Tính khả thi, khả năng áp dụng

Đề tài chỉ sử dụng kiến thứcnền rấtcơ bản (SGK),một số phép biến đổi tương đương, mối tương quan giữa đại số và hình học. Vì vậy, hầu như tất cả

các đối tượng học sinh đều có thể tiếp cận được phương pháp mới này. Bên

cacnhj đó, tác giả cũng đưa ra nhiều bài toán vận dụng ở mức độ cao dành cho đốitượnghọcsinhkhágiỏi.Tómlại, đề tài đơngiản trong cách dùngvàphong

phú đadạngtrongcáclĩnhvựckhiápdụng,khôngcần đếncác điềukiện để hạn chế sử dụngnêncóthể nóitínhkhả thicủa đètàilàtueong đối.

Đề tàikhôngchỉ vậndụng đượcchocácbàitoántrongchươngtrìnhsách

giáo khoa THPT hiện hành mà còn có thể áp dụng rộng rãi cho các bài toán

trongcácchuyên đề ônluyệnthiTHPTQuốcgia,...Vìvậy,cóthể nóikhả năng

ápdụngcủa đề tàirộng,phùhợpchomọi đốitượnghọcsinh,giáoviênlinhhoạt

biênsoạngiảngdạy.

3.1.3. khả năng phát triển của đề tài

Những khám phá từ lời giải của tác giả là hoàn toàn mới. Nhưng điều quan trọng hơn cả là: Vận dụng những ý tưởng khám phá từu sáng kiến không chỉ giảiquyếttrựctiếp bàitoáncầngiảimàtacòn mở rộng vàrútra đượccách giảitổngquátchomộtlớpbàitoán,tínhmới,tính sáng tạo,khả năng pháttriển củasángkiếnlà ở đây!Cònhơnthế nữamộtkhi đãhiểubàitoánmộtccahsthấu đáo, tường minh ta có thể tự điều chỉnh, tự sáng tác, phát triển để nhận được nhữngbàitoáncóchiềusâuhơn, độc đáohơn.

3.2. Các đề xuất khuyến nghị

- Đối với giáo viên: Mỗi giáoviên phảithường xuyên trao đổivề chuyên mônnghiệpvụ vớinhau,chútrọngtíchlũykinhnghiệmtronggiảngdạy,biếttổ chức cho học sinh học tập có nề nếp, có thói quen và lòng đam mê nghiên cứu khoa học,... và đặc biệt là phải biết lựa chọn cho mình phương pháp giảng dạy thích hợp nhất. Từ đó, để có thể gây hứng thú và kích thích học tập nhiều hơn chohọcsinh.

- Đới với lãnh đạo nhà trường: Lãnh đạo nhà trường mà trực tiếp là tổ chuyên môn phải là chỗ dựa vững chắc, đáng tin cậy cho giáo viên trong lĩnh vực chuyên môn, trong việc cải tiến phương pháp giảng dạy, trau dồi chuyên môn nghiệp vụ.Thư việnnhàtrườngphảithườngxuyên cậpnhật cácloạisách, tạpchícũngnhư cáctàiliệuthamkhảoliênquankhácchogiáoviên.

- Đới với cấp ngành: + Thường xuyên tổ chức các cuộc hội thảo, chuyên đề hơn nữa để giáo viêncó điềukiệngiaolưu,họchỏikinhnghiệmlẫnnhau.

Những giải pháp trong sáng kiến này của tôi được đúc kết qua thực tiễn giảng dạy, qua sách vở, tạp chí, cũng như tiếp thu được từ các thầy, cô giáo đi trước và quý đồng nghiệp. Vì vậy, bản thân tôi rất mong được sự góp ý đóng góp,xâydựngthẳngthắncủabangiámkhảocáccấp,củaquý đồngnghiệp,thầy côgiáovàtấtcả cácbạnnhằmgiúpcho đề tàicủatôingàycànghoànthiệnhơn.

KínhthưaBangiámkhảo!Quýbạn đọc!Dùbảnthântácgiả rấtcố gắng, miệtmài đầutư chuyênmôn,làmviệcnghiêmtúctrongmộtthờigianrấtdài để

có sáng kiến“ĐỀ XUẤT GIẢI PHÁP ĐỂ CHINH PHỤC BÀI TOÁN TÌM

MÔ ĐUN LỚN NHẤT, MÔ ĐUN NHỎ NHẤT TRONG SỐ PHỨC”này nhưng chắc chắn không tránh khỏi những khiếm khuyết, sai sót. Tác giả thành tâm đón nhận những ý kiến đóng góp và xây dựng để đề tài của tác giả hoàn thiệnhơn.

Tác giả chân thành cảm ơn!

Phù cát, ngày 5 tháng 3 năm 2020 Ngườithựchiện HuỳnhThị Trang

TÀILIỆUTHAMKHẢO

[1]Tuyểntậpcác đề thithử THPTQuốcgiatrêntoànquốcquacácnăm.

[2]Mộtsố trangwebvàtàiliệutừ Internet.

[3] Đề thiTHPTQuốcgiaquacácnăm.

[4]Tạpchítoánhọcvàtuổitrẻ,NXBGD-Bộ giáodục đàotạo.