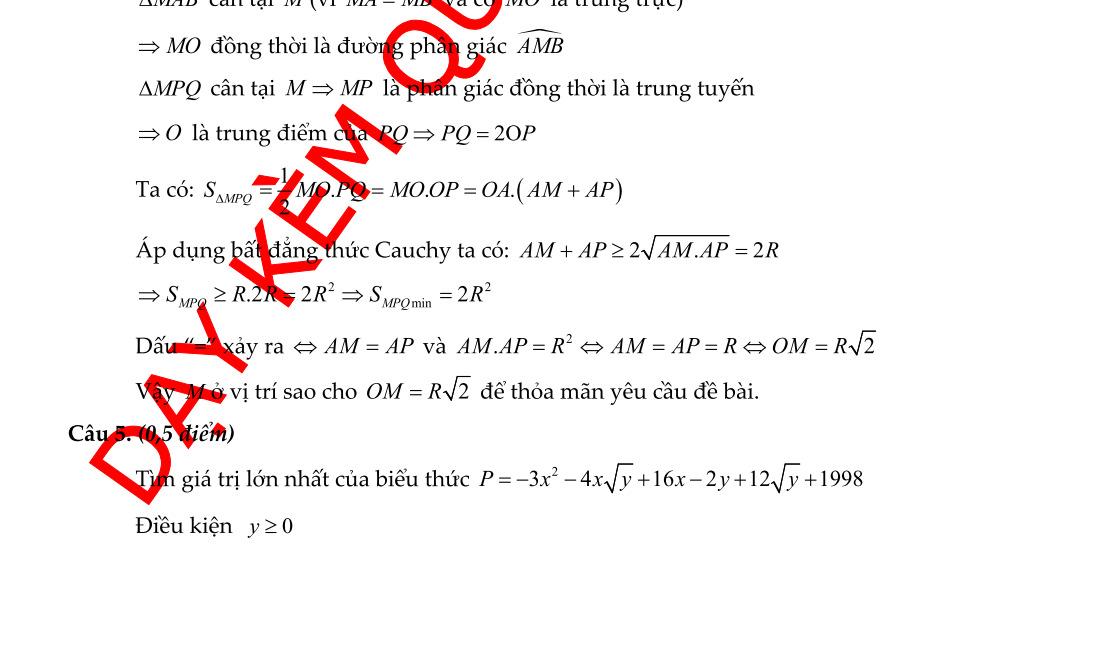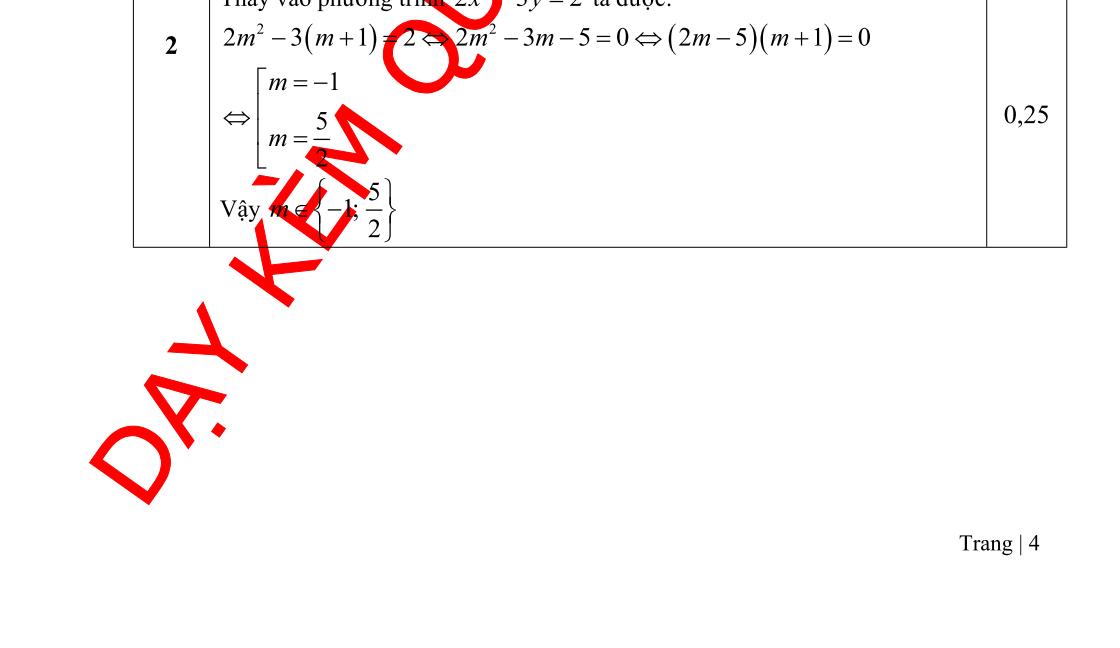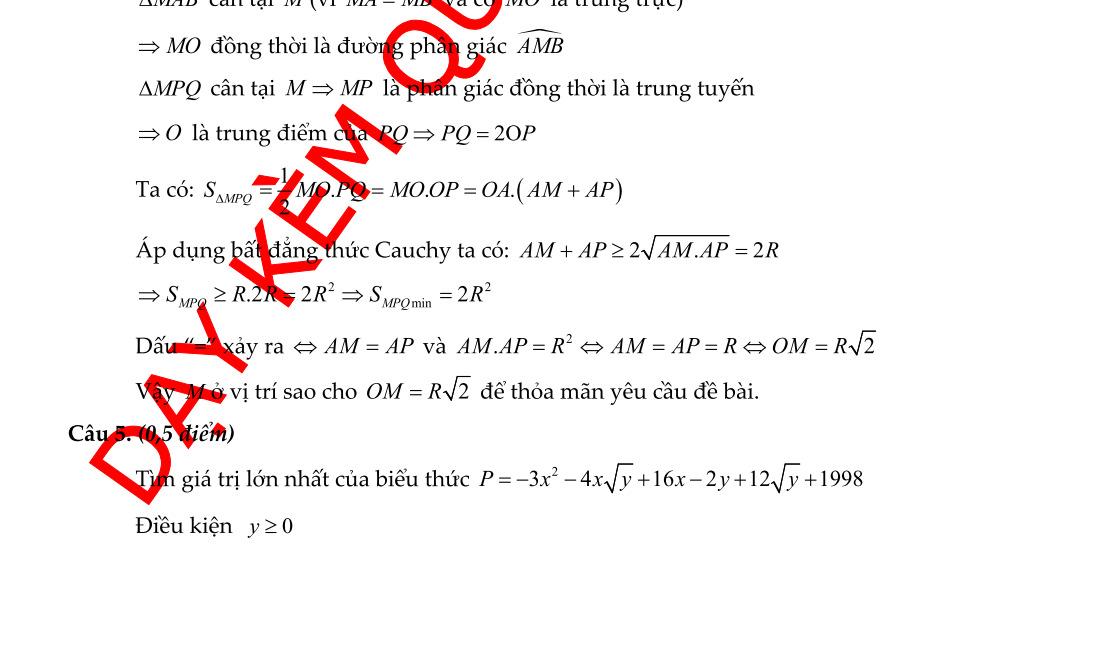ĐỀ THI TUYỂN SINH CHÍNH THỨC VÀO 10 MÔN TOÁN NĂM HỌC 2021-2022 CỦA 44 TỈNH - TP CẢ NƯỚC CÓ LỜI GIẢI by Dạy Kèm Quy Nhơn Official

ĐỀ THI TUYỂN SINH VÀO 10 MÔN TOÁN Ths Nguyễn Thanh Tú eBook Collection ĐỀ THI TUYỂN SINH CHÍNH THỨC VÀO 10 MÔN TOÁN NĂM HỌC 2021-2022 CỦA 44 TỈNH - TP CẢ NƯỚC CÓ LỜI GIẢI WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL.COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405

SỞ GIÁO DỤC - ĐÀO TẠO AN GIANG KỲ THI TUYỂN SINH VÀO 10 THPT Năm học 2021-2022 Khóa thi ngày 29/5/2021 Môn thi: TOÁN Thời gian làm bài: 120 phút , không kể thời gian phát đề

Bài 1. (3,0 điểm) Giải các phương trìnhvà hệ phương trìnhsau đây: a. . 2122 x

b. . 4260xx

c. . 211 4 xy xy 

 Bài 2. (2,0 điểm) Chohaihàm số có đồ thị làparabol và có đồ thị là đường thẳng . 2 yx   P 2yx  d a. Vẽ đồ thị và trêncùng một hệ trục tọa độ.  P d b. Bằng phéptính,tìm tọa độ giao điểm của và .  P d Bài 3. (2,0 điểm)

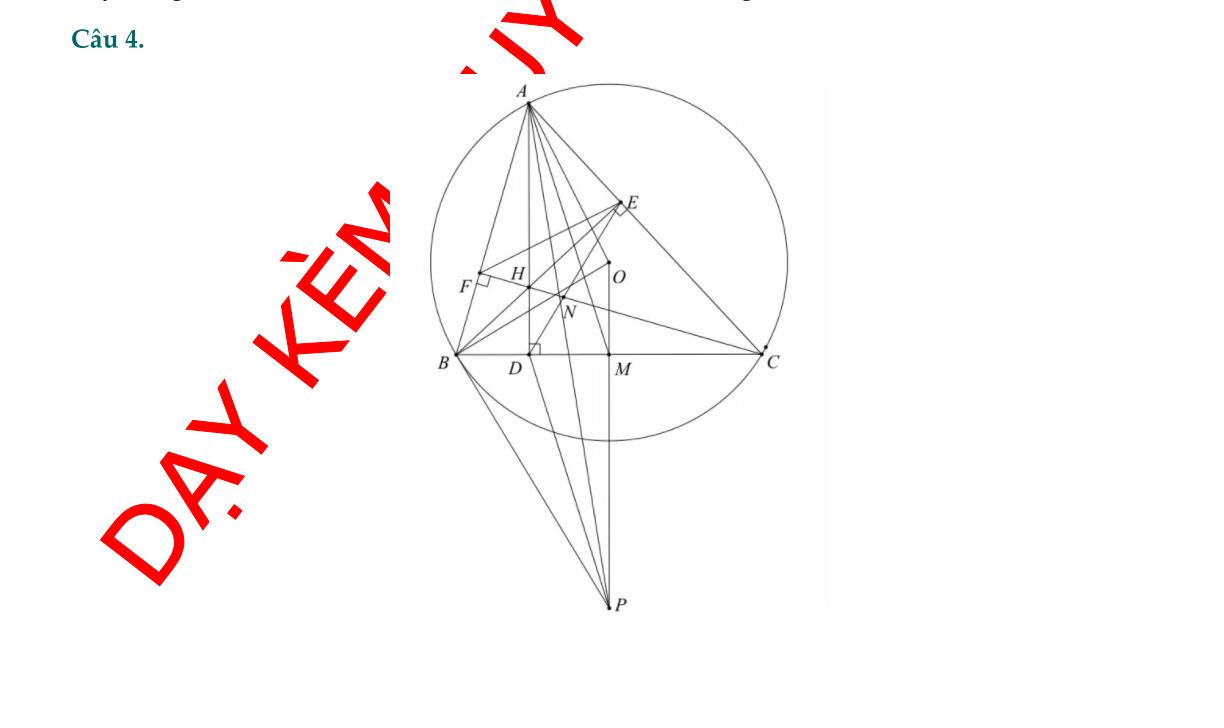
Cho phương trình bậc hai ( làtham số, là ẩn số). 2 2 21340xmxmm  m x a.Tìm để phương trìnhcóhai nghiệm phân biệt , . m 1x2x b. Đặt .Tính theo vàtìm để 22 1212 Axxxx  Amm18A Bài 4. Cho bốn điểm , , , theo thứ tự lần lượt nằm trên nửa đường tròn đường kính . Gọi làgiao điểm ABCD ADE của và . Kẻ vuônggóc với ( thuộc ). ACBDEF ADFAD a. Chứng minh tứ giác nội tiếp. ABEF b. Chứng

DẠYKÈMQUYNHƠNOFFICIAL







làtiaphângiác

. BD CBF

Một bức tường được xây bằng cácviên gạch

chữ

nhauvà được bố trỉ như hình

là phần ngoài của

6dm ĐỀ

minh

của góc

Bài 5.

hình

nhật bằng

vẽ bên. Phần sơn màu(tô đậm)

một hìnhtamgiáccó cạnh đáy 10dm và chiều cao .Tính diện tích phần tô đậm.

CHÍNH THỨC

DẠYKÈMQUYNHƠNOFFICIAL HƯỚNG DẪN GIẢI

x 



  Lời

x  

x  . 

2 2

x      



trình đã cho trở thành: . 260tt Tacó: . 2 141(6)250  Phương trìnhcóhai nghiệm phân biệt:  (thỏa điều kiện). 1 125 2 21 t     (không thỏa điều kiện). 2 125 3 21 t     Với . 2t 22x  2x  c. . 2113155 441 xy x x xy xyy                  Vậy hệ phương trìnhcó nghiệm . ;5;1xy Bài 2. (2,0 điểm) Chohaihàm số có đồ thị làparabol và có đồ thị là đường thẳng . 2 yx   P 2yx  d

Bài 1. (3,0 điểm) Giải các phương trìnhvà hệ phương trìnhsau đây: a. . 2122

b. . 4260xx

c. . 211 4 xy xy 

giải. a. 2122

2122

2221

2121

Vậy phương trìnhcó nghiệm: . 2x

b. 4260xx Đặt , điều kiện (). 2tx

0t Khi đó phương

a. Vẽ đồ thị và trêncùng một hệ trục tọa độ.  P d

b. Bằng phéptính,tìm tọa độ giao điểm của và .  P d

Lời giải.

a. Vẽ đồ thị và trêncùng một hệ trục tọa độ.  P d

Vẽ đồ thị hàm số • 2yx

Đồ thị hàm số là đường thẳng đi qua điểm và điểm 2yx (0;2)(1;1)

Vẽ đồ thị hàm số • 2 yx 

Tập xác định: D ,hàm số đồng biến khi ,hàm số nghịch biến khi . 10a 0x 0x

Bảng giá trị: x 2 1 0 1 2 2 yx  4 1 0 1 4 Đồ thị hàm số là đường congParabol đi qua gốc tọa độ và nhận làm trục đối xứng. 2 yx  OOy b. Bằng phéptính,tìm tọa độ giao điểm của và .  P d Phương trìnhhoành độ giao điểm: . 22xx

DẠYKÈMQUYNHƠNOFFICIAL

Với .24xy

Với .11xy Vậy toạ độ giao điểm của Parabol và đường thẳng là: và ). () P d(2;4)(1;1 Bài 3. (2,0 điểm)

Cho phương trình bậc hai ( làtham số, là ẩn số). 2 2 21340xmxmm  m x a.Tìm để phương trìnhcóhai nghiệm phân biệt , . m 1x2x b. Đặt .Tính theo vàtìm để 22 1212 Axxxx  Amm18A

Lời giải. a.Tìm để phương trìnhcóhai nghiệm phân biệt ,. m 1x2x (*). 2 2 21340xmxmm   . 22 2 2 '13421345 mmmmmmmm   Để phương trình(*)cóhai nghiệm phân biệt thì hay . '0 505m m  Vậy với thì phương trình đã chocóhai nghiệm phân biệt , 5m 1x2x b. Đặt .Tính

DẠYKÈMQUYNHƠNOFFICIAL

220xx  , hoặc 2x  1x

theo vàtìm để 22 1212 Axxxx  Amm18A Theo hệ thức Vi–ét,tacó:  12 2 12 2122 34 b xx mm a c xxmm a          Theo đề bài,tacó: 22 1212 Axxxx     2 121212 2 1212 22 2 2 2 2 3 223.34 4843912 16 xxxxxx xxxx mmm mmmm mm       Với 2 81618Amm

DẠYKÈMQUYNHƠNOFFICIAL    2 2 16180 20 210 22 0 . 101 mm mm mm mtm m m mtm              Vậy

2m 1m



hay  90  ABD  90 ABE Xét

giác

 9090180 

là

tổng haigóc đối diện bằng ) ABEF 180 b. Chứng minh làtiaphângiác của góc . BD CBF Vì là tứ giác nội tiếp (cmt) (haigóc nội tiếp cùng chắn cung ) ABEF  FBEFAE EF Hay .   CADFBD Lại có: (haigóc nội tiếp cùng chắn cung )   CBDCAD CD  ()CBDFBDCAD

và thỏa mãnyêu cầu bàitoán.

Bài 4. Cho bốn điểm , , , theo thứ tự lần lượt nằm trên nửa đường tròn đường kính . Gọi làgiao điểm ABCD ADE của và . Kẻ vuônggóc với ( thuộc ). ACBDEF ADFAD a. Chứng minh tứ giác nội tiếp. ABEF b. Chứng minh làtiaphângiác của góc . BD CBF Lời giải a. Chứng minh tứ giác nội tiếp. ABEF Tacó: làgóc nội tiếp chắn nửa đường tròn đường kính

ABD AD

tứ

tacó: ABEF

ABEAFE

tứ giác nội tiếp (tứ giáccó

Bài 5.

làphângiác của (đpcm).

FBC

Một bức tường được xây bằng cácviên gạch hình chữ nhật bằng nhauvà được bố trỉ như hình vẽ bên. Phần sơn màu(tô đậm) là phần ngoài của một hìnhtamgiáccó cạnh đáy và chiều cao .Tính diện tích phần tô 10dm6dm đậm.

Chiều rộng của một viên gạch là: .6:41,5() dm

Chiều dài của một viên gạch là: .10:52() dm

Diện tích của một viên gạch là: . 21,523 dm

Tồng số viên gạch để xây bức tường là: (viên). 234514 

Diện tích của bức tường đă xâylà. . 23.1442 dm

Diện tíchtamgiáctronghìnhlà: . 2 1 6.1030 2 dm

Diện tích phần sơn màulà: . 2423012 dm

DẠYKÈMQUYNHƠNOFFICIAL

BD 

DẠYKÈMQUYNHƠNOFFICIAL SỞ GIÁO DỤC VÀ ĐÀO TẠO BẮC

KỲ THI

Câu 1 (1,5 điểm) Rút gọn các biểu thức sau: a) 323250  A Tacó 323250 32162252 324252 (345)2 42         A Vậy 42A b) (với 11 : 242         x B xxx 0,4)xx Với ,tacó:0,4xx 11 : 242          x xxx B 21 : (2)(2)2     xx xxx 2 (2) (2)(2)    x xx 2 2  x Vậy , với . 2 2 B x 0,4xx Câu 2 (2, 5 điểm): a) Giải các phương trìnhsau 1) 240 x ĐỀ CHÍNH THỨC

KẠN

TUYỂN SINH LỚP 10 THPT NĂM HỌC 2021-2022 Môn thi: TOÁN Thời gianlàmbài:120phút (không tính thời gian phát đề)

c) Một người đi xemáy từ huyênNgân Sơn đến huyện Chợ Mới cáchnhau Khi về người đó tăng 100. km vận tốc thêm so với lúc đi, dodó thời gian về ít hơn thời gian đi là phút.Tính vận tốc đi của xe 10/kmh 30 máy.

Gọi vận tốc lúc đi của xemáylà (ĐK: ) (/)xkmh 0x

Lúc đi, xemáy đi hết (giờ) 100 x

Vận tốc lúc về của xemáylà 10(/) xkmh

Lúc về, xemáy đi hết (giờ) 100 10x

Dolúc về xemáy tăng tốc nên thời gian về ít hơn so với thời gian đi là phút nêntacó phương trình 30 1 2 h

DẠYKÈMQUYNHƠNOFFICIAL .240242 x xx Vậy phương trìnhcó nghiệm .2x 2) 42120 xx Đặt 2(0)txt Khi đó phương trình trở thành: . 2120 tt Tacó: nên phương trìnhcó2 nghiệm phân biệt 2 2 (1)4(12)4970  1724() 1723()       t tm t ktm Với tacó . 4t 2 2 4 2   x x x Vậy tập nghiệm của phương trìnhlà .{2;2}S b) Giải hệ phương trình 23 24    xy xy Tacó: 23235512 242482421                                xyxy y yx xyxyxyxy



Vậy hệ phương trình đã chocó nghiệm . (;)(2;1)

 xx 200(10)200(10)  x xxx

1001001 102

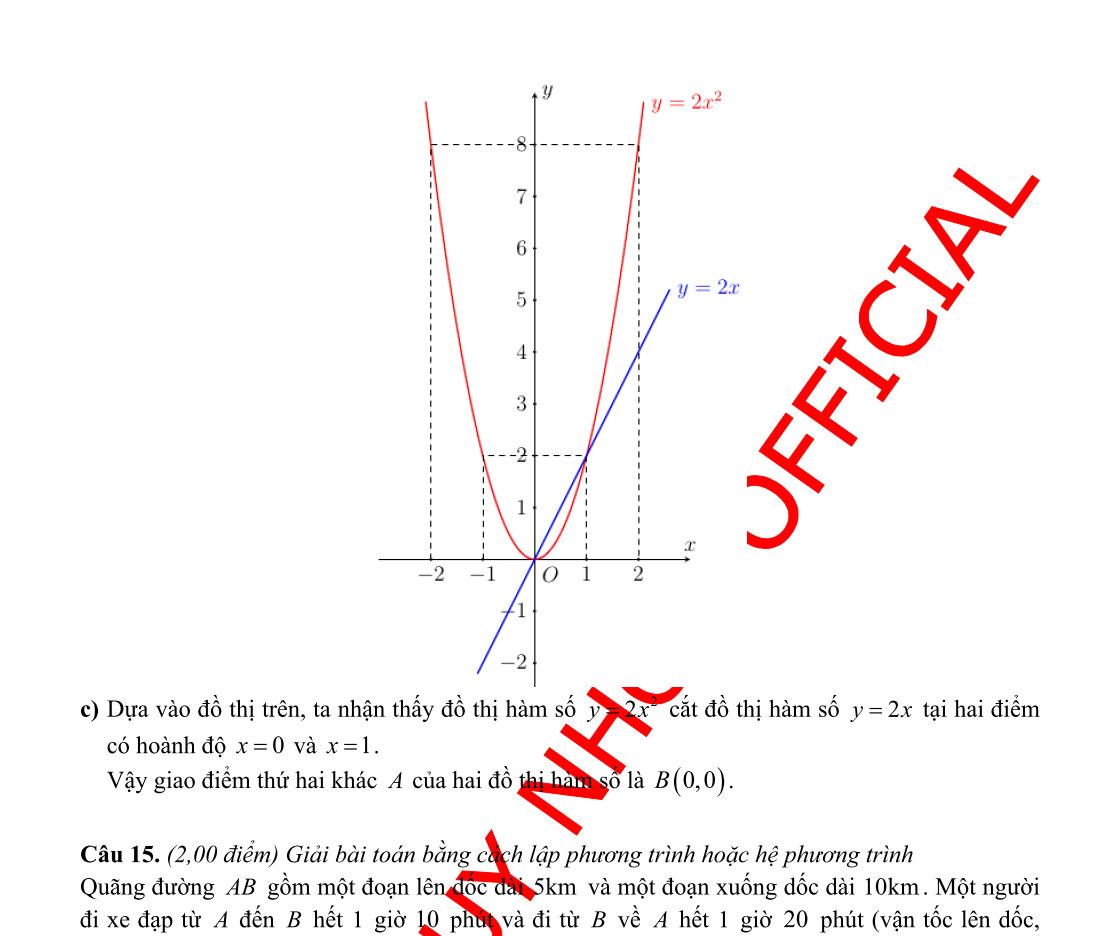
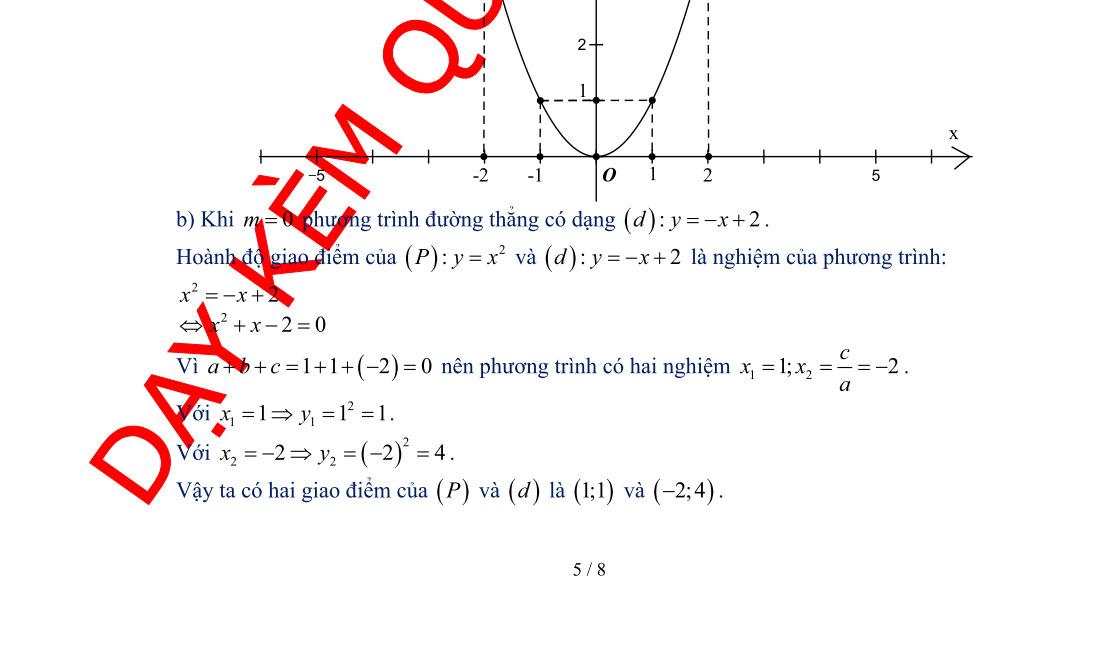
yx Đồ thị hàm số có hệ số nêncó bề lõm hướng lên, đồng biến khi , nghịch biến khi 22 yx 20a 0x 0x và nhận làm trục đối xứng. Oy Tacó bảng giá trị sau: x 2 1 0 1 2 22 yx 8 2 0 2 8 là đường cong đi quacác điểm . 22yx (2;8);(1;2);(0;0);(1;2);(2;8) +) Đường thẳng 2yx Tacó bảng giá trị sau: x 0 2 2yx 2 0 là đường thẳng đi quacác điểm 2 yx (0;2);(2;0) +) Vẽ đồ thị hàm số và đường thẳng trêncùng mặt phẳng tọa độ 22 yx 2yx Oxy

DẠYKÈMQUYNHƠNOFFICIAL 2 200200020010  x xxx 21020000 xx Tacó nên

2 2 520002025450   545140() 545150()          x tm x ktm Vậy



phương trìnhcó2 nghiệm phân biệt

vận tốc lúc đi của xemáylà . 40/kmh Câu 3 (1,5 điểm):

Vẽ đồ thị cáchàm số và đường thẳng trêncùng măt phẳng tọa độ . 22

yx 2yx Oxy +) Đồ thị hàm số

b)Tìm để đường thẳng đi qua điểm vàsongsong với đường thẳng , ab :   dyaxb (1;2)M . ():2 dyx Để thì Phương trình đường thẳng có dạng: '// dd 1 2    a b  d :   dyxb Lại có nênthay tọa độ điểm vào phương trình đường thẳng tacó: (1;2)   Md M  d 213() bbtm Vậy .1,3

DẠYKÈMQUYNHƠNOFFICIAL

nghiệm phân biệt khivà chỉ khi 22 0(1)40  mm 2 2 2140 mmm 230 m 3(*) 2  m Khi đó áp dụng định líVi-éttacó: 12 2 12 2(1) 4    xxm xxm Vì là nghiệm của phương trình(1)nêntacó . 2x 2 22 222 2 2 2(1)402(1)4 xmxm mxxm Khi đó tacó: 2 2 1 2 2(1)220 xmxm 222 2 124220 xxmm 222 1216 xxm

ab Câu 4 (1,5 điểm): Cho phương trình (với làtham số) 2 2 2(1)40(1) xmxm m a) Giải phương trình khi . (1)2 m Khi phương trình(1) trở thành: . 2m 2680 xx Tacó nên phương trìnhcóhai nghiệm phân biệt . 2 3810   314 312    x x Vậy khi thì phương trìnhcó tập nghiệm 2m {2;4}S b)Tìmgiá trị của để phương trình cóhai nghiệm phân biệt thỏa mãn m (1) 12 , xx 2 2 1 2 2(1)220 xmxm Phương trình(1)cóhai

DẠYKÈMQUYNHƠNOFFICIAL 2 2 1212216 xxxxm  222 4(1)2416 mmm 2 22 48428160 mmmm 28200 mm 2102200 mmm (10)2(10)0 mmm (10)(2)0 mm TH1: . 100 102 20    m m m TH2: . 10010 202       m m m m m Suyra . Kết hợp với điều kiện (*)tacó . 102  m 3 2 2  m Vậy 3 2 2  m Câu 5 (3,0 điểm): Chotamgiác cóbagócnhon nội tiếp đường tròntâm .Các đường cao của tamgiác ABC O ,, ADBECF cắt nhau tại ABC .H a) Chứng minhcác tứ giác , nội tiếp đường tròn. AEHFBFEC Xét tứ giác có nên là tứ giác nội tiếp (tứ giáccó tổng haigóc AEHF  9090180 AEHAFH AEHF đối bằng ). 180 Xét tứ giác có: là tứ giác nội tiếp (tứ giáccóhai đỉnh kề cùngnhình một BFEC  90  BFCBECBFEC cạnh dưới cácgóc bằng nhau).

b) Đường thẳng cắt đường tròntâm tại điểm khác điểm . Gọi làgiao điểm của hai đường AO OK AI thẳng và . Chứng minh làtrung điểm của đoạn thẳng . HKBC I BC Tacó (góc nội tiếp chắn nửa đường tròn) .

Mà () CHABgt (từ vuônggóc đến songsong) //CHBK

Chứng minh tương tự tacó: . // BHCK làhìnhbìnhhành (tứ giáccócác cặp cạnh đối songsong). BHCK Hai đường chéo và cắt nhau tại trung điểm mỗi đường.

DẠYKÈMQUYNHƠNOFFICIAL

 90 ABK ABBK

 AHBHCH ADBECF Đặt  AHBHCH P ADBECF 111 3       HDHEHF P ADBECF HDHEHF P ADBECF Tacó: 1 2 1 2      ABC AABC HHDBCS D ADAS DBC Chứng minh tương tự tacó: AHAC ,.     AHAB ABC ABC S S HE HF BESCFS 1       AHBCAHAC AHBCHACAHABABCAHAB ABCABCAABC ABC BC SSSSSSS HDHEHF ADBECFSSS S S Vậy 312 AHBHCH P ADBECF ----HẾT-----

 BCHK Mà .() IHKBCgt Vậy cũng làtrung điểm của (đpcm). I BC c)Tính .

SỞ GIÁO DỤC VÀ ĐÀO TẠO BẠC LIÊU

ĐỀ CHÍNH THỨC

Câu 1. (4,0 đ)

KỲ THI TUYỂN SINH VÀO LỚP 10 THPT

NĂM HỌC 2021 - 2022

MÔN THI: TOÁN

Thời gian làm bài: 120 phút

a)Rút gọn biểu thức: 286327A

b) Chứng minh rằng: với 1 : xyyx xy xyxy   0;0; xyxy 

Câu 2. (4,0 đ)

a) Giải hệ pt: 25 27 xy xy   

b)Chohàm số: có đồ thị (P)và đường thẳng (d): . Vẽ đồ thị (P) 21 4 yx  1 2 2 yx  vàtìm tọa độ giao điểm của (P) với đường thẳng (d) bằng phéptính. Câu 3. (6,0 đ)

Cho phương trình: (1) 2210xmxm

a) Giải pt(1) với m=-3.

b) Chứng tỏ pt(1)luôncó nghiệm với mọi số thực m.

c)Tìmm để ptcóhai nghiệm phân biệt là độ dàihai cạnh gócvuông của một 12 ; xx tamgiácvuôngcó độ dài đường cao ứng với cạnh huyền là . 2 5 h

Câu 4. (6,0 đ)

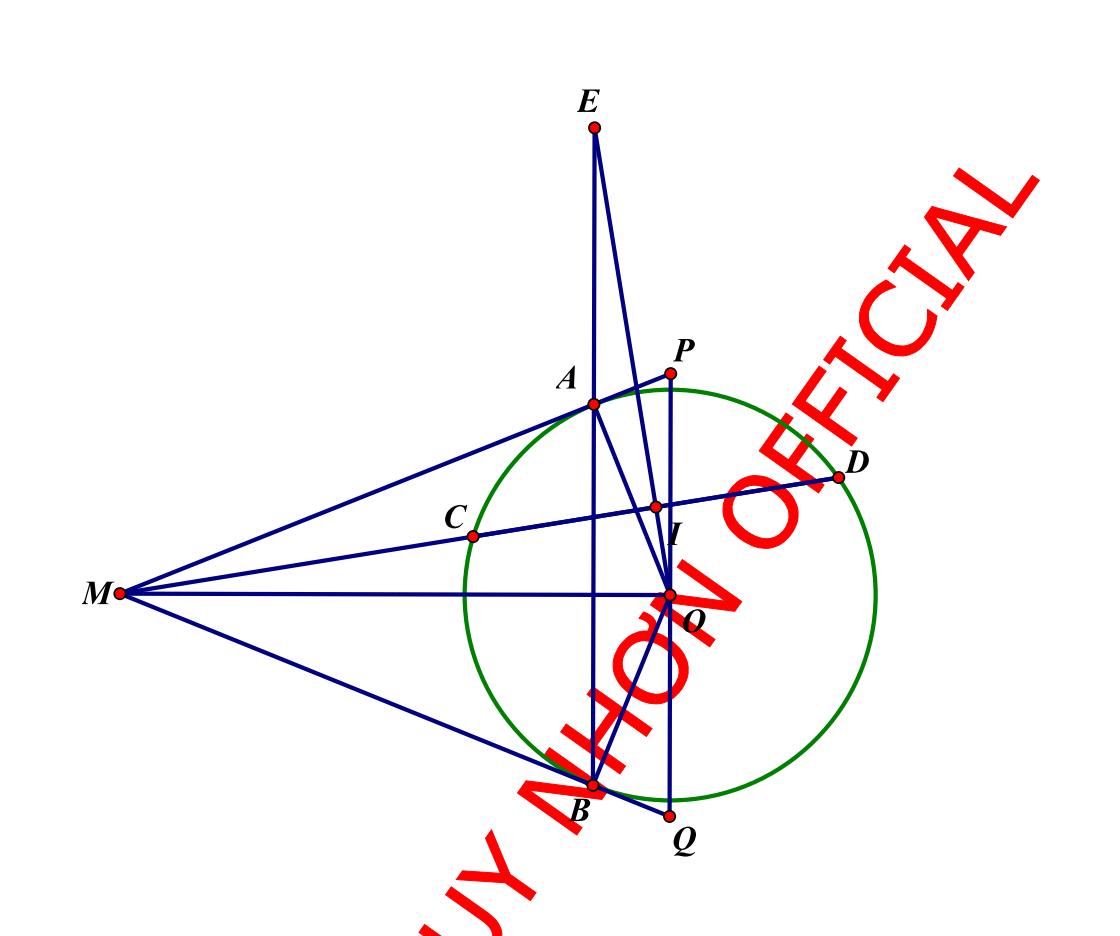
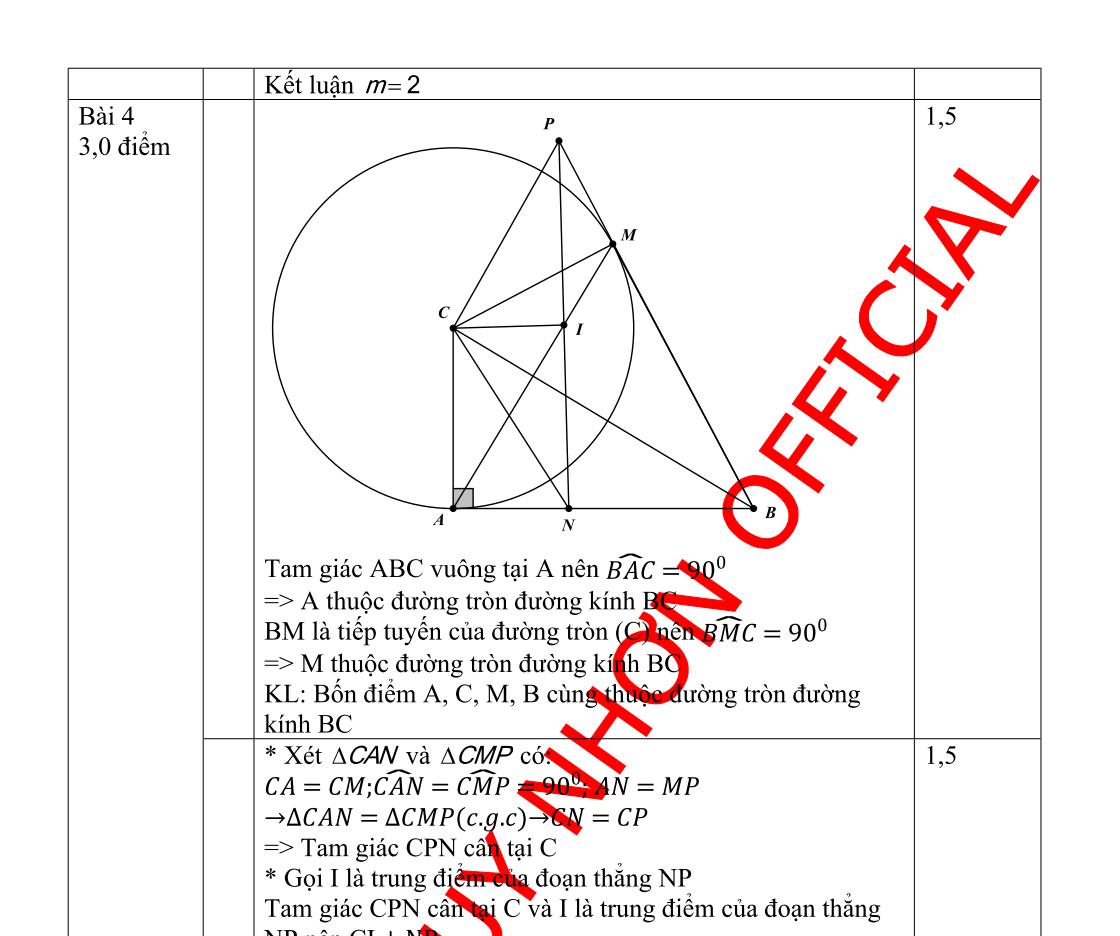
Cho đường tròn(O;R)và đường thẳng dkhông đi quaO cắt (O) tại hai điểm A;B. Trêntia đối của tiaBA lấy điểm M;quaM kẻ hai tiếp tuyến MC;MD với đường tròn(O)( C;Dlàcác tiếp điểm). Gọi Hlàtrung điểm của AB.

a) Chứng minh tứ giácOMCH nội tiếp.

b)OM cắt đường tròn(O) tại Ivà cắt CD tại K. Chứng minh 2OK.OM=R

c) Đường thẳng quaOvuônggóc với OM, cắt tiaMCvàMD lần lượt tại PvàQ. Tính độ dàiOMtheoRsaocho diện tíchtamgiácMPQ nhỏ nhất.

DẠYKÈMQUYNHƠN

OFFICIAL

DẠYKÈMQUYNHƠN OFFICIAL HƯỚNG

Câu 1. a) Rút gọn biểu thức: 286327A 28632727372737A   b) Chứng minh rằng: với 1 : xyyx xy xyxy   0;0; xyxy  1 : xyxy xyyx xyxyxyxy xyxyxy      Vậy với 1 : xyyx xy xyxy   0;0; xyxy  Câu 2. a) Giải hệ pt: 25 27 xy xy    Vậy 252410331 1 27272727(1)3 xyxy y y y xyxy xyx x                               S=3;1 b) Cho hàm số: có đồ thị (P) và đường thẳng (d): . Vẽ đồ thị (P) và 21 4 yx  1 2 2 yx  tìm tọa độ giao điểm của (P) với đường thẳng (d) bằng phép tính. + Vẽ (P): X -4 -2 0 2 4 21 4 yx  -4 -1 0 -1 -4 +Hoành độ giao điểm của (P)và(d)là nghiệm của pt:  22 2 2 1111 2 20280 2442 2 2480240 4 xxxx xx x xxx xx x     Với x=2ta được y=-1; với x=-4ta được y=-4. Vậy tọa độ giao điểm của (P)và(d)là: và  2;1 4;4

DẪN GIẢI

a) Giải pt (1) với m=-3. Khim=-3pt(1) trở thành: .Vì1+1+(-2)=0nênptcóhai nghiệm 220xx 121;2xx

b) Chứng tỏ pt (1) luôn có nghiệm với mọi số thực m. Tacó: với mọi m  2 2 2 24144440m mmmmm 

Vậy pt(1)luôncó nghiệm với mọi số thực m.

c) Tìm m để

cầu bàitoán.

m=1làgiá trị cần tìm.

4. (6,0 đ)

đường tròn(O;R)và đường thẳng dkhông đi quaO cắt (O) tại hai điểm A;B. Trêntia đối của tiaBA lấy điểm M;quaM kẻ hai tiếp tuyến MC;MD với đường tròn(O)( C;Dlàcác tiếp điểm). Gọi Hlàtrung điểm của AB. a) Chứng minh tứ giác OMCH nội tiếp. VìHlàtrung điểm của dâycungABnên

DẠYKÈMQUYNHƠN OFFICIAL

Câu 3. Cho phương trình: (1) 2210xmxm

  

  

pt có hai nghiệm phân biệt là độ dài hai cạnh góc vuông của 12 ; xx một tam giác vuông có độ dài đường cao ứng với cạnh huyền là . 2 5 h Theocâubtacó: 2 m Pt(1)cócóhai

12 ; xx vuông 2 12 12 00 0 020 1 10.0 m m xxm m m xx                Mặt kháctamgiácvuôngcó đường cao ứng với cạnh huyền nênáp dụng hệ thức 2 5 h tacó: 222 111 bch    22 2 2 12 121212 222 22 12 12 111 5 425 4 2 5 xx xxxxxx xx xx             Đối chiếu điều kiện ta  2 22 1 422151230 3 m mmmmm m         được

 OHMOCM90  

nghiệm phân biệt là độ dàihai cạnh gócvuông của một tamgiác

m=1 thỏa mãnyêu

Vậy

Câu

Cho

 OHABOHM=90   Tacó: nên tứ giácOMCH nội tiếp.

b) OM cắt đường tròn (O) tại I và cắt CD tại K. Chứng minh 2OK.OM=R

TamgiácODMvuông tại D(vì ). Mặt khác:(t/chai tiếp tuyến cắt

90ODM

MC=MD nhau); OMlà đường trung trực của đoạn thẳng CD.Trongtam OC=OD=R OMCD  giácvuôngODMáp dụng hệ thức tacó: . 2 b=a.b' 2 2OD=OK.OMOK.OM=R 

c) Đường thẳng qua O vuông góc với OM, cắt tia MC và MD lần lượt tại P và Q. Tính độ dài OM theo R sao cho diện tích tam giác MPQ nhỏ nhất. Theot/chai tiếp tuyến cắt nhautacóMOlàtiaphângiác của gócPMQ, mặt khác nêntamgiácPMQcân tại M. MOPQ

DẠYKÈMQUYNHƠN

OFFICIAL



 



Tacó .TrongtamgiácvuôngOMQtacó: PMQ 1 SMO.PQ=MO.OP 2  222222 111111 + + ODOPOMROPOM   Áp dụng bất đẳng thức Côsi: 22 22 2 PMQ 1111212 +2 OPOMOPOMOPOMRS    Dấu “=” xảy ra . 2 PMQ S2R  22 2 11 = OOM=OP=R2 MOP OM.OP=2R        Vậy đạt giá trị nhỏ nhất . PMQS OM=R2

PQ2OP

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH LỚP 10

TỈNH BẾN TRE Năm học: 2021 - 2022 Môn thi: TOÁN Thời gian làm bài: 120 phút (Không kể thời gian phát đề)

Bài 1. (1,0 điểm)

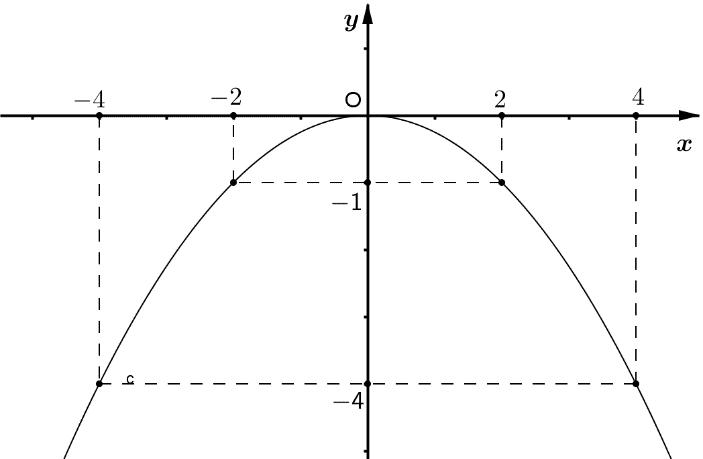
Dựa vàohình vẽ bên,hãy:

1) Viết tên tọa độ các điểm và MP

2)Xác định hoành độ điểm N

3)Xác định tung độ điểm Q

Bài 2. (1,0 điểm)

1)Tínhgiá trị của biểu thức 9.322A

2)Rút gọn biểu thức với 5 5 x B x   0x

Bài 3. (1,0 điểm)

Cho đường thẳng với làtham số ():(56)2021 dymx   m

OFFICIAL

1) Điểm có thuộc không?Vìsao? O(0;0)() d 2)Tìmcácgiá trị của để songsong với đường thẳng: m() d 45yx Bài 4. (1,0 điểm) Vẽ đồ thị hàm số 21 2 yx  Bài 5. (2,5 điểm)

DẠYKÈMQUYNHƠN

1 / 7

m làtham số. Tìmgiá 12 , xx 22(3)670xmxm trị nhỏ nhất của biểu thức: 2 1212()8 Cxxxx  Bài 6. (1,0 điểm) Cho tứ giácABCD nội tiếp đường tròn(O), biết (như hình vẽ bên).Tính số  0 030,40BACBCA   đo cácgóc .  ,, ABCADCAOC ĐỀ THI CHÍNH THỨC

1) Giải phương trình 2 56110 xx 2) Giải hệ phương trình 5 459 xy xy    3) Gọi làhai nghiệm của phương trình: với

Bài 7. (2,5 điểm)

Cho đường tròn và điểm saocho . Từ kẻ hai tiếp tuyến (;3) Ocm M 6 OMcm  M

đến đường tròn ( làcác tiếp điểm).Trên đoạn thẳng lấy điểm ( , MAMB () O, AB OA DD khác và , dựng đường thẳng vuônggóc với tại và tại A)O OADMBE

a) Chứng minh tứ giác nội tiếp đường tròn ODEB

b) Tứ giác làhìnhgì?Vìsao? ADEM

c) Gọi làgiao điểm của đường thẳng và saocho điểm nằm giữa và . K OM() O O MK

minh tứ giác làhìnhthoi AMBK

DẠYKÈMQUYNHƠN OFFICIAL

2 / 7

Chứng

= = = = = = =

= = = = = = = = = = = Hết = = = = = = = = = = = = = = = = = = =

Hướng dẫn giải

Bài 1. (1,0 điểm)

Dựa vàohình vẽ bên,hãy: 1) Viết tên tọa độ các điểm và MP 2)Xác định hoành độ điểm N 3)Xác định tung độ điểm Q Lời giải 1) Dựa vàohình vẽ tacó: ; 1;2M  3;3P 2) Dựa vàohình vẽ tacó: nênhoành độ điểm là  2;4N N2Nx 3) Dựa vàohình vẽ tacó: nêntung độ điểm là  1;1Q Q1Qy Bài 2. (1,0 điểm) 1)Tínhgiá trị của biểu thức 9322A 2)Rút gọn biểu thức với 5 5 x B x   0x Lời giải

DẠYKÈMQUYNHƠN OFFICIAL 3 / 7



x

5 x

x   (5)(5)5 5 xx x x    





số ():(56)2021 dymx   m 1) Điểm có thuộc không?Vìsao? O(0;0)() d 2)Tìmcácgiá trị của để songsong với đường thẳng: m() d 45yx Lời giải 1)Thay và vào phương trình đương thẳng ta được: 0x 0y ():(56)2021 dymx   (vôlý)0(56)0202102021 m  Vậy không thuộc đường thẳng . (0;0)O () d 2) Đường thằng songsong với đường thẳng () d 45yx 564 2 2021() 5luônđú m m ng      Vậy thỏa mãn đề bài. 2m Bài 4. (1,0 điểm) Vẽ đồ thị hàm số 21 2 yx 

1) 9322A

91622

34221222

112

2) Với thì0

Vậy với thì0x

5Bx

Bài 3. (1,0 điểm) Cho đường thẳng với làtham

DẠYKÈMQUYNHƠN OFFICIAL 4 / 7 Lời giải Tacó bảng giá trị sau: x -4 -2 0 2 4 21 2 yx  8 2 0 2 8 Bài 5. (2,5 điểm) 1) Giải phương trình 2 56110 xx 2) Giải hệ phương trình 5 459 xy xy    3) Gọi làhai nghiệm của phương trình: với m làtham số. 12 , xx 22(3)670xmxm Tìmgiá trị nhỏ nhất của biểu thức: 2 1212()8 Cxxxx  Lời giải 1) 2 56110 xx Tacó nên phương trìnhcó nghiệm phân biệt 56110abc 12 1; 11 5 c xx a  2) 544201116 459459511 xy xyy x xyxyxyy                        Vậy hệ phương trìnhcó nghiệm (;)(16;11) xy 3) Phương trình có với mọi 22(3)670xmxm 2 2 '(3)67160 mmm  m Suyra: phương trìnhtrênluôncóhai nghiệm phân biệt 12 , xx O

DẠYKÈMQUYNHƠN OFFICIAL 5 / 7 Theo

  Tacó: 2

 2

m m   2 424364856 mmm  2 47220 mm 2 4(1881)48120 mm 

2 4(9)344344, m m  

Dấu

xảy

 Vậy

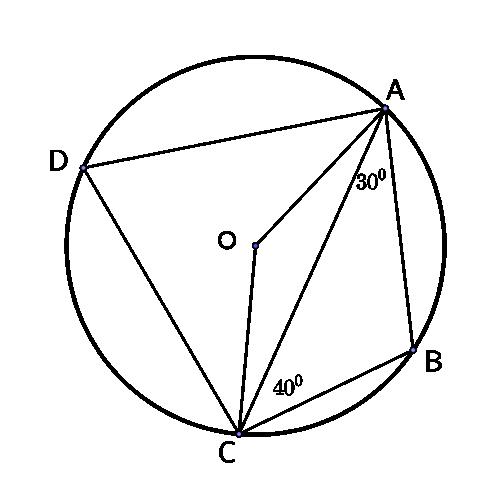
 Bài

vẽ

số  0 030,40BACBCA   đo cácgóc .  ,, ABCADCAOC Lời giải Xéttamgiác có: ABC (tổng 3góctrongtamgiác)  0180BACBCAABC Hay  00 0 03040180110 ABC ABC  Tứ giác nội tiếp đường tròn nên ABCD () O (tổng 2góc đối diện của tứ giác nội tiếp)  0180ABCADC Hay  0 0 011018070 ADC ADC  Tacó: (góc nội tiếp vàgóc ở tâmcùng chắn cung )  2 AOCADC  AC  00 270140AOC  Vậy  0 0 0110,70,140ABCADCAOC    Bài 7. (2,5 điểm) Cho đường tròn và điểm saocho . Từ kẻ hai tiếp tuyến (;3) Ocm M 6 OMcm  M đến đường tròn ( làcác tiếp điểm).Trên đoạn thẳng lấy điểm ( khác , MAMB () O, AB OADDA và , dựng đường thẳng vuônggóc với tại và tại )O OADMBE 1) Chứng minh tứ giác nội tiếp đường tròn ODEB 2) Tứ giác làhìnhgì?Vìsao? ADEM 3) Gọi làgiao điểm của đường thẳng và saocho điểm nằm giữa và . Chứng K OM() O O MK minh tứ giác làhìnhthoi AMBK Lời giải

định líVi-ettacó: 12 12 26 .67 xxm xxm 

1212()8 Cxxxx

(26)8(67)

(vì )

2 4(9)0, m m 

‘’=‘’

rakhivà chỉ khi .909m m

GTNN của Clà đạt tại 3449 m

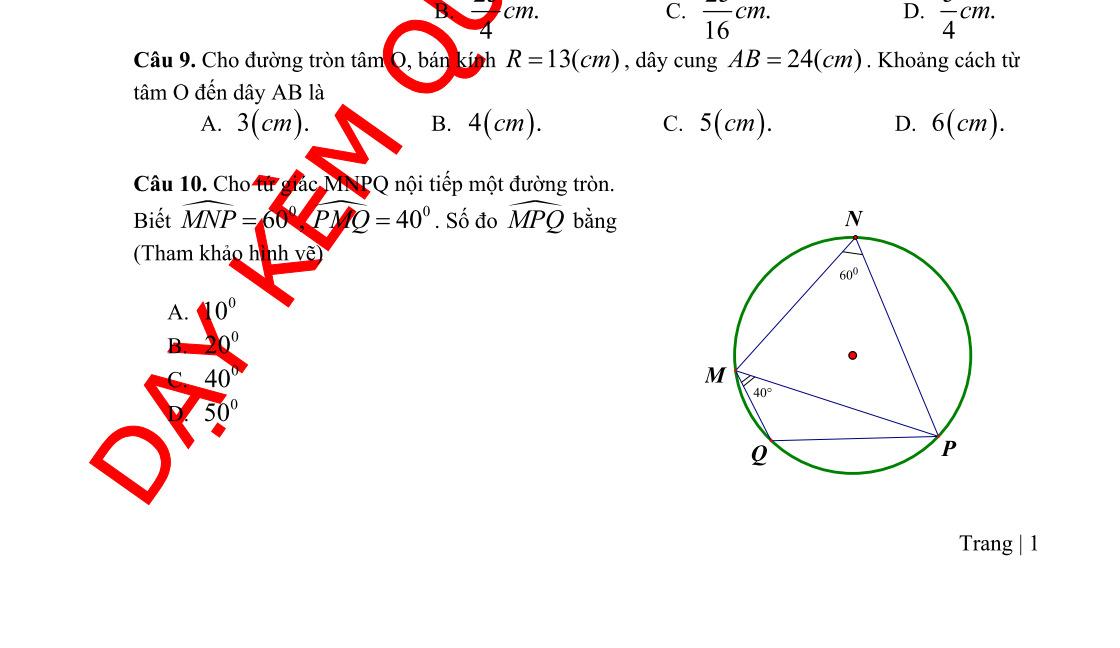
6. (1,0 điểm) Cho tứ giácABCD nội tiếp đường tròn(O), biết (như hình

bên).Tính

1) Chứng minh tứ giác nội tiếp đường tròn. ODEB Vì , là tiếp tuyến của nên MAMB () O  090OAMOBM Xét tứ giác có ODEB  000 9090180ODEOBE là tứ giác nội tiếp (tứ giáccó tổng haigóc đối bằng 1800). ODEB 2) Tứ giác làhìnhgì?vìsao? ADEM Tacó (từ vuônggóc đến songsong) () () AMOAgtAMDE DEOAgt      làhìnhthang ADEM Lại có nên làhìnhthangvuông.

ADEM

Gọi làgiao điểmcủa đường thẳng và saocho nằm giữa điểm và . K MO()OO MK Chứng minh tứ giác làhìnhthoi. AMBK

DẠYKÈMQUYNHƠN OFFICIAL 6 / 7





Gọi . HABOM  Tacó thuộc trung trực của . 3 OAOBcmO  AB làtrung trực của tại OM ABOMAB H làtrung trực của ,mà . MK ABMMKMAMB  Xéttamgiác vuông tại có đường cao ,áp dụng hệ thức lượng trongtamgiác OAM A AH vuôngtacó: 22 2 361,5()OA OHOMOAOH cm OM  Xéttamgiácvuông có: OAH

090DAMADE

Vậy làhìnhthoi (định nghĩa) (đpcm). AMBK

DẠYKÈMQUYNHƠN OFFICIAL 7 / 7   0 1,51sin 30 32

OAH

  0 000

   đều









AOH OA

90903060BAMOAH

MAB (1)MAMBAB Ta lại có (góc nội tiếp vàgóc tạo bởi tia tiếp tuyến vàdâycungcùng chắn cung ).

AKBBAM

AB đều

060AKB KAB (2)KAKBAB Từ (1)và(2)suyra: .MAMBKAKB

HỌC 2021 - 2022 Môn thi: TOÁN Ngày thi: 11/ 6/ 2020 Thời gian làm bài: 120 phút (không kể thời gian phát đề)

Bài 2. (2,0 điểm)

phương trình: (mlàtham số). Hãytìmgiá trị của 

xmxmm m để là nghiệm của phương trìnhvàxác định nghiệm còn lại của phương trình (nếu có). 3x 2.ChoParabol và đường thẳng (mlàtham số). Tìm 2 : Pyx  :212 dymxm 

3230

để cắt tại hai điểm phân biệt ; saocho . m P d  11 , Axy 22 , Bxy 12121yyxx  

Bài 3. (1,5 điểm)

Một xemáy khởi hành tại địa điểm đi đến địa điểm cách ,sau đó giờ, A BA160km1 một ôtô đi từ đến .Haixe gặp nhau tại địa điểm cách . Biết vận tốc của ô BA CB72km tô lớn hơn vận tốc của xemáy .Tính vận tốc của mỗi xe. 20/giêkm

4. (3,5 điểm)

DẠYKÈMQUYNHƠN OFFICIAL SỞ GIÁO DỤC VÀ ĐÀO TẠO BÌNH

Đề

KỲ THI

10 THPT

1.Cho

với . 112 : 1111 Px xxxx              0,0xx a)Rút gọn biểu

P b)Tìmgiá trị của khi .



 

ĐỊNH

chính thức

TUYỂN SINH VÀO LỚP

NĂM

Bài 1: (2,0 điểm)

biểu thức

thức

P423x

2. Giải hệ phương trình: 26 237 xy xy 

1.Cho

2 2



ABC  90ACB

cắt

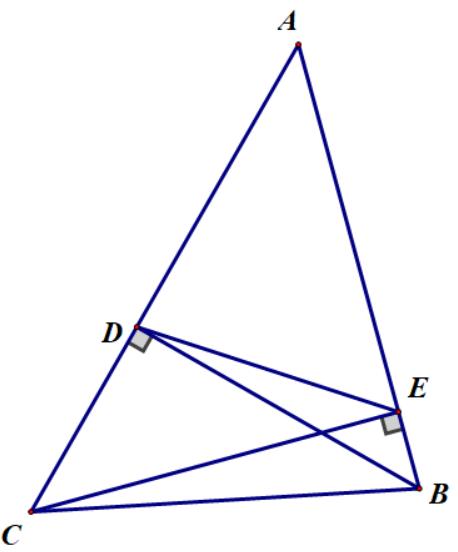
làchân BC OM  BCD  BCEF đường vuônggóc hạ từ xuống , làchân đường vuônggóc hạ từ xuống EABH B. AE a) Chứng minh tứ giác là tứ giác nội tiếp. BEHF b) Chứng minh .MFAE  c) Đường thẳng cắt tại . Đường thẳng cắt , lần lượt tại và MFACQ ECADAB I.K Chứng minh: và .  90EQA ECEK ICIK  Bài 5. (1,0 điểm) Cho làcác số dương thỏa . Chứng minh rằng: . ,, abc 111 2 111abc   1 8 abc …………………….

Bài

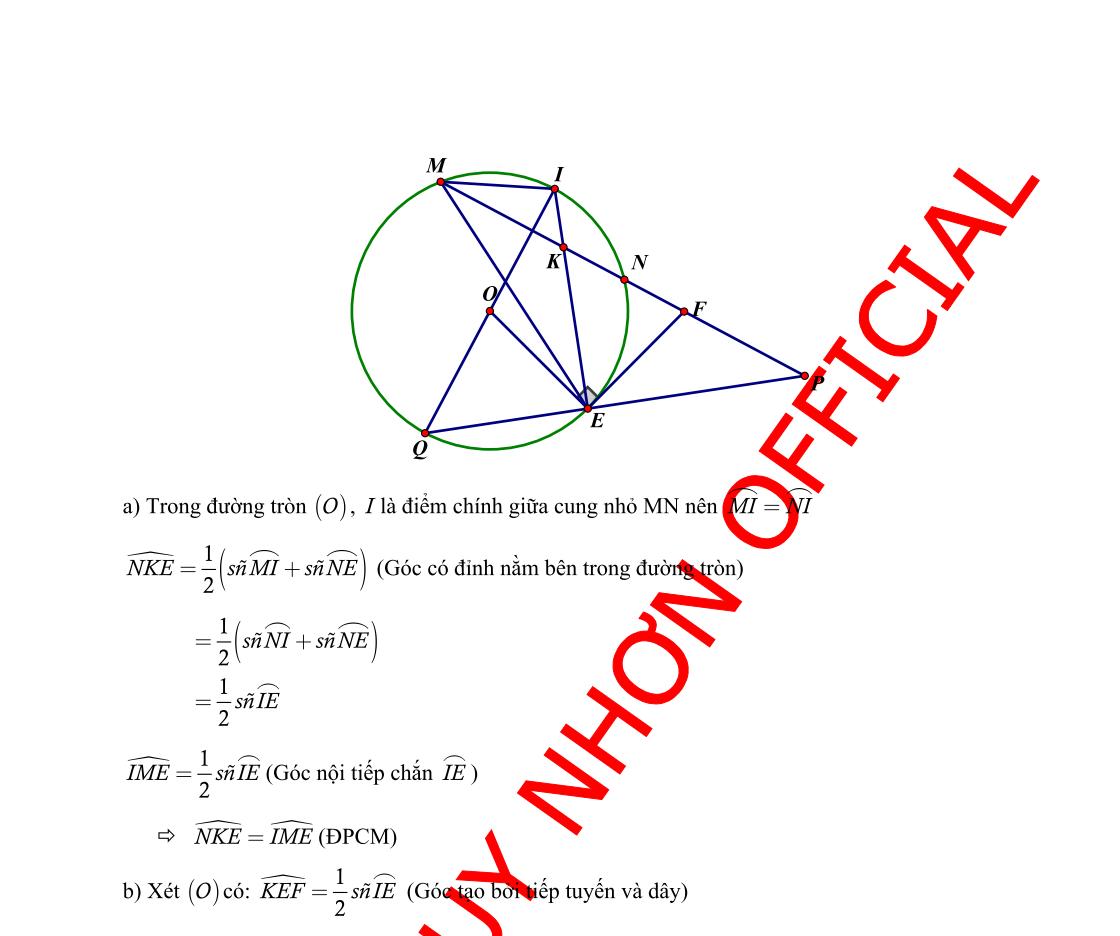
Chotamgiác có nội tiếp trong đường tròntâm . Gọi làtrung

 OM điểm , đường thẳng

cung nhỏ tại , cắt cung lớn tại . Gọi

DẠYKÈMQUYNHƠN OFFICIAL HƯỚNG DẪN CHẤM TUYỂN SINH VÀO 10 BÌNH ĐỊNH – NĂM HỌC 2021 - 2022 Bài Nội dung Điểm Bài 1 2,0 đ 1.Cho biểu thức với 112 : 1111 Px xxxx              0,0xx a)Rút gọn biểu thức P 112 : 1111 Px xxxx             1112 : 1 1 xxxx x x    0,25 11 11 xx xx    1 1 x x    0,25 b)Tìmgiá trị của khi . P423x Tacó: 423x 2 31  31x 0,25 Khi đó: 2 4231 311 P    523 3  536 3  0,25 2. Giải hệ phương trình: 26 237 xy xy    26 237 xy xy     2412 237    xy xy 0,5  26 5    xy y  4 5    x y 0,5 Bài 2 2,0 đ 1.Cho phương trình: (mlàtham số). Hãy 2 2 3230 xmxmm tìmgiá trị của để là nghiệm của phương trìnhvàxác định nghiệm m3x còn lại của phương trình (nếu có). Vì là một nghiệm của phương trìnhnên: 3x 2 2 333230 mmm    2 939230 mmm  2 20 m0m 0,25 Khi phương trình trở thành 0m 2 330 xx 330 xx hoặc . 0x 3x Vậy nghiệm còn lại là 0x 0,25 0,25

nhau tại địa điểm cách 1 BA C . Biết vận tốc của ôtô lớn hơn vận tốc của xemáy .Tính B72km 20/giêkm vận tốc của mỗi xe. Gọi là

DẠYKÈMQUYNHƠN OFFICIAL 2.ChoParabol và đường thẳng (mlà 2 : Pyx  :212 dymxm  tham số). Tìm để cắt tại hai điểm phân biệt ; m P d  11 , Axy 22 , Bxy saocho . 12121yyxx   Phương trìnhhoành độ giao điểm của và là:  P d2212 xmxm  22120xmxm  Tacó: = = 2 214.2 mm     2 441 mm221 m 0,25 Phương trìnhcóhai nghiệm phân biệt khi 0210 m 1 2 m 0,25 Theo hệ thức Vi-éttacó: 12 12 21 2 xxm xxm    0,25 Khi đó: 12121yyxx    22 12121xxxx   2 121231xxxx   2 213.210 mm   2 441610 mmm    2 420 mm 2210 mm hoặc 20 m 210 m (thỏa điều kiện) hoặc (không

kiện) 0m 1 2 m 0,25 Vậy với thì cắt tại hai điểm

0m P d 0,25 Bài 3 1,5 đ Một xemáy

tại

sau đó giờ, một ôtô đi

vận tốc của xemáy. Điều kiện: x / kmh 0x 0,25 Quãng đường xemáy đi đến lúc gặp nhaulà: 88 km Thời gianxemáy đi đến lúc gặp nhaulà: 88 x h 0,25 Vận tốc của ôtô đi là: 20x / kmh Quãng đường ôtô đi đến lúc gặp nhaulà: 72 km Thời gianôtô đi đến lúc gặp nhaulà: 72 20x h 0,25

thỏa điều

phân biệt thỏa điều kiện đã cho.

khởi hành

địa điểm đi đến địa điểm cách , A BA160km

từ đến .Haixe gặp

Giải phương trìnhta được: (nhận), (loại) 140x

244x 0,25 Vậy, vận tốc xemáylà , vận tốc xeôtôlà 40/kmh 60/kmh 0,25 Bài 4 3,5 đ Chotamgiác có nội tiếp trong đường tròntâm . Gọi ABC

90ACB OM làtrung điểm , đường thẳng cắt cung nhỏ tại , cắt cung lớn BC OM

BCD tại . Gọi làchân đường vuônggóc hạ từ xuống , làchân

BCEF EABH đường vuônggóc hạ từ xuốngB. AE a) Chứng minh tứ giác là tứ giác nội tiếp. BEHF

DẠYKÈMQUYNHƠN OFFICIAL

0,25 









b) Chứng

.MFAE  c) Đường

cắt

MFACQ ECADAB lượt tại và Chứng minh: và . I.K  90EQA ECEK ICIK  0,25 1 4 3 2 1 A B C O D E M F H 1 1 1 Q I K 0,25 0,5 a) Chứng minh tứ giác là tứ giác nội tiếp. BEHF Tacó: (gt)  BFE  90BHE  Hai điểm cùng nằm trên đường tròn đường kính hay tứ giác  , FH BE là tứ giác nội tiếp. BEHF 0,25 0,25 1,25 b) Chứng minh .MFAE  Vì làtrung điểm nên M BCOMBC   90EMB  thuộc đường tròn đường kính M EB 0,25

Theo đề tacó phương trình: 88721 20xx  

2 8817607220 xxxx



2417600xx 







minh

thẳng cắt tại Đường thẳng

, lần

DẠYKÈMQUYNHƠN OFFICIAL (cùng chắn cung )   FMEFBEABE   EF Mà (góc nội tiếp cùng chắn cung của đường tròntâm )  ABEADE   AE O Suyra: (1)  ADEFME // DAFM Lại có: (góc nội tiếp chắn nửa đường tròntâm )  90DAE  O (2) DAAE  Từ (1)và(2)suyra: (đpcm)MFAE  0,25 0,25 0,25 0,25 Cáchkhác Vì làtrung điểm nên M BCOMBC   90EMB  thuộc đường tròn đường kính M EB (cùng chắn cung )   11 FE   MB 1 Lại có: (cùng chắn cung của đường tròntâm )  11 AD   EB O Mà (vì ,góc nội tiếp chắn nửa đường tròn)  1190AB  90DBE  (vì )  1190DEBHAE  Suyra  11 BE  2 Từ và suyra  1 2  11 BF // MFBH Mặt khác BHAE  Suyra (đpcm)MFAE  1,5 c) Đường thẳng cắt tại . Đường thẳng cắt , lần lượt MFACQ ECADAB tại và Chứng minh: và . IK  90EQA ECEK ICIK  1,0 * Chứng minh:  90EQA  Tacó: (vì là điểm chính giữa cung )  34 AA D  AB làphângiáctronggóc AD  BAC Mà làphângiácngoàigóc ADAE AE  BAC  12 AA  cân tại (do vừa là đường cao vừa làphângiác) FAQ AAE AQAF  Xét và ,có: cạnh chung; ; AQE AFE AE  12 AA AQAF  = (c–g–c) AQE AFE   90EQAEFA  0,25 0,25 0,25 0,25 0,5 Chứng minh: ECEK ICIK 

DẠYKÈMQUYNHƠN OFFICIAL Tamgiác có:KAC làphângiáctrong đỉnh AI A ICAC IKAK   3 làphângiácngoài đỉnh AE A ECAC EKAK  4 Từ và suyra (đpcm)  3 4ICEC IKEK  0,25 0,25 Bài 5 1,0 đ Cho làcác số dương thỏa ,, abc 111 2 111abc    1 Chứng minh rằng: . 1 8 abc Từ tasuyra: 1 111 11 11111 bc abcbc        1 111 bc abc  2 11 bc bc   1 Tương tự tacó:  1 111 ac bac    2  1 111 ab cab   3 0,25 0,25 0,25 Nhâncác bất đẳng thức (cả hai vế dương) , , cùng chiều, ta được:  1 2 3  111 ..2.2.2 111111111 bcacab abc bcacab     222 222 1 8 111111 abc abcabc     8 111 abc abc (đpcm) 81 abc 1 8 abc  Dấu “=” xảy ra 111 2 111 abc abc       1 2 abc 0,25

DẠYKÈMQUYNHƠN OFFICIAL

ĐỀ THI CHÍNH THỨC

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH LỚP 10 TỈNH BÌNH DƯƠNGNăm học: 2021 - 2022 Môn thi: TOÁN Thời gian làm bài: 120 phút (Không kể thời gian phát đề)

Bài 1. (1,5 điểm) Rút gọn các biểu thức sau: a) 2 755(13)5A  b) 1061 5321 B 

Bài 2. (1,5 điểm) Cho hệ phương trình ( làtham số) 3210 2 xy xym    m a) Giải hệ phương trình đã chokhi .9m b)Tìm tất cả cácgiá trị của tham số để hệ phương trình đã chocó nghiệm thỏa m (x;y)x0,y0 

Bài 3. (2 điểm) ChoParabol và đường thẳng (d): 2():Pyx  56yx

a) Vẽ đồ thị (P). b)Tìm tọa độ cácgiao điểm của (P)và(d) bằng phéptính. c) Viết phương trình đường thẳng (d') biết (d')songsong(d)và(d') cắt (P) tại hai điểm phân biệt có hoành độ lần lượt là saocho . 12 , xx 12,24xx

Bài 4. (1,5 điểm) Một khu vườn hình chữ nhật có chiều dài gấp 3 lần chiều rộng. Người talàm một lối đi xungquanh vườn (thuộc đất trong vườn) rộng m.Tínhkích thước của vườn, biết rằng đất còn lại 1,5 trong vườn để trồng trọt là . 24329m

Bài 5. (3,0 điểm) Chotamgiác vuông tại nội tiếp trong đường tròntâm . Dựng ABC () AABAC  O đường thẳng qua songsong , đường thẳng qua songsong , gọi làgiao điểm dA BC 'dCBAD của và . Dựng vuônggóc ( nằm trên ), làgiao điểm của với đường tròn d' dAE BDE BDF BD . Chứng minh:  O a) Tứ giác nội tiếp được trong đường tròn. AECD b)  AOF2CAE  c) Tứ giác làhìnhbìnhhành. AECF d) . 2DFDB2AB 

DẠYKÈMQUYNHƠN

1 / 4

OFFICIAL

= = = = = = = = = = = = = = = = = = =

Hết

DẠYKÈMQUYNHƠN OFFICIAL 2 / 4 Hướng dẫn giải: Bài 1. a) 2 755(13)25.35|13|A  535(31)(130) do   .535355  b) 1061 5321 B  2(53)21 53(21)(21)   21 2 21  2(21) .221  Bài 2. a) Với hệ phương trình trở thành 9m 3210 29 xy xy    3210 4218 xy xy

 728 29 x yx  4

x y  Vậy

là . 9m  , xy 4,1 b) Tacó: 3210 2 xy xym      32101 22 xy yxm     Thay(2)vào(1)ta được  32210342107210 xxm xxmxm    210 7 m x   Thay vào(2)ta được . 210 7 m x   210443 29 77 m m y    Đề khivàchikhi . 0,0xy 210 0 7 443 0 7 m m          2100 4430 m m  5 43 4534 4 m m m      Vậy thỏa mãnyêu cầu bàitoán. 43 5 4 m  Bài 3. a) Vẽ đồ thị  P Đồ thị hàm số đi qua gốc tọa độ ,có bề lõm hướng xuống và nhận làm trục đối xứng. 2 yx  O Oy Bảng giá trị:



với hệ phương trìnhcó nghiệm

DẠYKÈMQUYNHƠN OFFICIAL 3 / 4 x 21 0 1 2 2 yx  41 0 14 Parabol đi quacác điểm , , , , .  2 : Pyx   2;4 1;1 0;0 1;1 2;4 Đồ thị Parabol : 2 : Pyx  2) Hoành độ giao điểm của đồ thị và là nghiệm của phương trình: () P() d 2 2 56560xxxx Tacó: nên phương trìnhcó2 nghiệm phân biệt 2 2 Δ454610bac   . 1 2 51 2 2 51 3 2 x x       Với . 2 1 1 2(2)4xy Với . 2 2 2 3(3)9xy Vậy tọa độ cácgiao điểm của và(d)là .  P  2;4,3;9AB Bài 4. Gọi chiều rộng hình chữ nhật là (m, đk: ). x 0x Khi đó chiều dàihình chữ nhật là (m). 3x Kích thước phần đất còn lại saukhilàm lối đi là .3;33 xmxm Theobài diện tích đất còn lại là nêntacó phương trình 24329m 3334329xx 2 33994329 xxx  2 31243200 xx  2414400xx 

Ptcóhai nghiệm phân biệt (t.m); (L) 1 238 40 1 x 

2 238 36 1 x

Vậy chiều rộng mảnh vườn là40m; chiều dài mảnh vườn là3.40=120m. Bài 5. a)tacó (góc nội tiếp chắn nửa đường tròn)

90BAC

Tứ giác làhìnhbìnhhành nên (haigócsoletrong) ABCD // ABCD

90AEDACD

// ABCDCDEABD 

; EC

AD90

AECD b) tứ giác nội tiếp (2góc nội tiếp chắn cung ) AECD  CAECDE EC (soletrong)

Suyra cùngnhìn dưới góc do đó tứ giác nội tiếp.

DẠYKÈMQUYNHƠN OFFICIAL 4 / 4

'414401444'38 





 



 



 



 CAEABD

Mà



 2.



đường tròn)(cùngvuônggóc với )  90BFC  // AECF BD Lại có  // AFBACBCADFECAFEC  Do đó tứ giác làhìnhbìnhhành. AECF d) Gọi giao điểm của và là ,do tứ giác làhìnhbìnhhànhnên ACBDI ABCD ;; IAICIBIDABCD  Xéttamgiác vuông tại có là đường caonên DCI CCF 2 2 CDDFDIABDFDI  mà do đó 2 22ABDFDI 2DIBD  22ABDFBD  = = = = = = = = = = = = = = = = = = = Hết = = = = = = = = = = = = = = = = = = =

90ACDBAC







làgóc ở tâm; làgóc nội tiếp chắn cung hay

ABD

AOF AF

AOFABD

AOFCAE

c)Tacó (góc nội tiếp chắn nửa

THI TUYỂN SINH LỚP 10 THPT NĂM 2021 Môn thi: TOÁN CHUNG Ngày thi: 7/6/2021 Thời gian làm bài: 120 phút, không kể thời gian giao đề

DẠYKÈMQUYNHƠNOFFICIAL SỞ GIÁO DỤC

ĐÀO

ĐỀ THI CHÍNH THỨC

Câu 1 (2,0 điểm): 1.Tínhgiá trị các biểu thức sau: 4925A 2275A 752A Vậy 2.A 25(35)B 5|35|B Do 535(B 350)  3B Vậy 3.B 2.Cho biểu thức với . 43 2 Pxxx x x    0x a.Rút gọn biểu thức . P Với tacó: 0x 43 2 Pxxx x x    (2)(2)(3) 2 Pxxxx x x      23Pxx

VÀ

TẠO BÌNH PHƯỚC

KỲ

Vậy với thì . 0x 21Px b.Tìmgiá trị của để . x5P Để thi . 5P2152424() x xxxtm

Vậy để thì . 5P 4x Câu 2 (2,0 điểm): 1.Choparabol và đường thẳng . 2():2 Pyx  ():1 dyx a) Vẽ parabol và đường thẳng trêncùng một hệ trục tọa độ () P d Oxy

Tập xác định: D ,hàm số đồng biến nếu ,hàm số nghịch biến nếu 20a 0x 0x Bảng giá trị x 2 1 0 1 2 22 yx  8 2 0 2 8 Đồ thị hàm số là đường congParabol đi qua điểm , nhận làm trục đối 22 yx  OOy xứng, bề lõm hướng lêntrên.

Tập xác định: D nênhàm số đồng biến trên 10a  Đồ thị hàm số là đường thẳng đi qua điểm và 1yx (0;1)(1;0)

DẠYKÈMQUYNHƠNOFFICIAL

21Px

DẠYKÈMQUYNHƠNOFFICIAL b)Tìm tọa độ giao điểm của và bằng phéptính. () P() d

độ giao điểm của và là nghiệm của phương trình () P() d . 2 2 21210 xxxx   Tacó nên phương trìnhcó2 nghiệm phân biệt 2110abc  1 1 . 2 x c x a      + Với 1112xy + Với 111 1 222xy Vậy tọa độ giao điểm của và là và . () P() d(1;2)11 ; 22    2.Không sử dụng máytinh cầm tay, giải hệ phuongtrinh: 24 27 xy xy    Tacó: 24428515 3 2727242 xy xy x x xyxy yxy                             

Hoành

Vậy nghiệm của hệ phương trìnhlà .(;)(3;2) xy Câu 3 (2,5 điểm): 1.Cho phương trình (1), với làtham số. 2(2)80xmx   m a) Giải phương trình(1)khi . 4m Thay vào phương trình(1)ta được: 4m 2280xx Tacó: nên phương trìnhcóhai nghiệm phân biệt: . 2 18930

Vậy phương trìnhcó tập nghiệm .{4;2}S

DẠYKÈMQUYNHƠNOFFICIAL

   



 2 2 1

11Qxx 

phương trình(1)luôncóhai nghiệm 2 (2)320 m m   phân biệt . 12 , xx Khi đó theoVi-éttacó: 12 12 2 8 xxm xx    Tacó:  2 2 1 2 11Qxx  2222 12121xxxx  2 22 1212 12 21xxxxxx  2 2 64(2)161(2)4949.Qm m m    Vậy . Dấu "=" xảy rakhi . max 49Q 2m Vậy giá trị lớn nhất của bằng 49khi . Q 2m 2.Haiôtô khởi hànhcùng một lúc tể đi từ địa điểm đến địa điểm cáchnhau A B Vận tốc ôtô thứ hai lớn hơn vận tốc ôtô thứ nhất là nênôtôthúhai 120. km 10/kmh đến trước ôtô thứ nhất 24phút.Tính vận tốc của mỗi ôtô. B Gọi vận tốc của ôtô thứ nhất là (ĐK: ). (/)xkmh 0x Suyra vận tốc của ôtô thứ hailà 10(/) xkmh 

  1 2 192 194 x x 

b)Tìm để phương trìnhcóhai nghiệm saocho biểu thức đạt m 12 , xx

giá trị lớn nhất. Phương trình(1)có: nên

Thởi gianôtô thứ nhất đi hết quãng đường là: AB120 x () h

Thời gianôtô thứ hai đi hết quãng đường là (h) AB120 10x

Vìôtô thứ hai đến trước ôtô thứ nhất 24phút giờ nêntacó phương trình: B 2 5

DẠYKÈMQUYNHƠNOFFICIAL

 2 2 2 1201202 105 600(10)6002(10) 6006000600220 22060000 1030000 xx x xxx x xxx xx xx           Tacó: nên phương trìnhcó2

2 2 (5)30003025550  1 2 55550() 55560() x tm x ktm      Vậy vận tốc của ôtô thứ nhất là và vận tốc của ôtô thứ hailà . 50/kmh 60/kmh Câu 4 (1,

9cmAB 12cmAC

Áp dụng định líPytagotrongtamgiácvuông tacó: ABC 2 2 2BCABAC  222 912BC  2225BC  22515(cm)BC  Áp dụng hệ thức lượng trongtamgiácvuông tacó: ABC

nghiệm phân biệt

0 điểm): Chotamgiác vuông tại có đường cao và đường trung tuyến Biết ABC A AH .AM , .Hãytính và diện tíchtamgiác .

,, BCAHAM ABM

Vì làtrung tuyến ứng với cạnh huyền của tamgiácvuông nên AM ABC (định lí đường trung tuyến trongtamgiácvuông). 11 2157,5(cm) 2 AMBC

Tacó .  2 1 111 . ..7,2.1527cm 2 224 ABM SAHBMAHBC

Vậy . 215cm,7,2cm,7,5cm,27cm ABM BCAH AM S

Câu 5 (2,5 điểm): Từ điểm nằm ngoài đường tròn kẻ hai tiếp tuyến là tiếp điểm). Kẻ A () O ,(, ABACBC cát tuyến không đi quatâm nằm giữa và và nằm về haiphíaso với AEF (E A; FOB cát tuyến ). Gọi làtrung điểm của . K EF



DẠYKÈMQUYNHƠNOFFICIAL 9.12 . 17,2(cm). 5 ABACABACAHBCAH BC

 

    

   



a) Chứng minh tứ giácOBAC nội tiếp đường tròn. Tacó: là tiếp tuyến của đường trònnên , ABAC   90 180 90 OAABABO ABOACO OCACACO           là tứ giác nội tiếp đường tròn đường kinh (dhnb). OBAC AO b) Chứnng minh làphângiác của . KA  BKC Vì là tiếp tuyến của đường trònnên (tính chất hai tiếp tuyến cắt nhau). , ABAC ABAC  Tacó làtrung điểm của nên (quan hệ vuônggóc giữa đường kínhvà K EFOKAK  dâycung).

90 OKAK AO ,,,, OKBAC thuộc một đường tròn. (góc chắn haicung bằng nhau)

thuộc đường tròn đường kính hay5 điểm cùng

11 22 BKAAKCsdABsdAC

Vậy làphângiác của . KA

BKC c) Kẻ dây vuônggóc saocho cắt tại .Chúngminh đi quatrung ED OBEDBCM FM điểm của đọn thẳng . I AB Gọi làgiao điểm của và J AKBC Gọi làgiao điểm của và .Ta sẽ chứng minh làtrung điểm của . I FMAB I AB

DẠYKÈMQUYNHƠNOFFICIAL







 ()

 đồng

ABJ

AKB AJAB ABAK  2 . ABAJAK Tương tự tacó: đồng dạng với ABE 2 ()ABAEAFBgg ABAEAF AFAB  (Vì làtrung điểm của ) .. AFAKAFAKFKEK AJAKAEAFAJAEAJAEEJEJ   K EF . AFAJ EKEJ  Ta lại có: (Định líTa-lét) ()// () ABAJ EMOBgt EMEJEMAB OBABgt AIAF EMEF                  11 222 2 AIAFAJABAB AI EMEKEJEM  Vậy làtrung điểm của (đpcm). I AB





Xéttamgiác và tacó: ABJAKB chung

BAK

ABJBKAACB

dạng với (g.g) (cặp cạnh tương ứng)



mặt phẳng

P  Oxy b)Tìm tất cả cácgiá trị của tham số để đường thẳng cắt tại hai điểm m ():21 dymx P phân biệt cóhoành độ thỏa mãn và . 12 , xx 12xx  212021xx

Bài 4. (1,0 điểm) Một phân xưởng phải may1200 bộ quần áotrong một thời gianquy định. Khi thực hiện, do cải tiến kĩ thuật nên mỗi ngàyphân xưởng maythêm được 10 bộ quần áovàhoànthành kế hoạch trước 4ngày. Hỏi theo kế hoạch mỗi ngàyphân xưởng maybaonhiêu bộ quần áo? Bài 5. (1,0 điểm) Một cốc nước dạng hình trụ có chiều caolà ,bánkính đáy là và lượng 15cm 3cm nước ban đầu trong cốc cao . Thả chìmhoàntoànvào cốc nước 5viênbi thủy tinhhình cầu có 10cm cùngbánkínhlà . Hỏi saukhi thả 5viênbi mực nước trong cốc cách miệng cốc một khoảng bằng 1cm baonhiêu?

(Giả sử độ dày của thành cốc và đáy cốc không đáng kể, kết quả làmtròn đến chữ số thập phân thứ hai)

DẠYKÈMQUYNHƠN OFFICIAL 1 / 5 SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH LỚP 10 TỈNH BÌNH THUẬN Năm học:

2022 Môn

Thời

) Bài 1. (2,0 điểm) Giải phương trìnhvà hệ phương trìnhsau: 1) 2340xx 2) 24 24 xy xy    Bài 2. (1,5 điểm) Rút gọn các biểu thức sau: 1)   2731223:3  2) (với ). 1562 : 3933 B xxx x      0;9xx



2021 -

thi: TOÁN

gian làm bài: 120 phút (Không kể thời gian phát đề

Bài 3. (1,5 điểm) Chohàm số có đồ thị 22 yx

 P a) Vẽ đồ thị trên

tọa độ 

(2,5 điểm) Từ điểm nằm bênngoài đường tròn vẽ các tiếp tuyến , với đường A  O ABAC tròn ( làcác tiếp điểm).  O, BC a) Chứng minh tứ giác nội tiếp. ABOC b) Từ vẽ cát tuyến đến đường tròn (với ). A AEF OAEAF  Chứng minh 2 . ACAEAF  c) cắt tại . Gọi làtrung điểm của đoạn thẳng ,tia cắt tại . Đặt OABCHM HBOMAEK Chứng minh  AOB 2 cos KB KA  Bài 7. (0,5 điểm) Ba bạn Đào, Mai,Trúc mặc ba chiếc áomàu trắng,hồng, xanhvà đeo

trang cũng màu trắng,

rằng: a)Trúc đeo khẩu

b) Chỉ có

c)Màuáovàmàu

Bài 6.

bacái khẩu

hồng, xanh. Biết

trangmàuxanh.

bạn Đào làcómàuáovàmàu khẩu trang giống nhau.

khẩu trang của bạn Mai đều không phải màu trắng. ĐỀ THI CHÍNH THỨC

Dựa vàocácthôngtintrên,emhãycho biết mỗi bạn Đào, Mai,Trúc mặc màugìvà đeo khẩu trang màugì?

2 / 5

DẠYKÈMQUYNHƠN OFFICIAL

= = = = = = = = = = = = = = = = = = = Hết = = = = = = = = = = = = = = = = = = =

DẠYKÈMQUYNHƠN OFFICIAL 3 / 5 Hướng dẫn giải: Bài 1. 1) 2340xx Cách1: 2 34.1.(4)250  Do đó phương trình đã chocóhai nghiệm phân biệt 1 2 325325 1; 4 2121 x x     Cách2:Vì 13(4)0abc Nên phương trình đã chocóhai nghiệm 12 4 1; 4 1 c xx a  2) 242000 24240242 xy x x x xyxy yy                        Vậy hệ phương trình đã chocó nghiệm (0;2) Bài 2. 1)   2731223:3    336323:3 73:37  2) (với ) 1562 : 3933 B xxx x      0;9xx  35363 . 9992 xx x xxx             351563 92 xx x x    6183 . 32 3 x x xx      633 .3 32 3 x x xx     Bài 3. a) x -2 -1 0 1 2 22 yx  8 2 0 2 8

Bài 4. Gọi là số bộ quần áophân xưởng may mỗi ngàytheo kế hoạch () x *xN  Thời gianphân xưởng may1200 bộ quần áotheo kế hoạch là (ngày) 1200 x Thực tế mỗi ngàyphân xưởng may được (bộ) 10x Nên thời gian thực tế phân xưởng may1200 bộ quần áolà (ngày) 1200 10x

DẠYKÈMQUYNHƠN OFFICIAL 4 / 5



x y P) 2 2 -2-1O1 8 b) Phương trìnhhoành độ giao điểm của và là  P d 2 2 2212210(1) xmxxmx   với mọi giá trị của 2 2 '()2(1)20 m m   m Nên phương trình(1)luôncóhai nghiệm phân biệt với mọi giá trị của . m Suyra luôn cắt tại hai điểm phân biệt với mọi giá trị của .  d  P m Theo định líViéttacó: 12 12 (2) 1 2(3) xxm xx    

Tacó mà suyra 12xx  12 1 0 2 xx 12 0 xx  Khi đó 212021xx 21()2021xx  212021xx  2021m 

Theo đề bàitacó phương trình 12001200 4 10xx   1200(10)12004(10) x xxx   2 440120000 xx  50() 60() xnhan xloai   Vậy theo kế hoạch mỗi ngàyphân xưởng may được 50 bộ quần áo. Bài 5. Thể tích của 5viênbilà 3 3 1 4420 541() 333 Vr cm      Mặt khác thể tích của 5viênbi bằng thể tích của nước dânglênnêntacó (với hlà chiều cao lượng nước dânglên) 220 20 33() 27 hhcm Chiều cao của nước saukhi thả 5viênbivàolà 20290 10 2727  cm

Mực nước cách miệng cốc một khoảng là 290115 154,26() 2727 cm

Vậy mực nước trong cốc cách miệng cốc là4,26 . cm Bài 6.

A (góc tạo bởi tia tiếp tuyến vàdâycungvàgóc nội tiếp cùng chắn một cung)

7. Vì chỉ có bạn Đào làcómàuáovàmàu khẩu trang giống nhaunênTrúc đeo khẩu trangmàu xanhthìTrúccómàuáolà hồng hoặc trắng. (1) Vìmàuáovàmàu khẩu trang của bạn Mai đều không phải màu trắng nênmàu khẩu trang của Mai chỉ có thể làmàu hồng, do đó khẩu trangvàáo của Đào làmàu trắng . Kết hợp với (1)nênTrúccómàuáo là hồng. Còn lại Maicómàuáolàxanh.

Vậy Trúc mặc áo hồng và đeo khẩu trangxanh, Đào mặc áo trắng và đeo khẩu trang trắng, Mai mặc áoxanhvà đeo khẩu trang hồng.

DẠYKÈMQUYNHƠN OFFICIAL 5 / 5

K H' M H E A O B C F













2ACAE ACAEAF AFAC  c)

H HO Khi

 2 ' coscoscos KBOHOHOHOB KAOAOAOBOA    

a)Tacó (tính chất của tiếp tuyến)

090OBAOCA

Tứ giác có ABOC

000 9090180OBAOCA Suyra tứ giác nội tiếp. ABOC b)Xét và có ACE AFC chung

ACEAFC

ACE AFC

Gọi làhình chiếu của qua '

đó là đường trungbình của

'HBH //BH'OM Hay //'OKBH Theo định lýThalestacó 'KBOH KAOA

Bài

SỞ GIÁO DỤC VÀ ĐÀO TẠO CÀ MAU

ĐỀ THI CHÍNH THỨC

KỲ THI TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2021 – 2022 Môn thi: TOÁN

Thời gian làm bài: 120 phút, không kể thời gian giao đề

Bài 1: (1,0 điểm)

a)Tínhgiá trị của biểu thức A = 2 731667  b)Rút gọn biểu thức B = (Với x ≥ 0, x ≠ 1) 2(2) 11   xxxxx x x

Bài 2: (1,0 điểm)

a) Giải phương trình 230 xx b)Cho hệ phương trình 2 1

      

x y ab y x ba

Tìmavàb biết hệ phương trình đã chocó nghiệm (x;y)=(3;2)

Bài 3: (1,5 điểm) Trong mặt phẳng tọa độ vuônggócOxy,choparabol(P): y = x2 . a) Vẽ (P). b)Tìmm để đường thẳng (d): y =(m – 1)x + m +4 cắt (P) tại hai điểm phân biệt nằm về haiphía của trục tung.

Bài 4: (1,5 điểm) Theocácchuyêngia về sức khỏe, người trưởng thành cần đi bộ từ 5000 bước mỗi ngày sẽ rất tốt cho sức khỏe. Để rèn luyện sức khỏe, anh Sơn và chị Hà đề ra mục tiêu mỗi ngày một người phải đi bộ ít nhất 6000 bước. Hai người cùng đi bộ ở côngviênvà thấy rằng, nếu cùng đi trong2phútthìanh Sơn bước nhiều hơn chị Hà20 bước. Hai người cùng giữ nguyên tốc độ đi như vậy nhưng chị Hà đi trong5phútthì lại nhiều hơn anh Sơn đi trong3 phútlà160 bước. Hỏi mỗi ngàyanh Sơn và chị Hàcùng đi bộ trong1 giờ thì họ đã đạt được số bước tối thiểu mà mục tiêu đề rahay chưa? (Giả sử tốc độ đi bộ hàngngày của hai người không đổi). Bài 5: (1,5 điểm) Cho phương trình (mlàtham số) 2 2 21470 

x(m)mm a)Tìmm để phương trình đã chocó nghiệm. b)Tìmm để phương trình đã chocóhai nghiệm âmphân biệt.

DẠYKÈMQUYNHƠN

OFFICIAL



Bài 6: (3,5 điểm) Chotamgiác nhọn ABC ( AB < AC) nội tiếp đường tròntâmO.Hai tiếp tuyến tại B và C của đường tròn(O) cắt nhau tại M,tia AM cắt đường tròn(O) tại điểm D.

a) Chứng minh rằng tứ giác OBMC nội tiếp được đường tròn.

b) Chứng minh MB2 = MD.MA

c) Gọi E làtrung điểm đoạn thẳng AD;tia CE cắt đường tròn(O) tại điểm F. Chứng minh rằng: BF // AM. ----- Hết -----

DẠYKÈMQUYNHƠN OFFICIAL

DẠYKÈMQUYNHƠN OFFICIAL 3 HƯỚNG DẪN GIẢI CHI TIẾT ĐỀ THI VÀO 10 MÔN TOÁN CÀ MAU – HỆ CHUNG Bài 1 (1 điểm): a) Tính giá trị của biểu thức A = 2 731667  Cách giải: 2 2 2 2 A731667 733237(7) 37(3+7) 3737 27        Vậy A= 27 b) Rút gọn biểu thức B = (Với x ≥ 0, x ≠ 1) 2(2) 11   xxxxx x x Cách giải: 2(2) 11 (1)44 (1)(1)1 54 11 44 1 4(1) 1 4             xxxxx B x x xxxxxx xx x xx xx x x x x Vậy với thìB=4. 0,1xx Bài 2 (1 điểm): a) Giải phương trình 230 xx

DẠYKÈMQUYNHƠN OFFICIAL 4 Cách giải: ĐKXĐ: 3 2 x 2 2 2 230 23 0 23 0 230 0 330 0 ()()0 0 3 1                 xx xx x xx x xx x xxx x x-3x+1 x x x (Thỏa mãn điều kiện) 3 x Vậy tập nghiệm của phương trìnhlàS={3} b) Cho hệ phương trình 2 1        x y ab y x ba Tìm a và b biết hệ phương trình đã cho có nghiệm (x;y) = (3;2) Cách giải: Điều kiện 0 0    a b Hệ phương trình đã chocó nghiệm (x;y)=(3;2)nêntacó hệ phương trình: 3232 2 2 2112 3 3                 abab baab Đặt . Hệ phương trình trở thành: 11 ,(0)uyu,v ab

Cách

y 0

yx2 b) Tìm m để đường thẳng (d): y = (m – 1)x + m + 4 cắt (P) tại hai điểm phân biệt nằm về hai phía của trục tung. Cách giải: Xét phương trìnhhoành độ giao điểm

4 3 2 1 2 1 -1 -2

DẠYKÈMQUYNHƠN OFFICIAL 5 55(TM)3222522 2323311(TM) 24                                 u u uvu uvuv u v v 152 2(TM) 5 1114 4(TM) 11                  ua a vb b Vậy 24 5,11 ab Bài 3: (1,5 điểm) Trong mặt phẳng tọa độ vuônggócO

xy,choparabol(P): y = x2

a) Vẽ

(P). của hai đồ thị hàm số và ():(1)4  dymxm tacó: 2(): Pyx 2(1)4 mxmx 2(1)40(*) xmxm Đường thẳng (d) cắt đồ thị hàm số (P) tại hai điểm phân biệt nằm về haiphía của trục tungkhivà chỉ khi phương trình(*)cóhai nghiệm trái dấu 0 ac 404 m m

giải: Tacó bảng giá trị : x -2 -1 0 1 2 y=x2 4 1 0 1 4 Vậy đồ thị hàm số (P):y=x2 làparabol đi quacác điểm (-2;4),(-1;1),(0;0),(1;1), (2;4). x

Vậy m>-4thì đường thẳng (d): y =(m – 1)x + m +4 cắt (P) tại hai điểm phân biệt nằm về haiphía của trục tung.

Bài 4: (1,5 điểm) Theo các chuyên gia về sức khỏe, người trưởng thành cần đi bộ từ 5000 bước mỗi ngày sẽ rất tốt cho sức khỏe.

Để rèn luyện sức khỏe, anh Sơn và chị Hà đề ra mục tiêu mỗi ngày một người phải đi bộ ít nhất 6000 bước. Hai người cùng đi bộ ở công viên và thấy rằng, nếu cùng đi trong 2 phút thì anh Sơn bước nhiều hơn chị Hà 20 bước. Hai người cùng giữ nguyên tốc độ đi như vậy nhưng chị Hà đi trong 5 phút thì lại nhiều hơn anh Sơn đi trong 3 phút là 160 bước. Hỏi mỗi ngày anh Sơn và chị Hà cùng đi bộ trong 1 giờ thì họ đã đạt được số bước tối thiểu mà mục tiêu đề ra hay chưa? (Giả sử tốc độ đi bộ hàng ngày của hai người không đổi).

Cách giải:

Gọi số bước anh Sơn đi bộ trong1phútlàx (bước) (x N*).

OFFICIAL

Gọi số bước chị Hà đi bộ trong1phútlày (bước) (y N*,y<x).

2phútanh Sơn đi được 2x (bước)

2phút chị Hà đi được 2y (bước)

Nếu đi cùngtrong2phútthìanh Sơn đi nhiều hơn chị Hà20 bước nêntacó phương trình:2x–2y=20 (1)

3phútanh Sơn đi được 3x (bước)

5phút chị Hà đi được 5y (bước)

Do chị Hà đi trong5phútthì nhiều hơn anh Sơn đi trong3phútlà160 bước nêntacó phương trình:5y–3x=160 (2)

DẠYKÈMQUYNHƠN

Từ (1)và(2)tacó hệ phương

22201010 1010105 531605316053(10)16021909595                                    xy xy xy xyxyx yx yx yy y y y Đối chiếu với điều kiện suyrax=105,y=95 Mỗi ngàyanh Sơn đi bộ trong1 giờ nên số bước anh Sơn đi là105.60=6300 (bước) Mỗi ngày chị Hà đi bộ trong1 giờ nên số bước chị Hà đi là95.60=5700 (bước) Vậy anh Sơn đạt được mục tiêu đề racòn chị Hàthìkhông đạt được mục tiêu đề ralà 6000 bước mỗi ngày. Bài 5: (1,5 điểm) Cho phương trình (m là tham số) 2 2 21470  x(m)mm a) Tìm m để phương trình đã cho có nghiệm.

trình:

Vậy với m> thì phương trình đã chocóhai nghiệm âm. 9 4 Bài 6: (3,5 điểm) Cho tam giác nhọn ABC ( AB < AC) nội tiếp đường tròn tâm O. Hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại M, tia AM cắt đường tròn (O) tại điểm D. Cách giải:

DẠYKÈMQUYNHƠN OFFICIAL 7 Cách giải: (1) 2 2 21470  x(m)mm 22 2 2 (21)4(47) 44141628 1227      mmm mmmm m Phương trình(1)có nghiệm 279 0122701227 124  m mm Vậy với thì phương trình đã chocó nghiệm. 9 4 m b) Tìm m để phương trình đã cho có hai nghiệm âm phân biệt. Cách giải: Phương trình (1) có hai nghiệm âm phân biệt 2 2 9 9 0 4 122704 19 0(21)021024 470(2)30 0                                        m m m b m m mm a mm m m c a

DẠYKÈMQUYNHƠN OFFICIAL 8 F E D M O B C A a) Chứng minh rằng tứ giác OBMC nội tiếp được đường tròn. TacóMB,MClàcác tiếp tuyến của đường tròn(O)nên   0 0 90 90        OBMBMBO OCMCMCO Xét tứ giácOBMCcó  000 9090180MBOMCO Mà làhaigóc đối nhaunên tứ giácOBMC nội tiếp.  , MBOMCO b) Chứng minh MB2 = MD.MA Tacó (góc tạo bởi tiếp tuyến vàdâycungvàgóc nội tiếp cùng chắn cung   DBMBAM BD). Xét MBDvà MABcó:   (g.g) chung      DBMBAM MBDMAB BMA # 2 . MBMD MBMAMD MAMB c) Gọi E là trung điểm đoạn thẳng AD; tia CE cắt đường tròn (O) tại điểm F. Chứng minh rằng: BF // AM. TacóElàtrung điểm của ADnênOE AD (mối quan hệ giữa đường kínhvàdây  cung)  090 OEM Xét tứ giácOEMCcó  000 9090180OEMOCM

DẠYKÈMQUYNHƠN OFFICIAL 9 Mà làhaigóc đối

tứ

 , OEMOCM (haigóc

 COMCEM Ta lại có sđ (tính chất

1 2 COMBOM  BC Mà sđ (tính chất góc nội tiếp) 1 2 BFC  BC (2)  COMBFC Từ (1)và(2)  MECBFC Màhaigóc và ở vị trí đồng vị .  MEC  BFC //hay//EMBFAMBF ----- Hết -----

nhaunên

giácOEMC nội tiếp.

nội tiếp cùng chắn cungCM) (1)

hai tiếp tuyến cắt nhau)

ĐỀ THI CHÍNH THỨC

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH LỚP 10 TỈNH CAO BẰNGNăm học: 2021 - 2022 Môn thi: TOÁN Thời gian làm bài: 120 phút (Không kể thời gian phát đề)

Bài 1. (4,0 điểm) 1) Thực hiện phéptính: . 22516 2) Chohai đường thẳng và Visao?Hãycho biết vitrí tương  1:32dyx   2:21dyx đối của hai đường thẳng trên? 3) Giải phương trình: .237 x 4) Giải hê phương trình: . 411 39 xy xy   

Bài 2. (2,0 điểm) Nhà bạn Hoàngcó một mảnh vườn hình chữ nhật, rộng 6m . Diện tích của mảnh vườn bằng Tính chiều rộng và chiều dài của mảnh vườn nhà bạn Hoàng. 2216m

Bài 3. (1,0 điểm) Chotamgiác vuông tại cócác cạnh . ABC A 9cm;12cmABAC  

1)Tính độ dài cạnh . BC

2) Kẻ đường cao .Tính độ dài đoạn thẳng AH AH

Bài 4. (1,5 điểm) Chotamgiác cóbagóc nhọn, . Vẽ các đường cao và của ABC  45BAC  BDCE tamgiác . Gọi làgiao điểm của và . ABCH BDCE

1) Chứng minh là tứ giác nội tiếp. ADHE

2)Tính tỉ số DE BC

Bài 5. (1,0 điểm) Cho phương trình:  2 22 12210mmxmmx   ( làtham số). Giả sử và làcác nghiệm của phương trìnhtrên.Tìmgiá trị lớn nhất vàgiá trị m 1x2x nhỏ nhất của biểu thức 12Sxx 

DẠYKÈMQUYNHƠN

1 / 4

OFFICIAL

= = = = = = = = = = = = = = = = = = =

Hết

Hướng dẫn giải: Bài 1.

1)Tacó: 22 225162542.546

chiều

hơn chiều rộng nên chiều dài mảnh vườn là: 6m  6.xm  Do diện tích của mảnh vườn là nêntacó phương trình: 2216m  2 621662160xx xx

Tacó: nên phương trìnhcó2 nghiệm phân biệt: '2 2 3216225150  Hoặc  131512tmx  231518ktmx Chiều rộng của mảnh vườn là và chiều dài của mảnh vườn là:

12m 12618m Vậy chiều rộng và chiều dài của mảnh vườn nhà bạn Hoàng lần lượt là métvà18mét. 12

DẠYKÈMQUYNHƠN OFFICIAL 2 / 4

 





x x xx 



39939323 xy y y y xyxyx x                      

phương trìnhlà  ;3;2xy Bài 2.

rộng

x

1)Tính độ dài cạnh . BC Áp dụng định lýPy-ta-gochotamgiác vuông tại tacó: ABC A 22222912225BCABAC 22515BC cm Vậy 15 BCcm  2) Kẻ đường cao Tính độ dài đọn thẳng .AH AH

Vậy 225166

2)Hai đường thẳng và cắt nhauvì  1d 2d 32

3)Tacó: 2372732105

Vậy nghiệm của phương trìnhlà 5.x

4) Tacó: 411222

Vậy nghiệm của hệ

Gọi chiều

của mảnh vườn nhà bạn Hoànglà: ĐK: ). (

Vì

dài lớn





Bài 3.

DẠYKÈMQUYNHƠN OFFICIAL 3 / 4 Áp dụng hệ thức lượng trongtamgiác vuông tại có đường cao ABC A .AH .9.12 .. 7,2 15 ABAC AHBCABACAH cm BC    Vậy 7,2. AHcm  Bài 4. 1) Chứng minh là tứ giác nội tiếp. ADHE Vì làcác đường cao của nên . , BDCE ABC  90AEHADH  Xét tứ giác có . ADHE  9090180AEHADH  là tứ giác nội tiếp (Tứ giáccó tổng 2góc đối bằng ). ADHE 0180 2)Tính tỉ số DE BC Vì là tứ giác nội tiếp nên (gócngoàivàgóctrong tại đỉnh đối diện của tứ giác ADHE  ADEABC  nội tiếp). Xét và có: ADE ABC chung;  BAC .   cmtADEABC  DEAD ADEggBCAB #ABC Xét có vuôngcân tại ADB    90,45Δ ADBgtBADgtABD      .D  2 coscos45 . 2 AD ADAD BAD AB ABAB    Vậy 2 . 2 DE BC 

DẠYKÈMQUYNHƠN OFFICIAL 4 / 4 Bài 5. Giả sử làcác nghiệm của phuoongtrìnhtrên.Tìmgiá trị lớn nhất vàgiá trị nhỏ nhất của 12 , xx biểu thức 12Sxx  Phương trình(1)cóhai nghiệm khivàchikhi 12 , xx (luôn đúng với mọi vì  2 2 2 022410 mmmm  m với mọi m). 2 2 13 1 0 24 mmm      Phương trình(1)luôncó2 nghiệm phân biệt 12,.xx Khi đó áp dụng định líVi-éttacó: 2 122 22 . 1 mmSxx mm    2 222mSmSSmm   2 1220*SmSmS   TH1: 1120101Sm mm  TH2:.Khi đó phương trình(*)có: 1S  2 *2412SSS  2 2 44432SSSS   2 384 SS Để tồn tại giá trị lớn nhất vàgiá trị nhỏ nhất của biểu thức thì phương trình(*) phải 12Sxx  có nghiệm. Khi đó tacó: 2 *03840 SS  2320SS  Hoặc Hoặc 20 320 S S  20 320 S S    2 2 3 S S      2 2 3 S S      Do đó giá trị nhỏ nhất của biểu thức bằng vàgiá trị lớn nhất của biểu thức 12Sxx  2 3 bằng 2. 12Sxx  Với tacó: 2 3 S  2 2 2 2 222 32221 13 mm mmmm mm    2440mm    2 202tmm m  Với tacó: 2S  2 2 2 2 22 22221 1 mm mmmm mm     200tmmm  Vậy giá trị nhỏ nhất của biểu thức bằng đạt được khi vàgiá trị lớn nhất 12Sxx  2 3 2m của biểu thức bằng 2 đạt được khi 12Sxx  0.m

2;4C b) Gọi làhình chiếu của điểm trên . Chứng minh rằng khi thay đổi H  4;4B  d k 0k thì diện tíchtamgiác không vượt quá ( đơn vị đo trêncáctruc tọa độ làxentimét). HBC 29cm Bài 3. (1,5 điểm)

Cho phương trình , với làtham số. 241120xmx   *m

a) Giải phương trình khi *2 m b)Tìm tất cả cácgiá trị của tham số để phương trình cóhai nghiệm phân biệt thỏa m  * 12 , xx mãn  2 1 2121242.4x 8.xmxxxx 

Bài 4. (1,5 điểm)

1)Tìmhai số tự nhiên, biết rằng tổng của chúng bằng 2021và hiệu của số lớn và số bé bằng 15.

Bài 5. (3,5 điểm)

DẠYKÈMQUYNHƠN OFFICIAL 1 / 9 SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH

10 THÀNH PHỐ ĐÀ NẴNG Năm

Môn

Thời

Bài 1. (2,0 điểm) 1)Tính 4312A 2)Cho biểu thức với 4 : 242 xxx B xxxx        0;4xx Rút gọn vàtìm tất cả cácgiá trị nguyên của để B xBx  Bài 2. (1,5 điểm)

có đồ

2 yx   P 

 a)

đồ

 P

LỚP

học: 2021 - 2022

thi: TOÁN

gian làm bài: 120 phút (Không kể thời gian phát đề)

Chohàm số

thị và đường thẳng

:x24dykk

Vẽ

thị Chứng minh rằng luôn đi qua điểm

 d 

Chotamgiác nhọn có

cắt

ABC

  ,,

 H a) Chứng minh rằng tứ giác

b) Gọi làtrung

của Đường tròn đường kính cắt tại điểm ( khác ). M .BC AHAMGGA Chứng minh rằng . .. AEABAGAM  c)Hai đường thẳng và cắt nhau tại Chứng minh rằng và đường DEBC .K  MACGCM  thẳng nối tâmhai đường tròn ngoại tiếp haitamgiác songsong với đường thẳng ,DMBEMC KG = = = = = = = = = = = = = = = = = = = Hết = = = = = = = = = = = = = = = = = = = ĐỀ THI CHÍNH THỨC

các đường cao

nhau tại

,ABAC

BDCEDACEAB

nội tiếp. BEDC

điểm

DẠYKÈMQUYNHƠN OFFICIAL 2 / 9 Hướng dẫn giải: Bài 1. (2,0 điểm) 1)Tính 4312A 2)Cho biểu thức với . 4 : 242 xxx B xxxx        0;4xx Rút gọn vàtìm tất cả cácgiá trị nguyên của để B xBx  Lời giải 1) Tính 43.12.A Tacó: 2 43122312236268A  2) Với .0;4xx 4 : 242 xxx B xxxx          2 4 : 22222 xx x x B xxxxxx              224 2.2 xxxxx B x xx      2222 2.2 x xx B xx xx      Vậy với thì 0;4xx 2 B x  Xét Bx  2 x x  22 xx  Mà và nên x0;4xx 1x Bài 2. (1,5 điểm) Chohàm số có đồ thị và đường thẳng 2 yx   P :x24dykk a) Vẽ đồ thị . Chứng minh rằng luôn đi qua điểm  P  d 2;4.C b) Gọi làhình chiếu của điểm trên . Chứng minh rằng khi thay đổi H  4;4B  d k 0k thì diện tíchtamgiác không vượt quá ( đơn vị đo trêncáctruc tọa độ làxentimét). HBC 29cm Lời giải a) Vẽ đồ thị Chứng minh rằng luôn đi qua điểm  P  d  2;4C * Vẽ đồ thị  P x -2 -1 0 1 2 y 4 1 0 1 4

DẠYKÈMQUYNHƠN OFFICIAL 3 / 9 Vậy đồ thị làparabol đi quacác điểm .  P  2;4,1;2,0;0,1;1,2;4 x y y=x 2 O 1 * Chứng minh rằng luôn đi qua điểm  d  2;4C Giả sử Cd  .24CC ykxk  4224 kk  ( đúng) 44 Vậy luôn đi qua điểm  d 2;4.C b) x y (d) y=x 2 H O B 1 C Tacó: làhình chiếu của điểm trên (vì ) H  4;4B  dBHHC Cd  vuông tại ( định lýpytago) HBC H222 BCBHHC Có: 1 2BHC SBHHC  Áp dụng bất đẳng thức ,ta được: 22 . 2 abab  22211 ... 2224BHC BHCHBCSBHHC     1 Mà  2466CBBCxx    2 Thay vào ta được:  2 1 2 9()BHC Scm  Dấu “=” xảy rakhivà chỉ khi 222 32 36 BHHC BHHC BHHCBC      Vậy khi thay đổi thì diện tíchtamgiác không vượt quá k 0k HBC 29cm

DẠYKÈMQUYNHƠN OFFICIAL 4 / 9

2

xmx   *m a)



 2 1 2121242.4x

xmxxxx 

a) Với thì

2m  *

   262120xxx   6260xxx   620xx             606 202 xx x x Vậy với thì

. 2m  *  6;2S b) Phương trình có nênluôncóhai nghiệm phân biệt trái dấu.  *   112120ac Theo định líVi-ettacó:     12 12 44 .12 xxm xx  1 Vì là nghiệm của phương trình nêntacó: 2x  * 2 2 2 41120xmx   2 22244120xmxx  2 22 2 44440xmxx    2 22244 44mxxx   2 2244 2mxx    2 222.4 2mxx   2224 2mxx 2 Màtheobàicó:  2 1 21212424x 8xmxxxx   3 Thay , vào ta được:  1 2 3  2 12 2.2.244128 xx m  2 1212 2.2484 xxxx m    22122444646416 m mm     2 2.1681644 mmm  216.2162 mm  222mm  2 422mm 

Bài 3. (1,5 điểm) Cho phương trình , với làtham số.

41120

Giải phương trình khi *2 m

b)Tìm tất cả cácgiá trị của tham số để phương trình cóhai nghiệm phân biệt thỏa m  * 12 , xx mãn

Lời giải

phương trình trở thành:

24120xx

phương trình có tập nghiệm là

số bé bằng 15.

2) Một địa phương lên kế hoạch xét nghiệm SARS-COV-2cho12000 người trong một thời gian quy định. Nhờ cải tiến phương phápnên mỗi giờ xét nghiệm được thêm1000 người. Vì thế, địa phương nàyhoànthành sớm hơn kế hoạch là16 giờ. Hỏi theo kế hoạch, địa phương này phải xét nghiệm trong thời gianbaonhiêu giờ? Lời giải 1) Gọi số lớn là , số bélà . x(15,) xx y y Tổng của hai số là2021nêntacó phương trình: 2021xy 1 Hiệu của số lớn và số bé bằng 15nêntacó phương trình: 15xy 2 Từ , tacó hệ phương trình:  1 2

 1018t/m202122036 1003t/m1515 x xy x y xy xy 

Vậy số lớn là1018, số bélà1003.

2) Gọi số người được xét nghiệm trong một giờ theo dự định là (người) x * (12000,) xx  

Theo kế hoạch, thời gian để địa phương đó xét nghiệm hết 12000 người là ( giờ) 12000 x

Thực tế, số người được xét nghiệm trong một giờ là (người) 1000x

Thực tế, thời gian địa phương đó xét nghiệm hết 12000 người là ( giờ) 12000 1000x

DẠYKÈMQUYNHƠN OFFICIAL 5 / 9  4 2 220mm   2 2 2210mm          2 2 2 2020 21210 m m m m                     202 213 211 m m m m m m Vậy 

1;2;3

Bài 4. (1,5 điểm) 1)Tìmhai số tự nhiên, biết rằng tổng của chúng bằng 2021và hiệu của số lớn và

              





Do địa phương

1200012000 16 1000xx     12000100012000161000 x xxx    2 1200012000000120001616000 x xxx   2 1616000120000000 xx  210007500000xx  215005007500000xxx  150050015000xx x   15005000xx             1500kh«ngtháamn15000 500tháam·n 5000 x x x x

hoànthành kế hoạch sớm hơn 16 giờ nêntacó phương trình:

Vậy theo kế hoạch, địa phương này cần (giờ) để xét nghiệm xong. 12000 24 500 

Bài 5. (3,5 điểm)

Chotamgiác nhọn có các đường cao cắt nhau tại ABC ,ABAC   ,, BDCEDACEAB  H

a) Chứng minh rằng tứ giác nội tiếp. BEDC

b) Gọi làtrung điểm của Đường tròn đường kính cắt tại điểm ( khác ). M .BC AHAMGGA Chứng minh rằng . .. AEABAGAM 

MACGCM  thẳng nối tâmhai đường tròn ngoại tiếp haitamgiác songsong với đường thẳng ,DMBEMC .KG Lời giải

c)Hai đường thẳng và cắt nhau tại Chứng minh rằng và đường DEBC .K

C a) Chứng minh tứ giác nội tiếp. BEDC Xét tứ giác có: BEDC (BDlà đường cao)

90oBDC

90oBEC

(CElà đường cao)

,màhaigócnày kề nhaucùngnhìn đoạn một góc bằng .

DẠYKÈMQUYNHƠN

6 / 9

OFFICIAL





 90oAEHADH ,màhaigócnày ở vị trí đối nhau.  9090180 oooAEHADH  là tứ giác nội tiếp đường tròn đường kính . AEHD AH (góc nội tiếp cùng chắn )  AGEADE  AE 1 Tacó: tứ giác nội tiếp (cma) (gócngoài của tứ giác nội tiếp) BEDC  EBCADE  2 Từ , hay  1 2  AGEEBC   AGEABM Xét và có: AGE ABM chung  A (cmt)   AGEABM



H E D





90oBDCBEC  BC 90o là tứ giác nội tiếp. BEDC b) Chứng minh . .. AEABAGAM  Xét tứ giác có: AEHD (gt)

DẠYKÈMQUYNHƠN OFFICIAL 7 / 9 (g-g) AGEABM  (đpcm) AGABAEABAGAM AEAM  c) G N M H E D A B C K J I Xét đường tròn đường

AH   AGDAED  AD Mà

đối

 AEDDCB  BEDC  AGDACBDCM Lại

 180oAGDDGM 

 là tứ giác nội tiếp GDCM (haigóc nội tiếp cùng chắn cung )  MGCMDC MC 1 Lại có: (định lí đường trung tuyến trongtamgiácvuông) cân tại 1 2 DMBCMC  MCD M (haigóc ở đáy của tamgiáccân)  MDCMCD  2 Từ , hay  1 2  MGCMCD  MGCMCA Xét và có: GCM CAM chung  AMC (cmt)  MGCMCA  (g-g) GCMCAM (haigóc tương ứng) (đpcm)  MACGCM Tacó: (cmb)hay   AGEABM   AGEEBM Mà: (kề bù),màhaigócnày ở vị trí đối nhau  180oAGEEGM  180oEBMEGM  là tứ giác nội tiếp EBGM  ** Tacóhai tứ giác làcác tứ giác nội tiếpĐường nối tâmhai đường tròn ngoại tiếp , EBGMGDCM  haitamgiác là đường nối tâmhai đường tròn ngoại tiếp hai tứ giác . , MBEMCD , EBGMGDCM

kính có: (góc nội tiếp cùng chắn )

(gócngoàivàgóctrong tại đỉnh

diện của tứ giác )

có: (kề bù),màhaigócnày ở vị trí đối nhau

180

DGMDCM

DẠYKÈMQUYNHƠN OFFICIAL 8 / 9









nội tiếp)  BACDFM  3 Mà (haigóc nội tiếp cùng chắn cung )  EDHEAH  EH 4 Lại có: (định lí đường trung tuyến trongtamgiácvuông) cân tại . 1 2 DMBCBM  MBD M hay  BDMDBM  HDMDBM Mà (cùng phụ với )  DBMHAD   ACB  HDMHAD  5 Từ ,, 3 4 5  EDMEDHHDMEAHHADBACDFMKDM  Xét và có: FDM DKM chung;  KMD (Cmt)  DFMKDM  (g-g) FDMDKM  2 . D MDFMMDFMKM KMM  Có: (cmt) GCMCAM 2 MCGMMCMGMA AMMC  Mà (cmt)MDMC  .. FMMAFMKMMGMA GMMK    (c-g-c) (haigóc ương ứng) FGMAKM  FGMAKM là tứ giác nội tiếp ( tứ giáccógocngoài bằng góctrong của đỉnh đối diện). AGFK (haigóc nội tiếp cùng chắn cung )  90oAFKAGK  AK hayKGAG KGGM  ** Từ , ***//IJKG Vậy đường tròn nối tâmhai đường tròn ngoại tiếp haitamgiác songsong với . , MBEMCD KG

Gọi làtâm đường tròn ngoại tiếp tứ giác , làtâm đường tròn ngoại tiếp tứ giác I EBGMJ GDCM Màgiao của hai tứ giác là , EBGMGDCMGM IJGM * Gọi FAHBC 

90oAFBCAFB  Xét tứ giác có: ,màhaigócnày ở vị trí kề nhau ADFB

90oAFBBDA

là tứ giác nội tiếp. ADFB

(gócngoàivàgóctrong tại đỉnh đối diện của tứ giác

9 / 9

DẠYKÈMQUYNHƠN OFFICIAL

DẠYKÈMQUYNHƠNOFFICIAL

 

  

P Câu

1)Trong

 2)Trong

đường thẳng và ():2(1)3 dymxm   12 , xx () d Parapol .Tìmgiá trị nhỏ nhất của biểu thức . () P 22 12Mxx  Câu 4. (3,5 điểm) Trên nửa đường tròntâm đường kính với , lấy điểm ( O AB 2022AB CC khác và ), từ kẻ vuônggóc . Gọi là điểm bất kìtrên đoạn ( ABCCH () ABHAB  D CHD khác và , đường thẳng cắt nửa đường tròn tại điểm thứ hai . C)H AD E 1) Chứng minh tứ giácBHDElà tứ giác nội tiếp. 2) Chứng minh: . ADECCDAC  3) Chứng minh: . 2..2022ADAEBHBA  

SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐẮK LẮK ĐỀ THI CHÍNH THỨC KỲ THI TUYỂN SINH LỚP 10 THPT NĂM 2021 - 2022 Môn thi: TOÁN Thời gian làm bài: 120 phút, không kể thời gian giao đề ĐỀ BÀI Câu 1. (1,5 điểm) 1) Giải phương trình: . 2 2530 xx 2)Chohàm số .Tìm tất cả giá trị của tham số để hàm số đồng biến (1)2021ymx

m trên . 3)Cho và .Tínhgiá trị của biểu thức . 12a 12b 2 Pabab  Câu 2. (2,0 điểm) Cho biểu thức: với 29321 5623 Pxxx xxxx  

0,4,9xxx 1)Rút gọn biểu thức . P 2)Tìm tất cả giá trị của để

3. (3,0 điểm)

mặt phẳng tọa độ , viết phương trình đường thẳng đi qua điểm Oxy ()  vàsongsong với đường thẳng . (1;2)A 21yx

mặt phẳng tọa độ ,choParapol và đường thẳng Oxy 2():Pyx 

Gọi lần lượt làhoành độ giao điểm của

4)Khi điểm di động trên nửa đường tròn( khác , và điểm chính giữa cung C CAB ),xác định vị trí điểm saochochuvitamgiác đạt giá trị lớn nhất. AB C COH

Câu 5. (1,0 điểm) Cho . Chứng minh rằng: . 1348,1348ab 22 2022() ababab  -------HẾT--------

ĐÁP ÁN THAM KHẢO

Câu 1. (1,5 điểm)

1)Xét phương trình 2 2530 xx Tacó nên phương trình đã chocóhai nghiệm: 2 54.2(3)490

DẠYKÈMQUYNHƠNOFFICIAL

1 2

; 3 2.222.2 x x    

khivàchikhi haylà (1)2021ymx    10m 1m Kết luận: 1m 3)Tacó: 2(12)(12)2(12)(12)Pabab  22(12)4 Vậy: 4P Câu 2. (2,0 điểm) 1) Với thì biểu thức xác dịnh vàta biến đổi như sau: 0,4,9xxx P P



5491549

Vậy, tập nghiệm của phương trình đã cholà . 1 3: 2 S   2)Hàm số đồng biến trên

DẠYKÈMQUYNHƠNOFFICIAL 29321 5623 29(3)(3)(21)(2) (2)(3)(2)(3)(2)(3) 29(3)(3)(21)(2) (2)(3) 29(9)(232) (2)(3) 2 (2)(3) (1)(2) (2)(3) Pxxx xxxx x xx xx P xxxx xx xxx xx P xx Pxxxx xx Pxx xx Pxx xx Px                    1 3x 2) Với thì 0,4,9xxx 1 4 110 10 039 3 3 x PP xx x x     Kết hợp với điều kiện ta được là tất cả giá trị cần tìm. 0,4,9xxx 9x x Câu 3. (2,0 điểm) 1)Vì đường thẳng songsong với đường thẳng nên phương trình đường ()  21yx  thẳng có dạng ()  với alà hằng số. Vì điểm thuộc đường thẳng điểm nên ():2yxa (1;2)A ()  hay 22.1a 4a Vậy: Phường trình đường thẳng .():24 yx 2) Phương trìnhhoành độ giao điểm của và là: () P() d 22(1)30(*)xmxm Vì làhoành độ giao điểm của và nên là nghiệm của phương trình 12 , xx () P() d 12 , xx (*).Do đó (luôn đúng) 2 2 * 37(1)(3)0 0 24 mm m      

DẠYKÈMQUYNHƠNOFFICIAL Theo hệ thức Vi-ettacó: .Khi đó: 12 12 2(1) 3 xxm xxm     2 22 2 2 1212 12 1 151524(1)2(3)(45) 4 44 Mxxxxxxm m m     Dấu "=" xảy rakhivà chỉ khi 5 4 m Vậy, giá trị nhỏ nhất của biểu thức là khi M15 4 5 4 m Câu 4. (3,5 điểm) 1)Xét tứ giác có: (góc nội tiếp chắn nửa đường tròn) BHDE  9)90 0(; DHAgtDEB     nên do đó tứ giácBHDE nội tiếp.  DHADEB  2)Xéthaitamgiác và có: chung; ADC ACE  CAD  90 ACDCAHCEA    Nên do đó hay . ~() ADCACEgg  ADAC DCCE  ADECCDAC  3)HD: Dựa vàoý(1) để chứng minh khi đó: ~(.) ADHABEgg . 2 22022ADAEBHBAABAEABBHAB  4)Tamgiác vuông tại nêntheo định líPytagotacó: CHO H 2 2 2 2 2 2 1 1 1 2()()() 2 2 OCOHHCOHHCOHHCOHHC  

DẠYKÈMQUYNHƠNOFFICIAL Haylà nên 2OHHCOC  (12)(12)1011 CHO CvOCOHHC OC  Dấu "=" xảy rakhivà chỉ khi điểm nằm trên nửa đường tròn saocho . C O  45ACD  Câu 5. (1,0 điểm) Để ý rằng  2 2 2 2 31 4()()0,1348 4 aabbababab    Nêntacó  2 2 2 33 4()(13481348)(),1348 4 aabbab abab  Haylà 2 22022(),1348aabbabab  Vậy, bất đẳng thức được chứng minhxong.

SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐẮK NÔNG

ĐỀ THI CHÍNH THỨC

KỲ THI TUYỂN SINH LỚP 10 THPT NĂM 2021 Môn thi: TOÁN (KHÔNG CHUYÊN)

Thời gian làm bài: 120 phút, không kể thời gian giao đề

ĐỀ BÀI

Bài 1 (2.0 điểm)

a)Cho phương trình (*).Hãyxác định các hệ số và giải phương trình 2560xx ,, abc (*). b) Giải hệ phương trình: . 5 1 xy xy   

Bài 2 (2.0 điểm): Rút gọn các biểu thức. a) . 32508  b) với 4 2 xxx xx    0x

Bài 3 (2.0 điểm):

a) Giải bàitoán bằng cách lập phương trình. Một mảnh đất hình chữ nhật có độ dài đường chéolà . Biết chiều dài mảnh đất lớn hơn chiều rộng là .Hãytính diện 13m 7m tích của mảnh đất hình chữ nhật đó. b)Cho phương trình: (1) với làtham số. Tìm tất cả cácgiá trị của 2210xmx m m để phương trình(1)cóhai nghiệm phân biệt thỏa mãn: 12 , xx 22 12127xxxx 

DẠYKÈMQUYNHƠNOFFICIAL

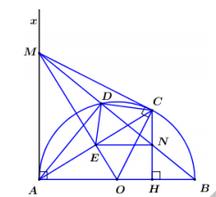
 Bài 4 (3.0 điểm): Cho nửa đường tròn đường kính . Vẽ tia tiếp tuyến củng () O AB Ax phía với nửa đường tròn đường kính . Lấy một điểm trêntia . Vẽ tiếp AB M () AxMA  tuyến với nửa đường tròn ( là tiếp điểm). Vẽ cắt tại , Vẽ cắt MC ()OC ACOMEMB nửa đường tròn tại . () O()DDB  a) Chứng minh: Tứ giác nội tiếp trong một đường tròn. AMDE b) Chứng minh: . 2 MAMDMB 

c) Vẽ vuônggóc với . Chứng minh rằng đi quatrung điểm của CH () ABHAB  MB đoạn thẳng . CH Bài 5 (1,0 điểm): Tìmgiá trị nhỏ nhất của biểu thức: với 2 2 2Aabc bccaab   ,,0 3 abc abc   

HƯỚNG DẪN GIẢI

Bài 1 (2,0 điểm) a)Cho phương trình (*).Hãyxác dịnh các hệ số và giải phương trình 2560xx ,, abc (*). Phương trình

DẠYKÈMQUYNHƠNOFFICIAL

có . 2560xx 1,5,6abc Vì nên phương trìnhcó2 nghiệm phân biệt 15(6)0abc 1 2 1 6 x c x a      Vậy tập nghiệm của phương trìnhlà . {1;6}S b) Giải hệ phương trình . 5 1 xy xy    Tacó: . 5263 1 12 xy x x xyyxy                      Vậy hệ phương trìnhcó nghiệm .(;)(3;2) xy Bài 2 (2,0 điểm): Rút gọn các biểu thức sau: a) 32508  2 2 325222  325222 (352)2 62

(2,0 điểm)

a) Giải bàitoán bằng cách lập phuơng trình

Một mảnh đất hình chữ nhật có độ dài đường chéolà . Biết chiều dài mảnh đất lớn 13m hơn chiều rộng là Hãytính diện tích mảnh dất hình chữ nhật đó. 7. m Gọi chiều rộng mảnh đất là (ĐK: ) Chiều dài mảnh đất là . ()xm 0x 7()xm  Vì độ dài đường

DẠYKÈMQUYNHƠNOFFICIAL

  

    



b) với . 4 2 xxx xx

0x Với tacó: 0x 4 2 xxx xx

(1)(2)(2) 2 xxxx x x

12xx 21 x

Vậy với thi . 0x 4 21 2 xxx x xx    Bài 3

của mảnh

2 22(7)13xx 221449169xxx  2 2141200 xx  27600xx  Ta có nên phương trình có 2 nghiêm phân biệt 2 2 74.(60)289170  71725() 717212() x tm x ktm          Chiều rộng của mảnh đất là , chiều dài của mảnh đất là

 5m 5712m

chéo

đất hình chữ nhật là nêntacó phương trình: 13m

DẠYKÈMQUYNHƠNOFFICIAL





 . 12 , xx Khi đó áp dụng định liVi-éttacó . 12 12 2 1 xxm xx    Theobàiratacó: 22 12127xxxx   2 12 12122 7xxxxxx  2 12 12 37xxxx  2 437 m  2 44 m  1m  Vậy

mãnyêu cầu bàitoán. 1m Bài 4 (3.0 điểm): Cho nửa đường tròn đường kính . Vẽ tia tiếp tuyến cùng () O AB Ax phía với nửa đường tròn đường kính . Lấy một điểm trêntia . Vẽ tiếp AB M () AxMA  tuyến với nửa đường tròn ( là tiếp điểm). Vẽ cắt tại , Vẽ cắt MC ()OC ACOMEMB nửa đường tròn tại . () O()DDB 

Vậy diện tích mảnh đất hình chữ nhật là . 25.1260mS

b)Cho phương trình (1)vói làtham số. 2210xmx m Tìm tất cả cácgiá trị của để phương trình(1)cóhai nghiệm phân biệt thỏa mãn m 12 , xx 22 12127xxxx 

Phương trình(1)có nên phương trình(1)luôncó2 nghiệm phân biệt 210,m m

thỏa

a) Chứng minh: Tứ giácAMDE nội tiếp trong một đường tròn.

Tacó: thuộc trung trực của . OAOCO  AC (tính chất 2 tiếp tuyến cắt nhau thuộc trung trực của . MAMC

)M AC làtrung trực của tại . OM ACOMAC 

90EAEM Tacó (góc nội tiếp chắn nửa đường tròn) .

90ADB

90ADM 

Xét tứ giác có là tứ giác nội tiếp đường tròn

DẠYKÈMQUYNHƠNOFFICIAL



 





AMDE  90() AEMADMcmtAMDE  đường kính (tứ giáccó2 đỉnh kề cùngnhìn dưới

. AM AM 90 b) Chứng minh . 2 , MAMDMB  Xét và có: MAD MBA chung;  AMB  90MDAMAB  cạnh tương ứng ~(.) (2MAMB MADMBAggMDMA   2 ) ..MAMDMB c) Vẽ vuônggóc với Chứng minh rằng đi quatrung điểm của đoạn CH ().ABHAB  MB thẳng . CH Gọi . {}MBCHN  Vì là tứ giác nội tiếp (cmt)nên (gócngoàivàgóctrong tại đinh đối AEDM  DECAMD  diện của tứ giác nội tiếp). Mà (cùng phụ với )nên (1).  AMDDAB   MAD  DECDAB  Tacó (đối đinh), mà (2).  DNCBNH    90 90 BNHNBH BNHDABDNCDAB DABNBH       Từ (1)và .  (2)DECDNC là tứ giác nội tiếp (tứ giáccó2 đỉnh kề cùngnhìn một cạnh dưới cácgóc bằng DENC nhau). (2góc nội tiếp cùng chắn cung ).  DNEDCE DE

một góc

Mà (2góc nội tiểp cùng chắn cung ).

DCEDCADBA

DA .Mà2gócnày nằm ở vị trí2góc đồng vị nên hay .

DNEDBA // ENAB// ENAH Lại có: làtrung điểm của (do làtrung trực của ). E ACOM , {}ACOMACE  làtrung điểm của (định lí đường trungbìnhtrongtamgiác ). N CH ACH Vậy đi qua làtrung điểm của (đpcm). MBN CH Bài 5 (1,0 điểm): Tìmgiá trị nhỏ nhất của

DẠYKÈMQUYNHƠNOFFICIAL





biểu thức với . 2 2 2Aabc bccaab   ,,0 3 abc abc    Áp dụng BĐT phụ: . Dấu "=" xảy rakhi . 2 2 2 2() xyxyz z abcabc    ,,,0xyzabc abc   Chúmgminh BĐT phụ: Áp dụng BĐT B.C.Schohai bộ số và tacó: ;; xyz abc      (;;) abc 222 2()() xyzabcxyz abc       2 2 2 2() xyxyz z abcabc    Khi đó tacó: 2 2 2 2 2()() 3 2()22 Aabcabcabcabc bccaabbccaababc        Vậ Dấu "=" xảy rakhivà chỉ khi . min 3 . 2 A 1abc



SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH LỚP 10 TỈNH ĐỒNG NAI Năm học: 2021 - 2022 Môn thi: TOÁN Thời gian làm bài: 120 phút (Không kể thời gian phát đề) Bài 1. (2,0 điểm) 1) Giải phương trình 23100xx 2) Giải phương trình 42 3250 xx 3) Giải hệ phương trình 231 24 xy xy    Bài 2. (2,25 điểm) 1) Vẽ đồ thị hàm số . 2: Pyx  2)Tìmgiá trị của tham số thực để Parabol và đường thẳng có m 2: Pyx  :23 dyxm  đúng một điểm chung. 3)Cho phương trình Gọi làhai nghiệm của phương trình.Không giải 2540xx 12 ; xx phương trình,hãytínhgiá trị biểu thức 22 1212 6 Qxxxx

Bài 4. (1,75 điểm)



   

1) Hằng ngày bạn Mai đi học bằng xe đạp, quãng đường từ nhà đến trường dài3km.Hômnay,xe đạp hư nênMai nhờ mẹ chở đi đến trường bằng xemáy với vận tốc lớn hơn vận tốc khi đi xe đạp là 24 km/h,cùng thời điểm khởi hành như mọi ngày nhưng Mai đã đến trường sớm hơn phút.tính vận tốc 10 của bạn Maikhi đi học bằng xe đạp.

ABC AC Bài 5. (3,0 điểm) Cho cóbagóc nhọn Ba đường cao cắt nhau tại ABC  ABAC  ,, ADBECF H 1) Chứng minh tứ giác nội tiếp. Xác định tâm của đường tròn ngoại tiếp tứ giác BFEC O BFEC 2) Gọi làtrung điểm của Chứng minh tiếp tuyến của đường tròn I AH IE  O 3) Vẽ cắt đường tròn tại (khác ), cắt tại Chứng minhba điểm CI OMMCEFADK thẳng hàng B,K,M = = = = = = = = = = = = = = = = = = = Hết = = = = = = = = = = = = = = = = = = = ĐỀ THI CHÍNH THỨC

DẠYKÈMQUYNHƠN

1 / 7

OFFICIAL





Bài 3. (1,0 điểm) Rút gọn biểu thức (với ). 42 : 2 Axxxx xx



0;4xx

2)Cho vuông tại , biết ( với là số thực dương). Tính thể tíchtheo ABC A ,2 ABaACa  a a của hìnhnón được tạo thànhkhiquay một vòng cạnh cố định.

2) Giải phương trình 42 3250 xx * Đặt 20xt Khi đó phương trình trở thành  * 2 3250 tt Ta thấy nên (nhận); (loại) 3250abc

11t

2 5 3 t

121;1xx Vậy phương trình cóhai nghiệm  * 121;1xx 3) Giải hệ phương trình 231 24 xy xy    231 24 xy xy    231 248 xy xy  231 77 xy y  2 1 x y 

Với ,tacó .Suyra . 1t

21x

Vậy hệ phương trìnhcó một nghiệm duy nhất  ;2;1xy Bài 2. (2,25 điểm) 1) Vẽ đồ thị hàm số . 2: Pyx  Tập xác định R x 2 1 0 1 2 y 4 1 0 1 4 Đồ thị hàm số là một Parabol đỉnh , nhận trục làm trục đối xúng, điểm là 2yx   0;0O Oy O điểm thấp nhất của đồ thị.

DẠYKÈMQUYNHƠN OFFICIAL 2 / 7



 

Hướng dẫn giải: Bài 1. (2,0 điểm) 1) Giải phương trình 23100xx  2 2 =b43411049 ac   497 Vậy phương trìnhcóhai nghiệm phân biệt ; 1 372 22 b x a  

2 375 22 b x a 





DẠYKÈMQUYNHƠN OFFICIAL 3 / 7



giải 2540xx 12 ; xx phương trình,hãytínhgiá trị biểu thức 22 1212 6 Qxxxx  Vì nên và trái dấu suyra phương trìnhcóhai nghiệm phân biệt. 1,4ac ac Theo hệ thức Vi-étcó 12 12 5 4 b xx a c xx a         2 2 22 121212 12 6 454.49Qxxxxxxxx  Bài 3. (1,0 điểm) Rút gọn biểu thức (với ). 42 : 2 Axxxx xx         0;4xx 42 : 2 Axxxx xx        

2)Tìmgiá trị của tham số thực để Parabol và đường thẳng có m 2: Pyx  :23 dyxm  đúng một điểm chung. Phương trìnhhoanh độ giao điểm của và :  P d 2 2 23230xxmxxm   2 ' 11313mm 

Để và có đúng một điểm chungthì  P d ' 10130 3 mm  3)Cho phương trình Gọi làhai nghiệm của phương trình.Không

Bài 4. (1,75 điểm) 1) Hằng ngày bạn Mai đi học bằng xe đạp, quãng đường từ nhà đến trường dài3km.Hômnay,xe đạp hư nênMai nhờ mẹ chở đi đến trường bằng xemáy với vận tốc lớn hơn vận tốc khi đi xe đạp là 24 km/h,cùng thời điểm khởi hành như mọi ngày nhưng Mai đã đến trường sớm hơn phút.tính vận tốc 10 của bạn Maikhi đi học bằng xe đạp. Giải

Gọi vận tốc của bạn Maikhi đi xe đạp từ nhà tới trường là (km/h) x 0x

Thời gianMai đi xe đạp từ nhà đến trường là (h). 3 x

Vận tốc xemáy mẹ Mai chở Mai từ nhà đến trường là (km/h) 24x

Thời gian mẹ chở mai đi học bằng xemáy từ nhà đến trường là (h) 3 24x

Vìhômnaymai đến sớm hơn phúthay (h)so với mọi ngày,tacó phương trình

DẠYKÈMQUYNHƠN OFFICIAL 4 / 7  22 2 : 2 xxxx A x x x              122Axx x  22Ax x 

101 6

   18241824 xxxx  2 2 184321824244320 xxxxxx   Có '2 ' 121.43257657624  (nhận); (loại). 1122412 1 x    1122436 1 x  Vậy vận tốc của bạn Maikhi đi xe đạp từ nhà đến trường là km/h12 2)Cho vuông tại , biết ( với là số thực dương). Tính thể tíchtheo ABC A ,2 ABaACa  a a của hìnhnón được tạo thànhkhiquay một vòng cạnh cố định. ABC AC Giải

331 246xx

Hìnhnón được tạo thànhcó . ;2 rABahACa  Thể tíchhìnhnón (đơn vị thể tích) 2 2 3112 .....2 333 Vrhaaa

Bài 5. (3,0 điểm) Cho cóbagóc nhọn Ba đường cao cắt nhau tại ABC  ABAC  ,, ADBECF H

1) Chứng minh tứ giác nội tiếp. Xác định tâm của đường tròn ngoại tiếp tứ giác BFEC O BFEC 2) Gọi làtrung điểm của . Chứng minh tiếp tuyến của đường tròn . I AH IE  O

3) Vẽ cắt đường tròn tại (khác ), cắt tại Chứng minhba điểm CI OMMCEFADK thẳng hàng B,K,M Chứng minh

DẠYKÈMQUYNHƠN OFFICIAL 5 / 7

  

  

F D

1) Chứng minh tứ giác nội tiếp. Xác định tâm của

tròn

BFEC

(là đường cao của )  090CFBCF ABC (là đường cao của )  090CEBBE ABC Mà và nằm cùngphía đối với nên tứ giác

EF CB BFEC Vì vuông tại

BEC E

O H E

đường

ngoại tiếp tứ giác

O BFEC

là tứ giác nội tiếp.

nêntâm của đường tròn ngoại tiếp tứ giác làtrung điểm của cạnh

BFEC O

DẠYKÈMQUYNHƠN OFFICIAL 6 / 7 2) Chứng minh tiếp tuyến của đường tròn IE  O I O H E F D A B C Tacó ( cân tại ).  EBOBEO  BOE O vuông tại có làtrung điểm của nên cân tại . AEH EI AHIEH  I  IHEIEH Mà (haigóc đối đỉnh)  IHEBHD  Và ( vuông tại ).  090EBOBHDHDB D Do đó  0 09090BEOIEHOEI  tại OEEIE Vậy là tiếp

đường tròntâm IE  O 3)



M K I O H E F D A B C

tuyến của

Vẽ cắt đường tròn tại (khác ), cắt tại Chứng minhba điểm CI

OMMCEFADK thẳng hàng B,K,M

DẠYKÈMQUYNHƠN OFFICIAL 7 / 7 và có (gócchung)và (cùng

).Do đó IEM ICE  EIMCIE   IEMICE   MEIEMICE  ∽ (g.g)  2.1IEIMIEIMIC ICIE  Tứ giác nội

) DCEH  0180HDCHEC hay  HDEHCE  IDEFCE  Mà

đó  FCEFEI   EF  FCEKEI   IDEKEI  và

KIE EID  KIEEID   IDEKEI  Suyra (g.g) KIEEID ∽  2.2IEIDIEIKID IKIE  Từ (1)và(2)suyra IDIMIMICIKID ICIK  Mặt khác và có (gócchung) DIC MIK  MIKDIC  Dodó (c.g.c) DICMIK ∽  090IDCIMK  tạiKMICM Vì (góc nội tiếp chắn nửa đường tròn) tại  090BMC BMICM Do đó trùngnhau thẳng hàng. , BMKM ,, BKM

chắn

tiếp (vì

(cùng chắn )hay .Do

có (gócchung)và

SỞ GD&ĐT HÀ GIANG

KỲ THI TUYỂN SINH VÀO LỚP 10 THPT

NĂM HỌC 2021 – 2022 Môn thi: Toán ( Dành cho mọi thí sinh) Thời gianlàmbài: 120 phút , không kể thời gian phát đề (Đề thi này có 01 trang)

Câu 1. (2,0 điểm)

Cho biểu thức A= ( 1 �� + 1 �� 1): ��+1 ( �� 1)2

a)Rút gọn biểu thức A.

b)Tìmcácgiá trị của x để biểu thức A>0.

Câu 2. (1,5 điểm)

Cho(P):y= và đường thẳng d:y= (mlàtham số) ��2 (��2 4)��+��2 3

a)Tìm toạ độ giao điểm của parabol(P) với đường thẳng dkhim=0.

b)Tìmcácgiá trị của tham số m để đường thẳng dluôn cắt (p) tại hai điểm phân biệt.

Câu 3. (2,0 điểm)

Haiphân xưởng của một nhàmáytheo kế hoạch phải làm tổng cộng 300 sản phẩm. Nhưng khi thực hiện thìphân xưởng I vượt mức 10%so với kế hoạch; phân xưởng II vượt mức 20%so với kế hoạch. Do đó cả haiphân xưởng đã làm được 340 sản phẩm. Tính số sản phẩm mỗi phân xưởng phải làmtheo kế hoạch.

Câu 4. (3,5 điểm)

Cho đường tròn(O,R)và đường thẳng dkhông đi quaO cắt đường tròn tại hai điểm A,B. Lấy một điểm Mtrêntia đối của tiaBA kẻ hai tiếp tuyến MC,MD với đường tròn (C,Dlà tiếp điểm). Gọi Hlàtrung điểm của AB.

a) Chứng minh rằng M,D,O,Hcùng nằm trên một đường tròn

b) Đoạn OM cắt đường tròn tại I.CMRIlàtâm đường tròn nội tiếp tamgiácMCD. c) Đường thẳng quaO,vuônggóc với OM cắt cáctiaMC,MDtheo thứ tự tại P,Q. Tìm

DẠYKÈMQUYNHƠNOFFICIAL

Câu 5. (1,0 điểm) Chocác số dương x,y,z thoả mãn ��2+��2+��2=3�� Chứng minh rằng ��2 ��4+�� + ��2 ��4+�� + ��2 ��4+�� ≤ 3 2 -------------------Hết----------------Thísinhkhông được sử dụng tài liệu. Cán bộ coithikhông giải thíchgìthêm. Họ vàtênthí sinh:…………………………………….Số báodanh……………………… Chữ kí của cán bộ coi thi 1:…………………Chữ kí của cán bộ coi thi 2:……………………..

vị trí của điểm Mtrêndsaocho diện tíchtamgiácMPQbé nhất.

Hướng dẫn giải Câu Lời giải sơ lược

DẠYKÈMQUYNHƠNOFFICIAL

Điể m

Vậy x>1thìA>0. 2. (1,5 đ) Cho(P):y= và đường thẳng d:y= (mlàtham ��2 (��2 4)��+��2 3 số) a)Xét phương trìnhhoành độ giao điểm của dvà(P): = - ��2 (��2 ―4)��+��2 ―3 ⇔��2 (��2 ―4)��―��2+3=0(1) Thaym=0vào phương trìnhtrênta được phương trình +4 ��2 ��+3=0 Tacó Δ′=4 3=1>0 Phương trìnhcóhai nghiệm phân biệt ⟹ ; . ��1= 2+ 1= 1 ��2= 2 1= 3 Với ��1= ―1⇒��1=1

a. ĐKXĐ: và ��>0 ��≠1 A= ( 1 �� + 1 �� 1): ��+1 ( �� 1)2 = = = ( 1 ��( �� 1)+ 1 �� 1): ��+1 ( �� 1)2 1+ �� ( �� 1). ( �� 1)2 ��+1 �� 1 �� Vây với và tacóA= ��>0 ��≠1 �� 1 �� 1 (2,0đ ) b. Với và ��>0 ��≠1 A>0 ⇔ �� 1 �� >0 với mọi và ) ⇔ ��―1>0(�� >0 ��>0 ��≠1 ⇔ ��>1 ⇔��>1 Kết hợp với ĐKXĐ ta được x>1 thoả mãn.

Với ��2= 3⇒��2=9

Vậy khim=0thìd cắt (P) tại hai điểm có toạ độ (-1;1)và(-3;9). b.Xét phương trìnhhoành độ giao điểm của dvà(P): = - ��2 (��2 4)��+��2 3 ⇔��2 (��2 4)�� 2+3=0(1)

Đường thẳng dluôn cắt (P) tại hai điểm phân biệt cóhai điểm phân ⇔(1) biệt ⇔Δ>0⇔(��2 ―4)2―4.(―��2+3)> 0

⇔��4 8��2+16+4��2 12>0 ⇔��4 4��2+4>0

⇔(��2 ―2)2 >0 ⇔��2 2 ≠0 ⇔�� ≠ ± 2 Vậy với thìd cắt (P) tại hai điểm phân biệt. �� ≠ ± 2 3 (2,0 đ)

Gọi số sản phẩm phân xưởng I phải làmtheo kế hoạch làx (sản phẩm) (�� ∈ ��∗;��<300) Số sản phẩm của phân xưởng II làm theo kế hoạch là 300 – x (sản ⟹ phẩm).

Vìkhi thực hiện thìphân xưởng I vượt mức 10%so với kế hoạch nên số sản phẩm phân xưởng Ilàm được làx+x.10%=x+0,1x=1,1x (sản phẩm) Phân xưởng II vượt mức 20%so với kế hoạch nên số sản phẩm phân xưởng IIlàm được là:300-x+(300–x).20%=(300–x).1,2 (sản phẩm)

DẠYKÈMQUYNHƠNOFFICIAL

Tổng số sản phầm của cả haiphân xưởng làm được là340 sản phẩm nênta có phương trình: 1,1x +(300–x).1,2 =340 ⇔1,1��+360 1,2��=340 ⇔0,1��=20 (tm) ⇔��=200 Vậy phân xưởng I cần làm200 sản phẩm vàphân xưởng II cần

200=100 sản

làm300–

phẩm.

DẠYKÈMQUYNHƠNOFFICIAL a.DoMDlà tiếp tuyến của (O)=> => MDOD   090MDO DoHlàtrung điểm của AB;dâyABkhông đi quatâmO nên ;=>OHAB   090MHO Xét tứ giácMHOD có  000 9090180MDOMHO  tứ giácMHOD nội tiếp  M,D,O,Hcùng nằm trên một đường tròn. b.DoMC,MDlà tiếp tuyến của (O) =>MOlàtiaphângiác của =>MIlàtiaphângiác của (*)  CMD  CMD OIlàtiaphângiác của => hay (1)  COD  COIDOI   CIDI  Mà ; (2)  1 d 2 MCIsCI   1 2 DCIsdDI  Từ 1,2=> =>CIlàphângiác của (**)  MCIDCI   MCD Từ (*),(**)=>Ilàtâm đường tròn nội tiếp tamgiácMCD 4. (3.5đ ) c.Tacó 11 ...2.. 22MPQ SMOPQMOOPMOOP    Mà (.)MCOMOPgg .. MOCO MOOPMPCO MPOP   22CO()CO2CO22 MPQ SMPMCCPMCCPOCR    Dấu “=” xảy rakhiMC=CP vuôngcân MOP  045PMO   090CMD 

DẠYKÈMQUYNHƠNOFFICIAL  MCODlàhìnhvuông cạnh R<=> OM=R 2 Vậy diện tíchtamgiácMPQbé nhất khiOM=R 2 5 (1.0đ ) Chocác số dương x,y,z thoả mãn ��2+��2+��2=3�� Chứng minh rằng ��2 ��4+�� + ��2 ��4+�� + ��2 ��4+�� ≤ 3 2  Áp dụng BĐT Cô–si đối với hai số vàyztacó 4 x 4 22 xyzxyz  Tương tự 4 2 4 2 2 2 yxzyxz zxyzxy       2 2 2 2 2 2 4 4 4 2 2 2222 xyz x y z xyzyxzzxyxyzyxzzxy          2 2 2 4 4 4 11111 ( )() 2 2 xyz xyz xyzyxzzxyxyyzzx xyz          Sử dụng BĐT 2222 (abc)3(abc)  Tacó 2 ( )3() xyzxyz   2222 ()3()9xyz xyzxyz   2 ()3 xyzxyz  => 2 4 ( )3()3.39 3 xyzxyzxyzxyz xyzxyz    2 2 2 4 4 4 4 4 133 22 xyz xyz xyzyxzzxyxyzxyz         Lại có 222 2 2 3 3 3 3()33()1 xyzxyzxyzxyzxyz    (Vìxyz>0)  xyz => 141xyz (đpcm) 2224 444 4 13333 22212 xyz xyz xyzyxzzxyxyzxyz      Dấu “=” xảy rakhivà chỉ khix=y=z=1.

Câu 2. (1,0 điểm) Trong mặt phẳng ,chohai đường thẳng và Oxy ():3m2 dymx .Tìmgiá trị của để hai đường thẳng và songsong với nhau.  1:1dyx m () d 1d Câu 3. (2,0 điểm) Cho phương trình ( làtham số) 2 2 2(m1)0x xm m

a) Giải phương trình với 1m b)Timgiá trị của để phương trình đã chocóhai nghiệm thỏa mãn: m 12 , xx 22 12 1264 xxxx 

Câu 4. (1,0 điểm) Giả sử giá tiền điện hàngtháng được tínhtheo bậc thang như sau: Bậc 1: Từ đến thìgiá điện là: 1500đ/kWh 1kWh100kWh Bậc 2: Từ đến thìgiá điện là: 2000đ/kWh 101kWh150kWh Bậc 3: Từ trở lênthìgiá điện là: 4000đ/kWh 151kWh (Vi dụ: Nếu dùng thicó tínhtheogiá bậc 1,có tínhtheogiábâck2và 170kWh100kWh 50kWh có tínhtheogiá bậc 3). 20kWh Tháng4 năm 2021 tổng số tiền điện của nhà bạn vànhà bạn là đ. So với tháng4thì A B560000 tháng5 tiền điện của nhà bạn tăng ,nhà bạn tăng ,dodó tổng số tiền điện của cả A30% B20% hainhàtrongtháng5là đ. Hỏi tháng4nhà bạn phải trả baonhiêu tiền điện vàdùng hết 701000 A baonhiêu ? (biết rằng số tiền điện ở trênkhôngtính thuế giá trị gia tăng). kWh Câu 5. (1.0 điểm) Chotamgiác vuông tại ,có độ dài cạnh , cạnh . ABC A 3cmAB 4cmAC Gọi là đường cao của tamgiác,tính diện tíchtamgiác . AH AHC Câu 6. (2,0 điểm) Chotamgiác nhọn nội tiếp đường tròntâm ; là điểm () ABCABAC  OE chính giữa cung nhỏ .BC

DẠYKÈMQUYNHƠNOFFICIAL

 b) với . 111 : 14

Q x xx        

xx

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ TĨNH ĐỀ THI CHÍNH THỨC MÃ ĐỀ 01 KỲ THI TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2021 - 2022 MÔN THI: TOÁN Thời gian làm bài: 90 phút Câu 1. (2,0 điểm) Rút gọn các biểu thức sau: a) . 45205P

2121

1 0, 4

a) Chứng minh .

CAEBCE  b) Gọi là điểm trên cạnh saocho khác làgiao điểm của với M AC ( EMECM  ); CN BM đường tròntâm ( khác ). Gọi làgiao điểm của với làgiao điểm của với ONBI BM; AEK AC Chứng minh tứ giác nội tiếp. EN EKMI Câu7.(1,0 điểm) Chocác số thực khôngâm thỏa mãn: .Timgiá trị lớn nhất ,, abc 2021abc vàgiá trị nhỏ nhất của biểu thức:

DẠYKÈMQUYNHƠNOFFICIAL

Pabbcca  ------------HẾT----------HƯỚNG DẪN GIẢI Câu 1. (2,0 điểm) Rútgoncác biểu thức sau: a) . 45205P 45205P 9.54.55P . 3525545P  Vây . 45P b) với . 111 : 142121 Q x xx         1 0, 4 xx 111 : 142121 Q x xx         21211 : 14(21)(21) Qxx x xx    41 : 4114Qx xx  4 4(14) (14)4 41 (14) x x Q x xx x x    Vậy , với . 4 Qx  1 0, 4 xx



Oxy ():32 dymxm .Tìmgiá trị của để hai đường thẳng ..và songsong với nhau.  1:1dyx m () d 1d Hai đường thẳng và songsong với nhaukhivà chỉ khi () d 1d

Câu 2. (1,0 điểm) Trong mặt phẳng , cho hai đường thẳng

phương trìnhcó2

khi tập

DẠYKÈMQUYNHƠNOFFICIAL

và

             



 Với

 2410xx Tacó



. 1 1 11 321 3 m m m m m

Vậy với thì và songsong với nhau. 1m() d 1d Câu 3. (2,0 điểm) Cho phương trình (mlàtham số)

2 2(m1)0

a) Giải phương trình với .1m

, phương trình đã cho trở thành . 1m

nên

nghiệm phân biệt . 2 2130 1 2 23 23 b x a b x a        

  



 Để phương trình đã chocó2 nghiệm thì . 12 , xx 1 0210 2 m m  Khi đó áp dụng định líVi-éttacó: . 12 2 12 2(1)xxm xxm    Theobàiratacó: 22 12 1264 xxxx  2 12 12 12264 xxxxxx  2 12 12 660xxxx  22 4(1)660 mm 

Vậy

nghiệm của phương trìnhlà . 1m

{23}S b)Tìmgiá trị của để phương trình đã chocóhai nghiệm thóamãn: m 12 , xx 22 12 1264 xxxx  Tacó: . 22 (1)21 mmm

Vậy có1giá trị của thỏa mãnlà . m 5m Câu 4. (1,0 điểm) Giả sử giá tiền điện hàngtháng được tínhtheo bậc thang như sau: Bậc 1: Từ đến thìgiá điện là: 1500đ/kWh 1kWh100kWh Bậc 2: Từ đến thìgiá điện là: 2000đ/kWh 101kWh150kWh

Bậc 3: Từ trở lênthìgiá điện là: 4000đ/kWh 151kWh

(Vi dụ: Nếu dùng thicó tínhtheogiá bậc 1,có tínhtheogiábâck2và 170kWh100kWh 50kWh có tínhtheogiá bậc 3). 20kWh

Tháng4 năm 2021 tổng số tiền điện của nhà bạn vànhà bạn là đ. So với tháng4thì A B560000 tháng5 tiền điện của nhà bạn tăng ,nhà bạn tăng ,dodó tổng số tiền điện của cả A30% B20% hainhàtrongtháng5là đ. Hỏi tháng4nhà bạn phải trả baonhiêu tiền điện vàdùng hết 701000 A baonhiêu ? (biết rằng số tiền điện ở trênkhôngtính thuế giá trị gia tăng). kWh

Gọi số tiền điện nhà bạn phải trả trongtháng4là (đồng) A (0)xx

Số tiền điện nhà bạn phải tràtrongtháng4là (đồng) B (0)yy

Theobàitacó tổng số tiền điện trongtháng4nhà bạn vànhà bạn phải trả là560000nênta A B có phương trình 560000(1)xy

Số tiền điện trongtháng5nhà bạn phải trả là (đồng) A 30%1,3 xxx 

Số tiền điện trongtháng5nhà bạn phải trả là: (đồng) B 20%1,2 yyy 

Theobàitacó

DẠYKÈMQUYNHƠNOFFICIAL





2 28100(1) mm

Tacó nên phương trìnhcó2 nghiệm phân biệt 28100abc . 1 2 1() 105() 2 mktm c m tm a    

tổng số tiền điện trongtháng5nhà

trình: 1,31,2701000(2) xy Từ (1)và(2)tacó hệ phương trình: 560000 1,31,2701000 xy xy    560000 560000 1,3(560000)1,27010007280000,1701000 x y x y yy y               560000 290000 0,127000270000 x yx y y              

bạn vànhà bạn phải trả là701000nênta A B có phương

Vậy số tiền điện nhà bạn phải trả trongtháng4là290000 đồng. A Nhận thấy: 290000100.150050.200010.4000   

Vậy số điện nhà bạn dùngtrongtháng4là . A 1005010160() kWh

Câu 5. (1,0 điểm) Chotamgiác vuông tại ,có độ dài cạnh , cạnh . ABC A 3cmAB 4cmAC Gọi là đường cao của tamgiác,tính diện tíchtamgiác . AH AHC

DẠYKÈMQUYNHƠNOFFICIAL

2 2 2 111 AHABAC  222 111 34AH  2 111 916AH  2 125 144AH  144 25 AH  12(cm) 5 AH  Áp dụng định liPytagotrongtamgiácvuông

2 22ACAHHC 

Áp dụng hệ thức lượng trongtamgiácvuông tacó: ABC

tacó: AHC

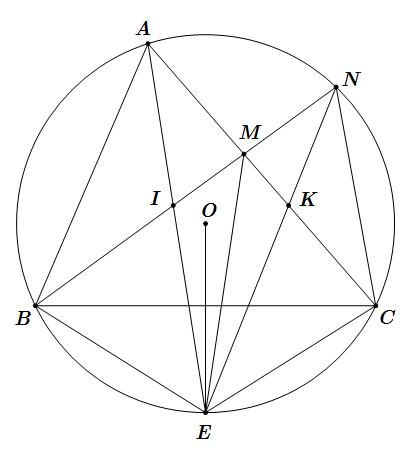
DẠYKÈMQUYNHƠNOFFICIAL 2 2 2 12 4 5 HC    2 144 16 25 HC  2256 25 HC  16(cm) 5 HC  Vitamgiác vuông tại nên . AHC H  2 1 1121696 .. cm 2 25525 AHC SAHHC     Câu 6. (2, 0 điểm) Chotamgiác nhọn nội tiếp đường tròntâm ; là điểm () ABCABAC  OE chính giữa cung nhỏ .BC a) Chứng minh .  CAEBCE  Vì là điểm chính giữa của cung nhỏ nên . E BCsdcsdcBECE 

(trong một đường tròn,haigóc nội tiếp chắn haicung bằng nhauthì bằng nhau).

CAEBCE b) Gọi là điểm trên cạnh saocho khác làgiao điểm của với M AC ( EMECM  ); CN BM đường tròntâm ( khác ). Gọi làgiao diểm của với làgiao diểm của với ONBI BM; AEK AC Chứng minh tứ giác nội tiếp. EN EKMI Vì ,mà (do ()EMECgt

DẠYKÈMQUYNHƠNOFFICIAL



EBM  MEBMEMB  Tacó: (2góc đối diện của tứ giác nội tiếp )  180EBMECN BECN (kề bù)  180EMBEMN .  ECNEMN Lại có (2góc nội tiểp chắn haicung bằng nhau)  ENCENM   ECNENCEMNENM  180180CENMEN  CENMEN làphângiác của . EK  MEC Màtamgiác cân tại nên đồng thời là đường cao . EMC() EEMEC  EK EKMC  90.EKM   90.EAKAEK  Mà (2góc nội tiểp chắn haicung bẳng nhau)  EAKEACBNE  vuông tại  90 90 BNEAEKBNIIENEIN  .I  90 90.EINEIM  Xét tứ giác có: . EKMI  9090180EKMEIM Vậy EKMIlà tứ giác nội tiếp (tứ giáccó tổng haigóc đối bằng ). 180 Câu7.(1,0 điểm) Chocác số thực khôngâm thỏa mãn: .Tìmgiá trị lớn nhất ,, abc 2021abc vàgiá trị nhỏ nhất của biểu thức: . Pabbcca  Tacó: Pabbcca 

 EBEC  ) .sdcEBsdcECEBEM   cân tại (2góc ở đáy).

DẠYKÈMQUYNHƠNOFFICIAL (BĐT Buniacopxki) 2 2 ( )3( )6.202112126Pabbccaabbcca  21212612126P P  Dấu "=" xảy ra . 2021 20212021 20212 3 ac caac ac b aa         Vậy max 2021 12126 . 3 P abc  

KỲ THI TUYỂN SINH LỚP 10 THPT NĂM 2021 - 2022 Môn thi: TOÁN Thời gian làm bài: 120 phút, không kể thời gian giao đề ĐỀ BÀI Bài 1 (1,5 điểm) Chohai biểu thức

2 5038(21);A

điểm)

DẠYKÈMQUYNHƠNOFFICIAL

 

Bxxxx

x   

 

 

Bài 3 (2,5

1.Cho

SỞ GIÁO DỤC VÀ ĐÀO TẠO HẢI PHÒNG ĐỀ THI CHÍNH THỨC 

(vói ). 1 11

0,1xx a)Rút gọn các biểu thức . , AB b)Tìmcácgiá trị của saocho . x AB  Bài 2 (1,5 điểm)

Giải hệ phương trình . 1 23 1 0 x y x y  



Bạn Nam hiện có50000 đồng. Để phục vụ cho việc học tập, bạn muốn mua một quyển sách tham khảo Toáncógiá trị 150000 đồng. Vì thế, bạn Nam đã lên kế hoạch mỗi ngày tiết kiệm 5000 đồng. Gọi số tiền bạn Nam tiết kiệm được sau (ngày) (gồm cả tiền hiện cóvà tiến tiết x kiệm được hàngngày)là (đồng). y a) Lập côngthíctính theo . yx b) Hỏi saubaonhiêungày bạn Namcó vừa đủ tiền để mua được quyển sáchtham khảo Toán?

phương trình (1)( làtham số, làtham số). 2 2 2(1)20xmxm

x m

a) Giải phuơng trình(1)khi 1m

b)Xác định cácgiá trị của để phương trình(1)cóhai nghiệm phân biệt thỏa mãn m 12 , xx điều kiện: 2 1 2 2(1)122xmxm 

2.Bàitoáncó nội dung thực tế:

Lúc9 giờ sáng, một xeôtô khởi hành từ đến với vận tốc không đổi trên cả quãng đường AB là Saukhixeôtônày đi dược 20phútthì cũng trênquãng đương đó, một xeôtô 55/. kmh khác bắt đầu đi từ về với vận tốc không đổi trên cả quãng đường là Hỏi haixe BA 45/. kmh ôtô găp nhaulúc mấy giờ? Biết quãng dường dài . AB135km

Bài 4 (0,75 điểm)

Một vật thể đặc bằng kim lọi dạng hình trụ cóbánkính đường tròn đáy và chiều cao đều bằng . Người takhoanxuyênquahai mặt đáy của vột thể đó theo phương vuônggóc với 6cm mặt đáy, phần bị khoanlà một lỗ hình trụ cóbánkính đường tròn đáy bằng (Hình1). 2cm Tính thể tích phần còn lại của vật thể đó.

DẠYKÈMQUYNHƠNOFFICIAL

Cho

() O , ADBECF cắt ABC nhau tại .H a) Chứng minhBCEFvàCDHElàcác tứ giác nội tiếp. b) Chứng minh làtiaphângiác của và đồng dạng với . EB  FEDBFE  DHE c)Giao điểm của với đường tròn là , cắt đường tròn tại Gọi AD () O()IIA IE () O().KKI  làtrung điểm của đọn thẳng . Chứng minh rằng ba điểm thẳng

M EF ,, BMK

Bài 5 (3 điểm)

cóbagóc nhọn nội tiếp đường tròn .Các đường cao và của ABC

hàng.

DẠYKÈMQUYNHƠNOFFICIAL Câu 6 (0,75 điểm) Choba số thực dương thỏa mãn điều kiện Tìmgiá trị nhỏ nhất của biểu ,, xyz 222 .xyz  thức: 222 2 22 1 11 2016. Pyzx x yz     ----------HẾT----------ĐÁP ÁN THAM KHẢO Bài 1 (1,5 điểm) a) 25038(21)A  2 2 52322|21|A  Do 523.2221(A  210)  (561)21A 1A Vậy .1A (vói ). 1 11 Bxxxx x x    0,1xx Với tacó: 0,1xx 1 11 Bxxxx x x    (1)(1)(1) 1 1 Bxxxx x x     1Bxx  21Bx  Vậy với thì . 0,1xx 21Bx 

DẠYKÈMQUYNHƠNOFFICIAL

                    

Vậy nghiệm của hệ phương trìnhlà (1;1) 2.a) Điều kiện: . ,50000xy  Sau ngày, bạn Nam tiết kiệm được số tiền là: (đồng). x 5000x Như vậy tổng số tiền bạn Namcósaukhi tiết kiệm được hàngngàylà: 500005000y x (đồng). Vậy đồng. 500005000y x b)KhibanNam đủ tiền muasáchthì bạn Nam cần có150000 đồng nêntacó phương trình: 500005000150000 x  5000100000 x  20()xtm

b) Điều kiện: 0,1xx Tacó: 121AB x 22 x  1x  1x  Kết hợp với điều kiện ta được thì . 1xAB  Vậy thì . 1xAB  Bài 2 (1,5 điểm) 1. Điều kiện . 0y Đặt 1(0) tt y  Khi đó tacó hệ phương trình: 23331 0 1() xt xx xt xtttm

1111() yytm y 

Vậy sau20ngàythì bạn Nam đủ tiền muasáchtham khảo mônToán. Bài 3 (2,5 điểm) 1.a)Thay vào phương trình tacó: 1m (1) 2 2 2 2(11)120430x x xx  Phương trìnhcó: 1430abc Phương trìnhcóhai nghiệm phân biệt và  11x 2 3.c x a  Vậy với thì phương trìnhcó tập nghiệm là: . 1m {1;3}S b)Xét phương trình (1) 2 2 2(1)20xmxm

DẠYKÈMQUYNHƠNOFFICIAL

Phương trình(1)cóhai nghiệm phân biệt 0  22 (1)20 mm  2 2 2120mmm  210 m  1 2 m  Với thì phương trình(1)cóhai nghiệm phân biệt . 1 2 m 12 , xx Áp dụng định líVi-éttacó: . 12 2 12 2(1) 2 xxm xxm    Theo đề bàitacó: 2 1 2 2(1)122xmxm  2 1122122xxxxm  2 2 1122122xxxxm  2 12 12122 122xxxxxxm  2 1212122xxxxm  22 4(1)2122 mm m   2 2 4842122 mmmm 

Quãng đường ôtô đi từ đến trong20phútlà: . AB 155 55() 33 km

Gọi thời gianôtô đi từ đến đi đến khi gặp ôtô đi từ đến là . BA AB(),(0)xhx Thời gianôtô đi từ đến đi đến khi gặp ôtô đi từ đến là: .  AB BA1() 3 xh 

Quãng đường ôtô đi từ đến đi được đến khi2xe gặp nhaulà:  AB . 155 5555() 33 x xkm   

Quãng đường ôtô đi từ đến đi được đến khi2xe gặp nhaulà: . BA 45() xkm Quãng đường dài AB135km Quãng đường ôtô đi từ đi trước ôtô đi từ là: A B

DẠYKÈMQUYNHƠNOFFICIAL 2 340 mm 



(34)0mm

0() 0 43403() mktm m m mtm            Vậy là thỏa mãnbàitoán. 4 3 m 2. Đổi 20phút .1() 3 h

155 55() 33

 Đến lúc phúthaixecòncáchnhaulà: 920 h 155350 353() 3 km Thời gianhaixe gặp nhaulà: 350 7 3:(5545)() 6 h Đổi giờ =1 giờ 10phút 7 6

Thời điểm haixe gặp nhaulà: 9 giờ 20phút giờ 10phút giờ 30phút 1 10

Vậy haixe gặp nhaulúc10 giờ 30phút. Bài 4 (0,75 điểm)

Thể tích của vật thể lúc đầu là: .  2 2 3 1 .6.6216VRh cm 

Thể tích của phần vật thể bị khoanlà: . 2 2 3 2 2624Vrh cm 

DẠYKÈMQUYNHƠNOFFICIAL





3 1221624192VVV cm    Vậy thể tích phần còn lại của vật thể đã cholà .3192cm Bài 5 (3 điểm) a)Tacó: lần lượt làcác đường cao của ,, ADBECF ABC  90 ADBC BEACADCBECBFC CFAB       Xét tứ giác tacó: BCEF  90()BECBFCcmt  



Thể tích phần còn lại của vật thể đã cholà: .  

là tứ giác nội tiếp. (Tứ giáccóhai đỉnh kề 1 cạnh cùngnhìn cạnh đối diện dưới các BCEF góc bẳng nhau).

Xét tứ giác tacó: CDHE

9090180CDHCEH

là tứ giác nội tiếp. (Tứ giáccó tổng haigóc đối diện bằng ). BCEF 180 b)Tacó: là tứ giác nội tiếp BCEF () cmt (haigóc nội tiếp cùng chắn cung )

FEBFCB BF Lại có: là tứ giác nội tiếp CEHD () cmt (haigóc nội tiếp cùng chắn cung )

() FEBBEDFCB làtiaphângiác của .(dpcm)

DẠYKÈMQUYNHƠNOFFICIAL



 

EB  FED

 FBEFCE EF Lại

tiếp cùng chắn cung )  HDEHCE EH Hay  FCEHDE   () FBEHDEFCE Xét và tacó: BFE DHE  ()FBEHDEcmt   ()FEBHEDcmt  đpcm . ~()(BFEDHEgg ) c) Chứng minh: 2 HIHD  BFFEBFFMBFEDHE DHHEHIHE  ∽ Lại có ()  BFEIHE   180oBCA

HEDHCD HD Hay

FEDFCB

Tacó: là tứ giác nội tiếp (cmt) BCEF (haigóc nội tiếp cùng chắn cung )

có: là tứ giác nội tiếp CEHD () cmt (haigóc nội

DẠYKÈMQUYNHƠNOFFICIAL Suyra  .. BFMIHEcgc ∽  FBMHIK Mà thẳng hàng.  HIKFBK  ,, BKM Câu 6 (0,75 điểm)  22 2 222 2 22 2 22 22 2 2 2 2222 22 2 2 22 2 222 22 1 11 4 2016 2016 32016 2 33 2021Min202122 yzx Pyzx x yz xyz Pyzxx xyzyz yzx xyz x xyz yz P P xyz                           