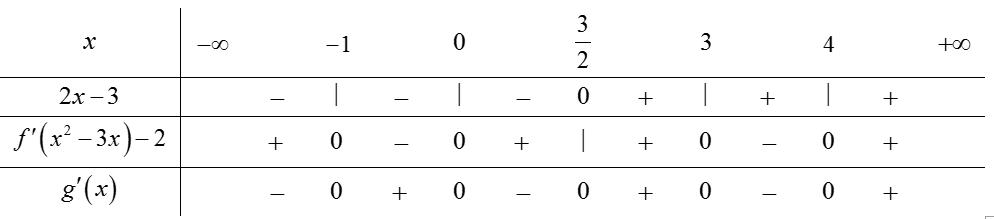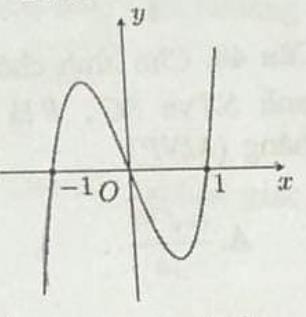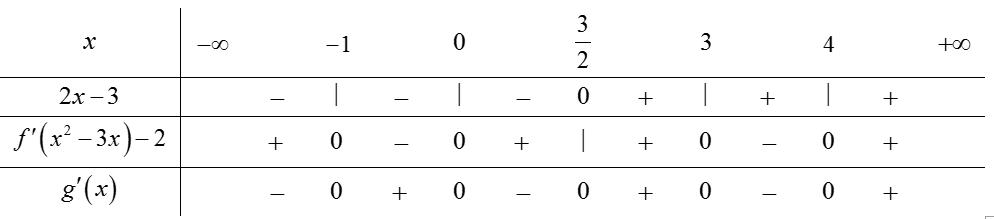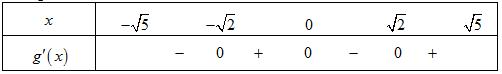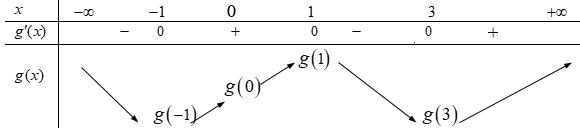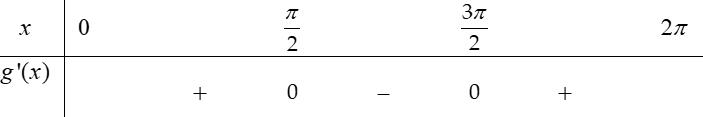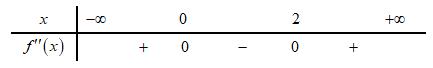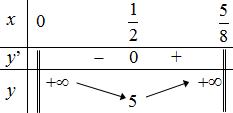CHUYÊN ĐỀ VẬN DỤNGVẬN DỤNG CAO MÔN TOÁN Ths Nguyễn Thanh Tú eBook Collection CHUYÊN ĐỀ VẬN DỤNG - VẬN DỤNG CAO LUYỆN THI TN THPT NĂM 2023 - GIẢI TÍCH 12 - CHUYÊN ĐỀ I ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ (667 TRANG) WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405

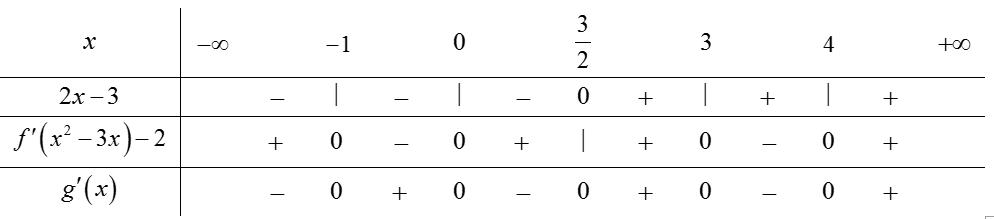



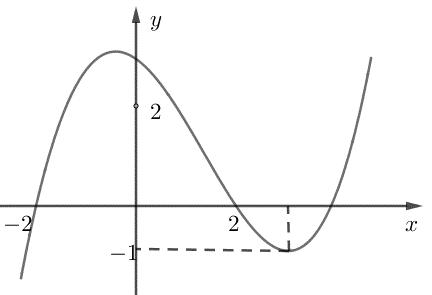
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 93 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn BÀI 1. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ – VD – VDC – PHẦN 2 Câu 66: Cho hàm số ( )fx liên tục trên . Hàm số ( )yfx = có đồ thị như hình bên dưới đây Hàm số ( ) ( ) 22326 gxfxxxx = + nghịch biến trên khoảng nào dưới đây? A. ( );0− . B. ( )0;4 . C. ( )1;0 . D. ( )0;1 . Lời giải Chọn D Ta có: ( ) ( )( ) ( ) ( ) 22 4 36 3 233 2 2 gxf x x x xx fxx −+=−−− =−− Xét ( ) 2 0 32 fx x − ( ) 2 2 2 4 34 31 3 2 303 0 x x f x x x x x x x − − − − . Ta có bảng xét dấu: CHƯƠNG I ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 94
đồ
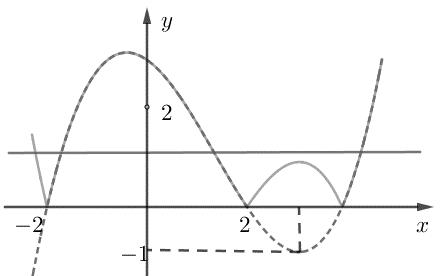
A. B. C. D. Lời giải Chọn C Cách 1: Ta có ( ) ( ) ( ) ( ) 2 2 14311618fxxxfxxx +=−++=+−++ Đặt 1 xa += ta được ( ) 2 68faaa =−+ . ( ) 2 2 680 4 a faaa a =−+ . Ta có ( ) ( ) ( ) ( ) 22232223yfxxxfxx =++=+++ . Hàm số đồng biến khi ( ) ( ) 2 22230 xfxx +++ TH1: ( ) 2 2 2 1 220 232 230 234 x x xx fxx xx − + ++ ++ ++ 1 1 12 12 12 x x x x x − = −+ −− −+ TH2: ( ) 2 2 220 1 230 2234 x x fxx xx + − ++ ++ 1 121 1212 x x x − −−− −−−+ Vậy hàm số đồng biến trên các khoảng ( ) 12; −++ và ( )12;1 . Cách 2: Đặt 1 xa += ta được ( ) 2 68faaa =−+ . ( ) 2 2 680 4 a faaa a = =−+= = ( )yfx = ( ) 2 143fxxx +=−+ ( ) 2 23yfxx=++ ( ) 1; −+ ( )12;0 ( ) 12; −++ ( )12;12−−−+
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
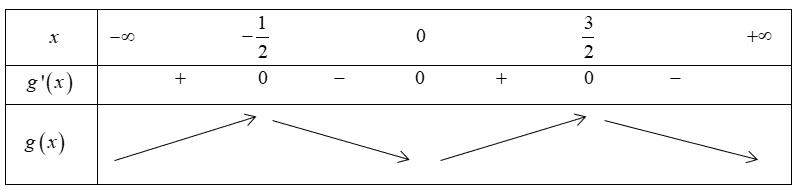
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Suy ra hàm số ( )gx nghịch biến trên các khoảng ( );1−− , 3 0; 2 , ( )3;4 Câu 67: Cho hàm số liên tục và xác định trên , biết rằng . Hàm số
ng biến trên khoảng nào dưới đây?
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 95
( ) ( ) 2 2223yxfxx =+++ . ( )2 2 2 1 1 10 0232 12 234 12 x x x yxx x xx x =− =− += =++= =−− ++= =−+ . Bảng
ấu
Vậ
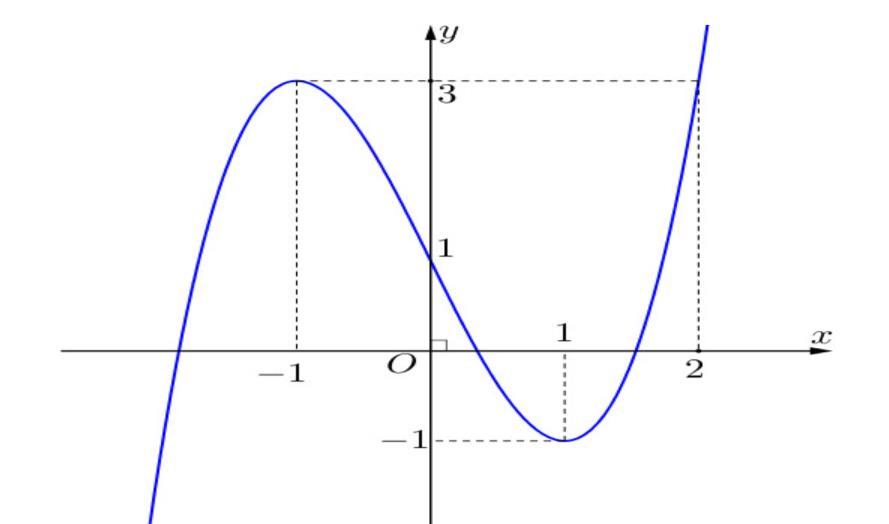
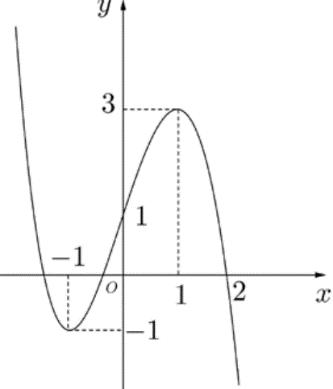
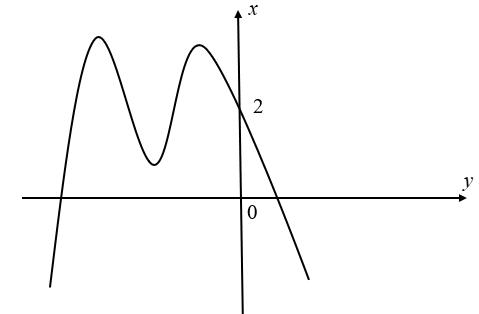
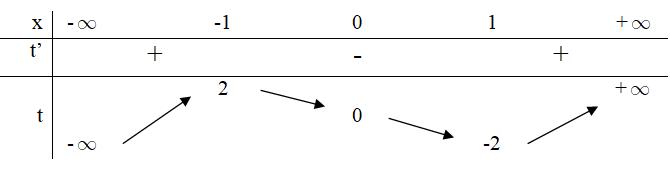
số đồng biến trên các khoảng ( ) 12; −++ và ( )12;1 Câu 68: Cho đồ thị hàm số như hình vẽ: Hỏi hàm số ( )yfx = nghịch biến trong khoảng nào? A. ( )2;5 . B. ( )2;2 . C. ( )5;10 . D. ( ) 10;+ . Lời giải Chọn A Từ đồ thị hàm số đã cho suy ra ( ) 3 20 10 12 x fx x − + Đặt 3 3 11txxt =+=− . Suy ra 3 3 21081071 ()0 11829 112 ttt ft tt t −−−−− − − . Vậy hàm số ( )yfx = nghịch biến trên mỗi khoảng ( )7;1 và ( )2;9 Cách khác ( ) 3 1 yfx =+
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
xét d
y
y hàm
Vậy hàm số ( )yfx = nghịch biến trên mỗi khoảng ( )7;1 và ( )2;9 .
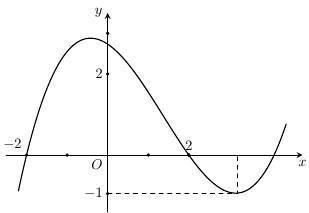
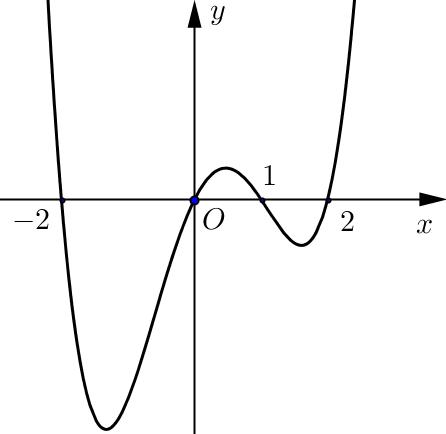
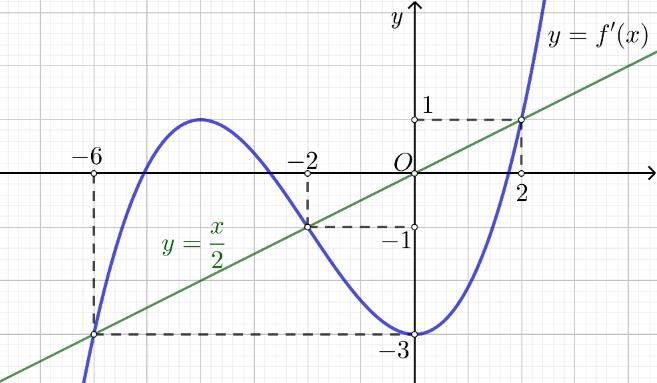
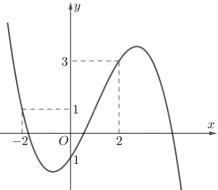
Câu 69: Cho hàm số đa thức ( )yfx = có đạo hàm trên . Biết đồ thị hàm số ( )yfx = như hình vẽ sau
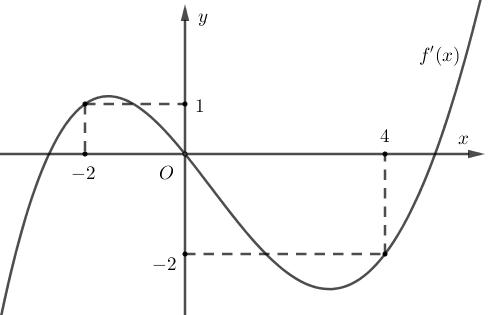
Hàm số ( ) ( ) 242412 gxfxxx =−+− nghịch biến trên khoảng nào trong các khoảng sau? A. ( )2;0 . B. ( );2−− . C. ( )1;2 . D. ( ) 2;+ . Lời giải Chọn C Ta có: ( ) ( ) 23 8.144 gxxfxxx =−+− ( ) 22 4211 xfxx =−+− ; ( ) ( ) 2 2
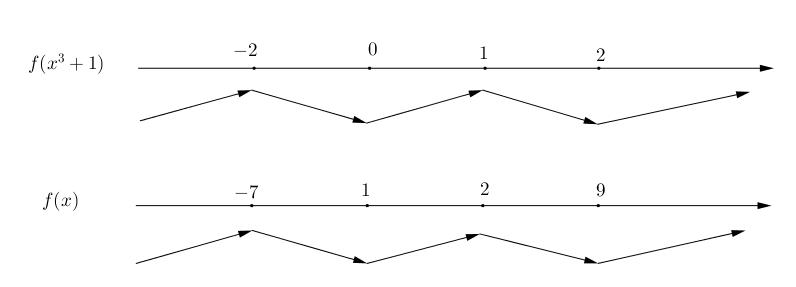
x gx x fx
0 01 1 2
= = −=− Vẽ đường thẳng 2 x y =− đi qua các điểm ( )2;1 , ( )0;0 và ( )4;2 . Nghiệm của phương trình ( ) 2 x fx =− là hoành độ giao điểm của đồ thị hàm số ( )yfx = với đường thẳng 2 x y =−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG
SÁT HÀM SỐ
ĐẠO HÀM ĐỂ KHẢO
Page 96
Vậy phương trình ( ) 0 gx = có các nghiệm đơn là: 0 x = , 1 x = , 5 x = nên ( )gx đổi dấu qua các nghiệm này. Có ( ) ( ) 324840gf=+ do ( ) ( ) ( ) 0,2;04; 2 x fxx +−+ .
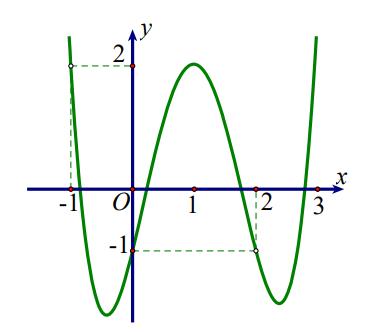
Bảng xét dấu ( )gx : Vậy hàm số ( )gx nghịch biến trên các khoảng ( );5−− , ( )1;0 và ( )1;5 . Câu 70: Cho hàm số ()yfx = có đạo hàm liên tục trên và có đồ thị hàm số ( ) 2 2 yfxx =− như hình vẽ Hỏi hàm số ( ) 23 2 11 3 yfxx =−++ đồng biến trên khoảng nào dưới đây? A. ( )3;2 B. ( )1;0 C. ( )1;2 D. ( )2;1 Lời giải

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
lớp
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 97
Chuyên luyện thi: Tuyển sinh vào
10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Quan sát hình vẽ trên, ta thấy ( ) 2 0 2 4 x x fxx x =− =−= = và ( ) 20 4 2 x x fx x − − . Khi đó ( ) 2 2 1 1 2 x fx −=− 2 2 2 12 10 14 x x x −=− −= −= 1 5 x x = =
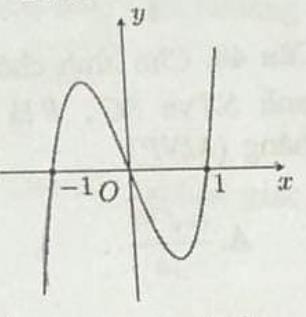
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 98
ọn D
2
( ) ( ) ( ) (
12
(2)21
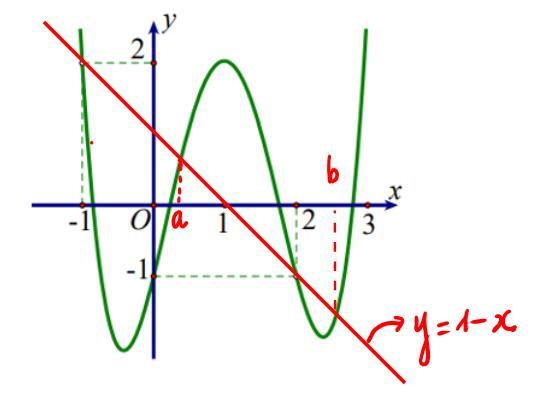
x t xa taa t x tbb xb =− =− =−− = = = = =− Bảng xét dấu ( )gx Suy ra: hàm số ( )gx đồng biến trên các khoảng ( ) ( ) ( ) 2;1;0;1;1; ab −−−+ Với ( )11;0 a −− và ( )11;2 b − chọn ( ) ( )2;12;1 a −−−− . Câu 71: Cho hàm số 432 () fxaxbxcxdxa =++++ có đồ thị hàm số ( )yfx = như hình vẽ bên. Hàm số ( ) ( ) ()122 ygxfxfx ==−− đồng biến trên khoảng nào dưới đây? A. 13 ; 22 . B. ( );0− . C. ( )0;2 . D. ( ) 3;+ .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ch
Ta có: ( ) ( )2 2 211yyfxxfx ==−=−− Xét hàm số ( ) ( ) 23 2 11 3 gxfxx=−++ : ( ) ( ) ( ) 22 2 20 2120 10 x gxxfxx fxx = =−+= −+= Đặt 1 xt=− phương trình ( )1 trở thành ( ) ( ) ( ) 22 11101112 fttftt −−+−=−−=− Vẽ đồ thị hàm số 1 yx =− lên cùng một đồ thị ( )
11 fx
)
0111;0
2311;2
− −+− =− =−+−=−+−=−+= =
. Do đó, hàm số ()gx nghịch biến trên ( );0− . ( ) ( ) ( ) 123;1 0;2 20;2 x x x
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 99 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn D Ta có 32 '()432 fxaxbxcxd =+++ , theo đồ thị thì đa thức '()fx có ba nghiệm phân biệt là 1,0,1 nên ( )( ) ( )2 3422 '()41144()21 fxaxxxaxaxfxaxaxaax =+−=−=−+=− Dựa vào đồ thị hàm số '()yfx = ta có 0 a nên ()0,\1fxx . ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) '()12'2122'2'12212'2 gxfxfxfxfxfxfxfxfx =−−+−−=−−−−−− Xét ( )122;0 13 ;13 222; 22 x x x −− − , dấu của '()fx không cố định trên 13 ; 22 nên ta không kết luận được tính đơn điệu của hàm số ()gx trên 13 ; 22 Xét ( ) ( ) ( ) ( ) ( ) 121;'120 ;0'()0 22;'20
xfx xgx xfx −+− −−−− . Do đó, hàm số ()gx đồng biến trên ( ) 3;+ Câu 72: Cho hàm số ()yfx = liên tục trên và 32 '()632 fxxx=−+− . Khi đó hàm số ( ) 2 ()3 gxfxx =− nghịch biến trên khoảng A. ( ) ; −+ . B. ( ) 1;+ . C. ( ) 2;+ . D. ( );1− . Lời giải Chọn C ( ) ( ) ( ) ( ) 22 ()323.3 gxfxxgxxfxx =−=−− . ( ) ( ) 2 3232 2 '()632'()06320420 4 x fxxxfxxxxx x
−− − , dấu của '()fx không cố định trên ( )3;1 và ( )0;2 nên ta không kết luận được tính đơn điệu của hàm số ()gx trên 13 ; 22 . Xét ( ) ( ) ( ) ( ) ( ) 12;5'120 3;'()0 2;1'20 xfx xgx xfx −−−− +

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 100 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) ( ) ( ) 22 2 3 ()323.302 30 x gxfxxgxxfxxgx fxx = =−=−−= −= 22 22 333 222 323201,2 343401,4 x xx xx xxxx xx xxxx = == == −=−−+= =−= −=−−= . Bảng xét dấu của ( )gx : Vậy chọn phương án C . Câu 73: Cho hàm số ( )yfx = liên tục trên và có đồ thị hàm số ( )yfx = như hình vẽ Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số ( ) ( ) 2 422021gxfxmxmx =−+−+ đồng biến trên khoảng ( )1;2 ? A. 0. B. 3. C. 2. D. 1. Lời giải Chọn C + Để ( )gx đồng biến trên khoảng ( ) ( ) ( )1;201;2 gxx ( ) ( ) ( )4.2201;2gxfxmxmx =−+− ( ) ( )1;2 2 xm fxmx −− ( ) + Đặt txm =− . Với ( ) ( ) 1;21;2 xtmm −− + Ta có: ( ) ( ) ( ) 1;2 2 t fttmm −−−
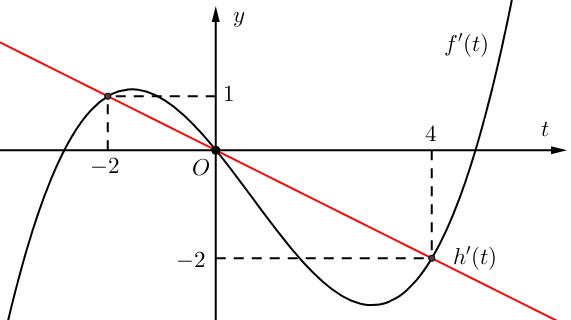
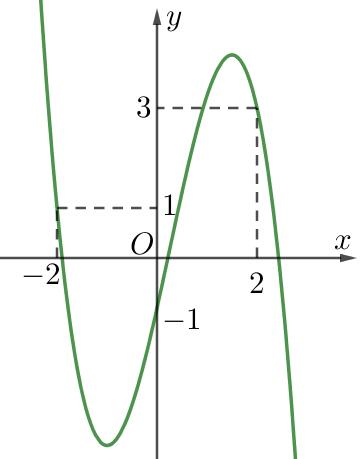
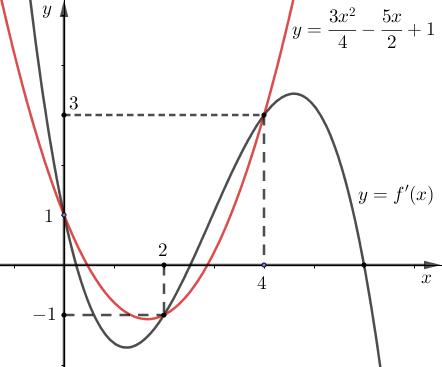
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 101 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn + Vẽ đồ thị hàm số ( )ft và ( ) 2 t ht =− trên cùng hệ trục ta được: Từ đồ thị ta có: ( ) ( ) 20 4 t ftht t − Nên để ( ) ( ) 1;2 2 t fttmm −−− ( ) ( ) ) 1;22;0 1;24; mm mm −−− −−+ 212023 143 mmm mm −−− −− Mà m nguyên dương 2;3 m . Vậy có 2 giá trị của m thỏa mãn đề bài. Câu 74: Cho hàm số ( )fx là hàm đa thức bậc bốn. Đồ thị hàm số ( )yfx = được cho bởi hình vẽ bên dưới đây Đặt hàm số ( ) ( ) 32 44 xx gxfxx =−−+ . Tập hợp tất cả các giá trị của tham số m để hàm số ( )gxm + nghịch biến trên khoảng ( ) 3;+ là A. ( ;5−− . B. ) 1; −+ . C. ( )5;1 . D. ( ) 1; −+ . Lời giải Chọn B
Bảng biến thiên: Xét hàm số ( )ygxm =+ có ( ) ( )( )( )22ygxmaxmxmxm =+=++++−
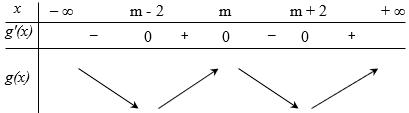
Ta có bảng biến thiên: Dựa vào bảng biến thiên ta thấy để hàm số nghịch biến trên khoảng ( ) 3;+ khi và chỉ khi 231mm −+− . Câu 75: Cho hàm số yfx có bảng xét dấu của đạo hàm như sau:


Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 102
x =− == =
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Xét ( ) ( ) 32 44 xx gxfxx =−−+ ( ) ( ) 2 31 1 42 gxfxxx =−−+ . ( ) 2 00 2 x gxx
Từ đó ta biểu diễn ( ) ( )( )22gxaxxx =+− trong đó 0 a .
Có bao nhiêu giá trị nguyên của tham số m thỏa mãn 2020 m − và hàm số 2 2 yfxxm đồng biến trên khoảng 0;1 ?
A. 17 B. 15 C. 16 D. 14 Lời giải Chọn C
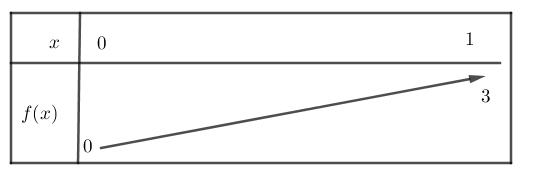

023,0;123,0;1 22,0;122,0;1 xxmxmxxmx xxmxxxmx . Xét hàm số 2 2 yxx , ta có bảng biến thiên Dựa vào bảng biến thiên ta có TH1: 2 0 23,0;1000 33 m mxxmxmm m . TH2: 2 22,0;1235 xxmxmm . Kết hợp với 2020 m −
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
suy
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page
103
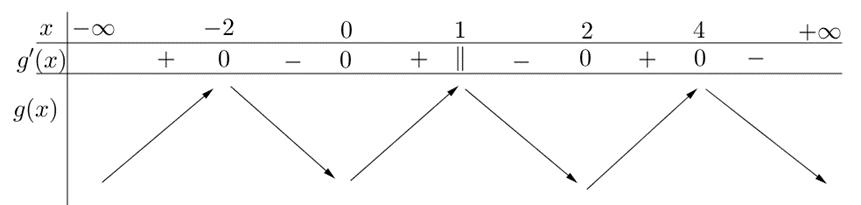
ra 20519;18;17;.....;5 mm −−−−−− Vậy có 16 số nguyên 2020 m − thỏa mãn yêu cầu
Câu 76: Cho hàm số đa thức bậc bốn ( )yfx = thỏa
( )
f =
ố (
có
Ta có 222 '22212 yxxmfxxmxfxxm Hàm số 2 2 yfxxm đồng biến trên khoảng 0;1 khi và chỉ khi 0,0;1yx và 0 y tại hữu hạn điểm. Khi đó ta có 2 2120,0;1 xfxxmx 2 20,0;1fxxmx 22 22 thị
bài toán.
mãn
1 0 2
, hàm s
)fx
đồ
như hình vẽ dưới đây?

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 104
=−−
đồ
−−
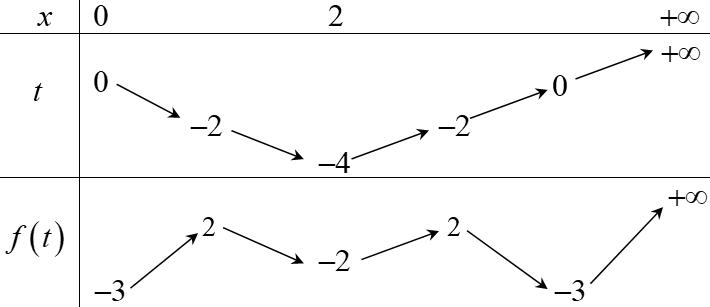
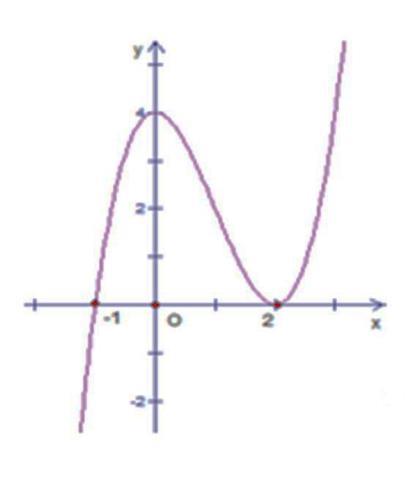
là hàm bậc ba có hai điểm cực trị 0,2xx== nên ( ) ( )2 fxaxx =− ( ) 32 3 a fxxaxb =−+ Dựa vào đồ thị ta có: ( ) 022fb == ; ( ) 2 10203 3 a fa =−+== ( ) 3232fxxx =−+ ( ) 43 11 2 42fxxxx =−++ Kiểm tra ( ) ( ) ( ) 12;32;22fff −=−==− đều được thỏa mãn. Đặt ( ) 2 1 28 xx hxf =−− ( ) ( ) 11 '1101* 22422222 hxfffxxxxxx =−−−=−−+=−=− Đặt 1 2 x t =− , trở thành ( ) 1 11 3 t fttt t =− =−= = . Khi đó ( ) 4 *0 4 x x x = = =− Ta có ( ) ( ) ( ) 11 0200 22fhf==−= ( ) ( ) ( ) ( ) ( ) ( ) 799 01;432;412 444hfhfhf==−=−=−=−−=− Bảng biến thiên của hàm số ( )hx
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Hàm số ( ) 2 1 28 xx gxf
ng biến trên khoảng nào dưới đây? A. ( );4
B. ( )0;2 C. ( )2;4 D. ( )4;0 Lời giải Ta có: ( )fx

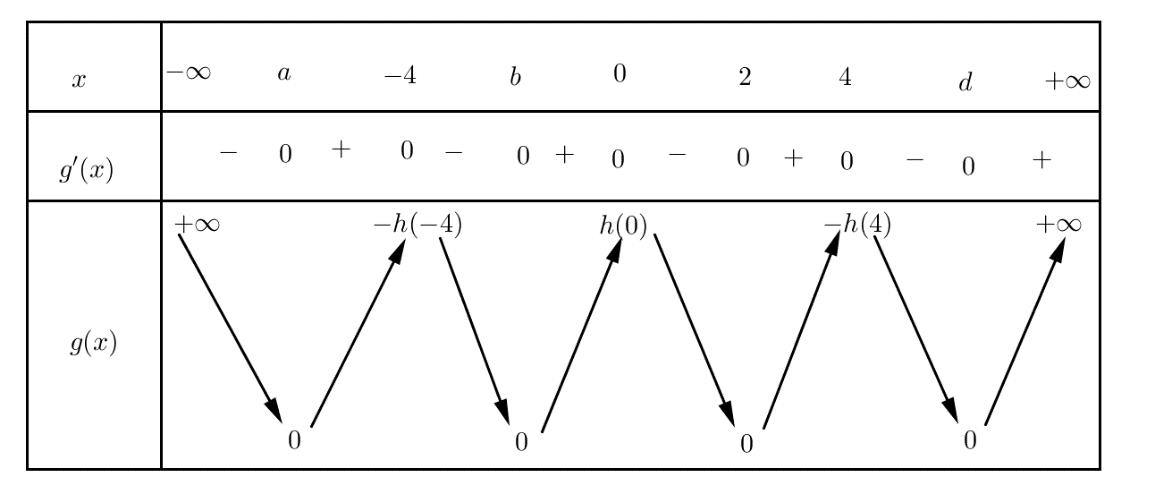
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 105
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
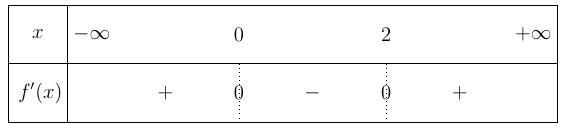
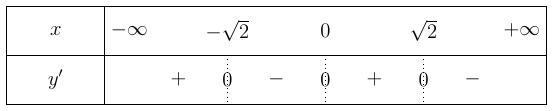
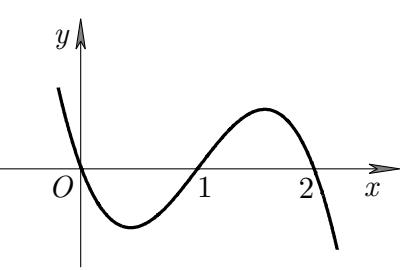
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vì vậy bảng biến thiên của hàm số ( )gx Hàm số ( ) 2 1 28 xx gxf =−− đồng biến trên khoảng ( )2;4 Câu 77: Cho hàm số ()yfx = có đồ thị như hình vẽ. Hàm số ( ) 2 2 yfx =− đồng biến trên khoảng: A. ( )2;1 B. ( ) 1;+ C. ( )1;0 D. ( )0;1 Lời giải Chọn D Từ đồ thị hàm số 0 ()()0 2 x yfxfx x = == = .
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 106
x
fx
= = = =−−=−== −= −= =−
D ( ) ( ) 22 sin3sin2gxfxxmm =+−++ ( ) ( ) ( ) ( ) ( ) 22 2sin.cos3cossin3sincos2sin3sin3sin gxxxxfxxmxxfxxm =++−=++− ( )gx đồng biến trên 25 ; 36 ( ) 25 0,; 36 gxx ( ) ( ) 2 25cos2sin3sin3sin0,; 36 xxfxxmx ++− ( ) 2 25sin3sin0,; 36 fxxmx +− . + Theo giả thiết: ( ) 2 1 230 3 x fxxx x =−−+ − , ta có:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Bảng xét biến thiên của hàm số ()yfx = Với ( ) ( ) 2222.2 yfxyxfx =−=−− . Khi đó ( ) ( ) 22 2 2 0 0 0 02.20202 20 22 2
x x yxfxxx
x x
. Bảng xét dấu đạo hàm của hàm số ( ) 2 2 yfx =− . Vậy hàm số ( ) 2 2 yfx =− đồng biến trên ( );2−− và ( )0;2 Suy ra hàm số ( ) 2 2 yfx =− đồng biến trên ( )0;1 . Câu 78: Cho hàm số ( )yfx = có đạo hàm ( ) 2 23fxxx =−−+ với x . Số giá trị nguyên của tham số m thuộc 10;10 để hàm số ( ) ( ) 22 sin3sin2gxfxxmm =+−++ đồng biến trên 25 ; 36 là A. 5 B. 6 C. 14 D. 15 Lời giải Chọn

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 107
(
2 2 2
xxmx
xxmx
+−
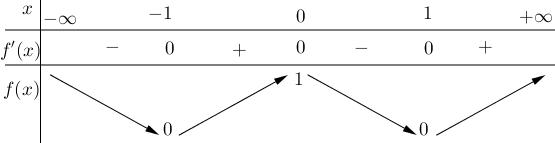
+−− 2 2 25sin3sin1,; 36 25sin3sin3,; 36 xxmx xxmx ++ +− . + Xét hàm số ( ) 2 sin3sin uxxx =+ trên 25 ; 36 , ta có ( ) 25 ; 36 363 max, 4 ux + = ( ) 25 ; 36 7 min 4 ux = , do đó 3631563 3 44 73 1 44 mm mm ++ − + , kết hợp với m và thuộc 10;10 ta được 10,9,...,0,7,...,10 m−− . Vậy có 15 số nguyên m thỏa mãn bài toán. Câu 79: Cho hàm số ( )yfx = xác định trên và có đồ thị hàm số đạo hàm ( )yfx = như sau: Hàm số ho hàm số 2 ()2(1)2212022 gxfxxxx=−+−−−+ nghịch biến trên khoảng nào dưới đây? A. (;1) −− . B. (1;2) . C. (1;1). D. (3;) + . Lời giải Chọn B Ta có 2 ()2(1)2212022 gxfxxxx=−+−−−+ ( ) ( ) ( ) 22 2 ()212212022 gxfxxxx =−+−−−+ ( ) 1 ()2111,1. 1 x gxfxxx x =−+−−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
)
25sin3sin1,; 2536sin3sin0,; 3625 sin3sin3,; 36
fxxmx
+−
ị hàm số ( )yft
đường thẳng
yt
ftt
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
luyện
lớp
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 108
Chuyên
thi: Tuyển sinh vào
10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ()0111 gxfxx =−=−−+ Đặt 1,0txt=− ta được phương trình ( ) 1 ftt =−+ Phương trình là phương trình hoành độ giao điểm của đồ th
= và
1
=−+ Vì 0 t nên ( ) 1 1 3 t
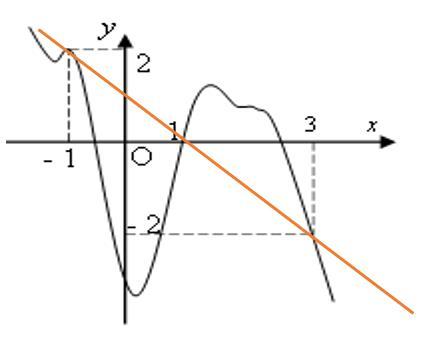
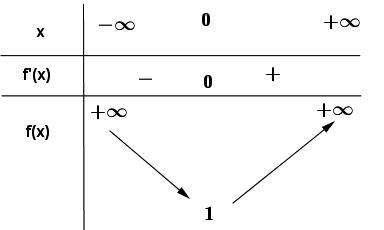
t = =−+ = 0 112 132 4 x x x x x x = −= = =− −= = Bảng biến thiên Dựa vào bảng biến thiên ta có hàm số nghịch biến trên ( )1;2 Câu 80: Cho hàm số ( )yfx = có bảng biến thiên như hình vẽ Hàm số ( ) 2 sin24sin21yfxx =−+ trên 0;2021 có ít nhất bao nhiêu khoảng đồng biến? A. 2042 B. 8084 C. 2021 D. 2020
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 109 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn B Hàm số sin2 yx = có chu kỳ T = , nên ta xét hàm số ( ) 2 sin24sin21yfxx =−+ trên 0; Ta có ( ) ( ) 2 sin24sin214cos2sin22 yfxxxx =−+− . Hàm số đồng
ế
2
−+− ( ) ( ) 2 cos2.sin24sin210 xfxx −+ Vì 2 1sin212sin24sin216 xxx −−−+ . Trường hợp 1: 3 cos202 22 xx ( ) ( ) 2 2 2 1sin24sin210 sin24sin210 1sin24sin216 xx fxx xx −−+ −+ −+ ( ) ( ) 11 arcsin22arcsin23 23sin2222222 1sin203 24 x x x x −−−− −− − . Trường hợp 2: 3 cos2020;;2 22 xx . ( ) ( ) 2 2 2 2sin24sin211 sin24sin210 0sin24sin211 xx fxx xx −−+− −+ −+ ( ) ( ) 1 22sin21arcsin2224 0sin22310arcsin23 2 x x x x − − − − .
bi
n ( ) ( )
sin24sin21.2cos2sin220 fxxxx
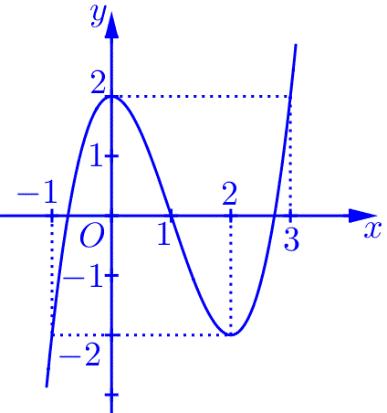
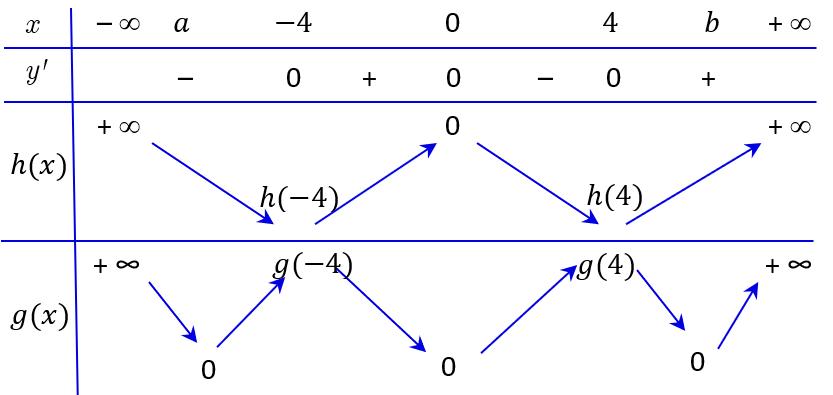
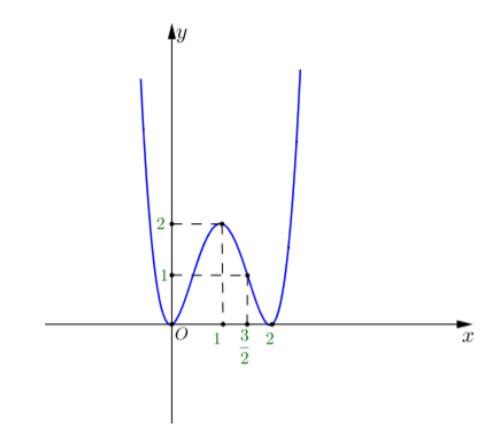
Suy ra hàm số ( ) 2 sin24sin21yfxx =−+ trên 0; có 4 khoảng đồng biến. Vậy hàm số ( ) 2 sin24sin21yfxx =−+ trên 0;2021 có ít nhất 8084 khoảng đồng biến. Câu 81: Cho hàm số bậc bốn ( )yfx = có ( ) 58 f và ( ) 10. f = Biết hàm số ( )yfx = có đồ thị như hình vẽ bên. Hàm số ( ) 2 1 28 xx gxf =−− nghịch biến trên khoảng nào dưới đây?
Khi đó ( ) ( ) 14 (3)'1010 34
tx ftttx tx
=−=− −−=== ==
Ta có bảng biến thiên của hàm số là
có
) ( ) ( )
xa hxx xbab
Ta có ( ) ( ) (0)1010 hff=−== ; suy ra ()00 (0)
= == =
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 110
ọn
=−−−=−−+=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. ( )8;4 B. ( ) 4;+ C. ( )2;4 D. ( )10;8 Lời giải Ch
D Xét hàm số ( ) 2 1 28 xx hxf =−− Ta có ( ) 11 '10'10 224222 hxffxxxx
(3) Đặt 11 22 xx tt −==−
T
Câu
ố ( )
đạ
.
ế
ằng
ậ
ợ
ấ
ả
ị
ủ
s
thì
ố
+
nghịch
ế
.
A. =1 S . B. = 3
S . C. =−1 S . D. =
S . Lờ
ả
Chọn D
Ta
(
2 88 81580 28 hff
−=−−=− , vì ( ) 58 f , suy ra 8 a − .
ừ đó ta có hàm số nghịch biến trên ( )10;8
82: Cho hàm s
fx có
o hàm ( ) 32 '44 fxxxx=−++−
Bi
t r
t
p h
p t
t c
cácgiá tr
c
a tham
ố ( ) \; mab
hàm s
( ) 2 3 1 1 hxfm x =−−
bi
n trên ( ) 2;+
Tính Sab =+
2
0
i gi
i
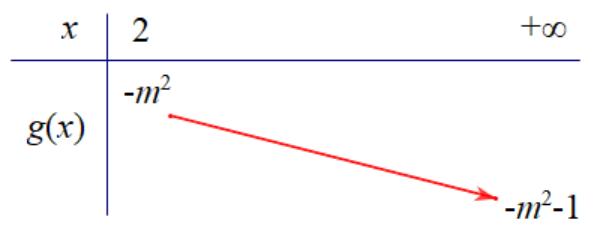
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 111 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có: ( ) 32 1 '0440 14 x fxxxx x − −++− Ta có: ( ) ( ) 2 2 33 '.'1 11 hxfm x x =−− + + Hàm số ( )hx nghịch biến trên ( ) 2;+
+ ( ) ( ) ( ) ( ) ( ) 2 2 2 2 2 33 .'10,2; 11 3 '10,2; 1 3 11 1,2;* 3 114 1 fmx x x fmx x m x x m x −−+ + + −−+ + −−− + + −− + Ta có bảng biến thiên của hàm số ( ) 2 3 1 1 gxm x =−− + trên ( ) 2;+ : Khi đó ( ) ( ) 2 2 2 2 11 1 *1\1;1 4 1 1 m m mm m m m −− − − − −− Suy ra 1; 1 ab=−= . Vậy 110 S =−+= Câu 83: Cho hàm số ( ) 4221fxxx=++ . Có bao nhiêu giá trị nguyên của tham số 0;10 m để hàm số ( ) ( ) 2 3 gxfxmm =−+ nghịch biến trên ( );1− ? A. 11 B. 5 C. 10 . D. 9 Lời giải Chọn C Xét hàm số ( ) 4221fxxx=++ Ta có ( ) 3 44 fxxx =+ ; ( ) 00fxx == Bảng biến thiên
( ) ( ) '0,2;hxx
Ta có ( ) ( ) ( ) 223.3 gxfxmmxmm =−+−+ = ( ) ( ) 2 3 3. xm fxmm xm −+ ( ) ( ) ( ) 2
−= = −+=
01 0 302 xm gx xmm
TH1: Nếu 0 m = phương trình ( ) 00gxx == không thỏa mãn nghịch biến trên khoảng ( );1− nên trường hợp này bị loại.
TH2: Nếu 0 m phương trình ( ) 0 gxxm == Ta có 2 301 xmmx −+ ( ) ( ) 2 30;1fxmmx −+− nên ( ) 0 gxxm hàm số ( )ygx = nghịch biến trên ( );1− ( ) ( )0;1gxx − ( ) ( ) ;1;1mm−− 1;2;3;4;5;6;7;8;9;10 m . Nên có 10 giá trị thỏa mãn. Câu 84: Cho hàm số ( )yfx = liên tục trên và hàm số ( ) ( )22gxfx=− có đồ thị như hình dưới. Có bao nhiêu số nguyên dương m để hàm số ( ) 4sincos2 yfxxm =+− nghịch biến trên khoảng 0; 2 ? A. 2 B. 3 C. 0 D. 1
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO
ĐỂ KHẢO SÁT HÀM SỐ
HÀM
Page 112
Lời giải Chọn B
Ta có ( ) ( ) ( ) ( ) ( )
=−= =−=== == Từ đó, ta có bảng biến thiên của hàm số ( )yfx = Đặt ( ) ( ) 4sincos2 hxfxxm =+−
xf gxfxxf xf
0'20 '2'2201'00 2'20
Khi đó ( ) ( ) '4cos.'sinx2sin2 hxxfx =−
Với ( ) ( ) ( ) cos,sin20 0;'00; sin0;1'sin0 22 xx xhxx xfx
Suy ra hàm số ( )hx nghịch biến trên 0; 2
đó, hàm
)yhx
ch biến trên kho
ng 0; 2
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 113
Do
số (
= nghị
ả
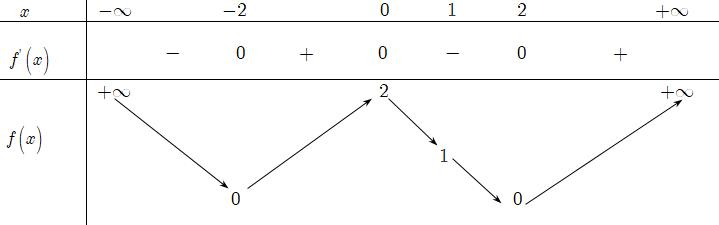
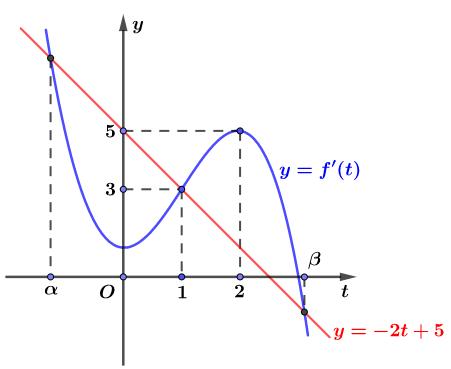
( ) 0 hx ( ) 0;04110303. 22 xhfmmm −−− Kết hợp với điều kiện nguyên dương của 1;2;3 mmcó 3 giá trị của m thỏa mãn yêu cầu bài toán. Câu 85: Cho hàm số ( )yfx = là hàm số đa thức bậc bốn, có đồ thị hàm số ( )yfx = như hình vẽ. Hàm số ( ) 2 52410 yfxxx =−+− đồng biến trên các khoảng nào sau đây?

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 114
gxfxx =−−+− Cho ()0gx = ( ) ( ) 25281005245 fxxfxx −−+−=−=− Đặt 52 tx =− ta có phương trình ( ) 25
=−+ Vẽ đồ thị hai hàm số ( )yft = và 25yt
ộ
ệ trụ
tọa độ Ta có hoành độ các giao điểm: ,0 1 5 ,2 t t t = = = 1 2 5 ; 2 2 5 ; 4 xx x xx =+ = =− . Do đó ()gx có bảng biến thiên như sau
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. ( )3;4 . B. 5 2; 2 . C. 3 ;2 2 . D. 3 0; 2 . Lời giải Chọn B Đặt ( ) 2 ()52410 gxfxxx =−+− ( ) ()252810
ftt
=−+ trên cùng m
t h
c
Căn cứ vào bảng biến thiên ta có hàm số đồng biến trên khoảng 5 2; 2
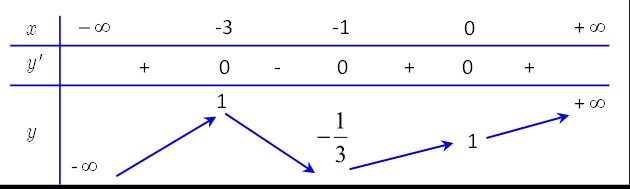
Câu 86: Cho hàm số ()yfx = liên tục trên và có đồ thị hàm số ()yfx = như hình vẽ dưới đây. Tìm tất cả các giá trị của tham số m để hàm số 2 1 ()()(1)2022 2 gxfxmxm=−−−++ đồng biến trên( )1;2 . A. 23 1 m m


Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO
ĐỂ
SÁT HÀM SỐ
HÀM
KHẢO
Page
115
− . B. 1 m − . C. 23 1 m m − . D. 23 m . Lời giải Chọn C Ta có ()()(1) gxfxmxm =−−−+ Vậy ()0()(1)0 gxfxmxm =−−−+= ()1(1)fxmxm −=−+ . Đặt txm =− , khi đó phương trình trở thành 222 ()100 222 txmxm ftttxmxm txmxm =−==+ =+=−== =−−=−=− . Bảng biến thiên của hàm số ()gx như sau:
− − + . Câu 87: Cho hàm số ( )yfx
Vậy hàm số ()gx đồng biến trên khoảng ( )1;2 khi 21 23 2 1 21 + =++−−=++−− ++++ Ta có 0;1 x nên 2 111 210 xx x −+− + . Yêu cầu bài toán ( ) 0,0;1gxx ( ) ( ) 2 2 2
m m m m m 480 10,0;1 2 fxxx mxx +−− ++
116

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn = có đồ thị ( )fx như hình vẽ Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ( ) ( ) ( ) 2 2 480 12021 2 gxfxx mxx =+−++ ++ nghịch biến trên ( )0;1 ? A. 4. B. 6. C. 7. D. 8. Lời giải Chọn C Do ()gx liên tục trên nên ()gx nghịch biến trên ( )0;1 ()gx nghịch biến trên 0;1 Ta có: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 22 2222 48021 480 211211 22 x gxxfxxxfxx mxxmxx

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 117 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) 2 22 480 21,0;1xxfxxx m +++− Dựa vào đồ thị ( )fx ta thấy khi 2 111 xx −+− thì ( ) ( ) 0 2 ;1 max14 x fxx +−= , dấu "" = xả
48015 (*)642 m m . Vì m là số nguyên dương nên ta có 7 giá trị m thỏa mãn đề bài. Câu 88: Cho hàm số đa thức ( )yfx = liên tục trên có đồ thị hàm số ( )yfx = như hình vẽ: Hàm số ( ) ( ) 2 424 gxfxxx =+−− nghịch biến trên khoảng nào dưới đây? A. ( )3;2 B. ( )0;1 C. ( )3;4 D. ( )1;0 Lời giải Chọn D Ta có ( ) ( ) 2 424 gxfxxx =+−− ( ) 2 4224 fxx =+−++ Đặt ( ) 2 ()44 hxfxx=−+ . ()4()24() 2 x hxfxxfx =−=− . Vẽ đồ thị hàm số ( )yfx = và đường thẳng 2 x y = trong cùng một mặt phẳng tọa độ:
y ra khi 1 x = Mà ( )2 2 0;1 max216 x xx ++= , dấu "" = xảy ra khi 1 x = . Nên ( ) ( ) 2 22 0;1 max214.1664 x xxfxx +++−== , dấu "" = xảy ra khi 1 x = Do đó
Từ hình vẽ ta suy ra bảng biến thiên của hàm ()hx :
Suy ra sự biến thiên của hàm ( ) ( ) 2 44hxfxx=−+ :
Từ đó suy ra sự biến thiên của hàm số ( ) ( ) ( ) 2 24224gxhxfxx=+=+−++ :
Ta thấy hàm số ( )gx nghịch biến trên mỗi khoảng ( );4−− , ( )2;0 .
Vậy hàm số nghịch biến trên khoảng ( )1;0 . Câu 89: Cho hàm số ( )yfx = có đạo hàm liên tục trên và ( ) 30 f −= và có bảng xét dấu đạo hàm như
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page
118
x−
(
x−
(
x−
sau:
6 22 +
)hx
0 +0 0 + ( )hx
20 2 +
) hx
4 20 + ( ) ( ) 2 gxhx=+
Hay ( ) ( ) ( ) ( ) ( ) ( ) ( ) 4242 12111121111213hxxxxxfxx =++−+++−−+++− .
Hay
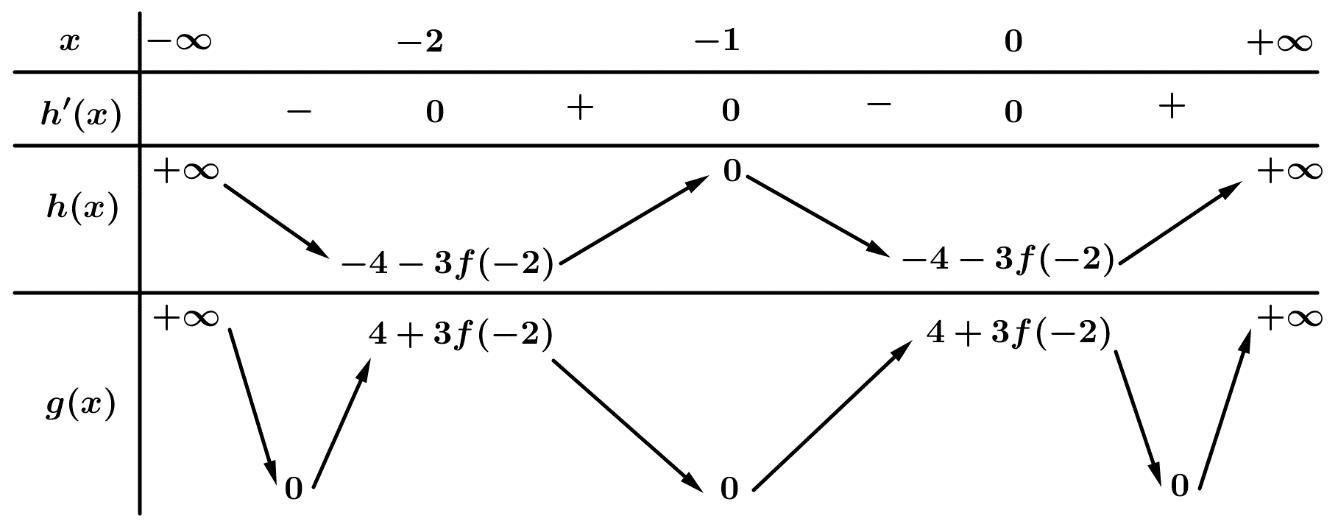
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 119 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Hỏi hàm số ( ) ( ) ( ) ( ) 62 432 21613442gxxxfxxx =+−+−−−−− đồng biến trên khoảng nào trong các khoảng sau? A. ( )1;2 B. ( )1;0 C. ( )0;1 D. ( ) 1;+ Lời giải Chọn B Xét hàm
ố ( ) (
(
62 432 21613442
. Khi
( ) (
= .
( ) ( ) ( ) ( ) ( ) 6242 216131213hxxxfxx=+−+−−+++− .
ra ( ) ( ) ( ) ( ) ( ) ( ) ( ) 5342 121121341411213hxxxxxfxx
s
) ( )
)
hxxxfxxx =+−+−−−−−
đó
)gxhx
Ta có
Suy
=+−+−−+++−+++− .
( ) ( ) ( ) ( ) ( ) ( ) 2242 121.11.111213hxxxxfxx =++−+++−+++− . Hay ( ) ( ) ( ) ( ) ( ) ( ) 242 121.2.111213hxxxxxfxx =+++++−+++− . Ta có ( ) ( ) ( ) 2 422 12131122, xxxx −+++−=−+−−− Từ bảng xét dấu suy ra ( ) ( ) 42 12130, −+++− fxxx Do đó, ( ) ( ) ( ) 242 1112130, xfxxx +++−+++− Vậy ( ) ( ) ( ) 1 0121.202 0 x hxxxxx x =− =++==− = và có bảng biến thiên: Từ bảng biến thiên có thể khẳng định hàm số ( )gx đồng biến trên khoảng ( )1;0 .
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo
42
Page 120
Câu
số ( )yfx = có đạo hàm liên tục trên và có đồ thị hàm số ( )yfx = như hình
. Xét hàm số ( ) ( )
21362021gxfxxx=+−−+
A. ( ) 1 0 2 gg B. ( ) 6 1 5 gg −− C. ( ) ( )21gg D. ( ) ( )54gg−− Lời giải Chọn B Ta có ( ) ( ) ( ) ( ) ( ) 2352233 6118186131 gxxfxxxxfxx =+−−=+−+ Suy ra ( ) ( ) ( ) ( ) 33 0 0 1311 x gx fxx = = +=+ Khi đó xét phương trình ( ) 1 30 1 t fttt t = == =− do vậy phương trình ( )1 có các nghiệm 3 0;1;2xxx==−=− . Và ( )gx có ba nghiệm trên đồng thời là các nghiệm bội lẻ Từ đó ta có ( ) 0 gx với ( ) ( ) 3 ;21;0 x −−− và ( ) 0 gx với ( ) ( ) 3 2;10; x −−+ .
viên: Huỳnh Văn Ánh
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
90: Cho hàm
vẽ
3632022
. Khẳng định nào sau đây đúng?
Vậy ( )gx đồng biến trên các khoảng ( ) ( ) 3 ;2;1;0−−− nghịch biến trên ( ) ( ) 3 2;1;0; −−+ .
Câu 91: Cho hàm số ( )yfx = liên tục trên có đồ thị hàm số ( )yfx = có đồ thị như hình vẽ
Hàm số ( ) ( ) 2 2122020gxfxxx =−−++ đồng biến trên khoảng nào A. ( )2;0 B. ( )3;1 C. ( )1;3 D. ( )0;1 Lời giải Chọn D

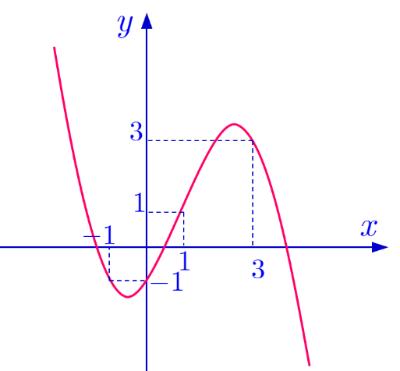
Ta có: ( ) ( ) ( ) ( ) ( )2 2 2220201 1 2202 1 1 gxfxgxx x f x x =++− + = Xét hàm số ( ) ( ) ( )2 12112021kxfxx−=−−−+ Đặt 1 tx=− Xét hàm số: ( ) ( ) 2 22021htftt=−+ ( ) ( ) 22 htftt =− Kẻ đường yx = như hình vẽ.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
121 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG
SÁT HÀM SỐ
ĐẠO HÀM ĐỂ KHẢO
Page
Khi
−
− Do đó: ( ) 110 10 11324 xx kx xx −− −−
đó: ( ) ( ) ( ) 00 htfttftt
1 13 t t
Ta có bảng biến thiên của hàm số ( ) ( ) ( )2 12112021kxfxx−=−−−+ Khi đó, ta có bảng biến thiên của ( ) ( ) ( )2 212021 1 gxfx x −+ = bằng cách lấy đối xứng qua đường thẳng 1 x = như sau:


CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 122
khoảng nào dưới đây? A. ( );1− . B. ( )1;2 . C. ( )3;4 . D. ( )2;3 . Lời giải Chọn C Ta có ( ) ( ) ( ) 2 32 yfxfxfx =− . Phương
( ) ( ) ( ) 0 00 2 fx yfx fx = == = . Dựa vào bảng biến thiên, ta thấy: ( ) 01;2;3;4fxx = ; ( ) 01fxxa== hoặc 4 x = ;
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vậy hàm số đồng biến trên ( )0;1 . Câu 92: Cho hàm số ( )fx có bảng biến thiên như sau: Hàm số ( ) ( ) 32 3 yfxfx =− đồng biến trên
trình
= =
=
( ) ( ) ( ) 1 21;2 3 4 = +== =
= t txftt t
= =+== = Vậy ( ) ( ) 112 0,0233 tt ftft tt . ( ) ( ) ( ) ( ) ( ) 22 220222222022 gxfxxmgxxfxxm =−+−+=−−+−+ .
=
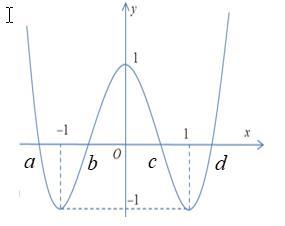
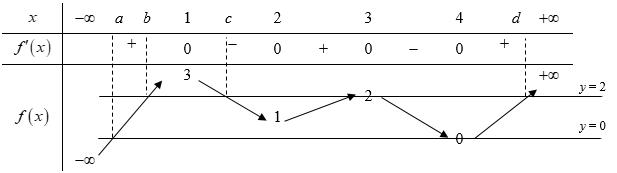
. Ta lập được bảng xét dấu của y : Từ bảng xét dấu, ta thấy hàm số đồng biến trên các khoảng ( ) ;a − ; ( );1b ; ( );2c ; ( )3;4 và ( ) ; d + Như vậy phương án đúng là C. Câu 93: Cho hàm số bậc bốn ( )yfx = . Biết hàm
hình bên.
22022 gxfxxm =−+−+ đồng biến
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page
số ( ) 1 yfx =+ có đồ thị như trong
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Có bao nhiêu số nguyên
123 2
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn trên ( )0;1 ? A. 2023 B. 2021 C. 2022 D. 2024 Lời giải Chọn A Dựa vào đồ thị hàm số ( ) 1 yfx =+ ta có ( ) 0 101 2
xbab xc fx x xd x fxx x Đặt ( ) 1 102. 3
dương m sao cho hàm số ( ) ( )
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 124 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Hàm số ( ) ( ) 2 22022 gxfxxm =−+−+ đồng biến trên ( )0;1 ( ) ( ) ( ) ( ) ( ) 22 22220220,0;1220220,0;1 xfxxmxfxxmx −−+−+−+−+ ( ) ( ) 22 22 22 22022122023 0;10;122022222024 22022322025 xxmmxx xxmmxxxx xxmmxx −+−+−+ −+−+−+ −+−+−+ 2022 20242024 m m . Vậy có 2023 số. Câu 94: Cho hàm số ()yfx = liên tục và có đạo hàm trên là ( ) 202122 ()(2)8 fxxxxmx =−++ . Gọi S là tập hợp tất cả các giá trị nguyên của (2020;) m−+ sao cho hàm số 202520242022132 ()()2021 202520241011 hxfxxxx=+−++ nghịch biến trên khoảng (;1) −− . Số phần tử của S là A. 2025 B. 2024
Lời giải Chọn A Ta
(
2024202320 2 2
21
x
=+−+ ( ) (
2
=−++++−− ( ) 2 90,;1xxmxx +++−− ( ) 2 9,;1mxxxx −−−−− ( ) 9 1,;1mxx x −−−−− Xét hàm số ( ) ( ) 9 1,;1gxxx x =−−−−− , tính đạo hàm lập bảng biến thiên ta tìm được ( );1 9 min153 xx x −− −−−==− Từ đó suy ra ( ) 9 1,;15mxxm x −−−−− . Do (2020;),2019;2018;...;5mmm −+−− . Suy ra có 5201912025 ++= số m . Câu 95: Cho hàm số ()yfx = liên tục và có đạo hàm trên là ( ) 202122 ()(2)8 fxxxxmx =−++ . Gọi S là tập hợp tất cả các giá trị nguyên của (2020;) m−+ sao cho hàm số 202520242022132 ()()2021 202520241011 hxfxxxx=+−++ nghịch biến trên khoảng (;1) −− . Số phần tử của S là A. 2025. B. 2024. C. 2026. D. 2027. Lời giải Chọn A
C. 2026 D. 2027
có
) ( ) ( )
202
213 ()()2.834 34 xxxm hxfxxx x
xx
=−+++−+
)
202122810,;1xxxmxxx
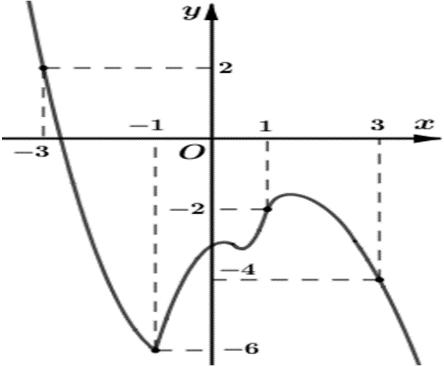
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 125 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có ( ) ( ) ( ) 2024202320 2 2 202 21 213 ()()2.834 34 xxxm hxfxxx x x xx =−+++−+ =+−+ ( ) ( ) 2 202122810,;1xxxmxxx =−++++−− ( ) 2 90,;1xxmxx +++−− ( ) 2 9,;1mxxxx −−−−− ( ) 9 1,;1mxx x −−−−− Xét hàm số ( ) ( ) 9 1,;1gxxx x =−−−−− , tính đạo hàm lập bảng biến thiên ta tìm được ( );1 9 min153 xx x −− −−−==− Từ đó suy ra ( ) 9 1,;15mxxm x −−−−− Do (2020;),2019;2018;...;5mmm −+−− . Suy ra có 5201912025 ++= số m Câu 96: Cho hàm số ( )yfx = là hàm đa thức bậc 4. Đồ thị hàm số ( )'2fx + được cho trong hình vẽ bên Hàm số ( ) ( ) 2642 4541gxfxxxx=−+−+ đồng biến trên khoảng nào sau đây? A. ( )4;3 . B. ( ) 2;+ . C. ( )2;2 . D. ( )2;1 . Lời giải Chọn A Ta có ĐTHS ( ) ' yfx = như sau.
suy ra ( ) 2 2 2
00 *22 42
Bảng xét dấu ( ) ' gx .
= = == = = .
x x xx x x
Từ bảng xét dấu của ( ) ' gx suy ra hàm số đồng biến trên ( );2−− nên hàm số cũng đồng biến trên ( )4;3
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 126
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có ( ) ( ) 254 '8.'6208 gxxfxxxx =−+− ( ) 242 35 8'1 42 xfxxx =−−+ Ta có ( ) ( ) ( ) 242 0 '035'1 * 42 x gx fxxx = = =−+ Từ đồ thị
A. 1 1;. 3 B. ( ) 2;0. C. ( ) 3;1. D.
Lời giải Chọn C Ta có ( ) ( )()221 gxfxx =++ . ( ) ( ) ( ) ( )( )()0101* gxfxxfxx =++==−+ . Số nghiệm của phương trình ( )* chính là số giao điểm của đồ thị hàm số ( )yfx = và đường thẳng ( )1 yx=−+ . Đường thẳng ( )1 yx=−+ đi qua các điểm ( ) ( ) ( ) ( )3;2,1;0,1;2,3;4 .
. Câu 97: Cho hàm số ()yfx = có đạo hàm liên tục trên R. Đồ thị hàm số '()yfx = như hình bên. Hàm số ( ) ( )2 ()21 gxfxx=++ nghịch biến trên khoảng:
( ) 1;3.
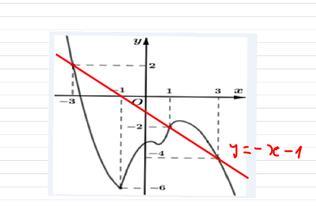
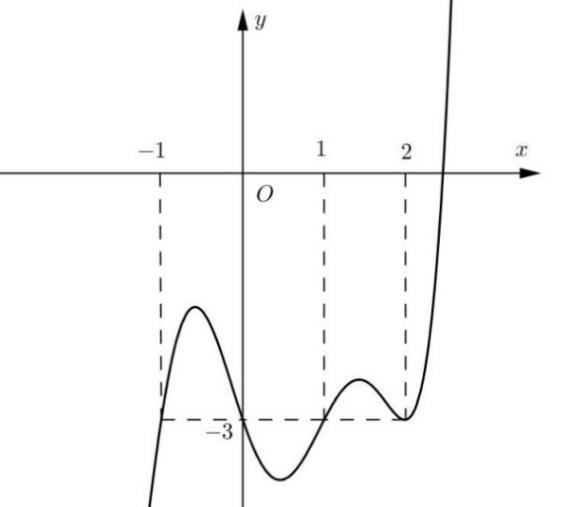
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 127 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Dựa vào đồ thị ( )* có ba nghiệm 3,1,3xxx=−== . Ta có bảng xét dấu Hàm số nghịch biến ( ) 31 0 3 x gx x − Câu 98: Cho hàm số ( )fx . Hàm số ( )yfx = có đồ thị như hình vẽ Hỏi hàm số ( ) ( ) 22 263 gxfxxxx =−+− đồng biến trên khoảng nào dưới đây? A. 1 ;0 4 B. 1 ;1 4 C. ( )0;1 D. ( );0− Lời giải Chọn A Ta có: ( ) ( ) 22 263 gxfxxxx =−+− ( ) ( ) ( ) 2 412123gxxfxxx =−−+− ( ) ( ) 2 4123 xfxx =−−+

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 128
x
−= = −=− (
2 2 2 2 1 4 21vônghiêm 21 20
x xx xx xx xx = −=− −= −= −= (
1 4 1 1 2 0 1 2 117nghiêmkép 4 117nghiêmkép 4 x x x x x x x = = =− = = + = = Ta có: ( ) ( )'29'(10)3gf−=−+ dựa vào đồ thì ( ) ' fx ta thấy ( ) ( ) '103'1030 ff−+ ( ) '20 g − . Vì ( ) ' gx không đổi dấu qua các nghiệm bội chẵn nên ta có bảng xét dấu như sau: Xét dấu ( )gx ta được ( ) 111117117 0,;0;1;; 24244 gxx ++ −+ . Suy ra ( )gx đồng biến trên các khoảng 1 ;0 2 và 11 ; 42 và ( ) 1;+ . Mà 11 ;0;0 42 −− nên hàm số ( ) ( ) 22 263 gxfxxxx =−+− đồng biến trên khoảng 1 ;0 4 Cách 2: Ta có: ( ) ( ) 22 263 gxfxxxx =−+− ( ) ( ) ( ) 2 412123gxxfxxx =−−+− ( ) ( ) 2 4123 xfxx =−−+ . Xét '()0 gx . TH1: ( ) ) ) 2 1 410411 '2311;1; ;0;1;42 22 x x x fxx x − + −− −−+ .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) 2 410 0 23
gx fxx
) ( )
22nghiêm kép
) ( )
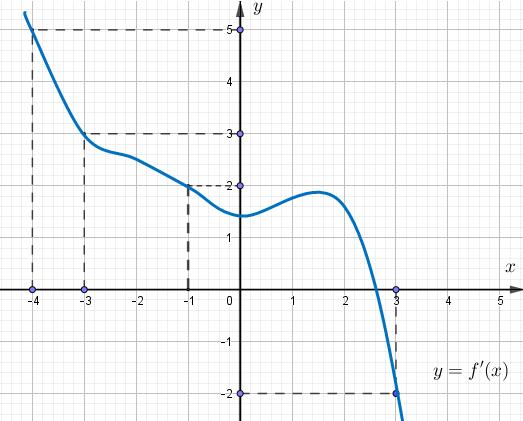
x x x fxx x Vậy ( ) ) 111 '0;0;1; 242 gxx −+ . Câu 99: Cho hàm số ( )fx . Biết hàm số ( )yfx = có đồ thị như hình bên. Trên khoảng ( );4−− và ( ) 3;+ hàm số ( )yfx = luôn nghịch biến. Có bao nhiêu số nguyên a thuộc đoạn 2022;2022 để hàm số ( ) ( ) ( )2 21 gxfxx =+− đồng biến trên khoảng ( );2022aa + ? A. 0. B. 2023. C. 4046. D. 4044. Lời giải Chọn A
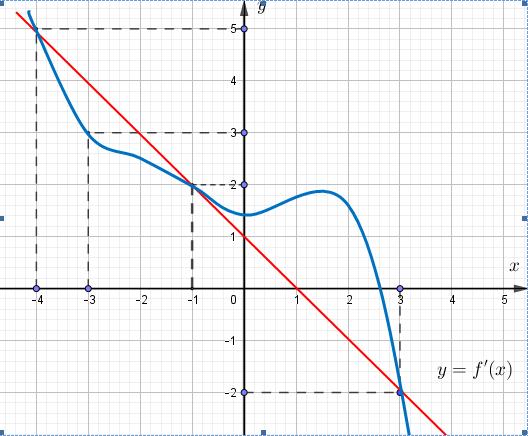
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 129
1
− − −−
−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn TH2: ( ) 2
41041 '2311;0 ;0;12 22
hình
kết
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 130
.
=
khoảng ( )
−− và (
1;3 . Hàm số ( )ygx = đồng biến
( )
aa + khi và chỉ khi ( ) ( );2022;4aa +−− hoặc ( ) ( )
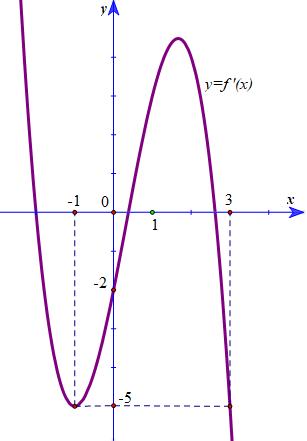
202242026 112026 202232019 aa a aa aa +−− − −− +− Mà a và 2022;2022 a− nên không có giá trị của a thỏa mãn. Câu 100: Cho hàm số ( )yfx = có đạo hàm liên tục trên . Bảng biến thiên của hàm số ( )yfx = được cho như hình vẽ bên dưới. Có bao nhiêu số nguyên ( )0;10 m để hàm số 2 x yfmx =−+ nghịch biến trên khoảng ( )1;3 ? A. 7 B. 3 C. 6 D. 2 Lời giải Chọn C Đặt ( ) 2 x gxfmx =−+ Ta có ( ) 1 1 22 x gxfm =−−+ Ta có ( ) 02 2 x gxfm − Từ bảng biến thiên ta có
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có ( ) ( ) ( ) 221 gxfxx =−− . ( ) ( ) ( ) ( ) 022101 gxfxxfxx −−− . Vẽ đồ thị hàm số 1 yx =− Từ
vẽ trên,
hợp với giả thiết là trên khoảng ( );4−− và ( ) 3;+ hàm số ( )yfx = luôn nghịch biến nên ta có ( ) 4 1 13 x fxx x − − −
Do đó hàm số ( )ygx
đồng biến trên hai
;4
)
trên khoảng
;2022
;20221;3aa +− hay
Suy ra hàm số 2 x yfmx =−+ nghịch biến trên hai khoảng ( );24 m −− và ( ) 22; ma−+
Do đó hàm số 2 x yfmx =−+ nghịch biến trên khoảng ( )1;3 khi và chỉ khi ( ) ( )1;3;24 m −−− hoặc ( ) ( ) 1;322; ma −−+ .
*TH1: ( ) ( )1;3;24 m −−− 7 324 2 mm −
Mà ( ),0;10mm nên 4;5;6;7;8;9 m
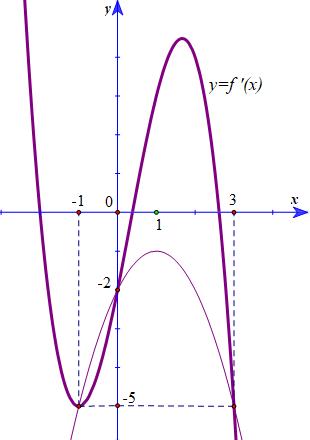
Trường hợp này có 6 số nguyên m thỏa mãn yêu cầu bài toán. *TH2: ( ) ( ) 1;322; ma −−+ 1 221 2 mama −−− . Mà 0 a suy ra 1 2 m − . Vậy có 6 số nguyên m thỏa mãn. Câu 101: Cho hàm số ( )yfx = có đồ thị hàm ( )yfx = như hình vẽ bên dưới. Hàm số ( ) ( ) 32 8 2441 3 gxfxxxx =+−++ đồng biến trên khoảng nào dưới đây? A. ( )0;1 . B. ( )1;0 . C. ( )0;3 . D. ( ) 3;+ . Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 131
− −
22422 222 2 x m xm x fm xmax ma
−
−
−
, với 0 a .
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 132
Chọn A
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
Ta có: ( ) ( ) 2 '2'2884 gxfxxx =+−+ ( ) ( ) ( ) 22 '02'28840'2442 gxfxxxfxxx =+−+==−+− Đặt 2, txx= trở thành ( ) 2 1 '220 3 t ftttt t =− =−+−=
=
( ) 1 212 '0200 233 2 x x gxxx x x =− =− === = = Bảng biến thiên: Vậy hàm số ( )gx đồng biến trên các khoảng 1 ; 2 −− và 3 0; 2 Mà ( ) 3 0;10; 2 nên hàm số đồng biến trên ( )0;1 Câu 102: Cho hàm số ( )fx liên tục trên . Hàm số ( )yfx = có đồ thị như hình bên dưới đây

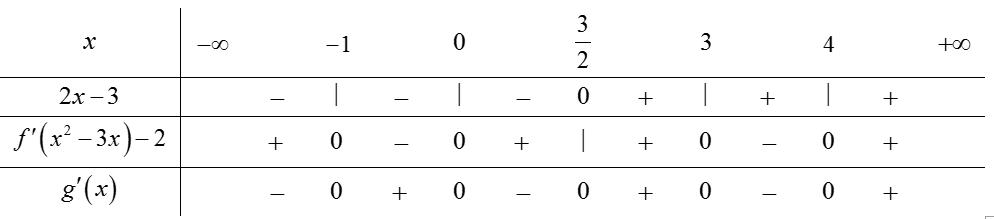
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 133
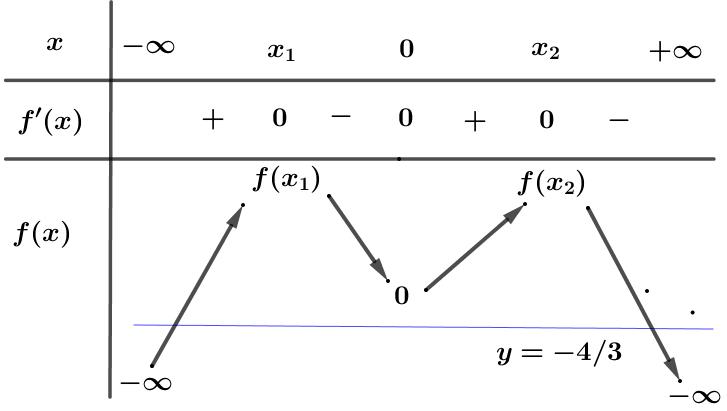
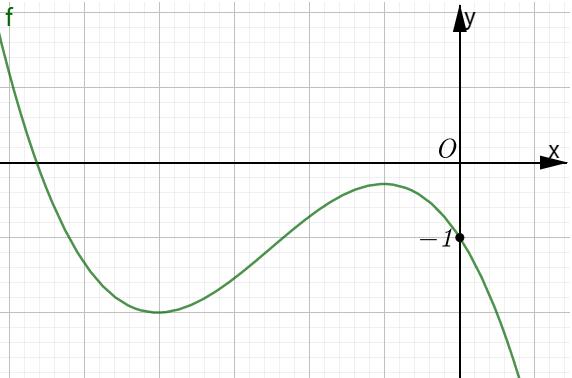
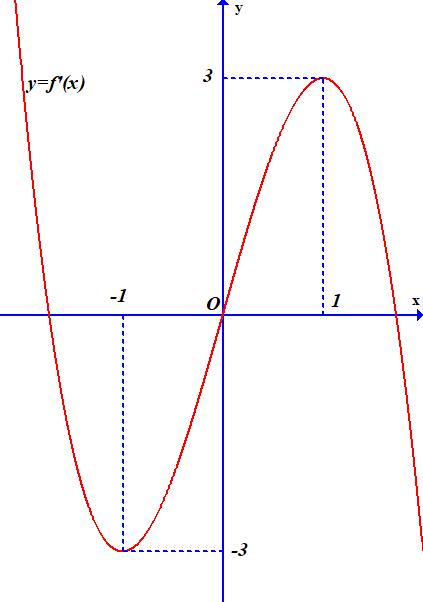
Hàm
ố ( ) (
22326 gxfxxxx = +
ị
ế
A. ( )
− . B. ( )0;4 . C.
. D.
. Lời giải Chọn C Ta có: ( ) ( )( ) ( ) ( ) 22 4 36 3 233 2 2
−+=−−− =−−
Xét
2
x − ( ) 2 2 2
x f x x x x x
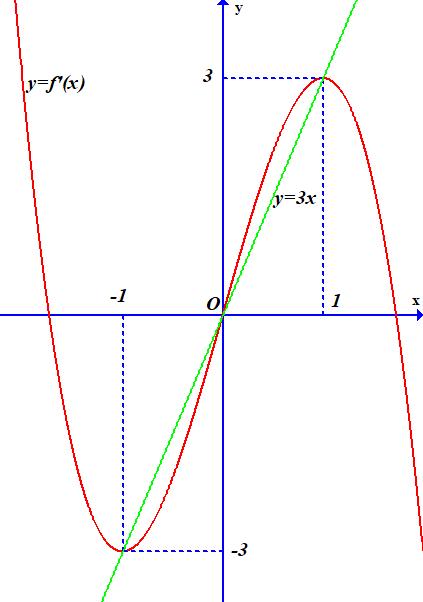
− − − − . Ta có bảng xét dấu: Suy ra hàm số ( )gx nghịch biến trên các khoảng ( );1−− , 3 0; 2 , ( )3;4 . Câu 103: Cho hàm số ( )yfx = nghịch biến trên . Tổng tất cả các giá trị nguyên của m để hàm số ( ) 32492021 3 m yfxmxx =+−++ nghịch biến trên . A. 0 B. 136 C. 68 D. 272 Lời giải Chọn B Ta có: 232 y'(2(4)9).'((4)92021) 3 m mxmxfxmxx =−−++−++
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
s
)
ngh
ch bi
n trên khoảng nào dưới đây?
;0
( )1;0
( )0;1
gxf x x x xx fxx
.
( )
0 3 2 fx
4 34 31 3 2 303 0 x
x x
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 134 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Để hàm số: ( ) 32492021 3 m yfxmxx =+−++ nghịch biến trên thì '0 yx 232 y'(2(4)9).'((4)92021)0 3 m mxmxfxmxxx =−−++−++ Lại
2 2(4)90 mxmxx −−+ 222 000 (4)901716017160 mmm mmmmmm −−−+−+ Vậy 1,2,3,...,15,16 m Tổng các giá trị nguyên của m thỏa mãn đề bài là: 123...1516136 +++++= Câu
Cho hàm số ( ) 9724 1 2321 9 yxxmmx =++−−+ . Tập các giá trị nguyên của m
ố
ến
1 2; 2 .
2 2
m mm m = −−= =− ,
ết
ợ
có: ( )yfx = nghịch biến trên suy ra '()0fx Nên để hàm số: ( ) 32492021 3 m yfxmxx =+−++ nghịch biến trên thì:
104:
để hàm s
đồng bi
trên là A.
B. 1 2; 2 . C. . D. 2 . Lời giải Chọn D TXĐ: HS đồng biến trên ( ) ( ) 3532 '72320 yxxxmmx =++−− ĐK cần: Ta thấy ( ) ( ) 3532 '7232 yxxxmm =++−− liên tục trên và có nghiệm x = 0. Để đạo hàm không đổi dấu trên thì ( ) 5327232xxmm ++−− có nghiệm 0 x = Suy ra
2320 1 2
k
h
p với điểu kiện m nguyên suy ra m=2 ĐK đủ: Thử lại, với m =2, ta có 86 '70 yxxx=+ , suy ra hàm số đồng biến trên . Vậy m = 2.
i Chọn C Ta có 2 363 yxxm =−++ Để hàm số nghịch biến trên khoảng ( ) 0;+ thì: ( ) 2 36300;yxxmx =−+++ . ( ) 2 2,0;mxxx −+ ( ) ( ) 2 0; min21.mxx + −=− Vậy 1 m − . Câu 106: Cho hàm số ( ) ( ) ( ) ( ) 34322311 132222021 42 fxmxmxmmxmmx =−++−++++ với m là tham số. Có bao nhiêu số nguyên 2022;2021 m− sao cho hàm
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 135
Câu
Tìm tất cả các giá trị của tham số m để hàm số 32331yxxmx =−++− nghịch biến trên khoảng (
+ A.
m B.
m C.
m − D. 2 m Lờ
ả
số ( )yfx = đồng biến trên khoảng ( )1;3 ? A. 2021 B. 2022 C. 2023 D. 2024 Lời giải Chọn D Ta có: ( ) ( ) ( ) 33223 '133222 fxmxmxmmxmm =−++−+++ 322333 33222 xmxmxmxmmxmx =+++++−− ( ) ( ) ( ) 3 33 22 xmxmmxmx =+++−+ Để hàm số ( )yfx = đồng biến trên khoảng ( )1;3 thì ( ) ( ) '0, 1;3 fxx hay ( ) ( ) ( ) ( ) 3 33 220,1;3xmxmmxmxx +++−+ ( ) ( ) ( ) ( ) 3322, 1;3 xmxmmxmxx ++++ Đặt ( ) ( ) 322;'320, gtttgttt =+=+ Do đó ( )gt đồng biến trên Suy ra ( ) ( ) ( ) ( ) , 1;3 gxmgmxx + ( ) ( ) ( ) , 1;31, 1;3 xmmxxmxxx +− ( ),1;3 1 x mx x
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
105:
) 0;
0
1
1
i gi
Xét ( ) 1 x hx x = trên ( )1;3 ; ( ) ( ) ( ) 2 1 '0, 1;3 1 hxx x =−

Do đó ( ) 1 x hx x = nghịch biến trên ( )1;3 hay ( ) ( )*3 2 *3 mh =
Kết hợp điều kiện m nguyên thuộc 2022;2021 ta được 2024 giá trị của m thỏa mãn.
Câu 107: Cho hàm số ( ) 4221fxxx=++ . Có bao nhiêu giá trị nguyên của tham số 0;10 m để hàm số ( ) ( ) 2 3 gxfxmm =−+ nghịch biến trên ( );1− ?
A. 11. B. 5. C. 10 . D. 9. Lời giải
Chọn C
hàm s
) 4221fxxx
có ( ) 3 44 fxxx
ảng biến thiên
; ( ) 00fxx
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG
SÁT HÀM SỐ
ĐẠO HÀM ĐỂ KHẢO
Page 136
== không
ỏa
nghịch
ế
khoảng ( );1− nên trường hợp này bị loạ
TH2: Nếu 0 m phương trình (
0 gxxm == Ta
2 301 xmmx −+ ( ) ( ) 2 30;1fxmmx −+− nên ( ) 0 gxxm hàm số ( )ygx = nghịch biến trên ( );1− ( ) ( )0;1gxx − ( ) ( ) ;1;1mm−− 1;2;3;4;5;6;7;8;9;10 m . Nên có 10 giá trị thỏa mãn. Câu 108: Cho hàm số ( )yfx = liên tục trên và hàm số ( ) ( )22gxfx=− có đồ thị như hình dưới.
Xét
ố (
=++ Ta
=+
== B
Ta có ( ) ( ) ( ) 223.3 gxfxmmxmm =−+−+ = ( ) ( ) 2 3 3. xm fxmm xm −+ ( ) ( ) ( ) 2 01 0 302 xm gx xmm −= = −+= TH1: Nếu 0 m = phương trình ( ) 00gxx
th
mãn
bi
n trên
i.
)
có


CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 137
=−= =−=== ==
Đặ
hxfxxm =+− Khi đó ( ) ( ) '4cos.'sinx2sin2 hxxfx =− Với ( ) ( ) ( ) cos,sin20 0;'00; sin0;1'sin0 22 xx xhxx xfx Suy ra hàm số ( )hx nghịch biến trên 0; 2
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Có bao nhiêu số nguyên dương m để hàm số ( ) 4sincos2 yfxxm =+− nghịch biến trên khoảng 0; 2 ? A. 2. B. 3. C. 0. D. 1. Lời giải Chọn B Ta có ( ) ( ) ( ) ( ) ( ) 0'20 '2'2201'00 2'20 xf gxfxxf xf
Từ đó, ta có bảng biến thiên của hàm số ( )yfx =
t ( ) ( ) 4sincos2
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 138 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do đó, hàm số ( )yhx = nghịch biến trên khoảng 0; 2 ( ) 0 hx ( ) 0;04110303. 22 xhfmmm −−− Kết hợp với điều kiện nguyên dương của 1;2;3 mmcó 3 giá trị của m thỏa
yêu cầu bài toán. Câu 109: Cho hàm số 2 32 1 31khi0 ()2 1 231 khi0 3 xxx fx xxxx ++ = +++ có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số 2 ()() gxfxm =+ đồng biến trên khoảng (1;1) A. 2. B. 1. C. 4. D. 0. Lời giải Chọn D Ta có: 2 3khi 0 '()43 khi 0 xx fx xxx + = ++ Cho 1 1 '()03 31 xy fx xy =−=− = =−= Ta có bảng biến thiên 2 '()2.'() gxxfxm =+ Xét tên khoảng ( )1;0 Để hàm số đồng biến trên ( )1;0 thì 2 '()0fxm+ Do đó ( ) 222 3131;1;0 xmxmxx −+−−−−−− ( )32;1;0 mx −−− 3;2 m =−− Thử lại:
mãn
+ 3 m =−
Ta có: 222 1001332'(3)0,(1;0) xxxfxx −−−−−−
Suy ra hàm số 2 ()() gxfxm =+ đồng biến trên khoảng (1;0)
+ 2 m =−
Ta có: 222 1001221'(3)0,(1;0) xxxfxx −−−−−−
Suy ra hàm số 2 ()() gxfxm =+ đồng biến trên khoảng (1;0)
Xét tên khoảng )0;1
Thử với: + 3 m =−
Ta có: ) 222 0101332'(3)0,0;1 xxxfxx −−−−
Suy ra hàm số 2 ()() gxfxm =+ nghịch biến trên khoảng )0;1
+ 2 m =−
Ta có: ) 222 0101221'(3)0,0;1 xxxfxx −−−−
Suy ra hàm số 2 ()() gxfxm =+ nghịch biến trên khoảng )0;1
Ta thấy trên )0;1 thì hàm số ()gx nghịch biến với 2 m =− và 3 m =− . Vậy không có m nguyên để hàm số đồng biến trên (1;1)
Câu 110: Gọi S là tập hợp chứa tất cả các giá trị của tham số nguyên 2021;2021 m− để hàm số ( ) 1232021 yxmxmxm =+−+−+ nghịch biến trên ( )2;34 . Số phần tử của tập S là: A. 2020 B. 2019 C. 2021 D. 2038 L
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 139
ời giải Chọn B Ta có: 33 3 22 xm ym x ++ =− + Hàm số nghịch biến trên ( )2;34 ( )02;34yx ( ) 33 302;34 22 xm mx x ++ − + ( )336202;34 xmmxx ++−+ Đặt ( ) ( ) 22;6xtt+= 2 2 xt=− Yêu cầu bài toán ( ) ( ) 2 323602;6 tmmtt −++− ( ) 2 33 2;6 61 t mt t
)gx đồng biến trên ( ) 3;+ ( ) ( ) 0,3;gxx + ( ) ( ) ( ) 2 3390,3; xmxx −+−++ ( ) 2 90,;0tmtt ++− ( ) 9 ,;0mtt t −−− .
Ta có trên ( );0− ta có t và 9 t đều là các số dương nên có 9 6 t t −− Vậy ( ) 9 ,;06mttm t −−− . Câu
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 140
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Xét hàm số ( ) 2 33 61 t ft t = trên ( )2;6 ( ) ( ) ( ) 2 2 18618 02;6 61 tt ftt t −+ = Hàm số ( )ft đồng biến trên ( )2;6 ( ) ( ) ( )632;6ftft= Do đó yêu cầu bài toán 3 m Vậy 3;4;...;2021 S = Tập S có 2019 phần tử. Câu 111: Cho hàm số ( )yfx = có đạo hàm ( ) ( ) ( ) 2 2 '19 fxxxxmx =−++ với mọi x . Có bao nhiêu số nguyên dương m để hàm số ( ) ( ) 3 gxfx =− đồng biến trên khoảng ( ) 3;+ ? A. 6 B. 7 C. 5 D. 8 Lời giải Chọn A Ta có ( ) ( ) ( )( ) ( ) ( ) ( ) 22 332339 gxfxxxxmx =−−=−−−+−+ . (
112: Có bao nhiêu giá trị nguyên dương của m để hàm số 22 2 4234 42 xxmxx y xx −+++− = −+ nghịch biến trên khoảng ( )4;0 ? A. 4. B. 3. C. 5. D. 17. Lời giải Chọn A Đặt ( ) 2 2 2 404;0 4 x txxtt xx =−=− t nghịch biến trên ( )4;0 ( )0;42 t
Khi đó bài toán trở thành tìm m nguyên dương để hàm số ( ) 2 32 2 ttm gt t +++ = + đồng biến trên ( )0;42 . Ta có ( ) ( ) ( ) ( ) 22 2 2 2 3244 04402 2 2 ttmttm gtgtttmtm t t +++++− ===++−=+= + + Do phương 0 m nên phương trình luôn có hai nghiệm phân biệt 2 xm =−
Hàm số đồng biên trên ( ) ;2 m −−− và ( ) 2; m −++ . Để hàm số ( )gt
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn x
A. 2 B. 3 C. 7
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO
SÁT HÀM SỐ
HÀM ĐỂ KHẢO
Page 141
đồng biến trên ( )0;42 ( ) ( ) 0;422; m −++ 2024 mmm −+ Câu 113: Cho hàm số ( ) ( ) 1 gxfx =− có đạo hàm ( ) ( ) ( ) ( ) 20212022 2 32236 gxxxxmxm =−++−−+ với mọi . Có bao nhiêu số nguyên ( )5;5 m− để hàm số ( )fx nghịch biến trên khoảng ( ) 0;+ ?
D.
(
(
2
. Từ
ra: (
−=
2
. Vậy, ( )
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 = ( ) ( ) ( ) 20212022 2 2325xxxmxm −+−−−+ Hàm số ( )fx nghịch biến trên khoảng ( ) 0;+ ( ) 0 fx ( ) 0; x + . Do ( ) ( ) 20212022 230xx −+− ( ) 0; x + nên ( ) 0 fx 2 250xmxm−−+ ( ) 0; x + . 2 5 2 x m x + + ) 0; x + . Đặt ( ) 2 5 2 x gx x + = + . Ta có: 2 5 2 x m x + + ) ( ) 0; mmingx + 2 m . Do m nguyên và (5;5) m− nên có 4;3;2;1;0;1;2 m−−−−
6 Lời giải Chọn C
) ( ) 1 gxfx =− Đặt 1 tx =− 1 xt=− . ( ) ( )gxft = ( ) ( )( ) ( ) 1 gxfttft =−=− . Mặt khác, ( ) ( ) ( ) ( ) ( )( ) 202120222 312112136 gxtttmtm =−++−−+−−−+ ( ) ( ) ( ) ( ) ( )( ) 202120222 312112136 gxtttmtm
=−++−−+−−−+
) ( ) ( ) ( ) 20212022
2325gxtttmtm
=+−−−+
và suy
)ft
( ) ( ) ( ) 20212022
2325 tttmtm +−−−+
fx
Vậy có 7 số nguyên m thỏa mãn yêu cầu bài toán. Câu 114: Cho hàm đa thức ( )yfx = có ( ) ( )( ) ( ) 2 125 fxxxx =+−− . Có bao nhiêu cặp số nguyên ( ) ; mn để hàm số ( ) ( ) 2 1cos yfmxn =+− nghịch biến trên khoảng ( ) 0; A. 11. B. 8. C. 9. D. 10. Lời giải Chọn A Xét ( ) ( )( ) ( ) 2 1 12502 5 − +−− Ta có bảng sau: Vậy có 11 cặp số nguyên ( ) ; mn . Câu 115: Cho hàm số ( )fx liên tục và có đạo hàm trên là ( ) ( ) ( ) 2 20212 '28 fxxxxmx =−++ . Gọi S là tập hợp tất cả các giá trị nguyên của ( ) 2020; m−+ sao cho hàm số ( ) ( ) 202520242022132 2021 202520241011 hxfxxxx=+−++ nghịch biến trên khoảng ( );1−− . Số phần tử của S là A. 2027. B. 2024. C. 2025. D. 2026. Lời giải Chọn C Ta có:

x fxxxxx x
=− =+−−== = . Bảng xét dấu Ta có ( ) ( ) ( ) ( ) ( ) 222 1cos1sin.1cos yfmxnymxfmxn =+−=−++− . Hàm số ( ) ( ) 2 1cos yfmxn =+− nghịch biến trên khoảng ( ) 0; nên ( ) 0,0;yx Khi đó, với mọi ( ) 0; x
: ( ) ( ) ( ) ( ) ( ) ( ) 2222 1sin.1cos01cos011cos5 mxfmxnfmxnmxn −++−+−−+− 22 22 110 40 154 mnmn n mnmn −−−−+
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 142
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 143 Chuyên luyện thi: Tuyển sinh
Sưu tầm và
( ) ( ) ( ) (
( ) ( ) (
( ) ( ) 2 20242023202120212202132 20212202122 2 20212 ''342834 2812 219. hxfxxxxxxxmxxxx xxxmxxxx xxxmx =+−+=−+++−+ =−++++− =−+++
ố nghịch biến trên
Xét hàm số ( ) 2 9 xx gx x = trên ( );1−− ta có ( ) 2 2 '9 x gx x −+ = ; ( ) ( ) ( ) 3;1 '0 3;1 x gx x =−− = =−−− Bảng biến thiên Để ( ) 2 9 ,;1 xx mx x −− khi và chỉ khi 5 m Do ( ) 2020; m−+ nên có tất cả 2025 giá trị nguyên của m Câu 116: Cho hàm số 5 2 ()(1)4029 5 x fxxmx =−+−− . Có bao nhiêu giá trị nguyên của để hàm số |(1)2022|yfx=−+ nghịch biến trên (;2) − ? A. 2005. B. 2006. C. 2007. D. 2008. Lời giải Chọn C Chọn C Đặt ( ) ( ) 12022 hxfx=−+ m
Giáo
Hòa
0984164935
vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12
biên soạn
)
) ( )( )
Hàm s
( );1−−
( ) '0hx , ( );1 x −− . ( ) ( ) ( ) 2 202122190,;1xxxmxx −+++−− ( ) ( ) 2 190,;1xmxx +++−− ( ) 2 9 ;1 xx mx x −−
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 144
Ta
ế
(
− (
− − ( ) ( ) ( ) 10044 1 5 10;2(2) m hxx −− ( ) ( ) ( ) ( ) 4 10044 1 5 12110;2(2) m xxmx −−−+−− Đặt 1, tx=− ( );1 t − , khi đó ta có ( ) ( ) 4 2210;1 ttmt −+−− ( ) 4 21;1ttmt −++− Đặt 4 ()211gttt=−++ '3 ()42gtt =−+
+
ọn D Ta có: ( ) ( ) ( ) 33223 '133222 fxmxmxmmxmm =−++−+++ 322333 33222 xmxmxmxmmxmx =+++++−− ( ) ( ) ( ) 3 33 22 xmxmmxmx =+++−+ Để hàm số ( )yfx = đồng biến
ảng
( ) ( ) ( ) (
3 33 220,1;3xmxmmxmxx +++−+
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
có ( ) 12022 yfx=−+ nghịch bi
n trên ( );2− thì
) ( ) ( ) 120220 ;2 0 fx x hx
−+
) ( ) ( ) 120220 ;2 10 f x hx +
. Xét '3 3 1 ()0420 2 gttt =−+== Nên 33 13 1 232 fmm
Từ và suy ra 3 310044 1 325 m + , mà m nên có 2007 giá trị m thỏa mãn yêu cầu bài toán. Câu 117: Cho hàm số ( ) ( ) ( ) ( ) 34322311 132222021 42 fxmxmxmmxmmx =−++−++++ với m là tham số. Có bao nhiêu số nguyên 2022;2021 m− sao cho hàm số ( )yfx = đồng biến trên khoảng ( )1;3 ? A. 2021. B. 2022. C. 2023. D. 2024. Lời giải Ch
trên kho
( )1;3 thì ( ) ( ) '0, 1;3 fxx hay
)
( ) ( ) , 1;31, 1;3 xmmxxmxxx +− ( ),1;3 1 x mx x
Xét ( ) 1 x hx x = trên ( )1;3 ; ( ) ( ) ( ) 2 1 '0, 1;3 1 hxx x =−
Do đó ( ) 1 x hx x = nghịch biến trên ( )1;3 hay ( ) ( )*3 2 *3 mh = Kết hợp điều kiện m nguyên thuộc 2022;2021 ta được 2024 giá trị của m thỏa mãn. DẠNG. Ứng dụng tính đơn điệu vào PT, BPT, HPT, BĐT Câu 118: Cho phương trình 3 32 332 xmmxxx ++=+++ với m là tham số thực. Gọi S là tập tất cả các giá trị nguyên của m sao cho phương trình đã cho có 3 nghiệm phân biệt. Tổng giá trị của phần tử S bằng: A. 9. B. 0. C. 3. D. 12. Lời giải Chọn A Ta có: 3 32 332 xmmxxx ++=+++ có 3 nghiệm phân bi
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 145
(
xmxmmxmxx ++++ Đặ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
) ( ) ( ) ( ) 3322, 1;3
t ( ) ( ) 322;'320, gtttgttt =+=+ . Do đó ( )gt đồng biến trên Suy ra ( ) ( ) ( ) ( ) , 1;3 gxmgmxx + ( )
ệt 3 32 33331(1) xmxmxxxx +++=+++++ có 3
ệm phân
ệt ( ) ( ) 33 3 3 331(1) xmxmxx +++=+++ có 3 nghiệ
ệt Xét ( ) ( ) 32310 ftttftttR =+→=+ nên hàm số đồng biến với tR Suy ra 3 31 xmx +=+ có 3 nghiệm phân biệt 32 3331 xmxxx +=+++ có 3 nghiệm phân biệt 3231mxx =++ có 3 nghiệm phân biệt Xét ( ) ( ) 322 31 360 =++=+= hxxxhxxx
nghi
bi
m phân bi
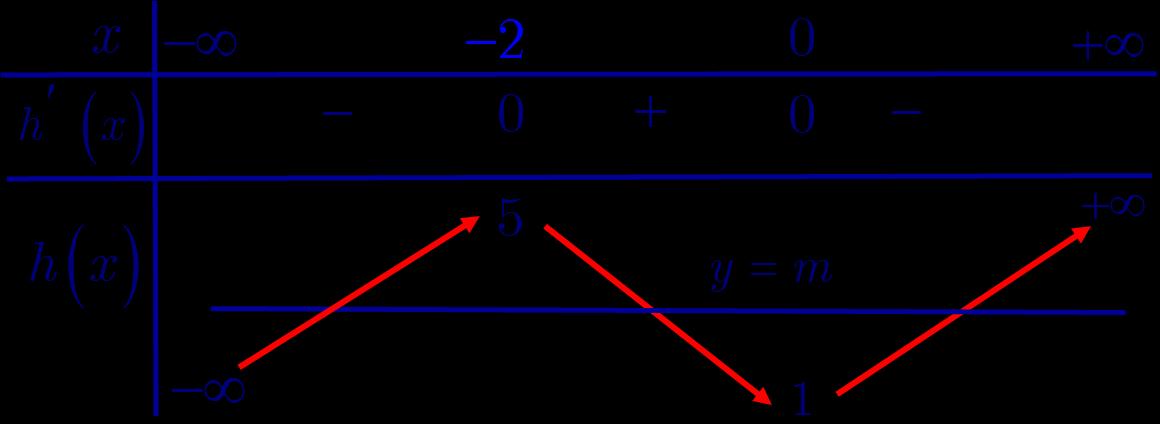
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 146
( ) 0
2 = += =− x xx x Ta
ả
ế
YCBT 15 2;3;4 m m mZ T
trị phần
ử
2349 ++= . Câu 119: Biết rằng tập tất cả các giá trị của tham số m để phương trình ( ) 22 425x8x24mxx++=++ có bốn nghiệm thực phân biệt là khoảng ( ) ; ab . Giá trị ab + bằng A. 28 3 . B. 25 3 . C. 4. D. 9. Lời giải
B Ta có: ( ) 22 425x8x24mxx++=++ ( ) ( ) ( ) 2 22 42442mxxxx ++=+++ *) Với 404xx+==− Khi đó ( ) ( ) 2 1420 x += vô nghiệm. *) Với 404xx+− . ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 22 442 442 1 2 4 422 xx xx mm x xxx +++ ++ ==+ + +++ Đặt 2 4 2 x t x + = + Xét hàm số ( ) 2 4 2 x fx x + = + ( ) ( ) ( ) 2 2 2 22 24 224 222 x xx x x fx x xx +−+ + == + ++
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
320
có B
ng bi
n thiên:
ổng giá
t
S là
Chọn
( ) 1 0240 2 fxxx =−==
Bảng biến thiên hàm số ( )fx
Từ bảng biến thiên ta được điều kiện của t là 13 t −
Vậy để có 2 nghiệm x ứng với 1 giá trị t thì 13 t
( )2 suy ra ( ) 4 ,1;3mtt t =+
Xét hàm số ( ) 4 gtt t =+ trên ( )1;3 . ( ) 2 4 1 gt t =− ; ( ) 2(n) 0 2(l) t gt t = = =− .

Bảng biến thiên thu gọn Từ BBT để phương trình có 4 nghiệm thực thì 13 4 3 m . Nên 13 4; 3 ab== . Vậy 25 3 ab+= Câu 120: Cho hàm số ( ) 2 4 fxxx =+− . Tìm tất cả giá
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 147
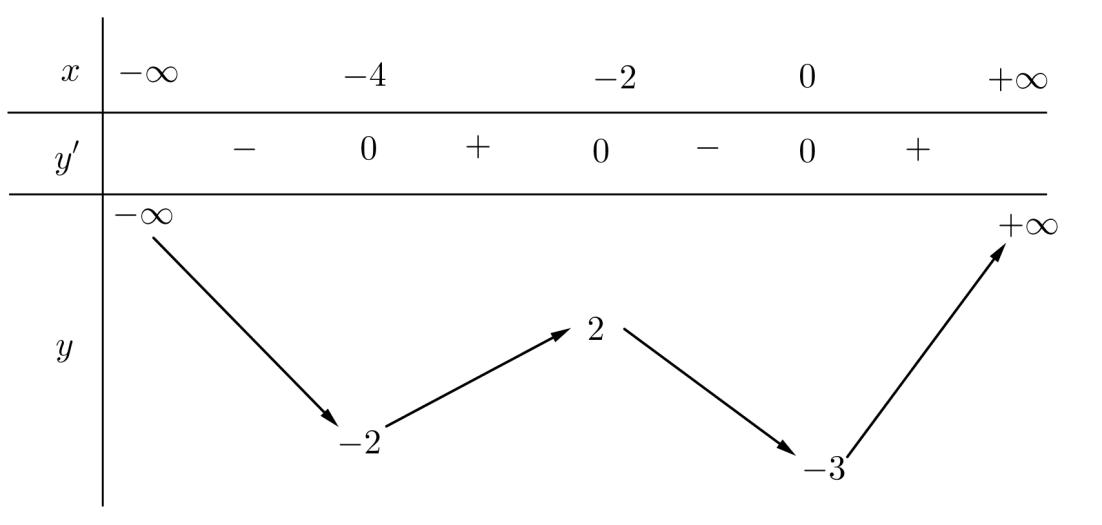
trị của tham số m để bất phương trình ( ) ( ) ( ) 2 2 26 224 3 x mxmfmxm fx −− nghiệm đúng với mọi x . Lời giải Ta có ( ) ( ) 2 40,0, fxxxxxxfxx =+−− và ( ) ( ) ( ) ( ) ( ) ( ) 22 4 .4.44, fxfxxxxxfxx fx −=+++−==− . 13
1 5
x y' y +
2 4
3
3
0
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 148
để
Chọn B Với \1;2;...;2022 xDR = , phương trình đã tương đương: ( ) ( ) ( ) ' 111 11...* 122022 fx mm fxxxx +=+=+++ Đặt ( ) ( ) 111 ...'0, 122022 gxgxxD xxx =+++ Từ bảng biến thiên của hàm số ( )gx ta kết luận được phương trình đã cho có 2022 nghiệm khi và chỉ khi 101 101 mm mm +− +− . Vậy có 4044 giá trị nguyên của 2022;2022 m− thỏa mãn yêu cầu bài toán. Câu 122: Cho hàm số ( )fx có đạo hàm liên tục trên , ( ) ( ) 1102,39ff== và có bảng xét dấu đạo hàm như sau:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do đó ( ) ( ) 2 2 4 3 3 fx fx =− , x Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 22 264 22432424 33 x mxmfmxmxmxmfmxm fxfx −−−−− ( ) ( ) ( ) ( ) ( ) 223.324.241 xfxmxmfmxm −−−− . Xét hàm số ( ) ( ) 22 .4, gttfttttt ==+− ( ) ( )2 2 222 2 222 4 2424 '420, 444 tt tttt gtttt ttt +− +−+ =++−== +++ . Suy ra hàm số ( )gt đồng biến trên , do đó ( ) ( ) ( ) ( ) 222 132432424302 gxgmxmxmxmxmxm −−−−−+− ( )2 nghiệm đúng với mọi x 2 '043013 mmm −+ Vậy 1;3 m Câu 121: Cho hàm số ( ) ( )( ) ( )12...2022fxxxx =−−− . Có bao nhiêu giá trị nguyên của
2022;2022 m−
phương trinh ( ) ( ) ( ) '1 fxmfx =+ có 2022 nghiệm phân biệt? A. 2022. B. 4044. C. 2023. D. 4045. Lời giải
bao nhiêu giá
nguyên
10;10
phương trình
1.111
( )1;3
. A. 20. B. 21. C. 12. D. 13. Lời giải Chọn D Đặt ( ) ( ) 1; axfxbmx =+= . Ta có ( ) ( ) ( ) ( ) ( ) 22 1.111 xfxxfxmxmxx +++++ Trở thành ( ) ( ) ( )( ) 332211100 axabxbabaabbxab
ệm đúng với m
Vì ( ) 22 10,1;3aabbxx ++++ Khi đó ta có ( ) ( ) ( ) ( ) ( ) 1 1,1;3 xfx xfxmxmx x + + Xét hàm số ( ) ( ) ( ) 2 1 xfx hx x + = ta có ( ) 2 11 gx xx =+ và ( )fx là hai hàm số dương cùng nghịch biến trên ( )1;3 nên hàm số ( ) ( ) ( ) 2 1 xfx hx x + = nghịch biến với mọi ( )1;3 x Từ bảng ta có: ( ) ( ) ( ) 1 ,1;32 xfx mxm x + .
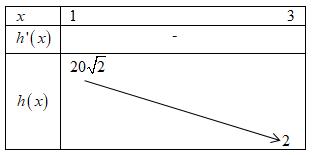
Mà m nguyên thuộc 10;10 nên 10,9,...,2 m−− . Vậy có 13 giá trị nguyên của m .
Chuyên luyện thi: Tuyển sinh vào lớp 10
Nghiệp THPT BDKT Toán 10; 11; 12
và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 149
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Tốt
Sưu tầm
Có
trị
thuộc
của m để bất
( ) ( ) ( ) ( ) ( ) 22
xfxxfxmxmxx +++++ nghi
ọi
x
++++−++++−




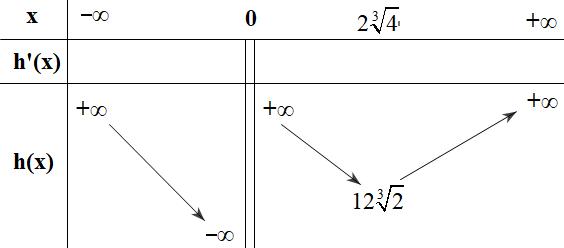
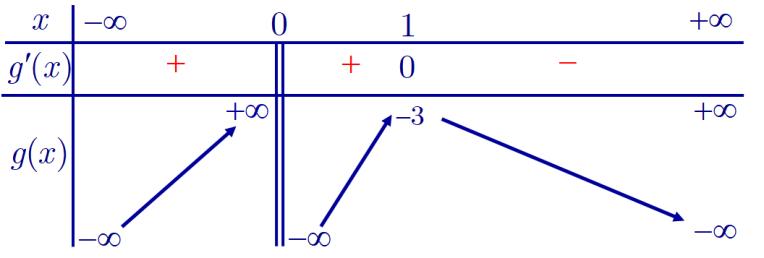
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 55 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12 BÀI 2: CỰC TRỊ CỦA HÀM SỐ VD VDC 01 HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: (MĐ 101-2022) Có bao nhiêu giá trị nguyên dương của tham số m để hàm số 42264 yxmxx =−+ có đúng ba điểm cực trị? A. 5 B. 6 C. 12 D. 11 Lời giải Chọn C Xét hàm số ( ) 42264 xmxx fx −+ = ( ) 3 464 4 f x x mx −+ = Ta có ( ) 0 fx = 3 0 4 464xmx−+= 2 16 mx x =+ Đặt ( ) ( ) ( ) 2 2 1616 202gxxgxxgxx xx =+=−== Bảng biên thiên Xét phương trình ( ) 42 3 0 2640 2640 0 f x xmxx x x mx = −+= −+= = Suy ra 32132 2640 2 xmxmx x −+==+ . Đặt ( ) ( ) ( ) 2 3 2 3 2 04 1322 2 hh x x xgxxxx x ==−= + = Bảng biên thiên CHƯƠNG I ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Nhận xét: Số cực trị hàm số ( )yfx = bằng số cực trị hàm số ( )yfx = và số nghiệm bội lẻ của phương trình ( ) 0 fx = Do đó yêu cầu bài toán suy ra hàm số ( )yfx = có 1 cực trị và phương trình ( ) 0 fx = có 2 nghiệm bội lẻ 3
12 12 122 m m m
. Vì tham số m nguyên dương nên 1;2;3;4;5;6;7;8;9;10;11;12 m Vậy có 12 giá trị nguyên dương của tham số m thoả mãn. Câu 2: (MĐ 102 2022) Có bao nhiêu giá trị nguyên âm của tham số a để hàm số 42 2 8x a yxx + =+ có đúng ba điểm cực trị? A. 2 B. 6 C. 5 D. 3 Lời giải Chọn D Xét hàm số ( ) ( ) 42 3 4 48 2 8 f xaxxx x fx ax ++ + = + = Ta có ( ) 0 fx = 3 0 4 8 4a xx + += 2 2 ax x =−− Đặt ( ) ( ) ( ) 2 2 22 201gxxgxxgxx xx =−−=−+== Bảng biến thiên Xét phương trình ( ) 42 3 020 0 8 280 x xxx xa fxa x
= += ++ + = = . Xét phương trình 3214 280 2 xaxax x ++==−− . Đặt ( ) ( ) ( ) 3 2 2 144 04 2 hx x x xhxhxx x =−=−+ == .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 56
B
Nhận xét: Số cực trị hàm số ( )yfx = bằng số cực trị hàm số ( )yfx = và số nghiệm bội lẻ của phương trình ( ) 0 fx = . Do đó yêu cầu bài toán suy ra hàm số ( )yfx = có 1 cực trị và phương trình ( ) 0 fx = có 2 nghiệm bội lẻ 3
− − −
3 3 32 a a a
Vì tham số a nguyên âm nên 1;2;3 a−−− . Vậy có 3 giá trị nguyên âm của tham số a thoả mãn. Câu 3: (MĐ103-2022) Có bao nhiêu giá trị nguyên âm của tham số a để hàm số 42 8 yxaxx =+− có đúng ba điểm cực trị? A. 5. B. 6. C. 11. D. 10. Lời giải
Chọn B
Xét hàm số ( ) 42 8 fxxaxx =+− ; ( ) 3 428fxxax =+− ( ) 3
0 0 80 x fx xax
= = +−=

Vì phương trình bậc ba luôn có tối thiểu 1 nghiệm nên để hàm số ( )yfx = có đúng ba điểm cực trị thì phương trình ( ) 0 fx = có 2 nghiệm phân biệt và ( ) 0 fx = có đúng 1 nghiệm bội lẻ. Đặt ( ) ( ) 32 83 gxxaxgxxa =+−=+ Để ( ) 0 gx = có 1 nghiệm duy nhất 0 ( )1 TH1: 2 30 xa+= vô nghiệm hoặc có nghiệm kép 0 a
=
a a x
TH2: 2 30 xa+= có hai nghiệm phân biệt 0 3
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 57
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
ảng biến thiên
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 58 Chuyên
ện thi:
ển sinh vào
ớp 10 Tốt
ệp
Quốc
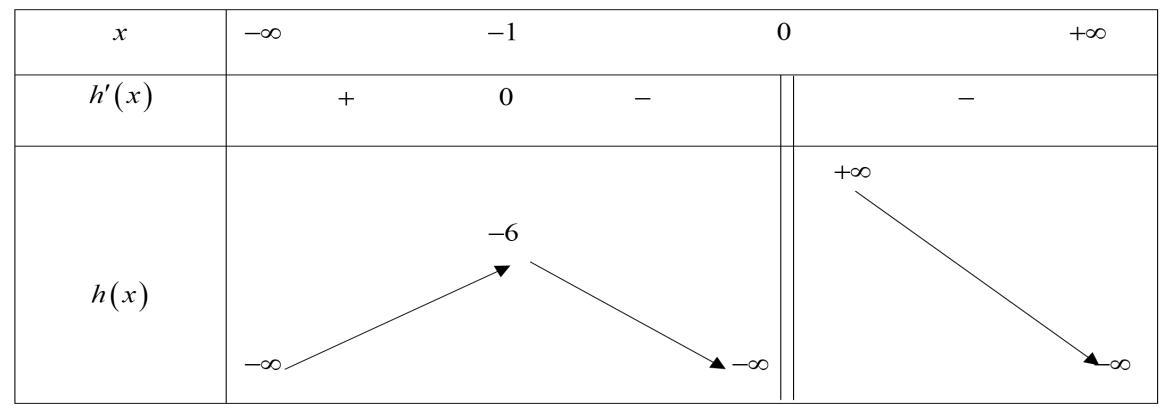
( ) 3 30806()13333 080316 3333 a aaa g a a asai aaa a a a g − −−+−− − −−−− − −− Suy ra 3 316 a − Để ( ) 0 fx = có đúng 1 nghiệm bội lẻ ( )2 TH1: 2 1220 xa+= vô nghiệm hoặc có nghiệm kép 0 a TH2: 2 1220 xa+= có hai nghiệm phân biệt 0 6 a a x = ( ) 6042806()26666 042806 6666 a aaa f a a asai aaa a a a f − −−+−− − − −−−− −− Suy ra 6 a − Vậy 6 a − thỏa ycbt với 6;5;4;3;2;1 aa−−−−−− . Cách 2: 42 8 yxaxx =+− ( )( ) ( )( ) 42333 4242 84282824 88 xaxxxaxxxaxxax y xaxxxaxx +−+−+−+− == +−+− Để hàm số 42 8 yxaxx =+− có đúng ba điểm cực trị phương trình 0 y = có đúng 3 nghiệm bội lẻ. Vì 0 x = không là nghiệm của các phương trình 3 80 xax+−= và 3 240 xax+−= Khi 0 x Ta có ( ) 3 3 8 80 x xaxagx x +−=== ( ) 3 3 2 82 04 x gxx x ===−
0984164935
luy
Tuy
l
Nghi
THPT
Gia BDKT 10; 11 môn Toán

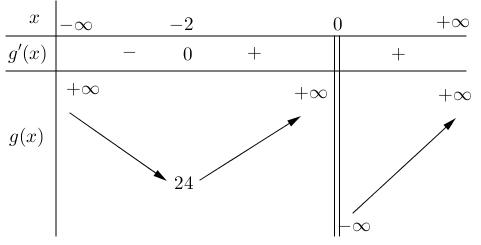
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 59 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12 Ta có ( ) 3 3 42 240 x xaxahx x +−=== ( ) 3 2 44 01 x hxx x ===− Yêu cầu bài toán 6 a − với 6;5;4;3;2;1 aa−−−−−− . Câu 4: (MĐ 104 2022) Có bao nhiêu giá trị nguyên dương của tham số m để hàm số 42 64 =−− yxmxx có đúng ba điểm cực trị? A. 23 B. 12 C. 24 D. 11 Lời giải Chọn C Xét ( ) 42 64 =−− fxxmxx . Ta có ( ) 32 32 426402 =−−==− fxxmxmx x Đặt ( ) ( ) ( ) 2 2 3232 2402 =−=+==− gxxgxxgxx xx
Xét phương trình ( ) 42 3
0 0640 640 = =−−= −−= x fxxmxx xmx

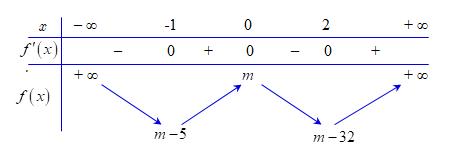
Xét 32 64 640 −−==−xmxmx x Đặt ( ) ( ) ( ) 2 3 2 6464 2032 =−=+==− hxxhxxhxx xx
m m mh . Vì m nguyên dương nên có 24 giá trị thỏa yêu cầu bài toán. Câu 5: (Tham khảo 2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số có điểm cực trị? 4323412 yxxxm =−−+ 7 3 5 6 4 ( ) 4323412 yfxxxxm ==−−+ ( ) 32 121224 fxxxx =−− ( ) 00fxx == 1 x =− 2 x =
24 24 3230,23 − A. B. C. D. Lời giải. Chọn D Ta có: .; hoặc hoặc .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 60
Ta có số điểm cực trị của hàm số ( ) = yfx bằng tổng số điểm cực trị của hàm số ( ) = yfx và số nghiệm bội lẻ của phương trình ( ) 0 = fx Suy ra yêu cầu bài toán trở thành hàm số ( ) = yfx có 1 điểm cực trị và phương trình ( ) 0 = fx có 2 nghiệm bội lẻ ( ) 3
Do hàm số có ba điểm cực trị nên hàm số có điểm cực trị khi
. Vậy có giá trị nguyên thỏa đề bài là .
Câu 6: (Mã 101, Năm 2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số
đạt cực tiểu tại ?
A. B. C.
D. Vô số Lời giải
Chọn C
Ta có .
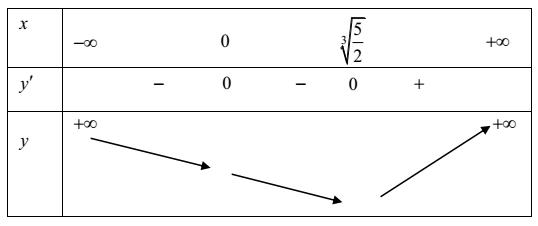
Xét hàm số có .
Ta thấy có một nghiệm nên có tối đa hai nghiệm
+ TH1: Nếu có nghiệm hoặc
Với thì là nghiệm bội của . Khi đó là nghiệm bội 7 của và đổi dấu từ âm sang dương khi đi qua điểm nên là điểm cực tiểu của hàm số. Vậy thỏa ycbt.
Với thì .
Bảng biến thiên
Dựa vào BBT không là điểm cực tiểu của hàm số. Vậy không thỏa ycbt.
+ TH2: . Để hàm số đạt cực tiểu tại
Do nên . Vậy cả hai trường hợp ta được 4 giá trị nguyên của thỏa ycbt. Câu 7: (Mã 102, Năm 2018) Có bao nhiêu giá trị nguyên của tham số để hàm số đạt cực tiểu tại
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 61
( )
( )
= 7 0
− 4 1;2;3;4
==== (
241yxmxmx =+−−−+ 0 x = 3 5 4 ( ) ( ) 8524241yxmxmx =+−−−+ ( ) ( ) 7423 85244 yxmxmx =+−−− 0 y = ( ) ( ) ( ) 342 852440xxmxm +−−−= ( ) ( ) ( ) 42 0 852440 x gxxmxm = =+−−−= ( ) ( ) ( ) 42 85244gxxmxm=+−−− ( ) ( ) 3 3252gxxm =+− ( ) 0 gx = ( ) 0 gx = ( ) 0 gx = 0 x = 2 m = 2 m =− 2 m = 0 x = 4 ( )gx 0 x = y y 0 x = 0 x = 2 m = 2 m =− ( ) 4 3 0 82005 2 x gxxx x = =−= = 0 x = 2 m =− ( ) 00 g 2 m 0 x = ( ) 00 g 2 4022mm −− m 1;0;1 m− m m 8524(1)(1)1yxmxmx =+−−−+ 0? x = 3 2 1
A. B. C. Vô số D.
fx
yfx
05 50 m m m
mmmm
) ( ) 8524
L
Chọn B
Ta có:
*Nếu thì , suy ra hàm số đạt cực tiểu tại
*Nếu thì , nhưng là nghiệm bội chẵn nên không phải cực trị
*Nếu : khi đó là nghiệmbội lẻ. Xét . Để là điểm cực tiểu thì . Vì nguyên nên chỉ có giá trị
Vậy chỉ có hai tham số nguyên để hàm số đạt cực tiểu tại là và . Câu 8: (Mã 103, Năm 2018) Có bao nhiêu giá trị nguyên của tham số để hàm số đạt cực tiểu tại A. B. Vô số C. D. Lời giải Chọn A
Ta có
Với
● Trường hợp :
Với . Suy ra là điểm cực tiểu của hàm số.
Với . Suy ra không là điểm cực trị của hàm số.
● Trường hợp :
Để hàm số đạt cực tiểu tại thì qua giá trị dấu của phải chuyển từ âm sang dương do đó
Kết hợp hai trường hợp ta được Do .
Vậy có giá trị nguyên của tham
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 62
ời giải
A. B. C. D.
7423 '85(1)4(1)1 yxmxmx =+−−−+
0 x = 1 m 0 x = ( ) ( ) 42 ()85141 gxxmxm=+−−− 0 x = 2 0 lim()4(1)0 x gxm → =−− 2 1011mm −− m 0 m = m 0 x = 0 m = 1 m = m ( ) ( ) 85244161yxmxmx =+−−−+ 0 x = 8 7 9 ( ) ( ) 7423'855416 yxmxmx =+−−− ( ) ( ) 342 854416xxmxm =+−−− ( ) 3 . xgx = ( ) ( ) ( ) 42 855416gxxmxm=+−−− 1 ( ) 004gm== 7 4'8 myx == 0 x = ( ) 43 4'85myxx=−=− 0 x = 2 ( ) 004gm 0 x = 0 x = ' y ( ) 0044gm− 44 m − 3;2;1;0;1;2;3;4 mm−−− 8 m m ( ) ( ) 8524391yxmxmx =+−−−+ 0 x = 4 7 6
số thỏa mãn. Câu 9: (Mã 104, Năm 2018) Có bao nhiêu giá trị nguyên của tham số để hàm số đạt cực tiểu tại ?
Vô số
( ) ( ) ( ) 342 85141xxmxm =+−−− ( ) ( ) 42 0 '0 851410(1) x y xmxm = = +−−−= 1 m = 7 '8 yx = 0 x = 1 m =− 4 0 '0 8100 x y xx = = −= 3 0 5 4 x x =
=
Chọn C Ta có
Xét hàm số có .
Ta thấy có một nghiệm nên có tối đa hai nghiệm
+) TH1: Nếu có nghiệm hoặc
Với thì là nghiệm bội của . Khi đó là nghiệm bội 7 của và đổi dấu từ âm sang dương khi đi qua điểm nên là điểm cực tiểu của hàm số. Vậy thỏa ycbt.
Với thì .
Bảng biến thiên
Dựa vào BBT không là điểm cực tiểu của hàm số. Vậy không thỏa ycbt.
+) TH2: . Để hàm số đạt cực tiểu tại
Do nên .
Vậy cả hai trường hợp ta được giá trị nguyên của thỏa ycbt.
Câu 10: (Mã 102, Năm 2019) Cho hàm số , bảng biến thiên của hàm số như sau: Số điểm cực trị của hàm s
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 63
ờ
L
i giải
ố là A.
( ) ( )
(
=+−−− 0 y = ( ) ( ) ( )
xxmxm +−−−= ( ) (
0
x
= =+−−−= ( )
) ( ) 42 85349gxxmxm=+−−− ( ) ( ) 3 3253gxxm =+− ( ) 0 gx = ( ) 0 gx = ( ) 0 gx = 0 x = 3 m = 3 m =− 3 m = 0 x = 4 ( )gx 0 x = y y 0 x = 0 x = 3 m = 3 m =− ( ) 4 3 0 830015 4 x gxxx x = =−= = 0 x = 3 m =− ( ) 00 g 3 m 0 x = ( ) 00 g 2 9033mm −− m 2;1;0;1;2 m−− 6 m ( )fx ( ) ' fx +∞ +∞ 1 3 ∞ ∞ + 1 1 f'(x) x 0 2 ( ) 2 2 yfxx =+ 3 9 5 7
. B. . C. . D. .
8524391yxmxmx =+−−−+
) ( ) 7423 85349 yxmxmx
342 853490
) ( ) 42
853490
gxxmxm
(
Lời giải
Chọn D Xét hàm số trên . Ta có Dựa vào bảng biến thiên của hàm ta được , trong đó . Do nên .
Khi đó phương trình vô nghiệm. Các phương trình mỗi phương trình đều có 2 nghiệm phân biệt và khác nhau, cùng khác . Suy ra phương trình có 7 nghiệm đơn. Vậy hàm số có 7 điểm cực trị
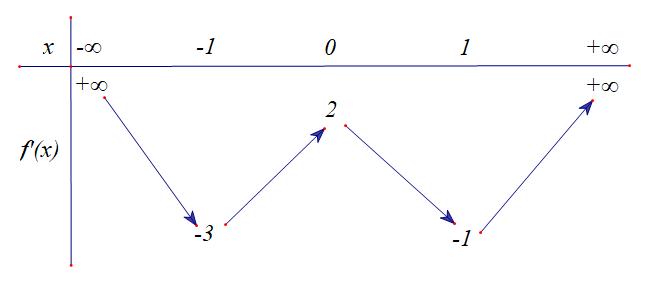
Câu 11: (Mã 103, Năm 2019) Cho hàm số , bảng biến thiên của hàm số như sau:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 64
Số điểm cực trị của hàm số là A. . B. . C. . D. . Lời giải Chọn C ( ) 2 2 yfxx =+ ( ) ( ) 2 '22'2 yxfxx =++ ( ) ' fx ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 2 2 2 2 2 1 1 111 2 '02112 2 113 2 114 x x xa xxa yxxbxb xxc xc xxd xd =− =− +=+ += =+=+=+ += +=+ += +=+ 101 abcd − 101 abcd − 10 10 10 10 a b c d + + + + ( )1 ( ) ( ) ( )2,3,4 1 '0y = ( ) 2 2 yfxx =+ ( )fx ( )fx ( ) 2 44 yfxx =− 9 5 7 3
Dựa vào bảng biến thiên ta có:
Ta có: , . Ta có khi và
Mặt khác: nên: vô nghiệm. có nghiệm phân biệt , . có nghiệm phân biệt , . có nghiệm phân biệt ,
Vậy phương trình có nghiệm bội lẻ phân biệt nên hàm số có điểm cực trị
Cách 2:
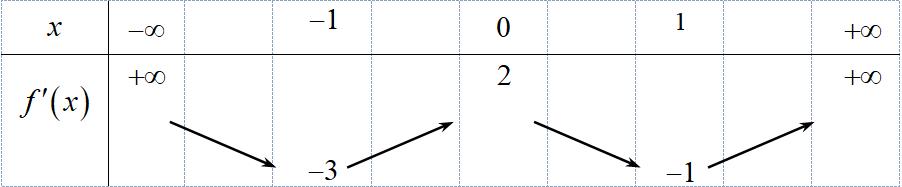
Gọi đại diện cho các tham số ta xét phương trình có ,
Vậy với mỗi giá trị thuộc khoảng đã cho phương trình có 6 nghiệm phân biệt.
Vậy phương trình có nghiệm bội lẻ phân biệt nên hàm số có điểm cực trị.
Câu 12: (Mã 104, Năm 2019) Cho hàm số , bảng biến thiên của hàm số như sau: Số điểm cực trị của hàm số
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 65
(
0;1 1; xa xb xc xd =−− =− = =+ ( ) ( ) 2 8444 yxfxx =−− 0 y = ( ) 2 840 440 x fxx −= −= ( ) ( ) ( ) ( ) 2 2 2 2 1 2 44;1 441;0 440;1 441; x xxa xxb xxc xxd = −=−− −=− −= −=+ 2 1 441 2 xxx=−=− ( ) 130 f −=− ( )2 2 442111 xxx−=−−− 2 44xxa −= 2 44xxb −= 2 1x 2x 2 44xxc −= 2 3x 4x 2 44xxd −= 2 5x 6x 0 y = 7 7 m 2 440 xxm−−= ( )'41 m =+ 01 m − ,, bcd ( ) 2 440fxx −= 0 y = 7 7 ( )fx ( )fx ( ) 2 44 yfxx =+ 5 9 7 3
là A. . B. . C. . D. . Lời giải ( ) 0 fx =
) ( ) ( ) ( ) ;1 1;0
Ta có . Dựa vào bảng biến thiên của nhận thấy .
Do đó . Lại có vô nghiệm vì ; ; ; . Vì do thuộc các khoảng khác nhau (như ) nên các nghiệm đều khác nhau và khác . Do đó có 7 nghiệm đơn phân biệt nên đổi dấu 7 lần suy ra hàm số có 7 điểm cực trị. Câu 13: (Đề tốt nghiệp 2020 Mã đề 101) Cho hàm số bậc bốn ( )fx có bảng biến thiên như sau:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 66
Chọn C
Số điểm cực trị của hàm số ( ) ( ) 2 4 1 gxxfx=+ là A. 11 B. 9 C. 7 D. 5 Lời giải Chọn B Ta chọn hàm ( ) 42 5103fxxx=−+ Đạo hàm ( ) ( ) 2 8444;0yxfxxy =++= ( ) ( ) 2 2 1 440440 8401 2 fxx fxx x x += += += =− ( )fx ( ) ( ) ( ) ( ) ( ) ;1 1;0 0 0;1 1; xa xb fx xc xd =−− =− = = =+ ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 2 2 44;1 441;0 440* 440;1 441; xxa xxb fxx xxc xxd +=−− +=− += += +=+ 2 44xxa += ( )2 2 442111, xxxx +=+−− 2 2 3 44 xx xxb xx = += = 4 2 5 44 xx xxc xx = += = 6 2 7 44 xx xxd xx = += = bcd ( )* 234567 ,,,,, xxxxxx 1 1 2 x =− 0 y = y
như sau:
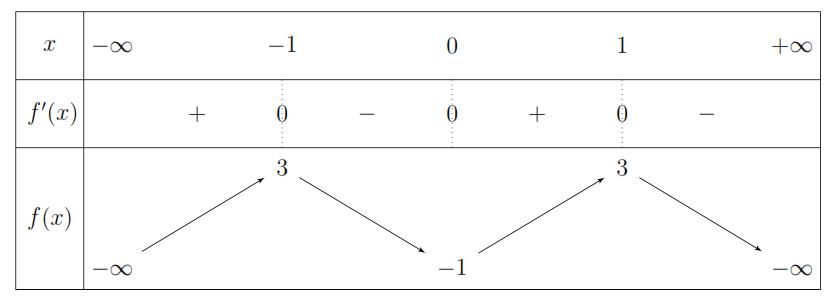
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 67 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 343 4121121211 gxxfxxfxfxxfxfxxfx =++++=++++ Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) 3 0 210 010 2110 2110 x xfx gxfx fxxfx fxxfx = += =+= +++= +++= . +) ( ) 10 fx += ( )* ( ) ( ) 4 5110130 xx+−++= 11,278 10,606 10,606 11,278 x x x x + + +− +− Phương trình có bốn nghiệ
− −
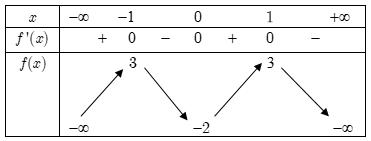
Số điểm cực trị của hàm số ( ) ( ) gxxfx=− 4 2 1 là A. 7 . B. 8 . C. 5 . D. 9 . Lời giải Chọn C Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 433 2 2.14112.1121 gxxfxxfxfxxfxfxxfx =−+−−=−−+− Vậy ( ) ( ) ( ) ( ) ( ) ( ) 0 0101 12102 x gxfx fxxfx = =−= −+−=
m phân biệt khác 0 +) ( ) ( ) ( ) ( )( ) 1 423 211025103120200 tx fxxfxttttt =+ +++=−++−−= 432 3020402060 tttt −−++= 1,199 0,731 0,218 1,045 t t t t
Phương trình có bốn nghiệm phân biệt khác 0 và khác các nghiệm của phương trình ( )* Vậy số điểm cực trị của hàm số ( )gx là 9. Câu 14: (Đề tốt nghiệpTHPT2020mãđê 102) Cho hàm số bậc bốn ( )fx có bảng biến thiên
Phương trình ( )1 có 4 nghiệm phân biệt
Phương trình ( )2 có ( ) ( ) ( ) ( ) ( ) 12121 fxxfxfxxfx −=−−=−+
Từ bảng biến thiên suy ra hàm ( )fx là bậc bốn trùng phương nên ta có ( ) fxxx=−+− 42 361 thay vào ( ) ( ) ( ) 21 fxxfx =−+ vô nghiệm
Vậy hàm ( )gx có 5 điểm cực trị
Câu 15: (Đề tốt nghiệpTHPT2020mãđề 103) Cho hàm số bậc bốn ()fx có bảng biên thiên như sau: Số điểm cực trị của hàm số 42 ()[(1)]gxxfx=− là A. 7. B. 5. C. 9. D. 11. Lời giải Chọn C Ta có : 422 ()483()16(1) fxxxfxxx =−+=− Ta có 3 ()2.(1).[2(1).(1)] gxxfxfxxfx =−−+− 3 0 ()0(1)0 2(1).(1)0
=

x gxfx fxxfx
Phương trình (1) có 0 x = (nghiệm bội ba). Phương trình (2) có cùng số nghiệm với phương trình ()0fx = nên (2) có 4 nghiệm đơn. Phương trình (3) có cùng số nghiệm với phương trình :
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ
O
HÀM SỐ
KHẢ
SÁT
Page 68
=−= −+−= (1) (2) (3)
++=−+++−= 432 2416321660 xxxx +−−+= có 4
ệm
ệ
Dễ thấy 9 nghiệm trên phân biệt nên
ố
=
ấ
ả
ự
trị
16: (Đề tốt nghiệp THPT 2020 mã đề
Số điểm cực trị của hàm số 4 2 ()(1)gxxfx=+ A. 7 B. 8 C. 9 D. 5
422 2()(1).()02(483)16(1)(1)0 fxxfxxxxxx
nghi
phân bi
t.
hàm s
()0gx
có t
t c
9 điểm c
c
Câu
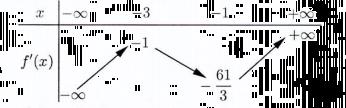
104) Cho hàm số bậc bốn ()fx có bảng biến thiên như sau
'()2(1)4(1).'(1)2(1).(1)2.'(1) gxxfxxfxfxxfxfxxfx =++++=++++ '()0gx = ta được
TH1: 0 x =
TH2:
xb fx xc
2 (1)0(2;1) (1;0) 0
=− =−− += =− = + TH3: (1)2.'(1)0 fxxfx+++= . Từ bảng biến thiên ta có hàm số thỏa mãn là 42 ()5102 fxxx=−+− ( ) (1)2.'(1)0(1)2(1).'(1)2'(1)0 fxxfxhxfxxfxfx +++==++++−+= Với 1 tx=+ ta có: 4233 ()51022(2020)2(2020)0 htttttttt =−+−+−+−−+= 432 4540504020 tttt −++−−= Lập bảng biến thiên ta suy ra có 4 nghiệm 4 t nghiệm x Vậy có 9 cực trị. Câu 17: (ĐTK 2020 2021) Cho ( )fx là hàm số bậc bốn thỏa mãn ( ) 00. f = Hàm số ( ) ' fx có bảng biến thiên như sau: Hàm số ( ) ( ) 3 3 gxfxx =− có bao nhiêu điểm cực trị? A. 3. B. 5. C. 4. D. 2. Lời giải
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo
ỳnh
ễn
Thuậ
Page 69
Lờ
ả
viên: Hu
Văn Ánh 42 Nguy
Cư Trinh
n Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12
i gi
i Chọn C
433 2
+
+
xa
xd
Ta có ()fx bậc ba có 2 điểm cực trị là 3,1xx nên ()(3)(1).fxaxx Suy ra 3 2 ()(23) 3 x fxaxxb Từ (3)1 f và 61 (1), 3 f giải ra 29 ,1 2 ab hay 3 2 29 ()(23)1. 23 x fxxx Do đó (0)10 f Đặt 3 ()()3 hxfxx thì 23 ()3()3hxxfx nên 3 2 1 ()0().hxfx x (*)
Trên (;0) thì ()0fx nên 3 ()0,0fxx , kéo theo (*) vô nghiệm trên (;0]. Xét 0 x thì ()fx đồng biến còn 2 1 x nghịch biến nên (*) có không quá 1 nghiệm. Lại có 3 2 0
1 lim(()) x fx x và 3 2 1 lim(()) x fx x nên (*) có đúng nghiệm 0. xc Xét bảng biến thiên của ()hx :
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ
ẢO SÁT HÀM SỐ
KH
Page 70
Vì (0)(0)0hf nên ()0hc và phương trình ()0hx có hai nghiệm thực phân biệt, khác .c Từ đó ()hx sẽ có 3 điểm cực trị. Câu 18: Cho hàm số ( ) ( ) 43212304 fxxxxmx =−++− với m là tham số thực. Có bao nhiêu giá trị nguyên m để hàm số ( ) ( ) gxfx = có đúng 7 điểm cực trị? A. 27. B. 31. C. 28. D. 30. Lời giải Xét hàm số ( ) ( ) 43212304 fxxxxmx =−++− .
Ta có ( ) 32 436604 fxxxxm =−++− . ( ) 32 0436604fxmxxx ==−++ Hàm số ( ) ( ) gxfx = có đúng 7 điểm cực trị Hàm số ( )fx có đúng 3 điểm cực trị dương Phương trình ( ) 0 fx = có 3 nghiệm dương phân biệt Phương trình 32 436604mxxx =−++ có 3 nghiệm dương phân biệt. (*)
Xét hàm số ( ) 32 436604hxxxx =−++
Ta có: ( ) 2 127260hxxx =−+ ; ( ) 1 0 5 x hx x
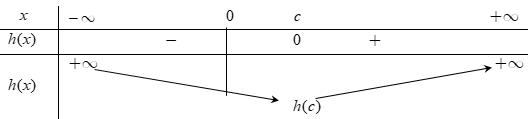
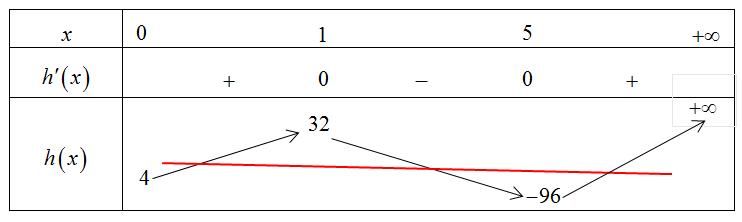
= = = .
Bảng biến thiên:
Dựa vào bảng biến thiên ta có ( ) *432 m .
Vì m nên 5;6;7;...;31 m .
Vậy có 27 giá trị m thỏa mãn yêu cầu bài toán.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 71
+ + =+++=+++ ++ . ( ) 0 gx
( ) 3 50fxxm ++= Đạo hàm không xác định tại 0 x = . Do đó điều kiện để ( )gx có ít nhất 3 điểm cực trị là phương trình ( ) 3 50fxxm ++= có ít nhất 2 nghiệm đơn hoặc bội lẻ khác 0. ( ) 3 50fxxm ++= Vậy
=
3 3 3 (
57 53 53
=−− fxxxx . Có bao nhiêu
++= ++= ++=− 6.36 .6 6 xxx fxxm xx
3 3 3 ++ =++ + . ( ) ( ) 3
+−=− +−=− ++=− Phương trình ( ) 3 50fxxm ++= có ít nhất 2 nghiệm bội lẻ khác 0 77mm −− x gx fxxm
có tất cả 6 giá trị nguyên m thỏa mãn. Câu 20: (MĐ 102 2020 2021 ĐỢT 1) Cho hàm số ( )yfx = có đạo hàm
) ( )( ) 2 89,
57 53 53 0 0 60
xxm xxm xxm = = ++=
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 72 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán Câu 19: (MĐ 101 2020-2021 ĐỢT 1) Cho hàm số ( )yfx = có đạo hàm ( ) ( )( ) 2 '79, fxxxx =−− . Có bao nhiêu giá trị
dương củ
số m để hàm số ( ) ( ) 3 5 gxfxxm =++ có í
nguyên
a tham
t nhất 3 điểm cực trị? A. 6 . B. 7 . C. 5. D. 4. Lời giải Ta có ( ) ( )( )( )733fxxxx =−−+ ( ) 7 03 3
x fxx x
= == =− . ( ) ( ) ( ) ( ) ( ) ( ) 2 3 2323 33
5 5 .355.355 55 xx xx gxxfxxmxfxxm xxxx
xxm xxm xxm giá trị nguyên dương của tham số m để hàm số ( ) ( ) 3 6 =++ gxfxxm có ít nhất 3 điểm cực trị? A. 5. B. 7. C. 8. D. 6 . Lời giải ( ) ( ) ( ) ( ) ( ) 333 66.6 gxfxxmgxxxmfxxm =++=++++ ( ) ( ) ( ) 32 3 3
Xét hàm số ( ) 3 6 hxxx =+ , vì ( ) 2 360, hxxx =+ nên ( )hx đồng biến trên . Ta có bảng biến thiên của hàm số ( ) ( ) 3 6 kxhxxx ==+ như sau: Hàm số ( ) ( ) 3 6 gxfxxm =++ có ít nhất 3 điểm cực trị khi phương trình ( ) 3 60fxxm ++= có ít nhất hai nghiệm khác 0. Điều này xảy ra khi và chỉ khi 80 m − hay 8 m Kết hợp điều kiện m nguyên dương, ta được 1;2;3...;7 m . Vậy có 7 giá trị của m thoả mãn.
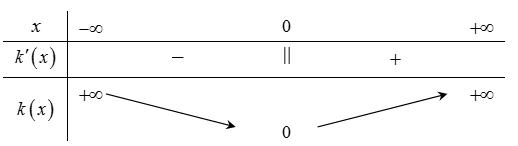
Câu 21: (MĐ 103 2020 2021 ĐỢT 1) Cho hàm số ( )yfx = có đạo hàm ( ) ( )( ) 2 1025, fxxxx =−− . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ( ) ( ) 3 8 gxfxxm =++ có ít nhất 3 điểm cực trị? A. 9 B. 25 C. 5 D. 10 Lời giải
Cách 1: Với mọi x ta có ( ) ( ) ( ) ( ) 3388 gxfxxmfxxmgx −=−−+=++= , do đó ( )gx là hàm số chẵn, suy ra đồ thị hàm số ( )ygx = nhận Oy làm trục đối xứng. Do đó số điểm cực trị của hàm số ( )gx bằng 21 a + với a là số điểm cực trị dương của hàm số ( ) ( ) 3 8 hxfxxm =++ Theo bài ra ta có 2131 aa+ , vì vậy ta cần tìm m để hàm số ( )hx có ít nhất một điểm cực trị dương.
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 73
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12 Ta có: ( ) 33 333 33 6868 606363 6363 xxmxxm fxxmxxmxxm xxmxxm ++=+=− ++=++=+=− ++=−+=−− .
(
( )( )( )1055fxxxx =−−+ ( ) 010,5fxxx === . ( ) ( ) ( ) 23 388 hxxfxxm =+++ , ( ) ( ) ( ) ( ) 3 3 3 8101 0852 853 xxm hxxxm xxm ++= =++= ++=− Đặt ( ) ( ) 328,380,0uxxxmuxxx =++=+ . Bảng
Ta có
)
biến thiên
Từ bảng biến thiên ta thấy (1), (2) và (3) nếu có nghiệm 0 x thì đó là nghiệm duy nhất. Phương trình ( ) 0 hx = có nghiệm 0 x khi và chỉ khi ít nhất một trong ba phương trình (1), (2) (3) có nghiệm 0 x , điều này tương đương với max5;5;1010 m −= Do m nguyên dương nên 1;2;,,,;9 m , vậy có 9 giá trị nguyên dương của tham số m cần tìm. Cách 2: Ta có: ( ) ( )( )

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 74
m là
ố
m . Vậ
9 giá trị
( ) (
(
2
.
( ) ( ) 3 7
=++
A. 16 B. 9 C. 4 D. 8 y=10
u + +∞ |
∞ u' x
2 10 0102505 5 = =−−== =− x fxxxx x Đặt ( ) 2 32 2 3800 88 3800 xkhix uxxmxxmu xkhix + =++=++= −− Bảng biến thiên của 3 8 =++ uxxm: Ta có ( ) ( ) .0yfuyufu === ( ) 0 fu = 10 5 5 u u u = = =− (1). Khi đó, để hàm số ( ) ( ) 3 8 =++ gxfxxm có ít nhất 3 điểm cực trị thì (1) có ít nhất hai nghiệm đơn hoặc bội lẻ khác 0 Suy ra 10 m . Mà
s
nguyên dương nên ta có: 1;2;...;9
y có
nguyên dương của tham số m cần tìm. Câu 22: (MĐ 104 2020 2021 ĐỢT 1) Cho hàm số ( )yfx = có đạo hàm
)
)
916, fxxxx
=−−
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số
gxfxxm
có ít nhất 3 điểm cực trị?
m
0
Có bao nhiêu giá

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 75
32 436603mxxx =−++ có
Đặ
( ) 32 436603
=−++
( ) 1 '0 5 x
x = = = . Bảng
ế
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12 Lời giải Ta có: ( ) ( ) ( ) ( ) 2 32 3 7 ''7..37 7 xx gxfxxmx xx + =+++ + Xét hệ pt: 3 3 3 74 74 79 0 xxm xxm xxm x +=−−
+=−
+=− = . Ta có BBT hàm số 3 7 yxx =+ Ycbt 901;2;...;8 m mm + − Câu 23: Cho hàm số 432 ()1230(3) fxxxxmx =−++− , với m là tham số thực.
trị nguyên của m để hàm số ( ) () gxfx = có đúng 7 điểm cực trị? A. 25 B. 27 C. 26 D. 28 Lời giải Ta có ( ) 32 '436603 fxxxxm =−++− Để hàm số ( ) () gxfx = có đúng 7 điểm cực trị thì hàm số 432 ()1230(3) fxxxxmx =−++− có đúng 3 cực trị dương. Hay ( ) 32 '04366030 fxxxxm =−++−= có 3 nghiệm dương phân biệt
3 nghiệm dương phân biệt.
t
hxxxx
( ) 2 '127260 hxxx =−+
hx
bi
n thiên
Từ BBT ta có 331 m và m nguyên nên có 27 giá trị nguyên thỏa mãn bài toán. Câu 24: (MĐ 103 2020 2021 ĐỢT 2) Cho hàm số ( ) ( ) 43210244 yfxxxxmx ==−++− . Có bao nhiêu giá trị nguyên của m để hàm số ( ) ( ) gxfx = có đúng 7điểm cực trị? A. 25 B. 22 C. 26 D. 21 Lời giải Hàm số ( ) ( ) gxfx = có đúng 7điểm cực trị khi và chỉ khi đồ thị hàm số ( )fx có 3 điểm cực trị có hoành độ dương Đồ thị hàm số ( )fx có 3 điểm cực trị có hoành độ dương khi và chỉ khi phương trình ( ) '0fx = có 3nghiệm dương phân biệt là nghiệm đơn. ( ) 3232 '04304840430484 fxxxxmxxxm =−++−=−++= Đặt ( ) 32 430484hxxxx =−++ Ta có ( ) 2 1 '1260480 4 x hxxx x
= =−+= = Suy ra để ( ) 0 fx = có 3nghiệm dương phân biệt khi 426 m
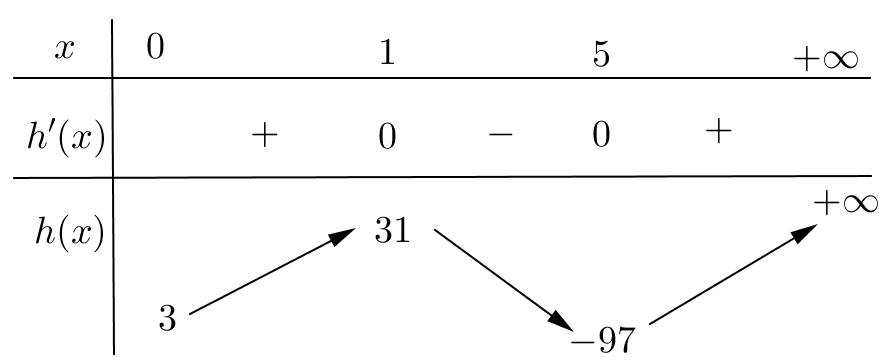
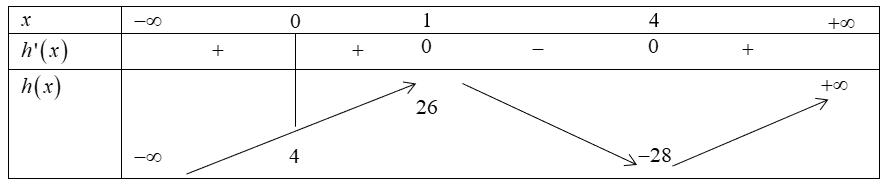
Vậy có 21 giá trị nguyên của m để hàm số ( ) ( ) gxfx = có đúng 7điểm cực trị Câu 25: (MĐ 104 2020 2021 ĐỢT 2) Cho hàm s
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán ố 432 ()1024(3) fxxxxmx =−++− , với m là tham số thực. Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) () gxfx = có đúng 7 điểm cực trị A. 21. B. 25. C. 24. D. 22. Lời giải Ta có 32 '()430483 fxxxxm =−++− Đồ thị hàm số ( ) () gxfx = gồm phần đồ thị hàm số ()yfx = bên phải trục tung và phần đối xứng của đồ thị hàm số ()fx bên phải trục tung sang bên trái qua trục tung. Do đó, hàm số
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 76
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
( ) () gxfx = có đúng 7 điểm cực trị khi và chỉ khi hàm số ()yfx = có đúng 3 điểm cực trị dương hay phương trình '()0fx = có ba nghiệm dương phân biệt Xét phương trình 32 32 '()04304830 430483 fxxxxm xxxm
= =−+= = Bảng biến thiên Từ BBT ta có phương trình '() fxm = có ba nghiệm dương phân biệt 325 m Vậy {4;5;...;24} m , có 21 số nguyên m thỏa mãn bài toán. DẠNG. BÀI TOÁN CỰC TRỊ HÀM SỐ CHỨA DẤU TRỊ TUYỆT ĐỐI Bài toán: Đồ thị hàm số () = yfx có bao nhiêu điểm cực trị (Áp dụng định nghĩa). 2 2 2().() ()() ()
=== fxfx yfxfxy fx ( ) ( ) 0()01 ()02 = = = fx y fx Sốnghiệm của ( )1 chính làsốgiaođiểm củađồ thị () = yfx và trụchoành 0 = y .Cònsố nghiệm của ( )2 là số cực trị của hàm số () = yfx , dựa vào đồ thị suy ra ( )2 . Vậy tổng số nghiệm bội lẻ của ( )1 và ( )2 chính là số cực trị cần tìm. Câu 26: Cho hàm số () = yfx có bảng biến thiên như sau. Hàm số ( ) 3 =−yfx có bao nhiêu điểm cực trị
=−++−= −++= Đặt 32 ()430483 hxxxx =−++ ta có 2 1 '()126048;'()0 4 x hxxxhx x A. 5 B. 6 C. 3 D. 1
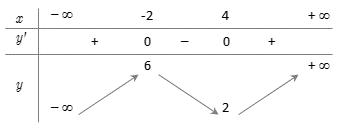
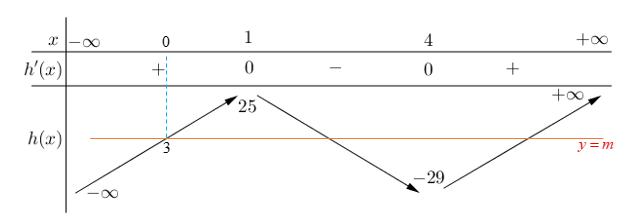
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 77
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12
nguyên c
tham
để
th
hàm s
2212yxmxmm có bảy điểm cực trị A. 1. B. 4. C. 0. D. 2. Lời giải Đồ thị hàm số 4222212yxmxmm có bảy điểm cực trị khi và chỉ khi đồ thị hàm số 4222212yxmxmm cắt trục hoành tại bốn điểm phân biệt 42222120xmxmm cóbốnnghiệmphânbiệt khivàchỉkhi

m m mm
mmm m mm 43 0 197197 44
2120 20 2120
22 2
197 3 4 m Vậy không có giá trị nguyên của tham số m để đồ thị hàm số 4222212yxmxmm có bảy điểm cực trị. Câu 28: Có bao nhiêu giá trị nguyên của tham số m để hàm số 43223412 yxxxm =−−+ có đúng 5 điểm cực trị? A. 5 B. 7 C. 6 D. 4
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 78 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán Lời giải Chọn C ( ) ( )31 =−yfx , Đặt |3|,0=−txt Thì (1) trở thành: ()(0)=yftt Có 2 2 3 (3)' (3) =−= x txt x Có () = xx ytft 33 0 0()02()7 ()041 == = ===−= = ==− x xx xx t ytfttLx ft tx Lấy x=8 có '(8)'(5)0 tf , đạo hàm đổi dấu qua các nghiệm đơn nên ta có bảng biến thiên: Dựa vào BBT thì
số ( ) 3 =−yfx có 3 cực trị
hàm
Câu 27: Tìm số các giá trị
ủa
số m
đồ
ị
ố 422
Lời giải Xét hàm số 4322()3412 fxxxxm =−−+ ; 32 ()121224 fxxxx =−− 123 ()00;1;2 fxxxx ===−= . Suy ra, hàm số ()yfx = có 3 điểm cực trị Hàm số 43223412 yxxxm =−−+ có 5 điểm cực trị khi đồthị hàm số ()yfx = cắt trục hoành tại 2 điểm phân biệt 4322 34120 xxxm−−+= có 2 nghiệm phân biệt. Phương trình 43224322 341203412 xxxmxxxm −−+=−++= (1). Xét hàm số 432g()3412 xxxx =−++ ; 32 g()121224 xxxx =−++ . Bảng biến thiên: Phương trình (1) cớ 2 nghiệm phân biệt 2 2
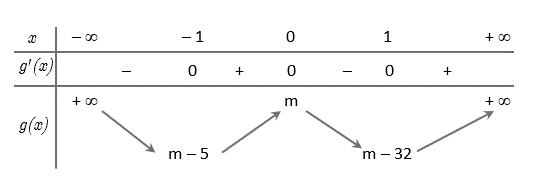
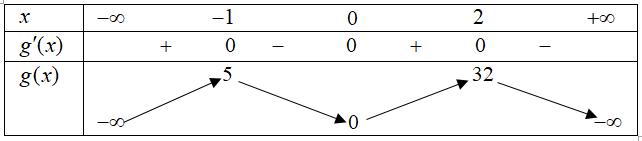
0 532 532 m m m Vậy 3;4;5;3;4;5 m−−− . Câu 29: Có bao nhiêu giá trị nguyên dương của tham số m để hàm số 4323412 yxxxm =−−+ có 5 điểm cực trị. A. 16 B. 44 C. 26 D. 27
Lời giải
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ
O
HÀM SỐ
Page 79
KHẢ
SÁT Chọn C Đặt: 432()3412 gxxxxm =−−+ Ta có: 32 232 '()121224015 0 xym gxxxxxym xym ==− =−−==−=− == Dựa vào bảng biến thiên, hàm số có ()ygx = có 5 điểm cực trị khi 0 0 50 532 320 m m m m m − − . Vì m là số nguyên dương cho nên có 26 số m thỏa đề bài Câu 30: Tập hợp các giá trị của m để hàm số 432 34121yxxxm =−−+− có 7 điểm cực trị là:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
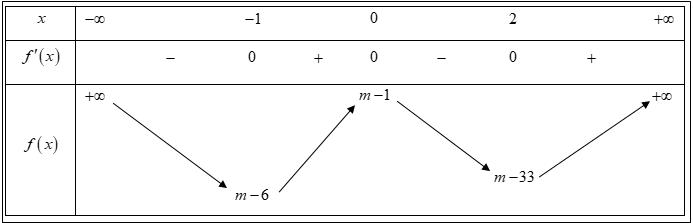
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 80 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT
11 môn Toán A. (0;6) B. (6;33) C.
Lời giải Chọn D Xét hàm số 432 ()34121 fxxxxm =−−+− , Có ( ) + = →+ x f x lim , ( ) + = →− x f x lim ( ) 322 ()121224122 fxxxxxxx =−−=−− 0 ()01 2 x fxx x =
=
A. 5 2 4 m B. 5 2 4 m − C. 5 2 4 m − D. 5 2 4
Lời giải Ta
( ) 2 '32212 yxmxm =−−+− Hàm số ()yfx = có 5 điểm cực trị khi chi khi hàm số ( )fx có hai cực trị dương. 0 0 0 S P ( ) ( ) ( ) 2 21320 221 0 3 2 0 3 mm m m −−− 2 450 1 2 2 mm m m −− 5 2 4 m Câu 32: Cho hàm số ( )yfx = có đạo hàm ( ) ( )( ) 32322 fxxxxx =−− với mọi x . Hàm số ( ) 12021 fx có nhiều nhất bao nhiêu điểm cực trị? A. 9 B. 2018 C. 2022 D. 11
10;
(1;33) D. (1;6)
==−
. Bảng biến thiên: Từ bảng biến thiên, ta có hàm số ()yfx = có 7 điểm cực trị đồ thị hàm số ()yfx = cắt Ox tại 4 điểm phân biệt 60116mmm −− Câu 31: Cho hàm số 32 ()(21)(2)2yfxxmxmx ==−−+−+ . Tìm tất cả các giá trị của tham số m để hàm số ()yfx = có 5 điểm cực trị
m
có:
Lời giải
Ta có ( ) ( )( ) 32220fxxxx =−−= có 4 nghiệm và đổi dấu 4 lần nên hàm số ( )yfx = có 4 cực trị. Suy ra ( ) 0 fx = có tối đa 5 nghiệm phân biệt. Do đó ( ) 12021 yfx =− có tối đa 9 cực trị.
Câu 33: Hình vẽ bên là đồ thị của hàm số ( )yfx =
Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số ( )1 yfxm =−+ có 5 điểm cực trị Tổng giá trị tất cả các phần tử của S bằng A. 9. B. 12. C. 18. D. 15. Lời giải Nhận xét: Số giao điểm của ( ) ( ) : Cyfx = với Ox bằng số giao điểm của ( ) ( ):1Cyfx =− với Ox .

Vì 0 m nên ( ) ( ):1 Cyfxm =−+ có được bằng cách tịnh tiến ( ) ( ):1Cyfx =− lên trên m đơn vị.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 81
TH1: 03 m . Đồ thị hàm số có 7 điểm cực trị. Loại.
TH2: 3 m = . Đồ thị hàm số có 5 điểm cực trị. Nhận.
TH3: 36 m . Đồ thị hàm số có 5 điểm cực trị. Nhận.
TH4: 6 m . Đồ thị hàm số có 3 điểm cực trị. Loại.
Vậy 36 m . Do * m nên 3;4;5 m .
Vậy tổng giá trị tất cả các phần tử của S bằng 12 Câu 34: Có bao nhiêu giá trị nguyên của tham số m để hàm số 4323412 2 m yxxx =+−+ có 7 điểm cực trị? A. 3 B. 9 C. 6 D. 4

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 82
Ta
432432 34123412 22 mm yxxxxxx =+−+=+−+ ( ) 32432 2 432 1212243412 2 3412 2 m xxxxxx y m xxx +−+−+ = +−+ ( ) ( ) 32 432 12122401 0 341202 2 xxx y m xxx +−= = +−+= . Từ ( ) 0 11 2 x x x = = =− . Vậy để hàm số có 7 điểm cực trị thì (2) phải có bốn nghiệm phân biệt khác 0;1;2 . Xét hàm số ( ) ( ) ( ) 43232 0 3412'121224'01 2 2 x m fxxxxfxxxxfxx x = =+−+=+−== =−
Lời giải
có 2
5
B. 3

C. 6
i gi
D. 4
Hàm s
yxxm
có 5 điểm c
th
hàm s
32 3 yxxm =−+ có hai điểm cực trị và nằm về hai phía của trục hoành phương trình ( ) 32301xxm−+= có ba nghiệm phân biệt. Xét bbt của hàm số 32 3 yxx =− 2 0 360 2 x yxx x
= =−= = Từ đó ta được ( )1 có ba nghiệm phân biệt 4004 mm −−
Vậy có 3 giá trị nguyên của m thỏa mãn. Câu 36: Có bao nhiêu giá trị nguyên của tham số m để hàm số 53 32560 yxxxm =−++ có 7 điểm cực trị? A. 42. B. 21. C. 40. D. 20. Lời giải
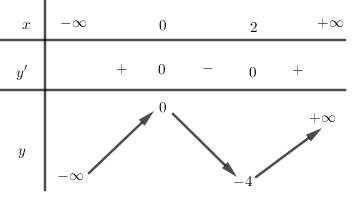
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 83 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12 Để (2) có 4 nghiệm phân biệt thì ( )fx cắt trục hoành tại 4 điểm phân biệt 50102010 0 0 2 m m m mm −+ Vậy có 9 giá trị nguyên của tham số m để hàm số 4323412 2 m yxxx =+−+ có 7 điểm cực trị. Câu 35: Có bao nhiêu giá trị nguyên của tham số m để hàm số 32 3 yxxm
ị
=−+ có 5 điểm cực tr
? A.
.
.
.
. Lờ
ải
ố 32 3
=−+
ực trị đồ
ị
ố
.
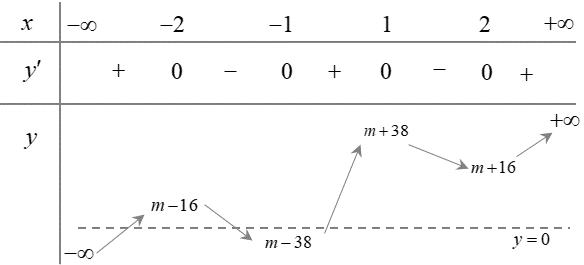

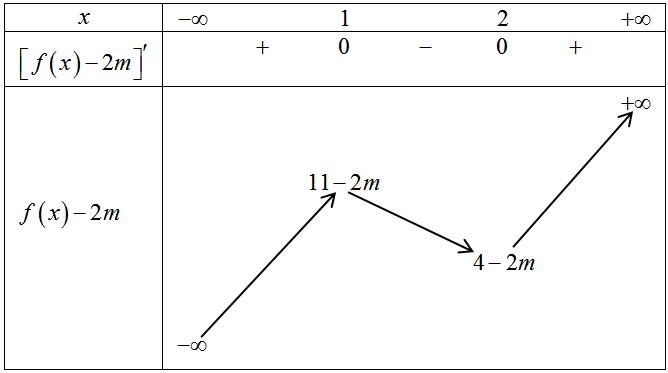
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 84 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán 53 42 2 2 32560 157560 216 1138 0 1 38 4 2 16 yxxxm yxx xym xxym y xym x xym =−++ =−+ =−=− ==−=− = ==+ = ==+ Suy ra 53 32560 yxxxm =−++ có 7 điểm cực trị 38016163817,37 160383816 37,17 mmmm mmm m −−= ++−− =−− Có tất cả 42 giá trị nguyên của .m Câu 37: Cho hàm số ( ) = yfx có bảng biến thiên như hình vẽ Đồ thị hàm số ( ) 2 =− yfxm có 5 điểm cực trị khi và chỉ khi A. ( )4;11 m B. 11 2; 2 m C. 3 = m D. 11 2; 2 m Lời giải Từ BBT của hàm số ( ) = yfx ta có bảng biến thiên của hàm số ( ) 2 =− yfxm như sau
Đồ thị hàm số ( ) 2 =− yfxm gồm hai phần:
+ Phần đồ thị của hàm số ( ) 2 =− yfxm nằm phía trên trục hoành.
+ Phần đối xứng với đồ thị của hàm số ( ) 2 =− yfxm nằm phía dưới trục hoành qua trục Ox
Do đó, đồ thị hàm số ( ) 2 =− yfxm có 5 điểm cực trị khi và chỉ khi ( )( ) 421120 mm −− 11 2; 2 m . Câu 38: Hình vẽ bên là đồ thị của hàm số ( )yfx = . Gọi S là tập hợp các giá trị nguyên dương của tham số m để đồ thị hàm số ( )2 yfxm =−+ có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng A. 15. B. 18. C. 9. D. 12. Lời giải
Cách 1: dùng đồ thị Nhận thấy: số giao điểm của ( ) ( ) : Cyfx = với Ox bằng số giao điểm của ( ) ( ) 1 :2Cyfx=− với Ox . Vì 0 m nên ( ) ( ) 2 :2 Cyfxm =−+ có được bằng cách tịnh tiến ( ) ( ) 1 :2Cyfx=− lên trên m đơn vị.

Đồ thị hàm số ( )2 yfxm =−+ có được bằng cách lấy đối xứng qua trục hoành Ox phần đồ thị ( ) 2C nằm phía dưới trục Ox và giữ nguyên phần phía trên trục Ox
Ta xét các trường hợp sau:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 85
+ Trường hợp 1: 03 m : đồ thị hàm số có 7 điểm cực trị (loại).
+ Trường hợp 2: 3 m = : đồ thị hàm số có 5 điểm cực trị (thỏa mãn).
+ Trường hợp 3: 36 m : đồ thị hàm số có 5 điểm cực trị (thỏa mãn).
+ Trường hợp 4: 6 m : đồ thị hàm số có 3 điểm cực trị (loại).
Vậy 36 m Do m + nên 3;4;5 m hay 3;4;5 S = .
Vậy tổng giá trị tất cả các phần tử của S bằng 12
* Cách 2: đạo hàm hàm số hợp.
Ta có: ( )2 yfxm =−+ ( ) 2 2 fxm =−+
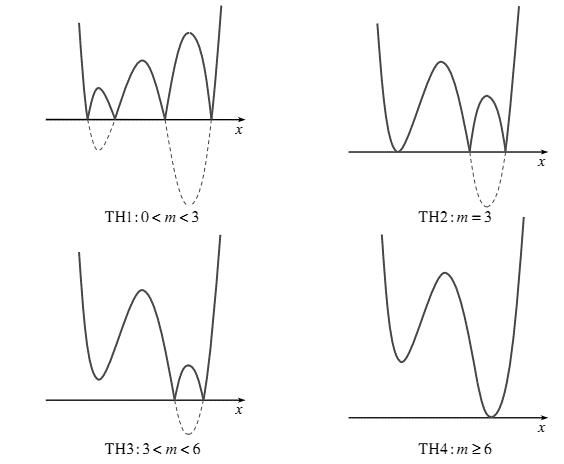
Xét ( ) 20 fx −= ( )1
−+− = −+
2.2 2 fxmfx y fxm
( ) ( ) ( ) ( ) 2
+ Do phương trình ( ) 0 fx = có 3 nghiệm phân biệt nên phương trình ( ) 20 fx −= cũng có 3 nghiệm phân biệt. - Xét ( ) 20fxm−+= ( )2 fxm−=− ( )2 + Nếu 63 m −−− 36 m thì phương trình ( )2 có 2 nghiệm phân biệt khác 3 nghiệm của ( )1 . + Nếu 3 m −=− 3 m = thì ( )2 có 3 nghiệm phân biệt (trong đó có 2 nghiệm đơn khác 3 nghiệm của ( )1 và 1 nghiệm kép trùng với 1 nghiệm của ( )1 ) Tóm lại : với 36 m thì hai phương trình ( )1 và ( )2 có tất cả 5 nghiệm bội lẻ phân biệt và y đổi dấu khi x đi qua các nghiệm đó, hay đồ thị hàm số ( )2 yfxm =−+ có 5 điểm cực trị. Lại do m + nên 3;4;5 m hay 3;4;5 S = Vậy tổng giá trị tất cả các phần tử của S bằng 12.
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 86
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Câu 39: Cho hàm số 32()3 fxxxm =−+ với 5;5 m− là tham số. Có bao nhiêu giá trị nguyên của m để hàm số ()fx có đúng ba điểm cực trị. A. 3. B. 0. C. 8. D. 6 . Lời giải Xét hàm số 32()3 gxxxm =−+ có 2 0 '()0360 2 x gxxx x


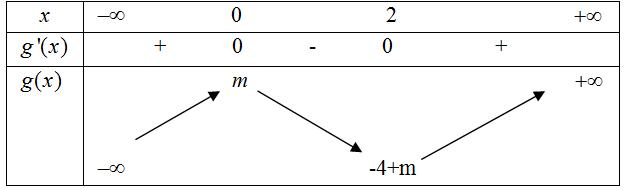
= =−= = . Bảng biến thiên Từ bảng biến thiên ta thấy để hàm số ()fx có đúng ba điểm cực trị thì đồ thị hàm số ()gx phải có đúng một giao điểm hoặc tiếp xúc với Ox Điều kiện này tương đương với 00 404 mm mm −+ . Kết hợp điều kiện 5;5 m− ta có 5;4;3;2;1;0;4;5 m−−−−− . Vậy có 8 giá trị thoả mãn. Câu 40: Cho hàm số ( )yfx = có bảng biến thiên như sau. Đồ thị hàm số ( ) 20172018 yfx=−+ có bao nhiêu điểm cực trị? A. 2 B. 3 C. 5 D. 4 Lời giải Có ( )2017 =−yfx bằng cách tịnh tiến sang bên phải 2017 đơn vị ta có bảng biến thiên của hàm số ( )2017 yfx=−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM
O
Ố
Page 87
ĐỂ KHẢ
SÁT HÀM S
Tịnh tiến đồ thị hàm số ( )2017 fx lên trên 2018 đơn vị và lấy trị tuyệt đối ta có bảng biến thiên của hàm số ( ) 20172018 yfx=−+
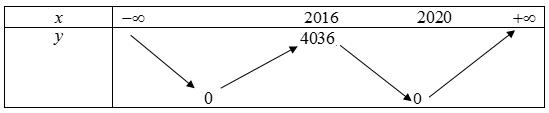
Từ bảng biến thiên, suy ra hàm số có 3 cực trị
Câu 41: Hàm số ( )fx có đạo hàm ( )fx trên . Hình vẽ bên là đồ thị của hàm số ( )fx trên .
Hỏi hàm số ( ) 2018 yfx=+ có bao nhiêu điểm cực trị? A. 5. B. 3. C. 2. D. 4. Lời giải
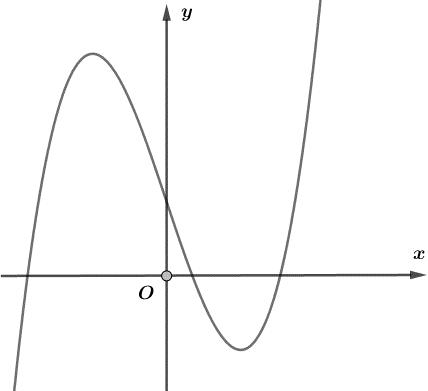
== Từ đồ thị hàm
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ
O
Ố
KHẢ
SÁT HÀM S
Page 88
số của ( )fx suy ra ( )fx cùng dấu với ( )( )( )123 xxxxxx với 1 0 x , 23 0 xx Suy ra: ( ) fx cùng dấu với ( )( )( ) 123 xxxxxx Do 1 0 xx− nên ( )( ) ( ) 22 2 x yfxxfx x == cùng dấu với ( )(
23 2 . x xxxx x Vậy
số (
trị.
ố
Cách 1: Từ đồ thị hàm số của ( )fx ta thấy ( )fx có hai cực trị dương nên hàm số ( ) yfx = lấy đối xứng phần đồ thị hàm số bên phải trục tung qua trục tung ta được bốn cực trị, cộng thêm giao điểm của đồ thị hàm số ( ) 2018 yfx=+ với trục tung nữa ta được tổng cộng là 5 cực trị. Cách 2: Ta có: ( ) ( ) 2 20182018yfxfx =+=+ . Đạo hàm: ( )( ) ( ) 22 2 . x yfxxfx x =
)
hàm
) 2018 yfx=+ có 5 cực
Câu 42: Cho hàm s
( )yfx
có bảng biến thiên như hình vẽ
Đồ thị hàm số ( ) 2 yfxm =− có 5 điểm cực trị khi và chỉ khi
A. ( )4;11 m B. 11 2; 2 m C. 3 m = D. 11 2; 2 m Lời giải Từ bảng biến thiên ta có đồ thị hàm số ( )yfx = có hai điểm cực trị. Để đồ thị hàm số ( ) 2 yfxm =− có 5 điểm cực trị thì đồ thị ( )yfx = cắt đường thẳng 2 ym = tại 523 −= điểm phân biệt 4211 m 11 2 2 m

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 89
DẠNG. SỐ ĐIỂM CỰC TRỊ CỦA HÀM HỢP
Bài toán: Cho hàm số ( )yfx = (Đề có thể cho bằng hàm, đồ thị, bảng biến thiên của ( ) ( ) ,' fxfx ). Tìm số điểm cực trị của hàm số ( )yfu = trong đó u là một hàm số đối với x
Ta thực hiện phương pháp tương tự xét số điểm cực trị của hàm số ( )yfx =
Bước 1. Tính đạo hàm ( ) ''.' yufu =
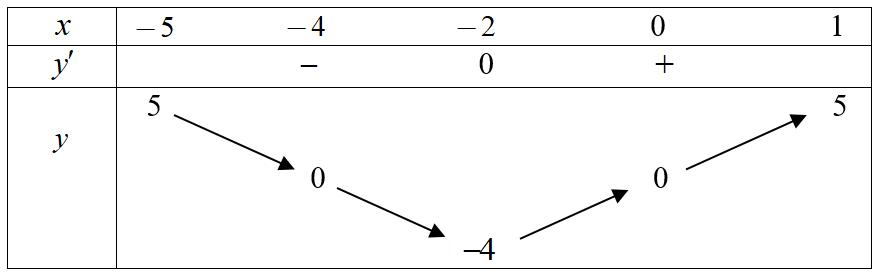
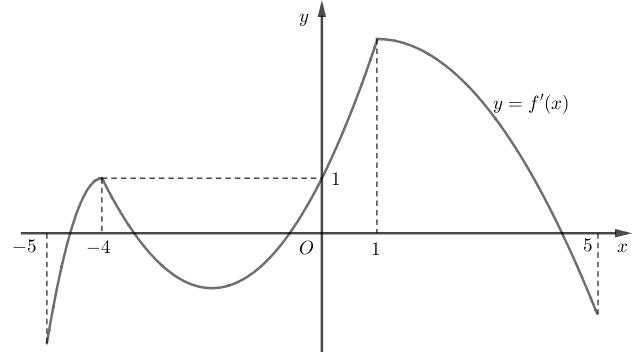
Bước 2. Giải phương trình ( ) '0 '0 '0 u y fu = = =
Bước 3.Tìm số nghiệm đơn và bội lẻ hoặc
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ
O
SỐ
KHẢ
SÁT HÀM
Page 90
( ) 2244 yfxxxx =+−− có bao nhiêu điểm cực trị thuộc khoảng ( )5;1 ? A. 5. B. 4. C. 6. D. 3. Lời giải Chọn A Đặt ( ) ( ) 2244 gxfxxxx =+−− ( ) ( ) ( ) ( ) ( ) ( ) 22 244242441 gxxfxxxxfxx =++−+=++− . Ta có ( ) ( ) 2 2 2 240 44(1) 0 40(2) 41;5(3) x xx gx xx xxa += +=− = += += . Xét phương trình ( ) 2 41;5xxa+= , ta có BBT của hàm số 2 4 yxx =+ trên ( )5;1 như sau:
các điểm mà ' y không xác định. Kết luận Câu 43: Cho hàm số ( )fx có đạo hàm liên tục trên . Đồ thị hàm số ( )yfx = như hình vẽ bên. Hàm số
Suy ra (1) có nghiệm kép 2 x =− , (2) có 2 nghiệm phân biệt 4;0xx=−= , (3) có 2 nghiệm phân biệt 12 ; xxxx == khác 2;0;4. Do đó phương trình ( ) 0 gx = có 5 nghiệm trong đó có 2 x =− là nghiệm bội ba, các nghiệm 4;0xx=−= ; 12 ; xxxx == là các nghiệm đơn. Vậy ( )gx có 5 điểm cực trị

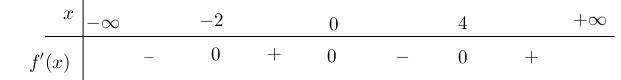
44: Cho hàm số ( )yfx = có đạo hàm đến cấp hai trên
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO
HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 91
− Bảng xét dấu ( )gx : Từ bảng xét dấu ( )gx ta suy ra hàm số đạt cực tiểu tại 3 x = . Câu 45: Cho hàm số ( ) = yfx xác định trên
có đồ thị ( )
Hàm số ( ) ( ) 3 =+ gxfxx đạt cực tiểu tại điểm 0x . Giá trị 0x thuộc khoảng nào sau đây O -1 3 2 y=f(x) x y
Câu
và có bảng xét dấu của hàm số ( ) ' yfx = như hình sau: Hỏi hàm số ( ) ( ) 3 2 123 3 x gxfxxx =−+−+ đạt cực tiểu tại điểm nào trong các điểm sau? A. 3 x = . B. 0 x = . C. 3 x =− . D. 1 x = . Lời giải Chọn A ( ) ( ) 2 143gxfxxx =−−+−+ . ( ) ( ) 12 1010 014 x fxfx x −−
−−− − 3 31 x x
,
fx như hình vẽ

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 92 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán A. ( )1;3 . B. ( )1;1 . C. ( )0;2 . D. ( ) 3;+ . Lời giải Chọn B Ta có ( ) ( ) ( ) ( ) ( ) 323 31 =+=++ gxfxxgxxfxx ( ) ( ) ( ) ( ) 3 233 3 00 03100 21 +== =++=+= = += xxx gxxfxxfxx x xx Do
(
( )
++++ gxxfxxfxxxxx
gxfxx đạt cực tiểu tại điểm 0 0 = x . Suy ra ( ) 0 1;1− x . Câu 46: Cho hàm số ( ) = yfx liên tục trên , có đồ thị ( ) fx như hình vẽ. Số điểm cực tiểu của hàm số ( ) ( ) 2 =−+ gxfxx là A. 1. B. 4. C. 3. D. 2. Lời giải Chọn A Ta có ( ) ( ) ( ) ( ) ( ) 22 21 =−+=−+−+ gxfxxgxxfxx . ( ) ( ) ( ) ( ) 22 2 2 1 2102 02100 0 2 = −+= =−+−+=−+= −+= −+= x x gxxfxxxx fxx xx 1 2 1 0 = = = x x x . Do đó ( ) ( ) ( ) ( ) ( ) 2 2 2 210 0 0210 210 0 −+ −+ −+−+ −+ −+ x fxx gxxfxx x fxx y=f'(x) O 2 x y
đó
) ( )
( ) 2333 031000201
Bảng biến thiên Vây hàm số ( ) ( ) 3 =+
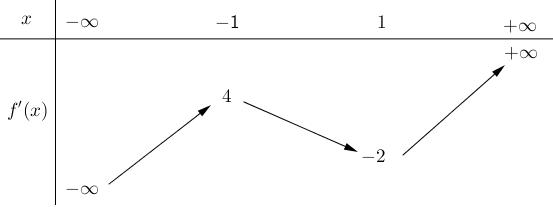
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 93 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12 2 2 2 11 22 210 001 1 112 22 0201 −+ −+ −+ x x xx x x x xx x x x x xx Bảng biến thiên x − 0 1 2 1 + ( ) gx + 0 0 + 0 ( )gx Vậy hàm số có 1 điểm cực tiểu. Câu 47: Cho hàm số ( )yfx = có đạo hàm liên tục trên , bảng biến thiên của hàm số ( ) ' fx như sau: Số điểm cực trị của hàm số ( ) 2 2 yfxx =+ là A. 4. B. 5. C. 1. D. 7. Lời giải Chọn B Ta có ( ) ( ) ( ) ( ) 2 2 1 '22'20 '201 x yxfxx fxx =− =++= += Từ BBT ta thấy phương trình ( ) ( ) ( ) ( ) ( ) 2 2 2 212 121;13 214 xxa xxb xxc +=− +=− += . Đồ thị hàm số 2 2 yxx =+ có dạng
Từ đồ thị hàm số 2 2 yxx =+ ta thấy phương trình (2) vô nghiệm; phương trình (3) ; phương trình (4) đều có 2 nghiệm phân biệt. Do đó '0y = có 5 nghiệm đơn phân biệt. Vậy hàm số ( ) 2 2 yfxx =+ có 5 điểm cực trị.
=
x xx xx xx
1 22 21 20
−=− −=− −=
x x x
1 0 2
= = = . Do 0 y = có một nghiệm bội lẻ ( 1 x = ) và hai nghiệm đơn ( 0 x = ; 2 x = ) nên hàm số ( ) 2 2 yfxx =− chỉ có ba điểm cực trị Câu 49: Cho hàm số yfx xác định trên và hàm số yfx có đồ thị như hình vẽ. Tìm số điểm cực trị của hàm số 2 3 yfx .
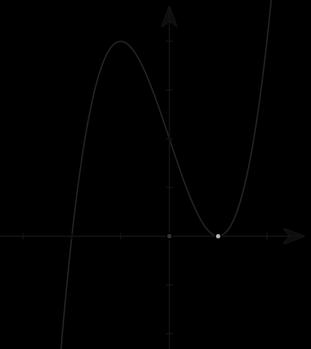

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 94
Câu 48: Cho hàm số ( )yfx = có đúng ba điểm cực trị là 2;1;0 và có đạo hàm liên tục trên . Khi đó hàm số ( ) 2 2 yfxx =− có bao nhiêu điểm cực trị? A. 3 B. 8 C. 10 D. 7 Lời giải Vì hàm số ( )yfx = có đúng ba điểm cực trị là 2;1;0 và có đạo hàm liên tục trên nên ( ) 0 fx = có ba nghiệm là 2;1;0 (ba nghiệm bội lẻ). Xét hàm số ( ) 2 2 yfxx =− có ( ) ( ) 2 22.2 yxfxx =−− ; ( ) ( ) 2 022.20yxfxx =−−= 2 2 2
A. 4 B. 2 C. 5 D. 3
Lời giải Chọn D Quan sát đồ thị ta có đổi dấu từ âm sang dương qua nên hàm số có một điểm cực trị là 2 x .
Ta có 2232.3yfxxfx 2 2
= = = 2 2

x
0 0 0 2 2 yfx 2
x x x x x yfx
0 0 0321 2 31
x x xx x x
= = = = = . Ta có bảng xét dấu: Từ đó suy ra hàm số ( ) 2yfx = có 3 điểm cực trị Câu 51: Cho hàm số bậc bốn ( )yfx = . Hàm số ( )yfx = có đồ thị như hình vẽ bên. Số điểm cực đại của hàm số ( ) 2 22yfxx=++ là
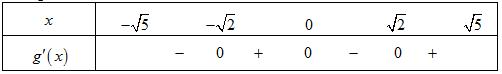
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG
O
Ố
ĐẠO HÀM ĐỂ KHẢ
SÁT HÀM S
Page 95
Mà 2 x là nghiệp kép, còn các nghiệm còn lại là nghiệm đơn nên hàm số 2 3 yfx có ba cực trị. Câu 50: Cho hàm số ( )fx có đạo hàm là ( )fx . Đồ thị của hàm số ( )yfx = như hình vẽ bên. Tính số điểm cực trị của hàm số ( ) 2yfx = trên khoảng ( )5;5 . A. 2 B. 4 C. 3 D. 5 Lời giải Xét hàm số ( ) ( ) ( ) ( ) 22 2 gxfxgxxfx == . ( ) ( ) 2
0 0 0 x gx fx



CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 96 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán A. 1. B. 2. C. 4. D. 3. Lời giải Từ đồ thị của ( )yfx = ta chọn ( ) ( )( )( )113fxxxx =+−− . Áp dụng công thức ( ) ( )yfuufu == với 2 22uxx=++ Ta có ( ) (
xx + =++=+++++−++− ++ (
xxxxxx xxxxxx ++++++− = ++++++++
=− ==−+ =−− Từ bảng biến thiên ta thấy hàm số có một điểm cực đại. Câu 52: Cho hàm số ( )yfx = xác định và liên tục trên có đồ thị như hình vẽ. Hàm số ( ) ( ) 2 24gxfxx=−− có bao nhiêu điểm cực tiểu? A. 1 B. 3 C. 2 D. 4 Lời giải Chọn B
)( )( ) 2222 2 1 22.221221223 22 x yfxxxxxxxx
)( )( ) ( ) ( )( ) 2 22 222 1221127 22221223
1 0122 122 x yx x
. Vì hàm số ( )yfx = đồng biến trên khoảng ( ) 0;+ do đó: ( ) 40 f
Suy ra: ( ) 20 g − . Theo tính chất qua nghiệm bội lẻ ( )gx đổi dấu, ta có bảng xét dấy ( )gx như sau: x − 15 13 1 13 + 15 + + ( )gx 0 + 0 0 + 0 0 +
Từ bảng xét dấu, suy ra hàm số ( )ygx = có 3 điểm cực tiểu.
Câu 53: Biết rằng hàm số ( )fx có đồ thị được cho như hình vẽ bên. Tìm số điểm cực trị của hàm số ( )yffx = .
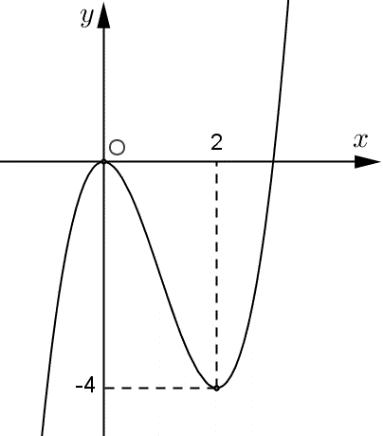
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 97 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12 Ta có: ( ) ( ) ( ) 2 2124gxxfxx =−−− ( ) ( ) ( ) ( ) 2 2 1 01240 240 x gxxfxx fxx = =−−−= −−= 2 2 1 113 24213 24015 15 x x x xxx xx x x = =+ = −−=−=− −−= =+ =−
−=−
(Tất cả đều là nghiệm bội lẻ). Ta chọn 2 x =− để xét dấu của ( )gx : ( ) ( ) ( )22.3.4gf
A. 5. B. 3. C. 4. D. 6. Lời giải Xét hàm số ( )yffx = , ( ) ( )yfxffx = ; ( ) ( ) ( ) ( ) ( ) ( ) 00 022 0 002; 2; xx fx xx y fxxa ffx fxxba == = == = ==+ = ==+ .
Với xb , ta có ( ) 2 fx ( ) 0 ffx
Với axb , ta có ( ) 02 fx ( ) 0 ffx
Với 0 xa hoặc 0 x , ta có ( ) 0 fx ( ) 0 ffx
BBT: Dựa vào BBT suy ra hàm số ( )yffx = có bốn điểm cực trị. Câu 54: Cho hàm số ( )yfx = liên tục và có đạo hàm trên 0;6 . Đồ thị của hàm số ( )yfx = trên đoạn 0;6 được cho bởi hình bên dưới. Hỏi hàm số ( ) 2 yfx = có tối đa bao nhiêu cực trị.
A. 3. B. 7. C. 6. D. 4. Lời giải Ta có ( ) ( ) 2 yfxfx = nên ( ) ( ) 0 0 0 fx y fx = = =

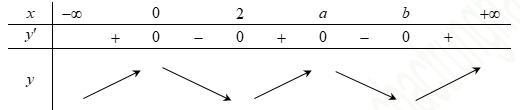
Từ đồ thị ta suy ra ( ) 0 fx = có tối đa 4 nghiệm, ( ) 0 fx = có tối đa 3 nghiệm. Do đó, hàm số ( ) 2 yfx = có tối đa 7 điểm cực trị nên có tối đa 7 cực trị.
Câu 55: Biết rằng hàm số ( )fx có đồ thị được cho như hình vẽ bên. Tìm số điểm cực trị của hàm số ( )yffx = ?
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 98
y -4
2 O x
x
y y=2 a -4
2 2 O b
= vì hàm số ( )fx có hai điểm cực trị 0;2xx== + ( ) ( ) ( ) ( ) 0 0 2 fx ffx fx = = = Quan sát đồ thị ta thấy phương trình ( ) 0 fx = có một nghiệm bội chẵn 0 x = và một nghiệm đơn hoặc bội lẻ 2 xa= Kẻ đường thẳng 2 y = nhận thấy phương trình ( ) 2 fx = có một nghiệm đơn hoặc bội lẻ xba = Do đó y có các điểm đổi dấu là 0;2,, xxxaxb ==== Vậy hàm số có 4 điểm cực trị. Câu 56: Cho hàm số ( )fx có đồ thị như hình vẽ bên dưới. Số điểm cực trị của hàm số ( ) ( ) ( ) gxffx = là.
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 99 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12 A. 5. B. 4. C. 3. D. 6. Lời giải Chọn B Ta có: ( ) ( ) ( ) ( ) ( ) '. yffxfxffx == ; ( ) ( ) ( ) 0 '0 0 fx y ffx = = = + ( ) 0 0 2 x fx x = =
A. 3. B. 7. C. 6. D. 5. Lời giải
Chọn C
Ta có ( ) ( ) ( ) ( ) ''.' gxfxffx = ( ) ( ) ( ) ( ) '0 '0 '0 fx gx ffx
= = = ( ) 0 '0 2 x fx x
= = = ( ) ( ) ( ) ( ) ( ) ( ) 0* '0 2** fx ffx fx = = =
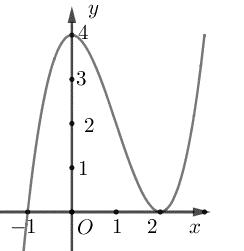
Dựa vào đồ thị suy ra: Phương trình (*) có hai nghiệm 1 2 x x
=− = . Phương trình ( **) có ba nghiệm ( ) ( ) ( )
=− = = ( ) '0gx = có nghiệm
Bảng biến thiên
xmn xnn xpp
10 01 2
=− = = = = =
x xm x xn x xp
1 0 2
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 100
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Nhìn bảng biến thiên ta thấy hàm số ( ) ( ) ( ) gxffx = có 6 cực trị
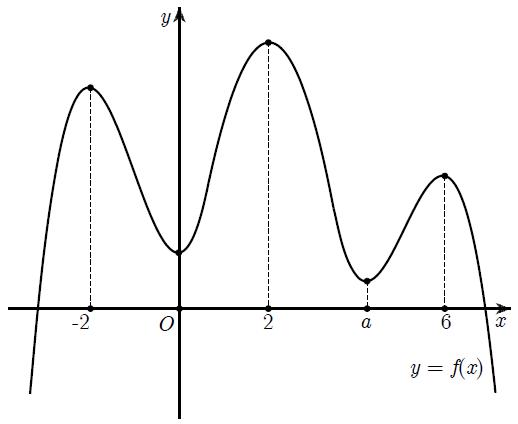
hàm
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 101
ọn B Từ đồ
ị
có 2; 0; 2; a ; 6 là tất cả các nghiệm của ( )fx . Ta có: ( ) ( ) ( ) ( ) 62562 3663 yfxxxxfxx =−=−− ( ) 5 62 660 '0 30 xx y fxx −= = −= 62 62 62 62 62 0,1 32 30 32 3 36 xx xx xx xx xxa xx == −=− −= −= −= −= 4 0,1 1 0,3 2 ,2 , xx x xx x xmm xnnm == = == = = = Ta có bảng biến thiên của hàm số ( ) 62 3 gxxx =−
Câu 57: Cho hàm số ( )yfx = có đồ thị như hình vẽ. Biết tất cả các điểm cực trị của
số ( )yfx = là 2; 0; 2; a ; 6 với 46 a . Số điểm cực trị của hàm số ( ) 62 3 yfxx =− là A. 8. B. 11. C. 9. D. 7. Lời giải Ch
th
ta
Dựa vào bảng biến thiên của hàm số ( ) 62 3 gxxx =− , ta suy ra 1 là nghiệm kép của phương trình 6232xx−=− và 0 là nghiệm kép của phương trình 6230xx−= . Do đó 1 và 0 là nghiệm kép của ( ) 62 3 fxx . Do vậy 1 và 0 là nghiệm bội ba của y . Các nghiệm khác 1 và 0 của y đều là nghiệm đơn. Vậy hàm số đã cho có 11 cực trị
x gxfxgxfxx x Bảng xét dấu của gx : Từ bảng xét dấu nhận thấy gx đạ + 0 2 0 -1 1 + x g'(x) 0 -∞ +∞
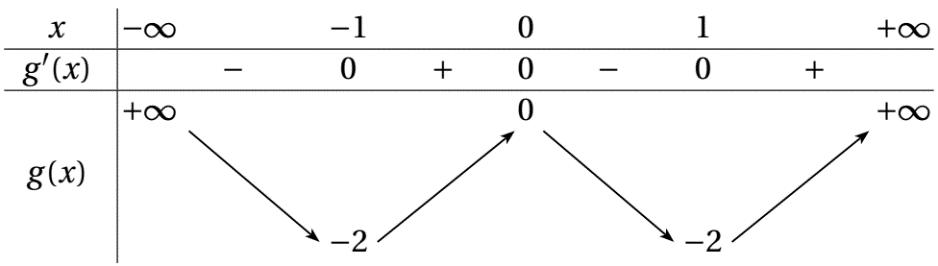

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 102
Câu 58: Cho hàm số (x) f xác định trên và có đồ thị ()fx như hình vẽ bên. Đặt ()() gxfxx . Hàm số đạt cực đại tại điểm thuộc khoảng nào dưới đây? A. 3 ;3 2 B. 2;0 C. 0;1 D. 1 ;2 2 Lời giải Ta có 1 1;011 2 t cực đại tại 12;0 x . Câu 59: Cho hàm số ( )yfx = có đạo hàm liên tục trên và đồ thị hàm số ( ) ' yfx = như hình vẽ bên. Số điểm cực trị của hàm số ( ) 201720182019yfxx =−−+ là. A. 3 B. 4 C. 1 D. 2 Lời giải Chọn C
Suy ra hàm số ( ) 201720182019yfxx =−−+ có 1 điểm cực trị.
Câu 60: Cho hàm số ( )yfx = có bảng biến thiên như sau
Hàm số ( ) 21yfx=+ đạt cực tiểu tại điểm A. 2 x = . B. 0 x = . C. 1 x = . D. 5 x = . Lời giải
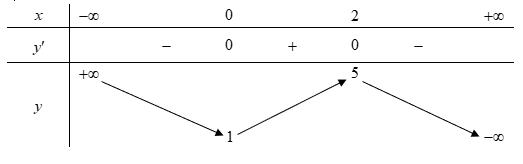

Ta có: ( ) 21yfx=+ ( ) 2 yfx = . Suy ra: Điểm cực tiểu của hàm số ( )yfx = cũng chính là điểm cực tiểu của hàm số ( ) 21yfx=+
Vậy: Hàm số ( ) 21yfx=+ đạt cực tiểu tại điểm 0 x = .
Câu 61: Cho hàm số ( )yfx = có đạo hàm liên tục trên . Đồ thị hàm số ( )yfx = như hình vẽ sau. Số điểm cực trị của hàm số ( ) 2 yfxx =+ là:
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 103
ệ
thi:
ển sinh vào
ớp 10 Tốt
ệp THPT Quốc Gia BDKT TOÁN 10; 11; 12 Ta có: ( ) ( ) ( ) 201720182019020172018020172018 fxxfxfx −−+=−−=−= Dựa vào đồ thị hàm số ( ) ' yfx = suy ra phương trình ( ) 20172018 fx −= có 1 nghiệm đơn
nhất.
Hòa
0984164935
Chuyên luy
n
Tuy
l
Nghi
duy



CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo
Page 104
=−
=−
viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán A. 4. B. 1. C. 3. D. 2. Lời giải Đặt ( ) ( ) 2 gxfxx =+ suy ra ( ) ( ) ( ) 0 1 0202 1 x gxfxfx xx
=+==−
. Dựa vào đồ thị ta có: Trên ( );1−− thì ( ) ( ) 220fxfx −+ . Trên ( ) 0 1;x thì ( ) ( ) 220fxfx −+ Trên ( ) 0; x + thì ( ) ( ) 220fxfx −+ . Vậy hàm số ( ) ( ) 2 gxfxx =+ có 1 cực trị. Câu 62: Cho hàm số ( )fx cóđồthị ( )fx nhưhình vẽdưới. Hàm số ( ) ( ) 3 2 252001 3 x gxfxxx =−+−+ có bao nhiêu điểm cực trị? A. 3 B. 1 C. 2 D. 0 Lời giải
Ch
Có ( ) ( ) 2 45gxfxxx =−+− ( ) ( ) 2 0 45 fx gx xx =− = +
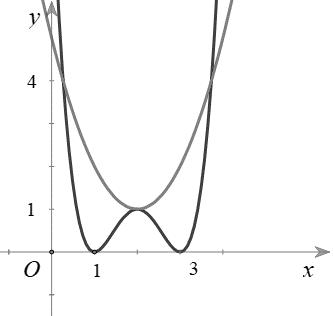
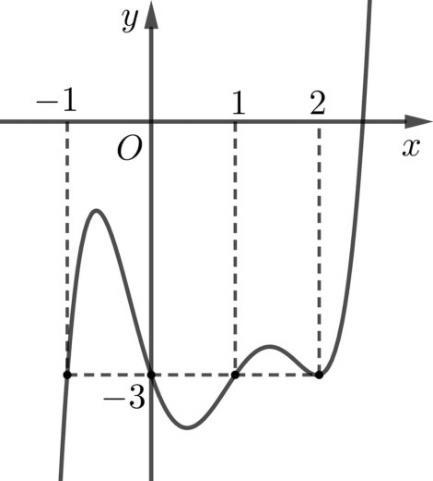
Ta có đồ thị hàm số 2 45yxx=−+ và đồ thị hàm ( )yfx = như hình vẽ dưới
Quan sát hình vẽ ta thấy ( ) 0 gx = có 3 nghiệm phân biệt trong đó chỉ có 1 nghiệm bội chẵn Vậy hàm số ( )gx có 2 điểm cực trị.
Câu 63: Cho hàm số đa thức ( )yfx = có đạo hàm trên , ( ) 00 f và đồ thị hình bên dưới là đồ thị của đạo hàm ( )fx . Hỏi hàm số ( ) ( ) 3 gxfxx =+ cóbao nhiêu cực trị?
đồ thị của hàm số ( )fx thì phương trình ( ) 3 fx =− có 4 nghiệm 1;0;1;2 Ta có bảng biết thiên
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 105
ọn C
ọ
=+
=+==−
A. 4. B. 5. C. 3. D. 6. Lời giải Ch
n B Đặt ( ) ( ) 3 hxfxx =+ ( ) ( ) 3 hxfx
( ) ( ) ( ) 0303hxfxfx
Theo
0 x h'(x) h(x)
1 1 +
+ +∞ +∞
2 0 f(0)
+ 0 0
0 x g(x)= h(x)
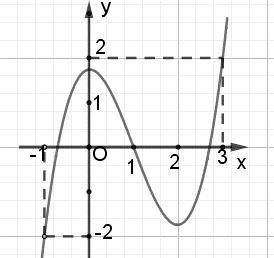
+ 0 ∞ ∞ x2 +∞ +∞ x 1 0 0 f(0)
Theo bảng biến thiên ta có phương trình ( ) 0 hx = có hai nghiệm 1 1; x − và 2 1 x (do có ( ) 00 f ) Khi đó ta có Vậy hàm số ( ) ( ) 3 gxfxx =+ có 5 cực trị Câu 64: Cho hàm số Cho hàm số ( )yfx = liên tục trên và hàm số ( ) ( ) 2 222019gxfxxx =−++ . Biết đồ thị hàm số ( )yfx = như hình vẽ Số điểm cực trị của hàm số ( ) x yg = là A. 5. B. 3. C. 2. D. 4. Lời giải Chọn A ( ) ( ) 222gxfxx =−+ , ( ) ( ) 01gxfxx ==− Đường thẳng 1 yx=− đi qua các điểm ( ) 1; 2 , ( )1;0 , ( )3;2
1 1 + ∞ ∞
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 106
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Quan sát vào vị trí tương đối của hai đồ thị trên hình vẽ, ta có BBT của hàm số ( )x yg = như sau Đồ thị hàm số ( ) x yg = nhận trục Oy làm trục đối xứng nên từ BBT trên ta suy ra BBT của hàm số ( ) x yg = như sau Vậy hàm số ( ) x yg = có 5 điểm cực trị.
Câu 65: Cho hàm số ()yfx = có đạo hàm trên và có đồ thị là đường cong như hình vẽ. Đặt ( ) ()3()4 gxffx=+ . Tìm số cực trị của hàm số ()gx A. 2. B. 8. C. 10. D. 6. Lời giải
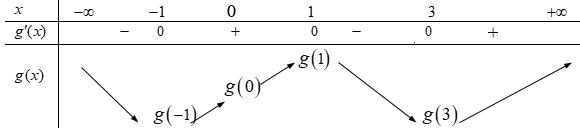
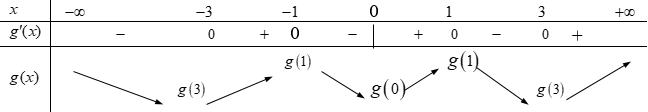
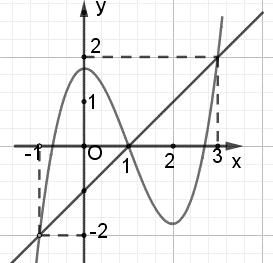
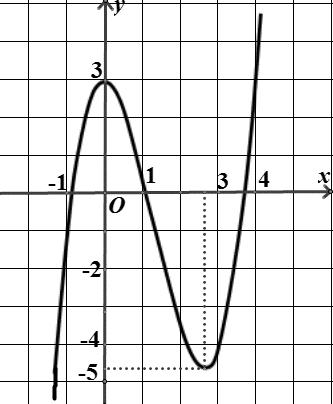
Chọn B
Ta có: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) '0 '3'.','03'.' '0 fx gxfxffxgxfxffx ffx
= == = . Từ đồ thị hàm số trên ta thấy:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 107
+ Phương trình ( ) '0fx = có 2 nghiệm phân biệt là 0; xx == với ( )1;3
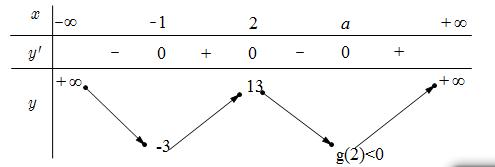
+ Phương trình ( ) ( ) ( ) ( ) 0 '0 fx ffx fx
= = = .

+ Phương trình ( ) 0 fx = có 3 nghiệm phân biệt khác 2 nghiệm trên.
+ Phương trình ( )fx = với ( )1;3 có 3 nghiệm phân biệt khác các nghiệm trên.
Vậy phương trình ( ) '0gx = có 8 nghiệm phân biệt và ( ) ' gx đổi dấu qua các nghiệm. Do đó hàm số ( )gx có 8 điểm cực trị Câu 66: Cho hàm số (x) yf = có đạo hàm trên , đồ thị hàm số ()yfx = là đường cong ở hình vẽ. Hỏi hàm số ( ) ( ) 2 ()41hxfxfx=−+ có bao nhiêu điểm cực trị?
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 108
( ) 2 ()41gxfxfx=−+ . Khi đó, ( ) ( ) ( ) ( )2 ()2 2().()401 0 2 xaa fx gxfxfxfxx fx x = = =−==− = = Do đó, ta có bảng biến thiên: Suy ra đồ thị hàm số ( )ygx = có ba điểm cực không nằm trên trục hoành và bốn giao điểm với Ox
A. 2 B. 3 C. 5 D. 7 Lời giải Chọn B Đặt ( )
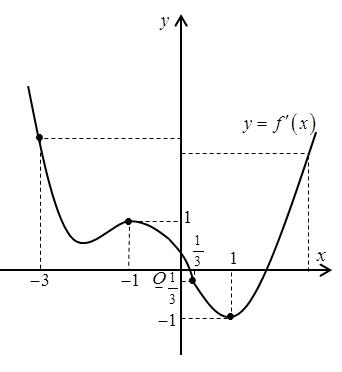
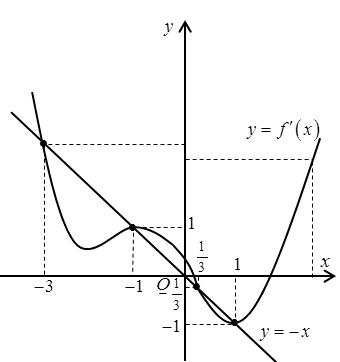
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 109 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12 Vậy đồ thị hàm số ( ) ( )yhxgx == có số cực trị là 347 += Câu 67: Cho hàm số ( )yfx = , hàm số ( )yfx = có đồ thị như
số 25sin1(5sin1) ()23 24 xx gxf =++ có bao nhiêu điểm cực trị trên
ảng
. A. 9 B. 7 C. 6 D. 8 Lời giải Chọn B Ta có: ( ) 5sin15 ()5coscos5sin1 22 x gxxfxx =+− . ( ) 5sin15 ()05coscos5sin10 22 x gxxfxx =+−=
hình bên. Hàm
kho
(0;2)
, ( Vì 02 x ).
==−
Suy phương trình ( ) 0 gx = có 9 nghiệm, trong đó có nghiệm 3 2 x = là nghiệm kép. Vậy hàm số ( )ygx = có 7 cực trị. Câu 68: Cho hàm số ( )yfx = liên tục trên có đạo hàm ( )fx liên tục trên và có bảng xét dấu như hình vẽ bên Hỏi hàm số ( ) 2 2 yfxx =− có tất cả bao nhiêu điểm cực trị? A. 4 B. 7 C. 9 D. 11 Lời giải Chọn C Tập xác định của hàm số: D = . * ( ) ( ) 2 2 yhxfxx ==−

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 110 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán cos0 5sin15sin1 22 x xx f = =− cos0 5sin1cos0 23cos0sin1 5sin16 5sin11 15sin12sin 25 5sin1121 5sin1sin 2333 5sin15sin123 1sin 25 x x x x x x x xx x x x x x x = = = =− =− −=− =−−=−=− −= = = −= = = 3 22 cos03 sin12 111 sinsin2sin 555 sin111 3sinsin33 sin333 5sinsin55 xx x x x xxarcxarc x xarcxarc x xarcxarc == = = =− =−=−−=+− = ==− =
Ta thấy phương trình ( ) 0 hx = có 8 nghiệm đơn ( )1 ( )hx không tồn tại tại 0 x = mà 0 x = thuộc tập xác định đồng thời qua đó ( )hx đổi dấu ( )2 . Từ ( )1 và ( )2 suy ra hàm số đã cho có 9 điểm cực trị Câu 69: Cho ( ) = yfx là hàm đa thức bậc 4 và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 12;12 để hàm số ( ) ( )21 =−+ gxfxm có 5 điểm cực trị? A. 13. B. 14. C. 15. D. 12. Lời giải Chọn C Đặt ( ) ( ) ( ) ( ) 21
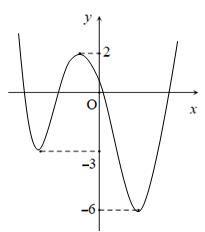
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 111 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12 ( ) ( ) ( ) 2 2..22. x yhxfxxx x ==−− ( ) 2 2 2 1 1 1 2 1 2 020 12 21 12 22 13 13 x x x x x x hxxx x xx x xx x x = =− = = =− =− =−= =+ −= =−−
−= =+ =−− .
m của ( ) = yhx với trục Ox khác với điểm cực trị của ( ) = yhx . Hàm số ( ) = yfx có 3 điểm cực trị. Suy ra hàm số ( ) = yhx cũng có 3 điểm cực trị. Hàm số ( )gx có 5 điểm cực trị khi và chỉ khi ( ) ( )01 2 =−=− m hxfx có 2 nghiệm phân biệt khác điểm cực trị của ( )hx .
=−+= hxfxmgxhx . Số điểm cực trị của ( )gx = số điểm cực trị của ( ) = yhx + số giao điể
Đồ thị hàm số ( )1=−yfx có được bằng cách tịnh tiến đồ thị hàm số ( ) = yfx sang bên phải 1 đơn vị. Dựa vào đồ thị, ta được: 2 2 − m hoặc 63 2 −−− m . ;12;12 4 612
mm m m có 15 giá trị m nguyên thỏa mãn yêu cầu bài toán.
và 0 a ) có đồ thị như hình vẽ. Số điểm cực trị của hàm số ( ) ( ) 2 24 gxfxx =−+ A. 2. B. 5. C. 4. D. 3. Lời giải. Chọn D Dựa vào đồ thị hàm số ( )yfx = có hai điểm cực trị là 2;0xx=−= ( ) ( ) 2 24 gxfxx =−+ liên tục trên ( ) ( ) ( ) 2 '44'24 gxxfxx =−+−+ ( ) 2 2
−+=
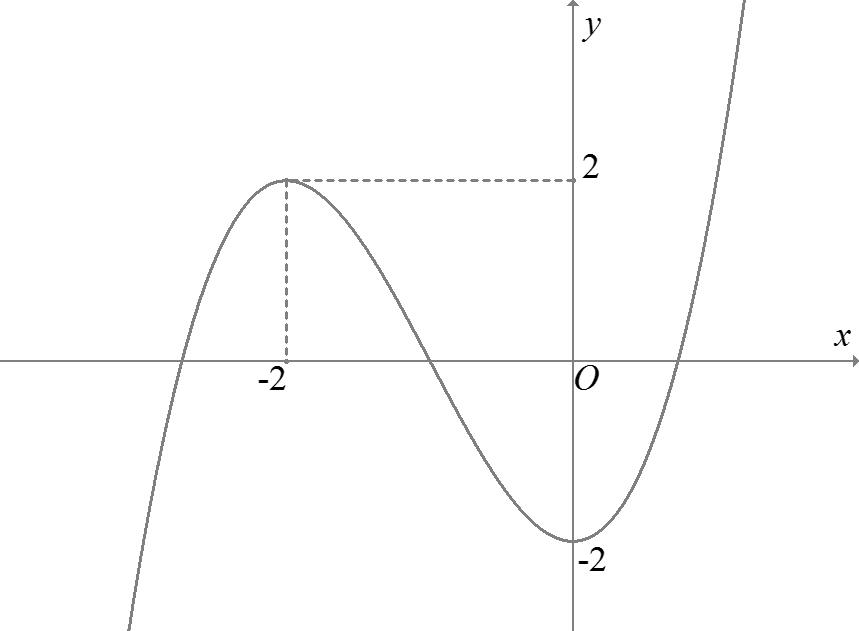

x gxxx xx
)gx có 3
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ
O SÁT HÀM SỐ
Page 112
KHẢ
− − ⎯⎯⎯⎯⎯⎯⎯→
=−+= −+=− ( )2 1 0 2 10 x x x x = = = −= Như vậy ( ) ' gx có 3 nghiệm, trong đó 1 là nghiệm bội 3, 0 và 2 là nghiệm đơn nên (
Câu 70: Cho hàm số ( ) 32 fxaxbxcxd =+++ (với ,,, abcd điểm cực trị. Câu 71: Cho hàm số bậc ba ( )yfx = có đồ thị như
vẽ Số điểm cực tiểu của hàm số ( )
440 '0240 242
hình
( ) 2 gxfxx =−+ bằng
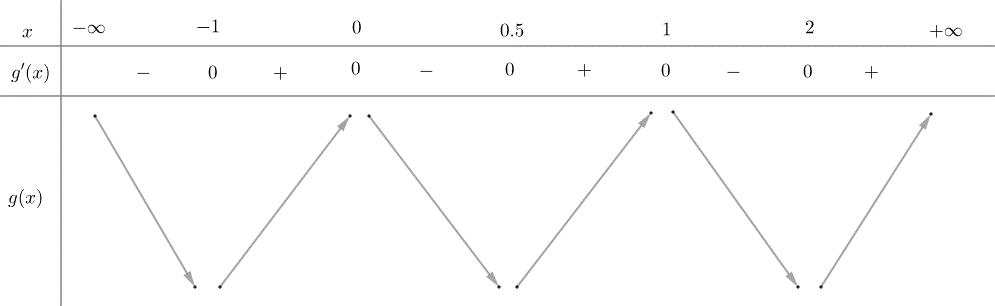
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 113 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12 A. 1. B. 5. C. 2. D. 3. Lời giải Chọn D Đặt ( ) 32 fxaxbxcxd =+++ . Khi đó ( ) 2 32 fxaxbxc =++ Theo đồ thị hàm số ( )yfx = , ta có ( ) ( ) ( ) ( ) 20124012401 0008443 22842200 02222 f abcaba f cabb abcdcc f ddd f −= −+=−==− = =−+=−=− −+−+=−== −=− === = Vậy ( ) 3232fxxx=−−+ . Khi đó, ta có ( ) ( ) 265323532gxfxxxxxx =−+=−+−+ . ( ) ( ) ( ) 43 1 0 1 325520 2 1 2 x x gxxxxxgxx x x =− = =−+−== = = Bảng biến thiên Suy ra, hàm số ( ) ( ) 2 gxfxx =−+ có ba điểm cực tiểu. Câu 72: Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số 4323412 yxxxm =−−+ có 5 điểm cực trị? A. 16 B. 28 C. 26 D. 27 Lời giải Chọn D Xét hàm số ( ) 4323412 fxxxxm =−−+ . Ta có ( ) 32 1212240fxxxx =−−= 0 1 2 x x x = =− = Bảng biến thiên:
Vậy với mọi m hàm số ( )fx luôn có ba điểm cực trị. Do đó để hàm số ( )yfx = có 5 điểm cực trị khi và chỉ khi phương trình ( ) 0 fx = có đúng hai nghiệm đơn hoặc nghiệm bội lẻ 0 50 320
m m m
− −
0 532 m m
Vì m là số nguyên dương cho nên có 27 số m thỏa đề bài. Câu 73: Cho hàm số ()yfx có bảng biến thiên như hình vẽ dưới đây: Hàm số (2)yfx đạt cực đại tại A. 1 2 x = B. 1 x =− C. 1 x = D. 2 x =− Lời giải Chọn C Đặt 2() txyft . Từ bảng biến thiên ta thấy hàm số ()yft đạt cực đại tại 1 121 2 222 1
tx x tx x . Vậy hàm số (2)yfx đạt cực đại tại điểm 1 x = và 1 2 x =− Câu 74: Cho hàm số ( )yfx = có đạo hàm liên tục trên và ( ) ( ) 00;44ff= . Biết hàm ( )yfx = có đồ thị như hình vẽ
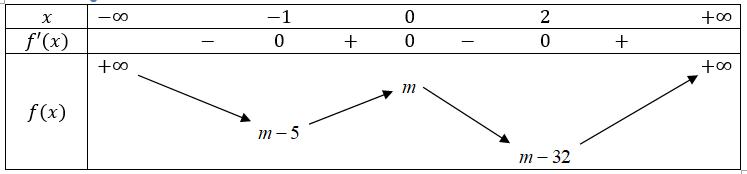
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
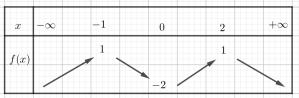
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 114
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
x
2
Số điểm cực trị của hàm số ( ) ( ) 2 2 gxfxx =− là A. 2. B. 1. C. 4. D. 3. Lời giải Chọn D Xét hàm số ( ) ( ) 2 2 hxfxx =− . Ta có: ( ) ( ) 2 22hxxfx =− ; ( ) ( ) 2 1 0 hxfx x == (vô nghiệm 0 x ). Đặt 2 ,0txxtt == .
Khi đó: ( ) 1 ft t = (*). Nhận thấy trên khoảng ( )0;1 thì ( ) 1 wt t = nghịch biến và ( )ft đồng biến, do đó (*) nếu có nghiệm là duy nhất.
Mặt khác: ( ) ( ) ( ) ( ) 0.1221280hhf =−−=− và ( )hx liên tục trên 0;1 nên ( ) ( ) 000;1:0xhx = . Vậy ( ) 0 hx = có nghiệm duy nhất ( ) 0 0;1 x và ( )hx có một điểm cực tiểu (vẽ bảng biến thiên). (1)
Xét phương trình: ( ) ( ) 2 020hxfxx =−= (**).
Ta có: ( ) ( ) 0000hfx=== là một nghiệm của (**).
Mặt khác: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )000101 .22440;2:0 hxhfxxfxxhx =−−= .
Nên (**) có nghiệm ( ) 10 ;2 xx
Vì ( )hx có một điểm cực trị, nên (**) có không quá 2nghiệm.
Vậy ( ) ( ) 2 20hxfxx=−= có hai nghiệm phân biệt. (2)
Từ (1) và (2) ta được: hàm số ( ) ( ) 2 2 gxfxx =− có 3 điểm cực trị
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 115
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
y
Câu 75: Cho hàm số ()yfx = đồng biến trên ( ) 4;+ có đồ thị như hình vẽ. Số điểm cực trị của hàm số (22)yfx=− bằng 5 3
1 4 O 1
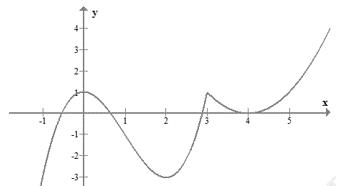


CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 116 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán A. 7. B. 5. C. 4. D. 9. Lời giải Chọn D ( ) ( ) ( ) ( )' ' '2'' (22)'22(22)22(22)(22) x gxfxgxxfxxfxfx x =−=−−=−−=− ( ) ( ) '' '0(22)0(22)00 x gxfxfxx x =−=−= Dựa vào đồ thị ta có ' 0 2 ()03 4 x x fx x x = = = = = ' 22011 22222 (22)05 2235 22 2243 3 x x x x x x fx x x x x x x = = −= = = −= →−= = −= = −= = = Ta có bảng xét dấu ( ) ' gx Suy ra hàm số (22)yfx=− có 9 điểm cực trị Câu 76: Cho hàm số ( )yfx = là một hàm đa thức có bảng xét dấu ( )fx như sau Số điểm cực trị của hàm số ( ) ( ) 2 gxfxx =− A. 5. B. 3. C. 1. D. 7.

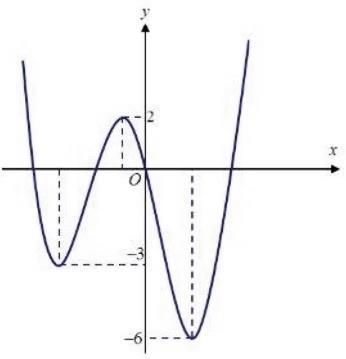
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên:
ỳnh
Ánh
ễn Cư
Thuậ
ế
Page 117
Lờ
ả
( )yfx = như hình vẽ dưới đây: Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m để hàm số ( ) 2 1 2018 3 yfxm =++ có 5điểm cực trị. Tổng tất cả các giá trị của các phần tử trong tập S bằng A. 6 B. 5 C. 7 D. 9 Lời giải Chọn C Đặt ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 1 20182018 201813 31 2018 3 fxfxm gxfxmgx fxm +++ =++= ++
Hu
Văn
42 Nguy
Trinh
n Hòa TP Hu
ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12
i gi
i Chọn A Ta có ( ) ( ) ( ) 2 2 gxfxxfxx =−=− . Số điểm cực trị của hàm số ( ) fx bằng hai lần số điểm cực trị dương của hàm số ( )fx cộng thêm 1. Xét hàm số ( ) ( ) ( ) ( ) ( ) 222 2 1 1 2 2 2101 15 1 2 x x hxfxxhxxfxxxx x xx = = =−=−−=−=− = −= Bảng xét dấu hàm số ( ) ( ) 2 hxfxx =− Hàm số ( ) ( ) 2 hxfxx =− có 2 điểm cực trị dương, vậy hàm số ( ) ( ) ( ) 2 2 gxfxxfxx =−=− có 5 điểm cực trị Câu 77: Cho đồ thị
−
m mm m
2 33;4 63 3
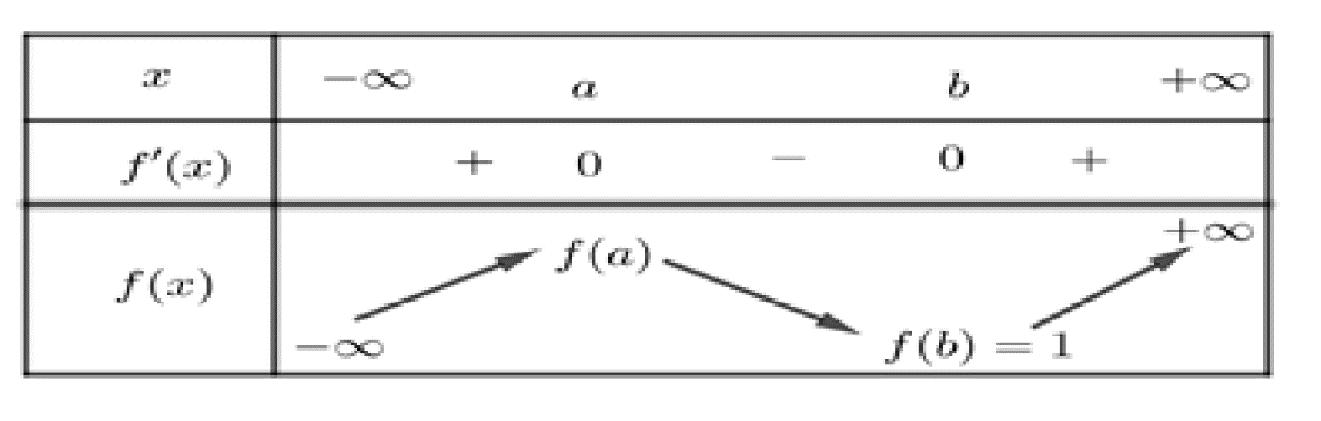

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 118
ể
Tốt
Phương
( ) ( ) (
(
2
0
3 fx gx m
+= = +=− Dựa
đồ thị ta thấy
Vậy
đồ
Hòa
0984164935
Chuyên luyện thi: Tuy −−− . Vậy tổng các phần tử là 7. DẠNG. TÌM MĐỂ HÀM SỐ ( ) ( ) fux THỎA MÃNĐIỀU KIỆN CHO TRƯỚC Câu 78: Cho hàm số bậc ba ( )yfx = có đồ thị của hàm đạo hàm ( )fx như hình vẽ và ( ) 1 fb = .Số giá trị nguyên của 5;5 m− để hàm số ( ) ( ) ( ) 2 4 gxfxfxm =++ có đúng 5 điểm cực trị là A. 8 B. 10 C. 9 D. 7 Lời giải Chọn C Cách 1: Ta có bảng biến thiên của ( ) fx : Xét hàm số ( ) ( ) ( ) 2 4 hxfxfxm =++
n sinh vào lớp 10
Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
trình
)
) ( )
201801
20182
fx
vào
phương trình ( )1 luôn có 3 nghiệm phân biệt.
để
thị hàm số ( )ygx = có 5 điểm cực trị thì phương trình ( )2 phải có 2 nghiệm đơn phân biệt ( ) 2 * 2
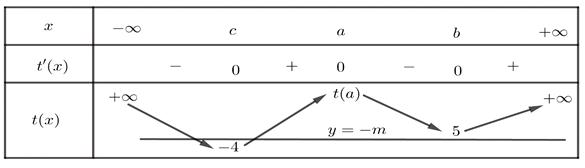
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 119
Pt
ệm
ệ
ị Xét
= (
+=− Để (
= có
ự
ị
ỉ khi PT
hoặc nghiệm bội lẻ phân biệt Xét hàm số ( ) ( ) ( ) 2 4 txfxfx =+ Ta có Bảng biến thiên của ( ) tx : Từ YCBT ( ) txm=− có hai nghiệm đơn hoặc nghiệm bội lẻ pb ( ) ( ) −−− − −−−− −− 55 54 4545 55;55 mtamta m mm m mmm 5;4;3;2;1;0;1;2;3. m −−−−− Cách 2: Ta có bảng biến thiên của hàm số ( ) = yfx :
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ''' '' '' ' 24 22 0220 ; 0 2 hxfxfxfx hxfxfx hxfxfx xaxb fx xcca fx =+ =+ =+= == = = =−
có 3 nghi
phân bi
t
có 3 điểm cực tr
( ) 0 hx
) ( ) ( ) 2 42fxfxm
) ( ) gxhx
5 điểm c
c tr
khi và ch
( )2 có 2 nghiệm đơn


CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 120 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán Xét hàm số ( ) ( ) ( ) 2 4 hxfxfxm =++ ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ''' '' '' ' 24 22 0220 ; 0 2 hxfxfxfx hxfxfx hxfxfx xaxb fx xcca fx =+ =+ =+= == = = =− Từ YCBT ( ) ( ) ( ) ( ) ==++ 2 4 gxhxfxfxm có 5 điểm cực trị khi: ( ) ( ) +− −++ − − − −−−−− 2 0 4(a)5 405 54 ;5;5 ;5;5 5;4;3;2;1;0;1;2;3 ha mfaf mm m mm mm m Câu 79: Cho hàm số ( )yfx = có đồ thị như hình vẽ bên dưới. Có bao nhiêu giá trị nguyên của tham số thực m để hàm số ( ) ( ) 2 2020 gxfxm =++ có 5 điểm cực trị?
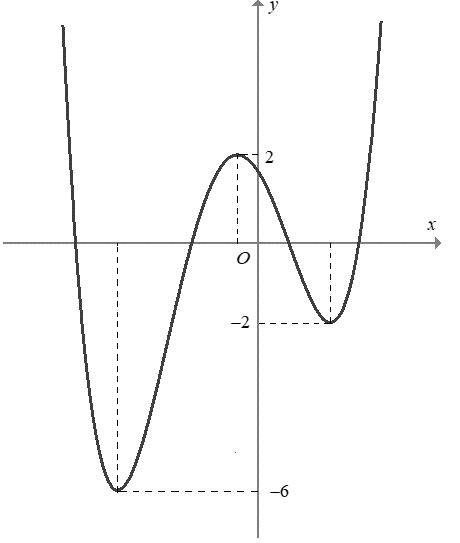
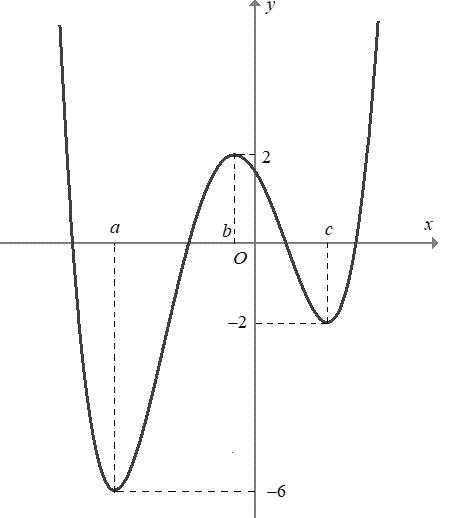

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 121 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc
TOÁN 10; 11; 12 A. 1. B. 2. C. 4. D. 5. Lời giải Chọn B Gọ
,, abc ( )abc là ba
ự
trị
ủ
= Khi
. Xét
2020
ớ
x .
( ) 2020 02020 2020 xa hxxb xc =− ==− =− Bảng biến thiên của hàm ( )hx Hàm
ố ( ) ( ) 2 2020
=++ có
ự
ị
2
Gia BDKT
i
điểm c
c
c
a hàm số ( )yfx
đó: ( ) ( ) ( ) 6;2;2fafbfc=−=−=
hàm ( ) ( )
hxfx=+ v
i
Khi đó: ( ) ( ) ( ) ( )2020.20202020hxfxxfx =++=+
s
gxfxm
5 điểm c
c tr
Phương trình ( )
20200fxm++= có đúng 2 nghiệm không thuộc
2020;2020;2020abc
Để hàm số ( )fx có đúng một điểm cực trị Phương trình ( )* vô nghiệm, có nghiệm kép hoặc có hai nghiệm phân biệt trong đó có nghiệm là 4. Trường hợp 1. Phương trình ( )* vô nghiệm 22 4243624724360 mmmm =++−−=− 33 m − 2 ;1; 0 ; 1; 2 m
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 122 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán 2 2 2 22 262 2626 m m mm m m = = =−−− . Vậy có 2 giá trị nguyên của m là 2 m = và 2 m =− thì hàm số ( ) ( ) 2 2020 gxfxm =++ có 5 điểm cực trị. Câu 80: Cho hàm số ( )fx có đạo hàm ( ) ( ) ( ) ( ) 43 222423618.fxxxxxmxm =++++++ Có tất cả bao nhiêu giá trị nguyên của m để hàm
B.
C.
D.
L
2 4
x
x
xmxm = = += =− = =− +=
m phân biệt 1x , 2x . Trong đó 1 4. x =− Phương trình có hai nghiệm phân biệt 2 12 3 , 4360 3 m xxm m − =− Theo định lí Viète ta có 122 122 426 .4.618 Sxxxm Pxxxm =+=−+=−− ==−=+ 2 2 22 39 225 39 22 22 xm mmm xm =−− −−=−−= =−− . Vậy 3;2 ;1; 0 ; 1; 2 ; 3; 5 m−−− thỏa mãn yêu cầu đề bài. Câu 81: Cho hàm số ( )yfx = có đồ thị như hình vẽ bên dưới
số ( )fx có đúng một điểm cực trị? B. 7
5
8
6
ời giải Chọn C Ta có ( ) ( ) ( ) ( ) ( ) ( )
3 2 2 00 202 0 404 236180 236180*
x x x fx x
xmxm
++++=
++++=
−− Trường hợp 2. Phương trình ( )* có nghiệm kép 2 3 4360 3 m m m = =−= =− . Trường hợp 3. Phương trình ( )* có hai nghiệ
Tìm tất cả các giá trị của tham số m để đồ thị hàm số ( ) ( ) ( ) 2 22 hxfxfxm =++ có đúng 3 điểm cực trị. A. 1 m B. 1 m C. 2 m D. 2 m Lời giải Chọ


CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 123
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12
ự
ị
ủ
trị
của
ị
( ) (
( ) 2 22=++ yxfxfxm và
y = . Xét
ố ( )
22
=++ (
=+=+ ( ) ( ) ( ) ( ) 01 03 1 0 x fx gxx fx x = = == = = BBT Hàm số ( )hx có 3 điểm cực trị 1 20 2 mm . Đáp án B là gần kết quả nhất Câu 82: Cho hàm số ( )fx có đạo hàm ( ) ( )( )3 2 1315fxxxax =−− . Tập hợp các giá trị của a để hàm số 2 5 4 x yf x = + có 6 điểm cực trị là A. 5515 ;\0; 4413 . B. 5515 ;\0; 4413 . C. 55;\0 44 . D. 5515 ;\ 4413 . Lời giải 23 22222 55555 .1315 44444 yfaxxxxx xxxxx ==−− +++++
n B Số c
c tr
c
a hàm số ( ) ( ) ( ) 2 22 hxfxfxm =++ bằng số cực trị của hàm số ( ) ( ) ( ) 2 22=++ yxfxfxm cộng với số giao điểm (khác điểm cực
)
đồ th
hàm số
)
0
hàm s
( ) ( ) 2
gxfxfxm
) ( ) ( ) ( ) ( ) ( ) 2221gxfxfxfxfxfx
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42
ễn Cư
Thuận
TP Huế
Page 124
Tố
ệ
= ( ) ( ) 3 2222 22 22 22 2052554156560 . 4444 xxaxxaxx xx xx −−+−−+− ++ ++ . 0 y = 2 2 0 3 4 3 540 (1) x x x x axxa = = = = −+−= ( 0 x =
ệ
đặt ( ) 2 54 gxaxxa =−+− Ycbt
ỏa
ệt khác 2;0;1;4 . (Nếu ( ) 00 = g thì 0 y = chỉ có 5 nghiệ
bội lẻ). Điều kiện: ( ) ( ) ( ) ( ) 2 0 54.40 20 20 00 30 4 0 3 =− −
a a a a a 55 44 0 15 13 a a a − Câu
Cho hàm số ( )yfx = có đạo
( ) ( ) ( ) 2 2 12 fxxxx =−− vớ
x .
giá trị nguyên dương của tham số m để hàm số ( ) 2 8 fxxm −+ có 5 điểm cực trị? A. 15 B. 17 C. 16 D. 18 Lời giải Đặt ( ) ( ) 2 8 gxfxxm =−+ ( ) ( ) ( ) 2 2 12 fxxxx =−− ( ) ( )( ) ( )( ) 2 222 2881882 gxxxxmxxmxxm =−−+−−+−+− ( ) 0 gx = ( ) ( ) ( ) 2 2 2 4 8101 802 8203 x xxm xxm xxm = −+−= −+= −+−= Các phương trình ( )1 , ( )2 , ( )3 không có nghiệm chung từng đôi một và ( )2 2 810xxm−+− với x
Nguy
Trinh
Hòa
ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10
t Nghi
p THPT Quốc Gia BDKT 10; 11 môn Toán
là nghi
m kép)
th
mãn khi phương trình 0 y
= có 6 nghiệm bội lẻ phương trình ( )1 có hai nghiệm phân bi
m
a aa g g g g g 0 55 44 5 4 0 15 13 −
83:
hàm
i
Có bao nhiêu
16 m . m nguyên dương và 16 m nên có 15 giá trị m cần tìm. Câu 84: Cho hàm số ()yfx = xác định trên và hàm số '()yfx = có đồ thị như hình bên. Biết rằng '()0fx với mọi ( ) ( ) ;3,49;. x−−+ Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ()()5 gxfxmx=−+ có đúng hai điểm cực trị A. 7. B. 8. C. 6. D. 5. Lời giải Chọn B '()'() gxfxm =− Số điểm cực trị của hàm số ()gx bằng số nghiệm đơn (bội lẻ) của phương trình '(). fxm =
Dựa và đồ thị ta có điều kiện 05 1013 m m
y 3 2 0 1
x
Vậy có 8 giá trị nguyên dương của m thỏa mãn. Câu 85: Cho hàm số ()yfx = . Hàm số ()yfx = có đồ thị như hình vẽ dưới đây. Tìm m để hàm số 2 ()yfxm =+ có 3 điểm cực trị A. ( ) 3; m+ . B. 0;3 m . C. )0;3 m . D. ( );0 m− . Lời giải Chọn C
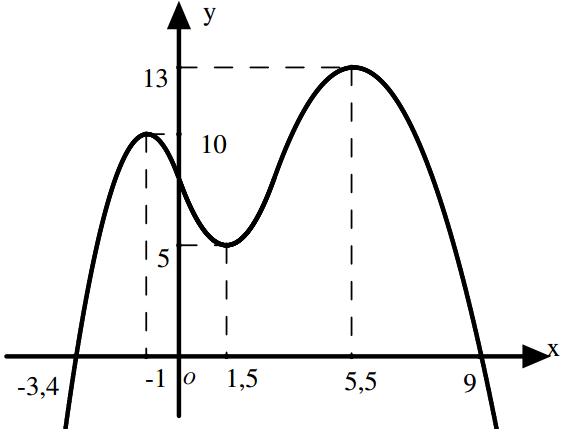
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo
ỳnh
ễn
Page 125
ố
Suy ra ( )gx có 5 điểm cực trị khi và chỉ
ệ
khác 4 160 1620 16320 163220 m m m m − −+ −+ −+− 16
viên: Hu
Văn Ánh 42 Nguy
Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 T
t Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12
khi ( )2 và ( )3 có hai nghiệm phân bi
t
18 16 18 m m m m
− − . Câu 86: Cho hàm số ( ) ( ) ( ) 2 2 243fxxxx =−−+ với mọi x . Có bao nhiêu giá trị nguyên dương của m để hàm số ( ) 2 109yfxxm =−++ có 5 điểm cực trị?
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 126 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán Do hàm số 2 ()yfxm =+ là hàm chẵn nên hàm số có 3 cực trị khi và chỉ khi hàm số này có đúng 1 điểm cực trị dương. ( ) 22()2 yfxmyxfxm =+=+ ( ) 22 2 22 22 00 0 0 0 0 11 33 xx x xmxm y fxm xmxm xmxm == = +==− = += +==− +==− Đồ thị
số (
=
ế
trục hoành tại điểm có hoành độ là 1 x = nên các nghiệm của pt 2 1 xm =− (nếu có) không làm ( ) 2 fxm + đổi dấu khi x đi qua, do đó các điểm cực
Ta
2 01 3 x
x = == =
=
( )
2 2 2 2100 10920
1091 1093 x xxm gx xxm xxm −= −++−= = −++= −++= ( ) ( ) ( ) 2 2 2 2 5 10920 10801 10602 x xxm xxm xxm = −++−= −++= −++= Hàm số ( ) 2 109yfxxm =−++ có 5 điểm cực trị khi và chỉ khi ( )gx đổi dấu 5 lần Hay phương trình ( )1 và phương trình ( )2 phải có hai nghiệm phân biệt khác 5
hàm
)yfx
ti
p xúc
trị của hàm số 2 ()yfxm =+ là các điểm nghiệm của hệ 2 2 0 3 x xm xm = =− =− Hệ trên có duy nhất nghiệm dương khi và chỉ khi 0 03 30 m m m
A. 18 B. 16 C. 17 D. 15 Lời giải Chọn B
có ( )
fxx
, 2 x
là nghiệm kép nên khi qua giá trị 2 x = thì ( )fx không bị đổi dấu. Đặt ( ) ( ) 2 109gxfxxm =−++ khi đó ( ) ( ) ( )'.210 gxfux =− với 2 109uxxm=−++ Nên ( )
2
0
của m để hàm số ( ) ( ) gxfx = có 5 điểm cực trị? A. 3. B. 5. C. 2. D. 4. Lời giải Chọn C Dựa vào cách vẽ đồ thị hàm số ( ) ( ) gxfx = , số điểm cực trị của đồ thị hàm số ( ) ( ) gxfx = bằng số điểm cực trị dương của đồ thị hàm số ( )yfx = cộng thêm 1. Để hàm số ( ) ( ) gxfx = có 5 điểm cực trị thì đồ thị hàm số ( )yfx = có 2 cực trị dương.
x fxx xmxm
= == −++−=
1 02. 2110*
Ta có ( ) ( ) ( ) 22
Có 2 x = là nghiệm bội 2, 1 x = là nghiệm đơn. Vậy ( ) 222110xmxm−++−= có hai nghiệm phân biệt, có một nghiệm dương 1 x , có một nghiệm 0 x
= −++−=−= = Với 1 m =− , có ( ) 222211000 xmxmxx −++−=== − − −++− Vì 0 mm= Vậy có hai giá trị nguyên của m thỏa mãn.
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 127 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12 ( ) ( ) ' 1 ' 2 0 0 50 50 h p , (Với ( ) 2 108hxxxm=−++ và ( ) 2 106pxxxm=−++ ). 170 190 17 170 190 m m m m m − − −+ −+ . Vậy có 16 giá trị nguyên dương m thỏa
Câu
ố ( )
=
ị
mãn.
87: Cho hàm s
yfx
có đạo hàm ( ) ( ) ( ) ( ) ( ) 2 22 21211fxxxxmxm
=−−−++− , x . Có bao nhiêu giá tr
nguyên
Trường hợp 1: Có nghiệm 0 x = khi đó ( ) 2222110101 xmxmmm −++−=−== Với 1 m = , có ( ) ( ) 222 0 211040TM 4 x xmxmxx x (Loại) Trường hợp 2: ( ) 222110xmxm−++−= có hai nghiệm phân biệt, có một nghiệm dương 1 x , có một nghiệm âm Điều kiện tương đương ( ) ( ) 2 22 101;1 121.11013 m m mm m
Câu 88: Cho hai hàm đa thức ( )yfx = , ( )ygx = có đồ thị là hai đường cong ở hình vẽ. Biết rằng đồ thị
hàm số ( )yfx = có đúng một điểm cực trị là A , đồ thị hàm số ( )ygx = có đúng một điểm cực trị là B và 7 4 AB = . Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng ( )5;5 để hàm số ( ) ( ) yfxgxm =−+ có đúng 5 điểm cực trị? A. 1 B. 3 C. 4 D. 6 Lời giải Chọn B Đặt ( ) ( ) ( )hxfxgx =− , ta có: ( ) ( ) ( )hxfxgx

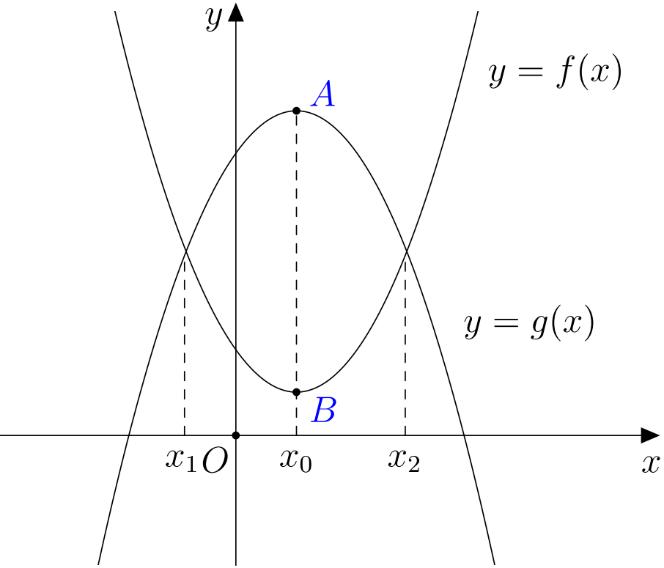

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT 10; 11 môn Toán
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ
O
Ố
KHẢ
SÁT HÀM S
Page 128
=− ; ( ) 0 0 hxxx == ; ( ) 1 0 hxxx == hoặc 2xx = ( 102 xxx ); ( ) ( ) ( ) 000 7 4 hxfxgx=−=− . Bảng biến thiên của hàm số ( )yhx = là:
Suy ra bảng biến thiên của hàm số ( ) ( ) ( )ykxfxgx ==− là: Do đó, hàm số ( ) ykxm =+ cũng có ba điểm cực trị. Vì số điểm cực trị hàm số ( ) ykxm =+ bằng tổng số điểm cực trị của hàm số ( ) ykxm =+ và số nghiệm đơn và số nghiệm bội lẻ của phương trình ( ) 0 kxm+= , mà hàm số ( ) ykxm =+ cũng có ba điểm cực trị nên hàm số ( ) ( ) yfxgxm =−+ có đúng năm điểm cực trị khi phương trình ( ) 0 kxm+= có đúng hai nghiệm đơn (hoặc bội lẻ). Dựa vào bảng biến thiên của hàm số ( )ykx = , phương trình ( ) 0 kxm+= có đúng hai nghiệm đơn (hoặc bội lẻ) khi và chỉ khi 7 4 m − 7 4 m − Vì m , 7 4 m − và ( )5;5 m − nên 4;3;2 m −−−
Câu 89: Cho hàm số ( ) ( ) ( ) 322122yfxxmxmx ==−−+−+ . Tập hợp tất cả các giá trị của tham số m để hàm số ( ) yfx = có 5 điểm cực trị là ; a c b , (với ,, abc là các số nguyên, a b là phân số tối giản). Giá trị của biểu thức 222 Mabc =++ là A. 40 M = B. 11 M = C. 31 M = D. 45 M = Lời giải Chọn D Hàm số ( ) ( ) ( ) 322122yfxxmxmx ==−−+−+ có đạo hàm là ( ) ( ) ( ) 2 32212 yfxxmxm ==−−+−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT Quốc Gia BDKT TOÁN 10; 11; 12
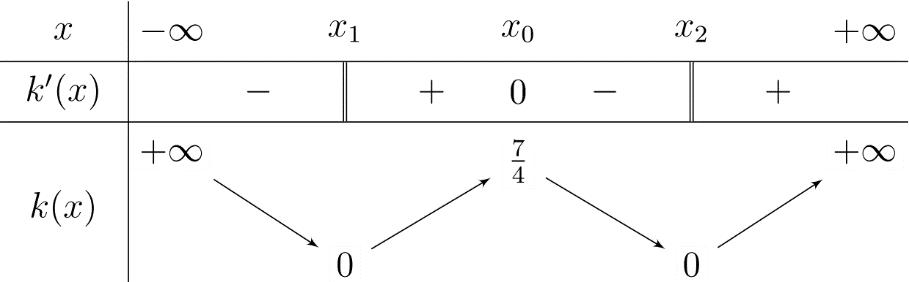
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 129
m cực trị thì hàm số ( )yfx = có hai điểm cực trị 12 , xx dương. Tương đương với phương trình ( ) 0 fx= có 2 nghiệm dương phân biệt. ( ) ( ) ( ) 2 21320 221 0 3 2 0 3 mm m S m P =−−− = = 2 450 1 2 2 mm m m −− 5 1 4 1 2 2 mm m m − 5 2 4 m . Suy ra 5 4 2 a b c = = = 222 45 Mabc =++ =
Để hàm số ( )yfx = có 5 điể
DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
p bảng biến thiên của hàm số ( ) = yfx khi biết đồ thị hàm số ( ) = yfx
B1. Xác định giao điểm của đồ thị hàm số ( ) = yfx với trục hoành B2: Xét dấu của hàm số ( ) = yfx , ta làm như sau
Phần đồ thị của ( )fx nằm bên trên trục hoành trong khoảng ( ) ; ab thì ( ) 0 fx , ( ) ; xab
Phần đồ thị của ( )fx nằm bên dưới trục hoành trong khoảng ( ) ; ab thì ( ) 0 fx , ( ) ; xab Lập bảng biến thiên của hàm số ( ) ( ) ( )gxfxux =+ khi biết đồ thị hàm số ( ) = yfx
B1: Đạ



CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 130 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn BÀI 2: CỰC TRỊ CỦA HÀM SỐ - VD VDC 02 HƯỚNG DẪN GIẢI CHI TIẾT TÌM CỰC TRỊ CỦA HÀM SỐ HỢP ( )fux HOẶC ( ) ( )fuxgx + KHI BIẾT ĐỒ THỊ HÀM SỐ ( )fx HOẶC ( )fx KIẾN THỨC CẦN NHỚ: Đạo hàm của hàm số hợp: ( ) ( ) ( ) ( ) ( ) == gxfuxgxuxfux . (
= =
ux
) ( ) ( ) 0 0 0
=
gx fux
Lậ
o hàm ( ) ( ) ( )gxfxux =+ . Cho ( ) ( ) ( ) 0 gxfxux ==− B2. Xác định giao điểm của
thị
số
=
và
thị
ố
=− B3: Xét
u củ
=
đồ
hàm
( )
yfx
đồ
hàm s
( )yux
dấ
a hàm số ( )ygx
, ta làm như sau Phần đồ thị của ( )fx
nằm bên trên đồ thị ( )ux trong khoảng ( ) ; ab thì ( ) 0 gx , ( ) ; xab
NG
Phần đồ thị của ( )fx nằm bên dưới đồ thị ( )ux trong khoảng ( ) ; ab thì ( ) 0 gx , ( ) ; xab
Câu 90: Cho hàm số ( )yfx = , hàm số ( )yfx = có đồ thị như hình sau: Hàm số ( ) ( ) 2 2122022gxfxxx =−−++ có bao nhiêu điểm cực trị? A. 3 B. 4 C. 5 D. 6 Lời giải
Chọn B
Ta có: ( ) ( ) 2122gxfxx =−−+ ( ) ( ) 011gxfxx =−=− .
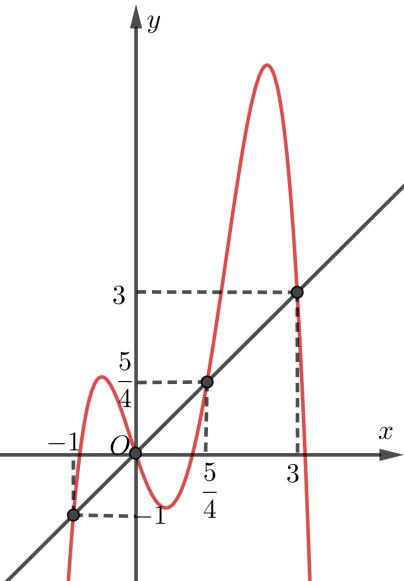
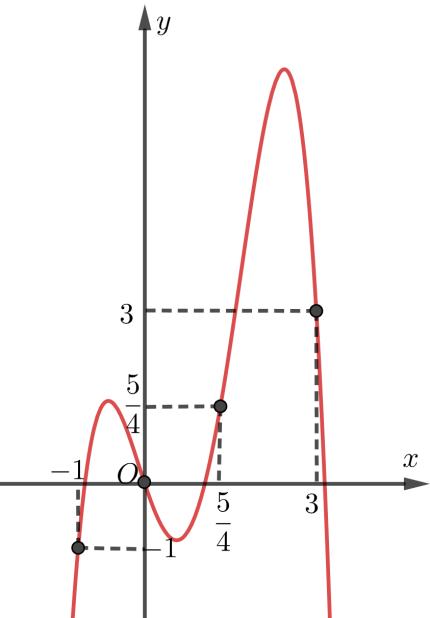
Đặt 1 tx=− . Khi đó phương trình trở thành ( ) ftt = .
Ta vẽ đồ thị hai hàm số ( )yft = và yt = trên cùng một hệ trục tọa độ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG D
HÀM ĐỂ KHẢO SÁT HÀM SỐ
ỤNG ĐẠO
Page 131
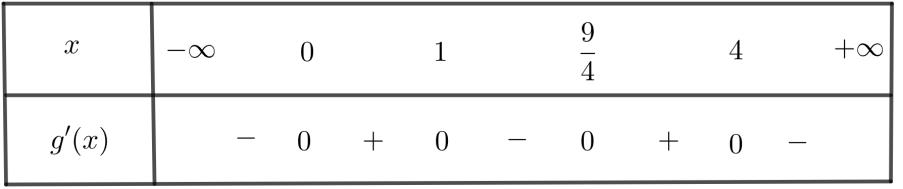
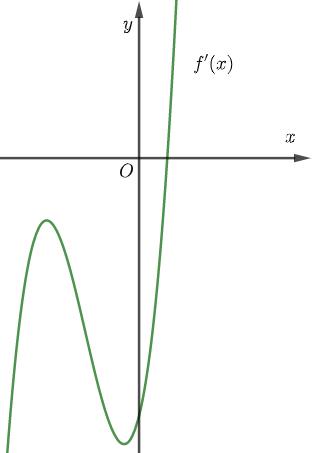
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 132 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Dựa vào đồ thị ta thấy ( ) 1110 0101 559 1 444 3134 txx txx ftt txx txx =−−=−= =−== = =−== =−== . Bảng xét dấu Vậy hàm số ( )ygx = có 4 cực trị Câu 91: Cho hàm số ( )yfx = có đồ thị ()fx như hình vẽ sau: Hỏi hàm số ( ) ( ) 3 62022hxfxx=−+ có bao nhiêu điểm cực trị? A. 1 B. 2 C. 4 D. 5 Lời giải Chọn A ( ) ( ) ( ) ( ) 3236202236hxfxxhxxfx =−+=− Ta có ( ) ( ) ( ) ( ) 3 2 2 0,01hxfxx x == Đặt 3 3 txxt == Từ ( )1 ta có: ( ) ( ) 3 2 2 ,2 ft t = Xét ( ) ( ) 3325 241 3 mtmt tt ==− Ta vẽ đồ thị hai hàm số ( )yft = và ( ) 3 2 2 ymt t == trên cùng một hệ trục tọa độ Lúc này ta có hình vẽ 2 đồ thị như sau


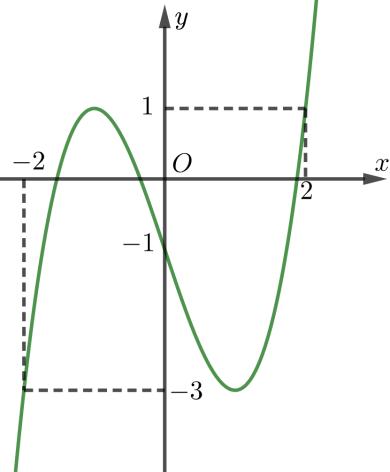
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 133 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Suy ra pt ( )2 có 1 nghiệm 0 0 tt= pt ( )1 có nghiệm 3 00 0 xtx== Bảng xét dấu Vậy hàm số ( )hx có 1 cực trị Câu 92: Cho ( )fx là liên tục trên và hàm số ( )fx có đồ thị như hình vẽ Hàm số ( ) ( ) ( ) ( ) 2 222 222022hxfxxxxxx =+−++++ có bao nhiêu điểm cực trị? A. 4. B. 5. C. 6. D. 7. Lời giải Chọn B ( ) ( ) ( ) ( )( ) ( ) 22 221221221 hxxfxxxxxx =++−++++ . ( ) ( ) ( ) ( ) 22 210 0 10* x hx fxxxx += = +−++= Đặt 2 txx =+ . Khi đó phương trình trở thành ( ) ( ) 101fttftt −+==− .
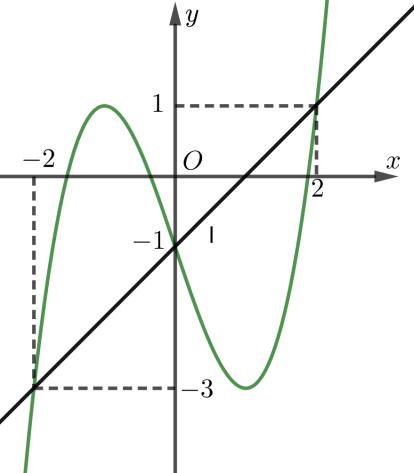


CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 134
2 2 2
t x
x t xx x =− += = = =−=+= =− =− +=− = Bảng xét dấu Vậy hàm số ( )hx có 5 cực trị. Câu 93: Cho hàm số bậc ba ( )yfx = có bảng biến thiên sau: Hàm số ( ) ( ) ( ) 2 42022hxfxfx=++ có bao nhiêu điểm cực trị? A. 3. B. 4. C. 5. D. 6. Lời giải Chọn A Ta có: ( ) ( ) ( ) ( ) ( ) ( ) 2422hxfxfxfxfxfx =+=+ ( ) ( ) ( ) ( ) ( ) ( ) 0 ; 0220 2 fx xaxb hxfxfx xcca fx = == =+= = =− . Suy phương trình ( ) 0 hx = có 3 nghiệm.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta vẽ đồ thị hai hàm số ( )yft = và 1 yt=− trên cùng một hệ trục tọa độ Dựa vào đồ thị ta thấy ( )
222 1 100 1 22 0 x xx
ftttxx
Vậy hàm số ( )yhx = có 3 cực trị Câu 94: Cho hàm số ( )yfx = , hàm số ( )yfx = có đồ thị như hình sau: Hàm số ( ) ( ) 2 coscs 202 o gx xx f + =− có bao nhiêu điểm cực trị trên khoảng 7 ;? 66 A. 6. B. 3. C. 8. D. 10. Lời giải Chọn B Ta có: ( ) ( ) ()scossscosin.inin.1 gxffxxxxx+=− =−−
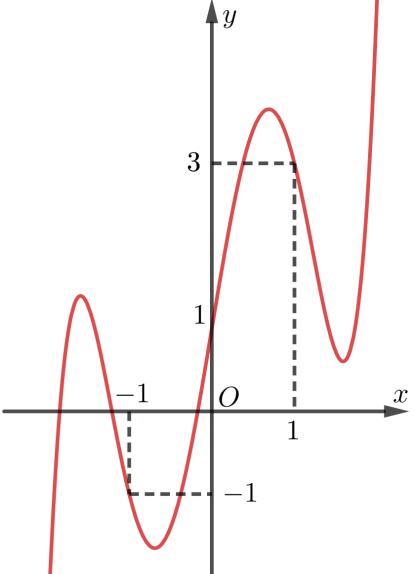
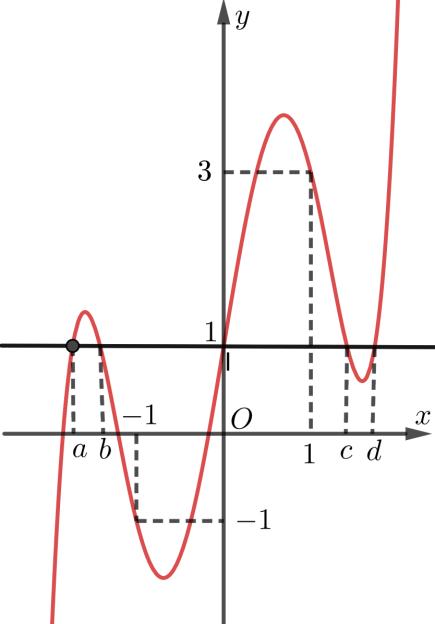
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 135
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935


CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 136
=
ảng xét dấu Vậy hàm số ( )ygx = có 3 cực trị Câu 95: Cho hàm số ( )yfx = là đa thức bậc 5 có đồ thị ( )fx như hình vẽ. Hàm số ( ) ( ) 22 2 gxfxxx =+− có bao nhiêu điểm cực trị? A. 3. B. 2. C. 4. D. 1. Lời giải Chọn A Ta có : ( ) ( ) ( ) 2 22.22 gxxfxxx =++− . ( ) ( ) 2 02 1 x gxfxx x =+= + , do 1 x =− không phải là nghiệm phương trình. Xét hàm số : ( ) 2 2 yfxx =+ ( ) ( ) 2 222 yxfxx =++ .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) in0 0 -1ptvnghim in0 -1ptvnghim 1 1ptvnghim 1ptvn s cos cos s ()0 cos cos ghim cos cos x x xaab x xbb x cc xdd g x c x f = = = = = = =
= «Ö «Ö «Ö «Ö Suy ra phương trình ( ) 0 gx = có 3 nghiệm trên khoảng 7 ; 66 là 0,,. 2 xxx === B
Khi đó, 2 2 2
x x xx yx xx x xx
=− =− +=− == +=− =− +=

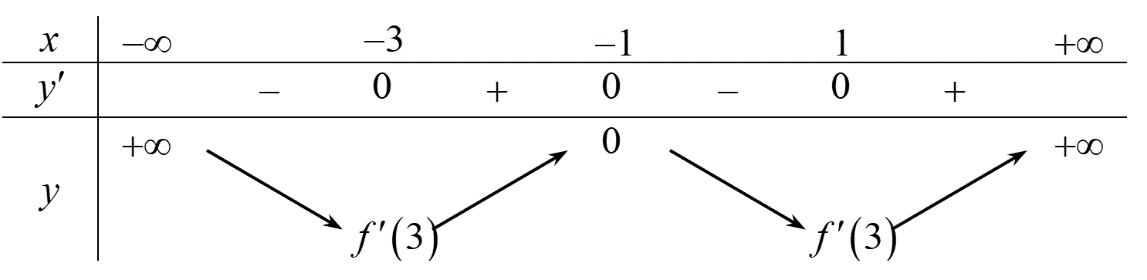
1 1 24 01 22 3 23
.
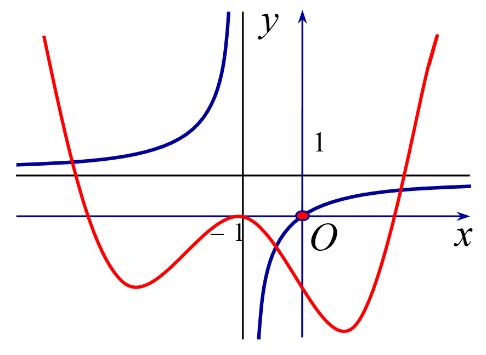
Bảng biến thiên : Xét hàm số: 1 x y x = + ( )2 1 0,1 1 yx x =− + Bảng biến thiên : Số nghiệm của phương trình: ( ) 2 2 1 x fxx x += + chính bằng số giao điểm của hai đồ thị hàm số ( ) 2 2 yfxx =+ và 1 x y x = +
Từ đồ thị suy ra phương trình ( ) 0 gx = có 3 nghiệm đơn, nên hàm số ( )gx có 3 điểm cực trị
Câu 96: Cho ( )fx là hàm số đa thức bậc bốn và hàm số ( )yfx = có đồ thị như hình dưới đây:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 137
Hỏi hàm số ( ) ( ) cos2 sin1 4 x gxfx=−+ có bao nhiêu điểm cực trị thuộc khoảng ( ) 0;2 ? A. 2 B. 5 C. 4 D. 3 Lời giải Chọn D Ta có ( ) ( ) ( ) sin2 cossin1cossin1sin 2 x gxxfxxfxx =−−=−− .
Khi đó, ( ) ( ) ( ) cos0 0 sin1sin0 * x gx fxx = = −−= .

= =
x x x
Trên khoảng ( ) 0;2 thì cos02 3 2
Đặt sin1tx=− thì phương trình ( )* trở thành ( ) 1 ftt =+ Vẽ đồ thị ( )yft = và đường thẳng 1 yt=+ trên cùng hệ trục tọa độ Oty như hình vẽ sau.
t fttt taa

1 11 , 1
Từ đồ thị ta có ( ) ( )
=− =+= = Với 1 t = thì sin11sin2 xx −== . Phương trình vô nghiệm.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 138
=
Với ta = thì sin1sin1 xaxa −==+ . Phương trình này vô nghiệm vì 12 a +
Với 1 t =− thì sin11sin0xxx −=−== .
Như thế phương trình ( ) 0 gx = có đúng 3nghiệm đơn thuộc khoảng ( ) 0;2 .
Vậy hàm số ( )gx có 3 điểm cực trị thuộc khoảng ( ) 0;2 .
Câu 97: Cho ( )yfx = là hàm bậc ba có ( ) 03 f =− Hàm số ( )yfx = có bảng xét dấu sau:
Hàm số ( ) ( ) 6 3432 9 3331 22 x ygxfxxmxxxx ==−+−+−−+− có bao nhiêu cực trị biết m là
giá trị lớn nhất của 3sin cos2 x P x = + . A. 10. B. 9. C. 7. D. 8. Lời giải

=− ==+− = . Mà ( ) ( ) ( )( ) 2 03331133 fkfxxxx =−==−+=− 23532 233 33
gxxfxxxxxx gxxfxxxx x gx fxxxx
=−−+−+−−+ =−−+−−+ = = −+=−+
3331312393 333131 1 0 3131 1
. Đặt 3 31 xxt −+= suy ra ( ) ( ) 2
− + = − =−= = −
x x t x ftttt x t x x
1,76137 1370,0602 13361,7011 1371,21796 60,76486 1,9828
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
.
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 139
Chọn D Từ bảng biến thiên ( ) ( ) ( )( ) 1 011 1 x fxfxkxx x . Theo bài ra 3sin3sincos2 cos2 x PxPxP x =−= + . Điều kiện P có nghiệm là ( )2 2 2311 PPP +− . Nên 1 m = . Khi đó ( ) ( ) 6 3432 9 31331 22 x ygxfxxxxxx ==−+−+−−+− . Ta có: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
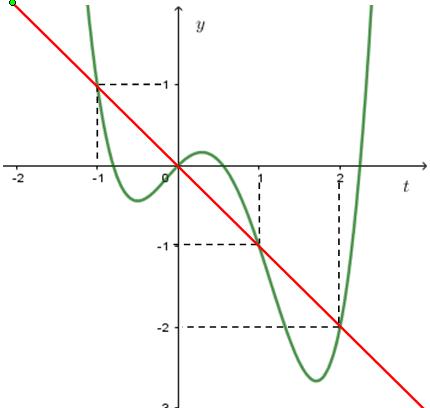

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO
HÀM SỐ
SÁT
Page 140
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do đó ( ) 0 gx = có 8 nghiệm đơn. Vậy hàm số ( )ygx = có 8 cực trị. Câu 98: Cho hàm số ( )yfx = có đạo hàm trên . Hàm số ( )yfx = đồ thị như hình vẽ bên dưới: Số điểm cực tiểu của hàm số ( ) ( ) 4 2322222021 2 x gxfxxxx =−+−++ là A. 3 B. 4 C. 5 D. 6 Lời giải Chọn B Ta có: ( ) ( ) ( ) 232 222264 gxxfxxxxx =−−+−+ . ( ) ( ) ( )( ) 22 212212 xfxxxxx =−−+−− ( ) ( ) ( ) 22 2122 xfxxxx =−−+− . Đặt 2 2 txx =− . Khi đó đồ thị hàm số ( )ft cắt đường thẳng yt =− tại bốn điểm phân biệt: 1 t =− , 0 t = , 1 t = , 2 t =
y hàm số ( )gx có bốn điểm cực tiểu. Cho đồ thị hàm số ( ) ( ) fux , ( ) ( ) fux hoặc bảng xét dấu của hàm, ( ) ( ) fux , ( ) ( ) fux . Xét cực trị của hàm ( ) ( ) fvx
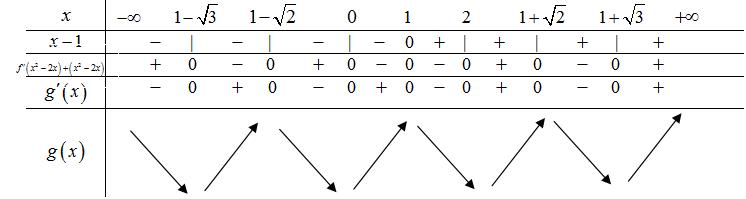
PHƯƠNG PHÁP
o Đạo hàm xét dấu thông thường. o Chọn hàm đại diện. o Đặt ẩn phụ. o Ghép trục. Nhắc lại quy tắc về dấu của tích, thương, tổng các biểu thức: ( )fx + + ( )gx + + ( ) ( )fxgx + + ( ) ( ) : fxgx + + ( ) ( )fxgx + + Chưa biết Chưa biết Câu99: Chohàmsố ( )yfx = bậc bốn cóđạohàmliêntụctrên .Hàmsố ( )31yfx =− có đồthịnhưhình dưới.
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 141 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Suy ra: ( ) 2 2 2 2 11 211 02002 2112 2213 x x xx x gxxxxx xx x xx x = = −=− = =−=== −= = −= = . Ta có: ( ) ( ) 2 222 2 221313 22021120212 21 xx xx fxxxxxxxx VN xx −+ − −−−−−+ −−
Khi đó BBT
Vậ
.
như sau:
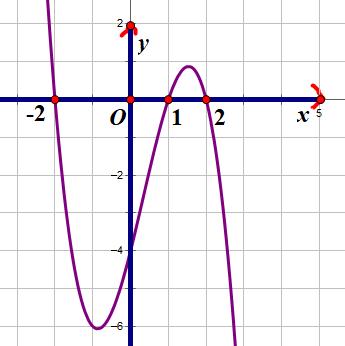

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 142 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Hàmsố ( ) 12 yfx =− cómấyđiểmcựcđại? A. 1 B. 3 C. 0 D. 2 Lời giải Chọn D Cách 1. Chọn hàm đại diện Quan sát đồ thị ta thấy ( )31yfx =− là hàm
ố bậ
ba
ệ
=−==
1111 212725 33327 ttt ftttt +++ =−+−−=−+−− ( ) (
1 725 27
=−+−−
. Xét
ố
=− ( )
12.122.12282124 27
=−−=−−=−++ Dấucủa y Ta suy ra hàm số ( ) 12 yfx =− có 2 điểm cực đạ
Cách 2. Xét dấu đạo
y . Xét ( ) 12 yfx =−
s
c
có 3 nghi
m 2,1,2xxx
Ta chọn: ( ) ( )( )( )31212fxxxx
−=−+−− [chưa chính xác 100% nhưng phù hợp trắc nghiệm] Đặt 1 31 3 t txx + =−= . ( ) ( )( )( )
)( )( )
fxxxx
Suy ra ( ) ( )( )( ) ( )( )( ) 11 12127122125282124 2727 fxxxxxxx
−=−−+−−−−=−++
hàm s
( ) 12 yfx
( ) ( ) ( )( )( ) 2
yxfxfxxxx
i.
hàm
Ta suy ra hàm số ( ) 12 yfx =− có 2 điểm cực đại. Câu 100: Cho hàm số ( )yfx = bậc bốn có đồ thị hàm số ( )1 yfx =+ như hình vẽ. Hàm số ( ) 2 3 yfx=− có bao nhiêu điểm cực trị?

A. 4. B. 2. C. 3. D. 1.

Lời giải
Chọn C
Cách 1. Chọn hàm đại diện. Hàm số
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 143 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) 12.122.12 yxfxfx =−−=−− ( ) ( )01201yfx =−= Theo đồ thị ( ) 2317 3101312 2315 xx fxxx xx =−−=− −==−= =−= ( ) 7 02 5 x fxx x =− == = Khi đó: ( ) 4 127 1 1122 2 1252 x x xx x x = −=− −==− −= =− ,cácnghiệm
trênđềulànghiệmbộilẻ Dấu y
ậ
=−
=
Ta
( ) (
) (
12112 fxxxfxxx +=−+−=−+−
=−=−−−=−−−+
( )yfx = b
c bốn, và quan sát đồ thị ta thấy ( )1 yfx =+ là hàm số bậc ba có hai nghiệm 2 x
, 1 x
, trong đó 1 x = là nghiệm bội chẵn.
chọn:
)(
) ( )( ) 22
[nếu tự luận thêm 0 k ]. Xét ( ) 2 3 yfx=− . ( ) ( )( ) ( )( ) ( ) 22 2 2222 232.252.255 yxfxxxxxxxx
. Ta có bảng xét dấu của hàm số ( ) 2 3 yfx=− .


CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 144 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Từ bảng biến thiên ta suy ra hàm số có 3 điểm cực trị. Cách 2. Xét dấu đạo hàm y Xét hàm số ( ) 2 3 yfx=− Ta có ( ) ( ) 22323yfxyxfx =−=− . ( ) ( ) 2 2 0 0230 30 x yxfx fx = =−= −= . Từ đồ thị của ( ) 211 10 112 xx fx xx =−+=− +==+= ( ) 1 0 2 t ft t =− = = , trong đó 2 t = là nghiệm bội chẵn. Khi đó ( ) 2 2 2 0 0 0 312 30 32 5 x x x xx fx x x = = = −=−= −= −= = , trong đó 5 x = là nghiệm bội chẵn. Ta có bảng biến thiên của hàm số ( ) 2 3 yfx=− Từ bảng biến thiên ta suy ra hàm số có 3 điểm cực trị Cách 3. Xét dấu đạo hàm y . Đồ thị ( ) ( ) 2 10 1 t yft tkep =− =+= = . Đặt 2 13tx+=− 2 2 4 x tx tx = =− Khi đó ( ) ( ) ( ) ( ) 2232.31.2.1 x yfxxfxfttxft =−=−=+=+ . 2 2 2422 01415 20200 x x t ytxx xxx = −=− =− ==−== === .
BBT của hàm số ( ) 2 3 yfx=− , nhờ ( ) ( ) ( ) 2 2.31.2.1 x yxfxfttxft =−=+=+


Từ bảng biến thiên ta suy ra hàm số có 3 điểm cực trị
Câu 101: Cho hàm số ( )yfx = có đạo hàm liên tục trên và có đồ thị hàm số ( )1 yfx =− như hình vẽ
Hỏi hàm số ( ) 2 1 yfx =− có bao nhiêu điểm cực trị?
A. 4. B. 2. C. 1. D. 3. Lời giải
Chọn D
Cách 1. Chọn hàm đại diện Quan sát đồ thị ta thấy ( )1 yfx =− là hàm số dạng bậc bốn có 3 nghiệm 2,0,2xxx=−== , trong đó 2 x =− là nghiệm bội chẵn.
Ta chọn: ( ) ( ) ( ) ( ) ( ) ( )( ) 22 122311 yfxxxxfxxxx =−=+−=++−
Xét ( ) 2 1 yfx =− . ( ) ( ) ( )( ) ( ) ( ) 22222 22 3 2 2321211 1 11 24 y x f x xxxx x xx =+ =−−−−−− +− =− Ta có bảng xét dấu của hàm số ( ) 2 1 yfx =− Từ bảng biến thiên ta suy ra hàm số có 3 điểm cực trị. Cách 2. Xét dấu đạo hàm y . Xét ( ) 2 1 yfx =− ta có ( ) 2 . 21fx x y =−− . ( ) ( ) 2 2
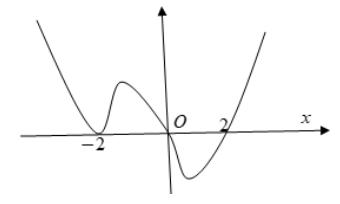
0 0210 0 . 1 x yfx fx x =
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 145
=−−= −=



CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 146 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Từ đồ thị hàm số ( )1 fx ta có ( ) 213 10011 211 xx fxxx xx =−−=− −==−=− =−= ( ) 3 01 1 x fxx x =− ==− = , trong đó 3 x =− là nghiệm bội chẵn. Khi đó ( ) 2 2 2 2 0 2 013 2 1011 0 11 x x x x x fx x x x = = = −=− = −= −=− = −= ,
ẻ Ta
ảng
dấu y . V
ị
ậc bốn (
=
ng
(
2 22
=++
ị
A. 4 B. 2 C. 1 D. 3 Lời giải Chọn D Từ bảng xét dấu của ( )2 yfx =− ta
ả
ấ
Ta có ( ) ( ) 2 2 1 22 22 x gxfxx xx + =++ ++ ( ) ( ) 2 10 0 220 x gx fxx += = ++= 2 2 2 10 221 221 223 x xx xx xx += ++=− ++= ++= 1 122 122 x x x =− =−+ =−− Bảng xét dấu:
trong đó 0,2xx== nghiệm bội l
có b
xét
ậy hàm số ( ) 2 1 yfx =− có 3 điểm cực tr
Câu 102: Cho hàm số b
)yfx
. Bả
xét dấu bên dưới là của đạo hàm ( )2 fx . Hàm số
) ( )
gxfxx
có bao nhiêu điểm cực tr
?
suy ra b
ng xét d
u của hàm số ( )yfx = .
Từ bảng xét dấu ta suy ra hàm số ( ) ( ) 2 22gxfxx=++ có 3 điểm cực trị.
Câu 103: Cho hàm số ( )yfx = có đạo hàm liên tục trên và có đồ thị hàm số ( ) 1 yfx =− như hình vẽ Số điểm cực trị của hàm số ( ) 2 22yfxx=−− là A. 3. B. 5. C. 7. D. 9. Lời giải Chọn C Cách 1. Chọn hàm đại diện Quan sát đồ th


Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 147
ị ta thấy ( ) 1 yfx =− là hàm số bậc ba có 3
ệm 2,0,1xxx=−== . Ta chọn: ( ) ( ) ( ) ( )( )( )12113111 yfxxxxxxx =−=+−=−−+−−+−−+ ( ) ( )( )31 fxxxx =−−− Xét ( ) 2 22yfxx=−− ( ) ( ) 2 22.22yxfxx =−−− ( )( )( )( ) 222 2222322122 xxxxxxx =−−−−−−−−−− ( )( )( )( ) 222 22252322 xxxxxxx =−−−−−−−− . 2 2 2 1 1 16 250 01 230 3 220 13 x x x xx yx xx x xx x = = = −−= ==− −−= = −−= = , đều là nghiệm bội lẻ. Vậy hàm số có 7 điểm cực trị. Cách 2. Xét dấu đạo hàm y .
nghi
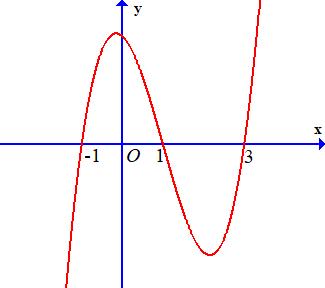
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 148 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Từ đồ thị hàm số ( ) 1 yfx =− suy ra ( ) 3 01 0 x fxx x = == = . Xét ( ) ( ) ( ) 22 2222.22 yfxxyxfxx =−−=−−− . +) 22 22 22 1 11 16 223250 01 221230 3 220220 13 x xx x xxxx yx xxxx x xxxx x = == = −−=−−= ==− −−=−−= = −−=−−= =
nghiệm đều là nghiệm bội lẻ +) Bảng xét dấu của y : Suy ra hàm số ( ) 2 22yfxx=−− có 7 điểm cực trị. Câu 104: Cho hàm số ( )yfx = xác định trên và hình vẽ dưới đây là đồ thị của hàm số ( ) 3 31yfxx =+− . Hàm số ( ) 2 2 yfxx =− có bao nhiêu điểm cực đại? A. 4. B. 3. C. 2. D. 5. Lời giải Chọn C Xét ( ) 2 2 yfxx =− , ta có ( ) ( ) 2 222 yxfxx =−−
, trong đó các

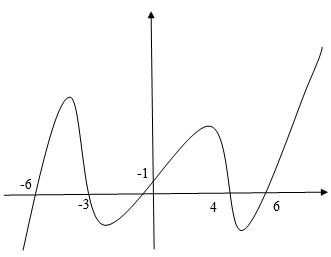
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn
42
ễn
Thuận
Huế ĐT:
Page 149 Chuyên
ố
12
và
ạn Từ đồ thị ta suy ra ( ) 3 33 3 1315 3101313 33135 xtxx fxxxtxx xtxx =−=+−=− +−===+−= ==+−= . Đặt 3 31txx=+− . Suy ra ( ) 5 03 35 t ftt t =−
= . Do đó ( ) 2 22 2 25 2023 235 xx fxxxx xx −=− −=−= −= .
2 2 2 11 1 25 03 23 7 2355 x x x xx yx xx x xx x = = =− −=− == −= = −= =−
Suy
số ( ) 2 2 yfxx =−
ố ( )
=
đạ
ụ
Số điểm cực trị của hàm số ( ) 2 23yfxx=−+ là A. 9. B. 7. C. 6. D. 5. Lời giải Chọn A Xét hàm số ( ) ( ) 2 23ygxfxx ==−+ Ta có: ( ) ( ) ( ) 2 2 1 22230 230 x yxfxx fxx = =−−+= −+= .
Ánh
Nguy
Cư Trinh
Hòa TP
0984164935
luyện thi: Tuyển sinh vào lớp 10 T
t Nghiệp THPT BDKT Toán 10; 11;
Sưu tầm
biên so
==
Suy ra
Bảng xét dấu:
ra hàm
có 2 điểm cực đại. Câu 105: Cho hàm s
yfx
có
o hàm liên t
c trên và có đồ thị hàm số ( ) 3 yfx
=− như hình vẽ
Phương trình ( ) 2 230fxx −+= có 7 nghiệm bội đơn phân biệt suy ra hàm số ( ) ( ) 2 23ygxfxx ==−+ có đúng 7 điểm cực trị trong đó có 4 điểm cực trị dương. Do đó hàm số ( ) 2 23yfxx=−+ có 9 điểm cực trị
Câu 106: Cho hàm số ( )fx xác định và liên tục trên , trong đó ( ) ( ) 1 gxfx =− là hàm số bậc ba có đồ thị như hình vẽ
Hàm số 1 2 x yf x = có tối đa bao nhiêu điểm cực trị? A. 7. B. 5. C. 3. D. 6. Lời giải
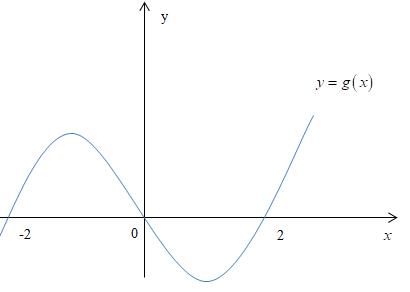
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 150 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Từ đồ thị ta có ( ) 6 3 31 4 6 x x yfxx x x =− =− =−=− = = Đặt ( ) 9 6 3'04 1 3 t t txftt t t = = =−== =− =−
( ) 2 2 22 2 2 239 236 230234 231 233 xx xx fxxxx xx xx −+= −+= −+=−+= −+=− −+=− 2 2 2 2 2 260 1 230 3 210 12 240 17 260 xx x xx x xx x xx x xx −−= =− −−= =
−−=
Do đó
= −+= = −+= .
sau: Suy ra đồ thị hàm số ( )yhx = có 2 điểm cực trị • Ta thấy đường thẳng 0 y = cắt đồ thị ( )yhx = tại nhiều nhất 4 điểm. Vậy hàm số ( ) 1 2 x yhxf x == có tối đa 6 điểm cực trị. Câu 107: Cho hàm đa thức ( )yfx = liên tục, có đạo hàm trên , có bảng xét dấu của ( )1 yfx =+ như sau: Số điểm cực đại của hàm số ( ) 2 1 yfxx=++ là A. 3 B. 2 C. 4 D. 1 Lời giải Chọn D Từ bảng xét dấu của ( )1 fx + ta có:


CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 151 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Chọn D • Từ đồ thị hàm số ( ) 1 yfx =− ta có: ( ) 2 100 2 x fxx x =− −== = Đặt 1 tx =− . Suy ra ( ) 3 01 1 t ftt t = == =−
• Xét ( ) 1 2 x hxf x = với mọi 2 x ( ) ( )2 11 22 x hxf x x = ( ) 1 1 23 1 2 01 5 2 1 2 3 2 x x x x hx x x x x =− = == = = • Ta có bảng biến thiên
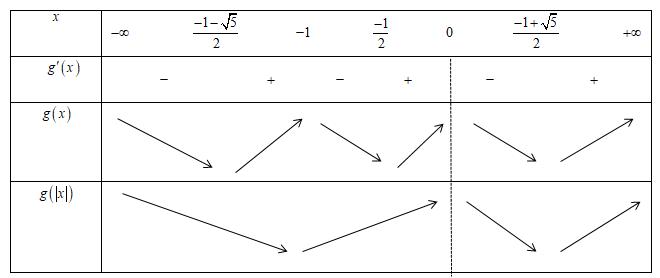

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 152 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) 1 100 1 x fxx x =− +== = . Đặt 1 tx=+ ta có ( ) 0 01 2 t ftt t = == = . Mặt khác ta có: ( ) ( ) ( ) ( ) ( ) 2212110gxfxxgxxfxx =++=+++= 2 2 2 0 1 2x10 15 10 2 11 15 2 12 1 2 x x x xx xx x xx x = =− += −+ = ++= ++= = ++= = Ta có bảng
Vì ( ) ( ) 2 1 ygxfxx ==++
(
2
ố
m
ực trị
ủa
ố
A. 3 B. 2 C. 4 D. 1
biên thiên sau:
và ( ) ( ) 2 1 gxfxx=++ đối xứng nhau qua trục tung nên hàm số
)
1 yfxx=++ có một điểm cực đại. Câu 108: Cho hàm số ( )yfx = có đạo hàm liên tục trên . Đồ thị hàm số ( )25yfx=+ như hình vẽ. Tìm s
điể
c
c
hàm s
( ) 3 2 yfx=− .

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 153 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn A ( ) ( ) ( ) ( ) 2 23 3 0 320 201 x yxfxy fx = =−= −= loaïi Ta có ( ) ( ) 1 1 250 2 4 x x fx x x =− = += = = loaïi . Đặt 25tx=+ . Suy ra ( ) 3 07 9 t ftt t = == = ( ) 3 33 33 3 33 3 2355 12799 291111 x xx xxx xx x = −== −=== −== = Vậy hàm số có 3 điểm cực trị Câu 109: Cho hàm số ( )fx thỏa mãn ( ) ( ) 30,20ff−= và có đồ thị ( ) ' yfx = là đường cong trong hình bên. Hàm số ( ) ( ) 42142411gxfxxxx =−+−+ có bao nhiêu điểm cực tiểu? A. 4. B. 7. C. 3. D. 5. Lời giải Chọn A Từ đồ thị của ( ) ' yfx = ta thấy ( )fx đồng biến trên 1;2 , suy ra ( ) ( ) 120ff= . Xét hàm số ( ) ( ) ( ) ( ) ( ) 423 142411;''42824hxfxxxxhxfxxx =−+−+=−−+ Vẽ đồ thị hàm số 3 42824yxx=−+ trên cùng mặt phẳng tọa độ, ta lập được bảng biến thiên của ( )hx và ( ) ( )gxhx =
Vậy hàm số ( ) ( ) 42142411gxfxxxx =−+−+ có 4 điểm cực tiểu. Câu 110: Cho hàm số ( ) 42 fxaxbxc =++ có đồ thị của hàm số ( )yfx = và ( )yfx = như hình vẽ bên dưới. Gọi ,, ABC là các điểm cực trị của đồ thị hàm số ( )yfx = có hoành độ lần lượt là 123 ,, xxx .
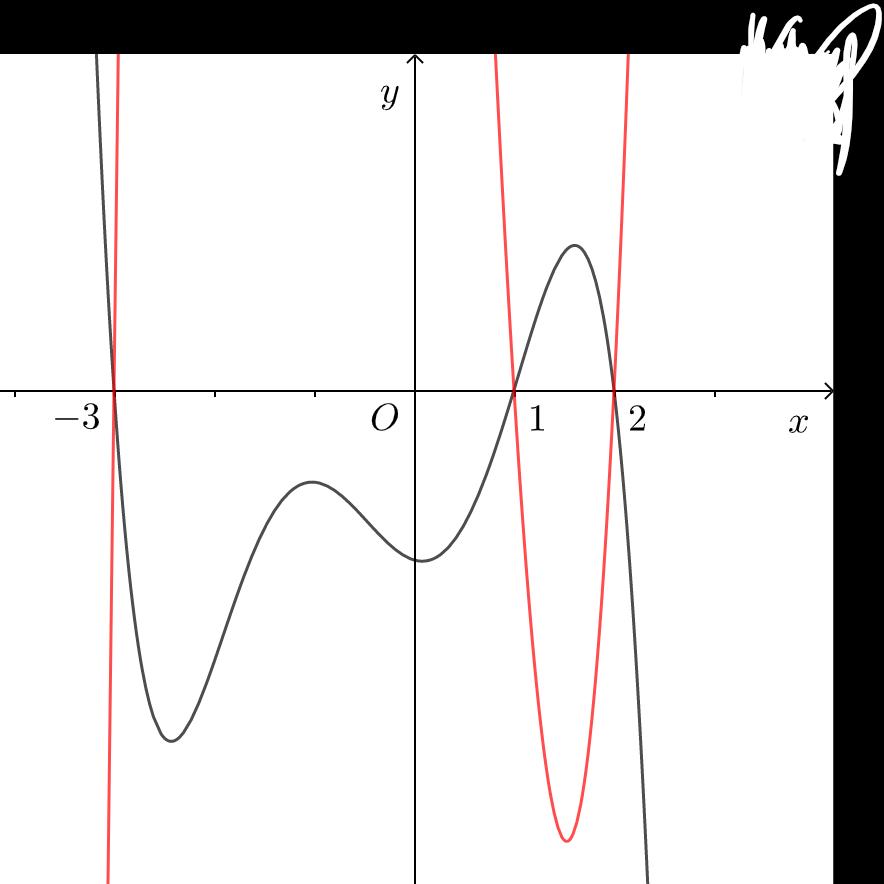


Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 154
Biết diện tích hình phẳng giới hạn bởi các đường ( ) 12,0,, yfxyxxxx ==== là 1S và diện tích của tam giác ABC là S . Tính 13Pxx = , với 1 1 S = và 1 S = . A. 0 P = . B. 1 P = . C. 1 P =− . D. 2 P = . Lời giải Chọn C
Ta có: 123 ,, xxx là các điểm cực trị của hàm số ( )yfx = , với 2 0 x = và 13xx
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
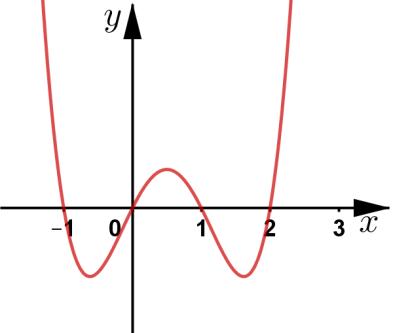
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 155
Theo giả thiết: ( ) ( ) ( ) 1 0 11 1d101 x Sfxxffx ==−= Và giả thiết: ( ) ( ) ( )311 1 1.01 2 ABC Sxxffx =−−= Ta có hệ: ( ) ( ) ( ) ( ) ( ) 1 31 1 311 3 13 13 01 2 1 1 01 1 0 2 0 ffx xx x xxffx x xx xx −= −= =− −−= = += += . Vậy 13.1Pxx==− . Câu 111: Cho ( )fx là đa thức bậc ba, biết hàm số ( ) 2 1 yfxx =−+ có đồ thị là đường cong trong hình vẽ Hỏi có bao nhiêu giá trị nguyên của tham số m thuộc 10;10 để hàm số ( ) 2 4 yfxm =+− có năm điểm cực trị? A. 8. B. 9. C. 10. D. 11. Lời giải Chọn B +) Ta có ( )fx là đa thức bậc ba nên ( ) ' fx là đa thức bậc hai ( ) 2
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 fxx −+ là đa thức bậc 4. Do đó từ đồ thị hàm số ( ) 2 1 yfxx =−+ ta có: ( ) ( ) ( )( ) 2 1112fxxaxxxx −+=+−− , với 0 a . ( ) ( )( ) ( )( ) 22222121311fxxaxxxxaxxxx −+=−−−=−+−−+− Suy ra ( ) ( )( ) '31, fxaxxx =−− +) Xét hàm số ( ) 2 4 yfxm =+− có ( ) 2 2 ''4 4 x yfxm x =+− +
1
nghiệm đó. 121mm+ . Mà m và 10;10 m− nên 2;3;4;...;10 m
số ()yfx = trên ( ;2−− , đồ thị hàm số ()yfx = trên đoạn 2;3 và đồ thị hàm số ()yfx = trên ) 3;+ . Số điểm cực trị tối đa của hàm số ()yfx = là A. 5. B. 6. C. 3. D. 7. Lời giải
Chọn A
Trên ( );2−− ta thấy ( )fx triệt tiêu và đổi dấu qua điểm 0xx = . Do đó trên miền này hàm số ()yfx = có 1 cực trị.
Trên ( )2;3 ta thấy ()fx đạt cực tiểu tại 1xx = và đạt cực đại tại 2xx = . Do đó trên miền này hàm số ()yfx = có 2 cực trị
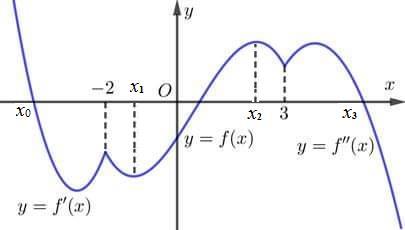

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 156
Vậy có 9 giá trị của m thỏ
ầ
Cho
số ()
=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) 2 0 '0 '40 x y fxm = = +−= 22 22 00 4141 4343 xx xmxm xmxm == +−=+=+ +−=+=+ Hàm số ( ) 2 4 yfxm =+− có 5 điểm cực trị '0y = có 5 nghiệm phân biệt và ' y đổi dấu khi x qua các
a mãn yêu c
u bài toán. Câu 112:
hàm
yfx
có đạo hàm cấp hai liên tục trên . Hình vẽ bên dưới là đồ thị hàm
Trên ( ) 3;+ ta thấy ( )fx triệt tiêu và đổi dấu từ dương sang âm khi đi qua 3xx = . Do đó trên miền này hàm số ()yfx = có tối đa 2 cực trị Vậy hàm số ()yfx = có tối đa 5 điểm cực trị
Câu 113: Cho hàm số đa thức bậc bốn ( )yfx = thỏa mãn ( ) 1 0 2 f = , hàm số ( )fx có đồ thị như hình vẽ


Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG D
HÀM ĐỂ KHẢO SÁT HÀM SỐ
ỤNG ĐẠO
Page
157
Số điểm cực trị của hàm số ( ) 2 181 3 x gxfx =−− là
.
.
Lời
ải Chọ
Xét hàm số ( ) 2 181 3 x hxfx =−− . Ta có: ( ) 6.12 3 x hxfx =−−− ( ) 01111 3333 hxffxxxx =−=−−=−− Dựa vào đồ thị ta thấy: 111 33 xx f −=−− 11 3 11 3 13 3 x x x −=− −= −= 6 0 6 x x x = = =−
.
A. 4
B. 3
C. 6. D. 7.
gi
n D


CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 158 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Từ đồ thị hàm số ( )yfx = là đồ thị hàm đa thức bậc ba, có hai điểm cực trị là ( )0;2 A và ( )2;2 B . Suy ra: ( ) ( ) 3243 1 322 4 fxxxfxxxxd =−+=−++
=−−=−−=−=− Bảng biến thiên: Vậy
ố ( )
x
=−− có
ị Câu
số ( ) ( ) 5432 0 yfxaxbxcxdxexfa ==+++++ và hàm số ( )yfx = có đồ thị như hình vẽ dưới đây Đặt ( ) ( ) 32 9 31962022 2 gxfxxxx =−−+−+ . Hàm số ( ) ygx = có bao nhiêu điểm cực trị? A. 3. B. 9. C. 5. D. 7. Lời giải Chọn A Ta có: ( ) ( ) ( ) ( ) ( ) 2 2 33127963313313316gxfxxxfxxx =−−+−=−−−−−−
0984164935
Do ( ) 1 0 2 f = nên 1 2 d = . Ta được: ( ) 43 11 2 42fxxxx=−++ Ta có: ( ) ( ) ( ) 181 6183361832182 42 hff −=−=−=−=− ( ) ( ) 63 01810 2 hf=−= ( ) ( ) ( ) 181 6181361812182 42 hff
hàm s
2 181 3
gxfx
7 điểm cực tr
114: Cho hàm
( ) ( ) ( ) ( ) 2 03131312gxfxxx =−=−+−+
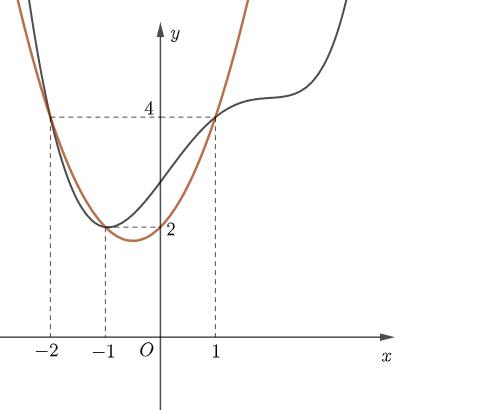
Đặt 31tx=− ta được phương trình: ( ) 2 2 fttt =++ Từ đồ thị của hai hàm số ( )yft = và hàm 2 2 ytt=++ ta có phương trình ( ) 2 2 fttt =++ có ba nghiệm 1 t =− , 1 t = và 2 t =− . Với 1 t =− thì 0 x = . Với 1 t = thì 2 3 x = . Với 2 t =− thì 1 3 x =
Khi đó phương trình ( ) 0 gx = có ba nghiệm 0 x = , 2 3 x = và 1 3 x =
Bảng biến thiên của hàm ( )ygx =
Từ bảng biến thiên của hàm ( )ygx = suy ra đồ thị hàm ( ) ygx = có 3điểm cực trị
Câu 115: Hình vẽ dưới đây là đồ thị của hàm số ()yfx = . Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số (1) yfxm =−+ có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 159
TH1: 03 m . Đồ thị hàm số có 7 điểm cực trị không thỏa mãn yêu cầu bài toán.
TH2: 3 m = . Đồ thị hàm số có 5 điểm cực trị thỏa mãn yêu cầu bài toán.


TH3: 36 m . Đồ thị hàm số có 5 điểm cực trị thỏa mãn yêu cầu bài toán.
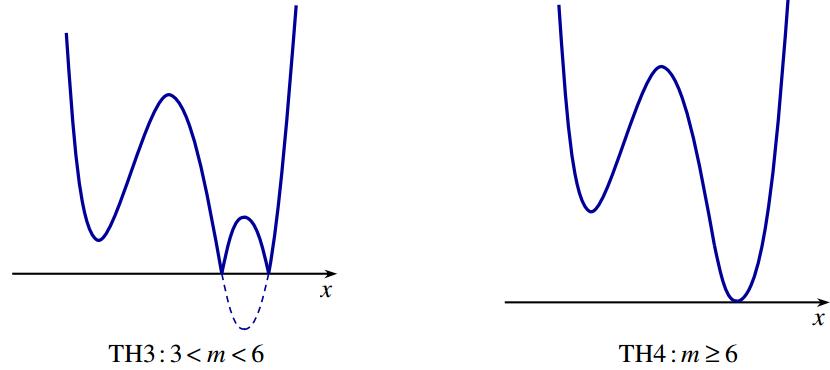
TH4: 6 m . Đồ thị hàm số có 3 điểm cực trị không thỏa mãn yêu cầu bài toán.
Vậy 36 m . Do * m nên }{3;4;5 m
Vậy tổng giá trị tất cả các phần tử của S bằng 12.
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
viên: Huỳnh Văn Ánh 42
ễn
Thuận
ế
Page 160
ện thi:
ể
ớ
Tố
ệ
12
và
ạn B. 15. B. 18. C. 12. D. 9. Lời giải
Nhận xét: Số giao điểm của ( ) ( ) : Cyfx = với Ox bằng số giao điểm của ( ) ( ):1Cyfx =− với Ox . Vì 0 m nên ( ) ( ):1 Cyfxm =−+ có được bằng cách tịnh tiến ( )
Cyfx =− lên
m
vị
Giáo
Nguy
Cư Trinh
Hòa TP Hu
ĐT: 0984164935
Chuyên luy
Tuy
n sinh vào l
p 10
t Nghi
p THPT BDKT Toán 10; 11;
Sưu tầm
biên so
Chọn C
( ):1
trên
đơn
nên theo tính chất hàm liên tục thì phương trình ( ) 0 fx = và ít nhất ba nghiệm và ( )fx là hàm bậc ba nên phương trình ( ) 0 fx = sẽ có ba nghiệm. Do đó hàm số ( )fx có hai điểm cực trị Hàm số ( )fx có 5 điểm cực trị. Câu 117: Biết Cho hàm số yfx liên tục trên . Đồ thị hàm số 3 fx được cho trong hình dưới. Hàm số 4 1 8 gxfxxx có tối đa bao nhiêu điểm cực đại. A. 3. B. 5. C. 2. D. 4. Lời giải
Chọn A Xét hàm số 4 1 8 hxfxxx liên tục trên Khi đó 3 1 1 2 hxfxx , nên 3 1 01 2 hxfxx . Đặt 3 3 xttx == , khi đó xét ( ) ( ) 3 1 '1 2 hxftt =−+
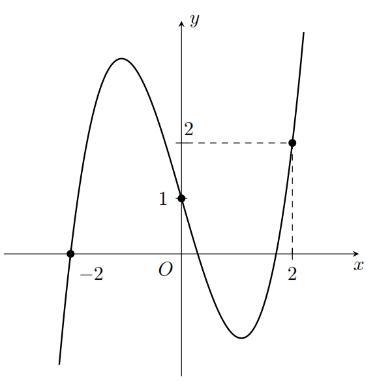
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 161 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 116: Cho hàm số ( ) 32 2 fxxbxcxd =+++ thỏa mãn 42160 bcd+++ và 9354 bcd−+ . Hàm số ( )yfx = có tất cả bao nhiêu điểm cực trị? A. 2 B. 3 C. 5 D. 4 Lời giải Chọn
Ta
( ) ( ) ( ) ( ) ( ) ( ) 32 32 limlim2 354930 242160 limlim2 xx xx fxxbxcxd fbcd fbcd fxxbxcxd →−→− →+→+ =+++=− −=−+−+ =+++ =+++=+
x
→− −
x
→+
C Ta có ( ) 32 2 fxxbxcxd =+++ ( )fx liên tục trên
có:
Ta có ( ) ( ) lim.30
fxf
, ( ) ( ) 320ff− , ( ) ( ) lim.20
fxf
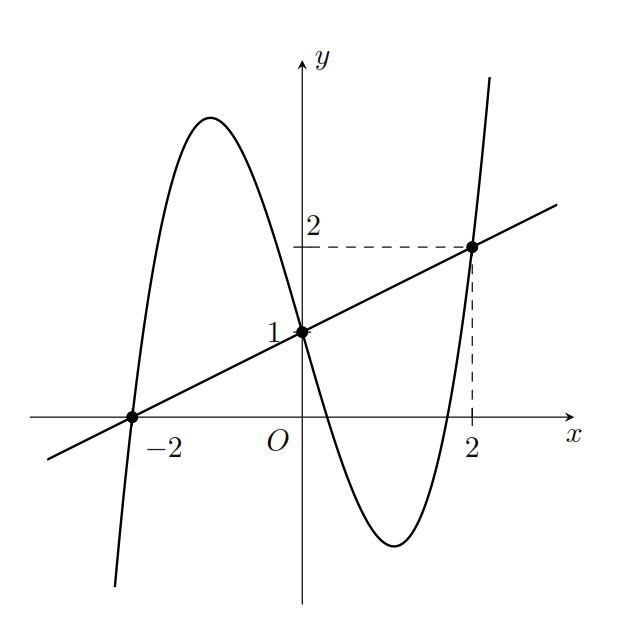

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 162
=−=− === = = Ta có bảng biến thiên của hàm số ( )hx như sau Vậy hàm số ( ) ( )gxhx = có tối đa 3 điểm cực đại. Câu 118: Cho hàm số ( ) 32 fxaxbxcxd =+++ , ( ) ,,, abcd thỏa mãn 0 a , 2022 d , 20220 abcd+++− . Tìm số điểm cực trị của hàm số ( ) 2022 yfx=− . A. 2. B. 1. C. 3. D. 5. Lời giải Chọn D Xét hàm số ( ) ( ) 2022 gxfx=− 32 2022 axbxcxd =+++− Ta có: ( ) ( ) 02022 12022 gd gabcd =− =+++− . Theo giả thiết, ta được ( ) ( ) 00 10 g g . Lại do: 0 a nên ( ) ( ) lim lim x x gx gx →+ →− =+ =− ( ) 1:0 g và ( ) 0:0 g .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vẽ đồ thị hàm số 1 1 2 yt=+ cùng hệ tọa độ với đồ thị hàm số ( ) 3 ' ft ta được như hình dưới Do đó ( ) 3 3 22 '000 2 2 tx hxtx t x
Do đó: ( ) ( ) ( ) ( ) ( ) ( )
( ) 0 gx = có 3 nghiệm phân biệt thuộc khoảng ( ) ; .
gg gg gg
.00 0.10 1.0
y O Khi đó đồ thị hàm số ( )ygx = có dạng f(x)=abs((1/3)*(x+1)*(2x-1)*(x-2)) -2 -1 1 2
y O Vậy hà
x
x m số ( ) 2022 yfx=− có 5 điểm cực trị Câu 119: Cho hàm số ( ) ( ) 432 0 fxaxbxcxdxea =++++ liên tục trên và thỏa mãn điều kiện: 0 168420 abcd abcd −+− +++ và ( ) ( ) gxfxe =− . Hỏi ( ) ( ) ggx có tối đa bao nhiêu điểm cực trị biết ( ) ( ) 00 lim.lim0 xx gxgx−+→→ ? A. 11. B. 8. C. 14. D. 17. Lời giải Chọn A Ta có: ( ) ( ) 432 gxfxeaxbxcxdx =−=++ Lại có: ( ) 00 g = mà ( ) ( ) 00 lim.lim0 xx gxgx−+→→ 0 x = là nghiệm kép của phương trình ( ) 0 gx = ( )gx đạt cực trị tại 0 x = Mặt khác: ( ) lim0 x gx →− ( ) 10 g − ( )gx đạt cực trị tại 0 x =
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 163
Hay hàm số ( )ygx = có đồ thị dạng f(x)=(1/3)*(x+1)*(2x-1)*(x-2) -2 -1 1 2
( ) 20 g ( ) lim0 x gx →+
Nên ta có thể phác họa bảng biến thiên của đồ thị ( )ygx = như sau:
Ta được bảng biến thiên của ( ) ygx = :
Ta được bảng biến thiên của ( ) ygx = : ( ) ygx= có 5 cực trị
= ==


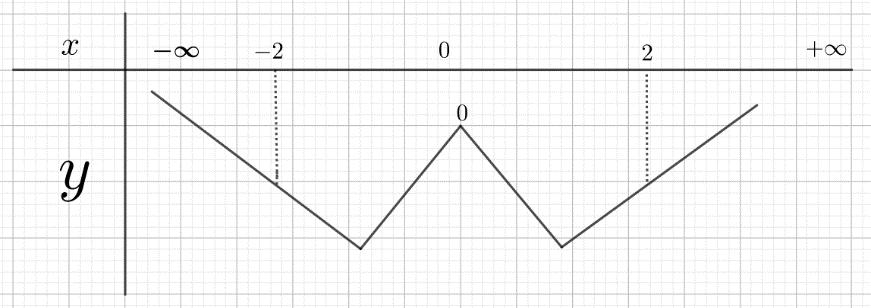
gx ggxgxggx ggx
Mặt khác: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 0 .0 0
Gọi các điểm cực trị của ( )gx là ( );0;10;02 abab− ( ) ( ) 0 gx = ( ) gxa = ( ) 0 gx = ( ) gxb =
Cho hàm số ( )yfx = có đạo hàm liên tục trên và có đồ thị hàm số ( )yfx = như hình vẽ bên dưới:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 164
=
Bảng biến thiên: Suy ra hàm số ( )yhx = có duy nhất một điểm
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
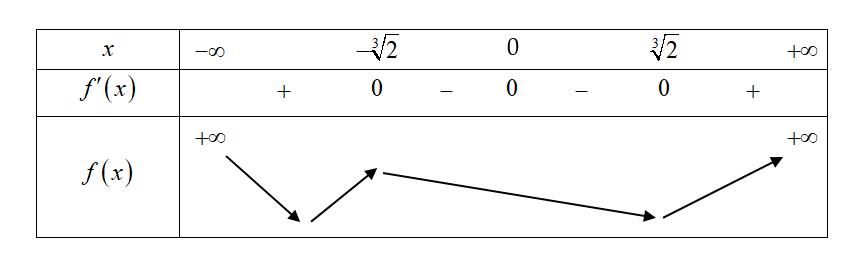
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 165
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Số điểm cực trị của hàm số ( ) ( ) 3 1 gxfx=+ là A. 3. B. 5. C. 4. D. 2. Lời giải Chọn A Đặt ( ) ( ) 3 1 hxfx=+ ( ) ( ) ( ) 3 1 gxhxfx ==+ . ( ) ( ) 3 3 23 3 3 3 0 2 11 3.100. 11 2 13 x x x hxxfxx x x x = =− +=− =+== += = +=
cực trị dương. Vậy số điểm cực trị của hàm số ( ) ( ) gxhx = là 3. Câu 120: Cho hàm số ( ) ( )( ) 2 156fxxxx =−−+ . Hỏi có bao nhiêu giá trị của
(
B.
D.
Lời
Đồ
( ) ( ) ( ) 2 2 2121211
=−−−+=−−−+−
x y 3 -1 O 1
tham số m để hàm số
) ( ) 2 212 gxfxxxm =−−−+ có đúng 9 điểm cực trị? A. 5
6 C. 7
3
giải Chọn B
thị hàm số
gxfxxxmfxxm
đối xứng qua đường thẳng 1 x = Xét hàm số ( ) 2 42,1yfxxmx =−++ .

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 166 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) 2 2 22 2 2 2 2 2 2 420 41 24420421 4 422 41 423 x x xxml xxm yxfxxmxxm xxm xxm xxm xxm = = −++= −+=− =−−++=−++= −=− −++= −−=− −++= Hàm số ( ) ( ) 2 212 gxfxxxm =−−−+ có đúng 9 điểm cực trị khi và chỉ khi đường thẳng ym =− cắt các đồ thị hàm số 22241,4,41 yxxyxxyxx =−−=−=−+ tại 3 điểm phân biệt có hoành độ lớn hơn 1 và khác 2 Ta có đồ thị Từ đồ thị, ta được: 22 137 0;;1;;2; 4334 222 mm m mm −− −−− . Câu 121: Cho hàm số ( ) 32 1 fxxmxnx=++− với , mn là các tham số thực thỏa mãn 0 72(2)0 mn mn + ++ . Tìm số cực trị của hàm ( ) yfx = . A. 2 B. 5 C. 9 D. 11 Lời giải Chọn D Ta có ( ) 32 1 fxxmxnx=++− là hàm đa thức nên liên tục trên , mặt khác ( ) ( ) ( ) ( ) 10 1.20 272(2)0 fmn ff fmn =+ =++ suy ra ( ) 0 fx = có ít nhất một nghiệm thuộc khoảng ( )1;2
Lời giải Chọn A Đặt ( ) ( ) ( ) 2 11211gxhxfxxm =−=−−−+− Do đồ thị hàm s
( )1 yhx
có được khi t
Ta có ( ) ( ) lim;lim xx fxfx →−→+ =−=+ ta có bảng biến thiên của hàm ( )yfx = Hàm số ( )yfx = có 2 cực trị dương nên hàm số ( ) yfx = có 5 cực trị. Mặt khác, đồ thị hàm số ( ) yfx = cắt trục Ox tại 6 điểm. Suy ra hàm số ( ) yfx = có 11 cực trị. Câu 122: Cho hàm đa thức ( )yfx = Hàm số ( )yfx = có đồ thị như hình vẽ sau: Có bao nhiêu giá trị của m để 0;6, m 2m để hàm số ( ) ( ) 2 212 gxfxxxm =−−−+ có đúng 9 điểm cực trị? A. 6. B. 5. C. 7 . D. 3. = = −+−=
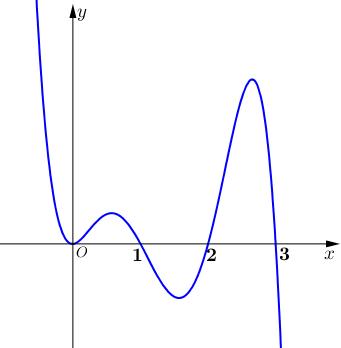
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 1 0 210* x y fxxm

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 167
ố
=−
ị
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 ột đơn vị nên số cực trị của hàm số ( )1 yhx=− bằng số cực trị hàm ( ) yhx = Như vậy, để hàm số ( )gx có 9 cực trị thì hàm số ( ) ( ) 2 21yhxfxxm ==−+− có 4 cực trị có hoành độ dương. Lại có: ( ) ( ) 2 2221.yxfxxm =−−+− ( ) ( ) 2
nh tiến đồ thị hàm số ( ) yhx = sang phải m
Để hàm số đã cho có 9 cực trị thì phương trình ( ) ( ) ( )1,2,3 phải có 3 nghiệm dương phân biệt khác 1. Khi đó, ta có: 112024 22134628 −−
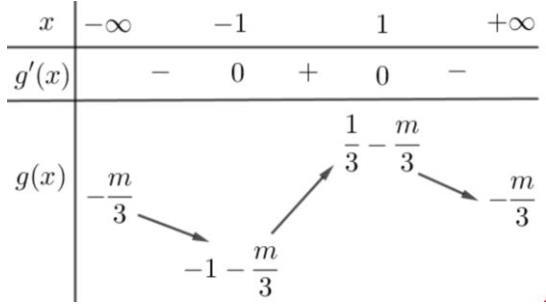
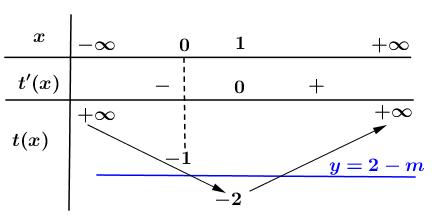
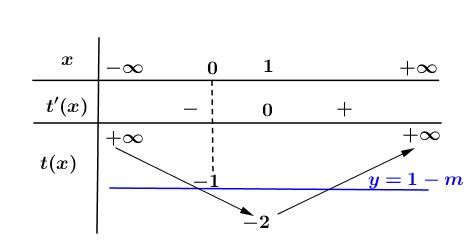
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 168 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( )* ( ) ( ) ( ) 2 2 22 2 2 2112111 2122122 2132133 xxm xxm xxmxxm xxm xxm −−=− −+−= −+−=−−=− −+−= −−=− Xét hàm số ( ) ( ) 2 2122txxxtxx =−−=−
−−− mmm mmm Do
Vậ
Xét
2
Ta
2
x gxx xx
2m
20;1;2;3;4;7. m
y có 6 giá trị m thỏa yêu cầu bài toán. Câu 123: Có bao nhiêu số nguyên m để hàm số 2 13 xm fx xx có ít nhất 3 điểm cực trị? A. 3 B. 5 C. 2 D. 4 Lời giải Chọn A
hàm số
13 xm gx xx
có
2 2 1 001. 1
Bảng biến thiên
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 169
) 2 4 gxffxfxm =−− có 17 điểm cực trị là A. 1652 B. 1653 C. 1654 D. 1651 Lời giải Chọn A Ta có: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 4 40 4 24 . fx x f x fx g xfxm ffxfxm ffxm = −−= ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 22 2 22 2 22 01 24022 4043 41 42424 42 42425 fx fxfx fxfxmfxfxm fxfxmvoly fxfxmfxfxm fxfxm fxfxmfxfxm = −== −−=−= −−=− −−=−=+ −−= −−=−−=− Dễ thấy ( )1 có 2 nghiệm đơn và ( )2 có 3 nghiệm đơn Vậy tổng số nghiệm đơn của phương trình ( ) ( ) ( )3;4;5 là 12 thì thỏa mãn Đặt ( ) ( ) ( ) ( ) ( ) ( ) 2 1;2 4220 ;; x uuxfxfxufxfxu xabc − ==−=−= .
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Hàm số gx có hai điểm cực trị 1, 1 xx với mọi m nên hàm số fxgx có ít nhất 3 điểm cực trị khi và chỉ khi phương trình 0 gx có nghiệm bội lẻ 1 10313332;1,0 0 0 3 mm m m m m Câu 124: Cho hàm số bậc ba ( )yfx = có đồ thị như hình vẽ Tổng tất cả các giá trị nguyên của tham số m để hàm số ( ) ( ) ( ) (
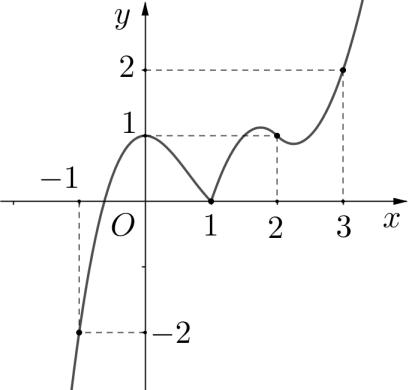
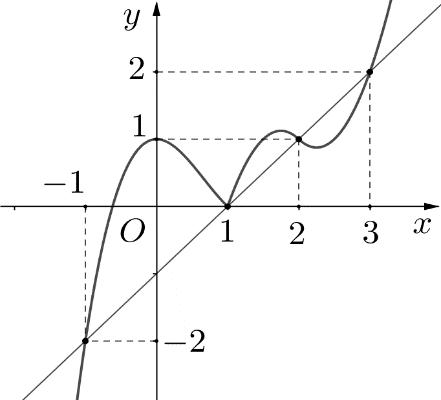
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 170 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Các nghiệm trên được sắp thứ tự từ nhỏ đến lớn như sau: 12 abc − Bảng biến thiên của hàm số ( ) ( ) 2 4 ufxfx =− Vậy số giao điểm của các đường thẳng 2;;2ymymym =−==+ với đồ thị ( )ux là 12 điểm phân biệt 3260 32601581;0;1;...;571652 m mmS m −− −−= −+ . Câu 125: Cho hàm số ()yfx = xác định trên có 9 (3)8,(4), 2 ff− 1 (2). 2 f Biết rằng hàm số () = yfx có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số ( )2 2()1=−−yfxx có bao nhiêu điểm cực trị? A. 4 B. 5 C. 6 D. 7 Lời giải Chọn B Đặt ( )2 ()2()1 gxfxx=−− . Ta xác định số điểm cực trị của hàm số () = ygx Ta có '()2'()2(1) =−−gxfxx Xét đường thẳng ():1 dyx=− . Đồ thị hàm số ()yfx = và đường thẳng () d có 4 điểm chung có hoành độ lần lượt 1;1;2;3 nhưng chỉ các điểm 1;2;3 là cực trị hàm số. ( )2 ()2()1 =−−gxfxx vì khi x đi qua điểm 1 thì '()gx không đổi dấu Bảng biến thiên của hàm số g 60 -3 -4 -4 -4 +∞ +∞ + + + 0 0 0 0 +∞ 0 c 2 b 1 a ∞ u u' x
Từ giả thiết ta thấy (2)0;(4)0,(3)0 −ggg nên phương trình ()0gx = có đúng 2 nghiệm Từ và suy ra đồ thị hàm số () = ygx có 5 điểm cực trị Câu 126: Cho hàm đa thức ( )yfx = , biết hàm số ( )yfx = có đồ thị như hình vẽ bên: Biết rằng ( ) 00 f = . Hỏi hàm số ( ) ( ) 63gxfxx =− có bao nhiêu điể

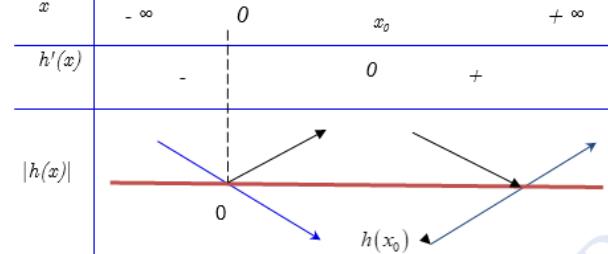
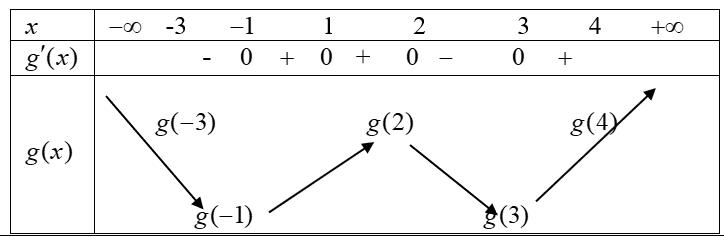
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 171
m cực đại? A. 2 B. 4 C. 3 D. 1 Lời giải Chon D ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 63562236 36 0 633210 210 x hxfxxhxxfxxxxfx xfx = =−=−=−= −= Đặt ( ) ( ) ( ) ( ) ( ) 362686 216120,. uxxfxuxxfxxfxx =−=+ và ( ) ( ) lim lim x x ux ux →− →+ =− =+ suy ra phương trình ( ) ( ) 36 210uxxfx =−= có nghiệm duy nhất. Giả sử ( ) ( ) ( ) 3636 1 210 2 uxxfxxfx =−== có nghiệm là 0x 3 0000xx Ta có bảng biến thiên sau:
Dựa vào bảng biến thiên ta thấy hàm số ( ) ( )gxhx = có 1 điểm cực đại.
Câu 127: Cho hàm số ( ) 32 yfxaxbxcxd ==+++ thỏa mãn 0,2021,20210adabcd +++− . Số điểm cực trị của hàm số ( ) 2021 yfx=− là A. 4. B. 2. C. 5. D. 6. Lời giải
Chọn C
Đặt ( ) ( ) 32 20212021gxfxaxbxcxd =−=+++− . Số cực trị của hàm số ( )ygx = bằng số cực trị của hàm số ( )ygx = cộng số nghiệm đơn của phương trình ( ) 0 gx =
Ta có ( ) ( ) 020210,120210 gdgabcd=−=+++−
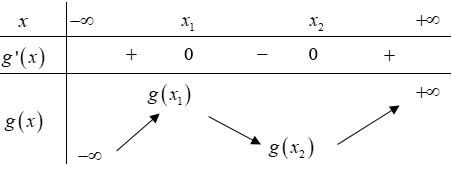
Giả sử hàm số ( )ygx = không có cực trị, kết hợp với 0 a ta có ( )gx đồng biến trên . Suy ra, ( ) ( )01gg Do đó, hàm số ( )ygx = có hai cực trị 12 , xx ( 12xx ).
Từ đây ta lập được bảng biến thiên của hàm số ( )ygx =
Chỉ có thể xảy ra một trong 5 trường hợp dưới đây.
Trường hợp 1: ( ) ( ) 12 001xxgg
Trường hợp 2: ( ) ( ) 12 101 xxgg
Trường hợp 3: ( ) ( ) ( ) ( ) ( ) 1 12 2
00 010 10 gxg xxgx gxg
=
có 3 nghiệm đơn. Do đó, hàm số ( )ygx = có 5 điểm cực trị.
=
nghiệm đơn. Do đó, hàm số
ygx
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO
Ố
HÀM ĐỂ KHẢO SÁT HÀM S
Page 172
có 3
( )
= có 5 điểm cực trị.
(
(
12 2
xxgx
= có
Trường hợp 4: ( ) ( ) ( ) ( ) ( ) 1 12 2 (
00 010 10 gxg xxgx gxg có
Trường hợp 5:
) ( )
) ( ) ( ) 1
00 010 10 gxg
gxg
3 nghiệm đơn. Do đó, hàm số
)ygx =
5 điểm cực trị. Vậy hàm số ( ) 2021 yfx=− có 5 điểm cực trị. Câu 128: Cho ( )fx là hàm bậc bốn thỏa mãn ( ) 00. f = Hàm số ( )fx đồ thị như hình vẽ
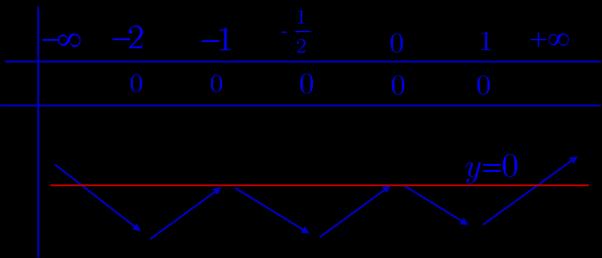
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 173 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Hàm số ( ) 2432 2()22 gxfxxxxxx =+−−++ có bao nhiêu điểm cực trị: A. 4 B. 6 C. 7 D. 5 Lời giải Chọn C Đặt ( ) 2432 2()22 hxfxxxxxx =+−−++ 232 22 ()2(21)()4622 2(21)()(1) hxxfxxxxx xfxxxx =++−−++ =++−+− 22 ()02(21)()(1)0 hxxfxxxx =++−+−= 22 1 2 ()(1)0 x fxxxx =− +−+−= Đặt 2 .txx =+ Ta được ()1ftt =− . Vẽ đồ thị hàm số ( )yft = và 1 yt=− trên cùng một hệ trục tọa độ ta được Dựa vào đồ thị suy ra: 2 2 2 0 2 2 1 00 1 2 2 2 x xx t x txx x t xx x = +=− =− =− =+= = = += =− Bảng biến thiên: x y 1 2 1 3 2 O 1 x y 1 2 1 3 2 O 1
0984164935
Qua bảng biến thiên ta thấy hàm số ( ) ()gxhx = có 7 cực trị.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 174
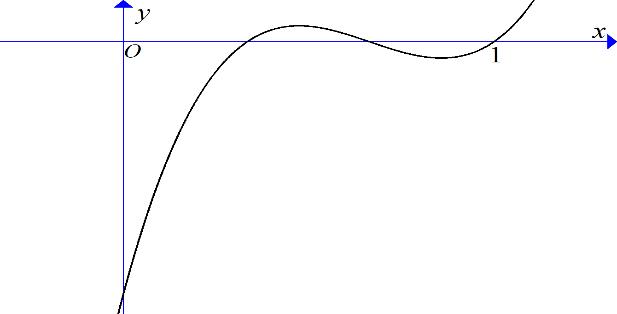
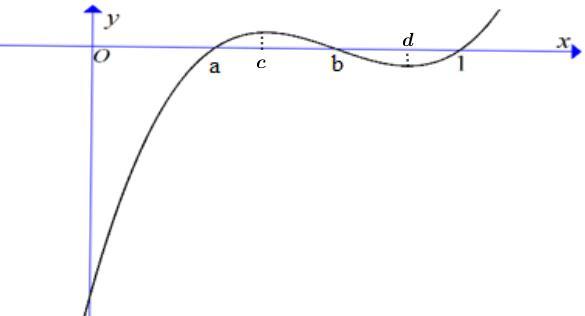



CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 175 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn BÀI 2: CỰC TRỊ CỦA HÀM SỐ HƯỚNG DẪN GIẢI CHI TIẾT Câu 129: Cho hàm số bậc ba ( )yfx = có đồ thị như hình vẽ Tìm số điểm cực trị của hàm số ( ) ( ) 2 yfgx = với ( ) 22 424 gxxxxx =−+− A. 17. B. 21. C. 23. D. 19. Lời giải Chọn D Xét hàm số ( ) 22 424 gxxxxx =−+− : TXĐ: 0;4 ( ) ( ) ( ) ( ) 2 22 2241 2422,0;4 44 x xx gxxxx xxxx =−+=− ; CHƯƠNG I ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Mỗi phương trình ( ) ( ) ( ) ( )4,5,7,8 có 4 nghiệm phân biệt Phương trình ( )6 có nghiệm kép 1 x = Phương trình ( )2 có 3 nghiệm phân biệt Tất cả các nghiệm của các phương trình ( ) ( ) ( ) ( ) ( )2,4,5,7,8 là phân biệt và y đổi dấu qua các nghiệm đó. y không đổi dấu qua 1 x = . Vậy hàm số đã cho có 19 điểm cực trị Câu 130: Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số là:
( )yfx = ( ) ( ) yffx =
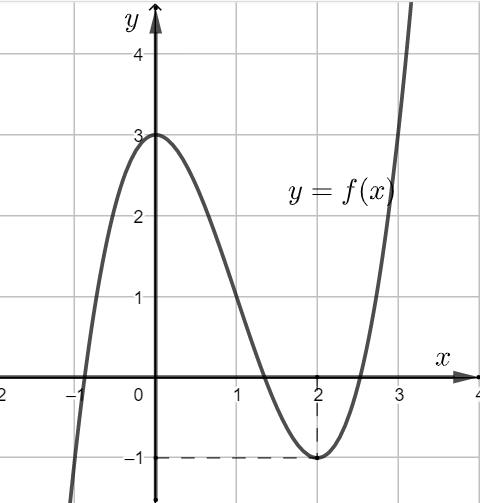
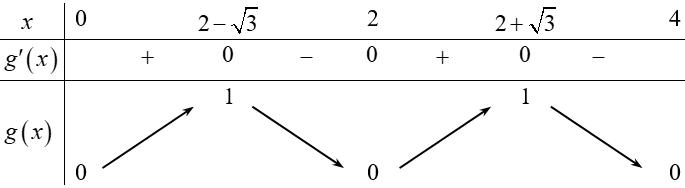
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 176
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) 2 22 0 4123 x x gx x xx = = = = −= ( ) ( ) 2 yfgx = ( ) ( ) ( ) ( ) ( ) 2. yfgxgxfgx= ; ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 01 002 03 fgx ygx fgx = == = ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 4 1501 16 gxa gxbab gx = = = ( ) ( ) ( ) ( ) ( )( ) 7 301 8 gxc acbd gxd = =
A. . B. C. ` D.
4 8 7 6
Chọn B
Ta có : Xét

Dựa vào đồ thị hàm số ta thấy:
Phương trình có 3 nghiệm
Phương trình có 3 nghiệm
Lời giải
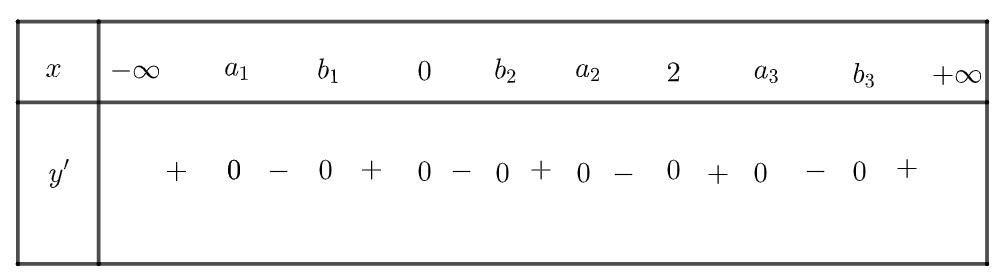
Trong đó và tất cả các nghiệm đều là nghiệm đơn. Khi đó ta có bảng xét dấu đạo hàm của hàm số như sau: Vậy hàm số có điểm cực trị. Câu 131: Cho hàm số ( )yfx = là hàm đa thức và có đồ thị hàm số ( ) 2 1 fx như hình vẽ. Hỏi hàm số ( ) 2 21fxx−+− có bao nhiêu điểm cực đại?
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 177
( ) ( ) ( ) ( ) ( ) yffxyfxffx == ( ) ( ) 0 0 2 0 ()0 ()0 ()2 x fx x y fx ffx fx = = =
= = = =
( ) 0 fx = 123 aaa ( ) 2 fx = 123 bbb 112233 02 abbaab ( ) ( ) yffx = 8


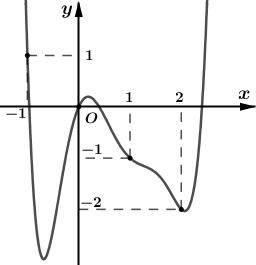
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 178 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 3. B. 2. C. 4. D. 15. Lời giải Chọn A Ta thấy ( ) 2242222 1(2)(2)(4)(1)2(1)3fxaxxxaxxaxx −=−+=−=−−−− ( ) 2 lim10 x fxa →+ −=− . Suy ra ( ) ( ) 2 23fxaxx =−− Đặt 2 21uxx=−+− 2 2 2 2 3,221,2 1, 1221, ()'()12 21, 3,11 11 1,21,1 1 xxx xx xxxxx uxux xx xxx xx xxx +− + −+− == −−− −−+− −− −+− ta thấy 1 '()02uxx== Câu 132: Cho hàm số ( )yfx = có đạo hàm trên . Đồ thị hàm số ( )yfx = như hình vẽ bên dưới. Số điểm cực tiểu của hàm số ( ) ( ) ( )( )2213gxfxxx =++++ là A. 2 B. 3 C. 1 D. 4 Lời giải
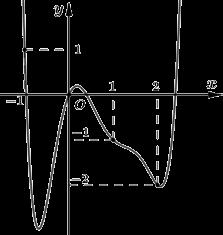
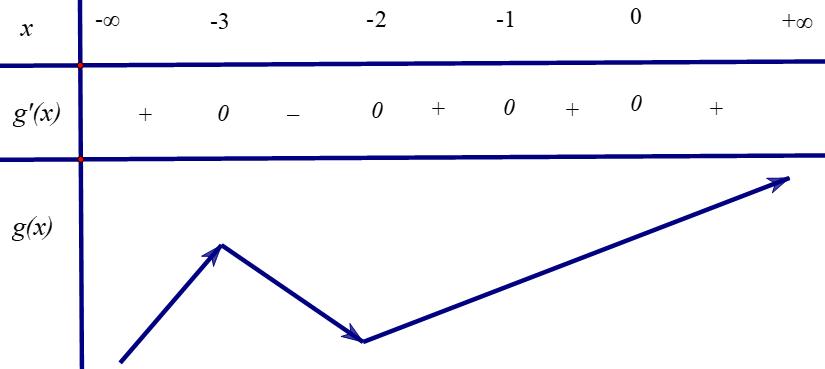
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 179 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Chọn C Xét ( ) ( ) ( )( ) ( ) ( )2 22132221gxfxxxfxx=++++=+++− Tập xác định D = ( ) ( ) ( )2222gxfxx =+++ . ( ) ( ) ( )022gxfxx =+=−+ 213 202 211 220 xx xx xx xx +=−=− +==−+==− +== Ta có ( ) ( ) ( )022gxfxx +−+ 12032 xx −+−− . Bảng biến thiên Dựa vào bảng biến thiên ta có hàm số ( )ygx = có một điểm cực tiểu là 2 x =− Vậy hàm số ( )ygx = có một điểm cực tiểu. Câu 133: Cho hàm số bậc ba ( )yfx = có đồ thị như hình vẽ
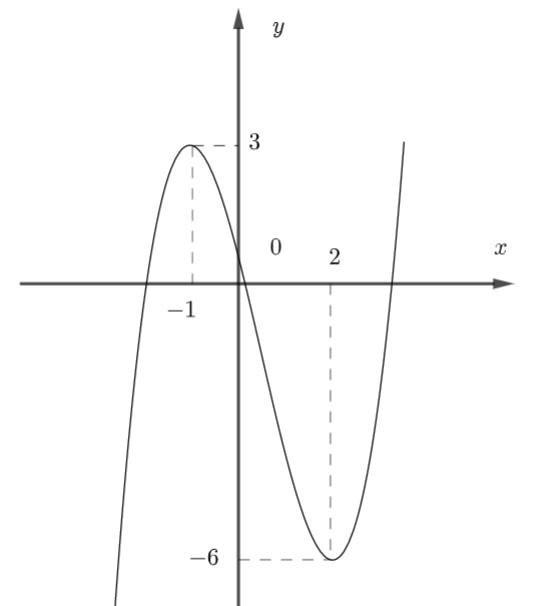
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 180 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Số các giá trị nguyên của tham số m để hàm số ( ) ( ) ( ) ( ) 2 4 gxffxfxm =−+ có 23 điểm cực trị là A. 0. B. 3. C. 4. D. 6. Lời giải
Đặt ( ) ( ) ( ) ( ) ( ) ( ) 2 1;2 4220 ;; x uuxfxfxufxfxu xabc − ==−=−= Trong đó: 12 abc − . Bảng biến thiên của hàm số ( ) ( ) 2 4 ufxfx =− . Ta có ( ) ( ) ( ) ( ) ( ) . gxfumgxumfum =+=++ . Do đó số điểm cực trị của hàm số ( ) ( ) ( ) ( ) 2 4 gxffxfxm =−+ chính là số nghiệm bội lẻ của hệ sau: ( ) ( ) 0 0;1;;2;;1;;2; 022;2 um umum umxabcxabc umm um fum += =−=− +=−− − + −−+ = += Suy ra số điểm cực trị của hàm số ( )gx phụ thuộc vào số giao điểm của các đường thẳng 2;2; ymymym =−−=−+=− với đồ thị ( )ux . 60 -3 -4 -4 -4 +∞ +∞ + + + 0 0 0 0 +∞ 0 c 2 b 1 a ∞ u u' x
0984164935
Chọn A
m mm m 2 2 2 2 2
là:
3. B. 9. C. 7. D. 5. Lời giải

gxfxx
có
−−−− 21 2,10 20 2,01 21
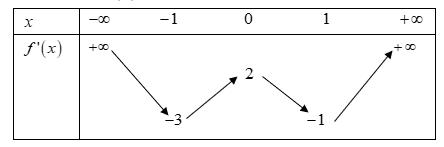
−−+− −−− . Câu 134: Cho hàm số ( )yfx = , bảng biến thiên của hàm số ( ) ' fx như sau: xxa xxbb fxx xxcc xxd
)
( )
) −=− −=− −= −= −= Ta có ( )2 2 2111xxx−=−−− 2 21xxa −=− vô nghiệm. Các phương trình ( ) 2 2,10xxbb−=− ; ( ) 2 2,01xxcc−= ; 2 21xxd−= này mỗi phương
yfxx hai nghiệm phân biệt, các nghiệm đều khác nhau và
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG D
HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 181
Số điểm cực trị của hàm số (
2 2
=−
A.
Chọn C Đặt ( ) (
2 2
=− Ta
( ) ( )
ỤNG ĐẠO 2
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 gxxfxx =−− . ( ) ( ) 2
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 1 '0 '20 x gx fxx
Mặt khác các nghiệm ;1;;2; xabc − là các nghiệm đơn, do đó yêu cầu bài toán trở thành tìm m nguyên để các đường thẳng trên cắt đồ thị ( )ux tại 18 điểm phân biệt 423 423 43 = = −= ( ) ( ) ( )
'22'2
trình đều có
khác 1
Vì khi đi qua các nghiệm của phương trình 3231xxm−+= dấu của ( ) 32 3 fxxm −+ không đổi nên dấu của ( )gx chỉ phụ thuộc các nghiệm của hai phương trình còn lại. Vậy hàm số ( )ygx = có 8 điểm cực trị khi và chỉ khi mỗi phương trình 3230xxm−+= và 3232xxm−+= phải có ba nghiệm phân biệt.
Xét hàm số ( ) 32 3 hxxx =−+ , ta có ( ) 2 36 hxxx =−+ ; ( ) 0 0 2 x hx x
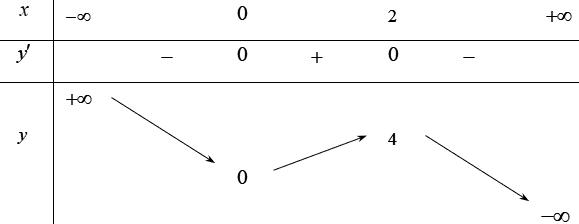
= = = .
Bảng biến thiên của hàm số ( )yhx =
Dựa vào bảng biến thiên, ta thấy điều kiện để mỗi phương trình 32 3 xxm−+= và 3232xxm −+=− phải có ba nghiệm phân biệt
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 182
Chọn D
0 ()01 2 x fxx x = == = , trong đó 1 x = là
ệm bộ
chẵ
x =
( ) ( ) ( ) 23236.3 gxxxfxxm =−−+ . ( ) 2 32 32 32 32 32 32 0 360 2 31 031 30 30 32 32 x xx x xxm gxxxm xxm xxm xxm xxm = −= = −+= =−+= −+= −+= −+= −+=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) 0 gx = có 7 nghiệm đơn ( ) ( ) 2 2 gxfxx=− có 7 điểm cực trị Câu 135: Cho hàm số ()fx có đạo hàm 2 ()(1)(2), fxxxxx =−− . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ( ) 32()3 gxfxxm =−+ có đúng 8 cực trị? A. 4. B. 3. C. 2. D. 1. Lời giải
Ta có
nghi
i
n, 0
và 2 x = là các nghiệm đơn.
là 02424 mmm − Vậy chỉ có một giá trị nguyên của m thỏa mãn là 3 m = . Câu 136: Cho hàm số ( )yfx = xác định trên , và có đồ thị ( ) ' fx như hình vẽ. Tìm m để hàm số ( ) 2 1 11 gxfxm x =++− có ít nhất 3 điểm cực trị.
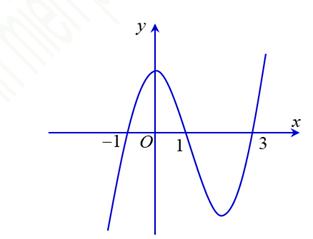
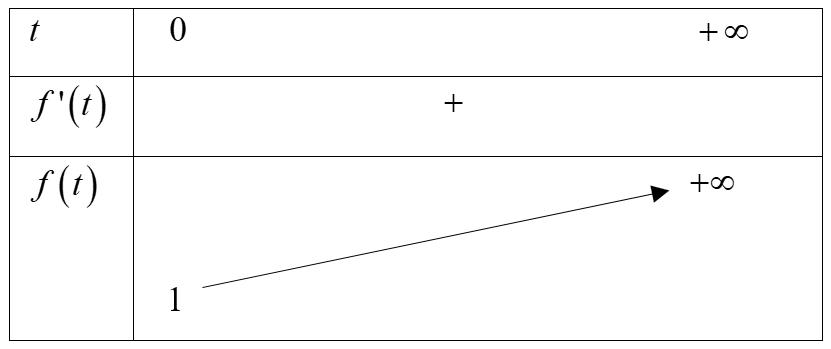
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 183
ạ
A. 2 m B. 0 m C. 0 m D. 2 m Lời giải
ập xác định của ( )
= . Nhận thấy
số
là hàm số chẵn. Xét trường hợp 0 x : ( ) ( ) 2 1.gxfxxm =++− ( ) ( ) 2 2
x gxfxxm x =++−+ +
c trị thì phương trình phải có ít nhất 2 nghiệm dương phân biệt. Do đó các phương trình,, phải có ít nhất 2 nghiệm dương phân biệt. Xét hàm số ( ) 2 1 fttt=++ có ( ) 2 10,0 1 t ftt t =+ + . Ta có bảng biến thiên: Suy ra để,, có ít nhất 2 nghiệm dương phân biệt thì 110mm+ .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên so
n
Chọn B T
:\0gxD
hàm
( ) 2 1 11 gxfxm x =++−
1.1 1
Xét phương trình ( ) ( ) ( ) 2 2 01.10* 1 x gxfxxm x =++−+= + ( ) ( ) ( ) 2 2 22 2 2 111 11 11112 13 133 xxm xxm xxmxxm xxm xxm ++=− ++−=− ++−=++=+ ++−= ++=+ Để hàm số ( ) 2 1 11 gxfxm x =++− có ít nhất 3 điểm cự
Câu 137: Cho hàm số ()fx là hàm bậc 5 và đồ thị hàm số ()fx như hình vẽ bên dưới. Có bao nhiêu số nguyên ( )10;10 m− để hàm số ( ) 2 yfxm =+ có đúng 5 điểm cực trị?
A. 3 B. 7 C. 10 D. 9 Lời giải
Chọn D
Ta có ()fx giao với trục hoành tại các điểm có hoành độ 0;2;3xxx=== , trong đó điểm có hoành độ 2 x = là điểm tiếp xúc với trục hoành do đó ( ) ( ) ( ) 2 23,fxaxxx =−− với 0, aa .
Khi đó ( ) ( )( ) ( ) 2 2222 2223. yxfxmaxxmxmxm =+=++−+−
TH1: Nếu 22 30;30, mxmxmx ++− khi đó y đổi dấu qua 0 x = , hàm số có đúng một điểm cực trị.
TH2: Nếu 0 m khi đó y đổi dấu qua 5 điểm là 0;;3 xxmxm ==−=− hàm số có đúng 5 điểm cực trị.
TH3: Nếu 2 030,mxmx + khi đó y đổi dấu qua 3 điểm là 0;3 xxm ==− , hàm số có đúng ba điểm cực trị.

Vì 0 m và ( )10;10 m− nên 9;8;7;6;5;4;3;2;1 m−−−−−−−−− . Vậy có tất cả 9 số nguyên m thỏa mãn
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM
Ố
ĐỂ KHẢO SÁT HÀM S
Page 184
yêu cầu bài
Câu 138: Cho hàm số ( ) 42 fxaxbxc =++ có đồ thị
ọ
số tự
ố điể
cực trị của hàm số ( ) ( ) ( ) 22 2022 gxffxm =− . Khi dó với mọi m ta
có ;, n . Giá trị của + bằng
toán.
như hình vẽ bên. G
i
nhiên n là s
m
luôn
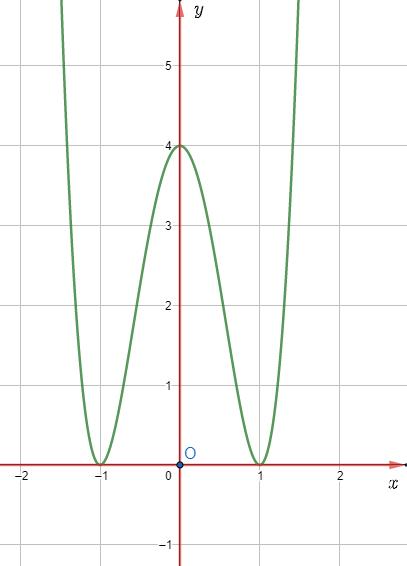
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 185 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 18. B. 25. C. 21. D. 15. Lời giải Chọn A Giả thiết suy ra ( ) ( )2 2 41fxx=− Ta có ( ) ( ) ( ) ( ) ( ) ( ) 22 22022.2022 gxffxmffxm =−− ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 22 2 22 222 22022.2022.2. 642022112022. ffxmffxmfxfx fxmxffxmfx =−− =−−−− Số cực trị của ( )gx chính là số nghiệm bội lẻ của ( ) ( ) ( ) ( ) ( ) 2 2 0 1;0;1 20220* 20221;0;1 fx x ffxm fxm = − −= −− Dễ dàng lập được bảng biến thiên của ( ) 2 fx
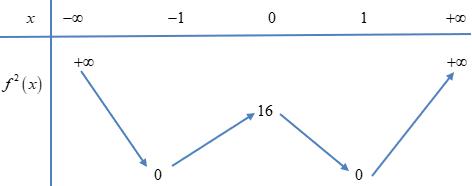
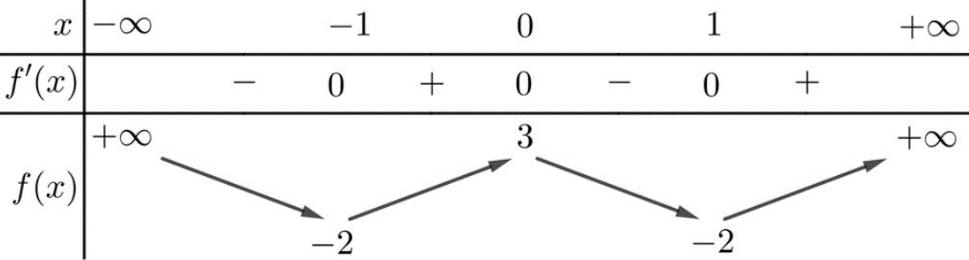
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 186 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do đó ( )* có tối đa 12 nghiệm đơn do đó hàm số ( )gx có tối đa 15 cực trị và có tối thiểu 3 cực trị. Vậy 18.+= Câu 139: Cho ( )fx là hàm đa thức và cho hàm đa thức bậc ba ( ) ( )1 gxfx=+ thỏa mãn ( ) ( ) ( ) ( )1312xgxxgx −+=++ . Số điểm cực trị của hàm số ( ) 2 245yfxx=−+ là A. 1. B. 3. C. 2. D. 5. Lời giải Chọn B ( ) ( ) ( ) ( )11gxfxgxfx =+=+ . ( ) ( ) ( ) ( )1312xgxxgx −+=++ hay ( ) ( ) ( ) ( )1413xfxxfx −+=++ Cho ( ) ( ) ( ) ( )( ) 40 1 34 1 30 f x fxaxx x f = = =−− =− = ( ) ( ) ( ) 22 24544.245 yfxxyxfxx =−+=−−+ ( ) 22 2 22 1 1122 4402 024542410 245022 24532420 2 1 x xx x x yxxxx fxx x xxxx x = == = −= =−+=−+= −+= + = −+=−+= = Vậy hàm số có 3 cực trị Câu 140: Cho hàm số đa thức bậc bốn ( )yfx = có bảng biến thiên như sau: Số điểm cực trị của hàm số ( ) ( ) ( ) 2 3 1 gxxxfx=−+ là A. 11. B. 8. C. 13. D. 10.
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 187 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn D Từ giả thiết ( )( ) 2 10yaxxa =− 42 2 a yaxxc =−+ Theo bài ra ( ) ( ) 42 3 03 20 5103 3 2 12 42 b y a yxx aa b b y = = = =−+ = −+=− =− . ( ) ( ) ( ) ( ) ( ) ( ) ( )( ) ( ) ( ) ( ) ( ) ( ) ( )( ) 22 323 23 1311211 131121 gxxxfxgxxfxfxxxfx gxfxxfxfxxx =−+=−+++−+ =+−+++− ( ) ( ) ( ) ( ) ( ) ( )( ) ( ) 23 102 0 3112103 fx gx xfxfxxx += = −+++−= + Giải ( ) ( )102 fx += . Dựa vào đồ thị phương trình có 4 nghiệm phân biệt 1234 ,,, xxxx + Giải ( ) ( ) ( )( ) ( ) 23 3112103 xfxfxxx −+++−= Hay ( ) ( ) ( ) ( ) ( ) ( ) 423 23 3151101340110 xxxxxxx −+−++++−+−= Đặt ( ) ( ) ( ) ( ) ( ) ( ) ( ) 423
Ta có (
(
(
(
(
( ) ( ) ( ) ( ) ( ) 3.20 2.10 1.0.50 0.5.00 0.0.50 0.5.10 hh hh hh hh hh hh −− −− −− − ( )yhx = liên tục trên nên ( )yhx = liên tục trên các đoạn 3,2,2;1,1;0.5,0.5;0,0;0.5,0.5;1 . Từ và phương trình có ít nhất 6 nghiệm đơn 5678910 32,21,10.5,0.50,00.5,0.51 xxxxxx −−−−−−− Mà phương trình bậc 6 có tối đa 6 nghiệm nên chỉ có 6 nghiệm phân biệt đơn nên đổi dấu
23 315110134011 hxxxxxxxx =−+−++++−+− ( )yhx = liên tục trên . ( ) ( ) ( ) ( ) ( ) ( ) ( ) 3731893 36878,222,16,0.5,02,0.5,186 6464 hhhhhhh −=−=−−=−===−=
)
)
) ( )
) ( )
)
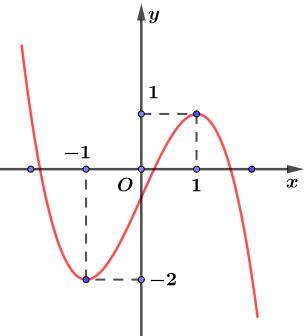
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 188
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vậy hàm số ( ) ( ) ( ) 2 3 1 gxxxfx=−+ có 10 điểm cực trị Câu 141: Cho hàm số yfx như hình vẽ. Hỏi hàm số 2 1 2 fx yfefxfx có tất cả bao nhiêu điểm cực trị? A. 5. B. 6 . C. 3 . D. 9 . Lời giải Chọn B 2 1 ''.'.1 2 fxfx yfefxfxfxefx 2 '0 '010 1 1 '0 2 2 fx fx fx yefx fefxfx . 1 '0 1 x fx x Đặt tfx . Giải 1:10. t et Xét 1'1tt htethte . '00htt . BBT:
Do đó 0 htt ht tiếp xúc với trục Ox . Pt 1 có nghiệm kép, nghiệm này không là cực trị
Giải 2 :
t t
2 2
ett ett .
1 1 3 2 1 1 4 2
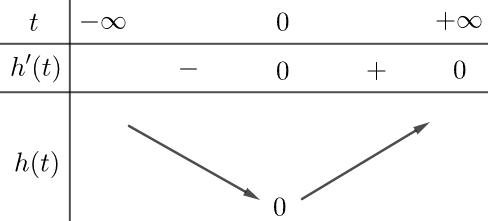
Giải 3: 2 1 10. 2 t ett
Xét 2 1 1'10 2 tt ktettktett '00ktt
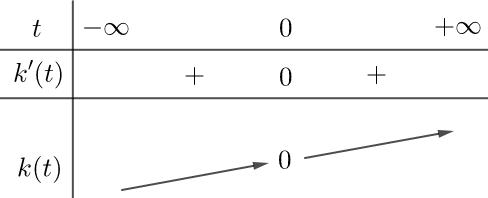
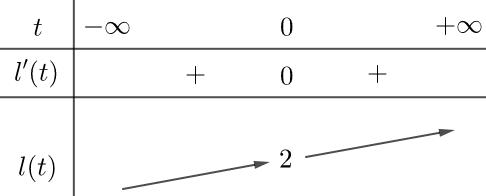
BBT: Pt 3 có nghiệm 00tfx .pt 3 có 3 nghiệm phân biệt 1231,0;1,1xxx .
Giải 4: 2 1 10. 2 t ett
Xét 2 1 1'10 2 tt ltettltett . '00 ltt
BBT:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 189
Nhận xét: 2 1 1 2 t ltett có 2.30ll 0 lt có 1 nghiệm 1 3;2 tt 1fxt có 1 nghiệm Pt 4 có 1 nghiệm.
Vậy '0gx có 6 nghiệm phân biệt.
Do vậy hàm số có 6 cực trị
Câu 142: Cho hàm số ()yfx = liên tục trên thoả mãn ( ) 20 f −= và đồ thị hàm số ( )yfx = được cho như hình vẽ bên dưới. Hỏi hàm số ( ) ( ) 2 2gxfxx=−− có bao nhiêu điểm cực tiểu? A. 3. B. 1. C. 0 . D. 2. Lời giải
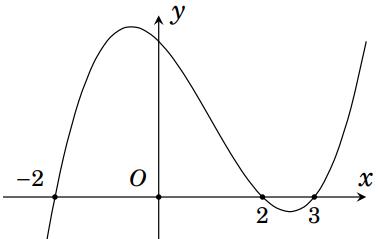

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO
HÀM SỐ
SÁT
Page 190
Bả
Xét ( ) ( ) ( ) ( ) 2 1 2 d222 f S fxxff ==−−= và ( ) ( ) ( ) 3 2 2 d23 S fxxff ==− Theo đồ thị ta thấy ( ) ( ) ( ) ( ) 12 22330Sff S ff − Ta có ( ) ( ) ( ) ( ) 22212.. =−−−−−− gxxfxxfxx ( ) ( ) ( ) 2 2 120 0 0 0 x fxx x gx fx += −−= −−= = Ta thấy:
Chọn D
ng biến thiên của ( )fx :
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 191 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 1 120 2 +==− xx ( ) ( ) ( ) 2 22 2 2 1 2 2 0 3 −−=− = −−= =− −−= −−= N xx x x xx x xx fxV VN Nhận xét đồ thị hàm số ( )fx tiếp xúc với
ố
ị
ố
ờ
Chọn C Ta có ( ) ( ) 34243618 =−−+ yxxfxxm Cho ( ) 42 3 180 0 4360 −+= = −= fxxm y xx . *) Với 3 0 4360 3 = −= = x xx x có 3 nghiệm đơn. *) Với ( ) 4242 42 4242 18018 180 18821882 −+=−=− −+= −+=−=−+ xxmxxm fxxm xxmxxm Xét hàm số ( ) 42 18=− gxxx . ( ) ( ) 3 0 436,0 3 = =−= = x gxxxgx x Ta có bảng biến thiên của hàm số ( ) 42 18=− gxxx
đường thẳng 0 = x nên phương trình ( ) 2 0 −−=fxx cho nghiệm bội chẵn, do đó ( ) 2fxx không đổi dấu khi đi qua các nghiệm của nó. Vậy ( )gx có ba điểm cực trị 1 ,1,2 2 == =− xx x . Vì ( ) ( ) 2 2 limlim →→ =−−=+ xx gxfxx nên ( )gx có số điểm cực đại không vượt quá số điểm cực tiểu. Do đó ( )gx có hai điểm cực tiểu. Câu 143: Cho hàm số ( ) = yfx có đạo hàm là ( ) 2 82 =− fxxx . Có bao nhiêu giá trị nguyên dương của tham số m để hàm s
( ) 42 18 =−+ yfxxm có đúng 7 cực tr
? A. 83. B. vô s
C. 80. D. 81. L
i giải
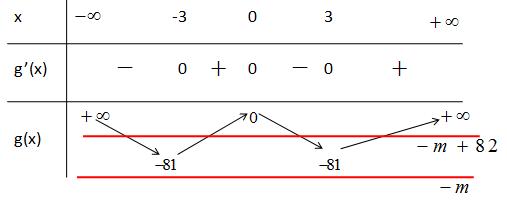
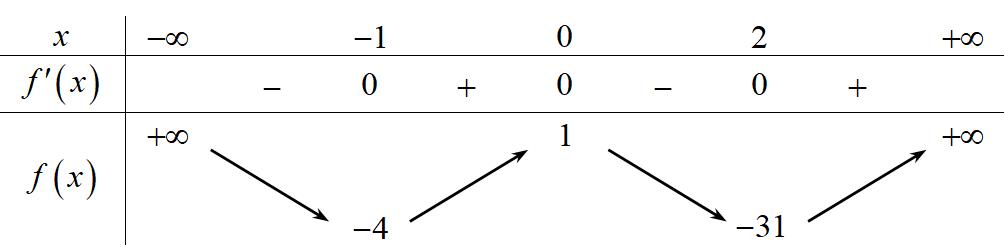
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 192 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Để hàm số ( ) 42 18 =−+ yfxxm có đúng 7 cực trị thì ( ) 42180 −+=fxxm phải có 4 nghiệm đơn khác 0,3 . Do đó dựa vào bảng biến thiên ta có 81 82163 81820 0 820 m m m m mm −− −−+ −+− Mà + m nên 83;84;...161;162 m nên có 80 giá trị. Câu 144: Cho hàm số ( ) 432 34121yfxxxx ==−−+ . Số điểm cực trị của hàm số ( ) ( ) yffx = bằng A. 13 B. 10 C. 3 D. 11 Lời giải Chọn A Ta có ( ) 32 121224 fxxxx =−− , ( ) 32 012122400,1,2 fxxxxxxx =−−===−=
=
= == = (
xxx =−== . ( ) ( ) ( ) ( ) 1(3) 20(4) 2(5) fx fx fx =− = = Theo
thiên thì và có bốn
và có
0 y = có 13
Bảng biến thiên Cách 1: Ta có ( ) ( ) ( )yffxfx
, ( ) ( ) ( ) ( ) ( ) ( ) 0(1) 0.0 0(2) fx yffxfx ffx
) 11;0;2
bảng biến
nghiệm phân biệt
hai nghiệm phân biệt. Do đó phương trình
nghiệm phân biệt và y
đổi dấu khi đi qua các nghiệm đó. Vậy hàm số đã cho có 13 điểm cực trị.
Cách 2: Sử dụng phương pháp ghép trục. Đặt ( ) ( ) ( ) gxffx = , ta có bảng biến thiên của ( )gx như sau Nhìn vào bảng biến thiên ta thấy hàm số đã cho có 13 điểm cực trị. Câu 145: Cho hàm số bậc bốn ( ) 432 fxaxbxcxdxa =++++ có đồ thị hàm số ( ) ' yfx = là đường cong như hình vẽ sau: Hàm số ( ) ( ) 2 212 yfxfxx =−− có bao nhiêu

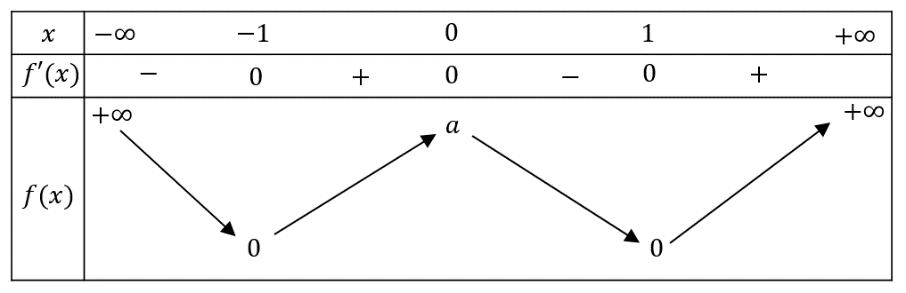

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 193
điểm cực trị? A. 3. B. 7. C. 4. D. 1. Lời giải Chọn B ( ) ( ) 43232432 fxaxbxcxdxafxaxbxcxd =++++=+++ Dựa vào đồ thị hàm số ( )fx ta có ( ) lim400. x fxaa →+ =+ Hàm số ( )fx cắt trục hoành tại 3 điểm có hoành độ lần lượt là 1;0;1 nên ta có hệ phương trình sau: ( ) ( ) 4242 00 43200221 43202 dd abcdbfxaxaxaaxx abcdca == −+−+===−+=−+ +++==− . Bảng biến thiên của hàm số ( )fx như sau: Đặt ( ) ( ) ( ) 2 212 gxfxfxx =−− .
Phương trình ( ) 0 gx = có bốn nghiệm nhưng đều là nghiệm bội chẵn.
Ta có ( ) ( ) limlim xx gxgx →+→− ==+ . Suy ra hàm số ( )ygx = có dạng như sau: Kết luậ

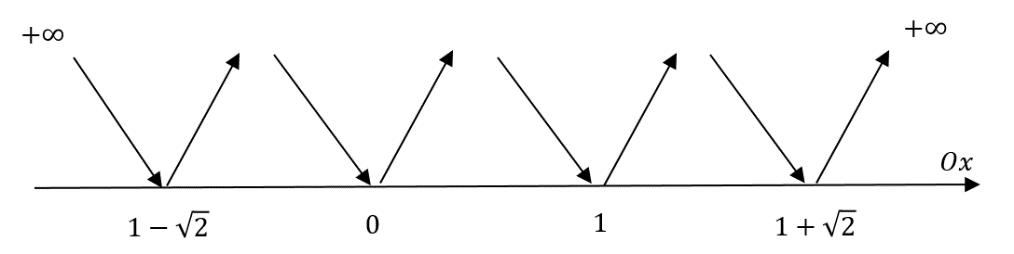
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 194
xxx
xx
= −=− −= = −= = −=−=+ −= −= =−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có ( ) ( ) ( ) 2 2 2 2110 2101 211 0 202112 2112 x x fx x x gx
fxx
x
.
ố (
=−−
Bả
ủ
Đặt ( ) ( ) 2 4 gxfxx =+
Ta
244
=++ ( ) ( ) 2 2 2 2 240 2 044 40 2 41 5 x x x gxxx fxx x xx =− += =− =+=− += =− += ( ) 2 4 fxx + không xác định khi 2 0 40 4 x xx x = += =− . Xét bất phương trình ( ) 2 2 2 42 20 440 40 25 41 25 x x xx fxx x xx x −− − −+ + −− + −+ Bảng xét dấu của ( )ygx =
n hàm s
) ( ) 2 212 yfxfxx
có 7 điểm cực trị. Câu 146: Cho hàm số ( )yfx = xác định và liên tục trên và có đạo hàm ( ) ( )( ) 3 14 '. xx fx x −+ = Hàm số ( ) 2 4 yfxx =+ có bao nhiêu điểm cực trị? Lời giải
ng xét dấu c
a ( )yfx
=
.
có ( ) ( ) ( ) 2
gxxfxx
Do hàm số ( )yfx = xác định và liên tục trên nên hàm số ( )ygx = xác định và liên tục trên , do đó hàm số ( ) 2 4 yfxx =+ có năm điểm cực trị. Câu 147: Cho hàm số ( )yfx = có đạo hàm là ( ) 2 16, fxxxx =+ . Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) 42 8 yfxxm =−+ có đúng 9 điểm cực trị? A. 16 B. xx xx xx yxx fxxm xxmxxm xxm xxm
== =−=− −= === −+= −+=−=− −+=− −=−− Xét hàm số ( ) ( ) ( ) 423 0 8416;02 2

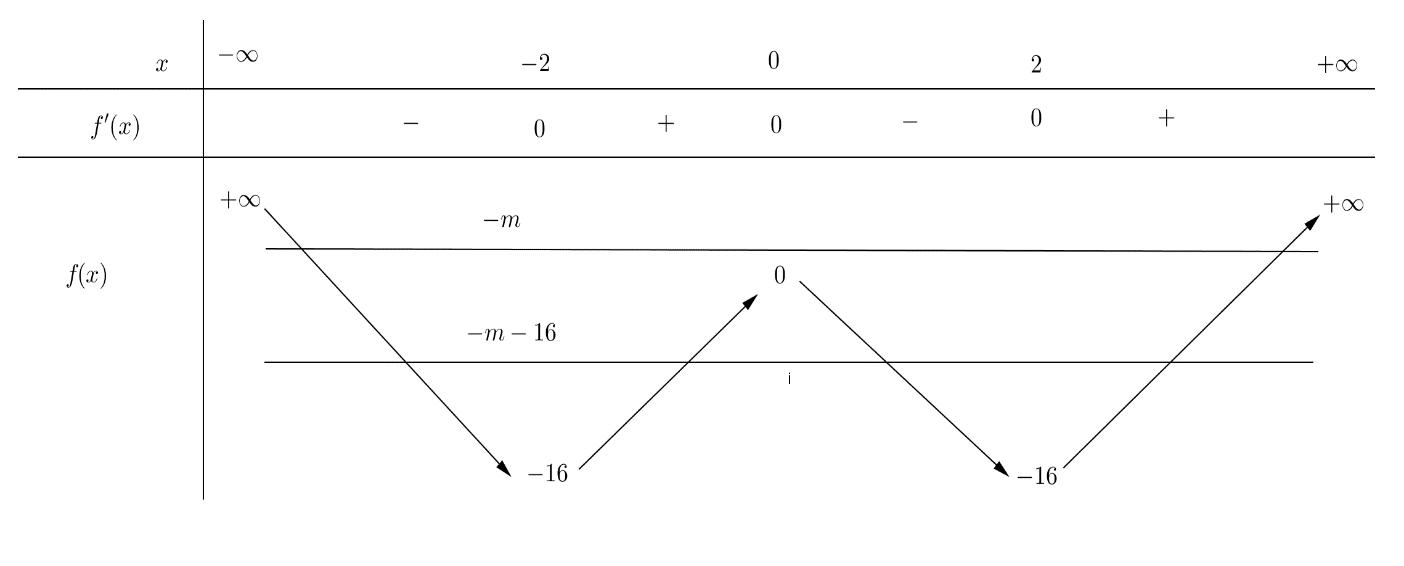
= =−=−==− = Nhận xét: 16, mmm −−− Có BBT
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 00 416022 022 80 808* 816816**
x fxxxfxxxfxx x
195 3 42 4242 42 42
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 9 C. 15 D. 10 Lời giải Chọn A Ta có ( ) ( ) 342416.8 yxxfxxm =−−+ ( ) ( ) ( )
Để hàm số đã cho có 9 cực trị thì phương trình ( )* có hai nghiệm phân biệt khác 2;0;2 và phương trình ( )** có bốn nghiệm phân biệt. Khi đó
TH1: 00 160 16016 mm m mm − − −−− .
TH2: 0 m = phương trình ( )* có ba nghiệm phân biệt trong đó có một nghiệm bằng 0 và phương trình ( )** có bốn nghiệm phân biệt thỏa mãn đề bài. Câu 148: Vậy 15;14;13;12;11;10;9;8;7;6;5;4;3;2;1;0 m−−−−−−−−−−−−−−− Cho hàm số
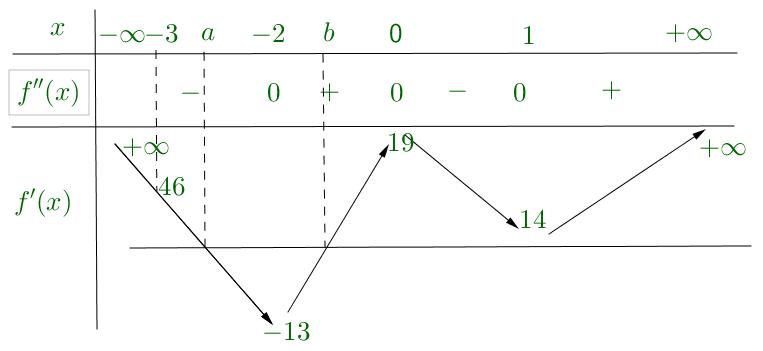
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ
O
SỐ
KHẢ
SÁT HÀM
Page 196
432
. Số cực trị của
số ('())
=
ằ
A. 4. B. 5. C.
Lời giải Chọn C ('())'''()'('()) yffxyfxffx == ''()0 '0 '('())0 fx y ffx = = = 432 '()341219 fxxxx=+−+ 32 2 ''()12122400(1) 1 x fxxxxx x =− =+−== = BBT '()(32) '('())0 '()(20) fxaa ffx fxbb =−− = =− '() fxa = (32) a −− có 2 nghiệm '() fxb = (20) b − có 2 nghiệm Từ, và suy ra hàm số đã cho có 7 cực trị vì các nghiệm này không trùng nhau.
'()341219 fxxxx=+−+
hàm
yffx
b
ng
7. D. 6.
Câu 149: Cho hàm số ( ) = yfx liên tục trên và có biểu thức đạo hàm ( ) 32310 =−− fxxxx. Hỏi có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số ( ) ( ) 2 223=−+−−gxfxmxm có 13 điểm cực trị? A. 2. B. 3 C. 4 D. 5
Lời giải
Chọn A
Hàm số ( ) = yfx đạt cực trị tại các điểm 5;0;2 ===−xxx
= = =−
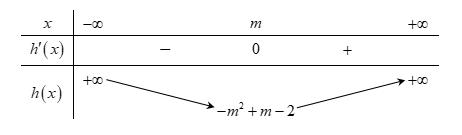
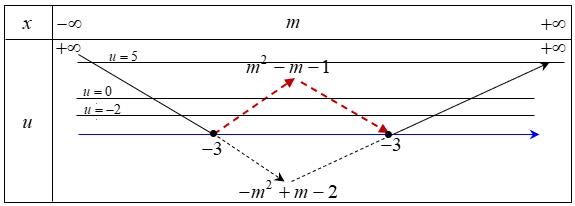
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG D
HÀM
KHẢO SÁT HÀM SỐ
Page 197
ỤNG ĐẠO
ĐỂ
u u
. Từ
ảng
ế
ấ
u
đơn
ủa 5 0 2 = = =− u u u phải bằng
Để
ệ
ộ
ẻ
5 = u phải
ằ
Xét hàm số ( ) ( ) 2 223=−+−−fufxmxm với 2 223=−+−−uxmxm Đặt ( ) 2 22=−+−hxxmxm , ta vẽ bảng biến thiên của hàm số ( )hx như sau: Nhận thấy 2 20−+− mm nên ta suy ra được bảng biến thiên của u như sau: Số điểm cực trị của ( ) = fu Số điểm cực trị của u + Số nghiệm đơn của 5 0 2 .
u
b
bi
n thiên ta th
y
có 3 điểm cực trị. Để hàm số ( )gx có 13 cực trị thì số nghiệm
c
10.
có 10 nghi
m b
i l
thì các đường thẳng 2;0=−=uu phải nằm dưới 2 1 mm và đường thẳng
n
m trên 2 1 mm

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 198 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Yêu cầu bài toán 2 2 15 102 152;3 2 1523 m m mm m m mmm + + −− ⎯⎯⎯→ −−− Câu 150: Cho hàm số 432 '()341219 fxxxx=+−+ . Số cực trị của hàm số ('())yffx = bằng A. 4. B. 5. C. 7. D. 6. Lời giải Chọn C ('())'''()'('()) yffxyfxffx == ''()0 '0 '('())0 fx y ffx = = = 432 '()341219 fxxxx=+−+ 32 2 ''()12122400(1) 1 x fxxxxx x =− =+−== = BBT '()(32) '('())0 '()(20) fxaa ffx fxbb =−− = =− '() fxa = (32) a −− có 2 nghiệm '() fxb = (20) b − có 2 nghiệm Từ, và suy ra hàm số đã cho có 7 cực trị vì các nghiệm này không trùng nhau. Câu 151: Cho hàm số (2)2022=+−yfx có đồ thị như hình bên dưới.
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
42
Page 199
ạ
Số giá trị nguyên của tham số m để
số
)
B. 4
Lời
+
ừ đồ thị ta thấy
Nên
33 33 11 0261126(1) 2613262(2) == =−++=−=− −++=−=− xx gxxxmxxm
y 2
-4 -1
Giáo viên: Huỳnh Văn Ánh
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên so
n
hàm
(
( ) 3 261 =−++ gxfxxm có 6 điểm cực trị là: A. 2
C. 6 D. 8
giải Chọn B
T
hàm số ( ) 22022=+−yfx có hai điểm cực trị là: 1,1=−=xx . Do đó, hàm số ( ) = yfx có hai điểm cực trị là 1,3==xx hay ( ) 1 0 3 = = = x fx x + Ta có ( ) ( ) ( ) 23 66261 =−−++ gxxfxxm
( )
xxmxxm . + Xét hàm số ( ) 3 26=− hxxx ta có đồ thị như hình vẽ x
-1 -2 O 1 x y
4 1
. + Bảng xét dấu ( )gx : + Dựa vào bảng xét dấu ta thấy hàm số
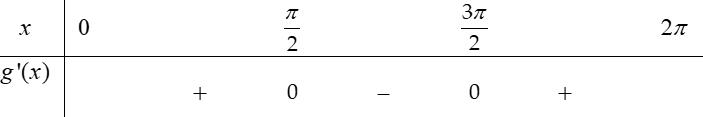
liên
hàm
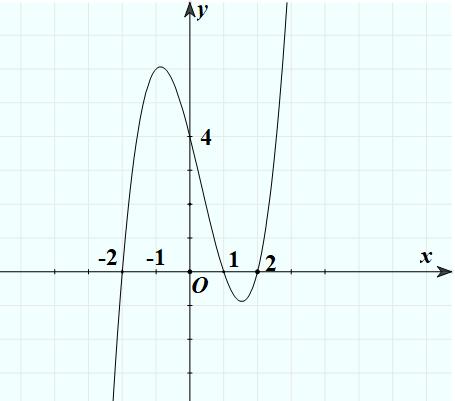
)yfx
đúng 4
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 200
−− −−
−− −− −−
( )ygx = có 2 điểm cực trị trong(0;2). Vậy hàm số ( ) ( )sin2gxfx=− trên khoảng ( ) 0;2022 có 2022điểm cực trị Câu 153: Cho hàm số ( )fx có đạo hàm
tục trên , đồ thị
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 số (
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do đó, ( ) = ygx có 6 điểm cực trị khi 424 4 46 3;2;4;5 42 44 24 m m m m m m m = có
điể
− Vậy có 4 giá trị nguyên của m Câu 152: Cho hàm số bậc ba ( )yfx = có đồ thị như hình vẽ dưới đây. Số điểm cực trị của hàm số ( ) ( )sin2gxfx=− trong khoảng ( ) 0;2022 là: A. 4044 B. 8088 C. 8078 D. 2022 Lời giải + Do ( )yfx = là hàm số bậc ba nên là hàm số liên tục và có đạo hàm luôn xác trên tập + Hàm số ( ) ( )sin2gxfx=− là hàm tuần hoàn với chu kì 2. Nên ta xét hàm số ( ) ( )sin2gxfx=− trong một chu kì (0;2]. + Mặt khác ( ) ( )cos.sin2gxxfx =− + Đặt sin2,tx=− do (0;2] x nên 3;1 t −− , dựa vào đồ thị hàm f thì ( ) 0,3;1ftt −− Hay ( ) ( sin20,0;2fxx − nên ( ) 0 gx = cos02 3 2 với trục hoành như hình vẽ bên dưới:
x x x
= = =
m chung
Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) 3 3 320212022 yfxxmm =−+++
có đúng 11 điểm cực trị?
A. 0. B. 3. C. 4. D. 1. Lời giải Chọn D
Với mỗi tham số m thì số điểm cực trị của hàm số ( ) 3 3 320212022 yfxxmm =−+++
và ( ) 3 32021yfxxm =−++ bằng nhau.

Do đó ta chỉ cần tìm giá trị nguyên của tham số m để hàm số ( ) 3 32021yfxxm =−++ có đúng 11 điểm cực trị.
Xét 0 x : Hàm số có dạng ( ) 3 32021yfxxm =−++
Khi đó ta có đạo hàm như sau: ( ) ( ) 23 3332021yxfxxm =−−++ .
Do nghiệm của phương trình 3 320214xxm−++= là các nghiệm bội bậc chẵn của phương trình 0 y = nên ta chỉ cần quan tâm đến các nghiệm còn lại. Tức là
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 201
0 y = ( ) 2 3 330 320210 x fxxm −= −++= ( ) 3 3 3 1do0 320211 320211 320212 xx xxm xxm xxm = −++=− −++= −++= ( ) 3 3 3 1do0 202131 202131 202132 xx mxx mxx mxx = +=−+− +=−++ +=−++ Vẽ đồ thị ba hàm số 3 31yxx=−+− ; 3 31yxx=−++ ; 3 32yxx=−++ với 0 x trên cùng một hệ trụ C.
Hàm số ( ) 3 32021yfxxm =−++ có đúng 11 điểm cực trị Hàm số ( ) 3 32021yfxxm =−++ có đúng 5 điểm cực trị dương Phương trình ( ) 3 320210fxxm −++= có đúng 4 nghiệm bội lẻ dương và khác 1 Đường thẳng 2021 ym=+ cắt đồ thị ba hàm số 3 31yxx=−+− ; 3 31yxx=−++ ; 3 32yxx=−++ tại 4 điểm phân biệt có hoành độ dương khác 1 120211 220213 m m −+ + 20222020 20192018 m m −− −− Do điều kiện m nguyên nên 2021 m =− . Vậy chỉ có 1 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Câu 154: Cho hàm số ( ) = yfx có đạohàm ( ) 3 4,. =−fxxxx Cóbaonhiêugiátrị nguyêncủatham số m để hàm số ( ) ( ) 322sin2 =++−++ gxfxxxxm có đúng 5 điểm cực trị? A. 3 B. 6 C. 4 D. 2 Lời giải Chọn D
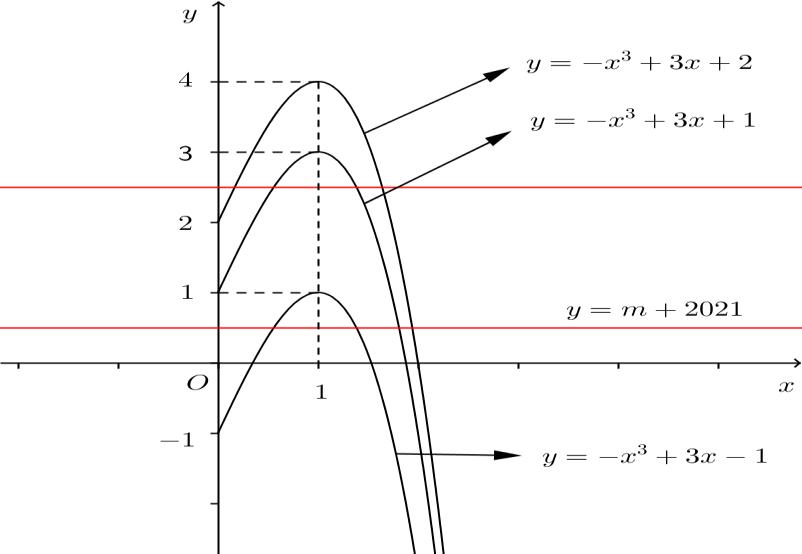
Ta có ( ) ( ), =−gxgxx nên hàm số ( )gx là hàm số chẵn trên . Do ( ) 3 2sin0,0;
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 202
+++xxxx
đúng 2 điểm cực trị dương. Ta có ( ) ( ) ( ) 232 322cos2sin2 =−++−++++ hxxxxfxxxxm Dễ thấy 2 322cos0,−++ xxxx và ( ) 2 00 2 = == =− x fxx x Suy ra ( ) ( ) 32 3232 32 2sin 02sin202sin2 2sin4 −++=− =−++++=−++=−− −++=−− xxxxm hxfxxxxmxxxxm xxxxm Đặt 3222sin322cos0, =−++=−++ uxxxxuxxxx , ta có bảng biến thiên
và không tồn tại ( ) ; ab để ( ) ( ) 0,; = gxxab nên hàm số ( )gx có đúng 5 điểm cực trị khi hàm số ( ) ( ) 32 2sin2 =−++++ hxfxxxxm có
nguyên cần tìm của m là 2. Cho hai hàm số ( ) ( ) ; gxfx , trong đó ( )gx là hàm số đa thức bậc ba thỏa mãn ( ) ( )1 gxfx=+ và ( ) ( ) ( ) ( )1312xgxxgx −+=++ . Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) 2 243 yfxxm =−+− có đúng ba cực trị. A. 2. B. 1. C. 3. D. 5. Lời giải

Chọn B
Theo giả thiết thì ( )gx là hàm số bậc ba thỏa mãn ( ) ( )1 gxfx=+ nên ta có ( )fx cũng là hàm số bậc ba. Suy ra ( ) 2 fxaxbxc =++ , do đó ( ) 0 fx = có tối đa hai nghiệm. Mặt khác ( ) ( ) ( ) ( ) 1 1 fx gxfxgx+= + = . Do đó ( ) ( ) ( ) ( )1312xgxxgx
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 203
20
40 −− −− −−
m m .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Qua bảng biến thiên ta thấy, hàm số ( )hx có đúng 2 điểm cực trị dương khi Câu 155:
)
4;2
m
Vậy số giá trị
Suy
( ) 3 0 4 x fx x = = = Ta có ( ) 2 243 yfxxm =−+− ( ) ( ) 2 44243 yxfxxm =−+ . 22 22 11 0243324. 2434241 xx yxxmxxm xxmxxm == =−+−=−= −+−=−=+ Hàm số ( ) 2 243 yfxxm =−+− có đúng ba cực trị khi và chỉ khi 0 y = có đúng 3 nghiệm đơn hoặc bội lẻ. Xét sự tương giao giữa đồ thị hàm số 2 24 yxx =− với hai đường ym = và 1 ym=+ như sau:
−+=++ ( ) ( ) ( ) ( ) 1413.xfxxfx−+= ++ Với ( ) 1240xf==
; ( ) 1230.xf
=−−=
ra
Do đó 0 y = có đúng 3 nghiệm đơn hoặc bội lẻ khi và chỉ khi 32 m −− .
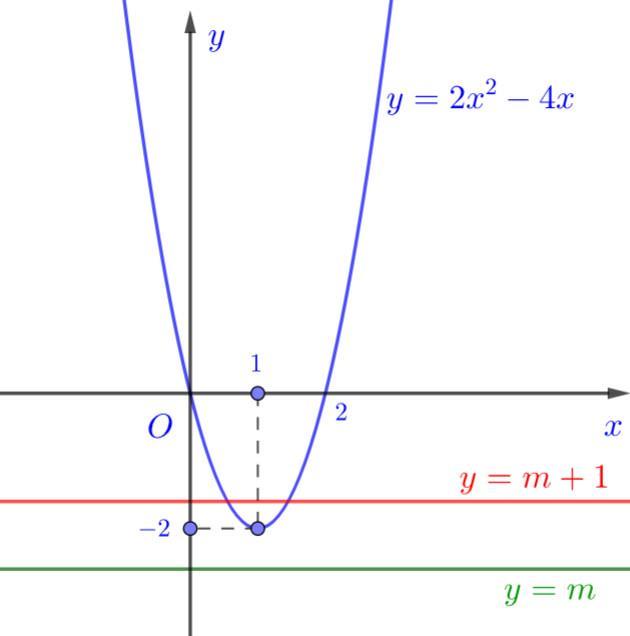
Vậy có một giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.
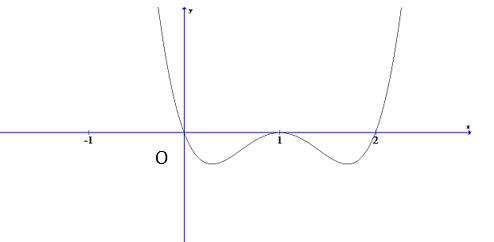
156:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 204
ị A. 15. B. 16.
Lời giải C
Ta có ( ) ( ) ( ) 2 248 gxxfxxm =−−+ ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 2 4 81 nghiem boi 2 02480. 80 1 822 x xxm gxxfxxm xxm xxm = −+= =−−+= −+= −+= Yêu cầu bài toán ( ) 0 gx = có 5 nghiệm bội lẻ mỗi phương trình ( ) (
1,2 đều
ệm phân
ệt khác 4. ( )*
Câu
Cho hàm số ( )yfx = có đạo hàm y = ( )fx với mọi . x và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ( ) ( ) 2 8 gxfxxm =−+ có 5 điểm cực tr
C. 17. D. 18.
họn A
)
có hai nghi
bi
−
−+
Vậy có 15 giá trị m nguyên dương thỏa mãn điều kiện.
Câu 157: Cho hàm số ( )yfx = . Đồ thị của hàm số ( )yfx = như hình bên. Đặt ( ) ( ) 4 2 2 x hxfx=− Hàm số ( )yhx = có bao nhiêu điểm cực trị?
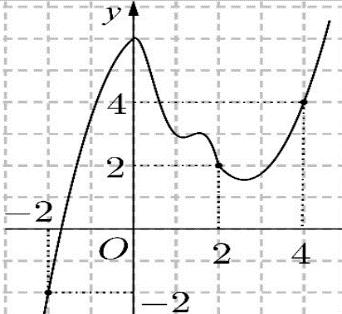
A. 4. B. 2. C. 3. D. 5. Lời giải Chọn D ( ) ( ) ( ) 2322222 hxxfxxxfxx =−=− , ( ) ( ) ( ) 2222 00 0 xx hx fxxfxx == = == Xét phương trình ( ) ftt = , dựa vào đồ thị, ta có: ( ) 2 2 4 t fttt t =− == =
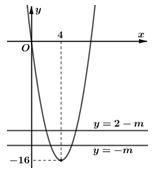
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 205
Cách 1: ( )*
160 1620 16 16 18
m m m m m
Vậy có 15 giá trị m nguyên dương thỏa mãn điều kiện.
Cách 2: Xét đồ thị ( )C của hàm số 2 8 yxx =− và hai đường thẳng 12 :,:2dymdym =−=−+
Khi đó ( ) 12 * , dd cắt ( )C tại bốn điểm phân biệt 1616.mm −−
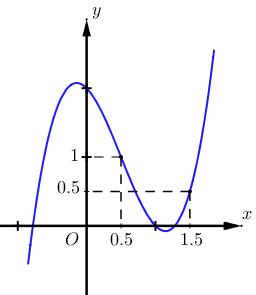
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 206
nh của hàm số ( )gx là ( ) 0; D =+ . + Ta có ( ) 2 12 2. 2 x gxxf x =− . Khi đó ( ) 2 2 11 0 2 x gxf x == Đặt 2 11 : 22 x tÐkt =− khi đó 2 1 2 xt=+ Phương trình trở thành ( ) 1 1 2 ft t = + ( ) 2 21 ft t = + . + Vẽ đồ thị ( )C của hàm số 2 21 y x = + với 1 2 x − .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do đó: ( ) 2 2 2 0 0 2 02 2 2 4 x x x hxx x x x = = =− == = = = . ( ) ( ) 12.1110hf =− . Ta có bảng xét dấu đạo hàm hàm ( )hx : Dựa vào bảng xét dấu, hàm số ( )yhx = có 5 điểm cực trị. Câu 158: Cho hàm số ( )fx . Hàm số ( )yfx = có đồ thị như hình bên dưới. Hàm số ( ) 2 1 2ln 2 x gxfx =− có bao nhiêu điểm cực trị? A. 5. B. 8. C. 6. D. 7. Lời giải Chọn C + Tập xác đị
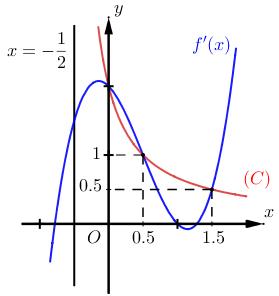

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 207 Chuyên
ện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT
10; 11; 12 Sưu tầm và biên soạn Dựa vào đồ thị ta thấy ( ) 2 2 2 1 2 0 2 2 2 0,511 21 1,5 2 2 x x t fttxx t t x x = = = ==== + = = = Kết hợp điều kiện 0 x , nên phương trình ( ) 0 gx = có 3 nghiệm đơn phân biệt nên hàm số ( )gx có 3 điểm cực trị. Câu 159: Cho hàm số ()yfx = là hàm số đa thức bậc bốn và có bảng biến thiên như hình vẽ. Tìm số điểm cực trị của hàm số ( ) 4 1 3 ()221. x gxfx=+ A. 7. B. 6. C. 5. D. 4. Lời giải Chọn D Ta có: ( ) 4 1 3 ()221. x gxfx=+ ( ) ( ) ( ) 44 2 11 3 5 ()22122 4ln2 3.11 22 xx gxfxfxfx x =+++ + ( ) ( ) ( ) 4 1 2 5 2ln2 ()2.221213210 x gxfxfxfx x =++++= ( ) ( ) ( ) ( ) 2 5 210 2ln2 213210* fx fxfx x += +++= Do các nghiệm của phương trình ( ) 2 210fx += là các nghiệm bội chẵn nên số điểm cực trị của hàm số ( )gx là số nghiệm bội lẻ của phương trình ( )* .
0984164935
luy
Toán

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 208
Chọn A
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Xét phương trình ( ) ( ) 5 2ln2 213210fxfx x +++= . Đặt 21tx=+ ta được ( ) 6 5 2.ln2()3()0 1 ftft t += . Từ bảng biến thiên ta thấy được phương trình ( ) 0 ft = có 4 nghiệm 1t , 2t , 3t , 4t . ( ) ( )( )( )( ) 1234 ftatttttttt =−−−− ( ) ( )( )( ) ( )( )( ) ( )( )( ) ( )( )( ) 234134124123 ftatttttttttttttttttttttttt =−−−+−−−+−−−+−−− Do 4 nghiệm 1t , 2t , 3t , 4t không là nghiệm của phương trình ( )* nên: ( ) ( ) ( ) 66 55 2.ln22.ln2()()3()030** () 11 ft ftft ft tt +=+= Thay ( )ft và ( )ft vào ( )** ta có: ( ) 6 5 1234 2ln23333 0 1 tttttttt t ++++= Xét hàm số ( ) ( ) 6 5 1234 2ln23333 1 ht tttttttt t =++++ với ( )1,1,4 i ttti= . ( ) ( ) ( ) ( ) ( ) ( ) ( ) 6 62222 1234 1,1,4 2.5.ln23333 0, 1 i t ht ttttttt t t t t i =++++ = Ta có bảng biến thiên của ( )ht : Từ bảng biến thiên ta thấy phương trình ( ) 0 ht = luôn có 4 nghiệm đơn phân biệt do đó hàm số ()gx có 4 điểm cực trị. Câu 160: Cho hàm số ( )yfx = có đạo hàm ( ) ( ) ( ) 2 2 3 fxxxx =+− với x . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ( ) 2 6 yfxxm =−+ có 5 điểm cực trị? A. 8 B. 9 C. 7 D. 6 Lời giải
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 209 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Xét ( ) ( ) 3 00 1 xnghiemboichan fxx x =− == = Đặt ( ) ( ) ( ) ( ) ( ) 22 626.6 gxfxxmgxxfxxm =−+=−−+ Hàm số ( )gx có 5 điểm cực trị mỗi phương trình và có hai nghiệm phân biệt khác 3 909 10010 9 909 10010 mm mm m mm mm − − −+ −+ Mà * 1;2;3;...;8 mm . Vậy có 8giá trị m thỏa mãn bài toán. Câu 161: Cho hàm số ( )yfx = có đạo hàm ( ) ( ) ( ) 2 2 1712, fxxxxx =−−+ .
ị
ố
A. 1 B. 2 C.
Lời giải Chọn B Ta có ( ) ( ) 1 03 4 xl fxx x = == = . ( ) ( ) ( ) ( ) ( ) 2333 3 3 11 333033331 34342 xx gxxfxxmxxmxxm xxm xxm == =−−+=−+=−−=− −+= −−=− Hàm số đã cho có đúng 6 điểm cực trị khi và chỉ khi ( ) ( )1,2 có tổng 4 nghiệm phân biệt 1 x . Ta vẽ đồ thị của hai hàm số 3333,34yxxyxx =−−=−− trên cùng một hệ tọa độ. ( ) ( ) ( ) ( ) 2 2 2 3 63 0 601 612 x xxmnghiemboichan gx xxm xxm = −+=− = −+= −+=
Có bao nhiêu giá tr
nguyên dương của tham s
m để hàm số ( ) ( ) 3 3 gxfxxm =−+ có đúng 6 điểm cực trị?
0 D. 3


CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 210
Từ đồ thị, ta có: 2112 2;5 6556 mm m mm −−− −−− Vậ
ố.
ố
ậ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
y có 2s
Câu 162: Cho hàm s
b
c bốn ( )yfx = có đạo hàm liên tục trên , hàm số ( )yfx = có đồ thị như hình vẽ. Gọi S là tập các giá trị nguyên của tham số m để hàm số ( )426yfxm =−+− có đúng 3 điểm cực tiểu. Tổng các phần tử của S bằng A. 18. B. 11. C. 2. D. 13. Lời giải Chọn B +) Ta có ( )426yfxm =−+− là hàm số chẵn với biến số 24 x nên đồ thị hàm số nhận đường thẳng 2 x = làm trục đối xứng. +) Xét hàm số ( ) 246yfxm =−+− ( )1 có ( )2210yfxm =+− Theo đầu bài 0 y = tại các điểm 1231;1;4xxx=−== .
Ta có 1 2 3
+−=− +−= +−=
xm xm xm
2101 2101 2104
ra hàm
ố
= = =
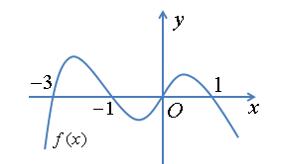
m x m x m x
1 2 3
9 2 11 2 14 2
( 123 ,, xxx là các nghiệm đơn).
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 211
ới 123 xxx và thỏa mãn 1 2 2 2 x x 9 2 2 11 2 2 m m 57 m 5;6 m 11 S = . Câu 163: Cho hàm số ()yfx = liên tục trên và có đồ thị có 3 điểm cực trị như hình vẽ dưới đây. Số điểm cực trị của hàm số 3 ()(32) gxfxx=−+ là: A. 5. B. 11. C. 9. D. 7. Lời giải Chọn D Ta có: ( ) ( ) ( ) 23 3332gxxfxx =−−+ , ( ) ( ) 3 3 330(1) 0 '320(2) x gx fxx −= = −+= (1)1 x = . Dựa vào đồ thị đã cho thì ( ) ( ) ( ) 3 3 3 323;1 (2)321;0 320;1 xxa xxb xxc −+=−− −+=− −+=
Suy
s
( )1 có 3 điểm cực trị +) Đồ thị hàm số ( )426yfxm =−+− gồm 2 phần: Phần 1: Đồ thị hàm số ( )1 phía bên phải đường thẳng 2 x = Phần 2: Lấy đối xứng phần 1 qua đường thẳng 2 x = . Do đó hàm số ( )426yfxm =−+− có 3 điểm cực tiểu thì hàm số ( ) 246yfxm =−+− có 3 cực trị 123 ,, xxx v
Xét hàm số ( ) ( ) 32 1 32330 1 x gxxxgxx x
= =−+=−= =− .

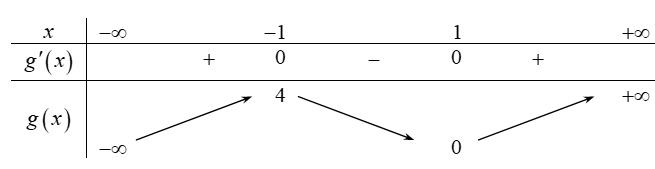
Ta có bảng biến thiên của hàm số ( )gx
Dựa vào bảng biến thiên ta có: phương trình ( ) 3 323;1xxa−+=−− có 1 nghiệm đơn phương trình ( ) 3 321;0xxb−+=− có 1 nghiệm đơn phương trình ( ) 3 320;1xxc−+= có 3 nghiệm phân biệt
= =−+= −+= Để hàm số ( )gx có 5 điểm cực trị khi và chỉ khi
3 021201 21242
x gxxxm xxm phương trình ( )1 và ( )2 , mỗi phương trình có hai nghiệm phân biệt khác 3. Xét hàm số ( ) 2 212 hxxx =− . Ta có: Dựa vào bảng biến thiên, để phương trình ( ) ( )1;2 có hai nghiệm phân biệt khác 3 1818 18 41822 mm m mm −− −− Vì * m nên có 17 giá trị của tham số m thỏa mãn đề bài.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 212
Ta có 5 nghiệm đơn trên đôi một khác nhau và khác 1 . Vậy hàm số có 7 điểm cực trị. Câu 164: Cho hàm số ( )fx có đạo hàm ( ) 2 4 fxxx =− . Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số ( ) ( ) 2 212 gxfxxm =−+ có đúng 5 điểm cực trị? A. 17. B. 19. C. 16. D. 18. Lời giải ( ) 2 0 40 4 x fxxx x = =−= = Ta có: ( ) ( ) ( ) 2 412212 gxxfxxm =−−+ ; ( ) ( ) ( ) 2 2
Ta có đồ thị ( )1C cắt đồ thị ( ) 2C tại 3 điểm nên phương trình ( ) ( )fxfx = có 3 nghiệm đơn phân biệt.

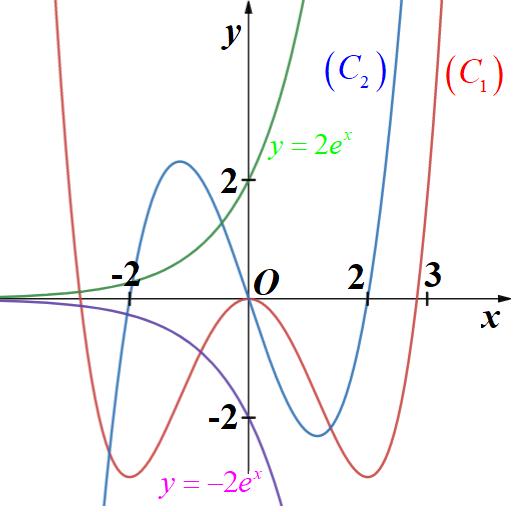
Ta có đồ thị ( )1C cắt trục hoành tại 2 điểm nên phương trình ( ) 0 fx = có 2 nghiệm đơn phân biệt.
Vẽ đồ thị các hàm số 2,2xx ee trên cùng một hình vẽ, ta có được:
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 213
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 165: Cho đồ thị hàm số bậc bốn ( )yfx = có đồ thị ( )1C và hàm số ( )yfx = có đồ thị ( ) 2C như hình vẽ bên. Số điểm cực đại của đồ thị hàm số ( ) ( ) x gxfefx = trên ( );3− là: A. 5 B. 3 C. 6 D. 4 Lời giải Chọn B
Ta có: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 0 20 0 02 22 x xx xx xx fxfxfxfx efxfx gxefxfxfefx efxfxe efxfxe −== =−= =−= ==− ==
Từ hình vẽ ta thấy được phương trình ( ) 2 xfxe = và ( ) 2 xfxe =− có 3 nghiệm đơn phân biệt. Vậy ( ) 0 gx = có 8 nghiệm đơn phân biệt nên hàm số ( )gx có 8 điểm cực trị. Hàm số có 4 điểm cực đại. Câu 166: Cho hàm số ( )fx có đạo hàm liên tục trên . Đồ thị của hàm số ( ) 52 yfx =− như
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
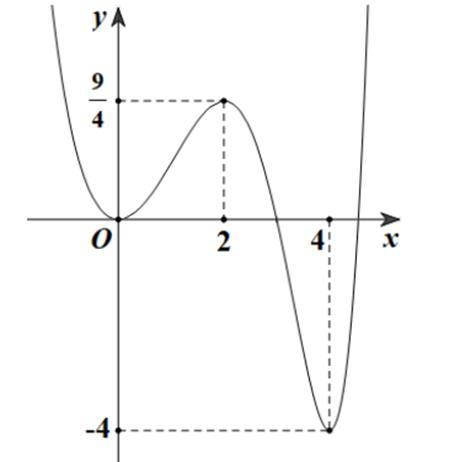
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM
Ố
ĐỂ KHẢO SÁT HÀM S
Page 214
Có bao nhiêu giá trị thực của
số 0;10 m để
ố
ự
trị? A. 6 B. 5 C. 4 D. 3 Lời giải Chọn A Ta có ( ) ( ) 52'2'52 yfxyfx =−=−− . Từ đồ thị, suy ra 0 '02 4 x yx x = == = . Đặt ( ) 5 5 52,'01 2 3 t t txxftt t = =−=== =− ( ) ( ) ( ) 22 2 2 2 2 2 2 ()241'16.'410 0 04 4154 411 4 4134 4 gxfxmgxxfxm x m x x xm m x xm xm m x =+−=+−= = + = = +−= = +−= +−=− =
hình vẽ bên dưới
tham
hàm s
( ) 2 241 yfxm =+− có 7 điểm c
c
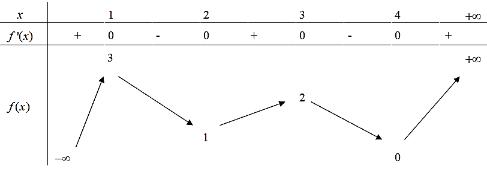
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 215
số ( ) ( ) ( ) ( ) 32 29122021ygxfxfxfx ==−++ liên tục trên Ta có ( ) ( ) ( ) ( ) ( ) 2 6..18.12 yfxfxfxfxfx =−+ ( ) ( ) ( ) 2 632 fxfxfx =−+ . Giải phương trình đạo hàm: ( ) ( ) ( ) ( ) ( ) ( ) '01 012 23 fx yfx fx = == = . Từ ( )1 , ta có ( ) 1 2 '0 3 4 x x fx x x = = = = = . Từ ( )2 , ta có ( ) ( ) ( ) ( ) ( ) =− = = = =+ ;1 2Nghieäm keùp 1 3;4 4; xa x fx xb xc Từ ( )3 , ta có ( ) ( ) ( ) ( ) ( ) = = = = =+ ;1 1;2 2 3nghieäm keùp ; xda xe fx x xuc .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn để hàm số ( ) 2 ()241 ygxfxm ==+− có 7 điểm cực trị thì '()0gx = có 7 nghiệm phân biệt và '()gx đổi dấu qua 7 nghiệm đó. Từ đó suy ra ( )ygx = có 7 cực trị khi 4 m vì, đồng thời theo đề 0;10 m . Vậy có 6 giá trị của m thỏa mãn yêu cầu bài toán . Câu 167: Cho hàm số ( )yfx = liên tục trên và có bảng biến thiên như sau: Hàm số ( ) ( ) ( ) 32 29122021yfxfxfx =−++
có bao nhiêu điểm cực đại? A. 5 B. 10 C. 7 D. 9 Lời giải Chọn A Hàm
Lập bảng xét dấu, ta có
Dựa vào bảng biến thiên, ta có hàm số ( )ygx = có 5 điểm cực đại.
Câu 168: Cho hàm đa thức ( )yfx = xác định trên và có bảng xét dấu của ( )fx như sau:
Hỏi hàm số ( ) ( ) 3 2 2 226 3 x gxfxxx =+++− đạt cực tiểu tại điểm nào dưới đây?
A. 3 B. 1 C. 3 D. 0 Lời giải
C
họn B
Từ bảng biến thiên của hàm ( )fx ta có ( ) 21221()(1)(1)(3) mnkfxpxxxx++ =+−− trong đó ,, mnk + và ()px là đa thức luôn dương.
Ta được ( ) 21221 ()(3)(1)(1)2(1)(3) mnk gxpxxxxxx ++ =++−+−+ ( ) 222 (1)(3)()(3)(1)(1)2 mnk gxxxpxxxx =−+++−+ Suy ra dấu của ()gx là dấu của ( )( )13xx−+ Do đó ( ) ( ) 3 2 2 226 3 x gxfxxx =+++− đạt cực tiểu tại 1 x = . Câu 169: Cho hàm số ( )yfx = xác định trên và hàm số ( )yfx = có đồ thị như hình vẽ: Hỏi đồ thị hàm số ( ) 3 fx y = có mấy điểm cực trị?


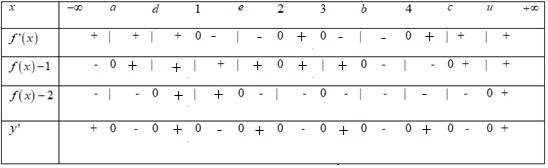
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 216
A. 3. B. 2. C. 0. D. 1. Lời giải
Chọn A
Xét hàm số ( ) 3 fx y = có tập xác định là
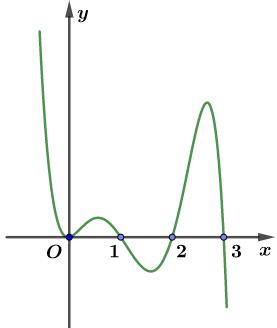
Ta có: ( ) ( ) .3.ln3 fx yfx = . Cho ( ) 00yfx == ( ) ( ) do3.ln30, fx x
Dựa vào đồ thị hàm số thì phương trình ( ) ( ) ( )
ảng xét dấ
ậy đồ th
xxx fxx xxx
,3;2 01 ,0;1
=−− ==− = .
11 22
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 217
ủ
mm để hàm số ( ) ( ) 2 2121gxfxxxm =−−−+− có đúng 9 điểm cực trị? A. 3. B. 5. C. 4. D. 2. Lời giải Chọn C Ta có: ( )( ) ( ) 2 2111 ()2121 1 xx gxfxxxm x =−−−+− ( ) 2 0 ()02 21210 x gxx fxxxm = == −−−+−= ; ( )gx không xác định tại 1 x =
B
u: V
ị hàm số ( ) 3 fx y = có 3 điểm cực trị. Câu 170: Cho hàm đa thức ()yfx = . Hàm số ()yfx = có đồ thị như hình vẽ sau Có bao nhiêu giá trị c
a ) 2;6;2
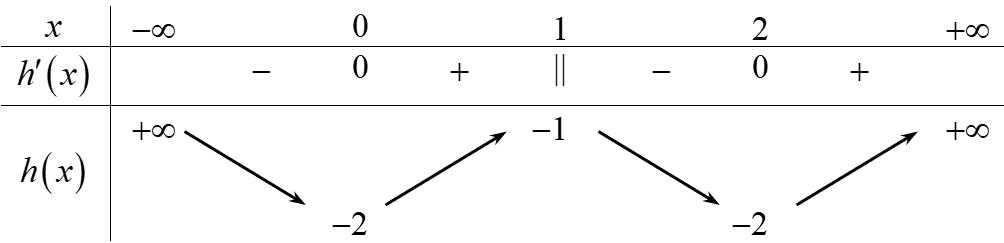
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 218 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Dựa vào đồ thị hàm số ( )fx , ta có ( ) 22 222 22 212112122 21210212122123 212132124 xxxmxxxm fxxxmxxxmxxxm xxxmxxxm −−−+−=−−−=− −−−+−=−−−+−=−−−=−
Xét
số ( ) 2 212
=−−− , ta
ả
ế
Hàm số đã cho có 9 cực trị 21 231 m m −− −−− 3 45 m m 59 2;3;; 22 m Vậy có bốn giá trị của m . Câu 171: Cho hàm số ( )yfx = có đạo hàm ( ) ( ) ( ) 2 2 2 yfxxxx ==−− , x
nên không phải là điểm cực trị của hàm số ( )yfx = +) Xét hàm số ( ) 2 1 6 2 ygxfxxm ==−+ ( ) ( ) 2 1 66 2 gxxfxxm =−−+ ( ) 2 6 01 60 2 x gx fxxm = = −+= 2 2 2 6 1 62 2 1 60 2 1 61 2 x xxm xxm xxm = −+= −+= −+=
−−−+−=−−−=−
hàm
hxxxx
có b
ng bi
n thiên sau
. Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m để hàm số 2 1 6 2 fxxm −+ có 5 điểm cực trị. Tính tổng tất cả các phần tử của S . A. 154. B. 17 C. 213 D. 153 Lời giải Chọn D +) Ta có ( ) 2 00 1 x fxx x =
== = , trong đó 2 x = là nghiệm bội chẵn
Nghiệm của phương trình 2 1 62 2 xxm−+= không phải là điểm cực trị của hàm số ( )ygx = Để hàm số ( )ygx = có 5 điểm cực trị thì phương trình 2 1 60 2 xxm−+= và 2 1 61 2 xxm−+= phải có 4 nghiệm phân biệt khác 6.
+) Xét hàm số ( ) 2 1 6 2 hxxx =− ( ) '6hxx=− . ( ) '06hxx== . Bảng biến thiên:

+) Số nghiệm phương trình 2 1 60 2 xxm−+= bằng số giao điểm của đồ thị hàm số ( )hx và đường thẳng ym =− .
+) Số nghiệm phương trình 2 1 61 2 xxm−+= bằng số giao điểm của đồ thị hàm số ( )hx và đường thẳng 1 ym=−+ .
Mà 1 mm −−+ nên để hai phương trình trên có 4 nghiệm phân biệt khác 6 thì 18 m −− 18 m
Tập các giá trị nguyên dương của m thỏa mãn yêu cầu bài toán là 1;...;17 S = Tổng tất các giá trị m của tập S là 1...17153 ++= . Câu 172: Cho hàm số ( )yfx = có đạo hàm ( ) 2 6 fxxx =+− . Có bao nhiêu giá trị nguyên của m để hàm số ( ) 3239 yfxxxm =−−+ có đúng 6 điểm cực trị. A. 7. B. 8. C. 9. D. 10. Lời giải Chọn D Ta có ( ) 2 3 60 2 x fxxx x
=− =+−= = .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page
219

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 220 Chuyên
ện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT
11; 12 Sưu tầm và biên soạn Ta có ( ) ( ) ( ) ( ) 232 32 32 1 3 369390 393 1 392 2 x x yxxfxxxm xxxm xxxm =− = =−−−−+= −−=−− −−=−+ . Xét ( ) ( ) 322 1 39; 3690 3 x hxxxxhxxx x =− =−−=−−=
−−+ −−− . V
Hỏi hàm số ( ) 4 32 462yfxx=−+ có bao nhiêu điểm cực đại? A. 4. B. 6. C. 9. D. 5. Lời giải Chọ
ố
ậ
ba
32
==+++ .
-2 -1
2 -4 -3 -2 -1 4
O 1 1
Hòa
0984164935
luy
Toán 10;
= , ta có bảng biến thiên Để hàm số ( ) 3239 yfxxxm =−−+ có đúng 6 điểm cực trị thì 25 2735 83 2429 2725 327 m m m m m m −+ −−− −−
ậy có 10 giá trị nguyên của m để hàm số ( ) 3239 yfxxxm =−−+ có đúng 6 điểm cực trị Câu 173: Cho hàm số bậc ba ( )yfx = có ( ) ( ) 130ff−+= và có đồ thị của hàm số ( )yfx = như sau:
n A Hàm s
b
c
( ) ( )
0 yfxaxbxcxda
x y y = f '(x)
4 3
3 2
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 221 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có 2 ()32 yfxaxbxc ==++ Đồ thị hàm số ()fx đi qua các điểm ( ) ( )0;0,2;0 và có hệ số 0 a . Ta có hệ phương trình 00 12403 cc abcba == ++==− ( ) 32 3 fxaxaxd =−+ . Ta lại có ( ) ( ) 1303272702 ffaadaadda −+=−−++−+== . Khi đó ( ) ( ) 3232fxaxx=−+ với 0 a Ta có ( ) 32 13 032013 1 x fxxxx x =− =−+==+ = . Đặt ( ) ( ) 4 32 462gxfxx=−+ . Ta có ( ) ( ) ( ) ( ) 3 32232 4.462.1212462 gxfxxxxfxx =−+−−+ ( ) ( ) ( ) 32 2 32 4620 012120 4620 fxx gxxx fxx −+= =−= −+= . ( ) ( ) ( ) 32 11 3232 22 32 462131.57 4620462130.57 462113131 222 xx xxx fxxxxxxx xx xxx −+=+ = −+=−+=−=− −+= −+ === 2 0 12120 1 x xx x = −= = . ( ) 32 32 32 1 46201()46202 462230() 2 xxkep xx fxx xx xxkep =−= −+= −+= −+= == . Phương trình ()0gx = có 9 nghiệm bội lẻ Ta thấy ( ) ( ) 3 (2)410.10.240 gff = . Vậy, hàm số ( ) ( ) 4 32 462gxfxx=−+ có 4 điểm cực đại.
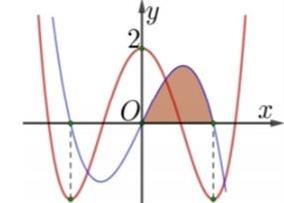
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO
HÀM SỐ
Page 222
nhiêu điểm cực trị. A. 2. B. 0. C. 3. D. 1. Lời giải Chọn C Nhận xét đồ thị hàm số yfx có 3điểm cực trị nên 0 a Ta có 3 2 0 20 22 x fxxax xaxa Dựa vào đồ thị hàm số ygx ta thấy 2 2 2 4 32 0 0 00 2.20 20.2.20 .20 21 2.2.202 20.2.20 24.222 3 83 ()d2.2 832 a a g aa d gabaca abac aa abac gabaca ab aaac xbc gxxxx Từ 1 và 2 ta có 0 0 b acca thay vào 3 ta có: 2 22 4 241622 8 a aaac . Khi đó 4 2 3 ()22 4 ()2 2 x fxx x gxx Vậy ( ) ( ) 423432 (2)(2)4824444842 yfxgxxxxxxxxx =−=−+−−+=+−−+ 32 16121640yxxx có 3 nghiệm phân biệt nên đồ thị hàm số có 3 điểm cực trị Câu 175: Cho hàm số ( ) = yfx có đồ thị của ( ) 32 yfx =− như hình vẽ sau:
SÁT
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 174: Cho hàm số 4 2 ()2 4 x fxax=++ và 3 2 () 2 x gxbxcxd =+++ có đồ thị như hình vẽ. Biết rằng diện tích miền tô đậm bằng 2 . Hỏi hàm số ( ) ( ) 22 yfxgx =− có bao
y 2 1 -2 O
x
15 10 5 5 10 15
= = =−== = =− Suy ra ( ) 3 3 3
x t fxftx t x
xxm gxxxm xxm
++= =++= ++=−
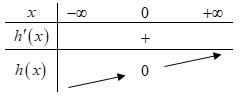
20217 020211 20211
3 3 3
+=− +=− +=−− Hàm số ( )gx có ít nhất 5 điểm cực trị khi và chỉ khi có ít nhất 2 trong 3 phương trình (1), (2),(3) có nghiệm dương. Xét hàm số ( ) 3 2021 hxxx =+ có ( ) 2 32021hxx =+ Ta có BBT của ( ) 8 6 4 2 2 4 6 8
xxm xxm xxm hx như sau: Vì 711mmm−−−− nên ta có 101. mm − Mà 2021;2021 m− nên 2021;...;0. m− Vậy có 2022 giá trị nguyên m thỏa mãn yêu cầu bài toán. Câu 176: Cho hàm số ()yfx = có đạo hàm 432 () fxaxbxcxdxe =++++ và ()fx có đồ thị như hình vẽ
20217(1) 20211(2). 20211(3)
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 223
Có bao nhiêu giá trị nguyên của tham số 2021;2021 m− để hàm số ( ) ( ) 3 2021 gxfxxm =++ có ít nhất 5 điểm cực trị? A. 2019. B. 2020. C. 2021. D. 2022. Lời giải Chọn D Vì ( ) ( ) 3 2021 gxfxxm =++ là hàm số chẵn nên số điểm cực trị của ( )gx bằng 2 lần số cực trị dương của ( ) 3 2021 fxxm ++ cộng với 1. Với 0, x ta có ( ) ( ) 3 2021;gxfxxm =++ ( ) ( ) ( ) 23 320212021. gxxfxxm =+++ Đặt 32 xt =− ta có 3 2 x t = và ( ) ( ) 7 2 3201. 1 1

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 224 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Biết đồ thị hàm số 2 ()2 yfxxx =+− tiếp xúc với trục hoành tại điểm có hoành độ 1 x = . Tích các điểm cực đại của hàm số ( ) 6 242 ()238 3 x
ờ
Chọ
Xét ( )
242 0 268(*) x fxxx = −=−+− Đặt 2 2 tx=− .
đó, ( ) 2 (*)2
t =−+
Từ đồ thị ta suy ra ( ) ( ) ( ) 2 2 0/ 202 1 222 2/ ttm x x tKTM x x ttm = −= = = = −= = Bảng xét dấu ()gx :
gxfxxx =−+−+ là A. 2 B. 1 C. 4 D. 2 L
i giải
n A
6 242 ()238 3 x gxfxxx =−+−+ có ( ) 253 ()2221216 gxxfxxxx =−+−+
( ) 242 ()022680 gxxfxxx =−+−+= ( )
Khi
ftt
. Các nghiệm của phương trình này là hoành độ giao điểm của hai đồ thị hàm số ()yft = và 2 2 ytt =−+ . Vẽ hai đồ thị hàm số trên cùng hệ trục ta được:
dưới đây
Đặt ( ) ( ) 32 9 31962022 2 gxfxxxx =−−+−+ . Hàm số ( ) ygx = có bao nhiêu điểm cực trị? A. 3. B. 9. C. 5. D. 7 . Lời giải Chọn A Ta có: ( ) ( ) ( ) ( ) ( ) 2 2 33127963313313316gxfxxxfxxx =−−+−=−−−−−− ( ) ( ) ( ) ( ) 2 03131312gxfxxx =−=−+−+ Đặt 31tx=− ta được phương trình: ( ) 2 2 fttt =++ Từ đồ thị của hai hàm số ( )yft = và hàm 2 2 ytt=++ ta có phương trình ( ) 2 2 fttt =++ có ba nghiệm 1 t =− , 1 t = và 2 t =− . Với 1 t =− thì 0 x = . Với 1 t = thì 2 3 x = . Với 2 t =− thì 1 3 x = Khi đó phương trình ( ) 0 gx = có ba nghiệm 0 x = , 2 3 x = và 1 3 x = Bảng biến thiên của hàm ( )ygx =


CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 225
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vậy các điểm cực đại của hàm số ()gx là 2 x = Câu 177: : Cho hàm số ( ) ( ) 5432 0 yfxaxbxcxdxexfa ==+++++ và hàm số ( )yfx = có đồ thị như hình vẽ
Từ bảng biến thiên của hàm ( )ygx = suy ra đồ thị hàm ( ) ygx = có 3điểm cực trị Câu 178: Cho ( )fx là hàm số đa thức bậc bốn và hàm số ( )yfx =

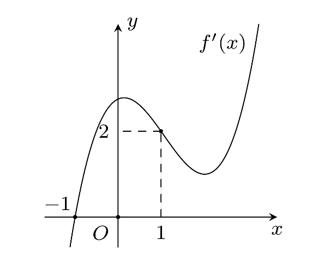
là đường cong như hình dưới đây.
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 226
có đồ thị
Hỏi hàm số ( ) ( ) cos2 sin1 4 x gxfx=−+
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 A. 3 B. 5 C. 4 D. 2 Lời giải Chọn A Ta có ( ) ( ) ( ) ( ) 21sin sin1cos.sin1sin.cos 42 x gxfxgxxfxxx =−+−=−− . Xét ( ) ( ) ( ) ( ) cos01 0 sin1sin02 x gx fxx = = −−= ( ) 1cos0, 2 xxkk ==+ . Vì ( ) 0;2020;1 2 xkk + . ( ) ( ) ( ) 2sin1sin0sin1sin fxxfxx −−=−= . Đặt ( ) ( )sin1,0;22;0txxt =−− . Khi đó: ( ) ( ) 1,2;01sin0, fttttxxkk =+−=−== . Vì ( ) 0;2021xkk
có bao nhiêu điểm cực trị thuộc khoảng ( ) 0;2
?
, với ( ) ( ) ( ) 42 85244gxxmxm=+−−− . Ta có ( ) ( ) ( ) 2 0 lim044 x gxgm
==−− Trường hợp 1: ( ) ( ) ( ) ( ) 2 00440;22; gmm−−−−+ Khi 0 x → thì ( ) 3.0yxgx + =→ ; khi 0 x + → thì ( ) 3.0yxgx =→ y đổi dấu từ dương sang âm qua 0 x = hàm số đạt cực đại tại 0 x = . Trường hợp 2: ( ) 00 g ( ) ( ) 2 4402;2 mm −−− Khi 0 x → thì ( ) 3.0yxgx =→ ; khi 0 x + → thì ( ) 3.0yxgx + =→ y đổi dấu từ âm sang dương qua 0 x = hàm số đạt cực tiểu tại 0 x = Trường hợp 3: ( ) ( ) 2 004402 gmm=−−== +) Với 2 m = , ta có 7 8 yx = y đổi dấu từ âm sang dương qua 0 x = hàm số đạt cực tiểu tại 0 x = . +) Với 2 m =− , ta có ( ) ( ) 3746 820820yxxxxx =−=− y không đổi dấu qua 0 x = hàm số không đạt cực trị tại 0 x = Như vậy hàm số đạt cực tiểu tại 0 x = ( 2;2 m− . Do m nguyên nên 1;0;1;2 m− Vậy có tất cả 4 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán. Câu 180: Cho hàm số ( ) 3222 32 yxxmxm =−−−+ ( ) m C . Biết rằng đồ thị hàm số cắt trục hoành tại ba điểm phân biệt ( ) ,, ABC ABCxxx và có hai điểm c
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 227
ọn D Tập xác định: D = . ( ) ( )
8524485244 yxmxmxxxmxm =+−−−=+−−−
=
ực trị , MN . Số các giá trị của tham số m để MNAC = là A. 1. B. 2. C. 0 . D. 3 Lời giải Chọn B Phương trình hoành độ giao điểm của ( ) m C và trục Ox là: ( ) 3222320xxmxm−−−+= ( )( ) 22 22 2 11 120 2011 x x xxxm xxm xm = = −−−= −−= =+ . Suy ra ( ) m C cắt trục Ox tại ba điểm phân biệt ( ) ( ) ( ) 22 11;0,1;0,11;0 AmBCm −+++ và 2 21 ACm =+
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vậy hàm số có 3 điểm cực trị thuộc khoảng ( ) 0;2 Câu 179: Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) ( ) 8524241yxmxmx =+−−−+ đạt cực tiểu tại 0 x = ? A. 3. B. 5. C. vô số. D. 4. Lời giải Ch
( ) ( ) 7423342
( ) 3 xgx
→

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 228 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có, 22 362yxxm =−−+ , ( ) 22 036201yxxm =−−+= , phương trình ( )1 luôn có 2nghiệm 12 , xx với mọi giá trị của tham số m Áp dung định lý Vi et ta có 12 2 12 2 2 . 3 xx
= . G
ị
Đườ
ẳng
điể
ự
ị
33
Nên
( ) ( ) ( ) ( ) ( ) ( ) 22 222 22 21212112 44 1114 99 MNxxmxxmxxxx =−++−=+++− ( ) ( ) ( ) ( ) 23 2222 44416 114211 93327 mmmm =++−−=+++ Theo giả thiết MNAC = ( ) ( ) ( ) ( ) ( ) 33 222222416416 11211141 327327 mmmmmm +++=++++=+ ( ) ( ) ( ) ( ) ( ) 322 22222 4164169 1141141 3273272 mmmmm +++=+++=+= 2 33 11 22 mm +==− Ta chọn đáp án B Câu 181: Cho hàm số bậc ba ( )yfx = có bảng biến thiên như sau Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số ( ) 2 21yfxxm =−++ có 3 điểm cực trị? A. 5 B. 2 C. 4 D. 3 Lời giải Chọn C Xét hàm số ( ) 2 21yfxxm =−++ có ( ) ( ) 2 2221yxfxxm =−−++ .
0984164935
m xx +=
−+
ọi hai điểm cực tr
là ( ) ( ) 1122 ;,; MxyNxy .
ng th
qua hai
m c
c tr
, MN là ( ) 2 2 222 1
m ymx + =−++ .
ta có
= =
x x yxxm fxxm xxm
=−++=−
−++=
( ) 2 2 2
1 1 0211 210 213
−++=
2 2
1 22 22
x xxm xxm
= −+−= −++= . Vẽ đồ thị hai hàm số ( ) 2 22ygxxx ==−+− và ( ) 2 22yhxxx ==−++ .
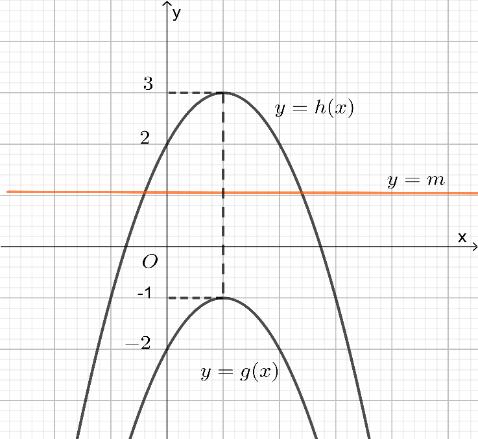
32 2
yxmxmx x y xmxm
=+−+ = = +−−= Để hàm số có tực tiểu mà không có cực đại khi và chỉ
4621 0 0 2310* khi TH1: ( )* vô nghiệm 2 09880mmm ++ . TH2: ( )* có một nghiệm 01.xm==− Vậy số giá trị nguyên của tham số m là 1. Câu 183: Cho hàm số 422 4832yxmxm =−++ . Tìm m để đồ thị hàm số có 3 điểm cực trị ,, ABC tạo thành một tam giác có tâm đường tròn nội tiếp nằm trên đường thẳng 20 xy+−= Lời giải Ta có 4223 48321616 yxmxmyxmx =−++=−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 229
Để hàm số ( ) 2 21yfxxm =−++ có 3 điểm cực trị thì đường thẳng ym = cắt đồ thị hai hàm số trên tại hai điểm phân biệt khác 1 hoặc 3 điểm phân biệt trong đó có một điểm có hoành độ bằng 1 x = 13 m − . Vì m nguyên nên 1,0,1,2 m− . Câu 182: Xét hàm số ( ) ( ) 4322122yfxxmxmxm ==+−++− . Số giá trị nguyên của tham số m để hàm số có cực tiểu mà không có cực đại là A. 1 B. Vô số C. 2 D. 3 Lời giải Chọn A Ta xét ( ) ( ) 4322122yfxxmxmxm ==+−++− ( ) ( )
3 2
0 016160 (*) x yxmx xm
= =−= =
Đồ thị hàm số có 3 điểm cực trị ,, ABC khi và chỉ khi phương trình 0 y = có 3 nghiệm đơn phân biệt, tức là phương trình có hai nghiệm phân biệt khác 00 m
Khi đó đồ thị hàm số có 3 điểm cực trị là ( ) 2 0;32Am + , ( ) 2 ;2Bmm−−+ , ( ) 2 ;2Cmm−+ .
Nhận xét: Tam giác ABC luôn cân tại A và có Oy là trục đối xứng. Gọi H là chân đường cao xuất phát từ đỉnh A của tam giác ABC suy ra AHOy và AH là đường cao cũng là đường phân giác trong góc A nên I là tâm đường tròn nội tiếp tam giác thì IAH hay IOy . Vì tam giác ABC có tâm đường tròn nội tiếp nằm trên đường thẳng 20 xy+−= nên I là giao điểm c
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 230
(
2020;2 xx I xyy == +−== Phương
đường thẳng 2
Phương
22
2 4320. +−−=
Do
tam giác nên ( ) ( ) ,, dIACdIBC = 2 2 3 3 (0) 161 = + m mm m 33 3 1 16131619 2 +=+== mmm Vậy 3 1 2 m = . Câu 184: Cho hàm số 3 5 yxmx=−+ , m là tham số. Hỏi hàm số đã cho có thể có nhiều nhất bao nhiêu điểm cực trị? A. 3 B. 1 C. 2 D. 4 Lời giải Chọn B Ta có: 3 6 55yxmxxmx =−+=−+ 553 2 6 633 . 2 xxx ymmm xxx x =−=−=− . 3 3 0 x ym x == . Đặt 2 3 2 330 () 30 xkhix x fx x xkhix == − Ta có bảng biến thiên hàm số ()fx như sau:
ủa đường thẳng 20 xy+−= với Oy . Suy ra tọa độ của I là nghiệm của hệ
) 00
trình
:2BCym=−+ .
trình đường thẳng : AC
22 3232 0 44 =+= xymxym mmmm
mmxym
I là tâm đường tròn nội tiếp
Từ bảng biến thiên ta thấy phương trình () fxm = có tối đa một nghiệm bội lẻ nên hàm số 3 5 yxmx=−+ có tối đa một điểm cực trị.
Câu 185: Cho hàm số ( )yfx = liên tục trên , biết ( ) 10 f = và ( ) 28 2 225 f =− Đồ thị hàm ( )yfx =

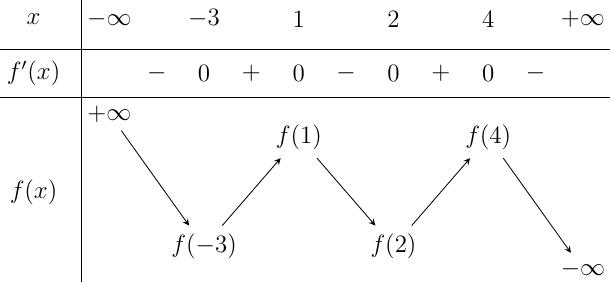
được cho bởi hình vẽ sau
Gọi S là tập hợp tất cả các số thực m là thỏa mãn 450m và hàm số ( ) yfxm =+ có nhiều điểm cực trị nhất. Số phần tử của S là A. 56. B. 57. C. 54. D. 55. Lời giải Chọn D Dựa vào đồ thị hàm ( )yfx = ta suy ra bảng biến thiên của hàm ( )yfx = như sau
Mặt khác, dựa vào đồ thị hàm ( )yfx = ta thấy
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page
231
ta suy ra b
ng bi
124141 41 xfxfxm gx fxm
+++ = ++

n thiên hàm ( ) yfxm =+ như sau Để hàm ( ) yfxm =+ có nhiều điểm cực trị nhất thì đồ thị hàm ( ) yfxm =+ cắt trục hoành tại nhiều điểm nhất. Dựa vào bảng biến thiên trên ta được 2828 00 225225 mmm − . Suy ra 045056 m mà 450m nên 4501;2;...;54;55 m Vậy có 55 giá trị thực m thỏa mãn yêu cầu đề bài. Câu 186: Cho hàm số ( )yfx = có đạo hàm liên tục trên và có bảng biến thiên như sau: Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) ( ) 3 41 gxfxm =++ có 7 điểm cực trị? A. Vô số. B. 3. C. 0. D. 1. Lời giải Chọn D Ta có: ( ) ( ) ( ) ( ) 233 3
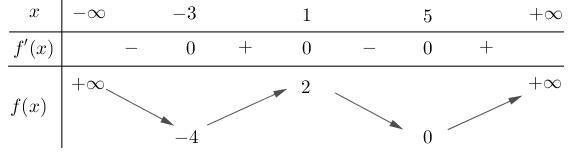
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 232 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 12 31 24 12 dd 131232 124214 dd fxxfxx ffffff ffffff fxxfxx − −−−− −− − .
=−
Kết hợp với bảng biến thiên hàm ( )yfx = và ( ) ( ) 10 28 2 225 f f =
,
ả
ế
Ta có bảng biến thiên: Để hàm số ( )gx có 7 điểm cực trị thì phương trình ( )* phải có 4 nghiệm bội lẻ khác 0 và 1 . Suy ra 0220 mm −− . Vậy có tất cả 1 giá trị nguyên của tham số m thỏa mãn. Câu 187: Chohàmsố ( )yfx = cóđạohàm ( ) ( )( ) 2 '916, fxxxx =−− .Cóbaonhiêugiátrịnguyên dương của tham số m để hàm số ( ) ( ) 3 7 gxfxxm =++ có ít nhất 3 điểm cực trị? A. 9. B. 16. C. 8. D. 4.
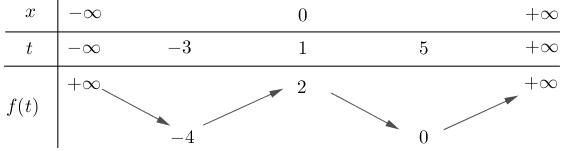
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 233
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Dễ thấy: 2 120,xx Từ bảng biến thiên ta có: ( ) 3 33 3 4130 4104111 4151 x x fxxx x x +=− = +=+==− = += . Ta có: ( ) 3 410fxm++= ( )* ( ) 3 41 fxm+=− . Đặt: 3 41tx=+ 2 1200txx ===
Chọ
C Ta có ( ) ( )( )( )944fxxxx =−−+ ( ) 9 04 4 x fxx x = == =− ( ) ( ) ( ) ( ) ( ) ( ) 2 3 2323 33 7 7 .377.377 77 xx xx gxxfxxmxfxxm xxxx + + =+++=+++ ++ . ( ) 0 gx = ( ) 3 0 70 x fxxm = ++= .
u kiện để
gx
Lời giải
n
Do đó điề
( )
có ít nhất 3 điểm cực trị là phương trình ( ) 3 70fxxm ++= có ít nhất 2 nghiệm bội lẻ khác 0.
( ) 3 70fxxm ++=
3 3 3
xxm xxm xxm
++= ++= ++=−

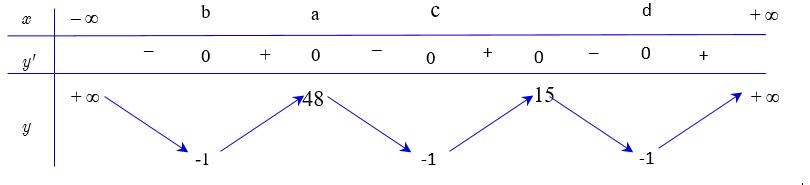
79 74 74
3 3 3
xxm xxm xxm
79 74 74
+−=− +−=− ++=− Phương trình ( ) 3 70fxxm ++= có ít nhất 2 nghiệm bội lẻ khác 0 99mm −− Vậy có tất cả 8 giá trị nguyên dương m thỏa mãn.
Câu 188: Cho hàm số bậc ba ( ) = yfx có đồ thị là một đường cong như hình bên dưới. Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) ( ) ( ) ( ) 2 2 =−− gxffxfxm có nhiều điểm cực trị nhất? A. 11. B. 10. C. 12. D. 13. Lời giải Chọn A *)Đặt: ( ) ( ) ( ) ( ) ( ) 2 221 =−=− ufxfxufxfx .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 234
bacd *)Bảng biến thiên của hàm số ( ) ( ) 2 2 ufxfx =− : *)Mặt khác: ( ) ( ) ( ) ( ) ( ) gxfumgxumfum =−=−− . Do đó số điểm cực trị của hàm số ( ) ( ) ( ) 2 2 gxffxfxm =−− chính là số nghiệm nghiệm bội lẻ của hệ: 2
;2 0 ;;
=
xa u xbcd trong đó 2
fum *)Hàm số ( ) ( ) ( ) ( ) 2 2 =−− gxffxfxm có nhiều điểm cực trị nhất khi và chỉ khi: 1215 113 1215 −− −+ m m m . Do m nguyên nên có 11 giá trị của m thỏa mãn. Câu 189: Cho hàm số ( )yfx = xác định trên và có đồ thị như hình bên dưới.Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ( )1 yfxm =++ có 5 điểm cực trị? A. 2 B. 1 C. 3 D. 0 Lời giải Chọn C Đồ thị hàm số ( )1 yfxm =++ được suy ra từ đồ thị hàm số ( )yfx = như sau: Tịnh tiến đồ thị hàm số ( )yfx = sang phải một đơn vị, sau đó tịnh tiến lên trên m đơn vị. Ta được đồ thị hàm số ( )C : ( )1 yfxm =++ Phần đồ thị ( )C nằm dưới trục hoành lấy đối xứng qua trục Ox ta được đồ thị của hàm số ( )1 yfxm =++ Ta được bảng biến thiên của hàm số ( )1 yfxm =++ như sau:
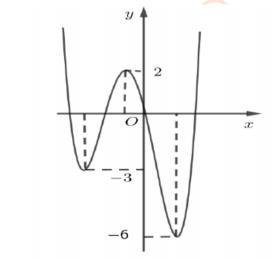
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 235
ạn ( ) ( ) 0 0;;;2;;;;2;
−= == −= −+ −= −= um umum umxbacdxbacd umm
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên so
022;2
um
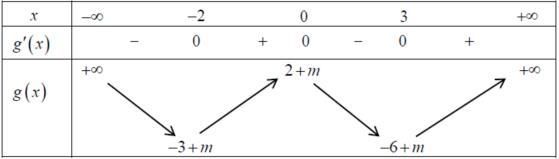

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 236
−+ −+
. Câu 190: Vậy có 3giá trị nguyên dương của m .Cho hàm số bậc ba ( ) = yfx có đồ thị như hình vẽ Tổng tất cả các giá trị nguyên của tham số m để hàm số ( ) ( ) ( ) ( ) 2 4 =−− gxffxfxm có 17 điểm cực trị bằng A. 1652 B. 1653 C. 1654 D. 1651 Lời giải Chọn A Đặt ( ) ( ) ( ) ( ) ( ) ( ) 2 1;2 4220 ;; x uuxfxfxufxfxu xabc − ==−=−= Các nghiệm trên được sắp thứ tự từ nhỏ đến lớn như sau: 12 − abc Bảng biến thiên của hàm số ( ) ( ) 2 4 =− ufxfx
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Để hàm số ( )1 yfxm =++ có 5 điểm cực trị thì đồ thị hàm số ( )C phải cắt trục Ox tại 2 hoặc 3 giao điểm. TH1: Tịnh tiến đồ thị ( )C lên trên. Khi đó 0 6036 30 m mm m
TH2: Tịnh tiến đồ thị ( )C xuống dưới. Khi đó 0 2 20 m m m − +
Do đó số điểm cực trị của hàm số ( )gx phụ thuộc vào số giao điểm của các đường thẳng 2;;2ymymym
với đồ thị ( )ux . Vì không tính điểm tiếp xúc nên các đường thẳng này chỉ có thể cắt đồ thị hàm số ( )ux tại 2 điểm; 4 điểm; 6 điểm hoặc không cắt đồ thị hàm số ( )ux Do đó yêu cầu bài toán trở thành tìm m nguyên để các đường thẳng trên cắt đồ thị ( )ux tại 12 điểm phân biệt
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 237 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có ( ) ( ) ( ) ( ) ( ) =−=−− gxfumgxumfum . Do đó số điểm cực trị của hàm số ( ) ( ) ( ) ( ) 2 4 =−− gxffxfxm chính là số nghiệm bội lẻ của hệ
( ) ( ) 0 0;1;;2;;1;;2; 022;2 um umum umxabcxabc umm um fum −= == −=−− −+ −= −= .
sau:
3260 32601581;0;1;...;571652 m mmS m −− −−= −+ Câu 191: Cho hàm số ()yfx = có đạohàm ( ) ( ) ( ) 3 22 11322 fxxxmxmm =−+−+− , x . Có bao nhiêu giá trị của tham số [5;5] m− để hàm số ( ) ( )gxfxm =+ có tối thiểu 3 cực trị. A. 8. B. 9. C. 10. D. 11. Lời giải Chọn D Ta có: ( ) ( ) ( ) 22 1 0 13220* x fx xmxmm = = +−+−= ( ) ( ) ( ) ( ) 22 2 * 134221 mmmm =−−−=+ . ( ) ( ). x gxfxm x =+ TH1: 1 m =− . ( ) 0 0 0 0 2 1 2 x x x gx x xm x = = = = = += = 60 -3 -4 -4 -4 +∞ +∞ + + + 0 0 0 0 +∞ 0 c 2 b 1 a ∞ u u' x
=−==+
x x x cực trị là 0;1;2xxx==−= . Hàm số ( )fxm + luôn có một điểm cực trị 0 x = . ( ) ( ) ( ) ( ) ( ) ;0 ;0 fxmx yfxm fxmx + =+= −+ Hàm số ( )fxm + có ba điểm cực trị là 1;;2 xmxmxm =−−=−=− . Hàm số ( )fxm −+ có ba điểm cực trị là 1;;2xmxmxm =+==− . Do đó hàm số ( )fxm + có tối đa 7 điểm cực trị là 0;1;;2;1;;2 xxmxmxmxmxmxm ==+==−=−−=−=−
= =− = . Do đó hàm số ( )fx có ba điểm
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 238 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vậy nhận 1 m =− TH2: 1 m − . Khi đó ( )* có 2 nghiệm phân biệt 1 m và 2m ( ) 00 11 0 11() 2 xx xmxm gx xmmxVN xmmxm == +==− =+=−=− +== TH2.1: 1 1 2 mmm − Yêu cầu bài toán 101 mm − . Vậy 5;5 1 5;4;3;2;0 2 1 m m m m − ⎯⎯⎯⎯→−−−− − TH2.2: 1 1 2 mmm − Yêu cầu bài toán 0 m Vậy 5;5 1 1;2;3;4;5 2 m mm − ⎯⎯⎯⎯→ Vậy có 11 giá
trị m thỏa mãn yêu cầu bài toán. Câu 192: Cho hàm số ( )yfx = có đạo hàm ( ) ( ) 2 '122 fxxxx=−− . Có bao nhiêu giá trị nguyên của tham số ( )10;10 m− để hàm số ( )yfxm =+ có 7 điểm cực trị? A. 8. B. 9. C. 10. D. 11. Lời giải Chọn A ( ) ( ) 2 '01220 fxxxx=−−= 0 1 2
Yêu cầu bài toán tương đương với
−− − −+ − + −
m m m m m m m
10 0 20 1 10 0 20
.
Câu 193: Vì m nguyên và ( )10;10 m− 9;8;...;2 m −−− .Vậy có 8 giá trị của tham số m thoả mãn yêu cầu bài toán. Hình vẽ dưới đây là đồ thị của hàm số yfx .
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số 10 yfxm có ít nhất 5 điểm cực trị? A. 6 B. 5 C. 7 D. 8 Lời giải Chọn B Nhận xét: Hàm số ()yfx=− có số điểm cực trị bằng số cực trị của hàm ()yfx = và số giao điểm của đồ thị hàm ()yfx = với đường thẳng y = Số điểm cực trị của hàm ()yfx = bằng số điểm cực trị của hàm ()yfxa =+ Từ nhận xét trên ta có: Hàm số (10)yfx=− có 3 cực trị. Vậy ta cần đường thẳng ym =− cắt đồ thị hàm số (10)yfx=− tại ít nhất 2 điểm khác cực trị. Từ đồ thị ta suy ra: 66mm −− . Do * m nên 1,2,3,4,5} m{ . Câu 194: Cho hàm số ( )yfx = có đạohàm ( ) 2 (5)(4), yfxxxxR ==−− .Có baonhiêugiátrị nguyên của m thuộc đoạn 100;100 để hàm số ( ) 3 ()3 ygxfxxm ==++ có ít nhất 3 điểm cực trị? A. 105 B. 106 C. 104 D. 103 Lời giải
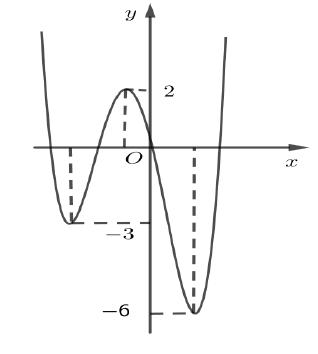
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page
239
ọn A
Ch
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 240 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có: ( ) ( )( ) ( )( ) ( ) ( )( ) ( ) ( ) ( ) 2 32 3 3 22 3 3 3 5405;2;2 333 ().3 3 333 .3 3 '030 fxxxxxx xxx gxfxxm xx xxx fxxm xx gxfxxm =−−====− ++ =++ + ++ =++ + =++= Do đạo hàm không xác định tại 0 x = nên để hàm số ( ) ( ) 3 3 ygxfxxm ==++ có ít nhất 3 cực trị thì 3 '(3)0fxxm++= có ít nhất hai nghiệm đơn hoặc nghiệm bội lẻ khác 0. (
333
xxmxxm ++=+=− ++=++=+=− ++=−+=−− Yêu
−− Vậy có tất cả 105 giá trị m thỏ
ầ
Câu
nhất
11 ; 212 A. 2 , 2 m B. 2 ,1 2 m C. 21,2 m D.
,2 2 m Lời giải Chọn C Co 2 3 03202 2 x fxxxx x sin3cos2sin 3 xxx
) 33
33 3535 '303232 3232 xxmxxm fxxmxxmxxm
cầu bài toán suy ra
505,,100;100 100;99;....4 mmmZm m −−
a mãn yêu c
u bài toán.
195: Cho hàm số yfx có đạo hàm 2 32 fxxxx . Tìm tất cả các giá trị thực không âm của tham số m để hàm số sin3cos gxfxxm có nhiều điểm cực trị
trên
2
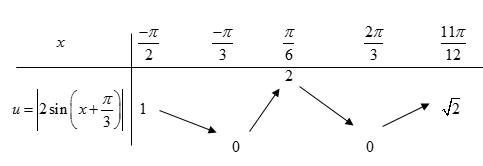
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 241 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 2 2sinsin3cos 3 gxxmfxxm 2 2sin.2cos 33 .2sin 3 2sin 3 xx gxfxm x cos0 3 cos02sin3 33 0 2sin02sin2 33 2sin2 3 x xxm gx fxmxm xm Xét 2sin 3 ux Để thỏa mãn yêu cầu đề bài thì các phương trình 1,2,3,4 có nhiều nghiệm nhất 11 ; 212 x , suy ra 2sin0,1 3 ux Khi đó 03143 021212 021212 mm mm mm . Vì 021,2mm . Do đó 21,2 m
Câu 196: Cho hàm số ( )yfx = xác định trên và có đồ thị ( ) ' yfx = như hình vẽ. Biết ( ) 11 f −= và ( ) 29 f =− . Tổng các giá trị nguyên của m để hàm số ( ) ( )2 gxfxxm =−−−+ có 5 điểm cực trị là? A. 4. B. 6. C. 7. D. 9. Lời giải
Chọn D
Đặt ( ) ( )2 hxfxx =−−− Số điểm cực trị của hàm số ( )gx = + Xét hàm số ( ) ( )2 hxfxx =−−− ( ) ( ) ''21hxfx =−−− Cho ( ) ( ) '0'21 hxfx=−=− . Đặt 2 tx=− . Suy ra ( ) '1(1)ft =− Vẽ đường thẳng ( ):1dy =− trên cùng hệ trục toạ độ với hàm số ( ) ' yfx =
t t t
Dựa vào đồ thị, ta có phương trình ( ) 1 10 2
=− = = Có ( ) ( ) 1112hf−=−−−=− và ( ) ( ) 2245hf=−−=
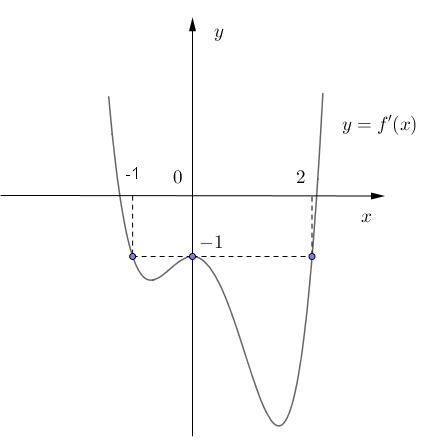
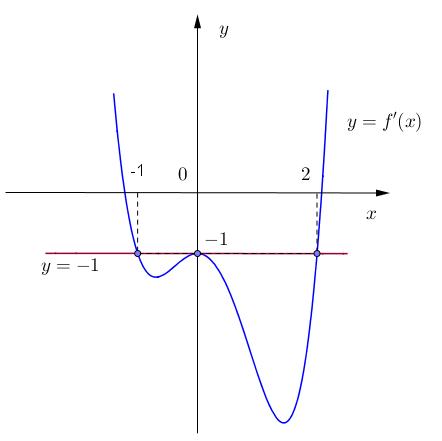
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ
O
Ố
KHẢ
SÁT HÀM S
Page 242
thiên
Dựa vào bảng biến thiên suy ra hàm số ( )hx có 2 cực trị. Suy ra hàm số ( )2 yfxxm =−−−+ cũng có 2 cực trị Hàm số ( )gx có 5 điểm cực trị khi và chỉ khi ( ) hxm =− có 3 nghiệm phân biệt khác điểm cực trị của ( )hx .
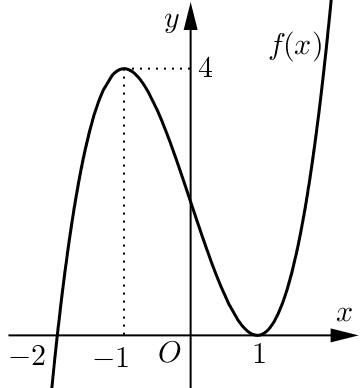
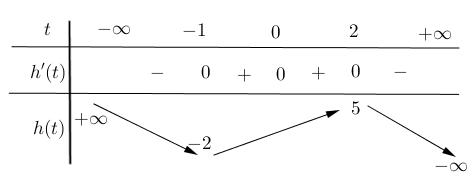
Dựa vào bảng biến thiên, ta có: 52 m − mà m Nên 4;3;2;1;0;1 m−−−− Tổng các giá trị m là: 4321019 −−−−++=− . Câu 197: Cho hàm số bậc ba ( )yfx = có đồ thị như hình vẽ bên dưới.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 243
Bảng biến
Có
ị
tham số 0;20 m để hàm số ( ) ( ) ( ) 2 2 gxfxfxm =−− có 9
m cực trị? A. 8 B. 9 C. 10 D. 11 Lời giải Chọn A Đặt ( ) ( ) ( ) ( ) ( ) ( ) 2 221hxfxfxmhxfxfx =−−=− Khi đó ( ) ( ) ( ) ( ) ( ) 1 1 0 02;1 1 0;1 1 x x fx hxxa fx xb xc = =− = ==−− = = = Ta có bảng biến thiên
bao nhiêu giá tr
nguyên của
điể
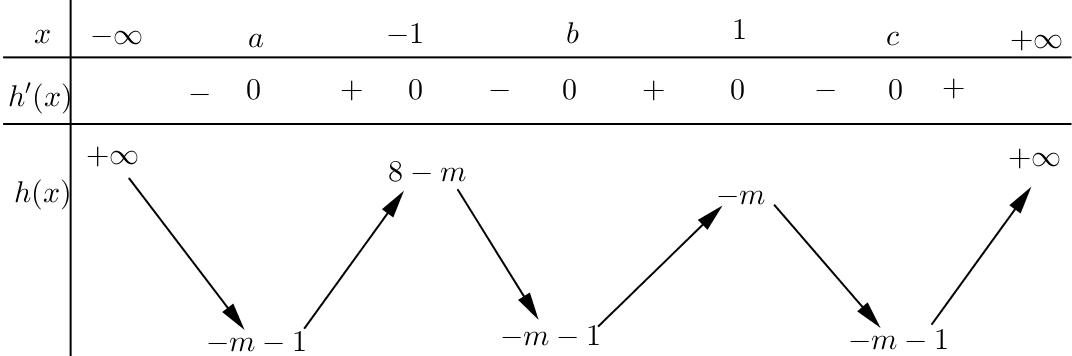
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
ỳnh
42
Page 244
ố
và
ạn Ta
)
có 5
trị.
=
0808mmm −− . Do
bán đường tròn ngoại tiếp tam giác ABC . Câu 199: 6,25,421210 4 ABC abc ABACBCSR S ====== .Cho hàm số ( )yfx = xác định và liên tục trên có ( ) 2 '(8).(815) fxxxx =−−+ Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) 422162 fxxm −−+ có nhiều cực trị nhất? A. 4. B. 5. C. 7. D. 8. Lời giải Chọn A Xét hàm số 422162 yxxm =−−+ có bảng biến thiên có dạng: x y 1 -3 3 D C B A 1
Giáo viên: Hu
Văn Ánh
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 T
t Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm
biên so
có (
hx
điểm cực
Vậy để thoả mãn thì ( ) 0 hx
có bốn nghiệm đơn hoặc bội lẻ hay
0;1;2;3;4;5;6;7 mm . Câu 198: Trong mặt phẳng tọa độ Oxy , gọi ,,, ABCD là bốn điểm cực trị của đồ thị hàm số 3 2 693yxxx =−+− với hoành độ đều khác 0. Bán kính đường tròn ngoại tiếp đi qua 4 điểm ,,, ABCD bằng A. 3 B. 10 C. 5 D. 2 Lời giải Chọn B Tọa độ bốn điểm cực trị của đồ thị hàm số 3 2 693yxxx =−+− là: ( ) ( ) ( ) ( )3;3,3;3,1;1,1;1ABCD Nhận thấy tứ giác ABCD là hình thang cân bán kính đường tròn ngoại tiếp tứ giác ABCD bằng
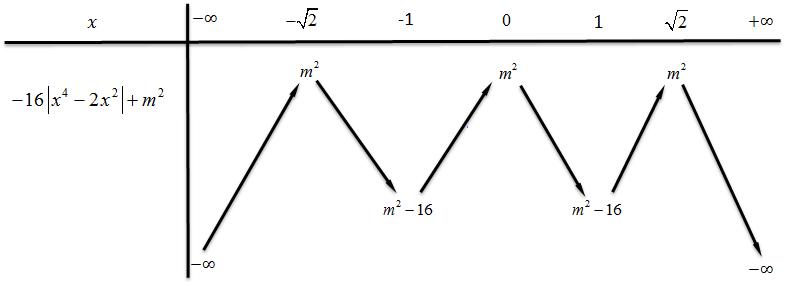


CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 245
YCBT
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Hàm số ( ) 2 '(8).(x815) fxxx=−−+ có 3 điểm cực trị là 3 x = , 5 x = ; 8 x = Số giao điểm tối đa của hàm số 422162 yxxm =−−+ với các đường thẳng 3 y = , 5 y = ; 8 y = thể hiện ở hình vẽ sau:
2 2 2 8 81922194,36 163 m mm m Vì 4;3;3;4 mm . Vậy có 4 giá trị nguyên m . Câu 200: Cho hàm số ( )fx có đạo hàm liên tục trên , đồ thị hàm số ( )yfx = có đúng 4 điểm chung với trục hoành như hình vẽ bên dưới:
Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) 3 3 320212022 yfxxmm =−+++
có đúng 11 điểm cực trị?
A. 0 . B. 2. C. 5. D. 1. Lời giải
Chọn D
Với mỗi tham số m thì số điểm cực trị của hàm số ( ) 3 3 320212022 yfxxmm =−+++
và ( ) 3 32021yfxxm =−++ bằng nhau.
Do đó ta chỉ cần tìm giá trị nguyên của tham số m để hàm số ( ) 3 32021yfxxm =−++ có đúng 11 điểm cực trị Xét 0 x : Hàm số có dạng ( ) 3 32021yfxxm =−++ . Khi đó ta có đạo hàm như sau: ( ) ( ) 23 3332021yxfxxm =−−++
= −++=− −++= −++=

( ) 3 3 3
xx xxm xxm xxm
1do0 320211 320211 320212
=
( ) 3 3 3
+=−+− +=−++ +=−++ Vẽ đồ thị ba hàm số 3 31yxx=−+− ; 3 31yxx=−++ ; 3 32yxx=−++ với 0 x trên cùng một hệ trụ C. Hàm số ( ) 3 32021yfxxm =−++ có đúng 11 điểm cực trị
1do0 202131 202131 202132
Hàm số ( ) 3 32021yfxxm =−++ có đúng 5 điểm cực trị dương
xx mxx mxx mxx
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM
Ố
ĐỂ KHẢO SÁT HÀM S
Page 246
Do nghiệm của phương trình 3 320214xxm−++= là các nghiệm bội bậc chẵn của phương trình 0 y = nên ta chỉ cần quan tâm đến các nghiệm còn lại. Tức là 0 y = ( ) 2 3
330 320210 x fxxm −= −++=
Phương trình ( ) 3 320210fxxm −++= có đúng 4 nghiệm bội lẻ dương và khác 1
Đường thẳng 2021 ym=+ cắt đồ thị ba hàm số 3 31yxx=−+− ; 3 31yxx=−++ ; 3 32yxx=−++ tại 4 điểm phân biệt có hoành độ dương khác 1 120211 220213 m m −+ + 20222020 20192018 m m −− −− . Do điều kiện m nguyên nên 2021 m =− Vậy chỉ có 1 giá trị nguyên của m thỏa mãn yêu cầu bài toán. Câu 201: Cho hàm s = == = . Đặt ( ) 5 5 52'01 2 3
ố ( )fx có đạo hàm liên tục trên . Đồ thị của hàm số ( ) 52 yfx =− như hình vẽ sau. Có bao nhiêu giá trị thực của tham số m thuộc khoảng ( )9;9 thỏa mãn 2m và hàm số t t txxftt t
? = =−=== =− Đặt ( ) ( ) ( ) ( ) 2 33 323 33 33
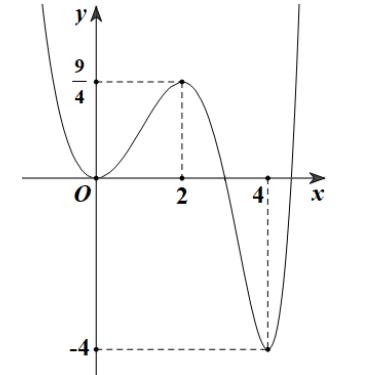
= +== =++−=+= +== +=−=− Từ đó suy ra ( )gx có 3 cực trị. Để ( )ygx = có 5 cực trị thì phương trình ( ) ( ) 3 12 041 4 m gxfx=+= có 2 nghiệm đơn phân biệt.
x xx gxfxmgxxfx xx xx
0 14151 241'24'410 24110 4131
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn x yx x
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 247
( ) 3 1 241 2 yfxm =++− có 5 điểm cực trị
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 A. 26 B. 25 C. 27 D. 24 Lời giải Chọn A Ta có ( ) ( ) 52'2'52 yfxyfx =−=−− . Từ đồ thị, suy ra 0 '02 4
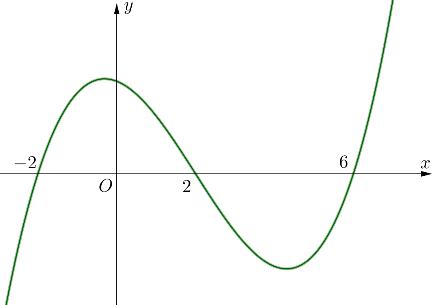
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 248 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Đặt 3 3 1 41 4 u uxx=+= và phương trình trở thành: ( ) 12 4 m fu = Từ đây, kết hợp với đồ thị ta có điều kiện là 129 4428 121217 40 4 m m mm −
−−−− −
trị của m thỏa mãn yêu cầu bài toán. Hết Câu 202: Cho hàm số ( )yfx = có đạo hàm trên . Biết hàm số ( )yfx = là hàm bậc 3 có đồ thị như hình vẽ Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) ( ) 3 231gxfxxm =+−+ có đúng 5 điểm cực trị? A. 4. B. 5. C. 6 . D. 7 . Lời giải Chọn A ( ) ( )( ) ( ) 23 3 3 6323 231 23 xxx gxfxxm xx ++ =+−+ + ( )gx không xác định tại 0 x = ( ) ( ) 3 02310gxfxxm =+−+= 3 3 3 2312 2312 2316 xxm xxm xxm +−+=− +−+= +−+= 3 3 3 233 231 235 xxm xxm xxm +=− +=+ +=+ ( )* ( ) 3 23 hxxx =+ có đồ thị
−
−
. Do ( )
217,16,,9,8 9;9,2 21,2,3,,16 m mm m
. Vậy có tất cả 26 giá
ị nguyên của tham số m thỏa điều kiện bài toán. Câu 203: Cho hàm số ( )yfx = xác định và liên tục trên có ( ) 324 '(8).(x815).(x2) fxxx=−−++ Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) 422162 fxxm −−+ có nhiều cực trị nhất? A. 4 B. 5 C. 7 D. 8 Lời giải Chọn A Xét hàm số 422162 yxxm =−−+ có bảng biến thiên có dạng: Hàm số ( ) 324 '(8).(x815).(x2) fxxx=−−++ có 3 điểm cực trị là 3 x = , 5 x = ; 8 x = Số giao điểm tối đa của hàm số 422162 yxxm =−−+ với các đường thẳng 3 y = , 5 y = ; 8 y = thể hiện ở hình vẽ sau:

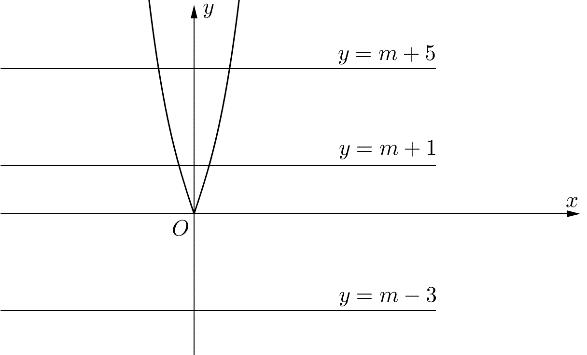
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 249
ạ
một cực trị là
x =
ự
ị
10 13 30 m m m + − − Vậ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên so
n Do ( )gx luôn có
0
nên ( )gx có 5 c
c tr
( )* có 4 nghiệm hoặc 5 nghiệm
y có 4 giá tr

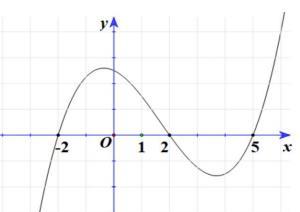
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 250 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn YCBT 2 2 2 8 81922194,36 163 m mm m Vì 4;3;3;4 mm . Vậy có 4 giá trị nguyên m Câu 204: Cho hàm số bậc bốn ( )yfx = có đồ thị ( )yfx = như hình vẽ Gọi S là tập hợp các giá trị nguyên thuộc đoạn 10;10 của tham số m để hàm số ( ) 2 2 yfxxm =+−− có đúng 3 điểm cực trị. Số phần tử của tập hợp S bằng A. 5 B. 3 C. 10 D. 6 Lời giải Chọn D ( ) 2 02 5 x fxx x =− == = ( )( ) ( ) 2 2 2 212 2 2 xxx yfxxm xx ++− =+−− +−
Ta có BBT của hàm số 2 2 txx=+− như sau: Để hàm số có đúng 3 điểm cực trị thì phương trình không có nghiệm đơn. Dựa vào BBT trên, phương trình không có nghiệm đơn 50 m + 5 m − Vì m , 10;10 m− 10;9;......5 m −−− . Vậy tập S có 6 phần tử. Câu 205: Cho hàm số ( )fx có đạo hàm liên tục trên . Đồ thị của hàm số ( ) 52 yfx =− như hình vẽ. Có bao nhiêu giá trị thực của tham số m thuộc khoảng ( )9;9 thỏa mãn 2m và hàm số ( ) 3 1 241 2 yfxm =++− có 5 điểm cực trị? A. 24. B. 25. C. 26. D. 27. Lời giải


CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 251 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Điểm đặc biệt: '0y = hoặc ' y không xác định ( ) 2 1 2 1 2 20(1) x x x fxxm =− = =− +−−= Ta thấy 1 ;1;2 2 xxx=−==− là các nghiệm
xxmxxm xxmxxm xxmxxm +−−=−+−=−
đơn của y 22 22 22 2222 (1)2222 2525
+−−=+−=+ +−−=+−=+
Chọn C
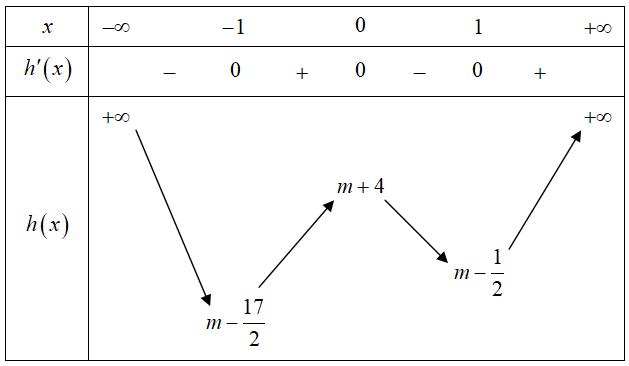
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 252 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn • Đặt ( ) ( ) 52 gxfx =− , khi đó đồ thị đã cho là của ( )gx . Có ( ) ( ) 515 222 fxgfxgxx ==− . ( ) 5 0 2 5 02 2 5 4 2 x x fx x = == = 5 1 3 x x x = = =− • Đặt ( ) ( ) 3 1 241 2 hxfxm =++− , có ( ) ( ) 23 2441hxxfx =+ . ( ) 2 3 3 3 0 415 0 411 413 x x hx x x = += = += +=− 0 1 1 x x x = =− = Bảng biến thiên: Từ BBT ta thấy ( )hx có 3 điểm cực trị, do đó hàm số ( ) ( ) 3 1 241 2 yfxmhx =++−= có 5 điểm cực trị khi và chỉ khi phương trình ( ) 0 hx = có đúng 2 nghiệm khác các điểm cực trị của ( )hx . Điều này tương đương với 404 171117 0 2222 mm mmm +− −− 28 1217 m m − . Mà 2m , ( )218;18 m− nên 217;16;...;81;2;...;16 m−−− Vậy có 26 giá trị m thỏa mãn. Câu 206: Cho hàm số bậc bốn ( )yfx = có đồ thị như hình vẽ dưới đây
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ( )1 yfxm =++ có 7 cực trị? A. 0. B. 3. C. 2. D. 1. Lời giải Chọn C Nhận xét: Hàm số ( )yfx α =− có số điểm cực trị bằng tổng số cực trị của hàm ( )yfx = và số giao điểm của đồ thị hàm ( )yfx = với đường thẳng y α = Số điểm cực trị của hàm ( )yfx = bằng số điểm cực trị của hàm ( )yfxa =+
Từ nhận xét trên ta có: Hàm số ( )1 yfx=+ có 3 cực trị Vậy ta cần đường thẳng ym =− cắt đồ thị hàm số ( )1 yfx=+ tại 4 điểm khác điểm cực trị.
Từ đồ thị ta suy ra: 3223 mm −−−
Do * m nên 1;2 m Câu 207: Cho hàm số ( ) ( ) 42 2 fxxmxm =−++ với m là tham số thực. Số giá trị nguyên của 2022;2022 m− để hàm số ( )yfx = có số điểm cực trị nhiều nhất là A. 2021. B. 2020. C. 2023. D. 2022. Lời giải
Chọn D
Hàm số ( )yfx = và hàm số ( )yfx = cùng có tập xác định là Lại có, hàm số ( )yfx = là hàm số đa thức bậc 4 trùng phương nên có tối đa 3 điểm cực trị là 1x , 2x , 3x và đồ thị hàm số ( )yfx = cắt trục hoành tại tối đa 4 điểm phân biệt có hoành độ là 4x , 5x , 6x , 7x .
Do đó, hàm số ( )yfx = có nhiều nhất là 7 điểm cực trị là các điểm 1x , 2x , 3x , 4x , 5x , 6x , 7x

Hàm số ( )yfx = có nhiều điểm cực trị nhất đồ thị hàm số ( )yfx = phải cắt trục hoành tại 4 điểm phân biệt
phương trình ( ) 2 20tmtm−++= phải có 2 nghiệm dương phân biệt
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 253
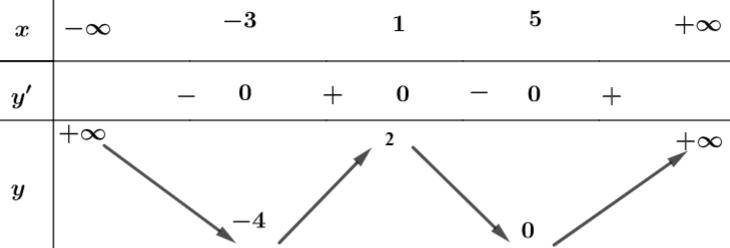

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 254 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt
ệp
12 Sưu tầm và biên soạn Δ0 0 0 S P ( )2 240 20 0 mm m m +− + 0 m Do 2022;2022 0 m m m −
Hòa
0984164935
Nghi
THPT BDKT Toán 10; 11;
nên 1;2;3;...;2022 m
. Câu 208: Cho hàm số ( )yfx = có đạo hàm liên tục trên và có bảng biến thiên như sau: Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) ( ) 3 41 gxfxm =++ có 7 điểm cực trị? A. 3 B. 1 C. 0 D. Vô số Lời giải Chọn B Ta có: ( ) ( ) ( ) ( ) 233 3 124141 41 xfxfxm gx fxm +++ = ++ . Dễ thấy: 2 120,xx . Từ bảng biến thiên ta có: ( ) 3 33 3 4130 4104111 4151 x x fxxx x x +=− = +=+==− = += Ta có: ( ) 3 410fxm++= ( )* ( ) 3 41 fxm+=− Đặt: 3 41tx=+ 2 1200txx === Ta có bảng biến thiên: Để hàm số ( )gx có 7 điểm cực trị thì phương trình ( )* phải có 4 nghiệm bội lẻ khác 0 và 1 . Suy ra 0220 mm −− . Vậy có tất cả 1 giá trị nguyên của tham số m thỏa mãn.
Câu 209: Cho hàm số ( )fx có đạo hàm liên tục trên . Đồ thị của hàm số ( ) 52 yfx =− như hình vẽ sau. Có bao nhiêu giá trị thực của tham số m thuộc khoảng ( )9;9 thỏa mãn 2m và hàm số ( ) 3 1 241 2 yfxm =++− có 5 điểm cực trị? A. 21. B. 26. C. 23. D. 27. = == = . Đặt 5 52 2 t txx=−= ( ) 5 01 3
Lời giải Chọn B Ta có ( ) ( ) 52252 yfxyfx t ftt t
=−=−− . Từ = == =− . Đặt ( ) ( ) 3 1 241 2 gxfxm =++− ( ) ( ) 23 24410gxxfx =+=
= +== +== +=−=−

x xx xx xx
2 33 33 33
0 4151 4110 4131
. Từ đó suy ra ( )gx có 3 cực trị. Để ( )ygx = có 5 cực trị thì phương trình ( ) ( ) 3 12 041 4 m gxfx=+= có 2 nghiệm đơn phân biệt. Đặt 3 3 42 5241 4 u uxx −=+= và phương trình trở thành: ( ) 12 52 4 m fu−= Từ đây, kết hợp với đồ thị ta có điều kiện là
129 4428 121217 40 4
m m mm
− − − . Do ( ) 217,16,,9,8 9;9,2 21,2,3,,16 m mm m
−−−− − . Vậy có tất cả 26 giá trị của m thỏa mãn yêu cầu bài toán. Câu 210: Cho hàm số ( )yfx = có đạo hàm ( ) 3 32, yfxxxx ==−− . Có bao nhiêu giá trị nguyên của tham số 30;30 m− để hàm số ( ) 42 8 yfxxm =−+ có đúng 7 điểm cực trị
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn x yx x
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 255
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 đồ thị, suy ra: 0 02 4
A. 1 B. 16 C. 2 D. 17 Lời giải
Chọn D
Ta có ( ) ( ) ( ) 2 3 3212yfxxxxx ==−−=+− , suy ra ( ) 0 fx = có nghiệm đơn là 2, nghiệm kép là 1.
Xét hàm số ( ) 42 8 hxxx =− có ( ) ( ) 32 41644hxxxxx =−=−
Suy ra ta có
=
gx fgx ygx gx gx
=−
= ==


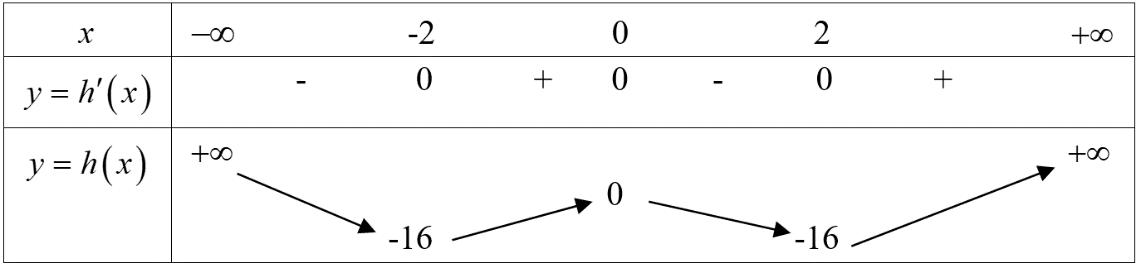
1(1) 0 02(2) 0 0(3)
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 256
Vậy ta thấy hàm số ( )gx có 5 điểm cực trị là 22;2;0;2;22 . Ta xét hàm số ( ) ( ) ( ) 42 8 yfxxmfgx =−+= ( ) ( ) ( )yfgxgx
( ) ( ) ( ) ( ) ( ) ( )
= =
Theo phần trên thì hàm số ( )gx có 5 điểm cực trị 22;2;0;2;22 , tương đương với phương trình có 5 nghiệm như trên; vậy điều kiện để hàm số ( ) ( ) ( ) 42 8 yfxxmfgx =−+= có 7 điểm cực trị là phương trình ( ) (2):2 gx = có 2 nghiệm bội đơn khác các số 22;2;0;2;22 vì ( ) 0 fx = có nghiệm kép là 1). Từ bảng biến thiên ta thấy yêu cầu bài toán tương đương với 16214 mm +− Kết hợp với điều kiện 30;30 m− , ta có 30;29;...;14 m−−− . Vậy ta có 17 giá trị thỏa mãn. Câu 211: Cho hàm số ( )yfx = có đồ thị như hình vẽ dưới đây.
( ) ( ) 1 0 2 fxxaa=−=
Suy ra hàm số ( )gx có 3 cực trị Để hàm số ( ) ( )hxgx = có đúng 3 cực trị thì phương trình ( ) 0 gx = vô nghiệm Xét phương trình ( ) ( ) ( ) 2 0 gxfxfxm =++= Đặt ( )tfx = , ta có: ( ) 2 0* ttm++= Từ đồ thị hàm số ( )yfx = , ta có với mỗi tR thì phương trình ( )tfx = luôn có nghiệm nên phương trình vô nghiệm 1 0140 4 mm − . Mà m nguyên thuộc đoạn 15;15 . Vậy có 15 giá trị của m. Câu 212: Cho hàm số 432 341221yxxxm =−−+− . Khi tham số m thay đổi thì hàm số đã cho có số điểm cực trị được chia thành ba mức là ,, abc với abc . Giá trị abc bằng A. 1 B. 15 C. 2 D. 3 Lời giải

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 257
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 15;15 để hàm số ( ) ( ) ( ) 2 hxfxfxm =++ có đúng 3 điểm cực trị? A. 16 B. 15 C. 17 D. 14 Lời giải Chọn B Xét hàm số ( ) ( ) ( ) 2 gxfxfxm =++ Ta có: ( ) ( ) ( ) ( ) ( ) ( ) ( )2.21gxfxfxfxfxfx =+=+ ( ) ( ) ( ) 0 01 2 fx gx fx = = =− +> ( ) 1 0 3 x fx x = = = +>
, phương trình ()0fx = có hai nghiệm đơn Hàm số ()yfx = có 5 điểm cực trị. TH3: 1 260213 2 mmm −− , phương trình ()0fx = có bốn nghiệm đơn Hàm số ()yfx = có 7 điểm cực trị. Theo giả thiết, ta có: 7,5ab== và 3 c = 1 abc−−=− Câu 213: Cho hàm số ( )fx có đạo hàm trên là ( )( )()34fxxx =+− . Tính tổng các giá trị nguyên của tham số [10;5] m

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 258
Chọn A
=−+ có nhiều điểm cực trị nhất? A. 54. B. 9. C. 54. D. 52. Lời giải Cách 1: ( )( ) ( ) 2 2 2 233 .3 3 xxxm yfxxm xxm −−+ =−+ −+ . y không xác định tại các điểm thỏa mãn 2 30(1)xxm−+= 2 2 230 033 34 x yxxm xxm −= =−+=− −+= 2 2 3 2 34(2) 34 x xxm xxm = −=− −=−−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
Xét hàm số: 432 ()341221 fxxxxm =−−+− Ta có: ( ) 322 ()121224122 fxxxxxxx =−−=−− Bảng biến thiên TH1: Nếu 33 2330 2 mm− , hàm số ()yfx = có 3 điểm cực trị. TH2: Nếu 33 23302632 2101 2 m mm m m −− −
− để hàm số ( ) 2 3 yfxxm
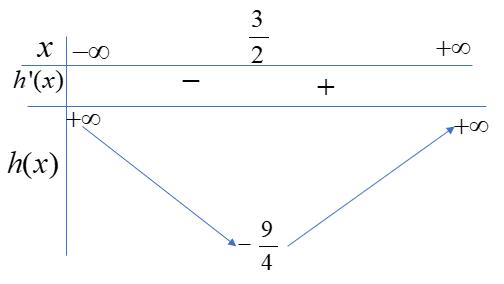
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo
Huỳnh Văn Ánh 42
ễn
Thuận
Huế
Page 259 Chuyên
ể
Tố
ệ
12 Sưu tầm và biên soạn Xét hàm số ( ) 2 3 hxxx =− có BBT Đề hàm số có nhiều điểm cực trị nhất thì số nghiệm phương trình và là nhiều nhất 97 4 44 mm −−−− . Mà
=−
a mãn 2 30(1)xxm−+= 2 2 230 033 34 x yxxm xxm −= =−+=− −+= 2 2 3 2 34(2) 34 x xxm xxm = −=− −=−− Đề hàm số có nhiều điểm cực trị nhấ
ố
2 2 2 3 34 34 xxm xxm xxm −=− −−=− −+=− có nhiều
ệ
ất Dựa vào đồ thị các hàm trên cùng
ệ tọa độ
viên:
Nguy
Cư Trinh
Hòa TP
ĐT: 0984164935
luyện thi: Tuy
n sinh vào lớp 10
t Nghi
p THPT BDKT Toán 10; 11;
[10;5] m− suy ra {10,9,8,...,2} m−−−− . Vậy tổng 54. S
Cách 2: ( )( ) ( ) 2 2 2 233 .3 3 xxxm yfxxm xxm −−+
=−+ −+ . y
không xác định tại các điểm thỏ
t thì s
nghiệm phương trình và là nhiều nhất
nghi
m nh
h
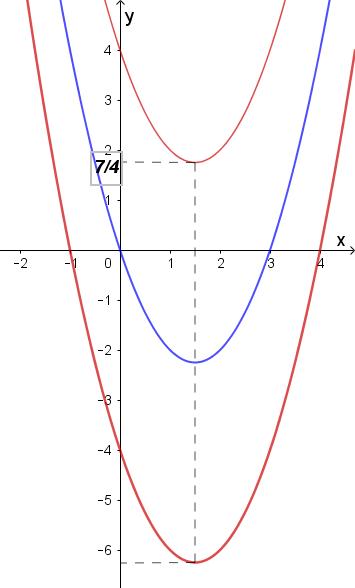
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 260 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Suy ra hàm số có nhiều điểm cực trị nhất khi 77 44 mm −− . Mà [10;5] m− suy ra {10,9,8,...,2} m−−−− . Vậy tổng 54. S =− Cách 3: ( )( ) ( ) 2 2 2 233 .3 3 xxxm yfxxm xxm −−+ =−+ −+ . y không xác định tại các điểm thỏa mãn 2 30(1)xxm−+= 2 2 230 033 34 x yxxm xxm −= =−+=− −+= 2 2 3 2 34(2) 34 x xxm xxm = −=− −=−− Đề hàm số có nhiều điểm cực trị nhất thì số nghiệm phương trình và là nhiều nhất 2 2 2 30 340 340 xxm xxm xxm −+= −−+= −++= có nhiều nghiệm nhất 1 2 3 940 7 91640 4 91640 m mm m =− =+−− =−− Mà [10;5] m− suy ra {10,9,8,...,2} m−−−− . Vậy tổng 54. S =− Câu 214: Cho hàm số ( )fx có đạo hàm trên ( ) ( )( )34fxxx =+− . Tính tổng các giá trị nguyên của tham số 10;5 m− để hàm số ( ) 2 3 yfxxm =−+ có nhiều điểm cực trị nhất? A. 54. B. 9. C. 52. D. 54. Lời giải Chọn D Ta có ( ) ( )( ) 3 340 4 x fxxx x =− =+−= = .
Suy ra.

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 261 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Tính đạo hàm, ( ) ( ) 2 2 2 3 323 3 xxm yfxxmx xxm −+ =−+− −+ . ( ) ( ) ( ) ( ) 2 2 2 2 2 2 2 2 2 3 3 3 2 2 2 30 31 30 0 33 342 34 34 343 34 x x x xxm xxm xxm y xxmVN xxm xxm xxm xxm xxm = = = −+= −=− −+= = −+=− −=− −+= −+=− −=−− −+=
Đặt ( ) 2 3 gxxx =− , khảo sát hàm
Chọ
Xét
(
=+−+ Tập
=
( ) 32 0 '12122401 2 x fxxxxx x = =+−== =− Bả
số ( )ygx = , ta được bảng biến thiên như bên dưới. Để hàm số có nhiều điểm cực trị nhất khi và chỉ khi 97 4 44 mm −−− Kết hợp với điều kiện 10;5 m− suy ra tập giá trị m là 10,9,8,...,2 S =−−−− . Vậy tổng các giá trị nguyên của tham số m bằng 54 Câu 215: Có bao nhiêu giá trị nguyên của tham số m để hàm số 432 34122 yxxxm =+−+ có 7 điểm cực trị? A. 4. B. 2. C. 3. D. 1. Lời giải
n B
hàm số
) 432 34122 fxxxxm
xác định: D
.
ng biến thiên:
Hàm số ( ) 432 34122 fxxxxm =+−+ luôn có 3 điểm cực trị nên hàm số
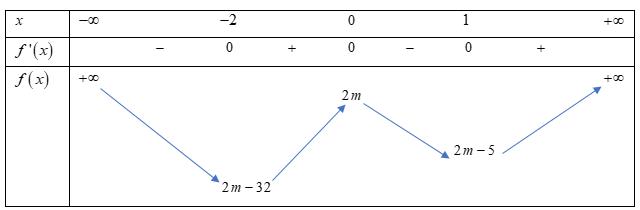
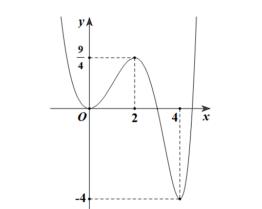
34122 yxxxmfx
)
có 7 điểm cực tr
đồ thị hàm số ( )yfx = cắt trục Ox
ại 4 điểm phân biệt 5 25020 2 mmm − . Vì m nên có 2 số nguyên thỏa mãn. Câu 216: Cho hàm số ( )fx có đạo hàm liên tục trên . Đồ thị hàm số ( )52x yf=− như hình vẽ bên. Có bao nhiêu giá trị thực của tham số m thuộc khoảng ( )9;9 thoả mãn 2m và hàm số ( ) 3 1 24x1 2 yfm =++− có 5 điểm cực trị. A. 26. B. 25. C. 27.
Chọn B Từ đồ thị ta có các bảng biến thiên của hàm ( )ft và ( )fu sau
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 262
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
(
432
=+−+=
ị
t
D. 24. Lời giải
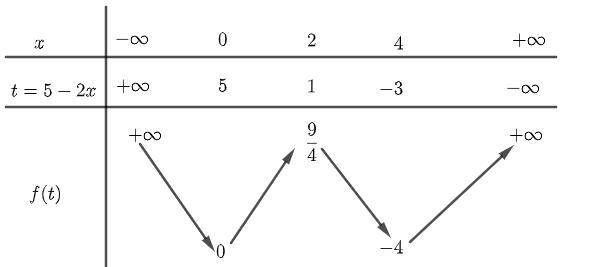
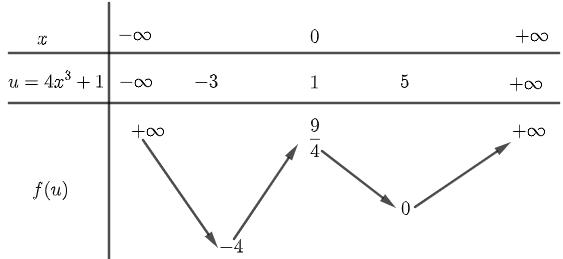
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 263 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Xét ( ) ( ) ( ) ( ) 323 1 24x124x'4x1 2 hxfmhxf =++−=+ ( ) 2 3 3 3 00 4x131 '0 4x110 4x151 xx x hx x x == +=−=− = +== +== ( ) ( ) 3 1 04x1 42 m hxf=+=− . Yêu cầu bài toán tương đương 1 401217 42 1928 424 m m mm −− − − . Kết hợp với điều kiện ta có ( ) 2 218;1821;2;3;...;1617;16;...;8 m m m −−− − . Vậy có 26 giá trị m thoả mãn yêu cầu bài toán. Câu 217: Cho hàm số ( )yfx = . Hàm số ( )yfx = có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m với 0;6 m để hàm số ( ) ( ) 2 212 gxfxxxm =−−−+ có đúng 9 điểm cực trị?
thẳng ym =− cắt các đồ thị hàm số 22241,4,41 yxxyxxyxx =−−=−=−+ tại 3 điểm phân biệt có hoành độ lớn hơn 1 và khác 2 Ta có đồ thị
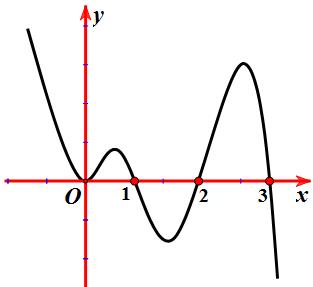
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 264
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 5 B. 3 C. 7 D. 6 Lời giải Chọn B Đồ thị hàm số ( ) ( ) ( ) 2 2 2121211 gxfxxxmfxxm =−−−+=−−−+− đối xứng qua đường thẳng 1 x = . Xét hàm số ( ) 2 42,1yfxxmx =−++ ( ) ( ) ( ) 2 2 22 2 2 2 2 2 2 420 41 24420421 4 422 41 423 x x xxml xxm yxfxxmxxm xxm xxm xxm xxm = = −++= −+=− =−−++=−++= −=− −++= −−=− −++= . Hàm số ( ) ( ) 2 212 gxfxxxm =−−−+ có đúng 9 điểm cực trị khi và chỉ khi đường

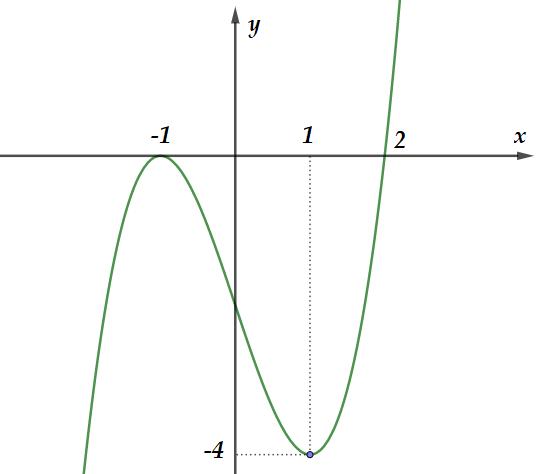
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 265 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Từ đồ thị, ta được: 22 0;1;2 4334 mm m mm −− −−− Câu 218: Cho hàm số ()yfx = có đồ thị hàm số '()yfx = như hình vẽ Số giá trị nguyên của tham số m để hàm số ( ) 2 ()243ygxfxxm ==−+− có 7 điểm cực trị. A. 1 B. 2 C. 4 D. 3 Lời giải Chọn A Ta có ( ) ( ) ( ) =−+−−+− 22 243.243 gxxxmfxxm . Suy ra ( ) 0 gx = ( ) ( ) −+ = −−+−22 0 243.243 xxmfxxm
2 2 2
24301 243 243 12 23 m



















xxm xx xxm .
−+−= −=−+
Xét phương trình ( ) ( ) −+−= 2 24301 xxm
ới ( ) 014401xxx −== .
ới ( ) 014401xxx +==− . Khi đó 1;0;1xxx=−== là 3 điểm cực trị của hàm số. +) Xét phương trình ( ) =− 2 2 243 1 x m x
Từ đồ thị suy ra phương trình ( )2 nếu có nghiệm thì nghiệm là bội chẵn nên hàm số ( )gx không đổi dấu nên không phải là cực trị.
+) Xét phương trình ( ) −−=−+ 2 24323 xxm
Yêu cầu bài toán suy ra phương trình ( )3 có 4 nghiệm phân biệt khác 0,1 . Xét hàm số 2 243yxx=−− có bảng biến thiên Từ bảng biến thiên suy ra 52357 mm −−+− . Vì m nguyên nên 6 m = . Vậy có 1 giá trị nguyên của tham số m thoả mãn.
219: Cho hàm số
) 322 2 yxmxmxm =+++− với m là tham số. Có bao nhiêu giá trị nguyên của m thoả mãn 15 m −
hàm số đã
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 266 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) = −+−= −+− 2 2 2430 2 0 43 xxm fxxm ( ) =− −+−= −+− −+−= 2 2 2 2430 243 24 1 32 xxm xxm xxm ( ) ( ) ( ) ( ) =−−
+)
V
V
Câu
(
để
cho có đúng 5 điểm cực trị? A. 6. B. 3. C. 5. D. 4. Lời giải Chọn D Hàm số ( ) 322 2 yxmxmxm =+++− có 5 điểm cực trị ( ) 322 2 yxmxmxm =+++− có hai điểm cực trị nằm về hai phía của trục hoành ( ) ( ) 322201xmxmxm+++−= có ba nghiệm phân biệt. Ta có ( ) 32220xmxmxm+++−= ( )( ) 2 20xmxxm ++−= ( ) 2 202 xm xxm =− +−= . x ∞ 1 0 1 + ∞ y' 0 + 0 0 + y + ∞ 5 3 5
Để ( )1 có ba nghiệm phân biệt thì ( )2 có hai nghiệm phân biệt khác m 2
10 30 m mm
+ − 1 0,3 m mm − .
Do m nguyên và 46 m − nên suy ra 1;2;4;5 m Vậy có 4 giá trị nguyên của m thỏa yêu cầu bài toán.
Câu 220: Gọi S là tập chứa tất cá các giá trị thực của tham số m để hàm số ( ) 2 214 yfxxmxx ==−++ có điểm cực đại với giá trị cực đại tương ứng nằm trong khoảng ( )3;4 và đồng thời thỏa mãn 10m là số nguyên. Tìm số phần tử của tập S . Lời giải Xét phương trình 2 210xmx−+= có 2 1 m =− . Trường hợp 1. Nếu 2 10 m =− thì ta có ( ) ( ) 22214221 yfxxmxxxmx ==−++=−−+ Dễ thấy hàm số này không tồn tại điểm cực đại. Trường hợp 2. Nếu 2 1 10 1 m m m − =− ; khi đó hai nghiệm phân biệt của phương trình 2 210xmx−+= lần lượt là 22 121;1xmmxmm =−−=+−
xx xx thì ( ) ( ) 22214221 yfxxmxxxmx ==−++=−−+ không có điểm cực đại. 2 121 2433;4 3434
Với 12 xxx xxmx mmmmm fmmm mm =+ −−++ +=++ ++ 2 2 2
đại m m m mmmm m mm m
thì ( ) ( ) 22214221 yfxxmxxxmx ==−+−+=−++− . 5 125 4342525254 4334 0
tri cực đại là: − − ++−−−+−−− − ++
. Suy ra ( ) 10251040 m −−− 42,310401042;414,2;4,1 mmmS −−−−−−= Vậy S có 2 phần tử. Câu 221: Tổng các giá trị nguyên của tham số m để hàm số 2 301yxxmx =−−++ có ba điểm cực trị là A. 22 B. 2 C. 21 D. 0 Lời giải Chọn D
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG D
ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
ỤNG
Page 267
Hàm số này có điểm cực
là: 2 xm=+ và giá
Với 1 2 ( ) 2 243yfmmm =+=++ Suy ra điều kiện: ( ) ( ) 22 12 2 2
Ta có: Hàm số có ba điểm cực trị khi và chỉ khi ( )* có 3 nghiệm phân biệt, tức là 1111 m − Mà 10;9;8;7;...;8;9;10 mm−−−− . Vậy tổng tất cả các giá trị nguyên của m là 0. Câu 222: Cho đồ thị hàm số ( )yfx = như hình vẽ. Gọi S là tập tất cả các giá trị nguyên dương của tham số m để hàm số ( ) 2 1 1 3 yfxm =++ có 5 điểm cực trị. Tổng tất cả các giá trị của các phần tử của tập S bằng: A. 7 B. 10 C. 8 D. 1 Lời giải


CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 268
(
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có: ( )2 22301301 yxxmxxxmx =−−++=−−++ .
)( ) ( ) ( )( ) 22 2 2 2 230213021 23030 xxxxxx ymm xx xx
=+=+ . ( )( ) ( )( ) ( ) 22 22 30213021 00* 3030 xxxxxx ymm xxxx
=+==− Nếu 2 30056xxxx −−− thì ( )( ) ( ) 2 2 3021 21 30 xxx mx xx =−=−− . Nếu 2 30056xxx −−− thì ( )( ) ( ) 2 2 3021 21 30 xxx mx xx =−=−
ọ
Ch
n A
ho m m
b −−− −

Hàm số ( )fx có 3 điểm cực trị. Đồ thị hàm số ( )1 fx + có được bằng cách tịnh tiến đồ thị hàm số ( )fx sang trái 1 đơn vị, nên hàm số ( )1 yfx=+ cũng có 3 điểm cực trị Do đó hàm số ( ) 2 1 1 3 yfxm =++ có 5 điểm cực trị ( ) 2 1 10 3 fxm ++= có 2 nghiệm đơn 1 63 3 1 2Loai 3
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 2 2
2
3 3 918 3232
m m m m
− − do m nguyên dương suy ra 332 m 3;4 S = . Tổng các phần tử của tập S là 7. Câu 223: Trong mặt phẳngtọađộ Oxy ,gọi ,,, ABCD là4điểm cựctrị củađồthị hàm số 3 2 693yxxx=−+− với hoành độ đều khác 0. Bán kính đường trờn ngoại tiếp đi qua 4 điểm ,,, ABCD bằng A. 3 B. 10 C. 5 D. 2 Lời giải Chọn B Xét ( ) 32693 x xx x f = +− Ta có ( ) ( ) ( ) 2 111;1 '31290 333;3 xyA fxxx xyB == =−+= ==−− Do hàm số ( )fx có 2 cực trị dương nên 3 2 693yxxx=−+− có 5 cực trị là ( ) ( ) ( ) ( ) ( )1;1,3;3,0;3,'1;1,'3;3 ABCAB Gọi đường tròn ngoại tiếp tứ giác là 22 220xyaxbyc +−−+=
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 269
ặc
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 ội lẻ ( ) 2 1 1 3 fxm+=− có 2 nghiệm đơn hoặc bội lẻ ( )
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 270 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có hệ 22 2220 222410 66186 abca abcbRabc abcc −−+=−= −+=−==+−= −−+=−= .



CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 271 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn BÀI 2: CỰC TRỊ CỦA HÀM SỐ - VD VDC - 04 HƯỚNG DẪN GIẢI CHI TIẾT Câu 224: Có bao nhiêu giá trị nguyên của m để đồ thị hàm số 2 3 3 mx yx x =+ + có các điểm cực trị thuộc hình tròn tâm O bán kính 130? R = A. 16 B. 18. C. 19. D. 17. Lời giải Chọn D 2 2 2 .3. '33 3 x mxmx x y x +− + =+ + ( ) ( ) ( ) 22 2222 .3 3 33 3333 mxmx m xxxx +− =+=+ ++++ Đặt 2 3 tx=+ 3 3 '3 m y t =+ . Cho '0y = 3 3 30 m t += 3 tm=− 2 3 3 xm+=− ( ) 3 22 3 0 xmm += 3 22 3 xm =− . Điều kiện để hàm số có các điểm cực trị: 3 2 30 m − 3 2 3 m 33 m − Khi đó 3 2 3 xm=− ( ) 3 2 3 2 333 3 mm yxxmx m x =+=+=− + Đặt 3 2 1 3, xm=− 3 2 2 3 xm=−− . Hai điểm cực trị ( ) ( ) 1122 ,,, AxyBxy , dễ thấy OAOB = Các điểm cực trị A , B thuộc hình tròn tâm O bán kính 130130ROAOB == 22 130 OAOB = ( ) ( ) 2 3322 313130 mm −+− Đặt 3 2 3 um=− ( ) 2 1130uu + 3 1300 uu +− 5 u 3 2 35 m − 2 512 m 5555 m − CHƯƠNG I ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Kết hợp với điều kiện 5533 m −− 22;21;...;6 m −−− Có 17 giá trị m . Câu 225: Cho hàm số ( )fx có đạo hàm liên tục trên . Đồ thị của hàm số ( ) 52 yfx =− như hình vẽ bên dưới Có bao nhiêu giá trị thực của tham số 0;10 m để hàm số ( ) 2 241 yfxm =+− có 7 điểm cực tr = == = . Đặt ( ) 5 5 52,'01 2 3
? A. 6 B. 5 C. 4 D. 3 t t txxftt t
, gxfxmgxxfxm x m x x xm m x xm xm m x
i ()241'16.'410 0 04 4154 411 4 4134 4
i gi = =−=== =− ( ) ( ) ( ) 22 2 2 2 2 2 2

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn x yx x
=+−=+−= = + = = +−= = +−= +−=− = để hàm số ( ) 2 ()241 ygxfxm ==+− có 7 điểm cực trị thì '()0gx = có 7 nghiệm phân biệt và '()gx đổi dấu qua 7 nghiệm đó. Từ đó suy ra ( )ygx = có 7 cực trị khi 4 m vì, đồng thời theo đề 0;10 m . Vậy có 6 giá trị của m thỏa mãn yêu cầu bài toán
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ
ẢO SÁT HÀM SỐ
KH
Page 272
ị
Lờ
ả
Chọn A Ta có ( ) ( ) 52'2'52 yfxyfx =−=−− . Từ đồ thị
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 suy ra 0 '02 4

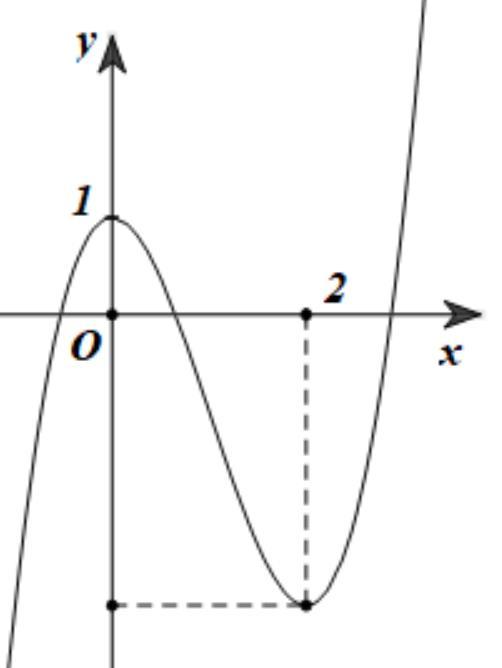
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo
Page 273
Câu
Tìm tất cả các giá trị của m để
ố
==+
trị và chúng đều là các số dương? A. 24 m . B. 03 m . C. 4 m . D. 34 m . Lời giải Chọn D Ta có: ( ) ( ) ( ) ( ) 2 2 2 1 '22.'2. 21 gxxfxxm fxxm =−−+ −++ ( ) 22 22 22 11 2222 '0 2121 2323 xx xxmxxm gx xxmxxm xxmxxm == =−+=−−=−− −+=−−=−− −+=−=− Ta có BBT của hàm số 2 2 yxx =− như sau x − 0 1 + 2 2 yxx =− + 0 1 + YCBT 13034 34 110 mm m mm −− −−− . Câu 227: Cho hàm số ( )yfx = có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 2021;2021 để hàm số ( ) ( ) 5 4 gxfxxm =++ có ít nhất 5 điểm cực trị? A. 2022 B. 2021 C. 2023 D. 2024
viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
226: Cho hàm số ( )yfx = có đạo hàm trên , bảng xét dấu của biểu thức ( )fx như bảng dưới đây.
hàm s
( ) ( ) ( ) 2 2 2 1 21 fxxm ygx fxxm −+
−++ có đúng 3 điểm cực
tại 0 x = và hàm số ( )gx có 1 cực trị tại điểm 0 x = Ta có ( ) 55 5 55

404 40 4242
xxmxxm fxxm xxmxxm
++=+=− ++=++=+=− . Xét hàm số ( ) 5 4 hxxx =+ , vì ( ) 4 560hxx =+ , x nên ( )hx đồng biến trên Khi đó bảng biến thiên của hàm số ( ) ( ) 5 4 kxhxxx ==+ như sau Hàm số ( ) ( ) 5 4 gxfxxm =++ có ít nhất 5 điểm cực trị khi phương trình ( ) 5 40fxxm ++= có ít nhất 4 nghiệm khác 0. Điều này xảy ra khi và chỉ khi 0 m − hay 0 m .
Kết hợp điều kiện 2021;2021 m− , ta được 2021;2020;...;1 m−−− Vậy có 2021 giá trị của m thoả mãn. Câu 228: Cho hàm số ( )fx có đạo hàm ( ) 2 2 ()(1)4 fxxxx
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 274 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn B ( ) ( ) ( ) ( ) ( ) 555 44.4 gxfxxmgxxxmfxxm =++=++++ ( ) ( ) ( ) 54 5 5 4.54 .4 4 xxx fxxm xx ++ =++ + ( ) ( ) 5 040gxfxxm =++= . ( )gx không xác định
0984164935
A. 18. B. 17. C. 16. D.
Lời giải Chọn B Ta có: ( ) 2 2 1 ()0(1)400 4 x fxxxxx x = =−−== = ,
x =
( ) ( ) ( ) ( ) 22 ()212412212 gxfxxmgxxfxxm =−+=−−+ Xét ( ) ( ) ( ) 2 04122120 xf x xxm g = −+=
=−− .Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ( ) 2 ()212 gxfxxm =−+ có đúng 5 điểm cực trị?
19.
trong đó 1
là nghiệm kép.
nên ta loại phương trình 2 2121 xxm−+= ) Xét hàm số 2 212 yxx =− có đồ thị, có đạo hàm '412yx=−
Ta có bảng biến thiên Để ( )gx có đúng 5 điểm cực trị thì mỗi phương trình ( ) ( )1;2 đều có hai nghiệm phân biệt khác 3. Do đó, mỗi đường thẳng 4 ym =− và ym =− phải cắt đồ thị tại 2 điểm phân biệt có hoành độ khác 3. Nhận xét: đường thẳng 4 ym =− luôn nằm trên đường thẳng ym =−
Suy ra 18 m−− 18 m . Câu 229: Vậy có 17 giá trị m nguyên dương. Cho hàm số ( )yfx = có đạo hàm ( ) ( )( ) 2 114fxxx =−− , x . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ( ) ( ) 3 321gxfxxm =++− có ít nhất 3 điểm cực trị? A. 5. B. 8. C. 6. D. 7. Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 275
−+= −+= −=− −+= −+=−=−
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) 2 2 2 2 22 3 3 2121() 2121 2121 2120 212421242 x x xxml xxm xxm xxm xxmxxm = =
++
+
ấ
ạ
=
gx đổi dấu khi qua 0 x = nên nếu ( ) 3 3210fxxm ++−= không tồn tại nghiệm bội lẻ bằng 0 thì 0 x = là một điểm cực trị của hàm số ( )gx Mặt khác ( ) 33 333 33 321113122 32103212312 3212332 xxmxxm fxxmxxmxxm xxmxxm ++−=+=− ++−=++−=−+=−− ++−=+=− . Xét hàm số ( ) 3 3 hxxx =+ , vì ( ) 2 330, hxxx =+ nên ( )hx đồng biến trên . Ta có bảng biến thiên của hàm số ( ) ( ) 3 3 kxhxxx ==+ như sau:
Chọn A ( ) ( ) ( ) ( ) ( ) 333 321321.321 gxfxxmgxxxmfxxm =++−=++−++− ( ) ( ) ( ) 32 3 3 3.33 .321 3 xxx fxxm xx
=++−
Ta th
y ( )gx xác định t
i 0 x
và ( ) '
Hàm số ( ) ( ) 3 321gxfxxm =++− có ít nhất 3 điểm cực trị khi phương trình ( ) 3 3210fxxm ++−= có ít nhất hai nghiệm bộ lẻ khác 0. Điều này xảy ra khi và chỉ khi 1220 m − hay 6 m Kết hợp điều kiện m nguyên dương ta được 1;2;3;4;5 m . Vậy có 5 giá trị của m thoả mãn. Câu 230: Có bao nhiêu giá trị nguyên của m để đồ thị hàm số m y x =+ + ( ) ( ) 3 3 222 '033,0 yxmxmm =+=−=− ( )1 Hàm số có điểm cực trị ( )1 có hai nghiệm phân biệt 3 2 3033 0 m m m
2 3 3 mx yx x =+ + có các điểm cực trị thuộc hình tròn tâm O bán kính 130 R = ? A. 16 B. 18 C. 19 D. 17 Lời giải Chọn D − − Với 33 m − , ta có ( ) 3 2 2 3 2 2
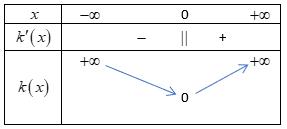
m xmy m xmy
33 3 1 33 3
=−==+ + =−−=−=−+ +
. Vậy hai điểm cực trị của đồ thị hàm số là 2 ;3 3 m A + + và 2 ;3 3 m B −−+ + Ta có ( ) ( ) 2 2 33 222 2 13313 3 m OAOBmm
==++=−+− + . Đặt ( ) 3 2 ,0tmt= , khi đó ( ) ( )2 32 31392830OAOBttttt ==−+−=−+− . 3232 928301309281600ycbtOARtttttt −+−−+−
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 3 '3 3
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 276
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Ta có ( )3 2
Suy ra 3 2 0816233 mm −− . Vì 22,24,...,6 mm−−− .
Vậy có 17 giá trị nguyên của m thỏa ycbt. Câu 231: Cho hàm số ( )yfx = có đạo hàm là ( ) ( )( ) 22 '99 fxxxx=+− , với mọi x . Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) ( ) 32 32 gxfxxmm =++− có không quá 6 điểm cực trị? A. 2. B. 5. C. 4. D. 7 . Lời giải
Chọn B
Ta có ( ) ( )( ) ( )( )( ) 22 '99339 fxxxxxxxx =+−=−++
Ta có ( ) ( )( ) ( ) ( ) 23 32 2 3
++ =++− + . ( ) ' gx không xác định 0 x = ( ) ( ) 32 3223 3223 3223 3223
333 '.'32 3
xxx gxfxxmm xx
=++−= ++−=−=+ ++−=−−=++ ++−=−=+− ++−=−−=++
gxfxxmm xxmmmmxx xxmmmmxx xxmmmmxx xxmmmmxx
'0'320 32023 323233 323233 329239
Ta vẽ đồ thị hàm số 3 3 yxx =+ như sau:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG D
ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
ỤNG
Page
277
08 t
đúng 9 điểm c
Nhìn vào đồ thị ta thấy hàm số ( ) ( ) 32 32 gxfxxmm =++− có không quá 6 điểm cực trị khi và chỉ khi 2 2313mmm −− . Mà 1;0;1;2;3 mm− nên có 5 giá trị thỏa mãn yêu cầu đề bài. Câu 232: Cho hàm số ()yfx = có đạo hàm là 2 ()10 fxxx =+ , x . Có bao nhiêu giá trị nguyên của tham số m để hàm s = −= =
278 = =+= =− Xét ( ) ( ) ( ) 424 3 2 84168 yfxxmyxxfxxm =−+=−−+ Cho ( ) 42
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 3 4160 0 80 xx y fxxm −= = −+= Xét phương trình: 3 0 4160 2 x xx x
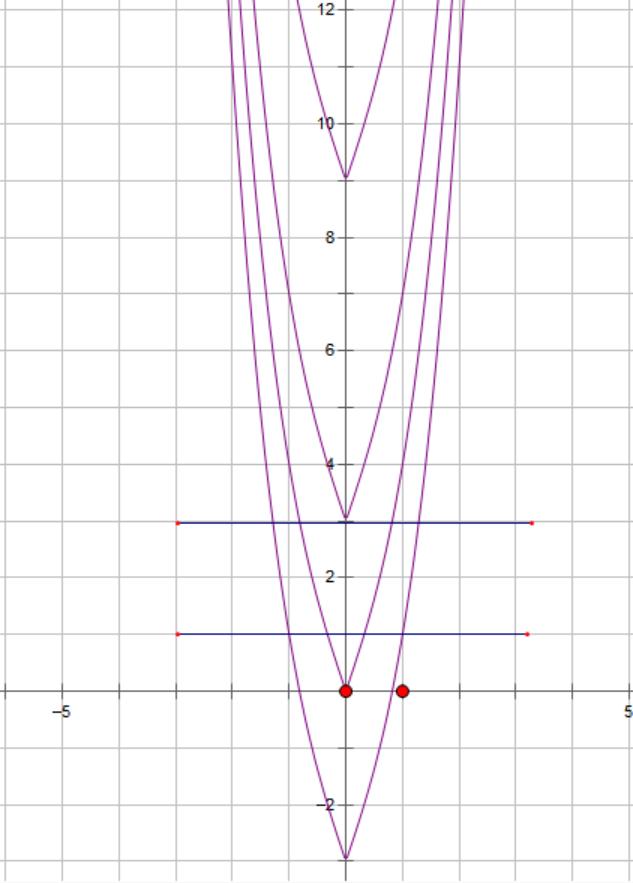
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page
ố ( ) 42 8 yfxxm =−+ có
ự
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 ị? A. 16. B. 9. C. 15. D. 10. Lời giải Chọn D Xét 2 0 ()100 10 x fxxx x
c tr
Xét phương trình: ( ) 4280fxxm −+= ( ) ( ) 42 42 4242
81 80 8108102 xxm xxm xxmxxm
. Đề hàm số ( ) 42 8 yfxxm =−+ có đúng 9 điểm cực trị thì phương trình ( ) 4280fxxm −+= cần có 6 nghiệm đơn 0 x và 2 x
Xét hàm số ( ) 42 8 gxxx + =− có ( ) 3 0 '160 2 x gxxx x
Ta có bảng biến thiên:
= =−+= =

Xét hai đường thẳng 12:,:10dymdym==+ song song với trục Ox . Vì ( ) 10 mmm+ , nên đường thẳng 2d nằm trên đường thẳng 1d
Phương trình có 2 nghiệm và phương trình có 4 nghiệm 01016 100 0 m m m + − . Vì m nên 9;...;1 m −− .
Vì 0 x = đã là cực trị của hàm số ( ) 42 8 yfxxm =−+ nên ta lấy cả trường hợp 0 m = . Câu 233: Vậy có 10 giá trị nguyên của tham số m thỏa mãn. Cho hàm số ( ) ( ) ( ) 2 2 243fxxxx =−−+ với mọi x . Có bao nhiêu giá trị nguyên dương của m để hàm số ( ) 2 109yfxxm =−++ có 5 điểm cực trị? A. 18. B. 16. C. 17. D. 15. Lời giải Chọn B Ta có ( ) 2 01 3
x fxx x
, 2 x = là nghiệm kép nên khi qua giá trị 2 x = thì ( )fx không bị đổi dấu. Đặt ( ) ( ) 2 109gxfxxm =−++ khi đó ( ) ( ) ( )'.210 gxfux =− với 2 109uxxm=−++ .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG
HÀM ĐỂ KHẢO SÁT HÀM SỐ
ĐẠO
Page 279
−+= −+= −+=−−+=+
= == =
Câu 234: Vậy có 16 giá trị nguyên dương m thỏa mãn. Cho hàm số ( )yfx = có đạo hàm ( ) ( ) ( )( ) 2020 22 320212 xx fxxxx =−−+− , x . Gọi S là tập các giá trị nguyên của tham số m để hàm số ( ) 2 8 yfxxm =−+ có đúng ba điểm cực trị 1x , 2x , 3x thỏa mãn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo
ỳnh
42
Page 280
ố
ạ
Nên ( ) ( )2 2 2 2 2100
0
x xxm gx xxm xxm −= −++−= = −++= −++= ( ) (
2 2 2 2 5
x xxm xxm xxm = −++−= −++= −++=
'
,. 170
− − −+ −+
. Lời giải Chọn D Ta có: ( ) ( ) ( )( ) 2020 22 03202120 xx fxxxx =−−+−= ( )* 2 2 3 3 202102 0 20 xx x x x x xx = = −+== = −= . Suy ra: ( ) ( ) 2 288 yxfxxm =−−+ , ( ) ( ) 2 02880yxfxxm =−−+= ( ) 2 280 80 x fxxm −= −+= ( ) ( ) ( ) 2 2 2 4 831 822 803 x xxm xxm xxm = −+= −+= −+= ( ) ( ) ( ) 2 2 2 4 831 822 83 x xxm xxm xxm = −=− −=− −=− Xét hàm số ( ) 2 8 yhxxx ==− , ( ) 28hxx =− , ( ) 02804hxxx =−== Ta có bảng biến thiên của hàm số ( )yhx = .
viên: Hu
Văn Ánh
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 T
t Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên so
n
10920
1091 1093
) ( )
10920 10801 10602
Hàm số ( ) 2 109yfxxm =−++ có 5 điểm cực trị khi và chỉ khi ( )gx đổi dấu 5 lần Hay phương trình ( )1 và phương trình ( )2 phải có hai nghiệm phân biệt khác 5 ( ) ( ) ' 1
2 0 0 50 50 h p
190 17 170 190 m m m m m
222 123 50 xxx++= . Khi đó tổng các phần tử của S bằng A. 17. B. 33. C. 35. D. 51

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 281
21618 1616
mm −− −− 16;17
Nếu 4 x = là nghiệm của
A. 8. B. 5. C.
Lời giải Chọn C Ta có: ( ) 0 '0 2 x fx x = = =− ( ) ( ) 23 2 33 3 33 '(33).'30 11 33011 '30303(*) 3232 yxfxxm xx x xx xxmxxm fxxm xxmxxm =−−+= == −= =−=− −+=−=− −+= −+=−−=−− Để hàm số ( ) 3 3 yfxxm =−+ có 4 điểm cực trị thì phải có 4 nghiệm bội lẻ. Xét ( ) 3 3 gxxx =−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vì 3 x = là nghiệm bội chẵn của phương trình ( ) 0 fx = nên nghiệm của phương trình ( )1 không phải là điểm cực trị của hàm số. Từ bảng biến thiên suy ra, hàm số có đúng ba điểm cực trị khi phương trình ( )2 có hai nghiệm phân biệt đồng thời phương trình ( )3 vô nghiệm hoặc có nghiệm duy nhất 4 x =
mm
m
phương trình ( )3 thì 16 m = , suy ra phương trình ( )2 2 42 8140 42 x xx x =− −+= =+ Nếu 17 m = thì phương trình ( )3 vô nghiệm, phương trình ( )2 2 3 8150 5 x xx x = −+= = Câu 235: Vậy 17 S = .Cho hàm số ()yfx = có đạo hàm là ( ) 2 '36 fxxx =+ , x . Có bao nhiêu giá trị nguyên của tham số 5;5 m− để hàm số ( ) 3 3 yfxxm =−+ có đúng 4 điểm cực trị?
6. D. 10.
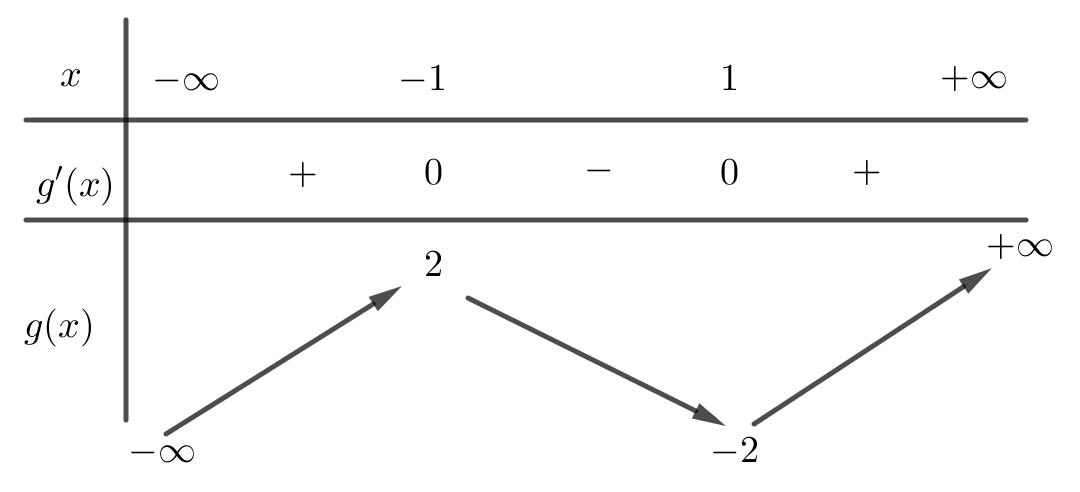
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo
Huỳnh Văn
42
ễn
ận
ế
Page 282
ể
ớ
Tốt
ệ
11; 12 Sưu
m và biên soạn ( ) 2 1 '330 1 x gxx x = =−= =− . Bảng biến thiên: Dựa vào bảng biến thiên, để có 4 nghiệm bội lẻ thì 2 22 224 22 m mm mm m −− − −−−−
−
( ) 0 gx = ( ) ( ) ( ) 22 2 2 4 (81)01 802 8203 x xxm xxm xxm = −+−= −+= −+−=
x
viên:
Ánh
Nguy
Cư Trinh Thu
Hòa TP Hu
ĐT: 0984164935
Chuyên luyện thi: Tuy
n sinh vào l
p 10
Nghi
p THPT BDKT Toán 10;
tầ
−−
Mà
5;4;2;3;4;5 5;5 m m m
−−
. Có 6 giá trị m . Câu 236: Cho hàm số ( )yfx = có đạo hàm ( ) ( ) ( ) 2 2 12 fxxxx
=−− với x . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ( ) 2 8 fxxm −+ có 5 điểm cực trị? A. 17 B. 15 C. 16 D. 18 Lời giải Chọn B Đặt ( ) ( ) 2 8 gxfxxm =−+ ( ) ( ) ( ) 2 2 12 fxxxx
=−− ( ) ( )( ) ( )( ) 2 222 2881882 gxxxxmxxmxxm =−−+−−+−+−
Các phương trình ( )1 , ( )2 , ( )3 không có nghiệm chung từng đôi một và ( )2 2 810xxm−+− với
m nguyên dương và 16 m nên có 15 giá trị m cần tìm. Câu 237: Cho hàm số ()yfx = . Hàm số ()yfx = có đồ thị như hình vẽ dưới đây. Tìm m để hàm s
Chọn C
Do hàm số 2 ()yfxm =+ là hàm chẵn nên hàm số có 3 cực trị khi và chỉ khi hàm số này có đúng 1 điểm cực trị dương. ( ) 22()2 yfxmyxfxm
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 283
−+
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Suy ra ( )gx có 5 điểm cực trị khi và chỉ khi ( )2 và ( )3 có hai nghiệm phân biệt khác 4 160 1620 16320 163220 m m m m −
−+
−+−
16 18 16 18 m m m m 16 m .
ố 2 ()yfxm =+ có 3 điểm cực trị. A. ;0. m B. 3; m . C. )0;3 m . D. 0;3 m . Lời giải
=+=+ ( ) 22 2 22 22 00 0 0 0 0 11 33 xx x xmxm y fxm xmxm xmxm == = +==− = += +==− +==− Đồ thị hàm số ( )yfx = tiếp xúc trục hoành tại điểm có hoành độ là 1 x = nên các nghiệm của pt 2 1 xm =− không làm ( ) 2 fxm + đổi dấu khi x đi qua, do đó các điểm cực trị của hàm số 2 ()yfxm =+ là các điểm nghiệm của hệ 2 2 0 3 x xm xm = =− =− Hệ trên có duy nhất nghiệm dương khi và chỉ khi 0 03 30 m m m − − . x y 3 2 0 1
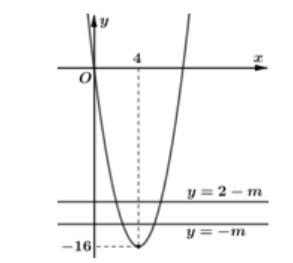
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 284
tấ
ả
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 238: Cho hàm số yfx có ( ) ( )( ) 2 121, fxxxxmxx
=+−+ với m là tham số thực. Hỏi có
t c
bao nhiêu số nguyên m không vượt quá 2022 sao cho hàm số ( ) ( ) 2 1 gxfx=− có 7 điểm cực trị? A. 2020. B. 2023. C. 2021. D. 2022. Lời giải
20 10 21220 x x xmxm = −= −+++= ( ) ( ) 42 0 1 21220* x x xmxm = = −+++= . Do 0 x là nghiệm bội lẻ và 1 x là các nghiệm đơn nên để gx có 7 điểm cực trị thì phương trình * phải có 4 nghiệm phân biệt khác 0 và khác 1 , hay phương trình ( ) 2 21220tmtm−+++= phải có 2 nghiệm dương phân biệt khác
ợ
ới
ờ
Chọn A Xét ( ) 22 ()0(1)20 fxxxx =−−= 1(
2) 0 2 x x x = = = Ta
( ) 2
=−−+
Chọn C Ta có: ( ) ( ) 2 2.1gxxfx =− ( ) ( ) 3242 212122 xxxmxm =−−+++ Khi đó ( ) 0 gx
= ( ) 3 2 42
1 ( ) ( ) 2 2 10 210 220 121.1220 m Sm Pm mm =− =+
=+ −+++ 1 1 1 1 10 m m m m − − −
1 m . Kết h
p v
điều kiện m nguyên, không vượt quá 2022 suy ra có 2021 giá trị của m . Câu 239: Cho hàm số ()yfx = có đạo hàm ( ) ( ) 2 2 ()12 fxxxx =−− với mọi x . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ( ) 2 ()8 gxfxxm =−+ có đúng 5 điểm cực trị? A. 15. B. 16. C. 17 . D. 18. L
i giải
nghiem boi
có:
()2(4).8 gxxfxxm
( ) 2 ()02(4)80 gxxfxxm =−−+=
2
81( nghiem boi 2) 80(1) 82(2)
Yêu cầu bài toán trở thành ()0gx = có 5 nghiệm bội lẻ hay mỗi phương trình, đều có hai nghiệm phân biệt khác 4. Xét đồ thị (C) của hàm số 2 8 yxx = và hai đường thẳng 1 : dym =− ; 2 2 : dym=−+ Khi đó xảy ra khi 12 , dd cắt (C) tại bốn điểm phân biệt 16 m −− 16 m
Vậy có 15 giá trị m nguyên dương thỏa mãn: {1,2,3,..,15}.
Câu 240: Cho hàm số ()yfx = . Hàm số ()yfx = có đồ thị như hình vẽ dưới đây. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số 2 ()yfxm =+ có 3 điểm cực trị. T
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 285
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
2
2 4
x xxm xxm xxm = −+= −+= −+=
Ta
( ) 22()2 yfxmyxfxm =+=+ ( ) 22 2 22 22 00 0 0 0 0 11 33 xx x xmxm y fxm xmxm xmxm == = +==− = += +==− +==− Đồ thị hàm số ( )yfx = tiếp xúc trục hoành tại điểm có hoành độ là 1 x = nên các nghiệm của phươngtrình 2 1 xm =− không làm ( ) 2 fxm + đổi dấu khi x đi qua, do đó các điểm cực trị của hàm số 2 ()yfxm =+ là các điểm nghiệm của hệ 2 2 0 3 x xm xm = =− =− x y 3 2 0 1
ổng các phần tử của S là: A. 3 B. 6 C. 1 D. 10 Lời giải Chọn A Do hàm số 2 ()yfxm =+ là hàm chẵn nên hàm số có 3 cực trị khi và chỉ khi hàm số này có đúng 1 điểm cực trị dương.
có:
Hệ trên có duy nhất nghiệm dương khi và chỉ khi 0 30030;1;2 m mm m −
. Vậy tổng các phần tử của S là 3 Câu 241: Cho hàm số ( )yfx = là hàm số bậc 5 và có đồ thị của hàm số ( )yfx = như hình vẽ dưới
Có bao nhiêu giá trị nguyên của ( )2022;2022 m− để hàm số
nghiệm kép của phương trình ( ) 0 gx = nên không sinh ra cực trị cho hàm số ( )ygx = . +) Dễ thấy ( ) ( ) ( )2,3,4 không có nghiệm chung. +) Phương trình ( )2 và ( )3 nếu có nghiệm thì sẽ có nghiệm dương
Cách 1: Từ đó suy ra để hàm số ( )ygx = có 3 điểm cực trị dương khi hai phương trình ( ) ( )2,3 có đúng 2 nghiệm dương khác 1011. Ta xét các khả năng có thể xảy ra:
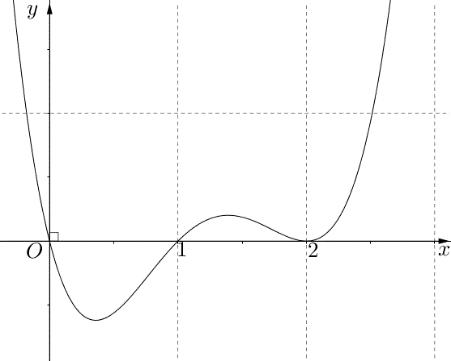
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO
HÀM SỐ
Page 286
SÁT
−
( ) 2 2022 yfxxm =−+ có 3 điểm cực trị dương. A. 4023 B. 2021 C. 2022 D. 4020 Lời giải Chọn B Từ đồ thị của hàm số bậc bốn ( )yfx =
ố
ta suy ra hàm s
( ) 0 01 2 x fxx x = == = trong đó 2 x = là nghiệm kép, 0 x = và 1 x = là nghiệm đơn. Đặt ( ) ( ) 2 2022 ygxfxxm ==−+ Ta có: ( ) ( ) ( ) 2 220222022 gxxfxxm =−−+ ( ) ( ) ( ) ( ) ( ) 2 2 2 10111 202202 0 3 202210 4 202220 x xxm gx xxm xxm = −+= = −+−= −+−= +) Phương trình ( )4 nếu có nghiệm thì các nghiệm là
phân biệt và ( )3 vô nghiệm.
Nhận thấy nếu các phương trình ( )2 và ( )3 có nghiệm thì luôn có nghiệm dương nên để hàm số đã cho có ba cực trị trị dương thì phương trình ( )2 và ( )3 có hai nghiệm trái dấu 0 m − 0. m Do ( )2022;2022 m− nên có 2021 số thỏa mãn yêu cầu bài toán. Câu 242: Cho hàm số ( )fx có đạo hàm ( ) 2 2 ()(1)4 fxxxx =+− .Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ( ) 2 ()212 gxfxxm =−+ có đúng 5 điểm cực trị?
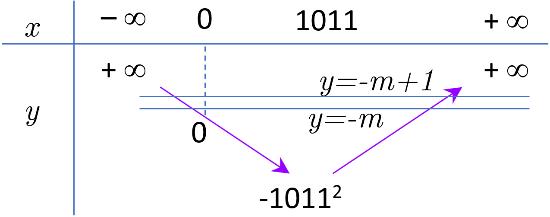
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 287 Chuyên
ện thi:
ển sinh
ớp 10 Tốt
ệp
12 Sưu tầm và biên soạn TH1: ( )2 và ( )3 có 2 nghiệm trái dấu khác 1011 2 2 0 10112022.10110 0. 10 10112022.101110 m m m m m −+ − −+− TH2: ( )2 có hai nghiệm dương
( ) 2 2 2 2 10110 1011 0 10111 101110 m m m m m − + −− .
0984164935
luy
Tuy
vào l
Nghi
THPT BDKT Toán 10; 11;
Không có m
phân biệt và ( )2 vô nghiệm. ( ) 2 2 2 2 10110 1011 0 10111 101110 m m m m m − + −− . Không có m . TH4: ( )2 và ( )3 cùng có
thì
( )
22 22 22 101110111 2022020222 0 3 20221020221
−+=−=− =−+−=−=−+ −+−=−=−−
TH3: ( )3 có hai nghiệm dương
nghiệm kép Vậy 0 m
hàm số có 3 cực trị dương. Do ( )2022;2022 m− nên có 2021 số thỏa mãn yêu cầu bài toán. Cách 2:
( ) ( ) ( ) ( )
4 20222020222 xx xxmxxm gx xxmxxm xxmxxm ==
Xét hàm số 2 2022 fxxx Bảng biến thiên:
hàm số 2 212 yxx =− có đồ thị. '412yx=− Ta có bảng biến thiên
Để ( )gx có đúng 5 điểm cực trị thì mỗi phương trình ( ) ( )1;2 đều có hai nghiệm phân biệt khác 3. Do đó, mỗi đường thẳng 4 ym =− và ym =− phải cắt đồ thị tại 2 điểm phân biệt có hoành độ khác 3. Nhận xét: đường thẳng 4 ym =− luôn nằm trên đường thẳng ym =− . Ta có: 18 m−− 18 m
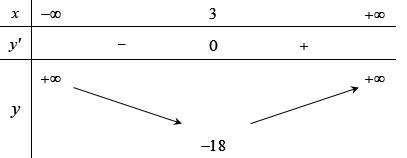
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 288 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 18 B. 17 C. 16 D. 19 Lời giải Chọn B Ta có: ( ) 2 2 1 ()0(1)400 4 x fxxxxx x =− =+−== = , trong đó 1 x =− là nghiệm kép. ( ) ( ) ( ) ( ) 22 ()212412212 gxfxxmgxxfxxm =−+=−−+ Xét ( ) ( ) ( ) 2 04122120 xf x x g xm = −+ −= ( ) ( ) 22 2 2 33 21202121 212421242 xx xxmxxm xxm xxm == −+=−=− −+= −=−
Xét
số
− để
A. 1 B. 7 C.
D.
Lời giải Chọn B ( ) 2 0 040 4 x fxxx x = =+= =−
. Vậy có 17giá trị m nguyên dương. Câu 243: Cho hàm số ( )fx có đạo hàm là ( ) 2 4, fxxxx =+ . Có bao nhiêu giá trị nguyên của tham
6;6 m
hàm số ( ) 32 3 yfxxm =−+ có đúng 4 điểm cực trị?
5
6

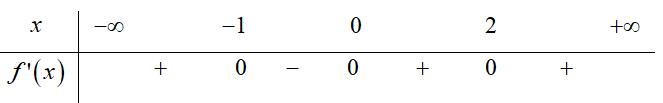
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 289 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) 232 3232 3232 36.3 00 22 0* 303 3434 yxxfxxm xx xx y xxmxxm xxmxxm =−−+ == == =−+=−=− −+=−−=−− Để hàm số ( ) 32 3 yfxxm =−+ có đúng 4 điểm cực trị thì ( )* phải có 4 nghiệm bội lẻ. Xét ( ) ( ) ( ) 32 2 3 36 0 0 2 gxxx gxxx x gx x =− =− = = = Bảng biến thiên
−− Mà 6;6 m m − nên 6;5;4;0;4;5;6 m =−−− . Câu 244: Cho hàm số ( )yfx = liên tục trên có bảng xét dấu ( ) ' fx như sau: Có bao nhiêu giá trị nguyên của m để hàm số ( ) 2 2 yfxxm =++ có 3 điểm cực trị? A. 5. B. 1. C. 2. D. 3. Lời giải Chọn B
Dựa và bảng biến thiên, để ( )* có 4 nghiệm bội lẻ thì 4 4 0 0 44 4 40 m m m m m m m −− − = −−− −
+= +=
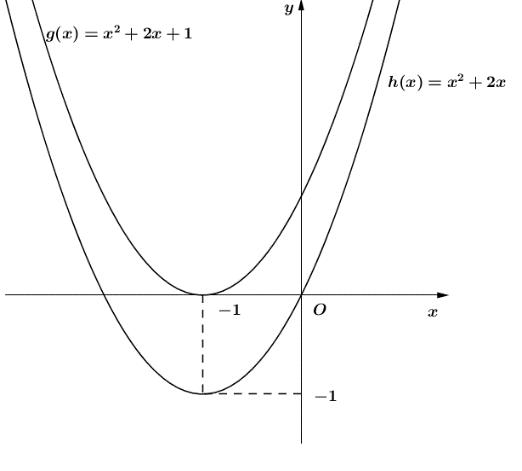
ẵn. Ta có: ( ) ( ) ( ) 22 2'22'2 yfxxmyxfxxm =++=+++ Suy ra ( ) ( ) ( ) ( ) 22 2 2 2
x x x yxxmxxm fxxm xxm xxm
=++=−++=−
++=
22011 220 '021212 '20 2023
+=−
Để hàm số ( ) 2 2 yfxxm =++ có 3 điểm cực trị thì các phương trình ( ) ( ) ( )1;2;3 phải sinh ra 3 nghiệm bội lẻ. Xét các phương trình ( ) ( )2;3 : 2 2
21 2 xxm xxm ++=− +=− Vẽ đồ thị hàm số ( ) ( ) 2221;2 gxxxhxxx =++=+ trên cùng hệ toạ độ ta có: Để '0y = có 3 nghiệm bội lẻ thì đường thẳng ym =− cắt đồ thị ( ) 2 21gxxx=++ và ( ) 2 2 hxxx =+ tại 2 điểm phân biệt, không tính tiếp xúc thoả mãn 1 x − . Khi và chỉ khi 1010 mm −− mà 0 mm= thoả mãn. Câu 245: Vậy có 1 giá trị m thoả mãn yêu cầu bài toán. Cho hàm số ( )yfx = có đạo hàm trên . Biết hàm số ( )yfx = là hàm bậc ba có đồ thị như hình vẽ bên dưới.
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 290 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Từ bảng xét dấu của ( ) ' fx ta thấy ( ) 1 '00 2 x fxx x =− == = trong đó 1 0 x x =− = là các nghiệm bội lẻ, 2 x = là nghiệm bội ch
=−
++=
Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) ( ) 3 231gxfxxm =+−+ có đúng 5 điểm cực trị?
A. 5 B. 7 C. 4 D. 6 Lời giải
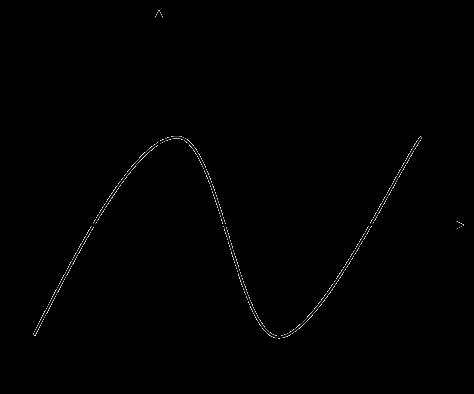
Chọn C
Hàm số ( ) ( ) 3 231gxfxxm =+−+ là hàm số chẵn nên đồ thị đối xứng qua trục Oy . Suy ra 0 x = là một điểm cực trị của hàm số. Đặt 3 23 txx =+ 2 630, txtx =+ đồng biến. Suy ra ứng với mỗi t chỉ có duy nhất một nghiệm x Ta có: ( ) ( )1 gtftm=−+ . ( ) ( ) 1; t gtftm t =−+ ( )0 t
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 291
(
123
165 tmtm gttmtm tmtm −+=−=−+ =−+==+ −+==+ . ( )* Hàm số ( ) ( ) 3 231gxfxxm =+−+ có đúng 5 điểm cực trị. Hệ phương trình ( )* có 4 nghiệm phân biệt khác 0. 30 3 10 113 50 5 15 m m m mm m m mm −+ + −− + − ++ . Vậy có 4 giá trị nguyên của m thỏa đề y x O 6 2 -2
Dựa vào đồ thị, ta có:
)
0121
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 292
c
( ) ( )( ) ( )( ) (
( )( ) (
( ) (
2 32 3 3 22 3 3 3
333 ().3 3 333 .3 3 '030
xxx gxfxxm xx xxx fxxm xx gxfxxm =−−====− ++ =++ + ++ =++ + =++= Do đạo hàm không xác định tại 0 x = nên để hàm số ( ) ( ) 3 3 ygxfxxm ==++ có ít nhất 3 cực trị thì 3 '(3)0fxxm++= có ít nhất hai nghiệm đơn hoặc nghiệm bội lẻ khác 0. ( ) 33 333 33 3535 '303232 3232 xxmxxm fxxmxxmxxm xxmxxm ++=+=− ++=++=+=− ++=−+=−− Yêu cầu bài toán suy ra 505,,100;100 100;99;....4 mmmZm m −− −− Vậy có tất cả 105 giá trị m thỏa mãn yêu cầu bài toán. Câu 247: Cho hàm số ( )yfx = có đạo hàm ( ) ( ) ( ) 2 2 12 fxxxx =−− với x . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ( ) 2 8 fxxm −+ có 5 điểm cực trị? A. 15. B. 17. C. 16. D. 18 Lời giải Chọn A Đặt ( ) ( ) 2 8 gxfxxm =−+ ( ) ( ) ( ) 2 2 12 fxxxx =−− ( ) ( )( ) ( )( ) 2 222 2881882 gxxxxmxxmxxm =−−+−−+−+−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 246: Cho hàm số ( )yfx = có đạo hàm ( ) 2 (5)(4), yfxxxxR ==−− .Cóbaonhiêugiátrị nguyên
ủa m thuộc đoạn 100;100 để hàm số ( ) 3 ()3 ygxfxxm ==++ có ít nhất 3 điểm cực trị? A. 104. B. 106. C. 105. D. 103. Lời giải Chọn C Ta có:
)
)
)
5405;2;2
fxxxxxx
xxm−+−
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 293 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) 0 gx = ( ) ( ) ( ) 2 2 2 4 8101 802 8203 x xxm xxm xxm = −+−= −+= −+−= Các phương trình ( )1 , ( )2 , ( )3 không có nghiệm chung từng đôi một và ( )2 2 810
với x . Suy ra
có 5 điểm
ự
trị
ỉ
160 1620 16320 163220 m m m m − −+ −+ −+− 16 18 16 18 m m m m 16 m Vì m nguyên dương và 16 m nên có 15 giá trị m cần tìm. Câu 248: Cho hàm s
Ta
( ) ( ) 1 00 2 xkép fxx x = == =
=
Xét
số ( ) 2 8 yfxxm =−+ . có ( ) ( ) 2 288 yxfxxm =−−+ Giải phương trình ( ) ( ) ( ) ( ) 2 2 2 2 2 2 4 4 28080 080 8082 820 81 x x x xxm ygxxxm fxxm xxm hxxxm xxmkép = = −= −+= ==−+= −+= −+= =−+−= −+= Để hàm số ( ) 2 8 yfxxm =−+ có 5 điểm cực trị thì ( ) ( ) ( ) ( ) ( ) 22 2 40 40 40 420 gx hx g h m m =− =−− 160 180 16 18 m m m m − − 16 m Do m nguyên dương nên 1;2;3;...15 m . Vậy có 15 giá trị của m
( )gx
c
c
khi và ch
khi ( )2 và ( )3 có hai nghiệm phân biệt khác 4
ố ( )yfx = có đạo hàm ( ) ( ) ( ) 2 2 12 fxxxx
=−− với mọi x
. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ( ) 2 8 yfxxm =−+ có 5 điểm cực trị? A. 15 B. 18 C. 16 D. 17 Lời giải Chọn A
có:
hàm số ( )yfx
đạt cực trị tại các điểm
hàm
Chọn A
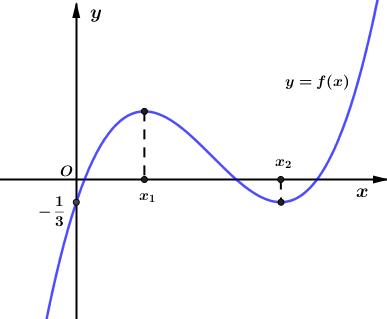
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 294
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 249: Cho hàm số ( ) ( ) 32 1 3,, yfxxbxcxdbcd ==+++ có đồ thị là đường cong như hình vẽ. Biết hàm số đạt cực trị tại 12 , xx thỏa mãn 12 21 xx−=− và ( ) ( ) 12 2 3 fxfx+= . Số điểm cực cực tiểu của hàm số ( ) ( ) ( )2 31 3 xfx yf x + = là A. 3 B. 5. C. 4. D. 2. Lời giải
lí Viet ta có 12 12 2 xxb xxc +=− = Mà theo giả thiết 12 21 xx−=− Suy ra ( )( ) ( ) 1 2 12 21 3 2141 14 1 39 b x bb b xc xxc = +− == = Từ giả thiết suy ra đồ thị hàm số có hai điểm cực trị là ( ) ( ) ( ) ( ) 1122 ;,; AxfxBxfx ( ) ( ) 12 12 1 ;; 223 fxfx xx Ib + + =− là tâm đối xứng của đồ thị Mà I thuộc đồ thị hàm số ( )fx nên ( ) 33 331122 23202 3333 bb bbcbbcc b −+−−=−−== Từ và suy ra:
Ta có ( ) 2 2 fxxbxc
=++ . Đồ thị hàm số đi qua điểm 1 0; 3 A nên 1 3 d =− . Gọi 12 , xx là hai nghiệm phân biệt của ( )fx . Áp dụng định

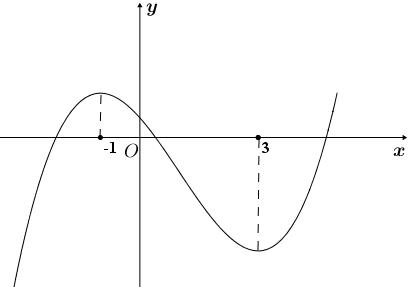
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 295 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( )( ) ( ) 332 2141322226023 bbbbbbbbc +−=−+−+==−= ( ) ( ) ( ) 3 2 2 1 23313 33 x fxxxfxxx =−+−+=− ( ) ( ) ( ) ( ) ( ) ( ) ( ) 22 2 31 2. 3 xfx ygxffxgxxfx x + ==== Ta
ấy ( ) 1 2 1 0 3 x
x = = = ( ) 2 2 0 0 011 3 3 x x gxxx x x = = === = =
ấu
ủa ( )gx : Vậy hàm số đã cho có 3 điểm cực tiểu. Câu 250: Cho hàm số bậc ba ( )yfx = có đồ thị như hình vẽ bên dưới. Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) ( ) 2 1 yfxm =−+ có 3 điểm cực trị? A. 2. B. 4. C. 3. D. 5. Lời giải Chọn B Đặt ( ) ( ) ( ) 2 1 gxfxm =−+ ( ) ( ) ( ) ( ) 2 211 gxxfxm =−−+ ( ) ( ) ( ) 2 2 1 011 13 x gxxm xm = =−=−− −=−
th
fx
Bảng xét d
c
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 296
m − Câu
nhiêu giá trị nguyên
ủa
số m để đồ thị
ố 2 3 3 mx yx x =+ + có
ự
trị nằm trong hình tròn tâm O , bán kính 130 R = ? A. 16 B. 18 C. 19 D. 17 Lời
ải
ọn D Ta có: ( )3 2 3 3 3 m y x =+ + . 0 y = ( )3 2 3 30 3 m x += + ( )3 2 3 xm +=− 2 3 3 xm +=− 3 22 0 3 m xm =− .
ố có cực trị 3 2 0 30 m m − (
m − .
(
ự
ị
số 2 3 3 mx yx x =+ + . 3 22 0 0 00 2 0 3 3 3 xm mx yx x =− =+ + ( ) 2 2 3 3 222 0 000 3 2 0 333 3 mx m yxxm m x =+=+=− + . Do điểm ( ) 00 ; Mxy nằm trong hình tròn tâm O , bán kính 130 R = nên ta có: 22 00 130 xy+ ( )3 332233130mm−+− ( ) ( ) 3 3322331300mm−+−− ( ) ( ) ( ) 2 33322235353260mmm −−−+−+ 3 2 8 m 2 512 m ( )1621622 m − . Từ ( )1 và ( )2 suy ra 16233 m −− Do m nguyên nên 22;21;...;6 m−−− . Vậy có 17 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vậy để hàm số ( )gx có 3 điểm cực trị khi ( )gx có đúng 3 nghiệm đơn hoặc bội lẻ 30 10 m m − −− 13 m − 1;0;1;2
251: Có bao
c
tham
hàm s
các điểm c
c
gi
Ch
Hàm s
)331
Giả sử điểm
) 00 ; Mxy là một điểm c
c tr
của đồ thị hàm



CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 25 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn BÀI 3: GIÁ TRỊ NHỎ NHẤT VÀ GIÁ TRỊ LỚN NHẤT CỦA HÀM SỐ VD VDC 01 HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: (MĐ 101 2022) Cho hàm số ( ) ( ) 42 121fxmxmx=−−+ với m là tham số thực. Nếu ( ) ( ) 0;3 min2 fxf = thì ( ) 0;3 max fx bằng A. 13 . 3 B. 4 C. 14 3 − D. 1 Lời giải Chọn B Có: ( ) ( ) 3 414 fxmxmx =−− Nếu
102 2022) Cho hàm số ( ) ( ) 42 21 fxmxmx =+− với m là tham số thực. Nếu ( ) ( ) 0;2 min1 fxf = thì ( ) 0;2 max fx bằng A. 2. B. 1. C. 4. D. 0. Lời giải Chọn C Vì ( ) ( ) 0;2 min1 fxf = nên suy ra ( ) 10 f = CHƯƠNG I ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
( ) ( ) 0;3 min2 fxf = thì điều kiện cần là ( ) 20 f = (Do ( )fx là hàm đa thức) Suy ra ( ) 4 20 3 fm == Điều kiện đủ: Với 4 3 m = , ta có ( ) 4218 1 33 fxxx=−+ ; ( ) 3 416 33 fxxx =− Nên ( ) ( ) 0 02 20;3 x fxx x =
== =− Ta có ( ) ( ) ( ) 13 01;34;2 3 fff===− Vậy ( ) ( ) 0;3 min2 fxf = ; ( ) 0;3 max4 fx = Câu 2: (MĐ
Ta có ( ) ( ) ( ) 3 1 44110 2 fxmxmxfm =+−== Với 1 2 m = thì ( ) 42 1 2 fxxx =−
Ta có ( ) ( ) 3 0 22;0 1 x fxxxfx x
= =−= = ( ) ( ) ( ) 1 00;1;24 2 fff==−= . Vậy ( ) 0;2 max4 fx = .
Câu 3: (MĐ 103-2022) Cho hàm số ( ) ( ) 42241fxaxax=++− với a là tham số thực. Nếu 0;2 max()(1) fxf = thì 0;2 min() fx bằng
A. 17. B. 16. C. 1. D. 3. Lời giải Chọn A
Ta có ( ) ( ) 3 444fxaxa =++ Theo giả thiết 0;2 max()(1) fxf = suy ra ( ) 10 f = . ( ) 44402 aaa ++==− .
x fxxxfxxxx x
Khi đó ( ) ( ) 423
= =−+−=−+==− = .
1 24188010;2 0
Ta có ( ) ( ) ( ) 01,11,217fff=−==− Vậy, 0;2 min()17 fx =−
Câu 4: (MĐ 104 2022) Cho hàm số ( ) ( ) 42 321fxaxax=+−+ với a là tham
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 26
số thực. Nếu ( ) ( ) 0;3 max2 fxf = thì ( ) 0;3 min fx bằng A. 9. B. 4. C. 1. D. 8. Lời giải Chọn D Ta có: ( ) ( ) 2 43, fxxaxax =+− Do ( ) ( ) 0;3 max2 fxf = nên ( ) 2031204faa =+==− Kiểm tra lại: 4 a =− thì ( ) 4281fxxx=−++ liên tục trên 0;3 .
Ta có: ( ) 217 f = , ( ) 01 f = và ( ) 38 f =−
Suy ra: ( ) ( ) 0;3 max217 fxf== và ( ) ( ) 0;3 min38 fxf==− .
Câu 5: (TK 2020 Lần 1) Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số ( ) 3 3 fxxxm =−+ trên đoạn 0;3 bằng 16. Tổng tất cả các phần tử của S là: A. 16 B. 16 C. 12 . D. 2 Lời giải Chọn A Xét 3 3 uxxm trên đoạn 0;3 có 2 033010;3uxx Khi đó 0;3 0;3
uuum uuum . Suy ra 0;3
max umax0,1,3maxm,m2,m1818 min umin0,1,3minm,m2,m182
m mm m Mfxmm m m mm
1816 1822 axmax2,181614 216 218
. Do đó tổng tất cả các phần tử của S bằng 16 Câu 6: (TK 2020 Lần 2) Cho hàm số ( ) 1 xm fx x + = + ( m là tham số thực). Gọi S là tập hợp tất cả các giá trị của m sao cho ( ) ( ) 0;1 0;1 maxmin2 fxfx+= . Số phần tử của S là A. 6. B. 2. C. 1. D. 4. Lời giải
Chọn B
Do hàm số ( ) 1 xm fx x + = + liên tục trên 0;1 . Khi 1 m = hàm số là hàm hằng nên ( ) ( ) 0;1 0;1 maxmin1 fxfx== Khi 1 m hàm số đơn điệu trên đoạn 0;1 nên + Khi ( ) ( )0;1ff cùng dấu thì ( ) ( ) ( ) ( ) 0;1 0;1
1 maxmin01 2 m fxfxffm + +=+=+ .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 27
Ta có: ( ) 3 416 fxxx =−+ và ( ) 00;3 020;3 20;3 x fxx x = == =− .
Phương
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 28
=
M ĐỂ GTLN-GTNN CỦA HÀM SỐ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI THỎA MÃN ĐIỀU KIỆN CHO TRƯỚC Dạng 1: Tìm m để ( ) ( ) ; max0. yfxmaa =+= Phương
Trước tiên
( ) ( )
) ; ;
== Kiể
tra
++=
+=−=−− =−−− +==−
mKa
mKmk += =+ ++
mka
mkmK += =+ ++
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn + Khi ( ) ( )0;1ff trái dấu thì ( ) 0;1 min0 fx = ,
( ) ( ) ( ) 0;1 1 maxmax0;1max; 2 m fxffm+ == . TH1: ( ) ( ) 1 0.10(1)0 0 m ffmm m − + . ( ) ( ) 0;1 0;1 1 1 maxmin225 2 3 m m fxfxm m = + +=+= =− (thoả mãn). TH2: ( ) ( ) 0.10(1)010 ffmmm +− ( ) ( ) 0;1 0;1 22 maxmin25 1 2 23 m m fxfxm m m = = +==− +
=
(không thoả mãn). Số phần tử của S là 2. DẠNG 1. ĐỊNH
pháp: Cách 1:
tìm
(
max;min. fxKfxkKk
m
max,. 222 mKmkmKmkKk mKmk ++++−−−
TH1: 2 Kk a Để
; max; mkamak yamakaK mKamaK
TH2: 2 Kk a
m . Cách 2: Xét trường hợp TH1:
MaxmK
TH2:
Maxmk
Dạng 2: Tìm m để
( ) ( ) ; min0. yfxmaa =+=
pháp: Trước tiên tìm ( ) ( ) ( ) ; ; max;min. fxKfxkKk
==
ng 3: Tìm m để ( ) ; max yfxm =+ không vượt quá giá trị M cho trước.
Phương pháp: Trước tiên tìm ( ) ( ) ( ) ; ; max;min. fxKfxkKk
pháp:
Dang 5: Tìm m để ( ) ; max ab yfxm =+ đạt min.
Phương pháp: Trước tiên tìm ( ) ( ) ( ) ; ; max;min. ab ab fxKfxkKk == Đề hỏi tìm . 2 Kk mm + =− Đề hỏi tìm min của ; max ab y giá trị này là . 2 Kk
Dạng 6: Tìm m để ( ) ; min ab yfxm =+ đạt min.
Phương pháp: Trước tiên tìm ( ) ( ) ( ) ; ; max;min. ab ab fxKfxkKk ==
Đề hỏi tìm ( )( ) 0 mmKmkKmk ++−− . Đề hỏi tìm min của ; min ab y giá trị này là 0.
Dạng 7: Cho hàm số ( ) yfxm =+ .Tìm m để
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 29 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Để ; min. 00 mkamKamakmaK ya mkmKmkmK +=+=−=−=−− = ++−− Vậy 12. mSS Dạ
Để ;
+− −−− +
==
max. mkM yMMkmMK mKM
Dạng 4: Tìm m để
( ) ; min yfxm
=+ không vượt quá giá trị a cho trước.
Phương
Trước tiên tìm ( ) ( ) ( ) ; ; max;min. fxKfxkKk == Để ( )( ) ; min0. 00 mkamKamakmaK yamKmkKmk mkmKmkmK ++−−−− ++−− ++−−
TH1: 1 cungdau . Kmkm Kmkm KmhkmmS ++ ++ ++⎯⎯⎯⎯⎯⎯→ TH2: 2 cungdau kmKm Kmkm kmhKmmS ++ ++ ++⎯⎯⎯⎯⎯⎯→ Vậy 12mSS Dạng 8: Cho
ố
( ) ; ; max.min0 ab ab yhyh hoặc max Min += Phương pháp: Trước tiên tìm
( ) ( ) ( ) ; ; max;min. ab ab fxKfxkKk ==
hàm s
( ) yfxm =+ . Phương pháp: Trước tiên tìm
( ) ( ) ( ) ; ; max;min. ab ab fxKfxkKk ==
BT1: Tìm m để ; ; minmax ab ab yymKmk +=+++=
BT2: Tìm m để ; ; min*max* ab ab yymKmk =++=
Câu 7: Tìm m để giá trị lớn nhất của hàm số 3 321yxxm=−+− trên đoạn 0;2 là nhỏ nhất. Giá trị của m thuộc khoảng nào? A. 3 ;1 2 . B. 2 ;2 3 . C. 1;0 . D. ( )0;1 . Lời giải
Chọn D
Xét hàm số ( ) 3 321yfxxxm ==−+− trên đoạn 0;2 . Ta có ( ) 2 '33010;2 1 x fxx x =− =−= = .
Ta có ( ) 021fm=− , ( ) 123fm=− và ( ) 221fm=+
Suy ra ( ) 0;2 21;23;2123;21 maxfxmaxmmmmaxmmP =−−+=−+= .
Trường hợp 1: Xét ( ) 1 23214420 2 mmmm −+−− .
Khi đó 232Pm=− , 1 2 m . Suy ra min 1 2 2 Pm== .
Trường hợp 2: Xét ( ) 1 23214420 2 mmmm −+−−
Khi đó 212Pm=+ , 1 2 m . Suy ra minP không tồn tại. Vậy 1 2 m =
Câu 8: Tính tổng tất cả các giá trị của tham số m sao cho giá trị lớn nhất của hàm số 2 2 yxxm =−+ trên đoạn 1;2 bằng 5 A. 1 B. 2
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 30
C. 2 D. 1 Lời giải Ta có 2 22 2 x y xxm = −+ , 01yx == Do đó yêu cầu bài toán tương đương ( ) ( ) ( ) max1,2,15 yyy−= max3,,15 mmm +−= . + Trường hợp 1 m − , ta có max3,,15352 mmmmm +−=+== . + Trường hợp 1 m − ta có max3,,15154 mmmmm +−=−==− Vậy tổng các giá trị m bằng 2.
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 31
. C. 2 a = . D. 5 a = . Lời giải Hàm số đã cho xác định và liên tục trên đoạn 2;1 . Ta có: ( ) ( ) 2 2 2415yxxaxa =++−=++− Đặt ( ) 2 1, 2;10;4txxa =+− . Lúc đó hàm số trở thành: ( ) 5 ftta=+− với 0;4 t Nên ( ) 0;40;4 2;1 0;4 maxmaxmax(0);(4)max5;1 tt x t yftffaa − ===−− 1515
−+−−+− =
ả
nhất của ( ) 0;4 max t ft là 2 khi 3 a = . Câu 10: Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất củ
ố 2 1 xmxm y x ++ = + trên 1;2 bằng 2. Số phần tử của tập S A. 3 B. 1 C. 4 D. 2 Lời giải Chọn D Xét 2 1 xmxm y x ++ = + . Ta có: ( ) ( ) 2 2 2 1 xx fx x + = + , ( ) 01;2 0 21;2 x fx x = = =− . Mà ( ) ( ) 1;2 21342134 1,f2max; 2323 x fymmmm ++++ === . Trường hợp 1: 1;2 3 212max2 25 2 x m m y m = + == =− . • Với 33417 2 236 m m + == • Với 5347 2 236 m m + =−=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 9: Cho hàm số 2 24yxxa=++− ( a là tham số ). Tìm a để giá trị lớn nhất của hàm số trên đoạn
2;1 đạt giá trị nhỏ nhất A. 1 a = . B. 3 a =
2 22 aaaa
Đẳng thức x
y ra khi 1523aaa −=−== . Do đó giá trị nhỏ
a hàm s
Mf Mf Mf
−
1 3 1
1 93 1
Mab Mab Mab 2 1 a b =− =− Ngược lại, khi 2 1 a b =− =− ta có, hàm số ( ) 2 21fxxx=−− trên 1;3 . Xét hàm số ( ) 2 21gxxx=−− xác định và liên tục trên 1;3 ( ) 22gxx =− ; ( ) 011;3gxx ==− M là giá trị lớn nhất của hàm số ( )fx trên 1;3 ( ) ( ) ( ) max1;3;1 Mggg=− =2 Vậy 2 1 a b =− =− . Ta có: 24ab+=− . Câu 12: Cho hàm số ( ) 322 127yxxmx =++++ . Giá trị lớn nhất của hàm số trên đoạn 3;1 có giá trị nhỏ nhất bằng A. 26 B. 18 C. 28 D. 16 Lời giải Chọn B
−+ ++ ++ 419321 Mababab −+++++−−− 1932(1) ababab −+++++−−− 48 M 2 M Nếu 2 M = thì điều kiện cần là 19312 ababab −+=++=−−−= và 1 ab−+ , 93ab++ , 1 ab cùng dấu 19312 19312 ababab ababab −+=++=−−−= −+=++=−−−=−
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 32 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Trường hợp 2: 1;2 2 343463max2 334610 3 x m m m y m m = += + == +=− =− . • Với 2217 2 326 m m + == • Với 102117 2 326 m m + =−=
Vậy có 2 giá trị của m thỏa mãn. Câu 11: Xét hàm số ( ) 2 fxxaxb =++ , với a , b là tham số. Gọi M là giá trị lớn nhất của hàm số trên 1;3 . Khi M nhận giá trị nhỏ nhất có thể được, tính 2 ab + . A. 2. B. 4. C. 4. D. 3. Lời giải Xét hàm số ( ) 2 fxxaxb =++ . Theo đề bài, M là giá trị lớn nhất của hàm số trên 1;3 Suy ra ( ) ( ) ( )
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
ỳnh
42
ễn
ậ
Page 33
ố
ạ
Xét (
uxxmx =++++
n
=+++ Do
( ) 2
==−=− ;
==−=− Do
==−−
ị nguyên của tham số m sao cho giá trị lớn nhất của hàm số 42119 3020 42 yxxxm =−++− trên đoạn 0;2 không vượt quá 20. Tổng các phần tử của S bằng A. 210. B. 195. C. 105. D. 300. Lời giải Xét hàm số ( ) 42119 3020 42 gxxxxm =−++− trên đoạn 0;2 Ta có ( ) 3 1930gxxx =−+ ; ( ) 50;2 02 30;2 x gxx x =− == = Bảng biến thiên
Giáo viên: Hu
Văn Ánh
Nguy
Cư Trinh Thu
n Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 T
t Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên so
n
) 322 127
trên đoạ
3;1 ta có: 22 3210, uxxmx
đó
3;1 max126 Auum
( ) 2 3;1 min363 auum
22 3;1 Mmaxmax26,63 ymm
và 22 43266372 Mmm−+− . Vậy 18 M . Dấu bằng xảy ra khi 22 26631822 mmm −=−== Câu 13: Có bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số 2 24yxxm=++− trên đoạn 2;1 bằng 4? A. 1. B. 2. C. 3. D. 4. Lời giải ( ) 2 24fxxxm=++− có ( ) 22fxx =+ , ( ) 01fxx ==− . Do đó 2 2;1 max24max1;4;5 xxmmmm ++−=−−− . Ta thấy 541mmm−−− với mọi m , suy ra 2;1 max y chỉ có thể là 5 m hoặc 1 m Nếu 2;1 max5 ym=− thì 54 51 m mm −= −− 1 m = . Nếu 2;1 max1 ym=− thì 14 15 m mm −= −− 5 m = Vậy 1;5 m Câu 14: Gọi S là tập tất cả các giá tr
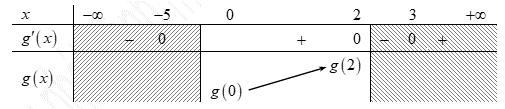
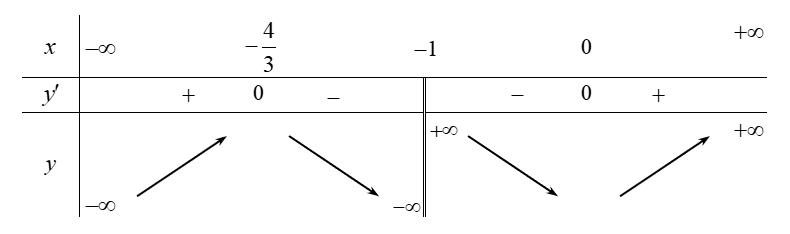
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 34 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) 020gm=− ; ( ) 26gm=+ . Để ( ) 0;2 max20 gx thì ( ) ( ) 020 220 g g 2020 620 m m − + 014 m . Mà m nên 0;1;2;...;14 m . Vậy tổng các phần tử của S là 105. Câu 15: Cho hàm số 4 1 xaxa y x ++ = + , với a là tham số thực. Gọi , Mm lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn 1;2 . Có bao nhiêu giá trị nguyên của tham số a để 2 Mm ? A. 10 B. 14 C. 5 D. 20 Lời giải Chọn B Xét hàm số 44 11 xaxax ya xx ++ ==+ ++ Ta có ( ) 43 2 4 34 03 10 x xx yy x x =− + == + = . Bảng biến thiên Dựa vào bảng biến thiên suy ra 116 max; 23 Maa =++ và min;116 23 maa =++ Trường hợp 1. 11 0 22 aa+− 1616 33 11 22 Maa maa =+=+ =+=+ . Khi đó 16113 22 323 Mmaaa ++ .
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 35 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Kết hợp điều kiện, ta có 113 23 a − có 5 giá trị nguyên thỏa mãn điều kiện. Trường hợp 2. 11 161622 0 331616 33 Maa aa maa =+=−− +− =+=−− 11661 22 236 Mmaaa −−−−− Kết hợp điều kiện ta có 6116 63 a −− . Suy ra có 5 giá trị nguyên của a thỏa mãn. Trường hợp 3. 1 0 2161 1632 0 3 a a a + −− + Nếu 11611635 232312 aaaaa ++−−+− thì 1 211667 22 162318 3 Ma Mmaaa ma =−− −−+− =+ . Kết hợp điều kiện, ta có 1667 318 a −− . Suy ra có 2 giá trị nguyên củ
mãn điều kiện. Câu 16: Gọi S là tập hợp tất cả các giá trị nguyên của tham số thực m sao cho giá trị lớn nhất của hàm số 42 1 144830 4 yxxxm =−++− trên đoạn 0;2 không vượt quá 30. Tổng giá trị các phần tử của tập hợp S bằng bao nhiêu? A. 120. B. 210. C. 108. D. 136. Lời giải Chọn D Đặt 42 1 ()144830 4 fxxxxm =−++− là hàm số xác định và liên tục trên 0;2 .
a a thỏa mãn điều kiện. Nếu 11611635 232312 aaaaa ++−−+− thì 16 316119 22 1329 2 Ma Mmaaa ma =+ +−−− =−− . Kết hợp điều kiện, ta có 191 92 a −− . Suy ra có 2 giá trị nguyên của a thỏa mãn điều kiện. Vậy có 14 giá trị nguyên của a thỏa
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 36 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Với mọi 0;2 x ta có 3 '()0284802 fxxxx =−+== . Suy ra 0;2 max()max(0);(2) fxff = . Theo đề 0;2 3030 14303030 max()30 14301430 3014 m mm m fx m m mm − +− − + + −+ 303030060 016 3014304416 mm m mm −− −+− Do 0;1;2;...;16. mmS= Vậy tổng tất cả 17 giá trị trong tập S là 136. Câu 17: Cho hàm số 432 2 yxxxa =−++ . Có bao nhiêu số thực a để 1;21;2 minmax10 yy+= ? A. 3. B. 5. C. 2. D. 1. Lời giải. Chọn C. Đặt 4322() yxxxafx =−++= . Xét hàm số ( ) 432 2 fxxxxa =−++ Khi đó 322 1 ()4622(231)00;;1 2 fxxxxxxxx =−+=−+= ( ) 0,1;2fxx và (1);(2)4 fafa==+ Ta có 1;2 x thì max,4 min,0,4 yaa yaa + + Xét các trường hợp + 0max4;min24103 ayayaaa =+=+== , nhận. + 4max;min44107 ayayaaaa −=−=−−−−−==− , nhận. + 0 4040min0;max4; a ayyaa a −=+− + 4106 1010 aa aa +== −==− . Vậy tồn tại hai giá trị a thỏa mãn. Câu 18: Biết giá trị lớn nhất của hàm số ( ) 3 21559 yfxxxmx ==−+−+ trên 0;3 bằng 60. Tính
0;3
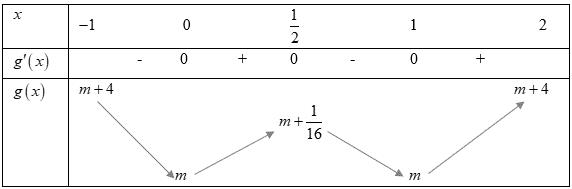
cho ( )
60.
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
ỳnh
Ánh 42
ễn
ận
Page 37
ổ
tất cả
trị củ
số thực m
ọ
Giáo viên: Hu
Văn
Nguy
Cư Trinh Thu
Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn t
ng
các giá
a tham
A. 48. B. 5. C. 6. D. 62. Lời giải Ch
n C Có
( ) ( ) 0;3 max6060,0;3 fxfxx = và 0
x sao
0
fx = Có ( ) 33 6021559602155609 fxxxmxxxmx −+−+−+−− 333 9602155609224552665,0;3. xxxmxxxmxxx −−+−−−+−−++ Có 3 266529,0;3 xxx −++ nên 3 2665,0;329.mxxxm −++ Tương tự 3 2245523 xx −+−− nên 3 22455,0;323. xxmxm −+−− Vậy 2329 m − thì ( ) 60,0;3.fxx Để 0 0;3 x sao cho ( ) 0 60 fx = thì 3 3 22455 2665 xxm xxm −+−= −++= có nghiệm trên 0;3. Hay 29 . 23 m m − Vậy 29 23 m m = =− thì ( ) 0;3 max60. fx = Khi đó tổng các giá trị của m là 29236. −= Câu 19: Cho hàm số ( ) 432 2 =−++ fxxxxm ( m là tham số thực). Gọi S là tập hợp tất cả các giá trị của m sao cho ( ) ( ) 1;2 1;2 minmax10 +=fxfx . Số phần tử của S là? A. 2. B. 3. C. 5. D. 1. Lời giải Chọn A Đặt ( ) ( ) 43232 0 1 24620 2 1 = =−++=−+== = x gxxxxmgxxxxx x Bảng biến thiên của hàm ( )gx
Dựa vào bảng biến thiên của ( )gx ta suy ra bảng biến thiên của ( ) ( ) 432 2 ==−++ fxgxxxxm . Ta có các trường hợp sau:
Trường hợp 1: 0 m . Bảng biến thiên của ( ) ( ) 432 2 ==−++ fxgxxxxm
Dựa vào bảng biến thiên ta có ( ) ( ) 1;2 1;2 minmax104103 +=++== fxfxmmm
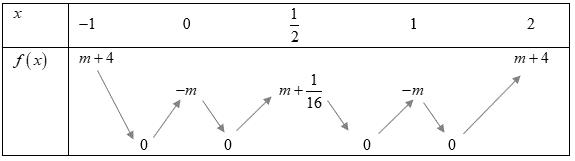
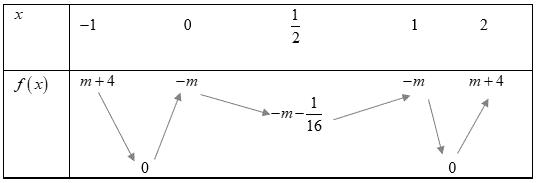
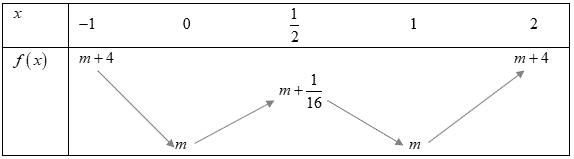
Trường hợp 2: 11 00 1616 +− mmm . Bảng biến thiên:
Dựa vào bảng biến thiên ta có ( ) ( ) 1;2 1;2 minmax1004106 +=++== fxfxmm
Trường hợp 3: 11 0 1616 +==−mm . Tương tự ta có: ( ) ( ) 1;2 1;2 minmax1004106 +=++== fxfxmm
Trường hợp 4: 11 044 1616 ++−− mmm . Bảng biến thiên:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 38
fxfx m m m m fxfx
Trường hợp 5: 404 +==−mm . Ta có: ( ) ( ) 1;2 1;2 minmax1001010 +=−==− fxfxmm
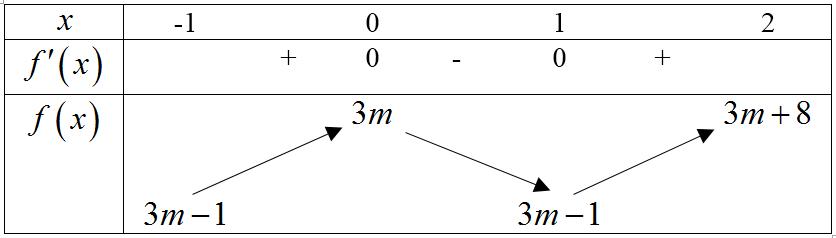
Trường hợp 6: 404 +−mm . Ta có:
)
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 39
Dụa vào bảng biến thiên ta có ( ) ( ) ( ) ( ) ( ) 1;2 1;2 1;2 1;2 minmax1004106 minmax1001010 += ++= = +−= =− +=
có ( ) ( ) 32 4441fxxxxx =−=− ( ) 0 0 1 x fx x = = = Bảng biến thiên của hàm số trên 1;2 : Vì 1;2 min2021 y = phương trình ( ) 0 fx = không có nghiệm thuộc 1;2 Trường hợp 1 : 1 310 3 mm− . Ta có 1;2 min31312021 ymm=−=−= 2022 3 m = Trường hợp 2 : 8 380 3 mm+− . Ta có 1;2 min38382021 ymm =+=−−= 2029 3 m =− . Vậy 12 202220294051 333 mm−=+= .
(
( ) 1;2 1;2 minmax104107 fxfxmmm +=−−−==− Vậy 7;3 m− Câu 20: Cho hàm số 4223 yxxm =−+ với m là tham số. Biết rằng có đúng hai giá trị 12 , mm của m để giá trị nhỏ nhất của hàm số đã cho trên 1;2 bằng 2021. Tính giá trị 12mm . A. 1 3 B. 4052 3 C. 8 3 D. 4051 3 Lời giải Chọn D Xét hàm số ( ) 4223 fxxxm =−+ , ta
fxmfxm
ế
303mm
thì
(
max17 fxm=+ ,
( ) 1;4 min3 fxm=− . Khi đó: ( ) ( ) ( ) 1;4 1;4 max3min173313 fxfxmmm +− +Nếu 17017mm+− thì ( ) 1;4 max3 fxm=−+ , ( ) 1;4 min17fxm =−− Khi đó: ( ) ( ) ( ) 1;4 1;4 max3min331727 fxfxmmm −+−−− . +Nếu ( )( ) 3170173mmm −+− thì ( ) ( ) 1;4 1;4 maxmax17,3max17,30;min0 fxmmmmfx =+−=+−= . Khi đó, không thỏa điều kiện ( ) ( ) 1;4 1;4 max3minfxfx . Do đó: 27 13 m m − kết hợp với 2020;2020 m− ta có 2020;2713;2020 m−− Vậy 4002 giá trị nguyên của m cần tìm. DẠNG 2. GIÁ TRỊ LỚN NHẤT GIÁ TRỊ NHỎ NHẤT HÀM ẨN, HÀM HỢP Câu 22: Cho hàm số ( )yfx = xác định và liên tục trên , đồ thị của hàm số ( )yfx = như hình vẽ Giá trị lớn nhất c
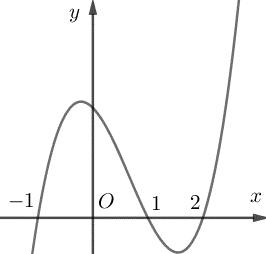
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 40
(
x =
= . (
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 21: Chohàmsố ( ) 3231fxxxm=−++ ( m làthamsốthực).Gọi S làtậphợptấtcảcácgiátrịnguyên của m thuộc đoạn 2020;2020 sao cho ( ) ( ) 1;4 1;4 max3minfxfx . Số phần tử của S là A. 4003 B. 4002 C. 4004 D. 4001 Lời giải Chọn B Xét hàm số ( ) ( ) 322 3136 yfxxxmyfxxx ==−++==−
) ( ) 2 0 0360 2 xl fxxx
=−=
) ( ) ( ) 11;23;417 fmfmfm =−=−=+ .
( )
( ) 1;4 1;4 max17;min3
=+=− +N
u
−
) 1;4
ủa hàm số ( )yfx = trên đoạn 1;2 là A. ( )1 f B. ( )1 f C. ( )2 f D. ( )0 f Lời giải
x fxx x
=− == =
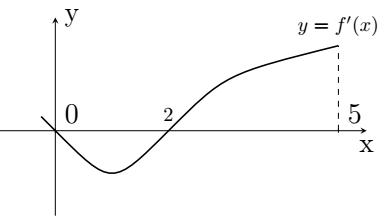
( ) 1 01 2
Từ đồ thị hàm yfx ta có bảng biến thiên
Từ đó suy ra giá trị lớn nhất của hàm số trên 1;2 là 1 f .
Câu 23: Cho hàm số ( )yfx = có đạo hàm là hàm ( )fx . Đồ thị của hàm số ( )yfx = được cho như hình vẽ. Biết rằng ( ) ( ) ( ) ( )0325ffff +=+ . Giá trị nhỏ nhất, giá trị lớn nhất của ( )yfx = trên đoạn 0;5 lần lượt là: A. ( )2 f ; ( )5 f B. ( )0 f ; ( )5 f C. ( )2 f ; ( )0 f D. ( )1 f ; ( )5 f Lời giải Dựa vào đồ thị hàm số ( )fx ta có bảng biến thiên. Khi đó: ( ) ( ) ( ) ( ) 0;5 min2 32

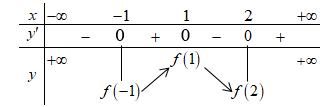
fxf ff
= , mà ( ) ( ) ( ) ( )0325ffff +=+ ( ) ( ) ( ) ( )0225ffff ++ ( ) ( )05ff . Vậy giá tr
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 41
ị nhỏ nhất, giá trị lớn nhất của ( )yfx = trên đoạn 0;5 lần lượt là: ( )2 f ; ( )5 f . Câu 24: Cho hàm số ( )fx có đạo hàm là ( )fx . Đồ thị của hàm số ( )yfx = được cho như hình vẽ bên. Biết rằng ( ) ( ) ( ) ( ) ( )012354 fffff +−=− . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của ( )fx trên đoạn 0;5 .
A. ( ) ( )5,3mfMf == B. ( ) ( )5,1mfMf == C. ( ) ( )0,3mfMf == D. ( ) ( )1,3mfMf == Lời giải
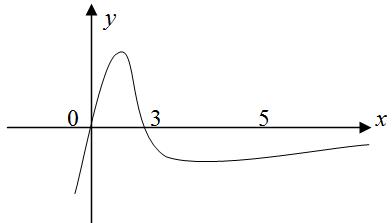
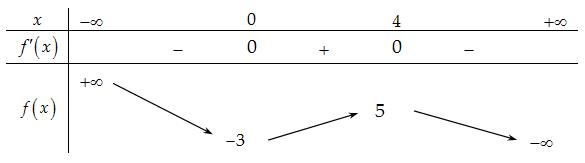

Ch
n A
b
bi
thiên của ( )fx trên đoạn
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 42
đây. Tìm giá trị lớn nhất của hàm số ( ) ( ) 23211 438 33gxfxxxxx =−+−++ trên đoạn 1;3 . A. 15. B. 25 3 C. 19 3 D. 12. Lời giải ( ) ( ) ( ) 22 42468gxxfxxxx =−−+−+ ( ) ( ) 2 2244xfxxx =−−+− . Với 1;3 x thì 40 x − ; 2 344 xx − nên ( ) 2 40fxx − Suy ra ( ) 2 2440 fxxx −+− , 1;3 x . Bảng biến thiên
ọ
Từ đồ thị ta có
ảng
ến
0;5 ( )3 Mf= và ( ) ( ) ( ) ( )13,43ffff ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )5013430505 ffffffffmf −=−+−= Câu 25: Cho hàm số ( )yfx = có bảng biến thiên như hình dưới
Suy ra ( ) ( ) 1;3 max2 gxg = ( ) 4712 f =+=
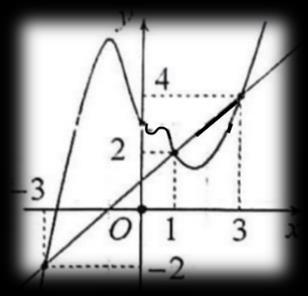
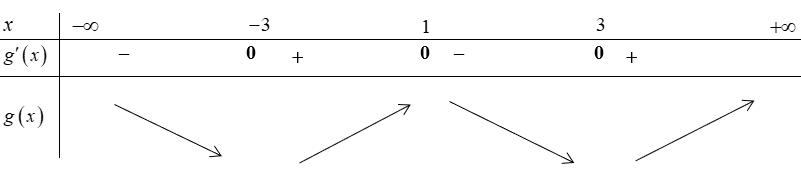
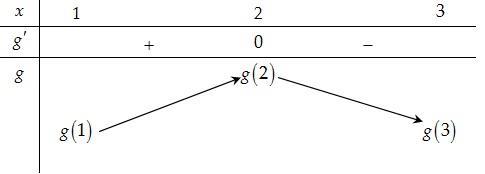
Câu 26: Cho hàm số ( )yfx = liên tục trên Đồ thị của hàm số ( )yfx = như hình bên. Đặt ( ) ( ) ( )2 21.gxfxx=−+ Mệnh đề dưới đây đúng. A. ( ) ( ) 3;3 max3. gxg = B. ( ) ( ) 3;3 min1. gxg = C. ( ) ( ) 3;3 max0. gxg = D. ( ) ( ) 3;3 max1. gxg = Lời giải Chọ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 43
n D ( ) (
(
Dựa vào đồ thị ta thấy ( ) ( ) 3 011 3 x gxfxxx x =− ==+= = Và với ( ) ( ) ( ) ;3:10xfxxgx −−+ với ( ) ( ) ( ) 3;1:10xfxxgx −+ , với ( ) ( ) ( ) 1;3:10xfxxgx + với ( ) ( ) ( ) 3;:10xfxxgx ++ Bảng biến thiên
)
) ( ) ( ) ( ) 2 21221 gxfxxgxfxx
=−+=−+
Dựa vào bảng biến thiên suy ra ( ) ( ) 3;3 max1. gxg =
Câu 27: Cho hàm số có đạo hàm cấp hai trên . Biết , và bảng xét dấu của như sau: Hàm số đạt giá trị nhỏ nhất tại điểm thuộc khoảng nào sau đây?
A. ( );2017−− B. ( ) 2017;+ C. ( )0;2 D. ( )2017;0 Lời giải Dựa vào bảng xét dấu của ( )fx ta có bảng biến thiên của hàm sồ ( )fx
Đặt 2017 tx=+
Ta có ( ) ( ) ( ) 2017201820182017.2018 yfxxfttgt =++=+−= ( ) ( ) 2018 gtft=+ .
( )yfx = ( ) 03 f = ( ) 22018 f =− ( )fx ( ) 20172018 yfxx =++ 0x ( ) 20172018 yfxx =++

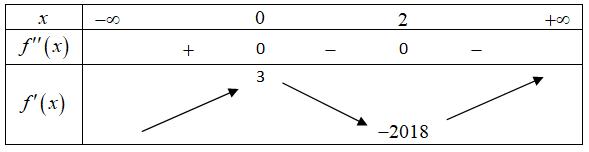
Dựa vào bảng biến thiên của hàm số ( )fx suy ra phương trình ( )gt có một nghiệm đơn ( );0− và một nghiệm kép 2 t = Ta có bảng biến thiên ( )gt Hàm số ( )gt đạt giá trị nhỏ nhất tại ( ) 0 ;0 t =− . Suy ra hàm số đạt giá trị nhỏ nhất tại 0x mà ( ) ( ) 002017;0;2017xx+−−− . Câu 28: Cho hàm số ( )fx có đạo hàm là ( )fx . Đồ thị của hàm số ( )yfx = được cho như hình vẽ dưới đây:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 44
Biết rằng ( ) ( ) ( ) ( )1012ffff −++ . Giá trị nhỏ nhất và giá trị lớn nhất của hàm số ( )yfx = trên đoạn 1;2 lần lượt là: A. ( )1 f ; ( )2 f . B. ( )2 f ; ( )0 f . C. ( )0 f ; ( )2 f . D. ( )1 f ; ( )1 f . Lời giải
Từ đồ thị của hàm số ( )yfx = ta có bảng biến thiên của hàm số ( )yfx = trên đoạn 1;2 như sau Nhận thấy ( ) ( ) 1;2 min1 fxf = Để tìm ( ) 1;2 max fx ta so sánh ( )1 f và ( )2 f Theo giả thiết, ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )10122101 ffffffff −++−−− . Từ bảng biến thiên, ta có ( ) ( ) 010ff− . Do đó ( ) ( ) ( ) ( )21021 ffff−−− Hay ( ) ( ) 1;2 max2 fxf = Câu 29: Cho hàm số ( )yfx = liên tục trên đoạn 7 0; 2 có đồ thị hàm số ( ) ' yfx = như hình vẽ

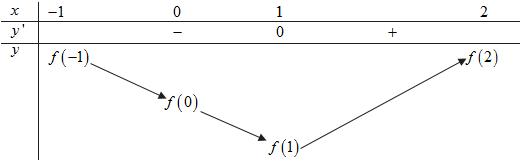
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 45
Hàm số ( )yfx = đạt giá trị nhỏ nhất trên đoạn 7 0; 2 tại điểm 0x nào dưới đây? A. 0 0 x = . B. 0 7 2 x = . C. 0 1 x = . D. 0 3 x = . Lời giải


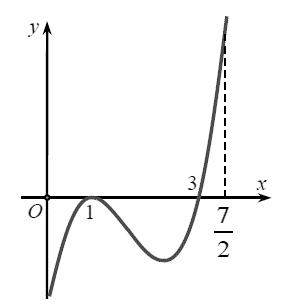

Chọn D
y x O
2 -1 1
Dựa vào đồ thị hàm số ( ) ' yfx = ta có bảng biến thiên trên đoạn 7 0; 2 như sau: Do đó hàm số đạt giá trị nhỏ nhất tại 0 3 x = . Câu 30: Cho hàm số ( )yfx = Đồ thị hàm ( )yfx = như hình vẽ Đặt ( ) ( ) 3 33 hxfxxx =−+ . Tìm mệnh đề đúng trong các mệnh đề sau: A. ( ) [3;3] max()31 hxf = B. ( ) [3;3] max()33 hxf=− C. ( ) [3;3] max()33 hxf = D. ( ) [3;3] max()30 hxf =
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 46
Lời giải
Chọn B
Ta có: ( ) ( ) 2 333hxfxx =−+ ( ) ( ) ( ) 2 31hxfxx =−− .
Đồ thị hàm số 2 1 yx=− là một parabol có toạ độ đỉnh ( )0;1 C , đi qua ( )3;2 A , ( )3;2 B .
Từ đồ thị hai hàm số yfx và 2 1 yx=− ta có bảng biến thiên của hàm số ( )yhx = .
h'(x)
x 0 0
h(x)
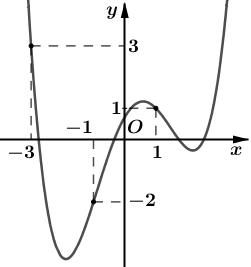




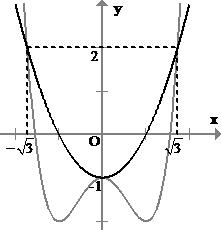
Với ( ) ( )333hf−=− , ( ) ( )333hf = .
Vậy [3;3] max()33 hxf Câu 31: Cho hàm số ( )yfx = có đồ thị ( )yfx = ở hình vẽ bên. Xét hàm số ( ) ( ) 32 133 2018, 342 gxfxxxx =−−++ mệnh đề nào dưới đây đúng? A. ( ) ( ) 3;1 min1 gxg=− . B. ( ) ( ) ( ) 3;1
31 min 2 gg gx −+ = . C. ( ) ( ) 3;1 min3 gxg=− D. ( ) ( ) 3;1 min1 gxg = Lời giải Chọn A
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 47
khoảng ( )3;1 đồ thị hàm số ( )fx nằm phía dưới ( )P nên ( ) ( ) 2 33 0 22 fxxxgx +−
Trên khoảng ( )1;1 đồ thị hàm số ( )fx nằm phía trên ( )P nên ( ) ( ) 2 33 0 22 fxxxgx +−
Trên khoảng ( ) 1;+ đồ thị hàm số ( )fx nằm phía dưới ( )P nên ( ) ( ) 2 33 0 22 fxxxgx +− .
Bảng biến thiên Từ bảng biến thiên, ta có ( ) ( ) 3;1 min1 gxg=− .
Câu 32: Cho hàm số ( )yfx = có đạo hàm liên tục trên R . Hàm số ( ) ' yfx = có đồ thị như hình sau:

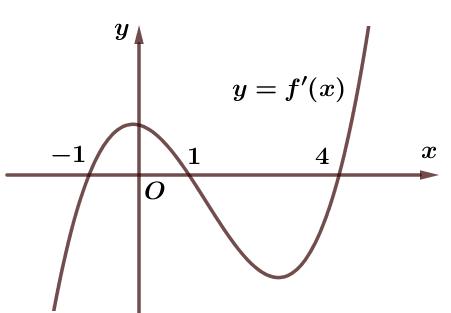
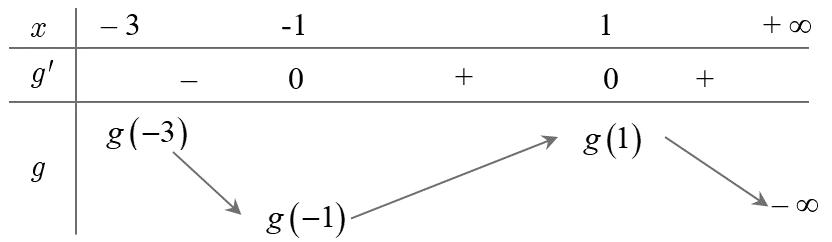
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 48 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có ( ) ( ) ( ) 223333 2222gxfxxxfxxx =−−+=−+− Vẽ parabol ( ) 2 33 : 22Pyxx=+− . Ta thấy ( )P đi qua các điểm có toạ độ ( )3;3 , ( )1;2 , ( )1;1 . Trên
Cho bốn mệnh đề sau: 1) Hàm số ( )yfx = có hai cực trị 2) Hàm số ( )yfx = đồng biến trên khoảng ( ) 1;+ 3) ( ) ( ) ( ) 124.fff 4) Trên đoạn 1;4 , giá trị lớn nhất của hàm số ( )yfx = là ( ) 1. f
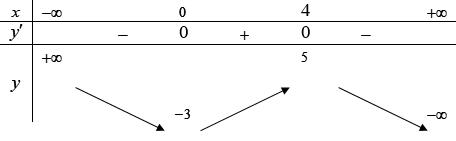
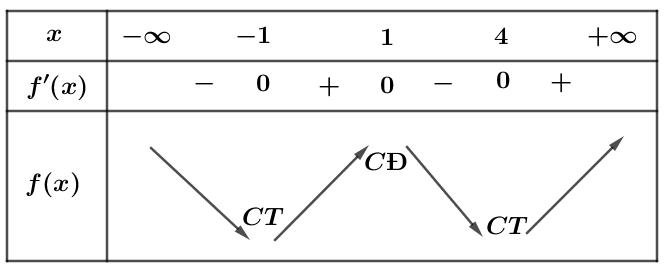
Số mệnh đề đúng trong bốn mệnh đề trên là: A. 3. B. 1. C. 4. D. 2. Lời giải
Chọn D
Dựa
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 49
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
vào đồ thị của hàm số ( ) ' yfx = ta thấy: ( ) 1 '01 4 x fxx x =− == = ( ) ( ) ( )'0;11;4fxx−− ( ) ( ) ( ) '01;14;fxx−+ Ta có bảng biến thiên của hàm số ( )yfx = Dựa vào bảng biến thiên đáp án đúng là mệnh đề số 3 và 4 Câu 33: Cho hàm số yfx có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số 23211 438 33gxfxxxxx trên đoạn 1;3. A. 25 . 3 B. 15. C. 19 . 3 D. 12.
gff gff g 132ggg Vậy 1;3 max12 gx tại 2. x Câu 34: Cho hàm số ( )yfx = . Hàm số ( )yfx = có bảng biến thiên như hình vẽ bên. Giá trị lớn nhất của hàm số ( ) ( ) 22sin gxfxx =− trên đoạ
n 1;1 là
)1 f


CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 50
A. (
B.
Lờ
giải Chọn B Ta có 1;122;2xx −− Từ bảng biến thiên của ( ) ' yfx = thì bảng biến thiên
yfx =
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Ta thấy 1;1 x − ta có ( ) ( ) ( ) 2 20 sin0sin0 fxf x −= , do đó ( ) ( ) (
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn gxgf = . Dấu “=” xảy ra khi 0 x =
Lời giải Chọn D Ta có 222 4 4.(42x)x6822(4) 2 x gxfxxxxfxx Xét thấy 22 1;3344(4)0xxxfxx Mặt khác 4 0 2 x 1;3 x Suy ra 02gxx 19171732 1(3)(4)53333 (3)(3)(4)519191934 3333 (2)5712.
( )0 f C. ( )2 f D. ( )1 f
i
( )
như sau:
)00
Câu 35: Cho hàm số ( )yfx = liên tục trên sao cho ( ) 1;2 max3 fx = . Xét hàm số ( ) ( )31 gxfxm =−+ . Tìm tất cả các giá trị của tham số m để ( ) 0;1 max10 gx =− . A. 13. B. 7. C. 13. D. 1. Lời giải
Chọn C
Đặt 31ux=− ( ) ( ) gxfum=+ . 0;11;2xu−
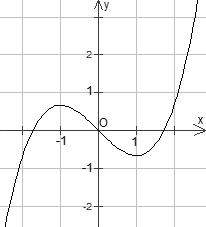
Do ( )fx liên tục trên nên ( ) ( ) ( )
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 51
Để (
==−
số (
yfx =
vẽ bên. Giá trị lớn nhất của hàm số sin3cos 2 xx yf + = trên đoạn 5 ; 66 bằng A. 3 f . B. ( )0 f . C. 5 6 f . D. 6 f . Lời giải Chọn A Đặt sin3cossin 23 xx tx + ==+ . Vì 5 ;;1;1 66322 xxt −+−− . Dựa vào đồ thị của hàm số ( )fx , ta có bảng biến thiên
( ) 0;11;21;2 maxmaxmax3 gxfumfumm =+=+=+
) 0;1 max1013 gxm
Câu 36: Cho hàm
)
có đạo hàm cấp 2 trên , hàm số ( )yfx = có đồ thị như hình
0;20;10xt . Ta có: ( ) ( ) ( ) 3232 0;20;20;20;2 maxmax2maxmax2 xxxx gxfxxxxmfxxxxm =+−++++−++ ( ) 0;10 max1 t ftm =++ ( ) 0;10 max1415 x fxmmm ++=++=+ .

Suy ra: ( ) 0;2
1 max51 2 x
x gxmx t
= =+= = . Theo giả thiết, ta có: ( ) 0;2 max8583 x gxmm =+==
Câu 38: Cho hai hàm số ( )yfx = , ( )ygx = có đạo hàm là ( )fx , ( )gx . Đồ thị hàm số ( )yfx = và ( )gx được cho như hình vẽ bên dưới.
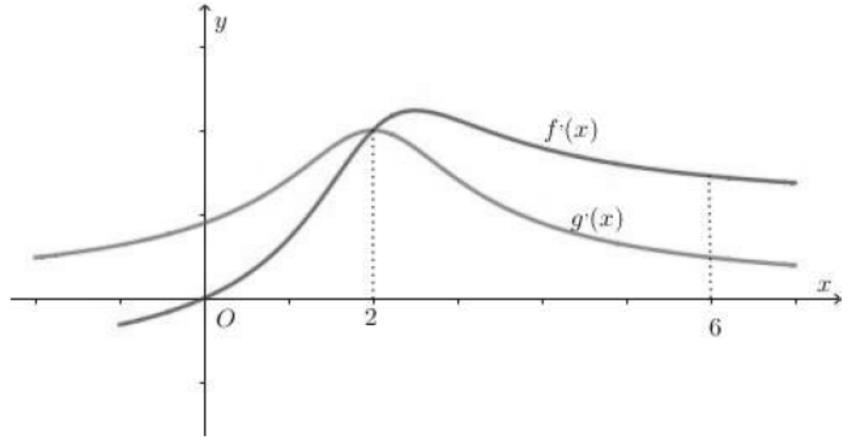
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 52 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có: ( ) 5 1;1 ; 66 sin3cos maxmax 2 xx fft + = 0sin0 33 txx =+==− Vậy 5 ; 66 sin3cos max 23 xx ff + =− Câu 37: Cho hàm số ( )yfx = liên tục trên sao cho ( ) ( ) 0;10 max24 x fxf == . Xét hàm số ( ) ( ) 32 2 gxfxxxxm =+−++ . Giá trị của tham số m để ( ) 0;2 max8 x gx = là A. 5 B. 4 C. 1 D. 3 Lời giải Chọn D Đặt 3 txx =+ . Vì
Biết rằng ( ) ( ) ( ) ( )0606ffgg −− . Giá trị lớn nhất, giá trị nhỏ nhất của hàm số ( ) ( ) ( )hxfxgx =− trên đoạn 0;6 lần lượt là: A. ( )6 h , ( )2 h B. ( )2 h , ( )6 h C. ( )0 h , ( )2 h D. ( )2 h , ( )0 h Lời giải
Ta có ( ) ( ) ( )hxfxgx =− ( ) 02hxx ==
Từ đồ thị ta có bảng biến thiên: Và ( ) ( ) ( ) ( )0606ffgg −− ( ) ( ) ( ) ( )0066fgfg −− . Hay ( ) ( )06hh Vậy ( ) ( ) 0;6 max6 hxh = ; ( ) ( ) 0;6 min2 hxh = Câu 39: Cho hàm số ( )fx liên tục trên , có đồ

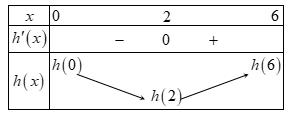
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 53
Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số 2 8 1 1 x yfm x =+− + có giá trị lớn nhất không vượt quá 2020? A. 4029. B. 4035. C. 4031. D. 4041. Lời giải Chọn C Đặt 2 8 1 x t x = + . Ta có: ( ) 2 2 2 88 1 x t x −+ = + ; 01tx == . BBT:
thị như hình vẽ

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 54
−
2
x
x =+− + trở
( ) ( )htft = . ( ) ( ) 00htft == 44;4 24;4 24;4 t t t =−− =−− =− Ta có: ( ) 40,810,2hmm −+−=− ; ( ) 4615hmm=+−=+ ; ( ) 21,610,6hmm −+−=+ ; ( ) 2415hmm =−+−=− . ( ) 4;4 MaxMaxyht = Max5;5 mm =+− . Yêu cầu bài toán 52020 52020 m m + − 202052020 202052020 m m −+ −− 20252015 20152025 m m − − 20152015 m − . Vậy có tất cả 4031 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán. Câu 40: Cho hàm số ( )yfx = liên tục trên có đồ thị ( )yfx = như hình bên. Đặt ( ) ( ) ( )2 21gxfxx=−−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
4;4 t
Hàm số
8 1 1
yfm
thành ( ) ( ) 1,4;4gtftmt=+−− . Đặt ( ) ( )
1,4;4htftmt=+−− , ta có:

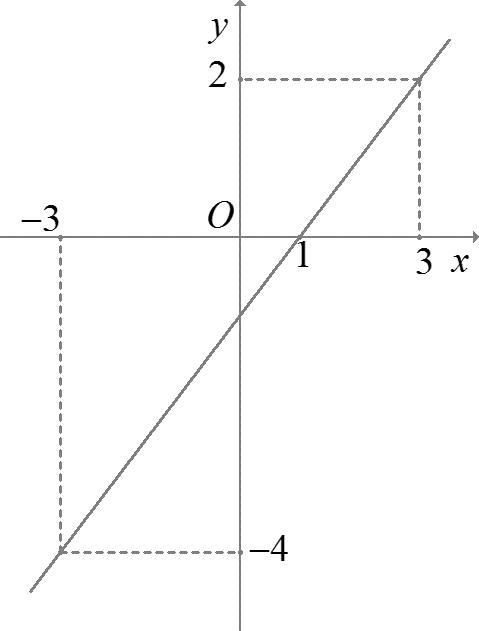
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 55 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Khi đó ( )ygx = đạt giá trị nhỏ nhất trên đoạn 3;3 tại A. 3 x =− . B. 3 x = . C. 0 x = . D. 1 x = . Lời giải. Chọn A Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2121 gxfxxgxfxx =−−=−− . Vẽ đồ thị hàm số 1 yx=− trên cùng hệ trục tọa độ với đồ thị hàm số ( )yfx = . Dựa vào đồ thị ta thấy + ( ) ( ) ( ) ( ) ( ) ( ) 13 31 013;013dd gxxgggxxgg − . Do đó ( )ygx = đạt giá trị nhỏ nhất trên đoạn 3;3 tại 3 x = hoặc 3 x =− + Phần hình phẳng giới hạn bởi ( );1;3;1yfxyxxx ==−=−= có diện tích lớn hơn phần hình phẳng giới hạn bởi ( );1;1;3yfxyxxx ==−== nên ( ) ( ) ( ) ( ) 13 31 33 dd gxxgxxgg − Vậy ( )ygx = đạt giá trị nhỏ nhất trên đoạn 3;3 tại 3 x =− .
Câu 41: Cho hàm số ( )fx . Biết hàm số ( )fx có đồ thị như hình dưới đây. Trên 4;3 , hàm số ( ) ( ) ( )2 21 gxfxx =+− đạt giá trị nhỏ nhất tại điểm A. 3 x =− . B. 4 x =− . C. 3 x = . D. 1 x =− . Lời giải
Chọn D
Xét hàm số
21 gxfxx
( ) ( )
có: ( ) ( ) ( ) 221 gxfxx
) ( ) 01 gxfxx ==−
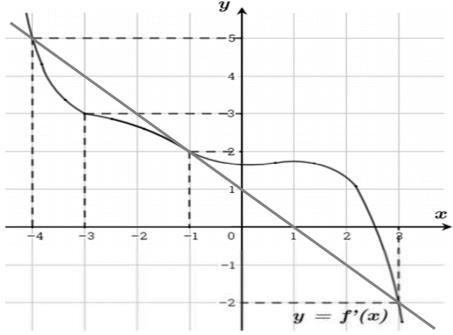
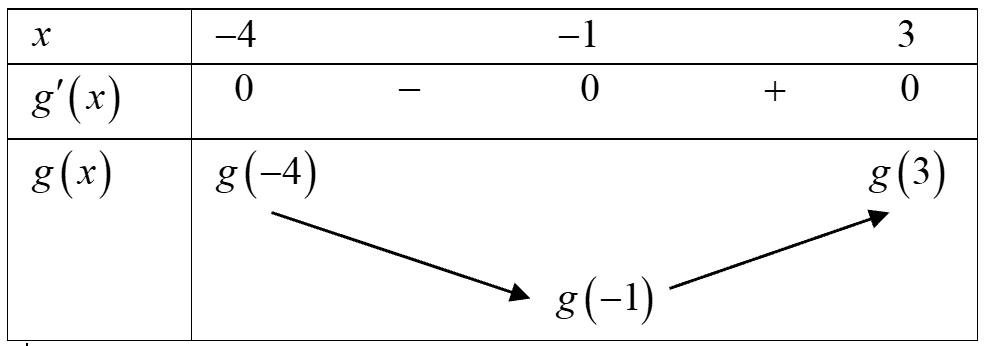
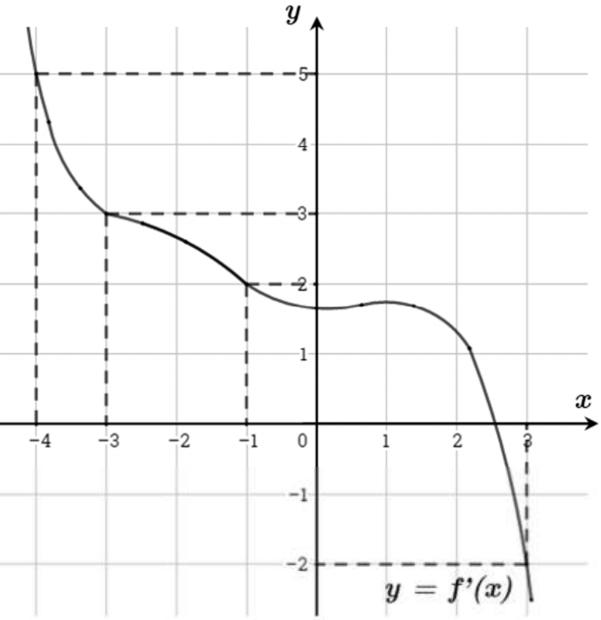
4;3
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 56
( )
2
=+− trên
Ta
=−− (
. Trên đồ thị hàm số ( )fx ta vẽ thêm đường thẳng 1 yx =− . Từ đồ thị ta thấy ( ) 4 11 3 x fxxx x =− =−=− = . Bảng biến thiên của hàm số ( )gx như sau: Vậy ( ) ( ) 4;3 min11 gxgx=−=− . Câu 42: Cho hàm số ( )yfx = có đạo hàm cấp hai trên . Biết ( ) ( ) ( ) 03,220180fff ==−= , và bảng xét dấu của ( )fx như sau
Hàm số ( )12018 yfx=−− đạt giá trị nhỏ nhất tại 0x thuộc khoảng nào sau đây? A. ( );2015−− . B. ( )1;3 . C. ( )1009;2 . D. ( )2015;1 . Lời giải.
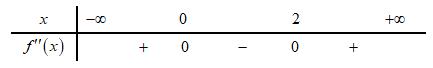

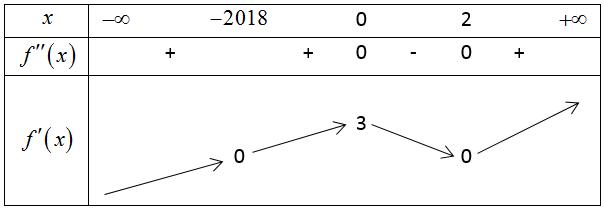
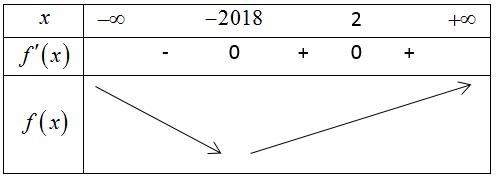
Chọn C
Từ bảng xét dấu của ( )fx và giả thiết ( ) ( ) ( ) 03,220180fff ==−= suy ra bảng biến thiên của hàm số ( )yfx = như sau
ừ đó
ra bảng biến thiên của hàm số ( )yfx
số ( )12018 yfx
t giá tr
)1011009;2
43: Cho hàm số ( )yfx
ỏ nhất khi và chỉ khi
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 57
T
suy
= : Hàm
=−− đạ
ị nh
120182018 x −−=− (
xx −==− . Câu
= có đạo hàm cấp hai trên . Biết ( ) 03 f = , ( ) 22020 f =− , ( ) lim x fx →− =− và bảng xét dấu của ( )fx như hình sau: Hàm số ( ) 20192020 yfxx =++ đạt giá trị nhỏ nhất tại điểm 0x thuộc khoảng nào sau đây? A. ( );2019−− B. ( )0;2 C. ( )2019;0 D. ( ) 2019;+ Lời giải Chọn A Theo giả thiết ta có
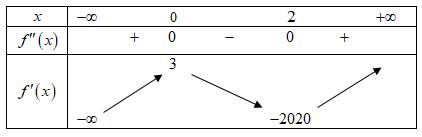

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 58 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có ( ) 20192020 yfx=++ ( ) 020192020yfx =+=− Từ bảng biến thiên trên ta có 20192019 0 201922017 xaxa y xx +==− =+==− , với 0 a Từ đó
x −− DẠNG 3. ỨNG DỤNG GTLN GTNN GIẢI
TẾ Câu 44:
số 0 a .
ố
ệ
ớ
ằng A. 2 3 3 a . B.
3 6 a .
Lời giải Chọn D Giả sử tam giác ABC vuông ở A thỏa mãn yêu cầu đề bài. Giả sử += ABBCa =−ABaBC Đặt 0 = ; BCxxa . =−ABax và ( )2 22 2 =−−=− ACxaxaxa Diện tích tam giác ABC là ( ) 2 11 2 22 ==−− . SABACaxaxa Xét hàm số ( ) ( ) 2 1 2 2 =−− fxaxaxa ( ) ( ) 2 2 1 2 22 =−−+− . a fxaxaax axa 222 2222 12123 2222 −++−− == . axaaaxaax xaxa
ta có bảng biến thiên của hàm số ( ) 20192020 yfxx =++ Từ bảng biến thiên có hàm số ( ) 20192020 yfxx =++ đạt giá trị nhỏ nhất tại 0 2019 xa=− . Vì 0 a nên ( ) 0 ;2019
BÀI TOÁN THỰC
Cho
Trong s
các tam giác vuông có tổng một cạnh góc vuông và cạnh huyền bằng a , tam giác có di
n tích l
n nhất b
2
C. 2 3 9 a . D. 2 3 18 a .
( ) 2 0 3 == a fxx Vậy diện tích lớn nhất của tam giác ABC là 2 2a3 318 == Sfa
Câu 45: Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ được cho bởi công thức ( ) 2 1 t ct t = + ( ) / mgL . Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất? A. 4 giờ B. 1 giờ C. 3 giờ D. 2 giờ Lời giải Xét hàm số ( ) 2 1 t ct t = + , (0) t . ( ) ( ) 2 2 2
1 1 t ct t = + . ( ) 1 0 1 t ct t = = =− Với 1 t = giờ thì nồng độ thuốc trong máu của bênh nhân cao nhất.
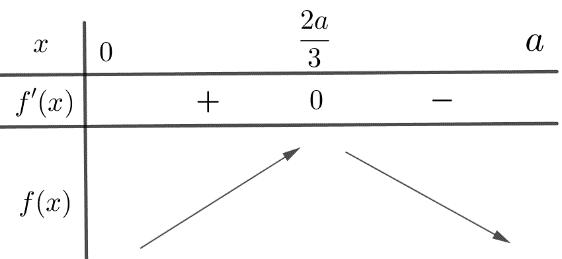

Câu 46: Cho một tấm nhôm hình vuông cạnh 12 cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x , rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 59
Thể tích của hình hộp là: ( )2 .122 VS x h x = = Xét hàm số: ( ) ( ) 2 .1220;6yxxx =− Ta có : ( ) ( ) ( )( ) 2 '1224122122126 yxxxxx =−−−=−− ; ( ) ( ) '0122.12602 yxxx =−−== hoặc 6 x = .

Suy
để làm thành một hình vuông và một hình tròn. Tính chiều dài của đoạn dây làm thành hình vuông được cắt ra sao cho tổng diện tích của hình vuông và hình tròn là nhỏ nhất? A. 56 4 + B. 112 4 + C. 84 4 + D. 92 4 + Lời giải Gọi chiều dài của đoạn dây làm thành hình vuông là x ( m ) => chiều dài của đoạn dây làm thành hình tròn là 28 x ( m ) +) Diện tích hình vuông là: 2 2 416 xx = +) Bán kính hình tròn là: R = 28 2 x
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 60 Chuyên
ện thi:
ể
ớ
Tốt
ệ
ạn A.
x = B.
x = C.
x = D.
x = Lời giải
( )
= là đường
ộp
ấm
c gấp lại tạo
ộp
ạnh
−
Giáo
Hòa
0984164935
luy
Tuy
n sinh vào l
p 10
Nghi
p THPT BDKT Toán 10; 11; 12 Sưu tầm và biên so
3
2
4
6
Chọn B Ta có :
hxcm
cao hình h
Vì t
nhôm đượ
thành hình h
nên c
đáy của hình hộp là: ( ) 122xcm Vậy diện tích đáy hình hộp ( ) ( ) 2 2 122 Sxcm =− . Ta có: ( ) 00 0;6 12206 xx x xx
ra với 2 x = thì thể tích hộp là lớn nhất và giá trị lớn nhất đó là ( ) 2128 y = . Câu 47: Một sợi dây có chiều dài 28m được cắt thành hai đoạn
48: Cho m
m nhôm hình chữ nhật có chiều dài bằng 10cm và chiều rộng bằng 8cm . Người ta cắt bỏ ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng ( )xcm , rồi gập tấm nhôm lại để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất. A. 8221 3 x = B. 1027 3 x = C. 921 9 x + = . D. 921 3 x = Lời giải Chọn D Ta có : ( )hxcm = là đường cao hình hộp Vì tấm nhôm được gấp lại tạo thành
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo
ỳnh
42
ễn
ậ
Page 61
ố
ạn => Diệ
2 2 2 2878456 24 xxx R −−+ == +) Tổng
ệ
22 2 78456414196 16416 xxx xx −++ +=−+
=
hình hộp nên cạnh đáy của hình hộp là: ( ) 102xcm và ( ) 82xcm Vậy diện tích đáy hình hộp ( )( )( ) 2 10282 Sxxcm =−− . Ta có: ( ) 0 0 10200;4 4 820 x x xx x x − − Thể tích của hình hộp là: ( ) ( ) .102.82 .S x V xx h == Xét hàm số: ( ) ( ) ( ).102.820;4yxxxx =−− Ta có : 2 '127280 yxx=−+ ;
viên: Hu
Văn Ánh
Nguy
Cư Trinh Thu
n Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 T
t Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên so
n tích hình tròn:
di
n tích hai hình:
Xét 2 ()414196 16 fxxx
+ =−+ . Nhận thấy ()fx đạt giá trị nhỏ nhất tại 2 b x a == ( ) 1416112 . 244
++ Vậy chiều dài của đoạn dây làm thành hình vuông để tổng diện tích của hai hình đạt giá trị nhỏ nhất là 112 4
+ m Câu
ột tấ

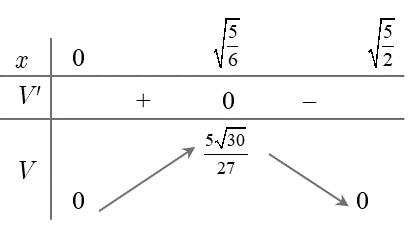
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 62
2 52 6 = x y x 23 2 5252 2 63 == xxx Vx x 2 56 3 = x V 2
=−= Vx 5
= x x 3 ma 530
27 =
V y x 2x
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) 921 4 '03 921 3 xl y xn + =
=
=
. Suy ra với 921 3 x = thì thể tích hộp là lớn nhất và giá trị lớn nhất. Câu 49: Ông A dự định sử dụng hết 2 5 m kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng Bể cá có dung tích lớn nhất bằng bao nhiêu? A. 3 1,01 m B. 3 0,96 m C. 3 1,33 m D. 3 1,51 m Lời giải Chọn A Gọi , xy lần lượt là chiều rộng và chiều cao của bể cá. Ta có thể tích bể cá 2 2 = Vxy . Theo đề bài ta có: 2 22.225 ++=xyxyx 2 625+= xyx
0560
6
1,01
m
C D A D' B C' B' A'
Câu 50: Một người nông dân có 15.000.000 đồng muốn làm một cái hàng rào hình chữ E dọc theo một con sông để làm một khu đất có hai phần chữ nhật để trồng rau. Đối với mặt hàng rào song song với bờ sông thì chi phí nguyên vật liệu là 60.000 đồng một mét, còn đối với ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu là 50.000 đồng một mét. Tìm diện tích lớn nhất của đất rào thu được A. 2 3125m B. 2 50 m C. 2 1250m D. 2 6250 m
Lời giải
x +
Chọn D
50 0 S' S
0
6250
+∞ 0
∞
Chọn D Gọi x là chiều dài 1 mặt hàng rào hình chữ E. Gọi y là chiều dài mặt hàng rào hình chữ E song song với bờ sông ( 0 y ). Số tiền phải làm là: 5005 .3.50000.6000015.000.000 2 x xyy +== Diện tích đất: 2 50055 ..250 22 x Sxyxxx ===− Ta có: '2505 Sx =− '0250550. Sxx =−= Bảng biến thiên: Vậy: ( ) 2 0; max6250 ()Sm + = khi 50. x = Câu 51: Ông Khoa muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích bằng 3 288m . Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là 500000 đồng/ 2 m . Nếu ông Khoa biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất. Hỏi ông Khoa trả chi phí thấp nhất để xây dựng bể đó là bao nhiêu?
A. 90 triệu đồng. B. 168 triệu đồng. C. 54 triệu đồng. D. 108 triệu đồng. Lời giải
Theo bài ra ta có để chi phí thuê nhân công là thấp nhất thì ta phải xây dựng bể sao cho tổng diện tích xung quanh và diện tích đáy là nhỏ nhất. Gọi ba kích thước của bể là a , 2a , c ( ) ( ) ( )0,0amcm .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 63

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 64
Chọ
C Kẻ đường cao BH , gọi số đo 2 góc ở đáy CD của hình thang là ( ) ,0;90xx Diện tích mảnh vườn là: ( ) ( ) ( ) 2 111 .sin2.2.cos2sinsin2 222 SBHABCDBCxABBCxABxx =+=+=+ Xét hàm số ( ) 2sinsin2 fxxx =+ với ( ) 000;90 x có ( ) 2cos2cos2 fxxx =+ Ta có: ( ) 2 1 cos 02cos2cos202coscos10 2 cos1 x fxxxxx x = =+=+−= =− Do ( ) 000;90 x nên ta nhận 0 1 cos60 2 xx== . Ta có bảng biến thiên: C D
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có diện tích cách mặt cần xây là 22 24226 Saacacaac =++=+ Thể tích bể 2 .2.2288Vaacac=== 2 144 c a = Suy ra 2222 3 2 144864432432432432 26.223.2..216 Saaaaa aaaaaa =+=+=++= . Vậy 2 min 216m S = , khi đó chi phí thấp nhất là 216.500000108 = triệu đồng. Câu 52: Một người nông dân có 3 tấm lưới thép B40, mỗi tấm dài ( ) 12 m và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân ABCD như hình vẽ Hỏi ông ta có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu 2 m ? A. 1003 B. 1063 C. 1083 D. 1203 Lời giải
n
B A
Từ bảng biến thiên ta thấy: ( ) ( ) 000;90 112 1 xx fx x
33 max 2 fx đạt được tại 060 x = ( ) 2 max1083Sm= khi góc ở đáy CD của hình thang bằng 060 ( ) 060 CD== Câu 53: Cho nửa đường tròn đường kính 2 AB = và hai điểm C , D thay đổi trên nửa đường tròn đó sao cho ABCD là hình thang. Diện tích lớn nhất của hình thang ABCD bằng A. 1 2 . B. 33 4 . C. 1. D. 33 2 . Lời giải Chọn B Gọi H là hình chiếu vuông góc của D lên AB , I là trung điểm của đoạn CD và O là trung điểm của AB . Đặt DHx = , −+− = ( ) 22 01120fxxx =−+−= Đặt 2 1 tx =− , khi đó phương trình trở thành 2 1 210 1 2
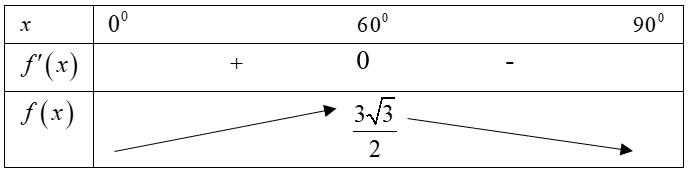
=− +−= = . 1 t =− loại. 1 2 t = ta có 22133 1 242 xxx −=== . Bảng biến thiên
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 01 x . Ta có 22222221 DCDIOHODDHx ===−=− Diện tích của hình thang ABCD là ( ) ( ) ( ) 2 11 2 ABCDDH Sfxxx + ===+− . Ta có ( ) 22 2
t tt t
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 65
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Vậy diện tích lớn nhất của hình thang ABCD bằng 33 4 .
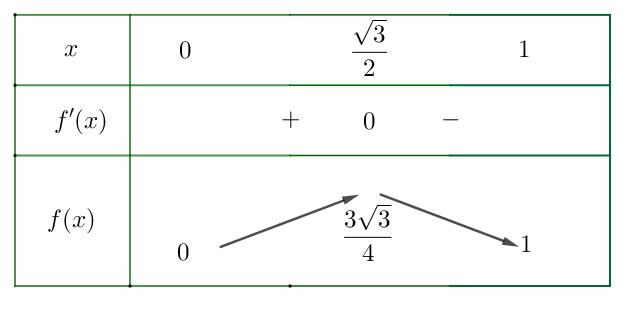
Câu 54: Một người đàn ông muốn chèo thuyền ở vị trí A tới điểm B về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng 3km Anh có thể chèo thuyền của mình trực tiếp qua sông để đến C và sau đó chạy đến B , hay có thể chèo trực tiếp đến B , hoặc anh ta có thể chèo thuyền đến một điểm D giữa C và B và sau đó chạy đến B . Biết anh ấy có thể chèo thuyền 6km/h, chạy 8km/h và quãng đường 8km BC = . Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Tính khoảng thời gian ngắn nhất để người đàn ông đến B . A. 3 2 . B. 9 7 . C. 73 6 . D. 7 1 8 + . Lời giải

Cách 1: Anh chèo thuyền của mình trực tiếp qua sông để đến C và sau đó chạy đến B Thời gian chèo thuyền trên quãng đường AC : 3 0,5 6 = Thời gian chạy trên quãng đường CB : 8 1 8 = Tổng thời gian di chuyển từ A đến B là 1,5 Cách 2: chèo trực tiếp trên quãng đường 22 3873 AB =+= mất h 73 126 6 . Cách 3:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 66
Gọi ( )km x là độ dài quãng đường BD; ( )8km x là độ dài quãng đường CD.
Thời gian chèo thuyền trên quãng đường 2 9 ADx=+ là: 2 9 6 x +
Thời gian chạy trên quãng đường DB là: 8 8 x
Tổng thời gian di chuyển từ A đến B là ( ) 2 98 68 xx fx +− =+
Xét hàm số ( ) 2 98 68 xx fx +− =+ trên khoảng ( )0;8
Ta có ( ) 2
1 8 69 x fx x =− + ; ( ) 2 9 0394 7 fxxxx =+==

Bảng biến thiên
Dựa vào BBT ta thấy thời gian ngắn nhất để di chuyển từ A đến B là h 7 1120 8 + .
Vậy khoảng thời gian ngắn nh
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 67
ất để người đàn ông đến B là h 7 1120 8 + . DẠNG 4. DÙNG PHƯƠNG PHÁP HÀM SỐ ĐỂ TÌM GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT CỦA BIỂU THỨC Câu 55: Cho ba số thực ,, xyz thỏa mãn 0,0,1xyz , 2 xyz++= .Biết giá trị lớn nhất của biểu thức Pxyz = bằng a b với * , ab và a b là phân số tối giản. Giá trị của 2ab + bằng A. 5. B. 43. C. 9. D. 6.
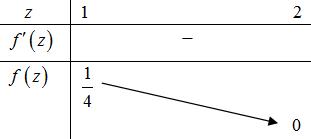
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 68
Lờ
===−+
1;426abab ==+= . Câu 56: Cho 22 2 xxyy−+= . Giá trị nhỏ nhất của 22 Pxxyy =++ bằng: A. 2 3 B. 1 6 C. 1 2 D. 2 Lời giải Chọn A Xét 2222 22 22 Pxxyyxxyy xxyy ++++ == −+ +nếu 0 y = thì 2 2 x = . Do đó 2 2 Px== suy ra min2 P = +nếu 0 y ta chia tử mẫu cho 2 y ta được 2 22 2 22 1 2 1 xx yy Pxxyy xxyy xx yy ++ ++ == −+ −+ Đặt x t y = , khi đó 2 2 1 21 Ptt tt ++ = −+ Xét ( ) ( ) ( ) 22 2 2 2 122 ' 1 1 ftftttt tt tt ++−+ == −+ −+
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
i giải Chọn D Ta có: ( ) 22 23 21 ..z44 224 xyz Pxyzzzzz +−
. Xét hàm số ( ) ( ) 23 1 44 4 fzzzz =−+ trên 1;2 Ta có: ( ) ( ) ( ) 2 2 1() 483;03 42 zloai fzzzfz z = =−+= = Bảng biến thiên: Dựa vào bảng biến thiên, ta có: 1 4 P . Vậy max 1 4 P = khi 1 1 2 z xy = ==
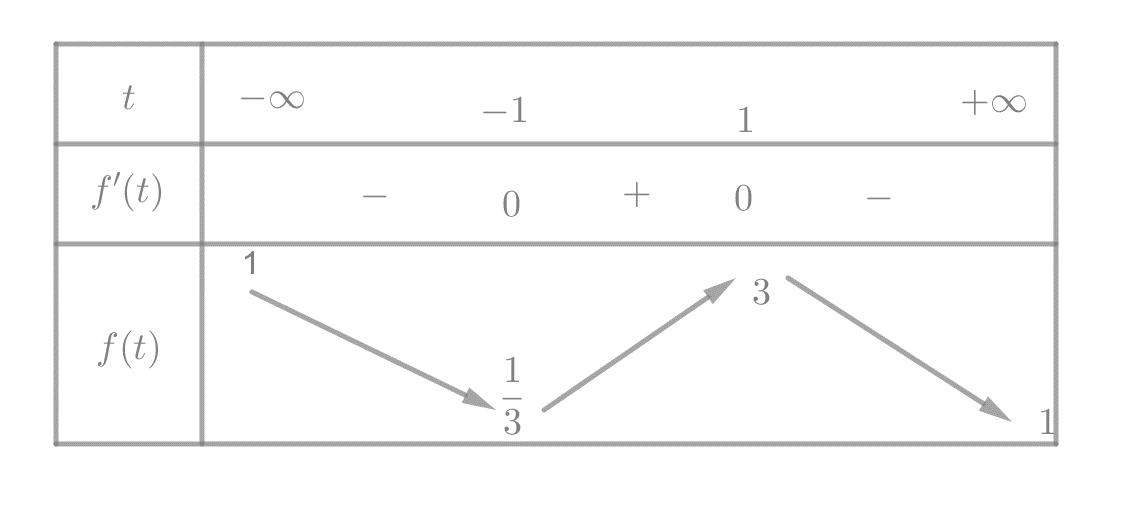
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 69
ỏ
ấ
ủ
Chọn C ( ) ( ) ( ) 2 2 121303 xyxyxyxy +=−++++ ( )( ) ( ) ( ) ( ) 2 22 211842284 Pxyxyxyxyxyxy =+++++−−=+++++−+ Đặt ( ) 4,1;2txyt =−+ . Ta có: ( ) ( ) ( ) 2 2242 4242810826fttttttt =−+−++=−++ . ( ) 3 4208fttt =−+ ( ) 2 21;2 2 0121;2 210 121;2 t t ftt tt t = = ==−+ +−= =−− ( ) ( ) 125;218ff== . Suy ra ( ) ( ) ( ) ( ) 1;2 1;2 min218;max125 mftfMftf ====== .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) 1 '0 1 t ft t = = =− Bảng biến thiên Khi đó 1 min 23 P = do đó 2 min 3 P = . Câu 57: Cho x , y là các số thực thỏa mãn 122xyxy +=−++ . Gọi M , m lần lượt là giá trị lớn nhất và nh
nh
t c
a ( )( ) 22 21184 Pxyxyxy =+++++−− . Tính giá trị Mm + A. 42 B. 41 C. 43 D. 44 Lời giải
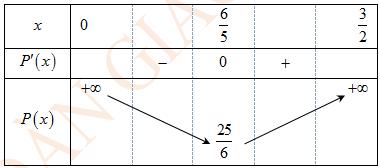
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 70 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vậy 43 Mm+= Câu 58: Cho x , 0 y thỏa mãn 3 2 xy+= và biểu thức 41 4 P xy =+ đạt giá trị nhỏ nhất. Tính 22 xy + A. 153 100 B. 5 4 C. 2313 1156 D. 25 16 Lời giải Chọn A Từ 3 2 xy+= suy ra 3 2 yx =− . Ta có: 3 0, 2 xy Xét hàm ( ) 41 3 4 2 Px x x =+ 41 64 xx =+ trên
ảng 3
2
ta
( ) ( )2 2 44 64 Px x x =−− . ( ) 0 Px = ( )2 2 44 64 x x = ( )2 2 64 xx=− 64 46 xx xx =− =− 6 5 2 x x = = Bảng biến thiên của ( )Px trên 3 0; 2 : Dựa vào bảng biến thiên ta thấy ( ) 3 0; 2 25 min 6 Px = khi 6 5 x = . Với 6 5 x = thì 3 10 y = Như vậy 25 min 6 P = khi 6 5 x = , 3 10 y = Khi đó, 22 153 100 xy+= Câu 59: Cho ,0xy và 5 4 xy+= sao cho biểu thức 41 4 P xy =+ đạt giá trị nhỏ nhất. Khi đó A. 22 25 32 xy+= B. 22 17 16 xy+= C. 22 25 16 xy+= D. 22 13 16 xy+= Lời giải Từ 55 44 xyyx +==− , nên 41 54 P xx =+ .
kho
0;
,
có:
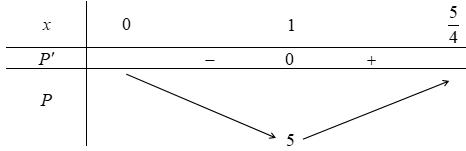
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 71
nhất của biểu thức ( )333 111 xyz xyz ++++ bằng: A. 20 B. 25 C. 15 D. 35 Lời giải Ta có: ( ) 2 44 5554 xyz xyz xyyzzx xyzxyzz +=− ++= ++= =−+=−+ Lại có: ( )2 4 xyxy + ( ) ( ) 2 2 2 44542 3 zzzz −−+ . Dấu "" = xảy ra khi xy = Và ( ) ( )( ) ( ) 3 333 33 xyzxyzxyzxyzxyxy ++=++++++++ ( ) ( ) 33334123 xyzxyzxyxy ++=−+−+ ( )( ) 2 64345zz=−−+ Ta có: ( )333 111 Pxyz xyz =++++ ( ) 32 32 5 312154 45 zzz zzz =−++ −+ Đặt 3245 tzzz =−+ , với 250 22 327 zt . Do đó xét hàm số ( ) 4 53 ft t =+ , với 50 2 27 t
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Xét hàm số 41 54 P xx =+ với 5 0 4 x ( )2 2 44 54 P x x =−+ ; ( )2 2 054 Pxx ==− 5 10; 4 55 0; 34 x x = = Bảng biến thiên Như vậy: min5 P = khi 1 x = ; 1 4 y = . Khi đó 22 17 16 xy+= . Câu 60: Xét các số thực dương , , xyz thỏa mãn 4 xyz++= và 5 xyyzzx++= . Giá trị nhỏ
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 72 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có ( ) 2 2050 0,;2 27 ftt t = nên hàm số ( )ft liên tục và nghịch biến. Do đó ( ) min 225 Pf== đạt tại 1 xy== , 2 z = . Câu 61: Cho , xy là các s
t xyyx + =+ . Ta
=+−+ ( )
ớ
. Khả
sát hàm số ( )ft với 5 2 t ta được ( ) 23 4 ft − . Vậy chọn C Câu 62: Cho các số thực dương x , y thỏa mãn 5 2 4 xy+= . Tìm giá trị nhỏ nhất minP của biểu thức 21 4 P xy =+ . A. min 34 5 P = . B. min 65 4 P = . C. minP không tồn tại. D. min 5 P = . Lời giải Từ giả thiết ta có 5 2 4 yx =− . Vì 0 y nên 55 20 48 xx − . Do đó 5 0 8 x . Ta có 2 21211015 5588542 4 x P xxxxx x =+=+= −−+ với 5 0 8 x ( ) ( )( ) ( ) ( ) ( ) 222 2222 15851651015120751602405075 8585 xxxxxxxxx P xxxx −−+−−+−−−−++− == −+−+
0984164935
ố thực dương thỏa mãn ( ) ( )( ) 22 22 xyxyxyxy ++=++ . Giá trị nhỏ nhất của biểu thức 3322 332249xyxy P yxyx =+−+ A. 25 4 . B. 5. C. 23 4 . D. 13. Lời giải Ta có ( ) ( )( ) 22 22 xyxyxyxy ++=++ ( )22 xyxy+ . Đặt 22 ; axybxy =+= ta được: ( ) ( ) 2 22 28244150 abbabaabb ++−− 5 2 a b . Suy ra: 22 55 22 xyxy
có: 3322 332249xyxy P yxyx
( ) ( ) 3232 4392491218 ttttttft =−−−=−−+= v
i 5 2 t
o
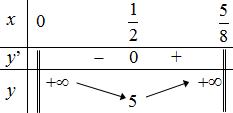
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 73
n ( ) 2 2 2 12016050 85 xx P xx −+− = −+ . Có 2
Pxx x
=−+−=
=
Bả
ế
Dựa vào bảng biến
ta
min 5 P = .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạ
55 0; 68 0120160500 15 0; 28 x
=
ng bi
n thiên
thiên
có
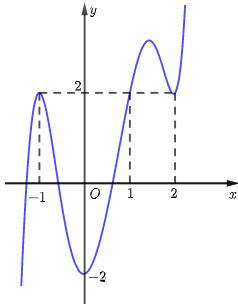



CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 74 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn BÀI 3: GIÁ TRỊ NHỎ NHẤT VÀ GIÁ TRỊ LỚN NHẤT CỦA HÀM SỐ VD VDC 02 HƯỚNG DẪN GIẢI CHI TIẾT Câu 63: Cho hàm số ( )yfx = có đồ thị hàm số ( )yfx = là đường cong trong hình vẽ Giá trị nhỏ nhất của hàm số ( ) ( ) 2143gxfxx=+−− trên đoạn 1 1; 2 bằng A. ( )0 f B. ( ) 11 f −+ C. ( ) 13 f D. ( ) 25 f Lời giải Chọn C Xét hàm số ( ) ( ) 2143gxfxx=+−− trên đoạn 1 1; 2 , ta có ( ) ( ) 2214gxfx =+− Suy ra ( ) ( ) 2111 02122110 2121 2 xx gxfxxx x x +=−=− =+=+== += = . Ta có BBT của hàm số ( ) ( ) 2143gxfxx=+−− trên đoạn 1 1; 2 như sau: CHƯƠNG I ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
0984164935
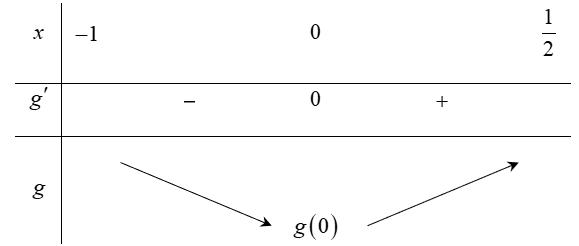
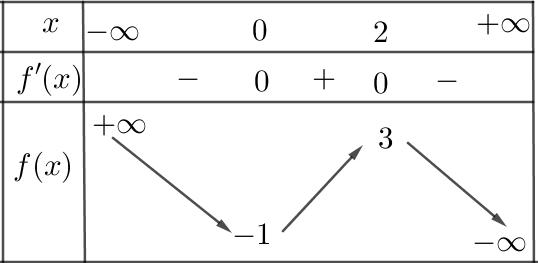
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 75 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vậy ( ) ( ) ( ) 1 1; 2 min013 gxgf ==− . Câu 64: Cho hàm số ( )yfx = có đạo hàm ( ) 2 36 yfxxx ==−+ . Biết ( ) 01 f =− , giá trị lớn nhất của hàm số ( ) ( ) 2 322022gxfxx=−++ trên đoạn 1 3; 2 bằng A. 21 2022 16 f + . B. 2024. C. 2025. D. 3 2022 2 f + . Lời giải Chọn C Hàm số ( )yfx = có đạo hàm ( ) 2 36 yfxxx ==−+ và ( ) 01 f =− nên hàm số: ( ) 3231yfxxx ==−+− ( ) 0 0 2 x fx x = = = Bảng biến thiên: Xét: ( ) ( ) ( ) 22 2 31 3; 22 1 13; 2302 1 23.32032023; 2 322 1 03; 2 1 33; 2 x x x gxxfxxxxx xx x x =− =− −= =−−+=−+==− −+= =− =− Bảng biến thiên của hàm số ( )ygx = trên đoạn 1 3; 2 là:
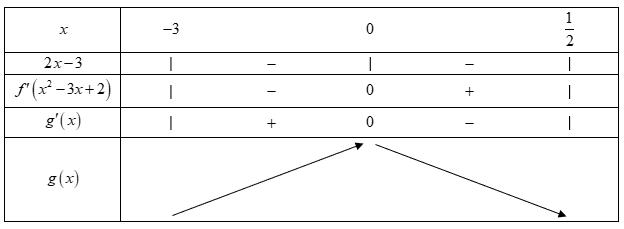
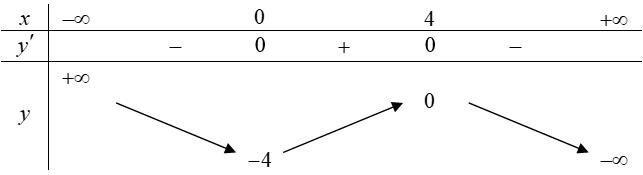
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 76 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Suy ra: ( ) ( ) ( ) 1 3; 2 max0220222025 gxgf ==+= Câu 65: Cho hàm số ( )yfx = có bảng biến thiên như hình dưới đây. Giá trị lớn nhất của hàm số ( ) ( ) 23211 438 33gxfxxxxx =−+−++ trên đoạn 1;3 bằng A. 12 B. 10 3 C. 4 3 D. 7 Lời giải Chọn D Ta có: ( ) ( ) ( ) 22 42468gxxfxxxx =−−+−+ = ( ) ( ) ( )( ) 2 22442 xfxxxx −−+−− = ( ) ( ) 2 2244xfxxx −−+− Ta thấy 2 344 xx − , 1;3 x ( ) 2 40fxx − . Hơn nữa, 40,1;3 xx − . Suy ra ( ) 2 2440 fxxx −+− . Do đó, ( ) 02gxx == Bảng biến thiên
Vậy ( ) ( ) ( ) 1;3 max247077 gxgf==+=+= .
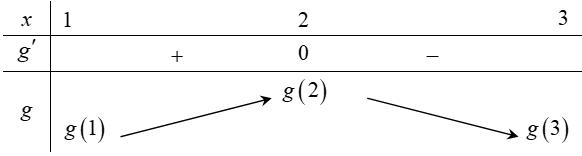
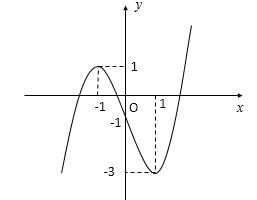
Câu 66: Cho hàm số ( )yfx = liên tục trên và có đồ thị như hình vẽ Đặt ( ) ( ) 22448gxxxfxx =−+−+ Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
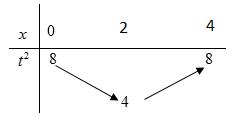
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 77
A Đặt ( ) (
==+++=++ Từ đồ thị hàm số ( )yfx = , ta có ( ) 011fd=−=− , suy ra ( ) 32 1 fxaxbxcx=++− . Ta cũng có ( ) ( ) ( ) 1121 1320 103203 f abca fabcb abcc f −= −+−== =−++=−= ++==− = . Như vậy ( ) 3 31yfxxx ==−− Đặt 2224848txxtxx =−+=−+ , 0;4 x . Ta có bảng biến thiên Suy ra 2 48222 tt
( )gx trên
0;4 là A. 1024 B. 1021 C. 102 D. 824 Lời giải Chọn
) 32232 yfxaxbxcxdfxaxbxc
Hàm số ( )gx thành ( ) ( ) 2 8 httft =−+ . Xét hàm số ( ) ( ) 2 8 httft =−+ trên 2;22 . Ta có: ( ) ( ) 20,2;22httftt =+ , .
Như vậy hàm số ( ) ( ) 2 8 httft =−+ đồng biến trên 2;22 , suy ra ( ) ( ) ( ) ( ) 0;4 2;22 min24823min; hthfgx ==−+=−= ( ) ( ) ( ) 0;4 2;22 max221021maxhthgx ==−= Vậy tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số ( )gx trên 0;4 là: 1024. Câu 67: Cho hai số thực , xy thỏa mãn ( ) 32 272131321 yyxxxy ++−=−++ . Tìm giá trị lớn nhất của biểu thức 2 Pxy =+ A. 8 P = B. 10 P = C. 6 P = D. 4 P = Lời giải Chọn D Điều kiện: 1 x Ta có ( ) 32 272131321 yyxxxy ++−=−++ ( ) ( ) 32 233112111 yyyyxxx −+−+−=−−+− ( ) ( )3 3 211211 yyxx −+−=−+−
Xét àm số ( ) 3 2 fttt =+ có ( ) 2 610, fttt =+ , suy ra ( )ft đồng biến trên Khi đó ( ) ( ) ( ) 2 *11112 fyfxyxxyy −=−−=−=− Khi đó ( )2 2 24424Pxyyyy =+=−+=−−
Đẳng thức xảy ra khi 2,0yx== Vậy max4 P = khi ( ) ( );0;2xy = .

68: Cho hàm số ( )yfx = . Hàm số
)fx
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page
78
Câu
(
có bảng biến thiên như hình vẽ sau: Giá trị lớn nhất của hàm số ( ) ( ) 22sin gxfxx =− trền đoạn [1;1] là A. ( )1 f . B. ( )0 f . C. ( )2 f . D. ( )1 f . Lời giải Chọn B ( ) ( ) ( ) 222sin.cos22sin2 fxxxfxx gx =−=− . Đặt 22;2txt=−
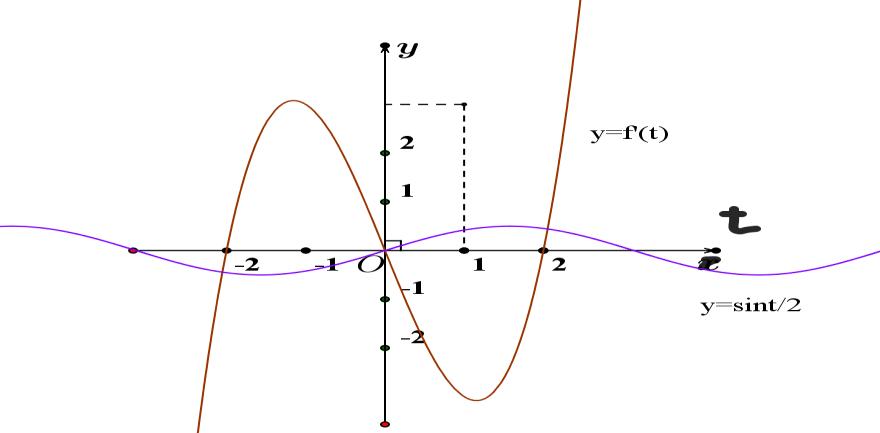


CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 79 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) sin 02sin0,2;2 2 t gtfttftt =−==− Vậy giá trị lớn nhất là ( ) ( )00gf = Câu 69: Cho hàm số ( )yfx = có bảng biến thiên như hình dưới đây. Giá trị lớn nhất của hàm số ( ) ( ) 23211 438 33gxfxxxxx =−+−++ trên đoạn 1;3 bằng A. 12 B. 10 3 . C. 4 3 . D. 7. Lời giải Chọn D Ta có: ( ) ( ) ( ) 22 42468gxxfxxxx =−−+−+ = ( ) ( ) ( )( ) 2 22442 xfxxxx −−+−− = ( ) ( ) 2 2244xfxxx −−+− . Ta thấy 2 344 xx − , 1;3 x ( ) 2 40fxx − Hơn nữa, 40,1;3 xx − Suy ra ( ) 2 2440 fxxx −+−
Do đó, ( ) 02gxx == Bảng biến thiên Vậy ( ) ( ) ( ) 1;3 max247077 gxgf==+=+= . Câu 70: Cho hàm số 32 ()3 fxaxbxxc =+−+ và 2 () gxdxe =+ có đồ thị như hình vẽ sau: Biết diện tích miền tô đậm như hình vẽ bằng 11 12 Giá trị lớn nhất của hàm số (1) yfxx =+− bằng A. 12 B. 12 + C. 1 D. 1 Lời giải
Chọn A
Từ đồ thị hàm số ()fx và (),gx ta có: 2 32 (0)11()1 . (0)11()31 gegxdx fcfxaxbxx ===+ ===+−+

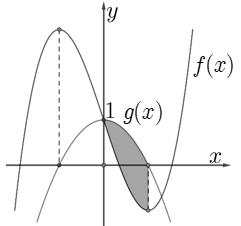
Từ đồ thị ta có hoành độ cực trị củ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 80
Khi
0 b = và có tỉ lệ 33 . 1 a da d ==− Suy ra: 3 ()31, fxaxx=−+ 2 ()1gxax=−+ và 2 ()10, a gxaxx a =−+== (0). a Mà 11 23 00 111111 121212()()d(3)d1. aa Sgxfxxaxaxxxa =−=−−+== Khi đó: 3 ()31. fxxx=−+ Xét (1) yfxx =+− với điều kiện [0;1], x ta có: 111 0 2212 x tx xx =−== 1 (0)(1)1,2 2 ttt === [1;2] t 3 ()31, [1;2]. yftttt ⎯⎯→==−+
a hàm số ()fx trùng với giao điểm của đồ thị hàm số ()gx với trục hoành ,Ox tức nghiệm của 2 ()3230fxaxbx =+−= và 2 ()10gxdx=+= trùng nhau.
đó
Ta có: 2 ()330, [1;2] fttt =− nên hàm số ()yft = luôn đồng biến trên [1;2]. Vậy [1;2] max()(2)12 ftf==−
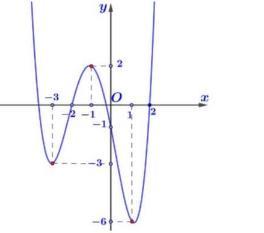

Câu 71: Cho hàm số ()yfx = , đồ thị của hàm số ()yfx = là đường cong trong hình bên. Giá trị nhỏ nhất của hàm số 2 ()(3)341 gxfxxx =+−+ trên đoạn 22 ; 33 bằng A. (0)1 f + . B. (6) f . C. 1 (2) 3 f . D. (3)8 f −+ .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 81
Lời giải Chọn C ( ) ( ) ( ) ( ) 2 ()(3)341336433234 gxfxxxgxfxxfxx =+−+=+−=+− ( ) ( ) ( ) ( ) ( ) 42 033234033 33 gxfxxfxx =+−==− Đặt 22 3,;2;2 33 txxt =− . Ta được phương trình ( ) 42 33 ftt =− Đặt ( )yft = , 42 : 33 dyt =− Bảng biến thiên
Hàm số 2 ()(3)341 gxfxxx =+−+ đạt giá trị nhỏ nhất 22 ; 33 khi ( ) ( ) 22 ; 33
221 23min2 333xxgxgf
====−

Câu 72: Cho hàm số ( )yfx = liên tục trên và có đồ thị như hình vẽ: Xét hàm số ( ) ( ) 3 214 gxfxxm =+−+ . Tìm m để ( ) 0;1 min5 gx =− A. 1 B. 2 C. 4 D. 0 Lời giải Chọn A Đặt ( ) 3 21txxx=+− với 0;1. x Ta có ( ) 2 320, 0;1 txxx =+ . Suy ra hàm số ( )tx đồng biến trên 0;11;2 t − . Từ đồ thị hàm số ta có ( ) ( ) 1;21;2 min1min414 ftftmm =−+=−+ Theo yêu cầu bài toán ta cần có: 1451 mm −+=−=− Câu 73: Cho hàm số ( )yfx = có bảng biến thiên như sau

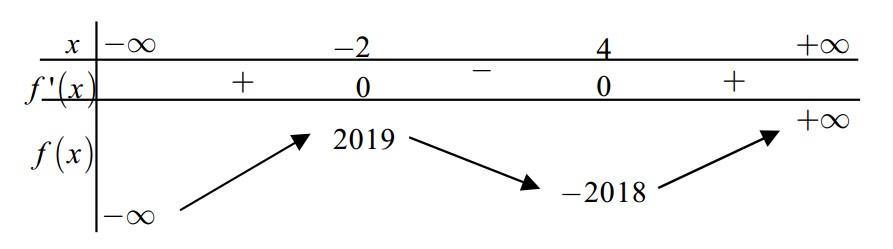
Tìm giá trị lớn nhất của hàm số ( ) ( ) 353122 33 5315gxfxxxxx =−−−+− trên đoạn 1;2 ? A. 2022 B. 2019 C. 2020 D. 2021 Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 82

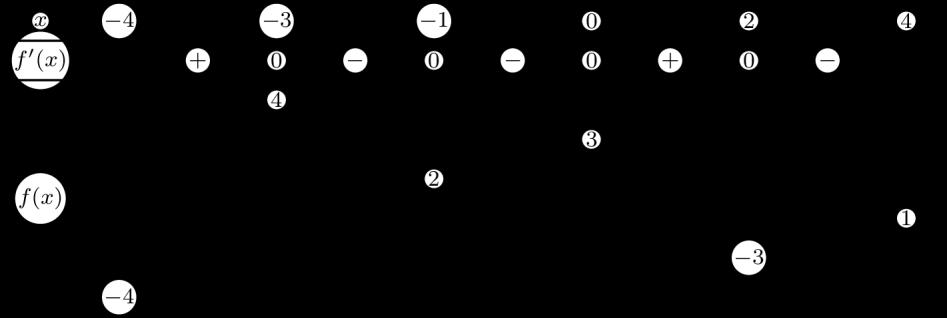
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 83 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Chọn D ( ) ( ) ( ) ( ) ( ) 2342232 333231333 gxxfxxxxxfxxx =−−−−+=−−−− ( ) ( ) 32 2 3330 0 10 fxxx gx x −−−= = −= Mà ( ) ( ) 3332 1;232;2303330 xxxfxxfxxx −−−−−−− , do đó ( ) 2 0101.gxxx =−== Ta có Vậy ( ) ( ) 1;2 max1222021 ygf==−+= Câu 74: Cho hàm số ( )fx có bảng biến thiên trên đoạn 4;4 như sau Có bao nhiêu giá trị của tham số 3;2 m− để giá trị lớn nhất của hàm số ( ) ( ) ( ) 3 3 gxfxxfm =++ trên đoạn 1;1 bằng 11 2 A. 3. B. 4. C. 2. D. Vô số. Lời giải Chọn A Đặt 3 3 txx =+ Xét hàm số ( ) 3 3 hxxx =+ , 1;1 x − ( ) 2 330hxx=+ , 1;1 x − . Bảng biến thiên của ( ) t x h =


CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 84
Vậy ( ) 0;4 0;4max3 t
= . Mặt
( ) ( ) ( ) ( ) (
)
1;10;4
maxmax
xt
− =−− =−− =+== =− =
ố ( )yfx = liên tục, có đạo hàm trên và có đồ thị như hình vẽ dưới đây: Ký hiệu ( ) ( ) gxfxxm =+−+221. Tìm tất cả các giá trị thực của tham
ố
( ) ( ) 0;10;1 4.maxgxmingx A. 1 3 m B. 1 3 m C. 15. m To D. − 5 3 m Lời giải Chọn B Đặt ( ) x txxtxxxt =+−→=++−⎯⎯→ 01 2 2217142111. Ta lại có ( ) ( ) ( )txxxxxx =+−=+−++−= 222 22122.122113. Khi đó ( ) ( ) gxftm =+ với t 1;3. Dựa vào đồ thị ta có ( ) ( ) ( ) ( ) == == 1;3 1;3 35 21 maxftf minftf Ycbt ( ) ( ) ( ) ++++ 1;31;3 1 4541. 3 maxfxmminfxmmmm
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
tft
khác
) ( ) (
( )
4;3 111153;1
2221;0 0;2
maa mbb gxftfmfm mcc mdd
; ; ; ; Vì
3;2 m− nên có tất cả 3 giá trị của m thỏa yêu cầu bài toán. Câu 75: Cho hàm s
s
m sao cho
Câu 76: Cho hai hàm số đa thức bậc bốn ()yfx = và ()ygx = có đồ thị như hình vẽ bên dưới, trong đó đường đậm hơn là đồ thị hàm số ()yfx = . Biết rằng hai đồ thị này tiếp xúc với nhau tại điểm có hoành độ là 3 và cắt nhau tại hai điểm nữa có hoành độ lần lượt là 1 và 3. Giá trị nhỏ nhất của hàm số ()()() uxfxgx =− trên đoạn [3;3]bằng A. 1283 9 B. 12103 9 C. 12103 9 D. 1283 9 Lời giải Chọn A Do đồ thị của hai hàm số tiếp xúc với nhau tại điểm có hoành độ là 3 và cắt nhau tại hai điểm nữa có hoành độ lần lượt là 1 và 3 nên ()()() uxfxgx =− có dạng 2 ()()()(3)(1)(3) uxfxgxkxxx =−=++−


Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG
HÀM
KHẢO SÁT HÀM SỐ
ĐẠO
ĐỂ
Page 85
+ (3 3 0 ') x ux x = =− = . BBT: Do
3;3 ()1283 9 minux = .
. (0)(0)(0).9.1.(3)(1) ufgk=−=− Mặt khác từ đồ thị ta có (0)(0)(0)1(2)1(2) ufg=−=−−−= Từ (1) và (2) ta được 1 1.9.1.(3)27 kk =−= . Do đó 2 1 ()()()(3)(1)(3) 27 uxfxgxxxx =−=++− Xét hàm ()ux ta có: 23211 (3)(1)(3))'(4121236)272 '()(7xxxxxx ux +−=+−− =
đó
Câu 77: Cho hàm số đathức ( )yfx = có đạohàm trên .Biết rằng ( ) 00 f = , ( )
3 24 ff −==− và đồ thị hàm số ( )yfx = có dạng như hình vẽ.
Hàm số ( ) ( ) 2 42 gxfxx =+ giá trị lớn nhất của ( )gx trên 3 2; 2 là
A. 2. B. 39 2 . C. 1. D. 29 2 . Lời giải
Chọn D
Xét hàm số ( ) ( ) 2 42 hxfxx =+ xác định trên
Hàm số ( )fx là hàm đa thức nên ( )hx cũng là hàm đa thức và ( ) ( ) 0402.00hf=+=
Khi đó ( ) ( ) ( ) ( ) 440' hxfxxhxfxx =+==− .


Dựa vào sự tương giao của đồ thị hàm số ( )yfx = và đường thẳng yx =− , ta có ( ) 3 03;0; 2 hxx =−
Ta có bảng biến thiên như sau:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 86
319
Từ đó ta có bảng biến thiên của hàm số ( ) ( )gxhx = như sau Vậy giá trị lớn nhất của ( )gx trên 3 2; 2 là 29 2 . Câu 78: Cho hàm số

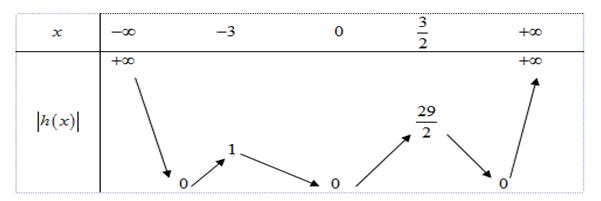

có đạo hàm và liên t
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 87
() = yfx
ụ
ỏ
ảng
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Giá trị nhỏ nhất của hàm số ( ) 42642 312152648 yfxxxxx =−+−++− trên đoạn 1;1 bằng A. 3. B. 0. C. 1. D. 2. Lời giải Chọn D Đặt ( ) 42642 ()312152648 ygxfxxxxx ==−+−++− ( ) ( ) 34253 ()122431215122496 gxxxfxxxxx =−+−+−++− ( ) ( ) ( )( ) 24222 122312151224 xxfxxxxx =−−−+−+−+ ( ) ( ) ( ) 2422 122312154 xxfxxx =−−−+−−+ . Vì ( )2 422 312153233 xxx −+−=−−−−
c trên th
a mãn ( ) 642 f −= và b
xét dấu đạo hàm như
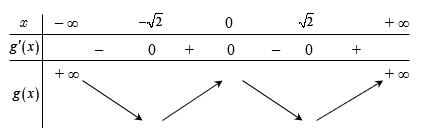
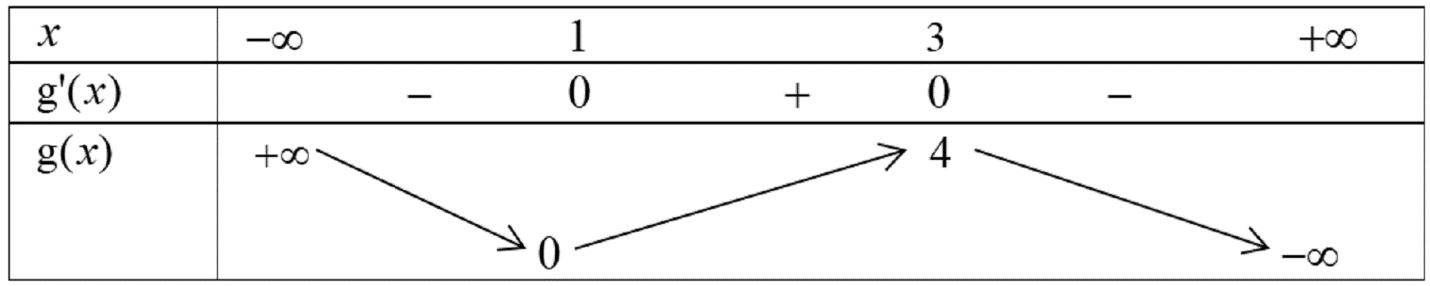

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 88
( ) (
fxxfxxx −+−−+−−+ ( )
x
x = =−== =− .
A. 2. B. 4. C. 9. D. 2. Lời giải Chọn B Bằng cách đổi biến ta rút được ( ) ( ) 12 fxgx=+− . Suy ra bảng biến thiên của hàm số ( )fx là: Đặt 3sincos2sin, 6 txxx =−=− ta có 0sin10;220;2 6 xtt −−+ Suy ra ( ) ( ) 3sincos222fxxft −−+=−+ , dấu "" = xảy ra được khi 6 x =
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
) ( ) 42422 3121503121540
3 0 0122402 2
gxxxx
Bảng biến thiên: Câu 79: Ta có ( ) ( ) ( ) ( ) min116402 gxggf=−==−−= . Cho hàm số bậc ba ( )yfx = có bảng biến thiên của hàm số ( ) ( ) 12 gxfx=−+ như sau Giá trị lớn nhất của hàm số ( ) 3sincos22cos24sin1 yfxxxx =−−+++− là:

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 89 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có ( ) ( )2 22 2cos24sin1212sin4sin14sin4sin12sin122 xxxxxxx +−=−+−=−++=−−+ Dấu "" = xảy ra được khi . 6 x = Suy ra ( ) 3sincos22cos24sin14yfxxxx =−−+++− , dấu "" = xảy ra được khi 6 x = Vậy giá trị lớn nhất của hàm số ( ) 3sincos22cos24sin1 yfxxxx =−−+++− là 4. Từ đồ thị ta có: 71 m − Vậy 6;5;4;3;2;1;0 S =−−−−−− Câu 80: Cho đồ thị hàm số ( )yfx = liên tục trên và có đồ thị như hình vẽ
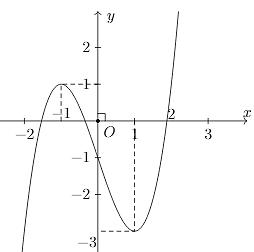
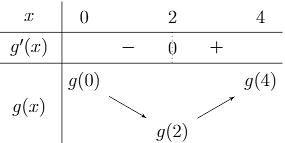
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 90
Đặ
ổ
trị
ớn
ất
trị
ỏ
ấ
ủ
(
đoạn
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
t ( ) ( ) 22448gxxxfxx =−+−+ . T
ng giá
l
nh
và giá
nh
nh
t c
a hàm số
)gx trên
0;4 là A. 1024 B. 1021 C. 102 D. 824 Lời giải Chọn A Dựa vào đồ thị hàm số đã cho ta tìm được ( ) 3 31yfxxx ==−− . Ta có ( ) ( ) 2 2 24 2448 248 x gxxfxx xx =−+−+ −+ . Cho ( ) ( ) ( ) 22 2 0 4824801 x gx fxxxx = = −++−+= Đặt 2 48uxx=−+ với 0;42;22xu ( ) ( ) 222 4824823230,2;22fxxxxfuuuuu −++−+=+=+− Nên phương trình ( )1 vô nghiệm. Khi đó: ( ) ( ) 224gf=− và ( ) ( ) ( ) 0422.ggf == Vậy tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số ( )gx trên đoạn 0;4 là ( ) ( ) ( ) ( ) 2022241110241024ggff+=+−=−+−=−
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 91
A.
Lờ
ả
Chọn B Điều kiện: ,1;1.xy − Đặt sin;sinxy== với ,;. 22 − Giả thiết ( ) sin..sin1sin1 coscos +=+= 2 += và ,0;. 2 Khi đó ( ) ( ) 22sin22sin2;22. 4 xymcosmmmm ++=++=++++ ( ) max max 22 22222 22;222 2222 22 m m m Kxymmaxmm m m m += + =−− =++=++= =− += + Vậy tích của các phần tử của S là ( )( ) 222222. −−−=+ Câu 82: Cho các số thực , xy thỏa mãn điều kiện 1 xy . Giá trị nhỏ nhất của biểu thức ( ) 22 log3log xy y x Tx y =+ là A. 15. B. 16. C. 13. D. 14. Lời giải Chọn A Ta có ( ) 2 2 22 1 log3log3log3 log xyy y x x Txx x y y =+=+− 2 2 2 1 loglog3log3 x y x x xy =+− 2 13 3 11log log22 x x y y =+− . Đặt logx ty = ; do 1 xy ( )0;1 t . Khi đó ( )2 43 3 1 T t t =+−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 81: Cho các số thực , xy thỏa mãn 22 111xyyx−+−= . Gọi S là tập hợp tất cả các giá trị thực của tham số thực m sao cho giá trị lớn nhất của ( ) 2 Kxym =++ bằng 2 . Tích các phần tử của S bằng
222 . B. 222 + . C. 222. D. 222−+ .
i gi
i
83:
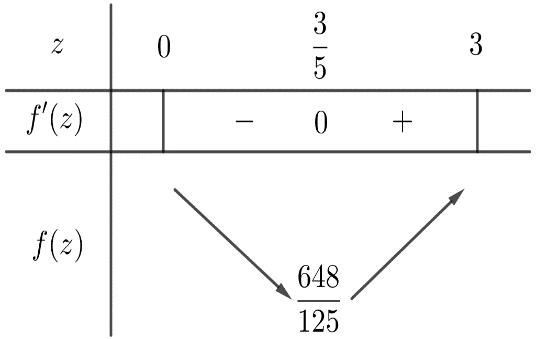
các
a mãn
xyz
Bi
ng a b , trong đó a , b là các số tự nhiên dương,
c
8 Pxyz

giá
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 92
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Xét hàm số ( ) ( ) 2 43 ()3,0;1 1 gtt t t =+− 32 ()83 (1) gt tt =− ; 1 ()03gtt == Suy ra (0;1) 1 min()15 3 gtg == Vậy min 15 T = , khi 3 1 log,(1) 3 x yyxyx == Câu
Cho
số thực dương x , y , z và thỏ
3
++= .
ểu thứ
444
=++ đạt
trị nhỏ nhất bằ
a b là phân số tối giản. Tính ab A. 234 B. 523 C. 235 D. 525 Lời giải Chọn C + Ta có 4 44 22 xyxy++ ( )4 44 1 8 xyxy ++ . Mà 3 xyz++= 3 xyz +=− . + ( )4 4444 1 838 8 Pxyzzz =++−+ . + Xét hàm số ( ) ( )4 4 1 38 8 fzzz =−+ , ( )0,3 z ( ) 32 6592727 2222fzzzz =−+− . ( ) 0 fz = 3 5 z = Bảng biến thiên hàm số ( )fz
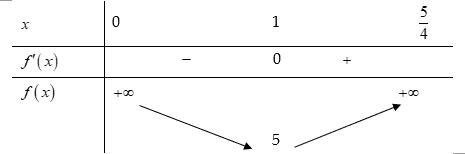
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 93
"" =
6
x
z = = =
0 4 x . Khi đó, 4141 545 4 4 P xxx x =+=− Đặt ( ) 41 45 fx xx =− , 5 0; 4 x , ( ) ( )2 2 44 45 fx x x =−+ , ( ) ( )2 22 0451540250fxxxxx =−=−+= 5 1 3 xx == Bảng biến thiên Dựa vào bảng biến thiên ta suy ra ( ) 5 0; 4 min5 x fx = khi 1 x = . Vậy min 5 P = khi 1 x = và 1 4 y =
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn + Suy ra ( ) ( ) min648 125 Pfzfz= . Dấu
xảy ra
5 6 5 3 5
y
+ Vậy min648 125 a P b == 523 ab−= Câu 84: Cho x và y là các số thực dương thỏa 5 4 xy+= . Tìm giá trị nhỏ nhất của biểu thức 41 4 P xy =+ . A. 5. B. 4 C. 34 5 D. 28 5 Lời giải Chọn A Cách 1: Ta có: 55 44 xyyx +==− . Vì ,0xy nên 5
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 94 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Cách 2: Áp dụng bất đẳng thức Schwarz Cho 12,,...,0 n bbb , ta có: ( )2 2 22 12 12 1212 ... ... n n nn aaa a aa bbbbbb +++ +++ +++ . Đẳng thức xảy ra khi 12 12 ... n n a aa bbb === Với 0,40xy , áp dụng bất đẳng thức
22 2 11 2 412225 4 P xyxyxy + =+=+= + Đẳng thức xảy ra
1 22 4 xy xy ==
1, 4 xy== Câu 85: Cho các số thực dương , ab thỏa mãn ( ) 22 2()(2) abababab ++=++ . Giá trị nhỏ nhất của biểu thức 3322 332249 abab P baba =+−+
cho ab ( ) 22 11 2()(2)21()2 ab ababababab baab ++=++++=+++ Áp dụng bất đẳng thức Cô Si cho hai số dương () ab + và 11 2 ab + : 1111 ()22().2222 ab abab ababba +++++=++ . Dấu "" = xảy ra khi 11 ()2 ab ab +=+ . Suy ra 21222 abab baba ++++ . Đặt ,(0). ab tt ba =+ Khi đó: 2 5 2122(2)4415023 2 t tttt t ++−− − . Do đó, ta có điều kiện 5 . 2 t
trên ta được:
khi
hay 1
thuộc khoảng nào? A. (6;5) B. (10;9) C. (11;9) D. (5;4) Lời giải Chọn A Vì , ab dương nên từ giả thiết ( ) 22 2()(2) abababab ++=++ , ta chia hai vế


CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo
ỳnh
42
ễn
ận
Page 95
Mặt
32 3322 3322
ababababab
=+−+=+−+−+− ( ) ( ) 3232 4392491218. tttttt =−−−=−−+ Đặt ( ) 322 5 491218'(t)1218120,. 2 fttttfttt =−−+=−− Bảng biến thiên Từ bảng biến thiên ta có, 5 2; 523 (). 24 t Minftf Vậy giá trị nhỏ nhất của biểu thức P là 23 4 khi 2 5 1 2 11 1 ()2 2 a ab b ba a ab ab b = += =
Có
nhiêu giá trị nguyên
ủ
ố 20;20
− để
ất
32
++
ệm đúng với mọi ( )
x− ? A.
B. 10.
Lờ
ả
Ta
( ) ( ) (
32 32 3 231;3 2 xxm
−++ ++−
viên: Hu
Văn Ánh
Nguy
Cư Trinh Thu
Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
khác:
494392
P bababababa
= +=+ = . Câu 86: Cho hàm số ( )yfx = liên tục trên và có đồ thị là đường cong như hình vẽ bên.
bao
c
a tham s
m
b
phương trình ( )
23 fxxmx
nghi
1;3
9.
C. 11. D. 12.
i gi
i Chọn B
có:
)
fxxmxfxx
và

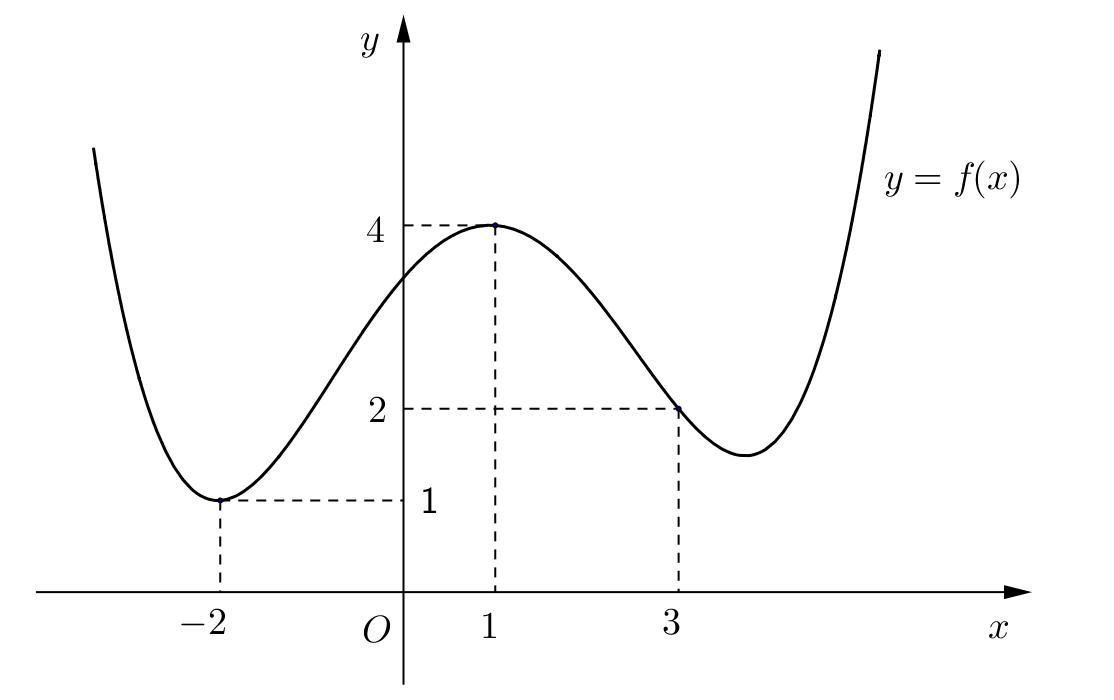
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 96
Có
trị
ủ
ố
vượt
ất
( ) ( ) ( ) 2 3 1 4
−− đúng
ọ
−
A. 1875 B. 1872 C. 1874 D. 1873 Lời giải Chọn D Điề
ệ
0
vì ( ) 0 2;30
−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Xét hàm số ( ) ( ) 322 0 336 0 2 22 x xxmxx gxgx x = −++−+ === = . Bảng biến thiên: Từ bảng biến thiên ta thấy được ( ) ( ) ( ) 1;3 4 max2 2 x m gxg − + == Ta có ( ) ( ) ( ) 1;3 min23 x fxf − ==− . Để ( ) ( ) ( ) ( ) ( ) 4 1;322310 2 m fxgxxfgm + −−− . Mà m nguyên
20;20 m− nên 20,19,...,11 m−−− . Vậy có 10 giá trị nguyên của m thoả mãn. Câu 87: Cho Cho hàm số ( )yfx = liên tục trên và có đồ thị như hình vẽ dưới đây:
bao nhiêu giá
nguyên c
a tham s
m không
quá 2022 để b
phương trình
m mfxfx fx
với m
i
2;3 x
?
u ki
n: ( )
mfx
fxxm
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 97 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 22 3 11 44 fx mmmfxfxmfxfx fxfx −−−++ ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 2 1 2 1 2 1 2 fx m fx fx fx m fx fx fx m fx fx −+ −+ −−+ ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 1 1 2 1 1 2 mfxfxfxfx mfxfxfxfx ++ −++ ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 1 max1 2 1 min1 2 mfxfxfxfx mfxfxfxfx ++ −++ ( ) 4217 2;3 4217 m x mvoly + − − ( )2 4217149,96 m + . Vì 2022 m . Nên có 202215011873 −+= Câu 88: Cho hàm số ( )ygx = thỏa mãn ( ) ( ) ( ) ( ) 32 2673231 gxgxgxxx −+=−−− . Tìm giá trị lớn nhất của biểu thức ( ) 2 Pgxx =+ A. 6 B. 0 C. 1 D. 4 Lời giải Chọn D Điều kiện xác định của phương trình là 1 x Ta có: ( ) ( ) ( ) ( ) 32 2673231 gxgxgxxx −+=−−− ( ) ( ) ( ) ( ) ( ) 32 266212211 gxgxgxgxxxx −+−+−=−−−+− ( ) ( ) ( ) ( ) 3 2112111 gxgxxxx −+−=−−+− ( ) ( ) ( ) ( )3 3 211211 gxgxxx −+−=−+− Xét hàm số ( ) 3 2 fttt =+ . Dễ thấy ( )ft đồng biến trên . Từ và suy ra ( ) 11 gxx −=− ( ) 11 gxx =+− Do đó 221 Pxx =+−+ Ta có 1 1 1 P x =+ ; 00Px ==
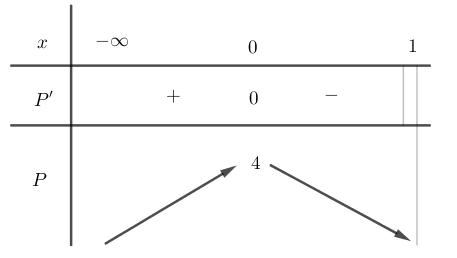
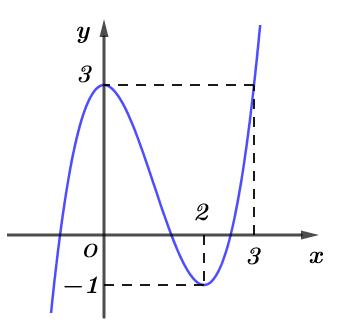
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 98
V
xxxx
++−+−+
. Gọi M là giá trị lớn nhất của ( )hx . Giá trị M thuộc khoảng nào sau đây A. ( )4;6 B. ( )2;4 C. ( )6;9 D. ( )0;2 Lời giải Chọn C ( ) 11422 11 2 22 xxxx xx gx xxxx ++−+−+ ++− ==+ −+−+ Ta có ( )( ) 111111 1 22 xx xx xxxx +++− ++− = −+−− dấu bằng xảy ra khi 0 x = . Do đó ( ) ( ) ( ) ( ) ( ) ( ) 222 22 33. 222121 110;1113 gxfgx xfxfx xfx ++−−+ −−−− ( ) 7 hx Đạt được khi 0 x = Câu 90: Gọi S làtập tất cảgiátrị củathamsố m saocho giá trị nhỏnhất củahàm số ( )2 3 3 yxxm =−+ trên đoạn 1;1 bằng 4. Tính tổng các phần tử của S A. 0. B. 5. C. 3. D. 6.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
ậy max40. Px== Câu 89: Cho hàm số ( ) ( ) 32 0 yfxaxbxcxda ==+++ có đồ thị như hình vẽ và hàm số ( ) 11422 2
gx xx
= −+ . Đặt ( ) ( ) ( ) ( ) ( ) 22 211 hxfgxfxfx =−++−−
Lời giải
Chọn A Đặt 3 3 txx =− . Với 1;12;2xt −−
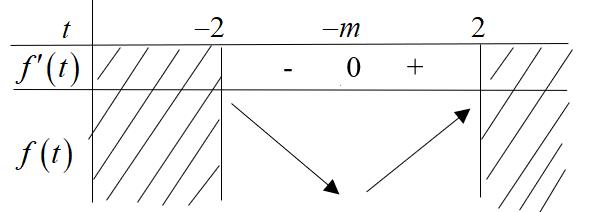
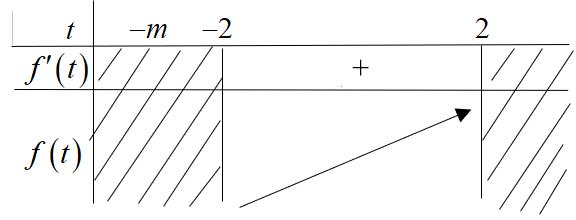
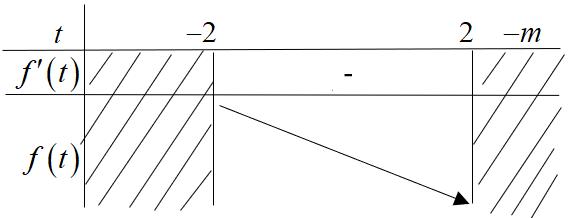
Ta được hàm số: ( ) ( )2 fttm =+ , xét trên đoạn 2;2
Ta có: ( ) 2()fttm =+ ; ( ) 0 fttm ==−
+) Trường hợp 1: Nếu 22mm −−
Ta có BBT:
Từ BBT suy ra: ( ) ( ) ( )2 [1;1][2;2] minmin22 yftfm ==−=−
Theo giả thiết: [1;1] min4 y = ( ) ( ) ( ) 2 0 24 4/ ml m mtm
= −= =
+) Trường hợp 2: Nếu 2222 mm −−−
Ta có BBT:
Từ BBT suy ra: ( ) ( ) [1;1][2;2] minmin0 yftfm ==−=
Theo giả thiết: [1;1] min4 y = không có m thỏa mãn. +) Trường hợp 3: Nếu 22mm −−
Ta có BBT:
Từ BBT suy ra: ( ) ( ) ( )2 [1;1][2;2] minmin22 yftfm ===+
Theo giả thiết: [1;1] min4 y = ( ) ( ) ( ) 2 0 24 4/ ml m mtm
= += =−
Vậy {4;4} S =− . Tổng các phần tử của S bằng 0
Câu 91: Cho biết hàm số ( ) 2 41 yfxxxm ==−−+ có giá trị lớn nhất bằng 3 khi 0;3 x . Số các giá trị của tham số m thỏa mãn là
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 99
vẽ dưới đây: Tính tổng tất cả các giá trị nguyên của tham số m để giá trị nhỏ nhất của hàm số ( ) 2 2x yfxm =++ trên đoạn 0;1 không lớn 4 A. 9. B. 0. C. 25. D. 39. Lời giải Chọn D Đặt 2 2x tx=+ , với 0;10;3.xt Ta quy về bài toán: Tính tổng tất cả các giá trị

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 100 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 2 B. 3 C. 1 D. 4 Lời giải Chọn A Đặt ( ) 2 41 gxxxm =−−+ . Ta có: ( ) ( ) 24;02gxxgxx =−== Ta có: ( ) ( ) ( ) 01;25;34 gmgmgm =−+=−+=−+ suy ra max 5;1 ymm =−+−+ . TH1: 51 51 2 2 53 8 mm mm m m m m −+−+ −+−+ = = −+= = TH2: 51 51 4 4 13 2 mm mm m m m m −+−+ −+−+ = = −+= =− . Vậy có 2 giá trị m thỏa mãn đề bài. Câu 92: Cho hàm số ( )yfx = liên tục, có đạo hàm trên và có đồ thị như hình
nguyên của tham số m để giá trị nhỏ nhất của hàm số ( ) yftm =+ trên đoạn 0;3 không lớn 4. Dựa vào đồ thị ta có ( ) ( ) ( ) ( ) ( ) 1;3 1;3 max035 . min21 ftff ftf === == Như vậy: ( ) ( ) 1;3 1;3 max5,min1. ftmmftmm +=++=+ + Trường hợp 1: 101.mm+− Khi đó ( ) 1;3 min1 ftmm+=+ .
Theo đề bài: ( ) 1;1 min4 ft nên 143.mm+
Kết hợp điều kiện: 13. m − Khi đó 1,0,1,2,3. m−
+ Trường hợp 2: 505.mm+− Khi đó ( ) 1;3 min5 ftmm+=−−
Theo đề bài: ( ) 1;1 min4 ft nên 549.mm −−−
Kết hợp điều kiện: 95. m −− Khi đó 9,8,7,6,5. m−−−−−
+ Trường hợp 3: ( )( ) 15051.mmm ++−− Khi đó ( ) 1;3 min0 ftm+= .
Suy ra ( ) 1;1 min4 ft hiển nhiên thỏa mãn.
Khi đó 4,3,2. m−−− Từ, và, suy ra 9,8,7,6,5,4,3,2,1,0,1,2,3. m−−−−−−−−− Vậy tổng tất cả giá trị nguyên của tham số m bằng 39.
Câu 93: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để 2 [0;3] max25 2 xxm + += . Tổng giá trị các phần tử của tập S bằng A. 2 . B. 4 . C. 4. D. 0. Lời giải Chọn D Đặt ( ) 2 22m g x x x = ++ với [0;3] x Ta có: ( ) 22gxx =+ ; ( ) 02201gxxx =+==− Ta có: ( ) 02 gm = ; ( ) 3215gm=+ . Suy ra giá trị lớn nhất của ( ) 2 22m f x x x = ++ trên [0;3] sẽ thuộc
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page
101
➢ Xét 55;10 2155 105;20 mA m mA =−= += =−= Ta
ấy
ị
ủ
ỏa mãn yêu cầu bài toán 2 [0;3] max25 2 xxm + += . ➢ Xét 5 20;5 252 5 10;5 2 mA m mA == = == Ta thấy không có giá trị nào của m thỏa mãn yêu cầu bài toán là 2 [0;3] max25 2 xxm + += . Vậy S = . Tổng giá trị các phần tử của tập S bằng 0.
215;2 Amm =+ .
th
không có giá tr
nào c
a m th
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 102 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 94: Cho hàm số ( ) 2 1 xm fx x = + trên 0;3 có giá trị lớn nhất bằng 5. Tích các giá trị của m bằng A. 5. B. 1. C. 2. D. 3. Lời giải Chọn A Với 0;3 x thì ( ) 2 2 11 xm xm fx xx == ++ . Hàm 2 1 xm y x = + đồng biến
2
0;3 3
====− ( ) 22 22 22 0;3 33 44 max5335340 2 mm mm fxmm ++− ==++−= 2 22 2 2 37 3 533735 5() 17() m mmm mtm ml −=−= = =− . Câu 95: Tìm tổng các giá trị của tham số m để giá trị lớn nhất của hàm số 32 69 yxxxm =−++− trên đoạn 0;1 bằng 5. A. 24 B. 10 C. 14 D. 5 Lời giải Chọn A Xét hàm số ( ) ( ) 322693260, gxxxxmgxxxx =−++−=−+ 0;1 maxmax9,15ymm =−− TH1: 4 95 14 14 915 915 m m m m mm mm = −= = = −− −− TH2: 10 155 20 10 915 915 m m m m mm mm = −= = = −− −− Vậy 10;14mm== thỏa mãn bài toán tổng các giá trị của tham số m bằng 24 Câu 96: Có bao nhiêu giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số ( ) ( ) 4232211 2 43 fxxmxmxm =+−−+ trên đoạn 0;2 luôn bé hơn hoặc bằng 5? A. 0. B. 4. C. 7. D. 8.
trên
0;3 nên
( )
( )
2 0;3
max3; min0 4 m yyyym
Lời giải Chọn B
Xét hàm số ( ) ( ) 4232211 2 43 gxxmxmxm =+−−+ trên đoạn 0;2. Ta có ( ) ( ) ( )( ) 322222220, 0;2. gxxmxmxxxxmx =+−−=−+ Suy ra hàm số ( )gx nghịch biến trên 0;2 Để giá trị lớn nhất của hàm số ( ) ( ) 4232211 2 43 fxxmxmxm =+−−+ trên đoạn 0;2 luôn bé
97: Cho hàm số ( ) 4221 fx xxm =−+− . Gọi S là tập hợp tất cả các giá trị của tham số m sao cho giá trị nhỏ nhất của hàm số trên đoạn 0;2 bằng 18. Tổng tất cả các phần tử của S bằng A. 5. B. 4 C. 14 D. 10 Lời giải Chọn A Xét hàm số ( ) 4221gxxxm=−+− liên tục trên đoạn 0;2 . ( ) 3 44 gxxx
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 103
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
hơn hoặc bằng 5 ( ) (
05 25 g g − ( ) 22 5 8 4245 3 m mmm +−−+− 31853185 88 m −+
m m ⎯⎯⎯→−
= 10;2 00;2 10;2 x x x =− = = ( ) 01gm=− , ( ) 12gm=− , ( ) 27gm=+ . ( ) 0;2 min2 x gxm =− , ( ) 0;2 max7 x gxm =+ . ( ) 0;2 minmin0,2,7 x fxmm =−+ . Trường hợp 1: 2 m . ( ) 0;2 min221820 x fxmmm =−−== Trường hợp 2: 707mm+−
)
1;0;1;2.
Câu
=− . ( ) 0 gx
t cả các phần tử của S bằng 5.
Câu 98: Có tất cả bao nhiêu giá trị của tham số m để giá trị nhỏ nhất của hàm số 2 42fxxxm trên 2;3 bằng 6. A. 4 B. 1 C. 3 D. 2 Lời giải Chọn D
Đặt 2 42gxxxm
+ Ta có: , 24gxx , 02402gxxx . + 210 26 35
gm gm gm
mingxm maxgxm
+ Suy ra 2;3 2;3
Ta xét các trường hợp sau:
6 10
+ Trường hợp 1: 6 m 2;3 6 minfxm 12 m . + Trường hợp 2: 10010mm . 2;3 10 minfxm 10616mm . + Trường hợp 3: 6010106mmm 2;3 0 minfx mà theo bài 2;3 6 minfx nên không có m thỏa mãn. Vậy có hai giá trị của tham số m thỏa mãn. Câu 99: Cho hàm số ( ) 633 2 fxxxmx =++− . Gọi S là tập tất cả các giá trị thực của tham số m để giá trị nhỏ nhất của hàm số ( )fx bằng 1. Tổng tất cả các phần tử của S bằng A. 1 4 B. 5 4 C. 2 D. 0
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 104
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
( ) 0;2 min771825 x fxmmm
=−−−−==− Trường hợp 3: ( )( ) 27072mmm −+− ( ) 0;2 min0 x fx = . Suy ra 20;25 m− . Vậy tổng tấ
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 105 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn B Tập xác định: ( ) 633 2 ==++− yfxxxmx Đặt 3tx = hàm số ban đầu trở thành hàm số ( ) 2 2 ==++− ygtttmt , t . Tam thức bậc hai ( ) 2 =++ htttm có biệ
Khi
( ) 2 22 111 2,t.
==++−=−+=−+−− ygtttmtttmtmm ( ) 11 minmin(). 24 ===− xt fxgtgm Theo đề 11 445 min()1. 154 1 44 x mm fxm mm == −== Trường hợp 2: 1 140 4 mm =− ( ) 2 =++htttm có 2 nghiệm phân biệt 1t , 2t ( ) 12tt Vì 12 12 12 0 10 0 +=− tt tt tt . +) Nếu 12 0 tt thì 12 0 Pttm== kết hợp với 1 4 m ta có 1 0 4 m . Khi đó: ( ) 13310min10 244 =+−+− t gmgtm +) Nếu 12 0 tt thì ( ) ( ) 2 22222220min0 =++−=− t gtttmttgt . Suy ra trong trường hợp 2 hàm số ( ) = ygt không thể có giá trị nhỏ nhất bằng 1 trên . Vậy 5 4 m = Suy ra tổng các phần tử của S là 5 4 Câu 100: Gọi S là tập tất cả giá trị của tham số m sao cho giá trị nhỏ nhất của hàm số ( )2 3 3 yxxm =−+ trên đoạn 1;1 bằng 4. Tính tổng các phần tử của S A. 0 B. 5 C. 3 D. 6 Lời giải
t thức 14m =− . Ta xét 2 trường hợp sau: Trường hợp 1: 1 140 4 mm =− ( ) 2 0,t.=++ htttm
đó,
244
Đặt 3 3 txx =− . Với 1;12;2xt −−



Ta được hàm số: ( ) ( )2 fttm =+ , xét trên đoạn 2;2
Ta có: ( ) 2()fttm =+ ; ( ) 0 fttm ==−
+) Trường hợp 1: Nếu 22mm −−
Ta có BBT:
Từ BBT suy ra: ( ) ( ) ( )2 [1;1][2;2] minmin22 yftfm ==−=−
Theo giả thiết: [1;1] min4 y = ( ) ( ) ( ) 2 0 24 4/ ml m mtm
= −= =
+) Trường hợp 2: Nếu 2222 mm −−−
Ta có BBT:
Từ BBT suy ra: ( ) ( ) [1;1][2;2] minmin0 yftfm ==−=
Theo giả thiết: [1;1] min4 y = không có m thỏa mãn. +) Trường hợp 3: Nếu 22mm −−
Ta có BBT:
Từ BBT suy ra: ( ) ( ) ( )2 [1;1][2;2] minmin22 yftfm ===+
Theo giả thiết: [1;1] min4 y = ( ) ( ) ( ) 2 0 24 4/ ml m mtm
= += =− Vậy {4;4} S =− . Tổng các phần tử của S bằng 0.
Câu 101: Cho hàm số ( ) 3 3 fxxx =−+ và ( ) ( ) 2sin gxfxm =++ ( m là tham số thực). Có bao nhiêu giá trị của m để ( ) ( ) maxmin50 gxgx+= ?
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 106
ọn A
Ch
max1818 2185017/ min22
gtmm mmmtm gtmm
TH1: Nếu 202mm −−− thì ( ) ( ) ( ) 1;3 1;3
=−=− −−+−==− =−−=−− .
=−=− ++−== =−−=+
min1818 2185033/ max22
gtmm mmmtm gtmm
TH2: Nếu 18018 mm − thì ( ) ( ) ( ) 1;3 1;3
)
=−−− =
)
4.
) 1;3 1;3
min0
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 107
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 0. B. 1. C. 2. D. 3. Lời giải Chọn C Đặt ( )
( ) ( ) 3 1;3 1;3 2sin1;33,1;3maxmin50 txgtttmtgtgt =+=−−+= Xét hàm số: 3233301;3yttmytt =−−=− ( ) ( ) ( ) ( ) ( ) 1;3 1;3 1;3 maxmax2;18 12,318minmin2;18 min0 gtmm gtmm ymym gt =−−− =−−− =−−=− =
B.
C.
2
D.
TH3: ờ
Nếu ( )( ) 2180218mmm −−−+−
thì (
(
maxmax2;18
gtmm gt
. Nhận xét: (
1;3 maxmax2;1850,2;18 gtmmmm =−−−− . Vậy 17;33 m− . Câu 102: Cho hàm số ( ) 42 4 fxxaxb =−+ , trong đó , ab là tham số thực. Biết rằng giá trị lớn nhất của hàm số ( )fx trên đoạn 1;1 bằng 1 2 . Tính ab + A. 1 2 .
7
.
9 2 . L
i giải Chọn D Ta có
( ) 1;1 1 max 2 fx = nên 42 1 4,1;1 2 xaxbx−+−
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 108 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Khi đó ta có: ( ) ( ) 1 1 2 1 0 2 21 22 f f f 11 44 22 11 22 111221 4.. 422 abab bb ab ab −+−+ −+− −+ . Suy ra 4224222 abbababbab −++−+−−+++−+− 24222 abbab −+++−+− Dấu '''' = xảy ra khi: * Trường hợp 1: 1 4 2 4 1 1 2 2 221 ab a b b ab −+= = = = −+−= Thử lại ta thấy giá trị lớn nhất củ
a ( ) 42 1 44 2 fxxx=−+ trên đoạn 1;1 bằng 1 2 * Trường hợp 2: 1 4 8 2 17 22 2211 2 ab a bb ab b −+=− = =−= −+−=− =− Vậy 9 2 ab+= . Câu 103: Cho hàm số bậc ba ( )yfx = có đồ thị như hình vẽ bên dưới. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 10;0 sao cho giá trị nhỏ nhất của hàm ( ) ( ) ( ) 243gxfxmfx=+−+− trên đoạn 1;3 lớn hơn 1? A. 9. B. 8. C. 10. D. 6 . Lời giải y x 2 3 1 O -2 -1
Ch
n
Đặt ,2;2fxtt 1;3 min11,1;3 gxgxx 2431,2;2 tmtt 2431 2431,2;2 tmt t tmt 244 242,2;2 tmt t tmt 244 244,2;2 2242
tmt tmtt ttmt 38 ,2;2 236
mt mtt tmt 14 14 2 2 40
m m m m mVL Do 10;010;9;...;3mm Vậy có 8 giá trị nguyên của m thỏa mãn yêu cầu bài toán. Câu 104: Biết rằng giá trị lớn nhất của hàm số ( ) 32 212989 yfxxxxmx ==−++++ trên đoạn 0;5 bằng 78. Tính tổng các giá trị của tham số m ? A. 6 B. 12 C. 7 D. 8 Lời giải Chọn D
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page
109
ọ
B
Do giá trị lớn nhất của hàm số ( ) 32 212989 yfxxxxmx ==−++++ ( m là tham số) trên đoạn 0;5 là 78 nên 32 212989780;5 xxxmxx −++++ và dấu bằng phải xảy ra tại ít nhất một điểm
trị lớn nhất của hàm số ( )cos1 yfxm =++ đạt giá trị nhỏ nhất. Tổng các phần tử của S bằng A. 4 B. 7 C. 7 2 D. 6 Lời giải Chọn C Đặt cos1,0;2txt=+ . Khi đó 42 2 yttm =−+ với 0;2 t . Xét ( ) 42 2 ftttm =−+ với 0;2 t . ( ) ( ) ( ) ( ) 3
t ftttt t
0nhan 4401nhan 1loai
= =−== =− . Ta có ( )0 fm = , ( ) 11 fm =−+ , ( ) 28 fm =+ . Do đó ( ) 0;2 max8ftm =+ , ( ) 0;2 min1 ftm=− Suy ra ( ) 0;2
8181279 max 22 mmmmm ft ++−++−+++ == . Ta có ( ) 0;2
2799 maxmax 22 m yft ++ == . Dấu bằng xảy ra khi và chỉ khi 7 270 2 mm+==− Câu 106: Tổng các giá trị của tham số m sao cho giá trị lớn nhất của hàm số 3 3 yxxm =−+ trên đoạn 0;2 bằng 5 là bao nhiêu? A. 6 B. 0 C. 8 D. 10 Lời giải Chọn B
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 110 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) 32 32 3232 32 0;5 32 0;5 212987890;5 78900;5 97821298789 2128621218700;5 max2128622 min212187030 x x xxxmxx xdungx xxxxmx xxmxxxx mxx m m mxxx −+++− − −−+++− −+−−+−+ −+− − −+−+ Và dấu bằng phải xảy ra nên 22 30 m m =− = . Vậy tổng tất cả giá trị m là 8 Câu 105: Cho hàm số ( ) 42 2 fxxx =− . Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá
Khi đó 253 mm −==− TH 2: 20 20 0 m m m + − . Khi đó : 2222 mmm −=−+ ( ) ( ) 0;2 22 maxfxmm =−−+=−
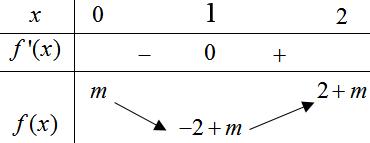
= + = =− . Câu 107: Cho hàm số
222(2) max5 2 mmmm fx +−+++−−+ == 3 24 5 3 2 m m m 2 2 21 2 xmx y xx −+ = −+ . Có tất cả bao nhiêu giá trị nguyên của tham số 10;10 m− để giá trị lớn nhất của hàm số lớn hơn hoặc bằng 4. A. 14 B. 10 C. 20 D. 18 Lời giải Chọn A Theo đề ra ta có 2 2 21 max4 2 xmx xx −+ −+
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 111
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Xét hàm số ( ) 3 3 fxxxm =−+ , ta có ( ) 2 33fxx =− . Ta có bảng biến thiên của ( )fx :
TH 1: 202 mm +− . Khi đó ( ) ( ) 0;2 22 maxfxmm =−−+=−
Khi đó 253 mm −==− . TH 3: 0 02 20 m m m −+ . Khi đó: 2222 mmm −=−+ ( ) 0;2 2 maxfxm=+ Khi đó 253 mm +== . TH 4: 202 mm −+ . Khi đó ( ) 0;2 2 maxfxm =+ 253 mm +== . Vậy tổng các giá trị của m là 0. Cách khác: Ta có ( ) 0;2 max2Afxm ==+ , ( ) 0;2 min2 afxm ==−+ Nên ( ) 0;2
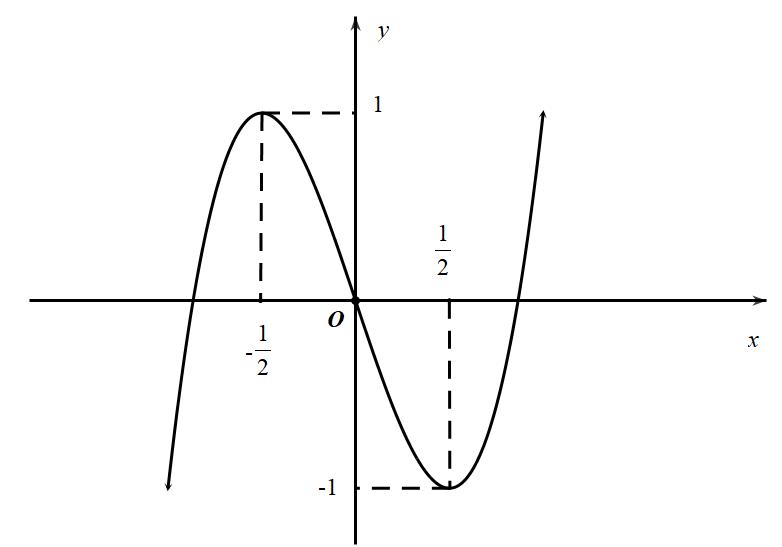
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 112 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT
10; 11; 12 Sưu tầm và biên soạn Ta có 2 2 21 lim1 2 x xmx xx → −+ = −+ do đó luôn tồn tại 2 2 21 max 2 xmx xx −+ −+ trên thoả yêu cầu bài
Ta
m để 2 2 21 max4, 2 xmx x xx −+ −+ Ta có 2 2 2 2 2 2 21 214, 4,2 221 4, 2 xmx x xmx xx x xx xmx x xx −+ − −+ −+ −+ −+ −+ ( ) ( ) 2 2 22 5x2490, 4410235235 3x2470,4170 221221 mxx mmm mxxmm m −++ +−−−−+ −−−−−− −+ 221235 m −−+ Khi đó 2 2 221 21 max4 2 235 m xmx xx m − −+ −+ −+ . Giá trị nguyên của tham số 10;10 m− là 10;9;...;3;5;6;...;10 m−−− . Câu 108: Cho hàm số ( )yfx = đồ thị như hình vẽ Đặt ( ) ( ) 1212 12 22 mm gxfxxf +−− =−−+ . Với giá trị nào của m thì giá trị nhỏ nhất của hàm số ( )gx là 0 A. Không tồn tại. B. 0. C. 1 2 . D. 1 2 . Lời giải Chọn D Điều kiện xác định của hàm số ( )gx là 11 120. 22 xx −−
Toán
toán.
tìm
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 113 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có: ( ) 0 fx và 121 x −−− Do đó: ( ) 121fxx−−− .Dấu bằng xảy ra khi: ( ) 0 0 121 fx x x = = −= ( ) 1212 1 22 mm gxf +−− − Để giá trị nhỏ nhất của hàm số ( )gx là 0thì: 1212 10 22 mm f +−− −= 1212 1 22 mm f +−− = Từ đồ thị hàm số 12121 2 22 mm+−− =− 12212 12222412 12122 11 11 22 22 mm mmm mm m m ++=− ++++=− +−−=− − − 2421 2421 11 210 22 1111 2222 mm mm mmm m m +=−− +=−− −−−=− − − Câu 109: Cho các số thực , xy thoả mãn 22 max5;972028 1 xyxyx y +−++ .Gọi , Mm lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 Pxy =− . Tính Mm A. 135 + . B. 22 . C. 122 + . D. 235 + . Lời giải Chọn A Từ giả thiết ta có ( ) 22 2 2 22 5 19 9725 222 xy xy xy + −+ −+− .
Tập hợp điểm ( ) , xy thoả mãn yêu cầu bài là phần được tô trên hình vẽ kể cả biên.
Ta thấy ( )1C cắt ( ) 3C tại hai điểm phân biệt trong đó có điểm ( )2,1 thoả mãn yêu cầu bài toán.
Xét đường thẳng đi qua ( ) , xy thoả mãn yêu cầu bài toán: 2 xyc −= . 2 xy đạt GTNN khi đi qua ( )2,1 nên 0 m = ( ) ( )2 222 2 :2819Cxyxxy+=+−+= + ( ) ( ) ( ) ( ) 2 212112.91351xyxy −=−+−++−+=+ 1 :21350 xy −−−= . 1 cắt ( ) 2C tại điểm thoả mãn bài toán. Khi đó 351 M =+ . Vậy 351 Mm−=+ . Câu
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page
114
110: Cho các số thực không âm
xy
ỏ
ị
ớ
của biểu thức ( )(
22
Sxyyxxy =+++ lần lượt là A. 25 ,12. 2 Mm== B. 191 12,. 16 Mm== C. 25191 ,.216 Mm== D. 25 ,0. 2 Mm== Lời giải Chọn C Do 0,0 1 xy xy += nên 0,1 1 xy yx =− Thay 1 yx =− vào biểu thức S ta được: ( ) ( ) ( ) ( ) ( ) 2 2 431413251 Sxxxxxx =+−−++− ( )( ) 222 4334542525 xxxxxx=−+−++− 432 163218212 xxxx =−+−+ Đặt ( ) 432 163218212SSxxxxx ==−+−+ với 01. x
,
th
a mãn 1. xy+= Giá tr
l
n nhất M và giá trị nhỏ nhất m
)
434325
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 115 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có ( ) 32 6496362.Sxxxx =−+− Xét phương trình ( ) 32 064963620Sxxxx =−+−= ( )( ) 2 21323220 xxx −−+= ( ) ( ) ( ) 1 0;1 2 23 0;1. 4 23 0;1 4 x x x = + = = Ta có ( ) ( ) 1252319123191 012;112;;;. 22416416 SSSSS +− ===== Do đó ( ) 0;1 125 max 22 SxS == và ( ) 0;1 2323191 min. 4416 SxSS −+ === Vậy 25 2 M = khi 1 2 xy== Và 191 16 m = khi 23 4 23 4 x y = + = hoặc 23 4 . 23 4 x y + = = Câu 111: Cho hai số thực , xy thay đổi và thỏa mãn ( )3 42xyxy++ . Giá trị nhỏ nhất của biểu thức ( ) ( ) 442222 542Axyxyxy =++−++ bằng A. 14 B. 15 16 C. 14 15 D. 14 Lời giải Chọn B Ta có, ( )2 4,, xyxyxy + , kết hợp với giả thiết ( )3 42xyxy++ suy ra ( ) ( ) 32 21.xyxyxy ++++ ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 442222 2 224422 2 22 2 2222 2 2222 542 5 42 2 5 42 22 15 42. 4 Axyxyxy xyxyxy xy xyxy xyxy =++−++ =+++−++ + ++−++ =+−++ Đặt ( )2 22 1 22 xy txy + =+
Do đó, 2 15 42 4 Att−+ Ta có bảng biến thiên của hàm số ( ) 2 15 42 4 fttt=−+ trên 1 ; 2 + như sau
Qua bảng biến thiên ta có ( ) 1 2;
115 min 216 t ftf +
== .
Tức là, 15 16 A , dấu “=” xảy ra khi 1 2 xy== Vậy giá trị nhỏ nhất của A bằng 15 16 . Câu 112: Cho các số
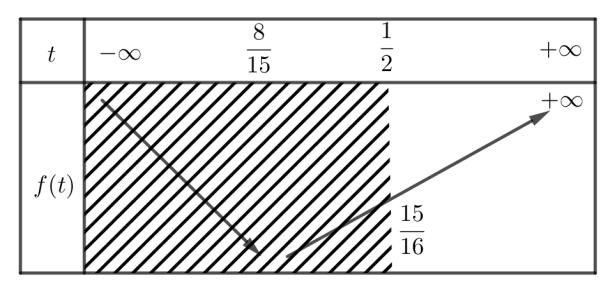
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page
116
ị
2
Vì 2,
1 b nên 2 log0 log20 a b b a . Từ đó suy ra: ( ) ( ) 2 22 log2log2log4log2 abab Pbaba +=+ 22 22 44 log2log.4 loglogaa aa Pbb bb =+= Dấu bằng xảy ra khi và chỉ khi 2 22 18 log216 a a a ab b b = = += = = Câu 113: Cho hai số thực 0;13xy thỏa mãn 2 2.21424 xy xyx . Tìm giá trị nhỏ nhất của biểu thức 22 2xy Pxy . A. 12 B. 3 C. 3 D. 1 Lời giải Chọn A
thực , ab thỏa mãn 2, a 1 b . Khi biểu thức ( ) 42 2 loglog416 a b Pbaa =+−+ đạt giá tr
nhỏ nhất thì tổng ab + bằng A. 4. B. 18. C. 14. D. 20. Lời giải Chọn B
a , ta có ( )2 2422 404164 aaaa −−+ . Dấu bằng xảy ra khi 2 a = . Ta có 1 b nên suy ra ( ) ( ) ( ) ( ) ( ) 2 42422 log4162log4162log42log24log2 bbbb b aaaaaaa −+=−+==
a
xyy Pxyyyy Xét hàm số 2 2 4 a gaa trên 2;4 2ln2 2 4 a gaa 2 2ln2 20,2;4 4 a gaa . ga luôn nghịch biến trên 2;4 [2;4] max2ln240 gag ga luôn nghịch biến trên 2;4 2;4 min412 gag Vậy min12 P khi 1437yyx . Câu =+++ =+++ =++−++ =−+ Đặt 2 410txyPtt ==−+
+ +++ 25254 41029 410329 410
xyxxyx xyxxyx 22 2233 3 22 22
xyxy xxxyxyx ( )( ) 22 25254 Pxyyxxy =+++ . Giá trị Mm bằng A. 1 16 . B. 1 15 . C. 1 14 . D. 1 19 . Lời giải Chọn A Ta có ( )( ) ( ) ( ) ( )
+=+++=++ +=+++=+++ Xét hàm số ( ) ( )2.1 t ftt=+ trên ( ) 0;+ ( ) ( ) ( ) 2.1ln220,0; tt fttt =+++ Hàm số ( )ft luôn đồng biến trên ( ) 0;+ ( ) *22121 xyxxy =++=+ 1 2 2212 2 22211 4 y Pxyyxxy xyxyxy xyxyxyxyxy xyxy
t c
a
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
117
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
Giả thiết cho 2 2.21424 xy xyx ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 221 21221 114: Cho ,0xy và 1 xy+= . Gọi , Mm lần lượt là giá trị lớn nhất và giá trị nhỏ nhấ
2.21222.2 2.212.22 2.2.212.2.22 2.212.211* ủ

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 118
đạt giá trị lớn nhất tại ; xy thỏa mãn phương trình 22 241xyxy A. 0 = S . B. 1=− S . C. 1 = S . D. 3 2 = S . Lời giải Chọn A Gọi đường tròn T 22 2410xyxy và điểm ; MxyT sao cho biểu thức 5214 1 yx P xy đạt giá trị lớn nhất. Ta có 5214 25140 1 yx PPxPyP xy . :25140MPxPyP Do đường thẳng và đường tròn T có điểm chung , dIR 2 22 46 2232629 25 P PPP PP 2 9100101PPP Có 1 PT tiếp xúc với đường thẳng :34150 xy Tọa độ tiếp điểm 118 ; 55 M
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Với ,0xy ta có 11 1200; 44xyxyxyt =+ Ta suy ra BBT Suy ra 1591 10; 1616 MmMm ==−= . Câu 115: Tính giá trị 18 Sxy sao cho biểu thức 5214 1 yx P xy
i Chọn D
Theo giả thiết 0 y nên ta có 3 4 21 1 xx y y + =+ + ( ) 3 4211 xxyy +=++ ( ) 3 822122 xxyy +=++ ( ) ( ) ( ) 3 3 222121 xxyy +=+++ .
Xét ( ) 3 fttt =+ . Ta có ( ) 2 310, fttt =+ nên hàm số ( )ft đồng biến trên Do đó ( ) ( )221fxfy=+ 221 xy =+ 2 421 xy =+ 2 1 2 2 yx =− Do 0 y và 221 xy=+ nên 1 2 x Khi đó 3 8 2 Sxy=−+ 2 822 xx =−+ ( ) 2 24410 xx =−−++ ( )2 102210 x =−−
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Huỳnh Văn Ánh 42
ễn
Thuận
Page 119
ố
và
ạn Vậy 1 5 180 18 5 x xy y
ố thực
ỏ
3 4 21 1 xx
y +
+
3 8 2 Sxy=−+ . A. 4 B. 7 C. 9 D. 10 Lời giả
Giáo viên:
Nguy
Cư Trinh
Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 T
t Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm
biên so
Câu 116: Cho hai s
dương , xy th
a mãn
y
=+
. Tính giá trị lớn nhất của biểu thức
Câu 117: Cho các số thực không âm , xy thay đổi. M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức ( ) ( ) ++ = ++ 22 22 9-422131 xyxyxyxy P xy . Giá trị của 812Mm + bằng A. 2. B. 0. C. 1. D. 2. Lời giải Chọn B Ta có: ( ) ( ) ( ) ( ) ( ) ( ) 22 22 2222 961441 942 21312131 xyyyxx xyxyxyxy P xyxy ++−++ −++− == ++++ ( ) ( ) 222131 xy xy =− ++ . Vì ( )2 0,0 21 x x x + , dấu bằng xảy ra khi 0 x =
Vậy max10 S = khi 2 x = .
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 120 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Nếu ( )2 11 0 1 8 2144 x x x x x = + ++ . Dấu bằng xảy ra khi 11 4 2 xx x == ( )2 1 0 218 x x + Vì ( )2 0,0 31 y y y + . Dấu bằng xảy ra khi 0 y = . Nế
−−−
====− 8120 Mm += . Câu 118: Cho các số thực , , xyz không đồng thời bằng 0 thỏa mãn điều kiện 222 3 xyz++ . Giá trị lớn nhất của biểu thức 222 2022 Pxyyzzx xyz =−−− ++ là A. 1. B. 3. C. 669. D. 671. Lời giải Chọn D Ta phải chứng minh 222 ,,, xyzxyyzzxxyz ++−− . Thật vậy, ta có ( ) ( ) ( ) 222 222 111 0 222 xyzxyyzzxxyzyxz ++−−−++++ . Khi đó 222 222222 20222022 Pxyyzzxxyz xyzxyz =−−−++− ++++ Đặt 222, 0;3 txyzt =++ . Khi đó, ta có ( ) 2022 Pftt t =− ( ) ( ( ) 2 2022 '10,0;3 fttft t =+ đồng biến và liên tục trên ( 0;3 Vậy ( ) 3671 Pf=− Do đó max671 P =− khi 1; 1 xyz===− hoặc 1; 1 xyz==−= . Câu 119: Người thợ làm một bể cá hai ngăn không nắp với thể tích 3 1296dm . Người thợ này cắt các tấm kính ghép lại một bể cá dạng hình hộp chữ nhật với 3 kích thước ,, abc để đỡ tốn kính nhất như hình vẽ và giả thiết rằng độ dày kính không đáng kể. Tính abc ++
u ( )2 11 0 31112 96 y y y y y = + ++ dấu bằng xảy ra khi 11 9 3 yy y == ( )2 1 0 3112 y y + . Suy ra ( ) ( ) 22 1111 128128 2131 xy P xy
++ . 11 ,min 812 MMaxPmP
A. 3,3 B. 3,6 C. 4,8 D. 3,9 Lời giải

Chọn B
Thể tích bể cá là: ( ) 3 ..1296 Vabcdm == Tổng diện tích các mặt của bể cá là: 32 Sabbcac =++
Ta có: 222 3 3236648Sabbcacabc =++= Dấu bằng xảy ra khi và chỉ khi: 33 22 abbcac abacbc == == .
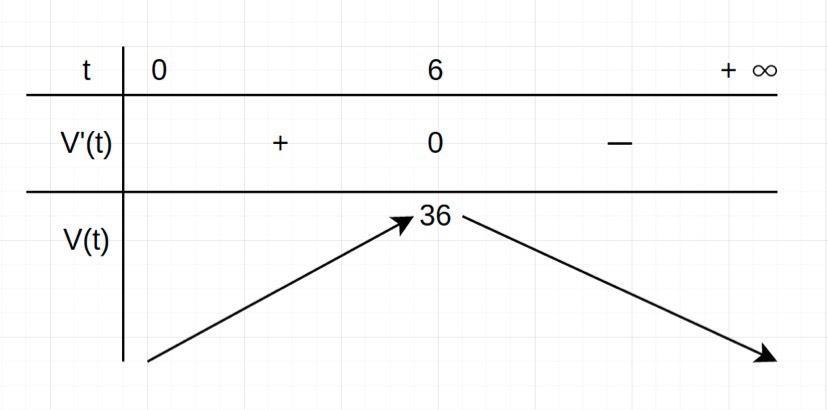
Thay vào thể tích ta được: ( ) 3 3.2.12962166 cccccdm === Suy ra ( ) 326363,6 abcccccdmm ++=++===
Câu 120: Một vật chuyển động theo quy luật 32 1 6 3 stt =−+ với t là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 7 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu? A. ( ) 180/. ms B. ( ) 24/. ms C. ( ) 144/. ms D. ( ) 36/. ms Lời giải Chọn D Ta có 2 '12'212vsttvt ==−+=−+ '021206. vtt =−+== max (6)36(/).vvms==
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
121 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page
Câu 121: Một cửa hàng bán vải Thanh Hà với giá bán mỗi kg là 50.000 đồng. Với giá bán này thì cửa hàng chỉ bán được khoảng 25kg. Cửa hàng này dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm 4000 đồng cho một kg thì số vải bán được tăng thêm là 50kg. Xác định giá bán để cửa hàng đó thu được lợi nhuận lớn nhất, biết rằng giá nhập về ban đầu mỗi kg là 30.000 đồng. A. 41.000 đồng. B. 34.000 đồng. C. 38.000 đồng. D. 45.000 đồng.
Lời giải
Chọn A
Gọi x đồng (30.00050.000 x ) là giá bán vải mới để cửa hàng thu được lợi nhuận lớn nhất.
Suy ra giá bán ra đã giảm là ( ) 50.000 x đồng.
Số lượng vải bán ra đã tăng thêm là ( ) 5050000 6250,0125. 4000 x x =− .
Tổng số vải bán được là 256250,0125.6500,0125. xx+−=−
Doanh thu của cửa hàng là ( ) 6500,0125.xx .
Số tiền vốn ban đầu để mua vải là ( ) 6500,0125.30000 x .
Vậy lợi nhuận của cửa hàng là
( ) ( ) 2 6500,0125.6500,0125.300000,0125102519500000 xxxxx −−−=−+− .
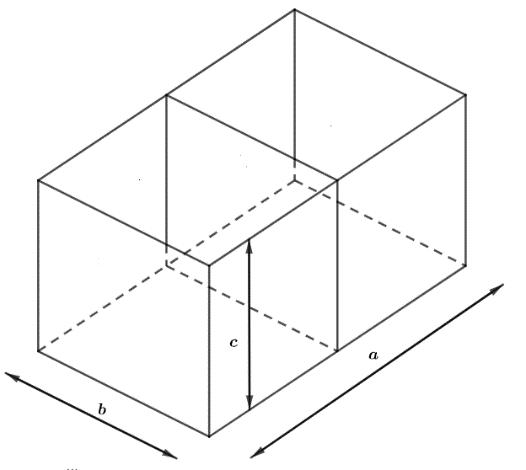
Ta có: ( ) ( )2 2 0,01251025195000000,01254100015125001512500fxxxx=−+−=−−+
Suy ra ( ) max1512500 fx = khi 41.000 x = đồng.
Vậy giá bán mỗi cân vải là 41.000 đồng thì cửa hàng thu được lợi nhuận lớn nhất.
Câu 122: Người ta cần làm một cái bể cá có hai ngăn, không có nắp ở phía trên với thể tích 3 1,296 m Người ta cắt các tấm kính ghép lại một bể cá có dạng hình hộp chữ nhật với ba kích thước là ,, abc . Người ta phải thiết kế các kích thước là bao nhiêu để đỡ tốn kính nhất .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 122
A. 1,2;1,2;0,9 ambmcm === . B. 3,6;0,6;0,6 ambmcm === . C. 2,4;0,9;0,6 ambmcm === D. 1,8;1,2;0,6 ambmcm === Lời giải Chọn D
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page
. B. 3 . C. 1 3 . D. 1 3 . Lời giải Chọn C Ta có ( ) 2 2 201 2 axb yyxaxyb x + =−+−= + Trường hợp 1: Nếu 0 y = Ta có ( ) 10 b axbx a −−==− Trường hợp 2: Nếu 0 y Phương trình có nghiệm khi và chỉ khi ( ) 222 420840ayybybya =−−−++ 2222 22 44 bbabba y −+++ Từ 2 trường hợp ta có: 2222 22 44 bbabba y −+++ Theo giả thiết ta có 22 22 2 2222 2 6 8 224 4 96 228 2 4 bba b bba a bbabba ++ = = ++= = −+−+=− =−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
123 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Thể tích bể cá là 1,296 Vabc== Kể cả miếng kính ở giữa, diện tích tổng các miếng kính là 23 Sabacbc =++ Suy ra 23123 . 1,296 SSabacbc Vabccba ++ ===++ Áp dụng Cô si cho 3 số 123 ;; cba ta có 3 3 1231236 3...3.5. 1,296 cbacba ++== Dấu "" = xảy ra khi 1,2961,8 1231,2. 0,6 a abc b c cba = = = == = Vậy để đỡ tốn kính nhất thì 1,8;1,2;0,6 ambmcm === Câu 123: Cho hàm số 2 2 axb y x + = + , với a khác 0 và , ab là các tham số thực. Biết max6,min-2 yy== . Giá trị của biểu thức 22 2 ab P a = bằng bao nhiêu? A. 3
Vậy 22 2 1 3 ab P a == .
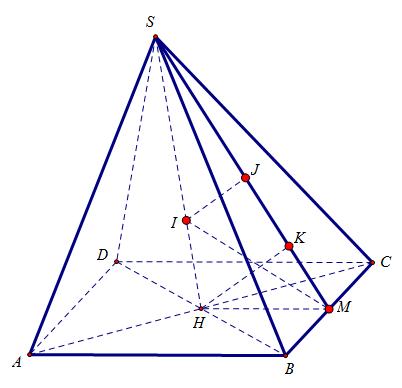
Câu 124: Một kiến trúc sư mốn thiết kế một mô hình kim tự tháp Ai Cập có dạng là một hình chóp tứ giác đều ngoại tiếp một mặt cầu có bán kính bằng 6m .Đề tiết kiệm nguyên liệu xây dựng thì kiến trúc sư đó phải thiết kế kim tự tháp sao cho có thể tích nhỏ nhất. Chiều cao của kim tự tháp đó là: A. 12m B. 18m C. 36m D. 24m Lời giải Ch
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 124
Từ
ạ
Theo Ta lét. 666 ;; 62 SIIJhha HKSHhHM SHHKhHKh ===== 222 2 .6 6 2 4 SHHMhah HK h SHHM a h == + + 2 2 2 1441441144 . 1212312 hhh aVh hhhh === Xét hàm 2 2 0 (24) ()'()'()0 24 12(12) h hhh fhfhfh h hh = === = Lập bảng biến thiên có Thể tích V đạt GTNN khi h =24 Câu 125: Trên mảnh đất hình chữ nhật ABCD có diện tích 2 25m , người chủ lấy một phần đất để trồng cỏ. Biết phần đất trồng cỏ này có dạng hình chữ nhật với hai đỉnh đối diện là A và H , với H
ọn D Giả sử kim tự tháp là hình chóp đều . SABCD , gọi M là trung điểm của BC Kẻ phân giác trong góc SMH cắt SH tại I I là tâm mặt cầu nội tiếp hình chóp đã cho
I h
IJ vuông góc ( )SBC , Từ H hạ HK vuông góc ( )SBC , IJ=R=6
thuộc cạnh .BD Hỏi số tiền lớn nhất người chủ cần chuẩn bị để trồng cỏ là khoảng bao nhiêu, với chi phí trồng cỏ là 70.000đồng 2 /m ?
A. 337.500đồng. B. 875.000đồng. C. 584.000đồng. D. 437.500đồng. Lời giải
Chọn D
Ta có ( ) 2 .25 ABADm = ; NHDN ABDA = Đặt ( ) .;1 NHDN xNHxABANxAD ABDA ====−
Diện tích đất trồng cỏ là: ( ) ( ) ..1..25..1 SANNHxxABADxx ==−=−
Diện tích lớn nhất khi ( ) .1 xx lớn nhất. Mà ( ) ( )2 1 1 .1 44 xx xx +− −=
Diện tích đất trồng cỏ lớn nhất 125 .25 44 S == Số tiền lớn nhất để trồng cỏ: 25 .70000437500 4 T == đồng.

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page
125
ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
sau đây là đường tiệm cận đứng của đồ thị hàm số ( ) 1 2 y fx = ? A. 1 x = . B. 2 x =− . C. 1 x =− . D. 2 x = . Lời giải ( ) 31 22 1 x fx x == 31221 xxx −=−=− Với ( ) 1 2 y fx = ta có ( ) ( )11 lim;lim xx yy +− →−→− =−=+
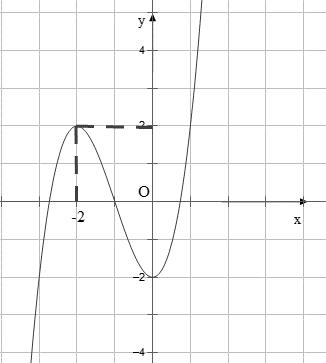
Vậy đồ thị hàm số ( ) 1 2 y fx = có đường tiệm cận đứng 1 x =− .
Câu 2: Cho hàm số ( )yfx = có đồ thị như hình vẽ
Số tiệm cận đứng của đồ thị hàm số ( ) 2019 1 y fx = là A. 1. B. 2. C. 3. D. 4. Lời giải Chọn C Từ đồ thị của hàm số ( )yfx = suy ra tập xác định của hàm số ( )yfx = là D =
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 1 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn BÀI 4. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ - VD - VDC HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: Cho đồ thị hàm số ( ) 31 1 x yfx x == . Khi đó đường thẳng nào
Do đó số đường tiệm cận đứng của đồ thị hàm số ( ) 2019 1 y fx = chính là số nghiệm của phương trình ( ) 1 fx = . Qua đồ thị ta có: Đường thẳng 1 y = cắt đồ thị hàm số ( )yfx = tại 3 điểm phân biệt nên phương trình ( ) 1 fx = có 3 nghiệm phân biệt. Vậy đồ thị hàm số ( ) 2019 1 y fx = có 3 đường tiệm cận đứng.
Câu 3: Cho hàm số ( )fx xác định và liên tục trên \1 có bảng biến thiên như sau: Hỏi đồ thị hàm số ( ) 1 y fx = có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
A. 4 B. 3 C. 2 D. 1 Lời giải
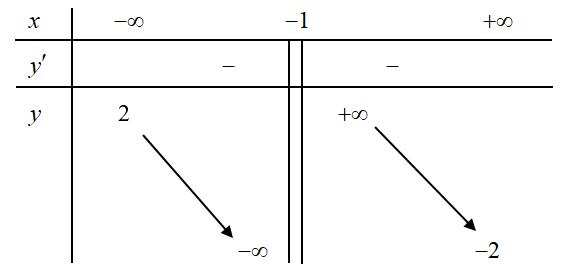
Chọn A
= lim01 lim 0 xx xx
=+ → và fx fx fxkhixx → →
fx fx fxkhixx → → ( ) ( ) ( ) 2 2 2
lim01 lim 0 xx xx
= =+ → Vậy đồ thị hàm số ( ) 1 y fx = có hai tiệm cận đứng là đường thẳng 1xx = và 2xx = Do đó Chọn A Câu 4: Cho hàm số ( )yfx = thỏa mãn ( ) lim1 x fx →− =− và ( ) lim x fxm →+ = . Có bao nhiêu giá trị thực của tham số m để hàm số ( ) 1 2 y fx = + có duy nhất một tiệm cận ngang. A. 1. B. 0. C. 2. D. Vô số. Lời giải Chọn C
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 2
Ta có: ( ) ( ) 11 lim2lim 2 xx fx fx →−→− == ; ( ) ( ) 11 lim2lim 2 xx fx fx →+→+ =−=− Suy ra đồ thị hàm số ( ) 1 y fx = có hai đường tiệm cận ngang là 1 2 y = và 1 2 y =− . Dựa vào bảng biến thiên của hàm số ( )yfx = ta thấy: phương trình ( ) 0 fx = có hai nghiệm phân biệt 12 1 xx − . Khi đó: ( ) ( ) 12 0 fxfx== Ta có: ( ) ( ) ( ) 1 1 1
Ta có ( ) 1 limlim1 2 xx y fx →−→− == + Đồ thị hàm số có tiệm cận ngang 1 y = . TH 1: Nếu 1 m =− thì ( ) 1 lim1 2 x fx →− = + và ( ) 1 lim1 2 x fx →+ = + thì đồ thị hàm số có một tiệm cận. TH 2: Nếu 1 m − Để đồ thị hàm số có một tiệm cận ngang ( ) 1 lim 2 x fx →+ + không có giá trị hữu hạn 202mm +==−
khi
m
hàm s
có duy nh
t m
t ti
m cận ngang. Câu 5: Cho hàm s
yfx
th
a mãn 4(tan)cos fxx = . Tìm tất cả các giá trị thực của m để đồ thị hàm số ()2019 () gx fxm = có hai tiệm cận đứng. A. 0 m B. 01 m C. 0 m D. 1 m Lời giải Chọn B ( ) 4 2 2
1 (tan)cos(tan) 1tan fxxfx x == + 22 1 ()(1)ft t = + Hàm số 22
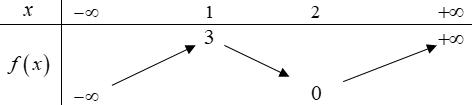
20192019()()1 () (1) gxgx fxm m x
== + Hàm số ()gx có hai tiện cận đứng khi và chỉ khi phương trình 22 1 0 (1) m x −= + có hai nghiệm phân biệt 22 1 (1)101 xm m += . Câu 6: Cho hàm số ( )yfx = xác định, liên tục trên và có bảng biến thiên như hình bên dưới: Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số ( ) 1 21 y fx = là: A. 4 B. 3 C. 1 D. 2 Lời giải Đặt ( ) ( ) 1 21 hx fx = *) Tiệm cận ngang:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 3
. Vậy
2;1
−− thì đồ thị
ố
ấ
ộ
ệ
ố ()
=
ỏ
Ta có: ( ) ( ) 1 limlim0 21 xx hx fx →+→+ == . ( ) ( ) 1 limlim0 21 xx hx fx →−→− == .
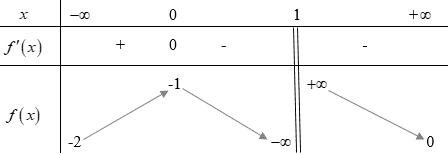
Suy ra đồ thị hàm số có một đường tiệm cận ngang 0 y = *) Tiệm cận đứng: Xét phương trình: ( ) 210 fx −= ( ) 1 2 fx = Dựa vào bảng biến thiên ta thấy phương trình ( ) 1 2 fx = có ba nghiệm phân biệt ,, abc thỏa mãn 12 abc Đồng thời ( ) ( ) ( ) limlimlim xaxbxc hxhxhx +−+ →→→ ===+ nên đồ thị hàm số ( )yhx = có ba đường tiệm cận đứng là xa = , xb = và xc = . Vậy tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số ( )yhx = là 4. Câu 7: Cho hàm số ()yfx = liên tục trên \1 và có bảng biến thiên như sau:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 4
Đồ thị ( ) 1 23 y fx = + có bao nhiêu đường tiệm cận đứng? A. 2. B. 0. C. 1. D. 3. Lời giải Chọn A Đặt ( ) ( ) 1 23 == + ygx fx có tử số là 10, x Ta có ( ) ( ) 3 230 2 fxfx+==−
Từ bảng biến thiên có phương trình có 2 nghiệm phân biệt: 12(;0),(0;1)xx−
Do đó đồ thị hàm số ( ) 1 23 y fx = + có 2 đường tiệm cận đứng.
Câu 8: Cho hàm số ( )yfx = liên tục trên \1 và có bảng biến thiên như sau:
Đồ thị hàm số ( ) 1 25 y fx = có bao nhiêu đường tiệm cận đứng? A. 0. B. 4. C. 2. D. 1. Lời giải
Ta có: ( ) ( ) ( ) 5 2501 2 fxfx−== . Phương trình ( )1 có 4 nghiệm phân biệt 1234 ,,,1xxxx và giới hạn của hàm số ( ) 1 25 y fx = tại các điểm 1234 ,,, xxxx đều bằng . Mặt khác ( ) 1
1 lim0 25 x fx → = nên 1 x = không phải tiệm cận đứng. Vậy đồ thị hàm số ( ) 1 25 y fx = có 4 đường tiệm cận đứng.
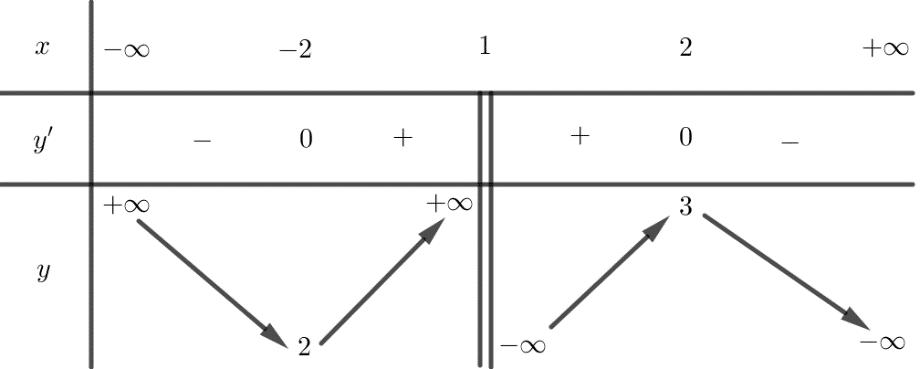

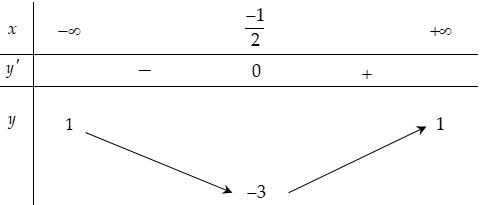
Câu 9: Cho hàm số ( )yfx = có bảng biến thiên như hình dưới đây.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 5
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số ( ) 1 21 y fx = là A. 0. B. 1. C. 2. D. 3. Lời giải Số tiệm cận đứng của đồ thị hàm số ( ) 1 21 y fx = đúng bằng số nghiệm thực của phương trình ( ) ( ) 1 210 2 fxfx−== Mà số nghiệm thực của phương trình ( ) 1 2 fx = bằng số giao điểm của đồ thị hàm số ( )yfx = với đường thẳng 1 2 y = Dựa vào bảng biến thiên ta thấy đường thẳng 1 2 y = cắt đồ thị hàm số ()yfx = tại 2 điểm phân biệt. Vậy đồ thị hàm số ( ) 1 21 y fx = có 2 tiệm cận đứng. Lại có ( ) 1 lim1 21 x fx → = đồ thị hàm số có một tiệm cận ngang là 1 y = . Vậy tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số ( ) 1 21 y fx = là 3. Câu 10: Chohàmbậcba ( )yfx = cóđồthị nhưhìnhvẽbên.Hỏiđồ thịhàmsố ( ) ( ) ( ) 22 2
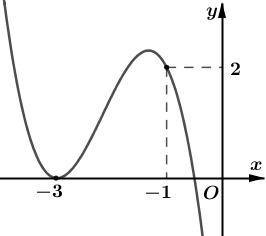
43 2 xxxx y xfxfx +++ = có bao nhiêu đường tiệm cận đứng? A. 2 B. 3 C. 4 D. 6 Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO
ĐỂ KHẢO SÁT HÀM SỐ
HÀM
Page 6
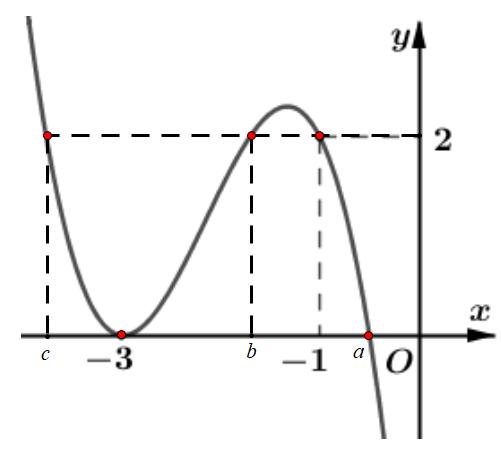
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 7 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT
12 Sưu tầm và biên soạn ( ) ( ) ( ) ( )( ) ( ) ( ) ( ) 22 2 43 131 ..2 2 xxxx xxxx y xfxfx xfxfx +++ +++ == Điều kiện tồn tại căn 2 xx + : 0 1 x x − Xét phương trình ( )
( ) 1 1 131 lim0 ..2 131 lim0 ..2 x x xxxx xfxfx xxxx xfxfx + →− →− +++ = +++ = nên 1 x =− không là tiệm cận đứng. ( )( ) ( ) ( ) ( ) 131 lim ..2 xb xxxx xfxfx + → +++ =+ nên xb = là tiệm cận đứng. ( )( ) ( ) ( ) ( ) 131 lim ..2 xc xxxx xfxfx + → +++ =+ nên xc = là tiệm cận đứng. Vậy đồ thị hàm số có 4 tiệm cận đứng.
0984164935
BDKT Toán 10; 11;
( ) ( ) ( ) 2 0 200 2 x xfxfxfx fx = −== = Với 0 x = ta có ( )( ) ( ) ( ) ( ) ( )( ) ( ) ( ) 00 131 131 limlim ..2 ..2 xx xxxx xxx xfxfx xfxfx ++ →→ +++ +++ ==+ . Suy ra 0 x = là tiệm cận đứng. Với ( ) 0 fx = 3 x =− hoặc xa = . Ta có: ( )( ) ( ) ( ) ( ) 3 131 lim ..2 x xxxx xfxfx + →− +++ =− nên 3 x =− là tiệm cận đứng. Với ( ) 2 fx = ( ) ( ) 1 31 3 x xbb xcc =− =−− =− . Ta có: ( )( ) ( ) ( ) ( ) 131 lim0 ..2 xb xxxx xfxfx + → +++ = ( )( ) ( ) ( ) ( ) ( )( ) ( ) ( )
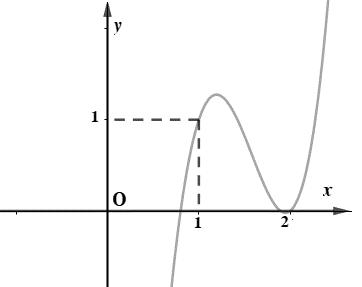
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 8
( ) ( ) (
2 2
=
có
A. 2 B. 4 C. 3 D. 5 Lời giải Chọn C Nhận xét 1: Với 0 1 x và ( ) 0 lim xx gx + → hoặc ( ) 0 lim xx gx → có kết quả là + hoặc − thì 0xx = là tiệm cận đứng của của đồ thị hàm số ( )gx Nhận xét 2: Dựa vào đồ thị hàm số ( )fx ta có: ( ) ( )( )2 1 2 fxaxxx=−− . Ta có ( ) ( ) ( ) ( ) 2 0 00 1 x xfxfxfx fx = −== = . ( ) 11 0,01 2 xxx fx x = = = ( ) 22 33 1 1,12 ,2 x fxxxx xxx = == = suy ra ( ) ( )( )( ) 23 11 fxaxxxxx −=−−− Khi đó ta có ( ) ( ) ( ) ( ) ( )( ) ( ) ( ) 2 2 321 121 .1 xxx xxx gx xfxfx xfxfx −+− == ( ) ( )( ) ( )( ) ( )( )( ) ( )( )( )( ) 2 2 123 123 121 1 2 .2.1 xxx x gx axxxxxxxx xaxxxaxxxxx == . 1 0, xxx == không phải tiệm cận đứng của đồ thị hàm số ( )ygx = không thỏa mãn điều kiện 0 1 x . Đồ thị hàm số ( )gx có 3 đường tiệm cận đứng là: 232,, xxxxx === Câu 12: Cho hàm số bậc ba ( ) 32 fxaxbxcxd =+++ có đồ thị như hình vẽ sau.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 11: Cho hàm số ( ) 32 fxaxbxcxd =+++ có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số
) ( )
321xxx gx xfxfx −+−
bao nhiêu tiệm cận đứng?
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 9
( )( )( )( )( ) 2 123 1 12 x axxxxxxxx = +−−−− Vậy đồ thị hàm số có 3 TCĐ 232;; xxxxx === . Câu 13: Cho hàm số ()yfx = là hàm số đa thức có đồ thì như hình vẽ dưới
t ( ) ( ) ( ) 2 2 2 = xx gx fxfx . Hỏi đồ thị hàm số (
= ygx có
nhiêu tiệm
ận
ng?
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Hỏi đồ thị hàm số ( ) ( ) ( ) ( ) ( ) 2 2 321 1 xxx gx xfxfx −+− = +− có bao nhiêu tiệm cận đứng? A. 5 B. 4 C. 6 D. 3 Lời giải Chọn D Ta có ( ) ( )( ) ( ) ( ) ( ) 121 11 xxx gx xfxfx = +− Đkxđ: ( ) ( ) 1 0 1 x fx fx
Dựa vào đồ thị hàm số ( )yfx = , ta có: ( ) 1 2 0 x fx xx = = = với 2 x = là nghiệm kép, ( ) 1 0;1 x . ( ) 2 3 1 1 x fxxx xx = == = với ( ) 231;2;2xx . Vậy ( ) ( )( ) ( )( ) ( )( )( )( ) 2 2 123 121 121 xxx gx axxxxxxxxx = +−−−−−
đây, đặ
)
bao
c
đứ
A. 5. B. 3. C. 4. D. 2. Lời giải Chọn C Ta xét phương trình ( ) ( ) ( ) ( ) 1 2 2 331
1 1 0 200 2 1 1,
x xx fx fxfx x fx xx xxxx
= =− = −= = = = =−
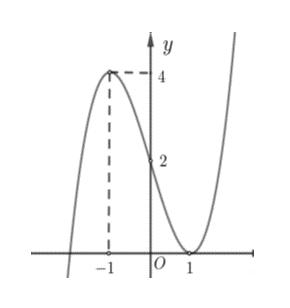
. Khi đó ( ) ( ) ( )( )( ) ( )( )( )( ) ( ) 2 2 123 123
1 ; 0 1 1 == xx gxa axxxxxxx axxxxxxxx . Vậy đồ thị hàm số ( ) = ygx có 4 đường tiệm cận đứng. Câu 14: Cho hàm số ( )yfx = xác định, liên tục trên và có bảng biến thiên như hình bên dưới.
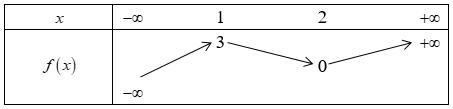
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 10
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số ( ) 3 1 3 y fxx = ++ là A. 2. B. 4. C. 3. D. 1. Lời giải
Chọn A Tính tiệm cận ngang.
y = .

Tính tiệm cận đứng.
Số đường tiệm cận đứng của đồ thị hàm số là số nghiệm của phương trình ( ) 3 30 fxx++=
ựa vào bảng biế
đứng.
= =− = =
y y y y
22 3 xxx y xfxfx 01 23 00 20
= = += +=−
1 0 1240 844
d c ab ab
a b c d
= =− = = Vậy ( ) 3231yfxxx ==−+ .
1 3 0 1
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 11
Ta có ( ) 3 3 1
x x xx
→+ →+ +⎯⎯⎯→+= ++ ( ) 3 3 1
x x xx
→− →− +⎯⎯⎯→−= ++
ậy
thị
ố
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
lim0 3
fxx
lim0 3
fxx
V
đồ
hàm s
có 1 tiệm cận ngang 0
D
n thiên ta có ( ) ( ) ( ) 333 00 303;;1fxxfxxxxxx++=+=−+=− Vì hàm số 3 yxx =+ đồng biến trên do đó ( ) 3 00;;1xxxx+=− có một nghiệm duy nhất. Vậy đồ thị hàm số ( ) 3 1 3 y fxx = ++ có 1 tiệm cần
Câu 15: Cho hàm số ( ) 32 yfxaxbxcxd ==+++ có đồ thị như bên dưới. Hỏi đồ thị hàm số ( ) ( ) ( ) ( ) 2 2 = có bao nhiêu đường tiệm cận đứng A. 4. B. 6. C. 3. D. 5. Lời giải Chọn C Ta có ( ) 2 32 yxaxbxc =++ . Dựa vào đồ thị hàm số, ta thấy hàm số đạt cực trị tại 0 x = , 2 x = . Do đó, ta có hệ ( ) ( ) ( ) ( )
= =− =
=
. Hàm số ( ) ( ) ( ) 2 2 232
22 lim 331 x
xxx xxxx + → −−+ ( ) ( ) ( ) 2 232 0
22 331 xxx y xxxx = −−+ có tập xác định ( 12;2\0;; Dxx =− . ( ) ( ) ( ) 2 2 232 0
22 lim 331 x
xxx xxxx + → = −−+ ( ) ( ) ( ) 2 32 0
xx xxxx + → ==− −−+
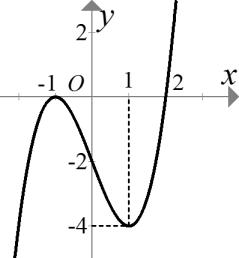
22 lim 331 x
2 2 232 A.
xxx xxxx + → =+ −−+ , ( ) ( ) ( ) 2
xxx xxxx + → =+ −−+ Suy ra 1xx = và 2xx = cũng là các đường tiệm cận đứng của đồ thị hàm số Câu 16: Cho hàm số 32 yaxbxcxd =+++ , ( )0 a có đồ thị như hình dưới đây. 0 1 430
22 lim 331 xx B. 1 C. 3 D. 4 Lời giải Điều kiện xác định: ( ) 2
22 lim 331 xx
Hỏi đồ thị hàm số ( ) ( ) ( ) ( ) 2 2 143 fx gx xxx = +−+ có bao nhiêu đường tiệm cận đứng? fx x xx
2 − −+
−
x x x x
2 1 1 3
2 3 x x . Ta có ( ) 3 lim x gx + →
fx xxx + → = +−+ =+ và ( ) 3 lim x gx →
( ) ( ) ( ) 2 2 3 lim 143 x
( ) ( ) ( ) 2 2 3 lim 143 x
fx xxx → = +−+ =−
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 12 Chuyên
ện thi:
ể
sinh
ớ
Tốt
ệ
và
ạn
đó ( ) ( ) ( ) ( ) 2 2 22 3 xxx y xfxfx = ( ) ( )( )( ) 2 3232 22 3313 xxx xxxxx = −−+− ( ) (
2 2
22
xxx xxxx = −−+ . Ta
( ) ( ) 2 2323310xxxx−−+= ( ) ( ) ( ) 1 2 3 0 3 1;0 0;1 2;3 x x xx xx xx =
Hòa
0984164935
luy
Tuy
n
vào l
p 10
Nghi
p THPT BDKT Toán 10; 11; 12 Sưu tầm
biên so
Khi
) ( )
232
331
có
Suy ra 0 x = là đường tiệm cận đứng. ( ) ( ) ( ) 1
2 2 232
Vậy đồ thị hàm số ( ) ( ) ( ) ( ) 2 2 143 fx gx xxx = +−+ có một đường tiệm cận đứng là: 3 x =
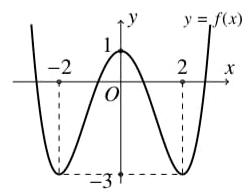
Câu 17: Cho hàm số trùng phương 42 yaxbxc có đồ thị như hình vẽ. Hỏi đồ thị hàm số 22 2
42 23 xxx y fxfx có tổng cộng bao nhiêu tiệm cận đứng?
liên t
c
và có đồ th
22 22 xxx y axxxxmxn Vậy hàm s ằng
như hình vẽ bên dưới. T
fxfx
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
s
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 13
ố có các tiệm cận đứng là 0;2;; xxxmxn Câu 18: Cho hàm số ( )yfx = có đạo hàm
ụ
trên
A. 5. B. 2. C. 3. D. 4. Lời giải Chọn D 22 2 ị
42 23 xxx y fxfx ổng
2 2 22 23 xxx fxfx Ta có: 2 230fxfx 1 3 fx fx ố đường tiệm cận đứng và ngang của đồ thị hàm số ( ) ( )( ) ( ) ( ) 2 2
2 0 2 2 2 11 4 xx gx
xmm x xnn x x Dựa vào đồ thị ta thấy các nghiệm 0;2xx là các nghiệm kép và đa thức 2 23fxfx có bậc là 8 nên 2 22 22 =
b
A. 4. B. 1. C. 2. D. 3. Lời giải


Chọn A
Tiệm cận đứng: Dựa vào đồ thị ta có: 2 1,0,1fxmxaxma 2 41,0,1.fxmxxbmb
Ta có: 22 22 2
1111 4 11
xxxx gx fxfx mxaxxxb 2 1 1 mxaxxb
Dễ thấy đồ thị hàm số có 3 tiệm cận đứng ,1, xaxxb .
Tiệm cận ngang: Ta có: limlim0. xx yy Đồ thị hàm số có 1 tiệm cận ngang 0 y Vậy đồ thị hàm số có 4 đường tiệm cận.
Câu 19: Cho hàm số bậc ba ( )yfx = có đồ thị như hình vẽ.
Có tất cả bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số ( ) ( ) 3
1 33 gx fxxm = có 8 tiệm cận đứng?
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 14
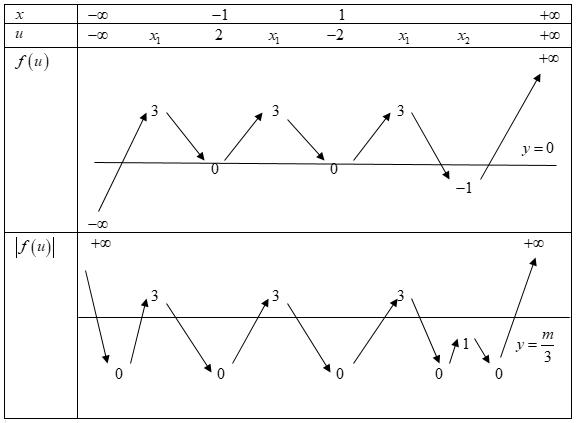
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 15
A. 4
Đặt
=−
. Từ đồ thị hàm số ( )yfx = ta có đồ thị
ố
ị
với 12202xx− . Bảng ghép trục Dựa vào bảng biến thiên, phương trình ( ) 3 3 3 m fxx−= có 8 nghiệm phân biệt khi và chỉ khi 1339 3 m m mà 4,5,6,7,8 mZm Vậy có 5 giá trị nguyên của tham số m Câu 20: Tất cả các giá trị của tham số m để đồ thị hàm số 2 2 2 2 xx y xxm +− = −+ có hai tiệm cận đứng là A. 1 8 m m − . B. 1 8 m m − . C. 1 m . D. 1 8 m m . Lời giải Chọn A
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
B. 6 C. 5 D. 3 Lời giải Chọn C Đồ thị hàm số ( ) ( ) 3 1 33 gx fxxm = có 8 tiệm cận đứng khi phương trình ( ) 3 33fxxm −= hay ( ) 3 3 3 m fxx−= có đúng 8 nghiệm phân biệt.
3 3 uxx
2 3301uxux
=−==
hàm s
có hai điểm cực tr
là ( ) ( ) 12 ;3,;1AxBx
m
Câu 21: G
sao cho đồ th
hàm số 2 3 29 x y xmx +
−+ có đúng hai tiện cận. Tính tổng các phần tử của S. A. 3. B. 3. C. 2. D. 0. Lời giải Chọn D 2 3 29 x y xmx + = −+ Ta có: lim0 x y → = suy ra tiệm cận ngang 0 y = . Để hàm số có đúng hai tiệm cận thì phải có đúng một tiệm cận đứng.
Trường hợp 1: Phương trình 2 290xmx−+= có nghiệm kép. 2 903mm =−==
=−
m m m m m m − −−−+= =− 3;3 S =− Tổng các phần tử của 0 S = Câu 22: Tính tổng tất cả các giá trị của tham số m để đồ thị hàm số 2 1 2 x y xxm + = −+ có đúng hai đường tiệm cận. A. 4 B. 2 C. 4 D. 5 Lời giải Chọn B Đặt ( ) 2 2 fxxxm =−+ Ta có lim0 x y →+ = , lim0 x y →− = nên hàm số 2 1 2 x y xxm + = −+ luôn có tiệm cận ngang 0 y = với mọi m .
3 90 3 32.390 3
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO
ĐỂ KHẢO SÁT HÀM SỐ
Page 16
(
0
− 10
− − +
−
HÀM
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Để đồ thị hàm số có hai đường tiệm cận đứng thì phương trình 2 20xxm−+= có hai nghiệm phân biệt khác nghiệm của phương trình 2 20 xx+−= . Hay phương trình ( ) 2 20fxxxm=−+= có hai nghiệm phân biệt khác 1 và 2. Khi đó ta có ( )
)
10 20 f f
10 80 m m m
1 1 8 m m m
81
− .
ọi S là tập hợp các số thực m
ị
=
Trường hợp 2: Phương trình 2 290xmx−+= có hai nghiệm phân biệt trong đó có một nghiệm bằng 3 ( ) ( ) 2 2
đứng. A. 1 m =− . B. 1 m = . C. 2 m =− . D. 2 m = . Lời giải
Chọn C Đồ thị hàm số ( ) ( ) 2 232 1 xmxm y x −+++ = + không có tiệm cận đứng khi phương trình ( ) 0 fx = có nghiệm 1 x =− Ta có ( ) ( ) ( ) 1012320fmm −=++++= 3602 mm +==−
Câu 24: Gọi S là tập hợp các giá trị thực của tham số m để đồ thị hàm số 2 2 32 4 xx y mxx −+ = + có một đường tiệm cận đứng và một đường tiệm cận ngang. Tổng các phần tử của S bằng A. 4. B. 4. C. 6. D. 2. Lời giải Chọn C Ta có 2 2 lim321
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 17 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Đồ thị hàm số 2 1 2 x y xxm + = −+ có đúng hai đường tiệm cận khi và chỉ khi phương trình ( ) 0 fx = có đúng 1 nghiệm hoặc phương trình ( ) 0 fx = có nghiệm 1
Suy ra ( ) 0101 10303. f mm mm f = −== +==− −= Vậy tổng tất cả các giá trị của tham số m để đồ thị
số 2 1 2 x y xxm + = −+ có đúng hai đường tiệm cận là ( ) 132 +−=− Câu 23: Xác định m để đồ thị hàm số ( ) ( ) 2 232 1 xmxm y x −+++ = + không có đường tiệm cận
x =− .
hàm
4 x xx mxxm → −+ = +
(
2 2 32(1)(2) 44 xxxx mxxxmx −+−− = ++
Để đồ thị hàm số có
tiệm cận đứng thì m thỏa mãn 404 2402 mm mm +==− +==− Từ và suy ra để đồ thị hàm số đã cho có một đường tiệm cận đứng và một đường tiệm cận ngang thì 4 2 m m =− =− . Vậy tổng các phần tử của S bằng 6 Câu 25: Có bao nhiêu giá trị của m để đồ thị hàm số ( )( ) 2 2 2 22 x y xxmxm + = −+− có 2 đường tiệm cận đứng? A. 1. B. 2. C. 4. D. 3. Lời giải Chọn D
. Suy ra để hàm số có một tiệm cận ngang thì 0 m . Lại có
)
.
một đường
Ta có: 2 20 x + x nên để đồ thị hàm số đã cho có 2 đường tiệm cận đứng thì ( )( ) 2 220xxmxm −+−= phải có 2 nghiệm phân biệt. 2 20xmxm +−= có nghiệm kép khác 2 hoặc có 2 nghiệm phân biệt trong đó có 1 nghiệm bằng 2.
nghiệm kép khác
Suy ra đồ thị hàm số có 1 tiệm cận ngang: ym = Đồ thị hàm số đã cho có đúng 2 đường tiệm cận Đồ thị hàm số đã cho có đúng 1 tiệm cận đứng
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO
KHẢO SÁT HÀM SỐ
HÀM ĐỂ
Page 18
−
=−
+=
m m − =− 4 3 m =− Vậy có tất cả 3 giá trị của m thỏa mãn ycđ B. Câu 26: Có bao nhiêu giá trị của tham số
2 2
32
xx = −+
cận?
Chọn A TXĐ: \1;2
= . Ta
2 2 2 2 1 1 limlimlim 32 32 1 xxx m mx x
===
TH1: 2 20xmxm+−= có
2 2 0 430 mm m += + 0 1 4 3 m m m = =−
0 1 m m =
TH2: 2 20xmxm+−= có 2 nghiệm phân biệt trong đó có 1 nghiệm bằng 2 2 0 430 mm m +
0 1 4 3 m
m để đồ thị hàm số
1
mx y
có đúng 2 đường tiệm
A. 2 B. 1 C. 4 D. 3 Lời giải
D
có
ym xx xx →→→
−+ −+ .
m m
= −= −= = .
Câu 27: Có baonhiêugiátrị nguyêndươngcủathamsố m đểđồthị hàm số 2 1 10 x y xxm + = ++ có 3đường tiệm cận? A. 24. B. 10. C. 25. D. 23. Lời giải Chọn D Ta có 22 11 limlim0 1010xx xx xxmxxm→−→+ ++ == ++++ nên đồ thị hàm số có một tiện cận ngang 0 y = .
1 10 1 410 4 m
m
Vậy có 2 giá trị của tham số m thỏa mãn yêu cầu bài toán.
Đồ thị hàm số có 3 đường tiệm cận khi và chỉ khi đồ thị hàm số có hai đường tiệm cận đứng phương trình 2 100xxm++= có hai nghiệm phân biệt khác 1 25025 909 mm mm m m m
có hai tiệm cận đứng , xaxb == sao cho 3 ab A. 5. B. 6. C. 7. D. 8. Lời giải C. 2 2 m m − D.
=− − . Kết hợp với điều kiện m nguyên dương ta có 1;2;3;...;8;10;...;24 m . Vậy có 23 giá trị nguyên dương m thỏa mãn đề bài. Câu 28: Cho hàm số 2 2 21 x y xmx = −+ . Hỏi có bao nhiêu giá trị nguyên của ( )10;10 m− để đồ thị hàm số − −
hàm 2 2 5 2
có hai đường tiệm cận đứng thì phương m m m
cần − Lời giải Chọn D Điều kiện: 2 10 xmx−+ . Ta có: 2 2 limlim00 1 xx
x yy xmx →→ === −+ là tiệm cận ngang của đồ thị hàm số. Đồ thị hàm số 2 2 1 x y xmx = −+ có đúng ba đường tiệm cận đồ thị hàm số 2 2 1 x y xmx = −+ có đúng hai đường tiệm cận đứng 2 10 xmx −+= có đúng hai nghiệm phân biệt khác 2
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO
KHẢO SÁT HÀM SỐ
Page 19
Chọn D Để đồ thị
số
HÀM ĐỂ trình ( ) 2 210gxxmx=−+= phải có hai nghiệm phân biệt , ab khác 2 tức là ( ) 2 2 1 0101 2022.2105 4 m m m g m m − − −+ Hệ thức Vi et 2 1 abm ab += = Ta
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 ( )( ) ( ) 5 33303901690 3 ababababmm −−−++−+ Kết hợp các điều kiện thì có 8 giá trị nguyên m thoả mãn yêu cầu bài toán. Câu 29: Tìm tất cả các giá trị thực của m để đồ thị hàm số 2 2 1 x y xmx = −+ có đúng ba đường tiệm cận. A. 22 m − B.
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 2 2 5 2
Câu 30: Có bao nhiêu giá trị của tham số m để đồ thị hàm số ( ) 22 1 213 x y xmxm = −++− có đúng hai đường tiệm cận? A. 1 B. 2 C. 3 D. 0 Lời giải Chọn C Đồ thị hàm số ( ) 22 1 213 x y xmxm = −++− có 1 tiệm cận ngang là 0 y = Đồ thị hàm số ( ) 22 1 213 x y xmxm = −++− có đúng hai đường tiệm cận Đồ thị hàm số ( ) 22 1 213 x y xmxm = −++− có đúng 1 tiệm cận đứng Phương trình ( ) 222130xmxm−++−= có nghiệm kép hoặc phương trình ( ) 222130xmxm−++−= có hai nghiệm phân biệt trong đó có một nghiệm bằng 1
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 20 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 2 2 22 4022 22105 5 22 m m m mm m m m − − =− −+
−++−= −−= =− Vậy có ba giá trị của m thỏa mãn yêu cầu đề bài. Câu 31: Tất cả các giá trị của tham số m để đồ thị hàm số 2 2 2 2 xx y xxm +− = −+ có hai tiệm cận đứng là A. 1 8 m m − B. 1 8 m m − C. 1 m D. 1 8 m m Lờigiải Để đồ thị hàm số có hai đường tiệm cận đứng thì phương trình 2 20xxm−+= có hai nghiệm phân biệt khác nghiệm của phương trình 2 20 xx+−= Hay phương trình ( ) 2 20fxxxm=−+= có hai nghiệm phân biệt khác 1 và 2 Khi đó ta có ( ) ( ) 0 10 20 f f − 10 10 80 m m m − − + 1 1 8 m m m − 81 m − .
( ) ( ) ( ) ( ) ( ) 2 2 2 2 2 2 02143013 4 0214303 121302301 mm m mm m mm mm m +−−= = =−
+−−
=
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 21 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 32: Có bao nhiêu giá trị nguyên của m thuộc 10;10 để đồ thị hàm số ( ) ( ) 2 2 13 12 xxx y xmxm −+ = ++−− có đúng ba đường tiệm cận? A. 19 B. 18 C. 17 D. 20 Lời giải Chọn B Xét 2 3030xxxx +− ( ) ( ) 2 2 2 2 2 1313 131.11.1 limlimlimlim1 121212 11 xxxx xx xxx xxxx y mm mm xmxm x xx xx →+→+→+→+ −+−+ −+ ==== +−− +−− ++−− ++ ++ . Đồ thị hàm số có tiệm cận ngang 1 y = ( ) ( ) ( ) 2 2 2 2 2 1313 131.11.1 limlimlimlim1 121212 11 xxxx xx xxx xxxx y mm mm xmxm x xx xx →−→−→−→+ −−+−−+ −+ ====− +−− +−− ++−− ++ ++ Đồ thị hàm số có tiệm cận ngang 1 y =− . Xét ( ) 2 1 120 2 x xmxm xm = ++−−= =−− Khi đó, đồ thị hàm số có đúng ba đường tiệm cận khi và chỉ khi 213 231 202 mm mm mm −−− −−−
có 18 giá trị m nguyên thỏa mãn yêu cầu bài toán. Câu 33: Tìm tất cả các giá trị của tham số sao cho đồ thị hàm số có đúng ba đường tiệm cận. A. B. C. . ` D. hoặc . Lời giải Chọn C Điều kiện xác định của hàm số . m ( ) 2 20202021 12 x y xmxm + = −−++ 2 m − 23 m 21 m −− 2 m − 1 m − ( ) 2 0 120 x xmxm −−++
−−− . Lại có m và 10;10 m− nên 1;1010;2\3 m−−− . Do vậy
Ta thấy nên đồ thị hàm số có đúng một đường tiệm cận ngang . Vậy yêu cầu bài toán tương đương đồ thị hàm số phải có hai đường tiệm cận đứng.
TH1) Phương trình có một nghiệm và một nghiệm dương, ta tìm được . Khi đó hàm số trở thành , hàm số chỉ có một tiệm cận đứng , suy ra không thỏa mãn. TH2) Phương trình có hai nghiệm dương phân biệt Ta có hệ điều kiện Câu 34: Có bao nhiêu số nguyên ( )2021;2021 m− để đồ thị hàm số 2 xm y x = có tiệm cận đứng? A. 2019 B. 2023 C. 2022 D. 2021 Lời giải Chọn B Điều kiện xác định 2 xm x Đồ thị hàm số có tiệm cận đứng ) 2;2 mm + Mà m nguyên và ( )2021;2021 m− nên 2020;2019;...;2 m−− nên có 2023 số. Câu 35: Đồ thị hàm số 2 4 2 x y x = có tổng số
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 22
đường tiệm cận ngang và đường tiệm cận đứng là A. 0. B. 3. C. 1. D. 2. Lời giải Chọn B Tập xác định của hàm số là ( ( ) ; 22; D =−−+ Ta có +) 2 222 42 limlimlim2 2 2 xxx xx yx x x +++ →→→ −+ ===+= là tiệm cận đứng của đồ thị hàm số. lim0 x y →+ = 0 y = ( ) 2 120xmxm−−++= 0 x = 2 m =− 2 2020202120202021 3(3) xx y xx xx ++ == 3 x = 2 m =− ( ) 2 120xmxm−−++= 12 12 0 0 .0 xx xx + ( ) ( ) 2 2 14206707 10121 1 20221 mm mm m mmm m mm m −−+ −− −−− − +− −
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 23 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn +) 2 22 44 411 limlimlimlim11 222 1 xxxx x x xx yy xx x →+→+→+→+ ===== là tiệm cận ngang của đồ thị hàm số. +) 2 22 44 411 limlimlimlim11 222 1 xxxx x x xx yy xx x →−→−→−→− ====−=− là tiệm cận ngang của đồ thị hàm số. Vậy tổng số tiệm cận đứng và ngang của đồ thị hàm số đã cho là 3. Câu 36: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số 22 73 x y x +− = +− là A. 0 B. 1 C. 2 D. 3 Lời giải Chọn B Điều kiện xác định: 7302 2 202 2 707 xx x xx x xx +− +− − +− ( )( ) ( )( ) 222 2473 22733limlimlim 73222 7922 xxx xx xx xx xx →→→ +−++ +−++ === +−++ +−++ 2 x = không là tiệm cận đứng của đồ thị hàm số 22 1 22 limlim11 7373 1 xx x x x y x x x →+→+ +− +− === +− +− là tiệm cận ngang của đồ thị hàm số. Vậy tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là 1 Câu 37: Cho hàm số 2 2 213 56 xxx y xx −−++ = −+ có đồ thị là ( )C . Xác định phương trình các đường tiệm cận đứng của ( )C A. 2 x = . B. 3 x = . C. 2 x = và 3 x = . D. 1 2 x = và 3 x = . Lời giải Chọn B TXĐ: \2,3 D =
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 24 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt
ệp
11; 12 Sưu tầm và biên soạn Ta có: ( )( ) 22 2 22 213352 56 56213 xxxxx y xx xxxxx −−++−− == −+ −+−+++ ( )( ) ( )( )( ) ( )( ) 22 231 31 232133213 xx x xxxxxxxxx −+ + == −−−+++−−+++ Dễ thấy: 22 limlim7 6 xx yy+−→→ ==− 2 x = không phải là tiệm cận đứng
33
xx
−+ →→
→+→+→+ ++ +=+=
ngang. Vậy hàm số ( )yhx = có 1 đường tiệm cận ngang. Câu 39: Đồ thị hàm số 2 511 2 xx y xx +−+ = + có tất cả bao nhiêu đường tiệm cận? A. 3 B. 0 C. 2 . D. 1 . Lời giải Chọn D Tập xác định: ) 1;\0 D =−+ . • lim x y →+ 2 511 lim 2 x xx xx →+ +−+ = + 234 5111 lim 2 1 x xxxx x →+ +−+ = + 0 = Suy ra đường thẳng 0 y = là đường tiệm cận ngang của đồ thị hàm số. • 0 lim x y → 2 0 511lim 2 x xx xx → +−+ = + ( ) ( )( ) 2 2 0 511 lim 2511 x xx xxxx → +−− = ++++ ( )( ) 2 2 0 259 lim 2511 x xx xxxx → + = ++++ ( )( ) 0 lim259 2511 x x xxx → + = −+++ 9 4 =
Hòa
0984164935
Nghi
THPT BDKT Toán 10;
của đồ thị hàm số.
lim;lim
yy
=−=+ 3 x = là tiệm cận đứng của đồ thị hàm số. Vậy đồ thị hàm số chỉ có một tiệm cận đứng là 3 x = Câu 38: Cho hàm số ( )yfx = liên tục trên ; ()0fx , x và ( ) lim3 x fx →− = và ( ) lim x fx →+ =+ . Số tiệm cận của hàm số ( ) ( ) 2 520221 15 x hx fxx + =+ + là A. 1. B. 4. C. 3. D. 2. Lời giải Chọn A Ta có: ( )yfx = liên tục trên ; ()0fx , x Mà 2 150, xx+ và 101xx+− Suy ra tập xác định của hàm số ( )yhx = : ) 1; D =−+ . Xét: ( ) ( ) 22 520221520221 limlimlim0 11xxx xx fxxfxx
++ Suy ra 0 y = là tiệm cận
có
Suy ra đường thẳng 0 x = không là đường tiệm cận đứng của đồ thị hàm số. Vậy đồ thị hàm số có tất cả 1 đường tiệm cận. Câu 40: Tìm tất cả các giá trị thực của tham số thực m để đồ thị hàm số 2 x yy mm m x
B. m C. ( ) 0; m+ D. ( );0 m 1 limlim555 933 3 xx
c
đúng
15 93 x mx y = có hai đường tiệm cận ngang. A. m →+→+ === là đường tiệm cận ngang khi x →+. 2
hàm x yy mm m x
n ngang.
TXĐ D
không →−→− === là đường tiệm cận ngang khi x →− . Khi đó đồ thị hàm số có hai đường tiệm ngang là 5 3 y m = Vậy 0 m thỏa yêu cầu bài toán. Câu 41: Có bao nhiêu giá trị nguyên của m thuộc 10;10 để đồ thị hàm số ( ) ( ) 2 2 1.3 12 xxx y xmxm −+ = ++−− có đúng ba đường tiệm cận? A. 19. B. 18. C. 17. D. 20. Lời giải Chọn A Đk: 0 3 x x − . Dễ thấy đồ thị hàm số luôn có 2 tiệm cận ngang 1 y = và 1 y =−
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG
HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 25
− Lời giải Chọn D Điều kiện: 22 930390 mxmx −− + Nếu 0 m = thì 15 3 x y = Ta có TXĐ D = Vì lim x y →+ =− ; lim x y →− =+ đồ thị hàm số đã cho không có tiệm cận ngang. + Nếu 0 m ta có 2 333 xx mmm − thì TXĐ 33 ; D mm =− Do đó không tồn tại lim x y →+ và lim x y →− đồ thị
số đã cho
có tiệm
ậ
+ Nếu 0 m ta có
với mọi x nên
ĐẠO = Ta
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 2
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 1 limlim555 933 3 xx
= và đạt cực tiểu tại 2 x =− . Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số ( )( ) ( ) ( ) 12 1
xx y fxf
−+ =
A. 5 . B. 2. C. 3 . D. 1. Lời giải
Chọn D
Điều kiện: 0 x Vì hàm số đạt cực đại tại 3 x = và đạt cực tiểu tại 2 x =− nên hệ số 0 a
Xét ( ) ( )1 xfxf →+−→− . Do đó hàm số đề bài không có tiệm cận ngang.
x fxffxfxa xb
= −===−+ =
Xét ( ) ( ) ( ) ( ) ) 1 10120; 3
Khi 1 lim0 0 x y → = : không xác định. lim xb y → =+ : đồ thị hàm số có tiệm cận đứng 3 xb= . Vậy đồ thị hàm số đề bài có duy nhất 1 tiệm cận đứng. Câu 43: Cho hàm số bậc ba 32 () fxaxbxcxd =+++ có đồ thị như hình vẽ. Với giá trị nào của m thì hàm số 2 ()()2() mx gx fxfx = có 5 tiệm cận đứng?

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 26 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT
10; 11; 12 Sưu tầm và biên soạn Xét phương trình ( ) 2 1 120 2 x xmxm xm = ++−−= =−− . Vì 1 x = là nghiệm của tử số nên đồ thị hàm số có ba đường đường tiệm cận khi và
0984164935
BDKT Toán
chỉ khi nó có một tiệm cận đứng nữa là 2 xm=−− Khi đó 202 231 mm mm −−− −−− Vì m nguyên thuộc 10;10 nên 10;9;8;....;2;1;2;...;10 m−−−− Vậy có 19 giá trị của m thỏa mãn yêu cầu bài toán Câu 42: Cho hàm số ( ) 32 fxaxbxcxd =+++ , biết hàm số đạt cực đại tại 3 x
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 27 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 2 m B. 2 m C. 2 m D. 2 m
Xét hàm số 2 () ()2() mx gx fxfx = Biểu thức mx xác định khi 0(1)mxxm − Ta có 2 1 2 ()2()0(2) (2;1) 0 ()0 (1;2) )2 1 2 fxfx xx x fx xx fx x x −= =−− = = = = =− = Hàm số có 5 tiệm cận đứng
5 nghiệm thỏa mãn điều kiện của (1) 2 m Câu 44: Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số ( ) 2 332 1294 1331 xx y mxxx +−+− = −+++ có đúng một đường tiệm cận. A. 4. B. 2. C. 3. D. 1. Lời giải Chọn B Điều kiện ( ) 2 332 2940 13310 xx mxxx −+− −+++ 3233 1 4 2 331 x xxxmx +++ ( )3 33 1 4 2 1 x xmx + 1 4 2 1 x xmx + . Do 1 4 2 x nên đồ thị hàm số đã cho không có tiệm cận ngang. Suy ra đồ thị có đúng một tiệm cận đứng khi và chỉ khi phương trình ( ) ( ) 332 133101 mxxx −+++= có đúng một nghiệm thuộc đoạn 1 ;4 2 . Ta có ( ) 15 11;3 4 x xmxm x + +== , 1 ;4 2 x
0984164935
Lời giải Chọn D
khi phương trình (2) có
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 28 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn So với điều kiện, suy ra 5 3 4 m Vậy có một giá trị nguyên 2 m = thỏa mãn. Câu 45: Đồ thị hàm số 2 4 2 x y x = có tổng số đường tiệm cận ngang và đường tiệm cận đứng là A. 0. B. 3. C. 1. D. 2. Lời giải Chọn B Tập xác định của hàm số là ( ( ) ; 22; D =−−+ . Ta có +) 2 222 42 limlimlim2 2 2 xxx xx yx x x +++ →→→ −+ ===+= là tiệm cận đứng của đồ thị hàm số +) 2 22 44 411 limlimlimlim11 222 1 xxxx x x xx yy xx x →+→+→+→+ ===== là tiệm cận ngang của đồ thị hàm số +) 2 22 44 411 limlimlimlim11 222 1 xxxx x x xx yy xx x →−→−→−→− ====−=− là tiệm cận ngang của đồ thị hàm số. Vậy tổng số tiệm cận đứng và ngang của đồ thị hàm số đã cho là 3. Câu 46: Có bao nhiêu số nguyên m để đồ thị hàm số 2 2 43 2 xx y xmx −+− = −+ có hai đường tiệm cận đứng? A. 0. B. 1. C. 2. D. 3. Lời giải Chọn B Ta có 2 43013xxx −+− . Đồ thị hàm số 2 2 43 2 xx y xmx −+− = −+ có hai đường tiệm cận đứng khi và chỉ khi phương trình 2 20 xmx−+= có hai nghiệm phân biệt thuộc [1;3]. 2 2 2 20() x xmxmfx x + −+=== 2 2 2 '();'()02 x fxfxx x ===
tiệm cận. A. 909. B. 908. C. 907. D. 906. Lời giải
Chọn B
Điều kiện xác định: 2
1 2 x xxm
+ Dựa vào điều kiện xác định ta suy ra hàm số đã cho không có giới hạn khi x →− . 2 1 lim0, 2 x
x m xxm →+ = +− . 0 y = là pt đường tiệm cận ngang.
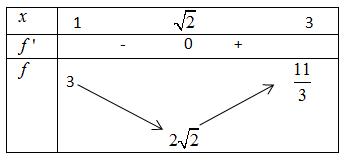
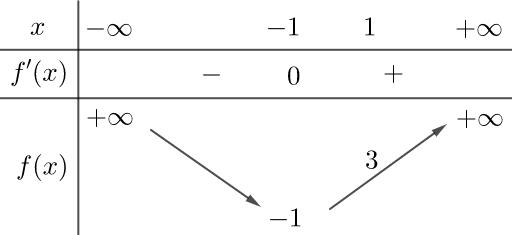
Cần tìm điều kiện để hàm số có 1 tiệm cận đứng.
Xét hàm số ( ) 2 2 fxxx =+ ( ) ( ) '22;'01 fxxfxx=+==− .
Dựa vào bảng biến thiên ta thấy:
Khi 3 m thì đồ thị hàm số không có tiệm cận đứng.
Khi 3 m thì đồ thị hàm số có 1 tiệm cận đứng.
Kết hợp đề bài, để đồ thị hàm số có đúng 2 đường tiệm cận thì 3;1000 m m .
Vậy có 908 giá trị nguyên của m .
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 29 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Bảng biến thiên Vậy 223 m . Câu 47: Tìm số giá trị nguyên thuộc đoạn 1000;1000 của tham số m để đồ thị hàm số 2 1 2 x y xxm = +− có đúng hai đường
0984164935
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo
Huỳnh Văn Ánh 42
ễn
Thuận
Huế ĐT:
Page 30 Chuyên
ệ
Tố
n Câu
trị
ủ
ố
− để đồ thị
số 2 2
x y
+ = −+ có
đường tiệm cận đứng? A.
Lờ
0 101
− −− −−−+ Mà m nguyên và 2021;2021 m− nên suy ra 2021;2020;...;3;2;1;0\8 m−−−−−− . Vậy có 2021 giá trị m thỏa mãn yêu cầu bài toán. Câu 49: Có bao nhiêu giá trị nguyên của 10;10 m− để đồ thị hàm số 2 2 (1)3x (1)2 xx y xmxm −+ = ++−− có đúng 2 đường tiệm cận? A. 19. B. 18 C. 17 D. 2 Lời giải Chọn D + ĐK: ( ) ( ) 2 2 2 30;30; 30;30; 1 (1)20 2 xxx xxx x xmxm xm +−−+ +−−+ ++−− −− + Do 2 2 2 13 (1)3x(1)11 (1)2(1)2 1 xx xx xx limlim mm xmxm xx →+→+ −+ −+ == ++ ++−− +− 2 2 2 13 (1)3x(1)11 (1)2(1)2 1 xx xx xx limlim mm xmxm xx →−→+ −−+ −+ ==− ++ ++−− +− Nên đồ thị hàm số luôn có 2 tiệm cận ngang với mọi giá trị của m . Do đó để đồ thị hàm số có đúng 2 tiệm cận thì đồ thị hàm số phải không có tiệm cận đứng. + Nhận thấy phương trình: 2 1 (1)20(1)(2)0 2 x xmxmxxm xm = ++−−=−++= =−− Để đồ thị hàm số không có tiệm cận đứng thì nghiệm ( ) 23;032021 xmmm =−−−−−−− + Vì m nguyên và 10;10 m− nên 1;0 m− . Vậy có 2 giá trị của .m Câu 50: Gọi S là tập các giá trị nguyên của tham số để đồ thị hàm số 22 32 2233 3 y m xmxmm xx −++ = có ít nhất một tiệm cận đứng tiếp xúc với đường tròn ( ) ( ) ( ) 22 :129Cxy−++= . Tính tổng các phần tử của tập S m
viên:
Nguy
Cư Trinh
Hòa TP
0984164935
luy
n thi: Tuyển sinh vào lớp 10
t Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạ
48: Có bao nhiêu giá
nguyên c
a tham s
2021;2021 m
hàm
2
xxm
hai
2020 B. 2021 C. 2022 D. 2019
i giải Chọn B Đồ thị hàm số 2 2 2 x y xxm + = −+ có hai đường tiệm cận đứng khi phương trình 2 20xxm−+= có hai nghiệm phân biệt và khác 2 ( ) ( ) 2
88 2220 mm mm m
A. B. 4 C. 2 D. Lời giải Chọn B Ta có ( ) 222233330mmmmm =−−+=−+− với mọi giá trị của m . Suy ra 2222330xmxmm−+−+ với mọi giá trị của xR . Gọi :0 xc += là đường thẳng tiếp xúc với đường tròn ( ) ( ) ( ) 22 :129Cxy−++= Khoảng cách từ tâm ( )1;2 I đến đường thẳng bằng bán kính 3 R = . Suy ra ( )
132 ;13134 cc dIc cc =+=+==
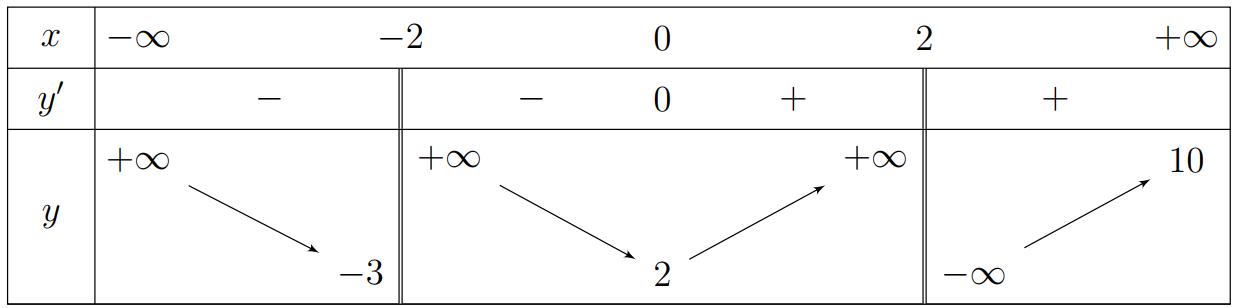
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 31
+=−=−
22
A. 6. B. 5. C.
. D.
. Lờ
ải Chọn D Đặt ( ) ( ) 1 26 gx fx = + , ta có
số xác
( ) 2; a+ . Khi đó ta có ( ) ( ) 1 lim0 2lim6 x x gx fx →− →− == + và ( )
lim
x x gx
→+ →+ == +
ậ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 6 5
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
Vậy đường thẳng có phương trình 202xx+==− hoặc 404xx−== Đồ thị hàm số
32 2233 3 y m xmxmm xx −++ = có ít nhất một đường tiệm đứng tiếp xúc với đường tròn ( ) ( ) ( ) 22 :129Cxy−++= Suy ra phương trình 3230xxm−−= có nghiệm 2 x =− hoặc 4 x = ( ) ( ) 32 32 20020 2320 16016 43.40 mm m mm m −−==− −−−−= −== −−= . Vậy tổng các phần tử của tập S là 20164−+=− . Câu 51: Cho hàm số ( )yfx = xác định và có đạo hàm trên \2 . Hàm số ( )fx có bảng biến thiên như hình vẽ dưới đây Tính tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số ( ) 1 26 y fx = + .
3
4
i gi
hàm
định trên \2;a , trong đó ( ) 3 fa =− và
( ) 11
2lim626
fx
nên 0 y = và 1 26 y = là hai đường tiệm c
n ngang.
Mặt khác ta có ( ) ( ) ( ) ( ) 2 2
1 lim2 2lim6 x x
gxx fx →− →−
1 lim02 2lim6 x x
gxx fx → →
==+=− + là tiệm cận đứng; ( ) ( ) 2 2
==+= + là tiệm cận đứng; Vậy đồ thị hàm số ( ) 1 26 y fx = + có 4 đường tiệm cận. Câu 52: Cho hàm số ( )yfx = là hàm số đa x fxxaa xbb
=== + không là tiệm cận đứng; ( ) ( ) 1 lim 2lim6 xa xa thức có đồ thị như hình vẽ dưới đây. Hỏi đồ thị hàm số ( ) 3 1 31 y fxx = có bao nhiêu đường tiệm cận đứng? A. 7 B. 3 C. 5 D. 6 Lời giải Chọn A Từ đồ thị ta thấy ( ) ( ) ( )
gxxa fx + + → → 1 112 2
= == = Xét ( ) ( ) ( ) ( ) ( ) ( ) ( )
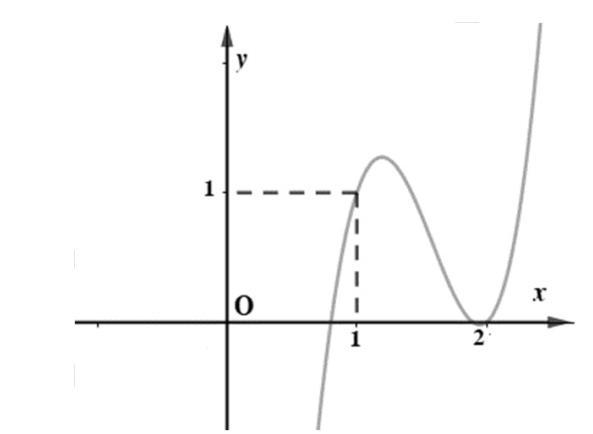
3 333 3
xx fxxfxxxxaa xxbb
311 310313122 323
−= −−=−=−= −= Ta có bảng biến thiên của hàm số ( ) 3 3 gxxx =− như sau. TừBBTsuyraphươngtrình có3nghiệmphânbiệt,phươngtrình có3nghiệmphânbiệt,phương trình có 1 nghiệm và 7 nghiệm này đều phân biệt. Vậy đồ thị hàm số đã cho có 7 tiệm cận đứng. Câu 53: Cho hàm số có bảng biến thiên: ( )yfx =
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 32
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Đồ thị hàm số có tất cả bao nhiêu đường tiệm cận đứng?
A. 5. B. 3. C. 6. D. 4. Lời giải Chọn D
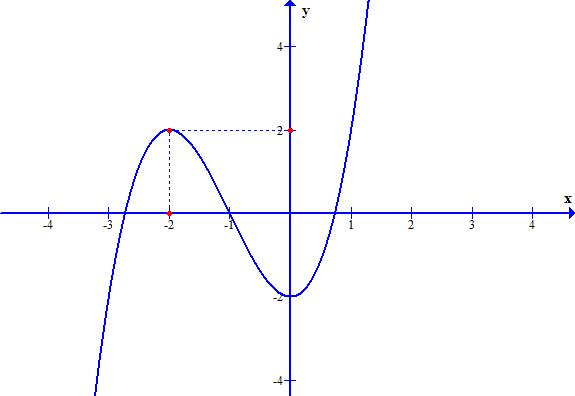
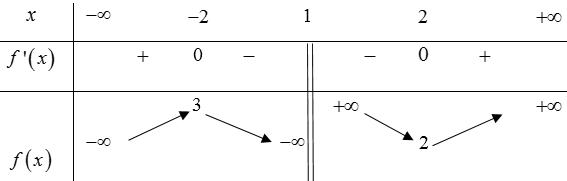
Ta có nên đường thẳng không là tiệm cận đứng. Ta có . đường thẳng là một tiệm cận đứng.
Xét tương tự ta có các đường thẳng là tiệm cận đứng. Vậy đồ thị hàm số có 4 tiệm
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 33
(
−+ →→ ==
(
(
xaa xbb
xcc xdd
=− −== = =
−+ →→ =−=+
cận đứng. Câu 54: Cho hàm số ( ) ( ) 32 0 fxaxbxcxda =+++ có đồ thị như hình vẽ ( ) 1 25 y fx =
) ( ) 11 11 limlim0 2525xxfxfx
1 x =
) ( )
) ( ) ( ) ( ) 2 521 250 212 2
fxfx
=−
( ) ( )lim;lim11 2525xaxafxfx
xa = ;; xbxcxd === ( ) 1 25 y fx =
Chọn C Ta có ( ) ( ) 1 limlim0
x gx fxm
= =− = có 3 giá trị của m.

== hàm số có tiệm cận ngang 0 y = . Để hàm số có đúng 3 tiệm cận ( )gx có 2 tiệm cận đứng phương trình ( ) 0 fxm−= có hai nghiệm phân biệt khác 1 hoặc có ba nghiệm trong đó có 1 nghiệm bằng 1. 2 2 0
m m m
Câu 55: Cho hàm số ( )yfx = có bảng biến thiên như sau: Đồ thị hàm số ( ) 2 1 1 y fx = có bao nhiêu đường tiệm cận đứng? A. 1. B. 2. C. 3 D. 4 Lời giải Chọn B Xét phương trình ( ) ( ) ( ) ( ) ( ) 2 11 10 12 fx fx fx = −= =− Dựa vào BBT ta nhận thấy, phương trình có 1 nghiệm và phương trình có 1 nghiệm. Do đó, đồ thị hàm số có 2 tiệm cận đứng.
Câu 56: Cho hàm số bậc ba ( ) ( ) 32 ;;; fxaxbxcxdabcd =+++ có đồ thị như hình vẽ dưới đây:
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 34
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Gọi Alà tập hợp tất cả các giá trị của tham số m để đồ thị hàm số ( ) ( ) 1 x gx fxm + = có đúng 3 đường tiệm cận. Số phần tử của A là A. 0. B. 2. C. 3. D. 4. Lời giải
xx
→→
42 44 x x
−=− −= 6 0 x x = = Giới hạn bên phải, bên trái của hàm số ( )gx tại các điểm 6 x = ; 0 x = bằng + hoặc − nên đồ thị hàm số ( )gx có 3 đường tiệm cận đứng Lại có ( ) 2 lim4 x x → −=− nên ( ) 2 lim43 x fx → −−= Khi đó ( ) lim0 x gx → = Đồ thị hàm số ( )gx có 1 đường tiệm cận ngang Vậy tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số ( )gx là 4.
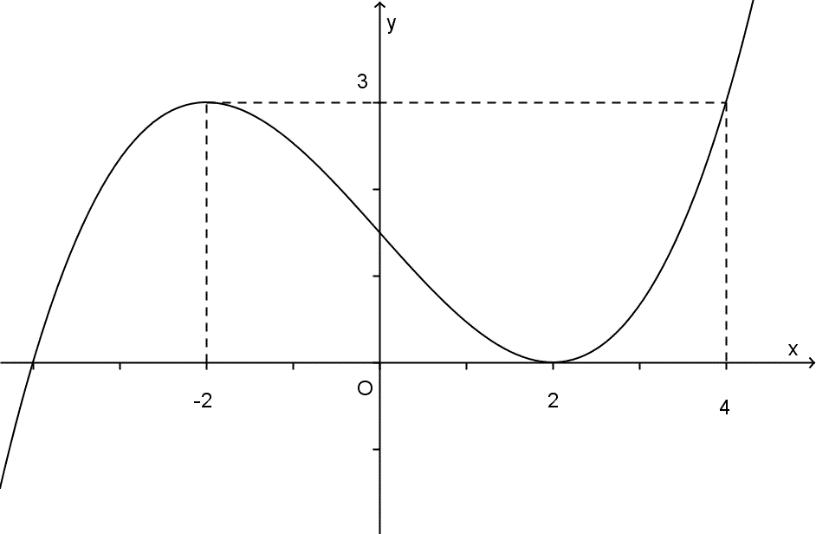
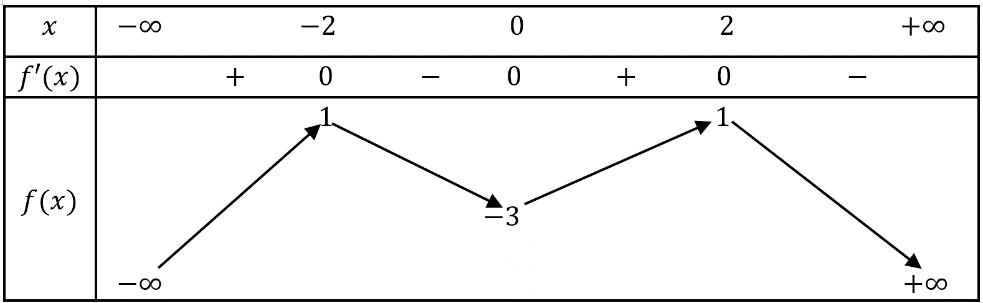
Câu 57: Cho ( )fx là hàm bậc bốn và có bảng biến thiên như hình vẽ
thị hàm số ( ) ( )( ) ( ) 2 42 1 xx gx fx = có mấy đường tiệm cận?
3
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 35
Đồ
A.
B.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 C.
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn D.
Tính tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số ( ) ( ) 2 1 43 gx fx = : A. 4. B. 5. C. 2. D. 3. Lời giải Chọn A Xét phương trình: ( ) 2 43fx−= 2 2 C
4
1
2 Lời giải
họn D Xét phương trình ( ) ( ) ( ) 22 10 22 xb fx xb = −= =− .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
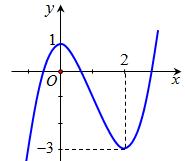
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 36
2 x =− là tiệm cận đứng của đồ thị hàm số. Vậy đồ thị hàm số ()gx có 2 đường tiệm cận. Câu 58: Cho hàm số bậc ba ( ) 32 fxaxbxcxd =+++ có đồ thị như hình vẽ. Hỏi đồ thị hàm số ( ) ( ) ( ) ( ) ( ) 2 2 22 33 xxx gx xfxfx = −+ có bao nhiêu đường tiệm cận đứng? A. 6. B. 3. C. 4. D. 5. Lời giải Chọn C ĐK xác định của 2 x là ( )2* x Ta có ( ) ( ) ( ) ( ) ( ) 2 3 3300 3 x xfxfxfx fx = −+== =− . * Ta có 3 x = không thỏa mãn * ( ) ( ) 0 00;2 2 xa fxxb xc = == = . Ta có xc = không thỏa mãn Ta có ( ) ( ) lim;lim xaxb gxgx ++ →→ =+=+ . Vậy ; xaxb == là các đường tiệm cận đứng. * ( ) 0 3 2 xd fx x = =− = . Ta có ( ) ( ) 2 lim;lim xdx gxgx +− →→ =+=+ .Vậy ;2xdx== là các đường tiệm cận đứng. Câu 59: Cho hàm số ( )yfx = liên tục trên \1 và có bảng biến thiên như sau
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do ( )fx làhàm sốbậcbốncó ( ) lim x fx →+ =− nên ( ) ( ) ( ) 22122 (0)fxaxxa −=+− Khi đó, ( ) ( )( ) ( ) ( ) ( ) 2 22 42 1 2 22 xx gx ax axx == + +− Do ( ) ( ) 1 limlim0 2 xx gx ax →+→+ == + và ( ) ( ) 1 limlim0 2 xx gx ax →+→+ == + , nên 0 y = là tiệm cận ngang của đồ thị hàm số. Và ( ) ( ) 22 1 limlim 2 xx gx ax ++→−→− ==− + và ( ) ( ) 22 1 limlim 2 xx gx ax →−→− ==+ + , nên
là
ngang
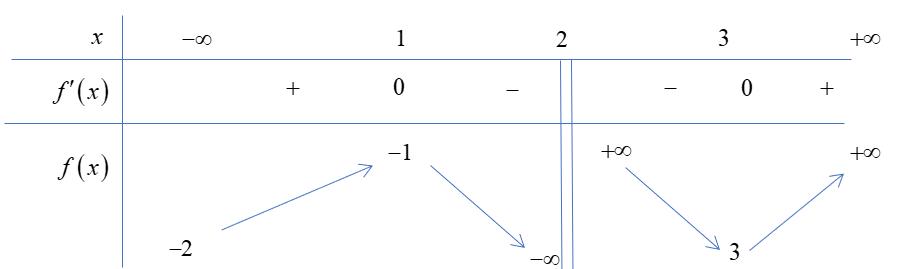

CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 37
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Tìm tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số ( ) 1 () 23 gx fx = A. 0. B. 1. C. 2. D. 3. Lời giải Chọn D Dựa vào bảng biến thiên ta có: Phương trình ( ) 230 fx −= ( ) ( ) ( ) 1 2 31;2 22; xx fx xx = = =+ ( ) 11 1 lim()lim 23 xxxx gx fx ++→→ ==+ , ( ) 22 1 lim()lim 23 xxxx gx fx ++→→ ==− Suy ra đường thẳng 1xx = và 2xx = là tiệm cận đứng của đồ thị hàm số ()ygx = . ( ) 1 lim()lim0 23 xx gx fx →+→+ == , ( ) 1 lim()lim0 23 xx gx fx →−→− == Đường thẳng 0 y = là tiệm cận ngang của đồ thị hàm số ()ygx = Vậy đồ thị hàm số ()ygx = có 2 đường tiệm cận đứng
1xx = ; 2xx = và 1 tiệm cận
là 0 y = . Câu 60: Cho hàm số ( )yfx = có đạo hàm là ( )yfx = và bảng biến thiên như hình vẽ dưới đây: Số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số ( ) ( ) 5 23 gx fx = + là A. 2 B. 3 C. 4. D. 5 Lời giải Chọn C
Dựa vào BBT ta thấy ( ) 230 fx += có hai nghiệm phân biệt là xa = và xb =
Khi đó: ( ) lim xa gx + → =+ và ( ) lim xa gxxa → =−= là đường TCĐ của đồ thị hàm số ( ) lim xb gx + → =− và ( ) lim xb gxxb → =+= là đường TCĐ của đồ thị hàm số ( ) lim55 x gxy →− =−=− là đường TCN của đồ thị hàm số ( ) lim00 x gxy →+ == là đường TCN của đồ thị hàm số Câu 61: Cho hàm số bậc ba ( ) 32 fxaxbxcxd =+++ , ( ) ,,, abcd có đồ thị như hình vẽ dưới đây. Hỏi đồ
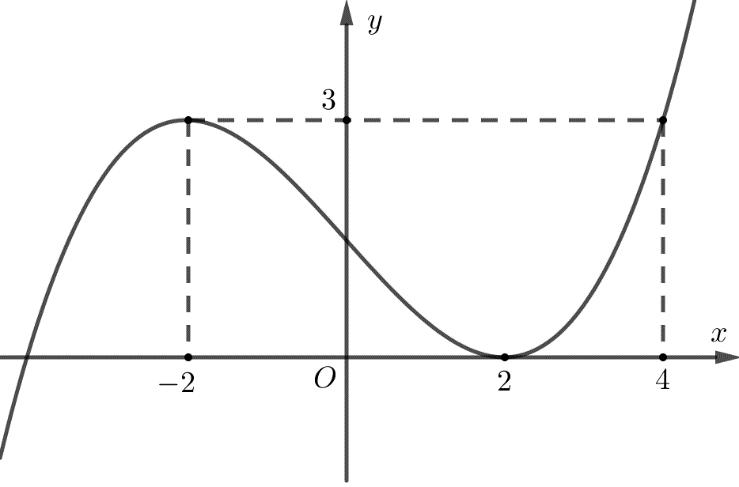
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO
ĐỂ KHẢO SÁT HÀM SỐ
HÀM
Page 38
Chọ
Từ đồ thị ta có ( ) 2 430
−−=
−= 2
−=− −= 2
= =
= đồ thị
ố
ng. Lại có ( ) 2 lim4 x fx → −=− ( ) lim0 x gx → = đường thẳng 0 y = là đường tiệm cận ngang của đồ thị hàm số. Vậy đồ thị hàm số có bốn đường tiệm cận. Câu 62: Cho hàm số ( )yfx = liên tục trên các khoảng xác định và có bảng biến thiên như hình vẽ dưới. Hỏi số đường tiệm cận đứng của đồ thị hàm số ( ) 2 1 e2 = fx y là bao nhiêu? ( )gx
thị hàm số ( ) ( ) 2 1 43 gx fx = có bao nhiêu đường tiệm cận đứng và tiệm cận ngang? A. 2. B. 3. C. 4. D. 5. Lời giải
n C
fx
( ) 2 43fx
2 42 44 x x
2 6 0 x x
6 0 x x =
hàm s
( )gx có ba đường tiệm cận đứ
A. 0. B. 3. C. 1. D. 2. Lời giải
Chọn D
Xét ( ) 2 e20 −= fx ( ) 2 ln2 fx = ( ) ( ) ln2 ln2 fx fx
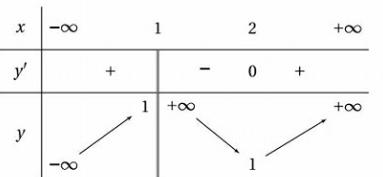
= =− .
Dựa vào bbt ta thấy: Đường thẳng ln2 y = cắt đồ thị ( )yfx = tại 1 điểm. Đường thẳng ln2 y =− cắt đồ thị ( )yfx = tại 1 điểm.
Suy ra phương trình ( ) 2 e20 −= fx có 2 nghiệm phân biệt. Vậy đồ thị hàm số ( ) 2
1 e2 = fx y có 2 đường tiệm cận đứng.
( )yfx = y' y
Câu 63: Cho hàm số có bảng biến thiên như sau
0 +∞
+ 0 0 +∞
x ∞ +∞ 2 2 0 + 1 2 2
Số đường tiệm cận đứng của đồ thị hàm số ( ) ( ) 2 1 x gx fx = là A. 4 B. 3 C. 2 D. 1 Lời giải Chọn B Dựa vào bảng biến thiên ta thấy ( ) ( ) 11 2 33
xxx fxfxxx xxx
=− −==== = Do đó đồ thị hàm số ( ) ( ) 2 1 x gx fx = có 3 đường tiệm cận đứng.
,2 1011 ,2
Câu 64: Cho hàm số ( ) 32 yfxaxbxcxd ==+++ ( ) ,,, abcd có đồ thị như hình bên dưới
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 39
Hỏi đồ thị hàm số ( ) ( ) ( ) 2 20221 2 x ygx fxfx == có bao nhiêu đường tiệm cận đứng?
A. 1. B. 0. C. 2. D. 3. Lời giải Chọn D
20221 12122 x xxxxx = +−−−− Tập xác định ( ) 1;\2,13 D =++ Ta có: ( ) ( )( ) ( ) 2 2 11 limlim2022 12122 xx gx xxxxx ++ →→ ==− +−−−− Vì 1 lim202220220 x + → = , ( )( ) ( ) 2 2 1 lim121220 x xxxxx + → +−−−−= và ( )( ) ( ) 2 2 121220xxxxx +−−−− khi 1 x + → . Nên 1 x = là tiệm cận đứng của đồ thị hàm số ( )gx . Nhận xét: Các giá trị 2 x = và 13 x =+ làm cho mẫu của ( )gx bằng +
1 y
y'
+ + 2
x + 2

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 40
Do đồ thị hàm ( )fx cắt và tiếp xúc với trục Ox lần lượt tại điểm có hoành độ 1 x =− và 2 x = nên ta suy ra hàm số có dạng: ( ) ( )( )2 12fxaxx=+− . Đồ thị hàm số đi qua điểm ( ) ( ) ( )( )2 1;211112221 faaa =+−=== Vậy ( ) ( )( )2 32 1234fxxxxx=+−=−+ ( ) ( ) ( ) ( )( ) 2 3232 2022120221 23432 xx gx xxxx fxfx == −+−+ ( )( ) ( )( ) 2 2 0 và tử của ( )gx khác 0 nên suy ra 2 x = và 13 x =+ là các tiệm cận đứng của đồ thị hàm số ( )gx . Vậy đồ thị hàm số ( )gx có 3 tiệm cận đứng. Câu 65: Cho hàm số ( )yfx = có bảng biến thiên sau Đồ thị hàm số ( ) 2 1 9 y fx = có bao nhiêu tiệm cận đứng?
A. 0. B. 3. C. 1. D. 2. Lời giải

Chọn D
Xét phương trình ( ) ( ) ( ) ( ) ( ) 2 31 90 32 fx fx fx = −= =−
Dựa vào BBT ta nhận thấy, phương trình có 1 nghiệm và phương trình có 1 nghiệm . Do đó, đồ thị hàm số có 2 tiệm cận đứng.
Câu 66: Cho hàm số ( )fx xác định và liên tục trên \1 có bảng biến thiên như sau:
Hỏi đồ thị hàm số ( ) 1 y fx = có tất cả bao nhiêu đường tiệm cận? A. 3. B. 4. C. 2. D. 1. Lời giải Chọn B Ta có: ( ) ( ) 11 lim2lim 2 xx fx fx →−→− == ; ( ) ( ) 11 lim2lim 2 xx fx fx →+→+ =−=− .
Suy ra đồ thị hàm số ( ) 1 y fx = có hai đường tiệm cận ngang là 1 2 y = và 1 2 y =− Dựa vào bảng biến thiên của hàm số ( )yfx = ta thấy: phương trình ( ) 0 fx = có hai nghiệm phân biệt 12 1 xx − Khi đó: ( ) ( ) 12 0 fxfx== .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 41
xx xx
→ → = =+ → và ( ) ( ) ( ) 2 2 2 lim01 lim 0 xx xx fx fx fxkhixx → → = =+ → Vậy đồ thị hàm số ( ) 1 y fx = có hai tiệm cận đứng là đường thẳng 1xx = và 2xx = . Câu 67: Cho hàm số 32 () yfxaxbxcxd ==+++ có đồ thị như hình bên dưới Hỏi đồ thị hàm số ( ) ( ) 2x ygx fx == có bao nhiêu đường tiệm cận đứng? A. 3. B. 1. C. 2. D. 0 . 2 2 + x + 1 y y'
Ta có: ( ) ( ) ( ) 1 1 1 lim01 lim 0
fx fx fxkhixx
Lời giải
Chọn A
Đk: ()0fx
Từ đồ thị ta thấy ()0fx = khi 4 x =− , 1 x =− và 2 x =
Khi đó ()(4)(1)(2) fxaxxx =++− có 3 nghiệm.
Do đó đồ thị hàm số ( )ygx = có 3 đường tiệm cận đứng.
Câu 68: Cho hàm số 32 yaxbxcxd =+++ có đồ thị như hình vẽ:
y 2
x
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số ( ) 2 1 54 y fxx = −+ A. 3. B. 4. C. 6 . D. 5. Lời giải Chọn C Vì hàm số ( )yfx = là hàm số bậc 3 do đó Dựa vào đồ thị ta có: ( ) 1 2 3
xx fxxx xx
3 2 00 3 2
=− === = Suy ra ( ) ( ) ( ) ( )
2 1 22 2 2 3
xxx fxxxxx xxx
541 540542 543
−+= −+=−+= −+= Xét phương trình 2 54 xxa −+= có nghiệm khi 9 4 a . Từ đó suy ra phương trình ( )1 , phương trình ( )2 và phương trình ( )3 đều có 2 nghiệm phân biệt nên đồ thị hàm số ( ) 2 1 54 y fxx = −+ có 6 đường tiệm cận đứng. Câu 69: Cho hàm số ( ) axb fx cxd + = + có bảng biến thiên như hình vẽ:
1 y
y'
2 1 O 1 +
x + 2
+ + 2
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 42
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số ( ) 3 29yfxx=+− là
A. 1. B. 2. C. 3. D. 4. Lời giải
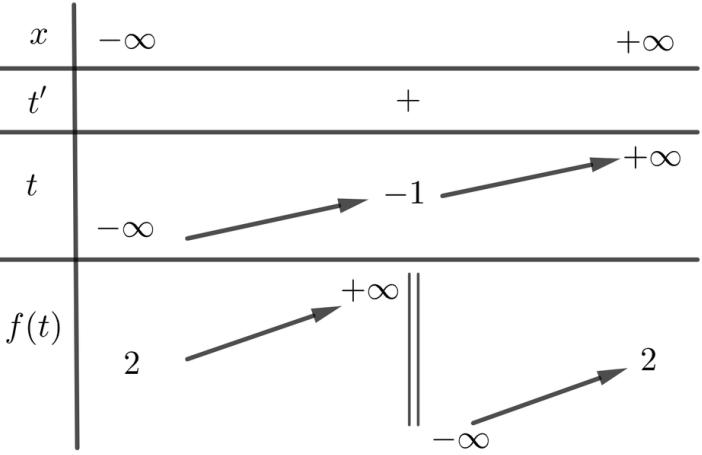

Chọn B
Đặt ( ) 3 29txxx=+− , thì ( ) 2 320txx =+ , x . Ta có bảng biến thiên của ( )yft = s Từ bảng biến thiên trên, ta thấy đồ thị hàm số ( ) 3 29yfxx=+− có một tiệm cận đứng và một tiệm cận ngang. Câu 70: Cho hàm số ( )yfx = có bảng biến thiên như sau Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số ( ) 1 2 y fx = là A. 4. B. 1. C. 3. D. 2. Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 43
x
→− ==
→+
Chọn D Ta có: +) ( ) 111 lim 2202122019
fx
, ( ) 1 lim 2 x fx
=− suy ra đồ thị hàm số ( ) 1 2 y fx = có một tiệm cận ngang: 1 2019 y = . +) Lại có: ( ) ( ) ( )202;3fxfxxa−===−−
Do đó: ( ) ( ) 11 lim;lim 22xaxafxfx +− →→ =−=+ , suy ra đồ thị hàm số ( ) 1 2 y fx = có một tiệm cận đứng: xa = . Vậy đồ thị hàm số ( ) 1 2 y fx = có 2 đường tiệm cận.
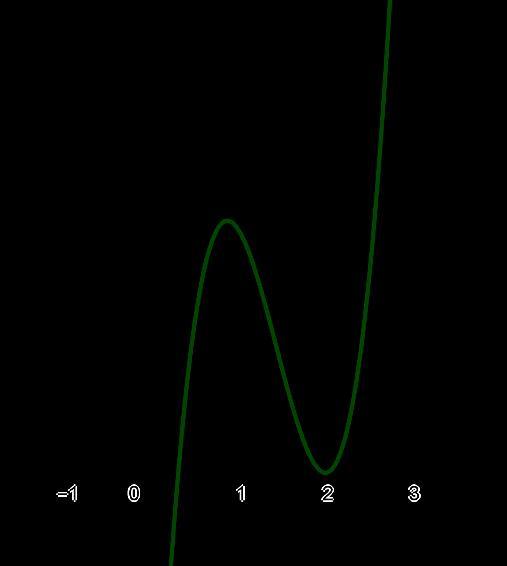
Câu 71: Cho hàm số ( )yfx = xác định và liên tục trên từng khoảng ( );1 và ( ) 1;+ , có bảng biến thiên như bên dưới Đồ thị hàm số ( ) 1 y fx = có tất cả bao nhiêu tiệm cận đứng?
A. 2 B. 4 C. 1 D. 3 Lời giải Chọn A Ta có phương trình ( ) 0 fx = có 2 nghiệm phân biệt, suy ra đồ thị hàm số ( ) 1 y fx = có 2 tiệm cận đứng. Câu 72: Cho hàm số bậc ba ( ) 32 fxaxbxcxd =+++ có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số ( ) ( ) ( ) ( ) 2 42
3221 54. xxx gx xxfx −++ = −+ có bao nhiêu đường tiệm cận đứng? A. 4 B. 3 C. 2 D. 6 Lời giải Chọn C
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 44
x − 21 3 + y+ 4 ++ 1 +
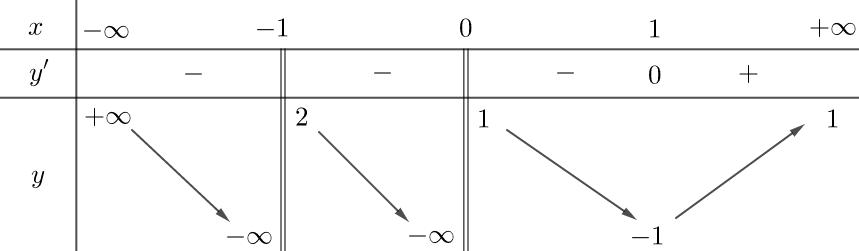
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 45
(
ố
0 1 ;\;1;2 2 Dx =−+ và ( ) ( )( )( ) ( ) 2 0 21 122 x gx axxxxx + = ++−− . Câu 73: Ta có ( ) ( ) // 0 2 lim,lim xxx gxgx+−+−→→ = =+ và 1 lim() x gx → hữu hạn
ị
ố
ệ
cận đứng là 0xx = và
x =
ố
T
đường
ệ
Vì
xx y
→−→− ==
Vì
xx
→+→+ ==
ị
ố
=
Vậy tổng số đường tiệm cận
ng
cận ngang của đồ thị hàm số 1 4()3 y fx = là 6. Câu 74: Cho hàm số ( ) ( ) 32 ,0yfxaxbxcxda ==+++ có đồ thị như hình bên. Gọi S là tập các giá trị nguyên của m thuộc khoảng ( )2019;2021 để đồ thị hàm số ( ) ( ) ( ) ( ) ( )( ) 2 1 222 xfx gx fxxmxm + = −−++ có 5 đường tiệm cận . Số phần tử của tập S là
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Quan sát đồ thị hàm số ( )fx ta thấy đồ thị hàm số cắt trục hoành tại điểm có hoành độ
) 0 0;1 x
, có hệ s
0 a và tiếp xúc với trục hoành tại điểm có hoành độ bằng 2. Từ đó suy ra ( ) ( )( )2 0 2 fxaxxx=−− . Suy ra ( ) ( ) ( ) ( ) ( ) ( ) ( )( ) 22 2 42 42 0 32213221 54. 54.2 xxxxxx gx xxfx xxaxxx −++−++ == −+ −+−− xác định trên
nên đồ th
hàm s
( )gx có 2 ti
m
2
Cho hàm s
()yfx = có bảng biến thiên như sau:
ổng số
ti
m cận đứng và tiệm cận ngang của đồ thị hàm số 1 4()3 y fx = là A. 3. B. 4. C. 5. D. 6. Lời giải Chọn D Dựa vào bảng biến thiên, phương trình 4()30 fx −= có 4 nghiệm 1234 ,,, xxxx thỏa ( ) 1 ;1 x −− , ( ) 2 1;0 x − , ( ) 3 0;1 x , ( ) 4 1; x + . Suy ra đồ thị hàm số 1 4()3 y fx = có 4 tiệm cận đứng là 1xx = , 2xx = , 3xx = , 4xx =
1 limlim0 4()3
fx
nên 0 y = là tiệm cận ngang của đồ thị hàm số 1 4()3 y fx = .
1 limlim1 4()3
y fx
nên 1 y = là tiệm cận ngang của đồ thị hàm số 1 4()3 y fx = Do đó đồ th
hàm s
1 4()3 y fx
có 2 tiệm cận ngang là 0 y = , 1 y = .
đứ
và tiệm
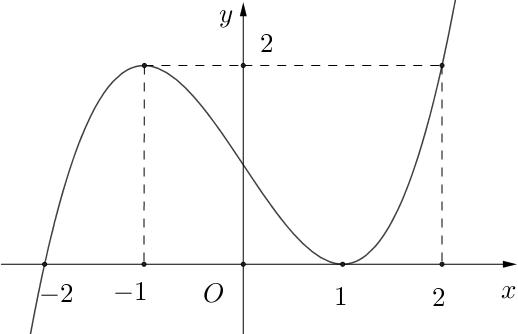
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 46 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
Lời giải Chọn C Đồ thị của hàm số ( )yfx = đi qua bốn điểm ( ) ( ) ( ) ( )2;0,1;2,1;0,2;2 nên ta có 1 84202 20 03 84222 1 a abcd abcdb abcd c abcd d = −+−+= −+−+== +++= =− +++= = Do đó, ( ) ( ) ( ) ( ) 2 2 11 3212 22 fxxxxx =−+=−+ . ( ) ( ) ( ) ( ) ( )( ) ( ) ( ) ( ) ( )( ) ( ) ( )( )( ) 2 32 2 2 2 2 1 112 2 1 3222 2 2112212 21222122 xxx gx xxxmxm xxx xx xxxmxm xxxmxm +−+ = −−−++ +−+ −+ == −+−++ −+−++ Điều kiện xác định của ( )gx là 2 2 2 1 220 x x x xmxm − − −++ Dễ thấy đồ thị hàm số ( )gx có duy nhất tiệm cận ngang là 0 y = , các đường thẳng 2;1xx==−
những tiệm cận đứng. Bởi th
0984164935
A. 4036. B. 4034. C. 2017. D. 2016.
là
ế, để đồ thị hàm số có 5 đường tiệm cận thì đồ thị này phải có thêm 2 tiệm cận đứng nữa. Tức là, phương trình 2 220xmxm−++= có hai nghiệm phân biệt khác 2;1;1 và cùng lớn hơn hoặc bằng 2 Đặt ( ) 2 22hxxmxm=−++ , điều kiện kể trên tương đương với

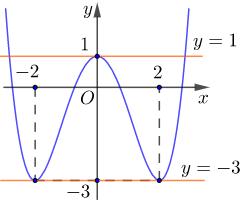
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 47 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) ( )( )( ) 2 12 2 '02012 21106333303 2;3;1 2065066 1 42455 2 m mm mm hhh mmm m mmm h m mm m xx m −− − − −−+ − − + −−− − +− −
trị nguyên của ( )2019;2021 m− thỏa yêu cầu bài toán là 4;5;...;2020, có 2017 giá trị nguyên. Câu 75: Cho hàm số trùng phương có đồ thị như hình vẽ. Hỏi đồ thị hàm số có tổng cộng bao nhiêu tiệm cận đứng? A. B. C. D. Lời giải Chọn B Xét phương trình Quan sát đồ thị, ta có: +) . +) Xét phương trình 42 yaxbxc =++ ( ) ( ) ( ) 3 2 4 23 xx y fxfx = +− 3 5 2 4 ( ) ( ) ( ) ( ) ( ) 2 1 230 3 fx fxfx fx = +−= =− ( ) ( ) 0 1 ,22 x fx xuuu = = =−− ( ) 32fxx=−= 3 0 40 2 x xx x = −= =
Vậy các giá
như hình vẽ bên. Hỏi đồ thị hàm số ( ) ( ) ( ) ( ) 2 2
1 O 1
y 2
x
3221xxx gx xfxfx −+− = có bao nhiêu đường tiệm cận đứng? A. 5. B. 4. C. 6 . D. 3. Lời giải Chọn B Ta có ( ) ( ) ( ) ( ) 2 2
x fx fx
0 0 0 x xfxfx fxfx = −= −= ( ) ( )
0 0 1
= = = 0 x = loại do điều kiện 1 2 x ( ) 0 fx = cho nghiệm 1 2 xa= ; 2 x = là nghiệm kép ( ) 1 fx = cho ba nghiệm đơn 1;; xxbxc === Khi đó có thể viết mẫu thành ( )( )( )( )( ) ( ) 2 12. xxaxbxxcxgx trong đó ( )gx vô nghiệm; tử phân tích thành ( )( ) 1221xxx Suy ra ( ) ( ) ( ) ( ) ( )( )( )( ) ( ) 2 2
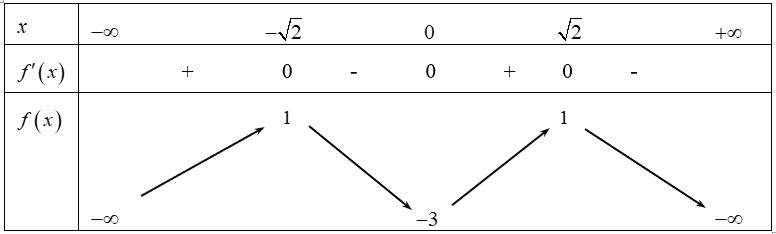
3221 21 2. xxx x gx xxaxbxcxgx xfxfx −+− ==
Ta dễ dàng kiểm tra được hàm sô có 4 tiệm cận đứng là ;;;2xaxbxcx ==== .
Câu 77: Cho hàm số ( )yfx = là hàm số bậc bốn và có bảng biến thiên như sau
Đồ thị hàm số ( ) ( ) ( ) 42 2 2 23 xx gx fxfx = +− có bao nhiêu đường tiệm cận A. 3. B. 4. C. 5. D. 6 . Lời giải
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 48
Vậy
ị
ố đã cho
đườ
ệm cận
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
đồ th
hàm s
có 5
ng ti
đứng. Câu 76: Cho hàm số bậc ba ( ) 32 fxaxbxcxd =+++ có đồ thị
==
2 42 22
2
22 2 23 22
+−
xxx xx gx fxfx xxxxaxb
1 limlim 22 xx gxyR xxxaxb →→ == +−−− nên đường thẳng 0 x = không phải là tiệm cận đứng của đồ thị ( )gx ii) ( ) ( )( )( )( ) (2)(2)
1 limlim 22 xx gx xxxaxb ++→−→− ==+ +−−− nên đường thẳng 2 x =− là tiệm cận đứng của đồ thị ( )gx . iii) ( ) ( )( )( )( ) (2)(2)
1 limlim 22 xx gx xxxaxb ++→→ ==− +−−− nên đường thẳng 2 x = là tiệm cận đứng của đồ thị ( )gx . iv) ( ) ( )( )( )( ) 1 limlim 22 xaxa gx xxxaxb ++→→ ==− +−−− nên đường thẳng xa = là tiệm cận đứng của đồ thị ( )gx v) ( ) ( )( )( )( ) 1 limlim 22 xbxb gx xxxaxb ++→→ ==+ +−−− nên đường thẳng xb = là tiệm cận đứng của đồ
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 49 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Chọn C + Mẫu của ( )gx là một đa thức bậc 8 nên ( ) () lim0 x x gx →− →+ = nên tiệm cận ngang của đồ thị hàm số ( )gx là đường thẳng 0. y = + ( ) ( ) ( ) ( ) (
2 2 2 1
3
x x fx fxfxx fx xaa xbb =− = = +−== =− =− =
( ) ( ) ( ) (
( )
) ( )
2300
,2 ,2
do đó
)( )
( ) ( )(
) thị ( )gx Vậy đồ thị hàm số ( )gx có 5 đường tiệm cận Câu 78: Cho hàm số ( ) 42 3 3231 x y xmxm + = −+++ . Có bao nhiêu giá trị nguyên thuộc đoạn 2019;2019 của tham số m để đồ thị hàm số có 5 đường tiệm cận? A. 2018. B. 2019 C. 2021 D. 2020 Lời giải Chọn B
2
+− +−−− nên i) ( ) ( )( )( )( ) 0 00
ra
n 2019;2019 của tham số m để đồ thị hàm số có 5 đường tiệm cận là 2019. Câu 79: Cho hàm số ( )yfx = có bảng biến thiên như sau: Số đường tiệm cận đứng của đồ thị hàm số ( ) ( ) 1 1 gx fx = + là A. 3. B. 4. C. 1. D. 2. Lời giải Chọn A Từ bảng biến thiên suy ra phương trình ( ) 1 fx =− có hai nghiệm phân biệt a và b Suy ra tập xác định của hàm số ( ) 1 1 y fx = + là \0;; Dab =
1 lim 1 x fx → =+ + ; ( ) 1 lim 1 xa fx + → =+ + ; ( ) 1 lim 1 xb fx + → =−
+ . Do đó, đồ thị hàm số ( ) ( ) 1 1 gx fx = + có 3 đường tiệm cận đứng.
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 50
−+++ 2 2
+ 2
+
→
310 311 319
m m + + + 1 3 0 8 3 m m m −
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Hàm số đã cho xác định khi: ( ) 4232310xmxm
1 31 x xm
1 31 x xm
. Ta có: ( ) lim0 x fx
= . Suy ra đồ thị hàm số có một TCN là đường thẳng 0 y = Vậy đồ thị hàm số có 5 đường tiệm cận khi nó có 4 đường TCĐ phương trình 2 31xm=+ có hai nghiệm phân biệt khác 1,3−
m
Suy
số giá trị nguyên thuộc đoạ
Câu
ố
m
ị
ố 2 2 43
xx
xmx −+− = −+
ệ
.
.
Chọn
Ta
2 43013xxx −+− +∞
∞ ∞
Ta có: ( ) 0 x ∞
80: Có bao nhiêu s
nguyên
để đồ th
hàm s
2
y
có hai đường ti
m cận đứng? A. 0. B. 1
C. 2. D. 3
Lời giải
B
có
1 + ∞ 0 2 1 0 +
y y'
Đồ thị hàm số 2 2 43 2 xx y xmx −+− = −+ có hai đường tiệm cận đứng khi và chỉ khi phương trình 2 20 xmx−+= có hai nghiệm phân biệt thuộc [1;3] 2 2 2 20() x xmxmfx x + −+=== 2 2 2 '();'()02 x fxfxx x === Bảng biến thiên Vậy 223 m
Câu 81: Cho hàm số axb y cxd + = + có đồ thị ( )C . Gọi giao điểm của hai đường tiệm cận là I . Điểm ( )000 ; Mxy di động trên ( )C , tiếp tuyến tại đó cắt hai tiệm cận lần lượt tại , AB và 2 IAB S = . Tìm giá trị 2 0IM sao cho 12 1 IAB

SS S
+ = A. 2

Chọn B
Nhận thấy kết quả bài toán không thay đổi khi ta tịnh tiến đồ thị ( )C theo IO . Khi đó hai tiệm cận của ( )C là hai trục tọa độ.
Và hàm số của đồ thị ( )C trở thành: ( ) 2 0 yy x x ==− .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 51
B. 41 20 C. 169 60 D. 189 60 Lời giải
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 52 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Gọi d là tiếp tuyến tại ( ) ( ) 000022 0000 2 ;: Mxydyxxx xxxx =−−+=−+ Suy ra: ( ) 0 2;0OxdAx = và 0 2 0; OydB x = 1 .2221 2 OAB SOAOBa ==== ( ) 0 2 000 0 11222 ,:,0;,; 2 x cydyxBC xxxx x ==−+ 0 0 10 2 00 0 2 1212131 22 x o x Sxdx xxxx x =−−−=− Và ( ) 0 0 2 200 2 0 0 11131 2 22 4 x x Sdxxx xx x =−−=− Theo giả thiết 22 12 1200 22 00 3354 112 45 4 IAB IAB SS SSSxy S xx + =+=+−=== Vậy 222 000 41 20 IMxy=+= . Câu 82: Số giá trị nguyên của tham số m sao cho đồ thị hàm số 2 1 2 x y xxm + = −+ có
ba
ng tiệm cận. A. 5. B. Vô số.
. D. 4. Lời giải Chọn C + 2 1 limlim0 2 xx x y xxm →+→+ + == −+ nên đồ thị hàm số có tiệm cận ngang 0. y = + Vậy để đồ thị hàm số 2 1 2 x y xxm + = −+ có đúng ba đường tiệm cận thì đồ thị hàm số có hai tiệm cận đứng 2 20xxm −+= có 2 nghiệm phân biệt 12 , xx lớn hơn hoặc bằng 1 ( )( ) ( ) ( ) 12 12 010 11021031. 11040 m xxmm xx − ++++− +++ Vì 2;1;0. mm−− Câu 83: Có bao nhiêu giá trị của m để hai đường tiệm cận của đồ thị hàm số ( ) 23 x fx xm + = tạo với hai trục toạ độ một hình chữ nhật có diện tích bằng 2022. A. 4 B. 1 C. 2 D. 3
đúng
đườ
C. 3
Lời giải Chọn C Để đồ thị hàm số ( ) 23 x fx mx + = có hai đường tiệm cận 3 2 m − . Khi đó đồ thị hàm số có tiệm cận ngang là 2 y =− và tiệm cận đứng là xm = Hai đường tiệm cận của đồ thị hàm số tạo với hai trục tọa độ một hình chữ nhật có kích thước là 2 và m . Để hình chữ nhật tạo thành có diện tích bằng 2022 2.2022 m = 10111011mm == . Câu 84: Cho hàm số 21 1 x y x = có đồ thị ( )C . Gọi (;)Mab là điểm thuộc đồ thị hàm số có hoành độ dương sao cho tổng khoảng cách từ M đến hai tiệm cận của ( )C nhỏ nhất. Khi đó tổng 2 ab + bằng A. 8. B. 5. C. 2. D. 7. Lời giải Chọn A Hàm số 21 1 x y x = có đường tiệm cận ngang 2 y = và đường tiệm cận đứng 1 x = . Khi đó: +) Khoảng cách từ (;)Mab đến tiệm cận ngang là: 211 22 11 a b aa −=−= ; +) Khoảng cách từ (;)Mab đến tiệm cận đứng là: 1 a Ta có 11 1212 12 aa aa −+−= . Vậy tổng khoảng cách nhỏ nhất là 2 khi
328
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 53
( ) ( ) 2 2 10 11120 12 al aaaa a a = −=−=−= = . Suy ra 2.21
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 21 bab ==+= . Câu 85: Cho hàm số ( ) 2 2 212 x y mxmxm = −−+− có đồ thị ( ) m C . Có bao nhiêu giá trị nguyên của tham số m để ( ) m C có đúng 2 đường tiệm cận? A. 2 B. 1 C. 0 D. 3 Lời giải Chọn A + TH1) 0 m = , ta được hàm số 2 22 x y x = , suy ra đồ thị hàm số có tiệm cận đứng 1 x = ; tiệm cận ngang 1 2 y = .
= −−+−= = . Để đồ thị hàm số ( ) m C có đúng 2 đường tiệm cận thì đồ thị hàm số ( ) m C chỉ có 1 tiệm cận đứng ( ) 2 2120mxmxm −−+−= hoặc có hai nghiệm phân biệt trong đó có một nghiệm bằng 2 hoặc có nghiệm kép ( )( ) ( ) 2 121212 1212
m m m m m mm xxxxxx xxxx
2 2 2 2 1 020 11010 20 1 2
Vậy có 2 giá trị nguyên của tham số m thỏa yêu cầu bài toán. Câu 86: Tìm tất cả các giá trị của tham số m sao cho đồ thị hàm số 2 12022 22 x y xmxm +− = −++ có đúng ba đường tiệm cận? A. 12 m − . B. 12 m − . C. 2 m . D. 2 m hoặc 1 m − . Lời giải Chọn C TXD: ) 1; D =−+ . Ta có lim0, x y →+ = đồ thị hàm số luôn có một đường tiệ m mmm m
= =− = −− +++++ +++ − ( ) ( ) ;12; 22102 220
xx lớn hơn hay bằng 1. −−+ +++ + Câu 87: Cho đồthị hai hàm số ( ) 1 1 x fx x + = và ( ) 1 2 ax gx x + = , 1 2 a − .Tìm tất cả cácgiátrị thựcdương của a để các tiệm cận của hai đồ thị hàm số tạo thành một hình chữ nhật có diện tích là 4 A. 2 a = . B. 4 a = . C. 3 a = . D. 5 a = . Lời giải Chọn D
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 54
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
+ TH2) 0 m , ta có: limlim00 xx yyy →+→− === là tiệm cận ngang của đồ thị hàm số. Xét phương trình: ( ) ( ) 2 1 212002 x mxmxmm m x m m cận ngang 0 y = . Để ĐTHS có ba đường tiệm cận ĐTHS có đúng hai đường tiệm cận đứng. phương trình 2 220xmxm−++= có hai nghiệm phân biệt 12 ,
Đồ thị hàm số ( ) 1 1 x fx x + = có hai đường tiệm cận là 1 x = và 1 y =
Đồ thị hàm số ( ) 1 2 ax gx x + = có hai đường tiệm cận là 2 x = và ya = .
Hình chữ nhật được tạo thành từ bốn đường tiệm cận của hai đồ thị trên có hai kích thước lần lượt là 1 và 1 a .
Theo giả thiết, ta có 1.14 a −= 5 3 a a
= =− . Vì 0 a nên chọn 5 a = .
Câu 88: Cho hàm số 2 1 2 mxx y x ++ = . Tìm để đồ thị hàm số có đúng hai tiệm cận ngang. A. 1 m . B. 0 m . C. 0 m = D. 1 m = Lời giải Chọn B
Vì 2 2 11 1 limlim 22 1 xx
++ ++ ==
xm mxx xx m x x x →+→+
11
m
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 55
2 3 x y xm = + có 3 tiệm cận. Tìm số phần tử của S A. Vô số. B. 1. C. 3. D. 2. Lời giải Chọn D Ta có: 2 2 3 31 limlim1 1 xx x x m xm x →−→− ==− + −+ và 2 2 3 31 limlim1 1 xx x x m xm x →+→+ == + + Do đó, đồ thị hàm số luôn có 2 tiệm cận ngang là 1 y =− ; 1 y = . Để đồ thị hàm số có 3 tiệm cận thì chỉ cần có thêm 1 tiệm cận đứng. Trường hợp 1: 2 0 xm+= có nghiệm kép khác 3, nên 0 m = Trường hợp 2: 2 0 xm+= có 2 nghiệm phân biệt, trong đó có 1 nghiệm 1 3 x = , nghiệm 2 3 x Vì 2 12 33093xmmx =+==−=− m
Và 2 2
1 limlim 22 1 xx xm mxx xx
x x x →−→− −++ ++ ==−
Vậy đồ thị hàm số có hai tiệm cận ngang khi 0 m Câu 89: Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số
Suy ra 9 m =− Vậy có 2 giá trị của m thỏa ycbt.
−+ = −++ có đúng ba đường tiệm cận? A. 2 m hoặc 1 m − B. 23 m C. 23 m D. 2 m Lời giải Ch = +−= =− Điều kiện để đồ thị hàm số 2 2 2 xx y xm +− = + có hai tiệm cận đứng là: Phương trình mẫu số 2 0 xm+= có hai nghiệm phân biệt khác 1 và 2 ( ) ( ) 2 2 2
giá tr
ọn B Ta có lim0, x y 00 101;0\4;1 204
= đồ thị hàm số luôn có 1 đường tiệm cậ xm m mmm m m
nguyên c
a tham s
91: S =− +−−−− − −+ Vì 2022;2022 m− và 2022;2021;2020;...;5;3;2 mm−−−−−− Vậy có 2020 số nguyên của m thỏa mãn yêu cầu bài toán.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 56
→+
n ngang 0 y = Để đồ thị hàm số có ba đường tiệm cận đồ thị hàm số có đúng 2 đường tiệm cận đứng phương trình 2 220xmxm−++= có hai nghiệm phân biệt 12 , xx lớn hơn 1 ( )( ) ( ) ( ) 12 12 '0 110 110 xx xx −− −+− ( ) ( ) ( ) 2 1212 12 ;12; 20 10221023 220 20 m mm xxxxmmm m xx −−+ −− −+++−+ − +− Câu
ố
ị
ủ
ố
Câu 90: Tìm tất cả các giá trị của tham số m sao cho đồ thị hàm số 2 − để
12022 22 x y xmxm số 2 2 2 xx y xm +− = + có hai tiệm cận đứng. A. 2018. B. 2020. C. 2022. D. 2023. Lời giải Chọn B Ta có 2 1 20 2 x xx x
2022;2022 m
đồ thị hàm
Câu 92: Cho hàm số ( ) ( ) 32 22
1221 146 mxmxmx y mxmx −+++ = +−− có đồ thị là ( )C . Tổng tất cả các giá trị nguyên của tham số m để đồ thị hàm số ( )C có tổng số đường tiệm cận đứng và tiệm cận ngang là 3. A. 1. B. 2. C. 3. D. 4.
Lời giải
Chọn A
TH1: Với 1 m = hàm số trở thành 2 2 221 246 xx y xx ++ = Khi đó đồ thị hàm số có 1 đường tiệm cận ngang là đường thẳng 1 y = và hai đường tiệm cận đứng có phương trình là 1 x =− và 3 x = nên 1 m = thoả mãn.
TH2: Với 1 m khi đó: ( ) lim x fx →− =− và ( ) lim x fx →+ =+ nếu 1 m hoặc ( ) lim x fx →− =+ và ( ) lim x fx →+ =− nếu 1 m
33 2221 x y xxmx = −−+−− với m là tham số. Có bao nhiêu số nguyên m thuộc đoạn x x
3;6 để đồ thị hàm số có 4 đường tiệm c y y
= − =
→+ →−
Đồ thị hàm số có 2 đường tiệm cận ngang. Khi đó đồ thị hàm số có 4 đường tiệm cận khi đồ thị hàm số có 2 đường tiệm cận đứng 2 22210 xxmx−−+−−= có 2 nghiệm phân biệt khác 1 Ta có ( ) 2 2
− −−+=+ −−+= Phương trình ( )* có 2 nghiệm phân biệt 12 , xx thỏa mãn 1 11 x − , 2 11 x −
1 2221 410 * x xxmx xxm
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO
KHẢO SÁT HÀM SỐ
HÀM ĐỂ
Page 57
Vậy đồ thị hàm số không có đường TCN. Đồ thị không thể có nhiều hơn 2 TCĐ. Kết luận 1 m = thì đồ thị hàm số ( )C có tổng số đường tiệm cận đứng và tiệm cận ngang là 3. Câu 93: Cho hàm số 2 ận? A. 7. B. 8. C. 9. D. 10. Lời giải Chọn B Ta có lim3 21 lim3 21
Khi đó 110 x +− nên đồ thị hàm số đã cho có đúng hai đường tiệm cận đứng khi phương trình 22404 xxmxxm −−=−= có hai nghiệm phân biệt thuộc ) 1;+ Bảng biến thiên của hàm số 2 4 yxx =− trên ) 1;+ như sau Dựa vào bảng biến thiên ta có giá trị m cần tìm là ( 4;3 m−− Câu 95: Cho hàm số 2 2 1 49 +− = ++ axx y xbx có đồ thị ( )C , trong đó a , b là các hằng số dương thỏa mãn .4 = ab Biết rằng ( )C có đường tiệm cận ngang = yc và có đúng 1 đường tiệm cận đứng. Tính tổng 324=+− Tabc . A. 11= T . B. 4 = T . C. 7 = T . D. 11=− T . Lời giải
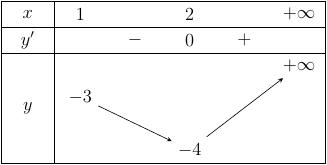
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 58 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( )( ) ( ) ( ) 2 12 1212 1 12 2 12 0303 14.11022 111010 120 110 m m m m m xx xxxx x xx x xx + − − − −−+ ++ +++ − ++ − +++ . Theo định lý vi et ta có 12 12 4 1 xx xxm += =−+ khi đó 1212 12 3 2 10 20 m m xxxx xx − − +++ ++ 3 2 1410 420 m m m − − −+++ + 3 22 636 420 m mm mm − −− − + . Do m nên 1;0;1;2;3;4;5;6 m− có 8 giá trị. Câu 94: Tập hợp các giá trị thực của tham số m để đồ thị hàm số 2 11 4 x y xxm +− = có đúng hai
ọ
đường tiệm cận đứng là A. ( ) 4; −+ B. 4;3 C. ( )4;3 D. ( 4;3 Lời giải Ch
n D Hàm số xác định khi 2 1 40 x xxm −−
.
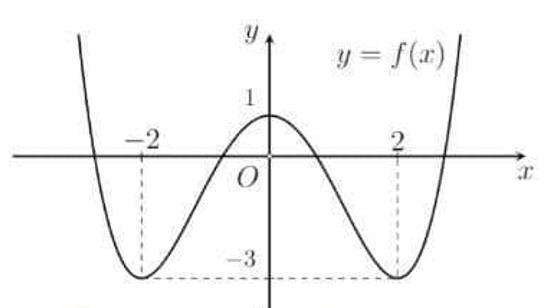
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 59
. Câu 96: Cho hàm trùng phương 42 yaxbxc =++ có đồ thị như hình vẽ. Hỏi đồ thị của hàm số ( )( ) ( ) ( ) 22 2 42 23 xxx y fxfx −+ = +− có tồng cộng bao nhiêu tiệm cận đứng? A. 3 B. 4 C. 2 D. 1 Lời giải Chọn A Xét tử: ( )( ) ( ) ( ) ( ) 22 01 42021 22 xb xxxxb xb = −+== =− .( )* Xét mẫu: ( ) ( ) ( ) ( ) 2 1 230 3 fx fxfx fx = +−= =− Với ( ) ( ) ( ) ( ) 02 121 21 xb fxxab xbb = ==− = . Kết hợp với ( )* suy ra: 0;; xxaxb === là tiệm cận đứng của đồ thị hàm số. Với ( ) ( ) ( ) 22 3 22 xb fx xb = =− =− . Kết hợp với ( )* suy ra: 2 x = là tiệm cận đứng của đồ thị hàm số Vậy có 3 đường tiệm cận.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Chọn D Theo giả thiết 0 a , 0 b Với 4 = ab ta có ( ) ( ) 2 22 22 22 4 1 1419 4949 4949 xx axxxbxbb b y xbxxbxbbxbxbxbx +− +−+−+ ====− ++++ ++++ . Đồ thị ( )C có đúng 1 đường tiệm cận đứng nên 2 490 ++=xbx có nghiệm kép Suy ra 2 4.4.9012=−== bb Ta có 4 = ab suy ra 1 3 = a ; 2 2 2 2 11 1 limlim 9 494 4 →+→+ +− +− === ++ ++ xx a axxa xx c b xbx xx suy ra 1 12 = c . Vậy 32411=+−=Tabc
Câu 97: Cho hàm trùng phương 42 yaxbxc =++ có đồ thị như hình vẽ. Hỏi đồ thị của hàm số ( )( ) ( ) ( ) 22 2
xxx y fxfx
42 23
−+ = +− có tồng cộng bao nhiêu tiệm cận đứng?
A. 3. B. 4. C. 2. D. 1. Lời giải
Chọn A
xb xxxxb xb
Xét tử: ( )( ) ( ) ( ) ( ) 22
= −+== =− ( )*

01 42021 22
02 121 21
xb fxxab xbb ủa đồ thị hàm số. Vậy có 3 đường tiệm cận. Câu 98: Có bao nhiêu giá trị của tham số để đồ thị hàm số 2 2 1 32 mx y xx = −+ có đúng 2 tiệm cận? A. 2. B. 1. C. 4. D. 3. Lời giải Chọn A + Ta có: 2 2 2 2
= ==− = . Kết hợp với ( )* suy ra: 0;; xxaxb === là tiệm cận đứng của đồ thị hàm số. Với ( ) ( ) ( ) 22 3 22 xb fx xb = =− =− . Kết hợp với ( )* suy ra: 2 x = là tiệm cận đứng c 1 1 limlimlim 32 32 1 xxx
m mx x ymym xx xx →−→−→− ==== −+ −+ là tiệm cận ngang của đồ thị hàm số.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO
ĐỂ KHẢO SÁT HÀM SỐ
HÀM
Page 60
Xét mẫu: ( ) ( ) ( ) ( ) 2 1 230 3 fx fxfx fx = +−= =− . Với ( ) ( ) ( ) ( )
+ Để đồ thị hàm số 2 2 1 32 mx y xx = −+ có đúng 2 tiệm cận 2 2 1 32 mx y xx = −+ có đúng 1 tiệm cận đứng. Ta có: 2 1 320 2 x xx x
= −+= =

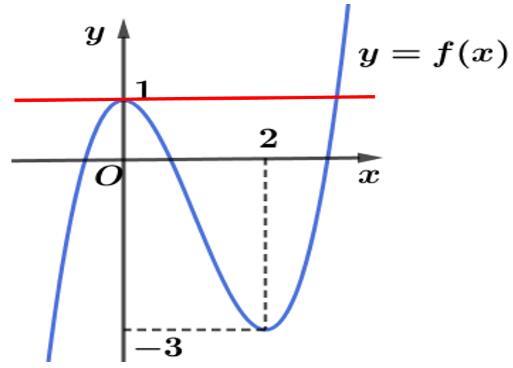
= = . Vậy có 2 giá trị tham số thỏa mãn yêu cầu đề bài. Câu 99: Cho hàm số ( ) 32 yfxaxbxcxd ==+++ có đồ thị như bên dướ
.110 .210 m m −= −= 1 1 4
2 i. Hỏi đồ thị hàm số ( ) ( ) ( ) ( ) 2 2 22 3 xxx y xfxfx = có bao nhiêu đường tiệm cận đứng A. B. 5 C. 4 D. 6 Lời giải Chọn A Điều kiện: ( ) ( ) 2 2 3 0 x x fxfx − Ta xét: ( ) ( ) ( ) ( ) ( ) ( ) 2 01 0 12 fx fxfx fx = −= = ( ) ( ) ( ) ( )( )( ) 1 2123 3 0 10;2 2 xx xxfxaxxxxxx xx = ==−−− = 3
m m
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 61
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
2
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 62
(
xxx = −=− =
+) ( )( ) 22 2 222 11 limlimlim 2 21 xxx xmxxmx y x xxmx +++ →−→−→− == + +−+ +) ( )( ) 22 2 222 11 limlimlim 2 21 xxx xmxxmx y x xxmx →−→−→− == + +−+ . Đồ thị hàm số nhận đường thẳng 2 x =− là đường tiệm cận đứng khi: ( ) ( ) ( ) ( ) 2 ,10;10 2 2.2103 22;1;...;10 2.202 mm m m m m m − −−−− − ⎯⎯⎯⎯⎯⎯→−− −−− − Như vậy có 13 giá trị nguyên của m thỏa mãn bài toán.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
) ( ) ( ) ( ) 2 4 43 0 21 xkép fxaxxx
Khi đó ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 22 2 2222 31 3 xxxxxx y xfxfx xfxfx == ( ) ( ) ( )( )( ) ( ) ( ) ( )( )( )( )( ) 22 12341234 2222 33 xxxxx xaxxxxxxaxxxaxxxxxxxxxx == Do 2 x nên đồ thị hàm số có 3 đường tiệm cận đứng là 120;; xxxxx === Câu 100: Trên đoạn 10;10 có tất cả bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số 2 1 2 xmx y x = + có đúng ba đường tiệm cận? A. 19. B. 7. C. 13. D. 9. Lời giải Chọn C Điều kiện: 2 0 2 xmx x − − Ta có +) lim11 x yy →+ == là TCN của đồ thị hàm số. +) lim11 x yy →− =−=− là TCN của đồ thị hàm số Suy ra đồ thị hàm số có đúng ba đường tiệm cận khi và chỉ khi đồ thị hàm số có đúng một đường tiệm cận đứng. Ta có:
Câu 101: Cho hàm số 22 23 x y x + = có đồ thị ( )C . Có bao nhiêu điểm M thuộc ( )C sao cho khoảng cách từ điểm M đến đường tiệm cận ngang bằng 10 lần khoảng cách từ điểm M đến đường tiệm cận đứng. A. 1. B. 2. C. 3. D. 4. Lời giải
Chọn B
) ( ) 2 2 2;6 2 23141280 1 1;4 M x xxx x M = −=−+= = .
Câu 102: Cho hàm số 2 2 22 x y xmxm = . Biết với a m b = ( , ab , a b tối giản) thì đồ thị hàm số có đúng 2 đường tiệm cận. Tính ab + . A. 7 ab+= B. 5 ab+= C. 8 ab+= D. 6 ab+= Lời giải Chọn A Để đồ thị hàm số có đúng 2 đường tiệm cận thì hoặc phương trình 2 220xmxm−−−= có nghiệm kép 2 x = hoặc phương trình 2 220xmxm−−−= phải có hai nghiệm . Do 2 '20,mmm =++ nên ta chỉ xét trường hợ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 63
ng tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số. ( ) 22 ; 23 x MCMx x + với 3 2 x Khoảng cách từ điể
Ta có các đường thẳng 3 2 x = và 1 y = lần lượt là đườ
m M đến đường tiệm cận đứng bằng 23 3 22 x x −= . Khoảng cách từ điểm M đến đường tiệm cận ngang bằng 225 1 2323 x xx + −= . Khi đó: 23 5 10. 232 x x = ( ) (
ứ
2 220
−−−= có hai nghiệm phân biệt. Thay 2 x = vào phương trình ta
c 2 5 m = Vậy 2,5,7abab==+= . Câu 103: Tập hợp các giá trị của m để đồ thị hàm số ( )( ) 22 20222021 21441 x y mxxxmx = −+++ có đúng 1 đường tiệm cận là A. ( ) ( ) ;101;. −−+ B. ( ) ( ) ;11;.−−+ C. D. 0.
p th
hai phương trình
xmxm
đượ
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 64 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT
10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn D Có lim0 x y → = . Nên hàm số luôn có 1 đường tiệm cận ngang 0 y = . Vậy ta tìm điều kiện để hàm số không có tiệm cận đứ
=− Cả 2
và đều vô nghiệm: 2 101 44011 m m m m m − − − Vậ
=
ả các giá trị của tham số m sao cho đồ thị hàm số 32 1 31 x y xxm = +++ có đúng một tiệm cận đứng. A. 4 0 m m − B. 5 1 m m − − C. 51 m −− D. 5 1 m m − − Lời giải Chọn D Đặt ( ) 3231 f xxxm = +++ ; ( ) ( ) 2 6; 2 0 0 3 xxx x x x f f + =− = = = Trường hợp 1: ( ) 1013105 gmm=+++==− . Khi đó ( ) ( )( )2 323412 g xxxxx +− = =−+ ( )( )2 1 12 x y xx = −+ ( )( )2 11 11 limlim 129 xx x y xx →→ == −+ ; ( )( )2 22 1 limlim 12 xx x y xx ++→−→− ==+ −+ ; ( )( )2 22 1 limlim 12 xx x y xx →−→− ==+ −+ Nên đồ thị hàm số chỉ có một tiệm cận đứng 2 x =− . Trường hợp 2: ( ) 1013105 gmm+++− .
0984164935
Toán
ng. Xét phương trình: ( )( ) 2 22 2 210 214410(1) 4410 (2) mxx mxxxmx xmx −+= −+++= ++= TH1: Xét 0 m = , ta được ( )( ) 2 2 211 41 2141 x y x xx ==− + −++ TH2: Xét 0 m . Có: 1 1 m =− và 2 2 44 m
phương trình
y 0 m
Câu 104: Tìm tất c
Đồ thị hàm số đã cho có đúng một tiệm cận đứng khi phương trình ( ) 0 g x = có nghiệm duy nhất ( ) ( ) ( )( ) 5 0.20150 1 m ggmm m − −++ − . Kết hợp hai trường hợp ta có những giá trị m cần tìm là: 5 1 m m − − Câu 105: Cho hàm số 322 3 3(21)xm = −++− x y xmxm . Có bao nhiêu giá trị nguyên thuộc đoạn 6;6 của tham số m để đồ thị hàm số có 4 đường tiệm cận? A. 8. B. 9. C. 12. D. 11. Lời giải Chọn B Gọi ( )C là đồ thị hàm số 322 3 3(21)xm = −++− x y xmxm .
x y xmxm nên đồ thị hàm số có 1 đường tiệm cận ngang là 0. = y Do đó ( )C có 4 đường tiệm cận khi và chỉ khi ( )C có 3 đường tiệm cận đứng ( ) ( ) 322321xm01−++−= xmxm có 3 nghiệm phân biệt khác 3 Ta có ( )( ) 2 (1)210 −−+= xmxmx −
−+= xm xmx . Phương trình (1) có 3 nghiệm phân biệt khác 3
22 2 3 10 210 3610
2 210 = m m m m ( ) ( ) 55 ;11;;33; 33 −−+ m Do 6;6−m , m nguyên nên 6;5;4;3;2;2;4;5;6−−−−−m . Vậy có 9 giá trị m thỏa mãn. Câu 106: Cho hàm số ( ) ( ) 2 2022 gx hxmm = với ( ) ( ) 432 ,,, hxmxnxpxqxmnpq =+++ . Hàm số ( )yhx = có đồ thị như hình vẽ bên dưới
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 65
2
− −+ −+
m
Ta có: ( ) 322 3 limlim0 321xm →→ == −++− xx 3 1 1 5 3
m
mm m
Tìm các giá trị m nguyên để số tiệm cận đứng của đồ thị hàm số ( )ygx = là 2. A. 11. B. 10. C. 9. D. 20. Lời giải Chọn B
Ta có ( ) 32 432 hxmxnxpxq =+++

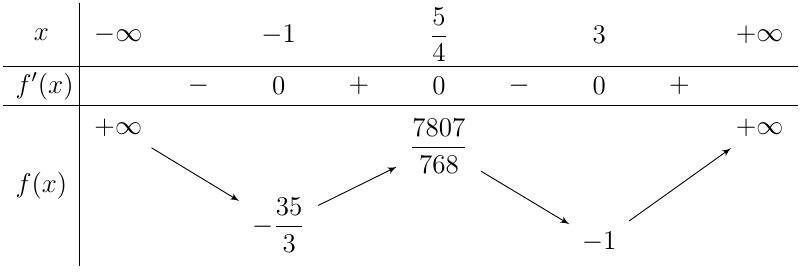
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 66
. Từ đồ
ị ta có ( ) 1 5 0 4 3 x
x =− == = và
.
432 13 15 3 hxmxmxmxmxC =−−++ . Từ đề bài ta có 0 C = Vậy ( ) 432 13 15 3 hxmxmxmxmx =−−+ Xét ( ) 2432 13 0151 3 hxmmmxxxx −−==−−+− . Xét hàm số ( ) ( ) 43232 1 135 1514132150 34 3 x fxxxxxfxxxxx x =− =−−+−=−−+== = . Bảng biến thiên Để đồ thị hàm số ( )gx có 2đường tiệm cận đứng phương trình ( ) 2 0 hxmm−−= có 2 nghiệm phân biệt phương trình 432 13 151 3 mxxxx =−−+− có 2 nghiệm phân biệt.
th
hxx
( )0 m
Suy ra ( ) ( ) ( ) 32 5 413413215 4 hxmxxxmxmxmxm
=+−−=−−+ Suy ra ( )
Từ bảng biến thiên kết hợp thêm điều kiện 0 m ta có 35 1 3 m −−
Do m nguyên nên 11;10;...;2 m−−− . Vậy có 10 số nguyên m thỏa mãn yêu cầu bài toán.
Câu 107: Tìm giá trị nguyên thuộc đoạn [2022;2022] của tham số m để đồ thị hàm số 2 3 = +− x y xxm có đúng hai tiệm tiệm cận. A. 2011 B. 2012 C. 2013 D. 2010 Lời giải
Chọn A
Ta có 2 3 lim0 →+ = +− x
x xxm suy ra đường thẳng 0 = y là tiệm cận ngang với mọi m Để đồ thị hàm số 2 3 = +− x y xxm có đúng hai tiệm cận thì phương trình ( ) 2 0* xxm+−= có nghiệm kép 3 x hoặc có hai nghiệm phân biệt trong đó 1 3 x và 2 3 x . Phương trình ( )* tương đương với ( ) 2 mfxxx ==+ , với 3 x Có ( ) ( ) 210 3 fxxfxx =+ . Suy ra hàm số ( )yfx = đồng biến trên ) 3;+ .
Khi đó yêu cầu bài toán tương đương với ( ) 312 mf= Suy ra 122022 m Vậy số giá trị m thỏa mãn là 2011.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ I GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 67