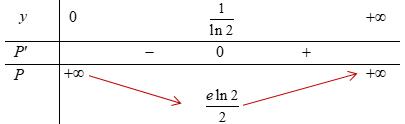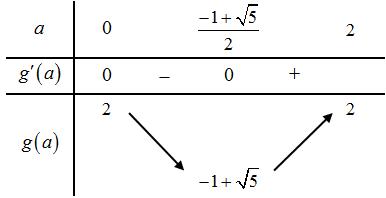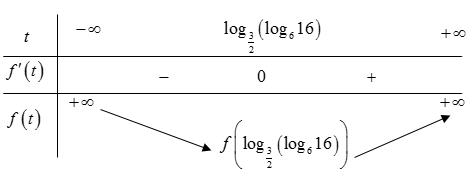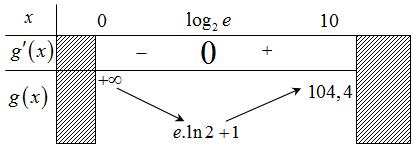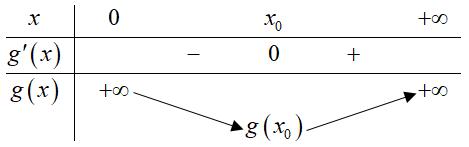CHUYÊN ĐỀ VẬN DỤNGVẬN DỤNG CAO MÔN TOÁN Ths Nguyễn Thanh Tú eBook Collection CHUYÊN ĐỀ VẬN DỤNG - VẬN DỤNG CAO LUYỆN THI TỐT NGHIỆP THPT NĂM 2023GIẢI TÍCH 12 - CHUYÊN ĐỀ II LŨY THỪAMŨ LOGARIT WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405



CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 1 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn LUỸ THỪA HÀM SỐ LUỸ THỪA LOGARIT HÀM SỐ MŨ HÀM SỐ LOGARIT MỨC ĐỘ VẬN DỤNG VẬN DỤNG CAO Câu 1: Cho ba số thực ,, xyz không âm thỏa mãn 2484 xyz++= . Gọi , MN lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 632 xyz S =++ . Đặt 26 TMN =+ , khẳng định nào sau đây là đúng? A. ( )1;2 T . B. ( )2;3 T . C. ( )3;4 T . D. ( )4;5 T . Lời giải Chọn A 23 24842224 xyzxyz ++=++= . Ta có 3 232323 2 64 42223.222363log3 27 xyzxyzxyz xyz ++++ =++++− . Khi đó 2 1 1log3 2 S − . Suy ra 2 1 1log3 2 M =− Đặt 2 2 2 3 2 2log 1 42log 2 1 82log 3 x yy yz axa byb czb == === === , khi đó 44 abcbca ++=+=− Do ,,0xyz nên ,,1abc , ta có ( )( ) ( ) ( ) 11014133 bcbcbcbcabcaabcaa −−+−−−−− Xét ( ) 2 3 fxaa =− đạt GTNN trên ) 1; a+ là 39 24 f = Suy ra 2 9 3 4 abcaa− . Mặt khác ( ) 22 119 loglog 632664 xyz Sabc =++= Khi đó ( ) 22 111 2log32log3 633 N =−=− . CHƯƠNG II HÀM SỐ LŨY THỪA - HÀM SỐ MŨ HÀM SỐ LOGARIT
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 2 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vậy ( ) 222 111 2621log36log3log31;2 233 TMNT =+=−+−=⎯⎯→ Câu 2: Cho các số thực , abthỏa mãn 1 ab và 11 2022. loglog baab += Giá trị của biểu thức 11 . loglogabab P ba =− A.
ờ
ả
Chọn A ⚫ 11 loglog2022loglog2022(*). ab ba ba ab +=+= ⚫ 11 logloglog()log()loglog. baba abab Pababab ba =−=−=− ⚫ Đặt loga tb = thì (*) trở thành: 2 202220181 2018 1 2
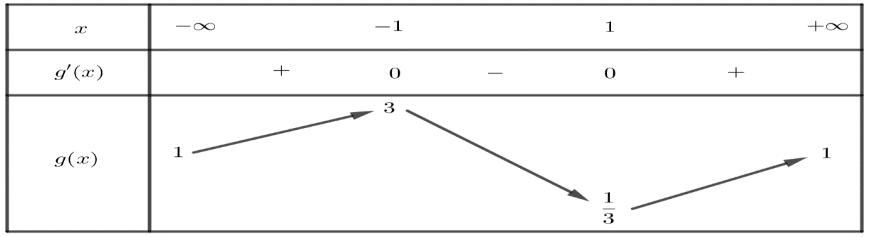
p thành một cấp số nhân . . Câu 4: Cho là ba số thực dương khác và . Biết . Khi đó giá trị của bằng bao nhiêu? ,, abc 64
++= ( ) ( ) 22 3loglog Pabbccaabc =++− 18 24 6 8 ,, abc 2acb= ( ) ( ) 22 3loglog Pabbccaabc =++− ( ) ( ) 22 22 3loglog. abbcbbb=++− ( ) ( ) 3 22 3loglogbabcb=++− ( ) 3 22 3log64logbb=− ( ) ( ) 3 3 22 log64logbb=− ( )3 6 2 3 2. log b b = 183 2 3log2.b b = 18 2 log218== ,, abc 1 1 abc log53,log54,log510 17 ababc === log5 c
2018. B. 2020. C. 2016. D. 2022. L
i gi
i
2022202210. 202220181 2018 2 tPt t ttt t tPt t + ==−=−
+=−+=
==−=
⚫ 10log1 a abb nên 11 01102018. tPtP tt =−= Câu 3: Cho ba số thực dương theo thứ tự lập thành một cấp số nhân và . Giá trị của biểu thức bằng: A. . B. . C. . D. . Lời giải Chọn A Ta có: theo thứ tự lậ
abc
33 log3logloglog16log22log2 888xxxxx x yyy yyy ==== ( ) 2log16log2log2 xxx = 2 1 16log24log2log416. 4 xx xx ==== Từ (*) suy log52 c = 1 log55 c = log567 60 c = log560 67 c = 5 1 log53log. 3 a a == 5 1 log54log. 4 b b == 5 1017 log5log. 1710 abc abc == 55555555 171167 loglogloglogloglogloglog 103460 abcabccabcab =++=−−=−−= log560 67 c =
323216 log2log16log2(*). log x xxy yyx ==== ( ) 3 ra 4 y = . Vậy 2222164240. Pxy=−=−= Câu 6: Cho các số thực dương 1,1xy thỏa mãn 2 loglog16 y x = và tích 64 xy = . Giá trị của biểu thức 2 2log y x A. 25 2 B. 20 C. 45 2 D. 25 Lời giải Chọn B
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 3
A. B. C. D. Lời giải Chọn D Ta có Khi đó: Vậy: . Câu 5: Cho , xy là hai số thực dương, 1 x thỏa mãn 3 2 332 log,log. 8 x y yx y == Tính giá trị của 22Pxy =− . A. 120 P = . B. 132 P = . C. 240 P = . D. 340 P = . Lời giải Chọn C Ta có: 2 2 2
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Ánh 42
Page 4
Đặt 2 loglog16 y xt == . Suy ra 4 2 2 2 2 2 4 4log2 log log2 2 4 t t t t t y y x x x x t t y y t = = = = = = = = Ta
4 6 4
t t xyt t ==+= . Ta
222 2 22 222 2 4164 logloglog81661620 y yxttt xttt =−=−=−+=+−=−= . Câu 7: Gọi , ab là các số thực lớn hơn 1 sao cho biểu thức ( ) 3 3 loglogb a Tba =+ đạt giá trị nhỏ nhất. Giá trị của biểu thức 4 log a Pab = bằng A. 1 2 B. 2. C. 2 3 D. 4. Lời giải Do , ab lớn hơn 1 nên log0 a b . Khi đó: ( ) 3 3 3 111 loglog27log3log3log3log ba a aaa Tbab bbb =+=+++ Do đó 3 4 111 427log...4 3log3log3log a aaa Tb bbb = Dấu bằng xảy ra khi 3 1 log 3 a bab == Khi đó 3 4 2 loglog 3 a b Pabb === . Câu 8: Có bao nhiêu số thực dương 1 n để log265 n là một số nguyên? A. 2 B. 4 C. 6 D. 8 Lời giải Chọn D Ta có: 8 2 8 log256log28log2 log nnn n === . Để log265 n là một số nguyên thì 2 log{1;2;4;8} n 1111 ;2;;4;;16;;256 2416256 n Vậy có tất cả 8 số thực dương 1 n thỏa mãn điều kiện bài toán. Câu 9: Cho các số thực , abthỏa mãn 1 ab và 11 2022. loglog baab += Giá trị của biểu thức 11 . loglogabab P ba =−
Giáo viên: Huỳnh Văn
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
có
642.226
có ( )
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 5 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 2018. B. 2020. C. 2016. D. 2022. Lời giải Chọn A ⚫ 11 loglog2022loglog2022(*). ab ba ba ab +=+= ⚫ 11 logloglog()log()loglog. baba abab Pababab ba =−=−=− ⚫ Đặt loga tb = thì (*) trở thành: 2 202220181 2018 1 2 2022202210. 202220181 2018 2 tPt t ttt t tPt t + ==−=− +=−+= ==−= ⚫ 10log1 a abb nên 11 01102018. tPtP tt =−= Câu 10: Biết x và y là hai số thực thỏa mãn ( ) 496 logloglog2. xyxy ==− Giá trị của x y bằng A. 2 2 3 log2 B. 1 C. 4 D. 2 Lời giải Chọn C Đk 0 0 2 x y xy Đặt ( ) 496 logloglog2xyxyt ==−= ( ) 2 4 1 3 42 942.9620 93 2 26 2 3 t t tt tttt t t x loai y xy = =− =−=−−= −= = Khi đó Câu 11: Với hai số thực dương , ab tùy ý và 35 6 3 log5loglog2 1log2 a b −= + . Khẳng định nào dưới đây là khẳng định đúng? A. 6 log2 ab = B. 36 ab = C. 230 ab+= D. 6 log3 ab = 2 42 4 93 tt x y ===
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 6
. Tính Amnpq = A. 42. B. 24. C. 8 D. 12 Lời giải Chọn B Ta có 333 22 24 2.32.32.3 log175log5.7log5log7 ==+ 33 575577 2121 log2.3log2.33.log2log33log2log3 =+=+ ++ Theo giả thiết ta có: 7 93 425 2 5 log3 2 log5log52 1 log7log72log3 2 log3 1 log2 2 c b aa bb a c ac = == === = = . Suy ra:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn B Ta có 35 6 3 log5loglog2 1log2 a b −= + 3 6 3 loglog2 log6 a b −= 66 loglog2 ab −= 6 log23636 aa ab bb === Câu 12: Ba số 248log3; log3; log3 aaa +++ theo thứ tự lập thành cấp số nhân. Công bội của cấp số nhân này bằng A. 1 4 B. 1 C. 1 3 D. 1 2 Lời giải Chọn C Theo giả thiết, ta có: ( ) ( )( ) ( ) ( ) 2 22 4282222 2 22 141 log3log3log3log3log3log3log3 233 11 log3log3312 aaaaa a +=+++=+ =− 2 1 log34 a =− Vậy: 22 4 2 22 11 log3log3log31 42 1 log33 log3log34 a q a −+ + === + −+ Câu 13: Cho 942 log5,log7,log3abc === . Biết 24 log175 mbnac pcq + = + với ,,, mnpq và q là số nguyên tố
24 21214242 log17531333333 222222
+ =+=+=+= ++ +++ ++
acbacb ccc ccc acabbacb
Câu 14: Cho x và y là hai số thực dương thỏa mãn 22 525244 xyxyxy ++=++ . Xét các hệ thức sau:
Hệ thức 1. ( ) ( ) ( ) 22 ln1ln1ln1 xyxy +++=++
Hệ thức 2. ( ) ( ) ( ) ( ) 22 ln1ln1ln1ln1 xyyx +++=+++ .
Hệ thức 3. ( ) ( ) ln31lnxyxyxy +++=+ .
Hệ thức 4. ( ) ( ) ln222lnxyxyxy +++=+
Trong các hệ thức trên, có bao nhiêu hệ thức đúng? A. 1 B. 4 C. 3 D. 2 Lời giải
Chọn D
Ta có 22 525244 xyxyxy ++=++ ( ) ( ) ( ) 2222 4421440 xxyyxxyy −++−++−+= ( ) ( ) ( ) 222 2120 xyxy −+−+−= ( ) ( ) ( )
−= = −= = −=
2 2 2
xy x x y y
20 1 10 2 20
.
Hệ thức 1. ( ) ( ) ( ) 22 ln1ln1ln1ln2ln3ln6 xyxy +++=+++= .
Hệ thức 2. ( ) ( ) ( ) ( ) 22 ln1ln1ln1ln1ln2ln3ln5ln2
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page 7
Vậy ta có: 2 4 24 1 3 m n mnpq p q = = = = =
xyyx +++=++++=+ Hệ thức 3. ( ) ( ) ln31lnln10ln3 xyxyxy +++=+= Hệ thức 4. ( ) ( ) ln222lnln92ln3 xyxyxy +++=+= . Vậy có 2 hệ thức đúng. Câu 15: Đặt 25 log3,log3ab== . Nếu biểu diễn ( ) 6 log45 () amnb bap + = + thì mnp ++ bằng: A. 3. B. 3. C. 6 . D. 4. Lời giải Chọn D Ta có:
333 6 333 log45log45log9log5 log6log2log3 + == + 2 3 5 3 2
1 1 log3 log32 (12) 11 (1) log31 log3
+ + + === + ++ .
ab b ba a
Theo bài ra: ( ) 6 log45 () amnb bap + = + .
Từ và ta có: 1,2,1mnp=== . Vậy 4 mnp++= Câu 16: Cho ba số thực dương ,, abc đều khác 1 thoả mãn log2log4log == abc bca và 2348++=abc
. Khi đó = Pabc bằng bao nhiêu? A. 243 B. 521 C. 512 D. 324 Lời giải
Chọn A
Do ,, abc đều khác 1 nên log,log,log abc bca đều khác 0.
Ta có: 2log2loglog.log2loglog2log abacbab bccbccc === 2log4loglog.log4loglog4log === acacccc bacbaba .
Nên 22log.log8log.log acbc cbca = 2log8log abba= 3 log8 a b = 2 log2 a bba== Mà 2 log2loglog2log===aba a bcbcbc .
lại có 2348abc++=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page 8
Ta
22 2348aaa ++= 2 5480 aa +−= 16 5 3 a a =− = . Do ,, abc đều là số thực dương nên 39abc=== Vậy 243 Pabc== . Câu 17: Có bao nhiêu số nguyên dương b sao cho ứng với mỗi b , có đúng 3 giá trị nguyên dương của a thoả mãn ( ) 2 2 log21 a a a ab ab + +− ? A. 1. B. 2. C. 3. D. 0. Lời giải Chọn A
Ta có ( ) ( ) ( ) 222 2 log21log22log1 a aaa a abaaabab ab + +−++++
Đặt ( ) 2 log,0ftttt=+ .
Ta có ( ) 1 100 ln2 ftt t =+
Nên từ suy ra 22 211 aa a aabbb aa ++−
Xét ( ) 2a ga a = , với a nguyên dương. Ta có ( ) 2 2ln2.2 0 aa a gaa a + = .
Theo yêu cầu bài toán ta có ( ) ( ) 11 3145 3 gbgb −
x x y Chọn B Điều kiện:
+ ? A. 21. B. 22. C. 23. D. 24. Lời giả 0 20 1
x y y
i x
− . + Trường hợp 1: ( ) 1 2 2
x x
1320 4 20log0
x x xy y
+ − − − + Trường hợp 2: ( ) 1 2 2
1320 4 20log
x x
x xy y
+ − − − Kết hợp điều kiện: 22 0;loglog10xy= . Ta có: ( )2 20logxy . Để có không quá 20 số nguyên x thì ( )2 20 22 1log201log2022 yyy 2;3;...;22 y . Có 22 số nguyên y. Câu 19: Cho hai số thực x , y thỏa mãn 2 xy+= . Giá trị nhỏ nhất của 2 1 2.3.3 24 yx A =+ là A. min 2 A = . B. min 81 8 A = . C. min 9 2 A = . D. min 51 8 A = . Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page 9
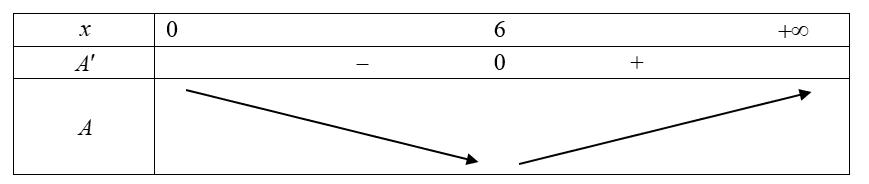
Mà b nên 4 b = . Vậy có 1 giá trị nguyên dương của b thoả mãn yêu cầu bài toán. Câu 18: Có bao nhiêu số nguyên dương y sao cho ứng với mỗi y có không quá 20 số nguyên x thỏa mãn 1 1 2 40 2
Chọn C Ta có: 22 xyyx +==− Xét: ( )2 222 11181 2.3.32.3.3.3 2424324 yxxxx x A =+=+=+ Đặt 3x t = , 0 t , khi đó ( ) 2 18 24 t Aft t =+= Xét: ( ) 2 18 06 12 t ftt t =−== . Bảng biến thiên của hàm số ( ) 2 18 24 t ft t =+ trên ( ) 0;+ Khi đó: A đạt giá trị nhỏ nhất tại ( ) min 9 66 2 tAf === .
Câu 20: Cho hai số thực dương x , y thỏa mãn ( )1 2 22log2 yy yxx +=++ . Giá trị nhỏ nhất của biểu thức x P y = bằng A. ln2 2 e + B. ln2 2 e C. ln2 2 e D. 2ln2 e Lời giải Chọn C Có ( )1 2 22log2 yy yxx +=++ ( ) 2 22log221 yy yxx +=++− . ( )1 Đặt ( ) 2 log22y tx=+ 222 yt x += 222ty x =−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page
10
. ( )1 trở thành: 2221 ytyyt +=−+− 1 212 ytyt + ++=+ . ( )2 Xét hàm số ( ) 2, x fxxx=+ ( ) 2ln210, x fxx =+ nên hàm số ( ) 2x fxx =+ luôn đồng biến trên . Kết hợp với ( )2 ta có: 1 ty=+ ( ) 2 log221 y xy +=+ 1 222yy x + += 1 2y x = Khi đó x P y = 1 2y y = 11 2 2ln22 yy y P y = .
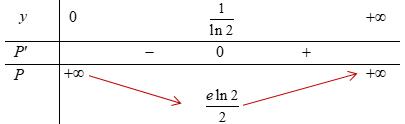
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 11
=
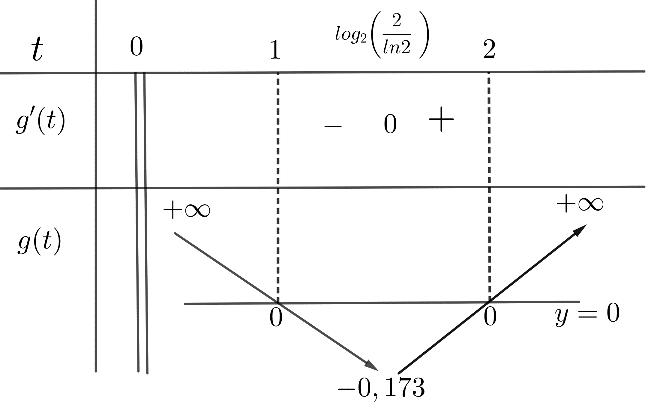
ee =+−=+ =+− =+ =−=− Do đó '0y = có nghiệm duy nhất 1 x = trên 1 ;e e ( ) ( ) 11 11 10 e y ee yeeMMme ym = =−=+=− == Câu 22: Gọi m là giá trị nhỏ nhất của hàm số ( ) ( ) 4222 xxfxa=+−+ trên đoạn 1;1 . Tất cả các giá trị của a để 1 m là A. 1 a B. 1 0 2 a − C. 1 2 a − D. 0 a Lời giải Chọn D
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Cho 0ln210Py
=−= 1 ln2 y
Bảng biến thiên: Vậy min ln2 2 e P = khi 2 e x = và 1 ln2 y = . Câu 21: Gọi , Mm lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số (1)ln yxx =− trên đoạn 1 ;e e . Khi đó Mm + bằng A. 2 1 e e . B. 1 e . C. 1 e . D. 1 e e . Lời giải Chọn C ( ) 2 2 1111 'ln1;''0; 1 'ln1 111 ''0; 11 '0;'20 yxyxe xxxe yx x yxe xxe yeye
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 12 Chuyên
thi: Tuyển sinh vào
10
và
Đặt: ( )20 x tt= . Với 1 1;1;2 2 xt − Xét
số ( ) ( ) 2 22gttat=+−+ , 1
2 t
Ta
( ) 22gtta =+− ; ( ) 2 0220 2 a gttat =+−==
(
. +
===
251 11 42 a ma + − Vậy 1 a . + TH2: 12 221 22 a a − . Khi đó ta có ( ) ( )2 1 ;2 2 228 min 24 a a mgtg −−+ === ( )2 28 1104 4 a ma −−+ Vậy 01 a . + TH3: 2 22 2 a a −− . Khi đó ta có ( ) ( ) 1 ;2 2 min222mgtga ===+ . 1 1221 2 maa+− . Suy ra không có giá trị nào của a thoả mãn. Kết luận: Vậy 0 a . Câu 23: Cho hai số thực ,1xy thỏa mãn ( ) ( ) 2222 222 log221loglog1 xxy =++ . Tính giá trị biểu thức ( ) 3log Pxy =+ A. 2 B. 1 C. 3 log2 D. 3 Lời giải Chọn B ( ) ( ) ( ) ( ) ( ) 2 2222222 222222 log221loglog11log21loglog1 xxyxxy =+++=++
0984164935
luyện
lớp
Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm
biên soạn
hàm
;2
có
;
) ( ) 22 0;0 22 aa gttgtt
TH1: 21 1 22 a a
. Khi đó ta có ( ) 1 ;2 2 min125 24 a mgtg
+
( ) ( ) ( ) 2 2 22 2 2 2 1log2log1* 1log x y x + =+ + Đặt ( ) 2 log,0txt= . Xét hàm số ( ) ( ) 2 2 1 (),0 1 t ftt t + = + , ta có: ( ) ( ) 2 2 2

22 1 t ft t = + , ( ) 01ftt == Bảng biến thiên Suy ra ( ) 2 ft ( )2 2 2 2 1log2 1log x x + + Lại vì ( ) 22 2 12log12yy+ nên ( ) 2 log1 * 1 tx y
== = 2 1 x y
= = 1 P = .
Câu 24: Cho các hàm số ( ) 3x fxx=+ và ( ) ( ) 322 13gxxmxmx =−++− với m là tham số thực. Gọi M là giá trị lớn nhất của hàm số ( ) ( ) 2 ygxfx =+ trên đoạn 0;1 . Khi M đạt giá trị nhỏ nhất thì giá trị của m bằng A. 3 B. 7 2 C. 5 2 D. 2 Lời giải Chọn A Đặt ( ) ( ) 233x hxxfxx =+=+ ( ) 33.ln30 x hx =+ Bảng biến thiên:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 13
đạt giá trị nhỏ nhất khi 3 m = .
2223 22
331218634436933 23112 3 =+++++++++=+ +++=+ Tập hợp các số , ab thỏa điều kiện ( )1 là nửa mặt phẳng tô đậm như hình vẽ. ( )2 là đường tròn tâm ( )2;3 I bán kính bằng 11 3 P + . Điều kiện ( ) ( )1,2 có điểm chung thì ( ) 7;PdI+ ( ) 6122 ;4 5 dI ==
PababaabbP P ab
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Ánh 42
Page 14
Với
x suy ra ( )
hx Xét
ố ( ) ( )
. ( ) ( ) ( )2 222222 321221210,
Suy
( ) ( ) (
2 22
==−+=−++=−+ M
Giáo viên: Huỳnh Văn
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
0;1
1;6
hàm s
322 13gxxmxmx =−++− trên
1;6
gxxmxmxmxmxxmxx
=−++=−+++=−++
ra
)
663621966914763147147Mgmmmmm
Câu 25: Với các số thực không âm , ab thỏa mãn 34 163.28 ab ba + + , giá trị nhỏ nhất của biểu thức 22 3312186Pabab =++++ bằng A. 15. B. 18. C. 25. D. 21. Lời giải Chọn A Đặt 34043 tabbta =+=− Ta có 34 163.284123.28 abt bataa + +−+ . Xét hàm số ( ) ( ) 4123.243.2.ln200,0. tt fttaaftata =−+=+ Suy ra hàm số ( )ft đồng biến trên khoảng ( ) 0;+ . Ta có ( ) ( ) ( ) ( )8223421ftftftab + ( ) ( ) ( ) ( ) ( )
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 15 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Suy ra 111615 3 P P + Câu 26: Đặt loga mab = Giá trị của m để biểu thức 2 2 loglog b a Paba =+ đạt giá trị nhỏ nhất là A. 0 B. 3 C. 3 2 D. 2 Lời giải Chọn B ▪ 1log1 a abb . ▪ 1 log1log 2 aa mabb ==+ log22 a bm =− 3 1 2 m . Ta có 2 2 loglog b a Paba =+ 22 2 loglog2logb aa aba=++ ( ) 12 122 222 m m =+−+ ( ) 1 113 1 m m =+−+ . Suy ra min 3 P = khi và chỉ khi ( )2 3 3 2 2 2 0 11 2 m m m m m m = = −= = Câu 27: Cho hàm đa thức ( )yfx = có đồ thị của hàm số ( )2 yfx =+ như hình vẽ
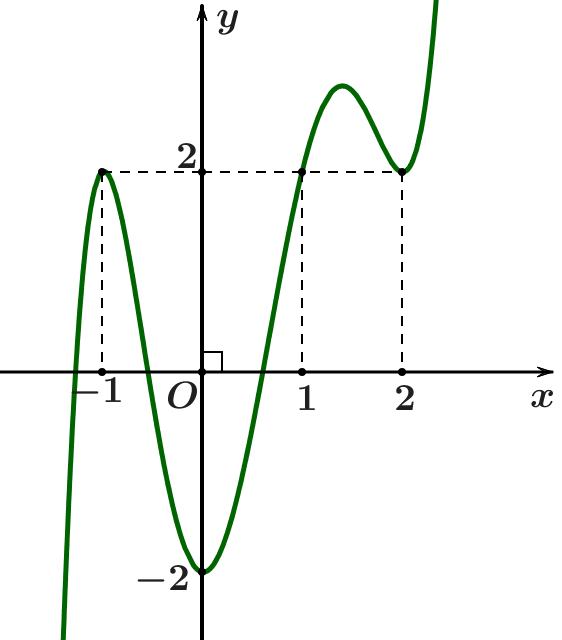
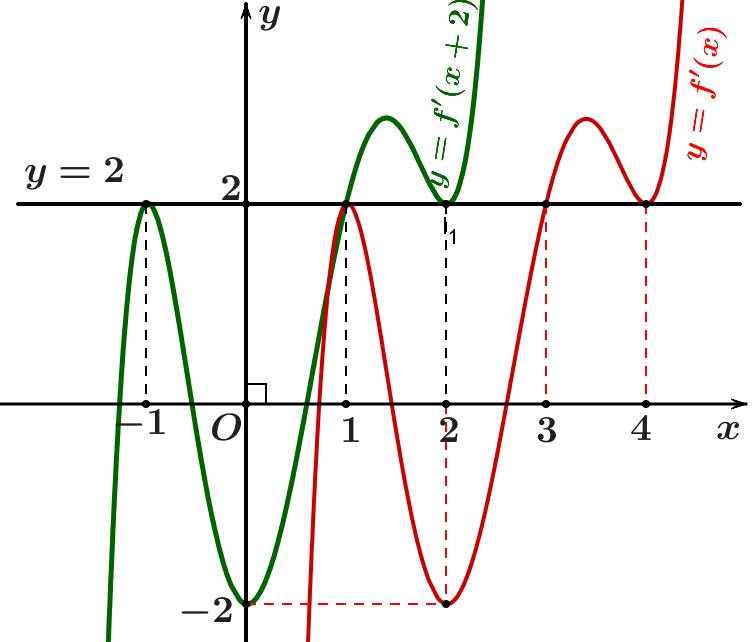
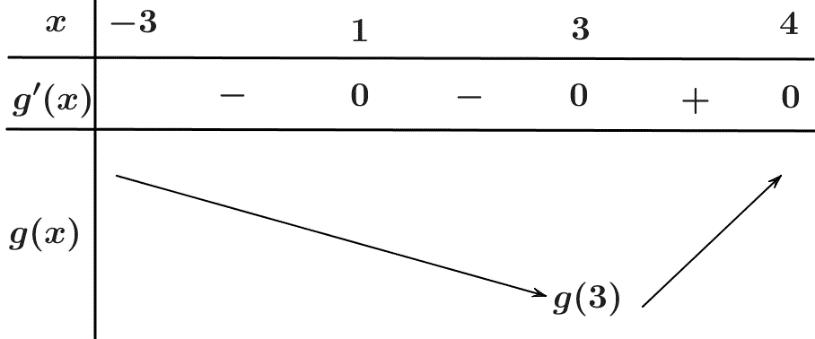
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 16 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Giá trị nhỏ nhát của hàm số ( ) ( ) 2 1 3 xfx gx = trên đoạn 3;4 là A. ( ) 1. g B. ( ) 3. g C. ( ) 3. g D. ( ) 4. g Lời giải Chọn C Xét hàm số ( ) ( ) ( ) ( ) ( ) ( ) 223ln3.2.3 fxxfxxgxgxfx =→=− Cho ( ) ( ) ( ) 0202gxfxfx =−== ( ) ( ) 1 3 4 xk x xk = = =
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 17
Câu
ọ
12 , xx
ệm c
2 12
xx
+ =
ớ
trị lớn nhất của
ểu
ứ
12
12
.
.
lnln0 lnln0log0;;1 a ba bab ba − Ta có ( ) 22 ln.2ln.ln02log.10 a axbxaxbx++=++= Theo định lý Vi ét, ta có: 12 12 2log 1 a xxb xx +=− + 12 12 12 2 21 2log2log2log2log aa aa xx Pxxbb xxbb =++=−+=−+ +− Vì 11 log0log22 2log2 aa a bb b += 1 2log22. 2log a a Pb b =−+− Dấu "" = xãy ra khi 2 2 1 log 2log a a bba b == Vậy giá trị lớn nhất của biểu thức 12 12 12 2xx Pxx xx =++ + bằng 22. Câu 29: Gọi , ab là các số thực lớn hơn 1 sao cho biểu thức ( ) 2 3 log6logb a Tba =+ đạt giá trị nhỏ nhất. Gía trị của 3 log a Pab = bằng A. 7 B. 1 C. 10 3 D. 2 Lời giải Chọn D Ta có ( ) ( ) 2 3 3 16log6loglog8logba a a Tbab b =+=+ ;Đặt ( )log;10 a xbdoabx = ( ) ( ) 4 32 22 1636362 8 0;00 882 x xL TxxTxT xxx x =− =+=−== = .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
28: G
i
là hai nghi
ủa phương trình
1
ab
v
i , ab là các số thực lớn hơn 1. Giá
bi
th
c
12
2xx Pxx xx =++ + bằng A. 4
B. 22
C. 4. D. 22 . Lời giải Chọn C Ta có: ( ) 22 12121ln0xxxx abab ++== ( ) 22 1ln2ln0ln.2ln.ln0 xaxbaxbxa ++=++= Phương trình có 2 nghiệm ( ) ( ) 22 lnln0 ba =−

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 18
Ta có
dương thay đổi thỏa mãn ( ) 22 2 log7223 c ccdd d ++−=+− . Giá trị nhỏ nhất của biểu thức ( ) ( ) 22 1 acbd −++− là A. 421. B. 291. C. 1255 5 . D. 855 5 . Lời giải Chọn B Ta
(
+− ( )2 2 22 log22log2121 1;01;2 cd cccddd dc dc −=− ++=++ ( )2 Đặt ( ) ; Mab và ( ) 1; Ncd . Theo ( )1 ta được M thuộc đường tròn tâm ( )3;4 I bán kính 1 R = ; theo ( )2 ta được N thuộc nửa đường thẳng 21yx=− ứng với 1 x . Khi đó ( ) ( ) 22 1 MNacbd =−++− .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
BBT Vậy ( ) 2 3 log6logb a Tba =+ đạt giá trị nhỏ nhất khi 2 2log2 a xbba === 23 3 22 loglog.log2 33aa a Pabaaa ==== Câu 30: Cho , ab là các số thực thay đổi thỏa mãn ( ) 22 20 log6841 ab ab ++ −−= và , cd là các số thực
có:
) 22 20 log6841 ab ab ++ −−= 22 20684abab ++=−− ( ) ( ) 22 341ab −++= ( )1 Lại có: ( ) 22 2 log7223 c ccdd d ++−=+− ( ) 22 2 2 log7223 230;,0() c ccdd d dddcgt
++−=+−

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo
Ánh 42
Page 19
V
Chọn A Ta có: ( 1;3 b :
+− Do đó: ( ) ( ) ( )
log99log3log3log aaaa bbbbb +−= Dấu “=” xảy ra 3 b = ( ) ( ) 22 log1log1 623log3122log1log1 aa a aa bb Pb bb +=+++ Theo BĐT Cô si ta có: ( ) ( ) 2 3 3 22 log1log1log1221 3.3 2222 log1log1 aaa aa bbb bb ++ ( ) 33 2 log1log1211 313.3193 2222 log1 aa a bb P b ++++=+
viên: Huỳnh Văn
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
ậy min1 291 MNNIR=−=− Câu 31: Cho các số thực ( ,1;3ab thỏa mãn ab . Biết giá trị nhỏ nhất của biểu thức ( ) 22 log996log ab a Pbba =+−+ là 3 1 9 n m + với , mn là các số nguyên dương. Tính 22Smn =+ A. 13 S = B. 8 S = C. 20 S = D. 29 S = Lời giải
22 993 bbb
223
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 20 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Dấu “=” xảy ra ( )2 3 log12 2log1 a a b b b = = ( )3 3 log14 a b b = −= 3 3 log314 a b = −= 3 14 3 3 b a + = = 3 1 14 3 3 b a + = = 2;313mnS === . Câu 32: Cho các số thực , ab thỏa mãn 1 1 3 ba .
giá trị nhỏ nhất của biểu thức ( ) 2 431 log8log 9 ab a b Pa =+ A. 7 B. 8 C. 6 D. 9 Lời giải Chọn B Vì 1 1 3 ba nên ( ) ( ) ( ) 2 22 431431 320loglog 99aa bb bbb − Ta có 2 2 1 8log8 log1 b a a a b = Đặt loga bx = . Vì 1 1 3 ba nên log1 a xb= . Khi đó ( ) ( ) 2 22 2 43118 log8loglog829log11aba a a b PabPx b x =+++ Mà ( ) ( ) ( ) ( ) ( ) ( ) ( ) 3 222 888 21123.1.1.28 111 xxxxx xxx +=−+−++−−+= Suy ra 8 P Dấu "" = xảy ra 3 2 3 2 3 b a = = Vậy min8 P = Câu 33: Tập hợp nào sau đây chứa tất cả các giá trị của tham số m để giá trị lớn nhất của hàm số 22 11 22 loglog yxxm =−+ trên đoạn 1 ;2 4 bằng 5? A. ( ) ( )5;31;3−− . B. ( ) ( )6;34;7−− . C. ( ) 0;+ . D. ( ) ( )9;50;3−− .
Tìm
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 21 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn A Xét 222 1111 2222 1 logloglog2log2 4 P xxxxx −=− = Đặt 1 2 log12txt =− . Ta được: ( ) 2 212Pttt=−− Khảo sát hàm số ( ) 2 2 fttt =− trên 1;2 , ta được ( ) 13 ft − 2222 1111 2222 loglogloglo 3 g 13113 Pmmm xxxx −−−++ + Vậy 22 11 22 22 11 22 22 11 2 1 2 4 1 2 4 1 2 4 2 mlogl a og loglog log3 log in1 mxmax1;3 max x x x mm mmm xx xx xx mm +=−+ +=−++ = ++ Yêu cầu bài toán 13 136() 154() 1313 352() 8() mm mm ml m mn mmmm m mn ml −++ −++ = −+= =− −++−++ += = =− Vậy ( ) ( )6;34;7−− chứa tất cả các giá trị m thỏa mãn Câu 34: Cho , xy là các số dương thỏa mãn ( ) ( ) ( ) log2loglogxyxy +=+ . Khi đó, giá trị nhỏ nhất của biểu thức 22 4 121 xy P yx =+ ++ là: A. 32 5 B. 29 5 C. 6. D. 31 5 Lời giải Chọn A Ta có: ( ) ( ) ( ) ( ) ( ) log2logloglog2log2 xyxyxyxyxyxy +=++=+= Mặt khác: ( ) ( ) 2 222808 xyxyxyxyxyxy =+−
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 22
(
Đặt
= suy ra ( )2
++
(
2
= +
. ( ) ( ) 2 2 4 0,8 2 tt ftt t + =
x
xy
+− + .
22
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Áp dụng bất đẳng thức cauchy Swat ta có:
) ( ) 22 22 2 4 121222 xyxy xy P yxxyxy + =+= +++++
xyt
2 22 xy t P xyt =
Xét hàm số
)
2 t ft t
, với ) 8; t +
+ , suy ra hàm số ( )ft đồng biến trên khoảng ( ) 8;+ ( ) ( ) 32 8 5 ftf = ( ) 32 5 Pft . 32 Min 5 P = khi 24 82 xyx xyy == == . Câu 35: Xét các số thực không âm
và y thỏa mãn 1 2.43
xy
Giá trị nhỏ nhất của biểu thức
46 Pxyxy =+++ bằng A. 33 4 B. 65 8 C. 49 8 D. 57 8 Lời giải Chọn B Nhận xét: Giá trị của , xy thỏa mãn phương trình ( ) 1 2431 xy xy +− += sẽ làm cho biểu thức P nhỏ nhất. Khi đó 11 0 (4 2 2 ()23 1):43xyxy xy xy yy +−+− ++− + = = Đặt axy =+ , từ ( )1 ta được phương trình ( ) 1 23 4.20* a a yy +−−= . Xét hàm số ( ) 1 23 4.2 a faa yy =+−− . Ta có ( ) 1 2 '4.ln40,0 a fay y =+ nên ( )fa hàm số đồng biến. Mặt khác, ( ) 0 73 lim0 4 a fa y → =−− , ( ) lim a fa →+ =+ . Do đó, phương trình ( )* có nghiệm duy nhất 33 22axy=+= . Ta viết lại biểu thức ( ) ( ) 2 1165 42 488 Pxyxyy =++++−−= . Vậy min 65 8 P =
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 23
++−+−= Đẳng thức xảy ra khi 5 3 4 2 1 32 4 y xy xy x = += +=+ = . Vậy 65 min 8 P = . Câu 36: Có bao nhiêu số nguyên m để ( ) ( ) 1;8 1;8 minmax2020 x x fxfx + với ( ) 2 2 5log1 log1 x fxm x + =+ + A. 2021. B. 2019. C. 2022. D. 2020. Lời giải Chọn D Đặt 2log Xx = , với 1;80;3xX . Khi đó ( ) ( ) 2 2 5log1 51 log11 x X fxmmgX xX + + =+=+= ++ . Có ( ) ( )2 4 0,1 1 gXX X =− + Nên với 0;3 X thì ( ) 14mgXm++ + Với 101mm+− thì ( ) ( ) 1;8 1;8 min11;max44 x x fxmmfxmm =+=+=+=+ . Suy ra 1420201007,5mmm +++ Vì m nên 0;1;2;...;1007 m có 1008 số nguyên m . + Với 404mm+− thì ( ) ( ) 1;8 1;8 min44;max11 x x fxmmfxmm =+=−−=+=−− Suy ra 4120201012,5mmm −−−−− . Vì m nên 1012;1011;...;5 m−− có 1008 số nguyên m
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Cách khác: Với mọi , xy không âm ta có 33 1 22 33 2.43.4.410 22 xyxy xy xyxyxyy +−+− +− +++−+− Nếu 3 0 2 xy+− thì ( ) 3 0 2 3 .410.410 2 xy xyyy +− +−+−+−= Vậy 3 2 xy+ . Áp dụng bất đẳng thức Bunhyakovski ta được ( ) ( ) 22 22 463213Pxyxyxy =+++=+++− ( ) 2 2 11365 513513 2228 xy
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 24
2 1
i Chọn C Ta có ( ) 212 1 2 2 202120202021 2020 22022202012021 y xy x xx yy y ++ == −+ −+ ( ) ( ) ( ) ( ) 2 21 202020212020120211 xyxyfxfy +=−+=− Với hàm số ( ) ( ) 22 20202021.20202021.2020 tttfttt=+=+ ( ) 2 2.2020.2020.ln20202021.2020.ln20200;0 ttt ftttt =++ Suy ra ( )ft là hàm đồng biến trên ( ) 0;+ mà ( ) ( ) 11fxfyxy =−+= Lại có ( )2 22 2122 11122 xyxy xyxxyyxy P yxxyxyxyxy +−+ +++− =+=== +++++++ Mà 1 12 4 xyxyxy =+ nên đặt 1 0; 4 uxy = khi đó ( ) 22 2 u Pgu u == + Xét hàm số ( ) 22 2 u gu u = + trên 1 0; 4 ta được ( ) ( )2 6 02 2 guu u =− + Nên hàm số ( )gu nghịch biến trên 1 0; 4 Do đó ( ) ( ) ( ) 11 0;0; 44 12 ax01; 43 MgugMingug ==== 2 1; 3 Mm == Suy ra 25 1 33 Mm+=+=
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn + Với ( )( ) 14041mmm ++−− thì ( ) ( ) 1;8 1;8 min0;max44 x x fxfxmm ==+=+ hoặc
( )
( ) 1;8 1;8 min0;max11 x x fxfxmm
==+=−− . Suy ra 042020 m ++ hoặc 012020 m −− với 41 m −− . Do đó với 41 m −− luôn thỏa mãn bài ra nên có 4 số nguyên m Câu 37: Vậy có 1008100842020 ++= số nguyên m Cho 0,1 xy thỏa mãn
2 2021 2020. 22022 xy x yy + = −+ Gọi , Mm lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 11 xy P yx =+ ++ . Khi đó Mm + bằng A. 4 3 . B. 2 3 . C. 5 3 . D. 7 4 . Lời giả
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo
Ánh 42
Page 25
Câu 38: Xét các số thực x , y thỏa mãn ( ) 22 122 222.4 xyx xyx ++ +−+ . Biết
trị lớn
thức 34 21 xy P xy = ++ bằng 113 ab + với , ab . Khi đó ab +
A. 3 B. 2 C.
D.
C
Ta
(
22 122 222.4 xyx xyx ++ +−+ 22 1 22 2 22 4 xy x xyx ++ +−+ 22 2122 222 xyx xyx +−+ +−+ ( ) ( ) ( ) 2 2 2 1 2 2111 xy xy −+ −++ Đặt ( )2 2 1,0uxyu=−+ . Khi đó ( ) ( )1212102 uu uu +−− Xét ( ) 21 u fuu=−− có ( ) ( ) (
22 1 2.ln210loglogln2
u fufuu =−===− . Bảng
Mà ( )
== ( )2 2 11xy −+ Khi đó tập hợp điểm ( ) ; Mxy là hình tròn ( )C tâm ( )1;0 I , bán kính 1 R = . Ta có ( ) ( ) ( ) 34 21342340 21 xy PxyPxyPxPyP xy =++=−−+++= ++ Khi đó tập hợp điểm ( ) ; Mxy là đường thẳng ( ) ( ) ( ) :2340 dPxPyP −+++= . Do vậy ( ) d và ( )C có điểm chung khi và chỉ khi ( ) ( ) ( ) ( ) 22 23 ;11 234 PP dId PP −+ −++ 2 315425 PPP −−+ ( )2 2 915425 PPP −−+ 2 414160 PP −− 71137113 44 P −+ .
viên: Huỳnh Văn
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
giá
nhất của biểu
bằng
0
1 Lời giải
họn B
có
)
)
ln2
biến thiên
( ) ( ) 010001 fffuu
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
Page 26
u thức 2 12 12 12
xx
xx =−−
+ . A. 3 32 B. 4 C. 32 D.
Lời giải Chọn D 1,1ab log0 b a . 2 1 1 xxab = ( ) 2 log.101 b xax +−= Phương trình (
Áp
ụng định
Vi
22 3 11
loglog AMGM bbb bb
=+=++ 3 34 S = khi 2 ,1 1 log2logb b ab a a = 3 ,1 1 log 2 b ab a = 3 1 2 1 ab = . Vậy 3 min34 S = . Câu 40: Xét các số nguyên dương , xy thỏa mãn ( ) 1 3814 x yz yzxyxz + +−=+− . Tìm giá trị nhỏ nhất của biểu thức ( ) 22 2 2 loglog2xyz ++ . A. 2 2log3 + . B. 2 5log3. C. 2 log11. D. 3 4log2 Lời giải Chọn B Ta có ( ) 14444 38143333 xxxyzyzyzyzxyxzxx yzyz +++ +−=+−−=−−=− ++ Xét hàm số ( ) 3t ftt =− với 0 t ta có ( ) 3ln310,0 t ftt =− hàm số ( ) 3t ftt =− đồng biến trên ( ) 0;+ . Do đó 4 44 33 x yz xx yzyz + −=−= ++ Mặt khác ta lại có ( ) ( ) 2 2 2222 132 .222 23 2 yzyzyzyz ++++ .
LŨY
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do đó 1 711317 4 max1132 7 444 4 a Pab b = + ==++= = . Câu 39: Cho hai số thực 1,1ab . Gọi 12 ; xx là hai nghiệm của phương trình 2 1 1 xxab = . Tìm giá trị nhỏ nhất của biể
44
Sxx
3 34
)1 luôn có hai nghiệm trái dấu 12 ; xx , với mọi 1,1ab .
d
lí
et cho ( )1 ta có:
4log2log2log34
Saaa aa
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Ánh 42
Page 27
Khi đó (
2
+
Vậy giá trị nhỏ nhất của biểu thức
thoả
14 ab . Tìm
1616bbb +− Do đó ( ) 23 log1616log3log aaa bbbb +−= ( )3 9log.161 27 log1 a a Pb b + ( ) ( ) ( ) ( )3 161 3log13log13log19 27 log1 aaa a Pbbb b −+−+−++ 4 16 4.3.3.3.9 27 P + 17 P . Vậy giá trị nhỏ nhất của biểu thức P là 17 Câu 42: Cho các số thực , ab thỏa mãn 1 ,1 2 ab . Khi biểu thức ( ) 42 2 loglog416 a b Pbaa =+−+ đạt giá trị nhỏ nhất thì tổng ab + bằng A. 4 B. 18 C. 14 D. 20 Lời giải Chọn B Do ( )2 4222416440aaaa−+− đúng 1 2 a . Dấu bằng xảy ra khi 2 a = . Suy ra: ( ) ( ) 2 2222 22 44 log2log2log4log2log2log.4 loglogababaa aa Pbababb bb +=+=+= Dấu bằng xảy ra khi và chỉ khi
Giáo viên: Huỳnh Văn
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
) ( ) ( ) ( )2 2222 222222
42 loglog22loglog242loglog5log3 3 xyzyzyzyz xy ++=++−+++=−
Câu 41:
( ) 22 2 2 loglog2xyz ++ bằng 2 5log3.Cho các số thực , ab
mãn
giá trị nhỏ nhất của biểu thức ( ) 23 16 3log1616log 27 ab a Pbba =+−+ B. 8 B. 18 C. 9 D. 17 Lời giải Chọn D Ta có: 14 b ( )( ) 2 1160bb −− 3216160bbb −−+ 32
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Huỳnh Văn Ánh 42
Cư Trinh Thuận
ĐT:
Page 28
10
2 2 2 2 22 418 loglog216 log a a a a a a ab b b b b = = = += = = = . Câu
Xét các số thực
xy thỏa
2022
xy xxyyxy
+
++
ị lớn nhấ
xyxyxyxyxyxy +++=+++++ Xét hàm số 2022 1 ()log,(0)()10,0 .ln2022 fuuuufuu u =+=+ () fu đồng biến trên (0;) + . Nên ta có: 22222 (*)0()() +=++++−−=+−+= xyxyxyxyxyxyxyxyxy Mặt khác: 2() 4 + xy xy 2 2 ()()() 4 + +−+ xy xyxy 2 34 ()()00 43 +−++ xyxyxy Đặt 4 0 3 xytt += . Ta có: 221219911 22 4 55519 5 3 +++ ===−−= ++++ + xyt P xytt Vậy giá trị lớn nhất của P bằng 11 19 khi 2 4 3 3 = == += xy xy xy
Giáo viên:
Nguyễn
Hòa TP Huế
0984164935
Chuyên luyện thi: Tuyển sinh vào lớp
Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
43:
dương ,
mãn
22 log(1)(1)
xyxy
=−+−+
. Tìm giá tr
t của biểu thức 221 5 ++ = ++ xy P xy A. 11 19 B. 1 C. 10 23 D. 1 5 Lời giải Chọn A Ta có: 2022 22 log(1)(1) xy xxyyxy xyxy + =−+−+ ++ 2222 20222022 log()log()xyxyxyxxyyxy +−++=−+−+ 2222 20222022 log()()log()()(*)
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 29
ố
của =+
L
3 1 log324 2 =++− + xy
ftt t Suy ra: ( ) ( ) ( ) 312 −=+ fxyfxy 332−=+xyxy 32 13 = + y x y Ta có 323 000 132 y yy y + 32 13 =+=+ + y Pxyy y với 3 0 2 y . ( )2 111 11 3 10 13 111 3 = =+= + −+ = y P y y Bảng biến thiên: Vậy min 2113 3 = P Câu 45: Cho hàm số 2 x yxae . Có bao nhiêu số nguyên dương a để hàm số có giá trị nhỏ nhất trên 1;3 nhỏ hơn 1? A. 2 B. 3 C. 4 D. 5
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 44: Xét các s
thực dương x , y thỏa mãn 3 1 log324 2 =++− + xy xyxy xy . Tìm giá trị nhỏ nhất minP
Pxy A. min 91119 9 = P . B. min 91119 9 + = P . C. min 181129 9 = P . D. min 2113 3 = P .
ời giải Chọn D
xyxy xy ( ) ( ) ( ) ( ) 33 log1log23121 −−+=−++− xyxyxyxy ( ) ( ) ( ) ( ) 33 log31log2312 −−+=−++ xyxyxyxy ( ) ( ) ( ) ( ) 33 log3131log22 −+−=+++ xyxyxyxy Xét ( ) 3log =+ fttt , ( )0 t ( ) 1 ln310,0 =+
Lời giải
Chọn A
Ta có 22222 xx yaxeexaxa 22212a x exaxa 0 2 xa y xa .

Vì a là số nguyên dương nên 22 a .
Ta có
Trường hợp 1: 13 a 31 a
Khi đó giá trị nhỏ nhất của hàm số trên 1;3 là 2 1;3 min.01 a yyaaae .
Do a nguyên dương suy ra 1 a Trường hợp 2: 1 a 1 a
Khi đó giá trị nhỏ nhất của hàm số trên 1;3 là 2 1;3
1 min1 a yy e .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 30
Ta có 2 2 1 11 a ae e 1 eae 11eae . Do a nguyên dương và 1 a suy ra 2 a Trường hợp 3: 33 aa . Từ, có 2 giá trị của a thỏa mãn yêu cầu.
Câu 46: `Cho x là số thực, y là số nguyên thỏa mãn 22 2320xyxyxy+−+−+ . Biết giá trị nhỏ nhất của biểu thức ( ) ( ) 232 3 ln11 2 Pxyxyxxy =++−+− bằng ln ac bd Giá trị của abcd +++ bằng A. 16 B. 14 C. 75 D. 20 Lời giải Chọn A Ta có ( ) 222223202320xyxyxyxyxyy +−+−++−+−+ . Nếu 2 3840 x yy =−+− thì nên Vế trái của BPT luôn không âm với mọi x vì 10 a = suy ra 2 2 38402 3 x yyy =−+− Do y là số nguyên nên 1 y = Thay 1 y = vào ( ) 222320xyxyy+−+−+ ta được 2 010xxx+− Xét hàm số ( ) 232 3 ln12 2 Pxxxx =++−− trên ( )1;0 + ( ) ( ) 2 22 211 63213 11 x Pxxxxx xxxx + =−−=+− ++++ Ta có 2 1 30 1 x xx − ++ vì ( )1;0 x− + ( ) 1 0 2 Pxx == Bảng biến thiên
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
31 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH
MŨ LOGARIT
12 LŨY THỪA
Page
Ta có giá trị nhỏ nhất của P bằng 31 ln 48 Vậy 3,4,1,8abcd==== 16 abcd +++= . Câu 47: Cho hai số x , y thỏa mãn 0 xy+ và 22 22 20212021 102021.log1002021.log2 xyxy xy xy ++ + ++ + . Tìm tổng của giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 22 1022Pxyxy =+−−+ A. 826 . B. 682 . C. 8. D. 12. Lời giải Chọn D
Ta có 22 2 22 0212021 12 100 02021.log2021.log + + ++ + + x y xy y x xy ( ) ( ) ( ) ( ) 22 2 20 2 212 2 021 *102021.log2021g210.lo + + +++ + x x y y xy y x Xét hàm số ( ) 2021 o 2021 .l 10g= + t ftt với 0 t . ( ) 20212021 0 10.ln100, ln10 + =
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 32
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
có: ( ) ( ) (
22 22 10225124***yxyP P xy x +−−+−+−− = = Gọi điểm ( ) ; Mxy , ( )5;1 K khi đó ta có điểm M thuộc hình tròn ( )1C có tâm ( )1;1 I , bán kính 2 r = và 2 24 PMK=− Vì 42==IKr nên điểm ( )5;1 K nằm bên ngoài ( )1C . Do đó minmin 42 PMKMKIKr=−=− 42 MaxMax PMKMKIKr=+=+ Suy ra min682,max826 =−−=−PP Vậy tổng của giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P bằng 12 .
t f t t t .
( )ft đồng biến trên khoảng ( ) 0;+ . Bất phương trình( ) ( ) ( ) ( ) ( ) 2222 *22 ++++ fxyfxyxyxy ( ) ( ) ( ) 22 112**−+− xy Lại
)
Câu 48: Cho các số thực không âm ,, abc thỏa mãn 39279 abc++= . Gọi , Mm lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 23 Sabc =++ Giá trị của biểu thức 3m M + bằng A. 10. B. 3. C. 7. D. 13. Lời giải
Chọn A
Đặt 23 3; 3; 3 abc xyz=== .

Khi đó 333 log,2log,3log axbycz === (,,1) xyz . Ta có ( ) 3log Sxyz = Ta có: 3 93273 xyzxyzxyzS =++ Vậy 3 MaxSM== khi 3 xyz=== Giả sử min;;13zxyzz = . Do ( )( ) 11018 xyxyxyz −−+−=− ( ) 87xyzzz −
ra
log7 S
, do đó
log7
minlog7mS
khi 1,7xzy
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page
33
trị nhỏ nhất, giá tr
u thức 1 12 P ab = + . Khi đó mM + bằng A. 10 3 B. 10 3 C. 7 3 D. 2 5 Lời giải Chọn A Ta có: ( ) 222 2221 ee1e0 abababb aabb ++++−+−−= 222 2221 e1e0 aabbb aabb −++ +−+−−= 22222212e2e1 aabbbaabbb−++ +−+=++ , ( )* Xét hàm số: ( ) e t ftt =+ ( ) e10 t ft =+ ( ) e t ftt =+ là hàm số đồng biến trên ( ) ( ) ( ) 22222222 *21211 faabbfbaabbbaabb −+=+−+=+−+=
Suy
3
3
==
=== . Vậy 3
3333710. m M +=+=+= Câu 49: Cho các số thực a , b thỏa mãn ( ) 222 2221 ee1e0 abababb aabb ++++−+−−= . Gọi m , M lần lượt là giá
ị lớn nhất của biể
Do đó: 22 22 1 12 aabb P abaabb −+ == +++ TH1: 01bP== TH2: ( )
2 2 2 2
1 1 0 1 1
aa xx bb bPgx xx aa bb
−+ −+ === ++ ++
22 1 x gx xx = ++ ; ( ) 1 0 1 x gx x
với a x b = ( ) ( ) 2 2 2
ảng biến thiên
= = =−
đó: min 1 3 mP== ;
3 MP== 10 3 mM
50: Gọi M và m tương ứng là giá trị lớn nhất,
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page 34
D Đặt sin,0;1txt= suy ra 2 1costx−= . Khi đó ( ) 2 1 22tt yft==+ , với 0;1 t Ta có ( ) 2 1 2 2ln22ln20 1 tt t ft t =−= ( ) 2 2 1 1 22 22 2ln22ln2* 11 tt tt t t tt == Đặt ( ) 2u gu u = với ( )0;1 u ; ( ) ( ) 2 2ln22 0,0;1 uu guu u − = . Do đó g đồng biến trên ( )0;1 . Nên ( ) 2222 12 *11 22 tttttt =−=−==
B
Do
max
+= Câu
giá trị nhỏ nhất của hàm số sincos22xx y =+ . Tính tổng 10102021 TMm =+ . A. 2 2 101026063 T =+ B. 2 2 202022021 T =+ C. 2 2 101022021 T =+ .D. 2 2 202026063 T =+ . Lời giải Chọn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 35 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có ( ) 03 f = , 222 222 2 2222 2 f =+= , ( ) 13 f = Do đó ( ) 0;1 maxmax3Myft=== , ( ) 2 2 0;1 minmin22myft=== . Vậy 2 2 10102021202026063TMm=+=+ . Câu 51: Xét các số thực dương ,, xyz thỏ
z xy
+
+−=+−
.
trị
ỏ
ấ
ủ
ứ
.
ọn
++
a mãn ( ) 1 5252
xyxzyz
Giá
nh
nh
t c
a biểu th
c ( ) 22 5 5 loglog4 Pzxy =++ bằng A. 2 1log3. B. 2 5log3. C. 2 1log3 + . D. 5 12log4−+
Lời giải Ch
D Phương trình: ( ) 12 2 525255 zzxyxyxyxzyzz xy
+−=+−−=− + Xét hàm số: ( ) ( ) 5,0; t fttt=−+ . Ta có ( ) ( ) 5ln510,0; t ftt =−+ do đó hàm số đồng biến ( ) 0;+ suy ra ( ) 22 fzfz xyxy ==++ thay lại ta được ( ) ( ) ( ) 22 22 55 2 5 244 loglog4log xy Pxy xy xy + =++= + + Ta có ( ) ( ) 2 2 22 15 2..14. 24xyxyxy +=++ do đó ( ) ( ) 22 555 2 4416 loglog12log4 5 xy P xy + ==−+ + . Dấu bằng xảy ra 2 4,. 5 yxz x == Câu 52: Xét các số thực dương , xy thỏa mãn ( ) ( )2 22 2 11 1log1xyxy xy ++++=− . Khi đó xy + đạt giá trị nhỏ nhất bằng bao nhiêu? A. 4 B. 8 C. 1 D. 9 2 Lời giải Chọn A Ta có
( ) ( ) ( ) ( )
2 22 2 2 22 2
11 1log1 1log21
xyxy xy xy xyxyxy xy
+ +++=−+ +++=+
++++=− + +++=−+ ( ) ( ) ( ) ( ) ( )
2 22 2 22 22
1log21 loglog
xy xyxyxy xy xyxyxyxy
Xét hàm số ( ) ( ) ( ) 2 1 log,0,'20,0. ln10 fttttfttt t =+=+
Từ đó suy ra ( ) ( ) ( ) 2 2 4 40 40 xy xy xyxyxyxy xy + + +=+−+ +
các số thực
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 36
số thực
.
ị
ỏ nhất của biểu thức ( ) 22222 55 2 19 loglog33 4 Pyzyz x =+++− A. 2 3 3log5 B. 5 4log3 C. 2 D. 1 Lời giải Chọn C 13 22 (2)327233332 xxyzyzyzxyxzx yz ++ +−=+−−=− + Đặt 3 2 t yz = + ta được 33 332 2 xtxtxtxyz yzx −=−===+ + . ( )2 2 2 2 2 2 4 9 33 42 y yy z x zzyz=++=+ +− Ta có ( ) ( ) ( )2 2 2222 2 25 5 yz yzyzyz + +++ ( ) ( ) ( ) ( ) ( ) 222222 5555 2 2 2 2 55 19 loglog33loglog 4 loglo 21 2 54 2221g2 yz yz Pyz x yz Pyzyz + =+++− ++ +++− − Câu 54: Cho các số thực , xy, 2 1 x thoản mãn ( ) 3 23x 3221 269221 xy xx xxxy −+− −+ +−++=+ . Tìm giá trị nhỏ nhất của biểu thức 3 34Pxyx=−−+ . A. 10 . B. 8 . C. 7 . D. 6 . Lời giải
Vì
dương , xy nên ( ) 44xyMinxy ++= Câu 53: Xét các
dương ,, xyz thỏamãn 1 2 (2)32723 x yz yzxyxz + +−=+−
Tìm giátr
nh
hàm số đồng biến trên , vì vậy 3322 uv uv+=+ ( ) ( ) ( )3 3 3232 fufvuvyxxyxx ==−=−=+−
Ta có ( ) ( ) ( ) 3 3333234323496834 Pxyxxxxxxxxxx =−−+=−+−−+=−−−++−+ 32 2664 xxx =−++ , 11 x − Xét hàm số ( ) 32 2664;11gxxxxx =−++− . Ta có ( ) ( )2 2 6126610gxxxx =−+=− Do đó hàm số đồng biến trên đoạn 1;1 . Vậy giá trị nhỏ nhất của P là ( ) 110 P −=− . Câu 55: Cho hàm số ()yfx = có đạo hàm trên và hàm số ( )yfx = có đồ thị như hình vẽ. Trên 2;4 , gọi 0x là điểm mà tại đó hàm số ( ) 2 ()1ln816 2 x gxfxx

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 37
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Chọn A Chia 2 vế của phương trình cho 2 2x ta được: ( ) 3 3x 322 26x9x+y82 y x x +−+=+ ( ) ( ) 3 3 3 3 2 3 2322 yx x yxx +−=+− Đặt 3 3, 2 uyxvx =−=− ta có 3322 uv uv+=+ Xét hàm số ( ) 3 2t ftt =+ . Ta có ( ) 0, ftt
Khi
0x
ảng
A. 1 ;2 2 B. 5 2; 2 C. 1 1; 2 D. 1 1; 2 Lời giải Chọn D Ta có 2 12812 '()11. 22816224gxffxxx xxx + =+−=+− +++
=+−++ đạt giá trị lớn nhất.
đó
thuộc kho
nào?
Cho ( ) 4 01 24 x gxf x =+= +
Đặt 10;3 2 x tt=+
Phương trình trở thành ( ) 42 221 ft tt == ++
Vẽ đồ thị 2 1 y x = + lên cùng một hệ tọa độ ta được:
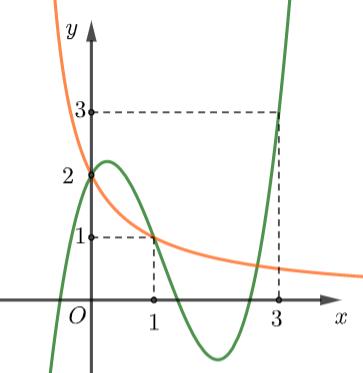
Từ đồ thị ta thấy hàm số đạt giá trị lớn nhất tại 10.tx==
Câu 56: Cho hai số thực dương ( ),1aba thỏa mãn 4 log2 a b = . Giá trị lớn nhất của biểu thức ( ) 3 3336ln42 2 a Pabb =+−− là số viết được dưới dạng ( )ln1xy với , xy là các số nguyên. Giá trị của xy + là A. 18. B. 6 . C. 12. D. 0 . Lời giải Chọn A
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 38
Ta có: 2244 log24 a aab bb === . Do ,0ab , áp dụng bất đẳng thức Cauchy: 3 33333632 28838624 abaababab +=++== Đặt 33 4 tab =+ thì 12 t Xét hàm số ( ) 6ln 2 t ftt=− với 12 t . Ta có ( ) 6161 0 2122 ft t =−−= với mọi 12 t nên ()ft là hàm số nghịch biến trên ) 12;+ Suy ra ( ) ( ) 126ln126,12ftft =− .
nhất một nghiệm trên ( )0;2 . Mà 1 x = là một nghiệm của phương trình ( ) 0 fx = nên phương trình ( ) 0 fx = có nghiệm duy nhất là 1 x
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 39
xy
+ ++−+++ ===
Câu 58: Xét các số thực dương ,, abc lớn hơn thỏa mãn ( ) 4loglog25log abab ccc += . Giá trị nhỏ nhất của biểu thức logloglog bac acb ++ bằng A. 8 B. 17 4 C. 3 D. 5 Lời giải Chọn D Ta có ( ) 4loglog25log41125loglogloglog abab cccc ccc abab +=+= + 1
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Đẳng thức xảy ra khi và chỉ khi 2,1ab== Vậy giá trị lớn nhất của P là ( )6ln1266ln121 −=− , suy ra 61218 xy+=+= Câu 57: Cho hai số thực dương , xy thỏa mãn ( ) ln ln ln5 2 2.52 xy xy + + = Tìm giá trị lớn nhất của biểu thức ( ) ( ) 1ln1ln Pxxyy =+++ A. max 10 P = B. max 0 P = C. max 1 P = D. max ln2 P = Lời giải Chọn B ln ln()ln5ln()ln2ln()ln5ln()ln()ln5ln2 2 2.522.522.52.2
xyxyxyxyxy
( ) ln ln10102 xy + = ( ) ln10ln()ln10.log2ln()log2ln()ln10.log2 xy xyxyee + +=+== log2 102xyxy +=+= Do đó ( ) ( ) ( ) 1ln3ln2 Pxxxx =++−− . Xét hàm số ( ) ( ) ( ) ( ) 1ln3ln2 fxxxxx =++−− ()lnln(2)ln1322 22(2) fxxxxxxx xxxxx +−− =+−−−=+ . ( ) ( ) ( ) ( ) 2 22 2 12244 .0,0;2 2 2 xxx fxx x x xx −−+ =−− Do đó ( ) 0 fx = có nhiều
= Lập bảng biến thiên ta được ( ) ( ) max0 fxfx==
) do ab . Hay log4 b a = . Mặt khác, theo giả thiết ta có logloglog42log.log bacac acbcb +++ logloglog42log baca acbb+++ 1 logloglog42 4 bac acb +++ logloglog5 bac acb ++ . Vậy giá trị nhỏ nh
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 40 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( )2 loglog 25 44loglog25log.log log.logloglog cc cccc cccc ab abab abab + =+= + ( ) loglog 4174loglog17 loglog cc ba cc ab ab ba +=+= 2 4log17log40 aa bb −+= log4 1 1log 4 log 4 a a a b b b = = = (
ất của biểu thức logloglog bac acb ++ bằng 5 khi 4 2 log4 loglog b ac a ab cb cb = = = = . Câu 59: Xét hai số thực , ab thỏa mãn (
+−+−+++ và
số thực , xy thỏ
( ) 22 2 log46101 xy xy ++ +−= . Giá trị nhỏ nhất của biểu thức (
22 2 Paxby
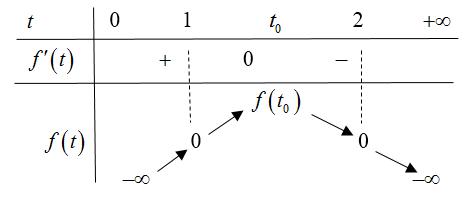
bằng A. 41125 5 . B. 942 . C. 1162 2 . D. 2185 5 . Lời giải Chọn D Đặt 0 tab=+ , ta có ( ) 1221 2 227log3 abab ab +−+−+++ trở thành 22 22 1111 .2.27log37log3.2.20 2222 tttt tt +++−− . Xét hàm số ( ) 2 2 11 7log3.2.20 22 tt ftt=+−− với 0 t Ta có ( ) 2 71.2ln22ln2 ln22 tt ft t =−− và ( ) ( ) ( ) 22 2 2 71.2ln22.2ln20 ln22 tt ft t =−−− với mọi 0 t . Suy ra ( ) ft nghịch biến trên ( ) 0;+ mà ( ) 10 f và ( ) 20 f nên ( ) 0 ft = có nghiệm duy nhất 0tt = . Ta có bảng biến thiên sau
) 1221 2 227log3 abab ab
hai
a mãn
) ( )
=−+−

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 41
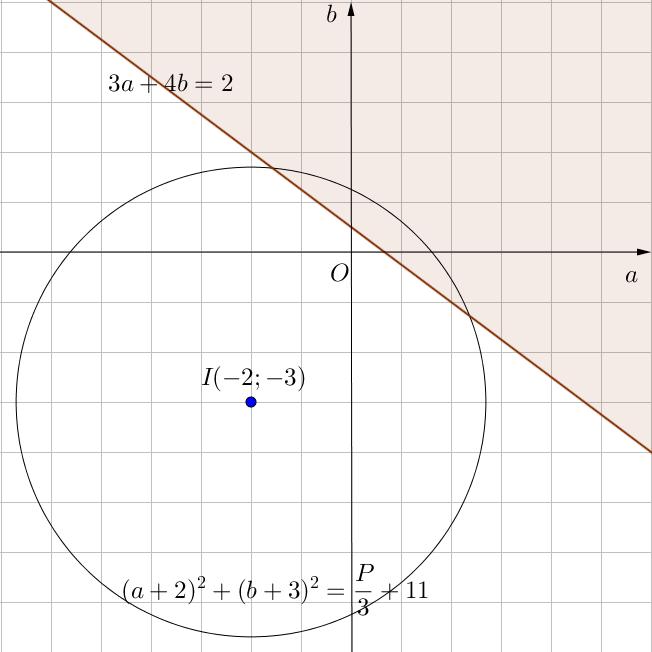
và ( ) 2 1 :2240 2 dxyxy+=+−= ,
điểm N thuộc đường tròn ( ) ( ) ( ) 22 :231Cxy−+−= Bài toán trở thành tìm giá trị nhỏ nhất 2 MN . Ta
Do ( ) ( ) 1 262 6 ,1 145 dId +− == + và ( ) ( ) 2 264 4 ,1 145 dId +− == + nên 2 MN nhỏ nhất bằng ( ) ( ) 2 2 2 42185 ,11 5 5 dId −=−= Câu 60: Cho hai đường cong 1 ():2, x Cy = 22 ():log. Cyx = Gọi S là tập hợp tất cả các giá trị
ự
tham số m sao cho đường thẳng yxm =−+ cắt trục
điểm ,A ,B ,C D sao cho
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Từ bảng biến thiên suy ra ( ) 012ftt hay ( ) 1221 2 227log3 abab ab +−+−+++ khi và chỉ khi ( ) 1 12122 2 abab ++ Ta có ( ) ( ) ( ) 22 22 22 2 log4610124610231 xy xyxyxyxy ++ +−=++=+−−+−= Xét điểm ( ) 2; Mab thỏa mãn ( ) 1 122 2 ab + và điểm ( ) ; Nxy thỏa mãn ( ) ( ) 22 231xy−+−= . Khi đó điểm M thuộc miền giới hạn bởi hai đường thẳng ( )1 1 :1220 2 dxyxy+=+−=
còn
có ( )C có tâm ( )2;3 I , bán kính 1 R = .
th
c của
tung, 1 (), C 2 () C và trục hoành lần lượt tại các
3 ADBC = như hình vẽ:
Tổng tất cả các phần tử của S bằng A. 42 B. 8. C. 9. D. 32.. Lời giải
Chọn C
Từ giả thiết suy ra ( ) 0; Am , ( );0Dm , ( ) 1 1;2x Bx , ( ) 222 ;log Cxx với 12,0xx và 0 m . , BC lần lượt là các giao điểm của ( ) ( ) 12 , CC với đường thẳng yxm =−+ nên ta có: 1 1 222
2 log
x xm xxm =−+ =−+ 1 1222 2log x xxx +=+ 122 log 1222log2 xx xx +=+ . Do hàm số ( ) 2t ftt=+ là hàm số đồng biến trên khoảng ( ) 0;+ nên 122 log xx= 1 2 2x x = ( ) ( ) 11 11 ;2,2; xx BxCx . 2 ADm = ; ( ) ( ) 111 2 111222222 xxx BCxxx =−=−=− Do 3 ADBC = nên 1 1 2 3 x m x −= Kết hợp với: 1 1 2x xm=−+ ta có hệ 1 1
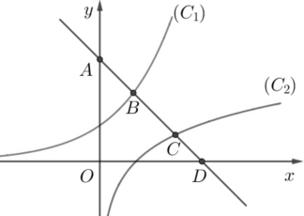
x x
m x xm
2 3 2
1 1
−= += 1 1 220 x x −= Xét hàm số ( ) 22 t gtt =− có ( ) 2.ln220 t gt =−= 2 2 log1,528 ln2 t =
Từ bảng biến thiên của hàm số ()gt và ( ) ( ) 120gg== suy ra PT có đúng 2 nghiệm là 1 1 x = và 1 2 x = .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 42
Với 1 1 x = thì 1 1 1 2213 x mx=+=+= Với 1 2 x = thì 1 2 1 2226 x mx=+=+= . Vậy 3;6 S = . Tổng tất cả các phần tử của S là 9.
Câu 61: Có bao nhiêu số nguyên dương b sao cho ứng với mỗi b , có đúng 3 giá trị nguyên dương của a thoả mãn ( ) 2 2 log21 a a a ab ab + +− ? A. 1. B. 2. C. 3. D. 0. Lời giải Chọn A
Ta có ( ) ( ) ( ) 222 2 log21log22log1 a aaa a abaaabab ab + +−++++
Đặt ( ) 2 log,0ftttt=+
Ta có ( ) 1 100 ln2 ftt t =+
Nên từ suy ra 22 211 aa a aabbb aa ++−
Xét ( ) 2a ga a = , với a nguyên dương. Ta có ( ) 2 2ln2.2 0 aa a gaa a + = .
Theo yêu cầu bài toán ta có ( ) ( ) 11 3145 3 gbgb −
Mà b nên 4 b = . Vậy có 1 giá trị nguyên dương của b thoả mãn yêu cầu bài toán.
Câu 62: Cho hai số thực dương ( ),1aba thỏa mãn 4 log2 a b = . Giá trị lớn nhất của biểu thức ( ) 3 3336ln42 2 a Pabb =+−− là số viết được dưới dạng ( )ln1xy với , xy là các số nguyên. Giá trị của xy + là A. 18 B. 6 C. 12 D. 0 Lời giải Chọn A Ta có: 2244 log24 a aab bb === Do ,0ab , áp dụng bất đẳng thức Cauchy: 3 33333632 28838624 abaababab +=++== . Đặt 33 4 tab =+ thì 12 t . Xét hàm số ( ) 6ln 2 t ftt=− với 12 t . Ta có ( ) 6161 0 2122 ft t =−−= với mọi 12 t nên ()ft là hàm số nghịch biến trên ) 12;+
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page 43
64:
Do đó ( ) ( ) ( ) 1ln3ln2 Pxxxx =++−− . Xét hàm số ( ) ( ) ( ) ( ) 1ln3ln2 fxxxxx =++−− ()lnln(2)ln1322 22(2) fxxxxxxx xxxxx +−−
=+−−−=+ . ( ) ( ) ( ) ( ) 2 22 2
−−+ =−− Do đó ( ) 0 fx = có nhiều nhất một nghiệm trên ( )0;2 . Mà 1 x = là một nghiệm của phương trình ( ) 0 fx = nên phương trình ( ) 0 fx
= có nghiệm duy nhất là 1 x = Lập bảng biến thiên ta được ( ) ( ) max0 fxfx== .
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 44
ln()ln5ln()ln2ln()ln5ln()ln()ln5ln2 2 2.522.522.52.2 xy xyxyxyxyxy + ++−+++ === ( ) ln ln10102 xy + = ( ) ln10ln()ln10.log2ln()log2ln()ln10.log2 xy xyxyee + +=+==
Câu
Cho các số thực , xy, 2
x thoản
(
giá trị nhỏ nhất của biểu thức 3 34
. A. 10 . B. 8 . C. 7 . D. 6 . Lờ
giải Chọn A Chia
vế của
2
x
c:
3
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 ( )
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Suy ra ( ) ( ) 126ln126,12ftft =− . Đẳng thức xảy ra khi và chỉ khi 2,1ab== Vậy giá trị lớn nhất của P là ( )6ln1266ln121 −=− , suy ra 61218 xy+=+= Câu 63: Cho hai số thực dương , xy thỏa mãn ( ) ln ln ln5 2 2.52 xy xy + + = Tìm giá trị lớn nhất của biểu thức ( ) ( ) 1ln1ln Pxxyy =+++ A. max 10 P = B. max 0 P = C. max 1 P = D. max ln2 P = Lời giải Chọn B ln 3 3 3 3 2 3
log2
102xyxy
+=+=
12244 .0,0;2 2 2 xxx fxx x x xx
1
mãn
) 3 23x 3221 269221 xy xx xxxy −+− −+ +−++=+ . Tìm
Pxyx=−−+
i
2
phương trình cho
2
ta đượ
( )
3x 322 26x9x+y82 y x x +−+=+
( )
2322 yx x yxx +−=+− .
Đặt 3 3, 2 uyxvx =−=− ta có 3322 uv uv+=+ Xét hàm số ( ) 3 2t ftt =+ . Ta có ( ) 0, ftt hàm số đồng biến trên , vì vậy 3322 uv uv+=+ ( ) ( ) ( )3 3 3232 fufvuvyxxyxx ==−=−=+− Ta có ( ) ( ) ( ) 3 3333234323496834 Pxyxxxxxxxxxx =−−+=−+−−+=−−−++−+ 32 2664 xxx =−++ , 11 x −
Xét hàm số ( ) 32 2664;11gxxxxx =−++− .

Ta có ( ) ( )2 2 6126610gxxxx =−+=−
đó hàm số đồng biến
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page
45
vẽ. Trên 2;4 , gọi 0x là điểm mà tại đó hàm số ( ) 2 ()1ln816 2 x gxfxx =+−++ đạt giá trị lớn nhất. Khi đó 0x thuộc khoảng nào? A. 1 ;2 2 B. 5 2; 2 C. 1 1; 2 D. 1 1; 2 Lời giải Chọn D Ta có 2 12812 '()11. 22816224gxffxxx xxx + =+−=+− +++ Cho ( ) 4 01 24 x gxf x =+= + Đặt 10;3 2 x tt=+
Do
trên đoạn 1;1 . Vậy giá trị nhỏ nhất của P là ( ) 110 P −=− . Câu 65: Cho hàm số ()yfx = có đạo hàm trên và hàm số ( )yfx = có đồ thị như hình

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 46
66: Xét các số thực dương ,, abc lớn hơn thỏa mãn ( ) 4loglog25log abab ccc += . Giá trị nhỏ nhất của biểu thức logloglog bac acb ++ bằng A. 8. B. 17 4 . C. 3. D. 5. Lời giải Chọn D Ta có ( ) 4loglog25log41125loglogloglog abab cccc ccc abab +=+= + ( )2 loglog 25 44loglog25log.log log.logloglog cc cccc cccc ab abab abab + =+= + ( ) loglog 4174loglog17 loglog cc ba cc ab ab ba +=+= 2 4log17log40 aa bb −+= log4 1 1log 4 log 4 a a a b b b = = = ( ) do ab . Hay log4 b a = Mặt khác, theo giả thiết ta có logloglog42log.log bacac acbcb +++ logloglog42log baca acbb+++ 1
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Phương trình trở thành ( ) 42 221 ft tt == ++ Vẽ đồ thị 2 1 y x = + lên cùng một hệ tọa độ ta được: Từ đồ thị ta thấy hàm số đạt giá trị lớn nhất tại 10.tx== Câu

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 47
ng
ế
hay ( ) 1221 2 227log3 abab ab +−+−+++ khi và chỉ khi ( ) 1 12122 2 abab ++ Ta có ( ) ( ) ( ) 22 22 22 2 log4610124610231 xy xyxyxyxy ++ +−=++=+−−+−= Xét điểm ( ) 2; Mab thỏa mãn ( ) 1 122 2 ab + và điểm ( ) ; Nxy thỏa mãn ( ) ( ) 22 231xy−+−= . Khi đó điểm M thuộc miền giới hạn bởi hai đường thẳng
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 1 logloglog42 4 bac acb +++ logloglog5 bac acb ++ Vậy giá trị nhỏ nhất của biểu thức logloglog bac acb ++ bằng 5 khi 4 2 log4 loglog b ac a ab cb cb = = = = Câu 67: Xét hai số thực , ab thỏa mãn ( ) 1221 2 227log3 abab ab +−+−+++ và hai số thực , xy thỏa mãn ( ) 22 2 log46101 xy xy ++ +−= . Giá trị nhỏ nhất của biểu thức ( ) ( ) 22 2 Paxby =−+− bằng A. 41125 5 B. 942 C. 1162 2 D. 2185 5 Lời giải Chọn D Đặt 0 tab=+ , ta có ( ) 1221 2 227log3 abab ab +−+−+++ trở thành 22 22 1111 .2.27log37log3.2.20 2222 tttt tt +++−− . Xét hàm số ( ) 2 2 11 7log3.2.20 22 tt ftt=+−− với 0 t . Ta có ( ) 2 71.2ln22ln2 ln22 tt ft t =−− và ( ) ( ) ( ) 22 2 2 71.2ln22.2ln20 ln22 tt ft t =−−− với mọi 0 t . Suy ra ( ) ft nghịch biến trên ( ) 0;+ mà ( ) 10 f và ( ) 20 f nên ( ) 0 ft = có nghiệm duy nhất 0tt = . Ta có bảng biến thiên sau Từ bả
bi
n thiên suy ra ( ) 012ftt
( )1 1 :1220 2 dxyxy+=+−= và ( ) 2 1 :2240 2 dxyxy+=+−= , còn điểm N thuộc đường tròn ( ) ( ) ( ) 22 :231Cxy−+−= .
Bài toán trở thành tìm giá trị nhỏ nhất 2 MN . Ta có ( )C có tâm ( )2;3 I , bán kính 1 R = . Do ( ) ( ) 1 262 6 ,1 145 dId +− == + và ( ) ( ) 2 264 4 ,1 145 dId +− == + nên 2 MN nhỏ nhất bằng ( ) ( ) 2 2 2 42185 ,11 5 5 dId −=−=

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 48



CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 1 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn LUỸ THỪA HÀM SỐ LUỸ THỪA LOGARIT HÀM SỐ MŨ HÀM SỐ LOGARIT MỨC ĐỘ VẬN DỤNG VẬN DỤNG CAO Câu 67: Cho các số thực a , b thỏa mãn 1 ab và 11 2020 loglog baab += . Giá trị của biểu thức 11 loglogabab P ba =− bằng A. 2014 . B. 2016 . C. 2018 . D. 2020 . Lời giải Chọn B Do 1 ab nên log0 a b , log0 b a và loglog baab . Ta có: 11 2020 loglog baab += loglog2020 baab += 22 loglog22020 baab ++= 22 loglog2018 baab += (*) Khi đó, loglogloglogloglogloglog babbaaba Pababababab =−=+−−=− Suy ra: ( )2 222loglogloglog22018220162016 baba PababP =−=+−=−== Câu 68: Tìm số nguyên dương n sao cho 3 22222 20182018 2018 20182018 log20192log20193log2019...log20191010.2021log2019 ++++= n n A. 2021 = n . B. 2019 = n . C. 2020 = n . D. 2018. = n . Lời giải 3 22222 20182018 2018 20182018 log20192log20193log2019...log20191010.2021log2019 ++++= n n 33322 20182018201820182018 log20192log20193log2019...log20191010.2021log2019 n ++++= ( ) 33322 20182018 123...log20191010.2021log2019 n ++++= 33322 123...1010.2021 n ++++= CHƯƠNG II HÀM SỐ LŨY THỪA - HÀM SỐ MŨ HÀM SỐ LOGARIT
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 2 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( )2 22 12...1010.2021 n +++= ( ) 2 22 1 1010.2021 2 nn + = ( )1 1010.2021 2 nn + = 2 2020.20210 nn +−= ( ) 2020 2021 n n = =− Câu 69: Cho hàm số 2 2 ()log117 24fxxxx . Tính 122018 ... 201920192019Tfff A. 2019 2 T B. 2019 T C. 2018 T D. 1009 T Lời giải Ta có: 2 2 22 117171(1)log111log2442 fxxxxxxx 22 22 1171711loglog2442 fxfxxxxxxx 22 2 log117171 2442 xxxxxx 2 log42 122018 ... 201920192019Tfff 120182201710091010 ... 201920192019201920192019 ffffff 1009.22018 Câu 70: Gọi a là giá trị nhỏ nhất của ( ) 3333 log2.log3.log4...log 9n n fn = với n và 2 n . Hỏi có bao nhiêu giá trị của n để ( ) fna = . A. 2 B. 4 C. 1 D. vô số Lời giải Chọn A ( ) 9999 3333 3333 log2.log3.log4...log 1 99log2.log3.log4...log n n fnn ==
Ta có: Nếu ( ) ( ) 99999 88 33333 1 230log1log2.log3.log4...log3 9 nkfnnf =
Nếu ( ) ( ) ( ) 9 99898 3 333.log33 nfff === Nếu ( ) ( ) ( ) ( ) 999 9999 333 3log13.log31...log3 nnfnfnf =+ Từ đó suy ra ( ) ( ) ( ) 98 33Minfnff == .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH
THỪA MŨ LOGARIT
12 LŨY
Page 3
++
9669241 log 2 ff T
T
T
Chọn B
f
fmnfmfnmn 96951951959596949596...12...9596
2 f
Câu 71: Cho x , y và z là các số thực lớn hơn 1 và gọi w là số thực dương sao cho log24 x w = , log40 y w = và log12 xyz w = . Tính logz w A. 52 B. 60 C. 60 D. 52 Lời giải Chọn C log24 x w = 1 log 24 w x = log40 y w = 1 log 40 w y = . Lại do log12 xyz w = ( ) 1 12 log w xyz = 1 12 logloglog www xyz = ++ 1 12 logloglog www xyz = ++ 1 12 11log 2440 w z =
1 log 60 w z = log60 z w = Câu 72: Cho 11 f , fmnfmfnmn với mọi * , mn . Tính giá trị của biểu thức
A. 9
B. 3
C. 10 T D. 4 T Lời giải
Có 11
,
fffffff 96.97 9612...95964656
i giải Chọn A Đặt 222 log;log;log axbycz === Ta có 1111 2020 abc ++= và 2020 abc++= ( ) ( )( ) ( )( )( ) 222222
111 1 0 0
abcabcabacbcabc abc abababcabcbcbcacac abbcca
++++=++++= +++++++= +++= Vì vai trò ,, abc như nhau nên giả sử 2020020202abcz +=== và 1 xy = ( ) ( ) ( ) ( ) 22 2 22
++−−−+=++−−−+ === Câu 74: Cho ba số thực dương , , xyz theo thứ tự lập thành một cấp số nhân, đồng thời với mỗi số thực dương (1)aa thì 3log,log,log a aa xyz theo thứ tự lập thành một cấp số cộng. Tính giá trị của biểu thức 1959201960 xyz P yzx . A. 60. B. 2019. C. 4038. D. 2019 2 . Lời giải Chọn C
log1log()11 log2log4040 xyzxyzxyyzzxzxyzyzzx zz
Ta có: , , xyz là ba số thực dường, theo thứ tự lập thành một cấp số nhân thì 2 . (1) yxz . Với mỗi số thực (1),aa 3log,log,log a aa xyz theo thứ tự lập thành một cấp số cộng thì 3 2logloglog4loglog3log (2) aaaaaa yxzyxz Thay (1) vào (2) ta được 2log.log3logloglog aaaaa xzxzxzxz Từ (1)ta suy ra yxz
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 4 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Tương tự 69.70 6912...68692415 2 f Vậy 9669241 46562415241 logloglog10003 22 ff T Câu 73: Cho các số thực dương ,, xyz thỏa mãn đồng thời 222 1111 logloglog2020 xyz ++= và 2 log()2020 xyz = . Tính ( ) ( ) 2 log1 xyzxyzxyyzzx ++−−−+ A. 4040 B. 1010 C. 2020 D. 22020 Lờ
0984164935
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
Page 5
(
= mn mn 2 14 log 21 = −−+ mn mnmn , vì 1+=mn 22 1411 loglog4.21 222 ==== mn mn Câu 76: Gọi n là số nguyên dương sao cho 23 33 333 1111190 logloglogloglog n xxxxx ++++= đúng với mọi x dương, 1 x . Tìm giá trị của biểu thức 23Pn=+ A. 32 P = . B. 23 P = . C. 43 P = . D. 41 P = . Lời giải Chọn D ( ) ( ) 23 33 333 1111190 logloglogloglog log32log33log3...log3190log3 log3123...190log3 123...190 1 190 2 n xxxxx xx xxxxx n n n nn ++++= ++++= ++++= ++++= + = 2 3800 nn +−= 19 19 20 n n n = = =− (do n nguyên dương) 2341Pn =+=
LŨY
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Thay vào giả thiết thì 19592019604038 P Câu 75: Cho hàm số ( ) 2 12 log 21 = x fx x và hai số thực , mnthuộc khoảng ( )0;1 sao cho 1+=mn Tính ( ) ( ) + fmfn A. 2 B. 0 C. 1 D. 1 2 Lời giải Chọn C
) ( ) 22 1212 loglog 2121 +=+ mn fmfn mn 22 122 loglog 211 =+ mn mn 2 122 log. 211
Câu 77: Cho x , y , z là ba số thực dương lập thành cấp số nhân; loga x , log a y , 3log a z lập thành cấp
số cộng, với a là số thực dương khác 1. Giá trị của 93xyz p yzx =++ là A. 13. B. 3. C. 12. D. 10. Lời giải
Chọn A
x , y , z là ba số thực dương lập thành cấp số nhân nên ta có 2 xzy = (1). loga x , log a y , 3log a z lập thành cấp số cộng nên: 3 loglog2log a aa xzy += log3log4log aaa xzy+= 34 xzy= (2). Từ (1) và (2) ta suy ra xyz == . Vậy 93 91313 xyz p yzx =++=++= .
Câu 78: Cho (1)1; f = ()()() fmnfmfnmn +=++ với mọi * , mnN . Tính giá trị của biểu thức ( ) ( ) 20192009145 log 2 ff T = A. 3 B. 4 C. 5 D. 10 Lời giải Chọn B Ta có (2019)(200910)(2009)(10)20090 ffff=+=++ Do đó (2019)(2009)145(10)20090145 fff−−=+− (10)(9)(1)9 (9)(8)(1)8 ................... (3)(2)(1)2
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH
THỪA MŨ LOGARIT
12 LŨY
Page 6
(2)(1)(1)1 fff fff fff fff =++ =++ =++ =++ Từ đó cộng vế với vế ta đượ
Vậy
logloglog100004. 22 ff −−−+ === Câu
Có bao nhiêu số nguyên dương n để log256 n là
ột số nguyên
A.
Lờ
ải Chọn C 2 log2568.log28 log nn n == là số nguyên dương 2 log1;2;4;82;4;16;256 nn .
c: (10)10.(1)12....8955.ff=+++++=
(2019)(2009)1452009014555
79:
m
dương?
2. B. 3. C. 4 D. 1
i gi
Vậy có 4 số nguyên dương.
Câu 80: Cho 2018! x = . Tính 2018201820182018 2320172018
1111 ... loglogloglog A xxxx =++++ . A. 1 2017 A = . B. 2018 A = . C. 1 2018 A = . D. 2017 A = . Lời giải 2018201820182018 2320172018
1111 loglogloglog A xxxx =++++ 2018201820182018 log2log3...log2017log2018 xxxx =++++ 2018.log22018.log3...2018.log20172018.log2018 xxxx =++++ ( )2018.log2log3...log2017log2018 xxxx =++++ ( )2018.log2.3.....2017.2018 x =
Câu 81: Tìm bộ ba số nguyên dương (;;) abc thỏa mãn log1log(13)log(135)...log(135...19)2log5040log2log3 abc+++++++++++−=++
(2;6;4) B. (1;3;2) C. (2;4;4) D. (2;4;3)
ời giải
có log1log(13)log(135)...log(135...19)2log5040log2log3 abc+++++++++++−=++ 222 log1log2log3...log102log5040log2log3 abc++++−=++
) 222 log1.2.3.102log5040log2log3 abc−=++
)2 log1.2.3.102log5040log2log3
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page 7
333
=++++
=
A.
L
Ta
(
(
abc−=++ ( ) 2log1.2.3.102log5040log2log3 abc−=++ ( ) ( ) 2log10!log7!log2log32log8.9.10log2log3 abcabc −=++=++ 26log24log3log2log3 abc++=++ Vậy 2 a = , 6 b = , 4 c = Câu 82: Tổng 32018 222 222 12log23log2....2018log2 S =++++ dưới đây. A. 221008.2018 . B. 221009.2019 . C. 221009.2018 . D. 22019 . Lời giải Ta có ( ) ( )2 3333 1 123... 4 nn n + ++++= . Mặt khác 32018 222 222 12log23log2....2018log2 S =++++ 111 232018 222 2 22 12log23log2....2018log2 =++++ 333 222 12log23log2....2018log2 =++++
123...2018
( ) 2 201820181 2 +
221009.2019 = .
Câu 83: Số 2016201720172018 có bao nhiêu chữ số? A. 147278481. B. 147278480. C. 147347190. D. 147347191. Lời giải Số chữ số của một số tự nhiên x là: log1 x + ( log x là phần nguyên của log x ). Vậy số chữ số của số 2016201720172018 là ( ) 20162017 log20172018120162017log201720181147278481. +=+=
Câu 84: Cho x-x 9+9=14 và x-x x+11-x 6+3(3+3)a = 2-3-3b với a b là phân số tối giản. Tính
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page 8
Pab A. 10. P B. 45. P C. 10. P D. 45. P Lời giải Chọn B Ta có 2222 2 991432.3.3316 3316334. xxxxxx xxxx 11 63(33)63(33)63(33) 23323.33.323.33 63.4189 45. 23.4105 xxxxxx xxxx xx a ab b Câu 85: Cho hai số thực dương , ab thỏa ( ) 469 logloglogabab ==+ . Tính a b . A. 1 2 B. 15 2 + C. 15 2 D. 15 2 −+ Lờigiải Chọn D Đặt ( ) 469 logloglog tabab ===+ 4 6469 9 t tttt t a b ab = =+= += 2 215 32 22 10 33 215() 32 t tt t L −+ = +−= = . 4215 632 t t t a b −+ === . Câu 86: Cho các số thực dương , xy thỏa mãn ( ) 694 logloglog22 xyxy ==+ . Tính tỉ số x y ?
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 9
thi: Tuyển sinh
10 Tốt
12 Sưu tầm và biên soạn A. 2 3 x y = . B. 2 31 x y = . C. 2 31 x y = + . D. 3 2 x y = . Lờigiải Chọn B Giả sử ( ) 694 logloglog22xyxyt ==+= . Ta có: 6(1) 9(2) 224(3) t t t x y xy = = += Khi đó 62 0 93 t t t x y == Lấy (1), (2) thay vào (3) ta có 2.62.94 ttt += 2 22 2.20 33 tt −−= 22 13 3 31 2 13 3 t t =+= =− (thoûa) (loaïi) Câu 87: Cho x , y là các số thực dương thỏa mãn 25159 logloglog24 xxy y + == và 2 xab y −+ = , với a , b là các số nguyên dương, tính ab + A. 14 ab+= . B. 3 ab+= . C. 21 ab+= . D. 34 ab+= . Lờigiải Chọn D Ta có 25 25 log 2 log 25159 2 925 15 logloglog24 15 loglog42 x x y xxy y xx = + == + = Đặt 25 log2.25 2 t x tx == , ta được 2.25154.9 ttt += 2 55 24 33 tt += 5 3 133 log 4 t −+ = 2.255133 2. 1532 t t t x y −+ === Do đó 1 a = , 33 b = nên 34 ab+= Bất đẳng thức Cauchy (AM GM) • ,0,ab thì 2.abab + Dấu "" = xảy ra khi: .ab = • ,,0,abc thì 3 3..abcabc ++ Dấu "" = xảy ra khi abc == Nhiều trường hợp đánh giá dạng: 2 2 ab ab + và 3 3 abc abc ++
Hòa
0984164935
Chuyên luyện
vào lớp
Nghiệp THPT BDKT Toán 10; 11;
Bất đẳng thức Cauchy Schwarz (Bunhiaxcôpki) • ,,,, abxy thì: 22222 (..)()(). axbyabxy +++ Dấu "" = khi ab xy = • ,b,c,x,y,za thì: 2222222 (...)()(). axbyczabcxyz ++++++ Dấu "" = xảy ra khi và chỉ khi: abc xyz == Nhiều trường hợp đánh giá dạng: 2222 ..()(x). axbyaby +++ Hệ quả. Nếu ,, abc là các số thực và ,, xyz là các số dương thì: 222 ()abab xyxy + + + và 2222 () abcabc xyzxyz ++ ++ ++ : bất đẳng thức cộng mẫu số
Câu 88: (Đề Tham Khảo 2020 Lần 2) Xét các số thực dương ,,, abxy thoả mãn 1,1ab và xy abab == . Giá trị nhỏ nhất của biểu thức 2 Pxy =+ thuộc tập hợp nào dưới đây? A. ( )1;2 B. 5 2; 2 C. )3;4 D. 5 ;3 2 Lời giải
Chọn D Đặt loga tb = Vì ,1ab nên 0 t
có: ( ) ( ) 11 log1log1 22 x aa aabxabbt ===+=+ . ( ) 111 log1log1 22 y bb babyaba t
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page
10
c nửa khoảng 5 ;3 2 Câu 89: (Đề Tham Khảo 2020 Lần 2) Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn ( ) 22 34 log()logxyxy +=+ ? A. 3 B. 2 C. 1 D. Vô số Lời giải Chọn B Cách 1: Đặt ( ) ( ) 22 34 22 3 log()log1 4 t t xy txyxy xy += =+=+ +=
Ta
===+=+
. Vậy ( ) 11 211 2 Pxyt t =+=+++ 313 2 222 t t =+++ Dấu đẳng thức xảy ra khi và chỉ khi 2 1 2 t ba t == . Giá trị nhỏ nhất của biểu thức 2 Pxy =+ bằng 3 2 2 + thuộ
=+
t y xxy y y
thuẫn với 3 2 o 22 lg2 4 xy + suy ra loại 1 x =−
t t
ậy có hai giá trị 0;1 x Cách 2: Đặt ( ) ( ) 22 34 22
3 log()log1 4
t t xy txyxy xy += =+=+ += Suy ra , xy là tọa độ của điểm M với M thuộc đường thẳng :3t dxy+= và đường tròn ( ) 22 :4t Cxy+= . Để tồn tại y tức tồn tại M nên ( ) , dC có điểm chung, suy ra ( ) , dOdR trong đó ( ) 0;0,2t OR = nên 3 2

t t t Khi đó ( ) 3 2 3 2 22
3 2log2 2
log2 log2
03 1 4
xy xy
+ + Minh họa quỹ tích điểm M như hình vẽ sau
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 11 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Áp dụng bất đẳng thức Cauchy, ta có ( ) ( ) 2 22 9 2 9 9242log2 4 t tt t xyxyt =++= Như vậy, 9 4 log2 2224441,891;0;1 tt xyxx +=− ➢ Trường hợp 1: 2 30 0 41 t t yt x y y == = = = . ➢ Trường hợp 2: 2 310 1 410 t t yt x y y =−= = = =− ➢ Trường hợp 3: 22 2 310 15 141312
t
=−+
=+ += mâu
V
h
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page 12
4
ba
= ( ) 2 241 log3211 4 a a ba + += = 2 3 3224 4 43 a aa ba b = = = = Vậy 327 26 44 ab+=+= . Câu 91: (Mã 101 - 2020 Lần 1) Xét các số thực không âm x và y thỏa mãn 1 2.43 xy xy +− + . Giá trị nhỏ nhất của biểu thức 22 46 Pxyxy =+++ bằng A. 33 4 . B. 65 8 . C. 49 8 . D. 57 8 .
Ta thấy có 3 giá trị x có thể thỏa mãn là 1;0;1xxx=−== . Thử lại: ➢ Trường hợp 1: 2 30 0 41 t t yt x y y == = = = . ➢ Trường
ợp 2: 2 310 1 410 t t yt x y y =−= = = =− ➢ Trường hợp 3: 22 2 310 15 141312 t t t t y xxy y y =+ =−+ =+ += mâu thuẫn với 3 2 o 22 lg2 4 xy + suy ra loại 1 x =− . Câu 90: (Mã 103 2018) Cho 0,0ab thỏa mãn ( ) ( ) 22 4518a1 log161log4512 abbabab++++++++= Giá trị của a2b + bằng A. 6 B. 27 4 C. 20 3 D. 9 Lời giải Chọn B Từ giả thiết suy ra ( ) 22 451 log1610 ab ab ++ ++ và ( ) 8a1 log4510 b ab + ++ Áp dụng BĐT Côsi ta có ( ) ( ) 22 4518a1 log161log451 abbabab++++++++ ( ) ( ) 22 4518a1 2log161.log451 abbabab+++ ++++ ( ) 8a1 22 2log161 b ab + =++ Mặt khác ( ) ( ) 2 22 16148a18a1,0 ababbbab ++=−+++ , suy ra ( ) 8a1 22 2log1612 b ab + ++ . Khi đó ( ) ( ) 22 4518a1 log161log4512 abbabab++++++++= ( ) ( ) 4518a1 log81log451
abbabab
++++=++
Lời giải
Chọn B
Cách 1: Nhận xét: Giá trị của , xy thỏa mãn phương trình ( ) 1 2431 xy xy +− += sẽ làm cho biểu thức P nhỏ nhất. Đặt axy =+ , từ ( )1 ta được phương trình 1 23 4.20 a a yy +−−= Nhận thấy 1 23 4.2 a ya yy =+−− là hàm số đồng biến theo biến a , nên phương trình trên có nghiệm duy nhất 33 22axy=+= . Ta viết lại biểu thức ( ) ( ) 2 1165 42 488 Pxyxyy =++++−−= . Vậy min 65 8 P = . Cách 2: Với mọi , xy không âm ta có 33 1 22 33 2.43.4.410 22 xyxy xy xyxyxyy +−+−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page 13
(1) Nếu 3 0 2 xy+− thì ( ) 3 0 2 3 .410.410 2 xy xyyy +− +−+−+−= (vô lí) Vậy 3 2 xy+ . Áp dụng bất đẳng thức Bunhyakovski ta được ( ) ( ) 22 22 463213Pxyxyxy =+++=+++− ( ) 2 2 11365 513513 2228 xy ++−+−= Đẳng thức xảy ra khi 35 24 321 4 y xy xy x = += +=+ = . Vậy 65 min 8 P = .
+− +++−+−
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Huỳnh
Ánh 42
Page 14
Câu 92: Xét các số thực , xy thỏa mãn ( ) 22 122 2224 xyx xyx ++ +−+ . Giá trị nhỏ nhất của biểu thức 4 21 y P xy = ++ gần nhất với số nào dưới đây? A. 2. B. 3. C. 5. D. 4. Lời giải Chọ
Ta
( ) 22221221222 2224222 xyxxyxxyxxyx ++++−+−++−+ ( ) ( ) 2 2 2 1 2 211 xy xy −+ −++ . Đặt ( ) (
2 2
=−+
Đồ thị hàm số 2t y = và đồ thị hàm số 1 yt=+ như sau: Từ đồ thị suy ra ( )2 2 210111 t ttxy +−+ . Do đó tập hợp các cặp số ( ) ; xy thỏa mãn thuộc hình tròn ( )C tâm ( ) 1;0,1IR = . Ta có ( ) 4 240 21 y PPxPyP xy =+−+= ++ là phương trình của đường thẳng d . Do d và ( )C có điểm chung ( ) ( ) ( ) 2 2 2 3 ,148160 44 P dIdRPP PP +− +− 1515 P −−−+ , suy ra giá trị nhỏ nhất của P gần nhất với 3 Câu 93: Cho các số thực , xy thỏa mãn bất đẳng thức ( ) 2249 log231 xy xy + + . Giá trị lớn nhất của biểu thức 3 Pxy =+ là A. 3 2 . B. 210 4 + . C. 510 4 + . D. 310 4 + . Lời giải Điều kiện 22 491 xy+
Giáo viên:
Văn
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
n B
có
)
10txyt
, ta được BPT: 21 t t +
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 15 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Trường hợp 1: 22 491 xy+ Ta có ( ) ( ) 22 21 231 31 x xy y + 13 31 22xyP ++ ( )1 Trường hợp 2: 22 491 xy+ . Khi đó ( ) 22 22 49 log2312349 xy xyxyxy + +++ 22 111 23 222xy −+− 1113 323 2224Pxyxy =+=−+−+ Áp dụng BĐT Bunhiacopski ta được: 2 22 1111115 23123 2224228 xyxy −+−+−+− Suy ra 1113310 23 22244Pxy + =−+−+ ( )2 Dấu bằng xẩy ra khi và chỉ khi 11 510 223 861 22 20 412310 5210 310 3 30 4 xy x xy xy y xy + −=− = −= +=+ + + = += . Từ ( )1 và ( )2 suy ra giá trị lớn nhất của P là 310 4 + Câu 94: (Chuyên Lam Sơn Thanh Hóa 2019) Cho các số thực , ab thay đổi, thỏa mãn
,1. 3 ab Khi biểu thức ( ) 42 3 loglog981 ab Pbaa =+−+ đạt giá trị nhỏ nhất thì tổng ab + bằng A. 2 39 + B. 3 92 + C. 292 + D. 332 + Lời giải Chọn A Do ( )2 4222981990aaaa−+− đúng 1 ; 3 a Dấu bằng xảy ra khi 3 a = Suy ra ( )2 33 loglog3log2log322 abab Pbaba +=+ Dấu bằng xảy ra khi và chỉ khi 2 3 33 log2log39 ab a a ba b = = = = Vậy, khi P đạt giá trị nhỏ nhất thì 2 39. ab+=+
1
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 16 Chuyên luyện thi: Tuyển sinh vào
10 Tốt
THPT
10; 11; 12 Sưu tầm và biên soạn Câu 95: Xét các số thực dương ,, abc lớn hơn 1 ( với ab ) thỏa mãn ( ) 4loglog25log abab ccc += . Giá trị nhỏ nhất của biểu thức logloglog bac acb ++ bằng A. 5 B. 8 C. 17 4 D. 3 Lời giải Chọn A Đặt
0984164935
lớp
Nghiệp
BDKT Toán
log,log ccaxby == Vì ,,1abc và ab nên suy ra loglog cc ab hay 0 xy Từ giả thiết suy ra: 111 425. logloglog ccc abab += 4425 xyxy += + ( )2 25 4 xy xy + = 17 4 xy yx += 4 1 4 x y x y = = 4 xy = ( vì xy ).
Do
Ta có: log1 loglogloglog loglog c bacc cc a acbb ba ++=++ = 1 x y yx ++ = 11 42.5 44 x yy yyy +++= . Dấu bằng xảy ra khi và chỉ khi 1 2 y = và 2 x = , tức là 22 ; accb == Vậy giá trị nhỏ nhất của biểu thức đã cho bằng 5. Cách khác Từ giả thiết suy ra: ( ) 4log.loglog25.log.log abbabb bccbc +=
( ) log 4loglog125log b ba b c cb ab += ( ) log0 4log125log1 b a b c b a =
+= +
,,1abc nên log0 b c ; suy ra ( )( ) 41log1log25 abba ++= 1 log 4 a b = . Khi đó: logloglog42log.log42log5 bacaca acbcbb +++=+= . Vậy giá trị nhỏ nhất của biểu thức bằng 5 đạt được khi và chỉ khi 422 ,, abaccb ===
Câu 96: Xét các số thực dương a , b, x,y thỏa mãn a1 , b1 và 2x3y66 abab == . Biết giá trị nhỏ nhất của biểu thức 42 Pxyxy =+− có dạng 165 mn + (với , mn là các số tự nhiên), tính =+ Smn A. 58 B. 54 C. 56 D. 60 Lời giải
Chọn C
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
LOGARIT
Page 17
LŨY THỪA MŨ
Vậy P đạt giá trị nhỏ nhất là 165 mn + khi 11 15 11 30log22loglog 15 aba babba === Ta có: 52 56 4 m mn n = += = Câu 97: Xét các số thực , xy thỏa mãn ( ) ( ) 22 log1log11 xy−+−= . Khi biểu thức 23 Pxy =+ đạt giá trị nhỏ nhất thì 323 xyab −=+ với , ab . Tính Tab = ? A. 9 T = B. 7 3 T = C. 5 3 T = D. 7 T = Lời giải Chọn C Điều kiện: 101 101 xx yy − − Khi đó: ( ) ( ) ( )( ) 22 22 log1log1111211 11xyxyyy xx −+−=−−=−==+ Suy ra: ( ) 66 2323215 11Pxyxx xx =+=++=−++ Cách 1: Dùng bất đẳng thức Áp dụng bất đẳng thức Côsi, ta có: ( ) ( ) 66 21221. 11 xx xx −+−
Theo bài ra ta có: 2x3y66 abab == 2x66 3y66 aab bab = = ( ) ( ) 66 a 66 b 2xlogab 3ylogab = = a b 2x66logb 3y66loga =+ =+ ( ) ( ) a b x31logb y21loga =+ =+ Vì a , b1 nên aa logblog10 = . Do đó: 4224(1log)(1log)66log22log abab Pxyxybaba =+−=++++−− 5230log22log52230log.22log524165 abab baba =+++=+

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
42
Page 18
( ) 6
1 xP x −++ D
ra
(
xN
−=−=−= =− 2233
+ =+= .
. Cách 2: Dùng bảng biến thiên Ta có: 6 23 1 Px x =++ ( )2 6 '2 1 P x =− ( ) ( ) 13 '0 13 xN P xL =+ = =− Bảng biến thiên Dựa vào bảng biến thiên, ta có: min 233 43513 3 Pxy + =+=+= . Do đó: ( ) 233555 323132131; 3333 xyabTab + −=+−=+==== . Câu 98: Cho 0,0ab thỏa mãn ( ) ( ) 22 4518a1 log161log4512 abbabab++++++++= . Giá trị của 2 ab + bằng A. 27 4 . B. 6. C. 20 3 . D. 9. Lời giải Chọn A
Giáo viên: Huỳnh Văn Ánh
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
2143435
ấu “=” xảy
( ) ( )
) ( ) 2 613 211313 113
xxx x xL
=+
1 3 3 y
Do đó: ( ) 233555 323132131; 3333 xyabTab + −=+−=+====
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 19 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có: 0,0ab Nên ( ) ( ) 22 451 81 log1610 4511 811 log4510 ab ab ab ab ab ab ++ + ++ ++ + ++ ( ) ( ) ( ) ( ) ( ) 2222 4518145181 22 81 log161log4512log161.log451 2log161 abababab ab Pabababab Pab ++++++ + =+++++++++ ++ Mặt khác: ( ) 2222 81 1612161812log812 ab abababPab + +++=++= Dấu bằng xảy ra khi và chỉ khi: 22 2 3 4 16 4 814512161 3 ab a ab ababbb b = = = +=+++=+ = Do đó 27 2 4 ab+= . Câu 99: Cho ,, abc là các số thực lớn hơn 1. Giá trị nhỏ nhất của biểu thức 3 404010108080 log log3logacab bc P a bc =++ bằng A. 2020. B. 16160. C. 20200. D. 13130. Lời giải Chọn C Ta có 3 404010108080404010108080 log2log11 log3loglog3.log 23 bc acab bc acab P aa bc bc =++=++ 2020log2020log8080log abc bcacab=++ ( ) ( ) ( ) 2020loglog2020loglog8080loglog aabbcc bcacab=+++++ 2020log2020log2020log8080log2020log8080log abacbc bacacb=+++++ Vì ,,1abc nên các số log,log,log,log,log,log0 abacbc bacacb Khi đó ta có 2 2020log2020log22020loglog4040 abab baba += 2 2020log8080log24040loglog8080 acac caca += 2 2020log8080log24040loglog8080 bcbc cbcb += Suy ra 40408080808020200 P ++=
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 20 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 100: Cho ,, abc là các số thực dương khác 1 thỏa mãn 22 logloglog2log3 abab cc bc bb +=−− . Gọi , Mm lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của loglog ab Pbc =− . Giá trị của biểu thức 3
=− bằng
ờ
ả
Chọn C Biến đổi đẳng thức đề bài ta được 2222 22 logloglog2log3loglogloglog2log1 logloglog.loglog2log1 abababaab ababab cc bcbccbc bb bcbcbc +=−−+=−−− +=−−− Đặt log;log ab ubvc == ta có phương trình 22 21uvuvuv +=−−− 2222221443uuvvuuvv −+++++++= 222 ()(1)(2)3 (*) uvuv −++++= Ta có bất đẳng thức quen thuộc 222 1 2()xyxy +− dấu bằng xảy ra khi xy =− , áp dụng bất đẳng thức này ta có 222222 11 (1)(2)(12)(1)(2)(1) 22 uvuvuvuv ++++−−+++−− (**) Từ (*) và (**) ta có 22 1 3()(1) 2 uvuv −−−− hay 222 3(1)3250115 23 PPPPP −−−−− Vậy 5 1, 3 mM=−= suy ra 36SmM=−=− Câu 101: Cho các số thực ,1xy và thỏa mãn điều kiện 4 xy . Biểu thức 2 2 4 2log8log 2 x y y Px=− đạt giá trị nhỏ nhất tại 00 , xxyy == . Đặt 44 00Txy =+ mệnh đề nào sau đây đúng A. 131 T = . B. 132 T = . C. 129 T = . D. 130 T = . Lời giải Chọn D Ta có 2 2 4 2log8log 2 x y y Px=− 2 2 2 2 22 log log8 2 log4log2 y x xy =− 22 22 3log2log1 2log2log1 xy xy +− =− ++
SmM
A. 16. B. 4. C. 6. D. 6 . L
i gi
i
102: Cho các s
= = Tổng mn + bằng A. 13. B. 16. C. 7.
1 4 7 4 ố
x y a ax byb cz c
= = Vậy 1744 44 44 00 22130 Txy =+=+= = = == = = , mà ( )1010.10.10101* xyz abcxyz ==++= . Ta có 5log.log2log.loglog.log52 Fabbccaxyyzzx =++=++ . Từ ( ) *1yxz=−− , thay vào biểu thức F , ta được: ( ) ( ) 22 512125625 Fxxzxzzxzzxxzzx =−−+−−+=−−−++ 2229115 262322 2222 zxxzzxxx =−−−−++−+−+ ( ) 222 91315 2344 44222 zxxzzxxx =−+++−−−−++
2 2 x y z
2 2 ố
x y ả
i gi
D. 10.
1 4 0 7 4 0 Lời giải Chọn C Đặt log10 log10 log10
n.
thực dương ,, abc thỏa mãn 10 abc = . Biết giá trị lớn nhất của biểu thức 5log.log2log.loglog.log Fabbcca =++ bằng m n với , mn nguyên dương và m n t
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
Page 21
LŨY
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
Đặt 2log xa = , 2log yb = ( ,0ab ), ta được 321 221 ab P ab +− =− ++ 12 221 ab =+ ++ . Vì 4 xy suy ra 22 loglog2 xy+ 202 abab +− Suy ra 1212 221421 P abbb =++ ++−+ Xét hàm 12 () 421 fb bb =+ −+ trên 0;2 ,ta có: ( ) ( ) 22 14 () 421 fb bb =− −+ ( ) ( )2 2 0214(4)0fbbb =+−−= 7 4 b = Ta có: ( ) ( ) 9978 0,2, 41049fff === . Suy ra trên đoạn 0;2 ta có: 8 min 9 P = 2 2
1 log 4 7 log 4
x y
= = . Câu
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 22 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) 2 2 31155 22 22222 zxx =−+−−−+ Vậy 5 max 2 F = khi và chỉ khi 13 2 31 02 22 205 2 xyz y zxx x z ++= = +−== −= =− Vậy 5,2527.mnmn==+=+= Câu 103: Cho các số thực dương ;; abc khác 1 thỏa mãn 22 3 loglog2loglog abba cc bc bab ++= . Gọi , Mm lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của loglog ab Pabbc =− . Tính giá trị biểu thức 2229 SmM =+ A. 28 S = . B. 25 S = . C. 26 S = . D. 27 S = . Lời giải Chọn D Đặt ( ) log;log,;0logloglog abaab xbycxycxyPabbcxyxPy ====−=−=+ Khi đó ta có ( ) ( ) ( ) ( ) 2222 3 2 2 22 loglog2loglog223 223 310 abba cc bcxyyxyx bab PyyyPyyPy yPyPP ++=++−=−− +++−=+−−+ +++++= . Phương trình có nghiệm khi 2 55 0325011;27 33 PPPmMS −++−=−== Nên giá trị nhỏ nhất của P là 1 1 4 4 2 0 44 00 77 44 2 0 1 log 2 2 8 4 130 7 9 log 22 4 x x x Txy y yy = = = =+= = == Câu 104: Cho 0,0ab thỏa mãn 22 45181 log(161)log(451)2 abababab . Giá trị của 2 ab bằng A. 9 B. 6 C. 27 4 D. 20 3 Lời giải Chọn C Theo bất đẳng thức Côsi với 0,0ab ta có: 222222 16121618116181 ababababab (*) Do 4511 ab nên từ (*) có: 22 4518145181 log(161)log(451)log(81)log(451) abababababababab
C. 3 1;
1 log(81)2 log(81) ab ab ab ab . Suy ra 22 45181 log(161)log(451)2 abababab . Đẳng thức xảy ra khi x a a y b a
ba ab a ababbb b abab . Vậy 27 2 4 ab Câu 105: Xét các số thực ,,, abxy thỏa mãn 1,1ab và xy a ab b == . Giá trị lớn nhất của biểu thức 2 Pxy =− thuộc tập nào dưới đây? A. 1 0; 2 =− == =− == Đặt loga tb = . Vì 1,1ab , nên 0 t Khi đó: ( ) 11313131322 112. 22222222 ttt Pt tttt =−−−=−−=−+−= Dấu bằng xảy ra khi và chỉ khi ( ) 1 2 0 2 t tt t == max 3221 0,0860; 22 P = Câu 106: Cho dãy số ( ) n u có số hạng đầu 1 1 u thỏa mãn ( ) ( ) 2222 212122 log5log7log5log7 +=+uu và 1 7 + = nn uu với mọi 1 n . Giá trị nhỏ nhất của n để 1111111 n u bằng: A. 11. B. 8. C. 9. D. 10. Lời giải Chọn D Ta có ( ) 1 7,1 + = nnn uunu là một cấp số nhân với số hạng đầu là 1u , công bội 7 = q ( ) ( ) 22 22 2121221221 log5log7log5loglog7log +=+++ uuuu 2222 222121222121 log52.log5.logloglog72.log7.loglog =+++++uuuu
35 ; 22
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 . B. 1 1; 2 .
23 2
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn . D.
22 45181451 451
1 log(161)log(451)log(81) log(81) ababab ab ababab ab Mặt khác 4511 ab và 811 ab nên: 451 451 . Lời giải Chọn A Từ giả thiết ta có: ( ) 1 log1log 2 11 log1 2log
22 2 4 16 3 45181260 4 3 ,0,0 aa xb ax bb aa y by b bb
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo
Huỳnh Văn Ánh 42 Nguyễn Cư Trinh
ĐT:
Page 24
Tốt
Sưu tầm và
soạn ( ) 222 21222122
=++++ uu 22222
=+++=+ uu (
2 2122121212
+=+= uuuu ( ) ( ) 1 21 1 212 212 log01loai1nhan loglog35035 loglog35 = = = += =− u u u u u Số hạng tổng quát của dãy số là 1112 1 111 ..7.7.7 355.75 ==== nnnn n uuq . 22 7 1 1111111.71111111755555552log5555555 5 − nn n un 7 log55555552+ n . Vì n nên giá trị nhỏ nhất của n bằng 10 Câu 107: Xét các số thực , xy thỏa mãn ( ) ( ) 22 log1log11 xy−+−= . Khi biểu thức 23 Pxy =+ đạt giá trị nhỏ nhất thì 323 xyab −=+ với , ab Tính Tab = A. 9 T = . B. 7 3 T = . C. 5 3 T = . D. 7 T = . Lời giải Chọn C Ta có ( ) ( ) 22 ,11 log1log11 22 11 11 xyx xy yy xx −+−= −==+ Khi đó ( ) 26 232312152125 11Pxyxx xx =+=++=−+++ , dấu bằng xảy ra khi và chỉ khi ( ) ( ) 1 13 6253 2132313211 2 13 1 3 3 2 1 1 x x xxy x y y x −= −=−=+−+=+ =+ =+ Vậy 5 1, 3 ab== nên 5 3 T = Câu 108: Xét các số thực a , b , 0 c thỏa mãn 3515 == abc . Giá trị nhỏ nhất của biểu thức 222 4()=++−++ Pabcabc thuộc tập hợp nào dưới đây? A. ( )1;2 B. )5;1 . C. )2;4 D. )4;6 Lời giải
viên:
Thuận Hòa TP Huế
0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10
Nghiệp THPT BDKT Toán 10; 11; 12
biên
2log2.log5log7.loglog5log7
212212222 2log2.log35.loglog5log7log5log7
)
2log2.log35.log02log.loglog350
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 25
ọn B
22
15 21log3log3 1log3log3 log3 log3 +− ++ +− ++ +− = ++ = =− a b c Câu 109: Xét các số thực dương a , b , c , x , y , z thỏa mãn 1 a , 1 b , 1 c và xyz abcabc === . Giá trị nhỏ nhất của biểu thức 1 2 Pxyz=+++ thuộc tập hợp nào dưới đây? A. )10;13 . B. )7;10 . C. )3;5 . D. )5;7 . Lời giải Chọn D Từ giả thiết ta có ( ) 1 1loglog 2 aa xbc =++ , ( ) 1 1loglog 2 bb yac =++ , ( ) 1 1loglog 2 cc zba =++ . Khi đó ta có 24loglogloglogloglog abacbc Pbacacb =++++++ . Vì 1 a , 1 b , 1 c nên log0 a b , log0 b c , log0 c a , log0 b a , log0 c b , log0 a c Áp dụng bất đẳng thức Cô Si ta được loglog2log.log abab baba + hay loglog2 abba+ . Tương tự loglog2 ac ca+ và loglog2 bccb+ .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ch
Đặt 3 5 15 log 35150log log = ==== =− abc at tbt ct . Khi đó 222 35153515 logloglog4(logloglog) =++−+− Ptttttt ( ) ( ) 222 35153515 log1log3log34log1log3log3 =++−+− tt ( ) ( ) 222 515515 1log3log341log3log3=++−+− XX , (với 3log Xt = ) ( ) 515 min 22 515 21log3log34 1log3log3 +− ==− ++ PP , khi ( ) ( )21log3log3 515 22 1log3log3 515 5 15 3 22 515 21log3log3 log3 1log3log3 +− ++ +− == ++ tt Suy ra ( ) ( ) ( ) 515 22 515 21log3log3 515 22 1log3log3 5 15 5 21log3log3 515
1log3log3 5 15
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 26 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do đó 210 P hay 5 P . Dấu "" = xảy ra khi và chỉ khi abc == Vậy giá trị nhỏ nhất min 5 P = . Câu 110: Xét các số thực dương ,,, abxy thỏa mãn 1,1ab và 22 . xy abab == . Giá trị nhỏ nhất của biể
A. 9 4 P = . B. 6 2 P =
C.
2
=
=
Lời giải Chọn B 22 2 2 11 log 22 11 log 22 a xy b xb abab ya =+ == =+ +)( )2 1111 loglog 2222 ab xyba =++ ( ) 111 loglog 424 abba =+++ 3 2 ( ,1log0,log0 ab abba ). Vì 6 0,0 2 xyxy . Dấu bằng xảy ra khi và chỉ khi ab =
2 2
=
B.
u thức Pxy = là
.
3
P
. D. 4 9 P
.
Câu 111: Xét các số thực dương ,,, abxy thỏa mãn 1,1ab và
x y y x abab == . Giá trị nhỏ nhất của biểu thức Pxy
là A. 2 P = .
4 P = . C. 3 P = . D. 1 P = . Lời giải Chọn B 2 2 2 2 1log 1log x a y y x b x b y abab y a x =+ == =+ . Ta có ( )( ) 22 .1log1log aa xy xybb yx ==++ 11loglog abba=+++ 4 ( ,1log0,log0 ab abba ). Dấu bằng xảy ra khi và chỉ khi ab = Câu 112: Xét các số thực dương ,,,,, abcxyz thỏa mãn 1,1,1,2abcy và 121xyz abcabc +−+ === . Giá trị nhỏ nhất của biểu thức Pxyz =++ là A. 13 P = . B. 3 P = . C. 9 P = . D. 1 P = .
1. Định lý: Nếu hàm số ( )yfx = đồng biến (hoặc luôn nghịch biến) và liên tục trên ( ) ; ab thì * ( ) ( ) ( ) ;;: uvabfufvuv == * Phương trình ( ) f x k = ( )kconst = có nhiều nhất 1 nghiệm trên khoảng ( ) ; ab
2. Định lý: Nếu hàm số ( )yfx = đồng biến (hoặc nghịch biến) và liên tục trên ( ) ; ab , đồng thời ( ) lim.lim()0 xaxb fxfx+−→→ thì phương trình ( ) ( )fxkkconst == có duy nhất nghiệm trên ( ) ; ab .
3. Tính chất của logarit:
1.1. So sánh hai logarit cũng cơ số: Cho số dương 1 a và các số dương , bc . Khi 1 a thì loglog aa bcbc . Khi 01 a thì loglog aa bcbc
2. Logarit của một tích: Cho 3 số dương 12,, abb với 1 a , ta có 1212log(.)loglog aaa bbbb =+
1.2. Hệ quả: Cho số dương 1 a và các số dương , bc . Khi 1 a thì log01 a bb . Khi 01 a thì log01 a bb loglog aa bcbc ==
3. Logarit của một thương: Cho 3 số dương 12,, abb với 1 a , ta có 1 12 2 logloglog aaa b bb b =− Đặc biệt: với ,0,1aba 1 loglog aa b b =− .
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 27 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn C 121 11loglog 21loglog 11loglog a b c a xyz b c xbc abcabcyac zba +−+ +=++ ===−=++ +=++ Ta có: 1213loglogloglogloglog acabbc xyzbccaba ++−+−=++++++ 36 xyz +++ 9 P ( ,,1log0,log0,log0,log0,log0,log0 aabbcc abcbcacab ). Dấu bằng xảy ra khi và chỉ khi abc == . SỬ DỤNG PHƯƠNG PHÁP HÀM SỐ (HÀM ĐẶC TRƯNG) GIẢI CÁC BÀI TOÁN
LOGARIT
4. Logarit của lũy thừa: Cho ,0,1aba , với mọi , ta có loglog aa bb = . Đặc biệt: 1 loglog n aa bb n = ( n nguyên dương).
Công th
s
dương
cơ số
abc
i
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page
28
ọn
Điều kiện: 2 0 0 xy xy + + . Đặt (
xyt +=
ta
2 4
t t xy xy + += (
2
tt t xx yx −− =− Nhận xét rằng
ố
=−
ế
ả
5.
ức đổi
: Cho 3
ố
,,
vớ
1,1ac , ta có loglog log c a c b b a = . Đặc biệt: 1 loglog a c c a = và 1 logloga a bb = với 0 . Câu 113: (Mã 102 - 2020 Lần 1) Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 242 số nguyên y thỏa mãn ( ) ( ) 2 43 loglogxyxy ++ ? A. 55. B. 28. C. 29. D. 56. Lời giải Ch
D
) 3log
,
có
3
)
43* 3
hàm s
( ) 43 tt ft
đồng bi
n trên kho
ng ( ) 0;+ và ( ) 0 ft với mọi 0 t Gọi n thỏa 2 43nn xx−=− , khi đó ( )* tn Từ đó, ta có 33 tn xyxx −=−− . Mặt khác, vì có không quá 242 số nguyên y thỏa mãn đề bài nên 3 3242log242 n n . Từ đó, suy ra 3 log242 2 4242 xx−− 27,428,4 x − Mà x nên 27,26,...,27,28 x−− . Vậy có 56 giá trị nguyên của x thỏa yêu cầu đề bài. Câu 114: (Mã 101 2020 Lần 1) Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 728 số nguyên y thỏa mãn ( ) 2 43 loglog() xyxy ++ ? A. 59. B. 58. C. 116. D. 115. Lời giải Chọn C Với mọi x ta có 2 xx Xét hàm số ( ) 2 34 ()log()log fyxyxy =+−+
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 29
Tập
định D(;) x =−+
2
−− ). ( ) 2
'()0,
+ +
f
. Ta
−+−
ọn D Ta
(
Đặ
*
( ) (
22
−+=−−+ Đạo hàm ( ) 2 11 ()0 ln2 ln3 gt t xxt =− −+ với mọi y . Do đó
gt
ng
ế
+ Vì mỗi x nguyên có không quá 127 giá trị * t nên ta có ( ) 2 23 (128)0log128log1280 gxx−−+ 27128344,845,8xxx −+− Như vậy có 90 giá trị thỏa yêu cầu bài toán Câu 116: (Mã 102 - 2020 Lần 1) Xét các số thực không âm x và y thỏa mãn 1 2.43 xy xy +− + . Giá trị nhỏ nhất của biểu thức 22 64 Pxyxy =+++ bằng A. 65 8 . B. 33 4 . C. 49 8 . D. 57 8 .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
xác
(do
yxyx
11
()ln3 ln4 fyxD xy xy =−
(do 2 0 xyxy++ ,ln4ln3 )
tăng trên D
có ( ) 2 34 (1)log(1)log10 fxxxxx −+=−+−−+ . Có không quá 728 số nguyên y thỏa mãn ( ) 0 fy ( ) 2 34 (729)0log729log7290 fxxx −+−−+ 2672940 xx
2 33670 xx−− 57,558,5 x − Mà x nên 57,56,...,58 x−− . Vậy có 58(57)1116 −−+= số nguyên x thỏa. Câu 115: (Mã 103 - 2020 Lần 1) Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 127 số nguyên y thỏa mãn ( ) ( ) 2 32 loglogxyxy ++ ? A. 89. B. 46. C. 45. D. 90. Lời giải Ch
có
) ( )( ) 2 32 loglog1 xyxy ++
t
txy=+ (do ,,0 xyxy+ )
) ( )
3223 (1)loglog()loglog02 xxttgttxxt
( )
đồ
bi
n trên ) 1;
Lời giải Chọn A Ta có 1222 2.43.232 xyxy xyyx +−+− +− ( ) ( ) 232 2.232.2* yxyx−
Hàm số ( ) .2t ftt = đồng biến trên , nên từ ( )* ta suy ra ( )23222301 yxxy −+−
Ta thấy ( )1 bất phương trình bậc nhất có miền nghiệm là nửa mặt phẳng có bờ là đường thẳng :2230dxy+−= (phần không chứa gốc tọa độ O ), kể cả các điểm thuộc đường thẳng d .
Xét biểu thức ( ) ( ) ( ) 22 22 6432132PxyxyxyP =++++++=+ Để P tồn tại thì ta phải có 13013PP+− .
Trường hợp 1: Nếu 13
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
30
V
Câu
(Đề Minh
ọa 2020 Lần 1) Có bao
ặ
ố
3 log3329y xxy ? A. 2019. B. 6. C.
.
. Lời giải Chọn D Cách 1: Ta có: 2 33 log3329log1123 yyxxyxxy . 1 Đặt 3 log113t xtx Phương trình 1 trở thành: 2
2 Xét
số 3u
trên .
P =− thì 3;2xy=−=− không thỏa ( )1 . Do đó, trường hợp này không thể xảy ra. Trường hợp 2: Với 13 P − , ta thấy ( )2 là đường tròn ( )C có tâm ( )3;2 I và bán kính 13 RP=+ Để d và ( )C có điểm chung thì ( ) 1365 ;13 8 22 dIdRPP + .
ậy 65 min 8 P =
117:
H
nhiêu c
p s
nguyên ; xy thỏa mãn 02020 x và
2020
D. 4
323tyty
hàm
fuu
13ln30, u fuu nên hàm số fu đồng biến trên
Do đó 222 ftfyty 3 log121991 yyxyxx
Vì 9 0202009120201920210log2021 yy xy 3 log20213,464
Do 0;1;2;3 yy , có 4 giá trị của y nên cũng có 4 giá trị của x
Vậy có 4 cặp số nguyên ; xy .
Cách 2:
Ta có: 2 33 log3329log1123 yyxxyxxy
Xét hàm số 3 log11fxxx với 0;2020 x .
Ta có 1 10,0;2020 1ln3 fxxx x Hàm số fx đồng biến trên đoạn 0;2020 . Suy ra 32 0log1120201log20212021 ffxxxffx 3 129log202120212028 y y Nếu 0 029991 yy yy 0 y Khi đó 292920279202722027 yyy yyyy 9 log20273,465 y 3 y 03 y 0;1;2;3 y . Do fx là hàm số luôn đồng biến nên với mỗi giá trị của y chỉ cho 1 giá trị của x . +) 3 0log1110yxxx +) 33 1log1111log1108 yxxxxx
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
31 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page
+) 33 2log1185log18480 yxxxxx +) 33 3log11735log1734729 yxxxxx Vậy có 4 cặp số nguyên ; xy . Câu 118: (Mã 103 - 2020 Lần 1) Xét các số thực không âm x và y thỏa mãn 1 2.43 xy xy +− + . Giá trị nhỏ nhất của biểu thức 22 24 Pxyxy =+++ bằng
GTNN của P là 41 8 khi 51 , 44xy==
Câu 119: (Mã 104 2020 Lần 1) Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 255 số nguyên y thỏa mãn ( ) ( ) 2 32 loglogxyxy ++ ? A. 80. B. 79. C. 157. D. 158 Lời giải Chọn D Ta có: ( ) ( ) 2 32 loglogxyxy ++ ( ) 2log 2 3 xy xy + + ( ) 2 log3 2 xyxy++ ( )1
Đk: 1 xy+ ( do , xy , 0 xy+ )
Đặt 1 txy=+ , nên từ ( ) 2 log3 2 1 xxtt −− ( )2
Để ( )1 không có quá 255 nghiệm nguyên y khi và chỉ khi bất phương trình ( )2 có không quá 255 nghiệm nguyên dương t .
Đặt ( )
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 32 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 33 8 B. 9 8 C. 21 4 D. 41 8 Lời giải Chọn D Ta có ( ) ( ) 11232 2.4323.4.402.2322 +−−−−+−+− xyxyyx xyxyyx (1) Xét TH: 3 320 2 − xx . (1) đúng với mọi giá trị 22 3 21 224 04 x Pxyxy y =+++
(2) Xét TH: 3 3200 2 − xx . Xét hàm số ( ) .2 = t ftt với 0 t ( ) 2.2.ln20 =+ ttftt với mọi 0 t (1) ( ) ( ) 232−fyfx 3 232 2 yxyx −− . Khi đó: ( ) 2 2222333 24223225 24Pxyxyxxxxxx =++++−++−=−+ 2 54141 2 488 x =−+ (3) So sánh (2) và (3) ta thấy
255 Mf = với ( ) 2 log3 fttt =− Vì f là hàm đồng biến trên ) 1,+ nên ( )2 ( ) 12 1 tfxx− khi 2 0 xx− . Vậy ( )2 có không quá 255 nghiệm nguyên ( ) 12 255 fxx − 2 255 xx − 7879 x − ( ) x Vậy có 158 số nguyên x thỏa mãn yêu cầu bài toán.
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 33 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 120: (Mã 104 - 2020 Lần 1) Xét các số thực không âm x và y thỏa mãn 1 2.43 +− + xy xy . Giá trị nhỏ nhất của biểu thức 22 42=+++ Pxyxy bằng A. 33 8 B. 9 8 C. 21 4 D. 41 8 Lời giải Chọn D Ta có ( ) ( ) 11232 2.4323.4.402.2322 +−−−−+−+− xyxyyx xyxyyx (1) Xét TH 3 320 2 − xx . (1) đúng với mọi giá trị 22 3 33 242 04 =+++ x Pxyxy y (2) Xét TH 3 3200 2 − xx Xét hàm số ( ) .2 = t ftt với 0 t ( ) 2.2.ln20 =+ ttftt với mọi 0 t (1) ( ) ( ) 232−fyfx 232 3 2 − − yx yx ( ) 2 2222321 424322 24 =++++−++−=−+ Pxyxyxxxxxx 2 14141 2 488 =−+ Px (3) So sánh (2) và (3) ta thấy GTNN của P là 41 8 khi 15 , 44 ==xy Câu
(Mã 102 2020 Lần 2) Có bao
ặp
ố
với mỗi cặp ( ) , mn tồn tại
ố thự
−
ỏ
( ) 2
m
−++ ? A. 16 B. 14 C. 15. D. 13 Lời giải Chọn D Đặt ( ) ( ) 2 2ln1 m faanaa=−++ , ta có ( ) 1 2 2 1 m n fama a =− + . ( ) 112 2 0201 12 mm famaaann m a =−=+= + phải có một nghiệm 0 1 a Suy ra 24 2 nn mm suy ra 0a
ệ
Ta
bảng biến
121:
nhiêu c
s
nguyên dương ( ) , mn sao cho 16 mn+ và ứng
đúng 3 s
c ( )1;1 a
th
a mãn
2ln1
anaa
là nghi
m duy nhất.
có
thiên
Ta thấy 0 là một nghiệm của phương trình ( ) 0 fa =
Nếu 1 m = suy ra để có nghiệm duy nhất thì 12 2 n n m (loại)
Nếu m lẻ và 1 m thì ta có a là một nghiệm thì a cũng là một nghiệm, do đó có đủ 3 nghiệm.
Nếu m chẵn thì phương trình chỉ có tối da 2 nghiệm (vì không có nghiệm âm).
Suy ra m lẻ. Để có 1 nghiệm dương thì theo BBT ta có ( ) ( ) ( ) 2 ln122,2 ln 2 2 0 1 1 fn n + + . Suy ra 1;2 n suy ra 3;5;;15 m . Suy ra có 13 cặp ( ) , mn (do 1521716 += ). Câu

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 34
n 2) Xét các số thực thỏ
mãn (
22 122 2224 xyx xyx ++ +−+ . Giá
ị
ớ
ấ
của biểu thức 84 21 x P xy + = −+ gần với giá trị nào sau
nhất? A. 9 B. 6. C. 7. D. 8. Lời giải Chọn C ( ) 22 122 222.4 xyx xyx ++ +−+ 22 122 2 222 x xy xyx ++ +−+ ( ) ( ) ( ) 2 2 2 1 2 11 201 xy xy −+ −−+− Đặt ( )2 2 1 txy =−+ ( ) ( )2 2 12100111 t ttxy −−−+ ( ) ( ) 84 28..40 21 x PPxPyP xy + =−−+−= −+ Yêu cầu bài toán tương đương:
122: (Mã 102 2020 Lầ
a
)
tr
l
n nh
t
đây
( ) ( )2 2 2 2
PP PPPP PP
284 1312285555 28
−+− −−+−+ −+ Câu 123: (Mã 103 2020 Lần 2) Có bao nhiêu cặp số nguyên dương ( ) ; mn sao cho 10 mn+ và ứng với mỗi cặp ( ) ; mn tồn tại đúng 3 số thực ( )1;1 a − thỏa mãn ( ) 2 2ln1 m anaa=++ ? A. 7 B. 8 C. 10 D. 9 Lời giải
Chọn D
Ta có ( ) ( ) 22 2 2ln1ln1 m m a anaaaa n =++=++ . Xét hai hàm số ( ) ( ) 2 ln1fxxx=++ và ( ) 2 m gxx n = trên ( )1;1
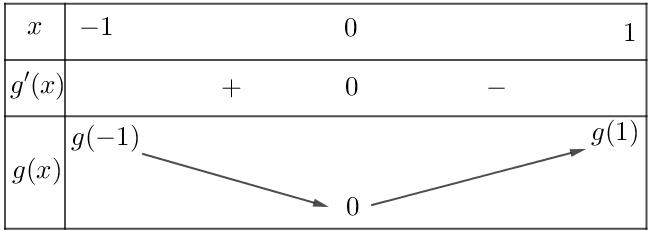
Ta có ( ) 2
1 0 1 fx x = + nên ( )fx luôn đồng biến và ( ) ( ) ( ) ( ) 22 2
1 ln1lnln1 1 fxxxxxfx xx −=−++==−++=− ++ nên ( )fx là hàm số lẻ
+ Nếu m chẵn thì ( )gx là hàm số chẵn và có bảng biến thiên dạng
Suy ra phương trình có nhiều nhất 2 nghiệm, do đó m lẻ + Nếu m lẻ thì hàm số ( )gx là hàm số lẻ và luôn đồng biến. Ta thấy phương trình luôn có nghiệm 0 x = . Dựa vào tính chất đối xứng của đồ thị hàm số lẻ, suy ra phương trình đã cho có đúng 3 nghiệm trên ( )1;1 khi có 1 nghiệm trên ( )0;1 , hay
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 35
( ) ( ) ( ) ( ) 22 11ln122,261;2 ln12 fgnn n + + Đối chiếu điều kiện, với 1 n = suy ra 1;3;5;7;9 m , có 5 cặp số thỏa mãn Với 2 n = thì 1;3;5;7 m có 4 cặp số thỏa mãn.
ố nào dưới đây A. 1 B. 2 C. 3 D. 4 Lời giải Chọn C Nhận xét 22 220; xyxxy +−+ Bất phương trình ( ) 22 122 222.4 xyx xyx ++ +−+ ( ) 22 1 22 2 2 22 2 xy x xyx ++ +−+

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Huỳnh
Ánh 42
Page 36
Vậy có 9 cặp số thỏa
ầ
ố thực
xy thỏa
( ) 22 122 222.4 xyx xyx ++ +−+
trị nhỏ nhất của biểu thức
x P xy + = −+ gần nhất vớ
( ) 22 2122 222 xyx xyx +−+ +−+ . Đặt 22 21txyx =+−+ Bất phương trình 21 t t + 210 t t −− Đặt ( ) 21 t ftt=−− . Ta thấy ( ) ( ) 010ff== . Ta có ( ) 2ln21 t ft =− ( ) 2 1 02ln21log0,52 ln2 t ftt === Quan sats BBT ta thấy ( ) 001ftt 22 0211 xyx +−+ ( )2 2 11xy −+ ( )1 Xét 84 284 21 x PPxPyPx xy + =−+=+ −+ ( ) 482 PPxPy−=−+ ( ) 4288228 PPPxPPy −+−=−+−+ ( )( )312821 PPxPy−=−−+
Giáo viên:
Văn
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
mãn bài toán. Câu 124: (Mã 103 2020 L
n 2) Xét các s
,
mãn
. Giá
84 21
i s
+ và ứng với mỗ
ặp (
tồn tại đúng
21 0 1 m m fxx n x =−= + Theo đề bài ( ) 0 fx = có ba nghiệm nên 1 2
1 ; 1 m yxy x == + , suy ra 1 m chẵn và 10 m −
m
Khi
( ) 0 fx
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 37 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( )( ) ( ) ( ) 2 22222312821821 PPxPyPPxy −=−−+−+−+ Thế ( )1 vào ta có ( )2 312 P ( )2 2 82PP −+ 2 440800 PP −+ 5555 P −+ . Dấu “=” xảy ra khi ( )2 2 8212 5 11 Px Py xy == −+= 2 2 1 5 2 1 5 xy y −= = 2 1 5 5 3 xy y −= = 1 3 5 3 5 3 5 3 x y x y = = = = Vậy giá trị nhỏ nhất của
là 552,76 − gần giá trị
ất.
Suy ra 3;5;7;9;11;13
.
đó
=
ệ
P Phương trình có 3 nghiệm ( ) (
3 nh 10
Câu f f − ( ) ( ) 2 ln21 21;2 2 ln21 n nn n + = −−
125: Có
bao nhiêu cắp số nguyên
dương ( ) , mn sao cho 14 mn
i c
) , mn
ba số thực ( )1;1 a − thỏa mãn ( ) 2 2ln1 m anaa=++ ? A. 14 B. 12 C. 11 D. 13 Lời giải Chọn C Xét ( ) ( ) 2 2 .ln1 m fxxxx n =−++ trên ( )1;1 Đạo hàm ( ) 1 2
21 1 m m x n x = + có ít nhất hai nghiệm Xét đồ thị của hàm 1 2
có nghi
m 1 2 0 0 x x
)
10
1;2 n và 3;5;7;9;11;13 m , do 14 mn+ nên ta có 11 cặp ( ) ; mn thỏa yêu cầu bài toán.
Câu 126: (Mã 104 - 2020 Lần 2) Có bao nhiêu cặp số nguyên dương (,) mn sao cho 12 mn+ và ứng với mỗi cặp (,) mn tồn tại đúng 3 số thực (1,1) a − thỏa mãn 2 2ln(1) m anaa=++ ? A. 12 B. 10 C. 11 D. 9 Lời giải
Chọn D
Ta có 22 2 2ln(1)ln(1)(*) mm anaaaaa n =++=++ .
Xét hàm 2 ()ln(1) faaa=++ trên (1,1) (dễ thấy hàm f lẻ, đồng biến trên R ), có BBT:
Xét hàm 2 (). m gaa n = trên (1,1)
Với m chẵn, ()ga là hàm chẵn và ()0, gaaR , do đó (*) không thể có 3 nghiệm.
Với m lẻ, ()ga là hàm lẻ, đồng biến trên R và tiếp tuyến của đồ thị tại điểm 0 a = là đường thẳng 0 y =
Dễ thấy (*) có nghiệm 0(1;1) a =− . Để (*) có đúng 3 nghiệm tức là còn có 2 nghiệm nữa là 0a với 0 01 a Muốn vậy, thì 222 (1).1(1)ln(12)2,261;2
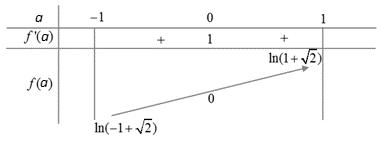
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH
LOGARIT
12 LŨY THỪA MŨ
Page
38
nn ===+== + Cụ thể: + 3;5;7;9 m thì 1;2 n : Có 8 cặp (,) mn + 11 m = thì 1 n : Có 1 cặp (,)
+
= :
thị hàm số ()ga là đường thẳng ( ();()2 gaagaa == ) không thể cắt đồ thị hàm số ()fa tại giao điểm 0 0 a được vì tiếp tuyến của hàm số ()fa tại điểm có hoành độ 0 a = là đường thẳng ya = Vậy có cả thảy 9 cặp (,). mn
ln(12) m gfnnn
mn
1 m
Đồ
2. Lời giải Chọn A
Ta có: ( ) ( ) 2222 1222122 22242211 xyxxxyxyxxxy ++−+++−+−+++ . Đặt 22210txxyt =−++ . Khi đó ta có 21 t t + , 0 t
Đặt ( ) 21,0 t fttt=−− , ta có: ( ) 2ln21 t ft =− , cho ( ) 0 ft = .
Ta nhận thấy phương trình ( ) 0 ft = có một nghiệm nên phương trình ( ) 0 ft = có tối đa hai nghiệm. Mặt khác ta có ( ) ( ) 010ff== . Suy ra phương trình ( ) 0 ft = có hai nghiệm 1 t = và 0 t = .
Khi đó ta có bảng xét dấu của hàm số ( )ft như sau:
Khi đó ( ) 00;1ftt . Suy ra ( )2 222 21111xxyxy −++−+ .
Khi đó tập hợp các điểm ( ) ; Mxy là một hình tròn ( )S tâm ( )1;0 I , bán kính 1 R = .
Ta có: ( ) 4 240 21 y PPxPyP xy =+−+= ++ .
24 PP PPP PP + −+ x y
2 135816 1 3 5 3
= =− Câu 128: (Mã 123 2017) Xét các số thực dương , xy thỏa mãn =++− + 3 1 log324 2 xy xyxy xy . Tìm giá trị nhỏ nhất minP của =+ Pxy A. = min 2113 3 P B. = min 91119 9 P C. = min 181129 21 P D. + = min 91119 9 P Lời giải

CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
Page 39
LŨY
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 127: (Mã 104 - 2020 Lần 2) Xét các số thực x và y thỏa mãn ( ) 22 122 2224 xyx xyx ++ +−+ . Giá trị lớn nhất của biểu thức 4 21 y P xy = ++ gần nhất với số nào dưới đây? A. 1. B. 0. C. 3. D.
Khi đó ta cũng có tập hợp các điểm ( ) ; Mxy là một đường thẳng ( ) :240 PxPyP +−+= . Để và ( )S có điểm chung, ta suy ra ( ) ,1dI . ( ) ( ) 2 22 +− 2 481601515 PPP +−−−−+ Ta suy ra max 15 P =−+ . Dấu "" = xảy ra khi
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 40
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Chọn A Với , xy dương và kết hợp với điều kiện của biểu thức =++− + 3 1 log324 2 xy xyxy xy ta được − 10 xy Biến đổi =++− + 3 1 log324 2 xy xyxy xy ( ) ( ) ( ) ( ) −−+=−−++− 333 log1log2312log3 xyxyxyxy ( ) ( ) ( ) ( ) −++−=+++ 333 log1log331log22 xyxyxyxy ( ) ( ) ( ) ( )( ) −+−=+++ 33 log3131log221 xyxyxyxy Xét hàm số ( ) =+ 3log fttt trên ( )=+ 0; D ( ) =+ 1 '10 .ln3 ft t với mọi xDnên hàm số ( ) =+ 3log fttt đồng biến trên ( )=+ 0; D Từ đó suy ra( ) ( ) ( ) −=+−=+= + 32 13123213 13 y xyxyyxyx y (do 0 y )
được −+ = 111 3 y Từ đó suy ra −+ == 111 mi 211 . 3 n 3 3 Pg Câu 129: (Mã 110 2017) Xét các số thực dương , ab thỏa mãn 2 1 log23 ab abab ab =++− + . Tìm giá trị nhỏ nhất minP của 2 Pab =+ A. min 3107 2 P = B. min 2101 2 P = C. min 2103 2 P = D. min 2105 2 P = Lời giải Chọn C
Theo giả thiết ta có 0,0xy nên từ = + 32 13 y x y ta được 3 0 2 y . −−+ =+=+= ++ 2 3233 1331 Pxyyyyy yy Xét hàm số ( ) −+ = + 2 33 31 yy gy y với 3 0 2 y ( ) ( ) +− == + 2 2 9610 '0 31 yy gy y ta
Điều kiện: 1 ab
Ta có ( ) ( ) ( ) ( ) ( ) 222 1 log23log2121log * ab abababababab ab =++−−+−=+++ + .

Xét hàm số ( ) 2log yfttt ==+ trên khoảng ( ) 0;+ .
Ta có ( ) 1 .ln210,0ftt t =+ . Suy ra hàm số ( )ft đồ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page
41
( ) ( ) ( )
*2121212
fabfababababba
−+ −=+−=++=−= +
Do 0, 0 ab nên 2 002 21 b b b −+ + . Khi đó: 2 22 21 b Pabb b −+ =+=+ + . Xét hàm số 2 ()2 21 b gbb b −+ =+ + trên khoảng ( )0;2 ( ) ( ) ( ) ( ) ( ) 2 2 210 0;2 55 4 2021 2 21 210 0;2 4 b gbb b b = =+=+= + −+ = Lập bảng biến thiên Vậy min 1022103 42 Pg == Câu 130: Cho hai số thực dương , xy thỏa mãn ( ) ln ln ln5 2 2.52 xy xy + + = . Tìm giá trị lớn nhất của biểu thức (1)ln(1)ln Pxxyy =+++ A. max 10 P = . B. max 0 P = . C. max 1 P = . D. max ln2 P = . Lời giải ln ln()ln5ln()ln2ln()ln5ln()ln()ln5ln2 2 2.522.522.52.2 xy xyxyxyxyxy + ++−+++ === ln()ln10102 xy + = ( ) ln10ln()ln10.log2ln()log2ln()ln10.log2 xy xyxyee + +=+== log2 102xyxy +=+= . Do đó ( ) ( ) ( ) 1ln3ln2 Pxxxx =++−− .
ng biến trên khoảng ( ) 0;+ Do đó
( ) ( ) 2
21 b
b
.
Xét hàm số ()(1)ln(3)ln(2) fxxxxx =++−− ()lnln(2)ln1322 22(2) fxxxxxxx xxxxx +−− =+−−−=+ . ( ) ( ) ( ) ( ) 2 22 2
−−+ =−−
12244 .0,0;2 2 2 xxx fxx x x xx
Do đó ( ) 0 fx = có nhiều nhất một nghiệm trên ( )0;2 Mà 1 x = là một nghiệm của pt ( ) 0 fx = nên phương trình ( ) 0 fx = có nghiệm duy nhất là 1 x = Lập bảng biến thiên ta được ( ) ( ) max10 fxf== .
Câu 131: Cho các số thực , xy thỏa mãn 0,1 xy và ( )( ) 3 log1120 1 xy xy xy + +++−= . Tìm giá trị nhỏ nhất của 2 Pxy =+ A. 2 B. 1 C. 1 2 D. 0 Lời giải Với điều kiện biểu thức đề bài có nghĩa, ta có ( )( ) ( ) ( ) 333 log1120loglog110 1 xy xyxyxyxyxy xy + +++−=+−−+++−= ( ) ( ) ( ) ( )( ) 33 loglog11* xyxyxyxy +++=−+− Xét hàm số ( ) 3log fxtt =+ trên ( )0;2 ( ) ( ) 1 ln310,0;2ftt t =+ nên hàm số ( )ft đồng biến trên ( )0;2 Do đó từ ( )* ta có ( ) 1 111 1 x xyxyyxxy x +=−+=−= + 1 22 1 x Pxyx x =+=+ + ( ) ( ) 2 2
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
42
20,0;1 1 Pxx x =− + Suy ra ( ) min01 PP== đạt được khi 0,1xy== . Câu 132: Cho các số thực , ab thỏa mãn 1. ab Biết rằng biểu thức 1 log log a ab a P ab =+ đạt giá trị lớn nhất khi kba = Khẳng định nào sau đây là sai A. 2;3 k . B. ( )0;1 k . C. 0;1 k . D. 3 0; 2 k . Lời giải
Ta có 1log0 a abb 1 loglogloglog1log1log. log aaaaaa ab
a Pababbb ab =+=+−=++− Đặt ( ) 2 1log 0log1aa tbtbt =−=− . Ta có: 2 2 Ptt=−++ trên ) 0;+ Bảng biến thiên t − 1 2 + P 9 2 Hàm số đạt giá trị lớn nhất tại 1 . 2 t = Với 3 4 1133 1loglog. 2244 aa tbbbak ==−=== Câu 133: Chohaisốthực , ab thỏamãn ( ) 2241 log281 ++ −= ab ab .Tính = a P b khibiểuthức 465=+−Sab đạt giá trị lớn nhất. A. 8 5 B. 13 2 C. 13 4 D. 17 44 Lời giải Chọn B ( ) 22 22 41 log2812841 ++ −=−=++ ab ababab Ta có:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 43
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 44 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 22 22 2 2 222 22 28412841 46565 4 6565 2841 44 65 4 8484012836251210606416 65 4 1002(586)210 −=++ −=++ −+ =+− = −+−+ −=++ −+ = −+−=++−+−++ −+ = +−+++= = abab abab Sb Sab a SbSbbb Sb a SbbSbSbSbb Sb a bSbSS S a 222 65 4 (586)100.(1)06489632640 173 −+ =−−+−−+ − b SSSS S Giá trị lớn nhất của S là: 13 5 3 2 5 = = a b Suy ra 13 2 = a b Câu 134: Cho a ,b là các số dương thỏa mãn 1 b và aba . Tìm giá trị nhỏ nhất của biểu thức log2log a b b a Pa b =+ A. 6 B. 7 C. 5 D. 4 Lời giải Chọn D Ta có: ( ) ( ) 11 4.log14.log11log1 1 log bb a b Paa b a =+−=+− Đặt logb ta = . Vì ( ) log1log112 2 bb t abaaatt . ( ) ( ) 1 4141 11 1 t Ptt t t =+−=+− với ( )1;2 t Xét hàm số ( )()41 1 t ftt t =+− với ( )1;2 t .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 45
u thức 22Tab =+ A. 1 2 B. 1 C. 3 2 D. 5 2 Lời giải ( ) ( ) 555 425 log34log425log34 ab abababab ab ++ =+−++=+++− + ( ) ( ) ( ) ( ) 55 log425425log55abababab +++++=+++ (*). Xét hàm ( ) 5 log,0fxxxx=+ . Đạo hàm ( ) 1 .ln510,0fxx x =+ . Suy ra hàm số ( )fx đồng biến trên ( ) 0;+ Phương trình (*) viết lại: ( ) ( ) ( ) ( ) 4255425535 fabfabababab ++=+++=++= . Mặt khác: ( ) ( ) ( ) 2 2222222 5 5313. 2 ababTab =+++=+ . Dấu "" = xảy ra 13 ab = 13 ; 22 ab== . 5 6 +∞ + 0 3 2 3 2 2 1 +∞ ∞ f (t) f '(t) t
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) 2 2 3 11 2 ()4,()01 1 4 1 2 ttm ftftt t tl = =+=−= = . Bảng biến thiên Từ bảng biến thiên suy ra: ( ) ( ) 1;2 3 minf5. 2 tf == Vậy giá trị nhỏ nhất của biểu thức P bằng 5 Câu 135: Cho a , b là hai số thực dương thỏa mãn 5 425 log34 ab ab ab ++ =+− + . Tìm giá trị nhỏ nhất của biể
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
Page 46
y xxy + = + ( ) ( ) 333 33.33.3(*) yxyxyxyx −+−=+ Xét ( ) .3t ftt = với 0 t . Ta có ( ) 3.3.ln30 ttftt =+ với 0 t , suy ra ( )ft đồng biến trên khoảng( ) 0;+ . Từ (*) ta có ( ) ( ) 333 fyfxyx −=+ với 330,30 yxyx −+ nên 3 333 3(1) x yxyxy x −=+= + . Ta có ( ) ( ) ( ) 3314 1 313133 xx Pxyxx xx =+=+=+++− ++ ( ) ( ) ( ) ( ) 4444434 121. 3133133 Pxx xx =++−+−= ++ . Vậy ( ) ( ) min 4 1 31233 43433 331231 0;013 x x x x Py x y xy += + = == + = . Câu 137: Xét các số thực dương x , y thỏa mãn ( ) 2 111 222 logloglogxyxy ++ . Tìm giá trị nhỏ nhất minP của biểu thức 3 Pxy =+ . A. min 9 P = B. min 8 P = C. min 252 4 P = D. min 17 2 P = Lời giải. Ta có: ( ) 2 111 222 logloglogxyxy ++ ( ) ( ) 22 11 22 loglogxyxyxyxy ++
LŨY
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 136: Xét các số thực dương , xy thỏa mãn 3 1 log334 3 y xyxy xxy =++− + . Tìm giá trị nhỏ nhất minP của Pxy =+ A. min 434 3 P = B. min 434 3 P + = C. min 434 9 P + = D. min 434 9 P = Lời giải Để 1 0 3 y xxy + mà từ giả thiết ,0xy suy ra 101 yy − . Vậy ĐKXĐ: 0;01xy . Ta có: 3 1 log334 3 y xyxy xxy =++− + 334 1 3 3 xyxy y xxy ++− = + ( ) 333 31 3 3 xyxy y xxy ++− = + ( ) 3 33 31 3 33 xyx y
− ( Vì ;0xy ).
y x xyy y y
( ) 2 2 11 1
Ta có: 2 1 3341 11 y Pxyyy yy =++=++ . Xét hàm số: ( ) 1 41;1 1 fyyy y =++ . Đạo hàm: ( ) ( ) / 2 1 4 1 fy y =− ( ) ( ) ( ) /
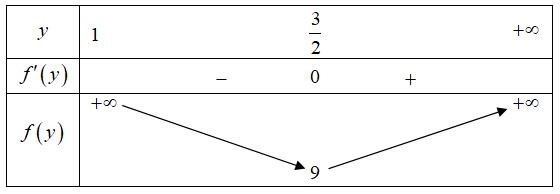
= = =
3 2 0 1 2
yn fy yl
. Bảng biến thiên.
Câu 138: Cho , xy là các số thực dương thỏa mãn ( ) 20192012 2 9019logloglog xy xy + + . Gọi minT là giá trị nhỏ nhất của biểu thức 2 Txy =+ . Mệnh đề nào dưới đây đúng? A. ( ) min 7;8 T
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
47
B. ( ) min 6;7 T C. ( ) min 5;6 T D. ( ) min 8;9 T Lời giải. Ta có: ( ) 20192012 2 9019logloglog xy xy + + ( ) 20192019 2 loglog xy xy+ 2 xyxy+ ( ) 2 1 yxx− 2 1 1 x y x x
Ta có: 2 1 2231 11 x Txyxx xx =++=++ . Xét hàm số: ( ) 1 31;1 1 fxxx x =++ .
Đạo hàm: ( ) ( ) / 2 1 3 1 fx x =− ( ) / 3 01(1) 3 fxxdox ==+ Bảng biến thiên. Do đó: min 423 T =+ . Câu 139: (Mã 105 2017) Xét hàm số ( ) = + 2 9 9 t t ft m với m là tham số thực. Gọi S là tập hợp tất cả các giá trị của m sao cho ( ) ( ) += 1 fxfy với mọi số thực , xy thỏa mãn ( ) + + xy eexy .Tìm số phần tử của S A. 0 B. Vô số C. 1 D. 2 Lời giải Chọn D Ta có ( ) ( ) + +==+==442 93 19loglog xy fxfymxymm Đặt +=,0xytt . Vì ( ) + +++− 1ln1ln0,0 xy t eexyeetttttt (1) Xét hàm ( ) =+− ln1 fttt với 0 t ( ) =−=== 11 100 t ftt tt Bảng biến thiên Dựa vào bảng biến thiên, ta có ( ) ( ) 1,0ftft +− 1ln0,0 ttt (2) Từ ( )1 và ( )2 ta có ==== 22 3 1log133 tmmm
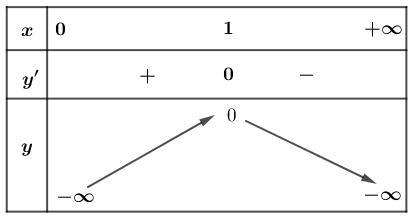
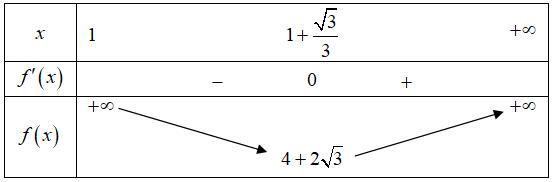
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
48
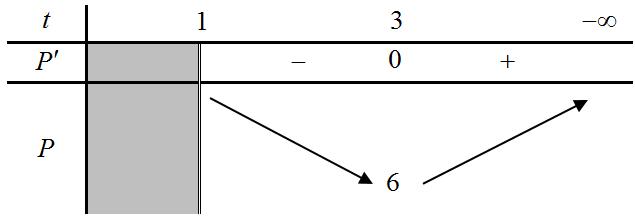
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 49 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 140: Cho ; xy là hai số thực dương thỏa mãn xy và 11 22 22 yx xy xy ++ . Giá trị nhỏ nhất của biểu thức 22 2 3 xy P xyy + = bằng A. 13 2 . B. 9 2 . C. 2. D. 6. Lời giải Chọn D Ta có ( ) ( ) 11 224141 22 yx xyxyyx xy ++++ ( ) ( ) ( ) ( )ln41ln41 ln41ln41 xy xyyx xy ++ ++ (vì ,0xy ). Xét hàm số ( ) ( )ln41 t ft t + = trên khoảng ( ) 0;+ . Ta có ( ) ( ) ( ) ( ) ( ) 2 2 4.ln4.ln414ln441ln41 41 0,0 41 t t tttt t t t ftt t t −+ −++ + == +
xy = Cách 2: Ta có 2 34 122426 11 t Pt tt + ==−+++= (AM GM). Suy ra, giá trị nhỏ nhất của P bằng 6 khi 3 t = hay 3 xy = Câu 141: Xét các số thực dương , xy thỏa mãn ( ) ( )2 22 2 221 24log4 2 xyxy xy ++++=− . Khi 4 xy + đạt giá trị nhỏ nhất, x y bằng
( )ft luôn nghịch biến trên khoảng ( ) 0;. + Lại có ( ) ( ) fxfyxy . Đặt x t y = , khi đó ( ) 1; t + 2 3 1 t P t + = Cách 1: Xét 2 3 1 t P t + = với ( ) 1; t + , ta có ( ) 2 2 231 1;03 t tt PP t t =− == = Bảng biến thiên Từ bảng biến thiên, suy ra giá trị nhỏ nhất của P bằng 6 khi 3 t = hay 3
A. 2 B. 4 C. 1 2 D. 1 4 Lời giải Chọn A
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH
LOGARIT
12 LŨY THỪA MŨ
Page 50
. Từ ( ) ( ) ( ) 12 2 xy fxyfxyxy +=+= . Ta có: ( ) 2 2(2)2;2 2 y xyxyxyyxy y +=−== ( ) ( ) 244 44104210242.18 222 y Pxyyyy yyy =+=+=+−++−= min 18 P = khi ( ) 4 42213 2 yyy y −=−== . 2 362 2 yx yx yy ==== . Câu 142: Cho , xy là các số thực dương thỏa mãn ( )( ) ( ) 2 22 334 log122141 ++ =+−+−−+ + xy xyxyxy xy Giá trị lớn nhất của biểu thức 532 21 +− = ++ xy P xy . A. 3. B. 1. C. 2. D. 4. Lời giải Chọn C • Ta có: ( )( ) ( ) 2 22 334 log122141 ++ =+−+−−+ + xy xyxyxy xy 22 2 22 334 log22333 ++ =+−−− + xy xyxy xy
Ta có: ( ) ( )2 22 2 221 24log4 2 xyxy xy ++++=− ( ) ( ) ( ) ( ) 22 22 1 2481loglog48 2 xyxyxyxyxyxy +−++++−=−+ ( ) ( ) ( ) 2 2 22 2log2log1 22 xyxy xyxy +++=+ . Xét hàm số ( ) 2 22log fttt =+ , với ( ) 0; t + ( ) 1 40,0 .ln2 fttt t =+ , suy ra hàm số ( )ft đồng biến trên khoảng ( ) 0;+
( ) ( ) 22 22 22 3332222 22333 3342 334.2.2 2
+ +++ ++ ++ =++=+ + xy xyxy xy xy xyxy xy ( ) ( ) 2233322222.334.22..2+++++=+xyxyxyxy ( ) ( ) 223342222334.222.2+++++=+xyxyxyxy ( )1
• Đặt ( ) ( ).20= t fttt
Ta xét: ( ) 2.2.ln20, 0 =+ tt fttt . Suy ra hàm số ( )ft đồng biến trên ( ) 0;+
Lúc đó; ( )1 có dạng: ( ) ( ) 2233422 ++=+ fxyfxy ( ) 222222334222342 ++=+++−+−=−+− xyxyxxyyxyxxyy ( ) ( ) ( ) 22 34 +−+−=−− xyxyxy ( ) ( ) 2 3401440 +−+−−++− xyxyxyxy • Khi đó: 5324 2202 2121 +−+− ==++= ++++ xyxy P xyxy • Vậy P đạt giá trị lớn nhất là 2, đạt đượ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
51 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
c khi
4
+= ++=+== −= xy xyxyxy xy . Câu 143: Cho các số thực , xy thỏa mãn 0,1 xy và ( )( ) 3 log1120 1 xy xy xy + +++−= . Tìm giá trị nhỏ nhất của P với 2 Pxy =+ A. 2 B. 1 C. 0 D. 1 2 Lời giải Chọn B Ta có ( )( ) 33 log1120log10 11 xyxy xyxyxy xyxy ++ +++−=+++−= ( ) ( ) 33 loglog11xyxyxyxy +++=−+− Xét hàm số đặc trưng ( ) 3log fttt =+ với 0 t Ta có ( ) 1 '10,0 ln3 ftt t =+ Hàm số ( )ft đồng biến với 0 t
22
334222 0
Có ( ) ( ) ( ) 1 1111 1 y fxyfxyxyxyxyyx y +=−+=−+=−= + Ta có ( ) 2244 2313211 111 y Pxyyyy yyy =+=+=−+++−++= +++ Vậy giá trị nhỏ nhất của P bằng 1
Câu 144: Cho , xy là các số thực dương thỏa mãn 3 4 log21. xy xy xy + =−+ + Tìm giá trị nhỏ nhất của biểu thức 42 2 322 () xyxyy P xxy ++ = + . A. 1 . 4 B. 1 . 2 C. 3 . 2 D. 2. Lời giải
Chọn D
Ta có 333 4 log21log(4)(x4y)log3()3() xy xyxyxyxy xy + =−++++=+++ + (1). Xét hàm số 3()log fttt =+ trên khoảng(0;) + Ta có 1 '()10,0 ln3 ftt t =+ . Suy ra hàm số ()ft đồng biến trên khoảng (0;) + . Từ (1) suy ra (4)(3()) fxyfxy +=+ và (4)0;3()0 xyxy ++ Do đó, (1)43()2 xyxyyx+=+=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page 52
+++ ===+=++ +
u "" = xảy ra 1 x = .Vậy 2. MinP = Câu 145: Xét các số thực dương ,,, abxy thỏa mãn 1,1ab và ( ) 22 2 xy abab == . Giá trị nhỏ nhất của biểu thức 22 Pxy =+ thuộc tập hợp nào dưới đây? A. )10;15 . B. )6;10 . C. ( )1;4 . D. )4;6 . Lời giải Chọn B Ta có: ( ) ( ) ( ) 2 22 2 log21log22log x aaa aabxabbxb ===+=+ ( ) ( ) ( ) 2 22 2 log21log22log y bbb babyabaya ===+=+ 2241log22log ab Pxyba =+=+++ .
. 4252 22 23 322612112166 662. 99 ()9 xyxyyxx Pxx xxx xxyx
Dấ

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 53
Bảng biến thiên của hàm số ( )ft . Từ bảng biến
(
+ ==
2 1 log2 33 66 a b ab xx yy = = == == . Câu 146: Xét các số thực dương x , y thỏa mãn ( ) 2 logloglogxyxy ++ . Biểu thức 8 Pxy =+ đạt giá trị nhỏ nhất của bằng: A. min 16 = P B. min 33 2 P = C. min 112 P = D. min 31 2 P = Lời giải Chọn A Từ đề bài 2 xyxy + ( ) 2 2 11 1 y x xyy y y − ( Vì ;0xy ). Ta có: 2 1 8891 11 y Pxyyy yy =++=++ .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Đặt ( )log0 a tbt= ta được: 2 412Pt t =+++ . Xét hàm số ( ) 2 412ftt t =+++ , với ( ) 0; t + ( ) ( ) 2 22 21212 ;00221 1212 22 ftfttt t tt tt tt =−=−=+=+ ++ ++ 44321 4218810 2 tttttt t +=++−−==
thiên suy ra
) ( ) ) 0; Minmin366;10 Pft
khi
Xét hàm số: ( ) 1 91;1 1 fyyy y =++ . Đạo hàm: ( ) ( ) / 2 1 9 1 fy y =− ( ) ( ) /
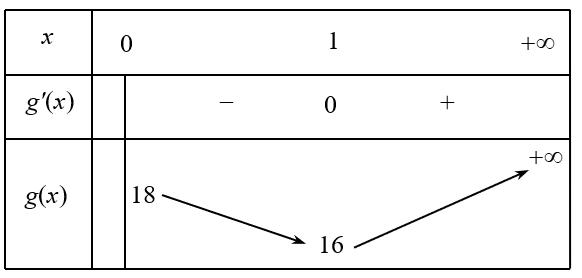
4 3 0 2 3
y fy yl
= = = Bảng biến thiên, ta thấy giá trị nhỏ nhất của ()fy là 4 16. 3 f = Vậy min 16 P = khi 16 3 x =
Câu 147: Cho hai số thực dương , xy thỏa mãn ( ) ( ) 22 loglog66 xxxyyx ++=−+ . Giá trị nhỏ nhất của biểu thức 3 3 Txy =+ là A. 16 B. 18 C. 12 D. 20 Lời giải
Chọn A Điều kiện: 0 x , 06 y . Ta có ( ) ( ) 22 loglog66 xxxyyx ++=−+ ( ) 2 22 loglog66xxyxxy +=−+− ( ) 2 2222 logloglog6log6xxxyxxxy ++=−++− ( ) ( ) ( ) 22 22 loglog66xxxyxy +=−+− ( )* Xét hàm số ( ) 2log fttt =+ trên ( ) 0;+ Ta có ( ) ( ) 1 10,0; .ln2 ftt t =++ nên hàm số ( )ft đồng biến trên ( ) 0;+ Khi đó ( ) ( ) ( ) ( ) 2 *6fxfxy =− ( ) 2 6 xxy=− 6 xy=− 6 yx=− . ( ) 3 36 Txx=+− ( ) 3 318 xxgx=−+= Xét hàm số ( ) 3 318gxxx=−+ trên ( ) 0;+ . Ta có ( ) 2 33gxx =− ; ( ) 0 gx = ( ) ( ) 10; 10; x x
=−+ =+ Bảng biến thiên:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page 54
Từ bảng biến thiên suy ra ( ) ( ) 116 Tgxg== . Dấu “=” xảy ra khi và chỉ khi 1 65 x yx
= =−= .
Câu 148: Xét các số thực dương , ab thoả mãn 2 1 log23 ab abab ab =++− + . Tìm giá trị nhỏ nhất minP của
Pab =+ . A. min 125 P =−+ . B. min 25 P =+ . C. min 15 P =−+ . D. min 125 P =+ . Lời giải Chọn C Điều kiện 101 abab −
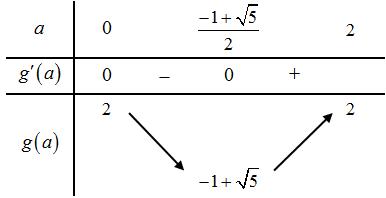
Ta có ( ) ( ) ( ) ( ) 222 1 log23log1log211 ab abababababab ab =++−−−+=+−−− + ( ) ( ) ( ) ( ) 22 log1121logabababab −++−=+++ ( ) ( ) ( ) ( ) ( ) 22 log2121log.1 abababab −+−=+++
Xét hàm số ( ) 2log fttt =+ với 0 t có ( ) 1 .ln210,0ftt t =+ nên hàm số ( ) 2log fttt =+ đồng biến trên khoảng ( ) 0;+
Ta có ( ) ( ) ( ) ( ) ( ) ( ) 2 12121221 21 a fabfababababab a −=+−=+−=+= + Do 2 ,0002 21 a aba a + Khi đó 2 222 2121 aa Paba aa −+ =+=+= ++
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH
MŨ LOGARIT
12 LŨY THỪA
Page
55
Vậ
. Câu 149: Cho các số thực x, y thỏa mãn 22 2 loglog225
x yxyxy x −=++− + . Hỏi giá trị nhỏ nhất củ
22
=++ là
Chọn D
Xét hàm ( ) 2 22 21 a ga a + = + ( ) ( ) ( ) 2 2 44415 0 212 aa gagaa a ===+−− + Bảng biến thiên
y min 15 P =−+
2
a
Pxyxy
bao nhiêu? A. 30202 . B. 33222 . C. 24162 . D. 36242 . Lời giải
Suy ra: ()ft là hàm đồng biến trên khoàng (0;) + Mà (42)(2) fxfyx−=+ nên 42 42(2) 2 x xyxy x −=+= + Vì 222 3() 4 Pxyxyxy =+++
Thay vào P ta có: 2 2 2 34234 4242 xx Px xx +=−+ ++
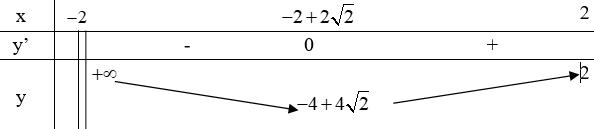
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 56
22
− ++
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Điều kiện xác định:
22 00 22 0 00 xx x xx y yy
Theo bài ra ta có:
22 222 22 22 2 loglog225 2 log(2)log(2)log2(2)(2)1 log(2)1(24)log(2)(2) log(42)(42)log(2)(2) x yxyxy x xxyxyx xxxyyx xxyxyx −=++− + −−+−=−++− −+−−=+++ −+−=+++ Xét hàm số 2 ()log(0) ftttt=+ : 1 '()100 .ln2 ftt t =+
Xét hàm số 2 4 2 x y x + = + trên khoảng (2;2): 22 22 2 2(2)(4)44 ' (2)(2) 222 '0440 222() xxxxx y xx x yxx xl +−++− == ++ =−+ =+−= =−− (Vì (2;2) x − ) Lập bảng biến thiên: Dựa vào bảng biến thiên, ta có min 442 y =−+ Vậy ( )2 min 3 44236242 4 P =−+=− Câu 150: Cho , xy là các số thực dương thỏa mãn ( ) 2 222 loglog1log2 xyxy +++ . Giá trị nhỏ nhất của biểu thức 2 xy + bằng A. 223 + B. 232 + C. 33 + D. 9
+ =
x y
(thỏa mãn điều kiện bài toán).
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 57
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn A Với 0;0.xy Ta có: ( ) ( ) ( ) ( ) 2 222 2 2 2 loglog1log2 1 22 2 21 10 2 1. xyxy xyxy yxx x x y x +++ + − − Đặt 2 mxy =+ ta có: ( ) ( ) ( ) 2 2 2 2 12 2 . 1 xmxxxm mxxx xx m x −−+ −− Xét hàm số ( ) 2 2 1 xx gx x = với 1 x Ta tìm thấy ( ) ( ) 1; min322 gx + =+ khi 22 2 x + = Vậy 322 m + , dấu + =
bằng xảy ra khi Vậy GTNN của 2 xy + là 322 + Câu 151: Cho các số thực , xy thuộc đoạn 0;1 thỏa mãn 2 1 2 2021 2020 22022 + = −+ xy x yy . Gọi , Mm lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 332 2639 ++− xyxxy . Tính Mm A. 5 2 . B. 5. C. 5. D. 3. Lời giải Chọn D Ta có 2 1 2 2021 2020 22022 + = −+ xy x yy ( ) 122 2020220222021 −+=+ xy yyx ( ) ( ) 2 12 20201202120202021 −+=+ yxyx . Ta có
22 2 432 4
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 58
=
M
===−
ố
ực
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) 2 20202021=+ t ftt với 0;1 t có ( ) ( ) 2 2020.ln2020.20212.2020.0 =++ tt fttt Do vậy ( ) ( ) 2 20202021=+ t ftt đồng biến trên khoảng 0;1 t . Suy ra ( ) ( ) 111 −==−=− fyfxxyyx Do vậy 332 2639 ++− xyxxy ( ) ( ) 3 32 261391 =+−+−− xxxxx 32322 2618186399 =+−+−+−+ xxxxxxx 32 430276 =−+−+ xxx Xét ( ) 32 430276 =−+−+ fxxxx với ( )0;1 x Mà ( ) 32 430276 =−+−+ fxxxx nên ( ) 2 1 2 1260270 9(loai) 2 = =−+−=
x fxxx x .
ặt khác ( ) ( ) 11 06,15, 22
fff . Do vậy 6 = M và 1 2 =− m . Vậy nên .3 =− Mm Câu 152: Xét các s
th
dương . xy thỏa mãn ( ) 2 111 222 logloglogxyxy ++ . Tìm giá trị nhỏ nhất minP của biểu thức 3 Pxy =+ . A. min 17 2 P = . B. min 8 P = . C. min 9 P = . D. min 252 4 P = . Lời giải Chọn C Ta có ( ) 2 111 222 logloglogxyxy ++ ( ) ( ) 2 11 22 loglogxyxy+ 2 xyxy+ ( ) 2 1 yxy− . Do 2 00yy ( ) 2 10yxy − . Mà 0 x nên 10 y − , hay 1 y . Khi đó ta có 2 1 y x y . Suy ra 2 33 1 y Pxyy y =++ Xét hàm số ( ) 2 3 1 y fyy y =+ trên ( ) 1;+ . Ta có ( ) ( ) 2 2 2 3 1 yy fy y =+ ( ) 2 2 483 1 yy y −+ = ; ( ) 0 fy = ( ) ( ) 1 1; 2 3 1; 2 y y =+ =+ Bảng biến thiên:
thỏa mãn 2 88 2 xyxy xy xy ++ = + . Khi 2 2 Pxyxy =+ đạt giá trị lớn nhất, giá trị của biểu thức 32xy + bằng A. 4. B. 2. C. 3. D. 5. Lời giải Chọn C
Ta có ( ) ( ) 2 22 88 22log88log xyxy xy xyxyxyxy xy ++ =++=−−+ + ( ) ( ) ( ) ( ) 22 log2121logxyxyxyxy −+−=+++ Xét hàm số ( ) 2log fttt =+ là hàm số đồng biến trên ( ) 0;+ Do đó từ ( )* ta có ( ) 2 21 21 y xyxyx y −=+= + Suy ra 22 min 221PxyxyyyP =+=−+= khi 1 1 3 yx== . Do đó 323 xy+=
Câu 154: Cho , xy là các số dương thỏa mãn ( ) ( ) ( ) log2loglogxyxy +=+ . Khi đó, giá trị nhỏ nhất

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 59
ả
ế
Dấu "" = xảy ra
ỉ
2 3 2
x
= ==
là
ố thực
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Từ b
ng bi
n thiên suy ra ( ) 3 9 2 fyf = . Vậy ( ) 9 Pfy
khi và ch
khi
9 12 y y
y
. Câu 153: Cho , xy
các s
dương
của biểu thức 22 4 121 xy P yx =+ ++ là: A. 31 5 B. 6 C. 29 5 D. 32 5 Lời giải Chọn D Ta có: ( ) ( ) ( ) ( ) ( ) log2logloglog2log2 xyxyxyxyxyxy +=++=+= Mặt khác: ( ) ( ) 2 222808 xyxyxyxyxyxy =+− Áp dụng bất đẳng thức cauchy Swat ta có: ( ) ( ) 22 22 2 4 121222 xyxy xy P yxxyxy + =+= +++++
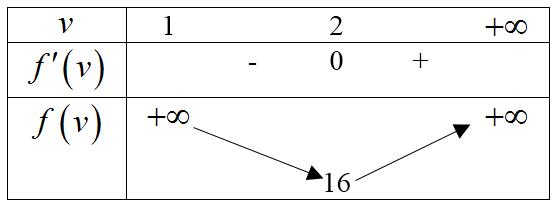
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo
Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 60
thi:
và
Đặt xyt = suy ra ( )2 2 22 xy t P xyt = ++ Xét
số ( ) 2 2 t ft t = + , vớ
8; t + ( ) ( ) 2 2 4 0,8 2 tt ftt t + = + , suy ra hàm số ( )ft đồng biến trên khoảng (
8;+ . ( ) ( ) 32 8 5 ftf =
. Giá trị nhỏ nhất của Mxy =+ là A. 22 B. 2. C. 4. D. 16. Lời giải Chọn C Với 0 xy , ta có ( ) ( ) ( ) 1 lnlnln 2 xyxyxy −+=+ ( ) ( ) ( ) 1 lnlnln 2 xyxyxy =+−− ( ) ln2ln
viên:
Hòa
0984164935
Chuyên luyện
Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm
biên soạn
hàm
i
)
)
( ) 32 5 Pft 32 Min 5 P = khi 24 82 xyx xyy == == Câu 155: Cho các số thực , xy thay đổi, thỏa mãn 0 xy và ( ) ( ) ( ) 1 lnlnln 2 xyxyxy −+=+
xy xy xy + = ( ) 2 lnln xy xy xy + = 2 xy xy xy + = ( ) ( ) 22 xyxyxy−=+ (*) Đặt 0 0 uxy vxy =+ = Ta có (*) ( ) 22 4 uvvu−= ( ) 2214 vuv−= ( ) 2 2 4 1 v ufv v == , (1) v ( ) ( ) ( ) ( ) ( ) 2 22 81442 11 vvvvv fv vv == , ( ) 02fvv == do 1 v Bảng biến thiên :

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 61
Vậ
4 2 0 xy
xy += = 22 22 x y =+ =−
là
ự
tr
nh
ấ
n thiên Từ đây ta suy ra 1 16 S , dấu bằng xảy ra khi 1 1 1 4 1 2 2 abc ab c c ab ++= == = = = Khi đó 4 2,2xyz=== . Câu 157: Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn ( ) 22 34 log()log2 xyxy +=+ ? A. 1 B. 3 C. 2 D. Vô số Phân tích Lời giải Chọn C Điều kiện: 0 xy+ .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
y min()min4 xyu+==
xy
Câu 156: Xét ,, xyz
các số th
c lớn hơn 1 thỏa mãn điều kiện 2 xyz = . Giá
ị
ỏ nh
t của biểu thức 333 222 1 logloglog 4 Sxyz =++ bằng A. 1 32 . B. 1 4 . C. 1 16 . D. 1 8 . Lời giải Chọn C Ta có ( ) 2222 log1logloglog1 xyzxyz =++= . Đặt 222 log,log,log axbycz === . Khi đó ta có ,,0abc và 1 abc++= ( )3 3333333 222 111 logloglog3() 444 Sxyzabcabababc =++=++=+−++ ( ) ( ) ( ) 2 3 3211 3()331 444 ab ababccc + +−++=−+ với 01 c . Đặt 2 ()331 fccc=−+ , 1 ()0630 2 fccc =−== . Ta có bảng biế
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 62 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Đặt ( ) 22 34 log()log2xyxyt +=+= , suy ra 22 3 24 t t xy xy += += ( ) ( ) 2 2 3 3241 t tt xy yy =− −+= Phương trình ( )1 2 32.3940 ttt yy−+−= . Phương trình phải có nghiệm nên: ( ) 2 331 93940 222 t ttt t =−− Do đó: 2 22 03 2 22 xy x xy + + 0;1 x ( vì x ) Thử lại: Với 4 9 4 9 2 log2 3log2 0 24 3 t t t y x y y = = = = = Với 2 130 1 1240 t t yt x y y +== = = += Với ( ) 2 31 12.94.33402 214 t ttt t y x y =+ =−++−= += Khi 094 tt t nên ( )2 vô nghiệm, khi 041 t t 140 t − nên ( )2 cũng vô nghiệ
Vậy 0;1 x . Câu 158: Có bao nhiêu cặp số nguyên dương ( ) ; xy thỏa mãn đồng thời hai điều kiện: 6110 x và ( ) 2 222 log1020201021 y xxyxx −+=+−+− ? A. 4. B. 2. C. 3. D. 1. Lời giải Chọn D Điều kiện: 2 1020200 xx−+ , đúng x Ta có ( ) 2 222 log1020201021 y xxyxx −+=+−+− ( ) ( ) 2 222 21log102210y xxxxy −++−+=+ ( ) ( ) 2 222 21log10log2210y xxxxy −+++−+=+ ( ) ( ) 2 222 22log2210y xxxxy −++−+=+ ( ) ( ) 2 2 log22 2210log2210 xx y xxy −+ +−+=+ (*).
m.
ỏa mãn).
Vậy có một cặp nguyên dương ( ) ( );4;1xy = thỏa mãn yêu cầu bài toán.
Câu 159: Có bao nhiêu số nguyên 10 y sao cho tồn tại số nguyên x thỏa mãn ( ) 2 2 221 5251 y y xxx x +−−−+=+− ? A. 10 B. 1 C. 5 D. Vô số Phân tích Phương trình dạng ( ) ( )fufv = . Phương pháp: Chứng minh ( )yft = đơn điệu trên ( ) ; ab . Từ phương trình suy ra uv = . Từ đó tìm sự liên hệ giữa 2 biến , xy và chọn , xy thích hợp. Lời giải
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 63
thi:
sinh
10
và
soạn Xét hàm ( ) 10t ftt =+ trên . Ta có ( ) 10.ln1010 t ft =+ , t . Do đó ( )ft đồng biến trên . Khi đó (*) ( ) ( ) 22log22 fxxfy −+= ( ) 22log22xxy−+= 2 2 2210y xx −+= ( ) 2 2 1110y x −+= . Vì 6110 x nên
Hòa
0984164935
Chuyên luyện
Tuyển
vào lớp
Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm
biên
( ) ( ) 2 2 2 6 111101011 y x −+=−+ ( ) 262 0log1011 y −+ Vì y + nên 1;2;3 y + Với 1 y = 2 2210xx −+= 2 280xx −−= 2(ktm) 4(tm) x x =− = + Với 2 y = 24 2210xx −+= 2 299980xx −−= (không có giá trị x nguyên nào thỏa mãn). +Với 3 y = 29 2210xx −+= 2 29999999980xx −−= (khôngcógiátrị x nguyên nào th
22
yyyy xxxxxx xxxx +−−−+−−− +=+−++−=+−
t ftt =+ đồng biến trên . Do đó từ phương trình trên suy ra: ( )2 2 22 2112212 yy yy xxxxx +−=−−=== . Do x nguyên nên ta có 22 y và 10 y nên 0;2;4;6;8 y Câu 160: Có bao nhiêu cặp số nguyêndương ( ) ; xy thoảmãn 12020 x và ( )1 2 22log2 yy yxx +=++
Chọn C Ta có: ( )
2 2212212 52515215
Xét: ( ) 1 5
Xét hàm số ( ) 22log fttt =+ , 0 t Vì ( ) 1 20 ln2 ft t =+ 0 t ( )ft đồng biến trên ( ) 0;+ nên( ) ( ) 1 2222 1222.222222 22 yy yyyyyy xx ffxxx ++ ===+== Do 12020 x nên 2 01log2020111,98 − yy Do * y nên 1;2;3;...;11 y , với mỗi giá trị y cho ta 1 giá trị x thoả đề. Vậy có 11 cặp số nguyên ( ) ; xy thoả mãn đề bài. Câu 161: Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 64
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 2021 B. 10 C. 2020 D. 11 Lời giải Chọn D Theo đề bài, ( )1 2 22log2 yy yxx +=++ ( ) 22 2 2log22log 2 y yy xx +=++ ( ) 22 22 22log222log 2 y yyyy x x + ++=++ ( ) ( ) 22 2222 2.2log22log22 yy yy xx ++ +=+ ( )1 .
Đặ
Suy ra: ( ) ( ) (
(
2 2 log13 2 22 22
t t t t xy xy xy xy ++ +=+ += +−= +=+ Ta
( ) ( ) ( ) 22 22 3 2loglog13log1 xyxy +−+=+− A. 1 B. 3 C. 2 D. 5 Lời giải Chọn C
t: ( ) ( ) ( ) 22 22 3 2loglog13log1 txyxy =+−+=+− .
)
)
213.2 1313
có:
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 65 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) ( ) 2 22 2 13.2213 132 13 2 1313 222 t t t t t t xyxy ++ ++ + + + + . Xét ( ) 13 22 t t ft =+ nghịch biến trên nên ( ) ( ) 1313 11 222 t t ftft + + . Do đó ( ) ( ) 2 log13 2 2 22 022log13 1313 t t xy xy ++ +=+ +=++ 0;1 x ( vì x ) Thử lại: Với 1 x = : ( ) ( ) ( ) ( ) 2 2 1321 3 132130 132213.2310 t t t t t tt y y =+− = +−−= +−+−+= Ta có: ( ) ( ) ( ) 132213.231 t tt gx =+−+−+ liên tục trên 0;1 thỏa mãn ( ) ( ) 010gg nên phương trình có nghiệm ( )0;1 t Do đó với 1 x = thì tồn tại số thực y thỏa mãn ( ) ( ) ( ) 22 22 3 2loglog13log1 xyxy +−+=+− Với 1 x =− : ( ) ( ) ( ) ( ) 2 2 1321 3 132130 132213.2310 t t t t t tt y y =++ = ++−= +++−+=
y y
2 2
=+ =+ +=+ +−−=
132 13 13231 132310
t t t t t t
Ta có: ( ) ( ) 132213.2310,1 t tt t +++−+ nên phương trình vô nghiệm. Do đó với 1 x =− thì không tồn tại số thực y thỏa mãn ( ) ( ) ( ) 22 22 3 2loglog13log1 xyxy +−+=+− Với 0 x = : ( ) ( ) ( )
Ta có: ( ) ( ) 13231 t t hx =+−− liên tục trên 1;0 thỏa mãn ( ) ( ) 100hh− nên phương trình có nghiệm ( )1;0 t − Do đó với 0 x = thì tồn tại số thực y thỏa mãn ( ) ( ) ( ) 22 22 3 2loglog13log1 xyxy +−+=+− . Vậy 0;1 x
x x
0 21 0210 0
. Vậy có 11 cặp ( ) ; xy thỏa mãn.
y x y y Ta có: PT ( ) 33 log2121log(*) xx yy−+−=+ Xét hàm số ( ) 3log fttt =+ trên ( ) 0;+ Khi đó ( ) 1 10 ln3 ft t =+ do đó hàm số ( ) 3log fttt =+ đồng biến trên ( ) 0;+ (*) có dạng ( ) ( ) 2121 xxffyy−==− Vì ( ) 2 0202002120201220210log2021 xx yx − ( ) 2 0log20210;1;2;3;4;5;6;7;8;9;10 x x x
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page 66
Câu 162: Có bao nhiêu cặp số nguyên ( ) ; xy thỏa mãn 02020 y và 3 21 log12? x x y y =+− A. 2019. B. 11. C. 2020. D. 4. Lời giải Chọn B Từ giả thiết ta có:
Câu 163: Xét các số thực ,, abx thoả mãn 1,1,01abx và 2 loglog() baxxab = . Tìm giá trị nhỏ nhất của biểu thức 22 lnlnln(). Pabab =+− A. 133 4 . B. 2 e . C. 1 4 . D. 322 12 + . Lời giải Chọn D
Ta có ( ) ( ) 22 loglog()loglog()lnlnlog.ln2.log.lnbaba xxxx ba ababxaxb === 22 ln log.ln2ln.ln2lnln2lnln2ln ln b a aabababab b ==== (vì 1,1ab ).

Thay ln2lnab = vào biểu thức P ta được ( ) ( ) 2222 lnlnln()3ln21ln321 Pababbbtt =+−=−+=−+ (với ln0tb= ). Đặt ( ) 2 ()321 fttt =−+ . Ta có ( ) 21 '()6210(0;) 6 fttt + =−+==+
BBT: Dựa vào BBT, suy ra ( ) 0; min()322 12 ft +
+ =− Vậy giá trị nhỏ nhất của P bằng 322 12 +
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page
67



CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 1 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 5. PHƯƠNG TRÌNH MŨ LOGARIT MỨC ĐỘ VẬN DỤNG VẬN DUNG CAO Câu 1: Gọi S là tổng các nghiệm của phương trình 222 3265237 2221 xxxxxx −++++++=+ . Khi đó S có giá trị là: A. 3. B. 6. C. 3. D. 5. Lời giải Chọn C Ta có ( ) ( ) 222 2373265 xxxxxx ++=−++++ . Khi đó . ( ) ( ) ( ) ( ) 222 2 22322 222 2 22 2 3265237 326565 326532 32 3265 65 2221 222.21 212210 210 21.120 120 xx xxxxxx xxxxxx xxxxxx xx xxxx xx −+ −+++++ −+++++ −+++−+ −+ −+++ ++ +=+ +=+ −−−= −= −−= −= 2 2 322 2 65 1 213202 216501 5 xx xx x xxx x xx x −+ ++ = =−+== =− ++= = =− Vậy 3 S =− . Câu 2: Có bao nhiêu giá trị nguyên của tham số ( )10;100 m− để tồn tại các số thực dương ,,, abxy thỏa mãn 1,1ab và ( ) 2 xmy xy abab + == A. 0 . B. 100 . C. 99. D. 98 . Lời giải Chọn A Đặt ( ) 2 xmy xy ababt + === CHƯƠNG II HÀM SỐ LŨY THỪA - HÀM SỐ MŨ – HÀM SỐ LOGARIT
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 2 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) 1 2 11 1 2 x xmy xy y xmy at bttt abt + + + = == = ( ) 1 11122 11 2220 m um myx u xmym x xyxy u y ++= ++=+++= = ( ) 2 2 222210 00 umum mumuu x x u u y y +−+= ++= = = Yêu cầu của bài toán được thực hiện khi phương trình có nghiệm dương ( )2 2180 0 322 000; 2 01 2 mm pmm S m −−
ọ
Ta
(
0
xxyxy y −−−+= ++−= Bài
tương
( )*
t nghiệm dương y . TH 1: Phương trình ( )* có 2 nghiệm trái dấu ( ) 2 201;2xxx −−− TH 2: Phương trình ( )* có nghiệm 12 '20 0 20 x yy Sx =+= = = vô nghiệm. TH 3: Phương trình ( )* có 2 nghiệm thỏa 2 12 20 02 20 xx yyx Sx −−= == = Vậy 0;1;2 x thỏa mãn đề bài.
Không có giá trị nguyên của m thỏa mãn yêu cầu bài toán. Câu 3: Có bao nhiêu số nguyên x sao cho tồn tại duy nhất số thực y thỏa mãn ( ) 2 3 3 log22logxxyxy++−= ? A. 5. B. 3. C. 4. D. 2. Lời giải Ch
n B
có ( )
) 22 2 3 3 220* log22log
yxyxx
toán
đương là phương trình
có đúng mộ
Câu 4: Có bao nhiêu giá trị nguyên của tham số m để phương trình 1 4.2360 xx mm + −+−= có hai nghiệm trái dấu A. 3. B. 5. C. 4. D. 2.
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 3
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Nên ta có ( )( ) 2 12 12 12 360 0 20 225 360 5 110 mm m ttm mm ttm m tt =−+ += =− −− Do 3;4 mm . Vậy có 2 giá trị của m. Câu 5: Cho hai hàm số , xxyayb == có đồ thị như hình vẽ Một đường thẳng bất kỳ song song với trục hoành cắt hai đồ thị lần lượt tại , BC sao cho = ABAC Tổng 2 nghiệm của phương trình: 4133.0 xx ab−+= là A. 3 logb B. 3 4 log a C. 3 4 logb D. 3 loga Lời giải Chọn B Đặt 12 12 ; xx yayb == Theo giả thiết: 21 ABACxx ==− * 12yy= 11 1 xx abb a ==
Lời giải Chọn D 1 4.2360(1) xx mm + −+−= Đặt 2,0 x tt= , pt trở thành: 2 2360(2)tmtm−+−= Phương trình có hai nghiệm trái dấu khi và chỉ khi pt có 2 nghiệm 12 , tt thỏa mãn 1201tt
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 4
x
x
=
=− =
ọ
+ +++= 1log1log1log
xxx++++= 1log1log1log
xxx+++ += 2 1log1log33 4.13.90 22 xx++ −+= Đặt 1log 3 ,0 2 x tt + = . Khi đó, phương trình trở thành: 2 9 41390 4 1 t tt t = −+= = Với 9 4 t = thì 1log1log2 3933 1log2log110 2422 xx xxx ++ ==+=== Với 1 t = thì 1log1log0 3331 11log0log1 22210 xx xxx ++ ==+==−= Tích tất cả các nghiệm của phương trình bằng: 10.1 10 = . Cách 2 Đk: 0 x 2 2log1loglog 4.39.478.6xxx+++= ( ) ( ) ( ) log10log10log104.99.413.6xxx +=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Phương trình: 2 3 4133.0413041330 −+=−+=−+= xxxxx x abaaa a 33 14 4 log log
a
a a x x a
=
Tổng hai nghiệm của phương trình là: 3 34 4 logloglog aaa −= Câu 6: Tìm tích tất cả các nghiệm của phương trình 2 2log1loglog 4.39.478.6xxx+++= A. 100. B. 1. C. 10. D. 1 10 . Lời giải Ch
n B Điều kiện: 0. x
Ta có: 2 2log1loglog 4.39.478.6xxx+++= ( ) 21log 1log1log4.39.413.6 x xx
4.99.413.6
946 4.9.13. 444
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 5 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) 2log10log1033 4.13.90 22 xx −+= ( ) ( ) ( ) ( ) log10 log10 3 1 1 log100 101 2 10 10100 log102 39 10 24 x x x x x x x x = = = = = = = = Tích các nghiệm bằng 1 Câu 7: Tìm tất cả các giá trị thực của m để phương trình 4.2250 xx mm −+−= có hai nghiệm trái dấu. A. 5 0; 2 . B. 5 ; 2 − . C. ( ) 0;+ . D. 5 ;4 2 . Lời giả
ọn D Đặ
x
=
− −+− 5 4 2 m . Câu 8: Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc khoảng ( )1000;1000 để phương trình ( ) ( ) 22 2 1 1011012.3 xx x m + ++−= có đúng hai nghiệm phân biệt? A. 1004. B. 1006. C. 1005. D. 1007. Lời giải Chọn C Chia hai vế của phương trình đã cho, cho 2 3x ta được ( ) 22 1101 61 1 33 0 xx m +− += Ta thấy 1 1111 33 00 +− = Do đó ta đặt ( ) 2 1 10 1 3 x tt + = thì 2 10 11 3 x t = Phương trình ( )1 trở thành ( ) 2 2 1 .6602 6 tmttmm tt t + −= + +==
i Ch
t 2
t
( )0 t
, phương trình có dạng: 2 250tmtm−+−= Đặt ( ) 2 25fttmtm=−+− . Để thỏa mãn yêu cầu đề bài thì đồ thị hàm số ( )ft cắt trục hoành tại hai điểm phân biệt có hoành độ 12 , tt thỏa mãn: ( ) ( ) 12 00 010 2 10 af S tt af 250 0 2 1250 m m mm
Để phương trình đã cho có đúng hai nghiệm phân biệt, thì phương trình ( )2 có 1 nghiệm lớn hơn
1
Xét hàm số ( ) ( ) 2 6,1ftttt=−+ Ta có ( ) 2603fttt =−+== Bảng biến thiên Từ bảng biến thiên suy ra 5 9 m m = là các giá trị thoả mãn yêu cầu bài toán. Do ( )1000;1000 m m
−
nên có 1005 giá trị của m tìm được.
Câu 9: Với giá trị nào của tham số m thì phương trình 1 4.220 xx mm + −+= có hai nghiệm 1x , 2x với 1x , 2x thỏa mãn 12 3 xx+= ? A. 4 m = . B. 2 m = . C. 1 m = . D. 3 m = .
Lời
giải
Chọn A Ta có: ( ) ( ) 2 1 4.22022.220* xxxx mmmm + −+=−+= Phương trình là phương trình bậc hai ẩn 2x có: ( )2 2 22 mmmm =−−=− Phương trình có nghiệm ( ) 2 2 2020 0 m mmmm m −− Áp dụng định lý Vi ét ta có: 1212 2.2222 xxxx mm + == Do đó 3 12 3224xxmm +=== . Thử lại ta được 4 m = thỏa mãn. Câu 10: Cho phương trình ( ) 22 3.25310.530 xx xx +−+−= . Gọi 1x , 2x 12 () xx là hai nghiệm của phương trình. Hiệu hai nghiệm 21Sxx =− bằng A. 2. B. 5 log3. C. 5 log3. D. 0. Lời giải Chọn B Xét ( ) 22 3.25310.530 xx xx +−+−= . Đặt 2 5x t = .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 6
0 3 t f'(t) f(t) 1 + + ∞ 9 ∞ 5
Phương trình trở thành ( ) 2 3310.30 txtx +−+−=
Giải phương trình này sẽ được nghiệm 1 1 3 t = ; 2 3 tx =−
Với 1 1 3 t = ta sẽ có 2 1 5 3 x = 152log3 x =−
Với 2 3 tx =− ta sẽ có 2 53 x x =− .
Nhận thấy 2 2 x = là một nghiệm của phương trình.
Vế trái là hàm đồng biến còn vế phải là hàm nghịch biến nên 2 x = là ngiệm duy nhất.
Vậy phương trình có hai nghiệm 152log3 x =− và 2 2 x = Hiệu hai nghiệm là S = 215log3 xx−= . Câu 11: Có bao nhiêu số tự nhiên m sao cho phương trình 21 42122 xxx m ++ −+−=+ có đúng 2 nghiệm thực phân biệt? A. 9 B. 10 C. 11 D. 8 Lời giải Chọn A ( ) ( ) 2 21 4212224.212.221 xxxxxx mm ++ −+−=+−+−=+ Đặt , phương trình ( )1 trở thành 22 2 22
( )20 x tt=
4.12263 4.12.2 4.12221 ttmtmtt ttmt ttmtmtt −+−=+=−++ −+−=+ −+−=−−=−+− ( )I Để phương trình đã cho có đúng hai nghiệm thực x thì ( )I có đúng hai nghiệm ( ) 0; t + Đặt ( ) ( ) 2263,21ftttgttt =−++=−+−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 7
Từ đồ thị, bài toán thỏa mãn 0 312 m m
= Mà 0;4;5;6;...;11 mm . Vậy có 9 giá trị của m thỏa mãn bài toán. Câu 12: Gọi S là tập hợp các giá trị nguyên của tham số m để phương trình 42230 xx m −−+= có hai nghiệm phân biệt thuộc khoảng ( )1;1 . Số tập hợp con của tập hợp S là A. 1. B. 0. C. 4. D. 2. Lời giải
Chọn A
Đặt 2x t = . Với ( ) 1 1;1;2 2 xt − Ta được phương trình ( ) ( ) 2 2 21212*ttmtm −+=−−=− Để phương trình đã cho có hai nghiệm phân biệt thuộc khoảng ( )1;1 thì phương trình ( )* phải có hai nghiệm phân biệt thuộc 1 ;2 2 . Ta có bảng biến thiên
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 8
19
44
Do m m . Do đó số tập con của tập S là 0 21 = Câu 13: Gọi S là tập hợp tất cả các giá trị của tham số m để phương trình 4(35).21240 xx mm −+++= có một nghiệm gấp hai lần nghiệm còn lại. Tổng tất cả các phần tử của S bằng A. 17 3 B. 2 3 C. 16 3 D. 13 3 Lời giải Chọn C 4(35).21240 xx mm −+++= . + Đặt 2x t = , phương trình trở thành 2 (35)1240tmtm−+++= Phương trình có hai nghiệm khi phương trình có hai nghiệm dương
Dựa vào bảng biến thiên, ta suy ra
022
mm − .
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 9 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 2 918901 3503 12401 mm m m m m =−+ + + Khi đó phương trình có hai nghiệm là 4 t = và 31tm=+ + Gọi 12 , xx là hai nghiệm của phương trình; gọi 12
ủa
Giả sử 12 2 2 1212 222xx xxtt === . ( ) 2 2 5 314 1 3 431 1 m m m m m = += = =+ =− Kết hợp điều kiện suy ra 1 ;5 3 m . Vậy tổng các phần tử của S là 16 3 . Câu 14: Tìm tất cả các giá trị của tham số m để phương trình 92.6.40 xxx m −+= có hai nghiệm trái dấu A. 01 m . B. 1 m − hoặc 1 m . C. 1 m . D. 1 m − . Lời giải Chọn A Phương
(
2 33
22 xx xxx mm −+=−+= Đặt 3 0 2 x t = , phương trình ( ) ( ) ( ) 2 120.2 gtttm =−+= Yêu cầu bài toán trở thành phương trình ( )2 có hai nghiệm 12 ; xx thỏa 1201xx . Khi đó ( ) 0 10 0 20 01 0 0 10 .10 g m S m P m m ag − − Vậy 01 m thỏa yêu cầu bài toán. Câu 15: Cho S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình ( ) ( ) 22 2721.9253.3510 xxx mmmm −−++−−+= có 3 nghiệm không âm phân biệt. Số phần tử của S là A. 18. B. 23. C. 19. D. 17. Lời giải Chọn D
, tt là hai nghiệm c
phương trình
trình
)
92.6.4020.1
Đặt 3x t = , 0 t , khi đó phương trình ( ) ( ) 22 2721.9253.3510 xxx mmmm −−++−−+= ( )1 trở thành: ( ) ( ) 322221253510tmtmmtm −−++−−+= ( ) ( ) ( ) 22 121510ttmtm −−−+−= ( ) ( ) 22 26 2520 6 2480826 8 11 2
1 215102 t tmtm m m m mmm m m m
= −−+−= Với 10tx== Bảng biến thiên hàm số ( ) ( ) 222151fttmtm=−−+− Đề phương trình ( )1 có 3 nghiệm không âm thì phương trình ( )2 có hai nghiệm phân biệt 12 1 tt Khi và chỉ − − −− − Vậy có 17 giá trị
ủa m thoả mãn. Đáp án D Câu 16: Có bao nhiêu giá trị nguyên của tham số m để phương trình 22 3 420 xx m + −−= có 4 nghiệm phân biệt A. 10 B. vô số C. 8 D. 9 Lời giải Chọn C Ta có 2222 3 42048.20 xxxx mm + −−=−−= Đặt 2 2x t = . Do 2 0 x nên 1 t Phương trình trở thành: 2 80ttm−−= 22808 ttmmtt −−==− Xét hàm số ( ) 2 8 fttt =− trên nửa khoảng ) 1;+ ta có ( ) ( ) 28;02804fttfttt =−=−== . Bảng biến thiên
nguyên c

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 10
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn khi 2
Để pt có 4 nghiệm phân biệt thì phải có 2 nghiệm t phân biệt lớn hơn 1. Ycbt 167 m −− Do nguyên dương nên có 8 giá trị.
Câu 17: Với giá trị nào của m thì phương trình 1 2 94.320 x x mm + −++= có hai nghiệm phân biệt 12 , xx thoả mãn 12 1 xx+= ? A. 3 4 m = B. 3 4 m =− C. 7 m = D. 1 m =− Lời giải Chọn C Đặt 30 x tt= . Ta được phương trình ( ) 2 34201 tmtm−++= Phương trình ban đầu có hai nghiệm phân biệt 12 , xx thoả mãn 12 1 xx+=

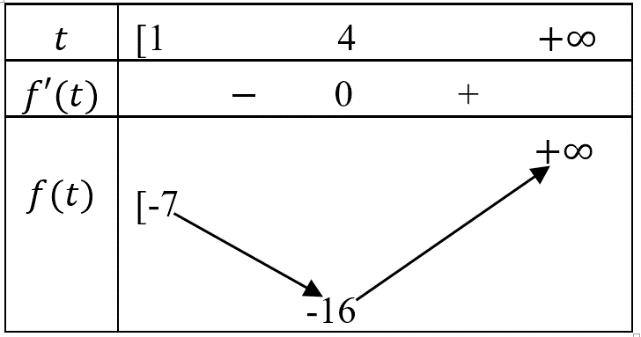
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
11
( ) ( ) 2 2 3105 023208 4360 3231057 37 38 7 m mm mm m m P m m m + −+ −− = + = = = = Câu 18: Tìm tất cả các giá trị của tham số m để phương trình 92.6.40 xxx m −+= có hai nghiệm trái dấu. A. 01 m . B. 1 m − hoặc 1 m .C. 1 m . D. 1 m − . Lời giải Chọn A Ta có: ( ) 2 33 92.6.402.01 22 xx xxx mm −+=−+= Đặt 3 ,0 2 x tt = Phương trình ( )1 trở thành: ( ) 2 202ttm−+=
12 12 33.3 xx tt + == Do đó phương trình ( )1 có hai nghiệm phân biệt 12 , tt thoả mãn 12.3tt =
+ 0 1 t phương trình 0 3 2
x t = có một nghiệm 30 2 log0xt=
+ 0 01 t phương trình 0 3 2
x t = có một nghiệm 30 2 log0xt=
+ 0 1 t = phương trình 0 3 2
x t = có một nghiệm 3 2 log10 x ==

Vậy để phương trình ( )1 có hai nghiệm trái dấu thì phương trình ( )2 có một nghiệm t thuộc khoảng ( )0;1 và một nghiệm 1. t Số nghiệm của phương trình ( )2 là số giao điểm của đồ thị hàm số ( ) 2 2 yfttt ==− và đường thẳng :. dym =− Lập bảng biến thiên của hàm số ( ) 2 2 yfttt ==− trên ( ) 0;. + Từ BBT ta suy ra 1001. mm −−
i
c
a tham số m thì phương trình
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
12
bậc hai ẩn 2x với ( )2 '222. mmmm=−−=− Phương trình (*) có nghiệm khi và chỉ khi: ( ) 2 2 '02020 0 m mmmm m −− Áp dụng định lý Vi ét ta có: 1212 2.2222 xxxx mm + == Do 12 3 xx+= nên ta có 3 22284 mmm === Vậy 4. m =
Câu 19: Vớ
giá trị nào
ủ
1 4.220 xx mm + −+= có hai nghiệm 12 , xx thỏa mãn 12 3? xx+= A. 1 m = B. 2 m = C. 3 m = D. 4 m = Lời giải Chọn D Ta có ( )2 1 4.22022.220 xxxx mmmm + −+=−+= (*) Phương trình (*) là phương trình
mm −+ . Câu 21: Tìm tất cả các giá trị thực của tham số m để phương trình + +++= 1 4.220 xxmm có hai nghiệm phân biệt 12 , xx thỏa mãn 12 2 xx+ . A. −−21. m B. −1. m C. −12.mm D. 2. m Lời giải Chọn A Ta có: ( ) ( ) 2 1 4.22022.220*. xxxx mmmm + +++=+++= Đặt 2,0 x tt= , phương trình ( )*
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 13 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 20: Tìm tất cả các giá trị thực của tham số m để phương trình ( ) ( ) 222 24221242 22466330 xxxxxx mm ++++++ +−−−= có hai nghiệm thực phân biệt A. 532532 m −+ B. 532 m + hoặc 532 m − C. 0 m hoặc 1 2 m . D. 1 0 2 m . Lời
Chọn D Phương trình đã cho tương đương với ( ) ( ) 222 212121 42466390 xxxxxx mm ++++++ +−−−= ( ) ( ) 22 212142 24630 93 xxxx mm ++++ +−−−= . Đặt ( ) ( 2 2 2110222 10;1 333 xxx tt +++ === . Phương
trở
=
=−+ Phương
02110
phương trình ( )
có hai nghiệm dương phân biệt 12 , tt thỏa mãn 12.4tt 2 02012 020021. 0402422 mmmm Smmm Pmm −−− −−− +− Câu 22: Có bao nhiêu giá trị nguyên của tham số m lớn hơn 10 để phương trình ( ) 162.12290 xxx m −++= có nghiệm dương?
giải
trình
thành ( ) ( ) 2 3 246303 21 t tmtm tm
+−−+=
trình có hai nghiệm phân biệt phương trình có đúng một nghiệm ( )0;1 t 1
2
trở thành: ( ) 2 220.1tmtm+++= Ta có: 1212 2 12 2222.24 xxxx xx + + Phương trình + +++= 1 4.220 xxmm có hai nghiệm phân biệt 12 , xx thỏa mãn 12 2 xx+
1
22220222.ttmttm −++=−=−− Xét ( ) 2 2,1.ftttt=− Ta có ( ) ( ) '22,'01. fttftt =−== Phương trình( )1 có nghiệm 0 x phương trình( )2 có nghiệm 1 t 211.mm −−−−

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 14
101 9;8;...;3;2. m m m −− ⎯⎯⎯⎯→−−−− Vậy có tất cả 8 giá trị m thỏa mãn bài
Câu 23: Tìm tích tất cả các nghiệm của phương trình 2 2log1loglog 4.39.478.6xxx+++= A. 100. B. 1. C. 10. D. 1 10 Lời giải Chọn B Điều kiện 0 x 2 2log1loglog22.logloglog loglog2loglog log log 4.39.478.64.3.39.4.478.6 933 0 10 log 3 36.3678.36.78.36 4222 3 2 1 3 22 3 23 1 log1 10 xxxxxx xxxx x x x x x x ++ = +=+= +=−+= = = = = = Do đó tích các nghiệm bằng 1. Câu 24: Cho phươngtrình 2256165.222.2 xxxx mm −+−−+=+ .Tìm m đểphươngtrình có 4nghiệ
ệ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 7. B. 8. C. 9. D. 10. Lời giải Chọn B Ta có ( ) ( ) 2 44 162.122902.201. 33 xx xxx mm −++=−++= Đặt 4 ,1. 3 x tt = Ta có phương trình: ( )
toán.
m phânbi
t.
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 15 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 11 ; 8256 m B. ( )0;2 m C. ( ) 1 0;2\ 8 m D. ( ) 11 0;2\; 8256 m Lời giải Chọn D 2256165.222.2 xxxx mm −+−−+=+ 2256175.222xxxx mm −+−− +=+ ( ) 2 562 22 1 561 .222 xx x xxx mm −+ +− −+− +=+ Đặt: ( ) 2 56 2 1 2 ;,0 2 xx x u uv v −+ = = Khi đó phương trình tương đương với: muvuvm +=+ ( )( ) 10uvm −−= 2 2 56 1 121 2 xx x u vm m −+ == = = ( ) 2 2 2 1 22 33 21log* x xx xx xm m == == =− = Để phương trình đã cho có 4 nghiệm phân biệt. phương trình có 2 nghiệm phân biệt khác 2 và 3. 2 2 2 0 1log0 1log4 1log9 m m m m − − − ( ) 0 2 111 0;2\; 88256 1 256 m m m m m Vậy: ( ) 11 0;2\; 8256 m . Câu 25: Cho bất phương trình ( ) ( )412201 xx mm +++ . Có bao nhiêu giá trị nguyên của tham số m thuộc 5;5 để bất phương trình ( )1 nghiệm đúng 1 x . A. 8. B. 9. C. 7 . D. 10. Lời giải Chọn C Đặt 2x t = Với 12xt
Bất phương trình trở thành: ( ) ( ) 2 1202tmtm+++ .
Bất phương trình ( )1 nghiệm đúng 1 x khi và chỉ khi bất phương trình ( )2 nghiệm đúng 2 t 2 2. 2 tt mt t + Xét hàm số ( ) 2 2 tt ft t = + trên khoảng ( ) 2; + ( ) ( ) 2 2 42 02. 2 tt ftt t = + ( ) ( ) 3 22. 2 ftft =−
đó ta phải có: 3 2 m −
ậy có 7 giá trị nguyên củ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 16
. Phương trình ( ) ( ) ( ) 32133 27 22 e fxfxfx m −++ = trở thành 32133 27 22 e ttt m −++ = Phương trình có nghiệm trên đoạn 0;2 khi và chỉ khi phương trình có nghiệm trên đoạn 15 1; 13 . Xét hàm số ( ) 32133 27 22 e ttt gt −++ = với 15 1; 13 t . 0 15 13 15 13 1 0 +∞ y' y ∞ +∞ 1 3 0 + ∞ x
Do
V
a m thỏa mãn điều kiện bài toán. Câu 26: Cho hàm số ( )yfx = có bảng biến thiên như sau: Tìm giá trị lớn nhất của m để phương trình ( ) ( ) ( ) 32133 27 22 e fxfxfx m −++ = có nghiệm trên đoạn 0;2 A. 15 13e B. 4 e C. 3 e D. 5 e Lời giải Chọn B Đặt ( )tfx = . Có ( ) 15 0;21; 13 xtfx =
Có ( ) ( ) 32133 22722 6137e ttt gttt −++ =−+ , ( ) 2 1 061370715 1; 613
t gttt t
= =−+= =
. Để phương trình đã cho có nghiệm dương g'(t) 1 15 13
+∞ t e 4 g(t)
−−= có nghiệm dương? A. 7 B. 4 C. 5 D. 6 Lời giải Chọn C Xét phương trình ( ) ( ) 77 11 77log10log1 xx mm −−==− Ta thấy 1 001 7 x g 15 13( )
x m x =
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
17 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
x
Ta có bảng biến thiên: Từ bảng biến thiên ta có phương trình có nghiệm trên đoạn 15 1; 13 khi 4 15 13 gme . Vậy giá trị lớn nhất của m thỏa mãn là 4 e m = Câu 27: Có bao nhiêu giá trị nguyên của tham số m để phương trình ( ) 7 1 log10 7 thì: ( ) 7 0log1111728 mmm −− Vì 3;4;5;6;7 mm . Vậy có 5 giá trị của tham số m thỏa mãn yêu cầu. Câu 28: Biết rằng nghiệm của phương trình 7337 xx = có dạng ( ) loglogab b xa = , với , ab là các số nguyên tố, ab . Tính 73 Sab =− . A. 43 B. 0 C. 4 D. 40 Lời giải Chọn D Ta có 7373 33 37log3log7 xxxx == . 3 73log7 xx= 3 7 log7 3
= −+−= =− . Suy ra 3 a = , 2 b = và 5 c = . Vậy
6
nhiêu nghi
m nguyên?
5 C. 3 D. 4
có:
( ) 73 3 loglog7 x = Từ đó 7;3ab== . Tính 7340Sab=−= Câu 29: Biết phương trình 2 52023xxx = có hai nghiệm dạng log4 a xb=− và xc = với a , b , c là các số nguyên và ( ),1;5ab . Khi đó 2 Tabc =++ bằng A. 3 T = . B. 4 T = . C. 13 T = . D. 12 T = . Lời giải Chọn D Ta có ( ) ( ) ( )( ) 2 5202 33 235log2205log254 xxx xxxxxx =−=−−−=−+ ( )( ) 3 3 1 25 1log226 2 242 x xx x
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
212Tabc=++= . Câu 30: Bất phương trình ( ) ( ) ( ) 2 log423 242 x xx −− có tất cả bao
ệ
A.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 B.
18 Lời giải Chọn D +) Ta
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) 2 log423 242 x xx −− ( ) ( ) ( ) ( ) ( ) ( ) 2 log423 22222 log2log42log42.log223log2 x xxxxx −−−−+− ( ) ( ) ( ) ( ) 2 22222 2log2.log223log2log(2)log220 xxxxx +−−+−−−−− ( ) 2
5 54log20 log24 x xx x − −− − Mà x nên 3;4;5;6 x . Vậy có 4 giá trị nguyên của x thỏa mãn yêu cầu bài toán. Câu 31: Có bao nhiêu số nguyên y sao cho tồn tại 1 ;6 3 x thỏa mãn ( ) 2 318 27127xxyx xy + =+ A. 19. B. 21. C. 20. D. 18. Lời giải Chọn C Ta có ( ) 2 318 27127xxyx xy + =+ 2 318 271 xxxy xy −+ =+ ( ) 2 27 318log1 xxxyxy−+=+
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 19 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt
ệp
12 Sưu tầm và biên soạn ( ) ( ) 2 27 318log1* xxxyxy −=+− . Xét
số ( ) ( ) 27 log1 guuu =+− với 1 u − . Ta có ( ) ( ) 0 11 1ln27ln271010,697guuu u =−==−=− + Bảng biến thiên Với 1 ;6 3 x ) 2 31827;0 xx −− . Dựa vào BBT và suy ra ( ) 27 21 028,02 27log10 10,957 xy xyxy uxyu −+− −− 21 28,02 0 10,957 y x uu y xxxx 084,06 30,1595 y y −− 2;1;1;2;...;84 yy−− Xét hàm số ( ) ( ) 2 27 318log1 fxxxxyxy =−−++ , 1 ;6 3 x Ta có ( ) ( ) 618 1ln27 y fxxy xy =−−+ + ; ( ) ( ) 2 2 1 60,;6 1ln273 y fxx xy =+ + . Do đó ( )fx là hàm số lõm nên ( ) 0 fx = có tối đa 2 nghiệm.
0984164935
Nghi
THPT BDKT Toán 10; 11;
hàm
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 20 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Dễ thấy 0 x = là nghiệm của nên để có nghiệm 1 ;6 3 x thì ( ) 60 1 0 3 f f 2727 2727 6log(16)0log(16)6y0 1720 log10log11 33333 yyy yyyy −++− −++−+ . Dựa vào bảng biến thiên và bấm máy tính Ta được 2;18\0 y − , Vì y nên 2;1;1;2;........18 y −− . Vậy có 20 giá trị của y thỏa mãn. Câu 32: Có bao nhiêu số nguyên y sao cho tồn tại 13 ; 62 x thỏa mãn ( ) 2 12218 271227xxyx xy + =+ . A. 27 B. 9 C. 11 D. 12 Lời giải Chọn C Ta có: ( ) ( ) 2 12218 2712271 xxyx xy + =+ ( ) ( ) 2 12182 120 1 27122 xxxy xy xy −+ + =+ *Với 0 y = , phương
22
xxxx−== 0 3 2 x x = = vô nghiệm vì 13 ; 62 x . * Khi 0, y vì 1 6 3 2 x và 1 2 xy − nên suy ra 1 3 3 y −− mà y là số nguyên nên 2;1 y −− . Với 1 y =− , phương trình thành: 2 1220 27(12)0 xx x −−= , có nghiệm trên 13 ; 62 vì 2 1220 1()27(12) xx gxx =−− liên tục trên 13 ; 62 và 11 13 .0 62gg . Với 2 y =− , phương trình thành: 2 1222 27(14)0 xx x −−= , có nghiệm trên 13 ; 62 vì 2 1222 2()27(14) xx gxx =−− liên tục trên 13 ; 62 và 22 13 .0 62gg
trình thành:
12181218 2710271
*Khi 1, y xét trên 1 6 3 ; 2 , ta có 2 1221 2 2 7 8 2 1 7(12)2718log(12 2 )2 xxyxxyxxxyxy + +−=+− = 27 log(12) 121820. xy xy x + −−+= Xét hàm 27 log(12) ()12182 xy gxxy x + =−−+ trên 13 ;. 2 6 Ta có 22 ln(12)213 '()1212120,;. ln27(12)ln273ln3l2 11 n3 2 6 xyy gxx xxxyx + =+−−− +
Do đó, hàm ()gx đồng biến trên 1 6 3 ; 2 . Vì thế phương trình ()0gx = có nghiệm trên 13 ; 62 khi và chỉ khi 1 . 6 3 ()0 2 gg Áp dụng bất đẳng thức ln(1)uu+ với mọi 0 u , ta có 27 log(16) 6 (3)1821820. 3n27 3 l y y gyy + =−+−+ Do đó 3 1 02log121601963 y gyy −++−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
21
. Vậy 2;1;1;2;...;9 y −− hay
trị y thỏa
Câu 33: Cho , ab là những số thực dương thỏa mãn điều kiện 22 ab+=
Có
ố
x sao cho tồn tại 10 1; 3 y để .9 3.3 2 y axbyx b a + =+ A. 4. B. 2. C. 7. D. 6. Lời giải Chọn A Ta có 2222 abba +==− . ( ) ( ) ( ) 222 2 .9 3.33.31.93.310 2 y axayaxy axbyxxyxy b aaaaa +−− +− =+=+−−+−= Đặt ( ) 23.310, att txyftaat =−=−+−= ( ) ( ) .3ln3.3ln3.ln3.3300 attatt ftaaat =−=−== . Ta có bảng biến thiên:
có 11 giá
đề
.
bao nhiêu s
nguyên
Suy ra ( ) 20 022; 3 ftxy == Vậy có 4 số nguyên x .
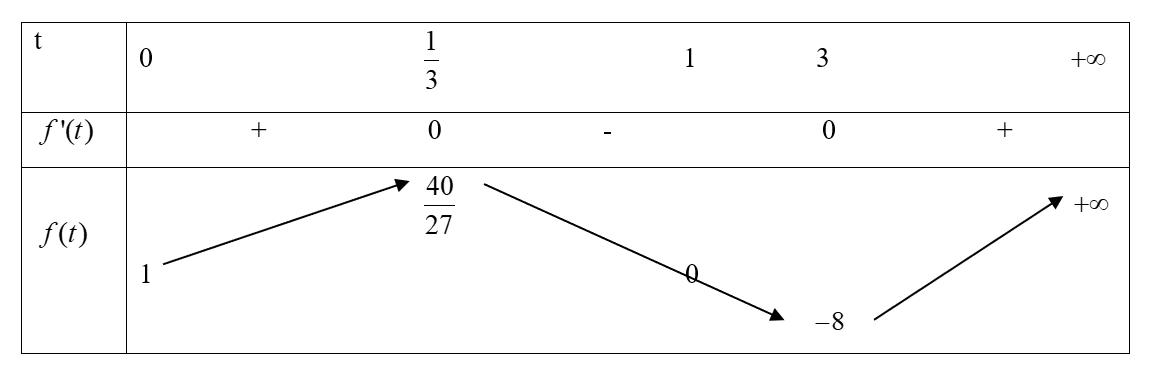
Câu 34: Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình 32 35.33.310 xxx m có ba nghiệm phân biệt 123 ,, xxx sao cho 123 01 xxx là A. 8. B. 7. C. 0. D. Vô số Lời giải
Chọn C
Đặt 30 x tt . Phương trình đã cho 325310(*).tttm Để phương trình đã cho có 3 nghiệm 123 ,, xxx thỏa mãn 123 01 xxx thì phương trình (*) phải có 3 nghiệm phân biệt 123 ,, ttt thỏa mãn 123 013(**). ttt 32 (*)531tttm
t fttttfttt t Bảng biến thiên :
Xét hàm 322 3 531'31030. 1 3
Từ bảng biến thiên ta thấy không có giá trị nào của m thỏa mãn bài toán.
Câu 35: Tìm tập hợp các giá trị của tham số thực m để phương trình ( ) 6320 +−−=xx mm có nghiệm thuộc khoảng ( )0;1 . A. 3;4 . B. 2;4 . C. ( )2;4 . D. ( )3;4 . Lời giải Chọn C
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
22
Ta có: ( ) 6320 +−−=xx mm ( )1 63.2 21 + = +
xx x m
Xét hàm số ( ) 63.2 21 + = +
xx x fx xác định trên .
Ta có ( ) ( )2 12.ln36.ln63.2.ln2 0, 21 ++ = +
xxx x fxx nên hàm số ( )fx đồng biến trên .
Với 01 x thì
Suy ra hàm số luôn đồng biến trên . Phương trình đã cho tương đương ( ) ( ) 333 4324323 fxxmfxmxxmxmxxm −+=−+−+=−+−+= Dễ thấy phương trình có đúng một nghiệm thực x khi và chỉ khi phương trình: 3 3 xxm−+= có đúng một nghiệm thực. Lập bảng biến thiên của hàm số ( ) 3 3 fxxx =−+ suy ra phương trình có đúng một nghiệm thực khi và chỉ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
23
( ) ( ) ( ) ( ) 0124 ffxffx . Vậy phương trình ( )1 có nghiệm thuộc khoảng ( )0;1 khi ( )2;4 m Câu 36: Có tất cả bao nhiêu giá trị nguyên của tham số 10;10 m− để phương trình ( ) 3 323 3.1xmxxm xxmee −−+−+=− có đúng một nghiệm thực x . A. 15 B. 16 C. 17 D. 18 Lời giải Chọn B Phương trình ( ) 3 323 3.1xmxxm xxmee −−+−+=− 3 3243 3 xmxxm xxmee −+−+−+=− ( ) ( ) 3 4332432xxmxm exxmexm −+−+ +−+=+−+ Xét hàm số ( ) ( ) ;'10tt ftettftet =+=+ .
khi 10;10 2103 2310 m mm mm − −− ⎯⎯⎯⎯→ − Vậy có tất cả 16 giá trị nguyên m thỏa mãn điều kiện đề bài. Câu 37: Có bao nhiêu giá trị nguyên của tham số m để phương trình ( ) ( ) 23 2 2121 xxxm −+− +=− có ba nghiệm phân biệt A. 0 B. 1 C. 2 D. 3 Lời giải Chọn B Vì ( ) ( ) 21.211 −+= nên
PT ( ) ( ) 23 2 2121 xxmx −+− +=+ 23 2 xxmx −+=− ( ) 32 2* mxxx =+−+
Ycbt tìm m nguyên để phương trình ( )* có 3 nghiệm phân biệt. Xét ( ) 32 2 yfxxxx ==+−+ Bảng biến thiên
Dựa vào bảng biến thiên suy ra 49 ;3 27 m , m nên 2 m = . Vậy có 1 giá trị m thỏa mãn đề bài.
Câu 38: Nghiệm của phương trình 22 32223 296435 xxxxxx xx+++=++ là A. 2 x = B. 6 x = C. 3 x = D. 2,3xx== Lời giải Chọn D 22222466424664 236235232346. xxxxxxxxxxxx PTxxxxx −++=−+−+−=−+−
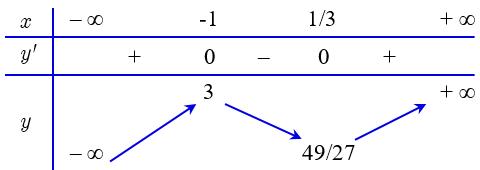
Đặt 2 ,46uxxvx=−=− ta có: 2323 uuvv uv−+=−+ .
Xét hàm số: ( ) ( ) 23tt fttt=−+ ta có: ( ) ( ) 2ln23ln310 tt ftt =++ Do đó ( ) ( ) 22 2 46560 3 x fufvuvxxxxx x
= ==−=−−+= = . Vậy phương trình có nghiệm là 2,3xx== .
Câu 39: Tìm m để phương trình sau có nghiệm: 930 xx m ++= .
A. 0 m . B. 0 m . C. 1 4 m . D. 1 4 m . Lời giải Chọn A
Đặt 3;0 x tt Phương trình trở thành: 22 0 ttmmtt ++==−− .
Xét hàm: ( ) 2 fttt =−− trên khoảng ( ) 0;+
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
24
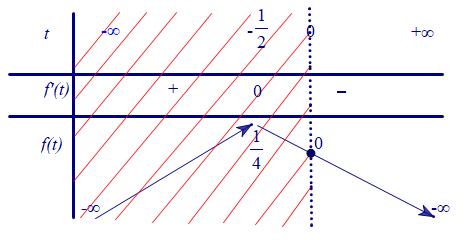

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 25 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có; ( ) 21ftt =−− ; ( ) 1 0 2 ftt ==− BXD: Dựa vào BXD, phương trình có nghiệm khi 0 m Vậy 0 m thoả yêu cầu bài toán. Câu 40: Cho hàm số ( ) 36 366 x x fx = + và đồ thị hàm số ( )ygx = như hình vẽ Số nghiệm thực của phương trình ( ) ( ) ( ) ( ) 211fgxfgx++= là A. 0. B. 1. C. 2. D. 3. Lời giải Chọn C TXĐ: D = Có ( ) ( ) 1 fafb+= 3636 1 366366 ab ab += ++ ( ) ( ) 2.3663636366363636 abababab ++ ++=+++ 36361 ab ab + =+= .
Do đó: ( ) ( ) ( ) ( ) 211fgxfgx++= ( ) ( ) 211gxgx ++= ( ) 0 gx = . Dựa vào đồ thị hàm số ( )ygx = ta có phương trình ( ) 0 gx = có 2 nghiệm phân biệt.
Câu 41: Cho phương trình 22 3.25(310).530 xx xx +−+−= , biết tổng các nghiệm của phương trình có dạng 5log abc + với (,,) abc . Tổng abc ++ là A. 7. B. 6. C. 12. D. 11.
Xét phương trình 22 53530(*)
xx =−−+= , đặt 2 ()53 x fxx =−+ Ta có 2 ()5ln510, x fxx =+ nên hàm số ()fx luôn đồng biết trên , mà (2)0 f = Nên phương trình ( )* có nghiệm duy nhất 2 x = . Vậy phương trình đã cho nghiệm là: 2 x = và 5 2log3 x =− Tổng các nghiệm của phương trình là: 5 4log3 suy ra 4,1,3abc==−= . Do đó 6 abc++= .
Câu 42: Cho phương trình: 9(41)33(41)0 xx mm −+++= . Có bao nhiêu giá trị m nguyên thuộc đoạn [10;10] để phương trình đã cho có nghiệm. A. 20. B. 19. C. 18. D. 8. Lời giải Chọn C Đặt: 3x = t
Phương trình đã cho trở thành: t2 t + 3 = 0 2 3 4(0,3) 3 tt mtt t −+ =
Phương trình đã cho có nghiệm khi đường thẳng 4 ym = cắt đồ thị hàm số 2 3 ()(0,3) 3 tt yfttt t −+ == ;
Ta có: 2 2 6 ' (3) tt y t =
Bảng biến thiên:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 26
1 3 3 t tx = =− suy ra 2 5 2 2 1
5 3 53 53 x x x x x x =− = =− =−
Lời giải Chọn B Đặt 2 5(0) x tt= ta có phương trình: 2 3(310)30 txtx +−+−=
2log3
xx
Từ bảng biến thiên suy ra, phương trình đã cho có nghiệm x khi: 1 4 m − hoặc 11 4 m Do m nguyên thuộc đoạn [10;10] nên {10,9,...1,3,4,...,10} m−−− . Vậy có 18 giá trị m Câu 43: Có bao nhiêu giá trị nguyên của m để phương trình 2 816.278.92.30 xxxx mm −+−−= có đúng hai nghiệm phân biệt? A. 4. B. 2. C. 3. D. 5. Lời giải Chọn A Ta có 2 816.278.92.3 xxxx mm−+=+ 4322 36.38.32.3 xxxx mm−+=+ Đặt 3x t = . Phương trình trên trở thành 4322 682 tttmtm −+=+ ( )2 23222 692 ttttmtm −+=++ ( ) ( ) 2 2 2 3 tttm−=+ 2 2
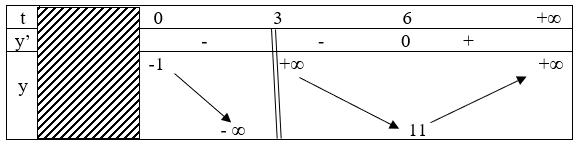
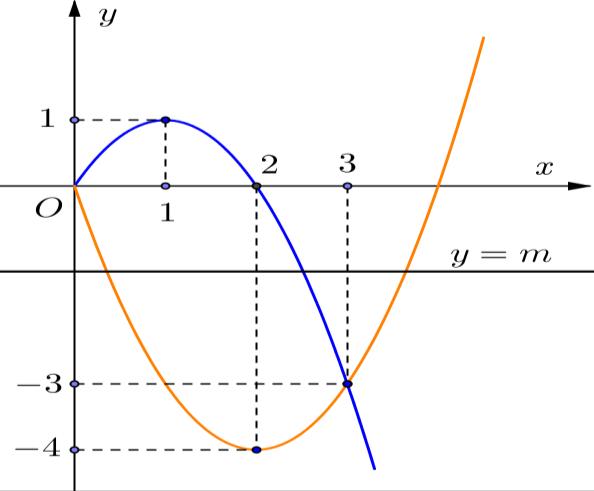
3 3 tmtt tmtt +=− +=−+
2 2
4 2 ttm ttm −= −+= .
Ta có đồ thị của hai hàm số ( ) 2 4 fttt =− và ( ) 2 2 gttt =−+ với 0 t
Để phương trình đã cho có đúng hai nghiệm phân biệt thì có đúng hai nghiệm dương phân biệt hay đường thẳng ym = cắt đồ thị hai hàm số tại hai điểm phân biệt có hoành độ dương.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 27
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo
ỳnh
42
ễn
Page 28
Dựa vào đồ thị ta có đường thẳng ym = cắt đồ thị hai
ố tại
điểm
m−− . Vậ
ị
ủ
m Câu
( )
1
xxxx
+ −+−+−+=
khoảng ( ) 0; là A.
. B.
.
Chọn A Ta có ( ) ( ) 1 42221sin2120 xxxx y + −+−+−+= ( ) ( ) ( ) 2 22.2.sin21122sin210 xxxx yy ++−−+−+−= ( ) ( ) 22 2sin211cos210 xxx yy ++−−++−= ( ) ( ) ( ) ( ) 21sin2121sin21 cos210sin211 xxxx xx yy yy =−+−=−+− +−=+−= ( ) ( ) 20 ()sin211 22 sin211 x x x x VN y y = +−= = +−=− ( ) 1 sin11 x y = +=− . Vậy phương trình đã cho có một nghiệm x trên ( ) 0; . Câu 45: Với a là tham số thực để bất phương trình 232 xx ax ++ có tập nghiệm là R , khi đó A. ( )1;3 a B. ( )0;1 a C. ( );0 a− D. ( ) 3; a+ Lời giải Chọn A 232 xx ax ++ 2320, xx axx +−− . Xét ()232 xx fxax=+−− liên tục trên R Ta có 00 (0)23.020fa =+−−= ()2ln23ln3 xx fxa =+− . Để ( ) ( ) ( ) 0,0, fxxfxfx 0 x = là điểm cực tiểu Vì 0 x = là điểm cực tiểu ( ) 00ln3ln2ln6 faa =+== Thử lại:
viên: Hu
Văn Ánh
Nguy
Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
hàm s
hai
có hoành độ dương khi
4;3;0;1
y có 4 giá tr
nguyên c
a
44: Số nghiệm của phương trình
( )
42221sin2120
y
( y là tham số) trong
1
2
C. 3. D. 4. Lời giải
afxx fx ==+−− =+−
( ) ( ) ln623ln6.2 2ln23ln3ln6
xx xx
Ta có vế trái ( ) 2ln23ln3 xx hx =+ đồng biến; vế phải ( ) ln6 kx = là hàm hằng. 0 x = Bảng biến thiên
Từ bảng biến thiên ( ) 0, fxx Vậy ln6 a = .
Câu 46: Cho hàm số ( ) 2x fx = . Số giá trị nguyên không dương của tham số m để bất phương trình ( ) ( ) 2 cos fxfm có nghiệm thuộc ( ) 0; là A. 1 B. 2 C. vô số D. 0 Lời giải Chọn A Đặt ( ) ( )cos,0;1;1txxt =−
Ta có: ( ) ( ) 2 cos fxfm có nghiệm thuộc ( ) 0; 2 22tm có nghiệm thuộc ( )1;1 2 tm có nghiệm thuộc ( )1;1 ( ) 2 1;1 min0tmm . Mà 0 m nên suy ra 0 m = .Vậy có 1 giá trị m cần tìm. Câu 47: Cho phươngtrình ( ) 2 33 2loglog150
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
29
x xxm −−−= Cótấtcảbaonhiêugiátrị nguyên dương của m để phương trình đã cho có đúng 2 nghiệm phân biệt? A. 125. B. 123. C. 122. D. 124. Lời giải Chọn B Điều kiện: ( ) 5 00 500log x x x xm mm − ( ) 2 33 2loglog150 x xxm −−−= ( ) 2 33 1 2loglog103,3 505 x x xx xx m fxm == −−= −= == Xét ( ) 5x fx = hàm số đồng biến trên ∞ + ∞ + ∞ + ∞ x f'(x) f(x) + 0 0 0

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 30 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Dựa vào bảng biến thiên, để phương trình có hai nghiệm phân biệt thì 1 3 1 5125 m m = , m + 01 3124 m m . Nên có 123 giá trị m thoả mãn. Câu 48: Cho hai số thực , xy với 0 x thỏa mãn 1 4 2 2 1 2log0 32 x x yy + += . Giá trị của 2021Sxy =+ bằng A. 3 2 . B. 3 2 . C. 1 2 . D. 0. Lời giải Chọn C Ta có: 11 44 2222 11 2log02log3232 xx xx yyyy ++ +==−
(
11
2 44 22
xx xx
++ =−−==−+
x x
Dấ
ằng xả
ra
(
4 2 1 10 x xx x
= = =− += . Giá trị của ( ) 2021 11 1 22 Sxy=+=+−= . Câu 49: Cho đồ thị hàm số ( ) 32 fxaxbxcxd =+++ có hai điểm cực trị là ( )0;3 A và ( )2;1 B . Số nghiệm của phương trình ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 423.23.2 ffxfxffxffx fx + −+= là A. 7. B. 6. C. 3. D. 9 Lời giải Chọn C Ta có: ( ) ( ) '000 '2030 f c ab f = = += −= và ( ) ( ) 033 2121 f d ab f = = +=− −= Do đó: 1;3;0;3abcd ==−== và ( ) 3233fxxx=−+ có đồ thì
;
) ( ) ( )
2
2log3202log41
yyy
; Ta có: 1 1 2. 4 4 222 x
x VT + == ( ) ( ) 2 22 log41log42VPy=−+=
u b
y
khi
) 1 1 0
y y
= +−+= = Ta có ( ) ( ) 22 303 xx mm−== Để phương trình ( ) ( )2 238330 x xx xm +−+−= có 2 nghiệm thì phương trình ( )2 3 x m = vô m m m
nghi m m m m m
c
thu . Vì 2021;2021 m− và m

)
) 23
nghi 1 1 1 981 981
nên có 2095 giá trị m nguyên cần tìm.
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 31 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 423.23.22322022 ffxfxffxffxffxffxffxfxfxfx + −+=+−== ( ) ( ) ( ) ( ) hinhve ffxfxfxx ==⎯⎯⎯→ 3 nghiệm. Câu 50: Gọi S là tập nghiệm của phương trình
ệm hoặc có
( ) ( )2 238330 x xx xm +−+−= Có tất cả bao nhiêu giá trị nguyên của 2021;2021 m− để tập hợp S có hai phần tử? A. 2095. B. 2092. C. 2093. D. 2094 Lời giải Chọn A Điều kiện: ( )2 30 x m − Ta có ( ) ( ) ( ) 2 2 ệm
23830 238330 30 ộ
x x
xx xx x xm m 1;2 (
+−+= +−+−= −= Xét hàm số ( ) 2383 xx fxx=+−+ , ta có ( ) 2ln23ln38 xx fx =+− ; ( ) ( ) ( ) 22 2ln23ln30, xx fxx =+ suy ra phương trình ( ) 0 fx = có nhiều nhất là 2 nghiệm Ta thấy 1 x = và 2 x = là hai nghiệm của phương trình, vậy 1 23830 2 xx x x x 1 1 1loglog2
Phương trình trở thành ( ).5.5** uvuv = . Xét hàm đặc trưng ( ) ( ) .5,0; x fxxx=+
Ta có ( ) ( ) 5.5ln50,0; xx fxxx =++ nên hàm số ( )fx đồng biến trên ( ) 0: + . Ta có ( ) ( ) ( ) **4255553 fufvuvxyxyyx ==++=+−=
Vì 0 y nên 05 x 5 log1 x Khi đó ( ) 2222 5555 log532log230log2log230 ymxmmxmxmm −−+−=−+−= Đặt ( ) 5 log1txt= . Khi đó ( ) 2222301tmtmm −+−= . Phương trình có nghiệm 222 02303003 mmmmmm −+− . Với 0;3 m , phương trình ( )1 có hai nghiệm 22 123,3 tmmmtmmm =−−=+− Phương trình ( )1 có nghiệm nhỏ hơn 1 ( ) 22 1 131132 tmmmmmm −−−−
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo
Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuậ
Huế
Page 32
ể
sinh
ạ
Câu
Có bao nhiêu giá trị nguyên của tham số mđể tồn tại cặp số thực dương ( ) ; xy thỏa
đẳng thức 34 425 5xy xy xy +− ++ = + và
A. 5 B.
+−
+− ++++++ === +++
xy
+
++ ++ =++=+ +
xy
viên:
n Hòa TP
ĐT: 0984164935
Chuyên luyện thi: Tuy
n
vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên so
n
51:
mãn
phương trình ( ) 22 55 log532log230 ymxmm −−+−= có nghiệm
2 C. 3 D. 4 Lời giải Chọn B ( ) ( )
+−++
34 55425 34 4254255425 55 5()555 xy xyxy
xyxyxy xyxyxy ( ) ( ) ( )
+++
55 42555 425 4255 425.555.5* 555 xy xyxy
xy xyxy xy Đặt 425 55 uxy vxy =++ =+ . Vì 0,0xy nên 0,0uv
Kết hợp điều kiện 0;3 m m , ta thấy 1;2 m thỏa mãn điều kiện ( )2 . Câu 52: Cho phương trình ( ) eln x xaa=++ , với a là tham số. Có bao nhiêu giá trị nguyên của a thuộc khoảng ( )0;19 để phương trình đã cho có nghiệm dương? A. 15. B. 18. C. 17. D. 16. Lời giải Chọn C Đặt ( ) lnet txaax =+=− với 0 x và ( )0;19 a .
Phương trình đã cho trở thành ee xtxt+=+
Xét hàm số ( ) e u guu =+
Ta có ( ) e10, u guu =+ nên hàm số ( )gu đồng biến trên
Suy ra ( ) ( ) ( ) * gxgtxt == ( ) ln xxa=+ e x xa=+ e x ax=−
Xét e x yx =− trên ( ) 0;+ có ( ) e10,0; x yx =−+
Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy phương trình đã cho có nghiệm dương 1 a .
Mà ( )0;19 a nên suy ra 2;3;4;...;18 a
Vậy có 17 giá trị a thỏa mãn.
Câu 53: Tìm số giá trị nguyên của tham số thực m để tồn tại các số thực , xy thỏa mãn 22 22 22 xymxyxym eexyxyxym +−++−+=++++−+ A. 9. B. 7 . C. 6 . D. 8. Lời giải Chọn A Ta có: 22 22 22 xymxyxym eexyxyxym +−++−+=++++−+ ( ) ( ) 22 22 110(*)xymxyxym exymexyxym +−++− −+−−+−++−−= . Đặt: ( ) 1 t ftet=−− với t ( ) 1 tfte =− ( ) 00ftt == . Bảng biến thiên:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 33

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 34
(
xym xyxym xymxyxymxy +−−=+++−= +−=
ệ
ộ
08 m Mà m nên
m V
ấ
ả
ố thực a , b thỏa mãn ( ) 222 2221 ee1e0
++++−+−−= . Gọ
t là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức 1 12 P ab = + . Khi đó mM + bằng A. 19 5 . B. 2 5 . C. 7 3 . D. 10 3 . Lời giải Ta có: ( ) 222 2221 ee1e0 abababb aabb ++++−+−−= 222 2221 e1e0 aabbb aabb −+++−+−−= 22222212e2e1 aabbbaabbb−+++−+=++ ( ) ( ) 222 21 faabbfb −+=+ , với ( ) e t ftt =+ Mà ( ) e10, t ftt =+ nên ( )ft là hàm đồng biến trên . Do đó 222 21 aabbb −+=+ 22 1 aabb−+= Khi đó, ta có:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Từ bảng biến thiên ta thấy ( ) 0 ftt và ( ) 00ftt== Do đó: ( ) ( ) ( ) 22 *0 fxymfxyxym +−+++−=
) ( ) ( ) ( ) ( ) 22 22 0(1)20230(**) 0(2) xyxymxyxym
++−= =−+=−+ Từ và ta có: ( ) ( ) 2 22 3 xyxyxyxyxyxy +=+++−+= ( ) ( ) ( ) ( ) ( ) 222 31 004 44 xyxyxyxyxyxy +−+++−++ Yêu cầu bài toán (**)
có nghi
m thu
c
0;4
0;1;...;8
ậy có t
t c
9 giá trị nguyên của m thỏa đề. Câu 54: Cho các s
abababb aabb
i m , M lần lượ
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo
Huỳnh Văn Ánh 42
ễn Cư
Thuận
ế
Page 35
ạn ( ) ( )2 2 11 31 333 ab ababab + +−==−− . 222221
+−+= Đặ
=
ra (
12
== + vớ
x
. Lại có ( ) ( )2 21
3 12 gxx x =−−
trình ( ) ( ) 1 42221sin2120 xxxx y + −+−+−+= thoả mãn ( ) ,0;2xy là A. 1. B. 2. C. 3. D. 4. Lời giải Chọn A ( ) ( ) 1 42221sin2120 xxxx y + −+−+−+= ( ) ( ) ( ) ( ) ( ) 2 22 21221sin21sin21cos210 xxxxx yyy −+−+−++−++−= ( ) ( ) ( ) 2 2 21sin21cos210 xxx yy −++−++−= ( ) ( ) 2 21sin210 cos210 xx x y y −++−= +−= ( ) ( ) ( ) 20 sin211 22 sin211 x x x x vn y y = +−= = +−=− 1 12, 2 x ykk = =−−+ Đối chiếu điều kiện ( ) ,0;2xy ta được ( ) 3 ;1;1 2 xy =− . Câu 56: Giá trị của tham số m sao cho phương trình ( ) 4 cos xx eemx += có một nghiệm thực duy nhất thuộc khoảng nào trong các khoảng sau? A. ( )14;15 B. ( )10;12 C. ( )13;14 D. ( )20;22 Lời giải Chọn A
viên:
Nguy
Trinh
Hòa TP Hu
ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên so
abababaabb
t abx
, suy
) 1
Pgx x
i 1 ;1 3
−
0,;1
+ , nên ( )gx nghịch biến trên 1 ;1 3 Do đó ( ) 11 3,1 33Mgmg =−=== . Vậy 10 3 mM+= . Câu 55: Số nghiệm ( ) ; xy của phương
phương trình
2cos
2
) 22 2cos
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 36
Ch
Đặ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có nhận xét nếu 0xx = là một nghiệm của phương trình ( ) 4 cos xx eemx += thì 0 4 x cũng là nghiệm của phương trình này. Để phương trình có một nghiệm thực duy nhất 00 4 xx =− 00 242 xx == . Thế vào
ta được 2
em = Thay 2 2em = ta được ( ) 42
xx eeex += (
xx eex+= 22222.2xxxxVTeeee=+= ( ) 2cos2VPx= Dấu “=” xảy ra khi ( ) 22 2 cos1 xx ee x x = = = . Vậy phương trình ( ) 4 cos xx eemx += có một nghiệm thực duy nhất 2 x = . Câu 57: Cho hàm số bậc ba yfx có đồ thị như hình vẽ: Cho phương trình 2 32230 fxm fxm . Số giá trị nguyên của tham số 20,20 m để phương trình có 4 nghiệm phân biệt nhỏ hơn 3 A. 1 B. 2 C. 10 D. 0 Lời giải
ọn A
t 2 tfxm Khi đó phương trình trở thành: 321 t t Xét hàm số 32 t gtt Ta có: 3ln32 t gt y x 1 O 2 -3
30 22 03ln3203logln3ln3 tt gttt
Bảng biến thiên của hàm số 32 t gtt
t g'(t) g(t)
Với 0 0,73 gt
∞+ ∞+ 0
Từ bảng biến thiên suy ra phương trình có đúng 2 nghiệm thực phân biệt t
Mặt khác ta có: 01 g , 11 g
Vậy phương trình 321 t t có 2 nghiệm thực phân biệt 120,1tt
Khi đó: 2 32230 fxm fxm 202 213 fxmfxm I fxmfxm
Từ đồ thị hàm số yfx suy ra 3231fxxx
Bảng biến thiên của hàm số 2 yfx , 3 yfx :
0 0 2 x y' y
0 +
t0 + + ∞ ∞ g t0 ( ) ∞
∞ 1 1
2 2 6
3 5
+
Từ bảng biến thiên suy ra giá trị của tham số m thỏa mãn yêu cầu bài toán là: 6556 22 mm mm
Vậy có 1 giá trị nguyên của tham số m thỏa mãn.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
37
ybbyabay +==+−= ( ) 333 3 12312.2231231232 xx yybayaby +=−=−−=
Từ ( )1 và ( )2 suy ra ( ) 3312123aabb +=+
Xét hàm số ( ) 3 12 fttt =+ , có ( ) 2 '3120 fttt=+
Từ ( )3 ab=
Suy ra 3 3

CHUYÊN ĐỀ II GIẢI TÍCH
LŨY THỪA MŨ LOGARIT
Page
12
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
38 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 58: Có bao nhiêu số nguyên y thuộc đoạn 2022;2022 sao cho tồn tại x thỏa mãn 3 3 12312.223 xx yy +=− A. 2022 B. 2027 C. 6 D. 2028 Lời giải Chọn D Đặt 2x a = , điều kiện 0 a và ( ) 33 3 312.23121231 x
3 12 312312 3 aa yaayaay +==−= với 0 a Ta có 2 '4ya=− với 0 a ; 2 '0402 yaa =−== Từ bảng biến thiên Ta có 16 3 y − , mà 2022;2022 y − nên có2028 giá trị nguyên y thỏa mãn Câu 59: Có bao nhiêu số nguyên y thuộc ( )2022;2022 để tồn tại duy nhất số thực dương x thỏa mãn ( ) ( ) 2 1 112 2 333.log1 xy xx xyxx +−−=+− ? A. 2020. B. 2022. C. 2021. D. 2019. Lời giải Chọn D Do 0 x và 2 10xx+− nên để ( ) 2 2 log1xyxx +− có nghĩa khi và chỉ khi 0 y . Ta có:
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 39
x + ++=++==+ Xét hàm số: ( ) 2 1 1 x gx x + =+ với 0 x , ta có: ( ) 22 1 0,0 1 gxx xx =− + Bảng biết thiên của ( )gx : x0()gx ()gx 2 Từ bảng biến thiên của ( )gx ta có: yêu cầu bài toán 2 y Mà ( ) 2022;20223;4;...;2021 y y y − . Vậy có 2019 số nguyên y thỏa mãn. Câu 60: Có bao nhiêu cặp số nguyên dương thỏa mãn 2021;2021xy và (1).3.27 xyxy += ? A. 2021. B. 673. C. 674. D. 2020. Lời giải Chọn C Ta có: ( ) 13 (1).3.273(1).33.271.33.3(*) xyxyxy xyxyxy + +=+=+= Xét hàm số: ( ) .3t ftt = với 0 t . Có ( ) 3.3ln30 ttftt =+ , với ( ) 0; t + Suy rahàm số ( ) .3t ftt = đồngbiếntrên ( ) 0;+ màphươngtrình ( )* códạng ( ) ( ) 1 fxfy += .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 2 1 112 2 1 2 2 12 22 12 22 333.log1 1 333.log 1 333log3log1 33log133log1 xy xx xxxy xxxy xxxy xyxx xy xx xyxx xxxy +− ++ ++ ++ −=+− −= ++ −=−++ +++=+ Xét hàm số ( ) ( ) ( ) 2 3 33log,03.ln30,0 .ln2 tt ftttftt t =+=+ Suy ra hàm số ( )ft đồng biến trên khoảng ( ) 0;+ . Có: ( ) ( ) ( ) 2 22 1 1111 x fxxfxyxxxyy
Do , xy nguyên dương suy ra: Phương trình ( ) 1 *13 3 x xyy + +== Do , xy nguyên dương và 1 3 2021;2021
x y xy suy ra có 2022 674 3 = số nguyên dương y thỏa mãn đề bài. Vậy có 674 cặp ( ) ; xy thỏa mãn đề bài. Câu 61: Có bao nhiêu số thực y thuộc khoảng 11 ; 55 sao cho ứng mỗi y có duy nhất số thực x th
ỏa mãn ( ) ( ) 2222 25 log31020log23 xxyyxxyy ++=++ ? A. 2. B. 4. C.
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
40 6. D. 8. Lời giải Chọn C Điều kiện: 22 22 310200 230 xxyy xxyy ++ ++ Đặt ( ) ( ) 2222 25 log31020log23xxyyxxyym ++=++= . Ta có hệ ( ) 22 22 310202 235 m m xxyy xxyy ++= ++= Nếu 0 y = thì 2 5 2 22 5 2 log3 log3 325 53.52 5 mm mmm m xx x x = == == = . Suy ra có hai số thực x thỏa mãn. Nếu 0 y thì đặt ( ) , xtyt= . Hệ trên trở thành ( ) ( ) ( ) ( ) 22 22 3102021 2352 m m ytt ytt ++= ++= Từ ( )1 và ( )2 suy ra ( ) 2 2 310202 235 m tt tt ++ = ++ Từ cách đặt suy ra ứng mỗi y có duy nhất số thực x khi và chỉ khi ( ) có nghiệm duy nhất. Xét hàm số ( ) 2 2 31020 23 tt ft tt ++ = ++ . Ta có ( ) ( ) ( ) 2 2 2 22115 ; 23 tt ft tt −++ = ++ ( ) 5 01 2 t ft t =− = =− . Bảng biến thiên:
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
Thay vào ( )2 ta được 22 55 log7log7 2 4.52.511 0,121; 9355yy==− .
TH2 : 2 5 log3 m = . Khi đó ( ) trở thành 2 2 3102011 3102069 234 tt ttt tt ++ =+=+=− ++ .
Thay vào ( )2 ta được 22 55 log3log3 2 16.54.511 0,169; 81955yy==− .
TH3 : 1 m =− . Khi đó ( ) có nghiệm duy nhất 5 t =−
Thay vào ( )2 ta được 2 1111 0,105; 9055 310 yy==−
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
ỳnh
42
ễn
Page 41
ạ
Từ bảng biến thiên suy ra ( ) có nghiệm duy nhất khi và chỉ khi 2 5 2 5 2 7 5log7 2 53log3 251 52 m m m m m m = = ==
Giáo viên: Hu
Văn Ánh
Nguy
Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên so
n
=− =
TH1 : 2 5 log7 m = . Khi đó ( ) có nghiệm duy nhất 1 2 t =− .
. Vậy có 6 số thực y thỏa đề. Câu 62: Có bao nhiêu số nguyên x sao cho tồn tại 1 ;2 2 y thỏa mãn ( ) 2 812.8 yxyy xy + =+ ? A. 3. B. 2. C. 1. D. 0. Lời giải Chọn C Phương trình đã cho tương đương với 2 333 212 yxyy xy +− =+
Suy ra 1 120 2 xyx y +− , mà 11 22 yx− . + Nếu 0 x = thay vào phương trình ban đầu ta được 2 881 yy y == + Nếu 1 x = thay vào phương trình ban đầu ta được ( ) 22 8128812 yyyyyy + =+=+ . Khảo sát hàm số ( ) 2 812 y fyy =−− ta có ( ) 2 1 2 11 '8.ln8.228.ln8.2.20, 22 y fyyy =−−
Do đó hàm số đồng biến trên 1 ;2 2 . Khi đó ( ) 1 0 2 fyf +) Nếu 2 x , xét phương trình tương đương là 2 333 212 yxyy xy +− =+
Khi đó ( ) 2 22 1 3333313.1 2 yxyyyyx +−=+−
Xét hàm ( ) 21 t gtt=−− . Khảo sát hàm số ta thấy ( ) 01gtt
Vì vậy 211 t tt + . Áp dụng bất đẳng thức này với 2 3331tyxyy =+−
ta có 2 3332 23331 yxyy yxyy +− +−+ Mà ( ) ( ) ( ) 2222 1 333121333330 2 yxyyxyyxyyyyxyyy +−+−+=+−=+−− . Suy ra 2 333 221 yxyy xy +− + nên phương trình ban đầu vô nghiệm. Vậy chỉ có 0 x
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
42
1
A.
B. 4. C. 5. D.
Lời giải Chọn B Ta có: 2 24 16(1)16 xxyx xy + =+ 2 24 1610 xxyx xy +− −−= Đặt 2 24 ()161 xxyx fxxy +− =−− . Ta tìm điều kiện của y để ()0fx = có nghiệm 1 ;2 2 x . +Với 5 y , 1 ;2 2 x thì 22 242(4)0 xxyxxxy+−=+− , Áp dụng bất đẳng thức Bernoulli: (1)1 r aar++ với 0,1 r − , ta có:
= thỏa mãn đề bài. Câu 63: Có bao nhiêu số nguyên y sao cho tồn tại
;2 2 x
thỏa mãn: 2 24 16(1)16 xxyx xy + =+
3.
6.
2 2422 ()(115)1115(24)1302(730) xxyx fxxyxxyxxyxxy +− =+−−++−−−=+−
Do đó, 5 y thì ()0fx , 1 ;2 2 x . Vì vậy 5 y không thỏa mãn.
+Với 2 y − , 2 24 ()0161 xxyx fxxy +− ==+ . Mà 1120, xyx +− 1 ;2 2 x .
Suy ra 2 y − không thỏa mãn.
+Từ đó ta xét 1;0;1;2;3;4 y −
Với mỗi giá trị 1;0;1;2;3;4 y − , ()fx liên tục trên
+ 1 y =− : 2 25 ()01610 xx fxx=+−= 1127 2256 f = ; (2)257 256 f = 1 .(2)0 2 ff ()0fx = có nghiệm 1 ;2 2 x hay 1 y =− thỏa mãn. + 0 y = : 2 24 ()0161 xx fx == 2 0 x x
= = + 1 y : 3 11 410 22 y fy =−− 1;2;3 y ; 2 (2)16120 y fy=−− 1;2;3 y 1 .(2)0 2 ff ()0fx = có nghiệm trên 1 ;2 2 x 1;2;3 y + 4 y = : 2 2 ()01614 x fxx ==+ ; 2 2 '()16.ln(16).440 x fxx=− 1 ;2 2 x ; mà 1 0 2 f ()0fx = không có nghiệm trên 1 ;2 2 x Vậy 1;1;2;3 y − Câu 64: Cho hàm số ( )yfx = có đồ thị là đường cong trong hình vẽ bên. Số nghiệm thực phân biệt của phương trình ( ) ( ) ( ) 1 fx fefx+= là
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
43
A. 8. B. 6. C. 4. D. 2. Lời giải
Chọn B
fx fx fx
efx fefx efx
+= += +=−
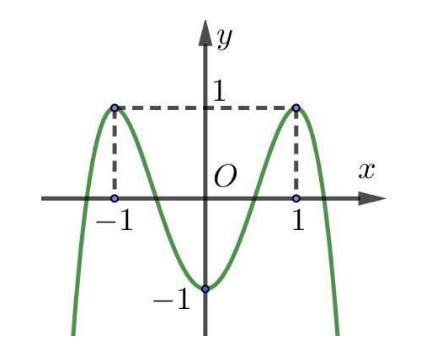
Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1 1 1 2
Xét hàm số ( ) , t gtett=+ ( ) '10, t tgte=+ hàm số ( )gt đồng biến trên hai phương trình và, mỗi phương trình có tối đa một nghiệm. Mặt khác ta có ( ) 01 g = nên ( ) ( ) 10 fx = , dựa vào đồ thị ta có phương trình có 4 nghiệm phân biệt.
Ta có hàm số ( ) 1 ygt=+ liên tục trên và ( ) ( ) ( ) ( ) ( ) ( ) 112102;1:1 ggcgc −+−+−−=−
Suy ra ( ) ( ) ( )2,2;1 fxcc =−− , dựa vào đồ thị ta có phương trình có 2 nghiệm phân biệt khác nghiệm của phương trình Vậy phương trình đã cho có 6 nghiệm phân biệt. Câu 65: Có bao nhiêu số nguyên y
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 44
ạ
10
thỏ
A. 9 B. 16 C. 18 D. 7 Lời giải Chọn B Ta có ( ) 22 27272 2021 21 021(1)2021202127log1 xxyxxxyxxyxxyxxy xy ++− =+ += +−=+ Ta xét ( ) ( ) 2 2021 27log1,1fxxxyxxyxy=+−−+− Ta có ( ) ( ) 47 ln2021.1 y fxxy xy =+−− + ( ) ( ) 2 2 40 ln2021.1 y fx xy =+ + nên hàm số ( )fx là
sao cho tồn t
i 1 ;4
x
a mãn 2 27 2021(1)2021? xxyx xy + =+
hàm lõm suy ra ( )fx có tối đa hai nghiệm. Và ( )fx luôn có một nghiệm là 0 x =
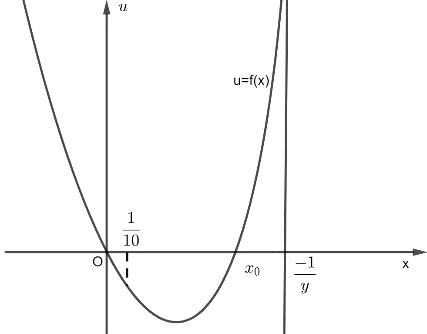
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 45
−
+−
=−
( )gy là hàm số đồng
ến trên nửa
ảng
+
. Từ, ta có 71,2,3...,7 1 yy TH2: 0 y mà ,10 y y − nên 1;2,...,9 y . từ ;4 10 1 11 xy x y , do đó tập xác định của ( )fx là 1 ; D y =−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có 1 1 x xy y
, mà 1 ;4 10 x
nên 1 0; 4 1 1 x −− suy ra 10 y − . TH1: 0 y mà 1 y y , từ 1 1 y xy x − , do đó tập xác định của ( )fx là 1 ; D y =+ Để ( )fx có nghiệm 1 ;4 10 x thì ( ) 1 0 10 40 f f
( ) ( ) ( ) 2021 2021 5345010log101 44log1402 yy yy −+
+ Xét ( )hy = 2021 534 log1 5010 yy −+ , có ( ) 11 00 10 10ln2021.(1) 10 hyy y =− + nên hàm số đồng biến, và 4 ( 5 ) , 0 7 hy y = . Do đó ( ) 17 0 h y y y Xét ( ) ( ) ( ) ( ) 2021 4 401, ln2021 44log1 14 4 gy gy y yy y =+
+ + do đó
bi
kho
[1;)
nên ( ) ( ) 101gygy
Xét hàm số ()7272 aa faa=+−− .
Ta có ()7ln72ln27 aa fa =+−
Ta có ( ) ( ) 22 ()7ln72ln20 aa fa =+ , a
Suy ra ()fa đồng biến trên , do đó ()0fa = có tối đa 1 nghiệm.
Mà (0)ln7ln270 f =+− và (1)7ln72ln270 f =+−
Suy ra ()0fa = có nghiệm duy nhất 0 (0;1) a
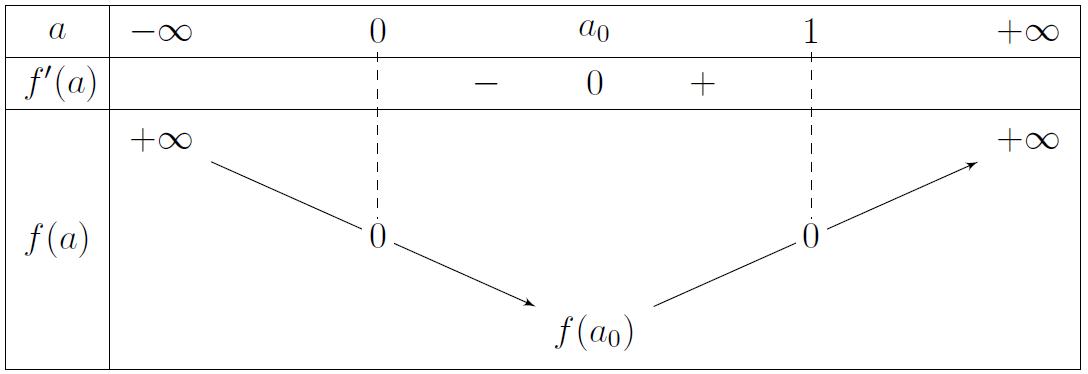
Suy ra ()0fa = có tối đa 2 nghiệm.
Bảng biến thiên của ()yfa =
Từ bảng biến thiên ta có ()0fa = có đúng 2 nghiệm 0 a = và 1 a =
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 46
f −+ luôn
với mọi 1;2,...,9 y Vậy 9,8,...,1,1,2,3...,6,7 y −−− nên có 16 giá trị của y thỏa mãn đề. Câu 66: Có bao nhiêu giá trị nguyên của tham số [10;10] m− để phương trình ( ) 22 323232 277214714273 mmm xxxxm xx +=−+− có bốn nghiệ
+=−+− +=−−+
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do 1 (0)0;lim() x y ffx → ==+ nên hàm số có nghiệm 1 ;4 10 x khi và chỉ khi hàm số có nghiệm 11 ; 10 x y khi và chỉ khi 2021 15340log10 105010 yy
đúng
m phân biệt trong đó có đúng hai nghiệm lớn hơn 1? A. 10 B. 9 C. 11 D. 8 Lời giải Chọn A Ta có ( ) ( ) 22 22 22 323232 22 2 33 23232 277214714273 72 714273 72 727232.() mmm mm mm xxxxm xxxx m xxxxm xx xx xx +=−+−
Đặt 2 23m xxa −−= . Khi đó () trở thành 727272720 aaaa aa +=++−−= .
=−−==− =−−==−− Để () có 4 nghiệm thực phân biệt trong đó có đúng hai nghiệm lớn hơn 1 thì () có 4 nghiệm thực phân biệt trong đó có đúng hai nghiệm lớn hơn 1 hay tương đương với đồ thị hàm số 3m y = cắt đồ thị các hàm số 2 2 yxx =− và 2 21yxx=−− tại 4 điểm phân biệt trong đó có đúng hai điểm có hoành độ lớn hơn 1.
ra
có 10
mm mm
331
m th
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Dựa vào đồ thị ta có
Page m m . Suy
47 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn {1;2;;10} m . Vậy
Từ đó 22 22 giá trị của
23032 () 231321. ỏa mãn bài toán. Câu 67: Cho hai số thực , xy thoả mãn 02020 x và 2 log(22)38y xxy++−= . Có tất cả bao nhiêu cặp số nguyên (;) xy thỏa mãn các điều kiện đã cho? A. 2018. B. 4. C. 2019. D. 1. Lời giải Chọn B Do 02020 x nên 10 x + . Ta có 33 222 log(22)38log(1)1log22 yyyxxyxx ++−=+ ++=+ Đặt ( ) 2 1 log1=101 .ln2 yttty t =++ hàm số ( ) 2 log1yttt=+ đồng biến Từ và ta được 33 1221 yyxx+==− Mà 3 8 020201220211820210log202103,6604 yy xyy
axxxx axxxx
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 48
( ) ( ) ( ) ( ) ( ) 3 3 3 3 332 3 3323 3323 3 3 33 3 3 32 31 3924 3 392433273 33327279 3333 33 92427 x mx x mxx mxx mxx xxxm xxxmxx mxxxx mxx mxx mxxxfx + +−++= +−++−+=+ +−=+−+− +−=+− −=− =−+−+= Xét ( ) 2 2 318240 4 x fxxx x = =−+−= = BBT Dựa vào BBT, để phương trình có 3 nghiệm phân biệt thì 711 m Vì 8,9,1027mmm == . Câu 69: Có tất cả bao nhiêu số nguyên dương y sao cho tồn tại số thực ( )1;8 x thỏa mãn ( )( ) ( ) 22 12 xx xeyyex −−=− ? A. 11 B. 14 C. 12 D. 13 Lời giải Chọn D Xét ( ) ( )( ) ( ) 22 12 xx fxxeyyex =−−−− trên ( )1;8 với y là tham số Ta có ( ) ( )( ) ( ) 2 2220 2 xxx y fxxeyeyyxeyxyfxx =−−+=+−== Nhận thấy ( ) ( ) 110fye=−− ( ) ( ) ( ) ( ) 828288 8726476414 feyyeyeye =−−−=−−−+ . Trường hợp 1: ( ) 120 2 y yfx . Bảng biến thiên
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Mà y nguyên nên 0,1,2,3yyyy ==== . Vậy có bốn cặp số nguyên (;) xy thỏa mãn. Câu 68: Cho phương trình ( ) 3 33323 3924.331 xmxxx xxxm −+−−+−++=+ . Tổng tất cả các giá trị nguyên của tham số m để phương trình trên có 3 nghiệm phân biệt là A. 38. B. 34 C. 27 D. 5 Lời giải Chọn C Ta có hệ sau: ( ) ( ) 3 33323 3924.331* xmxxx xxxm −+−−+−++=+ Phương trình ( )* tương đương:
Suy ra ( ) ( ) 288 80764140013.85 fyeyey −−−+ .
Do vậy 021;2 yy .
Trường hợp 2: ( ) ( ) ( ) 8160810 2 y yfxff khi đó phương trình vô nghiệm trên ( )1;8
Trường hợp 3: 18216 22 CT yy yx = . Bảng biến thiên
Suy ra ( ) ( ) 288 80764140013.85 fyeyey −−−+ .
vậy 213,853;4;...;13
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
49
4 3 . C. 0 . D. 1 3 . Lời giải Chọn A ( ) ( ) 222322 27641.9323210 xxxx xxxx =−+−−−= .( )1 Đặt 2 32xxt −= , 1 3 t − ( )1 3210 t t −−= . Đặt ( ) 321 t ftt=−− Ta có ( ) 3ln32 t ft =− là hàm số liên tục trên nửa khoảng 1 ; 3 −+ . Lại có ( ) 2 1 3ln30,; 3 t ftt =−+ nên suy ra ( )ft đồng biến trên 1 ; 3 −+
Do
yy . Vậy có 13 giá trị nguyên dương y thỏa mãn. Câu 70: Tổng các nghiệm nguyên của phương trình ( ) 2 2 27641.9 xx xx =−+ bằng bao nhiêu? A. 1. B.
Do ( ) 0ln320 f =− và ( ) 13ln320 f =− nên ( ) ( ) 0.10ff .

Suy ra phương trình ( ) 0 ft = có nghiệm duy nhất ( ) 0 0;1 t .
Ta có bảng biến thiên
Từ bảng biến thiên ta thấy phương trình ( ) 0 ft = có không quá hai nghiệm.
Mặt khác ( ) 00 f = , ( ) 10 f = nên suy ra phương trình đã cho có hai nghiệm 0 t = và 1 t =
Với 2 0 0320 2 3
ới
x txx x
= =−= = .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
50
thoả mãn ( ) !
y xx ++= ? A. 0. B. 1. C. 2. D. Vô số. Lời giải Chọn B Ta có: ( ) ( ) ! 3 111063!2.log11106 y xxxx y ++==++ . *Với 3 0!2log13xy== *Với 1 x = thì 3 !2.log2763 yy === *Với 2 x thì ta thấy (69) x + chia hết cho 9, (102)[(101)3] xx+=−+ không chia hết cho 9 Do đó: (11106) xx++ không chia hết cho 293 = Nên ( ) 3 !2.log11106xx y =++ là số không
2 x . Vậy, Tồn tại duy nhấy bộ ( )
xy =
V
22 1 13213210 1 3 x txxxx x = =−=−−= =− Vậy phương trình đã cho có 4 nghiệm: 12 0,1,, 33 xxxx ===−= Câu 71: Có bao nhiêu bộ ( ) ; xy với , xy là số tự nhiên
111063
nguyên khi
;(1;3)
thoả yêu cầu bài toán.
Câu 72: Có bao nhiêu số nguyên a sao cho ứng với mỗi a , tồn tại số thực ba thỏa mãn 42ab b =+ và đoạn ; ab chứa không quá 5 số nguyên? A. 5 B. 10 C. 6 D. 11 Lời giải
Chọn D Xét hàm số ( ) 2b fbb =+ có ( ) '2.ln210,. b fbb =+ Suy ra hàm số ( ) 2b fbb =+ đồng biến trên . Phương trình 42ab b =+ có nghiệm ba và đoạn ; ab chứa không quá 5 số nguyên khi và
Chọn D
Ta có: +−=+ 4 444816log x xyy +−=+ 4448164log x xyy +−=+ 1 4424log x xyy ( ) +−=+ 4 log4 1 4 414log4 y x xy .
Xét hàm số ( ) =+ 4t ftt . Ta có: ( ) =+ 14.ln40, t ftt
Suy ra hàm số ( )ft liên tục và đồng biến trên . Do đó ( ) ( ) ( ) ( ) −=−=−== 2 444 1log41log42log4x fxfyxyxyy . Vì ( )0;2020 y nên 2 42020 x −+44 2log20202log2020xx
Do + ; xy nên
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
51 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
ỉ khi 5 24420 425432.250 aaaa aaaa aa aa + +−− ++−−− Mà 5;4;...;5 aa−− . Vậy có
giá trị của a
ỏ
ch
11
th
a mãn yêu cầu đề bài. Câu 73: Có bao nhiêu cặp số nguyên dương thoả mãn 02020 y và +−=+ 4 444816log x xyy ? A. 9. B. 8. C. 7. D. 6. Lời giải
Ứ
ớ
ỗ
ặp
ố
Câu
ặ
ố
+−=+−
? A. 10.
11.
Lời
C
( ) ( )
++=+++++=+
(
2;3;4;5;6;7 x
ng v
i m
i giá trị nguyên của x cho ta giá trị nguyên của y Vậy có 6 c
s
nguyên thoả mãn yêu cầu bài toán.
74: Có bao nhiêu c
p s
nguyên ( ) ; xy thỏa mãn 02020 y và ( ) 2 log4412
x yxy
B.
C. 12. D. 2021.
giải
họn B
( ) 222 log4412log11log22
xxx yyxyy ( ) ; xy ( )*
)* 1 ( ) ; xy
Xét hàm số 2log fuuu Có 1 '10 ln2 fu u với 1 u fu đồng biến trên ) 1;+ 12x y Mặt khác 2 1120211220210log2021 x yx . Vì 0;1;2;3;4;5;6;7;8;9;10 xx Vậy có 11 cặp số nguyên thỏa mãn ycbt.
Câu 75: Số tất cả các giá trị nguyên dương a sao cho ứng với mỗi a , tồn tại ít nhất số thực b thỏa mãn ( ) ( )( ) 5 5 log5 log8 2224624 a abbbb +=+−+− là A. 10 B. 11 C. 9 D. 2022 Lời giải Chọn B Điều kiện 0 a , 22 b − Đặt 2 4 tbb =+− 22 424 tbb =+− 2 2 4 4 2 t bb −= . Đánh giá được 222,2;2. tb −− ( ) ( )( ) 5 5 log5 log8 2224624 a abbbb +=+−+−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
52
(
=+ , suy ra hàm số f đồng biến trên Nên ( ) ( ) 55 loglog 22aa fftt == . Để tồn tại ít nhất số thực b thì 5log 2222 a − 5 3 log55 2 aa Mà a nguyên dương nên 1;2;3;4;5;...;11 a Vậy có tất cả 11 số thỏa mãn. Câu 76: Có bao nhiêu số nguyên y thuộc đoạn 2022;2022 sao cho tồn tại x thỏa mãn 3 3 12.312.223 xx yy +=− ? A. 2022. B. 2021. C. 2028. D. 2027.
55 2 loglog 4 82.262 2 aa t t +=+ Phương trình trở thành: ( ) 55 3 loglog 3 11 22 22 aa tt+=+ Xét hàm số ( ) 3 1 2 fXXX =+
) 2 3 10 2 fXXX
Lời giải
Chọn C Đặt 2x t = , ( )0 t . Khi đó phương trình đã cho trở thành 3 3 12.3123 ytty +=− ( ) 3 3 31212.31212 ytyttt+++=+ ( )1
Xét hàm số ( ) 3 12 fuuu =+ . Ta có ( ) 2 3120fuu =+ , u .
Suy ra hàm số ( )fu luôn đồng biến trên
Khi đó ( ) ( ) ( ) 33 1312312fytftytt +=+= 3 312ytt+= 3 1 4 3 ytt=−
Xét hàm số ( ) 3 1 4 3 gttt =− với 0 t .
Ta có ( ) 2 4 gtt =− ; ( ) 0 gt = 2 40 t −= 2 2(L) t t = =− .

Bảng biến thiên:
Yêu cầu bài toán phương trình ( )1 có nghiệm 0 t 16 3 y − . Mà y và 2022;2022 y − nên 5;4;3;....;2022 y −−− . Vậy có 2028 số nguyên y thỏa mãn bài toán. Câu 77: Gọi S là tổng tất cả các số nguyên a sao cho ứng với mỗi a , tồn tại ít nh
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 53
( )( ) 33 log8log 22 1 2434 2 a abbbb +=+−+− ? A. 10. B. 15. C. 21. D. 28. Lời giải Chọn B Điều kiện 0 a , 22 b − . Đặt 2 4 tbb =+− 22 424 tbb =+− 2 2 4 4 2 t bb −= . Ta có 2 22 4 1. 44 bbb t bb =+= Do đó 2 222 00 042 42 bb tbbb bbb =−== −== .
ất số thực b thỏa mãn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 54
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Suy ra 2222;2. tb −− Ta có: ( ) ( ) 33333333 33 log8log3log2loglog2logloglog 1111 22222 2222 aaaaa aaa+=+=+=+ vì 33 log2log 2 a a = . ( )( ) 2 223 41 4343 22 t bbbbttt +−+−=+=+ . Phương trình trở thành: ( ) 33 3 loglog 3 11 22 22 aa tt+=+ Xét hàm số ( ) 3 1 2 fXXX =+ ( ) 2 3 10 2 fXXX =+ , suy ra hàm số f đồng biến trên . Nên ( ) ( ) 33 loglog 22aa fftt == . Để tồn tại ít nhất số thực b thì 3log 2222 a − 3 3 log33 2 aa . Mà a nguyên và 0 a nên 1;2;3;4;5 a Vậy 1234515 S =++++= Câu 78: Có bao nhiêu giá trị nguyên của m thuộc đoạn 100;100 để phương trình 20191 x mx =+ có hai n ghiệm phân biệt? A. 94 B. 92 C. 184 D. 100. Lời giải Chọn D *) TH1: 0 m + Vế trái của phương trình là hàm số đồng biến trên tập . + Vế phải của phương trình là hàm số nghịch biến trên tập . Nếu phương trình đã cho có nghiệm thì nghiệm đó là duy nhất *) TH2: 0 m = b 2 2 2 t + 0 t 2 22 2
Khi đó phương trình trở thành: 201910 x x ==
Vậy phương trình có nghiệm duy nhất 0 x =
*) TH3: 0 m
Xét hàm số ( ) 20191 x fxmx=−− trên ( ) 2019.ln2019m x fx =− ( ) 2019 0logln2019 m fxx == .

Đặt ( ) 20192019 aloga.log1 ln2019ln2019ln2019 mmm fm ==−− .
Bảng biến thiên của hàm số ( )yfx =
Để phương trình có hai nghiệm phân biệt thì đồ thị hàm số ( )yfx = phải cắt trục hoành tại hai điểm phân biệt. Điều đó tương đương với ( ) a0 f . Mà ( )()a (0)0 fxfx f = nên 2019 a0log0 ln2019 m 1ln2019 ln2019
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 55 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
ết luận: 0
m m
m thỏa mãn yêu cầu bài toán. Câu 79: Có bao nhiêu số nguyên y thuộc đoạn 2022;2022 sao cho tồn tại x thoả mãn 3 3 12.312.223 xx yy +=− A. 2027. B. 2022. C. 2021. D. 2028. Lời giải Chọn D Đặt 2;0 x tt= . Khi đó từ giả thiết ta có phương trình 3 3 12.3123 ytty +=− ( ) 3 3 31212.31212 ytyttt+++=+ Xét hàm số ( ) 3 12; 0 ftttt=+ có ( ) 2 3120; 0 fttt =+ ( )ft luôn đồng biến trên khoảng ( ) 0;+ .
m m K
ln2019
thỏa mãn yêu cầu bài toán. Do m và 100;100 m− nên 1;2;3...100 m
. Vậy có 100 giá trị
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 56 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Khi đó ( ) ( ) ( ) 3 1312fytft+= 3 312ytt+= 3 312 ytt=− . Đặt ( ) 3 12; 0 gtttt=− có ( ) 2 312gtt =− ; ( ) ( ) 2 0 2 t gt tL = = =− Bảng biến thiên Để tồn tại x ( )1 có nghiệm 0 t
−− . Vì
và
y −
−−−
ậ
ặ
ố
ả mãn đồng thời điều kiện 12022 x và 2 22 384.1286.863714 xxy yxx−+=−+
Chọn
Ta
2
xxy
+−+=+ 2
2
Cầ
số
[1;2022] x để y . Ta chứng minh: 2 713nn − 3 n Ta có n 31 3 32() nk k nk =+ =+ ( ) ( ) 22 22 71321142 71321289 nkk nkk −=++ −=++ . Ta có: 2 7(1)13 x 131 132() xk k xk −=+ −=+ . Ta có x và 1;2022 x 10;2021 x − Trên 0;2021 có 674 số chia hết cho 3 nên có 1348 số không chia hết cho 3. Vậy có 1348 cặp số nguyên (;) xy thoả mãn bài toán.
16 316 3 yy
y
2022;2022
nên
5;4;3;....;2022 y
. V
y có 2028 số nguyên y Câu 80: Có bao nhiêu c
p s
nguyên (;) xy tho
A. 674. B. 1348. C. 1346. D. 2022. Lời giải
B
có
22 384.12871466.83
xxy
7147231 3.271473.231(1) xxyxxy −+++−+=++ Xét hàm số ()3.2t ftt =+ có: ,()3.2.210 t ftlnt =+
(1) 2 714731 xxy−+=+
7(1)1 3 x y =
n tìm các
nguyên
Để phương trình đã cho có hai nghiệm dương phân biệt thì phương trình phải có hai nghiệm dương phân biệt. Xét 2 1 ()3(7141) 2 x fxxx =+−− , 0 x . Ta có: ()3.ln377 x fxx =+− ()03.ln37703.ln377 xx fxxx =+−==− . Vì vế trái là hàm đồng biến và vế phải là hàm nghịch biến nên phương trình ()0fx = có nghiệm duy nhất 0 0,67 xx= và 0 ()1,53fx − . Bảng biến thiên: Từ bảng biến thiên suy ra phương trình có hai nghiệm dương phân biệt khi 22 0 112222 ()(1)(1)2244fxmmm−+ −− Vì m nên 1 m =
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 57
x
== +−−=−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 81: Cho phương trình 2212211 9(714245)3(7141)(1)0 62 xx xxmmxxm + +−−+−−−−+−= . Có tất cả bao nhiêu giá trị nguyên của m để phương trình có hai nghiệm dương phân biệt? A. 1. B. 2. C. 3. D. 6. Lời giải Chọn A 2212211 9(714245)3(7141)(1)0 62 xx xxmmxxm + +−−+−−−−+−= 222211 9(7141)(1)13(7141)(1)0 22 xx xxmxxm +−−−−−−−−+−= ( ) 22 1 313(7141)(1)0 2 xx xxm −+−−−−= 22 310() 1 3(7141)(1)(*) 2
x xKTM xxm
Câu 82: Có bao nhiêu số nguyên y thuộc nửa khoảng )2022;2022 sao cho tồn tại x thỏa mãn 3 3 939.223 xx yy +=− ? A. 4. B. 2026. C. 2024. D. 2025. Lời giải Đặt 3 39.2x yu += , 20 x v = ( ) 3 391 yvu+= Phương trình 3 3 939.223 xx yy +=− ( )* trở thành 3 93uvy =− ( ) 3 932 uyv+=
Từ ( )1 và ( )2 33 399 yuvvu =−=− ( ) 3399**uuvv +=+
Xét hàm đặc trưng 3 ()9 fttt =+ có 2 ()390ftt =+ với t nên phương trình ( )** ( ) ( )fufv = có nghiệm duy nhất uv = 3 39yvv+= 3 39yvv=− ( )3 . Để tồn tại x thỏa mãn ( )* thì phương trình ( )3 phải có nghiệm 0 v
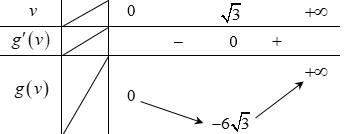
Xét hàm ( ) 3 9 gvvv =− với 0 v . ( ) 2 390gvv =−= 3 v = do 0 v Để phương trình ( )3 có nghiệm 0 v thì 363 y − 23 y − . Do y nguyên thuộc nửa khoảng )2022;2022 3;2021 y − có 2025 giá trị y thỏa mãn yêu cầu của bài toán. Câu 83: Gọi S là tập nghiệm của phương trình ( ) ( )2 238330 +−+−= x xx xm . Có tất cả bao nhiêu giá trị nguyên của 2021;2022−m để tập hợp S có hai phần tử? A. 2095. B. 2092. C. 2093. D. 2094. Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
58
+−+−= −= − x x x xx xx
xm
Ta có: ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 238301 238330I 302 30
+−+=
x
m m . *)Xét phương trình: ( )238301 +−+=xx x
Đặt: ( ) 2383=+−+ xx fxx với mọi x
Ta có: ( ) ( ) ( ) 22 '2.ln23.ln38;''2.ln23.ln30 =+−=+ xxxx fxfxx
Khi đó, bảng biến thiên của hai hàm số ( ) ( ) ';''== yfxyfx lần lượt như hình vẽ sau:
Theo bảng biến thiên ta thấy, phương trình: ( ) ( ) 10 = fx có nhiều nhất hai nghiệm.
Mặt khác nhận thấy: ( ) ( ) 120 ==ff . Vậy: ( ) 1 1 2 = = x x .
*)Xét phương trình: ( ) ( ) 2 302 −= x m .
+)Trường hợp 1: 1 m .
Phương trình: ( ) ( ) 2 302 −= x m vô nghiệm. Khi đó, hệ ( )I có đúng 2 nghiệm
Đặt: ( ) ( ) 2 3 =− x gxm với mọi x . Ta có: ( ) ( ) ( ) 2 '3.ln3.2.ln20= x x gxx .


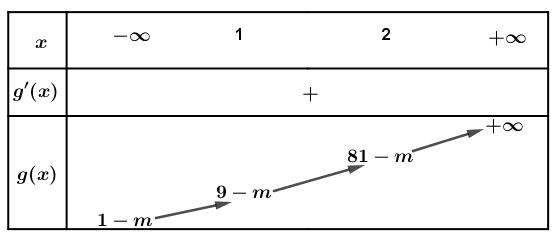
Bảng biến thiên của hàm ( ) = ygx :
+)Trường hợp 2: 10919. −− mmm
Phương trình ( )2 có 1 nghiệm nhỏ hơn 1, khi đó hệ ( )I có đúng 3 nghiệm.
+)Trường hợp 3: 9081981. −− mmm
Phương trình ( )2 có 1 nghiệm thuộc )1;2 , khi đó hệ ( )I có đúng 2 nghiệm
+)Trường hợp 4: 81081. − mm
Phương trình ( )2 có 1 nghiệm thuộc ) 2; + , khi đó hệ ( )I có đúng 1 nghiệm.
Do 2021;2022−m nên )2021;19;81 − m , mặt khác do m nguyên nên đếm được
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
59
2095 giá trị của tham số m thỏa mãn yêu cầu bài toán. Câu 84: Gọi S là tập nghiệm của phương trình ( ) 2 2230 x x xm −−= Có tất cả bao nhiêu giá trị nguyên 2021;2022 m− để tập hợp S có hai phần tử? A. 2093. B. 2095. C. 2094. D. 2096 Lời giải Chọn C Ta có: ( ) ( ) 2 2230* x x xm
−−= 2 2 220 30 30 x x x x m m −= −= − ( ) 2 2 2201 3 3 x x x x m m −=
1;2 hoặc chỉ có một trong hai
1;2 x thỏa điều kiện 2 30 x m − 12 21 12 22 22 22 3; 3 3; 3 33 mm mm m = = 9; 81 81; 9 981 mm mm m = = Vì m nguyên và 2021;2022 m− 2021;2020;...;1;09;10;...80 m−−−
60
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
Xét phương trình 220 x x −= với ( ) 22 x fxx =− ( ) '2ln22 x fx =− Cho ( ) 2 2 '0logln2fxx == nên ta có bảng biến thiên: x 2 2 logln2 + ( ) ' fx 0 + ( )fx + 2 2 logln2 f Vì 2 2 log0
ln2 f phương trình 220 x x −= có hai nghiệm 12xx==
Xét phương trình 2 332log x x mm== có nghiệm khi 1 m Ta có: 1 x = 2 39 x = ; 2 x = 2 381 x = + Nếu 19; 81 mmm nhận nghiệm 12xx== đồng thời phương trình 23 x m = vô nghiệm nên phương trình ( )* có 2 nghiệm thỏa yêu cầu bài toán. + Nếu 1 m phương trình 23 x m = có nghiệm nên phương trình ( )* có 2 nghiệm thỏa yêu cầu bài toán khi nghiệm của phương trình 23 x m = thuộc
Vậy có 2094 m nguyên và 2021;2022 m− thỏa đề.
Câu 85: Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 255 số nguyên y thoả mãn ( ) ( ) 2 52 loglogxyxy ++ ?
A. 1250 B. 1249 C. 625 D. 624 Lời giải Chọn A ( ) ( ) ( ) ( ) ( ) 22 5225 loglogloglog0,1 xyxyxyxy +++−+
Xét ( ) ( ) ( ) 2 25 loglog fyxyxy =+−+
Vì 2 xxx nên tập xác định của ( )fy là ( ) ;Dx=−+
Ta có ( ) ( ) ( ) ( ) 2 11 0, ln2 ln5 fyyDfy xy xy =− + + đồng biến trên ( ) ;x −+ .
Do y là số nguyên thuộc ( ) ;x −+ nên đặt , yxkk + =−+
Giả sử yxk =−+ là nghiệm bất phương trình ( )1 thì ( ) 0 fxk−+ Mà hàm số ( )fy đồng biến nên ( ) ( ) ( ) 12...0fxfxfxk −+−+−+ Lúc đó 1,2,..., xxxk −+−+−+ là các nghiệm của ( )1 Bảng biến thiên
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 61 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Để có không quá 255 số
( ) ( ) 2 25 2560log256log2560fxxx −+−−+ 2 1156147711561477 3903690 22 xxx −+ −− Mà
xx−−
nguyên y khi và chỉ khi
624;623;...;624;625
, có tất cả 1250 giá trị cần tìm.
Câu 86: Số nghiệm ( ) ; xy của phương trình ( ) ( ) 4221sin2120 +−+−+= xxx y thỏa mãn ( ) ,0,2 xy là. A. 1. B. 0. C. 2. D. 3. Lời giải Chọn A ( ) ( ) 4221sin2120 +−+−+= xxx y được biến đổi thành ( ) ( ) ( ) 2 2 21sin21cos21 −++−=−+− xxx yy
Vì vế trái không âm và vế phải không dương nên phương trình đã cho tương đương với ( ) ( ) 21sin21cos210 −++−=+−= xxx yy Tức là, ( ) cos210
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 62 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Giả thiết ( ) 22 22 4 42022log20220 xyxy xyxy +++−+ nên ( ) ; Mxy nằm trong đường tròn tâm ( ) 44 log2022log2022;2,7;2,7 22 I , 4 log202223,9 2 R = . Dùng đồ thị ta thấy có 8 giá trị là 1;0;1;2;3;4;5;6 x−
+−= x y và ( ) sin211 +−= x y hoặc ( ) sin211 +−=− x y . Kiểm tra lại thấy có ( ) cos210 +−= x y và ( ) sin211 +−=− x y là thỏa mãn. Giải ra được 1= x và 3 1 2 =− y Câu 87: Có bao nhiêu số nguyên x sao cho với mỗi x luôn tồn tại số thực y thỏa mãn 22 42022xyxy ++ A. 9 B. 7 C. 8 D. 6 Lời giải
Bước 2. Khảo sát sự biến thiên của hàm số ( )fx trên D . Bước 3. Dựa vào bảng biến thiên để xác định giá trị của tham số ( )Am để đường thẳng ( )yAm = nằm ngang cắt đồ thị hàm số ( )yfx = .
Bước 4. Kết luận các giá trị cần tìm của ( )Am để phương trình ( ) ( )fxAm = có nghiệm trên D . Lưu ý


Nếu hàm số ( )yfx = có giá trị lớn nhất và giá trị nhỏ nhất trên D thì giá trị ( )Am cần tìm là những m thỏa mãn: ( ) ( ) ( ) minmax xD xD fxAmfx . Nếu bài toán yêu cầu tìm tham số để phương trình có k nghiệm phân biệt, ta chỉ cần dựa vào bảng biến thiên để xác định sao cho đường thẳng ( )yAm = nằm ngang cắt đồ thị hàm số

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 1 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 5. PHƯƠNG TRÌNH MŨ LOGARIT MỨC ĐỘ VẬN DỤNG VẬN DUNG CAO PHƯƠNG PHÁP CHUNG Tìm m để ( ) ,0fxm = có nghiệm trên D? Bước 1. Tách m ra khỏi biến số và đưa về dạng ( ) ( )fxAm = .
( )yfx = tại k điểm phân biệt. Câu 88: Cho hàm số ( ) ( ) 22 271 3 3log231log130 xmxmxxm −++−+−+−= .Sốcácgiátrị nguyên của m để phương trình đã cho có hai nghiệm phân biệt 12 , xx thỏa mãn 12 15 xx− là: A. 14 B. 11 C. 12 D. 13 Lời giải Chọn D Ta có: ( ) ( ) 22 271 3 3log231log130 xmxmxxm −++−+−+−= ( ) ( ) 22 33 log231log13 xmxmxxm −++−=−+− CHƯƠNG II HÀM SỐ LŨY THỪA - HÀM SỐ MŨ – HÀM SỐ LOGARIT
ủa m thỏa mãn là 13. Câu 89: Gọi S là tập tất cả các giá trị nguyên của tham số m với 64 m để phương trình ( ) ( ) 15 5 loglog20 xmx ++−= có nghiệm. Tính tổng tất cả các phần tử của S . A. 2018. B. 2016. C. 2015. D. 2013. Lời giải Chọn C
x
2
x m
=
. Vì 2 x nên 2 22 2 m m − Kết hợp với 64 m . Khi đó 264 m − . Vì m nên 1;0;1...63 m =− có 65 giá trị. Vậy tổng S các giá trị
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 2 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) 2 22 130 23113 xxm xmxmxxm −+− −++−=−+− ( ) ( ) ( ) ( ) 2 2 2 130* 130* 2201 2 xxm xxm xm xmxm x −+− −+− = −++= = Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi phương trình có hai nghiệm phân biệt thỏa mãn 2 2 2 130 410 2113023 430 2 mmm mm mm m m −+− −+ −+−− − . Theo giả thiết ( )2 2 121212154225422101317 xxxxxxmmm −+−−−− Do đó 1323 m −− . Vậy số các giá trị
c
nguyên
Ta của m để phương trình có nghiệm là: ( ) 163.65 2015 2 S −+ == Câu 90: Cho phương trình ( ) 2 5 5 log612log2 −+=+ mx mx xxx , gọi S là tập hợp tất cả các giá trị của tham số m để phương trình đã cho có nghiệm duy nhất. Tìm số phần tử của S . A. 2 B. 0 C. 3 D. 1 Lời giải + Điều kiện 202 05156 +− − xx mxmx Với điều kiện trên, phương trình ( ) ( ) 2 5 5 log612log2* −+=+ mx mx xxx
có: ( ) ( ) 15 5 loglog20 xmx ++−= ( ) ( ) 55 loglog2xmx +=−
2 2
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 3 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) 2 55 log612log2 −+=+ mxmx xxx 2 2 6122 5 = −+=+ = x xxx x . 2 = x là nghiệm phương trình ( )* khi 5 5263 2 mm , vì mZ 4 m mZ . 5 = x là nghiệm phương trình ( )* khi 6 5561 5 mm , vì mZ 2 m mZ + Phương trình ( ) 2 5 5 log612log2 −+=+ mx mx xxx có nghiệm duy nhất khi 2 = m hoặc 3 m = Thử lại 2 = m : ( ) ( ) ( ) 22 252525 25 log612log2log612log2 −+=+−+=+ xxx x xxxxxx 2 6122 205 0251 −+=+ += − xxx xx x 3 m = : ( ) ( ) ( ) 22 353535 35 log612log2log612log2 xxx x xxxxxx −+=+−+=+ 2 6122 205 0451 xxx xx x −+=+ += − Vậy có hai giá trị mZ thỏa mãn ycbt. Câu 91: Cho phương trình ( ) 2222 25 52 log242log20 xxmmxmxm + −−+++−= . Hỏi có bao nhiêu giá trị nguyên của tham số m để phương trình đã cho có hai nghiệm 22 12 3 xx+= ? A. 1 B. 0 C. 3 D. 4 Lời giải Chọn B Phương trình đã cho tương đương với phương trình: ( ) ( ) 2222 2552 log242log20 xxmmxmxm +− −−+++−= ( ) ( ) 2222 5252 log242log20 xxmmxmxm ++ −−+−+−= ( ) 22 22 22 2222 220220 22421220 xmxm xmxm xmxmm xxmmxmxm +− +− −++−= −+−=+−
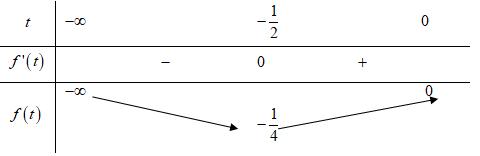
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 4 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 22 1 2 20 2 1 xmxm xm xm +− = =− Phương trình đã cho có hai nghiệm 12 , xx thỏa 22 12 3 xx+= ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 2 22 2 22 222040 1120210 2135220 mmmm m mmmmmm mm mm +− −+−−+− −−= +−= 0 1111 1 25 111111 ; 55 m mm mm −= −+ == Vậy không có giá trị nguyên nào của m thỏa yêu cầu đề bài Câu 92: Tìm tất cả các giá trị của tham số thực m để phương trình ( )2 21 2 4loglog0 xxm−+= có hai nghiệm phân biệt thuộ
c khoảng ( )0;1 . A. 1 0 4 m B. 1 0 4 m C. 1 4 m D. 1 0 4 m − Lời giải Ta có: ( ) ( ) ( ) ( ) 22 2 212222 2 4loglog02loglog0loglog 1 xxmxxmxxm −+=++=+=− Đặt 2log tx = với ( );0 t − ( ) 2 1 ttm+=− . Xét ( ) 2 fttt =+ ( ) ( ) '21 1 '0 2 ftt ftt =+ ==− Bảng biến thiên
Dựa vào bảng biến thiên 11 00 44 mm −− Câu 93: Tìm m đểphươngtrình 22 22 loglog3xxm −+= có nghiệm [1;8] x . A. 69 m B. 23 m C. 26 m D. 36 m Lời giải Chọn C 22 22 loglog3xxm −+= Điềukiện: 0 x pt ( )2 22log2log3 xxm −+ = Cách1: Đặt 2log tx = , với [1;8] x thì [0;3] t . Phương trình trở thành: 2 23 ttm −+= Để phương trình có nghiệm [1;8] x phương trình có nghiệm [0;3] t [0;3] [0;3] min()max() ftmft , trong đó 2 ()23fttt=−+ 26 m . Câu 94: Cho phương trình 2log12log1 2log12log1 2log12log1 mxx xmx mxx
( ) 2 222 log2loglog* xxmxm −−+= . Có bao nhiêu giá trị nguyên của tham ++=− −=++ ++=−+ 22 22
2019;2019 loglog1 loglog mxx mxx
phương trình có nghiệm? +=− +=− * TH1: 22 loglog mxx +=− ( ) 2 2 2 22 22
4038. −−= +=
2020.
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 0 log0 x mx + 22 222222 log2loglog4log8log4log4 xxmxmxxmxm −−+=−−+= ( ) 2 2222 4log4log14log4log1 xxmxmx −+=++++ ( ) ( )2 2 22 22 22
2021 log001 loglogloglog01 x x xxm mxx
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 5
số
m− để
A.
. B. 2019. C.
D.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Lời giải Điều kiện: 2
Đặt: ( ) 2 log0txt= , phương trình (1)trở thành: ( ) 2202ttmttm −−=−=
Đặt: ( 2 ()(;0gtttt=−− .Bài toán trở thành: Tìm giá trị của tham số m để phương trình
( )2 có ít nhất 1 nghiệm 0 t
Ta có: 2 ()()2100 gtttgttt =−=−

Ta có BBT: Dựa vào BBT, suy ra: để phương trình ( )2 có ít nhất 1 nghiệm 0 t thì 0 m * TH2: 22 loglog1mxx+=− 2 2 222
−+−=
log1 log3log103 x xxm
+=−+ ( ) 2 2 22
log1 loglog2log1 x mxxx
Đặt: ( ) 2 log1txt= , phương trình (1)trở thành: ( ) 22310314ttmmtt −+−==−+ Đặt: ) 2 ()1,1; gtttt=−++ Ta có: 2 ()31()23 gtttgtt =−+=− ) 3 ()02301; 2 gttt =−==+ Bài toán trở thành: Tìm giá trị của tham số m để phương trình ( )4 có ít nhất 1 nghiệm 1 t Ta có BBT:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 6
Dựa vào BBT, suy ra: để phương trình ( )4 có ít nhất 1 nghiệm 1 t thì 5 4 m − Kết hợp và, 2019;2019 m− 1;0;1;2;...;2019 m − Vậy có tất cả 2021 giá trị của m thỏa mãn ycbt Câu 95: Tìm tập hợp tất cả các giá trị thực của tham số m để phương trình ln0mxx−= có hai nghiệm phân biệt thuộc khoảng ( )2;3 A. ln2ln3 ; 23 B. ln2ln3 ;; 23 −+
C. ln21 ; 2 e D. ln31 ; 3 e Lời giải Chọn D ( ) ln ln0,2;3 x mxxmx x −== Đặt ( ) ( ) ln ,2;3 x fxx x = ( ) 2 1ln x fx x = ; ( ) 0 fxxe ==
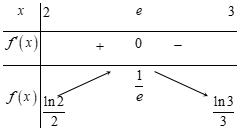
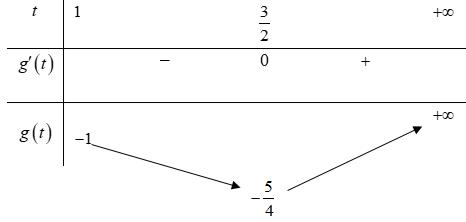
BBT
Để phương trình có hai nghiệm phân biệt thì ln31 ; 3 m e .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 7
Do các phương trình () a và () b là phương trình bậc hai nên để phương trình ban đầu có 3 nghiệm phân biệt ta có các trường hợp sau: TH1: 1 2 m = , chỉ có nghiệm kép bằng 0 và có 2 nghiệm phân biệt khác 0 TH2: 1 2 m , có 2 nghiệm phân biệt 21xm=− và có 2 nghiệm phân biệt trong đó có 1 nghiệm b
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 8
=−
ằng 21
− '0 (21)0gm −= '03 21 (21)01 m m gm m = −= = . + TH3: 1 2 m , có 2 nghiệm phân biệt 21xm=− và có nghiệm kép khác 21 m − '0 (21)0gm = − 3 3 2 12 m m m = = . Vậy tổng các giá trị của m là 13 13. 22 ++= Câu 97: Tìm tất cả các giá trị của m để phương trình ( ) ( ) lnlnsinsin mmxx ++= có nghiệm.
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 96: Tổng tất cả các giá trị của tham số m sao cho phương trình: ( ) ( ) ( ) 2 1 2 22 2.log234.log22 xm x xxxm −+=−+ có đúng ba nghiệm phân biệt là: A. 2. B. 3 2 C. 0 D. 3 Lời giải Tập xác định D = ( ) ( ) ( ) ( ) ( ) ( ) 2 2 1 2 22 2 1 2 22 2.234.22 2.(1)22.22(*) xm x xm x logxxlogxm logxlogxm −+=−+ −+=−+ Đặt 2 ()2log(2),0 t fttt=+ ; 2 1 '()2ln2.log(2)20,0 (2)ln2 tt fttt t =++ + . Vậy hàm số 2 ()2log(2) t ftt=+ đồng biến trên (0;) + Từ ta có 2 22 2 (1)2(1)22()(1) 2()(1) xmx fxfxmxxm xmx −=− −=−−=− −=−−
. 2 2 ()4120() 21() gxxxma xmb
=−++=
m
A. 1 1me1. e +− B. 1me1. − C. 1 1m1. e + D. 1me1. − Lời giải
Đặt ( ) lnsin umx =+ ta được hệ phương trình: ( ) ( ) sin
=+ =+ += =+
lnsinsin lnsin
Từ hệ phương trình ta suy ra: ( ) sin sin* ux euex +=+
u x
umx emx mux emu
Xét hàm số ( ) t ftet =+ có ( ) '10,. t ftet=+ Hàm số ( )ft đồng biến trên .
( ) ( ) ( ) *sinsin fufxux== Khi đó ta được: ( ) ( ) sin lnsinsinsin** x mxxexm +=−= Đặt sin,1;1.zxz=− Phương trình ( )** trở thành: ( )** z ezm −=
Xét hàm số: ( ) z gzez =− trên 1;1. Hàm số ( ) z gzez =− liên tục trên 1;1 và có ( ) ( ) ( ) ( ) 1;1 1;1 11,min01maxgzgegzg==−== Hệ phương trình ban đầu có nghiệm phương trình ( )** có nghiệm 11. me −
Câu 98: Số các giá trị nguyên của tham số m để phương trình 2 2 log(1)log(8) xmx −=− có hai nghiệm phân biệt là A. 5. B. Vô số. C. 4. D. 3. Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 9
ọ
2 29 xxmx−+= . Do
x nên suy ra 2 29xx m x −+ = Xét hàm số 2 ()29 xx fx x −+ = trên khoảng (1;). + 2 ' 2 9 () x fx x = , ' ()03.fxx== Bảng biến thiên Nhìn vào BBT ta thấy yêu cầu của bài toán là 48 m . Do m nguyên nên 5;6;7 m Vậy có 3 giá trị của m thỏa mãn yêu cầu bài toán. 0 x ' ()fx ()fx − 1 + 3 4 8 + +
Ch
n D Điều kiện: 1 x Ta có: 22 222 2 log(1)log(8)log(1)log(8)(1)8 xmxxmxxmx −=−−=−−=−
1
Câu 99: Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 2 ln2ln4 e x mmx
có nghiệm thuộc vào đoạn 1 ;1 e ?
A. 1. B. 2. C. 3. D. 4. Lời giải
Chọn A
Có 2 ln2ln4 e x mmx 2 ln12ln4mxmx 222ln4mmxm
1 .
• Với 2 20 mm 1 m 0 m , 1 0ln3 x Loại 1 m .
• Với 1 m , 1 2 ln 1 m x m 2
+ Hàm số ln yx đồng biến trên 1 ;1 e ln1;0 x .
+ Phương trình 2 có nghiệm thuộc đoạn 1 ;1 e khi 2 10 1 m m
m m m m
2 1 1 2 0 1
3 2 1 12
m m m
3 2 2 m 2 m Vậy có 1 giá trị nguyên dương của tham số m thỏa yêu cầu bài toán. Câu 100: Có bao nhiêu giá trị của tham số m để phương trình 2 366 4loglog20 6 x xm có hai nghiệm phân biệt 12 , xx thỏa mãn 1212 .72.12960xxxx A. 0. B. 1. C. 2. D. 3. Lời giải Chọn A 2 366 4loglog20 6 x xm 2 6 6 loglog20 xmxm Phương trình có hai nghiệm phân biệt khi 2 223 420 223 m mm m 12121212 .72.12960.36.1296 xxxxxxxx
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
10 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
6126162 log.4loglog44 xxxxm Câu 101: Tập hợp các giá trị thực của tham số m để phương trình ( ) ( ) 2 20191 2019 log4log210 xxm −++−= có hai nghiệm thực phân biệt là ( ) ; Tab = . Tính 2 Sab =+ A. 18 B. 8 C. 20 D. 16 Lời giải Chọn D Tập xác định ( ) 1 2;2; 2 m D =−+ .
Khi đó, phương trình đã cho trở thành 2 22 2019 4 log0421250(*) 21 x xxmxxm xm =−=+−++−= +− Phương trình (*) có 2 nghiệm phân biệt 2 11.(5)606(1) mmm =−−=−
Khi đó phương trình (1) có 2 nghiệm lần lượt là 1216;16 xmxm =−+−=−−−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
11 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
m − −+−− − −−−− . Từ và suy ra m . Vậy 56 m . Suy ra 5,6ab== 216 ab += Câu 102: Có bao nhiêu giá trị nguyên của m để phương trình ( ) 3 3 log3log916 x xm + ++= có hai nghiệm thỏa mãn 12 2 xx− A. 17 B. 16 C. 14 D. 15 Lời giải Chọn D Điều kiện xác định: 3 x − và 2 x − . Biến đổi phương trình đã cho về phương trình sau: ( ) ( ) 3 3 log34log3160 x xm + ++−= . ( ) ( ) 2 33 log316log340(1) xxm +−++= .
. TH1: 1 25 2 m m − ( )2;2 D =− . Phương trình có 2 nghiệm 12 , xxD 16263 5 16261 mm m mm −+−− −−−−− . Từ, và suy ra 56 m TH2: 1 2235 2 m m −− 1 ;2 2 m D = . Phương trình có 2 nghiệm 12 , xxD 162633 1335 1665 22 m mm m m mm mm
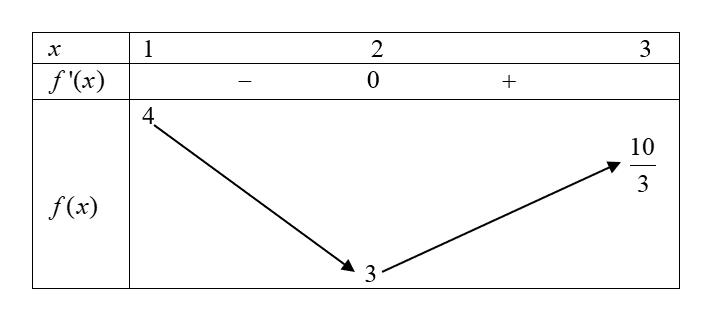
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 12
12 12 0 6440 160016 40 .40 m ttm m ttm − += = . Vậy có 15 giá trị nguyên m thỏa mãn. Câu 103: Tập hợp các số thực m để phương trình ( ) ( ) 2 ln31ln43 xmxxx −+=−+− có nghiệm là nửa khoảng ) ; ab . Tổng ab + bằng A. 10 3 B. 4. C. 22 3 D. 7. Lời giải Chọn D Ta có: ( ) ( ) 2 2 2 2 22 ln31ln43(1) 43013 31434 131313 444 1(2) xmxxx x xx xxmx xmxxx xx x xxxx xm mm x xx −+=−+− −+− −+= −+=−+− −+−+ +−= == Xét hàm số: ( ) 4 ()1; 1;3 fxxx x =+− có 2 4 '()1fx x =− ( ) ( ) 2 421;3(2)3 '()10 21;3 xf fx x x == =−= =− Bảng biến thiên:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Đặt ( ) 3 log3xt += phương trình ( )1 trở thành: ( ) 2 16402ttm−+= . Ta có: ( ) 3 log333 t xtx+==− . Theo điều kiện đề bài thì 2 x − nên 3320 t t −− Vậy để phương trình ( ) 3 3 log3log916 x xm + ++= có hai nghiệm thỏa mãn 12 2 xx− thì phương trình ( )2 phải có hai nghiệm t dương phân biệt
Dựa vào bảng biến thiên ta có: Phương trình có nghiệm. Phương trình có nghiệm thuộc khoảng ( )1;3 . )343;4 mm . Suy ra 3 347 4 a ab b = +=+= = . Câu 104: Cho phương trình 2 222 log2log41logxxxm −−−= , với m là tham số thực. Số các giá trị nguyên thuộc đoạn 2019;2019 của m để phương trình đã cho có nghiệm là A. 2021 B. 2024. C. 2023. D. 2020 Lời giải
Chọn B Điều kiện xác định: 22 1log0log102 xxx − Với điều kiện trên thì phương trình tương đương với ( )2 22 1log41log1xxm −−−−= ( )1
Đặt 21log tx =− , vì ( 0;2 x nên 0 t . Khi đó, ( )1 trở thành 4 41 ttm −−= ( )2 .
Để ( )1 có nghiệm ( 0;2 x thì ( )2 có nghiệm 0 t

Xét hàm số ( ) 4 41fttt=−− , ) 0; t + .
Ta có ( ) 3 44ftt =− . Cho ( ) ) 010;ftt ==+
Ta được bảng biến thiên của ( )ft như sau:
Theo BBT, để ( )2 có nghiệm 0 t thì 4 m − , mà 2019;2019 m− nên tập hợp các giá trị của m cần tìm là 4;3;2;1;0;1;;2019 Vậ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 13
y có tất cả 2024 giá trị nguyên của m thuộc đoạn 2019;2019 để phương trình đã cho có nghiệm. Câu 105: Tìm tất cả các giá trị thực của tham số m để phương trình ( ) ( )2 39 log1log91 m xxx+=+ có hai nghiệm phân biệt. A. ( )1;0 m− B. ( )2;0 m− C. ( ) 1; m−+ D. )1;0 m− Lời giải Chọn C Cách 1.
Điều kiện: 1 x −
Ta có pt: ( ) ( ) ( ) ( ) 2 3933 log1log91log11log1 m xxxxxmx +=++=++ ( ) ( ) 3 log11xmx −+= . Đặt: ( ) 3 log131 t xtx+==−

Ta có, Pt ( ) ( ) 1 31.131 ttmtftm t −−==−−= , với 0 t
Đặt: ( ) 1 31 t ft t =−− , với 0 t . ( ) ( ) ( ) 2 1 '3.ln30,;0,0; t ftt t =+−+
Suy ra, ( ) 1 31 t ft t =−− là hàm số đồng biến trên ( );0− và ( ) 0;+ .
Ta xét các giới sau: 1 lim311 t t t →−
−−=− , 1 lim31 t t t →+
1 lim31 t t t + →
−−=+ . 0
−−=− , 0
1 lim31 t t t →
−−=+ .
Ta có bảng biến thiên của hàm số ( ) 1 31 t ft t =−− , với ( ) ( ) ;0,0; t −+ .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 14
Ta có, số nghiệm của Pt cũng chính là số nghiệm của đồ thị hàm số ( ) 1 31 t ft t =−− và đồ thị hàm số ym = . Dựa, vào đồ thị ở hình vẽ trên, để phương trình ( ) ( )2 39 log1log91 m xxx+=+ có ba nghiệm khi ( ) 1; m−+ .
Cách 2. Điều kiện: 1 x − .
Ta có: ( ) ( )2 39 log1log91 m xxx+=+
Nhận thấy 0 x = không là nghiệm phương trình trên. Pt ( ) ( ) ( ) 3 3
1 log11 log1 xmxxm x −+=−= + Đặt: ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 3 3
11 '10,1; log1 1ln3.log1 fxxfxx x xx =−=+−+ + ++
Suy ra ( ) ( ) 3
1 log1 fxx x =− + là hàm số đồng biến ( ) 1; x −+ . Ta có BBT của hàm số ( ) ( ) 3
1 log1 fxx x =− +
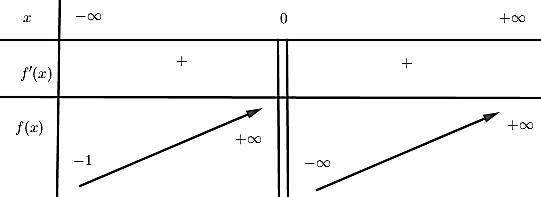

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 15
Dựa, vào BBT ở hình vẽ trên, để phương trình ( ) ( )2 39 log1log91 m xxx+=+ có ba nghiệm khi ( ) 1; m−+ .
5log.log4log3log20190
( ) ( ),1log.20190*
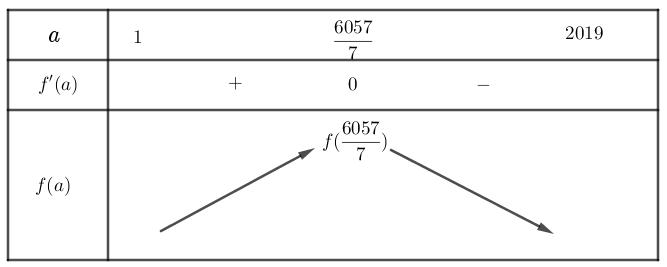
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
16
5log.log.log4log3log.log20190 5log.log43loglog20190* −−−= −−−= −+−= abab abaaba baba xxxx xaxxax axax Vì
− b
12 12
+ +== + ==−+ b aaa b
a
xxxx
a
xx ba xxaa aa Xét
5
ớ
Ta có ( ) '143 52019 =+ fa aa ; ( )
7 ==faa Bảng biến thiên Từ bảng biến thiên ta được giá trị lớn nhất của ( ) 12 ln..ln.ln4807636057 5757 =+ xx khi 6057 7 = a Từ đó suy ra 6057 = m ;
==+=+= nSmn Câu
Xét
Câu 106: Cho , ab là các số thực dương lớn hơn 1, thay đổi thỏa mãn 2019 +=ab để phương trình 5log.log4log3log20190 −−−= abab xxxx luôn có hai nghiệm phân biệt 12 ; xx . Biết giá trị lớn nhất của ( ) 12ln.xx bằng 34lnln 5757 + mn ; với , mn làcácsốnguyêndương.Tính 2 =+ Smn A. 22209 B. 20190 C. 2019 D. 14133 Lời giải Chọn A Theo bài ra ta có ( ) ( ) ( ) ( ) ( ) 2 ố nguyên dương
aba luôn có hai nghiệm phân biệt 12 ; xx Theo Viet ta có: ( ) ( ) ( ) ( ) ( ) 1212
ln 43log43. logloglog.ln 5logln 5 ln ln.4ln3ln1ln.4ln20193ln ln5ln5 +
a
b
a
b
( ) ( ) ( ) 1 4ln20193ln
=−+ faaa v
i ( )1;2019
a
6057 '0
8076260572.807622209
107:
các s
, ab sao cho phương trình 2 lnln50axbx++= có hai nghiệm phân
biệt 12 , xx và phương trình 2 5loglog0 xbxa++= có hai nghiệm phân biệt 34 , xx thỏa mãn 1234 xxxx . Tìm giá trị nhỏ nhất của 23 Sab =+ A. min 33 S = . B. min 30 S = . C. min 17 S = . D. min 25 S = . Lời giải Chọn B Điều kiện để hai phương trình 2 lnln50axbx++= và 2 5loglog0 xbxa++= có hai nghiệm phân biệt là: 2 200ba− Theo giả thiết ta có ++ +++=+ + có hai nghiệm phân biệt? A. 3. B. 1. C. 4 D. 2. Lời giải Chọn C Điều kiện: 2 210 20 xmx x ++ + 2 2 2 21 log212 2 xmx xmxx x
( ) ( ) 1212 12 5 3434 34 lnlnln logloglog 10 55 b a b bb xxxx xxe aa ++ +++=+ + ( ) 22 22 log21212log2 xmxxmxxx +++++=+++ Xét hàm số ( ) 2log fttt =+ trên khoảng ( ) 0;+ , có ( ) ( ) 1 ln210,0;ftt t =++ hàm số ( )ft đồng biến trên ( ) 0;+
Page +=−=− = +=−=− =
17 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn . Mà 5 1234 10 bb a xxxxe ln10 5 bb a −− 5 3 ln10 aa . Theo điều kiện có 2220020608babab − Từ và suy ra min 3 233030 8 a SabS b = =+= = . Câu 108: Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 2 2 2 21 log212 2 xmx xmxx x
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 bb xxxx xx
phương trình
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 18
− ++=+++=+
đã
thị hàm số ( ) 62.4 tt ft =− với đường thẳng ym = . Xét hàm số: ( ) 62.4 tt ft =− ( ) ( )6ln62.4ln423ln62.2ln4 ttttt ft =−=− ( ) ( ) 636 2 3 06ln62.4ln44log2log4log2 2 t tt ftt ==== +) ( ) ( ) 2 limlim62.4lim612. 3 t ttt ttt ft →+→+→+ =−=−=+ +∞ f( 4-m 2 ) ∞ +∞ 4-m 2 0 +∞ + f(x) f'(x) x
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Mà ( ) ( ) ( ) 22 2 2 212212 430 x fxmxfxxmxx xmx
+−−=
Do ( ) ( ) 2 43fxxmx=+−− là tam thức bậc hai nên có bảng biến thiên Phương trình
cho có hai nghiệm phân biệt khi và chỉ khi
( ) ( ) 2 430fxxmx=+−−= có hai nghiệm phân biệt lớn hơn 2. suy ra: 4 2 2 4 092 2 m m fm − − 2 8 99 . 22 4 30 2 m mm m − Do * 1;2;3;4 mm .Vậy có 4 giá trị của m . Câu 109: Số các giá trị nguyên nhỏ hơn 2018 của tham số m để phương trình ( ) ( ) 64 log2018log1009 xmx += có nghiệm là A. 2018. B. 2017. C. 2020. D. 2019. Lời giải Chọn C Đặt ( ) 4 log100910094t xtx== Phương trình đã cho có dạng ( ) 6 log2.42.4662.4 ttttt mtmm +=+==− Số nghiệm của phương trình bằng số giao điểm của đồ

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 19 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn +) ( ) ( ) limlim62.40 tt tt ft →−→− =−= Ta có bảng biến thiên: Với ( ) 36 2 log4log22,0136 f − Từ bảng biến thiên, để phương trình có nghiệm thì ( ) 36 2 log4log22,0136 mf − . Vậy 22018 m − . Có 2020 số nguyên m Câu 110: Có bao nhiêu số nguyên m để phương trình ( ) ( ) 2 35 log32log3 xx mm+=− có nghiệm? A.
.
.
2. D. 5. Lời giải Chọn A Đặt ( ) ( ) 2 35 2 323 log32log3 35 xt xx xt m mmt m += +=−= −= 2 235 tt mm +=− 2 21351 tt mm ++=−+ Xét hàm số ( ) 351 tt ft =−+ với t . Ta có: ( ) 3.ln35.ln5 tt ft =− Khi đó ( ) ( ) 330 5 3ln5 03.ln35.ln50loglog5 5ln3 t tt fttt =−==== Bảng biến thiên
3
B. 4
C.
giá trị thực của tham số m để phương trình 33 loglog1210 xxm ++−−= có ít nhất một nghiệm thực trong đoạn 1;27 A. ( )0;2 m . B. 0;2 m . C. 2;4 m . D. ( )0;4 m . Lời giải
Chọn B
Đặt 3 log1tx=+ . Với 1;27 x thì 1;2 t Phương trình đã cho trở thành 2 220ttm+−−= 2 22mtt +=+ ( )* Xét hàm số ( ) 2 fttt =+ trên đoạn 1;2
Ta có ( ) 210,1;2fttt =+ nên hàm số ( ) 2 fttt =+ đồng biến trên 1;2 . Bảng biến thiên: Để phương trình đã cho có ít nhất một nghiệm thực trong đoạn 1;27 thì phương trình ( )* phải có ít nhất một nghiệm thực trong đoạn 1;2 Từ bảng biến thiên, suy ra 2226 m + 02 m Câu 112: Có bao nhiêu giá trị nguyên của tham số m để phương trình

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
ỳnh
42
ễn
Page 20
Phương
có
ệm (
(
(
2
+−−−− Do 2;1;0 mm−− . Vậ
tr
ấ
Giáo viên: Hu
Văn Ánh
Nguy
Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
trình
nghi
)
)
) ( )
000 1112,0680,068 mftftmftm
y có 3 giá
ị nguyên của m thỏa mãn. Câu 111: Tìm t
t cả các
nghiệm 1;9 x . A. 1. B. 5. C. 3. D. 2. Lời giải Chọn A Điều kiện: 0 x Ta có: 222 3933 loglog20loglog20 −+−=−+−= xmxmxmxm Đặt 3log = tx , với 1;90;2xt . Phương trình đã cho trở thành: ( ) 2 2 2 201 1 + −+−== + t tmtmm t Xét hàm số ( ) 2 2 1 + = + t ft t với 0;2 t ta có: ( ) ( ) 2 2 22 1 +− = + tt ft t , ( ) 2 130;2 0220 130;2 =−+ =+−= =−− t fttt t .
22 39 loglog20 −+−= xmxm có
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 21
−+ m
ặ
+−
=+ =+=+ xx mxx mxxmxx Nhận xét với 0 = x không
Vớ
0 x thì ( ) (
2
1 + = x m x Xét
số ( ) (
2 1+ = x fx x vớ
x có ( ) ( ) 2 2 1 01=== x fxfxx x . Bảng biến thiên t()ft ()ft 2 0 13 22 223 0
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Bảng biến thiên: Khi đó: phương trình đã cho có nghiệm 1;9 x Phương trình ( )1 có nghiệm 0;2 t . 2232
M
t khác, do
m nên 2 = m . Vậy có một giá trị nguyên của tham số m thỏa yêu cầu bài toán. Câu 113: Có bao nhiêu giá trị nguyên của m để phương trình ( ) ( ) 2 2 loglog1 =+mxx vô nghiệm? A. 4. B. 6. C. 3. D. 5. Lời giải Chọn A Điều kiện 00 101
mxmx xx Ta có ( ) ( ) ( ) ( ) 222 2 loglog1log2log1 =+=+ mxxmxx ( ) ( ) ( ) ( ) ( ) 2 22 22 101 loglog1 111 +−
là nghiệm của phương trình.
i
)
1
hàm
)
i ( ) 1;\0−+
Phương trình đã cho vô nghiệm khi và chỉ khi 04 m . Do m nên 0;1;2;3 m .
Vậy có 4 giá trị nguyên của tham số m để phương trình ( ) ( ) 2 2 loglog1 =+mxx vô nghiệm.
Câu 114: Số các giá trị nguyên nhỏ hơn 2020 của tham số m để phương trình ( ) ( ) 64 log2020log1010 xmx += có nghiệm là A. 2020. B. 2021. C. 2019. D. 2022 Lời giải Chọn D Điều kiện xác định: 20200 10100 xm x + Đặt ( ) ( ) 64 log2020log1010xmxt +==
Suy ra ( ) 20206 1 10104
t t
xm x += = . Từ đó ( ) 62.4 2 tt m =− . Với mỗi nghiệm 0t của phương trình ( )2 thì 0 0 4 2010

t x = là nghiệm của hệ phương trình ( )1 đồng thời 0x thỏa mãn điều kiện ( )* . Do đó 0x là nghiệm của phương trình đã cho. Từ đó, điều kiện cần và đủ để phương trình đã cho có nghiệm là phương trình ( )2 có nghiệm. Xét hàm số ( ) 62.4 tt ft =− trên . Ta có ( ) 6.ln62.4.ln4 tt ft =− và ( ) ( ) 36 2 0loglog16:ftt === . Bảng biến thiên của hàm số ( )ft như sau:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 22
Dựa vào bảng biến thiên, ta có phương trình ( )2 có nghiệm khi và chỉ khi ( ) 2do mm− .
Vậy tất cả các giá trị nguyên của tham số m thỏa yêu cầu bài toán là các số nguyên thuộc tập hợp 2.1,0,1,2,....,2019 , có tất cả 2022 giá trị.
Câu 115: Xét các số nguyên dương , ab sao cho phương trình 2 lnln50axbx++= có hai nghiệm phân biệt 12 , xx và phương trình 2 5loglog0 xbxa++= có hai nghiệm phân biệt 34 , xx sao cho 1234 xxxx . Tìm giá trị nhỏ nhất của 23 Sab =+ . A. 30. B. 25. C. 33. D. 17. Lời giải Chọn A ( ) 2 lnln501axbx++= ( ) 2 5loglog02 xbxa++= Điều kiện để ( )1 có hai nghiệm phân biệt 12 , xx và ( )2 có hai nghiệm phân biệt 34 , xx là: 2220020 baba − Nhận xét:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
23 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
1234 ,,,0xxxx Do đó: ( ) ( ) ( ) ( ) 34 1234123412 log lnlnln log xx xxxxxxxxxx e ( ) 1234 lnlnlogloglog xxexx++ Mà 1234 lnln;loglog 5 bb xxxx a +=−+=− và , ab nguyên dương Nên log5log 5 bb eae a −− Vì a là số nguyên dương và 5log2,17 e nên 3 a 2 20606060(0) abbb Vì b là số nguyên dương và 607,75 nên 8 b Do đó: 2330Sab=+Giá trị nhỏ nhất của S là 30
ab== .
khi 3;8
xmxmm xm xm Để phương trình có 2 nghiệm phân biệt khi 1 41 3 mmm Khi đó phương trình có 2 nghiệm 4 41 1220,22.20 mmmxx Vì 4 12 16522.2165* mm xx Xét hàm số 43 2.8100ftttfttt Mà 23 m là nghiệm của * nên là nghiệm duy nhất. Suy ra 4 123,2.3162xx Suy ra 12 159 xx . Câu 117: Gọi 0m là giá trị thực nhỏ nhất của tham số m sao cho phương trình ( ) ( ) ( ) ( ) 2 11 33 1log35log310 mxmxm −−−−−+−= có nghiệm thuộc ( )3;6 . Khẳng định nào sau đây là đúng? A. Không tồn tại 0m B. 0 4 1; 3 m − C. 0 10 2; 3 m D. 0 5 5; 2 m −
Lời giải Chọn D Đặt ( ) 1 3 log3tx
Vì ( ) 3;61xt− . Phương trình trở thành: ( ) ( ) 2 1510mtmtm −−−+−= 22 51mtmtmtt
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
24 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH
THỪA MŨ LOGARIT
12 LŨY
Page
Câu 116: Cho phương trình 22 22 log51log40 xmxmm . Biết phương trình có 2 nghiệm phân biệt 12 , xx thỏa 12 165 xx . Giá trị của 12xx bằng A. 16 B. 119 C. 120 D. 159 Lời giải Chọn D 22 22 2 2 =−
log51log40 log log41 −+=−+
2 2 51 1 tt m tt −+ = −+
Xét hàm số ( ) 2 2 51 1 tt ft tt −+ = −+ ( ) ( )( ) ( )( ) ( ) ( ) 22 2 2222
tttttt t ft tttt
2512151 44 11
−−+−−−+ == −+−+ ( ) 01ftt == Bảng biến thiên: Để phương trình đã cho có nghiệm ( )3;6 x thì phương trình ( )* có nghiệm 1 t − . 3 m − . Vậy giá trị nhỏ nhất của m thỏa mãn yêu cầu bài toán là 0 5 35; 2 m =−−
Câu 118: Cho phương trình ( ) ln120mxx+−−= . Biết rằng tập hợp tất cả các giá trị của tham số m để phương trình đã cho có hai nghiệm 1x , 2x thỏa mãn 12024xx là khoảng ( ) ;a + . Khi đó a thuộc khoảng nào dưới đây? A. ( )3,7;3,8 B. ( )3,6;3,7 . C. ( )3,8;3,9 D. ( )3,5;3,6 . Lời giải Chọn A
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
25
=
Xét trên khoảng ( ) 0;+ phương trình: ( ) ( ) 2 ln120 ln1 x mxxm x + +−−== + Đặt ( ) ( ) ( ) 2 ,1;\0 ln1 x fxx x + =−+ + Với yêu cầu của đề bài ta xét ( )fx trên 2 khoảng ( )0;2 và( ) 4;+ ( ) ( ) ( ) ( ) 2 1 ln12 1 ln1 xx x fx x +−+ +
+ Đặt ( ) ( ) ( ) ( ) ( ) 1 ln12,x0;24; 1 gxxx x =+−++ +
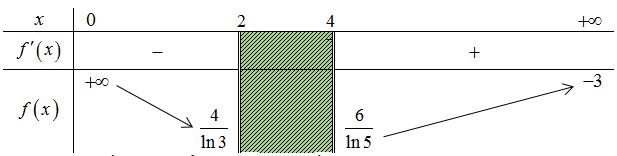
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
ỳnh
ễn
ậ
Page 26
ạ
( ) ( ) ( ) ( ) 2 11
x x =++ + +
(
(
(
(
(
4
3 6
5
=− =−++ T
ng
ựa
bảng biến
biệt thỏa 12024xx ( ) 6 ln53,728 m Câu 119: Tìm tất cả các giá trị của tham số a để phương trình 23 33 loglog10 xaxa+++= có nghiệm duy nh
u bài toán trở thành: Tìm tất cả các giá trị của tham số a để phương trình 2 23330 tata+++= có nghiệm duy nhất thuộc nửa khoảng ) 0;+ . Ta có: 2 2 23 233303,0 1 t tataat t +++== + . Xét hàm số: ( ) 2 23 1 t ft t = + trên nửa khoảng ) 0;+ Ta có:
Giáo viên: Hu
Văn Ánh 42 Nguy
Cư Trinh Thu
n Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên so
n
0,0;24; 1 1 gxx
Suy ra
)
)
) ( ) ( )
) ( )
) ( ) ( )
2ln30,0;20,0;2
5ln50,4;0,4;
gxgxfxx gxgxfxx
ừ đó ta có bả
biến thiên D
vào
thiên, để phương trình đề bài có 2 nghiệm phân
ất. A. Không tồn tại a . B. 1 a − hoặc 4210 a =− . C. 1 a D. 1 a = Lời giải Chọn B Điều kiện: 3 3 0 0 1 1 log0 x x x x x Khi đó phương trình 23 3333 loglog102log3log10 xaxaxaxa +++=+++= ( ) ( ) 33 2.3log33log3301 xaxa +++= . Đặt 3 3log,0 xtt= thì ( )1 trở thành: 2 23330 tata+++= Do đó, yêu cầ
1; 3 m − . B. 0 10 2; 3 m . C. 0 16 4; 3 m . D. 0 5 5; 2 m − . Lời gi
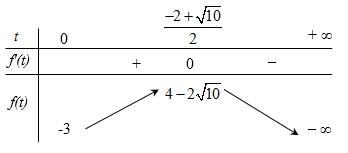
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 27
ải Chọn D Điều kiện: 2 x . Đặt ( ) 1 2 log2tx=− , với ( )2;4 x ( ) 1; t −+ Phương trình đã cho trở thành: ( ) ( ) 2 1510mtmtm −−−+−= ( ) 2222 51511 ttmtmtmttmtt −+=−+−+=−+ ( ) ( ) 2 2 2 51 1,10, 1 tt mttt tt −+ =−+ −+ Phương trình đã cho có nghiệm ( )1 có nghiệm 1 t − .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn +) ( ) ( ) 2 2 243 1 tt ft t −−+ = + . ( ) 2 210 210 2 02430 2 210 2 t ftttt t −+ = −+ =−−+== = . +) ( ) lim t ft →+ =− . +) Bảng biến thiên: Từ bảng biến thiên suy ra phương trình có một nghiệm duy nhất khi 331 42104210 aa aa −− =−+=−+ Đáp số: 1 a − hoặc 4210 a =−+ . Câu 120: Gọi 0m là giá trị nhỏ nhất của tham số thực m sao cho phương trình ( ) ( ) ( ) ( ) 2 11 22 1log25log210 mxmxm −−−−−+−= có nghiệm thuộc khoảng ( )2;4 . Khẳng định nào dưới đây đúng? A. 0 4
Xét hàm số ( ) ( ) 2 2 51 ,1 1 tt ftt tt −+ =− −+
Ta có: ( ) ( ) 2 2 2
44 1 t ft tt = −+ ( ) ( ) ( ) 2 113 04407 11 3
Bảng biên thiên hàm số ( )ft :
xf ftt xf
==− =−= =−−=−
−−+= = = −−= = = Theo giả thiết 1212 6246122 m xxmxxx +=+===−= . Câu 122: Tìm tất cả các giá trị của m để phương trình 2
loglog2log20 log 2 (log)(log2)0 m
xmxxm xm x xmx x x
22 2 loglog3−+= xxm có nghiệm 1;8 x . A. 26 m B. 36 m C. 69 m D. 23 m . Lời giải Chọn A Đặt 2log = tx . Khi 1;8 x thì 0;3 t . Bài toán trở thành: Tìm m để phương trình 2 23 −+= ttm có nghiệm 0;3 t . Xét hàm số ( ) 2 23=−+fttt với 0;3 t , ta có:
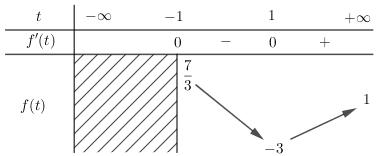
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 28
Dựa vào bảng biến thiên, phương trình ( ) ftm = có nghiệm 1 t − khi và chỉ khi 7 3 3 m − Vậy giá trị nhỏ nhất của tham số thực m để phương trình đã cho có nghiệm là 0 5 35; 2 m =−− . Câu 121: Giả sử phương trình 2 22 log(2)log20 xmxm −++= có hai nghiệm thực phân biệt 12 , xx thỏa mãn 12 6 xx+= . Giá trị biểu thức 12xx là A. 4. B. 3. C. 8. D. 2. Lời giải Chọn D Điều kiện 0 x . Phương trình đã cho tương đương 2 222 2 22 2 log2 4
( ) 2201 =−==fttt ; ( ) ( ) 0;3 min12 == t ftf ; ( ) ( ) 0;3 36 max == t ftf . Đồ thị hàm số ( ) 2 23==−+yfttt và đường thẳng = ym sẽ cắt nhau tại điểm có hoành độ 0;3 t nếu như ( ) ( ) 0;3 0;3 ma 6min x 2 t t ftmftm .
Câu 123: Tìm các giá trị thực của tham số m để phương trình 2 33 log3log270 xxm −+−= có hai nghiệm thực 1x , 2x thỏa mãn ( )( ) 123372xx++= . A. 9 2 m = . B. 3 m = . C. Không tồn tại. D. 61 2 m = . Lời giải Chọn A Đặt 3log tx = Phương trình đã cho trở thành ( ) 2 3270*ttm−+−= . Ứng với mỗi nghiệm t của phương trình ( )* có một nghiệm x . Vậy phương trình đã cho có hai nghiệm phân biệt khi phương trình ( )* có hai nghiệm phân biệt ( ) ( ) 2 37 03427098280 8 mmm −−−−+ Gọi 1t , 2t là hai nghiệm phương trình ( )* .
1292 .2 .2731 xxxt tt xxxt +===
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 29
Theo định lý Viét ta có: ( ) 12313231212 3loglog3log.3.27ttxxxxxx +=+=== Theo đề bài ( )( ) ( ) 12121212 3372.397212 xxxxxxxx ++=+++=+= Vậy ta có 1211 12 1222 = === . Theo định lý Viét ta có 12 9 .2227 2 ttmm ==−= . Kết luận: 9 2 m = thỏa mãn yêu cầu bài toán. Câu 124: Số các giá trị nguyên nhỏ hơn 2020 của tham số m để phương trình ( ) ( ) 64 log2020log1010 xmx += có nghiệm là A. 2022. B. 2020. C. 2019. D. 2021. Lời giải Chọn A Ta đặt ( ) ( ) 64 log2020log1010 xmx += t = . Khi đó 20206t xm+= và 10104t x = . Ta suy ra 246624 tttt mm +==−
125: Cho phương trình
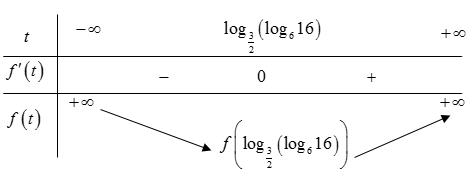
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 30
Chọn D ( ) ( ) (
x
−−−+=
( ) ( ) ( ) ( ) ( ) ( ) 2 01 102* 1003 14 x mx x mexm mxx + −−= =+ )* 0 m = thì pt vô nghiệm. )* 0 m thì hệ ( ) ( )2 0 10 *1 1 x x x m e x m x = + = .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Đặt ( ) 2.46 tt ft =−+ ( ) 6ln62.4.ln4 tt ft =− ( ) 0 ft = ( ) 636 2 32ln4log16loglog16 2ln6 t t ===
. Bảng biến thiên Phương trình ( ) ftm = có nghiệm khi và chỉ khi ( ) 36 2 loglog162,01 mf − . Hơn nữa, 2020 m m nên suy ra 22019 m m − . Vậy ta có 2022 giá trị m thỏa mãn. Câu
( ) ( ) ( ) 10log2log10 x mexmmxx−−−+= . ( m là tham số ). Có tất cả bao nhiêu giá trị nguyên của m để phương trình đã cho có ba nghiệm thực phân biệt? A. Vô số. B. 10. C. 11. D. 5. Lời giải
) 10log2log10
mexmmxx
+Xét ( ) 10 1 x
x fx e = và ( ) ( )2 1 1 2 x gxx xx + ==++ + ( ) ( ) ( ) ( ) ( ) 22 101.1010110 11
eex ex fx ee == Xét ( ) ( ) ( ) ( ) ( ) 10110101011000; xxxx uxexuxeexxex =−−=−+−=−+
xx x xx
= 10 * x mfx mgx
1 11 10. 1 x x gx x xx =−== =− Suy ra phương trình có ba nghiệm thực phân biệt 410. m Vì 5;6;7;8;9 mm= )* 0 m thì hệ ( ) ( ) ( )
− = = . Tương tự ta có ( ) ( ) ( ) ( ) 1 10
ee fxxfxfx eee +− →−→
−====
101010 01;0,lim,lim10 111 xx
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
31 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
Suy ra: Hàm số ( )ux nghịch biến trong khoảng ( ) ( ) ( ) 0;00 uxu += ( ) ( ) ( ) 00; fxxfx + nghịch biến trong khoảng ( ) 0;+ ( ) ( ) 0 lim10,lim0 x x fxfx + →+ → == + ( ) 2 22
( ) 2 22
= =−== =−
1 11 10. 1 x x gx x xx
Suy ra phương trình có nhiều nhất 1 nghiệm thực phân biệt, không thỏa mãn yêu cầu bài toán. Vậy có 5 giá trị m .
−+ 2 2
xm x xm x = 4210 120 xxm xm −++= +−= ( ) ( )

+
hàm 1 11 2 11 22 22
có xm xxm
+
( ) ( ) ( ) 1 1 2 2 2.ln22 2ln2 0,2. log2 t t t t ftt t += −+−= Khi đó ycbt phương trình ( )1 và ( )2 có tổng cộng 3 nghiệm thực phân biệt. Vẽ đồ thị hàm số ( ) 2 11 22fxx=+ và ( ) 2 11 2 22gxxx=−+− trên cùng một hệ trục tọa độ.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
32 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
−+
Xét
số ( ) ( ) 1 2 2 log2 t ft t = +
( )
−+−
Câu 126: Cho phương trình ( ) ( ) 2 22 1 2 2 4.log232.log220 xm xx xxxm −++−+= với m là tham số Tổng tất cả các giá trị của tham số m để phương trình đã cho có ba nghiệm phân biệt là A. 4. B. 1. C. 2. D. 3. Lời giải Chọn D Có ( ) ( ) 2 22 1 2 2 4.log232.log220 xm xx xxxm −+ −++−+= ( ) ( ) ( ) 2 2 12 11 22 2.log122.log220 xm x xxm −+−−+= ( ) ( ) ( ) 2 12 11 2 2 2 =−
22 log22log12 Phương trình đã cho ( ) ( ) ( ) 22 1212 fxfxmxxm −=−−=− ( )( ) 22412120xxmxm −+++−= 2 2
Đồ thị hàm số ( )fx và ( )gx tiếp xúc với nhau tại điểm có hoành độ 1. x = Dựa vào đồ thị ta có 13 ,1, 22 mmm=== thì phương trình đã cho có 3 nghiệm thực phân biệt. Vậy tổng các giá trị thực của m thỏa ycbt là 13 13. 22 ++=

Câu 127: Cho phương trình ( ) ( ) 2 33 log95log3100 xmxm−++−= . Số giá trị nguyên của tham số m để phương trình đã cho có hai nghiệm phân biệt thuộc 1;81 là A. 3 B. 5 C. 4. D. 2. Lời giải Chọn C Ta có ( ) ( ) ( ) ( ) ( ) 22 3333 log95log3100log1log360,1 xmxmxmxm −++−=−++−= Đặt 3log tx = , khi 1;81 x thì 0;4 t Khi đó ta có phương trình ( ) 2 3 1360 2 t tmtm tm = −++−= =− . Phương trình đã cho có hai nghiệm phân biệt thuộc 1;81 phương trình ( )1 có hai nghiệm phân biệt 235 0;4 02426 mm t mm −
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
33 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
nguyên của tham số m để phương trình đã cho có hai nghiệm phân biệt thuộc 1;81 . Chọn đáp án C. Câu 128: Cho , xy là hai số thực dương thỏa mãn 54 xy+= . Tổng tất cả giá trị nguyên của tham số m để phương trình 2 2 3 2 log310 xym xxym xy ++ +−−+−= + có nghiệm là A. 10. B. 5. C. 9. D. 2. Lời giải Chọn B
− . Suy ra có 4 giá trị
ết hợp với điều kiện 5445 xyyx +==− . Vì 4 ,00 5 xyx .
Ta có ( ) 22 4 *24024,0; 5 xxmmxxx ++−==−−+ .
+ ++= ++=
hàm
có
210ftt
với mọi 0 t , suy ra hàm số luôn đồng biế
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 34 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT
Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) 2 2 3 22 33 2 log310 log22log331 xym xxym xy xymxymxyxy ++ +−−+−= + +++++=+++ Vì ,0xy nên 0 xy+ . Xét hàm số ( ) 3log fttt =+ là hàm số đồng biến trên (
+ Khi đó ( )1 ( ) 2223330*xymxyxxym ++=+−−+= K
0984164935
BDKT
) 0;
. ( ) ( ) ( )2 *2222 xxxx mm +++=+ . Xét
số ( ) ( ) 2 0 ftttt=+ . Ta
( )
=+
n với mọi 0 t ( ) ( ) ( ) ( )
)
*222222** xxxxxx fmfmm +=+==+ . Đặt ( )20 x tt= ,
( )**
***
Hàm số 2 24yxx=−−+ nghịch biến trên 4 0; 5 nên 2 44 244 25 xx −−+ . Do vậy 2;3 m là các giá trị cần tìm Vậy tổng tất cả các giá trị m thỏa ycbt là 5. Câu 129: Biếtrằngđiềukiệncầnvàđủcủathamsố m đểphươngtrình ( ) 2 log22 x mmx ++= cónghiệm là a m b − với , ab là hai số nguyên dương và 7 b . Hỏi 2abb ++ bằng bao nhiêu? A. 31. B. 32. C. 21. D. 23. Lời giải Chọn C ( ) ( ) 2 2 −=
20 log22 22* Xét hàm ( ) ( ) 2 0 gtttt=− , ta có ( ) ( )
x x xx 2
m mmx mm =−== Bảng
(
2
khi đó phương trình
trở thành ( ) 2
ttm
.
1 210
gttgtt
biến thiên

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 35 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vậy để ( )*** có nghiệm 0 t thì 1 4 m − 2 1 21 4 a abb b = ++= = Câu 130: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 2 2 log(4)log240 xmxm−−−= có nghiệm thuộc đoạn 1;8 ? A. 1. B. 2. C. 5. D. 3. Lời giải Chọn D ĐK: 0 x ( ) ( ) ( )( ) ( ) ( ) ( ) ( ) 2 2 2 2 22 2 222 2 2 2 2 2 log4log240 2log2log240 log4log2log11 log;1;80;3 4 12 1 4 ;0;3 1 24 0,0;3 1 xmxm xmxm xxmx xtxt tt m t tt ftt t tt ftt t −−−= +−−−= +=+ = + = + + = + ++ = + ( ) ( ) 023 21 0,0,1,2 8 fmf mmm Câu 131: Cho hàm số bậc ba ( )yfx = có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số 5;5 m− sao cho phương trình ( ) ( ) ( ) ( ) ( ) ( ) 32 21 2 2 log1log128log120 fxfxmfxm +−++−++= có nghiệm ( )1;1 x − ?
trình đã cho có ( )1;1
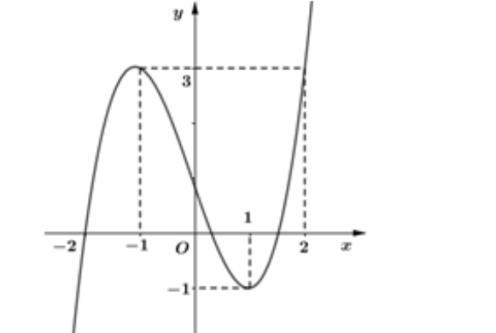
phương trình ( )* có nghiệm ( );2 t − Xét hàm số ( ) 2 2 fttt =− trên ( );2− có ( ) ( )2201;2fttt =−==− . Ta có bảng biến thiên của hàm số ( ) 2 2 fttt =− Từ bảng biến thiên suy ra phương trình ( )* có nghiệm ( );2 t − khi và chỉ khi 1 m − . Mà 5;51;0;1;2;3;4;5 m m m −

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 36 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 7. B. 5. C. 6. D. vô số. Lời giải Chọn A Với ( ) ( ) ( ) 1;113014xfxfx −−+ . Đặt ( ) ( ) ( ) ( ) 2 log1;2,1;1 tfxtx =+−− Khi đó phương trình đã cho trở
( )( ) (
222 2
t
ttm =− −−−=−−=−= −−=
− . Vậy có
giá
Câu 132: Cho phương trình 0 81 3).3 (2 9 = + + x x m (
a m để phương trình đã cho có hai nghiệm phân biệt 2 1, x x thỏa mãn 10 2 2 2 1 = + x x thuộc khoảng nào sau đây A. ( )10;5 B. ( )0;5 C. ( )15;10 D. ( )+;15 Lời giải Chọn C ( )9(23).38101 xx m −++= ( )2 3(23).3810 xx m −++= . Đặt ( )30 x tt= Phương trình trở thành: ( ) 2 (23)8102tmt−++=
thành: ( ) 324420ttmtm −−−+=
) ( )
2;2 220202* 20
tttmttmttm
Để phương
x−
7
trị của m thỏa mãn yêu cầu bài toán.
m là tham số thực). Giá trị củ
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 37 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) 22 234.8123324 mm =+−=+− Để phương trình ( )1 có hai nghiệm phân biệt thì phương trình ( )2 có hai nghiệm phân biệt dương: Điều kiện: ( )2 15 23182 0233240231833 023023182215 081032318212 232 23 2 m m m m mm m Smm m m P m m m + + +− −− +− + +− − − − − Áp dụng hệ thức Vi-ét: 12 12 23 .81 ttm tt +=+ = Vì 12 4 1212 .813.334 xx ttxx ==+= Do đó: ( )2 222 1212121212 102.1042.10.3 xxxxxxxxxx +=+−=−== Xét hệ phương trình 1211 12
30
xxxt
=== += +=== Nên (
Vậy Ch
+)
+) Để ( )
2
ệ
ệt
(
1222 .313
4327
tt xxxt
) 27 2330 2 mmTM +==
ọn C Câu 133: Cho phương trình ( ) ( ).1622.4301 xx mmm−−+−= . Tập hợp tất cả các giá trị dương của m để phương trình đã cho có hai nghiệm phân biệt là khoảng ( ) ;.ab Tổng 2 Tab =+ bằng: A. 14 B. 10 C. 11 D. 7 Lời giải Chọn C
Đặt: ( ) ( ) ( ) 2 4(0)1.22302 x ttmtmtm =−−+−=
1 có
nghi
m phân bi
thì
)2 phải có hai nghiệm dương phân biệt
135: Với giá trị nào của tham số
m sm pm
.22 2 xx tt + === 090 1 060 2 11 0 22
− = ==
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 38 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn = Điều kiện: ( ) ( ) ( ) 2 0 0 40 0 230 2 034 2 0 00() 0 0 3 30 0 m m m m mmm m m m m Sml m P m mm m −+ −−− − +) Vậy 3 34211 4 a mab b = += = Câu 134: Phương trình 1 43.20 xx m + −+= có hai nghiệm thực 12 , xx thỏa mãn 12 1 xx+=− . Giá trị của m thuộc khoảng nào sau đây? A. ( )5;0 . B. ( )7;5 . C. ( )0;1 . D. ( )5;7 .
Lời giải Đặt 2x t = . Ta có phương trình 2 60ttm−+= Phương trình đã cho có hai nghiệm 12 , xx thỏa mãn 12 1 xx+=− pt có hai nghiệm dương 12 , tt thỏa mãn 12 1 12 1
2.22230(1) xx m m −++= Đặt ( )20 x tt= , khi đó phương trình (1) trở thành: ( ) 2 2.2302 mtm t −++= .Phương trình ( )1 có hai nghiệm 12 ; xx khi và chỉ khi phương trình ( )2 có hai nghiệm 12 ; tt dương 2 0230 020 023 3 0 m m Sm m Pm −− + . Theo định lý Viet ta có 12 12 . 2 23 t t tt m m += =+ Với 2x t = ta có: 1 1212 2 1 12 2 213 .2.22321623 22 x xxxx x t ttmmm t + = =+==+= = . Câu 136: Phương trình 0 2 .2 4 1 = + + m m x x có hai nghiệm 2 1 , x x thỏa mãn 3 2 1 = + x x khi A. 4 m = B. 3 m = C. 2 m = D. 1 m = Lời giải
Câu
m để phương trình 1 4.2230 xx mm + −++= có hai nghiệm 12 ; xx thỏa mãn 12 4 x x += A. 5 2 m = . B. 2 m = . C. 8 m = . D. 13 2 m = . Lời giải Phương trình đã cho tương đương 2
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 39
Đặt 2x t = ,
t .
−+=
Ta
xx +
Ycbt
2 12 12 20 204 .28 mm ttmm ttm =− +== == . Câu 137: Tìm tất cả các giá trị của tham số m để phương trình ( ) ( ) 222 221242 4.42266330 xxxxxx mm +++++ +−−+= có hai nghiệm thực phân biệt. A. 432432 m −+ B. 432 m + hoặc 432 m − C. 1 m − hoặc 1 2 m D. 1 1 2 m − Lời giải Chọn D ( ) ( ) ( ) ( ) ( ) ( ) 222 222 22 221242 212121 2121 4.42266330(1) 42266390 42 22630 (2) 93 xxxxxx xxxxxx xxxx mm mm mm +++++ ++++++ ++++ +−−+= +−−+= +−−+= Đặt 2221(1)0222 1 333 xxx t +++ == = . Suy ra 01 t Pt trở thành: 2 (22)630(3)tmtm+−−−= 3() 21 tloai tm = =−− Để phương trình có
−− 1 1 2
− .
ý
ếu 1
= thì phương trình 2(1) 2 1 3 x+ = chỉ có nghiệm duy nhất là 1 x =− Câu 138: Biết rằng tập các giá trị của tham số m để phương trình( ) ( ) 3921310 xx mmm −++−−= có hai nghiệm phân biệt là một khoảng ( ) ; ab . Tính tích ab . A. 4 B. 3 C. 2 D. 3 Lời giải Chọn D Đặt: 3,(0) x tt = . Khi đó phương trình trở thành 2 (3)2(1)10(*) mtmtm −++−−=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
0
Phương trình viết thành ( ) 2 2201tmtm
.
có 1212 3 12 3222.28 xxxx
+=== .
tương đương phương trình ( )1 có hai nghiệm dương 12 , tt thỏa mãn 12.8tt =
2 nghiệm x phân biệt
Phương trình 2 (22)630tmtm+−−−= có đúng một nghiệm t thuộc khoảng ( )0;1
0211 m
m
Chú
: N
t
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 40 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Phương trình có hai nghiệm phân biệt khi phương trình có hai nghiệm dương phân biệt 0(1)(22)0 1 001 1 3.3 13 3 0 1 0 3 1 mm m Smab m m P m m mm +− + − −= − Câu 139: Có tất cả bao nhiêu số nguyên m để phương trình 4.2220190 xx mm −+−= có hai nghiệm trái dấu? A. 1008. B. 1007. C. 2018. D. 2017. Lời giải 4.2220190 xx mm −+−= Đặt ( )20 x tt= . Phương trình trở thành 2 220190tmtm−+−= Phương trình có hai nghiệm 12 ; xx thỏa 12 0 xx khi và chỉ khi phương trình có hai nghiệm 12 ; tt thỏa 1201tt ( )( ) ( ) ( ) 2 12 12 1212 12 4220190 0 0 0 0 0 2019 0220190 2 10 110 2201910 mm m Stt m Pttm m tttt tt mm −− =+ =− −++ −− −−+ ( ) 2 880760 0 2019 2018 2019 2 2 2018 mmm m m m m −+ . Do m nên 10102017 m Số giá trị nguyên m thỏa đề là 1008 Câu 140: Cho phương trình ( ) ( )( ) 4152141560 xx m +++−−= . Để phương trình có hai nghiệm phân biệt 12 , xx thỏa mãn 1220xx−= . Ta có m thuộc khoảng nào? A. ( )3;5 . B. ( )1;1 . C. ( )1;3 . D. ( );1−− . Lời giải Đặt ( )415 x t =+ , 0 t . Khi đó phương trình ban đầu trở thành: ( ) 2 21 606210,0 m tttmt t + +−=−++= Để phương trình có hai nghiệm phân biệt 12 , xx thỏa mãn 1220xx−= khi và chỉ khi phương trình có hai nghiệm dương phân biệt 12 , tt thỏa mãn ( ) (*) 2 12 0 1 04 2 0 ttSm P =−
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo
Huỳnh
Ánh 42
ễn
ậ
Page 41
ạ
Theo
( ) ( ) 12 12 3 122 22 3 12 1 6 6
21
+= += =+=+ = =+ ( ) ( ) 2 333 7 212162123;5 2 mmmm +++=+== . Câu 141: Phương trình ( ) ( )( ) 23122340 ++−−−=
. D. 3 2; −+ . Lời giải Đặt ( ) 23,0 x tt =+ Phương trình trở thành 2 12 404120 a ttta t +−=−+−= GT: Phương trình có 2 nghiệm phân
t 12
xx
( ) 12 12
+ −=+= xx xx Khi đó 12 3 = tt YCBT phương
2
12
=
12 1 12 2 12 12 12 0 320 0;0 3 3 41 2 1 1 .12 12 3 a tt t a tta t a tta tta tt + = − +==− = =− =− =− = Câu 142: Biết rằng tập các giá trị của tham số m để phương trình 3921310 xx mmm có hai nghiệm phân biệt là một khoảng ; ab . Tính tích ab A. 4 B. 3 C. 2 D. 3 Lời giải Đặt 3,(0), x tt phương trình đã cho trở thành 2 (3)(1)10* 2 () mtmtm Để phương trình đã cho có 2 nghiệm phân biệt thì phương trình có hai nghiệm dương phân biệt. 1220 '0 1 0013 3 0 1 0 3 mm m Sm m P m m
viên:
Văn
Nguy
Cư Trinh Thu
n Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên so
n
Viet, ta có:
.2121
tt tt ttmtm tt tm
xx a có 2 nghiệm phân biệt 12 , xx thỏa mãn 12 23 log3 + −=xx . Khi đó a thuộc khoảng A. 3 ; 2 −− . B. ( ) 0; + . C. 3 ;2 +
biệ
,
thỏa mãn
23 log3233
trình có
nghiệm dương phân biệt thỏa mãn
3
tt
Khi đó ;1;3ab Tích .3ab
Câu 143: Tìm tất cả các giá trị của mm để phương trình 92.320 xxmm −++= có hai nghiệm phân biệt A. 22 m − B. 2 m C. 2 m− D. 2 m Lời giải Đặt ( ) 30; x txt =+ và mỗi x cho ta một giá trị t tương ứng. Khi đó phương trình trở thành ( ) 2 220*tmtm−++= Để pt đã cho có 2 nghiệm phân biệt, tương
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
42 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
biệt 2 020 0202 020 mm Smm Pm −− + Câu 144: Xác định các giá trị của tham số m để phương trình ( ) ( ) 2 92264340 xxx mmm −++++= có hai nghiệm phân biệt? A. 2 m. − B. 3 m. − C. 1 m. −
Lờ
ả
Đặt ( ) 3 0 2 x t,t = khi đó phương trình trở
Phương trình có 2 nghiệm phân biệt khi và chỉ khi phương trình có 2 nghiệm dương phân biệt ( ) ( ) ( ) ( ) 2 2 12 2 12 2430 010 022021 0 31 430 mmm ttmmm. t.t m;; mm +−−− ++−− −−−+ ++ Câu 145: Biết rằng 0mm = là giá trị của tham số m sao cho phương trình ( ) ( ) 922133410 xx mm −++−= có hai nghiệm thực 12 , xx thỏa mãn( )( ) 122212xx++= . Khi đó 0m thuộc khoảng nào sau đây A. (3;9) B. ( ) 9;+ C. ( )1;3 D. ( )-2;0 Lời giải Chọn C ( ) ( ) 922133410(1) xx mm −++−= Đặt 3, 0 x tt= . Pt trở thành: ( ) ( ) 2 2213410tmtm−++−= 3 . 41 t tm = =−
đương phương trình ( )* có hai nghiệm dương phân
D. 2 m. −
i gi
i Xét phương trình: ( ) ( ) 2 92264340 xxx mmm −++++= Chia cả hai vế của phương trình cho 4x ta được ( ) 2 2 33 22430 22 xx mmm −++++=
thành: ( ) 2222430tmtmm −++++=
Để pt có 2 nghiệm thì điều kiện cần và đủ là 1 410 4 mm− Khi đó pt có hai nghiệm 1 1 x = và ( ) 23log41xm=− Từ giả thiết ( )( ) 122212xx++= ( ) ( ) 3 3log4-1212 m += ( ) 3 log412 m −= ( ) 2 15 .31 42 m =+= . Vậy ( ) 1;3. m Câu 146: Có bao nhiêu giá trị nguyên của tham số m để phương trình ( ) 16214380 −++−= xx mm có hai nghiệm trái dấu? A. 6 B. 7 C. 0 D. 3 Lởi giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
43 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
Đặ
−
giá trị nguyên? A. 1 B. 4 C. 9 D. 7 Lời giải Đặt ( )20 x tt= , khi đó phương tình có dạng ( ) 2 2102tmtm−++= Để phương trình ban đầu có nghiệm thì phương trình có nghiệm dương TH 1: Pt có 2 nghiệm trái dấu 1 210 2 mm +− TH 2: pt có 2 nghiệm dương 2 840 0420 210 mm mm m =−− + + Nên ) 11 ;420;\;420 22 SS =−−++=−+ . Vậy các số nguyên thỏa mãn là
Chọn A
t 4,0= x tt Phương trình đã cho trở thành ( ) 2 21380 −++−=tmtm ( )* Yêu cầu bài toán pt ( )* có hai nghiệm 12 , tt thỏa 1201tt ( )( ) 2 12 12 12 0 90 0 10 8 9 0 3 380 110 90 −+ + +
−− − mm tt m m tt m tt m Vậy m có 6 giá trị nguyên. Câu 147: Gọi S là tập hợp các giá trị thực của tham số m để phương trình4.2210 xx mm −++= có nghiệm. Tập \ S có bao nhiêu
0,1,2,3,4,5,6,7,8 hay đáp án C Câu 148: Cho phương trình ( ) ( ) 922133410 −++−= xx mm có hai nghiệm thực 12 , xx thỏa mãn ( )( ) 122212++=xx . Giá trị của m thuộc khoảng A. ( ) 9;+ B. ( )3;9 C. ( )2;0 D. ( )1;3 Lời giải
3
4 txx
Page 44
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Đặt
= x t , 0 t .
đã
có hai nghiệm dương phân biệt ( ) ( ) 2 1 04840 1 1 02210 1 2 0 4 3410 1 4 −+ +− − m mm m Smm m P m m . Khi
Vớ
=−
=−=− x mxm Với 3 = t thì 2 2 331 == x x Ta có ( )( ) 12122122 ++== xxx ( ) 3 log412 m −= 5 2
= . Vậy giá trị m cần tìm là 5 2 = m nên m thuộc
ảng
Câu 149: Có
=− với 0;4 x
t Đặt
t
= với
t
u
=−++
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
Phương trình đã cho trở thành: ( ) ( ) 2 2213410 −++−=tmtm Phương trình
cho có hai nghiệm thực 12 , xx khi và chỉ khi phương trình
đó phương trình có hai nghiệm là 41=−tm và 3 = t .
i 41
tm thì ( ) 1 13 341log41
m
kho
( )1;3
bao nhiêu giá trị nguyên của tham số m để phương trình 2244 94.3210 xxxx m −+−= có nghiệm? A. 27. B. 25. C. 23. D. 24. Lời giải ĐKXĐ: 0;4 x . Đặt 2
thì
0;2
3
u
0;2
thì
1;9
Khi đó, tìm m đề phương trình 2 4210uum−+−= có nghiệm thuộc đoạn 1;9 . 2 241 muu
, với
1;9 u
Xét hàm số ( ) 2 41fuuu=−++ .
( ) 2402fuuu =−+== .
Ta có, ( ) 14 f = , ( ) 25 f = , ( ) 944 f =− .

Do đó, phương trình có nghiệm khi và chỉ khi 5 442522 2 mm −−
Vậy có 25 số nguyên của tham số m .
Câu 150: Gọi ( ) ; ab là tập các giá trị của tham số m để phương trình 2 280 xx eem−−= có đúng hai nghiệm thuộc khoảng ( )0;ln5 Tổng ab + là A. 2. B. 4. C. 6. D. 14. Lời giải Đặt xte = ; ( )0;ln5 x tương ứng ( )1;5 t
Phương trình thành 2 28ttm −= . Xét hàm số ( ) 2 28 fttt =− với ( )1;5 t có ( ) 48ftt =−
Khi đó, phương trình đã cho có hai nghiệm phân biệt thuộc khoảng ( )0;ln5 khi phương trình ( ) ftm = có hai nghiệm ( )1;5 t 86 m −− .
Câu 151: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình ( ) ( ) 21218 xx m +−−= có hai nghiệm dương phân biệt. Số phần tử của S bằng A. 8. B. 7. C. 10. D. 9. Lời giải Đặt ( ) 21,0 x tt += . Vì ( ) ( ) 21.211 xx +−= nên ( ) 1 21 x t −= . Phương trình đã cho trở thành 2 88 m tttm t −=−= Phương trình đã cho có hai nghiệm dương phân biệt khi và chỉ khi có hai nghiệm phân biệt lớn hơn 1. Xét ( ) 2 8 fttt =− , trên ( ) 1;+ Ta có ( ) 28ftt =− .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 45 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
) 04ftt == Bảng biến thiên của hàm ( )ft Từ bảng biến thiên ta có có hai nghiệm phân biệt lớn hơn 1 khi và chỉ khi 167 m −− . Vậy số phần tử của S là 8. Câu 152: Tìm số giá trị nguyên của tham số ( )10;10 m− để phương trình ( ) ( ) 22 2 1 1011012.3 xx x m + ++−= có đúng hai nghiệm phân biệt? A. 14. B. 15. C. 13. D. 16. Lời giải ( ) ( ) 22 22 2 1 101101 1011012.36 33
xx xx x mm + +− ++−=+= (1) Đặt 22 1011011 ,0 33
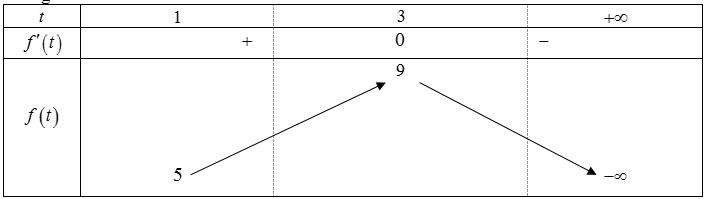
xx tt t +− == 2 1 (1).660 tmttm t +=−+= (2) Để (1) có đúng hai nghiệm phân biệt khi và chỉ khi (2) có một nghiệm lớn hơn 1. 2 (2)6 mtt=−+ . Xét hàm số 2 ()6 fttt =−+ trên khoảng (1;) + , ta có: ( ) ( ) 26;03fttftt =−+== . Bảng biến thiên: Dựa vào bảng biến thiên ta thấy 5 m hoặc 9 m = là giá trị thỏa mãn yêu cầu bài toán. Do ( )10;10 m− nên 9;8;7;6;5;4;3;2;1;0;1;2;3;4;9 m =−−−−−−−−− .
Suy ra có 15 giá trị m cần tìm.
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 46
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
(
thiên ta thấy, phương trình có nghiệm khi 1 425 2 mm−+ Câu 154: Số các giá trị nguyên của tham số m để phương trình: ( ) ( ) 1.16223.4650 xx mmm +−−++= có hai nghiệm trái dấu là A. 4. B. 8. C. 1. D. 2. Lời giải Cách 1. Đặt 4,0 x tt= , phương trình đã cho trở thành: ( ) ( ) 2 1223650mtmtm +−−++= 2 2 65 46 tt m tt ++ =− −+ .
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 47
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 153: Phương trình 11 .210 93 xx mm −++= có nghiệm khi m nhận giá trị: A. 1 2 m − B. 1 425 2 m −− C. 425 m + D. 1 425 2 mm−+ Lời giải Ta có phương trình: 11 .210 93 xx mm −++= Đặt 1 3 x t = , ( )0 t phương trình trở thành: 2 .210tmtm−++= Phương trình có nghiệm phương trình có nghiệm dương. 2 t = không là nghiệm của phương trình nên 2 1 () 2 t mft t + == 2 2 41 '() (2) tt ft t = , 2 2 2 4125()'()00410(2)25() tL tt fttt t tN =− ==−−= =+ Bảng biến thiên. Từ bảng biến
Phương trình đã cho có hai nghiệm 12 , xx trái dấu khi phương trình có hai nghiệm 12 , tt thỏa mãn: 1201tt
Đặt ( ) 2 2 65 46 tt ft tt ++ =− −+ ( ) ( ) 2 ' 2 2
Ta có bảng biến thiên:
10256 46 tt ft tt = −+ . Suy ra ( ) ' 1561 0 10 ftx ==
Từ bảng biến thiên, ta có phương trình có hai nghiệm 12 , tt thỏa mãn: 1201tt khi 41 m −− .
Vậy có hai giá trị nguyên của tham số m thỏa mãn bài toán là 3 m =− và 2 m =− Cách 2: Đặt 4,0 x tt= , phương trình đã cho trở thành:( ) ( ) 2 1223650mtmtm +−−++= .
Đặt ( ) ( ) ( ) 2 122365fxmtmtm =+−−++ Phương trình đã cho có hai nghiệm 12 , xx trái dấu khi phương trình có hai nghiệm 12 , tt thỏa mãn: 1201tt Điều đó xảy ra khi: ( ) ( ) ( ) ( )
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 48
) ( )(
41 11013120 1 41 1001650 5 6 m mfmm m m mfmm m −− +++ − −− +++ − Vậy có hai giá trị nguyên của tham số m thỏa mãn bài toán là 3 m =− và 2 m =− . Câu 155: Phương trình có nghiệm duy nhất. Số giá trị của tham số m thỏa mãn là A. Vô số B. 1 C. 2 D. 0 Lời giải Chọn B Ta có ( ) 412cos xx mx+= ( ) 22cos xx mx+= Ta thấy nếu 0xx = là một nghiệm của phương trình thì 0xx =− cũng là nghiệm của phương trình nên để phương trình có nghiệm duy nhất thì 0 0 x = . 412..cos() xx mx +=
( )(
)
Với 0 0 x = là nghiệm của phương trình thì 2 m = . Thử lại: Với 2 m = ta được phương trình ( ) ( ) 2 222cos* x x+= 2;2VTVP nên ( ) ( ) 2 222 *0 2cos2
x x x += = = thỏa mãn. Vậy 2 m = .
x 233 3 3
x x x x x x x x x 83.431.211(1) 22
=− xxmxmx xxmxmx
= +++=−+− +++=+ Xét hàm số ( ) 3 =+ fttt Ta có 2 =+ x tx mà 121024 01012103411034 010 +
xxx xx
=− = x x xxt x Xét hàm số ( ) ( ) 3 ,1;1034.=+ftttt ( ) ( ) 2 310,1;1034 =+fttt hay ( ) 3 =+ fttt đồng biến trên ( )1;1034 Suy ra ( ) 2 22 + +== x x x xmxm x
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 49
=− = =
=−
Câu 156: Cho phương trình ( ) 2.2.cos4 xxmx =− , với m là tham số. Gọi 0m là giá trị của m sao cho phương trình trên có đúng một nghiệm thực. Khẳng định nào sau đây là đúng? A. ) 0 5;1. m −− B. 0 5. m − C. ) 0 1;0. m − D. 0 0. m Lời giải Phương trình ( ) ( ) 2 4.2.cos422.cos xxxxmxmx =−+= Điều kiện cần: nếu 0x là một nghiệm của phương trình thì 0 2 x cũng là nghiệm. Vì phương trình có nghiệm duy nhất nên 0 1 x = Thay vào phương trình ta có: 4. m =− Điều kiện đủ: Với 4 m =− ta có ( ) ( ) ( ) 2 2 44.2cos4022cos4sin0 xxxxxx ++=++= ( ) ( ) ( ) ( ) ( ) ( ) 22cos 22cos 22 1 cos1 cos1 sin0 cos1 Vậy 4 m =− thỏa mãn Câu 157: Có bao nhiêu giá trị nguyên của tham số m để phương trình ( ) ( ) ( ) 233 83.431.211 xxx xxmxmx +++=−+− có đúng hai nghiệm phân biệt thuộc ( )0;10 A. 101 B. 100 C. 102 D. 103 Lời giải ( ) ( ) ( ) ( ) ( ) ( )
Xét hàm số ( ) ( ) 2 1,0;10.=+ x gxt x ( ) ( ) 22 2.ln21 .2ln22 == x xx x x gx xx ( ) 2 1 0log ln2 === gxxe BBT .ln21104,4ycbtem+ mà mZ nên 3,104. m = Có tất cả 102 số nguyên m thoả mãn. Câu 158: Tìmtấtcảcácgiátrịthựccủathamsố m đểphươngtrình ( )( ) 322 2111 +=+−+−mm eexxxx có nghiệm. A. 1 0;ln2 2 B. 1 ;ln2 2 − C. 1 0; e D. 1 ln2; 2 + Lời giải Đặt 2 2222 1 11211 2 t txxtxxxx =+−=+−−= . Ta có 2 2
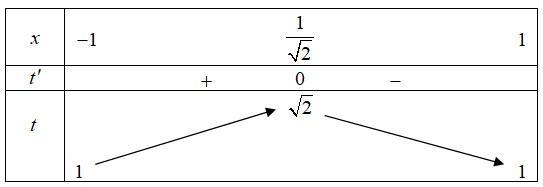
11 ','0 2 1 xx ttx x === Vậy 1;2 t − . Phương trình trở thành 2 333 1 21 2 mmmmm t eeteettet +=++=+= . Phương trình có nghiệm khi và chi khi 1 12ln2(;ln2] 2 m emm −− .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
50
3. C. 1. D. Vô số. Lời giải Chọn A Phương trình: ( ) ( ).21.21 xx xxxmm=−++− ( ) ( )( )2.1 x xmxmx −=−− ( )( ) 210 x xmx −−−= 210(2)
phương trình (2):210 x x −−= Đặt ()21 x fxx=−− '()2ln21 x fx =− 2 1 '()0logln2fxx
Bảng biến thiên của hàm số ()fx : Dựa vào bảng biến thiên ta có phương trình ()0fx = (2) có nhiều nhất 2 nghiệm. Mà (0)(1)0ff== phương trình (2) có đúng 2 nghiệm 0;1xx== . phương trình (1) có các nghiệm là 0;1; xxxm === . Để tập nghiệm của phương trình (1) có hai phần tử 0 1 m m
= = Số phần tử của A bằng 2. Câu 160: Giá trị của m để phương trình 1 420 xx m + −−= có nghiệm duy nhất là: A. 2 m = B. 0 m = C. 1 m = D. 1 m =− Lời giải Chọn D 1 420 xx m + −−= ( )1 . Đặt 2 x t = , 1 t Phương trình ( )1 trở thành: 22202 ttmmtt −−==− ( )2 Nhận xét: với 1 t = ta có duy nhất 1 nghiệm x tương ứng; với mỗi 1 t ta có 2 nghiệm x tương ứng.
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 51
thi: Tuyển sinh
ớ
ố
ạ
Câu 159: Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình ( ) ( ).21.21 xx xxxmm=−++− có hai phần tử. Số phần tử của A bằng A. 2. B.
Hòa
0984164935
Chuyên luyện
vào l
p 10 T
t Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên so
n
x xm x = −−= Xét
==
Phương trình ( )1 có duy nhất nghiệm Phương trình ( )2 có một nghiệm 1 1 t = và nghiệm còn lại 2 1 t . 1 1 t = là nghiệm của phương trình ( )2 101 mm −−==− Khi đó phương trình ( )2 trở thành: 2 2101ttt−+== . Vậy phương trình đã cho có nghiệm duy nhất khi và chỉ khi 1 m =− .
Câu 161: Gọi ; ab là tập hợp tất cả các giá trị thực của tham số m để phương trình 2 2e8e0 xx m có đúng hai nghiệm thuộc khoảng 0;ln5 . Giá trị của tổng ab là A. 2 B. 4 C. 6 D. 14 Lời giải
Chọn D
Đặt e x t . Khi đó 0ln50;ln5e;ext hay là 1;5 t .
Phương trình đã cho trở thành 2 28ttm, với 1;5 t
Vì với mỗi giá trị của 1;5 t ta có một và chỉ một giá trị tương ứng của 0;ln5 x . Do đó, yêu cầu bài toán xảy ra khi và chỉ khi phương trình 2 28ttm có hai nghiệm t phân biệt thuộc khoảng 1;5 .
Xét bảng biến thiên của hàm số 2 28 fttt có 48ftt trên đoạn 1;5 :
Dựa vào bảng trên ta thấy, phương trình 2 28ttm có hai nghiệm t phân biệt thuộc khoảng 1;5 khi và chỉ khi 86 m . Vậy phương trình 2 2e8e0 xx m có đúng hai nghiệm thuộc khoảng 0;ln5 khi và chỉ khi 8;6 m . Suy ra 8 a và 6 b , do đó 14 ab . Câu 162: Giá trị của tham số m thuộc
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
52 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
khoảng nào sau đây để phương trình 1 4.220 xx mm + −+= có hai nghiệm 1x , 2x thoả mãn 12 3 xx+= . A. 9 ;5 2 m . B. ( )2;1 m−− . C. ( )1;3 m . D. ( )3;5 m . Lời giải Chọn D ( ) 1 4.220 xx mm + −+= Đặt 20 x t = ( ) ( ) 2 220tmtm −+=
Giả sử phương trình ( ) có hai nghiệm 12 ; xx thỏa mãn đều kiện đề bài thì phương trình ( )** có hai nghiệm 12 ; tt thỏa: 1212 12.82.2828284 xxxx ttmm + ===== Thử lại phương trình ( ) ta có 4 m = thỏa mãn điều kiện.
Câu 163: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình 12 16.45440 xx mm −+−= có hai nghiệm đối nhau. Hỏi S có bao nhiêu phần tử? A. 2. B. 0. C. 1. D. 3. Lời giải Chọn B Ta có 12 16.45440 xx mm −+−= ( )2 2 4.45440 4 xx m m −+−= ( )1 . Đặt 4x
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
53 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
t = ( )0 t , phương trình có hai nghiệm 1x , 2x đối nhau 1212 0 12 4.4441 xxxx tt + ==== . Do đó ( )1 225440 4 m ttm−+−= phải có hai nghiệm dương phân biệt 1t , 2t th
= 0 0 1 S P = ( ) 2 2 2 45440 16 0 4 5441 m m m m −− −= 16291629 2929 0 3 m m m − = m . Vậy tập S
ử
ợ
m để phương trình 42.260 xx mm −−+= có hai nghiệm thực 12 , xx sao cho 12 3 xx . Tập hợp S có bao nhiêu phần tử? A. Vô số B. 3 C. 2 D. 1 Lời giải Chọn C Đặt 2x t = , 0 t ta được phương trình ( ) 2 2 6 2601 21 t tmtmm t + −−+== + . Ta có 12 3 12 32228 xx xx= . Phương trình ( )1 có hai nghiệm thỏa mãn 12 08 tt Đặt ( ) ( ) ( ) ( ) 2 2 2 6262 0 213 21 tt t t ftft t t t +− = + === =− + + Bảng biến thiên của ( )ft trên ( )0;8 :
ỏa 12 1 tt
không có phần t
Câu 164: Gọi S là tập h
p tất cả các giá trị nguyên của tham số
Từ bảng biến thiên ta thấy ( )1 có hai nghiệm 12 08 tt khi 70 2 17 m . Suy ra có hai giá trị nguyên của m là 3 m = và 4 m = . Câu 165: Giá trị thực của tham số m để phương trình ( ) 423.2640 xx m −++= có hai nghiệm thực 1x , 2x thỏa mãn ( )( ) 122224xx++= thuộc khoảng nào sau đây? A. 3 0; 2 . B. 3 ;0 2 . C. 2129 ; 22 . D. 1119 ; 22 m m m
. Lời giải Ch − −
n D Đặt 2x t = , điều kiện 0 t . Phương trình ban đầu trở thành ( ) ( ) 2 23.640*tmt−++= Để phương trình ban đầu có hai nghiệm thực 1x và 2x thì phương trình ( )* phải có hai nghiệm 1t , 2t dương 0 0 0 S P 13 2 m . Theo định lý Vi ét, ta có 12.64tt = 12 2.264 xx = 12 264 xx + = 12 6 xx += . Ta có ( )( ) 122224xx++= ( ) 1212 .2424xxxx +++= 12.8xx = . Từ 12 12
6 .8 xx xx += =
x x x x
1 2 1 2
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 19 2 13 2 3 2
54 2 4122470 230 mm m +− +

2 4 4 2
= = = = Khi đó, ta có 12 12 222023 xx ttm +=+==+ 17 2 m = Câu 166: Tìmtấtcảcácgiátrịthựccủathamsố m đểphươngtrình ( )( ) 322 2111 mm eexxxx +=+−+− có nghiệm. A. 1 0; e B. 1 0;ln2 2 C. 1 ;ln2 2 − D. 1 ln2; 2 +
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
ọ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
33 . mm eett +=+ Xét hàm số ( ) ( ) 32,310 fuuufuuu =+=+ do đó hàm số f đồng biến trên
Phương trình ( ) ( ) 33 mmmm eettfeftet +=+== .
Phương trình có nghiệm khi và chỉ khi 1202 mm ee − 1 ln2;ln2 2 mm − Câu 167: Tìm tất cả các giá trị thực của tham số m để phương trình 41.220 xx m có hai nghiệm 12 , xx thoả mãn 12 1 xx A. R m . B. 122;122mm . C. 122 m . D. 122 m . Lời giải Chọn D Đặt 2,0 x tt . Ta có phương trình 2 120tmt Phương trình đã cho có hai nghiệm 12 , xx khi phương trình có hai nghiệm 12,0tt . Khi đó 122122212 logloglog. xxtttt . Bài toán trở thành tìm m để phương trình có hai nghiệm dương phân biệt 12 , tt thoả mãn 212 log.1 tt
2 212
180 10 log1
m m tt 122 m
Câu 168: Cho hàm số yfx liên tục trên và có đồ thị như hình vẽ
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 55
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn C Điều kiện: 1;1 x− Đặt 2 1.xxt +−= Vì 1;11;2xt−− Ta có: ( ) 2 2 2222 1 11211. 2 t txxxxxx =+−=+−−= Phương trình đã cho trở thành:
Tập hợp tất cả các giá trị thực của m để phương trình 2 x fem có đúng 2 nghiệm thực là
A. 0;4 . B. 0;4 . C. 04; . D. 4; . Lời giải
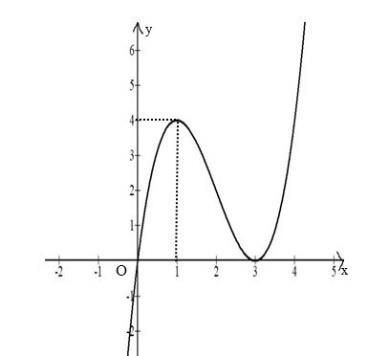
Chọn C Đặt 2 xte . Ta có 2 01xt , nếu 1 t thì 0 x và nếu 1 t thì ln xt . Phương trình trở thành phương trình
Sử dụng các nhận xét ở trên và đồ thị của hàm số ta có có đúng 2 nghiệm có đúng 1 nghiệm thuộc và nghiệm này lớn hơn 1.
Vậy tập hợp các giá trị nguyên của thỏa yêu cầu bài toán là
Câu 169: Tìm số giá trị nguyên của tham số để phương trình có đúng hai nghiệm phân biệt. A. B. C. D. Lời giải Chọn B Ta có: . Đặt , . Phương trình trở thành: . Phương trình có nghiệ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 56
Xét
ố
Ta
2
2
(
(
22 2
xx x m + ++−= 14 15 13 16 ( ) ( ) 22 22 2 1 101101 1011012.36 33 xx xx x mm + +− ++−=+= 2 101 3 x t + = 0 t 2 66 m tttm t +=−+= 2 1 ( ) 2 6 gttt =−+ ( ) 1;+ ( ) ( ) 2603gttgtt =−+==
m phân biệt phương trình có đúng nghiệm lớn hơn 1.
hàm s
: trên khoảng .
có: Bảng biến thiên:
1 x fem 2 ftm yfx 1
1; 0 4 m m m 04; ( )10;10 m−
)
)
1 1011012.3
Nhìn vào bảng biến thiên ta có: phương trình có đúng nghiệm lớn hơn 1 . Kết hợp điều kiện m nguyên và Có giá trị m thỏa yêu cầu đề
Câu 170: Tổng tất cả các giá trị
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
57 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
nguyên của để phương
có 3
ệm phân
ệt. A. B. C. D. Lời giải Chọn B Xét Dựa vào đồ thị: Câu 171: Cho số thực và hàm số có đồ thị như hình vẽ dưới đây. 1 5 m ( ) ( 10;1010;5mm−− 15 m ( ) 3 33323 3924.331 xmxxx xxxm −+−−+−++=+ 34 27 38 45 ( ) ( ) ( ) ( ) ( ) 3 3 3 33323 3 333 3 333 3 3333 3924.331 33273.331 33327331 3;3 132727.333 xmxxx xmxxx mxx baba xxxm xmx xmx axbmx baba −+−− −+−− +−++=+ +−++−=+ +−+−+=+ =−=− ++−=++=+ ( ) ( ) 32 3'3.ln330 tt fttftttR =+=+ ( ) ( ) ( ) 3 3 32 33 3392427 fafbabxmx mxxxxx ==−=− =−+=−+−+ ( ) ( ) ( ) 322 92427'318x24 '024 fxxxxfxx fxxx =−+−+=−+− === 7118,9,10. mm = m ( )yfx =
trình
nghi
bi
( ) 22
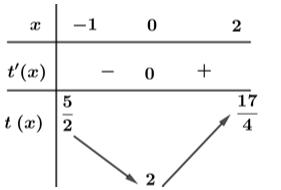
Phương trình có nhiều nhất bao nhiêu nghiệm phân biệt thuộc đoạn ?
A. . B. . C. . D. . Lời giải
Chọn B
Đặt , với
Hàm số liên tục trên và .
Bảng biến thiên:
Vậy với .
Với mỗi có 2 giá trị thỏa mãn .
Với mỗi có duy nhất 1 giá trị thỏa mãn
Xét phương trình với
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 58
Từ đồ thị trên ta thấy phương trình có số nghiệm nhiều nhất khi và chỉ khi phương trình có nghiệm , trong đó có . Do đó phương trình có nhiều nhất nghiệm phân biệt thuộc đoạn . xx fm += 1;2 2 3 4 5 ( ) 22xx ttx==+ 1;2 x − ( )ttx = 1;2 ( ) ( ) '2.ln22.ln2,'00 xx txtxx =−== 17 1;22; 4 xt − 5 2; 2 t x 22xx t =+ 517 2; 24 t x 22xx t =+ ( ) ftm = 17 2; 4 t ( ) 22xx fm += ( ) ftm = 2 12 , tt 12 5517 2;,; 224 tt ( ) 22xx fm += 3 1;2
Câu 172: Gọi là tổng các giá trị nguyên của tham số để phương trình
nghiệm . Chọn đáp án đúng. A. . B. . C. . D. . Lời giải
Chọn D Đặt thì phương trình đã cho trở thành với Khi đó phương trình có nghiệm có nghiệm , với
Ta có ; Bảng biến thiên: Dựa vào bảng biến thiên ta có: Vì nguyên nên . Suy ra .
Câu 173: Tập các giá trị của để phương trình có nghiệm là A. B. C. D. Lời giải Chọn D Điều kiện: . Đặt ; Phương trình trở thành: Đặt
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
59
có
S m 32 4726 xx mm + +=++
x 35 S =− 20 S = 25 S = 21 S =− 2x t = 22876 ttmm −+=+ 28 t 32 4726 xx mm + +=++ ( )
x ( ) 2 6 ftmm=+ ( )2;8 t ( ) 2 87
=−+ ( ) 28ftt =− ( ) ( )042;8ftt == 2 967 mm −+ 2 2 690 670 mm mm ++ +− 71 m m − 71 m − m 6;5;4;3;2;1;0 m−−−−−− ( ) 654321021 S =−++++++=− m ( ) 221111 422210 xx mm +−+−−+++= 9 ; 2 − 9 4; 2 ( );4− ) 4;+ 11 x − 2 112 x t +− = 1124 xt − 2 2 21 (2)210 2 tt tmtmm t −+ −+++== ( ) 22 2 2143()'()22 ftfttttt t t −+−+ ==
( )1;3
1;3
fttt
Phương trình có nghiệm có nghiệm
Câu 174: Cho hàm số , khi phương trình
có số nghiệm nhiều nhất thì giá trị nhỏ nhất của tham số có dạng Tính A. . B. . C. . D. . Lời giải Chọn C Đặt Khi đó Xét hàm số trên đoạn Ta có
2;4 t 4 m ( ) ( ) 47 31.2–63 xx fxxx =+++ ( ) 2 7469310fxxm−−+−= m a b Tab =+ 7 T = 11 T = 8 T = 13 T = ( ) 2 2 7469741313;7. txxx =−−=−−− ( ) 13. ftm =− ( ) ( ) 47 31263 tt fttt =++−+ 3;7. ( ) ( ) 477 3ln3212ln26; tttftt =+−+− ( ) ( ) ( ) ( ) 477722 3ln32ln22ln212ln2 ttttftt =−−++ ( ) ( )
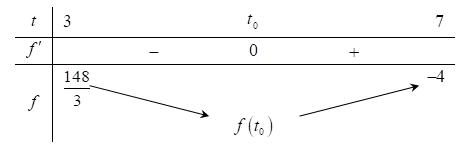

Suy ra hàm số đồng biến trên Lại có có nghiệm duy nhất thuộc
Dựa vào BBT, ta thấy phương trình có số nghiệm nhiều nhất
Suy ra giá trị nhỏ nhất của là nên .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
60
2 47 0,3;7 3ln321ln22ln20. tt t t =+−++ ( )ft ( ) 3;7. ( ) ( ) ( ) 30 0 70 f fx f = 0t ( ) 3;7. ( ) 13 ftm =− ( ) ( ) 0 0 1 5 134. 33 ft ftmm −− m 5 5 3 3 a b = ⎯⎯→ = 8 ab+=
Câu 175: Có bao nhiêu giá trị nguyên của tham số để phương trình có nghiệm thực? A. B. C. Vô số D. Lời giải Chọn B Ta có Đặt phương trình trở thành
Phương trình có nghiệm thực phương trình có nghiệm vì
Xét liên tục trên đoạn có
đồng biến trên đoạn .Có
Vậy phương trình có nghiệm thực Có 7 giá trị nguyên.
Câu 176: Cho hệ phương trình , là tham số. Gọi là tập các giá trị nguyên để hệ có một nghiệm duy nhất. Tập có bao nhiêu phần tử?
A. . B. . C. . D. . Lời giải
Chọn B
Điều kiện
Từ phương trình thứ nhất của hệ ta có .
Xét hàm số với Dễ thấy với mọi nên hàm số đồng biến trên
Do đó phương trình tương đương với . Thay vào phương trình thứ hai của hệ ta được Để hệ đã cho có nghiệm duy nhất thì phương trình phải có nghiệm duy nhất .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 61 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
m
5 7 3
( )1 3;9 t ( ) 2 311 11 22 tt mmt tt −+ ==−− 20 t − ( ) 1 1 2 ftt t =−− 3;9 ( ) ( ) ( ) 2 1 103;9 2 fttft t =+ 3;9 ( ) ( ) 55 31;9 7 ff== ( ) 221111 93.3210 xx mm +−+−−+++= 55 1; 7 m m 22 222 1 212.2.1 xyy xy xy my m S m 1 S 0 1 3 2 11;1yy 1 222 xyyxyy 2t yftt t 2.ln210 t y t yft 2 2 xyyxy 2 xy 1 22 412.2.13 yymy 3 1;1 y
( ) 221111 93.3210 xx mm +−+−−+++=
2 2211 0111112339 x xx +− −+− 2 113 x t +− = ( ) ( ) 2 3.2101tmtm−+++= ( ) 221111 93.3210 xx mm +−+−−+++=
t xx t
0 1;1 y 3 0022 0 412.2.1 2 1 12 2 2 2
yymy 415 20415111. 415
Giả sử là một nghiệm của thì . Khi đó nên cũng là nghiệm của . Suy ra . Thay vào ta được Thử lại: với thì viết thành Ta có , dấu bằng khi ; , dấu bằng khi Suy ra phương trình có nghiệm duy nhất là . Vậy thỏa mãn.
0000 2 222 00412.2.1412.2.1 yyyymymy 0y 3 000 0 yyy 0 y 3 0 m 0 m 3 22 1 412.2.12214 x xx x
+ −=+=== + 12 , xx 1220xx−= ( )* 12 , tt 2 12tt = ( ) 2 12
S P tt
0 0 0 1
= 08204. mm − 60 S = 1 210 2 Pmm=+− ( ) ( ) 12 12
62 .213 tt ttm += =+
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 62 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Câu 177: Chophươngtrình .Biếtphươngtrìnhcóhainghiệmphân biệt thỏa mãn . Khi đó thuộc khoảng nào sau đây? A. B. C. D. Lời giải Chọn A Đặt Phương trình trở thành: Do đó, phương trình đã cho có hai nghiệm phân biệt thỏa mãn khi và chỉ khi phương trình có hai nghiệm phân biệt dương thỏa mãn Tức là: +) +) luôn đúng. +) +) Theo Vi ét: 2 yyy y yy 42 VT 1 20 2 y y y 42 VP 0 y 4 0 y 0 m ( ) ( )( ) 4152141560 xx m +++−−= 12 , xx 1220xx−= m ( )3;5 ( )1;1 ( )1;3 ( );1−− ( ) ( ) ( ) 1 4150415 xx tt t +=−= ( ) 2 21 606210* m tttm t + +−=−++= ( ) ( ) ( ) 1 12 2
( )1 ( )3 ( )2 3 33 221212121.tmtmtm =+=+=+ ( )2 3 2 33 3
7 212 2121602 21314 mtm m mm m mktm
= += +++−= +=− =− ( ) 7 3;5. 2 m = S m 510254 xx m +=+ S 3 4 16 15 ( ) 510 510254 1 254
x xx x mm + +=+= + 0 m ( )1 0 m ( )2 2 510 (1)254 x x m + = + 5x t = 0 t ( )2 2 2 10 (2) 4 t m t + = + ( ) ( )2 2 10 4 t ft t + = + ( ) 0;+ ( ) ( ) 2 2 2
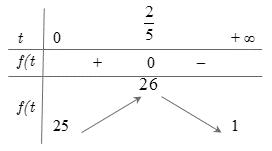
tl tt ftft ttm t
=− −−+ == = +
10() 2019280. ()0 . 2 () 4 5
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
63
Từ và suy ra: Thay vào ta được Vậy Câu 178: Gọi là tập hợp tất cả các giá trị nguyên của tham số để phương trình có nghiệm duy nhất. Số tập con của là A. B. C. D. Lời giải Chọn C . TH 1: . Phương trình vô nghiệm. TH 2: . Đặt , . Ta có: Xét hàm số trên khoảng Bảng biến thiên: ( ) ( ) ( )
( )1 ( )2
Đề phương trình có đúng một nghiệm Phương trình có đúng một nghiệm Do điều kiện Vậy , do đó số tập con của là
0 t
Câu 179: Tìm tập hợp tất cả các giá trị tham số để phương trình có 4 nghiệm phân biệt. A. . B. . C. . D. . Lời giải Chọn C
Xét phương trình: Đặt . Do đó, ta có . Điều kiện
. 125 m m = 0 2,3,4,5 m m m 2,3,4,5 S = S 4 216 = m 222122 4.2320 xxxx mm −+−+−+−= ( ) 1;+ ( ) ( ) ;12; −+ ( ) 2;+ ) 2;+ ( ) 22 1 2122 4.2320 xxxx mm −+−+−+−= ( )2 2 1 21 22 x xx t −+ == ( )2 21log xt −= ( )1 t ( )2 2 2320tmtm−+−= 1 t x 12 1 tt ( ) ( ) 2 2232 tmt −=− 3 2 t = 3 2, t ( ) 2 2 2 23 t m t = ( ) 2 2 23 t gt t = ( ) 3 1;\ 2 + ( ) ( ) 2 2 '264 23 tt gt t −+ = ( ) 1 '0 2 t gt t = = = 2 m
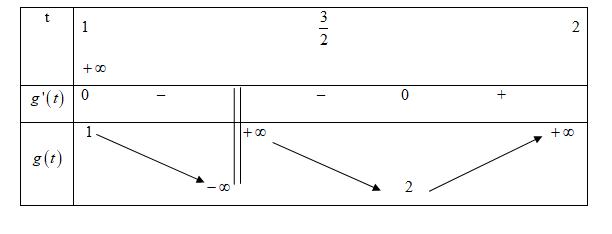
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
64 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
Ta có phương trình: trở thành: Ta nhận thấy mỗi giá trị cho hai giá trị tương ứng. Như vậy phương trình có 4 nghiệm phân biệt khi và chỉ khi phương trình có 2 nghiệm thỏa: . . Nhận xét: , không là nghiệm phương trình. Xét . Xét hàm trên ; Dựa vào bảng biến thiên, ta cần .
2 2
26
Câu 180: Cho phương trình: . Tập các giá trị để bất phương trình có ba nghiệm phân biệt có dạng . Tổng bằng: A. B. C. D. Lời giải
Chọn B
Ta có: Xét hàm số trên .
Ta có: Hàm số đồng biến trên
Mà .
Xét hàm số trên
Ta có: . . Bảng biến thiên: Phương trình có 3 nghiệm phân biệt phương trình có 3 nghiệm phân biệt .
Câu 181: Có bao nhiêu số nguyên để phương trình có đúng 3 nghiệm thực phân biệt? A. Vô số. B. . C. . D. . Lời giải
Chọn C
Ta có:
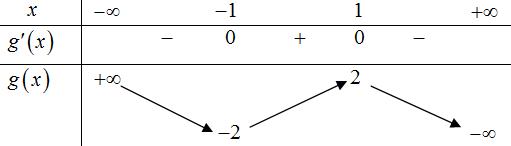
Đặt thì PT trở thành
Vậy bài toán trở thành tìm để phương trình có đúng 3 nghiệm thực phân biệt. Nhận thấy, nếu là một nghiệm của thì cũng là nghiệm của . Suy ra, điều kiện cần để phương trình có đúng 3 nghiệm thực phân biệt là có nghiệm
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
65
xxmxxxmxx +−+++−++−+−+=++−+=++ ( ) 2t ftt =+ ( ) 2ln210, t ftt =+ ( )ft ( ) ( ) ( ) 322322*22fxxxmfxxxxxmxx +−+=++−+=+ ( ) 33303**xxmmxx −+==−+ ( ) 3 3 gxxx =−+ ( ) 2 33gxx =−+ ( ) 01gxx == 32223 2230 xxxmxx xxm +−++−+−+= 2 2222 2 a mab b =− −+= = m ( ) 22 4 9.342133310 xx mxxm −+++++= 3 1 2 ( ) 22 4 9.342133.310 xx mxxm −+++++= ( ) ( ) 21 34133.310 x x mxm + −++++= ( ) 1 1 11 34133 33 x x mxm + + +=+++ 1 xt += ( ) 11 3433 33 t t mtm +=++ ( )* m ( )* o t ( )* o t ( )* ( )* ( )* 0 t =
32223 2230 xxxmxx xxm +−++−+−+= ( ) ; ab 2 ab + 1.2.4.0. ( ) 322322 232322 2230222* xxxmxxxxxmxx
+=++−=
3 m mmmm m =−
Thử lại: Với thì trở thành
.
Nhận thấy, , PT có nghiệm duy nhất nên không thỏa mãn.
Với thì trở thành
Xét hàm số với
Ta có, ; với mọi đồng biến trên có nhiều nhất 1 nghiệm có nhiều nhất 2 nghiệm .
Lại có, và Phương trình có 3 nghiệm là , Vậy thỏa mãn.
Câu 182: Có bao nhiêu giá trị nguyên của tham số để phương trình có đúng 3 nghiệm thực phân biệt? A. . B. C. D. . Lời giải Chọn C
Ta có phương trình .
( ) 2 2 1 11.3320 1 ln31 3ln30 3 3 t t ft t =++ 0 t ( )ft ( ) ( ) 0;0 ft += 0 t ( ) 0 ft = 0 t ( ) 10 f = ( ) 00 f = ( )** 0 t = 1 t = 1 m = 2019;2019 m 2121 20190 12 x xmxm xx 4038 2019. 2017. 4039 212121(2)1 2019020190 1212 xxxmxmxmx xxxx ++=++= +−+− 211121 201902019 1221 xxxx mm xxxx ++−==−− +−−+ 22 12113 212019'2019ln(2019)0;\1;2 (2)(1) xx x yyx xx xx =−−=−−−− −+ −+
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 66
=
(
t t
1
t
(
2
(
(
( ) ( )
Xét hàm số . Ta có bảng biến thiên 33 t t ftt=+−+ 0 t ( ) 3.ln3ln32 33 t t ft t =−− ( ) 2 2 3
2 m =− ( )*
) 12 343 33
t +=−
32 3 Cauchy t
VT =+
) 2 .32 3 VP −= 0 t =
m =− 1 m = ( )*
) 11 346 33 t t t +=+
) 12 3230 33 t t t +−+= ( )**
12 323
Vậy để phương trình có 3 nghiệm phân biệt thì mà .
Vậy ta có số nguyên cần tìm.
Câu 183: Gọi là tập hợp các giá trị của tham số sao cho hai phương trình và có nghiệm chung. Tính tổng các phần tử của .
A. B. . C. . D. . Lời giải
Chọn B
Vì hai phương trình đã cho có nghiệm chung nên hệ sau có nghiệm .
Xét hàm số xác định trên suy ra hàm đồng biến trên suy ra .
Xét hàm số xác định và liên tục trên
Ta có . Suy ra hàm số nghịch biến trên . Do đó có nhiều nhất là 3 nghiệm. Ta lại có . Suy ra phương trình Vậy Câu 184: Giá trị của tham số để phương trình có hai nghiệm thỏa mãn là A. B. C. D. Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
67
t Phương trình trở thành . Để phương trình ban đầu có 2 nghiệm thì phương trình phải có 2 nghiệm dương ;2 m 2019;2019; mm 2017 m S m 2 213m x += 2 321 x mxx=−+− S 6 3 1 5 2 ( ) ( ) 2 2 22 3 3 2 2 log21 213 log21321 321 321 m x x x mx x xxx mxx mxx =+ += +=−+− =−+− =−+− ( ) ( ) ( ) 2 3 log21 222 33 log212133log213 x xx xxxxx + +++=+++=+ ( ) 3t ftt =+ ( ) '3.ln310 t ft =+ ( ) 3t ftt =+ ( ) 22 3 log21213x xxx+=+= ( ) 2 213x gxx=+− ( ) ( ) ( ) 23 '43ln3''43ln3'''3ln30 xxx gxxgxgx=−=−=− ( ) '' gx ( ) 0 gx = ( ) ( ) ( ) 0120ggg=== 2 00 21311 22 x xm xxm xm == +=== == 3 S = m 1 4.220 xx mm + −+= 1, x 2x 12 3 xx+= 2 m = 3 m = 4 m = 1 m = 2, x t = 0. t 2 220tmtm−+= 2 020 0202. 020 mm Smm Pm −
Chọn C Đặ
Ta có
Kết luận
Câu 185: Tìm để phương trình có hai nghiệm trái dấu. A. B. C. D. Lời giải
Chọn D
Đặt , điều kiện:
Phương trình trở thành: Phương trình có 2 nghiệm phân biệt trái dấu có 2 nghiệm dương phân biệt thỏa mãn:
Phương trình có 2 nghiệm dương phân biệt .
Phương trình có một nghiệm lớn hơn và một nghiệm nhỏ hơn khi và chỉ khi .
Kết hợp các điều kiện thì ta được thỏa mãn yêu cầu bài toán.
Câu 186: Có bao nhiêu giá trị nguyên dương của tham số để phương trình có hai nghiệm phân biệt? A. . B. . C. . D. . Lời giải Chọn A
Phương trình tương đương Đặt , .
Phương trình trở thành ,
Phương trình đã cho có hai nghiệm phân biệt khi phương trình có hai nghiệm phân biệt dương. Vậy có 35 giá trị nguyên dương của tham số .
Câu 187: Gọi là tập hợp các số nguyên
ệm phân biệt. Hỏi tập có bao nhiêu phầ
phương trình
t
i
ả
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 68
= 1 1 ( )( ) 12110tt−− ( ) 1212 10 tttt −++ 210 m −+ 1 m 01 m m ( ) 1 92.63.40 + −+−= xxx m 35 38 34 33 ( ) 2 33 12.30 22 −+−= xx m 3 2 x t = 0 t ( ) 2 12.30 −+−=ttm 0 t '0390 39 030339 3 0120 m m Pmm m S − − m S m 12 4.235000 xx mm S 1 4 3 2
sao cho
có 2 nghi
n
ử A. B. C. D. Lờ
gi
i 1212 3 12123222.28.8284. xxxx xxttmm + +====== 4. m = m 1 420 xx m + −+= 0 m 1 m 11 m − 01 m 2x t = 0 t 2 20ttm−+= 1 420 xx m + −+= 2 20ttm−+= 12 , tt 12 1 tt 12 10 01 .0 m m ttm =−
Chọn C
Đặt khi đó phương trình trở thành: . Để có 2 nghiệm phân biệt khi và chỉ khi có 2 nghiệm dương phân biệt hay Vậy tập hợp các số nguyên là .
Câu 188: Tìm điều kiện của tham số để phương trình sau có nghiệm: Hãy chọn đáp án đúng nhất? A. . B. . C. . D. . Lời giải Chọn A
Đặt vì . Khi đó bài toán trở thành tìm điều kiện của tham số để phương trình có nghiệm trên đoạn Ta có . Vì không phải nghiệm của phương trình nên Xét Ta có thì phương trình bài ra có nghiệm.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 69
ủ
ng biến trên ℝ. 20 x tt 12 4.2350001 xx mm 222.350002tmtm 1 2 0 0 0 P S 22 2 35000 35000 20 mm m m 510510 101510151015 510 333 0 m mmm m m 13;14;15 S a ( ) 221111 92.3210. xx aa +−+−−+++= 64 4 7 a 64 2 9 a 50 3 3 a 50 1 3 a 2 113 x t +− = 2 01139 xt − a ( ) ( ) 2 2.210*tata−+++= 3;9 ( ) ( ) 2 *212 ttat −+=− 2 t = ( ) 2 21 * 2 tt a t −+ = ( ) ( ) ( ) 22 '' 214313;9 ;0 2233;9 t tttt ftftft tt t = −+−+ === = ( ) ( ) 6464 34;94 77ffa == m ( ) 2121 2 7720202020 2230 xxx x xmxm ++++ −+ −+++ 3. m − 21. m − 12. m − 2. m − ( ) ( ) ( ) 21212121 772020202071010.2171010.21* xxxxxx xxxx ++++++++ −+++++++ ()71010. t ftt =+
Câu 189: Điều kiện c
a để hệ bất phương trình có nghiệm là : A. B. C. D. Lời giải Chọn D Hàm số đồ
(
Suy ra :
Ycbt
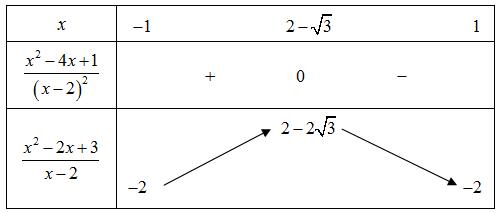
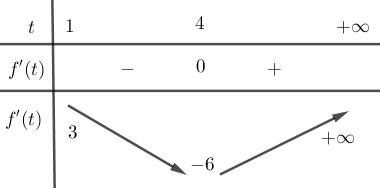
Từ bảng biến thiên ta có,
Câu 190: Cho phương trình Số giá trị nguyên của tham để phương trình đã cho có đúng hai nghiệm thực phân biệt là A. . B. . C. . D. . Lời giải Chọn C Đặt Khi đó phương trình đã cho trở thành Nghiệm cho một nghiệm Mỗi nghiệm cho hai nghiệm đối nhau. Do vậy phương trình đã cho có hai nghiệm thực phân biệt khi và chỉ khi phương trình có đúng một nghiệm , nghiệm còn lại phải nhỏ hơn 1. Xét hàm số . Bảng biến thiên
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
70
) ( ) ( )*2121 fxxfx ++++ 212111. xxxx ++++− ( ) 2 2 23 1;1: 2230. 2 xx xxmxmm x −+ −−+++ ( ) 2 23 1;1: ** 2 xx xm x −+ − ( ) **2. m − 22 1 162.410 xx m + −+= 10;10 m− 7 9 8 1 2 4,1 x tt= 2 810 ttm −+= 1 t = 0 x = 1 t x 1 t ( ) 2 810fttt=−+
Từ bảng biến thiên ta có phương trình có một nghiệm lớn hơn 1 khi . Suy ra số giá trị nguyên là 8.
Câu 191: Gọi là tập nghiệm của phương trình Có tất cả bao nhiêu giá trị nguyên của để tập hợp có hai phần tử? A. 2094. B. 2092. C. 2093. D. 2095. Lời giải.
Chọn A
Gọi là tập xác định của phương trình đã cho. Nếu thì nên . Nếu thì .
Xét hàm số có do đó phương trình có không quá 2 nghiệm. Mặt khác nên .
Lại có với , Nếu thì
Nếu thì có hai phần tử khi và chỉ khi
Vậy cóhaiphầntửkhivàchỉkhi .Sốcácgiátrịnguyêncủa thỏa mãn là
Câu 192: Gọi là tập tất cả các giá trị của để phương trình có đúng hai nghiệm phân biệt. Khi đó có A. tập con. B. Vô số tập con. C. tập con. D. tập con. Lời giải Chọn D Đặt , phương trình đã
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
71 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
cho trở thành . 3 6 m m =− 10;10 m− S ( ) ( )2 2230 x x xm −−= 2020;2020 m− S D 1 m 2 30 x mx − D = 1 m ( ) ) 23 loglog;Dm=+ ( ) ( ) ( ) ( ) ( ) 2 2 220 223 1 0 30 2 x x x x x xm m −= −−= −= ( ) 22 x fxx =− ( ) ( ) 2 2ln22;0 ln2 x fxfxx =−== ( ) 0 fx = ( ) ( ) 10;20ff== ( )1 1 2 x x = = 1 m ( ) ( ) 23g 2 lolog xm= 1 m 1;2 S = 1 m S ( ) 23 1loglog2981 mm S ( ) 1 * 981 m m 2020;2020 m− ( )* 1202018192094 +++−= S m 12 166.88.4.20 xxxx mm + −+−−= S 4 8 16 ( )2,0 x tt= ( ) 43226820*,0tttmtmt −+−−=
Phương trình đã cho có đúng hai nghiệm phân biệt khi và chỉ khi phương trình có đúng hai nghiệm dương phân biệt.
( )* ( ) ( ) ( ) ( ) ( ) 2 43222 2
Xét hai hàm số trên khoảng có đồ thị như sau
Dựa vào đồ thị hai hàm số này ta suy ra phương trình có đúng hai nghiệm dương phân biệt khi và chỉ khi hay có 4 phần tử
Vậy có tập con.
Câu 193: Tìm tập hợp các giá trị của tham số thực để phương trình có nghiệm thuộc khoảng . A. B. C. D. Lời giải Chọn C
Phương trình .
41 *6920 22 mtt ttttmtm mtt =− −+−++= =−+ ( ) ( ) 224;2 ftttgttt =−=−+ ( ) 0;+ ( )* 0;1;3;4 m−− S S 4 216 = m ( ) 6320 xx mm +−−= ( )0;1 3;4. 2;4. ( ) 2;4. ( ) 3;4. ( ) 63.2 6320 12
Xét hàm số liên tục trên .
xx xx x mmm + +−−== + ( ) 63.2 12
xx x fx + = + ( )0;1 ( ) ( ) ( ) 2 12ln36ln63.2ln2 '0,0;1. 12
xxx x fxx ++ = + ( ) 63.2 12
Ta có Suy ra hàm số đồng biến trên Do đó phương trình có nghiệm thuộc khoảng khi và chỉ khi , tức là
xx x fx + = + ( )0;1 ( ) 6320 xx mm +−−= ( )0;1 ( ) ( )01fmf 24. m
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
72
Câu 194: Tìm tập hợp các giá trị của tham số để phương trình: có hai nghiệm phân biệt thỏa mãn: A. . B. . C. . D. . Lời giải
Chọn A
m ( ) 2 22 loglog 2 323.330 xx mm −+++= 12 2 xx ( ) 1;\0−+ ( ) 0;+ \1;1 ( ) 1; −+ 0 x ( ) 2 22 loglog 2 323.330 xx mm −+++= ( )1 ( ) ( ) 22 2 loglog 2 323.330 xx mm −+++= 2log3 x t = ( )0 t 23 loglogxt = 3log2 t x = ( ) 222330tmtm−+++= +−+ + +
mm +=+ =+ 12.2xx 3132loglog 2.22 tt ( ) 312log. 22 tt ( ) 2 3 log3 22 m + ( ) 2 3 log31 m + 2 33 m + 2 0 m 0 m
)2 1 3 m m − − 1 m − ( ) 12 2 12
; tt 23 .3 ttm ttm
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
73 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
(
( )1 ( )2 12
0 0 0 S P ( ) ( ) ( ) 2 2 2 330 230 30
Điều kiện xác định: Ta có: Đặt: Khi đó: Phương trình có hai nghiệm phân biệt Phương trình có hai nghiệm phân biệt dương Theo hệ thức Vi et, ta có: Ta có: m m
Vậy .
1 0 m m − ( ) 55log x mxm
Câu 195: Cho phương trình . Có bao nhiêu giá trị nguyên trong khoảng để phương trình trên có nghiệm? A. . B. . C. . D. . Lời giải
Chọn B
Ta có phương trình với điều kiện Đặt thay vào phương trình ta có .
Từ và ta có hệ phương trình . Từ hệ phương trình ta suy ra
+=− m ( )20;20 15 19 14 17 ( ) 55log x mxm+=− 0 xm− ( ) 5log xmt −= 5t xm −= 5x mt+= 5(**) x tm −= 5 5 t x xm tm −= −= 55tx xt−=− 55 xtxt +=+ ( ) 5x fxx=+ ( ) 15.ln50 x fxx
Xét hàm số trên , ta có nên hàm số luôn đồng biến trên , do đó ta có thay vào phương trình ta có . Đặt ta có . Ta có . Ta có BBT với
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 74
Từ bảng biến thiên ta thấy phương trình có nghiệm khi hay . Ta suy ra có giá trị nguyên của thỏa mãn. Câu 196: Tổng tất cả các giá trị của tham số để phương trình có đúng 1 nghiệm là A. B. C. D. Lời giải Chọn D =+ ( ) 5x fxx=+ 55 xtxt+=+ ( ) ( ) fxftxt == 5x xm−= 5x xm−= ( ) 5x gxx=− ( ) 15.ln5 x gx =− ( ) 015.ln50 x gx =−= 1 5 ln5 x = 5 1 logln5 x = 55 111 loglogln5ln5ln5 g =− = 5x xm −= m 5 11 logln5ln5 m − 19 m m ( ) 22 2 452 46 2log1 ++− ++ =+ xxm xx m 2 1 4 0
Đặt , khi đó
Thế vào phương trình đã cho ta được phương trình sau
Vậy có đúng 1 nghiệm có đúng 1 nghiệm
Tổng tất cả các giá trị m bằng .
Câu 197: Tổng tất cả các giá trị của tham số để phương trình có đúng ba nghiệm phân biệt là: A. . B. . C. . D. . Lời giải Chọn B
ln22 3 ln23 xxxm xm xx −+−−+ −+ = −+ ( ) ( ) 2 22 232 3.ln233.ln22 xm xx xxxm −+
Phương trình tương đương .
( ) 3.ln,2 t fttt=
2322xxxm −+=−+ ( ) 2 2210gxxxxm =−−−+=

Xét hàm đặc trưng là hàm số đồng biến nên từ phương trình suy ra . Có và .
Xét các trường hợp sau:
TH1: ta có bảng biến thiên của như sau:
Phương trình chỉ có tối đa 2 nghiệm nên không có thoả mãn.
TH2: tương tự
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
75
−+ −+=−+
2
( )
2
TH3: , bảng biến thiên như sau:
2 45=++txx 1 t ( ) ( ) 2 22222ln12ln145 +=+=++=tmtmtmxxm ( ) 22 2 452 46 2log1 ++− ++ =+ xxm xx m 22450++−= xxm 2 10 =−= m 1 = m 0 m ( ) 2 2 212 23 3log22 xxxm xx xm −+−− −+ =−+ 2 3 1 0 ( ) ( ) 2 23(22) 2 == −+ ( ) 2 '0 0 xkhixm gx xkhixm = = = 0 m ( )gx m 2 m 02 m ( )
( )
2 42124 ' 212 xxmkhixmxkhixm gxgx xkhixm xmkhixm
−++−
gx
Phương trình có 3 nghiệm khi
Cả 3 giá trị trên đều thoả mãn, nên tổng của chúng bằng 3.

Câu 198: Có bao nhiêu giá trị nguyên của tham số trên đoạn để phương trình có nghiệm duy nhất. A. B. C. D. Lời giải
Chọn D
Điều kiện xác định
Phương trình tương đương với Đặt , ,
Phương trình đã cho viết lại thành +) Với thì ). +) Với có tương đương với , đồng biến và nghịch biến với Khi đó, đồng biến với .
Ta có Kết hợp, thì phương trình
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 76
có nghiệm duy nhất. ( )2 1 10 1 21023 2 21023 3 2 m m mmm mm m = −= −+=−= −+=− = a 10;10 ( ) ( ) ln1ln1 xax eexax + =++−+ 2 10 1 20 10 10 xa x ++ + ( ) ( ) ( ) ln1ln10 xax eexax + −−++−+= ( ) e xaxfxe + =− ( ) ( ) ( ) ln1ln1 gxxax =++−+ ( ) ( ) ( )Qxfxgx =− ( ) 0 Qx = 0 a = ( ) 0 Qx = 0 a 1 x − ( )fx ( )gx 1 x − ( )Qx 1 x − ( ) ( ) ( ) ( ) ( ) ( ) 111 1 limlimlnlimln1 11 limlimln 1 1 1 xaxxax xxx x a xx Qxeeeexaa xx a Qxe x e +++ ++ →−→−→− →+→+ ++ =−−=−−+=− ++ =−+=+ + ( ) 0 Qx =
+) Với có tương đương với , đồng biến và nghịch biến với .
Khi đó, nghịch biến với .
Ta có:
Kết hợp, suy ra có nghiệm duy nhất.
Do là số nguyên trên đoạn nên kết hợp 3 trường hợp trên thấy có 20 giá trị của thoả mãn điều kiện của bài.
Câu 199: Có bao nhiêu giá trị nguyên của tham số thuộc để phương trình có nghiệm?
A. . B. . C. . D. . Lời giải
Chọn A
Ta có
Xét hàm số với . Suy ra hàm số đồng biến trên .
Do đó
Xét hàm số
Bảng biên thiên
Từ bảng biên thiên suy ra phương trình có nghiệm khi và chỉ khi .
Mà nên
Vậy có 2019 giá trị nguyên của tham số thuộc để phương trình có nghiệm.
Câu 200: Có t
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 77
ất cả bao nhiêu giá trị thực của tham số sao cho phương trình có nghiệm nguyên duy nhất? A. . B. . C. . D. . 0 a 1 xa −− ( )gx ( )fx 1 xa −− ( )Qx 1 xa −− ( ) ( ) ( ) ( ) ( ) ( ) 111 1 limlimlnlimln1 11 limlimln 1 1 1 xaxxax xaxaxa x xx a Qxeeeexaa xx a Qxe x e +++ ++ →−−→−−→−− →+→+ ++ =−−=−−+=+ ++ =−+=− + ( ) 0 Qx = a 10;10 a m ( )2020;2020 ( ) ln22 x exmm =++ 2019 2020 2021 4039 ( ) ln22 x exmm =++ ( ) ln22 x exxmxm+=+++ ( ) ( ) ln2 ln2 xm x exexm + +=++ ( ) t ftet =+ t ( ) 10, t ftet =+ ( )ft ( ) ( ) ( ) ( ) ( ) *ln2ln222xx fxfxmxxmxmemex =+=++==− ( ) ( ) ( ) 100 xx gxexgxegxx =−=−== 1 21 2 mm ( ),2020;2020mm− 1;2;3;...;2019 m m ( )2020;2020 ( ) ln22 x exmm =++ 1;1 m− ( ) ( ) 2 22 2 1 loglog222 m xyxy + +=+− ( ) ; xy 3 2 1 0
Lời giải
Chọn B
Điều kiện: . Nhận xét: Vì có vai trò như nhau nên nếu phương trình có nghiệm thì cũng là một nghiệm của phương trình.
*) Điều kiện cần: Phương trình đã cho có nghiệm duy nhất
Thay vào phương trình ta được Vì . Lại có mà
*) Điều kiện đủ: Với thì phương trình đã cho trở thành
Suy ra phương trình đã cho có nghiệm duy nhất
Vậy có hai giá trị cần tìm là
Câu 201: Có bao nhiêu số nguyên để tồn tại số thực thỏa mãn ? A. B. C. D. vô số Lời giải Chọn B Đặt . Hệ có nghiệm đường thẳng và đường tròn có điểm chung . Do nên . Vì nên . Thử
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
78
lại: Với , hệ trở thành 22 0 10 xy xy + +− , xy
2
+
00421xx− ( ) ( )
22 22 002000 11 242log42log2log42 mm xxxxx ++ −−=− ( ) ( ) 00 0 0 2 4242 2 42 42 11 log1log2 log2 log1 xx x x m m + + 22121mm + 1;11mm−= 1 m = ( ) ( ) 22 22 loglog222 xyxy +=+− ( ) ( ) 22 22 1 222110 1 x xyxyxy y = +=+−−+−= = ( ) 1;1. m 1. m = y x ( ) ( ) 22 114 log3x4logyxy+=+ 3 2 1 ( ) ( ) 22 114 22 3x411 log3x4log 4 t t y yxyt xy += +=+= += :3x411t y += ( ) 22 :4t Cxy+= ( ) 11 2 1111 ,25log5 52 t t t dORt 22 4t xy+= 11 2 log5 221.9239767 t y y 1;0;1 y − 1 y =− 2 2 3x411 114 141218.11259.4 3 14 t t tttt t x −= + +=++= +=
( ) 00 ; xy ( ) 00 ; yx 00xy= ( ) ( )
2 020 1 log2log42 m xx
=−
( )
Nếu thì
Nếu . Vậy vô nghiệm.
Với thì hệ trở thành . - Với thì hệ trở thành
Xét hàm số , liên tục trên có nên phương trình luôn có nghiệm thuộc đoạn . Khi đó hiển nhiên sẽ tồn tại x thỏa mãn.
Vậy có 2 giá trị nguyên của thỏa mãn là .
Câu 202: Có bao nhiêu cặp số thực thỏa mãn đồng thời các điều kiện và A. . B. . C. . D. . Lời giải Chọn D
Ta có: Vì Với ta có: . Kết hợp với suy ra Thế vào ta được: Vậy các cặp số thực thỏa mãn là
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
79
ử là
nghi
m c
. Mệnh
0 t 2 114 4141 3 t tt + + ( ) 1214 012148114250 8.118.4 tt tttt tt t −+−+ 0 y = 11 2 log3 11 2 2 3x1112111 4log3 93 4 t t t t tx x = === = 1 y = 2 2 3x411 114 141218.11259.4 3 14 t t tttt t x += +=−+= += ()1218.11259.4 ttt ft =−+− 1 ;1 2 ( ) 1 10 2 ff ()0ft = 1 ;1 2 y 0,1yy== ( ) ; xy ( ) 2 3 23log5 4 35 xx y −+ = ( )2 4138? yyy−−++ 1 3 4 2 ( ) ( ) 22 3 23log523 43 3553.(*) xxxx yy −+−+ == ( ) 2 23 3 0 3351303. xx y yy −+ +− 3 y − ( ) ( ) ( ) 22 2 4138413830 yyyyyyyy −−++−+−+++ 30 y − 3 y − 3. y =− 3 y =− (*) 2 23 2 1 31230. 3 xx x xx x =− =−−= = ( ) ; xy ( ) ( ) 1;3;3;3. ( ) 00 ; xy ( ) ( ) 111 42sin21222sin21 xxxxx yy ++−+=++− 0 7 x 0 24 x − 0 47 x 0 52 x −−
Câu 203: Giả s
một
ệ
ủa phương trình
đề nào sau đây đúng? A. B. C. D.
Chọn B
Lời giải
( ) 1 2 12121 2 2 12121 2 121
xxxx xxxxx xxxxx xxx x
y yyy yyy yy
44.24.22.sin21440 22422sin214sin21cos210 222.22.2sin212sin214cos210 222sin214cos210 222sin2
−+−+−++= −+−+−++−++−= −+−+−++−++−= −++−++−= −+ ( ) ( ) 1 21
Ta có Vì .
x x
y y
Câu 204: Có bao nhiêu cặp số nguyên thỏa mãn và ? A. B. C. D. Lời giải Chọn A
+−= +−= ( ) ( ) 2121 cos210sin211 xx yy +−=+−= ( ) 21 sin21120 xx y +−== ( ) ( ) 21 0 sin2112422;4 xx yxx +−=−===− ( ) ; xy 04000 x ( ) ( )5 5 5252log14 y yxx +=++− 3 2 4 5 ( ) 5 log151 t xtx+==− ( ) ( ) 221 55251545251 ytytytyt +=−+−+=+− ( ) ( ) 55.ln510 uufuufu =+=+ ( ) ( ) ( ) 5 212121log1 fyftytytx =−=−+==+ 5 021log400102150;1;2 yyy ++= y x (;) xy , xy 1,2020 xy ( ) ( ) 32 221 248log236log23 yx xyxyxyxy yx + ++++−− +− 2017 4034 2 2017.2020
10 cos210
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
80 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
Đặt . Phương trình trở thành: . Xét hàm số nên hàm số luôn đồng biến. Vậy để Với mỗi nghiệm ta tìm được một nghiệm tương ứng. Câu 205: Có bao nhiêu bộ với nguyên và thỏa mãn ? A. B. C. D. Lời giải ( ) 111 42sin21222sin21 xxxxx yy ++−+=++− ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
Chọn B
Từ giả thiết kết hợp ĐKXĐ của bất phương trình ta có: ,.
Ta có:
Xét
+ Với thay vào ta được: và ).
Suy ra có 2017 bộ
+ Với thay vào ta thấy luôn đúng .
Suy ra có 2017 bộ . + Với Xét
Suy ra vô nghiệm và ). Vậy có 4034 bộ .
Câu 206: Cho x là số thực dương và y là số thực thỏa mãn . Giá trị của biểu thức bằng A. 2022. B. 2020. C. 2021. D. 2019. Lời giải Chọn C Áp dụng bất đẳng thức Cauchy ta có . Đặt thu được .
Dẫn đến Như vậy hai vế bằng
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
81 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
1 y = 32 221 3(4)log(3)log0 33 x xx x + +−− (;) xy 2 y = 4;2020 x (;) xy 3202020 yy − 333 22 g(y)logloglog0,3 222 yyyy y yyy ++ === +++ (;) xy 1 2 2log14(2)1 x x yy + =−−+ 22 2020 Pxyxy=+−+ 1 11 2.2,024 x x xxx xx + += 1,0ytt+= 232 14(2)114(3)31416(1)(2)16,0 yyttttttt −−+=−−=−++=−−+ 22 log14(2)1log164 yy −−+=
nhau khi dấu đẳng thức xảy ra tức là 12020;42020;,yxxyZ ( ) ( ) 32 221 248log236log23 yx xyxyxyxy yx + ++++−− +− ( ) ( ) 32 221 4(y2)log3(y2)log0 23 yx xx yx + +++−− +− 22 217 ()loglog20,4;2020 33 x fxx xx + ==+
t xxyPxyxy x x
1 1 1;020202021 0
= ====+−+= ( ) 2 222 3 log366321 y xxyxx −+=+−+− ( ) ; xy 02020;y x 5 6 7 4 ( ) ( ) 22 222222 33 log366321log322321 yy xxyxxxxyxx −+=+−+−−+=+−+− ( ) 2 222 3 1log22321 y xxyxx +−+=+−+− ( ) ( ) 2 222 3 log22223y xxxxy −++−+=+ ( ) 22 3 log22223z xxzxx−+=−+=
Câu 207: Cho phương trình . Hỏi có bao nhiêu cặp số và thỏa mãn phương trình đã cho? A. B. C. D. Lời giải Chọn D Đặt thì trở thành: Xét hàm số . Suy ra hàm số đồng biến trên . . Thay trở lại cách đặt ta có: . Xét hàm số: . . Bảng biến thiên: Suy ra: Do .
22 2 2 33 zyzy+=+ ( ) ( ) 33ln310, t ttfttft =+=+ ( )ft ( ) ( ) 22 fzfyzy == ( ) 2 222 3 log22223y xxyxx −+=−+= ( ) ( ) ( ) 2 22, 0;202022 =−+=− gxxxxgxx ( ) 01 ==gxx ( ) 2 2 3 140763621340763620log4076362 y gxy y 3 0log40763623,7 y 0;1;2;3 y
Page 82
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
( ) ( ) ( ) ( ) 4 9
1 3 3 3
.
Dựa vào bảng biến thiên của hàm số ta thấy mỗi phương trình trên có một nghiệm
Vậy có 4 cặp số thỏa mãn đề bài.
Câu 208: Có bao nhiêu cặp số nguyên thỏa mãn và ? A. . B. . C. . D. . Lời giải
Chọn D
Đặt . Suy ra , .
gx gx gx gx ( )gx 02020 x ( ) ; xy ( ) ; xy 22021 x ( )1 2 2log22 yyxxy−+=− 2020 9 2019 10 ( )1 2 log2y xt += 1 22 yt x += 1 22ty x =− ( )1 22222.22.2 ytyyt tyyt −=−−+=+ ( ) 2.2x gxx =+ ( ) 2.2ln210,
Phương trình đã cho trở thành: . Xét hàm số có nên hàm số luôn đồng biến.
Khi đó hay Suy ra Mà nên hay . Lại có là số nguyên nên tức 10 giá trị thỏa mãn.
Xét biểu thức , mỗi giá trị nguyên của cho tương ứng 1 giá trị nguyên của nên có 10 cặp số nguyên thỏa mãn yêu cầu đề bài.
Câu 209: Có bao nhiêu cặp số nguyên dương thảo mãn , với ? A. . B. . C. . D. . Lời giải Chọn D Ta có Ta thấy . Vì .
= = = = x gxx =+ ( )ygx = 2.22.2 ytytyt +=+= ( )1 2 log2y yx=+ 111 22222 yyyyyxx +==−= 22021 x 1 2 22202111log2021 y y − ( ) 2 2log20211 y + y 2,3,...,11 y 1 2y x = y x ( ) , xy ( ) ; xy ( ) ( ) 2333113 xyxyxxx + −−=+− 2020 x 13 15 6 7 ( ) ( ) ( ) ( ) ( )( ) 2322 33113331313130 xyxyyxxxy xxxxxxxx + −−=+−−−=−−−−−= ( )( ) 22 3 310,0313032log3 xxyyk xxxxxyxx −−−−−==== 6 202032020330;1;2;3;4;5;6 kk xk = , ab 3332.10.10, zzxyab ,, xyz log xyz 22 log1. xyz 22 11 ab
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 83
Câu 210: Biết là các số thực sao cho đồng thời là các số các số thực dương thỏa mãn và Giá trị của thuộc khoảng
A. . B. . C. . D. . Lời giải
Chọn D
(1;2) (2;3) (3;4) (4;5) 22 22 221
Ta có: Khi đó Đồng nhất hệ số ta được
Câu 211: Có bao nhiêu cặp số nguyên thỏa mãn và . A. B. . C. . D. . Lời giải
Chọn C
xyz xy xyxy xyz xy 3332 .10.10zzxyab 32 22 .10.10 zzxyxxyyab 2222322 .... xyxxyyaxybxyxxyyaxybxy 2222222222 .22. 1010 bb xxyyaxxyyxyxyxyaxyaxy 1 1 10 2 15 21 b a a b a 22 11144,0084;5. 225 ab ( ) ; xy 02020 y 3 33369log x xyy+−=+ 2020 9 7 8 (
z zz
Ta có: . Xét hàm số: .
log 10 10 log1 1010.10 ) ( ) ( ) 32log 3 333 3369log33293log33233log* y xxx xyyxyyxy + +−=++−=++−=+ ( ) ( )332 t ftt=+− ( ) 3.ln330, t ftt =+ ( )yft = ( ) ( ) ( ) 2 33 *2log2log3x fxfyxyy =+=+= 02020 y , xy 2 3 13202022log20202;3;4;5;6;7;8 x xx + x y ( ) ; xy ( ) ; xy 0;2020xyx +− ( ) 22 2 log2230 xyxyxyxy ++++−−= 20xy+
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 84
Ta có: . Suy ra hàm số đồng biến trên Khi đó: Do và nguyên nên: Ứng với mỗi giá trị có một giá trị của nên có 7 cặp số nguyên thỏa mãn yêu cầu bài toán. Câu 212: Có bao nhiêu cặp số nguyên thoả mãn và ? A. 19. B. 6 C. 10. D. 41. Lờigiải Chọn C + Điều kiện:
+ Ta có: nên
0 xy+ ( ) ( )( ) ( ) ( ) ( ) ( )
22 2 22 2 2222 22 2222 22
log2230 2 log230 log23log230 log2323log(1)
Xét hàm số: , ta có: nên hàm số đồng biến trên .
++++−−= ++ +++−−= + ++−++++−−= +++++=+++ ( ) 2log fttt =+ 1 '100; ln2 ftt t ( )ft ( ) 0; + ( ) ( ) (
Do đó: vì nên
+ Do suy ra
+ Do nên , với mỗi giá trị cho ta 1 giá trị thoả mãn YCBT.
Vậy có 10 cặp số nguyên thoả mãn YCBT.
Câu 213: Có bao nhiêu cặp số nguyên dương với thỏa mãn A. . B. . C. . D. . Lời giải Chọn C
Đặt , ta được
xyxyxyxy xyxy xyxyxy xy xyxyxyxyxyxy xyxyxyxyxyxy ) 2222 12323fxyxyfxyxyxyxy ++=+++=+ ( )( ) 21012 xyxyxy ++−==− 0 xy 10xyy 2020 x − 19 1 2 y y 9;8;...;1;0 y y x ( ) ; xy ( ) ; xy 2020 x ( ) ( ) ( ) 3 23319log21 y xyx −=+−− 1010 2020 3 4 ( ) 3 log21231 t xtx−==+ ( ) ( ) 22 33123133.33.32 tytyytty +−=+−+=+ ( ) ( ) 3.33.3ln310, uu fuufuu =+=+ ( )fu 2 ty= 2 231921 yy xx =+=− 9 202094039log4039 y xy y 1;2;3 y y x ( ) ; xy
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
85 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
Xét hàm số đồng biến trên . Do đó , vậy nên . Vì . Vì nguyên dương nên . Ta thấy với mỗi giá trị nguyên của thì tìm được 1 giá trị nguyên của . Vậy có 3 cặp thỏa mãn.



CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 1 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 5. PHƯƠNG TRÌNH –MŨ –LOGARIT MỨC ĐỘ VẬN DỤNG VẬN DUNG CAO Câu 214: Có tất cả bao nhiêu giá trị của tham số m để phương trình 22 33 log(2)log(1)62 xxmxmm +=−−+−+ có hai nghiệm trái dấu? A. 4 B. 3 C. vô số D. 5 Lời giải Chọn D Phương trình đã cho tương đương: 22 2 (1)622 x xmxmmx − −−+−+=+ ( ) 22 2 60* x xmxmm − −+−= Yêu cầu đề bài khi và chỉ khi phương trình ( )* có hai nghiệm 12 , xx thỏa 1220xx− ( )( ) ( ) 2 1212 2 121212 .0.06006 2202402 440 xxxx mmm xxxxxx m mm − +++++ −+ . Vì m nên 1;3;4;5 m Suy ra có 4 giá trị của tham số m thoả mãn điều kiện bài toán. Câu 215: Phương trình ( ) 22 9.log920 xxx −+−= có bao nhiêu nghiệm? A. 1. B. 4. C. 3. D. 2. Lời giải Chọn D Điều kiện: 2 2 9033 1103 920110110 x x x x xx − − − −+ +− . Ta có ( ) ( ) 2 22 2 2 3 903 9.log9202 log9209214 x x x xxxx xx xx x = = −= −+−==− +−= +−= = Kết hợp với điều kiện suy ra phương trình có 2 nghiệm 2;3xx=−= Câu 216: Có bao nhiêu số nguyên 10;10 m− để phương trình ( ) 2 12log0mxx−−= có hai nghiệm thực phân biệt? CHƯƠNG II HÀM SỐ LŨY THỪA - HÀM SỐ MŨ – HÀM SỐ LOGARIT
. Dễ thấy, phương trình ( )1 luôn có nghiệm 4 x = . Do đó để phương trình ( )1 có hai nghiệm phân biệt thì phương trình ( )2 phải có nghiệm duy nhất thỏa 04 x Bảng biến thiên của hàm số 1 y x = Từ bảng biến thiên ta thấy phương trình ( )2 có nghiệm duy nhất thỏa 04 x khi và chỉ khi 1 4 m . Kết hợp với điều kiện đầu bài, ta có 1 10 4 m . Do 1,2,3,4,5,6,7,8,9,10 mm Vậy có 10 giá trị thỏa mãn điề
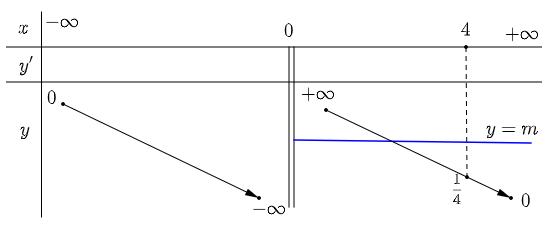
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 2
A. 20. B. 10. C. 9. D.
. Lờ
ải Chọn B Điều kiện: 2 0 0 04 2log0 4 x x x x x − Ta
2 2 1 10
12log0(1) 2log0
mx m mxx x x x −= = −−=
u kiện đầu bài. Câu 217: Biết rằng điềukiện cần và đủ của thamsố m đểphươngtrình ( ) 3 log32 x mmx ++= cónghiệm là a m b − với , ab là hai số nguyên dương và 7 b . Hỏi 2 2abb ++ bằng bao nhiêu? A. 31. B. 32. C. 22. D. 23. Lời giải Chọn C ( ) ( ) 3 2 30 log32 33* x x xx m mmx mm + ++= ++= . ( ) ( ) ( )2 *3333 xxxx mm +++=+
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
11
i gi
có ( )
(2)
4
−= =
Xét hàm số ( ) ( ) 2 0 ftttt=+ . Ta có ( ) 210ftt =+ với mọi 0 t , suy ra hàm số luôn đồng biến với mọi 0 t . ( ) ( ) ( ) ( ) ( ) 2 *333333** xxxxxx fmfmm +=+==+ Đặt ( )30 x tt= , khi đó phương trình ( )** trở thành ( ) 2 *** ttm −=
Xét hàm ( ) ( ) 2 0 gtttt=− , ta có ( ) ( ) 1 210 2 gttgtt =−== . Bảng biến thiên Vậy để ( )*** có nghiệm 0 t thì
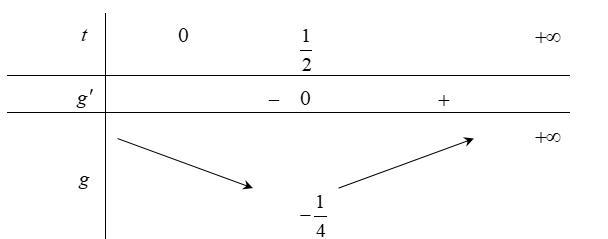
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 3
++= =
ấ
ả
. C. 1 2 m . D. 1 0 2 m . Lời giải Chọn A ( ) ( ) ( ) 202 ln2ln 212 x x xmx mx xmx − −= −=− −= . Phương trình ( ) ( ) ln2lnxmx −= có nghiệm phương trình ( ) 12mx−=− có nghiệm 2 x . Xét phương trình ( ) 12mx−=− Nếu 1 m = , vô nghiệm. Nếu 1 m , 2 1 x m =− có nghiệm 2 x 21 210001 111 m m mmm −+ Vậy 01 m thỏa mãn yêu cầu bài toán.
1 4 m − 2 1 222 4 a abb b =
Câu 218: Tìm t
t c
các giá trị của tham số m để phương trình ( ) ( ) ln2lnxmx −= có nghiệm A. 01 m . B. 1 m
Câu 219: Có bao nhiêu cặp số nguyên dương ( ) , xy thỏa mãn điều kiện ( ) log31. y x +
A. 8. B. 9. C. 10. D. 11. Lời giải
Chọn A
x x + + 3 10303100log10 yyxy − 1,2 yy + .
Với 1 y = thì 071,2,3,4,5,6,7 xx
Với 2 y
thì
y y
Bất phương trình đã cho tương đương với 30 310
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 4
Chọn A Điều kiện
xx xx − − . ( ) 2 21 22 2 3,1 log(1)42log(3)log1log32 xx xx xx −=+− −+−= ( ) ( ) 2 3,13,1 log132134 xxxx xxxx −−=−−= ( )( ) ( )( ) ( )( ) ( ) 2 2 3,13,1 3,1 134470 134 134410 xx xx xx xx xxvn xx xx xx −−= −+= −−= −−=− −−= 3,1 2525 25 xx x x x =− =− =+ Vậy phương trình có 1 nghiệm. Câu 221: Cho hai số thực a , b lớn hơn 1 thỏa mãn 2020 ab+= . Gọi m , n là hai nghiệm của phương trình ( )( ) loglog2log20 aba xxx−−= . Giá trị nhỏ nhất của biểu thức 4 mna + là A. 8076 B. 8077 C. 8078 D. 8079 Lời giải Chọn A
=
011 xx = Vậy có 8cặp số nguyên dương ( ) , xy thỏa mãn đề bài. Câu 220: Số nghiệm của phương trình 2 21 2 log(1)42log(3) xx −=+− là A. 1. B. 2. C. 3. D. 4. Lời giải
của phương trình 101 303
Ta xét phương trình ( )( ) 2 1 loglog2log20log2log20.(1) log abaaa a
xxxxx b −−=−−=
Do a , 1 b nên 1 0 loga b nên luôn có hai nghiệm.
Với m , n là nghiệm của phương trình, ta có 22 loglog2loglog()log. aaaaa mnbmnbmnb +===
Xét 2222 444(2020)48080(2)80768076. mnababbbbb +=+=+−=−+=−+ Như vậy giá trị nhỏ nhất của 4 mna + là 8076. Dấu bằng xảy ra khi 2018 a = và 2 b = Câu 222: Số nghiệm của phương trình ( ) ( ) ( ) 222 236 log1log1log1 xxxxxx −−++−=+− là A. 1 B. 0 C. 2 D. 3 Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 5
2 2 2
− −− +−
Ta
1 x = là nghiệm của phương
Với 1 x 2 110xx −+− . Vậy phương trình đã cho
Câu
phươngtrình ( ) ( ) ( ) 2 3 33 3 2log1log21log1 +=−++ xxx Tổng
ệmcủa
là A. 1. B. 2. C. 3. D. 4. Lời giải Chọn C
Chọn A Điều kiện:
10 101 10 x xxx xx
. Ta có: ( ) ( ) ( ) 222 236 log1log1log1 xxxxxx −−++−=+− ( ) ( ) ( ) 22 22 2 2 22 log1log1 log1log3log6 xxxx xx +−+− −+−+= ( ) 2 2 22 l1 log110 log3log6 xx +−−+−= ( ) 2 2 log10 xx +−= 2211110xxxx +−=−+−=
có:
trình.
có 1 nghiệm.
223: Cho
cácnghi
phươngtrình
là phương trình ( )* có đúng một nghiệm dương y . TH 1: Phương trình ( )* có 2 nghiệm trái dấu ( ) 2 201;2xxx −−− . TH 2: Phương trình ( )* có nghiệm 12 '20 0 20 x yy Sx =+= =
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 6 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ĐK 1 1 2 − x x . ( ) ( ) ( ) 2 3 33 3 2log1log21log1 +=−++ xxx ( ) ( ) 3 333 2log12log212log1 +=−++ xxx ( ) ( ) ( ) 33 33 log1log21.1121.1 +=−++=−+ xxxxxx . Nếu 1 1; 2 − x phương trình ( ) ( ) 332 0 121.1200 1 = +=−++++== =− x xxxxxxx x Nếu 1 ; 2 + x phương trình ( ) ( ) 332 1 121.1220 2 = +=−+−−+= = x xxxxxx
vô nghiệm. TH 3: Phương trình ( )* có 2 nghiệm thỏa 2 12 20 02 20 xx yyx Sx −−= == = . Vậy 0;1;2 x thỏa mãn đề bài. Câu 225: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m với 2021 m để phương trình ( ) ( ) 15 5 loglog20 xmx ++−= có nghiệm. Tập hợp S có tất cả bao nhiêu phần tử? A. 2020. B. 2023. C. 2022. D. 2021. Lời giải Chọn C
0984164935
x Vậy tổng nghiệm của phương trình là 3 Câu 224: Có bao nhiêu số nguyên x sao cho tồn tại duy nhất số thực y thỏa mãn ( ) 2 3 3 log22logxxyxy++−= ? A. 5 B. 3 C. 4 D. 2 Lời giải Chọn B Ta có ( ) ( ) 22 2 3 3 220* log22log 0 yxyxx xxyxy y −−−+= ++−= . Bài toán tương đương
=
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 7 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Điều kiện của phương trình là 2 xm x − khi đó ta có ( ) ( ) ( ) ( ) 1555 5 2 loglog20loglog22m xmxxmxx ++−=+=−= 2 22242 2 m mmmm −−−− . Vì 2021 m m nên tập 1,0,...,2020 S =− Tập hợp S có tất cả 2022 phần tử Câu 226: Tìm tất cả các giá trị thực của tham số m để phương trình ( ) ( ) 2 20221 2022 log1log240 xxm −++−= có hai nghiệm thực phân biệt. A. 321 . 28 m B. 521 . 28 m C. 521 . 28 m D. 521 . 28 m Lời giải Chọn A Phương trình tương đương: ( ) ( ) 2 2 20222022 2 10 log1log24 241 x xxm xmx − −=+− +−=− 2 11 25 x mxx − =−−+ Vậy phương trình 2 25 mxx=−−+ có hai nghiệm thực phân biệt trên ( )1;1 khi 21321 32 428 mm . Câu 227: Cho phương trình ( ) ( ) 2 22 log1log3250 +−−−+= xxxm . Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình đã cho có 2 nghiệm phân biệt? A. 8. B. 5. C. 4. D. 3. Lời giải
với , mn là các số nguyên dương và phân số m n tối giản. Tổng mn + bằng A. 11. B. 10. C. 12. D. 9. Lời giải Chọn A Ta có ( ) ( ) ( ) ( ) ( ) 22 2 22
log16log8 log16log8 loglog2 xx
xx xx xx == ( )( ) ( ) 22222 1 4log1loglog3loglog2 4 xxxxxx ++=+=−= . Vậy ( ) 1 4
1 log16log4log10 x x == , khi đó 1;1011mnmn ==+= . Câu 229: Cho phương trình ( ) 2 933 loglog61logxxm −−=− ( m là tham số thực). Có tất cả bao nhiêu giá trị nguyên của m để phương trình đã cho có nghiệm? A. 5 B. 7 C. 6 D. Vô số Lời giải Chọn A Ta có ( ) 2 933 loglog61logxxm −−=− , điều kiện 1 6 0
x m
Pt 33 11 loglog6161 xx xmxm == Xét ( ) 1 , 616 x fxx x = có ( ) ( )2 1 ' 61 fx x =
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 8 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Chọn C Ta có phương trình đã cho tương đương ( ) ( ) 2 22 22 11 log1log325 13254420(1) −− +=−−+ +=−−+−+−= xx xxxm xxxmxxm Phương trình đã cho có 2 nghiệm phân biệt khi và chỉ khi phương trình ( )1 có 2 nghiệm phân biệt lớn hơn 1 ( ) 0 209 10 920 22 110 − − − m S m m f Vậy có 4 giá trị nguyên của m thỏa mãn bài toán. Câu 228: Cho số thực dương 1 1, 2 xxx thoả mãn ( ) ( ) 2 log16log8 xx xx = . Giá trị ( ) log16 x x bằng log m n
Bảng biến thiên Phương trình có nghiệm 11 6 6 m m Kết hợp điều kiện 0; mm nên có 5 giá trị nguyên của m để phương trình có nghiệm.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
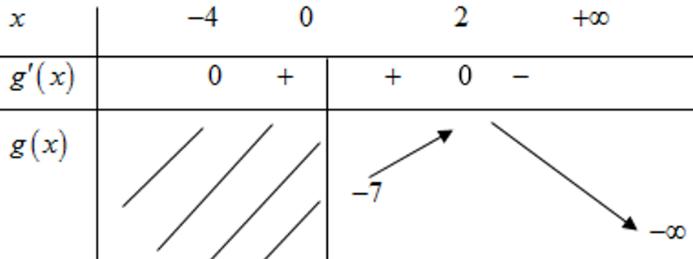
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 9
1 xx gx x −+− = + với 0 x ; ( ) ( ) 2 2 28 1 xx gx x −−+ = + ( ) 2 2 0280 4 x gxxx x = =−−+= =− , ( ) 23 g =− Từ BBT, nhận thấy phương trình 2 7 1 xx m x −+− = + có 1 nghiệm dương khi và chỉ khi 7 3 m m − =− Vậy số giá trị nguyên m thuộc 10;9 là 10;9;8;7;3 m−−−−−
Câu 230: Cho phương trình ( ) 2 5252 log7log0 xmxmx +− ++++= . Số giá trị nguyên m thuộc 10;9 để phương trình có nghiệm duy nhất là A. 3. B. 5. C. 4. D. 2. Lời giải Chọn B ( ) ( ) ( ) 1 22 525252 52 log7log0log7log0 xmxmxxmxmx +−+ + ++++=++++= ( ) ( ) ( ) ( ) 22 52525252 log7log0log7log xmxmxxmxmx ++++ +++−=+++= 2 2 7 7 1 0 0 xx xmxmx m x x x −+− +++= = + . Xét ( ) 2 7
trình đã cho có đúng 2 nghiệm phân biệt ? A. 1. B. 8. C. 4. D. 6.
u kiện của phương trình:
x m
10
4
m
4
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
ỳnh
ễn
Page 10
để
Điều kiện 3 2 33 3 00 001 log2log0log299 log01 x x x x x x x xx xx − Khi đó ta có 2 33 2 0202 log2log x xx m mm xx =−== ( ) ( ) 01 9 1;2 512; x x m m ⎯⎯⎯→ + mà m là số nguyên thuộc đoạn 2021;2021 nên có 1509 giá trị của m thỏ
Giáo viên: Hu
Văn Ánh 42 Nguy
Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 231: Có bao nhiêu số nguyên
2021;2021 m−
phương trình 2 33 2 0 log2log x m xx = có nghiệm? A. 1510. B. Vô số. C. 1512 D. 1509. Lời giải Chọn D
a mãn yêu cầu đề bài. Câu 232: Cho phương trình ( ) 222 31 3 3 log1log.log10 4 m xxx −++−= với m là tham số. Có bao nhiêu giá trị nguyên của m để phương
Lời giải Chọn C Điề
2
0
x 11 0
x
x ( ) 222 31 3 3 log1log.log10 4 m xxx −++−= ( ) ( ) 222 313 3 log1log.log10 4 m xxx −++−= 2 3 2 2 2 33 11,011,0411,0 44 log1000 log1log1444 44 m m xx m xx xx x x x m m xx mxx xx Phương trình đã cho có đúng 2 nghiệm phân biệt khi đường thẳng ym cắt parabol 2 444yxx tại 1 điểm phân biệt có hoành độ thuộc khoảng 1;1 khác 0 Xét hàm số 2 444,1;1,yxxx có 1 '210 2 yxx Bảng biến thiên
Từ đó suy ra bài toán được thỏa mãn khi 5 44,01 m mx + 1,2,3mmm thỏa mãn điều kiện 0 4 m x . Vậy có 4 giá trị của m . Câu 233: Cho phương trình 3 2 22 loglog0 4 x x xem −−= . Gọi S là tập hợp giá trị m nguyên với
10;10 m− để phương trình có đúng 2 nghiệm. Tổng giá trị các phần tử của S bằng A. 28 B. 3 C. 27 D. 12 Lời giải Chọn C Điều kiện: 0 x x em Ta có: 3 2 22 loglog0 4 x x xem −−= ( )1 3 2 22 loglog0 4 0 x x x em −= −= +) 3 2 22 loglog0 4 x x
11
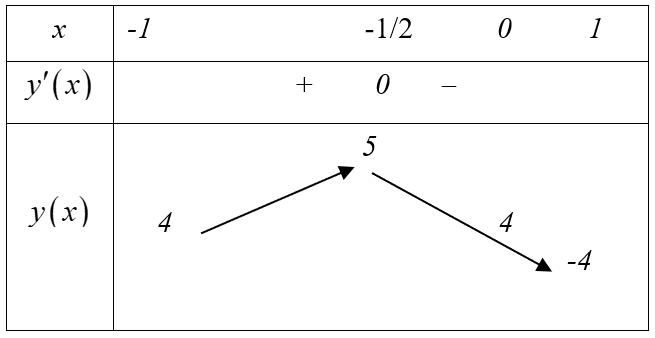
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
−= 2 22
xx −+= 2 2
= =
x x = = +) 0 x em−= x em= . Xét 3 trường hợp: +) Trường hợp
m
u kiện c
2 x =
x = +)
2
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 x =
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
log3log20
log1 log2 x x
2 4
1: 0
, điề
ủa phương trình là 0 x , phương trình ( )1 có 2 nghiệm là
và 4
Trường hợp 2: 01 m , điều kiện của phương trình là 0 x Khi đó, phương trình x em = có 1 nghiệm là ln0xm= nên phương trình ( )1 có 2 nghiệm là
x = và 4
+) Trường hợp 3: 1 m , điều kiện của phương trình là ln xm
Nên phương trình ( )1 có 2 nghiệm phân biệt 2ln4 m 24 eme .
Khi đó phương trình đã cho có 2 nghiệm là ln xm = và 4 x =
Suy ra, các giá trị m để phương trình có 2 nghiệm là 1 m và 24 eme . Do đó các giá trị nguyên 10;10 m− thỏa mãn yêu cầu bài toán là 10;9;8;7;6;5;4;3;2;1;0;1;8;9;10 S =−−−−−−−−−− . Vậy tổng giá trị các phần tử của S là 27 Câu 234: Số nghiệm của phương trình ( ) ( ) ( ) 222 236 log1log1log1
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
12
là
B.
Lờ
Chọ
u kiện 1 x . Câu 235: Cho phương trình ( ) 2 33 2loglog150 x xxm −−−= Có tất cả bao nhiêu giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt? A. 125. B. 123. C. 122. D. 124. Lời giải Chọn B Điều kiện 00 505 xx xx mm − .
xxxxxx −−++−=+−
A. 1
0 C. 2 D. 3
i giải
n B Điều kiện: 1. x Ta có: ( )( ) 22111xxxx −−+−= nên ( ) ( ) ( ) 222 236 log1log1log1 xxxxxx −−++−=+− ( ) ( ) ( ) 222 326 log1log1log1,(1) xxxxxx +−−+−=+− Đặt ( ) 2 3 log1txx =+− , phương trình trở thành: 2626 log3log3(1log3log3)00 tt ttt −=−−== 2 11 xx +−= : Phương trình này không có nghiệm x thỏa điề
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 13 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) 2 33 2 33 0,50 2loglog15050 2loglog10 x x x xm xxm m xx − −−−= −= −−= 5 1 2 3 3 0,50 0,50 log 50 1 log3 2 3 log1 x x x xm xm xm m xx x x − − = −= == = = + Khi 2 1log10mx=== vậy phương trình ( ) 2 33 2loglog150 x xxm −−−= có 2 nghiệm 1 2 3 3 x x = = + 51log mxm = là 1 nghiệm. Để phương trình có đúng 2 nghiệm thì 1 3 3 5 1 log3552,53125 3 mmm Câu 236: Cho , xy là các số thực dương thỏa mãn ( ) 235 log2log2logxyxy ==+ . Tính giá trị của 22Txy =− . A. 1 T =− . B. 175 T = . C. 28 T = . D. 13 T = . Lời giải Chọn B Vì ( ) 235 4 log2log2log23 5 t t t x xyxyty xy = ==+== += Ta có 43 4351 55 tt ttt +=+= Nhận xét rằng 2 t = là nghiệm của phương trình trên. Lại có 43 55 tt y =+ là hàm số nghịch biến nên 2 t = là nghiệm duy nhất của phương trình trên. 16 175 9 x T y = = = Câu 237: Biết x và y là hai số thực thoả mãn ( ) 496 logloglog2 xyxy ==− . Giá trị của x y bằng A. 2 2 3 log2. B. 1. C. 4. D. 2. Lời giải
( )2 cũng có 2 nghiệm tương ứng 131 log tx = , 232 log tx = . Khi đó ( ) 2 12313231212logloglog.2.39ttxxxxxx +=+==== . Mà ( )( ) ( ) 12121212 22721110 xxxxxxxx −−=−−+=−+= .
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 14 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Chọn C Đặt ( ) 496 4 logloglog29 26 t t t x xyxyty xy = ==−== −= 42 42.9620 93 tt ttt −=−−= Đặt 2 3 t u = , điều kiện
=
===
Câu
tất cả các giá trị của
ố
ệ
Suy
12 12
.9
xx += = 1 2 123132 1 2 1 9 .log.log0 9 1 x x ttxx x x = = == = = .
12 7 .270 2 ttmm =−== . Điều kiện đủ: Với 7 2 m = thay vào phương trình ( )2 ta được: 0 2 2 030 20 239 tx tt t x === −= = == Vậy phương trình ( )1 có hai nghiệm phân biệt là 0;9 thỏa mãn điều kiện đầu bài. Câu 239: Số nghiệm của phương trình ( ) 2 22 loglog3120 x xx−−= là A. 2. B. 1. C. 3. D. 0. Lời giải
0 u . Ta có phương trình: 2 1() 20 2 lo¹i u uu u =− −−=
. Ta có: 2 42 4 93 tt x y
238: Tìm
tham s
m để phương trình 2 33 log2log270 xxm −+−= có hai nghiệm thực phân bi
t 12 , xx thỏa mãn ( )( ) 12227.xx−−=− Lời giải Ta có 2 33 log2log270 xxm −+−= ( )1 Đặt 3log tx = , phương trình trở thành 2 2270ttm−+−= ( )2 . Điều kiện cần: Giả sử phương trình ( )1 có 2 nghiệm 1x , 2x khi đó phương trình
ra
10
xx
Theo phương trình ( )2 :
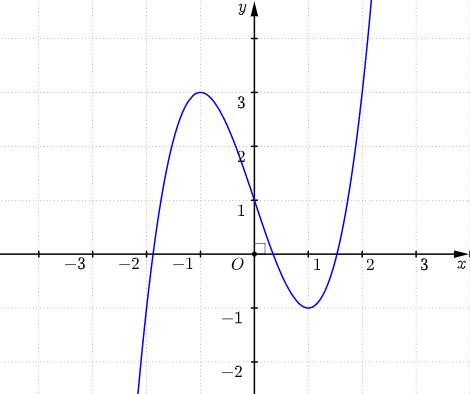
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 15
ọ
B
−= ==
ệm của
= . Câu
ố
ậ
ba
Số nghiệm của phương trình ( ) ( ) ( ) ( ) ( ) 32 21 2 2 log1log12log160 fxfxfx+−+−++= là A. 7 B. 5 C. 6 D. 8 Lời giải Chọn C Xét phương trình ( ) ( ) ( ) ( ) ( ) 32 21 2 2 log1log12log160 fxfxfx+−+−++= . Điều kiện: ( ) 1 fx −
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ch
n
Điều kiện 3 3 0 0 log12 log12 3120 x x x x x − Ta có ( ) 2 22 2 22 loglog0 loglog3120 3120 x x xx xx −= −−= −= + Xét phương trình 2 22 loglog0 xx−= ta có 2 2 22 2 log0 1 loglog0 log12 x x xx xx = =
+ Xét phương trình 3120 x −= ta có 3 31203120312log12 xxx x −=−=== So với điều kiện 3 log12 x ta nhận 3 log12 x = Vậy tập nghi
phương trình 3 log12 S
240: Cho hàm s
b
c
( )yfx = có đồ thị như hình vẽ
Dễ thấy số nghiệm phương trình ( )2 là số giao điểm của đồ thị hàm số ( )yfx = và 1 2 y =−

Suy ra phương trình có 3 nghiệm phân biệt. Tương tự phương trình ( )3 có nghiệm duy nhất và phương trình ( )4 có 2 nghiệm phân biệt. Hiển nhiên các nghiệm này phân biệt. Do dó phương trình ( )1 có 6 nghiệm phân biệt. Câu 241: Số giá trị nguyên âm của tham số thực m để phương trình ( ) 22 22 1log4log0mxxm ++−= có nghiệ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 16
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) 32 222 1log14log1log160 fxfxfx +−++++= . Đặt ( ) ( ) 2 log1tfx=+ , ta có ( ) ( ) ( ) ( ) ( ) ( ) 2 32 2 2 log11 1 4603log13 2 log12 fx t ttttfx t fx +=− =− −++==+= = += ( ) ( ) ( ) ( ) ( ) 1 2 2 ()73 34 fx fx fx =− =
=
m
ộc khoảng
0;1 là A. 4. B. 1. C. 2. D. 5. Lời giải Chọn B Đặt 2 log(;0)txt=− . Khi đó bài toán trở thành tìm m để phương trình ( ) 22140(*)mttm++−= có nghiệm thuộc (;0) − . Để phương trình có nghiệm ( ) 23 4140 mmmm =++=++
thu
( )
Câu 242: Giả sử phương trình 2 22 log2log20 xmxm có hai nghiệm thực phân biệt 12 ; xx thỏa mãn 12 6 xx . Giá trị của biểu thức 12xx là A. 4. B. 3. C. 8. D. 2. Lời giải
Chọn D
Đk: 0 x . Đặt 2log tx . Khi đó ta có phương trình: 2 (2)20tmtm . 2 220()2()0(2)()0 tmttmttmtmttm . 2 2
4 log2 2 log 2m
x x t tmxm x . Để phương trình có 2 nghiệm phân biệt 12 ; xx phương trình 2 (2)20tmtm có hai nghiệm phân biệt 2 m Ta có: 12 64261 m xxm . 12 422 xx .
Câu 243: Xét các số nguyên dương , ab sao cho phương trình ( ) 2 lnln501axbx++= có hai nghiệm phân biệt 12 ; xx và phương trình ( ) 2 5loglog02 xbxa++= có hai nghiệm phân biệt 34 ; xx sao cho 1234 ...xxxx Giá trị nhỏ nhất của 23 Sab =+ là A. 17 B. 25 C. 33 D. 30 Lời giải Chọn D
Điều kiện 0 x Đặt ln;log txux == Khi đó phương trình trở thành 2 50 atbt++= và phương trình trở thành 2 50 ubua++= Hai phương trình trên có hai nghiệm phân biệt khi 2 20 ba .
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 17
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Khi đó ta có được: 12 2 12 12 2 4 0 1 0 0 1 tt m tt m tt m += + = + . Vậy phương trình luôn có nghiệm thuộc (;0) − với tham số m thỏa 3 0 40Mà 1 m mmm m ++=−
Câu 244: Cho , ab thỏa mãn điều kiện 2
1 loglog3 ab
ba ba += . Tính giá trị của biểu thức ( ) 4 2 logab Tab = . A. 1 3 B. 3 2 C. 6 D. 2 3 Lời giải Chọn D 2 loglog3 abba+= 1 2log3 log a a
a a
b b
= = Do 1 ba nên 1 log 2 a b = . ( ) ( ) ( ) 4
b b += 2 2log3log10 a a bb −+= log1 1 log 2
ab b Tab b ab + ==== + .
2 2 4 loglog12log2 log14log3 a a ab a a
Câu 245: Cho phương trình ( ) 22 22 log2log30 xmmxm −−++= ( m là tham số thực). Gọi S là tập các giá trị của m để phương trình có 2 nghiệm phân biệt 12 , xx thỏa mãn 12.8xx = . Tổng các phần tử của S là A. 1. B. 2. C. 5. D. 2. Lời giải Chọn C Điều kiện: 0 x . Đặt 2 log2t txx == Khi đó ta có phương trình: ( ) ( ) 22 2.301tmmtm−−++= .
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 18
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có 1212 12 b tttt a xxeeee + === ; 1212 5 34.10.101010 b uuuu xx + === . 5 1234 5 10ln10 5ln10 bb a bb xxxxea a Mà a nguyên dương nên a3 . Vì 22206060babb . Mà b nguyên dương nên 8 b . Do đó 232.33.830Sab=++= . Dấu "" = xảy ra khi 3;8ab== . Vậy giá trị nhỏ nhất của 30 S = .
Để phương trình đã cho có 2 nghiệm phân biệt thì phương trình ( )1 có 2 nghiệm phân biệt, tương đương với ( ) ( ) 2 2 24.30mmm =−−−+
Giả sử phương trình ( )1 có 2 nghiệm 1 1 2t x = , 2 2 2t x = .
Yêu cầu bài toán 12 2 1212 1 .82.28323 3 tt m xxttmm m
=− ==+=−= =
Với 1 m =− thì 10= Với 3 m = thì 150=− . Vậy 1 S =− . Khi đó tổng các phần tử của S là 1
Câu 246: Cho phương trình ( ) 2 1 log1log45 x xm + ++= với tham số m . Số giá trị nguyên dương của m để phương trình đã cho có nghiệm là A. 4. B. 2. C. 3. D. 1. Lời giải
Chọn D
Ta có ( ) ( ) 221 1 log1log45log14log25 x x xmxm + + ++=++= Đặt 1 log2 x t + = phương trình trở thành ( ) 2 540,0ttmt−+= Điều kiện để phương trình có nghiệm là 25 025160 16 mm −
Vậy có 1 giá trị nguyên dương là 1 m =
Câu 247: Cho hai số thực , ab lớnhơn 1 thayđổi thỏamãn 15 ab+= .Gọi 12 , xx làhai nghiệm của phương trình 23 log.log2loglog0 baab axxbx−−= . Giá trị lớn nhất của biểu thức 12 . Txx = A. 196. B. 2744. C. 26244. D. 2021. Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 19
V
Chọn C Ta có ( ) 232 log.log2loglog0log.log23loglog10 baabbaba axxbxaxax −−=−+−= Đặt loga tx = . Khi đó phương trình có dạng ( ) ( ) 2 log.23log10* bb atat−+−= Do 1.log0 b a − nên phương trình luôn có hai nghiệm phân biệt 12tt
ới 12 2log3 23 1212 2log3. a b tt a ttbxxaaba + + +=+=== . Do 1515 abba +==− Xét ( ) ( )2 3 15 faaa =− với 114 a Khi đó ( ) ( ) ( ) ( ) 2 3 27222 15..,.15.15 8333 aaa faaaaa =−=−−
aaa aa +++−+− == Dấu "" = xảy ra khi 2 159 3 a aa =−= khi đó 6 b = . Vậy 12 . xx đạt giá trị lớn nhất bằng 26244
5 5 222 1515 272730 333 .26244 8585
Câu 248: Cho phương trình ( ) 2 1 log1log45 x xm + ++= với tham số m . Số giá trị nguyên dương của m để phương trình đã cho có nghiệm là A. 4 B. 2 C. 3 D. 1 Lời giải
Chọn D
Điều kiện: 10 x − Phương trình ( ) ( ) ( ) 221 1 log1log45log14log251 x x xmxm + + ++=++= TH1: Xét 0 m = thì ( ) ( ) 2 1log1531 xx +== nên là nghiệm của ( )pt1 . TH2: Xét 0 m Đặt ( ) 2 log1tx=+ , khi đó: ( ) ( ) 2 4 1545540 m tmttttm t +==−−+= ( 0 t = không là nghiệm của phương trình do 0 m ). Để ( )pt2 có nghiệm thì 25 25160 16 mm =− Kết hợp TH1 và TH2, ta có phương trình ( ) 2 1 log1log45 x xm + ++= có nghiệm khi 25 16 m Vì 1 mm + Câu 249: Xét phương trình ( ) ( ) 222 43 log3.log37. yy xxxxyy +−++=−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 20
sao cho tồn tại số thực x thỏa
phương
cho.
11. B. 10 . C. 9 . D. 8 . Lời giải Chọn C ( ) ( ) 222 433 log3.log3.log37 yy GTxxxxyy +−++=− ( ) 2 33 2 4 2 l 3 log3.log.og37 3 y y y xxyy xx ++=− ++ Đặt ( ) 2 3 log3y XxxX =++→
Có bao nhiêu số nguyên y
mãn
trình đã
A.
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
Câu
ồ
ạ
số thự
y thỏ
A. Vô số. B. 2. C. 3. D. 1. Lời giải Chọn B Đặt ( ) ( ) 22 34 loglog2xyxyt +=+= 22 3 24 t t xy xy += += ( )2 22 2 32421 4.93.42.9 13 1/23932 1 22 t t tttt xy y xt + =+== + . Suy ra 22 03 022 xy xy + + Ta có: 2222202220;1 xyxxx +− do x nguyên. Với 0 x = , ta có 4 9 log2 4 2 9 34 2.942log23249 t t tt t y ty y =
y 0;1 x− thì tồn tại số thực y thỏa mãn ( ) ( ) 22 34 loglog2 xyxy +=+ . Câu 251: Có bao nhiêu giá trị nguyên dương của tham số m nhỏ hơn 2022 để phương trình ( ) 3 log32 x mmx ++= có nghiệm thực? A. 2021. B. 2018. C. 2019. D. 2020. Lời giải Chọn A Vì xét m nguyên dương nên: ( ) 2 3 log3233 xxx mmxmm ++=++=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
21 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có ( ) ( ) ( ) ( ) 222 444 log3..7log3.log3.70 yXXyyXyXyy −=−−+−= Phương trình ( ) có nghiệm khi ( ) ( ) 2 2 44 log34.log3.70 yyy =−− ( ) 2 4 log34.280 yy −+ 08,73 y Mà 0;1;2;3;...;8 yy→ .
250: Có bao nhiêu số nguyên x sao cho t
n t
i
c
a mãn ( ) ( ) 22 34 loglog2 xyxy +=+
==== = . Với 1 x = , ta có ( )2 2 31 2.3141 241 t tt t y y =− −=− =− . ( )* Ta thấy 0 t = là nghiệm của ( )* Phương trình đã cho có nghiệm 1 y = Với 1 x =− , ta có 2 31 241 t t y y =+ =− Vì 22 4 311224414log51 tt yyyyt =+− . Vậ
Ta đặt: ( )30 x uu= và ( )30 x vmv=+ . Ta có hệ: 2 2
+= += .
mvu muv
Suy ra: ( )( ) 22 10 vuuvuvuvuv −=−−++==
Nên phương trình đã cho ban đầu có nghiệm thực khi phương trình: 2 muu += 2 0 uum −−= có nghiệm 0 u
Vì phương trình 2 0 uum−−= luôn có hai nghiệm trái dấu khi 0 m
Nên theo yêu cầu bài toán ta có: 0 20221;2;3;...;2021 m mm m
.
Vậy có 2021 giá trị m thỏa mãn yêu cầu bài toán.
Câu 252: Tính tích tất cả các nghiệm thực của phương trình 1 2 2 1 log25 2 x x x x + ++=
A. 1 2 . B. 2. C. 0. D. 1. Lời giải
Chọn A
ĐKXĐ: 0 x 1 2 2 1 log25 2 x x x x + ++= ( ) ( ) 1 21 2 fxf x += , với ( ) 2 log2t ftt=+ là hàm số đồng biến trên khoảng ( ) 0;+ Vậy ( ) 1 12 2 x x += 2 2410 xx −+= . Suy ra tích tất cả các nghiệm thực của phương trình đã cho bằng 1 2
Câu 253: Có bao nhiêu cặp số nguyên dương ( ) ; xy thỏa mãn: ( ) ( ) 22 3 log33? 2 xy xxyyxy xyxy + =−+−+ +++ A. 3. B. 2. C. 4. D. 8. Lời giải Chọn B
Ta có: ( ) ( ) 22 3 log33 2 xy xxyyxy xyxy + =−+−+ +++ ( ) ( ) ( ) ( ) 2222 33 log3333log22 xyxyxyxyxyxy +++=+++++++ ( ) ( ) 22 332 fxyfxyxy +=+++
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
22 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
Chọn B Ta có: ( ) ( ) 11 11 log11 log log 11 7 loglog777 x
y x y yxyx + =−+=− Đặt ( ) 11log 7 7 x ytt+= Phương trình trở thành: 1111 loglog77yytxxt=−=+ Ta có hệ phương trình 1111 1111
xx yt tyty xtxy =+=+ =+=+
loglog loglog 77 77
TH1: xét thấy 1 y = thì 8 x = {thỏa mãn} TH2: Xét 1 y Suy ra: 11111111 loglogloglog xttxtxyytyxy −=−+=+ Xét hàm đặc trưng ( ) 11log u fuyu =+ trên ( ) 0;+ . ( ) 11log ln .1 .ln11 u y fuy u =+ Xét: 1 y . Hàm số ( )fu đồng biến và liên tục trên ( ) 0;+ Do đó, ( ) ( ) fxftxt == Vì thế, ta đưa về xét phương trình: 111111 logloglog 777 xyyxyxxxx =+=+−=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 23
Xét hàm số ( ) 3 log fttt =+ trên khoảng ( ) 0;+ Ta có ( ) ( ) 2 10,0 ln3 fttft t =+ luôn đồng biến trên khoảng ( ) 0;+ Từ và suy ra ( ) ( ) ( ) ( ) 222 22 2333314 * xyxyxyxyxy +++=+−+−++= Mà * , xy nên ( ) ( )2 *414214 xyxy ++ Với 21xyxy +=== không thỏa ( )* Với 21 3 12 xx xy yy ==+=== thỏa ( )*
nguyên dương ( ) ; xy thỏa mãn.
giá trị nguyên dương
y
ồn tạ
số thực
+
ỏ
( ) 11 log() 11 7
x y yx + =− .
Vậy có 2 cặp số
Câu 254: Có bao nhiêu
của
sao cho t
i
( ) 7; x
th
a mãn:
loglog7
A. 9. B. 10. C. 8. D. 11. Lời giải
Chọn B
có
( ) ( ) ( ) ( ) 11 11 log 111111111111 11 −+ ++=+−+= ( ) ( ) ( ) 22 77 log2121log221 xxxx −+−=+ . Xét hàm số ( ) ( ) 7 log0ftttt=+ Có ( ) 1 10 ln7 ft t =+ với 0 t Hàm số đồng biến trên ( ) 0; + . Phương trình ( )1 trở thành ( ) ( ) ( ) ( ) 22
log7 log7log1; 7log0 log x xxxx x − suy ra: 11 log111 yy Kết luận: Ta được: 1,2,3,4...10 y x fxfxxx x
. Vậy, có 10 giá trị y thỏa mãn. Câu 255: Biết 1x , 2x là hai nghiệm của phương trình 2 2 7 441 log416 2 xx xx x −+ ++= và + = −=−= = Vậy ( ) ( ) 12
hai l xxabab tm
C. 11 ab
i gi
) 12 1 2 4 xxab +=+ v 95 4 29;59514. 95 4
13 ab
)
nguyên dương. Tính ab +===+=+= + Câu 256: Có bao nhiêu giá trị nguyên của tham số m sao cho phương trình 3 3 33loglog mmxx ++= có 3 nghiệm phân biệt? A. 2. B. 1. C. 3. D. 4. Lời giải Chọn C
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
(
ới a , b là
số
+ A. 16 ab+= . B. 14 ab+= .
+= . D.
+= . Lờ
ải
Điều kiện 0 1 2 x x Ta
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 (
24 2 2 22 77 44121
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 22 x xx xxxxx xx
log7 log7loglog7log.loglog log y x xxxxyy x −=−== Nhận xét: ( ) ( ) ( ) 11 111111 11 35 4 212212 35 4
log416log4412
Ta có: 3 3 33 33loglog33loglog mmxxmmxx ++=++= 3 3 3log33loglog3log mxmxxx +++=+ ( ) ( ) 3 3 333log33loglog3log1 mxmxxx+++=+
Xét hàm số ( ) ( ) 3 3 ftttt=+ Ta có: ( ) 2 330 fttt =+ Hàm số ( )ft đồng biến trên ( ) ; −+ , khi đó: ( ) 3 3 13logloglog3log mxxmxx+==−
Xét hàm số ( ) ( ) ( ) 2 3 3log1 log3log ln10 x gxxxgx x =−= .
+ +−+ + −− ( )1 có 3 nghiệm phân biệt khi và chỉ khi ( )2;2 m− mà m 1;0;1
m − .
257: Cho phương trình( ) ( ) ( ) 2 2 11 33 1 1log145log440 1 mxmm x −++−+−= + . Số giá trị nguyên dương
1 010 10 00 2 2 củ
x gx gx đoạn 2 ;2 3 . A. 3 B. 6 C. 2 D. 5 Lời giải Trên đoạn 2 ;2 3 thì phương trình luôn xác định. Do đó phương trình đã cho trở thành ( ) ( ) ( ) ( ) 2 11 33 41log145log1440 mxmxm −+−−++−= ( ) ( ) ( ) ( ) 2 11 33 1log15log110 mxmxm −+−−++−= Đặt ( ) 1 3 log1tx=+ , với 2 ;2 3 x − thì 11 t − . Ta có phương trình
a tham số m để phương trình đã cho có nghiệm thực trong
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 25
Điều kiện 0 x
Ta có: ( ) 10 log1 0 1 log1 10
x x gx x x
= = = =− = Bảng biến thiên: ( ) ( ) Câu
( ) ( ) ( ) 222 1510151 mtmtmmtttt −−−+−=−+=−+ 2 2 51 1 tt m tt −+ = −+ ( )* , vì 2 10,1;1ttt−+− . Xét hàm số ( ) 2 2 51 1 tt ft tt −+ = −+ với 11 t − Ta có ( ) ( ) 2 2 2
44 1 t ft tt = −+ ; ( ) 01ftt == ( ) 7 1 3 f −= , ( ) 13 f =−
Do đó ( ) 1;1 min3 ft =− và ( ) 1;1
7 minmax3 3 ftmftm − . Do m nguyên dương nên 1;2 m . Câu 258: Có bao nhiêu cặp số ( ) ; xy thỏa mãn điều kiện ( ) 22 2 2log615615 x yyx −+=−+ A. 1. B. 3. C. 4. D. 2. Lời giải
7 max 3 ft = . Phương trình đã cho có nghiệm thực trong đoạn 2 ;2 3 khi và chỉ khi phương trình ( )* có nghiệm 1;1 t − ( ) ( ) 1;1 1;1
A
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 26
toán là 12 x = và 59 y = . Câu 259: Cho hai số thực x , y thỏa mãn hệ thức 2 2 212log yx y x + = . Hỏi có tất cả bao nhiêu giá trị nguyên 2022;2022 m− để tồn tại duy nhất một số thực x thỏa mãn hệ thức 22 4101 yxmx=++ ? A. 2035 B. 2036 C. 2034 D. 2033 Lời giải Chọn A
Chọn
Ta có ( ) 22 2 2log615615 x yyx −+=−+ ( ) ( ) 22 2 2log615615 x xyy +=+++ ( ) 2 2 log615xy =+ 2 2615 x y =+ Vì [0;2022] y nên 22615[615;2022615][10;21]yx ++ Bảng giá trị tương ứng: Vậy ta có một cặp duy nhất thoả mãn bài
Điều kiện 0 211. x y +
Phương trình đã cho tương đương ( ) ( ) 2 2
21 21 2 2ln 2.ln212ln 2.2ln21 y y x x
+ + =+= +
x yx y
Xét hàm ( ) 2.ln t ftt = với 0 t . Ta có ( ) 1 2ln2.ln2.0 ttftt t =+ với 0 t nên ( ) ( ) 222121 fyfxyx +=+= suy ra 2 11xx .
Hơn nữa ( )2 222 2141 yxyx +==− nên ( )2 22223 4101110112 yxmxxxmxxxm =++−=++−=
Xét hàm ( ) 3 12 gxxx =− , ta có ( ) 2 312gxx =− ; ( ) 02gxx == .

Lập
bảng biến thiên
Dựa vào bảng biến thiên, ta thấy phương trình 22 4101 yxmx=++ có một nghiệm duy nhất khi 11 16. m m −
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
27
=− Vì
−
(
ng thời ,2021xy A. 15. B. 28. C. 22. D. 35. Lời giải Chọn C ( ) ( ) 2 41224 3log4423log21 xyxxxxy ++=+− ( ) ( )( ) 2 442221 3log4423log211 xxxyxxxy +++− ++=+− Xét ( ) 3.log t ftt = . ( ) 31 3ln3.log3ln3.log0,2 .ln10.ln10 t tt ftttt tt =+=+ . Do đó ( ) 22 144221423 xxxyyxx ++=+−=++ 2 1389713897 20214232021 44yxxx −−−+ ++ Vì ( )0;2022 x + nên 1;2;3;...;21;22 x
2022;2022 m
, ta có 2035 giá trị m thỏa yêu cầu bài toán. Câu 260: Có bao nhiêu cặp số nguyên dương ( ) , xy thoả mãn
) ( ) 2 41224 3log4423log21 xyxxxxy ++=+− đồ
Vì mỗi giá trị của x có đúng một giá trị của y nên có 22 cặp số nguyên dương ( ) , xy thoả mãn.
Câu 261: Tính tích tất cả các nghiệm thực của phương trình 1 2 2 2 21 log26 x x x x + + += .
A. 1 B. 0 C. 2 D. 1 2 Lời giải
Chọn D
Điều kiện: 2 21 00 x x x +
Phương trình đã cho tương đương với ( ) 2 21 2 2 2 21 log26* x x x x
+ + +=
Đặt 2 21 2 x t x + = . Điều kiện: 2 t vì 11 2.2 22 txx xx =+=
Phương trình ( )* trở thành: ( ) 2 log226 t t += Xét hàm số ( ) ( ) 2 log22t ftt=+ trên ) 2; +
Ta có: ( ) ) 1 .ln22.ln20,2; t ftt t =++
Hàm số ( )ft đồng biến trên ) 2; +
Nhận thấy ( ) ( ) 2 2 2log2.226 f =+= nên phương trình ( ) 6 ft = có đúng một nghiệm là 2 t = . Với 2 t = thì 2 2 21 22410 2 x xx x + =−+= .
Phương trình trên luôn có hai nghiệm phân biện thỏa mãn điều kiện 0 x nên
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
28
áp dụng hệ thức Vi ét, ta có: 12 1 2 xx = Câu 262: Cho hai số thực x và y thỏa mãn ( ) 33 2loglog5xy−= . Biết giá trị nhỏ nhất của biểu thức 1 3 25 x y P =+ là logb ac + trong đó ,, abc là các số tự nhiên, , bc là số nguyên tố. Tính giá trị của biểu thức 23 Tabc =++ . A. 22 T = . B. 23 T = . C. 17 T = . D. 8 T = . Lời giải Chọn A Ta có: ( ) ( ) 3333 2loglog52loglog5xyxy −==+
( ) 33 loglog5 222 3 2 11 33.33.log55 255 xyyy yy P =+=+=+ Xét ( ) ( ) 22 3 3.log55yy Pfyy ==+ ( ) ( ) 222222 3 2.3.ln3.log52.5.ln52.3.ln52.5.ln52.ln535 yyyyyy fy =−=−=− ( ) 22 03500 yy fyy =−== Bảng biến thiên: Vậy ( ) ( ) 3 minmin01log5 Pfyf===+ 1; 3; 52322abcTabc ====++= Câu 263: Cho các số thực , xy thoả mãn 22 2 loglog225 2 x yxyxy x . Giá trị nhỏ nhất của biểu thức 22 Pxyxy bằng: A. 33222. B. 36242. C. 30202. D. 24162. Lời giải Chọn B 22 2 loglog225 2 x yxyxy x 222 log2log2log225 xxyxyxy . 22 log2log2225 xyxyxyxy 22 log21422log2xxyxyyxy 22 log22422log2xxyxyyxy 22 log4242log22xxyxyyxy Đặt 2log fttt 1 '10 ln2 ft t ft đồng biến trên 0; Phương trình trở thành 422422240 fxfyxyxyxyxyxy

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
29
Đặt uxy , vxy 240 uv , ĐK: 2 4 uv 2 442 uu 2 8160uu 442442uu 2 222222415Pxyxyuvvuuu + Nếu 2 2 44213421342uuu + Nếu 2 2 44213421342uuu 2 2 15342536242 Pu Vậy min36242 P . Câu 264: Cho hai số thực dương , xy thỏa mãn 1 3ln933 3 xy xyxy xy ++ +=−− . Tìm giá trị nhỏ nhất của biểu thức Pxy = . A. 1. B. 1 9 C. 1 3 D. 9. Lời giải Chọn A ( ) 1 3ln9331 3 xy xyxy xy ++ +=−− ( ) ( ) ( ) ln131ln39 xyxyxyxy+++++=+ ( ) ( ) 13 fxyfxy++= , với ( ) ln3 fttt =+ là hàm số đồng biến trên khoảng ( ) 0;+ . Vậy ( ) ( )1132 xyxy++= Do ,0xy nên từ ( )2 ta có 3121 AMGM xyxyxy =+++ 3210 xyxy −− ( )13 Pxy = . Đẳng thức trong ( )3 xảy ra khi 1 xy== . Vậy giá trị nhỏ nhất của biểu thức Pxy = bằng 1. Câu 265: Với , xy là hai số thực và 0 y thỏa mãn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 ( ) ( ) 1 4 2 log6123.3 y y xx −−+= . Giá trị của biểu thức ( )2 651Pxyx=+−+ bằng A. 6. B. 18. C. 10. D. 32. Lời giải Chọn C Xét VP: Theo bđt Cosi ta có 11 2. 44yy yy + 1 4 33 y y + hay 3,0VPy Xét VT: Đặt 2 xt += ; 0 t . Khi đó ( ) 3 61236 xxtt −−+=−++ .
30
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
266:
Đặt ( ) 3 36fttt=−++ ; ( ) 2 33ftt =−+ ; ( ) 1 0 1 t ft t = = =− .
Bảng biến thiên của ( )ft trên ) 0;+
+==− +==
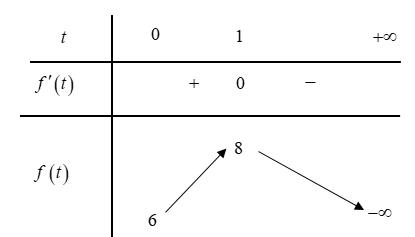
,
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
31 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
Vậy ( )2 65110Pxyx=+−+= . Câu
Cho phương trình ( ) ln0 x xmem+−+=
vớ
m
ự
2022;2022 m− để phương trình đã cho
tt ftetftet =+=+ Nên ta có: ()() ftfxtx == Phương trình xx emxexm −=−= có nghiệm khi và chỉ khi 1 m Vậy có: 2022 giá trị m . Câu 267: Có bao nhiêu số nguyên dương a sao cho tồn tại số thực x thỏa mãn phương
( ) ( ) ( ) 3log1 3 3log1 3 202120202020. x x xa xa + + +=+ A. 9.
5.
.
Dựa vào BBT ta thấy ( ) 8 ft ( ) 2 log3,0 ftt hay 3, VTx Theo giả thiết: ( ) 1 4 2 log6123 y y xx + −−+= chỉ có thể xảy ra khi 3 VPVT== . Dấu "" = xảy ra khi và chỉ khi 211 11 1 42 . Lờ
xx yy y ải
i
là tham số th
c. Có bao nhiêu giá trị nguyên
có nghiệm? A. 2022. B. 2021. C. 2019. D. 4042. Lời giải Chọn A Ta có: điều kiện: 0 xm+ ( ) ln t xtx x xme xmemtetex tme += +=−=+=+ += Xét hàm số: / ()()10()
trình
B.
C. 12
D. 8
i gi
Chọn A
x x
+ +
xa xa
x xa x xa
3log1 3 3log1 3
202120202020 2021202020212020
+ +
+=+ +=+
Ta có ĐK: 1 x − ( ) ( ) ( ) ( ) ( ) ( ) ( ) 3log1 3 3log1 3
Xét hàm số ( ) ( )20212020 t ftt=+ ( ) ( ) '20212020ln202120210,t(1;) ttftt=++−+
Suy ra hàm số ( ) ( )20212020 t ftt=+ đồng biến trên khoảng ( ) 1; −+ Từ đó ( ) ( ) ( ) ( ) ( ) 3log1 3 333log13log12021202020212020 x xx xa xaxa + ++ +=+=
ĐK: 3 00xx
Khi đó ( )3log1 3 log 3log3log(1).loglog log(1) x x xaxxaa x + ==+= + Hàm số log log(1) x y x = + có tập giá trị ( );1 T =− Để phương trình có nghiệm khi log1010 aa Vậy chọn đáp án
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
32
A. Câu
Tổng tất cả các giá trị nguyên của tham số m để
( ) 2cos4 62 20202020
2 m x m xx ++ +=++ có 5 nghiệm thuộc đoạn 4 ; 243 là A. 4 B. 2 C. 6 D. 5 Lời giải Chọn C Điều kiện: 3cos420220 2 m x ++ PT ( ) 2cos4.cossin4.sin 662 20202020 logsin420222021.log3cos42022 2 m xx m xx −+ +=++ ( ) 3cos4sin4 2 20202020 logsin420222021.log3cos42022 2 m xx m xx −+ +=++ ( ) 3cos42022 sin42022 2 20202020 2021.logsin420222021.log3cos42022 2 m x x m xx ++ + +=++ ( )1
268:
phương trình
logsin420222021.log3cos42022
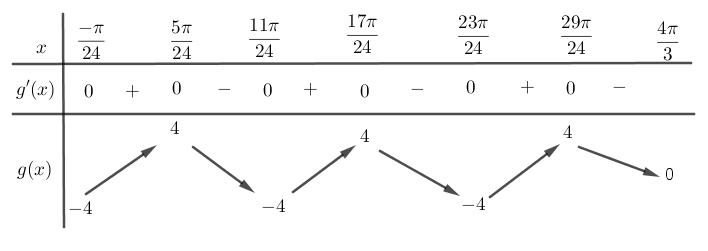
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 33
2
+=++ sin420223cos42022 2 m xx +=++ 2sin423cos44sin4 3 mxxmx =−=− Xét hàm số ( ) 4sin4 3 gxx =− trên 4 ; 243 ( ) 16cos4 3 gxx =− ; ( ) 0cos40 3 gxx =−= 5 244, k xk =+ Vì 4 ; 243 x − nên 511172329 ;;;;; 242424242424 x − Để phương trình có 5 nghiệm khi 40 m − Vì m nên 1;2;3mmm=−=−=− Tổng các giá trị nguyên bằng 6. Câu 269: Xét các số thực dương , xy thỏa mãn =++− + 3 1 log324 2 xy xyxy xy . Tìm giá trị nhỏ nhất minP của −+− =+ + 32 3561 31 yyy Px y A. = min 1 P B. = min 2 P C. = min 2 P D. =− min 21 P Lời giải Chọn A
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Xét hàm số ( ) 20202021.log t ftt = với 1 t Ta có ( ) 2020 1 2021.log.ln2021.20210,1 .ln2020 tt fttt t
=+ Suy ra, hàm số đồng biến và liên tục trên ( ) 1;+ Do đó, ( ) ( ) 1sin420223cos42022
m fxfx
Với , xy dương và kết hợp với điều kiện của biểu thức =++− + 3 1 log324 2 xy xyxy xy ta được − 10 xy
Biến đổi =++− + 3 1 log324 2 xy xyxy xy ( ) ( ) ( ) ( ) −−+=−−++− 333 log1log2312log3 xyxyxyxy ( ) ( ) ( ) ( ) −++−=+++ 333 log1log331log22 xyxyxyxy ( ) ( ) ( ) ( )( ) −+−=+++ 33 log3131log221 xyxyxyxy
Xét hàm số ( ) =+ 3log fttt trên ( )=+ 0; D ( ) =+ 1 '10 .ln3 ft t với mọi xD nên hàm số ( ) =+ 3log fttt đồng biến trên ( )=+ 0; D
Từ đó suy ra ( ) ( ) ( ) −=+−=+= + 32 13123213 13 y xyxyyxyx y
giả thiết ta có 0,0xy
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
34
= Câu 270: Có tất cả bao nhiêu số nguyên ,(2)aa để tồn tại các số thực x và y thỏa mãn 5() log 4 x a yx axyy+=+= ? A. 27. B. 26. C. 25. D. 28. Lời giải Chọn B Điều kiện: 0 y . Xét loglog()log()()xxxx aaa axyyaayyfafy +=++=+= Do hàm số ()loga fuuu =+ đồng biến trên ( ) 0;+ nên x ay =
Theo
nên từ = + 32 13 y x y ta được 3 0 2 y . −+−−−+− =+=+ +++ 3232 3561323561 313131 yyyyyyy Px yyy ( )( ) 2 2 3121 21 31 yyy yy y +−+ ==−+ + ( )2 111 Py =−+ Dấu bằng xảy ra khi 1 4 1 x y =
Khi đó 5()5() 44
x xxyxax axax +=+= 445590 xxx axaxax +=−=
ln(9) lnln(9)lnln(9)ln(), 0. x x axxaxagxx x ====

có:
1ln(9) ()0ln(9)1. 9
n
i
ph
i có nghi
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 35
Đặ
Ta
2
xe gxxx x ==== Để tồ
tạ
x thì ln() agx =
ả
ệm 9 9 ln027,41 e aae e . Do 2 a và a nên 2,3,..,27 a Câu 271: Có tất cả bao nhiêu số nguyên dương a để tồn tại các số thực x và y thỏa mãn 5() log 4 x a yx axyy+=+= ? A. 27. B. 26. C. 25 D. 28. Lời giải Chọn B Ta có: ,2,0.aay log loglog a y xx aa axyyaxay +=++=+ Đặt () t ftat =+ ta có ( )ft là hàm số đồng biến trên Do đó ( ) ()loglog x aa fxfyxyya === Đẳng thức ban đầu tương đương với ( ) 5 90 4 x xx ax axax +=−= .
t ()9 x gxax =− , ta có '()ln9 x gxaa=− ; '()0log9 ln a gxx a == . Bảng biến thiên
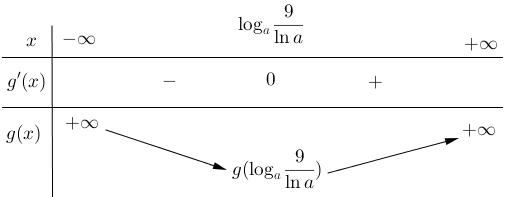
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 36 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do đó để phương trình ( ) 0 gx = có nghiệm thì 999 log09log0 lnlnln aa g aaa − 199loglnlog1lnlnln aa a aaa 9 999 ln1ln27,41 lnln eeaae aae . Vậy 2;3;4;...;27 a nên có 26 số nguyên dương a thỏa mãn yêu cầu bài toán. Câu 272: Có bao nhiêu giá trị nguyên của tham số m để phương trình ( ) 7 1 log10 7 x m −−= có nghiệm dương?
. Để
( ) 7 0log1111728 mmm −− Vì 3;4;5;6;7 mm . Vậy có 5 giá trị của tham số m thỏa mãn yêu cầu. Câu 273: Cho phương trình ( ) ( ) 22 1 5 log4log24.log50 aa xaxxax ++++++= . Gọi S là tập các giá trị nguyên của tham số a để phương trình có nghiệm duy nhất. Tổng các phần tử của S bằng A. 2 B. 3 C. 4 D. 0 Lời giải Chọn A Ta có 0 12 a aa a
A. 7 . B. 4 C. 5 D. 6 Lời giải Chọn C Xét phương trình ( ) ( ) 77 11 77log10log1 xx mm −−==− Ta thấy 1 001 7 x x
phương trình đã cho có nghiệm dương thì:
Đặt ( ) 2 20txaxt =++ Phương trình ( ) ( ) ( ) 22 1 5 log4log24.log501 aa xaxxax ++++++= trở thành: ( ) ( ) ( ) ( ) ( ) 2 5 2 54
=++ ++= Đặt ( ) ( ) ( ) 2 54 log4.log30ftttt =++ . Ta có ( ) ( ) ( ) ( ) ( ) 2 45 2 12 4ln5.log3log400 3ln4 t ftttt t t =+++ + + . Suy ra ( )ft đồng biến trong ( ) 0;+ nên ( ) ( ) ( ) ( ) 2111 ftftft === . ( ) ( ) 22 2
log4log4.log3 log4.log312 aa tt tt
12121 103 xaxxax xax
++=++= ++= Do đó ( )1 có đúng một nghiêm khi và chỉ khi ( )3 có nghiệm duy nhất khi và chỉ khi 2 402aa−== . Vậy tổng các phần tử của S bằng 2.
Câu 274: Cho phương trình ln() x exaa =++ , với a là tham số. Có bao nhiêu giá trị nguyên của a thuộc khoảng (0;19) để phương trình đã cho có nghiệm dương? A. 15. B. 18. C. 17. D. 16. Lời giải Chọn C + Xét ln() x exaa =++ Đặt ( ) ln t txaaex =+=− Ta được phương trình: ( ) xtxt etexexet =+−+=+ + Xét ( ) ( ) 10, uu fueufueu =+=+ Hàm số ( )fu đồng biến trên
Suy ra xt = ( ) ln x xxaaex =+=− + Xét ( ) x gxex =− ( ) 0100 x gxex =−== Ta có bảng biến thiên
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
37
Để phương trình có nghiệm dương thì đường thẳng ya = phải cắt đồ thị hàm số ( )gx tại điểm có hoành độ dương. Từ bảng biến thiên, suy ra 1 a Mà ( )0;19 a nên ( )1;19 x xx x
a + . Ta có 882 222 2222 2222
có bao nhiêu nghiệm nguyên? A. 1.
2. C. 3. D. 0. L
i giải
. V 2021log4loglog2021 14 2021logloglog2021 33 1441 2021loglogloglog2021 3333 1144 log20212021logloglog(2) 3333
y có 17 giá tr xxx xxx xxxx xxxx
a. Câu 275: Phương trình +−=− +−=− +−=−+ +++=+ Xét hàm số 2 () fttt =+ với 0 t . Vì '()210,0 fttt=+ nên 2 () fttt =+ là hàm số đồng biến trên ) 0;+ . Từ ta có 22 14 2021loglog 33 fxfx += Suy ra
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 4log0 2021log01 0
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 38
ậ
ị
882 2021log4loglog2021 xxx +−=−
B.
ờ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Chọn A Điều kiện xác định: 8 8
+++=
2021log4log0 2021log4log10 xx xxvn
Ta có 222 16ln4ln18ln416ln44ln184 xmxxmxmxxm +−=−+−+−=−+−
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 39
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 ( ) ( ) ( ) 2 2 16ln416ln42ln2ln0 xmxmxx +−++−−+= ( )( ) 16ln42ln16ln42ln10 xmxxmx +−++−−+= ( ) ( ) 16ln42ln1 16ln42ln12 xmx xmx +−=− +−=− Xét ( )1 pt 22 2ln01 4ln16ln44ln16ln4 xx mxxmxx − =−+=−+ Xét hàm số ( ) 2 4164fttt=−+ với ln0.tx= Ta có bảng biến thiên
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 2021 22222 1414 2021loglog2021logloglog20212 3333 xxxxxx +=+=== Vậy phương trình có 1 nghiệm nguyên. Cách 2 Điều kiện 8 log0 1 0 x x x
Ta có 882 2021log4loglog2021 xxx +−=− ( ) 8888 2021log4log2021log4log0 xxxx +−++−= ( )( ) 8888 2021log4log2021log4log10 xxxx +−+++= ( ) 88 88
+−=
2021 882 2021log4loglog20212 xxxx +===
Phương trình có môt nghiệm nguyên. Câu 276: Cho phương trình 22 16ln4ln18ln4xmxxm +−=−+− . Gọi S là tập hợp các giá trị nguyên của tham số m thuộc 2020;2021 để phương trình đã cho có đúng hai nghiệm thực phân biệt. Số phần tử của tập hợp S là A. 2018. B. 2034. C. 2042. D. 25. Lời giải Chọn B
Xét ( )2 pt 2 2
− =−+ =−+
2ln10 4ln20ln54ln20ln5 x xe mxx mxx
Xét hàm số ( ) 2 4164fuuu=−+ với 1 ln. 2 ux=
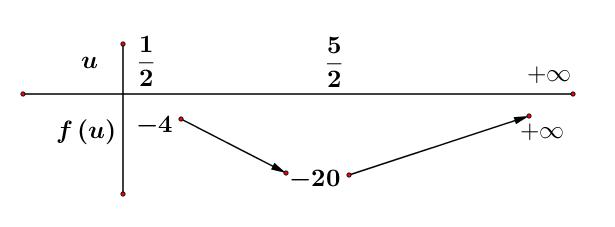
Ta có bảng biến thiên
Vậy yêu cầu bài toán 4 204 m m −− Vì 2020;2021 m− nên có 2034giá trị thỏa mãn Câu 277: Cho tham số m , khi bất phương trình 1 2 6280 x x m ++− có tập nghiệm là ( ) ; Sab = hãy xác định S sao cho ba đạt giá trị lớn nhất. A. 2 2 1 ;log64 S = . B. ( ) 2 6 log2;1 S = . C. 0 1 ;1 9 S = . D. 0 1 ;1 4 S
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
40
=
Lời
Chọn B ( ) 1 2 62801 x x m ++− . Điều kiện: 0 x . Đặt tx = , điều kiện: 0 t . Bất phương trình trên thành: ( ) 1 2 6282 t t m+−− Xét hàm số ( ) 1 628 t t ft =+− liên tục trên (0;) + . ( ) 1 2 1 '6ln62ln2 t t ft t =− ( ) 1 2 4 ln22 ''6ln62ln20(0;) t t t ftt t + =++ nên ( )
ft đồ
ế
.
.
giải
'
ng bi
n trên (0;) +
Ta lại có ( ) 0 lim' t ft + → =− và ( ) lim' t ft →+ =+ .
Suy ra có đúng một ( ) 0 0; t + sao cho ( ) 0 '0ft = .
Bảng biến thiên: Dựa vào bảng biến thiên, ta thấy phương trình ( ) 0 ft = có nhiều nhất là 2 nghiệm. Mà ( ) ( ) 6 1log20ff== nên phương trình ( ) 0 ft = có đúng 2 nghiệm là 6 1;log2tt== . ( )2 có tập nghiệm ( ) ; sao cho lớn nhất 2 00mm −== Khi đó ( )2 có tập nghiệm là ( ) 6 'log2;1 S = nên ( )1 có tập nghiệm là ( ) 2 6 log2;1 S = . Câu 278: Có bao nhiêu số nguyên y sao cho tồn tại 1 ;8 2 x thoả mãn 2 215 9(1).9? xxyx xy + =+ A. 17 B. 16 C. 18 D. 15 Lời giải
Chọn A
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
41
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
đồ
ế
=−−
=−−
có nghiệm 11 ;1;8 22 x nên 1 y =− thỏa mãn. ( ) 2 0 0:1215015 2 x yxx x = =−= = có nghiệm thuộc 1 ;8 2 suy ra 0 y = thỏa mãn. ( ) 1 115:08 2 yff khi đó có nghiệm 1 ;8 2 x 1 16'0 2 yf , mà '()fx đồng biến 11 '()'0, 22 fxfxxD Đặt: 3 11 ()14log1222 y gyfy ==−−+ ta có '()(ln31)2ln3 (2)ln3 y gy y −+ = + Ta có '()016() gyygy đồng biến trên ) 16;+ 1 2()(16)0fgyg = Suy ra: 1 2, xxD ta có: 1 ()0(1) 2 fxf không có nghiệm 1 ;8 2 x Vậy theo điều kiện đề bài ta có: 1;01,2,...15 y − ; Có 17 giá trị y thoả mãn.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
42 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) 2 2152 3 1 9(1).9215log101 2 xxyxxyxyxxy + =++−−+= Nếu có 1 ;8 2 x sao cho thoả mãn ta phải có 1 102 xyy x +−− mà y nên 1 y − Với mỗi y xét ( ) ( ) 2 3 1 ()215log1 2 fxxyxxy =+−−+ Tập xác định: {10}Dxxy=+ ; D là một khoảng theo y và hàm số ()fx liên tục trên D Ta có: '()4152(1)ln3 y fxxy xy =+−− + 2 2 ;''()40 2(1)ln3 y fxxD xy =+ + Suy ra: '()fx
ng bi
n trên D Ta có: 1 '13 2(2)ln3 y fy y
+ ; 3 11 14log1 222 y fy =−−+ ( ) 3 1 8848log(18) 2 fyy =+−+ 2 3 1 1:()216log(1);(;1) 2 yfxxxxD =−=−−−=− 3 111 15log0222 f
mà 1 lim()(1) x fx → =+
Câu 279: Có bao nhiêu giá trị nguyên dương của y để tồn tại số thực 1 x thỏa mãn phương trình
( ) 2 93 84 83loglog xy xyxyy x −+ −+−= ? A. 5. B. 4. C. 3. D. 6 . Lời giải Chọn A
( ) 2 93 84 83loglog xy xyxyy x −+ −+−=
Điều kiện: 1 840
x y xy , phương trình trở thành: ( ) 2 33 84 83log2log xy xyxyy x −+ −+−= ( ) 2 33 2 83loglog84 xy xyxyy x −+ −+−=
( ) ( ) 22 333 83loglog84log xyxyyxyx −+−=−+−
( ) ( ) ( ) ( ) 22 333 84loglog84log* xyxyyxyxy −+−=−+−
TH1: 1 y ( ) ( ) ( ) 2 33 *log83log0 xx +−= 2 831xxdox 419 419 xN xL Nhận 1 y
TH2: 1 y 3 log0 y +Nếu 2 84xyxy−+ thì *0 *0 VT VP Phương trình * vô nghiệm +Nếu 2 84xyxy−+ thì *0 *0 VT VP Phương trình * vô nghiệm
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 43
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
43
xm +−+= −+
A. 14. B. 13. C. 10. D. 5. Lời giải Chọn A Ta có 11 33 11 log33log33(),0 xx xx fxfxx xx =+−=−+−=− Ta có 1 2 11 ()3ln33ln30,0 ln3 x x fxx xx =++ hàm số ()fx đồng biến trên (0;) + . Do đó ( ) ( ) 222 1 470(4||3)474||347 4||3 ffxxfxmfxxxmxx xm +−+=−+=−+−+=−+ −+ 22 2 22 4444484 4||44 444444 xmxxmxx xmxx xmxxmx −=−+=−+− −=−+ −=−+−=+
44 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do đó: ( ) 2 *84 xyxy =−+ 2 84 1 x yfx x 2 2 2 '888 1 xx fx x 15 2 '0 15 2 xL fx xL Bảng biến thiên 2;3;4;5 YCBTy Vậy có 5 giá trị nguyên dương của y thỏa mãn yêu cầu bài toán. Câu 280: Cho hàm số ( ) 1 3 log33 x x fxx=+− Tổng bình phương các giá trị của tham số m để phương trình ( ) 2 1 470
ffxx
có đúng 3 nghiệm thực phân biệt bằng

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
ỳnh
42
ễn
Page 45
ạn Để phương trình ( ) 2 1 470 43 ffxx xm +−+= −+ chỉ có 3 nghiệm, dựa vào đồ thị ta có 4123 482 441 mm mm mm == == == Tổng bình phương các giá trị của m bằng: 222 12314 ++= Câu 281: Gọi S là tập các số nguyên 2022;2022 m để phương trình 2 22 2 logloglog xxmmx có đúng ba nghiệm phân biệt. Số phần tử của S bằng A. 2022. B. 1. C. 2021. D. 2. Lời giải Chọn C Điều kiện 2 0 log0 x mx Khi đó 2 22 2 logloglog xxmmx 22 2222222 log2loglogloglogloglog xxmmxxxmxmx Đặt 2 2 log log ux vmx , khi đó phương trình có dạng 22 10 uuvvuvuv 1 uv uv Xét 22 2 0 loglog u uvxmxumu uum .
Giáo viên: Hu
Văn Ánh
Nguy
Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên so
Xét 2 1 11 31 u uvumu uum .
Ta có đồ thị hai hàm số 2 ,0yuuu và 2 31,1yuuu trên cùng một hệ tọa độ như sau
Từ đồ thị để phương trình có 3 nghiệm phân biệt thì 1 0 4 m .
hàm s
hàm s m m = = = .
) 32 u fuu =+ là hàm đồng biến u nên suy ra ( ) ( ) 326913m ftfmtmxxx==−++=
) 32691fxxxx
−+++−=+− −+++−++=+ Đặt ( ) 3232 3 log6916913t txxxxxx =−++−++= . Khi đó ta có ( 0331 35log5
) 3232 3 2log691691323232 mtm xxxxxxmtm −+++−++=++=+ . m m
trên khoảng ( )2;2 có bbt:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
46
Xét
ố (
Vậy có 1 giá trị nguyên của tham số m thỏa mãn bài toán. Câu 282: Có bao nhiêu số nguyên dương m để phương trình ( ) ( )2 32 3 log6913321 m xxxxxm −+++−=+− có duy nhất một nghiệm thuộc khoảng ( )2;2 A. 4. B. 3. C. 1. D. 0. Lời giải Chọn C Ta có ( ) ( ) ( ) 2 32 3 3232 3 Xét
log6913321 2log69169132 ố (
m m =−++
xxxxxm xxxxxxm Để thỏa mãn ycbt thì 3
Vậy có duy nhất 1 giá trị nguyên dương của m thỏa ycbt.
Câu 283: Có bao nhiêu số nguyên dương m để phương trình ( ) 1 4 2log22 x xmm + =+++ có nghiệm 1;6. x− A. 30. B. 29. C. Đáp án khác. D. 28. Lời giải Chọn C
xx xm x
++ ++ +
Do m là số nguyên dương và 1;6. x− nên 20xm++ . ( ) ( ) ( ) ( ) 2
12 42 log22 2 2
2log222222log22 222log22
=+++++=+++++ ++=+++

xmmxxmxm xxm
Xét
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
47 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
+=++++==−− +=++ Xét hàm số ( ) ( ) 22 2212.ln201;6 xx gxxgxx ++ =−−+=−+− Bảng biến thiên Từ bảng biến
suy
trình có nghiệm khi và chỉ khi 622483124 mm . Mà 0 m và m nên 3;4;...;124 m Vậy có 122 giá trị nguyên dương của tham số m thoả mãn phương trình có nghiệm 1;6. x− . Câu 284: Có bao nhiêu số nguyên dương a để phương trình sau có ít nhất một nghiệm thực: ( )log loglog122 a xx aax ++=− A. 8. B. 1. C. 0. D. 9. Lời giải Chọn D Điều kiện 0 x . Vì loglogxa ax = nên đặt log 1 a xt += ta có log loglog log 1 22 21 a aa a xt xxtt ttx += +=+ +=− Vì ( ) log 1log02 a aafxxx =+ đồng biến trên ( ) 0; + . Vì vậy ( ) ( )fxft = xt=
hàm số ( ) 2t ftt =+ với t có ( ) 2.ln210, t ftt=+ Suy ra hàm số ( )yft = đồng biến trên .Ta có ( ) ( ) ( ) ( ) ( ) ( ) 22 2 2 2 02log22222222 2log22 t xx ftt ftxxmxmmx fxfxm ++ =+
thiên
ra phương
Hay log 1. a xx=−
Nếu 1 a = thay lại vào phương trình ta có 0 12xxx=−= . Vậy 1 a = thỏa mãn.
Nếu log 112 a axtx==+ . Vậy ( ) ln1ln log1 lnln x x a xx ==
Do vậy ( )0;10 a . Mà a nguyên dương và lớn hơn 1 nên 2,3,4,...,9 a
Vậy có 9 giá trị của a thỏa mãn điều kiện đầu bài.
Câu 285: Với x là số nguyên dương và y là số thực. Có tất c
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 48
ả
ặ
số
ỏ
( ) ln122310 xyyx ++=+− A. 10 B. Vô số C. 9 D. 11 Lời giải Chọn C Điều kiện: 1 120 2 x xyy + ++− . Ta luôn chứng minh được 1, x exx+ Xét hàm số ( ) ( ) 1100xx ygxexgxex ==−−=−== Bảng biến thiên: Suy ra ( ) 01 x gxxexx + Ta có: ( ) ( ) 2310 ln12231012231015 yx xyyxxyeyxx +− ++=+−++=+−+ Do x , nên 1;2;3;4;5 x . Lại có: ( ) ( ) ( ) ln122310ln12231000 xyyxxyyxfy ++=+−++−−+== Xét hàm số ( ) ( ) ln122310fyxyyx =++−−+ trên khoảng 1 ; 2 x + −+ Suy ra ( ) ( ) 21 2;0; 1222 xx fyfyy xy + =−==−−+ ++ . Bảng biến thiên của hàm số ( ) ( ) ln122310fyxyyx =++−−+ + 0 y' +∞ +∞ -∞ +∞ y=g(x) x 0 0
bao nhiêu c
p
( ) ; xy th
a mãn
Dựa vào bảng biến thiên ta nhận thấy: + Với một giá trị 1;2;3;4 x , phương trình ( ) ln1223100 xyyx ++−−+= theo ẩn y có 2 nghiệm phân biệt. + Với 5 x = phương trình ( ) ln122310 xyyx ++−−+ theo ẩn y có 1 nghiệm. Vậy có 9 nghiệm ( ) ; xy thỏa mãn bài toán.
Câu 286: Có tất cả bao nhiêu cặp số ( ) ; ab với , ab là các số nguyên dương thỏa mãn: ( ) ( ) ( ) ( ) 3 22 3 log3311 ababababab +++=+++−+ A. 1. B. 3. C. 2 . D. Vô số. Lời giải Chọn C
Với , ab là các số nguyên dương, ta có: ( ) ( ) ( ) ( ) 3 22 3 log3311 ababababab +++=+++−+ ( ) ( ) ( ) 33 3322 3 22 log3331 ab ababababababab abab + ++++=+−+++ +− ( ) ( ) ( ) ( ) 33332222 33 loglog331 abababababab +++=+−++− Xét hàm số: ( ) 3log fttt =+ trên ( ) 0;+ ( ) 1 '10,0 ln3 ftt t =+ nên hàm
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 49
số ( )ft đồng biến trên ( ) 0;+ . Khi đó, phương trình ( )1 trở thành : ( ) ( ) ( ) ( )( ) ( ) 3322332222 22 3330 0* 30 +=+−+=+−+−+−= +−= +−= fabfabababababababab abab ab Do * , ab nên phương trình ( )* vô nghiệm. Suy ra: 3 +=ab . + 10-2x f (y) x 2 0 y f '(y) +∞ x + 1 2 -∞ -∞
Mà , ab là các số nguyên dương nên *
= = += = =
a a b b ab a ab b
2 03 1 03 3 1 , 2
Vậy có hai cặp số ( ) ; ab thỏa mãn yêu cầu bài toán.
Câu 287: Có tất cả bao nhiêu số nguyên dương x sao cho tồn tại số thực 2022 y thỏa mãn ( ) 3 log9333 x yxy +=+− ? A. 6 B. 5 C. 7 D. 4 Lời giải
Chọn C Điều kiện: 1 930 3 yy+−
Ta có: ( ) 3 log9333 x yxy +=+− ( ) 3 log9333x yyx ++=+ ( ) ( ) 33 log3131log33xx yy +++=+ .
Xét hàm số ( ) 3log fttt =+ , với 1 t .
Ta có ( ) 1 ln310,1ftt t =+ , do đó hàm số ( )ft đồng biến trên ( ) 1;+ .
Vậy ( ) ( ) 313313 xxfyfy+=+= 331 x y =− .
Lại có 2022 y nên 36066 y 31606636067 xx − 3 log6067 x . Vì x nguyên dương nên 1;2;3;4;5;6;7 x . Vậy có 7giá trị x thỏa mãn.
Câu 288: Có bao nhiêu cặp số nguyên ( ) ; xy thỏa mãn các điều kiện 02020 x và 2 log(22)38y xxy++−= ? A. 2019. B. 2018. C. 1. D. 4. Lời giải Chọn D *) Do 02020 x nên 2 log(22) x + luôn có nghĩa. Ta có 2 log(22)38y xxy++−= 3 2 log(1)132 y xxy +++=+ 2 log(1) 3 2 log(1)232 x y xy + ++=+ (1)
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
50
*) Xét hàm số ()2t ftt=+ .
Tập xác định D = và ()12ln2 t ft =+ ()0ft t .
Suy ra hàm số ()ft đồng biến trên
Phương trình có dạng: ( ) ( ) 22 log(1)3log(1)3 fxfyxy +=+= 312 y x += 8 log(1)yx =+
Ta có 02020 x nên 112021 x + suy ra 88 0log(1)log2021 x +
Lại có 8 log20213,66 nên nếu y thì 0;1;2;3 y
Vì 3 21 y x =− nên ứng với 1 giá trị của y nguyên thì tồn tại duy nhất 1 giá trị x nguyên.
Vậy có 4 cặp số (;) xy nguyên thỏa yêu cầu bài toán.
Câu 289: Có bao nhiêu giá trị nguyên dương của tham số a nhỏ hơn 2022 để phương trình ( ) 2022 log2022x aax ++= có nghiệm thực?
A. 2021 B. 2022 C. 2018 D. 2023 Lời giải Chọn A Phương trình đã cho tương đương với phương trình 22 202220222022202220222022
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
51 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
Ta
x ax + . Xét
số
)
=++ (
đồ
biến trên ) 0;+ do đó ta có: 2 2022202220222022 xxxx aa +==− Đặt 2022x t = , 0 t . Ta có ( ) 2 agttt ==− . Với 0 t : 1 () 4 gt − . Phương trình đã cho có nghiệm 1 4 a − mà a nguyên dương nhỏ hơn 2022 nên 1;2;3;...;2021 a . Vậy có 2021 giá trị a thỏa mãn yêu cầu bài toán. Câu 290: Cho phương trình ( ) 33log x mxm+=− . Có bao nhiêu giá trị m nguyên trong khoảng ( )19;19 để phương trình có nghiệm. A. 15. B. 14. C. 18. D. 17.
xxxxxx aaaa ++=+++=+
có 20220,
hàm
( ) 2 fuuu =+ trên ) 0;+ . ( )
210,0;fuuu
)fu
ng
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 52
Lờ
•
−=
Tr
) ( ) 3333 xtxttxxtfxft−=−+=+= . • Với ( ) 3x fxx =+ ( ) 3.ln310. x fxx =+ Hàm số ( ) = yfx đồng biến trên . Phương trình ( ) ( ) = fxft có nghiệm duy nhất = xt • Với = xt ta có 33. xx mxxm +=−=− Xét hàm số ( ) 3x gxx =− ( ) ( ) 3 11 3.ln3103logln3ln3 xx gxgxx =−=== với 33 1111 loglog ln3ln3ln3ln3 mm −−−+ Do m là số nguyên và ( )19;19 m− nên {18;17;...;1} m . Vậy có 18 giá trị m thỏa mãn bài toán. Câu 291: Cho 02020 x và 9 log(918)29 y xxy++−= .Có bao nhiêu cặp số (;) xy nguyên thỏa mãn các điều kiện trên? A. 2019. B. 2018. C. 1. D. 3. Lời giải Chọn D Do 02020 x nên 3 log(918) x + luôn có nghĩa
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
i giải Chọn C
Đặt ( ) 33log x mxmt +=−= Ta có hệ phương trình: ( ) 3 333 log33 x xx tt mt mtmt xmt xmmx += +=+=
−=+=
ừ hai vế ta được: (
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 53
xy nguyên thỏa yêu cầu bài toán là các cặp (1;7), (2;79),(3;277) Câu 292: Tổng tất cả các giá trị nguyên của tham số m để phương trình ( ) 2cos4 62 20202020 logsin420222021.log3cos42022 2 m x m xx ++ +=++ có 5 nghiệm thuộc đoạn 4 ; 243 là A. 4. B. 2. C. 6. D. 5. Lời giải Chọn C Điều kiện : 3cos420220 2 m x ++ PT ( ) 2cos4.cossin4.sin 662 20202020 logsin420222021.log3cos42022 2 m xx m xx −+ +=++ ( ) 3cos4sin4 2 20202020 logsin420222021.log3cos42022 2 m xx m xx −+ +=++ ( ) 3cos42022sin42022 2 20202020 logsin420222021.log3cos42022 2 m xx m xx ++−− +=++ ( ) 3cos42022 sin42022 2 20202020 2021.logsin420222021.log3cos42022 2 m x x m xx ++ + +=++ ( )1 Xét hàm số ( ) 20202021.log t ftt = với 2021 t vì sin420222021,xx + . Ta có ( ) 2020 1 2021.log.ln2021.20210,2021 .ln2020 tt fttt t =+ Hàm số đồng biến trên [2021;) + . Từ ( ) ( ) 1sin420223cos42022 2 m fxfx +=++
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có 9 log(918)29 y xxy++−= 3 3 log(2)222 y xxy +++=+ 3 log(2) 2 3 log(2)323 x y xy + ++=+ (1) Xét hàm số ()3t ftt=+ . Tập xác định D = và ()13ln3 t ft =+ ()0ft t . Suy ra hàm số ()ft đồng biến trên . Do đó 3 (1)log(2)2xy+= 223 y x += Ta có 02020 x nên 222022 x + suy ra 2 232022 y 33 11 22log2log2022 y mà y thì 1;2;3 y Vậy có 3 cặp số (;)

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 54 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn sin420223cos42022 2 m xx +=++ sin420223cos42022 2 m xx +=++ sin43cos4 2 m xx =+ 2sin423cos4 mxx=− . Xét hàm số ( ) 2sin423cos4 gxxx =− trên 4 ; 243 ( ) 8cos483sin4 gxxx =+ ( ) 08cos483sin40gxxx =+= 3 tan4, 3244 k xxk =−=−+ . Vì 4 ; 243 x − nên 511172329 ;;;;; 242424242424 x − Để phương trình có 5 nghiệm khi 40 m − Vì m nên 1;2;3mmm=−=−=− . Tổng là 6. Câu 293: Gọi , xy là các số thực dương thỏa mãn 22 3 log(3)(3) 2 xy xxyyxy xyxy + =−+−+ +++ sao cho biểu thức 453 21 xy P xy +− = ++ đạt giá trị lớn nhất. Khi đó 20212022xy + bằng A. 6064. B. 4043. C. 6065. D. 8085. Lời giải Chọn A Ta có: 22 3 log(3)(3) 2 xy xxyyxy xyxy + =−+−+ +++ 2222 33 log()log(2)3() xyxyxyxyxyxy +−+++=++−+ 2222 33 log()3()2log(2)(2) xyxyxyxyxyxy ++++=+++++++
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 55 Chuyên
ện thi: Tuyển sinh vào lớp 10 Tốt
ệp
12 Sưu tầm và biên soạn 2222 33 log3()3()log(2)(2) xyxyxyxyxyxy +++=+++++++ , Xét hàm đặc trưng 3 ()log fttt =+ liên tục và đồng biến trên ( ) 0;+ . Khi đó ( ) ( ) 22 (*)3()2 fxyfxyxy +=+++ 22 3()2 xyxyxy +=+++ 22 444812120 xyxyxy +++−−= ( ) ( ) ( ) 22 2623150 xyxyy
(
(
Ta
==+
Suy ra : max 2 P = , xảy ra
102
yx xyy −== +== . Vậy: 202120226064 xy+= Câu 294: Tổng tất cả các giá trị nguyên của tham số m để phương trình ( ) 2cos4 62 20202020 logsin420222021.log3cos42022 2 m x m xx ++ +=++ có 5 nghiệm thuộc đoạn 4 ; 243 là A. 4. B. 2. C. 6. D. 5. Lời giải Chọn C Điều kiện : 3cos420220 2 m x ++ . PT ( ) 2cos4.cossin4.sin 662 20202020 logsin420222021.log3cos42022 2 m xx m xx −+ +=++ ( ) 3cos4sin4 2 20202020 logsin420222021.log3cos42022 2 m xx m xx −+ +=++ ( ) 3cos42022sin42022 2 20202020 logsin420222021.log3cos42022 2 m xx m xx ++−− +=++ ( ) 3cos42022 sin42022 2 20202020 2021.logsin420222021.log3cos42022 2 m x x m xx ++ + +=++ ( )1 . Xét hàm số ( ) 20202021.log t ftt = với 2021 t vì sin420222021,xx + . Ta có ( ) 2020 1 2021.log.ln2021.20210,2021 .ln2020 tt fttt t =+ Hàm số đồng biến trên [2021;) + .
0984164935
luy
Nghi
THPT BDKT Toán 10; 11;
+−++−+=
)
) 2 26250 xyxy +−++ 125 xy +
có: 45325 22 2121 xyxy P xyxy +−+−
++++ , ta có 250 xy+− ).
khi
251

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 56 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Từ ( ) ( ) 1sin420223cos42022 2 m fxfx +=++ sin420223cos42022 2 m xx +=++ sin420223cos42022 2 m xx +=++ sin43cos4 2 m xx =+ 2sin423cos4 mxx=− Xét hàm số ( ) 2sin423cos4 gxxx =− trên 4 ; 243 ( ) 8cos483sin4 gxxx =+ ( ) 08cos483sin40gxxx =+= 3 tan4, 3244 k xxk =−=−+ . Vì 4 ; 243 x − nên 511172329 ;;;;; 242424242424 x − . Để phương trình có 5 nghiệm khi 40 m − . Vì m nên 1;2;3mmm=−=−=− Tổng là 6. Câu 295: Xét các số thực dương x, y thỏa mãn ( ) 222 2022 221 24log(4) 2 xyxy xy ++++=− . Khi biểu thức 4 Pxy =+ đạt giá trị nhỏ nhất, giá trị của y x bằng A. 4. B. 2. C. 1 2 D. 1 4 Lời giải Chọn C Ta có: ( ) 222 2022 221 24log(4) 2 xyxy xy ++++=−
222 2022 2() 4(4)2log(4) xy xyxy xy + +++=− ( ) ( ) ( ) ( )2 22 202220224(2)2log22log xxyyxyxyxy ++++=+ ( ) ( ) ( ) ( ) ( ) ( ) 222 2 20222022 4()log4log1 xyxyxyxy +++=+
Ta xét hàm số ( ) 2022()log fttt =+ với (0) t ta có: ( ) ( ) 1 '10 ln2022 ft t =+ với 0 t Vậy ()ft là hàm đồng biến với 0 t từ đây ta suy ra được: ( ) ( ) 2 2 4()2xyxyxyxy +=+= 2 2 y x y = Vì ,0xy nên ta suy ra 20 y − hay 2 y
Ta có: ( ) ( ) ( ) 162 24 44104210218 222 y y Pxyyy yyy =+=+=++−+=
Dấu bằng xảy ra khi và chỉ khi ( ) ( )2 2136 4 4221 211() 2 yyx yy yyl y −=== =−−=−=−= Vậy 1 2 y x = Câu 296: Cho các số thực a không âm và b dương thỏa mãn ( ) 1 2 2log84 b b aa + =−+ . Tổng tất cả các giá trị nguyên của tham số m để
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 57
+
−+=−++++=−+++
.
phương trình sin2cos23 axbxm+=− có nghiệm là A. 9. B. 6 . C. 3. D. 4. Lời giải Vì 0 b
nên ta có: 1 1 2. 224(1) b b b b
= . Dấu “=” xảy ra 1 1 bb b == Lại có: ( ) ( )3 84(4)41214124 aaaaaaa
Đặt 4 ta=+ . Khi đó 2 t
Xét hàm: 3 ()12,2. ftttt=−+
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 58
27yx== Vậy có 2 điểm thỏa mãn yêu cầu là ( ) ( )1;0,1;1 Câu 298: Cho phương trình ( ) ( ) ( ) 222 22021 log1.log1log1 a xxxxxx −−−−=+− Có bao nhiêu giá trị nguyên thuộc khoảng ( )3;25 của tham số a sao cho phương trình đã cho có nghiệm lớn hơn 3? A. 16 B. 18 C. 19 D. 17
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có 2 ()3120,2 fttt =−+ . Do đó, ( ) ()216,2. ftft= ( ) 22 log84log164 (2) aa −+= . Dấu “=” xảy ra 20ta == . Từ và ta có: ( ) 1 2 0 2log84 1 b b a aa b + = =−+ = . Với 0,1ab== thì phương trình .sin2.cos23 axbxm+=− trở thành cos23 xm=− có nghiệm khi và chỉ khi 13124 mm −− . Vì m nguyên nên 2;3;4 m . Câu 297: Trong mặt phẳng với hệ tọa độ Oxy , điểm ( ) ; Mxy biểu diễn nghiệm của bất phương trình ( ) 3 log9183y xxy++=+ . Có bao nhiêu điểm M có tọa độ nguyên thuộc hình tròn tâm O bán kính 7 R = ? A. 7 B. 2 C. 3 D. 49 Lời giải Chọn B Điều kiện: 91802 xx+− ( ) ( ) 33 log9183log223 yyxxyxxy ++=++++=+ Đặt ( ) 3 log2tx=+ , t Khi đó ta có: ( )33* tyty+=+ Ta thấy hàm số ( ) 3x fxx=+ đồng biến trên Suy ra ( ) ( ) 3 *log223y tyxyx =+=+= Do M có tọa độ nguyên thuộc hình tròn tâm O bán kính 7 R = nên 22 49 , xy xy + Khi đó 02 171293330;1;2 y xxy −+ TH1: 01yx==− TH2: 11yx== TH3:
1 x
) ( ) ( ) ( ) 222 22021 log1.log1log11 a xxxxxx −−−−=+−
) ( ) ( ) 222 2202122 log1.log2.log1log2.log1 a xxxxxx −−+−=−−
2 2 2 2
log102 log1log20213 a
) ( ) ( ) ( )
xx xx
−−= +−= Ta có ( ) 22 211111 xxxxx −−=−=−= Vậy phương trình đã cho có nghiệm lớn hơn 3 khi phương trình ( )3 có nghiệm lớn hơn 3. Xét hàm số ( ) ( ) 2 2 log1fxxx=+− trên ( ) 3;+ ( ) 2
1 0,3 1 fxx x = . Suy ra hàm số đồng biến trên ( ) 3;+ . Mặt khác hàm số ( )fx liên tục trên ) 3;+ ; ( ) ( ) 2 3log322 f =+ ; ( ) lim x fx →+ =+ . Suy ra tập giá trị của hàm số ( )fx trên ( ) 3;+ là ( ) ( ) 2 log322;++
ậy phương trình ( )3 có nghiệm lớn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 59
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn A Điều kiện: 2 2 10 10 xx xx −−
+−
(
(
(
ả
ại
ứ
(
2261221212 22 .2.237log6log aaaa
+−=−+
A.
Chọn B Đặt 2 2 6 log02 0 y xaa ybb xy =− == + Ta được: 12212() 22 2.22.237log()2214log()60 yxyxxyxyxyxy −−++ +−=++−+−= Xét hàm số 2 2 ()2214log6 tt ftt =+−− , 0 t . 22 2 1414 ()4ln42ln2()4ln42ln20 .ln2ln2 ttttftft tt =+−=++ 0 t
V
hơn 3 khi: log2021322 a + ( ) ( ) ( ) 2 1 3;25 log322 2 2021 1 log3223202119,94 log a a a + + . Vậy có 16 giá trị nguyên của tham số a Câu 299: Có tất c
bao nhiêu số b nguyên dương sao cho tồn t
đúng hai số thực a thoả mãn đẳng th
c
)
bbaab
?
1024. B. 1023. C. 2047. D. 2048. Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 60
x
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ()0ft = có nhiều nhất hai nghiệm dương. Ta thấy (1)(2)0ff== . Do vậy ta được 2 2 2 2 ()011log16 22log16 baa txy ft txy baa =+− =+= = =+= =+− Từ đồ thị ta có 1011 2 10log1122 bb Câu 300: Cho hai số thực dương , xy thoả mãn ( )( ) 2 log2212 100 x yxyx y =−−+−+− . Giá trị lớn nhất của biểu thức ( ) 2 2022 ln2 y P x + = thuộc khoảng nào dưới đây? A. ( )700;800 B. ( )800;900 C. ( )500;600 D. ( )600;700 Lời giải Chọn A Điều kiện: 2 0
y
Ta có: ( )( ) 2 2 log221222log2log(1) 100 x yxyxxxxyyy y =−−+−+−−+−+−=++ Xét hàm số: 2 ()log(0) fttttt=++ Ta có: ( ) 1 '()2100 ln10 fttt t =++ Hàm số ( )ft đồng biến trên khoảng ( ) 0;+ . ( ) ( ) ( ) 122 fxfyyx −==−
( ) 2 20222022
+ == . Xét hàm số 2022
ln2 ln y x P xx
ln (),2 x Pxx x = ( )
2021 2022 2022 2 2022
11 '()0..ln02022ln0 2022 x Pxxxxx x x =−=−= 2022 xe=
1..ln 2022 .'() x xx x Px x = 2022 20222022 2021 2022
Bảng biến thiên: Vậy ( ) 2022 744700;800 maxP e =
301: Trong khoảng
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
61 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
Câu
( )10;20 có bao nhiêu giá trị m nguyên để phương trình ( ) ( )2 39 4log1log91 m xxx+=+ có đúng 2 nghiệm phân biệt. A. 8. B. 23. C. 20. D. 15. Lời giải Chọn B TXĐ: ( ) 1; D =−+ Phương trình: ( ) ( )2 39 4log1log91 m xxx+=+ ( ) ( ) 33 4log11log1 xxmx +=++ Với 0 x = thì pt 01 = Với 0 x thì pt ( ) ( ) 3 4log11 xmx−+= ( ) 3 1 4, log1 mx x =− + với ( ) 1;\0. x−+ Đặt ( ) ( ) 3 1 4 log1 fxx x =− + . với ( ) 1;\0 x−+ . ( ) ( ) ( ) ( )2 3 1 40 3 .1.log1 fx lnxx =+ ++ . Ta có: ( ) 1 lim4 x fx + →− =− ; ( ) lim x fx →+ =+ . Bảng biến thiên:


CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 62 Chuyên
ện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp
12 Sưu tầm và biên soạn Vậy để phương trình có 2 nghiệm phân biệt thì: 4 m − mZ và ( )10;20 m− 3;2;;19 m−− . Có 23 giá trị nguyên tham số m Câu 302: Số các giá trị nguyên của tham số [6;6] m −
==
0984164935
luy
THPT BDKT Toán 10; 11;
để phương trình ( ) ( ) 64 log2022log674 xmx += có hai nghiệm phân biệt là A. 3. B. 5. C. 6. D. 12. Lời giải Chọn C ĐK: 0 20220 x xm + Đặt ( ) ( ) ( ) 64 20226 log2022log6743.4663.41 6744 t tttt t xm xmxtmm x += +==+==− = Ta nhận thấy với mỗi nghiệm t của phương trình ( )1 thì tương ứng một nghiệm 4 674 t x = của phương trình đã cho. Nên bài toán trở thành tìm tham số m để phương trình ( )1 có hai nghiệm phân biệt. Xét hàm số ( ) 63.4 tt ft =− , có ( ) '6ln63.4ln4 tt ft =− ( ) '06ln63.4ln40 tt ft =−= 03 2 3ln4 log ln6 tt
. Bảng biến thiên:
Chọn D Với 12022 x , ta có: 32 2 7 2 2 7 22 77 22 77
xx xyx xyxy xx yx xy xyyx xxyy
231 log1437(1) 6123 (21)(1) log37(1) (21)(31) log(1)log(31)37(1) log7(1)7(1)log(31)31
−+ =+−+ +++ +− =−− ++ −−+=−− −+−=+++
Xét hàm số 7 log() ytt =+ ta có 1 '10(0) .ln7 yt t =+ Do đó: 22 77 22 log7(1)7(1)log(31)31 7(1)317(1)13 xxyy xyxy
−+−=+++ −=+−−= . Do y là số nguyên nên 2 7(1)1 x chia hết cho 3, suy ra 2(1) x không chia hết cho 3. Do đó, 1 x có hai dạng là: 131xk−=+ hoặc 132xk−=+ . () k TH1: 131xk−=+ ta có: 2222 7(1)17(31)17.97.67.113(21142)3() xkkkkkTM −−=+−=++−=++
Theo giả thiết: 12020 120221322022 33 xkk + . Do k suy ra, có 674số thỏa mãn. TH2: 132xk−=+ ta có: 2222 7(1)17(32)17.97.127.413(21289)3() xkkkkkTM −−=+−=++−=++
Theo giả thiết: 22019 120221332022 33 xkk + . Do k suy ra, có 673số thỏa mãn. Vậy, có tất cả 1347cặp số nguyên dương (;) xy thỏa mãn yêu cầu bài toán.
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 63
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Từ BBT suy ra, để ( )1 có hai nghiệm phân biệt thì ( ) 0 0 ftm . Do m nguyên và 6;6 m− 6;5;4;3;2;1 m −−−−−− Vậy có 6 giá trị của tham số m . Câu 303: Có bao nhiêu cặp số nguyên dương (;) xy thỏa mãn: 32 2 7 231 log1437(1) 6123 xx xyx xyxy −+ =+−+ +++ đồng thời 12022 x ? A. 1348 B. 674 C. 673 D. 1347. Lời giải
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 64
ab ab +− =−− + ( ) ( ) ( ) (
55 log425425log*
+−++−=+++ Xét
số ( ) 5 log,1ftttt=+ . ( ) 1 10, 1 .ln5 ftt t =+ . Suy
hàm số ( ) 5log
=+ đồng biến trên ( ) 1;+ Mặt khác ( ) ( ) ( ) *42542553 fabfabababba +−=++−=+=− Vì 4 1 3 ba . Vậy 4 1; 3 a ( ) ( ) 2 2222 31553315123040 abaaaaga ++=−++=−+= ( ) 4 1; 3 min585 44 gag == . Câu 305: Cho phương trình 1 2 53 log55.330100 62 xx xx x x + + ++−−= + . Gọi S là tổng bình phương tất cả các nghiệm của phương trình. Giá trị của S bằng A. 1 S = B. 2 S = C. 0 S = D. 5 S = Lời giải Chọn A Điều kiện: ( ) 1 620* 3 xx+− Khi đó ta có: ( ) ( ) ( ) ( ) ( ) 1 2 22 53 log55.330100 62 log53553log625621 xx xx xxxx x x xx + + ++−−= + +++=+++ Xét hàm số ( ) 2 log5,0yftttt ==+
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 304: Cho , ab là hai số thực lớn hơn 1 thỏa mãn 5 425 log350 ab ab ab +− ++−= + . Giá trị nhỏ nhất của biểu thức 22 315 ab++ bằng A. 10 3 B. 15 2 C. 45 2 D. 85 4 Lời giải Chọn D Ta có 5 425 log53 ab
)
abababab
hàm
ra
fttt
1 ln250,0yt t =+ nên hàm số đồng biến khi 0 t , do đó ( ) ( ) ( ) ( )1536253622 xxxx ffxx +=++=+ .
Xét hàm số ( ) 5362 xx gxx=+−− có ( ) ( ) 100gg== suy ra phương trình ( ) 0 gx = có hai nghiệm 1,0xx== .
Ta có ( ) ( ) ( ) ( ) 22 5ln53ln36,5ln53ln30, xxxx gxgxx =+−=+ nên ( ) 0 gx = có nhiều nhất một nghiệm, suy ra ( ) 0 gx = có nhiều nhất hai nghiệm. Vậy phương trình ( ) 0 gx = có hai nghiệm 1,0xx== suy ra 1 S = .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
65
Câu 306: Có bao nhiêu giá trị nguyên của tham số m để tồn tại cặp số thực dương ( ) ; xy thỏa mãn đẳng thức 34 425 5xy xy xy +− ++ = + và phương trình ( ) 22 55 log532log230 ymxmm −−+−= có nghiệm? A. 5. B. 2. C. 3. D. 4. Lời giải Chọn C Ta có ( ) ( ) 34 55 4255log425log34 xy xy xyxyxy xy +− ++ =++−+=+− + ( ) ( ) ( ) ( ) 55 log425log55425 xyxyxyxy ++−+=+−++ ( ) ( ) ( ) 55 log425425log55xyxyxyxy +++++=+++ Xét hàm số ( ) 5log fttt =+ trên ( ) 0;+ . Ta có ( ) 5 1 log10,0 ln5 ftttt t =+=+ nên hàm số đồng biến trên ( ) 0;+ , do đó ( ) ( ) ( ) 55 log425425log55xyxyxyxy +++++=+++ ( ) 42553553 xyxyxyxy ++=++==− Khi đó phương trình ( ) 22 55 log532log230 ymxmm −−+−= tương đương với 22 55 log2log230 xmxmm −+−= Đặt 5log tx = , do 0,0xy nên 535xy=− suy ra 1 t . Phương trình trở thành ( ) 222230fttmtmm =−+−= Phương trình có nghiệm khi phương trình có nghiệm 1 t . 222233 mmmmm =−+=−+ . Ta xét các trường hợp sau:
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 66 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Nếu 0 0 3 m m = = = Với 0 m = , có nghiệm kép 12 01 ttm=== Với 3 m = , có nghiệm kép 12 31 ttm=== Nếu 003 m , phương trình có hai nghiệm 12 1 tt khi và chỉ khi ( ) 2 517 1025104 517 2517411 224 1 m f mm m m S m m + −+ + Vậy phương trình có nghiệm 1 t khi và chỉ khi 03 517 51704 4 m m m + + . Mà m nguyên nên 1;2 m Do đó có ba giá trị nguyên của m thỏa mãn.
Chọn A + Ta có: 52(1)5320 xx mm −+−− đúng x ( ) ( )512320* x mm +++ đúng x TH1: 1 2 m =− . Bpt ( )* 5.020 x +
TH2: 1 2 m − . Bpt ( )* 32 5 12 x m m + − + .


TH3: 1 2 m − . Bpt ( )* 32 5 12 x m m + − + đúng x 323 0 122 m m m + −− + Theo giả thiết

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 1
6. BẤT PHƯƠNG
LOGARIT MỨC ĐỘ VẬN DỤNG VẬN DỤNG CAO
ả
ị
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
TRÌNH MŨ
Câu 1: Có tất c
bao nhiêu giá tr
nguyên của tham số [10;10] m− sao cho bất phương trình 52(1)5320 xx mm −+−− nghiệm đúng với mọi số thực x ? A. 9 B. 18. C. 20. D. 7. Lời giải
10;9;8;..2 [10;10] ; m m m − −−− Vậy có 9 giá trị nguyên của tham số m thỏa mãn. Câu 2: Số nghiệm nguyên của bất phương trình ( ) 2 2 216540 x xx −−+ là A. 4. B. 3. C. 2. D. 1. Lời giải Chọn A ĐK: 2 2 2 21604 2 x x x x − − CHƯƠNG II HÀM SỐ LŨY THỪA - HÀM SỐ MŨ – HÀM SỐ LOGARIT
3: Tìm số nguyên dương m sao cho tập nghiệm của bất phương trình .2.2440 xx xmxm−−+ chứa đúng 5 số nguyên dương A. 6 m = . B. 9 m = . C. 7 m = . D. 8 m = . Lời giải
Ta có: ( ) ( ) ( )( ) .2.2440240240 xxxx xmxmxmxmxm −−+−−−−− .
TH1: Nếu 2 m thì ( )( ) 2402 x xmxm−− .
Suy ra, ( ) 2; Sm = .
Suy ra, đúng 5 số nguyên dương thuộc S là 3;4;5;6;7;8 thì 9 m = .
TH2: Nếu 2 m thì ( )( ) 2402 x xmmx −− .
Suy ra, ( );2Sm = không chứa đúng 5 số nguyên dương.
TH3: Nếu 2 m = thì ( )( ) 2420 x x −− vô nghiệm.
Câu 4: Có bao nhiêu giá trị nguyên dương của tham số m để tập nghiệm của bất phương trình ( )( ) 4 33330 xx m + −− chứa không quá 9 số nguyên?
A. 3787. B. 729. C. 2188. D. 2187. Lời giải Chọn D Đặt ( )30 x tt= , bất phương trình ( )( ) ( ) 4 333301 xx m + −− trở thành:
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 2 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có: ( ) ( ) 2 2 2 2 2 2160 216540 2160 540 x x x xx xx −= −−+ − −+ ( ) 2 22 22 2 23 2 4 54014 x x x x x x x x x xx x = = = = − − = −+ . Vậy bất phương
( ) 2 2
x xx −−+
trình
216540
có 4 nghiệm nguyên. Câu
x mx
Trường hợp 1: 3 2103 210
x xm
+ −− −
Bất phương trình có nghiệm khi 3 m − .
x mx
Trường hợp 1: 3 2103 210
x xm
+ −− −
Bất phương trình có nghiệm khi 3 m − . Khi đó bất phương trình có nghiệm: 3 xm− . Để bất phương trình có nhiều nhất 20 nghiệm nguyên thì 31818 xm − Do 1;2;3;...;18
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 3
nghiệm của bất phương trình có không quá 9 số nguyên khi và chỉ khi 7 3 log703 mm . Do * m nên có 2187 giá trị của m Câu 5: Tính tổng tất cả các giá trị
ều
ấ
ọn A
(
(
(
33 33 3 3
mxmx xmxmx xmx +−+ ++− +−− +− ++ +−− −−− −−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( )( ) 81330 ttm −− 55 22 55 22 3;3 3;3 tmm mtm
. Do * m nên ( ) 5 2 3 5 133log 2 x mxm− Tập
nguyên dương của m để bất phương trình 33 2221 xmxm +−+++ có nhi
nh
t 20 nghiệm nguyên. A. 171 B. 190 C. 153 D. 210 Lời giải Ch
Ta có:
)
)
)( )
2221 21220 221210 21210 xmxm
mm + Vậy tổng tất cả các giá trị nguyên dương của m là: 123...18171. ++++= Câu 6: Tập hợp tất cả các giá trị thực của tham số m để bất phương trình ( ) ( ) ( ) 2 3121 2323 xxmx −−+ +− đúng x có dạng ( ) , ab . Tính Sab =+ ? A. 2. B. 5 2 . C. 2. D. 3. Lời giải Chọn D Ta có:
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 4 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) 2 3121 2323 xxmx −−+ +− ( ) ( ) ( ) 2 3121 2323 xxmx −−−+ ++ 2 3122xxmx−−−− ( ) 2 2310xmx +−+ Bất phương trình ( ) 2 2310xmx+−+ , x 2 10 0 0 41250 a mm −+ 15 22 m 15 3 22 Sab =+=+= . Câu 7: Số nghiệm nguyên của bất phương trình ( ) 95.66.412820 xxxx −−− là A. 44 B. 45 C. 48 D. 49 Lời giải Chọn A Điều kiện: 00 049 128207 x x x x x − + Với 49 x = không thỏa mãn bất phương trình đã cho. + Với 049 x
xxx
−−−−
K
ợp
Mà
có 44 giá trị nguyên của x . Vậy bất phương trình đã cho có 44 nghiệm nguyên. Câu 8: Có bao nhiêu số nguyên x thỏa mãn ( ) 2 3 412 2log 1 13810 3 xx x x −− ? A. Vô số. B. 6. C. 5. D. 7 . Lời giải Chọn B Điều kiện : 0 x . Xét ( ) ( ) 2 3 412 2log 1 1381,0 3 xx x fxxx =−−
, khi đó bất phương trình đã cho tương đương với 3 2 933 95.66.405.606log6 422 xxx
x
.
ết h
điều kiện ta được nghiệm của bất phương trình đã cho là 3 2 log649 x
x
nên 5;6;....;48 x
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 5 Chuyên
ện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp
11; 12 Sưu tầm và biên soạn Ta có: ( ) 2 3 412 2log 1 1 03 381 xx x fx x = = = ( ) 22 4124120 2 2 111 14120 333 6 xxxx xL xx x =− •==−−= = 33 2log2log 3333 381log3log812log4log xx xxxx•==−=+
xx =−= Bảng xét dấu: Vậy ( )
. Câu 9: Cho bất phương trình ( ) ( ) 22 717 7 log4log1log5 xxmx −++++ . Tổng các giá trị nguyên dương của tham số m sao cho bất phương trình đã cho nghiệm đúng
Chọn A Điều kiện: 2 40xxm −++ Ta có: ( ) ( ) 22 717 7
xxmx −++++ ( ) ( ) 22 777 log4log1log5 xxmx −++++ ( ) ( ) 22 77 log4log55 xxmx −+++ 222 22 455645 40 4 xxmxxxm xxmxxm −+++−+ −++− Bất phương trình đã cho nghiệm đúng 1;4 x khi và chỉ khi nghiệm đúng 1;4 x Đặt ( ) 2 645fxxx=−+ và ( ) 2 4 gxxx =− Khi đó nghiệm đúng 1;4 x ( ) ( ) 1;4 1;4 mMinfx mMaxgx 7 07 0 m m m . + f(x) 0 6 x 1 3 0 0 +
0984164935
luy
THPT BDKT Toán 10;
3 1 log1 3
1 06 3 fxx
, do đó có 6 số nguyên x thỏa mãn là: 1;2;3;4;5;6
1;4 x bằng A. 21. B. 28. C. 10. D. 11. Lời giải
log4log1log5
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 6
A. 28 B. 29 C.
D.
Lờ
Chọn A Điều kiện ( )0* x -Trường hợp 1: ( ) 2 2 22 5 1 log4log50;32
310;05; xx x xx x x −− − −+ Kết hợp với điều kiện ( )* ta được 5;32 x Trường hợp 2: ) 2 2 22 5 1 log4log50;32;1 20; 3102 0;5 xx x xx x x −+ −− − Kết hợp với điều kiện ( )* ta được 1 0; 2 x Vậy 1 0;5;32 2 x .Suy ra có 28 số nguyên x thỏa mãn bất phương trình đã cho Câu 11: Tìm tất cả giá trị của m để bất phương trình ( ) 9213320 xx mm −+−− nghiệm đúng với mọi số thực x . A. 3 2 m − B. 3 2 m − C. ( )523;523 m −−−+ . D. 2 m . Lời giải Chọn A Đặt 3x t = , 0 t . Khi đó, bất phương trình trở thành: ( ) 2 21320tmtm −+−− ( )( ) 1320ttm +−− 320−− tm 32+tm ( )1 Để bất phương trình đã cho nghiệm đúng với mọi x thì ( )1 phải nghiệm đúng với mọi ( ) 0; t +
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Mà m là số nguyên dương nên 1;2;3;4;5;6 m . Do đó tổng các giá trị nguyên dương của m là 21. Câu 10: Có bao nhiêu số nguyên x thỏa mãn ( )( ) 2 25 22 log4log5310 xx xx−−− ?
5
Vô số
i giải
25;32
Điều này tương đương với 320 + m 3 2 − m Vậy giá trị cần tìm của m là 3 2 m −
Câu 12: Có bao nhiêu giá trị nguyên thuộc đoạn 2021;2022 của tham số m để phương trình ( ) 2 923.330 xx mm −+++= có hai nghiệm phân biệt thỏa mãn: 12 2 xx+ A. 2021 B. 4042 C. 4040 D. 2020 Lời giải Chọn D Ta có: ( ) 2 923.330 xx mm −+++= ( ) 22 323.330 xx mm −+++= . Đặt 3x t = , 0 t
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 7
. Ta được
−+++= Nhận thấy: có hai nghiệm phân biệt khi và chỉ khi có
nghiệm
ệt
( ) 12 2 12 0 230 30 ttm ttm +=+ =+ ( )2 2 3(3)0 30 mm m +−+ + 6601 1 303 mm m mm +− − +− Khi đó: có
phương trình: ( ) 222330tmtm
hai
phân bi
dương
hai nghiệm 1t , 2t thỏa mãn: 2 12.3ttm=+ 2 1 2 3.33=+ xx m ( ) 12 22 123 33log3 xx mxxm + =++=+ . Từ ( ) 22 123 6 2log3239 6 m xxmm m +++ − . Kết hợp điều kiện ta được: 6 m . Do ,2021;2022mm− Các giá trị nguyên của m thỏa yêu cầu bài toán là: 3, 4,. 2021, 2022. Vậy có 2020 số thoả mãn yêu cầu. Câu 13: Có bao nhiêu số nguyên y sao cho ứng với mỗi y có nhiều nhất 5 số nguyên x thỏa mãn ( ) 3.2535.550 xx yy −++ A. Vô số B. 625. C. 3125. D. 225. Lời giải Chọn B Ta có ( ) ( ) 2 3.5355501 xx yy −++ . Đặt 50 x t = Khi đó, bất phương trình trở thành:
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 8 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( )( ) ( ) 2 335503502 tytytty −++−− . Do * y nên bất phương trình có nghiệm là 5 3 ty Từ đó suy ra 5 5 3 x y 55 5 loglog 3 xy . Ứng với mỗi số nguyên dương y có nhiều nhất 5 số nguyên x thỏa mãn 55 5 log;log 3 xy 5 0log4 y 1625 y Vậy có 625 số nguyên dương y thỏa mãn yêu cầu bài toán. Câu 14: Có bao nhiêu số nguyên x thoả mãn ( )( ) ( ) 2 2 2212122ln10 xxx x +−−−−+ A. 1. B. 2. C. 0. D. Vô số Lời giải Chọn C Điều kiện xác định: 21021 1 ln10ln1 00 xx xxx e xx − +− Ta có ( )( ) ( ) ( )( ) ( ) 2 2 2 2 ln10(1) 2212122ln10 22121220(2) xxx xxx x x + +−−−−+ +−−−− 1 (1) x e Giải Đặt ( ) 22 21,02121 xxxtttt −=−==+ Bất phương trình trở thành: ( ) ( )( ) ( ) ( )( ) ( ) ( ) ( )( ) ( ) 22222222 2 2 222 2 22 12121131 13 1131 1 2131 1. 11 tttttt tt tttt t t ttt t t t +−++−−+− ++ −++− +++ Do đó 211211221 xxx x −− Kết hợp điều kiện: 1 1 x e . Vậy bất phương trình có 0 nghiệm nguyên.
Câu 15: Có bao nhiêu giá trị nguyên dương của tham số m để tập nghiệm của bất phương trình ( )( ) 2 33320 xx m + −− chứa không quá 9 số nguyên? A. 1094. B. 3281. C. 1093. D. 3280. Lời giải Chọn D Đặt ( )3,0 x tt= bất phương trình ( )( ) ( ) 2 333201 xx m + −− trở thành ( )( ) ( )93202 ttm −− .
Nếu 3 2 9 m 3 1 18 m thì không có số nguyên dương m nào thỏa mãn yêu cầu bài toán. Nếu 3 2 9 m 3 18 m thì bất phương trình ( ) 3 22 9 tm
Khi đó tập nghiệm của bất phương trình ( )1 là ( ) 3 3;log2
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 9
2 Sm =− . Để S chứa không quá 9 số nguyên thì ( ) 8 3 3 log280 2 mm Vậy có 3280 số nguyên dương m thỏa mãn. Câu 16: Có bao nhiêu số nguyên x thỏa mãn ( ) ( ) 2 330.3813ln30 xx x −+− A. 1. B. 5. C. 4. D. 8. Lời giải Chọn B Điều kiện: ( ) 3 3 0 30 0 3ln30 3 3 x x e x e x x − Ta có ( ) ( ) ( ) 3 2 2 3ln30 330.3813ln302 330.3810;13; xx xx e x x x x −= = −+− −+ −+ Kết hợp với điều kiện, suy ra 1;3;4;5;6 x Vậy có 5 số nguyên x thỏa mãn yêu cầu bài ra. Câu 17: Có bao nhiêu số nguyên thoả mãn ? A. . B. . C. . D. . Lời giải Chọn D x ( ) ( ) 2 45.2642log40 xx x + −+− 22 25 23 24
Điều kiện xác định: . Bpt tương đương Kết hợp với điều kiện xác định ta được: .
Vậy có giá trị nguyên của thoả mãn yêu cầu bài toán.
Câu 18: Có bao nhiêu số nguyên thỏa mãn ? A. B. C. D. Lời giải Chọn B
Vì nên Vậy có số nguyên thỏa mãn bất phương trình đã cho.
Câu 19: Có bao nhiêu số nguyên thỏa mãn ? A. B. C. D. Lời giải Chọn C Vì nên Vậy có số nguyên thỏa mãn bất phương trình đã cho. Câu 20: Tổng tất cả các nghiệm nguyên của bất phương trình ( ) ( ) 2 24.5410log130
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
10 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
xxx x +−−+−
( ) 2log40 0 x x − 025 x ( ) ( )2 2 45.2640220.2640 2log404100 xx xx x x + −+ −+ −= = 242 2164 2525 x x x x xx == 02 425 x x 24 x x ( ) 1 2 2514.53lg0 25o xx x + −− 6 7 8 9 ( ) 2 1 2 2 1 3log0 4.53log03log0 4.5 25125 20 5125 xx xx x x x + + −= − −− − 8 08 525 x x x = 8 08 2 x x x = 8 28 x x = xZ 2;3;4;5;6;7;8 x 7 x ( ) 3 3 412822log0xx x + − 4 3 5 9 ( ) 3 3 3 3 3 2log0 412222llog0 8 412 0 80 og 2 xx xx x x x + + −= − −− 9 09 216 x x x = 9 09 4 x x x = 9 04 x x = xZ 1;2;3;4;9 x 5 17. 27. 26.
là A. 18. B. C. D.
++ 1.− x 2104.54−+−=xxx ( ) ( ) 215415 xxx ( )( )1524=−− xx ( ) ( )( ) ( ) 2 1524log130 xx fxx=−−+− 0 2104.54 2 = −+− = xxx x x ( ) 2 log1307 +−== xx ( )fx ( ) ( )1;02;7− 3;4;5;6 xx 18

Lời giải Chọn A Điều kiện Bất phương trình tương đương: Bảng xét dấu Suy ra tập nghiệm của bất phương trình là Vì tổng các nghiệm nguyên là Câu 21: Số nghiệm nguyên của bất phương trình ( ) 1 3 1log72.417.220 xx x + −+−+ là A. 3 B. 4 C. 6 D. 5 Lời giải Chọn D Điều kiện: 12 −+−+ ( )( ) 7073 228.2101 xx
xx + + −− −− Nếu 1 3 2.417.220 1 xx x x + =− −+= = ). Trường hợp này bất phương trình có nghiệm 3;1 x− Nếu 1 3 2.417.220 1 xx x x + − −+ . Bất phương trình đã cho ( ) ( ) 33 1log70log7174 xxx −++−− Do 6;5;4 xx−−− . Vậy cả 2 trường hợp ta được: 6;5;4;3;1 x−−−−− Câu 22: Có bao nhiêu giá trị nguyên của tham số 2022;2022 m− để bất phương trình ( ) ( ) 31.122.630 xxx mm++−+ có nghiệm đúng 0 x ? A. 2021. B. 4044. C. 2022. D. 2020. Lời giải Chọn A
7070 2.417.2208.217.220 xxxx x x x
11
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
Chia hai vế bất phương trình cho 3x , ta được ( ) ( ) 31.42.210 xx mm++−+
Đặt 2x t = ; vì 0 x nên 1 t .
Với 1 310 3 mm+==− , bất phương trình trở thành 7 10 3 t + .
Với 1 3 m − , bất phương trình trở thành ( ) ( ) ( ) ( ) 2 2 2
1 31.2.10,1 3 t mtmtmt tt −+ ++−+ .
761 3 tt gt tt +− = , ( ) 0,1gtt Suy ra ( )gt đồng biến trên khoảng ( ) 1;+ . Do đó ( ) 12 mg=− Vì 2022;2022 m− và m nên có 2021 giá trị thỏa mãn. Câu 23: Có bao nhiêu số nguyên x thỏa mãn ( ) ( ) 1 2 2
9318 0 g 6 lo2
+ +− −+ +
xx xx ? A. 5. B. 3. C. 1. D. 2. Lời giải Chọn D Xét bất phương trình: ( ) ( ) 1 2 2
9318 0 g 6 lo2 ĐKXĐ:
+ +− −+ + xxx xx
( ) 2 2 2 2 602323 12 log6202012 xx xx x
xx xx −++ −− − −++− −++− . Với 12 x − thì ( ) 2 2 log620 xx −++− , bất phương trình trở thành: 1 93180 xx+ +− 2 33.3180 xx+− ( )( ) 33360 xx−+ 33 x 1 x Kết hợp với điều kiện 12 x − ta có ( 1;1 x− . Mà x 0;1 x . Vậy có 2 giá trị nguyên x thỏa mãn. Câu 24: Có tất cả bao nhiêu giá trị nguyên của tham số m [10;10]− sao cho bất phương trình 52(1)5320 xx mm −+−− nghiệm đúng với mọi số thực x ? A. 9. B. 18. C. 20. D. 7 . Lời giải Chọn A 52(1)5320 xx mm −+−−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
12
Đặt ( ) ( )2 2
1 3 t gt tt −+ = ; ta có ( ) ( ) 2 2 2
( ) 12532 x mm+−−
TH1 : Nếu 1 120 2 mm +
Bất phương trình tương đương với 32 5 12 x m m + Để bất phương trình nghiệm đúng với mọi x thì không thể xảy ra nên TH 1 loại.
TH2 : Nếu 1 120 2 mm +
Bất phương trình tương đương với 32 5 12 x m m + Để bất phương trình nghiệm đúng với mọi x thì 32 0 12 m m + 1 2 m hoặc 3 2 m Kết hợp điều kiện ta được 3 2 m . Vì m và [10;10] m − nên m {10;9;...;2}−−− Vậy có 9 giá trị nguyên của m thỏa mãn yêu cầu bài toán. Câu 25: Tìm tất cả các giá trị của tham số m để bất phương trình ( ) 1 4210 xx m −+ nghiệm đúng với mọi x . A. ( ) 0; m+ . B.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 13
( ;0 m− . C. ( )0;1 m D. ( ) ( ) ;01; m−+ Lời giải Chọn B Ta có: ( ) ( ) 1 1 42104.2044.2401 4 xxxxxx mmmmm −+−−−− Đặt 2,0 x tt = . Bất phương trình trở thành: ( ) 2 440 2 tmtm−− . ( )1 đúng với mọi x khi và chỉ khi ( )2 đúng với mọi 0 t . Xét ( ) 2 44, 0 gttmtmt=−− ta có bảng biến thiên

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 14
− .
−
nguyên? A. 5. B. 3. C. 4. D. 6 . Lời giải Chọn D ( ) 25 1 242120 8 xxx −−− + Xét trường hợp 1: 5 5 10 0 2 5 x xx−= = = , thì ( )* 00 + Xét trường hợp 2: 5 055 120 x xx − Đặt 2x t = , 0 t Bất phương trình đã cho trở thành: ( ) ( )( ) ( ) 2 111 4022020 888 ttttttt −−+−−−− 2221 11 3 88 x tx Vậy tập nghiệm của bất phương trình đã cho là 3;15 S =− Từ đó ta có tập S chứa 6 số nguyên là: 3,2,1,0,1,5. Câu 27: Bất phương trình 2 35623xxx −−+ có tập nghiệm là A. ( ) 3 log18;3 . B. ( ) 3;+ . C. ( ) 3 ;log18− . D. ( ) 3 3;log18 .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn TH1: Nếu 020 mm : ( ) ( ) 2 0 ; 44 Mingtmm + =−− ( )2 đúng với mọi 0 t khi và chỉ khi ( ) ( ) ( ) 2 0 ; 001; 0 Mingtmmm + −−− . Kết hợp điều kiện ta được m TH1: Nếu 200 mm : ) ( ) ( ) 0 ; 04 Mingtgm + ==− . ( )2 đúng với mọi 0 t khi và chỉ khi ) ( ) 0 ; 0400Mingtmm + − Kết hợp điều kiện ta được ( ;0 m
Vậy ( ;0 m
Câu 26: Tập nghiệm của bất phương trình ( ) 25 1 242120 8 xxx −−− chứa bao nhiêu số
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 15 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn A Logarit hóa hai vế của phương trình ta được: ( ) 2 356 22 3log2log3xxx −−+ ( ) ( ) ( ) ( )( ) 2 222 3log256log3323log30 xxxxxx −−+−−−− ( ) ( ) 2 222 22 2 22 2 3 3 12log3 12log3log30log3 3.12log3log30 3 3 12log3 12log3log30 log3 x x x x xx x x x x + +− −+− + +− 3 3 3 3 log18 3 log18. 3 log18 x x x x x x Câu 28: Có bao nhiêu giá trị nguyên dương của tham số m để tập nghiệm của bất phương trình ( )( ) 3 33340 + −−xx m chứa không quá 6 số nguyên? A. 22. B. 19. C. 21.
Chọn D Bất phương
xx
( ) 3 3340 27 −− xx m 3 34 27 x m 33 3 loglog4 27 xm 3 5 log4 2 −xm Vậy tập nghiệm của bất phương trình là 3 5;log42 m . Vì tập nghiệm chứa không quá 6 số nguyên nên 3 log44 m 81 4 m . Do * m nên 1;2;...;20 m . Vậy có tất cả 20 số nguyên dương m thỏa mãn yêu cầu. Câu 29: Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a , có không quá 20 số nguyên b thỏa mãn 2 24.623 ababb ++ ++ ? A. 33. B. 32. C. 31. D. 30. Lời giải
D. 20. Lời giải
trình tương đương ( )( ) 27.33340 −−
m
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 16 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Chọn D ( ) ( ) 2 24.6232.2.4324.2.304.223230 ababbabbabbbabab ++ +++−−−−− ( )( ) 234.210 abb −− 3 3 3 * 230 log2 4.2102 2log2 log2 230 ( ) 2 4.210 ab b ab b ba b ba ba VNa b − −− − − − − Để có không quá 20 số nguyên b 32 log21919.log3 aa mà * a nên * 1;2...;30 aa . Vậy có 30 số nguyên dương a thỏa yêu cầu bài toán. Câu 30: Có tất cả bao nhiêu giá trị nguyên của tham số [10;10] m− sao cho bất phương trình 52(1)5320 xx mm −+−− nghiệm đúng với mọi số thực x? A. 9 B. 18 C. 20 D. 7 Lời giải Chọn A Ta có: 53 52(1)53202()
thực x 3 23 2 mm − . Do đó {10;9;8;7;6;5;4;3;2} m−−−−−−−−− . Câu 31: Cho bất phương trình 421230 xx mm . Có bao nhiêu giá trị nguyên của tham số m thuộc 5;5 để bất phương trình nghiệm đúng với mọi 2 x . A. 6 . B. 5. C. 7 . D. 8 . Lời giải
0984164935
51 x xx x mmmfx −+−−= + ( ) ( )2 2.5ln5 0, 51 x x fxxR = + Bảng biến thiên: Bất phương trình 52(1)5320 xx mm −+−− nghiệm đúng với mọi số
Chọn A
Ta có: 421230,2 xx mmx Đặt 2x t , 4 t . Khi đó phương trình đã cho trở thành: 2 2 23 2130 21 tt tmtmm t , 4 t
Xét hàm số 2 23 21 tt ft t , khi đó ft liên tục trên 4; 2 2 228 04 21 tt ftt t
Xét bảng biến thiên: Theo yêu cầu bài toán: 5 7 m . Vậy có 6 giá trị nguyên của tham số m thuộc 5;5
Câu 32: Tập nghiệm của bất phương trình ( ) ( ) 925.39210 xx xx −+++ là A. ) 0;12;+ . B. ( ) ;12; −+ .C. 1;2 . D. ( ) ;02; −+ . Lời giải Chọn A Đặt 3x t = , 0 t . Xét phương trình: ( ) ( ) 2 259210txtx−+++= ( )1 . Ta có ( ) ( ) ( ) 22 2 59218164 xxxxx =+−+=−+=− nên phương trình ( )1 luôn có nghiệm. Nếu 40 x == thì phương trình ( )1 có nghiệm kép 5 tx=+ . Do đó bất phương trình đã cho trở thành 35 x x + Nếu 40 x thì phương trình ( )1 có hai nghiệm phân biệt 21 9 tx t =+ = Xét các phương trình 392 x x == ( )1 và 3213210 xx xx =+−−= ( )2 . Đặt ( ) 321 x fxx=−− ; ta có ( ) 3ln32 x fx =− là hàm số đồng biến trên Lại có ( ) ( ) 010ff== và ( ) 00 f , ( ) 10 f nên ( )fx đổi dấu một lần duy nhất trong khoảng 0;1
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
17
Vậy phương trình ( )2 có đúng hai nghiệm 0 x = , 1 x = . Lập bảng xét dấu cho ( )1 và ( )2 ta được tập nghiệm của bất phương trình là: ) 0;12; S =+ .
Câu 33: Tìm tất cả
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
18
.
( ) (
212
−++−−+ −−
( ) (
2
=
( )
==−−−
ị
ủ
trình 222 sincossin 23.3xxx m + có nghiệm? A. 4. m B. 4. m C. 1. m D. 1. m Lời giải Chọn A Ta có 222 sincossin 23.3xxx m + 22 sinsin21 393.(1) xx m + Bất phương trình đã cho có nghiệm ( )1 có nghiệm ax mmy với 22 sinsin21 3. 39 xx y =+ Ta có: 2 22 2 sin sinsin 2 sin 2 1 3 21 sin03.1344 39 1 1 9 x xx x xy ++= Vậy bất phương trình có nghiệm khi 4 m .
các giá trị của m để bất phương trình ( ) 2 221.20 xx mm −++ nghiệm đúng với 0 x A. ( ;1−− . B. ( ;12− . C. ( ;0− . D. ( 1;16 . Lời giải Chọn A Đặt 2(1) x tt=
Khi đó, bất phương trình trở thành:
) 22 2 2 210220 2
21 tmtmtmttm tt tmttm t
Đặt
)
2 min. 21 tt gtmgt t
Ta có: ( ) ( ) 2 2 222 '0,1 21 tt gtt t −+ =
( ) ( min11;1 gtgm
Câu 34: Với giá tr
nào c
a m thì bất phương
Câu 35: Cho bất phương trình: ( ) ( )91.301 xx mm +−+ . Có bao nhiêu giá trị nguyên của tham số 2022;2022 m− để bất phương trình ( )1 nghiệm đúng 1 x A. 2021. B. 2024. C. 2022. D. 2023. Lời giải Chọn B Đặt 3x t = . Vì 13xt Bất phương trình đã cho thành: ( ) 2 1.0tmtm+−+ nghiệm đúng 3 t 2 1 tt m t − + nghiệm đúng 3 t . Xét hàm số ( ) ( ) ( ) 2 2 22 2,3,'10,3 111 tt gtttgtt tt t ==−+=− ++ + . Hàm số ()gt đồng biến trên ( ) 3;+ và ( ) 3 3 2 g = Yêu cầu bài toán tương đương 33 22 mm −− . bb aa fb = có tập xác định , và ( ) 451ln26ln50 54 4 5
Vì 2022;2022 m− nên có 2024giá trị nguyên m thỏa mãn. Câu 36: Có bao nhiêu số nguyên a sao cho ứng với mỗi a , tồn tại ít nhất bốn số nguyên ( )10;10 b− thỏa mãn 2 426 5abba +−+ ? A. 4 B. 6 C. 5 D. 7 bb a fb + = . Suy ra: ( )fb đồng biến trên . Ta có: * ( ) 22 22
giải 222 2 22
họn C 542614 20 55
) aaaa aa fa−== * ( ) 22 22
aaaa aa fa−== Do đó 2 2 ba =− là số nguyên lớn nhất để ( )* đúng. Theo đề: tồn tại ít nhất bốn số nguyên ( )10;10 b− , ta xét: 2222 12341;;1;2 babababa =−−=−=−=− và ( ) 1234 ,,,10;10bbbb − Suy ra: 2 9 a mà a nên 0;1;2 a .
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn bb abbaaa +−− +−− Xét hàm số ( ) 2 41 5.26. 4 55
333 2 33
5426994 30 55
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 19
Lời
C
Ta có (
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 22 41 42654.26.0* 5 5 5
Vậy có 5 giá trị nguyên a thỏa mãn đề bài. Câu 37: Có bao nhiêu số nguyên a sao cho ứng với mỗi a , tồn tại ít nhất bốn số nguyên 12;12 b thỏa mãn 2 4365 abba ? A. 4 . B. 6. C. 5. D. 7 . Lời giải Chọn D Chia cả hai vế cho 4b , ta được
2 131 654. 344 0 bb a a
(
7 giá tr
ị
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 20
+−
Đặt
) 2
a
=+− , với 11;11
− . Ta có ( )
a
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 =+−
(
131 654 344 bb a
fb
b
13311ln65ln0,11;11. 34444 bb
fbb
Do
đó
)fb nghịch biến trên 11;11 . Điều này dẫn đến yêu cầu bài toán trở thành ( ) 2 88 804365. aa f −+ Nếu 8 a − thì 2 884aa−−−+ . Suy ra ( ) 2 88848 4 488 44343413365. 4 aaaaaa =+−+
38: Có bao nhiêu số nguyên a sao cho ứng với mỗi a , tồn tại ít nhất 9 số nguyên 12;12 b thỏa mãn 2 3263 abba ? A. 4 B. 6 C. 5 D. 7 Lời giải Chọn C Chia cả hai vế cho 3b , ta được 2 11 . 2 0 3 2 3 633 bb a a +− Đặt ( ) 2 2 233 11 633 bb a a fb =+− , với 11;11 b− . Ta có ( ) 22 2333 111 ln63ln 3 0,11;11 bb a fbb =+− Do đó ( )fb nghịch biến trên 11;11 . Điều này dẫn đến yêu cầu bài toán trở thành
Nếu 8 a − thì do thì 8 31 a , mà a nên 2 82 4 4668log3;2;1;0;1;2;3. 66 a aa +−−− Thử lại tất cả
nguyên trên đều thỏa mãn yêu cầu. Câu
( ) 2 33 303263. aa f −+
Nếu 3 a − thì 2 336aa−−−+ . Suy ra ( ) 2 6 33 6 333 333331363. 3 aaaaa + = + =
Nếu 3 a − thì do thì 3 21 a và a nên 2 3 32 3633log632;1;0;1;2. a aa +−−
Thử lại tất cả 5 giá trị nguyên trên đều thỏa mãn yêu cầu.
Câu 39: Có bao nhiêu số nguyên a sao cho ứng với mỗi a , tồn tại ít nhất 8 số nguyên 10;10 b thỏa mãn 2 2 53624 abba ? A. 3 B. 6 C. 5 D. 7 Lời giải
Chọn A
Chia cả hai vế cho 5b , ta được 2 2 131 5 6245. 3 0 5
bb a a +− Đặt ( ) 2 131 64 3 5 25 5
bb a a fb =+− , với 9;9 b− . Ta có ( ) 13311ln624ln0,9;9. 5555 3
bb a fbb =+− Do đó ( )fb nghịch biến trên 9;9 . Điều này dẫn đến yêu cầu bài toán trở thành ( ) 2 211 1053624. aa f −+ Nếu 2 a − thì 2 2116 aa−−−+ . Suy ra ( ) 2 66 211111 55533513624. aaaaa +−+ Nếu 1 a − thì do thì 1 31 a và a nên 2 212 5. 1010 625241;0;1 2 1 2 a aaa −−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
21 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
Thử lại tất cả 3 giá trị nguyên trên đều thỏa mãn yêu cầu. Câu 40: Có bao nhiêu số nguyên a sao cho ứng với mỗi a , tồn tại ít nhất 8 số nguyên 10;10 b thỏa mãn 2 23 53598 aabba ? A. 4 . B. 6. C. 5. D. 7 . Lời giải Chọn B Chia cả hai vế cho 5b , ta được
+ Nếu 4 a thì do thì 1 327 a và a nên 2 2426254242;1;0;1;2;3;4.524 aa a aaa −−− Thử lại, ta thấy được 6 giá trị 1;0;1;2;3;4 thỏa mãn yêu cầu. Câu 41: Có bao nhiêu số nguyên a sao cho ứng với mỗi a , tồn tại ít nhất 8 số nguyên 8;8 b thỏa mãn 2 24 4337 aabba ? A. 4 . B. 6. C. 5. D. 7 . Lời giải
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 22
toán trở thành ( ) 2 241 1053598. aaa f −+ Nếu 4 a thì 2 2411aaa−−−+ . Suy ra 2 24111111 1 5625 5 . 7 598 553 2 5333359 3 8 27 aaaaaa a aa = =+
2
31 3374. 0 44 bb aa
+− Đặt ( ) 2 24 31 3374 44 bb aa a fb =+− , với 7;7 b− . Ta có ( ) . 444 3ln37l3311 4 n0,7;7 bb a fbb =+− Do đó ( )fb nghịch biến trên 7;7 . Điều này dẫn đến yêu cầu bài toán trở thành ( ) 2 24 004337. aaa f + Nếu 4 a thì 2 2411aaa−−−+ . Suy ra 2 2411111 1 1 464 4 37 5343 4 32 3333 7 7 27 aaaaaaa a a = = + + Nếu 4 a thì do thì 1 327 a và a nên 2 242 46331221221;0;1;2; 23 4 aa aaa a −+−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 2 23 31 35985. 0 55 bb aa a +− Đặt ( ) 2 23 31 35985 55 bb aa a fb =+− , với 9;9 b− . Ta có ( ) 3311 3ln598ln0,9;9. 5555 bb a fbb =+− Do đó ( )fb nghịch biến trên 9;9 . Điều này dẫn đến yêu cầu bài
Chọn C Chia cả hai vế cho 4b , ta được
24
a
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 23 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt
ệp
12
tầm và biên soạn Thử lại, ta thấy tất cả 5 giá trị trên đều thỏa mãn yêu cầu. Câu 42: Có bao nhiêu số nguyên x thỏa mãn bất phương trình ( ) 2121 55 log56log23220 x xx −+− ? A. 121 B. 0 C. 1 D. 122 Lời giải Chọn D Điều kiện 121 0 0126 232 x x x + TH1: ( ) 121 3220126 x xTM−== + TH2: 121 3220126 x x − Ta có BPT đã cho tương đương với ( ) 2 55 log56log20 xx−+ (
2 55
xx +−+ 2 55 log4log30 xx −+ 5 1log3 x ( ) 5125xTM . Mà 5;6;...;126 xx Vậy có 122 giá trị thỏa mãn yêu cầu đề bài. Câu 43: Số nghiệm nguyên của bất phương trình ( ) 2 232 42.1613.16 xxxx xx −−+ là: A. 4 B. 6 C. 3 D. 5 Lời giải Ta có: ( ) ( ) 22 232232 42.1613.16423.161 xxxxxxx xxxx
Xét trường hợp: 2 2301,3xxxx −−==−= VT
=+= ). Xét: 2 1 230 3 x xx x − −− ( ) 2 230 2 441 23.160 xx x xx = −− VT ( )1 1 Xét: 2 23013xxx−−− ( ) 2 230 2 441 23.160 xx x xx = −− VT ( )1 1 . Vậy: 2 2301;3.xxx−−− Tập nghiệm của bất phương trình là: 1;3 . Bất phương trình có 5 nghiệm nguyên. Câu 44: Biết phương trình 2 22 log(2)(21)log(2)40 xmxm −−+−++= có hai nghiệm 12 , xx thoả mãn 12122()28xxxx−+= . Số nghiệm nguyên thuộc khoảng (8;8) của bất phương trình 2 2512 xmxm eexxmm ++−+−+++− là A. 4 B. 5 C. 2 D. 15
0984164935
Nghi
THPT BDKT Toán 10; 11;
Sưu
)
1log6log20
−−++−− ( )1
( )1 0 401
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 24 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn C Từ giả thiết ( )( ) ( ) ( ) 1212122122 2()282232log2log25 xxxxxxxx −+=−−=−+−= 2152 mm +== . Thử lại 2 m = thỏa yêu cầu. Thay 2 m = vào ta được ( ) 42424242xxxx eexxexex +−+− +−+−+++−
xx
+−+++− 2 2 20 2 42405 50 444 x x xxxx xx xxx − +−+ − +−+
K
ợ
ới
u kiện
−
nh
. Ta
( ) ( ) ( ) 22 11 xxxxxx
+−+− −=−=−−=− Và
( ) ( ) ( ) 2222 1111 222 1.1.0 111 xxxxxxxxxx xxx fxeeeeeeeeee xxx +−+−++− =−++=++− +++ Nên hàm số ( ) ( ) 2 1 xxxfxeee +− =− đồng biến trên . Xét bất phương trình: ( ) ( ) 121212 707 111fmffmff mmm −+−−=− +++ 2 15 1265 70 1 11 m mm m m mm −+ −− − ++ Vì m nguyên dương nên 2;3;4 m . Câu 46: Số nghiêm nguyên của phương trình ( ) 2 232 5.13.225 25 xxxx xx + là
. Xét hàm số ( ) t ftet =+ , hàm số đồng biến trên . Suy ra ( ) 4242
exex
.
ết h
p v
điề
;(8;8)6;7xxx
. Câu 45: Cho hàm số ( ) ( ) 2 1 xxxfxeee +− =− . Có bao nhiêu số nguyên dương m thỏa mãn bất phương trình ( ) 12 70 1 fmf m −+ + ? A. Vô số B. 4 C. 3 D. 5 Lời giải Chọn C Xét hàm số ( ) ( ) 2 1 xxxfxeee +− =− xác đị
trên
có: ( )
fxeeeeeefx
có:
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 25 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 5 B. 4 C. 6 D. 3 Lời giải Chọn A Đặt 2 23txx=−− . Ta có ( )2 2 23144txxx =−−−− − = . Vậy ) 4; t −+ . Khi đó, phương trình trở thành 2 5.510 tx t + Đặt ( ) ( ) 22 5.51'5ln55 txtxfttft =+−=+
V
V
(
−−−−−
ủ
ị
ớ
i 0 t . ( ) 20212021 0 10.ln100, ln10 + = t f t t t . ( )ft đồng biến trên khoảng ( ) 0;+ . Bất phương trình( ) ( ) ( ) ( ) ( ) 2222 *22 ++++ fxyfxyxyxy ( ) ( ) ( ) 22 112**−+− xy . Lại có: ( ) ( ) ( ) 22 22 10225124***yxyP P xy x +−−+−+−− = = Gọi điểm ( ) ; Mxy , ( )5;1 K khi đó ta có điểm M thuộc hình tròn ( )1C có tâm ( )1;1 I , bán kính 2 r = và 2 24 PMK=−
04 t − .
ậy hàm số ( )ft là hàm đồng biến trên ) 4; −+
ới 0 t = ta có ( ) 00 f = . Dẫn đến
) ( ) ( ) 22 00101421213 4 f txxx t x
Vậy có 5 giá trị nguyên của x thỏa mãn ( ) 2 232 5.13.225 25 xxxx xx + Câu 47: Cho hai số , xy thỏa mãn 0 xy+ và 22 2 22 0212021 12 100 02021.log2021.log + + ++ + + x y xy y x xy . Tìm tổng c
a giá tr
l
n nhất và giá trị nhỏ nhất của biểu thức 22 1022. = +−+ P yxy x A. 12. B. 8. C. 682. D. 826. Lời giải Chọn A Ta có 22 2 22 0212021 12 100 02021.log2021.log + + ++ + + x y xy y x xy ( ) ( ) ( ) ( ) 22 2 20 2 212 2 021 *102021.log2021g210.lo + + +++ + x x y y xy y x Xét hàm số ( ) 2021 o 2021 .l 10g= + t ftt vớ
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
ỳnh
Page 26
Vì
==
nên điểm (
nằ
. Do
minmin 42 PMKMKIKr=−=− 42 MaxMax PMKMKIKr=+=+
Vậy tổng của giá trị lớn nhất và giá trị
ỏ
ấ
Theo
ta ( )20212021 m ; − và 0 m , suy ra 202010 ;
,;−− , tức là có 2021 giá trị
ỏa
Câu 49: Gọi S là tập hợp các số tự nhiên n có 4 chữ số thỏa mãn 2020 202020202323 n nn . Số phần tử của S là A. 8999 . B. 2019. C. 1010 . D. 7979. Lời giải Chọn C 2020 2020202020202020 23232020ln23ln23 n nnnn n 20202020 2020ln23ln230* nn fnn .
Giáo viên: Hu
Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
42
IKr
)5;1 K
m bên ngoài ( )1C
đó
Suy ra min682,max826 =−−=−PP
nh
nh
t của biểu thức P bằng 12 Câu 48: Tìm tất cả các giá trị nguyên của m trên ( )20212021 ; thỏa mãn ( )( ) 2 241432 3 mm mmm−++−+ . A. 2021. B. 2020. C. 1. D. 0. Lời giải Chọn A ( )( ) ( ) ( ) ( ) 2 2 24143243231313 mmmm m m m m m −++ −+− −+−+ − ( ) ( ) ( ) ( ) ( ) 22 432 3 131131432 m m m m mmmm −+−−−+−−++ +− Xét hàm số ( ) 2 30 fxxx, x =+− và ( ) 2 2 3 0 3 x xx fx, x +− =− + Mặt khác, ( ) 2 3 fxxx −=++ . Do đó, ( ) ( ) ( ) ( ) 1212210 mmm f m mm f −−−+− − Xét hàm số ( ) 21 x gxx=+− , ( ) 12ln20 x x gx, =+ và ( ) 00 g = . Như vậy, ( ) ( ) ( ) 00 g gm m
.
bài
m
m th
mãn.
Khảo sát hàm số yfn ,
2020 2ln23ln3ln23 23 22020ln2ln2332020ln3ln23 23 2ln3ln23 2ln33ln2 2323 2323 2020ln3.22020ln2.3 0, 23
fn n . Suy ra, fn là hàm nghịch biến. Ta có 20200 f . Khi đó *20202020 fnfn mà 1000,10002020nnn . Vậy có 1010 số tự nhiên n thỏa mãn yêu cầu bài toán.
nn nn nn nn nn nn nnnn nn nn
20202020 2020202020202020 20202020 20202020 2020202020202020
Câu 50: Với a là tham số thực để bất phương trình 232 xx ax ++ có tập nghiệm là . Khi đó: A. ( )1;3 a B. ( )0;1 a C. ( );0 a− D. ( ) 3; a+ Lời giải
Chọn A
Hàm số ( ) 232 xx fxax=+−− liên tục trên
Ta có ( ) ( ) '2ln23ln3;00 xx fxaf=+−=
Do đó ( ) ( ) ( ) 000fxxfxfxx = là điểm cực tiểu ( ) '00ln2ln30ln6 faa =+−== Thử lại: Với ln6 a = có ( ) '2ln23ln3ln6 xx fx =+− ( ) '02ln23ln3ln60 xx fxx =+== Bảng biến thiên: Bất phương trình ( ) 0 fx có tập nghiệm là

Câu 51: Cho hàm số 3 ()222022 xx fxx =−+ Biết rằng tồn tại số thực m sao cho bất phương trình ( ) ( ) ( ) 43737.20 xxfmxmfxm−++−− nghiệm đúng với mọi x . Hỏi m thuộc khoảng nào dưới đây? A. ( )30;50 . B. ( )10;30 . C. ( )50;70 . D. ( )10;10 .
27
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 có
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
. Suy ra hàm số ( )fx là hàm đồng biến trên .
fmxmfxm fmxmfxm mxmxm mxmxm mx
−+−−− −+−−− −+−−− −+−−− −+−
43737.2 43737.2 43737.2 43737.2 22370.
xx xx xx xx xx
Bất phương trình đã cho tương đương ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )( )
Xét phương trình 2370 x x +−= . Nhận xét phương trình có một nghiệm 5 x = . Xét hàm số ( ) 237 x gxx=+− , có ( ) 12ln20, x gxx =+ suy ra 5 x = là nghiệm đơn duy nhất. Suy ra ( )gx đổi dấu từ âm sang dương khi qua nghiệm 5 x =
Ta cũng có hàm số hàm số ( ) 2x hxm =− đồng biến trên nên từ giả thiết bất phương trình ( )( ) 22370 xx mx −+− nghiệm đúng với mọi x ta có ( ) 2x hxm =− đổi dấu từ âm sang dương khi x qua điểm 0 5 x = . Do đó ( ) 50 h = hay 32 m = Câu 52: Cho bất phương trình ( ) ( ) ( ) 233 273.9333131 xxx xxmxmx +++−+− . Số các giá trị nguyên của tham số m để bất phương trình trên có đúng7nghiệm nguyên dương phân biệt là A. 507. B. 508. C. 509. D. 510. Lời giải
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 28
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn A Xét hàm số 3 ()222022 xx fxx =−+ có tập xác định D = . Ta có Với mọi xDxD − và ( ) ( ) 3 222022 xx fxxfx −=−−=− . Suy ra ( )fx là hàm lẻ. Mặt khác ( ) 2 2ln22ln260660, xx fxxx =++
Chọn B Ta có ( ) ( ) ( ) 233 273.9333131 xxx xxmxmx +++−+− ( ) ( ) 32 21333 33.33.3333 xxxx xxmxxmxx + +++−+− ( ) ( ) 32 23133 33.33.3333 xxxx xxxxmxmx + ++++++ ( ) ( ) ( ) ( )( ) 3 3 33331 xx xxmxmx++++
Xét hàm số ( ) 3 3 fttt =+ , có ( ) 2 330ftt =+
Nên ( )ft đồng biến trên ( ) ; −+ , khi đó:( ) 3 131 x x xmxm x +− , do 0 x
Xét hàm số ( ) ( ) 2 33ln3.3 xxx x gxgx xx == , ta có ( ) 30 0log1gxxex ===
Ta có bảng biến thiên của hàm số ( )gx :
Nên để bất phương trình có đúng 7 nghiệm nguyên dương phân biệt thì ( ) ( ) 712187656121946569 1 817878 gm mm gm −
ậy có 508 giá trị nguyên của tham số m Câu 53: Gọi 0m là giá trị của tham số để bất phương trình 232 xx mx ++ có tập nghiệm là . Khi đó A. ( ) 0 ;0 m − . B. ( ) 0 3; m + . C. ( ) 0 0;1 m . D. ( ) 0 1;3 m . Lời giải
m
Chọn D +) Với 0 m : Bất phương trình không nhận các giá trị âm của x làm nghiệm.
Thật vậy, khi đó 232 xx+ và 22 mx + . Suy ra 0 m không thỏa mãn.
+) Với 0 m : Ta có 232 xx mx ++ 2320 xx mx +−− . Xét hàm số ( ) 232 xx fxmx=+−− trên . Khi đó ( ) 2ln23ln3 xx fxm =+− . Ta có ( ) 0 fx = 2ln23ln30 xx m +−= ( )2ln23ln31 xx m += . Xét hàm số ( ) 2ln23ln3 xx gx =+ trên ( ) 22 2ln23ln30, xx gxx =+ . Suy ra hàm số ( )gx đồng biến trên . Lại có ( ) lim0 x gx →− = và ( ) lim x gx →+ =+ Suy ra với mỗi giá trị 0 m thì phương trình ( )1 luôn có nghiệm duy nhất là 0x .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 29
− −
V
Ta có phương trình ( ) 0 fx = có nghiệm duy nhất là 0x .
Mà ( ) lim0 x fxm →−
=− và ( ) lim x fx →+
=+ nên ( ) 0 0, fxxx và ( ) 0 0, fxxx .


Bảng biến thiên của hàm số ( )fx :
Dựa vào bảng biến thiên ta thấy ( ) ( ) 0 min x fxfx =
Kết hợp điều kiện đề bài là ( ) ( ) ( ) 0 0,min0 x fxxfxfx = mà ( ) 00 f = . Suy ra 0 0 x = và 0 0 x = là giá trị duy nhất để ( ) 0 fx = Suy ra 0 0 x = là giá trị duy nhất để ( ) 0 fx = . Suy ra ( ) 0ln2ln30fm =+−= Vậy ( )ln2ln3ln61;3 m =+=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
30
Chọn D ( ) ( )
2
4 xx x mmx −−++−+ vớ
x ( ) ( ) ( ) 2
xxx mmx −++−−+ Xét hàm số ( )
x fcx=−+ ( ) '()4.4.ln441ln40 xxx
=−−=−+
ớ
Bảng xét dấu Với )0;1 x thì ( )
x x −+
Câu 54: Có bao nhiêu nghiệm nguyên của m thuộc đoạn [0;2022]để phương trình ( ) ( ) 1 2 1421.40 4 xx x mmx −−++−+ nghiệm đúng với mọi x thuộc )0;1 ? A. 2021 B. 1011 C. 2022 D. 1 Lời giải
1
1421.40
i
)0;1
142142..440
().44
fxxx
V
i )0;1 x
.440
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 31 Chuyên
ện thi: Tuyển sinh vào
ớp 10 Tốt
ệp
12 Sưu tầm và biên soạn Khi đó BPT tương đương với ( ) ( ) 2 1421420 xx mm−++− Với )0;1 x Đặt 4x t = )1;4 t ( ) ( ) ( ) 2 **12120 mtmt −++− 2 2 2 2 tt m tt −+ + Đặt 2 2 2 () 2 tt gt tt −+ = + Suy ra ) ( ) 1;4 1 min 2 m[0;2022] mgt m = 0 m = Câu 55: Có bao nhiêu giá trị nguyên m để bất phương trình 22 22 1423 3 211 22 2 mxx x xxm−−+ + nghiệm đúng với mọi giá trị thực của x
ời giải Chọn C Ta
22 22 22 22 1423 3 17622 17262
22 2 22211 217261 mxx x xmxx xmxx xxm xxm xmxx +−−− +−−− −−+ + +−−+ ++−+−−
−+=−+ Suy ra BPT ( )2 đúng với mọi giá trị thực của x khi và chỉ khi 2 10 m . Mà 3;2;1;0 mm . Vậy có 7 số nguyên thỏa mãn ycđ B. Câu 56: Có bao nhiêu số nguyên a sao cho ứng với mỗi a , tồn tại ít nhất bốn số nguyên ( )12;12 b− thỏa mãn 2 4365 abba +−+ ? A. 4. B. 6. C. 5. D. 7. Lời giải Chọn D Ta có: 2 4365 abba +−+ 2 43650 abba +− −− 2 365 40 44 ba a bb −−
0984164935
luy
l
Nghi
THPT BDKT Toán 10; 11;
A. 6. B. 9 C. 7 D. 8 L
có: ( )
211
Xét hàm số ( ) 2'2.ln210, tt fttyt =+=+ suy ra hàm số ( )ft luôn đồng biến trên Do đó BPT ( ) ( ) 2222 11762112 xmxxmxx +−−−−+ Có ( )2 2 21111010, xxxx
bb a a −−
2 311 4.65.0 434
Xét hàm số ( ) 2 311 4.65. 434
bb a a fb =−− , ( )12;12 b− .
Ta có ( ) 33111 ln..65.ln.0 44344
bb a fb =−− , ( )12;12 b −
Do đó ( )fb đồng biến trên ( )12;12 .
Ta có bảng biến thiên: Để có ít nhất 4 số nguyên ( )12;12 b− thỏa mãn ( ) 0 fb thì ( ) 80 f − 2 88 4365. aa + Suy ra 2 8 465 a 2 4 8log6511 a + . Do a nên 3;2;...;2;3 a−− . Vậy có 7 giá trị nguyên của a thoả mãn yêu cầu bài toán. Câu 57: Có bao nhiêu cặp số thực ( ) ; xy thỏa mãn đồng thời điề
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
32
u kiện ( ) 2 3 23log5 4 35 xx y −+ = và ( )2 4138 yyy−−++ ? A. 1 B. 2 C. 4 D. 3 Lời giải Chọn B Xét bất phương trình: ( )2 4138 yyy−−++ , + TH1: 0 y ( ) 0 2 41383030 y yyyyy −+−++−− . + TH2: 01 y ( ) 01 2 41381100 y yyyyy +−++−=
( )ft đồng biến trên khoảng ( ) 0;+ Do đó bất phương trình ( ) ( ) ( ) 133 yyfxfx . Vì 111 x nên 3 311log112,18 y y . Do y nguyên dương nên 1;2 y . +) TH 1: Với 1 y = khi đó 1 33xx 3;4;5;6;7;8;9;10;11 x . +) TH 2: Với 2 y = khi đó 2 39xx 9;10;11 x
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 33 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn + TH3: 1 y ( ) 1 2 973973 4138 22 y yyyy −−−+ −+++ loại TH3. Từ 3 trường hợp cho ta: 30 y − . Với 30 y − ta có: ( ) ( ) ( ) 2 22 3 23 3 23log52344331 35535 55 xx y xxxxyyy + −+−+−+ ==== Do 2 23 30 31 11 1 55 xx y+ = nên dấu bằng xảy ra 2 1;3 230 3;3 30 xy xx xy y =−=− −−= ==− += Vậy có 2 cặp số thực ( ) ; xy thỏa mãn. Câu 58: Có bao nhiêu cặp số nguyên dương ( ) ; xy thỏa mãn 111 x và 2 93yy xx+− ? A. 10. B. 11. C. 12. D. 13. Lời giải C
C Từ
thiết 2 93yy xx+− 2 93yy xx ++ Xét
( ) 2
=+ . Ta
(
=++
Câu
Cho , xy
ố
ự
ỏ
y sao cho với mỗi giá trị nguyên dương đó của y ta tìm được không quá 2021 giá trị nguyên của x ? A. 511060 B. 510049 C. 510048 D. 511059 Lời giải Chọn D Ta có: 22 1212 164442(21) yxyx xy ++−−− ( ) 22 22112 442.2442(1) yyxxyx −−−−− Xét hàm đặc trưng ()442 tt ygtt ==−− có ( ) '()44ln42 tt gt =+−
họn
giả
hàm số
; 0 ftttt
có
) ( ) 210; 0; fttt
Vậy có 12 cặp số nguyên dương ( ) ; xy thỏa mãn đầu bài.
59:
là các s
th
c th
a mãn 22 1212 164442(21) yxyx xy ++−−− . Có bao nhiêu số nguyên dương
Ta thấy: ( ) 442;ln4144ln420 tttt ++− nên suy ra hàm ()gt luôn đồng biến trên R ( ) ( ) 222 212121 gygxyxxy −−+ . Khi đó ta được 2121 yxy −++ , do đó yêu cầu bài toán trở thành 2 10111 211011511060 2 yy += .
Câu 60: Có bao nhiêu số nguyên y sao cho ứng với số nguyên y có tối đa 100 số nguyên x thỏa mãn 22 53log yx xy . A. 17 B. 18. C. 13. D. 20. Lời giải Chọn D Điều kiện: 2 xy Xét hàm số 22 53log yx fxxy ta có: 2 2 1 2.3.ln30 .ln5 yx fx xy Bảng biến thiên Từ bảng biến thiên trên ta có tập nghiệm của bất phương trình là 2 0 ; yx . Để có tối đa 100 số nguyên
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
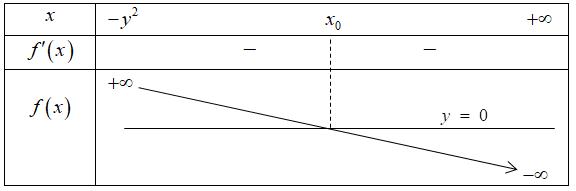
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
34
+−
x thì 2 1010 fy 22 22022202 55 3log10103log101 yyyy 2 35 2202loglog101010,339,83 yyy . Vậy có 20 giá trị nguyên của y Câu 61: Có bao nhiêu số nguyên a sao cho ứng với mỗi a , tồn tại ít nhất 9 số nguyên ( )12;12 b− thỏa mãn 2 3275 abba
+ ? A. 4 B. 6 C. 5 D. 7 Lời giải Chọn C Chọn. C. Chia cả hai vế cho 30 b , ta được
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 35 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 2 11 . 2 0 3 2 3 753 bb a a +− Giả sử ( ) 2 2 233 11 753 bb a a fb =+− là hàm số ẩn b và a là tham số với 11;11
− .
( ) 22 2333 111 ln75ln 3 0,11;11 bb a fbb =+− Do đó ( )fb nghịch biến trên 11;11 và
ít nhất 9 số nguyên ( )12;12 b− thỏa mãn đề bài nên điều này dẫn đến yêu cầu bài toán trở thành ( ) 2 33 303275. aa f −+ Nếu 3 a − thì 2 336aa
A.
B. 2019 C. 2018 D. 2020 Lời giải Chọn B Ta có: 2 22365603 baab + + 2 2 21 3656030 33 bb aa +− Xét hàm số ( ) 2 2 21 365603 33 bb aa fb =+− Bất phương trình trên trở thành ( ) 0, fb với ( )10;10 b− . Ta có ( ) 2211 ln.36560ln0 3333 bb a fb =+ , ( )10;10 b − Do đó ( )fb nghịch biến trên ( )10;10 khi đó ( ) ( ) ( )98...9fff −− khi đó để tìm được mười giá trị b nguyên thuộc ( )10;10 thỏa mãn ( ) 0 fb điều kiện là 2 2365603 aa + Mặt khác do a nguyên ( )0;2022 a nên 1 a suy ra
b
Ta có
có
−−−+ . Suy ra ( ) 2 3333 6633 6 333331331275. 3 aaaaaa +− + =+ Nếu 3 a − thì do thì 3 21 a và a nên 2 2 3 32 3753log2;1;0;1;2. 757 a aaa +− Thử lại tất cả 5 giá trị nguyên trên đều thỏa mãn yêu cầu. Câu 62: Có bao nhiêu số nguyên ( )0;2022 a sao cho ứng với mỗi a , tồn tại ít nhất mười số nguyên ( )10;10 b− thỏa mãn 2 22365603 baab + + ?
2021
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo
Page 36
2 3 2 3 1
aa a a + −− mà
Câu
Để 1 ;1 3 x đều là nghiệm của bất phương trình thì 11 133;4;...;19 3 mmm m . Câu 64: Có tất cả bao giá trị nguyên của tham số a thuộc ( )1999;2050 để 2022 2022 2022 11 22 22 a a a ++ . A. 29 B. 28. C. 30 D. 31 Lời giải Chọn B Ta có: 2022 2022 2022 11 22 22 a a a ++ ( ) ( ) 202220222022ln22ln22 aa a ++ ( ) ( ) 20222022ln22ln22 2022 aa a ++ ; vì ( )1999;2050 a
viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
log6563265633656032 1 log656322
a nguyên ( )0;2022 a
nên
3;4;5;...;2021 a
có 2019 số nguyên a .
63: Có bao nhiêu giá trị nguyên của tham số ( )1;20 m để 1 ;1 3 x đều là nghiệm của bất phương trình: loglog mx xm ? A. 18 B. 16 C. 17 D. 0 Lời giải Chọn C Điều kiện 01 x ( )2 1log1 logloglog0(*) loglog m mxm mm x xmx xx Do ( ) 1 ;1,1;20log03 m xmx Do đó 1 (*)1log1 m xxm m −
++ . 2022 a
. Kết hợp với điều kiện đề bài ta có 2022;2023;...;2049 a Vậy có 28 giá trị của a . Câu 65: Có bao nhiêu giá tr
nguyên



3920
)
5 nghi
m nguyên?
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
37
ị
của để ( )(
22
xxx m −− có
Xét hàm số ( ) ( ) ln22xx fx x ệ
+ = . Tập xác định \0 D = . ( ) ( ) ( ) ( ) ( ) 2 A.
22ln222ln22 22 −−++ = + Lờ
xxxxxx xx Chọn B *) Xét 2 2 1
x fx x Vì: ( ) ln2ln2ln22 =+xxx x và 02222xxxx−+ Suy ra ( ) ( ) 0 ' fxfx nghịch biến. Do đó: ( ) ( ) 20222022ln22ln22 2022 2 xx x xx x − −−− Từ
aa a . Vì ( )1;2 chỉ có hai số nguyên là 0 và 1 nên không có giá trị nào để bất phương trình có 5 nghiệm nguyên. Vậy có tất cả 65024giá trị thỏa mãn. Câu 66: Số nghiệm nguyên của bất phương trình 22 215102 22250 xxxx xx −+−+− là: A. 16. B. 23. C. 25. D. 24. Lời giải
65023 B. 65024 C. 65025 D. 65022
i giải
39020
suy ra: 22 2 2202log xx mmxm − Nếu 1 m thì BPT vô nghiệm. Nếu 1 m thì ( ) 22 2loglogmxm− Theo giả thiết, tập hợp ( ) 22 ;12;log;logmm −−+− có 5 giá trị nguyên Khi đó ta có: 2 3log451265536 mm . Suy ra có 65024giá trị m nguyên thỏa mãn. *) Xét 2 2 3902012 xx xxx −−−−
Chọn D
Ta có: 22 215102 22250 xxxx xx −+−+− ( ) 22 2151022 22215100 xxxx xxxx −+ −+−−+
Đặt 2 215 axx =− , 2 10 bxx =+ .
Khi đó bất phương trình trở thành: 220 ab ab −+− 22 abab++ ( )1
Xét hàm số ( ) 2t ftt =+ có ( ) 2ln210 t ft =+ với t
Suy ra ( )ft đồng biến trên Bất phương trình ( )1 ( ) ( ) fafbab 22 21510 xxxx−+ 2 250xx − . 025 x
x nên
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
38
++
Ta
++−− TH1: 2 1 1 1 1 280 2 2 20 0 21 x x x x x y x y + + + − − − − TH2: 2 1 280 2 x x + −− khi này để ( )( ) 21 2? 820xx y ++−− thì 11202 xx yy ++ − Ta thấy hàm số ( ) 1 2x fx + = đồng biến trên . Ta có bảng biến thiên của ( )fx trên 1 ; 2 −+ ( ) ( ) 1 2;,; 2 fxx+−+
Mà
1;2;...;24 x . Vậy bất phương trình có 24 nghiệm nguyên. Câu 67: Có bao nhiêu số nguyên dương y sao cho ứng với mỗi y có ít nhất 1 và tối đa 10 số nguyên x thỏa mãn ( )( ) 21 2? 820xx y
−− A. 1022 B. 2044 C. 2046 D. 2045 Lời giải Chọn C
có: ( )( ) 21 2? 820xx y
Vì đề bài yêu cầu tìm các giá trị nguyên dương của y sao cho ứng với mỗi y có ít nhất 1 và tối
đa 10 số nguyên x thỏa mãn 1 2x y + Mà hàm số ( ) 1 2x fx + = đồng biến trên
Suy ra y phải thỏa mãn: 111 223;2048 yy
Vì y nguyên dương nên có tất cả 2046 giá trị y thỏa mãn yêu cầu đề. Câu 68: Tìm tất cả các giá trị th
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
39 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
ực của tham số m để bất phương trình 222 sincoscos 45.7 + xxx m có nghiệm. A. 6 7 m . B. 6 7 m − . C. 6 7 m . D. 6 7 m − . Lời giải Chọn A Ta có 22 222 coscos sincoscos 15 45.74 287 ++ xx xxx mm Đặt 2 cos,0;1=txt thì BPT trở thành: 15 4 287 + tt m. Xét ( ) 15 4. 287 =+ tt ft là hàm số nghịch biến trên 0;1 Suy ra: ( ) ( ) ( ) ( ) 6 105 7 fftfft Từ đó BPT có nghiệm 6 7 m . Câu 69: Có bao nhiêu số nguyên a sao cho ứng với mỗi a , tồn tại ít nhất bốn số nguyên ( )10;10 b− thỏa mãn 2 426 5abba +−+ ? A. 4. B. 6. C. 5. D. 7. Lời giải Chọn C Ta có ( ) 22 41 42654.26.0* 5 5 5 bb abbaaa +−− +−− Xét hàm số ( ) 2 41 5.26. 4 55 bb aa fb = có tập xác định , và ( ) 451ln26ln50 54 4 5 bb a fb + = . Suy ra: ( )fb đồng biến trên . Ta có: * ( ) 22 22 222 2 22 542614 20 55 aaaa aa fa−==
* ( ) 22 22
aaaa aa fa−==
5426994 30 55
333 2 33
Do đó 2 2 ba =− là số nguyên lớn nhất để ( )* đúng. Theo đề: tồn tại ít nhất bốn số nguyên ( )10;10 b− , ta xét: 2222 1234112 babababa =−−=−=−=−
và 1234 ,,,9;8;7;;8;9bbbb −−− Suy ra: 22 4 268baa=−− mà a nên 0;1;2 a . Vậy có 5 giá trị nguyên a thỏa mãn đề bài. Câu 70: Có bao nhiêu số nguyên a sao cho ứng với mỗi a , tồn tại ít nhất ba số nguyên ( )8;8 b− thỏa mãn 2 5225 abba +−+ ? A. 4. B. 5. C. 6. D. 7 . Lời giải Chọn B
có: 22 211 5225.25.50
hàm s
211 .25.5
bb a a
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
40 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
Ta
525 bb abbaa a +− ++− . Xét
ố ( ) 2
525
fb =+− , với ( )8;8 b− , có ( ) ( ) 12211 ..ln25..ln0,8;8 25555 bb a fbb =+− hàm số ( )fb nghịch biến trên khoảng ( )8;8 BBT Để bất phương trình có ít nhất 3 nghiệm nguyên ( )8;8 b− thì ( 8; chứa ít nhất 3 số nguyên ( ) 2 55 55052250 aa f −−−− Sử dụng máy tính cầm tay ta được các giá trị nguyên của a là 2;1;0;1;2 . Vậy có tất cả 5 giá trị nguyên của a thỏa mãn yêu cầu bài toán.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
2 11 log0ln2ln2 − ()0, fuu Do đó 21021 vv vv −−− . Từ bảng biến thiên ở trên, ta thấy ()1fv = có nhiều nhất là 2 nghiệm. Dễ thấy 0,1vv== là hai nghiệm thỏa mãn 21 v v −= . 210101 v b vv a − . Nếu 0 a thì 010 b ba a . Tồn tại ít nhất 5 số nguyên b khi 5 a . Nếu 0 a thì 010 b ab a . Tồn tại ít nhất 5 số nguyên b khi 5 a − Kết hợp điều kiện ( ) 10;106;7;8;9;6;7;8;9aa −−−−− Câu 72: Có bao nhiêu số nguyên dương y để bất phương trình( )( ) 2023020222022 xx xy −+− có đúng 6 nghiệm x nguyên dương? A. 76 202220221 −+ B. 76 20222022 C. 76 20222023 D. 72022 Lời giải Chọn B
41 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 71: Có bao nhiêu số nguyên ( )10;10 a− sao cho ứng với mỗi a tồn tại ít nhất 5 số nguyên b thỏa mãn 22 21.21.2 abba abab aab bba + ++++ ? A. 8 B. 6 C. 10 D. 12 Lời giải Chọn A Điều kiện xác định: ,0ab Đặt ,.1 ab uvuv ba === Từ giả thiết ( ) ( ) ( ) 2.21.22.21210 uvvuuvv uuvuvvuv + ++++−−−−− ( )( ) 2210 uv uv −−− Ta chứng minh 20, u uu− . Thật vậy, xét hàm số ()2()2.ln21. uufuufu =−=− 2 11 ()02logln2ln2 u fuu === . Bảng biến thiên ()fu : Vì
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 42 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Xét hàm số ( ) 20222023 x fxx=−+ với 1 x . ( ) ( )2022ln2022101 x fxx =− . Hàm số đồng biến trên ) 1;+ Do đó 1 x ( ) ( ) 12022120230 fxf =−+ Khi đó bất phương trình:( )( ) 2023020222022 xx xy −+− 2022202202022log xx yyxy − . Do đó bất phương trình có đúng 6 nghiệm x nguyên dương ( ) 1;2;3;4;5;6 x khi và chỉ khi ( ) 67 2022 6log720222022yyy Vậy có 76 20222022 số. Câu 73: Có bao nhiêu số nguyên a sao cho ứng với mỗi số a , tồn tại ít nhất 3 số nguyên ( 7 b− ; )7 thỏa mãn: 2 54124 abba +−+ A. 4 B. 5 C. 6 D. 7 Lời giải Chọn B 2 22 5414 54124124.124.550 5555 bababa ab abbaabaa ba + +−−+ +++− Xét hàm số: ( ) ( ) 2 444 124.55.ln124.5.ln50 555 baba abaaabfbfb−+− =+−=− , b Vì hàm số ( )fb nghịch biến trên khoảng từ ( 7; )7 nên để tồn tại ít nhất 3 số nguyên b thỏa ( ) 0 fb thì ( ) 2 44 4054124 aa f −+ Với a , ta xét hai trường hợp TH1: 4 440041 a aa−−− . Suy ra 2 42 5 51244log1247 a a + Do a nên 2;1;0;1;2 a−− . TH2: 2 224 440455aa aaaaa −+−−− Lại có 44444 5625.55624.546244124,4 aaaaaa a ==+++− nên trường hợp này không xảy ra. Vậy có 5 giá trị nguyên của a thỏa mãn yêu cầu bài toán. Câu 74: Có bao nhiêu giá trị nguyên của ( )0;2022 m để bất phương trình 420 xx m +− nghiệm đúng với mọi 1;2 x ?
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 43
A. 6
ọ
Đặ
.
ất
1;22;4xt . Xét
ớ
( ) (
14.2 44.21 x xx m + ++ Đặt 2x t = . Khi đó 2 41 41 t m tt + ++ . Để
phương trình 2 41 41 t m tt + ++ nghiệm đúng 0 t Đặt ( ) ( ) ( ) 2 22 2 4142 0,0 4141 ttt ftftt tt tt ++ ==− ++ ++ . Hàm số nghịch biến trên ( ) 0;+ . Khi đó 2 41 41 t m tt + ++
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
B. 2021 C. 2015 D. 7 Lời giải Ch
n A
t 2,0 x tt =
B
phương trình trở thành: 22 0 ttmttm +−+
( ) 2 fttt =+ v
i
2;4 t
)
1 21;02;4 2 fttftt =+==− ( ) ( ) ( ) 2;4 26;420min6 fff=== . ( )mft , với 2;4 t . Bất phương trình đã cho nghiệm đúng với mọi 1;2 x ( ) 2;4 min6mftm Vì ( )0;2022 m có 6 giá trị cần tìm. Câu 75: Có bao nhiêu giá trị nguyên của ( )2021;2022 m− sao cho bất phương trình ( ) 2 .41.210 xx mmm + +−+− nghiệm đúng x A. 2022 B. 2021 C. 1 D. 0 Lời giải Chọn B Bất phương trình ( ) .441.210 xx mmm +−+− ( ) 44.2114.2 xxx m +++
bất phương trình ban đầu nghiệm đúng x thì bất
0 t khi và chỉ khi ( ) 01 mf= Vì ( )2021;2022 m− có 2021 giá trị cần tìm.
trị nguyên ( )12;12 b− thỏa mãn thì (8)0 f − 4388 43256 aa + .
Ta chứng minh các tính chất sau: “ Với hai số tự nhiên ;0xy thì 444 xyxy + + ”
Thật vậy, ta luôn có: ( )( ) 414104.44414441 xyxyxyxyxy + −−++++ .
Do ; xy nên 4xy + suy ra 444 xyxy + +
Xét bất phương trình: 4388 43256 aa+ Xét 2 a , ta luôn có: 34343 (1)44884 aaaaaa−+−−+ . Áp dụng tính chất trên ta có: 4333 884848 44443256 aaaa −−+−− ++ . Vậy vô nghiệm. Với 2 a khi đó 3 8 031 a , do đó 4 84 44
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo
Huỳnh Văn Ánh 42
ễn Cư
Thuậ
Page 44
Câu
ố
ứng
ớ
ỗ
ố
tồ
ạ
ít
ấ
ố
− thỏ
+++ .
Lờ
giải Chọn B Biến đổi 4343 31 4325643.2560
+−−
=−− .
3311 '()3.ln256ln'()0 4444 bb a fbfb =−− . Do đó hàm số luôn đồng biến trên ( )12;12 . Để ()0fb có ít nhất 4 giá
viên:
Nguy
Trinh
n Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
76: Có bao nhiêu s
nguyên a , sao cho
v
i m
i s
a
n t
i
nh
t 4 s
nguyên ( )12;12 b
a mãn: 43 43256 abab
A. 2. B. 3. C. 5. D. 7.
i
44 bb ababaa ++
Xét hàm số: 43 ()43.25631 44 bb aa fb
Ta có: 3
4256841212 a aa −− . Vì 1;0;1 aa− . Vậy có 3 giá trị nguyên của a Câu 77: Tập hợp tất cả các số thực x không thỏa mãn bất phương trình ( ) 2 422 94.20191 xx x +− là khoảng ( ) ; ab . Tính ba . A. 4. B. 5. C. 1 . D. 5. . Lời giải Chọn A TH1: 2 2 40 2 x x x − − .
Câu 78: Suy ra bất phương trình vô nghiệm. Khi đó tập hợp tất cả các số thực x không thỏa mãn bất phương
A
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 45 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Khi đó ta có ( ) 2 2 40 422 2 991 94.20191. 20190 x xx x x = +− Dấu "" = xảy ra khi và chỉ khi 2 40 2. 20 x x x −= = −= TH2: 2 4022xx−− Khi đó ta có ( ) 2 2 40 422 20 991 94.20191. 0201920191 x xx x x = +− =
(
2
xx x +−
−=
ố
ớ
trình
)
422 94.20191
là khoảng ( )2;2 . Suy ra 2;2.ab=−= Vậy 4 ba
Có bao nhiêu s
nguyên dương x sao cho ứng v
i mỗi x có đúng 9 số nguyên y thỏa mãn ( )( ) 12 230 yyxx + −− bằng A. 67 B. 64 C. 128 D. 53 Lời giải
− −
2 23
− 2 23 log1logxx− 232 2loglog2.log1 xx − 2 3
x
= TH2: 12 20 30 y y x x + − − (
2 32
xyx − Giả sử y là nghiệm nguyên nhỏ nhất. Khi đó để có đúng 9 số nguyên y thỏa ( )1 thì hệ sau ( ) 1 910 22 33 2 22 yy yy x x ++ có nghiệm. Vì y x nên dễ kiểm tra 04 7 y y thì hệ vô nghiệm, do đó hệ có nghiệm khi và chỉ khi 5;6 y Với 5 y = suy ra 45 15 7 2 33 22 x x 129;...;181 x có 53 số nguyên. Với 6 y = suy ra 56 15 8 2 33 22 x x 243;...;256 x có 14 số nguyên. Vậy có tất cả 67 số nguyên x
Chon
TH1: 12 20 30 y y x x +
12 2 3 y y x x +
2 2 3 1log log yx yx +
log1logxyx
1 log2log2
1 x
)
loglog11
Câu 79: Cho bất phươngtrình ( ) ( ) ( ) 233 83.4322121. xxx xxmxmx +++−+− Sốcácgiátrị nguyên của tham số m để bất phương trình trên có đúng 5 nghiệm nguyên dương phân biệt là A. 3. B. 4. C. 5. D. 6. Lời giải
Chọn B
Ta có ( ) ( ) ( ) 233 83.4322121 xxx xxmxmx +++−+− 21333 83.432222 xxxx xxmxxmxx + +++−+− ( ) ( ) ( ) ( ) 3 3 22221 xx xxmxmx++++
Xét hàm số ( ) 3 2 fttt =+ , có ( ) 2 320ftt =+ Nên ( )ft đồng biến trên ( ) ; −+ , khi đó: ( ) 2 121 x x xmxm x +− , do 0 x
Xét hàm số ( ) ( ) 2 22ln2.2 xxx x gxgx xx == , ta có ( ) 20 0log1gxxex ===
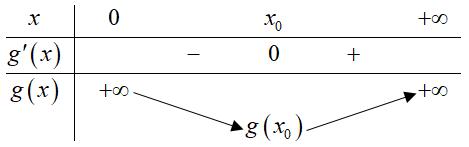
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
46
− . Câu 80: Xét các số thực x và y thỏa mãn ( ) 22 122 2224 xyx xyx ++ +−+ . Gọi ,m M tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 4 21 y P xy = ++ . Tính Mm + . A. 2 B. 25 C. 2 D. 25 Lời giải Chọn C Ta có ( ) ( ) 22221222122 22242211 xyxxyxxyxxyx +++−++−++−++ Đặt 22 210txyxt =+−+ . Khi đó ta có 21,0 t tt +
Ta có bảng biến thiên của hàm số ( )gx : Do ( ) ( ) ( )125fff = nên để bất phương trình có 5 nghiệm nguyên dương: ( ) ( ) 513735 6153 gm m gm −
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
ỳnh
Page 47
Từ đồ thị
ố
t y = và
+ Ta
Gọi ( )
là đường tròn ( ) (
2 2 11 xyC −+= có
−+ +− 222 958162401515 PPPPPP −++−−−−+ 15;152MmMm =−+=−−+=− . Câu 81: Biết nửa khoảng ) ( ) * ;,, mn Spppmn = là tập tất cả các số thực y sao cho ứng với mỗi y tồn tại đúng 6 số nguyên x thỏa mãn ( )( ) 22 2 32750 xxx y −− . Tổng mnp ++ bằng A. 46 mnp++= B. 66 mnp++= C. 14 mnp++= D. 30 mnp++= Lời giải Chọn A ( )( ) 22 2 32750 xxx y −− Th1: Xét 2 22 1 3270230 3 xx x xx x =− −=−−= = là nghiệm của bất phương trình Không đủ 6 nghiệm. Th2: Xét 2 22 1 3270230 3 xx x xx x − −−−
Giáo viên: Hu
Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
hàm s
2
1 yt=+ suy ra được 2101 t tt
có ( )2 22221111txyxxy =+−+−+
C
)
tâm là ( )1;0 I và bán kính là R1 = . Do đó các cặp số ( ) ; xy thỏa mãn thuộc hình tròn ( )C Lại có ( ) 4 240 21 y PPxPyP xy =+−+= ++ . Ta có và ( )C có điểm chung khi ( ) ( ) ( ) 2 2 2 2.14.0 ,135816 44 PPP dIRPPP PP +−+
Khi đó, 2 2 5 (1)5log(2) x yxy Nếu 01 y thì vô nghiệm. Không có y thỏa mãn. Nếu 1 y thì 55 (2)loglogyxy− Do đó, có đúng 6 nghiệm nguyên ( ) ( ) ( ) 55 ;13;log;log xyy −−+− 1625 55 4log516log2555 yyy . Suy ra ) ( ) 1625* 5;5,, Spmn = . Th3: Xét 2 22 327023013 xx xxx −−−− . Vì ( )1;3 chỉ có ba số nguyên nên không có giá trị y nào để bất phương trình có 6 nghiệm nguyên. Vậy ) ( ) 1625* 5;5,, Spmn = Nên 1625546 mnp++=++= Câu 82: Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 20 số nguyên y thỏa mãn 2 516 42512 xyxy −+−−+ và 0 xy+ ? A. 4. B. 5. C. 6. D. 20. Lời giải Chọn D Ta có: 2 516 42512 xyxy −+−−

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
48 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
+− Xét hàm số 2 516 ()42512 xyxy fy −+−− =+− ( ) ( ) 2 516 .4ln42ln20'()5 xyxy fy −+−− =− Vì 0 xyyx +− Hàm số ()fy nghịch biến trên đoạn từ ( ) ;x −+ Ta có BBT: Để hàm số ()fy có không quá 20 giá trị nguyên thõa mãn bài toán thì (21)0fx−+ 2 58921 425120 xx+−− +− 221 4 589log(5122)0xx +−−− ( ) ( )2121 44 53814log512253814log5122 22 12,47,5 x x −−+−−++− Vì xZ nên 12,11,.......,7 x−−
Vậy có 20 số nguyên x thỏa mãn bài toán.
Câu 83: Cho các số thực , xy thỏa mãn 22 1 1 22 2 4 22 xy x xyx và 20 xy . Giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 321Pxy lần lượt là M và m . Tính Mm A. 6 B. 10 C. 12 D. 18 Lời giải
Chọn D
Ta có: 2 22222111xyxxy , khi đó: 2222 22 11 1222122 2222 22 422222 222 xyxy xxyx x xyxxyx xyx .
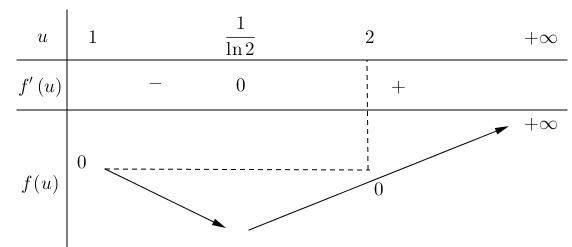
Lấy logarit cơ số e hai vế ta được: 222221ln2ln22xyxxyx
Đặt 22 22uxyx , 1 u *1ln2ln1ln2ln0 uufuuu 11 ln20 ln2 fuu u Bảng biến thiên của fu : Nhìn bảng biến thiên ta thấy 2 222 0121222011 fuuxyxxyC
Điểm ; Axy thỏa đề bài AC , xét :3210 xyP , đường thẳng song song hoặc trùng với đường thẳng 1 :320 xy Từ hình vẽ ta có điều kiện tồn tại , xy là đường thẳng có điểm chung với C .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
49
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 50 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do đó: 4 ;1413413 13 P dIP . Vậy 8 Mm Câu 84: Số các giá trị nguyên của ( )2021;2022 m− để loglog 5.3..log2 ab ba a abmb −+ với mọi ,(1;)ab+ là: A. 2021 B. 2022 C. 4044 D. 2020 Lời giải Chọn A Đặt 2 log,(0) x a xbbax == Khi đó loglog 5.3..log2 ab ba a abmb −+ ( ) 2 1 5.3..2 xx x aamx −+ 5.3..2 xx aamx −+ 2.2 x a m x . Xét 2.2 (),(0) x a fxx x = 2 ()2..ln22 xx axaa fx x −+ = . Đặt ( ) 2...ln22 xx gxaxaa=−+ với 0 x . Ta có ( ) 0 lim0 + → = x gx và ( ) ( )2 2...ln0,0 x gxaxax = ( ) 2...ln220,0 xx gxaxaax =−+
2 2..ln22 ()0,0 xx axaa fxx x −+ = ()fx đồng biến và liên tục trên ( ) 0, + 0 lim()2ln + → x mfxma , 0{2020;...;1;0}mm − . Câu 85: Tìm tất cả các giá trị thực của tham số m để bất phương trình ( ) ( ) 0,0220,02loglog31log x m + có nghiệm với mọi ( );0 x− A. 1. m B. 01. m C. 1. m D. 2. m Lời giải Đk: ;0xm Ta có: ( ) ( ) ( ) 0,0220,02 loglog31log,;0. x mx +− ( ) ( ) 2 log31,;0. x mx +− ( ) 312,;0. xm x +− Xét hàm ( ) 31 x fx =+ trên ( );0− . Ta có ( ) ( ) 3.ln30,;0. x fxx =− Bảng biến thiên: Để phương trình có nghiệm với mọi ( );0 x− ta phải có 22 m
1 m
Page
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Câu
ấ
= B.
=
=
=
Chọn C Ta có: ( ) ( ) 22 ln77ln4xmxxm +++ 22 2 774 40 xmxxm mxxm +++ ++ ( ) ( ) ( ) 2 2 74701 402 mxxm mxxm −−+− ++ Bất phương trình đã cho
với mọi x khi và chỉ khi
ất
vớ
ọi x Xét ( ) 2
−−+− ( )
. 1 2
∞ +
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 x
51 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
86: Gọi S là tổng t
t cả các giá trị nguyên của m để bất phương trình ( ) ( ) 22 ln77ln4xmxxm +++ nghiệm đúng với mọi x thuộc . Tính S . A. 14 S
0 S
C. 12 S
D. 35 S
Lời giải
đúng
các b
phương trình ( ) ( )1,2 đúng
i m
7470 mxxm
1
0
y y'
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
ỳnh
Page 52
(
− −− 5
. Xét 2 40mxxm−+ ( )2 . +
+
x 2 0 00 '022 40 m mm mm m − − 2 m ( ) Từ ( ) và ( ) ta có 25 m . Do mZ nên 3;4;5 m . Từ đó 34512 S =++= Câu 87: Có bao nhiêu giá trị nguyên dương của m để bất phương trình ( ) ( ) 22 22 log77log4xmxxm +++ nghiệm đúng với mọi x A. 5 B. 4 C. 0 D. 3 Lời giải Chọn D Cách 1: Bpt: ( ) ( ) 22 22 log77log4xmxxm +++ 22 2 774 40 xmxxm mxxm +++ ++ ( ) ( ) ( ) 2 2 7470 40 fxmxxm gxmxxm =−++− =++ Bpt đã cho nghiệm đúng với mọi x ( ) ( ) 0 , 0 , fxx gxx Trường hợp 1: 7 m = ( ) ( ) 2 040 07470 fx x xx gx ++ Vậy 7 m = không thỏa yêu cầu bài toán. Trường hợp 2: 0 m = ( ) ( ) 2 07470 040 fx xx x gx −+−
Giáo viên: Hu
Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn + Khi 7 m = ta có ( )1 trở thành 400 xx − . Do đó 7 m = không thỏa mãn. + Khi 7 m ta có ( )1 đúng với mọi x
)2 7 707 '059 470 m mm mm m
m ( )
Khi 0 m = ta có ( )2 trở thành 400 xx − . Do đó 0 m = không thỏa mãn.
Khi 0 m ta có ( )2 đúng với mọi
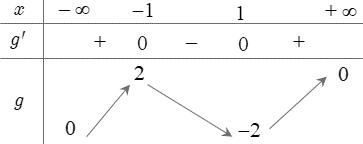
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 53 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vậy 0 m = không thỏa yêu cầu bài toán. Trường hợp 3: 0; 7 mm Khi đó: ( ) ( ) 0, 0, fx x gxx ( )2 2 070 0470 00 040 f f g g a m m a m m − −− − 7 59 0 22 m mm m mm − 25 m Do m nên 3;4;5 m . Cách 2: ( ) ( ) 22 22 log77log4xmxxm +++ 22 2 774 40 xmxxm mxxm +++ ++ ( ) 2 2 7470 40 mxxm mxxm −++− ++ ( ) ( ) 22 2 7471 14 xxmx mxx −++ +− 2 2 2 747 1 4 1 xx m x x m x −+ + + 22 22 44 77 11 44 11 xx mm xx xx mm xx +− ++ ++ Xét hàm số 2 4 () 1 x gx x = + trên 222 2222 4(1)4(1)44 '() (1)(1) xxxx gx xx −+++− == ++ 1 '()0 1 x gx x =− = = Bảng biến thiên Vậy đk 72 25 2 m m m −− Do m nên 3;4;5 m .
Câu 88: Tìm tất cả các giá trị thực của tham số m để bất phương trình 3 11 22 log1logxxxm có
1 0 x xxm Phương trình tương đương 333 11 22 log1log11 xxxmxxxmxm Khi đó ta có 3 1; 1,1min fxxmxmfx Ta có 2 3001;fxxx Bảng biến thiên Dựa vào bảng biến thiên và đề bài hỏi “có nghiệm” nên ta chọn m . Câu 89: Có tất cả bao nhiêu giá trị của tham số m để bất phương trình ( ) ( ) 22 22 log2log2 xmxmx++++ nghiệm đúng với mọi x . A. 2 B. 4 C. 3 D. 1 Lời giải Chọn D Ta thấy 2 20 xx+ Do đó bất phương trình ( ) ( ) 2222 22 log2log2220 xmxmxxmxmxmxm +++++++++ . Bất phương trình ( ) ( ) 22 22 log2log2 xmxmx

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
54 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
nghiệm. A. 2 m B. m C. 2 m D. Không tồn tại m Lời giải Chọn A Điều kiện 3 ++++ nghiệm đúng với mọi x khi và chỉ khi 00mxmxm += Câu 90: Tìm tập S tất cả các giá trị thực của số m để tồn tại duy nhất cặp số ( ) ; xy thỏa mãn ( ) 22 2 2 log4461 xy xym ++ +−+ và 22 2410xyxy++−+= . A. 5;1;1;5 S =−− . B. 1;1 S =− . C. 5;5 S =− D. 75;1;1;5;7 S =−−− Lời giải
phương trình có nghiệm thuộc khoảng ( ) 2; 2 1 -1 O
J I
của tham số m để y x 2
= = 1 5 m m = = Vậy 5;1;1;5 S =−− . Câu 91: Xét bất phương trình ( ) ( ) 2 22 log221log20 xmx−+− . Tìm tất cả các giá trị m -3
là nghiệm của phương trình 22 2410xyxy++−+= .
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 55
Chọn A
++
(
22
2 log4461 xy xym ++ +−+
+−+++ 222
+−−+−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
Nhận thấy 22 21 xy
với mọi , xy nên:
)
2
222 4462 xymxy
4480xyxym
( ) ( ) 22 2 22 xym−+− Khi 0 m = thì 2 2 x y =
= . Cặp ( )2;2 không
bất
Khi 0 m , tập hợp các điểm ( ) ; xy thỏa mãn là hình tròn tâm ( )2;2 J , bán kính là m . Trường hợp này, yêu cầu bài toán trở thành tìm m để đường tròn tâm ( )1;2 I , bán kính 2 và hình tròn tâm ( )2;2 J , bán kính m có đúng một điểm chung Điều này xảy ra khi 1 5 m m + . A. 3 ;0 4 m − B. ( ) 0; m+ C. ( );0 m− D. 3 ; 4 m =−+ Lời giải Chọn D Bất phương trình ( ) ( ) ( ) 22 2222 log221log20log2log101 xmxxmx −+−−− . Đặt 2log tx = , vì ( ) 1 2;; 2 xt ++ . Bất phương trình trở thành ( ) 2 22 1 2102122 t tmtmttm t −−− Đặt 2 1 t ft t với 1 ; 2 t .
Bất phương trình 1 có nghiệm thuộc khoảng ( ) 2;+ khi và chỉ khi bất phương trình 2 có
nghiệm thuộc khoảng 1 ; 2 +
Ta có ( ) 2 11 10; 2 ftt t =++

Bảng biến thiên
Từ bảng biến thiên suy ra bất phương trình đã cho có nghiệm thuộc khoảng ( ) 2;+ khi và chỉ khi 33 2 24 mm .
Câu 92: Cho bất phương
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
56
Chọn A Ta
( ) ( )
( ) ( )
22 77 22 77 log221log65,1;3 log71414log65,1;3 xxxxmx xxxxmx ++++++ +++++ ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 2 650,1;365,1;31 689,1;3689,1;32 mxxx xxmx xxmx xxmx −++ +++ ++ ++ Xét ( ) ( ) ( ) 2 65,1;3gxxxx=−++ , có ( ) ( ) ( ) ( ) 22 3413412,1;3gxxx =−++−++=− Do đó ( ) 112 m − . Xét ( ) ( ) 2 689,1;3hxxxx=++ , có ( ) ( ) 2 6.18.1923,1;3hxx ++= . Do đó ( ) 223 m Do m và 12;23 m− nên ta được tập các giá trị của m là 12;11;10;...;23 . Vậy có tổng cộng 36 giá trị của m thỏa yêu cầu bài toán.
trình ( ) ( ) 22 77 log221log65xxxxm ++++++ . Có tất cả bao nhiêu giá trị nguyên của m để bất phương trình có tập nghiệm chứa khoảng ( )1;3 ? A. 36 B. 34 C. 35 D. Vô số Lời giải
có:
( )
( )
Câu 93: Gọi S là tập hợp tất cả các điểm ( ) ; Mxy trong đó , xy là các số nguyên thoả mãn điều kiện ( ) 22 1 log221, xy xym ++ ++ với m là tham số. Có bao nhiêu số nguyên m thuộc đoạn 2020;2019 để tập S có không quá 5 phần tử? A. 1. B. 2020. C. 2021. D. 2019. Lời giải Chọn C ( ) 22 22 1 log221221 xy xymxymxy ++ ++++++ ( ) ( ) 22 111xym −+−+ Để bất phương trình có 5 phần t
ử thì 121mm+ Vậy có 2021 số nguyên m thuộc đoạn 2020;2019 để tập S có không quá 5 phần tử Câu 94: Có bao nhiêu số nguyên m sao
+++
+−+

xxmx mxx
5541 14
2 2 2
+− = + = + Hàm số ( )fx có bảng biến thiên: Hàm số ( )gx có bảng biến thiên: Từ bảng biến thiên suy ra để bất phương trình có tập nghiệm là khi 23 m . Vậy có 1 giá trị nguyên của m .
xx mfx x x mgx x
554 1 4 1
( ) ( )
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
cho bất phương trình ( ) ( ) 22 ln5ln1ln4xmxxm ++++ có tập nghiệm là . A. 3
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 57 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Ta có bất phương trình ( ) (
B. 4 C. 1 D. 2
) ( ) ( ) 2222 ln5ln1ln4ln55ln4 xmxxmxmxxm
+++++++ 22 2 554 40 xmxxm mxxm
++ ( ) ( ) 22 2
+−
1 4(1)20 xx mm + −++ 0. x ( ) ;12.− ( ;1.−− ( ;0.− ( 1;16.
) ( ) ;01;
. B. ( ;0 m− . C. ( ) 0; m+ D. ( )0;1 m Lời giải Bất phương trình ( ) 1 4210 xx m −+ ( )1 Đặt 2x t = , 0 t . Bất phương trình trở thành: ( ) 2 1 10 4 tmt−+ 2 440tmtm−− ( )2 .
Đặt ( ) 2 44 fttmtm =−− .
Đồ thị hàm số ( )yft = có đồ thị là một Parabol với hệ số a dương, đỉnh ( ) 2 2;44 Immm Bất phương trình ( )1 nghiệm đúng với mọi x Bất phương trình ( )2 nghiệm đúng với mọi 0 t hay ( ) 0,0ftt
TH1: 0 m ( ) 040fm=− 0 m thỏa mãn. TH2: 0 m 2 440 mm −− nên 0 m không thỏa mãn. Vậy 0 m .
Câu 97: Cho hàm số ( )yfx = . Hàm số ( )yfx = có bảng biến thiên như sau:
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 58
t BPT ( ) ( ) ( )
2 22 2 210212min 21
tmtmtmttmgtmgt t −++−−= Ta có ( ) ( ) ( ) ( ) ( 2 2 222 '0,111;1 21 tt gttMingtgm t −+ ===−−−
ìm tất cả các giá trị của
ố
để
ất
.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn DẠNG 2. BẤT PHƯƠNG TRÌNH MŨ CHỨA THAM SỐ Câu 95: Bất phương trình nghiệm đúng với mọi Tập tất cả các giá trị của m là A. B. C. D. Lời giải Chọn B Đặt 2x t = . ĐK: 1
( )
tt
Câu 96: T
tham s
m
b
phương trình ( ) 1 4210 xx m −+ nghiệm đúng với mọi x
A. (
m−+
Bất phương trình ( ) 2 3. x fxem + + có nghiệm ( )2;2 x− khi và chỉ khi: A. ( ) 23 mf−− B. ( ) 4 23 mfe −− C. ( ) 4 23 mfe − D. ( ) 23 mf−− Lời giải
Bất phương trình tương đương với ( ) ( ) 2 3. xmgxfxe + =− .
Ta có ( ) ( ) ( ) 222 3.33.0,2;2 x gxfxeex +−+ =−−=− .

Do đó ( ) ( ) ( ) ( ) 4 223.,2;2gxgfex=−− .
Vậy ( ) 4 23. mfe − thì phương trình có nghiệm trên khoảng ( )2;2 .
Câu 98: Cho hàm số bậc 3 ( )fx có đồ thị như hình vẽ bên.
Bất phương trình ( ) ( )32019xx feme+ có nghiệm ( )0;1 x khi và chỉ khi A. 4 1011 m − B. 4 32019 m e − + C. 2 1011 m − D. ( ) 32019 fe m e + Lời giải
Đặt xte = ( )0 t . Bất phương trình có dạng: ( ) ( )32019ftmt+ ( ) 32019 ft m t + .
Ta có: ( )0;1 x ( ) 1; x tee=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
59
Xét hàm ( ) ( ) 32019 ft gt t = + có ( ) ( )( ) ( ) ( )2 320193 32019 fttft gt t
+− = + .
Dựavàođồthịhàmsố ( )fx ,tathấy: ( )fx đồngbiếntrênkhoảng ( ) 1;e và ( ) 0 fx ( ) 1; xe ( ) ( ) 0 0 fx fx
( ) 1; xe ( ) 0 gt ( ) 1; te ( )gt đồng biến trên khoảng ( ) 1;e ( ) ( ) ( ) 1 ggtge ( ) 1; te .
Vậ
t cả giá trị của tham số thực m sao cho bất phương trình ( ) 921.3320 −+−− xx mm có nghiệm đúng với mọi số thực x là A. 3 2 − m . B. 2 m . C. 3 2 − m . D. m . Lời giải Chọn A Ta có: ( ) 921.3320 −+−− xx mm ( ) ( ) 2 32.3331.2−−+ xxx m ( )( ) ( ) 313331.2+−+ xxx m 332332 −+ xx mm Vậy, để ( ) 921.3320, −+−− xx mmx khi 3 320 2 +− mm Câu 100: Có bao nhiêu giá trị nguyên dương của tham số m để tập nghiệm của bất phương trình ( )( ) 2 33320
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
60
y bất phương trình ( ) ( )32019xx feme+ có nghiệm ( )0;1 x Bất phương trình ( ) 32019 ft m t + có nghiệm ( ) 1; te ( ) 42 1 20221011 mg =−=− . Câu 99: Tấ
xx m + −− khác rỗng và chứa không quá 9 số nguyên? A. 3281. B. 3283. C. 3280. D. 3279. Lời giải Chọn C Do m là số nguyên dương nên 2m >1 => 3 log20 m . 1 22 2 3 33033 2 xx x ++−===− 3 320log2 x mxm−== . Lập bảng biến thiên, ta kết luận: tập nghiệm bất phương trình này là 3 3;log22 m
Suy ra, 8 3 6561 log28233280.5 2 mmm= =>
Câu 101: Cho hàm số ( )yfx = . Hàm số ( )yfx = có bảng biến thiên như sau:
Bất phương trình ( ) 2x fxm + đúng với mọi ( )1;1 x − khi và chỉ khi:
A. ( ) 12 mf− . B. ( ) 12 mf− . C. ( ) 1 1 2 mf−− . D. ( ) 1 1 2 mf−− . Lời giải
Chọn B
( ) 2x fxm + , ( )1;1 x − ( ) 2x fxm− ( ) 2x fxm−
Xét hàm số ( ) ( ) 2x gxfx=− trên ( )1;1 .
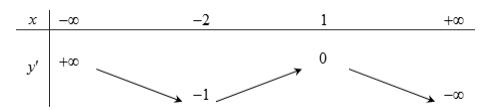
Ta có: ( ) ( ) 2.ln2 x gxfx =− .
Ta thấy: ( )1;1 x − thì ( ) 0 fx và 2.ln20 x
Do đó ( ) ( ) 2.ln20 x gxfx=− , ( )1;1 x − . Bảng biến thiên Từ bảng biến thiên ta có: ( ) ( ) 112mgmf− . Câu 102: Có bao nhiêu giá trị nguyên của tham số m để bất phương trình (
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
61 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
)( ) 22 3920 xxx m −− có 5 nghiệm nguyên? A. 65021. B. 65024 C. 65022. D. 65023. Lời giải Chọn B ( )( ) 22 3920 xxx m −− Th1: Xét 2 2 1 3902 2 xx x xx x =− −=−= = là nghiệm của bất phương trình Th2: Xét 2 2 1 3902 2 xx x xx x − −−
Khi đó, 2 2 2 (1)2log(2) x mxm Nếu 1 m thì vô nghiệm. Nếu 1 m thì 22 (2)loglogmxm− Do đó, có 5 nghiệm nguyên ( ) ( ) ( ) 22 ;12;log;logmm −−+− có 3 giá trị nguyên ) 2 log3;451265536 mm . Suy ra có 65024 giá trị m nguyên thỏa mãn. Th3: Xét 2 2 390212 xx xxx −−− . Vì ( )1;2 chỉ có hai số nguyên nên không có giá trị m nào để bất phương trình có 5 nghiệm nguyên. Vậy có tất cả 65024 giá trị m nguyên thỏa ycbt.
DẠNG 3. BẤT PHƯƠNG TRÌNH NHIỀU ẨN
Câu 103: Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 728 số nguyên y thỏa mãn ( ) 2 43 loglog() xyxy ++ ?
A. 59. B. 58. C. 116. D. 115. Lời giải
Chọn C
ới mọi x
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
62 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
−+=−+−−+ . Có
quá 728 số nguyên y
ỏ
( ) 2 34 (729)0log729log7290 fxxx −+−−+ 2672940 xx −+− 2 33670 xx−− 57,558,5 x − Mà x nên 57,56,...,58 x−− . Vậy có 58(57)1116 −−+= số nguyên x thỏa. Câu
Có bao nhiêu số nguyên x sao cho ứng
ớ
ỗ
x
(
2 43
V
ta có 2 xx Xét hàm số ( ) 2 34 ()log()log fyxyxy =+−+ . Tập xác định D(;) x =−+ ( ) 2 11 '()0, ()ln3 ln4 fyxD xy xy =− + + f tăng trên D Ta có ( ) 2 34 (1)log(1)log10 fxxxxx
không
th
a mãn ( ) 0 fy
104:
v
i m
i
có không quá 242 số nguyên y thỏa mãn
) ( )
loglogxyxy ++ ? A. 55. B. 28. C. 29. D. 56.
số ( ) 43 tt ft =− đồng biến trên khoảng ( ) 0;+ và ( ) 0 ft với mọi 0 t Gọi n thỏa 2 43nn xx−=− , khi đó ( )* tn
Từ đó, ta có 33 tn xyxx −=−−
Mặt khác, vì có không quá 242 số nguyên y thỏa mãn đề bài nên 3 3242log242 n n .
Từ đó, suy ra 3 log242 2 4242 xx−− 27,428,4 x − .
Mà x nên 27,26,...,27,28 x−−
Vậy có 56 giá trị nguyên của x thỏa yêu cầu đề bài. Câu 105: Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 127 số nguyên y thỏa mãn ( ) ( ) 2 32 loglogxyxy ++ ? A. 89. B. 46. C. 45. D. 90. Lời giải
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 63
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn D Điều kiện: 2 0 0 xy xy + + Đặt ( ) 3log xyt += , ta có 2 4 3 t t xy xy + += ( ) 2 43* 3 tt t xx yx −− =− . Nhận xét rằng hàm
gxx−−+ 27128344,845,8xxx −+− Như vậy có 90 giá trị thỏa yêu cầu bài toán Câu 106: Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 255 số nguyên y thỏa mãn ( ) ( ) 2 32 loglogxyxy ++ ? A. 80 B. 79 C. 157 D. 158 Lời giải Chọn D
Chọn D Ta có ( ) ( )( ) 2 32 loglog1 xyxy ++ Đặt * txy=+ ( ) ( ) ( ) 22 3223 (1)loglog()loglog02 xxttgttxxt −+=−−+ Đạo hàm ( ) 2 11 ()0 ln2 ln3 gt t xxt =− −+ với mọi y . Do đó ( )gt đồng biến trên ) 1;+ Vì mỗi x nguyên có không quá 127 giá trị * t nên ta có ( ) 2 23 (128)0log128log1280
Ta có: ( ) ( ) 2 32 loglogxyxy ++ ( ) 2log 2 3 xy xy + + ( ) 2 log3 2 xyxy++ ( )1
Đk: 1 xy+
Đặt 1 txy=+ , nên từ ( ) 2 log3 2 1 xxtt −− ( )2

Để ( )1 không có quá 255 nghiệm nguyên y khi và chỉ khi bất phương trình ( )2 có không quá 255 nghiệm nguyên dương t . Đặt ( )255 Mf = với ( ) 2 log3 fttt =− Vì f là hàm đồng biến trên ) 1,+ nên ( )2 ( ) 12 1 tfxx− khi 2 0 xx− . Vậy ( )2 có không quá 255 nghiệm nguyên ( ) 12 255 fxx − 2 255 xx − 7879 x − ( ) x Vậy có 158 số nguyên x thỏa mãn yêu cầu bài toán. Câu 107: Trong tất cả các cặp ( ) ; xy thỏa mãn ( ) 22 2 log4441 xy xy ++ +− . Tìm m để tồn tại duy nhất cặp ( ) ; xy sao cho 22 2220xyxym ++−+−= A. ( )2 102 m =− B. 102 m = C. 102 m =− D. ( )2 102 m = Lời giải
Chọn D Với mọi , xy , ta luôn có 22 221 xy++ nên BPT ( ) 22 2 log4441 xy xy ++ +− ( ) ( ) 22 22 4442222 xyxyxy +−++−+− ( )1 . BPT ( )1 mô tả hình tròn tâm ( )2;2 I và bán kính 1 2 R = Mặt khác, phương trình ( ) ( ) 22 22 222011 xyxymxym ++−+−=++−= ( )2 nên để ( )2 có nghiệm thì 0 m . • TH1: 0 m = . Khi đó, ( ) 1 2 1 x y
=− = không thỏa ( )1 nên loại 0 m =
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
64 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
• TH2: 0 m . Khi đó, ( )2 là phương trình đường tròn ( ) 2C tâm ( )1;1 J và bán kính 2 Rm = . Do đó, yêu cầu đề bài Hệ BPT ( ) ( ) ( ) ( )
222 11 xy xym
22 22
−+− ++−= có nghiệm duy nhất ( ) 2C tiếp xúc với đường tròn ( ) ( ) ( ) 22 1 :222Cxy−+−= cũng có tâm ( )2;2 I và bán kính 1 2 R = . Vì 1 102 IJR == nên ( )1C hoặc tiếp xúc ngoài, hoặc tiếp xúc trong với ( ) 2C . ➢ TH2a: ( )1C tiếp xúc ngoài với ( ) 212 102 CIJRRm =+=+ ( )2 102102mm =−=− ➢ TH2b: ( )1C tiếp xúc trong với ( ) 221 102CIJRRm =−=− ( )2 210102mm =+=+ . Vậy ( )2 102 m =
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
65 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page



CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 1 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 6. BẤT PHƯƠNG TRÌNH MŨ LOGARIT MỨC ĐỘ VẬN DỤNG VẬN DỤNG CAO Câu 108: Tính tổng T tất các nghiệm nguyên của bất phương trình 2 log103log1005 xx−− A. 50 T = . B. 45 T = . C. 110 T = . D. 55 T = . Lời giải Chọn D Điều kiện: 0 x . Bất phương trình đã cho tương đương với: ( ) ( ) 2 log103log10log105 xx−+− ( )2 log103log1020 xx −+ 1log102 x 110 x Do 1;101;2;...;10 x x x . Vậy ( )10.101 123...1055 2 T + =++++== Câu 109: Có bao nhiêu số nguyên x thoả mãn ( ) ( ) 2 3 24log2530? xx x −+− A. 24. B. 26. C. Vô số. D. 25. Lời giải Chọn B Ta có: ( ) ( ) 2 3 24log2530 xx x −+− ( ) ( ) 2 2 3 22log2530 xx x −+− ( ) ( ) 2 2 2 3 2 3 25 220 log2530 220 log2530 xx xx x x x − − +− − +− 2 2 25 20 2527 20 2527 x xx x xx x − − + − + 25 2 0 2 02 2 x x x x x x − CHƯƠNG II HÀM SỐ LŨY THỪA - HÀM SỐ MŨ – HÀM SỐ LOGARIT
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 2 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 250 2 2 x x x − = = 250 2 x x − = Vì x có 26 số nguyên thoả mãn yêu cầu bài toán. Trình bày Điều kiện: 25 x − Trường hợp 1: ( ) ( ) ( ) 22 2 2 333 240202 22 2 1 log2530log25log2722 xxxx x xx x x x xx − = +−+ Trường hợp 2: ( ) ( ) ( ) 22 2 2 333 0 24022 22 22 log2530log25log2720 2 xxxx x x xx x x x xx x = − +−+ Từ ( ) ( )1&2 và kết hợp điều kiện 25 x − , x nên 24;23;22;...;02 x−−− Vậy có 26 số nguyên x thỏa ycbt. Cách 3: ( ) ( ) 2 3 24log2530 xx x −+− Điều kiện: 25 x − ( ) ( ) ( ) ( ) ( )( )( )( ) ( ) 2 2 3 2 3 23 2 24log2530 22log2530 212312530 0 20 2 xx xx x x xxx x xx x −+− −+− −−−+− − = So sánh với điều kiện: 25 x − ta được 250 24;23;22;....;1;0;2 2 x x x x − ⎯⎯⎯→−−−− = Câu 110: Có bao nhiêu số nguyên x thỏa mãn ( ) ( ) 2 3 24log2530 xx x −+− ? A. 24 B. Vô số C. 25 D. 26 Lời giải Chọn D Ta xét: 22 22 2402220 xxxx xx −==−= 0 2 x x = =


CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo
Huỳnh Văn Ánh 42
ễn
ậ
ế
Page 3
ạn ( ) ( ) 33 25 log2530log2532 2527 x xxx x − +−=+== += . Bảng xét dấu: Suy ra 0 VT ( 25;02 x− . Vậy
ố
ỏ
ầ
Câu
ất
trình ( ) ( ) 3
−= = = =
=−
Vì 1;2;3 xx + Câu 112: Có bao nhiêu số nguyên x thỏa mãn bất phương trình sau? ( ) ( ) 222 3 321883273log180 xx x −+−+ . A. 4. B. 5. C. 6. D. 7. Lời giải Chọn D Trường hợp 1: ( ) ( ) 222 33 3log180log183903 xxxx −+=+=−== Thử lại với bất phương trình đề bài ta nhận 3 x =
viên:
Nguy
Cư Trinh Thu
n Hòa TP Hu
ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên so
có 26 s
th
a yêu c
u bài toán.
111: B
phương
9ln50xxx−+ có bao nhiêu nghiệm nguyên dương? A. 3. B. 7. C. 6. D. Vô số. Lời giải Chọn A Điều kiện: 5 x − Đặt ( ) ( ) ( ) 3 9ln5fxxxx=−+ . ( ) ( ) 3 3 900 0 ln503 4 x xx x fx x x x =−
+=
Bảng xét dấu: Dựa vào bảng xét dấu ta thấy ( ) 43 0 03 x fx x −−
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 4 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Trường hợp 2: ( ) ( ) 222 33 3log180log1839033 xxxx −++−− Ta có :( ) ( ) 222 3 321883273log180 xx x −+−+ 22 321883270 xx −+ ( )2 2188 33270 9 xx −+ 25 1 324333325 9 xx x − . So với điều kiện của trường hợp 2 ta nhận 23 x − Mà 2;1;0;1;2 xx−− . Kết hợp với trường hợp 1 ta nhận 3;2;1;0;1;2;3 x−−− . Vậy có tất cả 7 số nguyên x là nghiệm của bất phương trình. Câu 113: Bất phương trình có tổng tất cả các nghiệ
A. . B. . C. . D. . Lời giải Chọn C Ta có: Vì . Vậy tổng tất cả các
ệ
ằng Câu 114: Có bao nhiêu số nguyên x nhỏ hơn 2022 thoả mãn ( ) ( ) 2 2 2 2 log3.log2160,50 x xx−+− . A. 2020 B. 2021 C. 2022 D. 2023 Lời giải Chọn A Điều kiện: ( )2 160,50 0 x x − 2 0 x x − 0 x Ta có ( ) ( ) 2 2 2 2 log3.log2160,50 x xx−+− ( ) ( ) ( ) 2 2 2 2 160,501 2 log3.log20 x xx −= −+ + ( )2 (1)0,516242 x xx ==−=− ( ) ( ) ( ) 22 1 41log410 e xxxx −−−++ 6 8 4 10 ( ) ( ) ( ) 22 1 41log410 e xxxx −−−++ ( ) ( ) 2 2 1 2log410 e xxx −−++ ( ) 2 1 20 log410 e x xx − −++ 2 2 411 x xx −++ 2 2 40 x xx −+ 2 04 x x 1;3 xx 4
m nguyên là?
nghi
m nguyên b
ậy có 2020 số nguyên x thoả mãn đề bài. Câu 115: Cho hàm số ( ) 32 13 122022 2 xyfxxxxe ==−+−−− . Cho biết bất phương trình ẩn m sau đây ( ) ( ) ( ) 0,52 loglog2120210 fmff +− có bao nhiêu nghiệm nguyên? A. 14. B. 10. C. 11. D. 7. Lời giải Chọn D Điều kiện: 2. m ( ) 32 13 122022 2 xyfxxxxe ==−+−−− ( ) ( )2 2 ''31312320, xx yfxxxexxex ==−+−−=−−+− nênhàmsố ( )fx nghịchbiến trên . Do đó, ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 0,520,52 loglog2120210loglog21202102023 fmffmf+−+−=− ( ) ( ) ( ) 0,522 15 loglog2120log214121160
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 5
+ 2 2 log1 2
x x xx . Kế
ợ
với
u
ệ
ị
x
2 mmmm +−++ Vậy có 7 nghiệm nguyên. Câu 116: Số nghiệm nguyên của bất phương trình ( ) 2 loglog(46)1 x x − là A. 1. B. 0. C. 4. D. Vô số Lời giải Chọn B Điều kiện: ( ) 444 4 2 0,10,10,1 460log6log6log7 log460461log7 x x x xxxxxx xxx x − − − Ta có: ( ) 22 2 loglog(46)1log(46) 4624260 23log3 xx x xxxx x x x −− −−−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
(2) log24
t h
p
điề
ki
n, ta có các giá tr
nguyên thoả mãn trong trường hợp này là
1;24;5;6;....2021
V
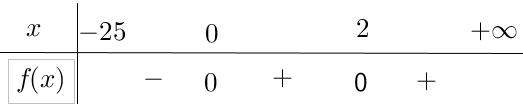
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 6
ế
ợ
ới
ệ
−=== =
01 m . Gọi ( ) ; ab là tập hợp các giá trị của m để bất phương trình ( ) ( ) log1821 x m mx−− có hữu hạn nghiệm nguyên. Tính ba A. 1. B. 321. C. 221. D. 421. Lời giải Chọn A Trường hợp 1: 1 m Ta có: ( ) ( ) 2222 log182118.810 xxxxx m mxmmmmm −−−+− 222 222 1641641640loglog x mm mmm mxx mmm +−+−+− −− . Rỏ ràng trong trường hợp này không thể có hữu hạn nghiệm nguyên Trường hợp 2:01 m Ta có: ( ) ( ) 22 22 .810 18 log1821 1 180 8 xx xx x m x x mmm mm mx m m +− − −− −
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn K
t h
p v
điều ki
n ta có: 42 log7log3 x Vì x
nên bất phương trình không có nghiệm nguyên. Câu 117: Có bao nhiêu số nguyên x thỏa mãn ( ) ( ) 2 3 24log2530 xx x −+− ? A. 24 B. 26 C. 25 D. Vô số Lời giải Chọn B Điều kiện: 25 x − . Đặt ( ) ( ) ( ) 2 3 24log253 xx fxx=−+− ◦ 22 22 0 240222 2 xxxx x xx x =
◦ ( ) ( ) 3 33 log2530log2532532 xxxx +−=+=+== Bảng xét dấu Từ bảng xét dấu, ( ) 250 0 2 x fx x − = . Vậy có 26 số nguyên x thỏa yêu cầu. Câu 118: Cho
u kiện
* * ,:,2020,:,2020 212 0,03,032
xyxy xyxy xy xy xy BPT cho có dạng ( )( ) ( )( ) 23 42 32log142log10 32 xy xyxy xy +− −−+++++ −+ + Xét 1 y = thì thành ( ) ( ) 23 42 3log134log0 33 x xx x + −−+++ , rõ ràng BPT này nghiệm đúng với mọi 3 x vì ( ) ( ) ( ) 223 42 30, log1log010, 340, log033 x xx x + −−++=+ .
Như vậy trường hợp này cho ta đúng 2017 bộ ( ) ( );;1xyx = với 42020,xx + Xét 2 y = thì thành ( ) 3 44log10 x + , BPT này cũng luôn đúng vớ
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 7 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 2 22 2 22 164 loglog164164 1 log8log8 log8 x mm mm m m mm m xx m mm xx x +− +−+− −− − Để bất phương trình có hữu hạn nghiệm nguyên thì: 222 222 1648163281632 log8log0log01 mmm mmm mmm +−+−+− + ( ) 224 816320,0;1 mmmm ++ Vậy 1 ba−= Câu 119: Có bao nhiêu bộ ( ) ; xy với , xy nguyên và 1,2020 xy thỏa mãn ( ) ( ) 32 221 248log236log23 yx xyxyxyxy yx + ++++−− +− ? A.
. B. 2017. C.
. D.
. Lời giải Chọn A + Điề
4034
2
2017.2020
i mọi x mà 42020,xx . Trường hợp này cho ta 2017 cặp ( ) ; xy nữa. + Với 2,3yx thì ( ) *0 VT nên không xảy ra. Vậy có đúng 4034 bộ số ( ) ; xy thỏa mãn yêu cầu bài toán. Câu 120: Có bao nhiêu giá trị nguyên dương của y để tập nghiệm của bất phương trình ( )( ) 2 log220 x xy−− có ít nhất 1 số nguyên và không quá 6 số nguyên? A. 2048. B. 2016. C. 1012. D. 2023.
TH1. Nếu 2
4 . log x xy Để bất phương trình có ít nhất 1 số nguyên và không quá 6 số nguyên thì 2 1 3log38. 8 yy −
Suy ra có 7 giá trị nguyên dương của y thỏa mãn TH2. Nếu 2
4 log x xy Để bất phương trình có ít nhất 1 số nguyên và không quá 6 số nguyên thì 2 5log11322048. yy
Suy ra có 204833 12016 1 += giá trị nguyên dương của y thỏa mãn. Từ, suy ra có 2023 giá trị nguyên dương của y thỏa mãn yêu cầu bài toán. Câu 121: Cho bất phương trình ( ) ( ) 22 3222 11 log321log1 mm xmxmxmmx ++ +−−−++− . Tập hợp các giá trị của m để bất phương trình trên có nghiệm ( ) ; ab . Giá trị của biểu thức 22ab + là A. 3. B. 8. C. 5. D. 9. Lời giải Chọn D Ta có
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 8
ện thi: Tuyển sinh
ớ
Tố
ệ
Sưu
và biên soạn Lời giải Chọn D Điều kiện: 0. x Ta có ( )( ) 2 2 2 2 2 log204 20log log220. log204 20log x x x x x xy y xy x x xy y − − −− −
Hòa
0984164935
Chuyên luy
vào l
p 10
t Nghi
p THPT BDKT Toán 10; 11; 12
tầm
−
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 9 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) ( ) ( )( ) ( ) ( ) ( ) ( ) ( ) ( ) 22 3222 11 3222 2 322 2 2 2 1;1 1;1 log321log1 3211 10 220 1;1 20 1;1 2 1;1 minmax2 1;1 0;3 mm xmxmxmmx xmxmxmmx x xmxmxmm x xmxm x xmx x xmx x m ++ +−−−++− +−−−++− − +−−−+ − −+− − − − − − 22 0 9 3 a ab b = += = Câu 122: Có bao nhiêu số nguyên x thỏa mãn ( ) ( ) ( )21 33 log1log313220 x xx +−+− ? A. Vô số B. 28 C. 26 D. 27 Lời giải Chọn D Điều kiện: 31 x − Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 33 1 21 33 2 33 1 log1log310 322 log1log313220 log1log3 2203 0 10 x x x xx xx xx +−+ +−+− +−+ 22 11 22 1 5 1 5 5 1310 6 22 5 3 6 6 1310 56 22 3 0 322 0 322 6 xx xx x xxx x x x x xxx x x x x − ++ − = ++ − . Kết hợp với điều kiện 31 x − ta có 315 6 x x −− = Vậy có 27 số nguyên x . Câu 123: Bất phương trình ( ) ( ) ( ) 2 2 loglog3330 xx xxx +−−− có tập nghiệm không là tập con của tập nào trong các tập hợp sau đây? A. ( )3;7 B. ( ) 3; −+ C. ( );5−− D. ( );0− Lời giải
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 10 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Chọn C ĐKXĐ: 2 1 01 0 3003 3 x x xx x x x x − − + − . Trường hợp 1: ( ) ( ) 2 2 22 22 loglog301 3230 3 330001 xx x xxx xxxxx x xxxx x +−− +−+− − − − Trường hợp 2: ( ) ( ) ( ) 2 2 22 22 31 loglog303230 13;0 33000 xx x xxx xxxxx x x xxxx x − +−− +−+− − − − Kết hợp với điều kiện ta được ( )3;1 x−− Vậy tập nghiệm của bất phương trình là ( )3;1 S =−− . Ta thấy S không là tập con của tập hợp ( );5−− Câu 124: Có bao nhiêu số nguyên dương y sao cho ứng với mỗi y có không quá 5 số nguyên x thỏa mãn ( )( ) 33ln10 x yx−− A. 2181. B. 2183. C. 2179. D. 2187. Lời giải Chọn D ĐK: 0 x TH 1: 33 3 log31log 33033 e1log ee ln10ln1 xx yxyx yy xy xx xx +− + − 7 3 ycbt1log83 yy + TH 2: 33 3 log31log 33033 1loge ee ln10ln1 xx yxyx yy yx xx xx +− + − 1 3 ycbt1log03 yy + Từ, và yêu cầu y nguyên dương ta có: 17 33 y có 2187 số y thỏa mãn. Câu 125: Cho bất phương trình ( ) ( ) 22 717 7 log4log1log5 xxmx −++++ . Tổng các giá trị nguyên dương của tham số m sao cho bất phương trình đã cho nghiệm đúng 1;4 x bằng A. 21. B. 28. C. 10. D. 11.
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 11 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn A Điều kiện: 2 40xxm −++ Ta có: ( ) ( ) 22 717 7 log4log1log5 xxmx −++++ ( ) ( ) 22 777 log4log1log5 xxmx −++++ ( ) ( ) 22 77 log4log55 xxmx −+++ 222 22 455645 40 4 xxmxxxm xxmxxm −+++−+ −++− Bất phương trình đã cho nghiệm đúng 1;4 x khi và chỉ khi nghiệm đúng 1;4 x Đặt ( ) 2 645fxxx=−+ và ( ) 2 4 gxxx =− . Khi đó nghiệm đúng 1;4 x ( ) ( ) 1;4 1;4 mMinfx
7 07 0 m m m Mà
ố
tất cả giá trị củ
ố m để bất
trình ( ) ( ) 22 log23log1 xxmx +++ có tập nghiệm là . A. 22 m − . B. 22 m . C. 2222 m − . D. 2 m . Lời giải Chọn A Ta có: ( ) ( ) 22 log23log1 xxmx +++ 2 22 10 231 xmx xxmx ++ +++ ( ) ( ) ( ) 2 2 101 * 202 xmx xmx ++ −+ Để bất phuương trình ( ) ( ) 22 log23log1 xxmx +++ có tập nghiệm là thì hệ ( )* có tập nghiệm 2 1 2 2 40 80 m m =− =− 22 m − Câu 127: Biết 9 4 x = là một nghiệm của bất phương trình ( ) ( ) 22 log2log23 aa xxxx −−−++ . Khi đó tập nghiệm của bất phương trình là A. 5 2; 2 T = . B. 5 ; 2 T =+ . C. ( );1 T =−− . D. 5 1; 2 T =− .
mMaxgx
m là s
nguyên dương nên 1;2;3;4;5;6 m
Do đó tổng các giá trị nguyên dương của m là 21. Câu 126: Tìm
a tham s
phương
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 12 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn A Thay 9 4 x = vào bất phương trình, ta được loglog1339 1616aa .( )1 Vì ( )1 là bất đẳng thức đúng nên 01 a Vì thế 22 2 223 20 xxxx xx −−−++ −− ( ) ( ) 2 2350 ;12; xx x −− −−+ ( ) ( ) 5 1; 2 ;12; x x − −−+ 5 2; 2 x . Vậy tập nghiệm của bất phương trình là 5 2; 2 T = . Câu 128: Số giá trị nguyên 2022;2022 x− thỏa mãn ( )
x
Điều
x x
x x
log x x + 2 log01 xx Với 2022;2022 x− và x suy ra 2;3;4;...;2022 x . Vậy có 2021 giá trị nguyên của x thỏa đề bài. Câu 129: Cho bất phương trình ( ) ( ) 22 log23log1 xxmx +++ . Có tất cả bao nhiêu giá trị nguyên của tham số m để bất phương trình nghiệm đúng với mọi x ? A. 5. B. Vô số. C. 4. D. 3. Lời giải Chọn D Ta có ( ) ( ) 22 log23log1,xxmxx +++ 22 2 231 , 10 xxmx x xmx + +++ +
( ) 2 42 log8loglog20
xx + là A. 2020 B. 2019 C. 2022 D. 2021 Lời giải Chọn D
kiện: ( ) 2 01011 1 log20212
x
. Ta có: ( ) ( ) 2 42 log8loglog20 x xx + ( ) ( ) ( ) 2 2 4 log201 log8log02 x x x = + +) ( ) 1 121 2 xx == . +) ( ) 4 8 1 22log0 log x x + ( ) 2 2 3 2log0 log x x + 2 2 2 3log 0
Xét
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 13 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) 2 2 201 , 102 x x xm mx x + ++ ( ) ( ) 1 2 0 0 2 2 80 40 m m − 2222 22 m m − 22 m − Vì m nên 1;0;1 m− . Vậy có 3 giá trị nguyên của tham số m thoả mãn. Câu 130: Có bao nhiêu cặp số nguyên không âm ( ) ; xy thỏa mãn điều kiện 2222 22 log1log65 469234 xyxy xyxy ++++ + ++++ ? A. 43 B. 49 C. 42 D. 45 Lời giải Chọn C Đặt 22 5;4680uxyvxy =++=++ Ta được 2222 22 log1log65 469234 xyxy xyxy ++++ + ++++ 2222 22 loglog65 469468
++++
++++
vv + + uv
xyxy xyxy
22 1 loglog 1 uu
hay ( ) ( ) 22 222 5468234xyxyxy ++++−+− 42406 xx −− vì ( ) ; xy là những số nguyên nên
V
Câu 131: Tập nghiệm của bất phương trình 2 log(45.28)0 xx x −−+ có dạng (;) ab . Giá trị ab + bằng A. 6. B. 4. C. 3. D. 5. Lời giải Chọn C Điều kiện: 45.280, xx x −+ . Bất phương trình:
0 x = có 7 cặp Xét 1 x = có 7 cặp Xét 2 x = có 8 cặp Xét 3 x = có 7 cặp Xét 4 x = có 7 cặp Xét 5 x = có 5 cặp Xét 6 x = có 1 cặp
ậy có 42 cặp số ( ) ; xy thỏa mãn đề bài.
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 14 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 2 2 log(45.28)0 log(45.28) 45.282 46.280 224 12 xx xx xxx xx x x x x −−+ −+ −+ −+ Vậy tập nghiệm của bất phương trình là: ( )1;2 . Câu 132: Số nghiệm nguyên của bất phương trình ( ) ( ) 6 332465ln30 xx x +−−+ là A. 144. B. 145. C. 146. D. 147. Lời giải Chọn B Ta có: ( ) ( ) ( ) ( ) 5 6 5 26 6 5 5 5 5ln303() 332465ln305ln3033 3324603246.330 3333 31 331. 53 32435 xx xx xx x x x xektm x x xe xe xe x x xe x −+= += +−−+ −+ −− −+ +− −− −− − − Vì x nên ta được số nghiệm nguyên của bất phương trình là 145. Câu 133: Gọi S là tập nghiệm của bất phương trình ( ) ( ) 22 log2log23 aa xxxx −−−++ . Biết ( ) ; Smn = và 7 3 thuộc S ,tính mn + A. 13 3 mn+= B. 7 2 mn+= C. 11 3 mn+= D. 9 2 mn+= Lời giải Chọn D Điều kiện: 2 2 20 23 230. 01 01 xx x xx a a −− −++ Do 7 3 x = là nghiệm của bất phương trình đã cho nên 1020 loglog01. 99aa a Vì 01 a nên bất phương trình 22223xxxx −−−++ 23 2 55 235012. 22 x xxxx −−−⎯⎯⎯→ Vì vậy 59 2 22 mn+=+=
Câu 134: Với m là tham số thực dương khác 1. Tìm tập nghiệm S của bất phương trình ( ) ( ) 22log3log2 mm xxxx ++− . Biết 1 x = là một nghiệm của bất phương trình đã cho. A. ( ) ( 1;01;3 S =−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12
THỪA MŨ LOGARIT
LŨY
Page
15
i Chọn D ( ) ( ) 22log3log2 mm xxxx ++− Với 1 x = , bpt: log5log101 mm m . Điều kiện: ( ) 2 2 30 1 ;0; 2 20 xx x xx ++ −+ − Bpt 22 32 xxxx ++− 2 230xx −++ 1;3 x − . Kết hợp với điều kiện ) 1 1;0;3 2 x − . Câu 135: Gọi S là tập chứa tất cả các giá trị nguyên của tham số m để
ất
( ) ( ) 2 log6012010103log11 xxmx ++−−+ có miền nghiệ
ứa
ệ
(
2
* 61210 x xxm − ++− . ( ) ( ) ( ) ( )
22 log6012010103log111log6121log11 xxmxxxmx ++−−++++−−+ ( ) ( ) ( ) 2233 log6121log161211 xxmxxxmx ++−+++−+ ( )1 ( ) 23232 6121331239 xxmxxxmxxxfx ++−+++−−−= . Từ ( )1 Hệ điều kiện ( )* trở thành: 1 x − . Xét hàm số ( ) 3239 fxxxx =−− trên khoảng ( ) 1; −+ . Ta có: ( ) 2 369fxxx =−− . ( ) 2 1 3690 3 x fxxx x =− =−−= =
. B. ) 1 1;0;2 2 S =− . C. ( ) 1 2;0;3 2 S =− D. ) 1 1;0;3 2 S =− Lời giả
b
phương trình
m ch
đúng 4 giá trị nguyên của biến x . Số phần tử của S là A. 11. B. 10. C. 9. D. 12. Lời giải Chọn A Điều ki
n
)
1
3
Bảng biến thiên: Để bất phương trình ( ) ( ) 2 log6012010103log11 xxmx ++−−+ có miền nghiệm chứa đúng 4 giá trị nguyên của biến x khi 112092 mm −−− . Vậy có 11 giá trị nguyên của tham số m thỏa mãn bài toán. Câu 136: Xét các số thực , xy thỏa mãn 22 1 xy+ và ( ) 22 log241 xy xy + + . Giá trị lớn nhất của biểu thức 3 Pxy =+ bằng A. 5210 + B. 545
C. 552 + D. 1025 + Lời
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
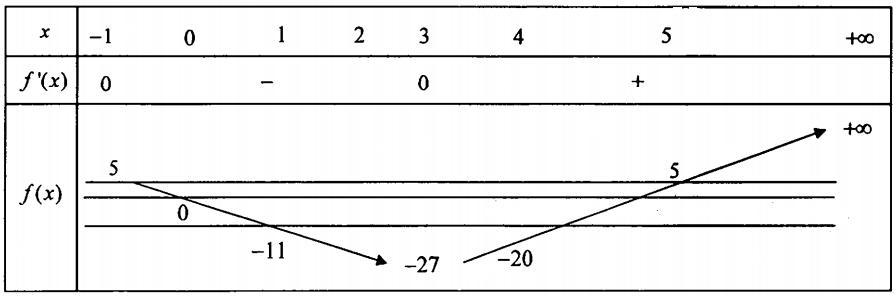
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 16
+
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 giải Chọn C Ta có 22 1 xy+ Khi đó ( ) ( ) ( ) 222222 22 log241log24log xyxyxyxyxyxy+++ +++ 22 24xyxy++ ( ) ( ) 2 2 2 2 21445512 x xxy y y −− + −− ++ + Khi đó ( ) ( ) ( ) ( )331255312 PxyPxyPxy =+=−+−+−=−+− Áp dụng BĐT Bunhiacopxki, ta có: ( ) ( ) ( ) ( ) ( ) 2 22 2 2 0 31 1 12 5 3 2 xy xy −+ +− −= + ( ) ( ) ( ) ( ) ( ) ( ) 2 22 2 2 253123 02 1 15 x Px y y −=−+−+ +−= Vậy ( )2 55052552552552 P PP −−− + Suy ra max552 P =+ . Dấu "" = xảy ra khi và chỉ khi 322 1,2 22xy=+=+ Câu 137: Cho bất phương trình ( ) ( ) 22 55 log441log23 xxmxx −++−++ với m là tham số. Có tất cả bao nhiêu giá trị nguyên của tham số m để bất phương trình nghiệm đúng với mọi x thuộc khoảng ( )1;3 ?
. * Xét ( ) 2 41411fxxx=++ trên ( )1;3 . Ta có ( ) 8140fxx =+ với ( )1;3 x . Vậy để thoả mãn thì ( ) 129 mf= * Xét ( ) 2 44gxxx=−+ trên ( )1;3 . Ta có bảng biến thiên của ( )gx trên ( )1;3
Vậy để thoả mãn thì 00mm − . Khi đó 029 m , suy ra có 30 giá trị nguyên của tham số m Câu 138: Có bao nhiêu giá trị nguyên m để bất phương trình 22 22 log(25)log540 xmxmm −++++ có ít nhất một nghiệm nguyên và không quá 1791 nghiệm nguyên? A. 10. B. 3. C. 9. D. 11. Lời giải Chọn D Điều kiện xác định của bất phương trình là 0 x . Đặt 2log , txt= Khi đó bất phương trình trở thành
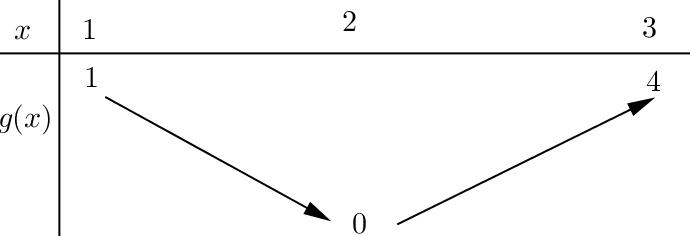
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 17
A. 30 B. 28 C. 29 D. Vô số Lời giải Chọn A Ta có ( ) ( ) (
2222 5555 log441log23log44log51015 xxmxxxxmxx −++−++−++++ (
(
22 22
xxxxm xx xxmxxm ++ ++−++
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
) ( )
)
) ( ) ( ) 2
5101544414111 1;31;3 440442 xxm
−++−+−
tmtmmtm −−−−++ 14 2 1log422mmmxmx ++++ Do 41 2214.2 mmm ++ −= , nên với 3 m − thì bất phương trình có ít nhất một nghiệm
Suy ra với 3 m − bất phương trình có ít nhất 1 nghiệm nguyên và không quá 1791 thì 2 1792 14.211791log7 14 m m −= Vậy 3;2;;7 m−− hay có 11 giá trị nguyên của tham số m thỏa mãn bài toán. Câu 139: Tập nghiệm của bất phương trình ( ) 41 4 log31.log313 164 x x − là A. ( ) 0;12;+ B. ( )1;2 C. 1;2 D. ( ) ;12; −+
( ) 2225540tmtmm −++++ . ( )( ) 14014
nguyên.
x x −−+− = −= 4 4
1 1 1
xe xe e e x ng 33 log2;log2 ab , ( ) , ab . Chọn khẳng định đúng. A. 2 ab+= . B. 1 ab−= . C. 7 ab−= . D. 12 ab+= . Lời giải Chọn D Điều kiện 1
= Kết hợp với điều kiện xác định ta được: 1 xe Vậy có 2 giá trị nguyên của x thoả mãn yêu cầu bài toán. Câu 141: Tập nghiệm của bất phương trình ( ) ( ) 1 33 log31.log3320 xx+ −−− có dạ 310 31 330
− − Ta có bất phương trình tương đương với ( ) ( ) ( ) ( ) 3333 log31.log3.3120log31.log31120 xxxx −−−−−+− . Đặt ( ) 3 log31 x t =− , bất phương trình trở thành ( ) 12021ttt +−− . Suy ra ( ) 3 110 2log31131334 99 xxx −−−
x x x+
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 18 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn A Điều kiện xác định 310 x x Khi đó bất phương trình đã cho tương đương với ( ) ( ) 444 log31.log31log163 4 xx −−−− , đặt ( ) 4 tlog31 x =− ( ) t ( )1 trở thành ( ) ( ) 4 2 4 33 log31 3182 3 22 20 111 4 312 log31 22 x x x x t x tt x t − − −+− − − Kết hợp điều kiện suy ra tập nghiệm của bất phương trình là ( ) 0;12;+ . Câu 140: Có bao nhiêu số nguyên x thoả mãn ( ) 2 ln3lnx4990 x x −−+− ? A. 2. B. 3. C. 4. D. 1. Lời giải Chọn A Điều kiện xác định: 990 0 x x − 1 x . Bpt tương đương 2 ln3lnx404lnx1
9901 x
3333 10 loglog4log1022log2 9 xx − Vậy tập nghiệm của bất phương trình đã cho là 33 log102;2log2 S =−
Câu 142: Bất phương trình ( )( ) 2 44 421loglog120 xx xx ++−− có tập nghiệm là 1 ;b a . Tính giá trị của biểu thức 4ab A. . B. . C. . D. . Lời giải Chọn A Điều kiện xác định Câu 143: Tính tổng các nghiệm nguyên của bất phương trình
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
19
+Đk: Câu 144: Có bao nhiêu số nguyên x thỏa mãn ( ) 2 2 25 log5log63log0 xxx −++− ? A. 64. B. 9. C. 65. D. 8. Lời giải Chọn C ( ) ( ) 2 2 25 log5log63log01 xxx −++− 2 5 5 2 2 log3 log3 log5log60 x x xx = −++ 5 2 125 log3 1log6 x x x = − 125 0125 1 64 2 x x x = 125 1 64 2 x x = 0 512 2049 16 2047 16 0 x ( ) 22 44444 1 42(loglog12)0log log1203log4256 64 1 x x xxxxxx −−−−− ++ 64,25640abab ==−= ( ) 2 22 loglog486420 x xx+−− 22 10 12 20 ( ) 2 22 loglog486420 x xx+−− 6 2 00 012 642022 x x x x x − 22 2222 2 1:12() 2:012(1)loglog480loglog60 1 3log24 8 1;2;3;4 12341222 THxtm THxxxxx xx KHDKx S += ++−+− − =++++=
A. B. C. D. Lời giải Chọn A
Suy ra có 65 số nguyên x thỏa mãn. Câu 145: Số nghiệm nguyên của bất phương trình 23 33 log(1)log(1)20 xx−−−+ là A. 7. B. 8. C. 9. D. 3. Lời giải Chọn A Điều kiện: 10 x − Ta có 23 33 log(1)log(1)20 xx−−−+ 2 33 log(1)3log(1)20 xx −−−+ 3 1log(1)2 x − 319 x − 410 x Vì 4;5;6;7;8;9;10 xx Vậy có 7 nghiệm nguyên dương
cho.
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 20
của bất phương trình đã
Câu
ổng các nghiệm
ủ
C
11 23216 48 xx . Vậy tổng tất cả các nghiệm
củ
ất
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Câu 147: Có tất cả bao nhiêu số nguyên dương m để bất phương trình ( ) 2 2 2 loglog32xxm + có nghiệm đúng với mọi ( ) 0;2? x A. 9. B. 8. C. 13. D. 12. Lời giải Điều kiện: 0 x . Ta có ( ) ( ) 22 222 2 loglog32log2log32xxmxxm ++ ( ) 2 22 log2log10xxm ++ Đặt 2 log,tx = với ( ) ( ) 0;2;1.xt− Khi đó ( ) 2 210. ttm++ Đặt ( ) 2 210fttt=++ . Ta có ( ) 2201.fttt =+==− Bảng biến thiên
146: T
nguyên c
a bất phương trình 32 22 2 log()log(2)130 18(2)x xx−+ ++ là A. 16. B. 8. C. 36. D. 136. Lời giải
họn D Điều kiện 0 x . Khi đó 32 32 22 22 2 log()log(2)130log()log(2)130 18(2)x xx xx −+ −+ ++ 3 22 22222 (2) loglog(2)130log(2)3log(2)1002log(2)5 8 x xxxx −+−++−
nguyên
a b
phương trình là 136
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
trình
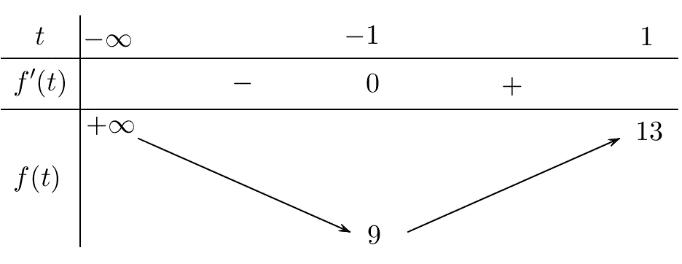
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
( ) 2 0;2 max20 −=xx Do đó 112 0256256 −− − mm mm . Vậy có 255 số m thỏa mãn đề bài. Câu 149: Có bao nhiêu số nguyên 2022;2022 x− thoả mãn ( ) 26 22 log23log7.2730 x xx −−− A. 2022. B. 2021. C. 8. D. 9. Lời giải Chọn D Điều kiện 663 00 0 09 63 273033 xx xx x x x − − Với 9 x = thoả mãn bất phương trình. Với 09 x suy ra 6 2730 x − Khi đó bất phương trình tương đương ( ) 2 22 log23log70 xx−− ( )2 22 log13log70 xx +−− ( )2 22 loglog60 xx −− 2 2log3 x − 1 8 4 x
21 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Yêu cầu bài toán 9. m Mà * 1;2;3;4;5;6;7;8;9 mm nên có tất cả 9 giá trị của m thỏa mãn. Câu 148: Có bao nhiêu giá trị nguyên của m sao cho với mỗi giá trị m , bất phương
( ) 22 24 log23log210 −++−+ xxmxxm nghiệm đúng với mọi giá trị 0;2 x ? A. 256 B. 252 C. 255 D. 253 Lời giải Chọn C Điều kiện ( ) 22 4 log2021 −+−+ xxmxxm . ( ) ( ) 222 224 1 log2log2log2 2 −+=−+=−+ xxmxxmxxm Đặt ( ) 2 4 log2 =−+ txxm . Điều kiện 0 t Bất phương trình trở thành: 2 3100+−tt 52− t Kết hợp với điều kiện ta được 02 t ( ) 2 22 4 2 21 0log2212256 2256 −+ −+−−− −+ xxm xxmmxxm xxm Đúng với mọi 0;2 x nếu giá trị nhỏ nhất của ( ) 2 0;2 min21−− xxm và
( ) 2 0;2 max2256−− xxm trên đoạn 0;2 . Với
( ) 2 0;2 min21 −=−xx ;
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 22
2
xx
−− ? A.
ố. B.
.
Lời giải Chọn B Điều kiện : 0 x Xét ( ) ( ) 2 3 412 2log 1 1381,0 3 xx x fxxx =−− Ta có: ( ) 2 3 412 2log 1 1 03 381 xx x fx x = = = ( ) 22 4124120 2 2 111 14120 333 6 xxxx xL xx x =− •==−−= = 33 2log2log 3333 381log3log812log4log xx xxxx•==−=+ 3 1 log1 3 xx =−= Bảng xét dấu: Vậy ( ) 1 06 3 fxx , do đó có 6 số nguyên x thỏa mãn là: 1;2;3;4;5;6. Câu 151: Có bao nhiêu số nguyên của x sao cho tồn tại số thực y thỏa mãn ( ) ( ) 22 32 2log1log221 xyxxy ++=+++ ? A. 2 B. 1 C. 3 D. 4 Lời giải Chon A Đặt ( ) ( ) 22 32 2log1log2212 xyxxyt ++=+++= + f(x)0 6 x 1 3 0 0 +
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vì x nguyên nên 1;2;3;4;5;6;7;8 x . Vậy bất phương trình có 9 nghiệm nguyên. Câu 150: Có bao nhiêu số nguyên x thỏa mãn ( )
3 412 2log 1 13810 3
x x
Vô s
6
C. 5. D. 7.
Ta thấy phương trình này có nghiệm 4 9 log2 3 y =
Nếu 2 x =− ta có phương trình ( ) ( ) 2 32 2log1log212 yyt −=+= ( ) 2
13 2.94.334* 214
t ttt t y y −= ++= += .
Ta có 2 421102.94 ttt yt =+ . Suy ra ( ) *4t VT nên phương trình vô nghiệm. Vậy có 2 giá trị nguyên của x thỏa mãn yêu cầu bài toán. Câu 152: Cho bao nhiêu số
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo
Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế
Page 23
ệ
ể
sinh
ớ
ố
ạn ( )2 22 2 1313 2214124 t t t t xy xy xxy xy ++= ++= +++= ++= Ta
( ) ( ) (
2 2 2 2 113
2 tt xyxyxy =++=+++++=
viên:
Hòa
ĐT: 0984164935
Chuyên luy
n thi: Tuy
n
vào l
p 10 T
t Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên so
có:
)
911.1.2112.4 22
931 422 t t Lại có ( ) ( ) 1 22 2 2 12414422;1;0 tt xyxx ++=+=−− . Nếu 0 x = ta có phương trình ( ) ( ) 2 32 2log1log21 yy+=+ . Ta thấy phương trình này có nghiệm 0 y = Nếu 1 x =− ta có phương trình 4 9 log2 2 324 2 9 3 2loglog222.94log23 24 t tt t y yytty y = ===== =
nguyên dương m để bất phương trình sau 2 2 3 2 21 log22 44 xx xxm xxm −+ −+− −+− có nghiệm A. 1. B. 3. C. 2. D. 4. Lời giải Chọn A Ta có 2 2 3 2 21 log22 44 xx xxm xxm −+ −+− −+− ( ) 2 22 3 2 21 log443211 44 xx xxmxx xxm −+ −+−−−+− −+− ( ) ( ) ( ) 2222 33 log321321log4444 xxxxxxmxxm −++−+−+−+−+−
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
( ) ( ) 3 5 6 1 3.log420 9 x x x + −+− . ( )1 A. 25. B. 26. C. 24. D. Vô số. Lời giải Chọn C Điều kiện xác định: 4 x − Với điều kiện 4 x − ta có: ( )1 ( ) ( ) ( ) 3 6 5 39.log420 xx x −+− ( ) ( ) ( ) 3 212 5 33.log420 xx x −+− . ( ) ( ) 3 212 5 3 212 5 330 log420 330 log420 xx xx x x − +− − +− 3 3 212 0425 212 425 xx x xx x −− + −− + ( ) ( ) 3 3 2120 2 421 2120 3 21 xx x xx x ++ − ++ Xét hàm số: ( ) 3 212fxxx=++ Ta có: ( ) 2 320 fxxx =+ Suy ra hàm số ( )fx đồng biến trên . Lại có ( ) 20 f −= do đó ( ) 2 2 421 x x − − 221 x − ( ) 2 3 21 x x − . Đối chiếu điều kiện x ta được 2;1;0;...;21 x−− Tổng số 24 giá trị nguyên của x thỏa mãn. Vậy chọn đáp án C.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
24 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Xét hàm ( ) 3log fttt =+ có ( ) 1 '10 ln3 ft t =+ nên đồng biến trên ( ) 0;+ Do đó: ( ) ( ) ( ) 2222 3214432144 fxxfxxmxxxxm −+−+−−+−+− 2 221mxx −++ Bất phương trình vô nghiệm 2 221, mxxx −++ Ta có: ( ) 2 3 221 2 Maxxx−++= ( ) 2 3 221 2 mMaxxx −++= Vậy bất phương trình có nghiệm khi 3 2 m Câu 153: Có bao nhiêu số nguyên x thỏa mãn
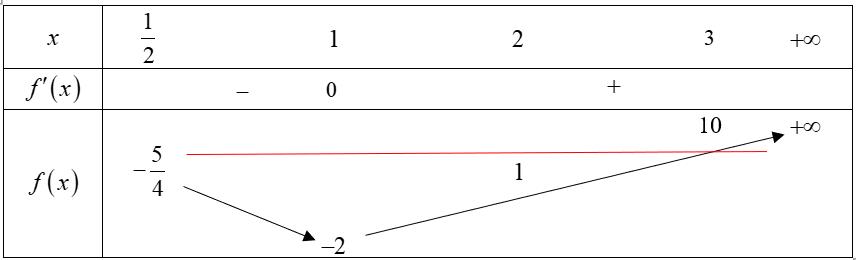
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
ỳnh
42
ễn
Page 25
Câu
bao
giá trị
ủ
ố m để
ậ
ệm
ủ
ất
( ) ( ) 2 22 log222log210 m xxx++−− chứa
B.
Lờ
giải Chọn C Ta có ( ) ( ) ( ) (
22 2222
mm xxxxxx ++−−++− ( )2 2 2 1 210 2 2221 2361 m m x x xxx xx − ++− −+ Xét hàm số ( ) 2 361fxxx=−+ trên 1 ; 2 + , ta có ( ) ( ) 66;01fxxfxx =−== . Bảng biến thiên Yêu cầu bài toán 2 12100log10 m m , 0;1;2;3 mm . Vậy có 4 giá trị nguyên của m thỏa mãn yêu cầu bài toán. Câu 155: Tổng tất cả các số nguyên x thỏa mãn 22 12 2ln4ln240 xxxx xx−−+ là A. 2. B. 1 C. 2. D. 1. Lời giải Chọn C Điều kiện: ( ) 0*. x 22 12 2ln4ln240 xxxx xx−−+ ( ) ( ) 22 22 2ln4ln240 ln24240 xxxx xxxx xx x −−+ −−− ( ) ( ) 2 24.ln10 xx x −− . Trường hợp 1:
Giáo viên: Hu
Văn Ánh
Nguy
Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
154: Có
nhiêu
nguyên c
a tham s
t
p nghi
c
a b
phương trình
đúng hai nghiệm nguyên. A. 10
9 C. 4 D. 3
i
)
log222log210log222log21
− −
Hệ bất phương trình vô nghiệm. Vậy tổng tất cả các số nguyên x thỏa mãn bất phương trình đã cho là 2. Câu 156: Cho hàm số bậc bốn ( )yfx = có đồ thị là đường cong trong hình vẽ. Gọi S là tập hợp các nghiệm thực của phương trình ( ) ( ) 2 log3ffx = . Số phần tử của tập S là A. 4 B. 6 C. 8 D. 10 Lời giải Chọn B Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 22 2 2 log22 log3log01 log22 fxfx ffxfxfx fx fx =−= ===
=
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 26 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 22 2 0 240220 2. ln10ln12 xxxx x x x xe xx xe − − Kết hợp với điều kiện
0984164935
( )* ta được 2 xe . Mà x suy ra 2 x = thỏa mãn. Trường hợp 2: 22 2 2402202 ln10ln1 =
xxxx x xe xx
+) ( ) 2 21 fx = , phương trình vô nghiệm. +) ( ) 1 fx = , phương trình có 2 nghiệm 1 x =
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Xét
(
. Ta
. Suy ra ( ) ( ) ( ) 22 *898918
. Câu 158: Có bao nhiêu số nguyên dương x thỏa mãn ( ) ( ) 2
x xxx +−−− ? A. 1. B. 2. C. 3. D. Vô số Lời giải Chọn A * ĐK: 2 0 30. 3 x xx x − * Ta có ( ) 325 x fxx=+− là hàm số đồng biến trên vì ( ) '3.ln320 x fxx=+ . Do ( ) 10 f = nên ( ) 01fxx và ( ) 01.fxx * Xét hai trường hợp Trường hợp 1: ( ) ( ) 2 2 2 2 2 325011 log320log3234 x x x x xx xx xx +− − −− −
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 27 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn +) ( ) ( ) 2 21;3 fx = , phương trình có 4 nghiệm phân biệt khác 1 . Vậy tập S có 6 phần tử. Câu 157: Có bao nhiêu số nguyên x thỏa mãn bất phương trình ( ) ( ) 22 2333 2log(21)log(42)log8log960 xx xxxx −+−++−+−+ ? A. 8 B. Vô số C. 7 D. 9 Lời giải Chọn A Điều kiện: 0 x Do 0 x nên 2 23 3 log(21)1log(21)log(42)2 log(42)1 x xx x + +++ +
23 2log(21)log(42)0 xx −+−+ Khi đó, ( ) ( ) 22 2333 2log(21)log(42)log8log960 xx xxxx −+−++−+−+ ( ) 22 33 log8log960 xxxx +−+−+ ( ) 22 33 log88log920 xxxx +++−−− ( ) ( ) 22 33 log88log99* xxxx++++
hàm số
) 3log fttt =+ liên tục trên ( ) 0; D =+
có ( ) 1 ln310, fttD t
=+ hàm số ()ft đồng biến trên D
fxfxxxx ++
2 325log320
38104 0 log1302 = ++−= Bảng biến thiên ( ) 024gxx . Suy ra có 3 số nguyên x thoả mãn. Câu 160: Bất phương trình 2 2332 66 loglog1loglog xx xx ++ có số nghiệm nguyên dương là A. vô nghiệm. B. 1 nghiệm. C. 2 nghiệm. D. 3 nghiệm.
x x gx x xx −= = =

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 28 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 2 1 1 11. 340 4 x x x x xx x − − −− Trường hợp 2: ( ) ( ) 2 2 2 2 2 325011 log320log3234 x x x x xx xx xx +− − −− − 2 1 1 14. 14 340 x x x x xx − −− Vậy kết hợp hai trường hợp ta có 1 x − hoặc 14 x . Đối chiếu với điều kiện ta được 1 x − hoặc 34 x . Theo yêu cầu của bài x là số nguyên dương nên 4 x = . Vậy có duy
nhất một giá trị x thỏa mãn yêu cầu. Câu 159: Có bao nhiêu số nguyên x thoả mãn ( ) 3 381log130 x xx −++− A. 2. B. 4. C. 1. D. 3. Lời giải Chọn D Điều Kiện: 1 x − . Xét hàm số ( ) ( ) 3 log13fxxx=++− với 1 x Ta có ( ) ( ) ( ) 1 10,1 1ln3 fxxfx x =+− + là hàm số đồng biến trên ( ) 1; −+ . Mà ( ) 20 f = nên phương trình ( ) 0 fx = có nghiệm duy nhất 2 x = Đặt ( ) ( ) 3 381log13 x gxxx =−++− ( ) ( ) 3

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 29
ỏ hơn 2020 sao cho tồn tại số thực dương x thỏa mãn đồng thời các điều kiện 2121 2772021.log yxy x ++++− và ( ) 2 2230xyxy−++− A. 6 B. 3 C. 2016 D. 2018 Lời giải Chọn D +)Điều kiện: 0 1 x y − +)Xét bất phương trình: ( ) 21211 22 22 772021.log7772021.log yxyy x xx +++++−− +)Với 01 x ta có: ( ) 1 22x 2 7770 2021.log0 y x + − nên thỏa mãn bất phương trình.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn B Điều kiện: 0. x BPT đã cho 2 23223 66 loglogloglog.log0 xxx xx +−− ( ) ( ) 2232 6 loglog1log1log0 xxx x −+− ( ) ( ) 223 6 log1loglog01 xx x −− Xét phương trình: ( ) 223 6 log1loglog0 xx x −−= 2 23 log10(1) 6 loglog0(2) x x x −= −= Giải(1): (1)2(/) xtm= Giải (2): 23 (2)loglog6 x x = 2 2 2 log6 log log3 x x = 2222 log3.loglog6logxx =− ( ) 222 log.1log3log6 x += ( ) 2222 log.log2log3log6 x += 2 log1 x = 2(/)xtm= Ta có bảng xét dấu Vậy BPT đã cho có nghiệm duy nhất 2. x = Câu 161: Có bao nhiêu số nguyên y nh
+)Với 1 x ta có: ( ) 1 22x 2
+ − nên bất phương trình vô nghiệm
y x
7770 2021.log0
+)Với 01 x xét bất phương trình: ( ) ( ) 2 22 23 2230223 2 xx xyxyyxxxy x −++−−−−
+)Xét hàm số ( ) 2 23 2 xx fx x = trên ( 0;1
Ta có: ( ) ( ) ( 2 2 47 0,0;1 2 xx fxx x −+ =
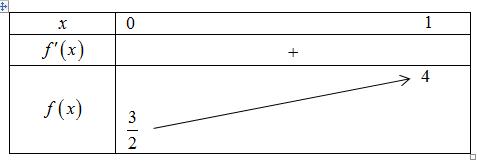
Bảng biến thiên: Dựa vào bảng biến thiên ta thấy để tồn tại số thực dương x thỏa mãn yêu cầu bài toán thì
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
30
dương (;) ab ,
đó
ab
2 1 22 22 b a b bb aa a + + + ? A. 5. B. 9. C. 10. D. 11. Lời giải Chọn C Đặt ;2b xay== , ta có 222 .1 2 yxyx xxyxy xyyxyxy + +++ Xét hàm 22 (;). yx xy fxy xyxy = ++ Khi (;)1xyfxy== Giả sử 22 2 224 (;).11(4) () xxx x xyxy xyfxyxyxy xyxyxy ==+ +++ Giả sử 2 224 (;).11 () yyy x xyxy xyfxy xyxyxy == +++
3 2 y . Do đó có 2018 số nguyên y nhỏ hơn 2020 thỏa mãn yêu cầu bài toán. Câu 162: Có bao nhiêu cặp số nguyên
trong
,1;2022
thỏa mãn
Vậy, (;)1(;)12b fxyfxyxya === Trên đoạn ,1;20222202211 b abb
Vậy, có 10 giá trị của b , và có 10 giá trị của a nên có 10 cặp (;) ab thỏa mãn. Câu 163: Có bao nhiêu giá trị nguyên của a sao cho ứng với mỗi a , tồn tại ít nhất năm số nguyên
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 31
−
A. 5. B. 4. C. 7 D. 6. Lời giải Chọn A 22554315 843158.30 8.488 bb abbaba babb +−+++−−− 2 5 1131 8.315.0 2488 bbb a a −−− . Đặt ( ) 2 5
bbb a a fb =−−− ( ) 5
bbb a
Dùng table solve suy ra có 5 giá trị nguyên của a Câu 164: Số nghiệm nguyên của bất phương trình ( ) ( ) ( )( ) 2 22 2log2log2115 xxxx +−−+− là A. 5 B. 6 C. 7 D. 4 Lời giải Chọn B Điều kiện: ( ) ( ) 2 2 2 2 2 2 2 2 2022 21021 2 log2021 2 log21021 21 1 211 1 x x x x x x x x x x x x x x x x x − − + − − + =− − − − + − − .
( )10;10 b
thoả mãn 2 5 84315 abbab +−+++ ?
1131 8.315. 2488
1113311 lnln.315.ln 2248888
fb
=−−− . ( ) ( )0,10;10fbb − . Để tồn tại ít nhất năm số nguyên ( )10;10 b− thì b thoả mãn ( ) 2 555 5 1131 508.315.0 2488 a a f −−−−
+ ++−+ ? A. 0 B. 1 C. 2 D. 7 Lời giải Chọn B ( ) 2 8 22 2 log2373 y xxyy + ++−+ ( ) ( ) 2 2 2 2 37 log231 8 yy xx y −++ ++ + Với mọi x ta có: ( ) ( ) ( ) 2 2 22 log23log121 xxx++=++ . Suy ra để ( )1 có nghiệm thì ta phải có 2 2 37 1 8 yy y −++ + 2 2310 yy −+ 1 ;1 2 y . Mà y nên 1 y = . Thay vào ( )1 ta được: ( ) 2 2 log2311 xxx++=−
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 32
) ( ) ( ) ( ) ( ) 2222 22 log4444log2121* xxxxxx +++++−+− Đặt 2 2 44 21 uxx vx =++ =− , khi đó ( )* có dạng 22 logloguuvv ++ . Xét hàm số 2(t)log ftt =+ có ( ) 2 22 log1 ()110 2log2.ln2.log t ft ttt =+=+ nên hàm số đồng biến trên khoảng ( ) 1;+ , do đó bpt 22 logloguuvvuv ++ . Khi đó 222442145015 xxxxxx ++−−−− . Kết hợp với điều kiện ta có 115xvx=− . Vì x nên 1;1;2;3;4;5 x− Chọn B Câu 165: Có bao nhiêu cặp số nguyên (,) xy thỏa mãn ( ) 2 8 22 2 log2373 y xxyy
Vậy có duy nhất cặp số nguyên (,) xy thỏa mãn. Câu 166: Có bao nhiêu số nguyên x thoả mãn ( ) 3 23 2log3log192.330 xx xxx −++−− A. 4096. B. 4095. C. 4094. D. 4097. Lời giải Chọn A Điều kiện: 0 0 311 92.330 33 x xx x x x x − −− Ta có
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có 1 x =− là một nghiệm của bất phương trình đã cho. Với 1 x , bất phương trình ( ) ( ) ( )( ) 2 22 2log2log2115 xxxx +−−+− ( ) ( ) ( ) ( ) ( ) ( ) 2222222 2222 log2log2145log2log212144 xxxxxxxxx +−−−−+−−−−++ (
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 33 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) 3 3 23 23 92.330(1) 2log3log192.3302log3log10 (2) 92.330 xx xx xx xxx xxx −−= −++−− −++ −− 31 (1)1. 33 x x x =− = = Giải. Đặt 2 log3 xt = 64t x = Ta được bất phương trình: ( ) ( ) 33 3log1846log1842 tttttt++++ 1849 ttt++ 184 1 999 ttt ++ . Đặt ( ) 184 999 ttt ft =++ . ( ) 118844lnlnln0 999999 ttt ft =++ , t Vậy ( )ft là hàm số nghịch biến trên . Lại có ( ) 21 f = . Từ 184 1 999 ttt ++ ( ) ( )2 ftf 2 t 26464 t 2 644096 x = Kết hợp điều kiện: 14096 x Vậy bất phương trình có 4096 nghiệm nguyên. Câu 167: Có bao nhiêu số nguyên x thoả mãn ( ) ( ) ( )( ) 2 33 2log2log2115 xxxx +−−+− ? A. 8 B. 7 C. 6 D. 5 Lời giải Chọn B ĐKXĐ: ) 2 21 1 11; 11 211 x x xD xx x + − =+ − − Ta có ( ) ( ) ( )( ) 2 33 2log2log2115 xxxx +−−+− ( ) ( ) ( ) ( ) 2222 33 log4444log2121 xxxxxx +++++−+− Đặt ( ) ( ) 3 3 11 log,1.10,1 .ln32log fttttftt t t =+=+ Suy ra ( )ft đồng biến trên ( ) 1;+ Suy ra ( ) ( ) 2222 4421442115 fxxfxxxxx ++−++−−
hàm
bi
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 34 Chuyên
ện thi: Tuyển sinh vào lớp 10 Tốt
ệp
12
tầm và biên soạn Vậy có 7 số nguyên x thoả mãn. Câu
Tính tổng tất cả các nghiệm nguyên của bất phương trình ( ) 22 22 log3log410 xxxx+−+−+ A. 4. B. 6. C. 5. D. 3. Lời giải Chọn B ĐKXĐ: 0 x Ta có ( ) ( )
Vớ
31 12 2212 x uxxxu x =++=+ + Và ( ) ( ) 3 1 log54
vxv xx =−−= Suy ra ( ) ( ) ( ) 0,0;4 fxxfx là hàm số đồng biến trên đoạn 0;4 . Để bất phương trình ( )* có nghiệm ( ) ( ) 0;4 min023mfxf == . Câu 170: Cho bất phương trình ( ) ( ) 22 55 log441log23 xxmxx −++−++ với m là tham số. Có tất cả bao nhiêu giá trị nguyên của tham số m để bất phương trình nghiệm đúng với mọi x thuộc khoảng ( )1;3 ? A. 30. B. 28. C. 29. D. Vô số. Lời giải
0984164935
luy
Nghi
THPT BDKT Toán 10; 11;
Sưu
168:
( ) ( ) 2222 2222 log3log410log33log44 xxxxxxxx +−+−+++++ Xét hàm số ( ) 2log fttt =+ trên khoảng ( ) 0;+ . Ta thấy
số ( )yft = luôn đồng
ến trên ( ) 0;+ Do đó ( ) ( ) ( ) 2222 22 log3log410343413 xxxxfxfxxxx +−+−+++ So sánh với điều kiện 0 x suy ra tập nghiệm nguyên của bất phương trình là 1;2;3 S = Vậy tổng các nghiệm nguyên của bất phương trình là: 1236 ++= . Câu 169: Tất cả các giá trị thực của m để bất phương trình 54 12.log3 x xxxm ++ có nghiệm: A. 23 m B. 3 12log5 m C. 23 m D. 2 212log5 m Lời giải Chọn C Điều kiện: 0;4 x . Ta thấy 54 44543log30 x xx −−− Khi đó bất phương trình trở thành ( ) ( ) ( ) ( ) 3 12.log54*mfxxxxx =++−−
i
2454.ln3
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 35 Chuyên
ện thi: Tuyển sinh vào lớp 10 Tốt
ệp
12 Sưu tầm và biên soạn Bất phương trình đã cho tương đương với ( ) ( ) 22 55 log441log23 xxmxx −+++++ ( ) ( ) 2 22 55 22 440 log44log51015 4451015 xxm xxmxx xxmxx −++ −++++ −++++ 2 2 44(1) 41411(2) xxm xxm −+− ++ . Để bất phương trình đã cho nghiệm đúng với mọi x thuộc khoảng ( )1;3 thì bất phương trình và phải nghiệm đúng với mọi x thuộc khoảng ( )
Ta có với ( )1;3 x thì 2 440xx−+ và 2 4141129 xx++ Do đó để bất phương trình và nghiệm đúng với mọi x thuộc khoảng ( )
thì 0 029 29 m m m − . Vì m nên 1;2;3;...;29 m có 29 giá trị nguyên của m . Vậy có 29 giá trị nguyên của m thỏ
Câu 171: Biết tập nghiệm của bất phương trình ( ) 222 22 log556log56 xxxxxxxxxx −−++−−+− là nửa khoảng (;] ab . Khi đó 6ab + bằng A. 19 2 . B. 9. C. 18. D. 13. Lời giải Chọn C Điều kiện: 2 0 0 03 23 60 x x x x xx − +− Ta có: ( ) 222 22 log556log56 xxxxxxxxxx −−++−−+− ( ) ( ) 22 22 1log516log56 xxxxxxxxxx −−−+−−+− ( )( ) ( ) 2 22 15log6log50 xxxxxxx −−++−− ( )( ) 2 2 5log160 xxxxx −−−+− ( )( ) ( ) 2 2 log51601 xxxxx −−−+− Đặt ( ) 2 log5fxxx=− ( ) ( ) ( ) 22 1 log0;(0;3]33log350 ln2 fxxxfxf =−=− ( ) 0 fx . Do đó,
0984164935
luy
Nghi
THPT BDKT Toán 10; 11;
1;3
1;3
a mãn bài ra.
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 36 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) 2 1160 xxx −−+− 2 61 xxx +−− ( )2 2 2 612350 11 xx xxx x x −− +−− 1 5 5 2 2 1 x x x x − Tập nghiệm của bất phương trình là: 5 ;3 2 S = 5 66.318. 2 ab +=+= Câu 172: Có bao nhiêu bộ ( ) ; xy với , xy nguyên và 1,15 xy thỏa mãn ( ) ( ) 32 221 248log236log. 23 yx xyxyxyxy yx + ++++−− +− A. 30 B. 11 C. 24 D. 16 Lời giải Chọn C Từ giả thiết 415 115 ; x y xy ( ) ( ) 32 221 248log236log23 yx xyxyxyxy yx + ++++−− +− ( )( ) ( )( ) ( ) 32 221 42log32log0* 23 yx xyxy yx + +++−− +− Xét ( ) ( ) 22 211 loglog20;4;151 33 x fxx xx + ==+ +Với 1 y = thay vào ( )* ta có: ( ) ( ) 32 221 34log3log0 33 x xx x + +−− luôn đúng 4;15 x Vậy có 12 bộ ( ) ; xy nguyên thỏa mãn. +Với 2 y = thay vào ( )* ta có: ( ) 3 44log10 x + luôn đúng 4;15 x
Vậy có 12 bộ ( ) ; xy nguyên thỏa mãn.
+Với 31520 yy +
Xét ( ) ( ) 333 22 logloglog0;3;152 222 yyyy hyy yyy ++ === +++
Từ ( )1 và ( ) ( )2* vô nghiệm.
Vậy có 24 bộ ( ) ; xy thỏa mãn.
Câu 173: Có bao nhiêu số tự nhiên x sao cho mỗi giá trị x tồn tại số y thoả mãn ( ) 22 36 log()log2 xyxy
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
37 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
−+ ? A.
B. 3
D. 6 Lời giải
ọn B Điều kiện: 0 xy− Đặt (
22 36
3
xy
−= +
xy yy =+ ++ Bất phương trình ( )1 2 32.3960 ttt yy++− muốn có nghiệm thì ( ) 22 939601 33 t ttt t =−− . Do đó: 2222660;1;2xyxx + Thử lại: * Với ( ) 2 3 2 3log20 0 2631;0 t t t t y x y y =− = =−− * Với ( )2 2 1313 1 12612136 t t t tt y y x y =− −= = + +− có nghiệm 0,0ty== * Với ( )2 2 23 2323 2 426968.3120 42236 t tt tttt tt y yy x y =− −==− = +−−+ +− có nghiệm 1,1ty==− Vậy 0;1;2 x Câu 174: Có tất cả bao nhiêu giá trị nguyên của y sao cho tương ứng với mỗi giá trị y luôn tồn tại không
1
C. 2
Ch
)
log()log2 txyxy =−+ , suy ra 22
26 t t
xy
( ) ( ) 2 2 3 3261 t tt
quá 15 số nguyên x thỏa mãn điều kiện ( ) ( ) ( ) 22 202120222 loglog16logxyyyxy ++++− ? A. 2021. B. 4042. C. 2020. D. 4041. Lời giải
Chọn D
Điều kiện 2 0 0 xy xy + −
2 0 xy xy +
Ta có bất phương trình ( ) ( ) ( ) 22 202120222 loglog16log0 xyyyxy ++++−−
Xét ( ) ( ) ( ) ( ) 22 202120222 loglog16log fxxyyyxy =++++−− với xy , y
Ta có: ( ) ( ) ( ) ( ) ( ) ( ) 2 22 '11ln2ln2021ln2ln2021 ln2 ln2021..ln2021.ln2 xyy fx xy xyxyxy =−= ++− .
Ta có: ( ) ( )ln2ln2021ln2ln2021xyxy −−
Suy ra ( ) ( ) 22 ln2ln2021ln2ln2021ln20210, xyyyyy −−−−− .
Do đó ( ) '0,, fxxyy
log16 log164 log2022 yy yy ++ +++ ( ) 2 2021 2022 + 2022
4 log162,00 1log2021 yy ++ 4 1log2021 2 1620212021,992020,99yyy + ++− Do y nên 2021;2020;...;2020 y −− Vậy có tất cả 4041 giá trị nguyên y thỏa yêu cầu bài toán. Câu 175: Có bao nhiêu số nguyên dương m để có không quá 2022 cặp ( ) , xy , với x, y là số tự nhiên thỏa mãn 2 log222xyxy ++− và xym + A. 63. B. 64. C. 22. D. 21. Lời giải Chọn A Ta xét 2 log222xyxy ++− , điều kiện 220 xy+− và x, y là các số tự nhiên
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 38
Ta có bảng biến thiên của ( )fx là: Yêu cầu bài toán ( ) 160 fy + ( ) ( ) 22 202120222 log16log16log16 yyyy +++++ ( ) ( ) 2 2021 2 2021 2021
( ) ( ) ( ) ( ) ( ) 22 12log22424log2210 xyxyxyyxy ++−+−++−−
Nếu 2240 xy −+− thì ( ) ( ) ( ) 2 24log2210 xyyxy +−++−− )
Nếu 240 xy+− , ta có ( ) ( ) ( ) ( ) ( ) ( ) 2 2
+− +−++−− +−−
240 24log2210 log2210 xy xyyxy yxy
Ta có ( ) 1240 xy +−
Với mỗi m nguyên dương, bất phương trình xym + có 2 2 mm + điểm ( ) ; xy với x,y là số tự nhiên.
Kết hợ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 39
1;2;3;....;63 m Câu 176: Tính ab + biết ; ab là tập hợp tất cả các giá trị của tham số m để bất phương trình ( ) 22 24 log24log25 xxmxxm −++−+ thỏa mãn với mọi 0;2 x A. 4 ab+= . B. 2 ab+= . C. 0 ab+= . D. 6 ab+= . Lời giải Chọn D Xét bất phương trình ( ) ( ) 22 24 log24log251 xxmxxm −++−+
p với điều kiện ta có số cặp ( ) ; xy thỏa điều kiện đề bài là: 2 6 2 mm + Theo đề ta có 2 2 6202240560 2 mm mm + −+− Mặt khác m nguyên dương nên
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 40 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có ( ) ( ) 22 22 1log24log252 xxmxxm −++−+ Điều kiện ( ) 2 2 2 20 * log20 xxm xxm −+ −+ Đặt 2 2 log2 txxm =−+ , bất phương trình ( )2 trở thành 2 45051ttt +−− Do đó ( ) 2 2 2 2 2 22 2 2 2 log21 log21 22 2 log2021 log25 xxm xxm xxm xxmxxm xxm −+ −+ −+ −+−+ −+− 2 2 24 21 xxm xxm −+ −+ ( )3 Xét hàm số ( ) 2 2 fxxxm =−+ trên 0;2 , ta có bảng biến thiên của ( )fx như sau Từ bảng biến thiên ta có, hệ ( )3 nghiệm đúng với mọi 0;2 x khi
chỉ khi ( ) ( ) 0;2 0;2 max4 24 min11 fxm m fxm = =−+ Suy ra 2 4 a b = = , vậy 6 ab+= Câu 177: Cho bất phương trình ( ) ( ) ( ) 222 22022 log1.log1log1 m xxxxxx −−−−+− Có bao nhiêu giá trị nguyên thuộc khoảng ( )1;2022 của tham số m sao cho bất phương trình đã cho nghiệm đúng với mọi x thuộc ) 5;+ ? A. 2022. B. 2021. C. 2012. D. 2010. Lời giải Chọn C Ta có: ( )( ) ( ) ) 222 2 111;log105;.xxxxxxx −−+−=+−+ PT ( ) ( ) ( ) ( ) 222 22022 log1.log1log11 m xxxxxx −−−−+−
và
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 41 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 22 22022 2 2 2 2 2022 2 2 2 22 2022 1 2 2 2022 2 log1 log1.log1log log11 .log1log log1 1 log1.log1log 1 log1log xx xx xxxx m xx xx m xx xxxx m xx m +− +− −−−− −− +− −−−− −−− ( ) ( ) 2 2022 2 1 log12 log xx m +− . Xét hàm s
á trị nguyên thuộc khoảng ( )1;2022 của tham số m thỏa mãn bài toán. Câu 178: Cho ,0xy , 30xy+ thỏa mãn 2222 2 2022log1334 xyxy xy xy ++ −+− + . Tổng của giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 22 1422022 P x x yy+−− = + bằng A. 4124 B. 4042 C. 4044 D. 4122 Lời giải Chọn A Ta có: 2222 2 2022log1334 xyxy xy xy ++ −+− + ( ) 2222 2 2022log3434 xyxy xy xy ++ +− + 2222 22 2022log2022log33 44 xyxy xyxy ++ ++++
ố ( ) ) 2 1,5;fxxxx=+−+ Có ( ) ) 2 105; 1 x fxx x =++ nên ( )fx đồng biến trên ) 5;+ . Suy ra ( ) ( ) ( ) ( ) 2 20222022 5log1log526fxfxx+−+ Để BPT ( )2 nghiệm đúng với mọi x thuộc ) 5;+ thì ( ) 526 log2022 20222 526 2 1 loglog526loglog2022210;11;...2021. mmm m + + + Vậy có 2022 gi
Xét hàm số: ( ) ( ) 22022log 0 ftttt=+ thì: ( ) 2 10 0 2022ln ftt t =+
Nên hàm số ( )ft đồng biến trên khoảng ( ) 0;+
Mà: ( ) 2222 22 33412 44 xyxy ffxyxyxyxy ++ ++++
Nên tập hợp các giá trị ( ) ; xy thỏa mãn thuộc hình tròn ( )C tâm ( )2;6 I bán kính 210 R = Ta có: ( ) ( ) 22 22 1422022711972yx P yxyP x +−−+−+=− =
• Nếu 1972 P = thì 7,1xy
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 42 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
== không thỏa mãn do: ( )7;1 M không thuộc hình tròn ( )C . • Nếu 1972 P . Để tồn tại , xy sao cho P đạt giá trị lớn nhất thì đường tròn ( ) C tâm ( )
1972
ải
điể
ớ
. Nên: 197221052 19722101972210 197221052 P PIJP P −− −−−+ −+ Vậy: ( ) ( ) 2 min minmax 2 max 197252210 4124 197252210 P PP P =+− += =++ Câu
Gọi S là tậ
ợ
(
2 3
+
tổng số phần tử thuộc S A. 7. B. 4. C. 1. D. 1. Lời giải Chọn D Điều kiện: 2 0 xy+ . Với mỗi số nguyên y , ta đặt 22 txyxty =+=− Bất phương trình ( ) 2 32log yx xy+ 2 32log yyt t +− 2 3 log20 yyt t +− − Đặt ( ) 2 3 log2,0 yyt fttt +− =− ; ( ) 2 1 .ln32.ln20,0 yyt ftt t +− =+ Suy ra ( )ft đồng biến trên ( ) 0;+ . Ta có bảng xét dấu sau: + f(11) f(10) f(1) t f'(t) f(t) 1 + 11 10 +
7;1 J bán kính
P ph
có
m chung v
i hình tròn ( )C
179:
p h
p các số nguyên y sao cho với mỗi yS
có đúng 10 số nguyên x thỏa mãn
)
2log yx xy
. Tính
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 43
Bất
(
2 3
yx xy+
x 2 3 log20 yyt t +− −
. 2 2 10 3 11 3 log1020 log1120 yy yy +− +− − − 2 2 10 3 11 3 2log10 2log11 yy yy +− +− ( ) ( ) 2 23 2 23 10loglog100 11loglog110 yy yy +−− +−− Từ hệ bất phương trình trên ta có 2 số nguyên 4 y =− ; 3 y = Vậy đáp án Chọn D Câu 180: Cho hàm số ( ) ( ) 2 202120212022ln1 xx fxxx =−+++ . Có bao nhiêu giá trị nguyên thuộc 2022;2022 của tham số m để bất phương trình ( ) ( ) 1 95230 xx ffm + ++−− có nghiệm thuộc đoạn 0;2 A. 1991 B. 2023 C. 2027 D. 1992 Lời giải Chọn C Xét hàm số ( ) ( ) 2 202120212022ln1 xx fxxx =−+++ TXĐ: D = ( ) ( ) 2 202120212022ln1 xx fxxx −=−++− (
2
xx xx =−+++ (
2
xx xx=−−++ ( ),
=− Vậy ( )fx là một hàm số lẻ trên D . ( ) 2 2 1 2021ln20212021ln202120221 1 xx x x fx xx + + =++ ++ 2 1 2021ln20212021ln202120220, 1 xx xD x =++ + hàm số đồng biến trên D Ta có: ( ) ( ) 1 95230 xx ffm + ++−− Vì ( )fx là hàm số lẻ nên ( ) ( ) ( ) 1 *95230 xx ffm + +−+ ( ) ( ) 1 9523 xx ffm + ++ ( )** Và do ( )fx là một hàm số đồng biến trên nên ( ) 1 **9523 xx m + ++ Bài toán trở thành tìm m để bpt 1 9523 xx m + ++ có nghiệm thuộc đoạn 0;2 Đặt 3x t = bài toán trở thành tìm m để bpt 2 56 ttm ++ có nghiệm thuộc đoạn 1;9 Xét bpt 2 56 ttm ++ 2 65 ttm−+ trên đoạn 1;9
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
phương trình
)
2log
có đúng 10 nghiệm nguyên
có đúng 10 nghiệm nguyên 0 t
) 1
202120212022ln1
)
202120212022ln1
fxxD
Ta có BBT của vế trái như sau: Vậy, bất phương trình có nghiệm thuộc đoạn 1;9 khi và chỉ khi 4 m − Mà 2022;2022 m m
nên 4;3;...;2022 m−− Vậy có ( ) 2022412027 −−+= giá trị của m thỏa đề.
Câu 181: Có bao nhiêu số nguyên dương b sao cho ứng với mỗi b, có đúng 3 giá trị nguyên dương của a thỏa mãn ( ) 2 2 log21 a a a ab ab + +− ? A. 1. B. 2 C. 3 D. 4 Lời giải Chọn A Vì 00ab . Với 0 b , ta có: ( ) ( ) ( ) 222 2 log21log2log2 a aaa a abaababa ab + +−+−+− ( ) ( ) ( ) ( ) 22 log22log1 aaaaabab ++++ Dễ thấy hàm số ( ) 2log gttt =+ đồng biến trên ( ) 0;+ nên ( ) ( ) 2 122 a a a aabb a + + Xét hàm số ( ) ( ) 2 ,0; a a faa a + =+ có ( ) ( ) 2 .2.ln221 ;0 ln2
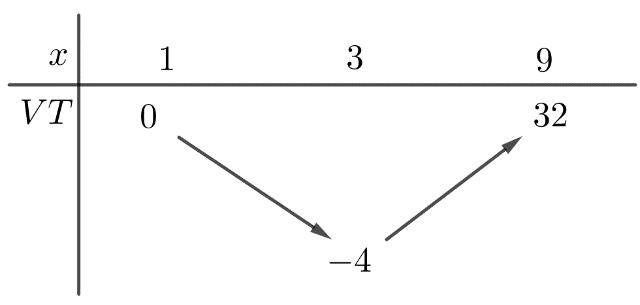
aa a fafaa a === . BBT.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
44
−
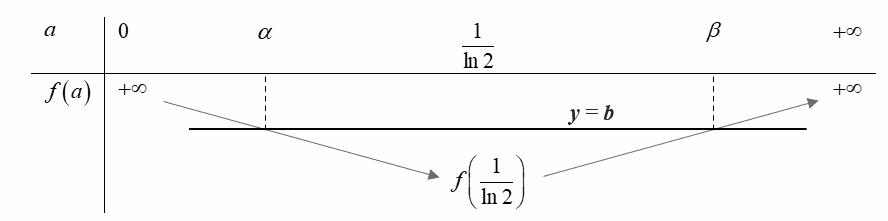
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 45 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Để ( )2 có nghiệm thì 1 2,88 ln2 bf . Để có đúng 3 giá trị nguyên a thỏa mãn ( )2 thì có hai trường hợp xảy ra TH1: ( ) ( ) ( ) 3 1 01 1111 35 34 33 4 5 b fb fbbb fb b . TH2: ( ) ( ) ( ) 1 3 1 45 45 37 5 5 fb b fbb fb b vô nghiệm. các giá trị b thỏa mãn yêu cầu bài toán là 11 5 3 b có đúng một số nguyên b thỏa mãn yêu cầu bài toán. Câu 182: Cho hàm số 220212023()ln(1) fxxxxx =++++ . Số nghiệm nguyên thuộc đoạn [2021;2021] của bất phương
+−
Lờ
giải Chọn D Xét hàm số 220212023()ln(1) fxxxxx =++++ Tập xác định DR Với mọi xD , ta có: ( ) ( ) ( ) ( ) ( ) ( ) 220212023ln1 fxxxxx −=−++−+−+− ( ) 220212023ln1xxxx =+−−− 20212023 2 1 ln 1 xx xx =−− ++ ( ) 220212023ln1xxxx =−++−− ( )fx =− .
trình (2)(3)0 x ffx
là A. 2021. B. 2020. C. 2022. D. 2023.
i
hàm s
fx
Mặt khác với m
hàm s
i xD , ta có:
suy ra: (3)(3) fxfx
fxxx
20202022
1 2021.2023.0
xx
Nên hàm số đồng biến trên tập xác định. Khi đó bất phương trình (2)(3)0(2)(3)0(2)(3) xxx ffxffxffx +−−−− 23230(*) xx xx −+− Xét hàm số ()23 x gxx=+− , ta có ()gx đồng biến trên R và (1)0g = nên bất phương trình 230 x x +− ( ) ( )1 gxg 1 x Do x nguyên thuộc [ 2021;2021] nên x nhận các giá trị thuộc tập Câu 183: 2021,2020,2019,...0,1 T =−−− vậy có 2023 giá trị cần tìm. Có bao nhiêu số nguyên 2022;2022 x− để ứng với mỗi x có tối thiểu 64 số nguyên y thỏa mãn ( ) 4 32 loglogxyxy ++ ? A. 3992. B. 3994. C. 3990. D. 3989. Lời giải Chọn A Điều kiện:
xy xy xy xy xy
4 4 4
0 0 0 0 0
+ + + + + Đặt kxy + =+ Xét hàm số ( ) ( ) 4 32 loglog0fyxyxy =+−+ . Suy ra ( ) ( ) ( ) 4 11 '0 ln2 2ln3 fy xy xy =− + + ( )fy nghịch biến. Xét hàm số ( ) ( ) ( ) 4 32 loglog gkfkxxkxk =−=+−− , k + . Do hàm số f nghịch biến nên hàm số g cũng nghịch biến. Giả sử 0k là nghiệm của phương trình ( ) 0 gk = Suy ra 0 0
1 64 kk k k +
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 46
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Vậy
ố ()
là
ố lẻ
-
ọ
2
2 (1)' '()2021.2023. 1 xx
xx ++ =++ ++ 20202022 2
1
x =++ +
Nên ( ) ( ) 4 32 640log64log64 gxx+− 2 log64 4 643 xx −+ ( ) 2 2 log64 4 643 xx −+ 26,99 26,99 x x − .
Với 26,992022 x ta có 1996 số nguyên x
Với 202226,99 x −− ta có 1996 số nguyên x
y có 3992
nguyên
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
47 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
. ( ) ( ) ( ) 3 3ln322 '3ln32.3ln310log2 ln2 32ln232ln2 x xx xx fxxa =−=−===+ Bảng biến thiên: Trong đó: ( ) 2 22 22log21,872 ln2ln2 fa =+−+ +∞ 3 y0 f(a) x0 + 0 a 1 f(x) f'(x) x
Vậ
số
x Câu 184: Có bao nhiêu giá trị nguyên lớn hơn 2 của y sao cho ứng với mỗi y tồn tại đúng 3 số nguyên dương x thỏa mãn ( ) 2 32log32 xx y −− A. 16. B. 51. C. 68. D. 66. Lời giải Chọn B Ta có: ( ) ( ) 22 32log3232log32 xxxx yy −−−− Đặt: ( ) ( ) 2 32log32 xx fx =−− Vì x nguyên dương nên ta xét hàm số ( )fx trên ) 1;+
Với 3 y tập nghiệm của bất phương trình xét trên ) 1;+ là 0 1; Sx = chứa đúng 3 số nguyên dương là 1; 2; 3 ( ) ( ) 0 468,39 3418,19,...,68 317,71 yf xy yf Vậy có 51 giá trị nguyên của y thỏa mãn yêu cầu bài toán
Câu 185: Có bao nhiêu giá trị nguyên thuộc khoảng ( )9;9 của tham số m để
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
48 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
bất phương trình ( ) ( ) 2 3log2log11 xmxxxx −−−− có nghiệm thực? A. 10. B. 7. C. 11. D. 6 . Lời giải Chọn B Điều kiện: 01 x Ta có: 44 11 1.1 2 2 xx xxxx +− −=−= Với điều kiện 01 x , ta có: ( ) ( ) 2 3log2log11 xmxxxx −−−− ( ) ( ) 2 loglog11 xxmxxxx −−−− ( ) 2 11 xxmxxxx −−−− . ( ) ( ) 33 1 .1 xx m xx +− . Xét ( ) ( ) 33 1 .1 xx xx +− ( )( ) 111 .1 xxxx xx +−−− = ( ) 44 2111 .1 xxxx xx ( ) 44 44 11 212 1 xxtft t xx −−=−= với 44 1 txx =− đk 1 0 2 t Ta có ( ) 2 20 ft t =−− ( )ft nghịch biến trên 1 0; 2 ( ) 1 0; 2 1 max2 2 ftf == Bất phương trình có nghiệm thực 2 m Do ( )9;9 m− nên 2;3;4;5;6;7;8 m .
Xét 1 y = thì thành ( ) ( ) 23 42 3log134log0 33 x xx x + −−+++ , rõ ràng BPT này nghiệm đúng với mọi 3 x vì ( ) ( ) ( ) 223 42 30, log1log010, 340, log033 x xx x + −−++=+
Như vậy trường hợp này cho ta đúng 2017 bộ ( ) ( );;1xyx = với 42020,xx .
+ Xét 2 y = thì thành ( ) 3 44log10 x + , BPT này cũng luôn đúng với mọi x mà 42020,xx . Trường hợp này cho ta 2017 cặp ( ) ; xy nữa.
+ Với 2,3yx thì ( ) *0 VT nên không xảy ra. Vậy có đúng 4034 bộ số ( ) ; xy thỏa mãn yêu cầu bài toán. Câu 187: Gọi a là số thực lớn nhất để bất phương trình ( ) 222ln10xxaxx−++−+ nghi
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 49
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có 7 giá trị của m cần tìm. Câu 186: Có bao nhiêu bộ ( ) ; xy với , xy nguyên và 1,2020 xy thỏa mãn ( ) ( ) 32 221 248log236log23 yx xyxyxyxy yx + ++++−− +− ? A. 2017 B. 4034 C. 2 D. 20172020 Lời giải Chọn B + Điều kiện * * ,:,2020,:,2020 212 0,03,032 xyxy xyxy xy xy xy BPT cho có dạng ( )( ) ( )( ) 23 42 32log142log10 32 xy xyxy xy +− −−+++++ −+ . +
ệm đúng với mọi x Mệnh đề nào sau đây đúng? A. ( 2;3 a . B. ( ) 8; a + . C. ( 6;7 a . D. ( 6;5 a−− . Lời giải Chọn C Đặt 2 2 13 1 24 txxx =−+=−+ suy ra 3 4 t Bất phương trình ( ) 222ln10xxaxx−++−+ ln10tat ++ ln1att −−
Trường hợp 1: 1 t = khi đó ln1att−− luôn đúng với mọi a
Trường hợp 2: 3 1 4 t
Ta có 313 ln1,;1,;1 4ln4 t atttat t −−
Xét hàm số ( ) ( ) 2
ln11 13 lnln40,;1 t t t ftftt tt ==−
t ata t
do đó 137 ,;1 3 ln4 4ln 4
Trường hợp 3: 1 t
Ta có ( ) ( ) 1 ln1,1;,1; ln t atttat t −−++
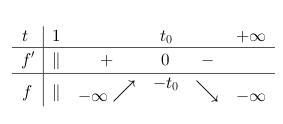
Xét hàm số ( ) ( ) ( ) 2
t t t ftftt tt ==−+ .
ln11 1 ,1; lnln
Xét hàm số ( )gt = ( ) 2 111 ln10 tgt ttt −−=+
Vậy ( ) 0 gt = có tối đa một nghiệm.
Vì ( ) ( ) 12;lim t ggt →+ =−=+ vậy ( ) 0 gt = có duy nhất một nghiệm trên ( ) 1;+
Do đó ( ) 0 ft = có duy nhất một nghiệm là 0t . Khi đó 0 0 0
1 ln t t t + = suy ra ( ) 00ftt =−
Bảng biến thiên
Vậy ( ) 0 1 ln,1; t atat t +−
Vậy 0 7 3 4ln 4
ta − .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
50
Vậy số thực a thỏa mãn yêu cầu bài toán là: ( 6;7 a .
Câu 188: Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 127 số nguyên y thỏa mãn ( ) ( ) 2 32 loglogxyxy ++ ? A. 45. B. 90. C. 89. D. 46. Lời giải
Chọn B
Ta có: ( ) ( ) 2 32 loglogxyxy ++ ( ) 2log 2 3 xy xy + + ( ) 2 log3 2 xyxy++ ( ) ( ) 2 log3 2 xxxyxy −+−+ ( )1 . Đặt txy =+ , ( )0 t thì ( )1 trở thành 2 2log3 xxtt −− ( )2 . Với mỗi x nguyên cho trước có không quá 127 số nguyên y thỏa mãn bất phương trình (1) tương đương với bất phương trình ( )2 có không quá 127 nghiệm t nguyên dương. Ta có hàm số ( ) 2 log3 fttt =− đồng biến trên ) 1;+ nên nếu 2 2log31281282059 xx−−= thì sẽ có ít nhất 127 nghiệm nguyên 1 t . Do đó yêu cầu bài toán tương đương với 2 2059 xx− 4445 x − . Vậy có 90 số nguyên x Câu 189: Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 255 số nguyên y thỏa mãn ( ) ( ) 2 52 loglogxyxy ++ ? A. 1250 B. 1249 C. 625 D. 624 Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
51 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
Điều kiện: 2 0 0 xy xy + + .
Chọn A Bất phương trình đã cho tương đương ( ) ( ) 2 25 loglog0 xyxy +−+ Xét hàm số ( ) ( ) 2 25 ()loglog fyxyxy =+−+ Tập xác định (;)Dx=−+ . Với mọi x ta có 2 xx nên ( ) ( ) 2 11 ()0, ln2 ln5 fyxD xy xy =− + + ()fy đồng biến trên khoảng (;) x −+ .
Do y là số nguyên thuộc (;) x −+ nên , yxkk + =−+ Giả sử yxk =−+ là nghiệm của bất phương trình thì ()()0 fyfxk=−+ .
Mà 12... xxxk −+−+−+ và ()fy đồng biến trên khoảng (;) x −+ , suy ra (1)(2)...()0 fxfxfxk −+−+−+ , nên các số nguyên 1,2,..., xxxk −+−+−+ đều là nghiệm của, hay nói cách khác bất phương trình sẽ có k số nguyên y thỏa mãn yêu cầu ứng với mỗi x Để có không quá 255 số nguyên y thì ( ) 2 25 (256)0log256log2560 fxxx −+−−+ 2 1156147711561477 3903690 22 xxx −+ −− . Mà x nên có 1250 số nguyên x thỏa yêu cầu bài toán. Câu 190: Có bao nhiêu số nguyên x sao cho ứng với mỗi số nguyên x có không quá 242 số nguyên y thoả mãn: ( ) ( ) 2 43 loglogxyxy ++
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
52
? A. 55. B. 56. C. 57. D. 58. Lời giải Chọn B Điều kiện: 2 0 0 xy xy + + Đặt ( ) 3log xyt += . Ta có: 22443 33 ttt tt xyxx xyyx +−− +==− Nhận xet: hàm số ( ) 43 tt ft =− đồng biến trên ( ) 0;+ và ( ) 0,0ftt Gọi n thoả mãn 2 43nn xx−=− , khi đó 2 434343 ttttnnxxtn −−−− Từ 033 tn xyxyxx +−=−− Mặt khác, không quá 242 số nguyên y thoả mãn đề bài nên 3 3242log242 n n 3 log242 2 43424227,428,427;26;...;28 nn xxxx −=−−−−− có 56 số nguyên x thoả mãn đề bài. Câu 191: Gọi S là tập hợp các số nguyên x thỏa mãn ( ) ( ) 2 2 l 2 66 og 2 222 4log2log12log x yxyxxx +−++ Có bao nhiêu giá trị nguyên của y để tập hợp S có nhiều nhất 32 phần tử? A. 16 B. 32 C. 19 D. 8 Lời giải Chọn C
Điều kiện: 0 x và 0 y
Bất phương trình tương đương với: ( ) ( ) 2 2log 2 22 2 6 2 6 4log12log2log x yxyxxx ++++ ( ) ( ) ( ) 2 2log 2 2 66 222 4log22log2log1 x yxyxxx +++++ ( ) ( ) ( ) 2 2 2 lg 2 6 o 22 6 4log42log1 x yxyxx +++ ( ) ( ) ( ) 2 2 2 2 log 2 2 66 4log42log 2 x x yxyx ++ ( ) ( ) ( ) 2 2 l 2 6 og 421 x fyxf .
Xét hàm đặc trưng ( ) 2 log,0ftttt=+
Ta có ( ) 1 10 ln2 ft t =+ với 0 t nên hàm số ( )ft đồng biến trên ( ) 0;+ . Khi đó ta được: 2 2log 2 6 (1)42 x yx 2 222 2log6loglog 2 yxx++ 2 222 loglog4log1() yxxgx−−= . Ta có ( ) 22 2 4 22 ()loglog ln2ln2ln2 gxxx xxx =−=−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
53
2 ()0log24 gxxx === Để tập S có nhiều nhất 32 phần tử thì ( ) ( )33 2 log3302019 g ygyy Vậy có 19 giá trị nguyên của y thỏa mãn yêu cầu bài toán Câu 192: Có bao nhiêu số nguyên a sao cho ứng với mỗi số a , tồn tại ít nhất 22 số nguyên ( )2022;2022 b− thỏa mãn: 2 762022 abba +−+ A. 91. B. 92. C. 93. D. 94. Lời giải Chọn A 2 22 7616 7620222022.2022.770 7777 bababa ab abbaabaa ba + +−−+ +++− Xét hàm số: ( ) 2 6 2022.77 7 ba abaa fb −+ =+− . 1 g(33) g(x) 1 0 0 33 5 4 0 + x g'(x)
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 54 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có ( ) 66.ln2022.7.ln70 77 ba ab fb =− , b Vì hàm số ( )fb nghịch biến trên khoảng ( )2022;2022 nên để tồn tại ít nhất 22 số nguyên b thỏa mãn ( ) 0 fb thì ( ) 22
nghiệm? A. 4. B. 1. C. 0 . D. 2. Lời giải Chọn B Ta có: 2 5sin5. x ( )2 211 m +−− nên 2 (2)11 22 77 log23log235. 22 m+−− ++++= Do đó phương trình đã cho 2 2 2 (2)1 2 2 5sin5 sin1 72. log22431 2 m x x m mm +− = = =− += ++=− Chọn đáp án B Câu
bao
ị
ủa
số m ( )10 m để
2000 200020002000 6 200002022.770762022 7 ++−−− −+−+ a aaaaa f . Với a , ta xét hai trường hợp: TH1: 2000 200020000061 a aa−−− . Suy ra 2 20222 7 720222022log20222025,9 a a + Do a nên 45;44;...;44;45 a−− TH2: 2 222000 200020000200077aa aaaaa −+−−− Lại có ( ) ( ) 2000200020002000200020002000 77.77717671 aaaaa ==+−+− 2000 762022,2000 aa a +− Suy ra 2 20002000 762022 aa+ nên trường hợp này không xảy ra. Vậy có 91 giá trị nguyên của a thỏa mãn yêu cầu bài toán. Câu 193: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 2(2)1 2 7 5sinlog23 2 m x +− =++ có
194: Có
nhiêu giá tr
nguyên c
tham
phương trìn ( ) 1 4 2log2=++ x xmm có nghiệm? A. 9 B. 10 C. 5 D. 4
Lời giải
Chọn A
ĐK: 20+xm
Ta có ( ) 1 4 2log2=++ x xmm ( ) 2 2log22 =++ x xmm
x t
Đặt ( ) 2 log2=+ txm ta có 22 22 =+ =+
tm xm 22 +=+ xtxt ( )1
Do hàm số ( ) 2 =+ u fuu đồng biến trên , nên ta có ( )1 =tx . Khi đó: 2222=+=− xx xmmx .
Xét hàm số ( ) 2 =− x gxx ( ) = gx 2ln210 −= x ( ) 2 logln2=− x
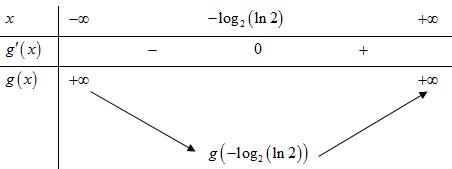
Bảng biến thiên: Từ đó phương trình đã cho có nghiệm khi và chỉ khi ( ) ( ) ( ) ( ) 2 2 logln2 2logln2 2 − g mgm 0,457 Do m nguyên và 10 m , nên 1,2,3,4,5,6,7,8,9 m . Câu 195: Có bao nhiêu số nguyên x sao cho ứng với mỗi
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
55 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
x có không quá 728 số nguyên y thỏa mãn ( ) ( ) 2 43 loglogxyxy ++ ? A. 115. B. 58. C. 59. D. 116. Lời giải Chọn D Điều kiện 2 0 0 , xy xy xy + + Khi đó ( ) ( ) 2 43 loglogxyxy ++ ( ) 3log 2 4 xy xy + + ( ) 3 log4 2 xyxy++ ( ) ( ) 3 log4 2 xyxyxy −+−+ . ( )1
Đặt 1 txyt=+ thì ( )1 được viết lại là 3 log4 2 xytt −− ( )2
Với mỗi x nguyên cho trước có không quá 728 số nguyên y thỏa mãn bất phương trình ( )1
Tương đương với bất phương trình ( )2 có không quá 728 nghiệm t .
Nhận thấy ( ) 3 log4 fttt =− đồng biến trên ) 1;+ nên nếu 3 log4 2 7297293367 xy−−= thì sẽ có ít
nhất 729 nghiệm nguyên 1 t Do đó yêu cầu bài toán tương đương với 2 33675758xxx −− .
Mà x nguyên nên x nhận các giá trị 57,56,...,57,58. Vậy có tất cả 116 số nguyên x thỏa yêu cầu bài toán.
Câu 196: Có bao nhiêu cặp số nguyên dương ( ) ; xy thỏa mãn điều kiện 2022 x và ( ) ( )3 3 3922log1 y yxx ++++ ?
A. 6. B. 2. C. 3776. D. 3778. Lời giải Chọn D
Ta có ( ) ( ) ( ) 3 33 3922log13.9623log1 yyyxxyxx ++++++++ ( ) ( ) ( ) 21 3 332113log1 y yxx + +++++
Xét hàm số ( ) 33 t ftt =+ có ( ) 3.ln330, t ftt =+
ra hàm số
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
56
mãn. Vậy có tất cả 3778 cặp số ( ) ; xy thỏa mãn đề bài. Câu 197: Xét các số , ab là các số nguyên dương nhỏ hơn 2022. Biết rằng với mỗi giá trị của b luôn có ít nhất 1000 giá trị của a thỏa mãn ( ) 2 1 22log41 abbab a b ++− + −− . Số giá trị b là A. 1019. B. 1020. C. 1021. D. 1022. Lời giải Chọn C Đặt 1,2cac=+ , khi đó ( ) ( ) 2 1 22log4122log22(1) abbabccbb ac bb ++−−− + −−−−
Suy
( ) 33 t ftt =+ đồng biến trên Do đó ( ) ( ) ( ) ( ) ( ) 21 33 *21log121log131 y fyfxyxx + ++++− Vì 2022 x nên 21 3 log20231 3120222,96 2 y y + − . Với giả thiết y nguyên dương suy ra 1;2 y . Với 1 y = có 262022 x suy ra có 1997 cặp số ( ) ; xy thỏa mãn. Với 2 y = có 2422022 x suy ra có 1781 cặp số ( ) ; xy thỏa
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 57 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn +) 1 b = , không thỏa mãn +) 2 2215 2 log4 cc b c = . •) 2 c = , không thỏa mãn •) 3 c , hàm ( ) 2 2 2 222(.ln2.ln1).2ln2.ln2 (),()0 log.ln2log ccccc cccc fcfc c cc −−++ == . Suy ra 15 ()(3),322021 4 fcfca .
=
ỏ
+) 2222 3,(1)(3)
ccbb b cb Hàm số 2 22 ()log tt ft t = đồng biến với mọi 3 t và 2 c = không thỏa mãn
3
Do đó 3 (3),(3)3202131022 202111000 b cbbbab b −+ Vậy 21022 b Câu 198: Gọi S là tập các số nguyên y sao cho với mỗi yS có đúng
x
2 3 2log() yx xy+
ổng
ần
ử
A.
ả
ọ
Điề
2
. Xét
2
fxxy =−+
ta
ấy (
ịch
ế
ả
và ( ) ( ) 2 lim,lim x xy fxfx →+ →− =+=− nên tồn tại ( ) 2 0 ; xy−+ sao cho
=
ừ đó ta được 2 0 ()0 fxyxx − Theo bài ra có đúng 10 số nguyên 2 2 (10)0 (11)0 fy x fy −+ −+ 2 2 10 3 11 3 2log100 2log110 yy yy +− +− − − 2 23 2 23 10log(log10)0 11log(log11)0 yy yy +−− +−− 2,86 3,86 4,013,01 y y y − − 4;3 y − Câu 199: Có bao nhiêu số nguyên dương b sao cho ứng với mỗi b , có đúng 3 giá trị nguyên dương a thỏa mãn ( ) 2 2 log21 a a a ab ab + +− ? A. 1. B. 2 . C. 3. D. 0. Lời giải
Do đó 2 b
th
a mãn.
lnln
nên
c
10 số nguyên
thoả mãn
Tính t
các ph
t
thuộc S
1 B. 7 C. 1 D. 4 Lời gi
i Ch
n C
u kiện:
xy −
hàm số
3 ()2log() yx
,
th
)fx ngh
bi
n trên kho
ng ( ) 2 ; y −+
( ) 0 0 fx
. T
Vì 00ab . Với 0 b , ta có: ( ) ( ) ( ) 222 2 log21log2log2 a aaa a abaababa ab + +−+−+− ( ) ( ) ( ) ( ) 22 log22log1 aaaaabab++++
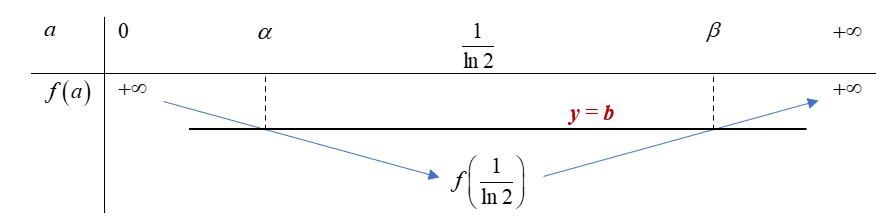
Dễ thấy hàm số ( ) 2log gttt =+ đồng biến trên ( ) 0;+ nên ( ) ( ) 2 122 a a a aabb a + +
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 58
Chọn A
Để ( )
ệ
1
bf . Để có đúng 3 giá trị nguyên a thỏa mãn ( )2 thì có hai trường hợp xảy ra TH1: ( ) ( ) ( ) 3 1 01 1111 35 34 33 4 5 b fb fbbb fb b . TH2: ( ) ( ) ( ) 13 1 45 45 537 5 fb b fbb fb b vô nghiệm. các giá trị b thỏa mãn yêu cầu bài toán là 11 5 3 b có đúng một số nguyên b thỏa mãn yêu cầu bài toán.
Xét hàm số ( ) ( ) 2 ,0; a a faa a + =+ có ( ) ( ) 2 .2.ln221 ;0 ln2 aa a fafaa a === BBT.
2 có nghi
m thì
ln22,88
Câu 200: Có bao nhiêu số nguyên a sao cho ứng với mỗi a , tồn tại ít nhất 7 số nguyên ( )0;10 b thỏa mãn ( ) ( ) 2 537 log16log13log34 bbaa ++−−− ? A. 9 B. 8 C. 11 D. 1 Lời giải Chọn D Ta có ( ) ( ) 2 537 log16log13log34 bbaa ++−−− ( ) ( ) 2 5337 log16loglog13log340 bbaa +++−−−− Đặt ( ) ( ) ( ) 2 5337 log16loglog13log34fbbbaa=+++−−−− , điều kiện 0 b ( ) ( ) 2 21 ln3 16ln5 b fb b b =+ + do 0 b nên ( ) 0 fb nên hàm số đồng biến trên ( )0;10 suy ra ( ) ( ) ( ) ( )123...9 ffff do vậy để có ít nhất 7 giá trị b nguyên thuộc ( )0;10 thì ( ) 30 f ( ) ( ) 37 log13log310* aa −−−− Đặt ( ) ( ) ( ) 37 log13log31,3;13gaaaa =−−−− bất phương trình trở thành ( ) 0 ga ( ) ( ) ( ) 11 0 213ln33ln7 ga aa =− hàm số nghịch biến. Mặt khác ( ) 40 g = bất phương trình ( )* trở thành ( ) ( )4 gag suy ra 4 a mà ( )3;13 a , a nguyên nên 4 a = . Vậy có duy nhất một giá trị nguyên 4 a = thỏa mãn bài toán. Câu 201:
Cho x là s
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
ố
ự
++−−
ủa biểu thức (
232 3
2
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 bằng ln ad bc + Giá trị abcd −+− bằng A. 0 . B. 1. C. 2 . D. 2022. Lời giải Chọn A Xét ( ) 2232201xyxyyx ++−− ( ) ( ) ( ) 2221302xyxyy +−+− . Suy ra, tồn tại ( ) ; xy thỏa mãn ( )1 khi ( )2 có nghiệm ẩn x ( ) ( ) 2 22 1 132101 2 x yyyyyy =−−−=−−+− 1 1; 2 y − . Do 0 yy= Thay 0 y = vào ( )2 ta được 2 2002xxx− ( )0;2 x .
59
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
th
c, y là số nguyên thỏa mãn 223220xyxyyx
. Biết giá trị nhỏ nhất c
) ( )
ln211
y Pxxeyxx =−++−−+
Câu 202: Có bao nhiêu số nguyên 11 a sao cho ứng với mỗi a tồn tại ít nhất 6 số nguyên ( )0;8 b thỏa mãn ( ) ( )( ) ( ) 2 435 log12log73log197. bbaa +++−++ A. 5. B. 4. C. 6. D. 7. Lời giải
Chọn A
Ta có ( ) ( )( ) ( ) 2 435 log12log73log197 +++−++ bbaa ( ) ( ) ( ) ( ) 2 4335 log12log7log3log1970. ++++−++− bbaa
Xét hàm ( ) ( ) ( ) ( ) ( ) 2 4335 log12log7log3log197fbbbaa =++++−++− trên ( )0;8 có ( ) ( ) ( ) ( ) 2 21 '0,0;8 7ln3 12ln4 b fbb b b =+ + + nên hàm số đồng biến trên ( )0;8 Suy ra ( ) ( ) ( )12...7fff , do đó để có ít nhất 6 số nguyên ( )0;8 b ta cần ( ) 20 f ( ) ( ) ( ) 35 log3log19301 aa −++− Xét hàm ( ) ( ) ( ) 35 log3log193gaaa=−++− trên ( )3;11 có ( ) ( ) ( ) ( ) 11 '0,3;11 3ln319ln5 gaa aa =+ −+ suy ra hàm ( )ga đồng biến trên ( )3;11 và có ( ) 60 g = , mặt khác ( ) ( ) ( ) 166 gaga , do đó 6,7,8,9,10 a .
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 60
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Với 0 y = ta có ( ) ( ) 232 3 ln121 2 Pxxxxfx =−++−+= . Xét hàm số ( )fx trên khoảng ( )0;2 : ( ) ( ) 2 22 211 63213 11 x fxxxxx xxxx =+−=−+ −+−+ ( ) 1 021 2 fxxx === BBT Vậy 137minln 248 Pf ==+ . Suy ra ( ) ( ) ;;;3;4;8;734870 abcdabcd=−+−=−+−=
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42
ễn Cư
Thuậ
ế
Page 61
ạ
Câu
Giả sử ( ) ; xy là cặp số nguyên thỏa mãn đồng thời 82022 x và ( )1 2 2log22 yyxxy−+=− . Tổng các giá trị của y
Chọn D + Ta có: ( ) ( ) 1 22 2log222.2122log22
++++ Xét 0 m = : hệ không nghiệm đúng với mọi x Xét 5 m = : hệ không nghiệm đúng với mọi x Xét 0; 5 mm Hệ nghiệm đúng với mọi x ( )2 (1) 2 (2) 5 5 50 7 '0 3 450 23 00 0 '0 2 40 2 m m m m m m m mm m m m m − −− − − Có 1 giá trị nguyên của m là 3
Nguy
Trinh
n Hòa TP Hu
ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên so
n
203:
bằng A. 60 B. 63 C. 2022 D. 49 Lời giải
yyyyy xxyyxx −+=−++=+++ ( ) ( ) 11 22 2log222log22* yyyy xx ++ +=+++ + Xét hàm số ( ) ( ) 2 log,0ftttt=+ là hàm số đồng biến trên ( ) 0;+ nên ( ) 11*2222 yyy xx +−=+= + ta có: 1 2 820228220224log2024410 y xyy Suy ra 4;5;6;7;8;9;10 y Câu 204: Có bao nhiêu giá trị nguyên của tham số m để bất phương trình ( ) ( ) 22 55 1log1log.4xmxxm ++++ nghiệm đúng với mọi x A. 1. B. 2. C. 0 . D. Vô số. Lời giải Chọn A ĐKXĐ: 2 .40mxxm++ Ta biến đổi BPT ( ) ( ) 22 55 log55log.4xmxxm +++ BPT nghiệm đúng với mọi x khi và chỉ khi hệ BPT sau nghiệm đúng với mọi x ( ) ( ) ( ) 2 22 22 55.45.4501 .40.402 mxxm xmxxm mxxmmxxm −−+− +++
Câu 205: Có tất cả bao nhiêu cặp số nguyên dương ( ) ; xy với 20 y thỏa mãn 43222 2022 1 log22. 1 x yyxyyx y + +−− +
111 log22log22 121 yx x yyxyyxyyyxx y yy Vì , 20 xy xy
. Suy ra hàm số đồng biến trên khoảng ( ) 0;+ . Khi đó ( ) ( ) ( ) ( ) ( ) 2222 111fyxfyyxy ++ . 201,2,3,...,20 191,2,3,...,19 21,2 11
+ + +−−+−− + + ( ) ( ) ( ) ( ) 22222222 20222022 11 log1log111 22yxyyyyyx +−++−+ ( ) ( ) ( ) ( ) ( ) 22222222 20222022 11 log11log11 1. 22yxyyyyyx ++++++ Xét hàm số ( ) ( ) 2022 11 log'10 24044.lnftttft t =+=+ + nên có các trường hợp sau
yx yx yx yx
== == == == Vậy cặp số tự nhiên thỏa mãn là: 123...1920210 +++++= Câu 206: Có bao nhiêu số nguyên x sao cho ứng với mỗi số nguyên x có đúng 5 số nguyên y thỏa mãn ( ) 2 2 2 3 3log23? yxy y xy + −+ A. 13 B. 11 C. 12 D. 10 Lời giải Chọn D + Ta có: ( ) ( ) ( ) 2 2 2
−+ −+ + ( ) ( ) 2 23 32 3.ln33.ln23 xy y yxy −+ + +−+ + Xét hàm số ( ) 3.ln t ftt = có ( ) 3 3.ln3.ln0 t t ftt t =+ nên hàm số đồng biến trên ( ) 3;+ .
3 2 23 32
+ −+ +
xy xy y
ln23 3 3log23 ln3 3 y yxy xy y
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
62 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
A. 200 B. 380 C. 210 D. 420 Lời giải Chọn C ( ) ( ) ( ) 2 2 43222222 20222022 2 2
+ Do đó: ( ) 2 2 2 22 3 3log233232(*) yxy y xyyxyyxy + −++−+−
TH1: 2 xy thì ( ) 2 *2xyy+ . Xét hàm số ( ) 2 2 gyyy =+ có bảng biến thiên
Để có 5 giá trị nguyên của y thỏa mãn bài toán thì điều kiện là ( ) ( ) 1238.gxgx
TH2: 2 xy thì ( ) 2 *2xyy−+ . Xét hàm số ( ) 2 2 hyyy =−+ có bảng biến thiên
Để có 5 giá trị nguyên của y thỏa mãn bài toán thì điều kiện là ( ) ( ) 4383. hxhx−−
Vậy có 10 giá trị nguyên của x thỏa mãn điều kiện của bài toán.
Câu 207: Có bao nhiêu số nguyên a sao cho ứng với mỗi a , tồn tại duy nhất số nguyên b thỏa mãn ( ) ( ) 2 2022 20222022 2022 2022 log202220211 a ba + −+− ? A. 2021. B. 2022 C. 2. D. 1. Lời giải Chọn D Ta có ( ) ( ) 2 2022 20222022 2022 2022 log202220211 a ba
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
63
(
Mặt khác ( )( )2022 20222022202220222022 1 2
20221 a b a −+−= +
vậy, để tồn tại b thoả mãn bất đẳng thức ( )* chỉ có duy nhất một giá trị 1 a = . Khi đó, có duy nhất một số nguyên 0 b = thoả mãn bất đẳng thức ( )* . Câu 208: Có bao nhiêu cặp số nguyên dương ( ) ; xy thỏa mãn điều kiện 2022 x và ( ) ( )3 3 392log12 y yxx +++− ? A.
Lời giải Chọn A
+ −+−
)( )2022 1 202220222 2022 202220212022 a ba −++ ( )*
20222021202220211
Do
3778 B. 3776. C. 2 D. 4044.
( ) ( )3 3 392log12 y yxx +++− ( ) ( ) ( ) 21 3 332113log1 y yxx + +++++ ( ) ( ) ( ) ( ) 3 21log11fyfx ++ , với ( ) 33 t ftt + là hàm số đồng biến trên Suy ra ( ) ( ) 3 121log1 yx ++ ( ) 21 312 y x + − . Do , xy nguyên dương và 2022 x nên từ ( )2 ta có: 21 312022 y+ − 3 log20231 12,97 2 y 1 2 y y
= =
Với 1 y = : Ta có 262022 x . Suy ra có 1997 cặp số nguyên dương ( ) ; xy thỏa mãn. Với 2 y = : Ta có 2422022 x . Suy ra có 1781 cặp số nguyên dương ( ) ; xy thỏa mãn. Vậy có 3778 cặp số nguyên dương ( ) ; xy thỏa mãn. Câu 209: Cho các số dương , xy thỏa mãn 5 1 log324 23 xy xy xy +− ++ + . Giá trị nhỏ nhất của biểu thức
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page
64
i Chọn A Đk: 1. xy+ + Ta có: ( ) ( ) 555 1 log324log11555log2323 23 xy xyxyxyxyxy xy +− +++−+++−+++ + ( ) ( ) ( ) 55 log555555log23231 xyxyxyxy +−++−+++ . + Xét hàm số ( ) 5 log,0.ftttt=+ + Ta có: ( ) 1 100 ln5 ftt t =+ + Do đó ( )ft là hàm số đồng biến trên ( ) 0;+ nên ( ) 1555233250 xyxyxy +−++− . + Ta có: ( )2 23 8949 628619 323232Axy xyxyxy + =+++++++= + .
49 62 Axy xy =+++ bằng A. 19. B. 113 . C. 272 2 . D. 316 4 . Lời giả
Ta có ( ) 1240 xy +− Với mỗi m nguyên dương, bất phương trình xym + có 2 2 mm + điểm ( ) ; xy với x,y là số tự nhiên.
Kết hợp với điều kiện ta có số cặp ( ) ; xy thỏa điều kiện đề bài là: 2 6 2 mm +
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 65
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Dấu "" = xảy ra khi 2 3, 3 2 x y = = . Áp dụng BĐT ( ) ( ) 2 22 ,0 ab ab xy xyxy + + + Câu 210: Có bao nhiêu số nguyên dương m để có không quá 2022 cặp ( ) , xy , với x, y là số tự nhiên thỏa mãn 2 log222xyxy ++− và xym + A. 63. B. 64. C. 22. D. 21. Lời giải Chọn A Ta xét 2 log222xyxy ++− , điều kiện 220 xy+− và x, y là các số tự nhiên ( ) ( ) ( ) ( ) ( ) 22 12log22424log2210 xyxyxyyxy ++−+−++−− Nếu 2240 xy −+− thì ( ) ( ) ( ) 2 24log2210 xyyxy +−++−− ) Nếu 240 xy+− , ta có ( ) ( ) ( ) ( ) ( ) ( ) 2 2 240 24log2210 log2210 xy xyyxy yxy +− +−++−− +−−
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 66
u
ệ
( )( ) ( )2224222 2 x xxmxx −+−+−++ ( )( ) ( )2224222 2 x mxxxx +−+−−++ ( )1 . + Ta thấy các nghiệm của ( )1 trong khoảng ( )1;2 luôn thỏa mãn ( )* . + Đặt ( )222,0txxt =−++ với ( )1;2 x − Xét ( ) 222fxxx=−++ với ( )1;2 x − ( ) ( )( ) 112222 2222 2222 xx fx xx xx −−−+ =+= −+ −+ . ( ) 022221fxxxx =−=+= . Bảng biến thiên:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Theo đề ta có 2 2 6202240560 2 mm mm + −+− Mặt khác m nguyên dương nên 1;2;3;....;63 m Câu 211: Gọi 0m là giá trị nhỏ nhất để bất phương trình ( ) ( ) ( ) 222 1log22log4222log1 2 x xmxxx +−−−+−++−+ có nghiệm. Chọn đáp án đúng trong các khẳng định sau A. ( ) 0 9;10 m . B. ( ) 0 8;9 m . C. ( ) 0 10;9 m −− . D. ( ) 0 9;8 m −− . Lời giải Chọn C + Điều kiện xác định: ( ) ( ) 1212 422204222 22 xx xx mxxmxx −− −+−++−−++ ( )* + Với điề
ki
n trên bất phương trình: ( ) ( ) ( ) 222 1log22log4222log1 2 x xmxxx +−−−+−++−+ ( )( ) ( ) 2 22 log221log4222 2 x xxmxx −+−+−++

CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 67
. +
2
==−−
. B
+
khi
19
Suy
( ) 0 19 10;9 2 m =−−− . Câu 212: Biết rằng tậpnghiệm củabất phươngtrình ( ) ( ) 2 3 43.22log3630 −+−−xx x
ảng (
ab . Khi đó 2022 ++ab có giá trị bằng A. 2024 B. 2025 C. 2027 D. 2023 Lời giải Chọn D Ta có:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Suy ra khi ( )1;2 x − thì ( 3;3 t . + Ta có ( )( ) ( )( ) 2 2 4 42222222 22 xt txxxxx =++−++−+= + ( )1 trở thành 2 2 4 4284 2 t mtmtt −−− ( )2 . + ( )1 có nghiệm ( )1;2 x − ( )2 có nghiệm ( 3;3 t
Xét hàm số ( )
84
ygttt trên ( 3;3
ảng biến thiên:
Do đó bất phương trình ( )2 có nghiệm ( 3;3 t
và chỉ khi
219 2 −−mm
ra
làkho
) ;
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 68 Chuyên
ện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT
12 Sưu tầm và biên soạn ( ) ( ) ( ) ( )( ) 2 22 33 2 2 2 360 43.22log3630log3630 43.220 36 9 21220 9 122 33 01 01 − −+−−−− −+ −− − xx xx xx x x xx x x x x x x Tập nghiệm của bất phương
. Kết hợp với điều kiện đề
ta
đượ
+++ ( )fx đồng biến trên . Ta thấy: ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 22021 22021 33 log4123log4123 fxxxxxxxfx −=−++−+−=++−=− Vậy ( )fx là hàm số lẻ. Khi đó: ( ) ( ) ( ) ( ) 222 1 1212122,0 fxfmxfxfmxxmxxmx x +−−+++ . Xét ( ) ( ) ( ) ( ) 2 111 ,010 1 xL gxxxgx xx xN =− =+=−= = Ta có bảng biến thiên của hàm số ( )ygx = : x 0 1 + ( )gx 0 + ( )gx + + 2
0984164935
luy
BDKT Toán 10; 11;
trình là ( )0;1
bài
tính
c: 20222023++=ab Câu 213: Cho hàm số ( ) ( ) 22021 3 log4123 fxxxx =+++ . Có tất cả bao nhiêu giá trị nguyên của m thuộc đoạn 2021;2021 để bất phương trình ( ) ( ) 2 120fxfmx++− nghiệm đúng với mọi ( ) 0; x+ . A. 2023. B. 4020. C. 4022. D. 2021. Lời giải Chọn A Tập xác định: Dx= . Ta có ( ) ( ) ( ) 2 2020 22 2412 60630 41412ln3 xx fxx xxx ++ =+
CHUYÊN ĐỀ II GIẢI TÍCH 12 LŨY THỪA MŨ LOGARIT
Page 69
++
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Theo yêu cầu bài toán thì 221. mm Vì 2021;2021 m−số giá trị của m bằng: ( ) ( ) 1202112023 −−+= Câu 214: Có bao nhiêu số nguyên dương a thỏa mãn ( )( ) 22 1lnln1(3)31 aaaa +++−+− ? A. 2 B. 1 C. 3 D. 4 Lời giải Chọn A ( )( ) ( ) ( ) 22 22 22 1lnln1(3)31 1lnln1(3)3 1lnln1(3)3(1) aaaa aaaa aaaa +++−+− +++−−− +++−+− Xét hàm số 2 ()1, ftttt=++ . Ta c 2 22 1 '()10, 11 ttt ftt tt ++ =+=
Suy ra hàm số ()ft đồng biến trên Khi đó (1)(ln)(3)ln3ln30(2) fafaaaaa −−−+ Xét hàm số ()ln3,0 gaaaa=−+ . Ta có 1 '()10,0 gaa a =+ Suy ra hàm sốg(a)đồng biến trên (0;) + Khi đó (2)()0()(2,21)2,21 gagaga . Vậy có 2 giá trị: 1 a = và 2 a = .