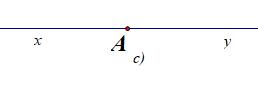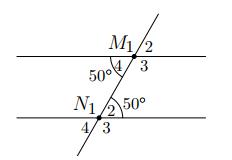CHUYÊN ĐỀ ĐẦY ĐỦ DẠY THÊM TOÁN 7 Ths Nguyễn Thanh Tú eBook Collection CHUYÊN ĐỀ ĐẦY ĐỦ DẠY THÊM TOÁN 7 DÙNG CHUNG 3 SÁCH KẾT NỐI TRI THỨC, CHÂN TRỜI SÁNG TẠO, CÁNH DIỀU (CƠ BẢNNÂNG CAO) - HÌNH HỌC - BẢN GV (518 TRANG) WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405
TIA PHÂN GIÁC CỦA MỘT GÓC
A. Lý thuyết
1. Góc ở vị trí đặc biệt
a) Hai góc kề nhau: Hai góc kề nhau là hai góc có chung đỉnh và chung 1 cạnh, hai cạnh còn lại nằm về 2 phía của đường thẳng chứa cạnh chung đó.
x O
y x O 50° y
z
b) Hai góc bù nhau: Hai góc bù nhau là hai góc có tổng số đo của hai góc là 180°
n A

c) Hai góc kề bù: hai góc vừa kề vừa bù gọi là hai góc kề bù
130°
y x O 4
x'
d) Hai góc đối đỉnh: Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh góc kia.
y x O
3 2 1 y'
x'
*) Tính chất: Hai góc đối đỉnh thì bằng nhau. Mỗi góc chỉ có duy nhất một góc đối đỉnh với nó. 2. Tia phân giác của một góc a) Tia phân giác của một góc: Là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau.
1
CHUYÊN ĐỀ: GÓC Ở VỊ TRÍ ĐẶC BIỆT.
x


Để vẽ tia phân giác Oz của xOy=64° . Ta thực hiện theo 2 bước.
Bước 1: Vẽ 64 xOy . Bước 2: Vẽ tia Oz nằm giữa hai tia , OxOy sao cho 64:232 xOz hoặc 64:232 yOz . Đường thẳng chứa tia phân giác của một góc được gọi là đường phân giác của góc đó. B. CÁC DẠNG TOÁN
Dạng 1: Góc ở vị trí đặc biệt
*) Phương pháp giải: Nhận biết và tính được một số góc kề bù, đối đỉnh
Bài 1:

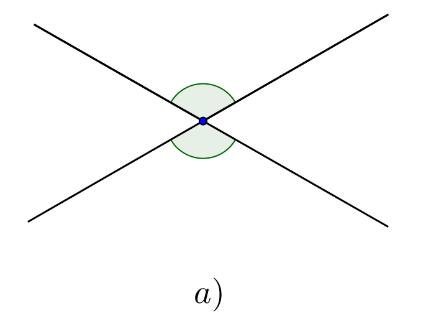
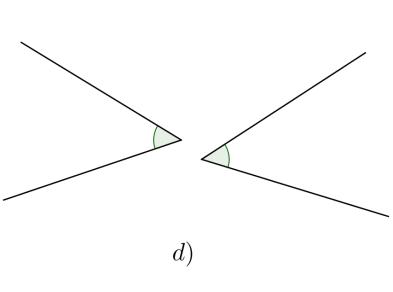
Trong các hình ),),),)abcd cặp góc nào đối đỉnh, cặp góc nào không đối đỉnh? Vì sao?
Lời giải
Vì hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh góc kia nên chỉ có hình a) là cặp góc đối đỉnh.
Bài 2: Hai đường thẳng 'xx và ' yy cắt nhau tại O như hình vẽ Hãy điền vào chỗ trống (…) trong các phát biểu sau:
1. Góc xOy và góc … là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh 'Ox và cạnh Oy là … của cạnh ' Oy .
2. Góc ' xOy và góc ' xOy là … vì cạnh Ox là tia đối của cạnh … và cạnh …
2 b) Cách vẽ:
O
y
z
Lời giải
1. xOy và ''xOy là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh 'Ox và cạnh Oy là tia đối của cạnh ' Oy .
2. ' xOy và ' xOy là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh 'Ox và cạnh Oy là tia đối của cạnh ' Oy .
Bài 3:
Vẽ ba đường thẳng cùng đi qua một điểm. Đặt tên cho các góc tạo thành.
1. Viết tên các cặp góc đối đỉnh. Chỉ ra các cặp góc bằng nhau
2. Viết tên các 3 cặp góc kề bù.
Lời giải
1. Các cặp góc đối đỉnh là aOb và ''aOb ; aOc và ''aOc ; bOc và ''bOc ; 'aOc và ' aOc ; 'aOb và ' aOb ; 'cOb và ' cOb. Các cặp góc đối đỉnh thì bằng nhau. 2. Các cặp góc kề bù là: aOb và 'aOb ; 'aOc và ''aOc ; bOc và ' cOb
Bài 4: Cho xBy có số đo bằng 60 . Vẽ góc đối đỉnh với xBy . Hỏi góc này có số đo bằng bao nhiêu độ ?
y x' x O
60° y'
Lời giải Vì hai góc đối đỉnh có số đo bằng nhau nên góc đối đỉnh với ''xBy cũng có số đo bằng 60 .
Bài 5: Hai đường thẳng MN và PQcắt nhau tại A tạo thành MAP có số đo bằng 30 .
1. Tính số đo góc NAQ
2. Tính số đo góc MAQ
3. Viết tên các cặp góc đối đỉnh.
4. Viết tên các cặp góc kề bù. Lời giải
30° A P Q M
N 30° A P Q M
N

3
1. Vì MAP và NAQ là hai góc đối đỉnh nên 30 MAPNAQ 2. Vì MAQ kề bù với MAP nên 180150MAQMAP . 3. Các cặp góc đối đỉnh: MAP và NAQ ; MAQ và PAN . 4. Các cặp góc bù nhau: MAP và MAQ ; MAP và PAN ; NAQ và MAQ ; NAQ và PAN .
Bài 6:

1. Vẽ ABC có số đo bằng 56 . 2. Vẽ ' ABC kề bù với ABC . Hỏi số đo của ' ABC ? 3. Vẽ ''CBA kề bù với ' ABC . Tính số đo ''CBA ?
Lời giải
1. Xem hình vẽ. 2. Vì ' ABC kề bù với ABC nên '180o ABCABC 18056 124
3. Vì ''CBA kề bù với ' ABC nên ''180' CBAABC 180124 56 .
Bài 7:
Cho hai góc kề nhau xOy và yOz có tổng số đo bằng 150 và 90 xOyyOz 1. Tính số đo các góc xOy và yOz 2. Vẽ các tia ', ' OxOy lần lượt là các tia đối của các tia , OxOy . Tính số đo các ''xOy , . , ' xOy . Lời giải 1. Ta có 90 xOyyOz . Thay vào 150 xOyyOz tìm được 30 yOz và 120 xOy . 2. ''120xOyxOy
4
, '180150 yOzyOz. Tương tự, ta tìm được '60xOy . Bài 8: Vẽ hai đoạn thẳng cắt nhau sao cho trong số các góc tạo thành có một góc bằng 47. Tính số đo các góc còn lại. Lời giải y' x' z y x O A C' C A' 47° B 56° C' C A' A B
Vì ''ABC và CBA là hai góc đối đỉnh nên ''ABC 47 CBA .
Vì 'CBA kề bù ''ABC nên '180CBACBA suy ra '180''133CBAABC .
Do 'CBA và ' ABC là hai góc đối đỉnh nên ''133CBAABC .
Bài 9:
Cho xOy . Vẽ tia Oz là phân giác xOy . Vẽ 'Oz là tia đối của tiaOz . Vẽ góc kề bù yOt với xOy . Khi đó hai ' zOt và xOz có phải là hai góc đối đỉnh không?
Lời giải Vì yOt kề bù với xOy nên , OxOt là hai tia đối nhau. Theo đề bài 'Oz là tia đối của tia Oz nên ' zOt và xOz là hai góc đối đỉnh.
Bài 10:

Cho mOn . Vẽ góc kề bù nOt với mOn . Vẽ mOz kề bù với mOn . Khi đó mOn và tOz có phải là hai góc đối đỉnh không?
Lời giải
Vì nOt kề bù với mOn nên Om và Ot là hai tia đối nhau; mOz kề bù với mOn nên On và Oz là hai tia đối nhau.
Do đó mOn và tOz là hai góc đối đỉnh.
Bài 11:
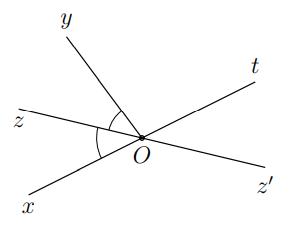
Cho xOy . Vẽ yOz kề bù với xOy . Vẽ xOt kề bù với xOy . Vẽ On là phân giác yOz . Vẽ
Om là phân giác xOt . Khi đó zOn và xOm có phải là hai góc đối đỉnh hay không?
Lời giải Vì yOz kề bù với xOy nên Ox và Oz là hai tia đối nhau, vì xOy kề bù với xOt nên Oy và
5
Ot là hai tia đối . Ta có yOzxOt (đối đỉnh).
Do On và Om lần lượt là phân giác yOz và xOt nên yOnnOz = xOmmOt . Lại có: 180 xOyxOt 180 xOyxOmmOt 180 xOyyOnxOm 180 xOnxOm hay xOn và xOm kề bù. Từ đó suy ra Om và On là hai tia đối nhau nên zOn và xOm là hai góc đối đỉnh.
Bài 12:
Cho góc bẹt xOy . Vẽ tia Oz sao cho góc 070 xOz a) Tính góc zOy b) Trên nửa mặt phẳng bờ Ox chứa Oz vẽ tia Ot sao cho 0140 xOt . Chứng tỏ Oz là tia phân giác của xOt c) Vẽ tia Om là tia đối của tia Oz , tia On là tia đối của tia Ot . Tính góc yOm và so sánh với xOn
Lời giải

z t y x O
70° 140° m n
a) Vì xOy là góc bẹt và 70 xOz 180110 O xOzzOy zy . b) Vì ba tia ,, OxOzOt cùng nằm trên một nửa mặt phẳng có bờ là Ox và xOzxOt nên tia Oz nằm giữa hai tia , OxOt . Lại có 1 2 xOzxOt nên tia Oz là tia phân giác của góc xOt c)Vì Vẽ tia Om là tia đối của tia Oz và 110 zOy .Vậy 70 yOmzOmzOy ; Vì tia On là tia đối của tia Ot và 140 xOt . Vậy 40 xOnnOtxOt Suy ra yOmxOn
6
BÀI TẬP TỰ LUYỆN
Bài 1:
Hai đường thẳng 'xx và ' yy cắt nhau tại O tạo thành xOy có số đo bằng 90 .
1. Tính số đo ''xOy
2. Tính số đo ' xOy .
3. Viết tên các cặp góc đối đỉnh.
Lời giải
1. Vì xOy đối đỉnh ''xOy nên ''90xOy
2. Vì xOy và ' xOy là hai góc kề bù nên '18090 xO y y xO .
3. xOy đối đỉnh ''xOy và ' xOy đối đỉnh ' xOy .
Bài 2:
1. Vẽ xOy có số đo bằng 80 .
2. Vẽ ''xOy đối đỉnh với góc xOy .
3. Vẽ tia phân giác Oz của xOy . Vẽ tia đối 'Oz của tia Oz . Kể tên các cặp góc đối đỉnh.
Lời giải
y'
y x

x' z
80° O
y x' x O z' y'
1. Vẽ tia Ox Đặt thước đo góc sao cho tâm của thước trùng với đỉnh O , tia Ox đi qua vạch 0O Vẽ tia Oy đi qua vạch 80 của thước. Ta vẽ được 80 yOx . Hình vẽ
2. Vẽ tia 'Ox là tia đối của tia Ox . Vẽ tia ' Oy là tia đối tia Oy ta được ''xOy đối đỉnh với xOy . Hình vẽ
3. Các cặp góc đối đỉnh là zOy và ''zOy ; xOz và ''xOz ; xOy và ''xOy ; ' zOx và ' zOx ; ' yOz và ' yOz ; ' xOz và ' xOz
7
Bài 3:
Cho góc bẹt AOB. Trên cùng một nửa mặt phẳng bờ AB , vẽ các tia , OCOD sao cho 80 AOC , 10 BOD . Tia OC và OD có vuông góc với nhau không? Tại sao ? Lời giải Vì AOC kề bù với COB suy ra 180100COBCOA . Vì OD nằm giữa hai tia OC và OB suy ra CODDOBCOB CODCOBDOB
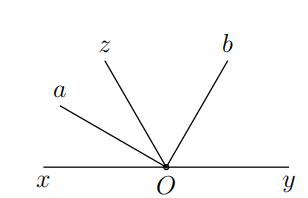
10010 COD 90 COD Hay đường thẳng chứa tia OC vuông góc với đường thẳng chứa tia OD
Bài 4:
Cho xOy là góc bẹt . Trên cùng một mặt phẳng bờ xy , vẽ tia Oz . Vẽ tia phân giác Oa của xOz , tia phân giác Ob của zOy . Tia Oa và Ob có vuông góc với nhau không? Vì sao? Lời giải Tia Oa là tia phân giác của xOz nên 2 xOz xOaaOz .

8
O
C D B
Tương tự 2 zOy zObbOy Vì Oz nằm giữa Oa và Ob nên 180 90. 222 xOyzOy aObaOzzOb
10° 80°
A
Dạng 2: Vẽ tia phân giác của một góc và áp dụng tính chất tia phân giác
*) Phương pháp giải:
+ Bước 1: biết vẽ góc với một số đo cho trước
+ Bước 2: biết áp dụng vẽ tia phân giác của góc theo số đo hoặc theo cách vẽ bằng thước hai lề.
*) Bài toán:
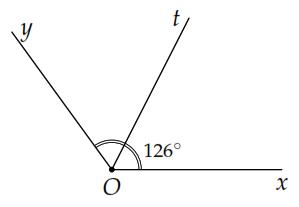
a) Vẽ góc xOy có số đo 126 .
b) Vẽ tia phân giác Ot của góc xOy ở ý trên.
Bài 1:
Lời giải
Cách vẽ
Vẽ tia Ox .
Đặt thước đo góc sao cho tâm của thước trùng với gốc O của tia Ox và tia Ox đi qua vạch 0 . Vẽ tia Oy đi qua vạch 126 của thước. Ta vẽ được 126 yOx
Vì tia Ot là tia phân giác của xOy nên ta có 63 2 xOy xOttOy
Đặt thước đo góc sao cho tâm của thước trùng với điểm O của tia Ox và tia Ox đi qua vạch 0 . Vẽ tia Ot đi qua vạch 63 và tia Ot nằm giữa hai tia Ox và Oy , ta được tia phân giác Ot của xOy .
Bài 2:
a) Vẽ góc xOy có số đo 44 . b) Vẽ tia phân giác Ot của góc xOy ở ý trên. Lời giải Cách vẽ: a) Vẽ tia Ox . Đặt thước đo góc sao cho tâm của thước trùng với điểm O của tia Ox và tia Ox đi qua vạch 0 Vẽ tia Oy đi qua vạch 44 của thước. Ta vẽ được 44 yOx .
t

y x O 44°
9
b) Vì tia Ot là tia phân giác của xOy nên ta có 22 2 xOy xOttOy
Đặt thước đo góc sao cho tâm của thước trùng với điểm O của tia Ox và tia Ox đi qua vạch O . Vẽ tia Ot đi qua vạch 22 và tia Ot nằm giữa hai tia Ox và Oy , ta được tia phân giác Ot của xOy .
Bài 3:
a) Vẽ xOy có số đo 90 b) Vẽ tia phân giác Ot của xOy ở ý trên.
45°
y t x O
Lời giải Cách vẽ Vẽ tia Ox Đặt thước đo góc sao cho tâm của thước trùng với điểm O của tia Ox và tia Ox đi qua vạch 0 .
Vẽ tia Oy đi qua vạch 90 của thước. Ta vẽ được 90 yOx
Vì tia Ot là tia phân giác của xOy nên ta có 45 2 xOy xOttOy
Đặt thước đo góc sao cho tâm của thước trùng với điểm O của tia Ox và tia Ox đi qua vạch 0 . Vẽ tia Ot đi qua vạch 45 và tia Ot nằm giữa hai tia Ox và Oy , ta được tia phân giác Ot của xOy .
Bài 4:
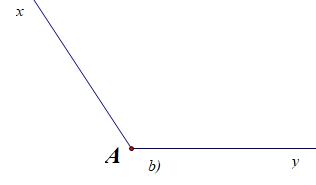
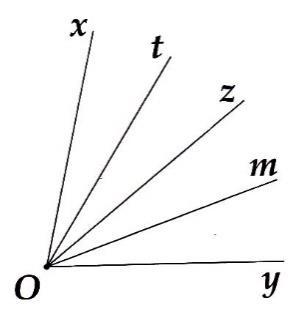
Vẽ tia phân giác của các góc được cho dưới đây:
Lời giải
Cách 1: Dùng thước kẻ hai lề vẽ tia phân giác dựa theo tính chất hình thoi có hai đường chéo là hai đường phân giác. Ta có các tia phân giác cần vẽ, riêng ý c) là góc bẹt vì vậy kẻ vuông góc ta có tia phân giác

10
Cách 2: Dùng thước đo góc ta tiến hành đo góc cần dựng tia phân giác áp dụng tính chất chia đôi góc ta vẽ góc nhỏ có số đo bằng một nửa góc đã cho có chung 1 cạnh, riêng ý c) là góc bẹt vì vậy kẻ vuông góc ta có tia phân giác
Bài 5:
Vẽ tia phân giác của K được cho dưới đây: Lời giải
Vẽ đường tròn tâm K bán kính R cắt hai cạnh của K tại , IJ Vẽ các đường tròn Tâm ; IJ có cùng bán kính r cắt nhau tại L Vẽ tia KL Khi đó tia phân giác của K là tia KL .
m



n z y x
O
11
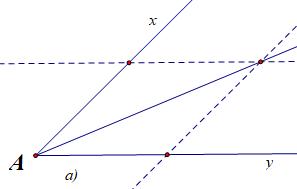
Bài 6: Cho hình vẽ. Biết 1234 ; OOOO và hai tia , OxOn đối nhau. Chỉ ra các tia phân giác trên hình bên; Tính số đo của mOy . 4 3 2 1
L

i giải Vì 12 OOOy là tia phân giác của xOz 34 OOOm là tia phân giác của nOz Ta có 1 18090 2 mOzzOymOy .
Bài 7:
Cho hai góc kề bù , xOyyOz sao cho 120 xOy . a) Tính yOz b) Gọi Ot là tia phân giác của yOz . Chứng tỏ 1 tOy=xOy 4 Lời giải a) Vì hai , xOyyOz là hai góc kề bù 18012060 yOz
Vậy 60 yOz
b) Vì Ot là tia phân giác của yOz có: 11 6030 22tOytOzyOz mà 120 xOy vậy 1 tOy=xOy 4 Bài 8:
Trên cùng một nửa mặt phẳng bờ chứa tia Ox , vẽ hai tia Oy và Ot sao cho 30; xOy 70 xOt a) Tính ? yOt Tia Oy có là tia phân giác của xOt không? Vì sao? b) Gọi tia Om là tia đối của tia Ox .Tính số đo của mOt ? c) Gọi Oz là tia phân giác của mOt . Tính số đo của yOz ? Lời giải
y t z O m
x
70° 30°
z t y x O
12
ờ
a) Vì (3070) xOyxOt Tia Oy nằm giữa hai tia Ox và Ot xOyyOtxOt 703040 yOt

Vậy 40 yOt Oy không là tia phân giác của xOt vì: (3040) xOyyOt b) Vì tia Om là tia đối của tia Ox nên tia Ot nằm giữa hai tia Om và Ox suy ra: xOttOmxOm 18070110 tOm
ậy 110 tOm
Vì Oz là tia phân giác của tOm nên 110:255 tOz
tia Ot
13
Vì ' Ot là tia phân giác của ' yOx 11 '''.11055 22tOxtOyyOx Vì Ot là tia phân giác của xOy 11 7035 22xOttOyxOy Vì Ox và ’Ox đối nhau Ot và ' Ot nằm giữa Ox và 'Ox '''180xOttOttOx ''180xOttOttOx '180–35–5590 tOt Có ' xOt và ''tOx là 2 góc kề bù ''180 '180–55125 xOttOxxOt y t t' x' x 70° O
V
c)
Mà
nằm giữa hai tia Oz và Oy nên ta có: 405595 yOzyOttOz Vậy 95 yOz Bài 9: Vẽ 2 góc kề bù xOy và ' yOx , biết 70 xOy Gọi Ot là tia phân giác của xOy , ' Ot là tia phân giác của ' xOy . Tính ';'; ' yOxtOtxOt Lời giải Ta có xOy và ' yOx là 2 góc kề bù '180xOyyOx '180–70110yOx
Bài 10: Cho AOB và BOC là hai góc kề bù. Biết 5. BOCAOB a) Tính số đo mỗi góc. b) Gọi OD là tia phân giác của BOC . Tính số đo AOD . Lời giải a) Vì AOB và BOC là hai góc kề bù nên: 180 AOBBOC
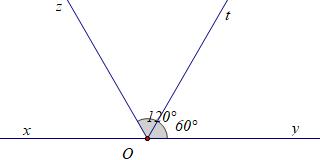

mà 56180BAOBAOB OC Do đó: 180:630; 5.30150 A OC O B B
b) Vì OD là tia phân giác của BOC nên 1 75 2 B DOCBO OD C Vì DOA và DOC là hai góc kề bù nên: 180 DC OADO Do đó 18018075105DODOC A Bài 11: Cho điểm O thuộc đường thẳng xy . Trên nửa mặt phẳng bờ xy , vẽ các tia Oz và Ot sao cho 60;120yOtyOz a) Tính số đo zOt . Từ đó suy ra Ot là tia phân giác của yOz . b) Tính số đo xOz và xOt . c) Tia Oz có phải tia phân giác của xOt không ? Vì sao ? Lời giải a) Ta có tia Oz và tia Ot cùng thuộc nửa mặt phẳng bờ là đường thẳng xy . Mà 60120yOtyOz
14
O A B D C
Suy ra tia Ot nằm giữa hai tia Oy và Oz (1) 1206060 yOzyOtzOtzOtyOzyOt 2 yOz zOtyOt (2) Từ (1) và (2) Ot là tia phân giác của .yOz
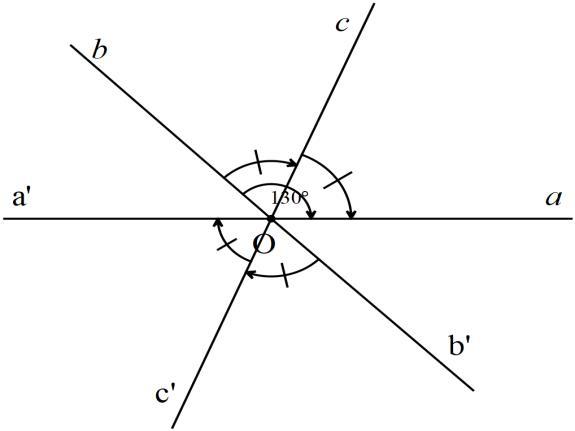
phân giác Oc của góc aOb và tia phân giác 'Oc của góc ''aOb . Hai tia Oc và 'Oc có phải là hai tia đối nhau không? Lời giải a) Ta có: 0''130aObaOb (đối đỉnh)

15
có: 0
(bù
do đó: 0000 '18018013050
0
(đối đỉnh)
thứ tự là
giác của hai góc aOb và a’Ob’ nên 1 2 aOccObaOb và 1 '''''' 2 aOccObaOb mà ''aObaOb . Do đó: 1 '''' 2 aOccObaOccObaOb '''''' cOccObbOaaOccObbOaaOc 0''180 bOaaOccObbOaaOb Suy ra: góc ' cOc là góc bẹt hay hai tia Oc và 'Oc là hai tia đối nhau.
b) Ta có xOz và yOz là hai góc có chung cạnh Oz , hai cạnh còn lại Ox và Oy là hai tia đối nhau xOz và yOz là hai góc kề bù . Ta có : 18018060yOzzOxxOzzOy Ta có xOt và yOt là hai góc có chung cạnh Ot , hai cạnh còn lại Ox và Oy là hai tia đối nhau xOt và yOt là hai góc kề bù: 180180120xOtyOtxOtyOt c) Ta có tia Oz và tia Ot cùng thuộc nửa mặt phẳng bờ là đường thẳng xy mà xOz=60<xOt=120 Suy ra tia Oz nằm giữa hai tia Ox và Ot 1206060 xOtxOzzOtzOtxOtxOz 2 xOt zOtxOz (4) Từ (3) và (4) Oz là tia phân giác của xOt . Bài 12: Cho hai đường thẳng ' aa và 'bb cắt nhau tại O . Biết 130 aOb . a) Tính các góc '';';' aObaObaOb b) Vẽ tia
Mặt khác ta cũng
'180aObaOb
nhau),
aObaOb
''50aObaOb
b) Oc, Oc’ theo
các tia phân
Bài 1:

Vẽ tia phân giác của các góc được cho dưới đây:
Lời giải Áp dụng cách vẽ ta có các tia phân giác là:
Bài 2:
Trên cùng một nửa mặt phẳng bờ chứa tia AB , vẽ tia AC , AD sao cho 50 BAC , 100 BAD . a) Trong ba tia AB , AC , AD thì tia nào nằm giữa hai tia còn lại? Vì sao? b) So sánh góc BAC và góc CAD c) Tia AC có phải là tia phân giác của góc BAD không? Vì sao?
Lời giải a) Vì AC , AD nằm trên một nửa mặt phẳng bờ chứa tia AB , mà BACBAD (do 50100) nên tia AC nằm giữa hai tia AB và AD . b) Theo tính chất cộng góc ta có 1005050. BADBACCADCADBADBAC Suy ra 50 BACCAD
16 BÀI TẬ
TỰ
Ệ
P
LUY
N
A N
b
A D
D M y x
a H N A M O 2 1 c H a b 21 z O y x 100°
C B
c) Do tia AC nằm giữa hai tia AB và AD lại có 50 BACCAD nên AC là phân giác của
BAD .
Bài 3: Trên cùng nửa mặt phẳng bờ chứa tia OA, vẽ 60 AOB ; 120 AOC a) Tính BOC b) Chứng tỏ tia OB là tia phân giác AOC . c) Vẽ tia OD là tia đối của tia OA. Tính DOC Lời giải Trên cùng nửa mặt phẳng bờ chứa tia OA ta có : 60 120 AOBAOC
D

120° 60°
Suy ra tia OB nằm giữa hai tia OA vàOC . AOBBOCAOC Hay 6012060 BOCBOC
Ta có: tia OB nằm giữa hai tia , OAOC và 60 AOBBOC
Suy ra tia OB là tia phân giác AOC . Vẽ tia OD là tia đối của tia OA (gt) ; AOCCOD là hai góc kề bù. 180 AOCCOD hay 12018060 DOCDOC
Bài 4:
17
Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ hai tia Oy và Ot sao cho 30;70xOyxOt a) Tính ? yOt Tia Oy có là tia phân giác của xOt không? Vì sao? b) Gọi tia Om là tia đối của tiaOx .Tính số đo của mOt c) Gọi Oz là tia phân giác của mOt . Tính số đo của yOz Lời giải a) Vì (3070) xOyxOt C B A
Tia Oy nằm giữa hai tia Ox và Ot xOyyOtxOt
703040 yOt Vậy 40 yOt Oy không là tia phân giác của xOt vì: (3040) xOyyOt b) Vì tia Om là tia đối của tia Ox nên tia Ot nằm giữa hai tia Om và Ox
O 70° 30° z m t O y x
suy ra: xOttOmxOm 18070110 tOm
Vậy 110 tOm c) Vì Oz là tia phân giác của tOm nên 110:255 tOz mà tia Ot nằm giữa hai tia Oz và Oy nên ta có: 405595 yOzyOttOz . Vậy 95 yOz
Bài 5:

Bên trong ,xOy vẽ tia Om sao cho 30 yOm và vẽ tia On sao cho 90. yOn
Cho 120. xOy

a) So sánh số đo các xOn và yOm . b) Gọi Ot là tia phân giác của xOy . Chứng tỏ Ot cũng là tia phân giác của mOn Lời giải a) Theo tính chất cộng góc, ta có: 30 30 xOnxOyyOm yOmxOyxOm
Vậy xOnyOm
b) Vì Ot là tia phân giác của xOy nên: 60 2 xOy xOtyOt
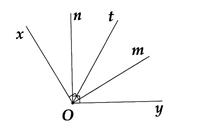
Từ đó, ta có ; 3030nOtxOtxOnmOtyOtyOm
Mặt khác, 60 mOnyOnyOm
Do đó, 2 mOn nOtmOt (cùng bằng 30°). Vậy Ot cũng là tia phân giác của mOn . Bài 6: Vẽ hai góc kề bù xOy và yOz , biết 70. xOy Vẽ Ot là tia phân giác của yOz a) Tính số đo yOz và yOt b) Tính số đo xOt . Lời giải
18
a) Sử dụng tính chất hai góc kề bù, suy ra 110. yOz Vì Ot là tia phân giác của yOz nên 55. 2 yOz yOt b) Ta có 55. zOtyOt Từ đó, suy ra 125. xOt
Bài 7:

Cho góc xOy . Vẽ tia Oz là tia phân giác của xOy Vẽ tia Ot là tia phân giác của xOz Vẽ tia Om là tia phân giác của .yOz a) Chứng tỏ tia Oz là tia phân giác của tOm b) Chứng tỏ 4 xOy tOz . c) Tính giá trị lớn nhất của góc tOm . Lời giải a) Theo tính chất tia phân giác của một góc, ta có: 1 2 xOzyOzxOy 1 2 xOttOzxOz (1) 1 2 zOmyOmyOz
Từ đó, suy ra tOzmOz Mặt khác, Ox và Ot cùng thuộc một nửa mặt phẳng bờ chứa tia ;; OzOyOm cùng thuộc nửa mặt phẳng còn lại. Do đó, tia Oz nằm giữa hai tia Ot và Om . Vậy tia Oz là tia phân giác của .tOm b) Từ (1), ta suy ra 1111 . 2224 tOzxOzxOyxOy Do đó, 4 xOytOz c) Từ ý a), suy ra 2 tOmtOz Kết hợp với ý b), ta có 1 2 tOmxOy Mà góc xOy có số đo lớn nhất bằng 180 (góc bẹt) nên góc tOm có số đo lớn nhất bằng 90. Nên 180(4545)90 tOm
19
A. Lý thuyết
1. Góc tạo bởi một đường thẳng cắt hai đường thẳng.
+ Cho đường thẳng c cắt hai đường thẳng a và b tại hai điểm , AB như hình vẽ bên
+ Có hai cặp góc so le trong là 1A và 3B ; 4A và 2B .
+ Có bốn cặp góc đồng vị là: 1A và 1B ; 2A và 2B ; 3A và 3B ; 4A và 4B .

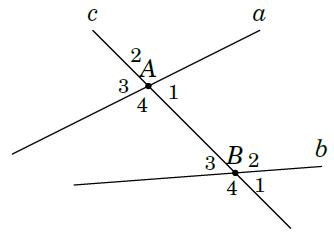
+ Có hai cặp góc trong cùng phía là 1A và 2B ; 4A và 3B .
+ Có hai cặp góc so le ngoài là 2A và 4B ; 3A và 1B .
2. Nhắc lại

+ Hai đường thẳng song song là hai đường thẳng không có điểm chung.
+ Hai đường thẳng phân biệt hoặc cắt nhau hoặc song song.
3. Dấu hiệu nhận biết hai đường thẳng song song
*) Nếu đường thẳng c cắt hai đường thẳng , ab và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc một cặp góc đồng vị bằng nhau) thì a và b song song với nhau.
B. CÁC DẠNG TOÁN
Dạng 1: Xác định cặp góc so le trong, cặp góc đồng vị, cặp góc trong cùng phía, cặp góc so le ngoài trên hình vẽ cho trước. Vẽ hai đường thẳng song song hoặc kiểm tra xem hai đường thẳng có song song với nhau không? Tính số đo góc .
I) Phương pháp giải:
+) Dựa vào vị trí của các cặp góc xác định đúng cặp góc so le trong, cặp góc đồng vị, cặp góc trong cùng phía, cặp góc so le ngoài trên hình vẽ cho trước.
+) Dùng góc nhọn của ê-ke (Áp dụng thực hành 1 hoặc thực hành 2) để vẽ hai góc so le trong hoặc hai góc đồng vị bằng nhau.
1 CHUYÊN ĐỀ: HAI ĐƯỜNG THẲNG SONG
VÀ DẤU HIỆU NHẬN BIẾT.
SONG
+) Dùng thước đo góc để kiểm tra xem hai góc so le trong hoặc hai góc đồng vị (các góc tạo bởi một đường thẳng cắt hai đường thẳng cần kiểm tra có song song hay không) có bằng nhau hay không.
II) Bài toán:
Cho hình sau:
a) Kể tên các góc so le trong. b) Kể tên các góc đồng vị. c) Kể tên các góc trong cùng phía.
Bài 1:

Lời giải
+ Các góc so le trong là: 2A và 2B ; 3A và 3B
+ Các góc đồng vị là: 1A và 2B ; 3A và 4B ; 4A và 3B ; 2A và 1B + Các góc trong cùng phía là: 3A và 2B ; 2A và 3B
Bài 2:
Chỉ ra các cặp góc so le trong, cặp góc đồng vị, cặp góc trong cùng phía, cặp góc so le ngoài trong các hình vẽ sau:
Hình 2a:
- Cặp góc so le trong: 1M và 3N ; 4M và 2N - Cặp góc so le ngoài: 2M và 4N ; 3M và 1N .
Lời giải
2
1 2 4 3 4
B
3 2
D C 4
3 2 1
A 2 3 4 1
1 4 m n l
3 2 1 4 3 2 1 x z y N M
- Cặp góc đồng vị: 4M và 4N ; 1M và 1N ; 2M và 2N 3M và 3N .
- Cặp góc trong cùng phía: 4M và 3N ; 1M và 2N Hình 2b:
- Cặp góc so le trong: 2C và 4D , 1C và 3D
- Cặp góc so le ngoài: 3C và 1D , 4C và 2D
- Cặp góc đồng vị: 1C và 1D , 2C và 2D , 3C và 3D , 4C và 4D
- Cặp góc trong cùng phía: 2C và 3D , 1C và 4D
Bài 3:
Vẽ hai đường thẳng xx , yy sao cho xx song song yy
x y y'
Hình vẽ tham khảo Lời giải
Sử dụng eke và thước vẽ như các bước ở thực hành 1 hoặc 2 ta được hình vẽ
Bài 4:
Cho hai điểm A và B . Hãy vẽ một đường thẳng a đi qua A và đường thẳng b đi qua B sao cho b song song với a
x' a b B
Hình vẽ tham khảo Lời giải
Sử dụng eke và thước vẽ như các bước ở thực hành 1 hoặc 2 ta được hình vẽ
A

3
Bài 5:
Chỉ ra các cặp góc so le trong, cặp góc đồng vị trong các hình vẽ bên.
Lời giải
ta có: - Cặp góc so le trong: 1E và 3F , 4E và 2F - Cặp góc đồng vị: 4E và 4F , 1E và 1F , 2E và 2F , 3E và 3F .

Bài 6:
Xem hình bên rồi điền vào chỗ trống (...) trong các câu sau:
1. IPO và POR là một cặp góc
2. OPI và TNO là một cặp góc ...
3. PIO và NTO là một cặp góc
4. OPR và POI là một cặp góc
1. IPO và POR là một cặp góc so le trong.
2. OPI và TNO là một cặp góc đồng vị.
3. PIO và NTO là một cặp góc đồng vị.
4. OPR và POI là một cặp góc so le trong
Lời giải
Bài 7:
Cho hình sau:
a, Đặt tên cho các góc trong hình.
b, Kể tên các góc bằng nhau có trong hình.
4
4 3 2 1 4 3 2 1 p o q F E 32°
Q
I
T
32°
P
P
N O R
Lời giải Vì 3P và 4P là 2 góc kề bù nên 34 180 PP Ta tính được 3 18032148 P
Vì 4P và 2P là 2 góc đối đỉnh nên 42 32 PP Vì 3P và 1P là 2 góc đối đỉnh nên 31 148 PP Tương tự ta có các góc tại đỉnh Q 13 148 QQ ; 24 32 QQ Vậy các góc bằng nhau có trong hình là: 4224 32 PPQQ 3113 148 PPQQ
Bài 8:

Cho hình sau.
a) Viết tên hai góc trong cùng phía tại A và B b) Viết tên các góc so le trong tại B và C .
c) Hai góc 1C và 1A là hai góc gì? d) Hai góc 2B và 2C là hai góc gì? Lời giải
a) Hai góc trong cùng phía tại A và B : 1A và 2B
b) Các góc so le trong tại B và C: 2C và 1B , 1C và 2B c) Hai góc 1C và 1A là hai góc đồng vị
d) Hai góc 2B và 2C là hai góc trong cùng phía.
5
4 2 3 1 3 4 2 1 32° 32° Q P 2 1 2 1 1 A B C
Vẽ lại các hình sau và tính số đo các góc còn lại.
Lời giải
Ta có: 2 3 180 KK (2 góc kề bù).
Thay số 2 70180 K . Suy ra 2 18070110 K
H
4

Thay số: 2 120180 H . Suy ra 2 18012060 H Suy ra 42 60 HH Bài 10: Cho hình vẽ bên:
K
2 3
70° 120° 1 4
3 2 1 a b

Ta có: 1 3 70 KK( 2 góc đối đỉnh) , 2 4 110 KK (2 góc đối đỉnh). - Tương tự: 3 1 120 HH (2 góc đối đỉnh) 12 180 HH (2 góc kề bù)
c
6
Bài 9:
1. Kể tên các cặp góc so le trong, các cặp góc đồng vị và các cặp góc trong cùng phía. 2.Tính số đo các cặp góc còn lại, biết: 11100,60OP , 2 40 Q Lời giải 1. Các cặp góc so le trong: 1O và 24 ; QO và 13 ; QO và 14 ; PO và 2P , 2Q và 4P , 3Q và 1P Các cặp góc đồng vị: 1O và 42 ; QO và 13 ; QO và 24 ; QO và 31 ; QO và 12 ; PO và 2; P 3O và 34 ; PO và 4P ; 1Q và 1P ; 2Q và 2P ; 3Q và 34 ; PQ và 4P
Các cặp góc trong cùng phía: 1O và 14 ; QO và 24 ; QO và 13 ; PO và 2P ; 2Q và 1P ; 3Q và 4P
2. Từ 1 100 O , suy ra: 324100,80OOO
Từ 1 60 P , suy ra: 324600 , 12 PPP
Từ 2 40 Q suy ra 41340,140QQQ
Bài 11:
Cho hình vẽ bên
a) Kể tên các cặp góc so le trong, các cặp góc đồng vị và các cặp góc trong cùng phía. b) Tính số đo các cặp góc còn lại, biết: 42 120 RS . Lời giải
a) - Cặp góc so le trong: 4S và 2R ; 3S và 1R . - Cặp góc đồng vị: 1S và 1R ; 4S và 4R , 3S và 3R , 1S và 1R - Cặp góc trong cùng phía: 4S và 1R ; 3S và 2R b) - Ta có: 42 120 SS (2 góc đối đỉnh). 2 3 180 SS (2 góc kề bù). Thay số 3 120180 S . Suy ra 3 18012060 S Suy ra 31 60 SS (2 góc đối đỉnh). - Tương tự: 24 120 RR(2 góc đối đỉnh) 12 180 RR (2 góc kề bù) Thay số: 1 120180 R . Suy ra 1 18012060 R Suy ra 31 60 RR
p S R
2 1 4 3
1 n

2 3 4
m
7
Bài 12:
Cho hình vẽ bên.
a) Kể tên các cặp góc so le trong, các cặp góc đồng vị và các cặp góc trong cùng phía.
b) Ghi tiếp số đo ứng với các góc còn lại.
c) Tính 32MN ; 41MN Lời giải
a) Cặp góc so le trong: 4M và 2N ; 3M và 1N Cặp góc đồng vị: 1M và 1N ; 4M và 4N , 3M và 3N , 1M và 1N .
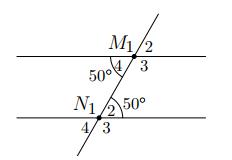
Cặp góc trong cùng phía: 4M và 1N , 3M và 2N b) 24 50 MM (2 góc đối đỉnh) ; 12 180 MM (2 góc kề bù). Suy ra 1 18050130 M Suy ra 31 130 MM (2 góc đối đỉnh) - Tương tự: 42 50 NN (2 góc đối đỉnh) ; 12 180 NN (2 góc kề bù). Suy ra 1 18050130 N Suy ra 31 130 NN (2 góc đối đỉnh) c) Từ kết quả đã tính ở ý b), ta có 32 180 MN ; 41 180 MN
BÀI TẬP TỰ LUYỆN
Bài 1:
Tìm các cặp góc so le trong (ngoài), đồng vị, góc trong (ngoài) cùng phía trên hình (H1). Lời giải
- Các cặp góc so le trong: 1A và 7B ; 4A và 6B .
b a
6 5 4 3 2 1 c
B A H1
8 7

8
- Các cặp góc so le ngoài: 2A và 8B ; 3A và 5B .
- Các cặp góc đồng vị: 1A và 5B ; 4A và 8B ; 3A và 7B ; 2A và 6B
- Các cặp góc trong cùng phía: 1A và 6A ; 4A và 7B
- Các cặp góc ngoài cùng phía: 2A và 5B ; 3A và 8B .
Bài 2:
Tính các giá trị ,,, xyzt trên hình sau (H2 )
Lời giải + Tính các giá trị ,,, xyzt trên hình 2 (H2) 60 x ( x đối đỉnh với góc 60 ) 120180 y ( y kề bù với góc 120 ) 180120 y 60 y 60180 z ( z kề bù với góc 60 ) 18060 z 120 z
z
y x
A 120o 60o x
B
H2
y x
z
A 120o 60o x
B
H2
Bài 3: Vẽ lại hình và tính các góc còn lại Lời giải
o 75 4 1 2 3
c 120o
a

4 3 2 1 F B
A E
y x'
x z' z b
110o y'
b) a)
9
Hình 3a. 2A kề bù với 1A nên tìm được 21180105AA . 31 75 AA (đối đỉnh) 42 ;105 AA (đối đỉnh).
Tương tự ta tìm được: 431324 18060;120;60BBBBBB
Hình 3b . Tương tự ý a ) ta tìm được: 90;110zExxEzzExxEzzFyyFz và 70 zFyyFz
Bài 4:
Cho hình vẽ bên:
1. Kể tên các cặp góc so le trong, các cặp góc đồng vị và các cặp góc trong cùng phía. 2. Tính số đo các cặp góc còn lại, biết 22 60 AB . Lời giải
1. Các cặp góc so le trong: 4A và 23 ; BA và 1B . Các cặp góc đồng vị: 1A và 12 ; BA và 2; B 3A và 34 ; BA và 4B . Các cặp góc trong cùng phía: 4A và 13 ; BA và 2B .
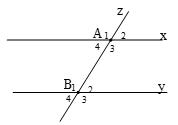
2. 2A kề bù với 1A nên tìm được 12180120AA 31 120 AA (đối đỉnh); 42 60 AA (đối đỉnh). Vì 22 60 AB nên 42 60 AB mà hai góc này ở vị trí so le trong nên theo tính chất ta có hai góc đồng vị bằng nhau. Từ đó, 1133120;120BABA và 44 60 BA .

10
Dạng 2: Nhận biết hai đường thẳng song song. Vận dụng tính số đo góc.
I. Phương pháp giải:
+) Dựa vào tính chất hai góc kề bù, đối đỉnh để chỉ ra hai góc so le trong hoặc hai góc đồng vị bằng nhau hoặc hai góc trong cùng phía bù nhau.
+) Áp dụng tính chất hai góc kề bù, đối đỉnh để lý luận và biến đổi tính góc.
II. Bài toán.
Cho hình vẽ bên. (Hình 1)
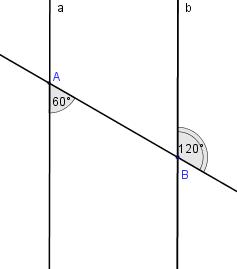
Bài 1:

Hai đường thẳng aa và bb có song song với nhau không? Vì sao?
Lời giải
Hình 1
Từ hình 1, ta có: cMaMNb Mà hai góc này ở vị trí đồng vị nên hai đường thẳng aa và bb song song với nhau (dhnb)
Bài 2:
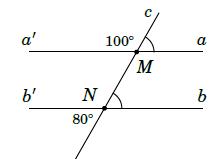
Cho hình vẽ bên. (Hình 2) Đường thẳng x , y có song song với nhau không? Tại sao?
3 2 1 2 1 125°
Lời giải
Ta có: 13 55 MM (2 góc đối đỉnh).
Suy ra 32 55125180 MN
Mà hai góc này ở vị trí hai góc trong cùng phía nên // xy (dhnb)
55° y
x M N
11
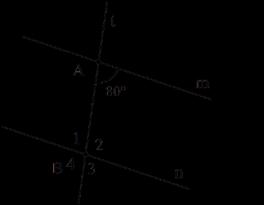
Bài 3:

Cho hình vẽ bên. (Hình 3) Đường thẳng a , b có song song với nhau không? Tại sao?
Lời giải Ta có: 12 180 PP (2 góc kề bù). 121801804040PP 0 11 40 PQ Mà hai góc này ở vị trí đồng vị nên // ab (dhnb)
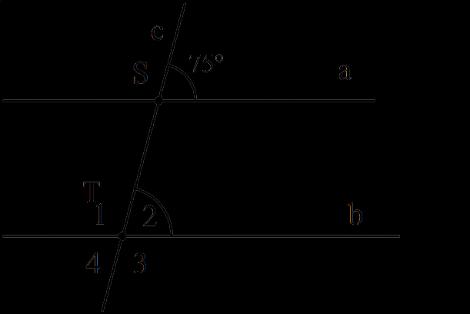
Bài 4:
Cho hình vẽ bên, biết hai đường thẳng a và b song song với nhau. Tính số đo các góc 1234 ,,, TTTT Lời giải Ta có 2 75 TcSa (hai góc đồng vị).
12
b c
Lại có 1T kề bù với 212180105TTT 42 75 TT (đối đỉnh) và 31 75 TT (đối đỉnh) Bài 5: Cho hình vẽ bên, biết hai đường thẳng m và n song song với nhau. Tính số đo các góc 1234 ,,, BBBB a
2 2 1 1 40° 140° Hình 3 Q P
Ta có 1 80 BBAm (hai góc so le trong). Lại có 1B kề bù với 211180120BBB . 42 120 BB (đối đỉnh) và 31 80 BB (đối đỉnh)
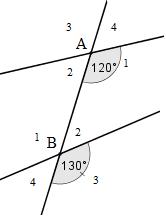
Bài 6:

Cho hình vẽ, biết 1 120 A ; 3 130 B thì hai đường thẳng a và b có song song với nhau không? Muốn // ab thì góc 1A hay 3B phải thay đổi thế nào? Lời giải Có 1A , 3B là hai góc đồng vị Và 13AB (do 120130 ) Vậy hai đường thẳng a và b không song song với nhau Muốn // ab thì góc 1 130 A hoặc 3 120 B
Bài 7:
Cho hình vẽ. Hãy chứng tỏ // ab bằng nhiều cách. Lời giải Có 12 180 AA (2 góc kề bù) Hay 2 60180 A 2 18060120 A
13 Lời giải

14 Tương tự ta có 32 180 BB (2 góc kề bù) Hay 3 120180 B 3 18012060 B Cách
3 1 60 A B . Và 1A ; 3B ở vị trí
// ab . Cách
2 2 120 A B . Và 2A ; 2B ở vị trí
ab . Cách 3: Có 3 2 12060180 A B . Và 2A ; 3B ở vị trí trong cùng phía. Vậy // ab Bài 8: Cho hình vẽ bên. Đường thẳng PQ và NO có song song với nhau không? Tại sao? Lời giải Kẻ tia Ox là tia đối của tia ON Ta có : 180 NOMMOx( 2 góc kề bù) Thay số : 130180 MOx . Suy ra 18013050 MOx Lại có : 110 MOxxOPMOP Suy ra 1105060 xOP Khi đó : 60120180 xOPOPQ Mà hai góc này ở vị trí trong cùng phía nên PQ // Ox hay PQ // NO (dhnb) Bài 9: x 130° 110° 120° P Q O N M
1: Có
so le trong. Vậy
2: Có
đồng vị. Vậy //
Và CAB ; ABD là hai góc trong cùng phía. Vậy // ACBC (dhnb).
Bài 10:
Cho 90 xOy , A là điểm nằm trên tia Ox Vẽ đường thẳng d vuông góc với Ox tại A Lời giải
Ta có 90 xOy Mà dOx tại A. Suy ra 1 90 A Suy ra 1 AxOy
Mà hai góc này ở vị trí đồng vị nên // dOy (dhnb)
Bài 11:
x y
1 A O

d 1

15
Cho hình vẽ. Hãy chứng tỏ // ACBD. Lời giải Có 3080110 ABDABCCBD Lại có 70110180 CABABD
Cho hình vẽ. Tìm trên hình các đường thẳng song song với OC Vì sao? Lời giải Có o90 CODEDO . Và COD ; EDO là hai góc so le trong. Suy ra // OCDE (dhnb) Vẽ // OGDE Ta có COD ; DOG là hai góc kề bù nên oooo 1801809090DOGCOD

16
A B O C D E
A B O C
Lại có DOGGOADOA Hay oo 90140 GOA ooo 1409050 GOA Nên ooo 50130180 OABGOA Mà OAB ; GOA là hai góc trong cùng phía. Nên // ABOG (dhnb) Suy ra // ABOC Vậy // OCDE và // OCAB Bài 12: 140° 130°
140° 130°
D E G
Và BAC ; ACD là hai góc so le trong. Vậy // ABCD BÀI TẬP TỰ LUYỆN Bài 1:


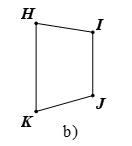
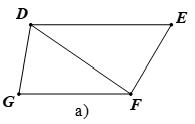
Cho điểm C nằm ngoài đường thẳng b . Vẽ đường thẳng a đi qua C sao cho a song song với b . Lời giải Bài 2: Kể tên các đoạn thẳng song song trong các hình vẽ sau: Lời giải

17
oooooo
Cho hình vẽ. Chứng tỏ rằng // ABCD . Lời giải Có o360 BACBAEEAC Hay ooo 100120360 BAC
360100120360220140 BAC
Do đó o140 BACACD
E
100° 140° 120° C D A
B
b) // .HKIJ
Bài 3:
Cho hình vẽ. Tìm trên hình các đường thẳng song song. Vì sao?
Lời giải
Có o 1 2 110 C C (đối đỉnh)

Có o 1 1 110 A B . Và 1A ; 1B là 2 góc đồng vị. Suy ra // ab
Có o 1 1 110 A C . Và 1A ; 1C là 2 góc đồng vị. Suy ra // ac
Có o 1 1 110 B C . Và 1B ; 1C là 2 góc đồng vị. Suy ra // bc
Bài 4:
Cho hình vẽ. Chứng minh: //// abc . Lời giải
18
// DEGF .
a)
o120 bBABAa . Và
ại có o360 bBCbBAABC Hay ooo 12080360 bBC oooooo 36012080360200160 bBC Do đó o160 bBCBCc 1
C A B
120° 120° 80° 160°
Có
bBA ; BAa là hai góc so le trong. Vậy // ab (1) L
1 2 1 110° 110° 110° c b a
c b a
C B A
Và bBC ; BCc là hai góc so le trong.
Vậy // bc (2)
Từ (1) và (2) suy ra //// abc
Bài 5:
Cho hình vẽ. Biết o60 mAx ; o120 mBy ; o150 BCz . Chứng minh: // // AxByCz . Lời giải
A

y
B
m x C
Có mAx ; BAx là hai góc kề bù. Nên oooo 18018060120BAxmAx
Suy ra o120 yBABAx . Và bBA ; BAa là hai góc so le trong. Suy ra // AxBy (1) Lại có o360 yBCyBAABC Hay ooo 12090360 yBC
z
Do đó o150 yBCBCz
Và yBC ; BCz là hai góc so le trong. Suy ra // ByCz (2)
Từ (1) và (2) suy ra //// AxByCz
19
oooooo 36012090360210150 yBC
CLÍT
A. Lý thuyết
+ Tiên đề Euclid: Qua một điểm ở ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.
Hình 1. Cho điểm M nằm ngoài đường thẳng a .
Ta vẽ đường thẳng b đi qua M sao cho //a b
+ Từ tiên đề Euclid ta suy ra được: Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cũng cắt đường thẳng còn lại.
+ Tính chất hai đường thẳng song song: Nếu một đường thẳng cắt hai đường thẳng song song thì:
* Hai góc so le trong bằng nhau.
* Hai góc đồng vị trong bằng nhau.
+ Nhận xét:
* Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
* Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.
II) CÁC DẠNG TOÁN
I. Phương pháp giải:
Dạng 1: Tính số đo góc
+ Dựa vào tính chất hai đường thẳng song song. Nếu biết số đo của một góc thì tính được số đo của góc kia.
II. Bài toán.
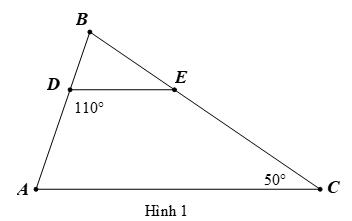
Bài 1:

Cho Hình 1, biết // DEAC , 110 ADE , 50 ACE . Hãy tính số đo các góc BDE và DEB L
1 CHUYÊN ĐỀ: TIÊN ĐỀ
ời giải b a M
Ta có: 180 ADEBDE (hai góc kề bù)
110180 BDE
180110 BDE 70 BDE
Ta có // DEAC suy ra BEDECA (hai góc đồng vị)
Nên 50 BED . Vậy 70 BDE , 50 BED
Cho Hình 2, biết //''xyxy , 65 xBC . Hãy tính số đo các góc ' BCy và ''xCz .
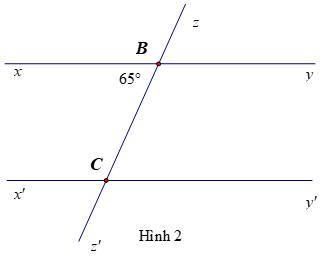
Bài 2:
Lời giải Ta có //''xyxy suy ra xBCBCy (hai góc so le trong)
Nên '65 BCy . Ta lại có: ''' xCzBCy (hai góc đối đỉnh)
Nên ''65xCz . Vậy '65 BCy , ''65xCz
Bài 3:
Cho Hình 3, biết // GxJy , 90 J , 47 IHx . Hãy tính số đo các góc JGH và HIJ
H G J
47° Hình 3
Lời giải
y
x I

2
Ta có: // GxJy và JyGJ
Nên Gx GJ
Nên 90 JGH .
Ta có // GxJy suy ra IHxHIJ (hai góc so le trong)
Nên 47 HIJ . Vậy 90 JGH , 47 HIJ .
Bài 4:
Cho Hình 4, biết // DEAC , 110 ADE , 50 ACE . Hãy tính số đo các góc DAC và DEC . Lời giải
Ta có: 180 ADEBDE (hai góc kề bù) 110180 BDE 180110 BDE 70 BDE
Ta có // DEAC suy ra BDEDAC (hai góc đồng vị)
Nên 70 DAC .
Ta có // DEAC suy ra BEDECA (hai góc đồng vị)
Nên 50 BED
Ta có: 180 BEDDEC (hai góc kề bù) 50180 DEC 18050 DEC 130 DEC . Vậy 70 DAC , 130 DEC .
D

110° E
50°
B A C
3
Cho Hình 5, biết 48 xBA , 48 BCD , 135 BCD .
a) Vì sao // ABCD? b) Hãy tính số đo góc ADC
Bài 5:
y x 135° 48° 48° A B C
Hình 5
Lời giải
a) Ta có 48 xBA , 48 BCD Suy ra xBABCD Mà ; xBABCD là hai góc đồng vị. Nên // ABCD. b) Ta có: 180 yABBAD (hai góc kề bù) 135180 yAB 180135 yAB 45 yAB Ta có // ABCDsuy ra yABADC (hai góc đồng vị) Nên 45 ADC .
Bài 6:
Cho Hình 6, biết 83 xFE , 83 FEH , 76 FGy

4
a) Vì sao // FGEH ? b) Hãy tính số đo góc xHy D
y' x' 83° 83° Hình 6 y x 76° H E G F
a) Ta có 83 xFE , 83 FEH
Suy ra xFEFEH
Mà ; xFEFEH là hai góc so le trong. Nên // FGEH .
b) Ta có: // FGEH nên FGyEHG (hai góc đồng vị)
Nên 76 EHG . Ta có EHGxHy (hai góc đối đỉnh) Nên 76 xHy .
Bài 7:
Cho Hình 7, biết 134 PQM , 76 QMy , 76 PNM . a) Vì sao // QM PN ? b) Hãy tính số đo góc xPz Lời giải
a) Ta có 76 QMy , 76 PNM
Suy ra QMyPNM
Mà ; QMyPNM là hai góc đồng vị. Nên // QM PN . b) Ta có: // QM PN nên PQMxPN (hai góc đồng vị)
Nên 134 xPN

Ta có 180 xPNxPz (hai góc kề bù) 134180 xPz 180134 xPz
z
76° N P
M Q
y x
134° 76° Hình 7
5
ờ
ả
L
i gi
i

6
E
46 xPz Nên 46 xPz Bài 8: Cho Hình 8, biết // AE BD , 90 ABD , 55 AED Hãy tính số đo các góc BAE và BDE . Lời giải + Ta có 90 ABD Suy ra DBAB tại B . Mà // AE BD Nên EAAB tại A Suy ra 90 BAE + Ta có: // AE BD nên ADEEDy (hai góc đồng vị) Nên 55 EDy Ta có 180 EDyEDB (hai góc kề bù) 55180 EDB 18055 EDB 125 EDB Nên 125 EDB Vậy 90 BAE , 125 EDB Hình8 y x 55° B A
D
Bài 9:
Cho Hình 9, biết 90 IHG , 90 FGH , 80 FIH
Hãy tính số đo góc IFG .
Lời giải
+ Ta có 90 FGH
Suy ra FGGH tại G . (1)
+ Ta có 90 IHG
Suy ra IHGH tại H . (2)
Từ (1) và (2) suy ra //FG HI
+ Ta có: //FG HI nên FIHIFx (hai góc so le trong)
Nên 80 IFx . Ta có 180 IFxIFG (hai góc kề bù) 80180 IFG 100 IFG Vậy 100 IFG
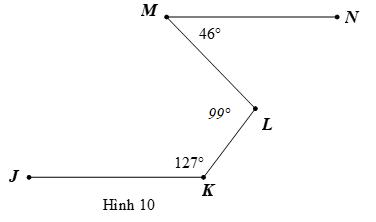
Cho Hình 10, biết // MN KJ , 46 NML , 127 JKL .
Bài 10:
Hãy tính số đo góc MLK Lời giải
x 80° Hình9 H
G F I 46° 127° Hình10
L
M N K J

7
+ Qua L vẽ xy sao cho // xyMN
Suy ra LMNMLx (hai góc so le trong)
Nên 46 MLx .
+ Ta có // xyMN (cách vẽ) Mà // KJMN Nên // xyKJ
Suy ra JKLKLy (hai góc so le trong) Nên 127 KLy . + Ta có 180 KLxKLy (hai góc kề bù) 127180 KLx 53 KLx + Ta có MLKKLxMLx 5346 MLK 99 MLK
Bài 11: Cho Hình 11, biết //AB ED, 118 BAC , 50 CDE . Hãy tính số đo góc ACD . Lời giải
+ Qua C vẽ xy sao cho // xyAB
Suy ra BACACx (hai góc so le trong)
Nên 118 ACx . + Ta có 180 ACxACy (hai góc kề bù) 118180 ACy 62 ACy
M N K J
46° 127° Hình 10
y x
L 50°

A B D E
118° Hình11
C
8
+ Ta có // xyAB
Mà //AB ED
Nên // xy ED
Suy ra EDCDCy (hai góc so le trong)
Nên 50 DCy + Ta có ACDACyDCy 6250 ACD 112 ACD .
Bài 12:
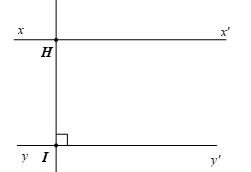
Cho Hình 12, biết //AB FG , 49 ABC , 120 EFG . Hãy tính số đo góc CEF . Lời giải + Qua E vẽ tia Ex sao cho // ExAB
Suy ra CBACEx (hai góc đồng vị) Nên 49 CEx . + Vẽ tia Fy là tia đối của tia FG Suy ra 180 EFGEFy (hai góc kề bù) 120180 EFy 60 EFy + Ta có // ExAB
Mà //AB FG Nên //Ex FG
A

y x 50° B
118° Hình11
9
Suy ra EFyFEx (hai góc so le trong)
D E C Hình12 120° 49° C E F G A B y x Hình 12 120° 49° C E F G A B
+ Ta có CEFCExFEx 4960 CEF 109 CEF .
BÀI TẬP TỰ LUYỆN
Bài 1:

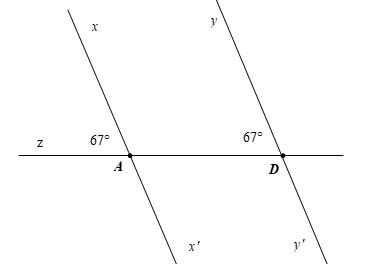
Cho Hình vẽ, biết 67 zAx , 71 zDy . Vì sao '// ' xx yy ?
a) Ta có 67 zAx , 71 zDy
Suy ra zAxzDy
Mà ; zAxzDy là hai góc đồng vị. Nên '// ' xx yy .
Lời giải
Bài 2:
Cho Hình 1, biết 134 ABC , 76 BCy , 76 ADC .
a) Vì sao // BC AD ?
b) Hãy tính số đo góc xAz
Lời giải
a) Ta có 76 BCy , 76 ADC
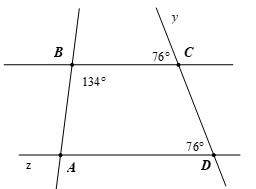
Suy ra BCyADC
Mà ; BCyADC là hai góc đồng vị Nên // BC AD .
10
Nên 60 FEx

11 b) Ta có: // BC AD nên ABCxAD (hai góc đồng vị) Nên
Ta
180
(hai
ề
180134
46
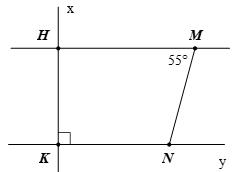
. Bài 3: Cho Hình 2, biết // HM KN , 90 HKN , 55
. Hãy tính số đo các góc
và
Lời
ải +
90
ạ
.
.
(hai
55180 MNK 18055
125
V
y
, 125
134 xAD
có
xADxAz
góc k
bù) 134180 xAz
xAz
xAz
Nên 46 xAz
HMN
KHM
KNM
gi
Ta có
HKN Suy ra KNKH t
i K Mà // HM KN Nên MHHK tại H
Suy ra 90 KHM + Ta có: // HM KN nên HMNMNy (hai góc đồng vị) Nên 55 MNy
Ta có 180 MNyMNK
góc kề bù)
MNK
MNK
ậ
90 KHM
MNK
Bài 4:
Cho Hình 4, biết // MxNy , 50 AMx , 40 ANy . Hãy tính số đo góc MAN .
+ Qua A vẽ tia Aa sao cho // AaMx
Suy ra xMAaAM (hai góc so le trong)
Nên 50 aAM
+ Ta có // AaMx (cách vẽ)
Mà // MxNy Nên // AaNy + Ta có // AaNy
Suy ra aANANy (hai góc so le trong)
Nên 40 aAM . + Ta có MANMAaNAa 5040 MAN 90 MAN .
Lời giải
M a
50° 40° y
A
x Hình4 N
M
x Hình4 N
A
50° 40° y

12
Dạng 2: Chứng minh hai đường thẳng song song, vuông góc.
I. Phương pháp giải:
* Chứng minh hai đường thẳng song song
+ Dựa vào dấu hiệu nhận biết hai đường thẳng song song.

+ Dựa vào tiên đề Euclid.
+ Dựa vào dấu hiệu: cùng vuông góc, cùng song song với đường thẳng thứ ba.
* Chứng minh hai đường thẳng vuông góc
+ Dựa vào dấu hiệu: Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
+ Dựa vào dấu hiệu: Hai đường thẳng cắt nhau trong bốn góc tạo thành có một góc vuông. II. Bài toán.
13
Bài 1: Cho Hình 1, biết 71 dAx , 71 ABy Vì sao // x y x y ? Lời giải + Ta có 71 dAx
, 71 ABy Suy ra dAxABy
Mà ; dAxABy
là hai góc đồng vị. Nên // x y x y
. Bài 2: Hình1 71° d 71° y' y x' x B A
Cho Hình 2, biết 71 xAB , 71 ABy . Vì sao // x y x y ?
Lời giải
+ Ta có 71 xAB , 71 ABy
Suy ra xABABy Mà ; xABABy là hai góc so le trong. Nên // x y x y .
Bài 3: Cho Hình 3, biết x H x I , y H y I . Vì sao // x y x y ?
Lời giải + Ta có x H x I , y H y I . Nên // x y x y .
Bài 4:
Cho Hình 4, biết // x y x y , y H y I , 65 yMz
a) Vì sao x H x I b) Tính số đo của góc xNz . Lời giải a) Ta có // x y x y , y H y I .
y x

x' x B
71°
71° y' y
Hình2
x' x I
A Hình3
y' y
M
65° I N H
H z x'
y' Hình4
14
Nên x H x I .
b) Ta có: // x y x y nên yMzxNz (hai góc đồng vị)
Nên 65 xNz

Bài 5:
Cho Hình 5, biết y H y I , 66 HJK , 66 JKy .
a) Vì sao // x y x y ? b) Vì sao x H x I ? Lời giải
a) Ta có 66 HJK , 66 JKy
Suy ra HJKJKy . Mà ; HJKJKy là hai góc so le trong. Nên // x y x y . b) + Ta có // x y x y , y H y I Nên x H x I
Bài 6:
Cho Hình 6, biết y H y I , 66 aJx , 66 JKy
a) Vì sao // x y x y ? b) Vì sao x H x I ?
x' x I
66° Hình 5 y' y
66°
H J K a 66°
x' x I
H J K
66° Hình6 y' y
15
a) Ta có 66 aJx , 66 JKy
Suy ra aJxJKy . Mà ; aJxJKy là hai góc đồng vị. Nên // x y x y . b) + Ta có // x y x y , y H y I . Nên x H x I . Bài 7: Cho Hình 7, biết 67 xAB , 67 ADC , 113 BCD . a) Vì sao // BC AD ? b) Vì sao //AB DC ? Lời giải a)Ta có 180 BCDBCy (hai góc kề bù) 113180 BCy 67 BCy + Ta có 67 BCy , 67 ADC
Suy ra ADCBCy .
Mà ; ADCBCy là hai góc đồng vị. Nên // BC AD . b) Ta có 67 xAB , 67 ADC
Suy ra ADCxAB
Mà ; ADCxAB là hai góc đồng vị. Nên //AB DC .
y x

B D
C
113° 67° 67° A
Hình7
16 Lời
ả
gi
i
Cho Hình 8, biết 50 xHG , 40 GFy , 90 HGF . Vì sao //Hx Fy ?
+ Vẽ tia Ga sao cho //Ga Hx
Suy ra xHGHGa (hai góc so le trong).
Nên 50 HGa . +Ta có HGFHGaFGa 9050 FGa
Nên 40 FGa . + Ta có 40 FGa , 40 GFy
Suy ra FGaGFy . Mà ; FGaGFy là hai góc so le trong. Nên //Ga Fy + Ta có: //Ga Fy ; //Ga Hx Nên //Hx Fy
Lời giải

17
Bài 8:
F
Bài 9: Cho Hình 9, biết 118 ABC , 112 BAD , 50 ADE . Vì sao // BC DE ? Lời giải + Qua A vẽ đường thẳng xy sao cho // xy BC Hình9 112° 50° 118° B A D C E 50° 40° y x Hình 8
G H a 50° 40° y x Hình 8 F G H
Suy ra xABCBA (hai góc so le trong).
Nên 118 ABx + Ta có 180 BAxBAy (hai góc kề bù) 118180 BAy
Nên 62 BAy +Ta có BADBAyDAy 11262 DAy
Nên 50 DAy . + Ta có 50 ADE , 50 DAy
Suy ra ADEDAy .
Mà ; ADEDAy là hai góc so le trong. Nên // xy DE . + Ta có: // xy DE ; // xy BC Nên // BC DE
Bài 10: Cho Hình 10, biết 99 MLK , 46 NML , 127 JKL Vì sao // MN KJ ? Lời giải + Qua L vẽ xy sao cho // xyMN
Suy ra LMNMLx (hai góc so le trong)
Nên 46 MLx .
+Ta có MLKMLxKLx 9946 KLx
Nên 53 KLx .
118°
y x

112° 50°
C E
B A D
Hình9
18
+ Ta có 180 KLxKLy (hai góc kề bù)
53180 KLy 127 KLy + Ta có 127 KLy , 127 JKL
Suy ra JKLKLy
Mà ; JKLKLy là hai góc so le trong.
Nên // xyKJ .
+ Ta có // xyMN (cách vẽ) Mà // xyKJ Nên // MN KJ Bài 11: Cho Hình 11, biết // IJFG , 45 JIH , 135 HGF . Chứng tỏ IHHG Lời giải + Qua H vẽ xy sao cho // xyIJ
Suy ra JIHIHx (hai góc so le trong)
Nên 45 IHx + Ta có // xy FG
Suy ra FGHGHy (hai góc so le trong)
Nên 135 GHy + Ta có 180 GHxGHy (hai góc kề bù) 135180 GHx
M
46° 127° Hình 10
y x

19
N K J L Hình 11 45° 135° I J H G F y x Hình 11 45° 135° I J H G F

20 45
C E
G
B
x
E F G A B
GHx + Ta có IHGIHxGHx 4545 IHG 90 IHG Nên. IHHG Bài 12: Cho Hình 12, biết 109 CEF , 49 ABC , 120 EFG . Chứng tỏ //AB FG . Lời giải + Qua E vẽ tia Ex sao cho // ExAB Suy ra CBACEx (hai góc đồng vị) Nên 49 CEx . + Ta có CEFCExFEx 10949 FEx 60 FEx + Vẽ tia Fy là tia đối của tia FG Suy ra 180 EFGEFy (hai góc kề bù) 120180 EFy 60 EFy Suy ra EFyFEx Mà ; EFyFEx là hai góc so le trong. Nên //Ex FG Hình12 120° 49°
F
A
y
Hình 12 120° 49° C

21 Mà // ExAB Do đó //AB FG . BÀI TẬP TỰ LUYỆN Bài 1: Cho Hình 4, biết // x y x y , y H y I . Vì sao x H x I . Lời giải Ta có // x y x y Mà y H y I Nên x H x I . Bài 2: Cho Hình 1, biết 134 ABC , 76 BCy , 76 ADC . a) Vì sao // BC AD ? b) Hãy tính số đo góc xAz . Lời giải z 134° 76° Hình 1 y x 76° D A C B

22
a) Ta có 76 BCy , 76 ADC Suy ra BCyADC Mà ; BCyADC là hai góc đồng vị Nên // BC AD . b) Ta có: // BC AD nên ABCxAD (hai góc đồng vị) Nên 134 xAD Ta có 180 xADxAz (hai góc kề bù) 134180 xAz 180134 xAz 46 xAz Nên 46 xAz . Bài 3: Cho Hình 2, biết 50 xCB , 40 BAy , 90 CBA . Vì sao // Cx Ay ? Lời giải + Qua A vẽ tia Aa sao cho // AaBx Suy ra aABxBA (hai góc so le trong) Nên 50 aAB . + Ta có BACBAaCAa 9050 CAa 40 CAa + Ta có 40 CAa , 40 BAy Suy ra CAaBAy Mà ; CAaBAy là hai góc so le trong. 90° 50° 40° y x Hình 3 A B C a 50° 40° y x Hình 3 C A B
Nên // Cy Aa .
+ Ta có: // AaBx (cách vẽ) Mà // Cy Aa Nên // Cx Ay
Bài 4:

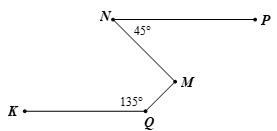
Cho Hình 11, biết // NPKQ , 45 NPM , 135 KQM . Chứng tỏ NMMQ Lời giải + Qua M vẽ xy sao cho // xyNP
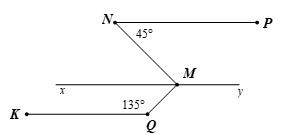
Suy ra PNMNMx (hai góc so le trong) Nên 45 NMx + Ta có // xyNP Mà // KQNP Nên // xy KQ
Suy ra KQMQMy (hai góc so le trong) Nên 135 QMy . + Ta có 180 QMxQMy (hai góc kề bù) 135180 QMx 45 QMx + Ta có NMQNMxQMx 5040 NMQ 90 NMQ Nên NMMQ
23

24
:
A. Lý thuyết
LÍ. CHỨNG MINH ĐỊNH LÍ
1. Định lí: Giả thiết và kết luận của định lí:
Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: “ Nếu … thì …”
Phần giữa từ “nếu” và từ “thì” là giả thiết của định lí.
Phần sau từ “thì” là kết luận của định lí.
2. Thế nào là chứng minh định lí
Chứng minh một định lí là dùng lập luận để từ giả thiết và những khẳng định đúng đã biết để suy ra kết luận của định lí.
B) Các dạng toán
I. Phương pháp giải:
Dạng 1: Xác định giả thiết và kết luận của định lí
Mỗi định lí thường được phát biểu dưới dạng: “ Nếu … thì …”
Phần giữa từ “nếu” và từ “thì” là giả thiết của định lí.
Phần sau từ “thì” là kết luận của định lí.
II. Bài toán.
Bài 1:

Hãy nêu giả thiết và kết luận của định lí sau: “ Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”
Lời giải
Giải thiết là: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba Kết luận là: chúng song song với nhau.
Bài 2:
Hãy phát biểu phần còn thiếu của giả thiết trong định lí sau: “ Hai góc ... thì bằng nhau”
Lời giải Phần thiếu là: đối đỉnh
Bài 3:
Hãy phát biểu phần còn thiếu của kết luận trong định lí sau: “ Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì ... ”
1
CHUYÊN ĐỀ
ĐỊNH
Lời giải
Phần thiếu là: chúng song song với nhau.
Bài 4:
Vẽ hình, ghi giả thiết và kết luận của định lí : “ Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau”
a b
Lời giải
GT c cắt a và b ; // ab KL 11 AB
Bài 5:
Hãy phát biểu định lí được diễn tả bằng hình vẽ sau:
Lời giải
c a // b
A

1
1 B
Nếu đường thẳng c cắt hai đường thẳng phân biệt ; ab . Và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì a và b song song với nhau.
2
a b
c 1 1 D
C
Bài 6:
Vẽ hình, ghi giả thiết và kết luận của định lí : “ Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông ” Lời giải GT xOy và O yz kề bù Om là tia phân giác của xOy On là tia phân giác của yOz KL 090 mOn
Bài 8: Định lí “ Hai góc đối đỉnh thì bằng nhau” có định lí đảo không ? Vẽ hình minh họa. Lời giải
a b
A G
3 2 1
4 3 2 1 B
Bài 7: Phần giả thiết: {};{} caAcbB 12 ,180 AB (tham khảo hình vẽ) là của định lý nào ? Lời giải Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc trong cùng phía bù nhau thì hai đường thẳng đó song song.
c 4

3
z y m x n O
H I K
Định lí “ Hai góc đối đỉnh thì bằng nhau” không có định lí đảo .
Hai góc bằng nhau nhưng không đối đỉnh.
Bài 9:
Phát biểu định lí đảo của định lí sau: “ Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song nhau”
Lời giải Định lí đảo “ Hai đường thẳng phân biệt song song nhau thì chúng cùng vuông góc với đường thẳng thứ ba”
Bài 10:

Cho hình vẽ với GT và LK sau. Có thể rút ra định lí nào. Lời giải GT // ab, ; caAcbB
Am là phân giác của BAa Bn là phân giác của ABb
KL AmBn Định lí: Nếu một đường thẳng cắt hai đường thẳng song song thì góc tạo bỡi hai tia phân giác của hai góc trong cùng phía là một góc vuông.
4
a
b c n m C B A
Bài 11:
Cho định lí: “Qua một điểm nằm ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó”, kết luận của định lí ứng với hình vẽ dưới đây là:
Lời giải Kết luận là: b đi qua A
Cho định lí: “Nếu một góc có hai cạnh là hai tia phân giác của hai góc kề bù thì đó là góc vuông”, kết luận của định lí ứng với hình vẽ dưới đây là:
Bài 12:
b A x
a

m t z y O
Lời giải Kết luận là: 90 zOt
BÀI TẬP TỰ LUYỆN
Bài 1: Hãy chỉ ra giả thiết và kết luận của định lí sau: “ Nếu M là trung điểm của đoạn thẳng AB thì 2 AB AMMB
Lời giải Giải thiết là: M là trung điểm của đoạn thẳng AB
Kết luận là: 2 AB AMMB
Bài 2: Điền vào chỗ trống để được định lí đúng: Nếu Ot là tia phân giác của xOy thì...
Lời giải Nếu Ot là tia phân giác của xOy thì O xOtyt
5
Bài 1:
Xác định giả thiết và kết luận của định lý sau:
“ Nếu hai góc xOy và ''xOy có một góc nhọn, một góc tù và //''OxOx , //''OyOy thì ''180o xOyxOy ”
Lời giải Giả thiết: hai góc xOy và ''xOy có một góc nhọn, một góc tù và //''OxOx , //''OyOy Kết luận: ''180o xOyxOy
Bài 3:
Cho hình vẽ với GT và LK sau. Có thể rút ra định lí nào. GT // ab, ; caAcbB
a b
c m n
A

Am là phân giác của cAa Bn là phân giác của nBb KL AmBn Lời giải Định lí: Nếu một đường thẳng cắt hai đường thẳng song song thì góc tạo bỡi hai đường phân giác của hai góc ngoài cùng phía là một góc vuông.
C B
6
minh định lí
I. Phương pháp giải:
Chứng minh một định lí là dùng lập luận để từ giả thiết và những khẳng định đúng đã biết để suy ra kết luận của định lí.
II. Bài toán.
Chứng minh định lí là gì ?
Bài 1:

Lời giải
Chứng minh một định lí là dùng lập luận để từ giả thiết và những khẳng định đúng đã biết để suy ra kết luận của định lí.
Bài 2:
Chọn đáp án đúng nhất trong các phát biểu sau: Khi chứng minh một định lí người ta cần:
a) Chứng minh định lí đó đúng trong một trường hợp cụ thể của giả thiết.
b) Chứng minh định lí đó đúng trong hai trường hợp cụ thể của giả thiết.
c) Chứng minh định lí đó đúng trong mọi trường hợp có thể xảy ra của giả thiết.
d) Chứng minh định lí đó đúng trong vài trường hợp cụ thể của giả thiết.
Lời giải
c) Chứng minh định lí đó đúng trong mọi trường hợp có thể xảy ra của giả thiết.
Bài 3:
Phát biểu sau có phải là một định lí . “Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia”
Lời giải
Không
Bài 4:
Diễn đạt bằng lời định lí sau: a
7
Dạng 2: Chứng
b
1
I
c
1
H
Lời giải
Nếu hai đường thẳng bị một đường thẳng thứ ba cắt và chúng tạo thanh một cặp góc trong cùng phai bù nhau thì hai đường thẳng đó song song với nhau
Bài 5:
Hãy sắp xếp các ý sau để hoàn thiện bài toán chứng minh định lí “ Hai góc đối đỉnh thì bằng nhau.
1/ Và 32 180o OO ( vì kề bù)
2/ Vậy 13 OO
3/ Có: 12 180o OO ( vì kề bù)
4/ Suy ra : 1232 OOOO
3/ Có: 12 180o OO ( vì kề bù)
1/ Và 32 180o OO ( vì kề bù)
4/ Suy ra : 1232 OOOO
2/ Vậy 13 OO
Lời giải
b a
4 3 2 O1
Bài 6:

Cho AD là tia phân giác của BAC . Vẽ BE song song với AD , EBA và BAD là hai góc so le trong. Chứng minh rằng EBADAC
Lời giải
Chứng minh: Có: 1 DACBAD ( vì AD là tia phân giác của BAC ) 2 EBABAD ( vì hai góc so le trong, // BEAD )
8
B A C E
D
Từ
Bài 7:
Cho hình vẽ biết DABE và ACBCBF .
Chứng minh rằng ABGF
Lời giải
Có ACBCBF
Và ; ACBCBF có vị trí so le trong.
Do đó: // EDGF
Lại có DABE
Vậy ABGF
Bài 8:

Ghi giả thiết kết luận và chứng minh định lý “ Hai góc cùng phụ với một góc thứ ba thì bằng nhau”
Lưu ý hai góc phụ nhau có tổng số đo bằng 090
Lời giải GT 090 AC , 090 BC
KL AB
Chứng minh: Ta có 90o AC 90o BC
Suy ra ACBC
Do đó AB
Vậy “Hai góc cùng phụ với một góc thứ ba thì bằng nhau”
9
(1) và (2) suy ra EBADAC
D G F
B E
A C
minh định lí sau: “ Hai tia phân giác của hai góc đối đỉnh là hai tia đối nhau”

10
Chứng
L
Ta
14 11 ''''' 22 tOtOxOyOxOyxOyxOy 111'''' 222 xOyxOyxOyxOy ( '' xOyxOy vì đối đỉnh) 1'''' 2 xOyxOyxOyxOy 00 1 .360180 2 Vậy
'''
Lờ
i GT ,'''
//''
//''
KL '''
x' y' x y 2 1 2 1 O' O x y t 4 3 2 1 t' y' x' O
Bài 9:
ời giải
có:
Ot và ' Ot là hai tia đối nhau Bài 10: Chứng minh rằng nêu hai góc nhọn ,''' xOyxOy có //''OxOx và //''OyOy thì
xOyxOy
i giả
xOyxOy nhọn
OxOx
OyOy
xOyxOy
Chứng minh: Vẽ tia 'OO , ta có:
Bài 11: Chứng minh rằng: Nếu ba điểm A,B,C thẳng hàng và A không nằm giữa B và C thì khoảng cách từ điểm A đến trung điểm M của đoạn thẳng BC bằng nửa tổng của hai đoạn thẳng AB và AC, tức là 2 ABAC AM
Lời giải GT Ba điểm A,B,C thẳng hàng và A không nằm giữa B và C M là trung điểm của đoạn thẳng BC
Vì điểm A không nằm giữa hai điểm B và C nên có hai trường hợp: Trường hợp 1: điểm B nằm giữa hai điểm A và C

11
11 'OO
( vì 11 ,'OO đồng vị , //''OxOx ) 22 'OO ( vì 22 ,'OO đồng vị , //''OyOy ) Suy ra 1212 ''OOOO Vậy '''xOyxOy
M C A B M A B C
KL 2 ABAC AM
Khi đó BCACAB
Và AMABBM
2 BC AMAB ( Vì M là trung điểm của BC ) 2 ACAB AMAB 2 ABAC AM
Trường hợp 2: điểm C nằm giữa hai điểm A và B
Bài 12:

Cho hai góc kề bù xOy và O yz . Gọi Ot là tia phân giác của xOy . Trong góc O yz vẽ tia ' Ot vuông góc với tia Ot . Chứng minh rằng ' Ot là tia phân giác của O yz Lời giải
GT xOy và O yz kề bù. Ot là tia phân giác của xOy Trong góc O yz vẽ tia ' Ot vuông góc với tia Ot . KL Chứng minh rằng ' Ot là tia phân giác của O yz Có
Và xOttOy
( vì Ot là tia phân giác của xOy ) Suy ra 'O' tOzyt Vậy ' Ot là tia phân giác của O yz
12 Khi đó BCABAC
Và AMACCM 2 BC AMAC ( Vì M là trung điểm của BC ) 2 ABAC AMAC 2 ABAC AM Vậy ta có điều phải chứng minh.
'90o xOttOz '90o tOyyOt
x y t' t z O
Bài 1: Phát biểu định lí đảo của định lí: “ Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông”
Lời giải Góc tạo bỡi hai tia phân giác của hai góc kề nhau là góc vuông thì hai góc đó là hai góc kề bù.
Bài 2: Hãy sắp xếp các ý sau để hoàn thiện bài toán chứng minh định lí “ Góc tạo bỡi hai tia phân giác của hai góc kề bù là một góc vuông” 1/ Do đó MON90o

13 BÀI TẬP TỰ LUYỆN
4/ AOBBOCAOBBOC
180
o o L
Sắp
(
4/ AOBBOCAOBBOC180 BOMBON90 2222 o o 1/
o C A B O N M
2/ AOB BOM 2
(vì OM là tia phân giác của AOB) 3/ BOC BON 2
(Vì ON là tia phân giác của BOC)
BOMBON 222
90 2
ời giải
xếp 2/ AOB BOM 2
vì OM là tia phân giác của AOB) 3/ BOC BON 2
( vì ON là tia phân giác của BOC)
Do đó MON90
Bài 3:
Hãy vẽ hình nêu giả thiết và kết luận và chứng minh bài toán sau: “ Cho AD là tia phân giác của BAC . Gọi EAG là góc đối đỉnh của BAD Chứng minh rằng DACEAG ”
Lời giải GT AD là tia phân giác của BAC . EAG đối đỉnh với BAD KL DACEAG Chứng minh: Có: 1 DACBAD ( vì AD là tia phân giác của BAC ) 2 EAGBAD ( vì hai góc đối đỉnh) Từ (1) và (2) suy ra DACEAG
Bài 4: Chứng minh rằng nêu hai góc tù ,''' xOyxOy có //''OxOx và //''OyOy thì '''xOyxOy
Lời giải GT ,''' xOyxOy tù //''OxOx //''OyOy KL '''xOyxOy Vẽ tia 'OO , ta có: 11 'OO ( vì 11 ,'OO đồng vị , //''OxOx ) 22 'OO ( vì 22 ,'OO đồng vị , //''OyOy ) Suy ra 1212 ''OOOO Vậy '''xOyxOy

14
G B C A E D
I. LÍ THUYẾT TRỌNG TÂM
1. Định lí tổng ba góc của một tam giác Tổng ba góc của một tam giác bằng 180o .
ABC có 180 ABC
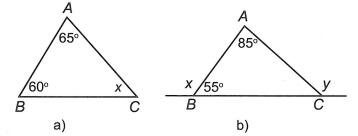
2. Áp dụng vào tam giác vuông Định nghĩa: Tam giác vuông là tam giác có một góc vuông. Định lý: Trong một tam giác vuông, hai góc nhọn phụ nhau. Tam giác ABC vuông tại A nên 90 BC Khi đó, hai góc nhọn được gọi là phụ nhau.
ABC vuông tại A 90 BC
3. Góc ngoài của tam giác Định nghĩa: Góc ngoài của tam giác là góc kề bù với một góc của tam giác ấy. Tính chất: Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.
ABC có ACx là góc ngoài đỉnh C ACxAB
II. CÁC DẠNG BÀI TẬP

Dạng 1: Tính số đo của một góc, so sánh các góc
I. Phương pháp giải:
* Lập các đẳng thức thể hiện:
+ Tổng ba góc của tam giác bằng 180 .
+ Trong tam giác vuông, hai góc nhọn phụ nhau.
+ Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó.
* Sau đó tính số đo góc phải tìm.
II. Bài toán.
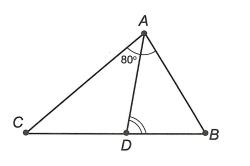
Ví dụ: Tính số đo x, y trong các hình vẽ sau: Hướng dẫn giải
1
Chuyên đề: TỔNG CÁC GÓC TRONG MỘT TAM GIÁC
A B C B
C x
A
B A C

2
Xét ABC có 180 ABC
L
xB .
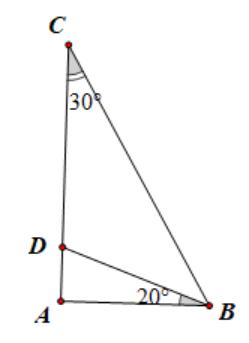
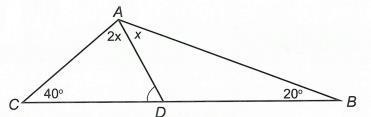
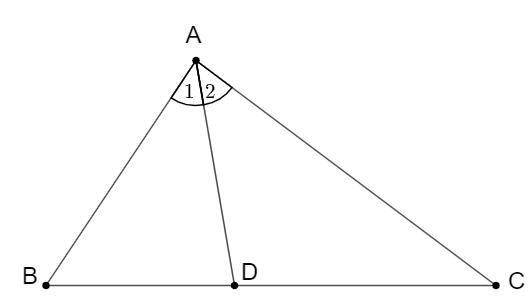
a ADB . Lời giải a) Xét ∆ABC có 180 ABC . Theo giả thiết 80 A nên 100 BC Mặt khác 20 BC (giả thiết). Suy ra: 10020 60 2 B 20602040 CB b) Do AD là tia phân giác góc A nên 11 .8040 22 BADDACA . Xét ∆ACD có ADB là góc ngoài đỉnh D nên 404080 ADBDACACD . Bài 2: Cho ∆ABC có 20,40BC a) Tam giác ABC là tam giác gì? b) Gọi AD là tia nằm giữa hai tia AB và AC Biết 2. CADBAD Tính
ố đo
a CDA.
a)
6560180 C 180656055 C b) Xét ∆ABC có y là góc ngoài tại đỉnh C. Suy ra 8555140 yAB
ại có 180 xB (hai góc kề bù). Suy ra 18018055125
Bài 1: Cho tam giác ABC có 80 A
và 20 BC a) Tính số đo các góc B, C của ∆ABC. b) Gọi AD là tia phân giác của A . Tính số đo củ
s
củ
Bài 4:

Cho tam giác ABC vuông tại B. Kết luận nào sau đây là sai?
ABC
3 Lời giải a) Xét ∆ABC có 180 ABC 1801802040120ABC . Do 90 A nên tam giác ABC là tam giác có một góc tù. b) Theo giả thiết, ta có 2. CADBAD 11111 .12040 212333 BADBADBAD BADA CADBADCADA Xét ∆ADB có ADC là góc ngoài đỉnh D nên 402060 ADCBADABDADC Bài 3: Tam giác ABC có số đo 75,45AB
. Góc C có số đo bằng A. 90 C . B. 60 C . C. 45 C . D. 75 C . Lời giải Xét ∆ABC có 180180180754560ABCCAB .
A. 90
. B. 90 AC . C. 90 BC . D. 90 CA . Lời giải Vì tam giác ABC vuông tại B nên 90 B (A đúng); 90 AC (B và D đúng). C. 90 BC sai vì 90 B nên 90 BC . Bài 5: Cho tam giác MNP có 80 M . Biết 40 NP . Số đo của N bằng A. 75 N . B. 45 N . C. 70 N D. 60 N Lời giải
Kết luận nào sau đây là đúng?
A. Một tam giác chỉ có tối đa hai góc nhọn.
B. Một tam giác chỉ có nhiều nhất một góc tù.
C. Trong một tam giác, có ít nhất hai góc có số đo nhỏ hơn 60°.
D. Trong một tam giác, số đo của mỗi góc luôn nhỏ hơn tổng số đo các góc còn lại. Lời giải

A. Sai vì luôn tồn tại tam giác có ba góc nhọn. Ví dụ tam giác có ba góc bằng 60°
B. Đúng. Giả sử tam giác có nhiều hơn 1 góc tù. Khi đó tổng ba góc trong tam giác lớn hơn 180° (mâu thuẫn với định lí tổng 3 góc trong tam giác).Vậy trong tam giác có nhiều nhất một góc tù.
C. Sai. Thật vậy xét tam giác ABC có 60,60,60ABC. Khi đó 180 ABC (mâu thuẫn với định lí tổng 3 góc trong tam giác).
D. Sai. Thậy vậy, xét ∆ABC có A tù. Khi đó góc ngoài 1A tại A là góc nhọn. Ta có 1ABCA (mâu thuẫn vì góc tù luôn lớn hơn góc nhọn).
4 Xét ∆MNP có 18018018080100MNPNPM . Mặt khác 40 NP . Suy ra 10040 70 2 N . Bài
6:
Bài 7: Cho tam giác ABC có 75 A và 2. BC . Số đo của góc C bằng A. 70 C B. 35 C C. 40 C . D. 50 C . Lời giải ∆ABC có 18018018075105ABCBCA . Mặt khác 2. BC nên 2105310535 CCCC


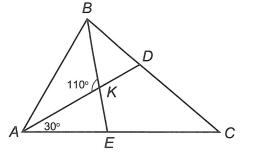
5
b)
. Lời giải a) Xét ∆ABC có 18018018075105ABCBCA . Mà 15 BC (giả thiết) nên 10515 60,1056045 2 BC b) Do BD là tia phân giác góc ABC nên 11 .6030 22 ABDDBCABC Xét ∆BCD có ADB là góc ngoài đỉnh D nên 304575 ADBDBCDCB Bài 9: Cho tam giác ABC có AD, BE lần lượt là tia phân giác trong các góc ,; ABDBCECA Biết AD cắt BE tại K và 110,30AKBKAC . Tính số đo các góc A, B, C của tam giác ABC. Lời giải Ta có 30 KAC Do AK là phân giác của BAC nên 30 KABKAC và 2.2.3060BACKAC Xét ∆ABK có 180301101801803011040KABKBAAKBKBAKBA Mà BK là phân giác của ABC nên 2.2.4080ABCABK . Xét ∆ABC có 1806080180180608040ABCCC . Vậy ∆ABC có 60,80,40ABC
Bài 8: Cho tam giác ABC có 75 A . Biết góc B có số đo lớn hơn số đo góc C là 15o . a) Tính số đo các góc B và C của tam giác ABC.
Gọi BD là tia phân giác của ABC với DAC
. Tính số đo của ADB

6 Bài 10:
A.
.
.
Lờ
Xét
a)
nên
BAC b)
ả thiết ::2:7:1
ABC ABC . Áp
ụng
chất dãy tỉ số bằng
ABCABC
.
t :3:2 32 AC AC . Áp
ụng
chất
ỉ số
ằ
Suy
3.2163;2.2142AC Bài 11: Tính số đo , xy trong hình vẽ dưới đây Lời giải Hình 1: Ta có: 12035180 x (định lý tổng ba góc trong một tam giác) 18012035 x 25 x . Vậy 25 x Hình 2: Hình2 60° y 70° Hình1 x 35° 120°
Cho tam giác ABC. Tính số đo các góc còn lại của tam giác biết
96 A và 32 C
B. ::2:7:1ABC
C. 75 B và :3:2AC
i giải
∆ABC có 180 ABC
Có 96,32AC
180180963252
Theo gi
271
d
tính
nhau, ta có: 180 18 27127110
Suy ra 2.1836;7.18126;1.1818ABC
c) Do 75 B nên ta có 18075105 AC Từ giả thiế
d
tính
dãy t
b
ng nhau, ta có: 105 21 32325 ACAC
ra
Ta có: 7060180 y (định lý tổng ba góc trong một tam giác) 1807060 y 50 y . Vậy 50 y
Bài 12:
Tính số đo x trong hình vẽ dưới đây
Cách 1:
Lời giải

x 55°
Ta có: 9055180 x (định lý tổng ba góc trong một tam giác) 1809055 x 35 x . Vậy 35 x
Cách 2:
Ta có 5590 x (trong tam giác vuông hai góc nhọn phụ nhau) 9055 x 35 x . Vậy 35 x
90° x 65°
Bài 13: Tính số đo x trong hình vẽ dưới đây Lời giải Ta có: 7065 x (góc ngoài của tam giác bằng tổng hai góc trong không kề với nó) 135 x . Vậy 135 x
x x
70° Hình 1
x
72° Hình2
x x Hình3
105° y x 40°
7
Bài 14: Tính số đo , xy trong hình vẽ dưới đây Lời giải
Hình 1:

Ta có: 72180 xx(định lý tổng ba góc trong một tam giác) 218072 x 2108 x 54 x . Vậy 54 x
Hình 2:
Ta có: 180 xxx (định lý tổng ba góc trong một tam giác) 3180 x 60 x . Vậy 60 x
Hình 3:
Ta có: 180105 x (hai góc kề bù) 75 x . Vậy 75 x Ta có: 4072180 y (định lý tổng ba góc trong một tam giác) 1807040 y 65 y . Vậy 65 y Bài 15: Tính số đo , xy trong hình vẽ sau: Biết 22 BAD và 90, ABD
8
Lời giải Hình 1 Xét ABD có 90, ABD 90 BADADB (tính chất tam giác vuông) 2290 ADB 9022 ADB 68 ADB Ta lại có 180112ADCADBADC . Trong ADC ta có 180 ADCDACACD . Mà 112218034DACACDxxx Hình 2 Ta có 180 EHFFHG (hai góc kề bù) 80180 EHF 18080 EHF 100 EHF Xét EHF có: 180 EHFFEHEFH (định lý tổng ba góc trong một tam giác) 10030180 FEH 50 FEH 50 x Ta lại có 80 yFGm (góc ngoài của tam giác). x x A B C D m y x 135° 80° 30° E F H G

9 80135 y 13580 y 55 y Bài 16: Cho hình vẽ. Chứng minh rằng: BCCD Lời giải Xét ABC có 90, BAC 90 ABCACB (tính chất tam giác vuông) 5090 ACB 9050 ACB 40 ACB Xét DEC có 90 DEC . 90 CDEDCE (tính chất tam giác vuông) 4090 DCE 9040 DCE 50 DCE Lại có ACEACBBCDDCE Mặt khác o180 ACE o 1804050oo BCD o90 BCD Hay BCCD Bài 17: Tính các góc của ABC , biết: 18 AB và 18 BC Lời giải Xét ABC có 1818 BCBC . Mà 181818ABAC 36 AC 36 AC Lại có: 180 ABC 3618180 CCC 3126 C 42 C 1842 B 60 B 78 A Bài 18: Tính các góc của tam giác ABC biết: a) 345 ABC . b) 26 ABC . 40° 50° C A E B D

10 Lời giải a) 345 ABC Ta có 35 , 34544 ABC ABCB . Mà 35 1801806045,75 44 ABCBBBBAC . b) 26 ABC . Ta có 266,3 ABCACBC Mà 1806318018108,54 ABCCCCCAB . Bài 19: Cho tam giác ABC , tia phân giác AD của góc A cắt BC tại D . Tính góc ADB biết 040 BC Lời giải Ta có 0180 BACBC (định lý tổng 3 góc của một tam giác) 0180 BACBC Vì AD là tia phân giác của góc BAC nên 00 12 1111 18090 2222 AAABCBC . Ta lại có 0 1 180 ABADB (định lý tổng 3 góc của một tam giác) 0000 1 111 1801809090 222 ADBABBCBBC 000 1 90.4070 2 Bài 20: Cho MNP . Tính các góc của tam giác biết a) 324 MNP . b) 2;36NMPM . Lời giải a) Áp dụng định lí tổng 3 góc trong một tam giác ta có:

11
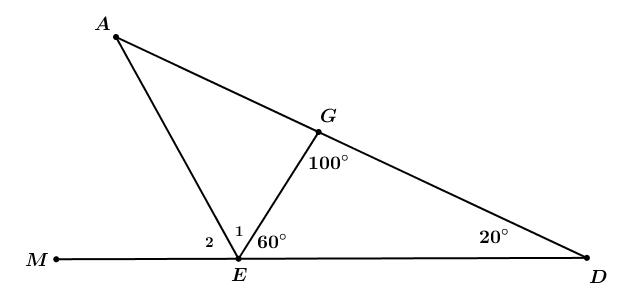
tại E cắt DG tại A . Tính DAE Lời giải a) Từ ::1:3:5DEG suy ra: 135 DEG mà 180 DEG ( tổng 3 góc trong một tam giác) Áp dụng tính chất của dãy tỉ số bằng nhau ta được: 180 20 1351359 DEGDEG
180 MNP Áp dụng tính chất của dãy tỉ số bằng nhau ta được: 180 20 3243249 MNPMNP 2060; 3 M M 2040; 2 N N 2080 4 P P . b) Ta có 2;36NMPM 2;36NMPM Áp dụng định lí tổng 3 góc trong một tam giác ta có: 180 MNP 236180MMM 436180 M 4144 M 36 M 22.3672;363672NMP Bài 21: Cho DEG biết ::1:3:5DEG . a) Tính các góc của tam giác DEG . b) Tia phân giác ngoài

12 2020 1 D D 2060 3 E E 20100 5 G G . b) Ta có 180 MEGGED 60180 MEG 120 MEG 12 120 EE (mà EA là phân giác ngoài tại E nên 12EE ) 1 2120 E 12 60 EE Ta có 2 EAD 6020 6020 40 A A A BÀI TẬP TỰ LUYỆN Bài 1: Tính số đo , xy trong hình vẽ dưới đây Lời giải Xét H1: Ta có: 12535180 x (định lý tổng ba góc trong một tam giác) 18012535 x 20 x . Vậy 20 x Xét H2: Ta có: 5565180 y (định lý tổng ba góc trong một tam giác) 1805565 y 60 y . Vậy 60 y Bài 2: Hình1 35° 125° x
Tính số đo , xy trong hình vẽ dưới đây
Lời giải

Hình 1:
Ta có: 18040 x (hai góc kề bù) 140 x .
Vậy 140 x
Ta có: 6040 y (góc ngoài của tam giác bằng tổng hai góc trong không kề với nó) 100 y .
Vậy 100 y
Hình 2:
Ta có: 7040 x (góc ngoài của tam giác bằng tổng hai góc trong không kề với nó) 110 x
Vậy 110 x
Ta có: 11040180 y (định lý tổng ba góc trong một tam giác) 18011040 y 30 y .
Vậy 30 y Bài 3:
13
Cho MNP . Tính các góc của tam giác biết a) 53;7415 MNMN . b) ;23 MNPMN Lời giải a) 74 53 352120 MNMN MN , áp dụng tính chất của dãy tỉ số bằng nhau ta được: 747415 15 212021201 MNMN 7 1545 21 M M 4 1575 20 N N Hình1 x 40° y 60° Hình2 y x 40° 70° 40° B A D C

14 -
,
: 180
4575180
120180
60 P b) ;23
-
, áp
ụng
180
180 PP
2180 P 90 P
90
Ta
23 32 MN MN , áp
ụng
ất củ
ỉ
Xét MNP
áp dụng định lý tổng 3 góc trong một tam giác ta được
MNP
P
P
MNPMN
Xét MNP
d
định lý tổng 3 góc trong một tam giác ta được:
MNP
MN
có:
d
tính ch
a dãy t
số bằng nhau ta được: 90 18 32325 MNMN
1854 3 M M 1836 2 N N Bài 4: Cho tam giác ABC có góc ngoài tại đỉnh C có số đo bằng 120 và 23AB . a) Tính các góc ,, ABC b) Hai tia phân giác của góc A và B cắt nhau tại I . Tính góc BIA. Lời giải a) Tính các góc ,, ABC . Ta có góc ngoài tại đỉnh C có số đo bằng 120 nên 1206060ACmACBC . Ta lại có 3 23 2 ABAB . x y m I B A C
b) Hai tia phân giác của góc A và B cắt nhau tại I . Tính góc BIA
Do tia Ax là tia phân giác của góc A 1 3636 2 BAxABAI
Do

15 Mà 3 180601804872
ABCBBBA
2
.
tia By là tia phân giác của góc B 1 2424 2 ABxBABI Ta lại có 1801803624120ABIBAIAIBAIB . Dạng 2: Các bài toán chứng minh góc
Phương pháp giải:
Sử dụng linh hoạt các tính chất về góc của một tam giác, góc ngoài tại một đỉnh hay tính chất tia phân giác của góc
Bước 1. Áp dụng tính chất tổng ba góc trong tam giác, tính góc trong yêu cầu của bài toán. Bước 2. Kết hợp tính chất đường phân giác để chứng minh hệ thức. Ví dụ: Cho tam giác MNP. Các đường phân giác trong các góc M, P cắt nhau tại I. Chứng minh rằng: 90 2 MNP MIP Hướng dẫn giải Xét ∆MIP có 180 MIPIMPIPM 180 MIPIMPIPM Lại có: 1 2 IMPNMP (do MI là phân giác của NMP ).

16
1 2 IPMNPM (do PI là phân giác của NPM ). Suy ra 1 180. 2 MIPNMPNPM . (1) Mặt khác, xét ∆MNP có 180 MNPNMPNPM 180 NMPNPMMNP (2) Thế (2) vào (1), ta được
1 180.180 2 MIPMNP 1 18090. 2 MIPMNP 90 2 MNP MIP (điều phải chứng minh)
Bài 1:

Cho tam giác ABC vuông tại A và AHBCHBC . a) Chứng minh BAHBCA b) Tia phân giác của CAH cắt CH tại K. Chứng minh AKBBAK Lời giải a) Xét ∆ABC có 9090BACABCACB Xét ∆ABH có 9090AHBABHBAH . Suy ra 90 ABCACBABHBAH ACBBAH (điều phải chứng minh). b) Ta có AK là tia phân giác của CAH nên 1 2 CAKKAHCAH . Mà ACBBAH (chứng minh câu a) nên suy ra ACBCAKBAHKAH ACBCAKBAK (1). Mặt khác AKB là góc ngoài đỉnh K của ∆AKC nên AKBACKCAK hay AKBACBCAK (2) Từ (1) và (2) ta có AKBBAK (điều phải chứng minh)
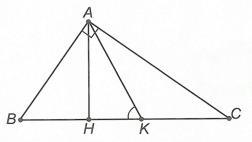
Bài 2:
Cho tam giác ABC vuông tại A . Kẻ AH vuông góc với BC HBC . Các tia phân giác góc ABC và góc HAC cắt nhau tại I. Chứng minh rằng 90 AIB .
Lời giải
Xét ∆ABC vuông tại A có 90 ABCACB . (1) Xét ∆AHC vuông tại H có 90 HACACH. (2) Từ (1) và (2), ta có 90 HACACHABCACBHACABC .
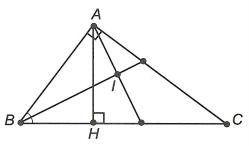
17
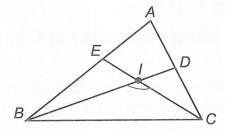
Bài 3: Cho tam giác ABC có BD , CE lần lượt là tia phân giác các góc B, C. Gọi I là giao điểm của BD và CE. a) Chứng minh rằng 90 2 A BIC

18
1
11 22
.
1801809090
Lại có
2 ABIABC
(do BI là phân giác của ABC ); 1 2 HAIHAC
(do AI là phân giác của HAC Suy ra
ABIHAIABCHACHAC
(do HACABC
). Xét ∆ABI có: 90 ABIIABABIIAHHABHACHABBAC
Mà 180 ABIIABAIB
. Suy ra
AIBABIIAB
(điều phải chứng minh).
1 2 IBAIBCB (do
). Xét ∆IBC có 180 BICIBCICB. Suy ra 111 180180180 222 BICIBCICBBCBC (1) Xét ∆ABC có 180180 ABCBCA (2) Thế (2) vào (1) ta có: 111 1801801809090 222 BICAAA (điều phải chứng minh). b) Từ chứng minh câu a, ta có: 11 9090.60120 22 BICBAC . Mà ta có 180 BIEBIC (hai góc kề bù). Suy ra 18018012060BIEBIC . c) Do BAC có số đo là trung bình cộng số đo của ABC và ACB nên
. b) Biết 60 BAC . Tính số đo của BIE . c) Tính số đo của BIC biết số đo góc BAC là trung bình cộng của hai góc , ABCACB . Lời giải a) Ta có
BI là tia phân giác B ), 1 2 ICAICBC
(do CI là tia phân giác C
Áp dụng chứng minh ở ý a ta có: 60 9090120 22 A BIC .
Bài 4:
Cho tam giác ABC và đường cao AH HBC . Biết rằng BAHBCA .
a) Chứng minh rằng tam giác ABC là tam giác vuông.
b) Biết rằng số đo góc ABC bằng trung bình cộng của hai góc , BACACB . Tính số đo các góc của tam giác ABC.
Lời giải
a) Xét ∆AHC vuông tại H có 90 HACHCA (1)
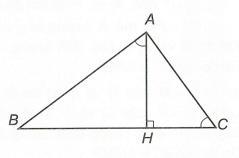
Theo giả thiết, ta có BAHBCA hya HABHCA
Theo (1), ta có: 9090 HACHABBACABAC
ậy tam giác ABC vuông

19 1 2 BACABCACB hay 2. BCA
Mà 180 ABC nên 180 3.18060 3 AA .
V
tại A. b) Do số đo góc ABC bằng trung bình cộng của hai góc BAC , ACB nên ta có 90 22 ACC ABC . (2) Tam giác ABC vuông tại A nên 9090 BCBC . (3) Từ (2) và (3) ta có: 90 90 2 C C . Giải phương trình ta tìm được 30 C . Khi đó, ta có 90903060BC . Vậy ∆ABC có 90;60;30ABC . Bài 5:
Cho ABC có ,90BC . Kẻ BD vuông góc với AC ( DAC ). Kẻ CE vuông góc với AB EAB . Gọi H là giao điểm của BD và CE . Chứng minh: 180o ADHE
Lời giải
Trong AEH vuông tại E , ta có: 11 90 AH (hai góc phụ nhau) (1) Trong ADH vuông tại D , ta có: 22 90 AH (hai góc phụ nhau) (2) Cộng (1) với (2) vế theo vế, ta có: 1212 9090 AAHH
Suy ra 180 AEHD
Bài 6:
Cho góc xOy , điểm A thuộc tia Ox . Kẻ AB vuông góc với Ox ( BOy ), kẻ BC vuông góc với Oy (COx ), kẻ CD vuông góc với Ox ( DOy ). Chứng minh: ABOACB và ABOCDO .

20
L
+
+
2
B
A
ời giải
Ta có: ABOACB
(cùng phụ với ABC )
Ta có: BAOx DCOx
(gt) Suy ra // ABCD Suy ra ABOCDO (đồng vị)
1 2 1 H D E
C
y x C D B O A

21
1.
2.
L
1. Xét ΔABH
ta có o
Xét Δ
o
Mà
. 2. Tương
a, ta
ABHHAC
Lời giải Gọi K là giao điểm của BE và AC Xét ABK ta có: 1 BKCBACABK Xét KEC ta có: 2 BECBKCKCE Từ 1;2 suy ra: BECBKCKCEBACABKKCE 90 BECBAC BEC là góc tù. H x
B
B
Bài 7: Cho ΔABC vuông tại A . Vẽ AH vuông góc với BC tại H . Vẽ Ax là tia đối của tia AC . Chứng minh:
BAHC
xAH và B bù nhau
ời giải
,
90. BAHABH
ABC , ta có
90. BCAABC
ABHABC
nên BAHBCA
tự câu
có
Mà xAH kề bù với HAC nên xAH bù với ABH Bài 8: Cho ABC vuông tại A , điểm E nằm trong tam giác đó. Chứng minh BEC là góc tù.
C A
K A C E
Cho tam giác MNP có NP .Vẽ phân giác MK . a) Chứng minh MKPMKNNP b) Đường thẳng chứa tia phân giác góc ngoài đỉnh M của tam giác MNP , cắt đường thẳng NP tại E . Chứng minh rằng: 2 NP MEP Lời giải a) Sử dụng tính chất góc ngoài. Ta được:
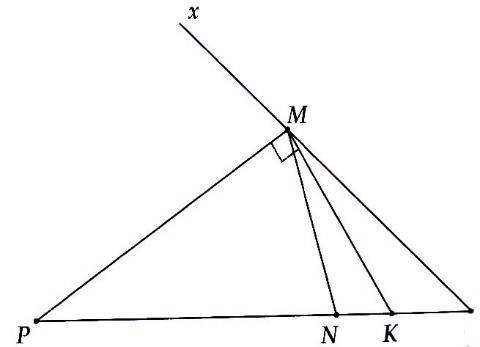
Cho tam giác ABC vuông tại A . Gọi d là đường thẳng vuông góc với BC tại C . Tia phân giác của góc B cắt AC ở D và cắt d ở E . Chứng minh rằng EDCDEC

22
Bài 9:
MKPMKNNP
MEPMExMPEP
. 22 MM MKNPMKPN
b) Ta có 2 NMx
Mà NMxNP . Từ đó suy 2 NP MEP Bài 10:
CEBEDCADB
Lời giải Ta có: 9;9 2 0 0 2 BB
Suy ra EDCDEC . d E D A C B
Bài 11:
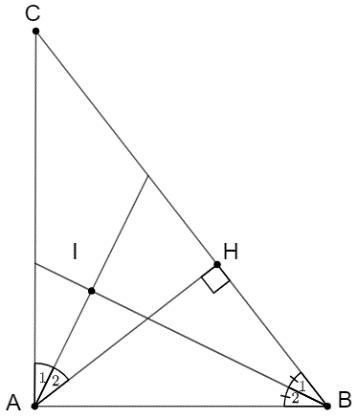
Cho tam giác ABC vuông tại A . Kẻ AH vuông góc với BC tại H . Các tia phân giác của B và HAC cắt nhau tại I . Chứng minh rằng 090 AIB Lời giải Ta có BI , AI lần lượt là tia phân giác của B và HAC Nên 12 1 2 BBABC và 12 1 2 AAHAC Mà ABCHAC (cùng phụ với C ) nên 21 BA Xét tam giác AIB có: 2 180 AIBIABB (định lý tổng 3 góc của một tam giác)

23
0 1801801809090 HACHABBAC Bài 12: Chứng minh rằng: Tổng ba góc ngoài ở ba đỉnh của một tam giác bằng 360 . Lời giải Giả sử : Xét ΔABC , cần chứng minh +360BAxCByACz Ta có: 180 BAxBAC 180 CByABC 180 ACzBCA Cộng vế theo vế ta có y x z C A B
22221180180180 AIBIABBAHABBAAHAB

24 3.180 BAxCByACzBACABCBCA Mà
b) ABC có BAxABCC (góc ngoài tam giác) 34 1 22 BC AABAx ACE có: 4 AEC (góc ngoài) 4 2 BC EACAEBC hay 2 BC AEB Bài 14: Cho
giác ABC, O là điểm nằm trong
a) Chứng minh rằng BOCAABOACO . b)
ết 90 2 A ABOACO và tia BO
tia
ủ
B. Chứng
ằng
ủ
. 2 1 4 3 2 1 B C A E D x 2 1 2 1 2 1 2 1 O A B C
180 BACABCBCA
3.180180360 BAxCByACz
Cách khác: Dựa vào tính chất góc ngoài tam giác, tính số đo từng góc ngoài ΔABC và thực hiện tương tự. Bài 13: Tam giác ABC có BC . Tia phân giác BAC cắt BC tại D. a) Chứng minh ADCADBBC . b) Đường thẳng chứa tia phân giác góc ngoài ở đỉnh A của tam giác ABC cắt đường thẳng BC tại E. Chứng minh rằng 2 BC AEB Lời giải a) ABD có 1 180 AABCADB ; ACD có 2 180 ACADC ; Mà 12 AA
nên CADCBADBADCADBBC
tam
tam giác.
Bi
là
phân giác c
a góc
minh r
tia CO là tia phân giác c
a góc C


25 Lời giải a) ABO có 11 OAABO (góc ngoài tam giác). ACO có 22 OAACO (góc ngoài tam giác). 1212 OOAAABOACO Hay BOCAABOACO . b) Từ 90 2 BAC ABOACO 2222 180 22 AABCACB BCBC 22 22 ABCACB BC mà BO là tia phân giác của ABC nên 1 2 ABC B suy ra 2 2 ACB C Hay CO là tia phân giác của góc ACB . BÀI TẬP TỰ LUYỆN Bài 1: Cho hình vẽ dưới đây. Chứng minh //C FAE biết rằng: 120;140;100.BAFABDBDE Lời giải Ta có: ABD là góc ngoài của 60 BCDBCD Hai góc trong cùng phía ; BCDFAC có tổng bằng 180 //C FAE C E A F B D
Bài 2:
Cho hình vẽ sau. Chứng minh rằng: AHBC
Lời giải ACK có 90 AC ; BHC có 90 HBCC
ABHC (cùng phụ C )
Bài 3:
Cho tam giác ABC có ˆ 90 A . Gọi d là đường thẳng đi qua C và vuông góc với BC Tia phân giác của góc B cắt AC ở D và cắt d ở E . Kẻ CH vuông góc với DE . Chứng minh rằng CH là tia phân giác của góc DCE
Lời giải

Ta có: 11 90 BD ; 12 90 CD mà 12DD 11 BC CMTT 22BC Mà 1212 BBCC CH là phân giác của DCE .
Bài 4: Cho tam giác ABC có ˆ 90 B , gọi D là một điểm nằm giữa A và C . Lấy điểm E thuộc tia đối của tia BD . Chứng minh rằng góc AEC là góc nhọn. Lời giải
26
H A K C B D 2 1 1 1 2 1 H E C B A 2 1 2 1 C A B D E

27 Chứng minh 1212 ; EBEB ( tính chất góc ngoài của tam giác) 90
.
AECABC
CHƯƠNG 4: TAM GIÁC BẰNG NHAU
Bài 2: HAI TAM GIÁC BẰNG NHAU
I. LÍ THUYẾT TRỌNG TÂM
1. Định nghĩa
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
2. Kí hiệu
Khi kí hiệu sự bằng nhau của hai tam giác, các chữ cái chỉ tên các đỉnh tương ứng được viết theo cùng thứ tự
Tam giác ABC và tam giác A’B’C’ bằng nhau Kí hiệu: ABCABC
Khi đó, hai tam giác có: Đỉnh A tương ứng với đỉnh A’. Đỉnh B tương ứng với đỉnh B’. Đỉnh C tương ứng với đỉnh C’.
II. CÁC DẠNG BÀI TẬP
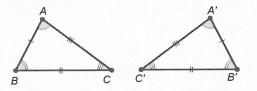

Dạng 1: Viết kí hiệu về sự bằng nhau của hai tam giác Phương pháp giải:
- Xác định các cặp đỉnh (góc) tương ứng của hai tam giác bằng nhau.
- Viết kí hiệu bằng nhau theo đúng thứ tự của các cặp đỉnh (góc) tương ứng.
Bước 1. Sử dụng cặp góc bằng nhau để chỉ ra cặp đỉnh tương ứng với nhau.
Bước 2. Xác định cặp đỉnh tương ứng thông qua giả thiết về cạnh (nếu có).
Bước 3. Viết kí hiệu bằng nhau của hai tam giác.
1
ế
,, ,, ABABBCBCCACA AABBCC
ABCABC
n
u
Ví dụ:
Cho hai tam giác bằng nhau: tam giác ABC (không có hai cạnh nào bằng nhau, không có hai góc nào bằng nhau) và tam giác có ba đỉnh là M , N, P . Biết , ABMNAM . Hãy viết kí hiệu về sự bằng nhau của hai tam giác đó.
Hướng dẫn giải
Theo giả thiết, ta có AM nên đỉnh A, M là hai đỉnh tương ứng với nhau trong hai tam giác. Mặt khác, ta có ABMN và A , M là hai đỉnh tương ứng với nhau nên B và N là hai đỉnh tương ứng.
Vậy, hai đỉnh còn lại là C và P là hai đỉnh tương ứng với nhau. Do đó ABCMNP
Bài 1:

Cho tam giác ABC và tam giác tạo bởi ba đỉnh M, T, H là hai tam giác bằng nhau. Biết rằng mỗi tam giác không có hai cạnh nào bằng nhau, không có hai góc nào bằng nhau. Viết kí hiệu về sự bằng nhau của hai tam giác trong các trường hợp sau: a) BT và AH . b) ABHT và BCMT . c) ACMT và CM .
Lời giải
a) Theo giả thiết BT và AH nên ta có B, T là hai đỉnh tương ứng; A và H là hai đỉnh tương ứng. Vậy cặp đỉnh tương ứng còn lại là C và M. Do đó ABCHTM
b) Ta có ABHT và BCMT nên hai đỉnh chung là B, T là hai đỉnh tương ứng. Từ đó, ta có cặp đỉnh A và H tương ứng với nhau; C và M tương ứng với nhau.
Do đó ABCHTM
c) Ta có CM nên C và M là hai đỉnh tương ứng. Mặt khác ACMT nên A và T là hai đỉnh tương ứng với nhau.
Vậy hai đỉnh tương ứng còn lại là B và H.
Do đó ABCTHM .
Phân tích
a) Từ hai cặp góc bằng nhau thì ta xác định được hai cặp đỉnh tương ứng. Cặp đỉnh còn lại của hai tam giác sẽ là tương ứng với nhau.
b) Từ hai cặp cạnh bằng nhau, ta xác định được đỉnh chung của hai cặp cạnh đó sẽ là cặp đỉnh tương ứng.
2
Bài 2:
Cho ABC và tam giác tạo bởi ba đỉnh H, I, K bằng nhau. Biết , ACIKBCHI . Cách viết nào sau đây là đúng?
A. ABCKHI B. ABCIKH C. ABCHKI . D. ABCKIH .
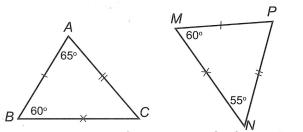
Lời giải Xét ∆ABC và ∆KHI có , ACIKBCHI nên C và I là hai đỉnh tương ứng. Suy ra A và K; B và H là hai cặp đỉnh tương ứng còn lại. Vậy ABCKHI
Bài 3:

Hai tam giác trong hình vẽ có bằng nhau không? Nếu
Suy ra hai tam giác đã cho bằng nhau. Ta có đỉnh A, M tương ứng với nhau; đỉnh B, P tương ứng với nhau và đỉnh C, N tương ứng với nhau.
Suy ra ABCMPN
Bài 4: Hai tam giác ABC và tam giác tạo bởi ba đỉnh M, N, P là hai tam giác bằng nhau. Biết rằng mỗi tam giác không có hai cạnh nào bằng nhau, không có hai góc nào bằng nhau. Viết kí hiệu bằng nhau của hai tam giác trong các trường hợp sau: a) AP và CAPN .
3
ệ
ề
ự
ằ
L
+)
.
Xét
;;
có hãy viết kí hi
u v
s
b
ng nhau của hai tam giác đó.
ời giải Áp dụng định lí tổng ba góc trong tam giác, ta có:
∆ABC có
180180606555CAB
+) ∆MNP có
180180605565MPN
∆ABC và ∆MNP có
65;60;55 ABMPBCPNACMN AMBPCN
b) BM và CP .
c) BCMN và CANP
a) Từ giả thiết, ta có
Lời giải

+) AP nên A và P là hai đỉnh tương ứng với nhau.
+) CAPN mà A tương ứng với đỉnh P nên hai đỉnh C và N tương ứng với nhau
Khi đó B và M là cặp đỉnh tương ứng còn lại.
Do đó ABCPMN .
b) Do BM nên B và M là hai đỉnh tương ứng.
Lại có CP nên C và P là cặp đỉnh tương ứng.
Suy ra A và N là cặp đỉnh tương ứng còn lại.
Do đó ABCNMP
c) Theo giả thiết ta có , BCMNCANP
Mà C là đỉnh chung của cặp cạnh BC, CA; N là đỉnh chung của cặp cạnh MN, NP. Do đó C và N là hai đỉnh tương ứng.
Đồng thời ta có B và M tương ứng với nhau; A và P là cặp đỉnh tương ứng còn lại
Do đó ta có kí hiệu ABCPMN . Dạng 2: Chứng minh các cạnh, các góc tương ứng bằng nhau Phương pháp giải: Sử dụng tính chất: Hai tam giác bằng nhau thì các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau Ví dụ 1: MNPABC
Ví dụ 2: Cho DEFOPQ
4
b) ,, ;; DEOPDFOQEFPQ DEFOPQ DOEPFQ
,, ;; MNABNPBCMPAC MANBPC
a) Tìm cạnh tương ứng với cạnh OP và góc tương ứng với góc E. b) Tìm các cạnh bằng nhau, tìm các góc bằng nhau. Hướng dẫn giải a) Cạnh tương ứng với cạnh OP là cạnh DE và góc tương ứng với góc E là góc P.

5
ằ
C.
.
. L
ả
ABCMNP nên ABMN (A
ACMP
AM (B sai) và BN (D đúng) Bài
Cho HIKHGF . Viết các cặp cạnh bằng nhau và các cặp góc bằng
Lời giải ;; ;; HIHGHKHFIKGF HIKHGF IGKFIHKGHF Bài
Cho ABCPQR . Biết 50 A và 50 BC a) Chứng minh rằng tam
b) Chỉ ra
cặ
ạ
ằ
Lờ
ải a) Xét ∆ABC có 180 ABC . Mà 50 A nên 18050130 BC . Ta lại có: 50 BC nên 13050 90 2 B . Do ABCPQR nên 90 QB Vậy ∆PQR có 90 Q nên ∆PQR là tam giác vuông tại Q. b) Do ABCPQR nên ta có các cặp cạnh bằng nhau gồm ,, ABPQBCQRCARP .
Bài 1: Cho tam giác ABC b
ng tam giác MNP . Khẳng định nào sau đây là sai? A. ABMN
B. AP
MPAC
D. BN
ời gi
i
đúng);
(C đúng);
2:
nhau.
3:
giác PQR là tam giác vuông.
các
p c
nh b
ng nhau của hai tam giác.
i gi
Dạng 3: Tính độ dài các đoạn thẳng, số đo góc, chu vi tam giác

Phương pháp giải:
Các nội dung cần lưu ý:
+) Tính chất bằng nhau giữa các cạnh tương ứng, các góc tương ứng của hai tam giác bằng nhau.
+) Tổng số đo ba góc trong một tam giác bằng 180°.
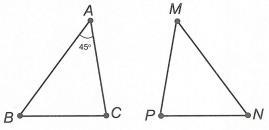
+) Tính chất của tỉ lệ thức và tính chất của dãy tỉ số bằng nhau.
Bước 1. Xác định cặp góc tương ứng bằng nhau giữa hai tam giác. Bước 2. Sử dụng tính chất về góc để tính số đo góc tương ứng. Ví dụ 1: Cho ABCMNP có 45,:2:3ABC . Tính các góc còn
6
ạ
củ
Do ABCMNP nên 45;; MANBPC . Xét ∆ABC có 180 ABC 18018045135BCA . Từ giả thiết, ta có 23 BC . Áp dụng tính chất dãy tỉ số bằng nhau, ta được 135 27 23235 BCBC 2.2754;3.2781BC Do đó 54;81NBPC . Ví dụ 2: Cho tam giác ABC và tam giác MNP bằng nhau. Biết số đo các góc như hình vẽ sau
l
i
a hai tam giác Hướng dẫn giải
ậy chu vi của tam giác ABC là
591226 ABC CABBCCAcm Nhận xét: + Hai tam giác bằng nhau có các cặp cạnh tương ứng bằng nhau. Do đó chu vi của các tam giác này cũng bằng nhau.
+ Bằng việc vận dụng các đặc điểm bằng nhau tương ứng của hai tam giác, ta có thể chỉ ra được nhiều thông số (chu vi, diện tích, đường phân giác, trung tuyến, đường cao,...).
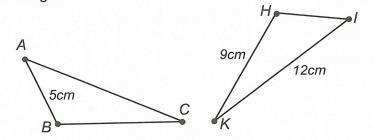
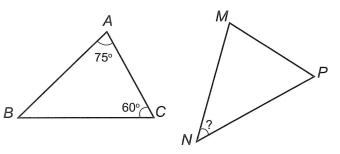
Bài 1:

Khẳng định nào sau đây là đúng?
A. Hai tam giác có các góc tương ứng bằng nhau là hai tam giác bằng nhau.
B. Hai tam giác có hai cặp góc tương ứng bằng nhau là hai tam giác bằng nhau.
C. Hai tam giác có các góc tương ứng bằng nhau, các cạnh tương ứng bằng nhau là hai tam
7
Lại có 45 ABCMNPBN Ch
Ví
Số đo góc MNP bằng A. 60°. B. 45°. C. 30°. D. 75°. Hướng dẫn giải Xét ∆ABC có
180180180756045ABCBAC
ọn B
dụ 3: Cho ,5,9 ABCIHKABcmHKcm và 12 IKcm . Tính chu vi tam giác ABC. Hướng dẫn giải Do ABCIHK nên ta có 9,12 BCHKcmCAIKcm
V
giác bằng nhau.
D. Hai tam giác có chu vi bằng nhau là hai tam giác bằng nhau. Lời giải
Hai tam giác có các góc tương ứng bằng nhau, các cạnh tương ứng bằng nhau là hai tam giác bằng nhau.
Bài 2: Cho ABCIHK . Biết 6,5,8 ABcmHKcmCAcm . Chu vi của ∆ABC bằng
A. 15 cm. B. 17 cm. C. 19 cm. D. 20 cm. Lời giải Vì ABCIHK nên 5 BCHKcm . Chu vi của ∆ABC là 65819 ABBCACcm
Bài 3:
Cho tam giác ABC có

8
ng 24 cm nên 242424816ABBCACBCACAB . Lại có :5:3 53 ACBC ACBC . Áp dụng tính chất dãy tỉ số bằng nhau, ta có 16 2 5388 ACBCACBC 5.210;3.26ACBC Mà ABCDEF nên 6 EFBCcm .
Cho
giác ABC và PQR
ằng
.
ằng
chu vi bằng 24cm, 8 ABcm và :5:3ACBC . Biết ABCDEF . Độ dài cạnh EF bằng A. 9 EFcm . B. 6 EFcm . C. 8 EFcm . D. 10 EFcm . Lời giải ∆ABC có chu vi bằ
Bài 4:
hai tam
b
nhau. Biết 8,5,2. ABcmBCcmPRQR
Chu vi của tam giác ABC b
A. 18 cm. B. 23 cm. C. 20 cm. D. 21 cm.

9 Lời giải ; ABCPQRACPRBCQR . Mà 2. PRQR nên 22.510 ACBCcm . Chu vi tam giác ABC là 851023 ABBCACcm Bài 5: Cho ABCDEG . Biết 15,70DEcmE và 40 AC a) Tính số đo các góc của hai tam giác. b) Tính độ dài cạnh AB. Lời giải a) Do ABCDEG nên 70 BE . Mà ∆ABC có 180 ABC nên 18070110 AC Do đó ta có 40 AC và 110 AC Suy
40110 75,40754035 2 ACA . Vậy 75,70,35DABEGC .
Vì ABCDEG nên ta có ABDE (hai cạnh tương ứng). Mà 15 DEcm nên 15 ABcm . Bài 6: Cho ABCMNP và BACGHK . Biết 2 7,9, 3 MNcmGKcmACBC . Chỉ ra các cạnh bằng nhau của ba tam giác trên. Tính chu vi của mỗi tam giác. Lời giải Theo giả thiết, ta có: BACGHKABCHGK Lại có ABCMNP . Suy ra ABCMNPHGK . Do đó ta có: 7,9; ABMNHGcmBCNPGKcmMPHKCA . Mặt khác 22 .966 33 ACBCACcmMPHKCAcm Vì các tam giác bằng nhau có cùng chu vi nên chu vi của các tam giác ;; ABCMNPHGK là 79622 ABBCCAcm .
ra
b)
Bài 7:
Cho tam giác ∆ABC và tam giác tạo bởi ba đỉnh H, I, K là hai tam giác bằng nhau biết , ACHKBCIH (trong mỗi tam giác không có bất kỳ hai cạnh nào bằng nhau, không có hai góc nào bằng nhau).
a) Viết kí hiệu bằng nhau của hai tam giác.
b) Biết rằng ::2:5:2IHK . Tính số đo các góc trong tam giác ABC.
Lời giải
a) Theo giả thiết: , ACHKBCIH .
Mà C là đỉnh chung của cặp cạnh AC, BC và H là đỉnh chung của cặp cạnh HK, IH. Do đó C và H là hai đỉnh tương ứng. Đồng thời A và K là tương ứng với nhau, B và I là hai đỉnh tương ứng còn lại. Vậy ABCKIH b) Xét ∆IHK có 180 IHK (tổng số đo ba góc trong tam giác). Từ giả thiết, ta có: 252 IHK Áp dụng tính chất dãy tỉ số bằng nhau, ta có: 180 20 2522529 IHKIHK
8:
Cho tam giác ABC và tam giác tạo bởi ba đỉnh K , N, P là hai tam giác bằng nhau (trong mỗi tam giác không có hai cạnh nào bằng nhau, không có hai góc nào bằng nhau). Biết 6,8 ABcmBCcm , tam giác PNK có chu vi bằng 24cm đồng thời độ dài các cạnh PK; KN; NP lần lượt tỉ lệ với 3 ; 5 ; 4. a) Tính độ dài các cạnh của tam giác PNK. b) Viết kí hiệu bằng nhau của hai tam giác nêu trên. Lời giải a) Vì chu vi của ∆PNK là 24cm nên 24 PNNKKPcm . Từ giả thiết, ta có: 344 PKKNNP .

10
. Suy ra: 2.2040;5.20100;2.2040 IHK Theo ý a) ta có ABCKIH nên 40;40;100AKBICH . Bài
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
b) Theo kết quả câu a, ta có 6,8 ABPKcmBCNPcm .
Ta thấy B là đỉnh chung của cặp đoạn thẳng AB và BC; P là đỉnh chung của cặp đoạn thẳng PK và NP.
Do đó B và P là hai đỉnh tương ứng
Suy ra A và K là hai đỉnh tương ứng với nhau; C và N tương ứng với nhau. Vậy ta kí hiệu ABCKPN .

11
24 2
PKKNNPPKKNNP
35435412
. Suy ra 2.36;2.510;2.48 PKcmKNcmNPcm
nhau c
a hai tam giác,
kí hi
b
ng nhau của hai tam giác suy ra các cạnh – góc bằng nhau. Viết kí hi
b
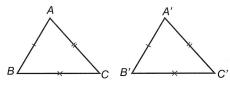

ng nhau của hai tam giác, từ kí hiệu bằng nhau của hai tam giác suy ra các cạnh – góc bằng nhau. I. Phương pháp giải:
Từ kí hiệu tam giác bằng nhau suy ra các cạnh và các góc bằng nhau đúng thứ tự tương ứng.
Ngược lại, khi viết kí hiệu tam giác bằng nhau lưu ý kiểm tra lại xem các góc hay cạnh tương ứng đã bằng nhau thỏa mãn yêu cầu đề
1
7: TRƯỜNG
ỢP BẰNG NHAU THỨ NHẤT CỦA TAM GIÁC
Bài
H
(cạnh – cạnh – cạnh)
ạ
ủ
Nếu ∆ABC và ∆A’B’C’ có: ABAB BCBC ACAC thì .. ABCABCccc
I. LÍ THUYẾT TRỌNG TÂM *) Trường hợp bằng nhau cạnh – cạnh – cạnh Nếu ba c
nh c
a tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
II. CÁC DẠNG BÀI TẬP
t
ệu về sự
ằ
Ví
,, ,, ABABBCBCACAC ABCABC AABBCC . +
bài chưa. II. Bài toán Bài 1: Cho biết ABCHIK . Hãy viết đẳng thức trên dưới một vài dạng khác. Lời giải Viết đẳng thức ABCHIK dưới một vài dạng khác: ACBKHI , CABKHI , ... Bài 2: Cho ABCDEF . Hãy chỉ ra các góc, các cạnh tương ứng bằng nhau.
Dạng 1: Viế
kí hi
b
ng
ủ
từ
ệu
ằ
ệu về sự
ằ
+
dụ:
Bài 3:
Cho MNPIHG . Hãy chỉ ra các góc, các cạnh tương ứng bằng nhau.
ời giả
Bài 4:
Cho hai tam giác bằng nhau: ABC và HIK . Viết kí hiệu về sự bằng nhau của 2 tam giác theo thứ tự đỉnh tương ứng, biết rằng: AH và BI
Lời giải
Hai tam giác ABC và HIK bằng nhau và AH ; BI thì kí hiệu bằng nhau của hai tam giác là: K ABC HI
Bài 5:
Cho hai tam giác bằng nhau: ABC và HIK . Viết kí hiệu về sự bằng nhau của 2 tam giác theo thứ tự đỉnh tương ứng, biết rằng: ;BC=KHABKI .
Lời giải
Hai tam giác ABC và HIK bằng nhau và ;BC=KHABKI thì kí hiệu bằng nhau của hai tam giác là: H ABC IK
Bài 6:

Cho hai tam giác bằng nhau: ABC và HIK . Viết kí hiệu về sự bằng nhau của 2 tam giác theo thứ tự đỉnh tương ứng, biết rằng: ; AKABIK
Lời giải
Hai tam giác ABC và HIK bằng nhau và ; AKABIK thì kí hiệu bằng nhau của hai tam giác là: H ABC KI .
2 Lời giải
,, ,, ABDEBCEFACDF ABCDEF ADBECF
L
i ,, ,, MNIHMPIG I MNP NPHG I MNHPG HG
BÀI TẬP TỰ LUYỆN DẠNG TOÁN
Bài 1:

Cho biết ABCMNP . Hãy viết đẳng thức trên dưới một vài dạng khác.
Lời giải Viết đẳng thức ABCMNP dưới một vài dạng khác: ACBMPN , CBAPNM , ...
Bài 2:
Cho MNPOPQ . Hãy chỉ ra các góc, các cạnh tương ứng bằng nhau. Lời giải ,, ,,
MNOPNPPQMPOQ
NMPPOQMNPOP N QM MPOP PO Q NQP
Bài 3:
Cho hai tam giác bằng nhau: ABC và HIK . Viết kí hiệu về sự bằng nhau của 2 tam giác theo thứ tự đỉnh tương ứng, biết rằng: AI và BK .
Lời giải
Hai tam giác ABC và HIK bằng nhau và AI ; BK thì kí hiệu bằng nhau của hai tam giác là: H ABC IK .
Bài 4:
Cho hai tam giác bằng nhau: ABC và PQR . Viết kí hiệu về sự bằng nhau của 2 tam giác theo thứ tự đỉnh tương ứng, biết rằng: ;BC=PRABPQ .
Lời giải Hai tam giác ABC và PQR bằng nhau và ;BC=PRABPQ thì kí hiệu bằng nhau của hai tam giác là: R ABC QP .
Bài 5:
Cho hai tam giác bằng nhau: MNP và HIK . Viết kí hiệu về sự bằng nhau của 2 tam giác theo thứ tự đỉnh tương ứng, biết rằng: ; NKMNIK
Lời giải
Hai tam giác MNP và HIK bằng nhau và ; NKMNIK thì kí hiệu bằng nhau của hai
3
.
tam giác là: H MNP IK .
Bài 6: Chứng minh rằng nếu: MNPNPM thì MNP có 3cạnh bằng nhau. Lời giải Vì MNPNPM nên , MNNPNPPM (các cạnh tương ứng) MNNPPM MNP có 3cạnh bằng nhau.
Dạng 2: Tìm hoặc chứng minh hai tam giác bằng nhau theo trường hợp cạnh - cạnh - cạnh Phương pháp giải: Bước 1. Kiểm tra ba điều kiện bằng nhau: cạnh - cạnh - cạnh
Bước 2. Kết luận hai tam giác bằng nhau.
Bài 1:

Cho hình vẽ. Chứng minh rằng ABDCDB
Xét ∆ABD và ∆CDB có ABCD (giả thiết) BD chung ADCB (giả thiết)
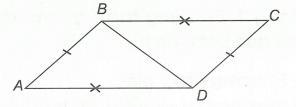
Suy ra .. ABDCDBccc
Lời giải
Bài 2:
Cho ∆ABC, M là trung điểm BC, N là một điểm trong tam giác sao cho NBNC . Chứng minh: NMBNMC
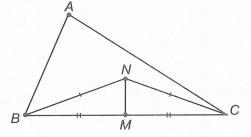
Lời giải
Xét ∆NMB và ∆NMC, ta có:
4
NM là cạnh chung.
NBNC (giả thiết). MBMC (do M là trung điểm của BC). Do đó NMBNMCccc

Bài 3: Quan sát hình bên. Để ABCDCB theo trường hợp cạnhcạnh - cạnh thì cần thêm điều kiện A. ACBC . B. ACDB . C. BDBC D. ABAD Lời giải Chọn B Xét ∆ABC và ∆DCB có ABCD ; BC chung. Do đó để ABCDCB thì cần thêm điều kiện về cạnh là ACBD
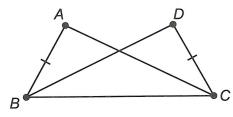
Bài 4: Cho ∆ABC và ∆A’B’C’ có ;' ABACACAB
. Trong các khẳng định sau khẳng định nào là khẳng định đúng? A. ABCACB
5
C. ABCBCA D. ABCBAC Lời giải Chọn A Xét ∆ABC và ∆A’B’C’ có ; ABACACAB và BCCB . Vì ; ABACACAB nên A và A'; B và C’; C và B' là các cặp đỉnh tương ứng. Suy ra ABCACB . Bài 5:
và BCCB
B. ABCABC
p tam giác bằng nhau trong hình v
Dạng 3: Biết hai tam giác bằng nhau và một số điều kiện, tính số đo góc, độ dài cạnh của tam giác
I. Phương pháp giải:
+ Từ kí hiệu tam giác bằng nhau suy ra các cạnh và các góc tương ứng bằng nhau.
+ Lưu ý các bài toán: tổng - hiệu, tổng - tỉ, hiệu – tỉ.
+ Sử dụng định lí tổng ba góc trong một tam giác.
II. Bài toán
Bài 1:

Cho ABCDEF với 7cm,5cm,ABBC . ,6cm DF Tính các cạnh còn lại của mỗi tam giác.
Lời giải Vì ABCDEF nên ,, ABDEBCEFACDF (các cạnh tương ứng). Mà 7cm,5cm,6cmABBCDF suy ra 7cm,5cm,6cmDEEFAC .
Bài 2:
Cho ABCDEF với 6cm,8cm,10cmBCABDF .
a) Tính các cạnh còn lại của mỗi tam giác. b) Tính chu vi của mỗi tam giác. Lời giải a) Vì ABCDEF nên ,, ABDEBCEFACDF (các cạnh tương ứng). Mà 6cm,8cm,10cmBCABDF suy ra 6cm,8cm,6cmEFDEAC . b) Chu vi ABC là: 8cm6cm10cm=24cm. ABBCAC Chu vi DEF là: 8cm6cm10cm=24cm. DEEFDF
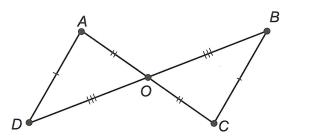
6 Chỉ ra cặ
ẽ
sau: Lời giải Xét ∆OAD và ∆OCB có ;; OAOCODOBADBC . Do đó .. OADOCBccc .
Bài 3:
Cho ABCIHK . Tính chu vi của mỗi tam giác, biết rằng 6cm AB , 8cm AC , 12cm HK .
Lời giải

Vì ABCIHK nên ,, ABIHBCHKACIK (các cạnh tương ứng).
Mà 6cm AB , 8cm AC , 12cm HK suy ra 6cm,8cm,12cmIHIKBC
Chu vi ABC là: 6cm12cm8cm=26cm. ABBCAC
Chu vi DEF là: 8cm6cm10cm=24cm. DEEFDF
Bài 4:
Cho ABCMNP , biết 65,30AP
a) Tìm các góc tương ứng bằng nhau. b) Tính các góc còn lại của hai tam giác. Lời giải
a) Vì ABCMNP ,, AMBNCP (các góc tương ứng). b) Vì AM mà 65 A nên 65 M Vì CP mà 30 P nên 30 C . Xét ABC có: 180 ABC (định lí tổng ba góc trong một tam giác) 180180653085BAC
7
Mà BN nên 85 N . Vậy 85 B , 30 C , 65 M và 85 N . Bài 5: Cho ABCDEF biết 50,70BD . Tính số đo góc C Lời giải Vì ABCDEF AD (các góc tương ứng) mà 70 D nên 70 A Vậy 60 C . Bài 6: Cho ABCMNP . Biết 7cm,3cm,4cmABBCMNNPMP . Tính độ dài các cạnh mỗi tam giác.
Vì ABCMNP nên ,, ABMNBCNPACMP (các cạnh tương ứng).
Mà 4cm MP 4cm AC , 3cm MNNP 3cm ABBC .
Lại có: 7cm ABBC suy ra: 73:25cm AB , 73:22cm BC 2cm,5cmNPBCMNAB . Vậy ABC có: 5cm,2cm,4cmABBCAC ; MNP có: 5cm,2cm,4cmMNNPMP
Bài 7:

Cho ABCIJK . Biết 9cm,2,5cmABBCIJJKAC . Tính chu vi mỗi tam giác. Lời giải Vì ABCIJK nên ,, ABIJBCJKACIK (các cạnh tương ứng).
Mà 5cm AC 5cm IK , 22 IJJKABBC . Lại có: 9cm ABBC 9:123cm,26cmBCABBC 6cm,3cmIJABIKBC .
Chu vi ABC là: 63514cm ABBCAC
8
Lời giải
.
ế
ABBCIJJKAC .
i Vì ABCIJK nên ,, ABIJBCJKACIK (các cạnh tương ứng). Mà 20cm AC 20cm IK , 5 3535 3 AB IJJKABBC BC . Lại có: 10cm ABBC 10:53.525cm,10:53.315cmABBC 25cm,15cmIJABIKBC . Chu vi ABC là: 25152060cm ABBCAC . Chu vi IJK là: 25152060cm IJJKIK
. Chu vi IJK là: 63514cm IJJKIK . Bài 8: Cho ABCIJK
Bi
t 10cm,35,20cm
Tính chu vi mỗi tam giác. Lời giả
giác.

9
Bài 9:
. Mà 3 PN nên 120:13120:430 N 33.3090
Suy ra: 30,90BNCP . Vậy: 30 B , 90 C , 60 M , 30 M , 90 N .
với 30,23 DBC . Tính số đo các góc của ABC . Lời giải Vì ABCDEF nên ,, ADBECF (các góc tương ứng). Mà 30 D nên 30 A . Xét ABC có: 180 ABC (định lí tổng
18018030150BCA . Mà 23BC 150:23.260 B và 150:23.390 C . Vậy 30,60,90ABC Bài 11: Cho ABCMNP , biết 40,10APN . Tính số đo các góc còn lại của MNP Lời giải Vì ABCMNP nên AM (hai góc tương ứng). Mà 40 A nên 40 M . Xét MNP có: 180 MNP (định lí tổng ba góc trong một tam giác)
Cho Cho ABCMNP , biết 60,3 APN . Tính số đo các góc còn lại của mỗi tam
Lời giải Vì ABCMNP nên ,, AMBNCP (các góc tương ứng). Vì AM mà 60 A nên 60 M . Xét MNP có: 180 MNP (định lí tổng ba góc trong một tam giác) 18018060120NPM
PN
Bài 10: Cho ABCDEF
ba góc trong một tam giác)

10 18018040140NPM . Mặt khác 10 PN 14010:275 P và 14010:265 N Vậy 40,65,75MNP .
Cho ABCMNP biết ::3:4:5ABC . Tính các góc của MNP . Lời giải Vì ::3:4:5ABC 3.,4.,5. 345 ABC kAkBkCk . Xét ABC có: 180 ABC (định lí tổng ba góc trong một tam
Vậy 45,60,75ABC . Bài 13: Cho ABCDEF . Biết 2 tia phân giác trong của góc B và C cắt nhau tại O, tạo 135 BOC ; 2 EF . Tính các góc của DEF . Lời giải Ta có: 180 BOCOBCOCB (tổng ba góc trong BOC bằng 180) 11 180 22 ABCACB (tính chất phân giác) 1 180 2 ABCACB 1 180180 2 BAC (tổng ba góc trong ABC bằng 180) 1 90 2 BAC . 135° O C A B
Bài 12:
giác) 3.4.5.180345.180 kkkk 12.180180:1215 kk 3.1545,4.1560,5.1575ABC

11 1 13590 2 BAC 13590.290 BAC . Do
nên
ứ
.
Mà
. Vậ
.
ế
.
.
. Vậy các cạnh của MNP là: 15cm,18cm,24cmMNNPMP BÀI TẬP TỰ LUYỆN DẠNG TOÁN Bài 1: Cho ABCIJK với 7cm,8cm,6cmABACJK . Tính các cạnh còn lại của mỗi tam giác. Lời giải Vì ABCIJK nên ,, ABIJBCJKACIK (các cạnh tương ứng). Mà 7cm,8cm,6cmABACJK suy ra 7cm,5cm,6cmIJIKBC Bài 2: Cho ABCMNP với 5cm,5cm,7cmBCMNAC .
ABCDEF
BACD
(hai góc tương
ng) 90 D
Xét DEF có 1801809090EFD (tổng ba góc trong DEF bằng 180).
2 EF
nên
90:1230 F 22.3060EF
y DEF
có: 90,60,30DEF
Bài 14: Cho ABCMNP bi
t ::5:6:8ABBCAC
Tính các cạnh của MNP biết tam giác này có chu vi là 57cm. Lời giải Vì ABCMNP nên ,, ABMNBCNPACMP (các cạnh tương ứng). Suy chu vi hai tam giác bằng nhau: 57cm ABBCACMNNPMP Vì ::5:6:8ABBCAC 5.,6.,8. 568 ABBCAC kABkBCkACk Ta có: 575685719573 ABBCACkkkkk .
55.315cm,66.318km,88.324km ABkBCkACk
15cm,18cm,24cmMNABNPBCMPAC
a) Tính các cạnh còn lại của mỗi tam giác.
b) Tính chu vi của mỗi tam giác.
Lời giải
a) Vì ABCMNP nên ,, ABMNBCNPACMP (các cạnh tương ứng).

Mà 5cm,5cm,7cmBCMNAC suy ra 5cm,5cm,7cmNPABMP
b) Chu vi ABC là: 5cm5cm7cm=17cm. ABBCAC Chu vi MNP là: 5cm5cm7cm=17cm. MNNPMP
Bài 3:
Cho ABCOPQ , biết 55,47AP
a) Tìm các góc tương ứng bằng nhau. b) Tính các góc còn lại của hai tam giác. Lời giải c) Vì ABCOPQ ,, AOBPCQ (các góc tương ứng). d) Vì AO mà 55 A nên 55 O
12
Mà CQ nên 78 Q Vậy 47 B , 78 C , 55 O và 78 Q Bài 4: Cho ABCPQR , biết 40,30BR . Tính các góc còn lại của mỗi tam giác. Lời giải Vì ABCPQR ,, APBQCR (các góc tương ứng). Vì BQ mà 40 B nên 40 Q . Vì CR mà 30 R nên 30 C . Xét ABC có: 180 ABC (định lí tổng ba góc trong một tam giác)
Vì BP mà 47 P nên 47 B . Xét ABC có: 180 ABC (định lí tổng ba góc trong một tam giác) 180180554778CAB
Mà AP nên 110 P . Vậy 110,30AC , 110 P , 40 Q .
Bài 5:
Cho ABCMNP biết =10cm BC , : =4:3 MNMP và +AC=14cm AB . Tính các cạnh của MNP .
Lời giải

Vì ABCMNP nên ,, ABMNBCNPACMP (các cạnh tương ứng).
Mà =10cm BC =10cm NP , : =4:3 MNMP : =4:3 ABAC Lại có: +AC=14cm AB 14:43.48cm,14:43.36cmABAC . 8cm,6cmMNABMPAC . Vậy MNP có: 8cm,10cm,6cmMNNPMP . Bài 6: Cho ABCMNP với 40,34 MBC .
13 1801804030110ABC
.
ố
ABC . Lờ
giả
Vì ABCMNP nên ,,
(các
ứng). Mà 40 M nên 40 A Xét ABC có: 180 ABC (định lí tổng ba góc trong
ột tam giác) 18018040140BCA Mà 34 43 BC BC 140:43.480 B và 140:43.360 C . Vậy 40,80,60ABC .
Cho
, biết 40,30
.
ố
ủ
Lời giải
Tính s
đo các góc của
i
i
AMBNCP
góc tương
m
Bài 7:
HIKMNP
HPN
Tính s
đo các góc còn lại c
a MNP

14 Vì HIKMNP nên HM (hai góc tương ứng). Mà 40 H nên 40 M . Xét MNP có: 180 MNP (định lí tổng ba góc trong một tam giác) 18018040140NPM Mặt khác 30 PN 14030:285 P và 14030:255 N Vậy 40,55,85MNP . Bài 8: Cho MNPIJK . Biết 2 tia phân giác trong của góc M và góc N cắt nhau tại O , tạo 120 MON . Tính các góc của IJK biết 3 IJ . Lời giải Ta có: 180 MONOMNONM (tổng ba góc trong MON bằng 180) 11 180 22 PMNPNM (tính chất phân giác) 1 180 2 PMNPNM 1 180180 2 MPN (tổng ba góc trong MNP bằng 180) 1 90 2 MPN 1 12090 2 MPN 12090.260 MPN Do MNPIJK nên MPNK (hai góc tương ứng) 60 K Xét IJK có 18018060120IJK (tổng ba góc trong IJK bằng 180). Mà 3 IJ nên 120:1330 J 33.3090IJ . Vậy IJK có: 90,30,60IJK . Dạng 3: Sử dụng trường hợp bằng nhau cạnh – cạnh – cạnh để chứng minh hai góc bằng nhau, hai cạnh bằng nhau, hai đường thẳng song song – vuông góc, đường phân giác, ba điểm thẳng hàng,….. 120° O N P M
I. Phương pháp giải:
+ Chỉ ra các tam giác có ba cạnh bằng nhau để suy ra tam giác bằng nhau.
+ Từ tam giác bằng nhau suy ra các cặp cạnh tương ứng bằng nhau, cặp góc tương ứng bằng nhau.
+ Nắm vững các khái niệm: tia phân giác của góc, đường cao của tam giác, đường trung trực của đoạn thẳng, hai đường thẳng song song, hai đường thẳng vuông góc; nắm vững định lí tổng ba góc trong một tam giác, tiên đề Ơ clit để giải các bài toán chứng minh.
II. Bài toán.
Bài 1: Tìm các tam giác bằng nhau trên hình vẽ, giải thích vì sao?
R S
Lời giải Xét PSR và RQP có: PR là cạnh chung, PSQR , SRPQ (theo giả thiết) PSRRQP (c.c.c).
Bài 2:
Tìm các tam giác bằng nhau trên hình vẽ, giải thích vì sao?
Q P N A B M
Lời giải
Xét AMB và ANB có: AB là cạnh chung, AMAN , BMBN (theo giả thiết) AMBANB (c.c.c).

15
I
Bài 3: Tìm các tam giác bằng nhau trên hình vẽ, giải thích vì sao? B C
A
Xét ABI và ACI có: AI là cạnh chung, ABAC , BICI (theo giả thiết) ABIACI (c.c.c).
Bài 4: Cho đoạn thẳng 6cm AB . Trên nửa mặt phẳng bờ AB , vẽ ABD sao cho 4cm AD , 5cm BD . Trên nửa mặt phẳng còn lại vẽ ABE sao cho 4cm BE , 5cm AE . Chứng minh: a) ABDBAE . b) ADEBED . Lời giải a) Xét ABD và BAE có: AB là cạnh chung, 4cm ADBE , 5cm BDAE ABDBAE (c.c.c). b) Xét ADE và BED có: DE là cạnh chung, 4cm ADBE , 5cm BDAE ADEBED (c.c.c).
D B A M
6cm
4cm 5cm 4cm 5cm E

Bài 5: Cho ABC có ABAC . Lấy M là trung điểm của BC . Chứng minh rằng: a) C AMB AM . b) BAMCAM . c) AMBC . Lời giải a) Xét AMB và AMC có: AM là cạnh chung, ABAC (theo giả thiết), BMCM (vì M là trung điểm BC ) C AMB AM (c.c.c) b) Vì C AMB AM (chứng minh trên) BAMCAM (hai góc tương ứng). c) Vì C AMB AM (chứng minh trên) BMACMA (hai góc tương ứng).
A B C
16 Lờ
ả
i gi
i
Bài 6:
Cho hình vẽ dưới đây. Chứng minh rằng: a) ABKKHA b) // ABHK c) // AHBK Lời giải
K H
a) Xét ABK và KHA có: AK là cạnh chung, ABHK , BKAH (theo giả thiết), ABKKHA (c.c.c)
b) Vì ABKKHA (chứng minh trên) BAKHKA (hai góc tương ứng). Mà hai góc này ở vị trí so le trong so với AB và HK nên AB // HK . c) Vì ABKKHA (chứng minh trên) HAKBKA (hai góc tương ứng). Mà hai góc này ở vị trí so le trong so với AH và BK nên AH // BK .
Bài 7:
A M

Cho ABC có ABAC . Gọi M là trung điểm của BC . Chứng minh rằng: a) AM là phân giác của góc BAC b) AM là trung trực của BC Lời giải a) Xét AMB và AMC có: AM là cạnh chung, ABAC (theo giả thiết), BMCM (vì M là trung điểm BC ) C AMB AM (c.c.c) BAMCAM (hai góc tương ứng) AM là phân giác của góc BAC .. b) Vì C AMB AM (chứng minh trên) BMACMA (hai góc tương ứng).
A B C
Mà 180 BMACMA (kề bù) 90 BMACMA AMBC Mặt khác M là trung điểm của BC AM là trung trực của BC
Bài 8:
17 Mà 180 BMACMA (kề
BMACMA
bù) 90
AMBC .
B
Cho ABC , đường cao AH . Trên nửa mặt phẳng bờ AC không chứa B vẽ DAC sao cho D ABC ; D CAB . CMR: AB // DC và DAHA .
Lời giải Xét ADC và CBA có: AC là cạnh chung, ADBC , CDAB (theo giả thiết) ADCCBA (c.c.c) DACCBA (hai góc tương ứng). Mà hai góc này ở vị trí so le trong so với AD và BC nên AD // BC . Lại có: AHBC ( AH là đường cao trong ABC ) AHAD (từ vuông góc tới song song).
Bài 9:
Cho ABC có ABACBC . Giả sử O là một điểm nằm trong tam giác sao cho OA=OBOC . Chứng minh rằng: O là giao điểm của 3 tia phân giác của ;; ABC . Lời giải Xét AOB và AOC có: chung cạnh AO , , OBOCABAC (giả thiết)
A

O C B
BAOCAO (hai góc tương ứng) AO là tia phân giác BAC . Chứng minh tương tự ta cũng có: BO là tia phân giác ABC , CO là tia phân giác ACB Suy ra O là giao điểm của 3 tia phân giác của ;; ABC .
Bài 10:
18
D H A B C
Cho ABC có ABAC Gọi D là trung điểm
của BC . Chứng minh rằng:
a) ADBADC
b) AD là phân giác của BAC , ADBC .
c) Trên nửa mặt phẳng bờ BC không chứa A lấy điểm E sao cho EBEC Chứng minh rằng: ,, AED thẳng hàng.
Lời giải
a) Xét ADB và ADC có: AD là cạnh chung, ABAC (theo giả thiết), BDCD (vì D là trung điểm BC )
C ADB AD (c.c.c)
b) Vì C ADB AD (chứng minh trên) BADCAD (hai góc tương ứng) AD là phân giác của BAC .
Vì C ADB AD (chứng minh trên) BDACDA (hai góc tương ứng).
Mà 180 BDACDA (kề bù) 90 BDACDA ADBC .
c) Xét EDB và EDC có: ED là cạnh chung, EBEC (theo giả thiết), BDCD (vì D là trung điểm BC )
EC DB ED (c.c.c) BDECDE (hai góc tương ứng).
Mà 180 BDECDE (kề bù) 90 BDECDE EDBC Vì qua điểm D chỉ có duy nhất một đường thẳng vuông góc với BC mà , EDBCADBC nên hai đường thẳng , EDAD trùng nhau hay ,, AED thẳng hàng.
Bài 11:
Cho ABC có ABAC và 80 BAC . Tính số đo các góc còn lại của ABC .

19
Lời giải D B A C
M C
B
E 80°
A
A

M C B
Xét AMB và AMC có: AM là cạnh chung, ABAC (theo giả thiết), BMCM (vì M là trung điểm BC ) C AMB AM (c.c.c) ABMACM (hai góc tương ứng) ACBABC Xét ABC có: 180 BACABCACB (tính chất tổng ba góc trong một tam giác) 18018080100ABCACBBAC Mà ACBABC nên 100:250 ACBABC . Bài 12: Cho ABC có ABACBC . Tính số đo các góc của ABC . Lời giải Lấy M là trung điểm của BC . Xét AMB và AMC có: AM là cạnh chung, ABAC (theo giả thiết), BMCM (vì M là trung điểm BC ) C AMB AM (c.c.c) ABMACM (hai góc tương ứng) ACBABC . Tương tự lấy N là trung điểm AC ta cũng chứng minh được ABNCBN (c.c.c)
BANBCN (hai góc tương ứng) BACBCA . Như vậy ABC có ba góc bằng nhau. Mà tổng ba góc trong tam giác bằng 180 nên các góc của ABC có số đo 60
Bài 13:
20
Lấy M là trung điểm của BC
Cho ∆ABC có ABAC . D,E thuộc cạnh BC sao cho BDDEEC . Biết ADAE .
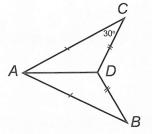
Chứng minh: EABDAC
Xét ∆ABE và ∆ACD có

ABAC AEAD BECD (vì cùng bằng 2 3 BC ).
Do đó ABEACDccc
Suy ra EABDAC (hai góc tương ứng).
Lời giải

Bài 14:
Tính số đo của góc B trong hình vẽ sau: Lời giải
Xét ∆ADC và ∆ADB có
ACAB (giả thiết)
CDBD (giả thiết) AD là cạnh chung. Do đó .. ADCADBccc . Suy ra ACDABD (hai góc tương ứng).
Mà 30 ACD nên 30 BABD .
Bài 315:
21
Cho bốn điểm A, B, C, D thuộc đường tròn (O) sao cho ABCD . Chứng minh rằng
a) AOBCOD . b) AOBCOD Lời giải a) Xét ∆AOB và ∆COD, ta có ABCD (giả thiết); OAOCR ; OBODR ; Do đó .. AOBCODccc . b) Theo câu a ta có AOBCOD nên AOBCOD (hai góc tương ứng).
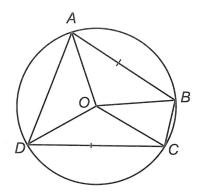
Bài 16:
Cho ∆ABC có ABAC . Trên cạnh BC lấy hai điểm M và N sao cho BMMNNC . Biết AMAN , chứng minh rằng a) AMBANC . b) ABNACM . Lời giải a) Xét ∆AMB và ∆ANC, ta có AMAN (giả thiết); MBNC (giả thiết); ABAC (giả thiết). Do đó AMBANCccc . b) Theo câu a) suy ra ABMACN (hai góc tương ứng) hay ABNACM .

Bài 17:

22
Cho hình vẽ bên.
Chứng minh rằng:
a) AODCOB . b) // ADBC .
a) Xét ∆AOD và ∆COB, ta có:
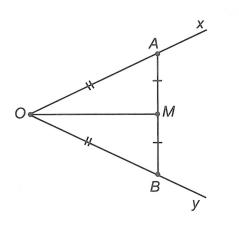
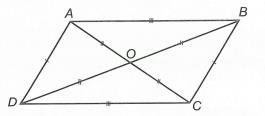
ADBC (giả thiết);
AOOC (giả thiết);
ODOB (giả thiết);
Do đó .. AODCOBccc
Lời giải

b) Theo câu a) suy ra ADOCBO (hai góc tương ứng). Mà hai góc này ở vị trí so le trong nên // ADBC Bài 18:
Cho góc xOy là góc nhọn. Trên tia Ox và Oy lần lượt lấy hai điểm điểm A và B sao cho
OAOB . Gọi M là trung điểm của đoạn thẳng AB. Chứng minh OM là tia phân giác của góc xOy. Lời giải
Xét ∆AOM và ∆BOM, ta có
OAOB (giả thiết); AMBM (giả thiết); OM là cạnh chung.
Do đó .. AOMBOMccc .
Suy ra AOMBOM (hai góc tương ứng). Suy ra OM là tia phân giác của xOy .
23
Cho ∆ABC, có ABAC . Lấy hai điểm D, E lần lượt thuộc cạnh BC sao cho
BDDEEC . Biết ADAE
a) Chứng minh EABDAC .
b) Gọi M là trung điểm của BC. Chứng minh
AM là phân giác của góc DAE. Lời giải
a) Vì BDDEEC nên 2 3 BECDBC .
Xét ∆ABE và ∆ACD, ta có
AEAD (giả thiết); ABAC (giả thiết);
BECD (chứng minh trên).
Do đó ABEACDccc .
Suy ra EABDAC (hai góc tương ứng).
b) Xét ∆ABM và ∆ACM ta có
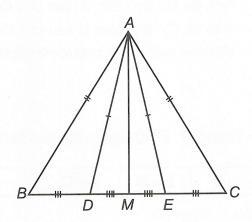
ABAC (giả thiết)
BMCM (do M là trung điểm của BC)

AM là cạnh chung. Do đó .. ABMACMccc
Suy ra BAMCAM (hai góc tương ứng)
Theo câu a) có BAECAD .
Ta có BAEBAMCADCAM
Suy ra EAMDAM Vậy AM là tia phân giác của DAE BÀI TẬP TỰ LUYỆN
24 Bài 19:
Bài 1:

Tìm các tam giác bằng nhau trên hình vẽ, giải thích vì sao?
Lời giải
+ Xét ABC và ADC có: AC là cạnh chung, ABAC , BCDC (theo giả thiết) ABCADC (c.c.c).
+ Xét ABI và ADI có: AI là cạnh chung, ABAC , BIDI (theo giả thiết) ABIADI (c.c.c).
+ Xét IBC và IDC có: IC là cạnh chung, IBIC , BCDC (theo giả thiết) IBCIDC (c.c.c).
Bài 2:
Tìm các tam giác bằng nhau trên hình vẽ, giải thích vì sao? Lời giải
Xét ORS và OPQ có: OROP , OSOQ (cùng là bán kính của đường tròn O , RSPQ (theo giả thiết) ORSOPQ (c.c.c).
Bài 3:
Cho hình vẽ: a) Chứng minh rằng MNPPQM b) Biết 20 MPN , tính số đo góc PMQ
25
I
B A C
P
Q
D
P Q O S R
M N
a) Xét MNP và PQM có: MN là cạnh chung, MNPQ , NPMQ (theo giả thiết), MNPPQM (c.c.c)
b) Vì MNPPQM (chứng minh trên) PMQMPN (hai góc tương ứng). Mà 20 MPN 20 PMQ .
Bài 4:
Cho ABC có 80 A . Vẽ cung tròn tâm B có bán kính bằng độ dài đoạn AC . Vẽ cung tròn tâm C có bán kính bằng độ dài đoạn AB . Hai cung tròn này cắt nhau tại D nằm khác phía của A đối với BC .
a) Chứng minh ABCB DC . Từ đó suy ra số đo góc BDC . b) Chứng minh AB // CD. Lời giải
a) Xét ABC và DCB có: BC là cạnh chung, ABCD , ACBD (theo giả thiết) ABCB DC (c.c.c) BDCCAB (hai góc tương ứng) 80 BDC .
Bài 5:
80°
D A C
b) Vì ABCB DC (chứng minh trên) ABCDCB (hai góc tương ứng). Mà hai góc này ở vị trí so le trong so với AB và CD nên AB // CD.
B I

Cho ABC có ABAC . Trên cạnh AC lấy điểm E sao cho CEAB . Gọi I là một điểm sao cho IAIC , IBIE . Chứng minh rằng: a) AIBCIE b) So sánh IAB và ACI . Lời giải a) Xét AIB và CIE có: IAIC , IBIE , ABCE (theo giả thiết)
A B C
E
26
ờ
L
i giải
E C A B D
AIBCIE (c.c.c) IABICE (hai góc tương ứng).
Mà E thuộc AC nên ICEACI . Vậy IABACI .
Bài 6:

Cho ABC có ABAC . Gọi M là trung điểm của BC .
a) Chứng minh rằng: AM là phân giác của BAC b) Chứng minh rằng: AM là đường trung trực của đoạn thẳng BC
c) Trên nửa mặt phẳng bờ BC chứa A lấy điểm E sao cho EBEC . d) Chứng minh rằng: ,, AEM thẳng hàng. Lời giải
a) Xét AMB và AMC có: AM là cạnh chung, ABAC (theo giả thiết), BMCM (vì M là trung điểm BC ) C AMB AM (c.c.c) BAMCAM (hai góc tương ứng) AM là phân giác của BAC
b) Vì C AMB AM (chứng minh trên) BMACMA (hai góc tương ứng).
Mà 180 BMACMA (kề bù) 90 BMACMA AMBC .
Mà M là trung điểm của BC nên AM là đường trung trực của đoạn thẳng BC . c) Xét EMB và EMC có: EM là cạnh chung, EBEC (theo giả thiết), BMCM (vì D là trung điểm BC ) EMC B EM (c.c.c) BMECME (hai góc tương ứng). Mà 180 BMECME (kề bù) 90 BMECME EMBC . Vì qua điểm M chỉ có duy nhất một đường thẳng vuông góc với BC mà , EMBCAMBC nên hai đường thẳng , EMAM trùng nhau hay ,, AEM thẳng hàng.
27
Bài 7: M E
A
B C
Cho ABC có ABAC và 60 BAC . Tính số đo các góc còn lại của ABC
Lời giải Lấy M là trung điểm của BC
Xét AMB và AMC có: AM là cạnh chung, ABAC (theo giả thiết), BMCM (vì M là trung điểm BC ) C AMB AM (c.c.c) ABMACM (hai góc tương ứng) ACBABC .
Xét ABC có: 180 BACABCACB (tính chất tổng ba góc trong một tam giác) 18018060120ABCACBBAC Mà ACBABC nên 120:260 ACBABC . Bài 8:
Cho tam giác nhọn ABC . Giả sử O là một điểm nằm trong tam giác sao cho OA=OBOC . Chứng minh rằng: O là giao điểm của ba đường trung trực của ba cạnh ABC Lời giải Lấy M là trung điểm AB . Xét AMO và BMO có: MO là cạnh chung, OAOB (theo giả thiết), MAMB (vì M là trung điểm AB ) O AMO BM (c.c.c) AMOBMO (hai góc tương ứng). Mà 180 AMOBMO (kề bù) 90 AMOBMO OMAB .

28
M
A
C B
O M B A C
Mà M là trung điểm của AB nên OM là đường trung trực của đoạn thẳng AB
Hay O thuộc đường trung trực của đoạn thẳng AB

Chứng minh hoàn toàn tương tự ta cũng có O thuộc đường trung trực của đoạn thẳng BC và AC .
Vậy O là giao điểm của ba đường trung trực của ba cạnh ABC .
29
I. LÍ THUYẾT TRỌNG TÂM
1. Trường hợp bằng nhau cạnh – góc – cạnh Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau. Xét ∆ABC

2. Hệ quả
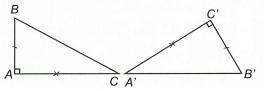
Trường hợp bằng nhau của hai tam giác vuông Nếu hai cạnh góc vuông của tam giác vuông này bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
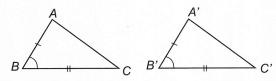
1 CHUYÊN ĐỀ
Ợ
TRƯỜNG H
P BẰNG NHAU THỨ HAI CỦA TAM GIÁC (cgc)
'
và ∆A’B’C’ có ABAB
BB
BCBC
Suy ra
ABCABCcgc
Xét
và 90 ABCA có ' ABAB ACAC . Suy ra ABCABC (hai cạnh góc vuông). II. CÁC DẠNG BÀI TẬP Dạng 1: Vẽ một tam giác khi biết độ dài
cạnh và góc
ữ
Phương
i: Vẽ ∆ABC biết độ dài hai cạnh , ABaBCb và B Bước 1. Vẽ
xBy
90 ABCA
hai
xen gi
a
pháp giả
góc
Bước 2. Xác định vị trí hai đỉnh còn lại của tam giác.
- Trên tia Bx, lấy điểm A sao cho ABa ;
- Trên tia By, lấy điểm C sao cho BCb .
Bước 3. Nối đoạn thẳng AC, ta được ∆ABC.
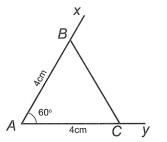

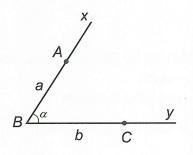
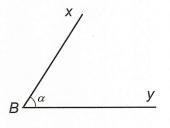
Bài 1:

Vẽ tam giác ABC có ABDAEC . Xác định độ dài cạnh BC.
Lời giải
- Vẽ góc 60 xAy .
- Trên tia Ax lấy điểm B sao cho 4 ABcm .
- Trên tia Ay lấy điểm C sao cho 4 ACcm .
- Vẽ đoạn thẳng BC ta được tam giác ABC. Dùng thước đo độ dài, ta đo được 4 BCcm .
2
Bài 2:
Vẽ tam giác ABC biết 90,3 AABcm và 4 ACcm

- Vẽ góc 90 xAy
- Trên tia Ax lấy điểm B sao cho 3 ABcm
- Trên tia Ay lấy điểm C sao cho 4 ACcm
- Vẽ đoạn thẳng BC ta được tam giác ABC.
Lời giải
Bài 3:
Vẽ tam giác MNP biết 4,5 MNcmMPcm và 45 M

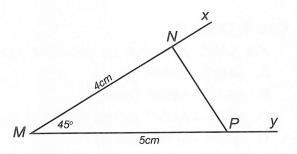
Lời giải
- Vẽ góc 45 xMy .
- Trên tia Mx lấy điểm N sao cho 4 MNcm .
- Trên tia My lấy điểm P sao cho 5 MPcm .
- Vẽ đoạn thẳng PN ta được tam giác MNP.
Bài 4:
Vẽ tam giác ABC có 50,3 CCACBcm .
Lời giải
- Vẽ góc 50 xCy .

3
- Trên tia Cx lấy điểm A sao cho 3 CAcm .
- Trên tia Cy lấy điểm B sao cho 3 BCcm .
- Vẽ đoạn thẳng AB ta được tam giác ABC
Dạng 2: Chứng minh hai tam giác bằng nhau theo trường hợp cạnh - góc - cạnh
Phương pháp giải: Bước 1. Kiểm tra ba điều kiện bằng nhau: cạnh - góc - cạnh.
Chú ý: Góc xen giữa hai cạnh
Bước 2. Kết luận hai tam giác bằng nhau.
Ví dụ: Cho ∆ABC và ∆ABD như hình vẽ. Chứng minh ABCABD .
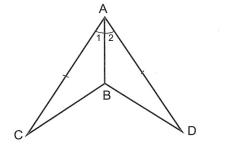
Hướng dẫn giải Xét ∆ABC và ∆ABD có

ACAD (giả thiết), 12 AA (giả thiết), AB là cạnh chung. Suy ra .. ABCABDcgc .
Bài 1. MĐ1 Trong các hình vẽ sau, có các tam giác nào bằng nhau? Vì sao?
Lời giải:
Các tam giác bằng nhau: ABDAED ; QMPNPM . Vì: + Xét ABD và AED có : ABAE (giả thiết); BADEAD (giả thiết); AD là cạnh chung
4
Q
N D B C A
P M E
ABDAED (c.g.c).
+ Xét QMP và NPM có: MNPQ (giả thiết); NMPQPM (giả thiết); MP là cạnh chung
QMPNPM (c.g.c).
Bài 5. MĐ2 Nêu thêm một điều kiện để mỗi hình dưới đây là hai tam giác bằng nhau theo trường hợp cạnh - góc - cạnh.
Lời giải: Để ABCADC theo trường hợp cạnh - góc - cạnh thì thêm điều kiện : ACBACD . Để EFIGHI theo trường hợp cạnh - góc - cạnh thì thêm điều kiện: IFIH Để MNPNMQ theo trường hợp cạnh - góc - cạnh thì thêm điều kiện: NPMQ
Bài 7. MĐ2 Qua trung điểm I của đoạn thẳng AB , kẻ đường thẳng vuông góc với AB , trên đường thẳng vuông góc đó lấy hai điểm C và D . Nối ,,, CACBDADB . Tìm các cặp tam giác bằng nhau. Lời giải:
Xét ACI và BCI có: AIBI ( I là trung điểm của AB ), CI là cạnh chung, 90 AICBIC
ACIBCI (c.g.c).

Xét ADI và BDI có:
AIBI ( I là trung điểm của AB ), DI là cạnh chung, 90 AIDBID
ADIBDI (c.g.c).
5
Q
I A H G E F M N B D C P 2 1 I A B C D
Vậy các cặp tam giác bằng nhau là: ACIBCI ; ADIBDI
Bài 8. MĐ2 Cho tam giác ABC , kẻ AH vuông góc với , BCHBC . Trên. tia đối của tia HA lấy điểm K sao cho HKHA , nối , KBKC . Tìm các cặp tam giác bằng nhau. Lời giải:
H A C
+ Xét ABH và KBH có: BH là cạnh chung; AHKH (giả thiết); 90 AHBKHB ABHKBH (c.g.c).
+ Xét CAH và CKH có: CH là cạnh chung; AHKH (giả thiết); 90 AHCKHC CAHCKH (c.g.c)
+ Xét ABC và KBC có: BC là cạnh chung, ACKC (vì CAHCKH ), ABKB (vì ABHKBH ) CAHCKH (c. c. c). Vậy các cặp tam giác bằng nhau: ABHKBH , CAHCKH , ABCKBC
Bài 9. MĐ2 Cho tam giác ABC có ABAC . Gọi AM là tia phân giác góc A . Chứng minh ABMACM .
Lời giải:
Xét tam giác ABM và tam giác ACM có : ABAC (giả thiết), BAMCAM ( AM là tia phân giác góc A ), AM là cạnh chung.

6
B K 2 1 2 1 M C B A
Suy ra ABMACM (c.g.c).
Bài 10. MĐ2 Cho tam giác ABC có BC . Gọi AM là tia phân giác góc A . Chứng minh ABMACM .
Lời giải:
2 1 2 M B C

1
Xét ABM có: 2 180 MAB (tổng ba góc trong một tam giác bằng 180 ).
Xét ACM có: 2 180 MAC (tổng ba góc trong một tam giác bằng 180 ).
Mà: BC ; 12 AA suy ra 12MM .
Xét tam giác ABM và tam giác ACM có : 12MM (chứng minh trên), AM là cạnh chung, 12 AA ( AM là tia phân giác góc A ). Suy ra ABMACM (c.g.c).
Bài 11. MĐ2 Cho Oz là tia phân giác góc xOy . Trên các tia ,, OxOyOz lần lượt lấy các điểm ,, ABC (khác O ) sao cho OAOB . Chứng minh OACOBC
Lời giải:
Xét OAC và OBC có: OAOB (giả thiết) AOCBOC (giả thiết) OC là cạnh chung OACOBC (c.g.c).
7
Bài 12. MĐ3 Cho góc xOy khác góc bẹt. Trên cạnh Ox lấy hai điểm A và B , trên cạnh Oy lấy hai điểm C và D , sao cho ; OAOCOBOD . A
y z x B A O C
a) Chứng minh OADOCB
b) Chứng minh ACDCAB
Lời giải:

C O A
x y D
a) Xét tam giác OAD và tam giác OCB , ta có: OAOC (giả thiết), AOC chung, ODOB (giả thiết) OADOCB (c.g.c).
b) Ta có : OBOAAB , ODOCCD . Mà ; OAOCOBOD nên ABCD . Lại có: OADOCB (chứng minh trên) suy ra ; B ADCBD (tương ứng).
Xét tam giác ACD và tam giác CAB có: ABCD , DB , ADCB (chứng minh trên) ACDCAB (c.g.c).
Bài 13. MĐ3 Cho ABC vuông ở A . Trên tia đối của tia AC lấy điểm D sao cho ADAC .
a) Chứng minh ABCABD .
b) Trên tia đối của tia AB lấy điểm M . Chứng minh MBDMBC . Lời giải:
a) Xét ABC và ABD có: ADAC (giả thiết), 90 BADBAC , AB là cạnh chung ABCABD (c.g.c).
b) Xét MBD và MBC có: ADAC (giả thiết), 90 MADMAC , AM là cạnh chung MBDMBC (c.g.c).
8
Bài 17. MĐ4 Cho ABC , kẻ BD vuông góc với AC , CE vuông góc với AB . Trên tia đối của tia BD , lấy điểm H sao cho BHAC . Trên tia đối của tia CE lấy điểm K sao cho CKAB . Chứng minh AHAK . Lời giải: B
D C A B M
Xét ABD vuông tại B (vì BDAC ) 1 90 BA . (1)
Xét ACE vuông tại E (vì CEAB ) 1 90 CA . (2) Từ (1) và (2) suy ra: 11 BC . Mà 1212180,180 BBCC 22BC .
Xét ABH và KCA có: ABCK (giả thiết), 22BC (chứng minh trên), BHAC (giả thiết) ABHKAC (c.g.c ) AHAK (hai cạnh tương ứng).
Bài 1:

Cho đoạn thẳng AB. Trên hai nửa mặt phẳng đối nhau bờ AB, vẽ các đoạn thẳng AC, BD bằng nhau và vuông góc với AB. Gọi M là trung điểm của AB. Chứng minh rằng AMCBMD .
Lời giải
Vì AC, BD vuông góc với AB nên 90 AB . Lại có M là trung điểm của AB nên MAMB . Xét ∆AMC và ∆BMD, có ACBD (giả thiết) 90 CAMDBM
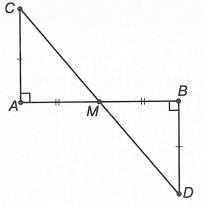
9
K
E D A
2 1 1 2
H
C B
Bài

Bài 3: Cho hình vẽ bên. Khẳng định nào
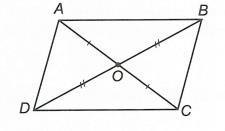

10 AMBM .
Suy ra AMCBMDcgc
.
.
.
2: Cho ∆ABC và ∆A’B’C’ như hình vẽ. Khẳng định nào sau đây đúng? A. ABCABC . B. ABCBAC
C. ABCCAB
D. ABCCBA
Lời giải Chọn D Xét ∆ABC và ∆A’B’C’ có ABBC
AC
ACAC
Do đó ABCCBAcgc
A.
B.
C.
. D.
. Lời giải
sát
vẽ, dễ chứng minh được: AOBCODcgc (B
AODCOBcgc (A
C sai). D.
sai
.
đúng?
AODBOC
AOBCOD
AODCOD
ADBADC
Quan
hình
đúng).
và
ADBDAC
do BDAC
Do đó chỉ có đáp án B đúng
Bài 4:

Cho hình vẽ bên. Khẳng định nào sai?
A. AHDAHE B. AHBAHC C. ABDAEC . D. ADBAEC . Lời giải
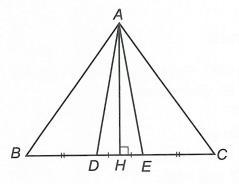
A. AHDAHE (đúng theo c.g.c). B. AHBAHC (đúng theo c.g.c). C. ABDAEC (sai vì ABAE ). D. ADBAEC (đúng theo c.g.c). Ở đáp án D, ta cần chỉ ra ; ADBAECADAE (điều này được suy ra từ AHDAHE ). Bài 5:
Cho ∆ABC và ∆MNP có ,, ABNMACNPAN . Trong các khẳng định sau, hãy chọn khẳng định sai
A. ABCNMP . B. BACMNP . C. ABCMNP D. CABPNM Lời giải Chọn C Xét ∆ABC và ∆MNP có ,, ABNMACNPAN . Suy ra ABCNMPcgc .
A. ABCNMP (đúng). B. BACMNP (đúng). C. ABCMNP (sai do đỉnh A, N không tương ứng). D. CABPNM (đúng). Bài 6:
11
Cho góc nhọn xAy . Trên tia Ax lấy hai điểm B và E, trên tia Ay lấy hai điểm D và C sao cho , ABADAEAC . Chứng minh rằng ABCADE
Lời giải

Xét ∆ABC và ∆ADE ta có ABAD (giả thiết), A chung, ACAE (giả thiết). Do đó .. ABCADEcgc .
BÀI TẬP TỰ LUYỆN
Bài 1. MĐ1 Trong các hình vẽ sau, có các tam giác nào bằng nhau? Vì sao? Lời giải: Xét ABC và DEF có: ABDE ; BE ; BCEF (theo giả thiết) ABCDEF (c.g.c).
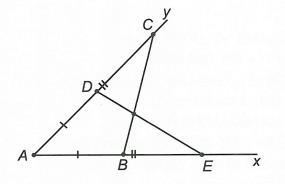
Bài 5. MĐ3 Cho góc xAy . Lấy điểm B trên Ax , điểm D trên Ay sao cho ABAD . Trên tia Bx lấy điểm E , trên tia Dy lấy điểm C sao cho BEDC . Chứng minh ABCADE .
giải:
12
Lời
B C A M P N D F E y x B C A E D
(giả thiết) nên AEAC
Xét ABC và ADE có: AEAC (chứng minh trên); A là góc chung; ABAD (giả thiết)
ABCADE (c.g.c).
Dạng 3: Chứng minh hai đoạn thẳng hoặc hai góc bằng nhau
Phương pháp giải:
Để chứng minh hai đoạn thẳng hoặc hai góc bằng nhau, ta có thể chứng minh hai tam giác bằng nhau có chứa hai đoạn thẳng hoặc hai góc đó.
Bước 1. Chọn hai tam giác có cạnh (hoặc góc) là hai đoạn thẳng (hoặc hai góc) cần chứng minh bằng nhau.
Bước 2. Chứng minh hai tam giác bằng nhau theo trường hợp cạnh - cạnh - cạnh hoặc cạnh - góc - cạnh (tùy theo giả thiết đề bài cho).
Bước 3. Suy ra cặp góc (cặp cạnh) tương ứng bằng nhau.
Ví dụ: Cho ∆ABC có ABAC . Tia phân giác của góc A cắt BC tại D. Chứng minh rằng BC và BDDC . Hướng dẫn giải
Xét ∆ADB và ∆ADC có
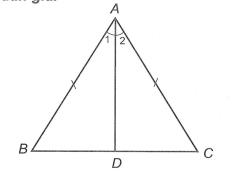
ABAC (giả thiết)
12 AA (do AD là tia phân giác)
AD là cạnh chung. Do đó ADBADC (c.g.c).
Suy ra:
BC (hai góc tương ứng); BDDC (hai cạnh tương ứng).

13 Ta có: AEABBE ; ACADDC Mà:
ABAD
; BEDC
Bài 1. MĐ1 Cho tam giác ABC có ABAC , tia phân giác của góc A cắt BC tại M . Chứng minh: BMCM Lời giải:
M C B
Xét tam giác ABM và tam giác ACM có: ABAC (giả thiết), BAMCAM ( AM là tia phân giác góc A ), AM là cạnh chung ABMACM (c.g.c) BMCM (hai cạnh tương ứng).
A O

x m y B
C
Bài 2. MĐ1 Cho góc nhọn xOy có Om là tia phân giác, COmCO . Trên tia Ox lấy điểm A , trên tia Oy lấy điểm B sao cho OAOB . Chứng minh:CACB Lời giải: Xét OAC và OBC có: OAOB (giả thiết), AOCBOC (giả thiết), OC là cạnh chung OACOBC (c.g.c) CACB (hai cạnh tương ứng).
Bài 3. MĐ1 Cho ABCMNP . Gọi O và G lần lượt là trung điểm của các cạnh BC và NP . Chứng minh AOMG Lời giải:
14
1 2
A
Ta có: ABCMNP ,, P B ABMNN NBC (tương ứng).
Mà O là trung điểm BC nên 1 2 BOBC , G là trung điểm NP nên 1 2 NGNP
Từ đó suy ra BONG

Xét ABO và MNG , ta có: ABMN BN , BONG (chứng minh trên) ABOMNG (c.g.c) AOMG (hai cạnh tương ứng).
Bài 5. MĐ2 Cho ABC có ABAC . Phân giác của góc A cắt cạnh BC tại điểm D . Trên cạnh AC lấy điểm E sao cho AEAB . Chứng minh:
a) BDED . b) DA là tia phân giác của góc BDE . Lời giải: a) Xét ADB và ADE có: AEAB (giả thiết), BADEAD ( AD là tia phân giác góc A ), AD là cạnh chung
ADBADE (c.g.c) BDCE (hai cạnh tương ứng).
b) Ta có: ADBADE (chứng minh trên) ADBADE (hai cạnh tương ứng) DA là tia phân giác của góc BDE
Bài 7. MĐ2 Cho ABC , M là trung điểm của BC . Trên tia đối của tia MA lấy điểm E sao cho MEMA . Chứng minh:
a) ABMECM .
b) ABCE và // ACBE . Lời giải:
15
G O A B C N P M
D A B C E
M C A
a) Xét ABM và ECM có:
AMEM (giả thiết),
BMCM ( M là trung điểm của BC ),
AMBEMC (hai góc đối đỉnh)
ABMECM (c.g.c).
b) Ta có: ABMECM (chứng minh trên) ABCE (hai cạnh tương ứng).
Xét AMC và EMB có:
AMEM (giả thiết), BMCM ( M là trung điểm của BC ),
AMCEMB (hai góc đối đỉnh)
AMCEMB (c.g.c)

ACMEBM (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong // ACBE .
Bài 8. MĐ3 Cho tam giác ABC có 80 A . Dựng AH vuông góc với BC ( HBC ). Trên tia đối tia HA lấy điểm D sao cho HDHA
a) Chứng minh: ACDC b) Chứng minh: ABCDBC c) Xác định số đo góc BDC
Lời giải:
E A 2 1 H C B D
a) Xét AHC và DHC có:
16
AHAD (giả thiết), B
HC là cạnh chung, 90 AHDDHC
AHCDHC (c.g.c)
ACDC (hai cạnh tương ứng).
b) Vì AHCDHC (chứng minh trên) 12CC (hai góc tương ứng).
Xét ABC và DBC có: ACDC (chứng minh trên), BC là cạnh chung, 12CC (chứng minh trên)
ABCDBC (c.g.c)
c) Vì ABCDBC (chứng minh trên) BDCBAC (hai góc tương ứng) 80 BDC
Bài 9. MĐ3 Cho ABC trên nửa mặt phẳng bờ AC không chứa điểm B , lấy điểm D sao cho // ADBC và ADBC . Chứng minh: a) ABCD b) // ABCD và ABDCDB
Lời giải:
O
B D
A C
a) Xét ABC và CDA có: ADBC (giả thiết), AC là cạnh chung, ACBDAC (hai góc so le trong) ABCCDA (c.g.c) ABCD (hai cạnh tương ứng). b) Vì ABCCDA (chứng minh trên) BACDCA (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong // ABDC
Xét ABD và CBD có: ADBC (giả thiết), BD là cạnh chung, ABDCBD (hai góc so le trong)
ABCCDA (c.g.c)

17
Bài 10. MĐ3 Cho ABC có 90 A , trên cạnh BC lấy điểm E sao cho BABE . Tia phân giác góc B cắt AC ở D .

a) Chứng minh: ABDEBD
b) Chứng minh: DADE . c) Tính số đo BED . d) Xác định độ lớn góc B để EDBEDC Lời giải:
a) Xét ABD và EBD có: BABE (giả thiết), 12BB ( BD là tia phân giác góc B ), BD là cạnh chung ABDEBD (c.g.c).
b) Vì ABDEBD (chứng minh trên) DADE (hai cạnh tương ứng). c) Vì ABDEBD (chứng minh trên) BADBED (hai cạnh tương ứng) 90 BED d) Để EDBEDC thì 2 EDBEDCBC 2 BC
18
V
. Bài 11. MĐ3 Cho ABC có ABAC . Kẻ tia phân giác
.
E sao cho
,
F sao cho
BDED
B
Mà 90 BC 60 B
ậy 60 B thì EDBEDC
AD của BAC
DBC
Trên cạnh AC lấy điểm
AEAB
trên tia AB lấy điểm
AFAC
. Chứng minh: a)
b) BFEC
c) BDFEDC d) ADFC Lời giải: 2 1 E D A C
a) Xét ABD và AED có: AD là cạnh chung, 12 AA ( AD là tia phân giác của BAC ), ABAE (giả thiết)
ABDAED (c.g.c) BDED (hai cạnh tương ứng).
b) Ta có: AFABBF , ACAEEC . Mà ACAF , ABAE (giả thiết) BFEC .
c) Vì ABDAED (chứng minh trên) 11 BE (hai góc tương ứng).
Ta có: 12 180 BB , 12 180 EE (kề bù). Mà 11 BE (chứng minh trên) 22BE .
Xét BDF và EDC có: BDED , 22BE , BFEC (chứng minh trên) BDFEDC (c.g.c)
d) Gọi H là giao điểm của AD và FC .
Xét AFH và ACH có: AH là cạnh chung, 12 AA ( AD là tia phân giác của BAC ), AFAC (giả thiết) AFHACH (c.g.c)
AHFAHC (hai góc tương ứng).

Lại có : 180 AHFAHC (kề bù) 90 AHFAHC ADFC .
Bài 14. MĐ4 Cho tam giác ABC nhọn. Vẽ đoạn thẳng AD vuông góc với AB và ADAB ( , DC khác phía so với AB ). Vẽ đoạn thẳng AE vuông góc với AC và AEAC ( , EB khác phía so với AC ). Chứng minh:
a) BEDC . b) BEDC . Lời giải:
19
1 2 2 1 2 1 H F D C B A E
a) Vì ADAB (giả thiết) nên 90 BAD ; AEAC (giả thiết) nên 90 CAE .
Ta có: 11 90 DACBADAA và 11 90 BAECAEAA DACBAE .
Xét DAC và BAE : ADAB , ACAE (giả thiết), DACBAE (chứng minh trên) DACBAE (c.g.c).
Vì DACBAE (chứng minh trên) nên DCBE , 1 CE ( tương ứng).
b) Gọi P là giao điểm AB và CD; I là giao điểm BE và CD
Ta có 90 ADCAPD (vì ADP vuông).

Lại có: DACBAE (chứng minh trên) ADCABE hay ADPPBI
90 ABEBPIBECD .
Bài 15. MĐ4 Cho tam giác ABC nhọn. Gọi , MN lần lượt là trung điểm của , ABAC . Lấy điểm , ED sao cho , MN là trung điểm của , CEBD
a) Chứng minh: // ADBC . b) Chứng minh: ,, AED thẳng hàng. Lời giải:
a) Xét AND và CNB :
NANC (vì N là trung điểm của AC ), NDNB (vì N là trung điểm của BD ),
ANDBNC (hai góc đối đỉnh)
ANDCNB (c.g.c) DANNCB (2 góc tương ứng).
20
P
B A
N
1
I
C
M D N E M A B C
Mà DAN và NCB là 2 góc so le trong nên // DABC .
b) Hoàn toàn tương tự ta chứng minh được: // AEBC . Như vậy: // AEBC , // DABC nên ,, ADE thẳng hàng (tiên đề Ơclít về đường thẳng song song).
Bài 1:

Cho ∆ABC. Gọi I là trung điểm của AC. Trên tia đối của tia IB lấy điểm E sao cho IEIB Chứng minh rằng:
a) AEBC . b) // AEBC Lời giải Xét ∆AIE và ∆CIB, ta có AICI (giả thiết);
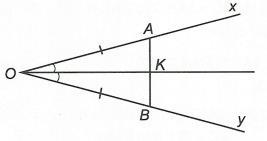
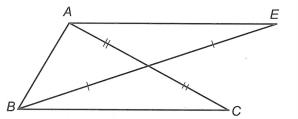
AIECIB (hai góc đối đỉnh); IEIB (giả thiết). Do đó (..)AIECIBcgc
Suy ra AEBC (hai cạnh tương ứng). b) Theo câu a) AIECIB
Suy ra EAIBCI (hai góc tương ứng) hay BCACAE . Mà hai góc này ở vị trí so le trong nên // AEBC .
Bài 2:
Cho góc xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OAOB . Gọi K là giao điểm của AB với tia phân giác của góc xOy. Chứng minh rằng: a) AKKB . b) OKAB . Lời giải
21
a) Xét ∆AOK và ∆BOK, ta có
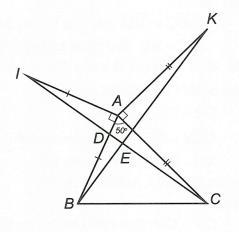
OAOB (giả thiết), AOKBOK (do AK là tia phân giác của góc O), OK là cạnh chung. Do đó AOKBOK (c.g.c). Suy ra AKBK (hai cạnh tương ứng). b) Theo câu a) ta có AOKBOK . Suy ra AKOBKO (hai góc tương ứng). Lại có 180 18090 2 AKOBKOAKOBKOOKAB .
Bài 3:

Cho ∆ABC có 50 A . Vẽ đoạn thẳng AI vuông góc và bằng AB (I và C khác phía đối với AB). Vẽ đoạn thẳng AK vuông góc và bằng AC (K và B khác phía đối với AC). Chứng minh rằng: a) ICBK b) ICBC Lời giải a) Ta có 9050140 IACIABBAC ; 9050140 BAKKACBAC Xét ∆AIC và ∆ABK, ta có AIAB (giả thiết), ACAK (giả thiết), 140 IACBAK . Do đó AICABK (c.g.c). Suy ra ICBK (hai cạnh tương ứng). b) Gọi D là giao điểm của IC và AB, E là giao điểm của IC và BK.
Vì AICABK nên AIDEBD (hai góc tương ứng). Lại có ADIEDB (hai góc đối đỉnh). Mà ∆AID vuông tại A nên 9090AIDADIEBDEDB
22
Bài 4:
Cho đoạn thẳng BC, điểm H nằm giữa B và C. Qua H kẻ đường thẳng vuông góc với BC, trên đường thẳng đó lấy các điểm A và K sao cho HAHK . Kẻ các đoạn thẳng AB, BK, KC, CA.
a) Chứng minh rằng BABK .
b) Chứng minh rằng BC là tia phân giác của góc ABK.
c) Kể tên các góc bằng góc BAH. d) ∆ABC bằng với tam giác nào? Vì sao? Lời giải
a) Xét ∆AHB và ∆KHB, ta có AHKH (giả thiết), 90 AHBKHB (do AKBC ), BH là cạnh chung. Do đó AHBKHBcgc

Suy ra BABK (hai cạnh tương ứng).
b) Theo câu a) ta có AHBKHB .
Suy ra ABHKBH (hai góc tương ứng)
Suy ra BC là tia phân giác của ABK .
c) Theo câu a ta có AHBKHB suy ra BAHBKH (hai góc tương ứng). d) ABCKBCcgc vì ABBK (chứng minh a); ABCKBC (do BC là tia phân giác của ABK ); BC chung
Bài 5:

23 Xét ∆BED có 1801809090BEDEBDEDB . Suy ra ICBK
Cho đoạn thẳng AB, điểm O nằm giữa A và B. Kẻ tia Ox vuông góc với AB. Trên tia Ox lấy các điểm C và D sao cho , OCOAODOB . Gọi M là trung điểm của AD,N là trung điểm của BC.
Chứng minh rằng: a) ADCB b) OMON , OM vuông góc với ON. Lời giải
a) Xét ∆AOD và ∆COB, ta có
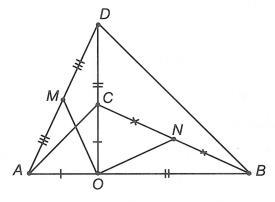

AOCO (giả thiết), 90 AODCOB (vì ODAB ), ODOB (giả thiết). Do đó .. AODCOBcgc . Suy ra ADBC (hai cạnh tương ứng).
b) Theo câu a) ta có AODCOB . Suy ra:
OBCODA (hai góc tương ứng); BCAD (hai cạnh tương ứng). Mà M, N lần lượt là trung điểm của AD, BC nên NBMD . Xét ∆OBN và ∆ODM có
OBOD (giả thiết), OBNODM (chứng minh trên), NBMD (chứng minh trên). Do đó OBNODM (c.g.c). Suy ra
ONOM (hai cạnh tương ứng);
NOBMOD (hai góc tương ứng).
Ta lại có 9090NOBNOCMODCON Vậy MOON .
24
Bài 6:
Cho ∆ABC. Gọi D, E theo thứ tự là trung điểm của AB, AC.
a) Trên tia đối của tia ED lấy điểm I sao cho
EIED . Chứng minh rằng AIDC
b) Chứng minh rằng: 1 ,// 2 DEBCDEBC . Lời giải
a) Xét ∆AEI và ∆CED ta có
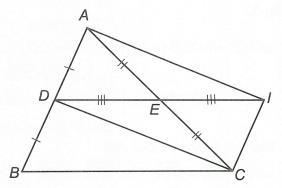
EAEC (giả thiết);
AEICED (hai góc đối đỉnh);
EIED (giả thiết). Do đó AEICEDcgc
Suy ra AICD (hai cạnh tương ứng).
b) Ta có AEICED (câu a)
Suy ra IAEDCE (hai góc tương ứng). Mà hai góc này ở vị trí so le trong nên // AIDC . Suy ra DAIBDC (hai góc đồng vị).
Xét BDC và ∆DAI ta có BDDA (giả thiết), BDCDAI (chứng minh trên), DCAI (chứng minh trên).
Do đó .. BDCDAIcgc . Suy ra DIBC (hai cạnh tương ứng). Mà 11 22 DEDIDEBC .

Ta lại có DBCADI (hai góc tương ứng). Mà hai góc này ở vị trí đồng vị nên // DEBC .
BÀI TẬP TỰ LUYỆN
Bài 15. MĐ4 Cho tam giác ABC nhọn. Gọi , MN lần lượt là trung điểm của , ABAC . Lấy điểm , ED sao cho , MN là trung điểm của , CEBD
a) Chứng minh: // ADBC b) Chứng minh: ,, AED thẳng hàng. Lời giải:
25
a) Xét AND và CNB :
NANC (vì N là trung điểm của AC ), NDNB (vì N là trung điểm của BD ), ANDBNC (hai góc đối đỉnh)
ANDCNB (c.g.c) DANNCB (2 góc tương ứng).
Mà DAN và NCB là 2 góc so le trong nên // DABC . b) Hoàn toàn tương tự ta chứng minh được: // AEBC . Như vậy: // AEBC , // DABC nên ,, ADE thẳng hàng (tiên đề Ơclít về đường thẳng song song).
Bài 6. MĐ4 Cho tam giác ABC có M và N lần lượt là trung điểm của cạnh AB và AC . Trên tia đối của tia NB lấy điểm D sao cho NDNB . Trên tia đối của tia MC lấy điểm E sao cho MEMC . Chứng minh :
a) ADBC b) // AEBC c) A là trung điểm của DE . Lời giải: a) Xét AND và CNB , ta có : ANNC ( N là trung điểm của cạnh AC ), 21NN (đối đỉnh), NDNB (giả thiết) ANDCNB (c.g.c) ADBC (hai cạnh tương ứng) b) Chứng minh tương tự ta có: AMEBMC (c.g.c), nên 11 EC (hai góc tương ứng). Mà 1E và 1C ở vị trí so le trong nên // AEBC . c) Vì ANDCNB nên 12DB (hai góc tương ứng).


26
D N E M A B
C 2 2 1 1 1 D N E M C B A C
Mà 1D và 2B ở vị trí so le trong nên // ADBC .
Ta có: // ADBC và // AEBC suy ra ,, DAE thẳng hàng (theo tiên đề Ơclit).
Vì AMEBMC AEBC (hai cạnh tương ứng).

Mà ADBC (chứng minh trên) AEAD . Suy ra A là trung điểm của ED Bài 7. MĐ4 Cho tam giác ABC có ba góc nhọn. Vẽ đoạn thẳng AMAB ; AMAB sao cho M và C khác phía đối với đường thẳng AB . Vẽ đoạn thẳng ANAC và ANAC sao cho N và B khác phía đối với đường thẳng AC . Gọi , IK lần lượt là trung điểm của BN và CM . Chứng minh : a) AMCABN . b) MCBN và MCBN c) AIAK và AIAK Lời giải: a) Vì AMAB (giả thiết) nên 90 BAM ; ANAC (giả thiết) nên 90 CAN . Ta có: 11 90 MACBAMAA và 11 90 BANCANAA MACBAN . Xét MAC và BAN : AMAB (giả thiết), ACAN (giả thiết), MACBAN (chứng minh trên) MACBAN (c.g.c). b) Gọi P là giao điểm AB và CM ; O là giao điểm BN và CM .
Ta có: 90 AMCAPM (vì AMP
27
). Lạ
AMCABN
ứ
AMPPBO 90 M
N .
.
vuông tại A
i có: MACBAN
(chứng minh trên)
(hai góc tương
ng) hay
ABPO BN B C
c) Ta có , KI lần lượt là trung điểm của , CMBN
Mà
CMBN (chứng minh trên) MKBI Xét AMK và ABI có:
AMKABN (chứng minh trên), AMAB
(chứng minh trên), 1 P K I O C A B N M
MKBI (chứng minh trên)
AMKABI (c.g.c)

AKAI (hai cạnh tương ứng) và MAKBAI (hai góc tương ứng).
Mà 90 MAKKAB 90 BAIKAB hay AIAK .
28
GÓC – CẠNH – GÓC (G.C.G)

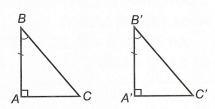
I. LÍ THUYẾT TRỌNG TÂM
Trường hợp bằng nhau góc – cạnh – góc
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau
Xét ∆ABC và ∆A’B’C’ có BB
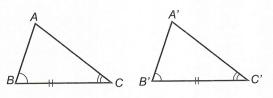
Hệ quả
Hệ quả 1: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Suy ra '(..)ABCABCgcg
BB
Suy ra ' ABCABC (cạnh góc vuông – góc nhọn kề).
Hệ quả 2: Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Trang 1 TRƯỜNG HỢP BẰNG NHAU THỨ BA CỦA TAM GIÁC
BCBC
CC
Xét 90 ABCA và 90 ABCA có ABAB
Xét 90 ABCA và 90 ABCA có BCBC
BB
II. CÁC DẠNG BÀI TẬP
Dạng 1: Vẽ tam giác biết một cạnh và hai góc kề Phương pháp giải Vẽ ∆ABC biết ,, AABaB
Bước 1. Vẽ đoạn thẳng ABa
Bước 2. Trên cùng nửa mặt phẳng bờ chứa AB vẽ hai tia Ax và By thỏa mãn , AB
Bước 1.
Bước 3. Xác định vị trí của đỉnh C: Giao của hai tia vừa vẽ.
Bước 2. Bước 3.
Ví dụ mẫu Ví dụ. Vẽ ∆ABC biết 3,90,30ACcmAC .
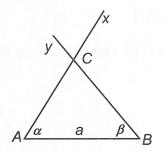
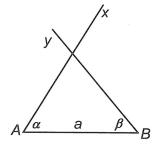

Hướng dẫn giải
- Vẽ đoạn thẳng 3 ACcm - Trên một nửa mặt phẳng bờ AC: + Vẽ tia Ax vuông góc với AC tại A + Vẽ tia Cy sao cho 30 ACy .
Trang 2
ền – góc
Suy ra ' ABCABC (cạnh huy
nhọn)
nhau
Ta được ∆ABC cần vẽ
Bài tập tự luyện dạng 1
Câu 1: Vẽ ∆ABC có 70,4,60BBCcmC
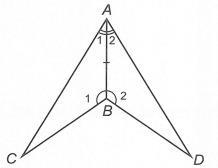
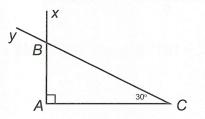
Câu 2: Vẽ ∆ABC có 30,3,60BBCcmC
Dạng 2: Chứng minh hai tam giác bằng nhau theo trường hợp góc - cạnh - góc Phương pháp giải
Ví dụ: Cho hình vẽ sau: Chứng minh rằng ABCABD
Bước 1. Xét hai tam giác cần chứng minh
Bước 2. Kiểm tra ba điều kiện bằng nhau: góccạnh – góc.
Chú ý: Hai góc kề cùng một cạnh.
Bước 3. Kết luận hai tam giác bằng nhau.
Ví dụ mẫu
Hướng dẫn giải
Xét ∆ABC và ∆ABD ta có
12 AA (giả thiết) AB là cạnh chung 12BB (giả thiết). Do đó .. ABCABDgcg
Ví dụ. Cho hình vẽ sau đây, chứng minh rằng ABDACE
Trang 3 - Ax và Cy cắ
t
tại B
Hướng dẫn giải
Ta có 1212180,180BBCC (hai góc kề bù). Mà 11 BC nên 22BC
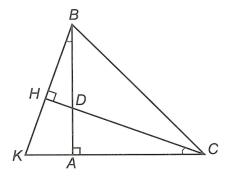
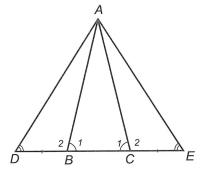
Xét ∆ABD và ∆ACE, ta có
DE (giả thiết)
BDCE (giả thiết) 22BC (chứng minh trên)
Do đó ABDACEgcg
Bài tập tự luyện dạng 2
Câu 1: Trong hình sau có các tam giác nào bằng nhau? Vì sao?
Câu 2: Cho hình vẽ sau biết ABAC . Chứng minh ABKACD

Trang 4
ng 3. Chứng minh hai đoạn thẳng bằng nhau
Phương pháp giải
Bước 1. Chọn hai tam giác có cạnh là hai đoạn thẳng cần chứng minh bằng nhau.
Bước 2. Chứng minh hai tam giác bằng nhau theo một trong ba trường hợp bằng nhau.
Bước 3. Suy ra hai cạnh tương ứng bằng nhau
Ví dụ: Cho hình vẽ sau với //,// ABCDADBC
Chứng minh rằng ABCD và ADBC Hướng dẫn giải Xét ∆ACD và ∆CAB ta có
11 AC (hai góc so le trong và // ADBC ) AC là cạnh chung 22AC (hai góc so le trong và // ABDC ) Do đó ACDCAB (g.c.g)
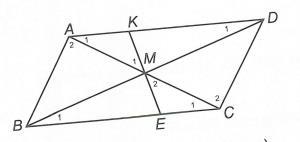

Suy ra: ABCD ADBC (hai cặp cạnh tương ứng)
Ví dụ mẫu Ví dụ. Cho cặp đoạn thẳng song song AD, BC bị chắn bởi hai đường thẳng song song AB, CD. Qua giao điểm M của AC và BD, kẻ đường thẳng bất kì cắt AD, BC theo thứ tự ở K, E. Chứng minh rằng: a) MAMC b) MKME Hướng dẫn giải a) Vì // ADBC nên 1111 ; ACDB (hai góc so le trong) Vì // ABCD nên 22AC (hai góc so le trong).
Trang 5 Dạ
Xét ∆ACD và ∆CAB, ta có
11 AC (chứng minh trên)
AC là cạnh chung
22AC (chứng minh trên)
Do đó ACDCABgcgADBC (hai cạnh tương ứng)
Xét ∆MAD và ∆MCB, ta có
11 AC (chứng minh trên)
ADBC (chứng minh trên)
11 DB (chứng minh trên)
Do đó .. MADMCBgcgMAMC (hai cạnh tương ứng)
Sơ đồ chứng minh.
Vận dụng tính chất song song //,// ADBCABCD Chứng minh .. ACDCABgcg
Chứng minh ADBC Chứng minh MADMCBgcg Chứng minh MAMC
b) Xét ∆MAK và ∆MCE, ta có
12MM (hai góc đối đỉnh) MAMC ( chứng minh trên)
11 AC (chứng minh trên) Do đó MAKMCEgcgMKME (hai cạnh tương ứng) Bài tập tự luyện dạng 3 Câu 1: Cho ∆ABC có 90 ABACA . Kẻ BD vuông góc với AC DAC . Kẻ CE vuông góc với AB EAB . Chứng minh rằng: BDCE Câu 2: Cho ∆ABC, điểm M thuộc cạnh BC. Đường thẳng đi qua M và song song với AB cắt AC ở D. Đường thẳng đi qua M và song song với AC cắt AB ở E. Chứng minh rằng ADME Dạng 4: Sử dụng nhiều trường hợp bằng nhau của tam giác Phương pháp giải Sử dụng nhiều trường hợp bằng nhau của hai tam giác đã học: +) Cạnh - cạnh - cạnh
Trang 6
+) Cạnh - góc - cạnh +) Góc - cạnh – góc. Ví dụ mẫu Ví dụ 1. Cho ∆ABC có ABAC . Trên hai cạnh AB, AC lần lượt lấy hai điểm D, E sao cho ADAE . Chứng minh rằng a) BEDC b) Gọi F là giao điểm của EB và DC. Chứng minh FDFE Hướng dẫn giải
a) Xét ∆ADC và ∆AEB, ta có ADAE (giả thiết) A là góc chung ABAC (giả thiết) Do đó .. ADCAEBcgc DCEB (hai cạnh tương ứng)
b) Theo câu a ta có 1122 ; ADCAEBBCED (hai góc tương ứng).
Vì 22 ED nên 11 ED (hai góc kề bù với hai góc bằng nhau)
Lại có ABAC và ADAEABADACAEDBCE
Xét ∆DFB và ∆EFC, ta có 11 11
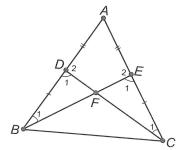
BC BDCE DE
(chứng minh trên)
Do đó DFBEFCgcgDFEF ( hai cạnh tương ứng).
Sơ đồ chứng minh câu b Sử dụng kết quả câu a Chứng minh 1111 ;; BCBDCEDE
Trang 7
ng minh .. DFBEFCgcg
Chứng minh DFEF
Ví dụ 2. Cho ∆ABC. Trên tia đối của tia AB lấy điểm D sao cho ADAB . Trên tia đối của tia AC lấy điểm E sao cho AEAC . Một đường thẳng đi qua A cắt các cạnh DE và BC theo thứ tự ở M và N.
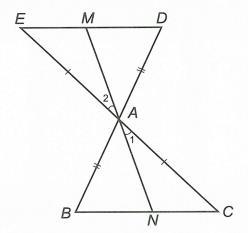
Chứng minh rằng AMAN Hướng dẫn giải
Xét ∆AED và ∆ACB, ta có
AEAC (giả thiết)
EADCAB (hai góc đối đỉnh)
ADAB (giả thiết)
Do đó AEDACBcgcEC (hai góc tương ứng)
Xét ∆AME và ∆ANC, ta có
12 AA (hai góc đối đỉnh)
AEAC (giả thiết)
EC (chứng minh trên)
Do đó AMEANCgcgAMAN (hai cạnh tương ứng)
Sơ đồ chứng minh
Chứng minh .. AEDACBcgc Chứng minh EC Chứng minh .. AMEANCgcg
Trang 8
Chứ
Bài tập tự luyện dạng 4
Câu 1: Cho ∆ABC ABAC . Trên tia đối của tia AB lấy điểm D sao cho ADAB . Trên tia đối của tia AB lấy điểm E sao cho AEAC . Gọi O là giao điểm của BC và DE. Chứng minh rằng
a) ADEABC b) ODOB c) OA là tia phân giác của COE
Câu 2: Cho ∆ABC có ABAC . Trên các cạnh AB và AC lấy các điểm D và E sao cho ADAE . Gọi K là giao điểm của BE và CD. Chứng minh rằng
a) BECD
b) KBCKCB
Câu 3: Cho ∆ABC có 60 A . Tia phân giác của góc B cắt AC ở D, tia phân giác của góc C cắt AB ở E. Các tia phân giác đó cắt nhau tại I. Chứng minh rằng IDIE
Trang 9 Chứng minh AMAN
Dạng 1. Vẽ tam giác biết một cạnh và hai góc kề
Câu 1:
- Vẽ đoạn thẳng 4 BCcm
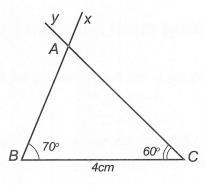
Trên cùng một nửa mặt phẳng bờ BC:
- Vẽ tia Bx sao cho 70 xBC
- Vẽ tia Cy sao cho 60 yCB
Bx và Cy cắt nhau tại A.
Ta được ∆ABC cần vẽ
Câu 2:
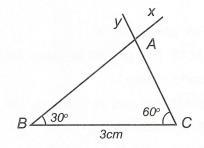
- Vẽ đoạn thẳng 3 BCcm
Trên nửa mặt phẳng bờ chứa đường thẳng BC:
- Vẽ góc 30 CBx
- Vẽ góc 60 BCy
Hai tia Bx và Cy cắt nhau tại A.
Ta được ∆ABC cần vẽ
Dạng 2. Chứng minh hai tam giác bằng nhau theo trường hợp góc - cạnh – góc
Câu 1:
Trang 10 ĐÁP ÁN
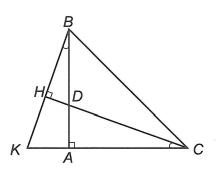
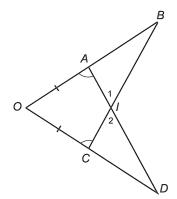
Trang 11 ..
vì
L
G
ủ
Xét
∆CID
V
..
..
OADOCBgcg
chung O OAOC OADOCB
OADOCBgcgODOB
(hai cạnh tương ứng) BD
(hai góc tương ứng) Mà OCOACDAB
ại có OADOCB
nên BADDCB
(hai góc kề bù với hai góc bằng nhau)
ọi I là giao điểm c
a AD và BC
∆AIB và
có BD ABCD BAIDCI
(chứng minh trên) Suy ra
AIBCIDgcg
ậy
OADOCBgcg và
AIBCIDgcg Câu 2: Xét ∆ABK vuông tại A và ∆ACD vuông tại A có: ABAC
ABKACD
Suy ra ABKACD (cạnh góc vuông - góc nhọn kề) Dạng 3. Chứng minh hai đoạn thẳng bằng nhau Câu 1:
Xét ∆ADB vuông tại D và ∆AEC vuông tại E, ta có

A chung
ABAC
Do đó ADBAEC (cạnh huyền - góc nhọn)
DBEC (hai cạnh tương ứng)
Câu 2:
Xét ∆AMD và ∆MAE, ta có
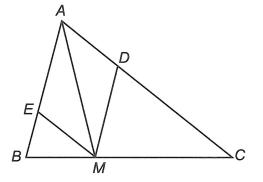
AMDMAE (hai góc so le trong, // MDAB )
AM là cạnh chung.
EMADAM (hai góc so le trong, // MEAC )
Do đó .. AMDMAEgcg
MEAD (hai cạnh tương ứng)
Dạng 4. Sử dụng nhiều trường hợp bằng nhau của tam giác
Câu 1:
Trang 12
a) Xét ∆ADE và ∆ABC, ta có
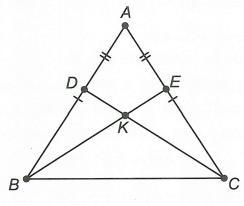
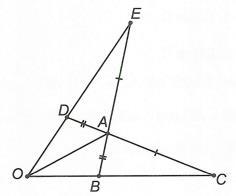
ADAB (giả thiết)
DAEBAC (hai góc đối đỉnh)
AEAC (giả thiết)
Do đó ADEABCcgc ADEABC (hai góc tương ứng)
b) Vì EDACBA nên ADOABO (tính chất hai góc kề bù). Lại có , AEACADAB nên AEABACAD hay BEDC
Xét ∆OBE và ∆ODC, ta có ,, OBEODCBEDCEC (do ADEABC ) Do đó .. OBEODCgcgODOB (hai cạnh tương ứng)
c) Xét ∆ODA và ∆OBA, ta có ,, ODOBADOABOADAB Do đó ODAOBAcgcDOABOA (hai góc tương ứng) OA là tia phân giác của COE
Câu 2:
a) Xét ∆AEB và ∆ADC, ta có , AEADA là góc chung, ABAC
Do đó .. AEBADCcgcBECD (hai cạnh tương ứng).
Trang 13
Xét ∆DBC và ∆ECB, ta có
DCBE (chứng minh trên), BC là cạnh chung, BDEC Do đó DBCECBccc
DCBEBC (hai góc tương ứng) hay KBCKCB
Câu 3:
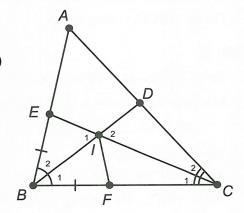
Xét ∆ABC ta có 18018060120BCA 11 60 BC (do BD và CE là tia phân giác của góc B và góc C) ∆BIC có 11 180120BICBC 12 60 II (hai góc đối đỉnh và cùng kề bù với BIC ).
Trên BC lấy điểm F sao cho BEBF Khi đó dễ dàng chứng minh được .. BEIBFIcgc IEIF (hai cạnh tương ứng) (1) 1 60 IBIF (hai góc tương ứng) 60 FICBICBIF
Xét ∆IFC và ∆IDC ta có 60 FICDIC (chứng minh trên), IC là cạnh chung, 12CC (do CI là phân giác của ACB ) Do đó IFCIDCccc . Suy ra IDIF (hai cạnh tương ứng). (2) Từ (1) và (2), suy ra IEID
Trang 14 b) Do ; ABACADAE nên BDEC
CÁC TRƯỜNG HỢP BẰNG NHAU THỨ HAI VÀ THỨ BA CỦA TAM
PHẦN I. TÓM TẮT LÍ THUYẾT
1. Trường hợp bằng nhau: cạnh - góc - cạnh Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau
(c.g.c) 2. Trường hợp bằng nhau: cạnh - góc - cạnh
một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
(g.c.g)

PHẦN II. CÁC DẠNG BÀI. Dạng 1. Tìm hoặc chứng minh hai tam giác bằng nhau
I. Phương pháp giải: + Xét hai tam giác. + Kiểm tra ba điều kiện bằng nhau cạnh - góc - cạnh, góc – cạnh - góc. + Kết luận hai tam giác bằng nhau.
II. Bài toán. Bài 2. MĐ1. Trong các hình vẽ sau, có hai tam giác nào bằng nhau? Vì sao?
Lời giải: Các tam giác bằng nhau: ADBADC ; EFGEHG . Thật vậy: + Xét ADB và ADC có:
ADBADC (giả thiết); AD là cạnh chung; BADCAD (giả thiết)
(g.c.g).
1 CHUYÊN ĐỀ.
GIÁC
và
ABAB AAABCABC ACAC
Xét ABC và ABC có: BB ABABABCABC AA
Xét ABC
ABC
có:
Nếu
ADBADC
A' C' B' B I A A C B B' C' A' B C F H A D E G
+ Xét EFG và EHG có:
FEGHEG (giả thiết); EG là cạnh chung; EGFEGH (giả thiết)
EFGEHG (g.c.g)

Bài 3. MĐ1 Trong các hình vẽ sau, có hai tam giác nào bằng nhau? Vì sao?
Lời giải: Các tam giác bằng nhau: GQHPHQ ; IKLIMN ; ABCDEF
Thật vậy:
+ Xét GQH và PHQ có:
GQHPHQ (theo giả thiết)
GHQPQH (hai góc so le trong, // GHQP ) QH là cạnh chung GQHPHQ (g.c.g)
+ Xét IKL và IMN có:
ILIK (theo giả thiết);
KILMIN (hai góc đối đỉnh);
KLIMNI (theo giả thiết)
IKLIMN (g.c.g)
Xét ABC và DEF có:
AD (theo giả thiết);
BE (theo giả thiết);
ABDE (theo giả thiết)
ABCDEF (g.c.g)
Bài 4. MĐ1 Trong các hình vẽ sau, có các tam giác nào bằng nhau? Vì sao?
Lời giải: Các tam giác bằng nhau: MNPMQO ; MNOMQP
2
QP
Q
G K
B
D E C F 2 1 2 1 P N Q
O
GH//
L H
P
M N
A
M
y:
+) Ta có: 12 180 PP (hai góc kề bù); 12 180 OO (hai góc kề bù)
Lại có : 21 PO 12PO
Xét MNP và MQO có: 12PO (chứng minh trên) ; NPQO (theo giả thiết); NQ (theo giả thiết)
MNPMQO (g.c.g)
+) Ta có: NONPPO ; QPQOOP . Mà NPQO NOQP .
+ Xét MNO và MQP có: MNMQ (vì MNPMQO - theo chứng minh trên), NQ (theo giả thiết), NOQP (chứng minh trên)
MNOMQP (c.g.c).
Bài 6. MĐ2 Nêu thêm một điều kiện để mỗi hình dưới đây là hai tam giác bằng nhau theo trường hợp góc - cạnh - góc.
A B C
D

M O
E P N
Lời giải: Để ABDAED theo trường hợp góc - cạnh - góc thì thêm điều kiện: ADBADE Để MNOMPO theo trường hợp góc - cạnh - góc thì thêm điều kiện: MONMOP Bài 14. MĐ3 Cho hình vẽ sau, trong đó // ABCD , ABCD . Chứng minh rằng: a) OABODC b) OACODB Lời giải: a) Xét OAB và ODC có: OABODC (hai góc so le trong), ABCD (giả thiết),
3 Thật vậ
O B D A C
OBAOCD (hai góc so le trong)
OABODC (g.c.g).
b) Vì OABODC (chứng minh trên) ; OAODOBOC (các cạnh tương ứng).
Xét OAC và ODB có: OAOD ,OBOC (chứng minh trên), AOBDOC (hai góc đối đỉnh) OACODB (c.g.c), Bài 15. CĐ4 Cho góc nhọn xOy có tia Oz là tia phân giác. Qua điểm A thuộc tia Ox , vẽ đường thẳng song song với Oy cắt Oz tại M . Qua M kẻ đường thẳng song song với Ox cắt Oy tại B .
a) Chứng minh OAMMBO b) Từ M vẽ MHOx ; MKOy . Chứng minh MHOMKO Lời giải:
a) Xét OAM và MBO , ta có : 11OM (hai góc so le trong), OM là cạnh chung, 22MO (hai góc so le trong) OAMMBO (g.c.g).
b) Ta có: 1 90 OOMH (hai góc nhọn phụ nhau), 2 90 OOMK (hai góc nhọn phụ nhau).

Lại có : 12OO (Oz là tia phân giác xOy ) OMHOMK .
Xét OMH và OMK , ta có: 12OO (chứng minh trên), OM chung, OMHOMK (chứng minh trên)
OMHOMK (g.c.g).
4
Bài 16. MĐ4 Cho tam giác ABC có 90 A và ABAC . Trên các cạnh AB và AC lần lượt lấy điểm D và E sao cho ADAE . Qua A và D kẻ đường vuông góc với BE cắt BC lần lượt tại M và N . Tia ND cắt tia CA tại I . Chứng minh rằng: a) AIDABE y z x 1 2 2 1 K H M B O A
Lời giải:

a) Gọi H là giao điểm của BE và IN
Ta có: AEB vuông tại A nên 90 ABEAEB ; DHB vuông tại H nên 90 DBHHDB .
Suy ra HDBAEB .
Mà HDBADI (hai góc đối đỉnh) suy ra ADIAEB
Xét ADI và ABE có: 90 DAIEAB , AEAD (giả thiết), ADIAEB (chứng minh trên).
Do đó AIDABE (g.c.g).
b) Ta có AMBE , INBE suy ra // AMIN
Qua N kẻ đường thẳng song song với AC cắt AM tại F // // ACNFAINF .
Xét AIN và NFA có:
IANFNA (so le trong, // AINF ), ANINAF (so le trong, // AMIN ), AN là cạnh chung AINNFA (g.c.g) NFAI (hai cạnh tương ứng).
Mà AIDABE (chứng minh trên) AIAB (hai cạnh tương ứng).
Lại có ABAC (giả thiết) NFAC
Lại có: // ACNF CAMMFN , ACMMNF (hai góc so le trong).
Xét MAC và MFN ta có: CAMMFN (chứng minh trên), ACMMNF (chứng minh trên), NFAC (chứng minh trên) MACMFN (g c g)
Dạng 2. Sử dụng trường hợp bằng nhau của tam giác để chứng minh một tính chất khác
I. Phương pháp giải: + Chọn hai tam giác có cạnh (góc) là hai đoạn thẳng (góc) cần chứng minh bằng nhau.
5
CMMN
b) Chứng minh
F
H
N D A B
E
I
M
C
+ Chứng minh hai tam giác ấy bằng nhau theo một trong hai trường hợp cạnh - góc - cạnh, góc - cạnh - góc rồi suy ra hai cạnh (góc) tương ứng bằng nhau.Kiểm tra ba điều kiện bằng nhau cạnh - góc - cạnh, góc - cạnh - góc .
+ Kết hợp với các tính chất đã học về tia phân giác, đường thẳng song song, đường trung trực, tổng ba góc trong một tam giác, ... để chứng minh một tính chất khác.
II. Bài toán.
Bài 4. MĐ2 Cho tam giác ABC có BC . Tia phân giác của góc A cắt BC tại D .
a) Chứng minh ABAC . b) Chứng minh ADBC . Lời giải:
A

2 1 1 2 D B C
a) Xét ADB có: 1 180 ABD (tổng ba góc trong tam giác)
Xét ADC có: 2 180 CBD (tổng ba góc trong tam giác).
Mà: 12 AA (vì AD là phân giác của BAC ), BC (giả thiết) 12 DD .
Xét ADB và ADC có: 12 AA ( AD là tia phân giác của góc BAC ), AD là cạnh chung, 12DD (chứng minh trên)
ADBADC (g.c.g) ABAC (hai cạnh tương ứng)
b) Ta có: 12 DD (chứng minh trên), mà 12 180 DD (hai góc kề bù) 12 90 DD ADBC Bài 6. MĐ2 Cho góc xOy khác góc bẹt và có Ot là tia phân giác. Lấy điểm C thuộcOt CO . Qua C kẻ đường vuông góc với Ot , cắt , OxOy theo thứ tự ở , AB a) Chứng minh:OAOB . b) Lấy điểm D thuộc Ct DC . Chứng minh: DADB và OADOBD . Lời giải:
6
t
y
a) Xét OAC có: 11 180 OAC(tổng ba góc trong một tam giác).
Xét OBC có: 22 180 OBC (tổng ba góc trong một tam giác)
Mà 12OO (vì Ot là phân giác xOy ), 90 AB nên 12CC .
Xét OAC và OBC có: 12OO (Ot là tia phân giác xOy ), OC là cạnh chung, 12CC (chứng minh trên)
OACOBC (g.c.g)

OAOB (hai cạnh tương ứng).
b) Xét OAD và OBD có: 12OO (Ot là tia phân giác xOy ), OD là cạnh chung, OAOB (chứng minh trên) OADOBD (c.g.c)
7
x
A C
D
F M
ADBD (hai cạnh tương ứng), OADOBD (hai góc tương ứng). Bài 12. MĐ4 Cho tam giác ABCABAC , tia Ax đi qua trung điểm M của BC . Kẻ BE và CF vuông góc với ) ( , AxEFAx a) Chứng minh: // BECF . b) So sánh BE và FC ; CE và BF . c) Tìm điều kiện về ABC để có BECE . Lời giải: B C
1 2 2 1 B
O
4 3 2 1 2 1 2 1 E
A
a) Ta có: BEAx , CFAx (giả thiết) // BECF (từ vuông góc đến song song)
b) Xét MBE và MCF có:
12BC (hai góc so le trong),
BMCM ( M là trung điểm của BC ),
13MM (hai góc đối đỉnh)
MBEMCF (g.c.g) BECF (hai cạnh tương ứng).
Xét MBF và MCE có:
21 BC (hai góc so le trong), BMCM ( M là trung điểm của BC ),
24MM (hai góc đối đỉnh)
MBFMCE (g.c.g) BFCE (hai cạnh tương ứng) d)
Giả sử BECE
Xét BEM và CEM có: BECE ; BMCM (cmt); EM là cạnh chung BEMCEM (c. c. c)
BMECME (hai góc tương ứng)
Mặt khác, 180 BMECME (hai góc kề bù) nên 90 BMECME
Suy ra EMBC hay AMBC
Xét BAM và CAM có: 90 BAMCAM ; BMCM (cmt); AM là cạnh chung BAMCAM (c. g. c) BACA (hai cạnh tương ứng)
ABC cân tại A . Vậy ABC cân tại A thì BECE .
D A
I

1 1 2 1 B C
2 1 M K
8
Bài 13. MĐ4 Cho tam giác ABC . Đường thẳng qua A song song với BC cắt đường thẳng qua C song song với AB ở D . Gọi M là giao điểm của BD và AC . a) Chứng minh ABCCDA . b) Chứng minh M là trung điểm của AC . c) Đường thẳng d qua M cắt các đoạn thẳng , ADBC lần lượt ở , IK . Chứng minh M là trung điểm của IK . Lời giải: a) Xét ABC và CDA có:
2 1
21 AC ( // ADBC ;hai góc so le trong),
AC là cạnh chung, 12AC ( // ABDC ; hai góc so le trong),
ABCCDA (g.c.g).

b) Vì ABCCDA (chứng minh trên) ADBC (hai cạnh tương ứng).
Xét AMD và CMB có: 21 AC ( // ADBC , hai góc so le trong), AC là cạnh chung, 11 BD ( //B ADC , hai góc so le trong)
AMDCMB (g.c.g) AMCM (hai cạnh tương ứng) M là trung điểm của AC c) Xét AMI và CMK có: 21 AC ( // ADBC , hai góc so le trong),
AMCM (chứng minh trên), 21MM (hai góc đối đỉnh) AMICMK (g.c.g) MIMK (hai cạnh tương ứng) M là trung điểm của IK Phần III. BÀI TẬP TỰ LUYỆN Dạng 1.
Bài 1. MĐ1 Trong các hình vẽ sau, có các tam giác nào bằng nhau? Vì sao?
Bài 2. MĐ1 Trên mỗi hình 1, hình 2, hình 3 có các tam giác nào bằng nhau? Vì sao?
Bài 3. MĐ1 Cho hình vẽ, chứng minh ABCMNP .
9
B C A M P N D F E Hình1 K F E G S Hình2 B D O A C Hình3 H C B
A
45° 70° C
B N
P

Bài 4. MĐ2 Cho ABCMNP . Gọi AD là đường phân giác góc A của tam giác ABC . Gọi ME là đường phân giác góc M của tam giác MNP . Chứng .ABDMNE
Bài 5. MĐ3 Cho góc xAy . Lấy điểm B trên Ax , điểm D trên Ay sao cho ABAD . Trên tia Bx lấy điểm E , trên tia Dy lấy điểm C sao cho BEDC . Chứng minh ABCADE .
Bài 6. MĐ4 Cho ABC có D là trung điểm của BC . Trên nửa mặt phẳng bờ BC không chứa điểm A , vẽ tia // BxAC , Bx cắt tia AD ở E
a) Chứng minh ADCEDB
b) Trên tia đối của tia AC , lấy điểm F sao cho AFAC . Gọi I là giao điểm của AB và EF Chứng minh AIFBIE .
Dạng 2.
Bài 1. MĐ1 Cho ABC có ABAC . Gọi , MN lần lượt là trung điểm của các cạnh AC , AB Chứng minh rằng : BMCN .
Bài 2. MĐ2 Cho ABC có ABAC , phân giác AMMBC . Chứng minh:
a) ABMACM .
b) M là trung điểm của BC và AMBC .
Bài 3. MĐ2 Cho tam giác ABC có : ABAC và M là trung điểm của BC .
10
a) Chứng minh AM là tia phân giác của góc BAC . b) Chứng minh AMBC . c) Qua C kẻ đường thẳng d song song với AB cắt tia AM tại N . Chứng minh M là trung điểm của AN . Bài 4. MĐ2 Cho ABC , có BC và ABAC . Tia phân giác của góc B cắt AC ở D . Tia phân giác của góc C cắt AB ở E . a) So sánh độ dài các đoạn thẳng BD và CE . b) Gọi I là giao điểm BD và EC . Chứng minh BIIC , IEID Bài 5. MĐ3 Cho ABC có ABAC . Trên nửa mặt phẳng bờ BC chứa điểm A , vẽ tia Bx , Cy lần lượt cắt hai cạnh AC , AB tại , DE sao cho ABDACE . a) Chứng minh ADAE . b) Gọi I là giao điểm của BD và CE . Chứng minh EBIDCI . c) Chứng minh AIBC Bài 6. MĐ4 Cho tam giác ABC có M và N lần lượt là trung điểm của cạnh AB và AC . Trên tia đối của tia NB lấy điểm D sao cho NDNB . Trên tia đối của tia MC lấy điểm E sao cho MEMC . Chứng minh : a) ADBC b) // AEBC A
65° 70° M
c) A là trung điểm của DE
Bài 7. MĐ4 Cho tam giác ABC có ba góc nhọn. Vẽ đoạn thẳng AMAB ; AMAB sao cho M và C khác phía đối với đường thẳng AB . Vẽ đoạn thẳng ANAC và ANAC sao cho N và B khác phía đối với đường thẳng AC . Gọi , IK lần lượt là trung điểm của BN và CM . Chứng minh : a) AMCABN b) MCBN và MCBN c) AIAK và AIAI .
ĐÁP SỐ BÀI TẬP TỰ LUYỆN
Dạng 1. Tìm hoặc chứng minh hai tam giác bằng nhau Bài 2. MĐ1 Trên mỗi hình 1, hình 2, hình 3 có các tam giác nào bằng nhau? Vì sao?
Lời giải: Hình 1

Xét FEK và SEK có: FEKSEK (giả thiết), EK là cạnh chung, FKESKE (giả thiết).
Vậy FEKSEK (g c g). Hình 2.
Xét OAD và OBC có: OADOBC (giả thiết), OAOB (giả thiết), O là góc chung.
Vậy OADOBC (g c g). Hình 3
Xét AHB và AHC có: 90 AHBAHC (giả thiết), HBHC (giả thiết), BC (giả thiết).
Vậy AHBAHC (g.c.g).
Bài 3. MĐ1 Cho hình vẽ, chứng minh ABCMNP .
11
Hình
S Hình
Hình
1 K F E G
2 B D O A C
3 H C B A
Lời giải: MNP có: 180 MNP (tổng ba góc trong một tam giác). Suy ra 180 MNP 180756545
Xét ABC và MNP có: 45 AM , ABMN (giả thiết), 70 BN . Vậy ABCMNP (g c g). Bài 4. MĐ2 Cho ABCMNP . Gọi AD là đường phân giác góc A của tam giác ABC . Gọi ME là đường phân giác góc M của tam giác MNP . Chứng ABDMNE Lời giải:
Ta có: ABCMNP suy ra ;; N BM A NA BM (tương ứng)

Mạt khác: AD là đường phân giác của A nên 1 1 2 A A , ME là đường phân giác của M nên 1 1 2 MM Do đó 11AM .
Xét tam giác ABD và tam giác MNE có: 11 ,, ABM M N BNA (chứng minh trên). Suy ra ABDMNE (g.c.g). Bài 6. MĐ4 Cho ABC có D là trung điểm của BC . Trên nửa mặt phẳng bờ BC không chứa điểm A , vẽ tia // BxAC , Bx cắt tia AD ở E
12
45°
A
M
. a) Chứng minh ADCEDB b) Trên tia đối của tia AC , lấy điểm F sao cho AFAC . Gọi I là giao điểm của AB và EF . Chứng minh AIFBIE . Lời giải: 65° 70°
70° C
B N
P 1 1 E D A B C P N M
a) Ta có // ACBE ACDDBE (2 góc so le trong).
Xét ADC và EDB có: ACDDBE (chứng minh trên), CDBD (giả thiết), ADCEDB (hai góc đối đỉnh).
Vậy ADCEDB (g.c.g).
b) Vì ADCEDB (chứng minh trên) ACEB (hai cạnh tương ứng).
Mà AFAC (giả thiết) AFBE .
Vì // ACBE (giả thiết), FAC // AFBE FAIIBE , AFIBEI (góc so le trong).
Xét AIF và BIE có: FAIIBE , AFBE , AFIBEI (chứng minh trên). Do đó AIFBIE (g c g). Dạng 2. Sử dụng trường hợp bằng nhau của tam giác để chứng minh một tính chất khác X Bài 3. MĐ2 Cho tam giác ABC có : ABAC và M là trung điểm của BC a) Chứng minh AM là tia phân giác của góc BAC b) Chứng minh AMBC c) Qua C kẻ đường thẳng d song song với AB cắt tia AM tại N . Chứng minh M là trung điểm của AN
Lời giải:

13
I
D B A C F
E
a) Xét tam giác ABM và tam giác ACM , ta có: ABAC (giả thiết), BMMC ( M là trung điểm của BC ), AM là cạnh chung
Suy ra ABMACM (c.c.c) 2 1 AA (hai góc tương ứng) hay AM là tia phân giác của góc BAC .
b) Ta có ABMACM nên 12MM (hai góc tương ứng). Mà 12 180 MM (kề bù) nên 12 90 MM. Hay AMBC .
c) Ta có // CNAB suy ra 11 BC (hai góc so le trong). Xét ABM và NCM , ta có: 13MM (hai góc đối đỉnh), MBMC ( M là trung điểm của BC ), 11 BC (chứng minh trên)
Suy ra ABMNCM (g.c.g) AMMN (hai cạnh tương ứng). Bài 4. MĐ2 Cho ABC , có BC và ABAC . Tia phân giác của góc B cắt AC ở D . Tia phân giác của góc C cắt AB ở E . a) So sánh độ dài các đoạn thẳng BD và CE b) Gọi I là giao điểm BD và EC . Chứng minh BIIC , IEID Lời giải:

14
1 2
M C B A
1 1 1 3 2 1
N
a) So sánh độ dài các đoạn thẳng BD và CE
Ta có: 12 2 ABC BB (vì BD là tia phân giác của ABC ), (1) 12 2 ACB CC (vì CE là tia phân giác của ACB ) , (2) ABCACB (giả thiết). (3) Từ (1), (2), (3) suy ra 1212 BBCC
Xét ABD và ACE có ABAC (giả thiết), BAC là góc chung, 11 BC (chứng minh trên).
Do đó ABDACE (g c g).
Suy ra BDCE (hai cạnh tương ứng).
b) Ta có ABAC (giả thiết), ADAE (vì ABDACE ).
Nên ABAEACAD BECD
Ta lại có ABDACE (cm câu a) ADBAEC (hai góc tương ứng).
Mặt khác: 180 ADBIDC (hai góc kề bù); 180 AECIEB (hai góc kề bù) nên IDCIEB .
Xét EBI và DCI có: 11 BC (chứng minh ở câu a), BECD (chứng minh trên), IDCIEB (chứng minh trên).
Do đó EBIDCI (g c g).
Suy ra BIIC , IEID (hai cạnh tương ứng).

Bài 5. MĐ3 Cho ABC có ABAC . Trên nửa mặt phẳng bờ BC chứa điểm A , vẽ tia Bx , Cy lần lượt cắt hai cạnh AC , AB tại , DE sao cho ABDACE
a) Chứng minh ADAE b) Gọi I là giao điểm của BD và CE. Chứng minh EBIDCI
15
D E
B A
2 1 1 2 I
C
c) Chứng minh AIBC
Lời giải:
1 2 1 2 I

D H C B
a) Xét ABD và ACE có: BAC là góc chung, ABAC (giả thiết), ABDACE (giả thiết) ABDACE (g – c – g) ADAE (hai cạnh tương ứng).
b) Ta có ABAC (giả thiết), ADAE (cm câu a).
Nên ABAEACAD BECD .
Ta lại có ABDACE (cm câu a) 11 ED (hai góc tương ứng).
Mặt khác: 12 180 EE ; 12 180 DD (hai góc kề bù) 22 ED .
Xét EBI và DCI có
EBIDCI (giả thiết), BECD (chứng minh trên), 22 ED (chứng minh trên), EBIDCI (g c g).
c) Gọi H là giao điểm của AI và BC
Xét AEI và ADI có: AI là cạnh chung, AEAD (chứng minh trên câu a), EIDI (vì EBIDCI ).
AEIADI (c.c.c) EAIDAI (hai góc tương ứng) hay BAHCAH .
Xét ABH và ACH có: AI là cạnh chung, BAHCAH (chứng minh trên), ABAC (giả thiết).
ABHACH (c.g.c) AHBAHC (hai góc tương ứng).
Mà 180 AHBAHC (hai góc kề bù) 180 90 2 AHBAHC
Vậy AHBC hay AIBC
16
A E y x

17
Dạng 1. Tìm hoặc chứng minh hai tam giác bằng nhau
I. Phương pháp giải:
+ Xét hai tam giác. + Kiểm tra ba điều kiện bằng nhau cạnh - góc - cạnh, góc – cạnh - góc. + Kết luận hai tam giác bằng nhau.
II. Bài toán.

Bài 1. MĐ1 Trong các hình vẽ sau, có các tam giác nào bằng nhau? Vì sao?
Bài 2. MĐ1 Trong các hình vẽ sau, có các tam giác nào bằng nhau? Vì sao?
Bài 3. MĐ1 Trong các hình vẽ sau, có hai tam giác nào bằng nhau? Vì sao?
Bài 4. MĐ1 Trong các hình vẽ sau, có các tam giác nào bằng nhau? Vì sao?
Bài 5. MĐ2 Nêu thêm một điều kiện để mỗi hình dưới đây là hai tam giác bằng nhau theo trường hợp cạnh - góc - cạnh.
18 PHIẾU BÀI TẬP
N D B C A Q P M E B C F H A D E G GH//QP L H Q P G K M N B A D E C F 2 1 2 1 P N Q M O
Bài 6. MĐ2 Nêu thêm một điều kiện để mỗi hình dưới đây là hai tam giác bằng nhau theo trường hợp góc - cạnh - góc.
Bài 7. MĐ2 Qua trung điểm I của đoạn thẳng AB , kẻ đường thẳng vuông góc với AB , trên đường thẳng vuông góc đó lấy hai điểm C và D . Nối ,,, CACBDADB . Tìm các cặp tam giác bằng nhau.
Bài 8. MĐ2 Cho tam giác ABC , kẻ AH vuông góc với , BCHBC . Trên. tia đối của tia HA lấy điểm K sao cho HKHA , nối , KBKC , KBKC . Tìm các cặp tam giác bằng nhau.
Bài 9. MĐ2 Cho tam giác ABC có ABAC . Gọi AM là tia phân giác góc A . Chứng minh ABMACM
Bài 10. MĐ2 Cho tam giác ABC có BC . Gọi AM là tia phân giác góc A . Chứng minh ABMACM .
Bài 11. MĐ2 Cho Oz là tia phân giác góc xOy . Trên các tia ,, OxOyOz lần lượt lấy các điểm ,, ABC (khác O ) sao cho OAOB . Chứng minh OACOBC .
Bài 12. MĐ3 Cho góc xOy khác góc bẹt. Trên cạnh Ox lấy hai điểm A và B , trên cạnh Oy lấy hai điểm C và D , sao cho ; OAOCOBOD a) Chứng minh OADOCB b) Chứng minh ACDCAB
Bài 13. MĐ3 Cho ABC vuông ở A . Trên tia đối của tia AC lấy điểm D sao cho ADAC a) Chứng minh ABCABD . b) Trên tia đối của tia AB lấy điểm M . Chứng minh MBDMBC . Bài 14. MĐ3 Cho hình vẽ sau, trong đó // ,DABCDABC . Chứng minh rằng: a) OABODC b) OACODB . Bài 15. MĐ4 Cho góc nhọn xOy có tia Oz là tia phân giác. Qua điểm A thuộc tia Ox , vẽ đường thẳng song song với Oy cắt Oz tại M . Qua M kẻ đường thẳng song song với Ox cắt Oy tại B a) Chứng minh OAMMBO . b) Từ M vẽ MHOx ; MKOy . Chứng minh MHOMKO Bài 16. MĐ4 Cho tam giác ABC có 90 A và ABAC . Trên các cạnh AB và AC lần lượt lấy điểm D và E sao cho ADAE . Qua A và D kẻ đường vuông góc với BE cắt BC lần lượt tại M và N . Tia ND cắt tia CA tại I . Chứng minh rằng: a) AIDABE

19
Q
A H G E F M N B
P
I
D C
D A B C E P N M O
Bài 17. MĐ4 Cho ABC , kẻ BD vuông góc với AC , CE vuông góc với AB . Trên tia đối của tia BD , lấy điểm H sao cho BHAC . Trên tia đối của tia CE lấy điểm K sao cho CKAB . Chứng minh AHAK Dạng 2. Sử dụng trường hợp bằng nhau của tam giác để chứng minh một tính chất khác
I. Phương pháp giải: + Chọn hai tam giác có cạnh (góc) là hai đoạn thẳng (góc) cần chứng minh bằng nhau. + Chứng minh hai tam giác ấy bằng nhau theo một trong hai trường hợp cạnh - góc - cạnh, góc - cạnh - góc rồi suy ra hai cạnh (góc) tương ứng bằng nhau.Kiểm tra ba điều kiện bằng nhau cạnh - góc - cạnh, góc - cạnh - góc .
+ Kết hợp với các tính chất đã học về tia phân giác, đường thẳng song song, đường trung trực, tổng ba góc trong một tam giác, ... để chứng minh một tính chất khác. II. Bài toán.
Bài 1. MĐ1 Cho tam giác ABC có ABAC , tia phân giác của góc A cắt BC tại M . Chứng minh: BMCM .
Bài 2. MĐ1 Cho góc nhọn xOy có Om là tia phân giác, COmCO . Trên tia Ox lấy điểm A , trên tia Oy lấy điểm B sao choOAOB . Chứng minh:CACB Bài 3. MĐ1 Cho ABCMNP . Gọi O và G lần lượt là trung điểm của các cạnh BC và NP . Chứng minh AOMG . Bài 4. MĐ2 Cho tam giác ABC có BC . Tia phân giác của góc A cắt BC tại D a) Chứng minh ABAC b) Chứng minh ADBC Bài 5. MĐ2 Cho ABC có ABAC . Phân giác của góc A cắt cạnh BC tại điểm D . Trên cạnh AC lấy điểm E sao cho AEAB . Chứng minh: a) BDED . b) DA là tia phân giác của góc BDE . Bài 6. MĐ2 Cho góc xOy khác góc bẹt và có Ot là tia phân giác. Lấy điểm C thuộcOt CO . Qua C kẻ đường vuông góc với Ot , cắt , OxOy theo thứ tự ở , AB . a) Chứng minh:OAOB b) Lấy điểm D thuộc Ct DC . Chứng minh: DADB và OADOBD Bài 7. MĐ2 Cho ABC , M là trung điểm của BC . Trên tia đối của tia MA lấy điểm E sao cho MEMA . Chứng minh: a) ABMECM b) ABCE và // ACBE Bài 8. MĐ3 Cho tam giác ABC có 80 A . Dựng AH vuông góc với BC ( HBC ). Trên tia đối tia HA lấy điểm D sao cho HDHA a) Chứng minh: ACDC b) Chứng minh: ABCDBC c) Xác định số đo góc BDC . Bài 9. MĐ3 Cho ABC trên nửa mặt phẳng bờ AC không chứa điểm B , lấy điểm D sao cho // ADBC và ADBC . Chứng minh: a) ABCD b) // ABCD và ABDCDB Bài 10. MĐ3 Cho ABC có 90 A , trên cạnh BC lấy điểm E sao cho BABE . Tia phân giác góc B cắt AC ở D . a) Chứng minh: ABDEBD . b) Chứng minh: DADE

20
b) Chứng minh CMMN
c) Tính số đo BED d) Xác định độ lớn góc B để EDBEDC

Bài 11. MĐ3 Cho ABC có ABAC . Kẻ tia phân giác AD của BAC DBC . Trên cạnh AC lấy điểm E sao cho AEAB , trên tia AB lấy điểm F sao cho AFAC . Chứng minh: a) BDED b) BFEC c) BDFEDC d) ADFC
Bài 12. MĐ4 Cho tam giác ABCABAC , tia Ax đi qua trung điểm M của BC . Kẻ BE và CF vuông góc với ) ( , AxEFAx . a) Chứng minh: // BECF b) So sánh BE và FC ; CE và BF c) Tìm điều kiện về ABC để có BECE
Bài 13. MĐ4 Cho tam giác ABC . Đường thẳng qua A song song với BC cắt đường thẳng qua C song song với AB ở D . Gọi M là giao điểm của BD và AC . a) Chứng minh ABCCDA . b) Chứng minh M là trung điểm của AC c) Đường thẳng d qua M cắt các đoạn thẳng , ADBC lần lượt ở , IK . Chứng minh M là trung điểm của IK Bài 14. MĐ4 Cho tam giác ABC nhọn. Vẽ đoạn thẳng AD vuông góc với AB và ADAB ( , DC khác phía so với AB ). Vẽ đoạn thẳng AE vuông góc với AC và AEAC ( , EB khác phía so với AC ). Chứng minh: a) BEDC . b) BEDC . Bài 15. MĐ4 Cho tam giác ABC nhọn. Gọi , MN lần lượt là trung điểm của , ABAC . Lấy điểm , ED sao cho , MN là trung điểm của , CEBD . a) Chứng minh: // ADBC b) Chứng minh: ,, AED thẳng hàng. Phần III. BÀI TẬP TỰ LUYỆN
Dạng 1. Tìm hoặc chứng minh hai tam giác bằng nhau Bài 1. MĐ1 Trong các hình vẽ sau, có các tam giác nào bằng nhau? Vì sao?
Bài 2. MĐ1 Trên mỗi hình 1, hình 2, hình 3 có các tam giác nào bằng nhau? Vì sao?
21
B
P
E Hình1 K F E G S Hình2 B D O A C Hình3 H C B A
C A M
N D F
Bài 3. MĐ1 Cho hình vẽ, chứng minh ABCMNP
45° 70° C
B N
P

Bài 4. MĐ2 Cho ABCMNP . Gọi AD là đường phân giác góc A của tam giác ABC . Gọi ME là đường phân giác góc M của tam giác MNP . Chứng ABDMNE
Bài 5. MĐ3 Cho góc xAy . Lấy điểm B trên Ax , điểm D trên Ay sao cho ABAD . Trên tia Bx lấy điểm E , trên tia Dy lấy điểm C sao cho BEDC . Chứng minh ABCADE
Bài 6. MĐ4 Cho ABC có D là trung điểm của BC . Trên nửa mặt phẳng bờ BC không chứa điểm A , vẽ tia // BxAC , Bx cắt tia AD ở E . a) Chứng minh ADCEDB b) Trên tia đối của tia AC , lấy điểm F sao cho AFAC . Gọi I là giao điểm của AB và EF Chứng minh AIFBIE
Dạng 2. Sử dụng trường hợp bằng nhau của tam giác để chứng minh một tính chất khác
Bài 1. MĐ1 Cho ABC có ABAC . Gọi , MN lần lượt là trung điểm của các cạnh AC , AB . Chứng minh rằng : BMCN
Bài 2. MĐ2 Cho ABC có ABAC , phân giác AM MBC . Chứng minh: a) ABMACM . b) M là trung điểm của BC và AMBC .
Bài 3. MĐ2 Cho tam giác ABC có : ABAC và M là trung điểm của BC . a) Chứng minh AM là tia phân giác của góc BAC b) Chứng minh AMBC c) Qua C kẻ đường thẳng d song song với AB cắt tia AM tại N . Chứng minh M là trung điểm của AN . Bài 4. MĐ2 Cho ABC , có BC và ABAC . Tia phân giác của góc B cắt AC ở D . Tia phân giác của góc C cắt AB ở E . a) So sánh độ dài các đoạn thẳng BD và CE b) Gọi I là giao điểm BD và EC . Chứng minh BIIC , IEID Bài 5. MĐ3 Cho ABC có ABAC . Trên nửa mặt phẳng bờ BC chứa điểm A , vẽ tia Bx , Cy lần lượt cắt hai cạnh AC , AB tại , DE sao cho ABDACE a) Chứng minh ADAE b) Gọi I là giao điểm của BD và CE. Chứng minh EBIDCI c) Chứng minh AIBC Bài 6. MĐ4 Cho tam giác ABC có M và N lần lượt là trung điểm của cạnh AB và AC . Trên tia đối của tia NB lấy điểm D sao cho NDNB . Trên tia đối của tia MC lấy điểm E sao cho MEMC Chứng minh :
a) ADBC b) // AEBC c) A là trung điểm của DE
22
Bài 7. MĐ4 Cho tam giác ABC có ba góc nhọn. Vẽ đoạn thẳng AMAB ; AMAB sao cho M và C khác phía đối với đường thẳng AB . Vẽ đoạn thẳng ANAC và ANAC sao cho N và B khác phía đối với đường thẳng AC . Gọi , IK lần lượt là trung điểm của BN và CM . Chứng minh : A
65° 70° M
a) AMCABN

b) MCBN và MCBN .
c) AIAK và AIAI .
23
PHẦN I. TÓM TẮT LÍ THUYẾT.
1. Trường hợp hai cạnh góc vuông
Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (theo trường hợp cạnh – góc – cạnh).
2. Trường hợp một cạnh góc vuông và một góc nhọn
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (theo trường hợp góc – cạnh – góc).
3. Trường hợp cạnh huyền và một góc nhọn
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( theo trường hợp g-c-g)
4. Trường hợp cạnh huyền và cạnh góc vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác đó bằng nhau.
1 CHUYÊN ĐỀ. CÁC TRƯỜNG HỢP BẰNG NHAU CỦA HAI TAM GIÁC VUÔNG
B A C
D E B A C F D E B A C F D E
F
PHẦN II. CÁC DẠNG BÀI.
Dạng 1. Tìm hoặc chứng minh hai tam giác vuông bằng nhau
I. Phương pháp giải: +) Xét hai tam giác vuông. +) Kiểm tra các điều kiện bằng nhau cạnh – góc – cạnh, góc – cạnh – góc, cạnh huyền – góc nhọn, cạnh huyền – cạnh góc vuông. +) Kết luận hai tam giác bằng nhau. II. Bài toán. Bài 1. Tìm các tam giác vuông bằng nhau trên hình dưới đây? Lời giải: +) Xét ABC và ADC có: 90 DB DACBAC ( gt) AC chung Do đó ABCADC ( cạnh huyền - góc nhọn) Bài 2. Tìm các tam giác vuông bằng nhau trên hình sau:
2
B A
F D E
C
C D B A
D C
Lời giải:
+) Xét ABC và BAD có: 90 ABCBAD
AB chung
BACABD (gt)
Do đó ABCBAD ( cạnh góc vuông - góc nhọn)
Bài 3. Tìm các tam giác vuông bằng nhau trên hình dưới đây?
A
Lời giải:
B C
D
+) Xét ABC và ADC có: 90 BD
BCDC ( gt)
AC chung
Do đó ABCADC ( cạnh huyền – cạnh góc vuông)
3
Bài 4. Tìm các tam giác vuông bằng nhau trên hình sau: A B
N F
Lời giải:
+) Xét MEF vuông tại M nên: 90 FMEF
+) Xét EMN vuông tại E nên: 90 NEMN
Mà FN ( gt)
Nên MEFEMN +) Xét MEF và EMN có: 90 EMFMEN MEFEMN (chứng minh trên) ME là cạnh chung
Do đó MEFEMN ( g-c-g).
Bài 5. Cho hình vẽ sau:
A
E D H B C
Lời giải:
a) Xét ABH vuông tại H và ACH vuông tại H có: BHCH (gt) AH là cạnh chung
4
b)
Chứng minh rằng: a) ABHACH ;
ADHAEH ; c) DBHECH .
Do đó ABHACH ( 2 cạnh góc vuông ) E M
b) Xét ADH vuông tại D và AEH vuông tại E có:
AH là cạnh chung
DAHEAH ( do ABHACH )
Do đó ADHAEH (cạnh huyền- góc nhọn)
c) Xét DBH vuông tại D và ECH vuông tại E có: BC ( do ABHACH ) BHCH (gt)
Do đó DBHECH ( cạnh huyền – góc nhọn )
Bài 6. Cho xOy . Tia Oz là tia phân giác xOy . Lấy điểm A thuộc tia ()OzAO . Kẻ AB vuông góc với , OxAC vuông góc với ) ( , OyBOxCOy . Chứng minh OABOAC .
Lời giải:
B x O y
C
+) Xét OAB vuông tại B và OAC vuông tại C có: OA là cạnh chung
AOBAOC ( do Oz là tia phân giác xOy )
A z G F E B C
Do đó OABOAC ( cạnh huyền – góc nhọn) Bài 7. Cho hình vẽ sau. Tìm các tam giác vuông bằng nhau trên hình?
A D
Lời giải:
+) Xét BFD vuông tại F và CGE vuông tại G ta có: BDCE (gt) BC (gt)
Do đó BFDCGE ( cạnh huyền – góc nhọn)
+) Xét AFD vuông tại F và AGE vuông tại G ta có:
5
ADAE (gt)
FDGE ( do BFDCGE )
Do đó AFDAGE (cạnh huyền – cạnh góc vuông)
Bài 8. Cho tam giác ABC có ABAC . Gọi D là trung điểm của cạnh BC . Kẻ DEAB ,
DFAC . Chứng minh:
a) DEBDFC ; b) DEADFA .
Lời giải:
A
F E D B C
a) Xét ABD và ACD có:
ABAC (gt)
AD là cạnh chung
DBDC ( D là trung điểm của cạnh BC )
Do đó ABDACD (c-c-c)
Nên BC và DABDAC
+) Xét DEB vuông tại E và DFC vuông tại F ta có: AD chung BC (chứng minh trên)
Do đó DEBDFC (cạnh huyền – góc nhọn)
b) Xét DEA vuông tại E và DFA vuông tại F ta có: AD là cạnh chung
DABDAC (chứng minh trên)
Do đó DEADFA (cạnh huyền – góc nhọn)
Bài 9. Cho tam giác ABC vuông tại A và ABAC Qua A kẻ đường thẳng d cắt BC . Vẽ , BMCN vuông góc với d . Chứng minh rằng : BAMACN .
Lời giải:
6
Vì ABC vuông tại A nên 90 BACBAMCAM Và ANC vuông tại N nên 90 ACNCAM Do đó BAMACN +) Xét BAM vuông tại M và ACN vuông tại N có: BAMACN (cmt) ABAC (gt) Nên BAMACN (cạnh huyền – góc nhọn ). Bài 10. Cho ABC có BC . Trên tia đối của tia BC lấy điểm , M trên tia đối tia của tia CB lấy điểm N sao cho .BMCN Kẻ (),() BEAMEAMCFANFAN Chứng minh rằng BMECNF Lời giải: Ta có: 180;180ABCABMACBACN ( kề bù) Mà ()ABCACBgt ABMACN +) Kẻ AIBC tại I . +) Xét ABI vuông tại I nên ta có: 90 BAIIBA +) Xét ACI vuông tại I nên ta có: 90 CAIICA
7
M
B
N C
A F E C I M N B A
Nên IABIAC
+) Xét ABI và ACI ta có: 90 AIBAIC AI chung IABIAC (chứng minh trên)
Do đó ABIACI (g-c-g)
Nên ABAC Xét ABM và ACN có: BMCN (gt) ABMACN (cmt) ABAC (cmt) ABMACN (c-g-c)
Nên MN +) Xét BME vuông tại E và CNF vuông tại F ta có: ()BMCNgt MN (cmt)
Do đó BMECNF ( cạnh huyền – góc nhọn).
Bài 11. Cho ABC . Từ A vẽ cung tròn có bán kính bằng BC , từ C vẽ cung tròn có bán kính bằng AB . Hai cung tròn này cắt nhau tại D ( D nằm khác phía của B đối với AC ). Kẻ AHBC () HBC và () CKADKAD . a) Chứng minh AHCCKA ; b) Chứng minh AHBCKD . Lời giải:
1 K H
1
D A B C
a) Vì cung tròn tâm A bán kính bằng BC cắt cung tròn tâm C có bán kính bằng AB tại D Nên ; ADBCCDAB +) Xét ABC và CDA có:
8 Mà ()IBAIABgt
nh chung
ADBC (cmt)
CDAB (cmt)
ABCCDA (c-c-c)
11 CA
+) Xét AHC vuông tại H và CKA vuông tại K có: 11 CA (cmt)
AC cạnh chung
Suy ra AHCCKA ( cạnh huyền- góc nhọn) b) Xét AHB vuông tại H và CKD vuông tại K có: AHCK ( do AHCCKA )
ABCD (cmt)
AHBCKD (cạnh huyền – cạnh góc vuông)
Dạng 2. Sử dụng các trường hợp bằng nhau của tam giác vuông để chứng minh hai đoạn thẳng bằng nhau, hai góc bằng nhau. Tính độ dài đoạn thẳng, số đo góc.
I. Phương pháp giải:
+ Chọn hai tam giác vuông có cạnh (góc) là đoạn thẳng (góc) cần tính hoặc chứng minh bằng nhau.
+ Tìm thêm hai điều kiện bằng nhau, trong đó có một điều kiện về cạnh, để kết luận hai tam giác bằng nhau.
+ Suy ra các cạnh (góc) tương ứng bằng nhau và kết luận.
II. Bài toán.
Bài 1. Cho hình vẽ sau. Chứng minh OK là phân giác của góc BOA
O
B K
A
Lời giải:
+) Xét OBK vuông tại B và OAK vuông tại A có: OK chung
9 AC cạ
OBOA (gt)
Do đó OBKOAK ( cạnh huyền – góc nhọn )
Suy ra BOKAOK (cặp góc tương ứng).
Vậy OK là phân giác của góc BOA
Bài 2. Cho ABC có ABAC . Kẻ ADBC . Chứng minh AD là tia phân giác của BAC . Lời giải:
ABAC (gt)
D B C
+) Xét ABD vuông tại D và ACD vuông tại D có: OD chung
Do đó ABDACD (cạnh huyền – góc nhọn)
Suy ra BADCAD (cặp góc tương ứng).
Vậy AD là phân giác của góc BAC
Bài 3. Cho ABC có BABC Qua A kẻ đường vuông góc với AB , Qua C kẻ đường vuông góc với CB , chúng cắt nhau ở K . Chứng minh BK là phân giác của góc B .
B
A C
A K
+) Xét ABK vuông tại A và CBK vuông tại C ta có:
()ABACgt
BK chung
10
ABKCBK (cạnh huyền – cạnh góc vuông)
Nên ABKCBK ( hai góc tương ứng ) Hay BK là phân giác của góc B .
Bài 4. Cho tam giác ABC , M là trung điểm cạnh BC . Vẽ BI , CK vuông góc với AM Chứng minh BICK . Lời giải:
+) Xét BIM và CKM có: MBMC ( M là trung điểm của BC ) 90 BIMCKM IMBKMC (đối đỉnh) Do đó BIMCKM (cạnh huyền – góc nhọn). Từ đó suy ra BICK (cặp cạnh tương ứng). Bài 5. Cho tam giác ABC vuông tại A Tia phân giác góc B cắt cạnh AC tại điểm M Kẻ ().MDBCDBC a) Chứng minh ;BABD b) Gọi E là giao điểm của hai đường thẳng DM và BA Chứng minh ABCDBE . Lời giải:
B A C
D M
E
a) Xét BMA vuông tại A và BMD vuông tại D ta có:
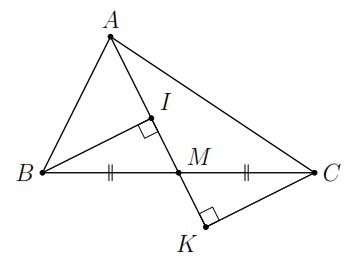
11 Do đó
BM cạnh chung
ABMDBM (do BM là phân giác của góc B )
Do đó BMABMD (cạnh huyền - góc nhọn)
Suy ra .BABD
b) Xét ABC và DBE ta có: 90 BACBDE BABD (chứng minh trên) B là góc chung Do đó (g-c-g). ABCDBE
Bài 6. Cho tam giác ABC có ABAC . Trên cạnh , ABAC lần lượt lấy các điểm , MN sao cho AMAN . Các đường thẳng vuông góc với , ABAC tại , MN cắt nhau ở O . AO cắt BC tại H . Chứng minh:
a) AMOANO ; b) HBHC và AHBC Lời giải:
A
N M H B C
O
a) Xét AMO vuông tại M và ANO vuông tại N ta có: AO là cạnh chung AMAN (gt) AMOANO (cạnh huyền- góc nhọn)
b) Xét AHB và AHC có:
ABAC (gt)
BAHCAH ( do AMOANO ) AH là cạnh chung
AHBAHC (c-g-c)
HBHC (hai cạnh tương ứng)
Và AHBAHC ( hai góc tương ứng ), mà hai góc này ở vị trí kề bù 180 90 2 AHCAHB
12
Bài 7. Cho tam giác ABC có ABAC . Đường thẳng vuông góc với AB tại B cắt đường thẳng vuông góc với AC tại C ở D . Gọi M là trung điểm cạnh BC . Chứng minh:
a) DABDAC ;
b) ,, AMD thẳng hàng.
Lời giải:
a) Xét DAB và DAC có: 90 DBAACD ABAC (gt) AD là cạnh chung
Do đó DABDAC (cạnh huyền -canh góc vuông).
b) Xét ABM và ACM ta có: ABAC (gt) MBMC ( M là trung điểm cạnh BC )
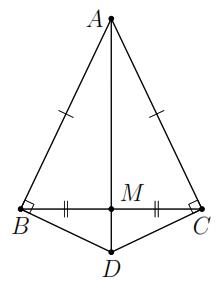
AM là cạnh chung
Nên ABMACM (c-c-c)
Do đó AMBAMC , mà hai góc này ở vị trí kề bù nên 180 2 AMBAMC .
Hay AMBC tại M (1)
+) Xét ABM và ACM , ta có: DBDC ( DABDAC )
MBMC ( M là trung điểm cạnh BC )
DM cạnh chung
Do đó DBMDCM ( c-c-c)
BMDCMD , mà hai góc này ở vị trí kề bù nên 180 90 2 BMDCMD
Hay DMBC tại M (2)
Từ (1) và (2) ta suy ra AM và DM cùng vuông góc với BC nên ,, AMD thẳng hàng.
13 Vậy AHBC
Bài 8. Cho ABC vuông tại A và ABAC . Tính số đo góc , BC ?
Lời giải:
Kẻ ()ADBCDBC +) Xét ABD vuông tại D và ACD vuông tại D , ta có: ()ABACgt AD chung
Suy ra ABDACD ( cạnh huyền – cạnh góc vuông )
Do đó BC ( hai góc tương ứng ) (1)
Vì ABC vuông tại A nên 90 BC (2) Từ (1) và (2) suy ra 45 BC
A M
C
Bài 9. Cho ABC vuông tại A . Từ điểm K trên cạnh AC , vẽ KHBC , biết KHKA . Chứng minh rằng BKAH
Lời giải: +) Xét ABK vuông tại A và HBK vuông tại H , ta có: BK chung KAKH (gt) ABKHBK (cạnh huyền – cạnh góc vuông) ; ABHBABKHBK +) Gọi M là giao điểm của BK và AH .
B A C
H K
14
D
B
15 +) Xét ABM và HBM , ta có: ABBH (chứng
ABMHBM
AM
ạnh
(.g.c)ABMHBMc
AMBHMB (
ứ
ị
ề
0 180 90 2 AMBHMB Vậy BKAH Bài 10. Cho ABC vuông tại A ABAC và các điểm M thuộc cạnh AC , H thuộc cạnh BC sao cho MHBC và MHHB . Chứng minh rằng AH là tia
giác của góc A . Lời giải: +) Kẻ HDABDAB và HEACEAC +) Xét DBH và EMH có: 90 HDBHEM HBHM (gt) HBDHME (cùng phụ ACB ) DBHEMH (cạnh huyền - góc nhọn) HEHD (hai cạnh tương ứng) +) Xét DAH và EAH có : 90 HDAHEA HDHE (chứng minh trên) AH là cạnh chung DAHEAH (cạnh huyền - cạnh góc vuông) DAHEAH (hai góc tương ứng) D E M H B A C
minh trên)
( do ABKHBK
)
c
chung
hai góc tương
ng), mà hai góc này ở v
trí k
bù
phân
là tia phân giác của góc BAC
Bài 11. Cho tam giác ABC . Các tia phân giác của góc B và C cắt nhau ở I . Kẻ ;; IDABIEACDABEAC . Chứng minh rằng ADAE Lời giải:
+) Kẻ HIBC
+) Xét BID vuông tại D và BIH vuông tại H , ta có: IBDIBH ( IB là phân giác của góc B ) IB là cạnh chung
Nên BIDBIH (cạnh huyền – góc nhọn)
Suy ra IDIH (hai cạnh tương ứng) 1
+) Xét CIE vuông tại E và CIH vuông tại H , ta có: ICEICH ( IC là phân giác của góc C )
IC chung
Do đó CIECIH (cạnh huyền – góc nhọn)
Suy ra IEIH (hai cạnh tương ứng) 2
Từ 1 và 2 suy ra IDIE
+) Xét IAD vuông tại D và IAE vuông tại E ta có: IDIE (chứng minh trên)
IA là cạnh chung
Do đó IADIAE (cạnh huyền – cạnh góc vuông)
Suy ra ADAE (hai cạnh tương ứng)
Bài 12. Cho ABC vuông tại A có ABAC . Vẽ () AHBCHBC D là điểm trên cạnh AC sao cho ADAB . Vẽ ()DEBCEBC . Chứng minh HAHE
Lời giải:
16 Vậy
AH
H
E I B
D
C A
+) Kẻ ()DKAHKAH
+) Xét HAB vuông tại H và KDA vuông tại K có: ADAB (gt)
BAHADK ( cùng phụ với KAD )
Do đó HABKDA ( cạnh huyền – góc nhọn)
HAKD (hai cạnh tương ứng)
Ta có KDAH ( cách vẽ)
Và EHAH ( do BCAH )
// KDEH KDHEHD (hai góc so le trong)
+) Xét KDH vuông tại K và EHD vuông tại E ta có: DH cạnh chung KDHEHD (cmt)
Do đó KDHEHD ( cạnh huyền – góc nhọn)
Suy ra HAHE ( hai cạnh tương ứng)
Bài 13 . Cho tam giác ABC có M là trung điểm của BC và AM là tia phân giác của góc A . Chứng minh ABAC Lời giải:
A
F E M B C
+) Từ M kẻ , MEABMFAC .
+) Xét MEA vuông tại E và MFA vuông tại F , ta có: MA là cạnh chung
17
K E D H A B C
MAEMAF (vì AM là tia phân giác của góc A )
Do đó MEAMFA ( cạnh huyền – góc nhọn)
Nên (1) AEAF và MEMF
+) Xét MEB vuông tại E và MFC vuông tại F , ta có MBMC ( vì M là trung điểm của BC ) MEMF (chứng minh trên)
Nên MEBMFC ( cạnh huyền – cạnh góc vuông)
Do đó (2) BECF Từ (1) và (2) ta suy ra AEBEAFCF hay ABAC
Phần III. BÀI TẬP TỰ LUYỆN
Dạng 1. Tìm hoặc chứng minh hai tam giác vuông bằng nhau Bài 1. Cho tam giác ABC nhọn có ABAC , vẽ BDAC tại D , CEAB tại E . Gọi M là giao điểm của BD và CE . Chứng minh:
a) DBAECA ; b) EBCDCB ; c) EAMDAM .
Bài 2. Cho ABC có ABAC . Trên nửa mặt phẳng bờ BC không chứa A lần lượt vẽ các tia , BxCy sao cho BxBA và CyCA . Gọi D là giao điểm của các tia , BxCy Chứng minh ABDACD
Dạng 2. Sử dụng các trường hợp bằng nhau của tam giác vuông để chứng minh hai đoạn thẳng bằng nhau, hai góc bằng nhau. Tính độ dài đoạn thẳng, số đo góc. Bài 1. Cho ABC nhọn có ABAC . Vẽ BHACHAC , CKABKAB .
a) Chứng minh: AHAK
giao
ng minh AI là tia phân giác c
a A
ABC
là một điể
trên cạnh AB , E là một điểm trên cạnh AC sao cho ADAE . Từ D và E hạ các đường , DMEN cùng vuông góc với BC . Chứng minh rằng: a) BC ; b) BMCN . Bài 3. Cho xOy . Trên tia Ox lấy điểm A , trên tia Oy lấy điểm B . Gọi M là trung điểm của đoạn thẳng AB . Từ A và B kẻ các đường thẳng , AEBF cùng vuông góc với tia OM . Chứng minh : AEBF . Bài 4. Cho góc xOy . Trên tia phân giác của góc đó lấy một điểm M , từ M hạ các đường thẳng vuông góc , MAMB xuống cạnh , OxOy .Chứng minh :
18
.
b) Gọi I là
điểm của BH và CK . Chứ
ủ
. Bài 2. Cho
có ABAC . D
m
a) MAOMBO ;
b) AB vuông góc với OM .
ĐÁP SỐ BÀI TẬP TỰ LUYỆN
Dạng 1. Tìm hoặc chứng minh hai tam giác vuông bằng nhau Bài 1.
A D
B C
a) DBAECA (cạnh huyền – góc nhọn). b) EBCDCB (cạnh huyền – góc nhọn). c) Từ DBAECA suy ra AEAD EAMDAM (cạnh huyền – cạnh góc vuông). Bài 2. Chứng minh được : ABDACD (cạnh huyền - cạnh góc vuông)
Dạng 2. Sử dụng các trường hợp bằng nhau của tam giác vuông để chứng minh hai đoạn thẳng bằng nhau, hai góc bằng nhau. Tính độ dài đoạn thẳng, số đo góc. Bài 1 .
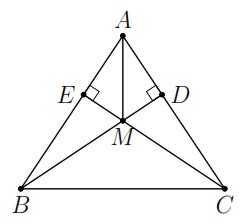
19
I
B C
a) Chứng minh được AHBAKC (cạnh huyền - góc nhọn) AHAK b) Chứng minh được AHIAKI (cạnh huyền - cạnh góc vuông)
20
H K
A
KAIHAI AI là tia phân giác của BAC Bài 2 . a) Gọi I là trung điểm của BC , khi đó ta chứng minh được () ABIACIccc Suy ra BC b) Chứng minh BDCE sau đó chứng minh BDMCEN (cạnh huyền – góc nhọn) Nên BMCN Bài 3 . Chứng minh MAEMBF ( cạnh huyền – góc nhọn) y
N M E I B C A D F E M x O
A B
21 Từ đó suy ra AEBF Bài
H
M x O
A
4 . a) MAOMBO ( cạnh huyền – góc nhọn) b) Gọi H là giao điểm của AB và OM . Ta có: BHOAHO ( c-g-c) Từ đó suy ra OHAOHB , mà hai góc này ở vị trí kề bù nên 90 OHAOHB Nên AB vuông góc với OM tại H
B
y
BÀI TẬP
Dạng 1. Tìm hoặc chứng minh hai tam giác vuông bằng nhau
Bài 1. Tìm các tam giác vuông bằng nhau trên hình sau:
D B
C
Bài 2. Tìm các tam giác vuông bằng nhau trên hình sau:
Bài 3. Tìm các tam giác vuông bằng nhau trên hình sau:
Bài 4. Tìm các tam giác vuông bằng nhau trên hình sau:
22
PHIẾU
A D A B C D A B C
Bài 5. Cho hình vẽ sau: Chứng minh rằng : a) ABHACH b) ADHAEH c) DBHECH
Bài 6. Cho xOy . Tia Oz là tia phân giác xOy . Lấy điểm A thuộc tia ()OzAO . Kẻ AB vuông góc với , OxAC vuông góc với ) ( , OyBOxCOy . Chứng minh OABOAC .
Bài 7. Cho hình vẽ sau. Tìm các tam giác vuông bằng nhau trên hình?
Bài 8.MD3. Cho tam giác ABC có ABAC . Gọi D là trung điểm của cạnh BC . Kẻ , DEABDFAC . Chứng minh:
a) DEBDFC b) DEADFA
Bài 9. Cho tam giác ABC vuông tại A và ABAC . Qua A kẻ đường thẳng d cắt BC . Vẽ , BMCN vuông góc với d . Chứng minh rằng : BAMACN .
23
N E
F E D
B C A G F E B
D
M
H
C A
Bài 10. Cho ABC có BC . Trên tia đối của tia BC lấy điểm , M trên tia đối tia của
lấy điểm N sao cho .BMCN Kẻ (),(), BEAMEAMCFANFAN ()AIBCIBC Chứng minh rằng BMECNF Bài 11. Cho ABC . Từ A vẽ cung tròn có bán kính bằng BC , từ C vẽ cung tròn có bán kính bằng AB . Hai cung tròn này cắt nhau tại D ( D nằm khác phía của B đối với AC ). Kẻ () AHBCHBC và () CKADKAD .
a) Chứng minh AHCCKA b) Chứng minh AHBCKD
Dạng 2. Sử dụng các trường hợp bằng nhau của tam giác vuông để chứng minh hai đoạn thẳng bằng nhau, hai góc bằng nhau. Tính độ dài đoạn thẳng, số đo góc.
Bài 1. Cho hình vẽ sau. Chứng minh OK là phân giác của góc BOA
O
B K
A
Bài 2. Cho ABC có ABAC . Kẻ ADBC . Chứng minh AD là tia phân giác của BAC . Bài 3. Cho ABC có BABC . Qua A kẻ đường vuông góc với AB , Qua C kẻ đường vuông góc với CB , chúng cắt nhau ở K . Chứng minh BK là phân giác của góc B ? Bài 4. Cho tam giác ABC , M là trung điểm cạnh BC . Vẽ BI , CK vuông góc với AM . Chứng minh BICK . Bài 5. Cho tam giác ABC vuông tại .A Tia phân giác góc B cắt cạnh AC tại điểm .M Kẻ ().MDBCDBC a) Chứng minh ;BABD b) Gọi E là giao điểm của hai đường thẳng DM và .BA Chứng minh ABCDBE . Bài 6. Cho tam giác ABC có ABAC . Trên cạnh , ABAC lần lượt lấy các điểm , MN sao cho AMAN . Các đường thẳng vuông góc với , ABAC tại , MN cắt nhau ở O . AO cắt BC tại H . Chứng minh a) AMOANO b) HBHC và AHBC .
24
tia CB
Bài 7. Cho tam giác ABC có ABAC . Đường thẳng vuông góc với AB tại B cắt đường thẳng vuông góc với AC tại C ở D . Gọi M là trung điểm cạnh BC . Chứng minh: a) DABDAC ; b) ,, AMD thẳng hàng.
Bài 8. Cho ABC vuông tại A và ABAC . Tính số đo góc , BC ? Bài 9. Cho ABC vuông tại A . Từ điểm K trên cạnh AC , vẽ KHBC , biết KHKA . Chứng minh rằng BKAH .
Bài 10. Cho ABC vuông tại A ABAC và các điểm M thuộc cạnh AC , H thuộc cạnh BC sao cho MHBC và MHHB . Chứng minh rằng AH là tia phân giác của góc A . Bài 11. Cho tam giác ABC . Các tia phân giác của góc B và C cắt nhau ở I . Kẻ ;; IDABIEACDABEAC . Chứng minh rằng ADAE
Bài 12. Cho ABC vuông tại A có ABAC . Vẽ () AHBCHBC . D là điểm trên cạnh AC sao cho ADAB . Vẽ ()DEBCEBC . Chứng minh HAHE
Bài 13 . Cho tam giác ABC có M là trung điểm của BC và AM là tia phân giác của góc A . Chứng minh ABAC
Phần III. BÀI TẬP TỰ LUYỆN Dạng 1. Tìm hoặc chứng minh hai tam giác vuông bằng nhau Bài 1. Cho tam giác ABC nhọn có ABAC , vẽ BDAC tại D , CEAB tại E . Gọi M là giao điểm của BD và CE . Chứng minh: a) DBAECA ; b) EBCDCB ; c) EAMDAM . Bài 2. Cho ABC có ABAC . Trên nửa mặt phẳng bờ BC không chứa A lần lượt vẽ các tia , BxCy sao cho BxBA và CyCA . Gọi D là giao điểm của các tia , BxCy . Chứng minh .ABDACD Dạng 2. Sử dụng các trường hợp bằng nhau của tam giác vuông để chứng minh hai đoạn thẳng bằng nhau, hai góc bằng nhau. Tính độ dài đoạn thẳng, số đo góc. Bài 1. Cho ABC nhọn có ABAC . Vẽ BHACHAC
25
a)
, CKABKAB . a) Chứng minh: AHAK b) Gọi I là giao điểm của BH và CK . Chứng minh AI là tia phân giác của A Bài 2. Cho ABC có ABAC D là một điểm trên cạnh AB , E là một điểm trên cạnh AC sao cho ADAE . Từ D và E hạ các đường , DMEN cùng vuông góc với BC . Chứng minh rằng:
BC
b) BMCN
Bài 3. Cho xOy . Trên tia Ox lấy điểm A , trên tia Oy lấy điểm B . Gọi M là trung điểm của đoạn thẳng AB . Từ A và B kẻ các đường thẳng , AEBF cùng vuông góc với tia OM Chứng minh : AEBF
Bài 4. Cho góc xOy . Trên tia phân giác của góc đó lấy một điểm M , từ M hạ các đường thẳng vuông góc , MAMB xuống cạnh , OxOy .Chứng minh:
a) MAOMBO . b) AB vuông góc với OM .
26
PHẦN I. TÓM TẮT LÍ THUYẾT.
1. Tam giác cân
a. Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau ABC cân tại A ABC ABAC b. Tính chất: Trong tam giác cân, hai góc ở đáy bằng nhau. Ngược lại một tam giác có hai góc ở đáy bằng nhau thì tam giác đó là tam giác cân. ABC cân tại A BC c. Dấu hiệu nhận biết:
- Tam giác có hai cạnh bằng nhau thì đó là tam giác cân. - Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.
2. Tam giác vuông cân
a. Định nghĩa: Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau. ABC vuông cân tại A 90 ABC A ABAC
b. Tính chất: Mỗi góc nhọn của tam giác vuông cân bằng 45o
ABC vuông cân tại A 45o BC

3. Tam giác đều
a. Định nghĩa: Tam giác đều là tam giác có ba cạnh bằng nhau ABC đều ABC ABBCCA
1 CHUYÊN ĐỀ: TAM GIÁC CÂN
ĐƯỜNG TRUNG TRỰC CỦA ĐOẠN THẲNG
A B C C B A
b. Tính chất: Trong tam giác đều mỗi góc bằng 60 .
c. Dấu hiệu nhận biết
- Tam giác có 3 cạnh bằng nhau thì tam giác đó là tam giác đều.
- Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.
- Nếu một tam giác cân có một góc bằng 60 thì tam giác đó là tam giác đều.
4. Đường trung trực của đoạn thẳng a. Định nghĩa đường trung trực: Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng ấy tại trung điểm của nó.
d

M A
B
Trên hình vẽ bên, d là đường trung trực của đoạn thẳng AB .
Ta cũng nói: A đối xứng B qua d .
b. Tính chất: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
c. Nhận xét: Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
MAMB M thuộc đường trung trực của AB .
d. Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.
PHẦN
II. CÁC DẠNG BÀI.
Dạng 1. Chứng minh tam giác cân, tam giác đều và sử dụng tính chất của tam giác cân, tam giác đều để giải quyết bài toán.
I. Phương pháp giải:
Dựa và dấu hiệu nhận biết của tam giác cân, tam giác đều. Dựa vào tính chất của tam giác cân, tam giác đều để tính số đo góc hoặc chứng minh các góc bằng nhau, các cạnh bằng nhau.
II. Bài toán.
2
A B C
Bài 1.
Trong các hình sau, hình nào là tam giác cân, hình nào là tam giác đều? Giải thích tại sao?
M C B
A F
80° 50° K E
D

I H G
Lời giải:
a) Xét ABC có: ABACBC nên ABC đều
Xét ACM có: ACCM nên ACM cân tại C
b) Trong DFK có 180 KDF
Ta có 18050KFD KF
DFK cân tại D .
c) Xét IGH có: IGGH nên IGH cân tại G
Mà 60 GIH nên IGH đều
Xét EGH có: EGEH nên EGH cân tại E Bài 2. Trong các hình sau, hình nào là tam giác cân, hình nào là tam giác đều? Giải thích tại sao?
F H
M
E D N L P O
Lời giải:
3
a) Trong DEH có DEDHDEH cân tại D . Ta có ;DEDH EFHG DEEFDHHG DFDG DFG cân tại D . b) Ta có MOMPPOMPO đều.
60° G

4 Lại có LOMOLOM
tại O
x D
A
cân
MPPNMPN cân tại P . Vì MOP đều nên 60 POMMPO Mà 180 MOPMOL (hai góc kề bù); 180 MPOMPN (hai góc kề bù) MOLMPN Xét MOL và MPN ta có: MOLMPN (cmt), OLPN (gt), MOMP (gt) Suy ra MOLMPN (c.g.c) Do đó MLMNLMN cân tại M Bài 3. Cho tam giác ABC cân tại A . Tính số đo các góc còn lại của tam giác ABC nếu biết: a) A = 40°; b) B = 50°; c) C = 60°. Lời giải: a) Trong ABC có 180 ABC 18018040140BCA Mà BC (Vì ABC cân tại A ) 140 70 2 BC b) Trong ABC có 180 ABC Mà ABC cân tại A 50 BC 1802.1082.5080AB c) Trong ABC có 180 ABC Mà ABC cân tại A 60 BC 1802.1802.6060AC Bài 4. Tìm số đo x trong hình vẽ sau: Lời giải:
C B

5 Trong ABC vuông tại A có ABAC nên ABC vuông cân tại A 45 ABCACB Xét ADC có ACDC nên ADC cân tại C CDACADx Ta lại có BCA là góc ngoài của ADC 2 BCACDACABxxx Do đó 24522,5 xx Bài 5. Cho tam giác ABD cân tại A có A = 40°. Trên tia đối của tia DB lấy điểm C sao cho DCDA . Tính số đo góc ACB . Lời giải: Trong ABC có 180 BADBADB 180140BADBBAD Mà BADB ( ABD cân tại A ) BADB 140 70 2 Ta có 180 ADBADC (hai góc kề bù) 110 ADC ADC có DCDA (gt) ADC cân tại D 180180110 35 22 ADC ACB Bài 6. Cho tam giác ABC vuông tại A, 30 B . Trên cạnh BC lấy M sao cho AMBM Chứng minh AMC đều. Lời giải: 40° C D B A
M
30° C
Ta có AMBM (gt) AMB cân tại M BAMB
Vì ABC vuông tại A 90 BC
Mà 90 BAMCAM ; BAMB (cmt)
Nên CAMC AMCcân tại M
Ta lại có 9060CB .
Suy ra AMC đều.
Bài 7. Cho tam giác ABC . Tia phân giác góc B cắt cạnh AC tại D . Qua D kẻ đường thẳng song song với BC , nó cắt cạnh AB tại E . Chứng minh tam giác EBD cân.
Lời giải:
A

B A E D C B
Vì // DEBC nên DBCEDB (vì hai góc so le trong)
Mà DBCDBE (vì BD là tia phân giác của ABC ) EBDEDB EDB cân tại E
Bài 8. Cho tam giác ABC vuông cân tại A. Tia phân giác góc A cắt cạnh BC tại D . Trên cạnh ABvà AC lần lượt lấy các điểm E và F sao cho AECF . Chứng minh ,, ABDADCAEF vuông cân.
6
Lời giải:

7
.
ứ
Lời
Ta có ABBCCA và AMBNCP ABAMBCBNCACP MBNCPA . Xét MBN và NCP ta có: 60 BC (vì ABC đều), BMCN (cmt),
Suy ra MBNNCP (c.g.c) MNNP (1) F E D B C A P N M C B A
Xét AEF vuông tại A có AEAF AEF vuông cân tại A Vì ABCvuông cân tại A 45 BC Ta lại có: AD là phân giác BAC 45 2 BAC BADCAD Xét ABD có 18090BDABBAD ADBC 90 ADC Xét ADB vuông tại D có 45 BDAB ADBvuông cân tại D Xét ADC vuông tại D có 45 CDAC ADC vuông cân tại D Bài 9. Cho tam giác ABC đều. Trên cạnh , , ABBCCA lần lượt lấy các điểm ,, MNP sao cho AMBNCP
Ch
ng minh tam giác MNPđều.
giải:
BNCP
(gt)
PMNP (2)
Từ (1) và (2) PMNPMN
Suy ra MNP đều.
Bài 10. Cho tam giác ABC cân tại A . Tia phân giác góc B cắt cạnh AC tại D , tia phân giác góc C cắt cạnh AB tại E . Chứng minh tam giác ADE cân.
Lời giải:
2 1 2 1
Vì BD , CE lần lượt là tia phân giác của ABC , ACB Nên 12 2 ABC BB , 12 2 ACB CC
Mà ABCACB (do tam giác ABC cân tại A )
Suy ra: 22BC
Xét ABD và ACE ta có: 22BC , A là góc chung, ABAC ( ABC cân tại A ) Suy ra ABDACE (g.c.g) ADAEADE cân tại A .
E D C B
Bài 11. Cho tam giác ABC cân tại A . Trên tia đối của tia BC lấy điểm D , trên tia đối của tia CB lấy điểm E sao cho BDCE . Chứng minh tam giác ADE cân.
Lời giải:
A

A 2 1 2 1 E D C B
Ta có: 12 180 BB , 12 180 CC (kề bù) 11 BC ( ABC cân tại A )
8 Chứng
tự ta có (..)PAMNCPcgc
minh tương

9 Nên 22BC Xét ABD và ACE ta có: 22BC (cmt) ABAC ( ABC cân tại A ) DBCE (gt) Suy ra ABDACE (g.c.g) ADAEADE cân tại A . Bài 12. Cho xOy = 120°, điểm A thuộc tia phân giác của xOy . Kẻ ABOx ( BOx ) và ACOy (COy ). Tam giác ABC là tam giác gì? Tại sao? Lời giải: Xét ABO và ACO ta có: 1 60 2 AOBAOCxOy (vì OA là tia phân giác của xOy ) O90ABOAC OA là cạnh chung Suy ra ABOACO (ch.gn) ABACABC cân tại A . Vì ABO vuông tại B 90 AOBBAO 906030 BAO Mà do BAOCAOABOACO 60 BAC Xét ABC cân tại A có 60 BAC ABC đều. Bài 13. Cho tam giác ABC cân tại A ( A < 90°). Kẻ BD vuông góc với AC tại D , kẻ CE vuông góc với AB tại E C B A O y x
a) Chứng minh tam giác ADE cân.
b) Chứng minh // DEBC .
c) Gọi I là giao điểm của BD và CE . Chứng minh IBIC .
d) Chứng minh AIBC

Lời giải:
Xét ABD và ACE ta có: 90 ADBAEC BAC là góc chung ABAC ( ABC cân tại A )
Suy ra ABDACE (ch.gn) ADAEADE cân tại A .
b) ABC cân tại A 2 180 BAC ACB (1) ADE cân tại A 2 180 BAC ADE (2)
Từ (1) và (2) ADEACB , mà hai góc này vị trí đồ
10
c)
I E D C B A
ng vị // DEBC
Ta có ABCABIIBC ; ACBACIICB Mà ABCACB ( ABC cân tại A ) ; ABIACI (vì ABDACE ) Nên IBCICB
IBC cân tại I IBIC d) Ta có ABAC ( ABC cân tại A ) A nằm trên đường trung trực của đoạn thẳng BC IBIC (cmt) I nằm trên đường trung trực của đoạn thẳng BC Do đó AI là đường trung trực của đoạn thẳng BC AIBC .

11 Bài
14. Cho tam giác ABC cân tại A. Lấy điểm M trên cạnh () BCMBMC . Trên tia đối của tia CB lấy điểm N sao cho BMCN . Đường thẳng qua M vuông góc với BC cắt AB tại E . Đường thẳng qua N vuông góc BC cắt AC tại F . a) Chứng minh: EMFN b) Qua E kẻ // EDAC ( DBC ). Chứng minh MBMD . c) EF cắt BC tại O . Chứng minh OEOF Lời giải: a) Ta có EBMACB ( ABC cân) mà FCNACB (đối đỉnh) nên EBMFCN Xét BEM và CFN ta có: EBMFCN (cmt) BMCN (gt) (90) EMBFNC Vậy BEMCFN (g.c.g) EMFN b) Ta có // EDACEDMACB (đồng vị) mà EBMACB nên EDMEBM Suy ra EBD cân tại E , do đó EBED Xét BME vuông tại M và DME vuông tại M , ta có EBED (cmt); EDMEBM (cmt) Suy ra BMEDME (ch.gn) E N F O M D C B A
c) Ta có // EMFN (cùng vuông góc với BC ) MEONFO (so le trong).
Xét MEO và NFO , ta có: MEONFO (cmt) EMFN (câu a) (90) EMOFNO
Suy ra MEONFO (g.c.g)
OEOF
Dạng 2. Vận dụng tính chất của đường trung trực để giải quyết bài toán
I. Phương pháp giải: Sử dụng tính chất: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
II. Bài toán.
Bài 1. Cho hai điểm A , B nằm trên đường trung trực của đoạn thẳng MN . Chứng minh MABNAB .
Xét MAB và NAB có: AMAN (cmt) BMBN (cmt) AB là cạnh chung
Do đó MABNAB (c.c.c).
A

N M
Lời giải: Do A , B nằm trên đường trung trực của đoạn thẳng MN nên AMAN , BMBN
d B
Bài 2. Cho ABC cân tại B . Lấy điểm D đối xứng với điểm B qua AC . Chứng minh ABDCBD .
Lời giải:
12 BMMD
Vì D đối xứng với điểm B qua AC nên AC là đường trung trực của BD Do A , C nằm trên đường trung trực của đoạn thẳng BD nên ABAD , BCDC
Xét ABD và CBD có: ABAD (cmt) BCDC (cmt) AC là cạnh chung Do đó ABDCBD (c.c.c).
Bài 3. Tam giác ABC vuông tại A có 30 C . Trên tia đối của tia AC lấy điểm D sao cho ADAC . Tính số đo góc BDA .
Lời giải:
B A

30° D C
Vì ABDC và ADAC nên AB là đường trung trực của DC BDBC
Suy ra DBC cân tại B 30 BDAC
Bài 4. Cho góc vuông xOy . Điểm M nằm trong góc đó. Vẽ điểm N và P sao cho tia Ox là đường trung trực của MN và Oy là đường trung trực của MP
a) Chứng minh ONOP b) Chứng minh ba điểm P , O , N thẳng hàng.
Lời giải:
13
D C B A
4 3 2 1
E
N O
a) Vì Ox là đường trung trực của MN nên OMON Vì Oy là đường trung trực của MP nên OMOP
Do đó ONOP b) Gọi E , F lần lượt là giao điểm của MN và Ox , MP và Oy
OMEONE (c.g.c) nên 12OO
OMFONP (c.g.c) nên 34OO

Ta có 12342322.90180PONOOOOOO
Do đó ba điểm P , O , N thẳng hàng.
Bài 5. Cho ABC vuông tại A . Đường trung trực của đoạn thẳng AC cắt AC tại H , cắt BC tại D . Nối A và D .
a) So sánh số đo góc DAB và DBA . b) Chứng minh D là trung điểm của BC
Lời giải:
H D
C B A
a) Từ giả thiết vì HD là đường trung trực của AC nên DCDA 1CA
14
F
P M
Vì ABC vuông tại A nên 21 90 AA , 90 BC 2 AB b) 2 AB nên ADB cân tại D DADB y
x 2 1

15 Mà DCDA ( vì HD là đường trung trực của AC ) DCDB Suy ra D là trung điểm của BC Bài 6. Cho ABC . Các đường trung trực của AB và AC cắt cạnh BC theo thứ tự ở M và N a) Biết 30 B , 45 C .
ố đo
MAN . b) Chứng minh
BAC
a) Ta có M nằm trên đường trung trực của đoạn thẳng AB MAMB AMB cân tại M 1 30 BA Tương tự N nằm trên đường trung trực của đoạn thẳng AC NANC ANC cân tại N 2 45 CA Trong ANC có 2 180180454590ANCCA nên 90 ANC . Suy ra ANBC . Xét ABC có 30 B , 45 C 180105BACBC . Vậy 12 304 1051 5 0530 MANAA b) Ta có: 12 ()()(180) MANBACAABACBCBACBAC 2180 BAC Vậy 2180MANBAC Bài 7. Cho góc vuông xOy . Trên các tia Ox , Oy lấy hai điểm A và B (không trùng với O ). Đường trung trực của các đoạn thẳng OA và OB cắt nhau ở M . Chứng minh: a) A , M , B thẳng hàng. b) M là trung điểm của AB . 2 1 45° 30° N M C B A
Tính s
góc BAC và
MAN = 2180
Lời giải:
a) Gọi 1M , 2 M lần lượt là giao điểm của trung trực đoạn OA, OB với AB Ta có 1M nằm trên đường trung trực của đoạn thẳng OA 11 MAMO 1 MOA cân tại 1M nên 1AO (1) Ta lại có 2 M nằm trên đường trung trực của đoạn thẳng OB 22 MBMO 2 MOB cân tại 2 M nên 2BO (2)
Từ (1) và (2) suy ra 12 OOAB Xét OAB vuông tại O nên 90 AB Do đó 12 90 OO (3) Ta lại có 1122 90 AOBOMOMO (4)

Từ (3) và (4) suy ra 1212 0 MOMMMM
Vậy A , M , B thẳng hàng.
Ta có M lần lượt
16 Lời giải:
a)
. b)
c)
2
M
M
B A O y x 2 1 M B A O y x
b)
nằm trên đường trung trực của đoạn OA, OB Nên MOMA , MOMB MAMB mà A , M , B thẳng hàng nên M là trung điểm của AB . Bài 8. ABC có BC = 30°. Đường trung trực của BC cắt AC ở K .
Chứng minh KBCKCB
Tính số đo góc ABK
Biết 3cm AB , 5cm AC
. Tính chu vi tam giác ABK . Lời giải:
1
2
1
a) K thuộc đường trung trực của BC KBKC BKC cân tại K KBCC b) Ta có: 30 ABKABCKBCABCC

c) Ta có: 5cm AKBKAKKCAC 8cm ABAKBK Vậy chu vi tam giác ABK là 8 cm Dạng 3. Chứng minh một điểm thuộc đường trung trực. Chứng minh một đường thẳng là đường trung trực của một đoạn thẳng.
I. Phương pháp giải: • Để chứng minh điểm M thuộc trung trực của đoạn thẳng AB , ta dùng nhận xét: Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó. MAMB M thuộc đường trung trực của AB .
• Để chứng minh đường thẳng d là đường trung trực của đoạn thẳng AB , ta chứng minh d chứahaiđiểm phân biệt cách đều A và B , hoặcdùngđịnhnghĩađườngtrungtrực.
II. Bài toán.
Bài 1. Cho đoạn thẳng 5cm AB . Vẽ đường tròn tâm A bán kính 4cm và đường tròn tâm B bán kính 3cm. Hai đường tròn này cắt nhau tại D , E . Chứng minh:
a) Điểm A thuộc đường trung trực của DE . b) AB là đường trung trực của DE
Lời giải:
17
K C B A E
B A
D
a) Từ giả thiết điểm D , E nằm trên đường tròn tâm A nên ADAE
Suy ra điểm A thuộc đường trung trực của DE .
b) Tương tự ý a), ta có điểm điểm B thuộc đường trung trực của DE Vậy AB là đường trung trực của DE .
Bài 2. Cho đoạn thẳng AB . Dựng các tam giác cân MAB , NAB lần lượt tại M và N ( M , N nằm khác phía so với AB ). Chứng minh:
a) Điểm M thuộc đường trung trực của AB ; b) MN là đường trung trực của AB Lời giải:
M
N

a) AMB cân tại M nên AMBM Suy ra điểm M thuộc đường trung trực của AB (1)
Ta lại có ANB cân tại N nên ANBN Nên điểm N thuộc đường trung trực của AB . (2)
Từ (1) và (2) suy ra: MN là đường trung trực của đoạn thẳng AB .
Bài 3. Cho ABC , đường phân giác AD . Trên tia AC lấy điểm E sao cho AEAB . Chứng minh: a) BDDE ; b) AD là đường trung trực của BE .
Lời giải:
E
B A D C B
18
a) Xét ABD và AED có: AD là cạnh chung
A
ABAE (gt)

Do đó ABDAED (c.g.c) nên BDDE
b) Vì BDDE (cmt) suy ra D nằm trên đường trung trực của BE (1).
Theo giả thiết: ABAE suy ra A nằm trên đường trung trực của BE (2). Từ (1) và (2) , suy ra AD là đường trung trực của BE .
Bài 4. Cho DEF có DEDF . Lấy điểm K nằm trong tam giác sao cho KEKF . Kẻ KP vuông góc với DE ( PDE ), KQ vuông góc với DF (QDF ). Chứng minh: a) K thuộc đường trung trực của EF và PQ ; b) DK là đường trung trực của EF và PQ . Từ đó suy ra // PQEF Lời giải: a) Ta có: DEDF KEKF
19 BADEAD
ủ
(Vì AD là tia phân giác c
a BAC )
Xét
PK
KEKF
12 DD Xét DPK và
90 DPKDQK 12DD
DK
ạ
Do
PKQK
2 1 Q P K F
D
nên K , D thuộc trung trực của EF .
DEK và DFK có:
là cạnh chung
(gt) DEDF
(gt) Do đó ABDAED
(c.g.c) nên BDDE
DQK
có:
(cmt)
là c
nh chung
đó DPKDQK
và DPDQ
E
Từ đó suy ra K , D thuộc trung trực của PQ
b) Ta có K , D thuộc trung trực của EF DK là đường trung trực của PQ
DKPQ (1)
Ta lại có K , D thuộc trung trực của PQ DK là đường trung trực của EF DK EF (2)
Từ (1) và (2) , suy ra // PQEF
Bài 5. Cho ABC cân tại A , M là trung điểm của BC ME vuông góc với AB , MF vuông góc với AC . Chứng minh:
a) AM là trung trực của của BC ; b) MEMF và AM là trung trực của EF ; c) // EFBC .
Lời giải:
A

F E M C B
a) Ta có ABC cân tại A ABAC (1)
Mà MBMC ( Vì M là trung điểm của BC ) (2) Suy ra , AM thuộc đường trung trực của BC
AM là trung trực của của BC
b) Vì ABC cân tại A nên BC .
Xét BEM và CFM có: 90 BEMCFM (gt) BMCM ( M là trung điểm của BC ) BC (Vì ABC cân tại A )
Do đó BEMCFM (ch-gn)
MEMF Ta có BEMCFM (ch-gn) BECF
20
AEAF Mặt khác, MEMF nên AM là đường trung trực của đoạn thẳng EF c) Ta có: AM là đường trung trực của BC và EF AMBC , AMEF // EFBC .
Bài 6. Cho góc xOy khác góc bẹt Oz là tia phân giác của xOy . Gọi M là một điểm bất kì thuộc tia Oz . Qua M vẽ đường thẳng a vuông góc với Ox tại A, cắt Oy tại C và vẽ đường thẳng b vuông góc với Oy tại B , cắt Ox tại D . Chứng minh: a) Điểm O thuộc đường trung trực của AB ; b) OM là đường trung trực của AB ; c) OM là đường trung trực của CD. d) // ABCD Lời giải:

21 Mà ABC cân tại A ABAC
Do đó ABBEACCF
12
OAOB
a) Xét OAM và OEM có: OM là cạnh chung
OO
(Vì Oz là tia phân giác của xOy ) 90 OAMOBM (gt) Do đó OAMOEM (ch-gn) nên
MAMB
Vì OAOB
nên O thuộc đường trung trực của AB . b) Vì MAMB nên M thuộc trung trực của AB Mà O thuộc trung trực của AB Suy ra OM là đường trung trực của AB . c) OBDOAC (c.g.c) 2 1 C D M B A z y O x
Nên ODOC O thuộc đường trung trực của CD (1)
OMDOMC (c.g.c)
Nên MDMC M thuộc đường trung trực của CD. (2)
Từ (1) và (2) suy ra OM thuộc đường trung trực của CD.
d) Ta có OM là đường trung trực của AB và CD
OMAB , OMCD // ABCD
Bài 7. Cho hai điểm A , B nằm cùng phía với đường thẳng d . Xác định vị trí điểm M trên đường thẳng d sao cho M cách đều hai điểm A và B Lời giải:
d M
Vì điểm M cách đều hai điểm A và B nên M thuộc đường trung trực của đoạn thẳng AB
Vậy điểm M là giao điểm của đường thẳng d với đường trung trực của AB .
Chú ý: Nếu A , B nằm sao cho ABd thì không tồn tại điểm cần tìm.
E
A
B A F C B D

22
Bài 8. Cho tam giác ABC cân tại A ( A < 90°). Đường trung trực của cạnh AC cắt tia CB tại điểm D . Trên tia đối của tia AD lấy điểm E sao cho AEBD . Chứng minh: a) Chứng minh CAD cân; b) Chứng minh DACABC ; c) Chứng minh ADCE ; d) Lấy F là trung điểm của DE . Chứng minh CF là đường trung trực của DE . Lời giải:
a) Vì D thuộc đường trung trực của AC nên DADC ADC cân. b) CAD cân DACDCA (1) Vì ABAC nên ABCDCA (2) Từ (1) và (2) DACABC c) Ta có : (180)EACDACDBAABC Mà DACDCA suy ra EACABD . Chứng minh được EACDBA (c.g.c) ADCE . d) Ta có: ADCE , DADC nên CECD Mà FEFD ( F là trung điểm của DE ). CF là đường trung trực của DE .
Bài 9. Cho ABC nhọn, đường cao AH . Lấy các điểm P và Q lần lượt đối xứng với H qua AB ; AC
a) Chứng minh APAQ
b) Gọi I , K lần lượt là giao điểm của PQ với AB , AC . Chứng minh APIAHI và AHKAQK .
c) Chứng minh HA là tia phân giác của IHK
d) Cho BAC = 60°. Tính số đo góc PAQ
Lời giải:
A

Q P
K I C B H
a) Ta có P đối xứng với H qua AB nên AB là đường trung trực của đoạn thẳng PH APAH
Ta lại có Q đối xứng với H qua AC nên AC là đường trung trực của đoạn thẳng QH
AQAH
Do đó APAQAH
b) Xét API và AHI ta có:
23
APAH ( A nằm trên đường trung trực của đoạn thẳng PH )
B A

D H E C
IPIH ( I nằm trên đường trung trực của đoạn thẳng PH ) AI cạnh chung Vậy APIAHI (c.c.c) APIAHI (1) Chứng minh tương tự: AHKAQK ( c.c.c) AHKAQK (2) c) Ta có APAQ PAQ cân tại A APIAQK (3). Từ (1), (2) và (3) có: AHIAHK HA là tia phân giác của IHK d) Ta có APIAHI PAIHAI AHKAQK HAKQAK Mà 2()2120PAQPAHHAQIAHHAKBAC Vậy 120 PAQ Bài 10. Cho tam giác ABC vuông tại A . Tia phân giác của B cắt AC tại E . Từ E kẻ EH vuông góc với BC tại H . a) Chứng minh: .ABEHBE b) Chứng minh BE là đường trung trực của đoạn thẳng AH . c) ẻ ()ADBCDBC . Chứng minh AH là tia phân giác của DAC Lời giải: a) Xét ABE và HBE ta có: 90 BAEBHE BE cạnh chung ABEDBE (gt)
24
b) Vì ABEHBE (cmt) BABH , EAEH
BABH (hai cạnh tương ứng) nên B thuộc đường trung trực của AH
EAEH (hai cạnh tương ứng) nên E thuộc đường trung trực của AH
Vậy BE là đường trung trực của đoạn thẳng AH
c) Ta có: // ADEH (cùng vuông góc với BC ) nên DAHEHA (so le trong)
Vì EAEH (cmt) nên tam giác EAH cân tại E nên EAHEHA
Vậy EAHDAH hay AH là tia phân giác của DAC
Phần III. BÀI TẬP TỰ LUYỆN
Dạng 1. Chứng minh tam giác cân, tam giác đều và sử dụng tính chất của tam giác cân, tam giác đều để giải quyết bài toán.
Bài 1: Trong các hình sau, hình nào là tam giác cân, hình nào là tam giác đều?
40° 70° J I

K 60° N M S R
Q G F D
Bài 2. Tìm số đo x trong hình vẽ sau:
Bài 3. Cho tam giác ABC vuông cân tại A. Trên đường thẳng AB lấy điểm D sao cho BDBC ( D và A khác phía so với B ). Tính số đo các góc của tam giác ADC
Bài 4. Cho ABC cân tại A . Trên các cạnh AC , AB lần lượt lấy M , N sao cho AMAN a) Chứng minh ABMACN . b) Gọi O là giao điểm của BM và CN . Chứng minh tam giác OBC cân. Bài 5. Cho xOy = 60°, điểm A thuộc tia phân giác của xOy . Kẻ ABOx ( BOx ) và ACOy (COy ). Tam giác OBC là tam giác gì? Tại sao?
25 Suy
ra ABEHBE (cạnh huyền - góc nhọn)
E 72° 36° 36° X 70° Y V S T
Bài 6. Cho tam giác ABC vuông tại A, 2 BCAB D là trung điểm cạnh . Đường thẳng vuông góc với tại cắt tại . Chứng minh
a) cân. b) đều.

Bài 7: Cho tam giác vuông tại . Tia phân giác góc cắt tại . Qua kẻ đường thẳng vuông góc với tại , cắt tại . Trên lấy điểm F sao cho . Chứng minh
a) ; b) là tam giác cân; c)
Dạng 2. Vận dụng tính chất của đường trung trực để giải quyết bài toán
Bài 1. Tam giác có điểm thuộc đường trung trực của . Biết . Tính số đo của các góc trong
Bài 2. Cho cân có . Các đường trung trực của và cắt cạnh theo thứ tự ở và và hai trung trực cắt nhau ở
a) Biết . Tính số đo góc
b) Chứng minh
c) Tính số đo .
Bài 3. Cho góc . Từ điểm nằm trong góc đó kẻ vuông góc với ( thuộc ) và vuông góc với ( thuộc ). Trên tia đối của tia lấy điểm sao cho . Trên tia đối của tia lấy điểm sao cho Chứng minh .
Bài 4. Cho vuông tại . là trung điểm của cạnh . Đường trung trực của cạnh cắt cạnh tại . Gọi là giao điểm của và
a. Chứng minh là tam giác cân. So sánh: và b. Chứng minh là trung điểm của c. Nếu , tính số đo của
Dạng 3. Chứng minh một điểm thuộc đường trung trực. Chứng minh một đường thẳng là đường trung trực của một đoạn thẳng.
Bài 1. Cho . Trên tia lấy điểm , trên tia lấy điểm . Kẻ đường trung trực của đoạn thẳng ( , ). Chứng minh thuộc đường trung trực của Bài 2. Cho tam giác có . Xác định điểm trên sao cho . Bài 3. Cho bốn điểm , , , tạo thành hình có và như hình vẽ. Giao điểm của và là . Từ vẽ vuông
26
góc với cắt cạnh , lần lượt tại , . Chứng minh là trung trực của và AC AC D BC E EAC ABE ABC () AABAC A BC D D BC D AC F AB AEAF ABCDEC DBF DBDE ABC A BC 40 B ABC ABC 90 A AB AC BC D E F 110 A DAE 2180 BACDAE DFE xOy A AH Ox H Ox AK Oy K Oy HA B HBHA KA C KCKA OBOC ABC A M AB AB BC N I CM AN ANB NAB NBA N BC IBIC ABC 90 xOy Ox A Oy B HM OA HOA MAB M OB ABC ABAC D AC DADBAC A B C D // ABCD // BCAD AC BD O O AC BC AD M N AC MN AMMCCNNA
N
D

Bài 4. Cho tam giác ABC vuông tại A. Tia phân giác của cắt AC tại E. Từ E kẻ EH vuông góc với BC tại H.
A B .ABEHBE
a) Chứng minh: b) Chứng minh BE là đường trung trực của đoạn thẳng AH. c) ẻ . Chứng minh AH là tia phân giác của
()ADBCDBC DAC ABC AI IBC IC H H AI AB E AC F EF A ABC H IC EF
27
M O
Bài 5. Cho tam giác cố định, đường phân giác ( ). Trên đoạn thẳng lấy điểm . Từ kẻ đường thẳng song song với , cắt kéo dài tại và cắt tại . Chứng minh: a) Đường trung trực của luôn đi qua đỉnh của tam giác ; b) Khi di động trên đoạn thẳng thì đường trung trực của đoạn thẳng luôn cố định. C B
Dạng 1. Nhận biết tam giác cân, tam giác đều. Vận dụng tính chất của tam giác cân, tam giác đều để tính số đo góc hoặc chứng minh các góc bằng nhau, các cạnh bằng nhau. Bài 1. Bài 1: Bài Bài 1. Trong các hình sau, hình nào là tam giác cân, hình nào là tam giác đều?
Lời giải: a) Trong có Ta có cân tại b) Ta có: có và đều. Suy ra (c.g.c) cân. c) Ta có Xét có suy ra cân

1 ĐÁP SỐ BÀI TẬP TỰ
Ệ
LUY
N
tại Xét có cân tại . Xét có cân tại . Bài 2. Tìm số đo x trong hình vẽ sau: Lời giải: Vì nên cân tại 40° 70° J I K 60° N M S R Q G F D E 72° 36° 36° KIJ 180 KIJ 18070KIJ KI IJK J QRS QRQS 60 QRSQRS QRNQSM QNQM QMN 72108;DGFDGE 36 DEF DEF 72 EDFEFD DEF E DFG 72 DGFDFGDFG D DGE 36 EDGDEGDGE G X 70° Y V S T TSTY TSY T

2 Vì TYYV nên cân tại YTVVx Ta có TYS là góc ngoài của nên 270TYSYTVVx 35 x Bài 3. Cho
ạ
.
Lời
Có Tam giác cân tại suy ra Suy ra Bài 4. Cho cân tại . Trên các cạnh , lần lượt lấy , sao cho a) Chứng minh b) Gọi là giao điểm của và . Chứng minh tam giác cân. Lời giải: a) Xét và ta có: 70 TYSS TYV Y TYV ABC A AB D BDBC D A B .ADC D B C A 45135.ABCACBCBD BCD B 180135 22,5 2 ADCBCD 67,5. ACD ABC A AC AB M N AMAN ABMACN O BM CN OBC N M C B A O AMB ANC
tam giác vuông cân t
i
Trên đường thẳng lấy điểm sao cho ( và khác phía so với ). Tính số đo các góc của tam giác
giải:
(gt) là góc chung ( cân tại ) Suy ra (c.g.c) b) Ta có: , Mà (cmt), ( cân tại ) Do đó Hay cân tại Bài 5. Cho = 60°, điểm thuộc tia phân giác của . Kẻ ( ) và ( ). Tam giác là tam giác gì? Tại sao? Lời giải: Xét và ta có: (vì là phân giác ) là cạnh chung Suy ra (ch.gn) cân tại có đều. Bài 6. Cho tam giác vuông tại , . là trung điểm cạnh . Đường thẳng vuông góc với tại cắt tại . Chứng minh a) cân. b) đều. Lời giải:

3
AMAN BAC ABAC ABC A AMBANC ABMACN ABCABMMBC ACBACNNCB ABMACN ABCACB ABC A MBCNCB OBCOCBOBC O xOy A xOy ABOx BOx ACOy COy OBC C B A y O x ABO ACO AOBAOC OA xOy O90ABOAC OA ABOACO OBOCOBC O OBC 60 BOC OBC ABC A 2 BCAB D AC AC D BC E EAC ABE

4
a)
b) là tam giác
Lời giải: a) Ta có suy ra . b) Xét và có: chung; . Suy ra (c.g.c). mà cân tại B E C D A EAD ECD ;DADC ;EDAEDC ED EDAECD EAECECA 90 ABEECA ECAEAC 90 ABEEAC BAEEBA BAE ABE E 2 AB ECBEEAAB ABE ABC () AABAC A BC D D BC D AC F AB AEAF ABCDEC DBF DBDE D F B C E A 90; ABCACB 90 ACBDEC ABCDEC FAD EAD AD ;FADEAD AFAE FADEDA ;DFADEA DFBDEC ABCDEC ABCDFB DBF D
a) Xét và có chung suy ra Suy ra cân. b) Ta có (cùng phụ góc ). Suy ra cân tại đều. Bài 7: Cho tam giác vuông tại . Tia phân giác góc cắt tại . Qua kẻ đường thẳng vuông góc với tại , cắt tại . Trên lấy điểm F sao cho . Chứng minh
;
cân; c) .
c) Ta có
Tam giác cân tại Từ và suy ra .
Dạng 2. Vận dụng tính chất của đƣờng trung trực để giải quyết bài toán.
Bài 1. Tam giác có điểm thuộc đường trung trực của . Biết . Tính số đo của các góc trong
Lời giải:
Vì nằm trên đường trung trực của nên Suy ra cân tại Tính được: , Bài 2. Cho cân tại có . Các đường trung trực của và cắt cạnh theo thứ tự ở và và hai trung trực cắt nhau ở a) Biết . Tính số đo góc b) Chứng minh c) Tính số đo . Lời giải: a) cân tại

5
FADEDA DEDF (1) DBF D DBDF (2) (1) (2) DBDE ABC A BC 40 B ABC 40° C B A A BC ABAC ABC A 40 ACB 100 BAC ABC A 90 A AB AC BC D E F 110 A DAE 2180 BACDAE DFE 3 2 1 F E D C B A ABC A 180180110 35 22 BAC BC D AB DADB
Ta có nằm trên đường trung trực của đoạn thẳng
cân tại
Tương tự nằm trên đường trung trực của đoạn thẳng cân tại
b) Ta có: Vậy
Bài 3. Cho góc . Từ điểm nằm trong góc đó kẻ vuông góc với ( thuộc ) và vuông góc với ( thuộc ). Trên tia đối của tia lấy điểm sao cho . Trên tia đối của tia lấy điểm sao cho . Chứng minh .
Lời

giải:
là đường trung trực của , Nên (1) Tương tự ta có là đường trung trực của , Nên (2) Từ (1) và (2) suy ra
Bài 4. Cho vuông tại . là trung điểm của cạnh . Đường trung trực của cạnh cắt cạnh tại . Gọi là giao điểm của và .
a. Chứng minh là tam giác cân. So sánh: và . b. Chứng minh là trung điểm của c. Nếu , tính số đo của . Lời giải:
6
ADB D 1 35 BA E AC EAEC AEC
E
35 CA 13 1102.3540 D BACAA AE 2213 180()2 DAEABCBACAAABACBACBACBAC 2180 BACDAE xOy A AH Ox H Ox AK Oy K Oy HA B HBHA KA C KCKA OBOC y x K H C B A O Ox AB OAB OAOB Oy AC OAC OAOC OBOC ABC A M AB AB BC N I CM AN ANB NAB NBA N BC IBIC ABC
3
a) Vì nằm trên đường trung trực của đoạn nên là tam giác cân tại đỉnh b) là tam giác cân tại đỉnh nên . vuông tại nên Mà Nên Suy ra cân tại Mà nên Do đó là trung điểm c) Nếu mà nên là đường trung trực của . Mà nên Khi đó vuông cân tại . Dạng 3. Chứng minh một điểm thuộc đƣờng trung trực. Chứng minh một đƣờng thẳng là đƣờng trung trực của một đoạn thẳng.
Bài 1. Cho . Trên tia lấy điểm , trên tia lấy điểm . Kẻ đường trung trực của đoạn thẳng ( , ). Chứng minh thuộc đường trung trực của . Lời giải: Ta có là

7
đường trung trực của đoạn thẳng nên cân tại I N M C B A 2 1 I N M C B A 2 1 N AB NANB ANB N ANB N 1BA ABC A 90 BACB 12 90 AA 2 AACB ANC N ANNC NANB NBNC N BC IBIC NBNC IN BC AIN ABAC ABC A 45 ABC 90 xOy Ox A Oy B HM OA HOA MAB M OB A x y O M B H 1 1 2 1 HM OA MAMO OMA M 1 2 OA

8 Mặt khác,
11 21
ABOO 11
ABC A
BC ABHACH
AH
//
I H
B A
AHBAHC
0
H
AH
ABH
. Vậy M thuộc trung trực của OB Bài 2. Cho tam giác có cân tại . Gọi là trung điểm của . a) Chứng minh rằng b) Chứng minh rằng là đường trung trực của c) Trên tia đối của tia lấy điểm sao cho . Chứng minh rằng: d) Chứng minh a) và có: (gt) cạnh chung ( là trung điểm ) Suy ra: (c-c-c) b) Ta có: ( 2 góc kề bù) Mà ( do ) Mà là trung điểm (gt) Nên là đường trung trực của c) và có: (gt) (đối đỉnh)
90
OB MOMB
H
BC HA I HAHI
ICAB CAHCIH
C
ABH ACH ABAC
AH HBHC
H BC ABHACH 180 AHBAHC
ABHACH
90 AHB
AHBC
BC
BC
IHC HAHI
AHBIHC
( là trung điểm )

Suy ra: (c-g-c)
Mà và ở vị trí so le trong Nên d) Ta có: ( do ) Mà ( cm trên) Nên Bài 3. Cho tam giác có . Xác định điểm trên sao cho Lời giải:
Ta có: . Nên thuộc đường trung trực của . Vậy là giao điểm của với đường trung trực của thì Bài 4. Cho bốn điểm , , , tạo thành hình có và như hình vẽ Giao điểm của và là . Từ vẽ vuông góc với cắt cạnh , lần lượt tại , . Chứng minh là trung trực của và .
9
Ch
(g.c.g)
Do
HBHC H BC ABHIHC
BAHCIH BAH CIH //
BAHCAH ABHACH BAHCIH CAHCIH ABC ABAC D AC DADBAC D C B A ACDADC DADBAC DADBADDC DBDC D BC D AC BC DADBAC A B C D // ABCD // BCAD AC BD O O AC BC AD M N AC MN AMMCCNNA N M O D C B A BACDCA BCAD BOCDOA OCAO // BCAD MCONAO
Lời giải:
ứng minh được:
nên ; (g.c.g) nên
nên (so le trong)
ICAB
tại trung điểm của nên là trung trực của . Suy ra
, và được cũng là trung trực của nên .
Suy ra .
Bài 5. Cho tam giác cố định, đường phân giác ( ). Trên đoạn thẳng lấy điểm . Từ kẻ đường thẳng song song với , cắt kéo dài tại và cắt tại . Chứng minh:
a) Đường trung trực của luôn đi qua đỉnh của tam giác ;
b) Khi di động trên đoạn thẳng thì đường trung trực của đoạn thẳng luôn cố định.
Lời giải:

a) Vì nên (đồng vị) và (so le trong). Mà , do đó cân tại Đường trung trực của luôn đi qua đỉnh của tam giác .
b) Vì nên đường trung trực của vuông góc với . Từ kết quả ý a), suy ra đường trung trực của luôn đi qua điểm và vuông góc với cố định. Vậy đường trung trực của đoạn thẳng luôn cố định.
10 ,
và
MOCNOAOMON ACMN MN AC MN AMAN CMCN MN AC AMMC AMMCCNNA ABC AI IBC IC H H AI AB E AC F EF A ABC H IC EF 1 2 1 E F H I C B A // HEAI 1EA 12 FA 12 AA 1EF AEF A AEAF EF A ABC // EFAI EF AI EF A AI EF
PHIẾU BÀI TẬP.
Dạng 1. Nhận biết tam giác cân, tam giác đều. Vận dụng tính chất của tam giác cân, tam giác đều để tính số đo góc hoặc chứng minh các góc bằng nhau, các cạnh bằng nhau.

11
Bài 1. Trong các hình sau, hình nào là tam giác cân, hình nào là tam giác đều? Giải thích tại sao?
Bài 2. Trong các hình sau, hình nào là tam giác cân, hình nào là tam giác đều? Giải thích tại sao?
Bài 3. Cho tam giác cân tại . Tính số đo các góc còn lại của tam giác nếu biết: a) = 40°; b) = 50°; c) = 60°.

Bài 4. Tìm số đo trong hình vẽ sau:
Bài 5. Cho tam giác cân tại có = 40°. Trên tia đối của tia lấy điểm sao cho . Tính số đo góc .
Bài 6. Cho tam giác vuông tại , . Trên cạnh lấy sao cho . Chứng minh đều.
Bài 7. Cho tam giác . Tia phân giác góc cắt cạnh tại . Qua kẻ đường thẳng song song với , nó cắt cạnh tại . Chứng minh tam giác cân.
Bài 8. Cho tam giác vuông cân tại . Tia phân giác góc cắt cạnh tại . Trên cạnh và lần lượt lấy các điểm
12
M C B A F 80° 50° K D I H G E 60° G F H E D N L P O M ABC A ABC A B C x x D C B A ABD A A DB C DCDA ACB ABC A 30 B BC M AMBM AMC ABC B AC D D BC AB E EBD ABC A A BC D AB AC E F AECF ,, ABDADCAEF
và sao cho . Chứng minh vuông cân.
Bài 9. Cho tam giác đều. Trên cạnh lần lượt lấy các điểm sao cho . Chứng minh tam giác đều.
Bài 10. Cho tam giác cân tại . Tia phân giác góc cắt cạnh tại , tia phân giác góc cắt cạnh tại . Chứng minh tam giác cân.
Bài 11. Cho tam giác cân tại . Trên tia đối của tia lấy điểm , trên tia đối của tia lấy điểm sao cho . Chứng minh tam giác cân.
Bài 12. Cho = 120°, điểm thuộc tia phân giác của . Kẻ ( ) và ( ). Tam giác là tam giác gì? Tại sao?
Bài 13. Cho tam giác cân tại ( < 90°). Kẻ vuông góc với tại , kẻ vuông góc với tại .
a) Chứng minh tam giác cân. b) Chứng minh . c) Gọi là giao điểm của và . Chứng minh . d) Chứng minh .
Bài 14. Cho tam giác cân tại . Lấy điểm trên cạnh . Trên tia đối của tia lấy điểm sao cho . Đường thẳng qua vuông góc với cắt tại . Đường thẳng qua vuông góc cắt tại .
a) Chứng minh: b) Qua kẻ ( ). Chứng minh . c) cắt tại Chứng minh
Dạng 2. Vận dụng tính chất của đƣờng trung trực để giải quyết bài toán
I. Phƣơng pháp giải: Sử dụng tính chất: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
II. Bài toán.

Bài 1. Cho hai điểm , nằm trên đường trung trực của đoạn thẳng , Chứng minh .
Bài 2. Cho cân tại . Lấy điểm đối xứng với điểm qua . Chứng minh .
Bài 3. Tam giác vuông tại có . Trên tia đối của tia lấy điểm sao cho . Tính số đo góc .
13
đườ
a)
b)
m , , thẳng hàng. ABC , , ABBCCA ,, MNP AMBNCP MNP ABC A B AC D C AB E ADE ABC A BC D CB E BDCE ADE xOy A xOy ABOx BOx ACOy COy ABC ABC A A BD AC D CE AB E ADE // DEBC I BD CE IBIC AIBC ABC A M () BCMBMC CB N BMCN M BC AB E N BC AC F EMFN E // EDAC DBC MBMD EF BC O OEOF A B MN MABNAB ABC B D B AC ABDCBD ABC A 30 C AC D ADAC BDA xOy M N P Ox MN Oy MP ONOP P O N
Bài 4. Cho góc vuông . Điểm nằm trong góc đó. Vẽ điểm và sao cho tia là
ng trung trực của và là đường trung trực của .
Chứng minh .
Chứng minh ba điể
Bài 5. Cho vuông tại . Đường trung trực của đoạn thẳng cắt tại , cắ
tại . Nối và .

a) So sánh số đo góc và .
b) Chứng minh là trung điểm của
Bài 6. Cho . Các đường trung trực của và cắt cạnh theo thứ tự ở và .
a) Biết , . Tính số đo góc và .
b) Chứng minh = .
Bài 7. Cho góc vuông . Trên các tia , lấy hai điểm và (không trùng với ). Đường trung trực của các đoạn thẳng và cắt nhau ở . Chứng minh:
a) , , thẳng hàng. b) là trung điểm của
Bài 8. có = 30°. Đường trung trực của cắt ở
a) Chứng minh
b) Tính số đo góc
c) Biết , . Tính chu vi tam giác
Dạng 3. Chứng minh một điểm thuộc đƣờng trung trực. Chứng minh một đƣờng thẳng là đƣờng trung trực của một đoạn thẳng.
Bài 1. Cho đoạn thẳng . Vẽ đường tròn tâm bán kính và đường tròn tâm bán kính . Hai đường tròn này cắt nhau tại , . Chứng minh:
a) Điểm thuộc đường trung trực của b) là đường trung trực của .
Bài 2. Cho đoạn thẳng . Dựng các tam giác cân , lần lượt tại và ( , nằm khác phía so với ). Chứng minh: a) Điểm thuộc đường trung trực của ; b) là đường trung trực của
Bài 3. Cho , đường phân giác . Trên tia lấy điểm sao cho . Chứng minh: a) ; b) là đường trung trực của .
Bài 4. Cho có . Lấy điểm nằm trong tam giác sao cho . Kẻ vuông góc với ( ), vuông góc với ( ). Chứng minh: a) thuộc đường trung trực của và ; b) là đường trung trực của và
14
t
. Từ đó suy ra . ABC A AC AC H BC D A D DAB DBA D BC ABC AB AC BC M N 30 B 45 C BAC MAN MAN 2180 BAC xOy Ox Oy A B O OA OB M A M B M AB ABC BC BC AC K KBCKCB ABK 3cm AB 5cm AC ABK 5cm AB A 4cm B 3cm D E A DE AB DE AB MAB NAB M N M N AB M AB MN AB ABC AD AC E AEAB BDDE AD BE DEF DEDF K KEKF KP DE PDE KQ DF QDF K EF PQ DK EF PQ // PQEF
5. Cho cân tại , là trung điểm của vuông góc với , vuông góc với . Chứng minh:
a) là trung trực của của ; b) và là trung trực của ; c) .
Bài 6. Cho góc khác góc bẹt là tia phân giác của . Gọi là một điểm bất kì thuộc tia . Qua vẽ đường thẳng vuông góc với tại A, cắt tại và vẽ đường thẳng vuông góc với tại , cắt tại . Chứng minh:
a) Điểm thuộc đường trung trực của ; b) là đường trung trực của ; c) là đường trung trực của d)

Bài 7. Cho hai điểm , nằm cùng phía với đường thẳng . Xác định vị trí điểm trên đường thẳng sao cho cách đều hai điểm và
Bài 8. Cho tam giác cân tại ( < 90°). Đường trung trực của cạnh cắt tia tại điểm . Trên tia đối của tia lấy điểm sao cho . Chứng minh.:
a) Chứng minh cân;
b) Chứng minh ;
c) Chứng minh ;
d) Lấy là trung điểm của . Chứng minh là đường trung trực của .
Bài 9. Cho nhọn, đường cao . Lấy các điểm và lần lượt đối xứng với qua ; .
a) Chứng minh . b) Gọi , lần lượt là giao điểm của với , . Chứng minh và . c) Chứng minh là tia phân giác của . d) Cho = 60°. Tính số đo góc Bài 10. Cho tam giác vuông tại . Tia phân giác của cắt tại . Từ kẻ vuông góc với tại . a) Chứng minh: b) Chứng
15
Bài
là
c) Kẻ . Chứng minh là
của Phần III. BÀI TẬP TƢƠNG TỰ TỰ GIẢI ABC A M BC ME AB MF AC AM BC MEMF AM EF // EFBC xOy Oz xOy M Oz M a Ox Oy C b Oy B Ox D O AB OM AB OM CD // ABCD A B d M d M A B ABC A A AC CB D AD E AEBD CAD DACABC ADCE F DE CF DE ABC AH P Q H AB AC APAQ I K PQ AB AC APIAHI AHKAQK HA IHK BAC PAQ ABC A B AC E E EH BC H .ABEHBE BE AH ()ADBCDBC AH DAC
minh
đường trung trực của đoạn thẳng
tia phân giác
ng 1. Nhận biết tam giác cân, tam giác đều. Vận dụng tính chất của tam giác cân, tam giác đều để tính số đo góc hoặc chứng minh các góc bằng nhau, các cạnh bằng nhau.
Bài 1: Trong các hình sau, hình nào là tam giác cân, hình nào là tam giác đều?
Bài 2. Tìm số đo trong hình vẽ sau:
Bài 3. Cho tam giác vuông cân tại . Trên đường thẳng lấy điểm sao cho ( và khác phía so với ). Tính số đo các góc của tam giác
Bài 4. Cho cân tại . Trên các cạnh , lần lượt lấy , sao cho a) Chứng minh b) Gọi là giao điểm của và . Chứng minh tam giác cân.

Bài 5. Cho = 60°, điểm thuộc tia phân giác của . Kẻ ( ) và ( ). Tam giác là tam giác gì? Tại sao?
Bài 6. Cho tam giác vuông tại , . là trung điểm cạnh . Đường thẳng vuông góc với tại cắt tại . Chứng minh a) cân. b) đều.
Bài 7: Cho tam giác vuông tại . Tia phân giác góc cắt tại . Qua kẻ đường thẳng vuông góc với tại , cắt tại . Trên lấy điểm F sao cho . Chứng minh a) b) là tam giác cân c) . Dạng 2. Vận dụng tính chất của đƣờng trung trực để giải quyết bài toán
16 Dạ
m thuộc đường trung trực của . Biết . Tính số đo của các góc trong 40° 70° J I K 60° N M S R Q G F D E 72° 36° 36° x X 70° Y V S T ABC A AB D BDBC D A B ADC ABC A AC AB M N AMAN ABMACN O BM CN OBC xOy A xOy ABOx BOx ACOy COy OBC ABC A 2 BCAB D AC AC D BC E EAC ABE ABC () AABAC A BC D D BC D AC F AB AEAF ABCDEC DBF DBDE ABC A BC 40 B ABC
Bài 1. Tam giác có điể
Bài 2. Cho cân có . Các đường trung trực của và cắt cạnh theo thứ tự ở và và hai trung trực cắt nhau ở
a) Biết . Tính số đo góc

b) Chứng minh c) Tính số đo .
Bài 3. Cho góc . Từ điểm nằm trong góc đó kẻ vuông góc với ( thuộc ) và vuông góc với ( thuộc ). Trên tia đối của tia lấy điểm sao cho . Trên tia đối của tia lấy điểm sao cho . Chứng minh
Bài 4. Cho vuông tại . là trung điểm của cạnh . Đường trung trực của cạnh cắt cạnh tại . Gọi là giao điểm của và .
a. Chứng minh là tam giác cân. So sánh: và . b. Chứng minh là trung điểm của c. Nếu , tính số đo của Dạng 3. Chứng minh một điểm thuộc đƣờng trung trực. Chứng minh một đƣờng thẳng là đƣờng trung trực của một đoạn thẳng.
Bài 1. Cho . Trên tia lấy điểm , trên tia lấy điểm . Kẻ đường trung trực của đoạn thẳng ( , ). Chứng minh thuộc đường trung trực của
Bài 2. Cho tam giác có . Xác định điểm trên sao cho Bài 3. Cho bốn điểm , , , tạo thành hình có và như hình vẽ. Giao điểm của và là . Từ vẽ vuông góc với cắt cạnh , lần lượt tại , . Chứng minh là trung trực của và
Bài 4. Cho tam giác C vuông tại . Tia phân giác của cắt C tại E. Từ E kẻ EH vuông góc với
17
C tại H. a) Chứng minh: b) Chứng minh E là đường trung trực của đoạn thẳng H. c) Kẻ . Chứng minh H là tia phân giác của ABC 90 A AB AC BC D E F 110 A DAE 2180 BACDAE DFE xOy A AH Ox H Ox AK Oy K Oy HA B HBHA KA C KCKA OBOC ABC A M AB AB BC N I CM AN ANB NAB NBA N BC IBIC ABC 90 xOy Ox A Oy B HM OA HOA MAB M OB ABC ABAC D AC DADBAC A B C D // ABCD // BCAD AC BD O O AC BC AD M N AC MN AMMCCNNA N M O D C B A B ABEHBE ()ADBCDBC DAC
Bài 5. Cho tam giác cố định, đường phân giác ( ). Trên đoạn thẳng lấ
ABC AI IBC IC H H AI AB E AC

điểm . Từ kẻ đường thẳng song song với , cắt kéo dài tại và cắt tại . Chứng minh:
F EF A ABC H IC EF
a) Đường trung trực của luôn đi qua đỉnh của tam giác ; b) Khi di động trên đoạn thẳng thì đường trung trực của đoạn thẳng luôn cố định.
18
y
PHẦN I. TÓM TẮT LÍ THUYẾT.
I. Góc đối diện với cạnh lớn hơn trong một tam giác
Định lí 1:

“ Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn “
VD: Cho , ABCACAB . Khi đó: + Cạnh AB là cạnh đối diện với góc C . + Cạnh AC là cạnh đối diện với góc B . ACABBC
II. Cạnh đối diện với góc lớn hơn trong một tam giác Định lí 2: “ Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn ”.
VD: Cho , ABCACAB . Khi đó:
+ Góc C là góc đối diện với cạnh AB. + Góc B là góc đối diện với cạnh AC BCACAB
Chú ý: + Đối diện với cạnh là góc, mà đối diện với góc là cạnh.
+ Trong tam giác tù hoặc tam giác vuông thì góc tù và góc vuông là góc lớn nhất nên cạnh đối diện với góc vuông (cạnh huyền), cạnh đối diện với góc tù là cạnh lớn nhất.
+ Định lí 1 và 2 chỉ đúng khi ta áp dụng trong 1 tam giác.
+ Trong tam giác cạnh nhỏ nhất đối điện với góc nhọn.
PHẦN II. CÁC DẠNG BÀI.
Dạng 1. So sánh các góc trong một tam giác
I. Phương pháp giải:
+ TH1: Nếu các góc cần so sánh nằm trong cùng một tam giác thì ta áp dụng định lí 1: So sánh các cạnh đối diện với các góc đó
+ TH2: Nếu các góc cần so sánh không cùng nằm trong cùng một tam giác
Thì ta dùng góc trung gian để so sánh
1 CHUYÊN ĐỀ:
ĐỐI DIỆN TRONG TAM GIÁC
QUAN HỆ GIỮA GÓC VÀ CẠNH
B A C
Bài toán.
Bài 1. So sánh các góc của ABC biết rằng: 4,6,5 ABcmBCcmCAcm
Lời giải:

ABC có (456)ABACBC CBA (Định lí 1 – quan hệ giữa góc và cạnh đối diện trong tam giác).
Bài 2. So sánh các góc của EFD biết rằng: 2,3cm4 DEcmDFEFcm .
Lời giải: EFD có (234)DEDFEF FED (Định lí 1 – quan hệ giữa góc và cạnh đối diện trong tam giác) Bài 3. So sánh các góc của ABC biết rằng: 22,11,3 ABcmBCcmCAcm
Lời giải: ABC có (22311)ABBCAC CAB (Định lí 1 – quan hệ giữa góc và cạnh đối diện trong tam giác). Bài 4. So sánh các góc của ABC biết độ dài các cạnh , , ABBCCA lần lượt tỉ lệ nghịch với 3,4,5 . Lời giải: ABC có: Độ dài các cạnh , , ABBCCA lần lượt tỉ lệ nghịch với 3,4,5. .3.4.5ABBCCA ABBCAC ACBBACABChayCAB (Định lý 1). Bài 5. So sánh các góc của ABC biết độ dài các cạnh , , ABBCCA lần lượt tỉ lệ với3,4,5 . Lời giải:
ABC có: Độ dài các cạnh , , ABBCCA lần lượt tỉ lệ với 3,4,5
ACBBACABChayCAB (Định lý 1) Bài 6. Sử dụng quan hệ giữa góc và cạnh đối diện để chứng minh định lí: Trong một tam giác cân, hai góc ở đáy bằng nhau. Lời giải: Cho ABCcân tại A nên ABACCB (Định lý 1) Vậy trong một tam giác cân, hai góc ở đáy bằng nhau.
2
II.
345 ABBCAC
ABBCAC
Bài 7. Sử dụng quan hệ giữa góc và cạnh đối diện để chứng minh định lí: Trong một tam giác đều, ba góc bằng nhau.
Lời giải: Cho ABCđều nên ABACBCCBA (Định lý 1)
Vậy trong một tam giác đều, ba góc bằng nhau.
Bài 8. Trong một tam giác, đối diện với cạnh nhỏ nhất là góc gì (nhọn, vuông, tù)? tại sao?
Lời giải: Trong một tam giác, đối diện với cạnh nhỏ nhất là góc nhỏ nhất. Góc nhỏ nhất của tam giác là góc nhọn (tam giác nào cũng có ít nhất một góc nhọn)
Bài 9. Cho tam giác ABC có ABAC . So sánh hai góc ngoài tại các đỉnh ; BC Lời giải: Trước hết ta so sánh các góc trong tại hai đỉnh ; BC
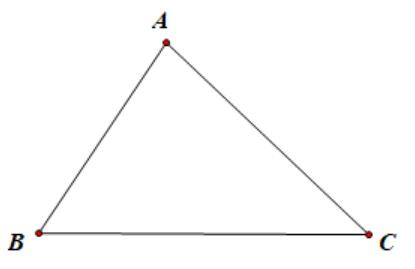
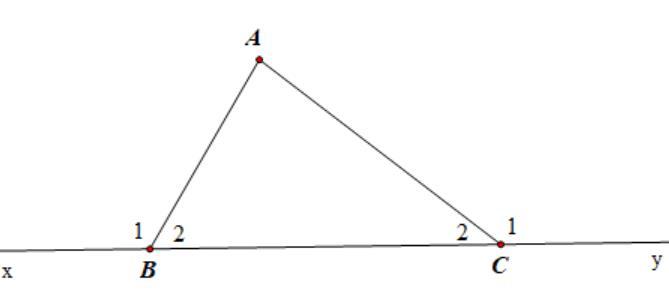

Vì ABAC nên 22 CB (Định lí 1) Mà 1212 180 BBCC (Tính chất hai góc kề bù) Do đó 11 CB
Bài 10. Cho tam giác ABC có ABlà cạnh nhỏ nhất. Chứng minh rằng 60 C Lời giải
Vì tam giác ABC có ABlà cạnh nhỏ nhất nên C là góc nhỏ nhất Do đó , CBCA
3
Suy ra 318060 CCBAC
Bài 11. Cho tam giác ABC có ba góc nhọn, ABAC . Kẻ BDvuông góc với AC tại D ,
vuông góc với ABtại E . So sánh DBC và ECB
Lời giải
Tam giác ABC có ABAC suy ra ACBABC ( quan hệ giữa cạnh và góc trong tam giác).
Tam giác DBC có 90 DBCACB (1).
( Trong tam giác vuông hai góc nhọn phụ nhau)
Tam giác ECB có 90 ECBABC(2)
( Trong tam giác vuông hai góc nhọn phụ nhau)
Mà ACBABC ( GT ) (3)
Từ (1),(2),(3) DBC ECB
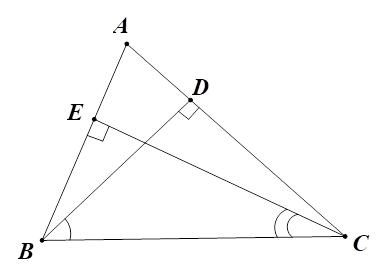

Bài 12. Cho tam giác ABC có ABAC . Gọi M là trung điểm của BC . Chứng minh MABMAC
Lời giải
A B C E
M
Trên tia đối của tia MAlấy điểm E sao cho AMME
ABMECM ( c.g.c )
ABEC ( hai cạnh tương ứng )
BAMCEM ( hai góc tương ứng) (1)
Xét AECcó CEAC ( vì ()ECABACgt )
EACAEC ( quan hệ giữa góc và cạnh đối diện trong tam giác ) (2)
4
CE

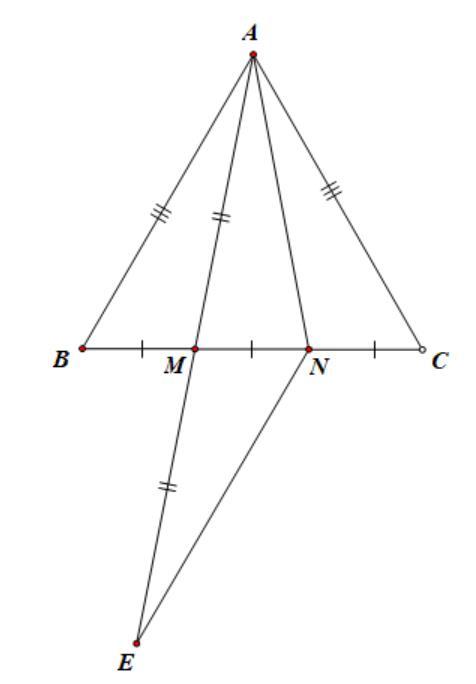
5 Từ (1),(2) MABMAC ( đ.p.c.m). Bài 13. Cho ABCđều. Trên cạnh BC lấy điểm M sao cho 1 3 BMBC . Chứng minh rằng 20 BAM Lời giải Gọi N là điểm trên BC sao cho BMMNNC ABCđều nên và 60 BACABCACB ABMACN ( c.g.c) BAMCAN ( hai góc tương ứng). Trên tia đối của tia MAlấy điểm E sao cho AMME (..)ABMENMcgc ABEN ( hai cạnh tương ứng). ABM có 60;30BBAM ( Vì ABCđều 1 32 BC BMBCBM nên 030 BAM ) 90 AMB ABMAMBAMAB ( quan hệ giữa cạnh và góc trong tam giác ) ENAM mà () AMANABMACN ENAN hay EANAENMANBAM Mà 60260BAMMANNACMANBAM Mặt khác 36020MANBAMBAMBAM ( đ.p.c.m )
góc tương ứng ) AECvà AOC có AC cạnh chung; AEAO và EACOAC Nên ECOC suy ra (1) EOCOEC AOE cân tại Anên (2) AOEAEO Từ (1), (2) AOCAEC, do đó

6 Bài 14. Cho ABCcân tại A. Gọi M là một điểm nằm trên cạnh BC sao cho MBMC . Lấy điểm O trên đoạn thẳng AM . Chứng minh rằng AOBAOC Lời giải Xét AMB và AMC có: ()ABACgt AM cạnh chung () MBMCgtMABMAC Trên nửa mặt phẳng bờ AC , không chứa điểm B , vẽ tia Ax sao cho Ax CMAB. Trên Ax lấy điểm E sao cho AEAO Ta có AECAOB (
ECOB ( hai cạnh
ứng ) AECAOB( hai
AOCAOB D
I.
+
+
Bài
L
x A B C M O E
c.g.c)
tương
ạng 2. So sánh các cạnh trong một tam giác
Phương pháp giải:
TH1: Nếu các cạnh cần so sánh nằm trong cùng một tam giác thì ta áp dụng định lí 2: So sánh các góc đối diện với các cạnh đó
TH2: Nếu các góc cần so sánh không cùng nằm trong cùng một tam giác Thì ta dùng góc trung gian để so sánh II. Bài toán.
1. So sánh các cạnh của ABC, biết: 00 45;55AB
ời giải
tại đỉnh A bằng 0120 000 18010080 A ABC có: 00 80;55AB Mà 0180 ABC (tổng 3 góc của một tam giác)
Bài 4. Chứng minh trong tam giác vuông, cạnh huyền lớn hơn mỗi cạnh góc vuông. Lời giải Trong tam giác vuông có một góc vuông và hai góc nhọn, góc vuông là góc lớn nhất, đối diện với góc vuông là cạnh huyền, hai cạnh còn lại là hai cạnh góc vuông . Nên trong tam giác vuông cạnh huyền là cạnh lớn nhất.
Bài 5. So sánh các cạnh của ABC△ , biết ABC cân tại A, 060 A .
Lời giải

ABCcân tại A .
BC (t/c tam giác cân) 0180 ABC (tổng 3 góc của một tam giác)
7
) BCACAB (Đị
Bài
Lời
ả
Vì
CC ABC(Vì
805545 ) BCACAB (Định
ABC có: 00 45;55AB Mà 0180 ABC (tổng 3 góc của một tam giác) 0000000 4555180180455580 CC CBA (Vì 000 805545 ) ABACBC (Định lý 2) Bài 2. So sánh các cạnh của ABCvuông tại A, biết 055 B Lời giải ABC có: 00 90;55AB Mà 090 BC (tổng 3 góc của một tam giác) 0 5560905535 CC ABC (Vì
000 905535
nh lý 2)
3. So sánh các cạnh của ABC, biết góc ngoài tại đỉnh A bằng 0100 , 055 B
gi
i
góc ngoài
0000000 8055180180805545
000
lý 2)

8 00 21801802 ABAB Mà
ABBB
Vì
ABC 234 ABC Theo tính chất dãy tỉ số bằng nhau: 0 0 180 20 2342349 ABCABC (tổng 3 góc của một tam giác) 002.2040 A 003.2060 B 004.2080 C ABC có: CBA (Vì 000 806040 ) ABACBC (Định lý 2) Bài 7: So sánh các cạnh của ABC biết rằng: 040 A và số đo góc , BC tỉ lệ với 3,4. Lời giải Ta có ABC biết rằng: 040 A và số đo góc , BC tỉ lệ với 3,4. 0180 ABC (tổng 3 góc của một tam giác) 00 4018018040140 BCBC Do đó 140 20 34347 BCBC Suy ra 3.2060,4.2080BC 406080 ABC BCACAB (Định lí 2) Bài 8: So sánh các cạnh của ABC biết rằng: 040 A và số đo góc , BC tỉ lệ nghịch với 3,4. Lời giải
00000 60180260120260
BCA (Vì 060 BCA)
ABC có B CA
ACABBC (Định lý 2) Bài 6. So sánh các cạnh của ABC△ , biết số đo các góc ,, ABC lần lượt tỉ lệ với 2,3,4 Lời giải
::2:3:4
So sánh các cạnh của tam giác ABC . b) Tam giác ABC còn gọi là tam giác gì? Vì sao? Lời giải a) Tam giác ABC cân tại A nên ˆˆ 45 CB ˆ 90 A . Vậy ˆ 9045ABC BCACAB
b) Tam giác ABC vuông cân tại A vì ˆ 90, ABC.
Bài 10: Cho ABC vuông tại A, điểm K nằm giữa A và C . So sánh BK và BC . Lời giải
Ta có AKCA (góc ngoài ABK ) nên 90 AKC
Xét BKC có 90 AKC nên BCBK
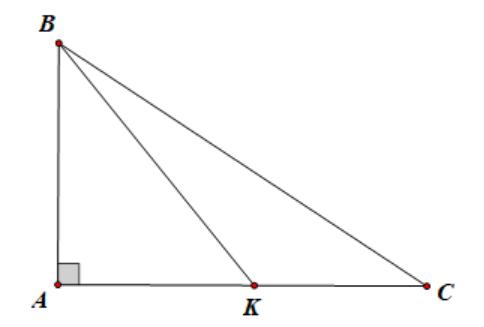
Bài 11: Cho tam giác ABC vuông tại A , 30 C . Điểm D thuộc cạnh AC sao cho 20 ABD . So sánh ,,,, BABDBCADDC Lời giải

9 Ta có ABC biết rằng: 040 A và số đo góc , BC tỉ lệ nghịch với 3,4. 0180 ABC (tổng 3 góc của một tam giác) 00 4018018040140 BCBC Do đó 34BC 140 20 43437 BCBC Suy ra 4.2080,3.2060BC 406080 ACB BCABAC (Định lí 2) Bài 9: Cho tam giác ABC cân tại A, biết 45 B a)

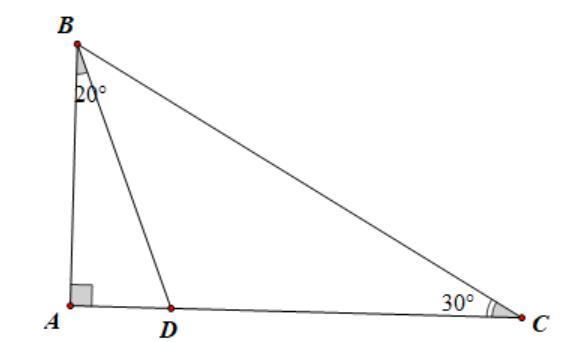
10 Tam giác ABC vuông tại A , 3090903060CABCC 602040 DBCABCABD Xét :180(3040)110BDCD (1104030)BDCDBCBCD BCDCBD Xét :902070ABDD (907020)BADADBABD BDABAD Vậy BCDCBDABAD Bài 12: Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt AC ở D . Kẻ DH vuông góc với BC tại H . So sánh: a) BA với BH b) DA với DC Lời giải a) Xét ABD và HBD có 90 BADBHD ABDHBD ( gt) BD cạnh chung ABDHBD ( Cạnh huyền-góc nhọn) BABH ( Hai cạnh tương ứng) b) HDCcó 90 DHCDCDH ( cạnh huyền , cạnh góc vuông) B A C D H
DCAD
Bài 13: Cho tam giác ABC có 90 A . Lấy điểm D thuộc cạnh AB điểm E thuộc cạnh AC Chứng minh rằng DEBC
Lời giải
Vì BDC là góc ngoài của DAC
Nên 90 BDCA . Do đó BC là cạnh lớn nhất của DBC
BCCD (1)
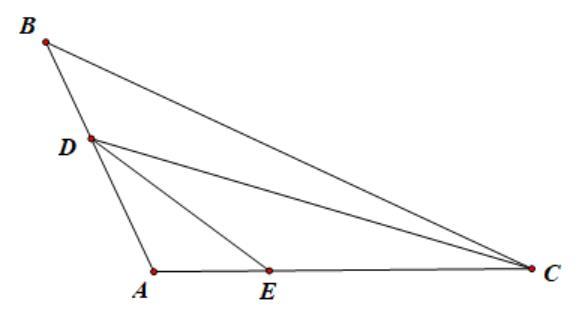

Mặt khác DEC là góc ngoài của ADE
Nên 90 DECA . Do đó DC là cạnh lớn nhất của DEC
DCDE (2)
Từ (1) và (2) suy ra DEBC
Bài 14. Cho tam giác ABC nhọn. Trên tia đối của tia BA lấy điểm D và trên tia đối của tia CA lấy điểm E sao cho CEBD . Chứng minh rằng: BCDE Lời giải
A D E
B C
Ta có ACDcó DCEADC ( góc ngoài của tam giác )
Xét BCD và CDE
Có BDCE (gt) CD : cạnh chung
11 Mà ADDH ( Vì ABDHBD )
Ph
cmt) DEBC ( Hai tam giác có hai cặp cạnh bằng nhau và hai góc tạo bởi các cạnh đó không bằng nhau thì góc nào lớn hơn thì có cạnh đối diện lớn hơn, ngược lại cạnh nào lớn hơn thì góc đối diện với cạnh đó lớn hơn).
BÀI TẬP TỰ LUYỆN
Dạng 1. Nhận biết đường vuông góc, đường xiên. Tìm khoảng cách của một điểm đến một đường thẳng.
Bài 1. Quan sát hình vẽ và cho biết: a) Các đường vuông góc kẻ đến ; ABBC b) Các đường xiên kẻ đến ; ABBC


H C B
D
Bài 2. Cho hình vuông ABCD có độ dài cạnh bằng 4cm, I là một điểm trên cạnh CD và cách C 1cm Tìm khoảng cách từ điểm I đến đường thẳng AD
Bài 3. Cho tam giác ABC vuông tại B có AD là tia phân giác của BAC ( DBC ). Kẻ DFAC tại F . Tính khoảng cách từ D đến đường thẳng AC , biết 2cm BD .
Bài 4. Một tấm gỗ xẻ có hai cạnh song song. Chiều rộng của tấm gỗ là khoảng cách giữa hai cạnh đó. Muốn đo chiều rộng của tấm gỗ, ta phải đặt thước như thế nào? Tại sao? Cách đặt thước trong hình dưới có đúng không?
Dạng 2. Quan hệ giữa đường vuông góc và đường xiên. Bài 1. Quan sát hình vẽ và cho biết đường nào là đường ngắn nhất? Vì sao?
A A E N D H M P d
Bài 2. Để tập bơi nâng dần khoảng cách, hàng ngày bạn Mai xuất phát từ M, ngày thứ nhất bạn bơi đến A, ngày thứ hai bạn bơi đến B, ngày thứ ba bạn bơi đến C, ... (Hình bên).
Bài 3. Cho tam giác ABC , điểm M nằm giữa B và C . Gọi H và K là chân các đường vuông góc kẻ từ M đến các đường thẳng AB và AC . So sánh BC và MHMK .
Vậy 2 BCMN BN
E
Bài 4. Cho tam giác ABC vuông tại A , M là trung điểm của AC . Gọi E và F là chân các đường vuông góc kẻ từ A và C đến đường thẳng BM . Chứng minh 2 BEF AB B .
ĐÁP SỐ BÀI TẬP TỰ LUYỆN
Dạng 1. Nhận biết đường vuông góc, đường xiên. Tìm khoảng cách của một điểm đến một đường thẳng.
Bài 1.
a) Các đường vuông góc kẻ đến AB là: CB , HE Các đường vuông góc kẻ đến BC là: AB , HD
b) Các đường xiên kẻ đến AB là , HAHB .
Các đường xiên kẻ đến BC là , HCHB
Bài 2.
Khoảng cách từ I đến đường thẳng AD là 413cm
khoảng cách giữa hai đường thẳng song song là độ dài của đoạn thẳng có hai đầu nằm trên hai đường thẳng và vuông góc với cả hai đường thẳng đó. Vì vậy muốn đo bề rộng của một tấm gỗ chính là xác định khoảng cách giữa hai đường thẳng song song ta phải đặt thước vuông góc với hai cạnh song song của tấm gỗ.
Xét ABD và AED có 90 BE AD chung 12 AA (Vì AD là tia phân giác của BAC ) ABDAED (Cạnh huyền – góc nhọn) BDED (hai cạnh tương ứng) Mà 2cm BD 2cm ED Vậy
ảng
từ D
ng thẳng AC
Bài
Bài 3.
kho
cách
đến đườ
là 2cm
4. Ta có
E D H C B A I D C B A 1cm 4cm 2 1 B C D E A
Cách đặt thước như trong hình dưới là sai.
Dạng 2. Quan hệ giữa đường vuông góc và đường xiên.
Bài 1.
AH là đường vuông góc kẻ từ A đến đường thẳng d , , , , APAMADANAE là các đường xiên kẻ từ A đến đường thẳng d
Do đó AH là đường ngắn nhất (Quan hệ giữa đường vuông góc và đường xiên).
Bài 2. Nhận thấy các điểm , , , ,...ABCD cùng nằm trên một đường thẳng. Gọi đường thẳng đó là đường thẳng d .
Theo định nghĩa: , , ,...
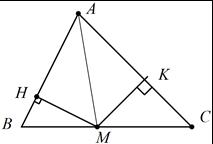
MBMCMD là các đường xiên kẻ từ M đến d .
MA là đường vuông góc kẻ từ M đến d
AB là hình chiếu của đường xiên MB trên d
AC là hình chiếu của đường xiên MC trên d
AD là hình chiếu cùa đường xiên MD trên d
Theo định lý MA là đường ngắn nhất trong các đường ,, , ,...MAMBMCMD Vì ABACAD nên MBMCMD Vậy MAMBMCMD nên bạn Mai đã tập đúng mục đích đề ra. Bài 3.
HM là đường vuông góc, BM là đường xiên nên HMBM
MK là đường vuông góc, MC là đường xiên nên MKMC Do đó MHMKMBMC B.MHMKC Bài 4.
A E
N D H M P d
PHIẾU BÀI TẬP
Dạng 1. Nhận biết đường vuông góc, đường xiên. Tìm khoảng cách của một điểm đến một đường thẳng.
Bài 1. Cho các hình vẽ sau. Hãy chỉ ra các đường vuông góc, các đường xiên kẻ từ điểm A trong hình 1 và điểm I trong hình 2
A H
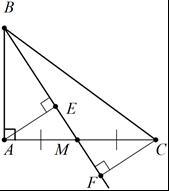
d C B
O Hình1
Hình2
B I C
Bài 2. Cho đường thẳng a và điểm O hãy vẽ đường vuông góc và ba đường xiên kẻ từ điểm O đến đường thẳng a . Chỉ ra các đường xiên và đường vuông góc vừa vẽ
Bài 3. Hãy chỉ ra các đường vuông góc, các đường xiên kẻ từ một điểm nằm ngoài đường thẳng EF đến đường thẳng đó trong hình vẽ sau:
Xét MAE và MCF có: ()AMCMgt AME CMF ( Hai góc đối đỉnh) 90 AEMCFM MAEMCFchgn MEMF - 2.BEBFBMMEBMMFBM Mặt khác 2 BEBF ABBMAB
Bài 4. Cho tam giác ABC vuông tại A . Gọi H là chân đường cao kẻ từ A đến cạnh BC
a) Tìm các đường vuông góc và đường viên trên hình. b) Tìm khoảng cách từ đỉnh , , ABC đến các cạnh của tam giác ABC .
Bài 5. Cho hình vuông ABCD. Hỏi trong bốn đỉnh của hình vuông
a) Đỉnh nào cách đều hai điểm D và B ? b) Đỉnh nào cách đều hai đường thẳng AD và DC ?
Bài 6. Quan sát hình dưới và cho biết:
a) Khoảng cách từ điểm I đến đường thẳng a , b , c b) Khoảng cách từ điểm P đến đường thẳng , bc .
Bài 7. Cho hình chữ nhật ABCD có độ dài các cạnh bằng 3cm,5cm, I là một điểm trên cạnh CD
a) Hãy chỉ ra các đường vuông góc và đường xiên kẻ từ A điểm đến đường thẳng CD b) Tìm khoảng cách từ điểm C đến đường thẳng AD .
B A
3cm
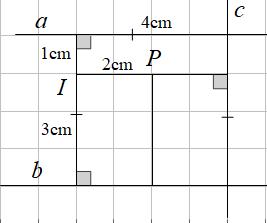
5cm I D C
Bài 8. Cho hình vuông ABCD có diện tích là 236cm . Tính khoảng cách từ đỉnh A đến cạnh CD
Bài 9. Cho hình thang cân có độ dài đáy nhỏ bằng 4cm, độ dài đáy lớn gấp đôi độ dài đáy nhỏ. Tính khoảng cách giữa hai đáy của hình thang cân, biết diện tích hình thang cân đó bằng 218cm
D
K M F E
Bài 10. Cho hình thang ABCD (Hình vẽ) có 7cm AB . Gọi E là hình chiếu của B lên cạnh CD. Biết ABED là hình vuông và diện tích hình thang ABCD gấp 2 lần diện tích hình vuông ABED . Hãy tính khoảng cách từ C đến đường thẳng BE .















Bài 11. Cho tam giác ABC cân tại A . Có M là trung điểm của đoạn thẳng BC . Chứng minh AM là khoảng cách từ A đến cạnh BC của tam giác ABC
Bài 12. Cho hình vẽ bên, biết ABCD , 90 BACBDC , 4cm DE . Tính khoảng cách từ E đến đường thẳng AB .
Dạng 2. Quan hệ giữa đường vuông góc và đường xiên.
Bài 1. Độ dài nào ngắn nhất trong các độ dài ,,, ABACADAE
Bài 2. Quan sát hình bên.
a) Tìm đoạn ngắn nhất trong các đoạn , , NMNENP
b) Tìm đoạn ngắn nhất trong các đoạn thẳng , , PMPNPD.
Bài 3. Bạn Bình xuất phát từ điểm I bên hồ bơi. Bạn ấy muốn tìm đường ngắn nhất để bơi đến thành hồ đối diện. Theo em, bạn Bình phải bơi theo đường nào?
Bài 4. Cho tam giác ABC , điểm D nằm giữa A và C ( BD không vuông góc với AC ). Gọi E và F là chân các đường vuông góc kẻ từ A và C đến đường thẳng BD . So sánh AC với tổng .AECF Bài 5. Cho hình vẽ. Chứng minh rằng: BDCEABAC
E C
D
4cm
D B A
C B A E P M D E N D C B A I
Bài 6. Cho tam giác IKL , IKIL . Lấy điểm M tùy ý nằm giữa K và L . Khi M thay đổi thì độ dài IM thay đổi. Xác định vị trí của M để độ dài IM nhỏ nhất. Bài 7. Cho ABC , điểm E nằm giữa , BC ( AE không vuông góc với BC ). Gọi H và K là chân các đường vuông góc kẻ từ B và C đến đường thẳng AE . a) So sánh BH và BE . b) Chứng minh BCBHCK . Bài 8. Cho MNP nhọn. Kẻ MDNPDNP , NEMPEMP
a) So sánh MN và MD . b) Chứng minh 2MNMDNE .
Bài 9. Cho ABC , kẻ AHBC tại H . Chứng minh rằng: a) 1 2 AHABAC b) Kẻ BKAC tại K , CLAB tại L . Chứng minh AHBKCLABBCCA
Bài 10. Cho ABC , các góc B và C nhọn. Điểm M nằm giữa B và C . Gọi d tổng các khoảng cách từ B và C đến đường thẳng AM .
a) Chứng minh rằng dBC . b) Xác định vị trí của M trên BC sao cho d có giá trị lớn nhất.
Bài 11. Hai tam giác: tam giác cân ABC và tam giác ADE Có chung góc ở đỉnh A có AEADABAC . Chứng minh rằng BCDE .
Bài 12. Cho ABC cân tại A , trên hai cạnh AB và AC lấy hai điểm M và N sao cho AMAN . Chứng minh rằng: 2 BCMN BN
BÀI TẬP TỰ LUYỆN
Dạng 1. Nhận biết đường vuông góc, đường xiên. Tìm khoảng cách của một điểm đến một đường thẳng. Bài 1. Quan sát hình vẽ và cho biết: a) Các đường vuông góc kẻ đến ; ABBC b) Các đường xiên kẻ đến ; ABBC Bài 2. Cho hình vuông ABCD có độ dài cạnh bằng 4cm, I là một điểm trên cạnh CD và cách C 1cm. Tìm khoảng cách từ điểm I đến đường thẳng AD .
E D C B A
E D H C B A
Bài 3. Cho tam giác ABC vuông tại B có AD là tia phân giác của BAC ( DBC ). Kẻ DFAC tại F . Tính khoảng cách từ D đến đường thẳng AC , biết 2cm BD .


Bài 4. Một tấm gỗ xẻ có hai cạnh song song. Chiều rộng của tấm gỗ là khoảng cách giữa hai cạnh đó. Muốn đo chiều rộng của tấm gỗ, ta phải đặt thước như thế nào? Tại sao? Cách đặt thước trong hình dưới có đúng không?
Dạng 2. Quan hệ giữa đường vuông góc và đường xiên.
Bài 1. Quan sát hình vẽ và cho biết đường nào là đường ngắn nhất? Vì sao?
A E N D H M P d
Bài 2. Để tập bơi nâng dần khoảng cách, hàng ngày bạn Mai xuất phát từ M, ngày thứ nhất bạn bơi đến A, ngày thứ hai bạn bơi đến B, ngày thứ ba bạn bơi đến C, ... (Hình bên).
Bài 3. Cho tam giác ABC , điểm M nằm giữa B và C . Gọi H và K là chân các đường vuông góc kẻ từ M đến các đường thẳng AB và AC . So sánh BC và MHMK .
Bài 4. Cho tam giác ABC vuông tại A , M là trung điểm của AC . Gọi E và F là chân các đường vuông góc kẻ từ A và C đến đường thẳng BM . Chứng minh 2 BEF AB B .
CẠNH CỦA MỘT TAM GIÁC
PHẦN I. TÓM TẮT LÍ THUYẾT.
*) Định lí: Trong một tam giác, độ dài của một cạnh bất kì luôn nhỏ hơn tổng độ dài hai cạnh còn lại.
A C

Ba hệ thức: , ,
B
ABBCAC ACABBC BCACAB
gọi là các bất đẳng thức tam giác.
- Tính chất: Trong một tam giác, độ dài của một cạnh bất kì luôn lớn hơn hiệu độ dài hai cạnh còn lại. - Nhận xét: Nếu kí hiệu ,, abc là độ dài ba cạnh tùy ý của một tam giác thì: bcabc .
1 CHUYÊN ĐỀ: QUAN HỆ GIỮA BA
PHẦN II. CÁC DẠNG BÀI. Dạng 1. Khẳng định có tồn tại hay không một tam giác biết độ dài ba cạnh I. Phương pháp giải: + Tồn tại một tam giác có độ dài ba cạnh là ,, abc nếu: abc bac cab
hoặc bcabc . + Trong trường hợp xác định được a là số lớn nhất trong ba số ,, abc thì điều kiện để tồn tại tam giác chỉ cần: abc . II. Bài toán. Bài 1. Bộ ba độ dài nào dưới đây có thể tạo thành độ dài của ba cạnh trong tam giác? a) 6cm;8cm;16cm b) 5,5cm;3,1cm;2,4cm c) 13,7cm;8,2cm;5,3cm d) 8m;12m;7m
Lời giải:
a) Không vì 1686
b) Có vì 5,53,12,4
c) Không vì 13,78,25,3 d) Có vì 1278
Bài 2. Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba đoạn thẳng có độ dài cho sau đây có thể tạo thành một tam giác hay không?
a) 3cm,4cm,6cm b) 2m,4m,8m c) 1cm,3cm,4cm

Lời giải:
a) Ta có 634 nên bộ ba đoạn thẳng này có thể là ba cạnh của một tam giác. b) Không vì 824 c) Không vì 413 .
Bài 3. Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác.
a) 3cm,3cm,7cm. b) 6m,10m,8m. c) 2m,6m,8m.
Lời giải: a) Không vì 733 b) Ta có 1068 nên bộ ba đoạn thẳng này có thể là ba canh của một tam giác. c) Không vì 862 . Bài 4. Một tam giác cân có một cạnh bằng 6cm. Tính hai cạnh còn lại, biết chu vi của tam giác đó bằng 20cm.
Lời giải: Nếu cạnh đã cho 6cm là cạnh đáy thì hai cạnh còn lại là 206:27cm , thỏa mãn bất đẳng thức tam giác. Nếu cạnh đã cho 6cm là cạnh bên thì hai cạnh còn lại là 6cmvà 202.68cm , thỏa mãn bất đẳng thức tam giác. Bài 5. Cho tam giác ABC có 1cm, =7cm.BCAC Tìm độ dài cạnh AB biết độ dài này là một số nguyên (cm). Lời giải: Theo bất đẳng thức tam giác, trong ABC có: 68ACBCABACBCAB Do AB là số nguyên nên 7cm AB Bài 6. Độ dài hai cạnh của một tam giác bằng 6cm và 2cm. Tính độ dài cạnh còn lại biết rằng số đo của cạnh đó theo cm là một số tự nhiên chẵn.
Lời giải: Giả sử ABC có 6cm,2cmABAC
2
Theo bất đẳng thức tam giác, ta có ABACBCABAC . Suy ra 48 BC . Mà BC có độ dài theo cm là một số tự nhiên chẵn. Do đó, 6cm BC .
Bài 7. Cho tam giác ABC có 4cm, 1cm ABAC . Hãy tìm độ dài cạnh BC biết rằng độ dài này là một số nguyên (cm)
Lời giải: Ta có 4cm, 1cm ABAC .
Theo bất đẳng thức tam giác, ta có ABACBCABAC . Suy ra 35 BC . Mà BC có độ dài theo cm là một số nguyên. Do đó, 4cm BC .
Bài 8. Tính chu vi của tam giác cân có hai cạnh bằng 4m và 8m
Lời giải:
Cách 1: Vì tam giác là tam giác cân nên sẽ có độ dại ba cạnh là
Th1 4m;4m;8m trường hợp này không xảy ra vì 4m+4m=8m
Th2 4m;8m;8m trường hợp này xảy ra vì 4m+8m>8m Vậy chu vi tam giác là 20m. Cách 2: Giả sử ABC có 4m,8mABAC . Theo bất đang thức tam giác, ta có ||ABACBCABAC
Do đó, 412 BC . Mà ABC cân nên suy ra 8m BC . Vậy chu vi tam giác ABC là 20m.
Bài 9. Tính chu vi của tam giác cân có hai cạnh bằng 3cm và 7cm. Lời giải: Giả sử ABC có 3cm,7cmABAC Theo bất đẩng thức tam giác, ta có ||ABACBCABAC . Do đó, 410 BC . Mà ABC cân nên suy ra 7cm BC . Vậy chu vi tam giác ABC là 17cm. Bài 10. Ba cạnh của một tam giác có độ dài bằng 1 2, 16, 2 x (đơn vị cm). Tìm x , biết rằng x là số tự nhiên và có giá trị nhỏ nhất có thể.
Lời giải:

3
Lời giải: Theo bất đẩng thức tam giác, ta có 11 |216|21613,518,5 22 xx Mà x là số tự nhiên và có giá trị nhỏ nhất có thể nên 14cm x Bài 11. Tam giác ABC có chu vi 18cm, .BCACAB Tính độ dài BC biết rằng độ dài đó là một số chẵn (đơn vị: cm).
Ta có: , BCABBCAC nên BCBCBCACABBC , tức là 3.18 BC
Vậy 6 BCcm 1

Ta có: BCACAB nên BCBCABACBC , tức là 2.18 BC .
Vậy 9cm BC 2
Do BC là số chẵn nên từ 1, 2 suy ra 8cm BC
Bài 12. Có bao nhiêu tam giác có độ dài hai cạnh là 7cm và 2cm còn độ dài cạnh thứ ba là một số nguyên (đơn vị cm)?
Lời giải:
Gọi độ dài cạnh còn lại của tam giác là: x ( cm ).
Theo bất đẳng thức tam giác, ta có: |72|7259 xx
Mà x là một số nguyên nên 6;7;8 x
Do đó có 3 tam giác thỏa mãn yêu cầu bài toán. Dạng 2. Chứng minh các bất đẳng thức về độ dài
I. Phương pháp giải: Sử dụng bất đẳng thức tam giác và các biến đổi về bất đẳng thức tam giác + Cộng cùng một số vào hai vế của bất đẳng thức: abacbc + Cộng từng vế hai bất đẳng thức cùng chiều: . ab acbd cd
4
II. Bài toán. Bài 1. Cho tam giác OBC cân tại O . Trên tia đối của tia CO lấy điểm A . Chứng minh ABAC . Lời giải: Vì A thuộc tia đối COnên C nằm giữa ; OA OAOC mà OBOCOAOB Xét tam giác OBA có AOOBAB (bất đẳng thức tam giác) ACOCOBAB . Lại có OBOC ( OBC cân tại O ) ACAB (điều phải chứng minh). B C O A
Bài 2. Cho tam giác ABC , điểm M thuộc cạnh AB
a) So sánh MC với AMAC . b) Chứng minh MBMCABAC
Lời giải:
A C
B
a) Áp dụng bất đẳng thức tam giác vào tam giác AMC ta có: MCAMAC b) Ta có: MCAMACMBMCMBMAACABAC
Bài 3. Cho tam giác ABC , trên tia đối của tia AC lấy điểm K .
a) So sánh AB với KAKB b) Chứng minh ABACKBKC .
M K
Lời giải:
C B
a) Áp dụng bất đẳng thức tam giác vào tam giác AKB ta có: ABKAKB . b) Ta có: A ABKBKABACKBKAACKBKC
Bài 4. Cho tam giác ABC , M là trung điểm của BC Chứng minh rằng: 2 ABACAM
A M B
Lời giải:
A C

5
D

6 Trên tia đối của tia MA lấy điểm D sao cho MDMA Xét MAB và MDC có MAMD AMBDMC (đối đỉnh) MBMC ( giả thiết ) (c.g.c) MABMDC ABDC (Hai cạnh tương ứng) Xét ADC có : CDACAD (bất đẳng thức trong tam giác) Do đó : ABACAD mà 2. ADAM 2 ABACAM (đpcm) Bài 5. Cho điểm M nằm trong ABC . Chứng minh rằng: MBMCABAC . Từ đó suy ra: .MAMBMCABACBC Lời giải: Kẻ BM cắt cạnh AC tại D . Xét ABD có : BDABADMBMDABAD 1 Xét MDC có : MCMDDC 2 Từ 1 và 2 suy ra : MBMCMDABADDCMD MBMCABAC CMTT ta có : MAMCABBC và MAMBACBC Do đó : 2.2.MAMBMCABACBC MAMBMCABACBC Bài 6. Cho tam giác ABC và M là một điểm nằm trong tam giác. Gọi I là giao điểm của đường thẳng BM và cạnh AC . So sánh MA với MIIA a) So sánh MA với MIIA . B A C D M
b) Chứng minh rằng MAMBIBIA
c) Chứng minh rằng IBIACACB
d) Chứng minh rằng MAMBCACB
Lời giải:

a) Xét AMI , theo bất đẳng thức tam giác, ta có MAMIIA b) Từ câu a), suy ra MAMBMIIAMB Do đó, MAMBIAIB c) Xét IBC , theo bất đẳng thức tam giác, ta có IBBCCI Do đó IAIBCACB . d) Từ câu a) kết hợp câu b) ta được MAMBCACB
Bài 7. Cho điểm K nằm trong tam giác ABC . Gọi M là giao điểm của tia AK với cạnh BC . a. Chứng minh rằng KAKBMAMBCACB . b. So sánh KBKC với ABAC . c. Chứng minh rằng KAKBKC nhỏ hơn chu vi tam giác ABC Lời giải:
7
I
K B C A M N P
B A C
M

8 a. Chứng minh tương tự bài tập 5 ta được KAKBMAMBCACB b.Gọi N là giao điểm của tia BK với AC Tương tự câu a) ta có KBKCNBNCABAC 1 Do đó, KBKCABAC c. Gọi P là giao điểm của tia CK với AB Ta có, KAKCPAPCBABC Do đó, KAKCBABC . 2 Từ câu a), suy ra KAKBCACB 3 Từ 1 , 2 và 3 , ta thấy 2()2() KAKBKCABACBC KAKBKCABACBC Vậy tổng KAKBKC nhỏ
.
8.
đỉnh A , lấy điểm M không trùng với A . Chứng minh rằng: MBMCABAC . Lời
Trên tia đối của tia AC lấy điểm D sao cho ABADABACADACCD 1 Xét AMB và AMD có: :MA chung; BAMDAM ( AM là tia phân giác của BAD ); MBMD (cách vẽ) .. AMBAMCcgc MBMD (hai cạnh tương ứng) MBMCMDMC 2 C B M A D
hơn chu vi tam giác ABC
Bài
Cho tam giác ABC . Trên đường phân giác của góc ngoài
giải:
Từ 1 , 2 , 3 suy ra MBMCABAC .
Bài 9. Cho hai điểm A và B nằm về hai phía của đường thẳng d . Tìm điểm C thuộc đường thẳng d sao cho tổng ACCB là nhỏ nhất.
Lời giải:
Giả sử C là giao điểm của đoạn thẳng AB với đường thẳng d . Vì C nằm giữa A và B nên ta có . 1 ACCBAB Lấy điểm 'C bất kỳ trên d ' CC . Nối ','ACBC . Áp dụng bất đẳng thức tam giác vào 'ABC , ta có ' '.2ACBCAB
Từ (1)và (2) suy ra '' ACBCACCB
Vậy C là điểm cần tìm. Bài 10. Cho đường thẳng d và hai điểm , AB nằm cùng về một phía của d và AB không song song với d . Một điểm H di động trên d . Tìm vị trí của H sao cho HAHB là lớn nhất. Lời giải:
d
Vì AB không song song với d nên AB cắt d tại .I Với điểm H bất kì thuộc d mà H không trùng với I thì ta có tam giác HAB . Xét tam giác HAB có HAHBAB .

9 Xét DMC , ta có: MCMDCD 3
Khi HI thì HAHBAB . d C B C' A
A I H B
t là b

ng AB , khi đó HI
là giao điểm của hai đường thẳng
Bài 11. Cho góc xOy nhọn, trên Ox lấy hai điểm A và B (điểm A nằm giữa hai điểm O và B ). Trên Oy lấy hai điểm C và D (điểm C nằm giữa O và D ). Chứng minh ABCDADBC
Lời giải:
Gọi F là giao điểm của AD và BC
Xét AFB , ta có ABAFFB (bất đẳng thức tam giác). (1) Xét CFD , ta có <+ CDCFFD (bất đẳng thức tam giác). (2) Từ 1,2 có +<+++=+ ABCDAFFBCFFDADBC hay +< ABCDADBC . (điều phải chứng minh).
Bài 12. Một trạm biến áp và một khu dân cư được xây dựng cách xa hai bờ sông tại hai địa điểm A và B . Hãy tìm trên bờ sông gần khu dân cư một địa điểm C để dụng một cột mắc dây đưa điện từ trạm biến áp về cho khu dân cư sao cho độ dài đường dây dẫn là ngắn nhất. Lời giải: Nếu ;; ABC thẳng hàng thì = ACBCAB Nếu ;; ABC không thẳng hàng thì ta có tam giác ABC lúc đó > ACBCAB Do đó: ACBC ngắn nhất khi ACBCAB , , ABC thẳng hàng và C nằm giữa ; AB
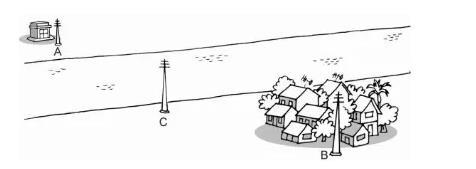
10 Vậy HAHB
ớ
ấ
và AB
l
n nh
ằ
d
y x F O C B A D
Vậy vị trí dặt một cột mắc dây điện từ trạm về cho khu dân cư sao cho độ dài đường dây dẫn ngắn nhất là C nằm giữa A và B (và , , ABC thẳng hàng)
Phần III. BÀI TẬP TỰ LUYỆN Dạng 1.
Bài 1. Bộ ba độ dài nào dưới đây có thể tạo thành độ dài của ba cạnh trong tam giác?
a) 6cm;7cm;15cm b) 4,2cm;3,5cm;2,5cm c) 3cm;7,2cm;5cm d) 3m;10m;7m

Bài 2. Cho tam giác ABC có cạnh 2cm AB và cạnh 7cm BC . Tính độ dài cạnh AC biết độ dài cạnh AC là một số nguyên tố.
Bài 3. Cho ABC cân. a) Tính , ACBC biết chu vi ABC là 23cm và 5cm. AB b) Tính chu vi ABC biết 5cm, 12cm. ABAC Bài 4. Có bao nhiêu tam giác có độ dài hai cạnh là 1cm và 3cm còn độ dài cạnh thứ ba là một số nguyên (đơn vị cm)?
Dạng 2.
Bài 1. Cho góc , xOyOz là tia phân giác của góc xOy . Từ điểm M ở trong góc xOz vẽ MH vuông góc với Ox ( H thuộc Ox ), MK vuông góc với Oy ( K thuộc Oy ). Chứng minh rằng: MHMK . Bài 2. Cho ABC có ( ABAC ) và AD là phân giác góc A ( DBC ). Gọi E là một điểm bất kỳ thuộc cạnh AD ( E khác A ). Chứng minh – –ACABECEB . Bài 3. Cho ABC cân tại A , góc A tù, trên cạnh BC lấy điểm D , trên tia đối của tia CB lấy điểm E sao cho BDCE , trên tia đối của tia CA lấy điểm I sao cho CICA a, Chứng minh rằng: ABDICE và ABACADAE . b, Từ D và E kẻ các đường thẳng cùng vuông góc với BC cắt , ABAI lần lượt tại M và N , Chứng minh rằng: BMCN . c, Chứng minh rằng: Chu vi ABC nhỏ hơn chu vi AMN Bài 4. Cho ABC vuông tại A , tia phân giác của góc B cắt AC tại D Chứng minh rằng BCBADCDA .
ĐÁP SỐ BÀI TẬP TỰ LUYỆN Dạng 1. Bài 1. a) Không vì 1567.
11
b) Có vì 4,23,52,5 c) Có vì 7,235 d) Không vì 1037 Bài 2. Áp dụng tính chất quan hệ ba cạnh của một tam giác vào tam giác ABC ta có: 59BCABACBCABAC
Mà độ dài cạnh AC là một số nguyên tố nên 7cm. AC Bài 3.
a) Tính , ACBC biết chu vi ABC là 23cm và 5cm. AB Cách 1: Vì là tam giác cân
TH1 : ta có ba cạnh là 5 ,5 13 cmcmvàcm không có tam giác có ban cạnh vậy Th2 : ta có ba cạnh là 5cm,x cm, x cm và chu vi bằng 23cm Lúc đó 5 5239 xxx thỏa mãn tam giác có ba cạnh này
Vì 5cm. AB nên 9cm. ACBC

Cách 2
* Nếu AB là cạnh bên và ABC cân tại A 5cm. ABAC 13cm BC (không thỏa mãn BĐT tam giác).
* Nếu AB là cạnh bên và ABC cân tại B 5cm ABCB . 13cm AC (không thỏa mãn BĐT tam giác).
*Nếu AB là cạnh đáy thì ABC cân tại C 235:29cm. ACBC (Thỏa mãn BĐT tam giác)
Vậy: 9cm ACBC b) Tính chu vi ABC biết 5cm, 12cm. ABAC
* Nếu 5cm ABBC là cạnh bên 12cm AC là cạnh đáy
Khi đó 12 5 5 ( không thỏa mãn BĐT tam giác).
Vậy 12cm ACBC là cạnh bên 5cm AB là cạnh đáy
12
Bài 4.
Gọi độ dài cạnh còn lại của tam giác là: x ( cm ).
Theo bất đẳng thức tam giác, ta có: |13|1324 xx
Mà x là một số nguyên nên 3 x
Do đó có 1 tam giác thỏa mãn yêu cầu bài toán.
Dạng 2 .
Bài 1.

Gọi A là giao điểm của MK với Oz . Vẽ AB vuông góc với Ox ( B thuộc Ox ). Nối B với M
x y O
B M A K
H z
Xét 0 (90)KOAK và 0 (90)BOAB có: OA chung
KOABOA (Oz là tia phân giác xOy ) KOABOA (cạnh huyền – góc nhọn)
AKAB (Hai cạnh tương ứng)
Xét ABM có BMABAM (Bất đẳng thức trong tam giác)
Do đó : BMAKAM hay BMMK
Mà MHBM (quan hệ giữa đường xiên và đường vuông góc ) MHMK ( đpcm )
Bài 2.
13 Chu vi ABC là : 1212529cm

14 Trên cạnh AC lấy điểm F sao cho AFAB Xét ABE và AFE có AF; EAE;EABBAFA chung . Do đó ABE AFE (c.g.c) BEEF Trong tam giác EFC có –FCECEF Mà BEEF nên –FCECEB 1 Lại có –FCACAF mà AFAB nên –FCACAB 2 Từ 1 và 2 suy ra – – .ABACECEB Bài 3. a, CM: c.g.c ABDICE , Ta có : ABACAI Vì ABDICEADEI Áp dụng BĐT trong : AEIAEEIAI hay AEADABAC b, CM: g.c.g BDMCEN BMCN c, Vì BMCNABACAMAN 1 Có BDCE (gt), BCDE Gọi O là giao của MN và BC OMOD MOONODOEMNDEMNBC ONOE 2 F D B C A E O B C A E N I D M
Bài 4.
Xét ADB và HDB có: : BD cạnh huyền chung; 12BB ( BD là tia phân giác của B ) DB ADB H (cạnh huyền-góc nhọn) ; BABHDADH (hai cạnh tương ứng)
Xét HDC vuông tại H có DCDH và HCDCDH (bất đẳng thức tam giác) Suy ra BCBHHCDCDA (vì DHDA ) Do đó, BCBADCDA (vì BHBA )
PHIẾU BÀI TẬP
Dạng 1:
Bài 1. Bộ ba độ dài nào dưới đây có thể tạo thành độ dài của ba cạnh trong tam giác?
a) 6cm;8cm;16cm b) 5,5cm;3,1cm;2,4cm d) 13,7cm;8,2cm;5,3cm c) 8m;12m;7m
Bài 2. Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba đoạn thẳng có độ dài cho sau đây có thể tạo thành một tam giác hay không? a) 3cm,4cm,6cm b) 2m,4m,8m c) 1cm,3cm,4cm Bài 3. Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác. a) 3cm,3cm,7cm . b) 6m,10m,8m. c) 2m,6m,8m.

15 Từ 1 và 2 ta
: chu
ủa ABC nhỏ hơn chu
a AMN
có
vi c
vi củ
2 H 1 C B A D
Bài 4. Một tam giác cân có một cạnh bằng 6cm. Tính hai cạnh còn lại, biết chu vi của tam giác đó bằng 20cm.
Bài 5. Cho tam giác ABC có 1cm, =7cm.BCAC Tìm độ dài cạnh AB biết độ dài này là một số nguyên (cm).

Bài 6. Độ dài hai cạnh của một tam giác bằng 6cm và 2cm. Tính độ dài cạnh còn lại biết rằng số đo của cạnh đó theo cm là một số tự nhiên chẵn.
Bài 7. Cho tam giác ABC có 4cm, 1cm ABAC . Hãy tìm độ dài cạnh BC biết rằng độ dài này là một số nguyên (cm)
Bài 8. Tính chu vi của tam giác cân có hai cạnh bằng 4m và 8m.
Bài 9. Tính chu vi của tam giác cân có hai cạnh bằng 3cm và 7cm.
Bài 10. Ba cạnh của một tam giác có độ dài bằng 1 2, 16, 2 x (đơn vị cm). Tìm x , biết rằng x là số tự nhiên và có giá trị nhỏ nhất có thể.
Bài 11. Tam giác ABC có chu vi 18cm, .BCACAB Tính độ dài BC biết rằng độ dài đó là một số chẵn (đơn vị: cm).
Bài 12. Có bao nhiêu tam giác có độ dài hai cạnh là 7cm và 2cm còn độ dài cạnh thứ ba là một số nguyên (đơn vị cm)?
Dạng 2:
Bài 1. Cho tam giác OBC cân tại O . Trên tia đối của tia CO lấy điểm A . Chứng minh ABAC . Lại có OBOC ( OBC cân tại O ) ACAB (điều phải chứng minh).
Bài 2. Cho tam giác ABC , điểm M thuộc cạnh AB c) So sánh MC với AMAC . d) Chứng minh MBMCABAC
Bài 3. Cho tam giác ABC , trên tia đối của tia AC lấy điểm K . c) So sánh AB với KAKB . d) Chứng minh ABACKBKC . Bài 4. Cho tam giác ABC , M là trung điểm của .BC Chứng minh rằng: 2 ABACAM Bài 5. Cho điểm M nằm trong ABC . Chứng minh rằng: MBMCABAC . Từ đó suy
16
ra: .MAMBMCABACBC Bài 6. Cho tam giác ABC và M là một điểm nằm trong tam giác. Gọi I là giao điểm của đường thẳng BM và cạnh AC . So sánh MA với MIIA a) So sánh MA với MIIA b) Chứng minh rằng MAMBIBIA c) Chứng minh rằng IBIACACB
d) Chứng minh rằng MAMBCACB
Bài 7. Cho điểm K nằm trong tam giác ABC . Gọi M là giao điểm của tia AK với cạnh BC .
a. Chứng minh rằng KAKBMAMBCACB .
b. So sánh KBKC với ABAC .
c. Chứng minh rằng KAKBKC nhỏ hơn chu vi tam giác ABC
Bài 8. Cho tam giác ABC . Trên đường phân giác của góc ngoài đỉnh A , lấy điểm M không trùng với A . Chứng minh rằng: MBMCABAC .
Bài 9. Cho hai điểm A và B nằm về hai phía của đường thẳng d . Tìm điểm C thuộc đường thẳng d sao cho tổng ACCB là nhỏ nhất.
Bài 10. Cho đường thẳng d và hai điểm , AB nằm cùng về một phía của d và AB không song song với d . Một điểm H di động trên d . Tìm vị trí của H sao cho HAHB là lớn nhất.
Bài 11. Cho góc xOy nhọn, trên Ox lấy hai điểm A và B (điểm A nằm giữa hai điểm O và B ). Trên Oy lấy hai điểm C và D (điểm C nằm giữa O và D ). Chứng minh ABCDADBC

Bài 12. Một trạm biến áp và một khu dân cư được xây dựng cách xa hai bờ sông tại hai địa điểm A và B . Hãy tìm trên bờ sông gần khu dân cư một địa điểm C để dụng một cột mắc dây đưa điện từ trạm biến áp về cho khu dân cư sao cho độ dài đường dây dẫn là ngắn nhất.
BÀI TẬ

17
P TỰ LUYỆN Dạng 1. Bài 1.
e)
f)
g)
h)
Bài 2.
Bài
Bộ ba độ dài nào dưới đây có thể tạo thành độ dài của ba cạnh trong tam giác?
6cm;7cm;15cm
4,2cm;3,5cm;2,5cm
3cm;7,2cm;5cm
3m;10m;7m
Cho tam giác ABC có cạnh 2cm AB
và cạnh 7cm BC
. Tính độ dài cạnh AC biết độ dài cạnh AC là một số nguyên tố
3. Cho ABC cân. a) Tính , ACBC biết chu vi ABC là 23cm và 5cm. AB
b) Tính chu vi ABC biết 5cm, 12cm. ABAC
Bài 4. Có bao nhiêu tam giác có độ dài hai cạnh là 1cm và 3cm còn độ dài cạnh thứ ba là một số nguyên (đơn vị cm)?
Dạng 2.

Bài 1. Cho góc , xOyOz là tia phân giác của góc xOy . Từ điểm M ở trong góc xOz vẽ MH vuông góc với Ox ( H thuộc Ox ), MK vuông góc với Oy ( K thuộc Oy ). Chứng minh rằng: MHMK
Bài 2. Cho ABC có ( ABAC ) và AD là phân giác góc A ( DBC ). Gọi E là một điểm bất kỳ thuộc cạnh AD ( E khác A ). Chứng minh – –ACABECEB .
Bài 3. Cho ABC cân tại A , góc A tù, trên cạnh BC lấy điểm D , trên tia đối của tia CB lấy điểm E sao cho BDCE , trên tia đối của tia CA lấy điểm I sao cho CICA a, Chứng minh rằng: ABDICE và ABACADAE b, Từ D và E kẻ các đường thẳng cùng vuông góc với BC cắt , ABAI lần lượt tại M và N , Chứng minh rằng: BMCN . c, Chứng minh rằng: Chu vi ABC nhỏ hơn chu vi AMN . Bài 4. Cho ABC vuông tại A , tia phân giác của góc B cắt AC tại .D Chứng minh rằng BCBADCDA
18
PHẦN I. TÓM TẮT LÍ THUYẾT.
1. Đường trung tuyến của một tam giác A B M C

Đoạn thẳng AM nối đỉnh A của ABC với trung điểm M của cạnh BC gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc ứng với cạnh BC ) của ABC . Đường thẳng AM cũng gọi là đường trung tuyến của ABC Mỗi tam giác có ba đường trung tuyến.
2. Tính chất đồng quy của ba đường trung tuyến Ba đường trung tuyến của một tam giác cùng đi qua một điểm (hay đồng quy tại một điểm). Điểm gặp nhau của ba đường trung tuyến gọi là trọng tâm của tam giác đó.
3. Vị trí của trọng tâm: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng 2 3 độ dài đường trung tuyến đi qua đỉnh ấy: 2 3 AGBGCG ADBECF
PHẦN II. CÁC DẠNG BÀI. Dạng 1. Sử dụng tính chất trọng tâm của tam giác
I. Phương pháp giải: Sử dụng linh hoạt các tỉ số liên quan đến trọng tâm tam giác.
II. Bài toán.
Bài 1. Chọn câu sai:
A. Trong một tam giác có ba đường trung tuyến.
B. Các đường trung tuyến của tam giác cắt tại một điểm.
C. Giao của ba đường trung tuyến của một tam giác gọi là trọng tâm của tam giác đó.
D. Một tam giác có hai trọng tâm.
Lời giải

1 CHUYÊN ĐỀ SỰ ĐỒNG QUY CỦA BA ĐƯỜNG TRUNG TUYẾN,
Một tam giác chỉ có một trọng tâm nên D sai.
Chọn đáp án D.
Bài 2. Điền số thích hợp vào chỗ trống: “Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng … độ dài đường trung tuyến đi qua đỉnh ấy”
A. 2 3 B. 3 2 C. 3. D. 2.
Lời giải
Chọn đáp án A.
Theo tính chất trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng 2 3 độ dài đường
trung tuyến đi qua đỉnh ấy. Số cần điền là 2 . 3
Bài 3. Cho hình vẽ sau. Tính tỉ số BG BE ?
Lời giải
F E D B
G
Ta có ,, ADBECF là ba đường trung tuyến của tam giác ABC và chúng cắt nhau tại G nên G là trọng tâm của tam giác ABC
Theo tính chất ba đường trung tuyến của tam giác ta có . 2 3 BG BE . 2 3 BGBE
Bài 4. Cho hình vẽ sau.Tình tỉ số AG GD ?
A C G
F E D B
A C

Lời giải
Ta có ,, ADBECF là ba đường trung tuyến của tam giác ABC và chúng cắt nhau tại G nên G là trọng tâm của tam giác ABC .
Theo tính chất ba đường trung tuyến của tam giác ta có:
2
Lời giải

3 2221 3333 AG AGADGDADAGADADAD AD 2 3
22 a bcabc m
Với AMB ta có: (1) AMMBAB Với AMC ta có: (2) AMMCAC Cộng từng vế của 1 2 và ta được: 2AMMBMCABAC Hay 2 a mabc 2 a bca m Chứng minh tương tự ta có 2 a bc m G M B A C a b c ma M B C A
2 1 3 AD AG GD AD 2. AGGD Bài 5. Tam giác ABC có trung tuyến 9cm AM và trọng tâm G Tính độ dài đoạn AG ? Lời giải Vì G là trọng tâm của tam giác ABC và AM là đường trung tuyến, nên 2 3 AGAM (Tính chất ba đường trung tuyến của tam giác), do đó: 2 .96cm 3 AG . Bài 6. Cho , , , .ABCBCaCAbABc Kẻ trung tuyến .AM Đặt a AMm Chứng minh rằng
Bài 7. Cho ABC có hai đường trung tuyến , BDCE
a) Tính các tỉ số , BGCG BDCE b) Chứng minh . 3 2 BDCEBC . Lời giải Gọi giao điểm của hai đường trung tuyến , BDCE là G GBC có: GBGCBC (bất đẳng thức tam giác). Mà 2 3 GBBD , 2 3 GC CE nên: 3 2 3 2 BDCEBC . Do đó 3 2 BDCEBC .
Bài 8. Cho ABC có 8 BCcm , các đường trung tuyến , BDCE cắt nhau tại G . Chứng minh 12 BDCEcm Lời giải
GBC có: GBGCBC (bất đẳng thức tam giác). Mà 2 3 GBBD , 2 3 GC CE nên: 3 2 3 2 BDCEBC

4 Khi đó ta có:
22 a bcabc m
Do đó 33 .812 22 BDCEBC G D E B C A G D E B C A
Bài 9. Cho tam giác ABC có hai đường trung tuyến , BPCQ cắt nhau tại G . Trên tia đối của tia . PB . lấy điểm E sao cho PEPG . Trên tia đối của tia QG lấy điểm F sao cho QFQG . Chứng minh: a) , GBGEGCGE ; b) EFBC và // EFBC . Lời giải a) Vì G là trọng tâm ABC nên 2, 2 BGGPCGGQ Lại có , PEPGQFQG nên 2, 2 GEGPGFGQ Do đó , .BGGECGGF b) Suy ra GBCGEF (c.g.c) Từ đó ta có EFBC và GEFGBC // EFBC .
Bài 10. Cho tam giác ABC có hai đường trung tuyến , ADBE cắt nhau tại G . Trên tia đối của tia DG lấy điểm M sao cho D là trung điểm của đoạn thẳng MG Trên tia đối của tia EG lấy điểm N sao cho E là trung điểm GN . Chứng minh: a) , ;GNGBGMGA b) ANMB và // ANMB Lời giải a) Vì G là trọng tâm ABC nên 2,A 2 BGGEGGD . Lại có 2, 2 GNGEGMGD .( D , E lần lượt là trung điểm của đoạn thẳng MG , GN ) Do đó , ;GNGBGMGA b) Suy ra GBMGNA (c.g.c)

5
G
G
P Q A C B E F
E D M N B A C
Dạng 2. Chứng minh một điểm là trọng tâm của tam giác
I. Phương pháp giải:
Để chứng minh một điểm là trọng tâm của tam giác, ta có thể dùng một trong hai cách sau:
+ Chứng minh điểm đó là giao điểm của hai đường trung tuyến trong tam giác.
+ Chứng minh điểm đó thuộc mộtđường trung tuyến của tam giác và thỏa mãn một trong các tỉ lệ về tính chất trọng tâmcủa tam giác.
II. Bài toán.

Bài 1. Cho hai đường thẳng ' ' xxvàyy cắt nhau tại O Trên tia Ox lấy hai điểm , AB sao cho A nằm giữa ,2. OvàBABOA Trên ' yy lấy hai điểm LvàM sao cho O là trung điểm của LM Nối B với , LB với M và gọi P là trung điểm của đoạn , MBQ là trung điểm của đoạn LB . Chứng minh rằng các đoạn thẳng LPvàMQ đi qua A . Lời giải
Ta có O là trung điểm của đoạn LM Suy ra BO là đường trung tuyến của 1 BLM Mặt khác BOBAAO vì A nằm giữa OvàB hay 23 OBOAOAOA Suy ra 2 2 3 BABO Từ 1,2 suy ra A là trọng tâm của BLM Mà LPvàMQ là các đường trung tuyến của BLM (vì P là trung điểm MB và O là trung điểm của đoạn LM ) Suy ra các đoạn thẳng LPvàMQ đi qua A (theo tính chất ba đường trung tuyến) Bài 2. Cho ABC với đường trung tuyến AD . Trên tia AD lấy điểm E sao cho ADDE , trên tia BC lấy điểm M sao cho BCCM . Chứng minh C là trọng tâm của AEM . Lời giải
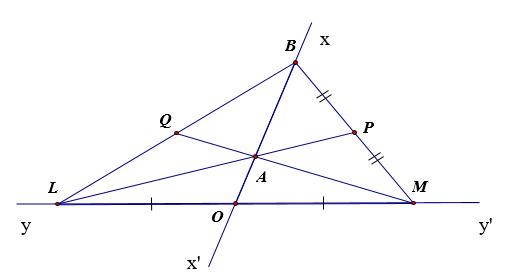
6 Từ đó ta có ANMB và GMBGAN
// ANMB
.
Theo đề bài ta có ADDE nên C thuộc MD là đường trung tuyến của tam giác AEM 1 Mặt khác ta có 2 BCCD và BCCM nên 2 CMCD 2 Từ 1 và 2 suy ra C là trọng tâm của AEM Bài 3. Cho ABC . Trên đường trung tuyến AM của tam giác đó, lấy hai điểm , DE sao cho ADDEEM . Chứng minh E là trọng tâm của ABC Lời giải Từ giả thiết ADDEEM ta có 2 3 AEAM . Mà E thuộc trung tuyến AM nên E là trọng tâm của ABC . Bài 4. Cho ABC . Vẽ trung tuyến BM . Trên tia BM lấy hai điểm , GK sao cho 2 3 BG BM và G là trung điểm của BK . Gọi E là trung điểm ; CKGE cắt AC tại I . Chứng minh: I là trọng tâm của KGC . Lời giải

7
D B C A E M
B
M
C A D E
I. Phương pháp giải: Chú ý những tính chất của tam giác vuông, tam giác cân, tam giác đều. II. Bài toán. Bài 1. Cho tam giác ABC cân tại A , trung tuyến AM . Chứng minh rằng AM vuông góc với BC . Lời giải

8
Theo đề bài 2 3 BG BM
. Suy ra 2 2 BGGMGKGM M
là trung điểm GK Do đó I là giao điểm ba đường trung tuyến trong KGC . Dạng 3. Vấn đề đường trung tuyến trong tam giác vuông, tam giác cân, tam giác đều
Xét
ABM có: ABACGT BMCMGT AM :
() ABMACMccc AMBAMC (Hai góc tương ứng)
180 AMBAMC nên 90 AMBAMC hay AMBC
có
đườ
I M
A G K
ABM
và
cạnh chung
Mà
Bài 2. Cho ABC
các
ng trung tuyến BDvàCE bằng nhau. Chứng minh rằng ABC là tam giác cân. Lời giải
B C
E M B C A
Gọi G là giao điểm của BDvàCE 22 ; 33 BGBDCGCE
Do BDCE nên ; BGCGGDGE BGECGD (c.g.c) BECD
Ta lại có: 11 ; 22 BEABCDCA

Do đó ABAC ABC cân tại A Bài 3. Cho tam giác ,ABC đường trung tuyến Gọi K là trung điểm của BM Trên tia đối của tia lấy KA điểm E sao cho .KEKA a) Điểm M là trọng tâm của tam giác nào? Vì sao? b) Gọi F là trung điểm của CE Chứng minh rằng ba điểm , , AMF thẳng hàng. Lời giải
K M B
C F
A C E
Xét ACE , ta có: ()KAKEgt CK là đường trung tuyến Mà 2 3 CMCK nên M là trọng tâm ACE .
Do F là trung điểm của ()ECgt nên AF là đường trung tuyến thứ ba của ACE Mà M là trọng tâm nên AF đi qua M Hay ba điểm ,, AMF thẳng hàng.
Bài 4. Cho ABC vuông tại A , trung tuyến AM . Trên tia đối của tia MA lấy điểm D sao cho MDMA
a) Tính ABD
9
D
E B A
G
b) Chứng minh ABDBAC c) Chứng minh 1 2 AMBC
Lời giải


a) AMCDMB (c.g.c) ADBDAC // BDAC Mà ABAC nên ABBD 90o ABD . b) ABDBAC (c.g.c). c) ABDBAC (c.g.c) ADBC Mà 1 2 AMAD 1 2 AMBC
Phần III. BÀI TẬP TỰ LUYỆN
Dạng 1. Sử dụng tính chất trọng tâm của tam giác Bài 1. Cho hình 1. Điền số thích hợp vào chỗ trống : ...;...; ...;...; ....
GDBDAGGE GDBGAEAG AEGE
Bài 2. Cho tam giác ABC , các đường trung tuyến BD và CE cắt nhau ởG . Cho biết BDCE Hãy so sánh GBC và GCB . Dạng 2. Chứng minh một điểm là trọng tâm của tam giác Bài 1. Cho tam giác ABC , đường trung tuyến AM . Gọi I là trung điểm BM . Trên tia đối của tia IA lấy điểm E sao cho IEIA . a) Điểm M là trọng tâm của tam giác nào? b) Gọi F là trung điểm của CE . Chứng minh rằng ba điểm ,, AMF thẳng hàng.
10
G E D A B C Hình 1
Bài 2. Cho ABC , M là trung điểm AC . Trên đoạn BM lấy điểm K sao cho
Điểm H thuộc tia đối của tia MK sao cho 2 BHBK . Gọi I là điểm thuộc cạnh AC và 1 3 ICCA . Đường KI cắt HC ở E . a)Chứngminh I làtrọngtâmcủa HKC và E làtrungđiểmcủa HC . b) Tính các tỉ số , IEIC IKMC . Chứng minh ba điểm , , HIF thẳng hàng ( I là trung điểm KC ) Bài 3. Cho hai đoạn thẳng AC và BD cắt nhau tại trung điểm O của mỗi đoạn. Gọi , MN lần lượt là trung điểm của , BCCD . Đoạn thẳng , AMAN cắt BD lần lượt tại I và K . Chứng minh: a) I là trọng tâm của ABC và K là trọng tâm của ADC ; b) BIIKKD . Bài 4. Cho tam giác ABC , đường trung tuyến BD . Trên tia đối của tia DB lấy điểm E sao cho DEBD . Gọi , PQ lần lượt là điểm trên BE sao cho BPPQQE . Chứng minh: a) , CPCQ cắt , ABAE tại trung điểm của , ABAE . b) // CPAQ và // CQAP . Dạng 3. Vấn đề đường trung tuyến trong tam giác vuông, tam giác cân, tam giác đều Bài 1. Cho tam giác . ABC . cân tại A. Trên đường trung tuyến BD lấy điểm E sao cho .DAEABD Chứng minh rằng .DAEECB
Bài 2. Cho tam giác ABC có các đường trung tuyến BD và CE bằng nhau. Chứng minh rằng : ABC là tam giác cân.
Bài 3. Cho ABC có ba đường trung tuyến , , AMBNCP cắt nhau tại G . Biết AMBNCP . Chứng mình ABC đều.
Bài 4. Cho ABC có ba đường trung tuyến , , AMBNCP cắt nhau tại G. Biết AGBGCG . Chứng minh ABC đều.
ĐÁP SỐ BÀI TẬP TỰ LUYỆN
Dạng 1. Sử dụng tính chất trọng tâm của tam giác Bài 1.

11
1 2 KMKB
G E D A B C
Bài 2. Hình 2. Xét ABC có BD và CE là 2 đường trung tuyến cắt nhau tại G (gt) 22 ; 33 BGBDCGCE (Tính chất ba đường trung tuyến của tam giác).
Mà BDCE (gt) BGCG .
Xét ∆ CGB có BGCG (cmt) GBCGCB ( Quan hệ giữa góc và cạnh trong một tam giác).
Vậy GBCGCB . Dạng 2 . Chứng minh một điểm là trọng tâm của tam giác
Bài 1. Hình 4.
Hình 2 Hình 4
a) Vì AM là đường trung tuyến của BC (gt) BMCM (Tính chất đường trung tuyến). Mà 1 2 BIIMBM ( vì I là trung điểm của BM ) 2 CMIM 2 2 3 CMCICMCMCI .
Xét ACE có



CI là đường trung tuyến (vì AIIE );

12
1 ;2; 3 13 ;; 22 3. GDBDAGGE GDBGAEAG AEGE
Hình
G E
B A
F E I M B A C
1
D C
Vậy M là trọng tâm của ACE ( tính chất ba đường trung tuyến của tam giác)
b) Xét ACE có

AF là đường trung tuyến của CE (vì F là trung điểm của CE ); M là trọng tâm của ACE AF đi qua điểm M (tính chất ba đường trung tuyến của tam giác)
Vậy ,, AFM thẳng hàng Bài 2.
a) M là trung điểm KH . Suy ra I là trọng tâm của HKC . Suy ra KI là trung tuyến HKC . b) 12 , 23 IEIC IKMC . Suy ra HI cũng là trung tuyến HKC . Bài 3. a) ABC có hai đường trung tuyến , BOAM cắt nhau tại I nên I là trọng tâm của ABC . Tương tự ta có K là trọng tâm của ADC . b) Từ ý a) suy ra ta có: 2 3 BIBO , DK = 2 3 DO Mặt khác BODO 21 33 BIDKBOBD 1 3 IKBC . Do đó BIIKKD Bài 4.
13 2 3 CMCI
I M B C A K H E K I M N O B D A C
a) Chứng minh được , PQ lần lượt là trọng tâm ABC , AEC .Suy ra ĐPCM.
b) Chú ý ADP = CQD và ADQCDP
Dạng 3. Vấn đề đường trung tuyến trong tam giác vuông, tam giác cân, tam giác đều Bài 1. Hình 5.
A

E D C B
Vẽ ,, AFBDCGBDCHAE .
Vì ABC cân tại A (gt) nên ABAC , ABCACB .
Xét ABF vuông và CAH vuông có ABAC ABFCAH
ABFCAH ( cạnh huyền – góc nhọn),
Suy ra AFCH ( hai cạnh tương ứng) (1).
Do BD là đường trung tuyến của ABC nên ADCD .
Xét ADF vuông và CDG vuông có
ADFCDG ( cạnh huyền – góc nhọn),
Suy ra AFCG (hai cạnh tương ứng) (2).
Từ (1) và (2) suy ra CHCG
Xét CEH vuông và CEG vuông có
CHCG (cmt); EC chung
CEHCEG (cạnh huyền – cạnh góc vuông),
14
ADCD ADFCDG
Q
D
E A C
G
P M N
B
F H


15 Suy ra CEHCEG
Lấy (3) trừ (4) theo từng
ế
.ECBEBAEBAECBEBAECB Mà DAEABD (gt) Vậy DAEECB Bài 2.
3. Gọi G là giao điểm của BD và CE
Xét ABC có BD và CE
22 , 33 BGBDCGCE (Tính
Do BDCE nên , BGCGGDGE Xét BGE và CGD có : GEGD EGBDGC BGCG BGECGD (c.g.c) BECD ( Hai cạnh tương ứng) Ta có 11 , 22 BEABCDAC (vì BD và CE là 2 đường trung tuyến) ABAC Vậy ABC là tam giác cân. Bài 3. G
D C B A
( hai góc tương ứng). Ta có CEGEBCECB (vì CEG là góc ngoài của BEC ), CEHEACECA (vì CEH là góc ngoài của AEC ), Do đó EBCECBEACECA (3). Mặt khác, EBAEBCECBECA (vì ABCACB ) (4)
v
và do EACEBA
(gt), ta được :
Hình
nên EGBDGC
(Hai góc đối đỉnh).
là 2 đường trung tuyến cắt nhau tại G (gt)
chất ba đường trung tuyến của tam giác).
E
Hình 3
PHIẾU BÀI TẬP

Dạng 1. Sử dụng tính chất trọng tâm của tam giác Bài 1. Chọn câu sai:
A. Trong một tam giác có ba đường trung tuyến.
B. Các đường trung tuyến của tam giác cắt tại một điểm.
C. Giao của ba đường trung tuyến của một tam giác gọi là trọng tâm của tam giác đó.
D. Một tam giác có hai trọng tâm.
Bài 2. Điền số thích hợp vào chỗ trống: “Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng … độ dài đường trung tuyến đi qua đỉnh ấy” A. 2 3 B. 3 2 C. 3. D. 2.
16
Ta có BNCP nên , GBGCGPGN . Ta chứng minh ABAC Tương tự, ta có ABBC Vậy .ABBCCA Suy ra ABC đều. Bài 4. Ta có AGBGCG và 2 3 AGAM , 2 3 BGBN , 2 3 CGCP AMBNCP . Tương tự Bài 3 suy ra ĐPCM.
G
A
P
M B C
N
G M B C A N P
Bài 3. Cho hình vẽ sau. Tính tỉ số BG BE ?
F E D B
Bài 4. Cho hình vẽ sau.Tình tỉ số AG GD ?
A C G
G
Bài 5. Tam giác ABC có trung tuyến 9cm AM và trọng tâm G . Tính độ dài đoạn AG ? Bài 6. Cho , , , .ABCBCaCAbABc Kẻ trung tuyến .AM Đặt a AMm Chứng minh rằng 22 a bcabc m Bài 7. Cho ABC có hai đường trung tuyến , BDCE a) Tính các tỉ số , BGCG BDCE b) Chứng minh 3 2 BDCEBC Bài 8. Cho ABC có 8 BCcm , các đường trung tuyến , BDCE cắt nhau tại G . Chứng minh 12 BDCEcm . Bài 9. Cho tam giác ABC có hai đường trung tuyến , BPCQ cắt nhau tại G . Trên tia đối của tia PB lấy điểm E sao cho PEPG . Trên tia đối của tia QG lấy điểm F sao cho QFQG . Chứng minh: a) , GBGEGCGE ; b) EFBC và // EFBC . Bài 10. Cho tam giác ABC có hai đường trung tuyến , ADBE cắt nhau tại G . Trên tia đối của tia DG lấy điểm M sao cho D là trung điểm của đoạn thẳng MG Trên tia đối của tia EG lấy điểm N sao cho E là trung điểm GN . Chứng minh: a) , ;GNGBGMGA b) ANMB và // ANMB . Bài 11. Cho hình 1. Điền số thích hợp vào chỗ trống :

17
F E D B A C
Bài 12. Cho tam giác ABC , các đường trung tuyến BD và CE cắt nhau ởG . Cho biết
BDCE . Hãy so sánh GBC và GCB
Dạng 2.Chứng minh một điểm là trọng tâm của tam giác
Bài 1. Cho hai đường thẳng ' ' xxvàyy cắt nhau tại .O Trên tia Ox lấy hai điểm , AB sao cho A nằm giữa ,2. OvàBABOA Trên ' yy lấy hai điểm LvàM sao cho O là trung điểm của .LM Nối B với , LB với M và gọi P là trung điểm của đoạn , MBQ là trung điểm của đoạn LB . Chứng minh rằng các đoạn thẳng LPvàMQ đi qua A .
Bài 2. Cho ABC với đường trung tuyến AD . Trên tia AD lấy điểm E sao cho ADDE , trên tia BC lấy điểm M sao cho BCCM . Chứng minh C là trọng tâm của AEM Bài 3. Cho ABC . Trên đường trung tuyến AM của tam giác đó, lấy hai điểm , DE sao cho ADDEEM . Chứng minh E là trọng tâm của ABC .
Bài 4. Cho ABC . Vẽ trung tuyến BM . Trên tia BM lấy hai điểm , GK sao cho 2 3 BG BM và G là trung điểm của BK . Gọi E là trung điểm ; CKGE cắt AC tại I . Chứng minh: I là trọng tâm của KGC .
Bài 5. Cho tam giác ABC , đường trung tuyến AM . Gọi I là trung điểm BM . Trên tia đối của tia IA lấy điểm E sao cho IEIA a) Điểm M là trọng tâm của tam giác nào? b) Gọi F là trung điểm của CE . Chứng minh rằng ba điểm ,, AMF thẳng hàng. Bài 6. Cho ABC , M là trung điểm AC . Trên đoạn BM lấy điểm K sao cho 1 2 KMKB . Điểm H thuộc tia đối của tia MK sao cho 2 BHBK . Gọi I là điểm thuộc cạnh AC và 1 3 ICCA . Đường KI cắt HC ở E a)Chứngminh I làtrọngtâmcủa HKC và E làtrungđiểmcủa HC . b) Tính các tỉ số , IEIC IKMC . Chứng minh ba điểm , , HIF thẳng hàng ( I là trung điểm KC )


18 ...;...; ...;...; GDBDAGGE GDBGAEAG AEGE
G E D A B C
Hình 1
Bài 7. Cho hai đoạn thẳng AC và BD cắt nhau tại trung điểm O của mỗi đoạn. Gọi , MN
lượt là trung điểm của , BCCD . Đoạn thẳng , AMAN cắt BD lần lượt tại I và K . Chứng minh: a) I là trọng tâm của ABC và K là trọng tâm của ADC ; b) BIIKKD . Bài 8. Cho tam giác ABC , đường trung tuyến BD . Trên tia đối của tia DB lấy điểm E sao cho DEBD . Gọi , PQ lần lượt là điểm trên BE sao cho BPPQQE . Chứng minh: a) , CPCQ cắt , ABAE tại trung điểm của , ABAE b) // CPAQ và // CQAP Dạng 3. Vấn đề đường trung tuyến trong tam giác vuông, tam giác cân, tam giác đều Bài 1. Cho tam giác ABC cân tại A , trung tuyến AM . Chứng minh rằng AM vuông góc với BC . Bài 2. Cho ABC có các đường trung tuyến BDvàCE bằng nhau. Chứng minh rằng ABC là tam giác cân.
Bài 3. Cho tam giác ,ABC đường trung tuyến AM Gọi K là trung điểm của BM Trên tia đối của tia lấy KA điểm E sao cho KEKA
a) Điểm M là trọng tâm của tam giác nào? Vì sao? b) Gọi F là trung điểm của CE Chứng minh rằng ba điểm , , AMF thẳng hàng. Bài 4. Cho ABC vuông tại A , trung tuyến AM . Trên tia đối của tia MA lấy điểm D sao cho MDMA
a) Tính ABD b) Chứng minh ABDBAC c) Chứng minh 1 2 AMBC
Bài 5. Cho tam giác ABC cân tại A. Trên đường trung tuyến BD lấy điểm E sao cho .DAEABD Chứng minh rằng .DAEECB Bài 6. Cho tam giác ABC có các đường trung tuyến BD và CE bằng nhau. Chứng minh rằng : ABC là tam giác cân. Bài 7. Cho ABC có ba đường trung tuyến , , AMBNCP cắt nhau tại G . Biết AMBNCP
. Chứng mình ABC đều. Bài 8. Cho ABC có ba đường trung tuyến , , AMBNCP cắt nhau tại G. Biết AGBGCG . Chứng minh ABC đều.
BÀI TẬP TỰ LUYỆN
Dạng 1. Sử dụng tính chất trọng tâm của tam giác Bài 1. Cho hình 1. Điền số thích hợp vào chỗ trống :

19
ần
l
Bài 2. Cho tam giác ABC , các đường trung tuyến BD và CE cắt nhau ởG . Cho biết BDCE . Hãy so sánh GBC và GCB Dạng 2. Chứng minh một điểm là trọng tâm của tam giác
Bài 1. Cho tam giác ABC , đường trung tuyến AM . Gọi I là trung điểm BM . Trên tia đối của tia IA lấy điểm E sao cho IEIA .
a) Điểm M là trọng tâm của tam giác nào?
b) Gọi F là trung điểm của CE . Chứng minh rằng ba điểm ,, AMF thẳng hàng. Bài 2. Cho ABC , M là trung điểm AC . Trên đoạn BM lấy điểm K sao cho 1 2 KMKB . Điểm H thuộc tia đối của tia MK sao cho 2 BHBK . Gọi I là điểm thuộc cạnh AC và 1 3 ICCA . Đường KI cắt HC ở E . a)Chứngminh I làtrọngtâmcủa HKC và E làtrungđiểmcủa HC . b) Tính các tỉ số , IEIC IKMC . Chứng minh ba điểm , , HIF thẳng hàng ( I là trung điểm KC ) Bài 3. Cho hai đoạn thẳng AC và BD cắt nhau tại trung điểm O của mỗi đoạn. Gọi , MN lần lượt là trung điểm của , BCCD . Đoạn thẳng , AMAN cắt BD lần lượt tại I và K . Chứng minh:
a) I là trọng tâm của ABC và K là trọng tâm của ADC ; b) BIIKKD . Bài 4. Cho tam giác ABC , đường trung tuyến BD . Trên tia đối của tia DB lấy điểm E sao cho DEBD . Gọi , PQ lần lượt là điểm trên BE sao cho BPPQQE . Chứng minh: a) , CPCQ cắt , ABAE tại trung điểm của , ABAE . b) // CPAQ và // CQAP . Dạng 3. Vấn đề đường trung tuyến trong tam giác vuông, tam giác cân, tam giác đề


20 ...;...; ...;...; GDBDAGGE GDBGAEAG AEGE
u G E D A B C Hình 1
Bài 1. Cho tam giác . ABC cân tại A. Trên đường trung tuyến BD lấy điểm E sao cho .DAEABD Chứng minh rằng .DAEECB
Bài 2. Cho tam giác ABC có các đường trung tuyến BD và CE bằng nhau. Chứng minh rằng : ABC là tam giác cân.
Bài 3. Cho ABC có ba đường trung tuyến , , AMBNCP cắt nhau tại G . Biết AMBNCP . Chứng mình ABC đều.
Bài 4. Cho ABC có ba đường trung tuyến , , AMBNCP cắt nhau tại G. Biết AGBGCG . Chứng minh ABC đều.
CHUYÊN ĐỀ 34.2. BA ĐƯỜNG
PHẦN I. TÓM TẮT LÍ THUYẾT.
1. Tia phân giác của một góc
PHÂN GIÁC TRONG MỘT TAM GIÁC
+ Định nghĩa tia phân giác của góc: Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau.
+ Đường thẳng chứa tia phân giác của một góc gọi là đường phân giác của góc đó.
+ Mọi điểm trên tia phân giác của một góc cách đều hai cạnh của góc đó. Ngược lại, mọi điểm nằm bên trong góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
A O M
2. Đường phân giác của tam giác
z B
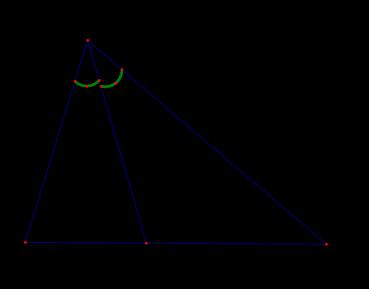

x y
- Trong tam giác ABC , tia phân giác của góc A cắt cạnh BC tại điểm M thì đoạn thẳng AM gọi là đường phân giác xuất phát từ đỉnh A của ABC
- Mỗi tam giác có ba đường phân giác.
3. Tính chất ba đường phân giác của tam giác: * Định lí: Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó.
21
PHẦN II. CÁC DẠNG BÀI.

Dạng 1. Chứng minh đoạn thẳng bằng nhau, góc bằng nhau, tính độ dài đoạn thẳng, số đo góc
I. Phương pháp giải: Sử dụng các tính chất:
+ Giao điểm của hai đường phân giác của hai góc trong tam giác nằm trên đường phân giác của góc thứ ba.
+ Giao điểm của các đường phân giác của một tam giác cách đều ba cạnh của tam giác + Tổng ba góc trong một tam giác bằng 180
II. Bài toán.
Bài 1. Tìm x trong mỗi hình vẽ sau biết CI và BI là hai phân giác của ACB và ABC , EH và FH là hai phân giác của DEF và DFE .
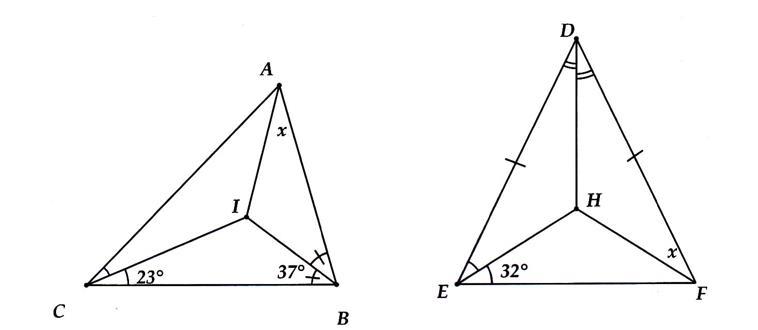
22
Lời giải a) Ta có + + 222()120BCIBCICBIBCICB = 180)180 (+ 12060 ABC Mà BI , CI lần lượt là tia phân giác của B và C nên I là giao điểm của ba đường phân giác trong ABC . AI là tia phân giác của 2 30 A Ax . b) Ta có DEF cân tại 264DFEHEF . H L K F E I
C A
B
Bài 2. Cho ABC có 120. A Các đường phân giác ,.ADBE Tính số đo góc BED . Lời giải
Gọi Ax là tia đối của AB Ta có: 1 60 2 BADDACBAC (vì AD là tia phân giác BAC ) nên 60 CAx Xét ABD có AE là tia phân giác góc ngoài đỉnh A , BE là tia phân giác của góc B và chúng cắt nhau tại E , nên DE là tia phân giác góc ngoài của góc D . Mà EDC là góc ngoài tại đỉnh D của BED , nên 2 BEDBEDC .
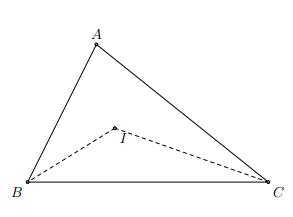

23 FH là tia
ủa DEF 32 2 DFEx
phân giác c
Do đó 22 30 222 ADCABCABDBADABCBAD BEDDB
Bài 3. Cho ABC . Gọi I là giao điểm của hai đường phân giác kẻ từ góc B và C . Tính số đo góc BIC trong các trường hợp: a) 80 BAC b) 120 BAC Lời giải a) 80 BAC C x 2 1 1 2 D E A B
Ta có BI là phân giác của ABC . Suy ra 1 2 IBCABC
Ta có CI là phân giác của ACB . Suy ra 1 2 ICBBCA
Xét IBC có : 180 BICIBCBCI
Suy ra 11 180 22 BICABCBCA
Suy ra 1 180 2 BICABCBCA
Suy ra 1 180 2 BICABCBCA
Suy ra 1 180180 2 BICBAC
Suy ra 1 90 2 BICBAC
Suy ra 1 90. 2 BICa
Suy ra 1 90.80 2 BIC
Suy ra 130 BIC
b) 120 BAC
Ta có 1 90.120 2 BIC

Suy ra 150 BIC .
Bài 4. Cho ABC , các tia phân giác của góc B và góc C cắt nhau ở I
a) Biết 70 A , tính số đo góc BIC b) Biết 140 BIC , tính số đo góc A . Lời giải
24
I B
C
A
a) Xét ABC , ta tính được 110 BC
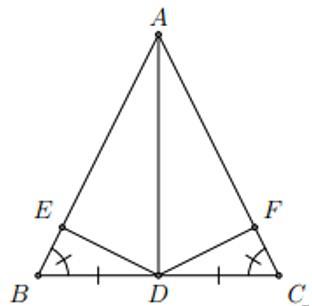
Do đó, 55 IBCICB .

Vậy 18055125 BIC
b) Xét BIC , từ giả thiết suy ra 40 IBCICB .
Do đó, ta có: 80 ABCACB .
Vậy 100 BAC .
Bài 5. Cho ABC cân tại A . Gọi D là trung điểm của BC ; E và F lần lượt là chân đường vuông góc kẻ từ D đến , ABAC . Chứng minh rằng DEDF . Lời giải
Xét ABC cân tại A có AD là đường trung tuyến đồng thời cũng là đường phân giác của góc A Ta có ; DEABDFACgt
Mà AD là đường phân giác của góc A (chứng minh trên) Suy ra DE = DF.
Bài 6. Cho ABC có 90 A các tia phân giác của BvàC cắt nhau tại .I Gọi , DE là chân các đường vuông góc hạ từ I đến các cạnh .ABvàAC
a) Biết 2cm ID . Tính IE ?
b) Biết 3 IDx , 23IEx . Tìm x ? Lời giải
25
D E I A B C
a) Xét ABC có các tia phân giác của BvàC cắt nhau tại .I Nên I là giao điểm của ba đường phân giác trong ABC , suy ra AI là đường phân giác của góc A và I cách đều ba cạnh của ABC (tính chất ba đường phân giác của tam giác).

Vì I là giao điểm của ba đường phân giác trong ABC nên 2cm IEID (tính chất ba đường phân giác của tam giác)
b) Ta có: IEID (chứng minh phần a) 233 xx 233 xx 6 x Bài 7. Cho ABC gọi I là giao điểm của hai tia phân giác góc A và góc .B Qua I kẻ đường thẳng song song với BC , cắt AB tại , M cắt AC tại N. Chứng minh rằng MNBMCN Lời giải Ba phân giác của một tam giác cùng đi qua một điểm nên CI là tia phân giác của góc C Vì // MNBC 12nênCI (so le trong) Mà 12CC nên 22nênCI Do đó NIC cân nên (1) NCNI Tương tự, ta có: (2) MBMI
26
Từ 1 2 và ta có: MIINBMCN hay MNBMCN 1 2 2 1 2 1 M N I B A C
Dạng 2. Chứng minh 3 đường đồng quy, 3 điểm
I. Phương pháp giải:
Sử dụng các tính chất:
thẳng hàng
+ Giao điểm của hai đường phân giác của hai góc trong tam giác nằm trên đường phân giác của góc thứ ba.
+ Giao điểm của các đường phân giác của một tam giác cách đều ba cạnh của tam giác
II. Bài toán.
Bài 1. Cho tam giác ABC cân tại A. Kẻ các tia phân giác BD, CE. Lấy M là trung điểm của BC.
a) Chứng minh AM là tia phân giác của góc BAC.
b) Ba đường thẳng AM, BD, CE đồng quy. Lời giải
a) Chứng minh được AMBAMC (c.c.c).
Từ đó suy ra AM là tia phân giác của góc BAC
b) Xét ABC có ,, AMBDCE là các tia phân giác. Từ tính chất ba đường phân giác trong tam giác, suy ra ba đường thẳng ,, AMBDCE đồng quy.
Bài 2. Cho tam giác ABC , tia phân giác AD . Các tia phân giác ngoài tại đỉnh B và C cắt nhau ở E . Chứng minh ba điểm ,, ADE thẳng hàng.
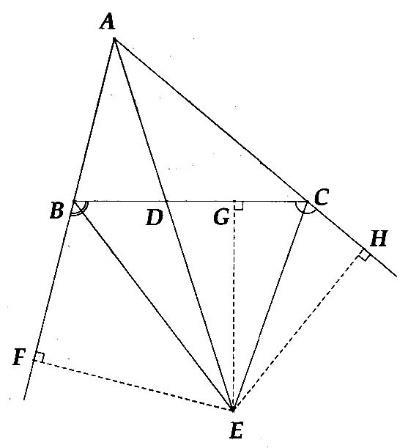
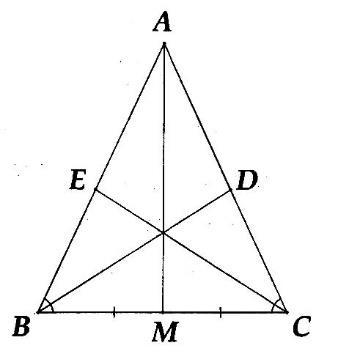
Lời giải

Gọi ,, FHG lần lượt là hình chiếu vuông góc của điểm E xuống các đường thẳng ,, ABACBC
Từ giả thiết suy ra EFEG và EHEG EFEH nên E thuộc tia phân giác của góc BAC . Mà AD là tia phân giác của góc BAC .
1
ba điểm ,, ADE thẳng hàng.
Bài 3. Cho tam giác ABC cân tại A . Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm ,, AGI thẳng hàng. Lời giải
Gọi , MN là trung điểm CAvàBA ABC cân tại A có , BMCN là đường trung tuyến ứng với cạnh , ACAB ⇒ BM=CN
Mà 22 ; 33 GBBMGCCN (Tính chất trọng tâm của tam giác) GBGC

Xét AGBvàAGC có AG chung ABAC (do ABC cân tại A ) GBGC (chứng minh trên) AGBAGCccc
BAGCAG (hai góc tương ứng)
G thuộc tia phân giác của BAC Theo đề bài I cách đều ba cạnh của tam giác I là điểm chung của ba đường phân giác I thuộc tia phân giác của BAC Vì , GI cùng thuộc tia phân giác của BAC nên , , AGI thẳng hàng. Bài 4. Cho tam giác ABC cân ở A có BM , CN là hai đường trung tuyến cắt nhau ở điểm G .
a) Chứng minh rằng: AG là tia phân giác của góc BAC b) CMR: GMGN c) CMR: đường thẳng AG là đường trung trực của đoạn thẳng MN . d) CMR: đường thẳng AG là đường trung trực của đoạn thẳng BC . e) Gọi P là trung điểm BC . CMR: ,, AGP thẳng hàng. Lời giải
2 Vậy
G N M
C B A
I
a) ABMACN (c.g.c)
ABMACN BGGC
Xét ABG và ACG có: ABAC ABGACG BGCG ABGACG (c.g.c) BAGCAG AG là phân giác của BAC b) AGNAGM (c.g.c) vì: : AG chung; ANAM ; NAGMAG GNGM c) ANAM AG GNGM là đường trung trực của MN

d) ABAC AG GBGC là đường trung trực của BC
Xét APB và APC có: ABAC AP chung BPPC APBAPC (c.c.c) BAPCAP (hai góc tương ứng)
AP là phân giác của BAC
Mà AG là phân giác của BAC Suy ra tia AP trùng với tia AG
3
G N M P B C A
ng hàng. Bài 5. Cho tam giác ABC . Phân giác trong của góc B và góc C cắt nhau tại I . Phân giác các góc ngoài tại đỉnh B và đỉnh C cắt nhau tại J , phân giác các góc ngoài tại đỉnh A và đỉnh C cắt nhau tại K , phân giác các góc ngoài tại đỉnh A và đỉnh B cắt nhau tại L .

4 Hay ,, APG
ẳ
Chứng
A
b) Ch
,,
ẳng hàng c) Chứng
ắt
ạ
ột
m. Lời giải a) BI là tia phân giác của góc 1 2 BIBCABC CI là tia phân giác của góc 1 2 CICBACB 1111 18090 22222 A IBCICBABCACBABCACBA Xét IBC có: 18090180 2 A BICIBCICBBIC 90 2 A BIC b) Kẻ ,, JMABJNBCJEAC J thuộc tia phân giác của CBxJMJN J thuộc tia phân giác của BCyJNJE L K E N M J B A C I
th
a)
minh 90 2
BIC
ứng minh ba điểm
AIJ th
minh ,, AJBKCL c
nhau t
i m
điể
thuộc tia phân giác của BAC (1)
Phân giác trong của góc B và góc C của tam giác ABC cắt nhau tại I Tia AI là phân giác của hay điểm I thuộc tia phân giác của BAC (2)

Từ (1) và (2) ba điểm ,, AIJ là ba điểm thẳng hàng.
c) Theo câu b ta có ba điểm ,, AIJ thẳng hàng nên đường thẳng AJ đi qua điểm I
Chứng minh tương tự đường thẳng BK đi qua và đường thẳng CL đi qua I Vậy ba đường thẳng ,, AJBKCL cắt nhau tại điểm I
Bài 6. Cho tam giác ABC có 120 A . Các tia phân giác của góc A và C cắt nhau ở O , cắt cạnh BC và AB lần lượt ở D và E . Đường phân giác góc ngoài tại đỉnh B của tam giác ABC cắt đường thẳng AC ở F . Chứng minh:
a) BOBF b) BDFADF c) Ba điểm ,, DEF thẳng hàng. Lời giải a) Vì O là giao điểm của hai đường phân giác nên BO cũng là đường phân giác của tam giác. Mà BF là đường phân giác ngoài nên 90 FBO BOBF b) 120 BAC nên 60 BAFDACDAB Phân giác trong của DAB vuông góc với AF AF là phân giác ngoài của DAB . Vậy F là giao điểm của các đường phân giác trong tam giác ABD DF là phân giác của ADB . Vậy BDFADF
5 JMJEJ
BAC
I O F E D C B A
c) Chứng minh tương tự, AE là phân giác ngoài của ACD mà CE là phân giác trong của tam giác. Nên E thuộc đường phân giác ngoài của ADC . Vậy ba điểm ,, DEF thẳng hàng. Dạng 3. Đường phân giác đối với tam giác đặc biệt (tam giác cân, tam giác đều)
I. Phương pháp giải: Sử dụng tính chất: trong tam giác cân, đường phân giác của góc ở đỉnh cũng đồng thời là đường trung tuyến, đường cao.
II. Bài toán.
Bài 1. Cho ABC cân tại A , đường phân giác AM Gọi D là một điểm nằm giữa .AvàM Khi đó BDC là tam giác gì?
Lời giải
D
A

M C B
Xét ABDvàACD có: ABAC (gt)
12 AA ( AM là đường phân giác)
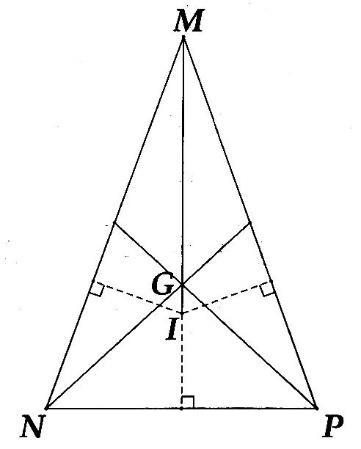
AD là cạnh chung
Nên ABDACD (c.g.c) BDCD (hai cạnh tương ứng).
Do đó BDC cân tại D .
Bài 2. Cho tam giác MNP cân tại M có G là trọng tâm. I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm ,, MGI thẳng hàng. Lời giải
I nằm trong tam giác và cách đều ba cạnh của tam giác nên MI là tia phân giác của góc M .
Do MNP cân tại M nên đường phân giác MI cũng là đường trung tuyến.
6
ng tâm c
MNP nên G nằm trên MI . Từ đó, suy ra ,, MGI thẳng hàng.
Bài 3. Tam giác ABC cân tại A . Tia phân giác của góc A cắt đường trung tuyến DB
Gọi I là trung điểm của AB . Chứng minh rằng ba điểm ,, IKC thẳng hàng.
Lời giải
Tam giác ABC cân tại A có:
C B

AK là tia phân giác của góc ở định nên đường thẳng AK là đường trung tuyến (1). BD là đường trung tuyến của tam giác ABC (2).
Từ (1) và (2) suy ra K là trọng tâm của tam giác ABC . Do đó C , K , I thẳng hàng.
Bài 4. Chứng minh rằng trong tam giác cân, trung điểm của cạnh đáy cách đều hai cạnh bên. Lời giải
A D I M
A B C
Xét tam giác ABC cân tại A , M là trung điểm của BC AM là tia phân giác của góc A nên M cách đều hai cạnh AB , AC .
Bài 5. Cho tam giác ABC có đường trung tuyến AM là đường phân giác của góc A . Chứng minh tam giác ABC cân tại A Lời giải
7 G là trọ
ủ
a
tại K .
K


8 Hạ , MDABMEAC . Vì AM là tia phân giác của A nên MDME . Do đó BDMCEM (cạnh huyền – cạnh góc vuông). Suy ra BC . Vậy ABC cân tại A Bài 6. Cho ABC có 2 AHBCvàBAHC Tia phân giác của góc B cắt AC tại E Tia phân giác của góc BAH cắt BE ở I . Chứng minh AIE là tam giác vuông cân tại E Lời giải XétAHB vuông ta có: 90 BAHABH mà 2 BAHC và 2 ABHIBH 2290 CIBH 290 CIBH 45 CEBH Xét BEC có AEI là góc ngoài tại đỉnh E nên 45 AEIECBEBC XétAHB có: 902290ABHHABIBAIAB 45 IBAIAB Xét AIB có AIE là góc ngoài tại đỉnh I nên 45 AIEIABIBA XétIAE có: 45 AIEAEI 18090EAIAEIAIE (tổng ba góc trong một tam giác) Vậy AIE là tam giác vuông cân tại E Bài 7. Cho tam giác ABC cân ở A có M là trung điểm cạnh BC và BD là đường phân giác ( D thuộc AC ). AM và BD giao nhau ở điểm I . a) CMR: Tia CI là tia phân giác của góc ACB . b) CMR: Tam giác BIC là tam giác cân. C I E H A B
( I nằm trên tia phân giác BD của ABC )
c) Gọi E là giao điểm của tia CI với cạnh AB . Chứng minh rằng: // EDBC d) Gọi H là giao điểm của AM và ED . CMR: H là trung điểm của ED . e) CMR: AMED f) Tìm điều kiện của tam giác ABC để điểm I và trọng tâm G của tam giác ABC trùng nhau. Lời giải a) Vì ABC cân tại A , có AM là đường trung tuyến nên AM là phân giác Có AM và BD giao nhau ở điểm I nên I là giao của 3 đường phân giác CI là đường phân giác của tam giác ABC b) Ta có 1 2 IBCABC
(CI là tia phân giác của ACB )

9
Mà
IBCICB IBC cân tại I c) Xét IEBvàIDC , có EBIDCI EIBDIC (2 góc đối đỉnh) IBIC IB = IC (do BIC cân tại I ) IEBIDC (g.c.g) BEDC AEAD AED cân tại A 180 2 A AED Mà 180 2 A ABC ( do ABC cân tại A ) H E
D M
A
1 2 ICBACB
ABCACB
( ABC cân tại A )
I
C B
Mà 2 góc ở vị trí so le trong của EDvàBC // EDBC d) AHEAHD (c.g.c) HEHD H là trung điểm của ED e) Có: AEAD AH HEHD
là đường trung trực của ED
AHED hay AMED f) I và trọng tâm G của ABC trùng nhau ABC đều Dạng 4. Chứng minh mối quan hệ giữa các góc I. Phương pháp giải: - Vận dụng các tính chất tia phân giác của một góc để tìm mối liên hệ giữa các góc. - Dùng định lí tổng ba góc trong một tam giác bằng 180 II. Bài toán.
Bài 1. Cho tam giác ABC có ba đường phân giác cắt nhau tại I . Chứng minh rằng: 90 IABIBCIAC Lời giải
A C

I B
Vì AI là phân giác BAC nên ta có: 1 2 IABBAC BI là phân giác ABC nên ta có: 1 2 IBCABC CI là phân giác BCA nên ta có: 1 2 ICABCA Do đó: 11 .18090 22 IABIBCIACBACABCBCA
Bài 2. Cho tam giác ABC có ba đường phân giác cắt nhau tại I và ABAC .
10
AEDABC
a) Chứng minh rằng: CBIACI
b) So sánh IB và IC Lời giải
I B

Vì BI là phân giác ABC nên ta có: 1 2 CBIABC
CI là phân giác BCA nên ta có: 1 2 ACIBCA
Mà ABAC nên ABCBCA (Quan hệ giữa góc và cạnh đối diện trong tam giác) CBIACI Bài 3. Cho hình vẽ.
a) Chứng minh ABDACD b) So sánh góc DBC và góc DCB
Lời giải
a) Căn cứ vào các kí hiệu đã cho trên hình vẽ ta có: ABDvàACD có: ABAC ; BADCAD ; AD là cạnh chung = ABDACD (c.g.c)
b) Vì ABDACD (chứng minh câu a)
BDCD (hai cạnh tương ứng) BCD cân tại D
DBCDCB (Tính chất tam giác cân)
11
A C B C D A

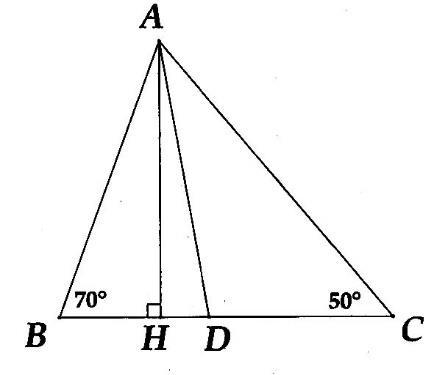
12 Bài 4. Cho ABC hai đường phân giác của góc B và góc C cắt nhau tại I Chứng minh rằng: 90 2 A BIC Lời giải I là giao điểm của hai đường phân giác góc B và góc C ⇒ Phân giác góc A là AI Ta có: 180 ABC 90 222 ABC 90 222 BCA Trong BIC có 180 22 BC BIC 18090 2 A Vậy 90 2 A BIC Bài 5. Cho tam giác ABC có BC . Từ đỉnh A kẻ đường cao AH và tia phân giác AD . a) Biết 70,50BC , tính số đo HAD b) Chứng minh 2 BC HAD Lời giải a) Từ giả thiết, ta tính được: 60 BAC 30 2 BAC DACDAB 80 ADHDACC Do đó, xét AHD ta tính được: Có thể tính BAH = 90° - 70° = 20°. I B A C

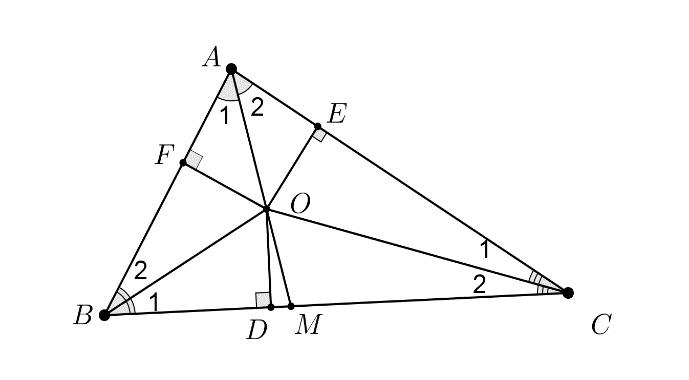
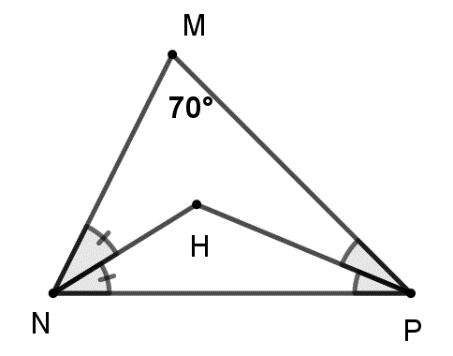
13 Vậy 302010 HAD
182
b) 90 90 2 H A A HDAC D
22 0 ACBC
Bài 6. Cho ABC các tia phân giác góc B và C cắt nhau ở O . Gọi ,, DEF lần lượt là chân đường vuông góc kẻ từ O đến ,, BCCAAB ,, DBCEACFAB . Tia AO cắt BC ở M a) Chứng minh: ODOEOF b) So sánh DOB và MOC ? MOB và DOC ? Lời giải a) Vì O là giao điểm các tia phân giác góc B và góc C của ABC
O cách đều 3 cạnh của ABC
ODOEOF
(Tính chất ba đường phân giác trong tam giác) b) Có 12 AA ( AO là tia phân giác BAC ) 21MOCAC ( MOC là góc ngoài AOC ) 0 0 180 90 222 BACACBABCABC (1) Xét BOD vuông ở D ta có 00 2 9090 2 ABC BODB (2) Từ (1), (2) BODMOC Chứng minh tương tự ta cũng có 0 (90) 2 ACB MOBDOC
Phần III. BÀI TẬP TỰ LUYỆN Dạng 1. Chứng minh đoạn thẳng bằng nhau, góc bằng nhau, tính độ dài đoạn thẳng, số đo góc Bài 1. Cho hình vẽ: H là giao điểm của hai đường phân giác xuất phát từ N và P của tam giác MNP .
a) Chứng minh rằng điểm H cách đều hai cạnh , MNMP
b) Tính số đo HMN , NHP ?
Bài 2. Cho ABC vuông ở A
Các tia phân giác góc B và C cắt nhau ở I .Gọi ,, DEF là hình chiếu của điểm I xuống ,, ABACBC
a) Chứng minh rằng ADAE
b) Trong trường hợp ABC cân ở A. Chứng minh DEF cân
Bài 3. Cho ABC , các tia phân giác của góc B và góc C cắt nhau ở I
a) Biết 80 A , tính số đo góc BIC .
b) Biết 120 BIC , tính số đo góc A .

Bài 4. Cho ABC có 90 A các tia phân giác của BvàC cắt nhau tại .I Gọi , DE là chân các đường vuông góc hạ từ I đến các cạnh ABvàAC
a) Biết 3cm ID . Tính IE ?
b) Biết 2 IDx , 24IEx . Tìm x ?
Dạng 2. Chứng minh 3 đường đồng quy, 3 điểm thẳng hàng
Bài 1. Cho hình vẽ :
CMR: ,, ABC thẳng hàng.
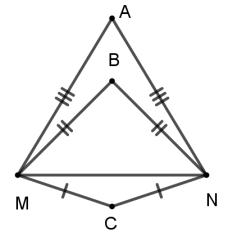
Bài 2. Cho tam giác ABC cân ở A có BM , CN là hai đường trung tuyến cắt nhau ở điểm G .
a) Chứng minh rằng: AG là tia phân giác của góc BAC .
b) CMR: GMGN
c) CMR: đường thẳng AG là đường trung trực của đoạn thẳng MN
d) CMR: đường thẳng AG là đường trung trực của đoạn thẳng BC
e) Gọi P là trung điểm BC . CMR: ,, AGP thẳng hàng.
14
Bài 3. Cho ABC các tia phân giác góc B và C cắt nhau tại I .Các đường phân giác góc ngoài tại đỉnh Bvà C cắt nhau ở K .Chứng minh ba điểm ,, AIK thẳng hàng
Bài 4. Cho tam giác ABC có 120 A . Các tia phân giác của góc A và C cắt nhau ở O , cắt cạnh BC và AB lần lượt ở D và E . Đường phân giác góc ngoài tại đỉnh B của tam giác ABC cắt đường thẳng AC ở F . Chứng minh:
a) BOBF
b) BDFADF c) Ba điểm ,, DEF thẳng hàng.
Dạng 3. Đường phân giác đối với tam giác đặc biệt (tam giác cân, tam giác đều)
Bài 1. Chứng minh rằng:
a) Trong tam giác cân, đường trung tuyến ứng với cạnh đáy cũng là đường trung trực của cạnh đáy.
b) Nếu tam giác có 1 đường vừa là đường trung trực của 1 cạnh, vừa là đường phân giác thì tam giác đó là tam giác cân.
Bài 2. Cho tam giác ABC cân ở A có M là trung điểm cạnh BC và BD là đường phân giác ( D thuộc AC ). AM và BD giao nhau ở điểm I
a) CMR: Tia CI là tia phân giác của góc ACB .
b) CMR: Tam giác BIC là tam giác cân.
c) Gọi E là giao điểm của tia CI với cạnh AB . Chứng minh rằng: ED // BC .
d) Gọi H là giao điểm của AM và ED . CMR: H là trung điểm của ED e) CMR: AMED f) Tìm điều kiện của tam giác ABC để điểm I và trọng tâm G của tam giác ABC trùng nhau. Bài 3. Cho tam giác ABC cân ở A có đường phân giác AD DBC và đường trung tuyến BE EAC cắt nhau tại O . a) Chứng minh: O là trọng tâm ABC b) Tam giác ABC cần có thêm điều kiện gì để O cũng là giao điểm 3 đường phân giác của tam giác ABC ?
Bài 4. Cho ABC cân ở A .Gọi G là trọng tâm tam giác, I là giao điểm các phân giác của tam giác, K là giao điểm hai đường phân giác góc ngoài tại đỉnh B và C .Chứng minh rằng bốn điểm ,,, AGIK thẳng hàng. Dạng 4. Đường phân giác đối với tam giác đặc biệt (tam giác cân, tam giác đều)
Bài 1. Cho ABC có góc 120 A các phân giác ,, ADBECF

15
a) Chứng minh rằng DE là tia phân giác góc ngoài đỉnh D của ABD b) Chứng minh rằng 90 EDF Bài 2. Cho ABC , 120 A .Các tia phân giác góc ; AC cắt nhau ở O , cắt các cạnh ; BCAB lần lượt ở D và E . Đường phân giác góc ngoài tại đỉnh B của ABC cắt đường thẳng AC ở F . Chứng minh: a) BOBF b) BDFADF c) 180 DEAFEA ĐÁP SỐ BÀI TẬP TỰ LUYỆN
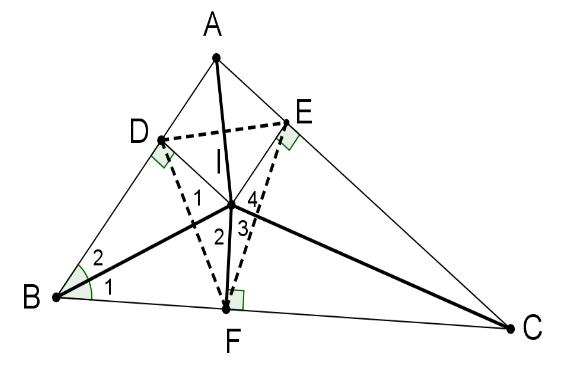
Dạng 1. Chứng minh đoạn

16
thẳng bằng nhau, góc bằng nhau, tính độ dài đoạn thẳng, số đo góc Bài 1. a) Vì H là giao điểm của hai đường phân giác của hai góc , NP nên MH là phân giác góc M Do đó, H cách đều hai cạnh , MNMP b) 11 =.7035 22 HMNNMP 1111 =180180180180 2222 NHPMNPMPNMNPMPNNMP 11 18018070180.110125 22 Bài 2. a) AI là phân giác góc A nên 45 IADIAE Hai AIE và AID là hai tam giác cân ở E và ở D nên AEEI và ADDI Vì AI là phân giác góc A nên IEID ADAE b) Nếu ABC vuông cân ở A thì BC nên 1212 BBCC 1234 DDDD . Do đó
Vậy EDF cân ở F
Bài 3.
I B
a) Xét ABC , ta tính được 100 BC
Do đó, 50 IBCICB .
Vậy 18050130 BIC
b) Xét BIC , từ giả thiết suy ra 60 IBCICB .
Do đó, ta có: 120 ABCACB .
Vậy 18012060 BAC .
Bài 4.
A C D E
B C
I A

a) Xét ABC có các tia phân giác của BvàC cắt nhau tại .I Nên I là giao điểm của ba đường phân giác trong ABC , suy ra AI là đường phân giác của góc A và I cách đều ba cạnh của ABC (tính chất ba đường phân giác của tam giác).
Vì I là giao điểm của ba đường phân giác trong ABC nên 3cm IEID (tính chất ba đường phân giác của tam giác) b) Ta có: IEID (chứng minh phần a) 242 xx 224 xx 6 x Dạng 2 . Đường phân giác đối với tam giác đặc biệt (tam giác cân, tam giác đều)
17 DIFEIF
DIFEIF (c.g.c) FDFE

18 Bài 1:
M H A B C G N M P B C A
Xét ABM và ABN có AB chung AMAN (gt) BMBN (gt)
ABMABNccc BAMNAB ( 2 góc tương ứng) AB là phân giác của MAN (1) Xét AMCvàANC , có
ACchung AMANgt MCNCgt AMCANCccc
MACNAC (2 góc tương ứng) AC là phân giác của MAN (2) Từ (1) và (2) AB trùng AC Bài 2. a) ABMACN (c.g.c)
ABMACN
Xét ABG và ACG có
ABAC ABGACG BGCG
ABGACG (c.g.c)

BAGCAG (hai góc tương ứng)
AG là phân giác của BAC b) AGNAGM (c.g.c) vì AG chung; ANAM ; NAGMAG GNGM (hai cạnh tương ứng)
c) ANAM AG GNGM
là đường trung trực của MN d) ABAC AG GBGC
là đường trung trực của BC
Xét APB và APC có: ABAC AP chung BPPC APBAPC (c.c.c) BAPCAP
AP là phân giác của BAC
Mà AG là phân giác của BAC APAG ,, APG thẳng hàng. Bài 3.
19
BGGC
I là giao điểm các phân giác của tam giác ABC nên I thuộc tia phân giác BAC (1) Hạ ,, KDBCKEACKFAB . Vì K thuộc tia phân giác của CBx nên KBKF , K lại thuộc tia phân giác BCy Nên KDKE . Suy ra KEKF . Điều này chứng tỏ K thuộc tia phân giác BAC (2) Từ (1) và (2) I và K cùng thuộc tia phân giác BAC .Vậy ba điểm ,, AIK thẳng hàng. Bài 4.

20
a) Gọi Bt là tia đối của tia BC Vì O là giao điểm của hai đường phân giác nên BO cũng là đường phân giác củ
1 2 OBACBA Mà BF là đường phân giác ngoài nên 1 2 ABFABt 11 .18090 22 OBAABFCBAABt Hay 090 FBO BOBF x y F E D K I A C B t F E D O A C B
Vì
a ABC
phân giác trong của DAB vuông góc với AF AF là phân giác ngoài của DAB Vậy F là giao điểm của các đường phân giác trong tam giác ABD DF là phân giác của ADB . Vậy BDFADF
c) Chứng minh tương tự, AE là phân giác ngoài của ACD mà CE là phân giác trong của tam giác. Nên E thuộc đường phân giác ngoài của ADC . Vậy ba điểm ,, DEF thẳng hàng. Dạng 3 . Đường phân giác đối với tam giác đặc biệt (tam giác cân, tam giác đều) Bài 1. a) Xét AMB và AMC , có ABAC

21 b)
120 BAC nên 060 BAFDACDAB
0
BC BMMC AMBAMC 090 AMBAMC AMBC mà AM là đường trung tuyến nên AM là đường trung trực của tam giác. b) Cũng chứng minh AMBAMC , chỉ ra ABAC ABC cân Bài 2. M C B A

22 a) Xét
EBIDCI EIBDIC
đỉnh) IBIC ( do BIC cân tại I ) IEBIDCgcg BEDC AEAD AED cân tại A 180 2 A AED Mà 180 2 A ABC ( do ABC cân tại A ) AEDABC Mà 2 góc ở vị trí so le trong của hai đường thẳng EDvàBC // EDBC d) AHEAHD (c.g.c) HEHD (hai cạnh tương ứng) H E I D M B C A
ABM
và ABM có:
ABACGT
BMCMGT
AM : cạnh chung () ABMACMccc AMBAMC (Hai góc tương ứng) AM là đường phân giác Có I là giao điểm của BD và AM I là giao của 3 đường phân giác CI là phân giác của ABC b) Ta có 1 2 IBCABC (t/c phân giác) 1 2 ICBACB
(t/c phân giác) Mà ABCACB
IBCICB IBC cân tại I (dhnb) c) Xét IEBvàIDC , có
(đối
H
là trung điểm của ED e) Có: AEAD AH HEHD là đường trung trực của ED AHED hay AMED f) I và trọng tâm G của ABC trùng nhau ABC đều
Bài 3.

a) ABDACD (c.g.c) BDCD (hai cạnh tương ứng) AD là trung tuyến O là giao điểm hai đường trung tuyến , ADBE nên O là trọng tâm b) ABC đều. Bài 4.
Gọi G là trọng tâm ABC G thuộc trung tuyến AM (1)
Mà AI là phân giác của ABC cân tại A AI là trung tuyến của ABC (2)
Từ (1) và (2) ,, AIG thẳng hàng (3) Theo đề bài AI là phân giác góc A mặt khác (theo bài 4) thì AK cũng là phân giác góc A nên ba điểm ,, AIK thẳng hàng (4)
23
O E D B C A
Dạng 4.
Bài 1.
a) Gọi Ax là tia đối của tia AB
Vì 120 ABC nên 60 CAx . Do AD là phân giác BAC nên 060 BADDACCAx Kẻ ;; MEABENADEPDB Xét ABD có BE là phân giác trong của góc B MEEP (tính chất tia phân giác), (1) AE là phân giác góc ngoài tại đỉnh A của tam giác ABD MENE (tính chất tia phân giác) (2) Từ (1) và (2) ta có EPNE . Do đó DE là phân giác góc ngoài tại đỉnh D của ABD b) Chứng minh tương tự ta có DF là phân giác góc ngoài đỉnh D của DEC Vì ; ADCADB là hai góc kề bù nên DEDF Hay 090 EDF
Bài 2.
y F E D
A

O B C
x
a) , BOBF là hai tia phân giác hai góc kề bù nên BOBF b) 180 FABBAC mà 120 BAC 60 FAB . AD là tia phân giác BAC nên
24 Từ
(3), (4) ,,, AIKG thẳng hàng
Từ đó suy ra BAFFAy
Xét ABD có hai đường phân giác góc ngoài đỉnh A và B cắt nhau ở F DF là phân giác
ABD
Vây BDFADF
c) Xét ACD có phân giác góc C và phân giác góc ngoài ở đỉnh A cắt nhau ở E DE là phân giác góc ngoài đỉnh D , DEDF đều là tia phân giác góc ADB Suy ra ba điểm ,, DEF thẳng hàng. Do đó, 180 DEAFEA
PHIẾU BÀI TẬP

Dạng 1. Chứng minh đoạn thẳng bằng nhau, góc bằng nhau, tính độ dài đoạn thẳng, số đo góc
Bài 1. Tìm x trong mỗi hình vẽ sau biết CI và BI là hai phân giác của ACB và ABC , EH và FH là hai phân giác của DEF và DFE

Bài 2. Cho ABC có 120. A Các đường phân giác ,.ADBE Tính số đo góc BED .
Bài 3. Cho ABC . Gọi I là giao điểm của hai đường phân giác kẻ từ góc B và C . Tính số đo góc BIC trong các trường hợp: a) 80 BAC b) 120 BAC Bài 4. Cho ABC , các tia phân giác của góc B và góc C cắt nhau ở I a) Biết 70 A , tính số đo góc BIC . b) Biết 140 BIC , tính số đo góc A Bài 5. Cho ABC cân tại A . Gọi D là trung điểm của BC ; E và F lần lượt là chân đường vuông góc kẻ từ D đến , ABAC . Chứng minh rằng DEDF .
Bài 6. Cho ABC có 90 A các tia phân giác của BvàC cắt nhau tại I Gọi , DE là chân các đường vuông góc hạ từ I đến các cạnh
25 60 BADDAC 60 FAyDAC (hai góc đối đỉnh)
.ABvàAC
a) Biết 2cm ID . Tính IE ?
b) Biết 3 IDx , 23IEx . Tìm x ?
Bài 7. Cho ABC gọi I là giao điểm của hai tia phân giác góc A và góc B Qua I kẻ đường thẳng song song với BC , cắt AB tại , M cắt AC tại N. Chứng minh rằng MNBMCN
Dạng 2. Chứng minh 3 đường đồng quy, 3 điểm thẳng hàng
Bài 1. Cho tam giác ABC cân tại A. Kẻ các tia phân giác BD, CE. Lấy M là trung điểm của BC.
a) Chứng minh AM là tia phân giác của góc BAC.
b) Ba đường thẳng AM, BD, CE đồng quy.

Bài 2. Cho tam giác ABC , tia phân giác AD . Các tia phân giác ngoài tại đỉnh B và C cắt nhau ở E . Chứng minh ba điểm ,, ADE thẳng hàng.
Bài 3. Cho tam giác ABC cân tại A . Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm ,, AGI thẳng hàng.
Bài 4. Cho tam giác ABC cân ở A có BM , CN là hai đường trung tuyến cắt nhau ở điểm G .
a) Chứng minh rằng: AG là tia phân giác của góc BAC
b) CMR: GMGN
c) CMR: đường thẳng AG là đường trung trực của đoạn thẳng MN .
d) CMR: đường thẳng AG là đường trung trực của đoạn thẳng BC .
e) Gọi P là trung điểm BC . CMR: ,, AGP thẳng hàng.
Bài 5. Cho tam giác ABC . Phân giác trong của góc B và góc C cắt nhau tại I . Phân giác các góc ngoài tại đỉnh B và đỉnh C cắt nhau tại J , phân giác các góc ngoài tại đỉnh A và đỉnh C cắt nhau tại K , phân giác các góc ngoài tại đỉnh A và đỉnh B cắt nhau tại L .
a) Chứng minh 90 2 A BIC
26
b) Chứng minh ba điểm ,, AIJ thẳng hàng c) Chứng minh ,, AJBKCL cắt nhau tại một điểm. Bài 6. Cho tam giác ABC có 120 A . Các tia phân giác của góc A và C cắt nhau ở O , cắt cạnh BC và AB lần lượt ở D và E . Đường phân giác góc ngoài tại đỉnh B của tam giác ABC cắt đường thẳng AC ở F . Chứng minh: a) BOBF b) BDFADF c) Ba điểm ,, DEF thẳng hàng. Dạng 3. Đường phân giác đối với tam giác đặc biệt (tam giác cân, tam giác đều)
Bài 1. Cho ABC cân tại A , đường phân giác AM Gọi D là một điểm nằm giữa .AvàM
Khi đó BDC là tam giác gì?
Bài 2. Cho tam giác MNP cân tại M có G là trọng tâm. I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm ,, MGI thẳng hàng.
Bài 3. Tam giác ABC cân tại A . Tia phân giác của góc A cắt đường trung tuyến DB tại K . Gọi I là trung điểm của AB . Chứng minh rằng ba điểm ,, IKC thẳng hàng.
Bài 4. Chứng minh rằng trong tam giác cân, trung điểm của cạnh đáy cách đều hai cạnh bên.
Bài 5. Cho tam giác ABC có đường trung tuyến AM là đường phân giác của góc A . Chứng minh tam giác ABC cân tại A .
Bài 6. Cho ABC có 2 AHBCvàBAHC . Tia phân giác của góc B cắt AC tại E . Tia phân giác của góc BAH cắt BE ở I . Chứng minh AIE là tam giác vuông cân tại E Bài 7. Cho tam giác ABC cân ở A có M là trung điểm cạnh BC và BD là đường phân giác ( D thuộc AC ). AM và BD giao nhau ở điểm I .
a) CMR: Tia CI là tia phân giác của góc ACB .
b) CMR: Tam giác BIC là tam giác cân. c) Gọi E là giao điểm của tia CI với cạnh AB . Chứng minh rằng: // EDBC
d) Gọi H là giao điểm của AM và ED . CMR: H là trung điểm của ED e) CMR: AMED
f) Tìm điều kiện của tam giác ABC để điểm I và trọng tâm G của tam giác ABC trùng nhau. Dạng 4. Chứng minh mối quan hệ giữa các góc

Bài 1. Cho tam giác ABC có ba đường phân giác cắt nhau tại I . Chứng minh rằng: 90 IABIBCIAC
Bài 2. Cho tam giác ABC có ba đường phân giác cắt nhau tại I và ABAC . a) Chứng minh rằng: CBIACI b) So sánh IB và IC
Bài 3. Cho hình vẽ. a) Chứng minh ABDACD b) So sánh góc DBC và góc .DCB
27
B C D A
Bài 4. Cho ABC hai đường phân giác của góc B và góc C cắt nhau tại I Chứng minh rằng: 90 2 A BIC
Bài 5. Cho tam giác ABC có BC . Từ đỉnh A kẻ đường cao AH và tia phân giác AD . a) Biết 70,50BC
, tính số đo HAD . b) Chứng minh 2 BC HAD Bài 6. Cho ABC các tia phân giác góc B và C cắt nhau ở O . Gọi ,, DEF lần lượt là chân đường vuông góc kẻ từ O đến ,, BCCAAB ,, DBCEACFAB . Tia AO cắt BC ở M a) Chứng minh: ODOEOF b) So sánh DOB và MOC ? MOB và DOC ? Phần III. BÀI TẬP TỰ LUYỆN
Dạng 1.Chứng minh đoạn thẳng bằng nhau, góc bằng nhau, tính độ dài đoạn thẳng, số đo góc Chứng minh đoạn thẳng bằng nhau, góc bằng nhau, tính độ dài đoạn thẳng, số đo góc
Bài 1. Cho hình vẽ:
H là giao điểm của hai đường phân giác xuất phát từ N và P của tam giác MNP .
a) Chứng minh rằng điểm H cách đều hai cạnh , MNMP
b) Tính số đo HMN , NHP ?
Bài 2. Cho ABC vuông ở A Các tia phân giác góc B và C cắt nhau ở I .Gọi ,, DEF là hình chiếu của điểm I xuống ,, ABACBC
a) Chứng minh rằng ADAE
b) Trong trường hợp ABC cân ở A. Chứng minh DEF cân Bài 3. Cho ABC , các tia phân giác của góc B và góc C cắt nhau ở I
a) Biết 80 A , tính số đo góc BIC b) Biết 120 BIC , tính số đo góc A .

Bài 4. Cho ABC có 90 A các tia phân giác của BvàC cắt nhau tại .I Gọi , DE là chân các đường vuông góc hạ từ I đến các cạnh .ABvàAC

28
a) Biết 3cm ID . Tính IE ?
b) Biết 2 IDx , 24IEx . Tìm x ?
Dạng 2. Chứng minh 3 đường đồng quy, 3 điểm thẳng hàng
Bài 1. Cho hình vẽ :
CMR: ,, ABC thẳng hàng.
Bài 2. Cho tam giác ABC cân ở A có BM , CN là hai đường trung tuyến cắt nhau ở điểm G .
a) Chứng minh rằng: AG là tia phân giác của góc BAC b) CMR: GMGN c) CMR: đường thẳng AG là đường trung trực của đoạn thẳng MN .
d) CMR: đường thẳng AG là đường trung trực của đoạn thẳng BC . e) Gọi P là trung điểm BC . CMR: ,, AGP thẳng hàng.
Bài 3. Cho ABC các tia phân giác góc B và C cắt nhau tại I .Các đường phân giác góc ngoài tại đỉnh Bvà C cắt nhau ở K .Chứng minh ba điểm ,, AIK thẳng hàng
Bài 4. Cho tam giác ABC có 120 A . Các tia phân giác của góc A và C cắt nhau ở O , cắt cạnh và lần lượt ở và . Đường phân giác góc ngoài tại đỉnh của tam giác cắt đường thẳng ở . Chứng minh:
a) b) c) Ba điểm thẳng hàng. Dạng 3. Đường phân giác đối với tam giác đặc biệt (tam giác cân, tam giác đều)


Bài 1. Chứng minh rằng:
a) Trong tam giác cân, đường trung tuyến ứng với cạnh đáy cũng là đường trung trực của cạnh đáy. b) Nếu tam giác có 1 đường vừa là đường trung trực của 1 cạnh, vừa là đường phân giác thì tam giác đó là tam giác cân.
Bài 2. Cho tam giác cân ở có là trung điểm cạnh và là đường phân giác ( thuộc ). và giao nhau ở điểm .
BC AB D E B ABC AC F BOBF BDFADF ,, DEF ABC A M BC BD D AC AM BD I
29
a) CMR: Tia là tia phân giác của góc
b) CMR: Tam giác là tam giác cân.
c) Gọi là giao điểm của tia với cạnh . Chứng minh rằng: // .
d) Gọi là giao điểm của và . CMR: là trung điểm của .
e) CMR: f) Tìm điều kiện của tam giác để điểm và trọng tâm của tam giác trùng nhau.
Bài 3. Cho tam giác cân ở có đường phân giác và đường trung tuyến cắt nhau tại .
a) Chứng minh: là trọng tâm
b) Tam giác cần có thêm điều kiện gì để cũng là giao điểm 3 đường phân giác của tam giác ?
Bài 4. Cho cân ở .Gọi là trọng tâm tam giác, là giao điểm các phân giác của tam giác, là giao điểm hai đường phân giác góc ngoài tại đỉnh và .Chứng minh rằng bốn điểm thẳng hàng.
Dạng 4. Đường phân giác đối với tam giác đặc biệt (tam giác cân, tam giác đều)
Bài 1. Cho có góc các phân giác a) Chứng minh rằng là tia phân giác góc ngoài đỉnh của b) Chứng minh rằng Bài 2. Cho , .Các tia phân giác góc cắt nhau ở , cắt các cạnh lần lượt ở và .Đường phân giác góc ngoài tại đỉnh của cắt đường thẳng ở . Chứng minh:

30
CI ACB BIC E CI AB ED BC H AM ED H ED AMED
ABC I G ABC ABC A AD
BE EAC O O ABC ABC O ABC ABC A G I K B C ,,,
ABC
,,
DE D
BOBF BDFADF
c) d) c)
DBC
AGIK
120 A
ADBECF
ABD
90 EDF ABC 120 A ; AC O ; BCAB D E B ABC AC F
180 DEAFEA
SỰ ĐỒNG QUY CỦA BA ĐƯỜNG TRUNG TRỰC, BA ĐƯỜNG CAO CỦA TAM
GIÁC
PHẦN I. TÓM TẮT LÍ THUYẾT.
1. Đường trung trực của tam giác:
Định nghĩa: Trong một tam giác, đường trung trực của mỗi cạnh được gọi là đường trung trực của tam giác đó.
Định lí 1: Ba đường trung trực của tam giác đồng quy tại một điểm. Điểm đó cách đều ba đỉnh của tam giác.
Nhận xét: Vì giao điểm của ba đường trung trực của tam giác cách đều ba đỉnh của tam giác nên là tâm đường tròn đi qua ba đỉnh tam giác đó. Tính chất: ΔABC cân tại A , AM là đường trung tuyến thì nó cũng là đường trung trực của BC Cụ thể:
a) Cho ABC , d là đường trung trực của cạnh BC thì d gọi là đường trung trực của ABC ứng với cạnh BC b) Trong hình sau, điểm O là giao điểm các đường trung trực của ABC Ta có OAOBOC Điểm O là tâm đường tròn ngoại tiếp ABC
d A B C B
A O C
c) ΔABC cân tại A , AM là đường trung tuyến thì cũng là đường trung trực của BC

1 CHUYÊN ĐỀ.
2. Đường cao của tam giác: Định nghĩa: Đoạn thẳng kẻ từ một đỉnh tam giác và vuông góc với cạnh đối diện gọi là đường cao của tam giác đó. Định lí 2: Ba đường cao của tam giác đồng quy tại một điểm. Điểm đó được gọi là trực tâm của tam giác.
Cụ thể:
a) AH là một đường cao của ABC AHBC
b) Trong hình vẽ ,, ADBECF là các đường cao, H là trực tâm của ABC

Chú ý:
a) ABC là tam giác nhọn thì H nằm trong tam giác.
2
C
A
H B C
M
B H B A C H F E D B A C H K L
A
b) ABC là tam giác vuông tại A thì điểm H trùng với điểm A
c) ABC là tam giác tù thì điểm H nằm ngoài tam giác.
3. Bổ sung:
Tính chất trong tam giác cân: ΔABC cân tại A, AM là đường cao thì nó cũng là đường trung trực, đường trung tuyến, đường phân giác.
PHẦN II. CÁC DẠNG BÀI. BA ĐƯỜNG TRUNG TRỰ
Dạng 1. Xác định tâm đường tròn ngoại tiếp tam giác
I. Phương pháp giải:
C

- Dựa vào định nghĩa và sự đồng quy của ba đường trung trực trong tam giác.
- Sử dụng tính chất giao điểm các đường trung trực trong tam giác thì cách đều ba đỉnh của tam giác đó.
3
I C B A≡H K L B A C I H A B C M
2. Điểm O là giao điểm các đường trung trực của .ABC Ta có .OAOBOC Điểm O là tâm đường tròn ngoại tiếp ABC
II. Bài toán.
A B C B
A O C
Bài 1. Chọn đáp án đúng. Điểm cách đều 3 đỉnh của tam giác là giao điểm của: A. 3 đường trung tuyến. B. 3 đường phân giác. C. 3 đường trung trực. D. 3 đường cao. Lời giải: Điểm nằm trong và cách đều 3 đỉnh của tam giác là giao điểm của 3 đường trung trực. Chọn đáp án C.
Bài 2. Chọn đáp án đúng. a) Cho ABC tù, giao điểm 3 đường trung trực của tam giác nằm: A. trong ABC .

4
1. Cho ABC , d là đường trung trực của cạnh BC thì d gọi là đường trung trực của ABC ứng với cạnh BC
d
B. ngoài ABC
C. trên 1 cạnh của ABC .
D. trùng với 1 đỉnh của ABC .
b) Cho ABC có 90 A thì tâm đường tròn ngoại tiếp tam giác:
A. nằm trong ABC
B. nằm ngoài ABC
C. là trung điểm của cạnh BC
D. trùng với đỉnh A của ABC
c) Cho ABC nhọn, giao điểm 3 đường trung trực của tam giác nằm:
A. trong ABC
B. ngoài ABC
C. trên một cạnh của ABC
D. trùng với một đỉnh của ABC
Lời giải:
a) Cho ABC nhọn, giao điểm 3 đường trung trực của tam giác nằm trong ABC . Chọn đáp án B
b) Cho ABC có 90 A thì tâm đường tròn ngoại tiếp tam giác là trung điểm của cạnh BC . Chọn đáp án C.
c) Cho ABC nhọn, giao điểm 3 đường trung trực của tam giác nằm trong ABC . Chọn đáp án A.
Bài 3. Cho ΔABC . Vẽ điểm O cách đều ba đỉnh ,, ABC và vẽ đường tròn đi qua 3 đỉnh của tam giác trong mỗi trường hợp sau:
a, ΔABC là tam giác nhọn. b, ΔABC vuông tại A . c, ΔABC là tam giác tù.
a, ΔABC là tam giác nhọn.
Lời giải:
b, ΔABC vuông tại A

5
c, ΔABC là tam giác tù.
Bài 4. Cho ,, ABC là ba điểm phân biệt không thẳng hàng. Xác định đường tròn đi qua ba điểm đó.
A
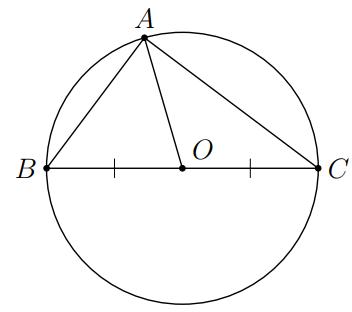

O B C
Lời giải: Gọi đường tròn đi qua ba điểm , , ABC có tâm O ta có .OAOBOC Ba điểm phân biệt , , ABC không thẳng hàng tạo thành tam giác .ABC
Vì OAOBOC nên O là giao điểm ba đường trung trực của tam giác ABC Vậy đường tròn đi qua ba điểm ,, ABC có tâm O là giao của ba đường trung trực của ABC và bán kính bằng .OA
Bài 5. Cho ABC có 90 A . Các đường trung trực của AB và của AC cắt nhau ở O và cắt BC theo thứ tự ở D và E . Nối ,,, ADAEOBOC . Tìm tam giác bằng OAD , bằng OAE
Lời giải:
6
OD là đường trung trực của AB suy ra , DADBOAOB Do đó OADOBD (c.c.c) Tương tự .OAEOCE Bài 6. Cho ABC vuông tại A , đường cao AH . Tia phân giác của các góc BAH và CAH cắt BC lần lượt ở D và E . Gọi O là giao điểm các đường phân giác của tam giác ABC . a) Chứng minh rằng đường tròn tâm O , bán kính OA đi qua ba điểm ,, ADE . b) Tính số đo góc DOE .
Lời giải: a) Ta có 090 BAEBACEACEAC

7
1 090 AEBHAE 2 Mà EACHAEgt , do đó từ 1,2 suy r BAEAEB nên AEB cân
ại B . Vì O là
điểm các đường phân giác của tam giác ABC nên BO là đường phân giác của tam giác cân ABE , do đó BO là đường trung trực của AE , suy ra OAOE 3 Chứng minh tương tự, CO là đường trung trực của AD , suy ra OAOD 4 Từ 3 và 4 suy ra OAODOE . Điều này chứng tỏ ba điểm ,, AED nằm trên đường tròn tâm O , bán kính OA hay đường tròn tâm O bán kính OA đi qua 3 điểm
AED . E D O B A C
t
giao
,,
x E D O H B A C
Bài 7. Tam giác ABC có A là góc tù. Các đường trung trực của các cạnh AB và AC cắt nhau ở O Các điểm B và C có thuộc đường tròn tâm O bán kính OA hay không? Vì sao? Lời giải
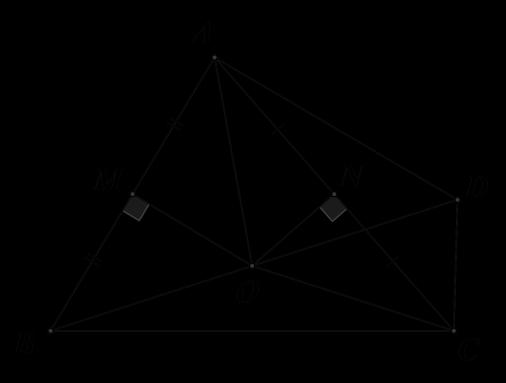

Từ giả thiết suy ra .OAOBOC Vậy các điểm B và C có thuộc đường tròn tâm O bán kính OA Bài 8. Cho ABC có ba góc nhọn, O là giao điểm hai đường trung trực của AB và AC . Trên tia đối của tia OB lấy điểm D sao cho OBOD
a) Chứng minh O thuộc đường trung trực của AD và CD b) Chứng minh các ABD , CBD vuông. c) Biết 70 ABC . Hãy tính số đo ADC . Lời giải
a) Vì O là giao điểm hai đường trung trực của AB và AC nên OAOBOC Mà ODOB nên ODOA và ODOC O thuộc đường trung trực của AD và CD
8 b) Từ 3 suy ra OAE cân tại O , nên OAEOEA . Vẽ tia
tia đố
của tia OA, ta có
Ox là
i
2 EOxOAEOEAxAE Tương tự, 2. xODxAD Do đó,
222 DOExADxAEDAEDAHHAE 0 2.2.90. 22 BAHHACBAC
Vậy 90 DOE
O B C A
ADCABC Bài 9. Tam giác ABC có ba đường trung tuyến cắt nhau tại O . Biết rằng điểm O cũng là giao điểm của ba đường trung trực trong tam giác ABC . Chứng minh tam giác ABC đều. Lời giải:
Cách 1:

Cho AO cắt BC tại F , BO cắt AC tại E , CO cắt AB tại D .
Suy ra ,, DEF lần lượt là trung điểm của ,, ABACBC .
Vì O là giao điểm 3 đường trung trực nên ODAB tại D , OEAC tại E , OFBC tại F
Suy ra ,, ADBECF là 3 đường trung trực của ABC
Vì AD đường trung trực của ABC nên ABAC (1)
Vì BE đường trung trực của ABC nên BABC (2)
9 b) Xét OAB cân tại O 0180 2 AOB OABOBA Xét OAD cân tại O 180 2 AOD OADODA 180180 22 AOBAOD OABOAD 180 18018090 22 AOBAOD 90 BAD ABD vuông tại A. Chứng minh tương tự CBD vuông tại C . c) Ta có ABD vuông tại A nên 90 ADBABD Ta có BCD vuông tại C nên 90 BDCCBD 180 ADOODCABOCBO 18018070110
C F A D E O B
Cách 2:
Cho AO cắt BC tại F , BO cắt AC tại E , CO cắt AB tại D .
Suy ra ,, DEF lần lượt là trung điểm của ,, ABACBC .
Vì O là giao điểm 3 đường trung trực nên ODAB tại D , OEAC tại E, OFBC tại F .
Suy ra ,, ADBECF là 3 đường trung trực của ABC .
Xét AFB và AFC có: AF chung 90 AFBAFC
BFCF (vì AF là trung trực của BC )
Do đó : AFBAFC (c.g.c)
ABAC
Chứng minh tương tự ta được: BABC
Do đó: ABACBC
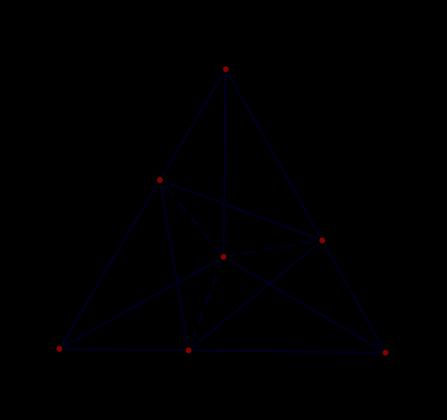

Vậy ABC là tam giác đều.
Bài 10. Cho ABC đều. Trên cạnh ,, ABBCCA lấy theo thứ tự ba điểm ,, MNP sao cho AMBNCP
a. Chứng minh MNP là tam giác đều b. Gọi O là giao điểm các đường trung trực của ABC Chứng minh rằng điểm O cũng là giao điểm các đường trung trực của MNP Lời giải: a) ABC đều nên ABBCCA Mà AMBNCP => BMCNAP Xét AMP và BNM có AMBN (gt) MAPNBM ( ABC đều)
10 Từ (1)
(2) suy ra ABACBC
suy ra ABC đều.
APBM (cmt)
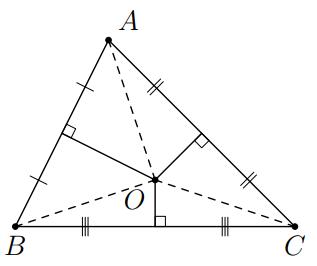

Do đó, (c.g.c)AMPBNM
=> MPMN (hai cạnh tương ứng) (1)
Tương tự: (c.g.c)AMPCPN Suy ra MPPN (2) Từ (1) và (2) ta có MPMNPN Vậy MNP là tam giác đều. b) Điểm O là giao điểm các đường trung trực của tam giác đều ABC nên OAOBOC đồng thời ,, AOBOCO cũng lần lượt là các tia phân giác của ,, BACABCACB . Xét MAO và NBO có: AMBN (gt) 11 22 MAONBOBACABC
(cmt)
(c.g.c) MAONBOOMON
(hai cạnh tương ứng)
tự : (c.g.c)OMOPMAOPCO . Vậy OMONOP . Do đó O là giao điểm các đường trung trực của MNP . Bài 11. Trong một buổi tổng vệ sinh sân trường, 3 tổ cần dọn cỏ và rác của 3 bồn cây ,, ABC ở 3 góc sân trường. Em hãy giúp 3 tổ chọn một vị trí O để đặt chiếc xe đẩy rác sao cho vị trí chiếc xe cách đều 3 bồn cây đó.
Lời giải:
Vì điểm O cách đều ba điểm ,, ABC nên O là giao của ba đường trung trực của tam giác ABC hay O là tâm đường tròn ngoại tiếp tam giác ABC Để xác định vị trí điểm O ta chỉ cần xác định giao điểm của hai trong ba đường trung trực của tam giác ABC .
Dạng 2. Chứng minh ba đường thẳng đồng quy, ba điểm thẳng hàng
I. Phương pháp giải:
Dựa vào định lí, tính chất về đường trung trực và sự đồng quy của ba đường trung trực trong tam giác.
11
OAOB
Tương
Bài toán.
Bài 1. Cho ABC cân tại A . Dựng tam giác BCD cân tại D biết D khác phía với A đối với đường đường thẳng BC . Gọi O là giao điểm của AB và AC . Chứng minh rằng ,, AOD thẳng hàng.
Lời giải:
ABC cân tại A ABAC .
BCD cân tại D DBDC
Suy ra AD là đường trung trực của BC Xét ABC , theo tính chất ba đường trung trực trong tam giác ta có các đường trung trực của AB và AC đồng quy với đường thẳng AD , hay ,, AOD thẳng hàng.
Bài 2. Cho ABC cân tại A . Gọi M là trung điểm của BC . Các đường trung trực của AB và AC cắt nhau ở E
Chứng minh ba điểm ,, AEM thẳng hàng.
Lời giải:
A B M
E
C

Theo gt, M là trung điểm của BC
AM là đường trung tuyến của tam giác cân ABC
AM cũng là đường trung trực của BC (1)
Xét ABC cân tại A có đường trung trực của AB và AC cắt nhau ở E
E thuộc đường trung trực của BC (theo tính chất ba đường trung trực của tam giác) (2)
12
II.
(1) và (2) suy ra, ba điểm ,, AEM thẳng hàng.
Bài 3. Cho tam giác ABC cân tại A . Gọi G là trọng tâm, O là giao điểm ba đường trung trực của tam giác ABC
a) Tam giác BOC là tam giác gì?
b) Chứng minh ba điểm ,, AOG thẳng hàng? Lời giải:
C
a) Do O là giao điểm ba đường trung trực của tam giác ABC nên ta có: OAOBOC
Suy ra tam giác BOC là tam giác cân tại O
b) Do O là giao điểm ba đường trung trực của tam giác ABC nên O thuộc đường trung trực của BC (1)
Do G là trọng tâm nên G thuộc đường trung tuyến của BC đi qua A (2)
Mà tam giác ABC cân tại A nên trung tuyến ứng với cạnh BC cũng là đường trung trực của BC
Suy ra G thuộc đường trung trực của BC (3)
Từ (1), (2) và (3) Suy ra ba điểm ,, AOG thẳng hàng








Bài 4. Cho tam giác ABC cân ở A . Gọi M là trung điểm của BC . Các đường trung trực của , ABAC cắt nhau ở E . Chứng minh ba điểm ,, AEM thẳng hàng.
Lời giải:
Chứng minh được: ABMACM (c.c.c).
Từ đó, suy ra AM là đường trung trực của BC .
Theo tính chất ba đường trung trực của tam giác, ta suy ra điểm E thuộc đường trung trực của BC
13 Từ
A B G O
ba điểm ,, AEM thẳng hàng.
Bài 5. Cho tam giác ABC cân tại A . Lấy điểm D sao cho tam giác BCD cân tại D ( D và A nằm khác phía đối với đường thẳng BC ). Chứng minh các đường trung trực của AB và AC đồng quy với đường thẳng AD
Lời giải:
Từ giả thiết, ta có: , ABACDBDC .
AD là đường trung trực của BC .
Xét ABC , theo tính chất ba đường trung trực trong tam giác ta có các đường trung trực của AB và AC đồng quy với đường thẳng AD Bài 6. Cho ABC vuông ở A , D là giao điểm hai đường trung trực của hai cạnh AB và AC . Chứng minh ,, BDC thẳng hàng.
Lời giải:

14
ậy
V
DAK
12 DD
Gọi I là trung điểm của AB , K là trung điểm AC ta có DIAB và DKAC Xét DAK và DCK có: DK cạnh chung
90º DKADKC
AKCK
(hình vẽ)
DCK (c.g.c)
CM tương tự: 34 DD
Ta lại có 2 90º DDAK
(hai góc phụ nhau) 4 3 1 2 B D I A K C
180º BCD ,, BDC thẳng hàng. Bài 7. Cho tam giác ABC cân tại A . M là trung điểm của BC . Kẻ ME vuông góc AB tại , EMF vuông góc với AC tại F
a) Chứng minh rằng AM là đường trung trực của EF ? b) Kẻ đường thẳng d vuông góc AB tại B , kẻ đường thẳng / d vuông góc với AC tại C , hai đường thẳng d và / d giao nhau giao tại D . Chứng minh rằng ba điểm ,, AMD thẳng hàng?
Lời giải:
A B M
F H E D
a) Gọi H là giao điểm của AM và EF
C










Xét tam giác ABC cân tại A M là trung điểm BCAM là trung tuyến ứng với BC AM là đường trung trực, cũng là đường phân giác của góc A
AEAF và EAHFAH
Xét hai tam giác EAH và FAH , có:
AEAF (cmt)
AH là cạnh chung
EAHFAH (cmt) Suy ra EAHFAH (c.g.c)
HEHF (2 cạnh tương ứng) (1) và AHEAHF (2 góc tương ứng)
Mà 180 AHEAHF (hai góc kể bù) 90 AHEAHF (2)
Từ (1) và (2) suy ra AH là đường trung trực của EF
15 3 90º DDAI (hai góc phụ nhau) 23 8 ºººº
DDDAIDAK
DDDDDD
180109090
12342322.90180ºº
Hay AM là đường trung trực của EF (đpcm)
b) Xét hai tam giác vuông ABD và ACD
AD là cạnh chung.
BADCAD ( AM là phân giác của góc A )
Suy ra ABDACD (cạnh huyền – góc nhọn)
Suy ra DBDC (2 cạnh tương ứng)

Suy ra D nằm trên đường trung trực AM của BC
Suy ra ba điểm ,, AMD thẳng hàng (đpcm)
Bài 8. Cho tam giác nhọn ABC . Gọi ,, HGO theo thứ tự là trực tâm, trọng tâm, giao điểm ba đường trung trực của tam giác. Tia AG cắt BC ở M . Gọi I là trung điểm của , GAK là trung điểm của GH . Chứng minh: a) 1 2 OMAH b) IGKMGO c) Ba điểm ,, HGO thẳng hàng d) 2 GHGO
Lời giải: a) Trên tia đối của tia OC lấy điểm N sao cho O là trung điểm của NC . Ta có: // OMBN và 1 2 OMBN . Vì // OMAH (cùng vuông góc với BC ) nên // AHNB Chứng minh tương tự // NABH . ANBBHA (c.g.c) do đó AHNB Mà 1 2 OMBN vì thế 1 2 OMAH
16
b) Tam giác AGH có I là trung điểm của , GAK là trung điểm của GH nên // IKAH và 1 2 IKAH Suy ra // IKOM và IKOM . Vì G là trọng tâm của tam giác ABC nên 1 2 GMGA , do đó GMGI IKGMGO (c.g.c). c) Vì IKGMGO (theo phần b) nên IKGMGO mà 180 IGKKGM do đó 180 KGMMGO Vậy ba điểm ,, KGO thẳng hàng, suy ra ba điếm ,, HGO thẳng hàng. d) IGKMGO nên GOGK mà 2 HGGK do đó 2 HGGO Chú ý: Đường thẳng đi qua ba điểm ,, HGO được gọi là đường thẳng Ơle Bài 9. Cho tam giác ABC cân ở A , đường phân giác AK . Các đường trung trực của AB và AC cắt nhau tại O . Kéo dài CO cắt AB ở D , kéo dài BO cắt AC ở E . a) Chứng minh ba điểm ,, AKO thẳng hàng. b) Chúng minh AK và các đường trung trực của AD và AE đồng quy.

17
a) Ta có: 1 2 ADAB (CD là trung trực của AB ) 1 2 AEAC ( BE là trung trực của AC ) Mà ABAC (tam giác ABC cân ở A ) ADAE Xét
ADOAEO (c
O
Lời giải:
hai tam giác vuông ADO và AEO có: ADAE
(cmt); : AO cạnh huyền chung
ạnh huyền – cạnh góc vuông). Suy ra DAOEAO
(hai góc tương ứng) AO
là đường phân giác của BAC Vậy ba điểm ,, AKO thẳng hàng.
D E K B C A
b) Ta có: ADAE (chứng minh phần a) (1).
Mặt khác, có ADOAEO (chứng minh phần a) ODOE (hai cạnh tương ứng) (2).
Từ (1) và (2) suy ra AO là đường trung trực của DE , hay AK là đường trung trực của DE . Xét ADE , theo tính chất ba đường trung trực của tam giác, ta có AK và các đường trung trực của AD và AE đồng quy.
Dạng 3. Vận dụng tính chất ba đường trung trực trong tam giác để giải quyết các bài toán khác
I. Phương pháp giải: Dựa vào tính chất về đường trung trực và sự đồng quy của ba đường trung trực trong tam giác.
1. Điểm M nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó:
M

2. ΔABC cân tại A, AM là đường trung tuyến thì cũng là đường trung trực của BC
II. Bài toán.
d I A B C M B
A B A
Bài 1. Cho ABC cân tại A , đường trung tuyến AM . Đường trung trực của AC cắt đường thẳng AM tại D . Chứng minh rằng DADB .
C M D K
18
Lời giải:
Cách 1:
Ta có ABC cân ở A nên trung tuyến AM cũng là đường trung trực của BC .
Vì D thuộc đường trung trực của AC nên DADC (1).
Vì D thuộc đường trung trực của BC nên DBDC (2).
Từ (1),(2) suy ra DADB .

Cách 2:
ABC cân tại A có AM là đường trung tuyến của cạnh đáy BC nên AM cũng là đường trung trực của BC
Ta lại có đường trung trực của AC cắt AM tại D
D là giao điểm của hai đường trung trực của cạnh BC và AC D thuộc đường trung trực của AB . Vậy DADB
Bài 2. Cho tam giác cân ABC có ABAC . Hai đường trung trực của hai cạnh ; ABAC cắt nhau tại O . Chứng minh: AOBAOC . Lời giải: Vì điểm O là giao điểm các đường trung trực của ABC nên O thuộc đường trung trực của BC .
ABC cân tại A ABAC A thuộc đường trung trực của BC .
Do đó AO là đường trung trực của BC
ABC cân tại A nên đường trung trực AO đồng thời là đường phân giác của A Xét AOB và AOC có: OA chung ABAC
( ABC cân tại A ) OABOAC
( AO là tia phân giác của BAC ) Do đó, AOBAOC (c.g.c) AOBAOC (hai góc tương ứng) Bài 3. Cho ABC , M là trung điểm của .BC Các đường trung trực của AB và AC cắt nhau tại O Tính số đo góc .OMB
19
Lời giải:
Từ giả thiết suy ra O thuộc đường trung trực của BC OM là đường trung trực của BC 90. OMB Bài 4. Cho ABC có góc 110. A Đường trung trực của các cạnh AB và AC cắt nhau tại I a) Chứng minh BIC cân. b) Chứng minh 2180 BICBAC và tính số đo góc BIC Lời giải: a) Từ giả thiết suy ra I thuộc đường trung trực của BC IBIC BIC cân. b) Có 2 1802;BIAA

20
1 1802. AICA BICBIAAIC 1218021802AA 2180. BAC Từ đó, suy ra 140. BIC Bài 5. Cho ABC có ˆ 60 A . Các đường trung trực của cạnh AB và AC lần lượt cắt BC ở E và F . Tính EAF . Lời giải: A B M C O 2 1 I B C A
Trước hết, do E nằm trên đường trung trực của AB nên EAB cân ở EBAEABE . Tương tự, ta có FAC cân ở FFACFCA . Ta có BCAFCAFABBAC FABBCABAC
Khi đó EAFBAEFABABCBCABAC 180218012060.EAFBAC Bài 6. Cho ABC cân tại A . Đường trung tuyến AM cắt đường trung trực của AC tại K . Chứng minh rằng .KAKBKC Lời giải ABC cân tại A nên đường trung tuyến AM cũng là đường trung trực. K là giao điểm các đường trung trực của , BCAC nên KAKBKC . Bài 7. Cho ABC cân tại A , 090 A . Các đường trung trực của AB và của AC cắt nhau tại O và cắt BC tại D và E . Chứng minh rằng: a) OA là đường trung trực của BC . b) BCCE . c) ODE là tam giác cân. Lời giải:

21
F E I K C B A
E D O C B
K M C B A K H
A
d c
t nhau
có

22 O là
ABCOBOC
i giải: Xét ABC vuông tạ
A. Vẽ
ng
trực 1d
ủ
ạ
ạ
ạ
Giả
ử
giao điểm các đường trung trực của .
ABC cân tại A ABAC Vậy AO là đường trung trực của BC . b) Gọi H là trung điểm của , ABK là trung điểm của AC . ... HBDKCEgcgBDCE c) HBDKCEHBDKEC ODEOEDODE cân tại O . Bài 8. Chứng minh rằng các đường trung trực của tam giác vuông cắt nhau tại trung điểm của cạnh huyền. Lờ
i
đườ
trung
c
a c
nh AB, cắt AB t
i I. vẽ đường trung trực 2d của cạnh AC, cắt AC t
i H
s
1d và 2
ắ
tại O. Ta
OAOB , do đó OAIOBI (c.g.c) Nên 12OO . Tương tự 34. OO Ta có // OIAC mà OHAC nên 90. IOH Do đó 0 12342322180.OOOOOOIOH Vậy ba điểm ,, BOC thẳng hàng. Mặt khác, OBOC nên O thuộc đường trung trực của BC . Vậy các đường trung trực của tam giác vuông cắt nhau tại trung điểm của cạnh huyền Bài 9. Cho tam giác đều ABC . Gọi D và E là hai điểm lần lượt trên hai cạnh AB và AC sao cho BDAE . Chứng minh rằng các đường trung trực của đoạn thẳng DE luôn đi qua một điểm cố định khi D và E di chuyển trên các cạnh AB và AC Lời giải: 4 3 2 1 O H I d2 d1 C B A
Ta nhận thấy rằng:
Nếu D trùng với B thì E trùng với A , đường trung trực của DE là đường trung trực của AB
Nếu D trùng với A thì E trùng với C , đường trung trực của DE là đường trung trực của AC .
Do đó, ta vẽ các đường trung trực của AB và cạnh AC , chúng ta cắt nhau tại O
Ta sẽ chứng tỏ rằng đường trung trực của DE đi qua O bằng cách chứng minh ODOE
Gọi H và I theo thứ tự là trung điểm của AB và AC . Từ đó suy ra HDIE rồi suy ra OHDOIE (c.g.c) để có .ODOE
Hoặc chứng minh OAEOBD rồi suy ra OAEOBD (c.g.c) để có ODOE
Bài 10. Cho ABC , ACAB . Hai điểm D và E theo thứ tự di chuyển trên các cạnh AB và AC sao cho BDCE . Chứng minh rằng các đường trung trực của DE luôn đi qua một điểm cố định.
Lời giải:

Trên cạnh AC lấy điểm G với CGAB thì điểm G cố định. Ta nhận thấy rằng:
Khi D trùng với B thì E trùng với C , đường trung trực của DE là đường trung trực của BC .
Khi D trùng với A thì E trùng với G , đường trung trực của DE là đường trung trực của AG .
Vẽ đường trung trực của BC và AG chúng cắt nhau tại I thì I là điểm cố định.
23
E D A
H I O
B C
I D E C B A G
nếu các đường trung trực của DE đi qua một điểm cố định thì điểm cố định đó
điểm I nói trên.
Thật vậy, I thuộc các đường trung trực của BC và AG nên ,. IBICIAIG
IABIGC (c.c.c), nên .IDIE
Điều này chứng tỏ rằng đường trung trực của DE luôn đi qua điểm I cố định.
BA ĐƯỜNG CAO
Dạng 1. Xác định trực tâm của một tam giác
I. Phương pháp giải:
- Để xác định trực tâm của một tam giác, ta cần tìm giao điểm hai đường cao của tam giác đó
- Dựa vào định nghĩa, định lí và nhận xét, tính chất về đường cao và sự đồng quy của ba đường cao trong tam giác.
1. AH là một đường cao của ABC AHBC
Chú ý:
2. Trong hình vẽ ,, ADBECF là các đường cao, H là trực tâm của ABC .
A C
A

K L
A C H F E D B H B C
24 Vì vậ
phải là
y
a) ABC là tam giác nhọn thì H nằm trong tam giác.
H B H
b) ABC là tam giác vuông tại A thì điểm H trùng với điểm A
II. Bài toán.
c) ABC là tam giác tù thì điểm H nằm ngoài tam giác.
H

≡H K L B
A C I
Bài 1. Cho ABC có 90 ABC , AHBC . Em chọn phát biểu đúng:
A. H là trực tâm của ABC
B. A là trực tâm của ABC
C. B là trực tâm của ABC
D. C là trực tâm của ABC
Lời giải: Vì ABC có 90 ABC nên ABC là tam giác vuông tại B B là trực tâm của ABC Đáp án đúng là C. Bài 2. Cho ABC , hai đường cao AM và BN cắt nhau tại H . Em chọn phát biểu đúng: A. H là trọng tâm của ABC .
B. 2 3 HAAM và 2 3 HBBN
C. H là trực tâm của ABC ; CH là đường cao của ABC .
D. CH là đường trung trực của ABC
Lời giải: ABC , hai đường cao AM và BN cắt nhau tại H CH là đường cao của ABC H là trực tâm của ABC
25
I C B
A
Đáp án đúng là C.
Bài 3. Cho ABC cân tại A có AMBC tại M . Chọn phát biểu đúng:
A. AM là đường trung tuyến của ABC
B. AM là đường trung trực của BC
C. AM là đường phân giác của BAC .
D. Cả A, B, C đều đúng.
Lời giải: Vì ABC cân tại A có AMBC nên AM là đường cao AM cũng là đường trung tuyến, đường trung trực và đường phân giác của ABC . Chọn đáp án D
Bài 4. Cho ABC vuông tại A . Lấy H thuộc AB , vẽ HEBC ở E . Tia EH cắt tia CA tại D . Khi đó
A. H là trọng tâm của BCD .
B. H là trực tâm của BCD .
C. H là giao ba đường trung trực của BCD .
D. H là giao ba đường phân giác của BCD
Lời giải:
D

A B C E
H
Trong BCD có: BACD tại A (do ABC vuông tại A ) BA là một đường cao của BCD DEBC tại E (do HEBC ) DE là một đường cao của BCD
Mà DE giao BA tại H
Do đó H là giao điểm của hai đường cao trong BCD
Suy ra H là giao điểm của ba đường cao trong BCD
Vậy H là trực tâm của BCD .
Chọn đáp án B
Bài 5. Cho tam giác ABC vuông tại ,A đường cao AH . Tìm trực tâm của các giác ,ABC ,AHB AHC
26
Tam giác ABC có hai đường cao là BA và AH . Từ đó suy ra trực tâm của tam giác ABC là A Chứng minh tương tự ta có trực tâm của tam giác , AHC đều là điểm H
Nhận xét: Trực tâm của tam giác vuông là đỉnh góc vuông của tam giác.
Bài 6. Cho H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác ,, HBCHABHAC
Lời giải

Gọi các đường cao tam giác là ,, AKBECF . Ta có: HBC có hai đường cao là , HKBF . Từ đó suy ra trực tâm của tam giác HBC là A
Chứng minh tương tự ta được trực tâm của tam giác ,HAB HAC lần lượt là C và B Bài 7. Cho ABC có 070 A , ABAC , đường phân giác góc A cắt BC tại D , BFAC tại F , H là giao điểm của BF và AD , E thuộc AC sao cho AEAB a) Xác định trực tâm của ABE . b) Tính số đo DHF . Lời giải
a) Gọi AD giao BE tại I Xét ABE có AEAB (gt)
D H
AHB I E F
B A C
27 Lời giải:
H C
A
B
Lại có: AD là tia phân giác góc A của ABC (gt) AIBE (tính chất của tam giác cân)
Mặt khác: BFAE và AD giao BE tại H nên H là trực tâm của ABE (tính chất 3 đường cao trong tam giác). b) Ta có: AD là tia phân giác của BAC (gt) ⇒ 0 1 35 2 HAFBAC
Dạng 2. Sử dụng tính chất trực tâm của tam giác để chứng minh hai đường thẳng vuông góc, ba đường thẳng đồng quy
I. Phương pháp giải: Nếu H là giao điểm hai đường cao kẻ từ B và C của tam giác ABC thì AHBC Nếu ba đường thẳng là ba đường cao của một tam giác thì chúng cùng đi qua một điểm.
II. Bài toán.
Bài 1. Cho ABC cân tại A , đường cao BE cắt đường trung tuyến AD ở H . Chứng minh CH tạo với AB một góc 90
Lời giải
A D

H E C B
Xét ABC cân tại A có: AD là đường trung tuyến (gt) AD cũng là đường trung cao. Lại có BE là đường cao mà BE cắt AD tại H H là trực tâm của ABC CHAB hay CH tạo với AB một góc 90 .
Bài 2. Cho tam giác ABC cân tại A . đường cao CH cắt tia phân giác của góc A tại D . Chứng minh rằng BDAC
28 ⇒ ABE
ạ
cân t
i A .
Vì AHF vuông tại F nên: 0000 90903555AHFHAF Vì DHF và AHF là 2 góc kề bù nên: 0000 18018055125DHFAHF
N

O Q P
M R
Kéo dài AD cắt BC tại E . Từ giả thiết suy ra AEBC . Do đó D là trực tâm của tam giác ABC Vậy BDAC Bài 3. Cho MNP vuông tại M . Trên cạnh MN lấy điểm Q , kẻ QRNPRNP . Gọi O là giao điểm của các đường thẳng PM và RQ . Chứng minh PQON . Lời giải: Ta có: ,NMPQ ORPN Mà NM giao OR tại Q Q là trực tâm của PON PQON .
Bài 4. Cho tam giác ABC cân tại A . Lấy điểm D sao cho A là trung điểm của BD Kẻ đường cao AE của tam giác ABC , đường cao AF của tam giác ACD . Chứng minh rằng .AEAF Lời giải:
Xét tam giác cân ABC có AE là đường cao, suy ra AE cũng là đường phân giác của BAC hay BAEEAC Tương tự trong tam giác cân ACD ta có CAFFAD . Từ đó ta được
29 Lời giải
hay .AEAF
Bài 5. Cho tam giác MNP có ba góc nhọn, các đường cao , NQPR cắt nhau tại S
a) Chứng minh MSNP b) Cho MNP = 65°. Tính SMR .
Lời giải:
a) Vì S là trực tâm MNP , do đó MSNP . b) Gọi H là giao điểm của MS với NP . Chú ý MHN vuông, từ đó tính được 25 SMR

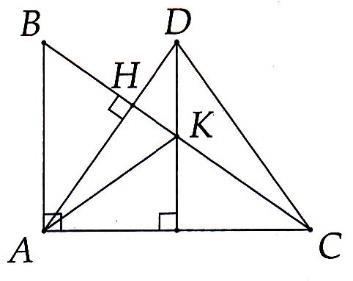
Bài 6. Cho tam giác ABC vuông tại A , kẻ đường cao AH . Lấy điểm K thuộc đoạn thẳng HC . Qua K kẻ đường thẳng song song với AB , cắt AH tại D . Chứng minh AKCD . Lời giải: Vì ABAC , do đó DKAC Bởi vậy K là trực tâm ADC , suy ra AKCD .
Bài 7. Cho tam giác ABC vuông cân tại B Trên cạnh AB lấy điểm H Trên tia đối của tia BC lấy điểm D sao cho BHBD Chứng minh a) DHAC b) CHAD Lời giải:
1 ()902 EAFEACCAFBACCAD
a) Kéo dài DH cắt AC tại M . Do BHBD và 90 DBA nên tam giác DBH vuông cân tại .B Suy ra 459090MDCCMDCCMDC DHAC b) ADC có hai đường cao AB và DM cắt nhau tại H nên H là trực tâm của tam giác đó. Do vậy, CHAD . Bài 8. Cho tam giác MNP vuông tại M MPMN . Trên cạnh MN lấy điểm Q sao cho MQMP , trên tia đối của tia MP lấy điểm R sao cho MRMN . Chứng minh: a) PQNR . b) RQNP . Lời giải:
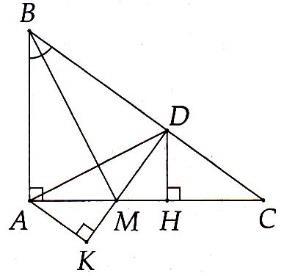
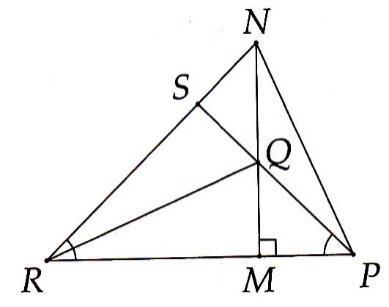

a) Gọi S là giao điểm của PQ và NR . Tính được 45 SPRSRP , từ đó PQNR . b) Từ kết quả ý a, ta có Q là trực tâm PNR RQNP Bài 9. Cho tam giác ABC vuông tại A , kẻ đường phân giác BM . Trên cạnh BC lấy điểm D sao cho BDBA . a) Chứng minh BMAD b) Gọi H là hình chiếu vuông góc của D trên , ACK là hình chiếu vuông góc của A trên DM Chứng minh ba đường thẳng ,, AKBMDH đồng quy. Lời giải:
a) Chú ý tam giác ABD cân tại B nên BM là đường phân giác cũng là đường cao, từ đó BMAD
31
b) Chú ý ,, AKBMDH là ba đường cao của AMD

Bài 10. Đoạn thẳng AB và điểm M nằm giữa A và () BMAMB . Vẽ tia đó lấy hai điểm C và D sao cho ,. MAMCMDMB Tia AC vuông cắt BD tại E . Chứng minh: a) AEBD b) C là trực tâm của tam giác ABD Lời giải: a) Do tia AC cắt BD tại E nên hai điểm C và D nằm cùng phía với AB Do MAMC và 90 AMC nên tam giác AMC vuông cân tại .M Tương tự ta có BMD vuông cân tại .M Từ đó suy ra 4590EDCDCECED ACBD
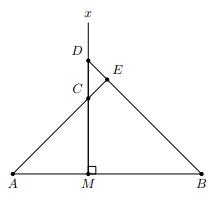

b) Trong tam giác ABD , hai đường cao AE và DM cắt nhau nên C là trực tâm của tam giác ABD .
Bài 11. Cho góc nhọn xOy . Trên tia Ox lấy điểm A , trên tia Oy lấy điểm B sao cho OAOB Kẻ ,(,) ACOyBDOxCOxDOy . Đường thẳng vuông góc với Ox tại A và đường thẳng vuông góc với Oy tại B cắt nhau tại M . Chứng minh: ,, OMACBD đồng quy. Lời giải:
Xét hai tam giác vuông AOM và BOM có: OM là cạnh chung. OAOB (giả thiết) Suy ra AOMBOM (cạnh huyền - cạnh góc vuông). Do đó, .AOMBOM
32
Vậy OM là tia phân giác của tam giác cân AOB . Suy ra OM là đường cao hay .OMAB
Xét trong tam giác AOB có ba đường cao ,, OMACBD do đó ,, OMACBD đồng quy.
Bài 12. Cho tam giác ABC vuông tại A có BD là đường phân giác. Trên cạnh BC lấy điểm E sao cho BABE Vẽ CHDB Chứng minh rằng ,, BADECH đồng quy.
Lời giải:
Gọi I là giao điểm của CH và .AB Ta có D là trực tâm của tam giác IBC suy ra IDBC (1)
Xét BAD và BED có:
ABAE (gt);
ABDEBD ( BD là đường phân giác)
BD : cạnh chung
BADBED (c.g.c)
90 BEDBAD (hai góc tương ứng)
DEBC (2)
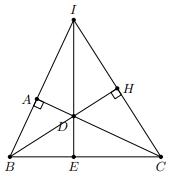
Từ (1) và (2) suy ra ,, IDE thẳng hàng hay ,, BADECH đồng quy.

33
ng 3. Vận dụng tính chất ba đường cao trong tam giác để giải quyết các bài
I. Phương pháp giải: Dựa vào định lí, tính chất về sự đồng quy của ba đường cao trong tam giác.
II. Bài toán. Bài 1. Cho ABC đều. a đường cao ,, AMBNCP c t nhau t i O . Chứng minh rằng:
a) OAOBOC b) O là tr ng t m của ABC c) AMBNCP Lời giải:

a) Vì ABC đều nên ABC cân ở cả 3 đinh nên ba đường cao ,, AMBNCP đồng thời là ba đường trung trực, ba đường trung tuyến của tam giác. Vì ,, AMBNCP là ba đường trung trực nên OAOBOC (1) b) Vì ,, AMBNCP là ba đường trung tuyến nên O là tr ng t m của ABC c) Vì O là tr ng t m của ABC suy ra 222 ,, 333 OAAMOBBNOCCP (2)
Từ (1) (2)suy ra AMBNCP Bài 2. Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nh n) bằng nhau thì tam giác đó là tam giác c n. Lời giải
Xét ABC có hai đường cao , BECF và BECF
Xét hai tam giác vuông CBF và CBE có: BC là c nh chung. BECF (giả thiết)
1 Dạ
khác
toán
M P N A B C O E F A B C
Suy ra CBFCBE (c nh huyền - c nh góc vuông).
Từ đó suy ra CBFBCE . Hay ABC cân t i A
Bài 3. Chứng minh rằng một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.
Lời giải
Xét tam giác ABC có hai đường cao ,, AHBECF và AHBECF
Xét hai tam giác vuông CBF và CBE có
BC là c nh chung.
BECF (giả thiết)
Suy ra CBFCBE (c nh huyền – c nh góc vuông).
Suy ra CBFBCE (1)
Xét hai tam giác vuông ABH va BAE có
AB là c nh chung. AHBE (giả thiết).
Suy ra ABH BAE (c nh huyền – c nh góc vuông).
Suy ra ABHBAE (hai c nh tương ứng) (2)
Từ (1) (2) suy ra CBFBCE BAE
Vậy ABC có ba góc bằng nhau nên ABC là tam giác đều. Bài 4. Cho ABC vuông t i A , kẻ đường cao AH và trung tuyến AM . Chứng minh trực tâm của ABC , MAB và MAC thẳng hàng. Lời giải
A
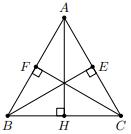

H B
Vì AH là đường cao của ABC nên trực tâm của ABC thuộc đường thẳng AH 1 Có: AH là đường cao của ABC
2
C M
Xét ABM có AHBM
Trực tâm của ABM thuộc đường thẳng AH 2
Xét ACM có AHCM Trực tâm của ACM thuộc đường thẳng AH 3 Từ 1;2;3 Trực tâm của ;; ABCABMACM thẳng hàng Bài 5. Cho tam giác ABC vuông t i A . Đường cao .AH Lấy I là trung điểm của .AC
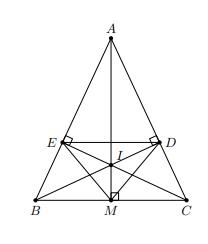
a) Chứng minh I là giao điểm của 3 đường trung trực AHC b) G i K và D lần lượt là trung điểm của AH và HC Chứng minh // KDAC . c) Chứng minh BKAD . Lời giải
a) Ta có HI là đường trung tuyến ứng với c nh huyền AC của tam giác vuông AHC nên IH 2 AC IAIC . Do đó, I là giao điểm của ba đường trung trực của .AHC
b) Do I là giao điểm của ba đường trung trực của AHC nên IDHC , suy ra // IDAH . Tương tự ta có //.IKHC

Từ đó ta chứng minh được IHKIDC (c.g.c). Suy ra ,. KHIDKIHD
Ta chứng minh được KHDIDC (c.g.c). Suy ra KDHICD , do đó //.KDAC
c) Do // KDAC nên KDAB . Trong ABD , hai đường cao KD và AH c t nhau t i K nên K là trực tâm của tam giác. Do đó .BKAD Bài 6. Cho tam ABC cân t i ,A hai đường cao BD và CE c t nhau t i ( ID ,) ACEAB . Tia AI c t BC t i M Chứng minh
a) M là trung điểm của BC
b) Tam giác MED là tam giác cân. Lời giải
, AHBCAHBMAHCM
a) Hai đường cao BC và CE c t nhau t i I nên I là trực tâm của tam giác .ABC Do đó .AIBC Hơn nữa, do tam giác ABC cân t i A nên đường cao AI cũng đồng thời là đường trung tuyến. Do đó, M là trung điềm của .BC b) Trong tam giác vuông ,BEC do EM là đường trung tuyến ứng với c nh huyền BC nên 1 2 EMBC . Tương tự, 1 . 2 DMBC Do đó ,EMDM suy ra MED là tam giác cân t i M Bài 7. Cho tam giác ABC cân t i ,A đường trung tuyến AM và đường phân giác BD c t nhau t i .K G i E là giao điểm của CK và .AB Chứng minh .BDCE Lời giải
ABC cân t i A nên đường trung tuyến AM cũng đồng thời là đường phân giác. Hai đường phân giác AM và BD c t nhau t i K . Do đó, CK là đường phân giác thứ ba của tam giác ABC ABC cân t i A nên .BC
Mà 1 2 DBCB ( BD là đường phân giác) 1 2 ECBC (CK là đường phân giác) DBCECB
Xét hai tam giác BDC và ECB có DBCECB (chứng minh trên) : BC c nh chung
EBCDCB ( ABC cân t i A )

Suy ra BDCECB (g.c.g)
Do đó, BDCE (hai c nh tương ứng)
Bài 8. Cho tam giác .ABC Hai đường cao , AHBK c t nhau t i .I
a) Chứng minh rằng .CIAB b) Khi 50, ACH hãy tính các góc ,.BIHHIK

4
a) Ta có I là trực tâm của tam giác chất đồng quy của ba đường cao, suy ra .CIAB b) Vì tam giác BKC vuông t i K nên 9040.KBCACB Mà tam giác BIH vuông t i H nên 9040BIHKBCBIH Vì hai góc HIK và BIH kề bù nên ta 180. HIKBIH Từ đó tính được 140 HIK Bài 9. Cho tam giác ABC cân t i A Hai đường cao xuất phát từ đỉnh B và đỉnh C c t nhau t i M Biết góc 120, BMC tính các góc của tam giác ABC Lời giải



G i , EF lần lượt là ch n đường cao h từ đỉnh , BC của tam giác .ABC Ta có 120 BMC nên góc 60 CME
Vì tam giác CME vuông t i E nên 90. MCACME Mặt khác tam giác AFC vuông t i F nên ta có 90. BACACF Suy ra 60. BACCME
5 Lời giải
Bài 10. Cho tam giác ABC cân t i , AM là trung điểm của ,.BC G i H và K lần lượt là chân các đường vuông góc kẻ từ M đến AB và .AC Chứng minh .MHMK
Lời giải

Tam giác ABC cân t i A nên AM đồng thời là đường trung tuyến và đường phân giác. L i có , MHABMKAC nên theo tính chất đường phân giác của một góc, có .MHMK
Phần III. BÀI TẬP TỰ LUYỆN
BA ĐƯỜNG TRUNG TRỰC
Dạng 1. Xác định tâm đường tròn ngoại tiếp tam giác
Bài 1. Cho ABC cân t i A , đường trung tuyến AM . Đường trung trực của AB c t AM ở O . Chứng minh rằng điểm O cách đều ba đỉnh của ABC Bài 2. Cho ABC cân t i A , O là giao điểm của ba đường trung trực. Lấy điểm D trên c nh AB , điểm E trên c nh sao cho ADCE . Chứng minh rằng a) OAOBOC b) Điểm O nằm trên đường trung trực của DE .
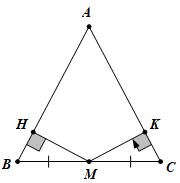
Bài 3. Nhà b n Nam có một mảnh vườn nhỏ trồng hoa và cỏ nhật. Bố của b n Nam nhờ Nam ch n vị trí để đặt vòi xoay phun tưới cây tự động sao cho vị trí đó cách đều ba khóm hoa ở ba góc vườn nhưng Nam l i chưa biết tìm như thế nào. Các em hãy giúp b n Nam giải quyết vấn đề này nhé.
Bài 4. Ông Hùng có ba cửa hàng ,, ABC không nằm trên một đường thẳng và đang muốn tìm địa điểm O để làm kho hàng. Phải ch n vị trí của kho hàng ở đ u để khoảng cách từ kho đến các cửa hàng bằng nhau?
Dạng 2. Chứng minh ba đường thẳng đồng quy, ba điểm thẳng hàng
6 Vì tam giác ABC cân t i A nên 60 ABCACB
Bài 5. Cho tam giác ABC cân ở ,A đường phân giác .AK Các đường trung trực của AB
AC c t nhau t i .O
a) Chứng minh rằng ba điểm , , AKO thẳng hàng.
b) Kéo dài CO c t AB ở ,D kéo dài BO c t AC ở .E Chứng minh rằng AK và các đường trung trực của AD và AE đồng quy.
Bài 6. Cho 90 xOy và điểm P nằm trong góc đó. Trên mặt phẳng đó lấy điểm A sao cho Ox là đường trung trực của đo n thẳng PA và điểm B sao cho Oy là đường trung trực của đo n thẳng PB .
a) Chứng minh ba điểm ,, OAB thẳng hàng.

b) Chứng minh O là giao điểm của ba đường trung trực của ABP từ đó suy ra ABP vuông.
Bài 7. Cho tam giác MNP cân ở M , đường cao MH . Các đường trung trực của MN và MP c t nhau ở D . Chứng minh ba điểm ,, MDH thẳng hàng.
Bài 8. Cho tam giác ABC cân có A là góc tù. G i M là trung điểm của BC N nằm trong tam giác ABC sao cho tam giác BNC cân t i N . Chứng minh đường thẳng AM và các đường trung trực của , NBNC đồng quy.
Dạng 3. Vận dụng tính chất ba đường trung trực trong tam giác để giải quyết các bài toán khác
Bài 9. Cho ABC có ˆ 110 A . Các đường trung trực của c nh AB và AC lần lượt c t BC ở E và F . Tính EAF .
Bài 10. Cho ABC cân t i A , 090 A . Các đường trung trực của AB và của AC c t nhau t i O và c t BC t i D và E Chứng minh rằng: a) OA là đường trung trực của BC . b) BDCE c) ODE là tam giác cân. Bài 11. Cho M là giao điểm 3 đường trung trực của tam giác ABC . Chứng minh rằng nếu M nằm trên một c nh của tam giác ABC thì ABC là một tam giác vuông. Bài 12. Cho ABC , đường ph n giác AIIBC . Trên đo n thẳng IC lấy điểm H , từ H kẻ đường thẳng song song với AI c t AB kéo dài t i E và c t AC t i F . Chứng minh rằng: a) Đường trung trực của đo n thẳng EF đi qua đỉnh A của ABC b) Đường trung trực của đo n thẳng EF vuông góc với AI . c) Khi H di động trên tia IC của ABC cố định thì đường trung trực của đo n thẳng EF cố định. Bài 13. Cho ABC có ba góc nh n. Các điểm ,, FKI lần lượt là trung điểm các c nh ,, BCBAAC . G i H là giao điểm các đường trung trực ABC . Trên tia đối của tỉa FH lấy
7
và
điểm 1A sao cho 1 AFFH . Trên tia đối của tia KH lấy điểm 1C sao cho 1KHKC . Trên tia đối của tia IH lấy điểm 1B sao cho 1IHIB
a) Chứng minh rằng hình lục giác 111 ACBACB có 6 c nh bằng nhau và 2 trong 6 c nh đó đôi một song song.
b) Chứng minh rằng: ABC = 111ABC BA ĐƯỜNG CAO
Dạng 1. Xác định trực tâm của một tam giác

Bài 14. Cho ABC , các đường cao ,, AKBNCM . Điểm H là trực t m của tam giác. Tìm trực t m của BHC , AHC , AHB Bài 15. Cho tam giác ABC , hai đường cao BD và CE . G i M là trung điểm của BC Chứng minh M thuộc trung trực của DE
Bài 16. Đo n thẳng AB và điểm M nằm giữa A và () BMAMB . Vẽ tia Mx vuông AB lấy hai điểm C và D sao cho ,. MAMCMDMB Tia AC vuông c t BD t i E . Chứng minh 1. AEBD
2. C là trực tâm của tam giác ABD .
Dạng 2. Sử dụng tính chất trực tâm của tam giác để chứng minh hai đường thẳng vuông góc, ba đường thẳng đồng quy
Bài 17. Cho tam giác LMN nh n và điểm S nằm trong tam giác. G i LS c t MN t i P , MS c t LN t i Q . Chứng minh rằng nếu LP vuông góc với MN và MQ vuông góc với LN thì NS vuông góc với ML .
Bài 18. Cho MNP cân t i M , đường cao PQ c t đường phân giác MS ở K . Chứng minh NKMP
Bài 19. Cho ABC vuông t i A , kẻ đường cao AH . Lấy điểm K thuộc đo n thẳng HC . Qua K kẻ đường thẳng song song với AB , c t AH t i D . Chứng minh AKCD .
Bài 20. Cho MNP vuông t i MMPMN . Trên c nh MN lấy điểm Q sao cho MQMP , trên tia đối của tia MP lấy điểm R sao cho MRMN . Chứng minh:
8
a) PQNR . b) RQNP . Dạng 3. Vận dụng tính chất ba đường cao trong tam giác để giải quyết các bài toán khác Bài 21. Cho MNP có ba góc nh n, các đường cao , NQPR c t nhau t i S. a) Chứng minh MSNP . b) Cho 065 MNP . Tính SMR . Bài 22. Cho ABC vuông t i A , kẻ đường phân giác BM . Trên c nh BC lấy điểm D sao cho BDBA a) Chứng minh BMAD .
b) G i H là hình chiếu vuông góc của D trên AC , K là hình chiếu vuông góc của A trên DM . Chứng minh ba đường thẳng ,, AKBMDH đồng quy.
ĐÁP SỐ BÀI TẬP TỰ LUYỆN
BA ĐƯỜNG TRUNG TRỰC
Dạng 1. Xác định tâm đường tròn ngoại tiếp tam giác
Bài 1.

ABC cân t i A có AM là đường trung tuyến của c nh đáy BC nên AM cũng là đường trung trực của BC
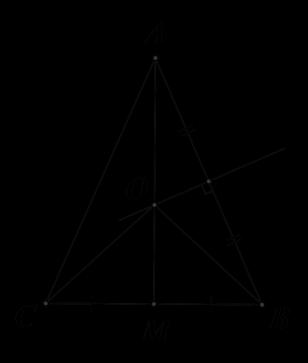
Vì đường trung trực của AB c t AM ở O ABC nên O là giao điểm của ba đường trung trực của ABC . Vậy O cách đều ba đỉnh của ABC
2.

9
m O là
điểm 3
ự
ủ
. b)
OAOC nên
21
(1)
A
12 AA (2) Từ (1) và (2) 111()ACA Xét
và OCE có: ADCE (gt) 11 AC (cmt)
Bài
a) Điể
giao
đường trung tr
c c
a ABC
nên OAOBOC
Ta có
AOC
cân t i O
AC
ABC
cân t i
, AO là đường trung trực nên AO là đường phân giác của BAC
OAD
Do đó, (c.g.c)OADOCE
ODOE (hai c nh tương ứng)
Vậy O nằm trên đường trung trực DE .
Bài 3.
G i vị trí ba khóm hoa đó lần lượt là ,, ABC và vị trí cần đặt vòi xoay phun tưới cây tự động là O thì điểm O cách đều ba điểm ,, ABC Do đó O là giao của ba đường trung trực của tam giác ABC hay O là t m đường tròn ngo i tiếp tam giác ABC Để xác định vị trí điểm O ta chỉ cần xác định giao điểm của hai trong ba đường trung trực của tam giác ABC .
Bài 4.

Vì điểm O cách đều ba điểm ,, ABC nên O là giao của ba đường trung trực của tam giác ABC hay O là t m đường tròn ngo i tiếp tam giác ABC .


Để xác định vị trí điểm O ta chỉ cần xác định giao điểm của hai trong ba đường trung trực của tam giác ABC
Dạng 2. Chứng minh ba đường thẳng đồng quy, ba điểm thẳng hàng
Bài 5.
10 OAOC
1 2 2 1
K
a) Ta có ABDACD (c.g.c). Từ đó suy ra AD là đường trung trực của .BC
Xét ABC , theo tính chất ba đường trung trực của tam giác nên O thuộc đường trung trực của BC Vậy ba điểm , , ADO thẳng hàng.
b) Ta có 21 , ABCACBBB 11. BC Chứng minh ADCAEB (g.c.g), suy ra 1. ADAE

Măt khác, có , OBOCBECD (vì ADCAEB ) nên 2. ODOE
Từ 1 và 2 suy ra AK là đường trung trực của BC
Xét ADE , theo tính chất ba đường trung trực của tam giác suy ra AK và các đường trung trực của AD và AE đồng quy.
Bài 6.

a) Xét AOP có: Ox là đường trung trực của PA nên , OAOPIAIP
Xét hai tam giác vuông OAI và OPI có: , OAOPIAIP
11
O
E D
OAI OPI (ch-cgv) 12OO (1) A
C B
Xét BOP có: Oy là đường trung trực của PB nên , OBOPEBEP
Xét hai tam giác vuông OBE và OPE có: , OBOPEBEP OBEOPE (ch-cgv) 34OO (2) Từ (1)(2) suy ra 1423 90 OOOO 1423232180AOBOOOOOO
Suy ra ba điểm ,, OAB thẳng hàng. b) Ta có OAOP và OBOP theo chứng minh c u a. OAOBOP O nằm trên đường trung trực của AB .
Xét ABP có:
Ox là đường trung trực của PA
Oy là đường trung trực của PB
O nằm trên đường trung trực của AB
Suy ra O là giao điểm của ba đường trung trực của ABP
Mà O nằm trên c nh AB của ABP nên ABP là tam giác vuông (Theo chứng minh Bài 1 mục III của chuyên đề này)
Bài 7.
Chứng minh được: MNHMPH (c nh huyền – c nh góc vuông).
Từ đó, suy ra MH là đường trung trực của NP .
Theo tính chất ba đường trung trực của tam giác, ta suy ra điểm D thuộc đường trung trực của NP .
Vậy ba điểm ,, MDH thẳng hàng.
Bài 8.

12
D D E H N P M
Từ giả thiết, ta có: , ABACNBNC . AN là đường trung trực của BC hay ,, ANM thẳng hàng. Xét NBC , theo tính chất ba đường trung trực trong tam giác ta có các đường trung trực của NB và NC đồng quy với đường thẳng AM Dạng 3. Vận dụng tính chất ba đường trung trực trong tam giác để giải quyết các bài toán khác Bài 9. Ta có E nằm trên đường trung trực của AB nên EAB cân ở EEABEBA Tương tự F nằm trên đường trung trực của AC nên FAC cân ở FFACFCA Ta có EAFBACBAECAF

13
M B C A N F
D E H K B C A
1107040 BACEBAFCA Bài 10.
E B C A

14
của
BHCK ABCACB
Vì
2
1
Trong
có 180
12 180 BAAC 12 180 BAAC Từ
12
1
B
C
a) Vì điểm O là giao điểm các đường trung trực của ABC nên O thuộc đường trung trực
BC . ABC cân t i A ABAC A thuộc đường trung trực của BC . Vậy AO là đường trung trực của BC . b) G i H là trung điểm của AB , K là trung điểm của AC Xét HBD và KCE có: 090 BHDCKE
( ABC cân t i A ) Do đó, (..)HBDKCEgcg BDCE (2 c nh tương ứng) c) HBDKCEHBDKEC
(2 góc tương ứng) mà , ODEOED lần lượt đối đỉnh với , HBDKEC ODEOEDODE cân t i O . Bài 11. Giả sử M nằm trên c nh BC của ABC
M là giao điểm 3 đường trung trực của tam giác ABC nên MAMBMC
Xét ABM có MAMB
nên ABM là tam giác cân.
BA (1) Xét ACM có MAMC
nên ACM là tam giác cân.
AC (2)
ABC
BAC
(1) (2) suy ra
22180 AA
2
M A
12 9090AAA ABC là tam giác vuông t i A.
Bài 12.








a) Ta có // AIEH 1 AE (đồng vị) và 21 AF (so le trong)
Mà 12AA (AI là tia ph n giác của BAC ) nên 1EF EAF là tam giác c n ở A AEAF điểm A thuộc đường trung trực của EF trung trực của đo n thẳng EF đi qua đỉnh A của ABC
b) G i đường trung trực của EF c t EF t i K .
Ta có // AIEH mà AKEH AKAI Vậy đường trung trực của đo n thẳng EF vuông góc với AI .
c) ABC cố định nên đường ph n giác AI cố định, Mà AKAI nên AK cũng cố định. Suy ra khi điểm H chuyển động trên IC thì AK luôn cố định hay đường trung trực của EF luôn cố định.
13.
15 12 2.180 AA
Bài
1 F K C H A I B E 1 2
+ Xét AKH và 1BKC là hai tam giác vuông có: AKKB , 1KHKC AKH 1BKC (hai c nh góc vuông) 1AHBC (1) và 1 1AB Vì 1 1AB và ở vị trí so le trong 1 // AHBC (2) + Xét AIH và 1CIB là hai tam giác vuông có: HIIB , AIIC AIH 1CIB (hai c nh góc vuông) 1AHCB (3) và 2 1AC Vì 2 1AC và ở vị trí so le trong 1 // AHCB (4) Từ (1)và (3) 11 // BCCB (//AH ) Từ (2)và (4) 11 = BCCB ( AH ) + Chứng minh tương tự ta có 11 // ACCA và 11 = ACCA ; 11 // BAAB và 11 = BAAB Mà H là giao điểm ba đường trung trực của ABC nên AHBHCH Do đó 111111 BCCBACCAABBA b)


16
Kẻ 11 , BBAA Xét 1BCB và 11B BC có: 11 = BCCB (chứng minh trên) 11 1BBCBBC (2 góc so le trong của 11 // BCC B ) 1BB là c nh chung 1BCB 11B BC (c.g.c) 11 = BCC B Chứng minh tương tự ta được 11 ABAB , 11ACAC
Xét 111ABC và ABC có: 11C BBC , 11 ABAB , 11ACAC 111ABC ABC (c.c.c) BA ĐƯỜNG CAO Dạng 1. Xác định trực tâm của một tam giác Bài 14. *) Các đường cao của BHC là: ,, HKBNCM c t nhau t i A .Vậy trực t m của BHC


17
là A .
N M B A C K H
*) Các đường cao của AHC là: , , HMANCK c t nhau t i B . Vậy trực t m của AHC là B
*) Các đường cao của AHB là: ,, HMAMBK c t nhau t i C . Vậy trực t m của AHB là C .
Bài 15.

Ta có EM là đường trung tuyến trong EBC vuông ở E , do đó 1 1 2 EMBC .
Tương tự ta có ED là đường trung tuyến trong DBC vuông ở D , do đó 1 2 2 DMBC
Từ (1),(2) suy ra MEMD , do đó M nằm trên đường trung trực của ED .
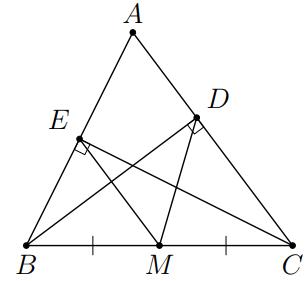
Bài 16.
x E D C A B M
a) Do tia AC c t BD t i E nên hai điểm C và D nằm cùng phía với AB
Do MAMC và 90 AMC nên tam giác AMC vuông cân t i .M Tương tự ta có BMD vuông cân t i .M
Từ đó suy ra 45 EDCDCECED 90. ACBD
b) Trong tam giác ABD , hai đường cao AE và DM c t nhau nên C là trực tâm của tam giác ABD Dạng 2. Sử dụng tính chất trực tâm của tam giác để chứng minh hai đường thẳng vuông góc, ba đường thẳng đồng quy Bài 17.
18

19
Vì MQ LN , LN MN S là trực t m của LMN NSML
() //AB(gt) ABACgt DK
(quan
ệ từ vuông
S Q
L S
C
Bài 18. Xét MPN cân t i M có MS là đường phân giác (gt) MSPN L i có PQMN K là trực tâm của MPN NKMP . Bài 19. Ta có:
DKAC
h
góc đến song song) L i có: CHAD và DK giaoCH t i K K là trực tâm của ADC AKCD Bài 20.
P M N
M P N Q K K H D
B A

20
M N Q S R
S N
P
a) G i RN giao PQ t i S Ta có: ()MQMPgt MPQ cân t i M Có 00 00 18090 9045 2 NMPSPR Tương tự: 000 0 18018090 45 22 RMN SRP L i có: 0180 RSPSRPSPR ( định lí tổng ba góc trong tam giác) 00 18090RSPSRPSPR PQNR . a) Xét PRN có: ()NMRPgt và ()PSRNcmt mà NM giao PS t iQ Q là trực tâm của PRN RQNP Dạng 3. Vận dụng tính chất ba đường cao trong tam giác để giải quyết các bài toán khác Bài 21. a) Xét MNP có: ()PRMNgt , ()NQMPgt S là trực tâm của MNP MSNP
P
M R H Q
Bài 22.
a) Ta có: ()BABDgt BAD cân t i B
L i có: BM là đường phân giác (gt) BMAD . b) Xét AMD có: BMAD AKMD DHAM
a đường thẳng ,, AKBMDH là ba đường cao của AMD a đường thẳng ,, AKBMDH đồng quy.
PHIẾU BÀI TẬP

BA ĐƯỜNG TRUNG TRỰC
Dạng 1. Xác định tâm đường tròn ngoại tiếp tam giác Bài 1. Ch n đáp án đúng. Điểm cách đều 3 đỉnh của tam giác là giao điểm của:
A. 3 đường trung tuyến. . 3 đường ph n giác. C. 3 đường trung trực. D. 3 đường cao. Bài 2. Ch n đáp án đúng.
a) Cho ABC tù, giao điểm 3 đường trung trực của tam giác nằm:
A. trong ABC B. ngoài ABC . C. trên 1 c nh của ABC .
21 b) G i MS giao NP t
H
i
MHNPNMH vuông t i H 090 SMRMNH 0000 90906525SMRMNH
K
C
H D M A B
D. trùng với 1 đỉnh của ABC
b) Cho ABC có 90 A thì t m đường tròn ngo i tiếp tam giác:
A. nằm trong ABC
. nằm ngoài ABC
C. là trung điểm của c nh BC
D. trùng với đỉnh A của ABC
c) Cho ABC nh n, giao điểm 3 đường trung trực của tam giác nằm:
A. trong ABC
B. ngoài ABC

C. trên một c nh của ABC
D. trùng với một đỉnh của ABC
Bài 3. Cho ΔABC . Vẽ điểm O cách đều ba đỉnh ,, ABC và vẽ đường tròn đi qua 3 đỉnh của tam giác trong mỗi trường hợp sau:
a) ΔABC là tam giác nh n.
b) ΔABC vuông t i A .
c) ΔABC là tam giác tù.
Bài 4. Cho ,, ABC là ba điểm phân biệt không thẳng hàng. Xác định đường tròn đi qua ba điểm đó.
Bài 5. Cho ABC có 90 A . Các đường trung trực của AB và của AC c t nhau ở O và c t BC theo thứ tự ở D và E . Nối ,,, ADAEOBOC . Tìm tam giác bằng OAD , bằng OAE
Bài 6. Cho ABC vuông t i A , đường cao AH . Tia phân giác của các góc BAH và CAH c t BC lần lượt ở D và E . G i O là giao điểm các đường phân giác của tam giác ABC
a) Chứng minh rằng đường tròn tâm O , bán kính OA đi qua ba điểm ,, ADE
b) Tính số đo góc DOE
Bài 7. Tam giác ABC có A là góc tù. Các đường trung trực của các c nh AB và AC c t nhau ở .O Các điểm B và C có thuộc đường tròn tâm O bán kính OA hay không? Vì sao? Bài 8. Cho ABC có ba góc nh n, O là giao điểm hai đường trung trực của AB và AC . Trên tia đối của tia OB lấy điểm D sao cho OBOD .
a) Chứng minh O thuộc đường trung trực của AD và CD
b) Chứng minh các ABD , CBD vuông.
c) Biết 70 ABC . Hãy tính số đo ADC .
Bài 9. Tam giác ABC có ba đường trung tuyến c t nhau t i O . iết rằng điểm O cũng là giao điểm của ba đường trung trực trong tam giác ABC . Chứng minh tam giác ABC đều.
22
Bài 10. Cho ABC đều. Trên c nh ,, ABBCCA lấy theo thứ tự ba điểm ,, MNP sao
a. Chứng minh MNP là tam giác đều
b. G i O là giao điểm các đường trung trực của ABC .
Chứng minh rằng điểm O cũng là giao điểm các đường trung trực của MNP
Bài 11. Trong một buổi tổng vệ sinh s n trường, 3 tổ cần d n cỏ và rác của 3 bồn cây ,, ABC ở 3 góc s n trường. Em hãy giúp 3 tổ ch n một vị trí O để đặt chiếc xe đẩy rác sao cho vị trí chiếc xe cách đều 3 bồn c y đó. Dạng 2. Chứng minh ba đường thẳng đồng quy, ba điểm thẳng hàng
Bài 1. Cho ABC cân t i A . Dựng tam giác BCD cân t i D biết D khác phía với A đối với đường đường thẳng BC . G i O là giao điểm của AB và AC . Chứng minh rằng ,, AOD thẳng hàng.
Bài 2. Cho ABC cân t i A . G i M là trung điểm của BC . Các đường trung trực của AB và AC c t nhau ở E .

Chứng minh ba điểm ,, AEM thẳng hàng.
Bài 3. Cho tam giác ABC cân t i A . G i G là tr ng tâm, O là giao điểm ba đường trung trực của tam giác ABC
a) Tam giác BOC là tam giác gì?
b) Chứng minh ba điểm ,, AOG thẳng hàng?
Bài 4. Cho tam giác ABC cân ở A . G i M là trung điểm của BC . Các đường trung trực của , ABAC c t nhau ở E . Chứng minh ba điểm ,, AEM thẳng hàng.
Bài 5. Cho tam giác ABC cân t i A . Lấy điểm D sao cho tam giác BCD cân t i D ( D và A nằm khác phía đối với đường thẳng BC ). Chứng minh các đường trung trực của AB và AC đồng quy với đường thẳng AD
Bài 6. Cho ABC vuông ở A , D là giao điểm hai đường trung trực của hai c nh AB và AC . Chứng minh ,, BDC thẳng hàng.
Bài 7. Cho tam giác ABC cân t i A . M là trung điểm của BC . Kẻ ME vuông góc AB t i , EMF vuông góc với AC t i F
a) Chứng minh rằng AM là đường trung trực của EF ?
b) Kẻ đường thẳng d vuông góc AB t i B , kẻ đường thẳng / d vuông góc với AC t i C , hai đường thẳng d và / d giao nhau giao t i D . Chứng minh rằng ba điểm ,, AMD thẳng hàng?
Bài 8. Cho tam giác nh n ABC . G i ,, HGO theo thứ tự là trực tâm, tr ng t m, giao điểm ba đường trung trực của tam giác. Tia AG c t BC ở M . G i I là trung điểm của , GAK là trung điểm của GH . Chứng minh:
a) 1 2 OMAH
23
cho AMBNCP
c) a điểm ,, HGO thẳng hàng

d) 2 GHGO
Bài 9. Cho tam giác ABC c n ở A , đường ph n giác AK . Các đường trung trực của AB và AC c t nhau t i O . Kéo dài CO c t AB ở D , kéo dài BO c t AC ở E .
a) Chứng minh ba điểm ,, AKO thẳng hàng.
b) Chúng minh AK và các đường trung trực của AD và AE đồng quy.
Dạng 3. Vận dụng tính chất ba đường trung trực trong tam giác để giải quyết các bài toán khác
Bài 1. Cho ABC cân t i A , đường trung tuyến AM . Đường trung trực của AC c t đường thẳng AM t i D . Chứng minh rằng DADB .
Bài 2. Cho tam giác cân ABC có ABAC . Hai đường trung trực của hai c nh ; ABAC c t nhau t i O . Chứng minh: AOBAOC
Bài 3. Cho ABC , M là trung điểm của .BC Các đường trung trực của AB và AC c t nhau t i O Tính số đo góc .OMB
Bài 4. Cho ABC có góc 110. A Đường trung trực của các c nh AB và AC c t nhau t i I a) Chứng minh BIC cân. b) Chứng minh 2180 BICBAC và tính số đo góc .BIC
Bài 5. Cho ABC có ˆ 60 A . Các đường trung trực của c nh AB và AC lần lượt c t BC ở E và F . Tính EAF
Bài 6. Cho ABC cân t i A . Đường trung tuyến AM c t đường trung trực của AC t i K . Chứng minh rằng .KAKBKC
Bài 7. Cho ABC cân t i A , 090 A . Các đường trung trực của AB và của AC c t nhau t i O và c t BC t i D và E . Chứng minh rằng: a) OA là đường trung trực của BC . b) BCCE
c) ODE là tam giác cân.
Bài 8. Chứng minh rằng các đường trung trực của tam giác vuông c t nhau t i trung điểm của c nh huyền.
Bài 9. Cho tam giác đều ABC . G i D và E là hai điểm lần lượt trên hai c nh AB và AC sao cho BDAE . Chứng minh rằng các đường trung trực của đo n thẳng DE luôn đi qua một điểm cố định khi D và E di chuyển trên các c nh AB và AC .
Bài 10. Cho ABC , ACAB . Hai điểm D và E theo thứ tự di chuyển trên các c nh AB và AC sao cho BDCE . Chứng minh rằng các đường trung trực của DE luôn đi qua một điểm cố định.
24
b) IGKMGO
Dạng 1. Xác định trực tâm của một tam giác
Bài 1. Cho ABC có 90 ABC , AHBC . Em ch n phát biểu đúng:
A. H là trực t m của ABC
B. A là trực t m của ABC
C. B là trực t m của ABC
D. C là trực t m của ABC
Bài 2. Cho ABC , hai đường cao AM và BN c t nhau t i H . Em ch n phát biểu đúng:
A. H là tr ng t m của ABC .
B. 2 3 HAAM và 2 3 HBBN
C. H là trực t m của ABC ; CH là đường cao của ABC
D. CH là đường trung trực của ABC .
Bài 3. Cho ABC c n t i A có AMBC t i M . Ch n phát biểu đúng:
A. AM là đường trung tuyến của ABC
B. AM là đường trung trực của BC .
C. AM là đường ph n giác của BAC .
D. Cả A, , C đều đúng.
Bài 4. Cho ABC vuông t i A . Lấy H thuộc AB , vẽ HEBC ở E . Tia EH c t tia CA t i D . Khi đó
A. H là tr ng t m của BCD
B. H là trực t m của BCD .
C. H là giao ba đường trung trực của BCD .
D. H là giao ba đường ph n giác của BCD
Bài 5. Cho tam giác ABC vuông t i ,A đường cao AH . Tìm trực tâm của các giác ,ABC ,AHB AHC
Bài 6. Cho H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác ,, HBCHABHAC
Bài 7. Cho ABC có 070 A , ABAC , đường phân giác góc A c t BC t i D , BFAC t i
F , H là giao điểm của BF và AD , E thuộc AC sao cho AEAB .
a) Xác định trực tâm của ABE .
b) Tính số đo DHF .
Dạng 2. Sử dụng tính chất trực tâm của tam giác để chứng minh hai đường thẳng vuông góc, ba đường thẳng đồng quy

25 BA ĐƯỜNG CAO
Bài 1. Cho ABC cân t i A , đường cao BE c t đường trung tuyến AD ở H Chứng minh CH t o với AB một góc 90
Bài 2. Cho tam giác ABC cân t i A . đường cao CH c t tia phân giác của góc A t i D Chứng minh rằng BDAC .
Bài 3. Cho MNP vuông t i M . Trên c nh MN lấy điểm Q , kẻ QRNPRNP . G i O là giao điểm của các đường thẳng PM và RQ . Chứng minh PQON .
Bài 4. Cho tam giác ABC cân t i A . Lấy điểm D sao cho A là trung điểm của BD Kẻ đường cao AE của tam giác ABC , đường cao AF của tam giác ACD . Chứng minh rằng .AEAF
Bài 5. Cho tam giác MNP có ba góc nh n, các đường cao , NQPR c t nhau t i S

a) Chứng minh MSNP b) Cho MNP = 65°. Tính SMR .
Bài 6. Cho tam giác ABC vuông t i A , kẻ đường cao AH . Lấy điểm K thuộc đo n thẳng HC . Qua K kẻ đường thẳng song song với AB , c t AH t i D . Chứng minh AKCD Bài 7. Cho tam giác ABC vuông cân t i B Trên c nh AB lấy điểm H Trên tia đối của tia BC lấy điểm D sao cho BHBD . Chứng minh a) .DHAC b) .CHAD Bài 8. Cho tam giác MNP vuông t i M MPMN . Trên c nh MN lấy điểm Q sao cho MQMP , trên tia đối của tia MP lấy điểm R sao cho MRMN . Chứng minh: a) PQNR . b) RQNP . Bài 9. Cho tam giác ABC vuông t i A , kẻ đường phân giác BM . Trên c nh BC lấy điểm D sao cho BDBA a) Chứng minh BMAD . b) G i H là hình chiếu vuông góc của D trên , ACK là hình chiếu vuông góc của A trên DM Chứng minh ba đường thẳng ,, AKBMDH đồng quy. Bài 10. Đo n thẳng AB và điểm M nằm giữa A và () BMAMB . Vẽ tia đó lấy hai điểm C và D sao cho ,. MAMCMDMB Tia AC vuông c t BD t i E . Chứng minh: a) AEBD b) C là trực tâm của tam giác ABD Bài 11. Cho góc nh n xOy . Trên tia Ox lấy điểm A , trên tia Oy lấy điểm B sao cho OAOB Kẻ ,(,) ACOyBDOxCOxDOy . Đường thẳng vuông góc với Ox t i A và đường thẳng vuông góc với Oy t i B c t nhau t i M . Chứng minh: ,, OMACBD đồng quy. Bài 12. Cho tam giác ABC vuông t i A có BD là đường phân giác. Trên c nh BC lấy điểm E sao cho BABE Vẽ CHDB Chứng minh rằng ,, BADECH đồng quy. Dạng 3. Vận dụng tính chất ba đường cao trong tam giác để giải quyết các bài toán khác
26
Bài 1. Cho ABC đều. a đường cao ,, AMBNCP c t nhau t i O . Chứng minh rằng:
a) OAOBOC . b) O là tr ng t m của ABC c) AMBNCP
Bài 2. Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nh n) bằng nhau thì tam giác đó là tam giác c n.
Bài 3. Chứng minh rằng một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.
Bài 4. Cho ABC vuông t i A , kẻ đường cao AH và trung tuyến AM . Chứng minh trực tâm của ABC , MAB và MAC thẳng hàng.
Bài 5. Cho tam giác ABC vuông t i A . Đường cao .AH Lấy I là trung điểm của .AC
a) Chứng minh I là giao điểm của 3 đường trung trực AHC b) G i K và D lần lượt là trung điểm của AH và HC Chứng minh // KDAC . c) Chứng minh BKAD .
Bài 6. Cho tam ABC cân t i ,A hai đường cao BD và CE c t nhau t i ( ID ,) ACEAB . Tia AI c t BC t i .M Chứng minh
a) M là trung điểm của BC b) Tam giác MED là tam giác cân.
Bài 7. Cho tam giác ABC cân t i ,A đường trung tuyến AM và đường phân giác BD c t nhau t i .K G i E là giao điểm của CK và .AB Chứng minh .BDCE
Bài 8. Cho tam giác ABC Hai đường cao , AHBK c t nhau t i I
a) Chứng minh rằng CIAB b) Khi 50, ACH hãy tính các góc ,.BIHHIK

Bài 9. Cho tam giác ABC cân t i A Hai đường cao xuất phát từ đỉnh B và đỉnh C c t nhau t i M Biết góc 120, BMC tính các góc của tam giác ABC
Bài 10. Cho tam giác ABC cân t i , AM là trung điểm của ,.BC G i H và K lần lượt là chân các đường vuông góc kẻ từ M đến AB và AC Chứng minh MHMK Phần III. BÀI TẬP
TỰ LUYỆN
BA ĐƯỜNG TRUNG TRỰC
Dạng 1. Xác định tâm đường tròn ngoại tiếp tam giác
Bài 1. Cho ABC cân t i A , đường trung tuyến AM . Đường trung trực của AB c t AM ở O . Chứng minh rằng điểm O cách đều ba đỉnh của ABC
Bài 2. Cho ABC cân t i A , O là giao điểm của ba đường trung trực. Lấy điểm D trên c nh AB , điểm E trên c nh sao cho ADCE . Chứng minh rằng a) OAOBOC
27
b) Điểm O nằm trên đường trung trực của DE
Bài 3. Nhà b n Nam có một mảnh vườn nhỏ trồng hoa và cỏ nhật. Bố của b n Nam nhờ Nam ch n vị trí để đặt vòi xoay phun tưới cây tự động sao cho vị trí đó cách đều ba khóm hoa ở ba góc vườn nhưng Nam l i chưa biết tìm như thế nào. Các em hãy giúp b n Nam giải quyết vấn đề này nhé.
Bài 4. Ông Hùng có ba cửa hàng ,, ABC không nằm trên một đường thẳng và đang muốn tìm địa điểm O để làm kho hàng. Phải ch n vị trí của kho hàng ở đ u để khoảng cách từ kho đến các cửa hàng bằng nhau?
Dạng 2. Chứng minh ba đường thẳng đồng quy, ba điểm thẳng hàng
Bài 5. Cho tam giác ABC cân ở ,A đường phân giác AK Các đường trung trực của AB và AC c t nhau t i .O
a) Chứng minh rằng ba điểm , , AKO thẳng hàng.
b) Kéo dài CO c t AB ở ,D kéo dài BO c t AC ở E Chứng minh rằng AK và các đường trung trực của AD và AE đồng quy.
Bài 6. Cho 90 xOy và điểm P nằm trong góc đó. Trên mặt phẳng đó lấy điểm A sao cho Ox là đường trung trực của đo n thẳng PA và điểm B sao cho Oy là đường trung trực của đo n thẳng PB
a) Chứng minh ba điểm ,, OAB thẳng hàng.

b) Chứng minh O là giao điểm của ba đường trung trực của ABP từ đó suy ra ABP vuông.
Bài 7. Cho tam giác MNP cân ở M , đường cao MH . Các đường trung trực của MN và MP c t nhau ở D . Chứng minh ba điểm ,, MDH thẳng hàng.
Bài 8. Cho tam giác ABC cân có A là góc tù. G i M là trung điểm của BC . N nằm trong tam giác ABC sao cho tam giác BNC cân t i N . Chứng minh đường thẳng AM và các đường trung trực của , NBNC đồng quy.
Dạng 3. Vận dụng tính chất ba đường trung trực trong tam giác để giải quyết các bài toán khác
Bài 9. Cho ABC có ˆ 110 A . Các đường trung trực của c nh AB và AC lần lượt c t BC ở E và F . Tính EAF . Bài 10. Cho ABC cân t i A , 090 A . Các đường trung trực của AB và của AC c t nhau t i O và c t BC t i D và E . Chứng minh rằng: a) OA là đường trung trực của BC . b) BDCE . c) ODE là tam giác cân. Bài 11. Cho M là giao điểm 3 đường trung trực của tam giác ABC . Chứng minh rằng nếu M nằm trên một c nh của tam giác ABC thì ABC là một tam giác vuông.
28
Bài 12. Cho ABC , đường ph n giác AIIBC . Trên đo n thẳng IC lấy điểm H , từ H kẻ đường thẳng song song với AI c t AB kéo dài t i E và c t AC t i F . Chứng minh rằng:
a) Đường trung trực của đo n thẳng EF đi qua đỉnh A của ABC
b) Đường trung trực của đo n thẳng EF vuông góc với AI .
c) Khi H di động trên tia IC của ABC cố định thì đường trung trực của đo n thẳng EF cố định.
Bài 13. Cho ABC có ba góc nh n. Các điểm ,, FKI lần lượt là trung điểm các c nh
,, BCBAAC . G i H là giao điểm các đường trung trực ABC . Trên tia đối của tỉa FH lấy điểm 1A sao cho 1 AFFH . Trên tia đối của tia KH lấy điểm 1C sao cho 1KHKC . Trên tia đối của tia IH lấy điểm 1B sao cho 1IHIB .
a) Chứng minh rằng hình lục giác 111 ACBACB có 6 c nh bằng nhau và 2 trong 6 c nh đó đôi một song song. b) Chứng minh rằng: ABC = 111ABC BA ĐƯỜ
NG CAO

Dạng 1. Xác định trực tâm của một tam giác
Bài 14. Cho ABC , các đường cao ,, AKBNCM . Điểm H là trực t m của tam giác. Tìm trực t m của BHC , AHC , AHB .
Bài 15. Cho tam giác ABC , hai đường cao BD và CE . G i M là trung điểm của .BC Chứng minh M thuộc trung trực của DE .
Bài 16. Đo n thẳng AB và điểm M nằm giữa A và () BMAMB . Vẽ tia Mx vuông AB lấy hai điểm C và D sao cho ,. MAMCMDMB Tia AC vuông c t BD t i E . Chứng minh 1. AEBD 2. C là trực tâm của tam giác ABD Dạng 2. Sử dụng tính chất trực tâm của tam giác để chứng minh hai đường thẳng vuông góc, ba đường thẳng đồng quy
Bài 17. Cho tam giác LMN nh n và điểm S nằm trong tam giác. G i LS c t MN t i P , MS c t LN t i Q . Chứng minh rằng nếu LP vuông góc với MN và MQ vuông góc với LN thì NS vuông góc với ML
Bài 18. Cho MNP cân t i M , đường cao PQ c t đường phân giác MS ở K Chứng minh NKMP
Bài 19. Cho ABC vuông t i A , kẻ đường cao AH . Lấy điểm K thuộc đo n thẳng HC . Qua K kẻ đường thẳng song song với AB , c t AH t i D . Chứng minh AKCD Bài 20. Cho MNP vuông t i MMPMN . Trên c nh MN lấy điểm Q sao cho MQMP , trên tia đối của tia MP lấy điểm R sao cho MRMN . Chứng minh: a) PQNR b) RQNP .
29
Dạng 3. Vận dụng tính chất ba đường cao trong tam giác để giải quyết các bài toán khác
Bài 21. Cho MNP có ba góc nh n, các đường cao , NQPR c t nhau t i S.

c) Chứng minh MSNP . d) Cho 065 MNP . Tính SMR .
Bài 22. Cho ABC vuông t i A , kẻ đường phân giác BM . Trên c nh BC lấy điểm D sao cho BDBA .
c) Chứng minh BMAD d) G i H là hình chiếu vuông góc của D trên AC , K là hình chiếu vuông góc của A trên DM . Chứng minh ba đường thẳng ,, AKBMDH đồng quy.
30
NHẬT VÀ HÌNH LẬP PHƢƠNG
PHẦN I. TÓM TẮT LÍ THUYẾT.
- Các kích thước của hình hộp chữ nhật là a,b,c (cùng đơn vị độ dài) thì:
Diện tích xung quanh: xq S 2(ab).c
Diện tích toàn phần: tpxqd SS2S
Thể tích: Vabc
- Kích thước của hình lập phương cạnh a là:
Diện tích xung quanh: xq S 24a
Diện tích toàn phần: 2 tp S6a
Thể tích: 3Va
PHẦN II. CÁC DẠNG BÀI.
Dạng 1. Một số yếu tố cơ bản, diện tích xung quanh, diện tích toàn phần của hình hộp chữ nhật và hình lập phƣơng:
I. Phƣơng pháp giải:
+ Nhận dạng hình, xác định được các yếu tố liên quan của hình hộp chữ nhật và hình lập phương.
+ Viết các công thức liên quan (công thức tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật và hình lập phương).
+ Thay số, tính và kết luận.
II. Bài toán.
Bài 1. Hoàn thành các công thức trong bảng sau: Hình Hình vẽ Diện tích xung quanh Thể tích Hình hộp chữ nhật xq S V
a

Hình lập phương xq S V
c b a
1 CHUYÊN ĐỀ. HÌNH
HỘP CHỮ
3Va Bài 2. Cho hình hộp chữ nhật ABCDMNHQ có độ dài NB3cm , BC4cm , MN6cm , Hãy xác định độ dài các cạnh còn lại của hình hộp chữ nhật. Lời giải: D
a) Ta có ABCDMNHQ là hình hộp chữ nhật nên các mặt ABCD, ABNM , AMQD , CHQD ,

HNMQ là các hình chữ nhật. Do đó theo tính chất hình chữ nhật ta có:
3. Cạnh của một hình lập phương bằng 2cm Tính diện tích toàn phần và diện tích xung quanh của hình lập phương đó. a c b a
2
Lời giải:
BCHN ,
NBAMDQCH , BCADMQNH , NMABCDHQ Mà NB3cm , BC4cm , MN6cm , Nên AMDQCH3cm ADMQNH4cm ABCDHQ6cm . Bài
B
Hình Hình vẽ Diện tích xung quanh Thể tích Hình hộp chữ nhật xq S2(ab).c tp S2abacbc M
Vabc Hình lập phương 2 xq S4a 2 tp S6a Q
A
N H
C
Lời giải:
Tính diện tích xung quanh của hình lập phương đó là: 22 xq S4a4.216 2 (cm)
Tính diện tích toàn phần của hình lập phương đó. 22 tp S6a6.224 2 (cm)
Bài 4. Cạnh của một hình lập phương bằng 5cm . Tính diện tích toàn phần và diện tích xung quanh của hình lập phương đó.
Lời giải:
Tính diện tích xung quanh của hình lập phương đó là: 22 xq S4a4.5100 2 (cm)
Tính diện tích toàn phần của hình lập phương đó. 22 tp S6a6.5150 2 (cm)
Bài 5. Cạnh của một hình lập phương bằng 2a(cm) . Tính diện tích toàn phần và diện tích xung quanh của hình lập phương đó.
Lời giải:

3
2a
2 5
Tính diện tích xung quanh của hình lập phương đó là: 22 xq S4.(2a)16a 2 (cm)
Tính diện tích toàn phần của hình lập phương đó. 2222 tp S6(2a)6.2.a24a 2 (cm)
Bài 6. Hình sau đây gồm bao nhiêu đơn vị diện tích và bao nhiêu đơn vị thể tích (mỗi hình nhỏ là một hình lập phương có cạnh là 1 đơn vị độ dài).
Lời giải:
Hình có kích thước là 4 ; 2 và 2 đơn vị dài. Diện tích hình gồm: + Bốn mặt hình chữ nhật kích thước 4.2 có diện tích là: 4.4.232 (đơn vị diện tích). + Hai mặt hình vuông kích thước 2.2 có diện tích là: 2.2.28 (đơn vị diện tích). Vậy hình có diện tích là: 32840 (đơn vị diện tích). Thể tích hình là V4.2.216 (đvtt)
Bài 7. Hình sau đây gồm bao nhiêu đơn vị diện tích và bao nhiêu đơn vị thể tích (mỗi hình nhỏ là một hình lập phương có cạnh là 1 đơn vị độ dài).
Lời giải:
Hình có lập phương kích thước là 4 đơn vị dài.
Diện tích toàn phần của hình là: 6.4.496 (đơn vị diện tích). Thể tích hình là 3 V464 (đvtt)
Bài 8. Hình sau đây gồm bao nhiêu đơn vị diện tích và bao nhiêu đơn vị thể tích (mỗi hình nhỏ là một hình lập phương có cạnh là 1 đơn vị độ dài).

4
Lời giải:
+ Hai mặt hình chữ nhật kích thước 4.2 có diện tích là: 2.4.216 (đơn vị diện tích).
+ Bốn bậc thang có diện tích là: 4.416 (đơn vị diện tích).
+ Hai mặt gồm 432110 hình vuông đơn vị có diện tích là: 2.1020 (đơn vị diện tích). Vậy hình có diện tích là: 16162052 (đơn vị diện tích). Thể tích hình là V(4321).210.220 (đvtt) Bài 9. Tìm số hình lập phương đơn vị (hình lập phương có cạnh là 1 đơn vị độ dài) để xếp được thành hình hộp chữ nhật sau:
5 6
Lời giải:
12

+ Trong hình mặt đáy là hình chữ nhật có chiều dài là 12cm , có thể chia thành 12 đơn vị, chiều rộng là 6cm. chia thành 6 đơn vị, và chiều cao của hình hộp chữ nhật là 5cm , chia thành 5 đơn vị. Do vậy số hình lập phương đơn vị có cạnh là 1 trên hình là: 6.12.5360 (hình)
Bài 10. Thể tích của hình lập phương là 3343cm . Tính diện tích toàn phần và diện tích xung quanh của hình lập phương đó.
Lời giải:
Gọi cạnh hình lập phương là a , ta có: 3 a343 , suy ra a7 .
Diện tích 6 mặt hình lập phương là: 26a 26.7 294 ( 2 cm ).
Diện tích xung quanh của hình lập phương là: 24a 2 4.7196 ( 2 cm )
Bài 11. Cho hình chữ nhật có thể tích 3 144cm, diện tích xung quanh là 2 168cm,diện tích toàn phần là 2 192cm. Tính các kích thước của hình hộp chữ nhật đó.
Lời giải:
5
Bài 12. Một căn phòng hình hộp chữ nhật có chiều dài 4,5m , chiều rộng 4m, chiều cao 3m Người ta muốn lăn sơn trần nhà và bốn bức tường. Biết rằng tổng diện tích các cửa là 211m Tính diện tích cần lăn sơn ?
Lời giải:

Diện tích trần nhà là 2 4,5 . 4 = 18 (m)
Diện tích bốn bức tường ( bao gồm cả diện tích các cửa) là : 2 2.4,5.3 + 2.4.3= 27 + 24 = 51(m)
Diện tích cần lăn sơn là 2 51 - 11 = 40 (m)
Bài 13: Một phòng học hình hộp chữ nhật có chiều dài 10m,chiều rộng 5m và chiều cao 4m. Người ta định sơn bốn bức tường căn phòng, biết giá công sơn là 25000 đồng một mét vuông.
6 Gọi các kích thước của hình hộp chữ nhật là a,b,c trong đó c là độ dài đường cao thì ta có: abc144 1 2abc2acbc168 2 2abbcca192 3 Từ 2 và 3 suy ra 2ab168192ab12 4 Từ 1 và 4 suy ra c12 Thay c12 vào 2 ta có: 2a.12b.12168ab7b7a Thay b7a vào (4) ta được: 2 a(7a)12a7a120(a3)(a4)0 a3 a4 Nếu a3 thì b4 Nếu a4 thì
V
b3
ậy các kích thước của hình hộp chữ nhật là: 3cm;4cm;12cm
4,5 3 4 A D H E F G C B
i

chi phí tiền công là bao nhiêu? cho biết căn phòng có 1 cửa chính cao 1,8m và rộng
hai cửa sổ có cùng chiều dài 80cm,chiều rộng 60cm.
Lời giải:
Diện tích xung quanh của hình phòng học là: 22.105.4120m
Diện tích cửa là: 21,8.20,8.0,6.24,56m
Diện tích cần sơn là 21204,56115,44m
Chi phí tiền công sơn: 25000.115,442886000 (đồng)
Bài 14. Thể tích của hình hộp chữ nhật là 3300dm . Tính diện tích toàn phần và diện tích xung quanh của hình hộp chữ nhật đó. Lời giải:
Chiều cao của hình hộp chữ nhật là: 300:10.65dm .
Diện tích toàn phần của hình hộp chữ nhật là: tp S2.106.52.10.6280 ( 2dm ).
Diện tích xung quanh của hình hộp chữ nhật là: xq S2ab.c 2106.5160 ( 2dm ).
Bài 15. Một căn phòng rộng 4,1m , dài 5,5m , cao 3m .Người ta muốn quét vôi trần nhà và bốn bức tường. Biết tổng diện tích các cửa bằng 12% tổng diện tích 4 bức tường và trần nhà. Hãy tính diện tích cần quét vôi.
Lời giải:
Diện tích bốn bức tường là: 2.4,15,5.357,6 ( 2 m ).
Diện tích trần nhà là: 4,1.5,522,55 ( 2 m ).
Diện tích 4 bức tường và trần nhà là: 57,622,5580,15 ( 2 m ).
Tổng diện tích các cửa là: 80,15.12%9,618 ( 2 m ).
Diện tích cần quét vôi là: 80,159,61870,532 ( 2 m ).
Bài 16. Một bể nước hình hộp chữ nhật có chiều rộng 1,6m . Lúc đầu bể không có nước. Người ta lắp một vòi nước, mỗi phút chảy được 24 lít nước. Sau 100 phút thì mực nước trong bể cao 0,6m. Tính chiều dài của bể nước
Lời giải: Lượng nước chảy vào bể sau 100 phút là 24.1002400 (lít) 32,4m . Chiều dài của bể là 2,4:0,6:1,52,5m . Bài 17. Các kích thước của một hình hộp chữ nhật tỉ lệ thuận với 5 ; 6 ; 7 . Thể tích của hình hộp là 31680m . Tính độ dài các kích thước của hình hộp chữ nhật đó.
Lời giải:
7 Hỏ
và
2m
Bài 18. Một bể bơi có chiều dài 12m, chiều rộng 5m và sâu 2,75m . Hỏi người thợ phải dùng bao nhiêu viên gạch men để lát đáy và xung quanh thành bể đó? Biết rằng mỗi viên gạch có chiều dài 25cm, chiều rộng 20 cm và diện tích mạch vữa lát không đáng kể.
Lời giải:
2,75m 5m
12m
Diện tích xung quanh và diện tích đáy bể là: 12 5 .2.2,75 93,5 2 m
Diện tích một viên gạch men là: 20 .25 500
Số viên gạch men cần dùng là: 93,5 : 0,05 1870 (viên) Đáp số: 1870 viên gạch men
Bài 19. Một bể cá dạng hình hộp chữ nhật làm bằng kính ( không có nắp) có chiều dài 80cm , chiều rộng 50cm, chiều cao 45cm
Mực nước ban đầu trong bể cao 35cm
a) Tính diện tích kính dùng để làm bể cá đó.
b) Người ta cho vào bể một hòn đá có thể tích 10dm3. Hỏi mực nước trong bể lúc này cao bao nhiêu xăng – ti-mét?
Lời giải:

8 Gọi các kích thước củ
hộp chữ nhật là
Đặt
Khi đó ta có 3 abc5k.6k.7k1680210k1680 3 k8k2 Với k2a10m;b12m;c14m
a hình
a,b,ca0,b0,c0 , ta có a:b:c5:6:7
và abc1680
Ta có abc a:b:c5:6:7 567
abc ka5k;b6k;c7k 567
45m 50cm
80cm
Diện tích xung quanh bể là: 2 80 50 .2.45 11700 cm
Diện tích đáy bể là: 2 80.50 4000 cm
Diện tích kính dùng để làm bể cá đó: 2 11700 4000 15700 cm
Đổi 3310dm 10000cm
Thể tích nước dâng lên chính là thể tích hòn đá do đó thể tích nước dâng lên là: 10000 cm3
Mực nước dâng lên số xăng – ti - mét là: 10000: 50x80 2,5 cm
Mực nước trong bể lúc này cao số xăng – ti - mét là: 2,5 35 37,5 cm
Đáp số: 2 15700cm;37,5cm

Bài 20. Một hình lập phương cạnh 5 cm được ghép bởi 125 hình lập phương nhỏ cạnh 1 cm Số các hình lập phương nhỏ giáp với 6 mặt của các hình lập phương nhỏ khác là
Lời giải: Số hình lập phương có 1 mặt không tiếp xúc với các hình lập phương khác là 25.215.29.250301898
(hình lập phương) Số hình lập phương nhỏ giáp với 6 mặt của các hình lập phương nhỏ khác là 1259827 (hình lập phương)
Bài 21. Có 512 hình lập phương đơn vị (cạnh dài một đơn vị). Hỏi cần phải thêm bao nhiêu hình lập phương đơn vị để xếp thành một hình lập phương có độ dài cạnh 10 đơn vị?
Lời giải:
Thể tích của 512 hình lập phương đơn vị là 3 512.1512 (đvtt)
Thể tích hình lập phương cạnh 10 đơn vị là 3 101000 (đvtt)
Thể tích cần tăng thêm 1000512488 (đvtt)
Số hình lập phương đơn vị cần tăng 3 488:1488 hình. Bài 22. Một bể chứa nước hình hộp chữ nhật có chiều dài 3m,chiều rộng 1,8m,chiều cao 1,2m.Khi bể không chứa nước, người ta cho một máy bơm, bơm nước vào bể mỗi phút bơm được 30 lít. Hỏi sau 3 giờ 15 phút bể đã đầy nước hay chưa?
Lời giải:
9
1,2m
3m
Thể tích bể nước hình hộp chữ nhật là: 33.1,8.1,26,48m
1,8m

Vì mỗi phút máy bơm được 30 lít nên sau 3 giờ 15 phút = 195 phút, máy bơm được lượng nước là: 33 30.1955850l5850dm5,85m
Vì 5,856,48 nên sau 3 giờ 15 phút bể vẫn chưa đầy nước.
Bài 24. Một thùng đựng hàng có nắp dạng hình hộp chữ nhật có chiều dài 2,5m, chiều rộng 1,8m và chiều cao 2m Người thợ cần bao nhiêu ki-lô-gam sơn để đủ sơn hai mặt của chiếc thùng đó ? Biết rằng mỗi ki-lô-gam sơn sơn được 25m mặt thùng.
Lời giải:
Diện tích xung quanh của thùng đựng hàng đó: 2 2,5 1,8 x2x2 17,2 m
Diện tích 2 đáy của thùng đựng hàng là: 2 2,5.1,8.2 9 m
Diện tích toàn phần của thùng đựng hàng đó: 2 17,2 9 26,2 m
Diện tích bề mặt cần quét sơn là: 2 26,2.2 52,4 m
Số ki-lô-gam sơn cần dùng là: 52,4:5 10,48 kg
Đáp số: 10,48 kg sơn.
Bài 25. Thiết bị máy được xếp vào các hình lập phương có diện tích toàn phần bằng 296dm . Người ta xếp các hộp đó vào trong một thùng hình lập phương làm bằng tôn không có nắp. Khi gò một thùng như thế hết 23,2m tôn (diện tích các mép hàn không đáng kể). Hỏi mỗi thùng đựng được bao nhiêu hộp thiết bị nói trên?
Lời giải:
Đổi 223,2m 320 dm
Diện tích 1 mặt của hộp thiết bị là: 96 : 6 = 16 (dm2)
Suy ra cạnh của hộp thiết bị là 4dm, vì 4 . 4 = 16
Diện tích một mặt của thùng đựng hàng là: 320 : 5 = 64 (dm2)
10
= 8 8 nên cạnh của thùng đựng hàng là 8dm
Thể tích một hộp đựng thiết bị là: 334 64 dm
Thể tích thùng đựng hàng là: 338 512 dm
Số hộp thiết bị đựng được trong một thùng là: 512 : 64 8 (hộp)
Xếp mỗi lớp 4 hộp và xếp được 2 lớp như thế
Đáp số: 8 hộp
Dạng 2. Thể tích của hình hộp chữ nhật và hình lập phƣơng:
I. Phƣơng pháp giải: + Áp dụng các công thức tính thể tích của hình hộp chữ nhật và hình lập phương. + Áp dụng giải các bài toán thực tế có liên quan
II. Bài toán.
Bài 1. Một bể bơi hình hộp chữ nhật dài 12m, rộng 4,5m ; chiều cao của nước trong bể 1,5m . Tính thể tích nước trong bể?
Lời giải: Thể tích của hình hộp chữ nhật là Va.b.h12.4,5.1,581
(cm)
Bài 2. Một hình hộp chữ nhật có các kích thước là 6cm; 8cm ; 12cm. Tính thể tích của hình hộp chữ nhật?
Lời giải:
Thể tích của hình hộp chữ nhật là Va.b.h6.8.12576
(cm)
Bài 3. Thể tích của một hình lập phương có độ dài cạnh bằng 5cm là: Lời giải: Thể tích của hình hộp lập phương là 33 Va5125
(cm)

Bài 4. Một bể bơi có hình dạng một hình hộp chữ nhật, có kích thước bên trong của đáy lần lượt là 6m và 25m . Dung tích nước trong hồ khi mực nước trong hồ cao 2m là?
Lời giải:
Dung tích nước trong hồ khi mực nước trong hồ cao 2m là Va.b.h6.25.2300
11 Vì
64
3
3
3
3
(m) 12 1,5 4,5
Bài 1. Hình hộp chữ nhật có ba kích thước lần lượt là a ; 2a; a 2 . Thể tích của hình hộp chữ nhật đó là
Lời giải: Thể tích của hình hộp chữ nhật là 3 a Va.2a.a 2 (đvdt)
Bài 5. Hình hộp chữ nhật có ba kích thước lần lượt là a ; a ; 2a Thể tích của hình hộp chữ nhật đó là
Lời giải: Thể tích của hình hộp chữ nhật là 3Va.a.2a2a (đvdt)
Bài 6. Cạnh của một hình lập phương bằng 5b ( cm). Tính thể tích của hình lập phương đó?
Lời giải: Thể tích của hình lập phương là 333 V(5b)125b(cm)
5b 2a

Bài 7. Tính thể tích của một hình lập phương có cạnh 2acm ?
Lời giải: Thể tích của hình lập phương là 333 V(2a)8acm
Bài 8. Một bể cá hình hộp chữ nhật có kích thước như sau chiều dài 1,2m ; chiều rộng 6dm; chiều cao 8dm . Tính thể tích của bể ?
Lời giải:
12
Đổi 1,2m12dm Thể tích của bể cá là 3V12.6.8675dm
1,2m
Bài 9. Một bể cá dạng hình hộp chữ nhật làm bằng kính (không nắp) có chiều dài 80cm , chiều rộng 50cm. Mực nước trong bể cao 35cm . Tính thể tích của mực nước trong bể theo đơn vị 3dm
Lời giải: Thể tích của mực nước trong bể là 33 V80.50.35140000(cm)140dm .
8dm 6dm 80cm

35cm 50cm
Bài 10. Cho biết một bể bơi tiêu chuẩn có chiều dài 50m , chiều rộng 25m và chiều cao 2,3m . Người ta bơm nước vào bể sao cho nước cách mép bể 0,3m . Tính thể tích nước trong bể và thể tích phần không chứa nước? Lời giải: Nước trong bể tạo thành một hình hộp chữ nhật có chiều dài 50m , chiều rộng 25m và chiều cao 2m . Thể tích nước trong bể là 3 1 V50.25.22500m Thể tích của cả bể là 3V50.25.2,32875m Thể tích phần bể không chứa nước là 3 21 VVV28752500375m
Bài 11. Một chiếc hộp hình lập phương không có nắp được sơn cả mặt trong và mặt ngoài. Diện tích phải sơn tổng cộng là 21690cm . Tính thể tích của hình lập phương đó.
Lời giải:
Chiếc hộp hình lập phương không có nắp gồm 5 hình vuông, mỗi hình vuông được sơn hai mặt nên diện tích của mỗi hình vuông là 21690:1019cm
13
Vì diện tích hình vuông bằng bình phương một cạnh nên cạnh của hình lập phương là 13cm Thể tích hình lập phương là 33 V132197cm .
Bài 12. Một bể cá dạng hình hộp chữ nhật làm bằng kính (không nắp) có chiều dài 1m , chiều rộng 70cm, chiều cao 80cm. Mực nước trong bể cao 30cm . Người ta cho vào bể một hòn đá thì thể tích tăng 314000cm . Hỏi mực nước trong bể lúc này là bao nhiêu? Lời giải: Đổi 1m100cm Thể tích phần nước ban đầu là 3V100.70.30210000cm . Sau khi cho vào một hòn đá thể tích tăng 314000cm . Khi đó thể tích phần bể chứa nước lúc sau là 3 1 VV14000224000cm Vì chiều dài và chiều rộng của bể nước không thay đổi nên sự thay đổi là do chiều cao mực nước thay đổi. Gọi chiều cao mực nước lúc sau là hcm. Ta có 1 1 V 224000 V70.100.hh32cm 100.70100.70
Bài 13. Một hình lập phương có cạnh bằng 1 . Người ta tăng mỗi cạnh của nó thêm 20 %. Thể tích của nó tăng bao nhiêu phần trăm?
Lời giải: Độ dài của mỗi cạnh hình lập phương sau khi tăng thêm là 11.20%1,2 (đvđd)
Thể tích ban đầu là 1 (đvtt)

Thể tích tăng thêm là 33 1,210,728 (đvtt)
Phần trăm thể tích tăng thêm là 0,728:1100%72,8%
Bài 14. Một bể cá hình hộp chữ nhật cao 50cm. Diện tích đáy bằng nửa diện tích xung quanh. Trong bể đang có nước cao đến 35cm. Hỏi thêm bao nhiều nước vào bể cá đó thì nước vừa đầy bể. Biết diện tích xung quanh của bể cá là 26400cm
Lời giải:
Gọi chiều dài, rộng, cao của bể cá hình chữ nhật lầm lượt là a,b,c
14
( cm,a,b,c0 ). Suy ra c20cm Do diện tích đáy bằng nửa diện tích xung quanh nên ta có xqdS2S hay xq S2ab suy ra ab6400:23200 Gọi V là thể tích của bể cá lúc đầy nước, 1V là thể tích bể cá với chiều cao nước là 35cm, 2V là thể tích lượng nước cần thêm để vừa đầy bể cá. Vậy lượng nước cần thêm vào để vừa đầy bể cá là: 2V 1VV 50.320035.3200 3200.5035 3200.15
348000cm

48000ml Bài 15. Cho một bể bơi tiêu chuẩn có chiều dài 50m, chiều rộng 25m và chiều cao 2,3m. Người ta bơm nước vào bể sao cho nước cách mép bể 0,5m. a) Tính thể tích nước trong bể b) Tính thể tích phần không chứa nước? Lời giải: a) Nước trong bể tạo thành một hình hộp chữ nhật có chiều dài 50m, chiều rộng 25m và chiều cao 1,8m.Do đó lượng nước trong bể là thể tích 3 1 V2250m b) Tính thể tích của bể là 3V2875m 3 2 V28752250625m là thể tích phần không chứa nước.
Bài 16. Hình lập phương A có cạnh bằng 2 3 cạnh của hình lập phương B . Hỏi thể tích hình lập phương A bằng bao nhiêu phần thể tích hình lập phương B ? Lời giải: Gọi chiều dài một cạnh của hình lập phương B là a . Vì hình lập phương A có cạnh bằng 2 3 cạnh của hình lập phương B nên chiều dài 1 cạnh của hình lập phương A là 2 a 3 Thể tích hình lập phương B là 3 B Va Thể tích hình lập phương A là 3 3 A 28 Vaa 327
AB 8 VV 27 Vậy thể tích hình lập phương A bằng 8 27 thể tích hình lập phương B Bài 17. Tính thể tích của một hình lập phương, biết diện tích toàn phần của nó là
15
2
.
294cm
Lời giải:

Hình lập phương có 6 mặt bằng nhau, vậy diện tích của mỗi mặt là 2294:649cm Độ dài cạnh hình lập phương là a497(cm) Thể tích hình lập phương là 33 V7343cm
Bài 18. Người ta xây một cái bể hình hộp chữ nhật có chiều dài 2m,chiều rộng 1,2m,chiều cao 1m.
a) Nếu lát kín các mặt xung quanh và mặt đáy bể bằng các viên gạch hình vuông cạnh 20cm thì cần bao nhiêu viên gạch?
b) Nếu dùng một chiếc thùng hình hộp chữ nhật có kích thước 30cm,40cm,50cm thì cần bao nhiêu thùng nước để đổ đầy bể? Lời giải: a) Diện tích mặt đáy của bể là: 22.1,22,4m Diện tích các mặt xung quanh của bể là: 21.2.21.1,2.26,4m Hoặc
16
21,22.2.16,4m 2m 1m 1,2m
(Áp dụng 1 trong 2 cách tính trên)

Tổng diện tích mặt đáy và các mặt xung quang của bể là: 22,46,48,8m
Vì các viên gạch hình vuông cạnh 20cm nên diện tích mỗi viên gạch là: 22 20.20400cm0,04m
Số viên gạch cần dùng là: 8,8:0,04220 (viên gạch)
b) Vì chiếc thùng hình hộp chữ nhật có kích thước 30cm,40cm,50cmnên thể tích chiếc thùng là: 33 30.40.5060000cm0,06m
Vì cái bể hình hộp chữ nhật có chiều dài 2m,chiều rộng 1,2m,chiều cao 1m nên thể tích bể là: 32.1,2.12,4m
Số thùng nước cần dùng để đổ đầy bể là: 2,4:0,0640 (thùng) Phần III. BÀI TẬP TỰ LUYỆN Dạng 1. Một số yếu tố cơ bản, diện tích xung quanh, diện tích toàn phần của hình hộp chữ nhật và hình lập phƣơng:
Bài 1. Cạnh của một hình lập phương bằng 3cm Tính diện tích toàn phần và diện tích xung quanh của hình lập phương đó.
Bài 2. Cạnh của một hình lập phương bằng 5a(cm). Tính diện tích toàn phần và diện tích xung quanh của hình lập phương đó.
Bài 3. Hình sau đây gồm bao nhiêu đơn vị diện tích và bao nhiêu đơn vị thể tích (mỗi hình nhỏ là một hình lập phương có cạnh là 1 đơn vị độ dài).
Bài 4. Một xí nghiệp làm bánh cần dùng 30 000 chiếc hộp bằng bìa cứng để đựng bánh. Hộp có đáy là một hình vuông cạnh 25cm và cao 6cm. Hỏi cần bao nhiêu mét vuông bìa để làm đủ số hộp kể trên, biết rằng các mép gấp dán hộp chiếm khoảng 8 100 diện tích hộp
Bài 5. Một căn phòng hình hộp chữ nhật dài 4,2m , rộng 3,6m và cao 3,4m . Người ta muốn quét vôi tường và trần nhà. Hỏi diện tích cần quét vôi là bao nhiêu mét vuông, biết rằng tổng diện tích các cửa bằng 25,8m .
Dạng 2. Thể tích của hình hộp chữ nhật và hình lập phƣơng:
17
Bài 1. Tính thể tích của một hình lập phương có độ dài cạnh bằng 3cm
Bài 2. Một bể cá dạng hình hộp chữ nhật làm bằng kính (không nắp) có chiều dài 60cm , chiều rộng 40cm. Mực nước trong bể cao 25cm . Tính thể tích của mực nước trong bể theo đơn vị 3dm
Bài 3. Một bể cá cảnh hình hộp chữ nhật có chiều dài 1,2m , chiều rộng 0,4m và chiều cao 0,6m . Mực nước trong bể cao 35cm . Sau khi thả hòn Non Bộ vào trong bể thì mực nước trong bể cao 47cm. Tính thể tích hòn Non Bộ.
Bài 4. Người ta xây một cái bể hình hộp chữ nhật có chiều dài 1,2m,chiều rộng 1m,chiều cao 1m.
a) Nếu lát kín các mặt xung quanh và mặt đáy bể bằng các viên gạch hình vuông cạnh 20cm thì cần bao nhiêu viên gạch?
b) Nếu dùng một chiếc thùng hình hộp chữ nhật có kích thước 30cm,40cm,50cm thì cần bao nhiêu thùng nước để đổ đầy bể?
ĐÁP

SỐ BÀI TẬP TỰ LUYỆN
Dạng 1. Một số yếu tố cơ bản, diện tích xung quanh, diện tích toàn phần của hình hộp chữ nhật và hình lập phƣơng: Bài 1. Cạnh của một hình lập phương bằng 3cm Tính diện tích toàn phần và diện tích xung quanh của hình lập phương đó.
Đáp số:
Tính diện tích xung quanh của hình lập phương đó là: 22 xq S4a4.336
Tính diện tích toàn phần của hình lập phương đó. 22 tp S6a6.354
Bài 2. Cạnh của một hình lập phương bằng 5a(cm). Tính diện tích toàn phần và diện tích xung quanh của hình lập phương đó.
Đáp số:
Tính diện tích xung quanh của hình lập phương đó là: 2222
18
2 (cm)
2 (cm)
xq S4(5a)4.5a100a 2 (cm) 3
Tính diện tích toàn phần của hình lập phương đó. 2222 tp S6(5a)6.5a150a 2 (cm)
Bài 3. Hình sau đây gồm bao nhiêu đơn vị diện tích và bao nhiêu đơn vị thể tích (mỗi hình nhỏ là một hình lập phương có cạnh là 1 đơn vị độ dài).
Đáp số: Hình có lập phương kích thước là 3 đơn vị dài. Diện tích toàn phần của hình là: 6.3.354 (đơn vị diện tích). Thể tích hình là 3 V327 (đvtt) Bài 4. Một xí nghiệp làm bánh cần dùng 30 000 chiếc hộp bằng bìa cứng để đựng bánh. Hộp có đáy là một hình vuông cạnh 25cm và cao 6cm. Hỏi cần bao nhiêu mét vuông bìa để làm đủ số hộp kể trên, biết rằng các mép gấp dán hộp chiếm khoảng 8 100 diện tích hộp Đáp số: Diện tích toàn phần của 30 000 chiếc hộp là: 2 1 S(4.0,25.0,062.0,25.0,25).300005550(m)

Diện tích các mép gấp dán của 30 000 chiếc hộp là: 2 2 8 S.5550444(m) 100
Diện tích bìa để làm số hộp trên là 2 12 SSS55504445994(m)
Bài 5. Một căn phòng hình hộp chữ nhật dài 4,2m , rộng 3,6m và cao 3,4m . Người ta muốn quét vôi tường và trần nhà. Hỏi diện tích cần quét vôi là bao nhiêu mét vuông, biết rằng tổng diện tích các cửa bằng 25,8m Đáp số: Diện tích tường cần quét vôi là: 2 tgxqc SSS(4,23,6).2.3,45.847,24(m) Diện tích cần quét vôi là: 2 tgtr SSS47,244,2.3,662,36(m) Dạng 2. Thể tích của hình hộp chữ nhật và hình lập phƣơng: Bài 1. Tính thể tích của một hình lập phương có độ dài cạnh bằng 3cm
19
Đáp số:
Thể tích của hình hộp lập phương là 33 Va327 3 (cm)
Bài 2. Một bể cá dạng hình hộp chữ nhật làm bằng kính (không nắp) có chiều dài 60cm , chiều rộng 40cm. Mực nước trong bể cao 25cm . Tính thể tích của mực nước trong bể theo đơn vị 3dm
Đáp số:
Thể tích của mực nước trong bể là 33 V60.40.2560000(cm)60dm .
Bài 3. Một bể cá cảnh hình hộp chữ nhật có chiều dài 1,2m , chiều rộng 0,4m và chiều cao 0,6m . Mực nước trong bể cao 35cm . Sau khi thả hòn Non Bộ vào trong bể thì mực nước trong bể cao 47cm. Tính thể tích hòn Non Bộ. Đáp số: Thể tích của hòn Non Bộ bằng thể tích phần nước đã dâng lên trong bể là: 3V1,2.0,4.(0,470,35)0,567m
Bài 4. Người ta xây một cái bể hình hộp chữ nhật có chiều dài 1,2m,chiều rộng 1m,chiều cao 1m.
a) Nếu lát kín các mặt xung quanh và mặt đáy bể bằng các viên gạch hình vuông cạnh 20cm thì cần bao nhiêu viên gạch?
b) Nếu dùng một chiếc thùng hình hộp chữ nhật có kích thước 30cm,40cm,50cm thì cần bao nhiêu thùng nước để đổ đầy bể?
Đáp số:
a) Số viên gạch cần dùng là: 135 (viên gạch) b) Vì chiếc thùng hình hộp chữ nhật có kích thước 30cm,40cm,50cm nên thể tích chiếc thùng là: 33 30.40.5060000cm0,06m Vì cái bể hình hộp chữ nhật có chiều dài 1,2m,chiều rộng 1m, chiều cao 1m nên thể tích bể là: 31.1,2.11,2m Số thùng nước cần dùng để đổ đầy bể là:

20
3

21 1,2:0,0620 (thùng)
Dạng 1. Một số yếu tố cơ bản, diện tích xung quanh, diện tích toàn phần của hình hộp chữ nhật và hình lập phƣơng:
Bài 1. Hoàn thành các công thức trong bảng sau: Hình Hình vẽ Diện tích xung quanh Thể tích Hình hộp chữ nhật xq S
a

lập phương xq S
Bài 2. Cho hình hộp chữ nhật ABCDMNHQ có độ dài NB3cm , BC4cm , MN6cm , Hãy xác định độ dài các cạnh còn lại của hình hộp chữ nhật.
c b a B A
Bài 3. Cạnh của một hình lập phương bằng 2cm . Tính diện tích toàn phần và diện tích xung quanh của hình lập phương đó.
22 PHIẾU BÀI TẬP
………….. V Hình
V
M N H Q D C
Bài 4. Cạnh của một hình lập phương bằng 5cm . Tính diện tích toàn phần và diện tích xung quanh của hình lập phương đó.
5 2a

Bài 5. Cạnh của một hình lập phương bằng 2a(cm) . Tính diện tích toàn phần và diện tích xung quanh của hình lập phương đó.
Bài 6. Hình sau đây gồm bao nhiêu đơn vị diện tích và bao nhiêu đơn vị thể tích (mỗi hình nhỏ là một hình lập phương có cạnh là 1 đơn vị độ dài).
Bài 7. Hình sau đây gồm bao nhiêu đơn vị diện tích và bao nhiêu đơn vị thể tích (mỗi hình nhỏ là một hình lập phương có cạnh là 1 đơn vị độ dài).
23
2
Bài 8. Hình sau đây gồm bao nhiêu đơn vị diện tích và bao nhiêu đơn vị thể tích (mỗi hình nhỏ là một hình lập phương có cạnh là 1 đơn vị độ dài).
Bài 9. Tìm số hình lập phương đơn vị (hình lập phương có cạnh là 1 đơn vị độ dài) để xếp được thành hình hộp chữ nhật sau:
Bài 10. Thể tích của hình lập phương là 3343cm . Tính diện tích toàn phần và diện tích xung quanh của hình lập phương đó.
Bài 11. Cho hình chữ nhật có thể tích 3 144cm, diện tích xung quanh là 2 168cm,diện tích toàn phần là 2 192cm. Tính các kích thước của hình hộp chữ nhật đó.

Bài 12. Một căn phòng hình hộp chữ nhật có chiều dài 4,5m , chiều rộng 4m, chiều cao 3m. Người ta muốn lăn sơn trần nhà và bốn bức tường. Biết rằng tổng diện tích các cửa là 211m . Tính diện tích cần lăn sơn ?
Bài 13: Một phòng học hình hộp chữ nhật có chiều dài 10m,chiều rộng 5m và chiều cao 4m. Người ta định sơn bốn bức tường căn phòng, biết giá công sơn là 25000 đồng một mét vuông. Hỏi chi phí tiền công là bao nhiêu? cho biết căn phòng có 1 cửa chính cao 1,8m và rộng 2m và hai cửa sổ có cùng chiều dài 80cm,chiều rộng 60cm.
Bài 14. Thể tích của hình hộp chữ nhật là 3300dm . Tính diện tích toàn phần và diện tích xung quanh của hình hộp chữ nhật đó.
Bài 15. Một căn phòng rộng 4,1m , dài 5,5m , cao 3m .Người ta muốn quét vôi trần nhà và bốn bức tường. Biết tổng diện tích các cửa bằng 12% tổng diện tích 4 bức tường và trần nhà. Hãy tính diện tích cần quét vôi.
24
12 5 6
Bài 16. Một bể nước hình hộp chữ nhật có chiều rộng 1,6m . Lúc đầu bể không có nước. Người ta lắp một vòi nước, mỗi phút chảy được 24 lít nước. Sau 100 phút thì mực nước trong bể cao 0,6m. Tính chiều dài của bể nước
Bài 17. Các kích thước của một hình hộp chữ nhật tỉ lệ thuận với 5 ; 6 ; 7 . Thể tích của hình hộp là 31680m Tính độ dài các kích thước của hình hộp chữ nhật đó.
.

Bài 18. Một bể bơi có chiều dài 12m, chiều rộng 5m và sâu 2,75m . Hỏi người thợ phải dùng bao nhiêu viên gạch men để lát đáy và xung quanh thành bể đó? Biết rằng mỗi viên gạch có chiều dài 25cm, chiều rộng 20 cm và diện tích mạch vữa lát không đáng kể.
Bài 19. Một bể cá dạng hình hộp chữ nhật làm bằng kính ( không có nắp) có chiều dài 80cm , chiều rộng 50cm, chiều cao 45cm .
Mực nước ban đầu trong bể cao 35cm
a) Tính diện tích kính dùng để làm bể cá đó.
b) Người ta cho vào bể một hòn đá có thể tích 10dm3. Hỏi mực nước trong bể lúc này cao bao nhiêu xăng – ti-mét?
Bài 20. Một hình lập phương cạnh 5 cm được ghép bởi 125 hình lập phương nhỏ cạnh 1 cm . Số các hình lập phương nhỏ giáp với 6 mặt của các hình lập phương nhỏ khác là
Bài 21. Có 512 hình lập phương đơn vị (cạnh dài một đơn vị). Hỏi cần phải thêm bao nhiêu hình lập phương đơn vị để xếp thành một hình lập phương có độ dài cạnh 10 đơn vị?
Bài 22. Một bể chứa nước hình hộp chữ nhật có chiều dài 3m,chiều rộng 1,8m,chiều cao 1,2m.Khi bể không chứa nước, người ta cho một máy bơm, bơm nước vào bể mỗi phút bơm được 30 lít. Hỏi sau 3 giờ 15 phút bể đã đầy nước hay chưa?
Bài 24. Một thùng đựng hàng có nắp dạng hình hộp chữ nhật có chiều dài 2,5m, chiều rộng 1,8m và chiều cao 2m Người thợ cần bao nhiêu ki-lô-gam sơn để đủ sơn hai mặt của chiếc thùng đó ? Biết rằng mỗi ki-lô-gam sơn sơn được 25m mặt thùng.
Bài 25. Thiết bị máy được xếp vào các hình lập phương có diện tích toàn phần bằng 296dm . Người ta xếp các hộp đó vào trong một thùng hình lập phương làm bằng tôn không có nắp. Khi gò một thùng như thế hết 23,2m tôn (diện tích các mép hàn không đáng kể). Hỏi mỗi thùng đựng được bao nhiêu hộp thiết bị nói trên?
Dạng 2. Thể tích của hình hộp chữ nhật và hình lập phƣơng: Bài 1. Một bể bơi hình hộp chữ nhật dài 12m, rộng 4,5m ; chiều cao của nước trong bể 1,5m Tính thể tích nước trong bể?
25
Bài 2. Một hình hộp chữ nhật có các kích thước là 6cm; 8cm ; 12cm. Tính thể tích của hình hộp chữ nhật?
Bài 3. Thể tích của một hình lập phương có độ dài cạnh bằng 5cm là:
Bài 4. Một bể bơi có hình dạng một hình hộp chữ nhật, có kích thước bên trong của đáy lần lượt là 6m và 25m . Dung tích nước trong hồ khi mực nước trong hồ cao 2m là?
Bài 1. Hình hộp chữ nhật có ba kích thước lần lượt là a ; 2a; a 2 . Thể tích của hình hộp chữ nhật đó là
Bài 5. Hình hộp chữ nhật có ba kích thước lần lượt là a ; a ; 2a. Thể tích của hình hộp chữ nhật đó là
Bài 6. Cạnh của một hình lập phương bằng 5b ( cm). Tính thể tích của hình lập phương đó?
Bài 7. Tính thể tích của một hình lập phương có cạnh 2acm ?
Lời giải:
Bài 8. Một bể cá hình hộp chữ nhật có kích thước như sau chiều dài 1,2m ; chiều rộng 6dm; chiều cao 8dm . Tính thể tích của bể ?
Bài 9. Một bể cá dạng hình hộp chữ nhật làm bằng kính (không nắp) có chiều dài 80cm , chiều rộng 50cm. Mực nước trong bể cao 35cm . Tính thể tích của mực nước trong bể theo đơn vị 3dm
Bài 10. Cho biết một bể bơi tiêu chuẩn có chiều dài 50m , chiều rộng 25m và chiều cao 2,3m Người ta bơm nước vào bể sao cho nước cách mép bể 0,3m . Tính thể tích nước trong bể và thể tích phần không chứa nước?
Bài 11. Một chiếc hộp hình lập phương không có nắp được sơn cả mặt trong và mặt ngoài. Diện tích phải sơn tổng cộng là 21690cm . Tính thể tích của hình lập phương đó.
Bài 12. Một bể cá dạng hình hộp chữ nhật làm bằng kính (không nắp) có chiều dài 1m , chiều rộng 70cm, chiều cao 80cm. Mực nước trong bể cao 30cm . Người ta cho vào bể một hòn đá thì thể tích tăng 314000cm . Hỏi mực nước trong bể lúc này là bao nhiêu?

Bài 13. Một hình lập phương có cạnh bằng 1 . Người ta tăng mỗi cạnh của nó thêm 20 %. Thể tích của nó tăng bao nhiêu phần trăm?
Bài 14. Một bể cá hình hộp chữ nhật cao 50cm. Diện tích đáy bằng nửa diện tích xung quanh. Trong bể đang có nước cao đến 35cm. Hỏi thêm bao nhiều nước vào bể cá đó thì nước vừa quanh của bể cá là 26400cm đầy bể. Biết diện tích xung
12 1,5 4,5
Bài 15. Cho một bể bơi tiêu chuẩn có chiều dài 50m, chiều rộng 25m và chiều cao 2,3m. Người ta bơm nước vào bể sao cho nước cách mép bể 0,5m. c) Tính thể tích nước trong bể d) Tính thể tích phần không chứa nước?
.
Bài 16. Hình lập phương A có cạnh bằng 2 3 cạnh của hình lập phương B . Hỏi thể tích hình lập phương A bằng bao nhiêu phần thể tích hình lập phương B ?
Bài 17. Tính thể tích của một hình lập phương, biết diện tích toàn phần của nó là 2294cm
Bài 18. Người ta xây một cái bể hình hộp chữ nhật có chiều dài 2m,chiều rộng 1,2m,chiều cao 1m.
a) Nếu lát kín các mặt xung quanh và mặt đáy bể bằng các viên gạch hình vuông cạnh 20cm thì cần bao nhiêu viên gạch?
b) Nếu dùng một chiếc thùng hình hộp chữ nhật có kích thước 30cm,40cm,50cm thì cần bao nhiêu thùng nước để đổ đầy bể?
Phần III. BÀI TẬP TỰ LUYỆN

Dạng 1. Một số yếu tố cơ bản, diện tích xung quanh, diện tích toàn phần của hình hộp chữ nhật và hình lập phƣơng:
Bài 1. Cạnh của một hình lập phương bằng 3cm Tính diện tích toàn phần và diện tích xung quanh của hình lập phương đó.
Bài 2. Cạnh của một hình lập phương bằng 5a(cm). Tính diện tích toàn phần và diện tích xung quanh của hình lập phương đó.
Bài 3. Hình sau đây gồm bao nhiêu đơn vị diện tích và bao nhiêu đơn vị thể tích (mỗi hình nhỏ là một hình lập phương có cạnh là 1 đơn vị độ dài).
27
Bài 4. Một xí nghiệp làm bánh cần dùng 30 000 chiếc hộp bằng bìa cứng để đựng bánh. Hộp có đáy là một hình vuông cạnh 25cm và cao 6cm. Hỏi cần bao nhiêu mét vuông bìa để làm đủ số hộp kể trên, biết rằng các mép gấp dán hộp chiếm khoảng 8 100 diện tích hộp
Bài 5. Một căn phòng hình hộp chữ nhật dài 4,2m , rộng 3,6m và cao 3,4m . Người ta muốn quét vôi tường và trần nhà. Hỏi diện tích cần quét vôi là bao nhiêu mét vuông, biết rằng tổng diện tích các cửa bằng 25,8m .

Dạng 2. Thể tích của hình hộp chữ nhật và hình lập phƣơng:
Bài 1. Tính thể tích của một hình lập phương có độ dài cạnh bằng 3cm .
Bài 2. Một bể cá dạng hình hộp chữ nhật làm bằng kính (không nắp) có chiều dài 60cm , chiều rộng 40cm. Mực nước trong bể cao 25cm . Tính thể tích của mực nước trong bể theo đơn vị 3dm
Bài 3. Một bể cá cảnh hình hộp chữ nhật có chiều dài 1,2m , chiều rộng 0,4m và chiều cao 0,6m . Mực nước trong bể cao 35cm . Sau khi thả hòn Non Bộ vào trong bể thì mực nước trong bể cao 47cm. Tính thể tích hòn Non Bộ.
Bài 4. Người ta xây một cái bể hình hộp chữ nhật có chiều dài 1,2m,chiều rộng 1m,chiều cao 1m.
a) Nếu lát kín các mặt xung quanh và mặt đáy bể bằng các viên gạch hình vuông cạnh 20cm thì cần bao nhiêu viên gạch?
b) Nếu dùng một chiếc thùng hình hộp chữ nhật có kích thước 30cm,40cm,50cm thì cần bao nhiêu thùng nước để đổ đầy bể?
28
VÀ HÌNH LĂNG TRỤ ĐỨNG TỨ GIÁC
PHẦN I. TÓM TẮT LÍ THUYẾT.
1.Hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác.
Trong hình lăng trụ đứng tam giác (tứ giác):
- Hai mặt đáy song song với nhau.
- Các mặt bên là những hình chữ nhật.
- Các cạnh bên song song và bằng nhau.
Độ dài một cạnh bên gọi là chiều cao của lăng trụ đứng.
*Chú ý: Hình hộp chữ nhật và hình lập phương cũng là các hình lăng trụ đứng tứ giác.
2.Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác.
a) Diện tích xung quanh của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác.
- Diện tích xung quanh của lăng trụ đứng bằng tích của chu vi đáy với chiều cao của nó.
Trong đó xq S : Diện tích xung quanh của hình lăng trụ, C : Chu vi một đáy của hình lăng trụ, h : chiều cao của lăng trụ.
b) Thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác. Thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác. day VSh
Trong đó: V : Thể tích của hình lăng trụ đứng, S : Diện tích một đáy của hình lăng trụ đứng, h : Chiều cao của hình lăng trụ đứng.

3. Diện tích toàn phần (mở rộng):
Diện tích toàn phần bằng diện tích xung quanh cộng diện tích hai đáy. 2 SSS xq tp d
Trong đó: tpS là diện tích toàn phần của hình lăng trụ. xq S : Diện tích xung quanh của hình lăng trụ.
1
ĐỀ
CHUYÊN
. HÌNH LĂNG TRỤ ĐỨNG TAM GIÁC
xq SCh
: Diện tích một đáy của hình lăng trụ đứng.
PHẦN II. CÁC DẠNG BÀI.
Dạng 1. Nhận biết các yếu tố của lăng trụ đứng tam giác, tứ giác.
I. Phương pháp giải:
+ Học sinh vẽ hình, quan sát để xác định các mặt, các cạnh, các đỉnh.
+ Để vẽ hình lăng trụ đứng , ta thường vẽ một đáy, sau đó vẽ các cạnh bên là các đoạn thẳng song song và bằng nhau.
II. Bài toán.
Bài 1.
Quan sát và gọi tên các đỉnh, mặt đáy, mặt bên, cạnh đáy, cạnh bên của hình lăng trụ đứng tam giác ở hình vẽ sau.
Lời giải:
Các đỉnh A , B , C , M , N , P

Các cạnh đáy: AB,AC,BC , MN,MP,NP
Các cạnh bên AM,BN,CP
Các mặt đáy là các tam giác ABC và MNP .
Các mặt bên là các hình chữ nhật ABNM , BCPN , ACPM .
Bài 2.
Quan sát và gọi tên các đỉnh, mặt đáy, mặt bên, cạnh đáy, cạnh bên của hình lăng trụ đứng tứ giác ở hình vẽ sau.
Lời giải:
Các đỉnh A , B , C , D , M , N , P , Q .
2 dS
P N M C B A Q P N M D C B A
Các cạnh đáy: AB,BC,CD,DA , MN,NP,PQ,QM

Các cạnh bên AM,BN,CP,DQ .
Các mặt đáy là các tứ giác ABCD và MNPQ .
Các mặt bên là các hình chữ nhật ABNM , BCPN , DCPQ , ADQM .
Bài 3. Trong hình lăng trụ đứng sau có bao nhiêu mặt, bao nhiêu đỉnh và bao nhiêu cạnh.
Lời giải:
Trong hình lăng trụ trên có 5mặt, 9cạnh, 6đỉnh; Bài 4. Cho hình lăng trụ đứng có đáy là hình thang vuông. Hãy kể tên: a) Các cạnh song song với AD ; b) Các cạnh song song với AB ;
Lời giải:
(b) H G F
D C B d a H.a
E
A c b
3
Các cạnh song song với AD là BC,FG,EH . Các cạnh song song với AB là EF . Bài 5. Điền đầy đủ các kích thước vào hình khai triển của các hình lăng trụ ở hình đưới đây:
Lời giải:
Bài 6.

Trong các hình khai triển đưới đây, hình nào gấp lại được thành một hình lăng trụ đứng?
Lời giải:
Hình khai triển a là hình gấp lại được thành một hình lăng trụ đứng tam giác.
Bài 7.
Trong các hình khai triển đưới đây, hình nào gấp lại được thành một hình lăng trụ đứng?
a) b) c) a) b) c)

Hình khai triển a,b là hình gấp lại được thành một hình lăng trụ đứng tam giác.
Bài 8.
Người ta cưa một khối gỗ có dạng một hình lập phương như hình vẽ và được hai hình lăng trụ. a) Đáy của lăng trụ đứng nhận được là tam giác vuông, tam giác cân, hay là tam giác đều? b) Các mặt bên của mỗi lăng trụ đứng nhận được có phải tất cả đều là hình vuông không?
4
Lời giải: c
a a
d d d c b
c d b
b
b c
H.a
a) Đáy của lăng trụ đứng nhận được là tam giác vuông cân.
b) Các mặt bên nhận được có hai hình vuông và một mặt nhận được.
Bài 9.
Từ hình khai triển trong hình vẽ sau có thể gấp theo các cạnh để có được một lăng trụ đứng hay không? ( Các tứ giác trên hình đều là những hình chữ nhật).
b) Trong hình vừa gấp được, xét xem các phát biểu dưới đây, phát biểu nào đúng:
- Cạnh AD vuông góc với cạnh AB
-EF và CF là hai cạnh vuông góc với nhau.
- Cạnh DE và cạnh BC vuông góc với nhau.
Lời

giải:
a) Gấp được thành một hình lăng trụ đứng.
b) Sau ghi gấp ta được một hình lăng trụ đứng như hình bên.
Các phát biểu trên đều là đúng.
Bài 10.
Quan sát các hình lăng trụ đứng trong các hình vẽ sau rồi điền số thích hợp vào các ô trống ở bảng dưới đây:
5
Hình a b c E
B D A F E
a) b) c)
F C
D C B A
Số mặt bên 4
Số đỉnh
Số cạnh bên 5
Lời giải: Bảng được điền như sau: Hình a b c
Số cạnh của một đáy 3 4 5
Số mặt bên 3 4 5
Số đỉnh 6 8 10

Số cạnh bên 3 4 5
Bài 11: Trong các hình sau đây, hình vẽ nào biểu diễn một hình lăng trụ đứng?
(1) (2) (3) (4) (5)
Lời giải: Hình 345 ;; biểu diễn một hình lăng trụ đứng.
Dạng 2. Tính diện tích, thể tích của hình lăng trụ đứng tam giác.
I. Phương pháp giải:
1. Diện tích xung quanh của hình lăng trụ đứng tam giác bằng tích của chu vi đáy với chiều cao của nó. . xq SCh Trong đó xq
S : Diện tích xung quanh của hình lăng trụ. C : Chu vi đáy của hình lăng trụ.
h : Chiều cao của lăng trụ.
2. Diện tích toàn phần: Diện tích toàn phần bằng diện tích xung quanh cộng diện tích hai đáy. 2 SSS xq tp d
6 Số cạ
ủa một
nh c
đáy 3
Trong đó:

tpS là diện tích toàn phần của hình lăng trụ. xq S : Diện tích xung quanh của hình lăng trụ. dS : Diện tích một đáy của hình lăng trụ đứng.
3. Thể tích của hình lăng trụ đứng tam giác bằng diện tích đáy nhân với chiều cao. .d VSh Trong đó V : Thể tích của hình lăng trụ đứng. dS : Diện tích một đáy của hình lăng trụ đứng. h : Chiều cao của hình lăng trụ đứng. II. Bài toán.
7
ải Chu vi ABC là: 33511 ABACBCcm Diện tích xung quanh của lăng trụ . ABCABC là: 2 .11.444 xq SChcm Diện tích ABC là: 1 .. 2 ABC SABAC 2 19 .3.3cm 22 Thể tích của lăng trụ đứng . ABCABC là: 3 9 ..418cm 2 ABC VSh . Bài 2. Một tấm lịch để bàn có dạng một lăng trụ đứng, ACB là một tam giác cân tại C . Tính diện tích miếng bìa để làm một tấm lịch như trên. C' B' A' C B A
Bài 1. Cho hình lăng trụ đứng ABCABC
, đáy ABC là tam giác vuông cân, 3cm ABAC
, 5 BCcm
4cm AA
. Tính diện tích xung quanh và thể tích hình lăng trụ đó. Lời gi
15cm 8cm C'
Lời giải: Do tam giác ACB cân ở C nên 15 CACBcm . Chu vi ACB là 8151538 Ccm
A'

22cm
B'
Diện tích miếng bìa để làm một tấm lịch chính là diện tích xung quanh của hình lăng trụ đứng, ta có: 2 3822836 xq SC.hC.BB'.cm . Vậy diện tích miếng bìa để làm một tấm lịch là 2 836cm .
B A
C B A C'
B' A'
C
8
Bài 3. Cho hình lăng trụ tam giác đều ABCABC có 4cm AB , '10cmAA . Tính diện tích xung quanh và thể tích lăng trụ đó. Lời giải: Chu vi ABC đều là: 3.412cm . Diện tích xung quanh của lăng trụ ABCABC là: 2 .12.10120 xq SChcm Bài 4. Thùng đựng của một máy cắt cỏ có dạng lăng trụ đứng tam giác. Hãy tính thể tích của thùng.
Lời giải:
100cm

60cm 70cm
Chu vi đáy của thùng đựng máy cắt cỏ là: 8060100240 Ccm .
80cm
Diện tích đáy của thùng đựng máy cắt cỏ là: 2 1 80602400 2 S.cm . Thể tích của thùng đựng máy cắt cỏ là: 3 240070168000 VS.h.cm . Bài 5. Quan sát hình lăng trụ đứng tam giác (H.4) rồi điền số thích hợp vào các ô trống ở bảng sau: acm 5 3 12 7 bcm 6 2 15 ccm 7 13 6 hcm 10 5 Chu vi đáy cm 9 21 2 xq Scm 80 63 Lời giải: acm 5 3 12 7 bcm 6 2 15 8 ccm 7 4 13 6 hcm 10 5 2 3 Chu vi đáy cm 18 9 40 21 2 xq Scm 180 45 80 63 Bài 6. Điền số thích hợp vào các ô trống ở bảng sau: Lăng trụ 1 Lăng trụ 2 Lăng trụ 3

9
Chiều cao của lăng trụ đứng tam giác 5cm 7cm
Chiều cao của tam giác đáy. 5cm
Cạnh tương ứng với đường cao của tam giác đáy. 3cm 5cm
Diện tích đáy 2 6cm 2 15cm
Thể tích lăng trụ đứng 3 49cm 0045,l
Lời giải: + Ở lăng trụ 1:
Chiều cao của tam giác đáy: 62 4 3 . cm
Thể tích: 3 4520.cm . + Ở lăng trụ 2:
Diện tích đáy: 2 4977:cm .
Chiều cao của tam giác đáy: 72 28 5 ,cm .
+ Ở lăng trụ 3: Chiều cao của lăng trụ: 45153:cm . Cạnh tương ứng: 152 6 5 cm .
Bài 7.
Hình vẽ sau biểu diễn một lưỡi rìu bằng sắt, nó có dạng một lăng trụ đứng, BDC là một tam giác cân.
a) Hãy vẽ thêm nét khuất, điền thêm chữ vào các đỉnh rồi cho biết AB song song với những cạnh nào? b) Tính thể tích lưỡi rìu.
A

Lời giải:
B
8cm 4cm 10cm D
C
10
a) AB song song với KD,IC .
b) Diện tích đáy: 2 4832.cm . Thể tích của lưỡi rìu: 3 3210320.cm
Bài 8.
Một lều trại có dạng hình lăng trụ đứng đáy là tam giác, thể tích phần không gian bên trong là 3 216,cm . Biết chiều dài CC' của lều là 24,m , chiều rộng BC của lều là 12,m . Tính chiều cao AH của lều.
A'
Lời giải:
A

C' B' H C B
Diện tích đáy của tam giác ABC là: 2 2162409 ABC SV:CC',:,,cm Chiều cao AH của lều là : 209 215 12 ABC ., AHS:BC,m ,
Bài 9.
Hình lăng trụ đứng ABC.A'B'C' có chiều cao 5m , đáy là tam giác vuông tại A và 2 ABm . Tính AC , biết thể tích của hình lăng trụ bằng 3 15m
Lời giải:
Diện tích đáy của tam giác vuông ABC là: 2 1553 ABC SV:h:m . Cạnh AC của tam giác ABC là: 23 23 2 ABC ACS:ABm .
Bài 10.
Diện thể tích của cái tủ tường hình lăng trụ đứng có các kích thước như trong hình vẽ sau.
11
I K D
B A
C
Lời giải:
Diện tích đáy của cái tủ tường là: 2 1 70702450 2 d S..cm .
Thể tích của cái tủ tường là: 3 2450180441000 d VS.h.cm .
Bài 11.
Một hình lăng trụ đứng ABCDEF có đáy ABC là một tam giác vuông tại A , chiều cao của lăng trụ
là 9cm. Độ dài hai cạnh góc vuông của đáy là 3cm và 4cm, cạnh huyền có độ dài là 5cm
a) Tính diện tích xung quanh của hình lăng trụ đứng. b) Tính diện tích toàn phần của hình lăng trụ đứng. c) Tính thể tích của hình lăng trụ đứng. Lời giải:
B

C A E D
F
a) Tính diện tích xung quanh của hình lăng trụ đứng. Chu vi ABC là: 34512 cm Diện tích xung quanh của lăng trụ ABCDEF là: 22.12.9108cm xq Sph . b) Tính diện tích toàn phần của hình lăng trụ đứng. Diện tích tam giác ABC là: 2 11 ...3.46cm 22 ABC SABAC . Diện tích toàn phần của lăng trụ ABCDEF là: 221082.6120cmtpxqABC SSS . c) Tính thể tích của hình lăng trụ đứng.
12
Thể tích lăng trụ . ABCDEF là: 3.6.954cm ABC VSh
Bài 12. Cho hình lăng trụ tam giác đều . ABCABC có 4 ABcm , 2 BHcm , 10 AA'cm . Tính diện tích

xung quanh và thể tích lăng trụ đó. Lời giải: Chu vi ABC đều là: 3.412cm C .
Diện tích xung quanh của lăng trụ ABCABC là: 2 .12.10120 xq Schcm . Diện tích ABC là: 2 11 424 22 ABC s.AB.BH..cm . Thể tích của lăng trụ đứng ABCABC là: 3.4.1040cm ABC VSh .
Dạng 3. Tính diện tích, thể tích của hình lăng trụ đứng tứ giác. I. Phương pháp giải:
1. Diện tích xung quanh của hình lăng trụ đứng tứ giác bằng tích của chu vi đáy với chiều cao của nó. . xq SCh Trong đó xq S : Diện tích xung quanh của hình lăng trụ. C : Chu vi đáy của hình lăng trụ. h : Chiều cao của lăng trụ.
2. Diện tích toàn phần: Diện tích toàn phần bằng diện tích xung quanh cộng diện tích hai đáy. 2 tpxqd SSS
Trong đó: tpS là diện tích toàn phần của hình lăng trụ.
13
C' B
C B' H
A'
A
S : Diện tích xung quanh của hình lăng trụ.
dS : Diện tích một đáy của hình lăng trụ đứng.
3. Thể tích của hình lăng trụ đứng tứ giác bằng diện tích đáy nhân với chiều cao.
.d VSh
Trong đó
V : Thể tích của hình lăng trụ đứng.
dS : Diện tích một đáy của hình lăng trụ đứng.
h : Chiều cao của hình lăng trụ đứng.
II. Bài toán.
Bài 1.

Cho hình lăng trụ đứng ABCDABCD có đáy là hình thoi cạnh 3cm và chiều cao bằng 5cm Tính diện tích xung quanh lăng trụ. Lời giải Lời giải: Chu vi của hình thoi ABCD là: 4312.cm . Diện tích xung quanh của lăng trụ đứng . ABCDABCD là: 2.12.560cm xq SCh .
Bài 2.
Cho hình lăng trụ đứng có đáy là hình thoi cạnh 6cm và diện tích xung quanh của hình lăng trụ là 2 192 cm . Tính chiều cao của hình lăng trụ.
Lời giải:
Chu vi đáy của hình lăng trụ là: 6424 C.cm Chiều cao của hình lăng trụ là 192248 xq hS:C:cm
14 xq
Bài 3. D' C' B' A' D C B A
Cho hình lăng trụ đứng có đáy là hình thoi. Biết chiều cao của hình lăng trụ 6cm và diện tích xung quanh của hình lăng trụ là 2 288cm . Tính cạnh đáy của hình lăng trụ.
Lời giải: Chu vi đáy của hình lăng trụ là: 288648 xq CS:h:cm
Do đáy của hình lăng trụ là hình thoi nên 4 cạnh bằng nhau. Cạnh đáy của hình lăng trụ đứng là: 48412:cm
Bài 4.
Tính diện tích xung quanh và thể tích của hình lăng trụ tứ giác đều ABCDABCD
A A'

C D
Lời giải: Vì . ABCDABCD là lăng trụ tứ giác đều nên tứ giác ABCD là hình vuông và có chiều cao 'AA Diện tích xung quanh của lăng trụ là: 24..'4.6.12288cm xq SABAA . Diện tích đáy ABCD là: 222 636cm ABCD SAB . Thể tích lăng trụ ABCDABCD là: 3.36.12432cm ABCD VSh Bài 5. Cho hình lăng trụ đứng tứ giác đều có thể tích là 3 392cm và chiều cao của hình lăng trụ là 8cm . Tính cạnh đáy của hình lăng trụ.
Lời giải: Diện tích xung quanh của hình lăng trụ đứng tứ giác đều là: 2 392849 xq SV:h:cm
Do lăng trụ đứng có đáy là tứ giác đều nên đáy là hình vuông. Vậy cạnh đáy của lăng trụ đứng là 7cm .
Bài 6.
Cho hình lăng trụ đứng tứ giác đều có thể tích là 3 2160cm và cạnh đáy của hình lăng trụ là 12cm. Tính chiều cao hình lăng trụ.
Lời giải:
15
có
6cm AB 12cm AA .
B' D' C' B