BÀI TẬP DẠY THÊM CẢ NĂM MÔN TOÁN Ths Nguyễn Thanh Tú eBook Collection BÀI TẬP DẠY THÊM CẢ NĂM TOÁN 10 SÁCH CHÂN TRỜI SÁNG TẠO (CHƯƠNG 15) (BẢN HỌC SINH) WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL.COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405
BÀI 1. MỆNH ĐỀ
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1. Mệnh đề và mệnh đề chứa biến
- Mệnh đề là một khẳng định đúng hoặc sai.
Một khẳng định đúng gọi là mệnh đề đúng.
Một khẳng định sai gọi là mệnh đề sai.
Một mệnh đề không thể vừa đúng vừa sai.
- Mệnh đề chứa biến không phải là mệnh đề, nhưng khi thay biến bởi giá trị nào đó thì nó trở thành mệnh đề.
Chú ý: Người ta thường sử dụng các chữ cái in hoa ,,,PQR đề kí hiệu mệnh đề.
2. Mệnh đề phủ định Phủ định của mệnh đề P là mệnh đề "Không phải P ", kí hiệu P . Mệnh đề P đúng khi P sai và P sai khi P đúng.
3. Mệnh đề kéo theo - Mệnh đề "Nếu P thì Q " được gọi là mệnh đề kéo theo, kí hiệu PQ . Mệnh đề PQ chỉ sai khi P đúng và Q sai. - Nếu mệnh đề PQ đúng (định lí) thì ta nói:
+P là giả thiết, Q là kết luận của định lí;
+P là điều kiện đủ để có Q ;
+Q là điều kiện cần để có P .
Chú ý:
a) Mệnh đề PQ còn được phát biểu là " P kéo theo Q " hoặc "Từ P suy ra Q ".
b) Để xét tính đúng sai của mệnh đề PQ , ta chỉ cần xét trường hợp P đúng. Khi đó, nếu Q đúng thì mệnh đề đúng, nếu Q sai thì mệnh đề sai.
4. Mệnh đề đảo, hai mệnh đề tương đương
- Mệnh đề đảo của mệnh đề kéo theo PQ là mệnh đề QP
ý: Mệnh
DẠYKÈMQUYNHƠNOFFICIAL
NG
Ậ
CHƯƠ
I. MỆNH ĐỀ VÀ T
P HỢP
-
đó, P là điều kiện cần và đủ đễ
ề
ệ
ầ
ệnh đề P và Q tương đương khi chúng cùng đúng hoặc cùng sai. 5. Mệnh đề chứa kí hiệu , ∀∃ - Mệnh đề “ ,()∀∈xMPx " đúng nếu với mọi ( )00 ,∈ xMPx là mệnh đề đúng. - Mệnh đề “ ,()∃∈xMPx " đúng nếu có 0 ∈ xM sao ( )0cho Px là mệnh đề đúng.
Chú
đề đảo của một mệnh đề đúng không nhất thiết là đúng. - Nếu cả hai mệnh đề PQ và QP đều đúng thì ta nói P và Q là hai mệnh đề tương dương, kí hiệu là ⇔ PQ
Khi
có Q (hay Q là đi
u ki
n c
n và đủ đễ có P ). Chí ý: Hai m
Dạng 1: Nhận biết mệnh đề, mệnh đề chứa biến
1. Phương pháp
Mệnh đề là một câu khẳng định đúng hoặc một câu khẳng định sai.
Một câu khẳng định đúng được gọi là một mệnh đề đúng, một câu khẳng định sai được gọi là mệnh đề sai.
Câu hỏi, câu cảm tháng, câu mệnh lệnh hoặc câu chưa xác định được tính đúng sai thì không phải là mệnh đề.
2. Các ví dụ rèn luyện kĩ năng Ví dụ 1: Các câu sau đây, câu nào là mệnh đề, câu nào không phải là mệnh đề? Nếu là mệnh đề hãy cho biết mệnh đề đó đúng hay sai.
(1) Ở đây đẹp quá!
(2) Phương trình 2 310xx−+= vô nghiệm
(3) 16 không là số nguyên tố
(4) Hai phương trình 2 430xx−+= và 2 310xx−++= có nghiệm chung.
(5) Số π có lớn hơn 3 hay không?
(6) Italia vô địch Worldcup 2006
(7) Hai tam giác bằng nhau khi và chỉ khi chúng có diện tích bằng nhau. Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Ví dụ 2: Cho các phát biểu sau, có bao nhiêu phát biểu là
DẠYKÈMQUYNHƠNOFFICIAL B. PHÂN LOẠI VÀ PH
NG PHÁP GIẢI BÀI TẬP
ƯƠ
i 3. Bài tập trắc nghiệm Câu 1. Phát biểu nào sau đây là một mệnh đề? A. Mùa thu Hà Nội đẹp quá! B. Bạn có đi học không? C. Đề thi môn Toán khó quá! D. Hà Nội là thủ đô của Việt Nam. Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 2. Câu nào sau đây không là mệnh đề?
mệnh đề? a) Hà Nội là thủ đô của Việt Nam. b) ,25.xx∈+> ℝ c) 65.x −≤ d) Phương trình 2 650xx−+= có nghiệm. A. 1. B. 2. C. 3. D. 4. Hướng dẫn giả
A. Tam giác đều là tam giác có ba cạnh bằng nhau.
B. 31 < . C. 451 −=
D. Bạn học giỏi quá!
Hướng dẫn giải
Câu 3. Cho các phát biểu sau đây:
1. “17 là số nguyên tố”
2. “Tam giác vuông có một đường trung tuyến bằng nửa cạnh huyền”
3. “Các em C14 hãy cố gắng học tập thật tốt nhé !”
4. “Mọi hình chữ nhật đều nội tiếp được đường tròn”
Hỏi có bao nhiêu phát biểu là một đề?
A. 4 B. 3 C. 2 D. 1
Hướng dẫn giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 4. Cho các câu sau đây:
1. “Phan-xi-păng là ngọn núi cao nhất Việt Nam”.
2. “ 2 9,86π < ”.
3. “Mệt quá!”.
4. “Chị ơi, mấy giờ rồi?”.
Hỏi có bao nhiêu câu là mệnh đề?
A. 1. B. 3 . C. 4 . D. 2 .
Hướng dẫn giải
Câu 5. Câu nào trong các câu sau không phải là mệnh đề?
A. π có phải là một số vô tỷ không?. B. 225 +=
C. 2 là một số hữu tỷ. D. 4 2 2 = . Hướng dẫn giải
Chọn A.
Câu 6. Trong các câu sau, câu nào không phải là mệnh đề?
A. Buồn ngủ quá!
B. Hình thoi có hai đường chéo vuông góc với nhau.
C. 8 là số chính phương.
D. Băng Cốc là thủ đô của Mianma.
Lời giải.
DẠYKÈMQUYNHƠNOFFICIAL
Câu 7. Trong các câu sau, có bao nhiêu câu là không phải là mệnh đề?
a) Huế là một thành phố của Việt Nam. b) Sông Hương chảy ngang qua thành phố Huế c) Hãy trả lời câu hỏi này! d) 51924. += e) 68125. += f) Bạn có rỗi tối nay không? g) 211.x += A. 1. B. 2. C. 3. D. 4. Lời giải.
Câu 8: Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Hãy đi nhanh lên! b) Hà Nội là thủ đô của Việt Nam. c) 57415. ++= d) Năm 2018 là năm nhuận. A. 4. B. 3. C. 1. D. 2. Lời giải.
Câu 9: Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Cố lên, sắp đói rồi! b) Số 15 là số nguyên tố. c) Tổng các góc của một tam giác là 180. ° d) x là số nguyên dương. A. 3. B. 2. C. 4. D. 1. Lời giải. .....................................................................................................................................................................
Câu 10: Trong các câu sau, câu nào là mệnh đề?
A. Đi ngủ đi!
B. Trung Quốc là nước đông dân nhất thế giới. C. Bạn học trường nào?
D. Không được làm việc riêng trong giờ học. Lời giải.
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
.....................................................................................................................................................................
Câu 11: Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
A. Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.
B. Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.
C. Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.
D. Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ. L
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
12: Mệnh đề 2 ,20xxa ∀∈−+> ℝ với a là số thực cho trước. Tìm a để mệnh đề đúng A. 2a ≤ . B. 2a < . C. 2a = . D. 2a > . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 13: Với giá trị nào của x thì 2 "10," xx−=∈ ℕ là mệnh đề đúng. A. 1x = . B. 1x =− . C. 1x =± . D. 0x = . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Dạng 2: Xét tính đúng sai của mệnh đề 1. Phương pháp Một câu khẳng định đúng là mệnh đề đúng, một câu khẳng định sai là mệnh đề sai. 2. Các ví dụ rèn luyện kĩ năng Ví dụ 1: Cho mệnh đề chứa biến ( ) 2 :"35"Pxxx +≤ với x là số thực. Mệnh đề nào sau đây là đúng: A. ( )3P B. ( )4P C. ( )1P D. ( )5P Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... Ví dụ 2: Trong các câu sau, câu nào là mệnh đề đúng? A. Nếu ab ≥ thì 22ab ≥ B. Nếu a chia hết cho 9 thì a chia hết cho 3. C. Nếu em chăm chỉ thì em thành công. D. Nếu một tam giác có một góc bằng 060 thì tam giác đó đều.
ời giải.
Câu
3. Bài tập trắc nghiệm
Câu 1: Chọn mệnh đề đúng trong các mệnh đề sau.
A. x ∀∈ℝ sao cho 1 xx +> B. x ∀∈ℝ sao cho xx = C. x ∃∈ ℝ sao cho 2-3 xx = D. x ∃∈ ℝ sao cho 2 0x < Lời giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 2. Trong các mệnh đề sau, mệnh đề nào đúng?
A. x ∀∈ℝ , 2 1x > 1x >− B. x ∀∈ℝ , 2 1x > 1x > C. x ∀∈ℝ , 1x >− 2 1x > D. x ∀∈ℝ , 1x > 2 1x > Hướng dẫn giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 3. Trong các mệnh đề sau, mệnh đề nào đúng?
A. 62 là số hữu tỷ
B. Phương trình 2 720xx+−= có 2 nghiệm trái dấu.
C. 17 là số chẵn.
D. Phương trình 2 70xx++= có nghiệm. Hướng dẫn giải .....................................................................................................................................................................
Câu 4: Trong các câu sau, câu nào là mệnh đề đúng?
A. Nếu ab ≥ thì 22ab ≥
B. Nếu a chia hết cho 9 thì a chia hết cho 3.
C. Nếu em chăm chỉ thì em thành công.
DẠYKÈMQUYNHƠNOFFICIAL Lời giải.
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL
ếu mộ
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
r7∃∈= ℚ . D. n, n4∀∈+ ℕ chia hết cho 4. Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 7: Hỏi trong các mệnh đề sau đây mệnh đề nào là mệnh đề đúng? A. 2 ",39" xxx∀∈> >ℝ . B. 2 ",39" xxx∀∈>− >ℝ . C. 2 ",93" xxx∀∈> >ℝ . D. 2 ",93" xxx∀∈> >−ℝ . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Dạng 3: Phủ định của mệnh đề 1. Phương pháp Cho mệnh đề P . Mệnh đề “Không phải P ” gọi là mệnh đề phủ định của P . Ký hiệu là P . Nếu P đúng thì P sai, nếu P sai thì P đúng . Cho mệnh đề chứa biến ()Px với xX ∈
D. N
t tam giác có một góc bằng 60° thì tam giác đó đều. Lời giải.
Câu 5: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai? A. 2 24.ππ −<−⇔< B. 2 416.ππ<⇔< C. 2352232.5. <⇒< D. 2352232.5. <⇒−>− Lời giải.
Câu 6: Trong các mệnh đề dưới đây mệnh đề nào đúng? A. 2x, x10∀∈+> ℝ B. 2 , xxx∀∈> ℝ C. 2r,
Mệnh đề phủ định của mệnh đề ",()" xXPx∀∈ là ",()" xXPx∃∈ Mệnh đề phủ định của mệnh đề ",()" xXPx∃∈ là ",()" xXPx∀∈ 2. Các ví dụ rèn luyện kĩ năng Ví dụ 1: Nêu mệnh đề phủ định của các mệnh đề sau, cho biết mệnh đề này đúng hay sai? :P " Hình thoi có hai đường chéo vuông góc với nhau" :Q " 6 là số nguyên tố" :R " Tổng hai c
DẠYKÈMQUYNHƠNOFFICIAL
:
:
:
L
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
1
∀∈ d) ( )∃∈ , xNPx Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Ví dụ 3: Dùng các kí hiệu để viết các
sau và viết
ệnh đề phủ định
ủ
a)
ủa ba số tự nhiên liên tiếp chia hết cho sáu b) Với mọi số thực bình phương của nó là một số không âm. c) Có một số nguyên mà bình phương của nó bằng chính nó. d) Có một số hữu tỉ mà nghịch đảo của nó lớn hơn chính nó. Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
ạnh của một tam giác lớn hơn cạnh còn lại"
S " 53 >− "
K " Phương trình 42220xx−+= có nghiệm "
H " ( )2 3312 = "
ời giải
Ví dụ 2: Cho mệnh đề chứa biến " ( ) 3: Pxxx > " , xét tính đúng sai của các mệnh đề sau: a) ( )1P b)
3 P
c) ( ), xNPx
câu
m
c
a nó.
Tích c
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... Ví dụ 4: Xác định tính đúng sai của mệnh đề sau và tìm phủ định của nó : a) A : " 2 ,0xRx ∀∈≥ " b) B: " Tồn tại số tự nhiên đều là số nguyên tố". c) C : " xN∃∈ , x chia hết cho 1x + " d) D: " 42
nNnn ∀∈−+ là hợp số " e) E: " Tồn tại hình thang là hình vuông ". f) F: " Tồn tại số thực a sao cho 1 12 1 a a ++≤ + " Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... 3. Bài tập trắc nghiệm Câu 1. Cho mệnh đề: “ 2 ,350xxx ∀∈++> ℝ ”. Mệnh đề phủ định của mệnh đề trên là A. 2 ,350xxx ∀∈++≤ ℝ B. 2 ,350xxx ∃∈++≤ ℝ C. 2 ,350xxx ∀∈++< ℝ D. 2 ,350xxx ∃∈++> ℝ Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 2. Cho mệnh đề “Có một học sinh trong lớp C4 không chấp hành luật giao thông”. Mệnh đề phủ định của mệnh đề này là A. Không có học sinh nào
ớp
ấ
ọ
ọ
ớ
ấ
ột họ
,1
trong l
C4 ch
p hành luật giao thông. B. M
i h
c sinh trong l
p C4 đều ch
p hành luật giao thông. C. Có m
c sinh trong lớp C4 chấp hành luật giao thông.
D. Mọi học sinh trong lớp C4 không chấp hành luật giao thông.
Hướng dẫn giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 3. Cho mệnh đề: “ Có một học sinh trong lớp 10A không thích học môn Toán”. Mệnh đề phủ định của mệnh đề này là:
A. “ Mọi học sinh trong lớp 10A đều thích học môn Toán”.
B. “ Mọi học sinh trong lớp 10A đều không thích học môn Toán”.
C. “ Mọi học sinh trong lớp 10A đều thích học môn Văn”.
D. “ Có một học sinh trong lớp 10A thích học môn Toán”.
Hướng dẫn giải .....................................................................................................................................................................
Câu 4. Mệnh đề phủ định của mệnh đề “ 2018 là số tự nhiên chẵn” là
A. 2018 là số chẵn.
C. 2018 không là số tự nhiên chẵn.
B. 2018 là số nguyên tố.
D. 2018 là số chính phương.
Hướng dẫn giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 5. Mệnh đề: “Mọi động vật đều di chuyển” có mệnh đề phủ định là
A. Có ít nhất một động vật di chuy
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... ..................................................................................................................................................................... Câu 6: Cho mệnh đề “ 2 ,70xRxx ∀∈−+< ”. Hỏi mệnh đề nào là mệnh đề phủ định của mệnh đề trên? A. 2 ,70xRxx ∃∈−+≥ B. 2 ,70xRxx ∀∈−+> C. 2 ,70xRxx ∀∈−+< D. 2 ,70xRxx ∃∈−+< Lời giải ..................................................................................................................................................................... B : sai là gì không dùng đúng kí hiệu của phủ định. C : sai là gì không dùng đúng ≥ D : sai kí hiệu không tồn tại. Câu 7: Cho mệnh đề: 2 "2350" xxx ∃∈−−< ℝ . Mệnh đề phủ định sẽ là
ển. B. Mọi động vật đều đứng yên. C. Có ít nhất một động vật không di chuyển. D. Mọi động vật đều không di chuyển. Hướng dẫn giải
A. 2 "2350" xxx ∀∈+−≥ ℝ . B. 2 "2350" xxx ∀∈+−> ℝ . C. 2 "2350" xxx ∃∈+−> ℝ . D. 2 "2350" xxx ∃∈+−≥ ℝ . Lời giải .....................................................................................................................................................................
Câu 8: Mệnh đề phủ định của mệnh đề: 2 ,50xRxx ∀∈++> là
A. 2 ,50xxx ∃∈++≤ ℝ . B. 2 ,50xxx ∀∈++≤ ℝ . C. 2 ,50xxx ∃∈++< ℝ . D. 2 ,50xxx ∀∈++< ℝ . Lời giải .....................................................................................................................................................................
Câu 9: Mệnh đề phủ định của mệnh đề “Phương trình ( )2 0 0axbxca++=≠ vô nghiệm” là mệnh đề nào sau đây?
A. Phương trình ( )2 0 0axbxca++=≠ có nghiệm.
B.. Phương trình ( )2 0 0axbxca++=≠ có 2 nghiệm phân biệt.
C. Phương trình ( )2 0 0axbxca++=≠ có nghiệm kép. D. Phương trình ( )2 0 0axbxca++=≠ không có nghiệm. Lời giải
DẠYKÈMQUYNHƠNOFFICIAL
.....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 10. Tìm mệnh đề phủ định của mệnh đề: 2 ,50xxx ∀∈++> ℝ . A. 2 ,50xxx ∃∈++< ℝ B. 2 ,50xxx ∀∈++< ℝ C. 2 ,50xxx ∀∈++≤ ℝ D. 2 ,50xxx ∃∈++≤ ℝ Hướng dẫn giải ..................................................................................................................................................................... Câu 11. Tìm mệnh đề phủ định của mệnh đề 2 ":" xxx∀∈> ℝ . A. 2 : xxx∀∈≤ ℝ B. 2 : xxx∃∈> ℝ C. 2 : xxx∃∈≤ ℝ D. 2 : xxx∃∈< ℝ Hướng dẫn giải
i mệnh đề nào là mệnh đề phủ định của mệnh đề trên?
A. 2 ,70∀∈−+> ℝ xxx . B. 2 ,70∃∈−+< ℝ xxx . C. 2 ,70∃∈−+≥ ℝ xxx . D. 2 ,70∃∈−+≤
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 12. Cho x là số tự nhiên. Phủ định của mệnh đề “ x∀ chẵn, 2 xx + là số chẵn” là mệnh đề:
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
A. x∃ lẻ, 2 xx + là số lẻ. B. x∃ lẻ, 2 xx + là số chẵn. C. x∀ lẻ, 2 xx + là số lẻ D. x∃ chẵn, 2 xx + là số lẻ Hướng dẫn giải
ệ
ℚ
2
xxx ∀∈−+≠ ℚ
ả
.....................................................................................................................................................................
Cho mệnh đề 2 “,70” ∀∈−+< ℝ xxx .
ỏ
Câu 13. Phủ định của m
nh đề 2 ":2520" xxx ∃∈−+= ℚ là A. 2 ":2520" xxx ∃∈−+> ℚ B. 2 ":2520" xxx ∃∈−+≠
C.
":2520"
D. 2 ":2520" xxx ∀∈−+= ℚ Hướng dẫn gi
i
Câu 14.
H
ng
..................................................................................................................................................................... .....................................................................................................................................................................
15. Mệnh đề phủ định của mệnh đề “ 2, 130xxx ∃∈++= ℝ ” là
“ 2, 130xxx ∀∈++≠ ℝ ”. B. “ 2, 130xxx ∃∈++> ℝ ”. C. “ 2, 130xxx ∀∈++= ℝ ”. D. “ 2, 130xxx ∃∈++≠ ℝ ”. Hướng dẫn giải ..................................................................................................................................................................... Câu 16. Tìm mệnh đề phủ định của mệnh đề 2 :";10"Pxxx∀∈+−> ℕ A. 2 :";10"Pxxx∀∈+−> ℕ B. 2 P:";10" xxx ∃∈+−≤ ℕ C. 2 :";10"Pxxx∃∈+−> ℕ . D. 2 :";10"Pxxx∀∈+−≤ ℕ . Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
ℝ xxx . Hướ
dẫn giải
Câu
A.
1. Phươ
2 m
pháp
nh đề P và
Mệnh đề “Nếu P thì Q ” gọi là mệnh đề kéo theo. Ký hiệu là PQ . Mệnh đề PQ chỉ sai khi P đúng Q sai, và đúng trong các trường hợp con lại. Cho mệnh đề PQ . Khi đó mệnh đề QP gọi là mệnh đề đảo của PQ . Mệnh đề “ P nếu và chỉ nếu Q ” gọi là mệnh đề tương đương, ký hiệu PQ ⇔ . Mệnh đề PQ ⇔ đúng khi cả hai mệnh
DẠYKÈMQUYNHƠNOFFICIAL
ạng 4:
ệ
đề
ệnh đề đảo và hai
ệnh đề
ương
ng
đề kéo theo PQ và QP đều đúng và sai trong các trường hợp còn lại. 2. Các ví dụ rèn luyện kĩ năng Ví dụ 1: Phát biểu mệnh đề PQ ⇒ và phát biểu mệnh đề đảo, xét tính đúng sai của nó. a) :P " Tứ giác ABCD là hình thoi" và :Q " Tứ giác ABCD AC và BD cắt nhau tại trung điểm mỗi đường" b) :"29"P > và :"43"Q < c) :P " Tam giác ABC
tại A" và :Q " Tam giác ABC có 2 AB = " d) :P " Ngày
ốc Khánh của nước Việt Nam" và :Q " Ngày
ngày thương binh liệt sĩ" Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Ví dụ 2: Phát biểu mệnh đề PQ ⇔ bằng hai cách và và xét tính đúng sai của nó a) :P "Tứ giác ABCD là hình thoi" và :Q " Tứ giác ABCD là hình bình hành có hai đường chéo vuông góc với nhau" b) :P " Bất phương trình 2 31xx−> có nghiệm" và :Q " ()() 2 13.11 −−−> " Hướng dẫn giải .....................................................................................................................................................................
D
M
nh
kéo theo, m
m
t
đươ
ng
Cho
ệ
Q .
vuông cân
2 tháng 9 là ngày Qu
27 tháng 7 là
3. Bài tập trắc nghiệm
Câu 1. Cho định lí “Nếu hai tam giác bằng nhau thì diện tích chúng bằng nhau”. Mệnh đề nào sau đây đúng?
A. Hai tam giác bằng nhau là điều kiện cần để diện tích chúng bằng nhau.
B. Hai tam giác bằng nhau là điều kiện cần và đủ để chúng có diện tích bằng nhau.
C. Hai tam giác có diện tích bằng nhau là điều kiện đủ để chúng bằng nhau.
D. Hai tam giác bằng nhau là điều kiện đủ để diện tích chúng bằng nhau.
Hướng dẫn giải .....................................................................................................................................................................
Câu 2: Trong các mệnh đề sau đây, mệnh đề nào có mệnh đề đảo là đúng?
A. Nếu a và b cùng chia hết cho c thì ab + chia hết cho c .
B. Nếu hai tam giác bằng nhau thì diện tích bằng nhau.
C. Nếu a chia hết cho 3 thì a chia hết cho 9
D. Nếu một số tận cùng bằng 0 thì số đó chia hết cho 5 .
Hướng dẫn giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 3: Trong các mệnh đề sau, mệnh đề nào không phải là định lí?
A. 2 , xx∃∈ ℕ chia hết cho 3 x chia hết cho 3 .
B. 2 , xx∃∈ ℕ chia hết cho 6 x chia hết cho 3 .
C. 2 , xx∀∈
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
ℕ
xx
ℕ
..................................................................................................................................................................... .....................................................................................................................................................................
Trong
mệnh đề
ệ
2 ,24xxx∀∈>− >ℝ . B. 2 ,24xxx∀∈> >ℝ .
chia hết cho 9 x chia hết cho 9 D. ,
∃∈
chia hết cho 4 và 6 x chia hết cho 12 Hướng dẫn giải
Câu 4:
các
sau, m
nh đề nào là định lí? A.
C. 2 ,42xxx∀∈> >ℝ . Lời giải
t số thực mà bình phương của nó bằng 3
C. Chỉ có một số thực có bình phương bằng 3 .
D. Nếu x là số thực thì 2 3=x . Hướng dẫn giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 2: Kí hiệu X là tập hợp các cầu thủ x trong đội tuyển bóng rổ, ( )Px là mệnh đề chứa biến “ x cao trên 180 cm ”. Mệnh đề ",()" ∀∈xXPx khẳng định rằng:
A. Mọi cầu thủ trong đội tuyển bóng rổ đều cao trên 180 cm
B. Trong số các cầu thủ của đội tuyển bóng rổ có một số cầu thủ cao trên 180 cm .
C. Bất cứ ai cao trên 180 cm đều là cầu thủ của đội tuyển bóng rổ.
D. Có một số người cao trên 180 cm là cầu thủ của đội tuyển bóng rổ Hướng dẫn giải
DẠYKÈMQUYNHƠNOFFICIAL D. Nếu ab + chia hết cho 3 thì , ab đều chia hết cho 3 . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Dạng 5: Mệnh đề với kí hiệu với mọi, tồn tại
Phương pháp • Kí hiệu ∀: đọc là với mọi, ∃: đọc là tồn tại •
ệnh đề phủ định của mệnh đề
•
ệ
đề
ủ định
ủa
ệ
Các
ụ rèn
ệ
ĩ
ă
ệ
đề 2
∃∈=
1.
M
", ()"∀∈xXPx là ", ()".∃∈xXPx
M
nh
ph
c
m
nh đề ", ()"∃∈xXPx là ", ()".∀∈xXPx 2.
ví d
luy
n k
n
ng Câu 1: M
nh
",3" xx
ℝ khẳng định rằng: A. Bình phương của mỗi số thực bằng 3 . B. Có ít nhất mộ
.....................................................................................................................................................................
3: Mệnh đề nào sau đây
ủ
nh
ủ
mệnh
ọ
ng
Mọi động
Mọ
độ
.....................................................................................................................................................................
Câu
là ph
đị
c
a
đề: “M
i độ
vật đều di chuyển”. A.
vật đều không di chuyển. B.
i
ng vật đều đứng yên. C. Có ít nhất một động vật không di chuyển. D. Có ít nhất một động vật di chuyển. Hướng dẫn giải
Câu 4: Phủ định của mệnh đề: “Có ít nhất một số vô tỷ là số thập phân vô hạn tuần hoàn” là mệnh đề nào sau đây:
A. Mọi số vô tỷ đều là số thập phân vô hạn tuần hoàn.
B. Có ít nhất một số vô tỷ là số thập phân vô hạn không tuần hoàn.
C. Mọi số vô tỷ đều là số thập phân vô hạn không tuần hoàn.
D. Mọi số vô tỷ đều là số thập phân tuần hoàn. Hướng dẫn giải
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
ℝ
ồ
tạ
2
.
..................................................................................................................................................................... .....................................................................................................................................................................
ậ
trắc nghiệm Câu 1. Tìm mệnh đề sai.
2
xxx ∀++> . B. 2
. C. 2
xxx ∃++= . D.
x
. Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 2: Mệnh đề nào sau đây đúng? A. 2 ,10xxx ∀∈−+> ℝ B. ,0nn ∃∈< ℕ C. 2 ,2nx ∃∈= ℚ . D. 1 ,0x x ∀∈> ℤ . Hướng dẫn giải ..................................................................................................................................................................... Câu 3. Mệnh đề nào sau là mệnh đề sai? A. 2 :0xx ∀∈> ℝ . B. 2 : xxx∃∈> ℝ C. 2 : nnn∃∈= ℕ D. n ∀∈ ℕ thì 2 nn ≤ Hướng dẫn giải ..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
Câu 5: Cho mệnh đề :A “ 2 ,70xxx ∀∈−+< ℝ ” Mệnh đề phủ định của A là: A. 2 ,70xxx ∀∈−+>
B. 2 ,70xxx ∀∈−+> ℝ C. Không t
n
i
:70xxx−+<
D. 2 ,-70xxx ∃∈+≥ ℝ . Hướng dẫn giải
3. Bài t
p
A.
";230"
";" xxx∀≥
";560"
1 ";" xx
∃<
Câu 4. Chọn mệnh đề sai.
A. “ 2 :0xx ∀∈> ℝ ”. B. “ 2 : nnn∃∈= ℕ ”. C. “ :2 nnn∀∈≤ ℕ ”. D. “ :1xx ∃∈< ℝ ”. Hướng dẫn giải .....................................................................................................................................................................
Câu 5. Tìm mệnh đề đúng.
A. 2 ";30" xx ∃+= B. 42 ";3x20" xx ∃++= C. 52";x "xx ∀∈> ℤ . D. ()( )2 ";2114" nn ∀∈+−ℕ⋮ Lời giải. .....................................................................................................................................................................
Câu 6. Trong các mệnh đề sau, mệnh đề nào sai?
n ∃∈ ℕ
2 112nn++
DẠYKÈMQUYNHƠNOFFICIAL
.....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
A.
,
chia hết cho 11 B. n ∃∈ ℕ , 2 1n + chia hết cho 4 C. Tồn tại số nguyên tố chia hết cho 5 D. n ∃∈ ℤ , 2 280 x −= Hướng dẫn giải
Câu 7. Trong các mệnh đề sau, mệnh đề nào đúng? A. x ∀∈ ℝ , ()2 11xx−≠− . B. ,3xx ∀∈< ℝ 3x ⇔< . C. 2 ,1nn ∃∈+ ℕ chia hết cho 4 D. 2 ,1nn ∀∈+ ℕ không chia hết cho 3 Hướng dẫn giải
..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1. Tập hợp và phần tử

- Mỗi tập hợp có các phần tử hoàn toàn xác định.
- Tập hợp không có phần tử nào gọi là tập rỗng, kí hiệu ∅ .
- Để chỉ a là phần tử của tập hợp A , ta viết ∈ aA ; ngược lại, ta viết ∉ aA .
- Người ta thường biểu thị tập hợp dưới dạng liệt kê các phần tủ hoặc chỉ ra tính chất đặc trưng của các phần tử.
Chú ý: Khi liệt kê các phần tử của tập hợp, ta có một số chú ý sau đây: a) Các phần tử có thể được viết theo thứ tự tuỳ ý. b) Mỗi phần tử chỉ được liệt kê một lần. c) Nếu quy tắc xác định các phần tử đủ rõ thì người ta dùng “..." mà không nhất thiết viết ra tất cả các phần tử của tập hợp. 2. Tập con và hai tập hợp bằng nhau A là tập con của B nếu mọi phần tử của A đều là phần tử của B , kí hiệu ⊂ AB .


Chú ý:
+⊂AA và ∅⊂ A với mọi tập hợp A .
+ Nếu A không phải là tập con của B thì ta kí hiệu ⊂ / AB (đọc là A không chía trong B hoặc B không chía A ).
+ Nếu ⊂ AB hoặc ⊂ BA thì ta nói A và B có quan hệ bao hàm. - Hai tập hợp A và B gọi là bằng nhau, kí hiệu = AB , nếu ⊂ AB và ⊂ BA
3. Một số tập con của tập số thực Sau này ta thường sử dụng các tập con của tập số thực sau đây ( a và b là các số thực, )< ab :
Trong các kí hiệu trên, kí hiệu −∞ đọc là âm vô cụcc (âm vô cùng), kí hiệu +∞ đọc là dương vô cưc (dương vô cùng).
DẠYKÈMQUYNHƠNOFFICIAL BÀI 2. TẬP HỢP
DẠYKÈMQUYNHƠNOFFICIAL B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP Dạng 1: Tập hợp và các phần tử của tập hợp 1. Phương pháp Cách liệt kê: Ghi tất cả các phần tử của tập hợp Cách nêu tính chất đặc trưng: Từ tất cả các phần tử của tậ hợp, nhận biết tính chất đặc trưng và ghi tính chất đặc trưng của các phần tử 2. Các ví dụ rèn luyện kĩ năng Ví dụ 1: Xác định các tập hợp sau bằng cách nêu tính chất đặc trưng { }0;1;2;3;4A = { }0;4;8;12;16B = { }1;2;4;8;16C = Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Ví dụ 2: Cho tập hợp 2 |2Axx x + =∈Ζ∈Ζ a) Hãy xác định tập A bằng cách liệt kê các phần tử b) Tìm tất cả các tập con của tập hợp A mà số phần tử của nó nhỏ hơn 3. Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... 3. Bài tập trắc nghiệm Câu 1: Trong các tập hợp sau đây, tập hợp nào có đúng một phần tử? A. { }; xy B. { }x C. { };x ∅ D. ∅ Lời giải Câu 2. Cho tập hợp { }|5Axx=∈≤ ℕ . Tập hợp A được viết dưới dạng liệt kê các phần tử là A. { }1;2;3;4A= B. { }1;2;3;4;5A= C. { }0;1;2;3;4;5A= . D. { }0;1;2;3;4A= . Lời giải ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL Câu 3. Cho tập ( )(){ }2 |410Xxxx=∈−−= ℝ . Tính tổng S các phần tử của tập X . A. 4S = . B. 9 2 S = . C. 9S = . D. 1S = . Lời giải Câu 4. Tập hợp { }2;5X = có bao nhiêu phần tử? A. 4 B. Vô số C. 2 D. 3 Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 5. Liệt kê phân tử của tập hợp { }22 |(2)(34)0Bxxxxx =∈−−−= ℕ . A. { }1;0;4B =− . B. { }0;4B = . C. 1 1;;0;4 2 B =− . D. { }0;1;4B = . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 6. Cho { }2 2530XxRxx=∈−+= , khẳng định nào sau đây đúng? A. { }1X = B. 3 1; 2 X = C. 3 2 X = D. { }0X = Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 7. Có bao nhiêu cách cho một tập hợp ? A. 2 B. 4 C. 3 D. 1 Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 8: Trong các tập hợp sau, tập hợp nào là tập hợp rỗng? A. { }/1xNx∈< . B. { }2 /6710xZxx ∈−+= . C. { }2 /420xQxx∈−+= D. { }2 /430xRxx∈−+= Lời giải .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL Câu 9: Cho hai tập hợp ( )( ){ } {}22 |2340,|4.AxxxxBxx =∈−−−==∈< ℤℕ Viết lại các tập A và
bằng
liệt kê các phần tử.
=−−
Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 10. Tìm số phần tử của tập hợp ()()( ){ }3 /1240Axxxxx =∈−+−= ℝ A. 5 B. 3 C. 2 D. 4 Lời giải Câu 11. Cho tập hợp ( )( ){ }22 |252160Axxxx =∈++−= ℤ . Tập hợp A được viết dưới dạng liệt kê là A. 1 4;;2;4 2 . B. { }4;2 . C. { }4± . D. { }4;2;4 . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 12. Hãy liệt kê các phần tử của tập hợp: { }2 /2x520Xxx=∈−+= ℤ A. { }0X = B. 1 2 X = C. { }2X = D. 1 2; 2 X = Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
B
cách
A. 3 2;1;2; 2 A =−− , { }0;1;2;3B = B. 3 2;1;2; 2 A
, { }1;2;3;4B = C. { }2;1;2A =−− , { }0;1;2;3B = D. { }2;1;2A =−− , { }1;2;3B =
DẠYKÈMQUYNHƠNOFFICIAL Câu 13. Cho tập ( )()( ){ }22 |412730Xxxxxx =∈−−−+= ℕ . Tính tổng S các phần tử của X . A. 9 2 S = B. 5S = C. 6S = D. 4S = Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 14. Trong các tập hợp sau, tập nào là tập rỗng? A. { }2 560xxx∈+−= ℝ . B. { }2 3520xxx∈−+= ℚ . C. { }2 10xxx∈+−= ℤ . D. { }2 510xxx∈+−= ℝ . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 15. Trong các tập hợp sau, tập hợp nào rỗng? A. { }2 40.Axx=∈−= ℕ B. { }2 50.Bxx=∈−= ℝ C. { }2 120.Cxxx=∈+−= ℚ D. { }2 230.Dxxx=∈++= ℝ Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 16. Cho { }* ,10,3Axxx =∈<ℕ⋮ . Chọn khẳng định đúng. A. A có 4 phần tử. B. A có 3 phần tử. C. A có 5 phần tử D. A có 2 phần tử Lời giải
DẠYKÈMQUYNHƠNOFFICIAL Câu 17. Tập hợp ()()( ){ }3 1240Axxxxx =∈−++= ℕ có bao nhiêu phần tử? A. 1. B. 3 . C. 5 . D. 2 . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 18. Trong các tập hợp sau, tập nào là tập rỗng? A. { }2 1 |340Txxx=∈+−= ℕ . B. { }2 1 |30Txx=∈−= ℝ C. { }2 1 |2Txx=∈= ℕ . D. ( )(){ }2 1 |1250Txxx=∈+−= ℚ . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 19. Hãy liệt kê các phần tử của tập hợp: { }2 ,10=∈++= ℝ Xxxx A. { }0=X . B. { }2=X . C. =∅X . D. 0=X . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 20. Hãy liệt kê các phần tử của tập hợp { }2 |2530Xxxx=∈−+= ℝ . A. { }1X = B. 3 2 X = C. { }0X = D. 3 1; 2 X = Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 21. Trong các tập hợp sau, tập nào là tập rỗng? A. { }2 560xxx∈+−= ℝ . B. { }2 3520xxx∈−+= ℚ . C. { }2 10xxx∈+−= ℤ . D. { }2 510xxx∈+−= ℝ . Lời giải .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL Câu 22. Xác định số phần tử của tập hợp { }|4,2017Xnnn=∈< ℕ⋮ . A. 505 . B. 503 . C. 504 . D. 502 . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Dạng 2: Tập hợp con và hai tập hợp bằng nhau 1. Phương pháp ( )ABxAxB ⊂⇔∀∈⇒∈ Các tính chất: + , AAA ⊂∀ + , AA∅⊂∀ + , ABBCAC ⊂⊂⇒⊂ • ( ABAB =⇔⊂ và ( )), BAxxAxB ⊂⇔∀∈⇔∈ 2. Các ví dụ rèn luyện kĩ năng Ví dụ 1: Cho { }4;2;1;2;3;4A =−−− và { }|4Bxx=∈Ζ≤ . Tìm tập hợp X sao cho a) AXB ⊂⊂ b) AXB ∪= với X có đúng bốn phần tử Lời giải 3. Bài tập trắc nghiệm Câu 1. Cho tập hợp { }, , , Aabcd = . Tập A có mấy tập con? A. 15 . B. 12 . C. 16 . D. 10 . Lời giải Câu 2. Tập hợp nào sau đây có đúng một tập hợp con?
DẠYKÈMQUYNHƠNOFFICIAL A. ∅ . B. { }1 . C. { }∅ . D. { }1;∅ . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
3. Cho tập hợp P . Tìm mệnh đề sai trong các mệnh đề sau? A. PP ⊂ . B. P∅⊂ . C. { }PP ∈ . D. PP ∈ . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 4. Tập hợp nào sau đây có đúng hai tập hợp con? A. { };x ∅ . B. { }x . C. { };;xy ∅ . D. { }; xy . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
5: Cho tập hợp A . Trong các mệnh đề sau, mệnh đề nào sai ? A. A∅⊂ B. { }AA ≠ C. AA ∈ D. AA ⊂ Lời giải Câu 6. Số tập con của tập hợp có n ( )1, nn≥∈ ℕ phần tử là A. 22 n + . B. 12 n . C. 12 n+ . D. 2n . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 7. Cách viết nào sau đây là đúng? A. [ ] ;.aab ⊂ B. { } [ ] ;.aab ⊂ C. { } [ ] ;.aab ∈ D. ( ] ;.aab ∈ Lời giải Câu 8. Cho tập hợp { }2*2,51 Axxx =+∈ ≤ℕ . Khi đó tập A bằng tập hợp nào sau đây? A. { }1;2;3;4A = . B. { }0;2;5A = .
Câu
Câu
C. { }2;5A = . D. { }0;1;2;3;4;5A = . Lời giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 9. Cho tập hợp { }1;2;8A= . Tập hợp A có tất cả bao nhiêu tập hợp con?
A. 9 B. 7 C. 8 D. 6 Lời giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 10: Trong các mệnh đề sau đây, mệnh đề nào sai?
A. AA ⊂ . B. A∅⊂ . C. A∈∅ . D. ∅⊂∅ . Lời giải
Câu 11: Cho hai tập hợp: { | Xnn =∈ ℕ là bội số của 4 và 6} và { | Ynn =∈ ℕ
DẠYKÈMQUYNHƠNOFFICIAL
ố
..................................................................................................................................................................... .....................................................................................................................................................................
}1;2; Aa = , { }1;2;;;; Babxy = . Hỏi có bao nhiêu tập hợp X thỏa AXB ⊂⊂ ? A. 8 . B. 7 . C. 6 . D. 2n . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 13: Hai tập hợp nào dưới đây không bằng nhau ? A. 11 |,, 28 k Axxkx ==∈≥ ℤ và 111 ;; 248 B = B. { }3;9;27;81A = và { }3|,14 n Bnn =∈≤≤ ℕ . C. { }|23Axx=∈−<≤ ℤ và { }1;0;1;2;3B =− . D. { }|5Axx=∈< ℕ và { }0;1;2;3;4B = Lời giải Câu 14: Cho tập hợp { }* |34Bxx=∈−<≤ ℕ . Tập hợp B có tất cả bao nhiêu tập hợp con? A. 16 . B. 12 . C. 8 . D. 4 .
là bội s
của 12}. Trong các mệnh đề sau, tìm mệnh đề sai? A. XY ⊂ B. YX ⊂ C. XY = D. : nnX∃∈ và nY ∉ Lời giải
Câu 12: Cho tập hợp {
Câu 15. Cho tập hợp { };; Axyz = và { };;;; Bxyztu = . Có bao nhiêu tập X thỏa mãn AXB ⊂⊂ ?
A. 16 B. 4 C. 8 D. 2 Lời giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 16. Có tất cả bao nhiêu tập X thỏa mãn { } { }1;21;2;3;4;5 X ⊂⊂ ? A. 8 . B. 1. C. 3 . D. 6 . Lời giải
Câu 17: Cho tập hợp { };; Axyz = và { };;;; Bxyztu = . Có bao nhiêu tập X thỏa mãn AXB ⊂⊂ ? A. 16 . B. 4 . C. 8 . D. 2 . Lời giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 18. Cho tập X có 1n + phần tử ( n ∈ N ). Số tập con của X có hai phần tử là
A. ( )1nn + . B. ( )1 2 nn C. 1n + D. ( )1 2 nn + Lời giải
DẠYKÈMQUYNHƠNOFFICIAL Lời giả
i
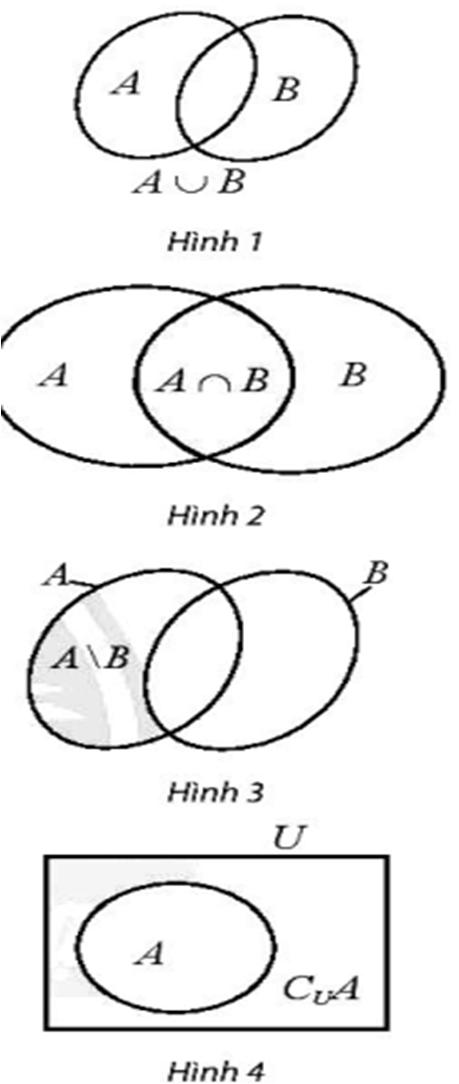
DẠYKÈMQUYNHƠNOFFICIAL BÀI 3. CÁC PHÉP TOÁN TRÊN TẬP HỢP A. KIẾN THỨC CƠ BẢN CẦN NẮM 1. Hợp của hai tập họp (Hình
{ ∪=∈ ABxxA ∣ hoặc }∈ xB 2. Giao
ủa
tập
ợp
{ và
∩=∈∈ ABxxAxB ∣ 3. Công
ức tính số phần tử Nếu A và B là các tập hợp hữu hạn thì ()()()(). ∪=+−∩ nABnAnBnAB 4. Hiệu của hai tập hợp (Hình
\{ và }.=∈∉ ABxxAxB ∣ 5. Phần bù của tập họp con (Hình 4) \{ và }==∈∉U CAUAxxUxA ∣ ( A là tập con của U ). B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP Dạng 1: Giao và hợp của hai tập hợp 1. Phương pháp Cần nắm chắc các định nghĩa {} | vaø ABxxAxB ∩=∈∈ ; {} | hoaëc ABxxAxB ∪=∈∈ 2. Các ví dụ rèn luyện kĩ năng Ví dụ 1: Cho các tập hợp sau ()() {} 22 |2320Axxxxx =∈−−+= ℝ và () {} |3131Bnnn=∈<+< ℕ Tìm AB ∩ Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... 3. Bài tập trắc nghiệm Câu 1: Cho {} ;; Aabc = và {} ;;; Bacde = . Hãy chọn khẳng định đúng. A. {} ; ABac ∩= . B. {} ;;;; ABabcde ∩= . C. {}ABb ∩= D. {} ; ABde ∩= Lời giải. ..................................................................................................................................................................... Câu 2: Cho hai tập hợp {} 0;2;3;5A = và {} 2;7B = . Khi đó AB ∩ A. {} 2;5AB∩= . B. {} 2AB∩= .
1)
c
hai
h
(Hình 2)
}.
th
3)
DẠYKÈMQUYNHƠNOFFICIAL C. AB∩=∅. D. { }0;2;3;5;7AB∩= . Lời giải. Câu 3. Cho hai tập hợp { }1;2;4;7;9X = và { }
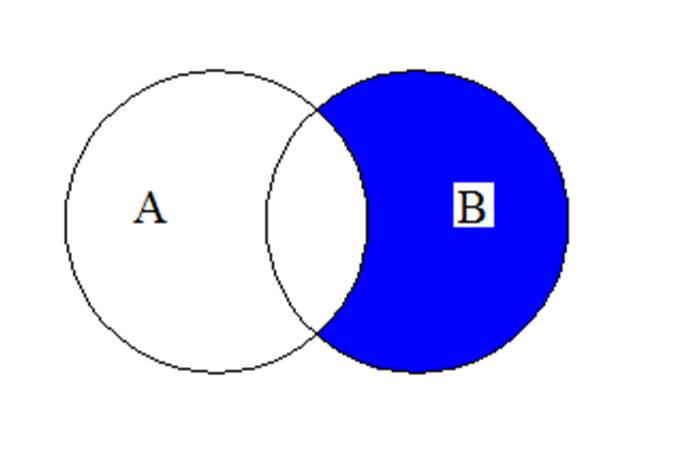
=−Y . Tập hợp XY ∪ có bao nhiêu phần tử? A. 9 . B. 7 . C. 8 . D. 10 . Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 4. Cho { }|3Axx=∈≤ ℕ , { }0;1;2;3B = . Tập AB ∩ bằng A. { }1;2;3 . B. { }3;2;1;0;1;2;3 . C. { }0;1;2 . D. { }0;1;2;3 . Lời giải. Câu 5. Cho A , B là hai tập hợp bất kì. Phần gạch sọc trong hình vẽ bên dưới là tập hợp nào sau đây? A. AB ∪ B. \ BA C. \ AB D. AB ∩ Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 6. Cho 2 tập hợp ( )( ){ }22 |22320Axxxxx =∈−−−= ℝ , { }2 |330Bnn=∈<< ℕ , chọn mệnh đề đúng? A. { }2AB∩= . B. { }5;4AB∩= . C. { }2;4AB∩= . D. { }3AB∩= . Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 7. Cho hai tập hợp { }1;2;; Aab = , { }1;; Bxy = với , xy khác ,,2,1ab . Kết luận nào sau đây đúng? A. ABB ∩= . B. AB∩=∅ . C. ABA ∩= . D. { }1AB∩= . A B
1;0;7;10
Câu 8: Cho hai đa thức ( )fx và ( )gx . Xét các tập hợp ( ){ }|0=∈= ℝ Axfx , ( ){ }|0=∈= ℝ Bxgx , ( ) ( ){ }22 |0 =∈+= ℝ Cxfxgx . Trong các mệnh đề sau, mệnh đề nào đúng? A. =∪ CAB B. =∩ CAB C. \.= CAB D. \.= CBA Lời giải.
Câu 9: Cho hai tập hợp ( ){ }|0=∈= ℝ Exfx , ( ){ }|0=∈= ℝ Fxgx . Tập hợp ( ) ( ){ }|0=∈= ℝ Hxfxgx . Trong các mệ
DẠYKÈMQUYNHƠNOFFICIAL Lời
ả
gi
i. .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
nh đề sau, mệnh đề nào đúng? A. =∩ HEF B. =∪ HEF C. \.= HEF D. \.= HFE Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... Dạng 2: Hiệu và phần bù của hai tập hợp 1. Phương pháp Cần nắm chắc các định nghĩa { }\| vaø ABxxAxB =∈∉ Nếu AE ⊂ thì \ A EEAC = . 2. Các ví dụ rèn luyện kĩ năng Ví dụ 1. Cho { }2;4;6;9A = và { }1;2;3;4B = . Tìm \ AB Lời giải { }\6;9AB = Ví dụ 2. Cho hai tập hợp { } { }1;2;4;6,1;2;3;4;5;6;7;8AB== . Tìm khi B CA Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... 3. Bài tập trắc nghiệm Câu 1. Cho hai tập hợp 2;4;6;9, {}{1;2;34. ;}AB== Tập hợp \ AB bằng tập hợp nào sau đây? A. {2;4} B. {1;3} C. {6;9} D. {6;9;1;3} Lời giải.
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 2: Phần tô đậm trong hình vẽ sau biểu diễn tập hợp nào? A. \ BA . B. \ AB . C. AB ∩ . D. AB ∪ . Lời giải. ..................................................................................................................................................................... Câu 3. Cho hai tập hợp {}{} 2;4;6;9,1;2;3;4AB== . Tập \ AB bằng tập hợp nào sau đây? A.{} 2;4 B. {} 1;3 C. {} 6;9 D. {} 6;9;1;3 Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 4. Cho A là tập hợp các hình thoi, B là tập hợp các hình chữ nhật và C là tập hợp các hình vuông. Khi đó A. \ BAC = . B. ABC ∪= . C. \ ABC = . D. ABC ∩= . Lời giải. ..................................................................................................................................................................... Câu 5. Cho hai tập hợp ,, MNMN ⊂ . Mệnh đề nào sau đây đúng? A. MNN ∩= B. \ MNN = C. MNM ∩= D. \ MNM = Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 6 . Cho hai tập hợp: {} 0;1;2;3;4A = và {} 2;4;6;8;10B = . Tập \ AB bằng A. {} 6;8;10 . B. {} 0;1;3 .
C. { }2;4 . D. { }0;1;2;3;4;6;8;10 . Lời giải. ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 7. Cho :A "Tập hợp các học sinh khối 10 học giỏi", :B “Tập hợp các học sinh nữ học giỏi”, :C “Tập hợp các học sinh nam khối 10 học giỏi”. Vậy tập hợp C là: A. AB ⊂ B. \ BA C. AB ∩ D. \ AB Lời giải. ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 8. Cho các tập hợp ,, ABC được minh họa bằng biểu đồ Ven như
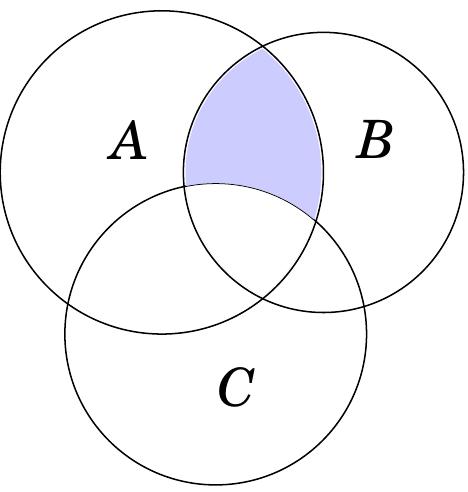
DẠYKÈMQUYNHƠNOFFICIAL
hình vẽ. Phần tô màu xám trong hình là biểu diễn của tập hợp nào sau đây? A. ABC ∩∩ B. ( ) ( )A\C\B A∪ C. ( ) B\ AC ∪ D. ( ) B\ AC ∩ Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 9: Cho {0;1;2;3;4}A = , {2;3;4;5;6}B = . Tính phép toán ( ) ( )\\ ABBA ∪ A. { }0;1;5;6 . B. { }1;2 . C. { }2;3;4 . D. { }5;6 . Lời giải. ..................................................................................................................................................................... Câu 10: Cho hai đa thức ( )fx và ( )gx . Xét các tập hợp ( ){ }|0=∈= ℝ Axfx , ( ){ }|0=∈= ℝ Bxgx , ( ) () |0 =∈= ℝ Cxfx gx . Trong các mệnh đề sau, mệnh đề nào đúng? A. =∪ CAB B. =∩ CAB C. \.= CAB D. \.= CBA Lời giải.
Dạng 3: Bài toán sử dụng biểu đồ Ven
1. Phương pháp
• Chuyển bài toán về ngôn ngữ tập hợp • Sử dụng biểu đồ ven để minh họa các tập hợp • Dựa vào biểu đồ ven ta thiết lập được đẳng thức(hoặc phương trình hệ phương trình) từ đó tìm được kết quả bài toán
Trong dạng toán này ta kí hiệu ( )nX là số phần tử của tập X . 2. Các ví dụ rèn luyện kĩ năng Ví dụ 1: Mỗi học sinh của lớp 10A1 đều biết chơi đá cầu hoặc cầu lông, biết rằng có 25 em biết chơi đá cầu , 30 em biết chơi cầu lông, 15 em biết chơi cả hai . Hỏi lớp 10A1 có bao nhiêu em chỉ biết đá cầu? bao nhiêu em chỉ biết đánh cầu lông?Sĩ số lớp là bao nhiêu?
Lời giải.
Ví dụ 2: Trong lớp 10C có 45 học sinh trong đó có 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Sử, 6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên.
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Bài tập trắc nghiệm Câu 1: Lớp 10A có 51 bạn học sinh trong đó có 31 bạn học tiếng Anh và 27 bạn học tiếng
ật.
ớ
10A có bao nhiêu bạn học cả tiếng Anh và tiếng
ật? A. 7 . B. 9 . C. 5 . D. 12 . Lờ
ả
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Lời giải.
3.
Nh
L
p
Nh
i gi
i.
Câu 2. Lớp 10A có 45 học sinh, trong đó có 15 học sinh được xếp loại học lực giỏi, 20 học sinh được xếp loại hạnh kiểm tốt, 10 em vừa được xếp loại học lực giỏi , vừa có hạnh kiểm tốt. Hỏi có bao nhiêu học sinh xếp loại học lực giỏi hoặc xếp loại hạnh kiểm tốt? A. 10 B. 35 C. 25 D. 45 Lời giải. .....................................................................................................................................................................
Câu 3. Trong số 50 học sinh của lớp 10A có 15 bạn được xếp loại học lực giỏi, 25 bạn được xếp loại hạnh kiểm tốt, trong đó có 10 bạn vừa được học sinh giỏi vừa được hạnh kiểm tốt. Khi đó, lớp 10A có bao nhiêu bạn được khen thưởng, biết rằng muốn được khen thưởng bạn đó phải có học lực giỏi hay hạnh kiểm tốt. A. 20 . B. 30 . C. 35 . D. 25 . Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 4: Lớp 110B có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 3 học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hóa, 2 học sinh giỏi cả Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn của lớp 110B là: A. 9. B. 10. C. 18. D. 28. Lời giải.
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Dạng 4: Tìm giao và hợp các khoảng, nửa khoảng, đoạn 1. Phương pháp • Để tìm AB ∩ ta làm như sau - Sắp xếp theo thứ tự tăng dần các điểm đầu mút của các tập hợp , AB lên trục số - Biểu diễn các tập , AB trên trục số (phần nào không thuộc các tập đó thì gạch bỏ) - Phần không bị gạch bỏ chính là giao của hai tập hợp , AB • Để tìm AB ∪ ta làm như sau
DẠYKÈMQUYNHƠNOFFICIAL -
ế
.....................................................................................................................................................................
Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... 3. Bài tập trắc nghiệm Câu 1. Tập ( ) [ );35;2−∞−∩− bằng A. [ )5;3 . B. ( ];5−∞− . C. ( );2−∞− . D. ( )3;2 . Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 2. Hình vẽ sau đây là biểu diễn của tập hợp nào? A. ( ) [ );25; −∞−∪+∞ . B. ( ) ( );25; −∞−∪+∞ . C. ( ] ( );25; −∞−∪+∞ D. ( ] [ );25; −∞−∪+∞ Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... 5 [ 2 )
Sắp x
p theo thứ tự tăng dần các điểm đầu mút của các tập hợp , AB lên trục số - Tô đậm các tập , AB trên trục số - Phần tô đậm chính là hợp của hai tập hợp , AB 2. Các ví dụ rèn luyện kĩ năng Ví dụ 1: Cho hai tập hợp ( ) ( )7;3, 4;5AB=−=− . Tìm ∩ AB , ∪ AB Lời giải.
Ví dụ 2: Cho số thực 0a < . Tìm a để () 4 ;9; a a −∞∩+∞≠∅
DẠYKÈMQUYNHƠNOFFICIAL
ết quả củ
L
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Cho
tập hợp [
=−
.
∩ .
AB∩=−+∞ .
∩= .
. L
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Cho
tập hợp [
=−M và (
N .
.
.
Lờ
ả
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 6. Cho ( ];2=−∞A , [ )2; =+∞B , (
0;3=C . Chọ
biểu sai. A. ( ]0;2AC∩= . B. ( )0;BC∪=+∞ . C. { }\2AB∪= ℝ D. [ )2;3BC∩= Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 7. Cho ( ];2=−∞−A , [ )3; =+∞B , ( ) 0;4.=C Khi đó tập ( ) ∪∩ ABC là A. ( ] ( );23; −∞−∪+∞ . B. ( ) [ );23; −∞−∪+∞ . C. [ )3;4 D. [ ]3;4
Câu 3. K
a [ ) ( ]4;12;3−∪− là A. ( )2;1 B. [ ]4;3 C. ( ]4;2 D. ( ]1;3
ời giải.
Câu 4.
hai
]2;3A
và ( )1;B =+∞
Tìm AB
A. [ )2;
B. ( ]1;3AB
C. [ ]1;3AB∩= . D. ( )1;3AB∩=
ời giải.
Câu 5.
các
]3;6
) ( );23; =−∞−∪+∞
Khi đó MN ∩ là A. ( ) [ ];23;6−∞−∪
B. ( ) [ );23; −∞−∪+∞
C. [ ) ( ]3;23;6−−∪ D. ( ) ( )3;23;6−−∪
i gi
i.
)
n phát
DẠYKÈMQUYNHƠNOFFICIAL Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 8. Cho ( ];5=−∞A , ( )0; =+∞B . Tìm ∩ AB A. [ )0;5AB∩= . B. ( )0;5AB∩= . C. ( ]0;5AB∩= D. ( );AB∩=−∞+∞ Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 9. Cho ( )1;9=A , [ )3; =+∞B , câu nào sau đây đúng? A. [ )1;AB∩=+∞ . B. ( )9;AB∩=+∞ . C. ( )1;3AB∩= . D. [ )3;9AB∩= . Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 10. Cho ba tập hợp: ( )4;3=−X , { }:240,5=∈+>< ℝ Yxxx , ( )( ){ }:340 =∈+−= ℝ Zxxx . Chọn câu đúng nhất: A. XY ⊂ . B. ZX ⊂ . C. ZXY ⊂∪ . D. ZY ⊂ . Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 11. Tập hợp nào dưới đây là giao của hai tập hợp { }:13Axx=∈−≤< ℝ , { }:2Bxx=∈< ℝ ? A. ( )1;2 B. [ )0;2 C. ( )2;3 D. [ )1;2 Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL
.....................................................................................................................................................................
Câu 12. Cho [ )1; =+∞A , { }2 |10=∈+= ℝ Bxx , ( )0;4=C . Tập ( ) ∪∩ ABC có bao nhiêu phần tử là số nguyên. A. 3 . B. 1. C. 0 . D. 2 . Lời giải.
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 13. Cho hai tập hợp ( )3;3=−A và ( )0; =+∞B . Tìm ∪ AB . A. ( )3;AB∪=−+∞ B. [ )3;AB∪=−+∞ C. [ )3;0AB∪=− . D. ( )0;3AB∪= . Lời giải.
−∞ . C. [ )1;1 . D. ( )1;1 . Lời giải. ..................................................................................................................................................................... Câu 15. Cho ( )2;A =+∞ , ( );Bm=+∞ . Điều kiện cần và đủ của m sao cho B là tập con của A là A. 2m ≤ . B. 2m = . C. 2m > . D. 2m ≥ . Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 16. Cho ( ];1=−∞+Am ; ( )1; =−+∞B . Điều kiện để ( ) ∪= ℝAB là A. 1m >− B. 2m ≥− C. 0m ≥ D. 2m >− Lời giải.
Câu 14. Kết quả của phép toán ( ) [ );11;2−∞∩− là A. ( )1;2 . B. ( );2
Câu 17. Cho các tập hợp khác rỗng 3 1; 2 m m + và ( ) [ );33;B =−∞−∪+∞ . Tập hợp các giá trị thực của m để AB∩≠∅ là A. ( ) [ );23; −∞−∪+∞ . B. ( )2;3 . C. ( ) [ );23;5−∞−∪ D. ( ) ( );94; −∞−∪+∞ Lời giải.
Câu 18. Cho hai tập hợp [ ]1;3A = và [ ];1Bmm=+ . Tìm tất cả giá trị của tham số m để BA ⊂ . A.
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
1m = . B. 12 m << . C. 12 m ≤≤ . D. 2m = . Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 19. Cho m là một tham số thực và hai tập hợp [ ]12;3Amm=−+ , { }|85 Bxxm =∈≥− ℝ . Tất cả các giá trị m để AB∩=∅ là A. 5 6 m ≥ . B. 2 3 m <− . C. 5 6 m ≤ . D. 25 36 m −≤< . Lời giải. ..................................................................................................................................................................... Câu 20. Cho hai tập 0;5A = ; (2;31Baa =+ , với 1a >− . Tìm tất cả các giá trị của a để A. B ∩≠∅ A. 5 2 1 3 a a < ≥− B. 5 2 1 3 a a ≥ <− C. 15 32 a −≤< D. 15 32 a −≤≤ Lời giải. ..................................................................................................................................................................... .....................................................................................................................................................................
Dạng 5: Xác định hiệu và ph
n bù các khoảng, đoạn, nửa khoảng 1. Phương pháp • Để tìm \ AB ta làm như sau - Sắp xếp theo thứ tự tăng dần các điểm đầu mút của các tập hợp , AB lên trục số - Biểu diễn tập A trên trục số(gạch bỏ phần không thuộc tập A ), gạch bỏ phần thuộc tập B trên trục số - Phần không bị gạch bỏ chính là
DẠYKÈMQUYNHƠNOFFICIAL
\ AB 2. Các ví dụ rèn luyện kĩ năng Ví dụ 1: Cho các tập hợp: { } { } { }|3|15|24 AxRxBxRxCxRx =∈<=∈<≤=∈−≤≤ a) Hãy viết lại các tập hợp , , ABC dưới kí hiệu khoảng, nửa khoảng, đoạn. b) Tìm ,,\ ABABAB ∪∩ c) Tìm ( ) ( )\ BCAC ∪∩ Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Ví dụ 2: Xác định các tập số sau và biểu diễn trên trục số: a) ( )4;20;4−∩ b) ( ) 0;31;4∪ c) 4;3\2;1 d) \1;3 ℝ Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
ầ
DẠYKÈMQUYNHƠNOFFICIAL Ví dụ 3: Cho các tập hợp ( ); Am =−∞ và 31;33Bmm=−+ . Tìm m để a) AB∩=∅ b) BA ⊂ c) ACB ⊂ ℝ d)
ℝ L
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... 3. Bài tập trắc nghiệm
ập
ợp
=− .
ậ
ợ
ằng
.
−∞−∪+∞ . Câu 2. Phần bù của [ )2;1 trong ℝ là A. ( ];1−∞ B. ( ) [ );21; −∞−∪+∞ C. ( );2−∞− D. ( )2; +∞ Lời giải. ..................................................................................................................................................................... Câu 3. Tập hợp nào sau đây chỉ gồm các số vô tỷ? A. *\ ℚℕ . B. \ ℝℚ . C. \ ℚℤ . D. { }\0ℝ . Lời giải. ..................................................................................................................................................................... Câu 4. Cho các tập hợp { }|3=∈< ℝ Axx , { }|15=∈<≤ ℝ Bxx , { }|24=∈−≤≤ ℝ Cxx . Khi đó ( ) ( )\ ∪∩ BCAC bằng A. [ )2;3 . B. [ ]3;5 . C. ( ];1−∞ . D. [ ]2;5 . Lời giải. ..................................................................................................................................................................... Câu 5. Cho ( ];1=−∞A ; [ )1; =+∞B ; ( ]0;1=C . Câu nào sau đây sai?
CAB∩≠∅
ời giải.
Câu 1. Cho t
h
)3;5A
T
p h
p CA ℝ b
A. ( ( );35; −∞−∪+∞
B. ( ) ( );35; −∞−∪+∞ . C. ( );35; −∞−∪+∞ . D. ( ) );35;
DẠYKÈMQUYNHƠNOFFICIAL A. ( ) ( ] ( )\C;01;AB∪=−∞∪+∞ . B. { }C1AB∩∩=− . C. ( )C;AB∪∪=−∞+∞ D. ( ) \CAB∩=∅ Lời giải. ..................................................................................................................................................................... Câu 6. Cho [ ]1;3=−A ; ( )2;5=B . Tìm mệnh đề sai A. [ )\3;5BA = . B. ( ]2;3AB∩= . C. [ ]\1;2AB =− D. [ ]1;5AB∪=− Lời giải. ..................................................................................................................................................................... Câu 7. Cho các tập { }|1=∈≥− ℝ Axx , { }|3=∈< ℝ Bxx . Tập ( )\ ∩ℝ AB là : A. ( ) [ );13; −∞−∪+∞ B. ( ]1;3 C. [ )1;3 . D. ( ] ( );13; −∞−∪+∞ . Lời giải. ..................................................................................................................................................................... Câu 8. Cho hai tập hợp ( )2;A =+∞ và 5 ; 2 B =−∞ . Khi đó ( ) ( )\ ABBA ∩∪ là A. 5 ;2 2 B. ( )2; +∞ C. 5 ; 2 −∞ D. 5 ; 2 −∞ Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 9. Cho ( )1;3=−A và [ ]0;5=B . Khi đó ( ) ( )\∩∪ ABAB là A. ( )1;3 . B. [ ]1;3 . C. ( ) { }1;3\0 . D. ( ]1;3 . Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
AB = . D. ( )\;0AB =−∞ . Lời giải. ..................................................................................................................................................................... Câu 14. Cho hai tập hợp { }|32Axx=∈−<≤ ℝ , ( )1; 3B =− . Chọn khẳng định đúng trong các khẳng định sau: A. ( ]1; 2AB∩=− . B. ( )\3;1AB =−− . C. ( ) [ );13;CB =−∞−∪+∞ℝ D. { }2;1;0;1;2AB∪=−− Lời giải.
Câu 10. Xác định phần bù của tập hợp ( );2−∞− trong ( );4−∞ . A. ( )2;4 B. ( ]2;4 C. [ )2;4 D. [ ]2;4 Lời giải.
Câu 11. Xác định phần bù của tập hợp ( ) ( ) { };1010;0−∞−∪+∞∪ trong ℝ . A. [ )10; 10 B. [ ] { }10; 10\0 C. [ ) [ )10;00; 10−∪ . D. [ ) ( )10;00; 10−∪ . Lời giải.
Câu 12. Cho hai tập hợp X , Y thỏa mãn { }\7;15XY = và ( )1;2XY∩=− . Xác định số phần tử là số nguyên của X . A. 2 B. 5 C. 3 D. 4 Lời giải.
Câu 13. Cho ( ];2=−∞A và ( )0; =+∞B . Tìm \ AB . A. ( ]\;0AB =−∞ B. ( )\2;AB =+∞ C. ( ]\0;2
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... Câu 15. Cho [ );1Aaa=+ . Lựa chọn phương án đúng. A. ( ] [ );1;CAaa=−∞∪++∞ℝ . B. ( ) [ );1;CAaa=−∞∪++∞ℝ . C. ( ] ( );1;CAaa=−∞∪++∞ℝ . D. ( ) ( );1;CAaa=−∞∪++∞ℝ . Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 16. Cho các tập hợp khác rỗng ( );=−∞ Am và [ ]22;22=−+Bmm . Tìm m ∈ ℝ để R CAB∩≠∅ A. 2m ≥ . B. 2m <− . C. 2m ≥− . D. 2m < . Lời giải. ..................................................................................................................................................................... Câu 17. Cho { }33Axmxmx =∈−=− ℝ , { }2 40Bxx=∈−= ℝ . Tìm m để \ BAB = . A. 33 22 m −≤≤ B. 3 2 m < C. 33 22 m −<< D. 3 2 m ≥− Lời giải. ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL BÀI TẬP CUỐI CHƯƠNG I
ập \ AB có bao nhiêu phần tử? A. 8. B. 1. C. 0 D. 12 Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 3. Cho hai tập hợp { } { }13;4AxxBxx =∈−≤≤=∈≤ ℤℕ . Tìm \.AB A. { } \1;0;1;2;3;4;6;8.AB =− B. [ )\1;0AB =− C. ( )\1;0AB =− D. { }\1AB =− Lời giải Câu 4. Viết tập hợp ()( ){ }2 21560Axxxx =∈+−+= ℕ bằng cách liệt kê phần tử. A. 1 ;2;3 2 A = B. { }2;3A = C. { }1;2A =− D. { }1;2;3A =− Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 5. Cho tập hợp [ ]3;5A =− .Viết lại tập hợp A bằng cách chỉ ra tính chất đặc trưng. A. { }35Axx=∈−≤≤ ℝ . B. { }35Axx=∈−≤≤ ℤ . C. { }35Axx=∈−≤≤ ℕ . D. { }35Axx=∈−<< ℝ . Lời giải Câu 6. Lập mệnh đề phủ định của mệnh đề: '';21'' n nn ∀∈≥+ ℕ A. '';21'' n nn ∃∈<+ ℕ . B. '';21'' n nn ∀∈<+ ℕ . C. '';21'' n nn ∃∈≤+ ℕ . D. '';21'' n nn ∀∈≤+ ℕ . Lời giải
A. TRẮC NGHIỆM Câu 1. Dùng kí hiệu khoảng, đoạn để viết lại tập hợp sau: 1 3 2 Bxx=∈−<≤ ℝ . A. 1 ;3 2 B =− . B. 1 ;3 2 B =− . C. 1 ;3 2 B =− . D. 1 ;3 2 B =− . Lời giải Câu 2. Cho tập hợp { }2;5;6;7;8A = và { }1;2;3;4;5;6;7B = . T
Câu 7. Trong các phát biểu sau, có bao nhiêu phát biểu là mệnh đề?
1/ Hải Phòng là một thành phố của Việt Nam.
2/ Bạn có đi xem phim không?
3/ 10 21 chia hết cho 11.
4/ 2763là hợp số. 5/ 2 320.xx−+= A. 3. B. 1. C. 2. D. 4. Lời giải .....................................................................................................................................................................
Câu 8. Cho tập hợp { }0;1;2;3X = và { } 1;0;1;2;3;5.Y =− Tìm Y CX
A. { } 1;5.Y CX =− B. { } 0;1;2;3.Y CX = C. .Y CX =∅ D. { } 1;0;1;2;3;5.Y CX =−
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
Lờ
ải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
ợ
Câu 10. Cho tập { }A=1;2;3;4 .Tìm các tập con của A A. 10 B. 12 C. 16 D. 8 Lời giải ..................................................................................................................................................................... Câu 11. Trong các tập hợp dưới đây, tập hợp nào là tập hợp rỗng? A. { }|215Nmm=∈≤≤ ℤ . B. { }2 |45Mxx=∈+= ℝ . C. { }|396Pnn=∈+= ℕ . D. { }|1Qxx=∈≤ ℕ . Lời giải
i gi
Câu 9. Cho tập h
p ( ] [ ) ;5,5;.AB=−∞=+∞ Tìm .AB ∪ A. ( ) ;5.AB∪=−∞ B. { } 5.AB∪= C. [ )5;AB∪=+∞ D. AB∪= ℝ Lời giải
Câu 12. Cho tập ( )(){ }2 |3230Axxxx =∈−++= ℕ và { }0;1;2;3;4;5B = . Có bao nhiêu tập X thỏa mãn AXB ∪= ?
A. 4 . B. 6 . C. 8 . D. 1. Lời giải
Câu 13. Trong mặt phẳng, cho A là tập hợp các tam giác đều, B là tập hợp các tam giác vuông, C là tập hợp các tam giác cân. Chọn khẳng định đúng.
A. CA ⊂ B. AB ⊂ C. BC ⊂ D. AC ⊂ Lời giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 14. Tìm mệnh đề đúng.
A. Điều kiện cần và đủ để một số tự nhiên chia hết cho 15 là số đó chia hết cho 5
B. Điều kiện cần để ab + là một số hữu tỉ là a và b đều là số hữu tỉ.
C. Điều kiện đủ để có ít nhất một trong hai số a , b là số dương là ab+> 0 .
D. Điều kiện cần và đủ để một tứ giác là hình chữ nhật là nó có hai đường chéo bằng nhau. Lời gi
DẠYKÈMQUYNHƠNOFFICIAL
Câu 15. Cho tập [ ]Am;m=++12 và tập [ ]B; = 01 . Tìm tất cả các giá trị thực của tham số m để CAB∩=∅ℝ . A. m ≥ 0 B. m =−1 C. m << 01 D. m <−1 Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 16. Cho tập { }Ax|x=∈−≤12ℝ và { }Bx|x=∈−<10ℝ . Tìm AB ∩ A. [ ]AB; ∩=−13 B. [ )AB; ∩=−11 C. ( )AB; ∩=−∞ 1 D. ( )AB; ∩=−12 Lời giải
ải
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 18. Tìm mệnh đề sai. A. ;(1)(2)nnnn ∀∈++ ℕ chia hết cho 6. B. 2 ;1nn ∀∈+ ℕ không chia hết cho 4. C. 2 ;1nn ∃∈+ ℕ chia hết cho 3. D. 2 ;0.xx ∃∈≤ ℝ Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 19. Cho hai tập hợp { }15; Axxkk =∈=∈ℤℤ và { }5; Bxxmm=∈=∈ℤℤ . Khẳng định nào sau đây đúng? A. BA ⊂ B. AB ⊂ C. AB ⊄ D. AB = Lời giải Câu 20. Cho mệnh đề chứa biến ( ) 32 :''320''Pxxxx−+= . Tìm tất cả các phần tử của x để ( )Px là một mệnh đề đúng ? A. 1,2xx=−=− B. 2,3xx=−=− C. 0,1,2xxx=== D. 4,2,3xxx==−= Lời giải .....................................................................................................................................................................
Câu 17. Lớp 10A có 45 học sinh. Trong đó có 12 học sinh có học lực giỏi, 30 học sinh có hạnh kiểm tốt, trong đó có 10 học sinh vừa lực giỏi vừa hạnh kiểm tốt. Học sinh được khen thưởng nếu được học lực giỏi hoặc hạnh kiểm tốt. Tìm số học sinh không được khen thưởng. A. 13. B. 35. C. 23. D. 32. Lời giải
DẠYKÈMQUYNHƠNOFFICIAL
21. Tìm mệnh đề sai.
( ) ,
⊂∪ với mọi tập , AB .
với mọi tập , AB . C. ( ) ,ABB ∩⊂ với mọi tập , AB . D.
với mọi tập , AB . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 24: Cho tập 11 | 22 Ax x =∈> ℝ và { }|12Bxx=∈≤≤ ℝ . Tìm ( ) ( )\ ABAB ∪∩ A. [ ] [ ] [ )2;10;12;4 −−∪∪ . B. [ ] ( ] ( )2;10;12;4 −−∪∪ C. [ ] [ ] [ ]2;10;12;4 −−∪∪ D. [ ] ( ) [ )2;10;12;4 −−∪∪ . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 25: Tìm mệnh đề sai. A. \A ∅=∅ , với mọi tập A B. AA ∪∅= , với mọi tập A C. A ∩∅=∅ , với mọi tập A . D. AAA ∩= , với mọi tập A . Lời giải BÀI TẬP TỰ LUẬN Bài 1. Xác định các tập hợp sau bằng cách nêu tính chất đặc trưng { }4;3;2;1;0;1;2;3;4A =−−−− , { }1; 3; 5; 7;9B = , { }0;1;4;9;16;25C = Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Bài 2. a) Trong các tập sau đây, tập nào là tập con của tập nào
Câu
A.
AAB
B. \, ABA ⊂
( ) ( ) ,ABAB ∪⊂∩
DẠYKÈMQUYNHƠNOFFICIAL { } { } ( ) { }2 1;2;34 0;2730 ABnNn CDxRx ==∈< =+∞=∈−+= b) Tìm tất cả các tập X thoả mãn bao hàm thức sau; { } { }1;21;2;3;4;5 X ⊂⊂ . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Bài 3: Cho tập hợp |14 36 Ax x =∈∈Ζ + ℝ a) Hãy xác định tập A bằng cách liệt kê các phần tử b) Tìm tất cả các tập con của tập hợp A . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Bài 4: Cho ( )( ){ }42 |1610Axxx =∈−−= ℝ và { }|290BxNx=∈−≤ . Tìm tập hợp X sao cho a) \ XBA ⊂ b) \ ABXA =∩ với X có đúng hai phần tử Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Bài 5: Cho tập { }1;1;5;8A =− , B ="Gồm các ước số nguyên dương của 16" a) Viết tập A dưới dạng chỉ ra tính chất đặc trưng của các phần tử. Viết tập B dưới dạng liệt kê các phần tử. b) Xác định các phép toán ,,\ ABABAB ∩∪ . Lời giải ..................................................................................................................................................................... .....................................................................................................................................................................
Bài 6: Cho các tập hợp {|17}ExNx=∈≤< ( )( )22 |9–5–0 {} 6AxNxxx =∈−= và {| BxNx =∈ là số nguyên tố nhỏ hơn 6}
a) Chứng minh rằng AE ⊂ và BE ⊂ b) Tìm ;; ()EEE CACBCAB ∪ c) Chứng minh rằng : ( ) ( )\\ \() EABEAEB ∩=∪ Lời giải .....................................................................................................................................................................
Bài 7: Xác định các tập hợp ,\, ABACABC ∪∩∩ và biểu diễn trên trục số các tập hợp tìm được biết:
a) { }13AxRx=∈−≤≤ , { }1BxRx=∈≥
DẠYKÈMQUYNHƠNOFFICIAL
, ( );1C =−∞ b) { }22AxRx=∈−≤≤ , { }3BxRx=∈≥ , ( );0C =−∞ Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Bài 8: Cho tập A = [-1; 2), B = (-3; 1) và C = (1; 4]. a) Viết tập A, B, C dưới dạng chỉ ra tính chất đặc trưng của các phần tử và biểu diễn chúng trên trục số b) Xác định các phép toán ,,\ ABBCAB ∩∪ . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Bài 9: Cho hai tập hợp ) { }0;4,/2ABxx ==∈≤ ℝ .Hãy xác định các tập hợp ,,\ ABABAB ∪∩ ) 0;4,2;2AB==− , )2;4AB ∪=− , 0;2AB∩= , ( )\2;4AB = Lời giải
DẠYKÈMQUYNHƠNOFFICIAL Bài 10: a) Cho A = { |15xRx∈−≤< } B={ |20xRx∈−<< hoặc 16 x <≤ } C={ |2xRx∈≥ } Tìm ,,\ ABACBC ∩∪ và biểu diễn cách lấy kết quả trên trục số b) Cho ( ) ,2,[21,)ABm =−∞−=++∞ . Tìm m để ABR ∪= Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Bài 11: a) Tìm m để ( ( )1;2; m ∩+∞≠∅ . b) Viết tập A gồm các phần tử x thỏa mãn điều kiện 3 10 0 x x x ≤ +≥ < dưới dạng tập số Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Bài 12: Cho tập hợp 1 1; 2 Amm + =− và ( ) );22;B =−∞−∪+∞ . Tìm m để a) AB ⊂ b) AB∩=∅ Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Bài 13: Cho hai tập khác rỗng : ( ( )
AmBm ==+ , với m ∈R. Xác định m để : a) AB∩≠∅ ; b) AB ⊂ ; c) BA ⊂ ; d) ()(1;3) AB∩⊂− Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL
–1;4, –2;22
b
ph
trinh
cho.
i c
p s
( )00 ; xy thoả mãn 00
++<axbyc gọi là một nghiệm
Nghi
các b
ph
trình
++>++≤ axbycaxbyc , 0++≥axbyc được định nghĩa tương tự. 3. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn - Trong mặt phẳng toạ độ ,Oxy tập hợp các điểm ( )00 ; xy sao cho 00 0++<axbyc được gọi là miền nghiệm của bất phương trình 0++<axbyc . - Để biểu diễn miền nghiệm của bất phương trinh 0++<axbyc trên mặt phẳng toạ độ ,Oxy ta làm như sau:
+ Bước 1: Trên mặt phẳng ,Oxy vẽ đường thẳng :0∆++= axbyc .
+ Bước 2: Lấy một điểm ( )00 ; xy không thuộc ∆ . Tính 00++ axbyc .
+ Bước 3: Kết luận
- Nếu 00 0++<axbyc thì miền nghiệm là nửa mặt phẳng (không kể bờ ∆ ) chứa điểm ( )00 ; xy
- Nếu 00 0++>axbyc thi miền nghiệm là nửa mặt phẳng (không kể bờ ∆ ) không chứa điểm ( )00 ; xy .
Chú ý: Đối với các bất phương
DẠYKÈMQUYNHƠNOFFICIAL CHƯƠNG II. BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN BÀI 1. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN A. KIẾN THỨC CƠ BẢN CẦN NẮM
ệ
ất
ương
ất
ẩn
ươ
cho trước; , ab không đồng thời bằng 0 và , xy là các ẩn. 2. Nghiệm của bất phương trình bậc nhất hai ẩn Xét bất phương trình 0++<axbyc . Mỗ
1. Khái ni
m b
ph
trình bậc nh
hai
Bất ph
ng trình bậc nhất hai ẩn , xy là bất phương trình có một trong các dạng 0;0;0;0 ++<++>++≤++≥ axbycaxbycaxbycaxbyc , trong đó ,, abc là những số
ặ
ố
0
của
ất
ương
đã
Chú ý:
ệm của
ất
ương
0,0
bờ B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP Dạng 1. Bất phương trình bậc nhất hai ẩn 1. Phương pháp Bất phương trình bậc nhất hai ẩn Bất phương trình bậc nhất hai ẩn , xy là mệnh đề chứa hai biến có một trong các dạng , axbyc axbyc axbyc axbyc +> +< +≥ ≤ + trong đó ,, abc là các số thực với 22 0ab+≠ . Nghiệm của bất phương trình Cặp số ( )00 ; xy để 00 axbyc +> là bất đẳng thức đúng được gọi là một nghiệm của bất phương trình axbyc +> Biểu diễn tập nghiệm của bất phương trình bậc nhất hai ẩn
trình bậc nhất hai ẩn dạng 0++≤axbyc (hoặc 0++≥axbyc ) thì miền nghiệm là miền nghiệm của bất phương trình 0++<axbyc (hoặc 0++>axbyc ) kể cả
Cũng như bất phương trình bậc nhất một ẩn, các bất phương trình bậc nhất hai ẩn thường có vô số nghiệm và để mô tả tập nghiệm của chúng, ta sử dụng phương pháp biểu diễn hình học. Trong mặt phẳng toạ độ ,Oxy tập hợp các điểm có toạ độ là nghiệm của bất phương trình được gọi là miền nghiệm của nó. Từ đó ta có quy tắc thực hành biểu diễn hình học tập nghiệm (hay biểu diễn miền nghiệm) của bất phương trình axbyc +≤ như sau (tương tự cho bất phương trình ).axbyc +≥
Bước 1. Trên mặt phẳng toạ độ Oxy vẽ đường thẳng :. axbyc∆+= Bước 2. Lấy một điểm ( )000 ; Mxy không thuộc ∆ (ta thường lấy gốc toạ độ ).O Bước 3. Tính 00axby + và so sánh 00axby + với .c Bước 4. Kết luận. +) Nếu 00 axbyc +< thì nửa mặt phẳng bờ ∆ chứa 0M là miền nghiệm của 00 .axbyc +≤ +) Nếu 00 axbyc +> thì nửa mặt phẳng bờ ∆ không chứa 0M là miền nghiệm của 00 .axbyc +≤ Chú ý: Miền nghi
DẠYKÈMQUYNHƠNOFFICIAL
ệm của bất phương trình 00 axbyc +≤ bỏ đi đường thẳng 00 axbyc += là miền nghiệm của bất phương trình 00 axbyc +< 2. Các ví dụ rèn luyện kĩ năng Ví dụ 1: Xác định miền nghiệm của các bất phương trình sau: a) 20. xy−≥ b) 221 . 23 xyxy−++ > Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Ví dụ 2: Xác định miền nghiệm của các bất phương trình sau: a) 30xy−≥ . b) 1 2 xy xy <++ Hướng dẫn giải
3. Bài tập trắc nghiệm
Câu 1. Bất phươngtrìnhnàosau đây làbất phươngtrình bậcnhất hai ẩn?
A. 2 230 xy+> B. 22 2xy+< C. 2 0xy+≥ D. 0xy+≥ Hướng dẫn giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 2. Chobấtphương trình 2360 xy+−≤ .Chọn khẳng định đúng trong cáckhẳng định sau:
A. Bất phương trình (1) chỉ có một nghiệmduy nhất. B. Bất phươngtrình (1) vônghiệm. C. Bất phương trình (1) luôn cóvô số nghiệm. D. Bất phương trình (1) cótậpnghiệm là ℝ
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
. Hướng dẫn giải Câu 3. Miền nghiệm của bất phương trình: 32(3)4(1)3 xyxy ++≥+−+ là nửa mặt phẳng chứa điểm: A. (3;0) B. (3;1) C. (2;1) D. (0;0) Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 4. Miềnnghiệmcủabấtphươngtrình: 3(1)4(2)53 xyx −+−<− lànửamặtphẳngchứa điểm: A. (0;0) B. (4;2) C. (2;2) D. (5;3) Hướng dẫn giải
Câu 5. Miềnnghiệmcủabấtphươngtrình 22(2)2(1) xyx −++−<− lànửamặtphẳng không chứa điểm nàotrong các điểm sau?
A. (0;0) B. (1;1) C. (4;2) D. (1;1) Hướng dẫn giải .....................................................................................................................................................................
Câu 6. Trongcáccặpsố sau đây,cặpnàokhôngthuộcnghiệmcủabấtphươngtrình: 450xy−+>
A. (5;0) B. (2;1) C. (0;0) D. (1;3) Hướng dẫn giải
Câu 7. Điểm (1;3)A là điểm thuộcmiềnnghiệm củabất phương trình: A. 3240 xy −+−> B. 30xy+< C. 30 xy−> D. 240 xy−+> Hướng dẫn giải .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
x y 2 2 O x
2 2
Câu 8. Cặp số (2;3) lànghiệm củabấtphương trình nào sau đây? A. 2310 xy−−> B. 0xy−< C. 43xy > D. 370xy−+< Hướng dẫn giải
Câu 9. Miềnnghiệmcủabấtphươngtrình 2xy+≤ làphần tô đậm tronghìnhvẽ củahình vẽ nào, trong cáchìnhvẽ sau? A. B.
y
O
DẠYKÈMQUYNHƠNOFFICIAL
H
ẫ
ải ..................................................................................................................................................................... Câu
ần tô đậm
ẽ
ể
ễntậ
ệmcủ
ấtphươngtrìnhnàotrongcácbất
ươ
A.
..................................................................................................................................................................... ..................................................................................................................................................................... x y 2 2 O x y 2 2 O 3 2 -3 O y x
C. D.
ướng d
n gi
10. Ph
tronghìnhv
sau,bi
udi
pnghi
ab
ph
ng trìnhsau?
23 xy−< B. 23 xy−> C. 23xy−< D. 23xy−> Hướng dẫn giải
A.KIẾNTHỨCCƠ BẢNCẦNNẮM
1.Kháiniệmhệ bấtphươngtrìnhbậcnhấthai ẩn Hệ bất phương trình bậc nhất hai ẩn là hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn ,.xy Mỗi nghiệm chung của tất cả các bất phương trình đó được gọi là một nghiệm của hệ bất phương trình đã cho.
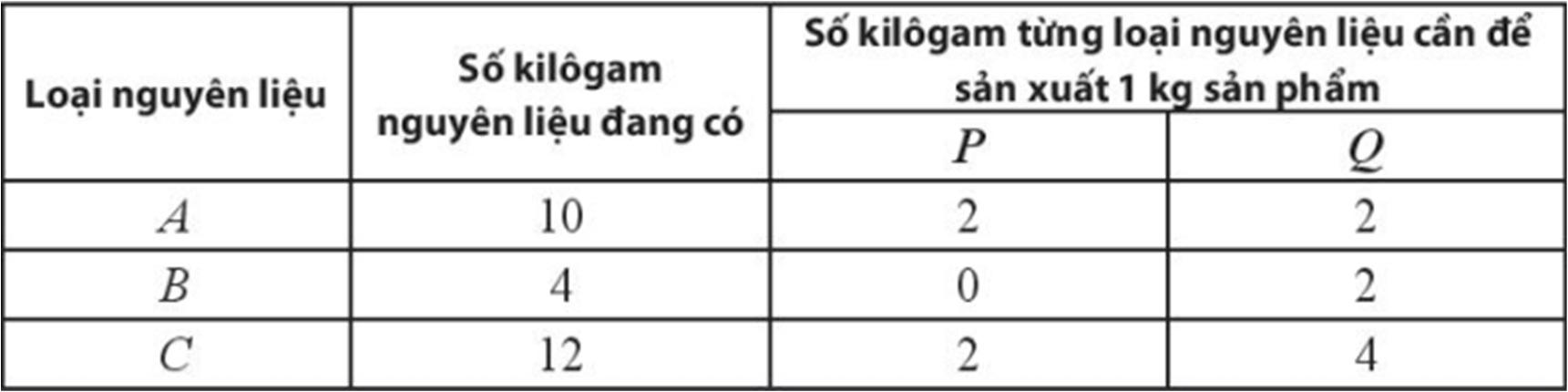
Trên mặt phẳng toạ độ ,Oxy tập hợp các điểm () 00 ; xy có toạ độ là nghiệm của hệ bất phương trình bậc nhất hai ẩn được gọi là miền nghiệm của hệ bất phương trinh đó. 2.Biểudiễnmiềnnghiệmcủahệ bấtphươngtrìnhbậcnhấthai ẩn Để biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng toạ độ ,Oxy ta thực hiện như sau:
- Trên cùng mặt phẳng toạ độ, biểu diễn miền nghiệm của mỗi bất phương trình của hệ
- Phần giao của các miền nghiệm là miền nghiệm của hệ bất phương trình. Chúý: Miền mặt phẳng toạ độ bao gồm một đa giác lồi và phần nằm bên trong đa giác đó được gọi là một miền đa giác. 3.Tìmgiátrị lớnnhấtvàgiátrị nhỏ nhấtcủabiểuthức =+ Faxby trênmộtmiền đagiác Hệ bất phương trình giúp ta mô tả được nhiều bài toán thực tế để tìm ra cách giải quyết tối uu, các bài toán này thường được đưa về việc tìm giá trị lớn nhất (GTLN) hoặc giá trị nhỏ nhất (GTNN) của biểu thức =+ Faxby trên một miền đa giác. Vídụ. Một người dùng ba loại nguyên liệu ,, ABC để sản xuất ra hai loại sản phẩm P và Q . Để sản xuất 1kg mỗi loại sản phẩm P hoặc Q phải dùng một số kilôgam nguyên liệu khác nhau. Tổng số kilôgam nguyên liệu mỗi loại mà người đó có và số kilôgam từng loại nguyên liệu cần thiết để sản xuất ra 1kg sản phẩm mỗi loại được cho trong bảng sau: Biết 1kg sản phẩm P lãi 3 triệu đồng và 1kg sản phẩm Q lãi 5 triệu đồng. Hãy lập phương án sản xuất hai loại sản phẩm trên sao cho có lãi cao nhất. Phươ
DẠYKÈMQUYNHƠNOFFICIAL
BÀI2.HỆ BẤTPHƯƠNGTRÌNHBẬCNHẤTHAI ẨN
ngphápgiải Để giải bài toán tìm phương án tối ưu ở trên, ta thực hiện các bước sau: Bước1. Đặt biến số , xy cho các đối tượng cần tìm. Ví dụ Đặt x là số kilôgam sản phẩm P và y là số kilôgam sản phẩm Q cần sản xuất. Bước2. Lập các hệ bất phương trình mô tả các điều kiện ràng buộc.
Bước3. Xây dựng hàm mục tiêu cho giá trị mà ta muốn đạt giá trị tối ưu.
Bước4. Biễu diễn miền nghiệm của hệ bất phương trinh (1) trên hệ trục toạ độ Oxy ta được một đa giác. Tìm toạ độ các đỉnh của đa giác. Vídụ. Miền nghiệm là ngũ giác ,OCBAD trong đó (0;0);(0;2);(2;2)OCB ;
Bước5. Do người ta đã chứng minh được F đạt GTLN hoặc GTNN tại một trong các đỉnh của đa giác nên ta chỉ cần tính các giá trị của hàm mục tiêu F tại các đỉnh của đa giác. Tìm ra đỉnh tại đó F đạt GTLN hoặc GTNN. Toạ độ của đỉnh này là phương án tối ưu cần tìm. Vídụ. Tính giá trị của F tại các đỉnh: Tại (0;0):3.05.00; =+=OF Tại (0;2):3.05.210 =+=CF ; Tại (2;2):3.25.216; =+=BF Tại (4;1):3.45.117 =+=AF ; Tại (5;0):355015 =⋅+⋅=DF . Tại đỉnh (4;1), AF đạt giá trị lớn nhất là 17 .

DẠYKÈMQUYNHƠNOFFICIAL Ví dụ. 22105 242 241226 00 00 +≤+≤ ≤≤ ⇔ +≤+≤ ≥≥ ≥≥ xyxy yy xyxy xx yy
Bước6. Nêu kết luận dựa trên ngôn ngữ thực tế của bài toán. Vídụ. Vậy phương án sản xuất tối ưu là làm ra 4kg sản phẩm P và 1kg sản phẩm Q . Khi đó sẽ có lãi cao nhất là 17 triệu đồng. B.PHÂNLOẠIVÀPHƯƠNGPHÁPGIẢIBÀITẬP Dạng1.Hệ bấtphươngtrìnhbậcnhấthai ẩn 1.Phươngpháp Tương tự hệ bất phương trình một ẩn, ta có hệ bất phương trình bậc nhất hai ẩn.
Trong mặt phẳng toạ độ, ta gọi tập hợp các điểm có toạ độ thoả mãn mọi bất phương trình trong hệ là miền nghiệm của hệ. Vậy miền nghiệm của hệ là giao các miền nghiệm của các bất phương trình trong hệ Để xác định miền nghiệm của hệ, ta dùng phương pháp biểu diễn hình học như sau: Với mỗi bất phương trình trong hệ, ta xác định miền nghiệm của nó và gạch bỏ (tô màu) miền còn lại.
Sau khi làm như trên lần lượt đối với tất cả các bất phương trình trong hệ trên cùng một mặt phẳng toạ độ, miền còn lại không bị gạch (tô đậm) chính là miền nghiệm của hệ bất phương trình đã cho.
Bàitoán: Tìm giá trị lớn nhất, nhỏ nhất của biểu thức (,) Txyaxby =+ với (;) xy nghiệm đúng một hệ bất phương trình bậc nhất hai ẩn cho trước.
Bước1: Xác định miền nghiệm của hệ bất phương trình đã cho. Kết quả thường được miền nghiệm S là đa giác.
Bước2: Tính giá trị của F tương ứng với (;) xy là tọa độ của các đỉnh của đa giác.
Bước3: Kết luận:
Giá trị lớn nhất của F là số lớn nhất trong các giá trị tìm được. Giá trị nhỏ nhất của F là số nhỏ nhất trong các giá trị tìm được. 2.Cácvídụ
DẠYKÈMQUYNHƠNOFFICIAL
rènluyệnkĩ năng Vídụ 1: Xác định miền nghiệm của hệ bất phương trình sau 20 330. xy xy +−≥ −+≤ Hướngdẫngiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Vídụ 2: Xác định miền nghiệm của hệ bất phương trình sau: 0 2360. 210 xy xy xy +> −+> −+≥ Hướngdẫngiải ..................................................................................................................................................................... ..................................................................................................................................................................... • •
DẠYKÈMQUYNHƠNOFFICIAL Vídụ 3: Xác định miền nghiệm của bất phương trình ( )33 ()0 xyxy−+≥ Hướngdẫngiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Vídụ 4: Cho biểu thức ( ) ;2 Fxyxy =+ trên miền xác định bởi hệ 290 0 10 xy xy y +−≤ −≤ −≤ . Tìm giá trị lớn nhất của F Hướngdẫngiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... 3.Bàitậptrắcnghiệm Câu1. Cho hệ bất phương trình 320 210
.....................................................................................................................................................................
xy xy +−≥ ++≤ . Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình? A. (0;1)M B. (1;1)N C. (1;3)P D. (1;0)Q Hướngdẫngiải
Câu2. Cho hệ bất phương trình 2510 250 10 xy xy xy −−> ++> ++< . Trong các điểm sau, điểm nào thuộc miền nghiệm
A. (0;0)O B. (1;0)M C. (0;2)N D. (0;2)P Hướngdẫngiải
A. (0;0)O B. (2;1)M C. (1;1)N D. (5;1)P Hướngdẫngiải
DẠYKÈMQUYNHƠNOFFICIAL
ủ
c
a hệ bất phương trình?
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Câu3. Miền nghiệm của hệ bất phương trình 10 23 0 13 2 22 xy x y x +−≥ ≥ +−≤ chứa điểm nào trong các điểm sau đây?
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
ệ
ất
ươ
39 3 28
xy xy yx y +≥ ≥− ≥− ≤ chứ
đ
ể
..................................................................................................................................................................... .....................................................................................................................................................................
ể
Câu4. Miền nghiệm của h
b
ph
ng trình
6
a
i
m nào trong các điểm sau đây? A. (0;0)O B. (1;2)M C. (2;1)N D. (8;4)P Hướngdẫngiải
Câu5. Đi
m (0;3)M thuộc miền nghiệm của hệ bất phương trìnhnào sau đây?
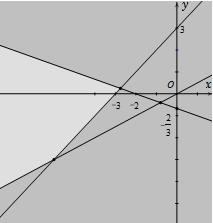
DẠYKÈMQUYNHƠNOFFICIAL A. 23 25128 xy xyx −≤ +≤+ B. 23 25128 xy xyx −> +≤+ C. 23 25128 xy xyx −>− +≤+ D. 23 25128 xy xyx −≤− +≥+ Hướngdẫngiải ..................................................................................................................................................................... Câu6. Cho hệ bất phương trình 20 2320 xy xy +−≤ −+> . Trong các điểm sau, điểm nào không thuộc miền nghiệm của hệ bất phương trình? A. (0;0)O B. (1;1)M C. (1;1)N D. (1;1)P Hướngdẫngiải ..................................................................................................................................................................... Câu7. Miền nghiệm của hệ bất phương trình 20 32 3 xy xy yx −< +>− −< là phần không tô đậm của hình vẽ nào trong các hình vẽ sau? A. B. C. D. Hướngdẫngiải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL Câu8. Miền nghiệm của hệ bất phương trình 10 2 23 xy y xy +−> ≥ −+> là phần không tô đậm của hình vẽ nào trong
A. B. C. D. Hướngdẫngiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu9. Phần không tô đậm trong
ẽ dưới đây
biểu diễ
ậ
ủ
ệ
ấ
ệ bất phương
A. 20 32 xy xy −≤ +≥− B. 20 32 xy xy −> +<− C. 20 32 xy xy −≤ +≤− D. 20 32 xy xy −< +>− Hướngdẫngiải ..................................................................................................................................................................... O y x1 2 1 -3 O y x1 2 1 -3 O y x1 2 1 -3 O y x1 2 1 -3 x y -2 2 1
các hình vẽ sau?
hình v
,
n t
p nghiệm c
a h
b
t phương trình nào trong các h
trình sau?
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
+≥ +≥ là A. min 23F = B. min 26F = C. 32mimF = D. min 67F = Hướngdẫngiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu12. Biểu thức (;) Fxyyx =− đạt giá trị nhỏ nhất với điều kiện 22 22 5 0 xy xy xy x −≥ −≤ +≤ ≥ tại điểm M có toạ độ là:
Câu10. Giá trị nhỏ nhất của biểu thức Fyx =− trên miền xác định bởi hệ 22 24 5 yx yx xy −≤ −≥ +≤ là A. min1 F = khi 2x = , 3y = . B. min2 F = khi 0x = , 2y = . C. min3 F = khi 1x = , 4y = D. min0 F = khi 0x = , 0y = Hướngdẫngiải
Câu11: Giá trị nhỏ nhất minF của biểu thức (;)43 Fxyxy =+ trên miền xác định bởi hệ 010 09 214 2530 x y xy xy ≤≤ ≤≤
DẠYKÈMQUYNHƠNOFFICIAL A. (4;1) B. 87 ; 33 C. 22 ; 33 D. (5;0) Hướngdẫngiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu13. Cho , xy thoả mãn hệ 21000 2800 0 0 xy xy x y +−≤ +−≤ ≥ ≥ Tìm giá trị lớn nhất max P của biểu thức (;)4000030000 Pxyxy ==+ A. max 2000000P = B. max 2400000P = C. max 1800000P = D. max 1600000P = Hướngdẫngiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu14. Giá trị lớn nhất max F của biểu thức (;)2 Fxyxy =+ trên miền xác định bởi hệ 04 0 10 2100 y x xy xy ≤≤ ≥ −−≤ +−≤ là A. max 6F = B. max 8F = C. max 10F = D. max 12F = Hướngdẫngiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Dạng2.Bàitoántối ưu
1.Phươngpháp
Vấn đề tìm miền nghiệm của hệ bất phương trình bậc nhất có liên quan chặt chẽ đến quyhoạchtuyến tính. Đó là một ngành toán học có nhiều ứng dụng trong đời sống và kinh tế. Lưu ý: Ta thừa nhận kết quả sau “Giá trị nhỏ nhất hay lớn nhất của biểu thức ( ); Pxyaxbyc =++
22 0ab+≠ trên miền đa giác lồi (kể cả biên) đạt được tại một đỉnh nào đó của đa giác”. 2.Cácvídụ rènluyệnkĩ năng Vídụ 1: Một công ty kinh doanh thương mại chuẩn bị cho một đợt khuyến mại nhằm thu hút khách hàng bằng cách tiến hành quảng cáo sản phẩm của công ty trên hệ thống phát thanh và truyền hình. Chi phí cho 1 phút quảng cáo trên sóng phát thanh là 800.000 đồng, trên sóng truyền hình là 4.000.000 đồng. Đài phát thanh chỉ nhận phát các chương trình quảng cáo dài ít nhất là 5 phút. Do nhu cầu quảng cáo trên truyền hình lớn nên đài truyền hình chỉ nhận phát các chương trình dài tối đa là 4 phút. Theo các phân tích cùng thời lượng một phút quảng cáo trên truyền hình sẽ có hiệu quả gấp 6 lần trên sóng phát thanh. Công ty dự định chi tối đa là 16.000.000 đồng cho quảng cáo. Công ty cần đặt thời lượng quảng cáo trên sóng phát thanh và truyền hình như thế nào để hiệu quả nhất? Hướngdẫngiải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Vídụ 2: Một xưởng sản xuất hai loại sản phẩm, mỗi kg sản phẩm loại một cần 2kg nguyên liệu và 30 giờ, đem lại mức lợi nhuận 40 000 đồng. Mỗi sản phẩm loại hai cần 4kg nguyên liệu và 15 giờ đem lại mức lợi nhuận là 30 000 đồng. Xưởng có 200kg nguyên liệu và 1200 giờ làm việc. Hỏi cần sản xuất mỗi loại sản phẩm bao nhiêu để có mức lợi nhuận cao nhất? Hướngdẫngiải
Vídụ 3: Một công ty điện tử sản xuất hai kiểu radio trên hai dây chuyền độc lập. Radio kiểu một sản xuất trên dây chuyền một với công suất 45 radio/ngày, radio kiểu hai sản xuất trên dây chuyền hai với công
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
suất 80 radio/ngày. Để sản xuất một chiếc radio kiểu một cần 12 linh kiện, để sản xuất một chiếc radio kiểu hai cần 9 linh kiện. Tiền lãi khi bán một chiếc radio kiểu một là 250 000 đồng, lãi thu được khi bán một chiếc radio kiểu hai là 180 000 đồng. Hỏi cần sản xuất như thế nào để tiền lãi thu được là nhiều nhất, biết rằng số linh kiện có thể sử dụng tối đa trong một ngày là 900?
A. Sản xuất 15 radio kiểu một và 80 radio kiểu hai.
B. Sản xuất 45 radio kiểu một và 40 radio kiểu hai.
C. Sản xuất 45 radio kiểu một.
D. Sản xuất 80 radio kiểu hai. Hướngdẫngiải
Vídụ 4: Trong một cuộc thi pha chế, mỗi đội chơi được sử
A. 7 lít nước đường.
B. 6 lít nước táo.
C. 3 lít nước đường, 6 lít nước táo.
ng t
i đa 24 g hương liệu, 9 lít nước và 210 g đường để pha chế nước cam và nước táo. Để pha chế 1 lít nước cam cần 30 g đường và 1 lít nước; pha chế 1 lít nước táo cần 10 g đường, 1 lít nước và 4 g hương liệu. Mỗi lít nước cam nhận được 20 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để được số tiền thưởng là lớn nhất?
D. 6 lít nước đường, 3 lít nước táo. Hướngdẫngiải
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
dụ
ố
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... 3.Bàitậptrắcnghiệm Câu1: Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9 lít nước và 210 g đường để pha chế nước cam và nước táo. ● Để pha chế 1 lít nước cam cần 30 g đường, 1 lít nước và 1 g hương liệu; ● Để pha chế 1 lít nước táo cần 10 g đường, 1 lít nước và 4 g hương liệu.
Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng.
Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?
A. 5 lít nước cam và 4 lít nước táo.
B. 6 lít nước cam và 5 lít nước táo.
D. 4 lít nước cam và 6 lít nước táo. Hướngdẫngiải .....................................................................................................................................................................
C. 4 lít nước cam và 5 lít nước táo.
Câu2: Một xưởng sản xuất hai loại sản phẩm
● Mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, đem lại mức lời 40 nghìn;
● Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, đem lại mức lời 30 nghìn.
Xưởng có 200 kg nguyên liệu và 1200 giờ làm việc. Nên sản xuất mỗi loại sản phẩm bao nhiêu để có mức lời cao nhất?
A. 30 kg loại I và 40 kg loại II. B. 20 kg loại I và 40 kg loại II. C. 30 kg loại I và 20 kg loại II. D. 25 kg loại I và 45 kg loại II. Hướngdẫngiải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Câu3: Một xưởng cơ khí có hai công nhân là Chiến và Bình.
i làm việc trong 2 giờ, Bình phải làm việc trong 6 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chi
DẠYKÈMQUYNHƠNOFFICIAL
sản phẩm I bán lãi
không thể làm việc quá 180 giờ và Bình không
ể
ệ
220
ờ. Số tiền
ớn nhất trong một tháng của xưởng là. A. 32 triệu đồng. B. 35 triệu đồng. C. 14 triệu đồng. D. 30 triệu đồng. Hướngdẫngiải ..................................................................................................................................................................... .....................................................................................................................................................................
Xưởng sản xuất loại sản phẩm I và II . Mỗi
500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đồng. Để sản xuất được một sản phẩm I thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ Để sản xuất được một sản phẩm II thì Chiến phả
ến
th
làm vi
c quá
gi
lãi l
Câu4. Một nhà khoa học đã nghiên cứu về tác động phối hợp của hai loại Vitamin A và B đã thu được kết quả như sau: Trong một ngày, mỗi người cần từ 400 đến 1000 đơn vị Vitamin cả A lẫn B và có thể tiếp nhận không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B . Do tác động phối hợp của hai loại vitamin trên nên mỗi ngày một người sử dụng số đơn vị vitamin B không ít hơn một nửa số đơn vị vitamin A và không nhiều hơn ba lần số đơn vị vitamin A . Tính số đơn vị vitamin mỗi loại ở trên để một người dùng mỗi ngày sao cho chi phí rẻ nhất, biết rằng mỗi đơn vị vitamin A có giá 9 đồng và mỗi đơn vị vitamin B có giá 7,5 đồng.
A. 600 đơn vị Vitamin A , 400 đơn vị Vitamin B B. 600 đơn vị Vitamin A , 300 đơn vị Vitamin B C. 500 đơn vị Vitamin A , 500 đơn vị Vitamin B D. 100 đơn vị Vitamin A , 300 đơn vị Vitamin B Hướngdẫngiải
Câu5. Công ty Bao bì Dược cần sản xuất 3 loại hộp giấy: đựng thuốc B1, đựng cao Sao vàng và đựng "Quy sâm đại bổ hoàn". Để sản xuất các loại hộp này, công ty dùng các tấm bìa có kích thước giống nhau. Mỗi tấm bìa có hai cách cắt khác nhau.
· Cách thứ nhất cắt được 3 hộp B1, một hộp cao Sao vàng và 6 hộp Quy sâm.
· Cách thứ hai cắt được 2 hộp B1, 3 hộp cao Sao vàng và 1 hộp Quy sâm. Theo kế hoạch, số hộp Quy sâm phải có là 900 hộp, số hộp B1 tối thiểu là 900 hộp, số hộp cao sao vàng tối thiểu là 1000 hộp.
Cần phương án sao cho tổng số tấm bìa phải dùng là ít nhất?
A. Cắt theo cách một 100 tấm, cắt theo cách hai 300 tấm.
B. Cắt theo cách một 150 tấm, cắt theo cách hai 100 tấm.
C. Cắt theo cách một 50 tấm, cắt theo cách hai 300 tấm.
D. Cắt theo cách một 100 tấm, cắt theo cách hai 200 tấm.
Hướngdẫngiải
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
Câu6. Một nhà máy sản xuất, sử dụng ba loại máy đặc chủng để sản xuất sản phẩm A và sản phẩm
B trong một chu trình sản xuất. Để sản xuất một tấn sản phẩm A lãi 4 triệu đồng người ta sử dụng máy I trong 1 giờ, máy U trong 2 giờ và máy MI trong 3 giờ. Để sản xuất ra một tấn sản phẩm
B lãi được 3 triệu đồng người ta sử dụng máy I trong 6 giờ, máy U trong 3 giờ và máy MI trong 2 giờ. Biết rằng máy I chỉ hoạt động không quá 36 giờ, máy hai hoạt động không quá 23 giờ và máy MI hoạt động không quá 27 giờ. Hãy lập kế hoạch sản xuất cho nhà máy để tiền lãi được nhiều nhất. A. Sản xuất 9 tấn sản phẩm A và không sản xuất sản phẩm B B. Sản xuất 7 tấn sản phẩm A và 3 tấn sản phẩm B C. Sản xuất 10 3 tấn sản phẩm A và 49 9 tấn sản phẩm B D. Sản xuất 6 tấn sản phẩm B và không sản xuất sản phẩm A Hướngdẫngiải
Câu7. Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kiogam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilogam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền một kg thịt bò là 160 nghìn đồng, một kg thịt lợn là 110 nghìn đồng. Gọi x , y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua. Tìm x , y để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn?
A. 0,3x = và 1,1y = B. 0,3x = và 0,7y = C. 0,6x = và 0,7y = . D. 1,6x = và 0,2y = . Hướngdẫngiải
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL
CÂUHỎITRẮCNGHIỆM
Câu1. Điểm nào dưới đây thuộc miền nghiệm của bất phương trình 210 +−<xy ? A. () 1;1Q . B. () 1;2M . C. () 2;2P . D. () 1;0N . Lờigiải
Câu2. Cho bất phương trình 250xy−+> có tập nghiệm là S . Mệnh đề nào sau đây là đúng? A. () 2;2 S−∈ B. () 2;2 S∈ C. () 2;4 S−∈ D. () 1;3 S∈ Lờigi
DẠYKÈMQUYNHƠNOFFICIAL BÀITẬ
Ố
PCU
ICHƯƠNG2
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
ải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu3. Hình vẽ nào sau đây biểu diễn miền nghiệm của bất phương trình 2360 xy−−≤ (miền không tô đậm kể cả bờ)? A. H1 B. H2 C. H3 D. H4 Lờigiải Câu4. Miền của bất phương trình 21 xy+> không chứa điểm nào sau đây? A. () 3;3C . B. () 1;1D . C. () 1;1A . D. () 2;2B . Lờigiải .....................................................................................................................................................................
Câu5. Cặp số ( )1;1 thuộc miền nghiệm của bất phương trình nào sau đây?
A. 30xy+−> B. 310xy −−−< C. 0xy −−< D. 310xy++<
Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu6. Điểm nào dưới đây thuộc miền nghiệm của bất phương trình 210 xy+−< ?
A. ( )1;1Q B. ( )1;2M C. ( )2;2P D. ( )1;0N Lờigiải
Câu7. Tập nghiệm của bất phương trình 3210 xy−+< là
A. Nửa mặt phẳng chứa gốc tọa độ, bờ là đường thẳng 3210 xy−+= (không bao gồm đường thẳng). B. Nửa mặt phẳng chứa gốc tọa độ, bờ là đường thẳng 3210 xy−+= (bao gồm đường thẳng).
C. Nửa mặt phẳng không chứa gốc tọa độ, bờ là đường thẳng 3210 xy−+= (bao gồm đường thẳng).
D. Nửa mặt phẳng không chứa gốc tọa độ, bờ là đường thẳng 3210 xy−+= (không bao gồm đường thẳng).
DẠYKÈMQUYNHƠNOFFICIAL
ờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu8. Cặp số nào dưới đây là một nghiệm của bất phương trình: 23 xy−> . A. ( )3;1 . B. ( )0;2 C. ( )1;1 . D. ( )2;1 . Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu9. Miền nghiệm của bất phương trình ( ) 529227 xxy +−<−+ không chứa điểm nào trong các điểm sau? A. ( )2;3 . B. ( )2;1 . C. ( )2;1 . D. ( )0;0 .
L
Câu10. Điểm nào dưới đây thuộc miền nghiệm của bất phương trình 210xy−−≤ ?
A. ( )0;1M B. ( )1;0Q C. ( )1;2N D. ( )1;1P Lờigiải
Câu11. Miền nghiệm của bất phương trình 250xy−+< là:
A. Nửa mặt phẳng chứa gốc tọa độ, bờ là đường thẳng 15 22yx=+ (bao gồm đường thẳng).
B. Nửa mặt phẳng không chứa gốc tọa độ, bờ là đường thẳng 15 22yx=+ (không bao gồm đường thẳng).
C. Nửa mặt phẳng chứa gốc tọa độ, bờ là đường thẳng 15 22yx=+ (không bao gồm đường thẳng).
D. Nửa mặt phẳng không chứa gốc tọa độ, bờ là đường thẳng 15 22yx=+ (bao gồm đường thẳng). Lờigiải .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL Lờigiải
.....................................................................................................................................................................
.....................................................................................................................................................................
ề
ệ
ủ
A. Nửa mặt phẳng I bỏ đi đường thẳng d B. Nửa mặt phẳng I kể cả bờ d C. Nửa mặt phẳng II kể cả bờ d D. Nửa mặt phẳng II bỏ đ
đường thẳng d Lờ
ả
.....................................................................................................................................................................
Câu12. Đường thẳng :22dxy−= chia mặt phẳng tọa độ thành hai miền I, II có bờ là đường thẳng d (hình vẽ bên). Xác định mi
n nghi
m c
a bất phương trình 22 xy−>
i
igi
i
Câu13. Tập nghiệm của bất phương trình 3210 xy−+<
A. Nửa mặt phẳng chứa gốc tọa độ, bờ là đường thẳng 3210 xy−+= (không bao gồm đường thẳng).
B. Nửa mặt phẳng chứa gốc tọa độ, bờ là đường thẳng 3210 xy−+= (bao gồm đường thẳng).
C. Nửa mặt phẳng không chứa gốc tọa độ, bờ là đường thẳng 3210 xy−+= (bao gồm đường thẳng).
D. Nửa mặt phẳng không chứa gốc tọa độ, bờ là đường thẳng 3210 xy−+= (không bao gồm đường thẳng).
Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... 3210 xy−+= (không bao gồm đường thẳng). Câu14. Đường thẳng :220dxy−−= chia mặt phẳng tọa độ thành hai miền I , II là hai nửa mặt phẳng có bờ là đường thẳng d (Hình vẽ bên). Xác định miền nghiệm của bất phương trình 220 xy−−≥ . A. Nửa mặt phẳng I bỏ đi đường thẳng d B. Nửa mặt phẳng I
DẠYKÈMQUYNHƠNOFFICIAL
ả
C. Nửa mặt phẳng II kể cả bờ d . D.
ẳ
. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu15. Hình dưới đây biểu diễn hình học miề
nghiệ
ủa
ấ
ươ
không gạch chéo và miền nghiệ
ứ
đườ
ẳ
x y
O
kể c
bờ d
Nửa mặt phẳng II bỏ đi đường th
ng d
n
m c
b
t ph
ng trình nào? (Miền nghiệm là miền
m không ch
a
ng th
ng)
d II I
-2 1
DẠYKÈMQUYNHƠNOFFICIAL A. 322 xy+> . B. 322 xy+< . C. 322 xy −+> . D. 322 xy −+< . Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu16. iá trị lớn nhất của biểu thức ( ) ;2 Fxyxy =+ , với điều kiện 04 0 10 2100 y x xy xy ≤≤ ≥ −−≤ +−≤ là A. 6 B. 12 C. 10 D. 8 Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu17. Điểm ( )0;0O không thuộc miền nghiệm của hệ bất phương trình nào sau đây? A. 30 240 xy xy +< ++> . B. 30 240 xy xy +≥ +−< . C. 360 240 xy xy +−< ++> . D. 360 240 xy xy +−< ++≥ . Lờigiải .....................................................................................................................................................................
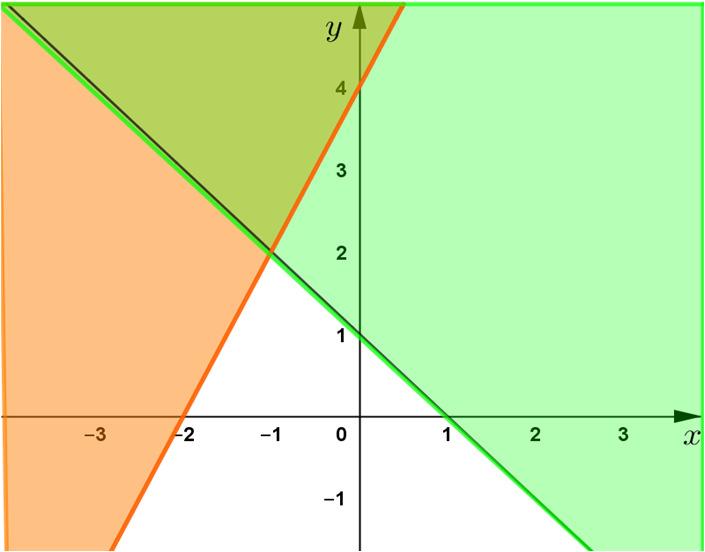
DẠYKÈMQUYNHƠNOFFICIAL Câu18. Miền không bị gạch chéo (kể cả đường thẳng 1d và 2d ) là miền nghiệm của hệ bất phương trình
A. 10 240 xy xy +−≥ −+≤ . B. 10 240 xy xy +−≥ −+≥ . C. 10 240 xy xy +−≤ −+≥ . D. 10 240 xy xy +−≤ −+≤ . Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu19. Miền nghiệm của hệ bất phương trình 34120 50 10 xy xy x −+≥ +−≥ +> là miền chứa điểm nào trong các điểm sau? A. () 1;3M B. () 4;3N C. () 1;5P . D. () 2;3Q . Lờigiải Câu20. Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình 260 350 10 xy xy x +−< −+> +> ? A. () 0;7M B. () 1;1N C. () 2;3P . D. () 1;2Q Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu21. Điểm nào trong các điểm sau thuộc miền nghiệm của hệ bất phương trình 34120 50 10 xy xy x −+≥ +−≥ +> ?
nào?
A. () 2;3Q . B. () 1;3M . C. () 4;3N . D. () 1;5P . Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Câu22. Miền nghiệm của hệ bất phương trình: 34120 50 10
xy xy x
−+≥ +−≥ +> là miền chứa điểm nào trong các điểm sau?
A. ()1;3.M B. ()4;3.N C. () 1;5P . D. () 2;3Q . Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Câu23. Điểm () 0;0O không thuộc miền nghiệm của hệ bất phương trình nào dưới đây?
A. 360 240 +−< ++> xy xy B. 30 240 +≥ +−< xy xy C. 30 240 +< ++> xy xy . D. 360 240 +−< ++≥ xy xy . Lờigiải .....................................................................................................................................................................
Câu24. Hai đường thẳng :230dxy++= và ':230dxy+−= chia mặt phẳng tọa độ thành 3 miền I,II, III có bờ là 2 đường thẳng d và 'd không kể các điểm nằm trên 2 đường thẳng đó: Xác định miền nghiệm của bất phương trình 23xy+< . A. Miền I và III B. Miền II C. Miền I D. Miền III Lờigiải
DẠYKÈMQUYNHƠNOFFICIAL
DẠYKÈMQUYNHƠNOFFICIAL Câu25. Gọi () S là tập hợp các điểm trong mặt phẳng tọa độ Oxy thỏa mãn hệ 10 490 230 xy xy xy −−≤ ++≥ −+≥ ( hình vẽ). Tìm tọa độ () ; xy trong miền () S sao cho biểu thức 324Txy=−− có giá trị nhỏ nhất. A. () 5;4 B. () 1;2 C. () 5;1 D. () 2;5 Lờigiải ..................................................................................................................................................................... Câu26. Giá trị lớn nhất của biểu thức ();2 Fxyxy =+ , với điều kiện 04 0 10 2100 y x xy xy ≤≤ ≥ −−≤ +−≤ là A. 6 B. 12 C. 10 D. 8 Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu27. Cho các giá trị , xy thỏa mãn điều kiện 20 210 320 xy xy xy −+≥ −−≤ −−≥ . Tìm giá trị lớn nhất của biểu thức 32 Txy =+ . A. 19 . B. 25 . C. 14 . D. Không tồn tại. Lờigiải
BÀITẬPTỰ LUẬN
Câu1. Cho bất phương trình: 20 xy−< . Trong các cặp số ( )1;2 , ( )2;0 , ( )0;1 , ( )3;2 , ( )1;2 , cặp nào là nghiệm của bất phương trình, cặp nào không phải là nghiệm của bất phương trình? Lờigiải .....................................................................................................................................................................
Câu2. Biểu diễn hình học tập nghiệm của bất phương trình 21xy−> ? Lờigiải
Câu3. Xác định miền nghiệm của các bất phương trình sau a) 20 xy−≥ . b) 221 23 xyxy−++ > Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
=− = là nghiệm của bất phương trình ( ) 12mxmy+−> . Lờigiải Câu6. Cho tam giác ABC có ( )1;2A , ( )3;1B và ( )3;4C . Tìm điều kiện của tham số m để điểm
5 ; 3 m Mm
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
Câu4. Tìm các nghiệm ( ); xy của bất phương trình 1 34 xy+≤ , trong đó x , y là số nguyên dương. Lờigiải Câu5. Tìm giá trị của tham số m sao cho 1 2 x y .....................................................................................................................................................................
nằm bên trong tam giác ABC ? Lờigiải
DẠYKÈMQUYNHƠNOFFICIAL Câu7. Xác định miền nghiệm của các hệ bất phương trình sau a) 20 330 xy xy +−≥ −+≤ b) 0 2360 210 xy xy xy +> −−+> −+≥ Lờigiải Câu8. Biểu diễn hình học tập nghiệm của hệ bất phương trình 20 33 xy xy −> +< . Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu9. Biểu diễn hình học tập nghiệm của hệ bất phương trình 26 4 0 0 xy xy x y −+≤ +≤ ≥ ≥ . Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL
Biểu diễn
học tập nghiệm của hệ bất phương trình 31 26 33 xy xy xy −≥− +≤ +> Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
Chocặp ( ); xy lànghiệm củahệ 31 26 33 xy xy xy −≥− +≤ +≥ (*).Tìm giátrị lớnnhất vànhỏ nhất củabiểu thứ
. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
ặ
ẳ
ẽ
ả
ố
ạ
x y D C B A O
Câu10.
hình
Câu11.
c ( ) ;231fxyxy=−+
Câu12. Trong m
t ph
ng Oxy , cho tứ giác ABCD có ( )2;0A ; ( )0;3B ; ( )3;2C và ( )3;2D (tham khảo hình v
). Tìm tất cả các giá trị của m sao cho điểm ( );1Mmm + nằm trên hình tứ giác ABCD tính c
b
n c
nh ,,, ABBCCDDA .
Câu13. Một hộ nông dân dự định trồng đậu và cà trên diện tích 8 ha. Nếu trồng đậu thì cần 20 công và thu 3 triệu đồng trên diện tích mỗi ha, nếu trồng cà thì cần 30 công và thu 4 triệu đồng trên diện tích mỗi ha. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu để thu về được nhiều tiền nhất, biết rằng tổng số công không quá 180. Lờigiải
Câu14. Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kg thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kg thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit.Biết rằng mỗi ngày gia đình này chỉ mua tối đa1.5kg thịt bò và 1kg thịt lợn, giá tiền 1kg thịt bò là200 nghìn đồng, 1kg thịt lợn là 100 nghìn đồng. Hỏi gia đình đó phải mua bao nhiêu kg thịt mỗi loại để số tiền bỏ ra là ít nhất. Lờigiải
DẠYKÈMQUYNHƠNOFFICIAL Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Câu15. Người ta định dùng hai loại nguyên liệu để chiết xuất ít nhất 120 kg hóa chất A và 9 kg hóa chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng có thể chiết xuất được 20 kg chất A và 0,6 kg chất B.Từ mỗi tấn nguyên liệu loại IIgiá3 triệu đồng có thể chiết xuất được10 kgchất Avà1,5 kg chất B. Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất.Biếtrằng cơ sở cungcấp nguyênliệuchỉ cóthể cung cấpkhôngquá10tấnnguyên liệuloại I và không quá 9 tấn nguyên liệu loại II. Lờigiải .....................................................................................................................................................................
Câu16. Có ba nhóm máy A, B,C dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị
dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và
máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được cho trong bảng sau: Nhóm Số máytrongmỗi nhóm
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
ạ
ả
Số máytrongtừngnhóm để sảnxuấtramột đơn vị sảnphẩm LoạiI LoạiII A 10 2 2 B 4 0 2 C 12 2 4 Một đơn vị sản phẩm I lãi ba nghìn đồng, một đơn vị sản phẩm loại IIlãi năm nghìn đồng. Hãy lập phương án để việc sản xuất hai loại sản phẩm trên có lãi cao nhất. Lờigiải
sản phẩm mỗi lo
i ph
i lần lượt
số
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL
1. Hàm số. Tập xác định và tập giá trị của hàm số Giả sử x và y làhai đạilượngbiếnthiênvà x nhậngiátrị thuộctậpsố D . Nếu với mỗi giá trị x thuộc D , ta xác định được một và chỉ một giá trị tương ứng y thuộc tập hợp số thực ℝ thìtacómộthàmsố.
Tagọi x làbiếnsố và y làhàmsố của x
Tậphợp D đượcgọilàtập xác địnhcủahàmsố
Tậphợp T gồmtấtcả cácgiátrị y (tương ứngvới x thuộc D )gọilàtậpgiátrị củahàmsố
Chú ý:
-Kíhiệu ()fx để chỉ giá trị y tương ứng với x , nên hàm số còn được viết là ()= yfx .
- Tập xác định của hàm số ()= yfx là tâp hợ tất cả các số thực x sao cho biểu thức ()fx có nghĩa.
2. Đồ thị hàm số Cho hàm số ()= yfx có tập xác định D Trên mặt phẳng tọa độ ,Oxy đồ thị () C của hàm số là tập hợp tất cả các điểm (;)Mxy với ∈ xD và ()= yfx Vậy (){(;()))} =∈ CMxfxxD ∣ Chú ý Điểm ( ), MMMxy thuộc đồ thị hàm số ()= yfx khi và chỉ khi ∈M xD và ( )= MMyfx .
3. Hàm số đồng biế
DẠYKÈMQUYNHƠNOFFICIAL
CHƯƠNG III: HÀM SỐ BẬC HAI VÀ ĐỒ THỊ BÀI 1. HÀM SỐ VÀ ĐỒ THỊ A. KIẾN THỨC CƠ BẢN CẦN NẮM
n, hàm số nghịch biến Vớ
số ()= yfx xác định trên khoảng
-
số đồng biến trên khoảng (;) ab nếu (
121212
∀∈< <
- Hàm số nghịch biến trên khoảng (;) ab nếu ( ) ( )121212 ,(;),.∀∈< > xxabxxfxfx Nhận xét: Khi hàm số đồng biến (tăng) trên khoảng (;) ab thì đồ thị của nó có dạng đi lên từ trái sang phải. Ngược lại, khi hàm số nghịch biển (giảm) trên khoảng (,) ab thì đồ thị của nó có dạng đi xuống từ trái sang phải. B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP Dạng 1: Tính giá trị của hàm số tại một điểm, điểm thuộc đồ thị 1. Phương pháp Thay trực tiếp các giá trị của biến số x vào hàm số. 2. Các ví dụ rèn luyện kĩ năng
i hàm
(;) ab , ta nói:
Hàm
) ( )
,(;),.
xxabxxfxfx
DẠYKÈMQUYNHƠNOFFICIAL
.....................................................................................................................................................................
iểm mà parabol đi qua. A. ( )4;2Q B. ( )3;1N C. ( )4;0P = D. ( )3;19M Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 4: Tìm m để đồ thị hàm số 41yxm=+− đi qua điểm ( )1;2A A. 6m = . B. 1m =− . C. 4m =− . D. 1m = . Lời giải Câu 5: Cho hàm số 2 2 1 52 1 1 xxkhix y x khix x −≥ = < Điểm nào sau đây thuộc đồ thị hàm số? A. ( )4;1 . B. ( )2;3 . C. ( )1;3 . D. ( )2;1 . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... 3. Bài tập trắc nghiệm Câu 1. Cho hàm số 1 1 x y x + = . Tìm tọa độ điểm thuộc đồ thị của hàm số và có tung độ bằng 2 . A. ( )0;2 B. 1 ;2 3 C. ( )2;2 D. ( )1;2
Câu 1: Điểm nào sau đây thuộc đồ thị hàm số () 1 2 x y xx + = ? A. ( )2;1M . B. ( )1;0N . C. ( )2;0P . D. 1 0; 2Q . Lời giải ..................................................................................................................................................................... Câu 2: Tọa độ giao điểm của đường thẳng 1yx=− và ( ) 2 :21Pyxx=−− là A. ( ) ( )1;1;3;2 . B. ( ) ( )0;1;3;2 . C. ( ) ( )0;1;3;2 . D. ( ) ( )1;1;3;2 . Lời giải .....................................................................................................................................................................
..................................................................................................................................................................... Câu 3: Cho () P có phương trình 2 24yxx=−+ . Tìm đ
DẠYKÈMQUYNHƠNOFFICIAL Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 2. Điểm nào sau đây thuộc đồ thị của hàm số 2 (1) x y xx = A. ( )0;1M . B. ( )2;1M . C. ( )2;0M . D. ( )1;1M . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 3. Cho hàm số () 2 223 khi2 1 2khi2 x fxx x xx ≥ = +< . Tính ( ) ( )22Pff=+− A. 3P = B. 2P = C. 7 3 P = D. 6P = Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 5. Đồ thị của hàm số () 21khi2 3khi2 xx yfx x +≤ == −> đi qua điểm nào sau đây: A. ( )0;3 . B. ( )3;7 . C. (2;3) . D. ( )0;1 . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 6. Cho hàm số: () ( ) 2 23khi11 1khi1 xx fx xx −−−≤≤ = −> . Giá trị của ( )1f ; ( )1f lần lượt là A. 8 và 0 B. 0 và 8 C. 0 và 0 D. 8 và 4 H Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 7. Cho hàm số 21khi3 7 khi3 2 xx y x x −+≤− = + >− . Biết ( )0 5fx = thì 0x là A. 2 . B. 3 . C. 0 . D. 1. Lời giải
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 8. Cho hàm số () 3 23 khi0 1 23 khi20 2 x x fxx x x x + ≥ + = + −≤< . Ta có kết quả nào sau đây đúng? A. () 1 1; 3f −= () 7 2 3f = B. ( ) 02;f = ( ) 37f −= C. ( )1f : không xác định; () 11 3 24f −=− D. ( ) ( ) 18;30ff−== Lời giải ..................................................................................................................................................................... Dạng 2: Tìm tập xác định của hàm số 1. Phương pháp Tìm tập xác định D của hàm số ( )= yfx là tìm tất cả những giá trị của biến số x sao cho biểu thức f(x) có nghĩa: { }=∈ DxRfxcoùnghóa () Điều kiện xác định của một số hàm số thường gặp: 1) Hàm số = Ax y Bx () () . Khi đó : { }=∈≠DxAx ℝ|() xaùc ñònh vaø A(x)0 2) Hàm số =∈ k yAxk ℕ 2* (), . Khi đó : { }=∈≥DxAx ℝ|() xaùc ñònh vaø A(x)0 3) Hàm số =∈ k Ax yk Bx ℕ* 2 () , () Khi đó : { }=∈ DxAxBx ℝ|(),() xaùc ñònh vaø B(x)>0 Chú ý: Đôi khi ta sử dụng phối hợp các điều kiện với nhau. A.B ≠0 ⇔ ≠ ≠ A B 0 0 Nếu = yfx() có tập xác định là D . Khi đó: = yfx() xác định trên tập X ⇔⊂XD = yfx() xác định trên tập X ⇔ fx() xác định với mọi ∈ xX 2. Các ví dụ rèn luyện kĩ năng Ví dụ 1 : Tìm tập xác định của hàm số 1yx=− Lời giải
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... Ví dụ 2: Tìm tập xác định của hàm số 126 yxx =+++ Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Ví dụ 3: Tập xác định của hàm số 2 x y x = Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Ví dụ 4: Tìm tập xác định của hàm số 1 1 3 yx x =+− Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Ví dụ 5: Tìm m để hàm số ( ) 231yxxm =−−− xác định trên tập ( )1; +∞ ? Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Ví dụ 6. Xác định tham số m để hàm số =− yxm 3 xác định trên tập ( )+∞1; Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Ví dụ 7. Xác định tham số m để hàm số =− yxm 2 xác định trên tập ( −∞− ;3 Lời giải .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... 3. Bài tập trắc nghiệm Câu 1. Tìm tập xác định D của hàm số () 1 1fxx x =++ A. { }\0D = ℝ . B. { }\1;0D =− ℝ . C. [ ) { }1;\0D =−+∞ . D. [ )1;D =−+∞ . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 2. Cho hàm số: 1 0 1 20 x yx xx ≤ = +> . Tập xác định của hàm số là tập hợp nào sau đây? A. [ )2; −+∞ B. ℝ C. { }\1ℝ . D. { }\1và2xxx ∈≠ ≥−ℝ . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 3. Tập xác định của hàm số 1 3 x y x + = là A. ( )3; +∞ . B. [ )1;+∞ . C. [ ) ( )1;33; −∪+∞ . D. { }\3ℝ . Lời giải ..................................................................................................................................................................... Câu 4. Tập xác định của hàm số 2 2 4 x y xx = là A. { }\0;2;4ℝ B. [ ]\0;4ℝ C. ( )\0;4ℝ D. { }\0;4ℝ Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL Câu 5. Tìm tập xác định D của hàm số () 1 1fxx x =++ A. { }\0D = ℝ . B. [ )1;D =+∞ . C. { }\1;0D =− ℝ . D. [ ) { }1;\0D =−+∞ . Lời giải Câu 6. Tìm tập xác định của hàm số 2 441yxx=−+ . A. 1 ; 2 +∞ . B. 1 ; 2 −∞ . C. ℝ . D. ∅ . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 7. Tập xác định của hàm số () 1 3 1 fxx x =−+ là A. ( ]1; 3D = B. ( ) [ );13;D =−∞∪+∞ C. [ ]1;3D = . D. D =∅ . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 8. Tập hợp nào sau đây là tập xác định của hàm số 15 72 x yx x =++ ? A. 17 ; 52 B. 17 ; 52 C. 17 ; 52 D. 17 ; 52 Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL Câu 9. Tập xác định của hàm số 2 2 9 68 x y xx = −+ là A. ( ) { }3;8\4 . B. [ ] { }3;3\2 . C. ( ) { }3;3\2 . D. ( ) { };3\2−∞ . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 10. Tập xác định của hàm số () 38khi2 71khi2 xxx yfx xx −++< == ++≥ là A. ℝ B. { }\2ℝ C. 8 ; 3 −∞ D. [ )7; −+∞ Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 11. Tìm tập xác định của hàm số 2 43 3 x yxx x =−+− A. ( ] ( );13; −∞∪+∞ . B. ( ) ( );13; −∞∪+∞ . C. ( )3; +∞ . D. ( )1;3 . Lời giải ..................................................................................................................................................................... Câu 12. Tập xác định của hàm số 2 31 56 xx y xx −++ = −+ là A. [ ) { }1;3\2 B. [ ]1;2 C. [ ]1;3 D. ( )2;3 Lời giải Câu 13. Tìm tập xác định của hàm số 2 252yxx=−+ .
DẠYKÈMQUYNHƠNOFFICIAL A. [ )1 ;2; 2 −∞∪+∞ . B. [ )2; +∞ . C. 1 ; 2 −∞ . D. 1 ;2 2 . Lời giải ..................................................................................................................................................................... Câu 14. Tìm m để hàm số 2331 5 xmx y xmxm −+− =+ −++ xác định trên khoảng ( )0;1 . A. 3 1; 2 m ∈ B. [ ]3;0m ∈− C. [ ] [ ]3;00;1m ∈−∪ . D. [] 3 4;01; 2 m ∈−∪ . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Dạng 3: Tính đồng biến, nghịch biến của hàm số 1. Phương pháp Cho hàm số f xác định trên K y = f(x) đồng biến trên K ⇔ ∀∈< < xxKxxfxfx 121212 ,:()() y = f(x) nghịch biến trên K ⇔ ∀∈< > xxKxxfxfx 121212 ,:()() Từ đó, ta có hai cách để xét tính đồng biến nghịch biến: Cách 1: ∀∈<xxKxx 1212 ,: . Xét hiệu số =− Afxfx 21 ()() Nếu >A 0 thì hàm số đồng biến Nếu <A 0 thì hàm số nghịch biến Cách 2: ∀∈≠xxKxx 1212 ,: . Xét tỉ số = Afxfx xx 21 21 ()() Nếu >A 0 thì hàm số đồng biến Nếu <A 0 thì hàm số nghịch biến 2. Các ví dụ rèn luyện kĩ năng Ví dụ 1. Khảo sát sự biến thiên của hàm số sau
DẠYKÈMQUYNHƠNOFFICIAL ( ) ( ) ()() =−+−∞+∞ =−−+−∞−−+∞ ayxx byxx 2 2 )46treânmoãikhoaûng ;2;2 )65treânmoãikhoaûng ;3;3; Lời giải Ví dụ 2. Khảo sát sự biến thiên của hàm số sau ()() ()() =−∞+∞ + =−∞−−+∞ + ay x byx x 3 )treânmoãikhoaûng ;1;1;1 1 )treânmoãikhoaûng ;2;2;24 Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Ví dụ 3. Khảo sát sự biến thiên và lập bảng biến thiên của hàm số sau =+= ayxby x 3 1 )3;) 1 Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Ví dụ 4: Tìm a để hàm số ( ) 1 fxaxa =−− đồng biến trên ℝ Lời giải ..................................................................................................................................................................... .....................................................................................................................................................................
3. Bài tập trắc nghiệm
Câu 1: Hàm số nào sau đây đồng biến trên tập xác định của nó?
A. 3 yx =− . B. 31yx=+ . C. 4y = . D. 2 23yxx=−+ Lời giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 2: Xét sự biến thiên của hàm số () 3 =fx x trên khoảng ( )0; +∞ . Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng ( )0; +∞
B. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng ( )0; +∞ C. Hàm số đồng biến trên khoảng ( )0; +∞ . D. Hàm số không đồng biến, không nghịch biến trên khoảng ( )0; +∞ Lời giải
Câu 3: Trong các hàm số sau, hàm số nào nghịch biến trên ℝ ? A. yx = . B. 2 yx =− . C. 2 yx = . D. 1 2 yx = Lời giải
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
= được gọi là nghịch biến trên K nếu 121212 ;, ()()xxKxxfxfx∀∈< < B. Hàm số ()yfx = được gọi là đồng biến trên K nếu 121212 ;, ()()xxKxxfxfx∀∈< ≤ C. Hàm số ()yfx = được gọi là đồng biến trên K nếu 121212 ;, ()()xxKxxfxfx∀∈< > D. Hàm số ()yfx = được gọi là đồng biến trên K nếu 121212 ;, ()()xxKxxfxfx∀∈< < Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 5. Tìm m để hàm số ( ) 217ymx=−+ đồng biến trên ℝ A. 1 2 m > B. 1 2 m ≥ C. 1 2 m = D. m ∈ ℝ Lời giải
.....................................................................................................................................................................
Câu 4. Chọn khẳng định đúng ? A. Hàm số ()yfx
DẠYKÈMQUYNHƠNOFFICIAL Câu 6. Tìm tất cả các giá trị của tham số m để hàm số ( ) 233ymxm =+++ nghịch biến trên ℝ . A. 3 2 m ≤− . B. 3 2 m ≥− . C. 3 2 m >− . D. 3 2 m <− . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 7. Tổng tất cả các giá trị nguyên dương của tham số m để hàm số ( )2 213yxmx =−+++ nghịch biến trên khoảng ( )1;5 là A. 6 . B. 3 . C. 1. D. 15 . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 8. Cho hàm số ( ) 22 ymxm =++− . Có bao nhiêu giá trị nguyên của m để hàm số đồng biến trên ℝ ? A. 2 . B. 3 . C. 4 . D. 5 . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 9. Tìm các giá trị thực của tham số m để hàm số 2xm y xm ++ = xác định trên ( )1;2 . A. 1 2 m m ≤− ≥ . B. 1 2 m m ≤− ≥ . C. 1 2 m m <− > . D. 12 m −<< . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Dạng 4: Dựa vào đồ thị tìm các khoảng đồng biến, nghịch biến 1. Phương pháp 2. Các ví dụ rèn luyện kĩ năng Câu 1: Cho hàm số ( )yfx = có tập xác định [ ]3;3 và đồ thị của nó được biểu diễn như hình dưới đây
O 11 3 1 1 4 3 2
x
Khẳng định nào sau đây đúng ?
A. Hàm số nghịch biến trên ( )1;0 . B. Hàm số đồng biến trên ( )3;1 và ( )1;4 .
C. Hàm số đồng biến trên ( )3;3 . D. Hàm số đồng biến trên ( )3;1 và ( )1;3 .
Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 2: Hàm số ( )yfx = có đồ thị như hình vẽ bên chỉ đồng biến trên tập
A. ( );1−∞− B. ( )1;+∞ C. ( );1−∞− và ( )1;+∞ . D. ( ];1−∞− và [ )1;+∞ .
Lời giải
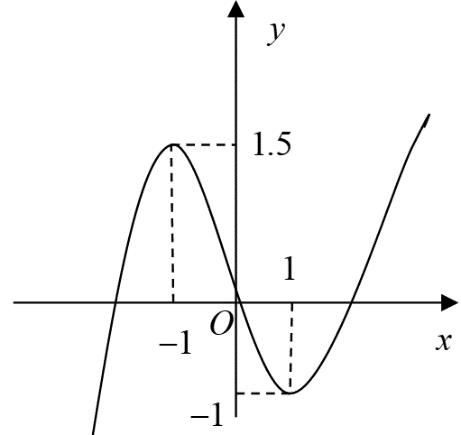
DẠYKÈMQUYNHƠNOFFICIAL
Câu 3: Cho hàm số ( )yfx = có tập xác định là [ ]3;3 , có đồ thị được biểu diễn bởi hình vẽ dưới đây. y
Khẳng định nào dưới đây là khẳng định đúng?
A. Đồ thị hàm số đi qua điểm ( )3;1A B. Đồ thị cắt trục hoành tại 3 điểm phân biệt.
C. Hàm số nghịch biến trên ( )2;1 .
D. Hàm số đồng biến trên ( )3;1 và ( )1;3 . Lời giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 4: Cho hàm số ( )yfx = có tập xác định [ ]3;3 và đồ thị của nó được biểu diễn như hình dưới đây.
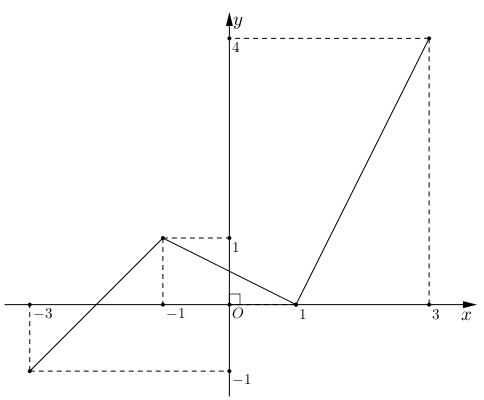
Khẳng định nào sau đây đúng ?
A. Hàm số nghịch biến trên ( )1;2 .
C. Hàm số đồ
B. Hàm số đồng biến trên ( )3;1 và ( )1;4 .
DẠYKÈMQUYNHƠNOFFICIAL
.....................................................................................................................................................................
ng biến trên ( )3;3 . D. Hàm số đồng biến trên
)3;1 và
)1;3 . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 5: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ ]3;3 để hàm số ( ) ( ) 12fxmxm=++− đồng biến trên 3. Bài tập trắc nghiệm Câu 1: Cho hàm số có đồ thị như hình bên dưới. x y O 11 3 1 1 4 3 2
(
(
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng ( )0;3 .
B. Hàm số đồng biến trên khoảng ( );1−∞
C. Hàm số nghịch biến trên khoảng ( )0;2 .
D. Hàm số đồng biến trên khoảng ( );3−∞
Lời giải .....................................................................................................................................................................
Câu 2. Cho hàm số ( )yfx = có tập xác định là [ ]3;3 và có đồ thị được biểu diễn bởi hình bên.
Khẳng định nào sau đây là đúng?
A. Hàm số ( ) 2018yfx=+ đồng biến trên các khoảng ( )3;1 và ( )1;3 .
B. Hàm số ( ) 2018yfx=+ đồng biến trên các khoảng ( )2;1 và ( )1;3
C. Hàm số ( ) 2018yfx=+ nghịch biến trên các khoảng ( )2;1 và ( )0;1 .
D. Hàm số ( ) 2018yfx=+ nghịch biến trên khoảng ( )3;2
Lời giải
Câu 3. Cho hàm số có đồ thị như hình bên dưới.
DẠYKÈMQUYNHƠNOFFICIAL
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng ( )0;3 .
B. Hàm số đồng biến trên khoảng ( );1−∞
C. Hàm số nghịch biến trên khoảng ( )0;2 .
D. Hàm số đồng biến trên khoảng ( );3−∞
Lời giải .....................................................................................................................................................................
Câu 4. Cho hàm số có đồ thị như hình vẽ.
Chọn đáp án sai.
A. Hàm số nghịch biến trên khoảng ( );1−∞− .
B. Hàm số đồng biến trên khoảng ( )1; +∞ .

C. Hàm số nghịch biến trên khoảng ( )1;1 .
D. Hàm số đồng biến trên khoảng ( )1;0
Lời giải .....................................................................................................................................................................
Câu 5. Hàm số ( )fx có tập xác định ℝ và có đồ thị như hình vẽ
DẠYKÈMQUYNHƠNOFFICIAL
Mệnh đề nào sau đây đúng ?
A. Đồ thị hàm số cắt trục hoành theo một dây cung có độ dài bằng 2 .
B. Hàm số đồng biến trên khoảng ( )0;5
C. Hàm số nghịch biến trên khoảng ( )0;3 .
D. ( ) ( )20192017ff <
Lời giải ..................................................................................................................................................................... .....................................................................................................................................................................
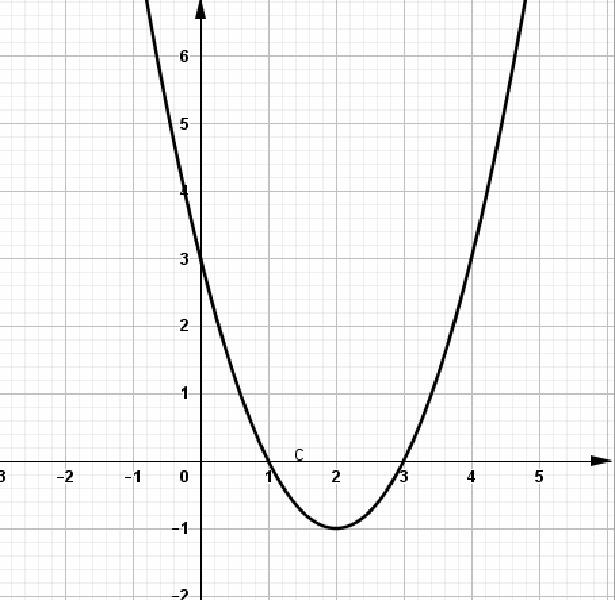
DẠYKÈMQUYNHƠNOFFICIAL
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1. Hàm số bậc hai
Hàm số bậc hai theo biến x là hàm số cho bởi công thức có dạng 2 (),==++ yfxaxbxc với ,, abc là các số thực và a khác 0 .
Tập xác định của hàm số bậc hai là ℝ
2. Đồ thị hàm số bậc hai
Trong mặt phẳng toạ độ ,Oxy đồ thị hàm số bậc hai 2 =++ yaxbxc (với 0≠a ) là một parabol () P :
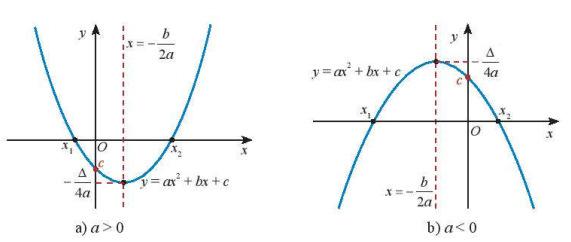
- Có đỉnh S với hoành độ 2 =− S b x a , tung độ 4 ∆ =− Sy a ;
- Có trục đối xứng là đường thẳng 2 =− b x a (đường thẳng này đi qua đỉnh S và song song với trục Oy nếu 0≠b , trùng với trục Oy nếu 0=b );
- Có bề lõm quay lên trên nếu 0>a , quay xuống dưới nếu 0<a ;
- Cắt trục tung tại điểm có tung độ bằng c , tức là đồ thị đi qua điểm có toạ độ (0;) c
Chú ý:
- Nếu 2 ′ = bb thì () P có đỉnh ; ′′ ∆ b S aa với 2′ ∆=−bac - Nếu phương trình 2 0++=axbxc có hai nghiệm 12 , xx thi đồ thị hàm số bậc hai 2 =++ yaxbxc cắt trục hoành tại hai điểm lần lượt có hoành độ là hai nghiệm này (xem Hình ).
DẠYKÈMQUYNHƠNOFFICIAL BÀI 2. HÀM
Ố BẬC
S
HAI
ẽ đồ
ị
ố
ậ
1) Xác định toa độ đỉnh ; 24 ∆ b S aa . 2) Vẽ trục đối xứng d là đường thẳng 2 =− b x a 3) Tìm toa độ giao điểm của đồ thị với trục tung (điểm (0;)Ac ) và giao điểm của đồ thị với trục hoành (nếu có). Xác định thêm điểm đồi xứng với A qua trục đối xứng d , là điểm ; b Bc a . 4) Vẽ parabol có đỉnh S , có trục đối xứng d , đi qua các điểm tìm được. 3. Sự biến thiên của hàm số bậc hai
- Cách v
th
hàm s
b
c hai 2 =++ yaxbxc (với 0≠a ):
Chú ý: Từ bảng biến thiên của hàm số bậc hai, ta thấy: - Khi 0>a , hàm số đạt giá trị nhỏ nhất bằng 4 −∆ a tại 2 = b x a và hàm số có tập giá trị là ; 4 ∆ =−+∞ T a . - Khi 0<a , hàm số đạt giá trị lớn nh
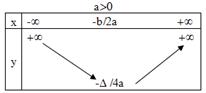
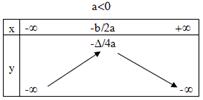

DẠYKÈMQUYNHƠNOFFICIAL Dự
đồ
ị
ố
ậ
a vào
th
hàm s
b
c hai 2 =++ yaxbxc (với 0≠a ), ta có bảng tóm tắt về sự biến thiên của hàm số này như sau:
4
tại 2 = b x a và hàm số có tập giá trị
; 4 ∆
=−∞− T a B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP Dạng 1: Bảng biến thiên, tính đơn điệu, GTLN và GTNN của hàm số bậc hai 1. Phương pháp Bảng biến thiên: Như vậy: Khi >a 0 hàm nghịch biến trên khoảng −∞− b a ; 2 , đồng biến trên khoảng −+∞ b a : 2 và có GTNN là ∆ a4 khi =− b x a2 Khi <a 0 hàm đồng biến trên khoảng −∞− b a ; 2 , nghịch biến trên khoảng −+∞ b a : 2 và có GTLN là ∆ a4 khi =− b x a2
ất bằng
−∆ a
là
DẠYKÈMQUYNHƠNOFFICIAL
Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Ví dụ 2: Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số ( ) 2 43yfxxx ==−−+ trên đoạn [ ] 0;4. Lời giải ..................................................................................................................................................................... Ví dụ 3: Tìm giá trị thực của tham số 0m ≠ để hàm số 2 232ymxmxm =−−− có giá trị nhỏ nhất bằng 10 trên .ℝ Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... 3. Bài tập trắc nghiệm Câu 1. Bảng biến thiên nào dưới đây là của hàm số 2 21yxx=−++ : A. x −∞ 1 +∞ y +∞ +∞ 2
* Chú ý: Nếu đề bài yêu cầu tìm GTLN, GTNN của hàm số trê [ ], cd ⊂ ℝ thì ta phải xem trục đối xứng 2 b x a =− có thuộc đoạn [ ], cd hay không? Từ đó phát thảo ra bảng biến thiên và dựa vào bảng biến thiên để tìm GTLL,GTNN 2. Các ví dụ rèn luyện kĩ năng Ví dụ 1: Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số ( ) 2 3 yfxxx ==− trên đoạn [ ] 0;2.
DẠYKÈMQUYNHƠNOFFICIAL B. C. D. Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 2. Trục đối xứng của parabol 2 53yxx=−++ là đường thẳng có phương trình A. 5 4 x = . B. 5 2 x =− . C. 5 4 x =− . D. 5 2 x = . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 3. Cho hàm số 2 23yxx=−+ . Chọn câu đúng. A.
số nghịch biến trên khoảng
+∞ . B.
số nghịch biến trên
ảng ( )
−∞ C.
số đồng biến trên ℝ . D.
số
Khẳng định nào sau đây đúng?
−∞
+∞
.
+∞ x −∞ +∞ y +∞ −∞ x −∞ 1 +∞ y 2 −∞ −∞ x −∞ +∞ y +∞ −∞
Hàm
( )1;
Hàm
kho
;1
Hàm
Hàm
đồng biến trên khoảng ( );1−∞ Lời giải ..................................................................................................................................................................... Câu 4. Xét tính đồng biến, nghịch biến của hàm số ( ) 2 45fxxx=−+ trên các khoảng ( );2−∞ và ( )2; +∞ .
A. Hàm số nghịch biến trên ( );2
, đồng biến trên ( )2;
B. Hàm số nghịch biến trên các khoảng ( );2−∞ và ( )2; +∞
C. Hàm số đồng biến trên ( );2−∞ , nghịch biến trên ( )2;
DẠYKÈMQUYNHƠNOFFICIAL D. Hàm số đồng biến trên các khoảng ( );2−∞ và ( )2; +∞ . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 5. Tìm giá trị nhỏ nhất của hàm số 2 41yxx=−+ . A. 3 . B. 1. C. 3 . D. 13 . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 6. Giá trị lớn nhất của hàm số () 2 2 59fx xx = −+ bằng A. 11 8 . B. 11 4 . C. 8 11 . D. 4 11 . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 8. Hàm số 2 43yxx=−+ đồng biến trên khoảng nào? A. ( )1;3 . B. ( );2−∞ . C. ( ); −∞+∞ . D. ( )2; +∞ . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 9. Cho parabol ( )P có phương trình 2 324=−+yxx . Tìm trục đối xứng của parabol A. 2 3 =−x B. 1 3 =−x C. 2 3 =x D. 1 3 =x Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 10. Cho hàm số 2 243yxx=−+ có đồ thị là parabol ( )P . Mệnh đề nào sau đây sai? A. ( )P không có giao điểm với trục hoành. B. ( )P có đỉnh là ( )1;1S . C. ( )P có trục đối xứng là đường thẳng 1y = D. ( )P đi qua điểm ( )1;9M Lời giải
DẠYKÈMQUYNHƠNOFFICIAL
ố 2
−+∞ .
−∞− .
.
−∞ . Lờ
ả
..................................................................................................................................................................... .....................................................................................................................................................................
ố 2
ị
.
đỉ
.
.
trục
xứ
x =
Lờ
..................................................................................................................................................................... .....................................................................................................................................................................
ố nào dưới đây
ng
ế
( )3;4 ? A. 21 21 2 yxx=−+ B. 2 72yxx=−+ C. 31yx=−+ D. 21 1 2 yxx=−+− Lời giải Câu 14. Hàm số nào sau đây có bảng biến thiên như hình bên? A. 2 52yxx=−++ . B. 21 2 yxx =−+ . C. 2 31yxx=−+ . D. 21 3 4 yxx=−+ . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 16. Bảng biến thiên của hàm số 2 241yxx=−++ là bảng nào sau đây? x −∞ 1 +∞ y −∞ 1 2 −∞
Câu 11. Hàm s
25yxx=−+− đồng biến trên khoảng: A. ( )1;
B. ( );1
C. ( )1; +∞
D. ( );1
i gi
i
Câu 12. Cho hàm s
24yxx=−+ có đồ th
( )P . Tìm mệnh đề sai
A. ( )P có
nh ( )1;3I
B. [ ]min4,0;3 yx=∀∈
C. ( )P có
đối
ng 1
D. [ ]max7,0;3 yx=∀∈
i giải
Câu 13. Hàm s
đồ
bi
n trên
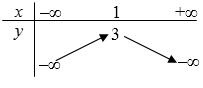
DẠYKÈMQUYNHƠNOFFICIAL A. . B. . C. D. Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 17. Tìm m để hàm số 2 223yxxm=−++ có giá trị nhỏ nhất trên đoạn [ ]2;5 bẳng 3 A. 3m =− B. 9m =− C. 1m = D. 0m = Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 18. Cho hàm số 2 1 2 yxmxm m =−++ ( )0m > xác định trên [ ]1;1 . Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên [ ]1;1 lần lượt là 1y , 2y thỏa mãn 12 8yy−= . Khi đó giá trị của m bằng A. 1m = . B. m ∈∅ . C. 2m = . D. 1m = , 2m = . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL Câu 19. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 4324103 =−−+− yxxxx trên đoạn [ ]1;4 là A. min 37 4 =−y , max 21=y B. max 37 4 =y , min 21=−y C. min 37 4 =y , max 21=y D. max 5=y , min 37 4 =−y Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Dạng 2: Xác định hàm số bậc hai 1. Phương pháp ( ) ∈⇔=++ MxyPyaxbxc 2 00000 ;() (P) có đỉnh () =− =− ⇔ =− =++ ∆ b xb Ixyax a y yaxbxc a 0 0 00 2 0 000 2; hoaëc: 2 4 (P) nhận = xx0 làm trục đối xứng ⇔=− b x a 0 2 (P) có giá trị nhỏ nhất (hay lớn nhất) bằng ⇔= ∆ yy a 00 4 2. Các ví dụ rèn luyện kĩ năng Ví dụ 1. Xác định Parabol 2 yaxbxc =++ đạt cực tiểu bằng 4 tại 2x =− và đồ thị đi qua ( )0;6A Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... Ví dụ 2. Parabol 2 yaxbxc =++ đi qua ( )8;0A và có đỉnh ( )6;12I . Xác định ,, abc Hướng dẫn giải ..................................................................................................................................................................... .....................................................................................................................................................................
Ví dụ 3. Tìm các hệ số abc ,, của ( )=++≠Pybxca 2 ():ax,0
a) (P) đi qua ( ) ( ) ( )ABC1;0;2;0;0;4 ;
b) (P) đi qua ( )A 1;2 và có đỉnh ( )I 1;2
Hướng dẫn giải
Ví dụ 4. Tìm các hệ số abc ,, của ( )2 ():ax,0 Pybxca=++≠
a) y nhận giá trị bằng -3 khi =x 2 và (P) cắt =+dyx:1 tại hai điểm có hoành độ bằng 0 và bằng 1.
i
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... 3. Bài tập trắc nghiệm Câu 1. Tìm khẳng định đúng trong các khẳng định sau? A. ( ) 2 325fxxx=+− là hàm số bậc hai. B. ( ) 24fxx=− là hàm số
ậ
hai. C. ( ) 3 321fxxx=+− là
b) (P) đ
qua hai điểm ( )A 1;6 , ( )B 4;3 và có trục đối xứng là =x 2 . Hướng dẫn giải
b
c
hàm số bậc hai.
DẠYKÈMQUYNHƠNOFFICIAL
ố
ậ
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Xác
nh
2
ế
ắ
trụ
ạ
ể
ằ
1 và có giá trị nhỏ nhất bằng 3
2 x = A.
: 2 1
=−++ B.
C.
2
.
. H
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Đồ thị của hàm số nào sau đây là parabol có đỉnh ( )1;3I . A. 2 243yxx=+− B. 2 1yxx=−+ C. 2 245yxx=++ D. 2 221yxx=−− Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 4. Cho parabol ( )P : 2 yaxbxc =++ có trục đối xứng là đường thẳng 1x = . Khi đó 42ab + bằng A. 1 B. 0 C. 1 D. 2 Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 5. Đồ thị hàm số 2222=−−− ymxmxm ( )0≠m là parabol có đỉnh nằm trên đường thẳng 3=−yx thì m nhận giá trị nằm trong khoảng nào dưới đây? A. ( )1;6 . B. ( );2−∞− . C. ( )3;3 . D. ( )0; +∞ . Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 6. Xác định a , b , c biết Parabol có đồ thị hàm số 2 =++ yaxbxc đi qua các điểm ( )0;1M , ( )1;1N , ( )1;1P . A. 2 1=−−yxx B. 2 1=−+yxx
D. ( ) 42 1fxxx=−+ là hàm s
b
c hai. Hướng dẫn giải
Câu 2.
đị
parabol ( )P :
yaxbxc =++ , 0a ≠ bi
t ( )P c
t
c tung t
i đi
m có tung độ b
ng
4 khi 1
( )P
yxx
( )P : 2 1yxx=−+
( )P :
221yxx=−+
D. ( )P : 2 0yxx=++
ướng dẫn giải
Câu 3.
Câu 7. Tìm parabol ( ) 2 :32Pyaxx=+− , biết rằng parabol có trục đối xứng 3.x =− A. 2 32yxx=+− B. 21 2 2 yxx=+− C. 21 32 2 yxx=−− D. 21 32 2 yxx=+− Hướng dẫn giải
DẠYKÈMQUYNHƠNOFFICIAL
C. 2 21=−−yx D. 2 1=−+−yxx Hướng dẫn giải ..................................................................................................................................................................... .....................................................................................................................................................................
. H
ng
ẫ
ả
..................................................................................................................................................................... Câu 9. Xác định phương trình của Parabol có đỉnh ( )0;1I và đi qua điểm ( )2;3A . A. ()21yx=− B. 2 1yx=+ C. ()21yx=+ D. 2 1yx=− Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 10. Tìm m để Parabol ( ) 2 :23Pymxx=−+ có trục đối xứng đi qua điểm ( )2;3A A. 2m = . B. 1m =− . C. 1m = . D. 1 2 m = . Hướng dẫn giải .....................................................................................................................................................................
..................................................................................................................................................................... Câu 8. Biết rằng hàm số ( )2 0yaxbxca =++≠ đạt cực tiểu bằng 4 tại 2x = và có đồ thị hàm số đi qua điểm ( )0;6A . Tính tích Pabc = . A. 6P =− . B. 3P =− . C. 6P = . D. 3 2 P =
ướ
d
n gi
i
Câu 11. Cho hàm số 2 21yxx=−−+ . Chọn câu sai
A. Đồ thị hàm số có trục đối xứng 1x =− .
B. Hàm số không chẵn, không lẻ
C. Hàm số tăng trên khoảng ( );1−∞− .
D. Đồ thị hàm số nhận ( )1;4I làm đỉnh.
Hướng dẫn giải
Câu 12. Cho parabol 2 4yaxbx=++ có trục đối xứng là đường thẳng 1 3 x = và đi qua điểm ( )1;3A
Tổng giá trị 2 ab + là A. 1 2 B. 1 C. 1 2 D. 1
Hướng dẫn giải .....................................................................................................................................................................
Câu 15. Để đồ thị hàm số 2221ymxmxm =−−− ( )0m ≠ có đỉnh nằm trên đường thẳng 2yx=− thì m nhận giá trị nằm trong
DẠYKÈMQUYNHƠNOFFICIAL
.....................................................................................................................................................................
.....................................................................................................................................................................
khoảng nào
ướ
đây?
−∞−
Câu 16. Cho parabol ( ) 2 :2.Pyaxbx=++ Xác định hệ số a , b biết (
P có đỉnh
I
=− , 4b =
=
=
=−
=−
ẫ
.....................................................................................................................................................................
d
i
A. ( )2;6 B. ( );2
C. ( )0;2 D. ( )2;2 Hướng dẫn giải
)
( )2;2
A. 1a
B. 1a
, 4b
C. 1a = , 4b
D. 4a = , 1b
Hướng d
n giải
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... Câu 17. Parabol ( ) 2:2 Pyxaxb =−−+ có điểm ( )1;3M với tung độ lớn nhất. Khi đó giá trị của b là A. 5 B. 1 C. 2 D. 3 Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 18. Xác định các hệ số a và b để Parabol ( ) 2 :4 Pyaxxb =+− có đỉnh ( )1;5I . A. 3 . 2 a b = =− B. 3 . 2 a b = = C. 2 . 3 a b = = D. 2 . 3 a b = =− Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 20. Cho hàm số ( ) 2 yfxaxbxc ==++ . Biểu thức ( ) ( ) ( )33231fxfxfx +−+++ có giá trị bằng A. 2 axbxc . B. 2 axbxc +− . C. 2 axbxc −+ . D. 2 axbxc ++ . Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Dạng 3: Đồ thị hàm số bậc hai 1. Phương pháp Để vẽ đường parabol =++ ybxc 2 ax ta có thể thực hiện các bước như sau: Xác định toạ độ đỉnh ∆b I aa ; 24 .
Xác định trục đối xứng =− b x a2 và hướng bề lõm của parabol.
Xác định một số điểm cụ thể của parabol (chẳng hạn, giao điểm của parabol với các trục toạ độ và các điểm đối xứng với chúng qua trục trục đối xứng). Căn cứ vào tính đối xứng, bề lõm và hình dáng parabol để vẽ parabol.
DẠYKÈMQUYNHƠNOFFICIAL
vẽ
ị
ư
Trước hết ta vẽ đồ thị =++ Pyaxbxc 2(): Ta có: () ++++≥ =++= −++++< axbxckhiaxbxc yaxbxc axbxckhiaxbxc 22 2 22 ,0 ,0 Vậy đồ thị hàm số =++ ybxc 2 ax bao gồm hai phần • Phần 1: Chính là đồ thị (P) lấy phần phía trên trục Ox • Phần 2: Lấy đối xứng phần đồ thị (P) phía dưới trục Ox qua trục Ox. Vẽ đồ thị hàm số P1 () và P2 () 2. Các ví dụ rèn luyện kĩ năng Câu 1. Đồ thị dưới đây là của hàm số nào sau đây? A. 2 23yxx=−−+ B. 2 22yxx=+− C. 2 242yxx=−− D. 2 21yxx=−− Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 2. Cho parabol ( ) ( )2 :,0Pyaxbxca=++≠ có đồ thị như hình bên. Khi đó 22abc ++ có giá trị là
Để
đồ th
hàm số =++ ybxc 2 ax ta lần lượt làm nh
sau:
DẠYKÈMQUYNHƠNOFFICIAL x y 3 -4 -1 2O 1 A. 9 . B. 9 . C. 6 . D. 6 . Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... 3. Bài tập trắc nghiệm Câu 1. Cho hàm số 2 yaxbxc =++ có đồ thị như hình bên dưới. Khẳng định nào sau đây đúng? ` x y O A. 0, 0, 0abc><< . B. 0, 0, 0abc><> . C. 0, 0, 0abc>>> . D. 0, 0, 0abc<<< . Hướng dẫn giải ..................................................................................................................................................................... Câu 2. Đồ thị hình bên dưới là đồ thị của hàm số nào? A. 2 231yxx=−+− B. 2 31yxx=−+− C. 2 231yxx=−+ D. 2 31yxx=−+ Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... O x y 1 1
DẠYKÈMQUYNHƠNOFFICIAL Câu 3. Cho hàm số 2 yaxbxc =++ có đồ thị như hình vẽ, thì dấu các hệ số của nó là A. 0,0,0abc<<> . B. 0,0,0abc<>> . C. 0,0,0abc>>> D. 0,0,0abc<>< Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 4. Hàm số 2 23yxx=−++ có đồ thị là
A. B. C. D. Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 5. Cho hàm số 2 yaxbxc =++ có đồ thị như hình bên. Khẳng định nào sau đây đúng? 1 1 3 4 1 1 25 4 2 O x y 3 5 6 1 1 3 4 1 1 2 3 42 O x y 3 1 1 3 4 1 1 2 3 42 O x y 13 1 3 4 1 1 2 3 42 O x y
hình nào trong các hình sau?

DẠYKÈMQUYNHƠNOFFICIAL
ab
.
.
.
. H
i Câu 6. Hàm số nào có đồ thị như hình vẽ sau A. 2 31yxx=−− .
2
. C. 2 251
=−−
Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 7. Cho hàm số 2 yaxbxc =++ có đồ thị như hình vẽ dưới đây. Mệnh nào sau đây
úng? A. 0a > , 0b = , 0c > . B. 0a > , 0b > , 0c > . C. 0a > , 0b < , 0c > . D. 0a < , 0b > , 0c > . Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... O x y O x y 1
A. 0,0,0
<>∆>
B. 0,0,0ab<<∆>
C. 0,0,0ab>>∆<
D. 0,0,0ab>>∆>
ướng dẫn giả
B.
251yxx=−+−
yxx
D. 2 25 yxx =−+
đ
DẠYKÈMQUYNHƠNOFFICIAL Câu 8. Cho hàm số 2 yaxbxc =++ có đồ thị như hình dưới đây. Khẳng định nào sau đây là đúng? A. 0
< , 0b > , 0c > B.
, 0
, 0c > C. 0
< , 0b > , 0c < .
,
,
c < . Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 9. Hàm số nào sau đây có đồ thị như hình bên? 2 2 4 6 5 y x 3 -3 1 2O 1
2
.
Hướng
ẫ
ả
..................................................................................................................................................................... Câu 10. Hàm số nào sau đây có đồ thị như hình bên x y 1 2 3 4 5 1 2 3 5 4 3 2 1 1 2 3 A. 2 33yxx=−− . B. 2
. O x y
a
0a >
b <
a
D. 0a >
0b >
0
A.
23yxx=−+−
B. 2 43yxx=−+− . C. 2 43yxx=−+ D. 2 23yxx=−−
d
n gi
i
53yxx=−+−
C. 2 33yxx=−−− .
D. 2 53yxx=−+− .
Hướng dẫn giải
Câu 11. Đồ thị hàm số 2 65yxx=−+
A. có tâm đối xứng ( )3;4I .
B. có tâm đối xứng ( )3;4I và trục đối xứng có phương trình 0x =
C. không có trục đối xứng.
D. có trục đối xứng là đường thẳng có phương trình 0x = Hướng dẫn giải .....................................................................................................................................................................
Câu 12. hàm số 2 yaxbxc =++ có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
y 1
O x
B. 0a < , 0b = , 0c < . C. 0a > , 0b > , 0c < D. 0a < , b0 > , c0 < Hướng dẫn giải
A. 0a < , 0b < , 0c < .
Câu 13. Cho parabol ( ) 2 : Pyaxbxc =++ ( )0a ≠ có đồ thị như hình bên. Tìm các giá trị m để phương trình 2 axbxcm ++= có bốn nghiệm phân biệt.
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Lựa chọn các kết luận cần thiết
Các ví dụ rèn luyện kĩ năng Ví dụ 1: Cho parabol ( ) 2 :21Pyxxm=−+− . Tìm tất cả các giá trị thực của m để parabol cắt Ox tại hai điểm phân biệt có hoành độ dương. Hướng dẫn giải
Ví dụ 2: Tìm tất cả các giá trị thực của tham số m để đường thẳng : dymx = cắt đồ thị hàm số ( ) 32 :69 Pyxxx =−+ tại ba điểm phân biệt. Hướng dẫn giải
Ví dụ 3: Tìm tất cả các giá trị thực của tham số m để phương trình 2 5720xxm−++= có nghiệm thuộc đoạn [ ]1;5 Hướng dẫn giải
DẠYKÈMQUYNHƠNOFFICIAL 1 2 3 1 2
x y 1 O2
1 2 3 4 I A.
−<< .
<< .
.
. H
ải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Dạng 4: Sự tương giao
.....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
3
3
13 m
B. 03 m
C. 03 m ≤≤
D. 13 m −≤≤
ướng dẫn gi
1. Phương pháp
Thiết lập phương trình hoành độ giao điểm
Khai thác các điều kiện
Xử lý phương trình hoành độ giao điểm
2.
.....................................................................................................................................................................
3. Bài tập trắc nghiệm
Câu 1. Cho hàm số ( )2 0yaxbxca =++≠ có đồ thị là parabol ( )P . Xét phương trình 2 0axbxc++= ( )1 . Chọn khẳng định sai:
A. Số giao điểm của parabol ( )P với trục hoành là số nghiệm của phương trình ( )1
B. Số nghiệm của phương trình ( )1 là số giao điểm của parabol ( )P với trục hoành.
C. Nghiệm của phương trình ( )1 là giao điểm của parabol ( )P với trục hoành.
D. Nghiệm của phương trình ( )1 là hoành độ giao điểm của parabol ( )P với trục hoành. Hướng dẫn giải
Câu 2. Tọa độ giao điểm của đường thẳng :4dyx=−+ và parabol 2 712yxx=−+ là
A. ( )2;6 và ( )4;8 B. ( )2;2 và ( )4;8 C. ( )2;2 và ( )4;0 D. ( )2;2 và ( )4;0
Hướng dẫn giải
DẠYKÈMQUYNHƠNOFFICIAL .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
ủ
ươ
2 yx = và 85yx=−− C. 2 yx = và 85yx=− D. 2 yx = và 85yx=+ Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 4. Giao điểm của parabol ( ) 2 :32Pyxx=−+ với đường thẳng 1yx=− là A. ( )1;2 ; ( )2;1 . B. ( )1;0 ; ( )3;2 . C. ( )2;1 ; ( )0;1 D. ( )0;1 ; ( )2;3 Hướng dẫn giải
Câu 3. Nghiệm c
a ph
ng trình 2 –850xx += có thể xem là hoành độ giao điểm của hai đồ thị hàm số: A. 2 yx = và 85yx=−+ B.
DẠYKÈMQUYNHƠNOFFICIAL .....................................................................................................................................................................
tọa độ
..................................................................................................................................................................... .....................................................................................................................................................................
Câu 5. Cho đường thẳng :1dyx=+ và Parabol ( ) 2 :2Pyxx=−− . Biết rằng d cắt ( )P tại hai điểm phân biệt A , B . Khi đó diện tích tam giác OAB bằng A. 4 B. 2 C. 3 2 D. 5 2 Hướng dẫn giải Câu 6. Biết đường thẳng : dymx = cắt Parabol ( ) 2 :1Pyxx=−+ tại hai điểm phân biệt A , B . Khi đó
trung điểm I của đoạn thẳng AB là A. 21 ; 22 mmm I ++ B. 2 123 ; 24 mmm I +−−+ C. 13 ; 24 I D. 1 ; 22 m I Hướng dẫn giải ..................................................................................................................................................................... Câu 7. Tìm tất cả các giá trị của tham số m để đường thẳng :23dyx=+ cắt parabol ( )2 2 yxmxm =++− tại hai điểm phân biệt nằm cùng phía với trục tung .Oy A. 3m >− . B. 3m <− . C. 3m > . D. 0m < . Hướng dẫn giải
Câu 8. Hỏi có bao nhiêu giá trị m nguyên trong nửa khoảng [ )10;4 để đường thẳng ( ) :12 dymxm=−+++ cắt Parabol ( ) 2 :2Pyxx=+− tại hai điểm phân biệt cùng phía với trục tung? A. 6 B. 5 C. 7 D. 8 Hướng dẫn giải
Câu 9. Tìm m để Parabol ( ) ( ) 22 :213Pyxmxm=−++− cắt trục hoành tại 2 điểm phân biệt có hoành độ 1x , 2x sao cho 12.1xx = A. 2m = B. Không tồn tại m C. 2m =− D. 2m =± Hướng dẫn giải
Câu 10. Cho hai hàm số ( )2 1 1 yxmxm =+−+ , 2 21yxm=++ . Khi đồ thị hai hàm số cắt nhau tại hai điểm phân biệt thì m có giá trị là A. 0m > . B. 0m < . C. m tùy ý. D. không có giá trị nào. Hướng dẫn giải .....................................................................................................................................................................
Câu 11. Đường thẳng ( ) :26 m dmxmy−+=− luôn đi qua điểm: A. ( )3;3 B. ( )2;1 C. ( )1;5 D. ( )3;1 Hướng dẫn giải
DẠYKÈMQUYNHƠNOFFICIAL
.....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
ả
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
O
2
..................................................................................................................................................................... ..................................................................................................................................................................... Câu 12. Tìm tất c
các giá trị m để đường thẳng 32 ymxm =+− cắt parabol 2 35yxx=−− tại 2 điểm phân biệt có hoành độ trái dấu. A. 3m <− . B. 34 m −<< . C. 4m < . D. 4m ≤ . Hướng dẫn giải
Câu 13. Cho parabol ( )2 0yaxbxca =++≠ , ( )P có đồ thị như hình vẽ:
x y
2
DẠYKÈMQUYNHƠNOFFICIAL Biết đồ thị ( )P cắt trục Ox tại các điểm lần lượt có hoành độ là 2 , 2 . Tập nghiệm của bất phương trình 0y < là A. ( ] [ );22; −∞−+∞ ∪ . B. ( )2;2 . C. [ ]2;2 D. ( ) (
−∞−+∞ ∪ Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 14. Giá trị nào của m thì phương trình ( ) ( ) ( )2 3310mxmxm −++−+= ( )1 có hai nghiệm phân biệt? A. { }\3m ∈ ℝ . B. (){}3 ;1;\3 5 m ∈−∞−∪+∞ . C. 3 ;1 5 m ∈− . D. 3 ; 5 m ∈−+∞ . Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 15. Có bao nhiêu giá trị thực của m để đường thẳng :42 dyxm =− tiếp xúc với parabol ( ) ( ) 2 :2231 Pymxmxm =−+−+ A. 3 . B. 1. C. 2 . D. 0 . Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 16. Cho hàm số ( )fx xác định trên R có đồ thị như hình vẽ. Phương trình ( ) 210 fx −= có bao nhiêu nghiệm? A. 1 B. 3 C. 2 D. 4
);22;
Câu 17. Cho hàm số ( )yfx = có bảng biến thiên như sau:
Với giá trị nào của tham số m thì phương trình ( ) 1 fxm −= có bốn nghiệm phân biệt. A. 1m = . B. 13 m << . C. 01 m << . D. 3m ≥ . Hướng dẫn giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 18. Cho hàm số ( ) 2 fxaxbxc =++ đồ thị như hình bên dưới. Hỏi với những giá trị nào của tham số m thì phương trình ( ) 1 fxm −= có đúng 3 nghiệm phân biệt. x
y O 2 −1
3
A. 22 m −<< B. 3m = C. 3m > D. 2m = Hướng dẫn giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 19. Cho hàm số ( ) 2 fxaxbxc =++ đồ thị như hình bên dưới. Hỏi với những giá trị nào của tham số m thì phương trình ( ) 1 fxm −= có đúng 2 nghiệm phân biệt.

DẠYKÈMQUYNHƠNOFFICIAL Hướng dẫn giải
..................................................................................................................................................................... .....................................................................................................................................................................
Câu 20. Hỏi có bao nhiêu giá trị m nguyên trong nửa khoảng ( ]0;2017 để phương trình 2 450xxm−−−= có hai nghiệm phân biệt?
A. 2016 . B. 2008 . C. 2009 . D. 2017 . Hướng dẫn giải
Câu 21. Hỏi có bao nhiêu giá trị m nguyên trong nửa khoảng ( ]0;2017 để phương trình 2 450xxm
DẠYKÈMQUYNHƠNOFFICIAL
y
3
x
O 2 −1
=−
A. 0 1 m m ≥
. B. 0 1 m m > =− . C. 1m ≥− . D. 0m ≥ . Hướng dẫn giải
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Dạng 4: Toán thực tế 1. Phương pháp 2. Các ví dụ rèn luyện kĩ năng Ví dụ 1: Khi nuôi cá thí nghiệm trong hồ, một nhà sinh học thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng ( ) 36010 Pnn =− . Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích để trọng lương cá sau một vụ thu được nhiều nhất? Hướng dẫn giải ..................................................................................................................................................................... .....................................................................................................................................................................
−−−= có hai nghiệm phân biệt? A. 2016 . B. 2008 . C. 2009 . D. 2017 . Hướng dẫn giải
Ví dụ 2: Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol . Biết khoảng cách giữa hai chân cổng bằng 162m. Trên thành cổng, tại vị trí có độ cao 43m so với mặt đất , người ta thả một sợi dây chạm đất . Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng Arch . Hướng dẫn giải
3. Bài tập trắc nghiệm
Câu 1. Một chiếc cổng hình parabol có phương trình 21 2 yx =− . Biết cổng có chiều rộng 5d = mét . Hãy tính chiều cao h của cổng.
O y x h
A. 4,45h = mét. B. 3,125h = mét. C. 4,125h = mét. D. 3,25h = mét. Hướng dẫn giải
Câu 2. Một của hàng buôn giày nhập một đôi với giá là 40 đôla. Cửa hàng ước tính rằng nếu đôi giày được bán với giá x đôla thì mỗi tháng khách hàng sẽ mua ( )120 x đôi. Hỏi của hàng bán một đôi giày giá bao nhiêu thì thu được nhiều lãi nhất? A. 80 USD. B. 160 USD. C. 40 USD. D. 240 USD. Hướng dẫn giải
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
Câu 3. Dây truyền đỡ trên cầu treo có dạng Parabol ACB như hình vẽ. Đầu, cuối của dây được gắn vào các điểm A , B trên mỗi trục AA′ và BB′ với độ cao 30m. Chiều dài đoạn AB′′ trên nền cầu bằng 200m . Độ cao ngắn nhất của dây truyền trên cầu là 5mOC = . Gọi Q′ , P′ , H ′ , O , I ′ , J ′ , K′ là các điểm chia đoạn AB′′ thành các phần bằng nhau. Các thanh thẳng đứng nối nền cầu với đáy dây truyền: QQ′ , PP′ , HH ′ , OC , II′ , JJ ′ , KK′ gọi là các dây cáp treo. Tính tổng độ dài của các dây cáp treo? A. Đáp án khác. B. 36,87m C. 73,75m D. 78,75m Hướng dẫn giải
Câu 4. M
doanh nghiệp t
nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp
p trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua vào một chiếc là 27 và bán ra với giá là 31 triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm 1 triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ tăng thêm 200 chiếc. Vậy doanh nghiệp
t
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
ột
ư
đang
ậ
BA
Q P H C I J K
B′ Q ′ P′ H ′ C ′ I ′ J ′ K ′ A′
phải định giá bán mới là bao nhiêu để sau khi đã thực hiện giảm giá, lợi nhuận thu được sẽ là cao nhất.
A. 30 triệu đồng.
B. 29 triệu đồng. C. 30,5 triệu đồng. D. 29,5 triệu đồng. Hướng dẫn giải
Câu 5. Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả là một cung parabol trong mặt phẳng với hệ tọa độ Oth ,trong đó t là thời gian , kể từ khi quả bóng được đá lên; h là độ cao của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2m . Sau đó 1 giây, nó đạt độ cao 8,5mvà 2 giây sau khi đá lên, nó ở độ cao 6m . Hãy tìm hàm số bậc hai biểu thị độ cao h theo thời gian t và có phần đồ thị trùng với quỹ đạo của quả bóng trong tình huống trên.
A. 2 4,912,21,2ytt=++ B. 2 4,912,21,2ytt=−++ C. 2 4,912,21,2ytt =−+− D. 2 4,912,21,2ytt=−−+ Hướng dẫn giải
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
BÀI TẬP CUỐI CHƯƠNG
PHẦN I: TRẮC NGHIỆM
Câu 1: Tính giá trị của hàm số () 1 2yfx x == tại 1x = .


A. ( ) 11f = B. ( ) 11f =− C. ( ) 10f = D. () 1 1 2f =
Hướng dẫn giải
Câu 3: Hàm số bậc hai 2 41yxx=−+ đồng biến trên khoảng nào trong các đáp án dưới đây?
A. ( ) 1;3. B. ( ) 0;2. C. ( ) 1;2. D. ( )2;3

Hướng dẫn giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 4: Đường nào trong các đáp án sau không thể là đồ thị của một hàm số y theo biến số ?x A. B. C. D. Hướng dẫn giải
Câu 5: Xác định tọa độ tất cả giao điểm của parabol 2 32yxx=−+ với trục hoành ( )Ox
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL
.....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Khẳng định nào
đ
<
A. ( ) ( ) 1;0,2;0.MN B. ( ) 0;2.M C. ( ) ( ) 0;1,0;2.MN D. ( ) 1;2.M Hướng dẫn giải Câu 6: Tìm tập xác định D của hàm số 3 1 x y x + = A. [ ) { } D3;\1. =−+∞ B. { } D\1;3. =− ℝ C. [ ) D3;. =−+∞ D. ( ) { } D3;\1. =−+∞ Hướng dẫn giải
Câu 7: Hình nào dưới đây cho ta đồ thị của hàm số 2 2 yxx =− ? A. B. C. D. Hướng dẫn giải
Câu 8:
dưới
ây là sai khi nói về sự biến thiên của hàm số A. Hàm số ( )yfx = gọi là nghịch biến (giảm) trên khoảng ( ); ab nếu ( ) 1212 ,;: xxabxx ∀∈< ( ) ( )21 fxfx
B. Nếu hàm số ( )yfx = nghịch biến (giảm) trên khoảng ( ); ab thì đồ thị “đi xuống’’ từ trái sang phải trên khoảng đó.
C. Hàm số ( )yfx = gọi là đồng biến (tăng) trên khoảng ( ); ab nếu ( ) 1212 ,;: xxabxx ∀∈< ( ) ( )21 .fxfx <
D. Nếu hàm số ( )yfx = đồng biến (tăng) trên khoảng ( ); ab thì đồ thị “đi lên’’ từ trái sang phải trên khoảng đó. Hướng dẫn giải .....................................................................................................................................................................
Câu 9: Biết rằng parabol ( ) 2 : =++ Pyaxbxc đi qua điểm ( )2;3A và có đỉnh ( )1;2I . Tính tổng bình phương các hệ số của ( )P A. 5. B. 30. C. 25. D. 14. Hướng dẫn giải .....................................................................................................................................................................
Câu 10: Gọi 0m là giá trị thực của tham số m để parabol ( ) 2 :23 Pyxxm =−+− cắt trục hoành ( )Ox tại hai điểm phân biệt , AB sao cho độ dài đoạn thẳng AB bằng 4. Mệnh đề nào sau đây là đúng? A. 0m ∈∅ B. ( )0 2;3.m ∈− C. ( )0 4;10.m ∈ D. ( )0 15;30.m ∈ Hướ
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
ng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 11: Tìm tất cả giá trị thực của tham số m để hàm số 2 1 x y xm = xác định trên khoảng ( ) 0;1. A. ( ) { } ;10.−∞−∪ B. ( ) ;1.−∞− C. ( ] ;1.−∞− D. ( ] { } ;10.−∞−∪ Hướng dẫn giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 12: Cho hàm số bậc hai ( )2 0yaxbxca=++≠ có đồ thị ( )P , đỉnh của ( )P được xác định bởi
công thức nào?
A. ; 4 b I aa ∆ B. ; 22 b I aa ∆ C. ; b I aa ∆ D. ; 24 b I aa ∆
Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 13: Cho hàm số ( ) 42 3.yfxxx==−+ Khẳng định nào sau đây đúng?
A. ( )fx
DẠYKÈMQUYNHƠNOFFICIAL
không chẵn không lẻ. B. ( )fx là hàm số chẵn. C. ( )fx là hàm số lẻ D. ( )fx là hàm số vừa chẵn vừa lẻ Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 14: Tậ
ủ
ố
=
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
15: Tọa độ giao điểm của :4dyx=− và ( ) 2 :7Pyxx=−− là: A. ( ) ( )3;1,1;5MN B. ( ) ( )3;1,1;5MN C. ( ) ( )3;1,1;5MN D. ( ) ( )3;1,1;5MN [ ] 1;6. Hướng dẫn giải ..................................................................................................................................................................... Câu 16: Cho hàm số 2 45=−−yxx .Trong các mệnh đề sau mệnh đề nào đúng? A. Hàm số đồng biến trên khoảng ( ) ;2.−∞ B. Hàm số nghịch biến trên khoảng ( );2−∞ và ( ) 2;. +∞ C. Hàm số đồng biến trên khoảng ( ) 3;. +∞
p xác định c
a hàm s
2 4y x
là: A. ℝ B. ( )4; +∞ C. { }\4ℝ D. ( );4−∞ Hướng dẫn giải
Câu
D. Hàm số nghịch biến trên khoảng ( ) 2;. +∞
Hướng dẫn giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 17: Một chiếc cổng hình parabol có phương trình 21 2 yx =− . Biết cổng có chiều rộng 5d = mét
(như hình vẽ). Hãy tính chiều cao h của cổng.
A. 3,125h = mét. B. 4,125h = mét. C. 4.45h = mét. D. 3,25h = mét. Hướng dẫn giải ........................................................................................................................................................ ........................................................................................................................................................
Câu 18: Cho hàm số 2 yaxbxc =++ có đồ thị như bên dưới. Khẳng định nào sau đây đúng?
A. a0,b0,c0. <<< B. a0,b0,c0. ><> C. a0,b0,c0. <>> D. a0,b0,c0. <<> Hướng dẫn giải
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... BÀI TẬP TỰ LU
N
Câu 19: Tập xác định D của hàm số 1 ()1fxx x =++ là: A. [ ) 1;.D =+∞ B. { } \1;0.DR=− C. [ ) { } 1;\0.D =−+∞ D. { } \0.DR = Hướng dẫn giải
Ậ
Câu 1. Cho parabol 2 42yxx=−+− và đường thẳng :2 dyxm =−+ . Tìm các giá trị m để
a) d cắt ( )P tại hai điểm phân biệt A , B . tìm tọa độ trung điểm của AB .
b) d và ( )P có một điểm chung duy nhất. Tìm tọa độ điểm chung này.
c) d không cắt ( )P d) d và ( )P có một giao điểm nằm trên đường thẳng 2y =− Hướng dẫn giải
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 2. Cho parabol ( ) 2 :43Pyxx=−+ và đường thẳng :3.dymx=+ Tìm các giá trị của m để a) d và ( )P tại hai điểm phân biệt A, B sao cho diện tích tam giác OAB bằng 9 2 . b) d cắt ( )P tại hai điểm phân biệt A, B có hoành độ 1x , 2x thỏa mãn 33 12 8xx+= . Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 3. Chứng minh rằng với mọi m , đồ thị của mỗi hàm số sau luôn cắt trục hoành tại hai điểm phân biệt và đỉnh I của đồ thị luôn chạy trên một đường thẳng cố định. a) 2 2 1 4 m yxmx=−+− b) 2221yxmxm =−+− Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 4. Chứng minh rằng với mọi m , đồ thị hàm số ( )2 2231ymxmxm =+−−+ luôn đi qua hai điểm cố định. Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 5. Chứng minh rằng các parabol sau luôn tiếp xúc với một đường thẳng cố định. a) ( ) 22 242183yxmxm =−−+− .
DẠYKÈMQUYNHƠNOFFICIAL b) ( )2 4141ymxmxm =−−+− ( )0m ≠ Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 6. Chứng minh rằng các đường thẳng sau luôn tiếp xúc vơi một parabol cố định. a) 2 242ymxmm =−++ ( )0m ≠ b) ( ) 2 4242ymxm =−−− 1 2 m ≠ Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 7. Một quả bóng được ném vào không trung có chiều cao tính từ lúc bắt đầu ném ra được cho bởi công thức ( ) 2 23httt=−++ (tính bằng mét), t là thời gian tính bằng giây ( )0t ≥ a. Tính chiều cao lớn nhất quả bóng đạt được.

DẠYKÈMQUYNHƠNOFFICIAL
Hãy tính xem sau bao lâu quả bóng sẽ rơi xuống mặt đất? Hướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 8. Độ cao của quả bóng golf tính theo thời gian có thể được xác định bằng một hàm bậc
ới các thông số cho trong bảng sau, hãy xác định độ cao quả bóng đạt được tại thời điể
ướng dẫn giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
b.
hai. V
m 3 giây? H
Câu 9. Một miếng nhôm có bề ngang 32 cm được uốn cong tạo thành máng dẫn nước bằng chia tấm nhôm thành 3 phần rồi gấp 2 bên lại theo một góc vuông như hình vẽ dưới. Hỏi x bằng bao nhiêu để tạo ra máng có có diện tích mặt ngang S lớn nhất để có thể cho nước đi qua nhiều nhất?
Hướng dẫn giải
Câu 10. Hai con chuồn chuồn bay trên hai quĩ đạo khác nhau, xuất phát cùng thời điểm.
Một con bay trên quỹ đạo là đường thẳng từ điểm
( )0;100A đến điểm ( )0;0O với vận tốc 5 m/s

Con còn lại bay trên quĩ đạo là đường thẳng từ ( )60;80B đến điểm ( )0;0O với vận tốc 10 m/s
Hỏi trong quá trình bay thì khoảng cách ngắn nhất hai con đạt được là bao nhiêu?
Hướng dẫn giải ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
.....................................................................................................................................................................
Câu 11. Một cửa hàng bán bưởi Đoan Hùng của Phú Thọ với giá bán mỗi quả là 50000 đồng. Với giá bán này thì mỗi ngày cửa hàng chỉ bán được 40 quả. Cửa hàng dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi quả 1000 đồng thì số bưởi bán tăng thêm được là 10 quả. Xác định giá bán để của hàng thu được lợi nhuận cao nhất, biết rằng giá nhập về ban đầu cho mỗi quả là 30000 đồng. Hướng dẫn giải
DẠYKÈMQUYNHƠNOFFICIAL .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................

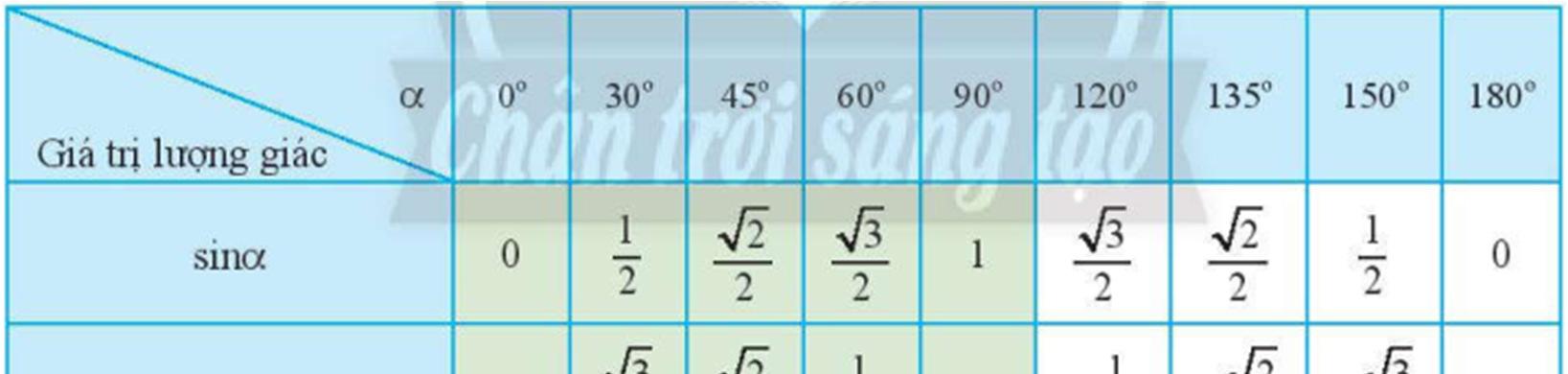

DẠYKÈMQUYNHƠNOFFICIAL BÀI 1. GIÁ TRỊ LƯỢNG GIÁC MỘT GÓC BẤT KỲ TỪ 0 ĐỘ ĐẾN 180 ĐỘ A. KIẾN THỨC CƠ BẢN CẦN NẮM 1. Giá trị lượng giác Với mỗi góc () 0180αα °° ≤≤ ta xác định được một điểm M duy nhất trên nửa đường tròn đơn vị sao cho α=xOM . Gọi () 00 ; xy là toạ độ điểm M , ta có: - Tung độ 0y của M là sin của góc α , kí hiệu là sin 0α = y ; - Hoành độ 0x của M là côsin của góc α , kí hiệu là 0cosα = x ; - Tỉ số ()0 0 0 0≠y x x là tang của góc α , kí hiệu là tan 0 0 α = y x ; - Tỉ số ()0 0 0 0≠ x y y là côtang của góc α , kí hiệu là 0 0 cot α = x y Các số sin,cos,tan,cotαααα được gọi là các giá trị lượng giác của góc α . 2. Tính chất - Mối liên hệ giữa các giá trị lượng giác của hai góc phụ nhau: ()() ()() cos90sin;sin90cos tan90cot;cot90tan αααα αααα °° °° −=−= −=−= - Mối liên hệ giữa các giá trị lượng giác của hai góc bù nhau: ()() ()()()() sin180sin;cos180cos; tan180tan90;cot180cot0180. αααα αααααα ° ° °°°°° −=−=− −=−≠−=−<< 3. Giá trị lượng giác các góc đặc biệt Chú ý: Trong bảng, ki hiệu "||" để chỉ giá trị lượng giác không xác định.
4. Sử dụng máy tính cầm tay để tính giá trị lượng giác của một góc
- Sau khi mở máy, ấn các phím SHIFTMENU để màn hình hiện lên bảng lựa chọn.

- Ấn phím 2 đế vào chế độ cài đặt đơn vị đo góc.
- Ân tiếp phím 1 để xác định đơnvị đo góc là "độ".
- Lại ấn phím MENU 1 đề vào chế độ tính toán.
DẠYKÈMQUYNHƠNOFFICIAL
TẬP Dạng 1 : Xác định giá trị lượng giác của góc đặc biệt. 1. Phương pháp giải. • Sử dụng định nghĩa giá trị lượng giác của một góc • Sử dụng tính chất và bảng giá trị lượng giác đặc biệt • Sử dụng các hệ thức lượng giác cơ bản 2. Các ví dụ. Ví dụ 1: Tính giá trị các biểu thức sau: a) 202020 sin90cos90cos180Aabc =++ b) 202020 3sin902cos603tan45B =−+− c) 2020202000 sin452sin503cos452sin404tan55.tan35C =−+−+ Hướng dẫn giải ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Ví dụ 2: Tính giá trị các biểu thức sau: a) 20202020 sin3sin15sin75sin87A =+++ b) 00000 cos0cos20cos40...cos160cos180B =+++++ c) 00000 tan5tan10tan15...tan80tan85C = Hướng dẫn giải ................................................................................................................................................................ ................................................................................................................................................................
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI
DẠYKÈMQUYNHƠNOFFICIAL ................................................................................................................................................................ ................................................................................................................................................................ Ví dụ 3: Tính theo hàm số lượng giác của các góc bé hơn 90 : sin100 , sin160 , cos170 , tan10345' , cot12415' . Hướng dẫn giải ................................................................................................................................................................ Dạng 2 : Xác định giá trị của một biểu thức lượng giác có điều kiện. 1. Phương pháp giải. • Dựa vào các hệ thức lượng giác cơ bản • Dựa vào dấu của giá trị lượng giác • Sử dụng các hằng đẳng thức đáng nhớ 2. Các ví dụ. Ví dụ 1: a) Cho 1 sin 3 α = với 00 90180 α << . Tính cosα và tan α b) Cho 2 cos 3 α =− . Tính sinα và cot α c) Cho tan22 γ =− . Tính giá trị lượng giác còn lại. Hướng dẫn giải ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Ví dụ 2: a) Cho 3 cos 4 α = với 00 090 α << . Tính tan3cot tancot A αα αα + = + . b) Cho tan2 α = . Tính 33 sincos sin3cos2sin B αα ααα = ++ Hướng dẫn giải ................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL ................................................................................................................................................................ ................................................................................................................................................................
Cho
góc α và β vớ
°
.
ị
ủ
ểu
ứ
=
=
=−
=
ẫ
ải ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 2: Cho hai góc α và β với 90αβ ° += .
giá trị của biểu thức coscossinsinP αββα=− A. 0.P = B.
P = C.
P =−
P =
ướng dẫn giải ................................................................................................................................................................
Cho
ẳng
đúng? A. sin0. α < B. cos0. α > C. tan0. α < D. cot0. α > Hướng dẫn giải ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 4: Cho hai góc nhọn α và β trong đó αβ < . Khẳng định nào sau đây là sai? A. coscos. αβ < B. sinsin. αβ < C. cotcot. αβ > D. tantan0. αβ+> Hướng dẫn giải ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 5: Khẳng định nào sau đây sai? A. cos75cos50. °° > B. sin80sin50. °° >
CÂU HỎI TRẮC NGHIỆM Câu 1:
hai
i 90αβ
+=
Tính giá tr
c
a bi
th
c sincossincosP αββα=+ A. 0.P
B. 1.P
C. 1.P
D. 2.P
Hướng d
n gi
Tính
1.
1.
D. 2.
H
Câu 3:
α là góc tù. Kh
định nào sau đây là
DẠYKÈMQUYNHƠNOFFICIAL
................................................................................................................................................................ ................................................................................................................................................................
Khẳng định nào
đ
đ
................................................................................................................................................................ ................................................................................................................................................................
Khẳng định nào sau đây đ
°°
ẫ
ả
................................................................................................................................................................ ................................................................................................................................................................ Câu 8: Chọn hệ thức đúng được suy ra từ hệ thức 22 cossin1? αα+= A. 22 1 cossin. 222 αα += B. 22 1 cossin. 333 αα += C. 22 1 cossin. 444 αα += D. 22 5cossin5. 55 αα += Hướng dẫn giải ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 9: Cho biết 3 sin. 35 α = Giá trị của 22 3sin5cos 33 P αα =+ bằng bao nhiêu? A. 105 25 P = B. 107 25 P = C. 109 25 P = D. 111 25 P = Hướng dẫn giải
C. tan45tan60. °° < D. cos30sin60. °° = Hướng dẫn giải
Câu 6:
sau
ây
úng? A. sin90sin100. °° < B. cos95cos100. °° > C. tan85tan125. °° < D. cos145cos125. °° > Hướng dẫn giải
Câu 7:
úng? A. sin90sin150.
< B. sin9015sin9030. °°′′ < C. cos9030cos100. °° ′ > D. cos150cos120. °° > Hướng d
n gi
i
DẠYKÈMQUYNHƠNOFFICIAL ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 10: Cho biết tan3. α =− Giá trị của 6sin7cos 6cos7sin P αα αα = + bằng bao nhiêu? A. 4 3 P = B. 5 3 P = C. 4 3 P =− D. 5 3 P =− Hướng dẫn giải ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 11: Cho biết 2 cos. 3 α =− Giá trị của cot3tan 2cottan P αα αα + = + bằng bao nhiêu? A. 19 . 13 P =− B. 19 . 13 P = C. 25 . 13 P = D. 25 . 13 P =− Hướng dẫn giải ................................................................................................................................................................ ................................................................................................................................................................ Câu 12: Cho biết cot5. α = Giá trị của 2 2cos5sincos1P ααα =++ bằng bao nhiêu? A. 10 26 P = B. 100 26 P = C. 50 26 P = D. 101 26 P = Hướng dẫn giải ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 13: Cho biết 3cossin1 αα−= , 00 090. α << Giá trị của tanα bằng A. 4 tan. 3 α = B. 3 tan. 4 α = C. 4 tan. 5 α = D. 5 tan. 4 α = Hướng dẫn giải ................................................................................................................................................................ ................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL
................................................................................................................................................................ ................................................................................................................................................................
................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
Câu 14: Cho biết 2cos2sin2 αα+= , 00 090. α << Tính giá trị của cot. α A. 5 cot. 4 α = B. 3 cot. 4 α = C. 2 cot. 4 α = D. 2 cot. 2 α = Hướng dẫn giải
Câu 15: Cho biết sincos. aαα+= Tính giá trị của sincos. αα A. 2 sincos. aαα = B. sincos2. aαα = C. 2 1 sincos. 2 a αα = D. 2 11 sincos. 2 a αα = Hướng dẫn giải
Câu 16: Cho biết 1 cossin. 3 αα+= Giá trị của 22 tancotP αα=+ bằng bao nhiêu? A. 5 . 4 P = B. 7 . 4 P = C. 9 . 4 P = D. 11 . 4 P = Hướng dẫn giải
Câu 17: Cho biết 1 sincos. 5 αα−= Giá trị của 44 sincosP αα=+ bằng bao nhiêu? A. 15 5 P = B. 17 5 P = C. 19 5 P = D. 21 5 P = Hướng dẫn giải
DẠYKÈMQUYNHƠNOFFICIAL
................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
................................................................................................................................................................
CÂU HỎI TRẮC NGHIỆM
Câu 1: Đẳng thức nào sau đây đúng? A. ( )o tan180tanaa+=− . B. ( )o cos180cosaa+=− . C. ( )o sin180sinaa+= . D. ( )o cot180cotaa+=− . Lời giải.
Câu 2: Trong các đẳng thức sau đây, đẳng thức nào đúng? A. ( ) sin180sinαα ° −=− . B. ( ) cos180cosαα ° −= C. ( ) tan180tanαα ° −= . D. ( ) cot180cotαα ° −=− Lời giải.
Câu 3: Cho α và β là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai? A. sinsinαβ = B. coscosαβ =− C. tantanαβ =− D. cotcotαβ = . Lời giải.
Câu 4: Cho góc α tù. Điều khẳng định nào sau đây là đúng? A. sin0 α < . B. cos0 α > . C. tan0 α > . D. cot0 α < . Lời giải.
DẠYKÈMQUYNHƠNOFFICIAL BÀI TẬP CUỐI CHƯƠNG 4
................................................................................................................................................................ ................................................................................................................................................................
................................................................................................................................................................ ................................................................................................................................................................
................................................................................................................................................................
................................................................................................................................................................
................................................................................................................................................................
................................................................................................................................................................
Câu 5: Hai góc nhọn α và β phụ nhau, hệ thức nào sau đây là sai? A. sincosαβ = . B. tancotαβ = . C. 1 cot cot β α = . D. cossinαβ =− Lời giải.
Câu 6: Cho 1 cos 2 x = . Tính biểu thức 22 3sin4cos Pxx =+ A. 13 4 . B. 7 4 . C. 11 4 . D. 15 4 . Lời giải.
DẠYKÈMQUYNHƠNOFFICIAL ................................................................................................................................................................ Câu 7: Biết 1 cos 3 α = . Giá trị đúng của biểu thức 22 sin3cosP αα=+ là: A. 1 3 B. 10 9 C. 11 9 D. 4 3 Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ Câu 8: Cho biết 2 cos 3 α =− và 0 2 π α << . Tính tanα? A. 5 4 B. 5 2 C. 5 2 D. 5 2 Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ Câu 9: Cho α là góc tù và 5 sin 13 α = . Giá trị của biểu thức 3sin2cosαα + là A. 3. B. 9 13 . C. 3 . D. 9 13 . Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 10: Cho 1 sin 3 α = , với 90180 α °<<° . Tính cosα A. 2 cos 3 α = . B. 2 cos 3 α =− . C. 22 cos 3 α = . D. 22 cos 3 α =− . Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL Câu 11: cosα bằng bao nhiêu nếu 1 cot 2 α =− ? A. 5 5 ± . B. 5 2 . C. 5 5 . D. 1 3 . Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 12: Nếu tan3 α = thì cosα bằng bao nhiêu? A. 10 10 . B. 1 3 . C. 10 10 ± . D. 10 10 . Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 13: Biết cot aα =− , 0a > . Tính cosα A. 2 cos 1 a a α = + . B. 2 1 cos 1 a α = + . C. 2 1 cos 1 a α =− + . D. 2 cos 1 a a α =− + . Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 14: Cho α là góc tù và 4 sin 5 α = . Giá trị của biểu thức 2sincosA αα=− bằng A. 7 5 . B. 7 5 . C. 1. D. 11 5 . Lời giải. ................................................................................................................................................................ ................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL ................................................................................................................................................................ Câu 15: Cho 4 sin, 5 α = với 90180 α °≤≤° . Tính giá trị của 3 sincos cos M αα α + = A. 25 27 M = B. 175 27 M = . C. 35 27 M = . D. 25 27 M =− . Lời giải Chọn D Ta có 2 22 cos1sin149 525 αα =−=−= Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ Câu 16: Cho biết 2 cos 3 α =− . Tính giá trị của biểu thức cot3tan 2cottan E αα αα + = + ? A. 19 13 . B. 19 13 . C. 25 13 . D. 25 13 Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 17: Cho biết cot5 α = . Tính giá trị của 2 2cos5sincos1E ααα =++ ? A. 10 26 . B. 100 26 . C. 50 26 . D. 101 26 . Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 18: Cho 1 3 cotα = . Giá trị của biểu thức 3sin4cos 2sin5cos A αα αα + = là: A. 15 13 . B. 13 . C. 15 13 . D. 13 . Lời giải.
DẠYKÈMQUYNHƠNOFFICIAL ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
................................................................................................................................................................ ................................................................................................................................................................
................................................................................................................................................................ ................................................................................................................................................................
................................................................................................................................................................
Câu 19: Cho biết 2 cos 3 α =− . Giá trị của biểu thức cot3tan 2cottan E αα αα = bằng bao nhiêu? A. 25 3 B. 11 13 C. 11 3 D. 25 13 . Lời giải.
Câu 20: Biết 1 cos 3 α = . Giá trị đúng của biểu thức 22 sin3cosP αα=+ là: A. 11 9 . B. 4 3 . C. 1 3 . D. 10 9 . Lời giải.
Câu 21: Cho tam giác ABC , mệnh đề nào sau đây đúng? A. 222 2cos abcbcA =++ . B. 222 2cos abcbcA =+− . C. 222 2cos abcbcC =+− D. 222 2cos abcbcB =+− Lời giải.
Câu 22: Cho tam giác ABC có 8,10ab== , góc C bằng 060 Độ dài cạnh c là? A. 321=c . B. 72=c . C. 211=c . D. 221=c . Lời giải.
Câu 23: Cho ∆ABC có 06,8,60bcA=== Độ dài cạnh a là: A. 213. B. 312. C. 237. D. 20. Lời giải.
Câu 24: Cho ∆ABC có 0 60,8,5.===Bac Độ dài cạnh b bằng: A. 7. B. 129. C. 49. D. 129 . Lời giải. ................................................................................................................................................................
Câu 25: Cho ABC∆ có 9AB = ; 8BC = ; 0B60 = . Tính độ dài AC .
A. 73 B. 217 C. 8 D. 113 Lời giải. ................................................................................................................................................................ ................................................................................................................................................................
Câu 26: Cho tam giác ABC có 2,1ABAC== và 0 60.A = Tính độ dài cạnh .BC A. 2.BC = B. 1.BC = C. 3.BC = D. 2.BC = Lời giải. ................................................................................................................................................................
Câu 27: Tam giác ABC có 0 8,3,60.acB=== Độ dài cạnh b bằng bao nhiêu? A. 49. B. 97 C. 7. D. 61. Lời giải. ................................................................................................................................................................ ................................................................................................................................................................
Câu 28: Tam giác ABC có 0 150,3,2. === CBCAC Tính cạnh AB ? A. 13 B. 3. C. 10 D. 1 Lời giải. ................................................................................................................................................................ ................................................................................................................................................................
Câu 29: Cho ;;cab là độ dài 3 cạnh của tam giác ABC . Biết 7=b ; 5=c ; 4 cos 5 A = . Tính độ dài của a A. 32 B. 72 2 C. 23 8 D. 6 Lời giải.
DẠYKÈMQUYNHƠNOFFICIAL ................................................................................................................................................................
Câu 30: Cho tam giác ABC có 4AB = cm, 7BC = cm, 9AC = cm. Tính cos A . A. 2 cos 3 A =− B. 1 cos 2 A = C. 1 cos 3 A = D. 2 cos 3 A = Lời giải. ................................................................................................................................................................ ................................................................................................................................................................
Câu 31: Cho tam giác ABC có 222 0abc+−> . Khi đó: A. Góc 090C > B. Góc 090C < C. Góc 090C = D. Không thể kết luận được gì về góc .C Lời giải. ................................................................................................................................................................ ................................................................................................................................................................
Câu 32: Cho tam giác ABC thoả mãn: 222 3 bcabc +−= . Khi đó: A. 0 30.A = B. 0 45.A = C. 0 60.A = D. 075A = . Lời giải. ................................................................................................................................................................ ................................................................................................................................................................
Câu 33: Cho các điểm (1;1),(2;4),(10;2). ABC Góc BAC bằng bao nhiêu? A. 090 . B. 0 60. C. 0 45. D. 0 30. Lời giải. ................................................................................................................................................................ ................................................................................................................................................................
Câu 34: Cho tam giác ABC , biết 24,13,15.abc=== Tính góc A ? A. 0 3334'. B. 0 11749'. C. 0 2837'. D. 0 5824'. Lời giải. ................................................................................................................................................................
Câu 35: Cho tam giác ABC , biết 13,14,15.abc=== Tính góc B ? A. 0 5949'. B. 0 537'. C. 0 5929'. D. 0 6222'. Lời giải. ................................................................................................................................................................ ................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL
................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL
t
ệ
° .
° .
° .
° . Lờ
ả
................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
37: Cho tam
ABC , chọn công thức đúng trong các đáp án sau: A. 222 2
a
m + =+ B. 222 2
a
m + =−
2
a
m + =− D.
2
a
m
= Lờ
ải ................................................................................................................................................................ ................................................................................................................................................................
ABC có 9AB = cm, 15BC = cm, 12AC = cm. Khi đó đường trung tuyến AM của tam giác có độ dài là A. 10 cm . B. 9 cm . C. 7,5 cm . D. 8 cm . Lời giải ................................................................................................................................................................ Câu 39: Cho tam giác ABC có 3,5ABBC== và độ dài đường trung tuyến 13BM = . Tính độ dài AC . A. 11 B. 4 C. 9 2 D. 10 Lời giải ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
Câu 36: Cho tam giác ABC biế
độ dài ba cạnh , , BCCAAB lần lượt là , , abc và thỏa mãn h
thức ( ) ( )2222 bbacca −=− với bc ≠ . Khi đó, góc BAC bằng A. 45
B. 60
C. 90
D. 120
i gi
i.
Câu
giác
24
bca
24
acb
C. 222
24
abc
222
22 4
cba
+−
i gi
Câu 38: Tam giác
DẠYKÈMQUYNHƠNOFFICIAL ................................................................................................................................................................ Câu 40: Cho ABC∆ vuông ở ,A biết 30,C =° 3.AB = Tính độ dài trung tuyến ?AM A. 3 B. 4 C. 5 2 D. 7 2 Lời giải ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 41: Tam giác ABC có 6,42,2.abc=== M là điểm trên cạnh BC sao cho 3BM = . Độ dài đoạn AM bằng bao nhiêu? A. 9. B. 9. C. 3. D. 1 108. 2 Lời giải ................................................................................................................................................................ ................................................................................................................................................................ Câu 42: Gọi 222 abc Smmm =++ là tổng bình phương độ dài ba trung tuyến của tam giác ABC . Trong các mệnh đề sau mệnh đề nào đúng? A. 2223 4()Sabc =++ B. 222 Sabc =++ C. 2223 () 2 Sabc =++ . D. 222 3()Sabc =++ . Lời giải ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 43: Cho tam giác ABC . Tìm công thức sai: A. 2. sin a R A = B. sin. 2 Aa R = C. sin2. bBR = D. sin sin. cA C a = Lời giải
Câu 44: Cho ABC∆ với các cạnh ,, ABcACbBCa === . Gọi ,, RrS lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp và diện tích của tam giác ABC . Trong các phát biểu sau, phát biểu nào sai? A. 4 abc S R = B. sin a R A = C. 1 sin 2 SabC = D. 222 2cos abcabC +−= Lời giải ................................................................................................................................................................ ................................................................................................................................................................
Câu 45: Cho tam giác ABC có góc 60BAC =° và cạnh 3BC = . Tính bán kính của đường tròn ngoại tiếp tam giác ABC . A. 4R = B. 1R = C. 2R = D. 3R =
DẠYKÈMQUYNHƠNOFFICIAL
................................................................................................................................................................
................................................................................................................................................................ ................................................................................................................................................................
................................................................................................................................................................ ................................................................................................................................................................
ABC∆ có 5AB = ; A40=° ; B60=° Độ dài BC gần nhất với kết quả nào? A. 3,7 . B. 3,3 . C. 3,5 . D. 3,1 . Lời giải ................................................................................................................................................................ Câu 48: Cho tam giác ABC thoả mãn hệ thức 2 bca += . Trong các mệnh đề sau, mệnh đề nào đúng? A. coscos2cos. BCA += B. sinsin2sin. BCA += C. 1 sinsinsin 2 BCA += D. sincos2sin. BCA += Lời giải ................................................................................................................................................................ ................................................................................................................................................................
Lời giải
Câu 46: Trong mặt phẳng, cho tam giác ABC có 4 cmAC = , góc 60A =° , 45B =° . Độ dài cạnh BC là A. 26 . B. 223 + . C. 232 . D. 6 . Lời giải
Câu 47: Cho
Câu 49: Tam giác ABC có 16,8a = ; 0 5613'B = ; 071C = . Cạnh c bằng bao nhiêu? A. 29,9. B. 14,1. C. 17,5. D. 19,9. Lời giải ................................................................................................................................................................ ................................................................................................................................................................
Câu 50: Chọn công thức đúng trong các đáp án sau: A. 1 sin. 2 SbcA = B. 1 sin. 2 SacA = C. 1 sin. 2 SbcB = D. 1 sin. 2 SbcB = Lời giải ................................................................................................................................................................ ................................................................................................................................................................
Câu 51: Cho hình thoi ABCD có cạnh bằng a . Góc 30BAD =° . Diện tích hình thoi ABCD là A. 2 4 a . B. 2 2 a . C. 2 3 2 a . D. 2 a . Lời giải ................................................................................................................................................................ ................................................................................................................................................................
Câu 52: Cho ∆ABC có 6,8,10.===abc Diện tích S của tam giác trên là: A. 48. B. 24. C. 12. D. 30. Lời giải ................................................................................................................................................................
Câu 53: Cho ∆ABC có 0 4,5,150.===acB Diện tích của tam giác là: A. 53. B. 5. C. 10. D. 103. Lời giải ................................................................................................................................................................
Câu 54: Một tam giác có ba cạnh là 13,14,15 . Diện tích tam giác bằng bao nhiêu? A. 84. B. 84. C. 42. D. 168. Lời giải ................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL
................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL ................................................................................................................................................................ Suy
=−−−=−−−= . Câu 55: Cho tam giác ABC có 4,6,8abc=== .
đó diện
củ
315.
3 Lời giải ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 56: Tam giác ABC có các trung tuyến 15 a m = , 12bm = , 9 c m = .Diện tích S của tam giác ABC bằng A. 72 B. 144 C. 54 D. 108 Lời giải 1 ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 57: Cho tam giác ABC∆ có 7;5;cos3 5 bcA === . Độ dài đường cao a h của tam giác ABC∆ là. A. 72 2 . B. 8 . C. 83 D. 803
ra: ()()()21(2113)(2114)(2115)84Sppapbpc
Khi
tích
a tam giác là: A. 915. B.
C. 105. D. 2 15.
Câu 58: Cho tam giác ABC đều cạnh 2a . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC A. 2 3 a . B. 4 3 a . C. 8 3 a . D. 6 3 a . Lời giải
Câu 59: Cho tam giác ABC có 6BC = , 2AC = và 31AB =+ . Bán kính đường tròn ngoại tiếp tam giác ABC bằng: A. 5 . B. 3 . C. 2 . D. 2 . Lời giải
Câu 60: Cho tam giác ABC có 3AB = , 4AC = , 5BC = . Bán kính đường tròn nội tiếp tam giác bằng A. 1. B. 8 9 . C. 4 5 . D. 3 4 .
Câu 61: Cho ∆ABC có 84,13,14,15.Sabc ==== Độ dài bán kính đường tròn ngoại tiếp R của tam giác trên là: A. 8,125. B. 130. C. 8. D. 8,5. Lời giải
DẠYKÈMQUYNHƠNOFFICIAL
ờ
L
i giải ................................................................................................................................................................
................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
................................................................................................................................................................
................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
Câu 62: Cho ∆ABC có 103S = , nửa chu vi 10=p Độ dài bán kính đường tròn nội tiếp r của tam giác trên là: A. 3. B. 2. C. 2. D. 3. Lời giải
Câu 63: Một tam giác có ba cạnh là 26,28,30. Bán kính đường tròn nội tiếp là: A. 16. B. 8. C. 4. D. 42. Lời giải
Câu 64: Một tam giác có ba cạnh là 52,56,60. Bán kính đường tròn ngoại tiếp là: A. 65 8 B. 40. C. 32,5. D. 65 4 Lời giải
Câu 65: Tam giác với ba cạnh là 5;12;13 có bán kính đường tròn ngoại tiếp là? A. 6. B. 8. C. 13 2 . D. 11 2 . Lời giải
DẠYKÈMQUYNHƠNOFFICIAL ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
................................................................................................................................................................ ................................................................................................................................................................
................................................................................................................................................................
................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
................................................................................................................................................................ ................................................................................................................................................................
................................................................................................................................................................
................................................................................................................................................................ ................................................................................................................................................................
................................................................................................................................................................
Câu 66: Tam giác với ba cạnh là 5;12;13 có bán kính đường tròn nội tiếp tam giác đó bằng bao nhiêu?
A. 2. B. 22. C. 23. D. 3.
DẠYKÈMQUYNHƠNOFFICIAL
................................................................................................................................................................ ................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL BÀI TẬP TỰ LUẬN Câu 1: Cho 3 cos 5 α =− . Hãy tính sin α , cosα , cosα Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 2: Biết rằng sin1562 4 = . Tính các giá trị lượng giác còn lại của góc 15 . Chứng minh 2sin15.cos15sin30 = Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 3: Cho tan2 α =− . Tính cosα và sin α Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 4: Cho 1 cos 2 α = , tính 22 3sin4cos Pxx =+ . Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 5: Cho 62 cos 4 x + = , tính 3sincos Pxx =+ Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 6: Cho tan2 α = , tính giá trị của biểu thức: a) 3sincos sincos A αα αα = + b) 2 22 2sin1 3sin2cos B α αα + = + Lời giải. ................................................................................................................................................................ ................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL ................................................................................................................................................................ Câu 7: Biết 2 sin 5 α = . Tính giá trị của biểu thức costan costan P αα αα = + Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 8: Chứng minh các đẳng thức sau(giả sử các biểu thức sau đều có nghĩa) a) 4422 sincos12sin.cos xxxx +=− b) 1cottan1 1cottan1 xx xx ++ = c) 32 3 cossin tantantan1 cos xx xxx x + =+++ Lời giải ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 9: Chứng minh rằng biểu thức sau đây không phụ thuộc vào x a) ()() 22sincossincos Axxxx =++− b) 442 sinos2sin1Bxcxx =−−+ Lời giải ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL Câu 10: Cho tam giác ABC. Chứng minh rằng a) ( )sinsinABC =+ b) ( )coscosABC =−+ c) sincos 22 ABC + = d) ( )tantanABC =−+ Lời giải ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 11: Chứng minh rằng nếu ( )( ) 1sin1sincoscos ABAB−−= thì ( )( ) 1sin1sincoscos ABAB++= Lời giải Vì 1sin0;1sin0 AB +>+> nên ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ( )( ) 1sin1sincoscos ABAB⇔++= Câu 12: Tam giác ABC có 22 bca += . Chứng minh rằng a) 2sinsinsinABC =+ . b) 211 abc hhh =+ Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL ................................................................................................................................................................ Câu 13: Tam giác ABC có 2bca = . Chứng minh rằng a) 2 sinsin.sinABC = b) 2 abc hhh = Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 14: Chứng minh rằng trong mọi tam giác ta đều có () 222222 3 4abc mmmabc ++=++ . Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 15: Gọi là trọng tâm tam giác ABC . Chứng minh () 222222 1 3 GAGBGCabc ++=++ Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 16: Chứng minh rằng tổng bình phương hai đường chéo của hình bình hành bằng tổng bình phương bốn cạnh của nó. Lời giải.
DẠYKÈMQUYNHƠNOFFICIAL ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 17: Cho tứ giác ABCD . Gọi , MN lần lượt là trung điểm hai đường chéo , ACBD . Chứng minh 2222222 4 ABBCCDADACBDMN +++=++ Lời giải. ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ Câu 18: Cho tam giác ABC có cạnh 23,2,30abC===° . Chứng minh ABC là tam giác cân. Tính diện tích và chiều cao a h của tam giác. Lời giải ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
Câu 21: Chứng minh tam giác ABC vuông tại A khi và chỉ khi 2225 abc mmm =+ Lời giải
DẠYKÈMQUYNHƠNOFFICIAL ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................ ................................................................................................................................................................
Câu 19: Xét dạng tam giác ABC thoả mãn 22 1cos2 sin 4 Bac B ac ++ = . Lời giải Ta có
Câu 20: Cho tam giác ABC có chiều cao ()a hppa =− .Chứng minh ABC là tam giác cân. Lời giải
Vectơ có độ dài bằng 1 gọi là vectơ đơn vị. 5. Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau. 6. Nếu hai vectơ cùng phương thì chúng chỉ có thể cùng hướng hoặc ngược hướng.
7. Ba điểm phân biệt ,, ABC thẳng hàng khi và chỉ khi hai vectơ AB và AC cùng phương.
8. Hai vectơ a và b được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài, ki hiệu = ab .
9. Hai vectơ a và b được gọi là đối nhau nếu chúng ngược hướng và có cùng độ dài, kí hiệu =− ab . Khi đó, vectơ b đượ goi là vectơ đối của vectơ a
10. Cho vectơ a và điểm O , ta luôn tìm được một điểm A duy nhất sao cho: = OAa 11. Với một điểm A bất ki, ta quy ước có một vectơ đặc biệt mà điểm đầu và điểm cuối đều là A . Vectơ
DẠYKÈMQUYNHƠNOFFICIAL BÀI 1. CÁC KHÁI NIỆM MỞ ĐẦU A. KIẾN THỨC CƠ BẢN CẦN NẮM 1. Cho đoạn thẳng .AB Nều ta chọn điểm A làm điềm đầu, điểm B làm điểm cuối thì ta được đoạn thẳng AB có hướng từ A đến B . Đoạn thẳng có định hướng AB được kí hiệu là AB và được goi là vectơ AB 2 . - Vectơ có điểm đầu là A, điểm cuối B được
ệu
,
ơ
. -
ng
ẳng đ
điểm
. -
ủa đoạn thẳng AB gọi
ủ
ơ AB
ệu là AB Như vậy ta có: ||= ABAB . 3. Một vectơ khi không cần chỉ rõ điểm đầu và điểm cuối có thể viết là ,,,,…abxy
kí hi
là AB
đọc là vect
(Hinh1)AB
Đườ
th
i qua hai
A và B gọi là giá của vectơ AB
Độ dài c
là độ dài c
a vect
và được ki hi
4.
0 ====… AABBCC vớ
mọi
ểm ,,,ABC 12. Vecto-không có độ dài bằng 0 và cùng hướng với mọi vectơ. B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP Dạng 1: Xác Định Một Vectơ; Phương, Hướng Của Vectơ; Độ Dài Của Vectơ 1. Phương pháp giải. • Xác định một vectơ và xác định sự cùng phương, cùng hướng của hai vectơ theo định nghĩa • Dựa vào các tình chất hình học của các hình đã cho biết để tính độ dài của một vectơ 2. Các ví dụ. Ví dụ 1: Cho tứ giác ABCD . Có bao nhiêu vectơ khác vectơ-không có điểm đầu và điểm cuối là đỉnh của tứ giác. Lời giải Ví dụ 2: Chứng minh rằng ba điểm ,, ABC phân biệt thẳng hàng khi và chỉ khi , ABAC cùng phương. Lời giải
này được kí hiệu là AA và gọi là vectơ-không. Ta ki hiệu vectơ-không là 0 . Như vậy
i
đi
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... Ví
ụ
ể
. Lời giải ..................................................................................................................................................................... Ví dụ 4: Cho hình vuông ABCD tâm O cạnh a . Gọi M là trung điểm của AB , N là điểm đối xứng với C qua D . Hãy tính độ dài của vectơ sau MD , MN Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Dạng 2: Chứng minh hai vectơ bằng nhau. 1. Phương pháp giải. • Để chứng minh hai vectơ bằng nhau ta chứng minh chúng có cùng độ dài và cùng hướng hoặc dựa vào nhận xét nếu tứ giác ABCD là hình bình hành thì ABDC = và ADBC = 2. Các ví dụ. Ví dụ 1: Cho tứ giác ABCD . Gọi M, N, P, Q lần lượt là trung điểm AB, BC, CD, DA. Chứng minh rằng MNQP = . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
d
3: Cho tam giác ABC . Gọi ,, MNP lần lượt là trung điểm của ,, BCCAAB . a) Xác định các vectơ khác vectơ - không cùng phương với MN có điểm đầu và điểm cuối lấy trong các điểm đã cho. b) Xác định các vectơ khác vectơ - không cùng hướng với AB có điểm đầu và điểm cuối lấy trong điểm đã cho. c) Vẽ các vectơ bằng vectơ NP mà có đi
m đầu , AB
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... Ví dụ 2: Cho tam giác ABC có trọng tâm G . Gọi I là trung điểm của BC . Dựng điểm 'B sao cho ' BBAG = . a) Chứng minh rằng BIIC = b) Gọi J là trung điểm của 'BB . Chứng minh rằng BJIG = . Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... CÂU HỎI TRẮC NGHIỆM Câu 1: Vectơ có điểm đầu là D , điểm cuối là E được kí hiệu là A. .DE B. .DE C. .ED D. .DE Lời giải ..................................................................................................................................................................... Câu 2: Cho tam giác .ABC Có bao nhiêu vectơ khác vectơ - không có điểm đầu và điểm cuối là các đỉnh , , ?ABC A. 3. B. 6. C. 4. D. 9. Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 3: Cho tứ giác ABCD . Có bao nhiêu vectơ khác vectơ - không có điểm đầu và cuối là các đỉnh của tứ giác? A. 4. B. 6. C. 8. D. 12. Lời giải
Câu 4: Mệnh đề nào sau đây đúng?
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
C. Có vô số vectơ cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ. Lời giải .....................................................................................................................................................................
Câu 5: Cho ba điểm , , ABC phân biệt. Khi đó:
A. Điều kiện cần và đủ để , , ABC thẳng hàng là AB cùng phương với AC
B. Điều kiện đủ để , , ABC thẳng hàng là với mọi ,M MA cùng phương với .AB
C. Điều kiện cần để , , ABC thẳng hàng là với mọi ,M MA cùng phương với AB D. Điều kiện cần để , , ABC thẳng hàng là .ABAC = Lời giải
Câu 6: G
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
ọi , MN lần lượt là trung điểm của các cạnh , ABAC
ủa tam giác
ABC
ỏ
ặ
ơ nào sau đây cùng hướng? A. MN và .CB B. AB và .MB C. MA và .MB D. AN và .CA Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 7: Cho lục giác đều ABCDEF tâm .O Số các vectơ khác vectơ - không, cùng phương với OC có điểm đầu và điểm cuối là các đỉnh của lục giác là A. 4. B. 6. C. 7. D. 9. Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 8: Với DE (khác vectơ - không) thì độ dài đoạn ED được gọi là
c
đều
. H
i c
p vect
A. Phương của .ED B. Hướng của .ED
C. Giá của ED D. Độ dài của ED Lời giải .....................................................................................................................................................................
Câu 9: Mệnh đề nào sau đây sai?
A. 0.AA = B. 0 cùng hướng với mọi vectơ C. 0.AB > D. 0 cùng phương với mọi vectơ
Lời giải .....................................................................................................................................................................
Câu 10: Hai vectơ được gọi là bằng nhau khi và chỉ khi
A. Giá của chúng trùng nhau và độ dài của chúng bằng nhau.
B. Chúng trùng với một trong các cặp cạnh đối của một hình bình hành. C. Chúng trùng với một trong các cặp cạnh đối của một tam giác đều. D. Chúng cùng hướng và độ dài của chúng bằng nhau. Lời giải
Câu 11: Cho bốn điểm phân biệt , , , ABCD và không cùng nằm trên một đường thẳng. Điều kiện nào trong các đáp án A, B, C, D sau đây là điều kiện cần và đủ để ABCD = ? A. ABCD là hình bình hành. B. ABDC là hình bình hành. C. .ACBD = D. .ABCD = Lời giải
DẠYKÈMQUYNHƠNOFFICIAL
.....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 12: Cho bốn điểm phân biệt , , , ABCD thỏa mãn ABCD = . Khẳng định nào sau đây sai?
A. AB cùng hướng .CD B. AB cùng phương .CD C. .ABCD = D. ABCD là hình bình hành. Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Câu 13: Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD . Đẳng thức nào sau đây sai?
A. ABDC = B. OBDO = C. OAOC = D. CBDA = Lời giải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... Câu
Cho hình vuông ABCD
Khẳng đị
A. .ACBD =
= C. ABBC =
Lờ
ải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu
Gọ
O là giao điểm của
đường
ữ
ậ
A.
=
14: Cho tứ giác ABCD Gọi , , , MNPQ lần lượt là trung điểm của ,AB ,BC ,CD DA Khẳng định nào sau đây sai? A. .MNQP = B. .QPMN = C. .MQNP = D. .MNAC = Lời giải Lời giải
15:
.
nh nào sau đây đúng?
B. .ABCD
D. Hai vectơ , ABAC cùng hướng.
i gi
16:
i
hai
chéo hình ch
nh
t ABCD . Mệnh đề nào sau đây đúng?
.OAOC
B. OB và OD cùng hướng.
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
C. AC và BD cùng hướng. D. ACBD = Lời giải
..................................................................................................................................................................... .....................................................................................................................................................................
a AM = Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 19: Cho hình thoi ABCD cạnh a và 60BAD =° . Đẳng thức nào sau đây đúng? A. .ABAD = B. BDa = C. .BDAC = D. .BCDA = Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 20: Cho lục giác đều ABCDEF có tâm .O Đẳng thức nào sau đây sai? A. .ABED = B. .ABAF = C. .ODBC = D. .OBOE = Lời giải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 21: Cho lục giác đều ABCDEF tâm O Số các vectơ bằng OC có điểm đầu và điểm cuối là các đỉnh của lục giác là A. 2. B. 3. C. 4. D. 6.
Câu 17: Gọi , MN lần lượt là trung điểm của các cạnh , ABAC của tam giác đều ABC Đẳng thức nào sau đây đúng? A. .MAMB = B. .ABAC = C. .MNBC = D. 2.BCMN = Lời giải Lời giải
Câu 18: Cho tam giác ABC đều cạnh a . Gọi M là trung điểm BC . Khẳng định nào sau đây đúng? A. .MBMC = B. 3 2 a AM = C. .AMa = D. 3 2
Câu 22: Cho tam giác ABC có trực tâm H . Gọi D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC . Khẳng định nào sau đây đúng? A. HACD = và ADCH = . B. HACD = và ADHC = . C. HACD = và ACCH = . D. HACD = và ADHC = và OBOD = . Lời giải
Câu 23: Cho 0AB ≠ và một điểm .C Có bao nhiêu điểm D thỏa mãn ?ABCD = A. 0. B. 1. C. 2. D. Vô số. Lời giải
Câu 24: Cho 0AB ≠ và một điểm C Có bao nhiêu điểm D thỏa mãn ?ABCD = A. 1. B. 2. C. 0. D. Vô số. Lời giải
DẠYKÈMQUYNHƠNOFFICIAL Lời giải ..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
.....................................................................................................................................................................
.....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
A.KIẾNTHỨCCƠ BẢNCẦNNẮM
1.Quytắcba điểm
Với ba điểm ,,,ABC ta có: += ABBCAC .
2.Quytắchìnhbìnhhành
Nếu OABC là hình bình hành thì ta có += OAOCOB
3.Tínhchấtcủaphépcộngcácvectơ
- Tính chất giao hoán: +=+ abba ;
- Tính chất kết hợp: ()() ++=++ abcabc ;
- Với mọi vectơ a , ta luôn có: 00 +=+= aaa


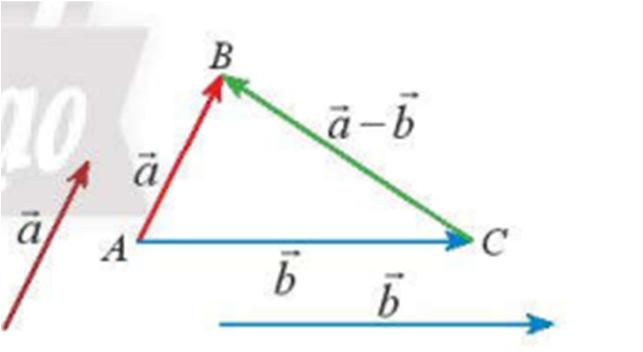
4.Hiệucủahaivecto
Cho hai vectơ a và b Hiệu của hai vecto' a và b là vectơ ()+− ab và ki hiệu ab . Chúý: Cho ba điểm ,, OAB ta có −= OBOAAB . 5.Tínhch

DẠYKÈMQUYNHƠNOFFICIAL BÀI2.TỔNGVÀHIỆU2VECTƠ
Điểm M
của đoạn thẳng AB khi và chỉ khi 0+=MAMB . Điểm G là trọng tâm của tam giác $A B C$ khi và chỉ khi 0++=GAGBGC B.PHÂNLOẠIVÀPHƯƠNGPHÁPGIẢIBÀITẬP Dạng1:Xác định độ dàitổng,hiệucủacácvectơ. 1.Phươngphápgiải. Để xác định độ dài tổng hiệu của các vectơ
ấtvectơ củatrung điểm đoạnthẳngvàtrọngtâmtamgiác
là trung điểm
DẠYKÈMQUYNHƠNOFFICIAL • Trước tiên sử dụng định nghĩa về tổng, hiệu hai vectơ và các tính chất, quy tắc để xác định định phép toán vectơ đó. • Dựa vào tính chất của hình, sử dụng định lí Pitago, hệ thức lượng trong tam giác vuông để xác định độ dài vectơ đó. 2.Cácvídụ. Vídụ 1: Cho tam giác ABC vuông tại A có 030=ABC và 5= BCa Tính độ dài của các vectơ + ABBC , ACBC và + ABAC . Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... b) Chứng minh rằng uMAMBMCMD =+−− không phụ thuộc vị trí điểm M . Tính độ dài vectơ u Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Dạng2:Chứngminh đẳngthứcvectơ. 1.Phươngphápgiải. • Để chứng minh đẳng thức vectơ ta có các cách biển đổi: vế này thành vế kia, biến đổi tương đương, biến đổi hai vế cùng bằng một đại lương trung gian. Trong quá trình biến đổi ta cần sử dụng linh hoạt ba quy tắc tính vectơ. Lưu ý: Khi biến đổi cần phải hướng đích , chẳng hạn biến đổi vế phải, ta cần xem vế trái có đại lượng nào để từ đó liên tưởng đến kiến thức đã có để làm sao xuất hiện các đại lượng ở vế trái. Và ta thường biến đổi vế phức tạp về vế đơn giản hơn. 2.Cácvídụ. Vídụ 1: Cho năm điểm ,,,, ABCDE . Chứng minh rằng
DẠYKÈMQUYNHƠNOFFICIAL a) ABCDEACBED ++=+ b) ACCDECAEDBCB +−=−+ Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Vídụ 2: Cho hình bình hành ABCD tâm O . M là một điểm bất kì trong mặt phẳng. Chứng minh rằng a) 0BADAAC++= b) 0OAOBOCOD+++= c) MAMCMBMD +=+ Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Vídụ 3: Cho tam giác ABC . Gọi M, N, P lần lượt là trung điểm của ,, BCCAAB . Chứng minh rằng a) 0BMCNAP++= b) 0APANACBM+−+= c) OAOBOCOMONOP ++=++ với O là điểm bất kì. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... O A D C B Hình 1.12
CÂUHỎITRẮCNGHIỆM
Câu1: Cho ba điểm , , ABC phân biệt. Khẳng định nào sau đây đúng?
A. ABACBC += B. MPNMNP += C. CABACB += D. AABBAB += Lờigiải
Câu2: Cho a và b là các vectơ khác 0 với a là vectơ đối của b . Khẳng định nào sau đây sai?
A. Hai vectơ , ab cùng phương. B. Hai vectơ , ab ngược hướng. C. Hai vectơ , ab cùng độ dài. D. Hai vectơ , ab chung điểm đầu. Lờigiải
Câu3: Cho ba điểm phân biệt ,, ABC Đẳng thức nào sau đây đúng? A. .CABABC −= B. .ABACBC += C. .ABCACB += D. .ABBCCA −= Lờigiải
Câu4: Cho ABCD =− . Khẳng định nào sau đây đúng? A. AB và CD cùng hướng. B. AB và CD cùng độ dài. C. ABCD là hình bình hành. D. 0.ABDC+= Lờigiải
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
Câu5: Tính tổng MNPQRNNPQR ++++ A. MR B. MN C. PR D. MP Lờigiải .....................................................................................................................................................................
Câu6: Cho hai điểm A và B phân biệt. Điều kiện để I là trung điểm AB là: A. IAIB = B. IAIB = C. IAIB =− D. AIBI = Lờigiải
Câu7: Điều kiện nào là điều kiện cần và đủ để I là trung điểm của đoạn thẳng AB ? A. IAIB = B. 0.IAIB+= C. 0.IAIB−= D. IAIB = Lờigiải
Câu8: Cho tam giác ABC cân ở A , đường cao AH . Khẳng định nào sau đây sai? A. .ABAC = B. .HCHB =− C. .ABAC = D. 2.BCHC = Lờigiải
Câu9: Cho hình vuông ABCD . Khẳng định nào sau đây đúng? A. ABBC = B. ABCD = C. ACBD = D. ADCB = Lờigiải
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
Mệnh đề nào
A. Nếu M là
ể
ạ
B. Nếu G là trọ
C. Nếu ABCD
Nếu
Câu10:
sau đây sai?
trung đi
m đo
n thẳng AB thì 0.MAMB+=
ng tâm tam giác ABC thì 0.GAGBGC++=
là hình bình hành thì .CBCDCA += D.
ba điểm phân biệt ,, ABC nằm tùy ý trên một đường thẳng thì .ABBCAC += Lờigiải
Câu11: Gọi O là tâm hình bình hành ABCD . Đẳng thức nào sau đây sai?
A. .OAOBCD −= B. .OBOCODOA −=− C. .ABADDB −= D. .BCBADCDA −=− Lờigiải
Câu12: Cho hình bình hành ABCD . Đẳng thức nào sau đây đúng? A. .ABBCDB −= B. .ABBCBD −= C. .ABBCCA −= D. .ABBCAC −= Lờigiải .....................................................................................................................................................................
Câu13: Gọi O là tâm hình vuông ABCD . Tính OBOC . A. OBOCBC −= B. OBOCDA −= C. OBOCODOA −=− D. OBOCAB −= Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu14: Cho tam giác ABC đều cạnh .a Mệnh đề nào sau đây đúng? A. ABBCCA == B. CAAB =− C. .ABBCCAa === D. .CABC =− Lờigiải
Câu15: Cho tam giác ABC với M là trung điểm BC Mệnh đề nào sau đây đúng? A. 0.AMMBBA++= B. .MAMBAB += C. .MAMBMC += D. .ABACAM += Lờigiải
Câu16: Cho tam giác ABC với ,, MNP lần lượt là trung điểm của ,, BCCAAB . Khẳng định nào sau đây sai?
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
Câu17: Cho ba điểm phân biệt ,,.ABC Mệnh đề nào sau đây đúng? A. ABBCAC += B. 0.ABBCCA++= C. ABBCCABC =⇔= D. ABCABC −= Lờigiải
Câu18: Cho tam giác ABC có ABAC = và đường cao .AH Đẳng thức nào sau đây đúng? A. .ABACAH += B. 0.HAHBHC++= C. 0.HBHC+= D. ABAC = Lờigiải
Câu19: Cho tam giác ABC vuông cân đỉnh
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
A. 0.ABBCCA++= B. 0.APBMCN++= C. 0.MNNPPM++= D. PBMCMP += Lờigiải
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
A , đường cao AH . Khẳng định nào sau đây sai? A. .AHHBAHHC +=+ B. .AHABAHAC −=− C. .BCBAHCHA −=− D. .AHABAH =− Lờigiải ..................................................................................................................................................................... Câu20: Gọi ,, MNP lần lượt là trung điểm các cạnh ,, ABBCCA của tam giác ABC Hỏi vectơ MPNP + bằng vectơ nào trong các vectơ sau? A. AP B. BP C. MN D. MBNB + Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu21: Cho bốn điểm phân biệt ,,,. ABCD Mệnh đề nào sau đây đúng? A. ABCDADCB +=+ B. ABBCCDDA ++= C. .ABBCCDDA +=+ D. .ABADCDCB +=+ Lờigiải
Câu24: Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Hỏi vectơ ( )AODO bằng vectơ nào trong các vectơ sau? A. .BA B. .BC C. .DC D. .AC Lờigiải
Câu25: Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Đẳng thức nào sau đây sai? A. 0.OAOBOCOD+++= B. ACABAD =+ C. .BABCDADC +=+ D. .ABCDABCB +=+ Lờigiải
Câu26: Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Gọi , EF lần lượt là trung điểm của , ABBC Đẳng thức nào sau đây sai? A. .DOEBEO =− B. .OCEBEO =+ C. 0.OAOCODOEOF ++++= D. 0.BEBFDO+−= Lờigiải
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
Câu22: Gọi O là tâm của hình vuông ABCD . Vectơ nào trong các vectơ dưới đây bằng ?CA A. .BCAB + B. .OAOC−+ C. .BADA + D. .DCCB Lờigiải
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Câu23: Cho lục giác đều ABCDEF có tâm .O Đẳng thức nào sau đây sai? A. 0.OAOCOE++= B. OAOCOBEB ++= C. 0.ABCDEF++= D. BCEFAD += Lờigiải
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... Câu27: Cho hình bình hành ABCD Gọi G là trọng tâm của tam giác ABC Mệnh đề nào sau đây đúng? A. .GAGCGDBD ++= B. .GAGCGDCD ++= C. .GAGCGDO ++= D. .GAGDGCCD ++= Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu28: Cho hình chữ nhật .ABCD Khẳng định nào sau đây đúng? A. ACBD = B. 0.ABACAD++= C. .ABADABAD −=+ D. .BCBDACAB +=− Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu29: Cho tam giác ABC đều cạnh a . Tính .ABAC + A. 3.ABACa += B. 3 . 2 ABACa += C. 2.ABACa += D. 23.ABACa += Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Câu30: Cho tam giác ABC vuông cân tại A có ABa = . Tính .ABAC + A. 2.ABACa += B. 2 . 2 ABACa += C. 2.ABACa += D. .ABACa += Lờigiải
Câu31: Cho tam giác ABC vuông cân tại C và 2.AB = Tính độ dài của ABAC + A. 5.ABAC+= B. 25.ABAC+= C. 3.ABAC+= D. 23.ABAC+= Lờigiải
Câu32: Cho tam giác ABC vuông tại A và có 3,4ABAC== . Tính CAAB + . A. 2.CAAB+= B. 213.CAAB+= C. 5.CAAB+= D. 13.CAAB+= Lờigiải
Câu33: Tam giác ABC có ABACa == và 120BAC =° . Tính .ABAC + A. 3.ABACa += B. .ABACa += C. 2 ABACa += D. 2.ABACa +=
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
.....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu34: Chotam giác ABC đều cạnh ,a H làtrung điểm của BC .Tính .CAHC A. 2 CAHCa −= B. 3 2 CAHCa −= C. 23 3 CAHCa −= D. 7 2 CAHCa −= Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu35: Gọi G là trọng tâm tam giác vuông ABC với cạnh huyền 12.BC = Tính độ dài của vectơ vGBGC =+ . A. 2.v = B. 23.v = C. 8.v = D. 4.v = Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu36: Chohìnhthoi ABCD có 2 ACa = và BDa = Tính ACBD + . A. 3.ACBDa += B. 3.ACBDa += C. 5.ACBDa += D. 5.ACBDa += Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
ạ
−=
−=
−=
−= Lờ
ải .....................................................................................................................................................................
A.
.
Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Chotam giác ABC có M thỏamãn điềukiện 0MAMBMC++= .Xác địnhvị trí điểm .M A. M là điểm thứ tư củahìnhbình hành .ACBM B. M làtrung điểm của đoạnthẳng .AB C. M trùngvới .C D. M làtrọngtâm tam giác .ABC Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Chotamgiác ABC Tậphợptấtcả các điểm M thỏamãn đẳngthứ
MBMCBMBA −=−
Câu37: Chohìnhvuông ABCD c
nh .a Tính ABDA A. 0.ABDA
B. ABDAa
C. 2.ABDAa
D. 2.ABDAa
igi
Câu38: Chohìnhvuông ABCD cạnh a ,tâm .O Tính OBOC + .
.OBOCa += B. 2.OBOCa += C.
2 OBOCa += D. 2 . 2 a OBOC+=
Câu39:
Câu40:
c
A. đường thẳng AB
B. trung trực đoạn .BC
C. đườngtròntâm ,A bánkính BC
D. đườngthẳngqua A vàsongsongvới BC
Lờigiải
Câu41: Cho hình bình hành ABCD . Tập hợp tất cả các điểm M thỏa mãn đẳng thức MAMBMCMD +−= là
A. một đường tròn.
B. một đườngthẳng. C. tập rỗng. D. một đoạn thẳng.
Lờigiải .....................................................................................................................................................................
Câu42: Chotamgiác ABC và điểm M thỏamãn MBMCAB += .Tìmvị trí điểm .M A. M làtrung điểm của AC B. M làtrung điểm của .AB C. M làtrung điểmcủa BC D. M là điểmthứ tư củahìnhbìnhhành .ABCM Lờigiải
DẠYKÈMQUYNHƠNOFFICIAL là
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Câu43: Cho tam giác ABC và điểm M thỏa mãn điều kiện 0MAMBMC−+= . Mệnh đề nào sau đây sai? A. MABC làhình bình hành. B. AMABAC += C. BABCBM += D. MABC = Lờigiải
b bất kì,với mọi số thực h và k ,tacó: ()+=+ kabkakb ()+=+ hkahaka , ()() = hkahka , 1. = aa , (-1), =− aa . 2. Điềukiện để haivectơ cùngphưong Hai vectơ a và ( bb khác 0) củngphươngkhi vàchỉ khi có một số k sao cho = akb .
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... .....................................................................................................................................................................
ỦAMỘTSỐ VỚIVECTƠ A.KIẾNTHỨCCƠ BẢNCẦNNẮM 1.Tíchcủ
ộtsố vớ
ộ
ơ
ấ
-Cho
Vect
ớ
ế
ớ
ẠIVÀPHƯƠNGPHÁPGIẢIBÀITẬP Dạng1:Dựngvàtính độ dàivectơ chứatíchmộtvectơ vớimộtsố. 1.Phươngphápgiải. Sử dụng địnhnghĩatíchcủamộtvectơ vớimộtsố vàcácquytắcvề phéptoánvectơ để dựngvectơ chứa tích một vectơ với một số, kết hợp với các định lípitago và hệ thức lượng trong tam giácvuông để tính độ dàicủachúng. 2.Cácvídụ. Vídụ 1: Cho tam giác đều ABC cạnh a điểm M là trung điểm BC . Dựng các vectơ sau và tính độ dài củachúng. a) 1 2 CBMA + b) 1 2 BABC c) 1 2 2 ABAC + d) 3 2,5 4 MAMB Lờigiải
BÀI3.TÍCHC
am
im
tvect
vàcáctínhch
t
số k khác0 vàvectơ a khác 0 .Tích củasố k vớivectơ a làmột vectơ,kí hiệu là ka
ơ ka cùng hướng v
i a n
u 0>k ,ngượchướng v
i a nếu 0<k vàcó độ dài bằng |||| ⋅ ka Quy ước: 00 =a và 00 =k . Với hai vectơ a và
3. Điềukiện để ba điểmthẳnghàng Ba điểm phânbiệt ,, ABC thẳng hàng khivàchỉ khi có số k khác0 đê = ABkAC B.PHÂNLO
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Vídụ 2: Chohình vuông ABCD cạnh a a) Chứng minh rằng uMAMBMCMD =−+− 432 khôngphụ thuộcvào vị trí điểm M. b)Tính độ dài vectơ u Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Dạng2:Chứngminh đẳngthứcvectơ.
1.Phươngphápgiải Sử dụng các kiến thức sau để biến đổi vế này thành vế kia hoặc cả hai biểu thức ở hai vế cùng bằng biểu thức thứ ba hoặc biến đổi tương đương về đẳng thức đúng:
• Cáctínhchất phéptoán vectơ
• Cácquytắc: quy tắcba điểm,quy tắchình bình hành vàquy tắcphéptrừ
• Tính chấttrung điểm:
M làtrung điểm đoạnthẳngAB MAMB ⇔+= 0
M làtrung điểm đoạnthẳngAB OAOBOM⇔+= 2 (Với O là điểm tuỳ ý)
• Tính chấttrọngtâm: G làtrọng tâmcủatam giácABC ⇔ GA +GB +GC =O G làtrọng tâmcủatam giácABC ⇔ OA +OB +OC =3OG (Với O là điểm tuỳ ý) 2.Cácvídụ. Vídụ 1: Cho tứ giác ABCD . Gọi I, J lần lượt là trung điểm của AB và CD, O là trung điểm của IJ .Chứngminh rằng:
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
a)
b) 0OAOBOCOD+++= c) MAMBMCMDMO +++= 4 vớiM là điểm bấtkì Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
ACBDIJ += 2
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Vídụ 2: Cho haitamgiác ABC và ABC111 cócùngtrọngtâm G.Gọi ,, GGG 123 lầnlượtlàtrọngtâm tam giác ,, BCAABCACB 111 .Chứngminhrằng GGGGGG++= 123 0 Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Vídụ 3: Chotam giác ABC có trựctâm H,trọng tâm G vàtâm đườngtrònngoạitiếp O.Chứng minh rằng a) HAHBHCHO ++= 2 b) OAOBOCOH ++= c) 20GHGO+= Lờigiải .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Dạng3:Phântíchmộtvectơ theohaivectơ khôngcùngphương. 1.Phươngphápgiả
Sử
ụng
chất phép toán vectơ, ba quy tắc phép toán vectơ và tính chất trung điểm, trọng tâm
Víd
== a)Hãy
== b)
c)Gọ
ể
ỏ
=
ứ
ẳ
ải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
i.
d
các tính
trong tam giác. 2.Cácvídụ.
ụ 1: Chotam giác ABC Đặt , aABbAC
dựng các điểm M,N thỏamãn: 1 , 23 AMABCNBC
Hãyphântích , , CMANMN quacácvéctơ a và b
i Ilà đi
m th
a: MICM
.Ch
ngminh ,, IAN th
nghàng Lờigi
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Vídụ 2: Chotam giác ABC ,trêncạnhBC lấyMsao cho 3 BMCM = ,trên đoạnAMlấyN saocho 25ANMN = .G làtrọngtâm tam giác ABC a) Phântích cácvectơ , AMBN quacácvéctơ AB và AC b)Phân tíchcácvectơ , GCMN quacácvéctơ GA và GB Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Vídụ 3: Cho hình bình hành ABCD . Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho , ABAMCDCN ==32 và G là trọng tâm tam giác MNB . Phân tích cácvectơ ANMNAG , , quacácvéctơ AB và AC Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
c thì M thuộc đường tròn tâm C, bán kính bằng kAB . .
-Nếu MAkBC = với A,B,C phân biệt vàklàsố thựcthay đổi thì
+M thuộc đường thẳng quaA songsongvới BC với kR ∈
+M thuộcnửa đường thẳng quaA song song vớiBC vàcùng hướng BC với k > 0
+M thuộcnửa đường thẳng quaA song song vớiBC vàngượchướng BC với k < 0
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Dạng4:Tìmtậphợp điểmthỏamãn điềukiệnvectơ chotrước.
ươngphápgiải. Để tìm tập hợp điểm M thỏamãnmãn điều kiện vectơ taquy về một trong
ạng
cthì M thuộc đường trungtrự
ủa
ướ
1.Ph
cácd
sau -Nếu MAMB = với A,B phân biệtchotrướ
cc
đoạn AB. - Nếu MCkAB = . với A, B, C phân biệt cho tr
ế
BC 2.Cácvídụ. Vídụ 1: Chotam giác ABC a) Chứng minh rằng tồn tại duy nhất điểm Ithỏa mãn: 2340 IAIBIC++= . b)Tìm quỹ tích điểm M thỏamãn : 234 MAMBMCMBMA ++=− . Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
- N
u MAkBCBC =≠ , với A, B, C thẳng hàng và k thay đổi thì tập hợp điểm M là đường thẳng
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Vídụ 2: Chotam giác ABC .Tìm tậphợp các điểm M thoả mãn điềukiệnsau : a) MAMBMAMC +=+ b) ( )MAMBkMAMBMC +=+−23 với k làsố thựcthay đổi Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Vídụ 3: Chotứ giác ABCD .Vớisố ktùyý,lấy các điểmMvàNsaocho , AMkABDNkDC == .Tìm tậphợp cáctrung điểm Icủa đoạnthẳngMN khi kthay đổi. Lờigiải
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... CÂUHỎITRẮCNGHIỆM Câu1: Chotam giác OAB vuông cân tại ,O cạnh OAa = Tính 2. OAOB A. a B. ( ) 12. a+ C. 5.a D. 22. a Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu2: Chotam giác OAB vuông cân tại ,O cạnh .OAa = Khẳng địnhnào sau đây sai? A. 345. OAOBa += B. 235. OAOBa += C. 725. OAOBa −= D. 1165. OAOBa −= Lờigiải .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu3: Chotam giác ABC có M làtrung điểmcủa , BCI làtrung điểmcủa .AM Khẳng định nào sau đây đúng? A. 20.IBICIA++= B. 20.IBICIA++= C. 20. IBICIA++= D. 0.IBICIA++= Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu4: Chotam giác ABC có M làtrung điểmcủa , BCI làtrung điểmcủa AM Khẳng định nào sau đây đúng? A. ( )1 . 4 AIABAC =+ B. ( )1 . 4 AIABAC =− C. 11 . 42 AIABAC =+ D. 11 . 42 AIABAC =− Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu5: Cho tam giác ABC có M là trung điểm của , BCG là trọng tâm củatam giác .ABC Khẳng định nàosau đây đúng? A. ( )2 3 AGABAC =+ B. ( )1 3 AGABAC =+ C. 12 32 AGABAC =+ D. 2 3. 3 AIABAC =+ Lờigiải
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu6: Cho tứ giác .ABCD Trên cạnh , ABCD lấy lần lượt các điểm , MN sao cho 32AMAB = và 32. DNDC = Tínhvectơ MN theohaivectơ ,.ADBC A. 11 33 MNADBC =+ B. 12 33 MNADBC =− C. 12 33 MNADBC =+ D. 21 33 MNADBC =+ Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu7: Cho hình thang ABCD có đáy là AB và CD Gọi M và N lần lượt là trung điểm của AD và BC Khẳng địnhnàosau đâysai? A. MNMDCNDC =++ B. MNABMDBN =−+ C. ( )1 . 2 MNABDC =+ D. ( )1 . 2 MNADBC =+ Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL Câu8: Chohìnhbìnhhành ABCD có M làtrung điểm của AB Khẳng định nào sau đây đúng? A. 1 . 2 DMCDBC =+ B. 1 . 2 DMCDBC =− C. 1 . 2 DMDCBC =− D. 1 . 2 DMDCBC =+ Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu9: Cho tam giác ,ABC điểm M thuộc cạnh AB sao cho 3 AMAB = và N là trung điểm của AC Tính MN theo AB và .AC A. 11 . 23 MNACAB =+ B. 11 . 23 MNACAB =− C. 11 . 23 MNABAC =+ D. 11 . 23 MNACAB =− Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu10: Chotamgiác .ABC Hai điểm , MN chiacạnh BC theobaphầnbằngnhau .BMMNNC == Tính AM theo AB và AC A. 21 . 33 AMABAC =+ B. 12 . 33 AMABAC =+ C. 21 . 33 AMABAC =− D. 12 . 33 AMABAC =− Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu11: Chotam giác ABC có M làtrung điểm của BC Tính AB theo AM và BC A. 1 2 ABAMBC =+ B. 1 2 ABBCAM =+ C. 1 2 ABAMBC =− D. 1 2 ABBCAM =− Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu12: Cho tam giác ABC , gọi M là trung điểm AB và N là một điểm trên cạnh AC sao cho 2 NCNA = .Gọi K làtrung điểm của MN .Khi đó A. 11 . 64 AKABAC =+ B. 11 . 46 AKABAC =− C. 11 . 46 AKABAC =+ D. 11 . 64 AKABAC =− Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu13: Chohìnhbìnhhành .ABCD Tính AB theo AC và .BD A. 11 . 22 ABACBD =+ B. 11 . 22 ABACBD =− C. 1 . 2 ABAMBC =− D. 1 . 2 ABACBD =− Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL Câu14: Chotam giác ABC và đặt ,. aBCbAC == Cặp vectơ nào sau đâycùng phương? A. 2,2. abab ++ B. 2,2. abab C. 5,102. abab +−− D. ,.abab +− Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu15: Cho tam giác ABC có G là trọng tâm và I là trung điểm của BC Đẳng thức nào sau đây đúng? A. 2.GAGI = B. 1 3 IGIA =− C. 2.GBGCGI += D. .GBGCGA += Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu16: Cho tam giác ABC có G là trọng tâm và M là trung điểm BC Khẳng định nào sau đây sai? A. 2 . 3 GAAM =− B. 3.ABACAG += C. .GABGCG =+ D. .GBGCGM += Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu17: Chotam giác ABC vuôngtại ,A M làtrung điểmcủa BC Khẳng địnhnào sau đây đúng? A. AMMBMC == B. MBMC = C. .MBMC =− D. . 2 BC AM = Lờigiải
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu18: Chotamgiác ABC Gọi M và N lầnlượtlàtrung điểmcủa AB và AC Khẳng địnhnàosau đây sai? A. 2.ABAM = B. 2.ACNC = C. 2.BCMN =− D. 1 . 2 CNAC =− Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu19: Chotam giác ABC có G làtrọngtâm.Mệnh đề nàosau đây đúng? A. 2 3 ABACAG += B. 3.BABCBG += C. CACBCG += D. 0.ABACBC++= Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu20: Chotam giác đều ABC và điểm I thỏamãn 2.IAIB = Mệnh đề nào sau đây đúng? A. 2 3 CACB CI = B. 2 3 CACB CI + =
DẠYKÈMQUYNHƠNOFFICIAL C. 2.CICACB =−+ D. 2 . 3 CACB CI + = Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu21: Chotam giác ABC vàmột điểm M tùyý.Mệnh đề nào sau đây đúng? A. 232. MAMBMCACBC +−=+ B. 232. MAMBMCACBC +−=+ C. 232. MAMBMCCACB +−=+ D. 232. MAMBMCCBCA +−=− Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu22: Chohìnhvuông ABCD cótâm là .O Mệnh đề nào sau đây sai? A. 2.ABADAO += B. 1 . 2 ADDOCA +=− C. 1 . 2 OAOBCB += D. 2.ACDBAB += Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu23: Chohìnhbìnhhành .ABCD Đẳngthứcnàosau đây đúng? A. 2.ACBDBC += B. .ACBCAB += C. 2. ACBDCD −= D. ACADCD −= Lờigiải .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Gọi G làtrọngtâmtamgiác ABC . Đặt , GAaGBb == .Hãytìm , mn để có BCmanb =+ A. 1,2.mn== B. 1,2.mn=−=− C. 2,1.mn== D. 2,1.mn=−=− Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu27: Cho ba điểm ,, ABC không thẳng hàng và điểm M thỏa mãn đẳng thức vectơ MAxMByMC =+ Tính giátrị biểuthức .Pxy =+
Câu24: Cho hình bình hành ABCD có M là giao điểm của hai đường chéo. Mệnh đề nào sau đây sai? A. ABBCAC += B. ABADAC += C. 2.BABCBM += D. .MAMBMCMD +=+ Lờigiải
Câu25: Chotamgiác ABC và điểm M thỏamãn 2. MAMBCA += Khẳng địnhnàosau đâylà đúng? A. M trùng .A B. M trùng .B C. M trùng C D. M làtrọng tâmcủatam giác ABC Lờigiải
Câu26:
DẠYKÈMQUYNHƠNOFFICIAL A. 0.P = B. 2.P = C. 2.P =− D. 3.P = Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu28: Cho hình chữ nhật ABCD và số thực 0.k > Tập hợp các điểm M thỏa mãn đẳng thức MAMBMCMDk +++= là A. một đoạn thẳng. B. một đường thẳng. C. một đường tròn. D. một điểm. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu29: Chohìnhchữ nhật ABCD và I làgiao điểmcủahai đườngchéo.Tậphợpcác điểm M thỏa mãn MAMBMCMD +=+ là A. trungtrựccủa đoạnthẳng .AB B. trung trựccủa đoạn thẳng AD C. đường tròn tâm ,I bánkính 2 AC D. đường tròn tâm ,I bánkính 2 ABBC + Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu30: Chohai điểm , AB phânbiệt vàcố định,với I làtrung điểmcủa .AB Tậphợpcác điểm M thỏamãn đẳng thức MAMBMAMB +=− là
A. đường tròn tâm ,I đường kính 2 AB B. đườngtròn đường kính .AB C. đường trung trựccủa đoạnthẳng .AB D. đường trung trực đoạn thẳng .IA Lờigiải
Chohai điể
DẠYKÈMQUYNHƠNOFFICIAL
.....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Cho tam giác đều ABC cạnh ,a trọng tâm G Tập hợp các điểm
thỏa mãn MAMBMAMC +=+ là A.
ng trung trựccủa đoạn BC . B.
C.
. Lờ
ả
Câu31:
m , AB phânbiệt vàcố định,với I làtrung điểmcủa .AB Tậphợpcác điểm M thỏamãn đẳng thức 22 MAMBMAMB +=+ là A. đường trung trựccủa đoạnthẳng AB B. đườngtròn đường kính AB C. đường trung trực đoạn thẳng .IA D. đường tròn tâm ,A bán kính .AB Lờigiải
Câu32:
M
đườ
đườngtròn đường kính BC .
đường tròn tâm G ,bán kính 3 a . D. đường trung trực đoạn thẳng AG
igi
i
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu33: Cho tam giác đều ABC cạnh a Biết rằng tập hợp các điểm M thỏa mãn đẳng thức 234 MAMBMCMBMA ++=− là đườngtròncố địnhcó bán kính .R Tínhbánkính R theo .a A. . 3 a R = B. . 9 a R = C. . 2 a R = D. . 6 a R = Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu34: Chotam giác ABC .Có baonhiêu điểm M thỏamãn 3MAMBMC++= ? A. 1. B. 2. C. 3. D. Vôsố. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
A.KIẾNTHỨCCƠ BẢNCẦNNẮM
1.Gócgiữahaivectơ
Chohai vectơ a và b đềukhác 0 .Từ một điểm O bất kì tavẽ , == OAaOBb
Góc AOB với số đo từ 0 ° đến 180 ° đượcgọi làgócgiữahai vectơ a và b .
Takí hiệugócgiữahai vectơ a và b là (,) ab .
Nếu (,)90 ° =ab thì tanói rằng a và b vuônggócvới nhau,kí hiệulà ⊥ ab
Chúý:
-Tử định nghĩatacó (,)(,) = abba .
-Gócgiữahai vectơ cùnghướngvàkhác 0 luônbằng 0 °
-Gócgiữahai vectơ ngượchướng vàkhác 0 luônbằng 180 ° .
- Trong trường hợp có it nhất một trong hai vectơ a hoặc b là vectơ 0 thi ta quy ước số đo góc giữa hai vectơ đó làtuỳ ý(từ 0 ° đến 180 ° ).
2.Tíchvôhướngcủahaivecto' Chohai vectơ a và b đềukhác 0
Tíchvô hướngcủa a và b làmột số,kihiệu là ab , đượcxác địnhbởi công thức: ||||cos(,)⋅=⋅⋅ ababab .
Chúý:
-Trường hợpitnhất một trong hai vectơ a và b bằng 0 ,taquy ước 0⋅=ab . -Với hai vectơ a và b đều khác 0 ,tacó 0⊥⇔⋅=abab - Khi = ab thi tich vô hướng ⋅ ab được ki hiệu là

DẠYKÈMQUYNHƠNOFFICIAL BÀI4.TÍCHVÔHƯỚNGHAIVECT
Ơ
2 a và được gọi là binh phrơng vô hiróng của vectơ a Tacó 22 ||||cos0|| ° =⋅⋅= aaaa Vậybìnhphươngvô hướng củamột vectơ luônbằngbìnhphương đô dài củavectơ đó. 3.Tínhchấtcủatíchvôhướng -Với bavectơ ,, abc bất kì vàmọi số k ,tacó: - ;⋅=⋅ abba ();•()()() ⋅+=⋅+⋅⋅=⋅=⋅ abcabackabkabakb . -Từ cáctính chất củatích vôhướngcủahai vectơ,tasuyra:222()2+=+⋅+ abaabb222()2−=−⋅+ abaabb22()()+⋅−=− ababab .
4.Ápdụngcủatíchvôhướng
Trong Vật li, tích vô hướng giúp tinh công sinhA bởi một lực F có độ dịch chuyển là vectơ d . Ta có công thức: =⋅ AFd . B.PHÂNLOẠIVÀPHƯƠNGPHÁPGIẢIBÀITẬP
Dạng1:Tínhtíchvôhướng2vectơ vàxác địnhgóccủahaivecto
1.Phươngphápgiải.
a) Để tínhtích vôhướng củahai vectơ,tacó thể sử dụng:
ab ab ab = 2.Cácvídụ. Câu1. Chotam giác ABC đều cạnh a ,tâm O .Hãy tính: a). . ABAC b). . ABBC c). ( )( )OBOCABAC +− d). ( )( )23 ABACABBC +− Lờigiải
Câu2. Chohìnhvuông ABCD cạnh a ,tâm O .Hãytính: a). ( )( ) ( )( ).; .; ; ABBCABBDABADBDBCABACADDADBDC ++++++
DẠYKÈMQUYNHƠNOFFICIAL
+Nếu có độ dài hai vectơ vàgócgiữachúng,tadùng định nghĩa ( )..cos, ababab = +Nếu làtích củatổng,hiệu cácvectơ tadùngtính chất củatích vôhướng + Nếu biết độ dài hai vectơ và độ dài của tổng hay hiệu của chúng, ta bình phương tổng hay hiệucủachúng +Nếu một vectơ cố định vàmột vectơ thay đổi ta cóthể dùng định lýhìnhchiếu. b) Để tính góccủahai vectơ,tasử dụng côngthức: () . cos, . ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL
.
ờ
ải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
đ
ỏ
ờ
ả
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
.
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
b). .; . ONABNAAB với N là điểm trêncạnh BC
c). .. MAMBMCMD + với M nằm trên đườngtrònnội tiếp hìnhvuông. L
igi
Câu3. Chohìnhthang ABCD có đáy lớn 3 BCa = ,
áynh
ADa = , đườngcao 2 ABa = a).Tính .; .; . ABCDBCBDACBD b).Gọi I làtrung điểm của CD . Hãytínhgócgiữa AI và BD . L
igi
i
Câu4. Chotam giác ABC đều cạnh a , đường cao AH .Tính: a). .; . ABACBAAH
b). ( )( )23 CBCACAAH Lờigiải
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu5. Chohìnhthoi ABCD tâm O cạnh bằng 7 ,góc 060BAC = .Tính: .; .; .; . ABACABOAACBDABOB Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu6. Chocácvectơ , ab có độ dài bằng1 vàthỏamãn điều kiện 233 ab−= .Tính ( )cos,ab . Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Cho các vectơ , ab có độ dài bằng 1 và góc tạo bởi hai vectơ bằng 060 . Xác định cosin góc giữahai vectơ u và v với 2, uabvab =+=−
Câu7.
DẠYKÈMQUYNHƠNOFFICIAL Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu8. Trong mặt phẳng Oxy cho ( ) ( ) ( )1;1,2;4,10;2ABC a).Chứng minh rằng ABC làtamgiácvuông. b).Tính . BABC suyra cosB Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu9. Chohai vectơ đơnvị , ab thỏamãn điềukiện 23 ab−= .Tính .; abab + Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... .....................................................................................................................................................................
ạ
ể
ứ
ọ
ủ
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
D
ng2:Bi
uth
ct
a độ c
atíchvôhướng. 1.Phươngphápgiải. • Cho axybxy == 1122(;), (;) .Khi đó +Tíchvô hướng hai vectơ là abxxyy =+1212. +Góccủahai vectơ đượcxác địnhbởi công thức ababxxyy abxyxy + == ++ 1212 2222 1122 .cos(,) Chú ý: ababxxyy ⊥⇔=⇔+= 1212 .00 • Để xác định độ dài một vectơ đoạnthẳngtasử dụng công thức +Nếu axy = (;) thì axy =+22 +Nếu AABB AxyBxy (;), (;) thì BABA ABxxyy =−+−22 ()() 2.Cácvídụ. Câu1: Cho tam giác ABC có ( ) ( ) ( );,;,;ABC122698 . a) Chứng minh tamgiác ABC vuôngtại A. b)TínhgócB củatamgiác ABC c) Xác địnhhìnhchiếu củaA lêncạnhBC Lờigiải
Câu2. Chocác điểm ( )43;1A , ( )0;3B , ( )83;3C a) Tính cáccạnh củatam giác ABC . b)Tính cácgóccủatam giác ABC .
Câu3. Chocác điểm ( )1;1A , ( )3;1B , ( )6;0C
a) Chứngminhba điểm ,, ABC khôngthẳnghàng. b)Tính góc B vàdiện tíchtam giác ABC Lờigiải .....................................................................................................................................................................
Câu4. Chocác điểm ( )1;3A , ( )4;2B
a) Tìm tọa độ điểm D nằm trên trục Ox vàcách đềuhai điểm A và B b)Tính chuvi và điệntích tam giác OAB . Lờigiải
Câu5. Cho các điểm ( )4;6A , ( )5;1B , ( )1;3C . Tìm tọa độ tâm và bán kính đường tròn ngoại tiếp tamgiác ABC .
Lờigiải
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu6. Cho tam giác ABC có ba đỉnh ( )3;0A , ( )3;0B , ( )2;6C . Tìm tọa độ trọng tâm G và trực tâm H củatam giác. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 7: Cho ba điểm AB(3;4),(2;1) và C(1;2). Tìm điểm M trên đường thẳng BC để góc AMB = 045 Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
C.CÂUHỎITRẮCNGHIỆM
Câu1. Cho và làhai vectơ cùng hướng và đều khácvectơ .Mệnh đề nào sau đây đúng? A. . B. . C. . D. . Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu2. Chohai vectơ và khác .Xác địnhgóc giữahaivectơ và khi A. B. C. D. Lờigiải .....................................................................................................................................................................
Câu3. Cho hai vectơ và thỏa mãn và Xác định góc giữa hai vectơ và A. B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu4.
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
Chohaivectơ và thỏamãn
ơ và
ớ
định góc giữahai vectơ và
Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu5. Chohai vectơ và . Đẳng thứcnào sau đâysai? A. B. C. D. Lờigiải a b 0 .. abab = .0ab = .1ab =− .. abab =− a b 0 α a b abab =− 0 180.α = 0 0.α = 0 90.α = 0 45.α = a b 3,a = 2b = .3.ab =− α a b 0 30.α = 0 45.α = 0 60.α = 0 120.α = a b 1ab== 2 3 5 uab =− vab =+ α a .b 0 90.α = 0 180.α = 0 60.α = 0 45.α = a b 22 21 2 ababab =+−− 2221 2 ababab =+−− 221 .. 2 ababab =+−− 221 .. 4 ababab =+−−
vàhaivect
vuônggócv
i nhau.Xác
A. B. C. D.
Câu6. Chotam giác đều có cạnhbằng Tínhtích vôhướng A. B. C. D. Lờigiải .....................................................................................................................................................................
Câu7. Cho tam giác đều cócạnhbằng Tính tíchvô hướng A. B. C. D. Lờigiải
Câu8. Cho tam giác vuôngcân tại vàcó Tính A. B. C. D. Lờigiải
Câu9. Cho tam giác vuôngtại vàcó Tính A. B. C. D. Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
giác
A. B.
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Câu10. Chotam
có Tính
C. D. Lờigiải ABC .a ..ABAC 2 .2.ABACa = 2 3 2 ABACa =− 2 .. 2 ABACa =− 2 .. 2 ABACa = ABC a ..ABBC 2 ..ABBCa = 2 3 2 ABBCa = 2 .. 2 ABBCa =− 2 .. 2 ABBCa = ABC A .ABACa == ..ABBC 2 ..ABBCa =− 2 ..ABBCa = 2 2 2 ABBCa =− 2 2 2 ABBCa = ABC A , .ABcACb == ..BABC 2BABCb = 2BABCc = 22BABCbc =+ 22BABCbc =− ABC 2cm, 3cm, 5cm.ABBCCA === ..CACB .13.CACB = .15.CACB = .17.CACB = .19.CACB =
ABC , , .BCaCAbABc === ( ) PABACBC =+ 22Pbc =− 22 . 2 cb P + = 222 . 3 cba P ++ = 222 2 cba P +− = ABC , , .BCaCAbABc === M BC AMBC 22 2 AMBCbc = 22 2 AMBCcb + = 222 3 cba AMBC ++ = 222 .. 2 AMBCcba +− = ABCD .a ..ABAC 2ABACa = 2 .2.ABACa = 22 2 ABACa = 21 2 ABACa = ABCD a ( )PACCDCA =+ 1.P =− 2 3.Pa = 2 3.Pa =− 2 2.Pa = ABCD .a ( ) ( )PABACBCBDBA =+++ 22.Pa = 2 2.Pa = 2Pa = 2 2.Pa =−
Câu11. Chotam giác có Tính A. B. C. D. Câu12. Chotamgiác có Gọi làtrung điểmcạnh Tính A. B. C. D. Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu13. Chohìnhvuông cạnh Tính A. B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu14. Chohìnhvuông cạnh .Tính A. B. C. D. Lờigiải ..................................................................................................................................................................... Câu15. Chohìnhvuông cạnh Tính A. B. C. D. Lờigiải .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
Câu16. Chohìnhvuông cạnh .Gọi là điểm đối xứng của qua Tính A. B. C. D. Lờigiải
ABCD a E D C AEAB 2 .2.AEABa = 2 .3.AEABa = 2 .5.AEABa = 2 .5.AEABa =
ABCD 8, 5.ABAD== ABBD .62.ABBD = .64.ABBD = .62.ABBD =− .64.ABBD =−
Câu17. Chohìnhchữ nhật có Tích A. B. C. D. Lờigiải .....................................................................................................................................................................
Câu18. Chohìnhthoi có và Tính A. B. C. D. Lờigiải
Câu19. Cho hình bình hành có , góc nhọn và diện tích bằng Tính A. B. C. D. Lờigiải
Câu20. Cho hình chữ nhật có và . Gọi là trung điểm của cạnh Tính A. B. C. D. Lờigiải .....................................................................................................................................................................
Câu21. Trong mặt phẳng tọa độ cho ba điểm Tính tích vô hướng
ABCD 8AC = 6.BD = ..ABAC .24.ABAC = .26.ABAC = .28.ABAC = .32.ABAC = ABCD 8cm, 12cmABAD== ABC 2 54cm. ( ) cos,. ABBC ( ) 27 cos,. 16 ABBC = ( ) 27 cos,. 16 ABBC =− ( ) 57 cos,. 16 ABBC = ( ) 57 cos,. 16 ABBC =− ABCD ABa = 2ADa = K AD BKAC .0.BKAC = 2 .2.BKACa =− 2 .2.BKACa = 2 .2.BKACa = ,Oxy ( ) ( ) ( )3;1, 2;10, 4;2.ABC
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
A. B. C. D. Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu22. Trong mặt phẳngtọa độ cho hai điểm và Tính tíchvô hướng A. B. C. D. Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu23. Trong mặt phẳngtọa độ cho hai vectơ và Tính tíchvô hướng A. B. C. D. Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu24. Trongmặtphẳngtọa độ chohaivectơ và Tìmtọa độ vectơ biết và A. B. C. D. Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu25. Trong mặt phẳngtọa độ cho bavectơ và Tính A. B. C. D. Lờigiải .....................................................................................................................................................................
40.ABAC = 40.ABAC = 26.ABAC = 26.ABAC = ,Oxy ( )3;1A ( )2;10B AOOB .4.AOOB =− .0.AOOB = .4.AOOB = .16.AOOB = ,Oxy 46 aij =+ 37.bij =− ab .30.ab =− .3.ab = .30.ab = .43.ab = ,Oxy ( )3;2a =− ( ) 1;7.b =−− c .9ca = .20.cb =− ( ) 1;3.c =−− ( ) 1;3.c =− ( ) 1;3.c =− ( ) 1;3.c = ,Oxy ( ) ( )1;2, 4;3ab== ( ) 2;3.c = ( )Pabc =+ 0.P = 18.P = 20.P = 28.P = ,Oxy ( )1;1a =− ( )2;0b = a b ( ) 1 cos,. 2 ab = ( ) 2 cos,. 2 ab =− ( ) 1 cos,. 22 ab =− ( ) 1 cos,. 2 ab =
Câu26. Trong mặt phẳng tọa độ cho hai vectơ và . Tính cosin của góc giữa hai vectơ và A. B. C. D. Lờigiải
DẠYKÈMQUYNHƠNOFFICIAL
ABAC
Câu27. Trongmặtphẳngtọa độ chohaivectơ và .Tínhcosincủagócgiữa hai vectơ và A. B. C. D. Lờigiải
Câu28. Trong mặt phẳng tọa độ cho hai vectơ và . Tính góc giữa hai vectơ và A. B. C. D. Lờigiải
Câu29. Trong mặt phẳng tọa độ cho hai vectơ và . Tính góc giữa hai vectơ và A. B. C. D. Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu30. Trongmặtphẳngtọa độ chohaivectơ và .Tínhgóc giữahaivectơ và A. B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu31. Trong mặt phẳng tọa độ cho vectơ . Vectơ nào sau đây không vuông
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
góc với vectơ ? A. B. C. D. Lờigiải ,Oxy (
a =−− (
b =− a .b ( ) 5 cos,. 5 ab =− ( ) 25 cos,. 5 ab =
= (
2
= ,Oxy
=
= α a .b O 90.α = O 60.α = O
α =
α = ,Oxy
α x y O 45.α = O
α =
,Oxy
=
=− α a b O 30.α = O 45.α = O
α =
α = ,Oxy
a = a ( )1 1;3.v =− (
2
v =−
=
v =−
)2;1
)4;3
( ) 3 cos,. 2 ab
) 1 cos,.
ab
( )4;3a
( )1;7b
45.
O 30.
( )1;2x = ( )3;1y =−−
60.
O 90.α = O 135.α =
( )2;5a
( )3;7b
60.
O 135.
( )9;3
)
2;6.
( )3 1;3.v
( )4 1;3.
Câu32. Trongmặtphẳngtọa độ choba điểm và .Tínhcosincủagócgiữa hai vectơ và A. B. C. D. Lờigiải
Câu33. Trong mặt phẳng tọa độ cho tam giác có và . Tính số đo góc củatam giác đãcho. A. B. C. D. Lờigiải
Câu34. Trongmặtphẳngtọa độ chohaivectơ và Tìm để vectơ vuông gócvới A. B. C. D. Lờigiải
Câu35. Trong mặt phẳng tọa độ cho hai vectơ và Tìm để vectơ và vectơ có độ dài bằng nhau. A. B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu36. Trong mặt phẳng tọa
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
độ cho ba vectơ và với ,Oxy ( ) ( )1;2, 1;1AB ( )5;1C AB AC ( ) 1 cos,. 2 ABAC =− ( ) 3 cos,. 2 ABAC = ( ) 2 cos,. 5 ABAC =− ( ) 5 cos,. 5 ABAC =− ,Oxy ABC ( ) ( )6;0, 3;1AB ( )1;1C B O 15. O 60. O 120. O 135. ,Oxy 1 5 2 uij =− 4 vkij =− k u v 20.k = 20.k =− 40.k =− 40.k = ,Oxy 1 5 2 uij =− 4.vkij =− k u v 37 . 4 k = 37 . 2 k = 37 . 2 k =± 5 8 k = ,Oxy ( ) ( )2;3, 4;1ab=−= ckamb =+ , .km ∈ ℝ
Bi
t rằngvectơ vuông gócvớivectơ .Khẳng địnhnàosau đây đúng? A. B. C. D. Lờigiải
Câu37. Trong mặt phẳng tọa độ cho hai vectơ và . Tìm vectơ biết và . A. B. C. D. Lờigiải
Câu38. Trongmặtphẳngtọa độ chobavectơ và với Tìm để vuônggócvới trụchoành. A. B. C. D. Lờigiải .....................................................................................................................................................................
Câu39. Trong mặt phẳngtọa độ chohai vectơ và Tìm để vectơ tạo với vectơ một góc A. B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Câu40. Trong mặt phẳngtọa độ tínhkhoảngcách giữ
DẠYKÈMQUYNHƠNOFFICIAL
ế
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
ahai điểm và A. B. C. D. Lờigiải ..................................................................................................................................................................... Trong mặt phẳng tọa độ cho tam giác có . Tính chu vi của tam giác đãcho. A. B. C. D. Lờigiải c ( )ab + 22. km = 32. km = 230. km+= 320. km+= ,Oxy ( )2;3a =− ( )4;1b = d .4ad = .2bd =− 56 77;.d = 56 77;.d =− 56 77;.d =− 56 77;.d =−− ,Oxy ( ) ( )4;1, 1;4uv== aumv =+ m ∈ ℝ m a 4.m = 4.m =− 2.m =− 2.m = ,Oxy ( )4;1u = ( ) 1;4.v = m amuv =+ bij =+ 0 45. 4.m = 1 2 m =− 1 4 m =− 1 2 m = ,Oxy ( )1;2M ( ) 3;4.N 4.MN = 6.MN = 36.MN = 213.MN = ,Oxy ABC ( ) ( ) ( )1;4, 3;2, 5;4ABC P 422.P =+ 442.P =+ 882.P =+ 222.P =+
Câu41. Trong hệ tọa độ ,cho vectơ Độ dài củavectơ bằng A. B. C. D. Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu42. Trongmặtphẳngtọa độ chohai điểm và Tìmtọa độ điểm thuộctrục hoành saocho tamgiác vuôngtại A. B. C. D. Lờigiải .....................................................................................................................................................................
Câu43. Trong mặt phẳng tọa độ cho hai điểm và Tìm tọa độ điểm thuộc trục tung saocho tamgiác vuôngtại A. B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Câu44. Trong mặt phẳng tọa độ cho ba điểm và Tìm điểm thuộc trụchoành sao cho A. B. C. D. Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
( );; Oij 34 55 aij =−− a 1 . 5 1. 6 . 5 7 . 5 ,Oxy ( )2;4A ( ) 8;4.B C ABC .C ( )6;0C ( ) 0;0,C ( )6;0C ( )0;0C ( ) 1;0.C ,Oxy ( )1;2A ( ) 3;1.B C ABC A ( )0;6C ( )5;0C ( )3;1C ( ) 0;6.C ,Oxy ( ) ( )–4;0, –5;0AB ( )3;0C M 0.MAMBMC++= ( ) –2;0.M ( ) 2;0.M ( ) –4;0.M ( ) –5;0.M ,Oxy ( )–2;2M ( )1;1N P ,, MNP ( )0;4P ( )0;–4P ( )–4;0P ( )4;0P
Câu45. Trongmặtphẳngtọa độ chohai điểm và Tìmtọa độ điểm thuộctrục hoành saocho ba điểm thẳnghàng. A. B. C. D. Lờigiải
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
Câu46. Trong mặt phẳng tọa độ tìm điểm thuộc trục hoành để khoảng cách từ đó đến điểm bằng A. B. C. D. Lờigiải
Câu47. Trong mặt phẳng tọa độ cho hai điểm và Tìm tọa độ điểm thuộc trục hoành saocho cách đều hai điểm và A. B. C. D. Lờigiải
Câu48. Trong mặt phẳng tọa độ cho hai điểm Tìm điểm thuộc trục hoàng saocho A. B. C. D. Lờigiải .....................................................................................................................................................................
Câu49. Trongmặtphẳngtọa độ chohai điểm và Tìm thuộctrụctungsaocho nhỏ nhất. A.
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu50. Trong mặt phẳng tọa độ cho hình bình hành biết Tìm tọa độ điểm ,Oxy M ( )1;4N 25. ( ) 1;0.M ( ) ( )1;0, 3;0.MM ( ) 3;0.M ( ) ( )1;0, 3;0.MM ,Oxy ( )1;3A ( ) 4;2.B C C A B 5;0. 3 C 5;0. 3 C 3;0. 5 C 3;0. 5 C ,Oxy
0 90?AMB = (
,Oxy
22MAMB + ( ) 0;1.M (
M 1 0;. 2 M 1 0;. 2 M ,Oxy ABCD
D
( ) ( ) 2;2,5;2.AB M
) 0;1.M ( ) 6;0.M ( ) 1;6.M ( ) 0;6.M
( )1;1A ( ) 3;2.B M
) 0;1.
( ) 2;0,A ( ) 2;5,B ( ) 6;2.C
A. B. C. D. Lờigiải
Câu51. Trong mặt phẳngtọa độ cho tamgiác có Tìmtọa độ trọng tâm củatam giác đãcho. A. B. C. D. Lờigiải .....................................................................................................................................................................
Trong mặt phẳng tọa độ cho tam giác có Tìm tọa độ tâm của đường tròn ngoại tiếptam giác đãcho. A. B. C. D. Lờigiải
Câu52. Trong mặt phẳngtọa độ chotam giác có và Gọi là tọa độ trựctâm
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
củatam giác đãcho.Tính A. B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu53. Trong mặt phẳng tọa độ cho tam giác có và Tìm toạ độ chân đườngcao kẻ từ đỉnh xuống cạnh A. B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ( ) 2;3.D ( ) 2;3.D ( ) 2;3.D ( ) 2;3.D ,Oxy ABC ( ) ( ) ( )1;3, 2;4, 5;3.ABC G 10 2;. 3 G 810 33;.G ( ) 2;5.G 410 33;.G ,Oxy ABC ( ) ( )4;1, 2;4,AB ( ) 2;2.C I 1 4;1.I 1 4;1.I 1 1;. 4 I 1 1;. 4 I ,Oxy ABC ( ) ( )3;0, 3;0AB ( ) 2;6.C ( ); Hab 6.ab + 65.ab+= 66.ab+= 67.ab+= 68.ab+= ,Oxy ABC ( ) ( )4;3,2;7AB ( ) 3;8.C 'A A BC ( ) '1;4.A ( ) '1;4.A ( ) '1;4.A ( ) '4;1.A
Câu54. Trongmặtphẳngtọa độ chotamgiác có Tìmtọa độ chân đường cao vẽ từ đỉnh củatam giác đãcho. A. B. C. D. Lờigiải
Câu55. Trong mặt phẳng tọa độ , cho ba điểm và Tìm tọa độ điểm để tứ giác làhìnhvuông. A. B. C. D. Lờigiải
Câu56. Trong mặt phẳngtọa độ cho hai điểm và Tìm t
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
ặ
ẳ
ọ
Tìm tọa độ điểm ,biết có tung độ âm. A. B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ,Oxy ABC ( ) ( )2;4, 3;1,AB ( ) 3;1.C 'A A 31 ';. 55 A 31 ';. 55 A 31 ';. 55 A 31 ';. 55 A Oxy ( ) ( )3;2, 3;6AB ( )
C D ABCD ( )
D (
D ( )
D (
D ,Oxy
ABC
(
,Oxy ABCD ( )1;1A ( )
B D D ( ) 0;1.D ( ) 2;3.D (
DD (
D
ọa độ điểm sao chotam giác vuôngcân tại A. B. C. D. Lờigiải
Câu57. Trong m
t ph
ng t
a độ cho hình vuông có và
11;0.
5;8.
) 8;5.
5;8.
) 8;5.
( )2;4A ( ) 1;1.B C
B
) 4;0.C ( ) 2;2.C ( ) ( )4;0, 2;2.CC ( ) 2;0.C
3;0.
) ( )2;3, 0;1.
) 2;3.
DẠYKÈMQUYNHƠNOFFICIAL
ặ
phẳng tọ
ớ
và
ọa độ đ
ể
ngphân
ủ
giác A. B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ,Oxy OAB ( )1;3A ( )4;2B E O OAB 55 22;.E = 31 22;.E =− ( ) 232;42.E =−++ (
232;42.E =−+−
Câu58. Trong m
t
a độ cho tam giác v
i
. Tìm t
i
m là chân đườ
giáctronggóc c
atam
)
A.KIẾNTHỨCCƠ BẢNCẦNNẮM
1.Gócgiữahaivectơ
Chohai vectơ a và b đềukhác 0 .Từ một điểm O bất kì tavẽ , == OAaOBb
Góc AOB với số đo từ 0 ° đến 180 ° đượcgọi làgócgiữahai vectơ a và b .
Takí hiệugócgiữahai vectơ a và b là (,) ab .
Nếu (,)90 ° =ab thì tanói rằng a và b vuônggócvới nhau,kí hiệulà ⊥ ab
Chúý:
-Tử định nghĩatacó (,)(,) = abba .
-Gócgiữahai vectơ cùnghướngvàkhác 0 luônbằng 0 °
-Gócgiữahai vectơ ngượchướng vàkhác 0 luônbằng 180 ° .
- Trong trường hợp có it nhất một trong hai vectơ a hoặc b là vectơ 0 thi ta quy ước số đo góc giữa hai vectơ đó làtuỳ ý(từ 0 ° đến 180 ° ).
2.Tíchvôhướngcủahaivecto' Chohai vectơ a và b đềukhác 0
Tíchvô hướngcủa a và b làmột số,kihiệu là ab , đượcxác địnhbởi công thức: ||||cos(,)⋅=⋅⋅ ababab .
Chúý:
-Trường hợpitnhất một trong hai vectơ a và b bằng 0 ,taquy ước 0⋅=ab . -Với hai vectơ a và b đều khác 0 ,tacó 0⊥⇔⋅=abab - Khi = ab thi tich vô hướng ⋅ ab được ki hiệu là

DẠYKÈMQUYNHƠNOFFICIAL BÀI4.TÍCHVÔHƯỚNGHAIVECT
Ơ
2 a và được gọi là binh phrơng vô hiróng của vectơ a Tacó 22 ||||cos0|| ° =⋅⋅= aaaa Vậybìnhphươngvô hướng củamột vectơ luônbằngbìnhphương đô dài củavectơ đó. 3.Tínhchấtcủatíchvôhướng -Với bavectơ ,, abc bất kì vàmọi số k ,tacó: - ;⋅=⋅ abba ();•()()() ⋅+=⋅+⋅⋅=⋅=⋅ abcabackabkabakb . -Từ cáctính chất củatích vôhướngcủahai vectơ,tasuyra:222()2+=+⋅+ abaabb222()2−=−⋅+ abaabb22()()+⋅−=− ababab .
4.Ápdụngcủatíchvôhướng
Trong Vật li, tích vô hướng giúp tinh công sinhA bởi một lực F có độ dịch chuyển là vectơ d . Ta có công thức: =⋅ AFd . B.PHÂNLOẠIVÀPHƯƠNGPHÁPGIẢIBÀITẬP
Dạng1:Tínhtíchvôhướng2vectơ vàxác địnhgóccủahaivecto
1.Phươngphápgiải.
a) Để tínhtích vôhướng củahai vectơ,tacó thể sử dụng:
ab ab ab = 2.Cácvídụ. Câu10. Chotam giác ABC đều cạnh a ,tâm O .Hãy tính: a). . ABAC b). . ABBC c). ( )( )OBOCABAC +− d). ( )( )23 ABACABBC +− Lờigiải
Câu11. Chohìnhvuông ABCD cạnh a ,tâm O .Hãytính: a). ( )( ) ( )( ).; .; ; ABBCABBDABADBDBCABACADDADBDC ++++++
DẠYKÈMQUYNHƠNOFFICIAL
+Nếu có độ dài hai vectơ vàgócgiữachúng,tadùng định nghĩa ( )..cos, ababab = +Nếu làtích củatổng,hiệu cácvectơ tadùngtính chất củatích vôhướng + Nếu biết độ dài hai vectơ và độ dài của tổng hay hiệu của chúng, ta bình phương tổng hay hiệucủachúng +Nếu một vectơ cố định vàmột vectơ thay đổi ta cóthể dùng định lýhìnhchiếu. b) Để tính góccủahai vectơ,tasử dụng côngthức: () . cos, . ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
ỏ
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
b). .; . ONABNAAB với N là điểm trêncạnh BC . c). .. MAMBMCMD + với M nằm trên đườngtrònnội tiếp hìnhvuông. Lờigiải
Câu12. Chohìnhthang ABCD có đáy lớn 3 BCa = , đáynh
ADa = , đườngcao 2 ABa = a).Tính .; .; . ABCDBCBDACBD b).Gọi I làtrung điểm của CD . Hãytínhgócgiữa AI và BD . Lờigiải
Câu13. Chotam giác ABC đều cạnh a , đường cao AH .Tính: a). .; . ABACBAAH . b). ( )( )23 CBCACAAH Lờigiải
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Chohìnhthoi ABCD tâm O cạnh bằng 7 ,góc 060BAC = .Tính: .; .; .; . ABACABOAACBDABOB Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Chocácvectơ , ab có độ dài bằng1 vàthỏamãn điều kiện 233 ab−= .Tính
cos,ab . Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Cho các vectơ , ab có độ dài bằng 1 và góc tạo bởi hai vectơ bằng 060 . Xác định cosin góc giữahai vectơ u và v với 2, uabvab =+=−
Câu14.
Câu15.
( )
Câu16.
DẠYKÈMQUYNHƠNOFFICIAL Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu17. Trong mặt phẳng Oxy cho ( ) ( ) ( )1;1,2;4,10;2ABC a).Chứng minh rằng ABC làtamgiácvuông. b).Tính . BABC suyra cosB Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu18. Chohai vectơ đơnvị , ab thỏamãn điềukiện 23 ab−= .Tính .; abab + Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL ..................................................................................................................................................................... .....................................................................................................................................................................
ạ
ể
ứ
ọ
ủ
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
D
ng2:Bi
uth
ct
a độ c
atíchvôhướng. 1.Phươngphápgiải. • Cho axybxy == 1122(;), (;) .Khi đó +Tíchvô hướng hai vectơ là abxxyy =+1212. +Góccủahai vectơ đượcxác địnhbởi công thức ababxxyy abxyxy + == ++ 1212 2222 1122 .cos(,) Chú ý: ababxxyy ⊥⇔=⇔+= 1212 .00 • Để xác định độ dài một vectơ đoạnthẳngtasử dụng công thức +Nếu axy = (;) thì axy =+22 +Nếu AABB AxyBxy (;), (;) thì BABA ABxxyy =−+−22 ()() 2.Cácvídụ. Câu1: Cho tam giác ABC có ( ) ( ) ( );,;,;ABC122698 . a) Chứng minh tamgiác ABC vuôngtại A. b)TínhgócB củatamgiác ABC c) Xác địnhhìnhchiếu củaA lêncạnhBC Lờigiải
Câu7. Chocác điểm ( )43;1A , ( )0;3B , ( )83;3C a) Tính cáccạnh củatam giác ABC . b)Tính cácgóccủatam giác ABC .
Câu8. Chocác điểm ( )1;1A , ( )3;1B , ( )6;0C
a) Chứngminhba điểm ,, ABC khôngthẳnghàng. b)Tính góc B vàdiện tíchtam giác ABC Lờigiải .....................................................................................................................................................................
Câu9. Chocác điểm ( )1;3A , ( )4;2B
a) Tìm tọa độ điểm D nằm trên trục Ox vàcách đềuhai điểm A và B b)Tính chuvi và điệntích tam giác OAB . Lờigiải
Câu10. Cho các điểm ( )4;6A , ( )5;1B , ( )1;3C . Tìm tọa độ tâm và bán kính đường tròn ngoại tiếp tamgiác ABC .
Lờigiải
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu11. Cho tam giác ABC có ba đỉnh ( )3;0A , ( )3;0B , ( )2;6C . Tìm tọa độ trọng tâm G và trực tâm H củatam giác. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu 7: Cho ba điểm AB(3;4),(2;1) và C(1;2). Tìm điểm M trên đường thẳng BC để góc AMB = 045 Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
C.CÂUHỎITRẮCNGHIỆM
Câu59. Cho và làhai vectơ cùng hướng và đều khácvectơ .Mệnh đề nào sau đây đúng? A. . B. . C. . D. . Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu60. Chohai vectơ và khác .Xác địnhgóc giữahaivectơ và khi A. B. C. D. Lờigiải .....................................................................................................................................................................
Câu61. Cho hai vectơ và thỏa mãn và Xác định góc giữa hai vectơ và A. B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu62.
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
Chohaivectơ và thỏamãn vàhaivectơ và
ới
định góc giữahai vectơ và
Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu63. Chohai vectơ và . Đẳng thứcnào sau đâysai? A. B. C. D. Lờigiải a b 0 .. abab = .0ab = .1ab =− .. abab =− a b 0 α a b abab =− 0 180.α = 0 0.α = 0 90.α = 0 45.α = a b 3,a = 2b = .3.ab =− α a b 0 30.α = 0 45.α = 0 60.α = 0 120.α = a b 1ab== 23 5 uab =− vab =+ α a .b 0 90.α = 0 180.α = 0 60.α = 0 45.α = a b 22 21 2 ababab =+−− 2221 2 ababab =+−− 221 .. 2 ababab =+−− 221 .. 4 ababab =+−−
vuônggócv
nhau.Xác
A. B. C. D.
Câu64. Chotam giác đều có cạnhbằng Tínhtích vôhướng A. B. C. D. Lờigiải .....................................................................................................................................................................
Câu65. Cho tamgiác đều cócạnh bằng Tính tíchvô hướng A. B. C. D. Lờigiải
Câu66. Cho tamgiác vuôngcân tại vàcó Tính A. B. C. D. Lờigiải
Câu67. Cho tamgiác vuôngtại vàcó Tính A. B. C. D. Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
Chotam giác có
B. C.
DẠYKÈMQUYNHƠNOFFICIAL .....................................................................................................................................................................
.....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Câu68.
Tính A.
D. Lờigiải ABC .a ..ABAC 2 .2.ABACa = 2 3 2 ABACa =− 2 .. 2 ABACa =− 2 .. 2 ABACa = ABC a ..ABBC 2 ..ABBCa = 2 3 2 ABBCa = 2 .. 2 ABBCa =− 2 .. 2 ABBCa = ABC A .ABACa == ..ABBC 2 ..ABBCa =− 2 ..ABBCa = 2 2 2 ABBCa =− 2 2 2 ABBCa = ABC A , .ABcACb == ..BABC 2BABCb = 2BABCc = 22BABCbc =+ 22BABCbc =− ABC 2cm, 3cm, 5cm.ABBCCA === ..CACB .13.CACB = .15.CACB = .17.CACB = .19.CACB =
ABC , , .BCaCAbABc === ( ) PABACBC =+ 22Pbc =− 22 . 2 cb P + = 222 . 3 cba P ++ = 222 2 cba P +− = ABC , , .BCaCAbABc === M BC AMBC 22 2 AMBCbc = 22 2 AMBCcb + = 222 3 cba AMBC ++ = 222 .. 2 AMBCcba +− = ABCD .a ..ABAC 2ABACa = 2 .2.ABACa = 22 2 ABACa = 21 2 ABACa = ABCD a ( )PACCDCA =+ 1.P =− 2 3.Pa = 2 3.Pa =− 2 2.Pa = ABCD .a ( ) ( )PABACBCBDBA =+++ 22.Pa = 2 2.Pa = 2Pa = 2 2.Pa =−
Câu69. Chotam giác có Tính A. B. C. D. Câu70. Chotamgiác có Gọi làtrung điểmcạnh Tính A. B. C. D. Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu71. Chohìnhvuông cạnh Tính A. B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... Câu72. Chohìnhvuông cạnh .Tính A. B. C. D. Lờigiải ..................................................................................................................................................................... Câu73. Chohìnhvuông cạnh Tính A. B. C. D. Lờigiải .....................................................................................................................................................................
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
ABCD a E D C AEAB 2 .2.AEABa = 2 .3.AEABa = 2 .5.AEABa = 2 .5.AEABa =
Câu74. Chohìnhvuông cạnh .Gọi là điểm đối xứng của qua Tính A. B. C. D. Lờigiải .....................................................................................................................................................................
ABCD 8, 5.ABAD== ABBD .62.ABBD = .64.ABBD = .62.ABBD =− .64.ABBD =−
Câu75. Chohìnhchữ nhật có Tích A. B. C. D. Lờigiải .....................................................................................................................................................................
Câu76. Chohìnhthoi có và Tính A. B. C. D. Lờigiải
Câu77. Cho hình bình hành có , góc nhọn và diện tích bằng Tính A. B. C. D. Lờigiải
Câu78. Cho hình chữ nhật có và . Gọi là trung điểm của cạnh Tính A. B. C. D. Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu79. Trong mặt phẳng tọa độ cho ba điểm Tính tích vô hướng
ABCD 8AC = 6.BD = ..ABAC .24.ABAC = .26.ABAC = .28.ABAC = .32.ABAC = ABCD 8cm, 12cmABAD== ABC 2 54cm. ( ) cos,. ABBC ( ) 27 cos,. 16 ABBC = ( ) 27 cos,. 16 ABBC =− ( ) 57 cos,. 16 ABBC = ( ) 57 cos,. 16 ABBC =− ABCD ABa = 2ADa = K AD BKAC .0.BKAC = 2 .2.BKACa =− 2 .2.BKACa = 2 .2.BKACa = ,Oxy ( ) ( ) ( )3;1, 2;10, 4;2.ABC
DẠYKÈMQUYNHƠNOFFICIAL
.....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
A. B. C. D. Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu80. Trong mặt phẳngtọa độ cho hai điểm và Tính tíchvô hướng A. B. C. D. Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu81. Trong mặt phẳngtọa độ cho hai vectơ và Tính tíchvô hướng A. B. C. D. Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu82. Trongmặtphẳngtọa độ chohaivectơ và Tìmtọa độ vectơ biết và A. B. C. D. Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu83. Trong mặt phẳngtọa độ cho bavectơ và Tính A. B. C. D. Lờigiải .....................................................................................................................................................................
40.ABAC = 40.ABAC = 26.ABAC = 26.ABAC = ,Oxy ( )3;1A ( )2;10B AOOB .4.AOOB =− .0.AOOB = .4.AOOB = .16.AOOB = ,Oxy 46 aij =+ 37.bij =− ab .30.ab =− .3.ab = .30.ab = .43.ab = ,Oxy ( )3;2a =− ( ) 1;7.b =−− c .9ca = .20.cb =− ( ) 1;3.c =−− ( ) 1;3.c =− ( ) 1;3.c =− ( ) 1;3.c = ,Oxy ( ) ( )1;2, 4;3ab== ( ) 2;3.c = ( )Pabc =+ 0.P = 18.P = 20.P = 28.P = ,Oxy ( )1;1a =− ( )2;0b = a b ( ) 1 cos,. 2 ab = ( ) 2 cos,. 2 ab =− ( ) 1 cos,. 22 ab =− ( ) 1 cos,. 2 ab =
Câu84. Trong mặt phẳng tọa độ cho hai vectơ và . Tính cosin của góc giữa hai vectơ và A. B. C. D. Lờigiải
DẠYKÈMQUYNHƠNOFFICIAL
ABAC
Câu85. Trongmặtphẳngtọa độ chohaivectơ và .Tínhcosincủagócgiữa hai vectơ và A. B. C. D. Lờigiải
Câu86. Trong mặt phẳng tọa độ cho hai vectơ và . Tính góc giữa hai vectơ và A. B. C. D. Lờigiải
Câu87. Trong mặt phẳng tọa độ cho hai vectơ và . Tính góc giữa hai vectơ và A. B. C. D. Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu88. Trongmặtphẳngtọa độ chohaivectơ và .Tínhgóc giữahaivectơ và A. B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu89. Trong mặt phẳng tọa độ cho vectơ . Vectơ nào sau đây không vuông
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
góc với vectơ ? A. B.
Lờigiải ,Oxy
=−−
=− a .b (
5
5
=−
=
,
a .
O
α = O
x
O
,
α a
O
α = O
α =
,Oxy
= a (
1
v =−
C. D.
( )2;1a
( )4;3b
)
cos,.
ab
( ) 25 cos,. 5 ab
( ) 3 cos,. 2 ab = ( ) 1 cos,. 2 ab =
Oxy ( )4;3a = ( )1;7b = α
b
90.
60.α = O 45.α = O 30.α = ,Oxy ( )1;2x = ( )3;1y =−− α
y
45.α = O 60.α = O 90.α = O 135.α =
Oxy ( )2;5a = ( )3;7b =−
b
30.
45.
O 60.α = O 135.α =
( )9;3a
)
1;3.
( )2 2;6.v =− ( )3 1;3.v = ( )4 1;3.v =−
Câu90. Trongmặtphẳngtọa độ choba điểm và .Tínhcosincủagócgiữa hai vectơ và A. B. C. D. Lờigiải
Câu91. Trong mặt phẳng tọa độ cho tam giác có và . Tính số đo góc củatam giác đãcho. A. B. C. D. Lờigiải
Câu92. Trongmặtphẳngtọa độ chohaivectơ và Tìm để vectơ vuông gócvới A. B. C. D. Lờigiải
Câu93. Trong mặt phẳng tọa độ cho hai vectơ và Tìm để vectơ và vectơ có độ dài bằng nhau. A. B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu94. Trong mặt phẳng tọa
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
độ cho ba vectơ và với ,Oxy ( ) ( )1;2, 1;1AB ( )5;1C AB AC ( ) 1 cos,. 2 ABAC =− ( ) 3 cos,. 2 ABAC = ( ) 2 cos,. 5 ABAC =− ( ) 5 cos,. 5 ABAC =− ,Oxy ABC ( ) ( )6;0, 3;1AB ( )1;1C B O 15. O 60. O 120. O 135. ,Oxy 1 5 2 uij =− 4 vkij =− k u v 20.k = 20.k =− 40.k =− 40.k = ,Oxy 1 5 2 uij =− 4.vkij =− k u v 37 . 4 k = 37 . 2 k = 37 . 2 k =± 5 8 k = ,Oxy ( ) ( )2;3, 4;1ab=−= ckamb =+ , .km ∈ ℝ
Bi
t rằngvectơ vuông gócvớivectơ .Khẳng địnhnàosau đây đúng? A. B. C. D. Lờigiải
Câu95. Trong mặt phẳng tọa độ cho hai vectơ và . Tìm vectơ biết và . A. B. C. D. Lờigiải
Câu96. Trongmặtphẳngtọa độ chobavectơ và với Tìm để vuônggócvới trụchoành. A. B. C. D. Lờigiải .....................................................................................................................................................................
Câu97. Trong mặt phẳngtọa độ chohai vectơ và Tìm để vectơ tạo với vectơ một góc A. B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Câu98. Trong mặt phẳngtọa độ tínhkhoảngcách giữ
DẠYKÈMQUYNHƠNOFFICIAL
ế
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
ahai điểm và A. B. C. D. Lờigiải ..................................................................................................................................................................... Trong mặt phẳng tọa độ cho tam giác có . Tính chu vi của tam giác đãcho. A. B. C. D. Lờigiải c ( )ab + 22. km = 32. km = 230. km+= 320. km+= ,Oxy ( )2;3a =− ( )4;1b = d .4ad = .2bd =− 56 77;.d = 56 77;.d =− 56 77;.d =− 56 77;.d =−− ,Oxy ( ) ( )4;1, 1;4uv== aumv =+ m ∈ ℝ m a 4.m = 4.m =− 2.m =− 2.m = ,Oxy ( )4;1u = ( ) 1;4.v = m amuv =+ bij =+ 0 45. 4.m = 1 2 m =− 1 4 m =− 1 2 m = ,Oxy ( )1;2M ( ) 3;4.N 4.MN = 6.MN = 36.MN = 213.MN = ,Oxy ABC ( ) ( ) ( )1;4, 3;2, 5;4ABC P 422.P =+ 442.P =+ 882.P =+ 222.P =+
Câu99. Trong hệ tọa độ ,cho vectơ Độ dài củavectơ bằng A. B. C. D. Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
Câu100. Trongmặtphẳngtọa độ chohai điểm và Tìmtọa độ điểm thuộctrục hoành saocho tamgiác vuôngtại A. B. C. D. Lờigiải .....................................................................................................................................................................
Câu101. Trong mặt phẳng tọa độ cho hai điểm và Tìm tọa độ điểm thuộc trục tung saocho tamgiác vuôngtại A. B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Câu102. Trong mặt phẳng tọa độ cho ba điểm và Tìm điểm thuộc trụchoành sao cho A. B. C. D. Lờigiải ..................................................................................................................................................................... .....................................................................................................................................................................
( );; Oij 34 55 aij =−− a 1 . 5 1. 6 . 5 7 . 5 ,Oxy ( )2;4A ( ) 8;4.B C ABC .C ( )6;0C ( ) 0;0,C ( )6;0C ( )0;0C ( ) 1;0.C ,Oxy ( )1;2A ( ) 3;1.B C ABC A ( )0;6C ( )5;0C ( )3;1C ( ) 0;6.C ,Oxy ( ) ( )–4;0, –5;0AB ( )3;0C M 0.MAMBMC++= ( ) –2;0.M ( ) 2;0.M ( ) –4;0.M ( ) –5;0.M ,Oxy ( )–2;2M ( )1;1N P ,, MNP ( )0;4P ( )0;–4P ( )–4;0P ( )4;0P
Câu103. Trongmặtphẳngtọa độ chohai điểm và Tìmtọa độ điểm thuộctrục hoành saocho ba điểm thẳnghàng. A. B. C. D. Lờigiải
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
Câu104. Trong mặt phẳng tọa độ tìm điểm thuộc trục hoành để khoảng cách từ đó đến điểm bằng A. B. C. D. Lờigiải
Câu105. Trong mặt phẳng tọa độ cho hai điểm và Tìm tọa độ điểm thuộc trục hoành saocho cách đều hai điểm và A. B. C. D. Lờigiải
Câu106. Trong mặt phẳng tọa độ cho hai điểm Tìm điểm thuộc trục hoàng saocho A. B. C. D. Lờigiải .....................................................................................................................................................................
Câu107. Trongmặtphẳngtọa độ chohai điểm và Tìm thuộctrụctungsaocho nhỏ nhất. A.
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu108. Trong mặt phẳng tọa độ cho hình bình hành biết Tìm tọa độ điểm ,Oxy M ( )1;4N 25. ( ) 1;0.M ( ) ( )1;0, 3;0.MM ( ) 3;0.M ( ) (
1;0, 3;0.MM ,Oxy ( )1;3A ( ) 4;2.B C C A B 5;0. 3 C 5;0. 3 C 3;0. 5 C 3;0. 5 C ,Oxy
0 90?AMB = (
,Oxy
22MAMB + ( ) 0;1.M (
1 0;. 2 M 1 0;. 2 M ,Oxy ABCD
D
)
( ) ( ) 2;2,5;2.AB M
) 0;1.M ( ) 6;0.M ( ) 1;6.M ( ) 0;6.M
( )1;1A ( ) 3;2.B M
) 0;1.M
( ) 2;0,A ( ) 2;5,B ( ) 6;2.C
A. B. C. D. Lờigiải
Câu109. Trong mặt phẳngtọa độ cho tamgiác có Tìmtọa độ trọng tâm củatam giác đãcho. A. B. C. D. Lờigiải .....................................................................................................................................................................
Trong mặt phẳng tọa độ cho tam giác có Tìm tọa độ tâm của đường tròn ngoại tiếptam giác đãcho. A. B. C. D. Lờigiải
Câu110. Trong mặt phẳngtọa độ chotam giác có và Gọi là tọa độ trựctâm
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
..................................................................................................................................................................... .....................................................................................................................................................................
củatam giác đãcho.Tính A. B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... Câu111. Trong mặt phẳng tọa độ cho tam giác có và Tìm toạ độ chân đườngcao kẻ từ đỉnh xuống cạnh A. B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ( ) 2;3.D ( ) 2;3.D ( ) 2;3.D ( ) 2;3.D ,Oxy ABC ( ) ( ) ( )1;3, 2;4, 5;3.ABC G 10 2;. 3 G 810 33;.G ( ) 2;5.G 410 33;.G ,Oxy ABC ( ) ( )4;1, 2;4,AB ( ) 2;2.C I 1 4;1.I 1 4;1.I 1 1;. 4 I 1 1;. 4 I ,Oxy ABC ( ) ( )3;0, 3;0AB ( ) 2;6.C ( ); Hab 6.ab + 65.ab+= 66.ab+= 67.ab+= 68.ab+= ,Oxy ABC ( ) ( )4;3,2;7AB ( ) 3;8.C 'A A BC ( ) '1;4.A ( ) '1;4.A ( ) '1;4.A ( ) '4;1.A
Câu112. Trongmặtphẳngtọa độ chotamgiác có Tìmtọa độ chân đường cao vẽ từ đỉnh củatam giác đãcho. A. B. C. D. Lờigiải
Câu113. Trong mặt phẳng tọa độ , cho ba điểm và Tìm tọa độ điểm để tứ giác làhìnhvuông. A. B. C. D. Lờigiải
Câu114. Trong mặt phẳngtọa độ cho hai điểm và
DẠYKÈMQUYNHƠNOFFICIAL
..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
.....................................................................................................................................................................
.....................................................................................................................................................................
.....................................................................................................................................................................
..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... ..................................................................................................................................................................... .....................................................................................................................................................................
Trong
ặt phẳng tọa độ
và Tìm tọa độ điểm ,biết có tung độ âm. A. B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ,Oxy ABC ( ) ( )2;4, 3;1,AB ( ) 3;1.C 'A A 31 ';. 55 A 31 ';. 55 A 31 ';. 55 A 31 ';. 55 A Oxy ( ) ( )
AB ( )
C D ABCD ( )
D (
D (
D (
D ,Oxy
,Oxy ABCD ( )
A ( )
B D D ( ) 0;1.D ( ) 2;3.D (
DD
D
Tìm tọa độ điểm sao chotam giác vuôngcân tại A. B. C. D. Lờigiải
Câu115.
m
cho hình vuông có
3;2, 3;6
11;0.
5;8.
) 8;5.
) 5;8.
) 8;5.
( )2;4A ( ) 1;1.B C ABC B ( ) 4;0.C ( ) 2;2.C ( ) ( )4;0, 2;2.CC ( ) 2;0.C
1;1
3;0.
) ( )2;3, 0;1.
( ) 2;3.
DẠYKÈMQUYNHƠNOFFICIAL
Trong mặt phẳng tọa độ
tam giác với và . Tìm tọa độ điể
là
đườngphân giáctronggóc củatam giác A. B. C. D. Lờigiải ..................................................................................................................................................................... ..................................................................................................................................................................... ,Oxy OAB ( )1;3A ( )4;2B E O OAB 55 22;.E = 31 22;.E =− ( ) 232;42.E =−++ ( ) 232;42.E =−+−
Câu116.
cho
m
chân