BÀI GIẢNG TOÁN 10 BỘ SÁCH CHÂN TRỜI SÁNG TẠO - BÀI TẬP TỰ LUẬN, TRẮC NGHIỆM THEO DẠNG (CHƯƠNG 1-3) by Dạy Kèm Quy Nhơn Official

BÀI GIẢNG TOÁN 10 BỘ CHÂN TRỜI SÁNG TẠO Ths Nguyễn Thanh Tú eBook Collection BÀI GIẢNG TOÁN 10 BỘ SÁCH CHÂN TRỜI SÁNG TẠO TÓM TẮT LÝ THUYẾT - BÀI TẬP TỰ LUẬN, TRẮC NGHIỆM THEO DẠNG (1831 TRANG) (CHƯƠNG 1 3) WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL.COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/30416001

BÀI1:MỆNHĐỀ

1. MỆNH ĐỀ, MỆNH ĐỀ CHỨABIẾN

a. Mệnh đề:

Mệnh đề là những khẳng định có tính đúng hoặc sai. Người ta gọi là một mệnh đề lôgic (gọi tắt là mệnh đề). Những câu không xác định được tính đúng sai không phải là mệnh đề.

OFFICIAL

Chú ý : Người ta thường sử dụng các chữ cái ,, PQR ,…để biểu thị các mệnh đề.

b. Mệnh đề chứa biến Xét câu “ n chia hết cho 2” (với n là số tự nhiên).

Ta chưa khẳng định được tính đúng sai của câu này, do đó nó chưa phải là một mệnh đề.

Tuy nhiên, nếu thay n bằng số tự nhiên cụ thể thì câu này cho ta một mệnh đề. Chẳng hạn:

• Với 5n = ta được mệnh đề “5 chia hết cho 2”. Đây là mệnh đề sai.

• Với 10n = ta được mệnh đề

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 1

“10 chia hết cho 2”. Đây là mệnh đề đúng. Ta nói rằng câu “ n chia hết cho 2” là một mệnh đề chứa biến. 2. MỆNH ĐỀ PHỦ ĐỊNH Để phủ định một mệnh đề P, người ta thường thêm (hoặc bớt) từ “không” hoặc “không phải” vào trước vị ngữ của mệnh đề P. Ta kí hiệu mệnh đề phủ định của mệnh đề P là P . 3. MỆNH ĐỀ KÉO THEO, MỆNH ĐỀ ĐẢO a. Mệnh đề kéo theo Mệnh đề PQ  chỉ sai khi P đúng và Q sai. CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP LÝ THUYẾT.I = Mỗi mệnh đề phải hoặc đúng hoặc sai. Một mệnh đề không thể vừa đúng vừa sai Mệnh đề P và mệnh đề P là hai phát biểu trái ngược nhau. Nếu P đúng thì P sai, còn nếu P sai thì P đúng. Mệnh đề ‘’Nếu P thì Q ’’ được gọi là một mệnh đề kéo theo và kí hiệu PQ 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 2 Các định lí toán học là những mệnh đề đúng và thường có dạng P . Khi đó ta nói: b. Mệnh đề đảo Nhận xét. Mệnh đề đảo của một mệnh đề đúng không nhất thiết là mệnh đề đúng. 4. MỆNH ĐỀ TƯƠNG ĐƯƠNG Nhận xét. Nếu cả hai mệnh đề PQ  và QP  đều đúng thì mệnh đề tương đương PQ  đúng. Khi đó ta nói “ P tương đương với Q ” hoặc “ P là điều kiện cần và đủ để có Q ” hoặc “ P khi và chỉ khi Q ”. 5. MỆNH ĐỀ CÓ CHỨAKÍ HIỆU ∀,∃ Kí hiệu  đọc là ''với mọi'' Kí hiệu  đọc là ''có một'' (tồn tại một) hay''có ít nhất một''(tồn tại ít nhất một). Cho mệnh đề ",()" xXPx  Mệnh đề phủ định của mệnh đề ",()" xXPx là mệnh đề ",()". xXPx  Mệnh đề phủ định của mệnh đề ",()" xXPx là mệnh đề ",()". xXPx Ví dụ: Câu ''Bình phương của mọi số thực đều lớn hơn hoặc bằng 0'' là một mệnh đề. Có thể viết mệnh đề này như sau 2 :0xx  hay 2 0,.xx Kí hiệu  đọc là ''với mọi'' Ví dụ: Câu ''Có một số nguyên nhỏ hơn 0'' là một mệnh đề. Có thể viết mệnh đề này như sau :0.nn  Kí hiệu  đọc là ''có một'' (tồn tại một) hay''có ít nhất một''(tồn tại ít nhất một).  Mệnh đề phủ định của mệnh đề ",()" xXPx là ",()". xXPx Ví dụ: Cho mệnh đề 2 “,70” xxx −+ . Tìm mệnh đề phủ định của mệnh đề trên? Lời giải Phủ định của mệnh đề 2 “,70” xxx −+ là mệnh đề 2 “,70” xxx −+  Mệnh đề phủ định của mệnh đề ",()" xXPx là ",()". xXPx Ví dụ: Cho mệnh đề 2 “,60” xxx −−= . Tìm mệnh đề phủ định của mệnh đề trên? Lời giải Phủ định của mệnh đề 2 “,60” xxx −−= là mệnh đề 2 “,60” xxx −− . P là giả thiết của định lí, Q là kết luận của định lí, hoặc “ P là điều kiện đủ để có Q ” hoặc “Q là điều kiện cần để có P ”. Mệnh đề QP  được gọi là mệnh đề đảo của mệnh đề PQ  Mệnh đề “ P nếu và chỉ nếu Q ” được gọi là một mệnh đề tương đương và kí hiệu là PQ  .

1.1. Trong các câu sau, câu nào là mệnh đề?

a) Trung Quốc là nước đông dân nhất thế giới;

b) Bạn học trường nào?

c) Không được làm việc riêng trong trường học;

d) Tôi sẽ sút bóng trúng xà ngang.

1.2. Xét tính đúng sai của các mệnh đề sau:

a) 10 3   ;

b) Phương trình370 x += có nghiệm;

c) Có ít nhất một số cộng với chính nó bằng 0;

d) 2022 là hợp số.

1.3. Cho hai câu sau:

P: “Tam giác ABC là tam giác vuông”;

OFFICIAL

Q: “Tam giác ABC có một góc bằng tổng hai góc còn lại”. Hãy phát biểu mệnh đề tương đương PQ  xét tính đúng sai của mệnh đề này.

1.4. Phát biểu mệnh đề đảo của mỗi mệnh đề sau và xác định tính đúng sai chúng.

P: “Nếu số tự nhiên n có chữ số tận cùng là 5 thì n chia hết cho 5”;

Q: “Nếu tứ giác ABCD là hình chữ nhật thì tứ giác ABCD có hai đường chéo bằng nhau”.

1.5. Với hai số thực a và b, xét các mệnh đề 22 :""Pab  và :"0"Qab  .

a) Hãy phát biểu mệnh

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 3

đề PQ  b) Hãy phát biểu mệnh đề đảo của mệnh đề ở câu a. c) Xác định tính đúng sai của mỗi mệnh đề ở câu a và câu b. 1.6. Xác định tính đúng sai của mệnh đề sau và tìm mệnh đề phủ định của nó. Q: “ n  , n chia hết cho n+1”. 1.7. Dùng kí hiệu ,  để viết các mệnh đề sau: P: “Mọi số tự nhiên đều có bình phương lớn hơn hoặc bằng chính nó”; Q: “ Có một số thực cộng với chính nó bằng 0”. HỆ THỐNG BÀI TẬP.II = BÀI TẬP. BÀI TẬP TỰ LUẬN.2 =

1. Các câu sau đây, có bao nhiêu câu là mệnh đề?

(1) Ở đây đẹp quá!

(2) Phương trình 2 310xx−+= vô nghiệm

(3) 16 không là số nguyên tố

(4) Hai phương trình 2 430xx−+= và 2 310xx−++= có nghiệm chung.

(5) Số  có lớn hơn 3 hay không?

(6) Italia vô địch Worldcup 2006

(7) Hai tam giác bằng nhau khi và chỉ khi chúng có diện tích bằng nhau.

(8) Một tứ giác là hình thoi khi và chỉ khi nó có hai đường chéo vuông góc với nhau.

Bài 2. Cho ba mệnh đề sau, với n là số tự nhiên

(1) 8n + là số chính phương

(2) Chữ số tận cùng của n là 4

(3) 1n là số chính phương

Biết rằng có hai mệnh đề đúng và một mệnh đề sai. Hãy xác định mệnh đề nào, đúng

Dung:

Quang:

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 4  DẠNG 1: XÁC ĐỊNH MỀNH ĐỀ VÀ MỆNH ĐỀ CHỨA BIẾN PHƯƠNG PHÁP Để xác định mệnh đề và mệnh đề chứa biến ta cần biết:  Mệnh đề là một câu khẳng định đúng hoặc sai. Một mệnh đề không thể vừa đúng hoặc vừa sai  Mệnh đề chứa biến là một câu khẳng định chứa biến nhận giá trị trong một tập X nào đó mà với mỗi giá trị chứa biến thuộc X ta được một mệnh đề. Bài

mệnh đề nào sai? Bài 3. Tại Tiger Cup 98 có bốn đội lọt vào vòng bán kết: Việt Nam, Singapor, Thái Lan và Inđônêxia. Trước khi thi đấu vòng bán kết, ba bạn Dung, Quang, Trung dự đoán như sau:

Singapor nhì, còn Thái Lan ba.

Việt Nam nhì, còn Thái Lan tư. Trung: Singapor nhất và Inđônêxia nhì. Kết quả, mỗi bạn dự đoán đúng một đội và sai một đội. Hỏi mỗi đội đã đạt giải mấy? Bài 4: Trong các phát biểu sau, phát biểu nào không phải là mệnh đề, giải thích? 1/ Hải Phòng là một thành phố của Việt Nam. 2/ Bạn có đi xem phim không?

Trong các phát biểu sau, phát bi

(I): “17 là số nguyên tố”

u nào là mệnh đề, xét tính đúng, sai của mệnh đề đó.

(II): “Tam giác vuông có một đường trung tuyến bằng nửa cạnh huyền”

(III): “Các em C14 hãy cố gắng học tập thật tốt nhé !”

(IV): “Mọi hình thoi đều nội tiếp được đường tròn”

Bài 6: Cho các câu sau đây:

(I): “Phan xi păng là ngọn núi cao nhất Việt Nam”.

(II): “ 2 9,86  ”.

(III): “Mệt quá!”.

(IV): “Chị ơi, mấy giờ rồi?”.

Hỏi có bao nhiêu câu là mệnh đề?

Bài 7: Trong các câu sau, có bao nhiêu câu là mệnh đề đúng

(I): Hãy cố gắng học thật tốt!

(II): Số 20chia hết cho 6.

(III): Số 5 là số nguyên tố.

(IV): Với mọi k  , 2k là số chẵn.

Bài 8: Trong các câu dưới đây, câu nào là mệnh đề, câu nào là mệnh đề chứa biến:

250 − .

Hãy tr

Bài

= 3.

Paris là th

i câu h

i này!.

đô nước

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 5 3/ 10 21 chia hết cho 11. 4/ 2763 là hợp số 5/ 2 320xx−+= . Bài 5:

ể

+ x

ả

ờ

ỏ

ủ

Ý.

9. Tìm tất cả các giá trị thực của x để mệnh đề :“211”Px − là mệnh đề đúng? Bài 10. Tìm tất cả các giá trị thực của x để mệnh đề :“210”Px − là mệnh đề sai? Bài 11. Tìm tất cả các giá trị thực của x để mệnh đề 2 :“540”Pxx++= là mệnh đề sai? Bài 12. Xét câu: ( ):Pn “n là số thự nhiên nhỏ hơn 50 và n chia hết cho 12”. Với giá trị nào của n sau đây thì ( )Pn là mệnh đề đúng. Khi đó số các giá trị của n bằng bao nhiêu?  DẠNG 2: XÉT TÍNH ĐÚNG SAI CỦA MỘT MỆNH ĐỀ PHƯƠNG PHÁP

Bài 3. Xét tính đúng, sai của m

P: “ 2 24.

Q: “ 2 416.

đề

Bài 4. Xét tính đúng, sai của mệnh đề sau:

M: “Số nguyên tố lớn hơn 2 là số lẻ”.

N: “Số tự nhiên có chữ số tận cùng

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 6 Để xét tính đúng, sai của một mệnh đề ta cần nhớ nội dung sau:  Một câu khẳng định đúng là mệnh đề đúng.  Một câu khẳng định sai là mệnh đề sai.  Không có mệnh đề vừa đúng vừa sai. Bài 1. Xét tính đúng, sai của mệnh đề sau: M: “π là một số hữu tỉ” N: “Tổng của độ dài hai cạnh một tam giác lớn hơn độ dài cạnh thứ ba” Bài 2. Xét tính đúng, sai của mệnh đề sau: A: “Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn” B: “Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn” . C: “Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ”. D: “Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ”

ệnh

 −− ”.

 ”.

là 0 hoặc 5 thì chia hết cho 5” . P: “Bình phương tất cả các số nguyên đều chia hết cho 2” Bài 5. Nêu mệnh đề phủ định của mỗi mệnh đề sau và xác định xem mệnh đề phủ định đó đúng hay sai: a) P : “Phương trình 2 10xx++= có nghiệm”. b) Q : “Năm 2020 là năm nhuận”. c) R : “327 chia hết cho 3”. Bài 6. Cho tam giác ABC với đường trung tuyến AM . Xét hai mệnh đề P : “Tam giác ABC vuông tại A ”; Q : “Trung tuyến AM bằng nửa cạnh BC ” a) Phát biểu mệnh đề PQ  và cho biết mệnh đề này đúng hay sai. b) Phát biểu mệnh đề PQ  và cho biết mệnh đề này đúng hay sai. Bài 7. Lập mệnh đề phủ định của mệnh đề: “ n  , 2 1nn++ là số nguyên tố”. Mệnh đề phủ định đó đúng hay sai?

Bài

Xét

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 7 Bài 8. Xét tinh đúng sai của mệnh đề 2 ",66" xxx .

9. Xét tinh đúng sai của mệnh đề “Với mọi giá trị n thuộc tập hợp số nguyên, 2 1n + không chia hết cho 3”.

10.

tinh đúng sai của mệnh đề “Tồn tại n thuộc tập hợp số nguyên, 2 1n + chia hết cho 4”.

11.

tinh đúng sai của mệnh đề “Nếu n  và 2 5n thì 5n ”. Bài 12. Xét tính đúng sai của mệnh đề: “ 32 ,341nnnn +−+ chia hết cho 6”. Bài 13. Xác định tính đúng, sai của mệnh đề A : " 2 ,0xx  " và tìm mệnh đề phủ định của nó. Bài 14. Viết mệnh đề phủ định của mệnh đề 2 :,4410 Axxx −+− và xét tính đúng, sai của mệnh đề đó. Bài 15. Xét mệnh đề chứa biến: ( ) 32 :"320"Pxxxx−+= . Có bao nhiêu giá trị của biến x để mệnh đề trên là mệnh đề đúng ?  DẠNG 3: PHỦ ĐỊNH MỘT MỆNH ĐỀ PHƯƠNG PHÁP  Để phủ định một mệnh đề ta thêm hoặc bớt từ “không” hoặc “không phải” trước vị ngữ của mệnh đề đó.  Ta có thể dùng từ thay thế hoặc đặt lại câu có cùng ý nghĩa.  Mệnh đề phủ định của mệnh đề ' )' ,( xXPx   là , ''(). xXPx    Mệnh đề phủ định của mệnh đề ' )' ,( xXPx   là , ''(). xXPx    Để phủ định mệnh đề kéo theo PQ  ta hiểu PQ  là “ ,()xXPx ta có ( )Qx ” nên mệnh đề phủ định là “ ,()xXPx ta có ( )Qx ” . Phủ định mệnh đề " P " là mệnh đề " không phải P ", kí hiệu P  Tính chất X thành không X và ngược lại.  Quan hệ = thành quan hệ  và ngược lại.  Quan hệ  thành quan hệ  và ngược lại.  Quan hệ  thành quan hệ  và ngược lại.  ( ), xXPx thành ( ), xXPx .  ( ), xXPx thành ( ), xXPx .

i mệnh đề sau a) 2 :250xxx ++= b) 2 :32xxx +

Bài 5. Lập mệnh đề phủ định của mỗi mệnh đề sau . :P “Phương trình 2 10x += có nghi

Bài 6. Xét tính đúng sai và nêu mệnh đề phủ định của mệnh đề

,21

là s

( )*2,1nnn − là bội số của 3”.

Bài 7. Xét tính đúng sai và nêu mệnh đề phủ định của mệnh đề “ 2 :650xxx −+= ”.

Bài 8. Xét tính đúng sai và nêu mệnh đề phủ định củ

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 8  ( ),,, xXyYPxy thành ( ),,, xXyYPxy .  ( ),,, xXyYPxy thành ( ),,, xXyYPxy Nếu P đúng thì P sai, nếu P sai thì P đúng. Bài 1. Nêu mệnh đề phủ định của các mệnh đề sau. :P " Trong tam giác tổng ba góc bằng 1800" :Q " 6 không phải là số nguyên tố" Bài 2. Lập mệnh đề phủ định của mỗi mệnh đề sau . a) Mọi hình vuông đều là hình thoi. b) Có một tam giác cân không phải là tam giác đều. Bài 3. Lập mệnh đề phủ định của mỗi mệnh đề sau . a) 2 :0xx  b) 2 : nnn . Bài 4. Lập mệnh đề phủ định của mỗ

ệm” :Q “

nNn +

ố

ẻ”

“

a mệnh đề “ ,:3xyyx =+ ”. Bài 9. Phát biểu mệnh đề phủ định của mệnh đề “ n chia hết cho 2 và cho 3 thì nó chia hết cho 6”. Bài 10. Phát biểu mệnh đề phủ định của mệnh đề “Hai tam giác bằng nhau thì diện tích của chúng bằng nhau”. Bài 11. Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của nó a) : nn chia hết cho n b) 2 :2xQx = c) :1xxx + d) 2 :31xRxx =+ Bài 12. Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của mệnh đề: ( )( ),12 nnnn ++ là số không chia hết cho 6 Bài 13. Phát biểu mệnh đề phủ định của mệnh đề sau. Cho biết tính đúng sai của mệnh đề phủ định a) ,,1aRbRab + . b) ( )2 22,,2 aRbRabaabb +=++ .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 9 c) 2 ,, aRbRab  d) ,, abc  mà 0abc++ thì 222 2 abc abbcca++ −++ .

kéo theo P ⟹ Q: Mệnh đề kéo theo P ⟹ Q chỉ sai khi P đúng và Q sai.

b. Xét tính đúng, sai của mệnh đề kéo theo:

P ⟹ Q chỉ sai khi P đúng và Q sai.

Phương pháp xét tính đúng sai của mệnh đề P ⟹ Q

Quan sát xem P, Q đúng hay sai

Khi đó P ⟹ Q rơi vào mẫu nào trong 4 mẫu sau

1. Đ⟹S→Sai 2. Đ⟹Đ 3. ��⟹Đ 4. ��⟹�� →Đúng Đặc biệ

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 10 Bài 14. Phát biểu mệnh đề phủ định của mệnh đề sau. Cho biết tính đúng sai của mệnh đề phủ định P : “ ( )( )( ) :1231nAnnnn =++++ không là số chính phương".  DẠNG 4: MỆNH ĐỀ KÉO THEO, MỆNH ĐỀ ĐẢO, MỆNH ĐỀ TƯƠNG ĐƯƠNG PHƯƠNG PHÁP 1. Mệnh đề kéo theo a. ĐN: Cho hai mệnh đề P và Q. Mệnh đề dạng: “Nếu P thì Q” được gọi là mệnh đề kéo theo Ký hiệu là: P ⟹ Q. Cách xét tính đúng sai của mệnh đề

t: Có hai trường hợp mà chỉ cần nhìn vào một trong hai mệnh đề P hoặc Q ta sẽ biết (P ⟹ Q) luôn đúng: TH1: P sai. TH2: Q đúng. Chú ý: P⟹QchínhlàP∩Q. 2. Mệnh đề tương đương a. Mệnh đề đảo: Mệnh đề Q⟹P được gọi là mệnh đề đảo của mệnh đề P⟹Q b. Mệnh đề tương đương - Điều kiện cần và đủ: Nếu cả hai mệnh đề "P⟹ Q" và "Q⟹P" đều đúng ta nói P và Q là hai mệnh đề tương đương và kí hiệu "P⟺Q" Lúc đó ta nói: P là điều kiện cần và đủ để có Q hay Q là điều kiện cần và đủ để có P. Hoặc P nếu và chỉ nếu Q Hay P khi và chỉ khi Q Hay Điều kiện cần và đủ để có P là Q. Cách xét tính đúng, sai của mệnh đề tương đương : Mệnh đề P ⇔ Q chỉ đúng khi cả hai mệnh đề kéo theo P ⟹ Q và Q ⟹ P đều đúng. Nói cách khác mệnh đề P ⇔ Q đúng nếu cả hai mệnh đề P và Q cùng đúng hoặc cùng sai. Bài 1. Lập mệnh đề PQ  và xét tính đúng sau của nó, với :"4"P   và 2 :"10"Q   . Bài 2. Phát biểu mệnh đề đảo của mệnh đề “Nếu 0A90 = thì ABC là tam giác vuông” và xét tính đúng sai của nó.

Cho mệnh

. L

p mệnh đề PQ

và xét tính đúng sai của nó.

Bài 4. Giả sử ABC là một tam giác đã cho. Lập mệnh đề PQ  và mệnh đề đảo của nó, rồi xét tính đúng sai của chúng với P: "Góc A bằng 90 ", Q: 222 "" BCABAC =+

Bài 5. Cho ABC . Xét mệnh đề P : “ ABC

OFFICIAL

Bài

ABCDlà t

Tổng số đo hai góc đối nhau bằng 180o .

Hãy phát biểu mệnh đề PQ  dưới dạng điều kiện cần và đủ.

Bài 10. Trên một hòn đảo, tôi đã gặp ba người A, B và C, một người là hiệp sĩ, một người khác là kẻ bất lương và người kia là gián điệp. Người hiệp sĩ luôn nói sự thật, kẻ bất lương luôn luôn nói dối và gián điệp có thể nói dối hoặc nói sự thật.

A nói: "Tôi là hiệp sĩ."

B nói, "Tôi là kẻ bất lương."

C nói: "Tôi là gián điệp."

Hỏi ai là gián điệp?

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 11 Bài 3.

đề :"23",Q:"46"P −−

ậ



là tam giác cân” và mệnh đề Q : “ ABC có hai đường trung tuyến bằng nhau”. Lập mệnh đề PQ  và xét tính đúng sai của nó. Bài 6. Phát biểu mệnh đề đảo của định lý: “Trong một tam giác cân, các đường cao ứng với các cạnh bên bằng nhau”. Mệnh đề đảo đó đúng hay sai? Tại sao? Bài 7. Cho mệnh đề chứa biến ( ):53Pnn + chia hết cho 3, với nN  , ( ): Qnn chia hết cho 3, với nN  Phát biểu mệnh đề “ ( ) ( ), nNPnQn ” và từ đó phát biểu mệnh đề đảo. Xét tính đúng sai của mệnh đề đảo.

8. Cho hai mệnh đề P và Q: P:

ứ giác nội tiếp. Q:

Bài 11. Ba anh em An, Bình, Vinh ngồi làm bài xung quanh một cái bàn được trải khăn mới. Khi phát hiện

có vết mực, bà hỏi thì các cháu lần lượt trả lời:

An: “Em Vinh không làm đổ mực, đấy là do em Bình.”

Bình: “Em Vinh làm đổ mực, anh An không làm đổ mực”.

Vinh: “Theo cháu, Bình không làm đổ mực, còn cháu hôm nay không chuẩn bị bài”.

Biết rằng trong 3 em thì có 2 em nói đúng, 1 em nói sai. Hỏi ai làm đổ mực?

Bài 12. Ếch hay cóc?

Trong một đầm lầy ma thuật, có hai loài lưỡng cư biết nói: cóc luôn luôn nói đúng và ếch luôn luôn nói sai.

Bốn loài lưỡng cư, Brian, Chris, LeRoy và Mike sống cùng nhau trong đầm lầy này và chúng đưa ra những tuyên bố sau:

OFFICIAL

Brian: "Mike và tôi là những loài khác nhau."

Chris: "LeRoy là một con ếch."

LeRoy: "Chris là một con ếch."

Mike: "Trong bốn người chúng tôi, ít nhất hai người là cóc."

Có bao nhiêu loài lưỡng cư là ếch?

Câu 1: Câu nào sau đây không là mệnh đề?

A. Tam giác đều là tam giác có ba cạnh bằng nhau.

B. 31 

Câu

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 12

. C. 451 −= . D. Bạn học giỏi quá!

2: Câu nào trong các câu sau không phải là mệnh đề? A.  có phải là một số vô tỷ không?. B. 225 += . C. 2 là một số hữu tỷ D. 4 2 2 = Câu 3: Trong các câu sau, câu nào là mệnh đề? A. 12là số tự nhiên lẻ B. An học lớp mấy? C. Các bạn có chăm học không? D. Các bạn hãy làm bài đi! Câu 4: Trong các câu sau, có bao nhiêu câu là mệnh đề? a) Cố lên, sắp tới nơi rồi! b) Số 15 là số nguyên tố. c) Tổng các góc của một tam giác là 180.  d) x là số nguyên dương. A. 3. B. 2. C. 4. D. 1. Câu 5: Trong các mệnh đề sau đây, mệnh đề nào có mệnh đề đảo là đúng? BÀI TẬP TRẮC NGHIỆM.2 =

bao nhiêu

A. 4.

Câu 8: Cho ba m

(1)

(2)

đề sau,

huy

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 13 A. “ Nếu I là trung điểm của AB thì IA = IB”. B. “ Nếu ABCD là hình bình hành thì ACABAD =+ ’’. C. “ Nếu x > 2 thì 2x  ” . D. “ Nếu , mn là 2 số nguyên dương và cùng chia hết cho 3 thì 22 mn + cũng chia hết cho 3”. Câu 6: Trong các mệnh đề dưới đây, các mệnh đề nào sai. M: “ 2 ,410rr = ”. N: “ 2 ,1nn + chia hết cho 8”. X: “ *,123 nn ++++ không chia hết cho 11”. Q: “ 2 ,1nnn + + là một số chẵn”. E: “ 32 2 263 , 21 xxx x x −+−  + ”. A. N, X, Q B. M, X, Q C. N, Q, E D. M, Q, E Câu 7: Cho các mệnh đề sau: (1) 2a và 3a 6a (2) 39aa  (3) 24aa  (4) 3a và 6a thì 18a (5) 00aba+ và 0b  . (6) 00aba== hoặc 0b = . (7) Hai tam giác bằng nhau khi và chỉ khi hai tam giác đó đồng dạng. (8) Một tam giác là tam giác vuông khi và chỉ khi đường trung tuyến ứng với cạnh

ền bằng một nửa cạnh huyền. Có

mệnh đề sai trong các mệnh đề trên?

B. 6. C.

ệnh

vớ

n là số tự nhiên:

8n + là số chính phương

Chữ số tận cùng của n là 4 (3) 1n là số chính phương Biết rằng có hai mệnh đề đúng và một mệnh đề sai. Hãy xác định mệnh đề nào đúng, mệnh đề nào sai? A. Mệnh đề (2) và (3) là đúng, còn mệnh đề (1) là sai B. Mệnh đề (1) và (2) là đúng, còn mệnh đề (3) là sai C. Mệnh đề (1) là đúng, còn mệnh đề (2) và (3) là sai D. Mệnh đề (1) và (3) là đúng, còn mệnh đề (2) là sai. Câu 9: Mệnh đề nào là sau đây sai? A. Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một góc bằng nhau.

B. Một tứ giác là hình chữ nhật khi và chỉ khi chúng có 3 góc vuông.

C. Một tam giác là vuông khi và chỉ khi nó có một góc bằng tổng hai góc còn lại

D. Một tam giác là đều khi và chỉ khi nó là tam giác cân và có một góc bằng 60. 

Câu 10: Mệnh đề nào dưới đây đúng?

A. Nếu tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác ABCD là hình bình hành.

B. Nếu tứ giác ABCD một cặp cạnh đối song song thì tứ giác ABCD là hình bình hành.

C. Nếu tứ giác ABCD có một cặp cạnh đối bằng nhau thì tứ giác ABCD là hình bình hành.

D. Nếu tứ giác ABCD có hai đường chéo vuông góc với nhau thì tứ giác ABCD là hình bình hành.

Câu 11: Mệnh đề nào sau đây sai?

A. 2 là số nguyên tố. B. 1 là số nguyên tố.

C. 5 là số nguyên

Câu 12: Trong các

đề sau,

đề nào là mệnh

sai?

A. Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một góc bằng nhau.

OFFICIAL

B. Một tứ giác là hình chữ nhật khi và chỉ khi chúng có 3 góc vuông.

C. Một tam giác là vuông khi và chỉ khi nó có một góc bằng tổng hai góc còn lại.

D. Một tam giác là đều khi và chỉ khi chúng có hai đường trung tuyến bằng nhau và có một góc bằng 60. 

Câu 13: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. Nếu số nguyên n có chữ số tận cùng là 5thì số nguyên n chia hết cho 5.

B. Nếu tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác ABCD là hình bình hành.

C. Nếu tứ giác ABCD là hình chữ nhật thì tứ giác ABCD có hai đường chéo bằng nhau.

D. Nếu tứ giác ABCD là hình thoi thì tứ giác ABCD có hai đường chéo vuông góc với nhau.

Câu 14: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. Nếu số nguyên n có tổng các chữ số bằng 9 thì số tự nhiên n chia hết cho 3.

B. Nếu xy  thì 22 xy 

C. Nếu xy = thì ... txty =

D. Nế

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 14

tố. D. 6 không phải là số nguyên tố.

mệnh

đề

u xy  thì 33 .xy  Câu 15: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai? A. "ABC là tam giác đều  Tam giác ABC cân". B. "ABC là tam giác đều  Tam giác ABC cân và có một góc 60".  C. "ABC là tam giác đều  ABC là tam giác có ba cạnh bằng nhau". D. "ABC là tam giác đều  Tam giác ABC có hai góc bằng 60".  Câu 16: Mệnh đề nào sau đây đúng? A. ( ):1nnn + là số chính phương. B. ( ):1nnn + là số lẻ. C. ( )( ):12nnnn ++ là số lẻ D. ( )( ):12nnnn ++ chia hết cho 6 Câu 17: Trong các mệnh đề sau, mệnh đề nào sai? A. 2 , xxx B. ,66xxx  C. 2 ,1nn + không chia hết cho 3. D. 2 ,7aa = .

Câu 18: Trong các

Câu 19: Trong các mệnh đề sau

nào

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 15

mệnh đề sau, mệnh đề nào đúng? A. 2 ,50xx += . B. 42 ,540xxx ++= . C. 3 , nnn− chia hết cho 3 D. 52 , xxx

mệnh đề

sai?

2399100 444....44 +++++ chia hết cho 5. B. 2 :1nn + không chia hết cho 4 .

:21 nnN − chia hết cho 7

3333 123....100 ++++ không chia hết cho 5050 Câu 20: Có bao nhiêu số nguyên n để mệnh đề “ 32 271 nnn+++ chia hết cho 21 n ” là đúng? A. 3. B. 2. C. 4. D. 5. Câu 21: Cho các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng? A. Nếu tứ giác ABCD là hình thang cân thì 2 góc đối bù nhau. B. Nếu ab = thì acbc = C. Nếu ab  thì 22ab  D. Nếu số nguyên chia hết cho 10 thì chia hết cho 5 và 2. Câu 22: Dùng kí hiệu ,  để phát biểu mệnh đề "Có một số hữu tỉ mà nghịch đảo của nó lớn hơn chính nó". A. 1 : nn n  B. 1 : nn n  C. 1 : nn n  D. 1 : nn n  Câu 23: Cho mệnh đề 2 1 “:” 4 Axx x =+− . Lập mệnh đề phủ định của mệnh đề A và xét tính đúng sai của nó. A. 2 1 “:” 4 Axxx=+− . Đây là mệnh đề đúng. B. 2 1 “:” 4 Axxx=+− . Đây là mệnh đề đúng. C. 2 1 “:” 4 Axxx=+− . Đây là mệnh đề đúng. D. 2 1 “:” 4 Axxx=+− . Đây là mệnh đề sai. Câu 24: Phủ định của mệnh đề: “Hình thoi có hai đường chéo vuông góc với nhau” là: A. “Hai đường chéo của hình thoi vuông góc với nhau”. B. “Hình thoi có hai đường chéo không vuông góc với nhau”. C. “Hình thoi có hai đường chéo bằng nhau”. D. “Hình thoi là hình bình hành có hai đường chéo vuông góc với nhau”. Câu 25: Phủ định của mệnh đề: “ 2 :1nn + không chia hết cho 3” là: A. “ 2 :1nn + chia hết cho 3”. B. “ 2 :1nn + không chia hết cho 3”. C. “ 2 :1nn + chia hết cho 3”. D. “  2 :1nn+ không chia hết cho 3”. Câu 26: Phủ định của mệnh đề: “ 2 :10xx + ” là: A. “ 2 :10xx + ” B. “ 2 :10xx + ”C. “ 2 :10xx + ”D. “ 2 :10xx += ”

di chuy

A. M

Câu 33: Cho n là s

nhiên,

A. :P ” (

Câu 34: Cho mệnh

ệnh

đây đúng

“Nếu 2ab+ thì một trong hai số a và b nhỏ hơn 1”. Phát biểu mệnh đề trên

bằng cách sử dụng khái niệm “điều kiện đủ”.

A. 2ab+ là

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 16 Câu 27: Phủ định của mệnh đề P: “ 2 :320xxx −+= ” là: A. P : “ 2 :320xxx −+ ” B. P : “ 2 :320xxx −+= ” C. P : “ 2 :320xxx −+ ” D. P : “ 2 :320xxx −+ ” Câu 28: Mệnh đề nào sau đây là phủ định của mệnh đề: “Mọi động vật đều

ển”.

ọi động vật đều không di chuyển. B. Mọi động vật đều đứng yên. C. Có ít nhất một động vật không di chuyển. D. Có ít nhất một động vật di chuyển. Câu 29: Phủ định của mệnh đề 2 ",531" xxx −= là A. 2" ,53"xxx− B. 2 ",531" xxx −= C. 2 "x,5x31" x − D. 2 ",531" xxx − Câu 30: Cho mệnh đề ( ):Px 2 ",10" xxx ++ . Mệnh đề phủ định của mệnh đề ( )Px là: A. 2 ",10" xxx ++ B. 2 ",10" xxx ++ C. 2 ",10" xxx ++ D. "  2 ,10"xxx++ Câu 31: Cho mệnh đề 2 “:”A xxx=  . Trong các mệnh đề sau, mệnh đề nào là phủ định của mệnh đề A? A. 2 “:” xxx B. 2 “:” xxx C. 2 “:” xxx D. 2 “:” xxx Câu 32: Cho mệnh đề 2 “:”A xxx=  . Trong các mệnh đề sau, mệnh đề nào là phủ định của mệnh đề A? A. 2 “:” xxx B. 2 “:” xxx C. 2 “:” xxx D. 2 “:” xxx

ố

ự

đề phủ định của mệnh đề nào sau

),1nnn + không là số chính phương”.

:Q ” ( ),1nnn + là số chẵn”

:R ” ( )( ),12nnnn ++ là số chẵn”.

:M ” ( )( ),12nnnn ++ không chia hết cho 6”

đề:

điều kiện đủ để một trong hai số a và b nhỏ hơn 1. B. Một trong hai số a và b nhỏ hơn 1 là điều kiện đủ để 2ab+ C. Từ 2ab+ suy ra một trong hai số a và b nhỏ hơn 1 D. Tất cả các câu trên đều đúng. Câu 35: Cho mệnh đề: “Nếu 2 góc ở vị trí so le trong thì hai góc đó bằng nhau”. Trong các mệnh đề sau đây, đâu là mệnh đề đảo của mệnh đề trên? A. Nếu 2 góc bằng nhau thì hai góc đó ở vị trí so le trong B. Nếu 2 góc không ở vị trí so le trong thì hai góc đó không bằng nhau C. Nếu 2 góc không bằng nhau thì hai góc đó không ở vị trí so le trong. D. Nếu 2 góc ở vị trí so le trong thì hai góc đó không bằng nhau.

Câu 36: Cho mệnh đề: “Nếu một tứ giác là hình thang cân thì tứ giác đó có hai đường chéo bằng nhau”.

Phát biểu mệnh đề trên bằng cách sử dụng khái niệm “điều kiện cần”.

A. Điều kiện cần để tứ giác là hình thang cân là tứ giác đó có hai đường chéo bằng nhau.

B. Điều kiện cần để tứ giác có hai đường chéo bằng nhau là tứ giác đó là hình thang cân.

C. Tứ giác là hình thang cân kéo theo tứ giác đó có hai đường chéo bằng nhau.

D. Cả a, b đều đúng.

Câu 37: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo là sai?

A. Tam giác cân có hai cạnh bằng nhau.

B. x chia hết cho 6 thì x chia hết cho 2 và 3.

C. ABCD là hình bình hành thì AB song song với CD.

D. ABCD là hình chữ nhật thì 90.ABC===

Câu 38: Mệnh đề nào dưới đây sai?

A. Tứ giác ABCD là hình chữ nhật khi và chỉ khi ABCD có ba góc vuông.

B. Tứ giác ABCD là hình bình hành khi và chỉ khi ABCD có hai cạnh đối song song và bằng nhau.

C. Tứ giác ABCD là hình thoi khi và chỉ khi ABCD có hai đường chéo vuông góc với nhau tại trung điểm mỗi đường.

OFFICIAL

D. Tứ giác ABCD là hình vuông khi và chỉ khi ABCD có bốn góc vuông.

Câu 39: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. Nếu số nguyên n có chữ số tận cùng là 5 thì số nguyên n chia hết cho 5.

B. Nếu tứ giác ABCDcó hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác ABCD là hình bình hành.

C. Nếu tứ giác ABCDlà hình chữ nhật thì tứ giác ABCDcó hai đường chéo bằng nhau.

D. Nếu tứ giác ABCDlà hình thoi thì tứ giác ABCDcó hai đường chéo vuông góc với nhau.

Câu 40: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. Nếu tổng hai số 2ab+ thì có ít nhất có một số lớn hơn 1.

B. Trong một tam giác cân hai đường cao bằng nhau.

C. Nếu tứ giác là hình vuông thì hai đường chéo vuông góc với nhau.

D. Nếu một số tự nhiên chia hết cho 6 thì nó chia hết cho 3.

Câu 41: Trong các mệnh đề sau đây, mệnh đề nào có mệnh đề đảo là đúng?

A. Nếu a và b cùng chia hết cho c thì ab + chia hết cho c

B. Nếu hai tam giác bằng nhau thì diện tích bằng nhau.

C. Nếu a chia hết cho 3 thì a chia hết cho 9

D. Nếu một số tận cùng bằng 0 thì số đó chia hết cho 5.

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 17

BÀI1:MỆNHĐỀ

1. MỆNH ĐỀ, MỆNH ĐỀ CHỨABIẾN

a. Mệnh đề:

Mệnh đề là những khẳng định có tính đúng hoặc sai. Người ta gọi là một mệnh đề lôgic (gọi tắt là mệnh đề). Những câu không xác định được tính đúng sai không phải là mệnh đề

OFFICIAL

Chú ý : Người ta thường sử dụng các chữ cái ,, PQR ,…để biểu thị các mệnh đề.

b. Mệnh đề chứa biến Xét câu “ n chia hết cho 2” (với n là số tự nhiên).

Ta chưa khẳng định được tính đúng sai của câu này, do đó nó chưa phải là một mệnh đề

Tuy nhiên, nếu thay n bằng số tự nhiên cụ thể thì câu này cho ta một mệnh đề. Chẳng hạn:

• Với 5n = ta được mệnh đề “5 chia hết cho 2”. Đây là mệnh đề sai.

• Với 10n = ta được mệnh đề

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 1

“10 chia hết cho 2”. Đây là mệnh đề đúng. Ta nói rằng câu “ n chia hết cho 2” là một mệnh đề chứa biến. 2. MỆNH ĐỀ PHỦ ĐỊNH Để phủ định một mệnh đề P, người ta thường thêm (hoặc bớt) từ “không” hoặc “không phải” vào trước vị ngữ của mệnh đề P. Ta kí hiệu mệnh đề phủ định của mệnh đề P là P . 3. MỆNH ĐỀ KÉO THEO, MỆNH ĐỀ ĐẢO a. Mệnh đề kéo theo Mệnh đề PQ  chỉ sai khi P đúng và Q sai. Các định lí toán học là những mệnh đề đúng và thường có dạng PQ  . Khi đó ta nói: CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP LÝ THUYẾT.I = Mỗi mệnh đề phải hoặc đúng hoặc sai. Một mệnh đề không thể vừa đúng vừa sai Mệnh đề P và mệnh đề P là hai phát biểu trái ngược nhau. Nếu P đúng thì P sai, còn nếu P sai thì P đúng. Mệnh đề ‘’Nếu P thì Q ’’ được gọi là một mệnh đề kéo theo và kí hiệu PQ 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 2 b. Mệnh đề đảo Nhận xét. Mệnh đề đảo của một mệnh đề đúng không nhất thiết là mệnh đề đúng. 4. MỆNH ĐỀ TƯƠNG ĐƯƠNG Nhận xét. Nếu cả hai mệnh đề PQ  và QP  đều đúng thì mệnh đề tương đương PQ  đúng. Khi đó ta nói “ P tương đương với Q ” hoặc “ P là điều kiện cần và đủ để có Q ” hoặc “ P khi và chỉ khi Q ”. 5. MỆNH ĐỀ CÓ CHỨAKÍ HIỆU ∀,∃ Kí hiệu  đọc là ''với mọi'' . Kí hiệu  đọc là ''có một'' (tồn tại một) hay''có ít nhất một''(tồn tại ít nhất một). Cho mệnh đề ",()" xXPx  Mệnh đề phủ định của mệnh đề ",()" xXPx là mệnh đề ",()". xXPx  Mệnh đề phủ định của mệnh đề ",()" xXPx là mệnh đề ",()". xXPx Ví dụ: Câu ''Bình phương của mọi số thực đều lớn hơn hoặc bằng 0'' là một mệnh đề. Có thể viết mệnh đề này như sau 2 :0xx  hay 2 0,.xx Kí hiệu  đọc là ''với mọi'' . Ví dụ: Câu ''Có một số nguyên nhỏ hơn 0'' là một mệnh đề. Có thể viết mệnh đề này như sau :0.nn  Kí hiệu  đọc là ''có một'' (tồn tại một) hay''có ít nhất một''(tồn tại ít nhất một).  Mệnh đề phủ định của mệnh đề ",()" xXPx là ",()". xXPx Ví dụ: Cho mệnh đề 2 “,70” xxx −+ . Tìm mệnh đề phủ định của mệnh đề trên? Lời giải Phủ định của mệnh đề 2 “,70” xxx −+ là mệnh đề 2 “,70” xxx −+  Mệnh đề phủ định của mệnh đề ",()" xXPx là ",()". xXPx Ví dụ: Cho mệnh đề 2 “,60” xxx −−= . Tìm mệnh đề phủ định của mệnh đề trên? Lời giải Phủ định của mệnh đề 2 “,60” xxx −−= là mệnh đề 2 “,60” xxx −− . P là giả thiết của định lí, Q là kết luận của định lí, hoặc “ P là điều kiện đủ để có Q ” hoặc “Q là điều kiện cần để có P ”. Mệnh đề QP  được gọi là mệnh đề đảo của mệnh đề PQ  Mệnh đề “ P nếu và chỉ nếu Q ” được gọi là một mệnh đề tương đương và kí hiệu là PQ 

1.1. Trong các câu sau, câu nào là mệnh đề?

a) Trung Quốc là nước đông dân nhất thế giới;

b) Bạn học trường nào?

c) Không được làm việc riêng trong trường học;

d) Tôi sẽ sút bóng trúng xà ngang.

Lời giải

Câu a) “Trung Quốc là nước đông dân nhất thế giới.” là mệnh đề là:

Câu b) là câu nghi vấn;

Câu c) là câu cầu khiến;

OFFICIAL

Câu d) là câu khẳng định chưa xác định được tính đúng sai)

1.2. Xét tính đúng sai của các mệnh đề

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 3

sau: a) 10 3   ; b) Phương trình370 x += có nghiệm; c) Có ít nhất một số cộng với chính nó bằng 0; d) 2022 là hợp số. Lời giải Xét tính đúng sai của các mệnh đề sau: a) 10 3   Mệnh đề đúng do 3,14  và 10 3,33 3  nên 10 3   . b) Phương trình370 x += có nghiệm. Vì phương trình370 x += có nghiệm hữu tỉ 7 3 x = nên mệnh đề là đúng. c) Có ít nhất một số cộng với chính nó bằng 0;Do tồn tại số thực 0 để 0 + 0 = 0 nên mệnh đề đúng. d) 2022 là hợp số. Ta có: 2022 1011.2= nên 2022 là hợp số hay mệnh đề đã cho là đúng. 1.3. Cho hai câu sau: P: “Tam giác ABC là tam giác vuông”; HỆ THỐNG BÀI TẬP.II = BÀI TẬP SÁCH GIÁO KHOA.1 =

Q: “Tam giác ABC có một góc bằng tổng hai góc còn lại”.

Hãy phát biểu mệnh đề tương đương PQ  xét tính đúng sai của mệnh đề này.

Lời giải

Mệnh đề tương đương PQ  : “Tam giác ABC là tam giác vuông khi và chỉ khi tam giác ABC có một góc bằng tổng hai góc còn lại”.

Mệnh đề PQ  đúng. Thật vậy:

+ PQ  đúng: Hiển nhiên.

+ Mệnh đề QP  : “Tam giác ABC có một góc bằng tổng hai góc còn lại thì tam giác ABC

là tam giác vuông”.

Không giảm tổng quát ta giả sử tam giác ABC có:

OFFICIAL

Nên tam giác ABC vuông tại A. Do đó mệnh đề QP  đúng.

1.4. Phát biểu mệnh

và xác định tính đúng sai chúng.

P: “Nếu số tự nhiên n có chữ số tận cùng là 5 thì n chia hết cho 5”;

Q: “Nếu tứ giác ABCD là hình chữ nhật thì tứ giác ABCD có hai đường chéo bằng nhau”.

Lời giải

Mệnh đề đảo của P: “Nếu số tự nhiên n chia hết cho 5 thì n có chữ số tận cùng là 5”. Mệnh đề sai vì số nguyên n cũng có thể có chữ số tận cùng là 0

Mệnh đề đảo của Q: “Nếu t

nhật”. Mệnh

giác ABCD có hai đường chéo b

sai (không th

a mãn

ng nhau thì tứ giác ABCD là

u hi

u nh

n bi

t hình ch

nhậ

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 4

0 00180 18090 ABC BCBCBC ABC  ++= +++=+= =+

đề đảo của mỗi mệnh đề sau

ứ

ằ

hình

ữ

đề

ỏ

dấ

ệ

ậ

ế

ữ

t). (Tứ giác có hai đường chéo bằng nhau là hình thangcân) 1.5. Với hai số thực a và b, xét các mệnh đề 22 :""Pab  và :"0"Qab  a) Hãy phát biểu mệnh đề PQ  . b) Hãy phát biểu mệnh đề đảo của mệnh đề ở câu a. c) Xác định tính đúng sai của mỗi mệnh đề ở câu a và câu b. Lời giải a) Mệnh đề PQ  : “Nếu 22ab  thì 0 ab ”.

b) Mệnh

c) Mệnh đề PQ

Mệnh đề QP

đúng.

1.6. Xác định tính đúng sai của mệnh đề sau và tìm mệnh đề phủ định của nó.

Q: “ n  , n chia hết cho n+1”.

Lời giải

Mệnh

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 5

đề đảo QP  : “Nếu 0 ab thì 22ab  ”.

 sai vì ví dụ có 22(3)4 − nhưng 304−



đề Q đúng do tồn tại 0n = để 0 chia hết cho 01 + . Mệnh đề phủ định: Q : “ n  , n không chia hết cho 1n + ”. 1.7. Dùng kí hiệu ,  để viết các mệnh đề sau: P: “Mọi số tự nhiên đều có bình phương lớn hơn hoặc bằng chính nó”; Q: “ Có một số thực cộng với chính nó bằng 0”. Lời giải Lời giải 2 :"," Pnnn  :",0"Qxxx+=

1. Các câu sau đây, có bao nhiêu câu là mệnh đề?

(1) Ở đây đẹp quá!

(2) Phương trình 2 310xx−+= vô nghiệm

(3) 16 không là số nguyên tố

(4) Hai phương trình 2 430xx−+= và 2 310xx−++= có nghiệm chung.

(5) Số  có lớn hơn 3 hay không?

(6) Italia vô địch Worldcup 2006

(7) Hai tam giác bằng nhau khi và chỉ khi chúng có diện tích bằng nhau.

(8) Một tứ giác là hình thoi khi và chỉ khi nó có hai đường chéo vuông góc với nhau.

Lời giải

Câu (1) và (5) không là mệnh đề(vì là câu cảm thán, câu hỏi)

Các câu (3), (4), (6), (8) là những mệnh đề đúng

Câu (2) và (7) là những mệnh đề sai.

Bài 2. Cho ba mệnh đề sau, với n là số tự nhiên

(1) 8n + là số chính phương

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 6  DẠNG 1: XÁC ĐỊNH MỀNH ĐỀ VÀ MỆNH ĐỀ CHỨA BIẾN PHƯƠNG PHÁP Để xác định mệnh đề và mệnh đề chứa biến ta cần biết:  Mệnh đề là một câu khẳng định đúng hoặc sai. Một mệnh đề không thể vừa đúng hoặc vừa sai  Mệnh đề chứa biến là một câu khẳng định chứa biến nhận giá trị trong một tập X nào đó mà với mỗi giá trị chứa biến thuộc X ta được một mệnh đề Bài

(2) Chữ số tận cùng của n là 4 (3) 1n là số chính phương Biết rằng có hai mệnh đề đúng và một mệnh đề sai. Hãy xác định mệnh đề nào, đúng mệnh đề nào sai? Lời giải Ta có số chính phương có các chữ số tận cùng là 0,1,4,5,6,9. Vì vậy Nhận thấy giữa mệnh đề (1) và (2) có mâu thuẫn. Bởi vì, giả sử 2 mệnh đề này đồng thời là đúng thì 8n + có chữ số tận cùng là 2 nên không thể là số chính phương. Vậy trong hai mệnh đề này phải có một mệnh đề là đúng và một mệnh đề là sai. BÀI TẬP TỰ LUẬN.2 =

Bài

Tương tự, nhận thấy giữa mệnh đề (2) và (3) cũng có mâu thuẫn. Bởi vì, giả sử mệnh đề này đồng thời là đúng thì 1n có chữ số tận cùng là 3 nên không thể là số chính phương.

Vậy trong ba mệnh đề trên thì mệnh đề (1) và (3) là đúng, còn mệnh đề (2) là sai.

Tiger Cup

có

vòng bán k

vòng

Nam, Singapor, Thái Lan và Inđônêxia. Trước khi thi

ba b

n Dung, Quang, Trung dự đoán như sau:

Dung: Singapor nhì, còn Thái Lan ba.

Quang: Việt Nam nhì, còn Thái Lan tư.

Trung: Singapor nhất và Inđônêxia nhì.

t qu

i b

(II):

(III):

(IV):

Câu

n d

đoán đúng một

i và sai m

độ

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 7

3. Tại

bốn đội lọt vào

bán kết: Việt

đấu

ết,

ạ

ế

ả,

ỗ

ạ

ự

độ

ột

i. Hỏi mỗi đội đã đạt giải mấy? Lời giải + Nếu Singapor nhì thì Singapor nhất là sai do đó Inđônêxia nhì là đúng(mâu thuẫn) + Như vậy Thái lan thứ ba là đúng suy ra Việt Nam nhì Singapor nhất và Inđônêxia thứ tư Bài 4: Trong các phát biểu sau, phát biểu nào không phải là mệnh đề, giải thích? 1/ Hải Phòng là một thành phố của Việt Nam. 2/ Bạn có đi xem phim không? 3/ 10 21 chia hết cho 11 4/ 2763 là hợp số. 5/ 2 320xx−+= Lời giải Các phát biểu không phải mệnh đề là 2 và 5 Câu 2 là câu hỏi. Câu 5 là mệnh đề chứa biến. Bài 5: Trong các phát biểu sau, phát biểu nào là mệnh đề, xét tính đúng, sai của mệnh đề đó. (I): “17 là số nguyên tố”

“Tam giác vuông có một đường trung tuyến bằng nửa cạnh huyền”

“Các em C14 hãy cố gắng học tập thật tốt nhé !”

“Mọi hình thoi đều nội tiếp được đường tròn” Lời giải

(I) là mệnh đề đúng.

(II) là mệnh đề đúng.

(III) không phải là mệnh đề.

(VI) là mệnh đề sai. Bài 6: Cho các câu sau đây:

(I):

(II):

(III):

(IV):

có

(I), (II) là

(III),

Bài 7: Trong các câu sau, có bao nhiêu câu là m

(I): Hãy

(II): S

(III): S

(IV): V

chia

OFFICIAL

Có hai mệnh đề đúng là (III) và (IV)

i gi

Bài 8: Trong các câu dưới đây, câu nào là mệnh đề, câu nào là mệnh đề chứa biến:

a) 250 − .

b) 4 + x = 3.

c) Hãy trả lời câu hỏi này!.

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 8

“Phan xi păng là ngọn núi cao nhất Việt Nam”.

“ 2 9,86  ”.

“Mệt quá!”.

“Chị ơi, mấy giờ rồi?”.

ỏi

bao nhiêu câu là mệnh đề?

ời giải

mệnh đề,

(IV) không là mệnh đề.

ệnh đề đúng

cố gắng học thật tốt!

ố 20

hết cho 6.

ố 5 là số nguyên tố.

ới mọi k  , 2k là số chẵn.

ờ

ả

d) Paris là thủ đô nước Ý. Lời giải a) Mệnh đề đúng. b) Mệnh đề chứa biến. c) Không phải là mệnh đề, câu mệnh lệnh. d) Mệnh đề sai. Bài 9. Tìm tất cả các giá trị thực của x để mệnh đề :“211”Px − là mệnh đề đúng? Lời giải Ta có 2111 211 2110 xx x xx − −−−  . Bài 10. Tìm tất cả các giá trị thực của x để mệnh đề :“210”Px − là mệnh đề sai? Lời giải Mệnh đề :“210”Px − sai khi và chỉ khi 210 x − đúng 1 2 x  Bài 11. Tìm tất cả các giá trị thực của x để mệnh đề 2 :“540”Pxx++= là mệnh đề sai?

Bài 1. Xét tính đúng, sai củ

là m

N: “Tổng của độ dài hai cạnh một tam giác lớn hơn độ dài cạnh thứ ba”

Lời giải

Mệnh đề M là một mệnh đề sai vì π là số vô tỉ

Mệnh đề N đúng.

Bài 2. Xét tính đúng, sai của mệnh đề sau:

A: “Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đề

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 9 Lời giải Mệnh đề 2 :“540”Pxx++= là mệnh đề sai khi thay giá trị x vào biểu thức 2 54xx++ ta được kết quả khác 0, ta thấy 1;4xx−− thỏa mãn. Bài 12. Xét câu: ( ):Pn “n là số thự nhiên nhỏ hơn 50 và n chia hết cho 12”. Với giá trị nào của n sau đây thì ( )Pn là mệnh đề đúng. Khi đó số các giá trị của n bằng bao nhiêu? Lời giải Các số thỏa mãn yêu cầu bài toán là 0;12;24;36;48.  DẠNG 2: XÉT TÍNH ĐÚNG SAI CỦA MỘT MỆNH ĐỀ PHƯƠNG PHÁP Để xét tính đúng, sai của một mệnh đề ta cần nhớ nội dung sau:  Một câu khẳng định đúng là mệnh đề đúng.  Một câu khẳng định sai là mệnh đề sai.  Không có mệnh đề vừa đúng vừa sai.

a mệnh đề sau: M: “π

ột số hữu tỉ”

u là số chẵn” . B: “Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn” C: “Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ”. D: “Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ”. Lời giải A là mệnh đề sai. Ví dụ: 134 += là số chẵn nhưng 1,3 là số lẻ. B là mệnh đề sai. Ví dụ: 2.36 = là số chẵn nhưng 3 là số lẻ. C là mệnh đề sai. Ví dụ: 134 += là số chẵn nhưng 1,3 là số lẻ. D là mệnh đề đúng. Bài 3. Xét tính đúng, sai của mệnh đề sau: P: “ 2 24. −− ”. Q: “ 2 416. ”.

Nêu mệnh đề

mệnh đề

và xác định xem mệnh đề phủ định đó đúng hay sai:

a) P : “Phương trình 2 10xx++= có nghiệm”.

b) Q : “Năm 2020 là năm nhuận”.

c) R : “327 chia hết cho 3”.

Lời giải

a) P : “Phương trình 2 10xx++= vô nghiệm”. P là mệnh đề đúng.

b) Q : “Năm 2020 không phải là năm nhuận”. Q là mệnh đề sai.

c) R : “327 không chia hết cho 3”. R là mệnh đề sai.

Bài 6. Cho tam giác ABC với đường trung tuyến AM . Xét hai mệnh đề

P : “Tam giác ABC vuông tại A ”;

Q : “Trung tuyến AM bằng nửa cạnh BC ”

a) Phát biểu mệnh đề PQ  và cho biế

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 10 Lời giải Ta có: Suy ra P sai. 2 416 . Suy ra Q đúng. Bài 4. Xét tính đúng, sai của mệnh đề sau: M: “Số nguyên tố lớn hơn 2 là số lẻ”. N: “Số tự nhiên có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5” . P: “Bình phương tất cả các số nguyên đều chia hết cho 2” . Lời giải M là mệnh đề đúng. Vì mọi số lớn hơn 2 mà chẵn thì đêuu chia hết cho 2, nên không thể là số nguyên tố. N là mệnh đề đúng. P là mệnh đề sai. Ví dụ: 2 39 = nhưng 9 không chia hết cho 2. Bài 5.

phủ đị

của mỗi

t mệnh đề này đúng hay sai. b) Phát biểu mệnh đề PQ  và cho biết mệnh đề này đúng hay sai. Lời giải a) “Nếu tam giác ABC đã cho vuông tại A thì trung tuyến AM bằng nửa cạnh BC ”. Mệnh đề này đúng. b) “Tam giác ABC đã cho vuông tại A nếu và chỉ nếu trung tuyến AM bằng nửa cạnh BC ”. Mệnh đề này đúng. Bài 7. Lập mệnh đề phủ định của mệnh đề: “ n  , 2 1nn++ là số nguyên tố”. Mệnh đề phủ định đó đúng hay sai? 2 4222.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 11 Lời giải Mệnh đề phủ định là: “ n  , 2 1nn++ không phải là số nguyên tố”. Mệnh đề phủ định đúng. Ví dụ với 4n = thì 2 121nn++= chia hết cho 3 nên là hợp số Bài 8. Xét tinh đúng sai của mệnh đề 2 ",66" xxx Lời giải Ta có 2 2 2 33 66 22 xx xx xx       Vậy mệnh đề đúng. Bài 9. Xét tinh đúng sai của mệnh đề “Với mọi giá trị n thuộc tập hợp số nguyên, 2 1n + không chia hết cho 3”. Lời giải Với ( ) 22 3191nkknk =+=+ không chia hết cho 3. Với ( ) 22 311961 nkknkk =++=++ không chia hết cho 3. Với ( ) 22 3219124 nkknkk =++=++ không chia hết cho 3. Do đó mệnh đề trên đúng. Bài 10. Xét tinh đúng sai của mệnh đề “Tồn tại n thuộc tập hợp số nguyên, 2 1n + chia hết cho 4”. Lời giải Với ( ) 22 2141nkknk =+=+ không chia hết cho 4. Với ( ) 22 211442nkknkk =++=++ không chia hết cho 4. Vậy mệnh đề trên sai. Bài 11. Xét tinh đúng sai của mệnh đề “Nếu n  và 2 5n thì 5n ”. Lời giải Giả sử n  và 2 5n mà ta có n không chia hết cho 5. Vì n không chia hết cho 5 nên n có thể biểu diễn theo một trong các dạng sau: 51nk= hoặc 52nk= Với 51nk= ta có 2225101nkk=+ không chia hết cho 5. Với 52nk= ta có 2225204nkk=+ không chia hết cho 5. Vậy mệnh đề trên đúng. Bài 12. Xét tính đúng sai của mệnh đề: “ 32 ,341nnnn +−+ chia hết cho 6”. Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 12 n  , ta có: ( ) ( )( )32234132611261 nnnnnnnnnnn +−+=++−+=++−+ . Vì ( )( )12nnn++ là tích 3 số tự nhiên liên tiếp nên ( )( )12nnn++ chia hết cho 6 Lại có 6n chia hết cho 6; 1 không chia hết cho 6. Do đó ( )( ) 1261nnnn++−+ không chia hết cho 6. Vậy mệnh đề đã cho là sai. Bài 13. Xác định tính đúng, sai của mệnh đề A : " 2 ,0xx  " và tìm mệnh đề phủ định của nó. Lời giải Mệnh đề A đúng và (Textranslationfailed) là mệnh đề sai. Bài 14. Viết mệnh đề phủ định của mệnh đề 2 :,4410 Axxx −+− và xét tính đúng, sai của mệnh đề đó. Lời giải Ta có 2 :",4410" Axxx−+− là mệnh đề sai vì ( ) 22 1 4410210 2 xxxx −+−−− Khi đó mệnh đề phủ định 2 :",4410" Axxx−+− là mệnh đề đúng. Bài 15. Xét mệnh đề chứa biến: ( ) 32 :"320"Pxxxx−+= Có bao nhiêu giá trị của biến x để mệnh đề trên là mệnh đề đúng ? Lời giải Ta có 323200,1,2xxxxxx −+==== . Vậy có ba giá trị của x .  DẠNG 3: PHỦ ĐỊNH MỘT MỆNH ĐỀ PHƯƠNG PHÁP  Để phủ định một mệnh đề ta thêm hoặc bớt từ “không” hoặc “không phải” trước vị ngữ của mệnh đề đó.  Ta có thể dùng từ thay thế hoặc đặt lại câu có cùng ý nghĩa.  Mệnh đề phủ định của mệnh đề ' )' ,( xXPx   là , ''(). xXPx    Mệnh đề phủ định của mệnh đề ' )' ,( xXPx   là , ''(). xXPx    Để phủ định mệnh đề kéo theo PQ  ta hiểu PQ  là “ ,()xXPx ta có ( )Qx ” nên mệnh đề phủ định là “ ,()xXPx ta có ( )Qx ” . Phủ định mệnh đề " P " là mệnh đề " không phải P ", kí hiệu P .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 13  Tính chất X thành không X và ngược lại.  Quan hệ = thành quan hệ  và ngược lại.  Quan hệ  thành quan hệ  và ngược lại.  Quan hệ  thành quan hệ  và ngược lại.  ( ), xXPx thành ( ), xXPx  ( ), xXPx thành ( ), xXPx .  ( ),,, xXyYPxy thành ( ),,, xXyYPxy  ( ),,, xXyYPxy thành ( ),,, xXyYPxy . Nếu P đúng thì P sai, nếu P sai thì P đúng Bài 1. Nêu mệnh đề phủ định của các mệnh đề sau. :P " Trong tam giác tổng ba góc bằng 1800" :Q " 6 không phải là số nguyên tố" Lời giải Ta có các mệnh đề phủ định là: :P "Trong tam giác tổng ba góc không bằng 1800 " :Q " 6 là số nguyên tố" Bài 2. Lập mệnh đề phủ định của mỗi mệnh đề sau . a) Mọi hình vuông đều là hình thoi. b) Có một tam giác cân không phải là tam giác đều. Lời giải Ta có các mệnh đề phủ định là: a) Có ít nhất một hình vuông không phải là hình thoi. b) Mọi tam giác cân đều là tam giác đều. Bài 3. Lập mệnh đề phủ định của mỗi mệnh đề sau . a) 2 :0xx  b) 2 : nnn . Lời giải Ta có các mệnh đề phủ định là: a) 2 :0xx  b) 2 : nnn Bài 4. Lập mệnh đề phủ định của mỗi mệnh đề sau a) 2 :250xxx ++= b) 2 :32xxx + Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 14 Ta có các mệnh đề phủ định là: a) 2 :250xxx ++ b) 2 :32xxx =+ Bài 5. Lập mệnh đề phủ định của mỗi mệnh đề sau . :P “Phương trình 2 10x += có nghiệm” :Q “ ,21nNn + là số lẻ” Lời giải Ta có các mệnh đề phủ định là: :P “Phương trình 2 10x += vô nghiệm” :Q “ ,21nNn + là số chẵn” Bài 6. Xét tính đúng sai và nêu mệnh đề phủ định của mệnh đề “ ( )*2,1nnn − là bội số của 3”. Lời giải Mệnh đề “ ( )*2,1nnn − là bội số của 3” là mệnh đề đúng vì ( ) ( ) ( ) 2* 1113, nnnnnn −=−+ . Phủ định của mệnh đề “ ( )*2,1nnn − là bội số của 3” là mệnh đề “ ( )*2,1nnn − không phải là bội số của 3”. Bài 7. Xét tính đúng sai và nêu mệnh đề phủ định của mệnh đề “ 2 :650xxx −+= ”. Lời giải Mệnh đề “ 2 :650xxx −+= ” là mệnh đề đúng vì 2 1 650 5. x xx x = −+=  = Phủ định của mệnh đề “ 2 :650xxx −+= ” là mệnh đề “ 2 :650xxx −+ ”. Bài 8. Xét tính đúng sai và nêu mệnh đề phủ định của mệnh đề “ ,:3xyyx =+ ”. Lời giải Mệnh đề “ ,:3xyyx =+ ” đúng vì ,3xyx =+ . Phủ định của mệnh đề “ ,:3xyyx =+ ” là mệnh đề “ ,:3xyyx + ”. Bài 9. Phát biểu mệnh đề phủ định của mệnh đề “ n chia hết cho 2 và cho 3 thì nó chia hết cho 6”. Lời giải Phủ định của mệnh đề “ n chia hết cho 2 và cho 3 thì nó chia hết cho 6” là mệnh đề “Có n chia hết cho 2 và cho 3 mà không chia hết cho 6” . Bài 10. Phát biểu mệnh đề phủ định của mệnh đề “Hai tam giác bằng nhau thì diện tích của chúng bằng nhau”. Lời giải

Phủ định của mệnh đề “Hai tam giác bằng nhau thì diện tích của chúng bằng nhau” là mệnh đề “Có

ai tam giác bằng nhau mà diện tích của chúng khác nhau” .

Bài 11. Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của nó

a) : nn chia hết cho n

2 :2xQx =

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 15

c) :1xxx + d) 2 :31xRxx =+ Lời giải a) : nNn không chia hết cho n . Mệnh đề phủ định đúng. b) 2 :2.xQx  Mệnh đề phủ định đúng. c) :1.xRxx + Mệnh đề phủ định sai. d) 2 :31.xRxx + Mệnh đề phủ định sai. Bài 12. Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của mệnh đề: ( )( ),12 nnnn ++ là số không chia hết cho 6 . Lời giải ( )( ),12 nnnn ++ là số chia hết cho 6. Mệnh đề này đúng vì ( )( ),12nnnn ++ là tích của 3 số tự nhiên liên tiếp, trong đó, luôn có một số chia hết cho 2 và một số chia hết cho 3 nên nó chia hết cho 2.36 = Bài 13. Phát biểu mệnh đề phủ định của mệnh đề sau. Cho biết tính đúng sai của mệnh đề phủ định a) ,,1aRbRab + . b) ( )2 22,,2 aRbRabaabb +=++ . c) 2 ,, aRbRab  d) ,, abc  mà 0abc++ thì 222 2 abc abbcca++ −++ . Lời giải a) Phủ định của mệnh đề là ,,1aRbRab + Mệnh đề phủ định này sai vì với 1;1ab== thì 21ab+= . b) Phủ định của mệnh đề là ( )2 22,,2 aRbRabaabb +++ Mệnh đề phủ định này sai. c) Phủ định của mệnh đề là 2 ,, aRbRab  Mệnh đề phủ định này đúng.

đề dạng: “Nếu P thì Q” được gọi là mệnh đề kéo theo.

Ký hiệu là: P ⟹ Q.

Cách xét tính đúng sai của mệnh đề kéo theo P ⟹ Q: Mệnh đề kéo theo P ⟹ Q chỉ sai khi P đúng và Q sai.

b. Xét tính đúng, sai của mệnh đề kéo theo: P ⟹ Q chỉ sai khi P đúng và Q sai Phương pháp xét tính đúng sai của mệnh đề

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 16 d) Phủ định của mệnh đề là ,, abc  mà 0abc++= thì 222 2 abc abbcca++ −=++ Mệnh đề phủ định này đúng vì 0abc++= ( )2 222 02220abcabcabacbc ++=+++++= 222 2 abc abbcca++ −=++ Bài 14. Phát biểu mệnh đề phủ định của mệnh đề sau. Cho biết tính đúng sai của mệnh đề phủ định P : “ ( )( )( ) :1231nAnnnn =++++ không là số chính phương". Lời giải P : “ ( )( )( ) :1231nAnnnn =++++ là số chính phương". P đúng vì ( )( )( ) ( )( ) ( ) 2222 :1231332131 nAnnnnnnnnnn =++++=++++=++  DẠNG 4: MỆNH ĐỀ KÉO THEO, MỆNH ĐỀ ĐẢO, MỆNH ĐỀ TƯƠNG ĐƯƠNG PHƯƠNG PHÁP 1. Mệnh đề kéo theo a. ĐN: Cho hai mệnh đề P và Q. Mệnh

P ⟹ Q Quan sát xem P, Q đúng hay sai Khi đó P ⟹ Q rơi vào mẫu nào trong 4 mẫu sau 1. Đ⟹S→Sai 2. Đ⟹Đ 3. ��⟹Đ 4. ��⟹�� →Đúng Đặc biệt: Có hai trường hợp mà chỉ cần nhìn vào một trong hai mệnh đề P hoặc Q ta sẽ biết (P ⟹ Q) luôn đúng: TH1: P sai TH2: Q đúng. Chú ý: P⟹QchínhlàP∩Q. 2. Mệnh đề tương đương a. Mệnh đề đảo: Mệnh đề Q⟹P được gọi là mệnh đề đảo của mệnh đề P⟹Q b. Mệnh đề tương đương Điều kiện cần và đủ: Nếu cả hai mệnh đề "P⟹ Q" và "Q⟹P" đều đúng ta nói P và Q là hai mệnh đề tương đương và kí hiệu "P⟺Q".

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 17 Lúc đó ta nói: P là điều kiện cần và đủ để có Q hay Q là điều kiện cần và đủ để có P. Hoặc P nếu và chỉ nếu Q Hay P khi và chỉ khi Q Hay Điều kiện cần và đủ để có P là Q. Cách xét tính đúng, sai của mệnh đề tương đương : Mệnh đề P ⇔ Q chỉ đúng khi cả hai mệnh đề kéo theo P ⟹ Q và Q ⟹ P đều đúng. Nói cách khác mệnh đề P ⇔ Q đúng nếu cả hai mệnh đề P và Q cùng đúng hoặc cùng sai. Bài 1. Lập mệnh đề PQ  và xét tính đúng sau của nó, với :"4"P   và 2 :"10"Q   Lời giải Ta có mệnh đề PQ  là: “Nếu 4  thì 2 10  ”. Vì P sai (và Q sai) nên mệnh đề PQ  là mệnh đề đúng. Bài 2. Phát biểu mệnh đề đảo của mệnh đề “Nếu 0A90 = thì ABC là tam giác vuông” và xét tính đúng sai của nó. Lời giải Ta có mệnh đề PQ  : “Nếu 090A = thì ABC là tam giác vuông” Mệnh đề đảo của mệnh đề trên là QP  : “ Nếu ABC là tam giác vuông thì 90A = ”. Mệnh đề QP  là mệnh đề sai, ví dụ trường hợp ABC vuông tại B Bài 3. Cho mệnh đề :"23",Q:"46"P −− . Lập mệnh đề PQ  và xét tính đúng sai của nó. Lời giải (): PQ  “Nếu 23  thì 46−− ”. Mệnh đề sai. Bài 4. Giả sử ABC là một tam giác đã cho. Lập mệnh đề PQ  và mệnh đề đảo của nó, rồi xét tính đúng sai của chúng với P: "Góc A bằng 90 ", Q: 222 "" BCABAC =+ . Lời giải Với tam giác ABC đã cho, ta có () PQ  : “Nếu góc A bằng 90o thì 222 BCABAC =+ ” là mệnh đề đúng. (): QP  “Nếu 222 BCABAC =+ thì ˆ 90oA = ” là mệnh đề đúng. Bài 5. Cho ABC . Xét mệnh đề P : “ ABC là tam giác cân” và mệnh đề Q : “ ABC có hai đường trung tuyến bằng nhau”. Lập mệnh đề PQ  và xét tính đúng sai của nó. Lời giải Ta có mệnh đề PQ  là: “ ABC là tam giác cân khi và chỉ khi tam giác đó có hai đường trung tuyến bằng nhau”. Vì PQ  và QP  đều là hai mệnh đề đúng nên mệnh đề PQ  đúng.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 18 Bài 6. Phát biểu mệnh đề đảo của định lý: “Trong một tam giác cân, các đường cao ứng với các cạnh bên bằng nhau”. Mệnh đề đảo đó đúng hay sai? Tại sao? Lời giải Mệnh đề đảo: “Trong tam giác, các đường cao ứng với các cạnh bên bằng nhau thì tam giác đó là tam giác cân”. Mệnh đề đảo trên đúng. (Hs tự chứng minh) Bài 7. Cho mệnh đề chứa biến ( ):53Pnn + chia hết cho 3, với nN  , ( ): Qnn chia hết cho 3, với nN  Phát biểu mệnh đề “ ( ) ( ), nNPnQn ” và từ đó phát biểu mệnh đề đảo. Xét tính đúng sai của mệnh đề đảo. Lời giải Mệnh đề: “ ,53nn + chia hết cho 3 thì n chia hết cho 3” Mệnh đề đảo: “ , nn chia hết cho 3 thì 53 n + chia hết cho 3”. Mệnh đề đảo trên đúng. Vì: n chia hết cho 3 suy ra 3, nkk= . Khi đó : 535.3.3153, nkkk +=+=+ 153 331533,. k kk +  Vậy 53 n + chia hết cho 3. Bài 8. Cho hai mệnh đề P và Q: P: ABCDlà tứ giác nội tiếp. Q: Tổng số đo hai góc đối nhau bằng 180o . Hãy phát biểu mệnh đề PQ  dưới dạng điều kiện cần và đủ. Lời giải Điều kiện cần : “ ABCDlà tứ giác nội tiếp là điều kiện cần để tổng số đo hai góc đối nhau bằng 180o ”. Điều kiện đủ: “Trong tứ giác ABCD, tổng số đo hai góc đối nhau bằng 180o là điều kiện đủ đề ABCDlà tứ giác nội tiếp.”

lương

người

A nói: "Tôi

Nếu A nói thật

A là hiệp sĩ.

B hoặc C là kẻ bất lương.

Nếu B là kẻ bất lương ⟹

t quả nhanh nhất, ta sẽ xét hiệp sĩ và gián điệp.

OFFICIAL

Bài 11. Ba anh em An, Bình, Vinh ngồi làm bài xung quanh một cái bàn được trải khăn mới. Khi phát hiện có vết mực, bà hỏi thì các cháu lần lượt trả lời:

An: “Em Vinh không làm đổ mực, đấy là do em Bình.”

Bình: “Em Vinh làm đổ mực, anh An không làm đổ mực”.

Vinh: “Theo cháu, Bình không làm đổ mực, còn cháu hôm nay không chuẩn bị bài”.

Biết rằng trong 3 em thì có 2 em nói đúng, 1 em nói sai. Hỏi ai làm đổ mực?

Lời giải

Nếu An nói đúng thì Bình là người làm đổ, suy ra Bình nói sai, theo đề bài ta có Vinh nói đúng. Nếu

Vinh nói đúng thì Bình không làm đổ mực. Suy ra mâu thuẫn.

Nếu Bình nói đúng, Vinh làm

Trong

Brian, Chris, LeRoy

nói: cóc luôn luôn nói đúng và

ch luôn luôn

Mike

cùng nhau trong đầm l

này và chúng đưa ra

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 19 Bài 10. Trên một hòn đảo, tôi đã gặp ba người A, B và C, một người là hiệp sĩ, một người khác là kẻ bất

và

kia là gián điệp. Người hiệp sĩ luôn nói sự thật, kẻ bất lương luôn luôn nói dối và gián điệp có thể nói dối hoặc nói sự thật.

là hiệp sĩ." B nói, "Tôi là kẻ bất lương." C nói: "Tôi là gián điệp." Hỏi ai là gián điệp? Lời giải Do tính đúng sai nên để xác định kế

⟹

B nói dối ⟹ Mâu thuẫn Nếu C là kẻ bất lương ⟹ C nói dối ⟹ Thỏa mãn Vậy A là hiệp sĩ, C là kẻ bất lương và B là gián điệp cần tìm.

đổ mực thì An nói sai. Dẫn đến Vinh nói đúng. Suy ra thỏa mãn. Vậy Vinh làm đổ mực. Bài 12. Ếch hay cóc?

một đầm lầy ma thuật, có hai loài lưỡng cư biết

ế

nói sai.

ốn loài lưỡng cư,

và

sống

ầy

những tuyên bố sau:

Brian: "Mike và tôi là những loài khác nhau."

Chris: "LeRoy là một con ếch."

LeRoy: "Chris là một con ếch."

Mike: "Trong bốn người chúng tôi, ít nhất hai người là cóc."

Có bao nhiêu loài lưỡng cư là ếch?

Cách 1: Trình bày lời văn:

Giả sử Brian là cóc (nói thật)

⟹ Mike là ếch (nói dối)

Lời giải

⟹ Chỉ có 1 con là ếch trong 4 con. Mà Mike đã là ếch

⟹ LeRoy và Chris là đều cóc (nói thật)

Nhưng Chris nói LeRoy là ếch ⟹ mâu thuẫn

Vậy Brian nói dối (là Ếch)

⟹ Brian và Mike cùng là loài ếch (nói dối)

⟹ Chỉ

LeRoy

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 20

có 1 con cóc và 3 con còn lại là ếch (*) • Nếu Chris là Cóc (nói thật) ⟹ LeRoy là ếch (nói dối) ⟹ Thỏa mãn (*) • Nếu LeRoy là Cóc (nói thật) ⟹ Chris là ếch (nói dối) ⟹ Thỏa mãn (*) Vậy có 3 loài lưỡng cư là ếch Cách 2: Dùng bảng Kí hiệu: Cóc : x Ếch: o Brian Chris

Mike x o o o Mâu thuẫn o x o o Thỏa mãn o o x o Thỏa mãn Vậy có 3 loài lưỡng cư là ếch. Câu 1: Câu nào sau đây không là mệnh đề? A. Tam giác đều là tam giác có ba cạnh bằng nhau. B. 31  C. 451 −= D. Bạn học giỏi quá! Lời giải BÀI TẬP TRẮC NGHIỆM.2 =

Câu

i là mệnh đề

Câu 4: Trong các câu sau, có bao nhiêu câu là mệnh đề?

a) Cố lên, sắp tới nơi rồi!

b) Số 15 là số nguyên tố

c) Tổng các góc của một tam giác là 180.  d) x là số nguyên dương.

A. 3. B. 2. C. 4. D. 1.

Chọn B

Câu a) không là mệnh đề

Câu d) là mệnh đề chứa biến Các câu b) c) là các mệnh đề

Câu 5: Trong các mệnh đề sau đây, mệnh đề nào có mệnh đề đảo là đúng?

A. “ Nếu I là trung điểm của AB thì IA = IB”.

B. “

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 21 Chọn D Vì “Bạn học giỏi quá!” là câu cảm thán không có khẳng định đúng hoặc sai. Câu 2: Câu nào trong các câu sau không phải là mệnh đề? A.  có phải là một số vô tỷ không?. B. 225 += C. 2 là một số hữu tỷ. D. 4 2 2 = . Lời giải Chọn A

3: Trong các câu sau, câu nào là mệnh đề? A. 12là số tự nhiên lẻ. B. An học lớp mấy? C. Các bạn có chăm học không? D. Các bạn hãy làm bài đi! Lời giải Chọn A

a) là câu cảm thán không phả

Lời

ả

Nếu ABCD là hình bình hành thì ACABAD =+ ’’. C. “ Nếu x > 2 thì 2x  ” . D. “ Nếu , mn là 2 số nguyên dương và cùng chia hết cho 3 thì 22 mn + cũng chia hết cho 3”. Lời giải Chọn D Đáp án A sai vì IA = IB thì IAB có thể là tam giác cân tại I. Đáp án B sai vì ACABAD =+ thì ,,, ABCD có thể thẳng hàng. Đáp án C sai vì 2x  thì 2x − hoặc 2x  Đáp án D đúng:

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 22 Nhận xét: 2 m ( 2 n ) là các số chính phương nên chia cho 3 có thể dư 0 hoặc 1 ( chứng minh bằng cách xét 3,31,32mkmkmk ==+=+ ) Do đó: Nếu 22 , mn cùng chia 3 dư 1 thì 22 mn + chia 3 dư 2 ( trái giả thiết) Nếu 1 trong 2 số 22 , mn có 1 số chia hết cho 3 và số còn lại chia hết cho 3 dư 1 thì 22 mn + chia 3 dư 1 ( trái giả thiết) Suy ra 22 , mn cùng chia hết cho 3. Mà 3 là số nguyên tố nên m, n cùng chia hết cho 3 Câu 6: Trong các mệnh đề dưới đây, các mệnh đề nào sai. M: “ 2 ,410rr = ”. N: “ 2 ,1nn + chia hết cho 8”. X: “ *,123 nn ++++ không chia hết cho 11”. Q: “ 2 ,1nnn + + là một số chẵn”. E: “ 32 2 263 , 21 xxx x x −+−  + ”. A. N, X, Q B. M, X, Q C. N, Q, E D. M, Q, E Lời giải Chọn A Mệnh đề M đúng, vì với 2 ,410 1 2 r r= = Mệnh đề N sai. Ta chứng tỏ mệnh đề phủ định “ 2 ,1nn + không chia hết cho 8” là đúng. + Nếu n chẵn thì 2 1n + là một số lẻ nên không chia hết cho 8 + Nếu n lẻ, ( )21 nkk=+ thì ( )2214424.12nkkkk +=++=++ chia 8 dư 2 vì ( )1kk + là số chẵn Mệnh đề X sai. Ta chứng tỏ mệnh đề phủ định “ *,123 nn ++++ chia hết cho 11”. Thật vậy, nếu *11n = thì 12+31166 +++= chia hết cho 11. Mệnh đề Q sai. Ta chứng minh mệnh đề phủ định “ 2 ,1nnn + + là một số lẻ” là đúng. + Nếu n chẵn 2 1nn++ là một số lẻ, + Nếu n lẻ, 21nk=+ thì 221463nnkk++=++ là số lẻ Mệnh đề E đúng vì ( )( )322 22 213263 ,3 2121 xxxxx xx xx −+−+− ==− ++ Câu 7: Cho các mệnh đề sau: (1) 2a và 3a 6a .

(2) 39aa  .

(3) 24aa 

(4) 3a và 6a thì 18a .

(5) 00aba+ và 0b 

(6) 00aba== hoặc 0b =

(7) Hai tam giác bằng nhau khi và chỉ khi hai tam giác đó đồng dạng.

(8) Một tam giác là tam giác vuông khi và chỉ khi đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.

Có bao nhiêu mệnh đề sai trong các mệnh đề trên?

A. 4. B. 6. C. 5. D. 7. Lời giải Chọn C

OFFICIAL

(1) đúng.

(2) sai, ví dụ 63 nhưng 69  .

(3) sai, vì 22 nhưng 24

(4) sai, vì 63 và 66 nhưng 618.

(5) sai, ví dụ a = 5, b = 7 có tổng a + b < 0 nhưng a > 0. (6) đúng.

(7) sai, 2 tam giác đồng dạng có thể không bằng nhau.

(8) đúng.

Câu 8: Cho ba mệnh đề sau, với n là số tự nhiên:

(1) 8n + là số chính phương

(2) Chữ số tận cùng của n là 4 (3) 1n là số chính phương

Biết rằng có hai mệnh đề đúng và một mệnh đề

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 23

sai. Hãy xác định mệnh đề nào đúng, mệnh đề nào sai? A. Mệnh đề (2) và (3) là đúng, còn mệnh đề (1) là sai B. Mệnh đề (1) và (2) là đúng, còn mệnh đề (3) là sai C. Mệnh đề (1) là đúng, còn mệnh đề (2) và (3) là sai D. Mệnh đề (1) và (3) là đúng, còn mệnh đề (2) là sai. Lời giải Chọn D Ta có số chính phương có các chữ số tận cùng là0,1,4,5,6,9. Vì vậy

đúng

này

có

Vậy trong hai m

n thấy giữa mệnh đề (2) và (3) cũng có mâu thuẫn. Bởi vì, giả sử mệnh đề này đồng thời là đúng thì 1n có chữ số tận cùng là 3 nên không thể là số chính phương.

Tương tự,

Vậy trong ba mệnh đề trên thì mệnh đề (1) và (3) là đúng, còn mệnh đề (2) là sai.

Câu 9: Mệnh đề nào là sau đây sai?

A. Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một góc bằng nhau.

B. Một tứ giác là hình chữ nhật khi và chỉ khi chúng có 3 góc vuông

C. Một tam giác là vuông khi và chỉ khi nó có một góc bằng tổng hai góc còn lại.

D. Một tam giác là đều khi và chỉ khi nó là tam giác cân và có một góc bằng 60. 

Lời giải

Chọn A

Vì hai tam giác đồng dạng thì luôn có các góc bằng nhau nên A sai

OFFICIAL

Các mệnh đề B, C, D đúng.

Câu 10: Mệnh đề nào dưới đây đúng?

A. Nếu tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác ABCD là hình bình hành.

B. Nếu tứ giác ABCD một cặp cạnh đối song song thì tứ giác ABCD là hình bình hành. C. Nếu tứ giác ABCD có một cặp cạnh đối bằng nhau thì tứ giác ABCD là hình bình hành. D. Nếu tứ giác ABCD có hai đường chéo vuông góc với nhau thì tứ giác ABCD là hình bình hành.

Chọn A

Theo định lý đã học suy ra Chọn A Các mệnh đề B, C, D sai.

Câu 11: Mệnh đề nào sau đây sai?

A. 2 là số nguyên tố B. 1 là s

C. 5 là số nguyên t

nguyên t

D. 6 không ph

i là s

ả

nguyên t

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 24

ận thấy giữa mệnh đề (1) và (2) có mâu thuẫn. Bởi vì, giả sử 2 mệnh đề này đồng thời là

thì 8n +

chữ số tận cùng là 2 nên không thể là số chính phương.

ệnh đề

phải có một mệnh đề là đúng và một mệnh đề là sai.

nhậ

ời gi

ố

ả

ố

ố Lời giải Chọn B Số nguyên tố là số tự nhiên lớn hơn 1, chỉ chia hết cho 1 và chính nó. Vậy B sai. Câu 12: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai? A. Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một góc bằng nhau. B. Một tứ giác là hình chữ nhật khi và chỉ khi chúng có 3 góc vuông. C. Một tam giác là vuông khi và chỉ khi nó có một góc bằng tổng hai góc còn lại. D. Một tam giác là đều khi và chỉ khi chúng có hai đường trung tuyến bằng nhau và có một góc bằng 60.  Lời giải Đáp án A sai vì hai tam giác đồng dạng thì các góc tương ứng bằng nhau. Hai tam giác đồng dạng bằng nhau khi chúng có cặp cạnh tương ứng bằng nhau.

Câu 13: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. Nếu số nguyên n có chữ số tận cùng là 5thì số nguyên n chia hết cho 5.

B. Nếu tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác ABCD là hình bình hành.

C. Nếu tứ giác ABCD là hình chữ nhật thì tứ giác ABCD có hai đường chéo bằng nhau.

D. Nếu tứ giác ABCD là hình thoi thì tứ giác ABCD có hai đường chéo vuông góc với nhau.

Lời giải

Xét mệnh đề đảo của đáp án A: “Nếu số nguyên n chia hết cho 5 thì số nguyên n có chữ số tận cùng là 5”. Mệnh đề này sai vì số nguyên n

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 25

cũng có thể có chữ số tận cùng là 0 Xét mệnh đề đảo của đáp án B: “Nếu tứ giác ABCD là hình bình hành thì tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường”. Mệnh đề này đúng. Câu 14: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng? A. Nếu số nguyên n có tổng các chữ số bằng 9 thì số tự nhiên n chia hết cho 3. B. Nếu xy  thì 22 xy  C. Nếu xy = thì ... txty = D. Nếu xy  thì 33 .xy  Lời giải Xét mệnh đề đảo của đáp án A: “Nếu số tự nhiên n chia hết cho 3 thì số nguyên n có tổng các chữ số bằng 9”. Mệnh đề này sai vì tổng các chữ số của n phải chia hết cho 9 thì n mới chia hết cho 9. Xét mệnh đề đảo của đáp án B: “Nếu 22 xy  thì xy  ” sai vì 22 xy xyxy xy    − . Xét mệnh đề đảo của đáp án C: “Nếu .. txty = thì xy = ” sai với 0,.txy= Câu 15: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai? A. "ABC là tam giác đều  Tam giác ABC cân". B. "ABC là tam giác đều  Tam giác ABC cân và có một góc 60".  C. "ABC là tam giác đều  ABC là tam giác có ba cạnh bằng nhau". D. "ABC là tam giác đều  Tam giác ABC có hai góc bằng 60".  Lời giải Mệnh đề kéo théo "ABC là tam giác đều  Tam giác ABC cân" là mệnh đề đúng, nhưng mệnh đề đảo "Tam giác ABC cân ABC là tam giác đều" là mệnh đề sai. Do đó, 2 mệnh đề "ABC là tam giác đều" và "Tam giác ABC cân" không phải là 2 mệnh đề tương đương. Câu 16: Mệnh đề nào sau đây đúng? A. ( ):1nnn + là số chính phương. B. ( ):1nnn + là số lẻ. C. ( )( ):12nnnn ++ là số lẻ. D. ( )( ):12nnnn ++ chia hết cho 6. Lời giải Chọn D

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 26 Ta có ( )( )12nnn++ là tích của 3 số tự nhiên liên tiếp nên ( )( )12nnn++ chia hết cho 3 và chia hết cho 2. Vậy ( )( )12nnn++ chia hết cho 6. Câu 17: Trong các mệnh đề sau, mệnh đề nào sai? A. 2 , xxx . B. ,66xxx  . C. 2 ,1nn + không chia hết cho 3. D. 2 ,7aa = . Lời giải Chọn D Câu 18: Trong các mệnh đề sau, mệnh đề nào đúng? A. 2 ,50xx += . B. 42 ,540xxx ++= . C. 3 , nnn− chia hết cho 3. D. 52 , xxx . Lời giải Chọn C Với * n thì ( )( )3 11nnnnn−=−+ là tích 3 số tự nhiên liên tiếp nên 3 nn chia hết cho 3. Với 0n = thì 3 0nn−= chia hết cho 3. Vậy 3 , nnn− chia hết cho 3. Câu 19: Trong các mệnh đề sau mệnh đề nào sai? A. 2399100 444....44 +++++ chia hết cho 5. B. 2 :1nn + không chia hết cho 4 C. :21 nnN − chia hết cho 7. D. 3333 123....100 ++++ không chia hết cho 5050 Lời giải Chọn D Phương án A đúng vì ( )2399100399399 444....444.54.5...4.5544...4 +++++=+++=+++ chia hết cho 5. Phương án B đúng vì +) TH1 : 2, nkk= Ta có : 22141nk+=+ không chia hết cho 4. +) TH1 : 21, nkk=+ Ta có : 221442nkk+=++ không chia hết cho 4. Vậy 2 :1nn + không chia hết cho 4 là mệnh đề đúng. Phương án C đúng vì với 3n = thì 217 n −= chia hết cho 7. Phương án D sai vì: ( ) ( ) ( )3333332333 123....1001100299...5060 ++++=++++++ chia hết cho 101 Lại có ( ) ( ) ( ) 333333233333 123....100199298...406050100 ++++=++++++++ chia hết cho 50. Vậy 3333 123....100 ++++ chia hết cho 5050.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 27 Câu 20: Có bao nhiêu số nguyên n để mệnh đề “ 32 271 nnn+++ chia hết cho 21 n ” là đúng? A. 3. B. 2. C. 4. D. 5. Lời giải Chọn C Ta có : ( )( )322 2714215 nnnnnn +++=++−+ 32 271 nnn+++ chia hết cho 21 n  5 chia hết cho 21 n 2111 2110 2153 2152 nn nn nn nn −==  −=−= −==  −=−=− Vậy có 4 giá trị nguyên của n . Câu 21: Cho các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng? A. Nếu tứ giác ABCD là hình thang cân thì 2 góc đối bù nhau. B. Nếu ab = thì .. acbc = . C. Nếu ab  thì 22ab  . D. Nếu số nguyên chia hết cho 10 thì chia hết cho 5 và 2. Lời giải Chọn D "Nếu số nguyên chia hết cho 10 thì chia hết cho 5 và 2" có mệnh đề đảo là "Nếu số nguyên chia hết cho 5 và 2 thì chia hết cho 10" là một mệnh đề đúng. Câu 22: Dùng kí hiệu ,  để phát biểu mệnh đề "Có một số hữu tỉ mà nghịch đảo của nó lớn hơn chính nó". A. 1 : nn n  B. 1 : nn n  C. 1 : nn n  D. 1 : nn n  Lời giải Chọn D Câu 23: Cho mệnh đề 2 1 “:” 4 Axx x =+− . Lập mệnh đề phủ định của mệnh đề A và xét tính đúng sai của nó. A. 2 1 “:” 4 Axxx=+− . Đây là mệnh đề đúng. B. 2 1 “:” 4 Axxx=+− . Đây là mệnh đề đúng. C. 2 1 “:” 4 Axxx=+− . Đây là mệnh đề đúng. D. 2 1 “:” 4 Axxx=+− . Đây là mệnh đề sai. Lời giải Chọn D 2 1 “:” 4 Axx x =+− vậy 2 1 “:” 4 Axx x =+− . Ta có 2 2 11 0, 42 xxxx  +−+   là mệnh đề đúng. Vậy mệnh đề A là mệnh đề sai.

Câu 24: Phủ định của mệnh đề: “Hình thoi có hai đường chéo vuông góc với nhau” là:

A. “Hai đường chéo của hình thoi vuông góc với nhau”.

B. “Hình thoi có hai đường chéo không vuông góc với nhau”.

C. “Hình thoi có hai đường chéo bằng nhau”.

D. “Hình thoi là hình bình hành có hai đường chéo vuông góc với nhau”.

Câu

góc” là

vuông góc”.

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 28

Lời giải

ọn B

ủ định của “vuông

“không

25: Phủ định của mệnh đề: “ 2

nn + không chia hết cho 3” là: A. “ 2 :1nn + chia hết cho 3”. B. “ 2 :1nn + không chia hết cho 3”. C. “ 2 :1nn + chia hết cho 3”. D. “  2 :1nn+ không chia hết cho 3”. Lời giải Chọn C Phủ định của  là  Phủ định của “không chia hết” là “chia hết” Câu 26: Phủ định của mệnh đề: “ 2 :10xx + ” là: A. “ 2 :10xx + ” B. “ 2 :10xx + ”C. “ 2 :10xx + ”D. “ 2 :10xx += ” Lời giải Chọn B Phủ định của  là  Phủ định của > là  Câu 27: Phủ định của mệnh đề P: “ 2 :320xxx −+= ” là: A. P : “ 2 :320xxx −+ ” B. P : “ 2 :320xxx −+= ” C. P : “ 2 :320xxx −+ ” D. P : “ 2 :320xxx −+ ” Lời giải Chọn D Phủ định của là  Phủ định của = là  Câu 28: Mệnh đề nào sau đây là phủ định của mệnh đề: “Mọi động vật đều di chuyển”. A. Mọi động vật đều không di chuyển. B. Mọi động vật đều đứng yên. C. Có ít nhất một động vật không di chuyển. D. Có ít nhất một động vật di chuyển. Lời giải Chọn C Phủ định của mệnh đề “Mọi động vật đều di chuyển” là mệnh đề “Có ít nhất một động vật không di chuyển”. Câu 29: Phủ định của mệnh đề 2 ",531" xxx −= là A. 2" ,53"xxx− B. 2 ",531" xxx −= C. 2 "x,5x31" x − D. 2 ",531" xxx − Lời giải Chọn C Phủ định của mệnh đề 2 ",531" xxx −= là mệnh đề 2 "x,5x31" x −

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 29 Câu 30: Cho mệnh đề ( ):Px 2 ",10" xxx ++ . Mệnh đề phủ định của mệnh đề ( )Px là: A. 2 ",10" xxx ++ B. 2 ",10" xxx ++ C. 2 ",10" xxx ++ D. "  2 ,10"xxx++ Lời giải Chọn C Phủ định của mệnh đề 2 ",10" xxx ++ là mệnh đề 2 ",10" xxx ++ Câu 31: Cho mệnh đề 2 “:”A xxx=  . Trong các mệnh đề sau, mệnh đề nào là phủ định của mệnh đề A? A. 2 “:” xxx B. 2 “:” xxx C. 2 “:” xxx D. 2 “:” xxx Lời giải Chọn B Trong mệnh đề phủ định,  đổi thành ,  đổi thành  Phủ định của  là . Câu 32: Cho mệnh đề 2 “:”A xxx=  . Trong các mệnh đề sau, mệnh đề nào là phủ định của mệnh đề A? A. 2 “:” xxx . B. 2 “:” xxx . C. 2 “:” xxx . D. 2 “:” xxx . Lời giải Chọn B Phủ định của  là  Phủ định của  là . Câu 33: Cho n là số tự nhiên, mệnh đề phủ định của mệnh đề nào sau đây đúng? A. :P ” ( ),1nnn + không là số chính phương”. B. :Q ” ( ),1nnn + là số chẵn” C. :R ” ( )( ),12nnnn ++ là số chẵn”. D. :M ” ( )( ),12nnnn ++ không chia hết cho 6” Lời giải Chọn D :P ” ( ),1nnn + là số chính phương” +) với ( ) 112nnn=+= không phải số chính phương A sai. :Q ” ( ),1nnn + là số lẻ”. +) với ( ) 112nnn=+= là số chẵn B sai. :R ” ( )( ),12nnnn ++ là số lẻ” TH1: n chẵn ( )( )12nnn ++ chẵn TH2: n lẻ ( )1n + chẵn ( )( )12nnn ++ chẵn

ab+

đủ để một trong hai số a và b nhỏ hơn 1. B. Một trong hai số a và b nhỏ hơn 1 là điều kiện đủ để 2ab+

C. Từ 2ab+ suy ra một trong hai số a và b nhỏ hơn 1

D. Tất cả các câu trên đều đúng.

Chọn A

Lời giải

Câu 35: Cho mệnh đề: “Nếu 2 góc ở vị trí so le trong thì hai góc đó bằng nhau”. Trong các mệnh đề sau đây, đâu là mệnh đề đảo của mệnh đề trên?

A. Nếu 2 góc bằng nhau thì hai góc đó ở vị trí so le trong

B. Nếu 2 góc không ở vị trí so le trong thì hai góc đó không bằng nhau

C. Nếu 2 góc không bằng nhau thì hai góc đó không ở vị trí so le trong.

D. Nếu 2 góc ở vị trí so le trong thì hai góc đó không bằng nhau.

ời giải

ọn A

Câu 36: Cho mệnh đề: “Nếu một tứ giác là hình thang cân thì tứ giác đó có hai đường chéo bằng nhau”.

Phát biểu mệnh đề

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 30 Vậy ( )( )12nnn++ chẵn n  C sai. :M ” ( )( ),12nnnn ++ chia hết cho 6”. +) ( ) ( ) 2* 6 3** P P P       ( )* Ở trên ta đã chứng minh P luôn chẵn 2P ( )** 3P TH1: 3n 3P TH2: n chia 3 dư 1 ( ) 23n + 3P TH3: n chia 3 dư 2 ( ) 13n + 3P Vậy 3P n  6P . Câu 34: Cho mệnh đề: “Nếu 2ab+ thì một trong hai số a và b nhỏ hơn 1”. Phát biểu mệnh đề trên bằng cách sử dụng khái niệm “điều kiện đủ”.

là điều kiện

trên bằng cách sử dụng khái niệm “điều kiện cần”. A. Điều kiện cần để tứ giác là hình thang cân là tứ giác đó có hai đường chéo bằng nhau. B. Điều kiện cần để tứ giác có hai đường chéo bằng nhau là tứ giác đó là hình thang cân. C. Tứ giác là hình thang cân kéo theo tứ giác đó có hai đường chéo bằng nhau. D. Cả a, b đều đúng. Lời giải Chọn A Câu 37: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo là sai? A. Tam giác cân có hai cạnh bằng nhau. B. x chia hết cho 6 thì x chia hết cho 2 và 3.

C. ABCD

ABCD

hình

Câu 38: Mệnh đề nào dưới đây sai

A. Tứ giác ABCD là hình chữ nhật khi và chỉ khi ABCD có ba góc vuông.

B. Tứ giác ABCD là hình bình hành khi và chỉ khi ABCD có hai cạnh đối song song và bằng nhau.

C. Tứ giác ABCD là hình thoi khi và chỉ khi ABCD có hai đường chéo vuông góc với nhau tại trung điểm mỗi đường.

D. Tứ giác ABCD là hình vuông khi và chỉ khi ABCD có bốn góc vuông.

Lời giải

Chọn D

Mệnh đề ở đáp án D không phải là một mệnh đề tương đương vì hình chữ nhật vẫn có bốn góc vuông nhưng không phải là hình vuông.

OFFICIAL

Câu 39: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. Nếu số nguyên n có chữ số tận cùng là 5 thì số nguyên n chia hết cho 5.

B. Nếu tứ giác ABCDcó hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác ABCD là hình bình hành.

C. Nếu tứ giác ABCDlà hình chữ nhật thì tứ giác ABCDcó hai đường chéo bằng nhau.

D. Nếu tứ giác ABCDlà hình thoi thì tứ giác ABCDcó hai đường chéo vuông góc với nhau.

Lời giải Chọn B

Đáp án A sai vì số nguyên n chi hết cho 5 thì số nguyên n có chữ số tận cùng là 5 và 0 ; Đáp án C sai vì hai đường chéo bằng nhau không suy ra được tứ giác là hình chữ nhật ; Đáp án D sai vì hai đường chéo vuông góc với nhau không suy ra được tứ giác là hình thoi.

Câu 40: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. Nếu tổng hai số 2ab+ thì có ít nhất có một số lớn hơn 1.

B. Trong một tam giác cân hai đường cao bằng nhau.

C. Nếu tứ giác là hình vuông thì hai đường chéo vuông góc với nhau.

D. Nếu một số tự nhiên chia hết cho 6 thì nó chia hết cho 3. Lờ

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 31

là

bình hành thì AB song song với CD. D.

là

chữ nhật thì 90.ABC=== Lời giải Chọn C

i giải Chọn B Tam giác có hai đường cao bằng nhau là tam giác cân là mệnh đề đúng. Câu 41: Trong các mệnh đề sau đây, mệnh đề nào có mệnh đề đảo là đúng? A. Nếu a và b cùng chia hết cho c thì ab + chia hết cho c B. Nếu hai tam giác bằng nhau thì diện tích bằng nhau. C. Nếu a chia hết cho 3 thì a chia hết cho 9 D. Nếu một số tận cùng bằng 0 thì số đó chia hết cho 5. Lời giải Chọn C Nếu a chia hết cho 9 thì a chia hết cho 3 là mệnh đề đúng.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 32

BÀI1:MỆNHĐỀ

Câu 1: Trong các câu dưới đây, câu nào không phải là mệnh đề?

A. 16 là số chính phương. B. Bạn bao nhiêu tuổi?

C. Năm 2021 là năm nhuận. D. Tổng các góc của một tứ giác bằng 0360 .

Câu 2: Câu nào sau đây không là mệnh đề?

A. 213 x + .

B. Mặt trời mọc ở hướng Tây.

C. Một tuần có bảy ngày.

D. Hình bình hành có một góc vuông là hình chữ nhật.

Câu 3: Phát biểu nào sau đây không phải là mệnh đề?

A. Bạn là học sinh khối 10 phải không?

B. Tổng ba góc của một tam giác bằng 180 .

C. 2 là số nguyên tố nhỏ nhất.

D. Năm 2022 là năm nhuận.

Câu 4: Trong các câu dưới đây, câu nào là mệnh đề?

A. Bạn có khỏe không?

C. Lớp bạn có bao nhiêu học sinh nữ?

B. Hôm nay trời nóng quá!

D. 111 không phải là số nguyên tố.

Câu 5: Trong các câu sau, câu nào không là một mệnh đề chứa biến?

A. 246 += B.

450

C. 520 xy−= D. 21

chia hết cho 3.

Câu 6: Trong các câu sau đây câu nào không phải là mệnh

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 18

xx−−=

x +

đề? A. Một năm có 365 ngày. B. Học lớp 10 thật vui. C. Pleiku là thành phố của Gia Lai. D. 236 += . Câu 7: Mệnh đề chứa biến 2 :''440"Pxx++= trở thành một mệnh đề đúng với. A. 2x =− . B. 1x =− . C. 1.x = D. 0x = . Câu 8: Trong các câu dưới đây có bao nhiêu câu là mệnh đề? (I) Số 2018 là số chẵn. (II) Hôm nay bạn có vui không? (III) Quảng Phú là một thị trấn của huyện CưMgar. (IV) Tiết 5 rồi, đói bụng quá! A. 4 B. 1 C. 2 D. 3 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.III ==

Câu 9: Cho các câu sau đây:

(I): “ Phan xi păng là ngọn núi cao nhất Việt Nam”.

(II): “ 2 9,86  ”.

(III): “ Mệt quá!”.

(IV): “ Chị ơi, mấy giờ rồi?”

Hỏi có bao nhiêu câu là mệnh đề?

A. 4 B. 3 C. 2 D. 1

Câu 10: Trong các câu sau, có bao nhiêu câu là mệnh đề?

a) Trời rét quá!

b) Việt Nam nằm ở khu vực Đông Nam Á.

c) 10244. −+=

d) Năm 2020là năm nhuận.

A. 1. B. 2. C. 3. D. 4.

Câu 11: Trong các phát biểu sau, phát biểu nào là mệnh đề?

A. 3 là số nguyên tố lẻ nhỏ nhất.

B. Đề thi hôm nay khó quá!

OFFICIAL

C. Một tam giác cân thì mỗi góc đều bằng 060 phải không?

D. Các em hãy cố gắng học tập!

Câu 12: Trong các phát biểu sau, phát biểu nào là mệnh đề?

A. 3 là số nguyên tố lẻ nhỏ nhất.

B. Đề thi hôm nay khó quá!

C. Một tam giác cân thì mỗi góc đều bằng 060 phải không?

D. Các em hãy cố gắng học tập!

Câu 13: Trong các câu sau, có bao nhiêu câu là mệnh đề?

a) 613 x + .

b) Phương trình 2 310xx+−= có nghiệm. c) ,51xx 

d) Năm 2018 là năm nhuận. e) Hôm nay thời tiết đẹp quá!

A. 4. B. 1. C. 2. D. 3.

Câu 14: Trong các câu sau, câu nào là mệnh đề?

A. Không được làm việc riêng trong giờ học. B. Đi ngủ đi. C. Trung Quốc là nước đông dân nhất thế giới. D. Bạn học trường nào?

Câu 15: Trong các câu sau, có bao nhiêu câu là mệnh đề?

a) Hãy đi nhanh lên!

b) Hà Nội là thủ đô của Pháp. c) 57415 ++=

3x  .

A. 4. B. 1. C. 2.

Câu 16: Trong các câu sau câu nào là mệnh đề?

A. Hãy đi nhanh lên!.

B. Hà nội là thủ đô của Việt Nam.

C. Nam ăn cơm chưa?.

D. Buồn ngủ quá!

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 19

Câu 17: Trong các câu sau câu nào là mệnh đề chứa biến?

A. 9 là số nguyên tố.

B. 18 là số chẵn.

C. ( )2 3, xxx+ .

D. Hình chữ nhật có hai đường chéo bằng nhau.

Câu 18: Cho mệnh đề chứa biến ( ) 2 :"511"Pxx với x là số nguyên tố. Tìm mệnh đề đúng trong các mệnh đề sau:

A. ( )3P . B. ( )2P . C. ( )7P . D. ( )5P .

Câu 19: Cho S là mệnh đề “ Nếu tổng các chữ số của một số n chia hết cho 6thì n chia hết cho 6”. Một giá trị của n để khẳng định S sai là:

A. 33. B. 40. C. 42. D. 30.

Câu 20: Trong các phát biểu sau, phát biểu nào là mệnh đề đúng?

A. Tổng của hai cạnh một tam giác lớn hơn cạnh thứ ba.

B. Hình thang có hai cạnh bên bằng nhau là hình thang cân.

C. Bạn có chăm học không?

D.  là một số hữu tỉ.

Câu 21: Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?

OFFICIAL

A. Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.

B. Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.

C. Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.

D. Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.

Câu 22: Trong các câu sau, câu nào một là mệnh đề đúng?

A. Hà nội là thủ đô của Việt Nam.

C. 7là một số tự nhiên chẵn.

Câu 23: Trong các mệnh đề sau, mệnh đề nào sai?

A. Hà nội là thủ đô của Việt Nam.

C. 5là một số tự nhiên lẻ.

B. 2là một số tự nhiên lẻ.

C.  là một số hữu tỷ.

B. 4là một số tự nhiên chẵn.

C.  là một số hữu tỷ.

Câu 24: Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị của x ?

A. 52xx  .

B. 52xx  .

C. 2252xx  . D. 52xx++ .

Câu 25: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?

A. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

B. Tam giác cân có một góc bằng 060 là tam giác đều.

C. Hình bình hành có hai đường chéo bằng nhau là hình vuông.

D. Tam giác có hai đường cao bằng nhau là tam giác cân.

Câu 26: Cho định lý “Nếu hai tam giác bằng nhau thì diện tích bằng nha”. Mệnh đề nào sau đây đúng?

A. Hai tam giác bằng nhau là điều kiện cần và đủ để chúng có diện tích bằng nhau.

B. Hai tam giác bằng nhau là điều kiện cần để diện tích chúng bằng nhau.

C. Hai tam giác có diện tích bằng nhau là điều kiện đủ để chúng bằng nhau.

D. Hai tam giác bằng nhau là điều kiện đủ để diện tích chúng bằng nhau.

Câu

Mệnh

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 20

27:

đề nào

đây là mệnh đề sai ? A. 2 :0xx  . B. 2 : nnn= . C. :2 nnn . D. 2 : xxx . Câu 28: Trong các mệnh đề sau, mệnh đề nào sai?

A. N

B. N

huy

C. V

hướ

D. Điể

ABC

OFFICIAL

) xBA  . D. ( ) xBA  .

Câu 32: Trong các mệnh đề sau, tìm mệnh đề sai?

A. Nếu a chia hết cho 9thì a chia hết cho 3 B. Nếu một tam giác có một góc bằng 60thì tam giác đó là tam giác đều.

C. Nếu 0ab thì 22ab  . D. Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân.

Câu 33: Cho mệnh đề chứa biến

các giá trị của x để ( )Px là một mệnh đề đúng.

Câu 34: Trong các

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 21

ếu m , n là các số vô tỉ thì mn cũng là số vô tỉ

ếu

là một tam giác vuông thì đường trung tuyến ứng với cạnh huyền bằng nửa cạnh

ền.

ới ba véctơ a , b , c đều khác véctơ 0 , nếu a , b cùng ngược hướng với c thì a , b cùng

ng.

là trọng tâm tam giác ABC khi và chỉ khi 0GAGBGC++= Câu 29: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng? A. Nếu hai số a , b cùng chia hết cho c thì ab + chia hết cho c B. Nếu một số nguyên chia hết cho 6 thì nó chia hết cho2 và 3. C. Nếu hai số x , y thỏa mãn 0xy+ thì có ít nhất một trong hai số x , y dương. D. Phương trình bậc hai ( )2 00axbxca++= có a , c trái dấu thì có hai nghiệm phân biệt. Câu 30: Cho hai đa thức ( )Px và ( )Qx . Xét các tập hợp ( ) 0AxPx== , ( ) 0BxQx== và ( ) ( ) 22 0CxPxQx =+=   . Trong các mệnh đề sau, mệnh đề nào đúng? A. CAB = B. CAB = C. \ CAB = D. \.CBA = Câu 31: Cho phần tử x thuộc tập B và tâp B là tập con của A . Trong các khẳng định sau khẳng định nào đúng? A. ( ) xBA  . B. ( ) xBA  . C. (

( ) 32 :"320"Pxxxx−+= . Tìm

A. 0,1,2xxx=== B. 2,3xx=−=− C. 1,2xx=−=− D. 4,2,3xxx==−=

mệnh đề sau, mệnh đề nào là mệnh đề sai? A. :33 n nn + B. 1267  C. 64107  D. ( )2 2:2 xxx − Câu 35: Xét mệnh đề kéo theo P: “Nếu 18 chia hết cho 3 thì tam giác cân có 2 cạnh bằng nhau” và Q: “Nếu 17 là số chẵn thì 25 là số chính phương”. Hãy chọn khẳng định đúng trong các khẳng định sau A. P đúng, Q sai. B. P đúng, Q đúng. C. P sai, Q đúng. D. P sai, Q sai. Câu 36: Trong các mệnh đề dưới đây, mệnh đề nào là mệnh đề đúng? A. 2 :10xx += . B. 2 :0xx  . C. 2 :210xx − . D. 2 :20xx −= . Câu 37: Mệnh đề nào sau đây là mệnh đề đúng? A. “ :22 x xx + ”. B. “ :21 x x + là số nguyên tố”. C. “ *2:1xx − là bội số của 3”. D. “ 2 :3xx = ”. Câu 38: Cho P Q là mệnh đề đúng. Khẳng định nào sau đây là sai? A. PQ  sai. B. PQ  đúng. C. QP  sai. D. PQ  sai.

Mệnh đề phủ định của mệnh

A. 2018không là một số lẻ.

2018là một số lẻ.

2018 là một số chẵn” là:

2018không là một số chẵn.

Câu 42: Mệnh đề nào sau đây là mệnh đề phủ định của mệnh đề: “Mọi động vật đều di chuyển”?

A. Có ít nhất một động vật di chuyển. B. Có ít nhất một động vật không di chuyển. C. Mọi động

Cho m

Cho mệnh đề "Có một học sinh trong lớp 11A không chấp hành luật giao thông " Mệnh đề phủ định của mệnh đề này là :

A. Không có học sinh nào trong lớp 11A chấp hành luật giao thông.

B. Mọi học sinh trong lớp 11A đều chấp hành luật giao thông.

C. Có một học sinh trong lớp 11A chấp hành luật giao thông. D. Mọi học sinh trong

hành luật giao thông.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 22 Câu 39: Số mệnh đề đúng trong các mệnh đề sau: ( ) 1 : Ixx x  . ( ) :20 nIIn . ( ) 2 :90IIIxx−= ( ) 2 :510IVnn+ chia hết cho 5 A. 1 B. 4 C. 2 D. 3 Câu 40: Lập mệnh đề phủ định của mệnh đề 2 ":20180" xxx ++ . A. 2 :20180xxx ++ B. 2 :20180xxx ++ C. 2 :20180xxx ++ D. 2 :20180xxx ++ Câu 41:

đề: “

vật đều không di chuyển. D. Mọi động vật đều đứng yên. Câu 43: Cho mệnh đề 2 :",12" Pxxx + . Mệnh đề nào sau đây là mệnh đề phủ định của mệnh đề P ? A. 2 :",12" Pxxx + . B. 2 :",12" Pxxx + . C. 2 :",12" Pxxx + . D. 2 :",12" Pxxx + . Câu 44:

ệnh đề 2 ",30" xxx −+ . Hỏi mệnh đề nào là phủ định của mệnh đề trên A. 2 ",30" xxx −+ . B. 2 ",30" xxx −+ . C. 2 ",30" xxx −+ . D. "  2 ,30"xxx−+ . Câu 45:

lớp 11A không chấp

Câu 46: Cho mệnh đề 2 :":70" Axxx−+ . Mệnh đề phủ định của A là: A. 2 :70xxx −+ B. 2 :70xxx −+ C. 2 :70xxx −+ . D. 2 :70xxx −+ . Câu 47: Cho mệnh đề: 2 ",20" xxx −+ . Mệnh đề phủ định là: A. 2 ",20" xRxx −+ B. 2 ",20" xxx −+ C. 2 ",20" xxx −+ D. 2 ",20" xxx −+ Câu 48: Cho mệnh đề: 2 ",20" xxx −+ . Mệnh đề phủ định sẽ là: A. 2 ",20" xxx −+ . B. 2 ",20" xxx −+ . C. 2 ",20" xxx −+ D. 2 ",20" xxx −+ Câu 49: Lập mệnh đề phủ định của mệnh đề : “ ,21 n nn + “ A. ,21 n nn + . B. ,21 n nn + . C. ,21 n nn + . D. ,21 n nn + . Câu 50: Cho mệnh đề 2 ",320" xxx ++ . Mệnh đề phủ định của mệnh đề trên là

Câu 51: Cho mệnh đề:”Có một học sinh trong lớp 10A không thích học môn Toán ”. Mệnh đề phủ định của mệnh đề này là:

A. ”Mọi học sinh trong lớp 10A đều thích học môn Văn ”.

B. ”Mọi học sinh trong lớp 10A đều không thích học môn Toán ”.

C. ”Có một học sinh trong lớp 10A thích học môn Toán ”.

D. ”Mọi học sinh trong lớp 10A đều thích học môn Toán ”.

Câu 52: Cho tứ giác ABCD. Xét hai mệnh đề

P: “ Tứ giác ABCDlà hình thoi”

Q: “ Tứ giác ABCDcó hai đường chéo vuông góc”.

Phát biểu mệnh đề PQ 

A. Tứ giác ABCDcó hai đường chéo vuông góc thì nó là hình thoi.

B. Tứ giác ABCDlà hình thoi thì nó có hai đường chéo vuông góc.

C. Tứ giác ABCDlà hình thoi khi và chỉ khi nó có hai đường chéo vuông góc.

D. Tứ giác ABCDlà hình thoi nếu nó có hai đường chéo vuông góc.

Câu 53: Trong các định lý sau, định lý nào không có định lý đảo?

A. Nếu tứ giác ABCDlà hình chữ nhật thì nó là hình bình hành có một góc vuông.

B. Nếu tứ giác ABCDlà hình vuông thì nó là hình thoi có hai đường chéo bằng nhau.

C. Nếu tứ giác ABCDlà hình bình hành thì nó là hình thang có hai cạnh bên bằng nhau.

D. Nếu tứ giác ABCDlà hình vuông thì nó là hình chữ nhật có hai cạnh kề bằng nhau.

Câu 54: Cho mệnh đề '''' PQ  . Phát biểu nào sau đây đúng?

A. P là điều kiện đủ để có Q. B. P là điều kiện cần và đủ để có Q.

C. Nếu P thì Q. D. P là điều kiện cần để có Q.

Câu 55: Cho định lí “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”. Mệnh đề nào sau đây đúng?

A. Hai tam giác bằng nhau là điều kiện cần và đủ để chúng có diện tích bằng nhau.

B. Hai tam giác có diện tích bằng nhau là điều kiện đủ đê chúng bằng nhau.

C. Hai tam giác bằng nhau là điều kiện cần để diện tích chúng bằng nhau.

D. Hai tam giác bằng nhau là điều kiện đủ để diện tích chúng bằng nhau.

Câu 56: Mệnh đề nào sau đây có mệnh đề đảo là mệnh đề đúng?

A. Nếu a và b cùng chia hết cho c thì ab + chia hết cho c .

B. Nếu ab  thì 22ab  .

C. Nếu số nguyên chia hết cho 14thì chia hết cho cả 7và 2

D. Hai tam giác bằng nhau có diện tích bằng nhau.

Câu 57: Trong các mệnh đề

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 23 A. 2 ,320xxx ++ B. 2 ,320xxx ++ C. 2 ,320xxx ++ D. 2 ,320xxx ++

sau, mệnh đề nào có mệnh đề đảo đúng. A. Nếu xy = thì txty = . B. Nếu xy  thì 33 xy  . C. Nếu số nguyên n có tổng các chữ số bằng 9thì số nguyên n chia hết cho 3. D. Nếu xy  thì 22 xy  Câu 58: Câu “Tồn tại ít nhất một số thực có bình phương không dương” là một mệnh đề. Có thể viết lại mệnh đề đó như sau. A. 2 :0xx  . B. 2 :0xx  . C. 2 :0xx = . D. 2 :0xx  . Câu 59: Mệnh đề ( ) 2 :",70"Pxxxx−+= . Phủ định của mệnh đề P là

biểu

lý “Với mọi số tự nhiên chia hết cho 5thì

chia hết cho

A. Với mọi số tự nhiên

, n chia hết cho 5là điều kiện cần để

1n và 2 1n + đều không chia hết cho 5

B. Với mọi số tự nhiên n , điều kiện cần để n chia hết cho 5là 2 1n và 2 1n + đều không chia hết cho 5.

C. Với mọi số tự nhiên n , điều kiện cần để 2 1n và 2 1n + đều không chia hết cho 5là n chia hết cho 5

D. Với mọi số tự nhiên n , n chia hết cho 5là điều kiện cần và đủ để 2 1n và 2 1n + đều không chia hết cho 5.

Câu 62: Phát biểu định lý đảo của định lý “ Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

A. Một tam giác là tam giác cân là điều kiện cần và đủ để có tam giác đó có hai góc bằng nhau

B. Một tam giác có hai góc bằng nhau khi và chỉ khi là tam giác đó là tam giác cân.

C. Một tam giác có hai góc bằng nhau là điều kiện đủ để có tam giác đó là tam giác cân.

D. Một tam giác là tam giác cân điều kiện đủ là tam giác đó có hai góc bằng nhau.

Câu 63: Tìm mệnh đề phủ định của mệnh đề: “Tất cả người dân Việt Nam đều được tiêm Vacxin ngừa Côvit.”

A. “Tất cả người dân Việt Nam đều không được tiêm Vacxin ngừa Côvit.”.

B. “Có người dân Việt Nam được tiêm Vacxin ngừa Côvit.”.

C. “Có một người dân Việt Nam không được tiêm Vacxin ngừa Côvit.”.

D. “Có ít nhất một người dân Việt Nam không được tiêm Vacxin ngừa Côvit.”

Câu 64: Cho mệnh

đề phủ định của mệnh đề Pvà tính đúng, sai của

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 24 A. 2 ,70xxx −+ B. 2 ,70xxx −+ C. 2 ,70xxx −+ D. 2 ,70xxx −+ Câu 60: Phủ định của mệnh đề 2 ":2520" xQxx −+= là A. 2 ":2520" xQxx −+ . B. 2 ":2520" xQxx −+ . C. 2 ":2520" xQxx −+ . D. 2 ":2520" xQxx −+= . Câu 61: Sử dụng thuật ngữ “điều kiện cần” để phát

định

2 1n và 2 1n + đều không

5”

đề 2 P:":10" xxx ++ . Mệnh

nó là: A. 2 P:":10" xxx ++= và P là mệnh đề sai. B. 2 P:":10" xxx ++= và P là mệnh đề đúng. C. 2 P:":10" xxx ++ và P là mệnh đề đúng. D. 2 P:":10" xxx ++= và P là mệnh đề sai.

Câu

Trong các câu dưới

A. 16 là s

Năm

chính phương.

BÀI1:MỆNHĐỀ

Câu 2: Câu nào sau đây không là mệnh đề?

A. 213 x +

B. Mặt trời mọc ở hướng Tây.

C. Một tuần có bảy ngày.

D. Hình bình hành có một góc vuông là hình chữ nhật.

Lời giải

Chọn A

213 x − không phải là mệnh đề.

Mặt trời mọc ở hướng Tây là mệnh đề sai.

Một tuần có bảy ngày là mệnh đề đúng.

Hình bình hành có một góc vuông là hình chữ nhật là mệnh đề đúng.

Câu 3: Phát biểu nào sau đây

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 1

đây, câu nào không phải là mệnh đề?

ố

B. Bạn bao nhiêu tuổi? C.

2021 là năm nhuận. D. Tổng các góc của một tứ giác bằng 0360 Lời giải Chọn B

không phải là mệnh đề? A. Bạn là học sinh khối 10 phải không? B. Tổng ba góc của một tam giác bằng 180 C. 2 là số nguyên tố nhỏ nhất. D. Năm 2022 là năm nhuận. Lời giải Chọn A “Bạn là học sinh khối 10 phải không?” là câu nghi vấn, không phải là một mệnh đề Câu 4: Trong các câu dưới đây, câu nào là mệnh đề? A. Bạn có khỏe không? B. Hôm nay trời nóng quá! C. Lớp bạn có bao nhiêu học sinh nữ? D. 111 không phải là số nguyên tố. Lời giải Chọn D Chọn D vì đây là câu khẳng định. Các câu A, C là các câu hỏi, câu B là câu cảm thán. Nên không phải là mệnh đề. CHƯƠNG I MỆNH ĐỀ - TẬP HỢP HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.III ==

Câu 5: Trong các câu sau, câu nào không là m

A. 246 += B. 2

C. 520 xy

Chọn A

Câu A là một mệnh đề

D. 21

t mệnh đề chứa bi

chia hết cho 3.

Lời giải

Câu B, C, D là mệnh đề chứa biến.

Câu 6: Trong các câu sau đây câu nào không phải là mệnh đề?

A. Một năm có 365 ngày. B. Học

OFFICIAL

đề: (I) và (III).

Câu 9: Cho các câu sau đây:

(I): “ Phan xi păng là ngọn núi cao nhất Việt Nam”.

(II): “ 2 9,86  ”.

(III): “ Mệt quá!”.

(IV): “ Chị ơi, mấy giờ rồi?”

Hỏi có bao nhiêu câu là mệnh đề?

A. 4 B. 3 C. 2 D. 1

Lời giải

Chọn C

Câu (I) là mệnh đề đúng.

Câu (II) là mệnh đề sai.

Câu (III) là câu cảm thán nên không phải là mệnh đề.

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 2

ộ

ế

450 xx−−=

−=

x +

lớp 10 thật vui. C. Pleiku là thành phố của Gia Lai. D. 236 += Lời giải Chọn B B. Vì đây là một câu cảm thán, không phải là một khẳng định có tính đúng hoặc sai nên B không phải là mệnh đề. Câu 7: Mệnh đề chứa biến 2 :''440"Pxx++= trở thành một mệnh đề đúng với. A. 2x =− . B. 1x =− . C. 1.x = D. 0x = . Lời giải Chọn A Ta có ( ) 22440202xxxx ++=+==− Vậy 2x =− . Câu 8: Trong các câu dưới đây có bao nhiêu câu là mệnh đề? (I) Số 2018 là số chẵn. (II) Hôm nay bạn có vui không? (III) Quảng Phú là một thị trấn của huyện CưMgar. (IV) Tiết 5 rồi, đói bụng quá! A. 4 B. 1 C. 2 D. 3 Lời giải Chọn C Ta có câu là mệnh

Câu (IV) là câu hỏi nên không

là mệnh đề.

Câu 10: Trong các câu sau, có bao nhiêu câu là m

a) Trời rét quá!

Việt Nam nằm ở khu vực Đông Nam Á.

10244.

Năm 2020là năm nhuận.

A. 1. B. 2

Chọn C

Câu b), câu c) và câu d) là mệnh đề

Câu a) là câu cả

Câu

Trong các phát

A. 3 là số nguyên tố l

Đề thi hôm nay khó quá!

C. 3

C. Một tam giác cân thì mỗi góc đều bằng 060 phải không?

D. Các em hãy cố gắng học tập!

Chọn A

Lời giải

Mệnh đề là những phát biểu có tính chất hoặc đúng hoặc sai, do đó phát biểu:”3 là số nguyên tố lẻ nhỏ nhất” là một mệnh đề đúng.

Câu 12: Trong các phát biểu sau, phát biểu nào là mệnh đề?

A. 3 là số nguyên tố lẻ nhỏ nhất.

B. Đề thi hôm nay khó quá!

C. Một tam giác cân thì mỗi góc đều bằng 060 phải không?

D. Các em hãy cố gắ

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 3

phải

ệnh đề?

−+= d)

4. Lời giải

m thán nên không phải là mệnh đề

11:

biểu sau, phát biểu nào là mệnh đề?

ẻ nhỏ nhất. B.

ng học tập! Lời giải Chọn A Mệnh đề là những phát biểu có tính chất hoặc đúng hoặc sai, do đó phát biểu:”3 là số nguyên tố lẻ nhỏ nhất” là một mệnh đề đúng. Câu 13: Trong các câu sau, có bao nhiêu câu là mệnh đề? a) 613 x + . b) Phương trình 2 310xx+−= có nghiệm. c) ,51xx  d) Năm 2018 là năm nhuận. e) Hôm nay thời tiết đẹp quá! A. 4. B. 1. C. 2. D. 3. Lời giải Chọn C

Câu 15: Trong các câu sau,

a) Hãy đi nhanh lên!

b) Hà Nội là thủ đô của Pháp

c) 57415 ++= d) 3x

A. 4. B. 1

Chọn C

Câu a) không phải là mệnh đề. Câu d) là mệnh đề chứa biến.

Câu 16: Trong các câu sau câu nào là mệnh đề?

A. Hãy đi nhanh lên!

B. Hà nội là thủ đô của Việt Nam. C. Nam ăn cơm chưa?. D. Buồn ngủ quá!

Chọn B

đề?

D. 3.

Lời giải

Đáp án B đúng vì nó là câu khẳng định có tính đúng sai.

Câu 17: Trong các câu sau câu nào là mệnh đề chứa biến?

A. 9 là số nguyên tố.

B. 18 là số chẵn.

C. ( )2 3, xxx+ .

D. Hình chữ nhật có hai đường chéo bằng nhau.

Lời giải

Chọn C

Đáp án A là mệnh đề sai. Đáp án

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 4 Trong các câu trên có các câu là mệnh đề: Phương trình 2 310xx+−= có nghiệm. Năm 2018 là năm nhuận. Có hai câu là mệnh đề chứa biến: 613 x + ; ,51xx  Và một câu là câu cảm thán. Câu 14: Trong các câu sau, câu nào là mệnh đề? A. Không được làm việc riêng trong giờ học. B. Đi ngủ đi. C. Trung Quốc là nước đông dân nhất thế giới. D. Bạn học trường nào? Lời giải Chọn C

có bao nhiêu câu là mệnh



. C. 2.

ời giải

B là mệnh đề đúng. Đáp án D là mệnh đề đúng. Đáp án C ta có với 0x = ta được mệnh đề đúng là 03. Ta có với 1x = ta được mệnh đề sai là 23. Nên tính đúng sai còn phụ thuộc giá trị của biến. Nó là mệnh đề chứa biến.

Câu 20: Trong các phát biểu sau, phát bi

nào là mệnh đề đúng?

A. Tổng của hai cạnh một tam giác lớn hơn cạnh thứ ba.

B. Hình thang có hai cạnh bên bằng nhau là hình thang cân.

C. Bạn có chăm học không?

D.  là một số hữu tỉ.

Chọn A

i giải

Câu 21: Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?

A. Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.

B. Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.

C. Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.

D. Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.

Lời giải

Chọn D

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 5 Câu 18: Cho mệnh đề chứa biến ( ) 2 :"511"Pxx với x là số nguyên tố. Tìm mệnh đề đúng trong các mệnh đề sau: A. ( )3P B. ( )2P C. ( )7P D. ( )5P Lời giải Chọn A ( ) 3:"5911"P  là mệnh đề đúng. Câu 19: Cho S là mệnh đề “ Nếu tổng các chữ số của một số n chia hết cho 6thì n chia hết cho 6”. Một giá trị của n để khẳng định S sai là: A. 33 B. 40 C. 42 D. 30 Lời giải Chọn A Ta có: 33n = có tổng các chữ số bằng 6thì chia hết cho 6nhưng số 33n = không chia hết cho 6 .

ểu

ờ

Câu 22: Trong các câu sau, câu nào một là mệnh đề đúng? A. Hà nội là thủ đô của Việt Nam. B. 2là một số tự nhiên lẻ. C. 7là một số tự nhiên chẵn. C.  là một số hữu tỷ. Lời giải Chọn A Ta thấy: Hà nội là thủ đô của Việt Nam là một mệnh đề đúng. 2là một số tự nhiên lẻ là một mệnh đề sai. 7là một số tự nhiên chẵn là một mệnh đề sai.  là một số hữu tỷ là một mệnh đề sai. Câu 23: Trong các mệnh đề sau, mệnh đề nào sai?

A. Hà nội là thủ đô của Việt

C. 5là một số tự nhiên lẻ.

Chọn C

Ta thấy:

là một số tự nhiên chẵn.

là một số hữu tỷ.

Hà nội là thủ đô của Việt Nam là một mệnh đề đúng.

4là một số tự nhiên chẵn là một mệnh đề đúng.

Trong các mệnh

nào

mệnh đề sai

OFFICIAL

A. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

B. Tam giác cân có một góc bằng 060 là tam giác đều.

C. Hình bình hành có hai đường chéo bằng nhau là hình vuông.

D. Tam giác có hai đường cao bằng nhau là tam giác cân.

Lời giải

Chọn C

Câu 26: Cho định lý “Nếu hai tam giác bằng nhau thì diện tích bằng nha”. Mệnh đề nào sau đây đúng?

A. Hai tam giác bằng nhau là điều kiện cần và đủ để chúng có diện tích bằng nhau.

B. Hai tam giác bằng nhau là điều kiện cần để diện tích chúng bằng nhau.

C. Hai tam giác có diện tích bằng nhau là điều kiện đủ để chúng bằng nhau.

D. Hai tam giác bằng nhau là điều kiện đủ để diện tích chúng bằng nhau.

Chọn D

Vì các định lí toán học là

Khi đó,

mệnh

Lời giải

và thường có dạng P

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 6

Nam. B. 4

C. 

Lời giải

5là một số tự nhiên lẻ là một mệnh đề đúng.  là một số hữu tỷ là một mệnh đề sai. Câu 24: Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị của x ? A. 52xx  . B. 52xx  . C. 2252xx  . D. 52xx++ . Lời giải Chọn D 5252xx++ điều này đúng với mọi x . Câu 25:

đề sau,

ệnh đề

là

những

đề đúng



ta nói: P là điều kiện đủ để có Q , Q là điều kiện cần để có P . Câu 27: Mệnh đề nào sau đây là mệnh đề sai ? A. 2 :0xx  . B. 2 : nnn= . C. :2 nnn . D. 2 : xxx . Lời giải Chọn A Ta có 2 0x  , x  Đáp án A sai. Câu 28: Trong các mệnh đề sau, mệnh đề nào sai? A. Nếu m , n là các số vô tỉ thì . mn cũng là số vô tỉ B. Nếu ABC là một tam giác vuông thì đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền. C. Với ba véctơ a , b , c đều khác véctơ 0 , nếu a , b cùng ngược hướng với c thì a , b cùng hướng. D. Điểm G là trọng tâm tam giác ABC khi và chỉ khi 0GAGBGC++=

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 7 Lời giải Chọn A Cho 2m = , 32n = là các số vô tỉ. Khi đó .6mn = là số hữu tỉ. Câu 29: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng? A. Nếu hai số a , b cùng chia hết cho c thì ab + chia hết cho c . B. Nếu một số nguyên chia hết cho 6 thì nó chia hết cho2 và 3 C. Nếu hai số x , y thỏa mãn 0xy+ thì có ít nhất một trong hai số x , y dương. D. Phương trình bậc hai ( )2 00axbxca++= có a , c trái dấu thì có hai nghiệm phân biệt. Lời giải Chọn B + Ta có 51 + chia hết cho3, tuy nhiên 5và 1không chia hết cho 3. Loại A + Nếu một số nguyên chia hết cho2 và 3thì nó chia hết cho 6. Chọn B + Ta có 10  , 20− , tuy nhiên ( ) 1210 +−=− . Loại C + Phương trình 2 0xx−= có hai nghiệm phân biệt, tuy nhiên a , c không trái dấu. Loại. D. Câu 30: Cho hai đa thức ( )Px và ( )Qx . Xét các tập hợp ( ) 0AxPx== , ( ) 0BxQx== và ( ) ( ) 22 0CxPxQx =+=   . Trong các mệnh đề sau, mệnh đề nào đúng? A. CAB = . B. CAB = . C. \ CAB = . D. \.CBA = . Lời giải Chọn A Vì ( ) ( ) 22 0PxQx +=  ( ) ( ) 0 0 Px Qx =    =  ( ) ( )xPxQx . Câu 31: Cho phần tử x thuộc tập B và tâp B là tập con của A . Trong các khẳng định sau khẳng định nào đúng? A. ( ) xBA  B. ( ) xBA  C. ( ) xBA  D. ( ) xBA  Lời giải Chọn B Câu 32: Trong các mệnh đề sau, tìm mệnh đề sai? A. Nếu a chia hết cho 9thì a chia hết cho 3. B. Nếu một tam giác có một góc bằng 60thì tam giác đó là tam giác đều. C. Nếu 0ab thì 22ab  D. Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân. Lời giải Chọn B Tam giác có một góc bằng 60thì có thể là tam giác vuông hoặc tam giác thường. Câu 33: Cho mệnh đề chứa biến ( ) 32 :"320"Pxxxx−+= . Tìm các giá trị của x để ( )Px là một mệnh đề đúng.

A. P đúng, Q sai.

Chọn

tam giác cân có 2 c

Hãy chọ

khẳng định đúng trong các khẳng định

nh bằng nhau” và Q: “Nế

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 8 A. 0,1,2xxx=== B. 2,3xx=−=− C. 1,2xx=−=− D. 4,2,3xxx==−= Lời giải Chọn A Những giá trị x làm cho ()Px là mệnh đề đúng là nghiệm của phương trình 32320xxx−+= . Do đó 0,1,2xxx=== là các giá trị cần tìm. Câu 34: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai? A. :33 n nn + . B. 1267  . C. 64107  D. ( )2 2:2 xxx − Lời giải Chọn D Với 1n = thì 33;34 n n =+= nên đáp án A là đúng. Ta có mệnh đề :"12"P  và mệnh đề :"67"Q  là mệnh đề sai nên mệnh đề PQ  hay mệnh đề 1267  là mệnh đề đúng. Đáp án B đúng. Ta có mệnh đề :"64"P  là mệnh đề sai và mệnh đề :"107"Q  là mệnh đề đúng nên mệnh đề PQ  hay mệnh đề 64107  là mệnh đề đúng. Đáp án C đúng. Với 1x =− thì ( )2 29x −= ; 2 1x = nên mệnh đề ( )2 2:2 xxx − là mệnh đề sai. Câu 35: Xét mệnh đề kéo theo P: “Nếu 18 chia hết cho 3 thì

ạ

là số chẵn thì 25 là số chính phương”.

B. P đúng, Q đúng. C. P sai, Q đúng. D. P sai, Q sai. Lời giải

B Mệnh đề PQ  sai khi P đúng, Q sai. Từ đó ta có hai mệnh đề trên đều đúng. Câu 36: Trong các mệnh đề dưới đây, mệnh đề nào là mệnh đề đúng? A. 2 :10xx += B. 2 :0xx  C. 2 :210xx − D. 2 :20xx −= Lời giải Chọn C  Ta có: 22011xx+ với x  . Vậy loạiA.  Ta có: 2 0x  với x  . Vậy loại B.  22 122 210 222 xxx −− , mà 0xx= . Vậy C đúng.  ( )2 202loaixx−== vì x . Vây loạiD. Câu 37: Mệnh đề nào sau đây là mệnh đề đúng? A. “ :22 x xx + ” B. “ :21 x x + là số nguyên tố”. C. “ *2:1xx − là bội số của 3”. D. “ 2 :3xx = ”. Lời giải Chọn A Giả sử chọn , ta được: 1 23  (đúng). Nhưng chọn 3x = , ta được: 85  (sai). 1x =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 9 Vậy :22 x xx + Câu 38: Cho P Q là mệnh đề đúng. Khẳng định nào sau đây là sai? A. PQ  sai. B. PQ  đúng. C. QP  sai. D. PQ  sai. Lời giải Chọn D P Q đúng suy ra PQ  đúng. Vậy mệnh đề sai là D Câu 39: Số mệnh đề đúng trong các mệnh đề sau: ( ) 1 : Ixx x  ( ) :20 nIIn ( ) 2 :90IIIxx−= . ( ) 2 :510IVnn+ chia hết cho 5. A. 1. B. 4. C. 2. D. 3. Lời giải Chọn B Ta có ( ) 1 : Ixx x  là mệnh đề đúng vì 2x =− thỏa mãn. Ta có ( ) :20 nIIn là mệnh đề đúng vì theo tính chất lũy thừa. Ta có ( ) 2 :90IIIxx−= là mệnh đề đúng vì 3x = . Ta có ( )22 51052 nn+=+ là số chia hết cho 5 mệnh đề ( )IV là mệnh đề đúng. Câu 40: Lập mệnh đề phủ định của mệnh đề 2 ":20180" xxx ++ . A. 2 :20180xxx ++ . B. 2 :20180xxx ++ . C. 2 :20180xxx ++ D. 2 :20180xxx ++ Lời giải Chọn D Mệnh đề phủ định của mệnh đề 2 ":20180" xxx ++ là mệnh đề 2 :20180xxx ++ Câu 41: Mệnh đề phủ định của mệnh đề: “2018 là một số chẵn” là: A. 2018không là một số lẻ. B. 2018không là một số chẵn. C. 2018là một số lẻ. D. 2018không là một số chẵn. Lời giải Chọn D Theo mệnh đề phủ định. Câu 42: Mệnh đề nào sau đây là mệnh đề phủ định của mệnh đề: “Mọi động vật đều di chuyển”? A. Có ít nhất một động vật di chuyển. B. Có ít nhất một động vật không di chuyển. C. Mọi động vật đều không di chuyển. D. Mọi động vật đều đứng yên. Lời giải Chọn B

A. Không có học sinh nào trong lớp 11A chấp hành luật giao thông.

B. Mọi học sinh trong lớp 11A đều chấp hành luật giao thông.

C. Có một học sinh trong lớp 11A chấp hành luật giao thông.

D. Mọi học sinh trong lớp 11A không chấp hành luật giao thông.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 10 Phủ định của “mọi” là “có ít nhất” Phủ định của “đều di chuyển” là “không di chuyển”. Do đó mệnh đề phủ định của mệnh đề: “Mọi động vật đều di chuyển” là “Có ít nhất một động vật không di chuyển” Câu 43: Cho mệnh đề 2 :",12" Pxxx + . Mệnh đề nào sau đây là mệnh đề phủ định của mệnh đề P ? A. 2 :",12" Pxxx + . B. 2 :",12" Pxxx + . C. 2 :",12" Pxxx + D. 2 :",12" Pxxx + Lời giải Chọn C Câu 44: Cho mệnh đề 2 ",30" xxx −+ . Hỏi mệnh đề nào là phủ định của mệnh đề trên A. 2 ",30" xxx −+ . B. 2 ",30" xxx −+ . C. 2 ",30" xxx −+ . D. "  2 ,30"xxx−+ . Lời giải Chọn C Câu 45: Cho mệnh đề "Có một học sinh trong lớp 11A không chấp hành luật giao thông " Mệnh đề phủ định của mệnh đề này là :

Lời giải Chọn B Câu 46: Cho mệnh đề 2 :":70" Axxx−+ . Mệnh đề phủ định của A là: A. 2 :70xxx −+ . B. 2 :70xxx −+ . C. 2 :70xxx −+ D. 2 :70xxx −+ Lời giải Chọn A Câu 47: Cho mệnh đề: 2 ",20" xxx −+ . Mệnh đề phủ định là: A. 2 ",20" xRxx −+ B. 2 ",20" xxx −+ C. 2 ",20" xxx −+ D. 2 ",20" xxx −+ Lời giải Chọn D Câu 48: Cho mệnh đề: 2 ",20" xxx −+ . Mệnh đề phủ định sẽ là: A. 2 ",20" xxx −+ . B. 2 ",20" xxx −+ . C. 2 ",20" xxx −+ D. 2 ",20" xxx −+ Lời giải

A. ”Mọi học sinh trong lớp 10A đều thích học môn Văn ”.

B. ”Mọi học sinh trong lớp 10A đều không thích học môn Toán ”.

C. ”Có một học sinh trong lớp 10A thích học môn Toán ”

D. ”Mọi học sinh trong lớp 10A đều thích học môn Toán ”.

Lời giải Chọn D

Câu 52: Cho tứ giác ABCD. Xét hai mệnh đề

P: “ Tứ giác ABCDlà hình thoi”

Q: “ Tứ giác ABCDcó hai đường chéo vuông góc”.

Phát biểu mệnh đề PQ 

A. Tứ giác ABCDcó hai đường chéo vuông góc thì nó là hình thoi.

B. Tứ giác ABCDlà hình thoi thì nó có hai đường chéo vuông góc.

C. Tứ giác ABCDlà hình thoi khi và chỉ khi nó có hai đường chéo vuông góc.

D. Tứ giác ABCDlà hình thoi nếu nó có hai đường chéo vuông góc.

Lời giải

Chọn C

Câu 53: Trong các định lý sau, định lý nào không có định lý đảo?

A. Nếu tứ giác ABCDlà hình chữ nhật thì nó là hình bình

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 11 Chọn A Ta có phủ định của mệnh đề ban đầu chính là: 2 ",20" xxx −+ Câu 49: Lập mệnh đề phủ định của mệnh đề : “ ,21 n nn + “ A. ,21 n nn + . B. ,21 n nn + . C. ,21 n nn + . D. ,21 n nn + . Lời giải Chọn A Mệnh đề: “ ( ), xDPx ” có mệnh đề phủ định là: “ ( ), xDPx ” . Nên mệnh đề : “ ,21 n nn + “ có mệnh đề phủ định là: “ ,21 n nn + ”. Câu 50: Cho mệnh đề 2 ",320" xxx ++ . Mệnh đề phủ định của mệnh đề trên là A. 2 ,320xxx ++ B. 2 ,320xxx ++ C. 2 ,320xxx ++ D. 2 ,320xxx ++ Lời giải Chọn B Phủ định của mệnh đề ( ) "," xpx là mệnh đề ( ) "," xpx Câu 51: Cho mệnh đề:”Có một học sinh trong lớp 10A không thích học môn Toán ”. Mệnh đề phủ định của mệnh đề này là:

hành có một góc vuông. B. Nếu tứ giác ABCDlà hình vuông thì nó là hình thoi có hai đường chéo bằng nhau. C. Nếu tứ giác ABCDlà hình bình hành thì nó là hình thang có hai cạnh bên bằng nhau. D. Nếu tứ giác ABCDlà hình vuông thì nó là hình chữ nhật có hai cạnh kề bằng nhau. Lời giải Chọn C

Câu

Nếu tứ giác

Cho m

Phát

Câu 55: Cho định lí “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”. Mệnh đề nào sau đây

C. Hai tam

D. Hai tam

Chọn D

Câu 56: Mệnh đề nào sau đây có mệnh đề đảo là mệnh đề đúng?

A. Nếu a và b cùng chia hết cho c thì ab + chia hết cho c .

B. Nếu ab  thì 22ab  .

C. Nếu số nguyên chia hết cho 14thì chia hết cho cả 7và 2

D. Hai tam giác bằng nhau có diện tích bằng nhau.

Lời giải

Chọn C

Ta kiểm tra các phương án:

A. Mệnh đề đảo là: “Nếu ab + chia hết cho c thì a và b cùng chia hết cho c ”. Là mệnh đề sai. Thật vậy, với 3,5,2abc=== ta có ab + chia hết cho c nhưng a không chia hết cho c .

B. Mệnh đề đảo là: “Nếu 22ab  thì ab  ”. Là mệnh đề sai. Thật vậy, với 6,5ab=−= ta có 22ab  nhưng ab 

C. Mệnh đề đảo là: “Nếu số nguyên chia hết cho cả 7và 2thì chia hết cho 14”. Là mệnh đề đúng.

Do 7 và 2 là hai nguyên tố cùng nhau nên một số nguyên nào đó chia hết cho 7 và 2 thì nó cũng chia hết cho 7.2, tức chia hết cho 14.

D. Mệnh đề đảo là: “Hai tam giác có diện tích bằng nhau thì bằng nhau ”. Là mệnh đề sai. Thật vậy,

vuông

3,2DEDF

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 12

ABCDlà hình thang có hai cạnh bên bằng nhau thì nó không là hình bình hành. Nó có thể là hình thang cân.

54:

ệnh đề '''' PQ  .

biểu nào sau đây đúng? A. P là điều kiện đủ để có Q. B. P là điều kiện cần và đủ để có Q. C. Nếu P thì Q. D. P là điều kiện cần để có Q. Lời giải Chọn C

đúng? A. Hai tam giác bằng nhau là điều kiện cần và đủ để chúng có diện tích bằng nhau. B. Hai tam giác có diện tích bằng nhau là điều kiện đủ đê chúng bằng nhau.

giác bằng nhau là điều kiện cần để diện tích chúng bằng nhau.

giác bằng nhau là điều kiện đủ để diện tích chúng bằng nhau.

ời giải

xét tam giác đều ABC có cạnh 4 23 và tam giác DEF

ở D ,

Dễ thấy hai tam giác đã cho có diện tích bằng nhau nhưng rõ ràng chúng không bằng nhau. Câu 57: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng. A. Nếu xy = thì txty = B. Nếu xy  thì 33 xy  C. Nếu số nguyên n có tổng các chữ số bằng 9thì số nguyên n chia hết cho 3. D. Nếu xy  thì 22 xy  Lời giải Chọn B * A sai khi 0t = .

2 1n và 2 1n + đều không chia hết cho 5.

B. Với mọi số tự nhiên n , điều kiện cần để n chia hết cho 5là 2 1n và 2 1n + đều không chia hết cho 5

C. Với mọi số tự nhiên n , điều kiện cần để

1n và

+ đều không chia hết cho 5là n chia hết cho

D. Với mọi số tự nhiên

họn

, n chia hết cho

là điều kiện

không chia

Lời

giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

A. Một tam giác là tam giác cân là điều kiện cần và đủ để có tam giác đó có hai góc bằng nhau

B. Một tam giác có hai góc bằng nhau khi và chỉ khi là tam giác đó là tam giác cân.

C. Một tam giác có hai góc bằng nhau là điều kiện đủ để có tam giác đó là tam giác cân

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 13 * B đúng vì ( )( )3322 0 xyxyxxyyxy −++ * C sai ví dụ như 114n = . * D sai khi 2;1xy=−= Câu 58: Câu “Tồn tại ít nhất một số thực có bình phương không dương” là một mệnh đề. Có thể viết lại mệnh đề đó như sau. A. 2 :0xx  B. 2 :0xx  C. 2 :0xx = D. 2 :0xx  Lời giải Chọn A Ta có mệnh đề 2 :0xx  Câu 59: Mệnh đề ( ) 2 :",70"Pxxxx−+= . Phủ định của mệnh đề P là A. 2 ,70xxx −+ B. 2 ,70xxx −+ C. 2 ,70xxx −+ . D. 2 ,70xxx −+ . Lời giải Chọn D Phủ định của mệnh đề ( ) 2 :",70"Pxxxx−+= là 2 :,70Pxxx−+ . Câu 60: Phủ định của mệnh đề 2 ":2520" xQxx −+= là A. 2 ":2520" xQxx −+ B. 2 ":2520" xQxx −+ C. 2 ":2520" xQxx −+ D. 2 ":2520" xQxx −+= Lời giải Chọn C Câu 61: Sử dụng thuật ngữ “điều kiện cần” để phát biểu định lý “Với mọi số tự nhiên chia hết cho 5thì 2 1n và 2 1n + đều không chia hết cho 5” A. Với mọi số tự nhiên n , n chia hết cho 5là điều kiện cần để

cần và đủ để 2 1n và 2 1n + đều

hết cho 5

giải C

B Với mọi số tự nhiên n , điều kiện cần để n chia hết cho 5là 2 1n và 2 1n + đều không chia hết cho 5. Câu 62: Phát biểu định lý đảo của định lý “ Nếu một tam

D. Một tam giác là tam giác cân điều kiện đủ là tam giác đó có hai góc bằng nhau.

Lời giải Chọn D

Một tam giác là tam giác cân điều kiện đủ là tam giác đó có hai góc bằng nhau.

Câu 63: Tìm mệnh đề phủ định của mệnh đề: “Tất cả người dân Việt Nam đều được tiêm Vacxin ngừa Côvit.”

A. “Tất cả người dân Việt Nam đều không được tiêm Vacxin ngừa Côvit.”.

B. “Có người dân Việt Nam được tiêm Vacxin ngừa Côvit.”.

C. “Có một người dân Việt Nam không được tiêm Vacxin ngừa Côvit.”.

nhất một người dân Việt Nam

được tiêm Vacxin ngừa

Câu

OFFICIAL

P:":10"

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 14

“

ó ít

không

Côvit.” Lời giải Chọn D

mệnh đề phủ định của mệnh đề “",()" xXPx là ",()" xXPx .

64: Cho mệnh đề 2 P:":10" xxx ++ . Mệnh đề phủ định của mệnh đề Pvà tính đúng, sai của nó là:

2 P:":10" xxx ++= và P là mệnh đề sai.

xxx ++= và P là mệnh đề đúng. C. 2 P:":10" xxx ++ và P là mệnh đề đúng. D. 2 P:":10" xxx ++= và P là mệnh đề sai. Lời giải Chọn A Mệnh đề phủ định của Plà 2 P:":10" xxx ++= . Xét phương trình 2 10xx++= vô nghiệm nên P là mệnh đề sai.

2:

HỢP

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP Page 31 BÀI

TẬP

1. Nhắc lại về tập hợp Như đã biết ở cấp Trung học cơ sở, trong toán học, người ta dùng từ tập hợp để chỉ một nhóm đối tượng nào đó hoàn toàn xác định. Mỗi đối tượng trong nhóm gọi là một phần tử của tập hợp đó. Tập hợp (còn gọi là tập) là một khái niệm cơ bản của toán học, không định nghĩa. Giả sử đã cho tập hợp A • Để chỉ a là một phần tử của tập hợp ,A ta viết aA  (đọc là a thuộc A ). • Để chỉ a không phải là một phần tử của tập hợp ,A ta viết aA  (đọc là P không thuộc A ). Cách xác định tập hợp Một tập hợp có thể được xác định bằng cách chỉ ra tính chất đặc trưng cho các phần tử của nó. Vậy ta có thể xác định một tập hợp bằng một trong hai cách sau • Liệt kê các phần tử của nó. • Chỉ ra tính chất đặc trưng cho các phần tử của nó. Người ta thường minh họa tập hợp bằng một hình phẳng được bao quanh bởi một đường kín, gọi là biểu đồ Ven. Tập hợp rỗng Tập hợp rỗng, kí hiệu là , là tập hợp không chứa phần tử nào. Nếu A không phải là tập hợp rỗng thì A chứa ít nhất một phần tử :. AxxA  2. Tập con và hai tập hợp bằng nhau Cho hai tập hợp A và B. Nếu mọi phần tử của A đều là phần tử của B thì ta nói tập hợp A là tập con của tập hợp B và kí hiệu A ⊂ B (đọc là A chứa trong B), hoặc B ⊃ A (đọc là B chứa A). Nhận xét: A ⊂ A và ∅⊂ A với mọi tập hợp A. CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP LÝ THUYẾT.I =

Trong toán học, người ta thường minh hoạ tập hợp bằng một hình phẳng được bao quanh bởi một đường cong kín, gọi là biểu đồ Ven (đặt theo tên nhà toán học, nhà triết học người Anh John Venn). Theo cách này, ta có thể minh hoạ A là tập con của B như Hình 1.

Chú ý:

Giữa các tập hợp số quen thuộc (tập số tự nhiên, tập số nguyên, tập số hữu ti, tập số thực),

cách

nhau nếu mỗi phần tử của tập hợp này cũng là phần tử

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP Page 32 Nếu A không phải là tập con của B thì ta kí hiệu A ⊄ B (đọc là A không chứa trong B hoặc B không chứa A). - Nếu A ⊂ B hoặc B ⊂ A thì ta nói A và B có quan hệ bao hàm. Như vậy ( ) :.ABxxAxB  Nếu A không phải là một tập con của ,B ta viết .AB 

ta có quan hệ bao hàm: N ⊂ Z ⊂ Q ⊂ R. Hai tập hợp A và B gọi là bằng nhau, kí hiệu .AB = , nếu AB  và BA  . ( ) :.ABxxAxB = Nói

khác, hai tập hợp A và B bằng

của tập hợp kia và ngược lại.

Tên

Tập

Đoạn

Khoảng

Nửa

Nửa khoảng

Khoảng

Biểu diễn trên

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP Page 33 3. Một số tập con của tập hợp số thực Sau này ta thường sử dụng các tập con của tập số thực sau đây ( a và b là các số thực, ab  ):

gọi và kí hiệu Tập hợp

trục số

số thực ( ); −+

 ; ab     ;|. abxaxb =

( ); ab ( )  ;| abxaxb =

khoảng  ); ab  )  ;| abxaxb =

khoảng (a;b] (   ;| abxaxb =

( ;a− (    ;|. axxa−= Nửa khoảng  );a +  )  ;| axax +=

( );a + ( )  ;| axax +=

( );a− ( )  ;| axxa−= Trong các ký hiệu trên, kí hiệu − đọc là âm vô cực, kí hiệu + đọc là dương vô cực.  DẠNG 1: XÁC ĐỊNH MỘT TẬP HỢP PHƯƠNG PHÁP Để xác định một tập hợp, ta có 2 cách sau:  Liệt kê các phần tử của tập hợp.  Chỉ ra tính chất đặc trưng của tập hợp. Bài 1. Viết lại tập hợp ( )( ) Axxxxx =−+−+= 22 253430 bằng cách liệt kê các phần tử của nó. Bài 2. Viết lại tập hợp ( )( ) Axxxxx =−+−+= 22 253430 bằng cách liệt kê các phần tử của nó. Bài 3. Viết lại tập hợp  Axx= 5 bằng cách liệt kê các phần tử của nó. HỆ THỐNG BÀI TẬP.II = BÀI TẬP TỰ LUẬN.1 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP Page 34 Bài 4. Viết mỗi tập hợp  A = 0;1;2;3;4 bằng cách chỉ rõ tính chất đặc trưng cho các phần tử của nó Bài 5. Viết mỗi tập hợp  A = 9; 36; 81; 144 bằng cách chỉ rõ tính chất đặc trưng cho các phần tử của nó Bài 6. Liệt kê tất cả các phần tử của tập hợp A gồm các số tự nhiên chia hết cho 3 và nhỏ hơn 25. Bài 7. Liệt kê các phần tử của tập hợp  2 2530=−+=Xxxx Bài 8. Viết tập hợp ( )( ) 22 9320 =−−+= Bxxxx dưới dạng liệt kê các phần tử. Bài 9. Viết tập hợp ( )( ) 22 5560 =−−+= Axxxx dưới dạng liệt kê các phần tử. Bài 10. Tính tổng tất cả các phần tử của tập hợp 3 2  =  Ax x Bài 11. Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi hóa, 6học sinh giỏi cả Toán và Lý, 5 học sinh giỏi cả Hóa và Lý, 4 học sinh giỏi cả Toán và Hóa, 3 học sinh giỏi cả ba môn Toán, Lý, Hóa. Tính học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A? Bài 12. Cho ( )2;A =+ , ( );Bm=+ . Tìm điều kiện cần và đủ của m để B là tập con của A ? Bài 13. Xác định số phần tử của tập hợp  |4,2017Xnnn= Bài 14. Cho hai tập hợp  1;3A = và  ;1Bmm=+ . Tìm tất cả giá trị của tham số m để BA  . Câu 15. Số phần tử của tập hợp  2 43220 =−++−= Axxxx Câu 16. Cho tập hợp ( ) 22123=+−=− Dxxxx . Hãy viết tập hợp D dưới dạng liệt kê các phần tử Câu 17. Tính tổng các phần tử của tập hợp 43 2 + = +  Axx x . Câu 18. Liệt kê các phần tử của  22 423423 =−+++ Axxxxx Câu 19. Liệt kê các phần tử của tập hợp  2238230 =+−++= Axxxxx . Câu 1. Cho tập hợp  2 10Axxx=++= .Các phần tử của tập A là: A. 0=A B.  0=A C. =A D.  =A Câu 2. Hãy liệt kê các phần tử của tập hợp  saocho 8MxNx = lµíccña A.  1;4;16;64M = . B.  0;1;4;16;64M = . C.  1;2;4;8M = D.  0;1;2;4;8M = BÀI TẬP TRẮC NGHIỆM.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP Page 35 Câu 3. Cho tập hợp ( )( ) 22–120Axxx =+= . Các phần tử của tập A là: A.  –1;1=A B. –2;–1; 2}{ 1;=A C. {1}=A D. {1}=A Câu 4. Cho 2 40Axx . Tập hợp A viết lại dạng liệt kê là A. . B.  . C.  )2; −+ . D.  )2;+ . Câu 5. Tập hợp nào là tập hợp rỗng, trong các tập hợp sau? A.  2 |6–710xxx += . B.  |1xx . C.  2 |420xxx−+= D.  2 |430xxx−+= Câu 6: Cho tập hợp ( )( ) 22930=−−= Bxxxx . Tập hợp B được viết dưới dạng liệt kê là A.  3;9;1;2=B . B.  3;9;0=−B . C.  9;9;0=−B . D.  3;3;0=−B . Câu 7: Cho tập hợp  3 90=−=Hxxx . Tập hợp H là tập con của tập hợp nào dưới đây ? A.  3;0;1;2=−A . B.  3;1;2;3=−B . C.  0;1;2=C . D.  3;0;2;3=−D . Câu 8: Tập hợp ( )( ) 23240=+−+= Axxxxx có bao nhiêu phần tử? A. 1. B. 3. C. 5. D. 2. Câu 9: Trong các tập hợp sau, tập hợp nào là tập rỗng? A.  2 560+−=xxx B.  2 3520−+= xxx . C.  2 10+−=xxx . D.  2 510+−=xxx . Câu 10: Cho tập hợp  2 1 =+Pnn và 33− n . Viết tập hợp P dưới dạng liệt liệt kê các phần tử A.  3;2;1;0;1;2;3=−−−P . B.  2;1;0;1;2=−−P . C.  1;2;5=P D.  0;1;4=P Câu 11. Cho tập hợp { Axx = là ước chung của 36và120}. Hãy liệt kê các phần tử của tập hợp A A.   1;2;3;4;6;12.A = B.   1;2;4;6;8;12.A = C.   2;4;6;8;10;12.A = D.   2;3;4;6;12.A = Câu 12. Số phần tử của tập hợp  2 1,2Akk k=+  là: A. 1. B. 2. C. 3. D. 5.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP Page 36 Câu 13. Trong các tập hợp sau, tập hợp nào rỗng? A.  2 40.Axx=−= B.  2 230.Bxxx=++= C.  2 50.Cxx=−= D.  2 120.Dxxx=+−= Câu 14. Trong các tập hợp sau, tập hợp nào là tập hợp rỗng? A.   1.Axx= B.  2 6710.Bxxx=−+= C.  2 420.Cxxx=−+= D.  2 430.Dxxx=−+= Câu 15. Cho hai tập hợp  0;2A = và   0;1;2;3;4.B = Có bao nhiêu tập hợp X thỏa mãn A XB A. 2 B. 4 C. 6 D. 8 Câu 16: Tổng tất cả các phần tử của tập hợp  216=+Axx bằng A. 3 B. 9 C. 0 D. 3 Câu 17: Cho tập ( ) ;, =Mxyxy và 22 0.+xy Hỏi tập hợp M có bao nhiêu phần tử? A. 1 B. 2 C. 0 D. Vô số Câu 18: Cho tập ( ) ( ) 2 43.0 =−+−= Mxxxxm . Có bao nhiêu giá trị của tham số m để tổng tất cả các phần tử của tập M bằng 4? A. 0. B. 1. C. 2. D. 3. Câu 19: Gọi A là tập hợp các số nguyên  7;7−m sao cho phương trình 2 0−+=xmxm có ít nhất một nghiệm dương. Số phần tử của tập hợp A là A. 9. B. 11. C. 10. D. 12. Câu 20: Cho tập hợp ( ) ( ) 2 ;256 =−=+ Axyxyy và , xy . Số phần tử của tập hợp A là A. 7. B. 5. C. 4. D. 6 .

BÀI 2: TẬPHỢP

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TOÁN HỌC TẬP HỢP Page 1

A là tập con của B như Hình 1.

Chú ý:

Giữa các tập hợp số quen thuộc (tập số tự nhiên, tập số nguyên, tập số hữu ti, tập

thực),

Nói cách

nhau nếu mỗi phần tử của tập hợp này cũng là phần tử

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TOÁN HỌC TẬP HỢP Page 2 Nếu A không phải là tập con của B thì ta kí hiệu A ⊄ B (đọc là A không chứa trong B hoặc B không chứa A). - Nếu A ⊂ B hoặc B ⊂ A thì ta nói A và B có quan hệ bao hàm. Như vậy ( ) :.ABxxAxB  Nếu A không phải là một tập con của ,B ta viết .AB 

hoạ

số

ta có quan hệ bao hàm: N ⊂ Z ⊂ Q ⊂ R. Hai tập hợp A và B gọi là bằng nhau, kí hiệu .AB = , nếu AB  và BA  . ( ) :.ABxxAxB =

khác, hai tập hợp A và B bằng

của tập hợp kia và ngược lại.

Tên

Tập

Đoạn

Khoảng

Nửa

Nửa khoảng

Nửa

Khoảng

Biểu

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TOÁN HỌC TẬP HỢP Page 3 3. Một số tập con của tập hợp số thực Sau này ta thường sử dụng các tập con của tập số thực sau đây ( a và b là các số thực, ab  ):

gọi và kí hiệu Tập hợp

diễn trên trục số

số thực ( ); −+

 ; ab     ;|. abxaxb =

( ); ab ( )  ;| abxaxb =

khoảng  ); ab  )  ;| abxaxb =

(a;b] (   ;| abxaxb =

( ;a− (    ;|. axxa−=

khoảng  );a +  )  ;| axax +=

( );a + ( )  ;| axax +=

( );a− ( )  ;| axxa−= Trong các ký hiệu trên, kí hiệu − đọc là âm vô cực, kí hiệu + đọc là dương vô cực.  DẠNG 1: XÁC ĐỊNH MỘT TẬP HỢP PHƯƠNG PHÁP Để xác định một tập hợp, ta có 2 cách sau:  Liệt kê các phần tử của tập hợp.  Chỉ ra tính chất đặc trưng của tập hợp. Bài 1. Viết lại tập hợp ( )( ) Axxxxx =−+−+= 22 253430 bằng cách liệt kê các phần tử của nó Lời giải HỆ THỐNG BÀI TẬP.II = BÀI TẬP TỰ LUẬN.1 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TOÁN HỌC TẬP HỢP Page 4 Ta có ( )( ) x xx x xxxx xx x x  =  −+= −+−+==  −+=  =  = 2 22 2 1 25343025303 4302 1 3 . Vì x  nên 3 1;;3 2 A Bài 2. Viết lại tập hợp ( )( ) Axxxxx =−+−+= 22 253430 bằng cách liệt kê các phần tử của nó. Lời giải Ta có ( )( ) x xx x xxxx xx x x  =  −+= −+−+==  −+=  =  = 2 22 2 1 25343025303 4302 1 3 Vì x  nên 1;3A . Bài 3. Viết lại tập hợp  Axx= 5 bằng cách liệt kê các phần tử của nó Lời giải Ta có x  5và x  nên 0;1;2;3;4x Vậy 0;1;2;3;4A Bài 4. Viết mỗi tập hợp  A = 0;1;2;3;4 bằng cách chỉ rõ tính chất đặc trưng cho các phần tử của nó Lời giải Ta nhận thấy các phần tử của tập hợp A là các số tự nhiên và nhỏ hơn 5. Do đó  Axx= 5 Bài 5. Viết mỗi tập hợp  A = 9; 36; 81; 144 bằng cách chỉ rõ tính chất đặc trưng cho các phần tử của nó Lời giải Ta có 293 , 2366 , 2819 , 214412 và các số 3,6,9,12 đều là bội của 3. Do đó ta viết lại tập hợp A bằng cách chỉ ra tính chất đặc trưng là 2 * 3,4Akkk . Bài 6. Liệt kê tất cả các phần tử của tập hợp A gồm các số tự nhiên chia hết cho 3 và nhỏ hơn 25. Lời giải Ta có  0;3;6;9;12;15;18;21;23=A

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TOÁN HỌC TẬP HỢP Page 5 Bài 7. Liệt kê các phần tử của tập hợp  2 2530=−+=Xxxx Lời giải Ta có 2 2530 xx−+= 1 3 2 x x =   = 3 1; 2  =   X Bài 8. Viết tập hợp ( )( ) 22 9320 =−−+= Bxxxx dưới dạng liệt kê các phần tử. Lời giải Ta có ( )( )22 9320 xxx −−+= 2 2 90 320 x xx  −=   −+= 3 3 1 2 =−  =  =  = x x x x . Vậy  3;1;2=B Bài 9. Viết tập hợp ( )( ) 22 5560 =−−+= Axxxx dưới dạng liệt kê các phần tử. Lời giải Ta có ( )( )22 5560 xxx −−+= 2 2 50 560 x xx  −=   −+= 5 3 2  = =   = x x x Vậy  2;3=A Bài 10. Tính tổng tất cả các phần tử của tập hợp 3 2  =  Ax x . Lời giải Ta có ( ) 213 2113 32 2352 231 xx xx x xxx xx −==  −−=−= −==  −=−=− . Vì x nên loại 1=−x . Suy ra  1;3;5=A . Vậy tổng tất cả các phần tử của tập hợp A là 1359 ++= . Bài 11. Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi hóa, 6 học sinh giỏi cả Toán và Lý, 5 học sinh giỏi cả Hóa và Lý, 4 học sinh giỏi cả Toán và Hóa, 3 học sinh giỏi cả ba môn Toán, Lý, Hóa. Tính học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A? Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TOÁN HỌC TẬP HỢP Page 6 Theo giả thiết đề bài cho, ta có biểu đồ Ven: Dựa vào biểu đồ Ven, ta có Số học sinh giỏi chỉ một môn Toán: 103313 −−−= Số học sinh giỏi chỉ một môn Lý: 103322 −−−= Số học sinh giỏi chỉ một môn Hóa: 113215 −−−= Vậy số học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A là: 325332119 ++++++= Bài 12. Cho ( )2;A =+ , ( );Bm=+ . Tìm điều kiện cần và đủ của m để B là tập con của A ? Lời giải Ta có: BA  khi và chỉ khi xBxA 2m  . Bài 13. Xác định số phần tử của tập hợp  |4,2017Xnnn= Lời giải Tập hợp X gồm các phần tử là những số tự nhiên nhỏ hơn 2017 và chia hết cho 4. Từ 0 đến 2015 có 2016 số tự nhiên, ta thấy cứ 4 số tự nhiên liên tiếp sẽ có duy nhất một số chia hết cho 4. Suy ra có 504 số tự nhiên chia hết cho 4 từ 0 đến 2015. Hiển nhiên 20164 Vậy có tất cả 505 số tự nhiên nhỏ hơn 2017 và chia hết cho 4 Bài 14. Cho hai tập hợp  1;3A = và  ;1Bmm=+ . Tìm tất cả giá trị của tham số m để BA  . Lời giải Ta có: 11 132 mm BA mm  +  . Vậy 12 m  . Câu 15. Số phần tử của tập hợp  2 43220 =−++−= Axxxx B= m;+∞( ) + ∞ - ∞ 2

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TOÁN HỌC TẬP HỢP Page 7 Lời giải Ta có 2 430−+xx và 220 −x nên 2 2 1 430 432201 3 220 1 = −+=  −++−== = −=  = x xx xxxx x x x . Vậy tập A có đúng 1 phần tử Câu 16. Cho tập hợp ( ) 22123=+−=− Dxxxx . Hãy viết tập hợp D dưới dạng liệt kê các phần tử. Lời giải Giải phương trình: ( )22123+−=− xxx (1) Điều kiện: 1 2 x (*) pt(1) 2 21321315−−=−+ xxx ( )( ) ( ) 2102 5235230 213213  =−−−−+= −+−+  x xxxx xx 5 2 23(2) 213 =   =− −+ x x x Ta có ( )( ) (2)232132 −−+= xx Đặt 21,t0=−tx Phương trình trở thành ( )( )2 232−+=tt ( ) ( ) ( ) 2 117 2 117 2   =−   =   −+ =  tl tl tn Với 117 2 −+ =t ta có 117 21 2 −+ −=x 9171117 21 24 −== xx Vậy 1117 5; 4   =    E . Câu 17. Tính tổng các phần tử của tập hợp 43 2 + = +  Axx x . Lời giải Ta có 25 254355 452 21222 21 x xx x xxxx x +=  ++=− =−+  ++++=  +=− 3 7 1 3 =  =−  =−  =− x x x x Suy ra  3;7;1;3=−−−A . Vậy tổng các phần tử của tập hợp A là ( ) ( ) ( ) 37138 +−+−+−=− .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TOÁN HỌC TẬP HỢP Page 8 Câu 18. Liệt kê các phần tử của  22 423423 =−+++ Axxxxx Lời giải Điều kiện: 3 230 2 +xx Ta có 22 423423 xxxx −+++ ( )( )2 12340234 ++−+− xxx 13 2342316213 2 ++ xxxx Vì x nên  0;1;2;3;4;5;6x Vậy  0;1;2;3;4;5;6=A Câu 19. Liệt kê các phần tử của tập hợp  2238230 =+−++= Axxxxx . Lời giải Đặt 2 30=+txx . Phương trình 2238230 +−++= xxxx trở thành 2 2 2802 4 = +−==  =− t ttt t + 2=t 22 1 32340 4 = +=+−=  =− x xxxx x . Vậy  1;4=−A . Câu 1. Cho tập hợp  2 10Axxx=++= .Các phần tử của tập A là: A. 0=A B.  0=A C. =A D.  =A Lời giải Chọn C Ta có:  2 10Axxx=++= . Vì phương trình 2 10xx++= vô nghiệm nên =A . Câu 2. Hãy liệt kê các phần tử của tập hợp  saocho 8MxNx = lµíccña . A.  1;4;16;64M = . B.  0;1;4;16;64M = . C.  1;2;4;8M = . D.  0;1;2;4;8M = . Lời giải Chọn A A. Đúng, căn bậc hai của các số trong tập M đều là ước của 8. B. HS hiểu nhầm số 0 là ước của mọi số tự nhiên. BÀI TẬP TRẮC NGHIỆM.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TOÁN HỌC TẬP HỢP Page 9 C. HS hiểu nhầm x là ước của 8. D. HS hiểu nhầm x là ước của 8 và 0 là ước của mọi số tự nhiên. Câu 3. Cho tập hợp ( )( ) 22–120Axxx =+= . Các phần tử của tập A là: A.  –1;1=A B. –2;–1; 2}{ 1;=A C. {1}=A D. {1}=A Lời giải Chọn A ( )( ) 22–120Axxx =+= . Ta có ( )( )22–120 +=xx ( ) 2 2 –10 20vn  =   +=  x x 1 1 =   =− x x   1;1.=− A Câu 4. Cho 2 40Axx . Tập hợp A viết lại dạng liệt kê là A. . B.  . C.  )2; −+ . D.  )2;+ . Lời giải Chọn A Ta có: 22404 xxx ( Vì 2 0, xx ). Câu 5. Tập hợp nào là tập hợp rỗng, trong các tập hợp sau? A.  2 |6–710xxx += . B.  |1xx . C.  2 |420xxx−+= . D.  2 |430xxx−+= . Lời giải Chọn C Ta có 2 22 420 22 x xx x  =+ −+=  =−  . Vì x nên x . Câu A sai là phương trình có 2 nghiệm hữu tỉ Câu B sai là bất phương trình có 1 nghiệm nguyên 0x = . Câu D sai là phương trình có 2 nghiệm là 1x và 3x . Câu 6: Cho tập hợp ( )( ) 22930=−−= Bxxxx . Tập hợp B được viết dưới dạng liệt kê là A.  3;9;1;2=B B.  3;9;0=−B C.  9;9;0=−B D.  3;3;0=−B Lời giải Chọn D

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TOÁN HỌC TẬP HỢP Page 10 Ta có 2 2 90 30 x xx  −=  −= 3 3 3 0 x x x x =−  =  =  = . Vậy  3;3;0=−B . Câu 7: Cho tập hợp  3 90=−=Hxxx . Tập hợp H là tập con của tập hợp nào dưới đây ? A.  3;0;1;2=−A . B.  3;1;2;3=−B . C.  0;1;2=C . D.  3;0;2;3=−D . Lời giải Chọn D Ta có ( )32 0 9090 3 = −=−=  = x xxxx x . Suy ra  0;3=H (vì x ). Câu 8: Tập hợp ( )( ) 23240=+−+= Axxxxx có bao nhiêu phần tử? A. 1. B. 3. C. 5. D. 2. Lời giải Chọn B Ta có ( )( ) ( )( )( )2322401240 +−+=−++= xxxxxxxx 01 102 200 ==  −==−  +==  xx xx xx (do 2 40, xx+ ). Vì x nên loại 2=−x . Suy ra  0;1=A . Vậy tập hợp A có 2 phần tử Câu 9: Trong các tập hợp sau, tập hợp nào là tập rỗng? A.  2 560+−=xxx B.  2 3520−+= xxx . C.  2 10+−=xxx D.  2 510+−=xxx Lời giải Chọn C Ta có 2 10+−=xx 15 2 − = x nên  2 10 +−==xxx . Câu 10: Cho tập hợp  2 1 =+Pnn và 33− n . Viết tập hợp P dưới dạng liệt liệt kê các phần tử. A.  3;2;1;0;1;2;3=−−−P . B.  2;1;0;1;2=−−P . C.  1;2;5=P . D.  0;1;4=P .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TOÁN HỌC TẬP HỢP Page 11 Lời giải Chọn C Ta có 2 1 33 0 1 2 =−  −=−  =   = =  n n n n n n n Suy ra  1;2;5=P . Câu 11. Cho tập hợp { Axx = là ước chung của 36và120}. Hãy liệt kê các phần tử của tập hợp A . A.   1;2;3;4;6;12.A = B.   1;2;4;6;8;12.A = C.   2;4;6;8;10;12.A = D.   2;3;4;6;12.A = . Lời giải Chọn A Ta có 22 3 362.3 1202.3.5  =  =  Do đó  1;2;3;4;6;12A = . Câu 12. Số phần tử của tập hợp  2 1,2Akk k=+  là: A. 1. B. 2. C. 3. D. 5. Lời giải Chọn D Vì k  và 2k  nên  2;1;0;1;2k  do đó ( )  2 11;2;5.k + Vậy A có 3 phần tử. Câu 13. Trong các tập hợp sau, tập hợp nào rỗng? A.  2 40.Axx=−= B.  2 230.Bxxx=++= C.  2 50.Cxx=−= D.  2 120.Dxxx=+−= Lời giải Chọn B Xét các đáp án:  Đáp án A. Ta có  2 2 402 2 x xA x = −==  =− .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TOÁN HỌC TẬP HỢP Page 12  Đáp án B. Ta có 2 230xx++= (phương trình vô nghiệm) B =  Đáp án C. Ta có  2 5055;5xxC −===− .  Đáp án D. Ta có  2 3 1204;3 4 x xxD x = +−==−  =− . Câu 14. Trong các tập hợp sau, tập hợp nào là tập hợp rỗng? A.   1.Axx= B.  2 6710.Bxxx=−+= C.  2 420.Cxxx=−+= D.  2 430.Dxxx=−+= Lời giải Chọn C Xét các đáp án:  Đáp án A. Ta có  1110xxA −= .  Đáp án B. Ta có  2 1 67101 1 6 x xxB x =  −+==  =  Đáp án C. Ta có 2 42022 xxxC −+=== .  Đáp án D. Ta có  2 3 4301;3 1 x xxD x = −+==  = Câu 15. Cho hai tập hợp  0;2A = và   0;1;2;3;4.B = Có bao nhiêu tập hợp X thỏa mãn A XB . A. 2 B. 4 C. 6 D. 8 Lời giải Chọn C Ta có A XB nên ; XAXB == ,  0;1;2X = ,  0;2;3X = ,  0;2;4X = ,  0;1;2;3X = ,  0;1;2;4X = ,  0;2;3;4X = Vậy có 8 tập X thỏa đề bài. Câu 16: Tổng tất cả các phần tử của tập hợp  216=+Axx bằng A. 3. B. 9. C. 0. D. 3. Lời giải Chọn D Ta có 75 2156216725 22 +−+−− xxxx . Vì x  nên  3;2;1;0;1;2−−−x . Suy ra  3;2;1;0;1;2=−−−A .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TOÁN HỌC TẬP HỢP Page 13 Vậy tổng tất cả các phần tử của tập hợp A là ( ) ( ) ( ) 3210123 −+−+−+++=− Câu 17: Cho tập ( ) ;, =Mxyxy và 22 0.+xy Hỏi tập hợp M có bao nhiêu phần tử? A. 1 B. 2 C. 0 D. Vô số Lời giải Chọn A Ta có 2 22 2 0, 0. 0,   +   xx xy yx Mà 22 0+xy nên chỉ xảy ra khi 22 00.+===xyxy Do đó ta suy ra ( ) 0;0=M nên tập hợp M có 1 phần tử. Câu 18: Cho tập ( ) ( ) 2 43.0 =−+−= Mxxxxm . Có bao nhiêu giá trị của tham số m để tổng tất cả các phần tử của tập M bằng 4? A. 0. B. 1. C. 2. D. 3. Lời giải Chọn D Ta có ( ) ( ) 2 2 1 430 43.03 0 x xx xxxmx xm xm = −+=  −+−==  −=  = Nếu 1 3 m m =  = thì  1;3=M . Khi đó tổng các phần tử bằng 4 (thỏa mãn). Nếu 1 3 m m    thì  1;3;= Mm . Khi đó 1340 ++== mm Vậy có 3 giá trị của tham số m để tổng tất cả các phần tử của tập M bằng 4. Câu 19: Gọi A là tập hợp các số nguyên  7;7−m sao cho phương trình 2 0−+=xmxm có ít nhất một nghiệm dương. Số phần tử của tập hợp A là A. 9 B. 11 C. 10 D. 12 Lời giải Chọn B TH1: Phương trình 2 0−+=xmxm có hai nghiệm trái dấu 00 acm . Mặt khác do  7;7−m và m nên  7;6;5;4;3;2;1 −−−−−−−m TH2: Phương trình 2 0−+=xmxm có nghiệm kép dương 0 0 =    S 4= m . TH3: Phương trình 2 0−+=xmxm có hai nghiệm dương phân biệt 120 xx

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TOÁN HỌC TẬP HỢP Page 14 0 0 0       S P 2 40 0 0 =−  =   = mm Sm Pm ( ) 40 04 0 −  =   = mm Smm Pm Từ các trường hợp trên suy ra  7;6;5;4;3;2;1;4;5;6;7=−−−−−−−A Vậy số phần tử của tập hợp A là 11. Câu 20: Cho tập hợp ( ) ( ) 2 ;256 =−=+ Axyxyy và , xy . Số phần tử của tập hợp A là A. 7. B. 5. C. 4. D. 6 Lời giải Chọn D Ta có ( )2 256−=+xyy ( ) 22316−+= xy ( )( ) 3316++−+= xyxy Vì 33++−+xyxy và 30++xy nên 30−+xy Do đó ( )( ) 3316++−+=xyxy khi các trường hợp sau xảy ra: TH1: 17 316 2 1531 3 2  ++==    −+= +=  x xy xy y loại do , xy TH2: 38 32 ++=   −+=  xy xy 5 33 =    +=  x y 5 33 =   += x y 5 0 6 =   =  =− x y y . TH3: 34 34 ++=   −+=  xy xy 4 30 =    +=  x y 4 3 =   =− x y . Do đó ( ) ( ) ( ) ( ) ( ) ( ) 5;0;5;6;5;0;5;6;4;3;4;3 =−−−−−−−A . Vậy tập hợp A có 6 phần tử.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP Page 31 BÀI 3: CÁC PHÉPTOÁNTRÊNTẬPHỢP 1. Hợp và giao của các tập hợp Cho hai tập hợp A và B. Tập hợp các phần tử thuộc A hoặc thuộc B gọi là hợp của hai tập hợp A và B, kí hiệu A ∪ B. A ∪ B = {x |x ∈ A hoặc x ∈ B}. xA xAB xB     Tập hợp các phần tử thuộc cả hai tập hợp A và B gọi là giao của hai tập hợp A và B, kí hiệu A∩B. A ∩ B = {x | x ∈ A và x ∈ B} xA xAB xB     Nhận xét: • Nếu A và B là hai tập hợp hữu hạn thì n(A ∪ B) = n(A) + n(B) + n(B) - n(A ∩ B). • Đặc biệt, nếu A và B không có phần tử chung, tức A ∩ B = ∅, thì n(��∪ B) = n(A) + n(B). 2. Hiệu của hai tập hợp, phần bù của tập con Cho hai tập hợp A và B Tập hợp các phần tử thuộc A nhưng không thuộc B gọi là hiệu của A và B, kí hiệu A\ B. A\B = {x | x ∈ A và x ∉ B} \ xA xAB xB     Nếu AU  thì hiệu \ UA được gọi là phần bù của A trong ,U kí hiệu .U CA CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP LÝ THUYẾT.I =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP Page 32 Chú ý: Trong các chương sau, để tìm các tập hợp là hợp, giao, hiệu, phần bù của những tập con của tập số thực, ta thường vẽ sơ đồ trên trục số. DẠNG : CÁC PHÉP TOÁN VỀ GIAO, HỢP, HIỆU CỦA HAI TẬP HỢP PHƯƠNG PHÁP Giao của hai tập hợp: ABxxAvaxB Hợp của hai tập hợp: ABxxAhoacxB . Hiệu cuả hai tập hợp: \ ABxxAvaxB . Phần bù: Cho BA thì \A CBAB . Bài 1. Cho hai tập hợp 1;2;3;7,2;4;6;7;8AB . Xác định các tập hợp AB , AB, \ AB , \.BA Bài 2. Cho tập {0;1;2;3;4;5}X = và tập {0;2;4}A = . Xác định phần bù của A trong X . Bài 3. Gọi n B là tập hợp các bội số của n trong . Xác định tập hợp 24BB ? Bài 4. Cho A là tập hợp tất cả các nghiệm của phương trình 2 43 0xx ; B là tập hợp các số có giá trị tuyệt đối nhỏ hơn 4 Xác định tập hợp \ AB ? Bài 5. Mỗi học sinh của lớp 10A1 đều biết chơi đá cầu hoặc cầu lông, biết rằng có 25 em biết chơi đá cầu, 30 em biết chơi cầu lông, 15 em biết chơi cả hai. Hỏi lớp 10A1 có bao nhiêu em chỉ biết đá cầu? Bao nhiêu em chỉ biết đánh cầu lông? Sĩ số lớp là bao nhiêu? Bài 6. Viết lại tập hợp {21| AxxZ và 24} x dưới dạng liệt kê Bài 7. Mỗi học sinh của lớp 10A1 đều biết chơi đá cầu hoặc cầu lông, biết rằng có 25 em biết chơi đá cầu , 30 em biết chơi cầu lông , 15 em biết chơi cả hai . Hỏi lớp 10A1 có bao nhiêu em chỉ biết đá cầu? bao nhiêu em chỉ biết đánh cầu lông? Sĩ số lớp là bao nhiêu? Bài 8. Cho các tập hợp: |3|15|24 AxRxBxRxCxRx HỆ THỐNG BÀI TẬP.II = BÀI TẬP TỰ LUẬN.1 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP Page 33 a) Hãy viết lại các tập hợp , , ABC dưới kí hiệu khoảng, nửa khoảng, đoạn. b) Tìm ,,\ ABABAB c) Tìm \ BCAC . Bài 9. Cho các tập hợp 3 1; 2 Amm +  =−  và ( )  );33;B =−−+ . Tìm tất cả các số thực m để AB= . Bài 10. Cho hai tập hợp ( 2;5E = và  23;22Fmm=−+ . Tìm tất cả các giá trị của tham số m để A hợp B là một đoạn có độ dài bằng 5 Bài 11. Cho khoảng 6 ; 2 A m  =−  và khoảng ( )1;Bm=−+ . Tìm tất cả các số thực m để \ ABA = . Bài 12. Cho các tập hợp ( )2;A =+ và )2 7;Bm  =−+  với 0m  Tìm tất cả các số thực m để \ AB là một khoảng có độ dài bằng 16 . Câu 1: Tập hợp nào sau đây chỉ gồm các số vô tỷ? A. *\ . B. \ . C. \ . D.  \0 . Câu 2: Cho tập hợp A . Trong các mệnh đề sau, tìm mệnh đề sai ?. A. AA B. AAA C. D. A Câu 3: Cho hai tập hợp ;;;;,;;;; AabcdmBcdmkl . Tìm AB . A. ; ABab . B. ;;;;;; ABabcdmkl . C. ; ABcd . D. ;; ABcdm . Câu 4: Cho , , ABC là ba tập hợp được minh họa như hình vẽ bên. Phần gạch sọc trong hình vẽ là tập hợp nào sau đây? A. \ ABC . B. \ ABC . C. \\ ACAB . D. ABC . Câu5: Cho hai tập hợp , MN thỏa mãn MN Mệnhđềnàosauđâyđúng? A. MNN B. \. MNN C. MNM D. \. MNM Câu 6: Số phần tử của tập hợp  2 23/,3Akkk =+ là: A. 7. B. 6. C. 5. D. 4. BÀI TẬP TRẮC NGHIỆM.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP Page 34 Câu 7: Tập hợp nào sau đây có đúng hai tập hợp con? A.  ;x  B.  x C.  ;;xy  D.  ; xy Câu 8: Cho tập X có biểu diễn trên trục số như hình sau: Khẳng định nào sau đây đúng. A. X là khoảng, ( )5;X =−+ . B. X là khoảng, ( );5X =−− . C. X là nửa khoảng, ( ;5X =−− . D. X là nửa khoảng,  )5;X =−+ . Câu 9: Tập hợp  ) ( 3;10;4− bằng tập hợp nào sau đây? A. ( )0;1 B.  0;1 C.  3;4 D.  3;0 Câu 10: Cho hai tập hợp  |20; 3Axxx = và  2 |50Bxxx=−= Xác định tập hợp AB  A.  0;3;6;9;12;15;18 . B.  0;3;5;6;9;12;15;18 . C.  3;6;9;12;15;18 D.  3;5;6;9;12;15;18 Câu 11: Cho hai tập hợp  4;1Am=− , ( 3; Bm =− khác rỗng. Tính tổng tất cả các giá trị nguyên của m để ABB = A. 13. B. 14. C. 12. D. 11. Câu 12: Chonửakhoảng  )5;3A =− vàđoạn  12;52 Bmm =−− .Tìmtấtcảcácsốthực m để AB= A. 15 m − . B. 1 5 m m −   . C. 1 5 m m −   . D. 1 5 m m −   . Câu 13: Cho nửa khoảng ( ; Am =−− và khoảng ( )25;23Bm=− . Gọi S là tập hợp các số thực m để ABA = . Hỏi S là tập con của tập hợp nào sau đây? A. ( );23−− . B. ( ;0− . C. ( )23; −+ . D.  . Câu 14: Cho hai tập hợp ( )1;8Am=− và ( )2;B =+ . Tìm tất cả các giá trị của số thực m để A khác tập rỗng và A. . B. . C. . D. . Câu 15: Cho , . Tìm để . A. B. C. D. \ AB = 3m  3m = 39 m  39 m   33Axmxmx =−=−  2 40Bxx=−= m \ BAB = 33 22 m − 3 2 m  33 22 m − 3 2 m −

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP Page 1 BÀI 3: CÁC PHÉPTOÁNTRÊNTẬPHỢP 1. Hợp và giao của các tập hợp Cho hai tập hợp A và B. Tập hợp các phần tử thuộc A hoặc thuộc B gọi là hợp của hai tập hợp A và B, kí hiệu A ∪ B. A ∪ B = {x |x ∈ A hoặc x ∈ B}. xA xAB xB     Tập hợp các phần tử thuộc cả hai tập hợp A và B gọi là giao của hai tập hợp A và B, kí hiệu A∩B. A ∩ B = {x | x ∈ A và x ∈ B} xA xAB xB     Nhận xét: • Nếu A và B là hai tập hợp hữu hạn thì n(A ∪ B) = n(A) + n(B) + n(B) - n(A ∩ B). • Đặc biệt, nếu A và B không có phần tử chung, tức A ∩ B = ∅, thì n(��∪ B) = n(A) + n(B). 2. Hiệu của hai tập hợp, phần bù của tập con Cho hai tập hợp A và B Tập hợp các phần tử thuộc A nhưng không thuộc B gọi là hiệu của A và B, kí hiệu A\ B. A\B = {x | x ∈ A và x ∉ B} \ xA xAB xB     Nếu AU  thì hiệu \ UA được gọi là phần bù của A trong ,U kí hiệu .U CA CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP LÝ THUYẾT.I =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP Page 2 Chú ý: Trong các chương sau, để tìm các tập hợp là hợp, giao, hiệu, phần bù của những tập con của tập số thực, ta thường vẽ sơ đồ trên trục số. DẠNG : CÁC PHÉP TOÁN VỀ GIAO, HỢP, HIỆU CỦA HAI TẬP HỢP PHƯƠNG PHÁP Giao của hai tập hợp: ABxxAvaxB Hợp của hai tập hợp: ABxxAhoacxB Hiệu cuả hai tập hợp: \ ABxxAvaxB Phần bù: Cho BA thì \A CBAB . Bài 1. Cho hai tập hợp 1;2;3;7,2;4;6;7;8AB Xác định các tập hợp AB , AB, \ AB , \.BA Lời giải Ta có 2;7,1;2;3;4;6;7;8,\1;3,\4;6;8ABABABBA Bài 2. Cho tập {0;1;2;3;4;5}X = và tập {0;2;4}A = . Xác định phần bù của A trong X . Lời giải Vì AX nên \{1;3;5)X CAXA . Bài 3. Gọi n B là tập hợp các bội số của n trong . Xác định tập hợp 24BB ? Lời giải HỆ THỐNG BÀI TẬP.II = BÀI TẬP TỰ LUẬN.1 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP Page 3 Ta có các tập hợp 2 4 2,2;4;6;8;10;... 4,4;8;12;16;... Bxxkk Bxxkk . Do đó 244 BBB . Bài 4. Cho A là tập hợp tất cả các nghiệm của phương trình 2 43 0xx ; B là tập hợp các số có giá trị tuyệt đối nhỏ hơn 4 Xác định tập hợp \ AB ? Lời giải Ta có 2 1 76 01;3 3 x xxA x 3;2;1;0;1;2;3B . Do đó \ AB Bài 5. Mỗi học sinh của lớp 10A1 đều biết chơi đá cầu hoặc cầu lông, biết rằng có 25 em biết chơi đá cầu, 30 em biết chơi cầu lông, 15 em biết chơi cả hai. Hỏi lớp 10A1 có bao nhiêu em chỉ biết đá cầu? Bao nhiêu em chỉ biết đánh cầu lông? Sĩ số lớp là bao nhiêu? Lời giải Dựa vào biểu đồ Ven ta suy ra số học sinh chỉ biết đá cầu là 251510 −= Số học sinh chỉ biết đánh cầu lông là 301515 −= . Do đó ta có sĩ số học sinh của lớp 10A1 là 10151540 ++= . Bài 6. Viết lại tập hợp {21| AxxZ và 24} x dưới dạng liệt kê Lời giải Ta có 242,1,0,1,2,3,4 xZ x x . Suy ra 3;1;1;3;5;7;9C Bài 7. Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi hóa, 6 học sinh giỏi cả Toán và Lý, 5 học sinh giỏi cả Hóa và Lý, 4 học sinh giỏi cả Toán và Hóa, 3 học sinh giỏi cả ba môn Toán, Lý, Hóa. Tính học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A? Lời giải Theo giả thiết đề bài cho, ta có biểu đồ Ven:

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP Page 4 Dựa vào biểu đồ Ven, ta có Số học sinh giỏi chỉ một môn Toán: 103313 −−−= Số học sinh giỏi chỉ một môn Lý: 103322 −−−= . Số học sinh giỏi chỉ một môn Hóa: 113215 −−−= . Vậy số học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A là: 325332119 ++++++= Bài 8. Cho các tập hợp: |3|15|24 AxRxBxRxCxRx a) Hãy viết lại các tập hợp , , ABC dưới kí hiệu khoảng, nửa khoảng, đoạn. b) Tìm ,,\ ABABAB c) Tìm \ BCAC . Lời giải a) Ta có: ;3 1;5 2;4ABC b) Suy ra ;5AB Suy ra 1;3AB Suy ra \;1AB 2;3AC và 2;5BC Suy ra ta có \3;5BCAC Bài 9. Cho các tập hợp 3 1; 2 Amm +  =−  và ( )  );33;B =−−+ . Tìm tất cả các số thực m để AB= . Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP Page 5 Đặt  )3;3XCBX==− AB= XA 13 43 3 2 m mm −−    +   Bài 10. Cho hai tập hợp ( 2;5E = và  23;22Fmm=−+ . Tìm tất cả các giá trị của tham số m để A hợp B là một đoạn có độ dài bằng 5 Lời giải Nhận xét: Kí hiệu X là độ dài của khoảng/nửa khoảng/đoạn X , khi đó 3E = ; 5F = * TH1: 35 232522 22 EFFEFmmm =−+ . * TH2: 5EFFEFF = . Vậy không có giá trị nào của m thỏa mãn TH2. Bài 11. Cho khoảng 6 ; 2 A m  =−  và khoảng ( )1;Bm=−+ . Tìm tất cả các số thực m để \ ABA = . Lời giải 2 6341\10 2224 ABAABmmmm mmm ==−−++−   ( )* Bài 12. Cho các tập hợp ( )2;A =+ và )2 7;Bm  =−+  với 0m  Tìm tất cả các số thực m để \ AB là một khoảng có độ dài bằng 16 . Lời giải Điều kiện để \ AB  là 22729 3 00 mm m mm −   Khi đó ( )2 \2;7ABm=− . Độ dài khoảng \ AB bằng 16 2 72165mm −−== (do 3m  ).

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP Page 6 Câu 1: Tập hợp nào sau đây chỉ gồm các số vô tỷ? A. *\ B. \ C. \ . D.  \0 . Lời giải Chọn B Tập hợp chỉ gồm các số vô tỷ là \ Câu 2: Cho tập hợp A . Trong các mệnh đề sau, tìm mệnh đề sai ?. A. AA. B. AAA. C. D. A . Lời giải Chọn A Ta có A . Câu 3: Cho hai tập hợp ;;;;,;;;; AabcdmBcdmkl . Tìm AB A. ; ABab . B. ;;;;;; ABabcdmkl . C. ; ABcd D. ;; ABcdm Lời giải Chọn D Tập hợp A và tập hợp B có chung các phần tử ,, cdm. Do đó ;; ABcdm . Câu 4: Cho , , ABC là ba tập hợp được minh họa như hình vẽ bên. Phần gạch sọc trong hình vẽ là tập hợp nào sau đây? A. \ ABC B. \ ABC C. \\ ACAB D. ABC Lời giải Chọn B Sử dụng phép toán giao hai tập hợp để tìm AB  , từ đó suy ra đáp án B. Câu5: Cho hai tập hợp , MN thỏa mãn MN Mệnhđềnàosauđâyđúng? A. .MNN B. \. MNN C. .MNM D. \. MNM Lời giải Chọn C BÀI TẬP TRẮC NGHIỆM.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP Page 7 Dựa vào biểu đồ Ven. Câu 6: Số phần tử của tập hợp  2 23/,3Akkk =+ là: A. 7. B. 6. C. 5. D. 4. Lời giải Chọn D  3;2;1;0;1;2;3k =−−−  3;5;11;21A = . Câu 7: Tập hợp nào sau đây có đúng hai tập hợp con? A.  ;x  B.  x C.  ;;xy  D.  ; xy Lời giải Chọn B. C1: Công thức số tập con của tập hợp có n phần tử là 2n nên suy ra tập  x có 1 phần tử nên có 1 22 = tập con. C2: Liệt kê số tập con ra thì  x có hai tập con là  x và   . Câu 8: Cho tập X có biểu diễn trên trục số như hình sau: Khẳng định nào sau đây đúng. A. X là khoảng, ( )5;X =−+ . B. X là khoảng, ( );5X =−− . C. X là nửa khoảng, ( ;5X =−− . D. X là nửa khoảng,  )5;X =−+ . Lời giải Chọn B Câu 9: Tập hợp  ) ( 3;10;4− bằng tập hợp nào sau đây? A. ( )0;1 B.  0;1 C.  3;4 D.  3;0 Lời giải Chọn C Ta có:  ) (   3;10;43;4 −=− . Câu 10: Cho hai tập hợp  |20; 3Axxx = và  2 |50Bxxx=−= Xác định tập hợp AB  A.  0;3;6;9;12;15;18 . B.  0;3;5;6;9;12;15;18 . C.  3;6;9;12;15;18 D.  3;5;6;9;12;15;18 Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP Page 8 Chọn B Ta có tập hợp  |20; 3Axxx =  0;3;6;9;12;15;18A = . Giải phương trình 2 0 50 5 x xx x = −=  = . Do x  nên  0;5B = .  0;3;5;6;9;12;15;18AB = Câu 11: Cho hai tập hợp  4;1Am=− , ( 3; Bm =− khác rỗng. Tính tổng tất cả các giá trị nguyên của m để ABB = . A. 13. B. 14. C. 12. D. 11. Lời giải Chọn B 34115ABBABmmm =−− . m   2;3;4;5m  tổng các giá trị nguyên của m là 234514 +++= . Câu 12: Cho nửa khoảng  )5;3A =− và đoạn  12;52 Bmm =−− . Tìm tất cả các số thực m để AB= A. 15 m − . B. 1 5 m m −   . C. 1 5 m m −   . D. 1 5 m m −   . Lời giải Chọn C 1231 5255 mm AB mm =−− −−  Vậy giá trị m cần tìm là 1 5 m m −   Câu 13: Cho nửa khoảng ( ; Am =−− và khoảng ( )25;23Bm=− . Gọi S là tập hợp các số thực m để ABA = . Hỏi S là tập con của tập hợp nào sau đây? A. ( );23−− . B. ( ;0− . C. ( )23; −+ . D.  . Lời giải Chọn B 252314 23 2323 mm ABABAm mm − =−  −−  Suy ra (  ( ;23;0S =−−− . Câu 14: Cho hai tập hợp ( )1;8Am=− và ( )2;B =+ . Tìm tất cả các giá trị của số thực m để A khác tập rỗng và A. B. C. D. Lời giải Chọn C Điều kiện: Để khi và chỉ khi , tức là Đối chiếu điều kiện, ta được . \ AB = 3m  3m = 39 m  39 m  189mm− \ AB = AB  213 mm − 39 m 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP Page 9 Câu 15: Cho , . Tìm để . A. . B. . C. . D. . Lời giải Chọn C Ta có: . Ta có: .  33Axmxmx =−=−  2 40Bxx=−= m \ BAB = 33 22 m − 3 2 m  33 22 m − 3 2 m − 30xAmx− 2 2 x xB x =   =− 0 00 3333 \20222 030 32 2 m m m m BABBAm m m m m =   =       ==−     −  − 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 1 TẬPHỢP.CÁCPHÉPTOÁNTRÊNTẬPHỢP DẠNG 1. PHẦN TỬ CỦA TẬP HỢP, CÁC XÁC ĐỊNH TẬP HỢP Câu 1: Ký hiệu nào sau đây dùng để viết đúng mệnh đề: “3 là một số tự nhiên”? A. 3  B. 3 C. 3  D. 3  Câu 2: Ký hiệu nào sau đây để chỉ 5 không phải là một số hữu tỉ? A. 5  B. 5  C. 5  D. 5  Câu 3: Cho tập hợp  1|,5Axxx=+ . Tập hợp A là: A.  1;2;3;4;5A = B.  0;1;2;3;4;5;6A = C.  0;1;2;3;4;5A = D.  1;2;3;4;5;6A = Câu 4: Hãy liệt kê các phần tử của tập hợp  2 |2310Xxxx=−+= A.  0X = B.  1X = C. 1 1; 2 X  =   D. 3 1; 2 X  =   Câu 5: Liệt kê các phần tử của phần tử tập hợp  2 |2530Xxxx=−+= A.  0X = B.  1X = C. 3 2 X  =   D. 3 1; 2 X  =   Câu 6: Trong các tập sau, tập nào là tập rỗng? A.  |1xx B.  2 |6710xxx −+= C.  2 :420xxx−+= D.  2 :430xxx−== Câu 7: Cho tập hợp ( ) ;|;,1Mxyxyxy =+= . Hỏi tập M có bao nhiêu phần tử? A. 0 B. 1 C. 2 D. 3 Câu 8: Cho tập hợp  2 1\,5Axxx =+ . Hãy liệt kê các phần tử của tập hợp A A.  0;1;2;3;4;5A = B.  1;2;5;10;17;26A = C.  2;5;10;17;26A = D.  0;1;4;9;16;25A = Câu 9: Hãy liệt kê các phần tử của tập hợp:  42 \680Xxxx=−+= . A.  2;4X = B.  2;2X =− CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.III ==

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 2 C.  2;2X = D.  2;2;2;2X =−− Câu 10: Cho tập hợp ( ) 22 ;\,,0Mxyxyxy=+ . Khi đó tập hợp M có bao nhiêu phần tử? A. 0 B. 1 C. 2 D. Vô số Câu 11: Số phần tử của tập hợp: ( ) 2 22 \21Axxxxx =+=−+ là: A. 0 B. 3 C. 1 D. 2 Câu 12: Số tập con của tập hợp: ( ) 2 22 \3220Axxxxx =+−−= là: A. 16 B. 8 C. 12 D. 10 Câu 13: Số phần tử của tập hợp: ( ) 2 22 \24441Axxxxx =+−=−+ là: A. 0 B. 2 C. 4 D. 3 Câu 14: Hãy liệt kê các phần tử của tập hợp  2 10Xxxx=++= : A. 0=X B.  0=X C. X = D.  X = Câu 15: Số phần tử của tập hợp  2 1/,2=+Akkk là: A. 1. B. 2. C. 3. D. 5. Câu 16: Trong các tập hợp sau, tập hợp nào là tập hợp rỗng: A.  xx1  . B.  2 x6710 xx −+= . C.  2 xx420 x −+= . D.  2 x430 xx −+= . Câu 17: Cho tập hợp ( )( ) 22–120Axxx =+= . Các phần tử của tập A là: A.  –1;1=A B. –2;–1; 2}{ 1;=A C. {1}=A D. {1}=A Câu 18: Trong các tập hợp sau, tập hợp nào là tập rỗng? A.  2 40Axx=−= B.  2 230Bxxx=++= C.  2 50Cxx=−= D.  2 120.Dxxx=+−= Câu 19: Trong các tập hợp sau, tập hợp nào khác rỗng? A.  2 10Axxx=++= B.  2 20Bxx=−= C. ( )( ) 32–310Cxxx=+= . D. ( ) 2 30Dxxx=+= . DẠNG 2. TẬP HỢP CON, TẬP HỢP BẰNG NHAU Câu 20: Cho hai tập hợp A và .B Hình nào sau đây minh họa A là tập con của B? A. B. C. D. Câu 21: Cho ba tập hợp E, F, G thỏa mãn: , EFFG  và GK  . Khẳng định nào sau đây đúng? A. GF  B. KG  C. EFG == D. EK  Câu 22: Cho tập hợp  0;3;4;6A = . Số tập hợp con gồm hai phần tử của A là:

Câu

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 3 A. 12 B. 8 C. 10 D. 6 Câu 23: Cho tập hợp  ;; Xabc = . Số tập con của X là A. 4 B. 6 C. 8 D. 12 Câu 24: Trong các tập hợp sau đây, tập hợp nào có đúng một tập hợp con? A.  B.  x C.   D.  , x Câu 25: Cho tập hợp  1;2A = và  1;2;3;4;5B = . Có tất cả bao nhiêu tập X thỏa mãn: AXB  ? A. 5 B. 6 C. 7 D. 8 Câu 26: Chotậphợp  1;2;5;7A = và  1;2;3B = .Cótấtcảbaonhiêutập X thỏamãn: XA  và XB  ? A. 2 B. 4 C. 6 D. 8 Câu 27: Cho tập hợp      1;3,3;,;;3 ABxCxy === . Để ABC == thì tất cả các cặp ( ); xy là: A. ( )1;1 B. ( )1;1 và ( )1;3 C. ( )1;3 D. ( )3;1 và ( )3;3 Câu 28: Cho tập hợp    1;2;3;4,0;2;4AB== ,  0;1;2;3;4;5C = . Quan hệ nào sau đây là đúng? A. BAC  B. BAC = C. AC BC    D. ABC =

29: Cho tập hợp A có 4 phần tử. Hỏi tập A có bao nhiêu tập con khác rỗng? A. 16 B. 15 C. 12 D. 7

30: Số các tập hợp con gồm hai phần tử của tập hợp  ;;;;; Babcdef = là: A. 15 B. 16 C. 22 D. 25

31: Số các tập hợp con có 3 phần tử có chứa a, b của tập hợp  ;;;;;; Cabcdefg = là: A. 5 B. 6 C. 7 D. 8 Câu 32: Trong các tập hợp sau đây, tập hợp nào có đúng hai tập hợp con? A.  ; xy B.  x C.  ;x D.  ;;xy Câu 33: Cho tập hợp  1,2,3,4,,= Axy . Xét các mệnh đề sau đây: ( )I : “3 A”. ( )II : “ 3,4  A”. ( )III : “ ,3, abA  ”. Trong các mệnh đề sau, mệnh đề nào đúng A. I đúng. B. , III đúng. C. , IIIII đúng. D. , IIII đúng. Câu 34: Cho  0;2;4;6=A . Tập A có bao nhiêu tập con có 2 phần tử? A. 4. B. 6. C. 7. D. 8. Câu 35: Cho tập hợp  1;2;3;4=X . Câu nào sau đây đúng? A. Số tập con của X là 16.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 4 B. Số tập con của X gồm có 2 phần tử là 8 C. Số tập con của X chứa số 1 là 6. D. Số tập con của X gồm có 3 phần tử là 2 Câu 36: Số các tập con 2 phần tử của  ,,,,, = Babcdef là: A. 15 B. 16 C. 22 D. 25 Câu 37: Số các tập con 3 phần tử có chứa ,  của  ,,,,,,,,, =C là: A. 8 B. 10 C. 12 D. 14 Câu 38: Trong các tập sau đây, tập hợp nào có đúng hai tập hợp con? A.  ; xy . B.  x . C.  ; x . D.  ;; xy . Câu 39: Cho tập hợp  ,,, Aabcd = . Tập A có mấy tập con? A. 16. B. 15. C. 12. D. 10. Câu 40: Khẳng định nào sau đây sai?Các tập AB = với , AB là các tập hợp sau? A. ( )( ) 1;3, 0} –1 {= 3ABxxx ==− . B.  1;3;5;7;9,21, ,04{} ABnnkkk ===+ . C.  2{1;2, 0} 23ABxxx  =−=−= . D.  2, 10ABxxx ==++= . Câu 41: Cho tập hợp    1;5,1;3;5XY== . Tập XY  là tập hợp nào sau đây? A.  1 B.  1;3 C. {1;3;5} D.  1;5 Câu 42: Cho tập    2;4;6;9,1;2;3;4XY== . Tập nào sau đây bằng tập \ XY ? A.  1;2;3;5 B.  1;3;6;9 C.  6;9 D.  1 Câu 43: Cho tập hợp    ;,;; XabYabc == XY  là tập hợp nào sau đây? A.  ;;; abcd B.  ; ab C.  c D. {;;} abc Câu 44: Cho hai tập hợp A và B khác rỗng thỏa mãn: AB  . Trong các mệnh đề sau mệnh đề nào sai? A. \ AB = B. ABA = C. \ BAB = D. ABB = Câu 45: Cho ba tập hợp: ( )  ( )  ( ) ( ) |0,|0,|0 FxfxGxgxHxfxgx =====+= . Mệnh đề nào sau đây là đúng? A. HFG = B. HFG = C. \ HFG = D. \ HGF = Câu 46: Cho tập hợp 2 2 |1 1 Axx x =  +  ; B là tập hợp tất cả các giá trị nguyên của b để phương trình 2 240xbx−+= vô nghiệm. Số phần tử chung của hai tập hợp trên là: A. 1 B. 2 C. 3 D. Vô số Câu 47: Cho hai tập hợp    1;2;3;4,1;2XY== X CY là tập hợp sau đây?

nhiêu học

54: Lớp 10A có 45 học sinh trong đó có 25 em học giỏi môn Toán, 23 em học giỏi môn Lý, 20 em học giỏi môn Hóa, 11 em học giỏi cả môn Toán và môn Lý, 8 em học giỏi cả môn Lý và môn Hóa, 9 em học giỏi cả môn Toán và môn Hóa. Hỏi lớp 10A có bao nhiêu bạn học giỏi cả ba môn Toán, Lý, Hóa, biết rằng mỗi học sinh trong lớp học giỏi ít nhất một trong 3 môn

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 5 A.  1;2 B.  1;2;3;4 C.  3;4 D.  Câu 48: Cho A, B, C là ba tập hợp được minh họa bằng biểu đồ ven như hình vẽ. Phần gạch sọc trong hình vẽ là tập hợp nào sau đây? A. ( ) \ ABC  B. ( ) \ ABC  C. ( ) ( )\\ ACAB  D. ( ) ABC  Câu 49: Cho hai tập hợp  0;2A = và  0;1;2;3;4B = . Số tập hợp X thỏa mãn AXB = là: A. 2 B. 3 C. 4 D. 5 Câu 50: Cho hai tập hợp  0;1A = và  0;1;2;3;4B = . Số tập hợp X thỏa mãn B XCA  là: A. 3 B. 5 C. 6 D. 8 Câu 51: Cho tập hợp  1;2;3;4;5A = . Tìm số tập hợp X sao cho  \1;3;5AX = và  \6;7XA = A. 1 B. 2 C. 3 D. 4 Câu 52: Ký hiệu X là số phần tử của tập hợp X. Mệnh đề nào sai trong các mệnh đề sau? A. ABABABAB =+=+ B. ABABABAB +=− C. ABABABAB +=+ D. ABABAB =+= Câu 53: Một lớp học có 25 học sinh giỏi môn Toán, 23 học sinh giỏi môn Lý, 14 học sinh giỏi cả môn Toán và Lý và có 6 học sinh không giỏi môn nào cả. Hỏi lớp đó có bao

sinh? A. 54 B. 40 C. 26 D. 68 Câu

Toán, Lý, Hóa? A. 3 B. 4 C. 5 D. 6 Câu 55: Cho tập hợp    1;2;3;4,0;2;4;6AB== . Mệnh đề nào sau đây là đúng? A.  2;4AB= B.  0;1;2;3;4;5;6AB= C. AB  D.  \0;6AB = Câu 56: Ký hiệu H là tập hợp các học sinh của lớp 10A. T là tập hợp các học sinh nam, G là tập hợp các học sinh nữ của lớp 10A. Khẳng định nào sau đây sai? A. TGH = B. TG= C. \ HTG = D. \ GT = Câu 57: Cho A, B, C là ba tập hợp. Mệnh đề nào sau đây là sai? A. ABACBC  B. \\ ABCACB  C. ABACBC  D. , ABBCAC  Câu 58: Cho tập hợp  ;; Aabc = và  ;;;; Babcde = . Có tất cả bao nhiêu tập hợp X thỏa mãn AXB  ? A. 5 B. 6 C. 4 D. 8 Câu 59: Cho hai tập hợp    1;2;3;4;5;1;3;5;7;9AB== . Tập nào sau đây bằng tập AB  ?

Câu

Cho

  6;9. D. .

Câu 67: Cho     0;1;2;3;4,2;3;4;5;6.AB== Tập hợp ( ) ( )\\ ABBA  bằng?

A.   0;1;5;6. B.   1;2. C.   2;3;4. D.

Câu 68: Cho

Câu

Cho

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 6 A.  1;3;5 B.  1;2;3;4;5 C.  2;4;6;8 D.  1;2;3;4;5;7;9 Câu 60: Cho tập hợp    2;4;6;9,1;2;3;4AB== . Tập nào sau đây bằng tập \ AB ? A.  1;2;3;5 B.  1;2;3;4;6;9 C.  6;9 D.  Câu 61: Cho các tập hợp    2 :760,:4AxxxBxx =−+== . Khi đó: A. ABA = B. ABAB = C. \ ABA  D. \ BA = Câu 62: Một lớp học có 25 học sinh chơi bóng đá, 23 học sinh chơi bóng bàn, 14 học sinh chơi cả bóng đá và bóng bàn và 6 học sinh không chơi môn nào. Số học sinh chỉ chơi 1 môn thể thao là? A. 48 B. 20 C. 34 D. 28 Câu 63: Trong các khẳng định sau khẳng định nào đúng: A. \ = . B. * = . C. * = . D. ** = . Câu 64: Chọn kết quả sai trong các kết quả sau: A. .= ABAAB B. .ABAAB = C. \. ==ABAAB D. \.BABAB== Câu 65: Cho  7;2;8;4;9;12X = ;  1;3;7;4Y = . Tập nào sau đây bằng tập  XY ? A.  1;2;3;4;8;9;7;12 B.  2;8;9;12 C.  4;7 D.  1;3

66:

hai tập hợp  2,4,6,9A = và  1,2,3,4B = .Tập hợp \ AB bằng tập nào sau đây? A.  1,2,3,5=A B.   1;3;6;9. C.

  5;6.

    0;1;2;3;4,2;3;4;5;6.AB== Tập hợp \ AB bằng: A.   0. B.   0;1. C.   1;2. D.   1;5.

69:

    0;1;2;3;4,2;3;4;5;6.AB== Tập hợp \ BA bằng: A.   5. B.   0;1. C.   2;3;4. D.   5;6. Câu 70: Cho     1;5;1;3;5.==AB Chọn kết quả đúng trong các kết quả sau A.   1.=AB B.   1;3.=AB C.   1;5.=AB D.   1;3;5.=AB Câu 71: Cho ( )( )   22*2 22320;330AxxxxxBnn =−−−== . Khi đó tập hợp  AB bằng: A.   2;4. B.   2. C.   4;5. D.   3. DẠNG 3. BIỂU DIỄN TẬP HỢP SỐ Câu 72: Cho tập hợp  \31Axx=− . Tập A là tập nào sau đây? A.  3;1 B.  3;1 C.  )3;1 D. ( )3;1 Câu 73: Hình vẽ nào sau đây (phần không bị gạch) minh họa cho tập hợp ( 1;4 ?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 7 A. B. C. D. Câu 74: Cho tập hợp  \,13Xxxx= thì X được biểu diễn là hình nào sau đây? A. B. C. D. Câu 75: Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp  49Axx= : A.   4;9.=A B. (  4;9.=A C.  ) 4;9.=A D. ( ) 4;9.=A DẠNG 4. CÁC PHÉP TOÁN TRÊN TẬP HỢP SỐ Câu 76: Cho tập hợp ( ;1A =−− và tập ( )2;B =−+ . Khi đó AB  là: A. ( )2; −+ B. ( 2;1 C. D.  Câu 77: Cho hai tập hợp  ) ( )5;3,1;AB=−=+ . Khi đó AB  là tập nào sau đây? A. ( )1;3 B. ( 1;3 C.  )5; −+ D.  5;1 Câu 78: Cho ( )  2;1,3;5AB=−=− . Khi đó AB  là tập hợp nào sau đây? A.  2;1 B. ( )2;1 C. ( 2;5 D.  2;5 Câu 79: Cho hai tập hợp (  ( 1;5;2;7AB== . Tập hợp \ AB là: A. ( 1;2 B. ( )2;5 C. ( 1;7 D. ( )1;2 Câu 80: Cho tập hợp ( )2;A =+ . Khi đó R CA là: A.  )2;+ B. ( )2;+ C. ( ;2− D. ( ;2−− Câu 81: Cho các số thực a, b, c, d và abcd  . Khẳng định nào sau đây là đúng? A. ( ) ( ) ( );;; acbdbc = B. ( ) ( ) ( ;;; acbdbc = C. ( )  )  );;; acbdbc = D. ( )  ) ( );;; acbdbc =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 8 Câu 82: Cho ba tập hợp      )2;2,1;5,0;1ABC =−== . Khi đó tập ( )\ ABC  là: A.  0;1 B.  )0;1 C. ( )2;1 D.  2;5 Câu 83: Cho tập hợp )3;8CA  =−  , ( ) ( ) 5;23;11.CB =− Tập ( )CAB  là: A. ( )3;3 . B.  . C. ( )5;11 . D. ( ) ( ) 3;23;8.− Câu 84: Cho   ( ) ( ) 1;4;2;6;1;2.ABC === Tìm :ABC  A.   0;4. B.  ) 5;. + C. ( ) ;1.− D.  Câu 85: Cho hai tập  342 Axxx =++ ,  5341Bxxx =−− Tất cả các số tự nhiên thuộc cả hai tập A và B là: A. 0 và 1. B. 1. C. 0 D. Không có. Câu 86: Cho  4;7A =− , ( ) ( );23;B =−−+ . Khi đó AB  : A.  ) (  4;23;7.−− B.  ) ( ) 4;23;7.−− C. (  ( ) ;23;.−+ D. ( )  ) ;23;.−−+ Câu 87: Cho ( ;2A =−− ,  )3;B =+ , ( ) 0;4.C = Khi đó tập ( ) ABC  là: A.   3;4. B. (  ( ) ;23;.−−+ C.  ) 3;4. D. ( )  ) ;23;.−−+ Câu 88: Cho  :20AxRx=+ ,  :50BxRx=− . Khi đó  AB là: A.  2;5 . B.  2;6 . C.  5;2 . D. ( )2; −+ . Câu 89: Cho    :20,:50AxRxBxRx =+=− . Khi đó \ AB là: A.  2;5 . B.  2;6 . C. ( )5;+ . D. ( )2;+ . Câu 90: Cho hai tập hợp  ) ( 2;7,1;9AB=−= . Tìm AB  . A. ( )1;7 B.  2;9 C.  )2;1 D. ( 7;9 Câu 91: Cho hai tập hợp  |51Axx=− ;  |33Bxx=− . Tìm AB  A.  5;3 B. ( )3;1 C. ( 1;3 D.  )5;3 Câu 92: Cho (  ( )1;5,2;7AB=−= . Tìm \ AB . A. ( 1;2 B. ( 2;5 C. ( )1;7 D. ( )1;2 Câu 93: Cho 3 tập hợp ( ;0A =− , ( )1;B =+ ,  )0;1C = . Khi đó ( ) ABC  bằng: A.  0 B. C.  0;1 D.  Câu 94: Cho hai tập hợp  4;7M =− và ( ) ( );23;N =−−+ . Khi đó MN  bằng: A.  ) ( 4;23;7−− B.  ) ( )4;23;7− C. (  ( );23; −+ D. ( )  );23; −−+ Câu 95: Cho hai tập hợp   ( )2;3,1;AB=−=+ . Khi đó ( )CAB  bằng: A. ( )1;3 B. (   );13; −+ C.  )3;+ D. ( );2−−

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 9 Câu 96: Chọn kết quả sai trong các kết quả sau: A. ABAAB = B. ABABA = C. \ ABAAB== D. \ ABAAB= Câu 97: Cho tập hợp )3;8 =− CA , ( ) ( ) 5;23;11.=−CB Tập ( )CAB  là: A. ( )5;11 . B. ( ) ( ) 3;23;8.− C. ( )3;3 . D.  . Câu 98: Cho 3 tập hợp: ( ;1A =− ;  2;2B =− và ( )0;5C = . Tính ( ) ( ) ?ABAC= A.  2;1 B. ( )2;5 C. ( 0;1 D.  1;2 DẠNG 5. CÁC BÀI TOÁN TÌM ĐIỀU KIỆN CỦA THAM SỐ Câu 99: Cho tập hợp    ;2,1;2AmmB=+− . Tìm điều kiện của m để AB  . A. 1m − hoặc 0m  B. 10 m − C. 12 m  D. 1m  hoặc 2m  Câu 100: Cho tập hợp ( )0;A =+ và  2 \430Bxmxxm =−+−= . Tìm m để B có đúng hai tập con và BA  . A. 03 4 m m   = B. 4m = C. 0m  D. 3m = Câu 101: Cho hai tập hợp   ( )2;3,;6ABmm =−=+ . Điều kiện để AB  là: A. 32 m −− B. 32 m −− C. 3m − D. 2m − Câu 102: Cho hai tập hợp ( 0;3X = và ( );4Ya = . Tìm tất cả các giá trị của 4a  để XY . A. 3 4 a a    B. 3a  C. 0a  D. 3a  Câu 103: Cho hai tập hợp   (   )\12;;2; AxxBmm ==−−+ . Tìm tất cả các giá trị của m để AB  . A. 4 2 m m   − B. 4 2 1 m m m   −  = C. 4 2 1 m m m   −  = D. 24 m − Câu 104: Cho số thực 0a .Điều kiện cần và đủ để ( ) 4 ;9; −+  a a là: A. 2 0. 3 − a B. 2 0. 3 − a C. 3 0. 4 − a D. 3 0. 4 − a Câu 105: Cho tập hợp    ;2,1;2AmmB=+=− với m là tham số. Điều kiện để AB  là: A. 12 m  B. 10 m − C. 1m − hoặc 0m  D. 1m − hoặc 2m  Câu 106: Cho tập hợp    );2,1;3AmmB=+= . Điều kiện để AB= là: A. 1m − hoặc 3m  B. 1m − hoặc 3m  C. 1m − hoặc 3m  D. 1m − hoặc 3m  Câu 107: Cho hai tập hợp    3;12;4A =−− , ( )1;2Bmm=−+ . Tìm m để AB

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 10 A. 5m  và 0m  B. 5m  C. 13 m  D. 0m  Câu 108: Cho 3 tập hợp ( ) ( )3;11;2A =−− , ( );Bm=+ , ( );2 Cm − . Tìm m để ABC . A. 1 2 2 m  B. 0m  C. 1m − D. 2m  Câu 109: Cho hai tập  0;5A = ; ( 2;31Baa=+ , 1a − . Với giá trị nào của a thì AB A. 15 32 a − B. 5 2 1 3 a a     −  C. 5 2 1 3 a a     −  D. 15 32 a − Câu 110: Cho 2 tập khác rỗng (  ( ) 1;4;2;22, AmBmm =−=−+ . Tìm m để AB A. 15 m − B. 15 m  C. 25 m − D. 3m − Câu 111: Cho số thực 0a .Điều kiện cần và đủ để ( ) 4 ;9; −+  a a là: A. 3 0. 4 − a B. 2 0. 3 − a C. 2 0. 3 − a D. 3 0. 4 − a Câu 112: Cho hai tập  0;5A = ; ( 2;31Baa=+ , 1a − . Với giá trị nào của a thì AB A. 5 2 1 3 a a     −  B. 15 32 a − C. 5 2 1 3 a a     −  D. 15 32 a − Câu 113: Cho  AxR\xm25 =− ;  BxR\x2020 = . Có bao nhiêu giá trị nguyên m thỏa AB= A. 3987. B. 3988. C. 3989. D. 2020. Câu 114: Cho 2 tập hợp  2;5Amm=−+ và  0;4B = . Tìm tất cả các giá trị thực của tham số m để BA  . A. 1m − . B. 12 m − . C. 12 m − . D. 2m  . Câu 115: Cho hai tập hợp (;1)Amm=+ và  1;3B =− . Tìm tất cả các giá trị của m để AB= A. 2 3 m m −   . B. 23 m − . C. 2 1 m m   − . D. 2 3 m m −   . Câu 116: Tìm m để AD  , biết (3;7)A =− và (;32) Dmm =− A. 3m =− B. 3m − C. 1m  D. 2m − Câu 117: Cho 2 tập hợp khác rỗng ( 1;4Am=− , ( )2;22Bm=−+ , với m . Tìm m để AB  . A. 15 m  B. 1m  C. 15 m − D. 21 m −− Câu 118: Cho ( )  )2 3;,;12; 4 m AmB +  =−=−−+   . Tìm m để AB= A. 14 2 3 m  B. 26 m  C. 26 m  D. 14 2 3 m 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 11 Câu 119: Cho số thực 0x  . Tìm x để ( ) 9 ;16; x x  −+   A. 3 0 4 x  . B. 3 0 4 x  . C. 3 0 4 x  . D. 3 0 4 x  . Câu 120: Cho hai tập hợpkhác rỗng ( 1;4Am=− và ( ) 2;22,.Bmm=−+ Có bao nhiêu giá trị nguyên dương của m để AB ? A. 5. B. 6. C. 4. D. 3. Câu 121: Cho ( ) ( );,0;AmB=−=+ . Điều kiện cần và đủ để AB= là: A. 0m  . B. 0m  . C. 0m  . D. 0m  . Câu 122: Cho hai tập hợp khác rỗng ( 1;4Am=− và ( )2;22Bm=−+ , m . Tìm tất cả các giá trị của m để AB A. 25 m − B. 3m − C. 3m − D. 35 m −

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 1 TẬPHỢP.CÁCPHÉPTOÁNTRÊNTẬPHỢP DẠNG 1. PHẦN TỬ CỦA TẬP HỢP, CÁC XÁC ĐỊNH TẬP HỢP Câu 1: Ký hiệu nào sau đây dùng để viết đúng mệnh đề: “3 là một số tự nhiên”? A. 3  B. 3 C. 3  D. 3  Lời giải Đáp án A sai vì kí hiệu “  ” chỉ dùng cho hai tập hợp mà ở đây “3” là một số Hai đáp án C và D đều sai vì ta không muốn so sánh một số với tập hợp. Đáp án B. Câu 2: Ký hiệu nào sau đây để chỉ 5 không phải là một số hữu tỉ? A. 5  B. 5  C. 5  D. 5  Lời giải Vì 5 chỉ là một phần tử còn là một tập hợp nên các đáp án A, B, D đều sai. Đáp án C. Câu 3: Cho tập hợp  1|,5Axxx=+ . Tập hợp A là: A.  1;2;3;4;5A = B.  0;1;2;3;4;5;6A = C.  0;1;2;3;4;5A = D.  1;2;3;4;5;6A = Lời giải Vì ,5xx nên    0;1;2;3;4;511;2;3;4;5;6xx += Đáp án D. Câu 4: Hãy liệt kê các phần tử của tập hợp  2 |2310Xxxx=−+= A.  0X = B.  1X = C. 1 1; 2 X  =   D. 3 1; 2 X  =   Lời giải Vì phương trình 2 2310 xx−+= có nghiệm 1 1 2 x x =   =  nhưng vì x  nên 1 2  . CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.III ==

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 2 Vậy  1X = . Đáp án B. Câu 5: Liệt kê các phần tử của phần tử tập hợp  2 |2530Xxxx=−+= . A.  0X = B.  1X = C. 3 2 X  =   D. 3 1; 2 X  =   Lời giải Vì phương trình 2 2530 xx−+= có nghiệm 1 3 2 x x =   =  nên 3 1; 2 X  =   Đáp án D. Câu 6: Trong các tập sau, tập nào là tập rỗng? A.  |1xx B.  2 |6710xxx −+= C.  2 :420xxx−+= D.  2 :430xxx−== Lời giải Xét các đáp án: Đáp án A: ,1110xxxx −= . Đáp án B: Giải phương trình: 2 1 6710 1 6 x xx x = −+=  =  . Vì 1xx= . Đáp án C: 2 42022xxx−+== . Vì x  Đây là tập rỗng. Đáp án C. Câu 7: Cho tập hợp ( ) ;|;,1Mxyxyxy =+= . Hỏi tập M có bao nhiêu phần tử? A. 0 B. 1 C. 2 D. 3 Lời giải Vì ; xy  nên x, y thuộc vào tập  0;1;2;... Vậy cặp ( ); xy là ( ) ( )1;0,0;1 thỏa mãn 1xy+= Có 2 cặp hay M có 2 phần tử. Đáp án C. Câu 8: Cho tập hợp  2 1\,5Axxx =+ . Hãy liệt kê các phần tử của tập hợp .A A.  0;1;2;3;4;5A = B.  1;2;5;10;17;26A = C.  2;5;10;17;26A = D.  0;1;4;9;16;25A = Lời giải Đáp án B.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 3 Ta có  2 1\,5Axxx =+ Vì ,5xx nên  0;1;2;3;4;5x  2 11;2;5;10;17;26x + . Câu 9: Hãy liệt kê các phần tử của tập hợp:  42 \680Xxxx=−+= A.  2;4X = B.  2;2X =− C.  2;2X = D.  2;2;2;2X =−− Lời giải Đáp án D. Giải phương trình 42680xx−+= 2 2 2 2 24 x x xx  = =    == . Câu 10: Cho tập hợp ( ) 22 ;\,,0Mxyxyxy=+ . Khi đó tập hợp M có bao nhiêu phần tử? A. 0 B. 1 C. 2 D. Vô số Lời giải Đáp án B. Vì 2 2 0 0 x y      nên 22 00xyxy+== Khi đó tập hợp M có 1 phần tử duy nhất là ( ) 0;0 . Câu 11: Số phần tử của tập hợp: ( ) 2 22 \21Axxxxx =+=−+ là: A. 0 B. 3 C. 1 D. 2 Lời giải Đáp án D. Giải phương trình ( )2 22 21xxxx+=−+ trên ( ) ( )2 2210xxx +−−= ( )( )22110xxxxxx +−+++−= ( )( )221210xxx ++−= 12 12 x x  =−−   =−+  .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 4 Câu 12: Số tập con của tập hợp: ( ) 2 22 \3220Axxxxx =+−−= là: A. 16 B. 8 C. 12 D. 10 Lời giải Đáp án A. Giải phương trình ( ) ( )2 22 320 xxxx+−+= Đặt 2 xxt += ta có phương trình 2 0 320 2 3 t tt t = −=  =  Với 0t = ta có 2 0 0 1 x xx x = +=  =− Với 2 3 t = ta có: 2 2 3 xx+= 2 333 3320 3 xxx − +−== Vậy A có 4 phần tử suy ra số tập con của A là 4 216 = Câu 13: Số phần tử của tập hợp: ( ) 2 22 \24441Axxxxx =+−=−+ là: A. 0 B. 2 C. 4 D. 3 Lời giải Đáp án C. Giải phương trình ( )2 22 24441 xxxx +−=−+ ( ) ( )2 22 2421 xxx +−=− 2 2 2421 2421 xxx xxx  +−=−   +−=−+ 2 2 1 3 230 2 12350 5 2 x x xx xxx x =−   = −−=    +−==   =− 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 5 Vậy A có 4 phần tử Câu 14: Hãy liệt kê các phần tử của tập hợp  2 10Xxxx=++= : A. 0=X B.  0=X C. X = D.  X = Lời giải Chọn C Phương trình 2 10xx++= vô nghiệm nên X = . Câu 15: Số phần tử của tập hợp  2 1/,2=+Akkk là: A. 1. B. 2. C. 3. D. 5. Lời giải Chọn C  2 1,2=+Akkk . Ta có ,2kk 22− k   1;2;5.= A Câu 16: Trong các tập hợp sau, tập hợp nào là tập hợp rỗng: A.  xx1  . B.  2 x6710 xx −+= . C.  2 xx420 x −+= . D.  2 x430 xx −+= . Lời giải Chọn C     xx10.== AA  2 x6710 =−+=Bxx . Ta có 2 6710 −+=xx 1 1 6 =   = x x   1.= B  2 xx420 =−+=Cx . Ta có 2 420−+=xx 22 22  =−   =+  x x = C  2 x430 =−+=Dxx . Ta có 2 430−+=xx 1 3 =   = x x   1;3.= D Câu 17: Cho tập hợp ( )( ) 22–120Axxx =+= . Các phần tử của tập A là: A.  –1;1=A B. –2;–1; 2}{ 1;=A C. {1}=A D. {1}=A Lời giải Chọn A ( )( ) 22–120Axxx =+= . Ta có ( )( )22–120 +=xx ( ) 2 2 –10 20vn  =   +=  x x 1 1 =   =− x x   1;1.=− A

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 6 Câu 18: Trong các tập hợp sau, tập hợp nào là tập rỗng? A.  2 40Axx=−= . B.  2 230Bxxx=++= . C.  2 50Cxx=−= . D.  2 120.Dxxx=+−= Lời giải Chọn B    2 402=−== AxxA  2 2 .30 =++==Bxxx B    2 5;5 50=−= =−CxxC    2 1203;4.=+−==− DxxxD Câu 19: Trong các tập hợp sau, tập hợp nào khác rỗng? A.  2 10Axxx=++= B.  2 20Bxx=−= C. ( )( ) 32–310Cxxx=+= . D. ( ) 2 30Dxxx=+= . Lời giải Chọn B  2 10=++=Axxx . Ta có ( )2 10vn++=xx = A  2 20=−=Bxx . Ta có 2 20−=x 2 = x  =B ( )( ) 32–310=+=Cxxx . Ta có ( )( )32–310 +=xx 3 3 = x = C ( ) 2 30=+=Dxxx . Ta có ( )2 30+=xx 0= x   0.= D DẠNG 2. TẬP HỢP CON, TẬP HỢP BẰNG NHAU Câu 20: Cho hai tập hợp A và .B Hình nào sau đây minh họa A là tập con của B? A. B. C. D. Lời giải Hình C là biểu đồ ven, minh họa cho AB  vì mọi phần tử của A đều là của B. Đáp án C. Câu 21: Cho ba tập hợp E, F, G thỏa mãn: , EFFG  và GK  . Khẳng định nào sau đây đúng? A. GF  B. KG  C. EFG == D. EK  Lời giải Dùng biểu đồ minh họa ta thấy EK  .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 7 Đáp án D. Câu 22: Cho tập hợp  0;3;4;6A = . Số tập hợp con gồm hai phần tử của A là: A. 12 B. 8 C. 10 D. 6 Lời giải Mỗi tập con gồm hai phần tử của A là:            0;3;,0;4,0;6,3;4,3;6,4;6 . Đáp án D. Câu 23: Cho tập hợp  ;; Xabc = . Số tập con của X là A. 4 B. 6 C. 8 D. 12 Lời giải Số tập con không có phần tử nào là 1 (tập  ) Số tập con có 1 phần tử là 3:      ,, abc . Số tập con có 2 phần tử là 3:      ;,;,; abacbc .  Số tập con có 3 phần tử là 1:  ;; abc . Vậy có 13318 +++= tập con. Đáp án C. Nhận xét: Người ta chứng minh được là số tập con (kể cả tập rỗng) của tập hợp n phần tử là 2n . Áp dụng vào Ví dụ 4 có 3 28 = tập con. Câu 24: Trong các tập hợp sau đây, tập hợp nào có đúng một tập hợp con? A.  B.  x C.   D.  , x Lời giải Vì tập  có tập hợp con là chính nó. Đáp án B có 2 tập con là  và  x . Đáp án C có 2 tập con là  và   . Đáp án D có 4 tập con. Đáp án A. Câu 25: Cho tập hợp  1;2A = và  1;2;3;4;5B = . Có tất cả bao nhiêu tập X thỏa mãn: AXB  ? A. 5 B. 6 C. 7 D. 8 Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 8 X là tập hợp phải luôn có mặt 1 và 2. Vì vậy ta đi tìm số tập con của tập  3;4;5 , sau đó cho hai phần tử 1 và 2 vào các tập con nói trên ta được tập X Vì số tập con của tập  3;4;5 là 3 28 = nên có 8 tập X. Đáp án D. Câu 26: Chotậphợp  1;2;5;7A = và  1;2;3B = .Cótấtcảbaonhiêutập X thỏamãn: XA  và XB  ? A. 2 B. 4 C. 6 D. 8 Lời giải Cách 1: Vì XA XB    nên ( )XAB  . Mà  1;2AB= Có 2 24 = tập X Cách 2: X là một trong các tập sau:      ;1;2;1;2 Đáp án B. Câu 27: Cho tập hợp      1;3,3;,;;3 ABxCxy === . Để ABC == thì tất cả các cặp ( ); xy là: A. ( )1;1 B. ( )1;1 và ( )1;3 C. ( )1;3 D. ( )3;1 và ( )3;3 Lời giải Ta có: 1 1 3 x ABC y y =  == =  = Cặp ( ); xy là ( ) ( )1;1;1;3 Đáp án B. Câu 28: Cho tập hợp    1;2;3;4,0;2;4AB== ,  0;1;2;3;4;5C = . Quan hệ nào sau đây là đúng? A. BAC  B. BAC = C. AC BC    D. ABC = Lời giải Đáp án C. Ta thấy mọi phần tử của A đều thuộc C và mọi phần tử của B đều thuộc C nên Chọn C Câu 29: Cho tập hợp A có 4 phần tử. Hỏi tập A có bao nhiêu tập con khác rỗng? A. 16 B. 15 C. 12 D. 7 Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 9 Đáp án B. Vì số tập con của tập 4 phần tử là 4 216= Số tập con khác rỗng là 16115 −= Câu 30: Số các tập hợp con gồm hai phần tử của tập hợp  ;;;;; Babcdef = là: A. 15 B. 16 C. 22 D. 25 Lời giải Đáp án A. Cách 1: Số tập con có 2 phần tử trong đó có phần tử a là 5 tập          ;,;,;,;,, abacadaeaf Số tập con có 2 phần tử mà luôn có phần tử b nhưng không có phần tử a là 4 tập:  ; bc ,  ; bd ,  ; be ,  ; bf . Tương tự ta có tất cả 5432115 ++++= tập. Câu 31: Số các tập hợp con có 3 phần tử có chứa a, b của tập hợp  ;;;;;; Cabcdefg = là: A. 5 B. 6 C. 7 D. 8 Lời giải Đáp án A. Tập con có 3 phần tử trong đó a, b luôn có mặt. Vậy phần tử thứ 3 sẽ thuộc một trong các phần tử c, d, e, f, g (5 phần tử) nên có 5 tập con. Câu 32: Trong các tập hợp sau đây, tập hợp nào có đúng hai tập hợp con? A.  ; xy B.  x C.  ;x D.  ;;xy Lời giải Đáp án B. Vì tập hợp  x có hai tập con là  và chính nó. Câu 33: Cho tập hợp  1,2,3,4,,= Axy . Xét các mệnh đề sau đây: ( )I : “3 A”. ( )II : “ 3,4  A”. ( )III : “ ,3, abA  ”. Trong các mệnh đề sau, mệnh đề nào đúng A. I đúng. B. , III đúng. C. , IIIII đúng. D. , IIII đúng. Lời giải Chọn A 3 là một phần tử của tập hợp A .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 10  3,4 là một tập con của tập hợp A . Ký hiệu:  3,4 A .  ,3, ab là một tập con của tập hợp A . Ký hiệu:  ,3, abA  . Câu 34: Cho  0;2;4;6=A . Tập A có bao nhiêu tập con có 2 phần tử? A. 4. B. 6. C. 7. D. 8. Lời giải Chọn B Có thể sử dụng máy tính bỏ túi để tính số tập con có 2 phần tử của tập hợp A gồm 4 phần tử là: 2 4 6C = Các tập con có 2 phần tử của tập hợp A là: 0;2 ,  0;4; ,  0;6 ,  2;4; ,  2;6 ,   4;6. Câu 35: Cho tập hợp  1;2;3;4=X . Câu nào sau đây đúng? A. Số tập con của X là 16. B. Số tập con của X gồm có 2 phần tử là 8 C. Số tập con của X chứa số 1 là 6 D. Số tập con của X gồm có 3 phần tử là 2. Lời giải Chọn A Số tập con của tập hợp X là: 4 216 = Số tập con có 2 phần tử của tập hợp X là: 2 4 6C = Số tập con của tập hợp X chứa số 1 là: 8  1 ,    1;2,1;3 ,  1;4 ,  1;2;3 ,  1;2;4 ,  1;3;4 ,   1;2;3;4. Số tập con có 3 phần tử của tập hợp X là: 3 4 4C = Câu 36: Số các tập con 2 phần tử của  ,,,,, = Babcdef là: A. 15. B. 16. C. 22. D. 25. Lời giải Chọn A Số các tập con 2 phần tử của  ,,,,, = Babcdef là 2 6 15C = (sử dụng máy tính bỏ túi). Câu 37: Số các tập con 3 phần tử có chứa ,  của  ,,,,,,,,, =C là: A. 8 B. 10 C. 12 D. 14 Lời giải Chọn A Các tập con 3 phần tử có chứa ,  của  ,,,,,,,,, =C là:  ,,  ,  ,,  ,  ,,  ,  ,,  ,  ,,  ,  ,,  ,  ,,  ,   ,,.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 11 Câu 38: Trong các tập sau đây, tập hợp nào có đúng hai tập hợp con? A.  ; xy . B.  x . C.  ; x . D.  ;; xy . Lời giải Chọn B  ; xy có 2 24 = tập con.  x có 1 22 = tập con là  x và  .  ; x có 2 24 = tập con.  ;; xy có 3 28 = tập con. Câu 39: Cho tập hợp  ,,, Aabcd = . Tập A có mấy tập con? A. 16 B. 15 C. 12 D. 10 Lời giải Chọn A Số tập con của tập A là: 4 216 = . Câu 40: Khẳng định nào sau đây sai?Các tập AB = với , AB là các tập hợp sau? A. ( )( ) 1;3, 0} –1 {= 3ABxxx ==− . B.  1;3;5;7;9,21, ,04{} ABnnkkk ===+ . C.  2{1;2, 0} 23ABxxx  =−=−= D.  2, 10ABxxx ==++= Lời giải Chọn C * {3} 1;=A , ( )( ) –130 ==− Bxxx  1;3= B =AB. 1;3;5; *} 9{ 7;=A ,  21, ,04==+ Bnnkkk  1;3;5;7;9= B =AB . *{;2} 1=−A ,  2 230=−=Bxxx  1;3=− B AB * =A ,  2 10=++=Bxxx = B =AB . Dạng 3. Các phép toán trên tập hợp Câu 41: Cho tập hợp    1;5,1;3;5XY== . Tập XY  là tập hợp nào sau đây? A.  1 B.  1;3 C. {1;3;5} D.  1;5 Lời giải Vì XY  là tập hợp gồm các phần tử vừa thuộc X và vừa thuộc Y nên Chọn D Đáp án D.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 12 Câu 42: Cho tập    2;4;6;9,1;2;3;4XY== . Tập nào sau đây bằng tập \ XY ? A.  1;2;3;5 B.  1;3;6;9 C.  6;9 D.  1 Lời giải Vì \ XY là tập hợp các phần tử thuộc X mà không thuộc Y nên Chọn C Đáp án C. Câu 43: Cho tập hợp    ;,;; XabYabc == XY  là tập hợp nào sau đây? A.  ;;; abcd B.  ; ab C.  c D. {;;} abc Lời giải Vì XY  là tập hợp gồm các phần tử thuộc X hoặc thuộc Y nên Chọn D Đáp án D. Câu 44: Cho hai tập hợp A và B khác rỗng thỏa mãn: AB  . Trong các mệnh đề sau mệnh đề nào sai? A. \ AB = B. ABA = C. \ BAB = D. ABB = Lời giải Vì \ BA gồm các phần tử thuộc B và không thuộc A nên Chọn C Đáp án C. Câu 45: Cho ba tập hợp: ( )  ( )  ( ) ( ) |0,|0,|0 FxfxGxgxHxfxgx =====+= Mệnh đề nào sau đây là đúng? A. HFG = B. HFG = C. \ HFG = D. \ HGF = Lời giải Vì ( ) ( ) ( ) ( ) 0 0 0 fx fxgx gx =  +=  =  mà ( ) ( ) |0 vµ FGxfxgx == Đáp án A. Câu 46: Cho tập hợp 2 2 |1 1 Axx x =  +  ; B là tập hợp tất cả các giá trị nguyên của b để phương trình 2 240xbx−+= vô nghiệm. Số phần tử chung của hai tập hợp trên là: A. 1 B. 2 C. 3 D. Vô số Lời giải Ta có: ( ) 222 2 21 121210101 1 x xxxxxx x +−+−= + Phương trình 2 240xbx−+= có 2 '4 b =− Phương trình vô nghiệm 2240422bbb −− Có 1b = là phần tử chung duy nhất của hai tập hợp. Đáp án A.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 13 Câu 47: Cho hai tập hợp    1;2;3;4,1;2XY== . X CY là tập hợp sau đây? A.  1;2 B.  1;2;3;4 C.  3;4 D.  Lời giải Vì YX  nên  \3;4X CYXY== Đáp án C. Câu 48: Cho A, B, C là ba tập hợp được minh họa bằng biểu đồ ven như hình vẽ. Phần gạch sọc trong hình vẽ là tập hợp nào sau đây? A. ( ) \ ABC  B. ( ) \ ABC  C. ( ) ( )\\ ACAB  D. ( ) ABC  Lời giải Vì với mỗi phần tử x thuộc phần gạch sọc thì ta thấy: ( ) \ xA xBxABC xC      Đáp án B. Câu 49: Cho hai tập hợp  0;2A = và  0;1;2;3;4B = . Số tập hợp X thỏa mãn AXB = là: A. 2 B. 3 C. 4 D. 5 Lời giải Vì AXB = nên bắt buộc X phải chứa các phần tử  1;3;4 và XB  Vậy X có 3 tập hợp đó là:        1;3;4,0;1;3;4,1;2;3;4,0;1;2;3;4 Đáp án C Câu 50: Cho hai tập hợp  0;1A = và  0;1;2;3;4B = . Số tập hợp X thỏa mãn B XCA  là: A. 3 B. 5 C. 6 D. 8 Lời giải Ta có  \2;3;4B CABA== có 3 phần tử nên số tập con X có 3 28 = (tập). Đáp án D.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 14 Câu 51: Cho tập hợp  1;2;3;4;5A = . Tìm số tập hợp X sao cho  \1;3;5AX = và  \6;7XA = . A. 1 B. 2 C. 3 D. 4 Lời giải Vì  \1;3;5AX = nên X phải chứa hai phần tử 2; 4 và X không chứa các phần tử 1; 3; 5. Mặt khác  \6;7XA = vậy X phải chứa 6; 7 và các phần tử khác nếu có phải thuộc A. Vậy  2;4;6;7X = . Đáp án A. Câu 52: Ký hiệu X là số phần tử của tập hợp X. Mệnh đề nào sai trong các mệnh đề sau? A. ABABABAB =+=+ B. ABABABAB +=− C. ABABABAB +=+ D. ABABAB =+= Lời giải Kiểm tra các đáp án bằng cách vẽ biểu đồ Ven cho hai trường hợp AB= và AB Đáp án C. Câu 53: Một lớp học có 25 học sinh giỏi môn Toán, 23 học sinh giỏi môn Lý, 14 học sinh giỏi cả môn Toán và Lý và có 6 học sinh không giỏi môn nào cả. Hỏi lớp đó có bao nhiêu học sinh? A. 54 B. 40 C. 26 D. 68 Lời giải Gọi T, L lần lượt là tập hợp các học sinh giỏi Toán và các học sinh giỏi Lý. Ta có: T : là số học sinh giỏi Toán L : là số học sinh giỏi Lý TL  : là số học sinh giỏi cả hai môn Toán và Lý Khi đó số học sinh của lớp là: 6TL+ . Mà 25231434TLTLTL =+−=+−= . Vậy số học sinh của lớp là 34640 += Đáp án B Câu 54: Lớp 10A có 45 học sinh trong đó có 25 em học giỏi môn Toán, 23 em học giỏi môn Lý, 20 em học giỏi môn Hóa, 11 em học giỏi cả môn Toán và môn Lý, 8 em học giỏi cả môn Lý và môn

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 15 Hóa, 9 em học giỏi cả môn Toán và môn Hóa. Hỏi lớp 10A có bao nhiêu bạn học giỏi cả ba môn Toán, Lý, Hóa, biết rằng mỗi học sinh trong lớp học giỏi ít nhất một trong 3 môn Toán, Lý, Hóa? A. 3 B. 4 C. 5 D. 6 Lời giải Gọi T, L, H lần lượt là tập hợp các học sinh giỏi môn Toán, Lý, Hóa. Khi đó tương tự Ví dụ 13 ta có công thức: TLHTLHTLLHHTTLH =++−−−+ 452523201189 TLH=++−−−+ 5TLH = Vậy có 5 học sinh giỏi cả 3 môn. Đáp án C. Câu 55: Cho tập hợp    1;2;3;4,0;2;4;6AB== . Mệnh đề nào sau đây là đúng? A.  2;4AB= B.  0;1;2;3;4;5;6AB= C. AB  D.  \0;6AB = Lời giải Đáp án A. Ta thấy  2;4AB= Câu 56: Ký hiệu H là tập hợp các học sinh của lớp 10A. T là tập hợp các học sinh nam, G là tập hợp các học sinh nữ của lớp 10A. Khẳng định nào sau đây sai? A. TGH = B. TG= C. \ HTG = D. \ GT = Lời giải Đáp án D. Vì \ GTG = . Câu 57: Cho A, B, C là ba tập hợp. Mệnh đề nào sau đây là sai? A. ABACBC  B. \\ ABCACB  C. ABACBC  D. , ABBCAC  Lời giải Đáp án B.

1;3;5

Đáp án

bằng t

1;2;3;4;5;7;9

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 16 Ta có thể dùng biểu đồ Ven ta thấy \\ ABCACB  Câu 58: Cho tập hợp  ;; Aabc = và  ;;;; Babcde = . Có tất cả bao nhiêu tập hợp X thỏa mãn AXB  ? A. 5 B. 6 C. 4 D. 8 Lời giải Đáp án C. Vì AX  nên X phải chứa 3 phần tử  ;; abc của A. Mặt khác XB  nên X chỉ có thể lấy các phần tử a, b, c, d, e Vậy X là một trong các tập hợp sau:    ;;,;;; abcabcd ,  ;;; abce ,  ;;;; abcde Câu 59: Cho hai tập hợp    1;2;3;4;5;1;3;5;7;9AB== . Tập nào sau đây

ập

 ?

 

B.  1;2;3;4;5 C.  2;4;6;8

 

Lời giải

A. Vì AB  gồm các phần tử vừa thuộc A vừa thuộc B. Câu 60: Cho tập hợp    2;4;6;9,1;2;3;4AB== . Tập nào sau đây bằng tập \ AB ? A.  1;2;3;5 B.  1;2;3;4;6;9 C.  6;9 D.  Lời giải Đáp án C. Vì  \| vµ ABxxAxB = Câu 61: Cho các tập hợp    2 :760,:4AxxxBxx =−+== . Khi đó: A. ABA = B. ABAB = C. \ ABA  D. \ BA = Lời giải Đáp án C. Ta có    1;6,\4ABxx ==     0;1;2;3\6\ BABABA == . Câu 62: Một lớp học có 25 học sinh chơi bóng đá, 23 học sinh chơi bóng bàn, 14 học sinh chơi cả bóng đá và bóng bàn và 6 học sinh không chơi môn nào. Số học sinh chỉ chơi 1 môn thể thao là? A. 48 B. 20 C. 34 D. 28 Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 17 Đáp án B. Gọi A là tập hợp các học sinh chơi bóng đá B là tập hợp các học sinh chơi bóng bàn C là tập hợp các học sinh không chơi môn nào Khi đó số học sinh chỉ chơi bóng đá là 225232.1420ABAB+−=+−= Câu 63: Trong các khẳng định sau khẳng định nào đúng: A. \ = . B. * = . C. * = . D. ** = . Lời giải Chọn D D đúng do *** = . Câu 64: Chọn kết quả sai trong các kết quả sau: A. .= ABAAB B. .ABAAB = C. \. ==ABAAB D. \.BABAB== Lời giải Chọn B B sai do ABAAB = Câu 65: Cho  7;2;8;4;9;12X = ;  1;3;7;4Y = . Tập nào sau đây bằng tập  XY ? A.  1;2;3;4;8;9;7;12 B.  2;8;9;12 C.  4;7 D.  1;3 Lời giải Chọn C    7;2;8;4;9;12,1;3;7;4==XY   7;4.= XY Câu 66: Cho hai tập hợp  2,4,6,9A = và  1,2,3,4B = .Tập hợp \ AB bằng tập nào sau đây? A.  1,2,3,5=A . B.   1;3;6;9. C.   6;9. D. . Lời giải Chọn C    2,4,6,9,1,2,3,4==AB   \6,9.= AB Câu 67: Cho     0;1;2;3;4,2;3;4;5;6.AB== Tập hợp ( ) ( )\\ ABBA  bằng? A.   0;1;5;6. B.   1;2. C.   2;3;4. D.   5;6. Lời giải Chọn A     0;1;2;3;4,2;3;4;5;6.==AB

Câu 68: Cho

Câu 69: Cho

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 18    \0;1,\5;6 ==ABBA ( ) ( )  \\0;1;5;6= ABBA

    0;1;2;3;4,2;3;4;5;6.AB== Tập hợp \ AB bằng: A.   0. B.   0;1. C.   1;2. D.   1;5. Lời giải Chọn B    0;1;2;3;4,2;3;4;5;6==

 \0;1= AB

    0;1;2;3;4,2;3;4;5;6.AB== Tập hợp \ BA bằng: A.   5. B.   0;1. C.   2;3;4. D.   5;6. Lời giải

ọn D    0;1;2;3;4,2;3;4;5;6==AB   \5;6.= BA Câu 70: Cho     1;5;1;3;5.==AB Chọn kết quả đúng trong các kết quả sau A.   1.=AB B.   1;3.=AB C.   1;5.=AB D.   1;3;5.=AB Lời giải Chọn C     1;5;1;3;5.==AB Suy ra   1;5.=AB Câu 71: Cho ( )( )   22*2 22320;330AxxxxxBnn =−−−== . Khi đó tập hợp  AB bằng: A.   2;4. B.   2. C.   4;5. D.   3. Lời giải Chọn B ( )( ) 22 22320 =−−−= Axxxxx  0;2= A  *2330=Bnn  1;2;3;4;5= B   2.AB = DẠNG 3. BIỂU DIỄN TẬP HỢP SỐ Câu 72: Cho tập hợp  \31Axx=− . Tập A là tập nào sau đây? A.  3;1 B.  3;1 C.  )3;1 D. ( )3;1 Lời giải Theo định nghĩa tập hợp con của tập số thực ở phần trên ta chọn ( )3;1 . Đáp án D.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 19 Câu 73: Hình vẽ nào sau đây (phần không bị gạch) minh họa cho tập hợp ( 1;4 ? A. B. C. D. Lời giải Vì ( 1;4 gồm các số thực x mà 14 x  nên Chọn A Đáp án A. Câu 74: Cho tập hợp  \,13Xxxx= thì X được biểu diễn là hình nào sau đây? A. B. C. D. Lời giải Giải bất phương trình:     1 1 133;11;3 1 3 33 x x xx x x x   −− −  −  Đáp án D. Câu 75: Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp  49Axx= : A.   4;9.=A B. (  4;9.=A C.  ) 4;9.=A D. ( ) 4;9.=A Lời giải Chọn A  49=Axx   4;9.= A DẠNG 4. CÁC PHÉP TOÁN TRÊN TẬP HỢP SỐ Câu 76: Cho tập hợp ( ;1A =−− và tập ( )2;B =−+ . Khi đó AB  là: A. ( )2; −+ B. ( 2;1 C. D. 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 20 Vì  \ hoac ABxxAxB = nên chọn đáp án C. Đáp án C. Câu 77: Cho hai tập hợp  ) ( )5;3,1;AB=−=+ . Khi đó AB  là tập nào sau đây? A. ( )1;3 B. ( 1;3 C.  )5; −+ D.  5;1 Lời giải Ta có thể biểu diễn hai tập hợp A và B, tập AB  là phần không bị gạch ở cả A và B nên ( )1;3x Đáp án A. Câu 78: Cho ( )  2;1,3;5AB=−=− . Khi đó AB  là tập hợp nào sau đây? A.  2;1 B. ( )2;1 C. ( 2;5 D.  2;5 Lời giải Vì với xA xAB xB     hay 21 21 35 x x x − − − Đáp án B. Câu 79: Cho hai tập hợp (  ( 1;5;2;7AB== . Tập hợp \ AB là: A. ( 1;2 B. ( )2;5 C. ( 1;7 D. ( )1;2 Lời giải   ( \\ va 1;2ABxxAxBx = Đáp án A. Câu 80: Cho tập hợp ( )2;A =+ . Khi đó R CA là: A.  )2;+ B. ( )2;+ C. ( ;2− D. ( ;2−− Lời giải Ta có: ( \;2R CAA==− . Đáp án C. Câu 81: Cho các số thực a, b, c, d và abcd  . Khẳng định nào sau đây là đúng? A. ( ) ( ) ( );;; acbdbc = B. ( ) ( ) ( ;;; acbdbc = C. ( )  )  );;; acbdbc = D. ( )  ) ( );;; acbdbc =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 21 Lời giải Đáp án A. Câu 82: Cho ba tập hợp      )2;2,1;5,0;1ABC =−== . Khi đó tập ( )\ ABC  là: A.  0;1 B.  )0;1 C. ( )2;1 D.  2;5 Lời giải Ta có:  ) ( )  )\2;1\0;1 ABABC =−= . Đáp án B. Câu 83: Cho tập hợp )3;8CA  =−  , ( ) ( ) 5;23;11.CB =− Tập ( )CAB  là: A. ( )3;3 . B.  . C. ( )5;11 . D. ( ) ( ) 3;23;8.− Lời giải Chọn C )3;8 =− CA , ( ) ( ) ( )5;23;115;11=−=−CB ( ) );38;  =−−+ A , (  ) ;511;.  =−−+ B (  );511;  =−−+ AB ( ) ( ) 5;11.=− CAB Câu 84: Cho   ( ) ( ) 1;4;2;6;1;2.ABC === Tìm :ABC  A.   0;4. B.  ) 5;. + C. ( ) ;1.− D. . Lời giải Chọn D   ( ) ( )1;4;2;6;1;2=== ABC ( 2;4= AB = ABC . Câu 85: Cho hai tập  342 Axxx =++ ,  5341Bxxx =−− Tất cả các số tự nhiên thuộc cả hai tập A và B là: A. 0 và 1. B. 1. C. 0 D. Không có. Lời giải Chọn A  342=++ Axxx ( ) 1;.=−+ A  5341 =−− Bxxx ( ) ;2.=− B ( )1;2=−AB   12.=− ABxx

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 22  12=− ABxx   0;1.= AB Câu 86: Cho  4;7A =− , ( ) ( );23;B =−−+ . Khi đó AB  : A.  ) (  4;23;7.−− B.  ) ( ) 4;23;7.−− C. (  ( ) ;23;.−+ D. ( )  ) ;23;.−−+ Lời giải Chọn A  4;7=−A , ( ) ( );23; =−−+B , suy ra  ) ( 4;23;7=−−AB Câu 87: Cho ( ;2A =−− ,  )3;B =+ , ( ) 0;4.C = Khi đó tập ( ) ABC  là: A.   3;4. B. (  ( ) ;23;.−−+ C.  ) 3;4. D. ( )  ) ;23;.−−+ Lời giải Chọn C ( ;2=−−A ,  )3; =+B , ( ) 0;4.=C Suy ra (   );23; =−−+AB ; ( )  ) 3;4.=ABC Câu 88: Cho  :20AxRx=+ ,  :50BxRx=− . Khi đó  AB là: A.  2;5 . B.  2;6 . C.  5;2 . D. ( )2; −+ . Lời giải Chọn A Ta có  :20=+AxRx  )2; =−+ A ,  :50=−BxRx ( ;5=− B Vậy   2;5.=− AB Câu 89: Cho    :20,:50AxRxBxRx =+=− . Khi đó \ AB là: A.  2;5 . B.  2;6 . C. ( )5;+ . D. ( )2;+ . Lời giải Chọn C Ta có  :20=+AxRx  )2; =−+ A ,  :50=−BxRx ( ;5=− B Vậy ( ) \5;.=+ AB Câu 90: Cho hai tập hợp  ) ( 2;7,1;9AB=−= . Tìm AB  A. ( )1;7 B.  2;9 C.  )2;1 D. ( 7;9 Lời giải Đáp án B.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 23  ) (   2;71;92;9 −=− Câu 91: Cho hai tập hợp  |51Axx=− ;  |33Bxx=− . Tìm AB  . A.  5;3 B. ( )3;1 C. ( 1;3 D.  )5;3 Lời giải Đáp án B.  ) (  ( )5;1,3;33;1ABAB =−=−=− Câu 92: Cho (  ( )1;5,2;7AB=−= . Tìm \ AB A. ( 1;2 B. ( 2;5 C. ( )1;7 D. ( )1;2 Lời giải Đáp án A. Vì \ AB gồm các phần tử thuộc A mà không thuộc B nên ( \1;2AB =− . Câu 93: Cho 3 tập hợp ( ;0A =− , ( )1;B =+ ,  )0;1C = . Khi đó ( ) ABC  bằng: A.  0 B. C.  0;1 D.  Lời giải Đáp án A. (  ( );01;AB=−+ ( )  0ABC = Câu 94: Cho hai tập hợp  4;7M =− và ( ) ( );23;N =−−+ . Khi đó MN  bằng: A.  ) ( 4;23;7−− B.  ) ( )4;23;7− C. (  ( );23; −+ D. ( )  );23; −−+ Lời giải Đáp án A.  ) ( 4;23;7MN=− Câu 95: Cho hai tập hợp   ( )2;3,1;AB=−=+ . Khi đó ( )CAB  bằng:

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 24 A. ( )1;3 B. (   );13; −+ C.  )3;+ D. ( );2−− Lời giải Đáp án D. Ta có:  )2;AB=−+ ( ) ( )\ CABAB = ( ) ( );2CAB =−− Câu 96: Chọn kết quả sai trong các kết quả sau: A. ABAAB = B. ABABA = C. \ ABAAB== D. \ ABAAB= Lời giải Đáp án D. Câu 97: Cho tập hợp )3;8 =− CA , ( ) ( ) 5;23;11.=−CB Tập ( )CAB  là: A. ( )5;11 . B. ( ) ( ) 3;23;8.− C. ( )3;3 . D.  . Lời giải Chọn A )3;8 =− CA , ( ) ( ) ( )5;23;115;11=−=−CB ( ) );38;  =−−+ A , (  ) ;511;.  =−−+ B (  );511;  =−−+ AB ( ) ( ) 5;11.=− CAB Câu 98: Cho 3 tập hợp: ( ;1A =− ;  2;2B =− và ( )0;5C = Tính ( ) ( ) ?ABAC= A.  2;1 . B. ( )2;5 . C. ( 0;1 . D.  1;2 . Lời giải Chọn A  2;1AB=− . ( 0;1AC= ( ) ( )  2;1ABAC=− . DẠNG 5. CÁC BÀI TOÁN TÌM ĐIỀU KIỆN CỦA THAM SỐ Câu 99: Cho tập hợp    ;2,1;2AmmB=+− . Tìm điều kiện của m để AB  . A. 1m − hoặc 0m  B. 10 m − C. 12 m  D. 1m  hoặc 2m  Lời giải Để AB  thì 122 mm −+ 11 10 220 mm m mm −− − + 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 25 Đáp án B. Câu 100: Cho tập hợp ( )0;A =+ và  2 \430Bxmxxm =−+−= . Tìm m để B có đúng hai tập con và BA  A. 03 4 m m   = B. 4m = C. 0m  D. 3m = Lời giải Để B có đúng hai tập con thì B phải có duy nhất một phần tử, và BA  nên B có một phần tử thuộc A. Tóm lại ta tìm m để phương trình 2 430mxxm−+−= (1) có nghiệm duy nhất lớn hơn 0. + Với 0m = ta có phương trình: 3 430 4 xx −−== (không thỏa mãn). + Với 0m  : Phương trình (1) có nghiệm duy nhất lớn hơn 0 điều kiện cần là: ( ) 2 1 '430340 4 m mmmm m =−−=−++==−  = +) Với 1m =− ta có phương trình 2 440xx −−−= Phương trình có nghiệm 2x =− (không thỏa mãn). +) Với 4m = , ta có phương trình 2 4410 xx−+= Phương trình có nghiệm duy nhất 1 04 2 xm== thỏa mãn. Đáp Án B. Câu 101: Cho hai tập hợp   ( )2;3,;6ABmm =−=+ . Điều kiện để AB  là: A. 32 m −− B. 32 m −− C. 3m − D. 2m − Lời giải Điều kiện để AB  là 236mm−+ 2 63 m m −   + 2 3 m m −   − 32 m −− Câu 102: Cho hai tập hợp ( 0;3X = và ( );4Ya = . Tìm tất cả các giá trị của 4a  để XY . A. 3 4 a a    B. 3a  C. 0a  D. 3a  Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 26 Ta tìm a để 3 34 4 a XYaXY a  =   là 3a  Đáp án B. Câu 103: Cho hai tập hợp   (   )\12;;2; AxxBmm ==−−+ . Tìm tất cả các giá trị của m để AB  A. 4 2 m m   − B. 4 2 1 m m m   −  = C. 4 2 1 m m m   −  = D. 24 m − Lời giải Giải bất phương trình:    122;11;2 xx −−    2;11;2A =−− Để AB  thì: 224 22 112 1 mm mm mm m   − −−   −−=   Đáp án B. Câu 104: Cho số thực 0a .Điều kiện cần và đủ để ( ) 4 ;9; −+  a a là: A. 2 0. 3 − a B. 2 0. 3 − a C. 3 0. 4 − a D. 3 0. 4 − a Lời giải Chọn A ( ) ( ) 44 ;9;09 aaa aa  −+   4 90 a a − 49² 0a a  49²0 0 a a −    2 0 3 − a

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 27 Câu 105: Cho tập hợp    ;2,1;2AmmB=+=− với m là tham số. Điều kiện để AB  là: A. 12 m  B. 10 m − C. 1m − hoặc 0m  D. 1m − hoặc 2m  Lời giải : Đáp án B. 122ABmm −+ 11 10 220 mm m mm −− − +  Câu 106: Cho tập hợp    );2,1;3AmmB=+= . Điều kiện để AB= là: A. 1m − hoặc 3m  B. 1m − hoặc 3m  C. 1m − hoặc 3m  D. 1m − hoặc 3m  Lời giải Đáp án C. 33 211 mm AB mm = +−  Câu 107: Cho hai tập hợp    3;12;4A =−− , ( )1;2Bmm=−+ . Tìm m để AB . A. 5m  và 0m  B. 5m  C. 13 m  D. 0m  Lời giải Đáp án A. Ta đi tìm m để AB= 235 145 011 22 mm mm mm m   +−−  −   −−=  + 55 0 m AB m −   hay 5 0 m m     

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 28 Câu 108: Cho 3 tập hợp ( ) ( )3;11;2A =−− , ( );Bm=+ , ( );2 Cm − . Tìm m để ABC A. 1 2 2 m  B. 0m  C. 1m − D. 2m  Lời giải Đáp án A. Ta đi tìm m để ABC= TH1: Nếu 20 mmm thì BC= ABC = TH2: Nếu 20 mmm ABC = 3 23 2 22 11 1 221 m m mm m m m   −    −−   Vì 0m  nên 1 0 2 2 m m      )1 ;2; 2 ABCm  =−+    1 2 2 ABCm  Câu 109: Cho hai tập  0;5A = ; ( 2;31Baa=+ , 1a − . Với giá trị nào của a thì AB

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 29 A. 15 32 a − . B. 5 2 1 3 a a     −  . C. 5 2 1 3 a a     −  . D. 15 32 a − . Lời giải Chọn D Ta tìm 5 255 2 A2 3101 1 1313 1 a a a B a a aa a       = +    −   −−−  − 15 32 ABa − Chọn A Câu 110: Cho 2 tập khác rỗng (  ( ) 1;4;2;22, AmBmm =−=−+ . Tìm m để AB A. 15 m − . B. 15 m  . C. 25 m − . D. 3m − . Lời giải Chọn C Đáp án A đúng vì: Với 2 tập khác rỗng A, B ta có điều kiện 145 25 2222 mm m mm − − +−− . Để 1223ABmmm −+− . So với kết quả của điều kiện thì 25 m − . Câu 111: Cho số thực 0a .Điều kiện cần và đủ để ( ) 4 ;9; −+  a a là: A. 3 0. 4 − a B. 2 0. 3 − a C. 2 0. 3 − a D. 3 0. 4 − a Lời giải Chọn B ( ) ( ) 44 ;9;09 aaa aa  −+   4 90 a a − 49² 0a a  49²0 0 a a −    2 0 3 − a . Câu 112: Cho hai tập  0;5A = ; ( 2;31Baa=+ , 1a − . Với giá trị nào của a thì AB A. 5 2 1 3 a a     −  . B. 15 32 a − . C. 5 2 1 3 a a     −  . D. 15 32 a − . Lời giải Chọn A Trước hết tìm a để AB=. Với 1231aaa−+ .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 30 Ta có 5 52 2 1310 3 a a AB a a  =  +  −  . Từ đó, kết hợp điều kiện ta có AB 5 2 1 3 a a     −  . Câu 113: Cho  AxR\xm25 =− ;  BxR\x2020 = . Có bao nhiêu giá trị nguyên m thỏa AB= A. 3987. B. 3988. C. 3989. D. 2020. Lời giải Chọn C Ta có:    AxR\xm25Am25;m25 =−=−+   (   )BxR\x2020B;20202020; ==−−+ Để AB= thì ( )2020m25m2520201 −−+ Khi đó ( ) m252020m1995 11995m1995 m252020m1995 −−− −  + . Vậy có 3989 giá trị nguyên m thỏa mãn. Câu 114: Cho 2 tập hợp  2;5Amm=−+ và  0;4B = . Tìm tất cả các giá trị thực của tham số m để BA  . A. 1m − . B. 12 m − . C. 12 m − . D. 2m  . Lời giải Chọn B Ta có 527mm+−+= . Để BA  20 12 54 m m m − −  + Câu 115: Cho hai tập hợp (;1)Amm=+ và  1;3B =− . Tìm tất cả các giá trị của m để AB=. A. 2 3 m m −   B. 23 m − C. 2 1 m m   − D. 2 3 m m −   Lời giải Chọn A 112 33 mm AB mm =+−−   .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 31 Vậy chọn đáp ánA. Câu 116: Tìm m để AD  , biết (3;7)A =− và (;32) Dmm =− . A. 3m =− B. 3m − C. 1m  D. 2m − Lời giải Chọn B Ta có: 333 3 732242 mmm ADm mmm −−− − −−−  . Câu 117: Cho 2 tập hợp khác rỗng ( 1;4Am=− , ( )2;22Bm=−+ , với m . Tìm m để AB  . A. 15 m  . B. 1m  . C. 15 m − . D. 21 m −− . Lời giải Chọn A Với 2 tập hợp khác rỗng ( 1;4Am=− , ( )2;22Bm=−+ ta có điều kiện 14 222 m m −  +− 5 2 m m    − 25 m − . AB 12 224 m m −−  + 1 224 m m −  + 1 1 m m −   1m  Kết hợp với điều kiện 25 m −15 m  . Câu 118: Cho ( )  )2 3;,;12; 4 m AmB +  =−=−−+   . Tìm m để AB= A. 14 2 3 m  . B. 26 m  . C. 26 m  . D. 14 2 3 m  . Lời giải Chọn A 142 3 34 14 3122 3 26 2 4 m mm ABmmm mm + −  =−−  +    . Câu 119: Cho số thực 0x  . Tìm x để ( ) 9 ;16; x x  −+   A. 3 0 4 x  . B. 3 0 4 x  . C. 3 0 4 x  . D. 3 0 4 x  . Lời giải Chọn D

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 32 Để ( ) 9 ;16; x x  −+   thì giá trị của số thực x phải thỏa bất phương trình 9 16x x  Ta có 29 16169 xx x  (do 0x  ) 2 1690 x − 33 44 x − So điều kiện 0x  , suy ra 3 0 4 x  . Câu 120: Cho hai tập hợpkhác rỗng ( 1;4Am=− và ( ) 2;22,.Bmm=−+ Có bao nhiêu giá trị nguyên dương của m để AB ? A. 5 B. 6 C. 4 D. 3. Lời giải Chọn C Ta có , AB là hai tập khác rỗng nên 145 25 2222 mm m mm − − +−− (*). Ta có 1223ABmmm −+− Đối chiếu với điều kiện (*), ta được 25 m − . Do m +  nên  1;2;3;4m . Vậy có 4 giá trị nguyên dương của m thỏa mãn yêu cầu. Câu 121: Cho ( ) ( );,0;AmB=−=+ . Điều kiện cần và đủ để AB= là: A. 0m  . B. 0m  . C. 0m  . D. 0m  . Lời giải Chọn C AB= 0m  . Câu 122: Cho hai tập hợp khác rỗng ( 1;4Am=− và ( )2;22Bm=−+ , m . Tìm tất cả các giá trị của m để AB . A. 25 m − B. 3m − C. 3m − D. 35 m − Lời giải Chọn A Điều kiện để hai tập ( 1;4Am=− và ( )2;22Bm=−+ khác tập rỗng là 14 222 m m −  +− 5 2 m m    − 25 m − ( )* Khi đó AB 122mm −+ 3m −

phương trình bậc nhất hai ẩn thường có vô số nghiệm và để mô tả tập nghiệm của chúng, ta sử dụng phương pháp biểu diễn hình học.

Trong mặt phẳng tọa độ ,Oxy tập hợp các điểm có tọa độ là nghiệm của bất phương trình ( )1 được gọi là miền nghiệm của nó. Từ đó ta có quy tắc thực hành biểu diễn hình học tập nghiệm (hay biểu diễn miền nghiệm) của bất phương trình axbyc + như sau (tương tự cho bất phương trình axbyc + )

Bước 1. Trên mặt phẳng tọa độ ,Oxy vẽ đường thẳng  : .axbyc +=

Bước 2. Lấy một điểm ( )000 ; Mxy không thuộ

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 51 BÀI 1. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN I. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Bất phương trình bậc nhất hai ẩn , xy có dạng tổng quát là ( )1axbyc + ( );; axbycaxbycaxbyc +++ trong đó ,, abc là những số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số. II. BIỂU DIỄN TẬP NGHIỆM CỦA BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Cũng như bất phương trình bậc nhất một ẩn, các bất

c  (ta thường lấy gốc tọa độ O ) Bước 3. Tính 00axby + và so sánh 00axby + với c Bước 4. Kết luận Nếu 00 axbyc + thì nửa mặt phẳng bờ  chứa 0M là miền nghiệm của 00 axbyc + Nếu 00 axbyc + thì nửa mặt phẳng bờ  không chứa 0M là miền nghiệm của 00 axbyc + Chú ý: Miền nghiệm của bất phương trình 00 axbyc + bỏ đi đường thẳng axbyc += là miền nghiệm của bất phương trình 00 .axbyc + CHƯƠNG II BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN LÝ THUYẾT.I =

Tương

phương

tìm

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 52 BÀI 2. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

tự hệ bất phương trình một ẩn

ệ bất

trình bậc nhất hai ẩn gồm một số bất phương trình bậc nhất hai ẩn , xy mà ta

ải

các nghiệm chung của chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ bất phương trình đã cho. Cũng như bất phương trình bậc nhất hai ẩn, ta có thể biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn. II. BIỂU DIỄN TẬP NGHIỆM CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Để biểu diễn miền nghiệm của hệ bất phương trình bậc nhất 2 ẩn ta làm nư sau: Trong cùng hệ toạ độ, biểu diễn miền nghiệm của mỗi bất phương trình trong hệ bằng cách gạch bỏ phần không thuộc miền nghiệm của nó. Phần không bị gạch là miền nghiệm cần tìm. III. ÁP DỤNG VÀO BÀI TOÁN THỰC TIỄN Giải một số bài toán kinh tế thường dẫn đến việc xét những hệ bất phương trình bậc nhất hai ẩn và giải chúng. Loại bài toán này được nghiên cứu trong một ngành toán học có tên gọi là Quy hoạch tuyến tính. 2.4. Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn? a) 0 0; x y    b) 2 0 1; xy yx  + − c) 0 0; xyz y ++   d) 2 2 23 431. xy xy −+  + 2.5. Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau trên mặt phẳng tọa độ: a) 1 0 0; yx x y −−     b) 0 0 24; x y xy     + c) 0 5 0. x xy xy   +  − 2.6. Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilôgam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn; giá tiền 1 kg thịt bò là 250 nghìn đồng; 1 kg thịt lợn là 160 nghìn đồng. Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn. a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm của hệ đó. b) Gọi F (nghìn đồng) là số tiền phải trả cho x kilôgam thịt bò và y kilôgam thịt lợn. Hãy biểu diễn F theo x và y. c) Tìm số kilôgam thịt mỗi loại mà gia đình cần mua để chi phí là ít nhất. HỆ THỐNG BÀI TẬP.II = BÀI TẬP.

DẠNG 1: CÁC BÀI TOÁN LIÊN BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Câu 1: Biểu diễn hình học tập nghiệm của bất phương trình 23 xy+

Câu 2: Biểu diễn hình học tập nghiệm của bất phương trình 320 xy −++ .

Câu 3: Biểu diễn hình học tậ

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 53

p nghiệm của bất phương trình 32(25)2(1) xyx +++− . Câu 4: Biểu diễn hình học tập nghiệm của bất phương trình ( ) ( ) 13132 xy +−− . DẠNG 2: CÁC BÀI TOÁN HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Câu 1: Biểu diễn hình học tập nghiệm của hệ bất phương trình 36 4 0 0 xy xy x y +  +     Câu 2: Tìm miền nghiệm của hệ bất phương trình 30 23 2 xy xy yx −  +−  + Câu 3: Tìm trị lớn nhất của biểu thức ( ) ;2 Fxyxy =+ , với điều kiện        +    2100 10 0 40 xy xy x y DẠNG 3: CÁC BÀI TOÁN THỰC TIỄN Bài toán: Tìm giá trị lớn nhất, nhỏ nhất của biểu thức , Txyaxby với ; xy nghiệm đúng một hệ bất phương trình bậc nhất hai ẩn cho trước. Bước 1: Xác định miền nghiệm của hệ bất phương trình đã cho. Kết quả thường được miền nghiệm S là đa giác. Bước 2: Tính giá trị của F tương ứng với ; xy là tọa độ của các đỉnh của đa giác. Bước 3: Kết luận: Giá trị lớn nhất của F là số lớn nhất trong các giá trị tìm được. Giá trị nhỏ nhất của F là số nhỏ nhất trong các giá trị tìm được. Câu 1: Một hộ nông dân định trồng đậu và cà trên diện tích 800m2. Nếu trồng đậu thì cần 20 công và thu 3.000.000 đồng trên 100m2 nếu trồng cà thì cần 30 công và thu 4.000.000 đồng trên 100 m2 Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được nhiều tiền nhất khi tổng số công không quá 180 Câu 2: Bạn An kinh doanh hai mặt hàng handmade là vòng tay và vòng đeo cổ. Mỗi vòng tay làm trong 4 giờ, bán được 40 ngàn đồng. Mỗi vòng đeo cổ làm trong 6 giờ, bán được 80 ngàn đồng. Mỗi tuần bạn An bán được không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong tuần An cần dùng để bán được ít nhất 400 ngàn đồng? BÀI TẬP TỰ LUẬN.2 =

ệc quá 220 giờ. Tính số tiền lãi lớn nhất trong một tháng của xưởng. Câu 4: Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kiogam thịt bò chứa 800 đơn vị protein và 200đơn vị lipit. Mỗi kilogam thịt lợn chứa 600đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền một kg thịt bò là 160 nghìn đồng, một kg thịt lợn là 110 nghìn đồng. Gọi x , y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua. Tìm x , y để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 54 Câu 3: Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm I và II Mỗi sản phẩm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đồng. Để sản xuất được một sản phẩm I thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ. Để sản xuất được một sản phẩm II thì Chiến phải làm việc trong 2 giờ, Bình phải làm việc trong 6 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá 180 giờ và Bình không thể làm vi

lượng protein và lipit trong thức ăn? Câu 5: Một hộ nông dân định trồng dứa và củ đậu trên diện tích 8ha . Trên diện tích mỗi ha , nếu trồng dứa thì cần 20 công và thu 3 triệu đồng, nếu trồng củ đậu thì cần 30 công và thu 4 triệu đồng. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu ha để thu được nhiều tiền nhất, biết rằng tổng số công không quá 180.

Câu 1: Bất phương trình ( ) 3–2–10 xyx + tương đương với bất phương trình nào sau đây?

A. –2–20xy  . B. 5–2–20 xy

. C. 5–2–10 xy

Câu 2: Cho bất phươngtrình ( ) ( ) 314253 xyx

A. Điể

4;2C thu

D. Điểm ( )5;3D thu

c mi

n nghi

nghi

a b

. D. 4–2–20 xy

. Khẳng định nào dưới đâylà khẳng định đúng?

cho.

phương trình đã cho.

Câu 3: Cho bất phương trình ( ) ( )322521 xyx +++− . Khẳng định nào dưới đây là khẳng định sai?

A. Điểm ( )3;4A thuộc miền nghiệm của bất phương trình đã cho.

B. Điểm ( )2;5B thuộc miền nghiệm của bất phương trình đã cho.

OFFICIAL

C. Điểm ( )1;6C thuộc miền nghiệm của bất phương trình đã cho.

D. Điểm ( )0;0O thuộc miền nghiệm của bất phương trình đã cho.

Câu 4: Cặp số ( )1;–1 là nghiệm của bất phương trình nào sau đây?

A. –30xy+

B. ––0 xy  C. 310xy++ D. ––3–10 xy 

Câu 5: Cặp số nào sau đây là nghiệm của bất phương trình ( ) –2–3 +xyy ?

A. ( )4;–4 B. ( )2;1 C. ( )–1;–2 D. ( )4;4

Câu 6: Cặp số nào sau đây không là nghiệm của bất phương trình ( ) 5210 −−xy ?

A. ( )0;1 B. ( )1;3 C. ( )–1;1 D. ( )–1;0

Câu 7: Miền nghiệm của bất phương trình 326 xy−− là

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 55



−+−−

m ( )0;0O thuộc miền nghiệm của bất phương trình đã cho.

Điểm ( )2;2B thuộc miền nghiệm của bất phương trình đã

Điểm ( )

ộ

ề

ệm

ủ

ất

ộ

ền

ệm củ

ất

A. B. C. D. BÀI TẬP TRẮC NGHIỆM.2 = O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 56 Câu 8: Miền nghiệm của bất phương trình 326 xy+ là A. B. C. D. Câu 9: Miền nghiệm của bất phương trình 326 xy−− là A. B. C. D. O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 57 Câu 10: Miền nghiệm của bất phương trình 326 xy+− là A. B. C. D. Câu 11: Miền nghiệm của hệ bất phương trình           + 6 82 3 93 y yx xy xy là phần mặt phẳng chứa điểm nào sau đây? A. ( )0;0 B. ( )1;2 C. ( )2;1 D. ( )8;4 Câu 12: Miền nghiệm của hệ bất phương trình 10 23 3 2(1)4 2 0 xy y x x  +−   −+     là phần mặt phẳng chứa điểm A. ( )2;1 . B. ( )0;0 . C. ( )1;1 . D. ( )3;4 . Câu 13: Trong các cặp số sau, tìm cặp số không là nghiệm của hệ bất phương trình    + + 0232 02 xy xy A. ( )0;0 . B. ( )1;1 . C. ( )1;1 . D. ( )1;1 . Câu 14: Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình 2310 540 xy xy +−  −+ ? A. ( )1;4 . B. ( )2;4 . C. ( )0;0 . D. ( )3;4 . O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

Hỏi khẳng định nào dưới đây là khẳng định đúng?

A. Điểm ( )2;1A thuộc miền nghiệm của hệ bất phương trình đã cho.

B. Điểm ( )0;0O thuộc miền nghiệm của hệ bất phương trình đã cho.

C. Điểm ( )1;1C thuộc miền nghiệm của hệ bất phương trình đã cho.

D. Điểm ( )3;4D thuộc miền nghiệm của hệ bất phương trình đã cho.

16: Cho h

phương

Hỏi khẳng định nào dưới đây là khẳng định đúng?

A. Điểm ( )0;0O thuộc miền nghiệm của hệ bất phương trình đã cho.

B. Điểm ( )1;0B thuộc miền nghiệm của hệ bất phương trình đã cho.

C. Điểm ( )0;2C thuộc miền nghiệm của hệ bất phương trình đã cho.

D. Điểm ( )0;2D thuộc miền nghiệm của hệ bất phương trình đã cho.

Câu 17: Điểm ( )0;0O

A. 360 240

trình nào sau đây?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 58 Câu 15: Cho hệ bất phương trình           + + 0 4 2)3(12 01 23 x y x xy

Câu

ệ

ất

trình: 2510 250 10 xy xy xy −−  ++  ++

thuộc miền nghiệm của hệ bất phương

+−  ++ xy xy . B. 360 240 +−  ++ xy xy . C. 360 240 +−  ++ xy xy . D. 360 240 +−  ++ xy xy . Câu 18: Cho hệ bất phương trình ( ) ( ) 3 211 2 4322 xy xy  −   − có tập nghiệm S . Mệnh đề nào sau đây là đúng? A. 1 ;1 4 S−−   B. ( ) ;|432Sxyxy=−= . C. Biểu diễn hình học của S là nửa mặt phẳng chứa gốc tọa độ và kể cả bờ d , với d là là đường thẳng 432 xy−= D. Biểu diễn hình học của S là nửa mặt phẳng không chứa gốc tọa độ và kể cả bờ d , với d là là đường thẳng 432 xy−= . Câu 19: Cho hệ 235(1) 3 25(2) xy xy +   +  . Gọi 1S là tập nghiệm của bất phương trình (1), 2S là tập nghiệm của bất phương trình (2) và S là tập nghiệm của hệ thì A. 12SS  . B. 21SS  . C. 2 SS = . D. 1 SS  .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 59 Câu 20: Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D? A. 0 326 y xy   + . B. 0 326 y xy   +− . C. 0 326 x xy   + . D. 0 326 x xy   +− . Câu 21: Miền tam giác ABC kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D? A. 0 5410 5410 y xy xy   −  + B. 0 4510 5410 x xy xy   −  + C. 0 5410 4510 x xy xy   −  + D. 0 5410 4510 x xy xy   −  + Câu 22: Cho hệ bất phương trình 2 3515 0 0 xy xy x y −  +     . Mệnh đề nào sau đây là sai? A. Trên mặt phẳng tọa độ Oxy , biểu diễn miền nghiệm của hệ bất phương trình đã cho là miền tứ giác ABCO kể cả các cạnh với ( )0;3A , 259 ; 88 B    , ( )2;0C và ( )0;0O B. Đường thẳng : xym+= có giao điểm với tứ giác ABCO kể cả khi 17 1 4 m − O C B 5 2 2A x O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 60 C. Giátrị lớnnhất củabiểuthức xy + ,với x và y thỏamãnhệbất phươngtrình đãcho là 17 4 D. Giátrị nhỏnhất củabiểuthức xy + ,với x và y thõamãn hệbất phươngtrìnhđãcholà0. Câu 23: Giá trị nhỏ nhất của biết thức trên miền xác định bởi hệ 22 24 5 yx yx xy −  −  + là. A. min 1F = khi 2,3xy== B. min 2F = khi 0, 2xy== C. min 3F = khi 1,4xy== . D. min 0F = khi 0, 0xy== . Câu 24: Biểu thức Fyx =− đạt giá trị nhỏ nhất với điều kiện         +  + 0 5 22 22 x xy xy xy tại điểm ; Sxy có toạ độ là A. ( )4;1 . B. ( )3;1 . C. ( )2;1 . D. ( )1;1 . Câu 25: Giá trị nhỏ nhất của biểu thức ( ) ;2 Fxyxy =− , với điều kiện         +   20 20 0 50 xy xy x y là A. 12. B. 10. C. 8. D. 6. Câu 26: Biểu thức Lyx =− , với x và y thỏa mãn hệ bất phương trình 2360 0 2310 xy x xy +−    −− , đạt giá trị lớn nhất là a và đạt giá trị nhỏ nhất là b . Hãy chọn kết quả đúng trong các kết quả sau: A. 25 8 a = và 2b =− B. 2a = và 11 12 b =− C. 3a = và 0b = D. 3a = và 9 8 b = Câu 27: Cho các giá trị , xy thỏa mãn điều kiện 20 210 320 xy xy xy −+  −−  −− . Tìm giá trị lớn nhất của biểu thức 32 Txy =+ A. 19 B. 25. C. 14 D. Không tồn tại. Câu 28: Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9 lít nước và 210 g đường để pha chế nước cam và nước táo. ● Để pha chế 1 lít nước cam cần 30 g đường, 1 lít nước và 1 g hương liệu; ● Để pha chế 1 lít nước táo cần 10 g đường, 1 lít nước và 4 g hương liệu. Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất? A. 5 lít nước cam và 4 lít nước táo. B. 6 lít nước cam và 5 lít nước táo. C. 4 lít nước cam và 5 lít nước táo. D. 4 lít nước cam và 6 lít nước táo.

Câu 29: M

● Mỗi kg

Xưởng

OFFICIAL

i 30 nghìn.

cao Sao vàng và đựng "Quy sâm đại bổ hoàn". Để sản xuất các loại hộp này, công ty dùng các tấm bìa có kích thước giống nhau. Mỗi tấm bìa có hai cách cắt khác nhau.

• Cách thứ nhất cắt được 3 hộp B1, một hộp cao Sao vàng và 6 hộp Quy sâm.

• Cách thứ hai cắt được 2 hộp B1, 3 hộp cao Sao vàng và 1 hộp Quy sâm. Theo kế hoạch, số hộp Quy sâm phải có là 900 hộp, số hộp B1 tối thiểu là 900 hộp, số hộp cao sao vàng tối thiểu là 1000 hộp. Cần phương án sao cho tổng số tấm bìa phải dùng là ít nhất?

A. Cắt theo cách một 20x − tấm, cắt theo cách hai 300 tấm.

B. Cắt theo cách một 150 tấm, cắt theo cách hai 100 tấm. C. Cắt theo cách một 50 tấm, cắt theo cách hai 300 tấm. D. Cắt theo cách một 100 tấm, cắt theo cách hai 200 tấm. Câu 32: Một nhà máy sản xuất, sử

máy

c ch

t t

n ph

t s

n phẩm A và sản phẩm B trong một chu trình s

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 61

ột xưởng sản xuất hai loại sản phẩm

sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, đem lại mức lời 40 nghìn;

sản phẩm loại II cần 4 kg nguyên liệu và

giờ, đem lại mức lờ

có 200 kg nguyên liệu và 1200 giờ làm việc. Nên sản xuất mỗi loại sản phẩm bao nhiêu để có mức lời cao nhất? A. 30kg loại I và 40 kg loại II. B. 20kg loại I và 40 kg loại II. C. 30kg loại I và 20 kg loại II. D. 25kg loại I và 45 kg loại II. Câu 30: Một nhà khoa học đã nghiên cứu về tác động phối hợp của hai loại Vitamin A và B đã thu được kết quả như sau: Trong một ngày, mỗi người cần từ 400 đến 1000 đơn vị Vitamin cả A lẫn B và có thể tiếp nhận không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B . Do tác động phối hợp của hai loại vitamin trên nên mỗi ngày một người sử dụng số đơn vị vitamin B không ít hơn một nửa số đơn vị vitamin A và không nhiều hơn ba lần số đơn vị vitamin A . Tính số đơn vị vitamin mỗi loại ở trên để một người dùng mỗi ngày sao cho chi phí rẻ nhất, biết rằng mỗi đơn vị vitamin A có giá 9 đồng và mỗi đơn vị vitamin B có giá 7,5 đồng. A. 600 đơn vị Vitamin A , 400 đơn vị Vitamin .B B. 600 đơn vị Vitamin A , 300 đơn vị Vitamin B C. 500 đơn vị Vitamin A , 500 đơn vị Vitamin .B D. 100 đơn vị Vitamin A , 300 đơn vị Vitamin .B Câu 31: Công ty Bao bì Dược cần sản xuất 3 loại hộp giấy: đựng thuốc B1

đựng

dụng ba

ại

đặ

ủng để

ả

xuấ

ả

ản xuất. Để sản xuất

ộ

ấn sả

ẩm A lãi 4 triệu đồng người ta sử dụng máy I trong 1 giờ, máy II trong 2 giờ và máy III trong 3 giờ. Để sản xuất ra một tấn sản phẩm B lãi được 3 triệu đồng người ta sử dụng máy I trong 6 giờ, máy II trong 3 giờ và máy III trong 2 giờ. Biết rằng máy I chỉ hoạt động không quá 36 giờ, máy hai hoạt động không quá 23 giờ và máy III hoạt động không quá 27 giờ. Hãy lập kế hoạch sản xuất cho nhà máy để tiền lãi được nhiều nhất. A. Sản xuất 9 tấn sản phẩm A và không sản xuất sản phẩm B B. Sản xuất 7 tấn sản phẩm A và 3 tấn sản phẩm .B C. Sản xuất 10 3 tấn sản phẩm A và 49 9 tấn sản phẩm B D. Sản xuất 6 tấn sản phẩm B và không sản xuất sản phẩm A

phương trình bậc nhất hai ẩn thường có vô số nghiệm và để mô tả tập nghiệm của chúng, ta sử dụng phương pháp biểu diễn hình học.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 1 BÀI 1. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN I. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Bất phương trình bậc nhất hai ẩn , xy có dạng tổng quát là ( )1axbyc + ( );; axbycaxbycaxbyc +++ trong đó ,, abc là những số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số. II. BIỂU DIỄN TẬP NGHIỆM CỦA BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Cũng như bất phương trình bậc nhất một ẩn, các bất

cho bất phương trình axbyc + ) Bước 1. Trên mặt phẳng tọa độ ,Oxy vẽ đường thẳng  : axbyc += Bước 2. Lấy một điểm ( )000 ; Mxy không thuộc  (ta thường lấy gốc tọa độ O ) Bước 3. Tính 00axby + và so sánh 00axby + với .c Bước 4. Kết luận Nếu 00 axbyc + thì nửa mặt phẳng bờ  chứa 0M là miền nghiệm của 00 .axbyc + Nếu 00 axbyc + thì nửa mặt phẳng bờ  không chứa 0M là miền nghiệm của 00 .axbyc + Chú ý: Miền nghiệm của bất phương trình 00 axbyc + bỏ đi đường thẳng axbyc += là miền nghiệm của bất phương trình 00 .axbyc + CHƯƠNG II BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN LÝ THUYẾT.I =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 2 BÀI 2. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN I. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Tương tự hệ bất phương trình một ẩn Hệ bất phương trình bậc nhất hai ẩn gồm một số bất phương trình bậc nhất hai ẩn , xy mà ta phải tìm các nghiệm chung của chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ bất phương trình đã cho. Cũng như bất phương trình bậc nhất hai ẩn, ta có thể biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn. II. BIỂU DIỄN TẬP NGHIỆM CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Để biểu diễn miền nghiệm của hệ bất phương trình bậc nhất 2 ẩn ta làm nư sau: Trong cùng hệ toạ độ, biểu diễn miền nghiệm của mỗi bất phương trình trong hệ bằng cách gạch bỏ phần không thuộc miền nghiệm của nó. Phần không bị gạch là miền nghiệm cần tìm. III. ÁP DỤNG VÀO BÀI TOÁN THỰC TIỄN Giải một số bài toán kinh tế thường dẫn đến việc xét những hệ bất phương trình bậc nhất hai ẩn và giải chúng. Loại bài toán này được nghiên cứu trong một ngành toán học có tên gọi là Quy hoạch tuyến tính. 2.4. Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn? a) 0 0; x y    b) 2 0 1; xy yx  + − c) 0 0; xyz y ++   d) 2 2 23 431. xy xy −+  + Lời giải a) 0 0; x y    d) 2 2 23 431. xy xy −+  + 2.5. Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau trên mặt phẳng tọa độ: a) 1 0 0; yx x y −−     b) 0 0 24; x y xy     + c) 0 5 0. x xy xy   +  − Lời giải a) 1 0 0; yx x y −−     HỆ THỐNG BÀI TẬP.II = BÀI TẬP.1 =

Bước 1: Vẽ đường thẳng

không thỏa mãn bất phương trình

Do đó miền nghiệm của của bất phương trình

là nửa mặt phẳng bờ 1d không chứa gốc tọa độ O không kể đường thẳng

Bước 2: Vẽ đường thẳng ( )2 :0dx

Vì 10

nên tọa độ điểm ( )1;0 thỏa bất phương trình

Do đó miền nghiệm của bất phương trình

Bước 3: Vẽ đường thẳng ( )3 :0dy =

là nửa mặt phẳng bờ Oy chứa điểm ( )1;0 không kể bờ Oy .

Vì 10− nên tọa độ điểm ( )0,1 thỏa bất phương trình 0y 

Do đó miền nghiệm của bất phương trình 0y  là nửa mặt phẳng bờ Ox chứa điểm ( )0;1 không kể bờ Ox .

Vậy miền nghiệm của hệ là miền không bị gạch.

b) 0

Bước 1: Vẽ đường thẳng ( )1 :0dx =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 3

( )1 :1dxy−+=− Vì 0001 −+=− nên tọa độ điểm ( )0;0O

1xy −+−



0x 



0 24; x y xy     +

2.6.

Vì 10  nên tọa độ điểm ( )1;0 thỏa bất phương trình 0x 

Do đó miền nghiệm của bất phương trình 0x  là nửa mặt phẳng bờ Oy và đường thẳng 0x = chứa điểm ( )1;0 .

Bước 2: Vẽ đường thẳng ( )2 :0dy =

Vì 10  nên tọa độ điểm ( )0,1 thỏa bất phương trình 0y 

Do đó miền nghiệm của bất phương trình 0y  là nửa mặt phẳng bờ Ox và đường thẳng 0y = chứa điểm ( )0;1 .

Bước 3: Vẽ đường thẳng ( )3 :24dxy+=

Vì 2.0004 += nên tọa độ điểm ( )0;0O thỏa mãn bất phương trình 24 xy+

Do đó miền nghiệm của của bất phương trình24 xy+ là nửa mặt phẳng bờ 3d và đường thẳng 24 xy+= chứa gốc tọa độ O .

Vậy miền nghiệm của hệ là miền không bị gạch.

gia

cầ

protein và

vị lipit trong th

i kilôgam th

vị protein và 200 đơn vị lipit. M

mỗi ngày. M

i kilôgam th

OFFICIAL

600 đơn vị protein và 400 đơn vị lipit. Bi

t 1,6 kg thịt bò và 1,1 kg th

gia đình này chỉ mua

n; giá tiền 1 kg thịt bò là 250 nghìn đồng; 1 kg thịt lợn là 160 nghìn đồng. Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.

a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm của hệ đó.

b) Gọi F (nghìn đồng) là số tiền phải trả cho x kilôgam thịt bò và y kilôgam thịt lợn. Hãy biểu diễn F theo x và y.

c) Tìm số kilôgam thịt mỗi loại mà gia đình cần mua để chi phí là ít nhất.

Lời giải

a) Gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giả sử gia đình này mua x kilôgam thịt bò và y kilôgam thịt lợn thì x và y cần thỏa mãn điều kiện: 01,6 x  và 01,1 y  .

Gia đình này cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 4

Một

đình

n ít nhất 900 đơn vị

400 đơn

ức ăn

ỗ

ịt bò

ứa 800 đơn

ỗ

ị

lợn

ứa

ết rằng

nhiều nhấ

ịt lợ

ăn mỗi ngày nên điều kiện tương ứng là 800600900 xy+ và 200400400 xy+ Hay 869 xy+ và 22xy+ Từ các bất phương trình biểu thị các điều kiện của bài toán, ta có hệ bất phương trình sau: 01,6 01,1 869 22 x y xy xy     +  + Biểu diễn miền nghiệm của hệ bất phương trình: ( ) ( ) ( ) ( ) 1 2 3 4 :1,6 :1,1 :869 :22 dx dy dxy dxy = = += +=

Miền nghiệm của hệ trên là miền tứ giác ABCD

(kể cả biên).

b) 250160 Fxy =+ (nghìn đồng)

c) ( ); Fxy đạt giá trị lớn nhất hoặc nhỏ nhất tại một trong các đỉnh của tứ giác ABCD.

( ) ( ) ( )23 0,3;1,1AddA  , ta có ( ) 0,3;1,1250.0,3160.0,191F =+= (nghìn đồng)

( ) ( ) ( )12 1,6;1,1BddB  , ta có ( ) 1,6;1,1250.1,6160.1,1576F =+= (nghìn đồng)

( ) ( ) ( )14 1,6;0,2CddC  , ta có ( ) 1,6;0,2250.1,6160.0,2432F =+= (nghìn đồng)

( ) ( ) ( )34 0,6;0,7DddD  , ta có ( ) 0,6;0,7250.0,6160.0,7262F =+= (nghìn đồng)

Vậy gia đình đó cần mua 0,3kg thịt bò và 1,1kg thịt

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 5

lợn để chi phí là ít nhất. DẠNG 1: CÁC BÀI TOÁN LIÊN BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Câu 1: Biểu diễn hình học tập nghiệm của bất phương trình 23 xy+ Lời giải Vẽ đường thẳng :23. xy += Lấy gốc tọa độ ( ) 0;0,O ta thấy O và có 2.003 + nên nửa mặt phẳng bờ  chứa gốc tọa độ O là miền nghiệm của bất phương trình đã cho (miền không bị tô đậm trong hình). Câu 2: Biểu diễn hình học tập nghiệm của bất phương trình 320 xy −++ Lời giải BÀI TẬP TỰ LUẬN.2 =

Trướ

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 6

c hết, ta vẽ đường thẳng ( ):320.dxy−++=

thấy ( )0;0 không là nghiệm của bất phương trình.

ậy miền nghiệm là nửa mặt phẳng bờ ( )d không chứa điểm ( ) 0;0. Câu 3: Biểu diễn hình học tập nghiệm của bất phương trình 32(25)2(1) xyx +++− Lời giải Đầu tiên, thu gọn bất phương trình đề bài đã cho về thành 34110. xy++ Ta vẽ đường thẳng ( ):34110.dxy++= Ta thấy ( )0;0 không là nghiệm của bất phương trình. Vậy miền nghiệm là nửa mặt phẳng (không kể bờ ( )d ) không chứa điểm ( ) 0;0. Câu 4: Biểu diễn hình học tập nghiệm của bất phương trình ( ) ( ) 13132 xy +−− Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 7 Trước hết, ta vẽ đường thẳng ( ) ( ) ( ) :13132.dxy +−−= Ta thấy ( )0;0 không là nghiệm của bất phương trình đã cho. Vậy miền nghiệm là nửa mặt phẳng bờ ( )d không chứa điểm ( ) 0;0. DẠNG 2: CÁC BÀI TOÁN LIÊN HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Câu 1: Biểu diễn hình học tập nghiệm của hệ bất phương trình 36 4 0 0 xy xy x y +  +     Lời giải Vẽ các đường thẳng ( ) ( ) 1 2 2 2 :36 :4 :0 :0 dxy dxy dxOy dyOx += += = = Vì điểm ( )0 1;1M có tọa độ thỏa mãn tất cả các bất phương trình trong hệ trên nên ta tô đậm các nửa mặt phẳng bờ ( )1 ,d ( )2 ,d ( )3 ,d ( )4d không chứa điểm 0M Miền không bị tô đậm (hình tứ giác OCIA kể cả bốn cạnh ,,, AIICCOOA) trong hình vẽ là miền nghiệm của hệ đã cho. Câu 2: Tìm miền nghiệm của hệ bất phương trình 30 23 2 xy xy yx −  +−  + . Lời giải Trước hết, ta vẽ ba đường thẳng: ( )1 :30dxy−= ( )2 :23dxy+=− ( )3 :2dxy+=

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 8 Ta thấy ( )1;0 là nghiệm của cả ba bất phương trình. Điều đó có nghĩa điểm ( )1;0 thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Câu 3: Tìm trị lớn nhất của biểu thức ( ) ;2 Fxyxy =+ , với điều kiện        +    2100 10 0 40 xy xy x y Lời giải Vẽ đường thẳng 1 :10dxy−−= , đường thẳng 1d qua hai điểm ( )0;1 và ( )1;0 Vẽ đường thẳng 2 :2100dxy+−= , đường thẳng 2d qua hai điểm ( )0;5 và ( )2;4 . Vẽ đường thẳng 3 :4dy = .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 9 Miền nghiệm là ngũ giác ABCOE với ( ) ( ) ( ) ( )4;3,2;4,0;4,1;0ABCE Ta có: ( ) 4;310F = , ( ) 2;410F = , ( ) 0;48F = , ( ) 1;01F = , ( ) 0;00F = . Vậy giá trị lớn nhất của biết thức ( ) ;2 Fxyxy =+ bằng 10 DẠNG 3: CÁC BÀI TOÁN THỰC TIỄN Bài toán: Tìm giá trị lớn nhất, nhỏ nhất của biểu thức , Txyaxby với ; xy nghiệm đúng một hệ bất phương trình bậc nhất hai ẩn cho trước. Bước 1: Xác định miền nghiệm của hệ bất phương trình đã cho. Kết quả thường được miền nghiệm S là đa giác. Bước 2: Tính giá trị của F tương ứng với ; xy là tọa độ của các đỉnh của đa giác. Bước 3: Kết luận: Giá trị lớn nhất của F là số lớn nhất trong các giá trị tìm được. Giá trị nhỏ nhất của F là số nhỏ nhất trong các giá trị tìm được. Câu 1: Một hộ nông dân định trồng đậu và cà trên diện tích 800m2. Nếu trồng đậu thì cần 20 công và thu 3.000.000 đồng trên 100m2 nếu trồng cà thì cần 30 công và thu 4.000.000 đồng trên 100 m2 Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được nhiều tiền nhất khi tổng số công không quá 180 Lời giải Gọi x là số 00x m2 đất trồng đậu, y là số 00y m2 đất trồng cà. Điều kiện 0x  , 0y  Số tiền thu được là 34 Txy =+ triệu đồng. Theo bài ra ta có 8 2030180 0 0 xy xy x y +  +      8 2318 0 0 xy xy x y +  +     Đồ thị: Dựa đồ thị ta có tọa độ các đỉnh ( )0;6A , ( )6;2B , ( )8;0C , ( )0;0O Câu 2: Bạn An kinh doanh hai mặt hàng handmade là vòng tay và vòng đeo cổ. Mỗi vòng tay làm trong 4 giờ, bán được 40 ngàn đồng. Mỗi vòng đeo cổ làm trong 6 giờ, bán được 80 ngàn đồng. Mỗi tuần bạn An bán được không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong tuần An cần dùng để bán được ít nhất 400 ngàn đồng? Lời giải

ờ, Bình phải làm việc trong 6 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 10 Gọi , xy  là số vòng tay và vòng đeo cổ trong tuần An làm được. Theo giả thiết ta có 4080400 015 04 xy x y +     Bài toán trở thành tìm nghiệm ( ), xy để 46 Lxy =+ nhỏ nhất. Miền nghiệm của hệ bất phương trình (1) là tam giác ABC với ( ) ( ) ( )0;50,10;0,2;4ABC kể cả miền trong tam giác đó. Tình giá trị của biểu thức 46 Lxy =+ tại tất cả các đỉnh của tam giác ABC ta thấy L nhỏ nhất khi 2,4xy== Vậy số giờ tối thiểu trong tuần An cần dung là 4.26.432L =+= Câu 3: Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm I và II . Mỗi sản phẩm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đồng. Để sản xuất được một sản phẩm I thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ. Để sản xuất được một sản phẩm II thì Chiến phải làm việc trong 2 gi

180 giờ và Bình không thể làm việc quá 220 giờ. Tính số tiền lãi lớn nhất trong một tháng của xưởng. Lời giải Gọi x , y lần lượt là số sản phẩm loại I và loại II được sản xuất ra. Điều kiện x , y nguyên dương. Ta có hệ bất phương trình sau: 32180 6220 0 0 xy xy x y +  +     Miền nghiệm của hệ trên là Tiền lãi trong một tháng của xưởng là 0,50,4 Txy =+ (triệu đồng). Ta thấy T đạt giá trị lớn nhất chỉ có thể tại các điểm A , B , C . Vì C có tọa độ không nguyên nên loại. Tại ( )60;0A thì 30T = triệu đồng. x y B 90 OA C

Câu 4: Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kiogam thịt bò chứa 800 đơn vị protein và 200đơn vị lipit. Mỗi kilogam thịt lợn chứa 600đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền một kg thịt bò là 160 nghìn đồng, một kg thịt lợn là 110 nghìn đồng. Gọi x , y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua. Tìm

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 11 Tại ( )40;30B thì 32T = triệu đồng. Vậy tiền lãi lớn nhất trong một tháng của xưởng là 32 triệu đồng.

x , y để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn? Lời giải Theo bài ra ta có số tiền gia đình cần trả là 160.110.xy + với x , y thỏa mãn: 01,6 01,1 x y    Số đơn vị protein gia đình có là 0,8.0,6.0,9 xy+ 869 xy + ( )1d . Số đơn vị lipit gia đình có là0,2.0,4.0,422 xyxy ++ ( )2d Bài toán trở thành: Tìm , xy thỏa mãn hệ bất phương trình 01,6 01,1 869 22 x y xy xy     +  + sao cho 160.110. Txy =+ nhỏ nhất. Vẽ hệ trục tọa độ ta tìm được tọa độ các điểm ( )1,6;1,1A ; ( )1,6;0,2B ; ( )0,6;0,7C ; ( )0,3;1,1D . Nhận xét: ( ) 377TA = nghìn, ( ) 278TB = nghìn, ( ) 173TC = nghìn, ( ) 169TD = nghìn. Vậy tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn thì 0,6x = và 0,7y = . Câu 5: Một hộ nông dân định trồng dứa và củ đậu trên diện tích 8ha . Trên diện tích mỗi ha , nếu trồng dứa thì cần 20 công và thu 3 triệu đồng, nếu trồng củ đậu thì cần 30 công và thu 4 triệu đồng. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu ha để thu được nhiều tiền nhất, biết rằng tổng số công không quá 180. Lời giải O x y A BC D 1 2 1 2 1,6x = 1,1y = 22xy+= 869 xy+=

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 12 Gọi , xy lần lượt là số ha trồng dứa và củ đậu. Có 08;08 xy  ; 8xy+ ; 20301802318 xyxy ++ Số tiền thu được là ( ) ,34 Txyxy =+ Ta có hệ 08 08 8 2318 x y xy xy     +  + Miền nghiệm của hệ là miền tứ giác OABC với ( ) ( ) ( )0;6,6;2,0;8ABC . Khi đó ( ), Txy đạt cực đại tại một trong các đỉnh của OABC. Có ( ) ( ) ( ) ( ) 0,00;0;624;6;226;8;024 TTTT==== . Vậy cần trồng 6 ha dứa và 2 ha củ đậu. Câu 1: Bất phương trình ( ) 3–2–10 xyx + tương đương với bất phương trình nào sau đây? A. –2–20xy  . B. 5–2–20 xy  . C. 5–2–10 xy  . D. 4–2–20 xy  . Lời giải Chọn B ( ) 3–2–10322205220 xyxxyxxy+−+−−− . Câu 2: Cho bất phương trình ( ) ( ) 314253 xyx −+−− . Khẳng định nào dưới đây là khẳng định đúng? A. Điểm ( )0;0O thuộc miền nghiệm của bất phương trình đã cho. B. Điểm ( )2;2B thuộc miền nghiệm của bất phương trình đã cho. BÀI TẬP TRẮC NGHIỆM.3 =

Cho b

phương trình

. Khẳng định nào dưới đây là khẳng định sai?

A. Điểm ( )3;4A thuộc miền nghiệm của bất phương trình đã cho.

B. Điểm ( )2;5B thuộc miền nghiệm của bất phương trình đã cho.

C. Điểm ( )1;6C thuộc miền nghiệm của bất phương trình đã cho.

D. Điểm ( )0;0O thuộc miền nghiệm của bất phương trình đã cho.

Lời giải

Chọn D

Lần lượt thay toạ độ điểm ở mỗi phương án vào bất phương trình đã cho, ta thấy ( ) ( )00;0;0xy =

không là nghiệm của bất phương trình đã cho.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 13 C. Điểm ( )4;2C thuộc miền nghiệm của bất phương trình đã cho. D. Điểm ( )5;3D thuộc miền nghiệm của bất phương trình đã cho. Lời giải Chọn A Lần lượt thay toạ độ điểm ở mỗi phương án vào bất phương trình đã cho, ta thấy ( ) ( )00;0;0xy = là nghiệm của bất phương trình đã cho. Câu 3:

ất

( ) ( )322521 xyx +++−

Câu 4: Cặp số ( )1;–1 là nghiệm của bất phương trình nào sau đây? A. –30xy+ . B. ––0 xy  . C. 310xy++ . D. ––3–10 xy  . Lời giải Chọn C ( ) ,31fxyxy=++ . Thay ( ) 1,113110f −=−+=− . Câu 5: Cặp số nào sau đây là nghiệm của bất phương trình ( ) –2–3 +xyy ? A. ( )4;–4 B. ( )2;1 C. ( )–1;–2 D. ( )4;4 Lời giải Chọn D ( ) ( )–2–32323* xyyxyyx +−++ Thay các đáp án vào bpt( )* để kiểm tra Câu 6: Cặp số nào sau đây không là nghiệm của bất phương trình ( ) 5210 −−xy ? A. ( )0;1 . B. ( )1;3 . C. ( )–1;1 . D. ( )–1;0 . Lời giải Chọn B Ta có ( ) 5210 −−xy 5220 xy −+ ; ta thay từng đáp án vào bất phương trình, cặp ( )1;3 không thỏa mãn bất phương trình vì 5.12.320 −+ là sai. Vậy Chọn B Câu 7: Miền nghiệm của bất phương trình 326 xy−− là

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 14 A. B. C. D. Lời giải Chọn C Trước hết, ta vẽ đường thẳng ( ):326.dxy−=− Ta thấy ( )0;0 là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng bờ ( )d chứa điểm ( ) 0;0. Câu 8: Miền nghiệm của bất phương trình 326 xy+ là O x y 2 3 O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 15 A. B. C. D. Lời giải Chọn A Trước hết, ta vẽ đường thẳng ( ):326.dxy+= Ta thấy ( )0;0 không phải là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng (không kể bờ ( )d ) không chứa điểm ( ) 0;0. Câu 9: Miền nghiệm của bất phương trình 326 xy−− là O 2 3 y x O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 16 A. B. C. D. Lời giải Chọn B Trước hết, ta vẽ đường thẳng ( ):326.dxy−=− Ta thấy ( )0;0 không phải là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng (không kể bờ ( )d ) không chứa điểm ( ) 0;0. Câu 10: Miền nghiệm của bất phương trình 326 xy+− là O x y 2 3 O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 17 A. B. C. D. Lời giải Chọn D Trước hết, ta vẽ đường thẳng ( ):326.dxy+=− Ta thấy ( )0;0 là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng (không kể bờ ( )d ) chứa điểm ( ) 0;0. Câu 11: Miền nghiệm của hệ bất phương trình           + 6 82 3 93 y yx xy xy là phần mặt phẳng chứa điểm nào sau đây? A. ( )0;0 . B. ( )1;2 . C. ( )2;1 . D. ( )8;4 . Lời giải O x 2 3 y O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 18 Chọn D Ta dùng máy tính lần lượt kiểm tra các đáp án để xem đáp án nào thỏa hệ bất phương trình trên. Câu 12: Miền nghiệm của hệ bất phương trình 10 23 3 2(1)4 2 0 xy y x x  +−   −+     là phần mặt phẳng chứa điểm A. ( )2;1 . B. ( )0;0 . C. ( )1;1 . D. ( )3;4 . Lời giải Chọn A Nhận xét: chỉ có điểm ( )2;1 thỏa mãn hệ Câu 13: Trong các cặp số sau, tìm cặp số không là nghiệm của hệ bất phương trình    + + 0232 02 xy xy A. ( )0;0 B. ( )1;1 C. ( )1;1 D. ( )1;1 Lời giải Chọn C Ta dùng máy tính lần lượt kiểm tra các đáp án để xem đáp án nào không thỏa hệ bất phương trình trên với mọi x Câu 14: Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình 2310 540 xy xy +−  −+ ? A. ( )1;4 . B. ( )2;4 . C. ( )0;0 . D. ( )3;4 . Lời giải Chọn C Nhận xét: chỉ có điểm ( )0;0 không thỏa mãn hệ Câu 15: Cho hệ bất phương trình           + + 0 4 2)3(12 01 23 x y x xy Hỏi khẳng định nào dưới đây là khẳng định đúng? A. Điểm ( )2;1A thuộc miền nghiệm của hệ bất phương trình đã cho. B. Điểm ( )0;0O thuộc miền nghiệm của hệ bất phương trình đã cho.

C. Điểm

)1;1

thuộc miền nghiệm

hệ bất phương trình đã cho.

D. Điểm ( )3;4D thuộc miền nghiệm của hệ bất phương trình đã cho.

Lời

Chọn A

Lần lượt thay toạ độ điểm ở mỗi phương án vào hệ bất phương trình đã

Hỏi khẳng định nào dưới đây là khẳng định đúng?

A. Điểm ( )0;0O thuộc miền nghiệm của hệ bất phương trình đã cho.

B. Điểm ( )1;0B thuộc miền nghiệm của hệ bất phương trình đã cho.

C. Điểm ( )0;2C thuộc miền nghiệm của hệ bất phương trình đã cho.

D. Điểm ( )0;2D thuộc miền nghiệm của hệ bất phương trình đã cho.

Lời giải

Chọn C

Lần lượt thay toạ độ điểm ở mỗi phương án vào hệ bất phương trình đã cho, ta thấy ( ) ( )00;0;2xy =− là nghiệm của hệ bất phương trình đã cho.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 19

(

của

giải

cho, ta thấy ( ) ( )00;2;1xy = là nghiệm của hệ bất phương trình đã cho. Câu 16: Cho hệ bất phương trình      ++ ++  10 250 2510 xy xy xy .

Câu 17: Điểm ( )0;0O thuộc miền nghiệm của hệ bất phương trình nào sau đây? A. 360 240 +−  ++ xy xy B. 360 240 +−  ++ xy xy C. 360 240 +−  ++ xy xy D. 360 240 +−  ++ xy xy Lời giải Chọn C Thay 0;0xy== vào từng đáp án ta được: 36060 24040 xy xy +−−   ++ (loại A. ); 36060 24040 xy xy +−−   ++ ( LoạiB. ) 36060 24040 xy xy +−−   ++ (thỏa mãn). Vậy Chọn C Câu 18: Cho hệ bất phương trình ( ) ( ) 3 211 2 4322 xy xy  −   − có tập nghiệm S . Mệnh đề nào sau đây là đúng? A. 1 ;1 4 S−−   .

c ti

p ta th

y ( )0;0 là nghi

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 20 B. ( ) ;|432Sxyxy=−= C. Biểu diễn hình học của S là nửa mặt phẳng chứa gốc tọa độ và kể cả bờ d , với d là là đường thẳng 432 xy−= D. Biểu diễn hình học của S là nửa mặt phẳng không chứa gốc tọa độ và kể cả bờ d , với d là là đường thẳng 432 xy−= . Lời giải Chọn B Trước hết, ta vẽ hai đường thẳng: ( )1 3 :21 2 dxy−= ( )2 :432dxy−= Thử

ự

ế

ấ

ệm của bất phương trình (2) nhưng không phải là nghiệm của bất phương trình (1). Sau khi gạch bỏ các miền không thích hợp, tập hợp nghiệm của hệ bất phương trình chính là các điểm thuộc đường thẳng ( ):432.dxy−= Câu 19: Cho hệ 235(1) 3 25(2) xy xy +   +  . Gọi 1S là tập nghiệm của bất phương trình (1), 2S là tập nghiệm của bất phương trình (2) và S là tập nghiệm của hệ thì A. 12SS  . B. 21SS  . C. 2 SS = . D. 1 SS  . Lời giải Chọn A Trước hết, ta vẽ hai đường thẳng: ( )1 :235dxy+= ( )2 3 :5 2 dxy+=

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 21 Ta thấy ( )0;0 là nghiệm của cả hai bất phương trình. Điều đó có nghĩa gốc tọa độ thuộc cả hai miền nghiệm của hai bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ Câu 20: Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D? A. 0 326 y xy   + . B. 0 326 y xy   +− . C. 0 326 x xy   + . D. 0 326 x xy   +− . Lời giải Chọn A Dựa vào hình vẽ ta thấy đồ thị gồm hai đường thẳng ( )1 :0dy = và đường thẳng ( )2 :326.dxy+= Miền nghiệm gồm phần y nhận giá trị dương. Lại có ( )0;0 thỏa mãn bất phương trình 326. xy+ Câu 21: Miền tam giác ABC kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D? O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 22 A. 0 5410 5410 y xy xy   −  + B. 0 4510 5410 x xy xy   −  + C. 0 5410 4510 x xy xy   −  + D. 0 5410 4510 x xy xy   −  + Lời giải Chọn C Dựa vào hình vẽ, ta thấy đồ thị gồm các đường thẳng: ( )1 :0dx = ( )2 :4510dxy+= ( )3 :5410dxy−= Miền nghiệm gần phần mặt phẳng nhận giá trị x dương (kể cả bờ ( )1d ). Lại có ( )0;0 là nghiệm của cả hai bất phương trình 4510 xy+ và 5410. xy− Câu 22: Cho hệ bất phương trình 2 3515 0 0 xy xy x y −  +     . Mệnh đề nào sau đây là sai? A. Trên mặt phẳng tọa độ Oxy , biểu diễn miền nghiệm của hệ bất phương trình đã cho là miền tứ giác ABCO kể cả các cạnh với ( )0;3A , 259 ; 88 B    , ( )2;0C và ( )0;0O B. Đường thẳng : xym+= có giao điểm với tứ giác ABCO kể cả khi 17 1 4 m − O C B 5 2 2A x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 23 C. Giátrị lớnnhất củabiểuthức xy + ,với x và y thỏamãnhệbất phươngtrình đãcho là 17 4 D. Giátrị nhỏnhất củabiểuthức xy + ,với x và y thõamãn hệbất phươngtrìnhđãcholà0. Lời giải Chọn B Trước hết, ta vẽ bốn đường thẳng: ( )1 :2dxy−= ( )2 :3515dxy+= ( )3 :0dx = ( )4 :0dy = Fyx =− Miền nghiệm là phần không bị gạch, kể cả biên. Câu 23: Giá trị nhỏ nhất của biết thức trên miền xác định bởi hệ 22 24 5 yx yx xy −  −  + là. A. min 1F = khi 2,3xy== B. min 2F = khi 0, 2xy== C. min 3F = khi 1,4xy== D. min 0F = khi 0, 0xy== Lời giải Chọn A Biểu diễn miền nghiệm của hệ bất phương trình 22 24 5 yx yx xy −  −  + trên hệ trục tọa độ như dưới đây:

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 24 Nhận thấy biết thức Fyx =− chỉ đạt giá trị nhỏ nhất tại các điểm , AB hoặc C . Ta có: ( ) ( ) ( ) 413;2;321FAFBFC=−===−= . Vậy min 1F = khi 2,3xy== Câu 24: Biểu thức Fyx =− đạt giá trị nhỏ nhất với điều kiện         +  + 0 5 22 22 x xy xy xy tại điểm ; Sxy có toạ độ là A. ( )4;1 . B. ( )3;1 . C. ( )2;1 . D. ( )1;1 . Lời giải Chọn A Cách 1: Thử máy tínhTa dùng máy tính lần lượt kiểm tra các đáp án để xem đáp án nào thỏa hệ bất phương trình trên loại được đáp án D. Ta lần lượt tính hiệu Fyx =− và min3 F =− tại 4,x = 1y = Cách 2: Tự luận: Tọa độ 78 ; 33 A   , 22 ; 33 B    , ( )4;1C . Giá trị F lần lượt tại toạ độ các điểm ,, BCA là 41 ,3; 33 . Suy ra min3 F tại 4;1.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 25 Câu 25: Giá trị nhỏ nhất của biểu thức ( ) ;2 Fxyxy =− , với điều kiện         +   20 20 0 50 xy xy x y là A. 12. B. 10. C. 8. D. 6. Lời giải Chọn B Vẽ các đường thẳng 1 :5dy = ; 2 :20dxy+−= ; 3 :20dxy−−= ; :0; :0OxyOyx== Các đường thẳng trên đôi một cắt nhau tại ( )0;5A Vì điểm ( )0 2;1M có toạ độ thoả mãn tất cả các bất pt trong hệ nên ta tô đậm các nửa mặt phẳng bờ 123,,,, dddOxOy không chứa điểm 0M . Miền không bị tô đậm là đa giác ABCD kể cả các cạnh (hình bên) là miền nghiệm của hệ pt đã cho. Kí hiệu ( ) ();2AAAA FAFxyxy ==− , ta có ()10,()4,()2;()3 FAFBFCFD=−=−==− , 10432 −−− Giá trị lớn nhất cần tìm là 10. Câu 26: Biểu thức Lyx =− , với x và y thỏa mãn hệ bất phương trình 2360 0 2310 xy x xy +−    −− , đạt giá trị lớn nhất là a và đạt giá trị nhỏ nhất là b Hãy chọn kết quả đúng trong các kết quả sau: A. 25 8 a = và 2b =− B. 2a = và 11 12 b =− C. 3a = và 0b = D. 3a = và 9 8 b = Lời giải Chọn B Trước hết, ta vẽ ba đường thẳng: 6 4 2 2 4 6 15 10 5 5 10 15 d3 d2 d1 h x( )=x 2 g x( )=2 x f x( )=5 B A D C O

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 26 ( )1 :2360dxy+−= ( )2 :0dx = ( )3 :2310dxy−−= Ta thấy ( )0;0 là nghiệm của cả ba bất phương trình. Điều đó có nghĩa gốc tọa độ thuộc cả ba miền nghiệm của cả ba bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ (kể cả biên). Miền nghiệm là hình tam giác ABC (kể cả biên), với ( ) 0;2,A 75 ;, 46 B    1 0;. 3 C    Vậy ta có 202,a =−= 5711 6412 b =−=− Câu 27: Cho các giá trị , xy thỏa mãn điều kiện 20 210 320 xy xy xy −+  −−  −− . Tìm giá trị lớn nhất của biểu thức 32 Txy =+ . A. 19. B. 25. C. 14. D. Không tồn tại. Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 27 Chọn B Miền nghiệm của hệ đã cho là miền trong tam giác ABC (Kể cả đường biên) trong đó ( )1;1A , ( )2;4B , ( )3;5C . Giá trị lớn nhất của 32 Txy =+ đạt được tại các đỉnh của tam giác ABC Do ( ) 1;13.12.15A TT==+= , ( ) 2;43.22.414B TT==+= và ( ) 3;53.32.525C TT==+= nên giá trị lớn nhất của 32 Txy =+ là 25 đạt được khi 3x = và 5y = . Câu 28: Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9 lít nước và 210 g đường để pha chế nước cam và nước táo. ● Để pha chế 1 lít nước cam cần 30 g đường, 1 lít nước và 1 g hương liệu; ● Để pha chế 1 lít nước táo cần 10 g đường, 1 lít nước và 4 g hương liệu. Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất? A. 5 lít nước cam và 4 lít nước táo. B. 6 lít nước cam và 5 lít nước táo. C. 4 lít nước cam và 5 lít nước táo. D. 4 lít nước cam và 6 lít nước táo. Lời giải Chọn C Giả sử , xy lần lượt là số lít nước cam và số lít nước táo mà mỗi đội cần pha chế Suy ra 3010xy + là số gam đường cần dùng; xy + là số lít nước cần dùng; 4 xy + là số gam hương liệu cần dùng. Theo giả thiết ta có 00 00 3010210321. 99 424424 xx yy xyxy xyxy xyxy    ++  ++  ++  ( )* Số điểm thưởng nhận được sẽ là 6080. Pxy =+ Ta đi tìm giá trị nhỏ nhất của biểu thức P với , xy thỏa mãn ( )* Câu 29: Một xưởng sản xuất hai loại sản phẩm ● Mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, đem lại mức lời 40 nghìn; ● Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, đem lại mức lời 30 nghìn. Xưởng có 200 kg nguyên liệu và 1200 giờ làm việc. Nên sản xuất mỗi loại sản phẩm bao nhiêu để có mức lời cao nhất? A. 30kg loại I và 40 kg loại II. B. 20kg loại I và 40 kg loại II.

phối hợp của hai loại vitamin trên nên mỗi ngày một người sử dụng số đơn vị vitamin B không ít hơn một nửa số đơn vị vitamin A và không nhiều hơn ba lần số đơn vị vitamin A . Tính số đơn vị vitamin mỗi loại ở trên để một người dùng mỗi ngày sao cho chi phí rẻ nhất, biết rằng mỗi đơn vị vitamin A có giá 9 đồng và mỗi đơn vị vitamin B có giá 7,5 đồng.

A. 600 đơn vị Vitamin A , 400 đơn vị Vitamin .B

B. 600 đơn vị Vitamin A , 300 đơn vị Vitamin .B

C. 500 đơn vị Vitamin A , 500 đơn vị Vitamin B

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 28 C. 30kg loại I và 20 kg loại II. D. 25kg loại I và 45 kg loại II. Lời giải Chọn B Gọi ( )0, 0 kgxy lần lượt là số sản phẩm loại I và loại II cần sản xuất. Khi đó, tổng số nguyên liệu sử dụng: 24200. xy+ Tổng số giờ làm việc: 30151200. xy+ Lợi nhuận tạo thành: 4030 Lxy =+ (nghìn). Thực chất của bài toán này là phải tìm 0,x  0y  thoả mãn hệ 24200 30151200 xy xy +  + sao cho 4030 Lxy =+ đạt giá trị lớn nhất. Câu 30: Một nhà khoa học đã nghiên cứu về tác động phối hợp của hai loại Vitamin A và B đã thu được kết quả như sau: Trong một ngày, mỗi người cần từ 400 đến 1000 đơn vị Vitamin cả A lẫn B và có thể tiếp nhận không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B . Do tác động

D. 100 đơn vị Vitamin A , 300 đơn vị Vitamin .B Lời giải Chọn D Gọi 0, 0xy lần lượt là số đơn vị vitamin A và B để một người cần dùng trong một ngày. Trong một ngày, mỗi người cần từ 400 đến 1000 đơn vị vitamin cả A lẫn B nên ta có: 4001000. xy + Hàng ngày, tiếp nhận không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B nên ta có: 600, 500.xy Mỗi ngày một người sử dụng số đơn vị vitamin B không ít hơn một nửa số đơn vị vitamin A và không nhiều hơn ba lần số đơn vị vitamin A nên ta có: 0,53. xyx  Số tiền cần dùng mỗi ngày là: ( ) ,97,5. Txyxy =+ Bài toán trở thành: Tìm 0, 0xy thỏa mãn hệ 0600,0500 4001000 0,53 xy xy xyx   +   để ( ) ,97,5 Txyxy =+ đạt giá trị nhỏ nhất.

Câu 31: Công ty Bao bì Dược cần sản xuất 3 loại hộp giấy: đựng thuốc B1, đựng cao Sao vàng và đựng "Quy sâm đại bổ hoàn". Để sản xuất các loại hộp này, công ty dùng các tấm bìa có kích thước giống nhau. Mỗi tấm bìa có hai cách cắt khác nhau.

• Cách

• Cách th

hai c

theo

và

vàng và 1 h

p Quy sâm.

p Quy sâm. Theo kế hoạch, số hộp Quy sâm phải có là 900 hộp, số hộp B1 tối thiểu là 900 hộp, số hộp cao sao vàng tối thiểu là 1000 hộp. Cần phương án sao cho

OFFICIAL

t chu trình sản xuất. Để sản xuất một t

n sản phẩm A lãi 4 triệu đồng người ta sử dụng máy I trong 1 giờ, máy II trong 2 giờ và máy III trong 3 giờ. Để sản xuất ra một tấn sản phẩm B lãi được 3 triệu đồng người ta sử dụng máy I trong 6 giờ, máy II trong 3 giờ và máy III trong 2 giờ. Biết rằng máy I chỉ hoạt động không quá 36 giờ, máy hai hoạt động không quá 23 giờ và máy III hoạt động không quá 27 giờ. Hãy lập kế hoạch sản xuất cho nhà máy

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 29

thứ nhất cắt được 3 hộp B1, một hộp cao Sao vàng

6 hộ

ứ

ắt đượ

2 hộp B1, 3 hộp cao Sao

ộ

tổng số tấm bìa phải dùng là ít nhất?

Cắt theo cách một 20x − tấm, cắt theo cách hai 300 tấm. B. Cắt

cách một 150 tấm, cắt theo cách hai 100 tấm. C. Cắt theo cách một 50 tấm, cắt theo cách hai 300 tấm. D. Cắt theo cách một 100 tấm, cắt theo cách hai 200 tấm. Lời giải Chọn A Gọi 0, 0xy lần lượt là số tấm bìa cắt theo cách thứ nhất, thứ hai. Bài toán đưa đến tìm 0, 0xy thoả mãn hệ 32900 31000 6900 xy xy xy +  +  += sao cho Lxy =+ nhỏ nhất. Câu 32: Một nhà máy sản xuất, sử dụng ba loại máy đặc chủng để sản xuất sản phẩm A và sản phẩm B trong mộ

ấ

để tiền lãi được nhiều nhất. A. Sản xuất 9 tấn sản phẩm A và không sản xuất sản phẩm .B B. Sản xuất 7 tấn sản phẩm A và 3 tấn sản phẩm B C. Sản xuất 10 3 tấn sản phẩm A và 49 9 tấn sản phẩm .B D. Sản xuất 6 tấn sản phẩm B và không sản xuất sản phẩm .A Lời giải Chọn B Gọi 0, 0xy (tấn) là sản lượng cần sản xuất của sản phẩm A và sản phẩm .B Ta có: 6 xy + là thời gian hoạt động của máy I 23xy + là thời gian hoạt động của máy .II 32xy + là thời gian hoạt động của máy III Số tiền lãi của nhà máy: 43 Txy =+ (triệu đồng).

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 30 Bài toán trở thành: Tìm 0, 0xy thỏa mãn 636 2323 3227 xy xy xy +  +  + để 43 Txy =+ đạt giá trị lớn nhất.

Câu 1: Điểm nào sau đây thuộc mi

A. ( )1;1A

Câu 2: Điểm (1;3)A là

A. 3240

Câu 3: Điể

m thu

n nghi

c mi

m c

a b

phương trình 3450 +−xy ?

phương trình:

Câu

Trong các

( )

OFFICIAL

240

A. Trong mặt phẳng tọa độ Oxy , tập hợp các điểm có tọa độ là nghiệm của bất phương trình axbyc + không được gọi là miền nghiệm của

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 1

ề

ệ

ủ

ất

B. ( )2;0B C. ( )1;2C D.

4;1D

điể

ộ

ền nghiệm của bất

−+− xy B. 30+xy C. 30 −xy D.

−+xy

m (0;3)A là điểm thuộc miền nghiệm của bất phương trình: A. 3240 xy −+− B. 30 xy− C. 240 xy−− D. 30xy+ Câu 4: Điểm nào sau đây không thuộc miền nghiệm của bất phương trình 450−+xy ? A. ( )5;0M B. ( )1;0N C. ( )1;3P D. ( )2;1Q

mệnh đề sau, mệnh đề nào đúng?

nó B. Biểu diễn tập nghiệm của bất phương trình 2310 xy−+ trên hệ trục Oxy là đường thẳng 2310 xy−+= . C. Trong mặt phẳng tọa độ Oxy , tập hợp các điểm có tọa độ là nghiệm của bất phương trình axbyc + được gọi là miền nghiệm của nó. D. Nghiệm của bất phương trình axbyc + là tập rỗng. Câu 6: Miền nghiệm của bất phương trình ( ) ( )22221 xyx −++−− là nửa mặt phẳng không chứa điểm nào trong các điểm sau? A. ( )0;0 . B. ( )1;1 . C. ( )4;2 . D. ( )1;1 . Câu 7: Miền nghiệm của bất phương trình ( ) ( ) 314253 xyx −+−− là nửa mặt phẳng chứa điểm nào trong các điểm sau? A. ( )0;0 B. ( )4;2 C. ( )2;2 D. ( )5;3 Câu 8: Miền nghiệm của bất phương trình ( ) ( )322521 xyx +++− là nửa mặt phẳng chứa điểm nào trong các điểm sau? A. ( )3;4 . B. ( )2;5 . C. ( )1;6 . D. ( )0;0 . CHƯƠNG II BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.III =

Câu 13: Trong các

( )0;0

Câu 14: Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?

A. 2530 xyz−+

Câu

2 3240 xx+−

253 xy+

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 2 Câu 9: Miền nghiệm của bất phương trình ( ) ( ) 415329 xyx −+−− là nửa mặt phẳng chứa điểm nào trong các điểm sau? A. ( )0;0 B. ( )1;1 C. ( )1;1 D. ( )2;5 Câu 10: Miền nghiệm của bất phương trình ( ) ( ) 323413 xyxy +++−+ là phần mặt phẳng chứa điểm nào trong các điểm sau? A. ( )3;0 . B. ( )3;1 . C. ( )1;1 . D. ( )0;0 . Câu 11: Miền nghiệm của bất phương trình ( ) 529227 xxy +−−+ là phần mặt phẳng không chứa điểm nào trong các điểm sau? A. ( )2;1 B. ( )2;3 C. ( )2;1 D. ( )0;0 Câu 12: Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình 21 xy+ ?

( )2;1 B. ( )3;7 C. ( )0;1 D. ( )0;0

cặp số sau đây, cặp nào không là nghiệm của bất phương trình 450xy−+ ?

( )5;0 . B. ( )2;1 . C. ( )1;3 . D.

C. 2

D. 235 xy+

15: Điểm nào sau đây thuộc miền nghiệm của bất phương trình 230 xy+− ? A. ( )1;3Q . B. 3 1; 2 M    . C. ( )1;1N . D. 3 1; 2 P    . Câu 16: Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi nửa mặt phẳng không bị gạch trong hình vẽ sau? A. 23 xy− . B. 3xy− . C. 23 xy− . D. 23 xy+ .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 3 Câu 17: Hình vẽ nào sau đây biểu diễn miền nghiệm là của bất phương trình nào sau đây? A. 21xy . B. 21xy . C. 2xy . D. 2xy . Câu 18: Miền nghiệm của bất phương trình 23xy+ là phần tô đậm trong hình vẽ của hình nào, trong các hình vẽ dưới đây? A. B. C. D. Câu 19: Miền nghiệm của bất phương trình 320 xy −++ không chứa điểm nào sau đây? A. ( )1;2A B. ( )2;1B C. 1 1; 2 C    D. ( )3;1D Câu 20: Miền nghiệm của bất phương trình 32(25)2(1) xyx +++− không chứa điểm nào sau đây? A. ( )1;2A . B. 12 ; 1111 B    . C. ( )0;3C . D. ( )4;0D . Câu 21: Miền nghiệm của bất phương trình 21 xy+ không chứa điểm nào sau đây? A. ( ) 1;1.A B. ( )2;2B C. ( )3;3C D. ( )1;1D Câu 22: Miền nghiệm của bất phương trình ( ) ( ) 13132 xy +−− chứa điểm nào sau đây? A. ( )1;1A B. ( )1;1B C. ( )1;1C D. ( )3;3D

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 4 Câu 23: Miền nghiệm của bất phương trình ( ) 22124xyx −+−+ chứa điểm nào sau đây? A. ( ) 1;1.A B. ( ) 1;5.B C. ( ) 4;3.C D. ( ) 0;4.D Câu 24: Miền nghiệm của bất phương trình 22220 xy−+− chứa điểm nào sau đây? A. ( ) 1;1.A B. ( )1;0B C. ( )2;2C D. ( ) 2;2.D Câu 25: Cho bất phương trình245 xy+ có tập nghiệm là S . Khẳng định nào sau đây là khẳng định đúng ? A. ( )1;1 S B. ( )1;10 S C. ( )1;1 S− D. ( )1;5 S Câu 26: Cho bất phương trình 250xy−+ có tập nghiệm là S . Khẳng định nào sau đây là khẳng định đúng? A. ( )2;2 S . B. ( )1;3 S . C. ( )2;2 S− . D. ( )2;4 S− . Câu 27: Miền nghiệm của bất phương trình 326 xy−− là A. B. C. D. O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 5 Câu 28: Miền nghiệm của bất phương trình 326 xy+ là A. B. C. D. Câu 29: Miền nghiệm của bất phương trình 326 xy+− là A. B. C. D. O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 6 Câu 30: Cho bất phương trình 2320 xy −++ có tập nghiệm là S Khẳng định nào sau đây là khẳng định đúng? A. ( )1;1 S . B. 2 ;0 2 S     . C. ( )1;2 S− . D. ( )1;0 S . Câu 31: Cặp số ( )(;) 2;3xy = là nghiệm của bất phương trình nào sau đây? A. 43xy  . B. –370xy + . C. 2–3–10 xy  . D. –0xy  . Câu 32: Cặp số ( )00 ; xy nào là nghiệm của bất phương trình 334 xy− . A. ( ) ( )00;2;2xy =− . B. ( ) ( )00;5;1xy = . C. ( ) ( )00;4;0xy =− . D. ( ) ( )00;2;1xy = . Câu 33: Cặp số ( ); xy nào sau đây là một nghiệm của hệ bất phương trình 20 ? 310 −  +− xy xy A. ( ) ( );2;1 =−−xy . B. ( ) ( );4;0 =xy . C. ( ) ( );1;2 =xy . D. ( ) ( );3;4 =−−xy . Câu 34: Trong mặt phẳng Oxy , điểm nào dưới đây thuộc miền nghiệm của hệ 31 22 xy xy −  + ? A. ( ) 1;0.P B. ( ) 1;1.N C. ( ) 1;1.M D. ( ) 0;1.Q Câu 35: Trong mặt phẳng với hệ trục tọa độ Oxy , điểm nào dưới đây thuộc miền nghiệm của hệ 210 3210 +−  ++ xy xy ? A. ( )1;1 B. ( )0;1 C. ( )1;0 D. ( )1;3 Câu 36: Miền nghiệm của hệ bất phương trình 39 3 xy xy +  − là phần mặt phẳng chứa điểm A. ( )1;2 B. ( )0;0 C. ( )2;1 D. ( )8;4 Câu 37: Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình 20 2320 xy xy +−  −+ là A. ( )0;0 . B. ( )1;1 . C. ( )1;1 . D. ( )1;1 . Câu 38: Miền nghiệm của hệ bất phương trình 10 23 3 2(1)4 2 0 xy y x x  +−   −+     là phần mặt phẳng chứa điểm nào trong các điểm sau? A. ( )2;1 B. ( )0;0 C. ( )1;1 D. ( )3;4

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 7 Câu 39: Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình 2310 540 xy xy +−  −+ ? A. ( )1;4 . B. ( )2;4 . C. ( )0;0 . D. ( )3;4 . Câu 40: Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình 2510 250 10 xy xy xy −−  ++  ++ ? A. ( )0;0 . B. ( )1;0 . C. ( )0;2 . D. ( )0;2 . Câu 41: Miền nghiệm của hệ bất phương trình 0 330 50 xy xy xy −  −+  +− là phần mặt phẳng chứa điểm A. ( )5;3 . B. ( )0;0 . C. ( )1;1 . D. ( )2;2 . Câu 42: Miền nghiệm của hệ bất phương trình 39 3 28 6 xy xy yx y +  −  −   là phần mặt phẳng chứa điểm A. ( )0;0 . B. ( )1;2 . C. ( )2;1 . D. ( )8;4 . Câu 43: Cho hệ bất phương trình 0 250 xy xy +  + có tập nghiệm là S . Khẳng định nào sau đây là khẳng định đúng? A. ( )1;1 S B. ( )1;1 S−− C. 1 1; 2 S −  D. 12 ; 25 S −  Câu 44: Miền nghiệm của hệ bất phương trình 36 3 28 4 xy xy yx y +  −  −   là phần mặt phẳng chứa điểm: A. ( )2;1 B. ( )6;4 C. ( )0;0 D. ( )1;2

Câu

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 8 Câu 45: Miền tam giác ABC kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn hệ bất phương trình dưới đây? A. 0 5410 5410 y xy xy   −  + B. 0 5410 4510 x xy xy   −  + C. 0 4510 5410 x xy xy   −  + D. 0 5410 4510 x xy xy   −  + Câu 46: Cho hệ bất phương trình 0 310 x xy    ++  có tập nghiệm là S Khẳng định nào sau đây là khẳng định đúng? A. ( )1;1 S− . B. ( )1;3 S− . C. ( )1;5 S− . D. ( )4;3 S− . Câu 47: Cho hệ bất phương trình 0 310 x xy    ++  có tập nghiệm là S . Khẳng định nào sau đây là khẳng định đúng? A. ( )1;2 S− B. ( )2;0 S C. ( )1;3 S− D. ( )3;0 S

48: Cho hệ bất phương trình 3 1 10 2 xy xy −   −+  có tập nghiệm S . Khẳng định nào sau đây là khẳng định đúng ? A. ( )1;2 S− B. ( )2;1 S C. ( )5;6 S− D. S = Câu 49: Cho hệ bất phương trình 3 21 2 432 xy xy  −   − có tập nghiệm S . Khẳng định nào sau đây là khẳng định đúng ? A. 1 ;1 4 S−−   . B. ( ) ;|432Sxyxy=−= . C. Biểu diễn hình học của S là nửa mặt phẳng chứa gốc tọa độ và kể cả bờ d , với d là là đường thẳng 432 xy−= . D. Biểu diễn hình học của S là nửa mặt phẳng không chứa gốc tọa độ và kể cả bờ d , với d là là đường thẳng 432 xy−= .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 9 Câu 50: Cho hệ 235(1) 3 25(2) xy xy +   +  . Gọi 1S là tập nghiệm của bất phương trình, 2S là tập nghiệm của bất phương trình và S là tập nghiệm của hệ thì A. 12SS  . B. 21SS  . C. 2 SS = . D. 1 SS  . Câu 51: Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D? A. 0 326 y xy   + B. 0 326 y xy   +− C. 0 326 x xy   + D. 0 326 x xy   +− Câu 52: Miền nghiệm của hệ bất phương trình 20 32 3 xy xy yx −  +−  − chứa điểm nào sau đây? A. ( )1;0A . B. ( )2;3B . C. ( )0;1C . D. ( ) 1;0.D Câu 53: Miền nghiệm của hệ bất phương trình 2360 0 2310 xy x xy +−    −− chứa điểm nào sau đây? A. ( ) 1;2.A B. ( )0;2B C. ( )1;3C D. 1 0;. 3 D    Câu 54: Miền nghiệm của hệ bất phương trình 210 350 x x − −+  chứa điểm nào sau đây? A. Không có B. 5 ;2. 3 B    C. ( ) 3;1.C D. 1 ;10 2 D    Câu 55: Miền nghiệm của hệ bất phương trình 30 2310 y xy −  −+ chứa điểm nào sau đây? A. ( )3;4A . B. ( )4;3B . C. ( )7;4C . D. ( ) 4;4.D O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 10 Câu 56: Miền nghiệm của hệ bất phương trình 20 32 xy xy −  +− không chứa điểm nào sau đây? A. ( ) 1;0.A B. ( ) 1;0.B C. ( )3;4C . D. ( ) 0;3.D Câu 57: Miền nghiệm của hệ bất phương trình 3260 3 2(1)4 2 0 xy y x x −−   −+    không chứa điểm nào sau đây? A. ( )2;2A . B. ( ) 3;0.B C. ( ) 1;1.C D. ( ) 2;3.D Câu 58: Miền nghiệm của hệ bất phương trình 0 33 5 xy xy xy −  −−  + không chứa điểm nào sau đây? A. ( ) 3;2.A B. ( ) 6;3.B C. ( ) 6;4.C D. ( ) 5;4.D Câu 59: Miền nghiệm của hệ bất phương trình 30 23 2 xy xy yx −  +−  + không chứa điểm nào sau đây? A. ( ) 0;1.A B. ( ) 1;1.B C. ( ) 3;0.C D. ( ) 3;1.D

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 11 Câu 60: Miền tam giác ABC kể cả ba cạnh ,, ABBCCA trong hình là miền nghiệm của hệ bất phương trình nào trong bốn hệ bất phương trình dưới đây? A. 20 20 220 xy xy xy +−  −+  −+ . B. 20 20 220 xy xy xy +−  −+  −+ . C. 20 20 220 xy xy xy +−  −+  −+ . D. 20 20 220 xy xy xy +−  −+  −+ . Câu 61: Giá trị nhỏ nhất của biểu thức Fyx =− trên miền xác định bởi hệ 22 24 5 yx yx xy −  −  + là A. min1 F = khi 2x = , 3y = B. min2 F = khi 0x = , 2y = C. min3 F = khi 1x = , 4y = . D. min0 F = khi 0x = , 0y = . Câu 62: Giá trị nhỏ nhất của biết thức Fyx =− trên miền xác định bởi hệ 22 2 54 xy xy xy +  −  +− là A. min 3F =− khi 1,2xy==− B. min0 F = khi 0,0xy== C. min 2F =− khi 42 , 33xy==− . D. min 8F = khi 2,6xy=−= . Câu 63: Cho hệ bất phương trình 2 3515 0 0 xy xy x y −  +     . Khẳng định nào sau đây là khẳng định sai? A. Trên mặt phẳng tọa độ Oxy , biểu diễn miền nghiệm của hệbất phương trình đã cho là miền tứ giác ABCO kể cả các cạnh với ( )0;3A , 259 ; 88 B    , ( )2;0C và ( )0;0O . B. Đường thẳng : xym+= có giao điểm với tứ giác ABCO kể cả khi 17 1 4 m − C. Giátrị lớnnhất củabiểuthức xy + ,với x và y thỏamãnhệbất phươngtrình đãcho là 17 4 . D. Giátrị nhỏnhất củabiểuthức xy + ,với x và y thõamãn hệbất phươngtrìnhđãcholà0.

ng tối đa 24g hương liệu, 9 lít nước và 210 g đường để pha chế nước cam và nước táo. Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu; pha chế 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu. Mỗi lít nước cam nhận được 60 điểm thưởng, m

lít nước táo nhận được 80 điểm thưởng. Đội A pha ch

và dành được điểm thưở

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 12 Câu 64: Giá trị lớn nhất của biết thức ( ) ;2 Fxyxy =+ với điều kiện 04 0 10 2100 y x xy xy     −−  +− là A. 6. B. 8. C. 10. D. 12. Câu 65: Giá trị nhỏ nhất của biết thức ( ) ;2 Fxyxy =− với điều kiện 05 0 20 20 y x xy xy     +−  −− là A. 10. B. 12. C. 8. D. 6. Câu 66: Biểu thức Fyx = đạt giá trị nhỏ nhất với điều kiện 22 22 5 0 xy xy xy x −+−  −  +   tại điểm ( ); Sxy có toạ độ là A. ( )4;1 . B. ( )3;1 . C. ( )2;1 . D. ( )1;1 . Câu 67: Biểu thức Lyx =− , với x và y thõa mãn hệ bất phương trình 2360 0 2310 xy x xy +−    −− , đạt giá trị lớn nhất là a và đạt giá trị nhỏ nhất là b . Hãy chọn kết quả đúng trong các kết quả sau: A. 25 8 a = và 2b =− B. 2a = và 11 12 b =− C. 3a = và 0b = D. 3a = và 9 8 b = Câu 68: Trong một cuộc thi pha chế, hai đội A, B được sử dụ

ỗi

ế được

lít nước cam và b lít nước táo

ng cao nhất. Hiệu số ab là A. 1. B. 3. C. 1. D. 6. Câu 69: Một hộ nông dân định trồng đậu và cà trên diện tích 2800 m . Nếu trồng đậu trên diện tích 2100 m thì cần 20công làm và thu được 3000000 đồng. Nếu trồng cà thì trên diện tích 2100 m cần 30 công làm và thu được 4000000 đồng. Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được nhiều tiền nhất khi tổng số công làm không quá 180 công. Hãy chọn phương án đúng nhất trong các phương án sau: A. Trồng 2600 m đậu; 2200 m cà. B. Trồng 2500 m đậu; 2300 m cà. C. Trồng 2400 m đậu; 2200 m cà. D. Trồng 2200 m đậu; 2600 m cà.

đa 24 gam hương liệu, 9 lít nước và 210 gam đường để pha chế nước ngọt loại I và nước ngọt loại II. Để pha chế 1 lít nước ngọt loại I cần 10 gam đường, 1 lít nước và 4 gam hương liệu. Để pha chế 1 lít nước ngọt loại II cần 30 gam đường, 1 lít nước và 1 gam hương liệu. Mỗi lít nước ngọt loại I được 80 điểm thưởng, mỗi lít nước ngọt loại II được 60 điểm thưởng. Hỏi số điểm thưởng cao nhất có thể của mỗi đội trong cuộc thi là bao

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 13 Câu 70: Một công ty TNHH trong một đợt quảng cáo và bán khuyến mãi hàng hóa (1 sản phẩm mới của công ty) cần thuê xe để chở trên 140 người và trên 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và

. Trong đó xe loại A có 10 chiếc, xe loại B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu, loại B giá 3 triệu. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất. Biết rằng xe A chỉ chở tối đa 20 người và 0,6 tấn hàng. Xe B chở tối đa 10 người và 1,5 tấn hàng. A. 4 xe A và 5 xe B . B. 5 xe A và 6 xe B . C. 5 xe A và 4 xe B . D. 6 xe A và 4 xe B Câu 71: Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilogam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilogam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền một kg thịt bò là 160 nghìn đồng, 1 kg thịt lợn là 110 nghìn đồng. Gọi , xy lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn. Tính 22 xy + A. 22 1,3xy+= B. 22 2,6xy+= C. 22 1,09xy+= D. 22 0,58xy+= Câu 72: Có hai cái giỏ đựng trứng gồm giỏ A và giỏ B, các quả trứng trong mỗi đều có hai loại là trứng lành và trứng hỏng. Tổng số trứng trong hai giỏ là 20 quả và số trứng trong giỏ A nhiều hơn số trứng trong giỏ B. Lấy ngẫu nhiên mỗi giỏ 1 quả trứng, biết xác suất để lấy được hai quả trứng lành là 55 84 Tìm số trứng lành trong giỏ A. A. 6. B. 14. C. 11. D. 10. Câu 73: Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối

nhiêu? A. 540. B. 600 . C. 640 . D. 720. Câu 74: Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm I và II Mỗi sản phẩm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đồng. Để sản xuất được một sản phẩm I thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ Để sản xuất được một sản phẩm II thì Chiến phải làm việc trong 2 giờ, Bình phải làm việc trong 6 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá 180 giờ và Bình không thể làm việc quá 220 giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là. A. 32 triệu đồng. B. 35 triệu đồng. C. 14 triệu đồng. D. 30 triệu đồng.

Câu 75: Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kiogam thịt bò chứa 800 đơn vị protein và 200đơn vị lipit. Mỗi kilogam thịt lợn chứa 600đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền một kg thịt bò là 160 nghìn đồng, một kg thịt lợn là 110 nghìn đồng. Gọi x , y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua. Tìm x , y để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn?

A. 0,3x = và 1,1y = B. 0,3x = và 0,7y = C. 0,6x = và 0,7y = D. 1,6x = và 0,2y =

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 14

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 1 DẠNG 1. TÌM NGHIỆM BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Câu 1: Điểm nào sau đây thuộc miền nghiệm của bất phương trình 3450 +−xy ? A. ( )1;1A B. ( )2;0B C. ( )1;2C D. ( )4;1D Lời giải Chọn A Thay tọa độ điểm ( )1;1A vào bất phương trình đã cho ta được: ( ) 3.14.150 +−− đúng. Do đó điểm ( )1;1A thuộc miền nghiệm của bất phương trình đã cho. Câu 2: Điểm (1;3)A là điểm thuộc miền nghiệm của bất phương trình: A. 3240 −+− xy B. 30+xy C. 30 −xy D. 240 −+xy Lời giải Chọn A Vì ( ) 3.12.340 −−+− là mệnh đề đúng nên ( )1;3A là điểm thuộc miền nghiệm của bất phương trình 3240 −+− xy . Câu 3: Điểm (0;3)A là điểm thuộc miền nghiệm của bất phương trình: A. 3240 xy −+− B. 30 xy− C. 240 xy−− D. 30xy+ Lời giải Chọn A Thay điểm (0;3)A vào từng đáp án, ta thấy A. 3.(0)2.(3)420 −+−=  nhận B. 3.(0)(3)30 −=− loại C. 2.(0)(3)470 −−=− loại D. (0)3.(3)90 += loại. Câu 4: Điểm nào sau đây không thuộc miền nghiệm của bất phương trình 450−+xy ? A. ( )5;0M . B. ( )1;0N . C. ( )1;3P . D. ( )2;1Q . Lời giải Chọn D CHƯƠNG II BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.III =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 2 Thay tọa độ điểm Q vào bất phương trình ta được 245010 −−+− . Do đó điểm Q không thuộc miền nghiệm của bất phương trình đã cho. Câu 5: Trong các mệnh đề sau, mệnh đề nào đúng? A. Trong mặt phẳng tọa độ Oxy , tập hợp các điểm có tọa độ là nghiệm của bất phương trình axbyc + không được gọi là miền nghiệm của nó B. Biểu diễn tập nghiệm của bất phương trình 2310 xy−+ trên hệ trục Oxy là đường thẳng 2310 xy−+= C. Trong mặt phẳng tọa độ Oxy , tập hợp các điểm có tọa độ là nghiệm của bất phương trình axbyc + được gọi là miền nghiệm của nó D. Nghiệm của bất phương trình axbyc + là tập rỗng Lời giải Chọn C Câu 6: Miền nghiệm của bất phương trình ( ) ( )22221 xyx −++−− là nửa mặt phẳng không chứa điểm nào trong các điểm sau? A. ( )0;0 . B. ( )1;1 . C. ( )4;2 . D. ( )1;1 . Lời giải Chọn C Ta có: ( ) ( )22221 xyx −++−− 22422 xyx−++−− 24xy + Dễ thấy tại điểm ( )4;2 ta có: 42.284 += . Câu 7: Miền nghiệm của bất phương trình ( ) ( ) 314253 xyx −+−− là nửa mặt phẳng chứa điểm nào trong các điểm sau? A. ( )0;0 . B. ( )4;2 . C. ( )2;2 . D. ( )5;3 . Lời giải Chọn A Ta có: ( ) ( ) 314253 xyx −+−− 334853 xyx −+−− 2480 xy −+ 240xy −+ Dễ thấy tại điểm ( )0;0 ta có: 02.0440 −+= Câu 8: Miền nghiệm của bất phương trình ( ) ( )322521 xyx +++− là nửa mặt phẳng chứa điểm nào trong các điểm sau? A. ( )3;4 B. ( )2;5 C. ( )1;6 D. ( )0;0 Lời giải Chọn D Ta có: ( ) ( )322521 xyx +++− 341022 xyx+++− 3480 xy ++ . Dễ thấy tại điểm ( )0;0 ta có: 3.04.080 ++ Câu 9: Miền nghiệm của bất phương trình ( ) ( ) 415329 xyx −+−− là nửa mặt phẳng chứa điểm nào trong các điểm sau? A. ( )0;0 B. ( )1;1 C. ( )1;1 D. ( )2;5

xét: chỉ có cặp số ( )2;3 không thỏa bất phương trình.

Câu 12: Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình 21 xy+ ?

A. ( )2;1 B. ( )3;7

C. ( )0;1 D. ( )0;0

Lời giải ChọnC.

Nhận xét: chỉ có cặp số ( )0;1 không thỏa bất phương trình.

Câu 13: Trong các cặp số sau đây, cặ

A. ( )5;0

Ta thay

nào

nghi

phương trình

xy−+

( )0;0

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 3 Lời giải Chọn D Ta có: ( ) ( ) 415329 xyx −+−− 4451529 xyx −+−− 25100 xy +− . Dễ thấy tại điểm ( )2;5 ta có: 2.25.5100 +− . Câu 10: Miền nghiệm của bất phương trình ( ) ( ) 323413 xyxy +++−+ là phần mặt phẳng chứa điểm nào trong các điểm sau? A. ( )3;0 . B. ( )3;1 . C. ( )1;1 . D. ( )0;0 . Lời giải ChọnC. Nhận xét: chỉ có cặp số ( )1;1 thỏa bất phương trình. Câu 11: Miền nghiệm của bất phương trình ( ) 529227 xxy +−−+ là phần mặt phẳng không chứa điểm nào trong các điểm sau?

( )2;1 . B. ( )2;3 . C. ( )2;1 . D. ( )0;0 . Lời giải ChọnC.

ận

không là

ệm của bất

450

B. ( )2;1 C. ( )1;3 D.

Lời giải ChọnB.

cặp số ( )2;1 vào bất phương trình 450xy−+ được 2450−−+ đo dó cặp số ( )2;1 không là nghiệm của bất phương trình 450xy−+ . Câu 14: Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn? A. 2530 xyz−+ B. 2 3240 xx+− C. 2 253 xy+ D. 235 xy+ Lời giải Chọn D Theo định nghĩa bất phương trình bậc nhất hai ẩn. Câu 15: Điểm nào sau đây thuộc miền nghiệm của bất phương trình 230 xy+− ? A. ( )1;3Q B. 3 1; 2 M    C. ( )1;1N D. 3 1; 2 P    Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 4 Chọn B Tập hợp các điểm biểu diễn nghiệm của bất phương trình 230 xy+− là nửa mặt phẳng bờ là đường thẳng 230 xy+−= và không chứa gốc tọa độ Từ đó ta có điểm 3 1; 2 M    thuộc miền nghiệm của bất phương trình 230 xy+− . Câu 16: Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi nửa mặt phẳng không bị gạch trong hình vẽ sau? A. 23 xy− . B. 3xy− . C. 23 xy− . D. 23 xy+ . Lời giải Chọn A Đường thẳng 23 xy−= đi qua điểm ( ) 3 0;3,;0 2    . Loại B Thay tọa độ điểm ( )0;0O vào vế trái của các bất phương trình ở đáp án A, C, D. Ta thấy đáp án A thỏa mãn. Câu 17: Hình vẽ nào sau đây biểu diễn miền nghiệm là của bất phương trình nào sau đây?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 5 A. 21xy B. 21xy C. 2xy D. 2xy Lời giải Chọn D Câu 18: Miền nghiệm của bất phương trình 23xy+ là phần tô đậm trong hình vẽ của hình nào, trong các hình vẽ dưới đây? A. B. C. D. Lời giải Trong mặt phẳng tọa độ vẽ đường thẳng :23dxy+= , ta thấy d chia thành 2 nửa mặt phẳng thì ta chọn nửa bên trái do 23xy+ . Câu 19: Miền nghiệm của bất phương trình 320 xy −++ không chứa điểm nào sau đây? A. ( )1;2A . B. ( )2;1B . C. 1 1; 2 C    . D. ( )3;1D . Lời giải Chọn A

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 6 Trước hết, ta vẽ đường thẳng ( ):320.dxy−++= Ta thấy ( )0;0 không là nghiệm của bất phương trình. Vậy miền nghiệm là nửa mặt phẳng bờ ( )d không chứa điểm ( ) 0;0. Câu 20: Miền nghiệm của bất phương trình 32(25)2(1) xyx +++− không chứa điểm nào sau đây? A. ( )1;2A B. 12 ; 1111 B    C. ( )0;3C D. ( )4;0D Lời giải Chọn B Đầu tiên, thu gọn bất phương trình đề bài đã cho về thành 34110. xy++ Ta vẽ đường thẳng ( ):34110.dxy++= Ta thấy ( )0;0 không là nghiệm của bất phương trình. Vậy miền nghiệm là nửa mặt phẳng không chứa điểm ( ) 0;0. Câu 21: Miền nghiệm của bất phương trình 21 xy+ không chứa điểm nào sau đây? A. ( ) 1;1.A B. ( )2;2B . C. ( )3;3C . D. ( )1;1D . Lời giải Chọn D

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 7 Trước hết, ta vẽ đường thẳng ( ):21.dxy+= Ta thấy ( )0;0 không là nghiệm của bất phương trình đã cho. Vậy miền nghiệm của bất phương trình là nửa mặt phẳng không chứa điểm ( ) 0;0. Câu 22: Miền nghiệm của bất phương trình ( ) ( ) 13132 xy +−− chứa điểm nào sau đây? A. ( )1;1A . B. ( )1;1B . C. ( )1;1C . D. ( )3;3D . Lời giải Chọn A Trước hết, ta vẽ đường thẳng ( ) ( ) ( ) :13132.dxy +−−= Ta thấy ( )0;0 không là nghiệm của bất phương trình đã cho. Vậy miền nghiệm là nửa mặt phẳng bờ ( )d không chứa điểm ( ) 0;0. Câu 23: Miền nghiệm của bất phương trình ( ) 22124xyx −+−+ chứa điểm nào sau đây? A. ( ) 1;1.A B. ( ) 1;5.B C. ( ) 4;3.C D. ( ) 0;4.D Lời giải Chọn B

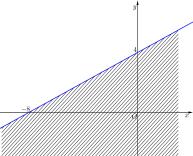
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 8 Đầu tiên ta thu gọn bất phương trình đã cho về thành 280.xy −+− Vẽ đường thẳng ( ):280.dxy−+−= Ta thấy ( )0;0 không là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng không chứa điểm ( ) 0;0. Câu 24: Miền nghiệm của bất phương trình 22220 xy−+− chứa điểm nào sau đây? A. ( ) 1;1.A B. ( )1;0B C. ( )2;2C D. ( ) 2;2.D Lời giải Chọn A Trước hết, ta vẽ đường thẳng ( ):22220.dxy−+−= Ta thấy ( )0;0 là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng bờ ( )d chứa điểm ( ) 0;0. Câu 25: Cho bất phương trình245 xy+ có tập nghiệm là S . Khẳng định nào sau đây là khẳng định đúng ? A. ( )1;1 S . B. ( )1;10 S . C. ( )1;1 S− . D. ( )1;5 S . Lời giải ChọnC. Ta thấy ( )1;1 thỏa mãn hệ phương trình do đó ( )1;1 là một cặp nghiệm của hệ phương trình. Câu 26: Cho bất phương trình 250xy−+ có tập nghiệm là S . Khẳng định nào sau đây là khẳng định đúng?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 9 A. ( )2;2 S B. ( )1;3 S C. ( )2;2 S− D. ( )2;4 S− Lời giải Chọn A Ta thấy ( )2;2 S vì 22.250 −+ . Câu 27: Miền nghiệm của bất phương trình 326 xy−− là A. B. C. D. Lời giải Chọn C Trước hết, ta vẽ đường thẳng ( ):326.dxy−=− Ta thấy ( )0;0 là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng bờ ( )d chứa điểm ( ) 0;0. Câu 28: Miền nghiệm của bất phương trình 326 xy+ là O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x O x y 2 3

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 10 A. B. C. D. Lời giải Chọn A Trước hết, ta vẽ đường thẳng ( ):326.dxy+= Ta thấy ( )0;0 không phải là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng không chứa điểm ( ) 0;0. Câu 29: Miền nghiệm của bất phương trình 326 xy+− là O 2 3 y x O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 11 A. B. C. D. Lời giải Chọn D Trước hết, ta vẽ đường thẳng ( ):326.dxy+=− Ta thấy ( )0;0 là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng chứa điểm ( ) 0;0. Câu 30: Cho bất phương trình 2320 xy −++ có tập nghiệm là S . Khẳng định nào sau đây là khẳng định đúng? A. ( )1;1 S . B. 2 ;0 2 S     . C. ( )1;2 S− . D. ( )1;0 S . Lời giải ChọnB. O x 2 3 y O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 12 Ta thấy 2 ;0 2 S     vì 2 2.3.020 2 −++= . Câu 31: Cặp số ( )(;) 2;3xy = là nghiệm của bất phương trình nào sau đây? A. 43xy  B. –370xy + C. 2–3–10 xy  D. –0xy  Lời giải Chọn D Ta có 2310 −=− nên Chọn D Câu 32: Cặp số ( )00 ; xy nào là nghiệm của bất phương trình 334 xy− . A. ( ) ( )00;2;2xy =− B. ( ) ( )00;5;1xy = C. ( ) ( )00;4;0xy =− D. ( ) ( )00;2;1xy = Lời giải Chọn B Thế các cặp số ( )00 ; xy vào bất phương trình: ( ) ( )00;2;2xy =− ( ) 334323.24 xy −−− ( ) ( )00;5;1xy = 3343.53.14 xy −− ( ) ( )00;4;0xy =− ( ) 3343.43.04 xy −−− ( ) ( )00;2;1xy = 3343.23.14 xy −− DẠNG 2. TÌM MIỀN NGHIỆM CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Câu 33: Cặp số ( ); xy nào sau đây là một nghiệm của hệ bất phương trình 20 ? 310 −  +− xy xy A. ( ) ( );2;1 =−−xy B. ( ) ( );4;0 =xy C. ( ) ( );1;2 =xy D. ( ) ( );3;4 =−−xy Lời giải Chọn C Thay các cặp số ( ); xy trong các phương án vào hệ bất phương trình trên, ta thấy ( ) ( );1;2 =xy thỏa mãn hệ bất phương trình. Câu 34: Trong mặt phẳng Oxy , điểm nào dưới đây thuộc miền nghiệm của hệ 31 22 xy xy −  + ? A. ( ) 1;0.P B. ( ) 1;1.N C. ( ) 1;1.M D. ( ) 0;1.Q Lời giải Chọn C Ta thấy tọa độ điểm M thỏa mãn hệ bất phương trình nên thuộc miền nghiệm của hệ bất phương trình

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 13 Câu 35: Trong mặt phẳng với hệ trục tọa độ Oxy , điểm nào dưới đây thuộc miền nghiệm của hệ 210 3210 +−  ++ xy xy ? A. ( )1;1 B. ( )0;1 C. ( )1;0 D. ( )1;3 Lời giải Chọn A Với 1 1 =−  = x y hệ phương trình 21000 321000 +−  ++  xy xy Câu 36: Miền nghiệm của hệ bất phương trình 39 3 xy xy +  − là phần mặt phẳng chứa điểm A. ( )1;2 B. ( )0;0 C. ( )2;1 D. ( )8;4 Lời giải Chọn D Ta có: ( ) ( ) 3.8491 8432 +   −  cả và đều đúng. Câu 37: Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình 20 2320 xy xy +−  −+ là A. ( )0;0 B. ( )1;1 C. ( )1;1 D. ( )1;1 Lời giải ChọnC. Ta thay cặp số ( )1;1 vào hệ ta thấy không thỏa mãn. Câu 38: Câu nào sau đây đúng?. Miền nghiệm của hệ bất phương trình 10 23 3 2(1)4 2 0 xy y x x  +−   −+     là phần mặt phẳng chứa điểm A. ( )2;1 . B. ( )0;0 . C. ( )1;1 . D. ( )3;4 . Lời giải Chọn A Nhận xét: chỉ có điểm ( )2;1 thỏa mãn hệ Câu 39: Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình 2310 540 xy xy +−  −+ ? A. ( )1;4 . B. ( )2;4 . C. ( )0;0 . D. ( )3;4 . Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 14 ChọnC. Nhận xét: chỉ có điểm ( )0;0 không thỏa mãn hệ. Câu 40: Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình 2510 250 10 xy xy xy −−  ++  ++ ? A. ( )0;0 . B. ( )1;0 . C. ( )0;2 . D. ( )0;2 . Lời giải ChọnC. Nhận xét: chỉ có điểm ( )0;2 thỏa mãn hệ Câu 41: Miền nghiệm của hệ bất phương trình 0 330 50 xy xy xy −  −+  +− là phần mặt phẳng chứa điểm A. ( )5;3 . B. ( )0;0 . C. ( )1;1 . D. ( )2;2 . Lời giải Chọn A Nhận xét: chỉ có điểm ( )5;3 thỏa mãn hệ Câu 42: Miền nghiệm của hệ bất phương trình 39 3 28 6 xy xy yx y +  −  −   là phần mặt phẳng chứa điểm A. ( )0;0 B. ( )1;2 C. ( )2;1 D. ( )8;4 Lời giải ChọnD. Nhận xét: chỉ có cặp số ( )8;4 thỏa bất phương trình 39 xy+ . Câu 43: Cho hệ bất phương trình 0 250 xy xy +  + có tập nghiệm là S . Khẳng định nào sau đây là khẳng định đúng? A. ( )1;1 S . B. ( )1;1 S−− . C. 1 1; 2 S −  . D. 12 ; 25 S −  . Lời giải Chọn C Thế đáp án, chỉ có 1 1; 2xy==− thỏa mãn hệ bất phương trình  chọn C Câu 44: Miền nghiệm của hệ bất phương trình 36 3 28 4 xy xy yx y +  −  −   là phần mặt phẳng chứa điểm:

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 16 Ta thấy ( )1;5 S− vì 10− . Câu 47: Cho hệ bất phương trình 0 310 x xy    ++  có tập nghiệm là S Khẳng định nào sau đây là khẳng định đúng? A. ( )1;2 S− B. ( )2;0 S C. ( )1;3 S− D. ( )3;0 S Lời giải ChọnD. Ta thấy ( )3;0 S vì 30 33.010    ++  . Câu 48: Cho hệ bất phương trình 3 1 10 2 xy xy −   −+  có tập nghiệm S . Khẳng định nào sau đây là khẳng định đúng ? A. ( )1;2 S− B. ( )2;1 S C. ( )5;6 S− D. S = Lời giải Chọn D Vì không có điểm nào thỏa hệ bất phương trình. Câu 49: Cho hệ bất phương trình 3 21 2 432 xy xy  −   − có tập nghiệm S . Khẳng định nào sau đây là khẳng định đúng ? A. 1 ;1 4 S−−   B. ( ) ;|432Sxyxy=−= C. Biểu diễn hình học của S là nửa mặt phẳng chứa gốc tọa độ và kể cả bờ d , với d là là đường thẳng 432 xy−= D. Biểu diễn hình học của S là nửa mặt phẳng không chứa gốc tọa độ và kể cả bờ d , với d là là đường thẳng 432 xy−= . Lời giải Chọn B

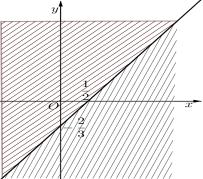
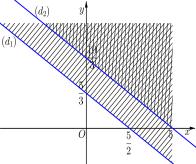
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 17 Trước hết, ta vẽ hai đường thẳng: ( )1 3 :21 2 dxy−= ( )2 :432dxy−= Thử trực tiếp ta thấy ( )0;0 là nghiệm của phương trình nhưng không phải là nghiệm của phương trình. Sau khi gạch bỏ các miền không thích hợp, tập hợp nghiệm của bất phương trình chính là các điểm thuộc đường thẳng ( ):432.dxy−= Câu 50: Cho hệ 235(1) 3 25(2) xy xy +   +  . Gọi 1S là tập nghiệm của bất phương trình, 2S là tập nghiệm của bất phương trình và S là tập nghiệm của hệ thì A. 12SS  . B. 21SS  . C. 2 SS = . D. 1 SS  . Lời giải Chọn B Trước hết, ta vẽ hai đường thẳng: ( )1 :235dxy+=

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 18 ( )2 3 :5 2 dxy+= Ta thấy ( )0;0 là nghiệm của cả hai bất phương trình. Điều đó có nghĩa gốc tọa độ thuộc cả hai miền nghiệm của hai bất phương trình. Say khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Câu 51: Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D? A. 0 326 y xy   + . B. 0 326 y xy   +− . C. 0 326 x xy   + . D. 0 326 x xy   +− . Lời giải Chọn A Dựa vào hình vẽ ta thấy đồ thị gồm hai đường thẳng ( )1 :0dy = và đường thẳng ( )2 :326.dxy+= Miền nghiệm gồm phần y nhận giá trị dương. Lại có ( )0;0 thỏa mãn bất phương trình 326. xy+ Câu 52: Miền nghiệm của hệ bất phương trình 20 32 3 xy xy yx −  +−  − chứa điểm nào sau đây? A. ( )1;0A . B. ( )2;3B . C. ( )0;1C . D. ( ) 1;0.D Lời giải Chọn D Trước hết, ta vẽ ba đường thẳng: ( )1 :20dxy−= ( )2 :32dxy+=− ( )3 :3dyx−= O 2 3 y x

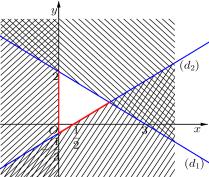
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 19 Ta thấy ( )0;1 là nghiệm của cả ba bất phương trình. Điều đó có nghĩa điểm ( )0;1 thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Câu 53: Miền nghiệm của hệ bất phương trình 2360 0 2310 xy x xy +−    −− chứa điểm nào sau đây? A. ( ) 1;2.A B. ( )0;2B . C. ( )1;3C . D. 1 0;. 3 D    Lời giải Chọn D Trước hết, ta vẽ ba đường thẳng: ( )1 :2360dxy+−= ( )2 :0dx = ( )3 :2310dxy−−= Ta thấy ( )1;1 là nghiệm của các ba bất phương trình. Điều này có nghĩa là điểm ( )1;1 thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ Câu 54: Miền nghiệm của hệ bất phương trình 210 350 x x − −+  chứa điểm nào sau đây? A. Không có B. 5 ;2. 3 B    C. ( ) 3;1.C D. 1 ;10 2 D    Lời giải Chọn A

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 20 Trước hết, ta vẽ hai đường thẳng: ( )1 :210dx −= ( )2 :350dx−+= Ta thấy ( )1;0 là không nghiệm của cả hai bất phương trình. Điều đó có nghĩa điểm ( )1;0 không thuộc cả hai miền nghiệm của hai bất phương trình. Vậy không có điểm nằm trên mặt phẳng tọa độ thỏa mãn hệ bất phương trình. Câu 55: Miền nghiệm của hệ bất phương trình 30 2310 y xy −  −+ chứa điểm nào sau đây? A. ( )3;4A B. ( )4;3B C. ( )7;4C D. ( ) 4;4.D Lời giải Chọn C Trước hết, ta vẽ hai đường thẳng: ( )1 :30dy−= ( )2 :2310dxy−+= Ta thấy ( )6;4 là nghiệm của hai bất phương trình. Điều đó có nghĩa điểm ( )6;4 thuộc cả hai miền nghiệm của hai bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 21 Câu 56: Miền nghiệm của hệ bất phương trình 20 32 xy xy −  +− không chứa điểm nào sau đây? A. ( ) 1;0.A B. ( ) 1;0.B C. ( )3;4C D. ( ) 0;3.D Lời giải Chọn B Trước hết, ta vẽ hai đường thẳng: ( )1 :20dxy−= ( )2 :32dxy+=− Ta thấy ( )0;1 là nghiệm của hai bất phương trình. Điều đó có nghĩa điểm ( )0;1 thuộc cả hai miền nghiệm của hai bất phương trình. Sau khi gạch bỏ phần không thích hợp, phần không bị gạch là miền nghiệm của hệ Câu 57: Miền nghiệm của hệ bất phương trình 3260 3 2(1)4 2 0 xy y x x −−   −+    không chứa điểm nào sau đây? A. ( )2;2A B. ( ) 3;0.B C. ( ) 1;1.C D. ( ) 2;3.D Lời giải Chọn C Trước hết, ta vẽ ba đường thẳng: ( )1 :3260dxy−−= ( )2 :43120dxy+−= ( )3 :0dx =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 22 Ta thấy ( )2;1 là nghiệm của cả ba bất phương trình. Điều đó có nghĩa điểm ( )2;1 thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Câu 58: Miền nghiệm của hệ bất phương trình 0 33 5 xy xy xy −  −−  + không chứa điểm nào sau đây? A. ( ) 3;2.A B. ( ) 6;3.B C. ( ) 6;4.C D. ( ) 5;4.D Lời giải Chọn A Trước hết, ta vẽ ba đường thẳng: ( )1 :0dxy−= ( )2 :33dxy−=− ( )3 :5dxy+= Ta thấy ( )5;3 là nghiệm của cả ba bất phương trình. Điều đó có nghĩa điểm ( )5;3 thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ miền không thích hợp, miền không bị gạch là miền nghiệm của hệ Câu 59: Miền nghiệm của hệ bất phương trình 30 23 2 xy xy yx −  +−  + không chứa điểm nào sau đây? A. ( ) 0;1.A B. ( ) 1;1.B C. ( ) 3;0.C D. ( ) 3;1.D Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 23 Chọn C Trước hết, ta vẽ ba đường thẳng: ( )1 :30dxy−= ( )2 :23dxy+=− ( )3 :2dxy+= Ta thấy ( )1;0 là nghiệm của cả ba bất phương trình. Điều đó có nghĩa điểm ( )1;0 thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Câu 60: Miền tam giác ABC kể cả ba cạnh ,, ABBCCA trong hình là miền nghiệm của hệ bất phương trình nào trong bốn hệ bất phương trình dưới đây? A. 20 20 220 xy xy xy +−  −+  −+ B. 20 20 220 xy xy xy +−  −+  −+ C. 20 20 220 xy xy xy +−  −+  −+ D. 20 20 220 xy xy xy +−  −+  −+ Lời giải FB Người gắn ID: Trần Lộc Chọn A Cạnh AB nằm trên đường thẳng 1 :20dxy+−= Cạnh AC nằm trên đường thẳng 2 :20dxy−+=

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 24 Cạnh BC nằm trên đường thẳng 3 :220dxy−+= Đường thẳng 1 :20dxy+−= chia mặt phẳng Oxy thành hai nửa mặt phẳng bờ 1d , thay tọa độ ( )0;0O vào vế trái 1d ta có 20− . Vậy nửa mặt phẳng chứa điểm O là miền nghiệm của bất phương trình 20xy+− . Tương tự nửa mặt phẳng chứa điểm O là miền nghiệm của bất phương trình 20xy−+ Nửa mặt phẳng không chứa điểm O là miền nghiệm của bất phương trình 220xy−+ . Từ (1),(2),(3) suy ra miền tam giác ABC kể cả ba cạnh ,, ABBCCA là miền nghiệm của hệ bất phương trình 20 20 220 xy xy xy +−  −+  −+ DẠNG 3. TÌM GIÁ TRỊ NHỎ NHẤT- GIÁ TRỊ LỚN NHẤT Câu 61: Giá trị nhỏ nhất của biểu thức Fyx =− trên miền xác định bởi hệ 22 24 5 yx yx xy −  −  + là A. min1 F = khi 2x = , 3y = . B. min2 F = khi 0x = , 2y = . C. min3 F = khi 1x = , 4y = D. min0 F = khi 0x = , 0y = Lời giải Chọn A Miền nghiệm của hệ 22 24 5 yx yx xy −  −  + là miền trong của tam giác ABC kể cả biên Ta thấy Fyx =− đạt giá trị nhỏ nhất chỉ có thể tại các điểm A , B , C .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 25 Tại ( )0;2A thì 2F = Tại ( )1;4B thì 3F = Tại ( )2;3A thì 1F = . Vậy min1 F = khi 2x = , 3y = Câu 62: Giá trị nhỏ nhất của biết thức Fyx =− trên miền xác định bởi hệ 22 2 54 xy xy xy +  −  +− là A. min 3F =− khi 1,2xy==− . B. min0 F = khi 0,0xy== . C. min 2F =− khi 42 , 33xy==− . D. min 8F = khi 2,6xy=−= . Lời giải Chọn C Biểu diễn miền nghiệm của hệ bất phương trình 22 2 54 xy xy xy +  −  +− trên hệ trục tọa độ như dưới đây: Giá trị nhỏ nhất của biết thức Fyx =− chỉ đạt được tại các điểm ( ) 4217 2;6,;,; 3333 ACB   . Ta có: ( ) ( ) ( ) 8;2;2FAFBFC==−=− . Vậy min 2F =− khi 42 , 33xy==− . Câu 63: Cho hệ bất phương trình 2 3515 0 0 xy xy x y −  +     . Khẳng định nào sau đây là khẳng định sai? A. Trên mặt phẳng tọa độ Oxy , biểu diễn miền nghiệm của hệbất phương trình đã cho là miền tứ giác ABCO kể cả các cạnh với ( )0;3A , 259 ; 88 B    , ( )2;0C và ( )0;0O B. Đường thẳng : xym+= có giao điểm với tứ giác ABCO kể cả khi 17 1 4 m −

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 26 C. Giátrị lớnnhất củabiểuthức xy + ,với x và y thỏamãnhệbất phươngtrình đãcho là 17 4 D. Giátrị nhỏnhất củabiểuthức xy + ,với x và y thõamãn hệbất phươngtrìnhđãcholà0. Lời giải Chọn B Trước hết, ta vẽ bốn đường thẳng: ( )1 :2dxy−= ( )2 :3515dxy+= ( )3 :0dx = ( )4 :0dy = Miền nghiệm là phần không bị gạch, kể cả biên. Câu 64: Giá trị lớn nhất của biết thức ( ) ;2 Fxyxy =+ với điều kiện 04 0 10 2100 y x xy xy     −−  +− là A. 6 B. 8 C. 10 D. 12 Lời giải Chọn C Vẽ đường thẳng 1 :10dxy−−= , đường thẳng 1d qua hai điểm ( )0;1 và ( )1;0 Vẽ đường thẳng 2 :2100dxy+−= , đường thẳng 2d qua hai điểm ( )0;5 và ( )2;4 . Vẽ đường thẳng 3 :4dy =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 27 Miền nghiệm là ngũ giác ABCOE với ( ) ( ) ( ) ( )4;3,2;4,0;4,1;0ABCE Ta có: ( ) 4;310F = , ( ) 2;410F = , ( ) 0;48F = , ( ) 1;01F = , ( ) 0;00F = . Vậy giá trị lớn nhất của biết thức ( ) ;2 Fxyxy =+ bằng 10. Câu 65: Giá trị nhỏ nhất của biết thức ( ) ;2 Fxyxy =− với điều kiện 05 0 20 20 y x xy xy     +−  −− là A. 10. B. 12. C. 8. D. 6. Lời giải Chọn A Biểu diễn miền ngiệm của hệ bất phương trình 05 0 20 20 y x xy xy     +−  −− trên hệ trục tọa độ như dưới đây:. Nhận thấy biết thức Fyx =− chỉ đạt giá trị nhỏ nhất tại các điểm ,, ABC hoặc D . Ta có: ( ) ( ) 7253;2510FAFB=−=−=−=− . ( ) ( ) 224,2202FCFD=−=−=−= . Vậy min 10F =− khi 0,5xy== .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 28 Câu 66: Biểu thức Fyx = đạt giá trị nhỏ nhất với điều kiện 22 22 5 0 xy xy xy x −+−  −  +   tại điểm ( ); Sxy có toạ độ là A. ( )4;1 . B. ( )3;1 . C. ( )2;1 . D. ( )1;1 . Lời giải Chọn A Biểu diễn miền ngiệm của hệ bất phương trình 22 22 5 0 xy xy xy x −+−  −  +   trên hệ trục tọa độ như dưới đây: Nhận thấy biết thức Fyx =− chỉ đạt giá trị nhỏ nhất tại các điểm , AB hoặc C . Chỉ ( )4;1C có tọa độ nguyên nên thỏa mãn. Vậy min 3F =− khi 4,1xy== Câu 67: Biểu thức Lyx =− , với x và y thõa mãn hệ bất phương trình 2360 0 2310 xy x xy +−    −− , đạt giá trị lớn nhất là a và đạt giá trị nhỏ nhất là b . Hãy chọn kết quả đúng trong các kết quả sau: A. 25 8 a = và 2b =− B. 2a = và 11 12 b =− C. 3a = và 0b = D. 3a = và 9 8 b = Lời giải Chọn B

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 29 Trước hết, ta vẽ ba đường thẳng: ( )1 :2360dxy+−= ( )2 :0dx = ( )3 :2310dxy−−= Ta thấy ( )0;0 là nghiệm của cả ba bất phương trình. Điều đó có nghĩa gốc tọa độ thuộc cả ba miền nghiệm của cả ba bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Miền nghiệm là hình tam giác ABC , với ( ) 0;2,A 75 ;, 46 B    1 0;. 3 C    Vậy ta có 202,a =−= 5711 6412 b =−=− DẠNG 4. ÁP DỤNG BÀI TOÁN THỰC TIỄN Câu 68: Trong một cuộc thi pha chế, hai đội A, B được sử dụng tối đa 24g hương liệu, 9 lít nước và 210 g đường để pha chế nước cam và nước táo. Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu; pha chế 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu. Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Đội A pha chế được a lít nước cam và b lít nước táo và dành được điểm thưởng cao nhất. Hiệu số ab là A. 1 B. 3 C. 1 D. 6 Lời giải Chọn C Gọi , xy lần lượt là số lít nước cam và nước táo mà mỗi đội cần pha chế ( )0;0xy Để pha chế x lít nước cam cần 30x g đường, x lít nước và x g hương liệu. Để pha chế y lít nước táo cần 10y g đường, y lít nước và 4y g hương liệu. Theo bài ra ta có hệ bất phương trình:

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 30 ( ) 3010210 9 * 424 0;0 xy xy xy xy +  +  +   . Số điểm đạt được khi pha x lít nước cam và y lít nước táo là ( ) ,y6080 Mxxy =+ . Bài toán trở thành tìm , xy để ( ), Mxy đạt giá trị lớn nhất. Ta biểu diễn miền nghiệm của hệ ( )* trên mặt phẳng tọa độ như sau: Miền nghiệm là ngũ giác ABCDE Tọa độ các điểm: ( )4;5A , ( )6;3B , ( )7;0C , ( )0;0D , ( )0;6E ( ), Mxy sẽ đạt giá trị lớn nhất, giá trị nhỏ nhất tại các đỉnh của miền nghiệm nên thay tọa độ các điểm vào biểu thức ( ), Mxy ta được: ( ) 4;5640M = ; ( ) 6;3600M = , ( ) 7;0420M = , ( ) 0;00M = , ( ) 0;6480M = . Vậy giá trị lớn nhất của ( ); Mxy bằng 640 khi 4;5xy== 4;51abab ==−=− Câu 69: Một hộ nông dân định trồng đậu và cà trên diện tích 2800 m . Nếu trồng đậu trên diện tích 2100 m thì cần 20công làm và thu được 3000000 đồng. Nếu trồng cà thì trên diện tích 2100 m cần 30 công làm và thu được 4000000 đồng. Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được nhiều tiền nhất khi tổng số công làm không quá 180 công. Hãy chọn phương án đúng nhất trong các phương án sau: A. Trồng 2600 m đậu; 2200 m cà. B. Trồng 2500 m đậu; 2300 m cà. C. Trồng 2400 m đậu; 2200 m cà. D. Trồng 2200 m đậu; 2600 m cà. Lời giải Chọn A Giả sử diện tích trồng đậu là x ;suy ra diện tích trồng cà là 8 x Ta có thu nhập thu được là ( ) ( ) ( )348.100001000032Sxxxx  =+−=−+  đồng. Tổng số công là ( ) 2030810240 xxx +−=−+ Theo giả thiết có 102401806 xx −+ x+y=9 x y E D≡O C B A 30x+10y=210 x+4y=24

Câu

Mà

t công

trong m

cáo và bán khuy

n mãi hàng hóa (1 sản phẩm mới c

a công ty) cần thuê xe để chở trên 140 người và trên 9 tấn

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 31

hàm số ( )Sx là hàm nghịch biến trên nên ( )Sx đạt giá trị lớn nhất khi 6x =

đó trồng 2600 m đậu, 2200 m cà.

70:

ộ

ty TNHH

ột đợt quảng

ế

ủ

hàng. Nơi thuê chỉ có hai loại xe A và B . Trong đó xe loại A có 10 chiếc, xe loại B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu, loại B giá 3 triệu. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất. Biết rằng xe A chỉ chở tối đa 20 người và 0,6 tấn hàng. Xe B chở tối đa 10 người và 1,5 tấn hàng. A. 4 xe A và 5 xe B . B. 5 xe A và 6 xe B . C. 5 xe A và 4 xe B . D. 6 xe A và 4 xe B . Lời giải Chọn D Gọi x là số xe loại A ( )010;xx  , y là số xe loại B ( )09;y y  . Khi đó tổng chi phí thuê xe là 43 Txy =+ Xe A chở tối đa 20 người, xe B chở tối đa 10 người nên tổng số người 2 xe chở tối đa được là 2010xy + Xe A chở được 0,6 tấn hàng, xe B chở được 1,5 tấn hàng nên tổng lượng hàng 2 xe chở được là 0,61,5xy + . Theo giả thiết, ta có 010 09 2010140 0,61,59 x y xy xy     +  + ( )* Biểu diễn miền nghiệm của hệ bất phương trình ( )* là tứ giác ABCD kể cả miền trong của tứ giác. Biểu thức 43 Txy =+ đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác ABCD.

gia đình cần

900 đơn

400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilogam thịt bò chứa 800

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 32 Tại các đỉnh ( ) ( ) ( )5 10;2;10;9;;9;5;4 2 ABCD    , ta thấy T đạt giá trị nhỏ nhất tại 5 4 x y =  = Khi đó min 32T = Câu 71: Một

ít nhất

vị protein và

đơn vị protein và 200 đơn vị lipit. Mỗi kilogam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền một kg thịt bò là 160 nghìn đồng, 1 kg thịt lợn là 110 nghìn đồng. Gọi , xy lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn. Tính 22 xy + A. 22 1,3xy+= . B. 22 2,6xy+= . C. 22 1,09xy+= . D. 22 0,58xy+= . Lời giải Chọn A Điều kiện: 01,6 x  ; 01,1 y  Khi đó số protein có được là 800600xy + và số lipit có được là 200400xy + Vì gia đình đó cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày nên điều kiện tương ứng là: 800600900à200400400 xyvxy ++ 869à22 xyvxy ++ 01,6 01,1 869 22 x y xy xy     +  + Miền nghiệm của hệ trên là miền nghiệm của tứ giác ABCD Chi phí để mua x kg thịt bò và y kg thịt lợn là 160110 Txy =+ Biết T đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác ABCD Tại A: 160.0,6110.0,7173T =+= Tại B: 160.1,6110.0,2278T =+= Tại C: 160.1,6110.1,1377T =+= Tại D: 160.0,3110.1,1169T =+=

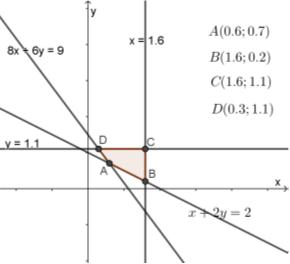
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 33 Vậy T đạt GTNN khi 0,3;1,1xy== 22220,31,11,3xy +=+= Câu 72: Có hai cái giỏ đựng trứng gồm giỏ A và giỏ B, các quả trứng trong mỗi đều có hai loại là trứng lành và trứng hỏng. Tổng số trứng trong hai giỏ là 20 quả và số trứng trong giỏ A nhiều hơn số trứng trong giỏ B. Lấy ngẫu nhiên mỗi giỏ 1 quả trứng, biết xác suất để lấy được hai quả trứng lành là 55 84 . Tìm số trứng lành trong giỏ A. A. 6. B. 14. C. 11. D. 10. Lời giải Chọn C Gọi a là số trứng lành, b là số trứng hỏng trong giỏ A. Gọi x là số trứng lành, y là số trứng hỏng trong giỏ B. Lấy ngẫu nhiên mỗi giỏ 1 quả trứng, xác suất để lấy được hai quả trứng lành: 55 84 ax abxy = ++ Do đó: ( ) ( )( ) ( )( ) ( )2 .55 1484 11 620 5 .55 100 2 ax abxyab a abxyxy x abxyabxyax    +++= = +++=+=  = +++  ++=   Suy ra: Giỏ A có 11 quả trứng lành. Câu 73: Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 gam hương liệu, 9 lít nước và 210 gam đường để pha chế nước ngọt loại I và nước ngọt loại II. Để pha chế 1 lít nước ngọt loại I cần 10 gam đường, 1 lít nước và 4 gam hương liệu. Để pha chế 1 lít nước ngọt loại II cần 30 gam đường, 1 lít nước và 1 gam hương liệu. Mỗi lít nước ngọt loại I được 80 điểm thưởng, mỗi lít nước ngọt loại II được 60 điểm thưởng. Hỏi số điểm thưởng cao nhất có thể của mỗi đội trong cuộc thi là bao nhiêu? A. 540. B. 600 . C. 640 . D. 720. Lời giải Chọn C

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 34 Gọi số lít nước ngọt loại I là x và số lít nước ngọt loại II là y. Khi đó ta có hệ điều kiện về vật liệu ban đầu mà mỗi đội được cung cấp: 10302103210 424424 99 ,0,0 xyxy xyxy xyxy xyxy ++ ++   ++    Điểm thưởng đạt được: 8060 Pxy =+ Bài toán đưa về tìm giá trị lớn nhất của biểu thức P trong miền D được cho bởi hệ điều kiện Biến đổi biểu thức 806080600PxyxyP =++−= đây là họ đường thẳng Δ trong hệ tọa độ Oxy Miền D được xác định trong hình vẽ bên dưới: Giá trị lớn nhất của P ứng với đường thẳng Δ đi qua điểm (5;4)A , suy ra: max 80.560.40640PPP+−=→== . Câu 74: Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm I và II . Mỗi sản phẩm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đồng. Để sản xuất được một sản phẩm I thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ. Để sản xuất được một sản phẩm II thì Chiến phải làm việc trong 2 giờ, Bình phải làm việc trong 6 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá 180 giờ và Bình không thể làm việc quá 220 giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là. A. 32 triệu đồng. B. 35 triệu đồng. C. 14 triệu đồng. D. 30 triệu đồng. Lời giải Chọn A Gọi x , y lần lượt là số sản phẩm loại I và loại II được sản xuất ra. Điều kiện x , y nguyên dương. x y O 5 6 9 4 3 6 7 9 Δ(P) A

Câu 75: Một gia đình cần ít nhất 900 đơn

protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kiogam thịt bò chứa 800 đơn vị protein và 200đơn vị lipit. Mỗi kilogam thịt lợn chứa 600đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền một kg thịt bò là 160 nghìn đồng, một kg thịt lợn là 110 nghìn đồng. Gọi x , y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua. Tìm x , y để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn? A. 0,3x = và 1,1y = B. 0,3x = và 0,7

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 35 Ta có hệ bất phương trình sau: 32180 6220 0 0 xy xy x y +  +     Miền nghiệm của hệ trên là Tiền lãi trong một tháng của xưởng là 0,50,4 Txy =+ Ta thấy T đạt giá trị lớn nhất chỉ có thể tại các điểm A , B , C . Vì C có tọa độ không nguyên nên loại. Tại ( )60;0A thì 30T = triệu đồng. Tại ( )40;30B thì 32T = triệu đồng. Vậy tiền lãi lớn nhất trong một tháng của xưởng là 32 triệu đồng.

vị

y = C. 0,6x = và 0,7y = D. 1,6x = và 0,2y = Lời giải Chọn A Theo bài ra ta có số tiền gia đình cần trả là 160.110.xy + với x , y thỏa mãn: 01,6 01,1 x y    Số đơn vị protein gia đình có là 0,8.0,6.0,9 xy+ 869 xy + ( )1d . Số đơn vị lipit gia đình có là0,2.0,4.0,422 xyxy ++ ( )2d . Bài toán trở thành: Tìm , xy thỏa mãn hệ bất phương trình 01,6 01,1 869 22 x y xy xy     +  + sao cho 160.110. Txy =+ nhỏ nhất. x y B 90 OA C

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 36 Vẽ hệ trục tọa độ ta tìm được tọa độ các điểm ( )1,6;1,1A ; ( )1,6;0,2B ; ( )0,6;0,7C ; ( )0,3;1,1D . Nhận xét: ( ) 377TA = nghìn, ( ) 278TB = nghìn, ( ) 173TC = nghìn, ( ) 169TD = nghìn. Vậy tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn thì 0,6x = và 0,7y = O x y A BC D 1 2 1 2 1,6x = 1,1y = 22xy+= 869 xy+=

S

C

i là tập xác định của hàm số.

Tập tất cả các giá trị y nhận được, gọi là tập giá trị của hàm số. Ta nói  ()| TfxxD = là tập

giá trị của ( )fx ( trên D ).

Chú ý: Cho KD  . Ta nói  ()|K TfxxK = là tập giá trị của ( )fx trên K .

Khi y là hàm số của x , ta có thể viết ( ) ( ) ,, ==

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 197 BÀI 1. HÀM SỐ VÀ ĐỒ THỊ 1. HÀM SỐ. TẬP XÁC ĐỊNH VÀ TẬP GIÁ TRỊ CỦA HÀM SỐ Cho một tập hợp khác rỗng D  . Giả sử x và y là hai đại lượng biến thiên và x nhận giá trị thuộc tập số D . Nếu với mỗi giá trị của x thuộc tập hợp số D có một và chỉ một giá trị tương ứng của y thuộc tập số thực thì ta có một hàm số Ta gọi x là biến số và y là hàm số của x . Tập hợp D gọ

yfxygx Khi một hàm số cho bằng công thức ( )yfx = mà không chỉ rỏ tập xác định thì ta quy ước: Tập xác định của hàm số ( )yfx = là tập hợp tất cả các giá trị của x để ( )fx có nghĩa. Một hàm số có thể cho bằng nhiều công thứccông thức. 2. ĐỒ THỊ HÀM SỐ Đồ thị của hàm số ( )= yfx xác định trên tập D là tập hợp tất cả các điểm ( )( ); Mxfx trên mặt phẳng toạ độ với mọi x thuộc D . Hay có thể diễn tả bằng: ( ) ( ) 0000 ;() MxyGyfx = với 0 xD  . CHƯƠNG III HÀM

Ố BẬ

HAI VÀ ĐỒ THỊ LÝ THUYẾT.I =

Hàm

(

Hàm

(

BÀI TẬP.

OFFICIAL

trường hợp nào thì y là hàm số của x ? a) 1xy+= ; b) 2 yx = ; c) 2 yx = ; d) 22 0xy−= .

6.2. Hãy cho một ví dụ về hàm số được cho bằng bảng hoặc biểu đồ. Hãy chỉ ra tập xác định và tập giá trị của hàm số đó.

6.3. Tìm tập xác định của các hàm số sau: a) 3 231yxx=++ ;b) 2 1 32 x y xx = −+ c) 11 yxx =++− .

6.4. Tìm tập xác định và tập giá trị của mỗi hàm số sau: a) 23yx=+ b) 22 yx =

6.5. Vẽ đồ thị các hàm số sau và chỉ ra các khoảng đồng biến, nghịch biến của chúng. a) 21yx=−+ ; b) 21 2 yx =−

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 198 3. SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ

số ( )yfx = xác định trên ( ); ab .

số ( )yfx = gọi là đồng biến (hay tăng) trên ( ); ab nếu

)12,; xxab và 12xx  ( ) ( )12 fxfx

số ( )yfx = gọi là nghịch biến (hay giảm) trên ( ); ab nếu

)12,; xxab và 12xx  ( ) ( )12 fxfx Nhận xét: + Hàm số ( )yfx = đồng biến trên ( ); ab khi và chỉ khi đồ thị hàm số “đi lên” trên khoảng đó. + Hàm số ( )yfx = nghịch biến trên ( ); ab khi và chỉ khi đồ thị hàm số “đi xuống” trên khoảng đó. 6.1. Xét hai đại lượng , xy phụ thuộc vào nhau theo các hệ thức dưới đây. Những

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 199 DẠNG 1. TÌM TẬP XÁC ĐỊNH CỦA HÀM SỐ Để tìm tập xác định D của hàm số ( )yfx = ta tìm điều kiện của x để ( )fx có nghĩa. Chú ý. Thông thường ( )yfx = cho bởi biểu thức đại số, ta xét một số trường hợp sau: + Hàm số ( ) () ()yfxux vx == có nghĩa khi ( )ux , ( )vx có nghĩa và ( ) 0vx  + Hàm số ( ) ( )yfxux == có nghĩa khi ( )ux có nghĩa và ( ) 0ux  . + Hàm số ( ) () () yfxux vx == có nghĩa khi ( )ux , ( )vx có nghĩa và ( ) 0vx  Câu 1. Tìm tập xác định của hàm số 21 1 x y x = Câu 2. Tìm tập xác định của hàm số 2 1 45y xx = ++ . Câu 3. Tìm tập xác định của hàm số 2 21 32 x y xx = −+ Câu 4. Tìm tập xác định của hàm số 22yx=− . Câu 5. Tìm tập xác định của hàm số 62 yx =− Câu 6. Tìm tập xác định của hàm số 31 22 x y x = . Câu 7. Tìm tập xác định của hàm số 3 62 x y x + = . Câu 8. Tìm tập xác định của hàm số 231yxx =−+−− Câu 9. Tìm tập xác định của hàm số ( ) 2 21 y xx = ++ . Câu 10. Tìm tập xác định của hàm số 21 x yx x =−− . HỆ THỐNG BÀI TẬP TỰ LUẬN.II == PHƯƠNG PHÁP.1 = BÀI TẬP.2 =

Câu

Tìm

Câu 12. Tìm

Câu 13. Tìm

Câu 14. Tìm

Câu 15. Tìm

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 200

11.

tập xác định của hàm số ( )2 2 324 y xxx = −++ .

tập xác định của hàm số ( )2 2 7624 x y xxx = +++

tập xác định của hàm số ( )2 5 893 x y xxx = .

tập xác định của hàm số 2 2442 x y xx = +−−

tập xác định của hàm số a) 31 22 x y x = −+ . b) ( )( ) 21 213 x y xx = +− . c) 2 1 45y xx = ++ . d) 3 21 32 x y xx + = −+ . Câu 16. Tìm tập xác định của hàm số a) 32yx=− b) 2 1yx=+ c) 211yxx =−+−− . d) 2 213yxxx =−++− . e) 22322221 yxxxx =++++−+− f) 2 1yxxx=+−+ Câu 17. Tìm tập xác định của hàm số a) ( ) 2 21 y xx = ++ . b) 21 x yx x =−− . c) 32 2 xx y x = + . d) ( )( ) 14 23 xx y xx −+− = . e) 1 1 1 yx xx =−+ + . f) 3322 2015 327 y xxx = −+−− . g) 1 827 1yxx x =++++ . h) ( )2 221yxxx =++−+ . DẠNG 2. TÌM ĐIỀU KIỆN ĐỂ HÀM SỐ XÁC ĐỊNH TRÊN MỘT TẬP K CHO TRƯỚC Bài toán. Cho hàm (,)= yfxm . Tìm tất cả các giá trị của m để hàm số xác định trên tập K . Bước 1: Tìm điều kiện xác định của hàm số (theo m ). Gọi D là tập xác định của hàm số. Bước 2: Hàm số xác định trên tập K khi và chỉ khi  KD. PHƯƠNG PHÁP.1 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 201 Một số lưu ý: + Hàm số (,) = A y fxm ( A là biểu thức luôn có nghĩa) xác định trên tập K khi và chỉ khi phương trình (,)0 =fxm vô nghiệm trên K . + Hàm số (,)= yfxm xác định trên tập K khi và chỉ khi bất phương trình (,)0 fxm nghiệm đúng với mọi  xK + Hàm số (,) = A y fxm ( A là biểu thức luôn có nghĩa) xác định trên tập K khi và chỉ khi bất phương trình (,)0 fxm nghiệm đúng với mọi  xK . + ( ) 1 12 2     KD KDD KD Câu 1. Cho hàm số 2 21 x y xxm + = ++ . Tìm tất cả các giá trị của m để hàm số xác định trên . Câu 2. Cho hàm số 2 yxm =− . Tìm tất cả các giá trị của m để hàm số có tập xác định là  )2;+ . Câu 3. Cho hàm số 356 1 xm y xm −+ = +− . Tìm tất cả các giá trị của m để hàm số xác định trên ( )0;+ Câu 4. Cho hàm số 21ymxxm =−+−+ . Tìm tất cả các giá trị của m để hàm số xác định trên ( )0;1 . Câu 5. Cho hàm số 4324(5)44 yxxmxxm =++++++ . Tìm tất cả các giá trị của m để hàm số xác định trên Câu 6. Tìm m để các hàm số sau đây xác định với mọi x thuộc khoảng ( )0;+ a) 21yxmxm =−+−− b) 234 1 xm yxm xm =−++ +− Câu 7. Tìm m để các hàm số a) 1 26yxm xm =+−++ xác định trên ( )1;0 . b) 2 1215yxmxm =−+++ xác định trên  1;3 . Câu 8. Tìm m để các hàm số BÀI TẬP.2 =

Câu

Tìm

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 202 a) 2 21 62 x y xxm + = −+− xác định trên b) 2 1 32 m y xxm + = −+ xác định trên toàn trục số DẠNG 3. TẬP GIÁ TRỊ CỦA HÀM SỐ Cho hàm số ( )yfx = có tập xác định D . Tập hợp ( ) TyfxxD == gọi là tập giá trị của hàm số ( )yfx =

tập giá trị của hàm số 54yx=−

2. Tìm tập giá trị của hàm số 23yx=+ . Câu 3. Tìm tập giá trị của hàm số 2 44yxx=−++ Câu 4. Tìm tập giá trị của hàm số 24 yx =− . Câu 5. Tìm tập giá trị của hàm số 2 1 45 y xx = −+ . DẠNG 4. TÍNH ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ * Phương pháp 1: Tìm tập xác định D của hàm số Với mọi 12 , xxD  , 12xx  . Tính ( ) ( )12 fxfx Nếu 12xx  12 ()()fxfx thì hàm số đã cho đồng biến (tăng). Nếu 12xx  12 ()()fxfx thì hàm số đã cho nghịch biến (giảm). * Phương pháp 2: PHƯƠNG PHÁP.1 = BÀI TẬP.2 = PHƯƠNG PHÁP.1 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 203 Tìm tập xác định D của hàm số Với mọi 12 , xxD  , 12xx  . Lập tỉ số ( ) ( )12 12 fxfx xx Nếu ( ) ( )12 12 0fxfx xx  thì hàm số đã cho đồng biến (tăng). Nếu ( ) ( )12 12 0fxfx xx  thì hàm số đã cho nghịch biến (giảm). Câu 1. Xét tính đồng biến và nghịch biến của hàm số ( ) 2 7fxx=− trên khoảng ( );0− và trên khoảng ( )0;+ Câu 2. Xét tính đồng biến và nghịch biến của hàm số ( ) 1fxx x = trên khoảng ( );1− và trên khoảng ( )1;+ . DẠNG 5. TÌM ĐIỀU KIỆN CỦA THAM SỐ ĐỂ HÀM SỐ ĐỒNG BIẾN (NGHỊCH BIẾN) TRÊN MỘT TẬP HỢP CHO TRƯỚC Hàm số đồng biến (nghịch biến) trên D . Ta xét ( ) ( )12 12 fxfx xx với mọi 12 , xxD  , 12xx  Để hàm số đồng biến thì ( ) ( )12 12 0fxfx xx  từ đó ta dễ dàng tìm được m thỏa mãn đề bài; ngược lại để hàm số nghịch biến thì ( ) ( )12 12 0fxfx xx  ta cũng dễ dàng tìm được m thỏa mãn đề bài Câu 1. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn  3;3 để hàm số ( ) ( ) 12fxmxm=++− đồng biến trên ? Câu 2. Tìm tất cả các giá trị thực của tham số m để hàm số ( ) 233ymxm =+++ nghịch biến trên Câu 3. Tìm tất cả các giá trị thực của tham số m để hàm số ( ) ( )2 12fxxmx=−+−+ nghịch biến trên khoảng ( )1;2 . BÀI TẬP.2 = PHƯƠNG PHÁP.1 = BÀI TẬP.2 =

chạy về vị trí hiện tại của tàu thứ nhất với vận tốc 7 hải lý/giờ. Hãy xác định thời điểm mà khoảng cách của hai tàu là nhỏ

3. Một của hàng buôn giày nhập một đôi với giá là USD. Cửa hàng ước tính rằng nếu đôi giày được bán với giá x USD thì mỗi tháng khách hàng sẽ mua ( )120 x đôi. Hỏi của hàng bán một đôi giày giá bao nhiêu thì thu được nhiều lãi nhất?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 204 DẠNG 6. BÀI TOÁN THỰC TẾ Bước 1: Lập biểu thức theo yêu cầu bài toán ( nếu cần); Bước 2: Khai thác giả thiết để xử lí bài toán phù hợp; Bước 3: Kết luận. Câu 1. Cho rằng diện tích rừng nhiệt đới trên trái đất được xác định bởi hàm số 718,34,6 St =− , trong đó S được tính bằng triệu hec ta, t tính bằng số năm kể từ năm 1990. Hãy tính diện tích rừng nhiệt đới vào các năm 1990 và 2018. Câu 2. Hai con tàu đang ở cùng một vĩ tuyến và cách nhau 5 hải lý. Đồng thời cả hai con tàu cùng khởi hành, một tàu chạy về hướng nam với 6 hải lý/giờ, còn tàu kia

nhất? Câu

40 PHƯƠNG PHÁP.1 = BÀI TẬP.2 =

S

C

i là tập xác định của hàm số.

Tập tất cả các giá trị y nhận được, gọi là tập giá trị của hàm số. Ta nói  ()| TfxxD = là tập

giá trị của ( )fx ( trên D ).

Chú ý: Cho KD  . Ta nói  ()|K TfxxK = là tập giá trị của ( )fx trên K .

Khi y là hàm số của x , ta có thể viết ( ) ( ) ,, ==

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 1 BÀI 1. HÀM SỐ VÀ ĐỒ THỊ 1. HÀM SỐ. TẬP XÁC ĐỊNH VÀ TẬP GIÁ TRỊ CỦA HÀM SỐ Cho một tập hợp khác rỗng D  . Giả sử x và y là hai đại lượng biến thiên và x nhận giá trị thuộc tập số D . Nếu với mỗi giá trị của x thuộc tập hợp số D có một và chỉ một giá trị tương ứng của y thuộc tập số thực thì ta có một hàm số Ta gọi x là biến số và y là hàm số của x . Tập hợp D gọ

Ố BẬ

HAI VÀ ĐỒ THỊ LÝ THUYẾT.I =

Hàm

(

OFFICIAL

trường hợp nào thì y là hàm s

a, b vì v

6.2. Hãy

i m

có duy

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 2 3. SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ

số ( )yfx = xác định trên ( ); ab .

số ( )yfx = gọi là đồng biến (hay tăng) trên ( ); ab nếu

)12,; xxab và 12xx  ( ) ( )12 fxfx

số ( )yfx = gọi là nghịch biến (hay giảm) trên ( ); ab nếu ( )12,; xxab và 12xx  ( ) ( )12 fxfx Nhận xét: + Hàm số ( )yfx = đồng biến trên ( ); ab khi và chỉ khi đồ thị hàm số “đi lên” trên khoảng đó. + Hàm số ( )yfx = nghịch biến trên ( ); ab khi và chỉ khi đồ thị hàm số “đi xuống” trên khoảng đó. 6.1. Xét hai đại lượng , xy phụ thuộc vào nhau theo các hệ thức dưới đây. Những

ố của x ? a) 1xy+= ; b) 2 yx = ; c) 2 yx = ; d) 22 0xy−= . Lời giải Ý

ớ

ỗ

x chỉ

nhất 1 giá trị y .

cho một ví dụ về hàm số được cho bằng bảng hoặc biểu đồ. Hãy chỉ ra tập xác định và tập giá trị của hàm số đó. Cách 1: Hàm số cho bằng bảng Ví dụ 1: Thống kê sô ca mắc covid trong 10 ngày đầu tháng 8 năm 2021 (theo bản tin dịch covid 19 của Bộ y tế). Ngày 1 2 3 4 5 6 7 8 9 10 Số ca 2025 2267 2173 935 1537 1497 2049 2002 1642 1466 Tập xác định : {1;2;3;4;5;6;7;8;9;10}D = Tập giá trị :  2025;2267;2173;935;1537;1497;2049;2002;1642;1466T = Cách 2: Hàm số cho bằng biểu đồ. BÀI TẬP.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 3 ➢Ví dụ 2: 6.3. Tìm tập xác định của các hàm số sau: a) 3 231yxx=++ ;b) 2 1 32 x y xx = −+ c) 11 yxx =++− . Lời giải a) 3 231yxx=++ ; Tập xác định : D = b) 2 1 32 x y xx = −+ Hàm số 2 1 32 x y xx = −+ xác định 2 1 320 2 x xx x  −+   . Vậy  \1;2D = c) 11 yxx =++− . Hàm số 11 yxx =++− xác định 10 11 10 x x x + −  − Vậy  1;1D =− 6.4. Tìm tập xác định và tập giá trị của mỗi hàm số sau: a) 23yx=+ b) 22 yx = Lời giải a) 23yx=+ Tập xác định : D = Tập giá trị :T = b) 22 yx = Tập xác định : D = Tập giá trị :  )0;T =+ . 6.5. Vẽ đồ thị các hàm số sau và chỉ ra các khoảng đồng biến, nghịch biến của chúng. a) 21yx=−+ ; b) 21 2 yx =− . Lời giải

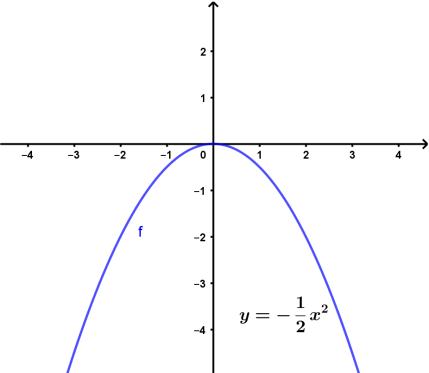
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 4 a) 21yx=−+ ; Hàm số luôn nghịch biến trên b) 21 2 yx =− Hàm số đồng biến trên khoảng ( );0− và nghịch biến trên khoảng ( )0;+ . 6.6. Giá thuê xe ô tô tự lái là 1,2 triệu đồng một ngày cho hai ngày đầu tiên và 900 nghìn đồng cho mỗi ngày tiếp theo. Tổng số tiền T phải trả là một hàm số của số ngày x mà khách thuê xe. a) Viết công thức của hàm số ( )TTx = b) Tính ( ) ( ) ( )2,3,5TTT và cho biết ý nghĩa của mỗi giá trị này. Lời giải a) Viết công thức của hàm số ( )TTx = . ( ) ( ) 1200000 02 24000009000002 2 xkhix Tx xkhix   =  +−  b) Tính ( ) ( ) ( )2,3,5TTT và cho biết ý nghĩa của mỗi giá trị này. ( ) 21200000.22400000.T == ( ) 324000009000003300000.T =+= ( ) 5240000027000005100000.T =+= DẠNG 1. TÌM TẬP XÁC ĐỊNH CỦA HÀM SỐ HỆ THỐNG BÀI TẬP TỰ LUẬN.II ==

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 5 Để tìm tập xác định D của hàm số ( )yfx = ta tìm điều kiện của x để ( )fx có nghĩa. Chú ý. Thông thường ( )yfx = cho bởi biểu thức đại số, ta xét một số trường hợp sau: + Hàm số ( ) () ()yfxux vx == có nghĩa khi ( )ux , ( )vx có nghĩa và ( ) 0vx  . + Hàm số ( ) ( )yfxux == có nghĩa khi ( )ux có nghĩa và ( ) 0ux  + Hàm số ( ) () () yfxux vx == có nghĩa khi ( )ux , ( )vx có nghĩa và ( ) 0vx  . Câu 1. Tìm tập xác định của hàm số 21 1 x y x = . Lời giải Hàm số xác định khi 101 xx − Vậy tập xác định của hàm số là  \1D = . Câu 2. Tìm tập xác định của hàm số 2 1 45y xx = ++ . Lời giải Ta có 2 45xx++= ( )2 210x ++ với mọi x . Vậy tập xác định của hàm số là D = Câu 3. Tìm tập xác định của hàm số 2 21 32 x y xx = −+ . Lời giải Hàm số xác định khi 3 320xx−+ ( )( )2 120xxx−+− 2 10 20 x xx −   +− 1 1 2 x x x      − 1 2 x x    − . Vậy tập xác định của hàm số là  \2;1D =− . PHƯƠNG PHÁP.1 = BÀI TẬP.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 6 Câu 4. Tìm tập xác định của hàm số 22yx=− . Lời giải Hàm số xác định 2201 xx − Vậy tập xác định của hàm số là  )1;D =+ Câu 5. Tìm tập xác định của hàm số 62 yx =− Lời giải Hàm số xác định 620263 xxx −−− . Vậy tập xác định của hàm số là ( ;3D =− . Câu 6. Tìm tập xác định của hàm số 31 22 x y x = Lời giải Hàm số xác định 2201 xx − Vậy tập xác định của hàm số là ( )1;D =+ Câu 7. Tìm tập xác định của hàm số 3 62 x y x + = . Lời giải Hàm số xác định 620263 xxx −−− . Vậy tập xác định của hàm số là ( );3D =− . Câu 8. Tìm tập xác định của hàm số 231yxx =−+−− Lời giải Hàm số xác định khi 230 10 x x −+  − 3 2 1 x x       3 1 2 x  . Vậy tập xác định của hàm số là 3 1; 2 D  =   . Câu 9. Tìm tập xác định của hàm số ( ) 2 21 y xx = ++ . Lời giải Hàm số xác định khi 20 10 x x +  + 2 1 x x −   − 1x − .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 7 Vậy tập xác định của hàm số là ( )1;D =−+ Câu 10. Tìm tập xác định của hàm số 21 x yx x =−− . Lời giải Hàm số xác định khi 2 10 0 x x  −  − 1 0 x x    (   ;0\1x−− Vậy tập xác định của hàm số là (   ;0\1D =−− . Câu 11. Tìm tập xác định của hàm số ( )2 2 324 y xxx = −++ Lời giải Hàm số xác định 2 1 320 2 40 4 x xx x x x  −+    +  − . Vậy tập xác định của hàm số là ( )  4;\1;2D =−+ . Câu 12. Tìm tập xác định của hàm số ( )2 2 7624 x y xxx = +++ . Lời giải Hàm số xác định 2 1 7601 6 2402 2 x xxx x xx x − − ++  −  +−  − . Vậy tập xác định của hàm số là ( )  2;\1D =−+− . Câu 13. Tìm tập xác định của hàm số ( )2 5 893 x y xxx = . Lời giải Hàm số xác định 2 1 8901 9 303 3 x xxx x xx x − − −−    −    Vậy tập xác định của hàm số là ( )  ;3\1D =−− . Câu 14. Tìm tập xác định của hàm số 2 2442 x y xx = +−− .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 8 Lời giải Hàm số xác định 240242 22 420242 0 2442024420 xxx x xxx x xxxxx +−−  −  −−−   +−−+−  . Vậy tập xác định của hàm số là    2;2\0D =− . Câu 15. Tìm tập xác định của hàm số a) 31 22 x y x = −+ b) ( )( ) 21 213 x y xx = +− c) 2 1 45y xx = ++ . d) 3 21 32 x y xx + = −+ . Lời giải a) Hàm số xác định khi 2201 xx −+ Vậy tập xác định của hàm số là  \1D = b) Hàm số xác định khi 2101 2 30 3 x x x x + −    −   . Vậy tập xác định của hàm số là 1 \;3 2 D  =−  c) Ta có ( ) 2245210xxx++=++ với mọi x Vậy tập xác định của hàm số là D = . d) Hàm số xác định khi ( )( )32320120xxxxx −+−+− 2 1 101 1 202 2 x x x x xxx x  −      +−−    − Vậy tập xác định của hàm số là  \2;1D =− . Câu 16. Tìm tập xác định của hàm số a) 32yx=− . b) 2 1yx=+ . c) 211yxx =−+−− . d) 2 213yxxx =−++− . e) 22322221 yxxxx =++++−+− f) 2 1yxxx=+−+ Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 9 a) Hàm số xác định khi 2 320 3 xx− . Vậy tập xác định của hàm số là 2 ; 3 D  =+  b) Ta có 2 10x + với mọi x . Vậy tập xác định của hàm số là D = c) Hàm số xác định khi 2303 3 21 10 12 x x x x x −+    −   . Vậy tập xác định của hàm số là 3 1; 2 D  =   d) Hàm số xác định khi ( ) 22 210 10 3 330 30 xxx x x xx x   −+ −  − −   Vậy tập xác định của hàm số là  )3;D =+ e) Ta có ( ) ( ) 22 222 3222212111 yxxxxxx =++++−+−=+++−+ 22 2111212 xxxx =+++−+=++−+ Hàm số xác định khi ( )( )2 22 101 220 10111 10110 101 101 xx xx xx xx x xxx xx xx −−  −+−   +− − −−+   −   +−     Vậy tập xác định của hàm số là  1;1D =− f) Hàm số xác định khi 2 2 2 2 2 1013 24 1 10 1 xx x xxx xxx xxx  −+ −+  −+− +−+ −+− 2 22 0 00 10 0 00 00 101 1 x xx xx x xxx xx xx xxx − −  −+    −   −   −+  −+ Vậy tập xác định của hàm số là D = .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 10 Câu 17. Tìm tập xác định của hàm số a) ( ) 2 21 y xx = ++ b) 21 x yx x =−− c) 32 2 xx y x = + d) ( )( ) 14 23 xx y xx −+− = e) 1 1 1 yx xx =−+ + f) 3322 2015 327 y xxx = −+−− g) 1 827 1yxx x =++++ h) ( )2 221yxxx =++−+ Lời giải a) Hàm số xác định khi 202 1 101 xx x xx +− − +− Vậy tập xác định của hàm số là ( )1;D =−+ . b) Hàm số xác định khi 2 101 10 00 xx x xx  −  − −  . Vậy tập xác định của hàm số là (   ;0\1D =−− . c) Hàm số xác định khi 202 22 202 xx x xx − − +− . Vậy tập xác định của hàm số là ( 2;2D =− . d) Hàm số xác định khi 101 14 404 2 202 3 303 xx x xx x xx x xx −  −   −   − Vậy tập xác định của hàm số là    1;4\2;3D = . e) Hàm số xác định khi 101 11 00 0 101 xx x xx x xx − −    +− . Vậy tập xác định của hàm số là (   1;1\0D =− . f) Hàm số xác định khi 3333 2222 3270327 xxxxxx −+−−−+− 22327933xxxxx −+− Vậy tập xác định của hàm số là  \3D = .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 11 g) Ta có ( )2 111 8277171 111yxxxx xxx =++++=+++=+++ . Hàm số xác định khi 707 101 xx xx +−   − Vậy tập xác định của hàm số là  )  7;\1D =−+ hoặc  ) ( )7;11;D =−+ h) Ta có ( ) ( ) ( )22221111 yxxxxx =++−+=++−+ Hàm số xác định khi ( ) ( ) ( ) 22 1110111 xxxx ++−++++ ( ) ( ) ( ) 2 22 10 11010 1010 111 x x x x xx xx +    ++ +     ++   +++ Vậy tập xác định của hàm số là D = DẠNG 2. TÌM ĐIỀU KIỆN ĐỂ HÀM SỐ XÁC ĐỊNH TRÊN MỘT TẬP K CHO TRƯỚC Bài toán. Cho hàm (,)= yfxm . Tìm tất cả các giá trị của m để hàm số xác định trên tập K Bước 1: Tìm điều kiện xác định của hàm số (theo m ). Gọi D là tập xác định của hàm số Bước 2: Hàm số xác định trên tập K khi và chỉ khi  KD. Một số lưu ý: + Hàm số (,) = A y fxm ( A là biểu thức luôn có nghĩa) xác định trên tập K khi và chỉ khi phương trình (,)0 =fxm vô nghiệm trên K + Hàm số (,)= yfxm xác định trên tập K khi và chỉ khi bất phương trình (,)0 fxm nghiệm đúng với mọi  xK + Hàm số (,) = A y fxm ( A là biểu thức luôn có nghĩa) xác định trên tập K khi và chỉ khi bất phương trình (,)0 fxm nghiệm đúng với mọi  xK . + ( ) 1 12 2     KD KDD KD PHƯƠNG PHÁP.1 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 12 Câu 1. Cho hàm số 2 21 x y xxm + = ++ . Tìm tất cả các giá trị của m để hàm số xác định trên Lời giải Điều kiện xác định của hàm số là 2 x0++xm . Hàm số xác định trên R  2 x0++xm , với mọi  xR  2 0++=xxm vô nghiệm  0  1 140 4 − mm Câu 2. Cho hàm số 2 yxm =− . Tìm tất cả các giá trị của m để hàm số có tập xác định là  )2;+ Lời giải Điều kiện xác định của hàm số là 2  m x . Khi đó tập xác định của hàm số là ; 2  =+  m D . Yêu cầu bài toán thỏa mãn  24 2 == m m Câu 3. Cho hàm số 356 1 xm y xm −+ = +− . Tìm tất cả các giá trị của m để hàm số xác định trên ( )0;+ Lời giải Điều kiện xác định của hàm số là 56 3 1     − m x xm (*) Hàm số xác định trên ( )0;+  (*) nghiệm đúng với mọi ( )0; +x  ( ) 56 0 3 10;     −+ m m  560 6 1 10 5 −  − m m m Câu 4. Cho hàm số 21ymxxm =−+−+ . Tìm tất cả các giá trị của m để hàm số xác định trên ( )0;1 . Lời giải BÀI TẬP.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 13 Điều kiện xác định của hàm số là 1 2      xm m x (*) Hàm số xác định trên ( )0;1  (*) nghiệm đúng với mọi ( )0;1x  1 11 0 2   =   m mm . Câu 5. Cho hàm số 4324(5)44 yxxmxxm =++++++ . Tìm tất cả các giá trị của m để hàm số xác định trên . Lời giải Ta có ( ) ( ) ( ) 43222 4x54x412 xmxmxxm ++++++=+++  Điều kiện xác định của hàm số là:( )2 20++xm (*) Hàm số xác định trên R  (*) nghiệm đúng với mọi xR  ( )22 +− xmxR  0 −m  0m Câu 6. Tìm m để các hàm số sau đây xác định với mọi x thuộc khoảng ( )0;+ a) 21yxmxm =−+−− b) 234 1 xm yxm xm =−++ +− Lời giải a) Hàm số xác định khi 0 2101 2 xm xm m xm x −    + −−    ( )* ● Nếu 1 1 2 m mm +  thì ( )* xm . Khi đó tập xác định của hàm số là  );Dm=+ Yêu cầu bài toán ( )  )0;; m ++ 0m  : không thỏa mãn 1m  ● Nếu 1 1 2 m mm +  thì ( ) *1 2 m x +  . Khi đó tập xác định của hàm số là 1 ; 2 m D +  =+  . Yêu cầu bài toán ( ) 11 0;;01 22 mm m ++ ++−   : thỏa mãn điều kiện 1m  Vậy 1m − thỏa yêu cầu bài toán.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 14 b) Hàm số xác định khi 234034 2 10 1 m xm x xm xm −+     +−  − Do đó để hàm số xác định với mọi x thuộc khoảng ( )0;+ , ta phải có 434 0 4 312 310 1 m m m m m     −   . Vậy 4 1 3 m  thỏa yêu cầu bài toán. Câu 7. Tìm m để các hàm số a) 1 26yxm xm =+−++ xác định trên ( )1;0 b) 2 1215yxmxm =−+++ xác định trên  1;3 Lời giải a) Hàm số xác định khi 0 26 26026 xmxm mxm xmxm − + −+++  . Do đó để hàm số xác định trên ( )1;0 , ta phải có 11 31 2603 mm m mm −− −− +− Vậy 31 m −− thỏa yêu cầu bài toán. b) Hàm số xác định khi 22 121502151 xmxmxmxm −++++++ . ( )* Bài toán được chuyển về việc tìm m để ( )* nghiệm đúng với mọi x thuộc đoạn  1;3 Điều kiện cần: Bất phương trình nghiệm đúng với mọi x thuộc đoạn  1;3 nên nghiệm đúng với 1x = , 2x = , tức là ta có 982171 12171 82213231 83231 3 m m m m m mm +−− −+  =− −+ +−−   . Điều kiện đủ: Với 8m =− , ta có ( ) 22 *287112871 xxxx −+−−+ ( ) 22 2 2 2 2880 20 430 2860 430 xx x xx xx xx  −+ − −+  −+ −+  ( )( ) 10 30 101 13013 30310 30 x x xx xxx xxx x −   − − −− − −   −  : thỏa mãn.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 15 Vậy 8m =− thỏa yêu cầu bài toán. Câu 8. Tìm m để các hàm số a) 2 21 62 x y xxm + = −+− xác định trên . b) 2 1 32 m y xxm + = −+ xác định trên toàn trục số. Lời giải a) Hàm số xác định khi ( ) 226203110xxmxm −+−−+− . Để hàm số xác định với mọi x  ( )2 3110xm−+− đúng với mọi x  11011mm− . Vậy 11m  thỏa mãn yêu cầu bài toán. b) Hàm số xác định khi 2 2 1 10 11 32030 33 m m xxm xm −+    −+−+−   . Để hàm số xác định với mọi x  2 1 11 30 33 m xm −    −+−  đúng với mọi x  1 1 1 03 3 m m m −   −  Vậy 1 3 m  thỏa mãn yêu cầu bài toán. DẠNG 3. TẬP GIÁ TRỊ CỦA HÀM SỐ Cho hàm số ( )yfx = có tập xác định D . Tập hợp ( ) TyfxxD == gọi là tập giá trị của hàm số ( )yfx = Câu 1. Tìm tập giá trị của hàm số 54yx=− PHƯƠNG PHÁP.1 = BÀI TẬP.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 16 Lời giải Tập xác định: D = Ta có 554, xxxx − Vậy tập giá trị của hàm số T = Câu 2. Tìm tập giá trị của hàm số 23yx=+ Lời giải Điều kiện xác định: 0x  . Tập xác định:  )0;D =+ . Ta có 020233, xxxxD + . Vậy tập giá trị của hàm số  )3;T =+ . Câu 3. Tìm tập giá trị của hàm số 2 44yxx=−++ . Lời giải Tập xác định: D = . Ta có ( ) 2244288, yxxxx =−++=−−+ Vậy tập giá trị của hàm số ( ;8T =− . Câu 4. Tìm tập giá trị của hàm số 24 yx =− . Lời giải Điều kiện xác định: 2 4022 xx −− . Tập xác định:  2;2D =− xD ta có 22204442xxx −− Mặt khác: 2 40 x − . Nên 2 042,xxD− . Vậy tập giá trị của hàm số  0;2T = Câu 5. Tìm tập giá trị của hàm số 2 1 45 y xx = −+ . Lời giải Điều kiện xác định: ( ) 22450210xxx−+−+ , đúng x  . Tập xác định: D =

* Phương pháp 1:

Tìm

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 17 Ta có ( ) 2245211xxx−+=−+ ( )2 2110x −+ ( )2 1 1 21x  −+ Mặt khác: ( )2 1 0 21x  −+ . Nên ( )2 1 01 21x  −+ , xD . Vậy tập giá trị của hàm số ( 0;1T = . DẠNG 4. TÍNH ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ

tập xác định D của hàm số. Với mọi 12 , xxD  , 12xx  . Tính ( ) ( )12 fxfx Nếu 12xx  12 ()()fxfx thì hàm số đã cho đồng biến (tăng). Nếu 12xx  12 ()()fxfx thì hàm số đã cho nghịch biến (giảm). * Phương pháp 2: Tìm tập xác định D của hàm số Với mọi 12 , xxD  , 12xx  . Lập tỉ số ( ) ( )12 12 fxfx xx . Nếu ( ) ( )12 12 0fxfx xx  thì hàm số đã cho đồng biến (tăng). Nếu ( ) ( )12 12 0fxfx xx  thì hàm số đã cho nghịch biến (giảm). Câu 1. Xét tính đồng biến và nghịch biến của hàm số ( ) 2 7fxx=− trên khoảng ( );0− và trên khoảng ( )0;+ Lời giải TXĐ: D = PHƯƠNG PHÁP.1 = BÀI TẬP.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 18 Với mọi 12 , xxD  , 12xx  , ta có ( ) ( ) 22 121277fxfxxx−=−−+ 22 121212 ()()xxxxxx =−=−+ Với mọi ( )12,;0xx − và 12xx  ta có 12 0xx− và 12 0xx+ . Suy ra ( ) ( )12 0fxfx− hay ( ) ( )12 fxfx  . Vậy hàm số đã cho nghịch biến trên khoảng ( );0− Với mọi ( )12,0;xx + và 12xx  ta có 12 0xx− và 12 0xx+ Suy ra ( ) ( )12 0fxfx− hay ( ) ( )12 fxfx  . Vậy hàm số đã cho đồng biến trên khoảng ( )0;+ Câu 2. Xét tính đồng biến và nghịch biến của hàm số ( ) 1fxx x = trên khoảng ( );1− và trên khoảng ( )1;+ Lời giải TXĐ:  \1D = . Với mọi 12 , xxD  , 12xx  , ta có: ( ) ( )12 fxfx 12 1211 xx xx =− 21 12 (1)(1) xx xx = Với mọi ( )12,;1xx − và 12xx  ta có 21 0xx− và 1 1x  , 2 1x  Suy ra ( ) ( )12 0fxfx− hay ( ) ( )12 fxfx  Vậy hàm số đã cho nghịch biến trên khoảng ( );1− . Với mọi ( )12,1;xx + và 12xx  suy ra ( ) ( )12 0fxfx− hay ( ) ( )12 fxfx  Vậy hàm số đã cho nghịch biến trên khoảng ( )1;+ DẠNG 5. TÌM ĐIỀU KIỆN CỦA THAM SỐ ĐỂ HÀM SỐ ĐỒNG BIẾN (NGHỊCH BIẾN) TRÊN MỘT TẬP HỢP CHO TRƯỚC Hàm số đồng biến (nghịch biến) trên D . Ta xét ( ) ( )12 12 fxfx xx với mọi 12 , xxD  , 12xx  Để hàm số đồng biến thì ( ) ( )12 12 0fxfx xx  từ đó ta dễ dàng tìm được m thỏa mãn đề bài; ngược lại để hàm số nghịch biến thì ( ) ( )12 12 0fxfx xx  ta cũng dễ dàng tìm được m thỏa mãn đề bài PHƯƠNG PHÁP.1 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 19 Câu 1. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn  3;3 để hàm số ( ) ( ) 12fxmxm=++− đồng biến trên ? Lời giải Tập xác định: D = Với mọi 12 , xxD  , 12xx  , ta có: ( ) ( )12 12 fxfx xx ( ) ( ) 12 12 1212mxmmxm xx ++−−++−   = 1m =+ Hàm số đồng biến trên 101mm +− Mà m và  3;3m− nên  0;1;2;3m Vậy có 4 giá trị nguyên của m thỏa mãn đề bài. Câu 2. Tìm tất cả các giá trị thực của tham số m để hàm số ( ) 233ymxm =+++ nghịch biến trên Lời giải Tập xác định: D = . Với mọi 12 , xxD  , 12xx  , ta có: ( ) ( )12 12 fxfx xx ( ) ( ) 12 12 233233 mxmmxm xx +++−+++   = 23 m =+ Hàm số nghịch biến trên 230 m + 3 2 m − Câu 3. Tìm tất cả các giá trị thực của tham số m để hàm số ( ) ( )2 12fxxmx=−+−+ nghịch biến trên khoảng ( )1;2 Lời giải Xét ( )1;2D = Với mọi 12 , xxD  , 12xx  , ta có: ( ) ( )12 12 fxfx xx ( ) ( )22 1122 12 1212xmxxmx xx  −+−+−−+−+  = ( )( ) ( )( )121212 12 1 xxxxmxx xx −−++−− = ( )12 1xxm =−++− . Hàm số nghịch biến trên khoảng ( )1;2 ( )12 10xxm −++− , ( )12,1;2xx  BÀI TẬP.2 =

718,34,6 St =− , trong

được tính

ta,

tính bằng số năm kể từ năm 1990. Hãy tính diện tích rừng nhiệt đới vào các năm 1990 và 2018.

Lời giải

Vào năm 1990 ứng với 0t = nên diện tích rừng nhiệt đới vào năm 1999 là: 718,34,6.0718,3S =−= (ha).

Vào năm 2018 ứng với 28t = nên diện tích rừng nhiệt đới vào năm 2018 là: 718,34,6.28589,5S =−= (ha).

Câu 2. Hai con tàu đang ở cùng một vĩ tuyến và cách nhau 5 hải lý. Đồng thời cả hai con tàu cùng khởi hành, một tàu chạy về hướng nam với 6 hải lý/giờ, còn

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 20 ( )12 1mxx ++ , ( )12,1;2xx  (1). Ta có ( )12,1;2xx  ( )12 13xx ++ (2). Từ (1) và (2) 3m  . Vậy 3m  DẠNG 6. BÀI TOÁN THỰC TẾ Bước 1: Lập biểu thức theo yêu cầu bài toán ( nếu cần); Bước 2: Khai thác giả thiết để xử lí bài toán phù hợp; Bước 3: Kết luận. Câu 1. Cho rằng diện tích rừng nhiệt đới trên trái đất được xác định bởi hàm số

đó S

bằng triệu hec

tàu kia chạy về vị trí hiện tại của tàu thứ nhất với vận tốc 7 hải lý/giờ. Hãy xác định thời điểm mà khoảng cách của hai tàu là nhỏ nhất? Lời giải Gọi d là khoảng cách của hai tàu sau khi xuất phát t (giờ), 0t  . Ta có: 22222222 1111(5)(57)(6)857025 dABAABBAAtttt =+=−+=−+=−+ . Suy ra 2 2 7180685()85702585 171717 ddtttt ==−+=−+   . PHƯƠNG PHÁP.1 = BÀI TẬP.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 21 Khi đó 685 17mind = . Dấu "" = xảy ra  7 17 t = . Vậy sau 7 17 giờ xuất phát thì khoảng cách hai tàu nhỏ nhất là nhỏ nhất. Câu 3. Một của hàng buôn giày nhập một đôi với giá là USD. Cửa hàng ước tính rằng nếu đôi giày được bán với giá x USD thì mỗi tháng khách hàng sẽ mua ( )120 x đôi. Hỏi của hàng bán một đôi giày giá bao nhiêu thì thu được nhiều lãi nhất? Lời giải Gọi y (USD) là số tiền lãi của cửa hàng bán giày. Ta có ( )( )12040yxx=−− 2 1604800xx =−+− ( )2 8016001600x =−−+ . Dấu "" = xảy ra 80x = . Vậy cửa hàng lãi nhiều nhất khi bán đôi giày với giá 80 USD. 40

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 1 BÀI 1. HÀM SỐ VÀ ĐỒ THỊ Câu 1: Tập xác định của hàm số 4220182019yxx=−− là A. ( )1; −+ B. ( );0− C. ( )0;+ D. ( ); −+ Câu 2: Trong các hàm số sau, hàm số nào có tập xác định là ? A. 3231yxx=+− . B. 2 2x y x + = . C. 2 23 x y x + = . D. 2 1 x y x + = . Câu 3: Tập xác định của hàm số 1 1 x y x + = là: A. . B. . C. . D. ( )1;+ . Câu 4: Tập xác định của hàm số 3 22 x y x = là A.  \1 B.  \3 C.  \2 D. ( )1;+ Câu 5: Tập xác định của hàm số ( )2 2 3 x y x + = là A. ( );3− B. ( )3;+ C.  \3 D. Câu 6: Tập xác định D của hàm số 31 22 x y x = là A. D = . B.  )1;D =+ . C. ( )1;D =+ . D.  \1DR = . Câu 7: Tập xác định của hàm số 2 5 1 =y x là A.  \1 . B.  \1;1 . C.  \1 . D. . Câu 8: Tập xác định của hàm số ()51 15fxxx xx +− =+ −+ là CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.III ==

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 2 A. D = . B. \1}. {D = C. \5{}.D =− D. \5;1. {}D =− Câu 9: Tập xác định của hàm số 2 3 56 x y xx = là A.  \1;6D =− B.  \1;6D =− C.  1;6D =− D.  1;6D =− Câu 10: Tìm tập xác định D của hàm số ( )( )2 1 14 x y xx + = +− . A.  \2D = B.  \2D = C.  \1;2D =− D.  \1;2D =− Câu 11: Tập xác định D của hàm số 31yx=− là A. ( )0;D =+ . B.  )0;D =+ . C. 1 ; 3 D  =+  . D. 1 ; 3 D  =+  . Câu 12: Tập xác định của hàm số 82 =−− yxx là A. ( ;4− B.  )4;+ C.  0;4 D.  )0;+ Câu 13: Tập xác định của hàm số 42yxx=−+− là A. ( )2;4D = B.  2;4D = C.  2;4D = D. ( ) ( );24;D =−+ Câu 14: Tập xác định của hàm số 34 1 x y x + = là A.  \1 . B. . C. ( )1;+ . D.  )1;+ . Câu 15: Tập xác định của hàm số 1 3 y x = là A.  ) 3;.D =+ B. ( ) 3;.D =+ C. (  ;3.D =− D. ( ) ;3.D =− Câu 16: Tìm tập xác định của hàm số 1 1 4yx x =−+ + A.  )  1;\4 + B. ( )  1;\4 + C. ( )4; −+ D.  )1;+ Câu 17: Tìm tập xác định D của hàm số 23yxx=+−+ A.  )3;D =−+ B.  )2;D =−+ C. D = D.  )2;D =+ Câu 18: Tìm tập xác định D của hàm số 631yxx=−−− A. ( )1;2D = . B.  1;2D = . C.  1;3D = . D.  1;2D =− . Câu 19: Tìm tập xác định D của hàm số 4 2 4 yx x =−− + .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 3 A.  4;2D =− . B. ( 4;2D =− . C.  )4;2D = . D. ( 2;4D =− . Câu 20: Tập xác định của hàm số 2 42 12 xx y xx −++ = là A.  2;4 B. ( ) ( )3;22;4−−− C. ( )2;4 D.  )2;4 Câu 21: Tập xác định của hàm số 1 3 3yx x =−+ là: A.  \3D = B.  )3;D =+ C. ( )3;D =+ D. ( );3D =− Câu 22: Tập xác định của hàm số 2 31 56 −++ = −+ xx y xx là A.  )  1;3\2 . B.  1;2 . C.  1;3 . D. ( )2;3 . Câu 23: Tập xác định của hàm số 52 (2)1 x y xx = là A. 5 1;\{2} 2     . B. 5 ; 2  +   . C. 5 1;\{2} 2    . D. 5 1; 2    . Câu 24: Tập xác định của hàm số ( ) 52 21 x y xx = là A.  5 12 2 ;\    B. 5 2 ;  +   C.  5 12 2 ;\   D. 5 1 2 ;    Câu 25: Tập xác định D của hàm số ( ) 22 fxxx x −++ = là A.    2;2\0D =− . B.  2;2D =− . C. ( )2;2D =− . D. D = . Câu 26: Tập xác định của hàm số 35 4 1 x y x + =− là ( ; ab với , ab là các số thực. Tính tổng ab + A. 8ab+=− . B. 10ab+=− . C. 8ab+= . D. 10ab+= . Câu 27: Tìm tập xác định của hàm số 123yxxx =+++++ . A.  ) 1;.−+ B.  )2; −+ C.  )3; −+ D.  ) 0;. + Câu 28: Tập xác định D của hàm số 243 yxx =++− là A. ( ) 2;3.D =− B.  ) 3;.D =−+ C. (  ;3.D =− D.   2;3.D =− Câu 29: Tập xác định của hàm số 2332 yxx =−−− là

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 4 A.  . B. 3 ;2 2    . C. 2;)[ + . D. 3 ;2 2    . Câu 30: Tìm tập xác định D của hàm số 6 43 = x y x A. 4 ; 3  =−  D . B. 34 ; 23  =   D . C. 23 ; 34  =   D . D. 4 ; 3  =+  D . Câu 31: Tập xác định của hàm số 1 9 25 yx x =+− là A. 5 ;9 2 D  =    . B. 5 ;9 2 D  =   . C. 5 ;9 2 D  =   . D. 5 ;9 2 D  =   . Câu 32: Tìm tập xác định D của hàm số ( ) 1 321 x y xx + = . A.  1 ;\3 2 D  =−+  . B. D = . C.  1 ;\3 2 D  =+  . D.  1 ;\3 2 D  =+  . Câu 33: Hàm số nào sau đây có tập xác định là ? A. 2 2 4 x y x = + B. 22 13yxx=−+− C. 2 3 4 x y x = . D. 2 213yxx=−−− . Câu 34: Tìm tập xác định của hàm số 2 31 1 (4)5 x yx xx =−− . A.    1;5\2 . B. (;5] − . C.  [1;5)\2 . D.  [1;)\2;5 + . Câu 35: Tập xác định D của hàm số ( ) 34 24 x y xx + = −+ là A. ( )  4;\2D =−+ B.  )  4;\2D =−+ C. D = D.  \2D = Câu 36: Tập xác định D của hàm số ( ) 4 132 x y xx + = +− là A. 3 4;. 2 D  =−  B. 3 4;. 2 D  =−  C. 3 ;. 2 D  =−    D.  ) 3 4;11;. 2 D  =−−−  Câu 37: Tập xác định của hàm số ( ) 1 3 1 fxx x =−+ là

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 5 A. ( 1;3D = . B. ( )  );13;D =−+ . C.  1;3D = D. D = Câu 38: Tìm tập xác định D của hàm số 4 6 510yx x =−+ . A. (   ;6\2D =− . B.  \2 . C.  )6;D =+ . D. ( ;6D =− . Câu 39: Cho hàm số ( ) 1 1 3fxx x =−+ . Tập nào sau đây là tập xác định của hàm số ( )fx ? A. ( )1;+ . B.  )1;+ . C.  ) ( )1;33;+ . D. ( )  1;\3 + . Câu 40: Tập xác định của hàm số ( ) 38khi2 71khi2 xxx yfx xx  −++ ==  ++  là A. B.  \2 C. 8 ; 3  −   D.  )7; −+ Câu 41: Tập xác định D của hàm số ( ) 1 2132 22yxx x =−−+ là A. 13 ; 22 D  =   . B.  13;\1 22 D  =    . C.  3 ;\1 2 D  =−    . D. 3 ; 2 D  =−  . Câu 42: Tập xác định của hàm số 3 21 y x = +− là A.  )  2;\1D =−+− B.  \1DR=− C.  )2;D =−+ D. ( )1;D =+ Câu 43: Tập xác định của hàm số ( )2 1 564 x y xxx + = −+− là A.  )   1;4\2;3. B.  ) 1;4. C. (    1;4\2;3. D. ( )   1;4\2;3. Câu 44: Tập xác định của hàm số 2 32 x y xx = −+ là: A.  )0;D =+ B.  \1;2D = C.  \1;2D + = D. ( )0;D =+ Câu 45: Tìm tập xác định D của hàm số: ( ) 23 0 2 10 khi khi x x yfxx xx   ==   − A.  \2D = B.  )  1;\2D =+ C. ( ;1D =− D.  )1;D =+ Câu 46: Tập xác định của hàm số 3 2 43 =++ x yx x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 6 A.  )2; =−+D . B.  ) 2;\;33 44  =−+−  D . C. 33 ; 44  =−  D . D. \;33 44  =−  D . Câu 47: Tìm tập xác định D của hàm số 326 43 xx y x −+ = A. 24 ; 33 D  =   . B. 34 ; 23 D  =   . C. 23 ; 34 D  =   . D. 4 ;. 3 D  =−  Câu 48: Giả sử ( ); Dab = là tập xác định của hàm số 2 3 32 x y xx + = −+− . Tính 22Sab =+ A. 7S = . B. 5S = . C. 4S = . D. 3S = . Câu 49: Hàm số 2 2 78 31 xx y xx −+ = −+ có tập xác định   \;;. Dabab = Tính giá trị biểu thức 33 4.Qabab =+− A. 11Q = B. 14Q = C. 14Q =− D. 10Q = Câu 50: Với giá trị nào của m thì hàm số 2 21 23 x y xxm + = xác định trên . A. 4m − . B. 4m − . C. 0m  . D. 4m  . Câu 51: Tập xác định của hàm số 35 4 1 x y x + =− là ( ; ab với , ab là các số thực. Tính tổng ab + A. 8ab+=− . B. 10ab+=− . C. 8ab+= . D. 10ab+= . Câu 52: Tập tất cả các giá trị m để hàm số 2 1 23 yxm xx =+− −−+ có tập xác định khác tập rỗng là A. ( );3− . B. ( )3; −+ . C. ( );1− . D. ( ;1− . Câu 53: Cho hàm số ( ) 2 20192020 ,2212fxx xxm + = −+− với m là tham số. Số các giá trị nguyên dương của tham số m để hàm số ( )fx xác định với mọi x thuộc là A. vô số. B. 9. C. 11. D. 10. Câu 54: Tìm tất cả các giá trị thực của tham số m để hàm số 2 22xm y xm ++ = xác định trên khoảng ( )1;0 . A. 0 1 m m   − . B. 1m − . C. 0 1 m m   − . D. 0m  . Câu 55: Tìm giá trị của tham số m để hàm số 1 21 x y xm + = −+ xác định trên nửa khoảng ( 0;1 .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 7 A. 1 2 1 m m     . B. 1 2 1 m m     . C. 1 2 1 m m     . D. 1 2 1 m m     . Câu 56: Tìm giá trị của tham số m để hàm số 2 1 2 y xxm = xác định trên   2;3. A. 0m  B. 03 m  C. 0m  D. 3m  Câu 57: Tìm tất cả các giá trị của m để hàm số 2 1 x y xm = −+ xác định trên khoảng ( )0;2 ? A. 13 m  . B. 1 5 m m    . C. 35 m  . D. 1 3 m m    . Câu 58: Tìm tất cả các giá trị của m để hàm số 1 232 24 x yxm xm + =−+++ +− xác định trên ( );2−− A.  2;4m− . B. ( 2;3m− . C.  2;3m− . D. ( ;2m−− . Câu 59: Tìm tất cả các giá trị thực của tham số m để hàm số 21 mx y xm = −+− xác định trên ( )0;1 . A. (   ;12m−− . B.  3 ;2 2 m  −    . C. (   ;12m− . D. (   ;13m− . Câu 60: Tìm tập hợp tất cả các giá trị của tham số m để hàm số 2 ()34yfxxmx ==−+ có tập xác định là D = . A. 4 3 m  B. 4 3 m  C. 4 3 m  D. 4 3 m  Câu 61: Tìm m để hàm số ( ) 231yxxm =−−− xác định trên tập ( )1;+ ? A. 2m  B. 2m  C. 2m  D. 2m  Câu 62: Tất cả các giá trị của tham số m để hàm số 2331 5 xmx y xm xm −+− =+ −++ xác định trên khoảng ( )0;1 là A.    3;00;1m− B. 3 1; 2 m     C.  3;0m− . D.   3 4;01; 2 m  −   . Câu 63: Tìm m để hàm số 2 21 2x1 x y xm + = +−+ có tập xác định là . A. 1m  B. 0m  C. 2m  D. 3m 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 8 Câu 64: Cho hàm số ( ) 22 1 212 x y xmxmm + = −+++ . Tập các giá trị của m để hàm số xác định trên  )0;1 là ( )  )  );;; Tabcd =−+ . Tính Pabcd =+++ . A. 2P =− . B. 1P =− . C. 2P = . D. 1P = . Câu 65: Tìm các giá trị thực của tham số m để hàm số 2xm y xm ++ = xác định trên ( )1;2 A. 1 2 m m −   B. 1 2 m m −   C. 1 2 m m −   D. 12 m − Câu 66: Tìm tất cả các giá trị của m để hàm số 12 yxmxm =−++− xác định với 0x  A. 1m  B. 0m  C. 0m  D. 1m  Câu 67: Tập hợp tất cả giá trị của tham số m để hàm số 21yxm=−+ xác định với mọi  1;3x  là: A.  2 . B.  1 . C. (;2] − . D. (;1] − . Câu 68: Tìm tất cả các giá trị của m để hàm số 1 2 5 yxm x =−++ có tập xác định  )0;5D = A. 0m  . B. 2m  . C. 2m − . D. 2m = . Câu 69: Tìm tất cả các giá trị của m để hàm số 2 1 32 m y xxm + = −+ có tập xác định D = . A. 1 1 3 m − . B. 1m − . C. 1 3 m  . D. 1 3 m  . Câu 70: Tìm điều kiện của m để hàm số 2 yxxm =−+ có tập xác định D = A. 1 4 m  . B. 1 4 m  . C. 1 4 −m . D. 1 4 m  . Câu 71: Tìm m để hàm số ( ) 2232 35 xmx y xm xm −+− =+ −++ xác định trên khoảng ( )0;1 A. 3 1; 2 m     B.  3;0m− C.    3;00;1m− D.   3 4;01; 2 m  −   Câu 72: Cho hàm số ( ) 2142 2 fxxmmx =+−+−− xác định với mọi  0;2x khi  ; mab . Giá trị của tổng ab + bằng A. 2 B. 3 C. 4 D. 5 Câu 73: Tìm m để hàm số 1 232 248 x yxm xm + =−+++ +− xác định trên khoảng ( );2−− .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 9 A.  2;4m− . B.  )2;3m− . C. ( 2;3m− . D.  2;3m− . Câu 74: Có bao nhiêu giá trị nguyên âm của tham số m để tập xác định của hàm số 2 712 2 ymx xm =++− chứa đoạn  1;1 ? A. 0 B. 1 C. 2 D. Vô số Câu 75: Cho hàm số 12 yxmx =++− với 2m − . Có bao nhiêu giá trị của tham số m để tập xác định của hàm số có độ dài bằng 1? A. 1 B. 2 C. 3 D. 4 Câu 76: Chọn khẳng định đúng? A. Hàm số ()yfx = được gọi là nghịch biến trên K nếu 121212 ;, ()()xxKxxfxfx  B. Hàm số ()yfx = được gọi là đồng biến trên K nếu 121212 ;, ()()xxKxxfxfx  C. Hàm số ()yfx = được gọi là đồng biến trên K nếu 121212 ;, ()()xxKxxfxfx  . D. Hàm số ()yfx = được gọi là đồng biến trên K nếu 121212 ;, ()()xxKxxfxfx  Câu 77: Trong các hàm số sau, hàm số nào là hàm đồng biến trên ? A. 12 yx =− B. 32yx=+ C. 2 21yxx=+− D. ( )223yx=−− Câu 78: Trong các hàm số sau, hàm số nào nghịch biến trên ? A. yx = B. 2 yx =− C. 2 yx = D. 1 2 yx = Câu 79: Xét sự biến thiên của hàm số ( ) 3 =fx x trên khoảng ( )0;+ . Khẳng định nào sau đây đúng? A. Hàm số nghịch biến trên khoảng ( )0;+ . B. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng ( )0;+ . C. Hàm số đồng biến trên khoảng ( )0;+ D. Hàm số không đồng biến, không nghịch biến trên khoảng ( )0;+ Câu 80: Hàm số 21 1 x y x + = nghịch biến trên khoảng nào trong các khoảng sau? A. ( );2− B. 1 ; 2  −+   C. 3 1; 2    D. ( )1;+ Câu 81: Cho đồ thị hàm số ()yfx = có bảng biên thiên như sau. Khẳng định nào sau đây sai?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 10 A. Hàm số đồng biến trên khoảng ( ) ;0.− B. Hàm số nghịch biến trên khoảng ( ) 1;. + C. Hàm số nghịch biến trên khoảng ( ) ;0.− D. Hàm số đồng biến trên khoảng ( ) 0;1. Câu 82: Cho hàm số ( )yfx = có bảng biến thiên như hình bên dưới. Khẳng định nào sao đây là đúng? A. Hàm số đồng biến trên khoảng ( ); −+ B. Hàm số đồng biến trên khoảng ( );1− . C. Hàm số đồng biến trên khoảng ( );0− D. Hàm số đồng biến trên khoảng ( )1;+ . Câu 83: Cho hàm số ( )yfx = có bảng biến thiên như hình dưới đây Hàm số ( )yfx = đồng biến trên khoảng A. ( );5−− B. ( )1; −+ C. ( );1−− D. ( )5; −+ Câu 84: Hàm số ( )yfx = có đồ thị như hình vẽ sau:

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 11 Hàm số ( )yfx = đồng biến trên khoảng nào dưới đây A. ( )0;1 . B. ( )4;2 . C. ( )1;3 . D. ( )1;3 . Câu 85: Cho hàm số ( )yfx = có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ( );0− . B. ( )0;1 C. ( )1;+ D. ( )1;0 Câu 86: Cho hàm số ( )fx có bảng biến thiên như sau Hàm số nghịch biến trong khoảng nào dưới đây? A. ( );0− B. ( )1;+ C. ( )2;2 D. ( )0;1 Câu 87: Cho hàm số có đồ thị như hình vẽ Chọn đáp án sai. A. Hàm số nghịch biến trên khoảng ( );1−− B. Hàm số đồng biến trên khoảng ( )1;+ C. Hàm số nghịch biến trên khoảng ( )1;1 . D. Hàm số đồng biến trên khoảng ( )1;0 Câu 88: Cho hàm số có đồ thị như hình bên dưới.

Khẳng

nào sau

là đúng?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 12

định

đây

A. Hàm số nghịch biến trên khoảng ( )0;3 B. Hàm số đồng biến trên khoảng ( );1− C. Hàm số nghịch biến trên khoảng ( )0;2 D. Hàm số đồng biến trên khoảng ( );3− Câu 89: Cho hàm số ( )yfx = xác định trên khoảng ( ); −+ có đồ thị như hình vẽ dưới đây. Mệnh đề nào sau đây đúng? A. Hàm số đồng biến trên khoảng ( )0;2 B. Hàm số nghịch biến trên khoảng ( )3;0 C. Hàm số đồng biến trên khoảng ( )1;0 D. Hàm số nghịch biến trên khoảng ( )0;3 Câu 90: Trong mặt phẳng Oxy , điểm (1;)Ay thuộc đồ thị hàm số 3yx=+ lúc đó giá trị của y bằng: A. 4y = . B. 2y = . C. 1y = . D. 3y = . Câu 91: Cho hàm số ( ) 2 21fxx=+ . Giá trị ( )2f bằng A. 3 B. 3 C. 4 D. Không xác định. Câu 92: Trong mặt phẳng Oxy , biết điểm 0 (1;)My thuộc đồ thị hàm số 47.yx=+ Giá trị của 0y bằng: A. 7 B. 1 C. 2 D. 3 Câu 93: Cho hàm số ( ) 75yfxx==−− Khẳng định nào sau đây là đúng?

Câu

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 13 A. ( ) 12f =− . B. ( ) 217f = . C. ( ) 29f −= . D. 5 10 7f  −=  . Câu 94: Cho hàm số ( ) 32 fxx =− . Giá trị của hàm số tại điểm 2x =− bằng A. 1. B. 3 . C. 7 . D. 7 . Câu 95: Trong các điểm sau đây điểm nào thuộc đồ thị của hàm số? A. ( )1 .2;3M B. ( )2 0; 1.M C. 3 11 ; . 22 M    D. ( )4 .1;0M Câu 96: Cho hàm số 3 32yxx=−+ . Điểm nào sau đây thuộc đồ thị hàm số đã cho? A. ( )2;0 B. ( )1;1 C. ( )2;12 D. ( )1;1 Câu 97: Cho () P có phương trình 2 24yxx=−+ . Điểm nào sau đây thuộc đồ thị () P . A. ( )4;2Q . B. ( )3;1N . C. ( )4;0P = . D. ( )3;19M . Câu 98: Điểm nào sau đây thuộc đồ thị hàm số ( ) 1 2 x y xx + = ? A. ( )2;1M B. ( )1;0N C. ( )2;0P D. 1 0; 2Q   

99: Điểm nào sau đây thuộc đồ thị hàm số 1 1y x = ? A. ( )1 2;1M . B. ( )2 1;1M . C. ( )3 2;0M . D. ( )4 0;2M .

100: Trong các điểm sau đây, điểm nào thuộc đồ thị hàm số 32yxx=++− ? A. ( )3;0M . B. ( )1;2N . C. ( )5;83P + . D. ( )5;8Q .

101: Điểm sau đây không thuộc đồ thị hàm số 2 44xx y x −+ = ? A. ( )2;0A . B. 1 3; 3 B    . C. ( )1;1C . D. ( )1;3D . Câu 102: Tìm m để đồ thị hàm số 41yxm=+− đi qua điểm ( )1;2A A. 6m = . B. 1m =− . C. 4m =− . D. 1m = . Câu 103: Đồ thị hàm số ( ) 2 232 32 xkhix yfx xkhix + ==  − đi qua điểm có tọa độ nào sau đây ? A. ( )0;3 B. ( )3;6 C. ( )2;5 D. ( )2;1

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 14 Câu 104: Đồ thị của hàm số ( ) 212 32 khi khi xx yfx x + ==  − đi qua điểm nào sau đây? A. ( )0;3 B. ( )3;7 C. ( )2;3 D. ( )0;1 Câu 105: Cho hàm số 2 2 1 52 1 1 xxkhix y x khix x  − =    Điểm nào sau đây thuộc đồ thị hàm số? A. ( )4;1 . B. ( )2;3 . C. ( )1;3 . D. ( )2;1 . Câu 106: Cho hàm số 2 2 1 52 1 1 xxkhix y x khix x  − =    Điểm nào sau đây thuộc đồ thị hàm số? A. ( ) 4;1. B. ( ) 2;3. C. ( ) 1;3. D. ( ) 2;1. Câu 107: Cho hàm số ( ) 2 5 fxxa x + = + có ( ) 413f −= . Khi đó giá trị của a là A. 11a = . B. 21a = . C. 3a =− . D. 3a = . Câu 108: Cho hàm số ( ) 2 31;1 2 ;1 xxkhix fx xkhix  ++ =  −+ . Tính ( )2f . A. 1 B. 4 C. 7 D. 0 Câu 109: Hàm số ( ) 2 223 khi x2 1 2khi x<2 x fx x x   =   + . Tính ( ) ( )22Pff=+− A. 3P = . B. 7 3 P = . C. 6P = . D. 2P = . Câu 110: Cho hàm số ( ) 2 223 khi2 1 1khi2 x fxx x xx  +−  =   + . Tính ( ) ( )22Pff=+− . A. 5 3 P = . B. 8 3 P = . C. 6P = . D. 4P = . Câu 111: Cho hàm số ( ) 2 21 khi0 3khi0 xx yfx xx − ==   . Giá trị của biểu thức ( ) ( )11Pff =−+ là: A. 2. B. 0. C. 1. D. 4. Câu 112: Cho hàm số 1 () 21 x fx x  =   1 1 x x   . Giá trị của biểu thức (1)(1)(5)Tfff =−++ là A. 2T =− B. 7T =− C. 6T = D. 7T =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 15 Câu 113: Cho hàm số ( ) 41 4 1 34 x fxkhix x xkhix  +−  =   − . Tính ( ) ( )55ff+− . A. 5 2 . B. 15 2 . C. 17 2 . D. 3 2 .

BÀI 1. HÀM S

Câu

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 1

Ố DẠNG 1. TẬP XÁC ĐỊNH CỦA HÀM SỐ Câu 1: Tập xác định của hàm số 4220182019yxx=−− là A. ( )1; −+ B. ( );0− C. ( )0;+ D. ( ); −+ Lời giải Chọn D Hàm số là hàm đa thức nên xác định với mọi số thực x

2: Trong các hàm số sau, hàm số nào có tập xác định là ? A. 3231yxx=+− B. 2 2x y x + = C. 2 23 x y x + = D. 2 1 x y x + = Lời giải Chọn A Hàm số 3231yxx=+− là hàm đa thức bậc ba nên tập xác định là . Câu 3: Tập xác định của hàm số 1 1 x y x + = là: A. . B. . C. . D. ( )1;+ . Lời giải Chọn C Điều kiện xác định: 101xx− Vậy tập xác định của hàm số 1 1 x y x + = là  D\1 = Câu 4: Tập xác định của hàm số 3 22 x y x = là A.  \1 . B.  \3 . C.  \2 . D. ( )1;+ . Lời giải Chọn A CHƯƠNG VI HÀM SỐ VÀ ĐỒ THỊ HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.III ==

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 2 Điều kiện xác định : 2201 xx− Nên tập xác định của hàm số là :  \1D = . Câu 5: Tập xác định của hàm số ( )2 2 3 x y x + = là A. ( );3− . B. ( )3;+ . C.  \3 . D. . Lời giải Chọn C Điều kiện: 303.xx− TXĐ:   \3. Câu 6: Tập xác định D của hàm số 31 22 x y x = là A. D = B.  )1;D =+ C. ( )1;D =+ D.  \1DR = Lời giải Chọn D Hàm số 31 22 x y x = xác định khi 1x  . Vậy  \1DR = Câu 7: Tập xác định của hàm số 2 5 1 =y x là A.  \1 B.  \1;1 C.  \1 D. Lời giải Chọn B Hàm số đã cho xác định khi 2 1 10 1  −  − x x x Vậy tập xác định của hàm số là  \1;1=−D Câu 8: Tập xác định của hàm số ()51 15fxxx xx +− =+ −+ là A. D = B. \1}. {D = C. \5{}D =− D. \5;1. {}D =− Lời giải Chọn D Điều kiện: 101 505 xx xx −   +− Vậy tập xác định của hàm số là:  \1;5D =− . Câu 9: Tập xác định của hàm số 2 3 56 x y xx = là

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 3 A.  \1;6D =− B.  \1;6D =− C.  1;6D =− D.  1;6D =− Lời giải Chọn A Điều kiện 2 1 560 6 x xx x − −−   Vậy  \1;6D =− . Câu 10: Tìm tập xác định D của hàm số ( )( )2 1 14 x y xx + = +− A.  \2D = B.  \2D = C.  \1;2D =− D.  \1;2D =− Lời giải Chọn D Điều kiện xác định: 2 101 402 x x xx + −   − . Vậy  \1;2D =− Lưu ý: Nếu rút gọn 2 1 4y x = rồi khẳng định  \2D = là sai. Vì với 1x =− thì biểu thức ban đầu ( )( )2 1 14 x xx + +− không xác định. Câu 11: Tập xác định D của hàm số 31yx=− là A. ( )0;D =+ B.  )0;D =+ C. 1 ; 3 D  =+  D. 1 ; 3 D  =+  Lời giải Chọn C Hàm số 31yx=− xác định 1 310 3 xx − . Vậy: 1 ; 3 D  =+  Câu 12: Tập xác định của hàm số 82 =−− yxx là A. ( ;4− B.  )4;+ C.  0;4 D.  )0;+ Lời giải Chọn A Điều kiện xác định của hàm số là 820 − x 4 x , nên tập xác định là ( ;4− . Câu 13: Tập xác định của hàm số 42yxx=−+− là A. ( )2;4D = B.  2;4D = C.  2;4D = D. ( ) ( );24;D =−+ Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 4 Chọn B Điều kiện: 40 20 x x −  − 4 2 x x     suy ra TXĐ:  2;4D = . Câu 14: Tập xác định của hàm số 34 1 x y x + = là A.  \1 B. C. ( )1;+ D.  )1;+ Lời giải Chọn C Điều kiện xác định của hàm số là 10 10 101 1010 x x xx xx − − − −−  Vậy tập xác định của hàm số là ( )1;D =+ . Cách khác: Điều kiện xác định của hàm số là 101−xx . Vậy tập xác định của hàm số là ( )1;D =+ . Câu 15: Tập xác định của hàm số 1 3 y x = là A.  ) 3;.D =+ B. ( ) 3;.D =+ C. (  ;3.D =− D. ( ) ;3.D =− Lời giải Chọn D Điều kiện xác định 303 xx − . Vậy tập xác định của hàm số 1 3 y x = là ( ) ;3.D =− Câu 16: Tìm tập xác định của hàm số 1 1 4yx x =−+ + . A.  )  1;\4 + . B. ( )  1;\4 + . C. ( )4; −+ . D.  )1;+ . Lời giải Chọn D Điều kiện xác định của hàm số: 101 404 xx xx −   +− Suy ra tập xác định của hàm số là  )1;+ . Câu 17: Tìm tập xác định D của hàm số 23yxx=+−+ . A.  )3;D =−+ . B.  )2;D =−+ . C. D = . D.  )2;D =+ . Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 5 Chọn B Hàm số xác định khi và chỉ khi 20 2. 30 x x x + − + Vậy  )2;D =−+ . Câu 18: Tìm tập xác định D của hàm số 631yxx=−−− A. ( )1;2D = B.  1;2D = C.  1;3D = D.  1;2D =− Lời giải Chọn B Hàm số xác định khi và chỉ khi 6302 101 xx xx −  −  Vậy  1;2D = . Câu 19: Tìm tập xác định D của hàm số 4 2 4 yx x =−− + A.  4;2D =− . B. ( 4;2D =− . C.  )4;2D = . D. ( 2;4D =− . Lời giải Chọn B Hàm số xác định khi và chỉ khi 202 . 404 xx xx −   +− Vậy ( 4;2D =− . Câu 20: Tập xác định của hàm số 2 42 12 xx y xx −++ = là A.  2;4 . B. ( ) ( )3;22;4−−− . C. ( )2;4 . D.  )2;4 . Lời giải Chọn D ĐKXĐ: 2 4 40 2 2024 3 120 4 x x x xx x xx x  −  −+−  − −−   . Vậy, tập xác định của hàm số là  )2;4D =− Câu 21: Tập xác định của hàm số 1 3 3yx x =−+ là: A.  \3D = . B.  )3;D =+ . C. ( )3;D =+ . D. ( );3D =− . Lời giải Chọn C Tập xác định của hàm số là những giá trị x thỏa mãn: 30 3 30 x x x −  − .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 6 Câu 22: Tập xác định của hàm số 2 31 56 −++ = −+ xx y xx là A.  )  1;3\2 B.  1;2 C.  1;3 D. ( )2;3 Lời giải Chọn A Hàm số xác định  )   2 3 30 1 101;3\2 3 560 2  −  − +−   −+   x x x xx x xx x . Vậy tập xác định  )  1;3\2=−D . Câu 23: Tập xác định của hàm số 52 (2)1 x y xx = là A. 5 1;\{2} 2     . B. 5 ; 2  +   . C. 5 1;\{2} 2    . D. 5 1; 2    . Lời giải Chọn A Hàm số xác định khi: 520 20 10 10 x x x x −  −  −  −  5 2 2 1 1 x x x x           5 1 2 2 x x      Câu 24: Tập xác định của hàm số ( ) 52 21 x y xx = là A.  5 12 2 ;\    . B. 5 2 ;  +   . C.  5 12 2 ;\   . D. 5 1 2 ;    . Lời giải Chọn A Hàm số có điều kiện xác định là: 5 520 52 1 202 2 2101 x x x xx xxx  −   −  −   Vây tập xác định của hàm số là:  5 12 2 D;\  =    . Câu 25: Tập xác định D của hàm số ( ) 22 fxxx x −++ = là A.    2;2\0D =− . B.  2;2D =− . C. ( )2;2D =− . D. D = .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 7 Lời giải Chọn A Điều kiện xác định của hàm số là 202 202 00 xx xx xx − +−    Tập xác định của hàm số    2;2\0D =− . Câu 26: Tập xác định của hàm số 35 4 1 x y x + =− là ( ; ab với , ab là các số thực. Tính tổng ab + A. 8ab+=− . B. 10ab+=− . C. 8ab+= . D. 10ab+= . Lời giải Chọn D Điều kiện xác định: 101 359 400 11 xx xx xx −   +−−   ( )( ) 1 19 910 x x xx    −− . * Tập xác định (  1;91,910Dabab =→==→+= . Câu 27: Tìm tập xác định của hàm số 123yxxx =+++++ A.  ) 1;.−+ B.  )2; −+ C.  )3; −+ D.  ) 0;. + Lời giải Chọn A 101 2021 303 xx xxx xx +− +−−  +−  Câu 28: Tập xác định D của hàm số 243 yxx =++− là A. ( ) 2;3.D =− B.  ) 3;.D =−+ C. (  ;3.D =− D.   2;3.D =− Lời giải Chọn D Để hàm số 243 yxx =++− xác định thì  202 3032;3. xx x xx +− − − Câu 29: Tập xác định của hàm số 2332 yxx =−−− là A.  . B. 3 ;2 2    . C. 2;)[ + . D. 3 ;2 2    . Lời giải Chọn D Điều kiện 2303 3 202;2 22 x x x x x −   −   

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 8 Câu 30: Tìm tập xác định D của hàm số 6 43 = x y x A. 4 ; 3  =−  D . B. 34 ; 23  =   D . C. 23 ; 34  =   D . D. 4 ; 3  =+  D . Lời giải Chọn A Điều kiện xác định: 4 430 3 − xx Câu 31: Tập xác định của hàm số 1 9 25 yx x =+− là A. 5 ;9 2 D  =    . B. 5 ;9 2 D  =   . C. 5 ;9 2 D  =   . D. 5 ;9 2 D  =   . Lời giải Chọn A Điều kiện xác định: 909 5 25059. 2 2 x x x x x −   −    Tập xác định: 5 ;9 2 D  =    Câu 32: Tìm tập xác định D của hàm số ( ) 1 321 x y xx + = . A.  1 ;\3 2 D  =−+  B. D = C.  1 ;\3 2 D  =+  D.  1 ;\3 2 D  =+  Lời giải Chọn C Điều kiện xác định: 303 2101 2 x x x x −    −    . Vậy tập xác định của hàm số đã cho là:  1 ;\3 2 D  =+  . Câu 33: Hàm số nào sau đây có tập xác định là ? A. 2 2 4 x y x = + B. 22 13yxx=−+− C. 2 3 4 x y x = . D. 2 213yxx=−−− . Lời giải Chọn B

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 9 2 2 4 x y x = + có tập xác định là ( )0; + . 2 3 4 x y x = có tập xác định là  \2;2 . 2 213yxx=−−− có tập xác định là  )1; + . Câu 34: Tìm tập xác định của hàm số 2 31 1 (4)5 x yx xx =−− A.    1;5\2 . B. (;5] − . C.  [1;5)\2 . D.  [1;)\2;5 + . Lời giải Chọn C Điều kiện xác định 2 10 (4)50 50 x xx x −  −−  −  x[1;5)\2 . Câu 35: Tập xác định D của hàm số ( ) 34 24 x y xx + = −+ là A. ( )  4;\2D =−+ . B.  )  4;\2D =−+ . C. D = . D.  \2D = . Lời giải Chọn A Hàm số ( ) 34 24 x y xx + = −+ xác định khi và chỉ khi 202 404 xx xx −   +− . Vậy tập xác định của hàm số là ( )  4;\2D =−+ Câu 36: Tập xác định D của hàm số ( ) 4 132 x y xx + = +− là A. 3 4;. 2 D  =−  B. 3 4;. 2 D  =−  C. 3 ;. 2 D  =−    D.  ) 3 4;11;. 2 D  =−−−  Lời giải Chọn D Để hàm số ( ) 4 132 x y xx + = +− xác định thì:  ) 404 3 1014;11; 2 3203 2 xx xxx x x   +−   +−−−−  −   .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 10 Câu 37: Tập xác định của hàm số ( ) 1 3 1 fxx x =−+ là A. ( 1;3D = B. ( )  );13;D =−+ C.  1;3D = D. D = Lời giải Chọn A Hàm số xác định khi 30 10 x x −  − 3 1 x x     13 x  . Vậy tập xác định của hàm số là ( 1;3D = Câu 38: Tìm tập xác định D của hàm số 4 6 510yx x =−+ A. (   ;6\2D =− . B.  \2 . C.  )6;D =+ . D. ( ;6D =− . Lời giải Chọn A ĐKXĐ: 60 5100 x x −  − 6 2 x x     . Vậy tập xác định của hàm số là (    ;6\2.D =− Câu 39: Cho hàm số ( ) 1 1 3fxx x =−+ . Tập nào sau đây là tập xác định của hàm số ( )fx ? A. ( )1;+ B.  )1;+ C.  ) ( )1;33;+ D. ( )  1;\3 + Lời giải Chọn C Tập xác định là 10 13 3 x x x −   Câu 40: Tập xác định của hàm số ( ) 38khi2 71khi2 xxx yfx xx  −++ ==  ++  là A. B.  \2 C. 8 ; 3  −   D.  )7; −+ Lời giải Chọn A Câu 41: Tập xác định D của hàm số ( ) 1 2132 22yxx x =−−+ là A. 13 ; 22 D  =   . B.  13;\1 22 D  =    . C.  3 ;\1 2 D  =−    . D. 3 ; 2 D  =−  . Lời giải Chọn C

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 11 Điều kiện xác định của hàm số trên là 3203 2 220 1 x x x x −     −   Vậy tập xác định:  3 ;\1 2 D  =−    Câu 42: Tập xác định của hàm số 3 21 y x = +− là A.  )  2;\1D =−+− . B.  \1DR=− . C.  )2;D =−+ . D. ( )1;D =+ . Lời giải Chọn A Hàm số xác định khi 20 21 x x +   +  2 1 x x −   − . Câu 43: Tập xác định của hàm số ( )2 1 564 x y xxx + = −+− là A.  )   1;4\2;3. B.  ) 1;4. C. (    1;4\2;3. D. ( )   1;4\2;3. Lời giải Chọn A ĐK:  )  2 1 10 2 5601;4\2;3. 3 40 4 x x x xxx x x x +−    −+−  −   Vậy TXĐ:  )   1;4\2;3.D =− Câu 44: Tập xác định của hàm số 2 32 x y xx = −+ là: A.  )0;D =+ B.  \1;2D = C.  \1;2D + = D. ( )0;D =+ Lời giải Chọn C Điều kiện xác định 2 0 0 1 320 2 x x x xx x    −+   . Vậy  \1;2D + = .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 12 Câu 45: Tìm tập xác định D của hàm số: ( ) 23 0 2 10 khi khi x x yfxx xx   ==   − . A.  \2D = B.  )  1;\2D =+ C. ( ;1D =− D.  )1;D =+ Lời giải Chọn C Với 0x  thì 20x − nên hàm số xác định với mọi 0x  . Với 0x  : Hàm số xác định khi 101 xx − Vậy (  (  ( ;00;1;1D =−=− Câu 46: Tập xác định của hàm số 3 2 43 =++ x yx x A.  )2; =−+D . B.  ) 2;\;33 44  =−+−  D . C. 33 ; 44  =−  D . D. \;33 44  =−  D . Lời giải Chọn B Điều kiện xác dịnh của hàm số 20 430 +   −  x x 2 3 4 3 4   −   −      x x x  ) 2;\;33 44  =−+−  D . Câu 47: Tìm tập xác định D của hàm số 326 43 xx y x −+ = . A. 24 ; 33 D  =   B. 34 ; 23 D  =   C. 23 ; 34 D  =   D. 4 ;. 3 D  =−  Lời giải Chọn C Điều kiện xác định: 2 320 324 430433 3 x x x x x  −   −    Vậy tập xác định của hàm số là 24 ; 33 D  =   Câu 48: Giả sử ( ); Dab = là tập xác định của hàm số 2 3 32 x y xx + = −+− . Tính 22Sab =+ A. 7S = B. 5S = C. 4S = D. 3S =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 13 Lời giải Chọn B Hàm số xác định khi 2 32012xxx −+− TXĐ: ( )1;2D = nên 221; 52 abSab ==+ == Câu 49: Hàm số 2 2 78 31 xx y xx −+ = −+ có tập xác định   \;;. Dabab = Tính giá trị biểu thức 33 4.Qabab =+− A. 11Q = B. 14Q = C. 14Q =− D. 10Q = Lời giải Chọn B Hàm số 2 2 78 31 xx y xx −+ = −+ xác định khi: 2 310xx−+ . Gọi , ab là 2nghiệm của phương trình 2 310xx−+= . Theo Vi et có 3 .1 ab ab +=  = . Có 33 4 Qabab =+− ( ) ( )3 34 abababab=+−+− 273.34=−− 14= Vậy 14Q = . Câu 50: Với giá trị nào của m thì hàm số 2 21 23 x y xxm + = xác định trên . A. 4m − . B. 4m − . C. 0m  . D. 4m  . Lời giải Chọn B Hàm số 2 21 23 x y xxm + = xác định trên khi phương trình 2 230xxm−−−= vô nghiệm Hay 404mm  =+− Câu 51: Tập xác định của hàm số 35 4 1 x y x + =− là ( ; ab với , ab là các số thực. Tính tổng ab + . A. 8ab+=− B. 10ab+=− C. 8ab+= D. 10ab+= Lời giải Chọn D Ta có ( ) 3535419 4. 111 xxxx y xxx ++−−−+ =−==

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 14 Điều kiện xác định của hàm số: ( ) ( ) 909 10 1019 0199 10 909 1 101 xx xTM xxx xx x xx xL xx −+   −− −+   −+ −+    −   TXĐ: (1;9]D = Vậy 1,910.abab==+= Câu 52: Tập tất cả các giá trị m để hàm số 2 1 23 yxm xx =+− −−+ có tập xác định khác tập rỗng là A. ( );3− . B. ( )3; −+ . C. ( );1− . D. ( ;1− . Lời giải Chọn C Hàm số xác định khi và chỉ khi 2 23031 0 xxx xmxm − −−+   − Để hàm số có tập xác định khác tập rỗng thì 1m  Câu 53: Cho hàm số ( ) 2 20192020 ,2212fxx xxm + = −+− với m là tham số. Số các giá trị nguyên dương của tham số m để hàm số ( )fx xác định với mọi x thuộc là A. vô số. B. 9. C. 11. D. 10. Lời giải Chọn B Hàm số ( )fx xác định với mọi x thuộc 2 22120,.xxmx −+−  Phương trình 2 22120xxm−+−= vô nghiệm ( ) 1212010. mm  =−− Vì m là số nguyên dương nên   1;2;3;...;8;9.m Vậy có 9 giá trị nguyên dương của m thỏa đề bài. Câu 54: Tìm tất cả các giá trị thực của tham số m để hàm số 2 22xm y xm ++ = xác định trên khoảng ( )1;0 . A. 0 1 m m   − B. 1m − C. 0 1 m m   − D. 0m  Lời giải Chọn C Hàm số đã cho xác định xm . Khi đó tập xác định của hàm số là: ( ) ( );; Dmm=−+ .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 15 Yêu cầu bài toán ( ) 0 1;01 m D m  −  − Câu 55: Tìm giá trị của tham số m để hàm số 1 21 x y xm + = −+ xác định trên nửa khoảng ( 0;1 A. 1 2 1 m m     . B. 1 2 1 m m     . C. 1 2 1 m m     . D. 1 2 1 m m     . Lời giải Chọn B Hàm số xác định khi 21021xmxm −+− . Hàm số xác định trên (  (  2101 0;1210;1 2 211 1 m m m m m − −  − . Câu 56: Tìm giá trị của tham số m để hàm số 2 1 2 y xxm = xác định trên   2;3. A. 0m  . B. 03 m  . C. 0m  . D. 3m  . Lời giải Chọn A Điều kiện:  2 20,2;3xxmx−− ( )   ( )2 11,2;3 *xmx −+ Ta có: 23 x  112 x − ( )2 114 x − ( )  2 11,2;3xx − , dấu bằng xảy ra khi ( )2 **x = Từ ( )* và ( )** , ta suy ra: 110mm+ Vậy 0.m  Câu 57: Tìm tất cả các giá trị của m để hàm số 2 1 x y xm = −+ xác định trên khoảng ( )0;2 ? A. 13 m  B. 1 5 m m    C. 35 m  D. 1 3 m m    Lời giải Chọn D

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 16 Hàm số 2 1 x y xm = −+ xác định khi 101xmxm −+− . Hàm số xác định trên khoảng ( )0;2 khi và chỉ khi 101 123 mm mm −  −  . Câu 58: Tìm tất cả các giá trị của m để hàm số 1 232 24 x yxm xm + =−+++ +− xác định trên ( );2−− A.  2;4m− B. ( 2;3m− C.  2;3m− D. ( ;2m−− Lời giải Chọn C Hàm số xác định 2320 240 xm xm −++   +− 32 2 42 m x xm +     − Hàm số xác định trên ( );2−− ( ) 32 2 2 42;2 m m + −    −−− 432 422 m m −+   −− 2 3 m m −    23 m − . Câu 59: Tìm tất cả các giá trị thực của tham số m để hàm số 21 mx y xm = −+− xác định trên ( )0;1 . A. (   ;12m−− B.  3 ;2 2 m  −    C. (   ;12m− D. (   ;13m− Lời giải Chọn C Hàm số xác định trên ( ) ( ) 20 0;10;1 210 xm x xm −+    −+−  ( ) ( ) 2 2 0;10;1 121 xm xm xx xmxm − −   −+−  202 1 112 2 101 mm m mm m mm −   −   = −   Vậy (   ;12m− . Câu 60: Tìm tập hợp tất cả các giá trị của tham số m để hàm số 2 ()34yfxxmx ==−+ có tập xác định là D = . A. 4 3 m  . B. 4 3 m  . C. 4 3 m  . D. 4 3 m  . Lời giải Chọn B Điều kiện: 2 340xmx−+ . YCBT  2 340, xmxx−+ .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 17 22 2 9164 00 443 m m a −−+   . Câu 61: Tìm m để hàm số ( ) 231yxxm =−−− xác định trên tập ( )1;+ ? A. 2m  . B. 2m  . C. 2m  . D. 2m  . Lời giải Chọn B ĐK: 11 ; 33 mm xD++ =+  Để hàm số xác định trên ( )1;+ thì ( ) 11 1;;1132 33 mm mm ++ +++   Câu 62: Tất cả các giá trị của tham số m để hàm số 2331 5 xmx y xm xm −+− =+ −++ xác định trên khoảng ( )0;1 là A.    3;00;1m− . B. 3 1; 2 m     . C.  3;0m− D.   3 4;01; 2 m  −   Lời giải Chọn D Điều kiện xác định của hàm số là: 23023 0 505 xmxm xmxm xmxm −+−  −  −+++  TH1. 2358 mmm−+ tập xác định của hàm số là: 8Dm= loại. TH2. 2358 mmm−+ TXĐ của hàm số là:  )  23;5\ Dmmm =−+ . Để hàm số xác định trên khoảng ( )0;1 thì ( )0;1 D . 3 230 402 514 3 1 00 2 11 m m m mm m mm mm  − −  +−           . Suy ra   3 4;01; 2 m  −   . Câu 63: Tìm m để hàm số 2 21 2x1 x y xm + = +−+ có tập xác định là A. 1m  B. 0m  C. 2m  D. 3m 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 18 Lời giải Chọn B Hàm số có tập xác định khi 2 210,1100 xxmxmm +−+=+− Câu 64: Cho hàm số ( ) 22 1 212 x y xmxmm + = −+++ . Tập các giá trị của m để hàm số xác định trên  )0;1 là ( )  )  );;; Tabcd =−+ . Tính Pabcd =+++ A. 2P =− B. 1P =− C. 2P = D. 1P = Lời giải Chọn A Hàm số xác định khi ( ) 222120 2 xm xmxmm xm  −+++  + Do đó tập xác định của hàm số là  \2; Dmm =+ Vậy để hàm số xác định trên  )0;1 điều kiện là:  ) 202 ;20;111 01210 mm mmmm mmm +−  +  +−  Câu 65: Tìm các giá trị thực của tham số m để hàm số 2xm y xm ++ = xác định trên ( )1;2 A. 1 2 m m −   B. 1 2 m m −   C. 1 2 m m −   D. 12 m − Lời giải Chọn B Hàm số xác định khi 0 xmxm − . Do đó hàm số xác định trên ( )1;2 ( ) 1 1;22 m m m − −   . Câu 66: Tìm tất cả các giá trị của m để hàm số 12 yxmxm =−++− xác định với 0x  A. 1m  B. 0m  C. 0m  D. 1m  Lời giải Chọn B Điều kiện 101 20 2 xm xm m xm x −+−    −    . Hàm số xác định với 10 00 0 2 m xm m −     

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 19 Câu 67: Tập hợp tất cả giá trị của tham số m để hàm số 21yxm=−+ xác định với mọi  1;3x  là: A.  2 B.  1 C. (;2] − D. (;1] − Lời giải Chọn D Hàm số xác định khi 21021xmxm −+− . Hàm số xác định với mọi  1;3x  thì 2111 mm− . Câu 68: Tìm tất cả các giá trị của m để hàm số 1 2 5 yxm x =−++ có tập xác định  )0;5D = . A. 0m  . B. 2m  . C. 2m − . D. 2m = . Lời giải Chọn D Điều kiện xác định của hàm số đã cho là 20 50 xm x −+  − 2 5 xm x −    Hàm số có tập xác định  )0;5D = 202.mm −== Câu 69: Tìm tất cả các giá trị của m để hàm số 2 1 32 m y xxm + = −+ có tập xác định D = . A. 1 1 3 m − B. 1m − C. 1 3 m  D. 1 3 m  Lời giải Chọn C Hàm số 2 1 32 m y xxm + = −+ có tập xác định D = 2 110 11 1 1'0130 3320, 3 m m mm m m xxmxm +− −−    − −+    . Câu 70: Tìm điều kiện của m để hàm số 2 yxxm =−+ có tập xác định D = A. 1 4 m  B. 1 4 m  C. 1 4 −m D. 1 4 m  Lời giải Chọn A Hàm số 2 yxxm =−+ có tập xác định D = 2 0, xxmx −+ ( )0 do 1 0,14 aÑa m  =   =−  1 4 m  .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 20 Vậy 1 4 m  thỏa yêu cầu bài. Câu 71: Tìm m để hàm số ( ) 2232 35 xmx y xm xm −+− =+ −++ xác định trên khoảng ( )0;1 . A. 3 1; 2 m     B.  3;0m− C.    3;00;1m− D.   3 4;01; 2 m  −   Lời giải Chọn D *Gọi D là tập xác định của hàm số ( ) 2232 35 xmx y xm xm −+− =+ −++ . * Dx  0 230 50 xm xm xm −+   −++ =   23 5 m xm x xm −     + =   . *Hàm số 2331 5 xmx y xm xm −+− =+ −++ xác định trên khoảng ( )0;1  ( )0;1 D ( ) 230 51 0;1 m m m  −  +    3 2 4 1 0 m m m m      −        3 4;01; 2 m  −   . Câu 72: Cho hàm số ( ) 2142 2 fxxmmx =+−+−− xác định với mọi  0;2x khi  ; mab . Giá trị của tổng ab + bằng A. 2. B. 3. C. 4. D. 5. Lời giải Chọn A Hàm số ()2142 2 fxxmmx =+−+−− xác định khi: 12 84 xm xm −  − Hàm số xác định trên [0; 2] nên 13 120284 22 mmm −−  13 ; 22 m     2ab += Câu 73: Tìm m để hàm số 1 232 248 x yxm xm + =−+++ +− xác định trên khoảng ( );2−− A.  2;4m− B.  )2;3m− C. ( 2;3m− D.  2;3m− Lời giải Chọn D Tập xác định của hàm số là tập hợp các giá trị của x thỏa mãn điều kiện:

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 21 2320 2480 xm xm −++  +− 32 2 42 m x xm +     − Để hàm số xác định trên khoảng ( );2−− cần có: 32 2 2 422 m m + −   −− 2 3 m m −     2;3m − . Câu 74: Có bao nhiêu giá trị nguyên âm của tham số m để tập xác định của hàm số 2 712 2 ymx xm =++− chứa đoạn  1;1 ? A. 0 B. 1 C. 2 D. Vô số Lời giải Đáp án A. Hàm số xác định khi và chỉ khi: 202 712071 2 xm xm m mx x −    + +−    Để tập xác định của hàm số chứa đoạn  1;1 thì ta phải có 71 11/7 2 1 211/2 2 211/2 m m mm m m m +      −  − Vậy không có giá trị nguyên âm nào của m thỏa mãn yêu cầu bài toán. Câu 75: Cho hàm số 12 yxmx =++− với 2m − . Có bao nhiêu giá trị của tham số m để tập xác định của hàm số có độ dài bằng 1? A. 1 B. 2 C. 3 D. 4 Lời giải Đáp án A. Điều kiện xác định của hàm số: 101 1 20 2 2 x x m mx mx x +−  − −    Vậy 1; 2 m D  =−  . Độ dài của D bằng 1 khi và chỉ khi ( ) 110 2 m m −−== Vậy có 1 giá trị của m thỏa mãn yêu cầu bài toán. DẠNG 2. XÁC ĐỊNH SỰ BIẾN THIÊN CỦA HÀM SỐ CHO TRƯỚC Câu 76: Chọn khẳng định đúng? A. Hàm số ()yfx = được gọi là nghịch biến trên K nếu 121212 ;, ()()xxKxxfxfx  .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 22 B. Hàm số ()yfx = được gọi là đồng biến trên K nếu 121212 ;, ()()xxKxxfxfx  C. Hàm số ()yfx = được gọi là đồng biến trên K nếu 121212 ;, ()()xxKxxfxfx  D. Hàm số ()yfx = được gọi là đồng biến trên K nếu 121212 ;, ()()xxKxxfxfx  . Lời giải Chọn D Lí thuyết định nghĩa hàm số đồng biến, nghịch biến Câu 77: Trong các hàm số sau, hàm số nào là hàm đồng biến trên ? A. 12 yx =− B. 32yx=+ C. 2 21yxx=+− D. ( )223yx=−− Lời giải Chọn B 32yx=+ đồng biến trên vì có hệ số góc 30a = Câu 78: Trong các hàm số sau, hàm số nào nghịch biến trên ? A. yx = B. 2 yx =− C. 2 yx = D. 1 2 yx = Lời giải Chọn B Hàm số yaxb =+ với 0a  nghịch biến trên khi và chỉ khi 0a  . Câu 79: Xét sự biến thiên của hàm số ( ) 3 =fx x trên khoảng ( )0;+ . Khẳng định nào sau đây đúng? A. Hàm số nghịch biến trên khoảng ( )0;+ . B. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng ( )0;+ C. Hàm số đồng biến trên khoảng ( )0;+ . D. Hàm số không đồng biến, không nghịch biến trên khoảng ( )0;+ . Lời giải Chọn A ( ) ( ) ( ) ( ) ( ) ( ) 1212 2121 21 21212121 ,0;: 3 333 0 + −=−==− xxxx fxfxxxfxfx xxxxxxxx Vậy hàm số nghịch biến trên khoảng ( )0;+ Câu 80: Hàm số 21 1 x y x + = nghịch biến trên khoảng nào trong các khoảng sau? A. ( );2− B. 1 ; 2  −+   C. 3 1; 2    D. ( )1;+ Lời giải Chọn D

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 23 Tập xác định:  \1D = Lấy ( )12;;1xx − sao cho 12xx  Xét ( )( ) ( ) ( )( ) 121212212121 12 121212 21212212213 111111 xxxxxxxxxxxx yy xxxxxx ++−+−−+−+ −=−== Với ( )12;;1xx − và 12xx  , ta có 21 0xx− ; 1 10x − ; 21212 100 xyyyy −− Do đó hàm số nghịch biến trên ( );1− Lấy ( )12;1;xx + sao cho 12xx  . Xét ( )( ) ( ) ( )( ) 121212212121 12 121212 21212212213 111111 xxxxxxxxxxxx yy xxxxxx ++−+−−+−+ −=−== Với ( )12;1;xx + và 12xx  , ta có 21 0xx− ; 1 10x − ; 21212 100 xyyyy −− Do đó hàm số nghịch biến trên ( )1;+ . DẠNG 3. XÁC ĐỊNH SỰ BIẾN THIÊN THÔNG QUA BẢNG BIẾN THIÊN HOẶC ĐỒ THỊ CỦA HÀM SỐ Câu 81: Cho đồ thị hàm số ()yfx = có bảng biên thiên như sau. Khẳng định nào sau đây sai? A. Hàm số đồng biến trên khoảng ( ) ;0.− B. Hàm số nghịch biến trên khoảng ( ) 1;. + C. Hàm số nghịch biến trên khoảng ( ) ;0.− D. Hàm số đồng biến trên khoảng ( ) 0;1. Lời giải Theo bảng biến thiên thì hàm số nghịch biến trên khoảng ( ) ;0.− Câu 82: Cho hàm số ( )yfx = có bảng biến thiên như hình bên dưới. Khẳng định nào sao đây là đúng? A. Hàm số đồng biến trên khoảng ( ); −+ . B. Hàm số đồng biến trên khoảng ( );1− C. Hàm số đồng biến trên khoảng ( );0− . D. Hàm số đồng biến trên khoảng ( )1;+ Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 24 Dựa vào bảng biến thiên: khoảng ( );0− có mũi tên hướng lên, diễn tả hàm số đồng biến. Câu 83: Cho hàm số ( )yfx = có bảng biến thiên như hình dưới đây Hàm số ( )yfx = đồng biến trên khoảng A. ( );5−− . B. ( )1; −+ . C. ( );1−− . D. ( )5; −+ Lời giải Chọn B Câu 84: Hàm số ( )yfx = có đồ thị như hình vẽ sau: Hàm số ( )yfx = đồng biến trên khoảng nào dưới đây A. ( )0;1 B. ( )4;2 C. ( )1;3 D. ( )1;3 Lời giải Hàm số ( )yfx = đồng biến trên khoảng ( )0;1 Câu 85: Cho hàm số ( )yfx = có đồ thị là đường cong trong hình bên.

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. ( );0− . B. ( )0;1 C. ( )1;+ D. ( )1;0

Lời giải

Vì đồ thị hàm số đi lên khi ( )0;1x  nên chọn đáp án B

Câu 86: Cho hàm số ( )fx có bảng biến thiên như sau

OFFICIAL

Hàm số nghịch biến trong khoảng nào dưới đây?

A. ( );0−

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 25

B. ( )1;+ C. ( )2;2 D. ( )0;1 Lời giải Ta thấy trong khoảng ( )0;1 , mũi tên có chiều đi xuống. Do đó hàm số nghịch biến trong khoảng ( )0;1 . Đáp án D. Câu 87: Cho hàm số có đồ thị như hình vẽ. Chọn đáp án sai. A. Hàm số nghịch biến trên khoảng ( );1−− B. Hàm số đồng biến trên khoảng ( )1;+ . C. Hàm số nghịch biến trên khoảng ( )1;1 .

Câu

D. Hàm

Hàm

n C

Khẳng định nào sau

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 26

số đồng biến trên khoảng ( )1;0 . Lời giải

ọ

ừ đồ thị hàm số ta thấy:

số nghịch biến trong các khoảng: ( );1−− và ( )0;1 .

số đồng biến trong các khoảng: ( )1;0 và ( )1;+

88: Cho hàm số có đồ thị như hình bên dưới.

đây là đúng?

Hàm số nghịch biến trên khoảng ( )0;3 . B. Hàm số đồng biến trên khoảng ( );1− . C. Hàm số nghịch biến trên khoảng ( )0;2 D. Hàm số đồng biến trên khoảng ( );3− Lời giải Chọn C Trên khoảng ( )0;2 , đồ thị hàm số đi xuống từ trái sang phải nên hàm số nghịch biến. Câu 89: Cho hàm số ( )yfx = xác định trên khoảng ( ); −+ có đồ thị như hình vẽ dưới đây. Mệnh đề nào sau đây đúng? A. Hàm số đồng biến trên khoảng ( )0;2 B. Hàm số nghịch biến trên khoảng ( )3;0 C. Hàm số đồng biến trên khoảng ( )1;0 D. Hàm số nghịch biến trên khoảng ( )0;3 Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 27 Đáp án C. Quan sát trên đồ thị ta thấy đồ thị hàm số đi lên trên khoảng ( )1;0 . Vậy hàm số đồng biến trên khoảng ( )1;0 . DẠNG 4. MỘT SỐ BÀI TOÁN LIÊN QUAN ĐẾN ĐỒ THỊ CỦA HÀM SỐ Câu 90: Trong mặt phẳng Oxy , điểm (1;)Ay thuộc đồ thị hàm số 3yx=+ lúc đó giá trị của y bằng: A. 4y = . B. 2y = . C. 1y = . D. 3y = . Lời giải Chọn B (1;)Ay thuộc đồ thị hàm số 3yx=+ nên ta có 132y =+= Đáp án B Câu 91: Cho hàm số ( ) 2 21fxx=+ . Giá trị ( )2f bằng A. 3 B. 3 C. 4 D. Không xác định. Lời giải Chọn B Ta có ( ) ( )2 22.213f −=−+= Câu 92: Trong mặt phẳng Oxy , biết điểm 0 (1;)My thuộc đồ thị hàm số 47.yx=+ Giá trị của 0y bằng: A. 7. B. 1. C. 2. D. 3. Lời giải Chọn D Điểm 0 (1;)My thuộc đồ thị hàm số 47yx=+ nên thay 1x =− vào 47yx=+ ta được: 0 4.(1)73y =−+= . Vậy 0 3.y = Câu 93: Cho hàm số ( ) 75yfxx==−− Khẳng định nào sau đây là đúng? A. ( ) 12f =− . B. ( ) 217f = . C. ( ) 29f −= . D. 5 10 7f  −=  . Lời giải Chọn C Ta có: ( ) 27.(2)59f −=−−−= Câu 94: Cho hàm số ( ) 32 fxx =− . Giá trị của hàm số tại điểm 2x =− bằng A. 1. B. 3 . C. 7 . D. 7 . Lời giải Chọn C Ta có: ( ) ( ) 23227f −=−−= .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 28 Vậy giá trị của hàm số tại điểm 2x =− bằng 7 . Câu 95: Trong các điểm sau đây điểm nào thuộc đồ thị của hàm số? A. ( )1 2;3M B. ( )2 0; 1.M C. 3 11 ; . 22 M    D. ( )4 1;0M Lời giải Chọn B Thay 0x = vào hàm số ta thấy 1y =− . Vậy ( )2 0;1M thuộc đồ thị hàm số. Câu 96: Cho hàm số 3 32yxx=−+ . Điểm nào sau đây thuộc đồ thị hàm số đã cho? A. ( )2;0 B. ( )1;1 C. ( )2;12 D. ( )1;1 Lời giải Chọn C Thay tọa độ điểm vào hàm số ta thấy chỉ có điểm ( )2;0 thỏa mãn. Câu 97: Cho () P có phương trình 2 24yxx=−+ Điểm nào sau đây thuộc đồ thị () P A. ( )4;2Q B. ( )3;1N C. ( )4;0P = D. ( )3;19M Lời giải Chọn D Thử trực tiếp thấy tọa độ của ( )3;19M thỏa mãn phương trình () P Câu 98: Điểm nào sau đây thuộc đồ thị hàm số ( ) 1 2 x y xx + = ? A. ( )2;1M . B. ( )1;0N . C. ( )2;0P . D. 1 0; 2Q    . Lời giải Chọn B Đặt ( ) ( ) 1 2fxx xx + = Ta có: ( ) ( ) 11 10 112f −+ −== . Câu 99: Điểm nào sau đây thuộc đồ thị hàm số 1 1y x = ? A. ( )1 2;1M . B. ( )2 1;1M . C. ( )3 2;0M . D. ( )4 0;2M . Lời giải Chọn A Đặt ( ) 1 1fx x = , ta có ( ) 1 21 21f == Câu 100: Trong các điểm sau đây, điểm nào thuộc đồ thị hàm số 32yxx=++− ?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 29 A. ( )3;0M . B. ( )1;2N . C. ( )5;83P + . D. ( )5;8Q . Lời giải Chọn C Đặt ( ) 32fxxx=++− , ta có ( ) 5535283f =++−=+ . Câu 101: Điểm sau đây không thuộc đồ thị hàm số 2 44xx y x −+ = ? A. ( )2;0A . B. 1 3; 3 B    . C. ( )1;1C . D. ( )1;3D . Lời giải Chọn C Đặt ( ) 32fxxx=++− , ta có ( ) 5535283f =++−=+ Câu 102: Tìm m để đồ thị hàm số 41yxm=+− đi qua điểm ( )1;2A A. 6m = B. 1m =− C. 4m =− D. 1m = Lời giải Chọn B Đồ thị hàm số 41yxm=+− đi qua điểm ( )1;2A suy ra 24.111 mm =+−=− Câu 103: Đồ thị hàm số ( ) 2 232 32 xkhix yfx xkhix + ==  − đi qua điểm có tọa độ nào sau đây ? A. ( )0;3 B. ( )3;6 C. ( )2;5 D. ( )2;1 Lời giải Chọn B Thay tọa độ điểm ( )0;3 vào hàm số ta được : ( ) 033f =− nên loại đáp án A Thay tọa độ điểm ( )3;6 vào hàm số ta được : ( ) 3936f =−= , thỏa mãn nên chọn đáp án B Câu 104: Đồ thị của hàm số ( ) 212 32 khi khi xx yfx x + ==  − đi qua điểm nào sau đây? A. ( )0;3 B. ( )3;7 C. ( )2;3 D. ( )0;1 Lời giải Với 02x = thì ( ) 02.011yf==+= . Vậy đồ thị của hàm số đã cho đi qua điểm ( )0;1 . Câu 105: Cho hàm số 2 2 1 52 1 1 xxkhix y x khix x  − =    Điểm nào sau đây thuộc đồ thị hàm số? A. ( )4;1 . B. ( )2;3 . C. ( )1;3 . D. ( )2;1 .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 30 Lời giải Chọn B Ta thấy ( )52.2 3 21 =− . Nên ( )2;3 thuộc đồ thị hàm số đã cho. Câu 106: Cho hàm số 2 2 1 52 1 1 xxkhix y x khix x  − =    Điểm nào sau đây thuộc đồ thị hàm số? A. ( ) 4;1. B. ( ) 2;3. C. ( ) 1;3. D. ( ) 2;1. Lời giải Chọn B Ta thấy ( )52.2 3 21 =− . Nên ( )2;3 thuộc đồ thị hàm số đã cho. Câu 107: Cho hàm số ( ) 2 5 fxxa x + = + có ( ) 413f −= . Khi đó giá trị của a là A. 11a = B. 21a = C. 3a =− D. 3a = Lời giải Chọn B Ta có ( ) ( )2.4 41321 45 a fa −+ −=== −+ Câu 108: Cho hàm số ( ) 2 31;1 2 ;1 xxkhix fx xkhix  ++ =  −+ . Tính ( )2f A. 1 B. 4 C. 7 D. 0 Lời giải Chọn A ( ) 2 31;1 2 ;1 xxkhix fx xkhix  ++ =  −+ ( ) ( ) ( )2 223.211f −=−+−+=− Câu 109: Hàm số ( ) 2 223 khi x2 1 2khi x<2 x fx x x   =   + . Tính ( ) ( )22Pff=+− A. 3P = B. 7 3 P = C. 6P = D. 2P = Lời giải Chọn A Ta có: ( ) ( )22Pff=+− ( )22223 22 21 =+−+  3= .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 31 Câu 110: Cho hàm số ( ) 2 223 khi2 1 1khi2 x fxx x xx  +−  =   + . Tính ( ) ( )22Pff=+− . A. 5 3 P = B. 8 3 P = C. 6P = D. 4P = Lời giải Chọn C ( ) ( ) ( )22223 22216 21Pff +− =+−=+−+= Câu 111: Cho hàm số ( ) 2 21 khi0 3khi0 xx yfx xx − ==   . Giá trị của biểu thức ( ) ( )11Pff =−+ là: A. 2 B. 0 C. 1 D. 4 Lời giải Chọn D ( ) ( )2 13.13f −=−= ( ) 12.111f =−= Vậy ( ) ( ) 11314Pff=−+=+= . Câu 112: Cho hàm số 1 () 21 x fx x  =   1 1 x x   . Giá trị của biểu thức (1)(1)(5)Tfff =−++ là A. 2T =− . B. 7T =− . C. 6T = . D. 7T = . Lời giải Chọn B Vì 11− nên (1)2.(1)13f −=−−=− , và (1)110f =−= Vì 51  nên (5)154f =−=− Vậy (1)(1)(5)3047Tfff=−++=−+−=− . Câu 113: Cho hàm số ( ) 41 4 1 34 x fxkhix x xkhix  +−  =   − . Tính ( ) ( )55ff+− . A. 5 2 . B. 15 2 . C. 17 2 . D. 3 2 . Lời giải Chọn C ( ) ( ) 541117 55358 5122ff +− +−=++=+=

S

B

C

1. ĐỊNH NGHĨA

Hàm s

trong

Chú

+ Khi

BÀI 2. HÀM SỐ BẬC HAI

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 216

ố bậc hai là hàm số cho bởi công thức: 2 ,=++ yaxbxc

đó x là biến số, ,, abc là các hằng số và 0a

ập xác định của hàm số bậc hai là

ý :

0a = , 0b  , hàm số trở thành hàm số bậc nhất ybxc =+ .

0ab== , hàm số trở thành hàm hằng yc = . 2. ĐỒ THỊ CỦA HÀM SỐ BẬC HAI a) Đồ thị hàm số 2,0yaxa= là một parabol có đỉnh là gốc tọa độ, có trục đối xứng là trục tung (là đường thẳng 0x = ). Parabol này quay bề lõm lên trên nếu 0a  , xuống dưới nếu 0a  b) Đồ thị hàm số 2 ,0yxbxcaa =++ là một parabol có: + Đỉnh ; 24 b I aa      . + Trục đối xứng là đường thẳng 2 b x a =− . + Bề lõm hướng lên trên nếu 0a  , hướng xuống dưới nếu 0a  + Giao điểm với trục tung là ( )0; Mc . + Số giao điểm với trục hoành bằng số nghiệm của phương trình 2 0axbxc++= . 0a  0a  CHƯƠNG III HÀM

Ố

Ậ

HAI VÀ ĐỒ THỊ LÝ THUYẾT.I =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 217 Để vẽ đường parabol 2 =++ yaxbxc ta tiến hành theo các bước sau: 1. Xác định toạ độ đỉnh ; 24     b I aa ; 2. Vẽ trục đối xứng 2 =− b x a ; 3. Xác định toạ độ các giao điểm của parabol với trục tung, trục hoành (nếu có) và một vài điểm đặc biệt trên parabol; 4. Vẽ parabol. 3. SỰ BIẾN THIÊN CỦA HÀM SỐ BẬC HAI Từ đồ thị ta suy ra bảng biến thiên của hàm số bậc 2 như sau: 0a  0a  + Khi 0a  , hàm số đồng biến trên khoảng ; 2 b a  −+   và nghịch biến trên khoảng ; 2 b a  −−   + Khi 0a  , hàm số đồng biến trên khoảng ; 2 b a  −−   và nghịch biến trên khoảng ; 2 b a  −+   . - Để vẽ đường parabol 2 =++ yaxbxc ta tiến hành theo các bước sau: 1. Xác định toạ độ đỉnh ; 24     b I aa ; 2. Vẽ trục đối xứng 2 =− b x a ; 3. Xác định toạ độ các giao điểm của parabol với trục tung, trục hoành (nếu có) và một vài điểm đặc biệt trên parabol; 4. Vẽ parabol. 4. ỨNG DỤNG CỦA HÀM SỐ BẬC HAI VÍ DỤ 1. Hai bạn An và Bình trao đổi với nhau. An nói: Tớ đọc ở một tài liệu thấy nói rằng cổng Trường Đại học Bách khoa Hà Nội (H.6.14) có dạng một parabol, khoảng cách giữa hai chân cổng là 8m và chiều cao của cổng tính từ một điểm trên mặt đất cách chân cổng 0,5m là 2,93 m. Từ đó tính ra được chiểu cao của cổng parabol đó là 12m. Sau một hồi suy nghĩ, Bình nói: Nếu dữ kiện như bạn nói, thì chiều cao của cổng parabol mà bạn tính ra ở trên là không chính xác. Dựa vào thông tin mà An đọc được, em hãy tính chiều cao của cổng Trường Đại học Bách khoa Hà Nội để xem kết quả bạn An tính được có chính xác không nhé!

OFFICIAL

VÍ DỤ 2. Quỹ đạo của một vật được ném lên từ gốc O (được chọn là điểm ném) trong mặt phẳng toạ độ Oxy là một parabol có phương trình 23 1000 =+ yxx , trong đó x (mét) là khoảng cách theo phương ngang trên mặt đất từ vị trí của vật đến gốc0, y (mét) là độ cao của vật so với mặt đất (H.6.15).

a) Tìm độ cao cực đại của vật trong quá trình bay. b) Tính khoảng cách từ điểm chạm đất sau khi bay của vật đến gốc O . Khoảng cách này gọi là tầm xa của qu

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 218

ỹ đạ

6.7. Vẽ các đường parabol sau: a) 2 32=−+yxx ; b) 2 223=−++yxx ; c) 2 21=++yxx ; d) 2 1=−+−yxx BÀI TẬP.

hai

6.9. Xác định parabol

1=++yaxbx

a) Đi qua hai điểm (1;0)A và (2;4)B ;

Đi qua điểm (1;0)A và có tr

ng h

a) () P nằm hoàn toàn phía trên trục hoành; b) () P nằm hoàn toàn phía dưới trục hoành; c) () P cắt trục hoành tại hai điểm phân biệt và có đỉnh nằm phía dưới trục hoành;

d) () P tiếp xúc với trục hoành và nằm phía trên trục hoành.

6.12. Hai bạn An và Bình trao đổi với nhau.

An nói: Tớ đọc ở một tài liệu thấy nói rằng cổng Trường Đại học Bách khoa Hà Nội (H.6.14) có dạng một parabol, khoảng cách giữa hai chân cổng là 8m và chiều cao của cổng tính từ một điểm trên mặt đất cách chân cổng 0,5m là 2,93 m. Từ đó tór tính ra được chiểu cao của cổng parabol đó là 12m.

Sau một hồi suy nghĩ, Bình nói: Nếu dữ kiện như bạn nói, thì chiều cao của cổng parabol mà bạn tính ra ở trên là không chính xác.

Dựa vào thông tin mà An đọc được, em hãy tính chiều cao của cổng Trường Đại học Bách khoa Hà Nội để xem kết quả bạn An tính được có chính xác không nhé!

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 219 6.8.

ừ các parabol đã vẽ ở Bài tập 6.7, hãy cho biết khoảng đồng biến và khoảng nghịch biến của mỗi hàm số bậc

tương ứng.

, trong mỗi trườ

ợp

ục đố

xứng 1=x ; c) Có đỉnh (1;2)I ; d) Đi qua điểm (1;6)A và có tung độ đỉnh 0,25 6.10. Xác định parabol 2 =++ yaxbxc , biết rằng parabol đó đi qua điểm (8;0)A và có đỉnh là (6;12)I 6.11. Gọi () P là đồ thị hàm số bậc hai 2 =++ yaxbxc . Hãy xác định dấu của hệ số a và biệt thức  , trong mỗi trường hợp

6.13. Bác Hùng dùng 40 m lưới thép gai rào thành một mảnh vườn hình chữ nhật để trồng rau.

OFFICIAL

a) Tính diện tích mảnh vườn hình chữ nhật rào được theo chiều rộng x (mét) của nó. b) Tìm kích thước của mảnh vườn hình chữ nhật có diện tích lớn nhất mà bác Hùng có thể rào được.

6.14. Quỹ đạo của một vật được ném lên từ gốc O (được chọn là điểm ném) trong mặt phẳng toạ độ Oxy là một parabol có phương trình 23 1000 =+ yxx , trong đó x (mét) là khoảng cách theo phương ngang trên mặt đất từ vị trí của vật đến gốc0, y (mét) là độ cao của vật so với mặt đất (H.6.15).

a) Tìm độ cao cực đại của vật trong quá trình bay. b) Tính khoảng cách từ điểm chạm đất sau khi bay của vật đến gốc O . Khoảng cách này gọi là tầm xa của quỹ đạo.

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 220

VẤN ĐỀ 1. TÌM ĐIỀU KIỆN ĐỂ HÀM SỐ 2 axx ybc =++ ĐỒNG BIẾN TRÊN KHOẢNG (;) ab HỆ THỐNG BÀI TẬP TỰ LUẬN.II = PHƯƠNG PHÁP.1 =

Câu 2. Tìm t

t c

các giá tr

a tham

Câu 3. Tìm tất cả các giá trị của tham số để hàm số 22 (1)41ymxmx =+−+ nghịch biến trên ( );1−

Câu 4. Tìm tất cả các giá trị của tham số m để hàm số 22(1)3ymxmx =−++ đồng biến trên ( )1;+ .

Câu 5. Tìm các giá trị của tham số m để hàm số 2 2(1)21ymxmxm =+−++ nghịch biến trên ( )1;2 .

Câu 6. Tìm tất cả các giá trị của tham số để hàm số ( ) 2 ()222019yfxmxmxm ==−−++ nghịch biến trên khoảng .

Câu 7. Tìm tất cả các giá trị của tham số để hàm số ( )2 ()213yfxmxmx

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 221 + Trường hợp 0a = : Yêu cầu của bài toán 0 0 a b =    + Trường hợp 0a  : Yêu cầu của bài toán ( ) 0 ;; 2 a b AB a      −+  + Trường hợp 0a  : Yêu cầu của bài toán ( ) 0 ;; 2 a b AB a      −−  . Lưu ý: Việc tìm điều kiện để hàm số 2 yaxbxc =++ nghịch biến trên khoảng (;) AB được làm tương tự Có thể dựa vào định nghĩa tính đồng biến, nghịch biến của hàm số để thực hiện các bài toán trên. Câu 1. Tìm tất cả các giá trị của tham số m để hàm số 2 -21yxmx=++ đồng biến trên ( );3− .

ấ

ả

ị củ

số để hàm số 22 442yxmxm =−+−+ nghịch biến trên ( )2; −+

==−++ đồng biến trên khoảng ( )2;3 . Câu 8. Cho hàm số: 2() yfxaxbxc ==++ với là các tham số, ( )0a  . Biết rằng ()fx đồng biến trên khoảng ( )2; −+ , hãy tìm giá trị lớn nhất của biểu thức 2 22 6 52 a P aabb = ++ . VẤN ĐỀ 2. XÁC ĐỊNH HÀM SỐ BẬC HAI Để xác định hàm số bậc hai ( ) 2 yfxaxbxc ==++ (đồng nghĩavới xácđịnh cáctham số ,, abc ) ta cần dựa vào giả thiết để lập nên các phương trình (hệ phương trình) ẩn là ,, abc . Từ đó tìm được ,, abc . Việc lập nên các phương trình nêu ở trên thường sử dụng đến các kết quả sau: Đồ thị hàm số đi qua điểm ( ) ( )0000 ; Mxyyfx = . Đồ thị hàm số có trục đối xứng 00 2 b xxx a =−= . m m m ( );3− m ,, abc BÀI TẬP.2 = PHƯƠNG PHÁP.1 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 222 Đồ thị hàm số có đỉnh là ( ) 2 ; 4 I II I b x Ixya y a  −=    −=   ( ) 2 I II b x a fxy   −=      =  Trên ,ta có: 1. ( )fx có giá trị lớn nhất 0a  . Lúc này gí trị lớn nhất của ( )fx là 42 fb aa   −=−  2. ( )fx có giá trị nhỏ nhất 0a  . Lúc này giá trị nhỏ nhất ( )fx là 42 fb aa   −=−  .

a nó

Câu 8. Tìm tất cả các

c tung

cho hàm s

có

yaxbxc

t giá tr

và

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 223 Câu 1. Xác định parabol ( ) 2 :2Pyaxbx=++ , biết rằng ( )P đi qua điểm ( )1;5M và có trục đối xứng là đường thẳng 1 4 x =− Câu 2. Xác định parabol ( ) 2 :2 Pyaxxc =++ , biết rằng 111 ; 22 I    là đỉnh của ( )P Câu 3. Tìm parabol ( )P : 2 yaxbxc =++ , biết rằng ( )P đi qua ba điểm ( )1;1A , ( )2;3B , ( )1;3C . Câu 4. Xác định hàm số 2 yaxbxc =++ với a , b , c là các tham số, biết rằng hàm số ấy đạt giá trị lớn nhất bằng 5 tại 2x =− và có đồ thị đi qua điểm ( )1;1M Câu 5. Tìm tất cả các giá trị của tham số m để parabol ( ) 2 :232Pymxmxm =−−− ( )0m  cắt đường thẳng 31yx=− tại đỉnh của nó. Câu 6. Tìm parabol ( ) 2 :4 Pyaxxc =−+ biết rằng hoành độ đỉnh của ( )P bằng 3 và ( )P đi qua điểm ( )2;1M . Câu 7. Tìm các tham số ,, abc sao

ố 2

=++ đạ

ị nhỏ nhấ

là 4

ại 2x =

đồ

ị củ

cắt trụ

tại điểm

tung độ là 6.

giá trị của ham số m sao cho parabol ( ) 2 :4 Pyxxm =−+ cắt trục Ox tại hai điểm phân biệt , AB thỏa mãn 3.OAOB = Câu 9. Cho hàm số ( ) 22424 yfxxmxmm ==+ . Tìm tất cả các giá trị của tham số m sao cho giá trị nhỏ nhất của ( ) 3fx = . VẤN ĐỀ 3. ĐỒ THỊ HÀM SỐ BẬC HAI Dạng 1. Cho parabol () P : 2 yaxbxc =++ . + Xác định trục đối xứng, tọa độ đỉnh của () P . + Tương giao của () P với trục Ox . + Tìm điều kiện để các giao điểm của () P và trục Ox thỏa mãn điều kiện nào đó. Thường dùng đến các kết quả sau: + Đường thẳng 2 b x a = là trục đối xứng của () P , điểm ; 24 b I aa −−    là đỉnh của () P . + Nghiệm (nếu có) của phương trình 2 0axbxc++= là hoành độ giao điểm của () P và trục Ox . + Giả sử ( ) ( );,; AABA AxyBxy là hai giao điểm của () P và trục Ox . Khi đó:, AB cùng ở bên trái đối với trục Oy 0 0 .0 AB AB xx xx   +    BÀI TẬP.2 = PHƯƠNG PHÁP.1 =

Xét phương trình

() P cắt trục hoành tại hai điểm phân bi

có hai nghiệm phân biệt.

() P và trục hoành có một điểm chung (còn gọi là tiếp xúc với nhau)  (*) có một nghiệm.

() P và trục hoành không có điểm chung  (*) vô nghiệm.

+ và () P tiếp xúc với nhau  2 axbxcmxn ++=+ có nghiệm kép.

Câu 1. Tìm tất cả các giá trị của tham số m để parabol ( ) 2 :3 Pyxxm =++ cắt trục hoành tại hai điểm phân

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 224 , AB cùng ở bên phải đối với trục Oy 0 0 .0 AB AB xx xx   +    . , AB cùng ở một bên đối với trục Oy 0 .0ABxx     , AB không ở cùng một bên đối với trục Oy .0ABxx  . Câu 1. Cho parabol Xác định trục đối xứng, tọa độ đỉnh của parabol () P , tọa độ giao điểm của parabol () P với trục hoành. Câu 2. Cho parabol ( ) 2 : Pyaxbxc =++ với Xét dấu của biết rằng cắt trục hoành tại hai điểm phân biệt có hoành độ âm. Dạng 2. Cho parabol ( ) 2 : Pyaxbxc =++ và đường thẳng : dymxn =+ + Biện luận số điểm chung của () P và trục hoành. + Tìm điều kiện để đường thẳng tiếp xúc với () P . +

2 0axbxc++= (*).

ệ

 (*)

biệt Câu 2. Tìm tất cả các giá trị của tham số để parabol ( ) 2 :21Pyxxm=−+− và trục Ox không có điểm chung. Câu 3. Cho parabol ( ) 2 :2Pyxx=++ và đường thẳng :1dyax=+ . Tìm tất cả các giá trị của tham số a để d tiếp xúc với ( )P . ( ) 2 :56.Pyxx=+− 0a  ,,bc ( )P d d m BÀI TẬP.2 = PHƯƠNG PHÁP.1 = BÀI TẬP.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 225 VẤN ĐỀ 4. TƯƠNG GIAO ĐỒ THỊ Dạng 1. Dựa vào đồ thị của hàm số ( )fx để biện luận theo tham số m số nghiệm của phương trình ( ) ( )fxgm = . Vẽ đồ thị ( )C của hàm số ( )fx . Tùy vào giá trị của ( )gm để chỉ ra số giao điểm của đường thẳng ( ): dygm = và( )C Số giao điểm của d và ( )C cũng chính là số nghiệm của phương trình ( ) ( )fxgm = . *Lưu ý: Đường thẳng ( ): dygm = là đường thẳng có phương ngang và cắt trục tung tại điểm có tung độ ( )gm . Câu 1. Cho hàm số 2 42yxx=−++ có đồ thị như hình vẽ bên dưới. Dựa vào đồ thị tìm các giá trị của tham số m để phương trình 2 42 xxm−++= có 2 nghiệm phân biệt. Câu 2. Cho hàm số 2 65yxx=−+ có đồ thị () P như nhình vẽ bên dưới. Dựa vào đồ thị, tìm các giá trị của tham số m để phương trình: 2 212610 xxm−+−= có 2 nghiệm phân biệt dương. Câu 3. Cho parabol ( ) 2 : Pyaxbxc =++ ( )0a  có đồ thị như hình bên. Tìm các giá trị của tham số m để phương trình 2 axbxcm ++= có bốn nghiệm phân biệt. PHƯƠNG PHÁP.1 = BÀI TẬP.2 =

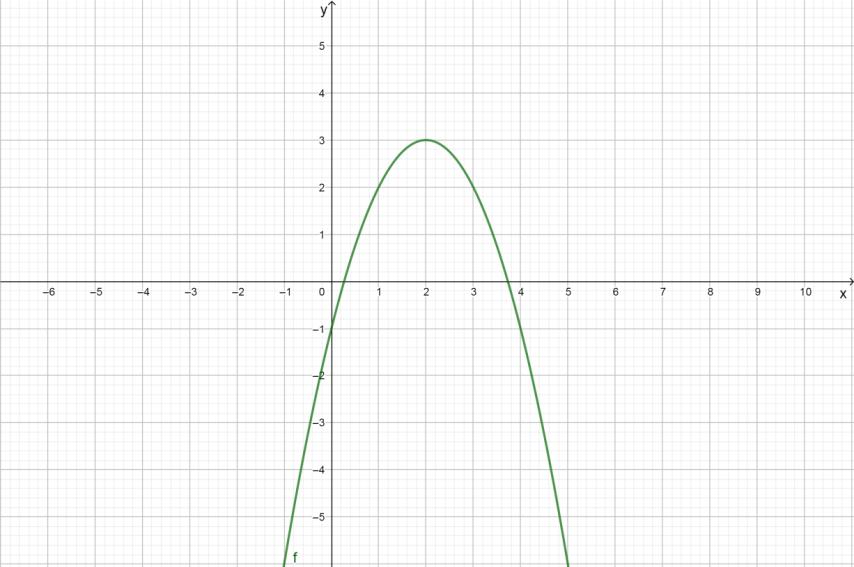
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 226 Câu 4. Cho phương trình ( )2 401xxm+−= . Tìm tất cả các giá trị của tham số m để phương trình ( )1 có đúng một nghiệm thuộc khoảng ( )3;1 . Câu 5. Có bao nhiêu giá trị m nguyên trong nửa khoảng ( 0;2019 để phương trình 2 450xxm−−−= có hai nghiệm phân biệt? Dạng 2. Sự tương giao của đồ thị hàm số bậc nhất và bậc hai Cho đồ thị ( )P của hàm số 2 yaxbxc =++ với 0a  và đồ thị d của hàm số ykxm =+ Toạ độ giao điểm của hai đồ thị( )P và d là nghiệm của hệ phương trình 2 yaxbxc ykxm  =++ =+ (1) Phương trình hoành độ giao điểm của ( )P và d là 2 axbxckxm ++=+ ( ) ( )2 02axbkxcm +−+−= Nhận xét: 1. Số giao điểm của ( )P và d bằng số nghiệm của hệ phương trình (1) và cũng bằng số nghiệm của phương trình (2). 2. Nếu phương trình (2) vô nghiệm thì ta nói d và ( )P không giao nhau. 3. Nếu phương trình (2) có nghiệm kép thì ta nói d và ( )P tiếp xúc với nhau. Lúc này ta nói d là tiếp tuyến của 4. Nếu phương trình (2) có 2 nghiệm phân biệt thì ta nói d và ( )P cắt nhau. Câu 1. Tìm tọa độ giao điểm của Parabol ( ) 2 :41Pyxx=−−+ và đường thẳng d : 3yx=−+ . Câu 2. Cho Parabol ( ) 2 :32Pyxx=−+ và đường thẳng :2dymx=+ . Tìm m để d tiếp xúc với ( )P Tìm tọa độ tiếp điểm khi đó. ( )P PHƯƠNG PHÁP.1 = BÀI TẬP.2 =

) ( )fxgx

(2), phương trình (2) được gọi là phương trình hoành độ giao điể

* Nhận xét:

i) Số giao điểm của ( )1P và ( )2P bằng số nghiệm của hệ (1) và bằng số nghiệm của phương trình (2). ii) ( )yfx = và ( )ygx = là các hàm số bậc hai nên phương trình (2) có nhiều nhất 2 nghiệm. iii) Các bài toán liên quan đến dạng này thường áp dụng đến nội dung định lý Vi et thuận, nhắc lại như sau. Cho phương trình bậc hai 2

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 227 Câu 3. Cho Parabol ( )P 2 24yxx=−+ và đường thẳng d : 22 ymxm =− ( m là tham số). Tìm các giá trị của m để d cắt ( )P tại hai điểm phân biệt có hoành độ là 1x , 2x thỏa mãn 22 122(1)316xmxm++=+ . Câu 4. Cho Parabol 21 ():2 Pyx = và đường thẳng ( ) 2 1 :1 2dymxm=+−− ( m là tham số). Tìm các giá trị của m thì đường thẳng d cắt Parabol ( )P tại hai điểm 1122 (;),(;) AxyBxy sao cho biểu thức 121212()Tyyxxxx =+−−+ đạt giá trị nhỏ nhất. Dạng 3. Sự tương giao của hai đồ thị hàm số bậc hai Cho hai hàm số ( )yfx = và ( )ygx = là các hàm số bậc hai có đồ thị lần lượt là các đường parabol ( )1P và ( )2P , khi đó tọa độ giao điểm của ( )1P và ( )2P là nghiệm của hệ phương trình ( ) ( ) yfx ygx =   =  . (1) Để giải hệ (1) ta cần giải phương trình (

m của ( )1P và ( )2P .

0axbxc++= có hai nghiệm 1x và 2x , ta luôn có 12 b xx a +=− và 12 c xx a = Câu 1. Biết rằng đồ thị hàm số 2 6 yxx =− cắt đồ thị hàm số 2 4yx=−− tại hai điểm ( ); AAAxy và ( ) ;.BBBxy Tính AByy + Câu 2. Biết rằng parabol 2 1yxx=−+ cắt parabol 2 24yxx=−++ tại hai điểm phân biệt có hoành độ lần lượt là 1x và 2x . Tính giá trị biểu thức 33 12Pxx =+ . Câu 3. Tìm tất cả các giá trị của m sao cho đồ thị hàm số ( ) 2 1232ymxxm =+++− cắt đồ thị hàm số 2 24yxmx=++ tại đúng hai điểm phân biệt có hoành độ lần lượt là 12 ; xx thỏa mãn 1221.xx+= Câu 4. Tìm tất cả các giá trị của m sao cho hai parabol ( ) 22 1yxmxm=+++ và ( ) ( )2 221yxmxm =−−+−+ cắt nhau tại hai điểm có hoành độ lần lượt là 12 ; xx thỏa mãn ( )1212 3 Pxxxx =−+ đạt giá trị lớn nhất. PHƯƠNG PHÁP.1 = BÀI TẬP.2 =

Câu

Tìm

đồ thị hàm số ( )m P : ( ) 222211ymxmxm =+−+− .

Câu 4. Cho hàm số ( )2 2354 yxmxm =+−+− . Chứng minh rằng với mọi giá trị của m , đồ thị ( )m P của hàm số đã cho và đường thẳng ( ) :243 m dymxm=−+ luôn có một điểm chung cố định. Câu 5. Cho các hàm số ( ) ( )2 :347 m Pyxmxm =−++− , ( ) ( )2 :3149 m Cymxmxm =−+−+ , ( ) ( ) :140 m dmxmym

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 228 VẤN ĐỀ 5. ĐIỂM CỐ ĐỊNH CỦA ĐỒ THỊ HÀM SỐ. Cho họ hàm số ( ) ;0fxm = ( m là tham số) có đồ thị ( )m P . Để tìm điểm cố định mà ( )m P luôn đi qua với mọi giá trị của m , ta thực hiện các bước sau: Bước 1: Giả sử điểm ( )00 ; Mxy là điểm cố định mà ( )m P luôn đi qua. Tọa độ điểm M thỏa mãn phương trình ( ) ;0fxm = Bước 2: Chuyển phương trình về phương trình ẩn m dạng 0AmB+= (hoặc 2 0AmBmC++= ). Phương trình nghiệm đúng với mọi m Khi đó ta có 0 0 A B =  = hoặc 0 0 0 A B C =  =  = . Tìm được ( )0000 ;; xyMxy  . Bước 3: Kết luận. Câu 1. Cho hàm số ( ) ( ) ( )2 1213 mymxmxmP =+−−+− . Chứng tỏ rằng ( )m P luôn đi qua một điểm cố định, tìm tọa độ điểm cố định đó.

2. Cho hàm số ( ) ( )2 1231 mymxmxmP =−+−+ . Tìm điểm cố định của họ đồ thị hàm số trên.

điểm cố định của

−++−= . Chứng minh rằng với mọi giá trị của m , các đồ thị của các hàm số đã cho luôn cùng đi qua một điểm cố định. VẤN ĐỀ 6: GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ BẬC HAI Dạng 1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên 1 tập cho trước Để tìm giá trị lớn nhất và nhỏ nhất của hàm số bậc hai, ta lập bảng biến thiên cho hàm số đó trên tập hợp đã cho. Dựa vào bảng biến thiên, ta kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số trên tập hợp đã cho. Câu 1. Cho hàm số 2 43yxx=−− . Tìm giá trị lớn nhất của hàm số đã cho trên  3;5 . Câu 2. Cho hàm số 2 243yxx=−++ . Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên  2;7 Câu 3. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 4243yxx=−− trên  1;2 PHƯƠNG PHÁP.1 = BÀI TẬP.2 = PHƯƠNG PHÁP.1 = BÀI TẬP.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 229 Câu 4. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 33422 221413yxxx =−+++++ Câu 5. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 4324322yxxxx =++−+ trên  2;4 Câu 6. Cho các số , xy thỏa mãn 22 1 xyxy +=+ . Tìm giá trị lớn nhất và giá trị nhỏ nhất của 4422 Pxyxy =+− Dạng 2. Tìm điều kiện của tham số để hàm số bậc hai đạt giá trị lớn nhất, giá trị nhỏ nhất Cho hàm số bậc hai: 2 yaxbxc =++ ( )0a  Nếu 0a  thì min 24yfb aa  =−=−   đạt tại hoành độ đỉnh 2I b x a =− . Nếu 0a  thì max 24yfb aa  =−=−   đạt tại hoành độ đỉnh 2I b x a =− Trường hợp tập xác định khác , ta kẻ bảng biến thiên của hàm số trên tập đó để có được giá trị lớn nhất, giá trị nhỏ nhất. Câu 1. Tìm giá trị thực của tham số 0m  để hàm số 2 232ymxmxm =−−− có giá trị nhỏ nhất bằng 10 trên Câu 2. Cho hàm số 2 yaxbxc =++ đạt giá trị nhỏ nhất bằng 2 khi 1x = và nhận giá trị bằng 3 khi 2x = . Tính abc Câu 3. Cho hàm số 2 21ymxxm=−−− . Tìm giá trị thực của tham số m để giá trị lớn nhất của hàm số đã cho đạt giá trị nhỏ nhất. Câu 4. Cho hàm số ( ) ( ) 22 2 12112 ymxmxm =−−+−++ . Với 1m  , tìm giá trị nhỏ nhất của biểu thức [0;2] [0;2] min max x x y B y   = PHƯƠNG PHÁP.1 = BÀI TẬP.2 =

DẠNG 1: Các bài toán thực tế mà mô hình thực tiễn chưa chuyển về mô hình toán học. Các bước làm như sau:

Bước 1: Dựa vào giả thiết và các yếu tố của đề bài, ta xây dựng mô hình toán học cho vấn đề đang

xét, tức là diễn tả

TẬP.

OFFICIAL

được cho b

i công th

c ( )

=−++ (tính b

ng mét), t là th

i gian tính bằng giây ( )0t  . a. Tính chiều cao lớn nhất quả bóng đạt được. b. Hãy tính xem sau bao lâu quả bóng sẽ rơi xuống mặt đất ?

Câu 2. Độ cao của quả bóng golf tính theo thời gian có thể được xác định bằng một hàm bậc hai. Với các thông số cho trong bảng sau, hãy xác định độ cao quả bóng đạt được tại thời điểm 3 giây ?

Câu 3. Một miếng nhôm có bề ngang 32 cm được uốn cong tạo thành máng dẫn nước bằng chia tấm nhôm thành 3 phần rồi gấp 2 bên lại theo một góc vuông như hình vẽ dưới. Hỏi x bằng bao nhiêu để tạo ra máng có có diện tích mặt ngang S lớn nhất để có thể cho nước đi qua nhiều nhất ?

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 230 VẤN ĐỀ 7: BÀI TOÁN THỰC TẾ

dưới “dạng ngôn ngữ toán học” cho mô hình mô phỏng thực tiễn. Căn cứ vào các yếu tố bài ra ta chọn biến số, tìm điều kiện tồn tại, đơn vị. Bước 2: Dựa vào các mối liên hệ ràng buộc giữa biến số với các giả thiết của đề bài cũng như các kiến thức liên quan đến thực tế, ta thiết lập hàm số bậc hai. Chuyển yêu cầu đặt ra đối với bài toán thực tiễn thành yêu cầu bài toán hàm số bậc hai. Bước 3: Dùng tính chất hàm số bậc hai để giải quyết bài toán hình thành ở bước 2. Lưu ý kiểm tra điều kiện, và kết quả thu được có phù hợp với bài toán thực tế đã cho chưa. DẠNG 2: Các bài toán thực tế đã mô hình hóa bằng một hàm số bậc hai. Thực hiện bước 3 của dạng 1. Câu 1. Một quả bóng được ném vào không trung có chiều cao tính từ lúc bắt đầu ném ra

ở

ứ

httt

ằ

ờ

PHƯƠNG PHÁP.1 = BÀI

2 =

Câu 4. Hai con chuồn chuồn bay trên hai quĩ đạo khác nhau, xuất phát cùng thời điểm. Một con bay trên quỹ đạo là đường thẳng từ điểm

( )0;100A đến điểm ( )0;0O với vận tốc 5m/s.

Con còn lại bay trên quĩ đạo là đường thẳng từ

( )60;80B đến điểm ( )0;0O với vận tốc 10m/s

Hỏi trong quá trình bay thì khoảng cách ngắn nhất hai con đạt được là bao nhiêu ?

Câu 5. Một cửa hàng bán bưởi Đoan Hùng của Phú Thọ vớ

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 231

i giá bán mỗi quả là 50000 đồng. Với giá bán này thì mỗi ngày cửa hàng chỉ bán được 40 quả. Cửa hàng dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi quả 1000 đồng thì số bưởi bán tăng thêm được là 10 quả. Xác định giá bán để của hàng thu được lợi nhuận cao nhất, biết rằng giá nhập về ban đầu cho mỗi quả là 30000 đồng. Câu 1. Cho hàm số 2 68yxx=−+ , có đồ thị là ( )P a) Lập bảng biến thiên và vẽ đồ thị ( )P . b) Biện luận theo m số nghiệm của phương trình ( ) 420xxm−−+= Câu 2. Vẽ đồ thị hàm số 2 4khi1 43khi1 xx y xxx    −+ = −+ . Câu 3. Xác định parabol 2 32yaxx=+− , biết rằng parabol đó a) Cắt trục hoành tại điểm có hoành độ bằng 2. b) Có trục đối xứng 3x =− c) Có đỉnh 111 ; 24 I    . d) Đạt cực tiểu tại 1x = Câu 4. Xác định parabol 2 2yaxbx=++ , biết rằng parabol đó a) Đi qua hai điểm ( )1;5M và ( )2;8N . b) Có đỉnh ( )2;2I c) Đi qua điểm ( )3;4A và có trục đối xứng 3 4 x =− . d) Đi qua điểm ( )1;6B và đỉnh có tung độ 1 4 . Câu 5. Xác định parabol 22 yxbxc =++ , biết rằng parabol đó a) Có trục đối xứng 1x = và cắt Oy tại điểm ( )0;4M . b) Có đỉnh ( )1;2I c) Đi qua hai điểm ( )0;1A và ( )4;0B . d) Có hoành độ đỉnh 2 và đi qua điểm ( )1;2N Câu 6. Xác định parabol 2 yaxc =+ , biết rằng parabol đó HỆ THỐNG BÀI TẬP TỰ LUẬN TỔNG HỢP.II =

Câu 7. Xác định parabol 2 4 yaxxc

a) Có hoành

b) Có

Câu 10. Xác định parabol

yaxbxc

parabol đó

hàm

Có giá trị nhỏ nhất bằng 4 tại 2x = và đồ thị hàm số đi qua điểm ( )0;6A

b) Có giá trị lớn nhất bằng 3 tại 2x = và đồ thị hàm số đi qua điểm ( )0;1B .

Câu 11. Cho hàm số 2 232ymxmxm =−−− ( )0m  . Xác định giá trị của m trong mỗi trường hợp sau

a) Đồ thị hàm số đi qua điểm ( )2;3A .

b) Có đỉnh thuộc đường thẳng 31yx=− .

c) Hàm số có giá trị nhỏ nhất bằng 10.

Câu 12. Cho parabol ( ) 2 :42Pyxx=−+− và đường thẳng :23 dyxm =−+ . Tìm các giá trị m để

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 232

Đi qua hai điểm ( )1;1M , ( )2;2B b) Có đỉnh ( )0;3I và một trong hai giao điểm với Ox là ( )2;0A .

=−+ , biết rằng

độ đỉnh là 3 và đi qua điểm ( )2;1M

trục đối xứng là đường thẳng 2x = và cắt trục hoành tại điểm ( )3;0A . Câu 8. Xác định parabol 2 yaxbxc =++ , biết rằng parabol đó a) Đi qua ba điểm ( ) ( ) ( )1;1, 1;3, 0;0ABO . b) Cắt trục Ox tại hai điểm có hoành độ lần lượt là 1 và 2, cắt trục Oy tại điểm có tung độ bằng 2. c) Đi qua điểm ( )4;6M , cắt trục Ox tại hai điểm có hoành độ lần lượt là 1 và 3 Câu 9. Xác định parabol 2 yaxbxc =++ , biết rằng parabol đó a) Có đỉnh ( )2;1I và cắt trục tung tại điểm có tung độ bằng 3 b) Cắt trục hoành tại hai điểm ( )1;0A , ( )3;0B và có đỉnh nằm trên đường thẳng 1y =− . c) Có đỉnh nằm trên trục hoành và đi qua hai điểm ( )0;1M , ( )2;1N d) Trục đối xứng là đường thẳng 3x = , qua ( )5;6M và cắt trục tung tại điểm có tung độ bằng 2 .

=++ , biết rằng

số a)

a) d cắt ( )P tại hai điểm phân biệt A , B . Tìm tọa độ trung điểm của AB . b) d và ( )P có một điểm chung duy nhất. Tìm tọa độ điểm chung này. c) d không cắt ( )P . d) d và ( )P có một giao điểm nằm trên đường thẳng 2y =− Câu 13. Cho parabol ( ) 2 :43Pyxx=−+ và đường thẳng :3dymx=+ . Tìm các giá trị của m để a) d cắt ( )P tại hai điểm phân biệt A , B sao cho diện tích tam giác OAB bằng 9 2 b) d cắt ( )P tại hai điểm phân biệt A , B có hoành độ 12 , xx thỏa mãn 33 12 8xx+= . Câu 14. Chứng minh rằng với mọi m , đồ thị hàm số ( )2 2231ymxmxm =+−−+ luôn đi qua hai điểm cố định. Câu 15. Chứng minh rằng các parabol sau luôn tiếp xúc với một đường thẳng cố định. a) ( ) 22 242183yxmxm =−−+− b) ( )2 4141ymxmxm =−−+− ( )0m 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 233 Câu 16. Chứng minh rằng các đường thẳng sau luôn tiếp xúc với một parabol cố định. a) 2 242ymxmm =−++ ( )0m  . b) ( ) 2 4242ymxm =−−− 1 2 m     .

S

B

C

1. ĐỊNH NGHĨA

Hàm s

trong

Tập

Chú

+ Khi

BÀI 2. HÀM SỐ BẬC HAI

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 1

ố bậc hai là hàm số cho bởi công thức: 2 ,=++ yaxbxc

đó x là biến số, ,, abc là các hằng số và 0a

xác định của hàm số bậc hai là

ý :

= , 0b  , hàm số trở thành hàm số bậc nhất ybxc =+ .

Ố

Ậ

HAI VÀ ĐỒ THỊ LÝ THUYẾT.I =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 2 Để vẽ đường parabol 2 =++ yaxbxc ta tiến hành theo các bước sau: 1. Xác định toạ độ đỉnh ; 24     b I aa ; 2. Vẽ trục đối xứng 2 =− b x a ; 3. Xác định toạ độ các giao điểm của parabol với trục tung, trục hoành (nếu có) và một vài điểm đặc biệt trên parabol; 4. Vẽ parabol. 3. SỰ BIẾN THIÊN CỦA HÀM SỐ BẬC HAI Từ đồ thị ta suy ra bảng biến thiên của hàm số bậc 2 như sau: 0a  0a  + Khi 0a  , hàm số đồng biến trên khoảng ; 2 b a  −+   và nghịch biến trên khoảng ; 2 b a  −−   + Khi 0a  , hàm số đồng biến trên khoảng ; 2 b a  −−   và nghịch biến trên khoảng ; 2 b a  −+   . - Để vẽ đường parabol 2 =++ yaxbxc ta tiến hành theo các bước sau: 1. Xác định toạ độ đỉnh ; 24     b I aa ; 2. Vẽ trục đối xứng 2 =− b x a ; 3. Xác định toạ độ các giao điểm của parabol với trục tung, trục hoành (nếu có) và một vài điểm đặc biệt trên parabol; 4. Vẽ parabol. 4. ỨNG DỤNG CỦA HÀM SỐ BẬC HAI VÍ DỤ 1. Hai bạn An và Bình trao đổi với nhau. An nói: Tớ đọc ở một tài liệu thấy nói rằng cổng Trường Đại học Bách khoa Hà Nội (H.6.14) có dạng một parabol, khoảng cách giữa hai chân cổng là 8m và chiều cao của cổng tính từ một điểm trên mặt đất cách chân cổng 0,5m là 2,93 m. Từ đó tính ra được chiểu cao của cổng parabol đó là 12m. Sau một hồi suy nghĩ, Bình nói: Nếu dữ kiện như bạn nói, thì chiều cao của cổng parabol mà bạn tính ra ở trên là không chính xác. Dựa vào thông tin mà An đọc được, em hãy tính chiều cao của cổng Trường Đại học Bách khoa Hà Nội để xem kết quả bạn An tính được có chính xác không nhé!

OFFICIAL

a) Tìm độ cao cực đại của vật trong quá trình bay. b) Tính khoảng cách từ điểm chạm đất sau khi bay của vật đến gốc O . Khoảng cách này gọi là tầm

của qu

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 3

ỹ đạ

6.7. Vẽ các đường parabol sau: a) 2 32=−+yxx ; b) 2 223=−++yxx ; c) 2 21=++yxx ; d) 2 1=−+−yxx BÀI TẬP.

hai

6.9. Xác định parabol

=++yaxbx

a) Đi qua hai điểm (1;0)A và (2;4)B ;

Đi qua điểm (1;0)A và có tr

ng h

d) () P tiếp xúc với trục hoành và nằm phía trên trục hoành.

6.12. Hai bạn An và Bình trao đổi với nhau.

Sau một hồi suy nghĩ, Bình nói: Nếu dữ kiện như bạn nói, thì chiều cao của cổng parabol mà bạn tính ra ở trên là không chính xác.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 4 6.8.

ừ các parabol đã vẽ ở Bài tập 6.7, hãy cho biết khoảng đồng biến và khoảng nghịch biến của mỗi hàm số bậc

tương ứng.

2 1

, trong mỗi trườ

ợp

ục đố

6.13. Bác Hùng dùng 40 m lưới thép gai rào thành một mảnh vườn hình chữ nhật để trồng rau.

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 5

VẤN ĐỀ 1. TÌM ĐIỀU KIỆN ĐỂ HÀM SỐ 2 axx ybc =++ ĐỒNG BIẾN TRÊN KHOẢNG (;) ab HỆ THỐNG BÀI TẬP TỰ LUẬN.II =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 6 + Trường hợp 0a = : Yêu cầu của bài toán 0 0 a b =    . + Trường hợp 0a  : Yêu cầu của bài toán ( ) 0 ;; 2 a b AB a      −+  . + Trường hợp 0a  : Yêu cầu của bài toán ( ) 0 ;; 2 a b AB a      −−  . Lưu ý: Việc tìm điều kiện để hàm số 2 yaxbxc =++ nghịch biến trên khoảng (;) AB được làm tương tự Có thể dựa vào định nghĩa tính đồng biến, nghịch biến của hàm số để thực hiện các bài toán trên. Câu 1. Tìm tất cả các giá trị của tham số m để hàm số 2 -21yxmx=++ đồng biến trên ( );3− . Lời giải Ta có 10a =− , 2 b m a −= nên hàm số đã cho đồng biến trên (;) m− . Do vậy, yêu cầu của bài toán  33 2 b m a − Kết luận: 3m  . Câu 2. Tìm tất cả các giá trị của tham số để hàm số 22 442yxmxm =−+−+ nghịch biến trên ( )2; −+ . Lời giải Ta có 40; 2a2 bm a =−−= nên hàm số đã cho nghịch biến trên ; 2 m  +   Do vậy, yêu cầu của bài toán  24 2 m m −− . Kết luận: 4m − Câu 3. Tìm tất cả các giá trị của tham số để hàm số 22 (1)41ymxmx =+−+ nghịch biến trên ( );1− Lời giải m m PHƯƠNG PHÁP.1 = BÀI TẬP.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 7 Ta có 2 10,am=+ 2 2 2a1 bm m −= + nên hàm số đã cho nghịch biến trên 2 2 ; 1 m m  −  +  . Do vậy, yêu cầu của bài toán  2 2 1 1 m m  +  2 (1)0 m −  1m = . Kết luận: 1m = . Câu 4. Tìm tất cả các giá trị của tham số m để hàm số 22(1)3ymxmx =−++ đồng biến trên ( )1;+ . Lời giải Ta có am = , 2 1 2a2 bm m + −= với 0m  . + Trường hợp 0m = : Hàm số đã cho trở thành 3yx=−+ , là hàm số nghịch biến trên nên không thể đồng biến trên ( )1;+ . Tức 0m = không thỏa mãn yêu cầu của bài toán. + Trường hợp 0m  : Ta có 0am= nên hàm số có BBT như sau: Dựa vào BBT thấy hàm số không thể đồng biến trên ( )1;+ . Tức 0m  bị loại. + Trường hợp 0m  : Ta có 0am= nên hàm số có BBT như sau: Dựa vào BBT thấy yêu cầu của bài toán  2 0 1 1 2 m m m    +    2 0 12 m mm   +  1m = Tóm lại: 1m = . Câu 5. Tìm các giá trị của tham số m để hàm số 2 2(1)21ymxmxm =+−++ nghịch biến trên ( )1;2 . Lời giải Ta có am = , 1 2 bm am −= với 0m  y x x y

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 8 + Trường hợp 0m = : Hàm số đã cho trở thành 21yx=−+ , là hàm số nghịch biến trên nên cũng nghịch biến trên ( )1;2 . Tức 0m = thỏa mãn yêu cầu của bài toán. + Trường hợp 0m  : Ta có 0am= nên hàm số nghịch biến trên 1 ; m m  +   Do vậy yêu cầu của bài toán  1 1m m −  1 0 m  , đúng với 0m  + Trường hợp 0m  : Ta có 0am= nên hàm số nghịch biến trên 1 ; m m  −   . Do vậy yêu cầu của bài toán 1 2m m   13 0m m   1 3 m  Tóm lại: 1 3 m  Câu 6. Tìm tất cả các giá trị của tham số để hàm số ( ) 2 ()222019yfxmxmxm ==−−++ nghịch biến trên khoảng . Lời giải + Trường hợp 242019myx==−+ , nghịch biến trên nên nghịch biến trên ( );3− . Tức 2m = thỏa mãn yêu cầu bài toán. + Trường hợp 2m  : Dựa vào sự biến thiên hàm bậc hai ta thấy ( )fx nghịch biến trên khoảng ( );3−  20 23 3 2 m mm m −     Từ các trường hợp trên, suy ra: 23 m  Vậy 23 m  Câu 7. Tìm tất cả các giá trị của tham số để hàm số ( )2 ()213yfxmxmx ==−++ đồng biến trên khoảng ( )2;3 . Lời giải + Trường hợp 0()3mfxx ==−+ nghịch biến trên . Tức 0m = không thỏa mãn yêu cầu bài toán. + Trường hợp 0m  : ( )fx đồng biến trên 21 ; 2 m m +  +   Do đó: ()fx đồng biến trên ( )2;3 211 2214 22 m mmm m + + . m ( );3− m

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 9 + Trường hợp 0m  : ()fx đồng biến trên 21 ; 2 m m +  −   . Do đó: ()fx đồng biến trên ( )2;3 211 3216 24 m mmm m + + (Không thỏa mãn 0m  ). Từ các trường hợp trên, suy ra 1 2 m  . Vậy 1 2 m  . Câu 8. Cho hàm số: 2() yfxaxbxc ==++ với là các tham số, ( )0a  . Biết rằng ()fx đồng biến trên khoảng ( )2; −+ , hãy tìm giá trị lớn nhất của biểu thức 2 22 6 52 a P aabb = ++ . Lời giải Do 0a  nên ()fx đồng biến trên ; 2 b a  −+   Từđâyta có: ( )fx đồng biếntrên ( )2; −+  24 2 bb aa − . Ta có 2 2 222 666 5225 25 a P aabbtt bb aa === ++++ ++   , với 4 b t a = . Có ( ) 22251429ttt++=++ , 4t  Dấu bằng xảy ra khi 4t = Do đó 6 29 MaxP = ,đạt được khi 4 b a = ,, abc

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 10 VẤN ĐỀ 2. XÁC ĐỊNH HÀM SỐ BẬC HAI Để xác định hàm số bậc hai ( ) 2 yfxaxbxc ==++ (đồng nghĩavới xácđịnh cáctham số ,, abc ) ta cần dựa vào giả thiết để lập nên các phương trình (hệ phương trình) ẩn là ,, abc . Từ đó tìm được ,, abc . Việc lập nên các phương trình nêu ở trên thường sử dụng đến các kết quả sau: - Đồ thị hàm số đi qua điểm ( ) ( )0000 ; Mxyyfx = Đồ thị hàm số có trục đối xứng 00 2 b xxx a =−= . Đồ thị hàm số có đỉnh là ( ) 2 ; 4 I II I b x Ixya y a  −=    −=   ( ) 2 I II b x a fxy   −=      =  . - Trên ,ta có: 1. ( )fx có giá trị lớn nhất 0a  . Lúc này gí trị lớn nhất của ( )fx là 42 fb aa   −=−  . 2. ( )fx có giá trị nhỏ nhất 0a  . Lúc này giá trị nhỏ nhất ( )fx là 42 fb aa   −=−  . Câu 1. Xác định parabol ( ) 2 :2Pyaxbx=++ , biết rằng ( )P đi qua điểm ( )1;5M và có trục đối xứng là đường thẳng 1 4 x =− . Lời giải Ta có: 25 1 24 ab b a ++=   −=−  3 2 ab ab +=   = 2 1 a b =   = Vậy ( )P có phương trình là 2 22yxx=++ . Câu 2. Xác định parabol ( ) 2 :2 Pyaxxc =++ , biết rằng 111 ; 22 I    là đỉnh của ( )P Lời giải PHƯƠNG PHÁP.1 = BÀI TẬP.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 11 Ta có : 21 22 4811 82 a c  −=   +−=   2 5 a c =−   = Vậy ( )P có phương trình là 2 225yxx=−−+ . Câu 3. Tìm parabol ( )P : 2 yaxbxc =++ , biết rằng ( )P đi qua ba điểm ( )1;1A , ( )2;3B , ( )1;3C Lời giải Ta có: ( ) ( ) 2 2 2 .1.11 .2.23 .113 abc abc abc  ++=−  ++=  −+−+=−  1 1 3 a b c =  =   =− ( ) 2 :3Pyxx =+− Vậy ( )P có phương trình là 2 3yxx=+− . Câu 4. Xác định hàm số 2 yaxbxc =++ với a , b , c là các tham số, biết rằng hàm số ấy đạt giá trị lớn nhất bằng 5 tại 2x =− và có đồ thị đi qua điểm ( )1;1M Lời giải Tập xác định D = Trên , do hàm số ( )1;1A đạt giá trị lớn nhất nên 0a  Do đó theo giả thiết, ta có: 2 2 425 1 b a abc abc  −=−  −+=  ++=−  2 3 8 3 7 3 a b c  =−   =−    =  (nhận) Vậy hàm số cần tìm là 2 287 333yxx=−−+ . Câu 5. Tìm tất cả các giá trị của tham số m để parabol ( ) 2 :232Pymxmxm =−−− ( )0m  cắt đường thẳng 31yx=− tại đỉnh của nó. Lời giải Đỉnh của ( )P là ( )1;42Im Theo giả thiết, I thuộc đường thẳng 31yx=− nên 423.111. mm −−=−=− Vậy 1m =− Câu 6. Tìm parabol ( ) 2 :4 Pyaxxc =−+ biết rằng hoành độ đỉnh của ( )P bằng 3 và ( )P đi qua điểm ( )2;1M .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 12 Lời giải Ta có: 4 3 2 481  −=−   ++= a ac 46 47 −=   +=− a ac 2 3 13 3 a c  =−     =−  . Vậy parabol ( )P có phương trình là 2 213 4 33yxx=−−− Câu 7. Tìm các tham số ,, abc sao cho hàm số 2 yaxbxc =++ đạt giá trị nhỏ nhất là 4 tại 2x = và đồ thị của nó cắt trục tung tại điểm có tung độ là 6. Lời giải Tập xác định: D = . Trên hàm số 2 yaxbxc =++ có giá trị nhỏ nhất nên 0a  Lại có đồ thị hàm số có đỉnh ( )2;4I . Do đó ta có: 1 2 42 2 4244222 666   −= = =−  ++=+=−=−  ===    b abaa abcabb ccc (nhận). Câu 8. Tìm tất cả các giá trị của ham số m sao cho parabol ( ) 2 :4 Pyxxm =−+ cắt trục Ox tại hai điểm phân biệt , AB thỏa mãn 3.OAOB = Lời giải Phương trình hoành độ giao điểm của ( )P và Ox là: 2 40.xxm−+= (*) ( )P cắt Ox tại hai điểm phân biệt , AB (*) có hai nghiệm phân biệt 404. mm  =− Gọi , ABxx là hai nghiệm của (*). Ta có 3 33. 3 = ==  =− AB AB AB xx OAOBxx xx  TH1: 33 341.34. .. ==  =+====  ==  ABA ABABBAB ABAB xxx xxxxxmxx xxmxxm  TH2: 36 342.124 =−=  =−+==−==−  ==  ABA ABABBAB ABAB xxx xxxxxmxx xxmxxm Vậy  12;3m− 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 13 Câu 9. Cho hàm số ( ) 22424 yfxxmxmm ==+ . Tìm tất cả các giá trị của tham số m sao cho giá trị nhỏ nhất của ( ) 3fx = . Lời giải Ta có 40=a nên đồ thị hàm số là một parabol có bề lõm hướng lên và có hoành độ đỉnh 2I m x = . • Nếu 24 2 m m −− thì 20Ix − . Suy ra ( )fx đồng biến trên đoạn  2;0 Do đó   ( ) ( ) 2 2;0 min2616 fxfmm =−=++ Theo yêu cầu bài toán: 2 6163mm++= (vô nghiệm). • Nếu 2040 2 m m −− thì  0;2Ix  . Suy ra ( )fx đạt giá trị nhỏ nhất tại 2I m x = . Do đó   ( )2;0 min 2 2 m fxfm  ==    . Theo yêu cầu bài toán 3 23 2 mm −==− (thỏa mãn 40 m − ). • Nếu 00 2 m m  thì 02Ix − . Suy ra ( )fx nghịch biến trên đoạn  2;0 Do đó   ( ) ( )2;0 2in0 2.m fxfm m= = Theo yêu cầu bài toán: 2 1 233 3 m mm m m =− −==  = ( Vì 0m  ). Từ các trường hợp trên, ta được 3 ;3 2 m     . VẤN ĐỀ 3. ĐỒ THỊ HÀM SỐ BẬC HAI Dạng 1. Cho parabol () P : 2 yaxbxc =++ . + Xác định trục đối xứng, tọa độ đỉnh của () P . + Tương giao của () P với trục Ox . + Tìm điều kiện để các giao điểm của () P và trục Ox thỏa mãn điều kiện nào đó. Thường dùng đến các kết quả sau: + Đường thẳng 2 b x a = là trục đối xứng của () P , điểm ; 24 b I aa −−    là đỉnh của () P . PHƯƠNG PHÁP.1 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 14 + Nghiệm (nếu có) của phương trình 2 0axbxc++= là hoành độ giao điểm của () P và trục Ox + Giả sử ( ) ( );,; AABA AxyBxy là hai giao điểm của () P và trục Ox . Khi đó: , AB cùng ở bên trái đối với trục Oy 0 0 .0 AB AB xx xx   +    , AB cùng ở bên phải đối với trục Oy 0 0 .0 AB AB xx xx   +    . , AB cùng ở một bên đối với trục Oy 0 .0ABxx     . , AB không ở cùng một bên đối với trục Oy .0ABxx  Câu 1. Cho parabol Xác định trục đối xứng, tọa độ đỉnh của parabol () P , tọa độ giao điểm của parabol () P với trục hoành. Lời giải + Ta có 5 22 b a −=− , 49 44 a  −=− , do vậy: ( )P có trục đối xứng là 5 2 x =− ; ( )P có đỉnh là 549 ; 24 I    . + Hoành độ giao điểm của ( )P với trục hoành là nghiệm của phương trình 2 1 560 6 x xx x = +−=  =− Vậy tọa độ giao điểm của ( )P với trục hoành là Câu 2. Cho parabol ( ) 2 : Pyaxbxc =++ với . Xét dấu của biết rằng cắt trục hoành tại hai điểm phân biệt có hoành độ âm. Lời giải đã cho cắt trục hoành tại hai điểm phân biệt có hoành độ âm khi và chỉ khi ( ) 2 :56.Pyxx=+− ( ) ( ) 1;0,6;0. 0a  ,,bc ( )P ( )P BÀI TẬP.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 15 0 0 0 S P      0 0 0 b a c a           0 0 0 b c       Dạng 2. Cho parabol ( ) 2 : Pyaxbxc =++ và đường thẳng : dymxn =+ + Biện luận số điểm chung của () P và trục hoành. + Tìm điều kiện để đường thẳng tiếp xúc với () P + Xét phương trình 2 0axbxc++= (*) () P cắt trục hoành tại hai điểm phân biệt  (*) có hai nghiệm phân biệt. - () P và trục hoành có một điểm chung (còn gọi là tiếp xúc với nhau)  (*) có một nghiệm. () P và trục hoành không có điểm chung  (*) vô nghiệm. + và () P tiếp xúc với nhau  2 axbxcmxn ++=+ có nghiệm kép. Câu 1. Tìm tất cả các giá trị của tham số m để parabol ( ) 2 :3 Pyxxm =++ cắt trục hoành tại hai điểm phân biệt Lời giải Phương trình hoành độ giao điểm của () P và trục hoành là (*). Yêu cầu của bài toán  (*) có hai nghiệm phân biệt  . Vậy 9 4 m  . Câu 2. Tìm tất cả các giá trị của tham số để parabol ( ) 2 :21Pyxxm=−+− và trục Ox không có điểm chung. Lời giải Phương trình hoành độ giao điểm của () P và trục Ox là 2 210xxm−+−= (*) Yêu cầu của bài toán  (*) vô nghiệm  020 m  − 2m  Vậy 2m  Câu 3. Cho parabol ( ) 2 :2Pyxx=++ và đường thẳng :1dyax=+ . Tìm tất cả các giá trị của tham số a để d tiếp xúc với ( )P Lời giải d d 2 30xxm++= 9 940 4 mm =− m PHƯƠNG PHÁP.1 = BÀI TẬP.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 17 Dựa vào đồ thị ta thấy, yêu cầu bài toán  6m  . Vậy 6m  . Câu 2. Cho hàm số 2 65yxx=−+ có đồ thị () P như nhình vẽ bên dưới. Dựa vào đồ thị, tìm các giá trị của tham số m để phương trình: 2 212610 xxm−+−= có 2 nghiệm phân biệt dương. Lời giải Phương trình: 2 212610 xxm−+−= 2 11 653 2 xxm −+=−+ (1). Phương trình (1) là phương trình hoành độ giao điểm của đồ thị hàm số ( )P 2 65yxx=−+ và đường thẳng ( ) 11 3 2dym=−+ Số nghiệm của phương trình (1) chính bằng số giao điểm của ( )P và ( )d . Dựa vào đồ thị ta thấy, yêu cầu bài toán  11 435 2 m −−+ 119 66 m  Vậy 119 66 m  Câu 3. Cho parabol ( ) 2 : Pyaxbxc =++ ( )0a  có đồ thị như hình bên. Tìm các giá trị của tham số m để phương trình 2 axbxcm ++= có bốn nghiệm phân biệt. Lời giải Đồ thị ( )C của hàm số 2 yaxbxc =++ bao gồm:

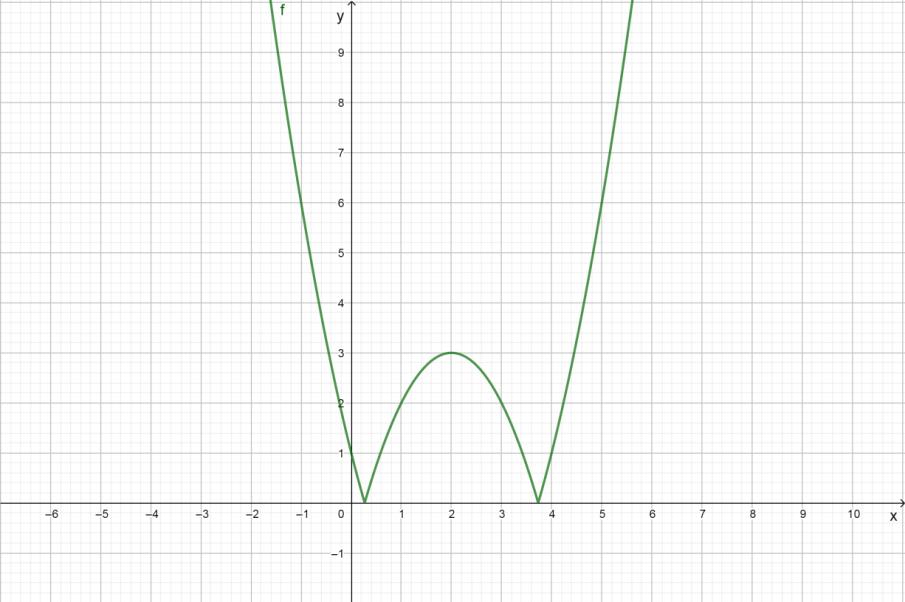
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 18 Phần 1: Là phần tính từ Ox trở lên của( )P Phần 2: Là phần đối xứng của phần phía dưới Ox của ( )P qua trục Ox . Phương trình 2 axbxcm ++= là phương trình hoành độ giao điểm của 2()Cyaxbxc =++ và đường thẳng : dym = Số nghiệm của phương trình 2 axbxcm ++= bằng số giao điểm của ( )C và ( )d . Dựa vào đồ thị ( )C ta thấy, yêu cầu của bài toán  suy ra 03 m  Vậy 03 m  Câu 4. Cho phương trình ( )2 401xxm+−= . Tìm tất cả các giá trị của tham số m để phương trình ( )1 có đúng một nghiệm thuộc khoảng ( )3;1 . Lời giải Phương trình ( )224041xxmxxm +−=+= ( )1 là phương trình hoành độ giao điểm của đồ thị ( )P của hàm số 2 4 yxx =+ và đường thẳng : dym = (cùng phương với trục Ox , cắt trục tung tại điểm có tung độ m ). Vẽ đồ thị ( )P Số nghiệm của phương trình (1) chính bằng số giao điểm của ( )P và ( )d

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 19 Dựa vào đồ thị, ta thấy phương trình 2 40xxm+−= có đúng một nghiệm thuộc khoảng ( )3;1 khi và chỉ khi 35 m − . Vậy 35 m − . Câu 5. Có bao nhiêu giá trị m nguyên trong nửa khoảng ( 0;2019 để phương trình 2 450xxm−−−= có hai nghiệm phân biệt? Lời giải PT: ( )22450451 xxmxxm −−−=−−= Số nghiệm phương trình ( )1 bằng số giao điểm của đồ thị ( )P của hàm số 2 45yxx=−− và đường thẳng ym = . Xét hàm số 2 45yxx=−− ta thấy nó có đồ thị ( )1P như hình sau đây: Xét hàm số 2 45yxx=−− ta thấy đây là hàm số chẵn nên đồ thị ( )2P của nó nhận Oy làm trục đối xứng. Mà 224545yxxxx =−−=−− nếu 0x  nên ( )2P gồm hai phần: Phần 1: Là phần bên phải Oy của ( )1P kể cả giao điểm của ( )1P và Oy . Phần 2: Là phần đối xứng của phần qua trục Oy . Tức ( )2P như hình sau đây: 1

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 20 Xét hàm số 2 45yxx=−− , ta có: ( ) ( ) ( ) 2 2 450 450 xxy y xxy  −− =  −−−  . Tức ( )P gồm hai phần: Phần 3: Là phần phía trên Ox của ( )2P kể cả các giao điểm của ( )2P và Ox Phần 4: Là phần đối xứng của phần phía dưới Ox của ( )2P qua trục Tức ( )P như hình sau đây Quan sát ( )P ta thấy: yêu cầu bài toán 9 0 m m    = . Do (   10;11;12;...;20190;2019 m m m      Vây có 2010 giá trị của tham số m thỏa yêu cầu bài toán Dạng 2. Sự tương giao của đồ thị hàm số bậc nhất và bậc hai Cho đồ thị ( )P của hàm số 2 yaxbxc =++ với 0a  và đồ thị d của hàm số ykxm =+ Ox PHƯƠNG PHÁP.1 =

phương

Nếu phương trình (2)

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 21 Toạ độ giao điểm của hai đồ thị( )P và d là nghiệm của hệ phương trình 2 yaxbxc ykxm  =++ =+ (1) Phương trình hoành độ giao điểm của ( )P và d là 2 axbxckxm ++=+ ( ) ( )2 02axbkxcm +−+−= Nhận xét: 1. Số giao điểm của ( )P và d bằng số nghiệm của hệ phương trình (1) và cũng bằng số nghiệm của phương trình (2). 2.

ếu

trình (2) vô nghiệm thì ta nói d và ( )P không giao nhau. 3.

có nghiệm kép thì ta nói d và ( )P tiếp xúc với nhau. Lúc này ta nói d là tiếp tuyến của . 4. Nếu phương trình (2) có 2 nghiệm phân biệt thì ta nói d và ( )P cắt nhau. Câu 1. Tìm tọa độ giao điểm của Parabol ( ) 2 :41Pyxx=−−+ và đường thẳng d : 3yx=−+ . Lời giải Phương trình hoành độ giao điểm của ( )P và d là 2 413xxx −−+=−+ 2 320xx ++= 1 2 x x =−   =− . Với 14xy=−= ; 25xy=−= . Tọa độ giao điểm của ( )P và d là ( ) ( )1;4,2;5AB Câu 2. Cho Parabol ( ) 2 :32Pyxx=−+ và đường thẳng :2dymx=+ Tìm m để d tiếp xúc với ( )P Tìm tọa độ tiếp điểm khi đó. Lời giải Phương trình hoành độ giao điểm của ( )P với d là 2 322xxmx−+=+ ( )2 30xmx −+= 0 3 x xm =   =+ . Để d tiếp xúc với ( )P thì 3m =− . Tọa độ tiếp điểm khi đó là (0;2)M ( )P BÀI TẬP.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 22 Nhận xét: Từ phương trình (1) ta tính ( )23m  =+ . Để d tiếp xúc với ( )P thì (1) có nghiệm kép 03 m  ==− . Câu 3. Cho Parabol ( )P 2 24yxx=−+ và đường thẳng d : 22 ymxm =− ( m là tham số). Tìm các giá trị của m để d cắt ( )P tại hai điểm phân biệt có hoành độ là 1x , 2x thỏa mãn 22 122(1)316xmxm++=+ Lời giải Xét phương trình hoành độ giao điểm của d và ( )P là ( ) 222140(1)xmxm−+++= . + Để d cắt ( )P tại hai điểm phân biệt có hoành độ là 12 ; xx thì 0   3 2 m  . Theo Viet ta có: 12 2 12 22 .4 xxm xxm +=+  =+ . Theo đề bài ta có 22 122(1)x316xmm++=+ ( ) 22 1122 316xxxxm ++=+ 222 1212 316xxxxm ++=+ ( )2 2 1212 316xxxxm +−=+ ( )2 22 224316 mmm +−−=+ 2m = . So sánh với điều kiện suy ra 2m = Câu 4. Cho Parabol 21 ():2 Pyx = và đường thẳng ( ) 2 1 :1 2dymxm=+−− ( m là tham số). Tìm các giá trị của m thì đường thẳng d cắt Parabol ( )P tại hai điểm 1122 (;),(;) AxyBxy sao cho biểu thức 121212()Tyyxxxx =+−−+ đạt giá trị nhỏ nhất. Lời giải Xét phương trình hoành độ giao điểm của ( )P và d ( ) 22 11 1 22 xmxm=+−− ( ) 2221210 (1)xmxm −+++= Để d cắt ( )P tại 2 điểm 1122 (;),(;) AxyBxy thì phương trình phải có 2 nghiệm 12 ; xx ( )2 2 0121002 mmm  +−− Vậy với 02 m  thì đường thẳng d cắt Parabol ( )P tại hai điểm 1122 (;),(;) AxyBxy Theo định lý Viet ta có: 12 2 12 22 .21 xxm xxm +=+  =+ Khi đó: ( ) ( ) 22 1122 11 1;1 22ymxmymxm =+−−=+−− . Ta có: ( ) ( ) ( )2 121212121212 1()21 Tyyxxxxmxxmxxxx =+−−+=++−−−−+ (1)

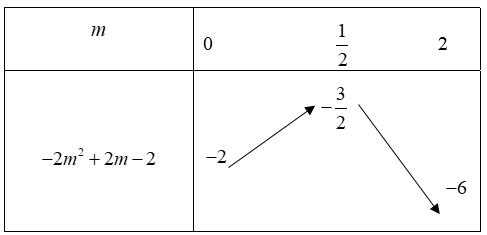
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 23 ( ) ( )2 22 214221222 Tmmmmm =+−−−+=−+− Bài toán trở thành tìm giá trị của tham số m để hàm số: 2 222Tmm=−+− đạt giá trị nhỏ nhất trên đoạn  0;2 . Ta có bảng biến thiên: Vậy giá trị nhỏ nhất của 6T =− đạt được khi 2m = . Dạng 3. Sự tương giao của hai đồ thị hàm số bậc hai Cho hai hàm số ( )yfx = và ( )ygx = là các hàm số bậc hai có đồ thị lần lượt là các đường parabol ( )1P và ( )2P , khi đó tọa độ giao điểm của ( )1P và ( )2P là nghiệm của hệ phương trình ( ) ( ) yfx ygx =   =  . (1) Để giải hệ (1) ta cần giải phương trình ( ) ( )fxgx = (2), phương trình (2) được gọi là phương trình hoành độ giao điểm của ( )1P và ( )2P * Nhận xét: i) Số giao điểm của ( )1P và ( )2P bằng số nghiệm của hệ (1) và bằng số nghiệm của phương trình (2). ii) ( )yfx = và ( )ygx = là các hàm số bậc hai nên phương trình (2) có nhiều nhất 2 nghiệm. iii) Các bài toán liên quan đến dạng này thường áp dụng đến nội dung định lý Vi et thuận, nhắc lại như sau. Cho phương trình bậc hai 2 0axbxc++= có hai nghiệm 1x và 2x , ta luôn có 12 b xx a +=− và 12 c xx a = Câu 1. Biết rằng đồ thị hàm số 2 6 yxx =− cắt đồ thị hàm số 2 4yx=−− tại hai điểm ( ); AAAxy và ( ) ;.BBBxy Tính AByy + . PHƯƠNG PHÁP.1 = BÀI TẬP.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 24 Lời giải Tọa độ giao điểm của hai đồ thị 2 5 yxx =− và 2 3yx=−− là nghiệm của hệ phương trình 222 22 664 44 yxxxxx yxyx =−−=−−    =−−=−−  2 2 2 1 1 5320 2 24 4 8 x x xxy x yxx yx y = =  =− −+=    =   =−−=    =−−=−  . Không mất tổng quát ta giả sử ( )1;5A và ( )2;8B , suy ra 13AByy+=− . Câu 2. Biết rằng parabol 2 1yxx=−+ cắt parabol 2 24yxx=−++ tại hai điểm phân biệt có hoành độ lần lượt là 1x và 2x . Tính giá trị biểu thức 33 12Pxx =+ . Lời giải Phương trình hoành độ giao điểm của hai parabol là 2221242330xxxxxx −+=−++−−= . (*) - Theo giả thiết ta có 12 , xx là hai nghiệm phân biệt của (*) nên 12 12 3 2 3 2 xx xx  +=    =−  Ta có ( )( ) ( ) ( ) 33222 12121122121212 3 Pxxxxxxxxxxxxxx =+=+−+=++−  2 33381 3 2228 P   =−−=      . Vậy 81 8 P = . Câu 3. Tìm tất cả các giá trị của m sao cho đồ thị hàm số ( ) 2 1232ymxxm =+++− cắt đồ thị hàm số 2 24yxmx=++ tại đúng hai điểm phân biệt có hoành độ lần lượt là 12 ; xx thỏa mãn 1221.xx+= Lời giải Phương trình hoành độ giao điểm của hai đồ thị đề bài cho là ( ) ( ) ( )222 12322421320 mxxmxmxmxmxm +++−=++−−+−= . (1) Phương trình (1) có đúng hai nghiệm phân biệt khi và chỉ khi ( ) ( )2 2 0 0 24101320 m m mmmmm      =−−−−++  . (2)

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 25 Với điều kiện (2), áp dụng định lý Viet cho phương trình (1) và giả thiết cho, ta có ( ) ( ) ( ) ( )( ) ( ) 11 12 1222 1212 2 3434 21 2122 323234232 (3) mm xxxxmm m mm xxxx mmm mmmmm xxxx mmmm  == +=   +===    ===  Giải phương trình (3) ta được 2m = và 2 3 m = đều thỏa mãn (2), nên đó là hai giá trị cần tìm của tham số m . Câu 4. Tìm tất cả các giá trị của m sao cho hai parabol ( ) 22 1yxmxm=+++ và ( ) ( )2 221yxmxm =−−+−+ cắt nhau tại hai điểm có hoành độ lần lượt là 12 ; xx thỏa mãn ( )1212 3 Pxxxx =−+ đạt giá trị lớn nhất. Lời giải Phương trình hoành độ giao điểm của hai parabol là ( ) ( ) ( ) ( )2 22221221221430xmxmxmxmxmxmm +++=−−+−++++++= . (1) Phương trình (1) có hai nghiệm khi và chỉ khi ( ) ( ) ( )( )2 2 12430150 mmmmm  =+−+++−− 10 50 51 10 50 m m m m m +  −−  −−  + −−  . (2) Với điều kiện (2), áp dụng định lý Viet cho phương trình (1), ta có ( ) ( ) ( )( ) 2 1212 4311 3311919 222 mm PxxxxPmmmmm ++ =−+=++=++=++ ( )( ) ( ) ( ) 2 1911 198 222 mm mm −−++  =−−+=   . (3) Dấu “=” ở bất đẳng thức (3) xảy ra khi và chỉ khi 19mm −−=+ hay 5m =− thỏa mãn (2). Vậy max8 P = đạt được khi 5m =− và do đó 5m =− chính là giá trị của tham số m cần tìm. VẤN ĐỀ 5. ĐIỂM CỐ ĐỊNH CỦA ĐỒ THỊ HÀM SỐ. Cho họ hàm số ( ) ;0fxm = ( m là tham số) có đồ thị ( )m P . Để tìm điểm cố định mà ( )m P luôn đi qua với mọi giá trị của m , ta thực hiện các bước sau: Bước 1: Giả sử điểm ( )00 ; Mxy là điểm cố định mà ( )m P luôn đi qua. PHƯƠNG PHÁP.1 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 26 Tọa độ điểm M thỏa mãn phương trình ( ) ;0fxm = Bước 2: Chuyển phương trình về phương trình ẩn m dạng 0AmB+= (hoặc 2 0AmBmC++= ). Phương trình nghiệm đúng với mọi m . Khi đó ta có 0 0 A B =  = hoặc 0 0 0 A B C =  =  = . Tìm được ( )0000 ;; xyMxy  Bước 3: Kết luận. Câu 1. Cho hàm số ( ) ( ) ( )2 1213 mymxmxmP =+−−+− . Chứng tỏ rằng ( )m P luôn đi qua một điểm cố định, tìm tọa độ điểm cố định đó. Lời giải Tập xác định: D = Giả sử điểm ( )00 ; Mxy là điểm cố định mà ( )m P luôn đi qua. Khi đó ( ) ( )2 0001213ymxmxm =+−−+− , m  ( ) 22 0000021230xxmxxy −+++−−= , m  . 2 00 2 000 210 230 xx xxy  −+=   +−−=  0 0 1 0 x y =   = . Vậy họ ( )m P luôn đi qua điểm cố định ( )1;0M . Câu 2. Cho hàm số ( ) ( )2 1231 mymxmxmP =−+−+ . Tìm điểm cố định của họ đồ thị hàm số trên. Lời giải Tập xác định: D = Giả sử điểm ( )00 ; Mxy là điểm cố định mà ( )m P luôn đi qua. Khi đó ( ) 2 0001231ymxmxm =−+−+ , m  . ( ) 22 00002310xxmxy +−−+−= , m  2 00 2 0o 230 10 xx xy  +−=   −+−=  0 00 2 0 1 3 1 x x yx  =  =−   =− 0 0 1 0 x y =   = hoặc 0 0 3 8 x y =−  =− . Vậy họ ( )m P luôn đi qua 2 điểm cố định ( )1 1;0M và ( )2 3;8M BÀI TẬP.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 27 Câu 3. Tìm điểm cố định của đồ thị hàm số ( )m P : ( ) 222211ymxmxm =+−+− Lời giải Tập xác định: D = . Giả sử điểm ( )00 ; Mxy là điểm cố định mà ( )m P luôn đi qua. Khi đó ( ) 222 000211ymxmxm=+−+− , m  ( ) 22 000012210xmxmxy ++−−−= , m  . ( ) 2 0 0 00 10 20I 210 x x xy  +=  =  −−−=  . Do phương trình 2 0 10x += vô nghiệm nên hệ ( )I vô nghiệm. Vậy không có điểm nào thỏa mãn yêu cầu bài toán. Câu 4. Cho hàm số ( )2 2354 yxmxm =+−+− . Chứng minh rằng với mọi giá trị của m , đồ thị ( )m P của hàm số đã cho và đường thẳng ( ) :243 m dymxm=−+ luôn có một điểm chung cố định. Lời giải Tập xác định của hai hàm số đã cho là D = . Giả sử điểm ( )00 ; Mxy là điểm cố định mà ( )m d luôn đi qua. Khi đó 00243ymxm=−+ , m  ( ) 00 2430 xmy −+−= , m  00 00 2402 303 xx yy −==−== ( )2;3M . Thay tọa độ điểm M và phương trình của ( )m P ta được ( )2 3223.254mm=+−+− 33= (đúng với mọi m ). Vậy ( )2;3M là điểm chung cố định của ( )m P và ( )m d Câu 5. Cho các hàm số ( ) ( )2 :347 m Pyxmxm =−++− , ( ) ( )2 :3149 m Cymxmxm =−+−+ , ( ) ( ) :140 m dmxmym −++−= Chứng minh rằng với mọi giá trị của m , các đồ thị của các hàm số đã cho luôn cùng đi qua một điểm cố định. Lời giải Tập xác định của hai hàm số đã cho là D = . Giả sử điểm ( )00 ; Mxy là điểm cố định mà ( )m d luôn đi qua. Khi đó ( ) 00 140mxmym −++−= , m  . ( ) 000140xymx +−+−= , m 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 28 000 00 104 403 xyx xy +−==   −==− ( )4;3M − . Thay tọa độ điểm M vào phương trình của( )m P ta được ( )2 343.447 mm −=−++− 33 (đúng với mọi m ). Thay tọa độ điểm M vào phương trình của ( )m C ta được ( )2 3.431.449 mmm −=−+−+ 33−=− (đúng với mọi m ). Vậy các đồ thị ( );m P ( );m C ( )m d luôn cùng đi qua một điểm cố định ( )4;3M . VẤN ĐỀ 6: GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ BẬC HAI Dạng 1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên 1 tập cho trước Để tìm giá trị lớn nhất và nhỏ nhất của hàm số bậc hai, ta lập bảng biến thiên cho hàm số đó trên tập hợp đã cho. Dựa vào bảng biến thiên, ta kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số trên tập hợp đã cho. Câu 1. Cho hàm số 2 43yxx=−− . Tìm giá trị lớn nhất của hàm số đã cho trên  3;5 . Lời giải Hàm số đã cho là hàm số bậc hai có hệ số: 1,4,3abc==−=− Ta có: 4 2 22.1 b a == ; 2 (4)4.(3)28 7 44.14 a −−−−− ===− . Vì 10a = nên hàm số nghịch biến trên (;2) − , đồng biến trên (2;) + . Do đó, ta có bảng biến thiên của hàm số trên  3;5 là: Dựa vào bảng biến thiên, vậy  3;5 min(2)7 x yy − ==− và  3;5 max(3)18 x yy − =−= Câu 2. Cho hàm số 2 243yxx=−++ . Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên  2;7 Lời giải Hàm số đã cho là hàm số bậc hai có 2,4,3abc=−== . PHƯƠNG PHÁP.1 = BÀI TẬP.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 29 Ta có: 4 1 22.(2) b a == ; 2 44.(2).3 5 44.(2) a −−− =−= Vì 20a =− nên hàm số đồng biến trên ( );1− , nghịch biến trên ( )1;+ . Do đó, ta có bảng biến thiên của hàm số trên  2;7 là: Dựa vào bảng biến thiên, vậy  2;7 min(7)67 x yy  ==− và  2;7 max(2)3 x yy  == Câu 3. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 4243yxx=−− trên  1;2 Lời giải Đặt 2tx = . Với  1;2x− ta có  0;4t  . Hàm số trở thành ( ) 2 43fttt=−− với  0;4t  . Bảng biến thiên: Dựa vào bảng biến thiên, ta có   ( )  1;2 0;4 maxmax3 x t yft −  ==− khi 0 4 t t =  = hay 0 2 x x =  = .   ( )  1;2 0;4 minmin7 x t yft −  ==− khi 2t = hay 2x = Câu 4. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 33422 221413yxxx =−+++++ . Lời giải Đặt ( ) 332242 1 121txttxx =+=++ . Hàm số trở thành ( ) 2 243fttt=−++ Bảng biến thiên: Dựa vào bảng biến thiên, ta có ( )  1; maxmax5 t yft + == khi 1t = hay 0x = Giá trị nhỏ nhất của y không tồn tại.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 30 Câu 5. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 4324322yxxxx =++−+ trên  2;4 . Lời giải Ta có: 43224422yxxxxx =++−−+ 222 (2)(2)2yxxxx =+−++ Đặt 2 2 txx =+ . Xét hàm số ( ) 2 2 txxx =+ với  2;4x− . Bảng biến thiên: Từ bảng biến thiên ta có:  1;24t − với  2;4x− Do đó, hàm số y ban đầu có giá trị lớn nhất, giá trị nhỏ nhất (nếu có) trên  2;4 bằng giá trị lớn nhất, giá trị nhỏ nhất của hàm số ( ) 2 2fttt=−+ với  1;24t − Bảng biến thiên: Dựa vào bảng biến thiên, ta có   ( )  2;4 1;24 maxmax 554 x t yft − − == khi 24t = hay 4x =   ( )  2;4 1;24 7minmin 4x t yft − − == khi 1 2 t = hay 2 126 2 22 xxx −+ +== . Câu 6. Cho các số , xy thỏa mãn 22 1 xyxy +=+ . Tìm giá trị lớn nhất và giá trị nhỏ nhất của 4422 Pxyxy =+− Lời giải Ta có: ( ) ( )2 2 22222222313221 Pxyxyxyxyxyxy =+−=+−=−++ Đặt txy = , khi đó 2 221Ptt=−++ Vì 22 22 2 2 xyxy xyxy  + +− nên 121 1 123 xyxy xy xyxy + − +− Do đó: 1 1 3 t −

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 31 Xét hàm số ( ) 2 221fttt=−++ trên 1 ;1 3    Bảng biến thiên: Dựa vào bảng biến thiên, ta có ( ) 1 ;1 3 1 minmin 9 t Pft  −  == khi 1 3 t =− hay 11 , 33 11 , 33 xy xy  ==−   =−=  ( ) 1 ;1 3 3 maxmax 2 t Pft  −  == khi 1 2 t = hay 102102 , 44 102102 , 44 xy xy  +−==   −+==  Dạng 2. Tìm điều kiện của tham số để hàm số bậc hai đạt giá trị lớn nhất, giá trị nhỏ nhất Cho hàm số bậc hai: 2 yaxbxc =++ ( )0a  Nếu 0a  thì min 24yfb aa  =−=−   đạt tại hoành độ đỉnh 2I b x a =− Nếu 0a  thì max 24yfb aa  =−=−   đạt tại hoành độ đỉnh 2I b x a =− Trường hợp tập xác định khác , ta kẻ bảng biến thiên của hàm số trên tập đó để có được giá trị lớn nhất, giá trị nhỏ nhất. Câu 1. Tìm giá trị thực của tham số 0m  để hàm số 2 232ymxmxm =−−− có giá trị nhỏ nhất bằng 10 trên . Lời giải Hoành độ đỉnh: 2 1 22I bm x am =−== , suy ra 42I ym=−− PHƯƠNG PHÁP.1 = BÀI TẬP.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 32 Để hàm số có giá trị nhỏ nhất bằng 10 khi và chỉ khi 0 2 4210 m m m  = −−=− ( Thỏa mãn) Câu 2. Cho hàm số 2 yaxbxc =++ đạt giá trị nhỏ nhất bằng 2 khi 1x = và nhận giá trị bằng 3 khi 2x = . Tính abc. Lời giải Để hàm số 2 yaxbxc =++ đạt giá trị nhỏ nhất bằng 2 khi 1x = và nhận giá trị bằng 3 khi 2x = khi và chỉ khi ( ) 0 0 1 120 22 1223 423 (2)3 a a ba ab a b fabc c abc f   = −= +=  =− ++=  = = ++==  . Vậy 1.(2).36abc =−=− . Câu 3. Cho hàm số 2 21ymxxm=−−− . Tìm giá trị thực của tham số m để giá trị lớn nhất của hàm số đã cho đạt giá trị nhỏ nhất. Lời giải Hoành độ đỉnh: 21 22I b x amm =−== , suy ra 2 2 111 .2.1I mm ymm mmm  =−−−=   TH1: Khi 0m  thì 2 1 max I mm yy m == tại điểm 1 Ix m = ( ) 222 121(1) 1111011I yfmmmmmm mmm −−−−−−−+ ==−+=+=++= . Vậy min1 Iy = tại điểm 1m =− . TH2: Khi 0m  thì hàm số đã cho không có giá trị lớn nhất, chỉ có giá trị nhỏ nhất. TH3: Khi 0m = thì hàm số 21yx=−− đã cho là hàm số bậc nhất, không có giá trị lớn nhất. Kết luận: 1m =− . Câu 4. Cho hàm số ( ) ( ) 22 2 12112 ymxmxm =−−+−++ . Với 1m  , tìm giá trị nhỏ nhất của biểu thức [0;2] [0;2] min max x x y B y   = . Lời giải Hoành độ đỉnh: ( ) ( ) 2 2 21 1 2 21 I bm x a m =−== , suy ra ( ) ( ) 22 2 121122I ymmmm =−−+−++=+ Do 2 (1)0, 1amm =−− nên ta có bảng biến thiên như sau:

DẠNG 1: Các bài toán thực tế mà mô hình thực tiễn chưa chuyển về mô hình toán học. Các bước làm như sau:

Bước 1: Dựa vào giả thiết và các yếu tố của đề bài, ta xây dựng mô hình toán học cho vấn đề đang xét, tức là diễn tả dưới “dạng ngôn ngữ toán học” cho mô hình mô phỏng thực tiễn. Căn cứ vào các yếu tố bài ra ta chọn biến số, tìm điều kiện tồn tại, đơn vị.

Bước 2: Dựa vào các mối liên hệ ràng buộc giữa biến số với các giả thiết của đề bài cũng như các kiến thức liên quan đến thực tế, ta thiết lập hàm số bậc hai. Chuyển yêu cầu đặt ra đối với bài toán thực tiễn thành yêu cầu bài toán hàm số bậc hai.

Bước 3: Dùng tính ch

n, và k

t hàm s

t qu

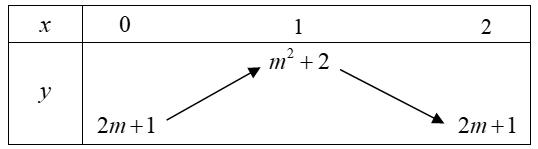
thu

hai

c có phù h

i quyết bài toán hình thành ở bước 2. Lưu ý kiểm tra điều ki

p v

i bài

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 33 Từ bảng biến thiên ta có:   2 0;2 max2 x ym  =+ tại 1x = ,  0;2 min21 x ym  =+ tại 0x = hoặc 2x = .     ( ) ( ) ( ) ( ) 0;2 0;2 2222 2 222 2 min111121m4422 211 2222 max2222 22 x x y mmmmm mm B ymmm m   ++−++−+ ++ =====− +++ + Vì ( ) ( ) ( ) 2 2 2 2 1 20, 0, , 222 m B m mm mm  + +− +  Vậy 1 min 2 B =− tại 2m =− . VẤN ĐỀ 7: BÀI TOÁN THỰC TẾ

ấ

ố

ậc

để

ả

ệ

ế

ả

đượ

ợ

ớ

toán thực tế đã cho chưa. DẠNG 2: Các bài toán thực tế đã mô hình hóa bằng một hàm số bậc hai. Thực hiện bước 3 của dạng 1. Câu 1. Một quả bóng được ném vào không trung có chiều cao tính từ lúc bắt đầu ném ra được cho bởi công thức ( ) 2 23httt=−++ (tính bằng mét), t là thời gian tính bằng giây ( )0t  a. Tính chiều cao lớn nhất quả bóng đạt được. b. Hãy tính xem sau bao lâu quả bóng sẽ rơi xuống mặt đất ? Lời giải a. Ta có: ( ) 2 23httt=−++  ( ) ( )2 14htt=−−+  ( ) ( ) max14 hth== . Vậy quả bóng đạt chiều cao lớn nhất bằng 4 m tại thời điểm 1t = giây. b. Ta có: 2 230tt −++=  1t =− (loại) hoặc 3t = (nhận). PHƯƠNG PHÁP.1 = BÀI TẬP.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 34 Vậy sau 3 giây quả bóng sẽ rơi xuống mặt đất. Câu 2. Độ cao của quả bóng golf tính theo thời gian có thể được xác định bằng một hàm bậc hai. Với các thông số cho trong bảng sau, hãy xác định độ cao quả bóng đạt được tại thời điểm 3 giây ? Lời giải Độ cao của quả bóng tính theo thời gian được xác định bởi hàm số ( ) 2 htatbtc =++ (tính bằng mét), t : giây, 0t  Với các thông số cho bởi bảng trên ta có: 0 11 28 42 48 420 c abc abc abc =   ++=   ++= ++=  16 64 0 a b c =−  =   = ( ) 2 1664 httt=−+ ( ) 348h = . Vậy độ cao quả bóng đạt được tại thời điểm 3 giây là 48 m. Câu 3. Một miếng nhôm có bề ngang 32 cm được uốn cong tạo thành máng dẫn nước bằng chia tấm nhôm thành 3 phần rồi gấp 2 bên lại theo một góc vuông như hình vẽ dưới. Hỏi x bằng bao nhiêu để tạo ra máng có có diện tích mặt ngang S lớn nhất để có thể cho nước đi qua nhiều nhất ? Lời giải Gọi ( )Sx là diện tích mặt ngang ứng với bề ngang x (cm) của phần gấp hai bên, ta có: ( ) ( )322 Sxxx =− , với 016 x  Diện tích mặt ngang lớn nhất khi hàm số ( )Sx đạt giá trị lớn nhất trên ( )0;16 Ta có: ( ) ( ) ( )22 23228128128, 0;16Sxxxxx =−+=−−+ . ( ) ( ) max8128 SxS == . Vậy 8x = cm thì diện tích mặt ngang lớn nhất.

Câu 4. Hai con chuồn chuồn bay trên hai quĩ đạo khác nhau, xuất phát cùng thời điểm. Một con bay trên quỹ đạo là đường thẳng từ điểm

( )0;100A đến điểm ( )0;0O với vận tốc 5m/s

Con còn lại bay trên quĩ đạo là đường thẳng từ

( )60;80B đến điểm ( )0;0O với vận

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 35

tốc 10m/s. Hỏi trong quá trình bay thì khoảng cách ngắn nhất hai con đạt được là bao nhiêu ? Lời giải Xét tại thời điểm t (giây),  0;10t  , con chuồn chuồn bay từ A về O có tọa độ là ( )0;1005 At  Con chuồn chuồn bay từ ( )60;80B về ( )0;0O trên quĩ đạo là đường thẳng có hệ số góc là 434tancos= , sin 355 k   === . Do đó tại thời điểm t , nó có tọa độ là 6010.cos 8010.sin xt yt   =−  =− 606 808 xt yt =−   =− ( )606;808 Btt  −− Ta có: ( )606;203 ABtt  =−−− . Khi đó, khoảng cách giữa hai con chuồn chuồn là: ( ) ( ) 22606203 dABtt  ==−++ 2 456004000dtt =−+ d nhỏ nhất khi hàm số ( ) 2 456004000fttt=−+ đạt giá trị nhỏ nhất trên  0;10 . Ta có: ( ) ( )  2 532020002000, 0;10fttt =−+   ( )0;10 20 min2000 3t ftf   ==   Vậy khoảng cách ngắn nhất của hai con chuồn chuồn trong quá trình bay là 2000205 = m. Câu 5. Một cửa hàng bán bưởi Đoan Hùng của Phú Thọ với giá bán mỗi quả là 50000 đồng. Với giá bán này thì mỗi ngày cửa hàng chỉ bán được 40 quả. Cửa hàng dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi quả 1000 đồng thì số bưởi bán tăng thêm được là 10 quả. Xác định giá bán để của hàng thu được lợi nhuận cao nhất, biết rằng giá nhập về ban đầu cho mỗi quả là 30000 đồng. Lời giải Gọi x là giá bán thực tế của mỗi quả bưởi Đoan Hùng ( x : đồng, 3000050000 x  ). Tương ứng với giá bán là x thì số quả bán được là: ( ) 101 4050000540 1000100 xx +−=−+ . Gọi ( )fx là hàm lợi nhuận thu được ( ()fx : đồng), ta có:

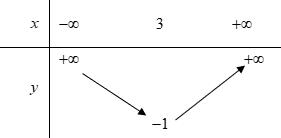
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 36 ( ) ( ) 211 540.3000084016200000 100100 fxxxxx  =−+−=−+−   Lợi nhuận thu được lớn nhất khi hàm ( )fx đạt giá trị lớn nhất trên  30000;50000 Ta có: ( )   21 420014400001440000, 30000;50000 10 fxxx  =−−+     ( ) ( )30000;50000 max 420001440000 x fxf  == . Vậy với giá bán 42000 đồng mỗi quả bưởi thì cửa hàng thu được lợi nhuận lớn nhất. Câu 1. Cho hàm số 2 68yxx=−+ , có đồ thị là ( )P a) Lập bảng biến thiên và vẽ đồ thị ( )P b) Biện luận theo m số nghiệm của phương trình ( ) 420xxm−−+= . Lời giải Lập bảng biến thiên và vẽ đồ thị hàm số 2 68yxx=−+ . Tọa độ đỉnh ( )3;1I Trục đối xứng 3x = . Hệ số d : bề lõm quay lên trên. Hàm số nghịch biến trên khoảng ( );3− và đồng biến trên khoảng ( )3;+ Bảng biến thiên Đồ thị hàm số cắt trục tung tại điểm ( )0;8A , cắt trục hoành tại hai điểm ( )4;0B và ( )2;0C HỆ THỐNG BÀI TẬP TỰ LUẬN TỔNG HỢP.II =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 37 x y   3     b) Ta có ( ) ( )( ) ( )( ) 42khi 20 42 42khi 20 xxx yxx xxx     −−− =−−=   hay ( ) 2 2 68khi 2 68khi 2y xxx xxx     −+ = −−+  . Do đó từ đồ thị hàm số ( ) 2 68yfxxx ==−+ suy ra đồ thị hàm số ( ) 42yxx=−− như sau: ● Đồ thị hàm số ( )yfx = phần bên phải đường 2x = ta giữ nguyên. ● Đồ thị hàm số ( )yfx = phần bên trái đường 2x = ta lấy đối xứng qua trục hoành. x y   3     Phương trình ( ) ( )420 42 xxmxxm −−+=−−=− là phương trình hoành độ giao điểm của đồ thị hàm số ( ) 42yxx=−− và đường thẳng ym =− (song song với Ox ). Do đó số nghiệm của phương trình bằng số giao điểm của đồ thị và đường thẳng. Dựa vào đồ thị, ta có ● 00 11 mm mm −    −−  : phương trình có 1 nghiệm duy nhất. ● 00 11 mm mm −==    −=−=  : phương trình có 2 nghiệm. ● 1001 mm −− : phương trình có 3 nghiệm. Câu 2. Vẽ đồ thị hàm số 2 4khi1 43khi1 xx y xxx    −+ = −+ Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 38 Khi 1x  thì 4yx=−+ . Cho 13xy== , ta được điểm ( )1;3A Cho 04xy== , ta được điểm ( )0;4B Khi 1x  thì 2 23yxx=+− . Tọa độ đỉnh ( )2;1I Hệ số 10a =− : bề lõm quay lên trên. Cho 10xy== , ta được điểm . ( )1;0M .. Cho 30xy== , ta được điểm ( )3;0N . x y O 3 1 3 2 4  Câu 3. Xác định parabol 2 32yaxx=+− , biết rằng parabol đó a) Cắt trục hoành tại điểm có hoành độ bằng 2. b) Có trục đối xứng 3x =− . c) Có đỉnh 111 ; 24 I    . d) Đạt cực tiểu tại 1x = Lời giải a) Vì parabol ( )P cắt trục hoành tại điểm có hoành độ bằng 2 nên điểm ( )2;0A thuộc ( )P . Thay 2x = , . 0y = . vào ( )P , ta được 04621 aa =+−=− . Vậy ( ) 2 :32Pyxx=−+− . b) Vì ( )P có trục đối xứng 3x =− nên 31 33 222 b a aa −=−−=−= . Vậy ( ) 21 :32 2 Pyxx=+−

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 39 c) Vì ( )P có đỉnh 111 ; 24 I    nên ta có 1 322 3 11119811 44 b abaa a aaa a  −=− == = =+= −=−  . Vậy ( ) 2 :332Pyxx=+− . d) Vì ( )P đạt cực tiểu tại 1x = nên suy ra 00 0 3 3 11 22 2 aa a b a aa       −=−= =−  : vô nghiệm. Vậy không có ( )P nào thỏa yêu cầu bài toán. Câu 4. Xác định parabol 2 2yaxbx=++ , biết rằng parabol đó a) Đi qua hai điểm ( )1;5M và ( )2;8N b) Có đỉnh ( )2;2I . c) Đi qua điểm ( )3;4A và có trục đối xứng 3 4 x =− d) Đi qua điểm ( )1;6B và đỉnh có tung độ 1 4 Lời giải a) Vì ( )P đi qua hai điểm ( )1;5M và ( )2;8N nên ta có 252 42281 aba abb ++==   −+== . Vậy ( ) 2 :22Pyxx=++ b) Vì ( )P có đỉnh ( )2;2I nên ta có 22 2 44 02 448161602 4 b baba aa bacaaab a  −= =−=− =    =− −=−=  −=−  hoặc 1 4 a b =  =− Do ( )P là parabol nên 0a  nên ta chọn 1 4 a b =  =− . Vậy ( ) 2 :42Pyxx=−+ c) Vì ( )P đi qua điểm ( )3;4A và có trục đối xứng 3 4 x =− nên ta có 4932432 9 3 3 2 24 2 3 ab ab a b ba ab ++=− +=− =−      −=− =  =−   .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 40 Vậy ( ) 2 42 :2 93 Pyxx=−−+ . d) Vì ( )P đi qua điểm ( )1;6B và có tung độ đỉnh bằng 1 4 nên ta có ( )2 22 26 4 44 16 1 12844 49360 44 ab ab abab a bacabbbbbb a −+= =+ −==+  =    −=−−+=+= −=−−=    hoặc 1 3 a b =  =− . • Với 16 12 a b =  = ta có ( ) 2 :16122Pyxx=++ • Với 1,3ab==− ta có ( ) 2 :32Pyxx=−+ . Vậy ( ) 2 :16122Pyxx=++ hoặc ( ) 2 :32Pyxx=−+ . Câu 5. Xác định parabol 22 yxbxc =++ , biết rằng parabol đó a) Có trục đối xứng 1x = và cắt Oy tại điểm ( )0;4M . b) Có đỉnh ( )1;2I . c) Đi qua hai điểm ( )0;1A và ( )4;0B . d) Có hoành độ đỉnh 2 và đi qua điểm ( )1;2N . Lời giải a) Vì ( )P có trục đối xứng 1x = nên 124 2 b bab a −==−=− Hơn nữa ( )P cắt trục Oy tại điểm ( )0;4M nên 2.0.044 bcc ++== Vậy ( ) 2 :244Pyxx=−+ . b) Vì ( )P có đỉnh ( )1;2I nên suy ra 2 1 2 442 168160482 4 b ba abb bacacc a  −=− = ==    −== −=  −=−  Vậy ( ) 2 :24 Pyxx =+ c) Vì ( )P đi qua hai điểm ( )0;1A và ( )4;0B nên suy ra 2.0.011 324031 4 bcc bc b ++=−=−    ++= =−   .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 41 Vậy ( ) 2 31 :21 4 Pyxx=−− . d) Vì ( )P có hoành độ đỉnh bằng 2 nên 248 2 b bab a −=−== Hơn nữa ( )P đi qua điểm ( )1;2N nên 2228212 bccc ++=−++=−=− . Vậy ( ) 2 :2812Pyxx=+− . Câu 6. Xác định parabol 2 yaxc =+ , biết rằng parabol đó a) Đi qua hai điểm ( )1;1M , ( )2;2B . b) Có đỉnh ( )0;3I và một trong hai giao điểm với Ox là ( )2;0A . Lời giải a) Vì ( )P đi qua hai điểm ( )1;1M , ( )2;2B nên suy ra 11 422 aca acc +==−   +=−= . Vậy ( ) 2 :2Pyx=−+ b) Vì ( )P có đỉnh ( )0;3I và giao với Ox tại ( )2;0A nên suy ra 33 403 4 c c ac a ==    += =−   Vậy ( ) 23 :3 4 Pyx=−+ . Câu 7. Xác định parabol 2 4 yaxxc =−+ , biết rằng parabol đó a) Có hoành độ đỉnh là 3 và đi qua điểm ( )2;1M b) Có trục đối xứng là đường thẳng 2x = và cắt trục hoành tại điểm ( )3;0A Lời giải a) Vì ( )P có hoành độ đỉnh bằng 3 và đi qua ( )2;1M nên suy ra 2 63 32 4814713 3 b baa a ac ac c  =− −=−=     +=−  ++= =−   . Vậy ( ) 2 213 :4 33Pyxx=−−− .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 42 b) Vì ( )P có trục đối xứng 2x = và cắt trục hoành tại ( )3;0A nên suy ra 412 2 91209123 b baa a acc ac  −==−=    +== −+= Vậy ( ) 2 :43Pyxx=−+ . Câu 8. Xác định parabol 2 yaxbxc =++ , biết rằng parabol đó a) Đi qua ba điểm ( ) ( ) ( )1;1, 1;3, 0;0ABO b) Cắt trục Ox tại hai điểm có hoành độ lần lượt là 1 và 2, cắt trục Oy tại điểm có tung độ bằng 2 c) Đi qua điểm ( )4;6M , cắt trục Ox tại hai điểm có hoành độ lần lượt là 1 và 3. Lời giải a) Vì ( )P đi qua ba điểm ( ) ( ) ( )1;1, 1;3, 0;0ABO nên suy ra 11 32 00 abca abcb cc ++==−  −+=−= ==  Vậy ( ) 2 :2 Pyxx =−+ b) Gọi A và B là hai giao điểm cuả ( )P với trục Ox có hoành độ lần lượt là 1 và 2. Suy ra ( )1;0A , ( )2;0B . Gọi C là giao điểm của ( )P với trục Oy có tung độ bằng 2. Suy ra ( )0;2C . Theo giả thiết, ( )P đi qua ba điểm , , ABC nên ta có 01 4201 22 abca abcb cc −+==  ++==− =−=−  . Vậy ( ) 2 :2Pyxx=−− c) Gọi E và F là hai giao điểm của ( )P với trục Ox có hoành độ lần lượt là 1 và 3. Suy ra ( )1;0E , ( )3;0F Theo giả thiết, ( )P đi qua ba điểm , , MEF nên ta có 16462 015368 9308206 abccaba abcabb abcabc ++=−=−−=−  ++=+=−=  ++=+==−  . Vậy ( ) 2 :286Pyxx=−+− . Câu 9. Xác định parabol 2 yaxbxc =++ , biết rằng parabol đó

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 43 a) Có đỉnh ( )2;1I và cắt trục tung tại điểm có tung độ bằng 3 b) Cắt trục hoành tại hai điểm ( )1;0A , ( )3;0B và có đỉnh nằm trên đường thẳng 1y =− c) Có đỉnh nằm trên trục hoành và đi qua hai điểm ( )0;1M , ( )2;1N d) Trục đối xứng là đường thẳng 3x = , qua ( )5;6M và cắt trục tung tại điểm có tung độ bằng 2 . Lời giải a) Vì ( )P có đỉnh ( )2;1I nên ta có 2 2 42 441 4 b aba baca a  −= =    −= −=−  . ( )1 Gọi A là giao điểm của ( )P với trục tung tại điểm có tung độ bằng 3. Suy ra ( )0;3A Theo giả thiết, ( )0;3A thuộc ( )P nên .0.033 abcc++=−=− . ( )2 Từ ( )1 và ( )2 , ta có hệ 2 4 0 16800 33 ba a aab cc = =  +== =−=−  hoặc 1 2 2 3 a b c  =−  =−  =−  . Do ( )P là parabol nên 0a  nên ta chọn 1 ;2;3 2 abc=−=−=− . Vậy ( ) 21 :23 2 Pyxx=−−− b) Vì ( )P cắt trục hoành tại hai điểm ( )1;0A , ( )3;0B nên 0.1.10 0.9.3930 abcabc abcabc =++++=   =++++= ( )1 Hơn nữa, ( )P có đỉnh thuộc đường thẳng 1y =− nên 2 1444 4 abaca a  −=−=−= ( )2 Từ ( )1 và ( )2 , ta có hệ 22 040 93030 04444 abcbaa abccab bacabacac ++==−=   ++===   −=−==  hoặc 1 4 3 a b c =  =−  = Do ( )P là parabol nên 0a  nên ta chọn Ox Vậy ( ) 2 :43Pyxx=−+ .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 44 c) Vì ( )P có đỉnh nằm trên trục hoành nên 2 0040 4 ba a  −==−= . ( )1 Hơn nữa, ( )P đi qua hai điểm ( )0;1M , ( )2;1N nên ta có 1 421 c abc =  ++= . ( )2 Từ ( )1 và ( )2 , ta có hệ 22 2 404010 1120 4214201 440 babaca ccbab abcabc aa   −=−===   ===−=   ++=+== −=  hoặc 1 2 1 a b c =  =−  = . Do ( )P là parabol nên 0a  nên ta chọn 1; 2; 1abc==−= . Vậy ( ) 2 :21Pyxx=−+ . d) Vì ( )P có trục đối xứng là đường thẳng 3x = nên 36 2 b ba a −==− ( )1 Hơn nữa, ( )P qua ( )5;6M nên ta có 6255abc=−+ ( )2 Lại có, ( )P cắt trục tung tại điểm có tung độ bằng 2 nên 2.0.02 abcc −=++=− ( )3 Từ ( )1 , ( )2 và ( )3 ta có hệ 6 848 253026;;2 5555 2 ba aaabc c =−  +−===−=−  =− Vậy ( ) 2 848 :2 5555 Pyxx=−− Câu 10. Xác định parabol 2 yaxbxc =++ , biết rằng hàm số a) Có giá trị nhỏ nhất bằng 4 tại 2x = và đồ thị hàm số đi qua điểm ( )0;6A . b) Có giá trị lớn nhất bằng 3 tại 2x = và đồ thị hàm số đi qua điểm ( )0;1B . Lời giải a) Vì hàm số giá trị nhỏ nhất bằng 4 tại 2x = và đồ thị hàm số đi qua điểm ( )0;6A nên ta có

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 45 22 2 2 44 0 441616800 4 6666 b a baba a bacaaab a ccc c  −= =−=− =    −=−=−−==   === =   hoặc 1 2 2 6 a b c  =  =−  =  . Do ( )P là parabol nên 0a  nên ta chọn 1 ,2,6 2 abc==−= Vậy ( ) 21 :26 2 Pyxx=−+ . b) Vì hàm số giá trị lớn nhất bằng 3 tại 2x = và đồ thị hàm số đi qua điểm ( )0;1B nên ta có 22 2 2 44 0 3412161600 4 1111 b a baba a bacaaab a ccc c  −= =−=− =    −=−=−+==  =−=−=− =−   hoặc 1 4 1 a b c =−  =  =− Do ( )P là parabol nên 0a  nên ta chọn 1, 4, 1abc=−==− . Vậy ( ) 2 :41Pyxx=−+− Câu 11. Cho hàm số 2 232ymxmxm =−−− ( )0m  . Xác định giá trị của m trong mỗi trường hợp sau a) Đồ thị hàm số đi qua điểm ( )2;3A b) Có đỉnh thuộc đường thẳng 31yx=− . c) Hàm số có giá trị nhỏ nhất bằng 10. Lời giải a) Đồ thị hàm số đi qua điểm ( )2;3A nên ta có 443231 mmmm +−−== . Vậy 1m = thỏa mãn yêu cầu bài toán. b) Ta có 2 1 22 bm x am =−== , suy ra 42ym=−− . Do đó tọa độ đỉnh ( )1;42Im Theo giả thiết, đỉnh I thuộc đường thẳng 31yx=− nên ta có 423.11 1mm −−=−=− . Vậy 1m =− thỏa mãn yêu cầu bài toán. c) Theo câu b) ta có tung độ đỉnh 42 4 ym a  =−=−− .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 46 Để hàm số có giá trị nhỏ nhất bằng 10 khi 0 0 2 421010 4 a m m m a   = −=−−−=−   . Vậy 2m = thỏa mãn yêu cầu bài toán. Câu 12. Cho parabol ( ) 2 :42Pyxx=−+− và đường thẳng :23 dyxm =−+ . Tìm các giá trị m để a) d cắt ( )P tại hai điểm phân biệt A , B . Tìm tọa độ trung điểm của AB b) d và ( )P có một điểm chung duy nhất. Tìm tọa độ điểm chung này. c) d không cắt ( )P . d) d và ( )P có một giao điểm nằm trên đường thẳng 2y =− . Lời giải Phương trình hoành độ giao điểm của d và ( )P là 22 4223 6320xxxmxxm −+−=−+−++= . ( )* a) Để d cắt ( )P tại hai điểm phân biệt , AB khi và chỉ khi phương trình ( )* có hai nghiệm phân biệt ( ) 7 '9320730 3 mmm =−+− Tọa độ trung điểm AB có dạng ; 22 ABAB Ixxyy ++    với , ABxx là hai nghiệm của ( )* Theo định lí Viet, ta có 6ABxx+= , suy ra 3 2 AB I xx x + == . Ta có ( ) ( ) ( )2323 363 22 ABAB AB yyxmxm xxmm +−++−+ ==−++=−+ . Vậy ( )3;63 Im −+ . b) Để d và ( )P có một điểm chung duy nhất khi và chỉ khi phương trình ( )* có nghiệm duy nhất ( ) 7 '9320730 3 mmm =−+=−== Với 7 3 m = , phương trình ( )* có nghiệm kép (nghiệm duy nhất) 3 2 b x a =−= . Thay 3x = vào hàm số 2 42yxx=−+− , ta được 1y = Vậy tọa độ điểm chung là ( )3;1 .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 47 c) Để d không cắt ( )P khi và chỉ khi phương trình ( )* vô nghiệm ( ) 7 '9320730 3 mmm =−+− d) Gọi ( ), MMMxy là giao điểm của d và ( )P . Giao điểm này nằm trên đường thẳng 2y =− suy ra 2My =− . Mặt khác M thuộc ( )P nên thay Mxx = và 2Myy==− vào ( )P , ta được ( ) ( ) 22 00;2 242 40 44;2 M MMMM M xM xxxx xM =− −=−+−−=  =−  • Với ( )0;2M . Vì M cũng thuộc d nên ta có 2 2.032 3 mm −+=−=− . • Với ( )4;2M . Vì M cũng thuộc d nên ta có 2.4322 mm −+=−= Vậy 2 3 m =− hoặc 2m = thỏa yêu cầu bài toán. Câu 13. Cho parabol ( ) 2 :43Pyxx=−+ và đường thẳng :3dymx=+ . Tìm các giá trị của m để a) d cắt ( )P tại hai điểm phân biệt A , B sao cho diện tích tam giác OAB bằng 9 2 . b) d cắt ( )P tại hai điểm phân biệt A , B có hoành độ 12 , xx thỏa mãn 33 12 8xx+= . Lời giải Phương trình hoành độ giao điểm của ( )P và d là ( )22 0 43340 4 x xxmxxmx xm = −+=+−+=  =+ . a) Để d cắt ( )P tại hai điểm phân biệt , AB khi 404 mm +− Với 0x = thì 3y = suy ra ( )0;3 AOy  . Với 4 xm =+ thì 2 43ymm=++ suy ra ( )2 4;43Bmmm+++ Gọi H là hình chiếu của B lên OA. Suy ra 4B BHxm ==+ Theo giả thiết bài toán, ta có 919191 ..3.443 222227OAB m SOABHmm m  =− ==+=+=  =− Vậy 1m =− hoặc 7m =− thỏa yêu cầu bài toán. b) Giả sử 1 0x = và 2 4 xm =+ . Theo giả thiết, ta có ( ) 333 12 8 048 42 2xxmmm +=++=+==− .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 48 Vậy 1m =− hoặc 7m =− thỏa yêu cầu bài toán. Cách 2. Áp dụng cho trường hợp không tìm cụ thể 1x , 2x Ta có ( ) ( )333 12121212838xxxxxxxx +=+−+= . ( )* Do 1x , 2x là hai nghiệm của phương trình ( )2 40xmx−+= nên theo định lý Viet, ta có 12 12 4 0 xxm xx +=+  = . Thay vào ( )* , ta được ( ) ( )3 43.0.48 2mmm +−+==− Câu 14. Chứng minh rằng với mọi m , đồ thị hàm số ( )2 2231ymxmxm =+−−+ luôn đi qua hai điểm cố định. Lời giải Gọi ( )00 ; Axy là điểm cố định của đồ thị hàm số ( )2 0002231ymxmxm =+−−+ , với mọi m ( )2 000023410mxxxy +−−−+= , với mọi m 2 000 000 1230 341 xxx xyy = +−=    −−+=−  hoặc 0 0 3 13 x y =−  = Vậy đồ thị luôn đi qua hai điểm cố định là ( )1 1;3A hoặc ( )2 3;13A với mọi giá trị của m Câu 15. Chứng minh rằng các parabol sau luôn tiếp xúc với một đường thẳng cố định. a) ( ) 22 242183yxmxm =−−+− b) ( )2 4141ymxmxm =−−+− ( )0m  Lời giải a) Gọi yaxb =+ là đường thẳng mà parabol luôn tiếp xúc. Phương trình trình hoành độ giao điểm ( ) 22 242183 xmxmaxb −−+−=+ ( ) 22 284830 xmaxmb −−++−−= ( )1 Yêu cầu bài toán  phương trình ( )1 luôn có nghiệm kép với mọi m ( ) ( )2 2 848830 mamb =−+−−−= , với mọi m ( ) ( ) ( )2 1644830 amab −++−+++= , với mọi m ( ) ( )2 40 4 34830 a a abb −+= =   −+++==−   Vậy parabol ( ) 22 242183yxmxm =−−+− luôn tiếp xúc với đường thẳng 43yx=− .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 49 b) Gọi yaxb =+ là đường thẳng mà parabol luôn tiếp xúc. Phương trình trình hoành độ giao điểm ( )2 4141 mxmxmaxb −−+−=+ ( )2 41410mxmaxmb −−++−−= ( )2 Yêu cầu bài toán  phương trình ( )2 luôn có nghiệm kép với mọi m ( ) ( )2 414410 mammb =−+−−−= , với mọi m ( ) ( ) ( )2 22 1681116410 mmaammb +−++−+−++= , với mọi m ( ) ( )2 42110 abma +−+−+= , với mọi m 2101 101 aba ab +−==   −+==−  Vậy parabol ( )2 4141ymxmxm =−−+− luôn tiếp xúc với đường thẳng 1yx=− . Câu 16. Chứng minh rằng các đường thẳng sau luôn tiếp xúc với một parabol cố định. a) 2 242ymxmm =−++ ( )0m  . b) ( ) 2 4242ymxm =−−− 1 2 m     . Lời giải a) Gọi 2 yaxbxc =++ , 0a  là parabol cần tìm. Phương trình trình hoành độ giao điểm 22242axbxcmxmm ++=−++ ( ) 222420axbmxcmm +−++−−= . ( )1 Yêu cầu bài toán  phương trình ( )1 luôn có nghiệm kép với mọi m ( ) ( )2 2 24420bmacmm =−−+−−= , với mọi m ( ) ( ) 22 4144480 ambambaca −−−+−+= , với mọi m 2 101 404 6480 aa bab bacac  −==   −==  −+== . Vậy đường thẳng 2 242ymxmm =−++ luôn tiếp xúc với parabol 2 46yxx=++ . b) Gọi 2 yaxbxc =++ , 0a  là parabol cần tìm. Phương trình trình hoành độ giao điểm ( ) 224242axbxcmxm ++=−−−

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 50 ( ) 2242420axbmxcm +−++++= ( )2 Yêu cầu bài toán  phương trình ( )2 luôn có nghiệm kép với mọi m ( ) ( )2 2 424420bmacm =−+−++= , với mọi m ( ) ( )2 2 424420 mbacm −+−++=   , với mọi m ( ) ( ) ( ) 22 161822480 ambmbaca −−+++−−= , với mọi m ( ) ( ) ( ) ( ) 22 2 161822480 101 202 24802 ambmbaca aa bb bacac −−+++−−=  −==   +==−   +−−==−  . Vậy đường thẳng ( ) 2 4242ymxm =−−− luôn tiếp xúc với parabol 2 22yxx=−− .

BÀI

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 1

2. HÀM SỐ BẬC HAI DẠNG 1. SỰ BIẾN THIÊN Câu 1: Hàm số 2 yaxbxc =++ , (0) a  đồng biến trong khoảng nào sau đậy? A. ;. 2 b a  −−   B. ;. 2 b a  −+   C. ;. 4a   −+   D. ;. 4a   −−   Câu 2: Hàm số 2 yaxbxc =++ , (0) a  nghịch biến trong khoảng nào sau đậy? A. ;. 2 b a  −−   B. ;. 2 b a  −+   C. ;. 4a   −+   D. ;. 4a   −−   Câu 3: Cho hàm số 2 41yxx=−++ . Khẳng định nào sau đây sai? A. Trên khoảng ( );1− hàm số đồng biến. B. Hàm số nghịch biến trên khoảng ( )2;+ và đồng biến trên khoảng ( );2− C. Trên khoảng ( )3;+ hàm số nghịch biến. D. Hàm số nghịch biến trên khoảng ( )4;+ và đồng biến trên khoảng ( );4− . Câu 4: Hàm số 2 411yxx=−+ đồng biến trên khoảng nào trong các khoảng sau đây? A. (2;) −+ B. (;) −+ C. (2;) + D. (;2) − Câu 5: Khoảng đồng biến của hàm số 2 43yxx=−+ là A. ( );2−− B. ( );2− C. ( )2; −+ D. ( )2;+ Câu 6: Khoảng nghịch biến của hàm số 2 43yxx=−+ là A. ( );4−− B. ( );4−− C. ( );2− D. ( )2; −+ Câu 7: Cho hàm số 2 43.yxx=−++ Chọn khẳng định đúng. A. Hàm số đồng biến trên . B. Hàm số nghịch biến trên . C. Hàm số đồng biến trên ( )2;+ . D. Hàm số nghịch biến trên ( )2;+ . CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.III ==

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 2 Câu 8: Hàm số ( ) 2 23fxxx=−+ đồng biến trên khoảng nào dưới đây? A. ( )1;+ . B. ( )2; −+ . C. ( );1− . D. 1 ; 2  +   . Câu 9: Hàm số 2 241yxx=−+ đồng biến trên khoảng nào? A. ( );1−− B. ( );1− C. ( )1; −+ D. ( )1;+ Câu 10: Hàm số 2 32yxx=−+− nghịch biến trên khoảng nào sau đây? A. 1 ;. 6  +   B. 1 ;. 6  −−   C. 1 ;. 6  −+   D. 1 ;. 6  −   Câu 11: Cho hàm số 2 61yxx=−+− . Hàm số đồng biến trên khoảng nào dưới đây? A. ( );3− B. ( )3;+ C. ( );6− D. ( )6;+ Câu 12: Cho hàm số 2231yxmxm=−++ ( )1 , m là tham số. Khi 1m = hàm số đồng biến trên khoảng nào? A. 3 ; 2  −   B. 1 ; 4  +   C. 1 ; 4  −   D. 3 ; 2  +   Câu 13: Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ( )2 213yxmx =−+− đồng biến trên khoảng ( )4;2018 ? A. 0 B. 1 C. 2 D. 3 Câu 14: Tìm tất cả các giá trị của b để hàm số 2 2(6)4yxbx=+++ đồng biến trên khoảng ( )6;+ . A. 0b  B. 12b =− C. 12b − D. 9b − Câu 15: Hàm số ( )2 213yxmx =−+−+ nghịch biến trên ( )1;+ khi giá trị m thỏa mãn: A. 0m  . B. 0m  . C. 2m  . D. 02 m  Câu 16: Tìm tất cả các giá trị của tham số m để hàm số 2 213yxmx =−++− nghịch biến trên ( ) 2;. + A. 3 1 m m −   B. 31 m − C. 31 m − D. 3 1 m m −   Câu 17: Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số 2 (1)21yxmxm đồng biến trên khoảng 2; . Khi đó tập hợp 10;10 S là tập nào? A. 10;5 B. 5;10 C. 5;10 D. 10;5 Câu 18: Tìm tất cả các giá trị dương của tham số m để hàm số ( ) 22 4 fxmxxm =−− luôn nghịch biến trên ( )1;2 .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 3 A. 1m  . B. 21 m − . C. 01 m  . D. 01 m  . Câu 19: Cho hàm số ( )22 2 yxmxmP =−+ . Khi m thay đổi, đỉnh của Parabol ( )P luôn nằm trên đường nào sau đây? A. 0y = B. 0x = C. yx = D. 2 yx = Câu 20: Cho hàm số ( )22 44 yxmxmP =−+ . Khi m thay đổi, đỉnh của Parabol ( )P luôn nằm trên đường nào sau đây? A. 0x = . B. 0y = . C. 22 yx = . D. 2 yx = . Câu 21: Tìm giá trị của tham số m để đỉnh I của đồ thị hàm số 2 6 yxxm =−++ thuộc đường thẳng 2019yx=+ A. 2020m = B. 2000m = C. 2036m = D. 2013m = DẠNG 2. XÁC ĐỊNH TOẠ ĐỘ ĐỈNH, TRỤC ĐỐI XỨNG, HÀM SỐ BẬC HAI THỎA MÃN ĐIỀU KIỆN CHO TRƯỚC. Câu 22: Cho hàm số bậc hai 2 =++ yaxbxc ( )0a có đồ thị ( )P , đỉnh của ( )P được xác định bởi công thức nào? A. ; 24     b I aa . B. ; 4     b I aa . C. ; 24 b I aa     . D. ; 24 b I aa     . Câu 23: Cho parabol ( ) 2 :321Pyxx=−+ . Điểm nào sau đây là đỉnh của ( )P ? A. ( )0;1I B. 12 ; 33 I    C. 12 ; 33 I    D. 12 ; 33 I    Câu 24: Trục đối xứng của đồ thị hàm số 2 yaxbxc =++ , (0) a  là đường thẳng nào dưới đây? A. 2 b x a =− B. 2 c x a =− C. 4 x a  =− D. 2 b x a = Câu 25: Điểm ( )2;1I là đỉnh của Parabol nào sau đây? A. 2 45yxx=++ B. 2 241yxx=++ C. 2 45yxx=+− D. 2 43yxx=−−+ Câu 26: Parabol ( ) 2: 263Pyxx=−−+ có hoành độ đỉnh là A. 3x =− B. 3 2 x = C. 3 2 x =− D. 3x = Câu 27: Tọa độ đỉnh của parabol 2 246yxx=−−+ là A. ( )1;8I . B. ( )1;0I . C. ( )2;10I . D. ( )1;6I . Câu 28: Hoành độ đỉnh của parabol ( ) 2 :243Pyxx=−+ bằng A. 2 B. 2 C. 1 D. 1

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 4 Câu 29: Parabol có phương trình trục đối xứng là A. . B. . C. . D. . Câu 30: Xác định các hệ số a và b để Parabol ( ) 2 :4 Pyaxxb =+− có đỉnh ( )1;5I . A. 3 2 a b =  =− B. 3 2 a b =  = C. 2 3 a b =  = D. 2 3 a b =  =− Câu 31: Biết hàm số bậc hai 2 =++ yaxbxc có đồ thị là một đường Parabol đi qua điểm ( )1;0A và có đỉnh ( )1;2I . Tính abc ++ . A. 3 B. 3 2 C. 2 D. 1 2 Câu 32: Biết đồ thị hàm số 2 yaxbxc =++ , ( ),,;0abca đi qua điểm ( )2;1A và có đỉnh ( )1;1I . Tính giá trị biểu thức 32 2 Tabc =+− . A. 22T = . B. 9T = . C. 6T = . D. 1T = . Câu 33: Cho hàm số 2 (0)yaxbxca =++ có đồ thị. Biết đồ thị của hàm số có đỉnh (1;1)I và đi qua điểm (2;3)A . Tính tổng 222 Sabc =++ A. 3 B. 4 C. 29 D. 1 Câu 34: Cho Parabol ( ) 2 : Pyxmxn =++ ( , mn tham số). Xác định , mn để ( )P nhận đỉnh ( )2;1I A. 4,3mn==− . B. 4,3mn== . C. 4,3mn=−=− . D. 4,3mn=−= . Câu 35: Cho Parabol: 2 yaxbxc =++ có đỉnh (2;0)I và () P cắt trục Oy tại điểm (0;1)M . Khi đó Parabol có hàm số là A. . B. . C. D. Câu 36: Gọi S là tập các giá trị 0m  để parabol ( ) 22 :22 Pymxmxmm =+++ có đỉnh nằm trên đường thẳng 7yx=+ . Tính tổng các giá trị của tập S A. 1 B. 1 C. 2 D. 2 Câu 37: Xác định hàm số 2 1yaxbxc biết đồ thị của nó có đỉnh 31 ; 24 I và cắt trục hoành tại điểm có hoành độ bằng 2. A. 2 32yxx . B. 2 32yxx . C. 2 32yxx . D. 2 32yxx . Câu 38: Hàm số bậc hai nào sau đây có đồ thị là parabol có đỉnh là      2 1 ; 2 5 S và đi qua ( )1;4A ? A. 582 =+ yxx . B. 21012 2 =+ yxx . 2 23yxx=−++ 1x =− 2x = 1x = 2x =− ( ) 21 :31 4 Pyxx=−−− ( ) 21 :1 4 Pyxx=−−− ( ) 21 :1 4 Pyxx=−+− ( ) 21 :21 4 Pyxx=−+−

C. yxx

Câu 39: Cho parabol ( )P có phương trình

yaxbxc

Tìm abc

, biết ( )P đi qua điểm ( )0;3A và có đỉnh ( )1;2I

A. 6abc++= B. 5abc

Câu 40: Parabol 2 yaxbxc =++ đạt c

A. 21 26 2 yxx=++

c tiểu b

ng 4 t

B. 2 26yxx

4abc

i 2x

D. 3abc

và đi qua ( )0;6A có phương trình là

C. 2 66yxx=++

D. 2 4yxx=++

Câu 41: Parabol 2 yaxbxc =++ đi qua ( )0;1A , ( )1;1B , ( )1;1C có phương trình là

A. 2 1yxx=−+ B. 2 1yxx

C. 2 1yxx=+− D. 2 1yxx=++

Câu 42: Parabol 2 2yaxbx=++ đi qua hai điểm (1;5)M và (2;8)N có phương trình là

A. 2 2yxx=++

22yxx

yxx=++ D. 2 2 yxx =+

Câu 43: Cho 2 ():1 Pyxbx=++ đi qua điểm ( ) 1;3.A Khi đó

A. 1.b =− B. 1.b

Câu

C. 3.b

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 5

52 = . D. 2 1 25 2 =++yxx .

=++ .

++= C.

++=

ự

ằ

ạ

=−

=++ .

=−−

=++ . C. 2 222

2.b =−

44: Cho parabol ( ) 2 : Pyaxbxc =++ đi qua ba điểm ( ) ( )1;4,1;4AB và ( )2;11C . Tọa độ đỉnh của ( )P là: A. ( )2;11 B. ( )2;5 C. ( )1;4 D. ( )3;6 Câu 45: Cho hàm số 2 yaxbxc =++ có bảng biến thiên dưới đây. Đáp án nào sau đây là đúng? A. 2 22.yxx=+− B. 2 22.yxx=−− C. 2 +32.yxx=− D. 2 22.yxx=−−− Câu 46: Cho parabol : có trục đối xứng là đường thẳng . Khi đó bằng A. B. C. D. Câu 47: Parabol 2 yaxbxc =++ đi qua ( )8;0A và có đỉnh ( )6;12I . Khi đó tích .. abc bằng A. 10368 B. 10368 C. 6912 D. 6912 Câu 48: Cho parabol 2 4yaxbx=++ có trục đối xứng là đường thẳng 1 3 x = và đi qua điểm ( )1;3A . Tổng giá trị 2 ab + là ( )P 2 yaxbxc =++ 1x = 42ab + 1 0 1 2

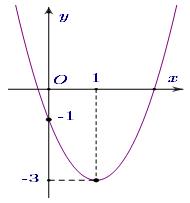
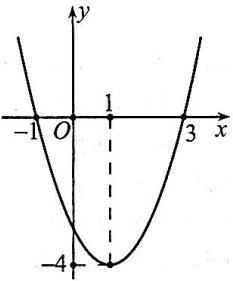
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 6 A. 1 2 . B. 1. C. 1 2 . D. 1. Câu 49: Cho parabol 2 yaxbxc =++ có đồ thị như hình sau Phương trình của parabol này là A. 2 1yxx=−+− . B. 2 241yxx=+− . C. 2 21yxx=−− . D. 2 241yxx=−− . Câu 50: Biết hàm số bậc hai 2 =++ yaxbxc có đồ thị là một đường Parabol đi qua điểm ( )1;0A và có đỉnh ( )1;2I Tính abc ++ A. 3. B. 3 2 . C. 2. D. 1 2 . Câu 51: Cho parabol 2():Pyaxbxc =++ , ( )0a  có đồ thị như hình bên dưới. Khi đó 22abc ++ có giá trị là: A. 9. B. 9. C. 6. D. 6. Câu 52: Cho hàm số ( )2 ..0yaxbxca =++ . Biết rằng đồ thị hàm số nhận đường thẳng 3 2 x = làm trục đối xứng, và đi qua các điểm ( ) ( )2;0,0;2AB . Tìm Tabc =−+ A. 1T = B. 3T = C. 0T = D. 6T = Câu 53: Cho hàm số ( ) 2 fxaxbxc =++ đồ thị như hình. Tính giá trị biểu thức 222 Tabc =++ .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 7 A. 0. B. 26. C. 8. D. 20. Câu 54: Xác định hàm số 2 yaxbxc =++ biết đồ thị của hàm số cắt trục tung tại điểm có tung độ là 3 và giá trị nhỏ nhất của hàm số là 25 8 tại 1 4 x = . A. 2 23yxx=−+− B. 2 1 .3 2 yxx=−+ C. 2 23yxx=−− D. 2 23yxx=+− Câu 55: Parabol 2 yaxbxc =++ đạt giá trị nhỏ nhất bằng 4tại 2x =− và đồ thị đi qua ( )0;6A có phương trình là: A. 2 66yxx=++ B. 2 4yxx=++ C. 21 26 2 yxx=++ D. 2 26yxx=++ . Câu 56: Cho parabol ( ) ( ) 2 :,0 Pyfxaxbxca ==++ . Biết ( )P đi qua ( )4;3M , ( )P cắt tia Ox tại ( )3;0N và Q sao cho MNQ có diện tích bằng 1đồng thời hoành độ điểm Q nhỏ hơn 3. Khi đó abc ++ bằng A. 24 5 . B. 12 5 . C. 5. D. 4. DẠNG 3. ĐỌC ĐỒ THỊ, BẢNG BIẾN THIÊN CỦA HÀM SỐ BẬC HAI Câu 57: Bảng biến thiên của hàm số 2 241yxx=−++ là bảng nào sau đây? A. B. C. D. Câu 58: Đồ thị nào sau đây là đồ thị của hàm số 2 23yxx=−−

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 9 A. 0.a  B. 0.a  C. 1.a = D. 2.a = Câu 63: Cho parabol 2 yaxbxc =++ có đồ thị như hình vẽ dưới đây. Khẳng định nào dưới đây đúng? A. 0,0,0abc B. 0,0,0abc C. 0,0,0abc D. 0,0,0abc Câu 64: Nếu hàm số 2 yaxbxc =++ có 0,0ab và 0c  thì đồ thị hàm số của nó có dạng A. . B. . C. . D. . Câu 65: Cho hàm số thì đồ thị của hàm số là hình nào trong các hình sau: A. Hình (1). B. Hình (2). C. Hình (3). D. Hình (4). Câu 66: Cho hàm số 2 yaxbxc =++ có đồ thị như hình bên dưới. Khẳng định nào sau đây đúng? ` A. 0, 0, 0abc . B. 0, 0, 0abc . C. 0, 0, 0abc . D. 0, 0, 0abc . Câu 67: Cho hàm số ( )2 ,0yaxbxca =++ có bảng biến thiên trên nửa khoảng  )0;+ như hình vẽ dưới đây: 2 ,(0,0,0)yaxbxcabc =++ x y O

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 10 Xác định dấu của a , b , c . A. 0,0,0abc B. 0,0,0abc C. 0,0,0abc D. 0,0,0abc Câu 68: Cho hàm số 2 yaxbxc =++ có đồ thị là parabol trong hình vẽ. Khẳng định nào sau đây là đúng? A. 0; 0; 0abc . B. 0; 0; 0abc . C. 0; 0; 0abc . D. 0; 0; 0abc . Câu 69: Cho hàm số 2 yaxbxc =++ có đồ thị như hình bên. Khẳng định nào sau đây đúng? A. 0a  , 0b  , 0c  . B. 0a  , 0b  , 0c  . C. 0a  , 0b  , 0c  .D. 0a  , 0b  , 0c  . Câu 70: Cho hàm số 2 yaxbxc =++ có đồ thị như bên. Khẳng định nào sau đây đúng? A. 0,0,0.abc B. 0,0,0.abc C. 0,0,0.abc D. 0,0,0.abc Câu 71: Cho hàm số 2 yaxbxc =++ . Có đồ thị như hình vẽ dưới đây. Hỏi mệnh đề nào đúng? x y O x y O 3 1 1

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 11 A. 0,0,0abc B. 0,0,0abc C. 0,0,0abc D. 0,0,0abc Câu 72: Cho đồ thị hàm số 2 yaxbxc =++ có đồ thị như hình vẽ bên dưới. Mệnh đề nào sau đây đúng? A. 0,0,0abc= . B. 0,0,0abc . C. 0,0,0abc . D. 0,0,0abc . Câu 73: Cho hàm số 2 yaxbxc =++ có 0;0;0abc thì đồ thị ( )P của hàm số là hình nào trong các hình dưới đây A. hình ( )4 B. hình ( )3 C. hình ( )2 D. hình ( )1 Câu 74: Cho hàm số 2 yaxbxc có đồ thị như hình vẽ dưới đây. Khẳng định nào sau đây là đúng? A. 0,0,0abc B. 0,0,0abc C. 0,0,0abc D. 0,0,0abc Câu 75: Hàm số nào có đồ thị như hình vẽ bên dưới?

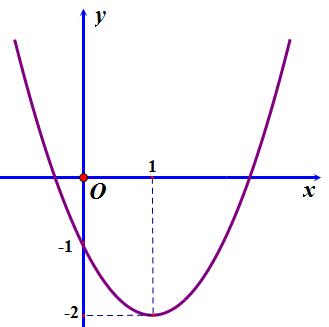
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 12 A. 2 43yxx=−+− B. 2 43yxx=−−− C. 2 23yxx=−−− D. 2 43yxx=−− Câu 76: Bảng biến thiên sau là của hàm số nào ? A. . B. . C. . D. . Câu 77: Bảng biến thiên sau là của hàm số nào? A. 2 4 yxx =− . B. 2 4 yxx =+ . C. 2 4 yxx =−+ . D. 2 4 yxx =−− . Câu 78: Đồ thị trong hình vẽ dưới đây là của hàm số nào trong các phương án A;B;C;D sau đây? A. 2 21yxx=+− . B. 2 22yxx=+− . C. 2 242yxx=−− . D. 2 21yxx=−− . Câu 79: Cho parabol 2 yaxbxc =++ có đồ thị như hình sau Phương trình của parabol này là 2 244yxx=−+ 2 361yxx=−+− 2 21yxx=+− 2 22yxx=−+

Phương

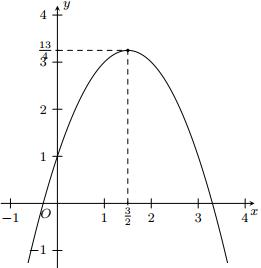
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 13 A. 2 1yxx=−+− . B. 2 241yxx=+− . C. 2 21yxx=−− . D. 2 241yxx=−− . Câu 80: Cho parabol 2 yaxbxc =++ có đồ thị như hình sau:

trình của parabol này là A. 2 1.yxx=−+− B. 2 241.yxx=+− C. 2 21.yxx=−− D. 2 241.yxx=−− Câu 81: Đồ thị hình bên dưới là đồ thị của hàm số bậc hai nào? A. 2 31yxx=−+ . B. 2 231yxx=−+ . C. 2 31yxx=−+− . D. 2 231yxx=−+− . Câu 82: Trên mặt phẳng tọa độ Oxy cho Parabol như hình vẽ. Hỏi parabol có phương trình nào trong các phương trình dưới đây? A. 2 31yxx=+− B. 2 31yxx=−− C. 2 31yxx=−−− D. 2 31yxx=−++ Câu 83: Cho parabol ( ) ( )2 :,0Pyaxbxca=++ có đồ thị như hình bên. Khi đó 22abc ++ có giá trị là x y -3 -1 O 1 O x y 1 1

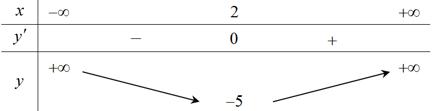
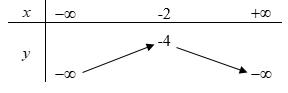
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 14 A. 9. B. 9. C. 6. D. 6. Câu 84: Hàm số nào sau đây có đồ thị như hình bên dưới A. 2 23yxx=−+− B. 2 43yxx=−+− C. 2 43yxx=−+ D. 2 23yxx=−− Câu 85: Bảng biến thiên ở dưới là bảng biến thiên của hàm số nào trong các hàm số được cho ở bốn phương án A, B, C, D sau đây? A. 2 4 yxx =−+ . B. 2 49yxx=−+− . C. 2 41yxx=−− . D. 2 45yxx=−− . Câu 86: Bảng biến thiên sau đây là bảng biến thiên của hàm số nào? A. 2 4 yxx =+ B. 2 48yxx=−−− C. 2 48yxx=−−+ D. 2 4 yxx =−− Câu 87: Cho parabol 2 yaxbcc =++ có đồ thị như hình vẽ Khi đó: x y 3 -4 -1 2O 1

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 15 A. 0,0,0abc . B. 0,0,0abc . C. 0,0,0abc . D. 0,0,0abc . Câu 88: Cho hàm số 2 yaxbxc =++ có đồ thị như hình bên dưới. Khẳng định nào sau đây đúng? ` A. 0, 0, 0abc B. 0, 0, 0abc C. 0, 0, 0abc D. 0, 0, 0abc Câu 89: Cho hàm số 2 yaxbxc =++ có đồ thị là parabol trong hình vẽ. Khẳng định nào sau đây là đúng? A. 0; 0; 0abc . B. 0; 0; 0abc . C. 0; 0; 0abc . D. 0; 0; 0abc . Câu 90: Cho hàm số 2 yaxbxc =++ có đồ thị như bên. Khẳng định nào sau đây đúng? A. 0,0,0.abc . B. 0,0,0.abc . C. 0,0,0.abc . D. 0,0,0.abc Câu 91: Cho hàm số 2 yaxbxc =++ . Có đồ thị như hình vẽ dưới đây. Hỏi mệnh đề nào đúng? A. 0,0,0abc B. 0,0,0abc C. 0,0,0abc D. 0,0,0abc Câu 92: Cho đồ thị hàm số 2 yaxbxc =++ có đồ thị như hình vẽ bên dưới. Mệnh đề nào sau đây đúng? x y O x y O

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 16 A. 0,0,0abc= B. 0,0,0abc C. 0,0,0abc D. 0,0,0abc Câu 93: Nếu hàm số 2 yaxbxc =++ có đồ thị như sau thì dấu các hệ số của nó là A. 0; 0; 0abc . B. 0; 0; 0abc . C. 0; 0; 0abc . D. 0; 0; 0abc . Câu 94: Cho parabol ( ) ( )2 :,0Pyaxbxca=++ có đồ thị như hình bên. Khi đó 42abc ++ có giá trị là: A. 3. B. 2. C. 3. D. 0 . Câu 95: Cho hàm số 2 yaxbxc =++ có đồ thị như hình dưới đây. Khẳng định nào sau đây là đúng?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 17 A. 0a  , 0b  , 0c  B. 0a  , 0b  , 0c  C. 0a  , 0b  , 0c  D. 0a  , 0b  , 0c  Câu 96: Cho parabol ( ) ( )2 :,0Pyaxbxca=++ có đồ thị như hình bên. Khi đó 22abc ++ có giá trị là A. 9. B. 9. C. 6. D. 6. Câu 97: Cho hàm số 2 yaxbxc =++ có đồ thị là đường cong trong hình vẽ dưới đây ? Giá trị của tổng 42 Tabc =++ là : A. 2T = B. 1T =− C. 4T = D. 3T = Câu 98: Cho đồ thị hàm số 2 43yxx có đồ thị như hình vẽ sau x y 3 -4 -1 2O 1 x y 3 2 3 -1 O 1

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 18 Đồ thị nào dưới đây là đồ thị của hàm số 2 43yxx A. Hình 2 B. Hình 4 C. Hình 1 D. Hình 3 Câu 99: Hàm số nào sau đây có đồ thị như hình bên? x y 1234 5 1 2 3 543211 2 3 A. 2 33yxx=−− B. 2 53yxx=−+− C. 2 33yxx=−−− D. 2 53yxx=−+− DẠNG 4. GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT Câu 100: Tìm giá trị nhỏ nhất của hàm số A. B. C. D. Câu 101: Giá trị nhỏ nhất của hàm số 2 23yxx=++ đạt được tại A. 2x =− . B. 1x =− . C. 0x = . D. 1x = . Câu 102: Giá trị nhỏ nhất của hàm số 2 23yxx=+− là A. 3 B. 2 C. 21 8 D. 25 8 2 41yxx=−+ 3 1 3 13

Câu

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 19

103: Khẳng định nào dưới đây đúng?

Hàm số 2 32yxx=−++ có giá trị lớn nhất bằng 25 12

Hàm số 2 32yxx=−++ có giá trị nhỏ nhất bằng 25 12

Hàm số 2 32yxx=−++ có giá trị lớn nhất bằng 25 3

Hàm số 2 32yxx=−++ có giá trị nhỏ nhất bằng 25 3 .

104: Giá trị lớn nhất của hàm số 2 321yxx=−++ trên đoạn  1;3 là: A. 4 5 B. 0 C. 1 3 D. 20

105: Giá trị lớn nhất của hàm số 2 2 59y xx = −+ bằng: A. 11 8 B. 11 4 C. 4 11 D. 8 11

106:

ổng giá trị nhỏ nhất và giá trị lớn nhất của hàm số 2 43yxx=−+ trên miền  1;4 là A. 1. B. 2. C. 7. D. 8. Câu 107: Giá trị nhỏ nhất của hàm số 2 2 yxx =− là: A. 1 B. 0 C. 1 D. 2 Câu 108: Giá trị nhỏ nhất của hàm số 2 43yxx=++ là: A. 1 B. 1 C. 4 D. 3 Câu 109: Cho hàm số 2 28 khi2 212khi2 xxx y xx  −− =  − . Gọi , Mm lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số khi  1;4x− . Tính Mm + . A. 14. B. 13. C. 4. D. 9. Câu 110: Tìm giá trị thực của tham số 0m  để hàm số 2 232ymxmxm =−−− có giá trị nhỏ nhất bằng 10 trên A. 1.m = B. 2.m = C. 2.m =− D. 1.m =− Câu 111: Hàm số 2 24yxxm=−++− đạt giá trị lớn nhất trên đoạn  1;2 bằng 3 khi m thuộc A. ( );5− . B.  )7;8 . C. ( )5;7 . D. ( )9;11 . Câu 112: Giá trị nhỏ nhất của hàm số 2 25yxmx=++ bằng 1 khi giá trị của tham số m là A. 4m = B. 4m = C. 2m = D. m

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 20 Câu 113: Giá trị của tham số m để hàm số 22232yxmxmm =−+−− có giá trị nhỏ nhất bằng 10 trên thuộc khoảng nào trong các khoảng sau đây? A.  )1;0m− B. 3 ;5 2 m    C. 5 ;1 2 m  −−  D. 3 0; 2 m     Câu 114: Tìm m để hàm số 2 223yxxm=−++ có giá trị nhỏ nhất trên đoạn  2;5 bằng 3 A. 0m = . B. 9m =− . C. 1m = . D. 3m =− . Câu 115:Tìm m để hàm số 2 223yxxm=−++ có giá trị nhỏ nhất trên đoạn  2;5 bằng 3. A. 3m =− . B. 9m =− . C. 1m = . D. 0m = . Câu 116: Tìm số các giá trị của tham số m để giá trị nhỏ nhất của hàm số ( ) ( ) 22211fxxmxm=+++− trên đoạn  0;1 là bằng 1. A. 0 B. 1 C. 2 D. 3 Câu 117: Cho hàm số ( ) 22 23132yxmxmm =−+++− , m là tham số. Tìm tất cả các giá trị của m để giá trị nhỏ nhất của hàm số là lớn nhất. A. 2m =− B. 1m = C. 3m = D. 5m = Câu 118: Gọi S là tập hợp tất cả các giá trị dương của tham số m để giá trị nhỏ nhất của hàm số ( ) 22 442 yfxxmxmm ==−+− trên đoạn  2;0 bằng 3. Tính tổng T các phần tử của .S A. 3T = B. 1 2 T = C. 9 2 T = D. 3 2 T =− DẠNG 5. SỰ TƯƠNG GIAO GIỮA PARABOL VỚI ĐỒ THỊ CÁC HÀM SỐ Câu 119: Giao điểm của parabol 2 ():32 Pyxx=−+ với đường thẳng 1yx=− là: A. ( ) ( )1;0;3;2 B. ( ) ( )0;1;2;3 C. ( ) ( )1;2;2;1 D. ( ) ( )2;1;0;1 Câu 120: Tọa độ giao điểm của ( ) 2 :4 Pyxx =− với đường thẳng :2dyx=−− là A. ( )0;2M , ( )2;4N . B. ( )1;1M , ( )2;0N . C. ( )3;1M , ( )3;5N D. ( )1;3M , ( )2;4N Câu 121: Tọa độ giao điểm của đường thẳng và parabol là A. và B. và C. và D. và Câu 122: Hoành độ giao điểm của đường thẳng 1 yx =− với 2 ():21 Pyxx=−+ là A. 0;1.xx== B. 1.x = C. 0;2.xx== D. 0.x = Câu 123: Gọi ( ); Aab và ( ); Bcd là tọa độ giao điểm của ( ) 2:2 Pyxx =− và :36 yx =− . Giá trị của bd + bằng. A. 7. B. 7. C. 15. D. 15. :4dyx=−+ 2 712yxx=−+ ( )2;6 ( )4;8 ( )2;2 ( )4;8 ( )2;2 ( )4;0 ( )2;2 ( )4;0

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 21 Câu 124: Cho hai parabol có phương trình 2 1yxx=++ và 2 22yxx=−− . Biết hai parabol cắt nhau tại hai điểm A và B ( ABxx  ). Tính độ dài đoạn thẳng AB. A. 42AB = B. 226AB = C. 410AB = D. 210AB = Câu 125: Giá trị nào của m thì đồ thị hàm số 2 3 yxxm =++ cắt trục hoành tại hai điểm phân biệt? A. 9 4 m − . B. 9 4 m − . C. 9 4 m  . D. 9 4 m  Câu 126: Hàm số 2 21yxx=+− có đồ thị như hình bên. Tìm các giá trị m để phương trình 2 20xxm++= vô nghiệm. A. 2m − B. 1m − C. 1m  D. 1m  Câu 127: Hỏi có bao nhiêu giá trị m nguyên trong nửa khoảng  )10;4 để đường thẳng ( ) :12 dymxm =−+++ cắt parabol ( ) 2 :2Pyxx=+− tại hai điểm phân biệt nằm về cùng một phía đối với trục tung? A. 6 B. 5 C. 7 D. 8 Câu 128: Cho parabol ( ) 2 : Pyxmx =− và đường thẳng ( ) ( ) :21dymx=++ , trong đó m là tham số Khi parabol và đường thẳng cắt nhau tại hai điểm phân biệt M, N, tập hợp trung điểm I của đoạn thẳng MN là: A. một parabol B. một đường thẳng C. một đoạn thẳng D. một điểm Câu 129: Cho hàm số 2 3 yxx =+ có đồ thị ( )P . Gọi S là tập hợp các giá trị của tham số m để đường thẳng 2 : dyxm =+ cắt đồ thị ( )P tại hai điểm phân biệt , AB sao cho trung điểm I của đoạn AB nằm trên đường thẳng :23dyx  =+ . Tổng bình phương các phần tử của S là A. 6. B. 4. C. 2. D. 1. Câu 130: Cho hàm số 2 235yxx=−− . Giá trị của tham số m để đồ thị hàm số ( )1 cắt đường thẳng 4 yxm =+ tại hai điểm phân biệt ( )11 ; Axy , ( )22 ; Bxx thỏa mãn 22 1212 2237 xxxx+=+ là A. 10 B. 10 C. 6 D. 9 Câu 131: Có bao nhiêu giá trị nguyên của m để đường thẳng 3ymx=− không có điểm chung với Parabol 2 1yx=+ ? A. 6 B. 9 C. 7 D. 8 x y 1 2 -2 -1 -2 -1 2O 1

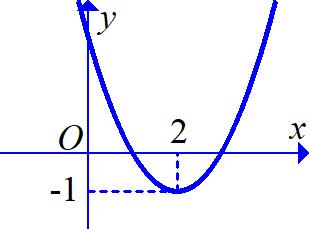
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 22 Câu 132: Tìm tất cả các giá trị m để đường thẳng 32 ymxm =+− cắt parabol 2 35yxx=−− tại 2 điểm phân biệt có hoành độ trái dấu. A. 3m − B. 34 m − C. 4m  D. 4m  Câu 133: Tìm để Parabol cắt trục hoành tại điểm phân biệt có hoành độ , sao cho . A. . B. Không tồn tại . C. . D. . Câu 134: Cho parabol ( ) 2 :25Pyxx=+− và đường thẳng :223 dymxm =+− . Tìm tất cả các giá trị m để ( )P cắt d tại hai điểm phân biệt nằm về phía bên phải của trục tung. A. 7 1 3 m  . B. 1m  . C. 7 3 m  . D. 1m  Câu 135: Gọi T là tổng tất cả các giá trị của tham số m để parabol ( ) 2 :4 Pyxxm =−+ cắt trục Ox tại hai điểm phân biệt , AB thỏa mãn 3 OAOB = . Tính T . A. 9T =− . B. 3 2 T = . C. 15T =− . D. 3T = . Câu 136: Tìm m để Parabol ( ) ( ) 22 :213Pyxmxm=−++− cắt trục hoành tại 2 điểm phân biệt có hoành độ 1x , 2x sao cho 12.1xx = A. 2m = . B. Không tồn tại m . C. 2m =− . D. 2m = . Câu 137: Cho parabol ( ) 2 : Pyaxbxc =++ . Tìm abc −+ , biết rằng đường thẳng 2,5y =− có một điểm chung duy nhất với ( )P và đường thẳng 2y = cắt ( )P tại hai điểm có hoành độ là 1 và 5. A. 2abc−−=− B. 2abc−−= C. 1abc−−= D. 1abc−−=− Câu 138: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 210xxm−+−= có bốn nghiệm phân biệt? A. 0 B. 1 C. 2 D. Vô số Câu 139: Biết ( ); Sab = là tập hợp tất cả các giá trị của tham số m để đường thẳng ym = cắt đồ thị hàm số 2 43yxx=−+ tại bốn điểm phân biệt. Tìm ab + . A. 1ab+= B. 1ab+=− C. 2ab+= D. 2ab+=− Câu 140: Cho hàm số có đồ thị như hình vẽ. Với những giá trị nào của tham số thì phương trình có đúng nghiệm phân biệt. m ( ) ( ) 22 :213Pyxmxm=−++− 2 1x 2x 12.1xx = 2m = m 2m =− 2m = ( ) 2 fxaxbxc =++ m ( ) fxm = 4

A. . B. . C. ; . D. .

Câu 141: Cho hàm số có đồ thị như hình vẽ. Hỏi với những giá trị nào của tham số thực thì phương trình có đúng 3 nghiệm phân biệt

A. . B. . C. . D. .

Câu 142: Tìm tất cả các giá trị thực của tham số m để parabol cắt đường thẳng tại 4 điểm phân biệt.

OFFICIAL

A. . B. . C. . D. .

Câu 143: Với giá trị nào của thì phương trình có 3 nghiệm thực phân biệt.

A. . B. . C. . D. .

Câu 144: Cho hàm số có đồ thị như hình vẽ

hàm

Tìm

các giá tr

a tham s

để đồ th

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 23

bên.

tất cả

ị

ủ

ố

ị

số cắt đường trên cùng một hệ trục tọa độ tại 4 điểm phân biệt là? A. . B. . C. . D. . Câu 145: Tìm tất cả các giá trị của để đồ thị hàm số cắt đường thẳng tại 4 điểm phân biệt. A. B. C. D. Câu 146: Cho hàm số có bảng biến thiên như sau: 01 m  10 m − 1m =− 3m = 3m  2 fxaxbxc m 1 fxm x y O 2   4m 0m 1m 2m ( ) 2 :21Pyxx=−− 3ym=− 21 m −− 12 m  21 m −− 12 m  m 2 54mxx=−+ 9 4 m  9 4 m  9 4 m = 0m = ( )yfx = m ( )yfx = 1y m= + 03 m−  0 3m  1 4m  21 m−  m 2 9 yxx =− ym = 3m − 81 4 m − 81 0 4 m − 0m  ( ) 2 fxaxbxc =++

Tìm tất cả các giá trị thực của tham số để phương trình có đúng ba nghiệm. A. . B. . C. . D. không tồn tại .

Câu 147: Cho hàm số có đồ thị như hình vẽ dưới đây Đặt ;gọi là tập hợp các giá trị nguyên của tham số m để phương trình có 8 nghiệm phân biệt. Số

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 24

phần tử của bằng A. . B. . C. . D. . DẠNG 6. ỨNG DỤNG THỰC TẾ LIÊN QUAN ĐẾN HÀM SỐ BẬC HAI Câu 148: Một chiếc ăng ten chảo parabol có chiều cao và đường kính miệng . Mặt cắt qua trục là một parabol dạng . Biết , trong đó m, n là các số nguyên dương nguyên tố cùng nhau. Tính . A. B. C. D. Câu 149: Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống. Biết rằng quỹ đạo của quả bóng là một cung parabol trong mặt phẳng với hệ tọa độ Oth, trong đó t là thời gian kể từ khi quả bóng được đá lên; h là độ cao của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2m. Sau đó 1 giây, nó đạt độ cao 8,5m và 2 giây sau khi đá lên, nó đạt độ cao 6m. Hỏi sau bao lâu thì quả bóng sẽ chạm đất kể từ khi được đá lên kể từ khi quả bóng được đá lên, là độ cao của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao và sau 1 giây thì nó đạt độ cao , sau 2 giây nó đạt độ cao . Tính tổng . A. B. C. D. m ( ) 201720182 fxm −−= 1m = 3m = 2m = m 2 43yxx=−+ ( ) 2 43fxxx=−+ S () fxm = S 0 1 2 4 0,5 hm = 4 dm = 2 yax = m a n = mn 7mn−= 7mn−=− 31mn−= 31mn−=− h 1,2 m 8,5m 6m abc 18,3abc 6,1abc 8,5abc 15,9abc

Câu 150: Một của hàng buôn giày nhập một đôi với giá là đôla. Cửa hàng ước tính rằng nếu đôi giày được bán với giá đôla thì mỗi tháng khách hàng sẽ mua đôi. Hỏi của hàng bán một đôi giày giá bao nhiêu thì thu được nhiều lãi nhất?

A. USD. B. USD. C. USD. D. USD.

Câu 151: Một quả bóng cầu thủ sút lên rồi rơi xuống theo quỹ đạo là parabol. Biết rằng ban đầu quả bóng được sút lên từ độ cao sau đó giây nó đạt

gì để có thể đi vào cổng mà không chạm tường?

OFFICIAL

A. . B. . C. . D. .

Câu 153: Trong số các hình chữ nhật có cùng chu vi bằng , hình chữ nhật có diện tích lớn nhất bằng bao nhiêu?

A. B. C. D.

Câu 154: Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 25

độ cao và giây nó ở độ cao Hỏi độ cao cao nhất mà quả bóng đạt được là bao nhiêu mét? A. B. C. D. Câu 152: Một chiếc cổng hình parabol có chiều rộng và chiều cao như hình vẽ. Giả sử một chiếc xe tải có chiều ngang đi vào vị trí chính giữa cổng. Hỏi chiều cao của xe tải thỏa mãn điều kiện

hình vẽ. Biết chiều cao cổng parabol là 4m còn kích thước cửa ở giữa là 3m x 4m. Hãy tính khoảng cách giữa hai điểm và A. 5m. B. 8,5m. C. 7,5m. D. 8m. Câu 155: Một chiếc cổng hình parabol dạng có chiều rộng . Hãy tính chiều cao của cổng. 40 x ( )120 x 80 160 40 240 1m 1 10m 3,5 6,25m 11m 12m 13m 14m 12 m 8 m 6 m h 06 h  06 h  07 h  07 h  16 64. 4. 16. 8. A B 21 2 yx =− 8 dm = h

ng nghiệm, rồi đổ thêm chất vào. Khi nồng độ chất đạt đến một giá trị nhất định thì chất mới tác dụng với chất . Khi phản ứng xảy ra, nồng độ cả hai chất đều giảm đến khi chất được tiêu thụ hoàn hoàn. Đồ thị nồng độ mol theo thời gian nào sau đây thể hiện quá

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 26 A. . B. . C. . D. . Câu 156: Cổng Arch tại thành phố St.Louis của Mỹ có hình dạng là một parabol. Biết khoảng cách giữa hai chân cổng bằng m. Trên thành cổng, tại vị trí có độ cao m so với mặt đất, người ta thả một sợi dây chạm đất. Vị trí chạm đất của đầu sợi dây này cách chân cổng một đoạn m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng Arch. A. m. B. m. C. m. D. m. Câu 157: Rót chất vào một ố

trình của phản ứng? A. . B. . C. D. Câu 158: Cô Tình có lưới muốn rào một mảng vườn hình chữ nhật để trồng rau, biết rằng một cạnh là tường, cô Tình chỉ cần rào cạnh còn lại của hình chữ nhật để làm vườn. Em hãy tính hộ diện tích lớn nhất mà cô Tình có thể rào được? A. . B. . C. . D. . 9 hm = 7 hm = 8 hm = 5 hm = 162 43 A 10 175,6 197,5 210 185,6 A B B A B B 60m 3 2400m 2450m 2350m 2425m

C

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 1 BÀI 2. HÀM SỐ BẬC HAI DẠNG 1. SỰ BIẾN THIÊN Câu 1: Hàm số 2 yaxbxc =++ , (0) a  đồng biến trong khoảng nào sau đậy? A. ;. 2 b a  −−   B. ;. 2 b a  −+   C. ;. 4a   −+   D. ;. 4a   −−   Lời giải Chọn B 0.a  Bảng biến thiên Câu 2: Hàm số 2 yaxbxc =++ , (0) a  nghịch biến trong khoảng nào sau đậy? A. ;. 2 b a  −−   B. ;. 2 b a  −+   C. ;. 4a   −+   D. ;. 4a   −−   Lời giải Chọn A 0.a  Bảng biến thiên Câu 3: Cho hàm số 2 41yxx=−++ . Khẳng định nào sau đây sai? A. Trên khoảng ( );1− hàm số đồng biến. B. Hàm số nghịch biến trên khoảng ( )2;+ và đồng biến trên khoảng ( );2− C. Trên khoảng ( )3;+ hàm số nghịch biến. D. Hàm số nghịch biến trên khoảng ( )4;+ và đồng biến trên khoảng ( );4− CHƯƠNG III HÀM SỐ BẬ

HAI VÀ ĐỒ THỊ HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.III ==

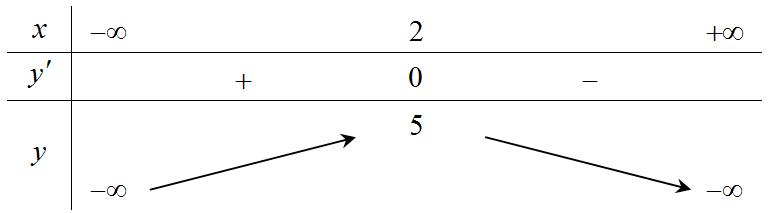
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 2 Lời giải Chọn D Đỉnh của parabol: 2 2I b x a =−= Bảng biến thiên của hàm số: Dựa vào bảng biến thiên suy ra khẳng định D sai. Câu 4: Hàm số 2 411yxx=−+ đồng biến trên khoảng nào trong các khoảng sau đây? A. (2;) −+ B. (;) −+ C. (2;) + D. (;2) − Lời giải Chọn C Ta có bảng biến thiên: Từ bảng biến thiên ta thấy, hàm số đồng biến trên khoảng (2;) + Câu 5: Khoảng đồng biến của hàm số 2 43yxx=−+ là A. ( );2−− . B. ( );2− . C. ( )2; −+ . D. ( )2;+ . Lời giải Chọn D Hàm số 2 43yxx=−+ có 10a = nên đồng biến trên khoảng ; 2 b a  −+   . Vì vậy hàm số đồng biến trên ( )2;+ . Câu 6: Khoảng nghịch biến của hàm số 2 43yxx=−+ là A. ( );4−− B. ( );4−− C. ( );2− D. ( )2; −+ Lời giải Chọn C Hàm số 2 43yxx=−+ có hệ số 10a = nên đồng biến trên khoảng ; 2 b a  −−  

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 3 Vì vậy hàm số đồng biến trên ( );2− Câu 7: Cho hàm số 2 43.yxx=−++ Chọn khẳng định đúng. A. Hàm số đồng biến trên . B. Hàm số nghịch biến trên . C. Hàm số đồng biến trên ( )2;+ D. Hàm số nghịch biến trên ( )2;+ Lời giải Chọn D Do 1a =− nên hàm số đồng biến trên ( );2− nghịch biến trên ( )2;+ Câu 8: Hàm số ( ) 2 23fxxx=−+ đồng biến trên khoảng nào dưới đây? A. ( )1;+ . B. ( )2; −+ . C. ( );1− . D. 1 ; 2  +   . Lời giải Chọn A Ta có hàm số ( ) ( ) 2 :23 ==−+ Pyfxxx là hàm số bậc hai có hệ số 1a = ;nên ( )P có bề lõm hướng lên. Hoành độ đỉnh của parabol 1 2I b x a == . Do đó hàm số đồng biến trên khoảng ( )1;+ . Câu 9: Hàm số 2 241yxx=−+ đồng biến trên khoảng nào? A. ( );1−− . B. ( );1− . C. ( )1; −+ . D. ( )1;+ . Lời giải Chọn D Hàm số bậc hai có 20;1 2 b a a =−= nên hàm số đồng biến trên ( )1;+ Câu 10: Hàm số 2 32yxx=−+− nghịch biến trên khoảng nào sau đây? A. 1 ;. 6  +   B. 1 ;. 6  −−   C. 1 ;. 6  −+   D. 1 ;. 6  −   Lời giải Chọn A ( ) ( ) 2 :32Pyfxxx ==−+− , TXĐ: D = . Có 3a =− , đỉnh S có hoành độ 1 6 x = . Nên hàm số ( )yfx = nghịch biến trong khoảng 1 ;. 6  +   Câu 11: Cho hàm số 2 61yxx=−+− . Hàm số đồng biến trên khoảng nào dưới đây? A. ( );3− B. ( )3;+ C. ( );6− D. ( )6;+ Lời giải

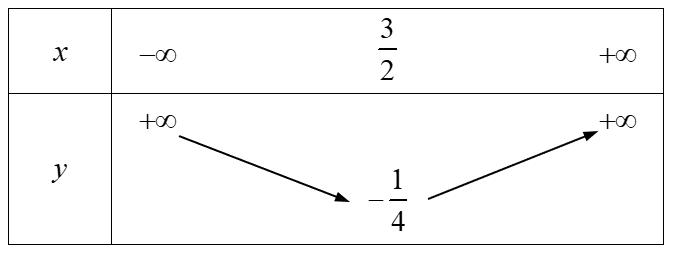
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 4 Ta có ( ) 6 10,3 22.1 b a a =−== . Suy ra hàm số đồng biến trên khoảng ( );3− Đáp án A. Câu 12: Cho hàm số 2231yxmxm=−++ ( )1 , m là tham số. Khi 1m = hàm số đồng biến trên khoảng nào? A. 3 ; 2  −   B. 1 ; 4  +   C. 1 ; 4  −   D. 3 ; 2  +   Lời giải Chọn D Khi 1m = , hàm số trở thành 2 32yxx=−+ Tập xác định: D = . Đỉnh 31 ; 24 I    Bảng biến thiên: Hàm số đồng biến trên 3 ; 2  +   . Câu 13: Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ( )2 213yxmx =−+− đồng biến trên khoảng ( )4;2018 ? A. 0 B. 1 C. 2 D. 3 Lời giải Hàm số có 10,1 2 b am a ==+ nên đồng biến trên khoảng ( )1;m ++ . Do đó để hàm số đồng biến trên khoảng ( )4;2018 thì ta phải có ( ) ( ) 4;20181;143 mmm +++ Vậy có ba giá trị nguyên dương của m thỏa mãn yêu cầu bài toán là 1, 2, 3. Đáp án D. Câu 14: Tìm tất cả các giá trị của b để hàm số 2 2(6)4yxbx=+++ đồng biến trên khoảng ( )6;+ . A. 0b  . B. 12b =− . C. 12b − . D. 9b − . Lời giải Chọn C

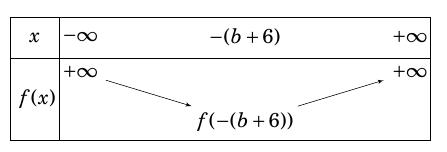
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 5 Hàm số 2 ()2(6)4yfxxbx ==+++ là hàm số bậc hai có hệ sô 10a = , 6 2 b b a =−− nên có bảng biến thiên Từ bảng biến thiên ta có: Hàm số đồng biến trên ( )6;+ thì ( ) ( ) 6;6;6612. bbb +−−+−−− . Câu 15: Hàm số ( )2 213yxmx =−+−+ nghịch biến trên ( )1;+ khi giá trị m thỏa mãn: A. 0m  . B. 0m  . C. 2m  . D. 02 m  Lời giảiss Chọn C Đồ thị hàm số có trục đối xứng là đường 1xm=− . Đồ thị hàm số đã cho có hệ số 2 x âm nên sẽ đồng biến trên ( );1 m −− và nghịch biến trên ( )1;m −+ . Theo đề, cần: 112mm− . Câu 16: Tìm tất cả các giá trị của tham số m để hàm số 2 213yxmx =−++− nghịch biến trên( ) 2;. + A. 3 1 m m −   . B. 31 m − . C. 31 m − . D. 3 1 m m −   . Lời giải Chọn C Hàm số 2 213yxmx =−++− có 10;1 2 b am a =−−=+ nên hàm số nghịch biến trên ( )1;m ++ Để hàm số nghịch biến trên ( )2;+ thì ( ) ( )2;1; m +++ 1221231 mmm +−+− Câu 17: Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số 2 (1)21yxmxm đồng biến trên khoảng 2; . Khi đó tập hợp 10;10 S là tập nào? A. 10;5 B. 5;10 C. 5;10 D. 10;5 Lời giải Chọn B Gọi ( )P là đồ thị của 2 (1)21yfxxmxm ( )yfx = là hàm số bậc hai có hệ số 1a

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 6 Gọi I là đỉnh của ( )P , có 1 2I m x = Nên hàm số đồng biến trên khoảng 1 ; 2 m Do đó để hàm số trên khoảng 2; khi 1 2 2 m 5m . Suy ra tập 5;S . Khi đó 10;105;10 S . Câu 18: Tìm tất cả các giá trị dương của tham số m để hàm số ( ) 22 4 fxmxxm =−− luôn nghịch biến trên ( )1;2 . A. 1m  . B. 21 m − . C. 01 m  . D. 01 m  . Lời giải Chọn C Với 0m  , ta có hàm số ( ) 22 4 fxmxxm =−− nghịch biến trên 2 ; m  −   , suy ra hàm nghịch biến trên ( )1;2 khi ( ) 22 1;2;201 m mm  −−   . Câu 19: Cho hàm số ( )22 2 yxmxmP =−+ . Khi m thay đổi, đỉnh của Parabol ( )P luôn nằm trên đường nào sau đây? A. 0y = . B. 0x = . C. yx = . D. 2 yx = . Lời giải Chọn A Tọa độ đỉnh I của Parabol là ( );0Im , nên I luôn thuộc đường thẳng 0y = . Câu 20: Cho hàm số ( )22 44 yxmxmP =−+ . Khi m thay đổi, đỉnh của Parabol ( )P luôn nằm trên đường nào sau đây? A. 0x = . B. 0y = . C. 22 yx = . D. 2 yx = . Lời giải Chọn B Tọa độ đỉnh I của Parabol là ( )2;0Im , nên I luôn nằm trên đường thẳng 0x = . Câu 21: Tìm giá trị của tham số m để đỉnh I của đồ thị hàm số 2 6 yxxm =−++ thuộc đường thẳng 2019yx=+ A. 2020m = B. 2000m = C. 2036m = D. 2013m = Lời giải Chọn D Đồ thị hàm số 2 6 yxxm =−++ là parabol có đỉnh ( )3;9 Im + .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 7 Đỉnh ( )3;9 Im + thuộc đường thẳng 20199320192013yxmm =++=+= DẠNG 2. XÁC ĐỊNH TOẠ ĐỘ ĐỈNH, TRỤC ĐỐI XỨNG, HÀM SỐ BẬC HAI THỎA MÃN ĐIỀU KIỆN CHO TRƯỚC. Câu 22: Cho hàm số bậc hai 2 =++ yaxbxc ( )0a có đồ thị ( )P , đỉnh của ( )P được xác định bởi công thức nào? A. ; 24     b I aa . B. ; 4     b I aa . C. ; 24 b I aa     . D. ; 24 b I aa     . Lời giải Chọn A Đỉnh của parabol ( ) 2 : =++ Pyaxbxc ( )0a là điểm ; 24     b I aa . Câu 23: Cho parabol ( ) 2 :321Pyxx=−+ . Điểm nào sau đây là đỉnh của ( )P ? A. ( )0;1I . B. 12 ; 33 I    . C. 12 ; 33 I    . D. 12 ; 33 I    . Lời giải Chọn B Hoành độ đỉnh của ( ) 2 :321Pyxx=−+ là 1 23 b x a =−= 2 112 32.1 333y  =−+=   . Vậy 12 ; 33 I    . Câu 24: Trục đối xứng của đồ thị hàm số 2 yaxbxc =++ , (0) a  là đường thẳng nào dưới đây? A. 2 b x a =− B. 2 c x a =− C. 4 x a  =− D. 2 b x a = Lời giải Chọn A Câu 25: Điểm ( )2;1I là đỉnh của Parabol nào sau đây? A. 2 45yxx=++ B. 2 241yxx=++ C. 2 45yxx=+− D. 2 43yxx=−−+ Lời giải Chọn A Hoành độ đỉnh là 2 2I b x a =−=− . Từ đó loại câu B. Thay hoành độ 2Ix =− vào phương trình Parabol ở các câu A, C, D, ta thấy chỉ có câu A thỏa điều kiện 1Iy = Câu 26: Parabol ( ) 2: 263Pyxx=−−+ có hoành độ đỉnh là

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 8 A. 3x =− . B. 3 2 x = . C. 3 2 x =− . D. 3x = . Lời giải Chọn C Parabol ( ) 2: 263Pyxx=−−+ có hoành độ đỉnh là 2 b x a =− ( ) 6 22 =− 3 2 =− Câu 27: Tọa độ đỉnh của parabol 2 246yxx=−−+ là A. ( )1;8I . B. ( )1;0I . C. ( )2;10I . D. ( )1;6I . Lời giải Chọn A Tọa độ đỉnh của parabol 2 246yxx=−−+ là ( ) ( ) ( ) ( ) 2 4 1 2.2 1;8 2.14.168 x I y  =−=− −  =−−−−+= Câu 28: Hoành độ đỉnh của parabol ( ) 2 :243Pyxx=−+ bằng A. 2. B. 2. C. 1. D. 1. Lời giải Chọn D 1 2 b x a =−= . Câu 29: Parabol có phương trình trục đối xứng là A. . B. . C. . D. . Lời giải Chọn C Parabol 2 23yxx=−++ có trục đối xứng là đường thẳng 2 b x a =− 1x = Câu 30: Xác định các hệ số a và b để Parabol ( ) 2 :4 Pyaxxb =+− có đỉnh ( )1;5I . A. 3 . 2 a b =  =− B. 3 . 2 a b =  = C. 2 . 3 a b =  = D. 2 . 3 a b =  =− Lời giải Chọn C Ta có: 4 112. 2I xa a =−−=−= Hơn nữa ( )IP  nên 543. abb −=−−= Câu 31: Biết hàm số bậc hai 2 =++ yaxbxc có đồ thị là một đường Parabol đi qua điểm ( )1;0A và có đỉnh ( )1;2I Tính abc ++ 2 23yxx=−++ 1x =− 2x = 1x = 2x =−

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 9 A. 3. B. 3 2 . C. 2. D. 1 2 . Lời giải Chọn C Theo giả thiết ta có hệ: 0 1. 2 2 −+=   −=  ++=  abc b a abc với 0a 1 0 1 2 2 23 2   =−+=   =−=−   ++=  =  abcb baa abc c Vậy hàm bậc hai cần tìm là 2 13 22 =−++yxx Câu 32: Biết đồ thị hàm số 2 yaxbxc =++ , ( ),,;0abca đi qua điểm ( )2;1A và có đỉnh ( )1;1I Tính giá trị biểu thức 32 2 Tabc =+− A. 22T = . B. 9T = . C. 6T = . D. 1T = . Lời giải Chọn A Đồ thị hàm số 2 ax ybxc =++ đi qua điểm ( )2;1A và có đỉnh ( )1;1I nên có hệ phương trình 421 42111 1224 2 1112 abc abccc b babab a abcabcaca ++= ++===   −==−=−=−   ++=−−+=−= ++=−  Vậy 32 222Tabc=+−= . Câu 33: Cho hàm số 2 (0)yaxbxca =++ có đồ thị. Biết đồ thị của hàm số có đỉnh (1;1)I và đi qua điểm (2;3)A . Tính tổng 222 Sabc =++ A. 3. B. 4. C. 29. D. 1. Lời giải Chọn C Vì đồ thị hàm số 2 (0)yaxbxca =++ có đỉnh (1;1)I và đi qua điểm (2;3)A nên ta có hệ: 112 4234234 203 1 2 abcabca abcabcb babc a   ++=++==   ++=++==− +==  −=  Nên 222 Sabc =++ =29 Câu 34: Cho Parabol ( ) 2 : Pyxmxn =++ ( , mn tham số). Xác định , mn để ( )P nhận đỉnh ( )2;1I

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 10 A. 4,3mn==− . B. 4,3mn== . C. 4,3mn=−=− . D. 4,3mn=−= . Lời giải Chọn D Parabol ( ) 2 : Pyxmxn =++ nhận ( )2;1I là đỉnh, khi đó ta có 421 253 244 2 mn mnn m mm ++=− +=−=   −==−=−   Vậy 4,3mn=−= . Câu 35: Cho Parabol: 2 yaxbxc =++ có đỉnh (2;0)I và () P cắt trục Oy tại điểm (0;1)M . Khi đó Parabol có hàm số là A. B. C. D. Lời giải Chọn C Parabol ( ) 2 : Pyaxbxc=++⎯⎯→ đỉnh 2 ; 24 bb Ic aa    Theo bài ra, ta có có đỉnh ( ) ( )22 2 42 2;01 4 0 4 b Iaba bbac c a  −= =−= −=  Lại có cắt Oy tại điểm ( )0;1M suy ra ( ) ( )0112yc=−=− Từ, suy ra 22 44 1 4 1;111 baba a babb ccbc =−=−  =−  =−=  =−=−==− Câu 36: Gọi S là tập các giá trị 0m  để parabol ( ) 22 :22 Pymxmxmm =+++ có đỉnh nằm trên đường thẳng 7yx=+ . Tính tổng các giá trị của tập S A. 1. B. 1. C. 2. D. 2. Lời giải Chọn A Khi 0m  thì ( ) 22 :22 Pymxmxmm =+++ có đỉnh là ( )2;1; 24 b IImm aa   −−−+   Vì đỉnh nằm trên đường thẳng 7yx=+ nên ( )22 2 1760 3 m mmmmTM m = +=−++−=  =− Vậy tổng các giá trị của tập S : ( ) 231 +−=− ( ) 21 :31 4 Pyxx=−−− ( ) 21 :1 4 Pyxx=−−− ( ) 21 :1 4 Pyxx=−+− ( ) 21 :21 4 Pyxx=−+−

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 11 Câu 37: Xác định hàm số 2 1yaxbxc biết đồ thị của nó có đỉnh 31 ; 24 I và cắt trục hoành tại điểm có hoành độ bằng 2. A. 2 32yxx . B. 2 32yxx . C. 2 32yxx . D. 2 32yxx . Lời giải Chọn D . Do đồ thị của nó có đỉnh 31 ; 24 I và cắt trụ hoành tại điểm có hoành độ bằng 2 nên ta có 3 22 301 931 96413 424 4202420 b a aba abcabcb abcabcc Vậy 2 32yxx Câu 38: Hàm số bậc hai nào sau đây có đồ thị là parabol có đỉnh là      2 1 ; 2 5 S và đi qua ( )1;4A ? A. 582 =+ yxx . B. 21012 2 =+ yxx . C. yxx 52 = D. 2 1 25 2 =++yxx Lời giải Chọn B Hàm số bậc hai cần tìm có phương trình: ( )02 =++yaxbxca Hàm số bậc hai có đồ thị là parabol có đỉnh là      2 1 ; 2 5 S và đi qua ( )1;4A ( ) 55 5a2222 222 254a4a4 14a11 10 424242 12444a4 bb ab a a bca b aaa abcabccc == =−   =−  −−+−+−  ====   ++=−++=−=−=−      Câu 39: Cho parabol ( )P có phương trình 2 yaxbxc =++ . Tìm abc ++ , biết ( )P đi qua điểm ( )0;3A và có đỉnh ( )1;2I . A. 6abc++= B. 5abc++= C. 4abc++= D. 3abc++= Lời giải Chọn A

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 12 ( )P đi qua điểm ( ) 0;33Ac= ( )P có đỉnh ( ) 211 1;26 2 21232 b baa Iabc a abaab  =−== −++=  −=−= −+= Câu 40: Parabol 2 yaxbxc =++ đạt cực tiểu bằng 4 tại 2x =− và đi qua ( )0;6A có phương trình là A. 21 26 2 yxx=++ . B. 2 26yxx=++ . C. 2 66yxx=++ . D. 2 4yxx=++ . Lời giải Chọn A Ta có: 24 2 b ba a −=−= Mặt khác : Vì ,()AIP  ( ) 2 2 4.(2).(2) 4.22 66.0.(0) abc ab abcc  =−+−+ −=−   =++=  Kết hợp, ta có : 1 2 2 6 a b c  =  =  =  Vậy ( ) 21 :26 2 Pyxx=++ Câu 41: Parabol 2 yaxbxc =++ đi qua ( )0;1A , ( )1;1B , ( )1;1C có phương trình là A. 2 1yxx=−+ . B. 2 1yxx=−− . C. 2 1yxx=+− . D. 2 1yxx=++ . Lời giải Chọn B Ta có: Vì ,,() ABCP  ( ) ( ) 2 2 2 1.0.0 1 1.1.(1)1 11.1.(1) abc a abcb abcc −=++ =  −=++=−   =−+−+=−  . Vậy ( ) 2 :1Pyxx=−− . Câu 42: Parabol 2 2yaxbx=++ đi qua hai điểm (1;5)M và (2;8)N có phương trình là A. 2 2yxx=++ B. 2 22yxx=++ C. 2 222yxx=++ D. 2 2 yxx =+ Lời giải Chọn B Parabol 2 2yaxbx=++ đi qua hai điểm (1;5)M và (2;8)N nên ta có hệ phương trình: 2 2 5.1.1231 42628.(2).(2)2 ababa ababb  =+++==    =−+−+−==  Vậy hàm số cần tìm là 2 22.yxx=++

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 13 Câu 43: Cho 2 ():1 Pyxbx=++ đi qua điểm ( ) 1;3.A Khi đó A. 1.b =− B. 1.b = C. 3.b = D. 2.b =− Lời giải Chọn A Thay tọa độ ( )1;3A vào 2 ():1 Pyxbx=++ . Ta được: ( )2 3111 bb =−−+=− . Câu 44: Cho parabol ( ) 2 : Pyaxbxc =++ đi quabađiểm ( ) ( )1;4,1;4AB và ( )2;11C .Tọađộ đỉnh của ( )P là: A. ( )2;11 B. ( )2;5 C. ( )1;4 D. ( )3;6 Lời giải Chọn B ( ) 2 : Pyaxbxc =++ đi qua ba điểm ( ) ( )1;4,1;4AB và ( )2;11C suy ra ( ) 2 41 44:41 42111 abca abcbPyxx abcc ++==−  −+=−==−++ −+=−=  Hoành độ của đỉnh của ( )P là 2 2 b x a == . Suy ra tung độ của đỉnh của ( )P là 2 24.215y =−++= . Câu 45: Cho hàm số 2 yaxbxc =++ có bảng biến thiên dưới đây. Đáp án nào sau đây là đúng? A. 2 22.yxx=+− B. 2 22.yxx=−− C. 2 +32.yxx=− D. 2 22.yxx=−−− Lời giải Chọn A Từ BBT ta có 0a  nên loại phương án D.Đỉnh ( )1;3I nên 1 a2 b −=− ,vậychọn A. Câu 46: Cho parabol : có trục đối xứng là đường thẳng . Khi đó bằng A. . B. . C. . D. . Lời giải Chọn B ( )P 2 yaxbxc =++ 1x = 42ab + 1 0 1 2

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 14 Do parabol ( )P : 2 yaxbxc =++ có trục đối xứng là đường thẳng 1x = nên 1 2 b a −= 2ab=− 20 ab += 420 ab += . Câu 47: Parabol 2 yaxbxc =++ đi qua ( )8;0A và có đỉnh ( )6;12I . Khi đó tích abc bằng A. 10368 B. 10368 C. 6912 D. 6912 Lời giải Chọn A Điều kiện 0.a  Từ giả thiết ta có hệ 6480 36612 6 2 abc abc b a   ++= ++=−  −=  3 36 96 a b c =  =−   = 10368abc =− . Câu 48: Cho parabol 2 4yaxbx=++ có trục đối xứng là đường thẳng 1 3 x = và đi qua điểm ( )1;3A Tổng giá trị 2 ab + là A. 1 2 . B. 1. C. 1 2 . D. 1. Lời giải Chọn B Vì parabol 2 4yaxbx=++ có trục đối xứng là đường thẳng 1 3 x = và đi qua điểm ( )1;3A nên ta có a43a13 1 2302 23 b ba b abb a ++= +=−=−   −=+==   . Do đó 2341ab+=−+= Câu 49: Cho parabol 2 yaxbxc =++ có đồ thị như hình sau Phương trình của parabol này là A. 2 1yxx=−+− B. 2 241yxx=+− C. 2 21yxx=−− D. 2 241yxx=−− Lời giải Chọn D

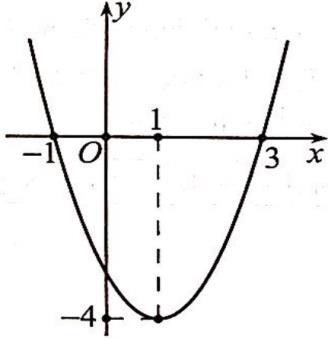
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 15 Đồ thị hàm số cắt trục tung tại điểm ( )0;1 nên 1c =− Tọa độ đỉnh ( )1;3I , ta có phương trình: 2 1 2 .1.113 b a ab  −=   +−=− 20 2 ab ab +=   +=− 2 4 a b =   =− . Vậy parabol cần tìm là: 2 241yxx=−− Câu 50: Biết hàm số bậc hai 2 =++ yaxbxc có đồ thị là một đường Parabol đi qua điểm ( )1;0A và có đỉnh ( )1;2I . Tính abc ++ . A. 3 B. 3 2 C. 2 D. 1 2 Lời giải Chọn C Theo giả thiết ta có hệ: 0 1. 2 2 −+=   −=  ++=  abc b a abc với 0a 1 0 1 2 2 23 2   =−+=   =−=−   ++=  =  abcb baa abc c Vậy hàm bậc hai cần tìm là 2 13 22 =−++yxx Câu 51: Cho parabol 2():Pyaxbxc =++ , ( )0a  có đồ thị như hình bên dưới. Khi đó 22abc ++ có giá trị là: A. 9. B. 9. C. 6. D. 6. Lời giải Chọn C Parabol 2 ():,(0) Pyaxbxca=++ đi qua các điểm (1;0),(1;4),(3;0) ABC

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 16 Do đó ta có hệ phương trình: 01 42 9303 abca abcb abcc −+==  ++=−=− ++==−  Khi đó: 222.122(3)6. abc++=−+−=− Câu 52: Cho hàm số ( )2 ..0yaxbxca =++ . Biết rằng đồ thị hàm số nhận đường thẳng 3 2 x = làm trục đối xứng, và đi qua các điểm ( ) ( )2;0,0;2AB . Tìm Tabc =−+ A. 1T = . B. 3T = . C. 0T = . D. 6T = . Lời giải Chọn D Ta có Đồ thị hàm số nhận đường thẳng 3 2 x = làm trục đối xứng ta được: ( )3 301 22 b ab a =+= Đồ thị hàm số đi qua các điểm ( ) ( )2;0,0;2AB ta được: ( )420 2 2 abc c ++=  = Từ ( ) ( )1,2 ta được: 1 36 2 a bT c =  =−=  = Câu 53: Cho hàm số ( ) 2 fxaxbxc =++ đồ thị như hình. Tính giá trị biểu thức 222 Tabc =++ . A. 0. B. 26. C. 8. D. 20. Lời giải Chọn B Do đồ thị hàm số có đỉnh là ( )2;1I ( ) 240 2 21421 b ab a fabc  = +=++=− =− ( )1 Do đồ thị hàm số đi qua điểm ( ) ( ) 0;3033 fc == ( )2

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 17 Từ ( )1 và( )2 1 4 3 a b c =  =−   = 26T = Câu 54: Xác định hàm số 2 yaxbxc =++ biết đồ thị của hàm số cắt trục tung tại điểm có tung độ là 3 và giá trị nhỏ nhất của hàm số là 25 8 tại 1 4 x = A. 2 23yxx=−+− B. 2 1 .3 2 yxx=−+ C. 2 23yxx=−− D. 2 23yxx=+− Lời giải Chọn C + Đồ thị cắt trục tung tại điểm ( )0; Ac 3c =− . + Giá trị nhỏ nhất của hàm số là 25 8 tại 1 4 x = nên đỉnh của đồ thị hàm số là 125 ; 48 I    Suy ra 1 240224 1125421 .3 1648 b aaba ababb  = +==   +=−=− +−=−  Vậy hàm số cần tìm là 2 23yxx=−− . Câu 55: Parabol 2 yaxbxc =++ đạt giá trị nhỏ nhất bằng 4tại 2x =− và đồ thị đi qua ( )0;6A có phương trình là: A. 2 66yxx=++ . B. 2 4yxx=++ . C. 21 26 2 yxx=++ . D. 2 26yxx=++ . Lời giải Chọn C Theo bài ra ta có ( ) 12424 422 2 24 2 666 02 yabc aba b a a cc c bb −=−+= −=−=  −=−  == = −=   =  . Câu 56: Cho parabol ( ) ( ) 2 :,0 Pyfxaxbxca ==++ . Biết ( )P đi qua ( )4;3M , ( )P cắt tia Ox tại ( )3;0N và Q sao cho MNQ có diện tích bằng 1đồng thời hoành độ điểm Q nhỏ hơn 3. Khi đó abc ++ bằng A. 24 5 . B. 12 5 . C. 5. D. 4. Lời giải Chọn A

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 18 Gọi điểm H là hình chiếu vuông góc của M lên trục Ox . Ta có ( )11 ..y.122 MNQMNQ SMHNQxx==−= ( ) 17 .331 23 QQ xx −== nên 7 ;0 3Q    Ta thu được: ( ) ( ) ( )7 4;3,3;0,;0 3 MNQP    1643 930 497 0 93 abc abc abc   ++= ++=    ++= 9 5 48 5 63 5 a b c  =   =    =  DẠNG 3. ĐỌC ĐỒ THỊ, BẢNG BIẾN THIÊN CỦA HÀM SỐ BẬC HAI Câu 57: Bảng biến thiên của hàm số 2 241yxx=−++ là bảng nào sau đây? A. B. C. D. Lời giải Chọn B Hàm số 2 241yxx=−++ có đỉnh ( )1;3I , hệ số 20a =− nên hàm số đồng biến trên khoảng ( );1− , nghịch biến trên khoảng ( )1;+ Câu 58: Đồ thị nào sau đây là đồ thị của hàm số 2 23yxx=−− A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4. Hình 2 x y O 1 Hình 3 x y O 1 Hình4 x y O 1

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 19 Lời giải Chọn D Dựa vào đồ thị có: ( ) ( ) 2 :23Pyfxxx ==−− ;có 10a = ;nên ( )P có bề lõm hướng lên ( )P có đỉnh I có 1Ix = Vậy ( ) ( ) 2 :23Pyfxxx ==−− có đồ thị là hình 4 Câu 59: Bảng biến thi của hàm số 4 241yxx=−++ là bảng nào sau đây? A. . B. . C. D. Lời giải Chọn C Hàm số 4 241yxx=−++ có hệ số 20a =− nên bề lõm quay lên trên vì vậy ta loại đáp án B, D. Hàm số có tọa độ đỉnh (1;3)I nên ta loại đáp án A. Vậy bảng biến thiên của hàm số 4 241yxx=−++ là bảng C. Câu 60: Bảng biến thiên của hàm số 2 21yxx=−+− là: A. B. C. . D. . Lời giải Chọn A 2 21=−+−yxx Có 10a =− , nên loại C và D. Tọa độ đỉnh ( )1;0I , nên nhận A.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 20 Câu 61: Bảng biến thiên nào dưới đây là của hàm số 2 22yxx=−++ ? A. B. C. D. Lời giải Chọn C '22yx=−+ '01yx== Hàm số đồng biến trên ( );1− ; nghịch biến trên ( )1;+ . Câu 62: Đồ thị hàm số 2 yaxbxc =++ , (0) a  có hệ số a là A. 0.a  B. 0.a  C. 1.a = D. 2.a = Lời giải Chọn B Bề lõm hướng xuống 0.a  Câu 63: Cho parabol 2 yaxbxc =++ có đồ thị như hình vẽ dưới đây. Khẳng định nào dưới đây đúng? A. 0,0,0abc B. 0,0,0abc C. 0,0,0abc D. 0,0,0abc Lời giải Chọn C Parabol quay bề lõm xuống dưới 0a  .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 21 Parabol cắt Oy tại điểm có tung độ dương 0c  . Đỉnh của parabol có hoành độ dương 00 2 bb aa  mà 0a  nên suy ra 0b  . Câu 64: Nếu hàm số 2 yaxbxc =++ có 0,0ab và 0c  thì đồ thị hàm số của nó có dạng A. B. C. D. Lời giải Chọn C Do 0a  nênParabol quaybềlõm lêntrên,suy raloại phươngán , AD .Mặt khácdo 0,0ab nên đỉnh Parabol có hoành độ 0 2a b x =− nên loại phương án B . Vậy chọn C . Câu 65: Cho hàm số thì đồ thị của hàm số là hình nào trong các hình sau: A. Hình (1) B. Hình (2) C. Hình (3) D. Hình (4). Lời giải Chọn C Vì nên đồ thị cắt trục tung tại điểm nằm phía trên trục hoành. Mặt khác nê hai hệ số này trái dấu, trục đối xứng sẽ phía phải trục tung. Do đó, hình là đáp án cần tìm. Câu 66: Cho hàm số 2 yaxbxc =++ có đồ thị như hình bên dưới. Khẳng định nào sau đây đúng? ` A. 0, 0, 0abc B. 0, 0, 0abc C. 0, 0, 0abc D. 0, 0, 0abc Lời giải Chọn A Parabol có bề lõm quay lên 0a  loại D. Parabol cắt trục tung tại điểm có tung độ âm nên 0c  loại B, C. Chọn A Câu 67: Cho hàm số ( )2 ,0yaxbxca =++ cóbảng biến thiêntrênnửakhoảng  )0;+ nhưhình vẽ dưới đây: 2 ,(0,0,0)yaxbxcabc =++ 0c  0,0ab x y O

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 22 Xác định dấu của a , b , c . A. 0,0,0abc B. 0,0,0abc C. 0,0,0abc D. 0,0,0abc Lời giải Chọn D Dựa vào bảng biến thiên ta có: Parabol ( )P có bề lõm quay xuống dưới; hoành độ đỉnh dương; cắt trục tung tại điểm có tung độ bằng 1 nên 0 0 00 2 100 a a b b a c c      =−  Câu 68: Cho hàm số 2 yaxbxc =++ có đồ thị là parabol trong hình vẽ. Khẳng định nào sau đây là đúng? A. 0; 0; 0abc . B. 0; 0; 0abc . C. 0; 0; 0abc . D. 0; 0; 0abc . Lời giải Chọn D Vì Parabol hướng bề lõm lên trên nên 0a  . Đồ thị hàm số cắt Oy tại điểm ( )0;c ở dưới 0Oxc . Hoành độ đỉnh Parabol là 0 2 b a − , mà 00ab Câu 69: Cho hàm số 2 yaxbxc =++ có đồ thị như hình bên. Khẳng định nào sau đây đúng? A. 0a  , 0b  , 0c  B. 0a  , 0b  , 0c  C. 0a  , 0b  , 0c  D. 0a  , 0b  , 0c  Lời giải x y O 3 1 1

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 23 Chọn D Dựa vào đồ thị, nhận thấy: * Đồ thị hàm số là một parabol có bề lõm quay xuống dưới nên 0a  * Đồ thị cắt trục tung tại tung độ bằng c nên 0c  * Đồ thị cắt trục hoành tại hai điểm có hoành độ 1 1x =− và 2 3x = nên 12 , xx là hai nghiệm của phương trình 2 0axbxc++= mà theo Vi et 12 2 b xx a +=−= 20bab =− . * Vậy 0a  , 0b  , 0c  . Câu 70: Cho hàm số 2 yaxbxc =++ có đồ thị như bên. Khẳng định nào sau đây đúng? A. 0,0,0.abc B. 0,0,0.abc C. 0,0,0.abc D. 0,0,0.abc Lời giải Chọn A Đồ thị cắt trục tung tại điểm có tung độ ( )c= âm nên 0c  . Suy ra loại B,. D. Đồ thị hướng bề lõm lên trên nên 0a  , hoành độ đỉnh 2 b a  =   dương nên 0,00 2 b ab a  Câu 71: Cho hàm số 2 yaxbxc =++ . Có đồ thị như hình vẽ dưới đây. Hỏi mệnh đề nào đúng? A. 0,0,0abc . B. 0,0,0abc . C. 0,0,0abc . D. 0,0,0abc . Lời giải Chọn A x y O

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 24 Nhận xét: +) Parabol có bề lõm quay xuống dưới nên 0a  +) Parabol cắt trục tung tại điểm có hoành độ bằng 0 và tung độ âm nên thay 0x = vào 2 yaxbxc =++ suy ra 0c  +) Parabol có trục đối xứng nằm bên phải trục tung nên 0 2 b x a =− mà 0a  nên 0b  Vậy 0,0,0abc . Câu 72: Cho đồ thị hàm số 2 yaxbxc =++ có đồ thị như hình vẽ bên dưới. Mệnh đề nào sau đây đúng? A. 0,0,0abc= B. 0,0,0abc C. 0,0,0abc D. 0,0,0abc Lời giải Chọn C Từ dáng đồ thị ta có 0a  . Đồ thị cắt trục Oy tại điểm có tung độ dương nên 0c  . Hoành độ đỉnh 0 2 b a − mà 0a  suy ra 0b  . Câu 73: Cho hàm số 2 yaxbxc =++ có 0;0;0abc thì đồ thị ( )P của hàm số là hình nào trong các hình dưới đây A. hình ( )4 . B. hình ( )3 . C. hình ( )2 . D. hình ( )1 . Lời giải Chọn C Vì 0a  nên đồ thị có bề lõm hướng xuống dưới  loại hình, hình.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 25 0;0ab  2 b a 0 nên trục đối xứng của ( )P nằm bên trái trục tung. Vậy hình thỏa mãn nên chọn đáp án C. Câu 74: Cho hàm số 2 yaxbxc có đồ thị như hình vẽ dưới đây. Khẳng định nào sau đây là đúng? A. 0,0,0abc B. 0,0,0abc C. 0,0,0abc D. 0,0,0abc Lời giải Chọn B Đồ thị hàm số cắt trục Oy tại điểm nằm phía dưới trục Ox nên 0C Đồ thị có bề lõm hướng lên do đó 0a Tọa độ đỉnh nằm ở góc phần tư thứ III nên 0 2 b a 0b . Câu 75: Hàm số nào có đồ thị như hình vẽ bên dưới? A. 2 43yxx=−+− . B. 2 43yxx=−−− . C. 2 23yxx=−−− . D. 2 43yxx=−− . Lời giải Chọn A Đồ thị có bề lõm quay xuống dưới nên 0a  . Loại phương án D. Trục đối xứng: 2x = do đó Chọn A Câu 76: Bảng biến thiên sau là của hàm số nào ? A. . B. . C. . D. . Lời giải Chọn A Dựa vào bảng biến thiên ta thấy 0a  . Loại .B 2 244yxx=−+ 2 361yxx=−+− 2 21yxx=+− 2 22yxx=−+

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 26 Tọa độ đỉnh ( )1;2I 10 2 b a −= . Suy ra 0b  . Loại. C Thay 12xy== . Loại .D Câu 77: Bảng biến thiên sau là của hàm số nào? A. 2 4 yxx =− . B. 2 4 yxx =+ . C. 2 4 yxx =−+ . D. 2 4 yxx =−− . Lời giải Chọn A Từ bảng biến thiên suy ra hệ số 0a  . Loại C, D Toạ độ đỉnh ( )2;4=−I loại B Câu 78: Đồ thị trong hình vẽ dưới đây là của hàm số nào trong các phương án A;B;C;D sau đây? A. 2 21yxx=+− . B. 2 22yxx=+− . C. 2 242yxx=−− . D. 2 21yxx=−− . Lời giải Chọn D Đồ thị cắt trục tung tại điểm có tung độ bằng 1 nên loại B và C Hoành độ của đỉnh là 1 2I b x a =−= nên ta loại A và Chọn D Câu 79: Cho parabol 2 yaxbxc =++ có đồ thị như hình sau Phương trình của parabol này là A. 2 1yxx=−+− . B. 2 241yxx=+− . C. 2 21yxx=−− . D. 2 241yxx=−− .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 27 Lời giải Chọn D Đồ thị hàm số cắt trục tung tại điểm ( )0;1 nên 1c =− . Tọa độ đỉnh ( )1;3I , ta có phương trình: 2 1 2 .1.113 b a ab  −=   +−=− 20 2 ab ab +=   +=− 2 4 a b =   =− Vậy parabol cần tìm là: 2 241yxx=−− . Câu 80: Cho parabol 2 yaxbxc =++ có đồ thị như hình sau: Phương trình của parabol này là A. 2 1.yxx=−+− B. 2 241.yxx=+− C. 2 21.yxx=−− D. 2 241.yxx=−− Lời giải Chọn D Do đồ thị cắt trục tung tại điểm có tung độ bằng 1 nên suy ra 1(1)c =− Đồ thị có tọa độ đỉnh ( );1;3 24 b II aa  −  nên ta có: 22 1 2222 (2)12 4120441203 4 b abababa a bacaaaca a  = =−=−=−   −=−−=−−= =−  Từ và ta có hệ phương trình 2 12 24 1480 ca bab aac  =−=   =−=− −==− . Ta được parabol có phương trình là 2 241.yxx=−− Câu 81: Đồ thị hình bên dưới là đồ thị của hàm số bậc hai nào? x y -3 -1 O 1

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 28 A. 2 31yxx=−+ B. 2 231yxx=−+ C. 2 31yxx=−+− D. 2 231yxx=−+− Lời giải Chọn B Dựa vào hình vẽ ta có hàm số bậc hai có hệ số 0a  nên ta loại đáp án C, D. Mặt khác đồ thị hàm số cắt trục hoành tại điểm có tọa độ ( )1;0 , mà điểm ( )1;0 thuộc đồ thị hàm số 2 231yxx=−+ và không thuộc đồ thị hàm số 2 31yxx=−+ nên ta Chọn B Câu 82: Trên mặt phẳng tọa độ Oxy cho Parabol như hình vẽ. Hỏi parabol có phương trình nào trong các phương trình dưới đây? A. 2 31yxx=+− . B. 2 31yxx=−− . C. 2 31yxx=−−− . D. 2 31yxx=−++ . Lời giải Chọn D Đồ thị hàm số là parabol có bề lõm quay xuống nên hệ số 0a  . Loại đáp án A, B. Đồ thị cắt trục tung tại điểm có tung độ dương nên loại đáp án C. Câu 83: Cho parabol ( ) ( )2 :,0Pyaxbxca=++ có đồ thị như hình bên. Khi đó 22abc ++ có giá trị là x y 3 -4 -1 2O 1 O x y 1 1

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 29 A. 9. B. 9. C. 6. D. 6. Lời giải Chọn C Parabol ( ) ( )2 :,0Pyaxbxca=++ đi qua các điểm ( )1;0A , ( )1; 4B , ( )3;0C nên có hệ phương trình: 0 4 930 abc abc abc −+=  ++=−  ++= 1 2 3 a b c =  =−   =− . Khi đó: ( ) 222.12236 abc++=−+−=− Câu 84: Hàm số nào sau đây có đồ thị như hình bên dưới A. 2 23yxx=−+− . B. 2 43yxx=−+− . C. 2 43yxx=−+ . D. 2 23yxx=−− . Lời giải Chọn B Đồ thị trên là của hàm số bậc hai với hệ số 0a  và có tọa độ đỉnh là ( )2;1I . Vậy đồ thị đã cho là đồ thị của hàm số 2 43yxx=−+− Câu 85: Bảng biến thiên ở dưới là bảng biến thiên của hàm số nào trong các hàm số được cho ở bốn phương án A, B, C, D sau đây? A. 2 4 yxx =−+ B. 2 49yxx=−+− C. 2 41yxx=−− D. 2 45yxx=−− Lời giải Chọn C Parabol cần tìm phải có hệ số 0a  và đồ thị hàm số phải đi qua điểm ( )2;5 . Đáp án C thỏa mãn. Câu 86: Bảng biến thiên sau đây là bảng biến thiên của hàm số nào?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 30 A. 2 4 yxx =+ . B. 2 48yxx=−−− . C. 2 48yxx=−−+ . D. 2 4 yxx =−− . Lời giải Chọn B Dựa vào BBT ta thấy: Parabol có bề lõm quay lên trên nên hệ số 0a   Loại A. Parabol có đỉnh ( )2;4I nên thay 2;4xy=−=− vào các đáp án B, C, D. Nhận thấy chỉ có đáp án B thỏa mãn. Câu 87: Cho parabol 2 yaxbcc =++ có đồ thị như hình vẽ. Khi đó: A. 0,0,0abc . B. 0,0,0abc . C. 0,0,0abc . D. 0,0,0abc . Lời giải Chọn A Đồ thị hàm số có bề lõm quay xuống nên 0,a  cắt trục tung tại điểm có tung độ dương nên 0.c  Đỉnh parabol có hoành độ âm nên 00 2 b b a  . Câu 88: Cho hàm số 2 yaxbxc =++ có đồ thị như hình bên dưới. Khẳng định nào sau đây đúng? ` A. 0, 0, 0abc . B. 0, 0, 0abc . C. 0, 0, 0abc . D. 0, 0, 0abc . Lời giải Chọn A Parabol có bề lõm quay lên 0a  loại D. Parabol cắt trục tung tại điểm có tung độ âm nên 0c  loại B, C. Chọn A Câu 89: Cho hàm số 2 yaxbxc =++ có đồ thị là parabol trong hình vẽ. Khẳng định nào sau đây là đúng? x y O

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 31 A. 0; 0; 0abc B. 0; 0; 0abc C. 0; 0; 0abc D. 0; 0; 0abc . Lời giải Chọn D Vì Parabol hướng bề lõm lên trên nên 0a  . Đồ thị hàm số cắt Oy tại điểm ( )0;c ở dưới 0Oxc Hoành độ đỉnh Parabol là 0 2 b a − , mà 00ab . Câu 90: Cho hàm số 2 yaxbxc =++ có đồ thị như bên. Khẳng định nào sau đây đúng? A. 0,0,0.abc . B. 0,0,0.abc . C. 0,0,0.abc . D. 0,0,0.abc Lời giải Chọn A Đồ thị cắt trục tung tại điểm có tung độ ( )c= âm nên 0c  . Suy ra loại B,. D. Đồ thị hướng bề lõm lên trên nên 0a  , hoành độ đỉnh 2 b a  =   dương nên 0,00 2 b ab a  Câu 91: Cho hàm số 2 yaxbxc =++ . Có đồ thị như hình vẽ dưới đây. Hỏi mệnh đề nào đúng? x y O

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 32 A. 0,0,0abc . B. 0,0,0abc . C. 0,0,0abc . D. 0,0,0abc . Lời giải Chọn A Nhận xét: +) Parabol có bề lõm quay xuống dưới nên 0a  . +) Parabol cắt trục tung tại điểm có hoành độ bằng 0 và tung độ âm nên thay 0x = vào 2 yaxbxc =++ suy ra 0c  . +) Parabol có trục đối xứng nằm bên phải trục tung nên 0 2 b x a =− mà 0a  nên 0b  . Vậy 0,0,0abc Câu 92: Cho đồ thị hàm số 2 yaxbxc =++ có đồ thị như hình vẽ bên dưới. Mệnh đề nào sau đây đúng? A. 0,0,0abc= . B. 0,0,0abc . C. 0,0,0abc . D. 0,0,0abc . Lời giải Chọn C Từ dáng đồ thị ta có 0a  . Đồ thị cắt trục Oy tại điểm có tung độ dương nên 0c  Hoành độ đỉnh 0 2 b a − mà 0a  suy ra 0b  Câu 93: Nếu hàm số 2 yaxbxc =++ có đồ thị như sau thì dấu các hệ số của nó là

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 33 A. 0; 0; 0abc B. 0; 0; 0abc C. 0; 0; 0abc D. 0; 0; 0abc Lời giải Chọn D Đồ thị hàm số có bề lõm hướng lên 0a  . Đồ thị hàm số cắt Oy tại điểm có tung độ âm 0c  . Loại A, C. Đồ thị hàm số có trục đối xứng bên trái Oy : 00 2 b b a − . Loại B. Câu 94: Cho parabol ( ) ( )2 :,0Pyaxbxca=++ có đồ thị như hình bên. Khi đó 42abc ++ có giá trị là: A. 3 B. 2 C. 3 D. 0 Lời giải Chọn A Vì đồ thị hàm số đi qua các điểm ( )0;1 , ( )1;2 , ( )2;3 nên thay vào phương trình Parabol ta có .0.011 24 4231 abca abcb abcc ++=−=−  ++== ++==−  423 abc ++= Vậy 423 abc++= Câu 95: Cho hàm số 2 yaxbxc =++ có đồ thị như hình dưới đây. Khẳng định nào sau đây là đúng? A. 0a  , 0b  , 0c  B. 0a  , 0b  , 0c  C. 0a  , 0b  , 0c  . D. 0a  , 0b  , 0c  . Lời giải Chọn C Nhìn vào đồ thị ta có:

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 34 • Bề lõm hướng xuống 0a  . • Hoành độ đỉnh 0 2 b x a =− 0 2 b a  0b  • Đồ thị hàm số cắt trục tung tại điểm có tung độ âm 0c  . Do đó: 0a  , 0b  , 0c  . Câu 96: Cho parabol ( ) ( )2 :,0Pyaxbxca=++ có đồ thị như hình bên. Khi đó 22abc ++ có giá trị là A. 9 B. 9 C. 6 D. 6 Lời giải Chọn C Parabol ( ) ( )2 :,0Pyaxbxca=++ đi qua các điểm ( )1;0A , ( )1; 4B , ( )3;0C nên có hệ phương trình: 0 4 930 abc abc abc −+=  ++=−  ++= 1 2 3 a b c =  =−   =− . Khi đó: ( ) 222.12236 abc++=−+−=− . Câu 97: Cho hàm số 2 yaxbxc =++ có đồ thị là đường cong trong hình vẽ dưới đây ? Giá trị của tổng 42 Tabc =++ là : A. 2T = . B. 1T =− . C. 4T = . D. 3T = . Lời giải Chọn B Đồ thị đã cho đi qua điểm ( )2;1I , ta có: 421 abc++=− . Vậy 1T =− . x y 3 -4 -1 2O 1 x y 3 2 3 -1 O 1

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 35 Câu 98: Cho đồ thị hàm số 2 43yxx có đồ thị như hình vẽ sau Đồ thị nào dưới đây là đồ thị của hàm số 2 43yxx A. Hình 2 B. Hình 4 C. Hình 1 D. Hình 3 Lời giải Chọn D Đồ thị hàm số y fx gồm hai phần Phần 1: ứng với 0y của đồ thị yfx Phần 2: lấy đối xứng phần 0y của đồ thị yfx qua trục Ox Câu 99: Hàm số nào sau đây có đồ thị như hình bên?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 36 x y 1234 5 1 2 3 543211 2 3 A. 2 33yxx=−− B. 2 53yxx=−+− C. 2 33yxx=−−− D. 2 53yxx=−+− Lời giải Chọn B Quan sát đồ thị ta loại A. và D. Phần đồ thị bên phải trục tung là phần đồ thị ( )P của hàm số 2 53yxx=−+− với 0x  , tọa độ đỉnh của ( )P là 513 ; 24    , trục đối xứng là 2,5x = . Phần đồ thị bên trái trục tung là do lấy đối xứng phần đồ thị bên phải của ( )P qua trục tung Oy . Ta được cả hai phần là đồ thị của hàm số 2 53yxx=−+− . DẠNG 4. GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT Câu 100: Tìm giá trị nhỏ nhất của hàm số . A. B. C. D. Lời giải Chọn A . Dấu xảy ra khi và chỉ khi . Vậy hàm số đã cho đạt giá trị nhỏ nhất là tại . Câu 101: Giá trị nhỏ nhất của hàm số 2 23yxx=++ đạt được tại A. 2x =− . B. 1x =− . C. 0x = . D. 1x = . Lời giải Chọn B Ta có: 2223(1)22, yxxxx =++=++ Dấu bằng xảy ra khi 1x =− nên chọn đáp án B. Câu 102: Giá trị nhỏ nhất của hàm số 2 23yxx=+− là A. 3 B. 2 C. 21 8 D. 25 8 Lời giải 2 41yxx=−+ 3 1 3 13 2 41yxx=−+ ( )2 233x =−−− "" = 2x = 3 2x =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 37 . Chọn A 2 12525 232 488yxx(x) =+−=+− 251 84ykhix== nên giá trị nhỏ nhất của hàm số 2 23yxx=+− là 25 8 . Câu 103: Khẳng định nào dưới đây đúng? A. Hàm số 2 32yxx=−++ có giá trị lớn nhất bằng 25 12 B. Hàm số 2 32yxx=−++ có giá trị nhỏ nhất bằng 25 12 C. Hàm số 2 32yxx=−++ có giá trị lớn nhất bằng 25 3 D. Hàm số 2 32yxx=−++ có giá trị nhỏ nhất bằng 25 3 . Lời giải Chọn A Ta có ( )2 14.3.225=−−= Vì 30a =− nên hàm số có giá trị lớn nhất là: 25 412 a − = Câu 104: Giá trị lớn nhất của hàm số 2 321yxx=−++ trên đoạn  1;3 là: A. 4 5 B. 0 C. 1 3 D. 20 Lời giải Chọn B Ta có 1 23 b a −= và 30a =− . Suy ra hàm số đã cho nghịch biến trên khoảng 1 ; 3  +   . Mà   1 1;3; 3  +  . Do đó trên đoạn  1;3 hàm số đạt giá trị lớn nhất tại điểm 1x = , tức là   ( ) ( )1;3 max10 fxf== . Câu 105: Giá trị lớn nhất của hàm số 2 2 59y xx = −+ bằng: A. 11 8 B. 11 4 C. 4 11 D. 8 11 Lời giải Chọn D Hàm số 2 59yxx=−+ có giá trị nhỏ nhất là 11 0 4  .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 38 Suy ra hàm số 2 2 59y xx = −+ có giá trị lớn nhất là 28 11 11 4 = Câu 106: Tổng giá trị nhỏ nhất và giá trị lớn nhất của hàm số 2 43yxx=−+ trên miền  1;4 là A. 1 B. 2 C. 7 D. 8 Lời giải Chọn C Xét trên miền  1;4 thì hàm số có bảng biến thiên là Từ bảng biến thiên suy ra: Giá trị lớn nhất của hàm số bằng 8 và giá trị nhỏ nhất của hàm số bằng 1 nên tổng giá trị lớn nhất và giá trị nhỏ nhất là ( ) 817 +−= Câu 107: Giá trị nhỏ nhất của hàm số 2 2 yxx =− là: A. 1 B. 0 C. 1 D. 2 Lời giải Chọn C Cách 1: Đặt ,0txt= . Hàm số ( ) 2 2 fttt =− đạt giá trị nhỏ nhất bằng 1 khi 10t = . Vậy hàm số 2 2 yxx =− đạt giá trị nhỏ nhất bằng 1 khi 11xx== . Cách 2: Ta có ( ) 222111 yxxxx =−=−−− ; 111yxx =−== . Vậy giá trị nhỏ nhất của hàm số là 1. Câu 108: Giá trị nhỏ nhất của hàm số 2 43yxx=++ là: A. 1 B. 1 C. 4 D. 3 Lời giải Chọn D Ta có 2 0 ,0 xxxx 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 39 Suy ra 2 433 xxx ++ . Dấu bằng xảy ra khi và chỉ khi 0x = . Vậy giá trị nhỏ nhất của hàm số đã cho là 3. Câu 109: Cho hàm số 2 28 khi2 212khi2 xxx y xx  −− =  − . Gọi , Mm lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số khi  1;4x− . Tính Mm + . A. 14 B. 13 C. 4 D. 9 Lời giải Chọn B BBT Dựa vào BBT ta có 4,9Mm=−=− Vậy ( ) 4913Mm+=−+−=− . Câu 110: Tìm giá trị thực của tham số 0m  để hàm số 2 232ymxmxm =−−− có giá trị nhỏ nhất bằng 10 trên . A. 1.m = B. 2.m = C. 2.m =− D. 1.m =− Lời giải Chọn B Ta có 2 1 22 bm x am =−== , suy ra 42ym=−− . Để hàm số có giá trị nhỏ nhất bằng 10 khi và chỉ khi 00 2 m m  0 2 4210 m m m  =  −−=− . Câu 111: Hàm số 2 24yxxm=−++− đạt giá trị lớn nhất trên đoạn  1;2 bằng 3 khi m thuộc A. ( );5− B.  )7;8 C. ( )5;7 D. ( )9;11 Lời giải Chọn C Xét hàm số 2 24yxxm=−++− trên đoạn  1;2

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 40 Hàm số đạt GTLN trên đoạn  1;2 bằng 3 khi và chỉ khi 33m −= 6m = Câu 112: Giá trị nhỏ nhất của hàm số 2 25yxmx=++ bằng 1 khi giá trị của tham số m là A. 4m = . B. 4m = . C. 2m = . D. m . Lời giải Chọn C Hàm số 2 25yxmx=++ có 10a = nên hàm số đạt giá trị nhỏ nhất khi 2 b x a =− . Theo đề bài ta có ( ) 22 11251 2 b yymmm a  −=−=−+=  2 42mm == Câu 113: Giá trị của tham số m để hàm số 22232yxmxmm =−+−− có giá trị nhỏ nhất bằng 10 trên thuộc khoảng nào trong các khoảng sau đây? A.  )1;0m− B. 3 ;5 2 m    C. 5 ;1 2 m  −−  D. 3 0; 2 m     Lời giải Chọn B Ta có ( ) 2222323232 yxmxmmxmmmx =−+−−=−−−−− . Đẳng thức xảy ra khi xm = . Vậy min32 ym=−− . Yêu cầu bài toán 8 3210 3 mm −−=−= . Câu 114: Tìm m để hàm số 2 223yxxm=−++ có giá trị nhỏ nhất trên đoạn  2;5 bằng 3. A. 0m = . B. 9m =− . C. 1m = . D. 3m =− . Lời giải Chọn D Ta có hàm số 2 223yxxm=−++ có hệ số 10,2ab==− , trục đối xứng là đường thẳng 1 2 b x a =−= nên có bảng biến thiên

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 41 Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên đoạn  2;5 suy ra giá trị nhỏ nhất trên đoạn  2;5 bằng ( )2f . Theo giả thiết ( ) 232333 fmm=−+=−=− . Câu 115:Tìm m để hàm số 2 223yxxm=−++ có giá trị nhỏ nhất trên đoạn  2;5 bằng 3. A. 3m =− . B. 9m =− . C. 1m = . D. 0m = . Lời giải Chọn A Vì 2 223yxxm=−++ có 10a = nên hàm số đồng biến trong khoảng ( )1;+ . Như vậy trên đoạn  2;5 hàm số đồng biến. Do đó giá trị nhỏ nhất của hàm số trên đoạn  2;5 là ( ) 223ym=+ ( ) 23y =− 233 m +=− 3m =− . Câu 116: Tìm số các giá trị của tham số m để giá trị nhỏ nhất của hàm số ( ) ( ) 22211fxxmxm=+++− trên đoạn  0;1 là bằng 1. A. 0 B. 1 C. 2 D. 3 Lời giải Chọn C Ta có ( )21 ;45 22 bm m a −+ −==+ Vì 0a  nên đồ thị hàm số là một parabol quay bề lõm lên trên và có điểm thấp nhất là đỉnh ; 24 b I aa −−    . Từ đó ta xét các trường hợp sau: * Trường hợp 1: ( ) ( )21 0;101 22 bm a −+  31 22 m  Khi đó   ( ) ( ) 0;1 45 min 44 m fx a −−+ == Vậy ta phải có ( )45 1 4 m −+ = 9 4 m = ). * Trường hợp 2: ( )21 1 00 222 bm m a −+  .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 42 Khi đó   ( ) ( ) 2 0;1 min01 fxfm==− . Ta phải có 2 112mm−== . Chỉ có 2m =− thỏa mãn ( )2 * Trường hợp 3: ( )21 3 11 222 bm m a −+  . Khi đó   ( ) ( ) 2 0;1 min121 fxfmm ==++ . Ta phải có 2 2110mmm++== hoặc 2m =− . Chỉ có 2m =− thỏa mãn ( )3 . Vậy  2;2m −− . Câu 117: Cho hàm số ( ) 22 23132yxmxmm =−+++− , m là tham số. Tìm tất cả các giá trị của m để giá trị nhỏ nhất của hàm số là lớn nhất. A. 2m =− B. 1m = C. 3m = D. 5m = Lời giải Chọn C Hàm số bậc hai với hệ số 20a = đạt giá trị nhỏ nhất tại ( )31 24 bm x a + =−= và ( ) 2 min 311325 4848 m yymm +  ==−+−   21 (3)228 m =−−−− Dấu bằng xảy ra khi 3m = . Câu 118: Gọi S là tập hợp tất cả các giá trị dương của tham số m để giá trị nhỏ nhất của hàm số ( ) 22 442 yfxxmxmm ==−+− trên đoạn  2;0 bằng 3. Tính tổng T các phần tử của .S A. 3T = . B. 1 2 T = . C. 9 2 T = . D. 3 2 T =− . Lời giải Chọn A Ta có đỉnh ;2 2 m Im   . Do 0m  nên 0 2 m  . Khi đó đỉnh  2;0I −

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 43 Giá trị nhỏ nhất của hàm số ( )yfx = trên đoạn  2;0 là ( ) 03y = tại 0x = 21 2 3 230 10 m mm m = −−=  =−  3S = . DẠNG 5. SỰ TƯƠNG GIAO GIỮA PARABOL VỚI ĐỒ THỊ CÁC HÀM SỐ Câu 119: Giao điểm của parabol 2 ():32 Pyxx=−+ với đường thẳng 1yx=− là: A. ( ) ( )1;0;3;2 B. ( ) ( )0;1;2;3 C. ( ) ( )1;2;2;1 D. ( ) ( )2;1;0;1 Lờigiải Chọn A Phương trình hoành độ giao điểm: 2 321xxx−+=− 2 430xx −+= 1 3 x x =   = . 110xyx==−= 312xyx==−= Hai giao điểm là: ( ) ( )1;0;3;2 . Câu 120: Tọa độ giao điểm của ( ) 2 :4 Pyxx =− với đường thẳng :2dyx=−− là A. ( )0;2M , ( )2;4N B. ( )1;1M , ( )2;0N C. ( )3;1M , ( )3;5N . D. ( )1;3M , ( )2;4N . Lời giải Chọn D Hoành độ giao điểm của ( )P và d là nghiệm của phương trình: 22 1 42320 2 x xxxxx x = −=−−−+=  = Vậy tọa độ giao điểm của ( )P và d là ( )1;3M , ( )2;4N Câu 121: Tọa độ giao điểm của đường thẳng và parabol là A. và B. và C. và D. và Lời giải :4dyx=−+ 2 712yxx=−+ ( )2;6 ( )4;8 ( )2;2 ( )4;8 ( )2;2 ( )4;0 ( )2;2 ( )4;0

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 44 Chọn D Phương trình hoành độ giao điểm: 22 22 7124680 40 xy xxxxx xy == −+=−+−+=  == . Câu 122: Hoành độ giao điểm của đường thẳng 1 yx =− với 2 ():21 Pyxx=−+ là A. 0;1.xx== B. 1.x = C. 0;2.xx== D. 0.x = Lời giải Chọn A Phương trình hoành độ giao điểm 22 0 1210 1 x xxxxx x = −=−+−=  = . Câu 123: Gọi ( ); Aab và ( ); Bcd là tọa độ giao điểm của ( ) 2:2 Pyxx =− và :36 yx =− . Giá trị của bd + bằng. A. 7. B. 7. C. 15. D. 15. Lời giải Chọn D Phương trình hoành độ giao điểm: 22 20 23660 315 xy xxxxx xy == −=−+−=  =−=− 15bd+=− Câu 124: Cho hai parabol có phương trình 2 1yxx=++ và 2 22yxx=−− . Biết hai parabol cắt nhau tại hai điểm A và B ( ABxx  ). Tính độ dài đoạn thẳng AB. A. 42AB = B. 226AB = C. 410AB = D. 210AB = Lời giải Chọn C Phương trình hoành độ giao điểm của hai parabol: 222 1 221230 3 x xxxxxx x =− −−=++−−=  = . 11;313xyxy =−=== , do đó hai giao điểm là ( )1;1A và ( )3;13B Từ đó ( ) ( ) 22 31131410AB =++−= Câu 125: Giá trị nào của m thì đồ thị hàm số 2 3 yxxm =++ cắt trục hoành tại hai điểm phân biệt? A. 9 4 m − B. 9 4 m − C. 9 4 m  D. 9 4 m  . Lời giải Chọn D Cho 2 30xxm++=

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 45 Để đồ thị cắt trục hoành tại hai điểm phân biệt khi phương trình có hai nghiệm phân biệt 2 9 0340940 4 mmm −− Câu 126: Hàmsố 2 21yxx=+− cóđồthịnhưhìnhbên.Tìmcácgiátrị m đểphươngtrình 2 20xxm++= vô nghiệm. A. 2m − B. 1m − C. 1m  D. 1m  Lời giải Chọn D 2220211 xxmxxm ++=+−=−− ( )* Số nghiệm của phương trình ( )* chính là số giao điểm của parabol 2 21yxx=++ và đường thẳng 1ym=−− Ycbt 1m  Câu 127: Hỏi có bao nhiêu giá trị m nguyên trong nửa khoảng  )10;4 để đường thẳng ( ) :12 dymxm =−+++ cắt parabol ( ) 2 :2Pyxx=+− tại hai điểm phân biệt nằm về cùng một phía đối với trục tung? A. 6 B. 5 C. 7 D. 8 Lời giải Chọn A Phương trình hoành độ giao điểm của d và ( )P : ( ) ( ) ( )22212240*xxmxmxmxm +−=−+++++−−= . d cắt ( )P tại hai điểm phân biệt nằm về cùng một phía đối với trục tung khi và chỉ khi ( )* có hai nghiệm phân biệt cùng đấu 2 08200 4 040 mm m P m   ++ −   −−  Vậy có 6 giá trị m nguyên trong nửa khoảng  )10;4 thỏa mãn ycbt. Câu 128: Cho parabol ( ) 2 : Pyxmx =− và đường thẳng ( ) ( ) :21dymx=++ , trong đó m là tham số. Khi parabol và đường thẳng cắt nhau tại hai điểm phân biệt M, N, tập hợp trung điểm I của đoạn thẳng MN là: A. một parabol B. một đường thẳng C. một đoạn thẳng D. một điểm x y 1 2 -2 -1 -2 -1 2O 1

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 46 Lời giải Chọn A Phương trình hoành độ giao điểm của ( )P và ( )d : ( )2 21xmxmx−=++ ( )2 2110xmx −+−= . có a, c trái dấu nên luôn có hai nghiệm phân biệt với mọi m. Do đó ( )P và ( )d luôn cắt nhau tại hai điểm phân biệt với mọi m. Khi đó , MNxx là hai nghiệm phân biệt của. Theo Viet ta có ( )21MN xxm+=+ . Ta có 1 2 MN I xx xm + ==+ Suy ra ( )( ) 211I ymm=+++ ( ) ( )2 2 1111 II mmxx =++++=++ Vậy I luôn thuộc parabol 2 1yxx=++ với mọi m. Chú ý: Cho hai điểm ( ); AAAxy , ( ); BBBxy . Trung điểm của đoạn thẳng AB là ; 22 ABAB Ixxyy ++    . Câu 129: Cho hàm số 2 3 yxx =+ có đồ thị ( )P . Gọi S là tập hợp các giá trị của tham số m để đường thẳng 2 : dyxm =+ cắt đồ thị ( )P tại hai điểm phân biệt , AB sao cho trung điểm I của đoạn AB nằm trên đường thẳng :23dyx  =+ . Tổng bình phương các phần tử của S là A. 6. B. 4. C. 2. D. 1. Lời giải Chọn B Phương trình hoành độ giao điểm của d và ( )P là: 2222320xxxmxxm +=++−= Đề d cắt ( )P tại 2 điểm phân biệt 2 010,mm  + Gọi 12 ; xx là 2 nghiệm của phương trình, khi đó ( )2 11 ; Axxm + , ( )2 22 ; Bxxm + 2 1212 2 ; 22 xxxxm I  +++    Theo Vi ét ta có 2 1212 2;. xxxxm +=−=− nên ( )2 1;1Im Vì I thuộc d nên 221122mmm−=== .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 47 Câu 130: Cho hàm số 2 235yxx=−− . Giá trị của tham số m để đồ thị hàm số ( )1 cắt đường thẳng 4 yxm =+ tại hai điểm phân biệt ( )11 ; Axy , ( )22 ; Bxx thỏa mãn 22 1212 2237 xxxx+=+ là A. 10. B. 10. C. 6. D. 9. Lời giải Chọn A Xét phương trình hoành độ giao điểm: 2 2354 xxxm −−=+ 2 2750 xxm −−−= Phương trình có hai nghiệm phân biệt khi và chỉ khi ( ) ( )2 74.250 m =−−−− 8890 m + 89 8 m − Gọi 1x , 2x là hai nghiệm phân biệt của nên theo Vi et ta có: 12 12 7 2 5 2 xx m xx  +=    =  22 1212 2237 xxxx+=+ ( )2 1212 2770 xxxx +−−= 2 75 27.70 22 m  −−=   7070 m += 10m =− Vậy 10m =− là giá trị cần tìm. Câu 131: Có bao nhiêu giá trị nguyên của m để đường thẳng 3ymx=− không có điểm chung với Parabol 2 1yx=+ ? A. 6 B. 9 C. 7 D. 8 Lời giải Chọn C Phương trình hoành độ giao điểm: 2 13xmx+=− 2 40xmx −+= Đường thẳng 3ymx=− không có điểm chung với Parabol 2 1yx=+  Phương trình vô nghiệm 0 2 160m − 44 m − . Vì  3;2;1;0;1;2;3mm−−− . Câu 132: Tìm tất cả các giá trị m để đường thẳng 32 ymxm =+− cắt parabol 2 35yxx=−− tại 2 điểm phân biệt có hoành độ trái dấu. A. 3m − B. 34 m − C. 4m  D. 4m  Lời giải Chọn C Phương trình hoành độ giao điểm: 2 3532 xxmxm −−=+−  ( ) ( )2 3280*xmxm−++−= Đường thẳng cắt parabol tại hai điểm phân biệt có hoành độ trái dấu khi và chỉ khi phương trình ( )* có hai nghiệm trái dấu  .0ac   280 m −  4m 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 48 Câu 133: Tìm đểParabol cắttrụchoànhtại điểmphânbiệtcóhoành độ , sao cho . A. . B. Không tồn tại . C. . D. . Lời giải Chọn A Phương trình hoành độ giao điểm của ( )P với trục hoành: Parabol cắt trục hoành tại điểm phân biệt có hoành độ , sao cho có nghiệm phân biệt , thỏa . Câu 134: Cho parabol ( ) 2 :25Pyxx=+− và đường thẳng :223 dymxm =+− . Tìm tất cả các giá trị m để ( )P cắt d tại hai điểm phân biệt nằm về phía bên phải của trục tung. A. 7 1 3 m  . B. 1m  . C. 7 3 m  . D. 1m  Lời giải Chọn C Phương trình hoành độ giao điểm của ( )P và d là ( ) ( )222522321730* xxmxmxmxm +−=+−+−−+= ( )P cắt d tại hai điểm phân biệt nằm về phía bên phải của trục tung khi và chỉ khi phương trình ( )* có hai nghiệm dương phân biệt ( ) ( ) 2 201730 5801 7 021010 73 370 3730 0 mm mm m b mmm a m mm c a    −+−  −+     −−−   − −+   Vậy 7 3 m  Câu 135: Gọi T là tổng tất cả các giá trị của tham số m để parabol ( ) 2 :4 Pyxxm =−+ cắt trục Ox tại hai điểm phân biệt , AB thỏa mãn 3 OAOB = . Tính T A. 9T =− . B. 3 2 T = . C. 15T =− . D. 3T = . Lời giải Chọn A Phương trình hoành độ giao điểm của () P và trục Ox là: 2 40(1)xxm−+= . m ( ) ( ) 22 :213Pyxmxm=−++− 2 1x 2x 12.1xx = 2m = m 2m =− 2m = ( ) 222130xmxm−++−= ( )1 ( )P 2 1x 2x 12.1xx =  ( )1 2 1x 2x 12.1xx = ( ) ( )2 2 2 130 2 2 231 mm m m mm   =+−− − =  −== 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 49 () P cắt trục Ox tại hai điểm phân biệt , AB thỏa mãn 3 OAOB =  phương trình (1) có hai nghiệm phân biệt 1x , 2x thỏa mãn 12 3 xx =  ' 12 12 0 3 3 xx xx   =  =−  12 12 40 3 3 m xx xx −  =  =−  12 12 4 3 3 m xx xx   =  =− . Mặt khác, theo định lý Viet cho phương trình (1)thì: 12 12 4xx xxm +=  = Với 12 3 xx = 1 3x = , 2 1x = 3m = thỏa mãn. Với 12 3 xx =− 1 6x = , 2 2x =− 12m =− thỏa mãn. Có hai giá trị của m là 3m = và 12m =− Vậy 9T =− . Chọn đáp án A. Câu 136: Tìm m đểParabol ( ) ( ) 22 :213Pyxmxm=−++− cắttrụchoànhtại 2 điểmphânbiệtcóhoành độ 1x , 2x sao cho 12.1xx = A. 2m = B. Không tồn tại m C. 2m =− D. 2m = Lời giải Chọn A Phương trình hoành độ giao điểm của ( )P với trục hoành: ( ) 222130xmxm−++−= ( )1 . Parabol ( )P cắt trục hoành tại 2 điểm phân biệt có hoành độ 1x , 2x sao cho 12.1xx =  ( )1 có 2 nghiệm phân biệt 1x , 2x thỏa 12.1xx = ( ) ( )2 2 2 130 2 2 231 mm m m mm   =+−− − =  −==  . Câu 137: Cho parabol ( ) 2 : Pyaxbxc =++ . Tìm abc −+ , biết rằng đường thẳng 2,5y =− có một điểm chung duy nhất với ( )P và đường thẳng 2y = cắt ( )P tại hai điểm có hoành độ là 1 và 5. A. 2abc−−=− B. 2abc−−= C. 1abc−−= D. 1abc−−=− Lời giải Chọn D Vì đường thẳng 2,5y =− có một điểm chung duy nhất với ( )P và đường thẳng 2y = cắt ( )P tại hai điểm có hoành độ là 1 và 5 nên suy ra tọa độ đỉnh của ( )P là: ( )15 ;2,52;2,5 2 −+  =  . Vậy ( )P đi qua ba điểm ( )2;2,5 , ( )1;2 và ( )5;2 Từ đó ta có hệ

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 50 1 102 4 2552 10 422,5 15 10 a abc abcb abc c  =−+=   ++==  ++=  =  . Vậy 1abc−−=− . Câu 138: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 210xxm−+−= có bốn nghiệm phân biệt? A. 0 B. 1 C. 2 D. Vô số Lời giải Chọn A Cách 1: ( )2221021* xxmxxm −+−=−+= . Số nghiệm của ( )* là số giao điểm của đồ thị hàm số 2 21yxx=−+ và đường thẳng ym = Dễ thấy hàm số 2 21yxx=−+ là một hàm số chẵn, do đó có đồ thị đối xứng qua trục Oy. Mặt khác ta có 222121yxxxx =−+=−+ với 0x  . Từ đó ta có cách vẽ đồ thị hàm số 2 21yxx=−+ như sau: Bước 1: Vẽ đồ thị hàm số 2 21yxx=−+ ; Bước 2: Xóa phần nằm bên trái trục tung của đồ thị hàm số 2 21yxx=−+ ; Bước 3: Lấy đối xứng phần nằm bên phải trục tung của đồ thị hàm số 2 21yxx=−+ qua trục tung. Quan sát trên đồ thị ta thấy đường thẳng ym = cắt đồ thị hàm số 2 21yxx=−+ tại bốn điểm phân biệt khi và chỉ khi 01 m  . Suy ra không có giá trị nguyên nào của m để phương trình đã cho có bốn nghiệm phân biệt. Cách 2: Đặt ,0txt= . Phương trình đã cho trở thành 2 210ttm−+−= . Ta thấy với 0t = thì 0x = , với 0t  thì xt =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 51 Do đó để phương trình đã cho có bốn nghiệm phân biệt thì phải có hai nghiệm dương phân biệt ( ) '0110 0 02001 1 010 m m Sm m Pm −−     −  . Do đó không có giá trị nguyên nào của m để phương trình đã cho có bốn nghiệm phân biệt. Câu 139: Biết ( ); Sab = là tập hợp tất cả các giá trị của tham số m để đường thẳng ym = cắt đồ thị hàm số 2 43yxx=−+ tại bốn điểm phân biệt. Tìm ab + . A. 1ab+= B. 1ab+=− C. 2ab+= D. 2ab+=− Lời giải Chọn A Ta có ( ) 22 2 22 43430 43 43430 khi khi xxxx yxx xxxx  −+−+ =−+=  −−+−+  . Từ đó ta có cách vẽ đồ thị hàm số 2 43yxx=−+ : Bước 1: Vẽ đồ thị hàm số 2 43yxx=−+ ; Bước 2: Giữ nguyên phần nằm trên trục Ox của đồ thị hàm số 2 43yxx=−+ ; Bước 3: Lấy đối xứng phần nằm dưới trục Ox của đồ thị hàm số 2 43yxx=−+ Quan sát đồ thị ta thấy đường thẳng ym = cắt đồ thị hàm số 2 43yxx=−+ tại bốn điểm phân biệt khi và chỉ khi 01 m  . Vậy ( )0;1S = . Suy ra 1ab+= . Câu 140: Cho hàm số ( ) 2 fxaxbxc =++ có đồ thị như hình vẽ. Với những giá trị nào của tham số m thì phương trình ( ) fxm = có đúng 4 nghiệm phân biệt. A. 01 m  B. 10 m − C. 1m =− ; 3m = D. 3m  Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 52 Chọn A Số nghiệm của phương trình ( ) fxm = là số giao điểm của đồ thị ( )yfx = và đường thẳng ym = . Ta có đồ thị hàm số ( )yfx = như hình vẽ dưới đây. Do đó phương trình ( ) fxm = có đúng 4 nghiệm phân biệt khi và chỉ khi 01 m  . Câu 141: Cho hàm số 2 fxaxbxc có đồ thị như hình vẽ. Hỏi với những giá trị nào của tham số thực m thì phương trình 1 fxm có đúng 3 nghiệm phân biệt A. 4m B. 0m C. 1m D. 2m Lời giải Chọn A Đồ thị hàm số cắt Oy tại 0;3 3c Đồ thị hàm số nhận 2;1 làm đỉnh nên ta có 2 2 421 b a abc 4 424 ba ab 1 4 a b Ta có 11fxmyfxm Ta có đồ thị hàm yfxC như hình vẽ x y O 2   4 2 2 4 15 10 5 x y -2 3 -1 2O

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 53 Số nghiệm của phương trình 1 fxm là số giao điểm của đồ thị hàm số C với đường thẳng 1ym 134mm Câu 142: Tìm tất cả các giá trị thực của tham số m để parabol cắt đường thẳng tại 4 điểm phân biệt. A. . B. . C. . D. . Lời giải Chọn B Hàm số có đồ thị được suy ra từ đồ thị hàm số bằng cách bỏ phần đồ thị phía trái trục tung và lấy thêm phần đối xứng của phần phía phải trục tung qua trục tung Đồ thị hàm số cắt đường thẳng tại điểm phân biệt khi và chỉ khi Câu 143: Với giá trị nào của m thì phương trình 2 54mxx=−+ có 3 nghiệm thực phân biệt. A. 9 4 m  . B. 9 4 m  . C. 9 4 m = . D. 0m = . Lời giải Chọn C Ta có: 22 2 22 54540 54 (54)540 xxkhixx yxx xxkhixx  −+−+ =−+=  −−+−+  Giữ nguyên đồ thị ( )P ứng với 0y  ta được đồ thị 1 () C Lấy đối xứng phần đồ thị ứng với 0y  ta được đồ thị 2 () C Vậy 12 ()()() CCC = ( ) 2 :21Pyxx=−− 3ym=− 21 m −− 12 m  21 m −− 12 m  2 2||1yxx=−− 2 21yxx=−− 2 2||1yxx=−− 3ym=− 4 23112 mm −−−

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 54 -2 -1 1 2 3 4 5 6 7 -1 1 2 3 4 5 x y y=m Số nghiệm của phương trình chính là số giao điểm nếu có của đồ thị hàm số 2 54yxx=−+ ( )C và đường thẳng ym = Yêu cầu bài ra  cắt tại 3 điểm phân biệt d là đường thẳng song song hoặc trùng với trục hoành Từ đồ thị hàm số ta suy ra cắt tại 3 điểm phân biệt khi 9 4 m = Câu 144: Cho hàm số ( )yfx = có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của tham số m để đồ thị hàm số ( )yfx = cắt đường 1y m= + trên cùng một hệ trục tọa độ tại 4 điểm phân biệt là? A. 03 m−  B. 0 3m  C. 1 4m  D. 21 m−  Lời giải Chọn D Từ đồ thị của hàm số ( )yfx = , ta suy ra cách vẽ đồ thị hàm số ( )yfx = như sau: Giữ nguyên phần đồ thị hàm số ( )yfx = ở phía trên trục hoành. Lấy đối xứng phần đồ thị dưới trục hoành qua trục hoành. Xóa phần đồ thị phía dưới trục hoành.

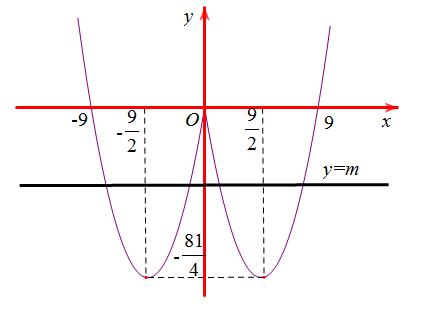
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 55 Dựa vào đồ thị hàm số ( )yfx = ta có đường thẳng 1ymx=+ cắt đồ thị hàm số ( )yfx = tại 4 điểm phân biệt 01312 mm +− . . Câu 145: Tìm tất cả các giá trị của m để đồ thị hàm số 2 9 yxx =− cắt đường thẳng ym = tại 4 điểm phân biệt. A. 3m − B. 81 4 m − C. 81 0 4 m − D. 0m  Lời giải Chọn C Cách 1: Xét phương trình hoành độ giao điểm: 22990xxmxxm −=−−= Đặt tx = , 0t  . 2 (1)90 ttm −−= Đồ thị hàm số 2 9 yxx =− cắt đường thẳng ym = tại 4 điểm phân biệt khi và chỉ khi phương trình có 2 nghiệm dương phân biệt 08140 81 0900 4 00 m Sm Pm +  −  −  Cách 2: Vẽ đồ thị hàm số 2 9 yxx =−

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 56 Dựa vào đồ thị suy ra đồ thị hàm số 2 9 yxx =− cắt đường thẳng ym = tại 4 điểm phân biệt khi và chỉ khi 81 0 4 m − Câu 146: Cho hàm số ( ) 2 fxaxbxc =++ có bảng biến thiên như sau: Tìm tất cả các giá trị thực của tham số m để phương trình ( ) 201720182 fxm −−= có đúng ba nghiệm. A. 1m = B. 3m = C. 2m = D. không tồn tại m Lời giải Chọn B Dựa vào BBT ta thấy hàm số ( ) 2 fxaxbxc =++ đạt GTNN bằng 1 tại 2x = và có hệ số 0a . Ta biểu diễn được: ( ) ( )2 2 21441fxaxaxaxa =−−=−+− Do đó ( ) ( )2 20172018201720201 −=−−fxax ( ) ( )2 201720182201720203 −−=−− fxax Vậy GTNN của ( ) 201720182 =−−yfx bằng 3 tại 2020 2017 x = . BBT của hàm số ( ) 201720182yfx=−− có dạng: Số nghiệm của phương trình ( ) 201720182 fxm −−= chính là số giao điểm của đồ thị hàm số ( ) 201720182yfx=−− và đường thẳng ym = . Dựa vào BBT ta thấy phương trình ( ) 201720182 fxm −−= có đúng ba nghiệm khi 3m = . Câu 147: Cho hàm số 2 43yxx=−+ có đồ thị như hình vẽ dưới đây

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 57 Đặt ( ) 2 43fxxx=−+ ;gọi S là tập hợp các giá trị nguyên của tham số m để phương trình () fxm = có 8 nghiệm phân biệt. Số phần tử của S bằng A. 0 B. 1 C. 2 D. 4 Lời giải Chọn A Số nghiệm của phương trình () fxm = chính là số giao điểm của đồ thị hàm số ( ) ( )ygxfx == và đường thẳng ym = . Xét ( ) ( ) 2 2 :43 ==−+Pyfxxx ;có ( )yfx = là hàm số chẵn;nên ( )2P nhận trục Oy làm trục đối xứng. Từđồ thị hàm số 2 1 43()yxxP =−+ ;tavẽđồ thị hàm số ( ) ( )2 243==−+ yfxxxP nhưsau: +) Giữ nguyên phần đồ thị 1 () P bên phải trục Oy . +) Lấy đối xứng phần đồ thị 1 () P bên phải trục Oy qua trục Oy Từ đồ thị hàm số ( ) 2 2 43()yfxxxP ==−+ ta vẽ đồ thị hàm số ( ) 2 3 43()ygxxxP ==−+ như sau +) Giữ nguyên phần đồ thị 2 () P nằm trên trục Ox . +) Lấy đối xứng phần đồ thị 2 () P nằm trên trục Ox qua trục Ox

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 58 Dựa vào đồ thị hàm số ( ) 2 3 43()ygxxxP ==−+ ta có phương trình () fxm = có 8 nghiệm phân biệt khi và chỉ khi 01 m  . Vậy không có giá trị nguyên của m thỏa mãn bài toán. DẠNG 6. ỨNG DỤNG THỰC TẾ LIÊN QUAN ĐẾN HÀM SỐ BẬC HAI Câu 148: Một chiếc ăng ten chảo parabol có chiều cao 0,5 hm = và đường kính miệng 4 dm = . Mặt cắt qua trục là một parabol dạng 2 yax = . Biết m a n = , trong đó m, n là các số nguyên dương nguyên tố cùng nhau. Tính mn A. 7mn−= B. 7mn−=− C. 31mn−= D. 31mn−=− Lời giải Chọn B Từ giả thiết suy ra parabol 2 yax = đi qua điểm 1 2; 2 I    . Từ đó ta có 2 11 .2 28 aa == . Vậy 187mn−=−=− . Câu 149: Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống. Biết rằng quỹ đạo của quả bóng là một cung parabol trong mặt phẳng với hệ tọa độ Oth, trong đó t là thời gian kể từ khi quả bóng được đá lên; h là độ cao của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2m. Sau đó 1 giây, nó đạt độ cao 8,5m và 2 giây sau khi đá lên, nó đạt độ cao 6m. Hỏi sau bao lâu thì quả bóng sẽ chạm đất kể từ khi được đá lên kể từ khi quả bóng được đá lên, h là độ cao của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2 m và sau 1 giây thì nó đạt độ cao 8,5m , sau 2 giây nó đạt độ cao 6m . Tính tổng abc. A. 18,3abc . B. 6,1abc . C. 8,5abc D. 15,9abc Lời giải

ban

bóng

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 59 Chọn C Từ giả thiết của bài toán ta có hệ phương trình 49 1,210 61 8,5 5 4261,2 a c abcb abc c  =−=   ++==  ++= =   17 2 abc ++= . Câu 150: Một của hàng buôn giày nhập một đôi với giá là đôla. Cửa hàng ước tính rằng nếu đôi giày được bán với giá x đôla thì mỗi tháng khách hàng sẽ mua ( )120 x đôi. Hỏi của hàng bán một đôi giày giá bao nhiêu thì thu được nhiều lãi nhất? A. 80 USD. B. 160 USD. C. 40 USD. D. 240 USD. Lời giải Chọn A Gọi là số tiền lãi của cửa hàng bán giày. Ta có . Dấu xảy ra . Vậy cửa hàng lãi nhiều nhất khi bán đôi giày với giá USD. Câu 151: Một quả bóng cầu thủ sút lên rồi rơi xuống theo quỹ đạo là parabol. Biết rằng

đầu

ả

được sút lên từ độ cao 1m sau đó 1 giây nó đạt độ cao 10m và 3,5 giây nó ở độ cao 6,25m Hỏi độ cao cao nhất mà quả bóng đạt được là bao nhiêu mét? A. 11m . B. 12m. C. 13m. D. 14m . Lời giải Chọn C Biết rằng quỹ đạo của quả bóng là một cung parabol nên phương trình có dạng 2 yaxbxc =++ Theo bài ra gắn vào hệ tọa độ và sẽ tương ứng các điểm A , B , C nên ta có 1 10 12,253,56,25 c abc abc =  ++=  ++= 3 12 1 a b c =−  =   = . 40 y ( )( )12040yxx=−− 2 1604800xx =−+− ( )2 8016001600x =−−+ "" = 80x = 80 12 10 8 6 4 2 5 y x O A B C

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 60 Suy ra phương trình parabol là 2 3121yxx=−++ . Parabol có đỉnh (2;13)I . Khi đó quả bóng đạt vị trí cao nhất tại đỉnh tức 13mh = Câu 152: Một chiếc cổng hình parabol có chiều rộng 12 m và chiều cao 8 m như hình vẽ. Giả sử một chiếc xe tải có chiều ngang 6 m đi vào vị trí chính giữa cổng. Hỏi chiều cao h của xe tải thỏa mãn điều kiện gì để có thể đi vào cổng mà không chạm tường? A. 06 h  . B. 06 h  . C. 07 h  . D. 07 h  . Lời giải Chọn D Chọn hệ trục tọa độ như hình vẽ. Parabol có phương trình dạng 2 yaxbx =+ Vì chiếc cổng hình parabol có chiều rộng 12 m và chiều cao, theo hình vẽ ta có parabol đi qua các điểm ( )12;0 và ( )6;8 , suy ra: 2 144120 9 36688 3 aba ab b  +==−    +=  =  . Suy ra parabol có phương trình 2 28 93yx=−+ . Do chiếc xe tải có chiều ngang 6 m đi vào vị trí chính giữa cổng nên xe sẽ chạm tường tại điểm ( )3;6A khi đó chiều cao của xe là 6. Vậy điều kiện để xe tải có thể đi vào cổng mà không chạm tường là 06 h  . Câu 153: Trong số các hình chữ nhật có cùng chu vi bằng 16, hình chữ nhật có diện tích lớn nhất bằng bao nhiêu?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 61 A. 64. B. 4. C. 16. D. 8. Lời giải Chọn C Gọi x là chiều dài của hình chữ nhật. Khi đó chiều rộng là 8 x Diện tích hình chữ nhật là ( )8 xx . Lập bảng biến thiên của hàm số bậc hai ( ) 2 8 fxxx =−+ trên khoảng ( )0;8 ta được ( ) ( ) ( )0;8 max416 fxf== Vậy hình chữ nhật có diện tích lớn nhất bằng 16 khi chiều dài bằng chiều rộng bằng 4 Câu 154: Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4m còn kích thước cửa ở giữa là 3m x 4m. Hãy tính khoảng cách giữa hai điểm A và B . A. 5m. B. 8,5m. C. 7,5m. D. 8m. Lời giải Chọn D Gắn hệ trục tọa độ Oxy như hình vẽ, chiếc cổng là 1 phần của parabol ( )P : 2 yaxbxc =++ với 0a  Do parabol ( )P đối xứng qua trục tung nên có trục đối xứng 000 2 b xb a =−== Chiều cao của cổng parabol là 4m nên ( )0;4G 4c = ( )P : 2 4yax=+

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 62 Lại có, kích thước cửa ở giữa là 3m x 4m nên ( ) ( )2;3,2;3EF 1 344 4 aa ===− . Vậy ( )P : 21 4 4 yx=−+ Ta có 2 14 40 44 x x x = −+=  =− nên ( )4;0A , ( )4;0B hay 8AB = Câu 155: Một chiếc cổng hình parabol dạng 21 2 yx =− có chiều rộng 8 dm = . Hãy tính chiều cao h của cổng. A. 9 hm = . B. 7 hm = . C. 8 hm = . D. 5 hm = . Lời giải Chọn C ( ) =− 21 : 2 Pyx , có 8d = . Suy ra 4 2 d = Thay 4x = vào 21 2 yx =− . Suy ra 8y =− . Suy ra ( )8 hcm = . Câu 156: Cổng Arch tại thành phố St.Louis của Mỹ có hình dạng là một parabol. Biết khoảng cách giữa hai chân cổng bằng 162m. Trên thành cổng, tại vị trí có độ cao 43m so với mặt đất, người ta thả một sợi dây chạm đất Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng Arch. A. 175,6m. B. 197,5m. C. 210m. D. 185,6m. Lời giải Chọn D

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 63 Gắn hệ toạ độ Oxy sao cho gốc toạ độ trùng với trung điểm của AB, tia AB là chiều dương của trục hoành Parabol có phương trình 2 y axc= + , đi qua các điểm: ( )81;0B và ( )71;43M nên ta có hệ 2 2 222 810 8143 185.6 8 . 17713 14 ac c ac  += =    += Suy ra chiều cao của cổng là 185,6c  m. Câu 157: Rót chất A vào một ống nghiệm, rồi đổ thêm chất B vào. Khi nồng độ chất B đạt đến một giá trị nhất định thì chất A mới tác dụng với chất B . Khi phản ứng xảy ra, nồng độ cả hai chất đều giảm đến khi chất B được tiêu thụ hoàn hoàn. Đồ thị nồng độ mol theo thời gian nào sau đây thể hiện quá trình của phản ứng? A. B. C. . D. . Lời giải Chọn B Theo giả thiết ta có: Từ khi bắt đầu rót chất B thì đã có chất A trong ống nghiệm, nên nồng độ chất A ban đầu lớn hơn chất B . Tức là ban đầu, đồ thị nồng độ chất A nằm “phía trên” đồ thị nồng độ chất B ( )1 . Khi chất B đạt đến một giá trị nhất định thì hai chất mới phản ứng với nhau. Điều này chứng tỏ có một khoảng thời gian từ khi rót chất B đến khi bắt đầu phản ứng xảy ra thì nồng độ chất A là một hằng số. Tức trong khoảng thời gian đó đồ thị nồng độ chất A là đồ thị của một hàm số hằng ( )2 . Khi phản ứng xảy ra, nồng độ hai chất đều giảm đến khi chất B được tiêu thụ hoàn toàn. Điều này chứng tỏ sau khi kết thúc phản ứng thì chất B được tiêu thụ hết và chất A có thể còn dư, kể từ khi ngừng phản ứng thì nồng độ chất A trong ống nghiệm không thay đổi nữa, nên đồ thị nồng độ chất A sau phản ứng phải là đồ thị của một hàm số hằng ( )3 Từ sự phân tích trên ta thấy chỉ có đồ thị của đáp án B. phù hợp.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HÀM SỐ BẬC HAI VÀ ĐỒ THỊ Sưu tầm và biên soạn Page 64 Câu 158: Cô Tình có 60m lưới muốn rào một mảng vườn hình chữ nhật để trồng rau, biết rằng một cạnh là tường, cô Tình chỉ cần rào 3 cạnh còn lại của hình chữ nhật để làm vườn. Em hãy tính hộ diện tích lớn nhất mà cô Tình có thể rào được? A. 2400m . B. 2450m . C. 2350m . D. 2425m . Lời giải Chọn B Gọi hai cạnh của hình chữ nhật có độ dài là , xy ; 0,60 xy  . Ta có 260602 xyyx +==− Diện tích hình chữ nhật là ( ) ( ) 112602 602.2602450 22 Sxyxxxxxx x +−  ==−=−=   . Vậy diện tích hình chữ nhật lớn nhất là ( )2450 m , đạt được khi 15,30xy== . y x x