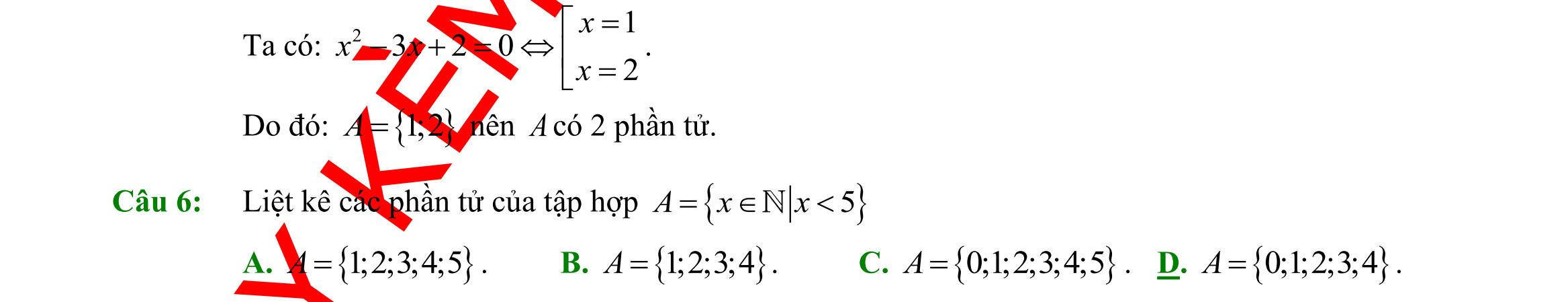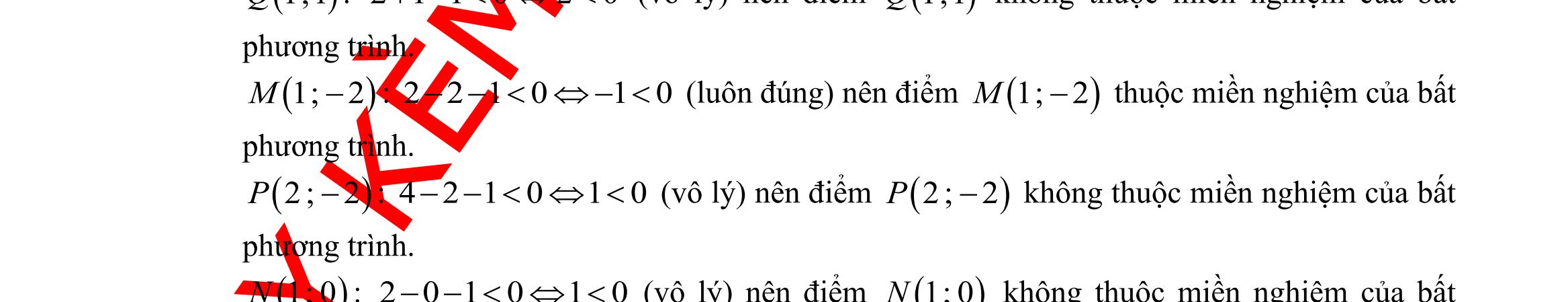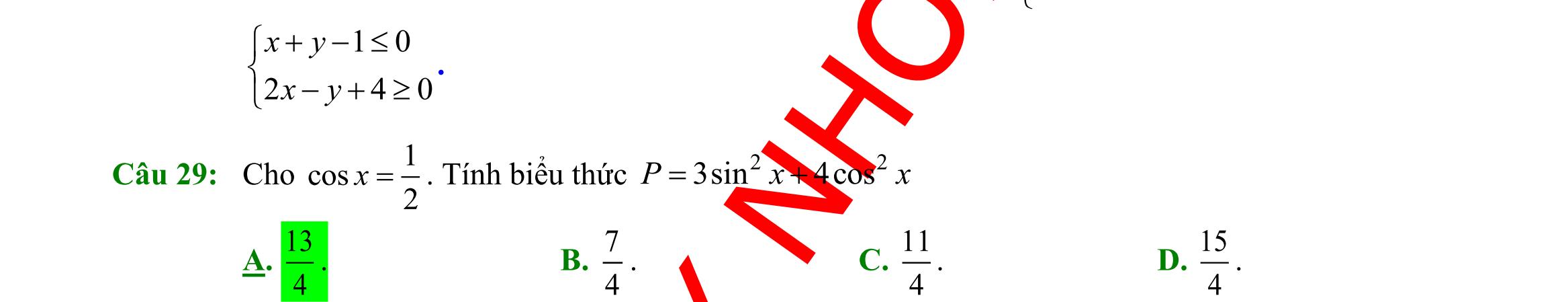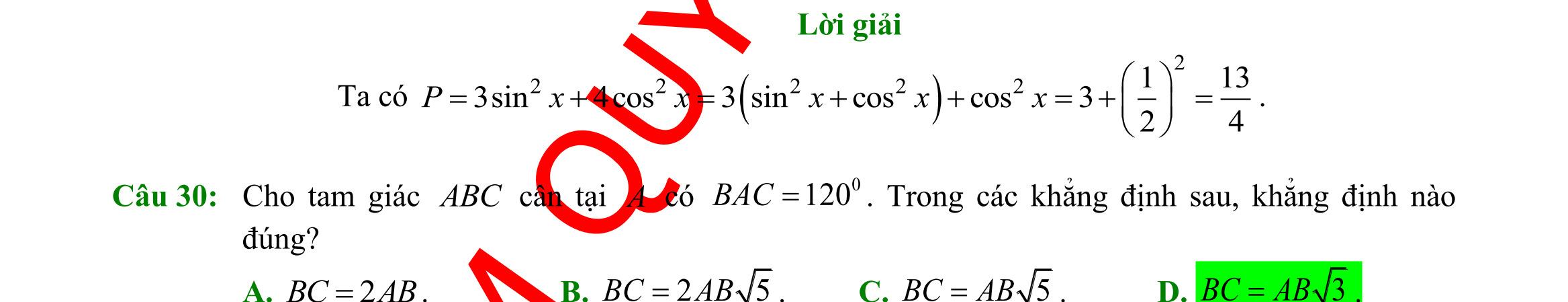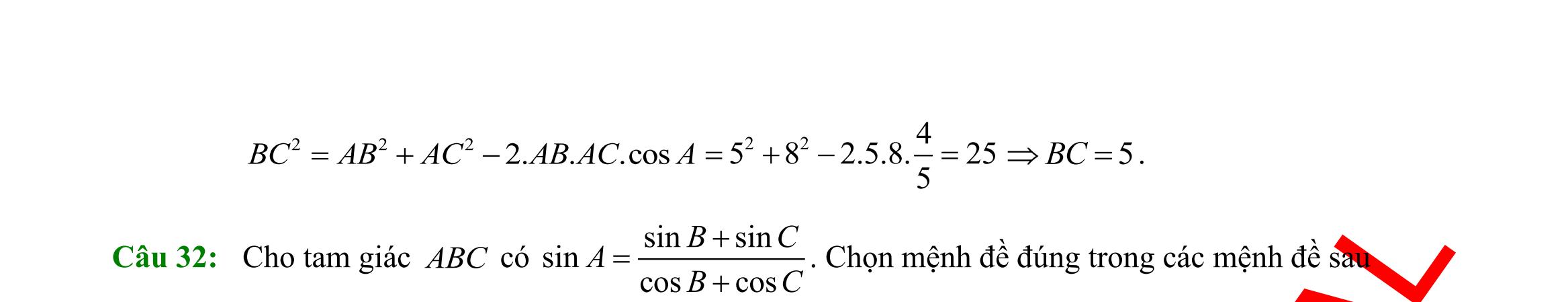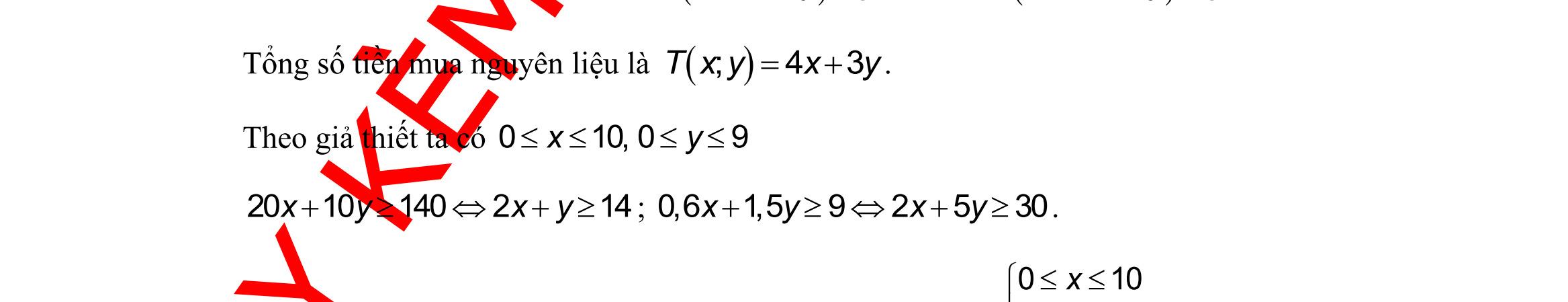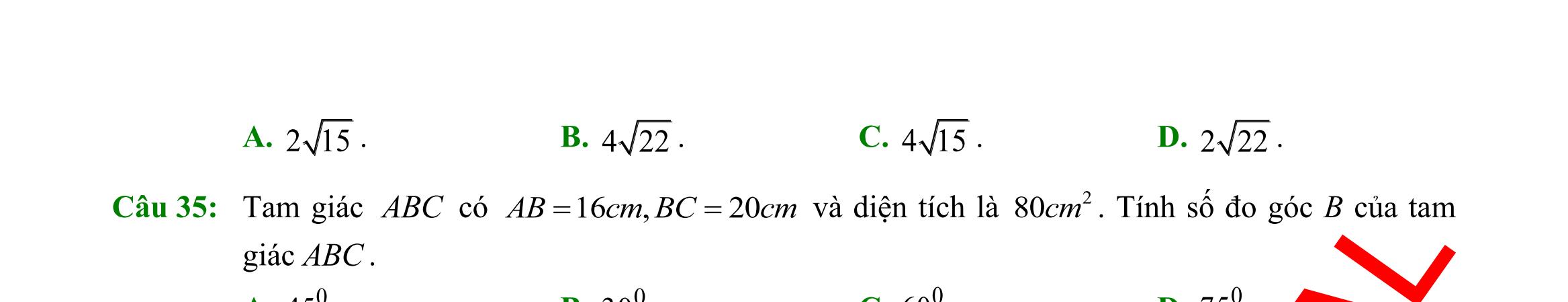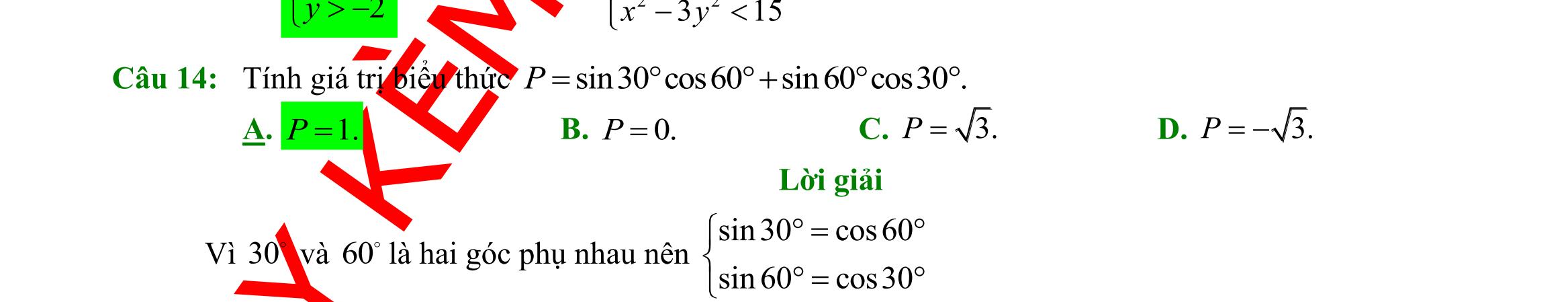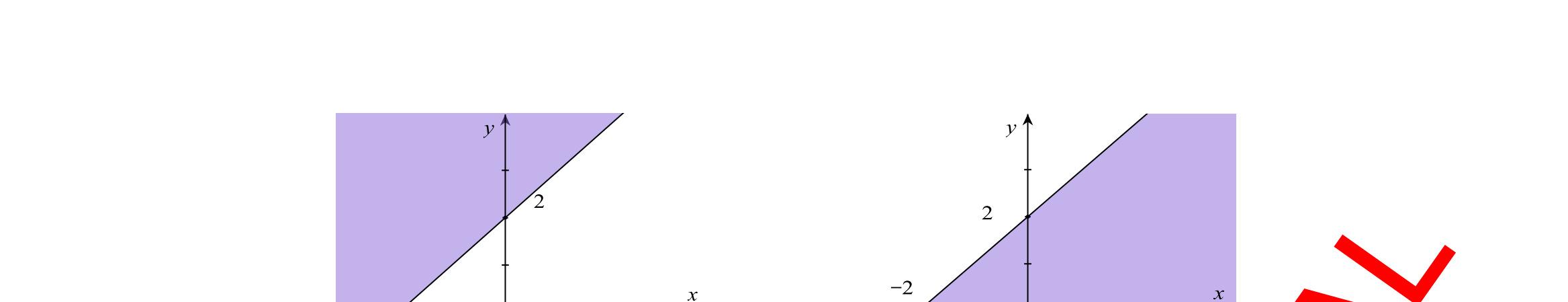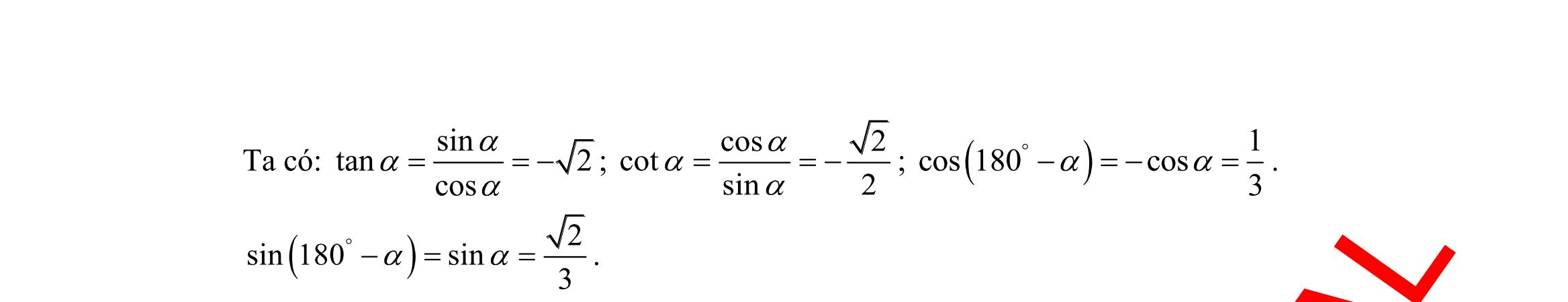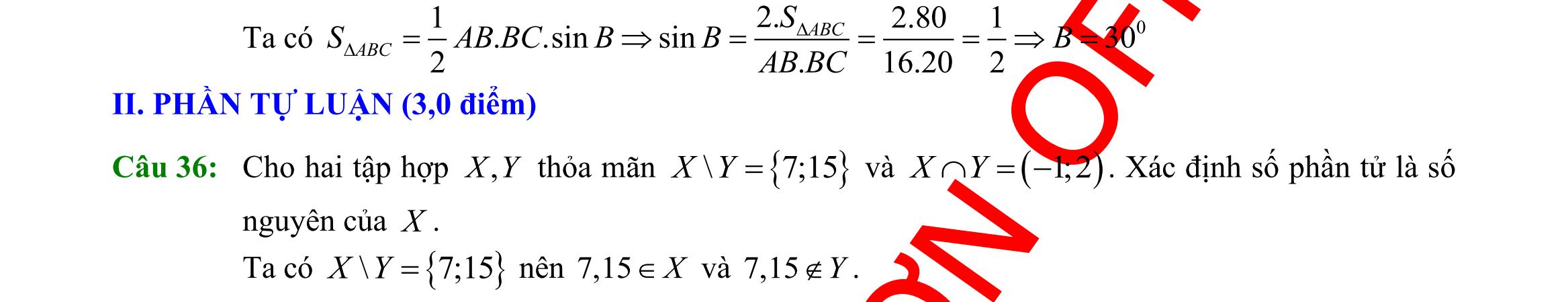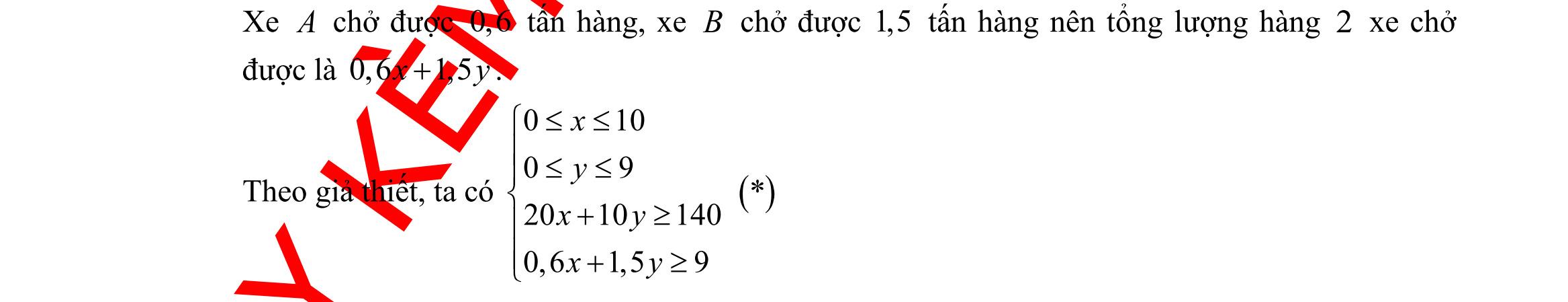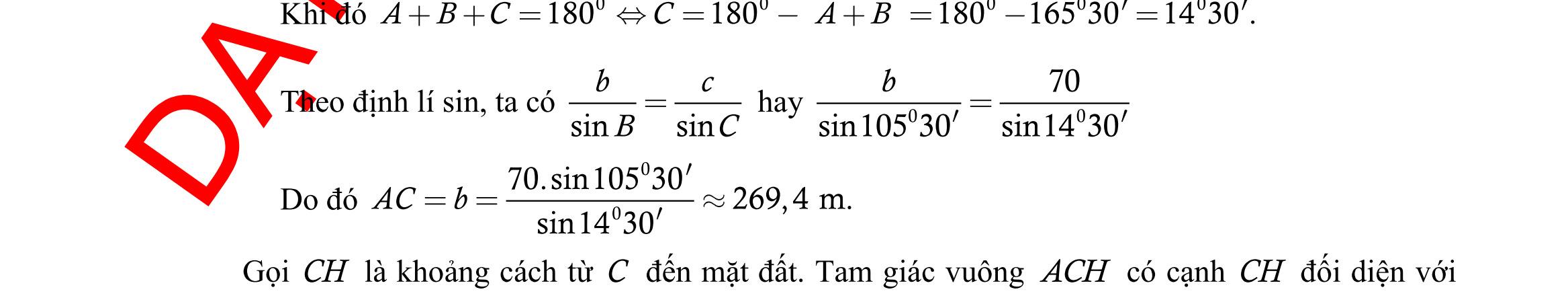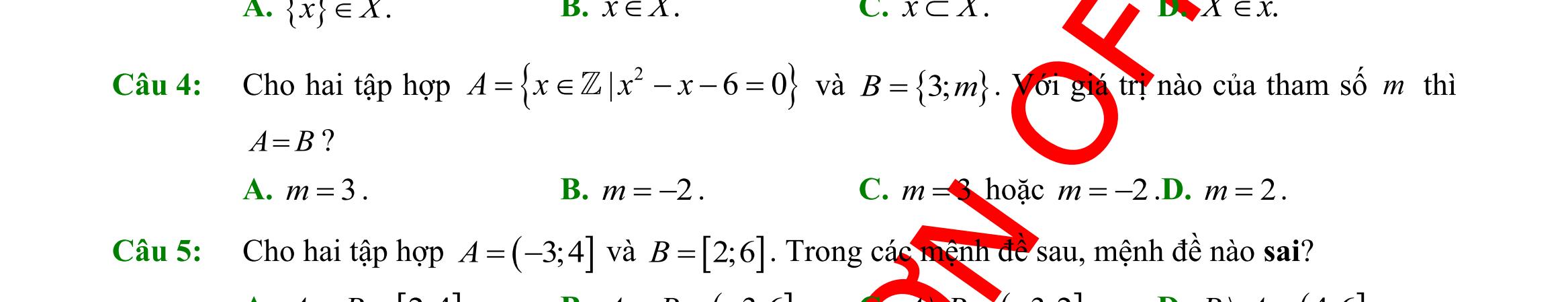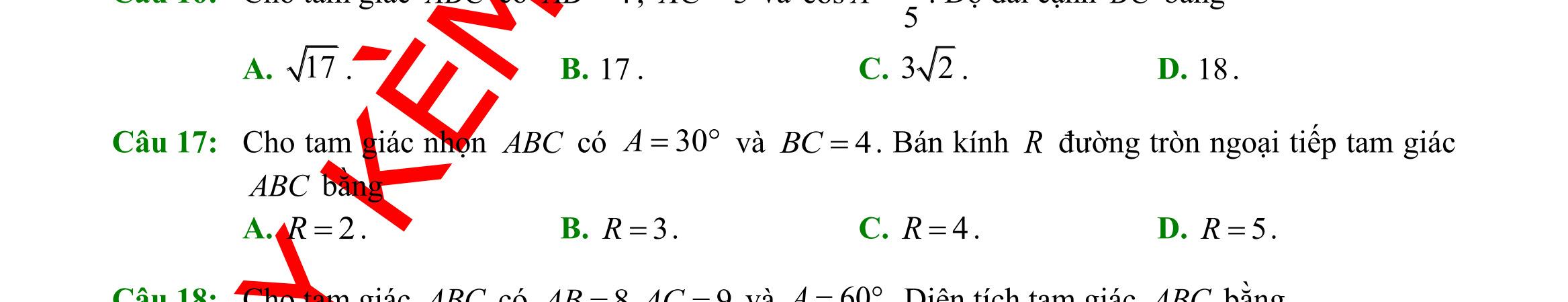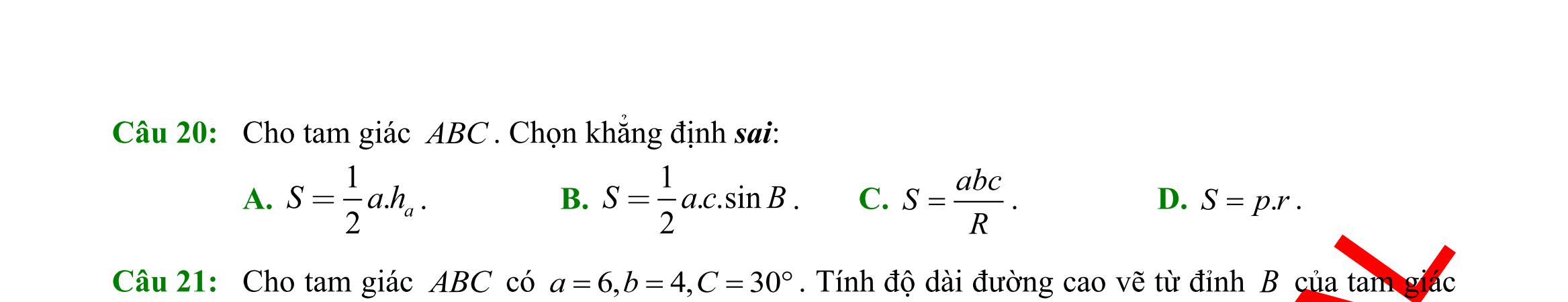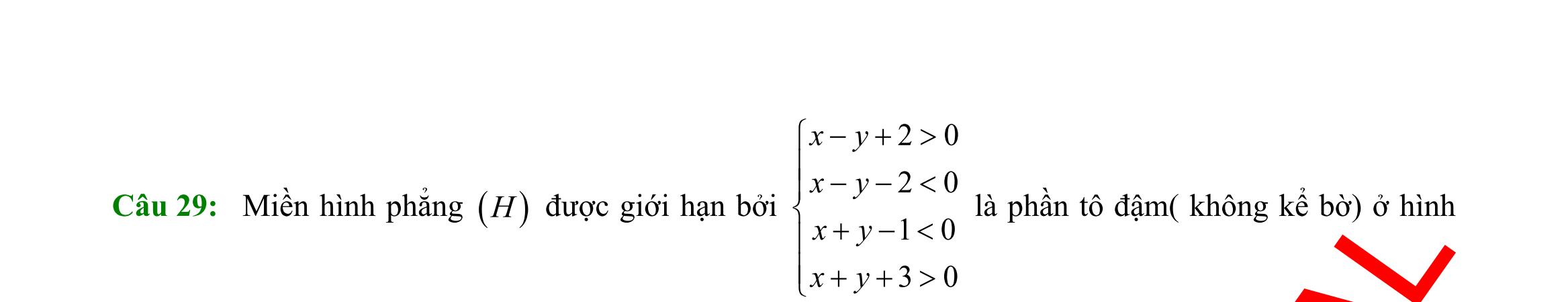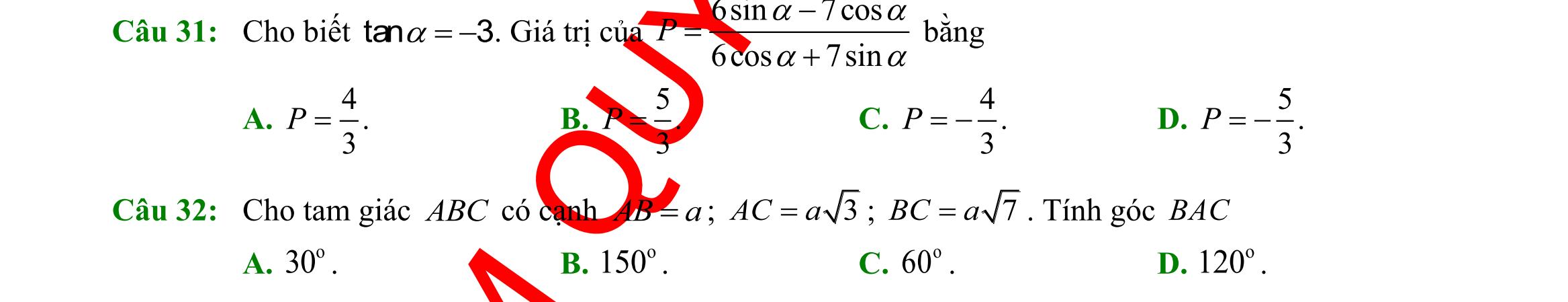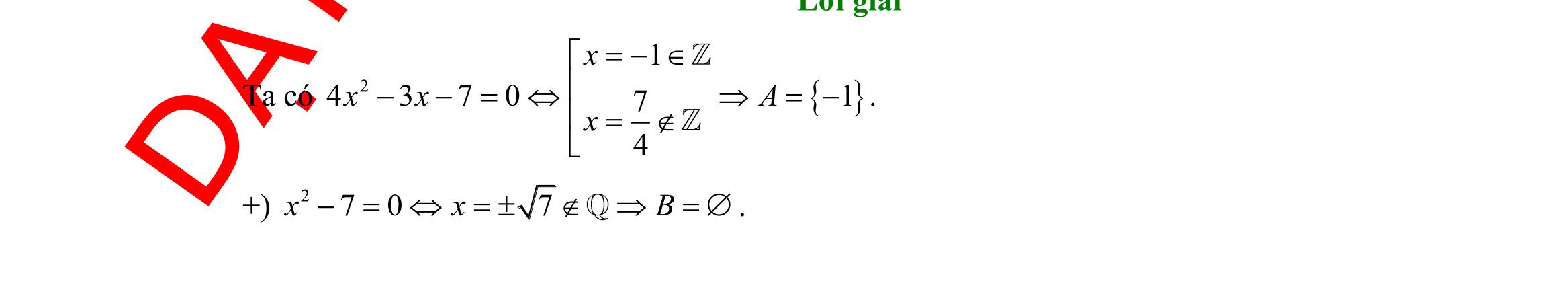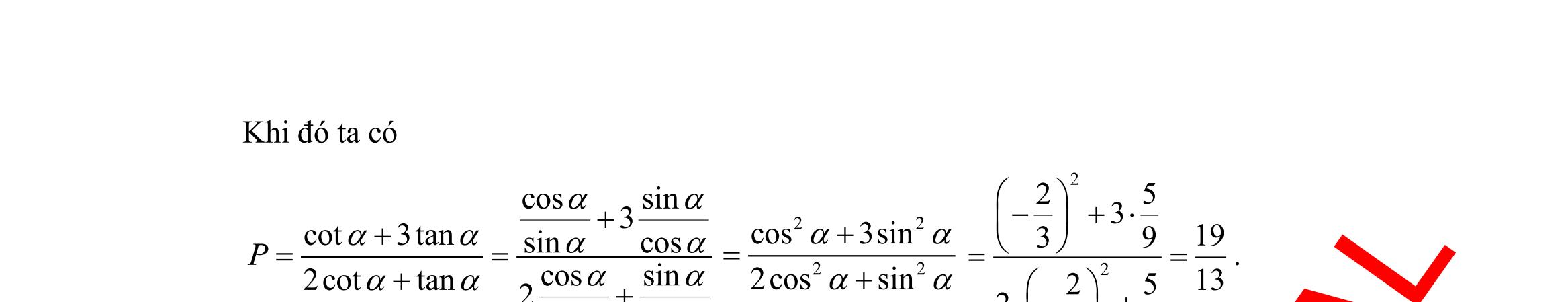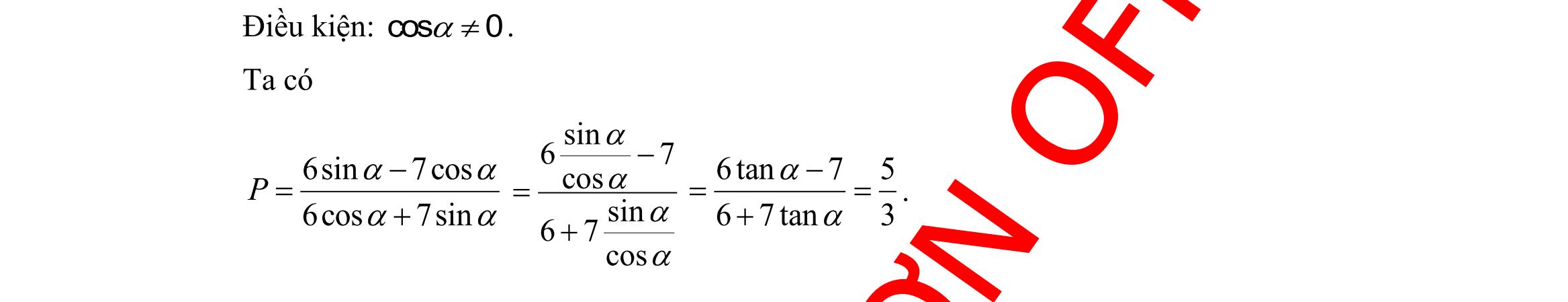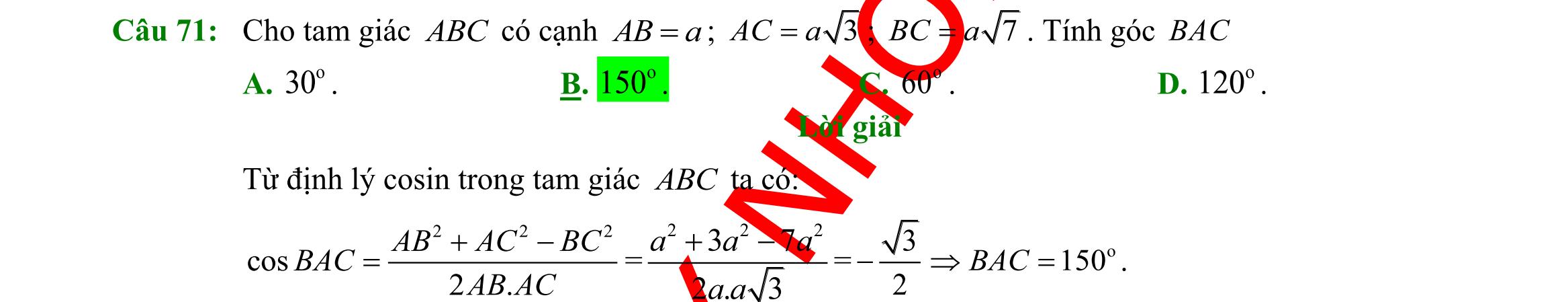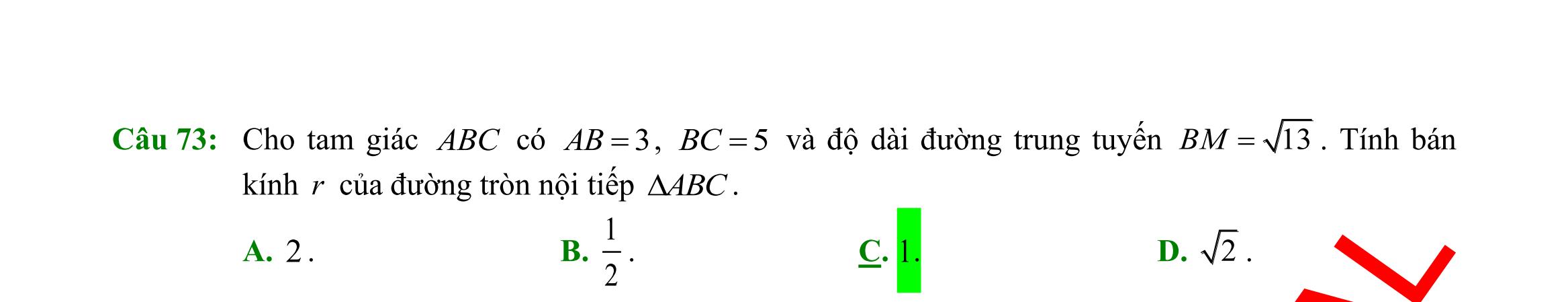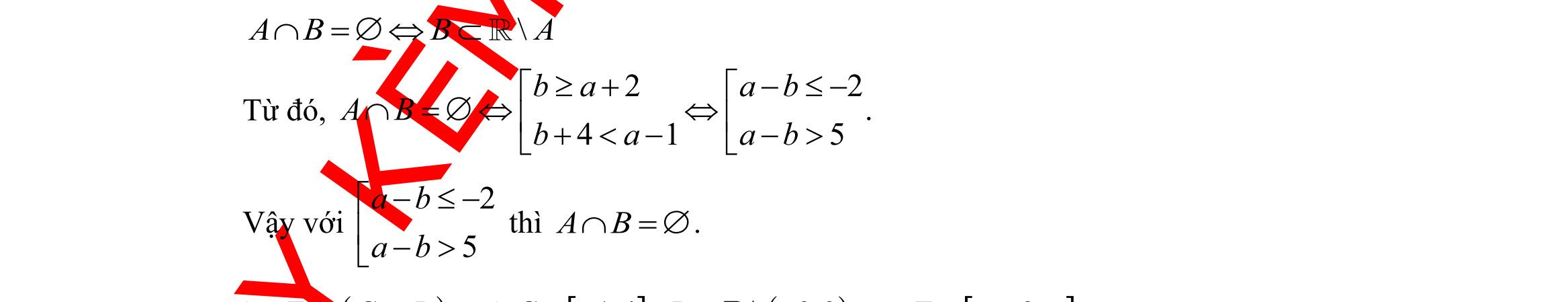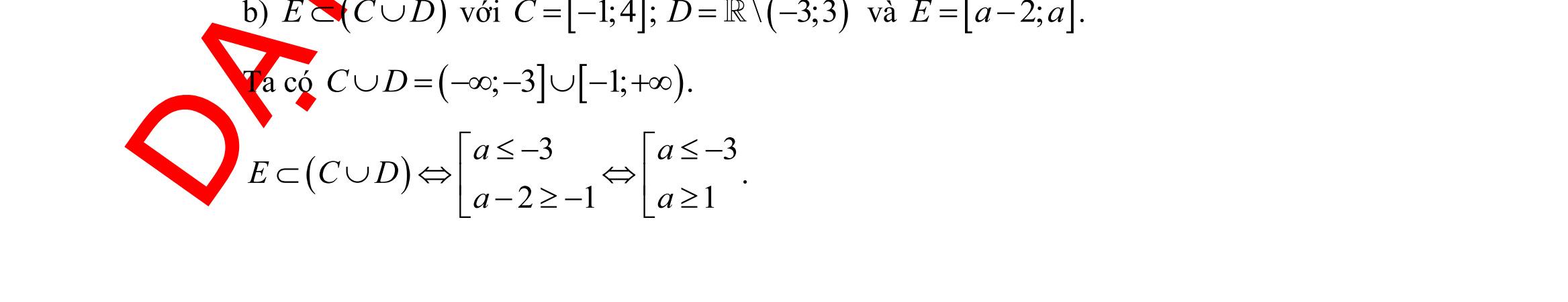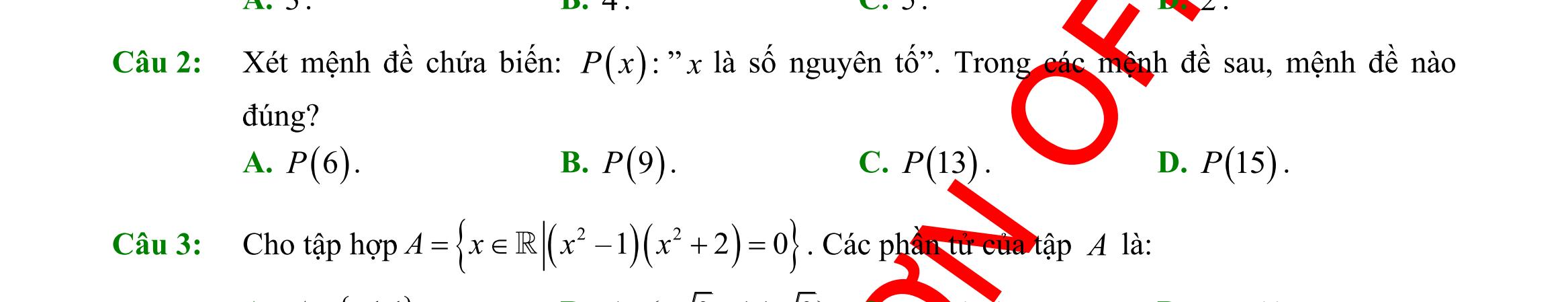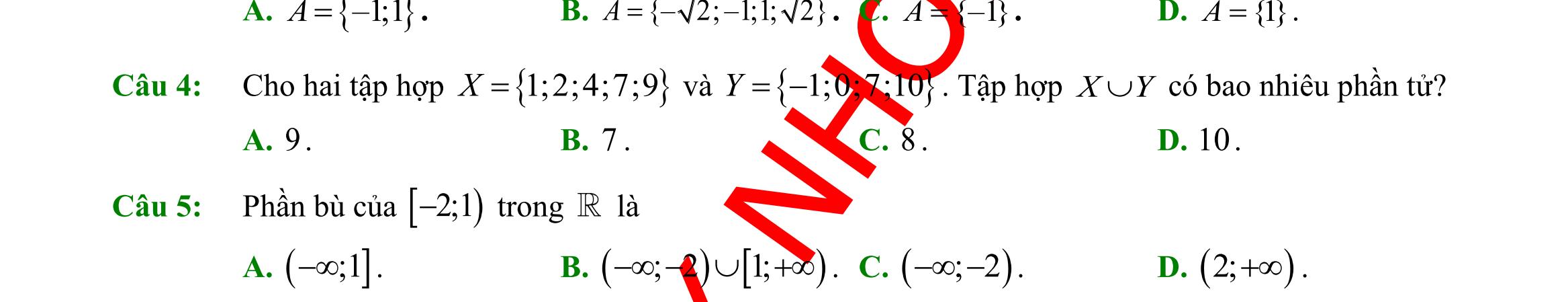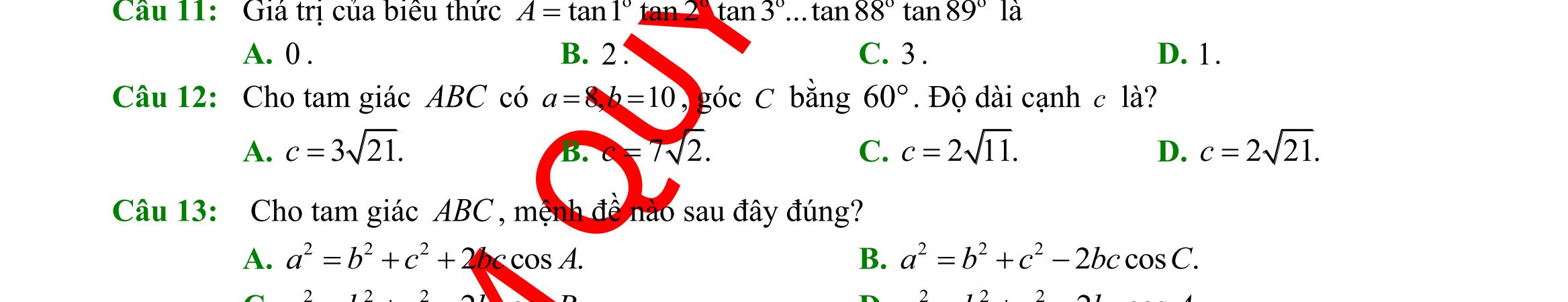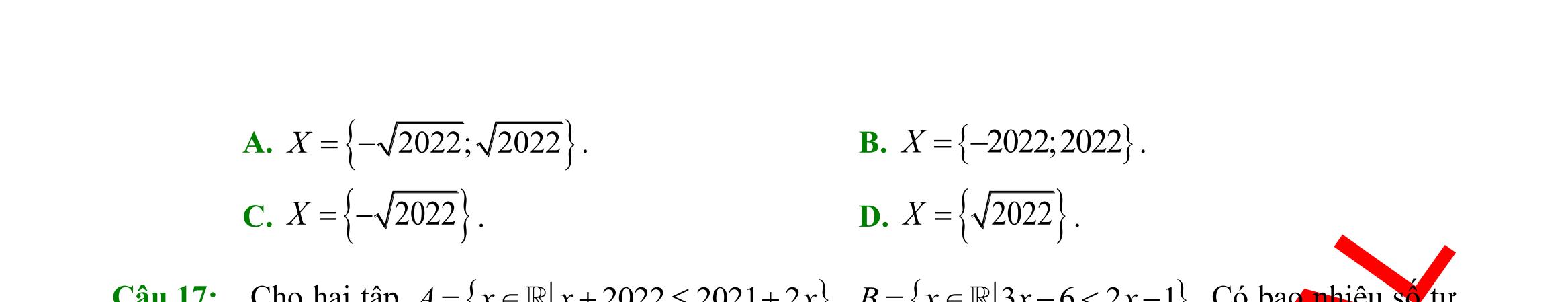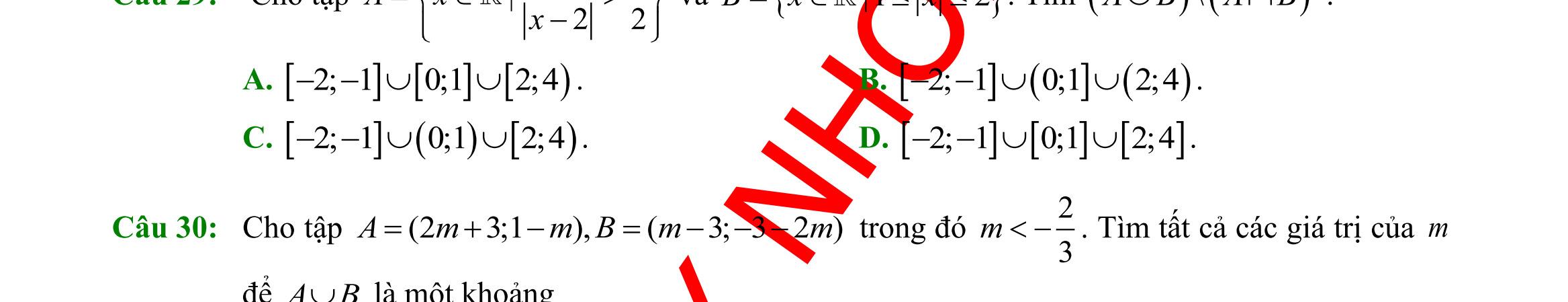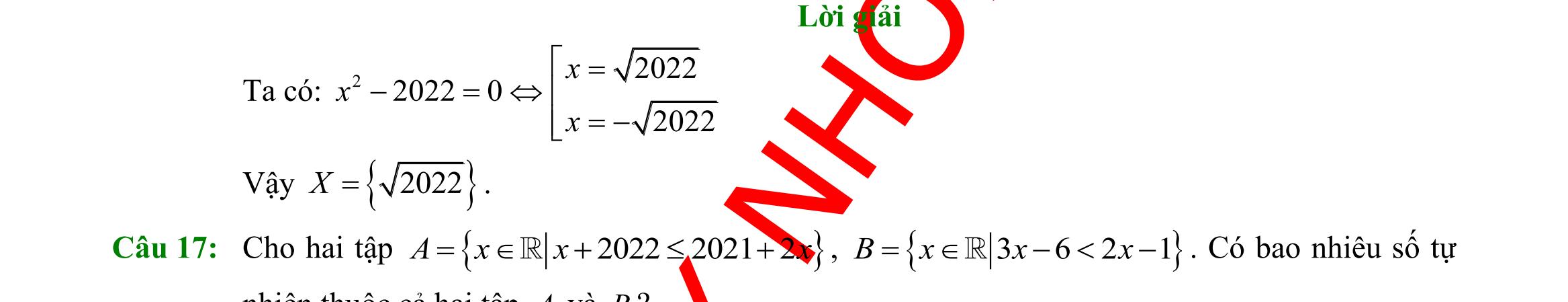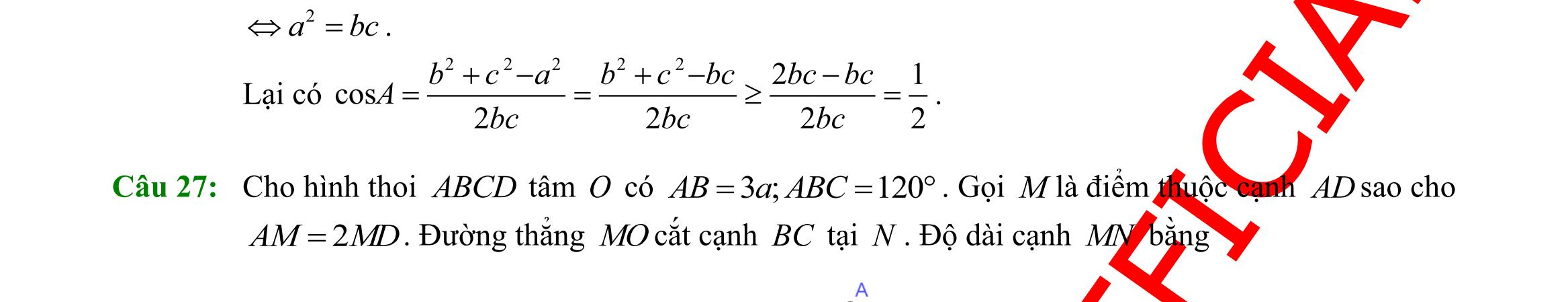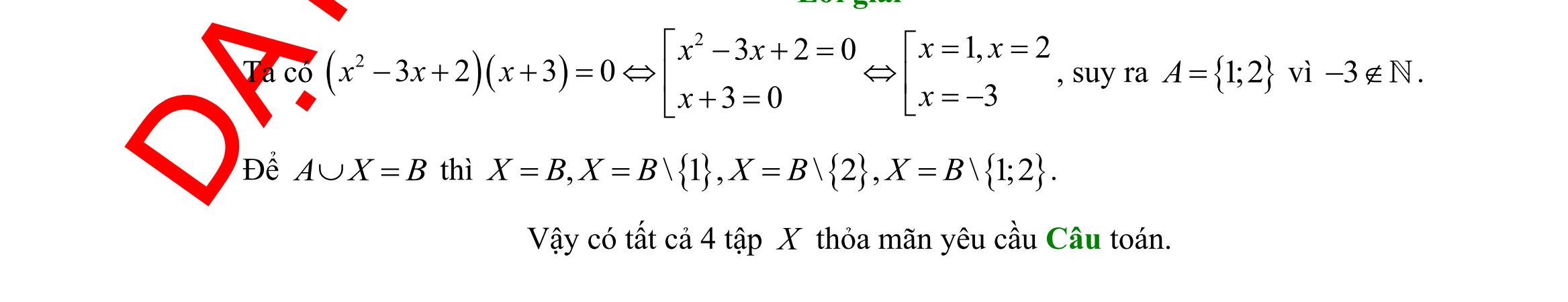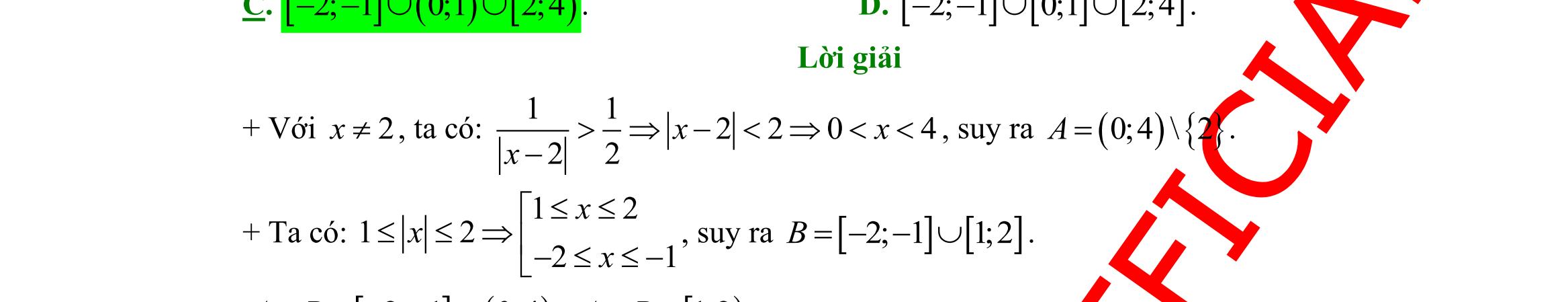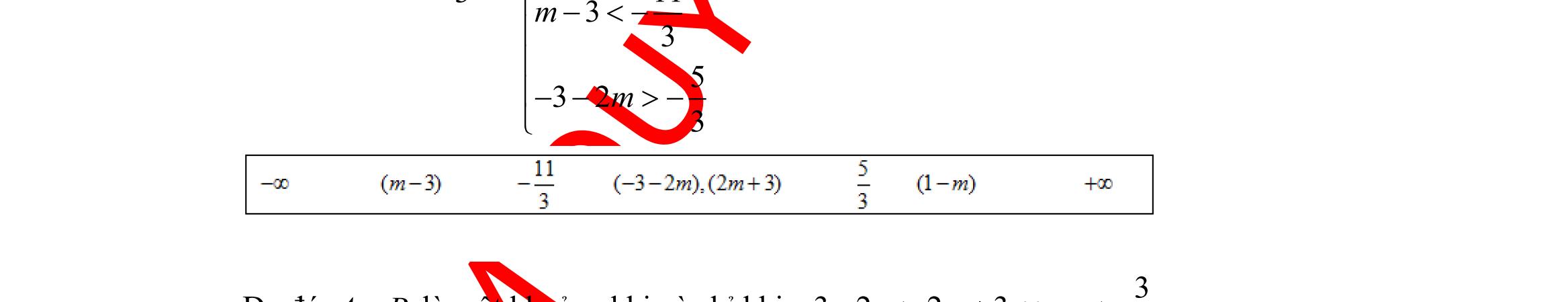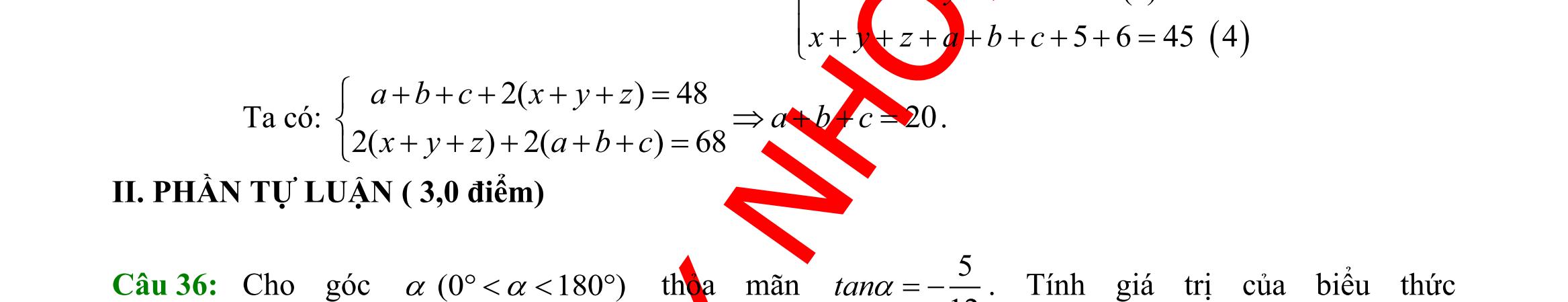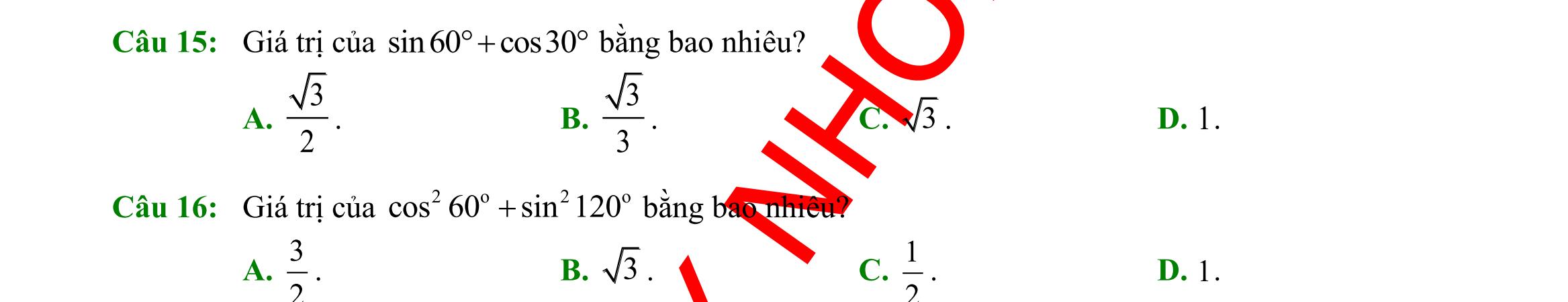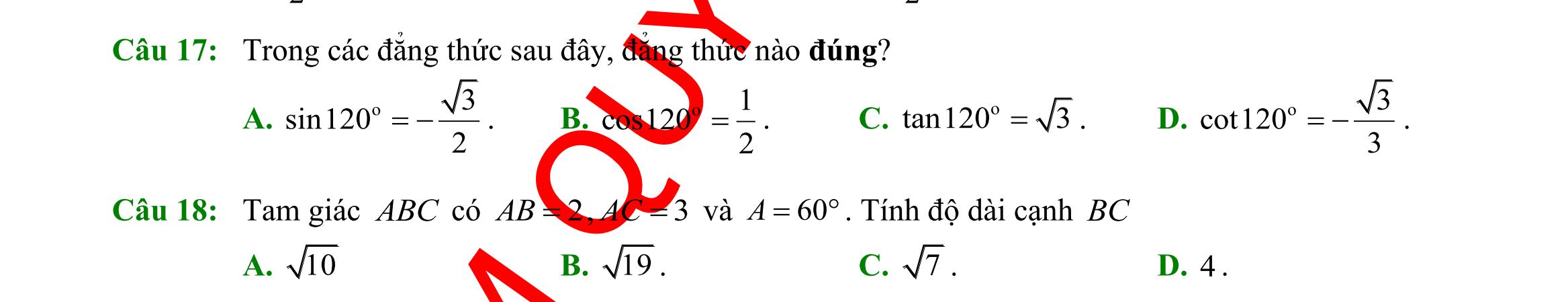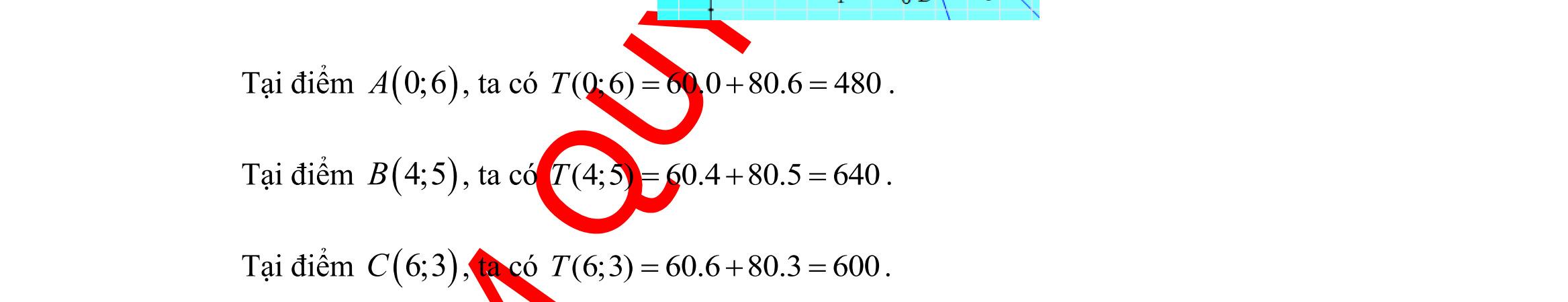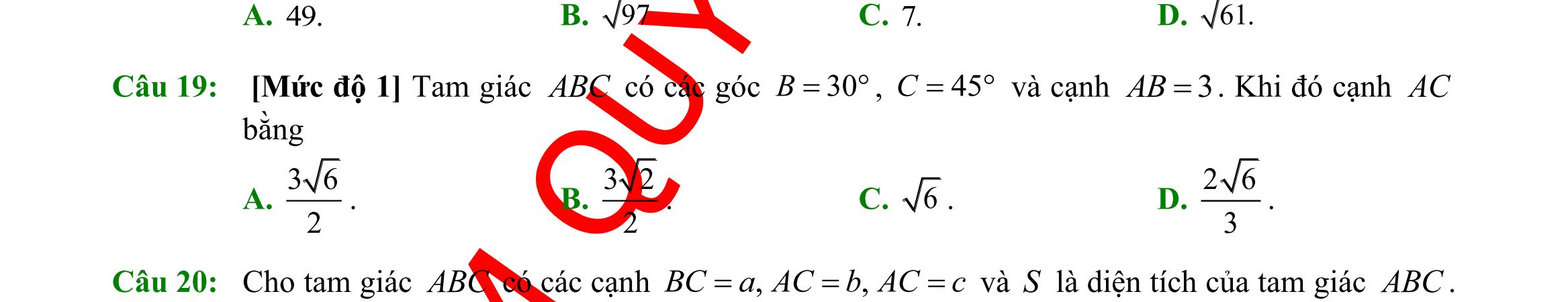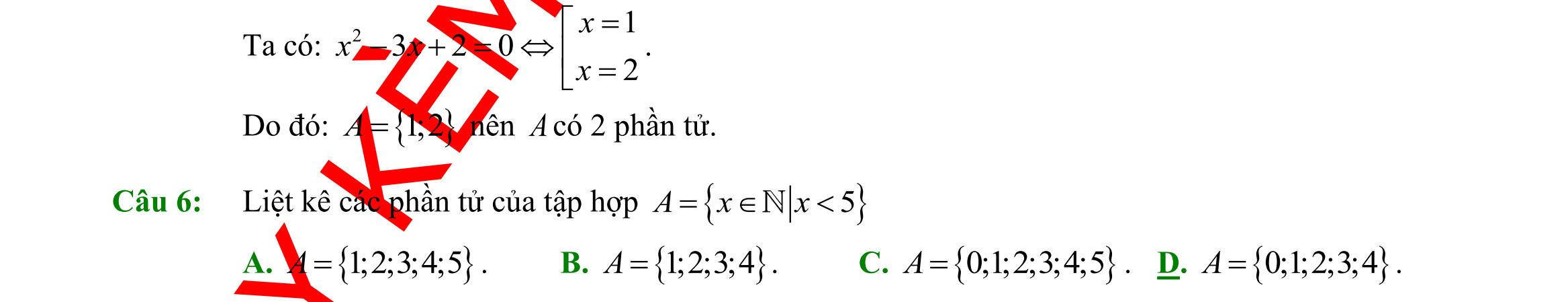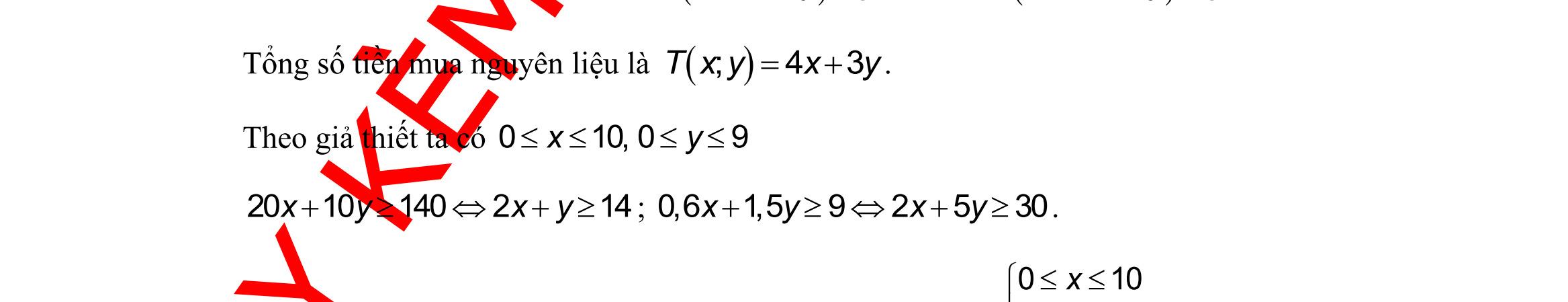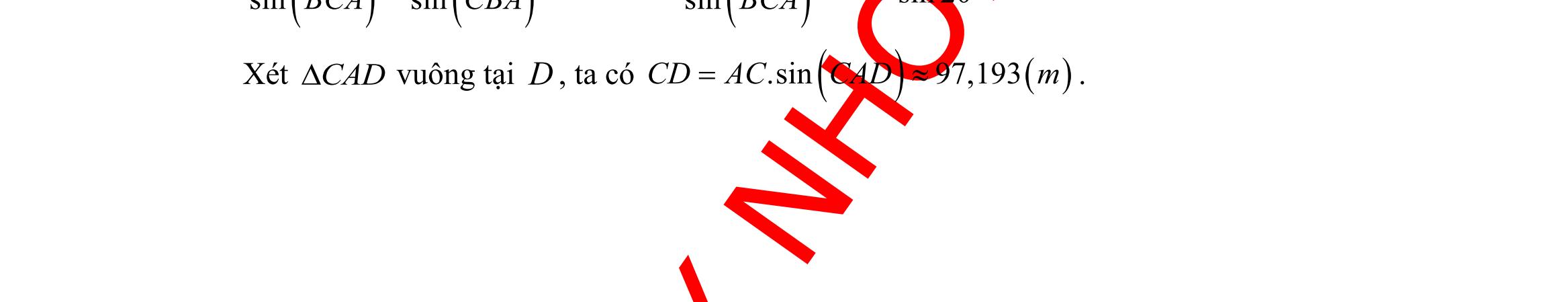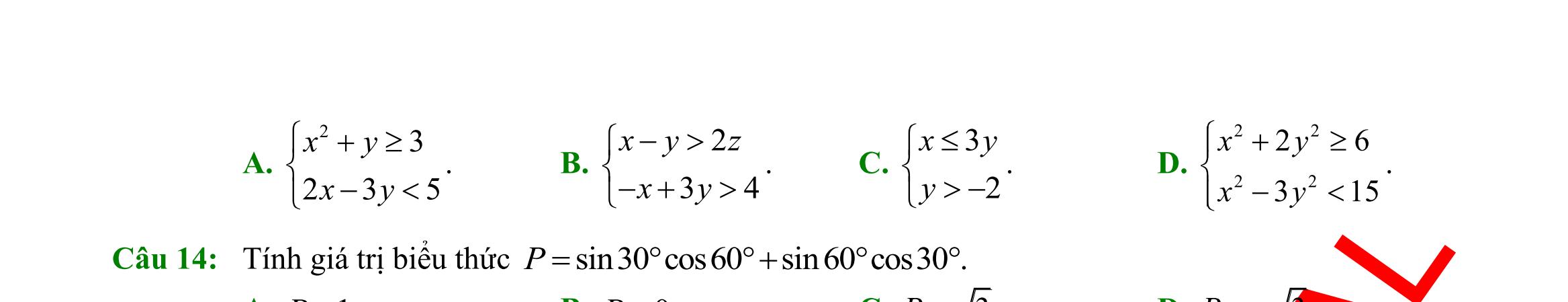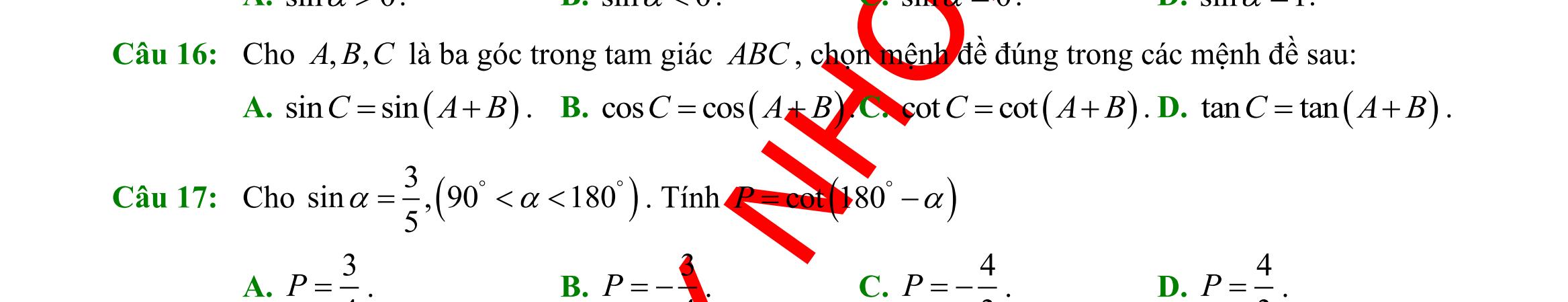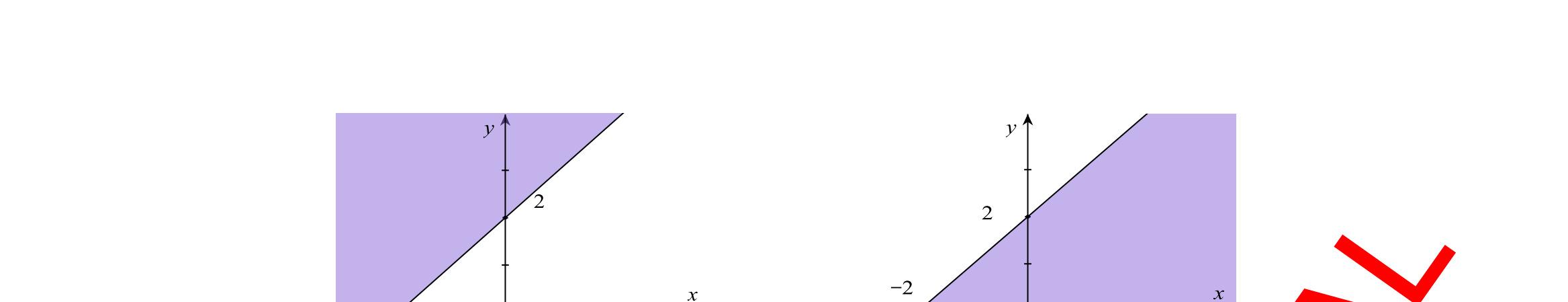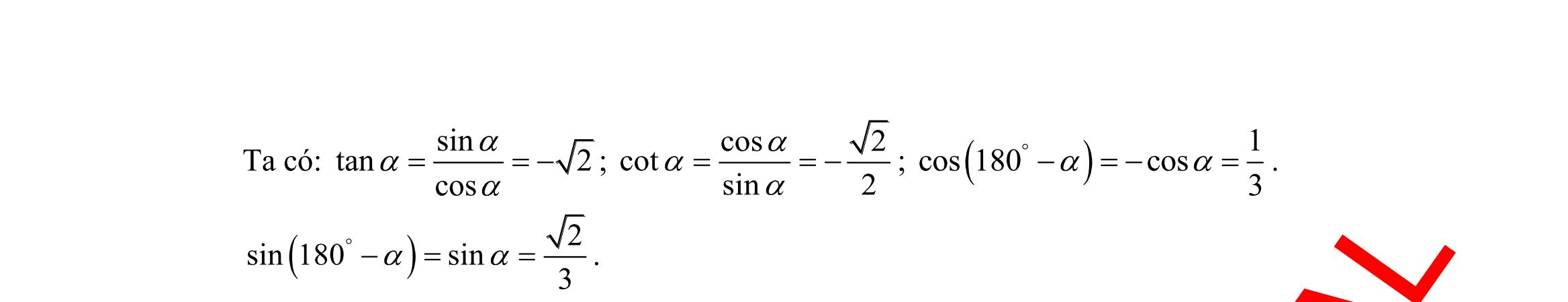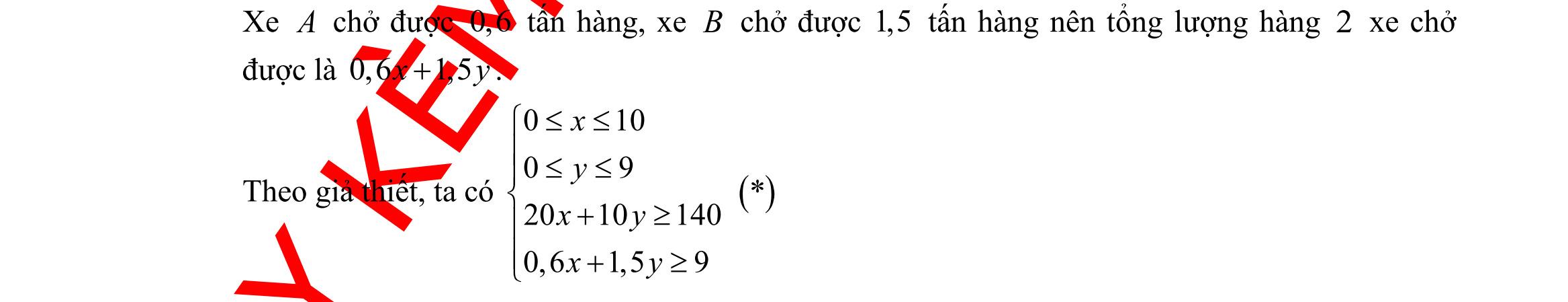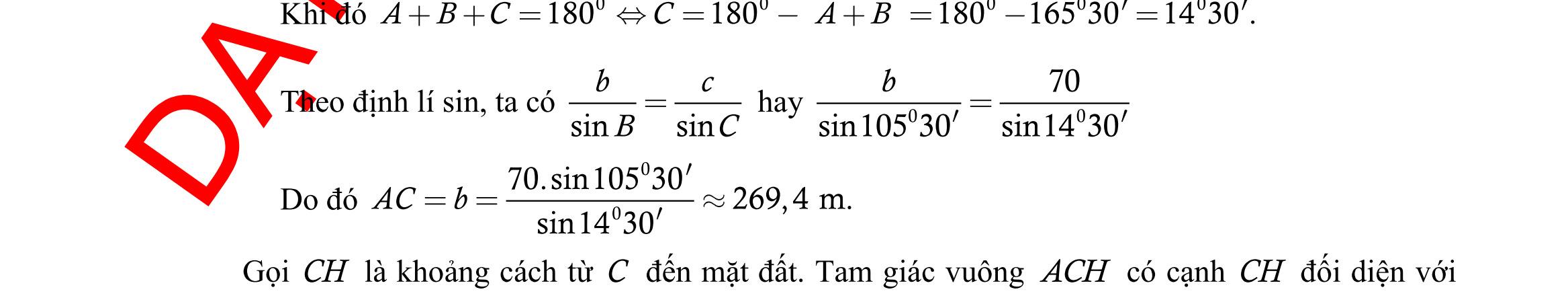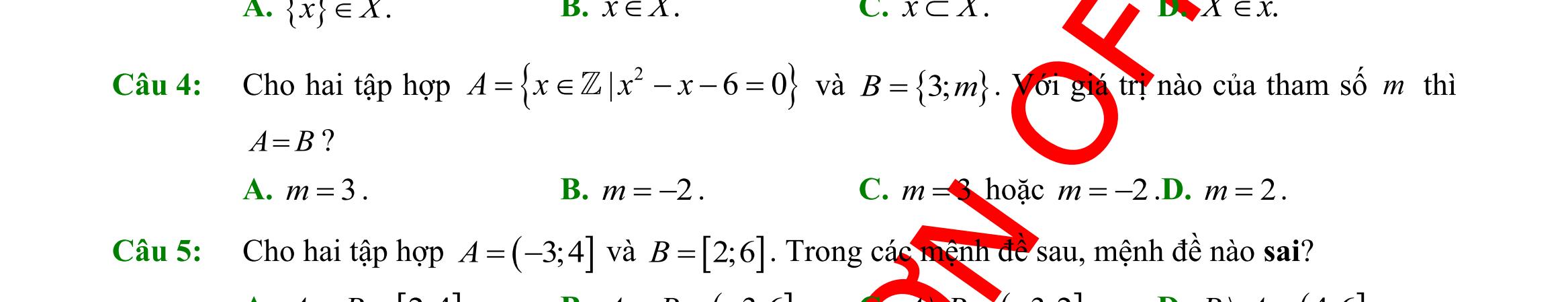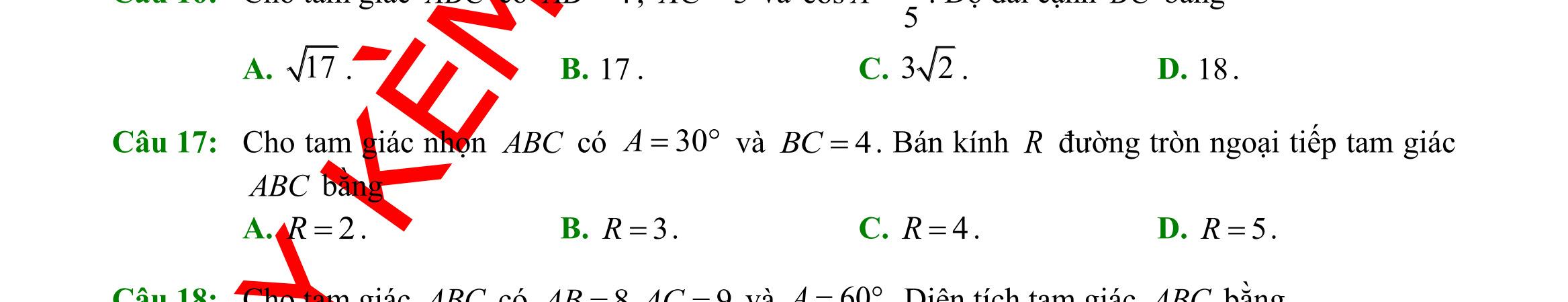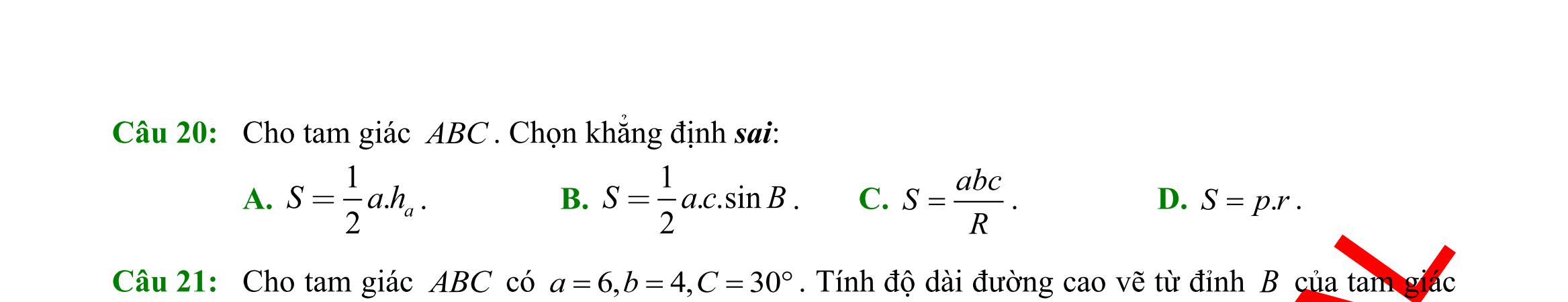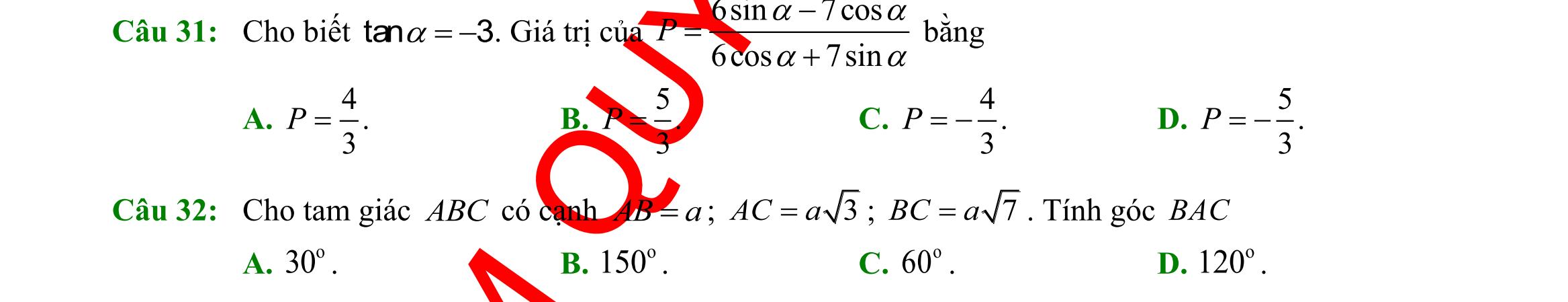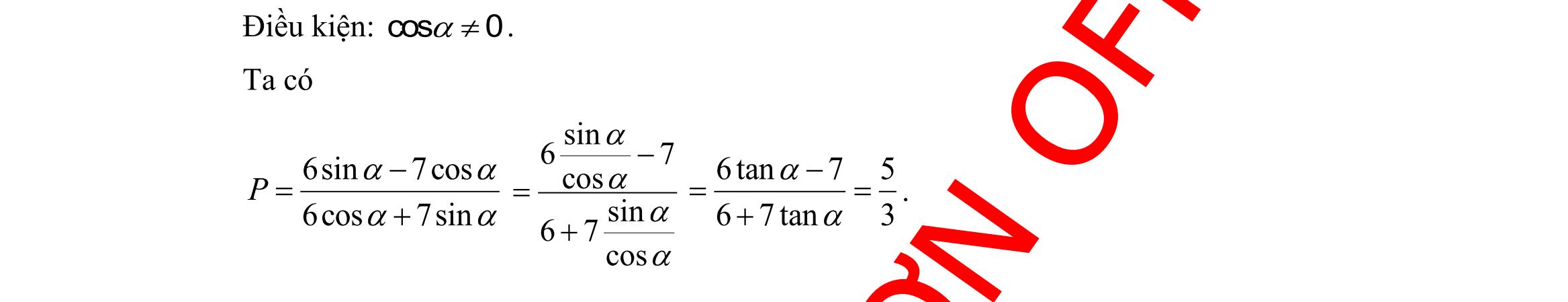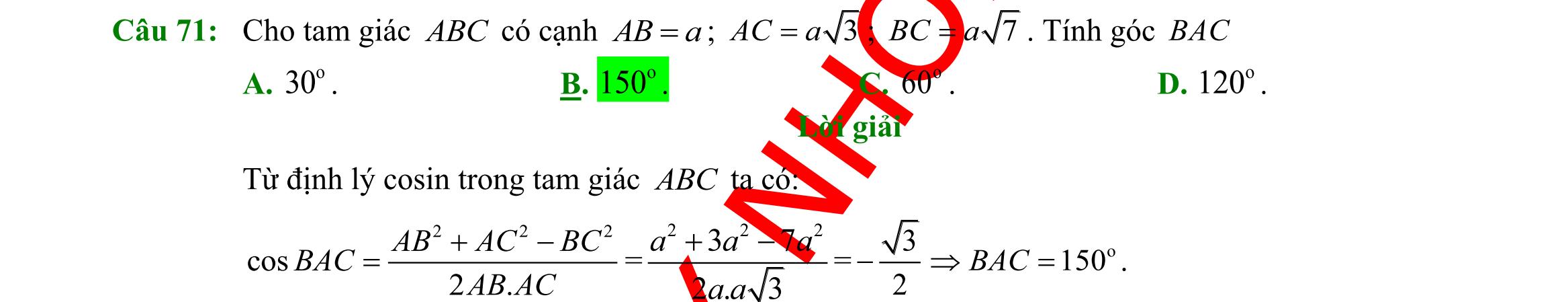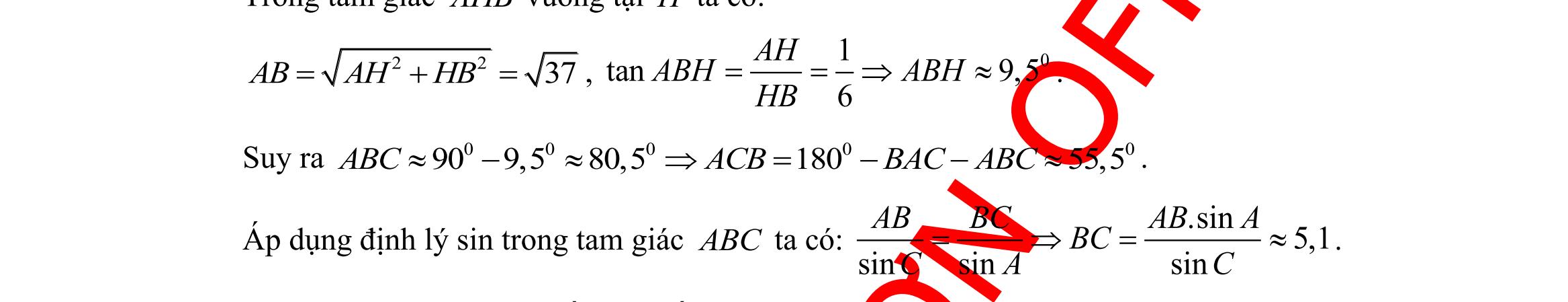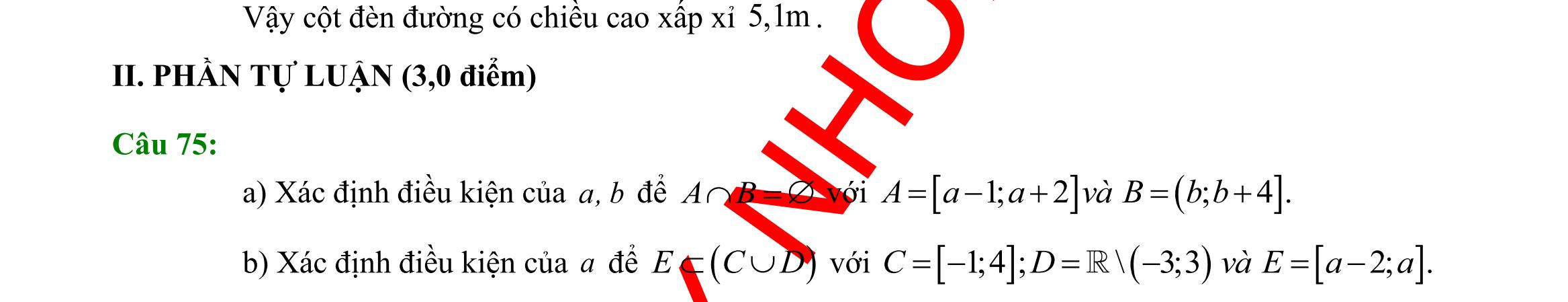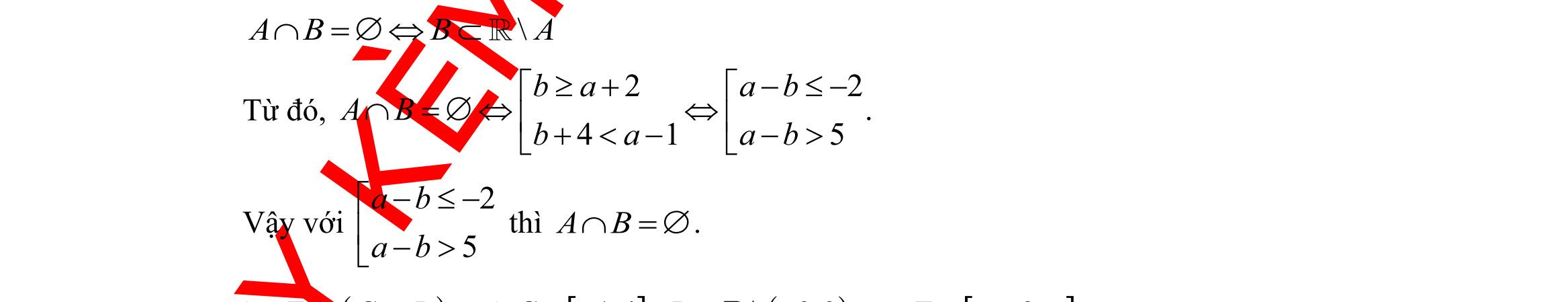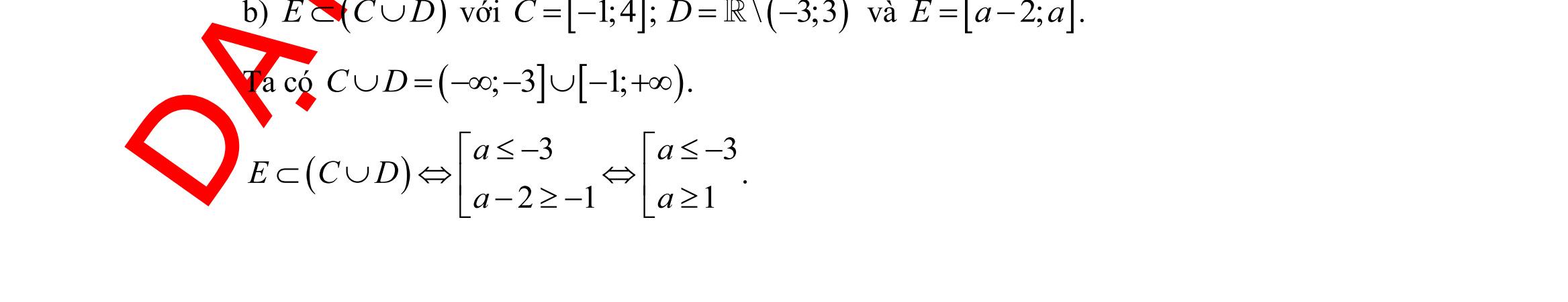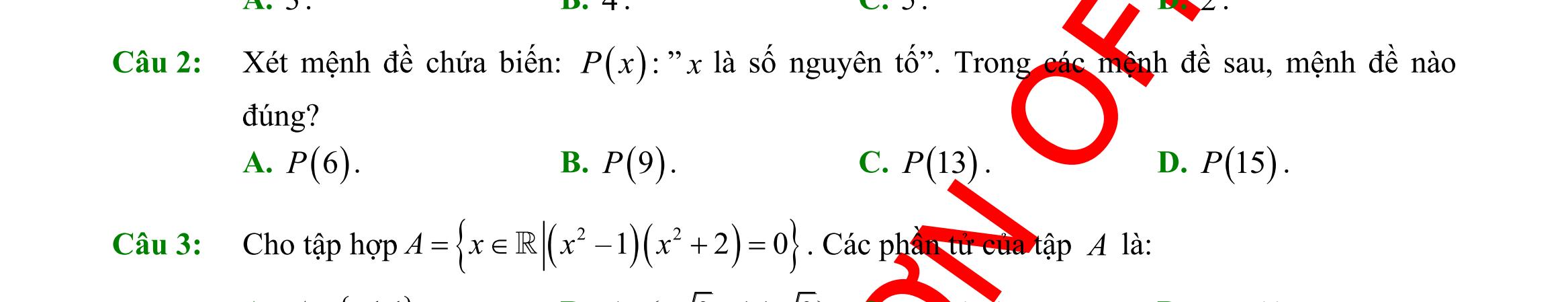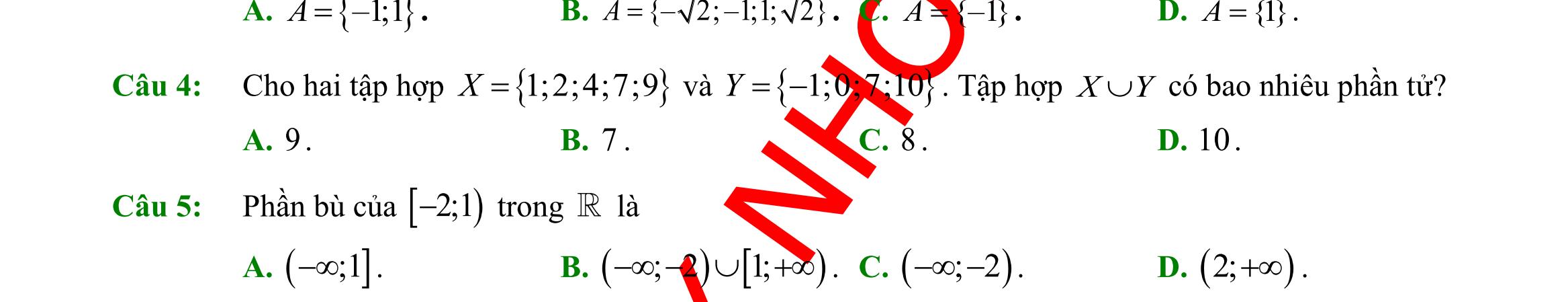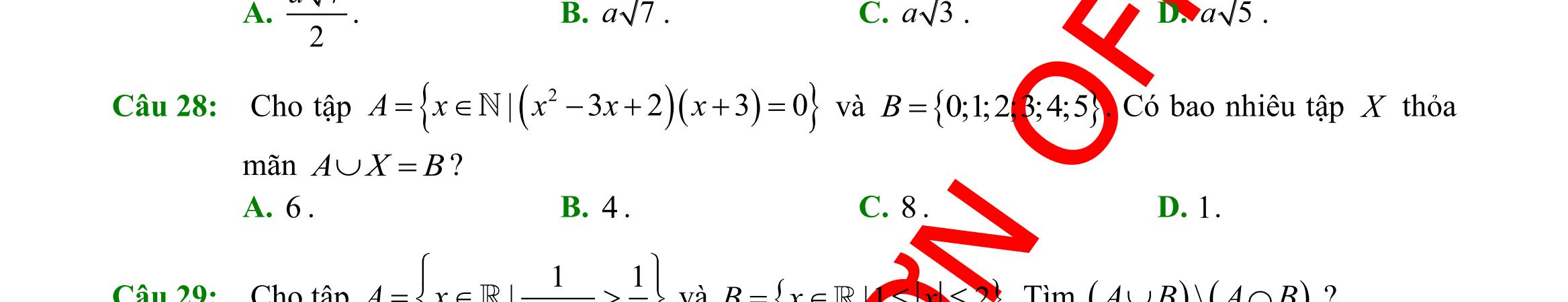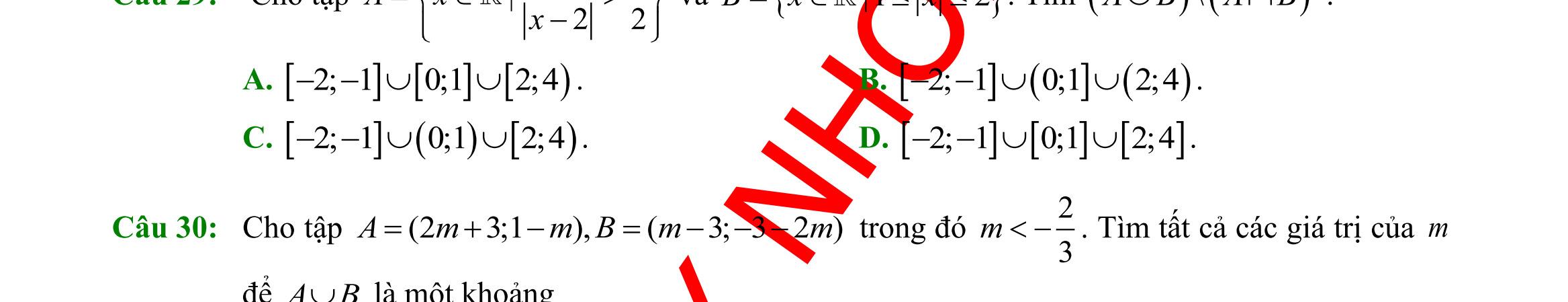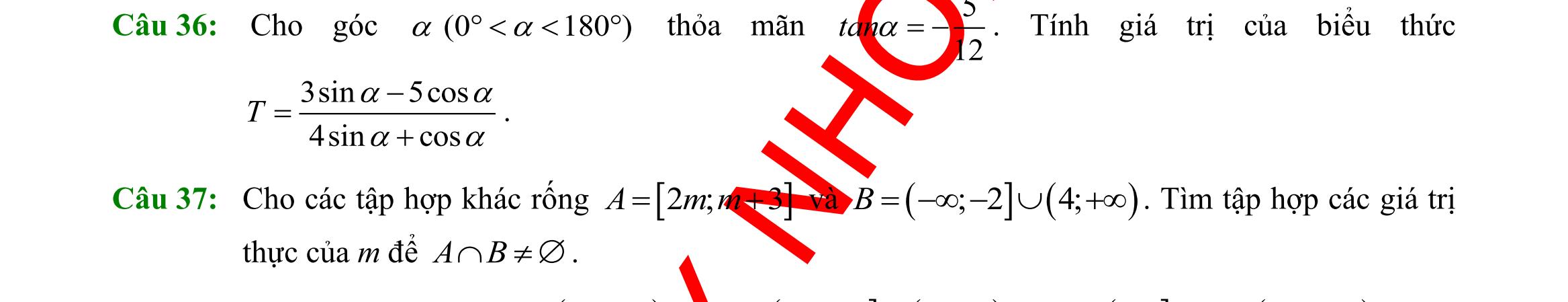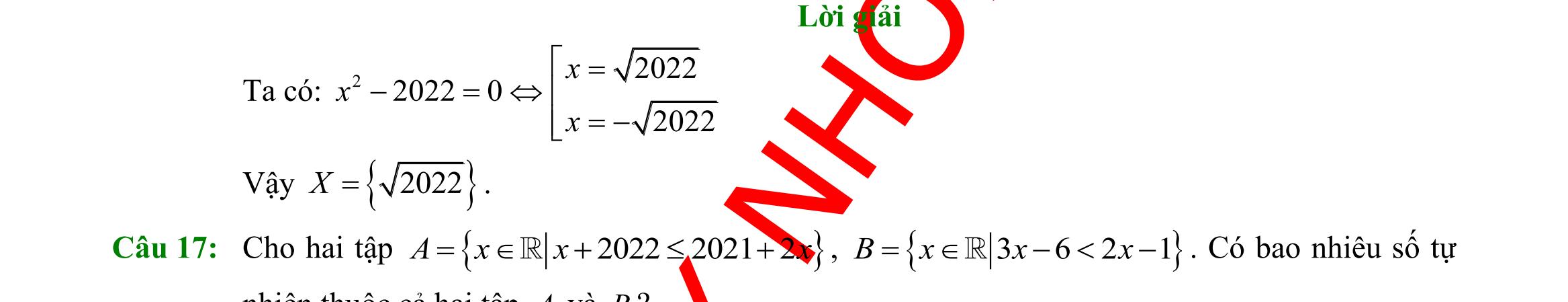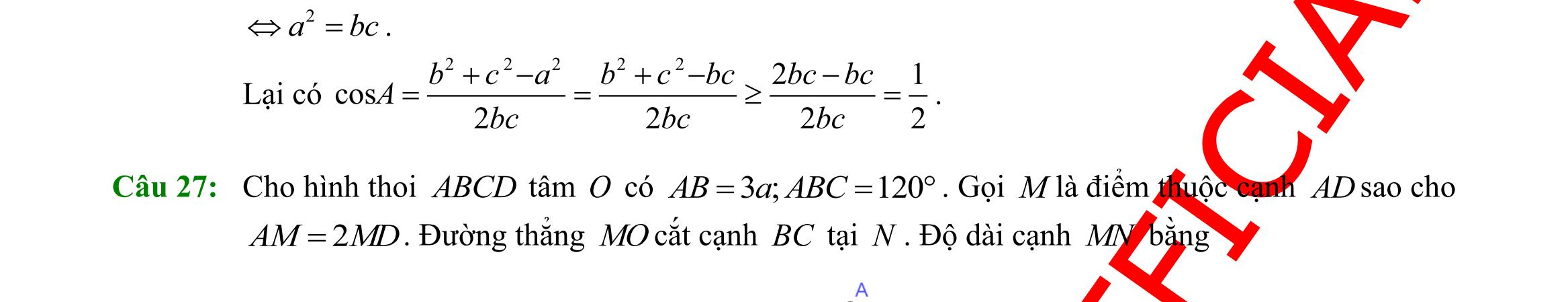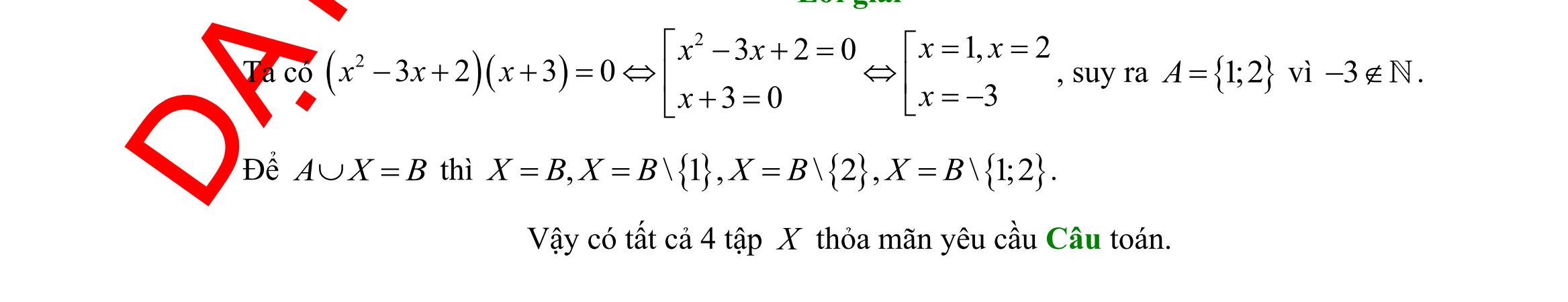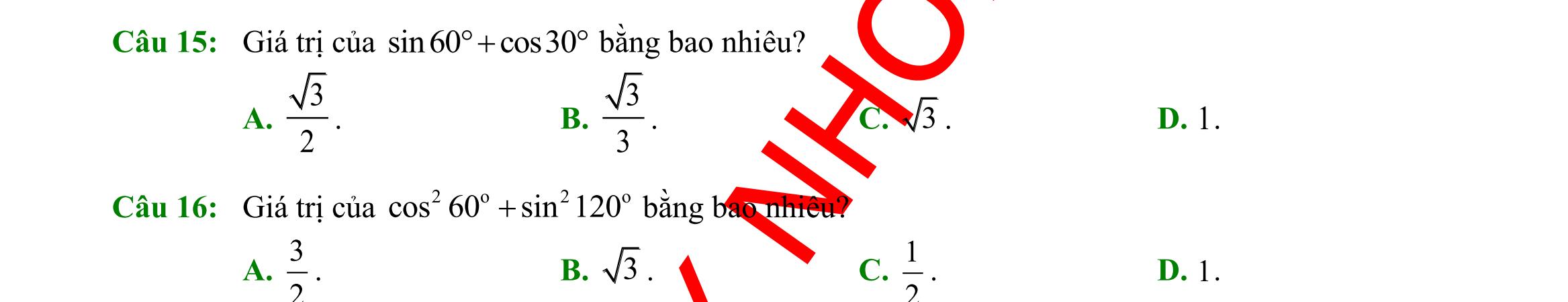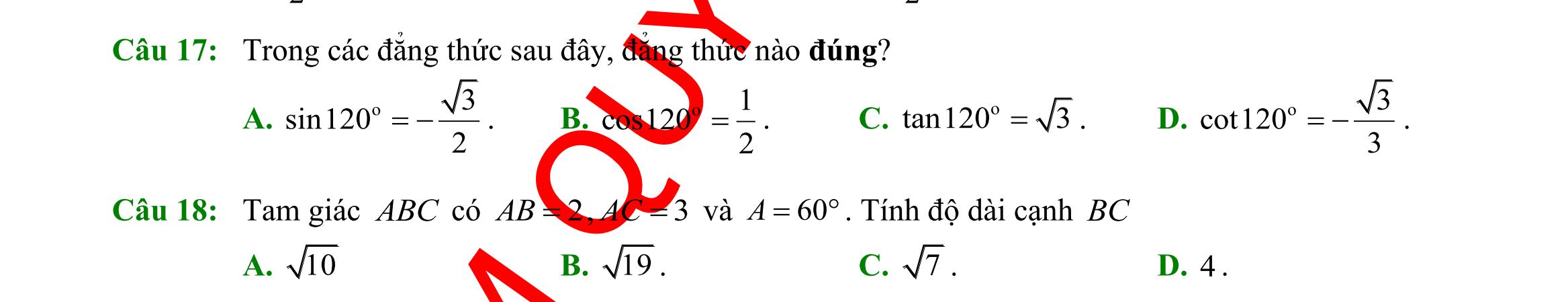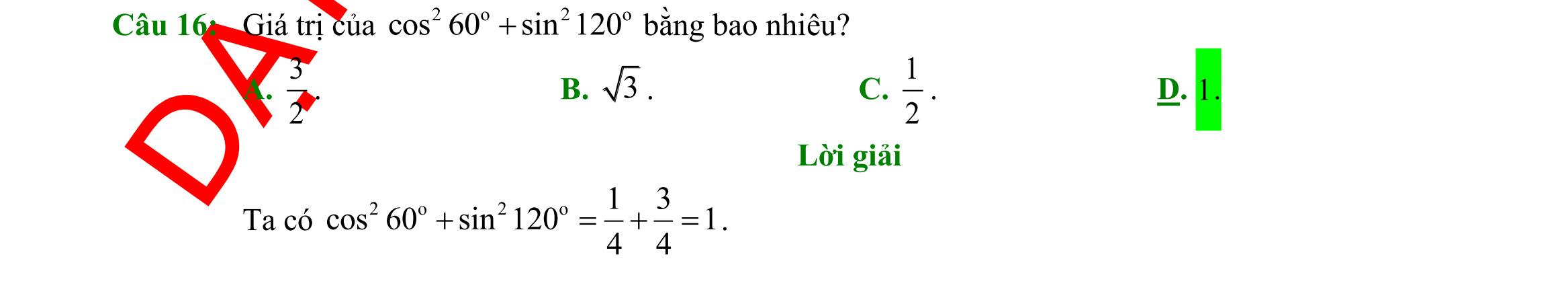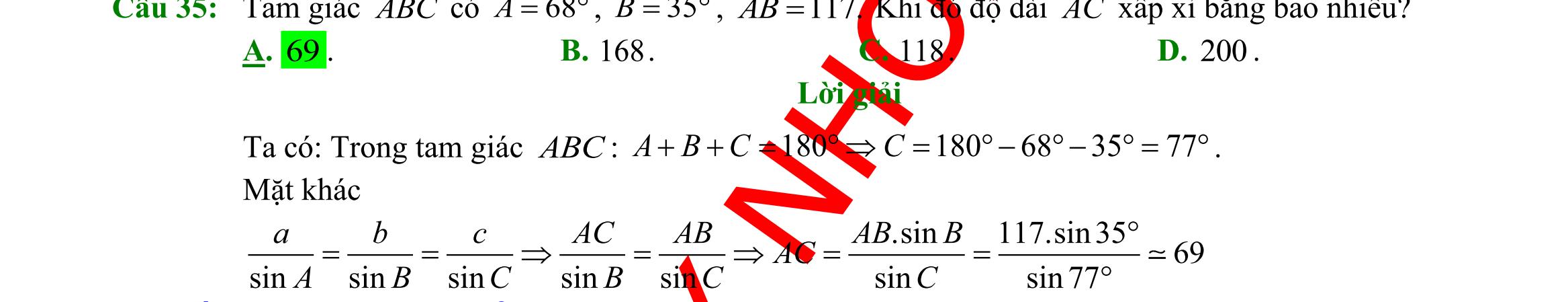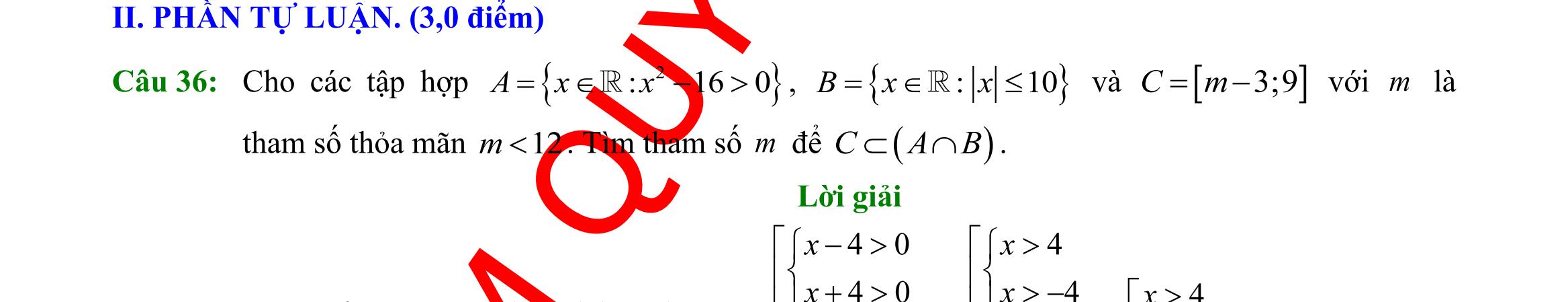BỘ ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI NĂM HỌC 2022 – 2023 MÔN TOÁN 10 (KẾT NỐI TRI THỨC) by Dạy Kèm Quy Nhơn Official

DẠYKÈMQUYNHƠN OFFICIALĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KỲ MÔN TOÁN Ths Nguyễn Thanh Tú eBook Collection BỘ 10 ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI NĂM HỌC 2022 2023 MÔN TOÁN 10 KẾT NỐI TRI THỨC CÓ LỜI GIẢI CHI TIẾT (35 CÂU TRẮC NGHIỆM + TỰ LUẬN) WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405

10 ĐỀ SỐ: 01

I. PHẦN TRẮC NGHIỆM (35 câu 7,0 điểm)

Câu 1: Phát biểu nào sau đây là một mệnh đề?

A. Trời hôm nay đẹp quá! B. New York là thủ đô của Việt Nam. C. Con đang làm gì đó? D. Số 3 có phải là số tự nhiên không?

Câu 2: Mệnh đề phủ định của mệnh đề: “ 2022 là một số chẵn” là:

A. 2022 không là một số chẵn.

C. 2022 là một số lẻ.

B. 2022 không là một số chẵn.

D. 2022 không là một số lẻ.

Câu 3: Cho mệnh đề: “Nếu tam giác có hai góc bằng 60o thì tam giác đó là tam giác đều”. Mệnh đề đảo của mệnh đề trên là:

A. Nếu tam giác có hai góc bằng 60o thì tam giác đó không là tam giác đều.

B. Nếu tam giác là tam giác đều thì tam giác đó có hai góc bằng 60o .

C. Tam giác là tam giác đều nếu và chỉ nếu tam giác đó có hai góc bằng 60o . D. Nếu một tam giác là tam giác đều thì tam giác đó có hai góc bằng nhau.

Câu 4: Viết mệnh đề sau bằng kí hiệu

: “Có một số nguyên bằng bình phương của chính nó” A. 2 ,0xxx

Câu 5: Viết tập hợp

Câu 6: Viết

hoặc

dạng liệt kê các phần tử.

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 1 ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI NĂM HỌC 2022 2023 MÔN: TOÁN





−= . B. 2 , xxx= . C. 2 , xxx= . D. 2 , xxx= .

 2 3720=−+= Axxx dưới

A. 1 ;2 3 A  =−  B. 1 ;2 3 A  =−−  C. 1 ;2 3 A  =   D.  2A =

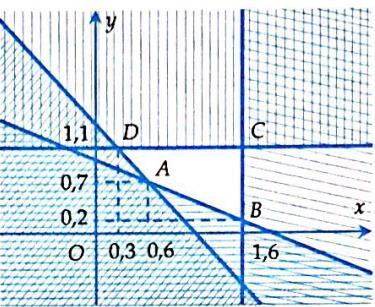
tập hợp  4;3;2;1;0;1;2;3;4A =−−−− bằng cách chỉ ra tính chất đặc trưng. A.  |4=Axx B.  |4=Axx C.  |44=−Axx D.  |4=Axx Câu 7: Số các tập con có hai phần tử của tập  2;1;1;3M =−− là A. 10. B. 4. C. 6. D. 16. Câu 8: Dùng các kí hiệu khoảng, đoạn, nửa khoảng viết lại tập hợp  |53Axx=− là A. ( )5;3 . B. ( 5;3 . C.  5;3 . D.  )5;3 . Câu 9: Kết quả của (  ( )1;4;3−− bằng A. ( ) 1;3. B.   3;4. C. (  ;4.− D. (  ;1.−− Câu 10: Phần bù của  )1;5 trong là A. ( ;1−− B. ( )  );15; −−+ C. ( );1−− D. ( )5;+ Câu 11: Cặp số 1;1 là nghiệm của bất phương trình A. 310.xy B. 0.xy C. 41.xy D. 20.xy

Câu 12: Bất phương trình nào sau đây là bất phương trình bậc nhất hai

Câu 13: Trong mặt phẳng Oxy , điểm nào dưới đây thuộc miền nghiệm của hệ

A. (

1;0.

Câu 14: Trong các hệ thức sau, hệ thức nào đúng

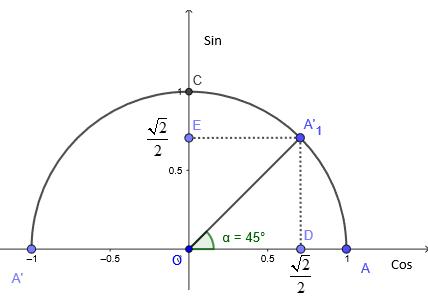
A. 1 sin150

Câu 18: Cho tam giác

Chọn mệnh đề

Câu 19: Tam giác

bán kính đường tròn ngoại tiếp. Hệ thức nào sau đây là

sin

Câu 20: Gọi ,,,,, abcrRS lần lượt là độ dài ba cạnh, bán kính đường tròn nội tiếp, ngoại tiếp và diện tích của ABC , 2 abc p ++ = . Khẳng định nào sau đây là đúng?

A. SpR = . B. 4 abc S R = . C. ( )( )( )1 2 Sppapbpc =−−− . D. 1 cos 2 SabC = .

Câu

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 2

ẩn?

2 230 xy− B. 43xy −+− C. 2 2xy+ D. 2246xy+

31 22 xy xy −  + ?

)

P B. ( ) 1;1.N C. ( ) 1;1.M D. ( ) 0;1.Q

2 = B. 1 cos150= 2 − C. tan1503 = D. 1 cot50 3 = Câu 15: Kết quả 3 2 là giá trị lượng giác của góc nào sau đây? A. sin30 . B. tan60 . C. cos30 . D. sin90 . Câu 16: Trong các khẳng định sau đây, khẳng định nào sai? A. sin30sin150 =− B. tan30tan150 =− C. cot30cot150 =− D. cos30cos150 =− Câu 17: Trong các đẳng thức sau đây, đẳng thức nào đúng? A. ( ) cot180cot−=− B. ( ) cos180cos−= C. ( ) tan180tan−=. D. ( ) sin180sin−=−.

ABC có ABc = , ACb = ,CBa = .

sai ? A. 222 2.cos abcbcA =+− . B. 222 2.cos bacacB =+− . C. 222 2.cos cababB =+− . D. 222 2.cos cbabaC =+− .

ABC có ;= BCa ;= ABc = ACb và có R là

sai? A. 2.

= a R A B. sin. 2 = Aa R C. .sin2. = bBR D. .sin sin. = cA C a

21: Xét mệnh đề kéo theo P: “Nếu 18 chia hết cho 3 thì tam giác cân có 2 cạnh bằng nhau” và Q: “Nếu 17 là số chẵn thì 25 là số chính phương”. Hãy chọn khẳng định đúng trong các khẳng định sau: A. P đúng, Q sai. B. P đúng, Q đúng. C. P sai, Q đúng. D. P sai, Q sai. Câu 22: Hình vẽ sau đây là biểu diễn của tập hợp nào? A. (;2)[5;) −−+ B. (;2)(5;) −−+ C. (;2](5;) −−+ D. (;2][5;) −−+ Câu 23: Cho hai tập hợp  )0;CA =+ , ( ) ( );52;CB =−−−+ . Xác định tập hợp  AB . A. ( )2;0AB=− . B. ( 5;0AB=− . C.  5;2AB=−− . D. ( )5;2AB=−− .

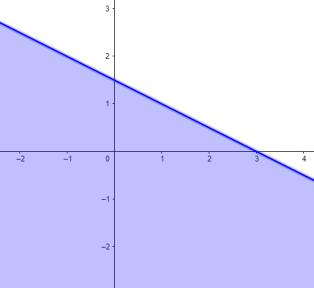
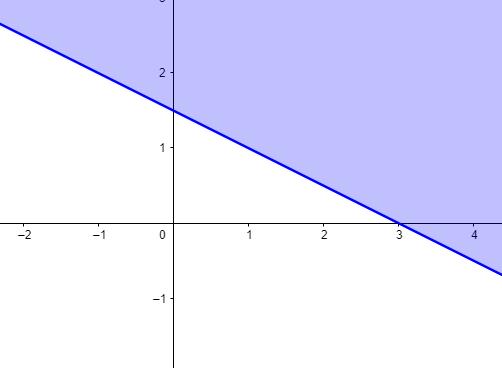
Câu 25: Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi nửa mặt phẳng không bị gạch trong hình vẽ sau?

A. 23 xy−

Câu 26: Hình

3xy

23 xy−

D. 23 xy+ .

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 3 Câu 24: Biết rằng  )3;11CA =− và ( 8;1CB =− . Khi đó ( )CAB  bằng A. ( )8;11 . B.  3;1= . C. (   );811; −−+ .D. ( ) ( );31; −−+ .

. B.

− . C.

vẽ nào sau đây biểu diễn miền nghiệm là của bất phương trình nào sau đây? A. 21xy B. 21xy C. 2xy D. 2xy Câu 27: Điểm ( )0;0O không thuộc miền nghiệm của hệ bất phương trình nào sau đây? A. 30 240 xy xy +  ++ . B. 30 240 xy xy +  +− . C. 360 240 xy xy +−  ++ . D. 360 240 xy xy +−  ++ . Câu 28: Miền tam giác ABC kể cả ba cạnh ,, ABBCCA trong hình là miền nghiệm của hệ bất phương trình nào trong bốn hệ bất phương trình dưới đây? A. 20 20 220 xy xy xy +−  −+  −+ . B. 20 20 220 xy xy xy +−  −+  −+ . C. 20 20 220 xy xy xy +−  −+  −+ D. 20 20 220 xy xy xy +−  −+  −+ Câu 29: Cho tan2  =− . Tính giá trị biểu thức 2sin3cos 3sin2cos P   + = . A. 1 8 P = . B. 7 4 P =− . C. 1 8 P =− . D. 7 4 P = .

Câu 30: Cho tam giác ABC có 8,10==BCCA , và 60 =ACB . Độ dài cạnh AB bằng

A. 321 B. 72 C. 211 D. 221

Câu 31: Tam giác ABC có 120A = thì đẳng thức nào sau đây đúng?

A. 222 3 abcbc =+− . B. 222 abcbc =++ . C. 222 3 abcbc =++ . D. 222 abcbc =+− .

Câu 32: Cho tam giác ABC có 60, 75BC== và 10AC = . Khi đó, độ dài cạnh BC bằng

A. 106 3 . B. 56 . C. 56 3 . D. 10.

Câu 33: Tam giác ABC có độ dài cạnh 3cm=AB ; 6cm=AC và 60 =A . Bán kính R của đường tròn ngoại tiếp tam giác ABC bằng

Câu 34: Cho tam giác ABC

Câu 35: Cho tam giác ABC

tích tam giác ABC

OFFICIAL

vi đường tròn ngoại tiếp tam giác ABC bằng

II. PHẦN TỰ LUẬN (3,0 điểm)

Câu 36: Cho hai tập khác rỗng

Câu 37: Cho hai tập hợp (1

AB

à A, B khác rỗng. Có bao nhiêu giá trị nguyên của m để \ AB = ?

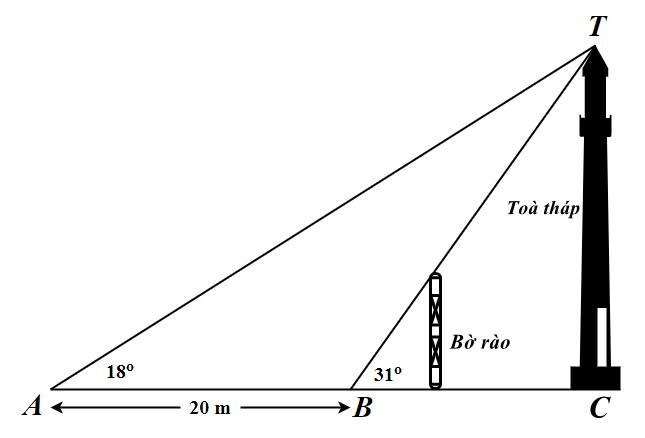
Câu 38: Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt

và biên soạn

DẠYKÈMQUYNHƠN

Sưu tầm

Page 4

3=R B. 33=R C. 3=R D. 6=R

có 6;9;60ABcmACcmBAC===. Diện

là

2273 2 Scm = B. 227 2 Scm = C. 2273 4 Scm = D. 227 4 Scm =

có ( )135, 102.BCBCcm +== Chu

A. ( )10 cm . B. ( )15 cm . C. ( )20 cm . D. ( )25 cm .

( –1;4Am = , ( )–2;22Bm=+ với m . Xác định m để

; 5]Am=− , (3 ; 20205) Bm =− v

đất sao cho ba điểm A, B, C thẳng hàng. Ta đo được AB = 24m, 063CAD = ; 048CBD = . Tính chiều cao h của khối tháp. Câu 39: Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140kg chất A và 9 kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng có thể chiết xuất được 20kg chất A và 0,6 kg chất B. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất được 10kg chất A và 1,5 kg chất B. Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất, biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II? ---------- HẾT ----------

HƯỚNG DẪN GIẢI CHI TIẾT

I. PHẦN TRẮC NGHIỆM

Câu 1: Phát biểu nào sau đây là một mệnh đề?

A. Trời hôm nay đẹp quá!

C. Con đang làm gì đó?

B là một mệnh đề.

B. New York là thủ đô của Việt Nam.

D. Số 3 có phải là số tự nhiên không?

Lời giải

Câu 2: Mệnh đề phủ định của mệnh đề: “ 2022 là một số chẵn” là:

A. 2022 không là một số chẵn.

B. 2022 không là một số chẵn.

C. 2022 là một số lẻ.

D. 2022 không là một số lẻ.

Chọn B

Lời giải

Câu 3: Cho mệnh đề: “Nếu tam giác có hai góc bằng 60o thì tam giác đó là tam giác đều”. Mệnh đề đảo của mệnh đề trên là:

OFFICIAL

A. Nếu tam giác có hai góc bằng 60o thì tam giác đó không là tam giác đều.

B. Nếu tam giác là tam giác đều thì tam giác đó có hai góc bằng 60o

C. Tam giác là tam giác đều nếu và chỉ nếu tam giác đó có hai góc bằng 60o

D. Nếu một tam giác là tam giác đều thì tam giác đó có hai góc bằng nhau.

Lời giải

Mệnh đề đảo của mệnh đề:: “Nếu tam giác có hai góc bằng 60o thì tam giác đó là tam giác đều” là “Nếu tam giác là tam giác đều thì tam giác đó có hai góc bằng 60o ”.

Câu 4: Viết mệnh đề sau bằng kí hiệu  hoặc : “Có

bằng bình

của chính nó”

Sưu

biên

DẠYKÈMQUYNHƠN

tầm và

soạn Page 5

một số nguyên

phương

A. 2 ,0xxx −= . B. 2 , xxx= . C. 2 , xxx= . D. 2 , xxx= . Lời giải Dựa vào mệnh đề: “Có một số nguyên bằng bình phương của chính nó” ta có mệnh đề: 2 , xxx= Câu 5: Viết tập hợp  2 3720=−+= Axxx dưới dạng liệt kê các phần tử. A. 1 ;2 3 A  =−  B. 1 ;2 3 A  =−−  C. 1 ;2 3 A  =   D.  2A = Lời giải Ta có 2 1 3720 3 2 x xx x  −+==  = Vậy  2A = Câu 6: Viết tập hợp  4;3;2;1;0;1;2;3;4A =−−−− bằng cách chỉ ra tính chất đặc trưng. A.  |4=Axx . B.  |4=Axx . C.  |44=−Axx . D.  |4=Axx . Lời giải

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 6 Tập hợp A gồm các số nguyên 4;3;2;1;0;1;2;3;4 nên  4=Axx . Câu 7: Số các tập con có hai phần tử của tập  2;1;1;3M =−− là A. 10 B. 4 C. 6 D. 16 Lời giải Các tập con có hai phần tử của tập  2;1;1;3M =−− là             2;1,2;1,2;3,1;1,1;3,1;3. Vậy số tập con cần tìm bằng 6. Câu 8: Dùng các kí hiệu khoảng, đoạn, nửa khoảng viết lại tập hợp  |53Axx=− là A. ( )5;3 B. ( 5;3 C.  5;3 D.  )5;3 Lời giải Áp dụng quy tắc viết các tập con của tâp số thực    ); Axaxbab == . Từ đó ta có    )|535;3Axx=−=− . Câu 9: Kết quả của (  ( )1;4;3−− bằng A. ( ) 1;3. B.   3;4. C. (  ;4.− D. (  ;1.−− Lời giải Ta có: (  ( ) ( )1;4;31;3 −−=− Câu 10: Phần bù của  )1;5 trong là A. ( ;1−− . B. ( )  );15; −−+ . C. ( );1−− . D. ( )5;+ . Lời giải  )  ( )  ) 1;5\1;5);15;.RC −=−=−−+ Câu 11: Cặp số 1;1 là nghiệm của bất phương trình A. 310.xy B. 0.xy C. 41.xy D. 20.xy Lời giải Chọn C Câu 12: Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn? A. 2 230 xy− B. 43xy −+− C. 2 2xy+ D. 2246xy+ Lời giải Ta thấy A,C,D là bất phương trình bậc 2 hai ẩn. Câu 13: Trong mặt phẳng Oxy , điểm nào dưới đây thuộc miền nghiệm của hệ 31 22 xy xy −  + ? A. ( ) 1;0.P B. ( ) 1;1.N C. ( ) 1;1.M D. ( ) 0;1.Q Lời giải Ta thấy tọa độ điểm M thỏa mãn hệ bất phương trình nên thuộc miền nghiệm của hệ bất phương trình Câu 14: Trong các hệ thức sau, hệ thức nào đúng? A. 1 sin150 2 = . B. 1 cos150= 2 − . C. tan1503 = . D. 1 cot50 3 = .

Lời

17: Trong

18: Cho tam giác

Chọn mệnh đề sai ?

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 7 Lời giải Ta có 1 sin150 2 = ; 3 cos150= 2 − ; 3 tan150 3 =− ; cot503 =− . Câu 15: Kết quả 3 2 là giá trị lượng giác của góc nào sau đây? A. sin30 B. tan60 C. cos30 D. sin90

giải Ta có 3 cos30 2 = . Câu 16: Trong các khẳng định sau đây, khẳng định nào sai? A. sin30sin150 =− . B. tan30tan150 =− . C. cot30cot150 =− D. cos30cos150 =−

giải Ta có ( ) sin30sin18030sin150 =−= Câu

các đẳng thức sau đây, đẳng thức nào đúng? A. ( ) cot180cot−=−. B. ( ) cos180cos−=. C. ( ) tan180tan−=. D. ( ) sin180sin−=−. Lời giải Ta có: ( ) sin180sin−= ( ) cos180cos−=− ( ) tan180tan−=− ( ) cot180cot−=− Câu

ABC có ABc = , ACb = ,CBa = .

A. 222 2.cos abcbcA =+− . B. 222 2.cos bacacB =+− . C. 222 2.cos cababB =+− . D. 222 2.cos cbabaC =+− Lời giải 222 2.cos cababB =+− là mệnh đề sai. Câu 19: Tam giác ABC có ;= BCa ;= ABc = ACb và có R là bán kính đường tròn ngoại tiếp. Hệ thức nào sau đây là sai? A. 2. sin = a R A B. sin. 2 = Aa R C. .sin2. = bBR D. .sin sin. = cA C a Lời giải Theo định lý sin trong tam giác 2. sinsinsin === abc R ABC Nên ta suy ra đáp án sai là .sin2 = bBR Câu 20: Gọi ,,,,, abcrRS lần lượt là độ dài ba cạnh, bán kính đường tròn nội tiếp, ngoại tiếp và diện tích của ABC , 2 abc p ++ = . Khẳng định nào sau đây là đúng? A. SpR = . B. 4 abc S R = .

giác cân có

cạnh bằng nhau” và

phương”. Hãy chọn khẳng định đúng trong các khẳng định sau:

A. P đúng, Q sai. B. P đúng, Q đúng. C. P sai, Q đúng. D. P sai, Q sai. Lời giải

Ta có P đúng vì cả hai mệnh đề giả thiết và kết luận đều đúng.

Q đúng vì giả thiết “17là số chẵn” là mệnh đề sai.

Câu 22: Hình vẽ sau đây là biểu

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 8 C. ( )( )( )1 2 Sppapbpc =−−− D. 1 cos 2 SabC = Lời giải SpR = sai vì Spr = với r là bán kính đường tròn nội tiếp ABC . ( )( )( )1 2 Sppapbpc =−−− sai vì ( )( )( )Sppapbpc =−−− với 2 abc p ++ = 1 cos 2 SabC = sai vì 1 sin 2 SabC = . 4 abc S R = đúng vì 4 abc S R = . Câu 21: Xét mệnh đề kéo theo P: “Nếu 18 chia hết cho 3 thì tam

: “Nếu 17 là số chẵn thì 25 là số chính

diễn của tập hợp nào? A. (;2)[5;) −−+ B. (;2)(5;) −−+ C. (;2](5;) −−+ . D. (;2][5;) −−+ . Lời giải Hình vẽ biểu diễn của tập hợp (;2)[5;) −−+ Câu 23: Cho hai tập hợp  )0;CA =+ , ( ) ( );52;CB =−−−+ . Xác định tập hợp  AB . A. ( )2;0AB=− . B. ( 5;0AB=− . C.  5;2AB=−− . D. ( )5;2AB=−− . Lời giải Ta có  )0;CA =+ nên ( );0A =− ( ) ( );52;CB =−−−+ nên  5;2B =−− Do đó  5;2AB=−− Câu 24: Biết rằng  )3;11CA =− và ( 8;1CB =− . Khi đó ( )CAB  bằng A. ( )8;11 . B.  3;1= . C. (   );811; −−+ . D. ( ) ( );31; −−+ . Lời giải Cách 1: + ( )  );311;A =−−+ , (  ( );81;B =−−+ . + (   );811;AB=−−+ . + ( ) ( )8;11CAB=− Cách 2: ( ) ( )8;11CABCACB==−

Câu

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 9

25: Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi nửa mặt phẳng không bị gạch trong hình vẽ sau? A. 23 xy− B. 3xy− C. 23 xy− D. 23 xy+ Lời giải Đường thẳng 23 xy−= đi qua điểm ( ) 3 0;3,;0 2    . Loại B Thay tọa độ điểm ( )0;0O vào vế trái của các bất phương trình ở đáp án A, C, D. Ta thấy đáp án A thỏa mãn. Câu 26: Hình vẽ nào sau đây biểu diễn miền nghiệm là của bất phương trình nào sau đây? A. 21xy . B. 21xy . C. 2xy . D. 2xy . Lời giải Chọn D Câu 27: Điểm ( )0;0O không thuộc miền nghiệm của hệ bất phương trình nào sau đây? A. 30 240 xy xy +  ++ . B. 30 240 xy xy +  +− . C. 360 240 xy xy +−  ++ D. 360 240 xy xy +−  ++ Lời giải Thay tọa độ O vào hệ ta được đáp án. Câu 28: Miền tam giác ABC kể cả ba cạnh ,, ABBCCA trong hình là miền nghiệm của hệ bất phương trình nào trong bốn hệ bất phương trình dưới đây?

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 10 A. 20 20 220 xy xy xy +−  −+  −+ . B. 20 20 220 xy xy xy +−  −+  −+ . C. 20 20 220 xy xy xy +−  −+  −+ . D. 20 20 220 xy xy xy +−  −+  −+ . Lời giải Cạnh AB nằm trên đường thẳng 1 :20dxy+−= Cạnh AC nằm trên đường thẳng 2 :20dxy−+= Cạnh BC nằm trên đường thẳng 3 :220dxy−+= Đường thẳng 1 :20dxy+−= chia mặt phẳng Oxy thành hai nửa mặt phẳng bờ 1d , thay tọa độ ( )0;0O vào vế trái 1d ta có 20− . Vậy nửa mặt phẳng chứa điểm O là miền nghiệm của bất phương trình 20xy+− Tương tự nửa mặt phẳng chứa điểm O là miền nghiệm của bất phương trình 20xy−+ . Nửa mặt phẳng không chứa điểm O là miền nghiệm của bất phương trình 220xy−+ . Từ (1),(2),(3) suy ra miền tam giác ABC kể cả ba cạnh ,, ABBCCA là miền nghiệm của hệ bất phương trình 20 20 220 xy xy xy +−  −+  −+ . Câu 29: Cho tan2  =− . Tính giá trị biểu thức 2sin3cos 3sin2cos P   + = A. 1 8 P = B. 7 4 P =− C. 1 8 P =− D. 7 4 P =

31: Tam giác

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 11 Lời giải Ta có: 2sin3cos 3sin2cos P   + = 23sincos coscos 32sincos coscos     + = 2tan3 3tan2   + = ( ) ( ) 223 1 3228 −+ == . Câu 30: Cho tam giác ABC có 8,10==BCCA , và 60 =ACB . Độ dài cạnh AB bằng A. 321. B. 72 . C. 211. D. 221. Lời giải Ta có: 222222..cos8102.8.10.cos6084 =+−=+−=ABBCCABCCAC 221= AB Câu

ABC có 120A = thì đẳng thức nào sau đây đúng? A. 222 3 abcbc =+− . B. 222 abcbc =++ . C. 222 3 abcbc =++ D. 222 abcbc =+− Lời giải Áp dụng định lí hàm số cos tại đỉnh A ta có: 222 2.cos abcbcA =+− . 222 2.os120abcbcc =+− 222 abcbc=++ . Câu 32: Cho tam giác ABC có 60, 75BC== và 10AC = Khi đó, độ dài cạnh BC bằng A. 106 3 . B. 56 . C. 56 3 . D. 10. Lời giải Ta có 180607545A =−−= . Áp dụng định lí Sin cho tam giác ABC , ta có: .sin10.sin45106 sinsinsinsin603 BCACACA BC ABB  ====  Câu 33: Tam giác ABC có độ dài cạnh 3cm=AB ; 6cm=AC và 60 =A . Bán kính R của đường tròn ngoại tiếp tam giác ABC bằng A. 3=R B. 33=R C. 3=R D. 6=R Lời giải Xét tam giác ABC ta có: 222 2..cos=+− BCABACABACA 222362.3.6.cos6027=+−= BC 222+=BCABAC Do đó tam giác ABC vuông tại B Vậy bán kính R của đường tròn ngoại tiếp tam giác ABC : ( )6 3cm 22 === AC R . Câu 34: Cho tam giác ABC có 6;9;60ABcmACcmBAC===. Diện tích tam giác ABC là

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 12 A. 2273 2 Scm = B. 227 2 Scm = C. 2273 4 Scm = D. 227 4 Scm = Lời giải 2113273 ...sin.6.9. 2224 SACABBACcm === . Câu 35: Cho tam giác ABC có ( )135, 102.BCBCcm +== Chu vi đường tròn ngoại tiếp tam giác ABC bằng A. ( )10 cm . B. ( )15 cm . C. ( )20 cm . D. ( )25 cm . Lời giải Ta có 13518013545.BCA+==−= Theo định lý sin trong tam giác ta có: ( )102 210. sin2.sin45 BC RRcm A ===  Chu vi đường tròn ngoại tiếp bằng: ( )22.1020 Rcm  == II. PHẦN TỰ LUẬN (3,0 điểm) Câu 36: Cho hai tập khác rỗng ( –1;4Am = , ( )–2;22Bm=+ với m . Xác định m để AB . Lời giải Điều kiện: 14 25 222 m m m − − −+ Ta có 221 3 42 mm ABm +− =−  − . Vậy 25 25 3 m ABm m − −  − . Câu 37: Cho hai tập hợp (1; 5]Am=− , (3 ; 20205) Bm =− và A, B khác rỗng. Có bao nhiêu giá trị nguyên của m để \ AB = ? Lời giải Vì , AB là hai tập hợp khác rỗng, nên ta có điều kiện: 156 32020520176 5 m m m m m −   −    Để \ AB = thì AB  ta có điều kiện: 314 4403 520205403 mm m mm −  − . Kết hợp điều kiện, 46. m  Vậy có 2 giá trị nguyên của m thỏa mãn. Câu 38: Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất sao cho ba điểm A, B, C thẳng hàng. Ta đo được AB = 24m, 063CAD = ; 048CBD = . Tính chiều cao h của khối tháp. Lời giải

chất A và 1,5 kg chất B. Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất, biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II?

giải Gọi số tấn nguyên liệu loại I, loại II được sử dụng lần lượt là ; xy Khi đó chiết xuất được ( )2010xy + kg chất A và ( )0,61,5xy + kg chất B.

số tiền mua nguyên liệu

giả

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 13 Ta có ( ) 000000 631171801174815CADBADADB===−+= Áp dụng định lý sin trong tam giác ABD ta có: .sin sinsinsin ABBDABBAD BD ADBBADADB == Tam giác BCD vuông tại C nên có: sin.sin CD CBDCDBDCBD BD == Vậy ( ) 00 0 .sin.sin24.sin117.sin48 sinsin1561,4m ABBADCBD CD ADB === . Câu 39: Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140kg chất A và 9 kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng có thể chiết xuất được 20kg chất A và 0,6 kg chấtB. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất được 10kg

Lời

Tổng

là ( ) ;43 Txyxy =+ Theo

thiết ta có 010,09 xy  2010140214 xyxy ++ ; 0,61,592530 xyxy ++ . Bài toán trở thành: Tìm , xy thỏa mãn hệ bất phương trình 010 09 214 2530 x y xy xy     +  + sao cho ( ) ;43 Txyxy =+ có giá trị nhỏ nhất. Miền nghiệm của hệ bất phương trình được biểu diễn bởi hình vẽ.

Suy ra miền nghiệm của là miền

Ta có ( ) ( ) (

giác lồi

5;4,10;2,10;9,;9

kể cả biên.

Thử lần lượt tọa độ các điểm trên vào biểu thức ( ) ;43 Txyxy =+ ta được ( ) 5;432T = là nhỏ nhất.

Vậy 5;4xy== . Nghĩa là sử dụng 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II thì chi phí thấp nhất.

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 14

tứ

ABCD,

) 5

2 ABCD  

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 1 ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI NĂM HỌC 2022 2023 MÔN: TOÁN 10 ĐỀ SỐ: 02 I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm) Câu 1: Phát biểu nào sau đây không là mệnh đề? A. 213 x + . B. Mặt trời mọc ở hướng Tây. C. Một tuần có bảy ngày. D. Hình bình hành có một góc vuông là hình chữ nhật. Câu 2: Cho tam giác ABC , khẳng định nào sau đây đúng? A. 222 2.cos abcbcA =++ . B. 222 2.cos abcbcA =+− . C. 222 .cos abcbcA =++ . D. 222 .cos abcbcA =+− . Câu 3: Giá trị cos150 bằng A. 3 2 . B. 1 2 . C. 3 2 . D. cos30 . Câu 4: Điểm ( )0;0O thuộc miền nghiệm của hệ bất phương trình nào sau đây? A. 360 240 +−  ++ xy xy . B. 360 240 +−  ++ xy xy . C. 360 240 +−  ++ xy xy . D. 360 240 +−  ++ xy xy . Câu 5: Cho  là góc tù. Mệnh đề nào đúng trong các mệnh đề sau? A. tan0.  B. cot0.   C. sin0.   D. cos0.   Câu 6: Cho mệnh đề chứa biến ( ) 2 :"1Pnn + chia hết cho 5". Mệnh đề nào sau đây sai? A. ( )4P B. ( )2P C. ( )3P D. ( )7P Câu 7: Miền nghiệm của bất phương trình 23xy+ là phần tô đậm trong hình vẽ của hình nào, trong các hình vẽ dưới đây? A. B. C. D. Câu 8: Cặp số ( )1;–1 là nghiệm của bất phương trình nào sau đây? A. –30xy+ . B. ––0 xy  . C. 310xy++ . D. ––3–10 xy  . Câu 9: Cho tam giác ABC có ,. ABcACb == Diện tích của tam giác ABC bằng A. cos. bcA B. sin. bcA C. 1 cos. 2 bcA D. 1 sin. 2 bcA

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 2 Câu 10: Mệnh đề phủ định của mệnh đề “ Có ít nhất một số thực x thỏa mãn điều kiện bình phương của nó là một số không dương” là A. 2 ":0".  xx B. 2 ":0" xx  . C. 2 ":0".  xx D. 2 ":0".  xx Câu 11: Tam giác ABC có 14,18,20abc=== Khẳng định nào sau đây đúng? A. 4250'B . B. 6056'B . C. 11904'B . D. 90 B . Câu 12: Số phần tử của tập hợp  2 |4410Axxx=−+= là A. 1. B. 2. C. 1 2 . D. 0. Câu 13: Cho hai tập hợp  )5;3A =− và ( 1;4B =− . Xác định tập hợp AB  A.  5;4AB=− . B.  )5;1AB=−− . C. ( )1;3AB=− . D. ( 3;4AB= . Câu 14: Cho tam giác ABC có 33,3,6ACABBC=== . Tính số đo góc B . A. 60 . B. 45 . C. 30 . D. 120 . Câu 15: Trong các đẳng thức sau đây, đẳng thức nào đúng? A. ( ) sin180sin−=−. B. ( ) cos180cos. −= C. ( ) tan180tan−=. D. ( ) cot180cot. −=− Câu 16: Trong các bất phương trình sau đây, bất phương trình nào là bất phương trình bậc nhất hai ẩn? A. 23. xy− B. 2 21.xy− C. 2 0.xy− D. 2323.xy− Câu 17: Mệnh đề nào sau đây đúng? A. 2 :39 xxx . B. 2 :39− xxx . C. 2 :93 xxx D. 2 :93 − xxx Câu 18: Viết tập hợp  4;3;2;1;0;1;2;3;4A =−−−− bằng cách chỉ ra tính chất đặc trưng. A.  |4=Axx . B.  |4=Axx . C.  |44=−Axx . D.  |4=Axx . Câu 19: Giá trị của cos30sin60 + bằng A. 3 3 . B. 3 2 . C. 3 . D. 1. Câu 20: Cho 2 tập hợp:    1;3;5;8;3;5;7;9XY== . Tập hợp XY  bằng tập hợp nào sau đây? A.   3;5. B.   1;3;5;7;8;9. C.   1;7;9. D.   1;3;5. Câu 21: Biết rằng  )3;11CA =− và ( 8;1CB =− . Khi đó, ( )CAB  bằng A. ( )8;11 B.  3;1= C. (   );811; −−+ . D. ( ) ( );31; −−+ . Câu 22: Cho mệnh đề:”Có một học sinh trong lớp 10A không thích học môn Toán ”. Mệnh đề phủ định của mệnh đề này là A. ”Mọi học sinh trong lớp 10A đều thích học môn Văn ”. B. ”Mọi học sinh trong lớp 10A đều không thích học môn Toán ”. C. ”Có một học sinh trong lớp 10A thích học môn Toán ”. D. ”Mọi học sinh trong lớp 10A đều thích học môn Toán ”.

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 3 Câu 23: Giá trị của tan5.tan10.tan15...tan80.tan85 =A là A. 2 B. 1 C. 0 D. 1 Câu 24: Cho tam giác ABC có bán kính đường tròn ngoại tiếp là R Đẳng thức nào sau đây đúng? A. 2. sin = a R A B. sin = a R A C. 3. sin = a R A D. 4. sin = a R A Câu 25: Trong mặt phẳng ,Oxy phần nửa mặt phẳng không tô đậm (không kể bờ) trong hình vẽ bên là biểu diễn hình học tập nghiệm của bất phương trình nào dưới đây? x y 2 3 -3 O A. 23. xy− B. 23. xy− C. 23.xy− D. 23.xy− Câu 26: Trong các tập hợp sau, tập hợp nào là tập hợp rỗng? A.   1.Axx= B.  2 6710.Bxxx=−+= C.  2 420.Cxxx=−+= D.  2 430.Dxxx=−+= Câu 27: Cho hệ bất phương trình 30 2360 xy xy +−  −+ . Trong các điểm sau, điểm nào không thuộc miền nghiệm của hệ bất phương trình trên? A. ( ) 0;0.O B. ( ) 6;0.P C. ( ) 1;1.N D. ( ) 1;1.M Câu 28: Tính diện tích tam giác có ba cạnh lần lượt là 5, 12, 13 A. 60. B. 30. C. 34. D. 75 . Câu 29: Cho biết 2 cos 3  =− . Tính giá trị của biểu thức cot3tan 2cottan E   + = + A. 19 13 =−E B. 19 13 =E C. 25 13 =E D. 25 13 =−E Câu 30: Cho A là tập hợp các hình thoi, B là tập hợp các hình chữ nhật và C là tập hợp các hình vuông. Khẳng định nào sau đây đúng? A. ABC = . B. ABC = . C. \ ABC = . D. \ BAC = . Câu 31: Cho các tập hợp { Mxx = là bội của 2} ; { Nxx = là bội của 6} ; { Pxx = là ước của 2} ; { Qxx = là ước của 6} . Khẳng định nào sau đây đúng? A. .MN  B. QP  C. .MNN = D. PQQ = Câu 32: Cho tam giác ABC có 4AB = cm, 7BC = cm, 9CA = cm. Giá trị cos A bằng A. 2 3 . B. 1 3 . C. 2 3 . D. 1 2 .

t bò ch

trong thức ăn mỗi ngày. Mỗi

200 đơn vị lipit. Mỗi kg thịt lợn chứa 600 đơn vị protein

400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn, giá tiền mỗi kg thịt bò là 250.000 đồng, giá tiền mỗi kg thị

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 4 Câu 33: Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D? A. 0 326 y xy   + B. 0 326 y xy   +− C. 0 326 x xy   + D. 0 326 x xy   +− Câu 34: Cho ABC có 45,75AB== . Tính tỉ số AB BC . A. 6 2 B. 13 2 + C. 632 6 + D. 6 3 Câu 35: Cho hai tập hợp  0;2A = và   0;1;2;3;4.B = Có bao nhiêu tập hợp X thỏa mãn ?A XB= A. 2. B. 3. C. 4. D. 5. II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm) Câu 36: (1,0 điểm). a) Cho hai tập hợp ( )( ) 2 2140Axxx=−−= và   3.Bxx= Xác định tập hợp .AB  b) Cho hai tập hợp ( )0;3M = và ) ;1.Nmm  =+  Tìm m để MNN = Câu 37: (1,0 điểm). a) Cho 1 sin 3  = với 90180.   Tính giá trị biểu thức 2tancos.P =+ b) Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit

kg thị

ứa 800 đơn vị protein và

và

t lợn là 85.000 đồng. Hỏi chi phí ít nhất để mua thịt mỗi ngày của gia đình đó là bao nhiêu? Câu 38: (1,0 điểm). Để đo chiều cao của một tòa nhà, người ta chọn hai điểm A và B thẳng hàng với chân C của tòa nhà, cách nhau 15m. Sử dụng giác kế, từ A và B tương ứng nhìn thấy đỉnh D của tòa nhà dưới các góc 35 và 40 so với phương nằm ngang. Hỏi chiều cao của tòa nhà đo được là bao nhiêu mét? HẾT O 2 3 y x

OFFICIAL

DẠYKÈMQUYNHƠN

Sưu tầm và biên soạn Page 5 HƯỚNG DẪN GIẢI CHI TIẾT I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm) Câu 1: Phát biểu nào sau đây không là mệnh đề? A. 213 x + B. Mặt trời mọc ở hướng Tây. C. Một tuần có bảy ngày. D. Hình bình hành có một góc vuông là hình chữ nhật. Lời giải: 213 x − không phải là mệnh đề Mặt trời mọc ở hướng Tây là mệnh đề sai. Một tuần có bảy ngày là mệnh đề đúng. Hình bình hành có một góc vuông là hình chữ nhật là mệnh đề đúng.  Chọn đáp án A. Câu 2: Cho tam giác ABC , khẳng định nào sau đây đúng? A. 222 2.cos abcbcA =++ . B. 222 2.cos abcbcA =+− . C. 222 .cos abcbcA =++ . D. 222 .cos abcbcA =+− . Câu 3: Giá trị cos150 bằng A. 3 2 B. 1 2 C. 3 2 D. cos30 Câu 4: Điểm ( )0;0O thuộc miền nghiệm của hệ bất phương trình nào sau đây? A. 360 240 +−  ++ xy xy . B. 360 240 +−  ++ xy xy . C. 360 240 +−  ++ xy xy . D. 360 240 +−  ++ xy xy . Lời giải: Thay 0;0xy== vào từng đáp án ta được: 36060 24040 xy xy +−−   ++ (loại A. ); 36060 24040 xy xy +−−   ++ ( LoạiB. ) 36060 24040 xy xy +−−   ++ (thỏa mãn).  Chọn đáp án C. Câu 5: Cho  là góc tù. Mệnh đề nào đúng trong các mệnh đề sau? A. tan0.  B. cot0.   C. sin0.   D. cos0.   Câu 6: Cho mệnh đề chứa biến ( ) 2 :"1Pnn + chia hết cho 5". Mệnh đề nào sau đây sai? A. ( )4P . B. ( )2P . C. ( )3P . D. ( )7P . Lời giải: Ta có: ( ) 417P = , ( ) 25P = , ( ) 310P = , ( ) 750P = .  Chọn đáp án A. Câu 7: Miền nghiệm của bất phương trình 23xy+ là phần tô đậm trong hình vẽ của hình nào, trong các hình vẽ dưới đây?

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 6 A. B. C. D. Lời giải: Trong mặt phẳng tọa độ vẽ đường thẳng :23dxy+= , ta thấy d chia thành 2 nửa mặt phẳng thì ta chọn nửa bên trái do 23xy+  Chọn đáp án B. Câu 8: Cặp số ( )1;–1 là nghiệm của bất phương trình nào sau đây? A. –30xy+ . B. ––0 xy  . C. 310xy++ . D. ––3–10 xy  . Lời giải: ( ) ,31fxyxy=++ . Thay ( ) 1,113110f −=−+=− Câu 9: Cho tam giác ABC có ,. ABcACb == Diện tích của tam giác ABC bằng A. cos. bcA B. sin. bcA C. 1 cos. 2 bcA D. 1 sin. 2 bcA Câu 10: Mệnh đề phủ định của mệnh đề “ Có ít nhất một số thực x thỏa mãn điều kiện bình phương của nó là một số không dương” là A. 2 ":0".  xx B. 2 ":0" xx  C. 2 ":0".  xx D. 2 ":0".  xx Lời giải: Theo giả thiết ta có mệnh đề: 2 ":0"Pxx= . Mệnh đề phủ định của P là 2 :":0" Pxx .  Chọn đáp án D. Câu 11: Tam giác ABC có 14,18,20abc=== Khẳng định nào sau đây đúng? A. 4250'B . B. 6056'B . C. 11904'B . D. 90 B . Lời giải: Ta có 22222214201817 cos 22.14.2035 acb B ac +−+− === Suy ra: 6056' oB   Chọn đáp án B. Câu 12: Số phần tử của tập hợp  2 |4410Axxx=−+= là A. 1 B. 2 C. 1 2 D. 0 Lời giải: 2 1 4410 2 xxx−+== . Số phần tử của tập hợp A là 1.

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 7  Chọn đáp án A. Câu 13: Cho hai tập hợp  )5;3A =− và ( 1;4B =− . Xác định tập hợp AB  A.  5;4AB=− . B.  )5;1AB=−− . C. ( )1;3AB=− . D. ( 3;4AB= . Lời giải:  ) (  ( )5;31;41;3AB=−−=− .  Chọn đáp án C. Câu 14: Cho tam giác ABC có 33,3,6ACABBC=== . Tính số đo góc B A. 60 B. 45 C. 30 D. 120 Lời giải: 222 cos 2. ABBCAC B ABBC +− = 936271 362 +− == Vậy số đo góc B là 60 .  Chọn đáp án A. Câu 15: Trong các đẳng thức sau đây, đẳng thức nào đúng? A. ( ) sin180sin−=−. B. ( ) cos180cos. −= C. ( ) tan180tan−=. D. ( ) cot180cot. −=− Câu 16: Trong các bất phương trình sau đây, bất phương trình nào là bất phương trình bậc nhất hai ẩn? A. 23. xy− B. 2 21.xy− C. 2 0.xy− D. 2323.xy− Câu 17: Mệnh đề nào sau đây đúng? A. 2 :39 xxx B. 2 :39− xxx C. 2 :93 xxx D. 2 :93 − xxx Câu 18: Viết tập hợp  4;3;2;1;0;1;2;3;4A =−−−− bằng cách chỉ ra tính chất đặc trưng. A.  |4=Axx . B.  |4=Axx . C.  |44=−Axx . D.  |4=Axx . Lời giải: Tập hợp A gồm các số nguyên 4;3;2;1;0;1;2;3;4 nên  4=Axx  Chọn đáp án D. Câu 19: Giá trị của cos30sin60 + bằng A. 3 3 . B. 3 2 . C. 3 . D. 1. Lời giải: 33 cos30sin603 22 +=+=  Chọn đáp án C. Câu 20: Cho 2 tập hợp:    1;3;5;8;3;5;7;9XY== . Tập hợp XY  bằng tập hợp nào sau đây? A.   3;5. B.   1;3;5;7;8;9. C.   1;7;9. D.   1;3;5. Câu 21: Biết rằng  )3;11CA =− và ( 8;1CB =− . Khi đó, ( )CAB  bằng A. ( )8;11 B.  3;1=

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 8 C. (   );811; −−+ D. ( ) ( );31; −−+ Lời giải: Cách 1: + ( )  );311;A =−−+ , (  ( );81;B =−−+ + (   );811;AB=−−+ + ( ) ( )8;11CAB=− Cách 2: ( ) ( )8;11CABCACB==−  Chọn đáp án A. Câu 22: Cho mệnh đề:”Có một học sinh trong lớp 10A không thích học môn Toán ”. Mệnh đề phủ định của mệnh đề này là A. ”Mọi học sinh trong lớp 10A đều thích học môn Văn ”. B. ”Mọi học sinh trong lớp 10A đều không thích học môn Toán ”. C. ”Có một học sinh trong lớp 10A thích học môn Toán ”. D. ”Mọi học sinh trong lớp 10A đều thích học môn Toán ”. Câu 23: Giá trị của tan5.tan10.tan15...tan80.tan85 =A là A. 2. B. 1. C. 0. D. 1. Lời giải: ( ) ( ) ( ) tan5.tan85.tan10.tan80...tan40.tan50.tan451 ==A Câu 24: Cho tam giác ABC có bán kính đường tròn ngoại tiếp là R Đẳng thức nào sau đây đúng? A. 2. sin = a R A B. . sin = a R A C. 3. sin = a R A D. 4. sin = a R A Câu 25: Trong mặt phẳng ,Oxy phần nửa mặt phẳng không tô đậm (không kể bờ) trong hình vẽ bên là biểu diễn hình học tập nghiệm của bất phương trình nào dưới đây? x y 2 3 -3 O A. 23. xy− B. 23. xy− C. 23.xy− D. 23.xy− Câu 26: Trong các tập hợp sau, tập hợp nào là tập hợp rỗng? A.   1.Axx= B.  2 6710.Bxxx=−+= C.  2 420.Cxxx=−+= D.  2 430.Dxxx=−+= Lời giải: Xét các đáp án:  Đáp án A. Ta có  1110xxA −= .  Đáp án B. Ta có  2 1 67101 1 6 x xxB x  =  −+==  =  .  Đáp án C. Ta có 2 42022 xxxC −+=== .

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 9  Đáp án D. Ta có  2 3 4301;3 1 x xxD x  = −+==  =  Chọn đáp án C. Câu 27: Cho hệ bất phương trình 30 2360 xy xy +−  −+ . Trong các điểm sau, điểm nào không thuộc miền nghiệm của hệ bất phương trình trên? A. ( ) 0;0.O B. ( ) 6;0.P C. ( ) 1;1.N D. ( ) 1;1.M Câu 28: Tính diện tích tam giác có ba cạnh lần lượt là 5, 12, 13. A. 60. B. 30. C. 34. D. 75 . Lời giải: Nửa chu vi của tam giác là: 51213 15 2p ++ == Diện tích của tam giác là: ( )( )( ) ( )( )( ) 51213151551512151330Spppp =−−−=−−−= .  Chọn đáp án B. Câu 29: Cho biết 2 cos 3  =− . Tính giá trị của biểu thức cot3tan 2cottan E   + = + A. 19 13 =−E B. 19 13 =E C. 25 13 =E D. 25 13 =−E Lời giải: ( ) ( ) 2 22 2 22 2 2 3 3tan122 cot3tan13tan32cos19 cos 1 2cottan13 2tan1cos 11tan 1 cos E        +− ++− ====== + ++ ++ + . Câu 30: Cho A là tập hợp các hình thoi, B là tập hợp các hình chữ nhật và C là tập hợp các hình vuông. Khẳng định nào sau đây đúng? A. ABC = . B. ABC = . C. \ ABC = . D. \ BAC = . Lời giải: Vì tứ giác vừa là hình thoi vừa là hình chữ nhật chính là hình vuông.  Chọn đáp án A. Câu 31: Cho các tập hợp { Mxx = là bội của 2} ; { Nxx = là bội của 6} ; { Pxx = là ước của 2} ; { Qxx = là ước của 6} . Khẳng định nào sau đây đúng? A. .MN  B. QP  C. .MNN = D. PQQ = Lời giải: Ta có các tập hợp             2,2;4;6;8;10;... 6,6;12;18;24;... 1;2 1;2;3;6 Mxxkk Nxxkk P Q    ===  ===   =  =  Do đó .NMMNN =  Chọn đáp án C. Câu 32: Cho tam giác ABC có 4AB = cm, 7BC = cm, 9CA = cm. Giá trị cos A bằng

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 10 A. 2 3 . B. 1 3 . C. 2 3 . D. 1 2 . Lời giải: Ta có: 222 222 2 2..coscos 2.3 ABACBC BCABACABACAA ABAC +− =+−== .  Chọn đáp án A. Câu 33: Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D? A. 0 326 y xy   + B. 0 326 y xy   +− C. 0 326 x xy   + D. 0 326 x xy   +− Lời giải: Dựa vào hình vẽ ta thấy đồ thị gồm hai đường thẳng ( )1 :0dy = và đường thẳng ( )2 :326.dxy+= Miền nghiệm gồm phần y nhận giá trị dương. Lại có ( )0;0 thỏa mãn bất phương trình 326. xy+  Chọn đáp án A. Câu 34: Cho ABC có 45,75AB== . Tính tỉ số AB BC A. 6 2 . B. 13 2 + . C. 632 6 + . D. 6 3 . Lời giải: Áp dụng định lí hàm số sin trong tam giác ABC , ta có ( )sin1804575 sinsin606 sinsinsinsin45sin452 ABBCABC CABCA −−  =====  .  Chọn đáp án A. Câu 35: Cho hai tập hợp  0;2A = và   0;1;2;3;4.B = Có bao nhiêu tập hợp X thỏa mãn ?A XB= A. 2. B. 3. C. 4. D. 5. Lời giải: Vì A XB= nên 1,3,4 .X Các tập X có thể là         1;3;4,1;3;4;0,1;3;4;2,1;3;4;0;2.  Chọn đáp án C. II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm) O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 11 Câu 36: (1,0 điểm). a) Cho hai tập hợp ( )( ) 2 2140Axxx=−−= và   3.Bxx= Xác định tập hợp AB  Lời giải: Ta có: ( )( )  2 2 1 2102 214022;2. 40 2 x x xxxA x x  = −=  −−==−=−  −=  =    3330;1;2;3. x xxB  −⎯⎯⎯→= Vậy   2;0;1;2;3.AB=− b) Cho hai tập hợp ( )0;3M = và ) ;1.Nmm  =+  Tìm m để .MNN = Lời giải: Ta có: MNNNM= (00 0130;2. 132 mm mmm mm  +  + Câu 37: (1,0 điểm). a) Cho 1 sin 3  = với 90180.   Tính giá trị biểu thức 2tancos.P =+ Lời giải: Ta có: 22 22 8cos 3 cos1sin. 9 22 cos 3     = =−=  =−  Do 90180   nên chọn 22 cos. 3  =− Ta có: sin222272 tan2tancos2. cos4436 P    ==−=+=−+−=−    b) Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kg thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kg thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn, giá tiền mỗi kg thịt bò là 250.000 đồng, giá tiền mỗi kg thịt lợn là 85.000 đồng. Hỏi chi phí ít nhất để mua thịt mỗi ngày của gia đình đó là bao nhiêu? Lời giải: Gọi x và y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó mua mỗi ngày. Khi đó, x và y phải thỏa mãn hệ bất phương trình: 869 244 01,6 01,1 xy xy x y +  +     Lượng tiền để mua thịt là 25085 Txy =+ (nghìn đồng). Miền nghiệm của hệ bất phương trình trên là miền tứ giác ABCD với ( )0,6;0,7A , ( ) 1,6;0,2,B ( )1,6;1,1C và ( )0,3;1,1D

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 12 Lập bảng: Đỉnh ( )0,6;0,7A ( )1,6;0,2B T 209.500417.000 Đỉnh ( )1,6;1,1C ( )0,3;1,1D T 493.500168.500 Vậy chi phí mua thịt ít nhất là 168.500 đồng. Câu 38: (1,0 điểm). Để đo chiều cao của một tòa nhà, người ta chọn hai điểm A và B thẳng hàng với chân C của tòa nhà, cách nhau 15m. Sử dụng giác kế, từ A và B tương ứng nhìn thấy đỉnh D của tòa nhà dưới các góc 35 và 40 so với phương nằm ngang. Hỏi chiều cao của tòa nhà đo được là bao nhiêu mét? Lời giải: Do 40CBD = , 35BAD = nên 40355ABD =−= (H.3.3). Áp dụng định lí sin cho tam giác ABD ta được 15 .sin.sin35 sinsin5 AB BDA D ==  . Từ đó suy ra chiều cao của tòa nhà bằng ( )15 .sin.sin3563,45m. sin5 ===  hCDBDCBD ____________________HẾT____________________ Huế, 09h40’ Ngày 26 tháng 9 năm 2022

I. PHẦN TRẮC NGHIỆM (35 câu 7,0 điểm)

Câu 1: Cho mệnh đề chứa biến ( )Px : 2 "540" xx−+= . Mệnh đề nào dưới đây đúng

A. ( )1P B. ( )5P C. ( )6P D. ( )7P

Câu 2: Trong các câu sau, câu nào là mệnh đề đúng?

A. 7là hợp số.

B. 102 chia hết cho 3.

C. 213 x +=

D. Sài Gòn là thủ đô của Việt Nam.

Câu 3: Cho mệnh đề: "Nếu hai tam giác bằng nhau thì diện tích hai tam giác đó bằng nhau". Trong các mệnh đề sau đây, đâu là mệnh đề đảo của mệnh đề trên?

A. "Nếu hai tam giác có diện tích không bằng nhau thì hai tam giác đó không bằng nhau".

B. "Nếu hai tam giác bằng nhau thì hai tam giác đó có chu vi bằng nhau."

C. "Nếu hai tam giác không bằng nhau thì diện tích hai tam giác đó không bằng nhau".

D. "Nếu hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau."

Câu 4: Mệnh đề phủ định của m

A. 2 ":7" xxx

C. 2 ":7"

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 1 ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI NĂM HỌC 2022 2023 MÔN: TOÁN 10 – ĐỀ SỐ: 03

ệnh đề 2 ":7" xxx + là:

+

2 ":7" xxx +

xxx +

2 ":7" xxx + Câu 5: Tập hợp  |5Nxx= có bao nhiêu phần tử? A. ( ) 0nN = . B. ( ) 6nN = . C. ( ) 4nN = . D. ( ) 5nN = . Câu 6: Trong các tập hợp sau, tập hợp nào là tập hợp rỗng. A.  |1xx . B.  2 |340xxx −−= . C.  2 |410xxx −+= D.  2 |2410xxx −−= Câu 7: Cho A = {1; 3; 5}. Tập hợp nào sau đây là tập con của tập A ? A.   . B.  0;1;5 . C.  1;3 . D.  1;3;5;6 . Câu 8: Hình vẽ nào sau đây minh họa cho tập hợp ( 1;4 ? A. . B. . C. D. Câu 9: Cho hai tập hợp    1;2;5;6,1;2;3;4;5;6;7;8AB== khi đó tập B CA là A.   1;2;4;6. B.   4;6. C.   3;4;7;8. D.   2;6;7;8. Câu 10: Phần bù của nửa khoảng  )2;1 trong là A. ( ;1− B. ( )  );21; −−+ C. (  ( );21; −−+ D. ( );2−− Câu 11: Bất phương trình nào sau đây không phải là bất phương trình bậc nhất hai ẩn? A. 3()2(4)0 xyy−−+ . B. 2 257 xy− . C. 23 356 xy+ D. –70xy +

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 2 Câu 12: Cặp số ( )1;–2 là nghiệm của bất phương trình nào sau đây? A. –50xy+ . B. –0xy  . C. 10xy++ . D. ––3–20 xy  . Câu 13: Trong các hệ sau, hệ nào không phải là hệ bất phương trình bậc nhất hai ẩn: A. 34 212 1 −  +   xy xy y B. 13 3  −  + x y C. 14 35 + −  xy x D. 2 4 215 −  + xy xy Câu 14: Trên nữa đường tròn đơn vị, cho góc  như hình vẽ. Hãy chỉ ra các giá trị lượng giác của góc  . A. Sin1  = ; 2 Cos 2  = ; Tan2  = ; 2 Cot 2  = . B. 2 Sin 2  = ; 2 Cos 2  = ; Tan1  = ; Cot1  = . C. Sin0.5  = ; 2 Cos 2  = ; 2 Tan 2  = ; Cot2  = . D. 2 Sin 2  = ; Cos1  = ; 2 Tan 2  = ; Cot2  = . Câu 15: Cho 00 0,180   và 0180+= . Khẳng định nào sau đây sai? A. sinsin0 += B. coscos0 += C. tantan0 += D. cotcot0 += Câu 16: Cho ( ) ( )00 cos90.sin180 Axx =−− . Khẳng định nào sau đây là khẳng định đúng? A. 2sin Ax = B. 2 cos Ax = C. sincos Axx = D. sincos Axx =− Câu 17: Cho góc xOM = với điểm 122 ; 33 M     trên nửa đường tròn đơn vị. Giá trị lượng giác của tan  là A. 1 tan 22  =− . B. tan22  =− . C. 221 tan 3  = . D. 22 tan 9  =− . Câu 18: Cho tam giác ABC có 7AC = , 8AC = và A60= . Kết quả nào trong các kết quả sau là độ dài của cạnh BC ? A. 7 B. 47 C. 57 D. 257 Câu 19: Cho tam giác ABC biết 45,60BC== . Tỉ số AB AC là A. 6 2 . B. 6 3 . C. 6 . D. 6 5 .

các

đảo đúng?

A. Nếu 2+ab thì có ít nhất một trong hai số , ab lớn hơn 1.

B. Nếu một số tự nhiên chia hết cho 6 thì số đó chia hết cho 3

C. Nếu tứ giác là hình vuông thì hai đường chéo vuông góc với nhau.

OFFICIAL

học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hóa, 2 học sinh giỏi cả Lý và Hóa, 1 học sinh giỏi cả ba môn Toán, Lý, Hóa. Số học giỏi ít nhất một môn của lớp 10A là A. 18 B. 10 C. 9 D. 28

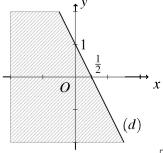
Câu 25: Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi nửa mặt phẳng không bị gạch trong hình vẽ sau?

DẠYKÈMQUYNHƠN

Sưu tầm và biên soạn Page 3 Câu 20: Cho ABC có 0 4,5,150.acB=== Diện tích của tam giác là: A. 53 . B. 10. C. 5. D. 103 . Câu 21: Trong

mệnh đề sau, mệnh đề nào có mệnh đề

D. Trong một tam giác cân hai đường cao bằng nhau. Câu 22: Sử dụng các kí hiệu đoạn, khoảng, nửa khoảng để viết tập hợp  3Axx= A.  )3;A =+ . B. (   );33;A =−−+ . C.  3;3A =− D. ( )3;3A =− Câu 23: Cho các tập hợp ( )4;2A =− ,  )1;5B =− . Biểu diễn trên trục số của tập hợp ( )\ AB  là hình nào dưới đây? A. B. . C. . D. . Câu 24: Lớp 10A có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 3

A. 320xy+− . B. 10xy+− . C. 320xy+− . D. 10xy+− .

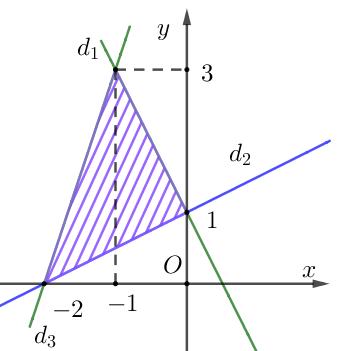
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 4 Câu 26: Bất phương trình nào sau đây có miền nghiệm là phần không bị gạch bỏ d trong hình vẽ A. 21 xy −+ . B. 21 xy− . C. 21 xy+ . D. 20 xy+ . Câu 27: Cặp số ( ); xy nào sau đây không phải là một nghiệm của hệ bất phương trình 5 2 22? 34 xy xy  −−   + A. ( ) ( );0;1xy = B. ( ) ( );4;0 =xy C. ( ) ( );2;2xy = D. ( ) ( );3;4xy = Câu 28: Cho miền gạch chéo như hình vẽ dưới đây Miền trên đây biểu diễn tập nghiệm của bất phương trình nào? A. 21 22 36 xy xy xy +  −+  − B. 21 22 36 xy xy xy +  −+  −− C. 21 22 36 xy xy xy +  −+  −− D. 21 22 36 xy xy xy +  −  − Câu 29: Cho góc  thỏa mãn 1 cos 3 = . Giá trị của biểu thức 1 sin cos P   =+ bằng A. 922 3 + . B. 43 2 . C. 322 3 + . D. 13 2 + . Câu 30: Tam giác có ba cạnh lần lượt là 5,8,9. Góc lớn nhất của tam giác có cosin bằng bao nhiêu? A. 1 10 . B. 1 10 . C. 2 5 . D. 1 2 . Câu 31: Tam giác ABC có 12BC = , 9CA = , 6AB = . Trên cạnh BC lấy điểm M sao cho 8BM = Tính độ dài đoạn thẳng AM A. 34. B. 17. C. 34 . D. 43. Câu 32: Cho tam giác ABC có cạnh 117,6812',3444'ABAB=== . Độ dài cạnh AC xấp xỉ là A. 68,4. B. 118. C. 200. D. 104,6.

OFFICIAL

DẠYKÈMQUYNHƠN

Sưu tầm và biên soạn Page 5 Câu 33: Ở giữa một cái hồ có một cái đảo nhỏ. Để tính khoảng cách từ điểm A trên đảo đến điểm B trên bờ hồ, người ta chọn điểm C . Sau đó thực hiện đo các góc B , C và khoảng cách BC . Biết ˆ 88B  = , ˆ 85C  = và 50mBC = , tính khoảng cách từ A đến B . A. 415,4. B. 412,7. C. 410. D. 408,7. Câu 34: Từ vị trí A người ta quan sát một cây cao. Biết 4 AHm = , 20 HBm = , 45BAC  = . Chiều cao của cây gần nhất với giá trị nào sau đây? A. 19 B. 15 C. 17. D. 14 Câu 35: Cho tam giác ABC có 3,5,6ABACBC=== . Tính bán kính đường tròn ngoại tiếp tam giác ABC . A. 4514 56 . B. 4514 14 . C. 414 45 . D. 4514 28 . II. PHẦN TỰ LUẬN Câu 36: Cho m là một tham số thực và hai tập hợp  12;3Amm=−+ ,  )85; Bm=−+ Tìm tất cả các giá trị m để AB=. Câu 37: Cho hai tập hợp (1; 5]Am=− , (3 ; 20205) Bm =− và A, B khác rỗng. Có bao nhiêu giá trị nguyên của m để \ AB = ?

Câu 38: Một tòa tháp đổ nát được rào lại vì lý do an toàn. Để tìm chiều cao của tháp CT , người đo đứng tại điểm A và

người đo đi thẳng 20 mét về phía chân tháp đến điểm B và đo được góc

góc

chiều cao của tháp, kết quả làm tròn đến hai chữ số thập phân.

OFFICIAL

Câu 39: Cho biết

cos.

Tính giá trị

bán lãi 500 nghìn đồng. Để sản

ất được một sản phẩm I thì Thành phải làm việc trong 4 giờ, Công phải làm việc trong 2 giờ. Để sản xuất được một sản phẩm II thì Thành phải làm việc trong 3 giờ, Công phải làm việc trong 5 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Thành không thể làm việc quá 200 giờ và Công không thể làm việc quá 240 giờ Tìm số tiền lãi lớn nhất trong một tháng của xưởng.

DẠYKÈMQUYNHƠN

Sưu tầm và biên soạn Page 6

đo

018CAT = . Sau đó

031CBT = . Tính

3  =−

của biểu thức cot3tan 2cottan P   + = + Câu 40: Một xưởng cơ khí có hai công nhân là Thành và Công. Xưởng sản xuất loại sản phẩm I và II Mỗi sản phẩm I bán lãi 600 nghìn đồng, mỗi sản phẩm II

---------- HẾT ----------

Lời

Câu 2: Trong các câu sau, câu nào là mệnh đề đúng?

là hợp

chia

Lời

"Nếu hai tam giác bằng nhau thì diện tích hai tam giác đó bằng nhau". Trong các mệnh đề sau đây, đâu là mệnh đề đảo của mệnh đề trên?

Cho mệnh

A. "Nếu hai tam giác có diện tích không bằng nhau thì hai tam giác đó không bằng nhau"

B. "Nếu hai tam giác bằng nhau thì hai tam giác đó có chu vi bằng nhau."

C. "Nếu hai tam giác không bằng nhau thì diện tích hai tam giác đó không bằng nhau".

D. "Nếu hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau."

Mệnh đề “Nếu A thì B ” có mệnh đề

Câu 4: M

Lời giải

là “Nếu B thì A

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 7 HƯỚNG DẪN GIẢI CHI TIẾT I. PHẦN TRẮC NGHIỆM (35 câu 7,0 điểm) Câu 1: Cho mệnh đề chứa biến ( )Px : 2 "540" xx−+= Mệnh đề nào dưới đây đúng A. ( )1P B. ( )5P C. ( )6P D. ( )7P

giải Chọn A

số. B. 102

hết cho 3. C. 213 x += D. Sài Gòn là thủ đô của Việt Nam.

giải Chọn B Câu 3:

đề:

đảo

”

ệnh đề

ủ định của mệnh đề 2 ":7" xxx + là: A. 2 ":7" xxx + B. 2 ":7" xxx + C. 2 ":7" xxx + D. 2 ":7" xxx + Lời giải Chọn D Câu 5: Tập hợp  |5Nxx= có bao nhiêu phần tử? A. ( ) 0nN = B. ( ) 6nN = C. ( ) 4nN = D. ( ) 5nN = Lời giải Ta có 5 x x     0;1;2;3;4x   0;1;2;3;4N = ( ) 5nN = . Câu 6: Trong các tập hợp sau, tập hợp nào là tập hợp rỗng. A.  |1xx B.  2 |340xxx −−= C.  2 |410xxx −+= . D.  2 |2410xxx −−= . Lời giải     |10.AxxA ==  2 |340Bxxx=−−= . Ta có 2 340 xx−−= 1 4 3 x x =−   =   1.B =−  2 |410Cxxx=−+= . Ta có 2 410xx−+= 23 23 x x  =−   =+  C =

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 8  2 |2410Dxxx=−−= . Ta có 2 2410 xx−−= 26 2 26 2 x x  +=   =  2626 ; 22 D  −+  =    Câu 7: Cho A = {1; 3; 5}. Tập hợp nào sau đây là tập con của tập A ? A.   B.  0;1;5 C.  1;3 D.  1;3;5;6 Lời giải Câu 8: Hình vẽ nào sau đây minh họa cho tập hợp ( 1;4 ? A. B. C. . D. Lời giải Vì ( 1;4 gồm các số thực x mà 14 x  nên Câu 9: Cho hai tập hợp    1;2;5;6,1;2;3;4;5;6;7;8AB== khi đó tập B CA là A.   1;2;4;6. B.   4;6. C.   3;4;7;8. D.   2;6;7;8. Lời giải Ta tìm tất cả các phần tử mà tập B có mà tập A không có. Câu 10: Phần bù của nửa khoảng  )2;1 trong là A. ( ;1− . B. ( )  );21; −−+ . C. (  ( );21; −−+ D. ( );2−− Lời giải Gọi  )2;1A =− , ta có: ( )  ) \;21;.CAA==−−+ Vậy ( )  ) ;21;.CA =−−+ Câu 11: Bất phương trình nào sau đây không phải là bất phương trình bậc nhất hai ẩn? A. 3()2(4)0 xyy−−+ . B. 2 257 xy− . C. 23 356 xy+ . D. –70xy + . Lời giải 3()2(4)0358 xyyxy −−+− là bất phương trình bậc nhất hai ẩn. 2 257 xy− không là bất phương trình bậc nhất hai ẩn. 23 35691256 xyxy ++ là bất phương trình bậc nhất hai ẩn. –70xy + là bất phương trình bậc nhất hai ẩn. Câu 12: Cặp số ( )1;–2 là nghiệm của bất phương trình nào sau đây? A. –50xy+ B. –0xy  C. 10xy++ D. ––3–20 xy  Lời giải Thay tọa độ ( )1;–2 vào các bpt, ta thấy bpt ––3–20 xy  thỏa mãn Câu 13: Trong các hệ sau, hệ nào không phải là hệ bất phương trình bậc nhất hai ẩn:

Lời

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 9 A. 34 212 1 −  +   xy xy y B. 13 3  −  + x y C. 14 35 + −  xy x D. 2 4 215 −  + xy xy

giải Hệ ở đáp án D không là hệ bất phương trình bậc nhất hai ẩn vì hệ này chứa một bất phương trình bậc hai 2 215+xy . Câu 14: Trên nữa đường tròn đơn vị, cho góc  như hình vẽ. Hãy chỉ ra các giá trị lượng giác của góc  . A. Sin1  = ; 2 Cos 2  = ; Tan2  = ; 2 Cot 2  = B. 2 Sin 2  = ; 2 Cos 2  = ; Tan1  = ; Cot1  = . C. Sin0.5  = ; 2 Cos 2  = ; 2 Tan 2  = ; Cot2  = D. 2 Sin 2  = ; Cos1  = ; 2 Tan 2  = ; Cot2  = Lời giải Ta có: 0 2 Sin 2y == ; 0 2 Cos 2 x == ; sin Tan1 cos    == ; cos Cot1 sin    == Câu 15: Cho 00 0,180   và 0180+= . Khẳng định nào sau đây sai? A. sinsin0 += B. coscos0 += C. tantan0 += D. cotcot0 += Lời giải Ta có 0180+= 0180 =− ( )0 sinsin180sin =−= sinsin0  −= . Vậy đáp án A sai. Câu 16: Cho ( ) ( )00 cos90.sin180 Axx =−− . Khẳng định nào sau đây là khẳng định đúng? A. 2sin Ax = B. 2 cos Ax = C. sincos Axx = D. sincos Axx =− Lời giải Ta có ( ) ( )00 cos90.sin180 Axx =−− sin.sinxx= 2sin x= .

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 10 Câu 17: Cho góc xOM = với điểm 122 ; 33 M     trên nửa đường tròn đơn vị. Giá trị lượng giác của tan  là A. 1 tan 22  =− B. tan22  =− C. 221 tan 3  = D. 22 tan 9  =− Lời giải Ta thấy 1 cos22 122sin 3 3 ;tan22 33cos1 22 sin 33 M       =−  −===−    =  . Câu 18: Cho tam giác ABC có 7AC = , 8AC = và A60= . Kết quả nào trong các kết quả sau là độ dài của cạnh BC ? A. 7 B. 47 C. 57 D. 257 Áp dụng định lý hàm số Cosin trong tam giác ABC ta có: 222 2..cos BCABACABACA =+− 22 782.7.8.cos60 =+− 57= 57BC = Câu 19: Cho tam giác ABC biết 45,60BC== . Tỉ số AB AC là A. 6 2 . B. 6 3 . C. 6 . D. 6 5 . Lời giải Áp dụng định lý sin trong tam giác ABC ta có: sinsin606 sinsinsinsin452 ABACABC CBACB  ====  . Câu 20: Cho ABC có 0 4,5,150.acB=== Diện tích của tam giác là: A. 53 . B. 10. C. 5. D. 103 . Lời giải Ta có: 011 ..sin.4.5.sin1505. 22ABC SacB  === MỨC 2 Câu 21: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng? A. Nếu 2+ab thì có ít nhất một trong hai số , ab lớn hơn 1 B. Nếu một số tự nhiên chia hết cho 6 thì số đó chia hết cho 3. C. Nếu tứ giác là hình vuông thì hai đường chéo vuông góc với nhau. D. Trong một tam giác cân hai đường cao bằng nhau. Lời giải “Tam giác có hai đường cao bằng nhau là tam giác cân” là mệnh đề đúng. Câu 22: Sử dụng các kí hiệu đoạn, khoảng, nửa khoảng để viết tập hợp  3Axx= . A.  )3;A =+ B. (   );33;A =−−+ C.  3;3A =− . D. ( )3;3A =− .

Lời giải

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 11 Lời giải Theo tính chất của bất đẳng thức chứa giá trị tuyệt đối ta có 333xx− Câu 23: Cho các tập hợp ( )4;2A =− ,  )1;5B =− . Biểu diễn trên trục số của tập hợp ( )\ AB  là hình nào dưới đây? A. B. . C. . D. . Lời giải Ta có: ( )  )1;2AB=− . ( ) ( )  )\;12; AB =−−+ Câu 24: Lớp 10A có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 3 học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hóa, 2 học sinh giỏi cả Lý và Hóa, 1 học sinh giỏi cả ba môn Toán, Lý, Hóa. Số học giỏi ít nhất một môn của lớp 10A là A. 18. B. 10. C. 9. D. 28.

Gọi A là tập hợp các học sinh giỏi Toán; B là tập hợp các học sinh giỏi Lý; C là tập hợp các học sinh giỏi Hóa. Học sinh giỏi ít nhất một môn là tập hợp ABC  Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )nABCnAnBnCnABnACnBCnABC =++−−−+ 756342110 ++−−−+= . Câu 25: Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi nửa mặt phẳng không bị gạch trong hình vẽ sau? A. 320xy+− . B. 10xy+− . C. 320xy+− . D. 10xy+− . Lời giải Đường thẳng qua điểm (2;0) nên loại đáp án B và D Điểm (0;0)O thuộc miền nghiệm của bất phương trình 320xy+− , do đó chọn đáp án A Câu 26: Bất phương trình nào sau đây có miền nghiệm là phần không bị gạch bỏ d trong hình vẽ

Thay

Suy

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 12 A. 21 xy −+ . B. 21 xy− . C. 21 xy+ . D. 20 xy+ . Lời giải Đường thẳng d đi qua 2 điểm 1 ;0 2    và ( )0;1 nên có phương trình: 21 xy+=

tọa độ của điểm ( )0;0O vào vế trái của đường thẳng d ta được: 01 

ra điểm O thuộc miền nghiệm của bất phương trình 21 xy+ Vậy miền không bị gạch bỏ kể cả bờ là miền nghiệm của bất phương trình 21 xy+ . Câu 27: Cặp số ( ); xy nào sau đây không phải là một nghiệm của hệ bất phương trình 5 2 22? 34 xy xy  −−   + A. ( ) ( );0;1xy = B. ( ) ( );4;0 =xy C. ( ) ( );2;2xy = . D. ( ) ( );3;4xy = . Lời giải Thay 4;0xy== vào hệ bất phương trình ta có : 5 22 22 3124 xy xy  −=−   += Vậy ( ) ( );4;0xy = không là một nghiệm của hệ bất phương trình. Câu 28: Cho miền gạch chéo như hình vẽ dưới đây Miền trên đây biểu diễn tập nghiệm của bất phương trình nào? A. 21 22 36 xy xy xy +  −+  − B. 21 22 36 xy xy xy +  −+  −− C. 21 22 36 xy xy xy +  −+  −− D. 21 22 36 xy xy xy +  −  − Lời giải

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 13 Lấy điểm ( )2;0A nằm trên đường thẳng 36 xy−= nhưng không nằm trên bất kỳ đường thẳng nào trong các đường thẳng 123 ,, ddd . Do đó ta loại A và D. Lấy điểm ( )1;1B thuộc miền gạch chéo thay vào B và C ta thấy C được thỏa mãn. Do đó loại B và Chọn C Câu 29: Cho góc  thỏa mãn 1 cos 3 = . Giá trị của biểu thức 1 sin cos P   =+ bằng A. 922 3 + B. 43 2 C. 322 3 + D. 13 2 + Lời giải Ta có: 2222 sincos1sin1cos +==− Với 1 cos 3 = 2 2 822 39 1 sin1sin 3   =−==   Vậy: 1122229 sin3. 22 cos31 3 3 3 P   + + =+==+= Câu 30: Tam giác có ba cạnh lần lượt là 5,8,9. Góc lớn nhất của tam giác có cosin bằng bao nhiêu? A. 1 10 B. 1 10 C. 2 5 D. 1 2 Lời giải Vì đối diện với cạnh lớn nhất là góc lớn nhất. Nên góc lớn nhất của tam giác có cosin bằng: 222 5891 2.5.810 +− = Câu 31: Tam giác ABC có 12BC = , 9CA = , 6AB = . Trên cạnh BC lấy điểm M sao cho 8BM = . Tính độ dài đoạn thẳng AM . A. 34 B. 17 C. 34 D. 43 Lời giải Xét tam giác ABC ta có 222 cos 2.. BCBAAC B BCBA +− = 222 126911 2.12.616 +− == Xét tam giác ABM , theo định lý hàm số Cosin ta có: 222 2...cos AMBABMBABMB =+− 22 11 682.6.8.34 16 =+−= 34AM = . Câu 32: Cho tam giác ABC có cạnh 117,6812',3444'ABAB=== . Độ dài cạnh AC xấp xỉ là A. 68,4 B. 118 C. 200 D. 104,6 Lời giải Ta có: 180774'CAB=−−= .

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 14 Áp dụng định lý sin trong tam giác ABC ta có: .sin117.sin3444' sinsinsinsin774'68,4 ABACABB AC CBC  ===  Câu 33: Ở giữa một cái hồ có một cái đảo nhỏ. Để tính khoảng cách từ điểm A trên đảo đến điểm B trên bờ hồ, người ta chọn điểm C . Sau đó thực hiện đo các góc B , C và khoảng cách BC Biết ˆ 88B  = , ˆ 85C  = và 50mBC = , tính khoảng cách từ A đến B . A. 415,4 B. 412,7 C. 410 D. 408,7 Lời giải Ta có ˆˆ ˆ 18018088857ABC  =−−=−−= Áp dụng định lí sin ta có: sin50sin85 408,7 sinsinsinsin7m. ABBCBCC AB CAA   === Câu 34: Từ vị trí A người ta quan sát một cây cao. Biết 4 AHm = , 20 HBm = , 45BAC  = . Chiều cao của cây gần nhất với giá trị nào sau đây? A. 19. B. 15. C. 17. D. 14. Lời giải Trong tam giác AHB ta có 41 tan1119 205 AH ABHABH BH  === Suy ra 907841.ABCABH  =− Suy ra 180()5619.ACBBACABC  =−+ Áp dụng định lý sin trong tam giác ABC , ta được sin 17m sinsinsin ABCBABBAC CB ACBBACACB  ==

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 15 Câu 35: Cho tam giác ABC có 3,5,6ABACBC=== . Tính bán kính đường tròn ngoại tiếp tam giác ABC . A. 4514 56 . B. 4514 14 . C. 414 45 . D. 4514 28 . Lời giải Ta có: 356 7 22 ABACBC p ++++ === Diện tích tam giác ABC là: ( )( )( ) ( )( )( ) 7737576214ABC SppABpACpBC  =−−−=−−−= Áp dụng công thức: 44ABC ABC ABACBCABACBC SR RS  == 3.5.64514 4.21456 R == . II. PHẦN TỰ LUẬN Câu 36: Cho m là một tham số thực và hai tập hợp  12;3Amm=−+ ,  )85; Bm=−+ . Tìm tất cả các giá trị m để AB=. Lời giải Ta có  12;3Amm=−+ ,  )85; Bm=−+ AB=  385 123 mm mm +−  −+  65 32 m m   −  5 6 2 3 m m      −   25 36 m − . Câu 37: Cho hai tập hợp (1; 5]Am=− , (3 ; 20205) Bm =− và A, B khác rỗng. Có bao nhiêu giá trị nguyên của m để \ AB = ? Lời giải Vì , AB là hai tập hợp khác rỗng, nên ta có điều kiện: 156 32020520176 5 m m m m m −   −    Để \ AB = thì AB  ta có điều kiện: 314 4403 520205403 mm m mm −  − Kết hợp điều kiện, 46. m  Vậy có 2 giá trị nguyên của m thỏa mãn. Câu 38: Một tòa tháp đổ nát được rào lại vì lý do an toàn. Để tìm chiều cao của tháp CT , người đo đứng tại điểm A và đo góc 018CAT = . Sau đó người đo đi thẳng 20 mét về phía chân tháp đến điểm B và đo được góc 031CBT = . Tính chiều cao của tháp, kết quả làm tròn đến hai chữ số thập phân.

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 16 Lời giải Ta có 0000 1803114913.ABTATB =−== Áp dụng định lí Sin vào tam giác :ABT 27,47. sinsin ABBT BTm ATBBAT = Tam giác BCT vuông tại C : 0 .sin3114,15. CTBTm = Vậy chiều cao của tháp xấp xỉ 14,15. m Câu 39: Cho biết 2 cos. 3  =− Tính giá trị của biểu thức cot3tan 2cottan P   + = + . Lời giải Ta có biểu thức 2222 5 sincos1sin1cos. 9  +==−= Ta có : 2 22 222 cossin25 33. cot3tancos3sin19 sincos39 cossin 2cottan2cossin13 225 sincos2.39 P       +−+ ++  ===== +++−+   Câu 40: Một xưởng cơ khí có hai công nhân là Thành và Công. Xưởng sản xuất loại sản phẩm I và II . Mỗi sản phẩm I bán lãi 600 nghìn đồng, mỗi sản phẩm II bán lãi 500 nghìn đồng. Để sản xuất được một sản phẩm I thì Thành phải làm việc trong 4 giờ, Công phải làm việc trong 2 giờ. Để sản xuất được một sản phẩm II thì Thành phải làm việc trong 3 giờ, Công phải làm việc trong 5 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Thành không thể làm việc quá 200 giờ và Công không thể làm việc quá 240 giờ Tìm số tiền lãi lớn nhất trong một tháng của xưởng. Lời giải Gọi x , y lần lượt là số sản phẩm loại I và loại II được sản xuất ra. Điều kiện x , y nguyên dương. Ta có hệ bất phương trình sau: 43200 25240 0 0 xy xy x y +  +     Miền nghiệm của hệ trên là

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 17 Tiền lãi trong một tháng của xưởng là 0,60,5 Txy =+ . Miền nghiệm của hệ là hình tứ giác OABC với ( )0;48A , ( )20;40B , ( )50;0C , ( )0;0O Vậy tiền lãi lớn nhất trong một tháng của xưởng là 32 triệu đồng.

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 1 ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI NĂM HỌC 2022 2023 MÔN: TOÁN 10 ĐỀ SỐ: 04 I. PHẦN TRẮC NGHIỆM (35 câu 7,0 điểm) Câu 1: Mệnh đề phủ định của mệnh đề :":10"Pxx+ là A. :":10"Pxx+ B. :":10".Pxx+ C. :":10".Pxx+ D. :":10".Pxx+ Câu 2: Cho góc  nhọn. Khẳng định nào sau đây đúng? A. sin0   . B. cos0   . C. tan0   . D. cot0   . Câu 3: Mệnh đề nào sau đây sai? A. Tam giác có ba góc bằng nhau thì có ba cạnh bằng nhau. B. Tổng ba góc trong một tam giác bằng 180.  C. Tam giác có tổng hai góc bằng góc còn lại là tam giác cân. D. Tam giác có ba cạnh bằng nhau thì có ba góc bằng nhau. Câu 4: Cho x là số thực, mệnh đề nào sau đây đúng? A. 2 :55xxx  hoặc 5.x − B. 2 :555.xxx − C. 2 :55.xxx  D. 2 :55xxx  hoặc 5.x − Câu 5: Trong các đẳng thức sau đây, đẳng thức nào đúng? A. ( ) sin180sin−=−. B. ( ) cos180cos. −= C. ( ) tan180tan−=. D. ( ) cot180cot. −=− Câu 6: Trung tuyến AM của tam giác ABC có độ dài bằng A. 222 24 + + bca . B. 222 24 + bca . C. 222 24 + bca . D. 222 24 + acb . Câu 7: Số phần tử của tập hợp  2 1,2Akk k=+  là A. 1. B. 2. C. 3. D. 5. Câu 8: Cho hệ 235(1) 3 25(2) xy xy  +  +  . Gọi 1S là tập nghiệm của bất phương trình (1), 2S là tập nghiệm của bất phương trình (2) và S là tập nghiệm của hệ thì A. 12SS  . B. 21SS  . C. 2 SS = . D. 1 SS  . Câu 9: Trong các đẳng thức sau đây, đẳng thức nào đúng? A. sin1503 2 =− B. 3 cos150 2 = C. 1 tan150 3 =− D. cot1503. = Câu 10: Cho tam giác ABC có 7b = ; 5c = và 3 cos 5 A = . Tính a A. 42 B. 2 C. 2 D. 3

Câu

OFFICIAL

DẠYKÈMQUYNHƠN

Sưu tầm và biên soạn Page 2

11: Kí hiệu X là tập hợp các cầu thủ x trong đội tuyển bóng rổ, ( )Px là mệnh đề chứa biến “ x cao trên 180 cm”. Mệnh đề ",()" xXPx khẳng định rằng:

Mọi cầu thủ trong đội tuyển bóng rổ đều cao trên 180 cm

Trong số các cầu thủ của đội tuyển bóng rổ có một số cầu thủ cao trên 180 cm .

Bất cứ ai cao trên 180 cm đều là cầu thủ của đội tuyển bóng rổ D. Có một số người cao trên 180 cm là cầu thủ của đội tuyển bóng rổ Câu 12: Xét mệnh đề :P 2 ":20" xxxm −+= với m là tham số. Tìm tất cả các giá trị của tham số m để mệnh đề P đúng. A. 1.m  B. 1.m  C. 1.m  D. 1.m  Câu 13: Cho tam giác ABC có 9,18ABAC== và 60 =BAC . Bán kính của đường tròn ngoại tiếp tam giác ABC là A. 3. B. 93 . C. 9. D. 6. Câu 14: Trong các cặp số sau, tìm cặp số không là nghiệm của hệ bất phương trình 20 2320 xy xy  +−  −+ A. ( )0;0 B. ( )1;1 C. ( )1;1 D. ( )1;1 Câu 15: Cho tập ( )( )( ) 22 |412730Xxxxxx =−−−+= . Tính tổng S các phần tử của X . A. 9 2 S = B. 5S = C. 6S = D. 4S = Câu 16: Cho tam giác ABC vuông tại .A Khẳng định nào sau đây sai? A. sincos. BC = B. sincos. 22 ABC+ =   C. ( ) sinsin. ABC =−+ D. ( ) coscos. ABC =−+ Câu 17: Trong mặt phẳng ( )Oxy , phần nửa mặt phẳng không tô đậm (kể cả bờ) trong hình vẽ dưới đây là biểu diễn hình học tập nghiệm của bất phương trình nào? A. 33xy− . B. 33 xy− . C. 33 xy−− . D. 33 xy−− . Câu 18: Trong các tập sau, tập nào là tập rỗng? A.  2 |0Mxx== . B.  |310Nxx=−= . C.  2 |1Pxx== D.  |210Qxx=−= Câu 19: Cho tập {,5}Xxx= . Tập X được viết dưới dạng liệt kê là A. {1;2;3;4}X = B. {0;1;2;3;4}X = C. {1;2;3;4;5}X = D. {0;1;2;3;4;5}X =

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 3 Câu 20: Cho tam giác ABC có ,. ABcACb == Diện tích của tam giác ABC bằng A. cos. bcA B. sin. bcA C. 1 cos. 2 bcA D. 1 sin. 2 bcA Câu 21: Cho 1 cot 3  = . Tính giá trị của biểu thức 3sin4cos . 2sin5cos A   + = A. 15 13 =−A . B. 13=−A . C. 15 13 =A . D. 13=A . Câu 22: Cho các tập hợp ,, ABC được minh họa bằng biểu đồ Ven như hình vẽ. Phần tô đậm trong hình là biểu diễn của tập hợp nào sau đây? A. ABC  B. ( ) ( )A\C\B A C. ( ) B\ AC  D. ( ) B\ AC  Câu 23: Trong các bất phương trình sau đây, bất phương trình nào là bất phương trình bậc nhất hai ẩn? A. 23. xy− B. 2 21.xy− C. 2 0.xy− D. 2323.xy− Câu 24: Trong các tập hợp sau, tập nào có đúng một tập hợp con? A.  B.   1. C.   D.   ;1. Câu 25: Khẳng định nào sau đây sai? A. = ABAAB B. ABAAB = C. \. ==ABAAB D. \.BABAB== Câu 26: Cặp số nào sau đây không là nghiệm của bất phương trình ( ) 5210 −−xy ? A. ( )0;1 B. ( )1;3 C. ( )–1;1 D. ( )–1;0 Câu 27: Cho tam giác ABC có 120.=BAC Đẳng thức nào sau đây đúng? A. 222 3 abcbc =+− . B. 222 abcbc =++ . C. 222 3 abcbc =++ . D. 222 abcbc =+− . Câu 28: Cho  3;4;7;8A = và  1;3;5;7;9B = . Chọn kết quả đúng trong các kết quả sau: A.  1;3;4;5;7;8;9AB= B.  1;3;5;7;9AB= C.  3;7AB= . D.  1;4AB= . Câu 29: Cho tam giác ABC có 4AB = , 5AC = , 6BC = . Tính ( )cos + BC A. 1 8 . B. 1 4 . C. –0,125. D. 0,75.

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 4 Câu 30: Miền nghiệm của bất phương trình 22xy+ là phần không tô đậm (kể cả biên) trong hình vẽ nào dưới đây? A. B. C. D. Câu 31: Cho tập hợp A . Mệnh đề nào sau đây đúng? A. \.A = B. \. AA= C. \. A= D. \.AA = Câu 32: Cho tam giác ABC có chu vi bằng 32 và bán kính đường tròn nội tiếp của ABC bằng 5. Tính diện tích Scủa tam giác ABC . A. = 32 5 S B. = 40.S C. = 160.S D. = 80.S Câu 33: Miền tam giác ABC kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D? A. 0 5410 5410 y xy xy    −  + . B. 0 4510 5410 x xy xy    −  + . C. 0 5410 4510 x xy xy    −  + . D. 0 5410 4510 x xy xy    −  + . Câu 34: Cho tancot m+= . Số giá trị của tham số m để 22 tancot7 += là A. Vô số B. 0 C. 1 D. 2 O C B 5 2 2A x

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 5 Câu 35: Cho tam giác ABC có 9,18ABAC== và 60 =BAC . Tính bán kính R của đường tròn ngoại tiếp tam giác .ABC A. 3=R B. 93=R C. 9=R D. 6=R II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm) Câu 36: (1,0 điểm). a) Cho hai tập hợp  2 320Axxx=−+= và   1;0;1.B =− Xác định các tập hợp ,\. ABBA  b) Cho hai tập hợp ( )0;8M = và ) ;.Nm  =+  Tìm m để tập hợp MN  có đúng 4 số nguyên. Câu 37: (1,0 điểm). a) Cho tan2 x =− với 90180. x  Tính giá trị biểu thức cot3cos. Pxx =− b) Cho tam giác ABC , biết 14,60,40cBACABC === . Tính ,.ab Câu 38: (1,0 điểm). a) Biểu diễn hình học tập nghiệm của hệ bất phương trình ( ) 20 1:10. 210 xy xy xy  ++  −−  −+ b) Tìm , xy thỏa mãn ( )1 sao cho biểu thức 23 Fxy =+ đạt giá trị lớn nhất, giá trị nhỏ nhất. HẾT

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 6 HƯỚNG DẪN GIẢI CHI TIẾT I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm) Câu 1: Mệnh đề phủ định của mệnh đề :":10"Pxx+ là A. :":10"Pxx+ B. :":10".Pxx+ C. :":10".Pxx+ D. :":10".Pxx+ Câu 2: Cho góc  nhọn. Khẳng định nào sau đây đúng? A. sin0   B. cos0   C. tan0   D. cot0   Câu 3: Mệnh đề nào sau đây sai? A. Tam giác có ba góc bằng nhau thì có ba cạnh bằng nhau. B. Tổng ba góc trong một tam giác bằng 180.  C. Tam giác có tổng hai góc bằng góc còn lại là tam giác cân. D. Tam giác có ba cạnh bằng nhau thì có ba góc bằng nhau. Lời giải: Tam giác có tổng hai góc bằng góc còn lại là tam giác cân là khẳng định sai vì Tam giác có tổng hai góc bằng góc còn lại là tam giác vuông.  Chọn đáp án C. Câu 4: Cho x là số thực, mệnh đề nào sau đây đúng? A. 2 :55xxx  hoặc 5.x − B. 2 :555.xxx − C. 2 :55.xxx  D. 2 :55xxx  hoặc 5.x − Lời giải: Đáp án A đúng vì 2 5 ,55 5 x xxx x      − .  Chọn đáp án A. Câu 5: Trong các đẳng thức sau đây, đẳng thức nào đúng? A. ( ) sin180sin−=− B. ( ) cos180cos. −= C. ( ) tan180tan−= D. ( ) cot180cot. −=− Câu 6: Trung tuyến AM của tam giác ABC có độ dài bằng A. 222 24 + + bca . B. 222 24 + bca . C. 222 24 + bca . D. 222 24 + acb . Lời giải: Theo công thức tính độ dài đường trung tuyến 222 22 24 + ==− a bca AMm .  Chọn đáp án B. Câu 7: Số phần tử của tập hợp  2 1,2Akk k=+  là A. 1. B. 2. C. 3. D. 5. Lời giải: Vì k  và 2k  nên  2;1;0;1;2k  do đó ( )  2 11;2;5.k + Vậy A có 3 phần tử.  Chọn đáp án C.

thấy (

0;0 là nghi

m c

a c

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 7 Câu 8: Cho hệ 235(1) 3 25(2) xy xy  +  +  . Gọi 1S là tập nghiệm của bất phương trình (1), 2S là tập nghiệm của bất phương trình (2) và S là tập nghiệm của hệ thì A. 12SS  B. 21SS  C. 2 SS = D. 1 SS  Lời giải: Trước hết, ta vẽ hai đường thẳng: ( )1 :235dxy+= và ( )2 3 :5 2 dxy+= Ta

)

ệ

ủ

ả hai bất phương trình. Điều đó có nghĩa gốc tọa độ thuộc cả hai miền nghiệm của hai bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ.  Chọn đáp án A. Câu 9: Trong các đẳng thức sau đây, đẳng thức nào đúng? A. sin1503 2 =− B. 3 cos150 2 = C. 1 tan150 3 =− D. cot1503. = Lời giải: Ta có: 1 tan150tan30. 3 =−=−  Chọn đáp án C. Câu 10: Cho tam giác ABC có 7b = ; 5c = và 3 cos 5 A = . Tính a . A. 42 B. 2 C. 2 D. 3 Lời giải: Áp dụng định lí hàm số Cosin vào tam giác ABC có 222 3 2..cos25492.5.7.32 5 BCABACABACA 42.BC  Chọn đáp án A. Câu 11: Kí hiệu X là tập hợp các cầu thủ x trong đội tuyển bóng rổ, ( )Px là mệnh đề chứa biến “ x cao trên 180 cm”. Mệnh đề ",()" xXPx khẳng định rằng: A. Mọi cầu thủ trong đội tuyển bóng rổ đều cao trên 180 cm. B. Trong số các cầu thủ của đội tuyển bóng rổ có một số cầu thủ cao trên 180 cm C. Bất cứ ai cao trên 180 cm đều là cầu thủ của đội tuyển bóng rổ D. Có một số người cao trên 180 cm là cầu thủ của đội tuyển bóng rổ.

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 8 Câu 12: Xét mệnh đề :P 2 ":20" xxxm −+= với m là tham số. Tìm tất cả các giá trị của tham số m để mệnh đề P đúng. A. 1.m  B. 1.m  C. 1.m  D. 1.m  Lời giải: Yêu cầu bài toán 2 20−+= xxm có nghiệm 04401. mm −  Chọn đáp án A. Câu 13: Cho tam giác ABC có 9,18ABAC== và 60 =BAC . Bán kính của đường tròn ngoại tiếp tam giác ABC là A. 3 B. 93 C. 9 D. 6 Lời giải: Trong tam giác ABC ta có 222 2..cos243BCABACABACA =+−= 93BC = Mặt khác 93 29 sin2sin2sin60 BCBC RR AA ====   Chọn đáp án C. Câu 14: Trong các cặp số sau, tìm cặp số không là nghiệm của hệ bất phương trình 20 2320 xy xy  +−  −+ A. ( )0;0 B. ( )1;1 C. ( )1;1 D. ( )1;1 Câu 15: Cho tập ( )( )( ) 22 |412730Xxxxxx =−−−+= . Tính tổng S các phần tử của X . A. 9 2 S = . B. 5S = . C. 6S = . D. 4S = . Lời giải: Ta có: ( )( )( ) 2 22 2 2 40 1 41273010. 3 2730 1 2 x x x xxxxx x xx x =  −= = −−−+=−=  =  −+=  =  Vì x nên  1;2;3X = . Vậy tổng 1236S =++= .  Chọn đáp án C. Câu 16: Cho tam giác ABC vuông tại A Khẳng định nào sau đây sai? A. sincos. BC = B. sincos. 22 ABC+ =   C. ( ) sinsin. ABC =−+ D. ( ) coscos. ABC =−+ Lời giải: Ta có: ( ) ( ) sinsin180sin. ABCBC  =−+=+  Vậy C sai.  Chọn đáp án C. Câu 17: Trong mặt phẳng ( )Oxy , phần nửa mặt phẳng không tô đậm (kể cả bờ) trong hình vẽ dưới đây là biểu diễn hình học tập nghiệm của bất phương trình nào?

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 9 A. 33xy− B. 33 xy− C. 33 xy−− D. 33 xy−− Câu 18: Trong các tập sau, tập nào là tập rỗng? A.  2 |0Mxx== B.  |310Nxx=−= C.  2 |1Pxx== . D.  |210Qxx=−= . Lời giải: Ta có 2 00xx== nên  0M = , A sai. Ta có 1 310 3 xx−== nên 1 3 N  =   , B sai. Ta có 2 11xx== nên  1;1P =− , C sai. Ta có 1 210 2 xx−== ( loại vì 1 2  ) .= Q  Chọn đáp án D. Câu 19: Cho tập {,5}Xxx= . Tập X được viết dưới dạng liệt kê là A. {1;2;3;4}X = . B. {0;1;2;3;4}X = . C. {1;2;3;4;5}X = . D. {0;1;2;3;4;5}X = . Lời giải: Vì tập X là các số tự nhiên nhỏ hơn hoặc bằng 5 nên {0;1;2;3;4;5}X = .  Chọn đáp án D. Câu 20: Cho tam giác ABC có ,. ABcACb == Diện tích của tam giác ABC bằng A. cos. bcA B. sin. bcA C. 1 cos. 2 bcA D. 1 sin. 2 bcA Câu 21: Cho 1 cot 3  = . Tính giá trị của biểu thức 3sin4cos 2sin5cos A   + = A. 15 13 =−A B. 13=−A C. 15 13 =A D. 13=A Lời giải: Do 1 cotsin0. 3 = Chia cả tử và mẩu của biểu thức A cho sin,  ta được: 3sin4sin.cot34cot 13 2sin5sin.cot25cot A   ++ ===  Chọn đáp án D. Câu 22: Cho các tập hợp ,, ABC được minh họa bằng biểu đồ Ven như hình vẽ. Phần tô đậm trong hình là biểu diễn của tập hợp nào sau đây?

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 10 A. ABC  . B. ( ) ( )A\C\B A . C. ( ) B\ AC  . D. ( ) B\ AC  . Lời giải: Phần tô xám trong hình là biểu diễn tập hợp các điểm vừa thuộc , AB mà không thuộc C . Chính là tập ( ) B\ AC   Chọn đáp án D. Câu 23: Trong các bất phương trình sau đây, bất phương trình nào là bất phương trình bậc nhất hai ẩn? A. 23. xy− B. 2 21.xy− C. 2 0.xy− D. 2323.xy− Câu 24: Trong các tập hợp sau, tập nào có đúng một tập hợp con? A.  B.   1. C.  . D.   ;1. Câu 25: Khẳng định nào sau đây sai? A. .= ABAAB B. .ABAAB = C. \. ==ABAAB D. \.BABAB== Lời giải: B sai do .ABAAB =  Chọn đáp án B. Câu 26: Cặp số nào sau đây không là nghiệm của bất phương trình ( ) 5210 −−xy ? A. ( )0;1 . B. ( )1;3 . C. ( )–1;1 . D. ( )–1;0 . Lời giải: Ta có ( ) 5210 −−xy 5220 xy −+ ; ta thay từng đáp án vào bất phương trình, cặp ( )1;3 không thỏa mãn bất phương trình vì 5.12.320 −+ là sai.  Chọn đáp án B. Câu 27: Cho tam giác ABC có 120.=BAC Đẳng thức nào sau đây đúng? A. 222 3 abcbc =+− . B. 222 abcbc =++ . C. 222 3 abcbc =++ . D. 222 abcbc =+− . Lời giải: Áp dụng định lí Côsin, ta có: 222 2.cos abcbcA =+− . 222 2.os120abcbcc =+− 222 abcbc=++  Chọn đáp án B. Câu 28: Cho  3;4;7;8A = và  1;3;5;7;9B = Chọn kết quả đúng trong các kết quả sau: A.  1;3;4;5;7;8;9AB= B.  1;3;5;7;9AB= C.  3;7AB= . D.  1;4AB= . Lời giải:

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 11 Ta có:   ;.= ABxxAxB Do đó  3;7AB= .  Chọn đáp án C. Câu 29: Cho tam giác ABC có 4AB = , 5AC = , 6BC = . Tính ( )cos .+ BC A. 1 8 . B. 1 4 . C. –0,125. D. 0,75. Lời giải: Ta có 4==cAB , 5==bAC , 6==aBC . Tính 8 1 2 cos 222 = + = bc bca A . Để ý 0,125 8 1 cos()cos+===BCA .  Chọn đáp án C. Câu 30: Miền nghiệm của bất phương trình 22xy+ là phần không tô đậm (kể cả biên) trong hình vẽ nào dưới đây? A. B. C. D. Câu 31: Cho tập hợp A . Mệnh đề nào sau đây đúng? A. \.A = B. \. AA= C. \. A= D. \.AA = Câu 32: Cho tam giác ABC có chu vi bằng 32 và bán kính đường tròn nội tiếp của ABC bằng 5. Tính diện tích Scủa tam giác ABC A. = 32 5 S B. = 40.S C. = 160.S D. = 80.S Lời giải: Ta có: 32 .580. 2 ===Spr  Chọn đáp án D. Câu 33: Miền tam giác ABC kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D?

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 12 A. 0 5410 5410 y xy xy    −  + . B. 0 4510 5410 x xy xy    −  + . C. 0 5410 4510 x xy xy    −  + . D. 0 5410 4510 x xy xy    −  + . Lời giải: Dựa vào hình vẽ, ta thấy đồ thị gồm các đường thẳng: ( )1 :0dx = ; ( )2 :4510dxy+= ; ( )3 :5410dxy−= Miền nghiệm gần phần mặt phẳng nhận giá trị x dương (kể cả bờ ( )1d ). Lại có ( )0;0 là nghiệm của cả hai bất phương trình 4510 xy+ và 5410. xy−  Chọn đáp án C. Câu 34: Cho tancot m+= . Số giá trị của tham số m để 22 tancot7 += là A. Vô số. B. 0. C. 1. D. 2. Lời giải: Ta có: ( ) 222 7tancottancot2  =+=+− 2 9m = 3m =  Chọn đáp án D. Câu 35: Cho tam giác ABC có 9,18ABAC== và 60 =BAC . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC A. 3=R . B. 93=R . C. 9=R . D. 6=R . Lời giải: Trong tam giác ABC ta có 222 2..cos243BCABACABACA =+−= 93BC = . Mặt khác 93 29 sin2sin2sin60 BCBC RR AA ====  .  Chọn đáp án C. II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm) Câu 36: (1,0 điểm). a) Cho hai tập hợp  2 320Axxx=−+= và   1;0;1.B =− Xác định các tập hợp ,\. ABBA  Lời giải: Ta có:  2 1 3201;2. 2 x xxA x  = −+==  = Suy ra:     1,\1;0.ABBA==− b) Cho hai tập hợp ( )0;8M = và ) ;.Nm  =+  Tìm m để tập hợp MN  có đúng 4 số nguyên. O C B 5 2 2A x

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 13 Lời giải: Yêu cầu bài toán 34. m  Câu 37: (1,0 điểm). a) Cho tan2 x =− với 90180. x  Tính giá trị biểu thức cot3cos. Pxx =− Lời giải: Ta có: 11 tan2cot. tan2 xx x =−==− Ta có: 22 22 5 111cos 5 1tancos. cos1tan5 5 cos 5 x xx xx x  = +=== + =−  Do 90180 x  nên chọn 515565 coscot3cos3. 52510 xPxx  −+ =−=−=−−−=    b) Cho tam giác ABC , biết 14,60,40cBACABC === . Tính ,.ab Lời giải: Ta có ( )ˆˆ 18080 ˆ =−+=CAB Áp dụng Định lí sin, ta có: 14 sin60sin40sin80 ==  ab Suy ra 14sin6014sin40 sin80sin8012,3;9,14.  ==  ab Câu 38: (1,0 điểm). a) Biểu diễn hình học tập nghiệm của hệ bất phương trình ( ) 20 1:10. 210 xy xy xy  ++  −−  −+ b) Tìm , xy thỏa mãn ( )1 sao cho biểu thức 23 Fxy =+ đạt giá trị lớn nhất, giá trị nhỏ nhất. Lời giải: a) Vẽ ba đường thẳng 123 :2;:1;:21. xyxyxy +=−−=−=− Tìm tọa độ giao điểm của ba cặp đường thẳng trên bằng cách giải ba hệ phương trình: (1): 1 20 2 103 2 x xy xy y  =− ++=    −−=  =−  (2): 102 . 2103 xyx xyy −−==−   −−==− (3): 2101 . 201 xyx xyy −+==−   ++==− Ta được ba giao điểm ( ) ( ) 13;;2;3;1;1. 22 ABC    Vì điểm ( )0;0O có tọa độ không thỏa mãn phương trình đâu và thỏa mãn hai bất phương trình cuối của hệ nên miền nghiệm của hệ ( )1 là miền tam giác ABC (kể cả biên).

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 14 x y C B A 3 2 1 O 1 b) Lập bảng: 13 ; 22 A   ( )2;3B ( )1;1C 23 Fxy =+ 11 2 F =− 13F =− 5F =− Vậy max 5F =− và min 13F =− ____________________HẾT____________________ Huế, 09h40’ Ngày 27 tháng 9 năm 2022

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 1 ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI NĂM HỌC 2022 2023 MÔN: TOÁN 10 ĐỀ SỐ: 05 I. PHẦN TRẮC NGHIỆM (35 câu 7,0 điểm) Câu 1: Cho tam giác ABC có diện tích là S Đẳng thức nào sau đây đúng? A. 1 cos. 2 = SabC B. 1 sin. 2 = SabC C. sin.= SabC D. cos.= SabC Câu 2: Trong các tập sau, tập nào là tập rỗng? A.  2 |0Mxx== . B.  |310Nxx=−= . C.  2 |1Pxx== D.  |210Qxx=−= Câu 3: Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn? A. 2530 xyz−+ B. 2 3240 xx+− C. 2 253 xy+ D. 235 xy+ Câu 4: Cách viết nào sau đây đúng? A. ;.aab  B.   ;.aab  C.   ;.aab  D. ( ;.aab  Câu 5: Trong các phát biểu sau, có bao nhiêu câu là mệnh đề? (1) Ly lước này nóng quá! (2) 2 22021.x += (3) Số 20 chia hết cho 3. (4) 233. + A. 3. B. 4. C. 1. D. 2. Câu 6: Cho hai tập hợp A và ,B phần tử x thỏa mãn: xA  hoặc xB  Khẳng định nào sau đây đúng? A. xAB  B. \.xAB  C. xAB  D. \.xBA  Câu 7: Cho hai tập hợp )1;4A =  và 2;8.B =  Tập hợp \ AB là A. 4;8.  B. 1;2.  C. ) 1;2.  D. ) 2;4.  Câu 8: Cho mệnh đề kéo theo: “Nếu tứ giác là hình chữ nhật thì nó có hai đường chéo bằng nhau.”. Sử dụng khái niệm “điều kiện cần”, “điều kiện đủ” để phát biểu mệnh đề trên. Phát biểu nào sau đây đúng? A. Tứ giác có hai đường chéo bằng nhau là điều kiện đủ để nó là hình chữ nhật. B. Tứ giác là hình chữ nhật là điều kiện đủ để nó có hai đường chéo bằng nhau. C. Tứ giác là hình chữ nhật là điều kiện cần để nó có hai đường chéo bằng nhau. D. Tứ giác là hình chữ nhật là điều kiện cần và đủ để nó có hai đường chéo bằng nhau. Câu 9: Cho góc  tù. Khẳng định nào sau đây đúng? A. sin0   . B. cos0   . C. tan0   . D. cot0   . Câu 10: Miền nghiệm của bất phương trình 326 −−xy là nửa mặt phẳng (kể cả bờ) được thể hiện theo phương án A, B, C, D nào dưới đây ?

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 2 A. B. C. D. Câu 11: Cho 4, 1 x Bxx x  = +  , khẳng định nào sau đây đúng? A.  0;1;2;3B = . B. 0;;;;1234 2345 B  =   . C.  0;1;2;3;4B = . D. 0;;;123 234 B  =   . Câu 12: Cho tam giác ABC có góc 60BAC = và cạnh 3BC = . Tính bán kính của đường tròn ngoại tiếp tam giác ABC A. 4R = B. 1R = C. 2R = D. 3R = Câu 13: Giá trị của tan30cot30 + bằng A. 4 3 . B. 13 3 + . C. 2 3 . D. 2. Câu 14: Mệnh đề nào sau đây đúng? A. 2 :1kkk ++ là số chẵn. B. 2 :.xxx C. :2. xnn D. 3 : nnn− không chia hết cho 3. Câu 15: Điểm nào dưới đây không thuộc miền nghiệm của hệ bất phương trình 2310 540 xy xy +−  −+ ? A. ( )1;4Q B. ( )2;4M C. ( )0;0P D. ( )3;4N Câu 16: Cho hai tập hợp:    1;3;5;8;3;5;7;9XY== . Tập hợp XY  bằng tập hợp nào sau đây? A.   3;5. B.   1;3;5;7;8;9. C.   1;7;9. D.   1;3;5. Câu 17: Miền nghiệm của bất phương trình ( ) ( )22221 xyx −++−− là nửa mặt phẳng không chứa điểm nào trong các điểm sau? A. ( )0;0M . B. ( )1;1Q . C. ( )4;2N . D. ( )1;1P . Câu 18: Rút gọn biểu thức ( ) ( ) 22 tancottancot=+−− Pxxxx ta được A. 4=P . B. 1=P . C. 2=P . D. 3.=P Câu 19: Cho tam giác ABC có 6,8,10.===abc Diện tích của tam giác ABC bằng A. 48. B. 24. C. 12. D. 30. Câu 20: Cho hai đa thức ( )fx và ( )gx . Xét các tập hợp ( ) |0Axfx== , ( ) |0Bxgx== , ( ) ( ) |0Cxfx gx   ==   . Khẳng định nào sau đây đúng? A. .CAB = B. .CAB = C. \B.CA = D. \.CBA = Câu 21: Cho A và B là hai tập hợp bất kì khác rỗng, thỏa mãn ABA = Khẳng định nào sau đây đúng? A. \. ABA = B. .ABA = C. .AB  D. .BA  O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 3 Câu 22: Cho tam giác ABC có 3,5ABBC== và độ dài đường trung tuyến 13BM = . Độ dài cạnh AC bằng A. 11. B. 4. C. 9 2 . D. 10 . Câu 23: Cho hai góc nhọn  và  ( )  . Khẳng định nào sau đây sai? A. coscos  B. sinsin  C. tantan0 + D. cotcot  Câu 24: Mệnh đề nào sau đây đúng? A. Nếu một tam giác có một góc bằng 060 thì tam giác đó đều. B. Nếu ab  thì 22ab  C. Nếu 2a chia hết cho 3 thì a chia hết cho 3. D. Nếu a chia hết cho 3 thì a chia hết cho 9. Câu 25: Xét góc  bất kì, hệ thức nào sau đây đúng? A. 22 sincos1 += . B. 22 sincos1 2  += . C. 22 sincos1 += D. 22 sin2cos21 += Câu 26: Tìm mệnh đề phủ định của mệnh đề 2 :":10".Pxxx+− A. 2 :":10".Pxxx+− B. 2 :":10".Pxxx+− C. 2 :":10".Pxxx+− D. 2 :":10".Pxxx+− Câu 27: Cho tập hợp  2 540.Axxx=−+= Khẳng định nào sau đây đúng? A. Tập hợp A có vô số phần tử. B. Tập hợp .A = C. Tập hợp A có một phần tử. D. Tập hợp A có hai phần tử. Câu 28: Cho tam giác ABC có 4AB = cm, 7BC = cm, 9AC = cm. Tính cos A A. 2 cos 3 A =− B. 1 cos 2 A = C. 1 cos 3 A = D. 2 cos 3 A = Câu 29: Cho tập hợp   1;2;3.A = Tập hợp nào sau đây bằng tập hợp ?A A. ) 2;4.−  B. ) 2;4.−  C. ) * 2;4.−  D. ) 2;4.−  Câu 30: Cho tam giác ABC , đẳng thức nào sau đây đúng? A. 222 2 24a bca m + =+ B. 222 2 24a acb m + =− C. 222 2 24a abc m + =− D. 222 2 22 4a cba m +− = Câu 31: Xét  là góc bất kì, đẳng thức nào sau đây sai? A. ( ) sin180sin−=. B. ( ) cos180cos. −= C. ( ) tan90cot−= D. ( ) cot180cot. −=− Câu 32: Cho 1 sin 3  = , với 90180   . Tính cos A. 2 cos 3  = . B. 2 cos 3  =− . C. 22 cos 3  = . D. 22 cos 3  =− . Câu 33: Giá trị nhỏ nhất của biết thức Fyx =− trên miền xác định bởi hệ 22 2 54 xy xy xy  +  −  +− là

Tam

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 4 A. min 3F =− khi 1,2xy==− B. min 0F = khi 0,0xy== C. min 2F =− khi 42 , 33xy==− . D. min 8F = khi 2,6xy=−= . Câu 34: Cho tam giác ABC thoả mãn hệ thức 2 bca += Mệnh đề nào sau đây đúng? A. coscos2cos. BCA += B. sinsin2sin. BCA += C. 1 sinsinsin 2 BCA += . D. sincos2sin. BCA += Câu 35: Cho tam giác ABC có các góc thỏa mãn sin2.sin.cosCBA = . Khẳng định nào sau đây đúng? A.

giác ABC cân tại .A B.

giác ABC cân tại .B C.

giác ABC cân tại .C D. Tam giác ABC không là tam giác cân. II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm) Câu 36: (1,0 điểm). a) Cho tập hợp ( )( ) 3 2140.Axxxx =−−= Liệt kê tất cả các tập con của tập hợp .A b) Cho hai tập hợp  03Mxx= và ) 2;.N  =+  Xác định các tập hợp ,.MNCN  Câu 37: (1,0 điểm). a) Biểu diễn hình học tập nghiệm của bất phương trình 23. xy− b) Cho góc  thỏa mãn tan2. = Tính giá trị biểu thức 33 sin sin3cos P   = + . Câu 38: (1,0 điểm). Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất sao cho ba điểm A, B, C thẳng hàng. Ta đo được AB = 24m, 63;CAD = 48CBD = (tham khảo hình vẽ). Tính gần đúng chiều cao h của khối tháp. HẾT

Câu

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 5 HƯỚNG DẪN GIẢI CHI TIẾT I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm) Câu 1: Cho tam giác ABC có diện tích là .S Đẳng thức nào sau đây đúng? A. 1 cos. 2 = SabC B. 1 sin. 2 = SabC C. sin.= SabC D. cos.= SabC Câu 2: Trong các tập sau, tập nào là tập rỗng? A.  2 |0Mxx== B.  |310Nxx=−= C.  2 |1Pxx== . D.  |210Qxx=−= . Lời giải: Ta có 2 00xx== nên  0M = , A sai. Ta có 1 310 3 xx−== nên 1 3 N  =   , B sai. Ta có 2 11xx== nên  1;1P =− , C sai. Ta có 1 210 2 xx−== ( loại vì 1 2  ) .= Q  Chọn đáp án D. Câu 3: Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn? A. 2530 xyz−+ . B. 2 3240 xx+− . C. 2 253 xy+ . D. 235 xy+ . Câu 4: Cách viết nào sau đây đúng? A. ;.aab  B.   ;.aab  C.   ;.aab  D. ( ;.aab 

5: Trong các phát biểu sau, có bao nhiêu câu là mệnh đề? (1) Ly lước này nóng quá! (2) 2 22021.x += (3) Số 20 chia hết cho 3. (4) 233. + A. 3. B. 4. C. 1. D. 2. Lời giải: Phát biểu (3), (4) là mệnh đề.  Chọn đáp án D. Câu 6: Cho hai tập hợp A và ,B phần tử x thỏa mãn: xA  hoặc .xB  Khẳng định nào sau đây đúng? A. .xAB  B. \.xAB  C. .xAB  D. \.xBA  Câu 7: Cho hai tập hợp )1;4A =  và 2;8.B =  Tập hợp \ AB là A. 4;8.  B. 1;2.  C. ) 1;2.  D. ) 2;4.  Lời giải: [ [ 28 4 ) ] 1 B A  Chọn đáp án C.

Câu 8: Cho mệnh đề kéo theo: “Nếu tứ giác là hình chữ nhật thì nó có hai đường chéo bằng nhau.”. Sử dụng khái niệm “điều kiện cần”, “điều kiện đủ” để phát biểu mệnh đề trên. Phát biểu nào sau đây đúng?

A. Tứ giác có hai đường chéo bằng nhau là điều kiện đủ để nó là hình chữ nhật.

B. Tứ giác

OFFICIAL

DẠYKÈMQUYNHƠN

Sưu tầm và biên soạn Page 6

là hình chữ nhật là điều kiện đủ để nó có hai đường chéo bằng nhau.

Tứ giác là hình chữ nhật là điều kiện cần để nó có hai đường chéo bằng nhau. D. Tứ giác là hình chữ nhật là điều kiện cần và đủ để nó có hai đường chéo bằng nhau. Câu 9: Cho góc  tù. Khẳng định nào sau đây đúng? A. sin0   . B. cos0   . C. tan0   . D. cot0   . Câu 10: Miền nghiệm của bất phương trình 326 −−xy là nửa mặt phẳng (kể cả bờ) được thể hiện theo phương án A, B, C, D nào dưới đây ? A. B. C. D. Lời giải: Trước hết, ta vẽ đường thẳng ( ):326.dxy−=− Ta thấy ( )0;0 là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng bờ ( )d chứa điểm ( ) 0;0.  Chọn đáp án C. Câu 11: Cho 4, 1 x Bxx x  = +  , khẳng định nào sau đây đúng? A.  0;1;2;3B = B. 0;;;;1234 2345 B  =   C.  0;1;2;3;4B = D. 0;;;123 234 B  =   Lời giải: Vì 4x  và x  nên  0;1;2;3x . Do đó, ta có 0;;;123 234 B  =   .  Chọn đáp án D. Câu 12: Cho tam giác ABC có góc 60BAC = và cạnh 3BC = . Tính bán kính của đường tròn ngoại tiếp tam giác ABC A. 4R = . B. 1R = . C. 2R = . D. 3R = . Lời giải: Ta có: 3 21 sin2sin 2.3 2 BCBC RR AA ==== .  Chọn đáp án B. Câu 13: Giá trị của tan30cot30 + bằng A. 4 3 B. 13 3 + C. 2 3 D. 2 Lời giải: O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 7 Ta có: 343 tan30cot303 33 +=+= .  Chọn đáp án A. Câu 14: Mệnh đề nào sau đây đúng? A. 2 :1kkk ++ là số chẵn. B. 2 :.xxx C. :2. xnn D. 3 : nnn− không chia hết cho 3. Lời giải: Với 1 2 x = thì 2 xx B đúng.  Chọn đáp án B. Câu 15: Điểm nào dưới đây không thuộc miền nghiệm của hệ bất phương trình 2310 540 xy xy +−  −+ ? A. ( )1;4Q . B. ( )2;4M . C. ( )0;0P . D. ( )3;4N . Lời giải: Nhận xét: chỉ có điểm ( )0;0P có tọa độ không thỏa mãn hệ.  Chọn đáp án C. Câu 16: Cho 2 tập hợp:    1;3;5;8;3;5;7;9XY== . Tập hợp XY  bằng tập hợp nào sau đây? A.   3;5. B.   1;3;5;7;8;9. C.   1;7;9. D.   1;3;5. Câu 17: Miền nghiệm của bất phương trình ( ) ( )22221 xyx −++−− là nửa mặt phẳng không chứa điểm nào trong các điểm sau? A. ( )0;0M B. ( )1;1Q C. ( )4;2N D. ( )1;1P Lời giải: Ta có: ( ) ( )22221 xyx −++−− 22422 xyx−++−− 24xy + . Dễ thấy tại điểm ( )4;2N ta có: 42.284 +=  Chọn đáp án C. Câu 18: Rút gọn biểu thức ( ) ( ) 22 tancottancot=+−− Pxxxx ta được A. 4=P . B. 1=P . C. 2=P . D. 3.=P Lời giải: ( ) ( )2222 tan2tan.cotcottan2tan.cotcot4 Axxxxxxxx =++−−+= .  Chọn đáp án A. Câu 19: Cho tam giác ABC có 6,8,10.===abc Diện tích của tam giác ABC bằng A. 48. B. 24. C. 12. D. 30. Lời giải: Nửa chu vi ABC là: 2 abc p ++ = . Áp dụng công thức Hê rông: ()()()12(126)(128)(1210)24Sppapbpc =−−−=−−−= .  Chọn đáp án B.

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 8 Câu 20: Cho hai đa thức ( )fx và ( )gx . Xét các tập hợp ( ) |0Axfx== , ( ) |0Bxgx== , ( ) ( ) |0Cxfx gx   ==   . Khẳng định nào sau đây đúng? A. CAB = B. CAB = C. \B.CA = D. \.CBA = Lời giải: Ta có ( ) ( ) ( ) ( ) 0 0 0 fxfx gx gx  = =    hay ( ) ( ) |0,0Cxfxgx == nên \B.CA =  Chọn đáp án C. Câu 21: Cho A và B là hai tập hợp bất kì khác rỗng, thỏa mãn .ABA = Khẳng định nào sau đây đúng? A. \. ABA = B. .ABA = C. .AB  D. .BA  Câu 22: Cho tam giác ABC có 3,5ABBC== và độ dài đường trung tuyến 13BM = . Độ dài cạnh AC bằng A. 11. B. 4. C. 9 2 . D. 10 . Lời giải: 13 5 3 M CB A Theo công thức tính độ dài đường trung tuyến;ta có: ( ) 222222 2 2 35 134 2424 BABCACAC BMAC ++ =−=−=  Chọn đáp án B. Câu 23: Cho hai góc nhọn  và  ( )  . Khẳng định nào sau đây sai? A. coscos  . B. sinsin  . C. tantan0 + . D. cotcot  . Câu 24: Mệnh đề nào sau đây đúng? A. Nếu một tam giác có một góc bằng 060 thì tam giác đó đều. B. Nếu ab  thì 22ab  C. Nếu 2a chia hết cho 3 thì a chia hết cho 3. D. Nếu a chia hết cho 3 thì a chia hết cho 9. Câu 25: Xét góc  bất kì, hệ thức nào sau đây đúng? A. 22 sincos1 += . B. 22 sincos1 2  += . C. 22 sincos1 += D. 22 sin2cos21 +=

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 9 Câu 26: Tìm mệnh đề phủ định của mệnh đề 2 :":10".Pxxx+− A. 2 :":10".Pxxx+− B. 2 :":10".Pxxx+− C. 2 :":10".Pxxx+− D. 2 :":10".Pxxx+− Câu 27: Cho tập hợp  2 540.Axxx=−+= Khẳng định nào sau đây đúng? A. Tập hợp A có vô số phần tử. B. Tập hợp .A = C. Tập hợp A có một phần tử. D. Tập hợp A có hai phần tử. Lời giải: Ta có:  2 1 5401;4. 4 x xxA x  = −+==  =  Chọn đáp án D. Câu 28: Cho tam giác ABC có 4AB = cm, 7BC = cm, 9AC = cm. Tính cos A A. 2 cos 3 A =− . B. 1 cos 2 A = . C. 1 cos 3 A = . D. 2 cos 3 A = . Lời giải: Ta có 222 cos 2.. ABACBC A ABAC +− = 222 4972 2.4.93 +− ==  Chọn đáp án D. Câu 29: Cho tập hợp   1;2;3.A = Tập hợp nào sau đây bằng tập hợp ?A A. ) 2;4.−  B. ) 2;4.−  C. ) * 2;4.−  D. ) 2;4.−  Câu 30: Cho tam giác ABC , đẳng thức nào sau đây đúng? A. 222 2 . 24a bca m + =+ B. 222 2 . 24a acb m + =− C. 222 2 24a abc m + =− D. 222 2 22 4a cba m +− = Câu 31: Xét  là góc bất kì, đẳng thức nào sau đây sai? A. ( ) sin180sin−= B. ( ) cos180cos. −= C. ( ) tan90cot−= D. ( ) cot180cot. −=− Lời giải: Ta có: ( ) cos180cos. −=− Vậy B sai.  Chọn đáp án B. Câu 32: Cho 1 sin 3  = , với 90180   . Tính cos . A. 2 cos 3  = B. 2 cos 3  =− C. 22 cos 3  = D. 22 cos 3  =− Lời giải: Ta có 22 cos1sin =− 2 22 18cos 13 39 22 cos 3    ==−=  =−  .

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 10 Mặt khác 90180   nên chọn 22 cos 3  =− .  Chọn đáp án D. Câu 33: Giá trị nhỏ nhất của biết thức Fyx =− trên miền xác định bởi hệ 22 2 54 xy xy xy  +  −  +− là A. min 3F =− khi 1,2xy==− . B. min 0F = khi 0,0xy== . C. min 2F =− khi 42 , 33xy==− . D. min 8F = khi 2,6xy=−= . Lời giải: Biểu diễn miền nghiệm của hệ bất phương trình 22 2 54 xy xy xy  +  −  +− trên hệ trục tọa độ như dưới đây: Giá trị nhỏ nhất của biết thức Fyx =− đạt được tại một trong các điểm ( ) 2;6,A 4217 ;,; 3333 CB   . Ta có: ( ) ( ) ( ) 8;2;2FAFBFC==−=− . Vậy min 2F =− khi 42 , 33xy==− .  Chọn đáp án C. Câu 34: Cho tam giác ABC thoả mãn hệ thức 2 bca += . Mệnh đề nào sau đây đúng? A. coscos2cos. BCA += B. sinsin2sin. BCA += C. 1 sinsinsin 2 BCA += D. sincos2sin. BCA += Lời giải: Ta có: 22 sinsinsinsinsinsin + ===== bc abcbc R ABCABC sinsin2sin. 2sinsinsin ++ =+= + bcbc BCA ABC  Chọn đáp án B. Câu 35: Cho tam giác ABC có các góc thỏa mãn sin2.sin.cosCBA = Khẳng định nào sau đây đúng? A. Tam giác ABC cân tại .A B. Tam giác ABC cân tại .B C. Tam giác ABC cân tại C D. Tam giác ABC không là tam giác cân. Lời giải: Áp dụng định lý sin và côsin, ta có:

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 11 sin2.sin.cos2cos CBAcbA == 222 2. 2 cbbca bc +− = 2222 cbca=+− ab= . Vậy tam giác ABC cân tại C  Chọn đáp án C. II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm) Câu 36: (1,0 điểm). a) Cho tập hợp ( )( ) 3 2140.Axxxx =−−= Liệt kê tất cả các tập con của tập hợp A Lời giải: Ta có: ( )( )  3 3 1 2102 0 21400;2. 40 2 2 x x x xxxA xx x x  =  −= = −−==  −= = =−  Các tập con của tập hợp Alà:     ;0;2;. A b) Cho hai tập hợp  03Mxx= và ) 2;.N  =+  Xác định các tập hợp ,.MNCN  Lời giải: Ta có:   ( 030;3.Mxx==  Suy ra: ( ) 2;3;;2.MNCN  ==−  Câu 37: (1,0 điểm). a) Biểu diễn hình học tập nghiệm của bất phương trình 23. xy− Lời giải: +) Vẽ đường thẳng :23. xy −= +) Thay tọa độ ( )0;0O vào bất phương trình ta thấy đúng nên miền nghiệm của bất phương trình đã cho là nửa mặt phẳng bờ , chứa điểm O tương ứng phần mặt phẳng không bị tô đen (kể cả bờ). x y O 1 b) Cho góc  thỏa mãn tan2. = Tính giá trị biểu thức 33 sin sin3cos P   = + . Lời giải: Do tan2cos0 = . Biến đổi 32 33333 33 sinsin1 sin. cos coscos sin3cossin3costan3 coscos P       === ++ + ( )2 3 tan1tan 10 . tan311   + == + Câu 38: (1,0 điểm).

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 12 Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất sao cho ba điểm A, B, C thẳng hàng. Ta đo được AB = 24m, 63;CAD = 48CBD = (tham khảo hình vẽ). Tính gần đúng chiều cao h của khối tháp. Lời giải: Ta có ( ) 631171801174815CADBADADB===−+= Áp dụng định lý sin trong tam giác ABD ta có: .sin sinsinsin ABBDABBAD BD ADBBADADB == Tam giác BCD vuông tại C nên có: sin.sin CD CBDCDBDCBD BD == Vậy .sin.sin24.sin117.sin48 61,4 sinsin15 ABBADCBD CDm ADB  ==  HẾT