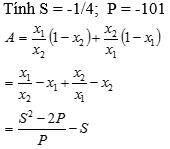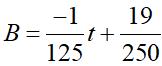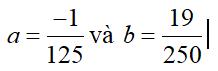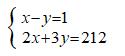ĐỀ THI TUYỂN SINH VÀO 10 MÔN TOÁN Ths Nguyễn Thanh Tú eBook Collection 63 ĐỀ THAM KHẢO TUYỂN SINH 10 THPT NĂM HỌC 2022 - 2023 MÔN THI TOÁN PHÒNG GD&ĐT 21 QUẬN - HUYỆN - THÀNH PHỐ SỞ GD&ĐT THÀNH PHỐ HỒ CHÍ MINH WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405
HOC: 2022 - 2023 MÔN: TOÁN 9

thi gồm 8 câu hỏi tự luân.
ời gian: 120 phút (không kể thời gian phát đề
DẠYKÈMQUYNHƠN OFFICIAL
ĐỀ
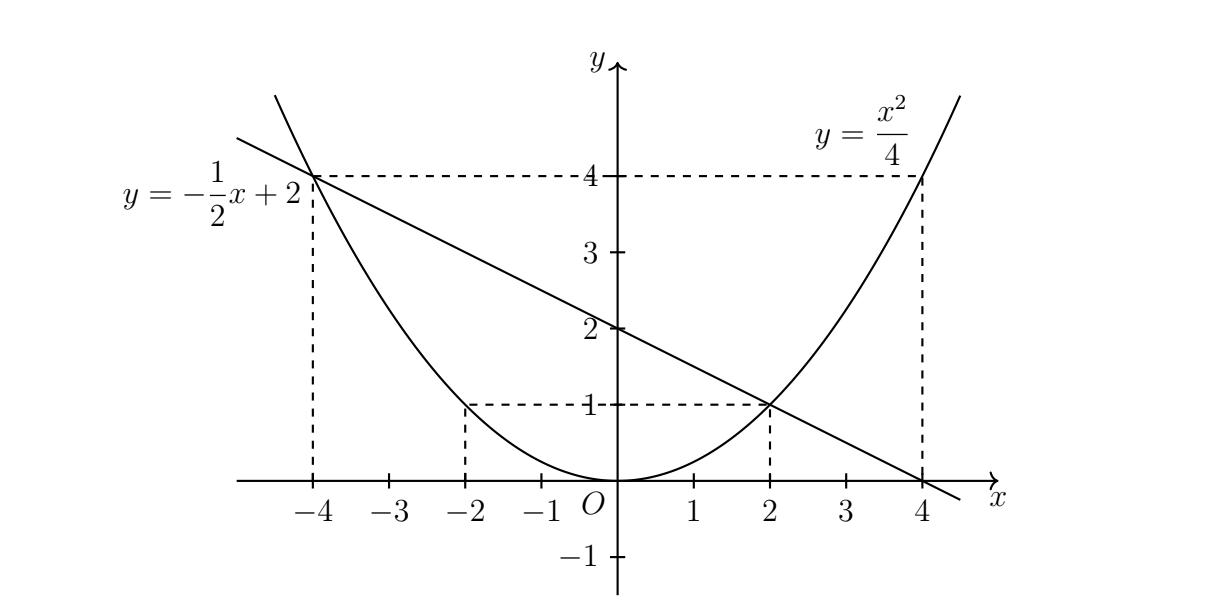
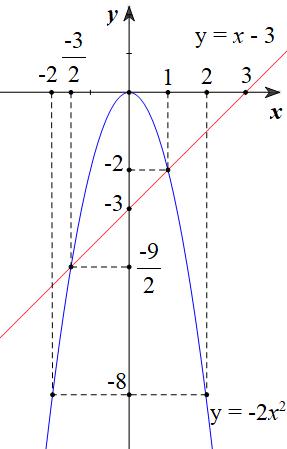
Câu 1. Cho hàm số 2 4 x y có đồ thị là parabol () P và hàm số 2 2 x y có đồ thị là đường thẳng () D . a) Vẽ đồ thị () P và () D trên cùng mặt phẳng tọa độ Oxy. b) Tìm tọa độ giao điểm của () P và () D bằng phép toán. Lời giải a) Học sinh tự vẽ. b) Phương trình hoành độ giao điểm 2 2 2 4. 42 x xx x Với 21xy Với 44xy Tọa độ giao điểm của () P và () D là (2;1) và (4;4). Câu 2. Gọi 12 , xx là các nghiệm của phương trình 2 120. xx Không giải phương trình, tính giá trị của biểu thức 12 21 11xx A xx . Lời giải Theo Vi-ét 12 12 1 12. xx xx Ta có 2 121212 12 !21 22 2 2 1 2 6 1241 12 13 xxxxxx xxxx AAA xxxx A . Câu 3. Để biết được ngày n tháng t năm 2020 là ngàythứ mấytrong tuần. Đầu tiên, đi tính giá trị biểu thức TnH , ở đây H được xác định như sau: Sau đó lấy T chia cho 7 ta được số dư r (0r6)
SỞ GD\&ĐT TP. HỒ CHÍ MINH PHÒNG GD\&ĐT HUYỆN BÌNH CHÁNH ĐỀ THAM KHẢO MÃ ĐỀ: Huyện Bình Chánh -1
THAM KHẢO TUYỂN SINH 10 NĂM
Đề
Th
Nếu 0 r
Nếu 1 r
Nếu 2 r
Nếu 3 r
thì ngày đó là ngày thứ Bảy
thì ngày đó là ngày Chủ Nhật
thì ngày đó là ngày thứ Hai
thì ngày đó là ngày thứ Ba
Nếu 6 r
thì ngày đó là ngày thứ Sáu
Hãy sử dụng quy tắc trên để xác định ngày 30/04/2020 là ngày thứ mấy? Bé An sinh vào tháng 12/2020. Biết rằng ngày sinh của bé An là một bội số của 5 và là Chủ Nhật. Hỏi ngày sinh c
c sinh cả lớp là học sinh khá, còn lại 18 em học sinh trung bình. Hỏi cuối học kì I lớp 9A có bao nhiêu học sinh ? Lời giải Gọi x là số học sinh lớp 9A . Suy ra số học giỏi là 4 15 x , số học sinh khá là 1 3 x Vậy ta có 41 1845 153 xxxx (em). Câu 5. Người ta nhấn chìm hoàn toàn một tượng đá nhỏ vào một lọ thuỷ tinh có nước dạng hình trụ; diện tích đáy của lọ thuỷ tinh là 29cm khi đó nước trong lọ dâng cao 4cm. Tính thể tích tượng đá.

Lời giải Thể tích tượng đá bằng với thể tích phần nước hình trụ dâng cao. Vậy thể là tượng đá là: 9.436 ( 2 cm ).
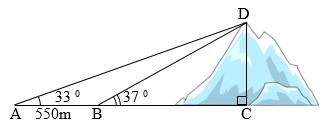
Câu 6. Tính chiều cao của một ngọn núi (làm tròn đến mét), cho biết tại hai điểm cách nhau 550 m, người ta nhìn thấy đỉnh núi với góc nâng lần lượt là 033 và 037 . Lời giải Xéttam giác DAC vàtamgiác DBC nhưhìnhvẽ,chiều cao núi chính là độ dài đoạn CD.
DẠYKÈMQUYNHƠN OFFICIAL
ủa bé An là ngày mấy? Lời giải Có 30,4,333ntHT chia 7 dư 5 nên đó là thứ năm. Có 12,2227171 tHTnnknk mà n là bội của 5 nên 20 n Câu 4. Cuối học kì I năm học 20182019 lớp 9A có số học sinh giỏi chiếm 4 15 học sinh cả
ớ
ố
ọ
l
p, 1 3 s
h
Ta có tan33 CD AC và tan37 CD BC suy ra tan33tan37 5 CDCD CD m.
Vậy chiều cao ngọn núi xấp xỉ 2584 mét.
Câu 7. Một vật rơi tự do từ độ cao so với mặt đất là 120 mét. Bỏ qua sức cản không khí, quãng đường chuyển động s (mét) của vật rơi sau thời gian t được biểu diễn gần đúng bởi công thức: 2 5 st , trong đó t là thời gian tính bằng giây.
a) Sau 3 giây vật này cách mặt đất bao nhiêu mét?
b) Sau bao lâu kể từ khi bắt đầu rơi thì vật này chạm mặt đất? (Làm tròn kết quả đến chữ số hàng đơn vị)
Lời giải
a) Khi 3 t thì 2 5 5.3 7 s mét.
Vậy vật cách mặt đất 75 mét.
b) Khi 120 s thì 22 15 2054226tt t giây. Vậy sau gần 5 giây kể từ khi bắt đầu rơi thì vật chạm mặt đất.
OFFICIAL
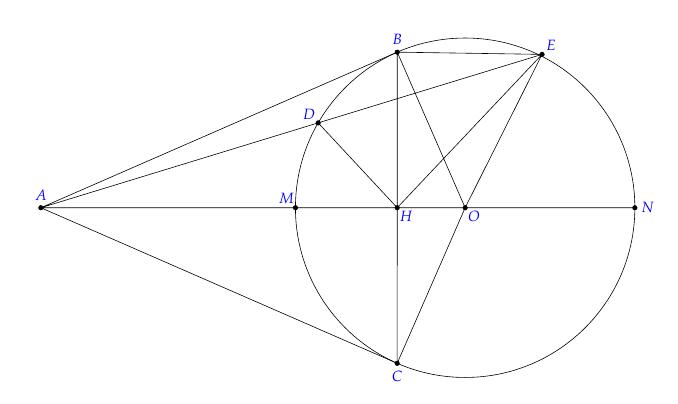
Câu 8. Cho đường tròn (;) OR và điểm A nằm ngoài đường tròn () O . Vẽ hai tiếp tuyến , ABAC của () O (,BC : Tiếp điểm) . Vẽ cát tuyến ADE của () O (,DE thuộc () O ; D nằm giữa A và E ; Tia AD nằm giữa hai tia AB và AO
a) Chứng minh 2 ABADAE b) Gọi H là giao điểm của OA và BC . Chứng minh tứ giác DEOH nội tiếp. c) Đường thẳng AO cắt đường tròn () O tại M và N (M nằm giữa A và )O . Chứng minh EHADMHAN Lời giải
DẠYKÈMQUYNHƠN
a) Ta có ABDAEB cùng
. Suy ra 2
ABDAEBAB
∽
b) Áp
ụng
ệ
Từ ()
chắn cung BD
ABAE
E AD A AB DA
()
d
h
thức lượng trong tam giác vuông 2 ABOABAO AH .
AHAOADAEDEOH
nội tiếp.
DẠYKÈMQUYNHƠN OFFICIAL c) Ta có 11 22 DEMDOMDEH
Suy ra EM là phân giác của góc AEH EHMH AEAM (1) ~ AEMAND (g-g) AEAM ANAD (2). Từ (1) và (2) suy ra: EHAEMHAM EHADMHAN AEANAMAD
(0.75 điểm) Chỉ số BMI còn được gọi là chỉ số khối lượng cơ thể (Body Mass Index). Dựa vào chỉ số BMI của một người, ta có thể biết được người đó béo, gầy hay có cân nặng lý tưởng. Chỉ số này được đề ra lần đầu tiên vào năm 1832 bởi một nhà khoa học người Bỉ. Công thức tính chỉ số BMI tương đối đơn giản, dựa vào hai chỉ số là chiều cao và cân nặng. Công thức cụ thể là 2 W BMI H Trong đó, W là khối lượng cơ thể tính theo đơn vị kilogam (kg), H là chiều cao tính theo đơn vị mét (m). Ta có bảng sau: Kết quả 18,5 BMI 18,524,9 BMI 2529,9 BMI 3040 BMI 40 BMI Phân loại Gầy Bình thường Béo phì độ I (nhẹ) Béo phì độ I (trung bình) Béo phì độ I (nặng) Ngoài ra, người ta có thể ước tính được tỉ lệ phần
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GD & ĐT QUẬN BÌNH TÂN NĂM HỌC
ng thẳng D . a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ; b) Tìm tọa độ giao điểm của P và D bằng phép
Bài 2: (1.0 điểm) Cho phương trình 2 2350 xx có 2 nghiệm là 12 ; xx . Không
ải
giá trị của biểu thức 22 12 Axx Bài 3:
tỉ lệ phần trăm khối lượng mỡ (so với khối lượng cơ thể), BMI là chỉ số khối lượng cơ thể, A là số tuổi và 1 G (nếu là giới tính nam) hoặc 0 G (nếu là giới tính nữ). Ví dụ, bạn nam 18 tuổi có chỉ số 20 BMI , thì theo công thức bạn có chỉ số 11,94 L , tức là cơ thể bạn nam có 11,94% khối lượng mỡ. Ta có bảng “tỉ lệ mỡ” như sau: Nam giới Nữ giới 2%4%: quá ít mỡ, cần thêm mỡ 6%13%: ít mỡ (vận động viên) 14%17%: người mẫu, fitness 18%25%: bình thường, chấp nhận được Trên 26%: béo phì 10%12%: quá ít mỡ, cần thêm mỡ 14%20%: ít mỡ (vận động viên) 21%24%: người mẫu, fitness 25%31%: bình thường, chấp nhận được Trên 32%: béo phì
2022-2023 ĐỀ THAM KHẢO MÔN : TOÁN 9 Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Quận Bình Tân – 1 Thời gian: 120 phút (không kể thời gian phát đề) Bài 1: (1.5 điểm). Cho hàm số 2 2
yx có đồ thị là parabol P và hàm số 24yx có đồ thị là đườ
toán.
gi
phương trình, hãy tính
trăm (%) khối lượng mỡ so với khối lượng cơ thể của một người khi áp dụng công thức sau: 1,2.0,23.10,8.5,4 LBMIAG Trong đó, L là
a) Một bạn nam năm nay 17 tuổi, cao 1,8m và có cân nặng là 63kg . Hãy tính tỉ lệ phần trăm % khối lượng mỡ (so với cơ thể) của bạn nam (làm tròn đến chữ số thập phân thứ nhất) và cho biết bạn nam thuộc dạng nào khi đối chiếu với bảng “tỉ lệ mỡ” đã cho ở trên.

b) Một bạn nữ năm nay 20 tuổi có chiều cao 1,68m và có t
OFFICIAL
c ngày 01/07/2016 xuống còn 40%, và có thể tiếp tục giảm xuống còn 35% kể từ ngày 01/01/2018 Ngày 01/07/2017. Một xe ô tô được chào bán với giá đã tính thuế là 581 triệu đồng. Giả sử giá gốc chưa tính thuế của xe không đổi, hãy tính:
a) Giá xe đó trước thuế vào thời điểm 01/07/2017.
b) Giá bán xe vào ngày 15/06/2016
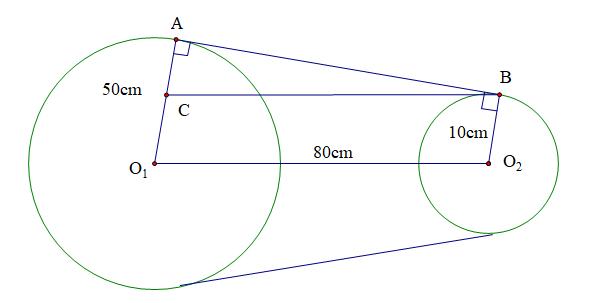
c) Giá bán xe vào ngày 01/01/2018 Bài 5: (1.0 điểm) Hình bên dưới biểu diễn một hệ thống ròng rọc gồm 1 sợi dây quấn quanh hai bánh xe. Khoảng cách giữa hai tâm của hai bánh xe là 80cm. Bán kính bánh xe lớn là 50cm, bán kính bán xe nhỏ là 10cm.
a) Tính chiều dài dây quấn quanh mỗi bánh xe (phần tiếp xúc với mỗi bánh xe).
b) Tính chiều dài toàn bộ dây của hệ thống ròng rọc.
(Lấy 3,14 và làm tròn các kết quả đến chữ số thập phân thứ 2)
Bài 6: (1.0
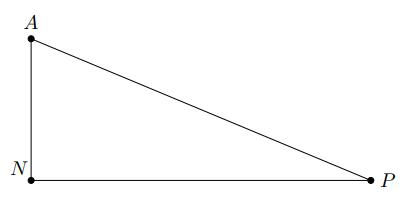
c 30/kmh . Nhà địa chất đang rất khát nước và ông biết rằng có một trạm xăng P ở vị trí xuôi theo đường 24km ( 24 NPkm) và ở đó có nước cho khách uống. a) Hỏi nhà địa chất tốn bao nhiêu phút để đi từ A đến P theo đường sa mạc?
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 78 -
đạ
n cần tăng thêm ít nhất bao nhiêu kilogam? Bài 4: (0.75 điểm) Cách tính thuế tiêu thụ đặc biệt và thuế nhập khẩu ô tô đã được điều chỉnh lại vào ngày 1 tháng 7 năm 2016, dẫn tới việc thay đổi mạnh trong cách tính giá xe. Trong tất cả các lại xe thì chỉ có xe cỡ nhỏ chở người dưới 10 chỗ
ế suấ
ớ
ệ
ỉ lệ mỡ là 20%.Bạn nữ này muốn cơ thể
t chuẩn người mẫu fitness (căn cứ theo bảng “tỉ lệ mỡ” ở trên) thì cơ thể cầ
, dung tích xi-lanh động cơ từ 3 1500 m trở xuống được giảm thu
t so v
i hi
n hành. Mức thuế xuất của loại xe này giảm từ 45% trướ
điểm) Nhà địa chất đang đi khảo sát và nghiên cứu tại một sa mạc. Ông ấy đang ở vị trí A trong sa mạc (xem hình vẽ minh hoạ) cách con đường nhựa 10km ( 10 ANkm). Trên con đường nhựa NP thì xe của nhà địa chất có thể chạy với vận tốc 50/kmh , nhưng trong sa mạc thì nó chỉ chạy đượ
Bài 7: (1.0 điểm) Một đoàn xe vận tải nhận chuyên chở 15 tấn hàng. Khi sắp khởi hành thì một xe phải điều đi làm công việc khác nên mỗi xe còn lại phải chở nhiều hơn 0,5 tấn hàng so với dự định. Hỏi thực tế có bao nhiêu xe tham gia vận chuyển (biết khối lượng hàng mỗi xe chở là như nhau)?
Bài 8: (3.0 điểm) Cho đường tròn ; OR với đường kính là AB và CD là một dây cung của đường tròn vuông góc với AB (CD không phải là đường kính của O ). Lấy điểm S tuỳ ý trên tia đối của tia BA. Đường thẳng SC cắt O tại M a) Chứng minh: SMASBC b) Các dây cung , AMBC cắt nhau ở N và các dây cung , ABDM cắt nhau tại P . Chứng minh rằng tứ giác BMNP nội tiếp và // NPCD c) Chứng minh rằng: 2 OSOPOM
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 79 -
có nhanh hơn
OFFICIAL
b) Nếu nhà địa chất đi từ A đến N , sau đó chạy trên con đường nhựa để đến P thì
không?
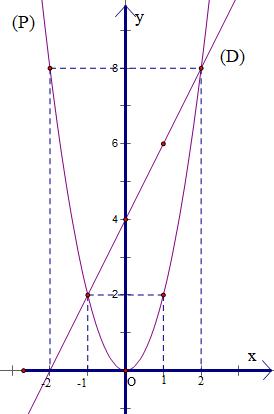
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 80HƯỚNG DẪN GIẢI Bài 1: (1.5 điểm). Cho hàm số 2 2 yx có đồ thị là parabol P và hàm số 24yx có đồ thị là đường thẳng D a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ; b) Tìm tọa độ giao điểm của P và D bằng phép toán. Lời giải a) Hàm số: 2 2 yx Bảng giá trị tương ứng của x và y : x 2 1 0 1 2 2 2 yx 8 2 0 2 8 Đồ thị hàm số là một Parabol đi qua các điểm 2;8 ; 1;2 ; 0;0 ; 1;2 ; 2;8 Hàm số: 24yx 04xy 16xy Đồ thị hàm số là đường thẳng đi qua 0;4 và 1;6 Vẽ: b) Hoành độ giao điểm của P và D là nghiệm của phương trình: 22 2242240 xxxx 2240 abc Phương trình có hai nghiệm phân biệt: 1 1 x ; 2 4 2 2 c x a + Với 1 1 x 1 2 y + Với 2 2 x 2 8 y Vậy toạ độ giao điểm của P và D là 1;2;2;8 .
tương
giản, dựa vào hai chỉ số là chiều cao và cân nặng. Công thức cụ thể là 2 W BMI H . Trong đó, W là khối lượng cơ thể tính theo đơn vị kilogam (kg), H là chiều cao tính theo đơn vị mét (m). Ta có bảng sau: Kết quả 18,5 BMI 18,524,9 BMI 2529,9 BMI 3040 BMI 40 BMI Phân loại Gầy Bình thường Béo phì độ I (nhẹ) Béo phì độ I (trung bình) Béo phì độ I (nặng) Ngoài ra, người ta có thể ước tính được tỉ lệ phần trăm (%) khối lượng mỡ so với kh
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 81Bài 2: (1.0 điểm) Cho phương trình 2 2350 xx có 2 nghiệm là 12 ; xx . Không giải phương trình, hãy tính giá trị của biểu thức 22 12 Axx Lời giải Ta có: 2;3;5 abc Phương trình có a và c trái dấu nên phương trình có hai nghiệm 12 ; xx Theo hệ thức Viet, ta có: 12 12 3 2 5 2 b Sxx a c Pxx a Ta có: 2 2 22222 121122121212 3529 22222. 224 AxxxxxxxxxxxxSP Bài 3: (0.75 điểm) Chỉ số BMI còn được gọi là chỉ số khối lượng cơ thể (Body Mass Index). Dựa vào chỉ số BMI của một người, ta có thể biết được người đó béo, gầy hay có cân nặng lý tưởng.
ỉ số
đề ra lần đầu tiên vào năm 1832 bởi một nhà khoa học người Bỉ. Công thức
ỉ số
của một người khi áp dụng công thức sau: 1,2.0,23.10,8.5,4 LBMIAG Trong đó, L là tỉ lệ phần trăm
mỡ (so với khối lượng cơ thể), BMI là chỉ số khối lượng cơ thể, A là số tuổi và 1 G (nếu là giới tính nam) hoặc 0 G (nếu là giới tính nữ). Ví dụ, bạn nam 18 tuổi có chỉ số 20 BMI , thì theo công thức bạn có chỉ số 11,94 L , tức là cơ thể bạn nam có 11,94% khối lượng mỡ. Ta có bảng “tỉ lệ mỡ” như sau: Nam giới Nữ giới 2%4%: quá ít mỡ, cần thêm mỡ 6%13%: ít mỡ (vận động viên) 14%17%: người mẫu, fitness 18%25%: bình thường, chấp nhận được Trên 26%: béo phì 10%12%: quá ít mỡ, cần thêm mỡ 14%20%: ít mỡ (vận động viên) 21%24%: người mẫu, fitness 25%31%: bình thường, chấp nhận được Trên 32%: béo phì
Ch
này được
tính ch
BMI
đối đơn
ối lượng cơ thể
khối lượng
a) Một bạn nam năm nay 17 tuổi, cao 1,8m và có cân nặng là 63kg. Hãy tính tỉ lệ phần trăm (%) khối lượng mỡ (so với cơ thể) của bạn nam (làm tròn đến chữ số thập phân thứ nhất) và cho biết bạn nam thuộc dạng nào khi đối chiếu với bảng “tỉ lệ mỡ” đã cho ở trên.
b) Một bạn nữ năm nay 20 tuổi có chiều cao 1,68m và
OFFICIAL
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 82 -
thêm ít nhất bao nhiêu kilogam? Lời giải a) Chỉ số BMI của bạn nam: 22 W63 19,4 1,8 BMI H Tỉ lệ phần trăm khối lượng mỡ so với cơ thể của bạn nam: 1,2.0,23.10,8.5,41,2.19,40,23.1710,8.15,410,9911,0% LBMIAG Vì 6%11,0%13% . Nên bạn nam thuộc dạng ít mỡ (vận động viên). b) Chỉ số BMI của bạn nữ: 1,2.0,23.10,8.5,4 201,2.0,23.2010,8.05,4 17,3 LBMIAG BMI BMI Khối lượng của bạn nữ: 22 2 W W.17,3.1,6848,8() BMIBMIHkg H Bạn nữ này muốn cơ thể đạt chuẩn người mẫu fitness, thì bạn tỉ lệ phần
LBMIAG BMI BMI Khối lượng của bạn nữ lúc này: 22 2 W W.18,2.1,6851,4() BMIBMIHkg H Khối lượng tối thiểu cần tăng thêm là: 51,448,82,6 kg Bài 4: (0.75 điểm) Cách tính thuế tiêu thụ đặc biệt và thuế nhập khẩu ô tô đã được điều chỉnh lại vào ngày 1 tháng 7 năm 2016, dẫn tới việc thay đổi mạnh trong cách tính giá xe. Trong tất cả các lại xe thì chỉ có xe cỡ nhỏ chở người dưới 10 chỗ, dung tích xi-lanh động
giảm thuế suất so với hiện hành. Mức thuế xuất của loạ
xe này giảm
ừ 45%
01/07/2016 xuống còn 40%, và có thể tiếp tục giảm xuống còn 35% kể từ ngày 01/01/2018. Ngày 01/07/2017. Một xe ô tô được chào bán với giá đã tính thuế là 581 triệu đồng. Giả sử giá gốc chưa tính thuế của xe không đổi, hãy tính: a) Giá xe đó trước thuế vào thời điểm 01/07/2017. b) Giá bán xe vào ngày 15/06/2016. c) Giá bán xe vào ngày 01/01/2018.
có tỉ lệ mỡ là 20%. Bạn nữ này muốn cơ thể đạt chuẩn người mẫu fitness (căn cứ theo bảng “tỉ lệ mỡ” ở trên) thì cơ thể cần cần tăng
trăm mỡ tối thiểu phải là 21%. Khi đó: Chỉ số BMI của bạn nữ lúc này: 1,2.0,23.10,8.5,4 211,2.0,23.2010,8.05,4 18,2
cơ từ 3 1500 m trở xuống được
i
t
trước ngày
a) Giá của xe trước thuế vào thời điểm 01/07/2017: 581:100%40%415 (triệu đồng)
b) Giá bán của xe vào ngày 15/06/2016: 415.100%45%601,75 (triệu đồng)
c) Giá bán xe vào ngày 01/01/2018: 415.100%35%560,25 (triệu đồng)
Bài 5: (1.0 điểm) Hình bên dưới biểu diễn một hệ thống ròng rọc gồm 1 sợi dây quấn quanh hai bánh xe. Khoảng cách giữa hai tâm của hai bánh xe là 80cm. Bán kính bánh xe lớn là 50cm, bán kính bán xe nhỏ là 10cm

a) Tính chiều dài dây quấn quanh mỗi bánh xe (phần tiếp xúc với mỗi bánh xe). b) Tính chiều dài toàn bộ dây của hệ thống ròng rọc. (Lấy 3,14 và làm tròn các kết quả đến chữ số th
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 83Lời giải
OFFICIAL
Lời giải a) Chiều dài
ấ
xe lớn: 2.502.50.3,14314,00 cm Chiề
ấ
xe nhỏ: 2.10.2.10.3,1462.80 cm b) Vẽ 12 // BCOO 12 OOBC là hình bình hành 121280;10 BCOOcmOCOBcm 11 501040 ACOAOCcm Xét ABC vuông tại A, có: 222 BCABAC (định lý Pytago) 222 222 2 8040 8040 4800 480069,28 AB AB AB ABcm Tổng chiều dài dây của hệ thống ròng rọc: 11 314,0062,8069,28.2314,00.62,80.703,76 22 cm Bài 6: (1.0 điểm) Nhà địa chất đang đi khảo sát và nghiên cứu tại một sa mạc. Ông ấy đang ở vị trí A trong sa mạc (xem hình vẽ minh hoạ) cách con đường nhựa 10km ( 10 ANkm). Trên con đường nhựa NP thì xe của nhà địa chất có thể chạy với vận tốc 50/kmh , nhưng trong sa mạc thì nó chỉ
ập phân thứ 2)
dây qu
n bánh
u dài dây qu
n bánh

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 84chạy được
.
địa chất đang rất
ông
ết rằ
ột trạm xăng P ở vị trí
222
N rồ
từ
đế
ẽ
điểm) Một đoàn xe vận tả
ậ
khởi hành thì một xe phải điều đi làm công việc khác nên mỗi xe còn lại phải chở nhiều hơn 0,5 tấn hàng so với dự định. Hỏi thực tế có bao nhiêu xe tham gia vận chuyển (biết khối lượng hàng mỗi xe chở là như nhau)? Lời giải Gọi số xe thực tế tham gia vận là x * x Số xe dự định là 1 x Khối lượng hàng mỗi xe chở thực tế: 15 x (tấn)
30/kmh
Nhà
khát nước và
bi
ng có m
xuôi theo đường 24km ( 24 NPkm) và ở đó có nước cho khách uống. c) Hỏi nhà địa chất tốn bao nhiêu phút để đi từ A đến P theo đường sa mạc? d) Nếu nhà địa chất đi từ A đến N , sau đó chạy trên con đường nhựa để đến P thì có nhanh hơn không? Lời giải a) Xét ANP vuông tại N, có :
APANNP (định lý Pytago) 222 2 1024 676 676 26
AP AP AP AP Quãng đường AP trong sa mạc dài 26km Thời gian đi trong sa mạc từ A đến P :
13 26:3052 15
h (phút) b) Thời gian đi từ A đến N : 1 10:3020 3
h (phút) Thời gian đi từ N đến P : 12 24:5028,8 25 h (phút) Tổng thời gian đi từ A đến N rồi từ N đến P : 2028,848,8 (phút) 52 (phút) Vậy đi từ A đến
i
N
n P s
nhanh hơn chạy thẳng từ A đến P. Bài 7: (1.0
i nh
n chuyên chở 15 tấn hàng. Khi sắp
a tia BA. Đường thẳng SC cắt O tại M
a) Chứng minh: SMASBC b) Các dây cung , AMBC cắt nhau ở N và các dây cung , ABDM cắt nhau tại P . Chứng minh rằng tứ giác BMNP nội tiếp và // NPCD
c) Chứng minh rằng: 2 . OSOPOM . Lời giải
a) Chứng minh: SMASBC Xét SMAvà SBC , có: S là góc chung SAMSCB (hai góc nội tiếp cùng chắn cung BM của O ) Do đó SMASBC (g.g)
b) Chứng minh rằng tứ giác BMNP nội tiếp và // NPCD

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 85Khối lượng hàng mỗi xe chở dự định: 15 1 x (tấn) Vì mỗi xe thực tế chở nhiều hơn dự định 0,5tấn hàng. Nên ta có phương trình: 2 2 1515 0,5 1 1510,51 15 111 151150,51 1515150,50,5 0,50,5150 5 6 xx xxx x xxxxxx xxxx xxxx xx xN xL Vậy thực tế có 5 xe tham gia vận chuyển. Bài 8: (3.0 điểm) Cho đường tròn ; OR với đường kính là AB và CD là một dây cung của đường tròn vuông góc với AB (CD không phải là đường kính của O ). Lấy điểm S tuỳ ý trên tia đối củ
AB là đường trung trực của CD (liên hệ giữa đường kính và dây cung)
ACAD(tính chất đường trung trực)
ACAD (hai cung bằng nhau căng hai dây bằng nhau)
AMDABC (hai góc nội tiếp chắn hai cung bằng nhau)
Hay NMPNBP
tứ giác BMNP nội tiếp (hai đỉnh kề cùng nhìn cạnh NP)
NPBNMB Hay NPAB Mà CDABgt Suy ra // NPCD (mối liên hệ giữa vuông góc và song song) c) Chứng minh rằng: 2 OSOPOM Vẽ đường kính MK của O (như hình)
(hai dây bằng nhau căng hai cung bằng nhau)(1)
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 86Vì
ABCDgt và AB là đường kính
Ta
ASC 2 sdACsdBM
1 2 KMDsdKD(tính chất góc nộ
tiếp) 2 sdADsdAK KMD (3) Mà ADAC (cmt)(4) Từ (1), (2) ,(3) và (4) ASCKMD hay OSMOMP Xét OSM và OMP
có: O : góc chung OSMOMP (cmt) Do đó OSMOMP
OSOM OMOP
ỉ
ố
2
Ta có: 090 AMB (góc nội tiếp chắn nửa đường tròn) Hay 090 NMB Mà tứ giác BMNP nội tiếp (cmt) 0180 NMBNPB (2 góc đối của tứ giác nội tiếp) 0000 1801809090
Xét AOK và BOM , có:
OAOBR
AOKBOM (hai góc đối đỉnh)
OKOMR
AOKBOMcgc
AKBM (hai cạnh tương ứng)
AKBM
có:
(góc có đỉnh nằm ngoài đường tròn) (2)
i
,
(g.g)
(t
s
đồng dạng)
OSOPOM
NHÓM WORD HÓA ĐỀ TOÁN - 87
DẠYKÈMQUYNHƠN OFFICIAL
chuy
472 lít
Khi bốc hai thùng lên xe tải thì phát hiện thùng thứ nhất có một lỗ mọt gần miệng thùng. Để tránh nước mắm bị rò rỉ ra ngoài, anh Mến đã lấy bớt 50 lít ở thùng một đổ vào thùng hai. Do đó, thùng thứ hai lúc này chứa nhiều hơn thùng thứ nhất 24 lít nước mắm. Hỏi lúc đầu mỗi thùng chứa bao nhiêu lít nước mắm? Bài 4: (1 điểm) Một máy bay cất cánh ở sân bay Tân Sơn Nhất (vị trí gốc tọa độ O) và bay theo một đường thẳng hợp với mặt đất Ox một góc 30và có phương trình yaxb với a, b là hằng số. Gọi y (m) là độ cao so với mặt đất, x (phút) là thời gian bay và có đồ thị như hình vẽ. a) Xác định hệ số a, b b) Tính quãng đường máy bay bay trong 5 phút Bài 5: (0.75 điểm) Một chủ vườn trồng sầu riêng không hạt thu hoạch cả mùa được 3000kg. Đầu mùa giá sầu riêng bán được là 50000 đồng/kg, giữa mùa giá giảm 30% so với đầu mùa, đến cuối mùa giá tang them 15% so với giữa mùa. Biết số lượng bán đầu mùa bằng 1 3 số lượng bán giữa mùa và bằng 1 2 số lượng bán cuối mùa. Tính
hai thùng
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GD & ĐT QUẬN BÌNH THẠNH NĂM HỌC 2022-2023 ĐỀ THAM KHẢO MÔN
9 Đề thi
MÃ ĐỀ : Quận Bình Thạnh – 1 Thời
Bài 1: (1.5 điểm) Cho hàm số 2 4 x y có đồ thị là parabol P và hàm số 1 yx có đồ thị là đường thẳng D . a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ; b) Tìm tọa độ giao điểm của P và D bằng phép tính. Bài 2: (1 điểm) Cho phương trình 2 714210 xx . Không giải phương trình, hãy tính giá trị của biểu thức 21 12 33xx A xx Bài 3: (1 điểm) Anh
ến đi làm
ở một
c mắm.
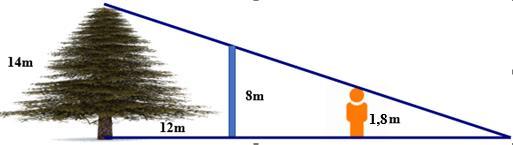
số tiền chủ vườn thu được vào đợt cuối mùa? Bài 6: (1.0 điểm) Một cái cây có chiều cao 14m, mọc ở phía sau một bức tường cao
và cách bức tường 12m. Hỏi người quan sát có chiều cao
ải đứng cách bức tường bao nhiêu mét để có thể nhìn thấy ngọn cây? x(
y(m) A 1 8000 O
: TOÁN
gồm 8 câu hỏi tự luận
gian: 120 phút (không kể thời gian phát đề)
M
thuê
hang nướ
Hôm nay, anh chuẩn bị vận
ển
nước mắm thành phẩm đựng trong
gỗ.
8m
1,8m ph
phút)
Bài 7: (0.75 điểm) Một hộp sữa lớn hình hộp chữ nhật có diện tích đáy là 20 2dm và chiều cao là 3 dm. Người ta rót hết sữa trong hộp ra những chai sữa nhỏ mỗi chai có thể tích là 0,35 3dm được tất cả 72 chai. Hỏi lượng sữa có trong hộp chiếm bao nhiêu phần trăm thể tích của hộp sữa?
Bài 8: (3.0 điểm) Cho đường tròn (O) và điểm A ở ngoài đường tròn Vẽ các tiếp tuyến AM, AN với (O) (M, N là các tiếp điểm). Qua A vẽ đường thẳng cắt đường tròn (O) tại hai điểm B và C phân biệt ( B nằm giữa A và C ). Gọi H là trung điểm BC
a) Chứng minh tứ giác AMHN nội tiếp và 2 AMABAC b) Gọi K là giao điểm của AO và (O). Chứng minh K là tâm của đường tròn nội tiếp AMN c) Đường thẳng qua B song song với AM cắt đoạn thẳng MN tại E. Chứng minh EH // MC
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 78 -
OFFICIAL
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI Bài 1: (1.5 điểm) Cho hàm số 2 4 x y có đồ thị là parabol P và hàm số 1 yx có đồ thị là đường thẳng D . a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ; b) Tìm tọa độ giao điểm của P và D bằng phép tính. Lời giải a) Hàm số: 2 4 x y Bảng giá trị tương ứng của x và y : x 4 2 0 2 4 2 4 x y 4 1 0 1 4 Đồ thị hàm số là một Parabol đi qua các điểm 4;4 ; 2;1 ; 0;0 ; 2;1 ; 4;4 Hàm số: 1 yx 01xy 10 12 xy xy Đồ thị hàm số là đường thẳng đi qua 0;1 ; 1;2 và 1;0 Vẽ: b) Hoành độ giao điểm của P và D là nghiệm của phương trình: 2 1 4 x x 2 440xx 2 (2)0202 xxx + Với 2 x 1 y Vậy tọa độ giao điểm của D và P là 2;1 Bài 2: (1.0 điểm) Cho phương trình 2 714210 xx . Không giải phương trình, hãy tính giá trị của biểu thức
đựng trong hai thùng gỗ. Khi bốc hai thùng lên xe tải thì phát hiện thùng thứ nhất có một lỗ mọt gần miệng thùng. Để tránh nước mắm bị rò rỉ ra ngoài, anh Mến đã lấy bớt 50 lít ở thùng một đổ vào thùng hai. Do đó, thùng thứ hai lúc này chứa nhiều hơn thùng thứ nhất 24 lít nước mắm. Hỏi lúc đầu mỗi thùng chứa bao nhiêu lít nước mắm? Lời giải
- Gọi x, y (lít) là số lít nước mắm lần lượt trong thùng 1, 2 lúc đầu (x, y > 0) - Vì ban đầu có tổng cộng 472 lít nước mắm 472(1) xy - Lúc sau lấy 50 lít ở thùng một đổ vào thùng hai nên lúc này thùng 1 chứa:
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 80Lời giải Phương trình đã cho là phương trình bậc hai của x có: 714210 abc Vậy phương trình đã cho luôn có hai nghiệm 1x ; 2x Theo định lý Vi-et, ta có: 12 12 2 3 b Sxx a c Pxx a Ta có : 21 12 2211 12 22 1212 12 2 33 (3)(3) 3 23 4 3 xx A xx xxxx A xx xxxx A xx SPS A P A Bài 3: (1 điểm) Anh Mến đi làm thuê ở một hãng nước mắm. Hôm nay,
ẩn bị vận
ể
c mắm thành
ẩm
anh chu
chuy
n 472 lít nướ
ph
ch
50 y
mắm. - Mà lúc này thùng 2 nhiều hơn thùng 1 là 24 lít nước mắm - (50)(50)2476(2) yxxy - Từ (1) và (2) ta có hệ phương trình: 476274 76198 xyx xyy - Vậy lúc đầu thùng 1 chứa 274 lít nước mắm, thùng 2 chứa 198 lít nước mắm Bài 4: (1 điểm) Một máy bay cất cánh ở sân bay Tân Sơn Nhất (vị trí gốc tọa độ O) và bay theo một đường thẳng hợp với mặt đất Ox một góc 30và có phương trình yaxb với a, b là hằng số. Gọi y (m) là độ cao so với mặt đất, x (phút) là thời gian bay và có đồ thị như hình vẽ. a) Xác định hệ số a, b b) Tính quãng đường máy bay bay trong 5 phút x(phút) y(m) A 1 8000 O
50 x lít nước mắm và thùng 2
ứa:
lít nước
b) Khi máy bay bay được 5 phút 5 x (phút) Thế 5 x vào phương trình 8000 yx 8000.540000() ym Vậy khi máy bay bay được
5: (0.75 điểm)

c 80000(m)
ng s
u riêng không h
ch cả mùa được 3000kg. Đầu mùa giá sầu riêng bán được là 50000 đồng/kg, giữa mùa giá giảm 30% so với đầu mùa, đến cuối mùa giá tang them 15% so với giữa mùa. Biết số lượng bán đầu mùa bằng 1 3 số lượng bán giữa mùa và bằng 1 2 số lượng bán cuối mùa. Tính số tiền chủ vườn thu được vào đợt cuối mùa?
Lời giải
- Giá tiền 1kg sầu riêng giữa mùa là: 50000(130%)35000 (đồng)
- Giá tiền 1kg sầu riêng giữa mùa là: 35000(115%)40250 (đồng)
- Gọi ()xkg là số lượng sầu riêng bán được đầu mùa (0) x
- Do số lượng bán đầu mùa bằng 1 3 số lượng bán giữa mùa và bằng 1 2 số lượng bán cuối mùa Nên số lượng bán giữa mùa và cuối mùa là: 3,2xx (kg) - Vì số lượng cả mùa là 3000kg 32300063000500() xxxxxkg
- Vậy số lượng sầu riêng đầu mùa, giữa mùa và cuối mùa lần lượt là: 500(kg), 1500(kg) và 1000(kg) - Số tiền chủ vườn thu được cuối mùa là: 500.500001500.350001000.40250117750000 (đồ
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 81Lời giải
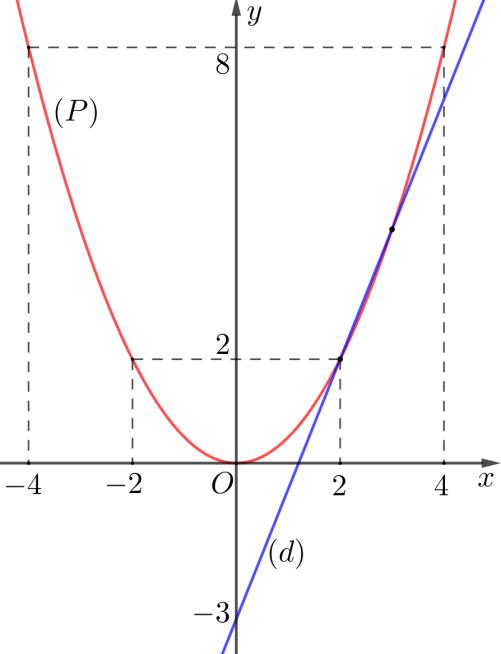
a) Đồ thị yaxb đi qua 2 điểm (1;8000);(0;0)AO 8000.180008000 0.000 ababa abbb
Vậy 8000;0ab và đồ thị có phương trình là 8000 yx
5 phút thì đạt độ cao 40000() m so với mặt đất Gọi C là vị trí của máy bay khi bay được 5 phút B là hình chiếu của C xuống mặt đất Vậy lúc này độ cao của máy bay là 40000() BCm và quãng đường máy bay bay được là OC Xét BCO vuông tại B có: 40000 sin80000() sinsin30 BCBC OOCm OCO Vậy sau 5 phút máy bay bay đượ
Bài
Một chủ vườn trồ
ầ
ạt thu hoạ
ng) Bài 6: (1.0 điểm) Một cái cây có chiều cao 14m, mọc ở phía sau một bức tường cao 8m và cách bức tường 12m. Hỏi người quan sát có chiều cao 1,8m phải đứng cách bức tường bao nhiêu mét để có thể nhìn thấy ngọn cây? 30 40000(m) B O C
sữa lớn hình hộp chữ nhật có diện tích đáy là 20 2dm và chiều cao là 3 dm. Người ta rót hết sữa trong hộp ra những chai sữa nhỏ mỗi chai có thể tích là 0,35 3dm được tất cả 72 chai. Hỏi lượng sữa có trong hộp chiếm bao nhiêu phần trăm thể tích của hộp sữa? Lời giải
- Thể tích của hộp sữa lớn là : 3 20.360() dm
- Thể tích sữa chứa trong 72 chai sữa nhỏ là: 3 72.0,3525,2() dm
- Thể tích sữa chứa trong hộp sữa lớn = Thể tích sữa chứa trong 72 chai sữa nhỏ là 3 25,2() dm và chiếm 25,2.10042%
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 82Lời giải - Gọi AB là chiều cao cây. - CD là chiều cao tường. - MN là chiều cao người quan sát - AM cắt BN ở O - Xét ODC và OBA có: DC // BA ( cùng OB ) ODDC OBBA ( hệ quả Ta-lét ) 84 147 12 4 477433 4.416() OD OB ODOBOBODBD ODm - Xét OMN và OCD có: MN // CD ( cùng OB ) ONMN ODCD ( hệ quả Ta-lét) 1,816.1,8 3,6() 1688 ON ONm Vậy để nhìn thấy ngọn cây người quan sát cần cách bức tường 1 khoảng là : 163,612,4() DNODONm Bài 7: (0.75 điểm) Một hộp
tròn. Vẽ các tiếp tuyến AM, AN với (O) (M, N là các tiếp điểm). Qua A vẽ đường thẳng cắt đường tròn (O) tại hai điểm B và C phân biệt ( B nằm giữa A và C ). Gọi H là trung điểm BC a) Chứng minh tứ giác AMHN nội tiếp và 2 AMABAC b) Gọi K là giao điểm của AO và (O). Chứng minh K là tâm của đường tròn nội tiếp AMN c) Đường thẳng qua B song song với AM cắt đoạn thẳng MN tại E. Chứng minh EH // MC Lời giải 14m 12m 8m 1,8m N D B A O C M
60 thể tích hộp sữa lớn Bài 8: (3.0 điểm) Cho đường tròn (O) và điểm A ở ngoài đường
a) Xét tứ giác AMON có: ˆˆ 90 AMOANO ( do AM, AN là 2 tiếp tuyến (O)) ˆˆ 180 AMOANO Vậy tứ giác AMON nội tiếp đường tròn đường kính AO ,,, AMON đường tròn đường kính AO (1) Ta có: + OH là 1 phần bán kính (O) + H là trung điểm dây cung BC của (O) OH vuông góc BC OHA vuông tại H ,, OHA đường tròn đường kính AO (2) Từ (1) và (2) ,,,, OHAMN đường tròn đường kính AO
Tứ giác AMHN nội tiếp đường tròn đường kính AO
AMB và ACM có:
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 83 -
OFFICIAL
+ ˆ
chung + ˆ ˆ AMBACM (góc tạo bởi tiếp tuyến và dây với góc nội tiếp cùng chắn cung MB) AMB đồng dạng ACM (gg) AMAB ACAM (tsđd) 2 AMABAC b) Ta có: + AMAN ( tính chất 2 tiếp tuyến cắt nhau tại A ) +OMON bán kính (O) OA là trung trực MN OA vuông góc MN ở I là trung điểm MN Xét OKM có: OKOM bán kính (O) OKM cân tại O ˆˆ OKMOMK (3) Lại có: I E B H K N M A O C
Xét
: NAC
90 OMKKMAOMA (do AM là tiếp tuyến (O)) (5) Từ (3), (4), (5)
IMKKMA Xét AMN có: +MK là phân giác ˆ NMA ( do ˆˆ IMKKMA ) +AI là phân giác ˆ NMA ( tính chất 2 tiếp tuyến cắt nhau tại A) +MK cắt AI ở K
K là tâm đường tròn nội tiếp AMN c) Ta có:
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 84+ ˆˆ
ˆˆˆ
+ ˆˆ
ˆˆ BENBHN Xét
ứ
ˆˆ
Tứ
ˆˆ EHBENB Mà ˆ ˆ
ˆ ˆ EHBMCB
90 OKMIMK ( do IMK vuông tại I) (4) +
ˆˆ
+ ˆˆ BENAMN
( 2 góc đồng vị do BE // AM )
AMNAHN
( 2 góc nội tiếp cùng chắn cung AN của đường tròn đường kính OA)
t
giác BEHN có:
BENBHN
giác BEHN nội tiếp
MCBENB
( 2 góc nội tiếp cùng chắn cung MB của (O))
EH // MC ( do 2 góc trên nằm ở vị trí đồng vị )
PHÒNG GD-ĐT HUYỆN CẦN GIỜ
TRƯỜNG THCS BÌNH KHÁNH
ĐỀ ĐỀ NGHỊ TUYỂN SINH 10
Năm học: 2022–2023
MÔN: TOÁN – LỚP: 9
Thời gian: 120 phút (không kể thời gian phát đề)
Câu 1. (1,5 điểm)
Cho Parabol (P): và đường thẳng (D):
a) Vẽ (P) và (D) trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán.
Câu 2. (1,0 điểm)
Cho phương trình: 20x2 + 5x – 2020 = 0
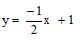
Không giải phương trình trên, hãy tính giá trị của biểu thức sau:
Câu 3. (1,0 điểm)
Trong đợt dịch Covid-19, học sinh hai lớp 9A và 9B trường THCS BK ủng hộ 212 chiếc khẩu trang cho những nơi cách li tập trung. Biết rằng số học sinh lớp 9A nhiều hơn số học sinh lớp 9B là 1 học sinh và mỗi học sinh lớp 9A ủng hộ 2 chiếc khẩu trang, mỗi học sinh lớp 9B ủng hộ 3 chiếc khẩu trang. Tìm số học sinh mỗi lớp.
Câu 4. (1,0 điểm)
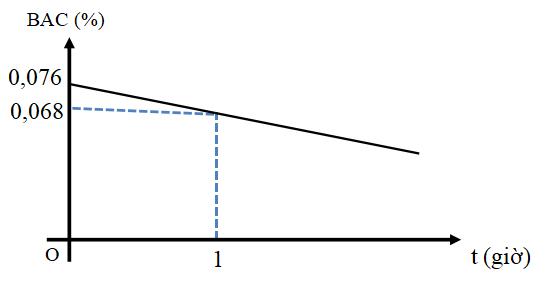
Nồng độ cồn trong máu (BAC) được định nghĩa là phần trăm rượu (rượu ethyl hoặc ethanol) trong dòng máu của một người. BAC 0,05% có nghĩa là có 0,05 gam rượu trong 100 ml máu. Càng uống nhiều rượu bia thì nồng độ cồn trong máu càng cao và càng nguy
DẠYKÈMQUYNHƠNOFFICIAL
hiểm khi tham gia giao thông. Nồng độ BAC trong máu của một người được thể hiện qua đồ thị sau:
a) Viết công thức biểu thị mối quan hệ giữa nồng độ cồn trong máu (B) sau t giờ sử dụng
b) Theo nghị định 100/2019/NĐ-CP về xử phạt vi phạm hành chính, các mức phạt (đối với xe máy).Hỏi sau 3 giờ, nếu người này tham gia giao thông thì sẽ bị xử phạt ở mức độ nào?
Câu 5. (1,0 điểm)
Một siêu thị chạy chương trình khuyến mãi cho nước tăng lực có giá niêm yết là 9000 (đ/lon) như sau:
- Nếu mua 1 lon thì không giảm giá. - Nếu mua 2 lon thì lon thứ hai được giảm 500 đồng - Nếu mua 3 lon thì lon thứ hai được giảm 500 đồng và lon thứ ba được giảm giá 10%.
- Nếu mua trên 3 lon thì lon thứ hai được giảm 500 đồng, lon thứ ba được giảm 10% và những lon thứ tư trở đi đều được giảm thêm 2% trên giá đã giảm của lon thứ ba.
a) Hùng mua 3 lon nước tăng lực trên thì phải thanh toán số tiền là bao nhiêu?
DẠYKÈMQUYNHƠNOFFICIAL
b) Vương phải trả 422 500 đồng để thanh toán khi mua những lon nước tăng lực trên. Vương đã mua bao nhiêu lon nước?
Câu 6. (1,0 điểm)
Tính chiều cao của một ngọn núi (làm tròn đến mét), cho biết tại hai điểm cách nhau 550m, người ta nhìn thấy đỉnh núi với góc nâng lần lượt là 330 và 370 .
Câu 7. (1,0 điểm)
Trong hình vẽ dưới đây, hai địa điểm A và B cách nhau 100km. Một xe ô tô khởi hành từ B đến A với vận tốc 40 km/h. Cùng lúc đó, một xe đạp điện cũng khởi hành từ A trên đoạn đường vuông góc với AB với vận tốc 20 km/h. Hỏi sau 90 phút hai xe cách nhau bao xa?
Câu 8. (2,5 điểm)
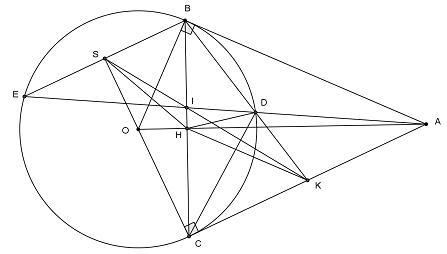
Từ điểm A ở ngoài đường tròn (O) (OA > 2R), vẽ hai

DẠYKÈMQUYNHƠNOFFICIAL
điểm
ủ
a)
b)
c)
ọ
tiếp tuyến AB, AC của (O). Gọi K là trung
c
a AC, KB cắt (O) tại D, OA cắt BC tại H.
Chứng minh HK // AB và tứ giác CHDK nội tiếp
Tia AD cắt (O) tại E. Chứng minh KC2 = KD. KB và BE // AC
G
i I là giao điểm của BC và AE, tia KI cắt BE tại S. Chứng minh BD. BK = 2HS2 . HẾT
PHÒNG GD-ĐT HUYỆN CẦN GIỜ TRƯỜNG THCS BÌNH KHÁNH
ĐÁP ÁN ĐỀ ĐỀ NGHỊ TUYỂN SINH 10
Năm học: 2022–2023 MÔN: TOÁN – LỚP: 9 Thời gian: 120 phút (không kể thời gian phát đề) Câu Hướng dẫn chấm Điểm 1a Vẽ đúng (P) và (D) 1 1b Tìm được giao điểm (-2; 2) và 0,5 2
20x2 + 5x – 2020 = 0 CM pt có nghiệm 0,25 0,5 0,25
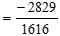
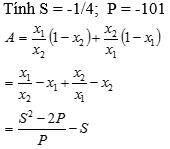
DẠYKÈMQUYNHƠNOFFICIAL
3
Gọi x, y (hs) lần lượt là số học sinh của lớp 9A và 9B
(x > y > 0; x, y N)
Do số học sinh lớp 9A nhiều hơn số học sinh lớp 9B là 1 học sinh nên ta có pt: x – y = 1 ( 1 )

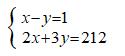

Do mỗi học sinh lớp 9A ủng hộ 2 chiếc khẩu trang, mỗi học sinh lớp 9B ủng hộ 3 chiếc khẩu trang và hai lớp ủng hộ được 212 khẩu trang nên ta có pt : 2x + 3y = 212 ( 2 )
Từ (1 ) và (2 ) ta lập được hệ pt: Giải hệ pt ta được : KL: Vậy lớp 9A có 43 học sinh , lớp 9B có 42 học sinh .
0,25 đ 0,25 đ 0,25 đ 0,25 đ
a) Gọi B= at + b là công thức biểu thị nồng độ cồn trong máu sau t giờ sử dụng Từ các tọa độ điểm (0; 0,076) và (1; 0,068), ta tìm được và 0,25 +0,25 đ 4b b) Ta có công thức Sau 3 giờ kể từ khi sử dụng, nồng độ cồn trong máu là 0,25 đ
4a
DẠYKÈMQUYNHƠNOFFICIAL
5a
Vì 50<52<80 nên sẽ bị xử phạt ở mức 2
a/ Hùng mua 3 lon nước ngọt trên thì phải trả số tiền là: 9000 + 8500 + ( 9000 – 10%.9000) = 25 600 ( đồng)
b/ Giá tiền của lon nước tăng lực thứ 4 trở đi. (9000 – 10%.9000) – 2%.(9000 – 10%.9000) = 7938 (đồng) Gọi n ( lon) là số lon nước tăng lực thứ 4 trở đi ( n>0, nguyên)
0,25 đ
0,25
5b
6
Vì Vương phải trả 422 500 đồng để thanh toán khi mua những lon nước tăng lực trên. Nên ta có : 7938n + 25 600 = 422 500 Suy ra : n = 50 ( TĐK) Vậy Vương đã mua 53 lon nứơc tăng lực.
AB = AC – BC

AB = CD.cotCAD – CD.cotCBD 550 = CD(cot33o – cot37o) CD = 550 : (cot33o – cot37o) CD = 2584,3…≈ 2584 (m) Vậy: Chiều cao ngọn núi xấp xỉ 2584 (m)
0,25 0,25 0,25
0,25 0,5 0,25
7
Quãng đường xe ô tô đi được: BC = 40.1,5 = 60 (km) 0,25đ

Quãng đường xe đạp đi được: AD = 20. 1,5 = 30 (km) 0,25đ
Quãng đường AC = AB – BC = 100 – 60 = 40 (km) Tam giác ADC vuông tại A: 22 DC304050 0,5đ
DẠYKÈMQUYNHƠNOFFICIAL
Vậy xe đạp cách ô tô là 50 km. 8
8a Chứng minh HK // AB và tứ giác CHDK nội tiếp - OA là đường trung trực của BC suy ra H là trung điểm của BC - HK là đường trung bình của ∆ABC suy ra HK // ABCHDK nội tiếp
8b Chứng minh KC2 = KD. KB và BE // AC - ∆KCD ~ ∆KBC suy ra KC2 = KD. KB và KA2 = KD. KB - ∆KAD ~ ∆KBA (c – g – c) -
0,25 0,25 0,5
0,5 0,5
8c - S là trung điểm của BE suy ra CO ^ BE tại S - BC = 2BH = 2HS - BD.BK = BH.BC = 2BH2 = 2HS2 0,25 0,25 HẾT
DẠYKÈMQUYNHƠNOFFICIAL
ĐỀ THAM KHẢO MÔN : TOÁN 9 -------------------- Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Huyện Củ Chi – 01 Thời gian: 120 phút (không kể thời gian phát đề)
Câu 1. Cho Parabol 2 (P): 4 x y và đường thẳng (D):2 2 x y
a) Vẽ (P) và (D) trên cùng một mặt phẳng tọa độ. b) Tìm tọa độ giao điểm của (P) và (D) và bằng phép toán. Câu 2. Cho phương trình: 2 310xx . Không giải phương trình, tính giá trị của biểu thức: 33 12Axx Câu 3. Ông Ba mua một ký khoai tại vườn là 5.000 đồng một ký, tiền xe vận chuyển từ vườn đến nơi tiêu thụ là 2.000.000 đồng một chuyến. Gọi x (kg) là số kg khoai ông Ba mua mỗi chuyến, y (đồng) là tổng chi phí cho một chuyến khoai.
a) Lập công thức tính y theo x. b) Biết sau một chuyến khoai, ông Ba thu được 30 triệu đồng và lãi được 8 triệu đồng. Hỏi ông Ba đã mua bao nhiêu kg khoai và đã bán ra với giá bao nhiêu tiền 1 ký?
Câu 4. Bạn Nam nhặt được một tấm gỗ bị gãy là một phần của hình tròn (hình 1). Nam muốn biết bán kính của hình tròn chứa tấm gỗ là bao nhiêu, nên bạn ấy đã kẻ một dây AB bất kỳ trên tấm gỗ, sau đó dựng đường trung trực của AB và xác định các điểm C và điểm H (hình 2). Nam đo được AH=6cm,CH=4cm. Em hãy giúp bạn ấy tính bán kính của hình tròn chứa tấm gỗ.
Câu 5. Ngày thứ 3 giá một ký thịt Lợn giảm 10% so với ngày thứ 2, nhưng giá một ký thịt Lợn trong ngày thứ 4 lại tăng 5% so với ngày thứ 3. Biết giá một ký thịt Lợn ở ngày thứ 4 là 94.500 đồng một ký. a) Tính một ký thịt Lợn ở ngày thứ 2 b) Thứ 5 giá một ký thịt Lợn tăng %x so với ngày thứ 4. Ngày thứ 6, giá một ký thịt Lợn giảm %x so với ngày thứ 5. Giá một ký thịt Lợn ở ngày thứ 6 là 94.000 đồng. Hãy tìm x (làm tròn đến chữ số thập phân thứ 2) Câu 6. Hôm qua, bà Tư bán 20 kg gà và 25 kg vịt được tổng cộng 3.050 .000 đồng. Hôm nay giá gà tăng 5% và giá vịt giảm 10% nên bà bán 30kg gà và 35kg vịt thu được tổng cộng 4.410.000 đồng. Tính giá một kg gà, một kg vịt của ngày hôm qua. Câu 7. Bạn Bình đổ 11 lít nước vào một cái nón lá thì đầy nón. Bình đo được đường kính vòng tròn đáy của nón
40cm Biết công thức tính thể tích hình nón là 2 1 3 Vrh
. Với r là bán kính đáy, h là chiều cao hình nón. Độ dài đường sinh BC của hình nón bằng bao nhiêu dm? (làm tròn còn 1 chữ số thập phân).
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10
OFFICIAL
PHÒNG GD & ĐT HUYỆN CỦ CHI NĂM HỌC 2022-20232
lá là
OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 78Câu 8. Cho (;) OR và dây 2 CDR . Gọi B là điểm chính giữa cung nhỏ CD, kẻ đường kính BA, trên tia đối của tia AB lấy S, SC cắt () O tại M, MD cắt AB tại K, AC cắt MB
DẠYKÈMQUYNHƠN
tại H a) Chứng minh MAKH nội tiếp b) Chứng minh HK // CD c) Chứng minh 2OKOSR
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI
a) Hàm
ố
Bả
ị
ủ
x
2 0 2 4 2 4 x y 4 1 0 1 4 Đồ
điểm (4;4);(2;1);(0;0);(2;1);(4;4) Hàm số: 2 2 x y 02xy 04yx Đồ thị hàm số là đường thẳng đi qua 0;2 và 4;0 Vẽ: b) Hoành độ giao điểm của P và D là nghiệm của phương trình: 2 2 42 xx 2 20 42 xx 2 280xx 2 11.890 Phương trình có hai nghiệm phân biệt: 1 2 x ; 2 4 x + Với 1 2 x 1 1 y + Với 2 4 x 2 4 y Vậy D cắt P tại hai điểm phân biệt là 2;1 và 4;4 .
Câu 1. Cho Parabol 2 (P): 4 x y
và đường thẳng (D):2 2 x y a) Vẽ (P) và (D) trên cùng một mặt phẳng tọa độ. b) Tìm tọa độ giao điểm của (P) và (D) và bằng phép toán. Lời giải
s
: 2 4 x y
ng giá tr
tương ứng c
a x và y :
4
thị hàm số là một Parabol đi qua các
ký khoai
ký,
chuyển từ vườn đến nơi tiêu thụ là 2.000.000 đồng một chuyến. Gọi x (kg) là số kg khoai ông Ba mua mỗi chuyến, y (đồng) là tổng chi phí cho một chuyến khoai.
a) Lập công thức tính y theo x. b) Biết sau một chuyến khoai, ông Ba thu được 30 triệu đồng và lãi được 8 triệu đồng. Hỏi ông Ba đã mua bao nhiêu kg khoai và đã bán ra với giá bao nhiêu tiền 1 ký? Lời giải
a) Vì khoai có giá 5.000 đồng 1 ký nên x (kg) khoai ông Ba mua mỗi chuyến sẽ có giá là 5.000x Tiền xe vận chuyển từ vườn đến nơi tiêu thụ là 2.000.000 đồng một chuyến nên tổng chí phí cho mỗi chuyến khoai là: y=5.000x+2.000.000 b) Số tiền mà ông Ba đã bỏ ra để mua khoai là 30822 (triệu) Số kg khoai mà ông Ba đã mua là: y=5.000x+2.000.000=22.000.000 x=4000(kg) Số tiền mà ông Ba đã bán ra cho 1 ký khoai là: 30.000.000:40007500 (đồng).
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 80Câu 2. Cho phương trình: 2 310xx . Không giải phương trình, tính giá trị của biểu thức: 33 12Axx Lời giải a) Phương trình đã cho là phương trình bậc hai của x có: 224(3)4.1.150bac Vậy phương trình đã cho có hai nghiệm phân biệt 1x ; 2x b) Theo định lý Vi-et, ta có : 12 12 3 1 1 1 1 3 b xx a c xx a Do đó: 2 3322 12121122121212 3 Axxxxxxxxxxxxxx 2 (3)(3)313618 Vậy giá trị của biểu thức 18 A Câu 3. Ông
Ba mua một
tại vườn là 5.000 đồng một
tiền xe vận
Vậy ông Ba đã bán 1 ký khoai với giá là 7500
ng). Câu 4. Bạn Nam nhặt được một tấm gỗ bị gãy là một phần của hình tròn (hình 1). Nam muốn biết bán kính của hình tròn chứa tấm gỗ là bao nhiêu, nên bạn ấy đã kẻ một dây AB bất kỳ trên tấm gỗ, sau đó dựng đường trung trực của AB và xác định các điểm C và điểm H (hình 2). Nam đo được AH=6cm,CH=4cm. Em hãy giúp bạn ấy tính bán kính của hình tròn chứa tấm gỗ.
(đồ
Câu 5. Ngày thứ 3 giá một ký thịt Lợn giảm 10% so với ngày thứ 2, nhưng giá một ký thịt Lợn trong ngày thứ 4 lại tăng 5% so với ngày thứ 3. Biết giá một ký thịt Lợn ở ngày thứ 4 là 94.500 đồng một ký. a) Tính một ký thịt Lợn ở ngày thứ 2 b) Thứ 5 giá một ký thịt Lợn tăng %x so với ngày thứ 4. Ngày thứ 6, giá một ký thịt Lợn giảm %x so với ngày thứ 5. Giá một ký thịt Lợn ở ngày thứ 6 là 94.000 đồng. Hãy tìm x (làm tròn đến chữ số thập phân thứ 2) Lời giải
a) Gọi a là giá một ký thịt lợn ở ngày thứ 2 (đơn vị: đồng), (a>0)
Ngày thứ 3 giá một ký thịt Lợn giảm 10% so với ngày thứ 2 nên giá thịt lợn ngày thứ 3 là: 90%.a=0,9a (đồng) Giá một ký thịt Lợn trong ngày thứ 4 lại tăng 5% so với ngày thứ 3 nên giá thịt lợn ngày thứ 4 là: 105%.0,9a=0,945a (đồng) Vì giá một ký thịt Lợn ở ngày thứ 4 là 94.500 đồng một ký nên ta có phương trình
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 81Lời giải Gọi bán kính của hình tròn chứa tấm gỗ là R Ta có: 222 OAOHAH 22() OCCHAH 222 (4)6RR 22 81636RRR 6,5() Rcm Vậy bán
.
kính của tấm gỗ là 6,5(cm)
0,945a94.500a100.000 (đồng) (nhận) Vậy giá 1 ký thịt Lợn ở ngày thứ 2 là 100.000 đồng b) Thứ 5 giá một ký thịt Lợn tăng %x so với ngày thứ 4 nên giá thịt lợn ngày thứ 5 là: 94.5001 100 x (đồng) Ngày thứ 6, giá một ký thịt Lợn giảm %x so với ngày thứ 5 nên giá thịt lợn ngày thứ 6 là: 94.5001.1 100100 xx (đồng) Vì giá một ký thịt Lợn ở ngày thứ 6 là 94.000 đồng nên ta có phương trình: 2 2 2 94.500(1)(1)94.000 100100 188 1 189 100 10000 189 xx x x H C B A O
:
Vậy 7,27 x . Câu 6. Hôm qua, bà Tư bán 20 kg gà và 25 kg vịt được tổng cộng 3.050 .000 đồng. Hôm nay giá gà tăng 5% và giá vịt giảm 10% nên bà bán 30kg gà và 35kg vịt thu được tổng cộng 4.410.000 đồng. Tính giá một kg gà, một kg vịt của ngày hôm qua. Lời giải
Gọi giá một kg gà và một kg vịt của ngày hôm qua lần lượt là x (đồng) và y (đồng) (>0) x,y
Vì bà Tư bán 20 kg gà và 25 kg vịt được tổng cộng 3.050.000 đồng nên ta có phương trình: 20+25y=3.050.000 x (1)
Hôm nay giá gà tăng 5%nên giá gà là 105%1,05xx (đồng) Hôm nay giá vịt giảm 10%nên giá vịt là 90%0.9yy (đồng)
Vì hôm nay bà đã bán 30kg gà và 35 kg vịt thu được tổng cộng 4.410.000 đồng nên ta có phương trình: 30.1,0535.0,94.410.00031,531,54.410.000 (2) xyxy
nhËn nhËn Vậy giá một kg gà là 90.000 đồng và giá một kg vịt là 50.000 đồng. Câu 7. Bạn Bình đổ 11 lít nước vào một cái nón lá thì đầy nón. Bình đo được đường kính vòng tròn đáy của nón lá là 40cm. Biết công thức tính thể tích hình nón là 2 1 3 Vrh . Với r là bán kính đáy, h là chiều cao hình nón. Độ dài đường sinh BC của hình nón bằng bao nhiêu dm? (làm tròn còn 1 chữ số thập phân) Lời giải Ta có đường kính vòng trong đáy của nón lá là 40cm nên bán kính của nó sẽ là r = 20cm = 2dm. Bình đổ 11 lít nước vào một nón là thì đầy nón nghĩa là 11 lít sẽ là thể tích của nón lá =11(lít) V
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 82 -
100 321 100 321 x x
(nhËn) (lo¹i)
Từ
1 và 2 ta có hệ phương trình: 5 2 31,31,54.410. 0+25y=3.050.00 000 0 x xy ) 50.000 =90.00 ) 0( ( y x
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 83Theo đề bài ta có phương trình: 2 1 11 3 33 2 4 hh (dm) Độ dài đường sinh BC của hình nón là: 2 222222 33 210,9 4 10,93.3 () BCOCOBhr BCdm Câu 8. Cho (;) OR và dây 2 CDR . Gọi B là điểm chính giữa cung nhỏ CD, kẻ đường kính BA, trên tia đối của tia AB lấy S, SC cắt () O tại M, MD cắt AB tại K, AC cắt MB tại H. a) Chứng minh MAKH nội tiếp b) Chứng minh HK // CD c) Chứng minh 2 . OKOSR Lời giải a) Vì B là điểm chính giữa cung nhỏ CD nên BCBD Xét tứ giác AMHK có: HMKHAK (2 góc nội tiếp của (O) chắn 2 cung bằng nhau) AMHK là tứ giác nội tiếp (tứ giác có 2 đỉnh cùng nhìn cạnh HK dưới 2 góc bằng nhau) b) Ta có: 90 BMA (góc nội tiếp chắn nửa đường tròn tâm O) 90 HMA Tứ giác AMHK là tứ giác nội tiếp 180 HMAHKA 1809090 HKA ABHK (1) Xét (O; R), ta có B là điểm chính giữa cung nhỏ CD ABCD (2) Từ (1) và (2) // HKCD
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 84c) Ta có: COBBC s® (góc ở tâm chắn cung BC) (3) 2 CMDCD s® (góc nội tiếp của (O) chắn cung CD) Mà 2. CDBC (B là điểm chính giữa cung nhỏ CD) 2 22 CMDCD.BCBC s® .s® (4) Từ (3) và (4) COBCMD CMKO là tứ giác nội tiếp (tứ giác có góc ngoài bằng góc đối trong) SCOOKD (góc ngoài bằng góc đối trong) Ta có: 180 180 COBCOS DOBDOK (2 gãc kÒ bï) (2 gãc kÒ bï) Mà: COBDOB (2 góc ở tâm chắn 2 cung bằng nhau) COSDOK Xét SCO và DKO có: COSDOK SCOOKD SCODKO(gg) 2OK.OSOC.ODR OS OD OC OK )(ts®d
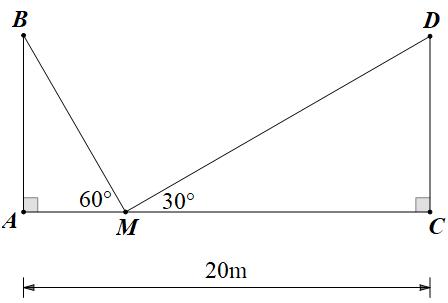
các giá trị của m để phương trình có 2 nghiệm 1x ; 2x thỏa mãn 121 2238 xxx . Bài 3: (0.75 điểm) Hai trụ điện cùng chiều cao được dựng thẳng đứng hai bên lề đối diện một đại lộ rộng 20m. Từ một điểm M nằm giữa hai trụ điện người ta nhìn thấy đỉnh 2 trụ điện với hai góc nâng lần lượt là 60 AMB và 30 DMC .
a) Tính chiều cao của các trụ điện và khoảng cách từ điểm M đến gốc mỗi trụ điện. b) Nếu chiều cao của mỗi trụ điện là 8m, hãy xác định vị trí của điểm M để 90 BMD Bài 4: (0.75 điểm) Công thức Lozent tính cân nặng lý tưởng theo chiều cao dành cho nữ là 150 100 2 T FT
(với T là chiều cao (cm) và F là cân nặng lý tưởng (kg)).
a) Bạn Hoa có cân nặng 56 kg. Hỏi bạn Hoa phải đạt chiều cao bao nhiêu để có cân nặng lý tưởng? b) Một công ty người mẫu đưa ra yêu cầu tuyển người mẫu nữ cao từ 1,7 m trở lên với cân nặng lý tưởng theo công thức Lozent. Hỏi nếu người mẫu cao 1,7 m thì cân nặng là bao nhiêu kg để đủ điều kiện tiêu chuẩn người xét tuyển? Bài 5: (1.0 điểm).
a) Nếu giảm bớt thời gian thắp sáng của 1 bóng điện 60 W một giờ mỗi ngày thì x hộ gia đình sẽ tiết kiệm được bao nhiêu tiền biết giá điện 1800 đồng/kWh. Hãy viết công thức tính tiền tiết kiệm được. b) Trong tháng 10/2021 thành phố A hưởng ứng chương trình tiết kiệm năng lượng điện theo hình thức trên, biết thành phố có khoảng 1,9 triệu hộ gia đình. Tính tổng số tiền tiết kiệm điện trong tháng đó. Bài 6: (1.0 điểm) Nhân dịp lễ 30/4, siêu thị điện máy Nguyễn Kim đã giảm giá nhiều mặt hàng để kích cầu mua sắm. Giá niêm yết tổng số tiền một tivi và một máy giặt là 25,4 triệu đồng. Trong đợt này giá một tivi giảm 40%, giá một máy giặt giảm 25%, nên bác Hai mua một tivi và một máy giặt với tổng
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GD & ĐT QUẬN 1 NĂM HỌC 2022-20232 ĐỀ THAM KHẢO MÔN :
9 -------------------- Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Quận Gò Vấp – 1 Thời gian: 120 phút (không kể thời gian phát đề) Bài 1: (1.5 điểm). Cho hàm số 2 2 yx có đồ thị P và hàm số 3 yx có đồ thị D . a) Vẽ đồ thị P và D trên cùng mặt phẳng tọa độ; b) Tìm tọa độ giao điểm của P và D bằng phép toán. Bài 2: (1.0 điểm) Cho phương trình 2240xxm ( x là ẩn số, m là tham số). a) Chứng tỏ rằng phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m . b) Tìm
TOÁN
n là 16,7 triệu đồng. Hỏi giá một chiếc tivi, một chiếc máy giặt khi chưa giảm giá là bao nhiêu triệu đồng? (làm tròn kết quả đến chữ số thập phân thứ nhất)
Bài 7: (1.0 điểm) Một chiếc nón ông già Noel thường có 3 phần: hình trụ làm đế nón, phần mũ chính là hình nón, trên đỉnh nón là quả bông trắng có hình cầu và có các kích thước tương ứng như hình vẽ. Tính tổng diện tích phần vải để may nón (kết quả làm tròn đến hàng đơn vị)
Bài 8: (3.0 điểm) Cho đường tròn ; OR . Lấy điểm A nằm ngoài đường tròn sao cho 2 OAR , vẽ các tiếp tuyến AD , AE đến O ( D , E là tiếp điểm) Lấy C trên cung lớn DE , vẽ DHCE ( HCE ); P là trung điểm của DH , CP cắt đường tròn O tại Q , AQ cắt O tại M
a) Chứng minh 2 . AQAMAD và tính . AQAM theo R . b) Gọi I là giao điểm của OA và DE . Chứng minh tứ giác QDPI nội tiếp đường tròn. c) Chứng minh AO là tiếp tuyến của đường tròn ngoại tiếp ADQ .

DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 78 -
ố
OFFICIAL
s
tiề
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI Bài 1: (1.5 điểm). Cho hàm số 2 2 yx có đồ thị P và hàm số 3 yx có đồ thị D . a) Vẽ đồ thị P và D trên cùng mặt phẳng tọa độ; b) Tìm tọa độ giao điểm của P và D bằng phép toán. Lời giải a) Hàm số: 2 2 yx Bảng giá trị tương ứng của x và y : x 2 1 0 1 2 2 2 yx 8 2 0 2 8 Đồ thị hàm số là một Parabol đi qua các điểm 2;8 ; 1;2 ; 0;0 ; 1;2 ; 2;8 Hàm số: 3 yx 03xy 03yx Đồ thị hàm số là đường thẳng đi qua 0;3 và 3;0 Vẽ: b) Hoành độ giao điểm của P và D là nghiệm của phương trình: 2 23 xx 2 230 xx 2 14.2.3250 Phương trình có hai nghiệm phân biệt: 1 3 2 x ; 2 1 x + Với 1 1 x 1 2 y + Với 1 3 2 x 2 9 2 y Vậy D cắt P tại hai điểm phân biệt là 1;2 và 39 ; 22 Bài 2: (1.0 điểm) Cho phương trình 2240xxm ( x là ẩn số, m là tham số). a) Chứng tỏ rằng phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m b) Tìm các giá trị của m để phương trình có 2 nghiệm 1x ; 2x thỏa mãn 121 2238 xxx .

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 80Lời
xxxx 2 2.438 m 2 00mm Vậy với 0 m thì phương trình có 2 nghiệm 1x ; 2x thỏa mãn 121 2238 xxx . Bài 3: (0.75 điểm) Hai trụ điện cùng chiều cao được dựng thẳng đứng hai bên lề đối diện một đại lộ rộng 20m. Từ một điểm M nằ
trụ điện và khoảng cách từ điểm M đến gốc mỗi trụ điện. b) Nếu chiều cao của mỗi trụ điện là 8m, hãy xác định vị trí của điểm M để 90 BMD . Lời giải a) Gọi chiều cao mỗi trụ điện là h Xét ABM vuông tại A có: tan tan60 ABh AMBAM AM Xét CMD vuông tại C có: tan tan30 CDh CMDCM CM Mà 11 2020:53 tan60tan30tan60tan30 hh AMCMAChm b) Xét ABM vuông tại A có: 8 tan tan AB AMBAM AM AMB Xét CMD vuông tại C có: 8 tan tan CD CMDCM CM CMD Mà 88 20 tantan AMCMAC AMBCMD , vì 90 BMD AMB phụ CMD Suy ra 5 tancottancot 2 CMDAMBAMBAMB Đặt 1 tancot xAMBAMB x phương trình được đưa về ẩn x là: 2 2 15 5201 2 2 x xxx x x
giải a) Phương trình đã cho là phương trình bậc hai của x có:
2 22 44.1.1640 mm với mọi giá trị của m Vậy phương trình đã cho luôn có hai nghiệm phân biệt 1x ; 2x với mọi giá trị của m . b) Theo định lý Vi-et, ta có: 12 2 12 4 xx xxm
Do đó: 121 2238 xxx 1212 238
m giữa hai trụ điện người ta nhìn thấy đỉnh 2 trụ điện với hai góc nâng lần lượt là 60 AMB và 30 DMC . a) Tính chiều cao của các
(với T là chiều cao (cm) và F là cân nặng lý tưởng (kg)).
a) Bạn Hoa có cân nặng 56 kg. Hỏi bạn Hoa phải đạt chiều cao bao nhiêu để có cân nặng lý tưởng? b) Một công ty người mẫu đưa ra yêu cầu tuyển người mẫu nữ cao từ 1,7 m trở lên với cân
thức tính tiền tiết kiệm được.
b) Trong tháng 10/2021 thành phố A hưởng ứng chương trình tiết kiệm năng lượng điện theo hình thức trên, biết thành phố có khoảng 1,9 triệu hộ gia đình. Tính tổng số tiền tiết kiệm điện trong tháng đó. Lời giải
a) Số tiền tiết kiệm được là: 1800.0,06.108xx (đồng) b) Tổng số tiền tiết kiệm điện trong tháng 10/2021 của thành phố A là: 1800.0,06.31.19000006361200000 (đồng) Bài 6: (1.0 điểm) Nhân dịp lễ 30/4, siêu thị điện máy Nguyễn Kim đã giảm giá nhiều mặt hàng để kích cầu mua sắm. Giá niêm yết tổng số tiền một tivi và một máy giặt là 25,4 triệu đồng. Trong đợt này giá một tivi giảm 40%, giá một máy giặt giảm 25%, nên bác Hai mua một tivi và một máy giặt với tổng số tiền là 16,7 triệu đồng. Hỏi giá một chiếc tivi, một chiếc máy giặt khi chưa giảm giá là bao nhiêu triệu đồng? (làm
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 81 88 4 2 tan AMm AMB hoặc 88 16 0,5 tan AMm AMB
Vậy điểm M cách A một khoảng là 4m hoặc 16m thì góc 90 BMD . Bài 4: (0.75 điểm) Công thức Lozent tính cân nặng lý tưởng theo chiều cao dành cho nữ là 150 100 2 T FT
tưởng theo công thức Lozent.
ỏi nếu người mẫu cao 1,7
ặng
để đủ điều kiện tiêu chuẩn người xét tuyển? Lời giải a) Chiều cao bạn Hoa để có cân nặng lý tưởng là: 150 561001122200150162 2 T TTTTcm b) Số cân nặng để đủ điều kiện tiêu chuẩn người xét tuyển là: Với 170 T thì 170150 17010060 2 Fkg . Bài 5: (1.0 điểm) a) Nếu giảm bớt thời gian thắp
của 1
điện 60
ộ
ờ mỗ
nặng lý
H
m thì cân n
là bao nhiêu kg
sáng
bóng
W m
t gi
i ngày thì x hộ gia đình sẽ tiết kiệm được bao nhiêu tiền biết giá điện 1800 đồng/kWh. Hãy viết công
p phân thứ nhất). Lời giải Gọi x (triệu đồng) là giá một chiếc tivi khi chưa giảm giá, y (triệu đồng) là giá một chiếc máy giặt khi chưa giảm giá ( 0 x ; 0 y ) Tổng số tiền một tivi và một máy giặt khi chưa giảm là 25,4 triệu đồng nên ta có phương trình: 25,4 xy 1 Giá một tivi giảm 40%, giá một máy giặt giảm 25%, nên bác Hai mua một tivi và một máy giặt với tổng số tiền là 16,7 triệu đồng ta có phương trình: 140%125%16,7 xy 2 Từ 1 và 2 ta có hệ phương trình:
tròn kết quả đến chữ số thậ
Vậy giá một chiếc tivi khi chưa giảm giá là 15,7 triệu đồng và giá một chiếc máy giặt khi chưa giảm giá là 9,7 triệu đồng Bài 7: (1.0 điểm) Một chiếc nón ông già Noel thường có 3 phần: hình trụ làm đế nón, phần mũ chính là hình nón, trên đỉnh nón là quả bông trắng có hình cầu và có các kích thước tương ứng như hình vẽ. Tính tổng diện tích phần vải để may nón (kết quả làm tròn đến hàng đơn vị). Lời giải

DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 82 -
xyx xyy (thỏa
OFFICIAL
25,415,7 0,60,7516,79,7
mãn)
nón: 22 2 3232732 22..10.45101876 2222 RhRlcm Vậy diện tích vải dùng để may nón là 2 1876cm Bài 8: (3.0 điểm) Cho đường tròn ; OR . Lấy điểm A nằm ngoài đường tròn sao cho 2 OAR , vẽ các tiếp tuyến AD , AE đến O ( D , E là tiếp điểm). Lấy C trên cung lớn DE , vẽ DHCE ( HCE ); P là trung điểm của DH , CP cắt đường tròn O tại Q , AQ cắt O tại M . a) Chứng minh 2 . AQAMAD và tính . AQAM theo R . b) Gọi I là giao điểm của OA và DE . Chứng minh tứ giác QDPI nội tiếp đường tròn. c) Chứng minh AO là tiếp tuyến của đường tròn ngoại tiếp ADQ . Lời giải
Diện tích vải dùng để may nón gồm: diện tích vải để may phần đế nón hình trụ, diện tích vải để may phần mũ chính hình
I là trung điểm của DE . Xét DHE có: P là trung điểm của HD , I là trung điểm của DE Suy ra IP là đường trung bình của DHE // IPHE CEDDIP (hai góc đồng vị) mà CEDCQD (cùng chắn CD ) Suy ra DIPDQP Xét tứ giác QDPI có DIPDQP suy ra tứ giác QDPI nội tiếp (tứ giác có hai đỉnh liên tiếp cùng nhìn mộ

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 83a) Xét ADQ và AMD có: 1 2 ADQAMD sđ DQ ; DAQ chung ADQ đồng dạng AMD (g.g) ADAQ AMAD 2 ADAQAM Xét ADO vuông tại D : 222 AOADODpitago 2 22222 23 ADAOODRRR 2 .3 AQAMR b) Ta có: ODOER và ADAE
chất hai tiếp tuyến
ắ
ng
ự
ủ
ạ
t cạnh dưới góc bằng nhau). c) Xét ADO vuông tại D có DI là đường cao suy ra 2 . ADAIAO mà 2 . ADAQAM suy ra .. AIAM AIAOAQAM AQAO Xét AIQ và AMO có: IAQ chung, AIAM AQAO suy ra AIQ đồng dạng AMO (c.g.c) suy ra AIQAMO Ta có: AIQ phụ DIQ , DIQDPQ (cùng chắn DQ ), DPQCPH (đối đỉnh), CPH phụ QCE , QCEQME (cùng chắn QE ), suy ra QMOQME hay 3 điểm M , O , E thẳng hàng. 90 MDE (góc nội tiếp chắn nửa đường tròn) suy ra // MDOA (cùng vuông với DE ) OAQDMQ (hai góc so le trong) mà ADQDMQ suy ra OAQADQ suy ra AO là tiếp tuyến của đường tròn ngoại tiếp ADQ
(tính
c
t nhau) AO
là đườ
trung tr
c c
a DE AODE t
i I và
định. Nếu xe chạy mỗi giờ nhanh hơn 10km thì đến nơi sớm hơn dự định 3 giờ, nếu xe chạy chậm lại mỗi giờ 10km thì đến nơi chậm mất 5 giờ. Tính vận tốc của xe lúc đầu, thời gian dự định và chiều dài AB Bài 4: (0.75 điểm) Sản lượng cà phê xuất khẩu của Việt Nam hàng năm được xác định theo hàm số 100900Tn . Với T là sản lượng (đơn vị: nghìn tấn) và n là số năm kể từ năm 2005.
a) Hãy tính sản lượng cà phê xuất khẩu năm 2007.
b) Theo hàm số trên thì sản lượng cà phê xuất khẩu đạt 1800 nghìn tấn vào năm nào?
Bài 5: (1.0 điểm) Bài toán từ cuốn sách Số học của Mat-nhit-xki (Nga). Một người hỏi thầy giáo: “Lớp của thầy có bao nhiêu học trò?”, thầy đáp: “Nếu thêm vào cả số học trò tôi có, rồi lại thêm nửa số học trò của tôi, rồi thêm 1 4 số học trò và cả con trai của ông nữa vào thì sẽ là 100”. Hỏi thầy có bao nhiêu học trò?
Bài 6: (1.0 điểm) Có 2 can đựng dầu, can thứ nhất đang chứa 38 lít và can thứ hai đang chứa 22 lít. Nếu rót từ can thứ nhất sang cho đầy can thứ hai thì lượng dầu trong can thứ nhất chỉ còn lại nửa thể tích của nó. Nếu rót từ can thứ hai sang cho đầy can thứ nhất thì lượng dầu trong can thứ hai chỉ còn lại 1 3 thể tích của nó. Tính thể tích của mỗi can.

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG
MÔN
. b)
ủ
trình, hãy tính giá trị của biểu thức 12 21 11 11 xx A xx Bài 3: (0.75 điểm) Một xe ô tô dự định đi từ A đến B trong một thời gian nhất
GD & ĐT HUYỆN HÓC
NĂM HỌC 2022-2023 ĐỀ THAM KHẢO MÔN : TOÁN 9 -------------------- Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Huyện Hóc Môn – 1 Thời gian: 120 phút (không kể thời gian phát đề) Bài 1: (1.5 điểm) Cho parabol 2 1 (): 2 Pyx và đường thẳng 5 ():3 2 dyx a) Vẽ () P và () d trên cùng hệ trục tọa độ
Tìm tọa độ giao điểm c
a () P và () d bằng phép toán. Bài 2: (1.0 điểm) Cho phương trình 2 3410 xx có hai nghiệm 12 , xx . Không giải phương
Bài 7: (1.0 điểm) Một xe chở xăng dầu, bên trên có chở một bồn chứa hình trụ chiều dài 2,6 mét và đường kính đáy là 1,4 mét. Theo tiêu chuẩn an toàn, thì bồn chỉ chứa tối đa 80% thể tích khi xe di chuyển trên đường. Vậy bồn đó có thể chứa được nhiều nhất là bao nhiêu lít nhiên liệu? (làm tròn đến hàng đơn vị).
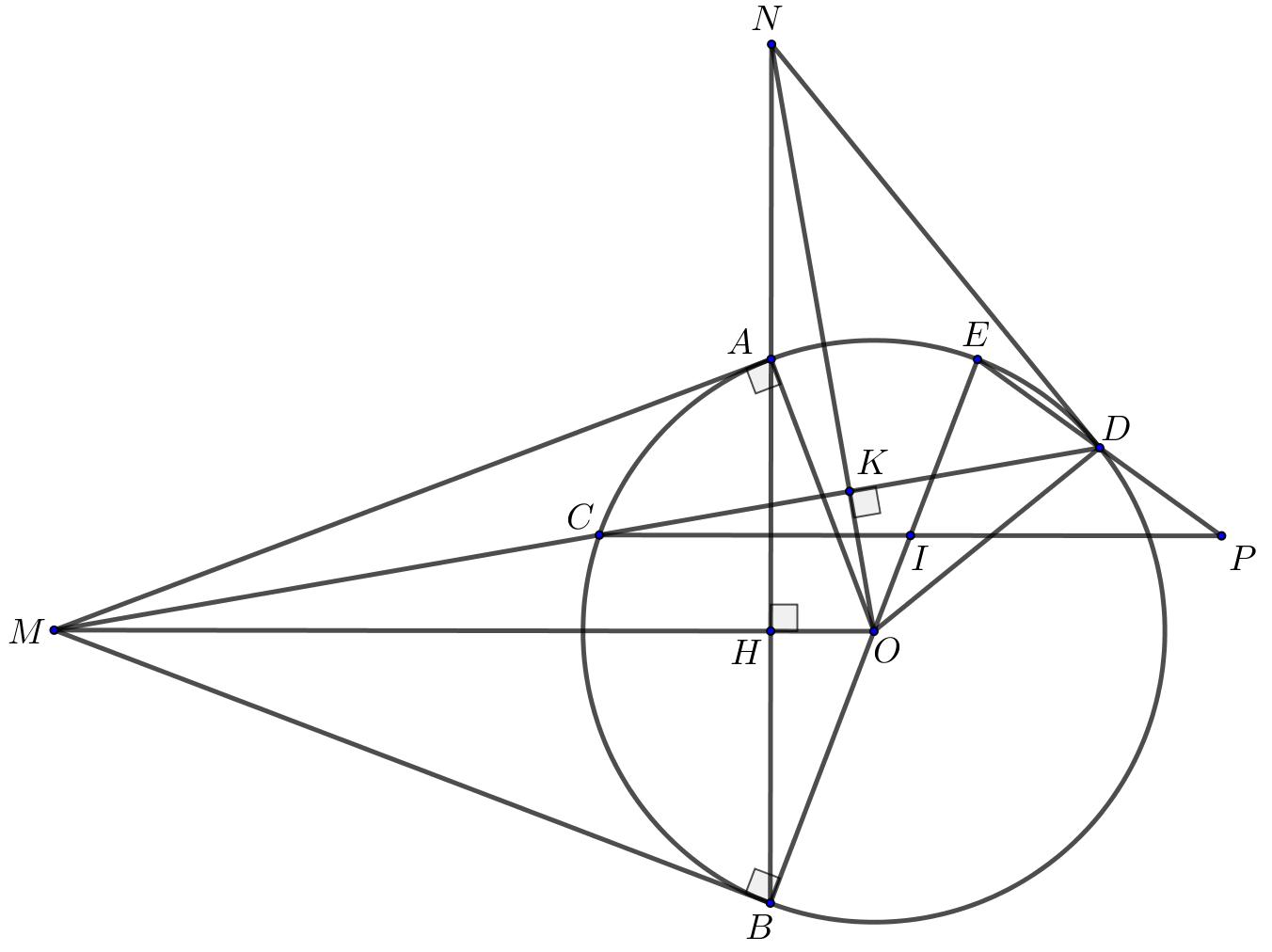
Bài 8: (3.0 điểm) Cho điểm M nằm ngoài đường tròn (;) OR . Qua M kẻ hai tiếp tuyến MA và MB và cát tuyến MCD ( ,,, ABCD cùng thuộc đường tròn () O ), tia MC nằm giữa tia MO và MA. Gọi H là giao điểm của MO và AB
a) Chứng minh tứ giác MAOB nội tiếp. b) Gọi K là trung điểm của CD. Chứng minh 5 điểm ,,,, MKAOB cùng thuộc một
DẠYKÈMQUYNHƠN
- 78 -
OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN
đường
ra KM là
giác của AKB . c) Đường thằng OK cắt đường thẳng AB tại N . Chứng
ND là tiếp tuyến của đường tròn () O d) Vẽ đường kính BE của đường tròn () O . Từ C vẽ đường thẳng song
với OM cắt
ng thẳng BE và ED lần lượt tại
.
ứng
m CP
tròn. Suy
phân
minh
song
các đườ
, IP
Ch
minh I là trung điể
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI Bài 1: (1.5 điểm) Cho parabol 2 1 (): 2 Pyx và đường thẳng 5 ():3 2 dyx a) Vẽ () P và () d trên cùng hệ trục tọa độ b) Tìm tọa độ giao điểm của () P và () d bằng phép toán. Lời giải a) Hàm số: 2 1 2 yx Bảng giá trị tương ứng của x và y : x 4 2 0 2 4 2 1 2 yx 8 2 0 2 8 Đồ thị hàm số là một Parabol đi qua các điểm 4;8 ; 2;2 ; 0;0 ; 2;2 ; 4;8 Hàm số: 5 3 2 yx 03xy 22xy Đồ thị hàm số là đường thẳng đi qua 0;3 và 2;2 Vẽ: b) Hoành độ giao điểm của P và d là nghiệm của phương trình: 2 15 3 22 xx 2 56xx 2 560xx 2 54.1.610 Phương trình có hai nghiệm phân biệt: 1 3 x ; 2 2 x + Với 1 3 x 1 9 2 y + Với 2 2 x 2 2 y Vậy d cắt P tại hai điểm phân biệt là 9 3; 2 và 2;2
3 giờ, nếu xe chạy chậm lại mỗi giờ 10km thì đến nơi chậm mất 5 giờ. Tính vận tốc của xe lúc đầu, thời gian dự định và chiều dài AB . Lời giải Gọi vận tốc của xe lúc đầu là x ( 0 x , đơn vị: km/h) và thời gian dự định là y ( 0 y , đơn vị: giờ).
Nếu xe chạy mỗi giờ nhanh hơn 10km thì đến nơi sớm hơn dự định 3 giờ nên ta có phương trình: 103 xyxy (1) N
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 80Bài 2: (1.0 điểm) Cho phương trình 2 3410 xx có hai nghiệm 12 , xx . Không giải phương trình, hãy tính giá trị của biểu thức 12 21 11 11 xx A xx Lời giải - Phương trình đã cho là phương trình bậc hai của x có: 22444.3.(1)280bac Vậy phương trình đã cho có hai nghiệm phân biệt 1x ; 2x - Theo định lý Vi-et, ta có: 12 12 4 3 1 3 xx xx Do đó: 2 2 22 12 1212 12 21121212 41 1122 11222 33 41 111113 1 33 xx xxxx xx xxxxxxx A x Vậy giá trị của biểu thức 2 3 A Bài 3: (0.75 điểm) Một xe ô tô dự định đi từ A đến B trong một thời gian nhất định. Nếu xe chạy mỗi giờ nhanh hơn 10km thì đến nơi sớm hơn dự định
i mỗi giờ 10km
đến
chậ
ấ
ờ
Từ (1) và (2) ta có hệ phương trình: 1033103040 1055105015 xyxy xyx xyy xyxy (thoả mãn) Vậy vận tốc của xe lúc đầu là 40 km/h, thời gian dự định là 15 giờ và chiều dài AB là 600 xy km. Bài 4: (0.75 điểm) Sản lượng cà phê xuất khẩu của Việt Nam hàng năm được xác định theo hàm số 100900Tn . Với T là sản lượng (đơn vị: nghìn tấn) và n là số năm kể từ năm 2005. a) Hãy tính sản lượng cà phê xuất khẩu năm 2007. b) Theo hàm số trên thì sản lượng cà phê xuất khẩu đạt 1800 nghìn tấn vào năm nào? Lời giải a) Năm 2007, ta có 2 n nên sản lượng cà phê xuất khẩu năm này là: 100.29001100 T (nghìn tấn) Vậy sản lượng cà phê xuất khẩu năm 2007 là 1100 nghìn tấn. b) Với 1800 T , ta có 18001009009 nn
ếu xe chạy chậm lạ
thì
nơi
m m
t 5 gi
nên ta có phương trình:
105 xyxy
(2)
lượng cà phê xu
kh
đạt 1800 nghìn tấn vào năm 2014. Bài 5: (1.0 điểm) Bài toán từ cuốn sách Số học của Mat-nhit-xki (Nga). Một người hỏi thầy giáo: “Lớp của thầy có bao nhiêu học trò?”, thầy đáp: “Nếu thêm vào cả số học trò tôi có, rồi lại thêm nửa số học trò của tôi, rồi thêm 1 4 số học trò và cả con trai của ông nữa vào thì sẽ là 100”. Hỏi thầy có bao nhiêu học trò? Lời giải
th
hai thì lượng dầu trong can thứ nhất chỉ còn lại nửa thể tích của nó. Nếu rót từ can thứ hai sang cho đầy can thứ nhất thì lượng dầu trong can thứ hai chỉ còn lại 1 3 thể tích của nó. Tính thể tích của mỗi can. Lời giải Gọi phần thể tích còn trống của can thứ nhất và can thứ hai lần lượt là x và y ( ,0xy , đơn vị: lít) Suy ra thể tích của can thứ nhất và can thứ hai lần lượt là: 38 x (lít) và 22 y (lít). Nếu rót từ can thứ nhất sang cho đầy can thứ hai thì lượng dầu trong can thứ nhất chỉ còn lại nửa thể tích của nó nên ta có phương trình: 1 3838 2 yx (1) Nếu rót từ can thứ hai sang cho đầy can thứ nhất thì lượng dầu trong can thứ hai chỉ còn lại 1 3 thể tích của nó nên ta có phương trình:
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 81 -
ậ
Theo đề bài: “Nếu
ả
ố
ọ
học trò và cả con trai của ông nữa vào thì sẽ là 100”, nên ta có phương trình: 1111 11009936 244 xxxxxx (thoả mãn). Vậy số học trò của lớp thầy giáo là 36 người Bài 6: (1.0 điểm) Có 2 can đựng
ầu, can
ứ
ứ
ừ
ứ
ất
1
3 xy
Từ (1) và (2) ta có hệ phương trình: 1 383823810 2 134414 2222 3 yx xyx xyy xy (thoả mãn) Vậy thể tích can thứ nhất là 103848 (lít) và can thứ hai là 142236 (lít) Bài 7: (1.0 điểm) Một xe chở xăng dầu, bên trên có chở một bồn chứa hình trụ chiều dài 2,6 mét và đường kính đáy là 1,4 mét . Theo tiêu chuẩn an toàn, thì bồn chỉ chứa tối đa 80% thể tích khi xe di chuyển trên đường. Vậy bồn đó có thể chứa được nhiều nhất là bao nhiêu lít nhiên liệu? (làm tròn đến hàng đơn vị). Lời giải Bán kính của bồn chứa hình trụ là: 1,4 0,7 2 Rm . Đổi đơn vị: 7 Rdm , 26 hdm . Thể tích của bồn chứa hình trụ là: 22.7.261274 VRh (dm3) = 1274 (lít)
OFFICIAL
V
y sản
ất
ẩu
Gọi x là số học trò lớp thầy có (người) ( x
)
thêm vào c
s
h
c trò tôi có, rồi lại thêm nửa số học trò của tôi, rồi thêm 1 4 số
d
th
nhất đang chứa 38 lít và can th
hai đang chứa 22 lít. Nếu rót t
can th
nh
sang cho đầy can
ứ
2222
(2)
Theo tiêu chuẩn an toàn bồn chỉ chứa tối đa 80% thể tích khi xe di chuyển trên đường do đó
nhiên liệu nhiều nhất mà bồn chứa được là: .80%1274.80%3202V (lít) Vậy bồn đó có thể chứa được nhiều nhất khoảng 3202 lít nhiên liệu.
Bài 8: (3.0 điểm) Cho điểm M nằm ngoài đường tròn (;) OR . Qua M kẻ hai tiếp tuyến MA và MB và cát tuyến MCD ( ,,, ABCD cùng thuộc đường tròn () O ), tia MC nằm giữa tia MO và MA. Gọi H là giao điểm của MO và AB a) Chứng minh tứ giác MAOB nội tiếp. b) Gọi K là trung điểm của CD. Chứng minh 5 điểm ,,,, MKAOB cùng thuộc một đường tròn. Suy ra KM là phân giác của AKB c) Đường thằng OK cắt đườ
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA
- 82 -
OFFICIAL
ĐỀ TOÁN
số lít
ng thẳng AB tại N . Chứng minh ND là tiếp tuyến của đường tròn () O d) Vẽ đường kính BE của đường tròn () O . Từ C vẽ đường thẳng song song với OM cắt các đường thẳng BE và ED lần lượt tại , IP . Chứng minh I là trung điểm CP . Lời giải a) Vì , MAMB là các tiếp tuyến của đường tròn O nên , MAOAMBOB . Ta có 9090180 MAOMBO , do đó tứ giác MAOB nội tiếp đường tròn đường kính MO b) Vì K là trung điểm của CD nên OKCD 90 MKO K thuộc đường tròn đường kính MO , theo câu a) ta có 5 điểm ,,,, MKAOB cùng thuộc một đường tròn Ta có: - AKMMBA (góc nội tiếp cùng nhìn cung AM ) (1) - BKMMAB (góc nội tiếp cùng nhìn cung BM ) (2) Mặt khác, do , MAMB là hai tiếp tuyến của O nên MAMB MAB cân tại M nên MABMBA (3)
Từ (1), (2) và (3) dẫn đến AKMBKM hay KM là phân giác của AKB
c) Xét OHN và OKM , có 90 HK và MOKNOH nên ~ OHNOKM (g,g)
Suy ra .. OKONOHOM (4)
Mặt khác áp dụng hệ thức lượng trong tam giác vuông MAO ta có 222 OHOMOAROD (5)
Từ (4) và (5) suy ra 2 . OKONOD , do đó ~ OKDODN (c.g.c)
Mà 9090OKDODN . Vì thế ND là tiếp tuyến của đường tròn O .
d) Vì // ICOM nên ICKOMK (đồng vị) (6)
Lại có OMKOBK (góc nội tiếp cùng nhìn cung OK ) (7)
Từ (6) và (7) ta có ICKOBK , do
DẠYKÈMQUYNHƠN
NHÓM WORD
- 83 -
OFFICIAL
HÓA ĐỀ TOÁN
đó tứ giác IBCK nội tiếp, vì vậy IKDEBC Mà EBCEDC (2 góc nội tiếp cùng chắn cung CE của
IKDEDC Do đó //// IKDEIKPD . Mặt khác, vì K là trung điểm CD nên IK là đường trung bình của CDP I là trung điểm CP
(O))
a) Nếu bạn Hùng mua 44 cái bánh nói trên ở cửa hàng bánh A thì phải trả bao nhiêu tiền?
b) Tại cửa hàng B (gần cửa hàng A) bán cùng loại bánh nói trên (chất lượng như nhau) đồng giá 15.000 đồng 1 cái nhưng nếu mua 3 cái bánh chỉ phải trả 40.000 đồng. Hỏi bạn Hùng mua 44 cái bánh nói trên ở cửa hàng nào để tổng số tiền phải trả ít hơn? Câu 5: (0.75 điểm) Qua nghiên cứu, người ta nhận thấy rằng với mỗi người trung bình nhiệt độ môi trường giảm đi 10C thì lượng calo cần tăng thêm khoảng 30 calo. Tại 210C, một người làm việc cần sử
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GD & ĐT HUYỆN NHÀ BÈ NĂM HỌC 2022-2023 ĐỀ THAM KHẢO MÔN : TOÁN 9 -------------------- Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Nhà bè – 01 Thời gian: 120 phút (không kể thời gian phát đề) Câu 1: (1.5 điểm) Cho hàm số 2 4 x y có đồ thị là Parabol P và hàm số 2 2 x y có đồ thị là đường thẳng d a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ; b) Tìm tọa độ giao điểm của P và d bằng phép toán. Câu 2: (1.0 điểm) Gọi 12 , xx là các nghiệm của phương trình 2 120xx . Không giải phương trình, tính giá trị của biểu thức 12 21 11xx A xx . Câu
(0.75 điểm) Quy tắc sau đây cho ta biết CAN, CHI của năm X
Để xác định
ần
ố
r
chia X cho
ả
ậu Tuấ
ợ
ử dụng quy tắc trên
CAN, CHI của năm 2022; b) Bạn Loan nhớ rằng mẹ bạn ấy sinh năm Giáp Thìn nhưng không rõ là năm bao nhiêu. Hãy xác định năm sinh của mẹ bạn Loan. Câu 4: (0.75
3:
nào đó.
CAN, ta c
tìm s
dư
trong phép
10 và tra vào b
ng 1.
Để xác định CHI, ta tìm số dư s trong phép chia X cho 12 và tra vào bảng 2. Ví dụ: Năm 1982 có CAN là Nhâm, có CHI là Tuất. Bảng 1 r 0 1 2 3 4 5 6 7 8 9 CAN Canh Tân Nhâm Quý Giáp Ất Bính Đinh Mậu Kỷ Bảng 2 s 0 1 2 3 4 5 6 7 8 9 10 11 CHI Thân D
t H
i Tí Sửu Dần Mão Thìn Tỵ Ngọ Mùi a) Em hãy s
để xác định
điểm) Bạn Hùng mua bánh liên hoan cuối niên học cho lớp. Tại cửa hàng bánh A giá bánh bạn Hùng muốn mua là 15.000 đồng 1 cái bánh, nhưng nếu mua trên 10 cái bánh sẽ được cửa hàng bánh giảm 10% trên tổng số tiền mua bánh.
a) Xác định hệ số , ab ;
b) Nếu một người làm việc ở sa mạc Sahara trong nhiệt độ 500C thì cần bao nhiêu calo?
Câu 6: (1.0 điểm) Tháp đồng hồ có phần dưới có dạng hình hộp chữ nhật, đáy là hình vuông có cạnh dài 5m, chiều cao của hình hộp chữ nhật là 12m. Phần trên của tháp có dạng hình chóp đều, các mặt bên là các tam giác cân chung đỉnh. Mỗi cạnh bên của hình chóp dài 8m.
a) Tính theo mét chiều cao của tháp đồng hồ. (làm tròn đến chữ số thập phân thứ nhất) b) Cho biết thể tích của hình hộp chữ nhật được tính theo công thức VSh , trong đó S là diện tích mặt đáy, h là chiều cao của hình hộp chữ nhật. Thể tích của hình chóp được tính theo công thức 1 3 Sh , trong đó S là diện tích mặt đáy, h là chiều cao của hình chóp. Tính thể tích của tháp đồng hồ này (Làm tròn đến hàng đơn vị).
Câu 7: (1.0 điểm) Trong đợt dịch Covid- 19, học sinh hai lớp 9A và 9B trường THCSX ủng hộ 217 chiếc khẩu trang cho những nơi cách li tập trung. Biết rằng số học sinh lớp 9A nhiều hơn số học sinh lớp 9B là 4 học sinh và mỗi học sinh lớp 9A ủng hộ 3 chiếc khẩu trang, mỗi học sinh lớp 9B ủng hộ 2 chiếc khẩu trang. Tìm số học sinh

DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 78dụng khoảng
mỗi
Người ta thấy mối
ệ giữa
đại
là một hàm số bậc
ất
OFFICIAL
3000 calo
ngày.
quan h
hai
lượng này
nh
yaxb ( x là đại lượng biểu thị cho nhiệt độ môi trường và y là đại lượng biểu thị cho lượng calo).
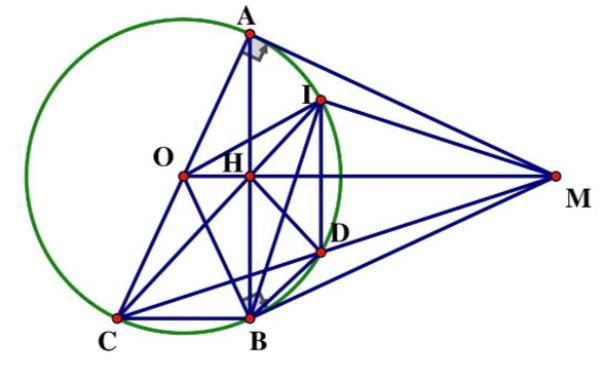
mỗi lớp. Câu 8: (3.0 điểm) Cho đường tròn (,) OR , từ điểm M nằm ngoài () O vẽ hai tiếp tuyến MA và (, MBAB là tiếp điểm). Vẽ đường kính AC của (),OMC cắt () O tại ( DD khác )C , OM cắt AB tại H . a) Chứng minh tứ giác MAOB nội tiếp và 2 MBMCMD b) Chứng minh..MOMHMCMD c) CH cắt ( II khác )C . Chứng minh tứ giác COIM nội tiếp.

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI Bài 1: (1.5 điểm) Cho hàm số 2 4 x y có đồ thị là Parabol P và hàm số 2 2 x y có đồ thị là đường thẳng d . a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ; b) Tìm tọa độ giao điểm của P và d bằng phép toán. Lời giải a) Hàm số: 2 4 x y Bảng giá trị tương ứng của x và y : x 4 2 0 2 4 2 4 x y 4 1 0 1 4 Đồ thị hàm số là một Parabol đi qua các điểm 4;4 ; 2;1 ; 0;0 ; 2;1 ; 4;4 Hàm số: 2 2 x y 02xy 04yx Đồ thị hàm số là đường thẳng đi qua 0;2 và 4;0 Vẽ: b) Hoành độ giao điểm của P và d là nghiệm của phương trình: 2 2 42 xx 2 28xx 2 280xx 2 11.890 Phương trình có hai nghiệm phân biệt: 1 2 x ; 2 4 x . + Với 1 2 x 1 1 y + Với 2 4 x 2 4 y Vậy d cắt P tại hai điểm phân biệt là 2;1 và 4;4 . Bài 2: (1.0 điểm) Gọi 12 , xx là các nghiệm của phương trình 2 120xx . Không giải phương trình, tính giá trị của biểu thức 12 21 11xx A xx .
CHI, ta tìm s
dư s trong phép chia X cho 12 và tra vào bảng 2. Ví dụ: Năm 1982 có CAN là Nhâm, có CHI là Tuất.
ảng 1
0 1 2 3 4 5 6 7 8 9 CAN Canh Tân Nhâm Quý Giáp Ất Bính Đinh Mậu Kỷ Bảng 2
0 1 2 3 4 5 6
8 9 10 11
Thân Dậu Tuất Hợi Tí Sửu Dần Mão Thìn Tỵ Ngọ Mùi a) Em hãy sử dụng quy tắc trên để xác định CAN, CHI của năm 2022; b) Bạn Loan nhớ rằng mẹ bạn ấy sinh năm Giáp Thìn nhưng không rõ là năm bao nhiêu. Hãy xác định năm sinh của mẹ bạn Loan. Lời giải a) Vì 2022 chia cho 10 dư 2 và 2022 chia cho 12 dư 6 nên năm 2022 có CAN là Nhâm, có CHI là Dần. b) Gọi năm sinh của mẹ bạn Loan là x ( * x ). Vì Mẹ bạn Loan sinh năm Giáp Thìn nên x chia cho 10 dư 4 và chia cho 12 dư 8. 16 x chia hết cho cả 10 và 12 hay 16 x là một bội chung của 10 và 12.
là một giá tr
hợp lí.
m
b
Loan sinh năm 1964 Bài 4: (0.75 điểm) Bạn Hùng mua bánh liên hoan cuối niên học cho lớp. Tại cửa hàng bánh A giá bánh bạn Hùng muốn mua là 15.000 đồng 1 cái bánh, nhưng nếu mua trên 10 cái bánh sẽ được cửa hàng bánh giảm 10% trên tổng số tiền mua bánh.
a) Nếu bạn Hùng mua 44 cái bánh nói trên ở cửa hàng bánh A thì phải trả bao nhiêu tiền?
b) Tại cửa hàng B (gần cửa hàng A) bán cùng loại bánh nói trên (chất lượng như nhau) đồng giá 15.000 đồng 1 cái nhưng nếu mua 3 cái bánh chỉ phải trả 40.000 đồng. Hỏi bạn Hùng mua 44 cái bánh nói trên
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 80Lời giải Theo định lý Vi-et, ta có: 12 12 1 12 b Sxx a c Pxx a 12 21 11xx A xx 22 2 1212 12 2 xxxx SPS xxP 2 1212113 126 Bài
.
ự
3: (0.75 điểm) Quy tắc sau đây cho ta biết CAN, CHI của năm X nào đó.
Để xác định CAN, ta cần tìm số dư r trong phép chia X cho 10 và tra vào bảng 1.
Để xác định
ố
B
r
s
7
CHI
Mà
BCNN10,1260
16B600;60;120;180;;1920;1980;2040; x
44;104;164;;1904;1964;2024; x
Th
c tế ta thấy 1964 x
ị
Vậy
ẹ
ạn
mua trên 10 cái bánh sẽ được cửa
giảm
trên tổng số tiền
ố tiền bạn Hùng phải trả khi
ở
ử
ở cửa hàng nào để tổng số tiền phải trả ít hơn? Lời giải a) Số tiền mua bánh khi chưa giảm giá là: 1500044660000 (đồng) Vì
hàng bánh
10%
mua bánh nên s
mua 44 cái bánh
c
a hàng A là: 66000090%594000 (đồng). b) Ta có 441432 nên bạn Hùng mua 42 cái bánh ở cửa hàng B với giá 40000 đồng 3 cái và 2 cái bánh với giá 15000 đồng 1 cái. Do đó số tiền bạn Hùng phải trả khi mua 44 cái bánh ở cửa hàng B là:
Bài 5: (0.75 điểm) Qua nghiên cứu, người ta nhận thấy rằng với mỗi người trung bình nhiệt độ môi trường giảm đi 10C thì lượng calo cần tăng thêm khoảng 30 calo. Tại 210C, một người làm việc cần sử dụng khoảng 3000 calo mỗi ngày. Người ta thấy mối quan hệ giữa hai đại lượng này là một hàm số bậc nhất yaxb ( x là đại lượng biểu thị cho nhiệt độ môi trường và y là đại lượng biểu thị cho lượng calo).
a) Xác định hệ số , ab ; b) Nếu một người làm việc ở
ậy 30,3630ab .
Từ kết quả câu a , ta có hàm số 303630yx
Một người làm việc ở sa mạc Sahara trong
C, tức
x
Thay 50 x
vào hàm số ta được: 305036302130 y . Vậy người đó cần 2130 calo. Bài 6: (1.0 điểm) Tháp đồng hồ có phần dưới có dạng hình hộp chữ nhật, đáy là hình vuông có cạnh dài 5m, chiều cao của hình hộp chữ nhật là 12m. Phần trên của tháp có dạng hình chóp đều, các mặt bên là các tam giác cân chung đỉnh. Mỗi cạnh bên của hình chóp dài 8m.
a) Tính theo mét chiều cao của tháp đồng hồ. (làm tròn đến chữ số thập phân thứ nhất)
b) Cho biết thể tích của hình hộp chữ nhật được tính theo công thức VSh , trong đó S là diện tích mặt đáy, h là chiều cao của hình hộp chữ nhật. Thể tích của hình chóp được tính theo công thức 1 3 Sh , trong đó S là diện tích mặt đáy, h là chiều cao của hình chóp. Tính thể tích của tháp đồng hồ này (Làm tròn đến hàng đơn vị).
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 811440000215000590000 (đồng) Vì 594000590000 nên bạn Hùng phải mua bánh ở cử
để tổ
ố tiền phải trả ít hơn.
a hàng B
ng s
sa mạc Sahara trong nhiệt độ 500C thì cần bao nhiêu calo? Lời giải a) Tại 210C, một người làm việc cần sử dụng khoảng 3000 calo mỗi ngày, tức là khi 21 x thì tương ứng 3000 y . Khi nhiệt độ môi trường giảm đi 10C thì lượng calo cần tăng thêm khoảng 30calo, tức là khi 20 x thì tương ứng 3030 y Từ đó
aba abb V
ta có hệ phương trình: 21300030 2030303630
b)
.
nhiệt độ 500
50
.
Trong đợt dịch
- 19 , học sinh hai lớp 9A và 9B trường THCSX ủng hộ 217 chiếc khẩu trang cho những nơi cách li tập trung. Biết rằng số học sinh lớp 9A nhiều hơn số học sinh lớp 9B là 4 học sinh và mỗi học sinh lớp 9A ủng hộ 3 chiếc khẩu trang, mỗi học sinh lớp 9B ủng hộ 2 chiếc khẩu trang. Tìm số học sinh mỗi lớp.

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 82Lời giải Gọi các đỉnh lần lượt là .. SABCDABCD với , OACBDOACBD a) Ta có: 22 52m BDBCCD 152 22 ODBCOD 22 206 2 SOSDOD . Chiều cao tháp: 19,2m SOOO . b) 3 1206 5.5.12.5.5.359,8(m) 32 ABCDABCDSABCDVVV Bài 7: (1.0 điể
Lời giải Gọi học sinh lớp 9A là * , aa , khi đó học sinh lớp 9B là 4 a . Theo đề bài ta có: .44.221745 aaa Vậy: 9A có 45 học sinh, 9B có 41 học sinh. Bài 8: (3.0 điểm) Cho đường tròn (,) OR , từ điểm M nằm ngoài () O vẽ hai tiếp tuyến MA và (, MBAB là tiếp điểm). Vẽ đường kính AC của (),OMC cắt () O tại ( DD khác )C , OM cắt AB tại H . a) Chứng minh tứ giác MAOB nội tiếp và 2 . MBMCMD . b) Chứng minh..MOMHMCMD . c) CH cắt I ( I khác )C . Chứng minh tứ giác COIM nội tiếp. Lời giải
m)
Covid
a) Xét tứ giác MAOB: 9090180 MAOMBO (giả thiết) Suy ra tứ giác MAOB nội tiếp.
Xét MDB và MBC có: BMC là góc chung; MBDMCB (cùng chắng BD ) MDBMBC ∽ (g – g) 2 MBMD MBMDMC MCMB b) Ta có: MAMB và OAOB (tính chất hai tiếp tuyến cắt nhau) MO là đường trung trực AB MOAB. MOB vuông tại B có đường cao BH 2 . MBMHMO . Mà 2 MBMCMD (chứng minh trên) .. MOMHMCMD c) MOB vuông tại B có đường cao BH 2 OBOHOM Mà OBOCR 2 . OCOHOM OCOM OHOC
Xét COH và MOC có: COM là góc chung; OCOM OHOC (chứng minh trên). COHMOC ∽ (c – g – c) OCHOMC . OIC cân tại O (OCOIR), OCHOIC OMCOIC Suy ra tứ giác COIM nội tiếp.
NHÓM WORD HÓA ĐỀ TOÁN - 83 -
DẠYKÈMQUYNHƠN OFFICIAL
(1)
minh phương trình (1) luôn có hai nghiệm trái dấu. b) Tìm giá trị của biểu thức 12 21 2022 11
xx A
Bài 3: (0.75 điểm) Một người mua hai loại hàng và phải trả tổng cộng 2,17 triệu đồng, kể cả thuế giá trị gia tăng (VAT) với mức 10% đối với loại hàng loạt hàng thứ nhất và 8% đối với loại hàng thứ hai. Nếu thuế VAT là 9% đối với cả hai loại hàng thì người đó phải trả tổng cộng 2,18 triệu đồng. Hỏi nếu không kể thuế VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại hàng?
Bài 4: (0.75 điểm) Để tìm Hàng CHI của một năm ta dùng công thức sau rồi đối chiếu kết quả với bảng sau: Để tìm Hàng CAN của một năm ta dùng công thức sau rồi đối chiếu kết quả với bảng sau: Hàng CAN = Chữ số tận cùng của năm dương lịch 3

lãi của năm đầu được gộp vào với tiền vốn để tính lãi năm sau và lãi suất vẫn như cũ. Hết 2 năm bác Bình An phải trả tất cả 605 triệu đồng. Hỏi lãi suất cho vay của ngân hàng đó là bao nhiêu phần trăm trong 1 năm?
Bài 6: (1.0 điểm) Sóng cực ngắn có tần số 3030000MHz . Năng lượng rất lớn, không bị tầng điện ly hấp thụ, truyền đi rất xa (2200) km theo đường thẳng. Dùng trong thông tin liên lạc vũ trụ, ra đa và truyền hình. Tại một thời điểm có hai vệ tinh đang ở hai vị trí A và B cùng cách mặt đất 230km,
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG
ĐỀ
--------------------
.
2
dyx a) Vẽ đồ thị P và d trên
hệ trục tọa độ; b)
ọa
m của P và d
ằ
xx
GD & ĐT QUẬN 1 NĂM HỌC 2022-2023
THAM KHẢO MÔN : TOÁN 9
Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Quận 1 – 1 Thời gian: 120 phút (không kể thời gian phát đề) Bài 1: (1.5 điểm)
Cho
():
Pyx và ():2
cùng
Tìm t
độ giao điể
b
ng phép toán. Bài 2: (1.0 điểm) Cho phương trình 2 250
a) Chứng
xx
số tận
Hàng
Giáp Âtt
Mã số 1 2 3 4 5 6 7 8 9 10(0) Em hãy sử dụng quy tắc trên để xác định CAN, CHI của năm 2022. Bài 5: (1.0 điểm) Bác Bình An vay ở một ngân hàng 500 triệu đồng để sản xuất trong thời
1 năm sau bác
1
(Nếu chữ
cùng của năm đang xét nhỏ hơn 3 thì ta sẽ cộng thêm 10)
CAN
Bính Đinh Mậu Kỷ Canh Tân Nhâm Quý
hạn 1 năm. Lẽ ra đúng
phải trả cả tiền vốn lẫn tiền lãi, song bác đã được ngân hàng cho kéo dài thời hạn thêm
năm nữa, số tiền
một tín hiệu (truyền bằng sóng cực ngắn) được truyền đi từ vệ tinh A truyền đến vệ tinh B theo phương AB . Hỏi vệ tinh B có nhận được tín hiệu đó không? Biết khoảng cách giữa A và B theo đường thẳng là 2200km và bán kính Trái Đất là 6400km
Bài 7: (1.0 điểm) Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao trong bằng 3 lần đường kính trong của đáy; một viên bi hình cầu và một khối nón đều bằng thủy tinh. Biết viên bi và khối nón đều có đường kính bằng đường kính trong của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài. Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu.
Bài 8: (3.0 điểm) Cho đường tròn tâm O đường

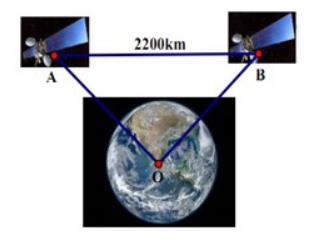
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA
TOÁN - 78
OFFICIAL
ĐỀ
-
kính AB . Trên đường tròn () O lấy điểm C không trùng B sao cho ACBC . Các tiếp tuyến của đường tròn () O tại A và tại C cắt nhau tại D . Gọi H là hình chiếu vuông góc của C trên , ABE là giao điểm của hai đường thẳng OD và AC a) Chứng minh OECH là tứ giác nội tiếp. b) Gọi F là giao điểm của hai đường thẳng CD và AB . Chứng minh 290 BCFCFB . c) Gọi M là giao điểm của hai đường thẳng BD và CH ; gọi T là hình chiếu vuông góc của O lên BC Chứng minh ba điểm ,, EMT thẳng hàng. --------------------------------------------
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI Bài 1: (1.5 điểm). Cho 2 (): Pyx và ():2 dyx a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ; b) Tìm tọa độ giao điểm của P và d bằng phép toán. Lời giải a) Hàm số: 2 yxP Bảng giá trị tương ứng của x và y : x 2 1 0 1 2 2 yx 4 1 0 1 4 Đồ thị hàm số là một Parabol đi qua các điểm 2;4 ; 1;1 ; 0;0 ; 1;1 ; 2;4 Hàm số: 2 yx 02xy 02yx Đồ thị hàm số là đường thẳng đi qua 0;2 và 2;0 Vẽ: b) Hoành độ giao điểm của P và d là nghiệm của phương trình: 2 2 xx 2 20 xx Vì 1120 abc Phương trình có hai nghiệm phân biệt: 1 1 x ; 2 2 x + Với 1 1 x 1 1 y + Với 2 2 x 2 4 y Vậy d cắt P tại hai điểm phân biệt là 1;1 A và 2;4 B Bài 2: (1.0 điểm) Cho phương trình 2 250 xx (1). a) Chứng minh phương trình (1) luôn có hai nghiệm trái dấu. b) Tìm giá trị của biểu thức 12 21 2022 11 xx A xx . Lời giải 6 4 2 y = -x + 2 y = x2 2 1 1 -2 -1 y x O
cộng 2,17 triệu đồng, kể cả thuế giá trị gia tăng (VAT) với mức 10% đối với loại hàng loạt hàng thứ nhất và 8% đối với loại hàng thứ hai. Nếu thuế VAT là 9% đối với cả hai loại hàng thì người đó phải trả tổng cộng 2,18 triệu đồng. Hỏi nếu không kể thuế VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại hàng? Lời giải Gọi số tiền không kể thuế của loại hàng thứ nhất là x (triệu đồng), của loại hàng thứ hai là y (triệu đồng) ( 0,0xy ) Tổng số tiền phải trả là 2,17 triệu đồng, kể cả thuế giá trị gia tăng (VAT) với mức 10% đối với loại hàng loạt hàng thứ nhất và 8% đối với loại hàng thứ hai nên ta có phương trình: 8%10%2,171,081,12,17 xxyyxy (1); Nếu thuế VAT là 9% đối với cả hai loại hàng thì người đó phải trả tổng cộng 2,18 triệu đồng nên ta có phương trình: 9%9%2,181,091,092,18 xxyyxy
Hàng CAN của một năm ta dùng công thức sau rồi đối chiếu kết quả với bảng sau: Hàng CAN = Chữ số tận cùng của năm dương lịch 3 (Nếu chữ số tận cùng của năm đang xét nhỏ hơn 3 thì ta sẽ cộng thêm 10) Hàng CAN Giáp Ất Bính Đinh Mậu Kỷ Canh Tân Nhâm Quý Mã số 1 2 3 4 5 6 7 8 9 10(0)

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 80Xét phương trình 2 250 xx (1). a) Phương trình (1) có .1.550ac phương trình (1) luôn có hai nghiệm phân biệt trái dấu 12 , xx . b) Phương trình (1) luôn có hai nghiệm phân biệt trái dấu 12 , xx Theo hệ thức Vi-et, ta có: 12 12 2 5 xx xx 1122 1212 212112 11 202220222022 11111 1 xxxx xxxx A xxxxxx 22 22 121212 1122 12121212 22252 202220222022 11521 xxxxxx xxxx xxxxxxxx 4102 2022820222014 521 Bài 3: (0.75 điểm) Một người mua hai
Vậy ta có hệ: 1,081,12,17 1,091,092,18 xy xy . Giải hệ phương trình
được: 1,5 0,5 x y (thỏa mãn). Vậy không kể thuế VAT thì loại hàng thứ nhất phải trả 1,5 triệu đồng, loại hàng thứ hai phải trả 0,5 triệu đồ
Bài
tìm
Để
loại hàng và phải trả tổng
(2);
ta
ng.
4: (0.75 điểm) Để
Hàng CHI của một năm ta dùng công thức sau rồi đối chiếu kết quả với bảng sau:
tìm
2101239
CAN, CHI
gi
năm 2022
nên năm 2022 có CAN là Nhâm, và 202242018

chia cho 12 dư
cộng 1 bằng 3 nên năm 2022 có CHI là Dần Bài 5: (1.0 điểm) Bác Bình An vay ở một ngân hàng 500 triệu đồng để sản xuất trong thời hạn 1 năm. Lẽ ra đúng 1 năm sau bác phải trả cả tiền vốn lẫn tiền lãi, song bác đã được ngân hàng cho kéo dài thời hạn thêm 1 năm nữa, số tiền lãi của năm đầu được gộp vào với tiền vốn để tính lãi năm sau và lãi suất vẫn như cũ. Hết 2 năm bác Bình An phải trả tất cả 605 triệu đồng. Hỏi lãi suất cho vay của ngân hàng đó là bao nhiêu phần trăm trong 1 năm?
(triệ
đồng).
sau hai năm bác Bình An phải trả 605 triệu đồng nên ta có phương trình: 22 500100050060550010001050 xxxx
Giải phương trình ta được 1 0,1 x (thỏa mãn); 2 2,1 x (loại). Vậy lãi suất mỗi năm của ngân hàng đó là 0,110% . Bài 6: (1.0 điểm) Sóng cực ngắn có tần số 3030000MHz . Năng lượng rất lớn, không bị tầng điện ly hấp thụ, truyền đi rất xa (2200) km theo đường thẳng. Dùng trong thông tin liên lạc vũ trụ, ra đa và truyền hình. Tại một thời điểm có hai vệ tinh đang ở hai vị trí A và B cùng cách mặt đất 230km, một tín hiệu (truyền bằng sóng cực ngắn) được truyền đi từ vệ tinh A truyền đến vệ tinh B theo phương AB . Hỏi vệ tinh B có nhận được tín hiệu đó không? Biết khoảng cách giữa A và B theo đường thẳng là 2200km và bán kính Trái Đất là 6400km
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 81 -
sử dụ
tắc
Lời giải Gọi lãi suất của ngân
là x ( 0 x ). Ta có: Số tiền phải trả sau năm thứ nhất là: 500500x
ệu
ng). S
Lời giải Kẻ OHAB tại H , OAB có 64002306630 OAOBkm nên OAB cân tại OOH cũng là trung tuyến của 2200 1100 22 AB OABHAHBkm H A B O
Em hãy
ng quy
trên để xác định
của
Lời
ải Vì
2
hàng đó
(tri
đồ
ố tiền phải trả sau năm thứ hai là: 2 5005005005005001000500 xxxxx
u
Vì
.
7: (1.0 điểm) Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao trong bằng 3 lần đường kính trong của đáy; một viên bi hình cầu và một khối nón đều bằng thủy tinh. Biết viên bi và khối nón đều có đường kính bằng đường kính trong của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài. Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu.
Tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu là tỉ số thể tích của hiệu thể tích hình trụ với tổng thể tích hình nón và hình cầu với thể tích của hình trụ.
Chiều cao của hình trụ là : ����
Chiềucaocủahìnhnónlà :���� ����=����

Ta có: Thể tích hình trụ là: ���� =��������=�� ���� ����=�������� Thể tích viên bi là: 3 2 4 3 VR
Thể tích hình nón là:
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 82Áp dụng định lý Pi-ta-go cho OHA vuông tại H , ta có: 2222222663011006538 OAOHHAOHOAAHkm . Vậy 6400 OH nên tín hiệu truyền từ vệ tinh A đến được vệ tinh B mà không bị trái đất cản lại.
Bài
Lời giải
223 3 114 ..4 333 VRhRRR Th
ạ
trong
là: 3333 4123 4410 6 333 VVVVRRRR . Tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu là: 3 4 3 1 10 5 3 9 6 R V V R . Bài 8: (3.0 điểm) Cho đường tròn tâm O đường kính AB . Trên đường tròn () O lấy điểm C không trùng B sao cho ACBC . Các tiếp tuyến của đường tròn () O tại A và tại C cắt nhau tại D . Gọi H là hình chiếu vuông góc của C trên , ABE là giao điểm của hai đường thẳng OD và AC a) Chứng minh OECH là tứ giác nội tiếp. b) Gọi F là giao điểm của hai đường thẳng CD và AB . Chứng minh 290 BCFCFB c) Gọi M là giao điểm của hai đường thẳng BD và CH ; gọi T là hình chiếu vuông góc của O lên BC Chứng minh ba điểm ,, EMT thẳng hàng. Lời giải
ể tích nước còn l
i
bình
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 83 -
̂
CD và AB . Chứng minh 290 BCFCFB . Ta có: 2.BCFCOB (góc tạo bởi tia tiếp tuyến và dây cung và góc ở tâm
chắn BC ); Mà OCCDOCF vuông tại 90 CCOBCFB ; Vậy 290 BCFCFBCOBCFB c) Gọi M là giao điểm của hai đường thẳng BD và CH ; gọi T là hình chiếu vuông góc của O lên BC . Chứng minh ba điểm ,, EMT thẳng hàng. E H D B O A C F E H D B O A C
a) Chứng minh OECH là tứ giác nội tiếp. DADC (tính chất hai tiếp tuyến cắt nhau); OAOC (bán kính O ) OD là trung trực của ACODAC tại trung điểm E của AC 90 OEC ; Tứ giác OECH có: ������
=����° (chứng minh trên) 90 OHC ( H là hình chiếu vuông góc của C lên AB )
tứ giác OECH nội tiếp đường tròn đường kính OC . b) Gọi F là giao điểm của hai đường thẳng
cùng
Gọi G là giao điểm của BC và AD; Vì 90 ACB góc nội tiếp chắn nửa đường tròn 90 ACG ; Trong ACG vuông tại C , ta có: DACDCA ( DAC cân tại D ) 9090DACDCADGCDCGDCG cân tại DDCDGDAD là trung điểm của AG; Vì // CHGA (cùng vuông góc với AB ) nên theo hệ quả của định lý T-let, ta có: MHBMMC DABDDG mà DADGMHMCM là trung điểm của CH ; OBC cân tại O có OT là đường cao nên cũng là trung tuyến T là trung điểm của BC ; Theo a) ta có E là trung điểm của AC . Vậy EM là đường trung bình của // CAHEMAH hay // EMAB ; ET là đường trung bình của // CABETAB ; Theo tiên đề Ơ-clit ,, EMETEMT thẳng hàng.
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 84 -
G T
F
OFFICIAL
M
E H D B O A C
ng loạt giảm giá các sản phẩm. Trong đó có chương trình nếu mua một gói kẹo thứ hai trở đi sẽ được giảm 10% so với giá ban đầu là 50000 đồng. a) Nếu gọi số gói kẹo đã mua là x, số tiền phải trả là y. Hãy biểu diễn diễn y theo x. b) Bạn Thư muốn mua 10 gói kẹo thì hết bao nhiêu tiền Bài 4: (1.0 điểm) Trong kỳ thi HKII môn toán lớp 9. Một phòng thi của trường có 24 thí sinh dự thi. Các thí sinh đều phải làm bài trên giấy thi của trường phát. Cuối buổi thi, sau khi thu bài, giám thị coi thi đếm được tổng số tờ giấy thi là 53 tờ. Hỏi trong phòng thi đó có bao nhiêu thí sinh làm bài 2 tờ giấy thi, bao nhiêu thí sinh làm bài 3 tờ giấy thi? Biết rằng có 3 thí sinh chỉ làm 1 tờ giấy thi. Bài 5: (1.0 điểm) Trong một phòng họp có 360 người họp, được sắp xếp ngồi đều trên các dãy ghế. Nếu bớt đi 3 dãy ghế thì mỗi dãy ghế phải xếp thêm 4 ghế mới đủ chỗ. Hỏi lúc đầu có bao nhiêu dãy ghế và mỗi dãy xếp mấy ghế? Bài 6: (1.0 điểm) Để ước lượng khối lượng của cây gỗ trồng trong rừng người ta cần xác định chiều cao h của cây (đo bằng mét) và chu vi C của vòng tròn thân cây ngang t
m ngực (đo bằng mét). Theo cách đo đạc trong lâm nghiệp, độ cao ngang tầm ngực là 1,4 mét tính từ mặt đất. Từ đó người ta có thể quấn thước dây vòng quanh thân cây ở độ cao này và ghi lại số đo chu vi C.
a) Áp dụng công thức thể tích hình trụ V = S.h trong đó S là diện tích vòng tròn thân cây có chu vi C nói trên và h là chiều cao của cây sẽ tính được thể tích của cây. Nếu một cây có chu vi C của vòng tròn thân cây ngang tầm ngực là 1,28m và chiều cao là

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GD & ĐT QUẬN 3 NĂM HỌC 2022-20232 ĐỀ THAM KHẢO MÔN : TOÁN 9 -------------------- Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Quận 3 – 1 Thời gian: 120 phút (không kể thời gian phát đề) Bài 1: (1.5 điểm). Cho P : 2 yx và đường thẳng D : 34yx a) Vẽ P và D trên cùng một hệ trục. b) Tìm tọa độ giao điểm của P và D bằng phép tính Bài 2: (1.0 điểm) Cho phương trình bậc hai: 2 210xmx 1 a) Chứng minh rằng phương trình 1 luôn có hai nghiệm phân biệt 1x và 2x b) Tìm các giá trị m để 22 1212 7 xxxx Bài 3: (1.0 điểm) Một cửa hàng đồ
ầ
20,4m thì cây có thể tích bao nhiêu (làm tròn đến chữ số thập phân thứ nhất)?
b) Cho biết loại cây nói trên có khối lượng riêng là D = 1,05 tấn/m3 khối lượng m = V . D. Hãy ướ
lượng khối lượng của cây đó tính theo đơn vị là kg (làm tròn đến hàng trăm).
OFFICIAL
Bài 7: (1.0 điểm) Một cửa hàng Pizza có chương trình khuyến mãi: giảm 30% cho bánh Pizza hải sản có giá bán ban đầu là 210000 đồng/cái. Nếu khách hàng có thẻ VIP thì sẽ được giảm thêm 5% trên giá đã giảm. Hỏi một nhóm nhân viên văn phòng đặt mua 60 cái bánh Pizza hải sản ở cửa hàng trong đó có 25 cái dùng thẻ VIP thì phải trả tất cả bao nhiêu tiền (làm tròn nghìn đồng)? Bài 8: (2.5 điểm) Từ điểm A ở ngoài đường tròn ; OR vẽ hai tiếp tuyến AB, AC với đường tròn O , BC là tiếp điểm . Gọi H là giao điể
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA
TOÁN - 78 -
ĐỀ
c
m của
.
ọ
là
m của AB.
ừ B kẻ đường
ẳng
vớ
tạ
ẳ
ại D (D khác B). a) Chứng minh tứ giác ABOC nội tiếp và .. OKOIOHOA . b) Đường tròn ; 2 AB I cắt AC tại E. Gọi F là giao điểm của BE và OA. Chứng minh F đối xứng với O qua H. c) Chứng minh đường tròn ngoại tiếp AFB đi qua điểm K
AO và BC
G
i I
trung điể
T
th
vuông góc
i OI
i K, đường th
ng này cắt đường tròn
O t
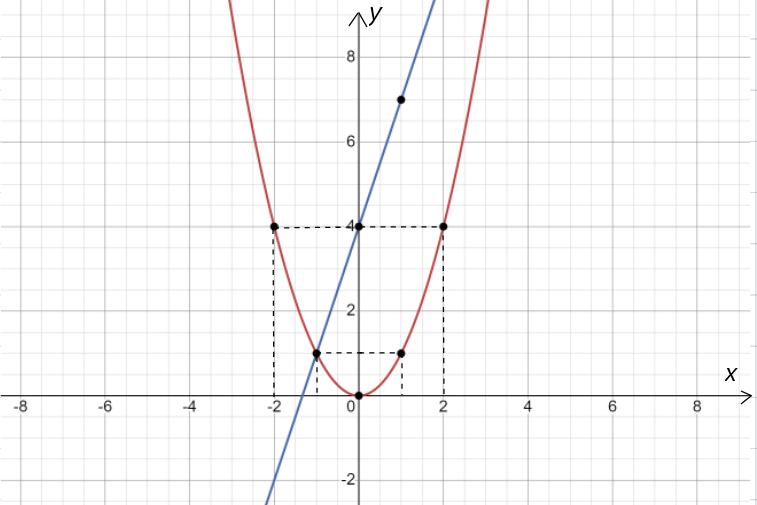
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI Bài 1: (1.5 điểm). Cho P : 2 yx và đường thẳng D : 34yx a) Vẽ P và D trên cùng một hệ trục. b) Tìm tọa độ giao điểm của P và D bằng phép tính Lời giải a) Hàm số: 2 yx Bảng giá trị tương ứng của x và y : x –2 -1 0 1 2 2 yx 4 1 0 1 4 Đồ thị hàm số là một Parabol đi qua các điểm ( ��;��); ( ��;��); 0;0 ; (��;��); (��;��) Hàm số: 34yx 04xy 11xy Đồ thị hàm số là đường thẳng đi qua 0;4 và 1;1 Vẽ: b) Hoành độ giao điểm của P và D là nghiệm của phương trình: 2 34xx 2 340xx 1,3,4abc 1(3)(4)0 abc Phương trình có hai nghiệm phân biệt: 1 1 x ; 2 4 x + Với 1 1 x 1 1 y + Với 2 4 x 2 16 y Vậy D cắt P tại hai điểm phân biệt là 1;1 và 4;16 . Bài 2: (1.0 điểm) Cho phương trình bậc hai: 2 210xmx 1 a) Chứng minh rằng phương trình 1 luôn có hai nghiệm phân biệt 1x và 2x . b) Tìm các giá trị m để 22 1212 7 xxxx . Lời giải a) Cách 1: Phương trình đã cho là phương trình bậc hai của x có:
c
ng có 24 thí sinh d
thi. Các thí sinh đều phải làm bài trên giấy thi của trường phát. Cuối buổi thi, sau khi thu bài, giám thị coi thi đếm được tổng số tờ giấy thi là 53 tờ. Hỏi trong phòng thi đó có bao nhiêu thí sinh làm bài 2 tờ giấy thi, bao nhiêu thí sinh làm bài 3 tờ giấy thi? Biết rằng có 3 thí sinh chỉ làm 1 tờ giấy thi. Lời giải Gọi x là số thí sinh làm bài 2 tờ giấy thi, y là số thí sinh làm bài 3 tờ giấy thi ,,0,21 xyxy
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 8022 ()1.(1)11 mmm 0 m Vậy phương trình đã cho
m 1x ; 2x với mọi
trị của m . Cách
:
trái
ấu
ệt b) Theo
12 12 2 1 xxm xx Do đó: 22 1212 7 xxxx 2 121237xxxx 2
m 2 437 m 2 44 m 2 1 m 1 m Vậy với 1 m thì phương trình có hai nghiệm 1x ; 2x thỏa mãn 22 1212 7 xxxx Bài 3: (1.0 điểm) Một cửa hàng đồng loạt giảm giá các sản phẩm. Trong đó có chương trình nếu mua một gói kẹo thứ hai trở đi sẽ được giảm 10% so với giá ban đầu là 50000 đồng. a) Nếu gọi số gói kẹo đã mua là x, số tiền phải trả là y. Hãy biểu diễn diễn y theo x b) Bạn Thư muốn mua 10 gói kẹo thì hết bao nhiêu tiền. Lời giải a) Giá một gói kẹo thì gói thứ hai trở đi: (100%10%).5000045000 đồng Số gói kẹo đã mua là x, số tiền phải trả là y. Theo đề bài ta có: 50000450001450005000 yxyx b) Bạn
xy Vậy số tiền bạn Thư phải trả khi mua 10 gói kẹo là 455000 đồng Bài
(1.0
ỳ
ớ
ột
Vì
tờ giấy thi nên
xy Tổng số tờ giấy thi của các thí sinh làm 2 tờ và 3 tờ giấy thi là
xy Ta có hệ phương trình: 212242813 23502350218 xyxyyx xyxyxyy (thỏa mãn) Vậy có 13 thí sinh làm bài 2 tờ giấy thi, có 8 thí sinh làm bài 3 tờ giấy thi. Bài 5: (1.0 điểm) Trong một phòng họp có 360 người họp, được sắp xếp ngồi đều trên các dãy ghế. Nếu bớt đi 3 dãy ghế thì mỗi dãy ghế phải xếp thêm 4 ghế mới đủ chỗ. Hỏi lúc đầu có bao nhiêu dãy ghế và mỗi dãy xếp mấy ghế? Lời giải Gọi x là dãy ghế ban đầu (x nguyên dương, 3 < x < 360) Số ghế mỗi dãy ban đầu là 360 x Số dãy ghế lúc sau là: x – 3. Số ghế mỗi dãy lúc sau là: 360 3 x Vì mỗi dãy ghế phải xếp thêm 4 ghế so mới đủ chỗ nên ta có phương trình:
luôn có hai nghiệ
giá
2
vì a, c
d
nên phương trình luôn có 2 nghiệm phân bi
định lý Vi-et, ta có:
23.(1)7
Thư mua 10 gói kẹo 1045000.105000455000
4:
điểm) Trong k
thi HKII môn toán l
p 9. M
phòng thi
ủa trườ
ự
có 3 thí sinh làm bài 1
ta có 24321
2353350
Bài 6: (1.0 điểm) Để ước lượng khối lượng của cây gỗ trồng trong rừng người ta cần xác định chiều cao h của cây (đo bằng mét) và chu vi C của vòng tròn thân cây ngang tầm ngực (đo bằng mét). Theo cách đo đạc trong lâm nghiệp, độ cao ngang tầm ngực là 1,4 mét tính từ mặt đất. Từ đó người ta có thể quấn thước dây vòng quanh thân cây ở độ cao này và ghi lại số đo chu vi C
a) Áp dụng công thức thể tích hình trụ V = S.h trong đó S là diện tích vòng tròn thân cây có chu vi C nói trên và h là chiều cao của cây sẽ tính được thể tích của cây. Nếu một cây có chu vi C của vòng tròn thân cây ngang tầm ngực là 1,28m và chiều cao là 20,4m thì cây có thể tích bao nhiêu (làm tròn đến chữ số thập phân thứ nhất)?
b) Cho biết loại cây nói trên có khối lượng riêng là D = 1,05 tấn/m3 khối lượng m = V . D. Hãy ước lượng khối lượng của cây đó tính theo đơn vị là kg (làm tròn đến hàng trăm). Lời giải
a) Gọi R (m) là bán kính vòng tròn thân cây ngang tầm ngực (R > 0) Chu vi vòng tròn thân cây ngang tầm ngực là: 1,28 20,2() 22 C CRRm Diện tích vòng tròn thân cây ngang tầm ngực: 222 .0,20,126()SRm
Thể tích cây là: 3 .0,126.20,42,6() VShm b) Khối lượng của cây: .2,6.1,052,73mVD (tấn) 2700 (kg) Bài 7: (1.0 điểm) Một cửa hàng Pizza có chương trình khuyến mãi: giảm 30% cho bánh Pizza hải sản có giá bán ban đầu là 210000 đồng/cái. Nếu khách hàng có thẻ VIP thì sẽ được giảm thêm 5% trên giá đã giảm. Hỏi một nhóm nhân viên văn phòng đặt mua 60 cái bánh Pizza hải sản ở cửa hàng trong đó có 25 cái dùng thẻ VIP thì phải trả tất cả bao nhiêu tiền (làm tròn nghìn đồng)?
Lời giải
Giá một cái bánh Pizza hải sản trong chương trình khuyến mãi: (100% – 30%).210000 = 147000 (đồng)
Giá một cái bánh Pizza hải hải trong chương trình khuyến mãi và có dùng thẻ VIP : (100% – 5%).147000 = 139650 (đồng)
Nhóm nhân viên văn phòng đặt mua 60 cái bánh Pizza hải sản trong đó có 25 cái dùng thẻ VIP thì s
là : 147000.(60-25) + 139650.25 = 8636250 (đồng)
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 812 360360360(3)4(3)360 4 3(3)(3) 3601080412360 xxxx xxxxxx xxxx 2 1 4121080015 xxx
ạ
x
(lo
i) ; 2 18
(nhận) Vậy lúc đầu có 18 dãy ghế và mỗi dãy có 360 20 18 (ghế)
ả
trả
8: (2.5 điểm) Từ điểm A ở ngoài đường tròn ; OR vẽ hai tiếp tuyến AB, AC với đường tròn O , BC là tiếp điểm . Gọi H là giao điểm của AO và BC. Gọi I là trung điểm của AB. Từ B kẻ đường thẳng vuông góc với OI tại K, đường thẳng này cắt đường tròn O tại D (D khác B). a) Chứng minh tứ giác ABOC nội tiếp và .. OKOIOHOA . b) Đường tròn ; 2 AB I cắt AC tại E. Gọi F là giao điểm của BE và OA. Chứng minh F đối xứng với O qua H.
ố tiền ph
i
Bài
c) Chứng minh đường tròn ngoại tiếp AFB đi qua điểm K. L
a) Ta có , OBABOCAC (AB, AC là tiếp tuyến của (O) ) Suy ra 9090180 ooo ABOACO Do đó tứ giá ABOC nội tiếp. Lại có: AO là phân giác góc BAC và AB = AC (AB, AC là tiếp tuyến của đường tròn (O)) Suy ra AO là phân giác cũng là đường cao của tam giác cân ABC AOBC tại H. ∆OBA vuông tại B có đường cao BH 2 OBOHOA ∆OBI vuông tại B có đường cao BK 2 OBOKOI Vậy: OHOAOKOI b) Xét đường tròn ; 2 AB I
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 82 -
ời giải
Ta
2
Mà
OBF Mà BHOF Do đó ∆OBF cân tại B có BH là phân giác cũng là đường cao và đường trung tuyến Suy ra H là trung điểm OF hay F đối xứng O qua H. c) Ta có .. OHOAOKOI (chứng minh ở câu a) OAOI OKOH Đồng thời ∆OKA và ∆OAI có AOI chung nên OKHOAI ” (c.g.c) OKHOAI Tứ giác AHKI nội tiếp IKAIHA (1) Lại có 1 2 IHIAAB (∆ABH vuông tại H, HI là trung tuyến) nên ∆IHA cân tại I IHAIAH mà IAHOBH (cùng phụ BOH ) và OBHHBF (chứng minh trên)
:
có: 1
E HAEH H BEsđ
(góc nội tiếp chắn cung HE)
HAEOBH
(cùng nhìn cạnh OC của tứ giác nội tiếp OBAC) HBEOBH
BH là phân giác
OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 83nên
(2) Từ
(2)
M
Do
V
DẠYKÈMQUYNHƠN
IHAHBF
(1) và
IKAHBF
ặt khác: 90o BFAHBFBHFHBF (góc ngoài ∆BHF) 90o BKAIKABKIIKA
đó BFABKA
và cùng nhìn cạnh AB
ậy tứ giác BKFA nội tiếp hay đường tròn ngoại tiếp ∆BFA đi qua K.
3: (0.75 điểm) Một năm bình thường sẽ có 12 tháng và 365 ngày. Khi một năm có số ngày hoặc số tháng tăng lên (theo Dương lịch hoặc theo Âm lịch) thì sẽ được gọi là năm nhuận, trong đó có những ngày nhuận và tháng nhuận. Năm nhuận là năm có 29 ngày tháng 2 Dương lịch (không nhuận là 28 ngày). Cách tính năm nhuận theo Dương lịch là những năm dương lịch nào chia hết cho 4 thì đó sẽ là năm nhuận.
Ví dụ: 2016 chia hết cho 4 nên năm 2016 là năm nhuận. Ngoài ra, đối với thế kỷ (những năm có 2 số cuối là số 0) thì ta sẽ lấy số năm đó chia cho 400, nếu như chia hết thì đó sẽ là năm nhuận (hoặc hai số đầu trong năm chia hết cho 4).
Ví dụ: 1600 và 2000 là các năm nhuận nhưng 1700, 1800 và 1900 không phải năm nhuận.
a) Em hãy dùng quy tắc trên để xác định năm 2022 có phải là năm nhuận dương lịch không?
b) Bạn Hòa nhớ rằng sinh nhật lần thứ 15 của bạn vào ngày 2/6/2022 là ngày thứ năm. Bạn thắc mắc ngày mình sinh ra là ngày thứ mấy? Em hãy giúp bạn giải đáp thắc mắc đó.
Bài 4: (0.75 điể
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GD & ĐT QUẬN 4 NĂM HỌC 2022-2023 ĐỀ THAM KHẢO MÔN:
Đề
MÃ ĐỀ: Quận 4 – 1 Thời
Bài 1: (1.5 điểm) Cho Parabol (): P 2 1 2 yx và đường thẳng ():4 dyx a) Vẽ đồ thị của hàm số () P và () d trên cùng một hệ
ị
ủ
=
TOÁN 9
thi gồm 8 câu hỏi tự luận
gian: 120 phút (không kể thời gian phát đề)
trục tọa độ b) Tìm tọa độ giao điểm của () P và () d bằng phép tính. Bài 2: (1.0 điểm) Cho phương trình 2 520xx có hai nghiệm là 12 , xx . Không giải phương trình, hãy tính giá tr
c
a biểu thức: A
22 1212 xxxx
Bài
ột xe ôtô chuyển
gian
được quãng đường dài bao nhiêu km? b) Đến lúc mấy giờ thì xe đi được quãng đường dài 34 km (tính từ lúc 7h00)? Bài 5: (1.0 điểm) Một người mua 3 đôi giày với hình thức khuyến mãi như sau: Nếu bạn mua một đôi giày với mức giá thông thường, bạn sẽ được giá giảm 30% khi mua đôi
với một nửa giá ban
ban đầu
ủ
30◦.
m) M
động theo hàm số S = 30t + 4t2, trong đó S (km) là quãng đường xe đi được trong thời
t (giờ); t là thời gian chuyển động của xe tính từ lúc 7h00 sáng. Xem như xe chuyển động đều trên một đoạn đường thẳng và không nghỉ. a) Hỏi từ lúc 7h30 phút đến lúc 8h15 phút xe đã đi
thứ hai, và mua một đôi thứ ba
đầu. Bạn Anh đã trả 1.320.000 cho 3 đôi giày. a) Giá
c
a một đôi giày là bao nhiêu? b) Nếu cửa hàng đưa ra hình thức khuyến mãi thứ hai là giảm 20% mỗi đôi giày. Bạn Anh nên chọn hình thức khuyến mãi nào nếu mua ba đôi giày. Bài 6: (1.0 điểm) Đổ nước vào một chiếc thùng hình trụ có bán kính đáy là 20 cm. Nghiêng thùng cho mặt nước chạm vào miệng cốc và đáy cốc (như hình vẽ) thì mặt nước tạo với đáy cốc một góc
a) Tính chiều cao của chiếc thùng hình trụ
b) Tính thể tích của chiếc thùng? (Kết quả làm tròn hai chữ số thập phân)
Bài 7: (1.0 điểm) Một đoàn y tế của Bệnh viện Chợ Rẫy, TP HCM gồm các bác sĩ và y tá tăng cường về tỉnh Cà Mau để khám chữa bệnh cho người dân trong tỉnh. Đoàn gồm 135 người và có tuổi trung bình là 40 tuổi. Tính số bác sĩ và y tá biết tuổi trung bình của các bác sĩ là 50 tuổi và tuổi trung bình của các y tá là 35 tuổi.
Bài 8: (3.0 điểm) Từ điểm A ở ngoài đường tròn tâm O, vẽ hai tiếp tuyến AB, AC với (O) (B, C là hai tiếp điểm). Vẽ cát tuyến AEF với (O) sao cho AE < AF và tia AF nằm giữa tia OA và tia OC. Gọi D là trung điểm của EF.
a) Chứng minh tứ giác AODC nội tiếp.
b) Gọi K là giao điểm của AF và BC. Chứng minh AD AK = AE AF
c) Đường thẳng OD cắt các tia AB, AC lần lượt tại hai điểm M và N. Đường thẳng vuông góc với MN tại O cắt BC tại G, AG cắt MN tại H. Chứng minh H là trung điểm của MN. HẾT
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 78 -
OFFICIAL
Đồ thị hàm số là đường thẳng đi qua 2;2 và (1;3).

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI
�� ��
�� �� ��
Bài 1: (1.5 điểm) Cho Parabol (): P 2 1 2 yx và đường thẳng ():4 dyx a) Vẽ đồ thị của hàm số () P và () d trên cùng một hệ trục tọa độ. b) Tìm tọa độ giao điểm của () P và () d bằng phép tính. Lời giải a)
Hàm số (): P 2 1 2 yx Bảng giá trị tương ứng của x và y : x �� �� �� �� �� (P): y = �� �� ���� ��
0
Đồ thị hàm số là một Parabol đi qua các điểm 2;2 ; 1 1; 2 ; 0;0 ; 1 1; 2 ; 2;2
Hàm số ():4 dyx x = -2 ⇒ y = 2 x = -1 ⇒ y = 3
Vẽ đồ thị hàm số () P và (d) trên cùng một hệ trục tọa độ.
điểm) Một năm bình thường sẽ có 12 tháng và 365 ngày. Khi một năm có số ngày hoặc số tháng tăng lên (theo Dương lịch hoặc theo Âm lịch) thì sẽ được gọi là năm nhuận, trong đó có những ngày nhuận và tháng nhuận. Năm nhuận là năm có 29 ngày tháng 2 Dương lịch (không nhuận là 28 ngày). Cách tính năm nhuận theo Dương lịch là những năm dương lịch nào chia hết cho 4 thì đó sẽ là năm nhuận.
Ví dụ: 2016 chia hết cho 4 nên năm 2016 là năm nhuận. Ngoài ra, đối với thế kỷ (những năm có 2 số cuối là số 0) thì ta sẽ lấy số năm đó chia cho 400, nếu như chia hết thì đó sẽ là năm nhuận (hoặc hai số đầu trong năm chia hết cho 4).
Ví dụ: 1600 và 2000 là các năm nhuận nhưng 1700, 1800 và 1900 không phải năm nhuận.
a) Em hãy dùng quy tắc trên để xác định năm 2022 có phải là năm nhuận dương lịch không?
b) Bạn Hòa nhớ rằng sinh nhật lần thứ 15 của bạn vào ngày 2/6/2022 là ngày thứ năm. Bạn thắc mắc ngày mình sinh ra là ngày thứ mấy? Em hãy giúp bạn giải đáp thắc mắc đó. Lời giải
a) Năm 2022 không phải là năm nhuận, vì 2022 : 4 dư 2.
b) Hòa sinh nhật lần thứ 15 vào ngày 2/6/2022, suy ra ngày sinh của Hòa là: 2/6/2007. Từ năm 2007 đến năm 2020, có số năm nhuận là: 15 4 = 3.75 (năm) ⇒ Có 3 năm nhuận trong 15 năm tuổi của Hòa. Tổng số ngày từ ngày 2/6/2007 đến 2/6/2022 là: (15 – 3) . 365 + 3 . 366 = 5478 (ngày) Ta có: 5478 : 7 dư 4, đồng nghĩa với Hòa sinh trước thứ năm 4 ngày, tức là chủ nhật.
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 80b) Hoành độ giao điểm của P và (d) là nghiệm của phương trình: 2 1 4 2 xx ⇔ 2 1 40 2 xx ∆ = 2 1 (1)4..(4)9 2 > 0 + Với 1x = 4 ���� = 8 + Với 2x = �� ���� = ��. Bài 2: (1.0 điểm) Cho phương trình 2 520xx có hai nghiệm là 12 , xx . Không giải phương trình, hãy tính giá trị của biểu thức: A = 22 1212 xxxx Lời giải A = 2222 1212121212()2552.(2)34xxxxxxxxxx Theo định lý Vi-et, ta có: 12 12 5 .2 xx xx Bài 3: (0.75
Bài 4: (0.75 điểm) Một xe ôtô chuyển động theo hàm số S = 30t + 4t2, trong đó S (km) là quãng đường xe đi được trong thời gian t (giờ); t là thời gian chuyển động của xe tính từ lúc 7h00 sáng. Xem như xe chuyển động đều trên một đoạn đường thẳng và không nghỉ
a) Hỏi từ lúc 7h30 phút đến lúc 8h15 phút xe đã đi được quãng đường dài bao nhiêu km?
b) Đến lúc mấy giờ thì xe đi được quãng đường dài 34 km (tính từ lúc 7h00)?
Lời giải
a) Thời gian từ 7h30 phút đến 8h15 phút là: 8h15p – 7h30 = 0.75 (h)
Quãng đường xe chạy trong 0.75h là: S = 30 . 0.75 + 4 . (0.75)2 = 24.75 (km)
b) Thời gian xe đi được quãng đường 34km là: 34 = 30t + 4t2
⇒ t = 1 (h)
Từ lúc 7h xe đi 34km, thời gian xe đến là: 7h + 1h = 8h Vậy xe đến lúc 8h.
OFFICIAL
Bài 5: (1.0 điểm) Một người mua 3 đôi giày với hình thức khuyến mãi như sau: Nếu bạn mua một đôi giày với mức giá thông thường, bạn sẽ được giá giảm 30% khi mua đôi thứ hai, và mua một đôi thứ ba với một nửa giá ban đầu. Bạn Anh đã trả 1.320.000 cho 3 đôi giày.
a) Giá ban đầu của một đôi giày là bao nhiêu? b) Nếu cửa hàng đưa ra hình thức khuyến mãi thứ hai là giảm 20% mỗi đôi giày. Bạn Anh nên chọn hình thức khuyến mãi nào nếu mua ba đôi giày. Lời giải a) Gọi x là giá một đôi giày. Theo hình thức khuy
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 81 -
(100%30%).(100%50%).2.2 xxxx Mà bạn Anh đã trả 1.320.000, ta có: 2.2x = 1.320.000 ⇒ x = 600.000
Giả sử giảm 20% mỗi đôi
600.000 . 3 . (100% –
⇒ Bạn Anh nên chọ
ến mãi, số tiền bạn Anh mua 3 đôi giày tính theo x là:
b)
giày, bạn Anh mua 3 đôi giày sẽ có giá là:
20%) = 1.440.000 > 1.320.000
n hình thức khuyến mãi ban đầu.
Bài 6: (1.0 điểm) Đổ nước vào một chiếc thùng hình trụ có bán kính đáy là 20 cm. Nghiêng thùng cho mặ
nước chạm vào miệng cốc và đáy cốc (như hình vẽ) thì mặt nước tạo với đáy cốc một góc 30◦
a) Tính chiều cao của chiếc thùng hình trụ
b) Tính thể tích của chiếc thùng? (Kết quả làm tròn hai chữ số thập phân)
a) Đường kính đáy là: 20 . 2 = 40 (cm) Xét �������� vuông tại B, có �� ̂ = 30o, ta có: AB = tan �� ̂ . BC = 40 3 ≈ 23.09 (cm)

b) Diện tích đáy thùng hình trụ là: 2 .R = 3.14 . 202 = 1256.64 (cm2) Thể tích chiếc thùng là: Vthùng = Sđáy ABh ≈ 1256.64 . 23.09 ≈ 29015.82 (cm3)
Bài 7: (1.0 điểm) Một đoàn y tế của Bệnh viện Chợ Rẫy, TP HCM gồm các bác sĩ và y tá tăng cường về tỉnh Cà Mau để khám chữa bệnh cho người dân trong tỉnh. Đoàn gồm 135 người và có tuổi trung bình là 40 tuổi. Tính số bác sĩ và y tá biết tuổi trung bình của các bác sĩ là 50 tuổi và tuổi trung bình của các y tá là 35 tuổi.
Lời giải
Tổng số tuổi của đoàn y tế là: 135 .
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 82 -
OFFICIAL
t
40
Gọi x là số bác sĩ trong
ng số
ổ
Gọi y là số y tá trong
tổng số tuổ
ủ
Từ tổng số tuổi và tổng số người
50355400 135 xy xy Suy ra 45 x (bác sĩ); 90 y
= 5400 (tuổi).
đoàn, tổ
tu
i của bác sĩ là: 50x (tuổi).
đoàn,
i c
a y tá là: 35y (tuổi).
trong đoàn, ta có hệ phương trình:
(y tá).
Bài 8: (3.0 điểm) Từ điểm A ở ngoài đường tròn tâm O, vẽ hai tiếp tuyến AB, AC với (O) (B, C là hai tiếp điểm). Vẽ cát tuyến AEF với (O) sao cho AE < AF và tia AF nằm giữa tia OA và tia OC. Gọi D là trung điểm của EF.

a) Chứng minh tứ giác AODC nội tiếp.
b) Gọi K là giao điểm của AF và BC. Chứng minh AD AK = AE AF.
c) Đường thẳng OD cắt các tia AB, AC lần lượt tại hai điểm M và N. Đường thẳng vuông góc với MN tại O cắt BC tại G, AG cắt MN tại H. Chứng minh H là trung điểm của MN. L
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 83 -
OFFICIAL
a) Gọi I là trung điểm AO. D là trung điểm dây cung EF () O ODEF , 90o ODA Xét tứ giác ADOC, có: 90o ODA 90o OCA (do OC là tiếp tuyến (O) tại C) Tứ giác ADOC nội tiếp (I, IO), các điểm A, D, O, C cùng thuộc (,) IIO . (1) b) �������� vuông tại B , suy ra (,)BIIO . (2) Từ (1), (2) A, D, O, C, B cùng thuộc(,) IIO . Xét �������� và ��������, có: AKCBKD (đối đỉnh)
ời giải

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 84 -
��������
AKKC
..
Xét
EKCBKF
CEFFBC
��������
EKKC BKKF EKKFBKKC
Từ
(4): AKKDEKKF .()().() AKADAKAKAEAFAK 22 .... AKADAKAKAFAKAEAFAEAK .. AEAFAKAFADAE .. AEAFAKDFAE Mà DFDE , AEDEAD AEAFAKAD c) Kẻ đường thẳng a qua G song song với MN, lần lượt cắt các cạnh AM tại U, AN tại V. Xét tứ giác CGOV, có: 90o OCV (góc tiếp tuyến, với V tiếp tuyến tại C của (O)) 90o OGV (do OG MN, UV//MN, nên OG UV) CGOV nội tiếp (2 góc cùng chắn cung). OCGOVG (cùng chắn cung OG ) (5) Xét tứ giác UBOG, có: 90o OGU 90o OBU UBOG nội tiếp (2 góc đối bù nhau). GUOGBO (cùng chắn cung OG ) (6)
CAKDBK
(cùng chắn cung CD (,) IIO )
�������� (g.g)
BKKD
AKKDBKKC
(3)
�������� và ��������, có:
(đối đỉnh)
(cùng chắn cung CF (;) OOB )
�������� (g.g)
(4)
(3),
Xét �������� cân tại O và đường tròn (O;R), có:
OBCOCB (7)
Từ (5); (6); (7), suy ra OUGOVG
Suy ra �������� cân tại O, mà OG là đường cao ��������
Suy ra OG đồng thời là đường trung tuyến, G là trung điểm UV.
Xét �������� có VG // HN, theo định lí Thales ta có: VGAG HNGH
(8)
Xét �������� có VG // HN, theo định lí Thales ta có: GUAG HNGH
Từ (7), (8), suy ra: GUVG HMHN
Mà GU = VG, suy ra HM = HN. Suy ra H là trung điểm MN.
(8)
NHÓM WORD HÓA ĐỀ TOÁN - 85 -
DẠYKÈMQUYNHƠN OFFICIAL
GD & ĐT QUẬN 1 NĂM HỌC 2022-2023 ĐỀ THAM KHẢO MÔN : TOÁN 9 -------------------- Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Quận 5 – 1 Thời gian: 120 phút (không kể thời gian phát đề) Bài 1: (1.5 điểm) Cho parabol 2 : 2 x Py và đường thẳng :46dyx a) Vẽ đồ thị
P và
d trên cùng hệ trục tọa độ; b) Tìm tọa độ giao điểm của P và d bằng phép toán. Bài 2: (1.0 điểm) Cho phương trình 2 1 101 2 xx
Không giải phương trình hãy tính giá trị của biểu thức sau:
ới
, xx là hai nghiệm của phương trình (1). Bài 3: (0.75 điểm) Để tính múi giờ của một địa điểm ta làm như sau: - Ở Đông bán cầu (kí hiệu là Ð): múi giờ = kinh độ Đông: 15 - Ở Tây bán cầu (kí hiệu là T): múi giờ (= 360 Kinh độ Tây): 15 (Kết quả làm tròn đến hàng đơn vị) Để tính giờ của một địa điểm, ta tính theo công thức: TGMTH với T là
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT
Ồ
ĐỀ THAM KHẢO TUYỂN SINH 10
Múi giờ 0 1 2 3 4 5 6 7 8 9 10 11 H 0 1 2 3 4 5 6 7 8 9 10 11 Múi giờ 13 14 15 16 17 18 19 20 21 22 23 H 12 11 10 9 8 7 6 5 4 3 2 1 a) Lúc 1900 h ở Hà Nội 105Ð ngày 15/6/2021 thì lúc đó ở Los Angeles 120T là mấy giờ? b) Một chiếc máy bay cất cánh ở sân bay tại New York 75 T với vận tốc 750/kmh trên quãng đường chim bay dài 14250 km để hạ cánh xuống sân bay Tân Sơn Nhất của Việt Nam 105Ð đúng 2 giờ sáng ngày 01/10/2021. Hỏi máy bay cất cánh tại New York ngày nào? Lúc mấy giờ? Bài 4: (0.75 điểm) Áp suất của nước P (đơn vị: atm ) lên một người thợ lặn ở độ sâu d (tính theo feet) là một hàm số bậc nhất () Pdadb có đồ thị như hình bên
TP.H
CHÍ MINH
PHÒNG
12 12 21 xx Axx xx v
12
giờ tại nơi đó, GMT là giờ gốc, H được quy đổi như sau:
a) Tính các hệ số a và b biết các điểm 0;1 A và 33;2 B thuộc đồ thị hàm số. b) Tính áp suất của nước lên người thợ lặn ở độ sâu 100 feet (kết quả làm tròn đến hàng đơn vị). Biết feet là đơn vị đo độ dài, 10,3048. feetm
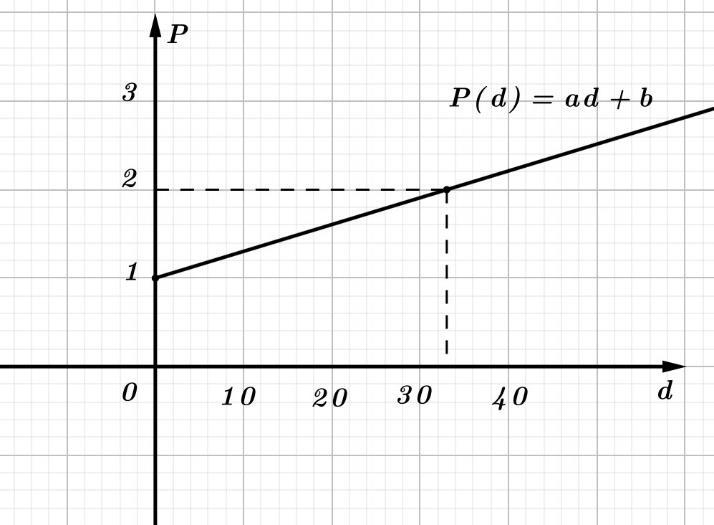
Bài 5: (1.0 điểm) Hãng viễn thông Văn có ba phương án trả tiền cước điện thoại cho mỗi cuộc gọi:
- Phương án I: Trả tổng cộng 99 cent cho 20 phút đầu, sau đó từ phút 21 trở đi thì mỗi phút trả 5. cent
- Phương án II: Kể từ lúc đầu tiên, mỗi phút trả 10 .cent
- Phương án III: Trả 25 cent tiền thuê bao, sau đó kể từ phút đầu tiên mỗi phút trả 8 cent
Anh Toán là nhân viên Sale bất động sản. Trung bình thì mỗi tháng anh Toán thực hiện 200 cuộc gọi với 10% cuộc gọi 1 phút, 10% cuộc gọi 5 phút, 30% cuộc gọi 10 phút, 30% cuộc gọi 20 phút, 20% cuộc gọi 30 phút. Hỏi anh Toán nên chọn phương án nào của hãng viễn thông Văn để có lợi nhất?
Bài 6: (1.0 điểm) Thầy Bảo, nhân viên y tế, được trường phân công mua một số hộp khẩu trang để phục vụ cho công tác phòng chống dịch Covid của nhà trường. Thầy dự định mua một số hộp khẩu trang tại nhà thuốc Pharmacity. Khi tham khảo giá trên thì tổng số tiền thầy sẽ trả là 600 nghìn đồng. Tuy nhiên, khi đến mua trực tiếp, Pharmacity có chương trình khuyến mãi mỗi hộp khẩu trang được giảm 2 nghìn đồng nên thầy quyết định mua thêm 2 hộp. Khi đó tổng số tiền phải trả là 672 nghìn đồng. Hỏi thầy Bảo đã mua tất cả bao nhiêu hộp khẩu trang?
Bài 7: (1.0 điểm) Một bồn nước hình trục có bán kính đáy là 3 m, chiều cao là 4 m. Người ta đổ nước vào trong bồn
cao của nước bằng đúng một nửa chiều cao của bồn và tiếp tục đặt vào trong b
c có dạng hình cầu bằng kim loại không thấm nước có bán kính là 50 cm và chìm hoàn toàn trong nước.
a) Hỏi khi đó mực nước trong bồn cao bao nhiêu mét (làm tròn đến chữ số thập phân thức ba)?
b) Sau đó, người ta lại bơm thêm nước vào bồn bằng một vòi có công suất chảy là 3 0,0024 cm cho mỗi giây. Hỏi sau bao nhiêu phút thì bồn đầy nước (làm tròn đến hàng đơn vị)?
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 78 -
OFFICIAL
sao cho chiều
ồn một phao nướ
a) Chứng minh tứ giác ABHE nội tiếp và GD song song BC
b) Gọi N là giao điểm giữa HE và .AC Chứng minh tam giác AHN vuông tại .N
c) Tia phân giác của góc BAC cắt đường tròn O tại .F Gọi M là giao điểm của OF và , BCK là trung điểm của , ABI là giao điểm của KM và HE . Chứng minh rằng ... ABEIAEEM
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79Bài 8: (3.0 điểm) Cho tam giác ABC nhọn ABAC nội tiếp đường tròn O . Kẻ AD là đường kính của
,
của
O
AH vuông góc với BC tại , HBE vuông góc với AD tại E Gọi G là giao điểm
AH với O

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 80HƯỚNG DẪN GIẢI Bài 1: (1.5 điểm) Cho parabol 2 : 2 x Py và đường thẳng :46dyx a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ; b) Tìm tọa độ giao điểm của P và d bằng phép toán. Lời giải a) x 2 1 0 1 2 2 2 x y 2 1 2 0 1 2 2 x 1 2 46yx 2 2 b) Phương trình hoành độ giao điểm của parabol () P và đường thẳng : d 2 2 46 2 8120 22 618 x x xx xy xy Vậy () P và d cắt nhau tại hai điểm 2;2 M và 6;18 N Bài 2: (1.0 điểm) Cho phương trình 2 1 101 2 xx Không giải phương trình hãy tính giá trị của biểu thức sau: 12 12 21 xx Axx xx với 12 , xx là hai nghiệm của phương trình (1). Lời giải Áp dụng định lí Vi-ét ta có: 12 12 2 2 xx xx Khi đó: 2 2 22 1212 1212 121212 211212 2222 22 2 xxxx xxxx Axxxxxx xxxxxx Bài 3: (0.75 điểm) Để tính múi giờ của một địa điểm ta làm như sau: - Ở Đông bán cầu (kí hiệu là Ð): múi giờ = kinh độ Đông: 15 - Ở Tây bán cầu (kí hiệu là T): múi giờ = (360 Kinh độ Tây): 15 (Kết quả làm tròn đến hàng đơn vị)
2 giờ sáng ngày 01/10/2021. Hỏi máy bay cất cánh tại New York ngày nào? Lúc mấy giờ? Lời giải
a) Hà Nội thuộc múi giờ: 105:157 Los Angeles thuộc múi giờ: (360120):1516 Chênh lệch giờ từ Hà Nội đến Los Angeles là; 1679 Giờ của Los Angeles là 19928244 giờ ngày 16/6/2021
b) Thời gian để máy bay đi hết quãng đường là 14250:75019 giờ Vậy để hạ cánh lúc 2 giờ ngày 01/10/2021 thì cất cánh lúc 7 giờ ngày 30/09/2021. Bài 4: (0.75 điểm) Áp suất của nước P (đơn vị: atm ) lên một người thợ lặn ở độ sâu d (tính theo feet) là một hàm số bậc nhất () Pdadb có đồ thị như hình bên a) Tính các

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 81Để tính giờ của một địa điểm, ta tính theo công thức: TGMTH với T là giờ tại nơi đó, GMT là giờ gốc,
được
đổi
sau: Múi
ờ 0 1 2 3 4
2 3 4
11
H
quy
như
gi
5 6 7 8 9 10 11 H 0 1
5 6 7 8 9 10
Múi giờ 13 14 15 16 17 18 19 20 21 22 23 H 12 11 10 9 8 7 6 5 4 3 2 1 a) Lúc 1900 h ở Hà Nội 105Ð ngày 15/6/2021 thì lúc đó ở Los Angeles 120T là mấy giờ? b) Một chiếc máy bay cất cánh ở sân bay tại New York 75 T với vận tốc 750/kmh trên quãng đường chim bay dài 14250 km để hạ cánh xuống sân bay Tân Sơn Nhất của Việt Nam 105Ð đúng
hệ số a và b biết các điểm 0;1 A và 33;2 B thuộc đồ thị hàm số b) Tính áp suất của nước lên người thợ lặn ở độ sâu 100 feet
ết quả làm tròn đến
đơn
t feet
đơn vị đo độ
Lờ
ả
(k
hàng
vị). Biế
là
dài, 10,3048. feetm
i gi
i
tiền cước điện tho
i
m
i
Phương án I: Trả tổng cộng 99 cent cho 20 phút đầu, sau đó từ phút 21 trở đi thì mỗi phút trả 5. cent - Phương án II: Kể từ lúc đầu tiên, mỗi phút trả 10 .cent - Phương án III: Trả 25 cent tiền thuê bao, sau đó kể từ phút đầu tiên mỗi phút trả 8 cent . Anh Toán là nhân viên Sale bất động sản. Trung bình thì mỗi tháng anh Toán thực hiện 200 cuộc gọi với 10% cuộc gọi 1 phút, 10% cuộc gọi 5 phút, 30% cuộc gọi 10 phút, 30% cuộc gọi 20 phút, 20% cuộc gọi 30 phút. Hỏi anh Toán nên chọn phương án nào của hãng viễn thông Văn để có lợi nhất? Lời giải Giả sử người đó có 100 cuộc gọi trong một tháng Theo phương án I, người đó phải trả: 99.1003020.20.510900() cent Theo phương án II, người đó phải trả: 1.105.1010.3020.3030.20.1015600() cent Theo phương án III, người đó phải trả: 25.1001.105.1010.3020.3030.20.814980() cent Như vậy, phương án I cho tiền cước lợi nhất. Bài 6: (1.0
ng số tiền thầy sẽ trả là 600 nghìn đồng. Tuy nhiên, khi đến mua trực tiếp, Pharmacity có chương trình khuyến mãi mỗi hộp khẩu trang được giảm 2 nghìn đồng nên thầy quyết định mua thêm 2 hộp. Khi đó tổng số tiền phải trả là 672 nghìn đồng. Hỏi thầy Bảo đã mua tất cả bao nhiêu hộp khẩu trang? Lời giải Gọi giá tiền mỗi hộp khẩu trang dự định mua là x (nghìn đồng), điều kiện 2. x Giá tiền mỗi hộp khẩu trang thực tế là 2 x (nghìn đồng)
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 82a) Vì 0;1 A và 33;2 B thuộc đồ thị
số
a
b)
V
Bài
ụ
vụ
phòng chống
ị
thuốc Pharmacity.
hàm
nên: 1 .01 33 .332 1 ab
ab b
Phương trình hàm số 1 ()1 33 Pdd
Với 100100.0,304830,48 feetm
ới 30,48 dm
thì áp suất của nước lên người thợ lặn là
1 30,48.30,4812() 33 Patm
5: (1.0 điểm) Hãng viễn thông Văn có ba phương án trả
ạ
cho
ỗ
cuộc gọi: -
điểm) Thầy Bảo, nhân viên y tế, được trường phân công mua một số hộp khẩu trang để ph
c
cho công tác
d
ch Covid của nhà trường. Thầy dự định mua một số hộp khẩu trang tại nhà
Khi tham khảo giá trên thì tổ
c vào trong bồn sao cho chiều cao của nước bằng đúng một nửa chiều cao của bồn và tiếp tục đặt vào trong bồn một phao nước có dạng hình cầu bằng kim loại không thấm nước có bán kính là 50 cm và chìm hoàn toàn trong nước.
a) Hỏi khi đó mực nước trong bồn cao bao nhiêu mét (làm tròn đến chữ số thập phân thức ba)?
b) Sau đó, người ta lại bơm thêm nước vào bồn bằng một vòi có công suất chảy là 3 0,0024 cm cho mỗi giây. Hỏi sau bao nhiêu phút thì bồn đầy nước (làm tròn đến hàng đơn vị)? Lời giải
a) Thể tích nước có sẵn trong bồn: 23 .3.218()Vm Thể tích quả cầu kim loạ
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 83Ta có: 2 600672 2 2 600(2)2(2)672 0 (2) 27612000 50 12 xx xxxx xx xx x x Vậy giá tiền mỗi hộp khẩu trang thực tế là: 50248 nghìn đồng Số hộp khẩu trang đã mua là: 672:4814 hộp Bài 7: (1.0 điểm) Một bồn nước hình trục có bán kính đáy là 3 m, chiều cao là 4 m. Người ta đổ nướ
i 3 3 41 '() 326 Vm Lượng nước có trong bồn khi đó 3 109 '() 6 VVm Chiều cao mực nước là 109 :92,0185() 6 m Mực nước dâng lên được 0,0185() m b) Thời gian đầy bồn nước là 2 .3(42,0185)23343,997630' 0,0024 Th Bài 8: (3.0 điểm) Cho tam giác ABC nhọn ABAC nội tiếp đường tròn O . Kẻ AD là đường kính của O , AH vuông góc với BC tại , HBE vuông góc với AD tại E Gọi G là giao điểm của AH với O . a) Chứng minh tứ giác ABHE nội tiếp và GD song song BC b) Gọi N là giao điểm giữa HE và AC Chứng minh tam giác AHN vuông tại N c) Tia phân giác của góc BAC cắt đường tròn O tại .F Gọi M là giao điểm của OF và , BCK là trung điểm của , ABI là giao điểm của KM và HE . Chứng minh rằng ... ABEIAEEM Lời giải
()90 ()90 AHBCgtAHB BEADgtAEB 090 AHBAEB (hai đỉnh kề của một tứ giác cùng nhìn một cạnh với một góc bằng nhau) Suy ra tứ giác ABHE nội tiếp Ta có: 090 AGD (góc nội tiếp chắn nửa đường tròn () O AGGD (1) Mà ()AGBCgt (2) Từ (1) và (2) suy ra // GDBC b) Vì // BCGD (chứng minh trên) CBDBDG
tương ứng)
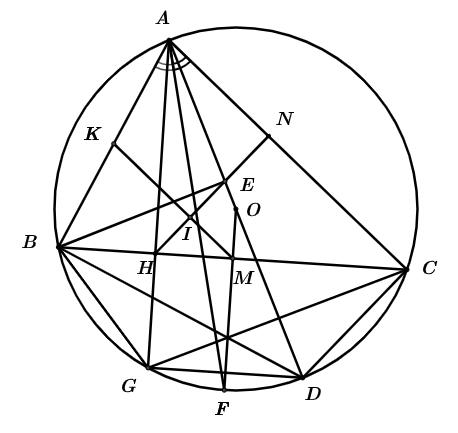
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 84 -
a) Xét tứ giác ABHE có: 0 0 (so le trong) CDBGsdCDsdBG Ta có: 1 2 BAGsdBG (góc nội tiếp) 1 2 CADsdCD (góc nội tiếp) Suy ra: BAGCAD Xét AEN và ABH có: BAGCAD ABHAEN ( ABHE là tứ giác nội tiếp) AENCADgg 090 AHBANE (2 góc
c) Vì AF là tia phân giác của BACBAFCAFBFFCFOBC M là trung điểm BC KM là đường trung bình của tam giác // ABCKMAC (3) Mà HNAC (4)
Từ (3) và (4) suy ra HNKM hay 0 90. EIM
Tứ giác ABHE là tứ giác nội tiếp OEMMEHHBOOBA (5)
khác: 000 9090180 BEOOMB
tứ giác nội tiếp
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 85 -
N
OFFICIAL
HNANAHN
vuông tại
Mặt
BEOM là
OEMOBM (2 góc nội tiếp cùng chắn cung ) OM (6) Từ (5) và (6) suy ra: IEMABO (7) Mặt khác: ABO cân tại OOBAOAB (8) Từ (7) và (8) suy ra IEMOAB Xét ABE và MEI có + 090 AEBEIM (chứng minh trên) + IEMOAB (chứng minh trên) ()ABEEMIgg ABAE ABEIAEEM EMEI (điều phải chứng minh).
QUẬN 6 (ĐỀ 1) (đề thi gồm 02 trang)
NĂM HỌC: 2022 - 2023
MÔN THI: TOÁN
Bài 1: (1,5 điểm) Cho Parabol (P): 2 yx và đường thẳng (d):y3x4
a) Vẽ (d) và (P) trên cùng hệ trục toạ độ.
b) Tìm toạ độ các giao điểm của (P) và (d) bằng phép tính. Bài 2: (1 điểm) Cho phương trình: 4x2 + 3x – 1 = 0 có hai nghiệm x1, x2 Không giải phương trình, tính giá trị biểu thức A = (x1 – 2)(x2 – 2)
Bài 3: (0,75 điểm) Trong kết quả xét nghiệm lượng đường trong máu có bệnh viện tính theo đơn vị là mg/dl nhưng cũng có bệnh viện tính theo đơn vị là mmol/l. Công thức chuyển đổi là 1mmol/l = 18 mg/dl. Hai bạn Châu và Lâm nhịn ăn sáng sau khi thử đường huyết tại nhà có chỉ số đường huyết lần lượt là 110mg/dl và 90mg/dl. Căn cứ vào bảng sau, em hãy cho biết tình trạng sức khỏe của hai bạn Châu và Lâm: Tên xét nghiệm Hạ đường huyết Đường huyết bình thường
Giai đoạn tiền tiểu đường
Chẩn đoán bệnh tiểu đường Đường huyết lúc đói (x mmol/l) x < 4.0 mmol/l 4.0 x 5.6 mmol/l 5.6 < x < 7.0 mmol/l x 7.0 mmol/l
Bài 4: (1 điểm) Minh đến nhà sách mua một quyển tập và một quyển sách thì phải thanh toán số tiền là 25 000 đồng. Nếu Minh mua thêm 1 quyển tập cùng loại nữa thì số tiền phải thanh toán là 30 000 đồng. Biết rằng mối liên hệ giữa số tiền phải thanh toán y (đồng) cho nhà sách và số tập x (quyển) mà Minh mua là một hàm số bậc nhất có dạng y = ax + b (a 0).
a) Xác định các hệ số a và b. b) Minh mang theo khi đến nhà sách là 70 000 đồng thì có thể mua được bao nhiêu quyển tập và giá của quyển tập mà Minh mua là bao nhiêu tiền? Bài 5: (0,75 điểm) Vào cuối học kì I, trường trung học cơ sở A có tỉ lệ học sinh xếp loại học lực trung bình trở lên ở khối 7 là 90% học sinh toàn khối 7 và ở khối 9 là 84% học sinh toàn khối 9. Nếu tính chung cả hai khối thì số học sinh xếp loại học lực trung bình trở lên là 864 em, chiếm tỉ lệ 86,4% số học sinh cả khối 7 và khối 9. Hãy cho biết mỗi khối trên có bao nhiêu học sinh?
Bài 6: (1 điểm) Các viên kẹo mút có dang hình cầu, bán kính 1,6cm. Người ta dùng môt
DẠYKÈMQUYNHƠN
SỞ GIÁO
O TẠO
OFFICIAL
DỤC VÀ ĐẠ
THÀNH PHỐ HỒ CHÍ MINH
ĐỀ THAM
10 THPT
KHẢO TUYỂN SINH
que nhựa hình trụ tròn, bán kính 0,2cm cắm vào đến phân nửa viên kẹo để người dùng dễ sử dụng.
a) Tính thể tích phần ống nhựa hình trụ cắm vào phân nửa viên kẹo. b) Tính thể tích thực của viên kẹo sau khi trừ phần ống nhựa cắm vào.
Bài 7: (1 điểm) Thống kê điểm một bài kiểm tra môn toán của lớp 9A, người ta đã tính được điểm trung bình kiểm tra của lớp là 6,4. Nhưng do sai sót khi nhập liệu, số học sinh đạt điểm 6 và điểm 7 đã bị mất. Dựa vào bảng thống kê dưới đây em hãy tìm lại hai số bị mất đó , biết lớp 9A có 40 học sinh. Điểm 3 4 5 6 7 8 9 10 Số học sinh 1 2 7 6 2 1 Bài 8: (3 điểm) Cho điểm A nằm ngoài đường tròn tâm O. Kẻ hai tiếp tuyến AB và AC (B, C là tiếp điểm) và một cát tuyến AHK (AH < AK) với đường tròn Lấy điểm I thuộc đoạn BC (IB < IC), I không thuôc cát tuyến AHK. Kẻ OM AI tại M.
OFFICIAL
a) Chứng minh: 5 điểm M, O, C, B, A cùng thuộc một đường tròn.
b) Chứng minh: AI.AM = AB2 và tứ giác MIHK nội tiếp đường tròn. c) Kẻ KI cắt đường tròn (O) tại N (khác K) và AN cắt đường tròn (O) ở E. Chứng minh H, I, E thẳng hàng HẾT
DẠYKÈMQUYNHƠN
CÂU ĐÁP ÁN
a) Bảng giá trị
Vẽ (P) và (d)
b) Phương trình hoành độ giao điểm của (P) và (d): – x2 = 3x – 4
Câu 1 : (1,5 điểm)
- x2 – 3x + 4 = 0 [�� =1 �� = 4
Vậy tọa độ giao điểm của (P) và (d) là: (1; -1); (-4; -16)
Ta có: a và c trái dấu nên PT luôn có 2 nghiệm.
Khi đó theo định lý Viet, ta có :{�� =��1 +��2 = 3 4 �� =��1.��2 = 1 4
Câu 2 : (1 điểm)
Ta có : A = (x1 – 2) ( x2 – 2) A = x1.x2 – 2( x1 + x2) + 4 A = P – 2S + 4 A = 1 4 2. 3 4 +4= 21 4
Chỉ số đường huyết của Châu là: 110mg/dl = 1 18 .110= 55 9 ≈6,1 mmol/l Chỉ số đường huyết của Lâm là: 90mg/dl = 1 18 90=5 mmol/l Căn cứ vào bảng đề cho, ta có thể kết luận bạn Lâm đường huy
ĐIỂM
0.5 điểm 0.5 điểm 0.25 điểm 0.25 điểm
0.5 điểm 0.25 điểm 0.25 điểm
ết bình thường, còn bạn Châu thuộc giai đoạn tiền tiểu đường 0.25 điểm 0.25 điểm 0.25 điểm Câu 4 : (0,75
DẠYKÈMQUYNHƠN
OFFICIAL
điể
a) a) Xác định các hệ số a và b. b) a = 5 000; c) b = 20
d) b) Số
ập
ể
với giá
Câu 3 : (0,75 điểm) Tổng
m)
000
t
mua được là 10 quy
n
5 000 đồng/quyển 0.25 điểm 0.25 điểm 0.25 điểm Câu 5 :
số học sinh khối 7 và khối 9 :
(1 điểm)
864 : 86,4% = 1000 (học sinh)
Gọi x là số học sinh khối 7 (x > 0) 1000 x là số học sinh khối 9
Tỉ lệ học sinh xếp loại học lực trung bình trở lên của khối 7
là 90% và của khối 9 là 84%.
Nên ta có phương trình 0,9 x + 0,84(1000 x) = 864 x = 400
Vậy số học sinh khối 7 là 400 em, khối 9 là 600 em.
a) Thể tích phần ống nhựa hình trụ cắm vào viên kẹo: �� = ����2ℎ =�� 0,22 1,6=0,064��(����3)
Câu 6 : (1 điểm)
b) Thể tích hình cầu có bán kính 1,6cm: �� = 4 3 ����3 = 4 3��.1,63 = 4 3��4,096=5,46��(����3) Thể tích thực của viên kẹo: 5,46�� 0,064�� =5,396��(����3)
Gọi x là số học sinh đạt điểm 6 y là số học sinh đạt điểm 7( x; y ∈ N*, x, y < 40)
0.25 điểm
Câu 7 : (1 điểm)
Theo đề bài ta có hê pt: { ��+�� =21 6��+7�� =134 {�� =13 �� =8 Vậy có 13 học sinh đạt 6 điểm, 8 học sinh đạt 7 điểm
0.25 điểm
0.25 điểm 0.25 điểm
0.5 điểm 0.25 điểm 0.25 điểm
0.25 điểm 0.5 điểm 0.25 điểm
DẠYKÈMQUYNHƠN
OFFICIAL
Câu 8 : (3 điểm)
a) Do ABO ̂ =ACO ̂ =AMO ̂ =900 (gt)
Nên 5 điểm A, B, C, O, M cùng thuôc đường tròn đường kính AO
b) Chứng minh: ∆������ đồng dạng ∆AMB (g –g)
=> AI . AM = AB2 Chứng minh: AH . AK = AB2 => AI . AM = AH . AK Chứng minh: ∆AIH đồng dạng ∆AKM ( c – g – c) => ������ ̂ =������ ̂ => Tứ giác IMKH nội tiếp c) Chứng minh: IA . IM = IB . IC = IN. IK Chứng minh: ∆INA đồng dạng ∆IMK ( c – g –c) Tứ giác ANMK nội tiếp Do đó: ������ ̂ =1800 ������ ̂ =1800 ������ ̂ =������ ̂ = ������ ̂ Vậy H; I; K thẳng hàng
0.5 điểm 0.25 điểm 0.25 điểm 0.25 điểm 0.25 điểm 0.25 điểm 0.25 điểm 0.25 điểm 0.25 điểm 0.25 điểm 0.25 điểm
DẠYKÈMQUYNHƠN OFFICIAL
E N
H C B O A K I
M
TRƯỜNG THCS NTT ĐỀ THAM KHẢO THI TUYỂN SINH 10 NĂM HỌC 2022 -2023 MÔN TOÁN – LỚP 9 Thời gian: 120 phút (không kể thời gian phát đề)
Bài 1: (1,5 điểm) Cho Parabol (P): ��= 1 2 ��2 và đường thẳng (d): �� = 2��+2. a. Vẽ (P) và (d) trên cùng một mặt phẳng tọa độ b. Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Bài 2. (1 điểm) Cho phương trình: 2��2 3�� 4=0 có 2 nghiệm là ��1,��2. Không giải phương trình, hãy tính giá trị của biểu thức �� = 1 ��1 2 + 1 ��2 2. Bài 3. (1 điểm) Càng lên cao không khí càng loãng nên áp suất khí quyển càng giảm. Với những độ cao không lớn lắm thì ta có công thức tính áp suất khí quyển tương ứng với độ cao so với mực nước biển như sau: �� =760 2ℎ 25 Trong đó: ��: Áp suất khí quyển (mmHg) ℎ: Độ sao so với mực nước biển (m) Ví dụ các khu vực ở Thành phố Hồ Chí Minh đều có độ cao sát với mực nước biển (ℎ = 0��) nên có áp suất khí quyển là �� =760mmHg.
a) Hỏi Thành phố Đà Lạt ở độ cao 1500m so với mực nước biển thì có áp suất khí quyển là bao nhiêu mmHg?
b) Dựa vào mối liên hệ giữa độ cao so với mực nước biển và áp suất khí quyển người ta chế tạo ra một loại dụng cụ đo áp suất khí quyển gọi là “cao kế”. Một vận động viên leo núi dùng “cao kế” đo được áp suất khí quyển là 540mmHg. Hỏi vận động viên leo núi đang ở độ cao bao nhiêu mét so với mực nước biển?
Bài 4 ( 1 điểm ) Một người mua 3 đôi giày với hình thức khuyến mãi như sau: Nếu bạn mua một đôi giày với mức giá thông thường, bạn sẽ được giá giảm 30% khi mua đôi thứ hai, và mua một đôi thứ ba với một nửa giá ban đầu. Bạn Anh đã trả 1320000 cho 3 đôi giày.
a) Giá ban đầu của một đôi giày là bao nhiêu?
b) Nếu cửa hàng đưa ra hình thức khuyến mãi thứ hai là giảm 20% mỗi đôi giày. Bạn An nên chọn hình thức khuyến mãi nào nếu mua ba đôi giày. Bài 5 ( 1 điểm ): Một lớp học có 40 học sinh, trong đó nam nhiều hơn nữ. Trong giờ ra chơi, cô giáo đưa cả lớp 260000 đồng để mỗi bạn nam mua một ly Coca giá 5000 đồng/ly, mỗi bạn nữ mua một bánh phô mai giá 8000 đồng/cái và được căn – tin thối lại 3000 đồng. Hỏi lớp có bao nhiêu học sinh nam và bao nhiêu học sinh nữ?
DẠYKÈMQUYNHƠNOFFICIAL
Bài 6 ( 0.75 điểm ) Một công ty xăng dầu có hai bể chứa xăng hình cầu có thể tích bằng nhau, bán kính của bể xăng là R=6m, biết rằng bể thứ nhất chỉ còn 50% xăng trong bể, bể thứ hai còn 75%lượng xăng trong bể. Công ty chở xăng đến các cây xăng bằng xe thùng, thùng xe hình trụ dài 5,5m bán kính đáy của thùng xe là r=2m. Hỏi công ty cần phải chở tối thiểu bao nhiêu chuyến xe để hết lượng xăng trong hai bể xăng. Bài 7: (0.75 điểm) Để hòa chung với không khí World Cup, ở một thành phố tổ chức giải bóng đá lứa tuổi THCS bao gồm 32 đội tham gia chia thành 8 bảng. Ở vòng bảng, 2 đội có thứ hạng cao nhất sẽ được đi tiếp vào vòng trong (vòng loại trực tiếp). Thắng được 3 điểm, hòa được 1 điểm, thua 0 điểm. Nếu hai đội cùng điểm sẽ so hiệu số bàn thắng –thua. Ở bảng A, đội Phượng Hoàng của bạn An nằm trong bảng hạt giống sau 2 lượt đấu số hạng như sau :
1. Đội Báo Đen : 4 điểm
2. Đội Thỏ Trắng : 2 điểm
3. Đội Sư Tử : 2 điểm
4. Đội Phượng Hoàng 1 điểm
Ở lượt đấu diễn ra song song 2 trận Báo Đen – Sư Tử và Thỏ Trắng – Phượng Hoàng. Các em hãy tính xác suất vào vòng trong của đội Phượng Hoàng biết rằng đội Phượng Hoàng luôn có hiệu số bàn thắng thấp nhất ? Xác suất = (số khả năng vào vòng trong): (số khả năng xảy ra). 100% Bài 8 ( 3 điểm )Từ điểm A ở ngoài đường tròn (O, R) vẽ hai tiếp tuyến AB và AC và một cát tuyến ADE không đi qua tâm (O) (B, C là các tiếp điểm và AD < AE).
a) Chứng minh tứ giác ABOC nội tiếp được đường tròn, xác định tâm và bán kính của đường tròn đó ?
b) Gọi H là giao điểm của OA và BC. Chứng minh AH.AO = AD .AE = AB2
c) Gọi I là trung điểm của DE. Qua B vẽ dây BK // DE. Chứng minh ba điểm K, I, C thẳng hàng.
DẠYKÈMQUYNHƠNOFFICIAL
DẠYKÈMQUYNHƠNOFFICIAL Đáp án sơ lược: Bài 1: Bảng giá trị 0.25 x 2 Vẽ đồ thị 0.25 x 2 Đúng giá trị x: 0.25 Kết luận đúng tọa độ giao điểm 0.25 Bài 2: Tổng ��1 +��2 = 3 2 0,25 Tích ��1��2 = 2 0,25 �� = (��1+��2)2 2��1��2 (��1��2)2 = (3 2)2 2( 2) ( 2)2 = 25 16 0,25 x 2 Bài 3: Giải. a) Hỏi Thành phố Đà Lạt ở độ cao 1500m so với mực nước biển thì có áp suất khí quyển là bao nhiêu mmHg? �� =760− 21500 25 =640mmHg 0,5đ b) 540=760 2ℎ 25 ⟺ℎ =2750m 0,5đ Bài 4: Gọi x(đồng) giá ban đầu của một đôi giày(x>0) Theo đề bài ta có pt: (100%30%)(100%50%)1320000 0,70,51320000 2,21320000 600000 xxx xxx x x
Vậy giá ban đầu của một đôi giày 600
ng b)tổng số tiền khi mua 3 đôi giày được giảm 20% là 600 000. 3 .(100%-20%)=1440 000 đồng Vậy Bạn An nên chọn hình thức khuyến mãi thứ nhật nếu mua ba đôi giày.(1 320 000 đồng < 1 440 000 đồng) 0.25 điểm Bài 5 : Gọi x là số học sinh nam , y là số học sinh nữ 0.25 điểm x4 Theo đề bài, ta lập hệ phương trình xy40 5x8y257 21 19 x y
0.75 điểm
000 đồ
Vậy có 21 học sinh nam và 19 học sinh nữ
Bài 6: Thể tích của một bể xăng là V= 3 4 288 3 R 3 m 0.25 đ
Số xăng còn lại của hai bể là 3 50%.28875%.288360 m 0.25 đ
Thể tích của thùng xe là 2 1 .22Vrh
Ta có 1
360 16,36 22 V V
Vậy công ty phải chở ít nhất là 17 xe thì sẽ hết lượng xăng trong hai bể 0.25 đ
Bài 7: Số khả năng xảy ra là 9 Số khả năng PH vào là 2 0.25 TH : BĐ thắng ST và TT thua PH : PH vào TH : BĐ hòa ST và TT thua PH : PH vào 0.25 Vậy xác suất để PH được vào vòng trong là 2/9x100%=22,2% 0.25 Câu 8. (1,0 điểm ):
a) Chứng minh tứ giác ABOC nội tiếp được đường tròn, xác định tâm và bán kính của đường tròn đó ? Xét tứ giác ABOC có: góc ABO + góc ACO = 1800 Suy ra tứ giác ABOC nội tiếp đường tròn có tâm là trung điểm OA, bán kính bằng OA :
b) Gọi H là giao điểm của OA và BC. Chứng minh AH.AO = AD .AE = AB2 Chứng minh được hai tam giác ABD và AEB đồng dạng (g-g) Suy ra được AB2 = AD.AE
Chứng minh được OA là đường trung trực của BC Sử dụng hệ thức lượng trong tam giác vuông suy ra AB2 = AH . AO Từ đó suy ra AD. AE = AH.AO
c) Gọi I là trung điểm của DE. Qua B vẽ dây BK // DE. Chứng minh ba điểm K, I, C thẳng hàng. (0,25 x 4)
- Chứng minh được tứ giác BKED là hình thang cân
- Chứng minh được tam giác IBK cân tại I
- Chứng minh được góc IKB = góc CKB
- Suy ra ba điểm K, I, C thẳng hàng.
DẠYKÈMQUYNHƠNOFFICIAL
H
K B
DẠYKÈMQUYNHƠNOFFICIAL
C I D O A E
THAM KHẢO TUYỂN SINH 10 NĂM HỌC 2022 – 2023 MÔN TOÁN Thời gian làm bài: 120 phút (không kể thời gian phát đề)
Bài 1: (1.5 điểm) Cho parabol 2 :2 Pyx và đường thẳng :1dyx . a) Vẽ P và d trên cùng hệ trục tọa độ b) Tìm tọa độ giao điểm của P và d bằng phép tính. Bài 2: (1 điểm) Cho phương trình 2 2760 xx có hai nghiệm 12 , xx . Không giải phương trình, hãy tính giá trị biểu thức 12 2122 xx A xx Bài 3: (0.75 điểm) Quy tắc sau đây cho ta biết CAN, CHI của năm X nào đó. Để xác định CAN, ta tìm số dư r trong phép chia X cho 10 và tra vào bảng 1. Để xác định CHI, ta tìm số dư s trong phép chia X cho 12 và tra vào bảng 2. Ví dụ: năm 2020 có CAN là Canh, có CHI là Tí. Bảng 1 r 0 1 2 3 4 5 6 7 8 9 CAN Canh Tân Nhâm Quý Giáp Ất Bính Đinh Mậu Kỷ Bảng 2 s 0 1 2 3 4 5 6 7 8 9 10 11 CHI Thân Dậu Tuất Hợi Tí Sửu Dần Mẹo Thìn Tỵ Ngọ Mùi a) Em hãy sử dụng quy tắc trên để xác định CAN, CHI của năm 1984? b) Trần Hưng Đạo (còn gọi là Hưng Đạo Đại Vương), tên thật là Trần Quốc Tuấn, là một nhà chính trị, nhà quân sự lỗi lạc của dân tộc Việt Nam. Vào năm Mậu Tí cuối thế kỉ thứ13,ôngđãchỉ huyquân dân tađánh bại cuộcxâmlượccủa quân Nguyên – Mông lần thứ ba. Em hãy xác định chính xác sự kiện trên xảy ra vào năm bao nhiêu?
Bài 4: (0.75 điểm) Cửa hàng A thực hiện chương trình giảm giá cho khách hàng mua sỉ tập vở học sinh loại thùng tập 100 quyển/thùng như sau: Nếu mua 1 thùng thì giảm 5% so với giá niêm yết. Nếu mua 2 thùng thì thùng thứ nhất giảm 5% còn thùng thứ hai được giảm10% so với giá niêm yết. Nếu mua 3 thùng trở lên thì thì ngoài hai thùng đầu được hưởng chương trình giảm giá như trên thì từ thùng thứ ba trở đi mỗi thùng sẽ được giảm 20% so với giá niêm yết. Biết giá niêm yết của mỗi thùng tập loại 100 quyển/thùng là 450 000 đồng.
a) Cô Lan mua 5 thùng tập loại 100 quyển/thùng ở cửa hàng A thì sẽ phải trả bao nhiêu tiền?
b) Cửa hàng B lại có hình thức giảm giá khác cho loại thùng tập nêu trên là: nếu mua từ 3 thùng trở lên thì sẽ giảm 14% cho mỗi thùng. Nếu anh Tùng mua 5 thùng tập thì
DẠYKÈMQUYNHƠN OFFICIAL QUẬN 8 - ĐỀ SỐ 1 ĐỀ
nên mua ở cửa hàng nào để số tiền phải trả là ít hơn? Biết giá niêm yết ở hai cửa hàng là bằng nhau.
Bài 5: (1 điểm) Một tiệm bánh có chương trình giảm 5% trên tổng hóa đơn khi mua hàng chỉ trong ngày 09/01/2021, bạn My mua 5 hộp bánh bông lan cùng loại trong ngày 09/01/2021, số tiền bạn phải trả là 375 250 đồng. Ngày 12/01/2021, bạn Uyên mua 6 hộp bánh bông lan cùng loại với bạn My đã mua thì trả số tiền là 470 000 đồng. Biết số tiền phải trả (khi chưa có chương trình khuyến mãi) và số hộp bánh bông lan liên hệ bằng công thức: yaxb , y (đồng) là số tiền phải trả và x là số hộp bánh bông lan cùng loại. a) Viết hàm số biểu diễn y theo x b) Hỏi vào ngày 12/01/2021, bạn Nhân mua bao nhiêu hộp bánh bông lan cùng loại với bạn My? Biết số tiền Nhân trả là 320 000 đồng.
OFFICIAL
Bài 6: (1 diểm) Một cái cốc hình hộp cao 10cm có đáy là hình vuông cạnh 6 cm đang chứa một lượng nước cao 4cm. Người ta thả vào 5 viên bi thủy tinh có dạng hình cầu với đường kính 4cm. Biết cả 5 viên bi chìm hoàn toàn.
a) Hỏi mực nước trong cốc dâng cao bao nhiêu cm? (Làm tròn đến chữ số thập phân thứ nhất. Biết thể tích của hình cầu được tính theo công thức 3 4 3 VR với R là bán kính hình cầu. b) Hỏi cần thả thêm ít nhất bao nhiêu viên bi cùng loại như trên thì nước trong cốc tràn ra ngoài?
Bài 7: (1 điểm) Hai trường THCS A và B của một thị trấn có 210 học sinh thi đậu vào lớp 10 THPT, đạt tỉ lệ trúng tuyển 84%. Tính riêng thì trường A đậu 80% và trường B đậu 90%. Hỏi mỗi trường có bao nhiêu học sinh thi đậu vào lớp 10?
Bài 8: (3 điểm) Cho đường tròn ; OR , điểm A nằm ngoài đường tròn với 2 OAR
DẠYKÈMQUYNHƠN
giao điểm của BC và OA. a) Chứng minh: tứ giác AOBC nội tiếp và KB = KC. b) Vẽ BH vuông góc dây cung CD ( H thuộc CD), gọi I là trung điểm của BH; DI cắt đường tròn O tại điểm thứ hai là N, AN cắt đường tròn O tại điểm thứ hai là M. Chứng minh: 2 .3 AMANR và AKNONM . c) Chứng minh: AO là tiếp tuyến của đường tròn ngoại tiếp tam giác ABN HẾT.
, vẽ hai tiếp tuyến , ABAC với đường tròn (B, C là các tiếp điểm), D thuộc cung lớn BC, BDDC ( ,, DOC không thẳng hàng), K là
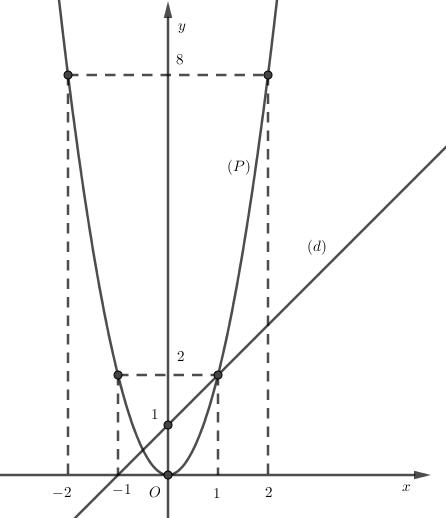
DẠYKÈMQUYNHƠN OFFICIAL Đáp án Thang điểm Bài 1: a) Vẽ P và d trên cùng hệ trục tọa độ Bảng giá trị: x 0 1 1 yx 1 2 x 2 1 0 1 2 2 2 yx 8 2 0 2 8 Vẽ đồ thị: b) Tìm tọa độ giao điểm của P và d bằng phép tính. Phương trình hoành độ giao điểm của d và P là: 0.25 0.25 0.25
DẠYKÈMQUYNHƠN OFFICIAL 2 21 xx 2 210 xx 1() 11 22 xL xy Vậy tọa độ giao điểm là (1; 2) và 11 ; 22 . 0,25 0.25 0.25 Bài 2: 2 2760 xx Áp dụng định lý Vi-et, ta có: 12 7 2 b Sxx a và 12.3 c Pxx a . Ta có: 12 2122 xx A xx 1122 21 22 22 xxxx xx 2 22 42 SSP SP 15 8 0.25 0.25 0.25 0.25 Bài 3: a) Vì 1984 chia 10 dư 4 nên CAN là Giáp Vì 1984 chia 12 dư 4 nên CHI là Tí b) Vì CAN của năm Mậu Tí là Mậu nên suy ra chữ số tận cùng của năm đó là chữ số 8. Mặt khác do năm đó xảy ra vào cuối thế kỉ 13 nên năm đó sẽ có dạng là 128 c ( c là các chữ số 5,6,7,8 hoặc 9) Vì CHI của năm Mậu Tí là Tí nên 12412 c . Do đó năm cần tìm là 1288 0.25 0.25 0.25
0.5 0.25 Bài 5: a) Bạn My mua 5 hộp bánh bông lan cùng loại trong ngày 09/01/2021, khi đó có chương trình khuyến mãi 5% hóa đơn, số tiền bạn phải trả là 375 250 đồng nên ta có: 37525095%5ab Ngày 12/01/2021, bạn Uyên mua 6 hộp bánh bông lan cùng loại với bạn Uyên thì trả số tiền là 470 000 đồng nên ta có: 4700006ab Ta có hệ phương 0.25 0.25 0.25 0.25 Bài 6: a) Thể tích nước khi cho 5 viên bi vào cốc là: 3 23 44160 4.65..144() 323 cm Chiều cao mực nước trong cốc là: 2
160 144 38,7() 6 cm
b) Thể tích còn lại của cốc là: 23 6.108,746,8() cm Ta có : 3 46,8 1,4 44 32 Vậy cần thả thêm ít nhất 2 viên bi cùng loại như trên thì nước trong cốc tràn ra ngoài
0.25 0.25 0.25 0.25 Bài 7: Gọi , xy lần lượt là số học sinh thi đậu vào lớp 10 của trường A và B. Theo giả thiết ta có: 210 xy . Vì số học sinh đậu đạt 84% nên tổng số học sinh của hai trường là 210:(84%)250 (học sinh). 0.25 0.25
DẠYKÈMQUYNHƠN OFFICIAL
Bài 4: a)Số tiền cô Lan cần trả khi mua 5 thùng tập ở cửa hàng A là: 95%90%3.80%.4500001912500(đồng) b) Số tiền cô Lan cần trả khi mua 5 thùng tập ở cửa hàng B là: 5.86%.4500001935000 Vậy cô Lan nên mua bên cửa hàng A trình: 4,750,9537525075000 647000020000 aba abb Vậy: 7500020000yx b) Nhân mua 4 hộp
DẠYKÈMQUYNHƠN OFFICIAL
Bài 8: \ a) Xét tứ giác OBAC , ta có: 90o OBA ( AB là tiếp tuyến tại B của đường tròn O ) 90o OCA ( AC là tiếp tuyến tại C của đường tròn O ) Vậy 0180 OBAOCA Do đó, tứ giác OBAC nội tiếp. Cm: OA là trung trực của BC Suy ra: KB = KC b) Xét tam giác OAB vuông tại B ( AB là tiếp tuyến tại B của O ) 222 2 22 222 22 2 4 3 OAOBAB RRAB RRAB ABR (1) Xét ABN và AMB , ta có: BAM : chung 0.25X2 0.25X2 0.25 K M N I H C O A B D
Tính riêng trường A đậu 80% nên tổng số hs trường A là :80% 0,8 x x . Tương tự, tổng số học sinh trường B là 0,9 y . Suy ra: 250 0,80,9 xy Từ đó ta có hệ: 210 120 25090 0,80,9 xy x xy y . Vậy trường A thi đậu 120 người và tổng số học sinh là 150 Trường B thi đậu 90 người và tổng số học sinh là 100. 0.25 0.25
ABNAMB (góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn cung BN )
Suy ra: ABNAMB (g-g)
Suy ra: 2 ABAN ABAMAN AMAB (2)
Từ (1) và (2), suy ra: 2 .3 AMAMR (đpcm) Cm: AKNAMO
Cm: OMNONM
Suy ra: AKNONM c) (tinhchat2tieptuyencatnhautaiA) OBOCR ABAC
Suy ra: OA là đường trung trực của BC K là trung điểm của BC Mà I là trung điểm của BH (gt) Nên IK là đường trung bình của tam giác BHC
Suy ra: // // IKHC IKHB
Vì // IKHC nên NIKNDC (hai góc đồng vị)
Mà NDCNBC (hai góc nội tiếp cùng chắn cung NC )
Nên NIKNBC . Xét tứ giác IBNK có: NIKNBC (cmt)
Suy ra, tứ giác IBNK nội tiếp ( tứ giác có hai đỉnh , IB liên tiếp cùng nhìn KN dưới góc bằng nhau)
Trong tứ giác IBNK nội tiếp có 90o BIK , suy ra 90o BNK
Ta có: NKANBC (do cùng phụ BKN )
Mà NCANBC (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung NC ).
Vậy NCANKA
Xét tứ giác KNAC có: NCANKA (cmt)
Vậy tứ giác KNAC nội tiếp ( tứ giác có hai đỉnh , KC liên tiếp cùng nhìn NA dưới góc bằng nhau)
Ta có NAONCK (hai góc nội tiếp cùng chắn cung NK trong tứ giác NAKC nội tiếp)
Mà ABNNCK (góc nội tiếp-góc tạo bởi tia tiếp tuyến và dây cùng chắn cung BN )
Nên ABNNAO
Vậy AO là tiếp tuyến của đường tròn ngoại tiếp tam giác ABN .
0.25 0.25 0.25 0.25 0.25 0.25 0.25
DẠYKÈMQUYNHƠN
OFFICIAL
3:
điểm) Cô Phượng mua 200 cái áo với giá mua 1 áo là 120 000 đồng. Cô bán 70 cái áo, mỗi áo so với giá mua lãi được 15%. Với 40 cái áo kế tiếp, cô bán giá 1 cái áo bằng giá vốn. Còn 90 cái áo còn lại, mỗi áo phải báo lỗ với giá vốn 10%. Hỏi sau việc mua và bán 200 cái áo, cô Phượng lãi hay lỗ bao nhiêu tiền?
Bài 4: (0.75 điểm) Bạn Thắng tính xếp một tháp domino 10 tầng với thứ tự tầng một có 1 quân domino, tầng hai có 2 quân domino và cứ thế cho đến tầng thứ mười. Nếu một bộ cờ domino có tất cả 28 quân cờ, hỏi bạn Thắng cần ít nhất bao nhiêu bộ domino để có thể hoàn thành tòa tháp nêu trên.

Bài 5: (1.0 điểm) Thực hiện chương trình khuyến mãi tháng mua sắm lộc vàng, một siêu thị trong thành phố đã giảm giá cho một lô hàng quần kaki gồm 50 cái với giá bán lẻ lúc đầu 320 000 đồng/cái quần, một số phần trăm. Sau khi bán 50% lô quần kaki trong hai tuần đầu của tháng, cửa hàng quyết định giảm thêm một số phần trăm như vậy cho số quần kaki còn lại, và bây giờ giá quần kaki có giá 180 000 đồng/cái. Do đó trong hai tuần còn lại của tháng, cửa hàng đã bán hết lô hàng quần kaki. Hỏi:
a) Mỗi một lần chiếc quần kaki đã được siêu thị giảm giá bao nhiêu phần trăm trong tháng khuyến mãi b) Tính số tiền siêu thị thu được khi bán hết lô hàng quần kaki.
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GD & ĐT QUẬN 10 NĂM
ĐỀ
Đề
MÃ ĐỀ
1 Thời
P : 2 1 2 yx
ẳ
. a) Vẽ đồ thị P và d trên
hệ trục tọa độ b) Tìm tọa độ giao điểm của P và d
ằ
Bài 2: (1.0 điểm) Cho phương trình 2 2370 xx có
ệ
22 1212 Axxxx
HỌC 2022-2023
THAM KHẢO MÔN : TOÁN 9
thi gồm 8 câu hỏi tự luận
: Quận 10 –
gian: 120 phút (không kể thời gian phát đề) Bài 1: (1.5 điểm) Cho parabol
và đường th
ng
:4 dyx
cùng
b
ng phép toán.
nghi
m là 12;.xx Không giải phương trình: Tính
Bài
(0.75
Bài 6: (0.75 điểm) Một viên gạch hình vuông 4040 cmcm được trang trí họa tiết như hình trên, tính diện tích phần tô màu? (kết quả làm tròn đến hàng đơn vị)
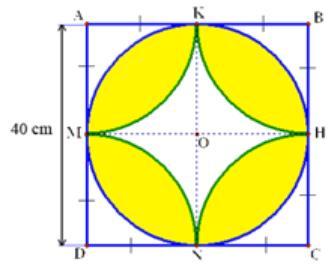
Bài 7: (0.75 điểm) Một cổng trường được thiết kế theo hình dạng Parapol 2 yx , khoảng cách giữa hai chân cổng là 4m . Hỏi một chiếc xe tải có chiều rộng 2,4m và chiều cao là 2,5mcó thể đi qua cổng được không? Bài 8: (3.0 điểm) Cho điểm A nằm ngoài đường tròn O . Qua A kẻ tiếp tuyến AB ( B
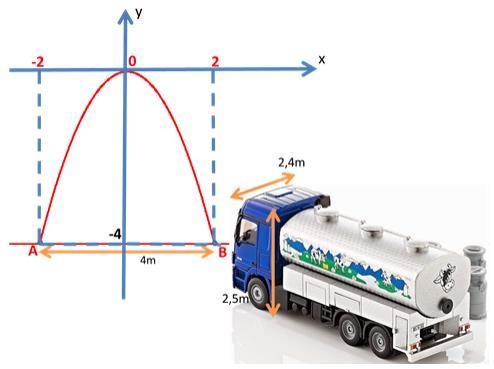
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN
OFFICIAL
là tiếp điểm) và cát tuyến ACD(C nằm giữa , AD) với đường tròn O sao cho C và B nằm khác phía với OA. Gọi H là trung điểm của CD a) Chứng minh rằng: Bốn điểm ,,, ABOH thuộc một đường tròn. b) Gọi E là giao điểm của tia
và O ( , EB
trung trực
c) Chứng
rằng:
HO
cùng thuộc nửa mặt phẳng bờ chứa cát tuyến ACD). Đường
của BC cắt CE tại S . Chứng minh rằng: 2
BOEBCE . Suy ra tứ giác BEOS nội tiếp.
minh
AS là tia phân giác của BAC và // ASBE .
SOFC nội tiếp. HẾT
NHÓM WORD HÓA ĐỀ TOÁN d) Qua D kẻ
song với BE cắt đường tròn O tại F . Chứng
rằng: Tứ giác
DẠYKÈMQUYNHƠN OFFICIAL
đường thẳng song
minh

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN HƯỚNG DẪN GIẢI
Bài 1: (1.5 điểm) Cho parabol P : 2 1 2 yx và đường thẳng :4 dyx . a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. b) Tìm tọa độ giao điểm của P và d bằng phép toán. Lời giải a) Hàm số: 2 1 2 yx Bảng giá trị tương ứng của x và y : x 4 2 0 2 4 2 1 2 yx 8 2 0 2 8
Đồ thị hàm số là một Parabol đi qua các điểm
4;8 ;
2;2 ;
0;0 ;
2;2 ; 4;8
Hàm số: 4 yx Bảng giá trị tương ứng của x và y : x 0 1 4 yx 4 5 Đồ thị hàm số là đường thẳng đi qua 0;4 và 1;5
Vẽ:

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN b) Hoành độ giao điểm của P và d là nghiệm của phương trình: 2 1 4 2 xx 2 28 xx 2 280 xx 2 11.890 Phương trình có hai nghiệm phân biệt: 1 2 x ; 2 4 x + Với 1 2 x 1 2 y + Với 2 4 x 2 8 y Vậy d cắt P tại hai điểm phân biệt là 2;2 và 4;8 Bài 2: (1.0 điểm) Cho phương trình 2 2370 xx có nghiệm là 12;.xx Không giải phương trình: Tính 22 1212 Axxxx . Lời giải a) Phương trình đã cho có hai nghiệm 1x ; 2x Theo định lý Vi-et, ta có : 12 12 3 2 7 2 b xx a c xx a Do đó: 22 1212 Axxxx 2 121212 2 2 373 2 222 31 4 xxxxxx Bài 3: (0.75 điểm) Cô Phượng mua 200 cái áo với giá mua 1 áo là 120 000 đồng. Cô bán 70 cái áo, mỗi áo so với giá mua lãi được 15%. Với 40 cái áo kế tiếp, cô bán giá 1 cái áo bằng giá vốn. Còn 90 cái áo còn lại, mỗi áo phải báo lỗ với giá vốn 10%. Hỏi sau việc mua và bán 200 cái áo, cô Phượng lãi hay lỗ bao nhiêu tiền? Lời giải Số tiền cô Phượng mua 200 cái áo: 200.12000024000000 (đồng) Số tiền cô Phượng bán 200 cái áo: 70.120000.115%40.12000090.120000.110%24180000 (đồng) Số tiền cô Phượng lãi sau khi bán 200 cái áo: 2418000024000000180000 (đồng) Câu 4: (0,75 điểm). Bạn Thắng tính xếp một tháp domino 10 tầng với thứ tự tầng một có 1 quân domino, tầng hai có 2 quân
WORD
domino và cứ thế cho đến tầng thứ mười. Nếu một bộ cờ domino có tất cả 28 quân cờ, hỏi b
Thắng cần ít nhất bao nhiêu bộ domino để có thể hoàn thành tòa tháp nêu trên. Lời giải Số quân domino cần để xếp tháp domino: 1234567891055 (quân) Số bộ cờ domino cần: 55 55:28 28 (bộ) Vậy bạn Thắng cần ít nhất 2 bộ cờ domino (vì 55 2 28 ) Câu 5: (1,0 điểm). Thực hiện chương trình khuyến mãi tháng mua sắm lộc vàng, một siêu thị trong thành phố đã giảm giá cho một lô hàng quần kaki gồm 50 cái với giá bán lẻ lúc đầu 320 000 đồng/cái quần, một số phần trăm. Sau khi bán 50% lô quần kaki trong hai tuần đầu của tháng, cửa hàng quyết định giảm thêm một số phần trăm như vậy cho số quần kaki còn lại, và bây giờ giá quần kaki có giá 180 000 đồng/cái. Do đó trong hai tuần còn lại của tháng, cửa hàng đã bán hết lô hàng quần kaki. Hỏi:
a) Mỗi một lần chiếc quần kaki đã được siêu thị giảm giá bao nhiêu phần trăm trong tháng khuyến mãi. b) Tính số tiền siêu thị thu được khi bán hết lô hàng quần kaki Lời giải a) Gọi x là số phần trăm cửa hàng giảm giá mỗi đợt. 01 x
Giá của một cái quần sau khi giảm giá lần 1: 320000.1 x (đồng)
Giá của một cái quần sau khi giảm giá lần 2: 2 320000.1 x (đồng) Theo đề bài, ta có:
DẠYKÈMQUYNHƠN
NHÓM
n
OFFICIAL
HÓA ĐỀ TOÁN
ạ
2 2 320000.1180000 10,5625 10,75 0,25 10,75 10,75 1,75 x x x xN x x xL Vậy số phần trăm cửa hàng giảm giá mỗi đợt là 25%. b) 50% lô quần kaki: 50%.5025 (cái quần) Số tiền siêu thị thu được khi bán hết lô quần kaki: 25.320000.125%25.18000010500000 (đồng)
Câu 6: (0,75 điểm). Một viên gạch hình vuông 4040 cmcm được trang trí họa tiết như hình trên, tính diện tích phần tô màu? (kết quả làm tròn đến hàng đơn vị) Lời giải Bán kính hình tròn: 40:220 cm Diện tích 1 4 hình tròn: 2 2 .20 100 4 cm Diện tích OKH : 2 2 20 200 2 cm Diện tích phần tô màu: 2 100200.2.4913 cm Câu 7: (0,75 điểm). Một cổng trường được thiết kế theo hình dạng Parapol 2 yx , khoảng cách giữa hai chân cổng là 4


DẠYKÈMQUYNHƠN
OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN
m . Hỏi một chiếc xe tải có chiều rộng 2,4m và chiều cao là 2,5mcó thể đi qua cổng được không? Lời giải Ta có đồ thị hàm số của cổng trường như hình vẽ. Khi đó cổng trường có chiều cao 4 hm Chiều rộng của xe tải là: 2,4m (hay 2,4 CDm) 2,4:21,2 Dx và 1,2 Cx (do tính chất đối xứng của parabol) 2 1,21,44 DCyy (hay độ dài 1,44 OHm) Chiều cao tối đa của xe tải có thể đi qua cổng HK là: 41,442,56 m Vậy xe tải có thể đi qua cổng trường 2,52,56 mm
Câu 8: (3,0 điểm). Cho điểm A nằm ngoài đường tròn O . Qua A kẻ tiếp tuyến AB ( B là tiếp điểm) và cát tuyến ACD(C nằm giữa , AD) với đường tròn O sao cho C và B nằm khác phía với OA. Gọi H là trung điểm của CD
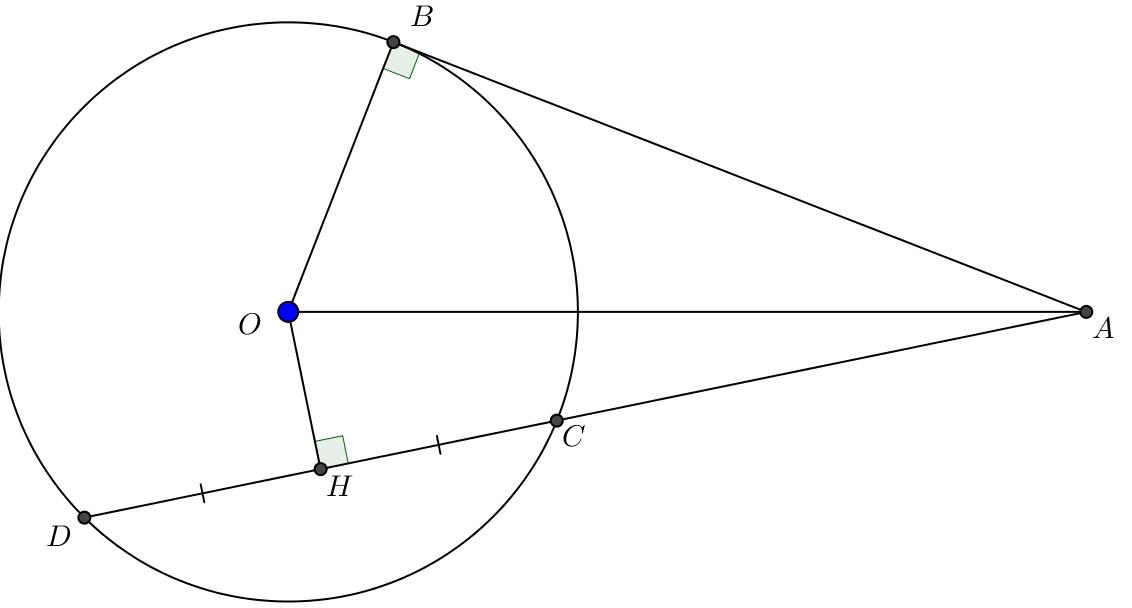
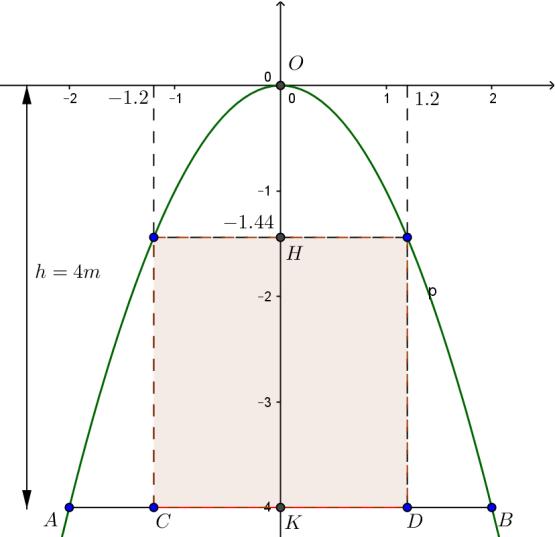
a) Chứng minh rằng: Bốn điểm ,,, ABOH thuộc một đường tròn.
b) Gọi E là giao điểm của tia HO và O ( , EB cùng thuộc nửa mặt phẳng bờ chứa cát tuyến ACD).
Đường trung trực của BC cắt CE tại S . Chứng minh rằng: 2 BOEBCE . Suy ra tứ giác BEOS nội tiếp.
c) Chứng minh rằng: AS là tia phân giác của BAC và // ASBE .
d) Qua D kẻ đường thẳng song song với BE cắt đường tròn O tại F . Chứng minh rằng: Tứ giác SOFC nội tiếp. Lời giải
a) Chứng minh rằng: Bốn điểm ,,, ABOH thuộc một đường tròn. Xét O có: H là trung điểm CD
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN
OFFICIAL
OH là một phần của đường kính OHCD (liên hệ đường kinh và dây cung) Xét tứ giác ABOH có: 000 9090180ABOAHO ( AB là tiếp tuyến O và OHCD). Tứ giác ABOH nội tiếp (tổng 2 góc đối bằng 0180 )
,,, ABOH thuộc một đường tròn.(đpcm) b) Gọi E là giao điểm của tia HO và O ( , EB cùng thuộc nửa mặt phẳng bờ
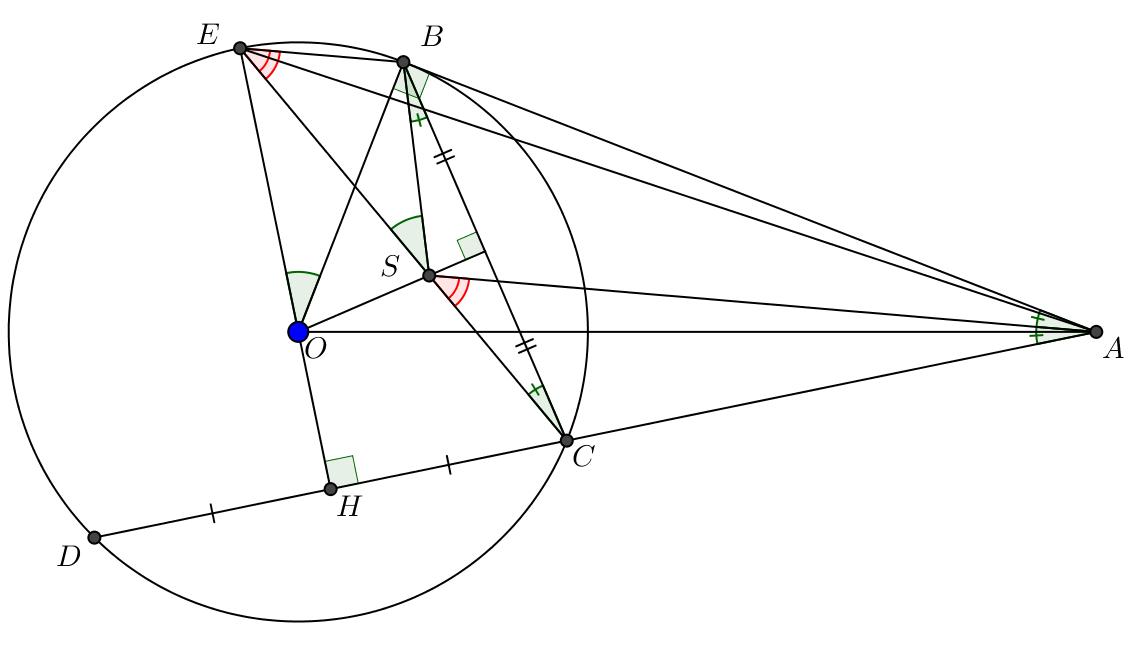
DẠYKÈMQUYNHƠN
OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN
chứa cát tuyến ACD). Đường trung trực của BC cắt CE tại S . Chứng minh rằng: 2 BOEBCE . Suy ra tứ giác BEOS nội tiếp Xét O có: BOE sđ BE (góc ở tâm chắn cung BE ) BCE 1 2 sđ BE (góc nội tiếp chắn cung BE ). 2 BOEBCE (đpcm) Đường trung trực của dây cung BC đi qua S SBC cân tại S BCSCBS Ta có: BSEBCSCBS (góc ngoài của SBC ) 2. BCE BOE Xét tứ giác BEOS có: BSEBOEcmt Tứ giác BEOS nội tiếp (Tứ giác có 2 đỉnh liên tiếp cùng nhìn một cạnh bằng nhau).(đpcm)
c) Chứng minh rằng: AS là tia phân giác của BAC và // ASBE Ta có: BOEBAH (tứ giác ABOH nội tiếp)
BSEBAC (vì BSEBOEcmt ) Xét tứ giác ABSC có BSEBAC
Tứ giác ABSC nội tiếp (góc ngoài bằng góc đối trong)
BASBCS (góc nội tiếp chắn cung BS ).
BACcmt
AS là tia phân giác góc BAC (đpcm) Ta có:
BEC 1 2 sđ BC (góc nội tiếp chắn cung BC )
ABC 1 2 sđ BC (góc tạo bởi tiếp tuyến và dây cung BC ).
BECABC
ASC (góc nội tiếp chắn cung SC ) //
ASBE (hai góc đồng vị bằng nhau).(đpcm) d) Qua D kẻ đường thẳng song song với BE cắt đường tròn O tại F . Chứng minh rằng: Tứ giác SOFC nội tiếp.
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN
1 2
BSEcmt
1 2
SACFDC (sole trong bằng nhau)
FBC (cùng chắn cung CF )
SACSBC ( AS là tia phân giác của BAC )
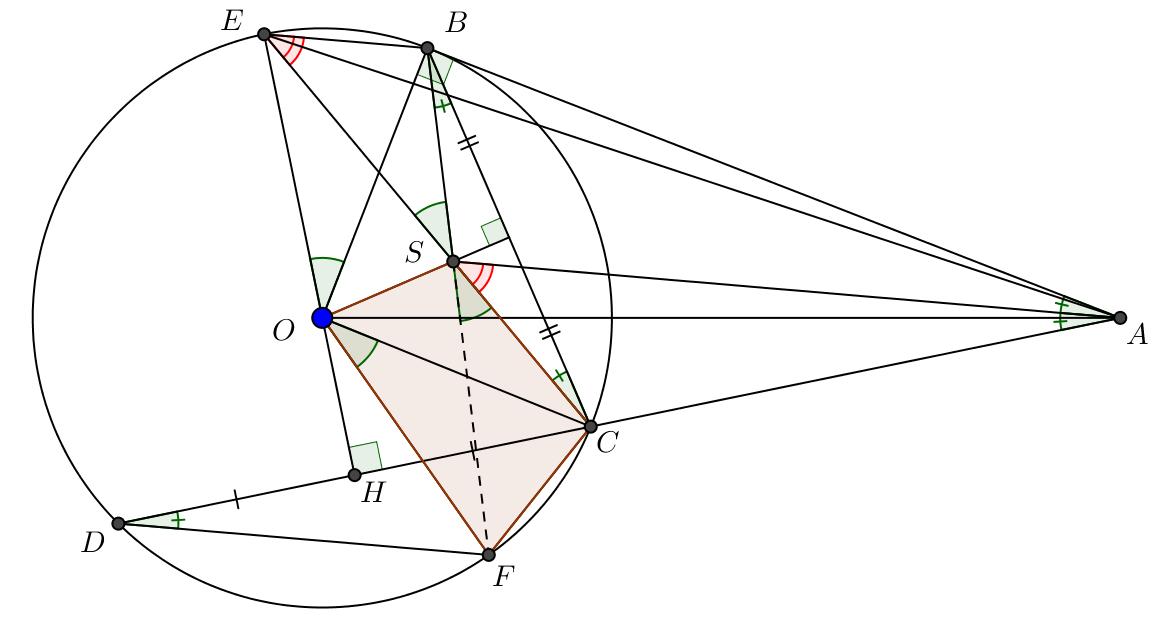
Ba điểm ,, BSF thẳng hàng. Ta có:
FSCBSE (đối đỉnh).
(góc ở tâm chắn cung CF ; góc nội tiếp chắn cung CF ).
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN
2
2
Ta có: // // //
ASBE ASDF DFBE (từ vuông góc đến song song). Ta lại có :
Mà:
FBCSBC
BCEcmt
FBCcmt
FOC
Xét tứ giác SOFC có: FSCFOC
Tứ giác SOFC nội tiếp (tứ giác có 2 đỉnh liên tiếp cùng nhìn một cạnh bằng nhau)
ĐỀ THAM KHẢO TUYỂN SINH 10 NĂM HỌC 2022- 2023
Bài 1: Trong mặt phẳng tọa độ Oxycho Parabol (P): 2 yx và đường thẳng (d): y = 2x + 3 a) Vẽ (P) và (d) trên cùng một hệ trục tọa độ. b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Bài 2: Cho phương trình 2 x–3x m 0 (1) (m là tham số). Tìm m để phương trình (1) có hai nghiệm x1, x2 thoả mãn mãn 1212 2x2x3xx7
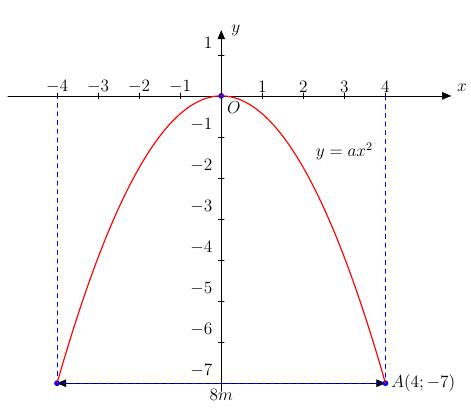
Bài 3: Diện tích của một tam giác có thể được tính theo công thức
với a,b,c là số đo ba cạnh; p là nửa chu vi của tam giác. Cho một tam giác có số đo ba cạnh là: a7, b13, c12. Hãy tính diện tích của tam giác theo công thức trên.
Bài 4: Một quyển tập giá 12.000 đồng, một hộp bút giá 30.000 đồng. Bạn An cần mua một số quyển tập và một hộp bút.
a) Gọi x là số quyển tập An mua và y là số tiền phải trả (bao gồm tiền mua tập và một hộp bút). Viết công thức biểu diễn y theo x. b) Nếu bạn An có 400.000 đồng để mua tập và một hộp bút thì tối đa bạn An mua được bao nhiêu quyển tập?
Bài 5: Trường tiểu học Lushan do kiến trúc sư Zaha Hadid thiết kế là nơi học tập của 120 học sinh. Các khu nhà được thiết kế với mái vòm hình parabol theo công thức (P): y = ax2 và được định hướng để cung cấp điều kiện ánh sáng tối ưu nhất.
Biết rằng cổng có độ cao 7m và chiều rộng 8m. Hãy xác định phương trình của parabol (P).

DẠYKÈMQUYNHƠN OFFICIAL UỶ BAN NHÂN DÂN QUẬN 11 TRƯỜNG THCS LÊ QUÝ ĐÔN QUẬN 11
Sppapbpc
Bài 6: Một vật sáng AB cao 6 cm đặt vuông góc với trục chính x’x của một thấu kính hội tụ và cách thấu kính 15cm. Thấu kính có tiêu cự OF = OF’= 10cm . Xác định chiều cao và vị trí của ảnh A’B’.
Bài 7: Thùng của một xe tải có dạng của một hình lăng trụ đứng (như hình vẽ) Các kích thước được cho trên hình
a) Tính thể tích của thùng chứa. b)Nếu 1m3 cát nặng 1,6 tấn và xe chở đến 3 4 tải trọng thì khối lượng của cát lúc đó là bao nhiêu kg?
Bài 8: Cho đường tròn (O; R). Từ điểm A bên ngoài đường tròn, kẻ các tiếp tuyến AB, AC (B,C là tiếp điểm của (O) và cát tuyến ADE không qua tâm (D nằm giữa A và E, AE cắt đoạn thẳng OB). Gọi I là trung điểm của ED.
a) Chứng minh 5 điểm A, B, I, O, C cùng thuộc 1 đường tròn b) BC cắt AE tại K. Chứng minh AB2 = AK.AI
c) Từ D vẽ DJ // AB ( J thuộc BC). Chứng minh IJ //EB HẾT
DẠYKÈMQUYNHƠN
OFFICIAL
6cm B' O x' x B A I F F' A'
Bài 1: Trong mặt phẳng tọa độ Oxycho Parabol (P): 2 yx và đường thẳng (d): y = 2x + 3.

a) Vẽ (P) và (d) trên cùng một hệ trục tọa độ. b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Giải
Bảng giá trị của (P) x 2 1 0 1 2 2 yx 4 1 0 1 4
DẠYKÈMQUYNHƠN OFFICIAL HƯỚNG
DẪN
Bảng giá trị của (d) x –1 0 y2x3 1 3
Phương trình hoành độ giao điểm của D và P : 2 x2x3 2 x2x30 x3hayx1 2 x3y39 2 x1y11 Vậy toạ độ giao điểm của D và P là: 3;9 và 1;1
tam giác. Cho một tam giác có số đo ba cạnh là: a7,
b13,
c12.
Hãy tính diện tích của tam giác theo công thức trên. Giải Nửa chu vi của tam giác : p = abc71312 16 22
Diện tích của tam giác:
(đơn vị độ dài)
Bài 4: Một quyển tập giá 12.000 đồng, một hộp bút giá 30.000 đồng. Bạn An cần mua một số quyển tập và một hộp bút.
a) Gọi x là số quyển tập An mua và y là số tiền phải trả (bao gồm tiền mua tập và một hộp bút). Viết công thức biểu diễn y theo x. b)Nếu bạn An có 400.000 đồng để mua tập và một hộp bút thì tối đa bạn An mua được bao nhiêu quyển tập?
Giải
a) Công thức biểu diễn y theo x: y = 12 000x + 30 000
b) Thay y = 400 000 vào công thức trên ta được : 400 000 = 12 000x + 30 000
x = 30,8(3)
Vậy An mua được tối đa 30 quyển tập
DẠYKÈMQUYNHƠN OFFICIAL Bài 2: Cho phương trình 2 x–3x m 0 (1) (m là tham số). Tìm m để phương trình (1) có hai nghiệm x1, x2 thoả mãn mãn 1212 2237 xxxx Giải 2 34.1.m94m Để phương trình (1) có 2 nghiệm x1, x2 9 094m0m 4 Theo hệ thức Viet ta có : 12 Sxx3 12 Px.xm Theo để bài ta có : 1212 2x2x3xx7 2S3P7 1 2.33.m7m 3 (nhận so với điều kiện 9 m 4 ) Vậy 1 m 3 thì phương trình (1) có hai nghiệm x1, x2 thoả mãn mãn 1212 2237 xxxx Bài 3: Diện tích của một tam giác có thể được tính theo công thức Sppapbpc với a,b,c là số đo ba cạnh;
nửa chu
p là
vi của
Sppapbpc
1616716131612 243
Bài 5: Trường tiểu học Lushan do kiến trúc sư Zaha Hadid thiết kế là nơi học tập của 120 học sinh. Các khu nhà được thiết kế với mái vòm hình parabol theo công thức (P): y = ax2 và được định hướng để cung cấp điều kiện ánh sáng tối ưu nhất. Biết rằng cổng có độ cao 7m và chiều rộng 8m. Hãy xác định phương trình của parabol (P). Giải Vì điểm A(4 ; –7) thuộc (P): y = ax2

Vậy phương trình của parabol (P): 2 7 yx 16 Bài 6: Một vật sáng AB cao 6 cm đặt vuông góc với trục chính x’x của một thấu kính hội tụ và cách thấu kính 15cm. Thấu kính có tiêu cự OF = OF’= 10cm . Xác định chiều cao và vị trí của ảnh A’B’.

DẠYKÈMQUYNHƠN
OFFICIAL
Xét OAB,A'B'//AB A'B'OA' ABOA (hệ quả định lý Ta
A'B'OA' 615 (1) 6cm B' O x' x B A I F F' A'
2 7a.4 7 a 16
Giải
lét)
A'F'A'B'
106 2 OA'10A'B' Từ (1),(2) OA'OA'10 1510 OA'30 cm A'B'30 A'B'12 615 cm Bài 7: Thùng của một xe tải có dạng của một hình lăng trụ đứng với các kích thước: 7mx3,1mx1,6m (như hình vẽ) . a) Tính thể tích của thùng chứa. b) Nếu 1m3 cát nặng 1,6 tấn và xe chở đến 3 4 tải trọng thì khối lượng của cát lúc đó là bao nhiêu kg?
lét) 10AB OA'OF'A'B'
(hệ quả
Giải
a) Thể tích của thùng chứa : 37.3,1.1,634,72m b) Cân nặng của 34,72m3 cát : 34,72 . 1,6 = 55,552 (tấn)
Khối lượng của cát lúc xe chở đến 3 4 tải trọng là: 3 55,55241,664 4 (tấn)
Bài 8: Cho đường tròn (O; R). Từ điểm A bên ngoài đường tròn, kẻ các tiếp tuyến AB, AC (B,C là tiếp điểm của (O) và cát tuyến ADE không qua tâm (D nằm giữa A và E, AE cắt đoạn thẳng OB). Gọi I là trung điểm của ED.
a) Chứng minh 5 điểm A, B, I, O, C cùng thuộc 1 đường tròn b) BC cắt AE tại K. Chứng minh AB2 = AK.AI c) Từ D vẽ DJ // AB ( J thuộc BC). Chứng minh IJ //EB Giải

DẠYKÈMQUYNHƠN OFFICIAL Xét
OFI',A'B'//OI
OF'OI
định lý Ta
a) Chứng minh 5 điểm A, B, I, O, C
cùng thuộc 1 đường tròn
Ta có: I là trung điểm của ED OIED 0OIA90
Ta có: 0OBAOCA90 (tiếp tuyến vuông góc bán kính) Mà 3 đỉnh B, I, C cùng nhìn cạnh OA dưới 1 góc vuông 5 điểm A, B, I, O, C cùng thuộc đường tròn đường kính OA
b) Chứng minh AB2 = AK.AI
Ta có AB = AC (tính chất 2 tiếp tuyến cắt nhau)
Xét đường tròn đường kính AO: Ta có: ABAC (AB = AC)
ABCAIB
ABKAIB Xét ABK và AIB có: A: góc chung ABKAIB (chứng minh trên) ABKAIB (g – g)
ABAK AIAB (các cạnh tương
OFFICIAL
DẠYKÈMQUYNHƠN
ứ
ỉ lệ
2 ABAI.AK c) Chứng minh IJ //EB Ta có: DJ // AB JDIBAI (đồng vị) Xét đường tròn đường kính OA: 1 BCIBAIsBI 2 ñ JDIBCIBAI JDIJCI 2 đỉnh D, C cùng nhìn cạnh IJ dưới 2 góc bằng nhau tứ giác IJDC nội tiếp 1 JIDJCDsJD 2 ñ JIDBCD Mà 1 BCDBEDsBD 2 ñ JIDBED IJ // EB (2 góc đồng vị bằng nhau) HẾT J K D I C B A O E
ng t
)
ệm phân biệt thỏa 22 1212 55 0 22
Bài 3: Một con mèo của Hà ăn 1 3 lon thức ăn vào mỗi buổi sáng và 1 4 lon thức ăn vào buổi chiều. Buổi sáng thứ Hai, trước khi cho mèo ăn, Hà mở một cái hộp chứa 6 lon thức ăn của mèo. Hỏi vào ngày nào trong tuần con mèo có thể ăn hết số thức ăn trong hộp đó? Bài 4: Một cửa hàng cho thuê sách cũ có quy định: Nếu khách hàng là hội viên của cửa hàng thì phải đóng phí 70000 đồng/năm và được thuê sách với giá 6000 đồng/quyển, còn nếu khách hàng không là hội viên phải thuê sách với giá 10000 đồng/quyển. Gọi y (đồng) là tổng số tiền khách hàng phải trả trong một năm và x là số quyển sách thuê trong một năm.
a) Lập hàm số của y theo x với khách hàng là hội viên và với khách hàng không là hội viên của cửa hàng.
b) Anh Nam là một hội viên của cửa hàng, năm vừa rồi anh Nam trả cho cửa hàng tổng cộng 322000 đồng. Hỏi nếu anh Nam không là hội viên của cửa hàng thì năm vừa rồi anh phải trả cho cửa hàng bao nhiêu tiền?
Bài 5: Một vé xem phim có giá 60000 đồng. Khi có đợt giảm giá, mỗi ngày số lượng người xem tăng lên 50%, do đó doanh thu cũng tăng 25%. Hỏi giá vé khi được giảm là bao nhiêu?
Bài 6: Một dụng cụ trộn bê tông gồm một phần có dạng hình trụ, phần còn lại có dạng hình nón. Các kích thước cho trên hình bên. Hãy tính
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GD & ĐT QUẬN 12 NĂM HỌC 2022-2023 ĐỀ THAM KHẢO MÔN : TOÁN 9 Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Quận 12 – 1 Thời gian: 120 phút (không kể thời gian phát đề) Bài 1: Cho Parabol 2 1 : 2 Pyx và đường thẳng d : 3 2 2 yx a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. b) Tìm tọa độ giao điểm của P và d bằng phép toán. Bài 2: Tìm m để phương trình 222230 xmxmm có hai nghi
xxxx
a) Thể tích của dụng cụ này. b) Diện tích mặt ngoài của dụng cụ (không tính nắp đậy).
Bài 7: Sau khi xem bảng báo giá trên tờ rơi quảng cáo ở siêu thị, mẹ bạn Bình đưa bạn 370000 đồng ra siêu thị mua 1 gói bột ngọt loại 1kg và một chai dầu ăn loại 5 lít thì vừa đủ tiền. Hôm nay vì trúng đợt có chương trình khuyến mãi, dầu ăn được giảm bớt 20000 đồng/chai 5 lít và bột ngọt được giảm giá 10% so với giá niêm yết, do đó bạn Bình chỉ phải trả 337500 đồng. Hỏi giá niêm yết trên bảng báo giá hai mặt hàng này là bao nhiêu?
Bài 8: Cho tam giác ABC nhọn ( ABAC ) nội tiếp đường tròn O các đường cao BF và CK của tam giác ABC cắt nhau tại H . Tia FK cắt tia CB tại M , AH cắt BC và đường tròn O lần lượt tại D và E ( EA). a) Chứng minh tứ giác BKFC nội tiếp và MKMFMBMC b) AM cắt đường tròn O tại N ( NA). Chứng minh: AKNAFN . c) Gọi I là hình chiếu của E lên AC Tia EI cắt DC và đường tròn O lần lượt tại G và Q ( QE ). Chứng minh I là trung điểm của QG và 3 điểm N , F , Q thẳng hàng.

DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 78 -
OFFICIAL
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI Bài 1: Cho Parabol 2 1 : 2 Pyx và đường thẳng 3 :2 2 dyx a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ. b) Tìm tọa độ giao điểm của P và d bằng phép toán. Lời giải a) 2 1 : 2 Pyx x 2 1 0 1 2 y 2 1 2 0 1 2 2 b) Phương trình hoành độ giao điểm của P và d là 2 2 2 13 2 22 13 20 22 340 1 4 xx xx xx x x Với 1 x , ta có: 2 11 .1 22 y . Với 4 x , ta có: 2 1 .48 2 y Vậy tọa độ giao điểm của P và d là 1 1; 2 , 4;8 Bài 2: Tìm m để phương trình 222230 xmxmm có hai nghiệm phân biệt thỏa 22 1212 55 0 22 xxxx . Lời giải Ta có: 2 222 '1.232323 mmmmmmm . Phương trình 222230 xmxmm có hai nghiệm phân biệt khi và chỉ khi '0 230 3 2 m m
ứa 6 lon thức ăn của mèo. Hỏi vào ngày nào trong tuần con mèo có thể ăn hết số thức ăn trong hộp đó? Lời giải Trong một ngày, một con mèo của Hà ăn được: 11437 34121212 (lon thúc ăn). Để ăn hết 6 lon thức ăn, một con mèo của Hà cần: 772 6:10,29 127 (ngày). Do đó, cần ít nhất 11 ngày để con mèo của Hà ăn hết 6 lon thức ăn. Ta có: 117.14 Vậy vào ngày thứ 5 trong tuần con mèo có thể ăn hết số thức ăn trong hộp đó. Bài 4: Một cửa hàng cho thuê sách cũ có quy định: Nếu khách hàng là hội viên của cửa hàng thì phải đóng phí 70000 đồng/năm và được thuê sách với giá 6000 đồng/quyển, còn nếu khách hàng không là hội viên phải thuê sách với giá 10000 đồng/quyển. Gọi y (đồng) là tổng số tiền khách hàng phải trả trong một năm và x là số quyển sách thuê trong một năm. a) Lập hàm số của y theo x với khách hàng là hội viên và với khách hàng không là hội viên của cửa hàng.
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 80Với 3 2 m , theo định lý Viet, ta có: 12 2 2 12 2 2 1 23 .23 1 m Sxxm mm Pxxmm Ta có: 22 1212 22 1212 2 121212 2 2 22 2 2 55 0 22 5 .0 2 5 2.0 2 5 22.23.20 2 424650 24650 260 2 (n) 3 (l) 2 xxxx xxxx xxxxxx mmmm mmmm mmm mm m m Vậy 2 m . Bài 3: Một con mèo của Hà ăn 1 3 lon thức ăn vào mỗi buổi sáng và 1 4 lon thức ăn vào buổi chiều. Buổi sáng thứ Hai, trước khi cho mèo ăn, Hà mở một cái hộp ch
b) Anh Nam là một hội viên của cửa hàng, năm vừa rồi anh Nam trả cho cửa hàng tổng cộng 322000
đồng. Hỏi nếu anh Nam không là hội viên của cửa hàng thì năm vừa rồi anh phải trả cho cửa hàng bao nhiêu tiền?
Lời giải
a) Với khách hàng là hội viên của cửa hàng, ta có: 700006000. yx;
Với khách hàng không là hội viên của cửa hàng, ta có: 10000. yx.
b) Vì anh Nam là một hội viên của hàng hàng và năm vừa rồi anh Nam trả cho cửa hảng tổng cộng 322 000 đồng nên ta có: 322 00070 0006 000. x . Suy ra: số sách mà anh Nam đã thuê trong năm vừa rồi là 42 (quyển).
Nếu anh Nam không là hội viên của cửa hàng thì năm vừa rổi anh phải trả cho cửa hàng số tiền là 10000.42420000 (đồng).
OFFICIAL
Bài 5: Một vé xem phim có giá 60000 đồng. Khi có đợt giảm giá, mỗi ngày số lượng người xem tăng lên 50%, do đó doanh thu cũng tăng 25%. Hỏi giá vé khi được giảm là bao nhiêu? Lời giải Giá vé (đồng) Số vé bán được Doanh thu (đồng) Trước đợt giảm giá 60 000 x 60 000.x Trong đợt giảm giá 125%.60000. 150%. x x 150%.x 125%.60 000.x Gọi x ( x ) là số vé xem phim bán được trước đợt giảm giá. Khi đó: Số vé xem phim bán được trong đợt giảm giá 150%.x (vé).
Doanh thu trước đợt giảm giá là 60000.x (đồng).
Doanh thu trong đợt giảm giá là 125%.60000.x (đồng).
Giá vé trong đợt giảm giá là :125%.60000. 50000 150%. x x Vậy giá vé khi được giảm là 50000 đồng. Bài 6: Một dụng cụ trộn bê tông gồm một phần có dạng hình trụ, phần còn lại có dạng hình nón. Các kích thước cho trên hình bên. Hãy tính
a) Thể tích của dụng cụ này. b) Diện tích mặt ngoài của dụng cụ (không tính nắp đậy). Lời giải
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 81 -
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 82a) Thể tích của dụng cụ đó là 22 22 32 3 1,47011,4701 .....1,6.0,7.0,7..0,7.0,9 2100321003 .0,70,3..0,7 49 1,5393804m 100 b) Diện tích mặt ngoài của dụng cụ (không tính nắp đậy) là 2 1,4701,470 2.....1,60,98.0,63.1,61.5,06m 21002100 . Bài 7: Sau khi xem bảng báo giá trên tờ rơi quảng cáo ở siêu thị, mẹ
ạn
ị
1 gói
ột ngọt
ạ
Lời giải Gọi x , y (đồng) 0,370 xy lần lượt là giá niêm yết của 1 gói bột ngọt loạ
ộ
370000 110%20000337500 370000 0,9357500 125000 245000 xy xy xy xy x y Vậy giá niêm yết của 1 gói bột ngọt loại 1kg và một chai dầu ăn loại 5 lít lần lượt là 125000 đồng và 245000 đồng. Bài 8: Cho tam giác ABC nhọn ( ABAC ) nội tiếp đường tròn O các đường cao BF và CK của tam giác ABC cắt nhau tại H . Tia FK cắt tia CB tại M , AH cắt BC và đường tròn O lần lượt tại D và E ( EA). a) Chứng minh tứ giác BKFC nội tiếp và MKMFMBMC . b) AM cắt đường tròn O tại N ( NA). Chứng minh: AKNAFN c) Gọi I là hình chiếu của E lên AC . Tia EI cắt DC và đường tròn O lần lượt tại G và Q ( QE ). Chứng minh I là trung điểm của QG và 3 điểm N , F , Q thẳng hàng. Lời giải
b
Bình đưa bạn 370000 đồng ra siêu th
mua
b
lo
i 1kg và một chai dầu ăn loại 5 lít thì vừa đủ tiền. Hôm nay vì trúng đợt có chương trình khuyến mãi, dầu ăn được giảm bớt 20000 đồng/chai 5 lít và bột ngọt được giảm giá 10% so với giá niêm yết, do đó bạn Bình chỉ phải trả 337500 đồng. Hỏi giá niêm yết trên bảng báo giá hai mặt hàng này là bao nhiêu?
i 1kg và m
t chai dầu ăn loại 5 lít. Theo đề bài, ta có hệ phương trình:
a) Tứ giác BKFC có 90 BKCBFC nên tứ giác BKFC nội tiếp đường tròn đường kính BC .
Suy ra: KFBKCB (góc nội tiếp cùng chắn KB ) hay MFBMCK .
Xét KMB và CMF có: FMC : chung MFBMCK (cmt)
Suy ra: KMBCMF (g.g).
Do đó: MKMC MBMF . Suy ra: MKMFMBMC (1) (đpcm).
b) Ta có: tứ giác NACB nội tiếp đường tròn O
Suy ra: MNBMCA

Xét MNB và MCA có: CMA: chung MNBMCA (cmt)
Suy ra: MNBMCA (g.g).
Do đó: MNMC MBMA . Suy ra: .. MNMAMBMC (2).
Từ (1) và (2), suy ra: MKMFMNMA. Suy ra: MKMN MAMF .
Xét MKA và MNF có: FMA: chung MKMN MAMF (cmt)
NHÓM WORD HÓA ĐỀ TOÁN - 83 -
DẠYKÈMQUYNHƠN OFFICIAL
Suy ra: MKAMNF (c g.c)
Suy ra: NFKNAK .
Tứ giác NAFK có NFKNAK . Suy ra tứ giác NAFK là tứ giác nội tiếp (3).
Suy ra: AKNAFN (góc nội tiếp cùng chắn AN ).
c) Vì H là giao điểm hai đường cao BF , CK của tam giác ABC nên H là trực tâm của ABC .
Do đó: AD là đường cao của ABC . Hay AEBC tại D hay 90 EDC .
Tứ giác EDIC có 90 EICEDC
Suy ra: tứ giác EDIC nội tiếp đường tròn đường kính EC
Suy ra: DEIDCI (góc nội tiếp cùng chắn DI ).
Mặc khác: DEIAEQACQICQ (góc nội tiếp cùng chắn AQ ).
Do đó: GCIQCI .
Tam giác GCQ có đường cao CI cũng là đường phân giác góc GCQ
OFFICIAL
Suy ra: GCQ cân tại C . Hay CI cùng là đường trung tuyến của GCQ .
Do đó: I là trung điểm của GQ (đpcm).
Tứ giác KAFH có 90 AKHAFH
Suy ra: Tứ giác KAFH nội tiếp đường tròn đường kính AH (4).
Từ (3) và (4), suy ra: 5 điểm N , A, F , H , K cùng thuộc đường tròn đường kính AH
Suy ra: NAHNFH (góc nội tiếp cùng chắn NH ).
Mặc khác: NAHNAENQE (góc nội tiếp cùng chắn NE ).
Suy ra: NFHNQE .
Ta có : // HFEQ (vì cùng vuông góc với AC ).
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 84 -
180 NQEHFQ (2 góc
) Mà NFHNQE 180 NFHHFQ ,, NFQ thẳng hàng
trong cùng phía
(đpcm).
Trường THCS Hoàng Hoa Thám ĐỀ THAM KHẢO TUYỂN SINH 10 – Năm học 2022 – 2023
Bài 1: Cho Parabol (P): 2 1 2 yx và đường thẳng (d): 2 yx a/ Vẽ (P) và (d) lên cùng một mặt phẳng tọa độ b/ Tìm tọa độ giao điểm của (P) và (d) bằng phép tính Bài 2: Cho phương trình: 2 2x7x50 có 2 nghiệm 1x và 2x . Không giải phương trình, hãy tính giá trị biểu thức: 1221 P3x5x3x5x Bài 3: Ba thành viên trong đội bóng nữ lớp 9 trường trung học cơ sở Hoàng Hoa Thám nói chuyện với nhau vào dịp thi đua phong trào cho ngày 20-11-2020. Hạnh: Tớ vừa nhận ra số áo của bọn mình đều là những số nguyên tố có hai chữ số.

Bích Thủy : Tổng hai số áo của các bạn là ngày sinh của tớ vừa diễn ra trong tháng này.
Cúc : Ừ, vui thật, tổng hai số áo của các cậu lại là ngày sinh của tớ vào cuối tháng này.
Hạnh: Và tổng số áo của các cậu lại đúng bằng ngày hôm nay.
Vậy Cúc mặc áo số mấy?
Bài 4: Có 45 người gồm bác sĩ và luật sư có tuổi trung bình của họ là 40 tuổi. Tính số bác sĩ và luật sư, biết tuổi trung bình của bác sĩ là 35 và tuổi trung bình của luật sư là 50.
Bài 5: Bác Tâm đền thế giới di động để mua một chiếc điện thoại. Tại đây, cửa hàng để giá 6 000 000 đồng chưa tính thuế VAT ( thuế 10% tính trên giá gốc).
a/ Hỏi nếu lấy chiếc điện thoại đó thì Bác Tâm phải trả bao nhiêu tiền? b/ Bác Tâm lấy chiếc điện thoại này và mua thêm phụ kiện. Tổng số tiền bác phải trả cho cửa hàng là 7 920 000 đồng ( đã bao gồm thuế VAT 10%). Hỏi phụ kiện chưa tính thuế VAT là bao nhiêu?
Bài 6: Một chụp nhựa bảo vệ chuông điện có cấu trúc gồm một phần hình trụ có bán kính R, chiều cao 6cm và một bán cầu bán kính R (hình vẽ bên). Cho biết diện tích mặt xung quanh khối chụp 2 120 cm . Tính thể tích khối chụp (kết quả làm tròn đến chữ số thập phân thứ nhất).
Bài 7: Hội phụ huynh lớp 9A dự định phát đều 300 quyển vở cho tất cả học sinh tiên tiến của lớp.Nhưng khi phát có 3 học sinh vắng mặt, vì vậy mỗi học
DẠYKÈMQUYNHƠN
OFFICIAL
sinh được nhận thêm 5 quyển vở so với dự tính ban đầu. Hỏi số học sinh tiên tiến của lớp 9A?
Bài 8: (3đ) Cho M nằm ngoài (O) vẽ tiếp tuyến MA, MB và cát tuyến MCD nằm trên nửa mặt phẳng bờ là tia OM chứa điểm A. Gọi E là trung điểm của CD.
a) CMR: MAEB là tgnt, xác định tâm S b) AB cắt CD tại I. CMR: EA.EB = EI.EM c) Từ C vẽ đường thẳng vuông góc OA, cắt AE tại K. CMR: IK // AC Hướng dẫn giải
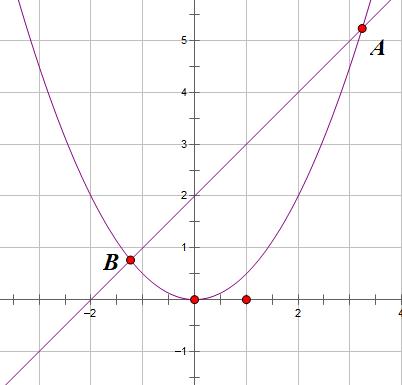
DẠYKÈMQUYNHƠN
OFFICIAL
b/
2 2 12 1 2 2 240 15;15 xx xx xx Thay 1 15 x vào (d) 1 35 y Thay 2 15 x vào (d) 2 35 y Vậy tọa độ giao điểm của (P) và (d) là 15;35;15;35 Bài 2: (1 điểm) Cho phương trình: 2 2x7x50 có 2 nghiệm 1x và 2x . Không giải phương trình, hãy tính giá trị biểu thức: 1221 P3x5x3x5x Theo hệ thức Vi-ét ta có : 12 12 b7 xx a2 c5 xx a2 Khi đó : 1221 P3x5x3x5x 22 121212 P9xx15x15x25xx 22 1212 P34xx15xx
Bài 1: Cho Parabol (P): 2 1 2 yx
và đường thẳng (d): 2 yx a/ Vẽ (P) và (d) lên cùng một mặt phẳng tọa độ
Tìm tọa độ giao điểm của (P) và (d) bằng phép tính Phương trình hoành độ giao điểm của (P) và (d)
2 121212 P34xx15xx2xx 2 575 P34.152. 222 1375 P 2
Bài 3: Số ngày lớn nhất trong một tháng là 31, và các số nguyên tố có hai chữ số nhỏ nhất là 11, 13, 17 (các số nguyên tố tiếp theo bị loại vì tổng của nó với số nguyên tố có hai chữ số bất kỳ lớn hơn 31).
Vậy ba số áo 11, 13, 17, và ba tổng đôi một của chúng là 24, 28 và 30.
Vì tất cả các ngày nói đến trong câu chuyện nằm trong cùng một tháng quý 4, nên ngày sinh của Cúc lớn nhất, tức là bằng 30, ngày hôm nay là 28 và ngày sinh của Bích Thủy là 24.
Từ đó dễ dàng tìm được số áo của Hạnh là 13, của Bích Thủy là 17 còn Cúc mang áo số 11.
Bài 4:
Gọi x(người) là số bác sĩ x > 0 Y (người là số luật sư y> 0
Có 45 người bác sĩ và luật sư nên x + y = 45
Tổng số tuổi của bác sĩ là 35x
DẠYKÈMQUYNHƠN OFFICIAL
Tu
Ta có hpt 45 35501800 xy xy 30 15 x y Vậy có 30 bác sĩ và 15 luật sư
a) Số tiền bác Tâm phải trả là: 6
b) Số tiền phụ kiện bác Tâm
7
Tổng số tuổi của luật sư là 50y
ổi trung bình của 45 người là 40 tuổi nên ta có 3550 40 45 xy
=> 35x+50y = 1800
Bài 5:
000 000 (1+10%) = 6 600 000 (đồng)
phải trả là:
920 000 – 6 600 000 = 1 320 000 ( đồng)

DẠYKÈMQUYNHƠN OFFICIAL Số tiền phụ kiện chưa tính thuế VAT là: 1 320 000 : (1+10%) = 1 200 000 (đồng) Bài 6: Ta có diện tích xung quanh 2 2 2 2.2 120122 6600 369 SRhR RR RR R Thể tích khối chụp 233 2 .845,1() 3 VRhRcm
7: Gọi x( học sinh) là số học sinh tiên tiến lớp
x thuộc
*
ọc sinh
ặ
ậ
Giải phương trình ta được : x=15(nhận);x= -12(loại) Vậy số học sinh tiên tiến lớp 9A là 15 học sinh Bài 8: a) * Xét (O), ta có: CD là dây cung không đi qua tâm và E là trung điểm của CD OE CD tại E (định lí đường kính – dây cung) * Ta có: 0MAO90 (MA là tiếp tuyến của (O)) 0MBO90 (MB là tiếp tuyến của (O)) 0MEO90 (OE CD) A, B, E cùng nhìn cạnh OM dưới góc 900 M, A, E, O, B cùng thuộc đường tròn đường kính OM MAEB nội tiếp đường tròn đường kính OM Khi đó, tâm S của đường tròn là trung điểm của OM I K E C B A O M D
Bài
9A.Đk:
N
và x>3 Số h
có m
t nh
n phần tập: x-3 Số quyển vở 1 học sinh dự định nhận được: 300 x Số quyển vở 1 học sinh thực tế nhận được: 300 3 x Theo đề bài ta có phương trình: 300300 5 3 xx
b) * Xét (S), ta có: MA = MB (t/c 2 tiếp tuyến cắt nhau)
MAMB
, mà 1 .MA 2 MEA
; 1 .MB 2 MEB
Xét MAE và BIE, ta có: MEAMEB
MAE BIE (g.g) EAEM EIEB
có:
(1)
Ta có: 0180 AKCCKE , 0180 CIBBIE , mà CKEBIE
Ta có: ACKMAC
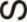
(slt, CK // MA), MACIBC
Xét ACK và CBI, ta có: AKCCIB
(KCE IBE)
(cùng chắn cung AC)
Xét ACE, ta có: EKKA EIIC
IK // AC (talet đảo)
DẠYKÈMQUYNHƠN OFFICIAL
I
D
MEAMEB
*
, AMEIBE
EA.EB = EI.EM c) * Ta có: KCEAME , mà AMEABE KCEABE * Xét KCE và IBE, ta
KCEIBE , KECIEB
KCE IBE (g.g) EKKC EIIB
*
AKCCIB
*
ACKIBC
*
, ACKIBC
ACK CBI (g.g) KAKC ICIB
(2) Từ (1) & (2) EKKA EIIC
*
K E C B A O M
SỞ GD & ĐT TP.HỒ CHÍ MINH
ĐỀ THAM KHẢO TUYỂN SINH 10
PHÒNG GD & ĐT QUẬN TÂN PHÚ NĂM HỌC 2022-2023 ĐỀ THAM KHẢO MÔN : TOÁN 9 Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Quận 1 – 1 Thời gian: 120 phút (không kể thời gian phát đề) Câu 1(1,5 điểm) Cho Parabol (P): 2 1 2 yx và đường thẳng (d): 1 3 2 yx
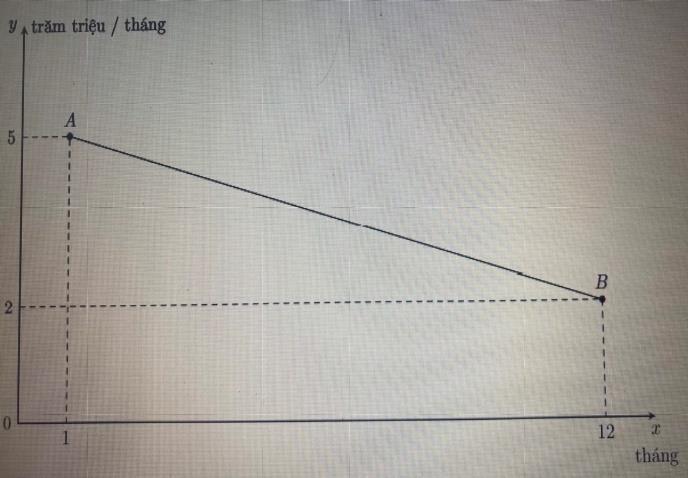
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ. b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Câu 2(1 điểm) Cho phương trình: 2 2510 xx có 2 nghiệm 12 ; xx . Không giải phương trình hãy tính giá trị của biểu thức 122122xxxx .
Câu 3: Giáo viên muốn chia lớp thành 8 nhóm để hoạt động học nhóm trong các tiết học của môn mình, giáo viên cho học sinh chia nhóm ngẫu nhiên dựa vào số thứ tự của học sinh trong lớp. Học sinh lấy số thứ tự chia cho 8, được số thương q và số dư là r, nếu số dư là 0 thì thuộc nhóm 1, số dư là 1 thì thuộc nhóm 2, số dư là 2 thì thuộc nhóm 3..., số dư là 7 thì thuộc nhóm 8. Và sắp thứ tự trong nhóm mới dựa vào q, nếu q = 0 thì số thứ tự là 1, q = 1 thì số thứ tự là 2, q = 2 thì số thứ tự là 3...
a) An và Bình có số thứ tự trong lớp lần lượt là 13 và 24 thì An và Bình thuộc nhóm mấy và số thứ tự bao nhiêu trong nhóm của mình?
b) Em hãy tính số thứ tự trong lớp của một học sinh. Biết lớp có 42 học sinh và học sinh ấy. Câu 4: Do ảnh hưởng của dịch bệnh, thu nhập của một công ty bị giảm dần trong năm 2021. Các số liệu thống kê được thể hiện bằng đồ thi trong hình vẽ bên
DẠYKÈMQUYNHƠNOFFICIAL
a) Tìm hàm số thể hiện sự liên quan của các đại lượng y ( trăm triệu/ tháng) theo đại lượng x ( tháng)
b) Biết một số sảm phẩm bán được công ty có lợi nhuận là 100 ngàn đồng. Em hãy tính số sản phẩm công ty bán được trong tháng 9 năm 2021( làm tròn đến hàng đơn vị)
Câu 5( 1 điểm) Có hai loại quặng sắt chứa 60% sắt, quặng loại B chứa 50% sắt. Ngưới ta trộn một lượng quặng loại A với một lượng quặng loại B thì được hỗn hợp chứa 8 10 sắt.Nếu lấy tăng hơn lúc đầu là 10 tấn quặng loại A và lấy giảm hơn lúc đầu là 10 tấn quặng loại B thì đươc hỗn hợp quặng chứa 17 30 sắt. Tính khối lượng kim loại đem trộn lúc đầu.
Câu 6: Một bình nước hình hộp chữ nhật có chiều rộng, chiều dài đáy bình và chiều cao lần lượt tỉ lệ với 2; 3 và 5. Biết chiều cao của bình là 20 cm.
a) Tính thể tích tối đa mà bình chứ đựng.
b) Bình nước được rót vào cái ly hình trụ có đường kính đáy là 5cm, chiều cao 12 cm. Biết bình đựng đầy nước và rót vào ly 90% thể tích của ly.Tính số ly nước nhiều nhất có thể rót ra được ( chỉ tính các ly có đủ lượng nước cần).
Câu 7 ( 1 điểm) Trước ngày kết thúc năm học tập thể các học sinh lớp 9A muốn mua quà tặng cho giáo viên giảng dạy lớp mình trong suốt năm học để tỏ lòng tri ân, mỗi món quà tặng cho thầy với giá 50 ngàn đồng, mỗi món quà tặng cho cô có giá là 65 ngàn đồng, biết lớp tặng cho 15 giáo viên tất cả và tổng số tiền mà lớp mua quà là 870 ngàn đồng. Em hãy tính số thầy giáo và cô giáo lớp 9A dự định mua quà tặng.
Câu 8 ( 3 điểm)Cho tam ABC nhôn nội tiếp đường tròn(O;R) có 3 đường cao AD, BE, CF cắt nhau tại H. Gọi M, N lần lượt là giao điểm của BE, CF với (O).
a) Chứng minh: OAMN
b) Chứng minh: AH . AD + BH . BE = AB2
c) Tia phân giác của góc BAC cắt (O) tại K và BC tại I. Gọi J là tâm của đường tròn ngoại iếp tam giác AIC. Chứng minh KO và CJ cắt nhua tại điểm thuộc đường tròn (O).
DẠYKÈMQUYNHƠNOFFICIAL
UBND THÀNH PHỐ THỦ ĐỨC ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC: 2022 – 2023 MÔN THI: TOÁN ĐỀ 1 Thời gian làm bài: 120 phút (Không kể thời gian phát đề) Câu1. (1,5 điểm) Cho hàm số 2 yx có đồ thị là parabol (P) và hàm số y2x3 có đồ thị là đường thẳng (D) a) Vẽ đồ thị (P) và (D) trên cùng một hệ trục toạ độ. b) Tìm toạ độ các giao điểm của (P) và (D) bằng phép tính. Câu 2. (1 điểm) Cho phương trình 2 311150 xx có 2 nghiệm là 12 , xx Không giải phương trình, hãy tính giá trị của biểu thức 12 21


33xx A xx Câu 3. (0,75 điểm) Tượng đài Bà mẹ Việt Nam anh hùng đã trở thành một điểm đến mới thu hút đông đảo du khách trong và ngoài nước, đem lại những lợi ích thiết thực cho sự phát triển kinh tế, xã hội của địa phương. Quan trọng hơn cả, Tượng đài là một điểm về nguồn mang giá trị lịch sử và nhân văn vô cùng to lớn, góp phần giáo dục truyền thống uống nước nhớ nguồn, giáo dục lòng yêu nước với mọi tầng lớp nhân dân, nhất là đối với thế hệ trẻ ngày hôm nay. Địa phương xây tượng đài là tỉnh Quảng Nam, tỉnh có nhiều Bà mẹ Việt Nam anh hùng nhất với 11.234 người. Theo định hướng, tượng đài lấy nguyên mẫu từ hình ảnh mẹ Việt Nam anh hùng Nguyễn Thị Thứ (xã Điện Thắng, huyện Điện Bàn, tỉnh Quảng Nam), Bà có 9 con trai, một con rể và hai cháu ngoại hy sinh trong hai cuộc đấu tranh chống Pháp và Mỹ Tượng đài Bà mẹ Việt Nam anh hùng có tổng diện tích 15 ha. Phía trước khuôn viên tượng đài là quảng trường tiền môn rộng lớn. Giữa quảng trường có 8 trụ huyền thoại, mỗi trụ cao 11,2m, đường kính gần 2m. Trên các cột trụ khắc họa hình ảnh các bà Mẹ ở mọi miền đất nước. Đây vừa là cổng chào, biểu tượng cô đọng về vẻ đẹp của các Bà mẹ Việt Nam anh hùng cũng như toàn thể phụ nữ Việt Nam. . Tính thể tích mỗi cột trụ. (làm tròn đến hàng đơn vị).
Biết thể tích hình trụ: 2 VRh
DẠYKÈMQUYNHƠN
OFFICIAL
Câu 4. (1 điểm) Đại dịch COVID-19 còn được gọi là đại dịch coronavirus, là một đại dịch bệnh truyền nhiễm với tác nhân là virus SARS-CoV-2, đang diễn ra trên phạm vi toàn cầu. Khởi nguồn vào cuối tháng 12 năm 2019 với tâm dịch đầu tiên được ghi nhận tại thành phố Vũ Hán thuộc miền Trung Trung Quốc. Tại Việt Nam, theo thống kê đến 6 giờ ngày 31/5/2021. Tổng số người tiếp xúc gần và nhập cảnh từ vùng dịch đang được theo dõi sức khỏe (cách ly): 150 471 người gồm 3 đối tượng cách ly là cách ly tại nhà; cách ly tại bệnh viện và cách ly tập trung khác. Biết số người cách ly tại bệnh viện ít hơn số người cách ly tập trung khác là 25 240 người. Số người cách ly tại bệnh viện và cách ly tập trung khác ít hơn số người cách ly tại nhà là 79 723 người. Tính số người cách ly ở mỗi đối tượng. Câu 5. (1 điểm) Bạn Bình muốn mua một đôi giày thể thao mới. Hiện tại bạn đang có sẵn một số tiền nhưng không đủ để mua. Vì vậy bạn lên kế hoạch tiết kiệm tiền từ ngày 1/2/2020 đến ngày 31/3/2020. Tháng Tư, Bình rủ An đến cửa hàng để mua giày. Sau khi mua giày xong, Bình mua hai thêm hai ly trà sữa với giá 30 000 đồng một ly thì Bình còn dư lại 60 000 đồng. Gọi y (đồng) là số tiền bạn Bình có sẵn, x (đồng) là số tiền bạn để dành mỗi ngày từ 1/2/2020 đến 31/3/2020.

OFFICIAL
a) Lập hàm số y theo x biết giá đôi giày bạn mua là 680 000 đồng.
b) Biết số tiền bạn Bình có sẵn do ông bà lì xì Tết là 200 000 đồng. Hỏi để có tiền mua giày thì mỗi ngày Bình phải tiết kiệm bao nhiêu tiền ? Câu 6. (1 điểm)
“Trăng cứ tròn vành vạnh kể chi người vô tình ánh trăng im phăng phắc đủ cho ta giật mình” (Trích Ánh Trăng, Nguyễn Duy)
(tiếng Anh: Moon) là
tinh tự nhiên duy

DẠYKÈMQUYNHƠN
Mặt Trăng
vệ
nhất của Trái Đất và là vệ tinh tự nhiên lớn thứ năm trong Hệ Mặt Trời; có đường kính bằng 27,3% đường kính Trái Đất. a) Một quả địa cầu mô hình có đường kính 16 cm (Tỷ lệ: 1/80 000 000). Tính bán kính thực tế của Trái đất khoảng bao nhiêu km?
b) Tính khối lượng của Mặt Trăng biết Mặt Trăng là một hình cầu và tỉ trọng trung bình 3,334 g/cm3 . Biết công thức tính thể tích khối cầu: V = 3 4 3 π.r (π = 3,14). Câu 7 (0,75 điểm) Ba ông Phát, Hưng, Thịnh góp vốn theo tỉ lệ 2;3;5 để mở công ty chuyên sản xuất bao bì.
a) Năm 2019, công ty lời 60 tỷ đồng. Số tiền lời được chia theo tỷ lệ góp vốn của mỗi người .Tính số tiền lời của mỗi người.
b) Năm 2020, công ty làm ăn thua lỗ (do dịch bệnh nên hàng làm ra ít,tiền lương của công nhân vẫn phải trả). Số tiền lỗ được chia theo tỉ lệ góp vốn của mỗi người, riêng số tiền lỗ của ông Thịnh là 12 tỷ đồng. Tính số tiền lỗ của công ty năm 2020.
Câu 8. (3 điểm) Cho ABC nhọn (AB < AC) nội tiếp trong đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H. Tia EF cắt tia CB tại K. a) Chứng minh tứ giác BFEC nội tiếp và KF.KE = KB.KC b) Đường thẳng KA cắt (O) tại M. Chứng minh tứ giác AEFM nội tiếp. c) Gọi N là trung điểm của BC. Chứng minh M, H, N thẳng hàng.
OFFICIAL
DẠYKÈMQUYNHƠN
-
HƯỚNG DẪN CHẤM – ĐỀ 1 Câu NỘI DUNG ĐIỂM 1a a) Vẽ đồ thị (P) và (D) trên cùng mặt phẳng toạ độ Oxy. Bảng giá trị : x – 2 – 1 0 1 2 2 yx 4 1 0 1 4 x 0 1 y2x3 3 1 Vẽ : Vẽ đúng (P) và (d) 0,25x2 0,25x2 1b b) Tìm toạ độ giao điểm của (P) và (D) bằng phép toán. Phương trình hoành độ giao điểm của (P) và (D) là : 0,25
Hết -
DẠYKÈMQUYNHƠN OFFICIAL 2 2 12 x2x3 x2x30 x1;x3 Thay x = 1 và x3 vào y2x3 x1 suy ra y1 x3 suy ra y9 Vậy tọa độ giao điểm của (P) và (D) là (1 ; –1 ) và (–3 ; –9) 0,25 2 2 311150 xx Theo định lí Vi - ét ta có: 12 12 b11 Sxx a3 c15 Px.x5 a3 2 12 21 33 3(2) xx SP A xxP 211 15 0,5 0,25 0,25 3 Bán kính cột trụ là : 2:11() Rm Thể tích mỗi cột trụ: 223 .1.11,235()VRhm 0,5 0,25 4 Gọi x (người) là số người cách ly tại bệnh viện (x ∈ N*) Gọi y (người) là số người cách ly tại nhà (y ∈ N*) Số người cách ly tập trung khác là: x + 25240 Tổng số người bị cách ly là 150471 nên 25240 150471 2 1252311 xxy xy Số người cách ly tại bệnh viện và cách ly tập trung khác ít hơn số người cách ly tại nhà là 79723 người nên: – 25240 797 2 23 2+ 104963 yxx xy Ta có hệ phương trình: 2 125231 2 + 10 5 496 067 1150 3 97 xy x x y y (nhận) Vậy: Số người cách ly tại bệnh viện là: 5067 người Số người cách ly tại nhà là 115097 người. Số người cách ly tập trung khác là 5067 + 25240 = 30307 0,25 0,25x2 0,25
5a
người
a) Vì năm 2020 là năm nhuận nên tháng 2 có 29 ngày.
Từ ngày 1/2 đến 31/3/2020 có 29 + 31 = 60 ngày. Số tiền bạn Bình tiết kiệm trong 60 ngày là 60x (đồng) Số tiền bạn Bình có là 680000 + 2.30000 + 60000 =800000 (đồng)
Vậy hàm số y = 800000 – 60x.
5b Thay y = 200000 vào y = 800000 – 60x 10000 x
0,25 0,25
Vậy mỗi ngày bạn Hằng tiết kiệm 10000 đồng. 0,25 0,25
0,25 0,25 6b lời ông Phát được chia là: 1 60.12 5 (tỷ đồng). Số tiền lời ông Hưng được chia là: 3 60.18 10 (tỷ đồng). Số tiền lời ông Thịnh được chia là: 1 60.30 2 (tỷ đồng).
b) Bán kính Mặt Trăng là : (27,3%.1280000000):2 174720000() cm Thể tích Mặt Trăng là: 3253 4 .3,14.174720000 2,23303869.10 () 3 cm Khối lượng Mặt Trăng là : 2525 22 2,23303869.103,334 7,444950992.10 7,444950992.10 g kg 0,25 0,25 7b b) Số tiền lỗ của công ty năm 2020 :
0,25 0,25 7a a) Ông Phát góp vốn chiếm 1 5 (số vốn) Ông Hưng góp vốn chiếm 3 10 (số vốn) Ông Thịnh góp vốn chiếm 1 2 (số vốn) Số tiền
DẠYKÈMQUYNHƠN
OFFICIAL
6a a) Đường kính thực tế của Trái đất là : 16.80000000 1280000000() cm Bán kính thực tế của Trái đất là 1280000000 : 2 640000000() 6400() cmkm Vậy bán kính thực tế của Trái đất là khoảng 6400km
a.Chứng minh tứ giác BFEC nội tiếp và KF.KE = KB.KC Ta có: 090 BFCBEC (vì CF, BE là đcao của ABC )
BFEC nội tiếp (2 đỉnh kề cùng nhìn 1 cạnh dưới góc 900)
1 12:24 2 (tỷ đồng). 0,25 8a
KFBKCE (góc ngoài bằng góc đối trong) Xét KFB và KCE, ta có: FKB chung KFBKCE (cmt) Vậy KFBKCEgg . . KFKEKBKC
0,25 0,25 0,25 0,25 8b
b. Chứng minh tứ giác AEFM nội tiếp (1đ) Xét KBA và KMC, ta có: AKC chung KABKCM (2 góc nội tiếp cùng chắn cung MB) Vậy KBA KMC (g-g)
KM. KA = KB. KC Mà KF.KE = KB. KC (cmt) KM.KA=KF.KE (cùng = KB.KC) Xét KFM và KAE, ta có: AKE chung
0,25 0,25
DẠYKÈMQUYNHƠN OFFICIAL
KMKF KEKA (vì KM. KA=KF. KE) Vậy KFM KAE (c-g-c)
KFMKAE (2 góc tương ứng)
AEFM nội tiếp (góc ngoài = góc đối trong)
c. Chứng minh M, H, N thẳng hàng (1đ) Kẻ đường kính AQ của (O)
090 ABQ ; 090 ACQ
AB ⊥ BQ, AC ⊥ CQ Ta có: AB ⊥ BQ, AB⊥ CF CF// BQ. AC ⊥ CQ, AC⊥BE BE// CQ
BHCQ là hình bình hành N là trung điểm của HQ
0,25 0,25 8c
H,N,Q thẳng hàng (1) AEFM nội tiếp (cmt) và AEHF nội tiếp A,E,H,F,M cùng thuộc 1 đường tròn. AEHM nội tiếp 090 AMHAEH HM⊥AM Mà QM⊥AM( vì 090 QMA ) Q, H, M thẳng hàng (2) Từ (1), (2) suy ra H, M, N thẳng hàng.
0,25 0,25 0,25 0,25
Lưu ý: - Khi học sinh giải và trình bày cách khác thì giáo viên dựa trên thang điểm chung để chấm. - Học sinh không vẽ hình bài hình học thì không chấm. Hết
DẠYKÈMQUYNHƠN OFFICIAL
DẠYKÈMQUYNHƠN OFFICIAL




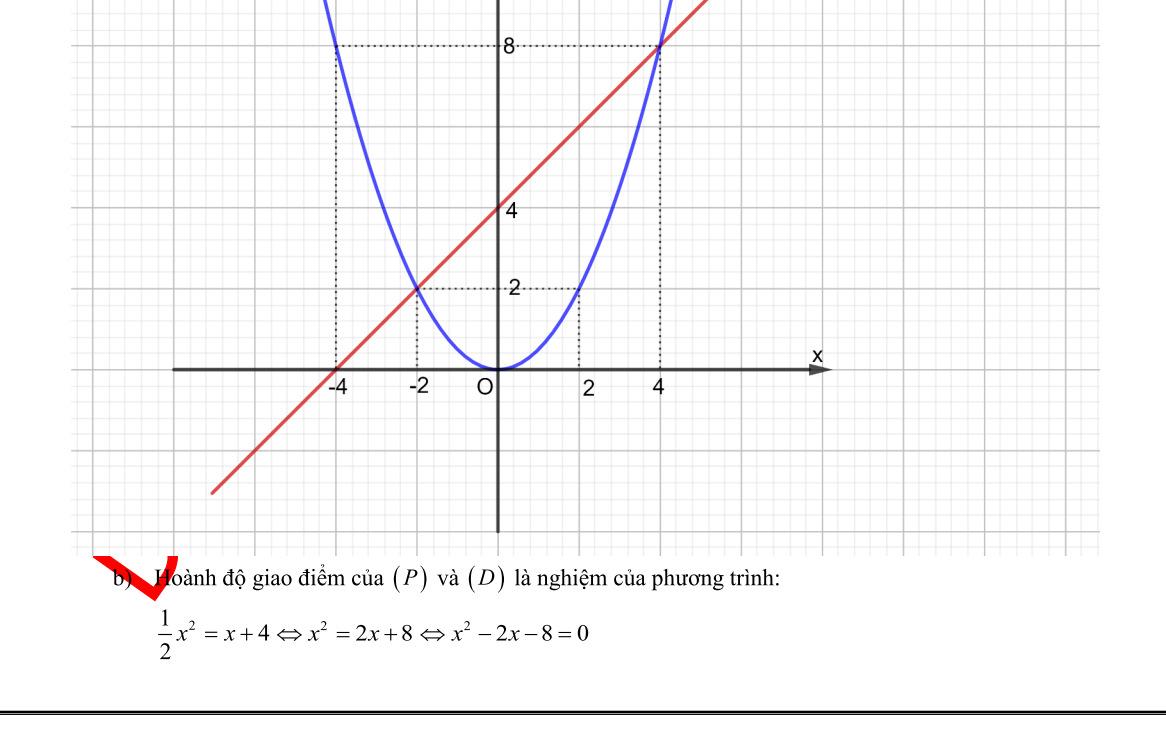





















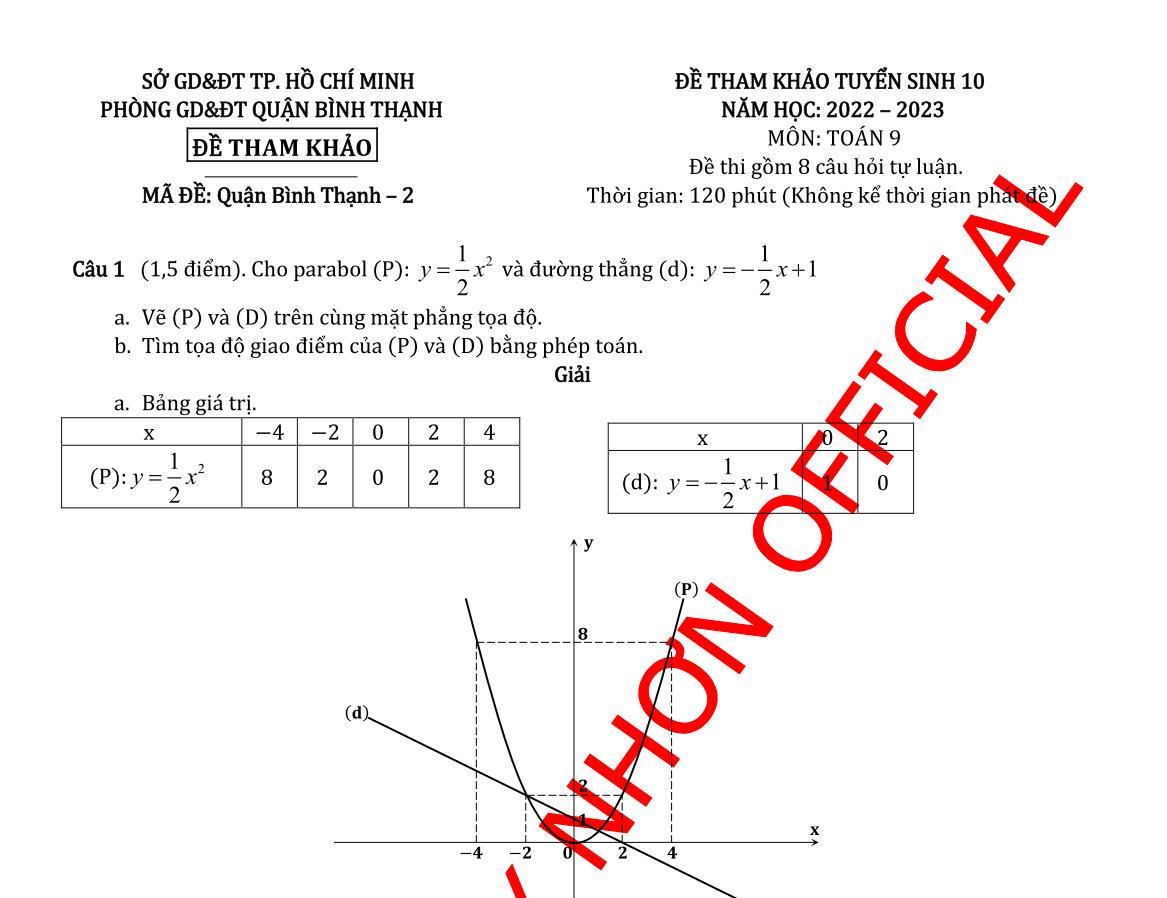


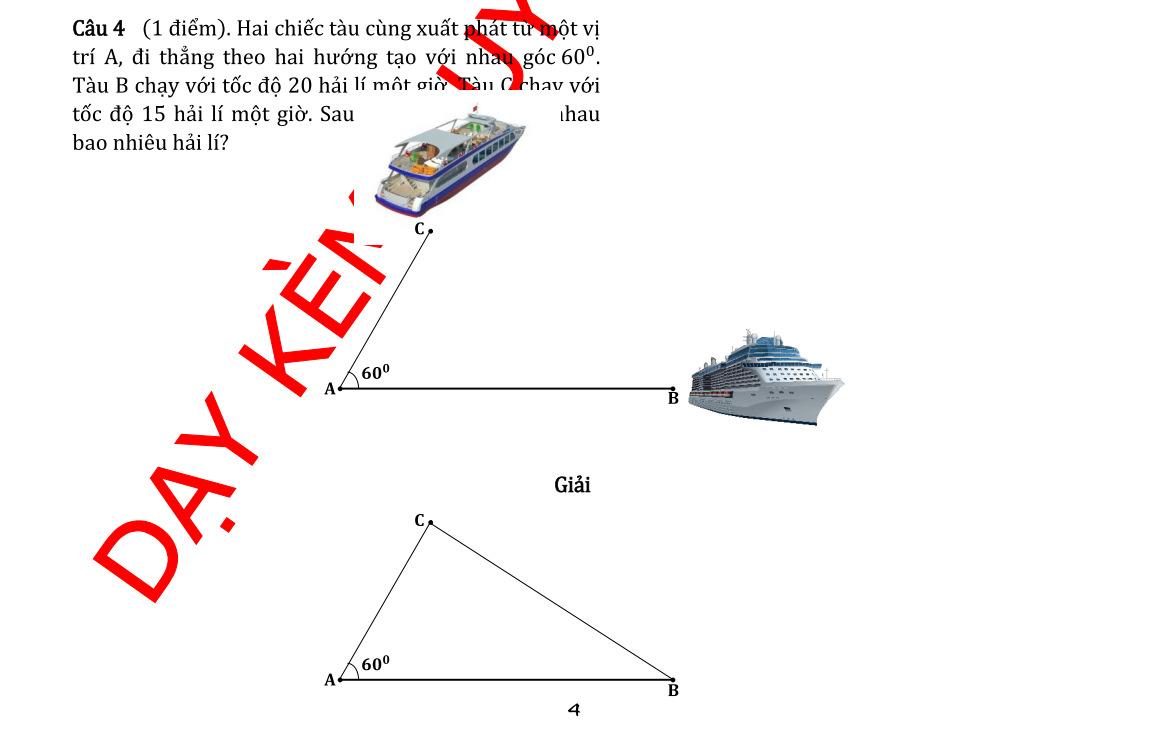



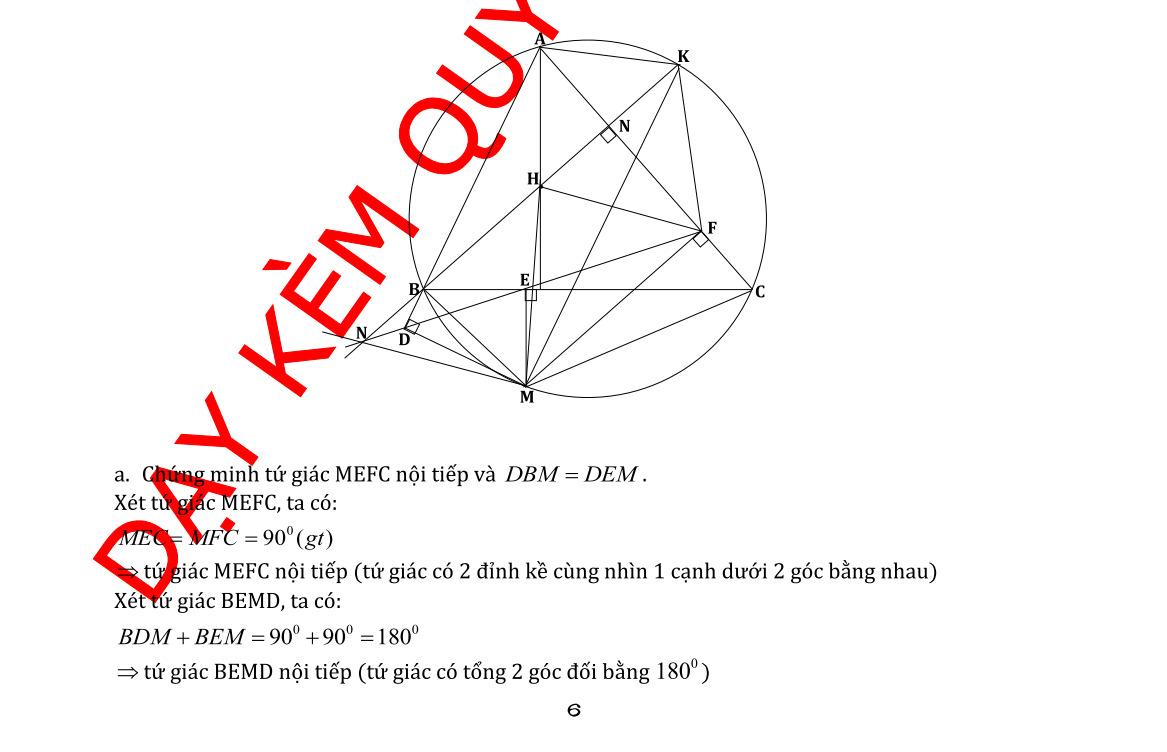




























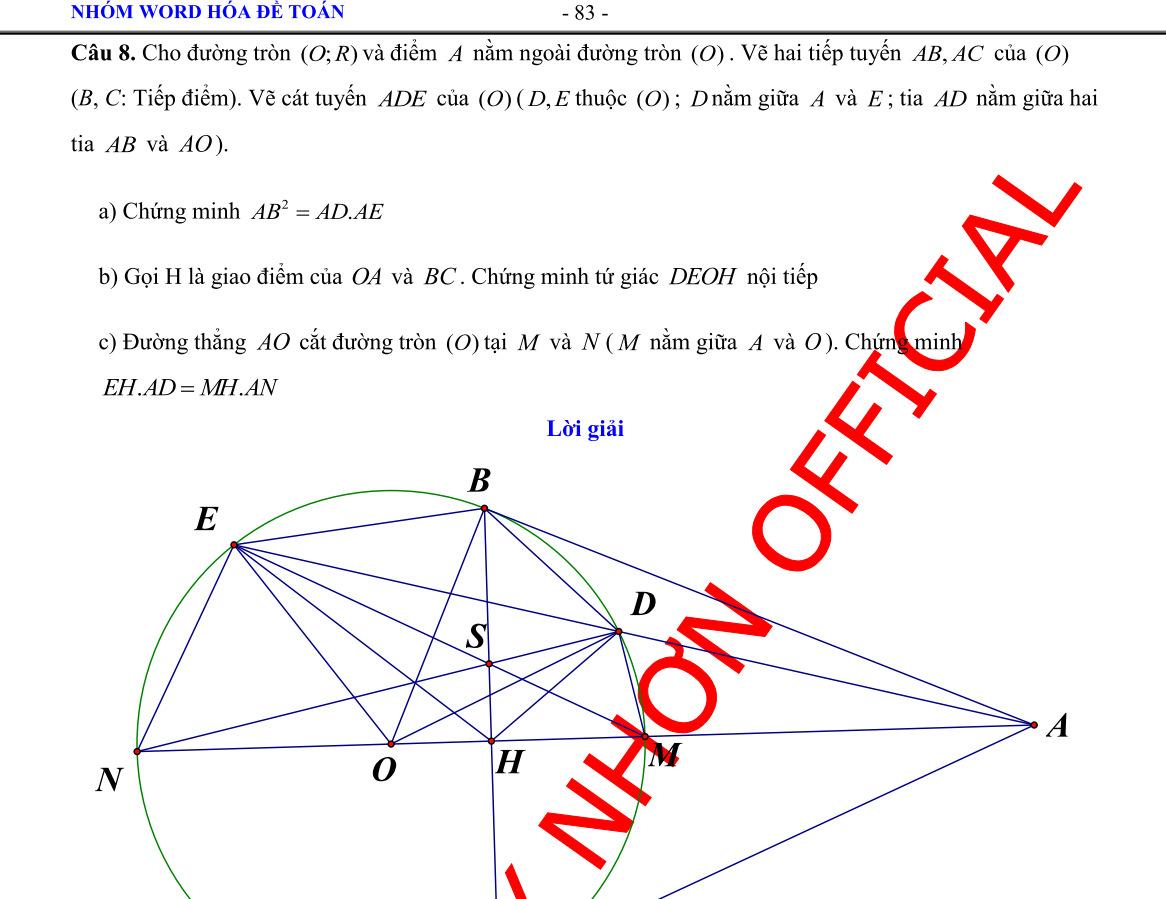










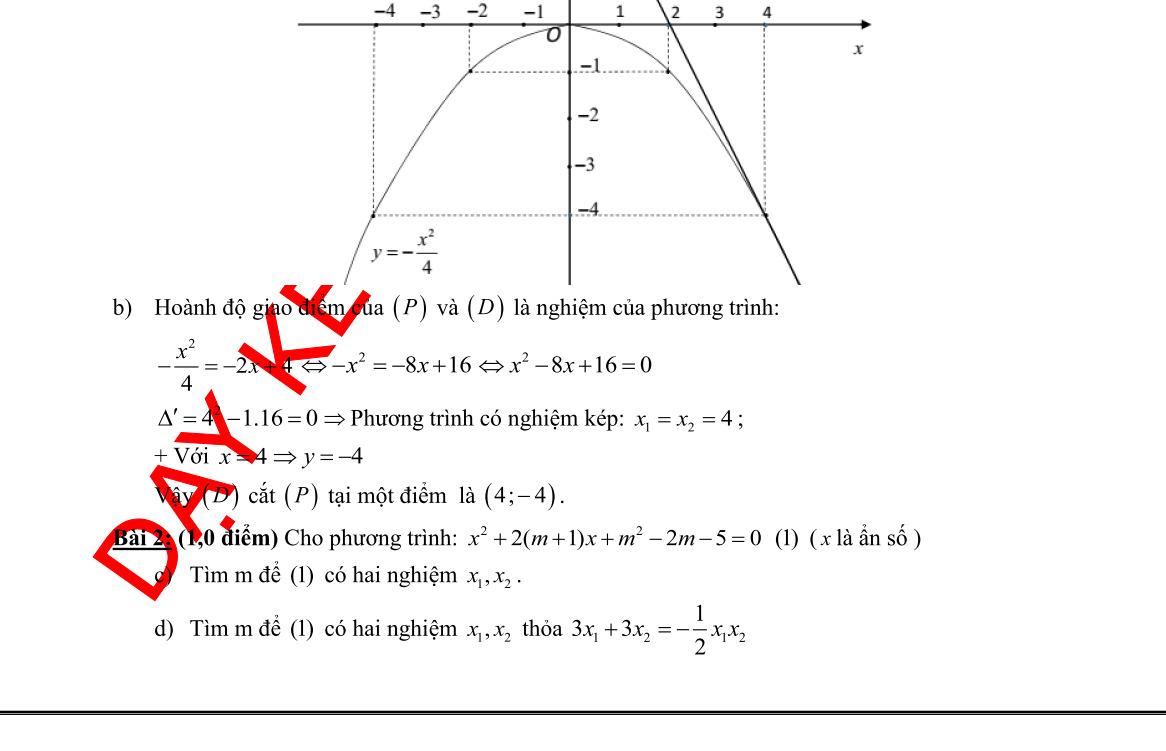





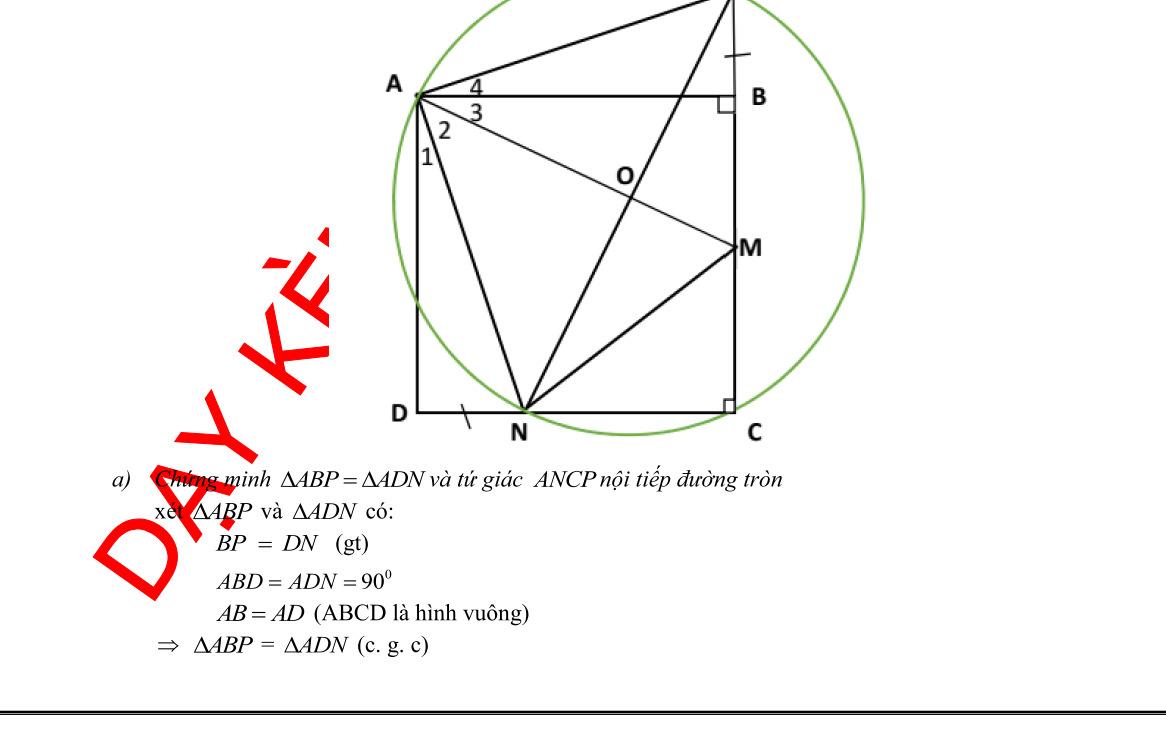







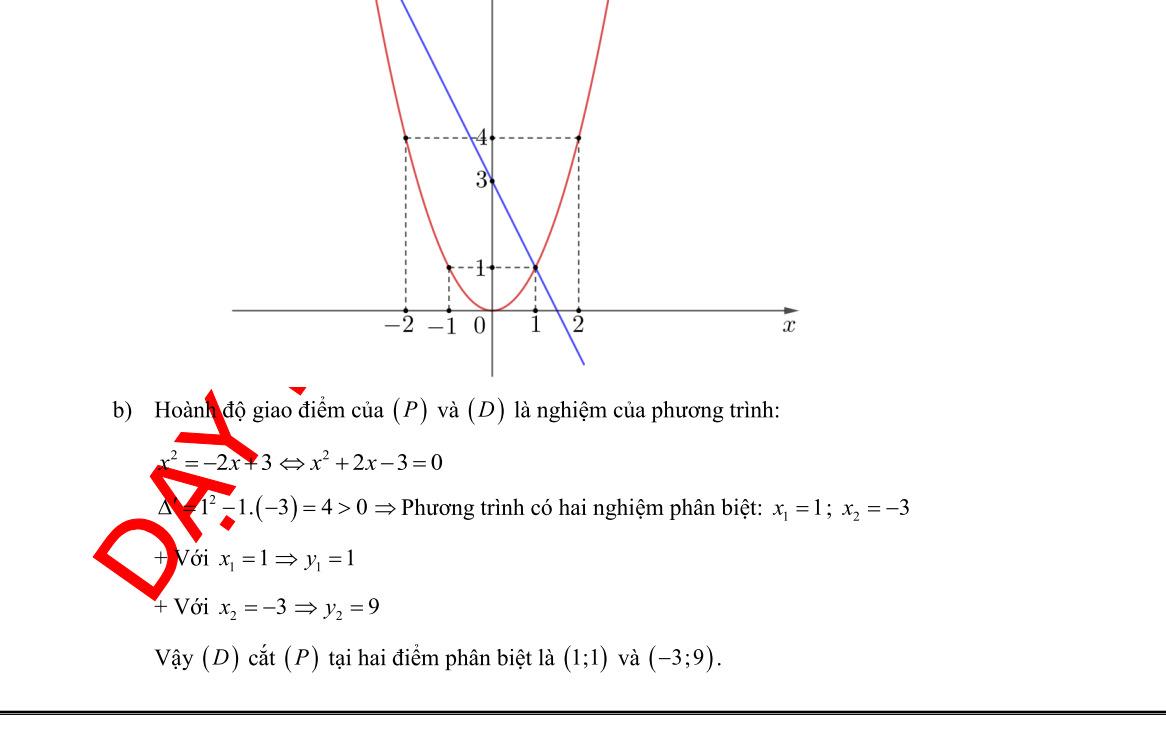






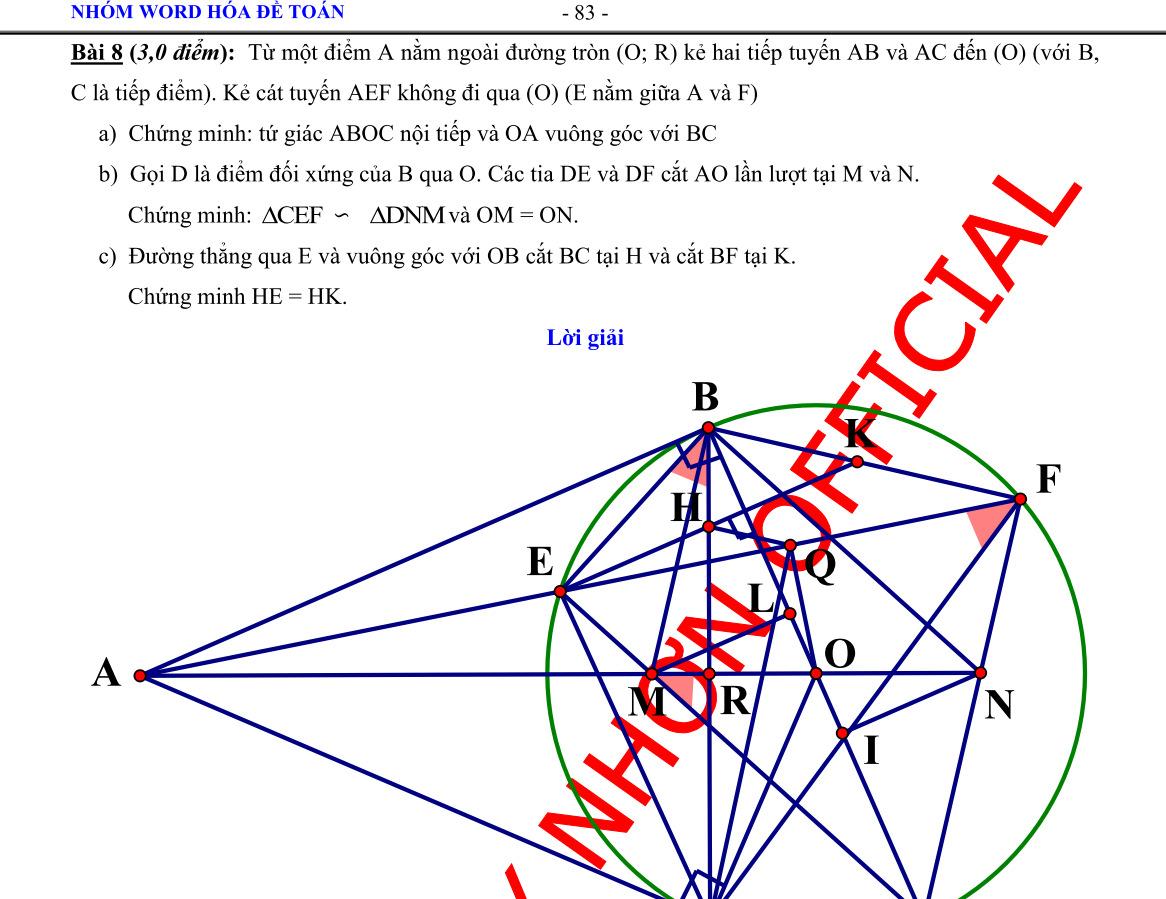














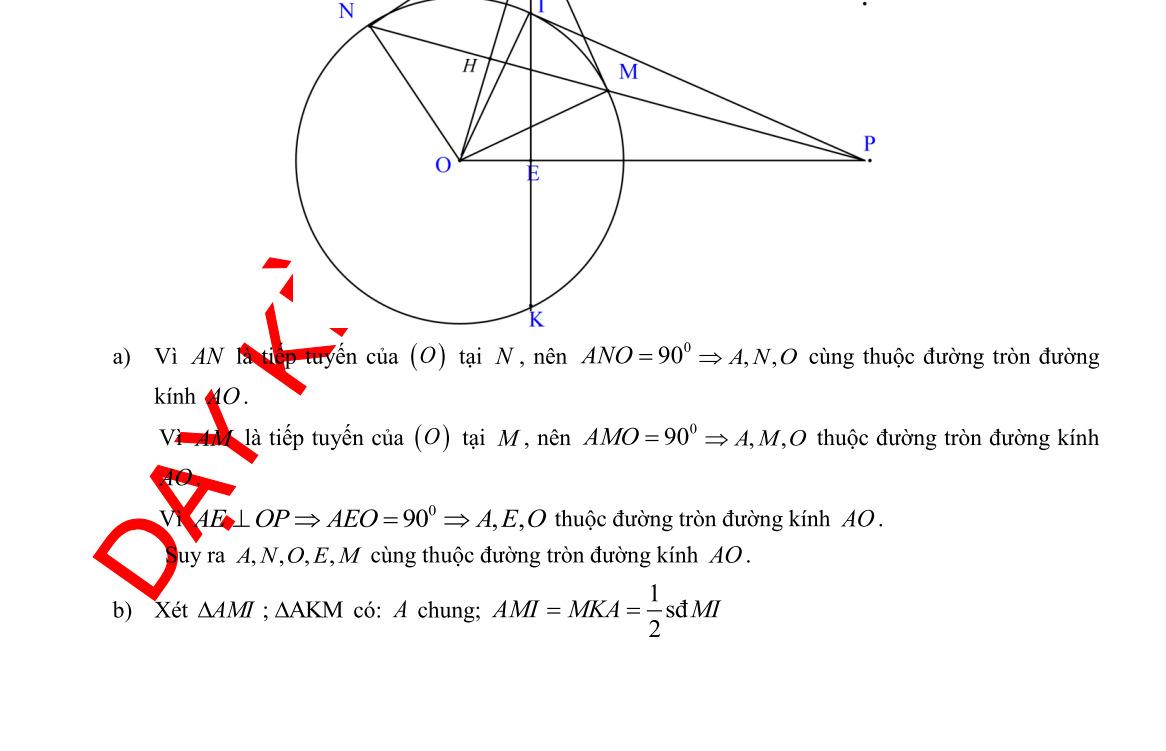















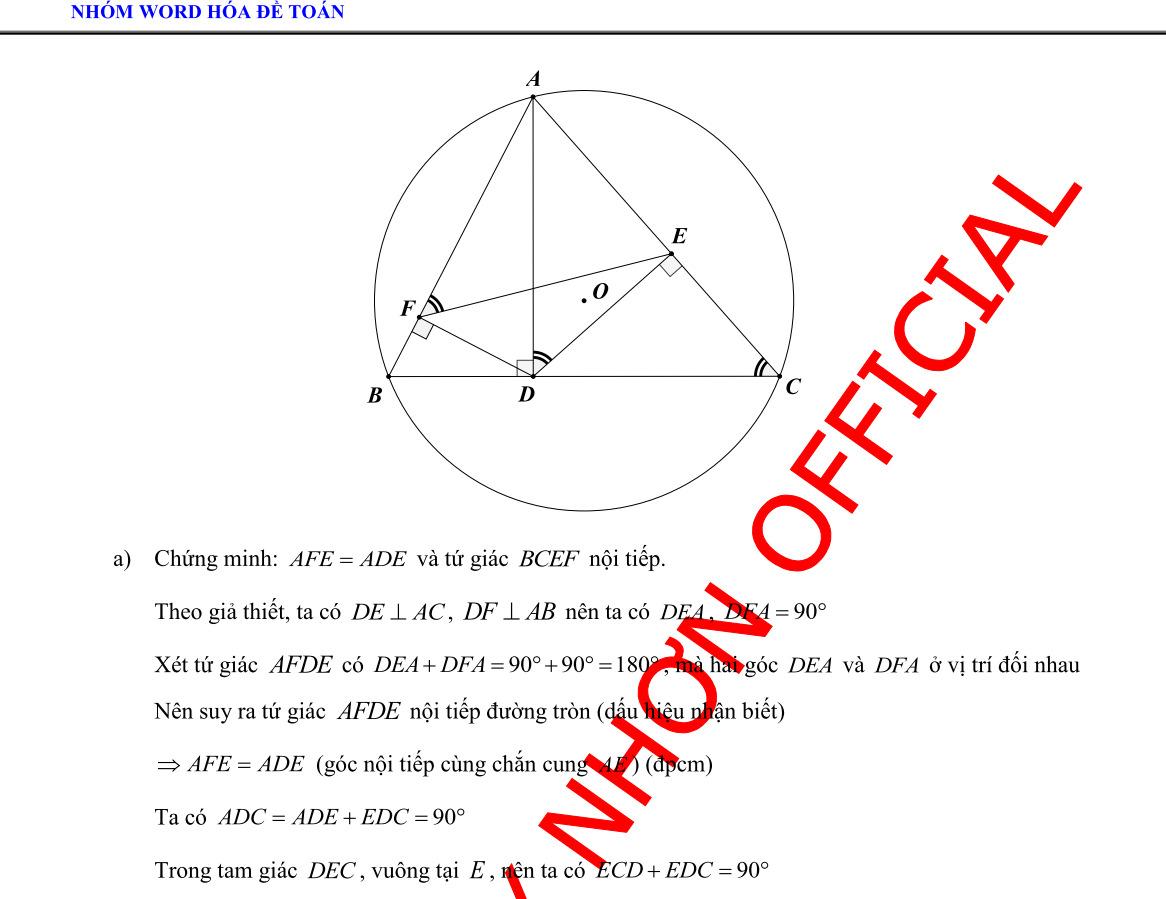

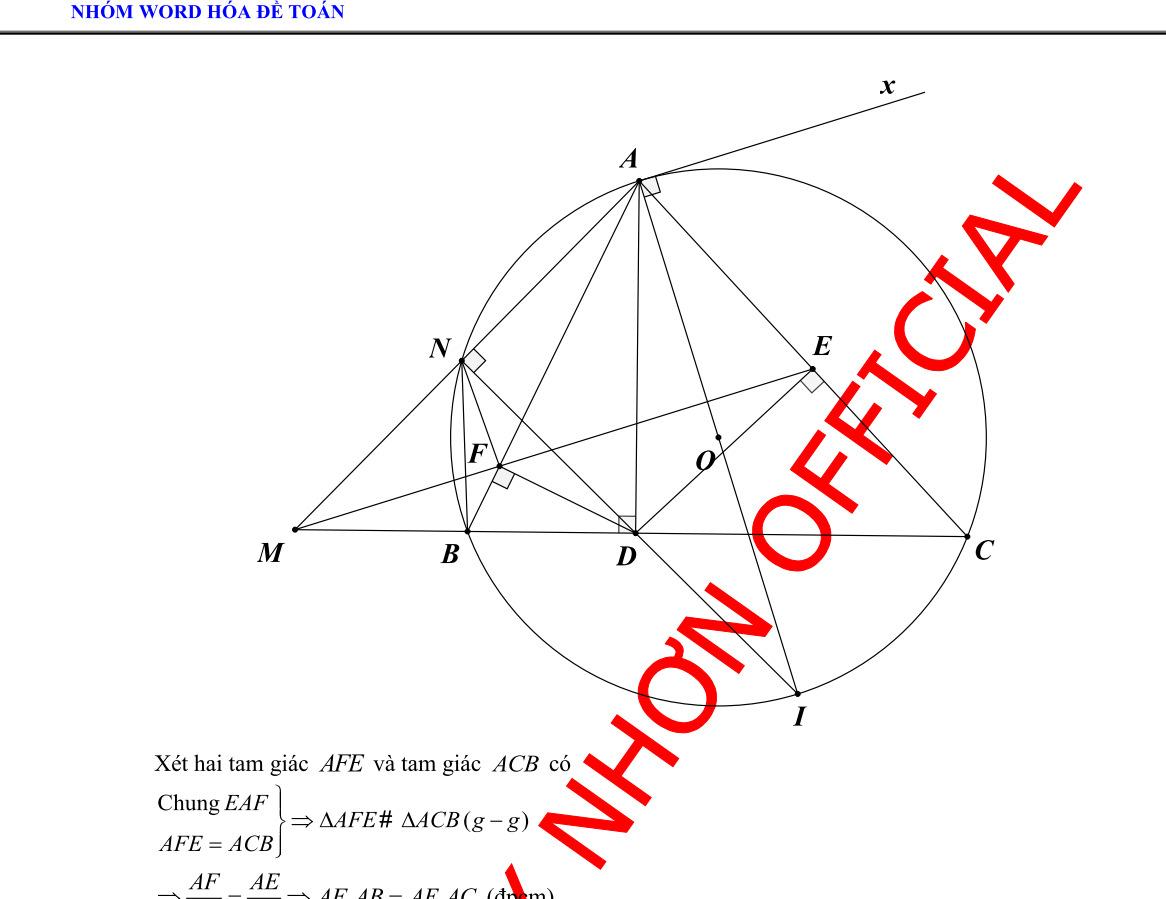










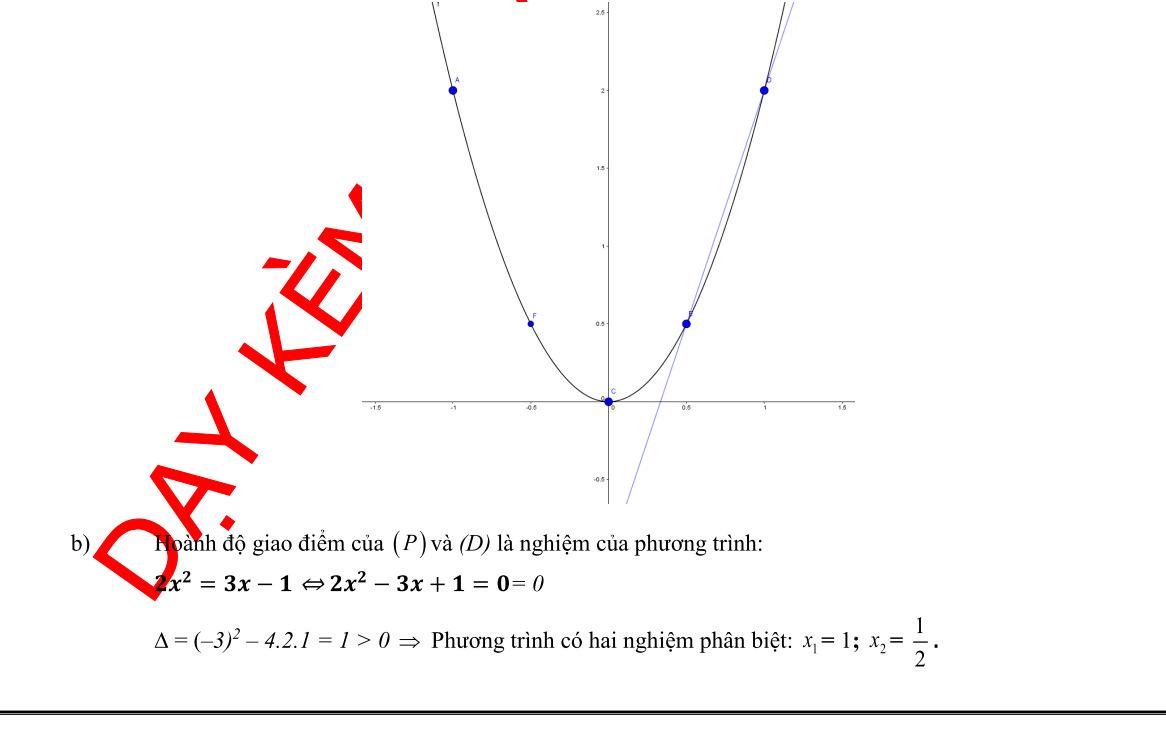






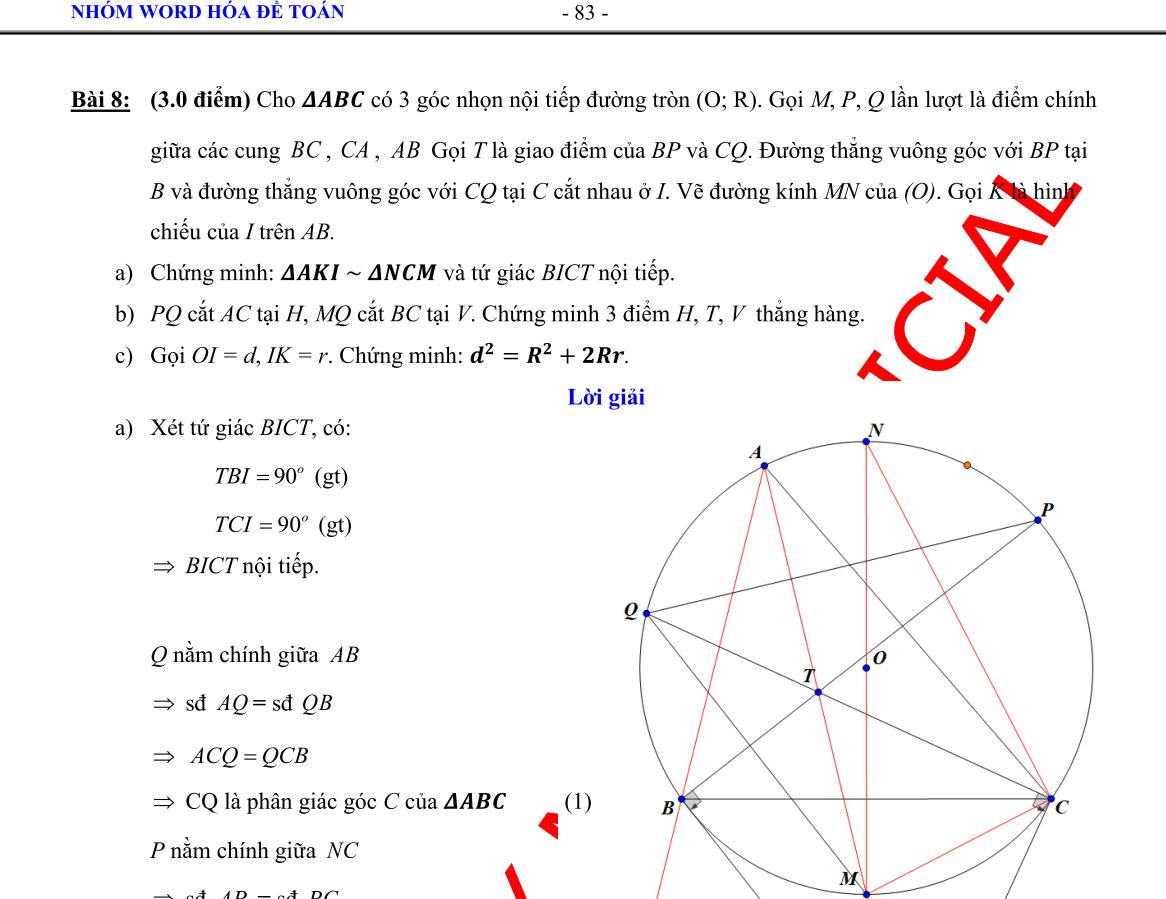
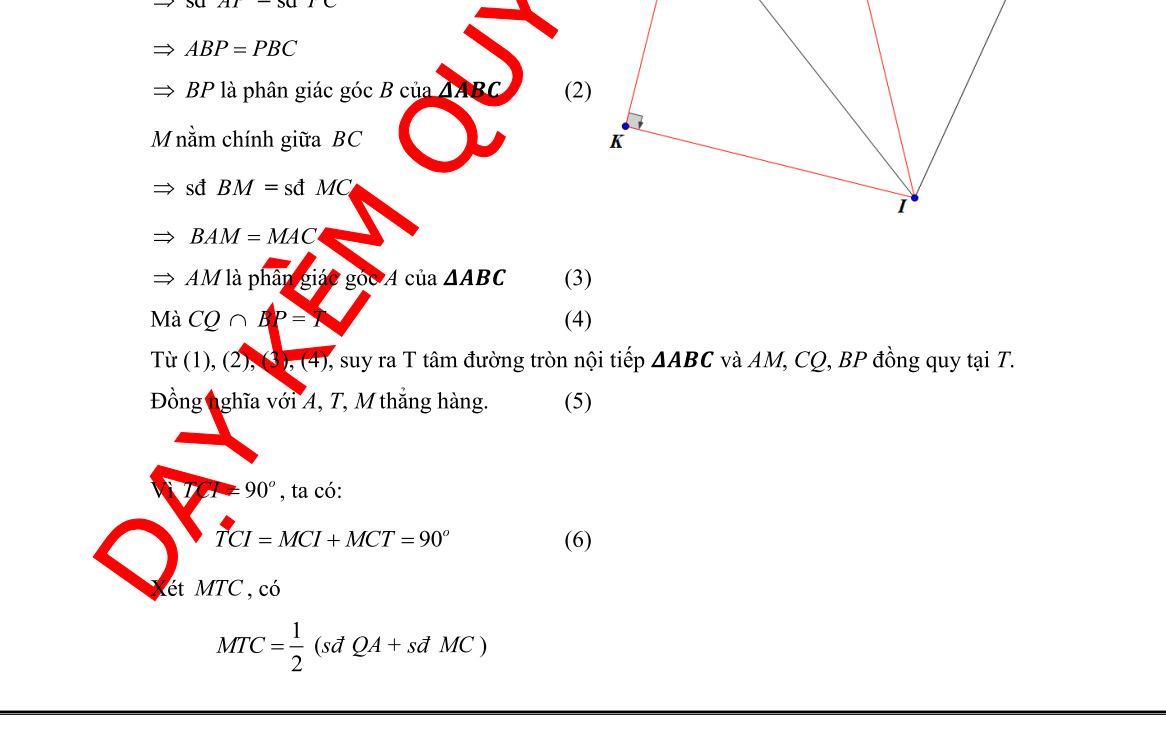

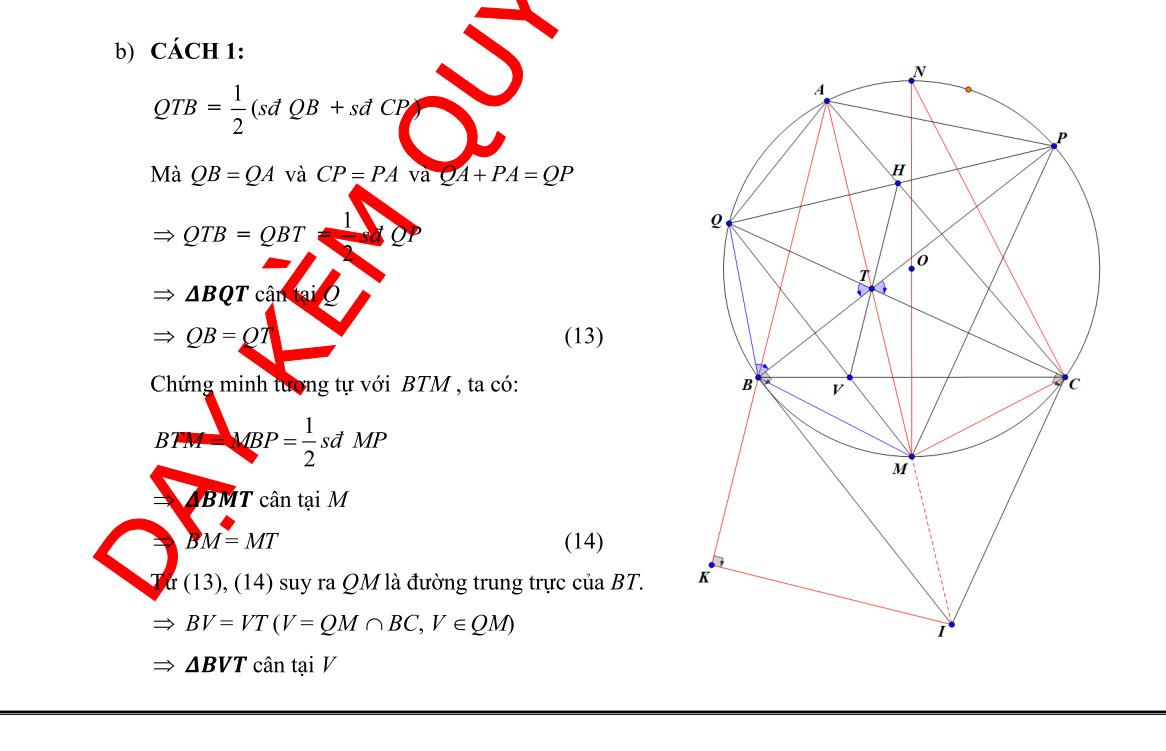


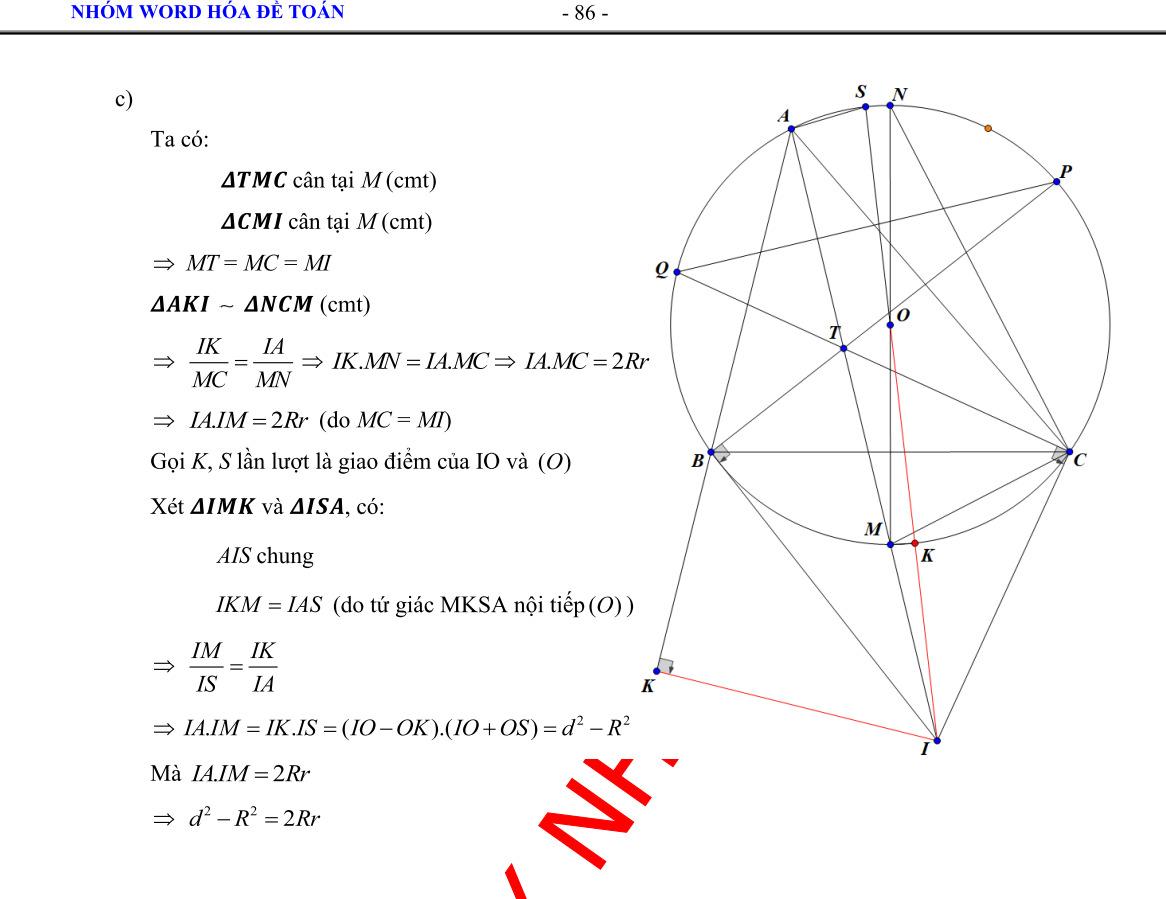











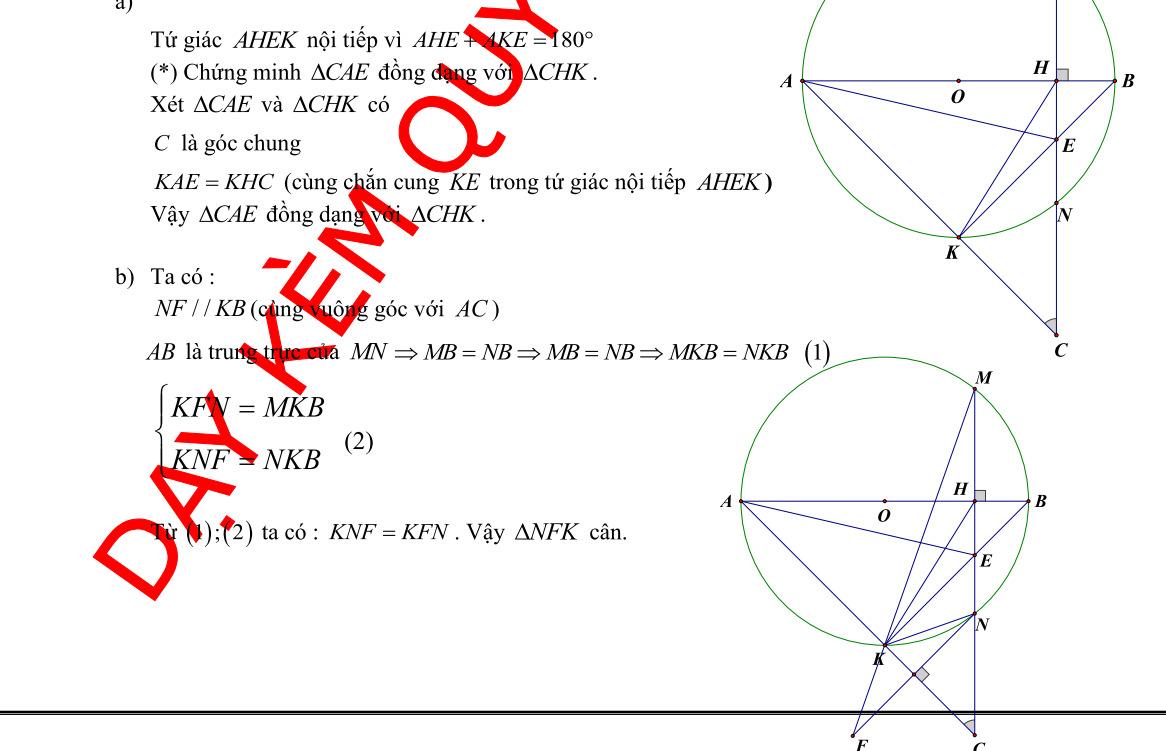
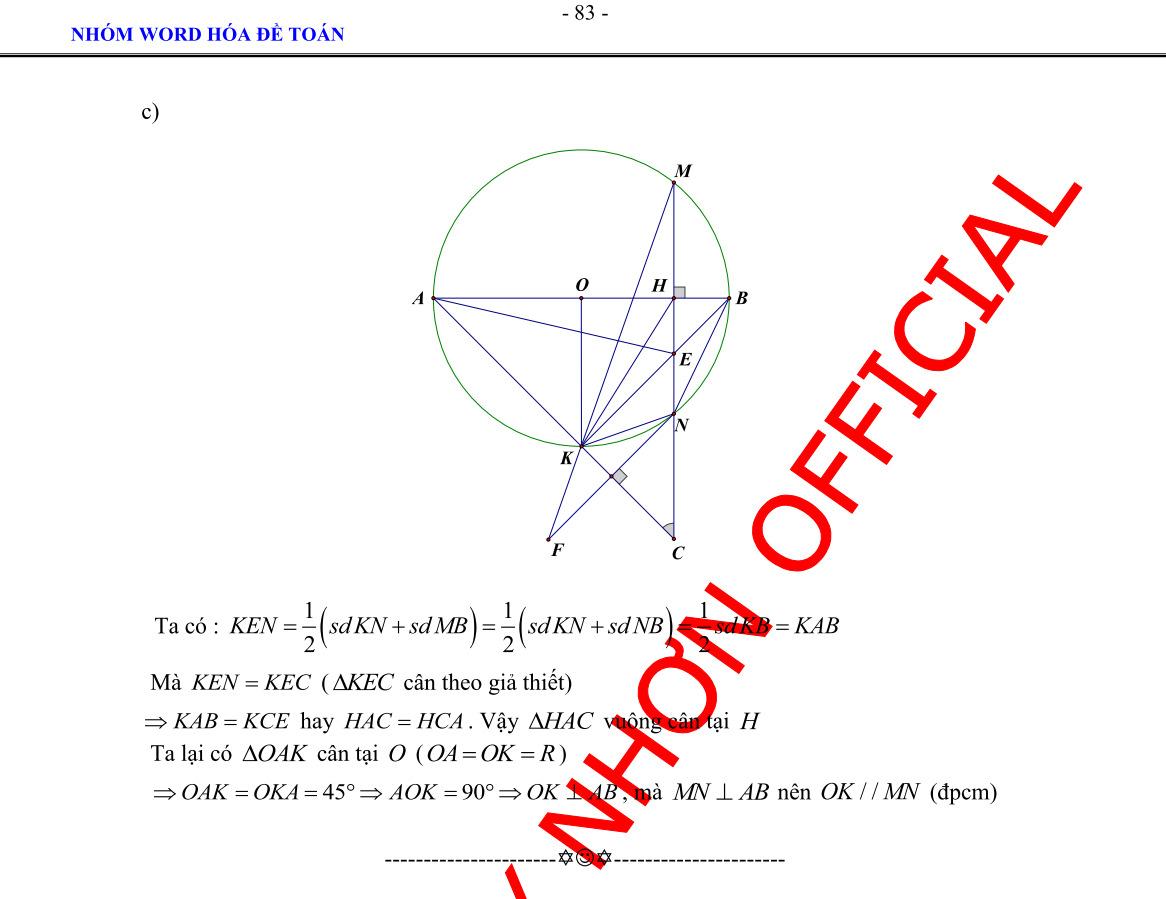





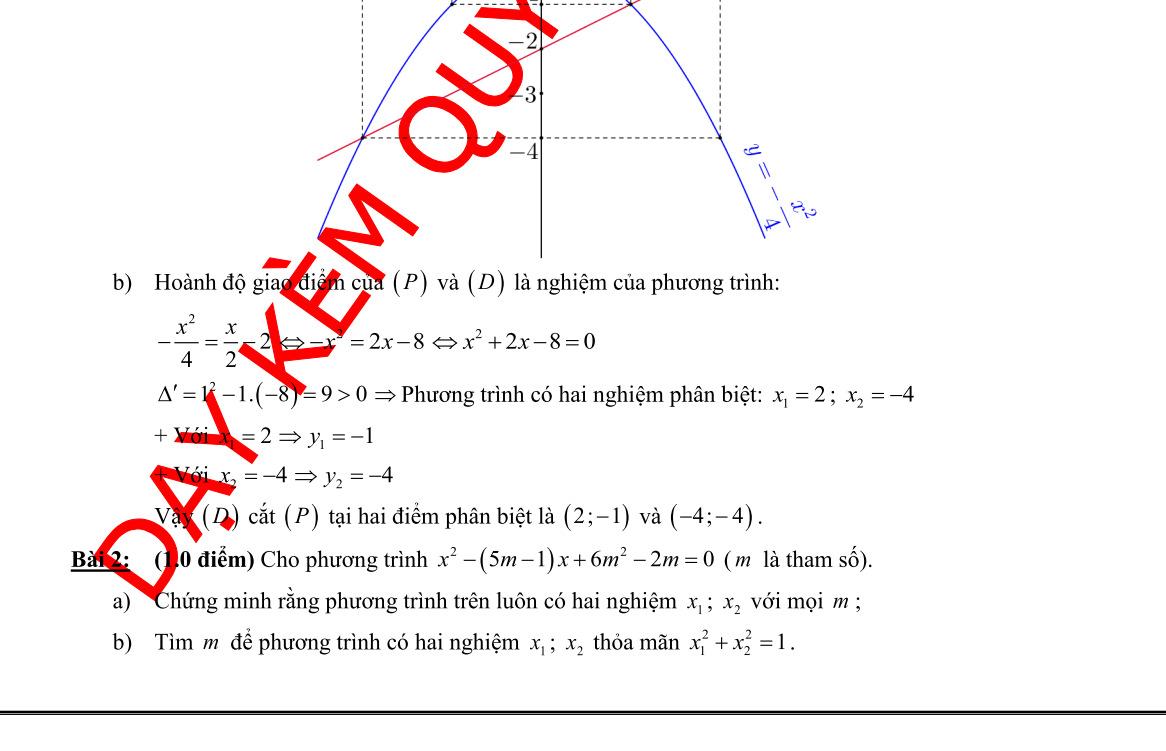














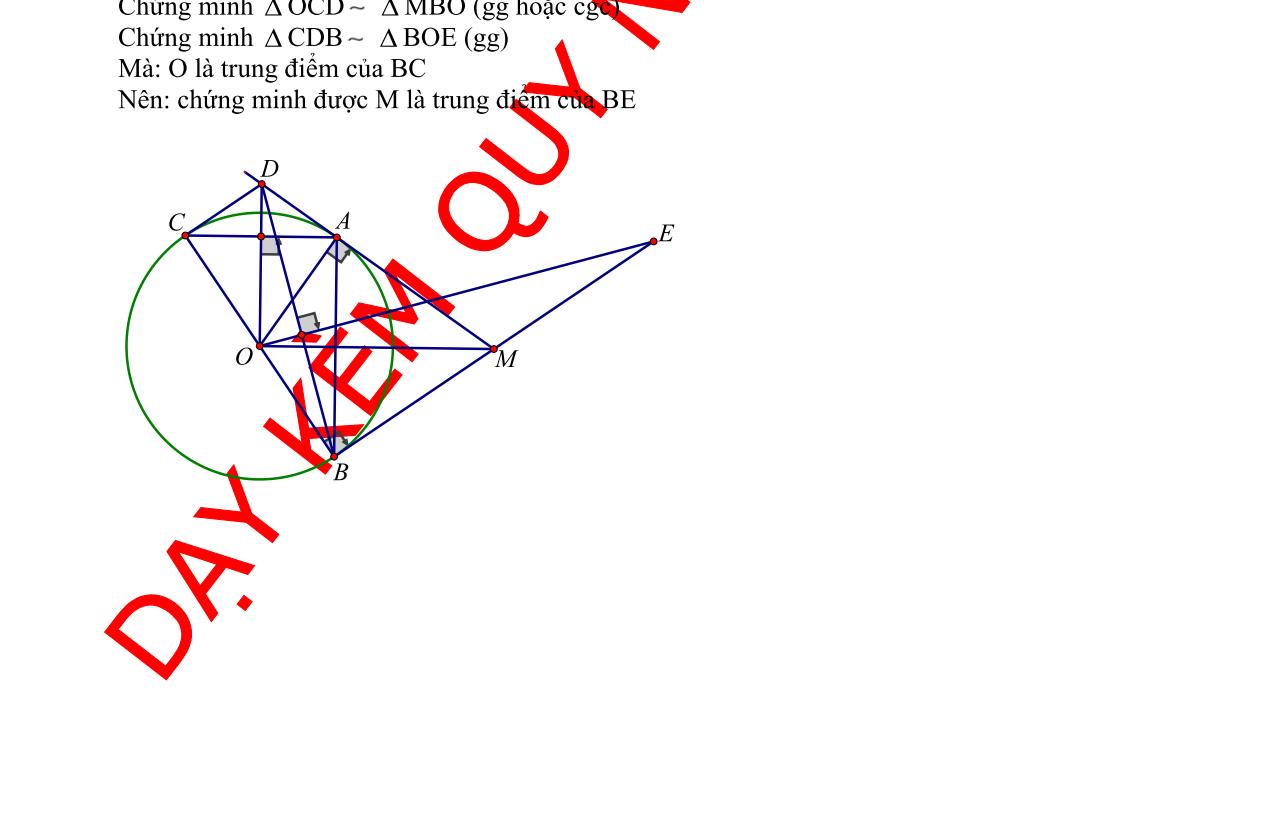







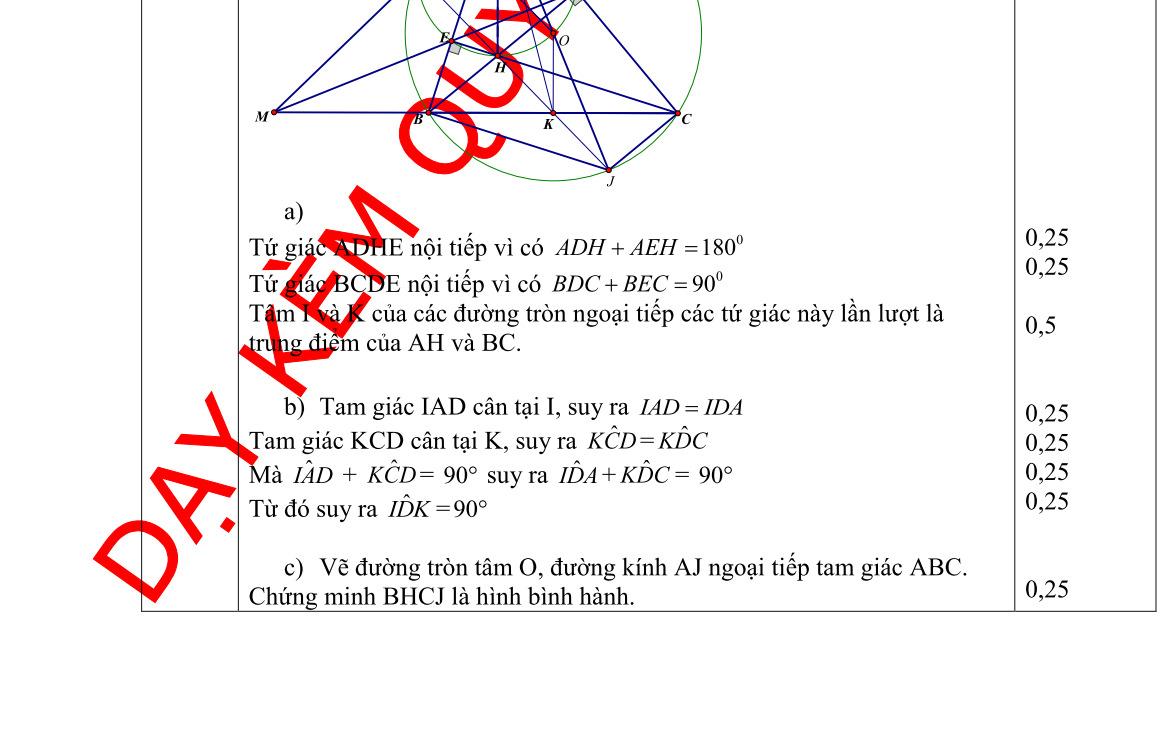











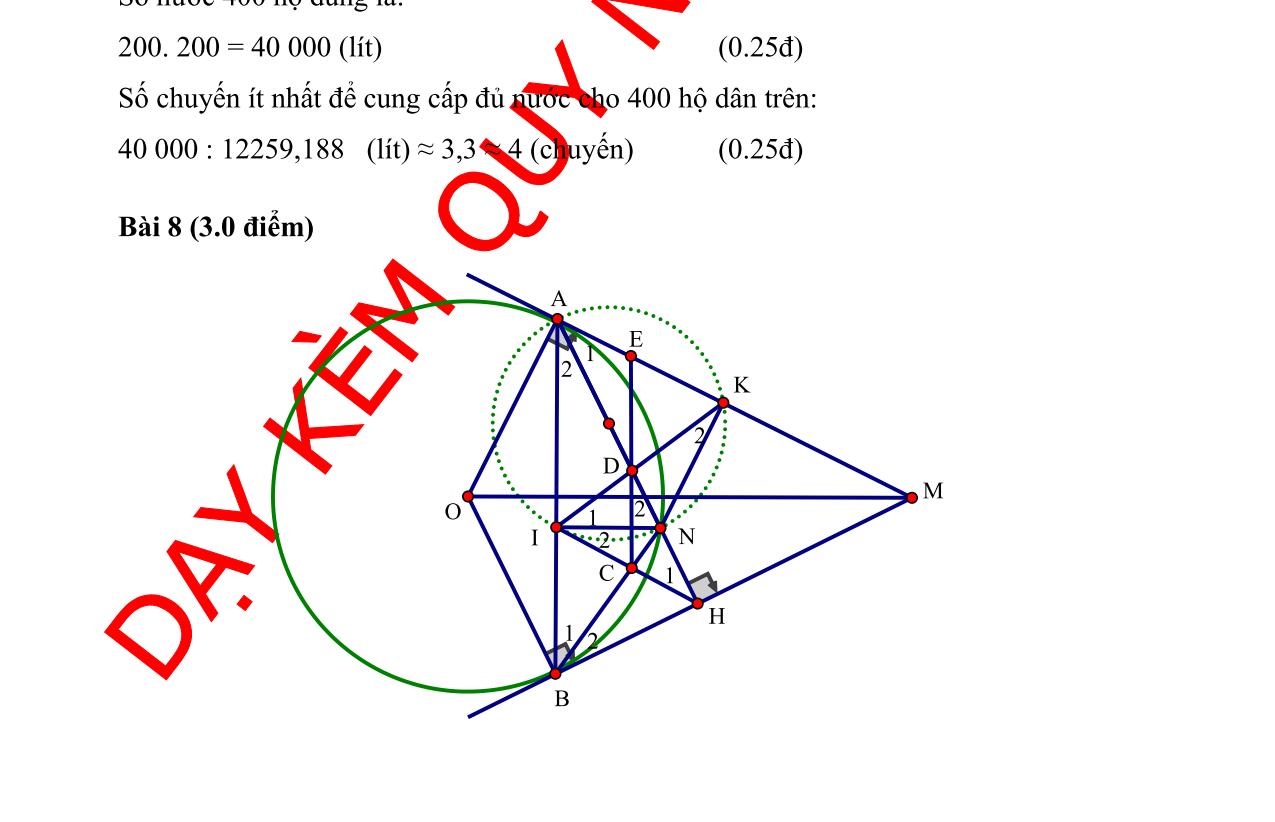






































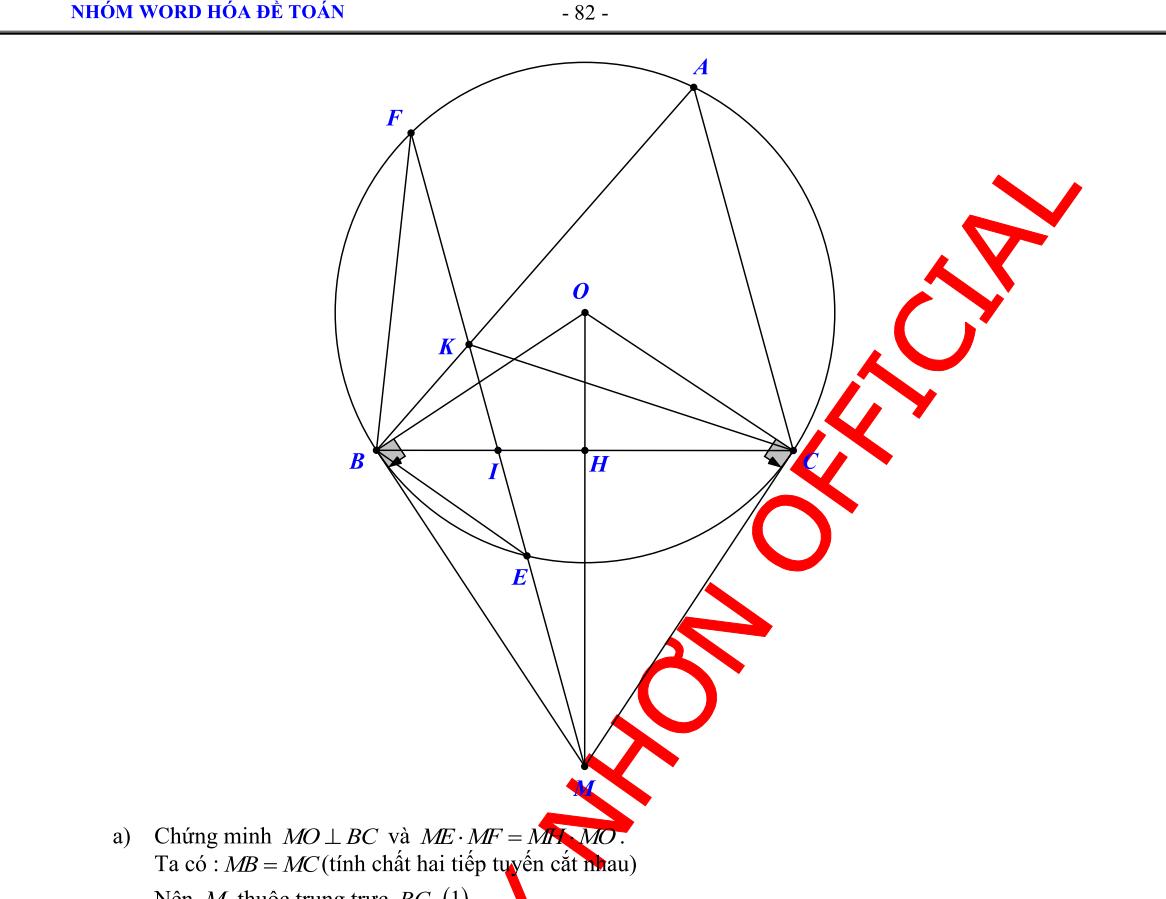

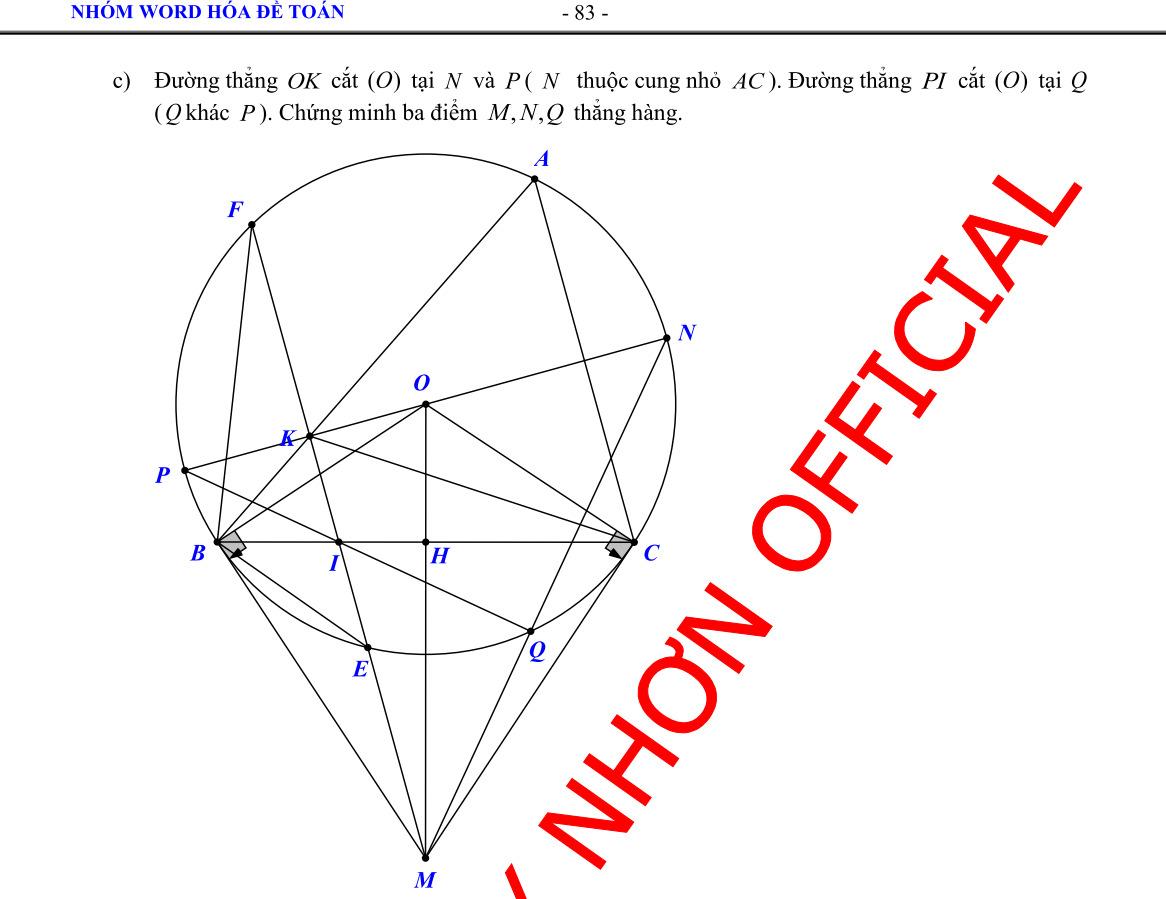








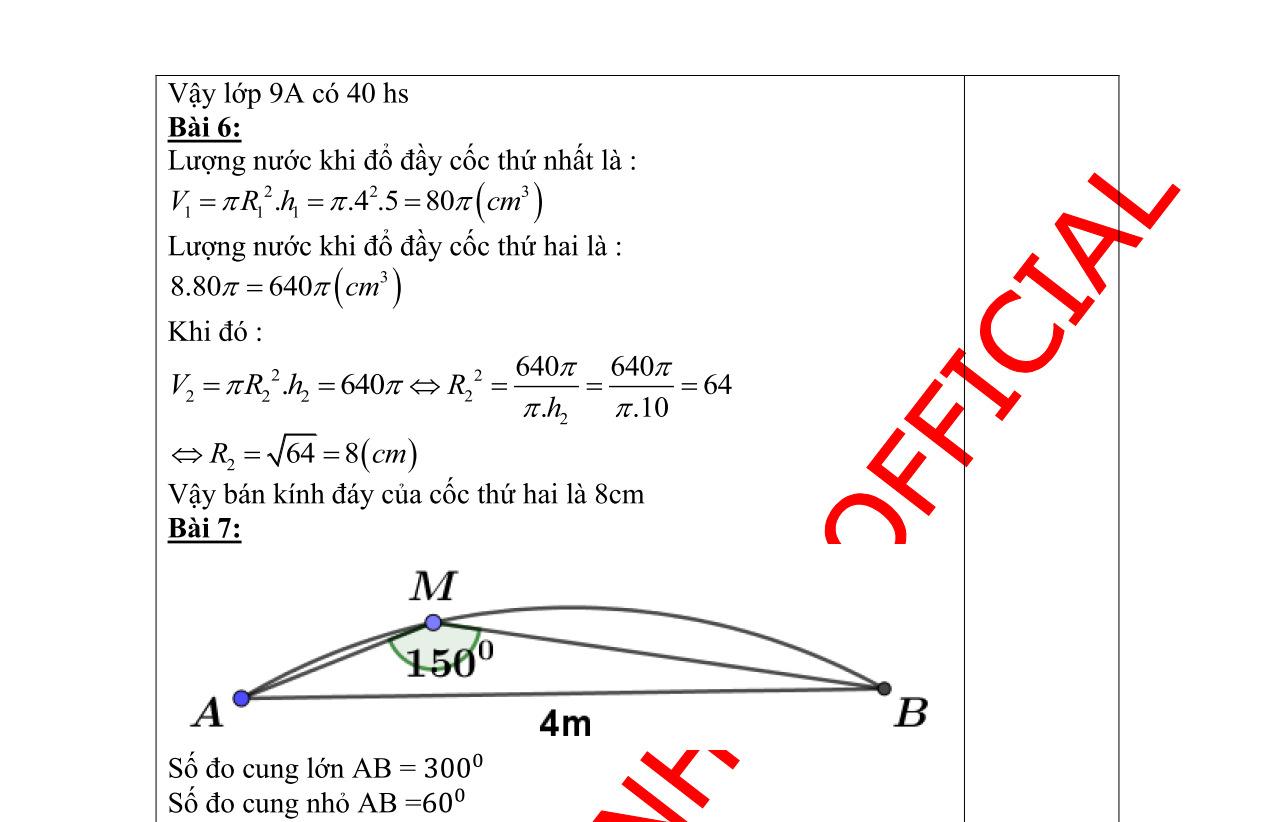










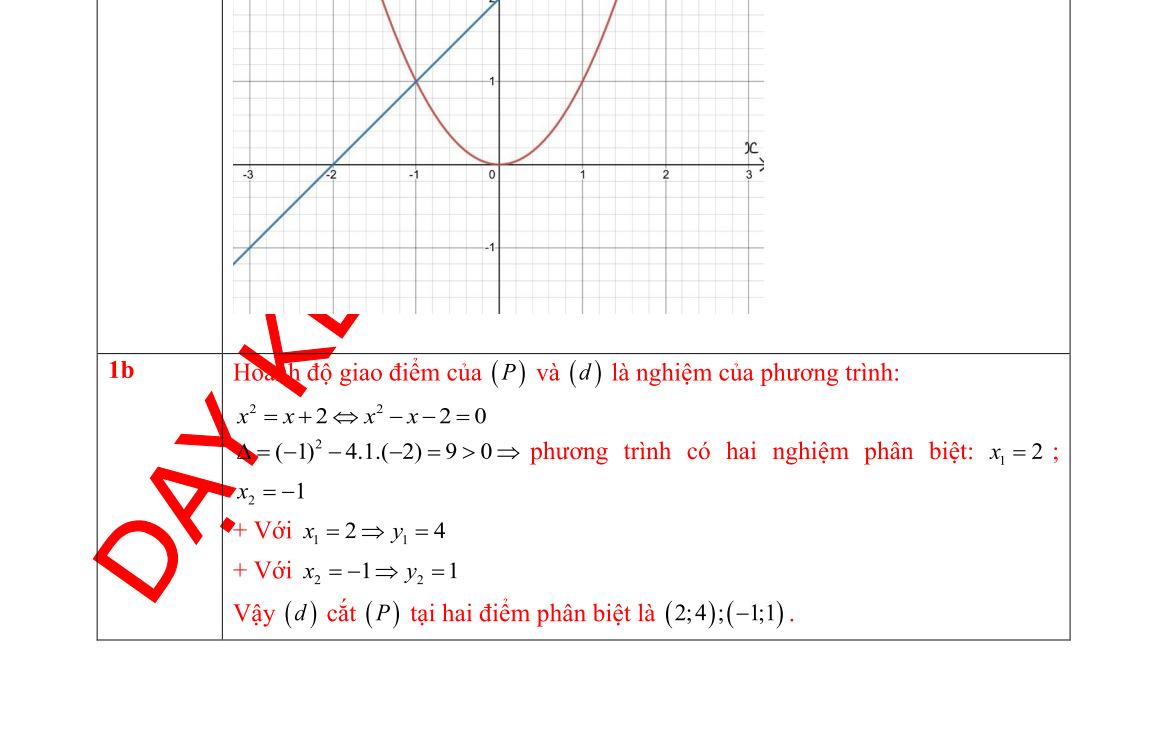









3:
điể


đây hơn 1 thế kỷ, nhà khoa học người Hà Lan Hendrich Lorentz đưa ra công thức tính số cân nặng lí tưởng của con người theo chiều cao như sau: 150 100 T MT N (công thức Lorentz). Trong đó: M là số cân nặng lí tưởng (kg), T là chiều cao (cm), N = 4 với nam và N = 2 với nữ.
a) Bạn Huy (là nam ) chiều cao là 1,75m. Hỏi cân nặng của bạn nên là bao nhiêu kg để đạt lí tưởng (làm tròn kết quả đến kg)?
b) Với chiều cao bằng bao nhiêu thì số cân nặng lí tưởng của nam giới và nữ giới bằng nhau (làm tròn kết quả đến chữ số thập phân thứ nhất)?
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10
--------------------
a)
b)
12
xx .
ủ
PHÒNG GD & ĐT QUẬN 1 NĂM HỌC 2022-20232 ĐỀ THAM KHẢO MÔN : TOÁN 9
Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : BÌNH CHÁNH – 3 Thời gian: 120 phút (không kể thời gian phát đề) Bài 1: (1.5 điểm) Cho parabol và đường thẳng
Vẽ () P và () D trên cùng mặt phẳng tọa độ Oxy .
Tìm giao điểm của () P và () D bằng phép toán Bài 2: (1.0 điểm) Cho phương trình 2 3x–2x–2=0có hai nghiệm
,
Hãy tính giá trị c
a biểu thức 12 21 xx + x- 1x D= - 1 Bài
(0.75
m) Cách
nhiệt độ theo F ( Fahrenheit ). Công thức để đổi từ C sang F có dạng yaxb trong đó x là số chỉ C và y là số chỉ của F tương ứng. Biết rằng nhiệt độ của nước đá đang tan ( C0 ) tương ứng F32 và nhiệt độ của nước đang sôi ( C100 ) tương ứng F212 . Em hãy cho biết nhiệt độ của một người bình thường ( C37 ) sẽ là bao nhiêu F ? Bài 5: (1.0 điểm). Cận thị trong học sinh ngày càng tăng. Lớp 9A có 35 học sinh, trong đó chỉ có 1 4 số học sinh nam và 1 5 số học sinh nữ không bị cận thị. Biết tổng số học sinh nam và học sinh nữ không bị cận thị là 8 học sinh. Tính số học sinh nữ không bị cận thị?
Bài 4: (0.75 điểm) Ở các nước như Anh, Mỹ người ta thường tính
Bài 6: (1.0 điểm). Một người mua 3 đôi giày với hình thức khuyến mãi như sau: Nếu bạn mua một đôi giày với mức giá thông thường bạn sẽ được giá giảm 30% khi mua đôi thứ hai và mua một đôi thứ ba với một nửa giá ban đầu. Bạn Anh đã trả tổng cộng
1320000 cho 3 đôi giày.
a) Hỏi Giá ban đầu của một đôi giày là bao nhiêu?
b) Nếu cửa hàng đưa ra hình thức khuyến mãi thứ hai là giảm 20%mỗi đôi giày. Bạn An nên chọn hình thức khuyến mãi nào nếu mua ba đôi giày Bài 7: (1.0 điểm) Một dụng cụ trộn bê tông gồm một phần có dạng hình trụ, phần còn lại có dạng hình nón. Các kích thước cho trên hình bên.
a) Tính thể tích của dụng cụ này. b) Tính diện tích mặt ngoài của dụng cụ (không tính nắp đậy). Bài 8: (3.0 điểm) Cho tam giác ABC nhọn AB<AC nội tiếp đường tròn O , các đường cao BF và CK của tam giác ABC cắt nhau tại H. Tia FK cắt tia CB tại M, AH cắt BC và đường tròn O lần lượt tại D và E EA . a) Chứng minh: Tứ giác BKFC nội tiếp và MK.MF=MB.MC. b) AM cắt đường tròn O tại N NA . Chứng minh : AKN=AFN c) Gọi I là hình chiếu của E lên AC . Tia EI cắt DC và đường tròn O lần lượt tại G và Q QE . Chứng minh : I là trung điểm của QG và 3 điểm N,F,Q thẳng hàng.
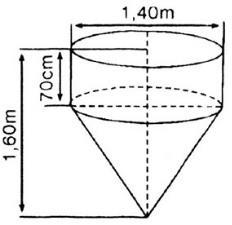
DẠYKÈMQUYNHƠN
OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN


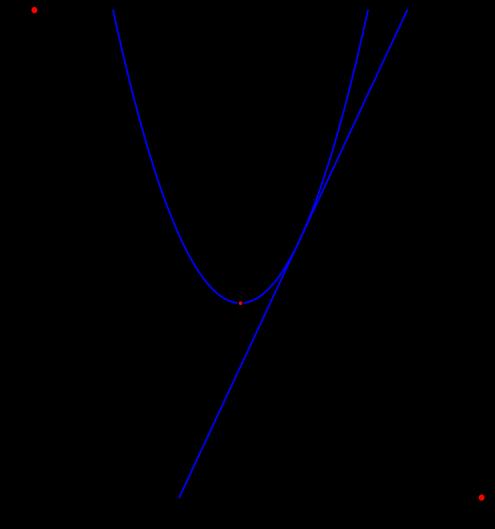
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN HƯỚNG DẪN GIẢI
phương trình(D):y=2x-1 ta được: y=2.1-1=1 Vậy tọa độ giao điểm của () P và () D là: 1;1 A Bài 2: (1.0 điểm) Cho phương trình 2 3x–2x–2=0có hai nghiệm 12 , xx Hãy tính giá trị của biểu thức 12 21 xx + x- 1x D= - 1 Lời giải Vì a = 3, c = - 2 nên a và c trái dấu. Suy ra phương trình đã cho có 2 nghiệm Ta có: 12 12 2 3 2 . 3 xx xx x 0 1 21yx -1 1
Bài 1: (1.5 điểm) Cho parabol và đường thẳng a) Vẽ () P và () D trên cùng mặt phẳng tọa độ Oxy b) Tìm giao điểm của () P và () D bằng phép toán Lời giải a) (0,75 đ) x -2 -1 0 1 2 2 yx 4 1 0 1 4 b) Phương trình hoành độ giao điểm của () P và (D) là: 2 21xx
2 210xx
2 10 x 10 x 1 x Thay 1 x vào
)6 33
Bài 3: (0.75 điểm) Cách đây hơn 1 thế kỷ, nhà khoa học người Hà Lan Hendrich Lorentz đưa ra công thức tính số cân nặng lí tưởng của con người theo chiều cao như sau: 150 100 T MT N
(công thức Lorentz). Trong đó: M là số cân nặng lí tưởng (kg), T là chiều cao (cm), N = 4 với nam và N = 2 với nữ a) Bạn Huy (là nam ) chiều cao là 1,75m. Hỏi cân nặng của bạn nên là bao nhiêu kg để đạt lí tưởng (làm tròn kết quả đến kg)?
b) Với chiều cao bằng bao nhiêu thì số cân nặng lí tưởng của nam giới và nữ giới bằng nhau (làm tròn kết quả đến chữ số thập phân thứ nhất)?
Lời giải a/ Bạn Huy (là nam ) chiều cao là 1,75m nên cân nặng của bạn để đạt lí tưởng là: b/ Vì cân nặng lý tưởng cùa nam và nữ bằng nhau và với nam là N = 4, nữ là N = 2 ta có: Bài 4: (0.75 điểm) Ở các nước như Anh, Mỹ người ta thường tính nhiệt độ theo F ( Fahrenheit ). Công th
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN
D=
22 121212 2112 2 2 121212 1212 xxx+x-(x+x) += x - 1x - 1(x-1).(x-1) 2-22 -2×(x+x)-2xx-(x+x)-5 333 === xx-(x+x22
t rằng nhiệt độ của nước
) tương ứng F212 .
ế
ệt độ của một người bình thường ( C37 ) sẽ là bao nhiêu F ? Lời giải Công thức để đổi từ C sang F có dạng yaxb trong đó x là số chỉ C và y là số chỉ của F tương ứng. ( C0 ) tương ứng F32 suy ra a.0+b=321 ( C100 ) tương ứng F212 suy ra 100.a+b=2122 Từ (1) và (2) có hệ phương trình : 0.321,8 100a21232 aba bb Vậy công thức đổi từ C sang F là : y,x1832 150175150 10017510056,2556() 4 T MTkg N 150150 100100 42 2300150150 () TT TT TTTcm
ức để đổi từ C
sang F có dạng yaxb trong đó x là số chỉ C và y là số chỉ của F tương ứng. Biế
đá đang tan ( C
0 ) tương ứng F
32 và nhiệt độ của nước đang sôi ( C
100
Em hãy cho bi
t nhi
Bài 5: (1.0 điểm). Cận thị trong học sinh ngày càng tăng. Lớp 9A có 35 học sinh, trong đó chỉ có 1 4 số học sinh nam và 1 5 số học sinh nữ không bị cận thị. Biết tổng số học sinh nam và học sinh nữ không bị cận thị là 8 học sinh. Tính số học sinh nữ không bị cận thị? Lời giải
Gọi x là số học sinh nam lớp 9A ( * x ) Số học sinh nữ là 35 x
Số học sinh nam không bị cận thị là 1 4 x
Số học sinh nữ không bị cận thị là 1 35 5 x Theo đề bài, ta có phương trình :
Vậy số học sinh nữ không bị cận thị là 1 35203 5
học sinh.
Bài 6: (1.0 điểm). Một người mua 3 đôi giày với hình thức khuyến mãi như sau: Nếu bạn mua một đôi giày với mức giá thông thường bạn sẽ được giá giảm 30% khi mua đôi thứ hai và mua một đôi thứ ba với một nửa giá ban đầu. Bạn Anh đã trả tổng cộng 1320000 cho 3 đôi giày.
a) Hỏi Giá ban đầu của một đôi giày là bao nhiêu? b) Nếu cửa hàng đưa ra hình thức khuyến mãi thứ hai là giảm 20%mỗi đôi giày. Bạn An nên chọn hình thức khuyến mãi nào nếu mua ba đôi giày Lời giải
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN Do đó khi x 37 thì y,., 183732986
ậ
OFFICIAL
V
y nhiệt độ bình thường của con người là C
37 hay ,F
986 .
xxxn
11 358...20 45
a) Gọi x(đ)là giá ban đầu của một đôi giày x>0 Theo đề bài ta có pt: x+(100%-30%)x+(100%-50%)x=1320000 x+0,7x+0,5x=1320000 2,2x=1320000 x=600000 Vậy giá ban đầu của một đôi giày 600000đ b) Tổng số tiền khi mua 3 đôi giày được giảm 20% là 600000.3.100%-20%=1440000đ Vậy Bạn An nên chọn hình thức khuyến mãi thứ nhật nếu mua ba đôi giày. 1320000đ<1440000đ
M, AH cắt BC và đường tròn
O lần lượt tại D và E EA . a) Chứng minh: Tứ giác BKFC nội tiếp và MK.MF=MB.MC. b) AM cắt đường tròn O tại N NA . Chứng minh : AKN=AFN. c) Gọi I là hình chiếu của E lên AC . Tia EI cắt DC và đường tròn O lần lượt tại G và Q QE . Chứng minh : I là trung điểm của QG và 3 điểm N,F,Q thẳng hàng. Lời giải

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN
hình nón 23 2 1 .0,7.0,90,147() 3 Vm . Vậy Thể tích của dụng cụ này: 3 12 0,3430,1470,49 VVVm b) Diện tích xung quanh dụng cụ là: 2.. xqhthn SSSrhrl 222 497130 2.0,7.0,7.0,7.0,70,9 50100 m . Bài 8: (3.0 điểm) Cho tam giác ABC nhọn AB<AC nội tiếp đường tròn O , các đường cao BF và CK của tam giác ABC cắt nhau tại H. Tia FK cắt tia CB tại
G D Q I E H N M K F O B C A
Bài 7: (1.0 điểm) Một dụng cụ trộn bê tông gồm một phần có dạng hình trụ, phần còn lại có dạng hình nón. Các kích thước cho trên hình bên. a) Tính thể tích của dụng cụ này. b) Tính diện tích mặt ngoài của dụng cụ (không tính nắp đậy). Lời giải Thể tích phần hình trụ: 23 1 .0,7.0,70,343()
Vm Thể tích phần
ABC nhọn ABAC nội tiếp đường tròn O
BF và CK là đường cao của tam giác ABC cắt nhau tại H
GT Gọi I là hình chiếu của E lên AC
KL a) Chứng minh: Tứ giác BKFC nội tiếp và MKMFMBMC
b) Chứng minh : AKNAFN .
c) Chứng minh : I là trung điểm của QG và 3 điểm ,, NFQ thẳng hàng.
a) Xét tứ giác BKFC , có:
90 BKC (CKAB , CK là đường cao của ABC ) 90 BFC ( BFAC , BF là đường cao của ABC )
Do đó: 90 BKCBFC
Mà 2 đỉnh , KF cùng nhìn cạnh CB dưới 1 góc vuông
Suy ra tứ giác BKFC nội tiếp.
Xét MKB và MCF , có:
FMC : chung ( góc trong bằng góc ngoài đối diện, tứ giác BKFC nội tiếp)
Vậy MKBMCFgg ∽ MKMC MBMF MKMFMBMC

Chứng minh được : MN.MA = MB.MC
Xét MBN và MAC , có: AMC : chung MNBMCA ( góc trong bằng góc ngoài đối diện, tứ giác BNAC nội tiếp)
Vậy MNBMCAgg ∽ MNMC MBMA .. MNMAMBMC Mà MKMFMBMC Nên .. MNMF MNMAMKMF MKMA
Xét MNK và MFA , có: AMF : chung MNMF MKMA (chứng minh trên)
Vậy MKNMAFcgcMNKMFA
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN
OFFICIAL
∽ suy ra, tứ giác KFAN nội tiếp (góc trong bằng góc ngoài đối diện) AKNAFN Chứng minh : I là trung điểm của QG và 3 điểm ,, NFQ thẳng hàng. Trong ABC có , BFCK là hai đường cao cắt nhau tại H nên H là trực tâm của ABC suy ra ADBC tại D Suy ra DEGICG mà ICQDEG . Suy ra ICGICQ Từ đó chứng minh được IGIQ . Suy ra I là trung điểm của QG . Chứng minh : 3 điểm ,, NFQ thẳng hàng. Ta có ICGICQ mà ICGAKF và AKFANF . Suy ra ANFICQ . Mà ICQANQ . Suy ra ANFANQ .
NHÓM WORD HÓA ĐỀ TOÁN Suy ra 2 tia NF và NQ trùng nhau nên ba điểm ,, NFQ thẳng hàng.
DẠYKÈMQUYNHƠN OFFICIAL
3: (0.75
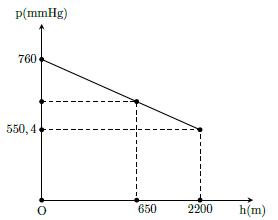
vì m
chu k
quay c
a Mặt Trăng quanh Trái Đất là khoảng 29,53 ngày nên một năm âm lịch chỉ có khoảng 354 ngày (làm tròn). Do vậy, cứ sau một vài năm âm lịch thì người ta phải bổ sung một tháng (tháng nhuận) để đảm bảo năm âm lịch tương đối phù hợp với chu kỳ của thời tiết. Cách tính năm nhuận âm lịch như sau: Lấy số năm chia cho 19, nếu số dư là một trong các số: {0;3;6;9;11;14;17} thì năm âm lịch đó có tháng nhuận. Ví dụ:
2017 là năm nhuận âm lịch vì 2017 chia 19 dư 3. 2015 không phải là năm nhuận âm lịch vì 2015 chia 19 dư 1.
a) Em hãy sử dụng quy tắc trên để xác định năm 1995 và 2030 có phải năm nhuận âm lịch hay không?
b) Năm nhuận dương lịch là năm chia hết cho 4. Ngoài ra, những năm chia hết cho 100 chỉ được coi là năm nhuận dương lịch nếu chúng cũng chia hết cho 400 (ví dụ 1600 là năm nhuận dương lịch nhưng 1700 không phải năm nhuận dương lịch). Hỏi trong các năm từ năm 1895 đến năm 1930, năm nào vừa là năm nhuận âm lịch vừa là năm nhuận dương lịch?
Bài 4: (0.75 điểm) Càng lên cao không khí càng loãng nên áp suất khí quyển càng giảm. Ví dụ ở khu vực thành phố Hồ Chí Minh có độ cao sát mực nước biển nên có áp suất khí quyển là 760 pmmHg , còn ở thành phố Puebla, Mexico có độ cao 2200 hm thì có áp suất khí quyền là 550,4 pmmHg Với những độ cao không lớn lắm thì ta có công thức tính áp suất khí quyển tương ứng với độ cao so với mực nước biển là một hàm số bậc nhất pahb có đồ thị như hình bên dưới.
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GD & ĐT BÌNH TÂN NĂM HỌC 202
ị của biểu
ứ
2-20232 ĐỀ THAM KHẢO MÔN : TOÁN 9 -------------------- Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Quận Bình Tân - 3 Thời gian: 120 phút (không kể thời gian phát đề) Bài 1: (1.5 điểm) Cho parabol 2 1 (): 2 Pyx và đường thẳng ():34 dyx . a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ Oxy . b) Tìm tọa độ giao điểm của P và d bằng phép toán. Bài 2: (1.0 điểm). Cho phương trình 2 3520 xx có hai nghiệm 12 , xx . Không giải phương trình, hãy tính giá tr
th
c 12 2111 xx A xx
Bài
điểm) Theo âm lịch,
ột
ỳ
ủ
a) Xác định hệ số a và b b) Hỏi cao nguyên Lâm Đồng có độ cao 650m so với mục nước biển thì có áp suất khí quyển là bao nhiêu mmHg? (làm tròn đến chữ số thập phân thứ nhất) Bài 5: (1.0 điểm) Trong kỳ thi HKII môn toán lớp 9, một phòng thi của trường có 24 thí sinh dự thi. Các thí sinh đều phải làm bài trên giấy thi của trường phát. Cuối buổi thi, sau khi thu bài, giám thị coi thi đếm được tổng số tờ là 53 tờ giấy thi. Hỏi trong phòng thi đó có bao nhiêu thí sinh làm bài 2 tờ giấy thi, bao nhiêu thí sinh làm bài 3 tờ giấy thi? Biết rằng có 3 thí sinh chỉ làm 1 tờ giấy thi.?
Bài 6: (1.0 điểm) Phần trên của cối xay gió có dạng một hình nón. Chiều cao của hình nón là 42cm và thể tích của nó là 3 17600cm . Em hãy giúp chàng Đôn-ki-hô-tê tính bán kính đáy của hình nón (làm tròn kết quả đến chữ số thập phân thứ nhất). Biết công thức tính thể tích hình nón là: 2 1 3 VRh

Bài 7: (1.0 điểm) Sau buổi lễ chào mừng "Ngày nhà giáo Việt Nam 20/11" lớp 9A cùng nhau đi ăn kem ở một quán gần trường. Nhân dịp quán mới khai trương nên có khuyến mãi, bắt đầu từ ly thứ 5 giá mỗi ly kem giảm 4000 đồng so với giá ban đầu. Lớp 9A mua 40 ly kem, khi tính tiền chủ cửa hàng thấy lớp mua nhiều nên giảm thêm 5% số tiền trên hóa đơn, vì vậy số tiền lớp 9A chi phải trả là 471200 đồng.
a) Tính số tiền chủ cửa hàng đã giảm thêm 5% trên hóa đơn cho lớp 9A
b) Hỏi giá của một ly kem ban đầu là bao nhiêu?
Bài 8: (3.0 điểm) Từ điểm A ở ngoài đường tròn () O , kẻ hai tiếp tuyến , ABAC tới đường tròn ( , BC là các tiếp điểm). Đường thẳng qua A cắt đường tròn () O tại D và E (D nằm giữa A và E , dây
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 78 -
OFFICIAL
DE
qua tâm
a) Chứng minh tứ giác
ộ
ABOC b) Chứng minh HA là
c) Chứng minh:
.
không
O ). Gọi H là trung điểm của , DEAE cắt BC tại K .
ABOC n
i tiếp đường tròn. Xác định tâm I của đường tròn ngoại tiếp tứ giác
tia phân giác của BHC
211 AKADAE
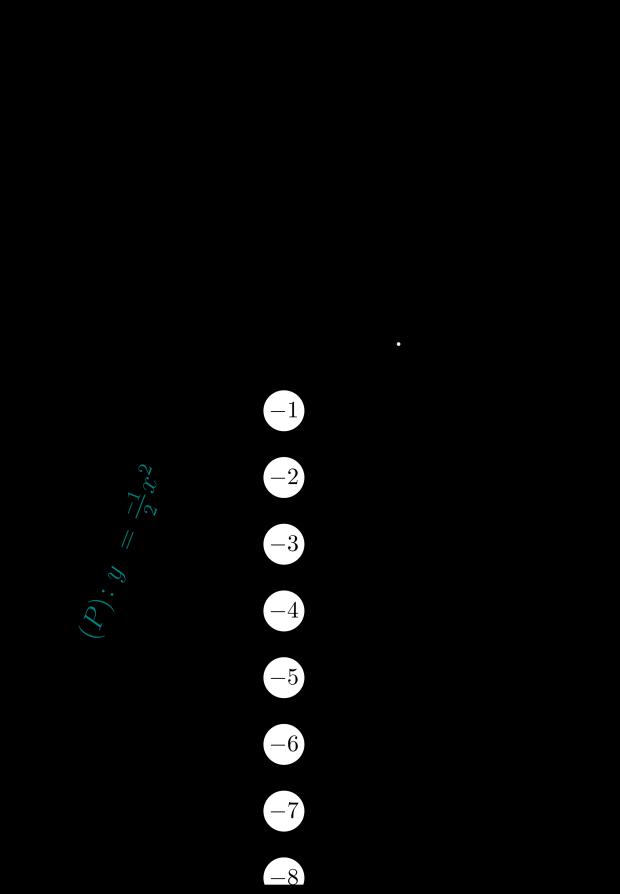
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI Bài 1: (1.0 điểm) Cho parabol 2 1 (): 2 Pyx và đường thẳng ():34 dyx . a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ Oxy . b) Tìm tọa độ giao điểm của P và d bằng phép toán. Lời giải a) Hàm số: 2 2 x y Bảng giá trị tương ứng của x và y : x 4 2 0 2 4 2 2 x y 8 2 0 2 8 Đồ thị hàm số là một Parabol đi qua
điểm 4;8 ; 2;2 ; 0;0 ; 2;2 ; 4;8 Hàm số: 34yx 04xy 04/3yx Đồ thị hàm số là đường thẳng đi qua 0;4 và 4/3;0 Đồ thị như hình bên b) Hoành độ giao điểm của P và d là nghiệm của phương trình: 2 34 2 x x 2 68xx 2 680xx 2 31.810 Phương trình có hai nghiệm phân biệt: 1 2 x ; 2 4 x + Với 1 2 x 1 2 y + Với 2 4 x 2 8 y Vậy D cắt P tại hai điểm phân biệt là 2;2 và 4;8 Bài 2: (1.0 điểm) Cho phương trình 2 3520 xx có hai nghiệm 12 , xx . Không giải phương trình, hãy tính giá trị của biểu thức 12 2111 xx A xx Lời giải Theo định lý Vi-et, ta có: 12 12 5/3 2/3 xx xx
các
bổ sung một tháng (tháng nhuận) để đảm bảo năm âm lịch tương đối phù hợp với chu kỳ của thời tiết. Cách tính năm nhuận âm lịch như sau: Lấy số năm chia cho 19, nếu số dư là một trong các số: {0;3;6;9;11;14;17} thì năm âm lịch đó có tháng nhuận.

Ví dụ:
2017 là năm nhuận âm lịch vì 2017 chia 19 dư 3.
2015 không phải là năm nhuận âm lịch vì 2015 chia 19 dư 1.
a) Em hãy sử dụng quy tắc trên để xác định năm 1995 và 2030 có phải năm nhuận âm lịch hay không?
b) Năm nhuận dương lịch là năm chia hết cho 4. Ngoài ra, những năm chia hết cho 100 chỉ được coi là năm nhuận dương lịch nếu chúng cũng chia hết cho 400 (ví dụ 1600 là năm nhuận dương lịch nhưng 1700 không phải năm nhuận dương lịch). Hỏi trong các năm từ năm 1895 đến năm 1930, năm nào vừa là năm nhuận âm lịch vừa là năm nhuận dương lịch? Lời giải
a) Vì 199519.105 nên 1995 chia hết cho 19. Suy ra năm 1995 là năm nhuận âm lịch Vì 203019.10616 nên 2030 chia cho 19 dư 16 Suy ra năm 2030 không là năm nhuận âm lịch.
b) Gọi k là số tự nhiên sao cho 189536.1930 k (1). Phương trình (1) tương đương 5253 k hay 53 k
Suy ra từ năm 1895 đến năm 1930 có 1 năm chia hết cho 4 và 19. Do đó, từ năm 1895 đến năm 1930, năm 53.191908 vừa là năm nhuận âm lịch vừa là năm nhuận dương lịch. Vậy có 1 v
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 80 1122 12 2112 2 22 1212121212 12121212 2 2 25 2 11 1111 5 34 2515 33 33 x xx A xxx xxxxx xxx xxxx xxxxx xxx x x Vậy, 4 15 A Bài 3: (0.75 điểm) Theo âm lịch, vì một chu kỳ quay của Mặt Trăng quanh Trái Đất là khoảng 29,53 ngày nên một năm âm lịch chỉ có khoảng 354 ngày (làm tròn). Do vậy, cứ sau một vài năm âm lịch thì người ta phải
lên
t khí quyển càng giảm. Ví dụ ở khu vực thành phố
ồ Chí Minh có độ cao sát mực nước biển nên có áp suất khí quyển là 760 pmmHg , còn ở thành phố
có độ cao
550,4
.
ị
ừa là năm nhuận âm lịch vừa là năm nhuận dương lịch, từ năm 1895 đến năm 1930 Bài 4: (0.75 điểm) Càng
cao không khí càng loãng nên áp suấ
H
Puebla, Mexico
2200 hm
thì có áp suất khí quyền là
pmmHg
Với những độ cao không lớn lắm thì ta có công thức tính áp suất khí quyển tương ứng với độ cao so với mực nước biển là một hàm số bậc nhất pahb có đồ th
như hình bên dưới.
a) Xác định hệ số a và b . b) Hỏi cao nguyên Lâm Đồng có độ cao 650m so với mục nước biển thì có áp suất khí quyển là bao nhiêu mmHg? (làm tròn đến chữ số thập phân thứ nhất) Lời giải a) Từ đẳng thức pahb và 760 p tại 0 h ta được 760 b . Dựa và đồ thị đã cho ta có 550,4.2200760 a . Suy ra 0.095 a Vậy, 0.095 a
và 760 b . b) Từ câu a) ta có 0.095760ph . Tại 650 h , ta được 0.095*650760 p hay 698.3 p . Áp suất khí quyển của cao nguyên Lâm Đồng là 698.3 mmHg. Bài 5: (1.0 điểm) Trong kỳ thi HKII môn toán lớp 9, một phòng thi của trường có 24 thí sinh dự thi. Các thí sinh đều phải làm bài trên giấy thi của trường phát. Cuối buổi thi, sau khi thu bài, giám thị coi thi đếm được tổng số tờ là 53 tờ giấy thi. Hỏi trong phòng thi đó có bao nhiêu thí sinh làm bài 2 tờ giấy thi, bao nhiêu thí sinh làm bài 3 tờ giấy thi? Biết rằng có 3 thí sinh chỉ làm 1 tờ giấy thi.? Lời giải Số thí sinh làm bài thi 2 tờ giấy và 3 t
tích của nó là 3 17600cm . Em hãy giúp chàng Đôn-ki-hô-tê tính bán kính đáy của hình nón (làm tròn kết quả đến chữ số thập phân thứ nhất). Biết công thức tính thể tích hình nón là:

DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 81 -
OFFICIAL
. 1 Tổng số tờ là 53 tờ giấy nên ta được 23533 xy 2350 xy 2 Từ 1 và 2 ta có hệ phương trình: 212242813 23503350218 xyxyyx xyxyxyy (thỏa mãn) Vậy có 13 thí sinh làm bài 2 tờ giấy thi và 8 thí sinh làm bài 3 tờ giấy thi. Bài 6: (1.0 điểm) Phần trên của cối xay gió có dạng một hình nón. Chiều cao của hình nón là 42cm và thể
. Lời giải Theo giả thuyết, ta có 2 1 1760042 3 R . Suy ra 76000.3 20.01 42 R cm. Vậy,
m)
ờ giấy là 24321
. Gọi x là số thí sinh làm bài 2 tờ giấy thi, y là số thí sinh làm bài 3 tờ giấy thi ( x ; y nguyên dương, x ; 21 y ). Khi đó, ta có 21 xy
2 1 3 VRh
bán kính đáy của hình nón bằng 20.01 cm. Bài 7: (1.0 điể
Sau buổi lễ chào mừng "Ngày nhà giáo Việt Nam 20/11" lớp 9A cùng nhau đi ăn kem ở một quán gần trường. Nhân dịp quán mới khai trương nên có khuyến mãi, bắt đầu từ ly thứ 5 giá
mỗi ly kem giảm 4000 đồng so với giá ban đầu. Lớp 9A mua 40 ly kem, khi tính tiền chủ cửa hàng thấy lớp mua nhiều nên giảm thêm 5% số tiền trên hóa đơn, vì vậy số tiền lớp 9A chi phải trả là 471200 đồng.
a) Tính số tiền chủ cửa hàng đã giảm thêm 5% trên hóa đơn cho lớp 9A
b) Hỏi giá của một ly kem ban đầu là bao nhiêu?
Lời giải
a) Số tiền chủ cửa hàng đã giảm thêm 5% trên hóa đơn cho lớp 9A là 471200 524800 95 đồng.
b) Số tiền lớp phải trả nếu không giảm thêm 5% là 47120024800496000 Gọi x là giá mỗi ly kem ban đầu ( 0 x ). Theo giả ta có 4.(404).(4000)496000 xx Suy ra, ta có phương trình 40. - 144000 = 496000 16000. x x Vậy, giá của một ly kem ban đầu là 16000 đồng. Bài 8: (3.0 điểm) Từ điểm A ở ngoài đường tròn () O , kẻ hai tiếp tuyến , ABAC tới đường tròn ( , BC là các tiếp điểm). Đường thẳng qua A cắt đường tròn () O tại D và E (D nằm giữa A và E , dây DE không qua tâm O ). Gọi H là trung điểm của , DEAE cắt BC tại K c) Chứng minh tứ giác ABOC nội tiếp đường tròn. Xác định tâm I của đường tròn ngoại tiếp tứ giác ABOC .
d) Chứng minh HA là tia phân giác của BHC .
c) Chứng minh: 211 AKADAE . Lời giải
a) Ta có 90 AMBACM (do AB và AC là các tiếp tuyến). Suy ra tứ giác ABOC nội tiếp đường tròn đường kính OA. Do đó, tâm I của đường tròn ngoại tiếp tứ giác ABOC là trung diểm của OA.
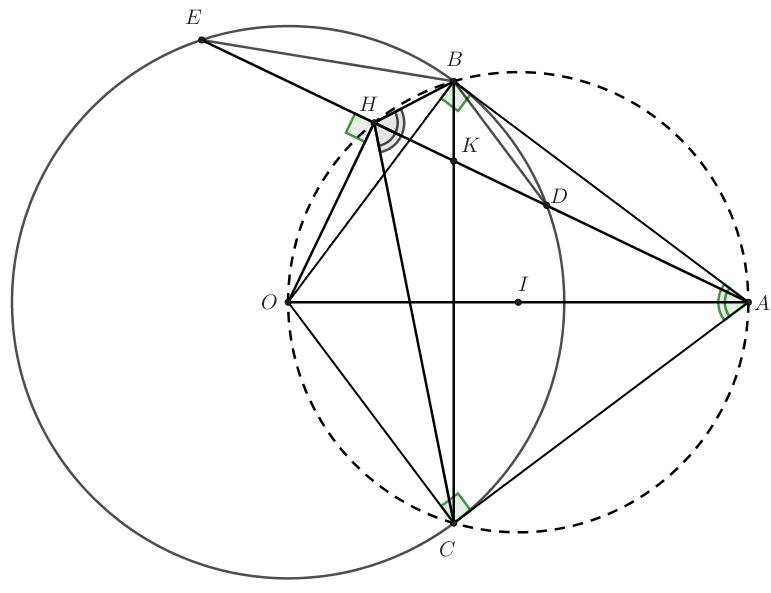
DẠYKÈMQUYNHƠN
- 82
OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN
-
b) Do H là trung điểm của dây cung DE nên 90 OHA .
Suy ra H nằm trên đường tròn ngoại tiếp tứ giác ABOC .
Do đó, 1 2 BHA sđ 1 2 AC sđ (180)90OCCOB (1), 1 2 CHA sđ 1 2 AB sđ (180)90OBBOA (2).
Mặt khác, theo tính chất của tiếp tuyến, ta có BOACOB (3).
Từ (1), (2) và (3), ta được BHACHA
Vậy, HA là tia phân giác của BHC . c) Xét 2 tam giác ABD và AEB ta có 1 2 BEADBA sđ BD. BADBAE
Suy ra ABDAEB ∽
Do đó, ABAE ADAB hay 2 . ADAEAB (1).
Mặt khác, xét 2 tam giác AKB và ABH , ta có 1 2 KBACHD sđ CD.
Suy ra KBABHA (câu b)
Do đó, AKBABH ∽ .
Từ đó, AKAB ABAH hay 2AKAHAB Từ (1) và (2), ta được
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 83 -
OFFICIAL
1 . 2 ..2. 211 AKAHADAE AKADAEADAE AKADAKAEADAE AKAEAD
SỞ GD&ĐT TP. HỒ CHÍ MINH PHÒNG GD &ĐT QUẬN BÌNH THẠNH ĐỀ THAM KHẢO MÃ ĐỀ: Quận Bình Thạnh- 3 -------------------------
ĐỀ THAM KHẢO TUYỂN SINH 10
NĂM HỌC: 2022- 2023 MÔN THI: TOÁN 9 Đề thi gồm 8 câu hỏi tự luận. Thời gian: 120 phút( không kể thời gian phát đề)
Câu 1 (1,5 điểm): Cho parabol (P): �� = 1 3 ��2 và đường thẳng (d): ��= ��+6.
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Câu 2 (1 điểm): Cho phương trình bậc hai (ẩn x) 2��2 4�� 1=0 . Không giải phương trình trên, hãy tính giá trị của biểu thức sau ��=��1(��2 2 +2)+��2(��1 2 +2).
Câu 3(1 điểm): Một ô tô có bình xăng chứa b (lít) xăng. Gọi y là số lít xăng còn lại trong bình xăng khi ô tô đã đi quãng đường x (km), y là hàm số bậc nhất có biến số là x cho bởi công thức y=ax+b thỏa bảng giá trị sau: x (km) 60 180 y (lít) 7 21
a) Tìm các hệ số a và b của hàm số bậc nhất trên.
b) Xe ô tô có cần đổ thêm xăng vào bình hay không khi chạy hết quãng đường dài 700 km, nếu cần đổ thêm xăng thì phải đổ thêm mấy lít xăng?
Câu 4 (1 điểm): Một người quan sát đứng cách một tòa nhà khoảng 25 m (điểm A). Góc nâng từ chỗ anh ta đứng đến nóc tòa nhà (điểm C) là 360
a) Tính chiều cao của tòa nhà ( làm tròn đến 0,1 mét ).
b) Nếu anh ta đi thêm 5 m nữa, đến vị trí D nằm giữa A và B thì góc nâng từ D đến nóc tòa nhà là bao nhiêu (làm tròn đến phút)?
Câu 5 (0,75 điểm): Một hồ bơi tràn có dạng là một lăng trụ đứng với đáy là hình thang vuông. Mặt hồ là một hình chữ nhật có chiều rộng AA’ là 20 m. Chiều sâu của hồ tăng dần từ 1 m đến 3 m theo chiều dài DC của đáy hồ. Khi người ta dùng một máy bơm với lưu lượng là 28 ��3/phút thì sẽ bơm đầy hồ mất 50 phút. Tính chiều dài AB của mặt hồ.
DẠYKÈMQUYNHƠN
OFFICIAL
Câu 6 (1 điểm): Một địa phương cấy 10 ha giống lúa loại I và 8 ha giống lúa loại II. Sau một mùa vụ, địa phương đó thu hoạch và tính toán sản lượng thấy: Tổng sản lượng của hai giống lúa thu về là 139 tấn và sản lượng thu về từ 4 ha giống lúa loại I nhiều hơn sản lượng thu về từ 3 ha giống lúa loại II là 6 tấn. Hãy tính năng suất lúa trung bình ( đơn vị: tấn/ ha) của mỗi loại giống lúa. Câu 7 (0,75 điểm): Cô giáo có dự định chuẩn bị 1 buổi tiên tất niên cho lớp 9A có 48 học sinh như sau: mỗi bạn 1 lon nước giải khát và 1 phần bánh. Mỗi phần bánh 35000 đồng, nhưng mua trên 30 phần được giảm 10%. Nước giải khát giá bán lẻ là 8000 đồng/ lon, nhưng nếu mua nguyên thùng 24 lon thì giá 178000 đồng/ thùng. Vậy nếu cô giáo mua vừa đủ phần bánh và nước cho các bạn học sinh thì phải trả bao nhiêu tiền? Câu 8 (3 điểm): Cho đường tròn (O; R) có hai đường kính AB và CD vuông góc với nhau, vẽ dây MN vuông góc với đoạn OB tại H ( M thuộc cung nhỏ BC). Gọi E là giao điểm của BC và MN. a) Chứng minh tứ giác AEHC nội tiếp và ����⋅����=����⋅���� b) Hai tia AC và NM cắt nhau tại K, đường thẳng qua K và song song với AB, cắt tia NC tại I. Chứng minh ���� ⊥���� và ����2 =����⋅���� c) Chứng minh ����2 +����2 =4��2
OFFICIAL
DẠYKÈMQUYNHƠN
……………HẾT……………
Câu 1 (1,5 điểm): Cho parabol (P): �� = 1 3 ��2 và đường thẳng (d): ��= ��+6.
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Bài giải:
a) Bảng giá trị ( P) : �� = 1 3 ��2 x -3 -2 0 2 3 �� = 1 3 ��2 3 4 3 0 4 3 3 Đồ thị (P) là parabol đi qua các điểm (-3;3), ( 2;4 3), (0;0), (2;4 3), (3;3) Bảng giá trị ( d) : ��= ��+6. x 0 6 �� = ��+6 6 0 Đồ thị (d) là đường thẳng đi qua các điểm (0; 6), (6; 0) Hình vẽ ( HS tự vẽ đồ thị)
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Phương trình hoành độ giao điểm (P) và (d) có dạng 1 3 ��2 = ��2 +6 ⇔��2 +3��+18=0⟺��1 = 6ℎ��ặ����2 =3 Thay �� = 6 vào phương trình của (d) ta được �� =0 Thay �� =3 vào phương trình của (d) ta được ��=3 Vậy tọa độ giao điểm của (P) và (d) là ( 6;0), (3;3) Câu 2 (1 điểm): Cho phương trình bậc hai (ẩn x) 2��2 4�� 1=0 . Không giải phương trình trên, hãy tính giá trị của biểu thức sau ��=��1(��2 2 +2)+��2(��1 2 +2).
DẠYKÈMQUYNHƠN
BÀI GIẢI CHI TIẾT
OFFICIAL
Theo định lý Vi- ét, ta có: �� =��1 +��2 = �� �� = 4 2 =2 �� =��1 ��2 = �� �� = 1 2 ��=��1(��2 2 +2)+��2(��1 2 +2)=��1��2 2 +2��1 +��2��1
+2��
=��1��2(��1 +��2)+2(��1 +��2
Câu 3(1
:
ô
Bài giải: 2��2 4�� 1=0
2
2
)= 1 2 2+2.2=3
điểm)
Một
tô có bình xăng chứa b (lít) xăng. Gọi y là số lít xăng còn lại trong bình xăng khi ô tô đã đi quãng đường x (km), y là hàm số bậc nhất có biến số là x cho bởi công thức y=ax+b thỏa bảng giá trị sau: x (km) 60 180 y (lít) 7 21 a) Tìm các hệ số a và b của hàm số bậc nhất trên.
b) Xe ô tô có cần đổ thêm xăng vào bình hay không khi chạy hết quãng đường dài 700 km, nếu cần đổ thêm xăng thì phải đổ thêm mấy lít xăng?
Bài giải:
a) Lượng xăng tiêu hao khi ô tô đi được 1 km là: (27 – 21): (180 – 60) = 0, 05 lít a = – 0,05

Thay x = 60, y = 27 và a = –0,05 vào hàm số y = ax + b b = 30.

b) Thay x = 700 vào hàm số y = – 0,05 x + 30 y = –5 < 0 Xe ô tô cần đổ thêm 5 lít xăng vào bình xăng khi chạy hết quãng đường x = 700 (km)
Câu 4 (1 điểm): Một người quan sát đứng cách một tòa nhà khoảng 25 m (điểm A). Góc nâng từ chỗ anh ta đứng đến nóc tòa nhà (điểm C) là 360
OFFICIAL
a) Tính chiều cao của tòa nhà ( làm tròn đến 0,1 mét ). b) Nếu anh ta đi thêm 5 m nữa, đến vị trí D nằm giữa A và B thì góc nâng từ D đến nóc tòa nhà là bao nhiêu (làm tròn đến phút)? Bài giải: a) �������� vuông tại B Ta có: tan������ ̂ = ���� ���� ⟺tan360 = ���� 25 ⟺���� =25.tan360 ≈18,2�� b) �������� vuông tại B DB=AB AD=25 5=20m tan������ ̂ = ���� ���� = 18,2 20 ≈0,91 ⟹������ ̂ ≈42018′ Câu 5 (0,75 điểm): Một hồ bơi tràn có dạng là một lăng trụ đứng với đáy là hình thang vuông. Mặt hồ là một hình chữ nhật có chiều rộng AA’ là 20 m. Chiều sâu của hồ tăng dần từ 1 m đến 3 m theo chiều dài DC của đáy hồ. Khi người ta dùng một máy bơm với lưu lượng là 28��
thì sẽ bơm đầy hồ mất 50 phút. Tính chiều dài AB của mặt hồ.
DẠYKÈMQUYNHƠN
Bài giải: Do máy bơm có lưu lượng 28��3/phút mất 50 phút để đầy hồ nên ta có: Thể tích của cả hồ: �� =2850=1400��3 Hồ có dạng hình lăng trụ đứng đáy là hình thang vuông nên chiều cao là 20m Diện tích đáy của lăng trụ: �� =��⋅ℎ⇒��= �� ℎ = 1400 20 =70��2 Mà �� = (����+����)⋅���� 2
3/phút
Vậy chiều dài AB của mặt hồ là 35m Câu 6 (1 điểm): Một địa phương cấy 10 ha giống lúa loại I và 8 ha giống lúa loại II. Sau một mùa vụ, địa phương đó thu hoạch và tính toán sản lượng thấy: Tổng sản lượng của hai giống lúa thu về là 139 tấn và sản lượng thu về từ 4 ha giống lúa loại I nhiều hơn sản lượng thu về từ 3 ha giống lúa loại II là 6 tấn. Hãy tính năng suất lúa trung bình ( đơn vị: tấn/ ha) của mỗi loại giống lúa. Bài giải: Gọi năng suất lúa trung bình của loại I và loại II trên mỗi ha lần lượt là x và y (tấn/ha) (x,y> 0)
10 ha giống lúa loại I thu về sản lượng 10x (tấn)
8ha giống lúa loại II thu về sản lượng 8y (tấn)
Tổng sản lượng thu về là 139 tấn, nên ta có pt: 10��+8�� =139(1)
4ha giống lúa loại I thu về sản lượng 4x (tấn)
3ha giống lúa loại II thu về sản lượng 3y (tấn)
Vì sản lượng thu về từ 4 ha giống lúa loại I nhiều hơn sản lượng thu về từ 3 ha giống lúa loại II là 6 tấn, nên ta có pt: 4�� 3�� =6(2) Từ (1) và (2) ta có hệ phương trình: { 10��+8�� =139 4�� 3��=6 (*) Giải hệ phương trình (*) được nghiệm là: { �� =7,5 �� =8 Vậy năng suất lúa trung bình của loại I: 7,5��ấ��/ℎ�� và loại II 8��ấ��/ℎ�� Câu 7 (0,75 điểm): Cô giáo có dự định chuẩn bị 1 buổi tiên tất niên cho lớp 9A có 48 học sinh như sau: mỗi bạn 1 lon nước giải khát và 1 phần bánh. Mỗi phần bánh 35000 đồng, nhưng mua trên 30 phần được giảm 10%. Nước giải khát giá bán lẻ là 8000 đồng/ lon, nhưng nếu mua nguyên thùng 24 lon thì giá 178000 đồng/ thùng. Vậy nếu cô giáo mua vừa đủ phần bánh và nước cho các bạn học sinh thì phải trả bao nhiêu tiền? Bài giải:
Ta có: Số học sinh là 48 lớn hơn 30 phần
⇒
Mua trên 30 phần được giảm 10% tiền bánh
Số tiền phải trả khi mua 48 phần bánh là: 35000 × 48 = 1680000 (đồng)
Số tiền phải trả khi mua bánh được giảm giá là: 1680000 × (100% - 10%) = 1512000 (đồng)
Vì lớp có 48 học sinh nên cô giáo phải mua 2 thùng
⇒
Số tiền phải trả khi mua đủ phần nước ngọt là: 178000 .2 = 356000 (đồng)
Số tiền phải trả khi mua bánh và nước ngọt là: 1512000 + 356000 = 1868000 (đồng)
Vậy nếu cô giáo mua đủ phần bánh và nước cho các bạn học sinh thì phải trả 1868000 đồng.
DẠYKÈMQUYNHƠN
⇔70=(1+3)����
⇒���� = 70.2
=35(��)
OFFICIAL
2
4
Câu 8 (3 điểm): Cho đường tròn (O; R) có hai đường kính AB và CD vuông góc với nhau, vẽ dây MN vuông góc với đoạn OB tại H ( M thuộc cung nhỏ BC). Gọi E là giao điểm của BC và MN.
a) Chứng minh tứ giác AHEC nội tiếp và ����⋅����=����⋅����
b) Hai tia AC và NM cắt nhau tại K, đường thẳng qua K và song song với AB, cắt tia NC tại I. Chứng minh ���� ⊥���� và ����2 =����⋅����
c) Chứng minh ����2 +����2 =4��2
Bài giải:
a) Xét tứ giác AHEC , có: ������ ̂ =900 (����) ������ ̂ =900 (����) ⟹ ������ ̂ +������ ̂ =900 +900 =1800 ⟹Tứ giác AHEC nội tiếp ( tứ giác có tổng 2 góc đối bằng 1800 )
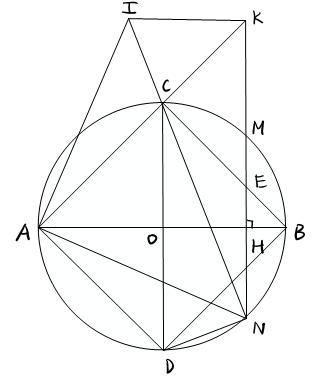
b) Ta có: ������ ̂ +������ ̂ =900 (��ì������������ô������ạ����) ������ ̂ +������ ̂ (��ì��đ���� ̂ =��đ���� ̂ ) Nên ������ ̂ +������ ̂ =900 Mà ������ ̂ +������ ̂ =900
Suy ra: ������ ̂ =������ ̂ Do đó: A, I cùng phía và cùng nhìn NK dưới 1 góc không đổi ⟹Tứ giác ANKI nội tiếp ⟹���� ⊥���� ∗ CM: ����2 =���� ���� Xét �������� và �������� có: ���� =���� ������ ̂ =������ ̂ (��ù������ù������ ̂ ) ������ ̂ =������ ̂ (��ù������ℎụ������ ̂ ) ⟹�������� =��������(�� �� ��) ⟹���� =����(1) Xét �������� và �������� có: ������ ̂ ��ℎ������ ������ ̂ = 1 2(��đ���� ̂ +��đ����̂) = 1 2(��đ���� ̂ +��đ����)= ������ ̂
DẠYKÈMQUYNHƠN
OFFICIAL
⟹��������~��������(��.��) ⇒ ���� ���� = ���� ���� ⇒����2 =����⋅����(2) Từ (1) (2) ⇒����2 =����⋅���� c) Ta có: �������� =��������(������) ⟹���� =���� Xét �������� vuông tại N có: ����2 =����2 +����2 (đị��ℎ��í������������) ⟹ ����2 +����2 =4��2
i nhuận y(đồng) của một cửa hàng thu được khi bán x hộp sữa loại 900 g được cho bởi phương trình : yaxb .Biết rằng trong tháng 10 cửa hàng bán được 95 hộp sữa thu được lợi nhuận 4 870 00 đồng ,tháng 11 bán được 180 hộp sữa thu được lợi nhuận 9 120 000 đồng .Tính hệ số a và b. Bài 4: (1 điểm) Theo âm lịch thì do một chu kỳ quay của Mặt Trăng quanh Trái Đất là khoảng 29,53 ngày nên một năm âm lịch chỉ có khoảng 354 ngày (làm tròn).Do vậy ,cứ sau một vài năm âm lịch thì người ta phải bổ sung một tháng (tháng nhuận) để đảm bảo năm âm lịch tương đối phù hợp với chu kì của thời tiết ,là yếu tố phụ thuộc vào chu kỳ quay của Trái Đất xung quanh Mặt Trời .Cách tính năm nhuận âm lịch như sau :Lấy số năm chia cho 19 ,nếu số dư là một trong các số :0;3;6;9;11;14;17 thì năm âm lịch đó có tháng nhuận . Ví dụ : 2017 là năm nhuận âm lịch vì 2017 chia cho 19 dư 3 2015 không phải năm nhuận âm lịch vì 2015 chia 19 dư 1 a) Em hãy sử dụng qui tắc trên để xác định năm 1995 và 2030 có phải năm nhuận âm lịch hay không ? b)Năm nhuận dương lịch là năm chia hết cho 4.Ngoài ra những năm chia hết cho 100 chỉ được coi là năm nhuận dươnglịch nếu chúng cũng chia hết cho 400 (vídụ : 1600là năm nhuận dương lịch
DẠYKÈMQUYNHƠN OFFICIAL SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GD & ĐT HUYỆN CẦN GIỜ NĂM
2022-2023 ĐỀ THAM
MÔN
9 Đề
MÃ ĐỀ : Huyện cần giờ – 3 Thời
120
đề) Bài 1: (1.5 điểm) Cho hàm số 2 2 x y có đồ thị là parabol P và đường thẳng D : 4 yx a) Vẽ đồ thị P và D trên cùng mặt phẳng tọa độ; b) Tìm tọa độ giao điểm của P và D bằng phép toán. Bài 2: (1.0 điểm) Cho phương trình 2 7120xx có 2 nghiệm 1x , 2x .Không giải phương trình ,hãy tính giá trị biểu thức 22 1212 Axxxx . Bài 3: (1 điểm) Trong một tháng khoảng lợ
,năm nào vừa là
dương lịch? Bài 5: (1.0 điểm) Tháng 6 / 2021 ,gia đình ông Hai thu nhập 15 000 000 đồng và chi tiêu 12 000 000 đồng .Tháng 7 / 2021,gia đình ông Hai có thu nhập giảm 10% mà chi tiêu lại tăng 13 %.Hỏi gia đình ông Hai có để dành được tiền trong tháng 7 / 2021 được không?
HỌC
KHẢO
: TOÁN
thi gồm 8 câu hỏi tự luận
gian:
phút (không kể thời gian phát
nhưng 1700 không phải năm nhuận dương lịch ).Trong các năm từ năm 1895 đến năm 1930
năm nhuận âm lịch vừa là năm nhuận
Bài 6: (1.0điểm)Mộtbểkínhnuôicácódạnghìnhhộpchữnhậtcóchiềudài100cm,chiềurộng50cm,chiều cao 60 cm.Mực nước trong bể cao bằng 3 4 chiều cao bể .Tính thể tích nước trong bể đó (độ dày kính không đáng kể ).Công thức tính thể tích nước trong bể là VSh với S là diện tích mặt đáy bể và h là chiều cao mực nước trong bể.
Bài 7: (1.0 điểm) Bà nội dành dụm được một số tiền để thưởng cho các cháu của bà .Nếu bà thưởng cho mỗi cháu 140 000 đồng thì bà còn dư 40 000 đồng ,nếu bà thưởng cho mỗi cháu 60 000 đồng thì bà còn thiếu 60 000 đồng .Hỏi bà nội dành dụm được bao nhiêu tiền và có bao nhiêu cháu? Bài 8: (3.0 điểm) Từ điểm A ở ngoài đường tròn , OR ,vẽ hai tiếp tuyến AB ,AC và cát tuyến AMN với đường tròn (B,C là các tiếp điểm ) ,AM < AN và tia AM nằm giữa hai tia AB ,AO .Gọi I là hình chiếu của O trên AN,H là giao điểm của OA và BC.
a)Chứng minh tứ giác OABI nội tiếp và xác định tâm của đường tròn ngoại tiếp tứ giác OABI
b)Chứng minh IA là tia phân giác của BIC .
c)Chứng minh điểm H thuộc đường tròn ngoại tiếp OMN .
DẠYKÈMQUYNHƠN
OFFICIAL
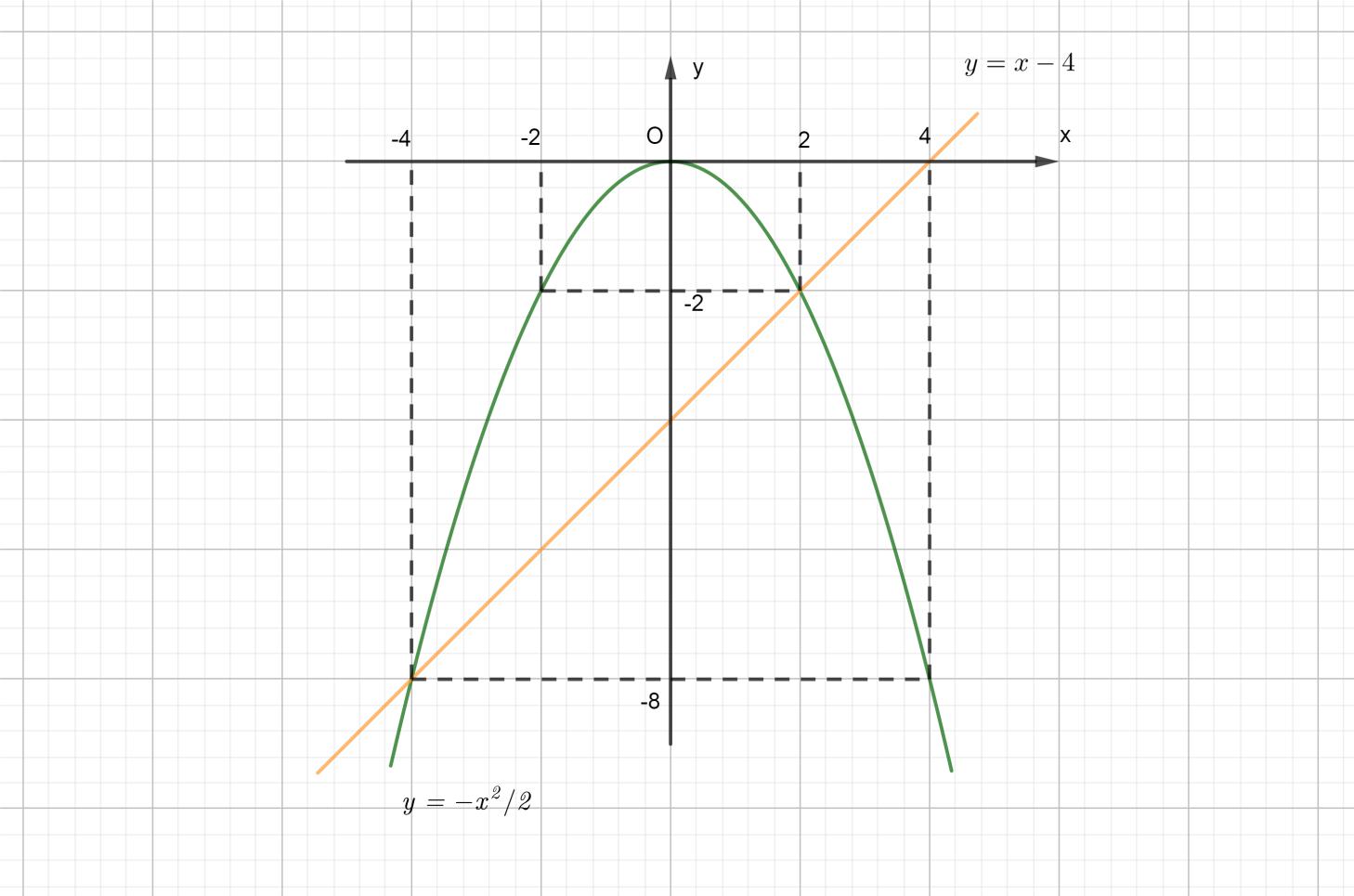
DẠYKÈMQUYNHƠN OFFICIAL HƯỚNG DẪN GIẢI Bài 1: (1.5 điểm). Cho hàm số 2 2 x y có đồ thị là parabol P và đường thẳng D : 4 yx a) Vẽ đồ thị P và D trên cùng mặt phẳng tọa độ; b) Tìm tọa độ
điểm của P và D bằng
Lời giải a) Hàm số: 2 2 x y Bảng giá trị tương ứng của x và y : x 4 2 0 2 4 2 2 x y 8 2 0 2 8 Đồ thị hàm số là một Parabol đi qua các điểm 4;8 ; 2;2 ; 0;0 ; 2;2 ; 4;8 Hàm số: 4 yx 04xy 04yx Đồ thị hàm số là đường thẳng đi qua 0;4 và 4;0 Vẽ: b) Hoành độ giao điểm của P và D là nghiệm của phương trình: 2 4 2 x x 2 28xx 2 280xx
giao
phép toán.
DẠYKÈMQUYNHƠN OFFICIAL 2 11.890 Phương trình có hai nghiệm phân biệt: 1 2 x ; 2 4 x + Với 1 2 x 1 1 y + Với 2 4 x 2 8 y Vậy D cắt P tại hai điểm phân biệt là 2;2 và 4;8 . Bài 2: (1.0 điểm) Cho phương trình 2 7120xx có 2 nghiệm 1x , 2x .Không giải phương trình ,hãy tính giá trị biểu thức 22 1212 Axxxx . Lời giải Vì phương trình đã cho có 2 nghiệm 1x , 2x nên Theo định lý Vi-et, ta có: 12 12 7 12 xx xx Gía trị biểu thức : 22 1212 Axxxx 2 121212 ()2() Axxxxxx 2 (7)2.127 A 18 A Bài 3: (1 điểm) Trong một tháng khoảng lợi nhuận y(đồng) của một cửa hàng thu được khi bán x hộp sữa loại 900 g được cho bởi phương trình : yaxb .Biết rằng trong tháng 10 cửa hàng
đượ
95
ộp sữa thu đượ
Từ (1) và (2) ta có hệ phương trình: 954870000 1809120000 ab ab Giải hệ phương trình ta có : 50000,120000ab Bài 4: (1 điểm) Theo âm lịch thì do một chu kỳ quay của Mặt Trăng quanh Trái Đất là khoảng 29,53 ngày nên một năm âm lịch chỉ có khoảng 354 ngày (làm tròn).Do vậy ,cứ sao một vài năm âm lịch thì người ta phải bổ
ờ
tiết
ế
:0;3;6;9;11;14;17
Ví dụ : 2017
2015
bán
c
h
c lợi nhuận 4870000đồng ,tháng 11 bán được 180 hộp sữa thu được lợi nhuận 9120000 đồng .Tính hệ số a và b. Lời giải Lợi nhuận của cửa hàng trong tháng 10 (95,4870000) xy : 487000095ab (1) Lợi nhuận của cửa hàng trong tháng 11 (180,9120000) xy : 9120000180ab (2)
sung một tháng (tháng nhuận) để đảm bảo năm âm lịch tương đối phù hợp với chu kì của th
i
,là y
u tố phụ thuộc vào chu kỳ quay của Trái Đất xung quanh Mặt Trời .Cách tính năm nhuận âm lịch như sau :Lấy số năm chia hết cho 19 ,nếu số dư là một trong các số
thì năm âm lịch có tháng nhuận .
là năm nhuận âm lịch vì 2017 chia cho 19 dư 3
không phải năm nhuận âm lịch vì 2015 chia 19 dư 1
Lời giải
a) Em hãy sử dụng qui tắc trên để xác định năm 1995 và 2030 có phải năm nhuận âm lịch hay không ?
b)Năm nhuận dương lịch là năm chia hết cho 4.Ngoài ra những năm chia hết cho 100 chỉ được coi là năm nhuận dương lịch nếu chúng chia hết cho 400(ví dụ : 1600 là năm nhuận dương lịch nhưng 1700 không phải năm nhuận dương lịch ).Trong các năm từ năm 1895 đến năm 1930 ,năm nào vừa là năm nhuận âm lịch vừa là năm nhuận dương lịch?
a) Năm 1995là năm nhuận âm lịch vì 1995chia 19dư 0 Năm 2030không phải năm nhuận âm lịch vì 2030chia 19dư 16
b) Từ năm 1895 đến năm 1930,các năm chia hết cho 4 là : 1896,1900,1904,1908,1912,…..,1928 tổng cộng sẽ có 19281896 19 4
Vì 1900chia hết cho 100 nhưng không chia hết cho 400 nên chỉ có 8 năm nhuận âm lịch
1896chia cho 19 dư 15
1904 chia cho 19 dư 4
1908 chia cho 19 dư 8
1912 chia cho 19 dư 12
1916 chia cho 19 dứ 16
1920 chia cho 19 dư 1
1924 chia cho 19 dư 5
1928 chia cho 19 dư 9
OFFICIAL
Do đó không có năm nào từ năm 1895 đến 1930 vừa là năm nhuận âm lịch vừa là năm nhuận dương lịch Bài 5(1.0 điểm) Tháng 6 /2021 ,gia đình ông Hai thu nhập 15 000 000 đồng và chi tiêu 12 000 000 đồng .Tháng 7 / 2021,gia đình ông Hai có thu nhập giảm 10% mà chi tiêu lại tăng 13 %.Hỏi gia đình ông Hai có để dành được tiền trong tháng 7 / 2021 được không? Lời giải
Số tiền gia đình ông Hai dành được trong tháng 6/2021 : 15000000120000003000000 đồng
Số tiền thu nhập của ông Hai trong tháng 7/2021: 15000000.(100%10%)13500000 đồng
Số tiền chi tiêu của ông Hai trong tháng 7/2021:12000000.(100%13%)13560000 đồng > 13500000 đồng Vậy trong tháng 7 ông Hai không để dành được tiền Bài 6: (1.0điểm)Mộtb
DẠYKÈMQUYNHƠN
ểkínhnuôicácódạnghìnhhộpchữnhậtcóchiềudài100cm,chiềurộng50cm,chiều cao 60 cm.Mực nước trong bể cao bằng 3 4 chiều cao bể .Tính thể tích nước trong bể đó (độ dày kính không đáng kể ).Công thức tính thể tích nước trong bể là VSh với S là diện tích mặt đáy bể và h là chiều cao mực nước trong bể.
Lời giải -Chiều cao của mực nước trong bể là: 3 6045 4 cm -Thể tích nước trong bể là:100.50.45225000 3 cm Bài 7: (1.0 điểm) Bà nội dành dụm được một số tiền để thưởng cho các cháu của bà .Nếu bà thưởng cho mỗi cháu 140 000 đồng thì bà còn dư 40 000 đồng ,nếu bà thưởng cho mỗi cháu 60 000 đồng thì bà còn thiếu 60 000 đồng .Hỏi bà nội dành dụm được bao nhiêu tiền và có bao nhiêu cháu? Lời giải Gọi x,y lần lượt là số tiền bà nội dành dụm được và số cháu của bà ( * , xyN ) -Khi thưởng cho mỗi cháu 140 000 đồng thì bà dư 40 000 đồng: 14000040000yx
14000040000xy

(1) -Khi thưởng cho mỗi cháu 60 000 đồng thì bà thiếu 60 000 đồng: 16000060000yx

u của O trên AN,H là giao điểm của OA và BC.
a)Chứng minh tứ giác OABI nội tiếp và xác định tâm của đường tròn ngoại tiếp tứ giác OABI
b)Chứng minh IA là tia phân giác của BIC .
c)Chứng minh điểm H thuộc đường tròn ngoại tiếp OMN . Lời giải
DẠYKÈMQUYNHƠN OFFICIAL
Từ (1) và (2) ta có hệ phương trình: 14000040000 1600060000 xy xy Giải hệ phương trình ta có : 740000(),5() xnyn Vậy số tiền bà nội dành dụm được là 740000đồng Số cháu của bà nội là 5 cháu Bài 8: (3.0 điểm) Từ điểm A ở ngoài đường tròn , OR ,vẽ hai tiếp tuyến AB ,AC và cát tuyến AMN với đường tròn (B,C là các tiếp điểm ) ,AM < AN và tia AM nằm giữa hai tia AB ,AO .Gọi I là hình chiế
16000060000xy
(2)
B
a) Chứng minh tứ giác OABI nội tiếp và xác định tâm của đường tròn nội tiếp tứ giác OABI :
Ta có : 090 OCA (AB là tiếp tuyến của (O))
090 AIO (I là hình chiếu của O trên AN) 090 OBAAIO Tứ giác OABI nội tiếp đường kính AO (2 đỉnh kề nhau cùng nhìn 1 cạnh dưới 1 góc vuông) Tâm đường tròn ngoại tiếp tứ giác OABI là trung điểm của OA b)Chứng minh IA là tia phân giác của BIC :
Ta có : 090 OCA (AC là tiếp tuyến của (O))
090 AIO (I là hình chiếu của O trên AN) 090 OCAAIO Tứ giác OCAI nội tiếp đường kính AO (2 đỉnh kề nhau cùng nhìn 1 cạnh dưới 1 góc vuông)
AICAOC (cùng chắn cung AC) Mà : AIBAOB (cùng chắn cung AB) AOBAOC (tính







DẠYKÈMQUYNHƠN
OFFICIAL
AICAIB IA là tia phân giác của BIC c)Chứng minh điểm H thuộc đường tròn ngoại tiếp OMN : Ta có: 1 2 ABMsdMB (góc tạo bởi tiếp tuyến và dây cung) 1 2 ANBsdMB (góc nội tiếp) ABMANB Xét ABM và ANB ta có: BAN chung ABMANB (cmt) (.)ABMANBgg A C M N O I H
chất 2 tiếp tuyến cắt nhau)
DẠYKÈMQUYNHƠN OFFICIAL AMAB ABAN (tỉ số đồng dạng) 2 ABAMAN (1) Ta cũng chứng minh được : (.)ABHAOBgg AHAB ABAO (tỉ số đồng dạng) 2 ABAHAO (2) Từ (1) và (2) ta có: AHAOAMAN AMAO AHAN Xét AMH và AON ta có: NAOchung AMAO AHAN (..)AMHAONcgc AMHHON Mà: 090 AMHNHM (kề bù) 090 HONNHM Tứ giác MHON nội tiếp Điểm H thuộc đường tròn ngoại tiếp OMN
An ra nhà sách và mang theo một số tiền vừa đủ để mua 10 quyển tập và 6 cây bút. Nhưng khi ra đến nơi, giá của một quyển tập mà bạn An dự định mua đã tăng thêm 500 đồng một quyển còn giá một cây bút thì giảm 1000 đồng một cây so với dự định. Vậy để mua 10 quyển tập và 6 cây bút như dự định ban đầu thì bạn An còn thừa hay thiếu số tiền là bao nhiêu?
Bài 4: Nhân ngày “Phụ nữ Việt Nam 20/10”, cửa hàng bán túi xách và ví da giảm giá 30% cho tất cả các sản phẩm và ai có thẻ “Khách hàng thân thiết” sẽ được giảm tiếp 10% trên giá đã giảm
a) Hỏi mẹ bạn An có thẻ khách hàng thân thiết khi mua 1 cái túi xách trị giá 500.000 đồng thì phải trả bao nhiêu tiền?
b) Mẹ bạn An mua túi xách trên và thêm 1 cái ví da nên phải trả tất cả 693.000 đồng. Hỏi giá ban đầu của cái ví da là bao nhiêu?
Bài 5: Ảnh hưởng của viêm đường hô hấp cấp do chủng mới của virus corona (nCoV) gây ra nên nông sản Việt, đặc biệt là thanh long, dưa hấu đang tắc đường xuất khẩu qua Trung Quốc. Trước tình hình đó, bắt đầu từ ngày 5/2/2020, hệ thống siêu thị Big C đã triển khai chương trình chung tay hỗ trợ nông dân trồng dưa hấu, thanh long, bán hàng không lợi nhuận đối với sản phẩm thanh long và dưa hấu, nhằm kích cầu tiêu thụ, mua sắm của người dân. Big C đã đưa ra con số giải cứu dự kiến khoảng 1.200 tấn thanh long, 2.000 tấn dưa hấu hỗ trợ nông dân, mang sản phẩm bán trên toàn hệ thống siêu thị và các cửa hàng thuộc thương hiệu GO!. Với giá dưa hấu ruột đỏ chỉ 4.900 đồng/kg, thanh long ruột đỏ miền Tây và thanh long ruột trắng Bình Thuận được bán với giá 10.900 đồng/kg. Nếu hoàn thành dự kiến đưa ra thì Big C sẽ đem lại cho nông dân bao nhiêu tiền lợi nhuận? Biết rằng tiền đầu tư (công chăm sóc, giống, phân bón, …) trung bình vào mỗi sào dưa hấu hết 6 triệu đồng và thu hoạch được 2 tấn; mỗi sào thanh long hết 12 triệu đồng và thu được 1,5 tấn. Bài 6: Một cốc nước hình trụ cao 15 cm, đường kính đáy là 6 cm. Lượng nước ban đầu cao 10cm. Thả vào cốc 5 viên bi hình cầu cùng đường kính 2 cm. Hỏi sau khi thả 5 viên bi thì mực nước cách miệng cốc bao nhiêu cm? (Làm tròn lấy 2 chữ số thập phân)
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GD & ĐT HUYỆN CỦ CHI NĂM HỌC 2022-2023 ĐỀ THAM KHẢO MÔN :
9 -------------------- Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Huyện Củ Chi – 03 Thời gian: 120 phút
thời gian phát đề) Bài 1: a) Vẽ đồ thị hàm số 2 1 (P): 4 yx và 1 (D):2 2 yx trên cùng hệ trục tọa độ b) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán. Bài 2: Cho phương trình 2 31250 xx có hai nghiệm là 12 , xx . Không giải phương trình,
trị của
: 2 1212 2 1212 4 4 xxxx T xxxx Bài
TOÁN
(không kể
hãy tính giá
biểu thức
3: Bạn
Bài 7: Trong kì thi học kì II môn toán 9, một phòng thi của trường có 24 thí sinh dự thi. Các thi sinh đều phải làm bài trên giấy thi của trường phát cho. Cuối buổi thi, sau khi thu bài, giám thị coi thi đếm được tổng số tờ là 53 tờ giấy thi. Hỏi trong phòng thi đó có bao nhiêu thi sinh làm bài 2 tờ giấy thi, bao nhiêu thí sinh làm bài 3 tờ giấy thi? Biết rằng có 3 thí sinh chỉ làm 1 tờ giấy thi.
Bài 8: Cho điểm A nằm ngoài (O; R), kẻ tiếp tuyến AB, AC của (O) (B, C là tiếp điểm). AO cắt BC tại H, kẻ cát tuyến ADE của (O) cắt đoạn BH, kẻ OIDE tại I a) Chứng minh ABIO nội tiếp và 2OHOAR b) Tiếp tuyến tại E của (O) cắt OI tại K. Chứng minh D, K, E, O, H cùng thuộc một đường tròn c) Chứng minh K, B, C thẳng hàng
OFFICIAL
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 78 -

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI Bài 1: a) Vẽ đồ thị hàm số 2 1 (P): 4 yx và 1
2
trên
ệ trục tọa độ b)
tọa độ
điểm của
ằ
Lờ
giải a) Hàm số: 2 1 4 yx Bảng giá trị tương ứng của x và y : x 4 2 0 2 4 2 1 4 yx 4 1 0 1 4 Đồ thị hàm số là một Parabol đi qua các điểm 4;4 ; 2;1 ; 0;0 ; 2;1 ; 4;4 Hàm số: 1 2 2 yx 02xy 04yx Đồ thị hàm số là đường thẳng đi qua 0;2 và 4;0 Vẽ: b) Hoành độ giao điểm của P và D là nghiệm của phương trình: 2 11 2 42 xx 2 28xx 2 280xx 2 11.890 Phương trình có hai nghiệm phân biệt: 1 1 x ; 2 4 x + Với 1 2 x 1 1 y + Với 2 4 x 2 4 y Vậy D cắt P tại hai điểm phân biệt là 2;1 và 4;4
(D):2
yx
cùng h
Tìm
giao
(P) và (D) b
ng phép toán.
i
Bài 3: Bạn An ra nhà sách và mang theo một số tiền vừa đủ để mua 10 quyển tập và 6 cây bút. Nhưng khi ra đến nơi, giá của một quyển tập mà bạn An dự định mua đã tăng thêm 500 đồng một quyển còn giá một cây bút thì giảm 1000 đồng một cây so với dự định. Vậy để mua 10 quyển tập và 6 cây bút như dự định ban đầu thì bạn An còn thừa hay thiếu số tiền là bao nhiêu? Lời giải
Gọi x (đồng) là giá tiền của một quyển tập (x > 0) y (đồng) là giá tiền của một cây bút (y > 1000)
Tổng giá tiền mà An phải trả theo dự định ban đầu: 106xy (đồng)
Giá tiền của một quyển tập sau khi tăng giá: 500 x (đồng)
⟹ Giá tiền của 10 quyển tập sau khi tăng giá: 10500 x (đồng)
Giá tiền của một cây bút sau khi giảm giá: 1000 y (đồng)
⟹ Giá tiền của 6 cây bút sau khi giảm giá: 61000 y (đồng)
Tổng giá tiền mà An phải trả: 10500610001061000 xyxy (đồng)
Vậy để mua 10 quyển tập và 6 cây bút An còn thừa 1000 đồng.
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 80Bài 2: Cho phương trình 2 31250 xx có hai nghiệm là 12 , xx . Không giải phương trình, hãy tính giá trị của biểu thức: 2 1212 2 1212 4 4 xxxx T xxxx Lời giải - Phương trình đã cho là phương trình bậc hai của x có: 224(12)4.3.52040bac Vậy phương trình đã cho có hai nghiệm phân biệt 1x ; 2x - Theo định lý Vi-et, ta có : 12 12 3 4 12 5 3 b xx a c xx a Do đó: 22 112212 1212112212 22 1212 12121212 42 442 4 44 xxxxxx xxxxxxxxxx T xxxx xxxxxxxx 12121212 1212 5 4.42. 4424()2 29 3 444()4.424 xxxxxxxx xxxx Vậy giá trị của biểu thức 29 24 T
Bài 4: Nhân ngày “Phụ nữ Việt Nam 20/10”, cửa hàng bán túi xách và ví da giảm giá 30% cho tất cả các sản phẩm và ai có thẻ “Khách hàng thân thiết” sẽ được giảm tiếp 10% trên giá đã giảm
a) Hỏi mẹ bạn An có thẻ khách hàng thân thiết khi mua 1 cái túi xách trị giá 500.000 đồng thì phải trả bao nhiêu tiền?
b) Mẹ bạn An mua túi xách trên và thêm 1 cái ví da nên phải trả tất cả 693.000 đồng. Hỏi giá ban đầu của cái ví da là bao nhiêu? Lời giải
a) Giá tiền của túi xách trị giá 500.000 đồng nhân ngày “Phụ nữ Việt Nam 20/10”: 70%.500000350000
(đồng) Mẹ An có thẻ khách hàng thân thiết nên số tiền mẹ An phải trả khi mua túi xách này: 90%.350000315000
(đồng) Vậy mẹ bạn An có thẻ khách hàng thân thiết thì phải trả 315000 đồng. b) Giá tiền của ví da mà mẹ An phải trả khi có thẻ khách hàng thân thiết: 693000315000378000 (đồng) c) Giá tiền của ví da mà mẹ An phải trả khi không có thẻ khách hàng thân thiết: 378000:90%420000 (đồng) Giá tiền ban đầu của ví da: 420000:70%600000 (đồng) Vậy giá ban đầu của cái ví da là 600000 đồng
Bài 5: Ảnh hưởng của viêm đường hô hấp cấp do chủng mới của virus corona (nCoV) gây ra nên nông sản Việt, đặc biệt là thanh long, dưa hấu đang tắc đường xuất khẩu qua Trung Quốc. Trước tình hình đó, bắt đầu từ ngày 5/2/2020, hệ thống siêu thị Big C đã triển khai chương trình chung tay hỗ trợ nông dân trồng dưa hấu, thanh long, bán hàng không lợi nhuận đối với sản phẩm thanh long và dưa hấu, nhằm kích cầu tiêu thụ, mua sắm của người dân. Big C đã đưa ra con số giải cứu dự kiến khoảng 1.200 tấn thanh long, 2.000 tấn dưa hấu hỗ trợ nông dân, mang sản phẩm bán trên toàn hệ thống siêu thị và các cửa hàng thuộc thương hiệu GO!. Với giá dưa hấu ruột đỏ chỉ 4.900 đồng/kg, thanh long ruột đỏ miền Tây và thanh long ruột trắng Bình Thuận được bán với giá 10.900 đồng/kg. Nếu hoàn thành dự kiến đưa ra thì Big C sẽ đem lại cho nông dân bao nhiêu tiền lợi nhuận? Biết rằng tiền đầu tư (công chăm sóc, giống, phân bón, …) trung bình vào mỗi sào dưa hấu hết 6 triệu đồng và thu hoạch được
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 81 -
OFFICIAL
12
đồng và thu
1,5
Lời giải Đổi: 1.200 tấn = 1.200.000 kg 2.000 tấn = 2.000.000 kg Số tiền thu được sau khi bán ra 1.200 tấn thanh long, 2.000 tấn dưa hấu là: 1200000.109002000000.490022880000000 (đồng) Số tiền đầu tư vào dưa hấu là: 2000.6 6000 2 (triệu đồng) Số tiền đầu tư vào thanh long là: 1200.12 9600 1,5 (triệu
2 tấn; mỗi sào thanh long hết
triệu
được
tấn.
đồng)
Tổng số tiền đầu tư: 6000960015600 (triệu đồng) 15 600 000 000 (đồng)
Số tiền lợi nhuận sau khi hoàn thành dự kiến: 22880000000156000000007280000000 (đồng) Vậy nếu hoàn thành dự kiến đưa ra thì Big C sẽ đem lại cho nông dân 7 280 000 000 đồng tiền lợi nhuận
Bài 6: Một cốc nước hình trụ cao 15 cm, đường kính đáy là 6 cm. Lượng nước ban đầu cao 10cm. Thả vào cốc 5 viên bi hình cầu cùng đường kính 2 cm. Hỏi sau khi thả 5 viên bi thì mực nước cách miệng cốc bao nhiêu cm? (Làm tròn lấy 2 chữ
Bài 7: Trong kì thi học kì II môn toán 9, một phòng thi của trường có 24 thí sinh dự thi. Các thi sinh đều phải làm bài trên giấy thi của trường phát cho. Cuối buổi thi, sau khi thu bài, giám thị coi thi đếm được tổng số tờ là 53 tờ giấy thi. Hỏi trong phòng thi đó có bao nhiêu thi sinh làm bài 2 tờ giấy thi, bao nhiêu thí sinh làm bài 3 tờ giấy thi? Biết rằng có 3 thí sinh chỉ làm 1 tờ giấy thi.
DẠYKÈMQUYNHƠN
OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 82 -
Lời giải Bán kính của cốc nước
trụ là: 6:23() Rcm Thể tích lượng nước ban đầu có trong cốc hình trụ là: 223 .3.1090()VRhcm níc ban ®Çu Bán kính của viên bi hình cầu là: 2:21() rcm Thể tích viên bi hình cầu là: 3 33 bi 44.14 () 333 Vrcm Thể tích nước sau khi bỏ 5 viên bi vào: 3 4290 905.() 33 Vcm níc lóc sau Chiều cao của mức nước lúc này 2 2 ':.3290290() 327 V hcm R níc lóc sau Mực nước cách miệng hồ: 290115 154,26() 2727 cm
số thập phân)
hình
Gọi
lần lượt
Vì có 3 học sinh làm 1 tờ giấy thi và một
thi có 24 thí sinh dự thi nên ta có phương trình: 32421xyxy (1) Vì có 3 học sinh làm 3 tờ giấy và có tổng số tờ là 53 tờ giấy thi nên ta có phương trình: 233532350 xyxy (2) Từ (1) và (2) ta có: 235013 218()xyx n xyy Vậy có 13 thí sinh làm 2 tờ, 8 thí sinh làm 3 tờ.
Lời giải
x, y (học sinh)
số thí sinh làm 2 tờ và 3 tờ giấy thi ( * x, y )
phòng
cát tuyến ADE của (O) cắt đoạn BH, kẻ OIDE tại I a) Chứng minh ABIO nội tiếp và 2 . OHOAR b) Tiếp tuyến tại E của (O) cắt OI tại K. Chứng minh D, K, E, O, H cùng thuộc một đường tròn c) Chứng minh K, B, C thẳng hàng L

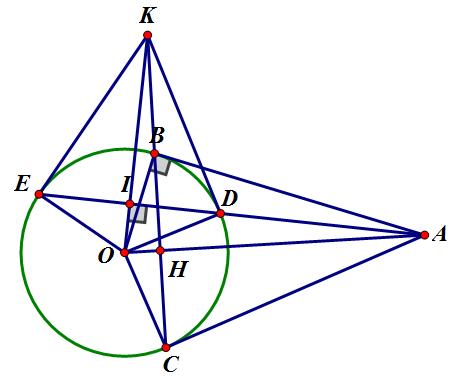
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 83 -
H, kẻ
ời giải a) Theo đề ta có: OIED tại I nên I là trung điểm của ` Xét tứ giác ABIO ta có : 90() 90 OIA OBA gi¶ thiÕt (AB lµ tiÕp tuyÕn) OIAOBA Tứ giác ABIO nội tiếp (tứ giác có đỉnh liền kề cùng nhìn cạnh OA dưới 2 góc bằng nhau) Ta có : ( () ABAC OBOCR tÝnh chÊt 2 tiÕp tuyÕn c¾t nhau) OA là đường trung trực của BC OABC tại H và H là trung điểm của BC Xét OBA vuông tại B có BH là đường cao nên 2 OBOHOA (hệ thức lượng) Mà OBR nên 2 . OHOAR b) Ta có OIED tại trung điểm I của ED nên OI là đường trung trực của ED. Suy ra KD = KE Dễ dàng chứng minh được : (..)90OEKODKcccOEKODK Tứ giác OEKD nội tiếp đường tròn đường kính OK (1) Xét OEK vuông tại E có EI là đường cao nên 2 . OEOIOK (hệ thức lượng)
Bài 8: Cho điểm A nằm ngoài (O; R), kẻ tiếp tuyến AB, AC của (O) (B, C là tiếp điểm). AO cắt BC tại



DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 84Mà OER nên 2OIOKR Ta lại có : 2 . OHOAR (chứng minh câu a) Suy ra OIOA OIOKOHOA OHOK Suy ra (..)OHKOIAcgc 90 OHKOIAOHK vuông tại Tam giác OHK nội tiếp đường tròn đường kính OK (2) Từ (1) và (2) 5 điểm D, K, E, O, H cùng thuộc đường tròn đường kính . c) Theo chứng minh trên ta có: () () OAKHOHHK OABHOABC K, B, H thẳng hàng Vậy thẳng hàng
PHÒNG GD & ĐT QUẬN GÒ VẤP NĂM HỌC 2022-2023 ĐỀ THAM KHẢO MÔN : TOÁN 9 -------------------- Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Quận Gò Vấp – 3 Thời gian: 120 phút (không kể thời gian phát đề)
Câu 1: (1,5 điểm). Cho Parabol 2 1 : 2 Pyx và đường thẳng 1 :3 2 Dyx
a) Vẽ (P) và (D) trên cùng hệ trục tọa độ b) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán Câu 2: (1 điểm). Cho phương trình 2 3410 xx . Gọi x1; x2 là hai nghiệm của phương trình trên. Không giải phương trình hãy tính giá trị của biểu thức 12 21
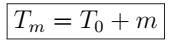
11xx A xx Câu 3: (0,75 điểm). Một chiếc máy bay cất cánh tại sân bay Tân Sơn Nhất lúc 10h ngày 01/03/2021, máy bay hạ cánh tại Tokyo sau 7h bay. Biết Hà Nội ở khoảng kinh tuyến số 105oĐ, Tokyo ở khoảng kinh tuyến số 135oĐ; Los Angeles ở khoảng kinh tuyến số 120oT.
a) Tính số thứ tự theo kinh tuyến của múi giờ ở Hà Nội, Tokyo và Los Angeles?
b) Máy bay hạ cánh tại Tokyo lúc mấy giờ, ngày nào? Biết công thức tính giờ:
Trong đó: - Tm: giờ địa phương (múi giờ). - T0: giờ GMT (giờ gốc). - m: là số thứ tự theo kinh tuyến của múi giờ Thiết lập công thức tính múi giờ: - Ở Đông bán cầu: m = (kinh tuyến Đông): 15 . - Ở Tây bán cầu: m = (360 – kinh tuyến Tây) : 15
Tính ngày: - Điểm cùng bán cầu không đổi ngày - Khi ở khác bán cầu sẽ có sự thay đổi không chỉ giờ mà cả ngày cũng khác. Quy luật đổi ngày sẽ tính từ kinh tuyến 180o. Nếu từ Đông sang Tây cộng them 1 ngày, ngược lại từ Tây sang Đông tính lùi 1 ngày.
Câu 4: (0,75 điểm). Tại một địa điểm nhiệt độ đo được ở mặt đất khoảng 26oC. Biết rằng cứ lên 1km thì nhiệt độ sẽ giảm 6oC. a) Hãy lập hàm số T theo h, biết rằng mối liên hệ giữa nhiệt độ T(oC) và độ cao h (km) là hàm số bậc nhất.
b) Hãy tính nhiệt độ khi ở độ cao 2,5 km so với mặt đất. Câu 5 (1 điểm). Một cửa hàng chuyên bán điện thoại di dộng. Để phục vụ nhu cầu mua sắm dịp Tết Nguyên Đán đã nhập về lô hàng gồm điện thoại của hai hãng Op và SS. Sau một thời gian mở bán với giá niêm yết thì cửa hàng khuyến mãi giảm giá 5% khi mua điện thoại Op; giảm 6% khi mua điện thoại SS. Lúc này, anh Nam đến cửa hàng mua 3 chiếc điện thoại Op và 5 chiếc điện thoại SS để tặng người thân. Anh dự tính phải trả là 49685000 đồng. Nhưng khi tính tiền anh Nam được cửa hàng thông báo khi mua điện thoại SS, bắt đầu từ chiếc thứ 4 sẽ không thực hiện khuyến mãi trên mà giảm ngay 900000 đồng mỗi chiếc so với giá niêm yết. Do đó anh Nam đã trả số tiền là 48797000 đồng. Hỏi giá niêm yết của mỗi chiếc điện thoại của hãng Op; hãng SS là bao nhiêu?
Câu 6 (1 điểm). Một xí nghiệp làm gia công thiết bị điện tử qui định trung bình mỗi ngày một công nhân phải làm được 400 sản phẩm thì mới đạt chỉ tiêu. Khi đó công nhân sẽ nhận được mức lương là 8 triệu đồng/tháng. Ngoài ra, nếu làm vượt chỉ tiêu sẽ được thưởng 2000 đồng cho mỗi sản phẩm vượt chỉ tiêu.
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT
Ồ CHÍ
ĐỀ THAM KHẢO TUYỂN SINH 10
TP.H
MINH
Trong tháng 4/2022, anh Minh lãnh được tiền lương là 9,5 triệu đồng. Hỏi trong tháng 4/2022 anh Minh làm được bao nhiêu sản phẩm? Biết xí nghiệp nghỉ làm các ngày Chủ nhật và các ngày lễ, và 1/4/2022 là thứ sáu.
Câu 7 (1 điểm). Để trải nghiệm về thức uống được tốt nhất và hấp dẫn với khách hàng, người chủ quán yêu cầu nhân viên pha chế phải giữ cho khoảng cách của mực nước trong cốc cách mép cốc ít nhất 2 cm. Biết rằng cốc của quán sử dụng có dạng một hình trụ cao 9 cm, đường kính 6 cm. Mặt đáy phẳng và dày 1 cm, thành cốc dày 0,2 cm. Nhân viên đã đổ vào cốc 120 ml thức uống. Hỏi nếu người nhân viên này bỏ thêm vào 5 viên đá dạng hình cầu, đường kính 2 cm thì mực nước trong cốc có phù hợp với yêu cầu đã đặt ra không? (Các kết quả làm tròn đến chữ số thập phân thứ hai sau dấy phẩy).
Câu 8 (3 điểm). Cho ∆ABC vuông tại A, đường cao AH. Vẽ (O) đường kính AH, đường tròn này cắt AB, AC lần lượt tại D, E.
a) Chứng minh tứ giác ADHE là hình chữ nhật.
b) Chứng minh AD · AB = AE · AC và tứ giác BDEC nội tiếp . Gọi I, K, F lần lượt là tâm đường tròn nội tiếp ∆ABH, ∆ABC, ∆AHC. Chứng minh AK ⊥ IF.
OFFICIAL
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 78 -

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI Bài 1: (1.5 điểm) Cho hàm số 2 1 2 yx có đồ thị là parabol P và hàm số 1 3 2 yx có đồ thị là đường thẳng D a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ; b) Tìm tọa độ giao điểm của P và D bằng phép tính Lời giải a) Hàm số: 2 1 2 yx Bảng giá trị tương ứng của x và y : x 4 2 0 2 4 2 1 2 yx 8 2 0 2 8 Đồ thị hàm số là một Parabol đi qua các điểm 4;8 ; 2;2 ; 0;0 ; 2;2 ; 4;8 Hàm số: 1 3 2 yx 03xy 22 24 xy xy Đồ thị hàm số là đường thẳng đi qua 0;3 ; 2;2 và 2;4 Vẽ: b) Hoành độ giao điểm của P và D là nghiệm của phương trình: 2 11 3 22 xx 2 60 xx 3 2 x x
Bài 3: (0,75 điểm). Một chiếc máy bay cất cánh tại sân bay Tân Sơn Nhất lúc 10h ngày 01/03/2021, máy bay hạ cánh tại Tokyo sau 7h bay. Biết Hà Nội ở khoảng kinh tuyến số 105oĐ, Tokyo ở khoảng kinh tuyến số 135oĐ; Los Angeles ở khoảng kinh tuyến số 120oT. a) Tính số thứ tự theo kinh tuyến của múi giờ ở Hà Nội, Tokyo và Los Angeles?
b) Máy bay hạ cánh tại Tokyo lúc mấy giờ, ngày nào?
Biết công thức tính giờ:
Trong đó: - Tm: giờ địa phương (múi giờ). - T0: giờ GMT (giờ gốc). - m: là số thứ tự theo kinh tuyến của múi giờ
Thiết lập công thức tính múi giờ: - Ở Đông bán cầu: m = (kinh tuyến Đông): 15 - Ở Tây bán cầu: m = (360 – kinh tuyến Tây) : 15 .
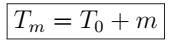
Tính ngày: - Điểm cùng bán cầu không đổi ngày
- Khi ở khác bán cầu sẽ có sự thay đổi không chỉ giờ mà cả ngày cũng khác. Quy luật đổi ngày sẽ tính từ kinh tuyến 180o. Nếu từ Đông sang Tây cộng them 1 ngày, ngược lại từ Tây sang Đông tính lùi 1 ngày.
Lời giải
a) Vì Hà Nội và Tokyo ở Đông bán cầu Nên số thứ tự theo kinh tuyến của múi giờ tại:
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 80+ Với 2 x 2 y + Với 3 x 9 2 y Vậy tọa độ giao điểm của d và P là 2;2 ; 9 3; 2 Bài 2: (1.0 điểm) Cho phương trình 2 3410 xx . Gọi x1; x2 là
12 21 11xx A xx Lời giải Phương trình đã cho là phương trình bậc hai của x có: 3410 abc Vậy phương trình đã cho luôn có hai nghiệm 1x ; 2x Theo định lý Vi-et, ta có: 12 12 4 3 1 3 b Sxx a c Pxx a Ta có : 12 21 1122 12 22 1212 12 2 11 (1)(1) 2 2 3 xx A xx xxxx A xx xxxx A xx SPS A P A
hai nghiệm của phương trình trên. Không giải phương trình hãy tính giá trị của biểu thức
- Hà Nội: 105:157 m Hà Nội thuộc múi giờ số 7
- Tokyo: 135:159 m Tokyo thuộc múi giờ số 9
Vì Los Angeles ở Tây bán cầu Nên số thứ tự theo kinh tuyến của múi giờ tại Los Angeles: (360120):1516 m Los Angeles thuộc múi giờ số 16
b) Lúc 10h ngày 1/3/2021 tại sân bay Tân Sơn Nhất có múi giờ số 7, theo công thức tính giờ ta có: 0001073 m TTmTT
ậy giờ GMT là 3h Khi máy bay cất cánh tại sân bay Tân Sơn Nhất thì lúc đó, ở Tokyo có múi giờ số 9 có giờ địa phương là: 0 3912 mmm TTmTT Vậy khi máy bay cất cánh thì lúc đó, tại Tokyo là 12h Mà máy bay hạ cánh tại Tokyo sau 7h bay nên đáp lúc 19h ngày 1/3/2021 Bài 4: (0,75 điểm). Tại một địa điểm nhiệt độ đo được ở mặt đất khoảng 26oC. Biết rằng cứ lên 1km thì nhiệt độ sẽ giảm 6oC.
a) Hãy lập hàm số T theo h, biết rằng mối liên hệ giữa nhiệt độ T(oC) và độ cao h (km) là hàm số bậc nhất.
b) Hãy tính nhiệt độ khi ở độ cao 2,5 km so với mặt đất. Lời giải
a) Cứ lên cao 1 km thì nhiệt độ giảm 6oC nên tại độ cao h (km) thì nhiệt độ giảm đi 6.h ( C ) Hàm số tính nhiệt độ T(oC) theo độ cao h (km) là: 266 Th
b) Khi ở độ cao 2,5 km so với mặt đất thì h = 2,5 (km) Thế h = 2,5 vào hàm số, ta được: 266.2,511 T Vậy nhiệt độ khi ở độ cao 2,5 km so với mặt đất là 11 C
Bài 5: (1 điểm). Một cửa hàng chuyên bán điện thoại di dộng. Để phục vụ nhu cầu mua sắm dịp Tết Nguyên Đán đã nhập về lô hàng gồm điện thoại của hai hãng Op và SS. Sau một thời gian mở bán với giá niêm yết thì cửa hàng khuyến mãi giảm giá 5% khi mua điện thoại Op; giảm 6% khi mua điện thoại SS. Lúc này, anh Nam đến cửa hàng mua 3 chiếc điện thoại Op và 5 chiếc điện thoại SS để tặng người thân. Anh dự tính phải trả là 49685000 đồng. Nhưng khi tính tiền anh Nam được cửa hàng thông báo khi mua điện thoại SS, bắt đầu từ chiếc thứ 4 sẽ không thực hiện khuyến mãi trên mà giảm ngay 900000 đồng mỗi chiếc so với giá niêm yết. Do đó anh Nam đã trả số tiền là 48797000 đồng. Hỏi giá niêm yết của mỗi chiếc điện thoại của hãng Op; hãng SS là bao nhiêu? Lời giải
- Gọi x, y (đồng) là giá niêm yết của mỗi chiếc điện thoại của hãng Op; hãng SS (x, y > 0)
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 81 -
OFFICIAL
V
i củ
- Anh Nam mua 3 chiếc điện thoại Op và 5 chiếc điện thoại SS dự tính phải trả là 49685000 đồng 3.0,955.0,96496850002,854,749685000(1) yxy - Khi mua điện thoại SS, bắt đầu từ chiếc thứ 4 sẽ không thực hiện khuyến mãi trên mà giảm ngay 900000 đồng Khi mua 5 chiếc điện thoại SS anh Nam phải trả: 52.90000051800000 yy Nên tổng số tiền anh phải trả số tiền là 48797000 đồng 3.0,9551800000487970002,85550597000(2) xyxy Từ (1) và (2) ta có hệ phương trình là: 2,854,74968500012420000 2,855505970003040000 xyx xyy Vậy giá niêm yết của mỗi chiếc điện thoại của hãng Op; hãng SS là 12420000 đồng và 3040000 đồng
- Giá tiền chiếc điện thoại của hãng Op sau giảm giá 5% là: (15%)0,95 xx - Giá tiền chiếc điện thoạ
a hãng SS sau giảm giá 5% là: (16%)0,94 yx
NHÓM
Bài 6: (1 điểm). Một xí nghiệp làm gia công thiết bị điện tử qui định trung bình mỗi ngày một công nhân phải làm được 400 sản phẩm thì mới đạt chỉ tiêu. Khi đó công nhân sẽ nhận được mức lương là 8 triệu đồng/tháng. Ngoài ra, nếu làm vượt chỉ tiêu sẽ được thưởng 2000 đồng cho mỗi sản phẩm vượt chỉ tiêu. Trong tháng 4/2022, anh Minh lãnh được tiền lương là 9,5 triệu đồng. Hỏi trong tháng 4/2022 anh Minh làm được bao nhiêu sản phẩm? Biết xí nghiệp nghỉ làm các ngày Chủ nhật và các ngày lễ, và 1/4/2022 là thứ sáu.
Lời giải
Ta có: 1/4/2022 là thứ sáu 3/4/2022 là Chủ Nhật Vậy trong tháng 4/2022, anh Minh được nghỉ các ngày Chủ Nhật rơi vào ngày 3, 10, 17, 24, 31 và lễ Quốc Khánh 30/4 Số ngày anh Minh phải làm trong tháng 4 là: 31625 (ngày) Tổng số sản phẩm đạt chỉ tiêu trong tháng 4 là: 25.40010000 (sản phẩm) Số tiền thưởng cho sản phẩm vượt chỉ tiêu là: 950000080000001500000 (đồng) Số sản phẩm vượt chỉ tiêu là: 1500000:2000750 (sản phẩm) Tổng số sản phẩm anh Minh làm trong tháng 4/2022 là: 7501000010750 (sản phẩm) Bài 7: (1 điểm). Để trải nghiệm về thức uống được tốt nhất và hấp dẫn với khách hàng, người chủ quán yêu cầu nhân viên pha chế phải giữ cho khoảng cách của mực nước trong cốc cách mép cốc ít nhất 2 cm. Biết rằng cốc của quán sử dụng có dạng một hình trụ cao 9 cm, đường kính 6 cm. Mặt đáy phẳng và dày 1 cm, thành cốc dày 0,2 cm. Nhân viên đã đổ vào cốc 120 ml thức uống. Hỏi nếu người nhân viên này bỏ thêm vào 5 viên đá dạng hình cầu, đường kính 2 cm thì mực nước trong cốc có phù hợp với yêu cầu đã đặt ra không? (Các kết quả làm tròn đến chữ số thập phân thứ hai sau dấy phẩy).
OFFICIAL
ời giải - Thể tích nước tối đa cho phép đổ vào ly là :
2 33 6 .0,2.91247,04()147,78() 2 Vcmcm
- Thể tích 5 viên đá hình cầu là: 3 3 4220 5.() 323 cm - Sau khi bỏ 5 viên đá hình cầu vào 120 ml thức uống thì lúc này thể tích chứa nước và đá trong ly là: 33 20 120()140,93() 3 cmcm - Do thể tích nước và đá chứa trong ly lúc này ít hơn thể tích nước tối đa cho phép đổ vào ly nên mực nước trong cốc phù hợp
DẠYKÈMQUYNHƠN
82
WORD HÓA ĐỀ TOÁN -
-
với yêu cầu đã đặt ra. Bài 8: (3.0 điểm) Cho ∆ABC vuông tại A, đường cao AH. Vẽ (O) đường kính AH, đường tròn này cắt AB, AC lần lượt tại D, E a) Chứng minh tứ giác ADHE là hình chữ nhật. b) Chứng minh AD · AB = AE · AC và tứ giác BDEC nội tiếp . Gọi I, K, F lần lượt là tâm đường tròn nội tiếp ∆ABH, ∆ABC, ∆AHC. Chứng minh AK ⊥ IF Lời giải
L
a) - Ta có: ˆˆ 90 ADHAEH (Góc nội tiếp chắn nửa (O))
- Xét tứ giác ADHE có: ˆ ˆˆ 90 DAHADHAEH (cmt) Tứ giác ADHE là hình chữ nhật b) - Xét AHB vuông tại H có HD là đường cao 2 AHADABhtl (1)
- Xét AHC vuông tại H có HE là đường cao 2 .2AHAEAChtl
- Từ (1) và (2) AD.AB=AE.AC
- Xét ADE và ACB có + ˆ BAC chung + ADAE ACAB (do AD.AB=AE.AC) ADE đồng dạng ACB (c-g-c) ˆ ˆ ADEACB - Xét tứ giác BDEC có ˆ ˆ ADEACB (cmt) Tứ giác BDEC nội
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 83 -
OFFICIAL
tiếp c) -
+
ˆ AHB
+ HF
ˆ AHC
+ ˆˆ 180 AHBAHC(kề bù) HIHF - Ta có: + HI là phân giác ˆ AHB(do I là tâm đường tròn nội tiếp AHB ) + HF là phân giác ˆ AHC (do F là tâm đường tròn nội tiếp AHC ) + ˆˆ 90 AHBAHC ˆˆˆˆ 45 IHBIHAFHAFHC - Ta có: + ˆˆ BAHACH (cùng phụ ˆ ABC ) N M F I K E D O H B C A
Ta có:
HI là phân giác
(do I là tâm đường tròn nội tiếp AHB )
là phân giác
(do F là tâm đường tròn nội tiếp AHC )
+ 1 ˆˆ 2 IAHBAH (do AI là phân giác của ˆ BAH ) + 1 ˆˆ 2 FCHACH (do CF là phân giác của ˆ ACH ) ˆˆ IAHFCH - Xét IAH và FCH có: + ˆˆ IAHFCH (cmt) + ˆˆ 45 IHAFHC (cmt) IAH đồng dạng FCH (g-g) ˆˆ AIHCFH - CF cắt AI tại N - Xét tứ giác INFH có ˆˆ NIHCFH (cmt) Tứ giác IEFH nội tiếp
180 INFIHF - Mà ˆ 90 IHF (cmt) ˆ 90 INF FNAI - Ta có: + ˆ ˆ CAHABC (cùng phụ ˆ ACB ) + 1 ˆˆ 2 FAHCAH (do AF là phân giác của ˆ CAH ) + 1 ˆˆ 2 IBHABC (do BI là phân giác của ˆ ABC )
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 84 -
HFAHIB - BI cắt AF ở M - Xét tứ giác IMFH có: + ˆˆ HFMHIB (cmt) Tứ giác IMFH nội tiếp ˆˆ 180 IMFIHF - Mà ˆ 90 IHF (cmt) ˆ 90 IMF IMAF - Xét AIF có + FN là đường cao thứ nhất (do FNAI ) + IM là đường cao thứ hai (do IMAF ) + IM cắt FN tại K K là trực tâm của AIF AK là đường cao thứ 3 AKIF
ˆˆ
ˆ ˆ FAHIBH - Xét FAH và IBH có: + ˆ ˆ FAHIBH (cmt) + ˆˆ 45 FHAIHB (cmt) FAH đồng dạng IBH ˆˆ
tính giá trị c
a biểu th
c 12 2122 xx C xx .` Bài 3. (0,75 điểm) Bạn An dự dịnh đem vừa đủ số tiền để mua 20 quyển tập tại nhà sách Nguyễn Văn Cừ. Tuy nhiên, hôm nay nhà sách có chương trình khuyến mãi đầu năm giảm giá 20% mỗi quyển tập. Hỏi với số tiền bạn An đem có thể mua được tất cả bao nhiêu quyển tập?
Bài 4. (0,75 điểm) Hiện tại bạn Bình đã để dành được một số tiền là 800000000 đồng. Bạn Bình đang có ý định mua một căn chung cư là 2000000000 đồng. Nên hàng tháng bạn Bình có mức lương 50 triệu đồng một tháng, sau khi trừ chi phí ăn uống, tiền thuê nhà, cho ba mẹ... tổng cộng hết là 30 triệu đồng, số tiền còn lại bạn đều để dành để mua nhà. Gọi m (triệu đồng) là số tiền bạn Bình tiết kiệm được sau t (tháng) (tính luôn cả 800 triệu đã tiết kiệm trước đó).
a) Thiết lập hàm số của m theo t .
b) Hỏi sau bao nhiêu năm kể từ ngày bắt đầu tiết kiệm thì Bình có thể mua được căn chung cư đó?
Bài 5. (1,0 điểm) Phòng học lớp 6A gắn máy lạnh. Lớp có 49 học sinh, trong đó có 40 bạn học bán trú. Biết rằng các bạn học bán trú thì đóng tiền điện 100%, các bạn không học bán trú thì đóng 50%. Trong 4 tháng lớp đã xài hết 700 Kwh điện, biết mỗi Kwh điện giá 2000 đồng. Tính số tiền mỗi học sinh bán trú và không bán trú cần phải đóng? (làm tròn đến chữ số hàng nghìn).
Bài 6. (1,0 điểm) Nhà bạn An có một xô đựng nước có dạng hình nón cụt. Đáy xô có đường kính là 28cm , miệng xô là đáy lớn của hình nón cụt có đường kính là 36 cm. Hỏi Nếu cần 78 lít nước thì bạn An phải xách tối thiểu là bao nhiêu lần nếu chiều cao của xô là 32cm ?
32
18 14
Bài 7. (1,0 điểm) Nhu cầu mua hàng online hiện nay rất lớn. Để vận chuyển các món hàng đó đến tay khách hàng không ai khác chính là các shipper. Ngày 5/1/2022 công ty A cần nhờ các shipper vận chuyển một số hàng. Theo dự định mỗi shipper sẽ vận chuyển 30 món hàng thì sẽ chở hết số hàng
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GD
HÓC MÔN
. b) Tìm tọa độ giao điểm của () P và () d bằng phép toán. Bài 2. (1,0 điểm) Cho phương trình 2 580xx có
ệm 12 , xx . Không giải
& ĐT HUYỆN
NĂM HỌC 2022-2023 ĐỀ THAM KHẢO MÔN : TOÁN 9 -------------------- Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Hóc Môn – 3 Thời gian: 120 phút (không kể thời gian phát đề) Bài 1. (1,5 điểm) Cho parabol 2 1 (): 2 Pyx và đường thẳng ():34 dyx a) Vẽ () P và () d trên cùng hệ trục tọa độ
hai nghi
phương trình, hãy
ủ
ứ
trên. Nhưng thực tế mỗi shipper vận chuyển 36 món hàng. Do đó số shipper vận chuyển số hàng đó giảm đi 3 người. Tính số hàng mà công ty A đã giao cho khách.
Bài 8. (3,0 điểm) Cho (;) OR và điểm A ở ngoài () O kẻ hai tiếp tuyến ,(, AMANMN là hai tiếp điểm). Kẻ đường kính , MDAD cắt () O tại . KNK cắt AH tại I .
a) Chứng minh: tứ giác ANOM nội tiếp và 2 AIIKIN .
b) Chứng minh: AIMMHD ∽
c) MI cắt () O tại G . Chứng minh 3 diểm ,, DHG thẳng hàng.
DẠYKÈMQUYNHƠN OFFICIAL
78
NHÓM WORD HÓA ĐỀ TOÁN -
-
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI
2
L
x 4 2 0 2 4 2 1 2 yx 8 2 0 2 8 Vẽ: b.
ọa độ
m củ
Phương trình hoành độ
ủ
2 1 34 2 xx 2 68xx 2 680xx
Bài 1. (1,5 điểm) Cho parabol
1 (): 2 Pyx
và đường thẳng ():34 dyx a) Vẽ () P và () d trên cùng hệ trục tọa độ. b) Tìm tọa độ giao điểm của () P và () d bằng phép toán. Lời giải a. Vẽ () P và () d trên cùng hệ trục tọa độ Bảng giá trị: x 0 1 2 34yx 4 1 2
ại có:
Tìm t
giao điể
a () P và () d bằng phép toán.
giao điểm c
a
d và
P là
c tất cả bao nhiêu quyển tập? Lời giải
Gọi giá tiền mua một quyển tập khi chưa giảm là 0 x (đồng) Số tiền mà bạn An đem theo là 20x (đồng).
Nên hàng tháng bạn Bình có mức lương 50 triệu đồng một tháng, sau khi trừ chi phí ăn uống, tiền thuê nhà, cho ba mẹ... tổng cộng hết là 30 triệu đồng, số tiền còn lại bạn đều để dành để mua nhà. Gọi m (triệu đồng) là số tiền bạn Bình tiết kiệm được sau t (tháng) (tính luôn cả 800 triệu đã tiết kiệm trước đó).
a) Thiết lập hàm số của m theo t
b) Hỏi sau bao nhiêu năm kể từ ngày bắt đầu tiết kiệm thì Bình có thể mua được căn chung cư đó? Lời giải
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 802 4 x x Với 2 x thì 2 1 2 2 yx Với 4 x thì 2 1 8 2 yx . Vậy tọa độ giao điểm của đường thẳng d và C là 2;2 và 4;8 Bài 2. (1,0 điểm) Cho phương trình 2 580xx có hai nghiệm 12 , xx . Không giải phương trình, hãy tính giá trị của biểu thức 12 2122 xx C xx .` Lời giải Xét phương trình 2 580xx 1 Có 1;5;8abc . Phương trình 1 có 22454.1.8570bac Nên phương trình 1 có hai nghiệm phân biệt 1x , 2x Áp dụng định lí Viete cho phương trình 1 ta được: 12 5 b Sxx a 12 8 c Pxx a Ta có: 12 2122 xx C xx 22 1122 12 22 22 xxxx C xx 2 121212 1212 22 224 xxxxxx xxxx 2 22 24 SPS PS 17 2 Vậy 17 2 C . Bài 3. (0,75 điểm) Bạn An dự dịnh đem vừa đủ số tiền để mua 20 quyển tập tại nhà sách Nguyễn
Tuy
nhà sách có
ỏi với số tiền bạn An đem
Văn Cừ
nhiên, hôm nay
chương trình khuyến mãi đầu năm giảm giá 20% mỗi quyển tập. H
có thể mua đượ
Vậy
Bình đã để dành được một số tiền
ạn
định mua một căn chung cư
Số tiền một quyển tập sau khi giảm giá là 120%0,8xx (đồng).
nên số quyển tập sau khi giảm giá mà bạn An có thể mua là 20 25 0,8 x x (quyển tập) Vậy với số tiền đem theo thì bạn An mua được 25 quyển tập sau khi giảm giá. Bài 4. (0,75 điểm) Hiện tại bạn
là 800000000 đồng. B
Bình đang có ý
là 2000000000 đồng.
a.
Số tiền mà Bình tiết kiệm được trong một tháng là 503020 (triệu đồng).
Số tiền mà Bình tiết kiệm được trong t (tháng) là 20t (triệu đồng).
Số tiền mà Bình có được sau t (tháng) là 20800mt (triệu đồng).
b.
Để mua được căn chung cư, số tiền Bình cần có được là 2000000000 đồng hay 2000 (triệu đồng) nên 200020800 t 2000800 60 20 t (tháng). Vậy mất 5 năm tiết kiệm thì Bình mua được căn chung cư. Bài 5. (1,0 điểm) Phòng học lớp 6A gắn máy lạnh. Lớp có 49 học sinh, trong đó có 40 bạn học bán trú. Biết rằng các bạn học bán trú thì đóng tiền điện 100%, các bạn không học bán trú thì đóng 50%. Trong 4 tháng lớp đã xài hết 700 Kwh điện, biết mỗi Kwh điện giá 2000 đồng. Tính số tiền mỗi học sinh bán trú và không bán trú cần phải đóng? (làm tròn đến chữ số hàng nghìn). Lời giải Gọi x (đồng) là số tiền điện mỗi học sinh học bán trú phải đóng 0 x . Gọi y (đồng) là số tiền điện mỗi học sinh không học bán trú phải đóng 0 y Vì các bạn học bán trú thì đóng tiền điện 100%, các bạn không học bán trú thì đóng 50% Nên ta có phương trình: 11 0 22
Tổng số tiền mà các bạn phải đóng là: 700.20001400000
(đồng)
Vậy số tiền mỗi học sinh bán trú phải đóng là: 31000 (đồng). Vậy số tiền mỗi học sinh không bán trú phải đóng là: 16000 (đồng).
Bài 6. (1,0 điểm) Nhà bạn An có một xô đựng nước có dạng hình nón cụt. Đáy xô có đường kính là 28cm , miệng xô là đáy lớn của hình nón cụt có đường kính là 36 cm. Hỏi Nếu cần 78 lít nước thì bạn An phải xách tối thiểu là bao nhiêu lần nếu chiều cao của xô là 32cm ?
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 81 -
OFFICIAL
Từ
yxxy
1
Thế nên 4091400000 xy
2
1 và (2) ta có hệ pt 1 0 2 4091400000 xy xy
31000 16000 x y
L
ời giải
Đáy lớn của xô có bán kính 36 18 2 Rcm 18 14 32
(lít). Để múc được tổng cộng 78 (lít) nước thì ta cần 78:25,873,01
(lần xách) Vậy cần ít nhất 4 lần xách thì mới có thể có đủ 78 lít nước.
Bài 7. (1,0 điểm) Nhu cầu mua hàng online hiện nay rất lớn. Để vận chuyển các món hàng đó đến tay khách hàng không ai khác chính là các shipper. Ngày 5/1/2022 công ty A cần nhờ các shipper vận chuyển một số hàng. Theo dự định mỗi shipper sẽ vận chuyển 30 món hàng thì sẽ chở hết số hàng trên. Nhưng thực tế mỗi shipper vận chuyển 36 món hàng. Do đó số shipper vận chuyển số hàng đó giảm đi 3 người. Tính số hàng mà công ty A đã giao cho khách. Lời giải
Gọi x (món hàng) là số hàng công ty A giao cho khách * x
Số shipper khi mỗi người vận chuyển 30 món hàng là: 30 x (người) Số shipper khi mỗi người vận chuyển 36 món hàng là: 36 x (người) Vì số shipper vận chuyển số hàng đó giảm đi 3 người nên ta có phương trình: 3 3036 xx
11 3 3036 x 3 540 11 3036
x (món hàng) Vậy số hàng của công ty A là 540 món hàng. Bài 8. (3,0 điểm) Cho (;) OR và điểm A ở ngoài () O kẻ hai tiếp tuyến ,(, AMANMN là hai tiếp điểm). Kẻ đường kính , MDAD cắt () O tại KNK cắt AH tại I a) Chứng minh: tứ giác ANOM nội tiếp và 2 AIIKIN b) Chứng minh: AIMMHD ∽ . c) MI cắt () O tại G . Chứng minh 3 diểm ,, DHG thẳng hàng. Lời giải
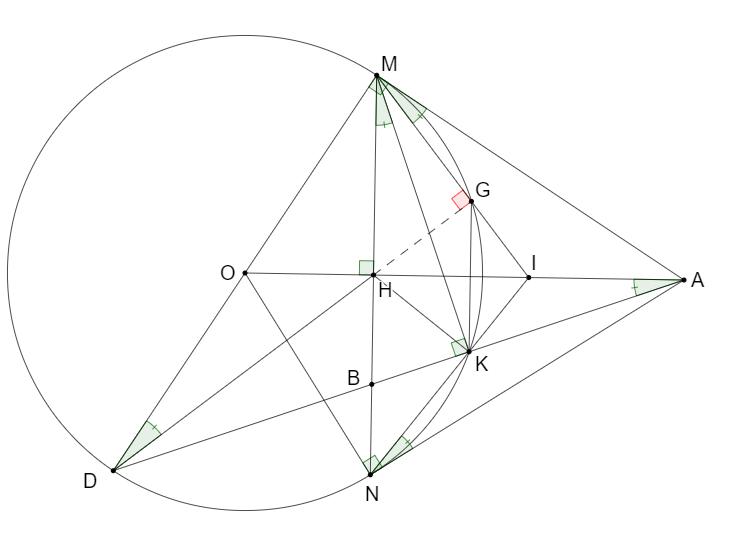
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 82 Đáy bé của xô nước có bán kính 28 14 2 rcm Thể
ủa
tích c
xô nước là:
22 1 3 VRrRrh
Nên
22 1 ..141814.18.32 3 V
3 25870 cm
25,87
Ch
ng minh: tứ giác ANOM nội
Ta có:
OMON (bán kính O )
AMAN (tính chất hai tiếp tuyến cắt nhau)
Nên OA là đường trung trực của đoạn thẳng MN .
Suy ra OAMN tại H Lại có: DKM nội tiếp đường tròn tâm O đường kính MD.
Nên DKM vuông tại K Suy ra MKDK tại K Xét tứ giác AMON ta có: 90 OMA ( AM là tiếp tuyến tại M của O ) 90 ONA ( AN là tiếp tuyến tại N của O )
Nên 90 OMAONA
Suy ra tứ giác OMAN là tứ giác nội tiếp đường tròn đường kính OA. Gọi B là giao điểm của AD và MN
Ta có: BMKBAH (cùng phụ với góc HBK ) Mà NMKINA (góc nội tiếp và góc được tạo bởi tia tiếp tuyến và dây cung chắn NK của O ).
Suy ra BAHINA Xét IKA và IAN ta có: NIA là góc chung IAKINA (cmt) Suy ra IKAIAN gg .
Nên IKIA IAIN Suy ra 2 IAIKIN . b. Chứng minh: AIMMHD ∽ Cách 1: Sử dụng đồng dạng theo trường hợp góc – góc. Xét tam giác ONA vuông tại N có đường cao NH , ta có: 2 ONOHOA Mà ONODR Nên 2 . ODOHOA
Suy ra ODOA OHOD Xét OHD và ODA , ta có:
DOA là góc chung ODOA OHOD (cmt) Suy ra OHDODA cgc
Nên ODHOAD (hai góc tương ứng)
Ta có: I nằm trên OA là đường trung trực của MN .
Suy ra IMIN
Nên MIN cân tại I . Nên IMNINM
Lại có AMAN nên AMN cân tại A Nên AMNANM . Ta có: IMNIMAAMN INMINAANM
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 83 -
tiế
và 2 AIIKIN
OFFICIAL
a.
ứ
p
.
Lại có AMNANM và IMNINM (cmt)
Nên INAIMA
Ta có: INAIMA (cmt)
ODHOAD (cmt)
Lại có: INAOAD (cmt)
Suy ra IMAODH
Xét MHD và AIM , ta có: IAMOMH (cùng phụ với HMA )
IMAODH (cmt)
Suy ra MHDAIMgg
Suy ra IMAMDH (hai góc tương ứng).
Cách 2: Sử dụng đồng dạng theo trường hợp góc – cạnh – góc.
Xét tam giác MOA vuông tại M có đường cao MH , ta có: 2 AMAHAO (hệ thức lượng)
Xét tam giác AMK và tam giác ADM , ta có: MAD là góc chung
AMKADM (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn MK của O ).
Nên AMKADMgg
Suy ra AMAK ADAM Suy ra 2 AMAKAD Mà 2 . AMAHAO (cmt)
Nên .. AKADAHAO Nên AKAO AHAD
Xét AKH và AOD ta có:
DAO là góc chung AKAO AHAD (cmt) Nên AKHAOD cgc Suy ra ADOAHK
Mà MDKMNK (góc nội tiếp chắn cung MK của O ). Nên AHKMNK
IHK và INH ta có: HIN là góc chung IHKINH
Xét MHA và OHM , ta có: 90 MHOMHA MAHOMH
(cmt) Nên MHAOHMgg
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 84 -
OFFICIAL
. Xét
(cmt) Suy ra IHKINH Suy ra 90 IHNHKN và IHIK INIH Nên 2 IHINIK
Mà 2 . IAIKIN
Suy ra IAIH
Suy ra AHAM MHMO
Mà 2 1 2
IAAM MH MD IAAM MHMD
Xét IAM và HMD , ta có: IAMOMH (cùng phụ với HMA )
IAAM MHMD (cmt)
Nên IAMHMD cgc
Suy ra IMAMDH (hai góc tương ứng).
c. MI cắt () O tại G . Chứng minh 3 diểm ,, DHG thẳng hàng.
Ta có: IMAMDG (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn MG của O )
Mà IMAMDH (cmt)
Nên MDGMDH Mà hai góc trên nằm ở nửa mặt phẳng có bờ là cạnh MD
Suy ra D , H , G thẳng hàng.
NHÓM WORD HÓA ĐỀ TOÁN - 85 -
DẠYKÈMQUYNHƠN OFFICIAL
11xx A xx
Bài 3: (1,0 điểm) Một hãng taxi có giá cước tính như sau - Ở km đầu tiên cước: 15.000 đồng. - Từ km thứ 2 đến km thứ 20 giá cước: 13.500/km - Từ km thứ 21 trở đi giá cước: 11.500/km Gọi y (đồng) là số tiền phải trả, x (km) là quãng đường đi Taxi.
a) Viết biểu thức y theo x trong trường hợp đi ít hơn hoặc bằng 20km và trên 20km.
b) Một người đi Taxi phải trả 300.250 đồng. Hỏi người đó đã đi quãng đường dài bao nhiêu?
Bài 4: (1,0 điểm) Có một quả bóng được khâu từ 32 miếng da: Các miếng hình lục giác màu trắng và các miếng hình ngũ giác màu đen. Mỗi miếng màu đen ráp với năm miếng màu trắng. Mỗi miếng màu trắng ráp với ba miếng màu đen và ba miếng màu trắng. Hỏi có bao nhiêu miếng màu trắng?
Bài 5: (1.0 điểm) Trường THCS A dự định tổ chức đi học tập ngoại khóa cho học sinh gồm: Khối 6 có 64 học sinh, khối 7 có 72 học sinh, khối 8 có 64 học sinh, khối 9 có 81 học sinh và 16 giáo viên phụ trách. Trường THCS A sẽ thuê 7 chiếc xe gồm 2 loại: Loại 30 chỗ ngồi và loại 45 chỗ ngồi (không kể tài xế). Hỏi nhà trường phải thuê bao nhiêu xe mỗi loại? (Biết rằng có một xe còn dư 3 chỗ ngồi, các xe còn
đó nhận được bao nhiêu tiền lương? Biết rằng tiền lương tăng ca bằng 150% tiền lương cơ bản.
Bài 7: (1.0 điểm) Có một bình thủy tinh hình trụ phía bên trong có đường kính đáy là 30 cm, chiều cao 20 cm đựng một nửa bình nước và một khối thủy tinh hình trụ có bán kính đáy là 14 cm và chiều cao 11 cm. Hỏi nếu bỏ lọt khối thủy tinh vào bình thủy tinh thì lượng nước trong bình có bị tràn ra ngoài
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GD & ĐT HUYỆN NHÀ BÈ NĂM
202
ĐỀ
--------------------
.
ố 2
1
ị
đường thẳng d a) Vẽ đồ thị P và d trên cùng mặt phẳng tọa độ; b) Tìm tọa độ giao điểm của P và d bằng phép
Bài 2: (1,0 điểm) Gọi 12 , xx là các nghiệm của phương trình 2 60 xx . Không giải
trình,
giá trị của biểu thức 12 21
HỌC
2-2023
THAM KHẢO MÔN : TOÁN 9
Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Huyện Nhà Bè - 03 Thời gian: 120 phút (không kể thời gian phát đề) Bài 1: (1,0 điểm)
Cho hàm s
1 2 yx
có đồ thị là parabol P và hàm số
1 2 yx
có đồ th
là
tính.
phương
tính
ới mức lương cơ bản là
ngàn đồng cho
giờ làm việc trong một ngày. Nếu trong một
ngày
ngày thì người
lại không còn chỗ trống). Bài 6: (1.0 điểm) Một công nhân làm việc v
200.000
8
tháng người đó làm 26
và tăng ca thêm 3 giờ/ngày trong 10
hay không? Tại sao? (Cho thể tích hình trụ tính theo công thức: 2 VRh với R là bán kính đáy, h là chiều cao của hình trụ).
Bài 8: (3.0 điểm) Cho đường tròn và điểm nằm ngoài đường tròn (;) OR . Vẽ hai tiếp tuyến , ABAC của ()(,OBC là hai tiếp điểm). Vẽ cát tuyến ADE của ()(,ODE thuộc ());OD nằm giữa A và E ; tia AD nằm giữa hai tia AB và AO
a) Chứng minh 2 ABADAE
b) Gọi H là giao điểm của OA và BC . Chứng minh tứ giác DEOH nội tiếp.
c) Đường thẳng AO cắt đường tròn () O tại M và N ( M nằm giữa A và )O Chứng minh .. EHADMHAN .
NHÓM WORD HÓA ĐỀ TOÁN - 78 -
DẠYKÈMQUYNHƠN OFFICIAL
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI Bài 1: (1,0 điểm). Cho hàm số 2 1 2 yx có đồ thị là parabol P và hàm số 1 1 2 yx có đồ thị là đường thẳng d . a) Vẽ đồ thị P và d trên cùng mặt phẳng tọa độ; b) Tìm tọa độ giao điểm của P và d bằng phép tính. Lời giải a) Hàm số: 2 1 2 yx Bảng giá trị tương ứng của x và y : x 4 2 0 2 4 2 1 2 yx 8 2 0 2 8 Đồ thị hàm số là một Parabol đi qua các điểm 4;8 ; 2;2 ; 0;0 ; 2;2 ; 4;8 Hàm số: 1 1 2 yx 01xy 20xy Đồ thị hàm số là đường thẳng đi qua 0;1 và 2;0 Vẽ: b) Hoành độ giao điểm của P và d là nghiệm của phương trình: 2 11 1 22 xx 2 20 xx 90 Phương trình có hai nghiệm phân biệt: 1 1 x ; 2 2 x + Với 1 1 x 1 1 2 y + Với 2 2 x 2 2 y Vậy d cắt P tại hai điểm phân biệt là 1 1; 2 và 2;2 g x = 1 2 x 1 f x = 1 2 x2 -1 -8 -2 4 2 -2 -4 0 x y
biểu thức y theo x trong trường hợp đi ít hơn hoặc bằng 20km và trên 20km
b) Một người đi Taxi phải trả 300.250 đồng. Hỏi người đó đã đi quãng đường dài bao nhiêu? Lời giải
a) Trường hợp đi ít hơn hoặc bằng 20 km: 150001.135 0 00135 1 0 50 0 yx x Trường hợp đi trên 20 km: 1500019.1350020 0 .1150011500 4150 yx x .
b) Vì 3002501500019.13500 nên người đó đi trên 20 km. Ta có phương trình: 4150030025022,5 11500xx . Vậy người đó đi quãng đường dài 22,5 km.
Bài 4: (1,0 điểm) Có một quả bóng được khâu từ 32 miếng da: Các miếng hình lục giác màu trắng và các miếng hình ngũ giác màu đen. Mỗi miếng màu đen ráp với năm miếng màu trắng. Mỗi miếng màu trắng ráp với ba miếng màu đen và ba miếng màu trắng. Hỏi có bao nhiêu miếng màu trắng? Lời giải Ta gọi số miếng trắng là x ( * 2 , 3 xx ) gọi số miếng đen là y ( *,2 3 yy ) Vì tổng có 32 miếng nên ta có 32 xy .
Ta xét các đoạn thẳng là các cạnh của ngũ giác và lục giác. Ta tính tổng số đoạn thẳng theo hai cách: Có
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 80Bài 2: (1,0 điểm) Gọi 12 , xx là các nghiệm của phương trình 2 60 xx . Không giải phương trình, tính giá trị của biểu thức 12 21 11xx A xx . Lời giải Ta
xx . Theo
12 12 1 6 xx xx . Do
12 21 11xx A xx 2 22 2 112 1 xxxx xx 11212 12 2 2 2. xxxxxx xx 2 3 2.(6) 1 6 17 . Bài 3: (1,0 điểm) Một hãng taxi có giá cước tính như sau - Ở km đầu tiên cước: 15.000 đồng. - Từ km thứ 2 đến km thứ 20 giá cước: 13.500/km - Từ km thứ 21 trở đi giá cước: 11.500/km. Gọi y (đồng) là số tiền phải trả, x (km) là quãng đường đi Taxi. a) Viết
có: 250, nên phương trình đã cho có hai nghiệm phân biệt 12 ,
định lý Vi-et, ta có:
đó:
ếng trắng và mỗ
c lặp hai lần nên số đoạn
Có y miếng đen và mỗi miếng có 5 đoạn thẳng, nhưng trong đó mỗi đoạn thẳng mà nối hai đỉnh gần nhất của hai ngũ giác được lặp hai lần nên số đoạn thẳng có là: 55:215:2 yyy . Từ đó ta có 35xy . Mà 55160 xy nên 8160 x nên 20 x . Vậy có 20 miếng da màu trắng
x mi
i miếng có 6 đoạn thẳng, nhưng trong đó mỗi miếng có 3 đoạn thẳng mà đượ
thẳng có là: 63:29:2 xxx
học sinh, khối 7 có 72 học sinh, khối 8 có 64 học sinh, khối 9 có 81 học sinh và 16 giáo viên phụ trách. Trường THCS A sẽ thuê 7 chiếc xe gồm 2 loại: Loại 30 chỗ ngồi và loại 45 chỗ ngồi (không kể tài xế). Hỏi nhà trường phải thuê bao nhiêu xe mỗi loại? (Biết rằng có một xe còn dư 3 chỗ ngồi, các xe còn lại không còn chỗ trống). Lời giải Gọi , xy lần lượt là số xe 30 chỗ, 45 chỗ ( * , xy ).
Ta có: 7 xy .
Tổng số học sinh và giáo viên là: 6472648116297.
Tổng số ghế xe: 2973300 (do có dư 3 chỗ ngồi).
Do đó ta có: 45300 30xy .
Ta có hệ phương trình: 71 306 45300xy xxy y . Vậy nhà trường thuê 1 xe 30 chỗ và 6 xe 45 chỗ.
Bài 6: (1.0 điểm) Một công nhân làm việc với mức lương cơ bản là 200.000 ngàn đồng cho 8 giờ làm việc trong một ngày. Nếu trong một tháng người đó làm 26 ngày và tăng ca thêm 3 giờ/ngày trong 10 ngày thì người đó nhận được bao nhiêu tiền lương? Biết rằng tiền lương tăng ca bằng 150% tiền lương cơ bản. Lời giải Với mức lươnng cơ bản, mỗi giờ người đó nhận được 200000825000 đồng. Nên mỗi giờ tăng ca người đó nhận được 150 2500037500 100 đồng. Tổng số tiền người đó nhận được trong một tháng: 200000.263.10.37500 6325000 đồng. Bài 7: (1.0 điểm) Có một bình thủy tinh hình trụ phía bên trong có đường kính đáy là 30 cm, chiều cao 20 cm đựng một nửa bình nước và một khối thủy tinh hình trụ có bán kính đáy là 14 cm và chiều cao 11 cm. Hỏi nếu bỏ lọt khối thủy tinh vào bình thủy tinh thì lượng nước trong bình có bị tràn ra ngoài hay không? Tại sao? (Cho thể tích hình trụ tính theo công thức: 2 VRh với R là bán kính đáy, h là chiều cao của hình trụ) Lời giải Thể tích còn trống của bình thuỷ tinh : 2 1 .207068,6 1 .15 2 V (cm3). Thể tích khối thuỷ tinh : 2 2 .116773,3 .14 V (cm3). Do 21 VV nên nếu bỏ
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 81 -
ối 6 có
OFFICIAL
Bài 5: (1.0 điểm) Trường THCS A dự định tổ chức đi học tập ngoại khóa cho học sinh gồm: Kh
64
lọt khối thủy tinh vào bình thủy tinh thì lượng nước trong bình không bị tràn ra ngoài Bài 8: (3.0 điểm) Cho đường tròn và điểm nằm ngoài đường tròn (;) OR . Vẽ hai tiếp tuyến , ABAC của ()(,OBC là hai tiếp điểm). Vẽ cát tuyến ADE của ()(,ODE thuộc ());OD nằm giữa A và E ; tia AD nằm giữa hai tia AB và AO . a) Chứng minh 2 ABADAE b) Gọi H là giao điểm của OA và BC . Chứng minh tứ giác DEOH nội tiếp.
a) Chứng minh 2 ABADAE .
Xét ABD và AEB ta có: BAD : góc chung ABDAEB (cùng chắn BD ) ABDAEB ∽ (g – g) 2 ABAD ABADAE AEAB (đpcm)
b) Chứng minh tứ giác DEOH nội tiếp.
Ta có: ABO vuông tại B có BH là đường cao 2 . ABAHAO 2 .. AHAOADAEAB AHDAEO ∽ AHDAEO
Suy ra tứ giác DEOH nội tiếp.
c) Chứng minh EHADMHAN
Ta có: 2 DOM DEM (cùng chắn DM ) 22 DOHDEH DEM DEMMEH
EM là phân giác của EAH EHMH AEAM (1).
Ta có: AEMAND ∽ (g – g) AEAM ANAD (2).
Từ (1) và (2) suy ra: .. EHAEMHAM AEANAMAD EHMH ANAD .. EHADANMH (đpcm).
OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 82 -
DẠYKÈMQUYNHƠN
c) Đường thẳng AO cắt đường tròn () O tại M và N ( M nằm giữa A và )O Chứng minh .. EHADMHAN . Lời giải
N M H D C O A B E
GD & ĐT QUẬN 1 NĂM HỌC 2022-20232 ĐỀ THAM KHẢO MÔN : TOÁN 9

Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Quận 1 – 3 Thời gian: 120 phút (không kể thời gian phát đề) Bài 1: (1.5 điểm) Cho parabol
P : 2 4
x y và đường thẳng d : 2 2 x y a) Vẽ đồ th
P và
d trên cùng hệ trục tọa độ; b) Tìm tọa độ giao điểm c
a
P và
d bằng phép toán. Bài 2: (1.0 điểm) Cho phương trình 2 2610
có hai nghiệm là 12 ; xx . Không giải phương trình, hãy tính giá trị của biểu thức: 12 21
22 11 xx A xx Bài 3: (0.75 điểm) Càng lên cao không khí càng loãng nên áp suất khí quyển càng giảm. Gọi y là đại lượng biểu thị cho áp suất khí quyển (tính bằng mmHg) và x là đại lượng biểu thị cho độ cao so với mặt nước biển (tính bằng mét). Người ta thấy với độ cao không lớn lắm thì mối liên hệ giữa hai đại lượng này là một hàm số bậc nhất yaxb có đồ thị như hình vẽ sau: a) Hay xác định các hệ số a và b . b) Một vận động viên leo núi đo được áp suất khí quyển là 540 mmHg. Hỏi vận động viên leo núi đang ở độ cao bao nhiêu mét so với mực nước biển. Bài 4: (0.75 điểm) Bạn An đến siêu thị mua hai món hàng phải trả tổng cộng 480000 đồng, trong đó đã tính 40000 đồng thuế VAT (thuế giá trị gia tăng). Biết rằng thuế VAT đối với mặt hàng thứ nhất là 10% và thuế VAT với mặt hàng thứ hai là 8%. Hỏi nếu không tính thuế VAT thì giá niêm yết mỗi món hàng là bao nhiêu?
Bài 5: (1.0 điểm) Cho cốc rượu, phần phía trên là một hình nón có chiều cao 6 cm và đáy là đường tròn bán kính 3 cm. Biết trong cốc có chứa rượu với mực nước đang cách miệng cốc là 2 cm. Tính thể tích rượu trong ly. (kết quả làm tròn đến chữ số thập phân nhứ nhất)
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT
Ồ CHÍ
ĐỀ THAM KHẢO TUYỂN SINH 10
TP.H
MINH
PHÒNG
--------------------
ị
ủ
xx
Bài 6: (1.0 điểm) Một chiếc ti vi trong một đợt khuyến mãi, cửa hàng đã giảm giá 20% trên giá niêm yết. Đợt khuyến mãi thứ hai của hàng giảm giá tiếp 30% trên giá đã giảm ở đợt một. Nhưng đợt thứ ba cửa hàng tăng giá trở lại 25% trên giá đã giảm ở đợt hai và giá hiện tại của chiếc ti vi là 10500000 đồng. Hỏi giá niêm yết ban đầu của chiếc ti vi là bao nhiêu? Bài 7: (1.0 điểm) Hai tổ của một nhà máy sản xuất khẩu trang trong một ngày sản xuất được 1500 chiếc khẩu trang. Để đáp ứng nhu cầu khẩu trang trong dịch cúm do chủng mới virut Corona gây ra nên mỗi ngày tổ một vượt mức 75%, tổ hai vượt mức 68%, cả hai tổ sản xuất được 2583 chiếc khẩu trang. Hỏi ban đầu trong một ngày mỗi tổ sản xuất được bao nhiêu chiếc khẩu trang? Bài 8: (3.0 điểm) Từ một điểm A ở ngoài đường tròn O , kẻ hai tiếp tuyến , ABAC ( , BC là tiếp điểm) và cát tuyến ADE đến đường tròn (tia AE nằm trong góc OAB và điểm D nằm giữa A và E ).
a) Chứng minh: OA vuông góc với BC tại H và AHAOADAE .
b) Chứng minh: tứ giác OHDE nội tiếp đường tròn và HB là tia phân giác của góc DHE c) Gọi I là giao điểm của BC với AE . Qua I kẻ đường thẳng song song với AC , cắt CD và CE lần lượt tại M và N . Chứng minh: CDEC CHEH và I là trung điểm của MN .
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 78 -
OFFICIAL

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI Bài 1: (1.5 điểm) Cho parabol P : 2 4 x y và đường thẳng d : 2 2 x y a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ; b) Tìm tọa độ giao điểm của P và d bằng phép toán. Lời giải a) Hàm số: 2 4 x y Bảng giá trị tương ứng của x và y : x 4 2 0 2 4 2 4 x y 4 1 0 1 4 Đồ thị hàm số là một Parabol đi qua các điểm 4;4 ; 2;1 ; 0;0 ; 2;1 ; 4;4 Hàm số: 2 2 x y 02xy 04yx Đồ thị hàm số là đường thẳng đi qua 0;2 và 4;0 Vẽ: b) Hoành độ giao điểm của P và d là nghiệm của phương trình: 2 2 42 xx 2 28 xx 2 280 xx 2 11.890 Phương trình có hai nghiệm phân biệt: 1 2 x ; 2 4 x + Với 1 2 x 1 1 y + Với 2 4 x 2 4 y Vậy d cắt P tại hai điểm phân biệt là 2;1 và 4;4 . Bài 2: (1.0 điểm) Cho phương trình 2 2610 xx có hai nghiệm là 12 ; xx . Không giải phương trình, hãy tính giá trị của biểu thức: 12 21 22 11 xx A xx .
và x là đại lượng biểu thị cho độ cao so với mặt nước biển (tính bằng mét). Người ta thấy với độ cao không lớn lắm thì mối liên hệ giữa hai đại lượng này là một hàm số bậc nhất yaxb có đồ thị như hình vẽ sau:
a) Hãy xác định các hệ số a và b . b) Một vận

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 80Lời giải Phương trình đã cho là phương trình bậc hai của x có: .2.10 ac phương trình đã cho có hai nghiệm 1x ; 2x 1122 12 2112 2121 22 1111 xxxx xx A xxxx 22 1212 1212 34 .1 xxxx xxxx 2 121212 1212 234 1 xxxxxx xxxx Theo định lý Vi-et, ta có: 12 12 3 1 2 xx xx Suy ra 2 1 32.3.34 22 1 31 2 A . Bài 3: (0.75 điểm) Càng lên cao không khí càng loãng nên áp suất khí quyển càng giảm. Gọi y là đại lượng biểu thị cho áp suất khí quyển (tính bằng mmHg)
động viên leo núi đo được áp suất khí quyển là 540 mmHg. Hỏi vận động viên leo núi đang ở độ cao bao nhiêu mét so với mực nước biển. Lời giải a) Dựa vào đồ thị hàm số ta thấy đồ thị hàm số yaxb đi qua các điểm 0;760,1600;632AB Ta có hệ phương trình: 760 760.0 2 6321600. 25 b ab ab a Vậy 2 25 760 a b . b) Theo phần a) ta có 2 760 25 yx với y là đại lượng biểu thị cho áp suất khí quyển (tính bằng mmHg) và x là đại lượng biểu thị cho độ cao so với mặt nước biển (tính bằng mét). Một vận động viên leo núi đo được áp suất khí quyển là 540 mmHg
Vậy vận động viên leo núi đang ở độ 2750 mét so với mực nước biển.
Bài 4: (0.75 điểm) Bạn An đến siêu thị mua hai món hàng phải trả tổng cộng 480000 đồng, trong đó đã tính 40000 đồng thuế VAT (thuế giá trị gia tăng). Biết rằng thuế VAT đối với mặt hàng thứ nhất là 10% và thuế VAT với mặt hàng thứ hai là 8%. Hỏi nếu không tính thuế VAT thì giá niêm yết mỗi món hàng là bao nhiêu? Lời giải
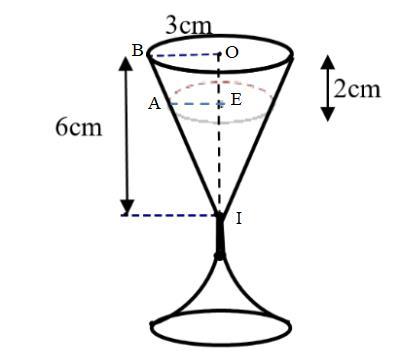

DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 81 -
xx .
OFFICIAL
2 5407602750 25
lượt là , xy (đồng) với 0,0xy Bạn An đến siêu thị mua hai món hàng phải trả tổng cộng 480000 đồng, trong đó đã tính 40000 đồng thuế VAT 4400001 xy Biết rằng thuế VAT đối với mặt hàng thứ nhất là 10% và thuế VAT với mặt hàng thứ hai là 8% 10%8%400000,10,08400002 xyxy Từ 1 và 2 ta có hệ phương trình: 440000240000 0,10,0840000200000 xyx xyy Vậy giá tiền niêm yết khi không tính thuế VAT của mỗi món hàng lần lượt là 240000 đồng và 200000 đồng. Bài 5: (1.0 điểm) Cho cốc rượu, phần phía trên là một hình nón có chiều cao 6 cm và đáy là đường tròn bán kính 3 cm. Biết trong cốc có chứa rượu với mực nước đang cách miệng cốc là 2 cm. Tính thể tích rượu trong ly. (kết quả làm tròn đến chữ số thập phân nhứ nhất) Lời giải Thể tích rượu trong ly 2 1 3 VAEIE Có 4cm IEIOEO
Gọi giá tiền niêm yết khi không tính thuế VAT của mỗi món hàng lần
Thể tích rượu trong ly 23 1 4.233,5cm 3 V
Bài 6: (1.0 điểm) Một chiếc ti vi trong một đợt khuyến mãi, cửa hàng đã giảm giá 20% trên giá niêm yết. Đợt khuyến mãi thứ hai cửa hàng giảm giá tiếp 30% trên giá đã giảm ở đợt một. Nhưng đợt thứ ba cửa hàng tăng giá trở lại 25% trên giá đã giảm ở đợt hai và giá hiện tại của chiếc ti vi là 10500000 đồng. Hỏi giá niêm yết ban đầu của chiếc ti vi là bao nhiêu? Lời giải Gọi giá niêm yết ban đầu của chiếc ti vi là x (đồng) ( 0 x ) Đợt khuyến mãi thứ nhất cửa hàng đã giảm giá 20% trên giá niêm yết suy ra giá của chiếc ti vi trong đợt khuyến mãi thứ nhất là : .20%0,8 xxx (đồng). Đợt khuyến mãi thứ hai cửa hàng giảm giá tiếp 30% trên giá đã giảm ở đợt một suy ra giá của chiếc ti vi trong đợt khuyến mãi thứ hai là : 0,830%.0,8.0,8.0,7.0,56 xxxx (đồng). Đợt thứ ba cửa hàng tăng giá trở lại 25% trên giá đã giảm ở đợt hai suy ra giá hiện tại của chiếc ti vi là : 0,5625%.0,561,25.0,560,7 xxxx (đồng). Theo bài ra ta có : 0,71050000015000000 xx (đồng). Vậy giá niêm yết ban đầu của chiếc ti vi là 15000000 đồng. Bài 7: (1.0 điểm) Hai tổ của một nhà máy sản xuất khẩu trang trong một ngày sản xuất được 1500 chiếc khẩu trang. Để đáp ứng nhu cầu khẩu trang trong dịch cúm do chủng mới virut Corona gây ra nên mỗi ngày tổ một vượt mức 75%, tổ hai vượt mức 68%, cả hai tổ sản xuất được 2583 chiếc khẩu trang. Hỏi ban đầu trong một ngày mỗi tổ sản xuất được bao nhiêu chiếc khẩu trang? Lời giải Gọi x là số khẩu trang ban đầu tổ một sản xuất được mỗi ngày 0 x Gọi y là số khẩu trang ban đầu tổ hai sản xuất được mỗi ngày 0 y . Hai tổ của một nhà máy sản xuất khẩu trang trong một ngày sản xuất được 1500 chiếc khẩu trang suy ra ta có phương trình: 15001 xy Nhưng mỗi ngày tổ một vượt mức 75%, tổ hai vượt mức 68%, cả hai tổ sản xuất được 2583 chiếc khẩu trang suy ra ta có phương trình: 75%68%25831,751,6825832
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 82.4.3 2cm 6 AEIEIEBO IAEIBOAE BOIOIO
OFFICIAL
xxyyxy Từ 1 và 2 ta có hệ phương trình: 1500900 1,751,682583600 xyx xyy . Vậy ban đầu trong một ngày tổ một sản xuất được 900 chiếc khẩu trang, tổ hai sản xuất được 600 chiếc khẩu trang. Bài 8: (3.0 điểm) Từ một điểm A ở ngoài đường tròn O , kẻ hai tiếp tuyến , ABAC ( , BC là tiếp điểm) và cát tuyến ADE đến đường tròn (tia AE nằm trong góc OAB và điểm D nằm giữa A và E ). a) Chứng minh: OA vuông góc với BC tại H và AHAOADAE . b) Chứng minh: tứ giác OHDE nội tiếp đường tròn và HB là tia phân giác của góc DHE c) Gọi I là giao điểm của BC với AE . Qua I kẻ đường thẳng song song với AC , cắt CD và CE lần lượt tại M và N . Chứng minh: CDEC CHEH và I là trung điểm của MN . Lời giải
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 83a) Ta có ABAC (tính chất hai đường tiếp tuyến cắt nhau) OBOC (cùng bằng bán kính) OA là trung trực của BCOABC tại H . Xét ABO vuông tại B có 2 . BHOAABAHAO (1) Xét ABD và AEB có BAE chung ABDAEB (cùng chắn BD ) g.g ABDAEB 2 .2 ABAE ABADAE ADAB Từ (1) và (2) suy ra .. AHAOADAE . b) Xét AHD và AEO có: AHAD AEAO (câu a), OAE chung 3 AHDAEOAHDAEO Có 0 1804OHDAHD Từ (3) và (4) 0180 OHDAEO tứ giác OHDE nội tiếp đường tròn. Tứ giác OHDE nội tiếp đường tròn 5 OHEODE ODE cân tại O 6 ODEOEDAEO Từ (3), (5) và (6) AHDOHE (7) Lại có: 0 908 AHDDHI Và 0 909 OHEEHI Từ (7), (8) và (9) DHIEHIHI là tia phân giác của góc DHE. c) Có ADHEOH (cùng bù với EDH ) và AHDOHE (chứng minh trên). Suy ra .. DHHA ADHEOHHOHAHDHE OHEH . Xét trong tam giác vuông 22 HCHE OCAHOHAHCHCHDHE HDHC , mà CHDCHE (do HI là tia phân giác của góc DHE) I H D O C A M B E N
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 84 CDCHCDEC CDHECH ECEHCHEH . Có HI là phân giác trong của tam giác 10 IEHE EDH IDHD Mà HAHIHA là phân giác ngoài của tam giác 11 AEHE EDH ADHD Từ (10) và (11) suy ra 12 IEAEIEID IDADAEAD Có // MNAC áp dụng định lý Talet ta có: 13 INEI ACEA IMID ACAD Từ (12) và (13) suy ra INIM INIMI ACAC là trung điểm của MN .
Tổng điều tra dân số và nhà ở năm 2019 được tiến hành vào thời điểm 0 giờ ngày 1/4/2019 theo Quyết định số 772/QD-TTg ngày 26/6/2018 của Thủ tướng Chính phủ. Đây là cuộc Tổng điều tra dân số và nhà ở lần thứ năm ở Việt Nam kể từ khi đất nước thống nhất vào năm 1975. Theo kết quả của cuộc tổng điều tra nói trên, tổng dân số của Việt Nam là 96.208.984 người, trong đó nam ít hơn nữ là 446.862 người và dân tộc Kinh chiếm 85,3% dân số cả nước.
a) Dân tộc Kinh có bao nhiêu người (làm tròn đến hàng đơn vị)?
b) Tính số nam và số nữ của Việt Nam.
Bài 4: Một xí nghiệp cần bán thanh lý b sản phẩm. Số sản phẩm y còn lại sau x ngày bán được xác định bởi hàm số: yaxb có đồ thị như bên
a) Hãy dựa vào đồ thị hãy xác định , ab và hàm số y .
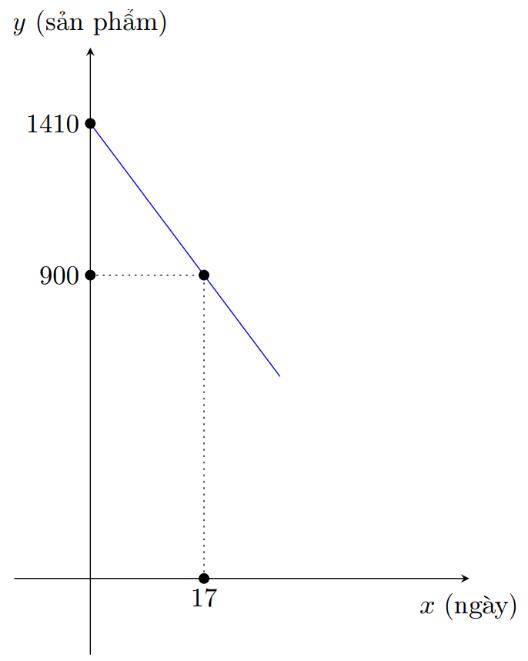
b) Xí nghiệp cần bao nhiêu ngày để bán hết số sản phẩm cần thanh lý?
Bài 5: Các bạn học sinh của lớp 9A dự định đóng góp một số tiền để mua tặng cho mỗi em ở Mái ấm tình thương ba món quà (giá tiền các món quà đều như nhau). Khi các bạn đóng đủ số tiền như dự trù thì Mái ấm đã nhận chăm sóc thêm 9 em và giá tiền mỗi món quà lại tăng thêm 5% nên số tiền có được
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GD & ĐT QUẬN 3 NĂM HỌC 2022-2023 ĐỀ THAM KHẢO MÔN
9 -------------------- Đề thi
8
tự
MÃ ĐỀ : Quận 3 – 3 Thời gian: 120 phút
thời
phát đề) Bài 1: Cho 2 (): Pyx và đường thẳng ():34 dyx a) Vẽ () P và () d trên cùng mặt phẳng tọa độ. b) Tìm tọa độ giao điểm của () P và () d bằng phép tính. Bài 2: Cho phương trình 2 253 xx có hai nghiệm 12 , xx . Không giải phương trình hãy tính giá trị của biểu thức 1221 33 Axxxx . Bài
: TOÁN
gồm
câu hỏi
luận
(không kể
gian
3:
vừa đủ để tặng mỗi em
ấm
Bài 6: Coi cả Trái Đất và Mặt Trăng đều có dạng hình cầu và biết bán kính của Trái Đất là khoảng 6371 km, bán kính của mặt trăng là khoảng 1737 km a) Hãy tính diện tích bề mặt của Trái Đất và diện tích bề mặt của Mặt Trăng.
hai món quà. Hỏi có bao nhiêu em ở Mái
lúc tặng quà?
b) Biết 70,8% diện tích bề mặt Trái Đất là nước. Hãy tính phần diện tích này? (Làm tròn kết quả
hàng triệu)
Bài 7: Giá của một mặt hàng là 800.000 đồng. Nếu bán mặt hàng này với giá bằng một nửa giá niêm yết thì lợi nhuận là 20%. Hỏi phải bán với giá bao nhiêu thì được lợi nhuận 60%?
Bài 8: Cho tam giác ABC nhọn () ABAC nội tiếp đường tròn tâm O có ba đường cao , , ADBECF cắt nhau tại H
a) Chứng minh AEHF và ABDE là các tứ giác nội tiếp.
b) Đường thẳng EF cắt đường tròn () O tại các điểm , MN ( M thuộc cung nhỏ AB ). Kẻ đường kính AK của đường tròn O . Chứng minh tia EB là tia phân giác của góc DEF và KMN cân.
c) Đường trung trực của CE cắt MK tạiQ . Chứng minh MA là tiếp tuyến của () MEC và OQ vuông góc với MC .
OFFICIAL
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 78 -
n
đế
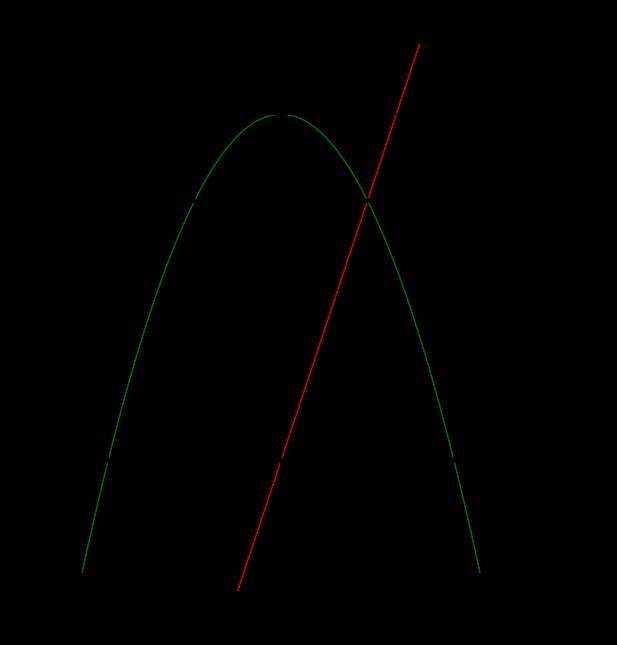
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI Bài 1:
2
ẳ
.
2;4 ; 1;1 ; 0;0 ; 1;1 ; 2;4 . Hàm số: 34yx x 0 1 34yx 4 1 Đồ thị hàm số là đường thẳng đi qua 0;4 và 1;1 . Vẽ: b) Hoành độ giao điểm của P và D là nghiệm của phương trình: 22 1 34340 4 x xxxx x + Với 1 1 x 1 1 y + Với 2 4 x 2 16 y Vậy D cắt P tại hai điểm phân biệt là 1;1 và 4;16 Bài 2: Cho phương trình 2 253 xx có hai nghiệm 12 , xx . Không giải phương trình hãy tính giá trị của biểu thức 1221 33 Axxxx Lời giải Ta có: 22 2532530 xxxx . 2 54.2.310 Phương trình có hai nghiệm phân biệt.
Cho
():
Pyx và đường th
ng ():34
dyx
a) Vẽ () P và () d trên cùng mặt phẳng tọa độ. b) Tìm tọa độ giao điểm của () P và () d bằng phép tính. Lời giải a) Hàm số: 2 yx
Bảng giá trị tương ứng của x và y : x 2 1 0 1 2 2 yx 4 1 0 1 4
Đồ thị hàm số là một Parabol đi qua các điểm
3: Tổng điều tra dân số và nhà ở năm 2019 được tiến hành vào thời điểm 0 giờ ngày 1/4/2019 theo Quyết định số 772/QD-TTg ngày 26/6/2018 của Thủ tướng Chính phủ. Đây là cuộc Tổng điều tra dân số và nhà ở lần thứ năm ở Việt Nam kể từ khi đất nước thống nhất vào năm 1975. Theo kết quả của cuộc tổng điều tra nói trên, tổng dân số của Việt Nam là 96.208.984 người, trong đó nam ít hơn nữ là 446.862 người và dân tộc Kinh chiếm 85,3% dân số cả nước. a) Dân tộc Kinh có bao nhiêu người (làm tròn đến hàng đơn vị)?

Vậy số nam là 47881061 và số nữ là 48327923 Bài 4: Một xí nghiệp cần bán thanh lý b sản phẩm. Số sản phẩm y còn lại sau x ngày bán được xác định bởi hàm số: yaxb có đồ thị như bên
a) Hãy dựa vào đồ thị hãy xác định , ab và hàm số y b) Xí nghiệp cần bao nhiêu ngày để bán hết số sản phẩm cần thanh lý? L
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 80Theo định lí Vi-et: 12 12 5 2 3 2 xx xx Khi đó: 2 2222 12211212 5399 331031032343.4. 224 AxxxxxxxxPSPSP .
L
xy Ta
Bài
b) Tính số nam và số nữ của Việt Nam.
ời giải a) Số người dân tộc Kinh là: 96208984.85.3%82066263
người. b) Gọi số nam và số nữ lần lượt là x và y
,
có hệ phương trình: 9620898447881061 44686248327923 xyx xyy
.
ả
a) Nhìn vào hình ta có đồ thị hàm số yaxb đi qua hai điểm 0;1410 và 17;900 . Thay 0;1400 vào 14100. yaxbab Thay (17; 900) vào y = ax +b 900 = 17a +b Ta có hệ pt: 1410 0. 0. 1410 900 17 0 17 900 30 141 a b abab abab . Vậy 301410yx b) Số ngày xí nghiệp bán hết số sản phẩm cần thanh lý: 030 141047xx Vậy số ngày xí nghiệp bán hết số sản phẩm cần thanh lý là 47 ngày.
ời gi
i
Bài 5: Các bạn học sinh của lớp 9A dự định đóng góp một số tiền để mua tặng cho mỗi em ở Mái ấm tình thương ba món quà (giá tiền các món quà đều như nhau). Khi các bạn đóng đủ số tiền như dự trù thì Mái ấm đã nhận chăm sóc thêm 9 em và giá tiền mỗi món quà lại tăng thêm 5% nên số tiền có được vừa đủ để tặng mỗi em hai món quà. Hỏi có bao nhiêu em ở Mái ấm lúc tặng quà?
i gi
i
là s
em
mái ấm lúc chưa có thêm 9 em
i
là giá tiề
một món quà lúc chưa tăng giá. Ta có phương trình:
.3.9.2..15%21 xaxax
Vậy có 21 em ở Mái ấm lúc tặng quà. Bài 6: Coi cả Trái Đất và Mặt Trăng đều có dạng hình cầu và biết bán kính của Trái Đất là khoảng 6371 km, bán kính của mặt trăng là khoảng 1737 km.
a) Hãy tính diện tích bề mặt của Trái Đất và diện tích bề mặt của Mặt Trăng. b) Biết 70,8% diện tích bề mặt Trái Đất là nước. Hãy tính phần diện tích này? (Làm tròn kết quả đến hàng triệu) Lời giải a) Diện tích bề mặt của Trái Đất: 222 44.6371510000000kmSR Diện tích bề mặt của Mặt Trăng: 222 44.173738000000kmSR b) Diện tích nước bao phủ bề mặt Trái Đất là: 2510000000.70,8%361000000km Bài 7: Giá của một mặt

DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 81 -
OFFICIAL
Lờ
ải Gọ
x
ố
ở
x . Gọ
a
n
hàng là 800.000 đồng. Nếu bán mặt hàng này với giá bằng một nửa giá niêm yết thì lợi nhuận là 20%. Hỏi phải bán với giá bao nhiêu thì được lợi nhuận 60%? Lời giải Giá gốc của mặt hàng đó: 800000:2.1–20%320000 (đồng) Giá bán lần sau: 320000.160%512000 (đồng). Bài 8: Cho tam giác ABC nhọn () ABAC nội tiếp đường tròn tâm O có ba đường cao , , ADBECF cắt nhau tại H . a) Chứng minh AEHF và ABDE là các tứ giác nội tiếp. b) Đường thẳng EF cắt đường tròn () O tại các điểm , MN ( M thuộc cung nhỏ AB ). Kẻ đường kính AK của đường tròn O . Chứng minh tia EB là tia phân giác của góc DEF và KMN cân. c) Đường trung trực của CE cắt MK tạiQ . Chứng minh MA là tiếp tuyến của () MEC và OQ vuông góc với MC Lời giải
a) Xét tứ giác AEHF có o90 AFHAEH ( BE và CF là các đường cao) o180 AFHAEH
Tứ giác AEHF nội tiếp đường tròn đường kính AH Xét tứ giác ABDE có o90 ADBAEB ( AD và BE là các đường cao)
Tứ giác ABDE nội tiếp đường tròn đường kính AB .
b) Tứ giác AFHE nội tiếp 1 FAHFEH Tứ giác ABDE nội tiếp 2 FAHBED . Từ 1 và 2 FEHBED hay EB là tia phân giác của góc DEF . Xét tứ giác BFEC có o90 BECBEC
Tứ giác BFEC nội tiếp đường tròn đường kính BC .
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 82 -
đ 11 ss đ đ đss 22 ANBMAMMB ANAM AKMN tại trung điểm của MN AK là đường trung trực của MN KMKN hay KMN cân tại K c) Ta có: 1 đs 2 E ANAMAMEA M CM ME là dây của đường tròn MEC MA là tiếp tuyến của MEC . o90 AMKAMMA tại M Tâm đường tròn (MEC) thuộc MK mà Q là giao điểm MK và đường trung trực của EC Q là tâm đường tròn (MEC) QM = QC mà OM = OC (= bk(O)) OQ là đường trung trực MC Vậy OQ MC. Q N M K H F E D O B C A
AFEACB
đó, P là áp suất khí quyển () mmHg ; h là độ cao so với mực nước biển () m . Hỏi thành phố Bảo Lộc ở độ cao 1200m so với mực nước biển thì áp suất của khí quyển là bao nhiêu mmHg ? Bài 4: (0.75 điểm) Một công ty chuyên cung cấp dịch vụ Internet với mức phí ban đầu lắp đặt là 300.000 đồng. Cước phí y (đồng) là số tiền mà người sử dụng Internet cần trả hàng tháng và phụ thuộc vào thời gian sử dụng x tháng. Công thức biểu thị môi liên hệ giữa hai đại lượng này là một hàm số bậc nhất yaxb . Xác định hệ số a và b . Biết rằng sau 2 tháng sử dụng thì cước phí phải trả là 440.000đồng. Bài 5: (1.0 điểm) Chuẩn bị cho một buổi liên hoan chung vui cuối tuần của lớp 9A có 38 học sinh. Giáo viên chủ nhiệm xuất quỹ 410.000 đồng và giao cho mỗi nam sinh mua một hộp bánh Tôm có giá 15.000 đồng/1 hộp. Mỗi nữ sinh mua một lố có vài chai nước nhỏ có giá 6000 đồng/1 lố. Tính số nam sinh và nữ

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GD & ĐT QUẬN 4 NĂM HỌC 2022-2023 ĐỀ THAM KHẢO MÔN : TOÁN 9 Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Quận 4 – 3 Thời gian: 120 phút (không kể thời gian phát đề) Bài 1: (1.5 điểm) Cho Parabol 2 1 (): 4 Pyx và đường thẳng 1 ():3 4 dyx a) Vẽ đồ thị hàm số () P và () d trên cùng một hệ trục tọa độ. b) Tìm tọa độ giao điểm của () P và () d bằng phép tính. Bài 2: (1.0 điểm) Cho phương trình 2 3260 xx có 2 nghiệm 1x , 2x . Tính giá trị của biểu thức: 12 21 11 22 xx M xx . Bài 3: (0.75 điểm) Khi càng lên cao thì áp suất khí quyển càng giả
suất khí quyển ở độ cao
so với mặt nước biển
ng
ử
ụ
2 760 25 h P .
(1.0 điểm) Một hồ bơi hình chữ nhật
chiều
ều rộng 10,2m và đường chéo của hồ này là 53,1m. (Làm tròn kết quả đến một chữ số thập phân). a) Thể tích của hồ bơi này. b) Để bơm nước đầy hồ một máy bơm mỗi giờ bơm lượng nước 372,9m . Hỏi bao lâu bơm nước đầy hồ bơi?
m do không khí loãng dần. Để tính áp
không quá cao
thườ
s
d
ng công thức:
Trong
a sinh của lớp 9A, biết sau khi đã mua xong tiền căn-tin thối lại là 2000đồng. Bài 6:
có
dài 52m; chi
Bài 7: (1.0 điểm) Trong dịp tổ chức sinh nhật cho 1 bạn trong lớp. Nhóm học sinh cần mua một số lượng bánh ở một tiệm bánh có khuyến mãi, cứ mua kể từ bánh thứ 17 sẽ được giảm 800 đồng theo giá mỗi cái bánh. Nhóm học sinh mua 25 cái bánh với số tiền 192 800 đồng. Hỏi giá tiền mỗi cái bánh ban đầu là bao nhiêu?
Bài 8: (3.0 điể
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 78 -
OFFICIAL
m) Cho ; OR đường kính EF . Trên tia FE lấy điểm Asao cho 2 OAR , từ Avẽ ; ABAC lần lượt là hai tiếp tuyến của O a) Chứng minh tứ giác ABOC nội tiếp và OABC tại H . b) Vẽ đường thẳng qua H song song với BF lần lượt cắt , BEBA tại I và K . Chứng minh BHBK và EKAB . c) Chứng minh đường thẳng AI đi qua trung điểm BF . HẾT
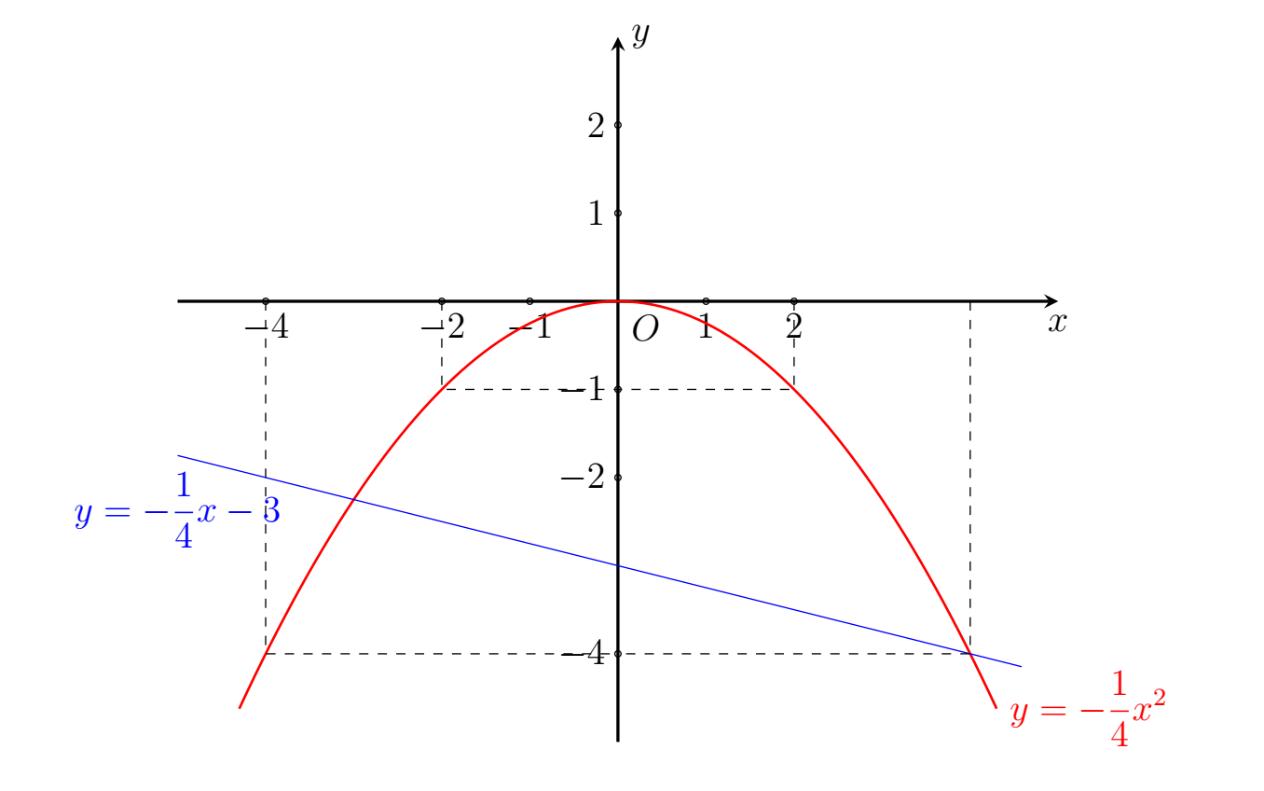
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI Bài
.5 điể
2
và đườ
ẳ
a)
a)
2
. B
x
2 0 2 4 2
1 0 1 4 Đồ thị hàm số là một Parabol đi qua các điểm 4;4 ; 2;1 ; 0;0 ; 2;1 ; 4;4 . Hàm số: 1 3 4 yx . 03xy 012yx Đồ thị hàm số là đường thẳng đi qua 0;3 và 12;0 . Vẽ đồ thị hàm số () P và () d trên cùng một hệ trục tọa độ. b) Hoành độ giao điểm của P và d là nghiệm của phương trình: 2 11 3 44 xx 2 12 xx 2 120 xx . 2 14.12490 Phương trình có hai nghiệm phân biệt: 1 3 x ; 2 4 x . + Với 1 3 x 1 9 4 y . + Với 2 4 x 2 4 y .
1: (1
m) Cho Parabol
1 (): 4 Pyx
ng th
ng 1 ():3 4 dyx
Vẽ đồ thị hàm số () P và () d trên cùng một hệ trục tọa độ b) Tìm tọa độ giao điểm của () P và () d bằng phép tính. Lời giải
Hàm số:
1 (): 4 Pyx
ảng giá trị tương ứng của x và y :
4
1 (): 4 Pyx
4
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 80Vậy d cắt P tại hai điểm phân biệt là 9 3; 4 và 4;4 . Bài 2: (1.0 điểm) Cho phương trình 2 3260 xx có 2 nghiệm 1x , 2x . Tính giá trị của biểu thức: 12 21 11 22 xx M xx . Lời giải 2 22 1212 1212 211212 2 1131 111 222222 xxxx xxxx M xxxxxx . Theo định lý Vi-et, ta có: 12 12 2 3 3 xx xx Do đó: 2 22(3) 3132923 3 22322754 M . Bài 3: (0.75 điểm) Khi càng lên cao thì áp suất khí quyển càng giảm do không khí loãng dần. Để tính áp suất khí quyển ở độ cao không quá cao so với mặt nước biển thường sử d
2.1200 760664() 25 PmmHg . Bài 4: (0.75 điểm) Một công ty chuyên
ấp dịch vụ
ớ
ức
đầu lắp đặt là 300.000 đồng. Cước phí y (đồng) là số tiền mà người sử dụng Internet cần trả hàng tháng và phụ thuộc vào thời gian sử dụng x tháng. Công thức biểu thị môi liên hệ giữa hai đại lượng này là một hàm số bậc nhất yaxb . Xác định hệ số a và b . Biết rằng sau 2 tháng sử dụng thì cước phí phải trả là 440.000đồng. Lời giải Theo đề ta có: Với cước phí ban đầu là 300.000 đồng thì 0 x . Do đó: 300000.0300000 abb . Sau 2 tháng sử dụng, cước phí được xác định: .230000044000070000 aa .
ụng công thức: 2 760 25 h P
. Trong đó, P là áp suất khí quyển () mmHg ; h là độ cao so với mực nước biển () m . Hỏi thành phố Bảo Lộc ở độ cao 1200m so với mực nước biển thì áp suất của khí quyển là bao nhiêu mmHg ? Lời giải Theo công thức tính áp suất khí quyển: 2 760 25 h P . Với độ cao của thành phố Bỏa Lộc là 1200m, áp suất khí quyển là:
cung c
Internet v
i m
phí ban
b
300000.
Bài 5: (1.0 điểm) Chuẩn bị cho một buổi liên hoan chung vui cuối tuần của lớp 9A có 38 học sinh. Giáo viên chủ nhiệm xuất quỹ 410.000 đồng và giao cho mỗi nam sinh mua một hộp bánh Tôm có giá 15.000 đồng/1 hộp. Mỗi nữ sinh mua một lố có vài chai nước nhỏ có giá 6000 đồng/1 lố. Tính số nam sinh và nữa sinh của lớp 9A, biết sau khi đã mua xong tiền căn-tin thối lại là 2000đồng. Lời giải
Gọi , xylần lượt là số nam và nữ sinh của lớp 9A ( ,*xyN và ,38xy ).
Số học sinh lớp 9A: 38 xy (học sinh) (1)
Số tiền bánh Tôm đã mua: 15000x (đồng).
Số tiền mua nước: 6000y (đồng)
Theo đề ta có phương trình: 1500060004100002000408000. xy (2)
Từ (1) và (2) ta có hệ pt: 38 150006000408000. xy xy
Giải hệ ta được: 20 18. x y
Vậy số học sinh nam: 20.
Số học sinh nữ: 18. Bài 6: (1.0 điểm) Một hồ bơi hình chữ nhật có chiều dài 52m; chiều rộng 10,2m và đường chéo của hồ này là 53,1m. (Làm tròn kết quả đến một chữ số thập phân).

a) Thể tích của hồ bơi này. b) Để bơm nước đầy hồ một máy bơm mỗi giờ bơm lượng nước 372,9m . Hỏi bao lâu bơm nước đầy hồ bơi? Lời giải

DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 81 -
OFFICIAL
Vậy 7000
a
Gọi các điểm như trên hình vẽ. Theo đề ta có hồ bơi là 1 hình hộp chữ nhật nên ABCDlà hình chữ nhật. Suy ra 10,2 52 ABCDm BCADm Xét ACD vuông tại D ta có: 222 ACADCD (theo định lí Py – ta – go). 222 2 5210,2 2808,04 AC AC Ta có mp EAABCD (ABCD.EFGH là hình hộp chữ nhật).
a)
tích c
a hồ bơi là: 3 ..3,4.52.10,21803,361803,4 VAEADABm b) Thời gian để bơm nước đầy hồ bơi là: 1803,4:72,9=24,7(giờ). Bài 7: (1.0 điểm) Trong dịp tổ chức sinh nhật cho 1 bạn trong lớp. Nhóm học sinh cần mua một số lượng bánh ở một tiệm bánh có khuyến mãi, cứ mua kể từ bánh thứ 17 sẽ được giảm 800 đồng theo giá mỗi cái bánh. Nhóm học sinh mua 25 cái bánh với số tiền 192 800 đồng. Hỏi giá tiền mỗi cái bánh ban đầu là bao nhiêu? Lời giải Gọi x (đồng) là giá tiền của một cái bánh ban đầu ( 800 x ). Giá của một cái bánh sau khi mua kể từ bánh thứ 17 là: 800 x (đồng). Vì nhóm học sinh mua 25 cái bánh với tổng
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 82 -
ại A
16.2516.800192800 1697200192800 251928007200 25200000 200000:258000 () xx xx x x xN Vậy giá tiền của mỗi cái bánh ban đầu là 8000 đồng Bài 8: (3.0 điểm) Cho ; OR đường kính EF . Trên tia FE lấy điểm Asao cho 2 OAR , từ Avẽ ; ABAC lần lượt là hai tiếp tuyến của O a) Chứng minh tứ giác ABOC nội tiếp và OABC tại H . b) Vẽ đường thẳng qua H song song với BF lần lượt cắt , BEBA tại I và K . Chứng minh BHBK và EKAB . c) Chứng minh đường thẳng AI đi qua trung điểm BF . Lời giải
Suy ra EAACAEC
vuông t
Suy ra 222 ECAEAC (theo định lí Py – ta – go).
222 22 2 53,12808,04 11,57 11,573,4 m. AEECAC AE AE AE
Thể
ủ
số tiền là 192 800 đồng nên ta có phương trình:
a)
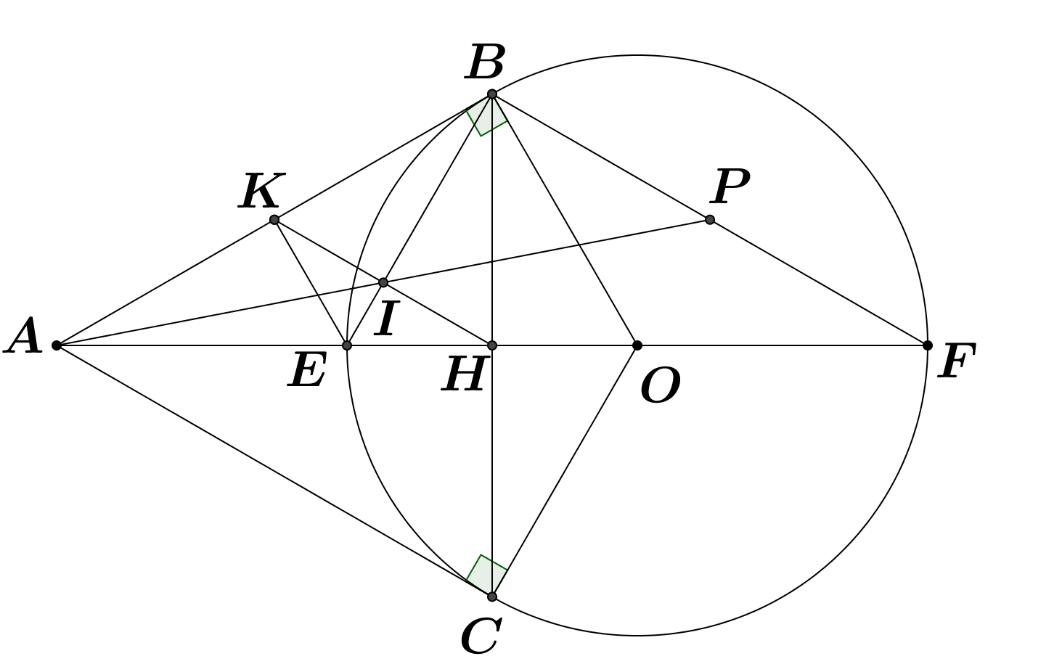
Xét tứ giác ABOC có: 90 ABO ( AB là tiếp tuyến của (O)). 90 ACO ( AC là tiếp tuyến của (O)).
Suy ra 9090180 ABOACO .
Suy ra tứ giác ABOC nội tiếp (tứ giác có tổng hai góc đối bằng 180 ).
Ta có: ABAC (tính chất hai tiếp tuyến cắt nhau). và OBOCR Suy ra OA là đường trung trực của BC Suy ra OABC tại H
b)
Ta có: 90 EBF (góc nội tiếp chắn nửa (O)).
Suy ra BEF vuông tại B 90 EBHFBH (1)
Ta lại có: BHF vuông tại H (OABC tại H ). 90 BFHFBH (phụ nhau). (2) Từ (1) và (2) suy ra EBHBFH . Hay EBHBFE Mặt khác: BFEABE (góc nội tiếp bằng góc giữa tiếp tuyến và dây cung cùng chắn cung BE). EBHABE .
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 83 -
OFFICIAL
Hay IBHIBK Ta có: // BFKH (gt) và BEBF ( BEF vuông tại B ). KHBE . Hay KHBIIBE . Xét BKH có BI là đường cao KHBI Mà BI cũng là đường phân giác ( IBHIBK , BI nằm giữa BK và BH ). Suy ra BKH là tam giác cân tại BBKBH (đpcm). Xét KBE và HBE có BKBH (chứng minh trên) KBEHBE , EBHABEKAB . BEcạnh chung. Suy ra KBEHBE (c – g – c) 90 BKEBHE (hai góc tương ứng). Suy ra EKAB .
Gọi P là giao điểm của AI và BF
Xét PAF có: // IHPF //, , BFKHIKHPBF
và , IAPHAF (gt).
Suy ra IHAI PFAP (hệ quả định lí Ta – lét). (3)
Xét ABP có: // IKPB //, , BFKHIKHPBF
và , IAPKAB (gt).
Suy ra IKAI PBAP (hệ quả định lí Ta – lét). (4)
Từ (3) và (4) suy ra IHIK PFPB (5)
Xét BKH cân tại B (chứng minh trên) có BI là đường cao KHBI
Mà BI cũng là đường trung tuyến IHIK (6) Từ (5) và (6) PFPB Mà PBF ( P là giao điểm của AI và BF ).
Suy ra P là trung điểm của BF
NHÓM WORD HÓA ĐỀ TOÁN - 84c)
DẠYKÈMQUYNHƠN OFFICIAL
ếu có của phương trình đã cho.
Bài 3: (0.75 điểm) Một nhà máy sản xuất xi măng có sản lượng hang năm được xác định theo hàm số 12,5360Tn . Với T là sản lượng (đơn vị tấn) và n là số năm tính từ năm 2010. a) Hãy tính sản lượng xi măng của nhà máy vào năm 2020. b) Theo hàm số trên thì nhà máy đạt sản lượng 510 tấn vào năm nào?
Bài 4: (0.75 điểm) Trong tháng Giêng hai tổ công nhân đã may được 800 chiếc áo. Tháng Hai, tổ 1 may vượt mức 15%, tổ hai may vượt mức 20%so với tháng Giêng do đó cả hai tổ đã may được 945 cái áo. Hỏi trong tháng Giêng mỗi tổ đã may được bao nhiêu chiếc áo?
Bài 5: (1.0 điểm) Trong tháng 4 năm 2021, một công nhân được nhận tiền lương là 7 800 000 đồng gồm tiền lương trong 24 ngày làm việc bình thường và 4 ngày làm việc đặc biệt (gồm chủ nhật và ngày lễ). Biết tiền lương của một ngày làm việc đặc biệt nhiều hơn tiền lương của một ngày bình thường là 200 000 đồng. Tính tiền lương của một ngày làm việc bình thường. Bài 6: (1.0 điểm) Quãng đường giữa hai thành phố A và B dài 120 km. Lúc 6 giờ sáng, một ô tô xuất phát từ A đi về B. Người ta thấy mối liên hệ giữa khoảng cách của ô tô so với A và thời điểm đi của ô tô
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG
ĐỀ
--------------------
Bài
.5
m) Cho hàm số 2 2 x y có đồ thị là
P và
ố 4 yx có đồ thị là đường thẳng D a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ; b) Tìm tọa độ giao điểm của P và D bằng phép toán. Bài 2: (1.0 điểm) Cho phương trình 2 53150 xx .Không giải phương trình. Hãy tính giá trị biểu thức 2 1212 22 Axxxx với 12 ; xx là hai nghiệm n
GD & ĐT QUẬN 5 NĂM HỌC 2022-20232
THAM KHẢO MÔN : TOÁN 9
Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Quận 5 – 3 Thời gian: 120 phút (không kể thời gian phát đề)
1: (1
điể
parabol
hàm s
a) Xác định các hệ số a, b?
b) Lúc 8 giờ sáng ôtô cách B bao xa?
Bài 7: (1.0 điểm) Một cái ly thủy tinh hình nón, bán kính đáy bằng 2 cm và chiều cao bằng 6 cm
a) Tính thể tích cái ly (biết bề dày của cái ly không đáng kể)( làm tròn đến chữ số thập phân thứ nhất) b) Người ta rót rượu vào ly, biết chiều cao của rượu trong ly bằng 3 cm. Tính thể tích rượu chứa trong ly ( làm tròn đến chữ số thập phân thứ nhất).
Bài 8: (3.0 điểm) Cho tam giác ABC nhọn (AB < AC). Đường tròn tâm O đường kính BC cắt AB, AC lần lượt tại E và F. Gọi H là giao điểm của BF và CE. Gọi D là giao điểm của AH và BC. Gọi M là trung điểm của HC. Gọi I là giao điểm của DF và CE. a) Chứng minh: AHBC và FHCBAC b) Chứng minh 2 FDEFCE và IEIMIDIF c) Qua I vẽ đường thẳng song song với MF cắt HF , AC lần lượt tại K và S. Lấy T đối xứng K qua I. Chứng minh tứ giác SHTC nội tiếp.

DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 78là một hàm số bậc nhất yaxb có đồ thị như hình sau:
OFFICIAL
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI Bài 1: (1.5 điểm) ) Cho hàm số 2 2 x y có đồ thị là parabol P và hàm số 4 yx có đồ thị là đường thẳng D a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ; b) Tìm tọa độ giao điểm của P và D bằng phép toán. Lời giải a) Học sinh tự vẽ b) Hoành độ giao điểm của P và D là nghiệm của phương trình: 2 4 2 x x 2 28xx 2 280xx 2 11.890 Phương trình có hai nghiệm phân biệt: 1 2 x ; 2 4 x + Với 1 2 x 1 1 y + Với 2 4 x 2 4 y Vậy D cắt P tại hai điểm phân biệt là 2;1 và 4;4 Bài 2: (1.0 điểm) Cho phương trình 2 53150 xx .Không giải phương trình. Hãy tính giá trị biểu thức 2 1212 22 Axxxx với 12 ; xx là hai nghiệm nếu có của phương trình đã cho. Lời giải Vì 12 ; xx là hai nghiệm của phương trình. Áp dụng định lý vi-et: 12 12 3 5 3 b Sxx a c Pxx a 2 1212 2 121212 2 22 42 33321 4.32. 5525 Axxxx Axxxxxx A Bài 3: (0.75 điểm) Một nhà máy sản xuất xi măng có sản lượng hang năm được xác định theo hàm số 12,5360Tn . Với T là sản lượng (đơn vị tấn) và n là số năm tính từ năm 2010. a) Hãy tính sản lượng xi măng của nhà máy vào năm 2020. b) Theo hàm số trên thì nhà máy đạt sản lượng 510 tấn vào năm nào? Lời giải a) Sản lượng xi măng vào năm 2020 là: 12,520202010360485 T (tấn) b) Theo đề bài ta có: 51012,536012 nn (năm) Vậy nhà máy đạt sản lượng 510 tấn vào năm 2022
Bài 4: (0.75 điểm) Trong tháng Giêng hai tổ công nhân đã may được 800 chiếc áo. Tháng Hai, tổ 1 may vượt mức 15%, tổ hai may vượt mức 20%so với tháng Giêng do đó cả hai tổ đã may được 945 cái áo. Hỏi trong tháng Giêng mỗi tổ đã may được bao nhiêu chiếc áo? Lời giải Gọi x (chiếc áo) là số chiếc áo của tổ 1 may trong tháng Giêng. y (chiếc áo) là số chiếc áo của tổ 2 may trong tháng Giêng. ( ,*xy ) Theo đề bài ta có hệ phương trình: 800300 115%120%945500 xyx xyy Vậy tổ 1 may được 300 chiếc áo, tổ 2 may được 500 chiếc áo.

bình thường là 200 000 đồng. Tính tiền lương của một ngày làm việc bình thường.
i Gọi x (đồng) là tiền lương ngày làm việc đặc biệt y (đồng) là tiền lương ngày làm việc bình thường ( ,0xy ) Theo đề bài ta có hệ phương trình: 200000450000 4247800000250000
Vậy tiền lương của một ngày làm việc bình thường là 250000 đồng Bài 6: (1.0 điểm) Quãng đường giữa hai thành phố A và B dài 120 km. Lúc 6 giờ sáng, một ô tô xuất phát từ A đi về B. Người ta thấy mối liên hệ giữa khoảng cách của ô tô so với A và thời điểm đi của ô tô là một hàm số bậc nhất yaxb có đồ thị như hình sau:
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 80 -
OFFICIAL
Lời gi
a) Xác định các hệ số a, b? b) Lúc 8 giờ sáng ôtô cách B bao xa? Lời giải a) Theo đề bài ta có hệ phương trình sau : 6040 9120240 aba abb Vậy 40,240.ab Hàm số : 40240yx b) Thay 8 x vào 40240yx
Bài 5: (1.0 điểm) Trong tháng 4 năm 2021, một công nhân được nhận tiền lương là 7 800 000 đồng gồm tiền lương trong 24 ngày làm việc bình thường và 4 ngày làm việc đặc biệt (gồm chủ nhật và ngày lễ). Biết tiền lương của một ngày làm việc đặc biệt nhiều hơn tiền lương của một ngày
ả
xyx xyy
Bài 7: (1.0 điểm) Một cái ly thủy tinh hình nón, bán kính đáy bằng 2 cm và chiều cao bằng 6 cm
OAOB OAOC OB OBcm
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 8140.824080 y Vậy lúc 8h
ô
B :
km
OFFICIAL
sáng
tô cách
1208040()
a) Tính thể tích cái ly (biết bề dày của cái ly không đáng kể)( làm tròn đến chữ số thập phân thứ nhất) b) Người ta rót rượu vào ly, biết chiều cao của rượu trong ly bằng 3 cm. Tính thể tích rượu chứa trong ly ( làm tròn đến chữ số thập phân thứ nhất). Lời giải a) Thể tích cái ly : 2 3 .2.6 25,1() 3 cm b) Theo đề bài ta có hình vẽ sau : Xét OAC có : O’B // OC '' 3' '1() 62 n (AB < AC). Đường tròn tâm O đường kính BC cắt AB, AC lần lượt tại E và F. Gọi H là giao điểm của BF và CE. Gọi D là giao điểm của AH và BC. Gọi M là trung điểm của HC. Gọi I là giao điểm của DF và CE. a) Chứng minh: AHBC và FHCBAC b) Chứng minh 2 FDEFCE và IEIMIDIF c) Qua I vẽ đường thẳng song song với MF cắt HF , AC lần lượt tại K và S. Lấy T đối xứng K qua I. Chứng minh tứ giác SHTC nội tiếp. Lời giải
Thể tích rượu chứa trong ly : 2 3 .1.3 3,1 3 cm Bài 8: (3.0 điểm) Cho tam giác ABC nhọ
a) Chứng minh BEC vuông tại E và BFC vuông tại F Suy ra H là trực tâm ABC => AHBC Tứ giác AEHF nội tiếp => FHCBAC b) Ta có: EDHECF (tứ giác AEDC nội tiếp) HDFHCF ( tứ giác HDCF nội tiếp) EDHHDF
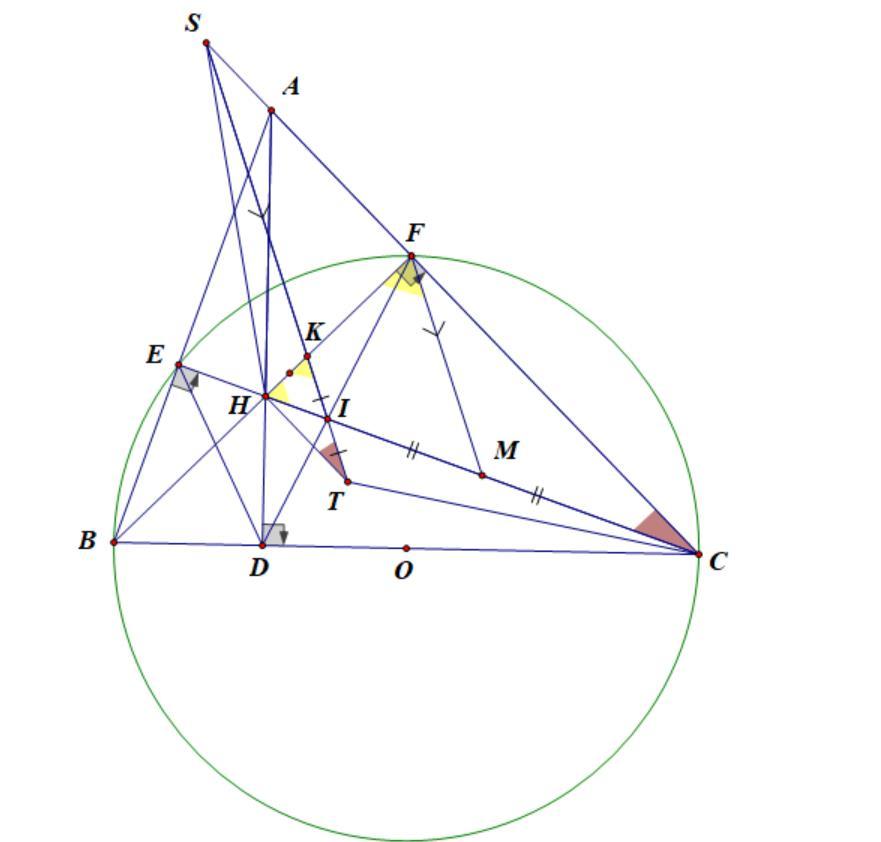
HD là phân giác của EDF
2 EDFECF Ta có: 2 EMFECF ( góc ngoài FMC ) ()EDIFMIgg IEIMIDIF
c) Ta có: FHMHFM ( HFM cân tại M) HFMHKI (2 góc đồng vị, FM // KI)
KHIHKI
HKI cân tại I => HI = KI => HIT cân tại I
HKT vuông tại H
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 82 -
∽
HTSHCS (cùng phụ FHC ) Tứ giác HTCS nội tiếp
SỞ GIÁO DỤC VÀ ĐẠO TẠO
THÀNH PHỐ HỒ CHÍ MINH QUẬN 6 (ĐỀ 3) (đề thi gồm 02 trang)
Bài 1. (1,5 điểm)
ĐỀ THAM KHẢO TUYỂN SINH 10 THPT
NĂM HỌC: 2022 - 2023 MÔN THI: TOÁN
Cho parabol (P): y = x2 và đường thẳng (d): y = x + 2.

a) Vẽ (P) và (d) trên cùng hệ trục tọa độ. b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Bài 2. (1,0 điểm)
Cho phương trình: 2x2 – x – 3 = 0 có 2 nghiệm là x1, x2. Không giải phương trình, hãy tính giá trị của biểu thức
Bài 3. (0,75 điểm)
Anh An làm việc cho một công ty sản xuất hàng cao cấp, anh được trả năm triệu bảy trăm sáu mươi ngàn đồng cho 48 tiếng làm việc trong một tuần. Sau đó để tăng thêm thu nhập, anh An đã đăng ký làm thêm một số giờ nửa trong tuần, mỗi giờ làm thêm này anh An được trả bằng 150% số tiền mà mỗi giờ anh An được trả trong 48 giờ đầu. Cuối tuần sau khi xong việc, anh An được lãnh số tiền là bảy triệu hai trăm ngàn đồng. Hỏi anh An đã làm thêm bao nhiêu giờ trong tuần đó?
Bài 4. (0,75 điểm)
Một cửa hàng bán lại bánh A như sau: nếu mua không quá 3 hộp thì giá 35 nghìn đồng mỗi hộp, nếu mua nhiều hơn 3 hộp thì bắt đầu từ hộp thứ tư trở đi giá mỗi hộp sẽ giảm đi 20% giá ban đầu.
a) Viết công thức tính y (số tiền mua bánh) theo x (số hộp bánh mua trong trường hợp nhiều hơn 3 hộp)
b) Lan và Hồng đều mua loại bánh A với số hộp nhiều hơn 3. Hỏi mỗi bạn mua bao nhiêu hộp biết rằng số hộp bánh Lan mua gấp đôi số hộp Hồng mua, đồng thời số tiền mua bánh của Lan nhiều hơn Hồng 140 nghìn đồng.
Bài 5. (1,0 điểm)
Một trường THPT nhận được 650 hồ sơ đăng ký tuyển sinh vào lớp 10 với hai hình thức: đăng ký trực tuyến và đăng ký trực tiếp tại nhà trường. Số hồ sơ đăng ký trực tuyến nhiều hơn số hồ sơ đăng ký trực tiếp là 120 hồ sơ. Hỏi nhà trường đã nhận được bao nhiêu hồ sơ đăng ký trực tuyến?
Bài 6. (1,0 điểm)
Hình vẽ biểu diễn một sợi dây chuyền có dạng hình trụ. Phần A và C được làm bằng bạc trong khi phần B được làm bằng vàng. Thể tích của sợi dây chuyền là 80 mm3
DẠYKÈMQUYNHƠN
OFFICIAL
2222 1212 Axxxx2022 .
a) Tìm độ dài của phần B theo mm, làm tròn đến 4 chữ số sau dấu thập phân. b) Tìm khối lượng theo gam của sợi dây chuyền đã cho biết khối lượng riêng của bạc và vàng lần lượt là 10,49 g/cm3 và 19,3 g/cm3. (làm tròn đến 2 chữ số phần thập phân, biết thể tích hình trụ bằng diện tích đáy nhân đường cao)
Bài 7. (1,0 điểm)
Mục tiêu là để rèn luyện sức khỏe, anh An và anh Bình đề ra mục tiêu mỗi ngày một người phải đi bộ ít nhất 6000 bước. Hai người cùng đi bộ ở công viên và thấy rằng, nếu cùng đi trong 2 phút thì anh An bước nhiều hơn anh Bình 20 bước. Hai người cùng giữ nguyên tốc độ như vậy nhưng anh Bình đi trong 5 phút thì lại nhiều hơn anh An đi trong 3 phút là 160 bước. Hỏi mỗi ngày anh An và anh Bình cùng đi bộ trong 1 giờ thì họ đã đạt được số bước tối thiểu mà mục tiêu đề ra hay chưa? (Giả sử tốc độ đi bộ hàng ngày của hai người không đổi).
Bài 8. (3,0 điểm)
Cho đường tròn (O; R) và điểm S nằm ngoài đường tròn (O) (SO < 2R). Từ S vẽ hai tiếp tuyến SA , SB (A, B là tiếp điểm) và cát tuyến SMN không qua tâm (M nằm giữa S và N) tới đường tròn (O). a) Chứng minh: SA2 = SM.SN b) Gọi I là trung điểm của MN. Chứng minh: IS là phân giác của góc AIB. c) Gọi H là giao điểm của AB và SO. Hai đường thẳng OI và BA cắt nhau tại E. Chứng minh: OI.OE = R2 . Hết
OFFICIAL
DẠYKÈMQUYNHƠN
Bài 1. (1,5 điểm) Cho parabol (P): y = x2 và đường thẳng (d): y = x + 2.
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Hướng dẫn:
a) Vẽ (P) (0,5 đ) Vẽ (d) (0,25 đ)
b) Phương trình hoành độ giao điểm cho 2 nghiệm
x = –1 ; x = 2. (0,25đ) Với x = –1 thì y = 1 A(–1 ; 1) (0,25 đ) Với x = 2 thì y = 4 B(2 ; 4) (0,25 đ) Bài 2. (1 điểm) Cho phương trình: 2x2 – x – 3 = 0 có 2 nghiệm là x1, x2. Không giải phương trình, hãy tính giá trị của biểu thứ
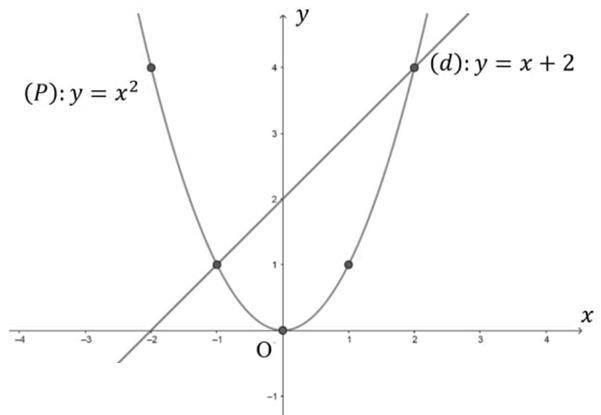
(0,25 đ) Bài 3. (0,75 điểm) Anh An làm việc cho một công ty sản xuất hàng cao cấp, anh được trả năm triệu bảy trăm sáu mươi ngàn đồng cho 48 tiếng làm việc trong một tuần. Sau đó để tăng thêm thu nhập, anh An đã đăng ký làm thêm một số giờ nửa trong tuần, mỗi giờ làm thêm này anh An được trả bằng 150% số tiền mà mỗi giờ anh An được trả trong 48 giờ đầu. Cuối tuần sau khi xong việc, anh An được lãnh số tiền là bảy triệu hai trăm ngàn đồng. Hỏi anh An đã làm thêm bao nhiêu giờ trong tuần đó?
Höôùng daãn :
Số tiền mỗi giờ anh An làm trong 48 giờ đầu: 5.760.000 : 48 = 120.000 (đồng)
Số tiền anh An làm thêm là: 7.200.000 – 5.760.000 = 1.440.000 (đồng)
Số tiền mỗi giờ làm thêm anh An được trả là: 120.000 150% = 180.000 (đồng)
Số giờ mà anh An làm thêm là: 1.440.000 : 180.000 = 8 (giờ)
Bài 4. (0,75 điểm) Một cửa hàng bán lại bánh A như sau: nếu mua không quá 3 hộp thì giá 35 nghìn đồng mỗi hộp, nếu mua nhiều hơn 3 hộp thì bắt đầu từ hộp thứ tư trở đi giá mỗi hộp sẽ giảm đi 20% giá ban đầu.
a) Viết công thức tính y (số tiền mua bánh) theo x (số hộp bánh mua trong trường hợp nhiều hơn 3 hộp).
b) Lan và Hồng đều mua loại bánh A với số hộp nhiều hơn 3. Hỏi mỗi bạn mua bao nhiêu hộp biết rằng số hộp bánh Lan mua gấp đôi số hộp Hồng mua, đồng thời số tiền mua bánh của Lan nhiều hơn Hồng 140 nghìn đồng.
DẠYKÈMQUYNHƠN
OFFICIAL ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
2222 1212 Axxxx2022 Hướ
ẫn:
222222 1212121212 Axxxx(xx)2xx(xx)2022
22133 22022120222023 222
c
ng d
S = x1 + x2 = 1 2 (0,25 đ) P = x1.x2 = 3 2 (0,25 đ)
(0,25 đ)
Hướng dẫn :
a) Giá tiền mỗi hộp bánh khi giảm 20% là: 28000 35000 80% (đồng)
Giá tiền 3 hộp bánh là: 3 35.000 = 105.000 (đồng)
Công thức tính y (số tiền mua bánh) theo x (số hộp bánh mua trong trường hợp nhiều hơn 3 hộp) là: 105000 3) 28000(x y
hay 21000 28000x y
b) Gọi x (hộp) là số hộp bánh Hồng mua. (x > 3) 2x (hộp) là số hộp bánh Lan mua.

Theo giả thiết, ta có:
140000 21000 x 28000 21000 2x 28000
5 x 140000 28000x 140000 28000x 56000x
(nhận) Vậy số hộp bánh Hồng mua là 5 hộp và số hộp bánh Lan mua là 10 hộp.
Bài 5. (1 điểm)
Một trường THPT nhận được 650 hồ sơ đăng ký tuyển sinh vào lớp 10 với hai hình thức: đăng ký trực tuyến và đăng ký trực tiếp tại nhà trường. Số hồ sơ đăng ký trực tuyến nhiều hơn số hồ sơ đăng ký trực tiếp là 120 hồ sơ. Hỏi nhà trường đã nhận được bao nhiêu hồ sơ đăng ký trực tuyến?
Hướng dẫn:
Gọi số hồ sơ đăng kí trực tuyến là x (hồ sơ) (điều kiện: x N*, x < 650). Vì trường THPT nhận được 650 hồ sơ nên số hồ sơ đăng kí trực tiếp tại nhà trường là: 650 – x (hồ sơ) Vì số hồ sơ đăng kí trực tuyến nhiều hơn số hồ sơ đăng ký trực tiếp là 120 hồ sơ nên ta có phương trình: x – (650 – x) = 120 2x – 650 = 120 2x = 770 x = 385 (thỏa mãn) Vậy số hồ sơ đăng kí trực tuyến là 385 hồ sơ.
Bài 6. (1,0 điểm)
Hình vẽ biểu diễn một sợi dây chuyền có dạng hình trụ. Phần A và C được làm bằng bạc trong khi phần B được làm bằng vàng. Thể tích của sợi dây chuyền là 80 mm3 .
a) Tìm độ dài của phần B theo mm, làm tròn đến 4 chữ số sau dấu thập phân. b) Tìm khối lượng theo gam của sợi dây chuyền đã cho biết khối lượng riêng của bạc và vàng lần lượt là 10,49 g/cm3 và 19,3 g/cm3. (làm tròn đến 2 chữ số phần thập phân, biết thể tích hình trụ bằng diện tích đáy nhân đường cao)
DẠYKÈMQUYNHƠN
OFFICIAL
a) Thể tích hình trụ: 22 22 V80 VRh1,5..hh11,31768 1,5.1,5. Độ dài của Phần B là xấp xĩ 11,31768 – 10 1,3177 mm. b) Thể tích của phần A và C : r2 × × 6 + r2 × × 4 = (1,5)2 × × 6 + (1,5)2 × × 4 70,68583 mm3 = 0,07068583 cm3 . Khối lượng của phần A và C: 0,07068583 × 10,49 0,741494 gam Thể tích của phần B = 80 – 70,68583 = 9,31417 mm3 = 0,00931417 cm3 . Khối lượng của phần B = 0,00931417 × 19,3 0,179763 gam khối lượng mặt dây chuyền xấp xĩ 0,741494 + 0,179763 0,921 gam.
Hướng dẫn :
Bài 7. (1 điểm) Mục tiêu là để rèn luyện sức khỏe, anh An và anh Bình đề ra mục tiêu mỗi ngày một người phải đi bộ ít nhất 6000 bước. Hai người cùng đi bộ ở công viên và thấy rằng, nếu cùng đi trong 2 phút thì anh An bước nhiều hơn anh Bình 20 bước. Hai người cùng giữ nguyên tốc độ như vậy nhưng anh Bình đi trong 5 phút thì lại nhiều hơn anh An đi trong 3 phút là 160 bước. Hỏi mỗi ngày anh An và anh Bình cùng đi bộ trong 1 giờ thì họ đã đạt được số bước tối thiểu mà mục tiêu đề ra hay chưa? (Giả sử tốc độ đi bộ hàng ngày của hai người không đổi). Hướng dẫn: Gọi số bước anh An đi bộ trong 1 phút là x (bước) (x N*). Gọi số bước anh Bình đi trong 1 phút là y (bước) (x N*). Vì nếu cùng đi trong 2 phút thì anh An bước nhiều hơn anh Bình 20 bước nên ta có phương trình: 2x – 2y = 20 x – y = 10 anh Bình đi trong 5 phút thì lại nhiều hơn anh An đi trong 3 phút là 160 bước nên ta có phương trình: 5y – 3x = 160 Ta có hệ phương trình: xy10x105() 5y3x160y95()
OFFICIAL
Mỗi ngày anh An và anh Bình cùng đi bộ trong 1 giờ nên số bước anh An đi là 105.60 = 6300, anh Bình đi được 95.60 = 5700 bước. Vậy anh An đạt được mục tiêu đề ra còn anh Bình thì không.
Bài 8. (3 điểm) Cho đường tròn (O ; R) và điểm S nằm ngoài đường tròn (O) (SO < 2R). Từ S vẽ hai tiếp tuyến SA , SB (A, B là tiếp điểm) và cát tuyến SMN không qua tâm (M nằm giữa S và N) tới đường tròn (O). a) Chứng minh: SA2 = SM.SN. b) Gọi I là trung điểm của MN. Chứng minh: IS là phân giác của góc AIB. c) Gọi H là giao điểm của AB và SO. Hai đường thẳng OI và BA cắt nhau tại E. Chứng minh: OI.OE = R2 . Hướng dẫn : a) Chứng minh: SA2 = SM.SN. Xét SAM và SNA : Ta có: góc ASN chung góc SAM = góc SNA (cùng chắn cung AM)

SAM và SNA đồng dạng (g ; g) SMSN SA SA SM SN SA 2
b) Chứng minh: IS là phân giác của góc AIB Vì I là trung điểm của dây MN trong đường tròn (O)
MN OI góc OIS = 900 góc OAS = 900 (SA là tiếp tuyến) góc OBS = 900 (SB là tiếp tuyến) Ba điểm I, A, B cùng nhìn OS dưới một góc vuông nên cùng nằm trên đường tròn đường kính OS. Năm điểm A, I, O, B, S cùng thuộc đường tròn đường kính SO Do SA = SB (t/c 2 tiếp tuyến cắt nhau) cung SA = cung SB góc AIS = góc SIB
IS là phân giác của góc AIB. c) Chứng minh: OI.OE = R2 . Ta có: SA = SB (cmt) và OA = OB = R
DẠYKÈMQUYNHƠN
nhan nhan
SO là đường trung trực của AB BE SO tại H
Tứ giác IHSE nội tiếp (vì góc EHS = góc EIS = 900) góc OHI = góc SEO
OHI và OES đồng dạng (vì góc EOS chung ; góc OHI = góc SEO)
OSOH OIOE OS OI OE OH
(3)
Áp dụng hệ thức lượng trong AOS vuông tại A có đường cao AH
Ta có: OA2 = OH.OS (4)
Từ (3) và (4) OI.OE = OA2 = R2 Hết
DẠYKÈMQUYNHƠN OFFICIAL
PHÒNG GIÁO DỤC & ĐÀO TẠO QUẬN 7 ĐỀ THAM KHẢO TUYỂN SINH LỚP 10 TRƯỜNG TH, THCS, THPT VIỆT ÚC
Môn: TOÁN - Thời gian: 120 phút Năm học: 2021 - 2022
Bài 1: (1,5 điểm)
Cho hàm số y = x2 và y = x + 2
a) Vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ Oxy b) Tìm tọa độ các giao điểm A, B của đồ thị hai hàm số trên bằng phép tính
Bài 2: (1,5 điểm)
Cho phương trình x2 – 2x – 3m2 = 0, với m là tham số a) Giải phương trình khi m = 1. b) Tìm tất cả các giá trị của m để phương trình có hai nghiệm x1, x2 khác 0 và thỏa điều kiện 12 21
8 3 xx xx .
Bài 3: (1 điểm)
Trứng vịt rẻ hơn 200đồng/quả, nặng hơn trứng gà mà hàm lượng protein giống nhau. Nếu biết cách mua, trứng vịt cũng thơm ngon không kém gì trứng gà.
Dưới đây là khảo sát về trứng vịt.
- Giá: 2.300 đ/1 quả
- Trọng lượng trung bình: 55g
- Tỷ lệ trọng lượng: lòng đỏ: 31,9%, lòng trắng 55,8%, vỏ 11,9%, màng vỏ 0,4%. Hỏi: a) 25 quả trứng gà bao nhiêu tiền biết rằng mua 1 chục trứng thì được bớt 1 nghìn đồng? b) 10 quả trứng vịt khi sử dụng phải bỏ đi phần vỏ (vỏ, màng vỏ) bao nhiêu gam?
Bài 4: (1 điểm)
Hai người cùng làm chung một công việc trong 12 5 giờ thì xong. Nếu mỗi người làm một mình thì người thứ nhất hoàn thành công việc trong ít hơn người thứ hai là 2 giờ. Hỏi nếu làm một mình thì mỗi người phải làm trong bao nhiêu thời gian để xong công việc?
Bài 5: (1 điểm)
Một xe lửa chạy qua một cái cầu dài 181m hết 47 giây, cùng vận tốc đó, xe lửa lướt qua một người đi bộ ngược chiều với nó trong 9 giây; vận tốc người đi bộ 1m/s. Tính vận tốc và chiều dài của xe lửa?
Bài 6: (1 điểm)
Từ một tấm thiếc hình chữ nhật ABCD có chiều rộng AB= 3,6 dm , chiều dài AD =4,85 dm, người ta cắt một phần tấm thiếc để làm mặt xung quanh của một hình nón với đỉnh là
DẠYKÈMQUYNHƠNOFFICIAL
A và đường sinh bằng 3,6 dm, sao cho diện tích mặt xung quanh này lớn nhất.Mặt đáy của hình nón được cắt trong phần còn lại của tấm thiếc hình chữ nhật ABCD.
a) Tính thể tích của hình nón được tạo thành.
b) Chứng tỏ rằng có thể cắt được nguyên vẹn hình tròn đáy mà chỉ sử dụng phần còn lại của tấm thiếc ABCD sau khi đã cắt xong mặt xung quanh hình nón nói trên.
Bài 7: (1 điểm)
Một cái cây bị sét đánh trúng giữa thân cây làm thân cây ngã xuống đất xuống đất tạo với mặt đất một góc là 400. Biết rằng khúc thân cây còn đứng cao 3m. Tính chiều cao lúc đầu của cây.
Bài 8: (2 điểm)
Cho tam giác ABC có các góc đều nhọn, BAC = 450. Vẽ các đường cao BD và CE của tam giác ABC. Gọi H là giao điểm của BD và CE.
a) Chứng minh tứ giác ADHE nội tiếp được trong một đường tròn.
b) Chứng minh: HD = DC.
c) Tính tỉ số: DE BC .
DẠYKÈMQUYNHƠNOFFICIAL
ĐÁP ÁN – HƯỚNG DẪN CHẤM ĐIỂM
Bài Câu Nội dung Điểm 1 a a) Vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ Oxy Lập bảng : x 0 - 2 y = x + 2 2 0 x - 2 - 1 0 1 2 y = x2 4 1 0 1 4
0,75 2 a Khi m = 1, phương trình thành 0,75
thay x1 = -1 y1 = x2 = (-1)2 = 1; x2 = 2 y2 = 4 Vậy tọa độ giao điểm cần tìm là A( - 1; 1) , B(2; 4) 8 3 xx xx 22 12123()8 xxxx 3(x1 + x2)(x1 – x2) = 8x1x2 Ta có : a.c = -3m2 0 nên 0, m Khi 0 ta có : x1 + x2 = 2 b a và x1.x2 = 2 3 c m a 0 Điều kiện để phương trình có 2 nghiệm 0 mà m 0 > 0 và x1.x2 < 0 x1 < x2 Với a = 1 x1 = '' b và x2 = '' b x1 – x2 = 2 2'213 m Do đó, ycbt 22 3(2)(213)8(3) mm và m 0 22132 mm (hiển nhiên m = 0 không là nghiệm)
DẠYKÈMQUYNHƠNOFFICIAL
0,75 b Hoành độ giao điểm của đường thẳng (d) và Parabol (P) là nghiệm của phương trình: x2 = x + 2 ⟺ x2 – x – 2 = 0 ( a = 1 , b = – 1 , c = – 2 ) có a – b + c = 1 – ( – 1 ) – 2 = 0 1 1 x ; 2 2 2 1 c x a : x2 – 2x – 3 = 0 x = -1 hay x = 3 (có dạng a–b + c = 0) 0,75 b Với x1, x2 0, ta có : 12 21
3
4m4 – 3m2 – 1 = 0 m2 = 1 hay m2 = -1/4 (loại) m = 1
Mua 25 trứng gà chỉ trả: 2500.25 – 2.1000 = 60500 (đồng)
Phần sử dụng của 10 quả trứng vịt là: 10.55.(31,9%+55,8%) = 482,35 (gam)
4 Gọi thời gian người thứ nhất hoàn thành một mình xong công việc là x (giờ), ĐK 12 5 x
Thì thời gian người thứ hai làm một mình xong công việc là x + 2 (giờ) Mỗi giờ người thứ nhất làm được 1 x (cv), người thứ hai làm được 1 2 x (cv)
Vì cả hai người cùng làm xong công việc trong 12 5 giờ nên mỗi giờ cả hai đội làm được 12 1: 5 = 5 12 (cv)
1,0
DẠYKÈMQUYNHƠNOFFICIAL
115 xx212 25 (2)12 xx xx 5x2 – 14x –
’ = 49 +
=> 7136 55 x (loại) và 71320 4 55 x (TMĐK) Vậy người thứ nhất làm xong công việc trong 4 giờ, người thứ hai làm xong công việc trong 4+2 = 6 giờ. 1,0 5 Gọi v là vận tốc xe lửa; a là chiều dài xe lửa thì Với vận tốc v đi 47 giây xe lửa đã chạy 181 + a nên 47v = 181 + a(1) Xe lửa lướt qua một người đi bộ ngược chiều nghĩa là xe và người đi hết quãng đường bằng chiều dài xe lửa đi ngược 1,0
Do đó ta có phương trình
24 = 0
120 = 169, , 13
chiều trong 9 giây, nên có 9.(v+ 1) = a (2)

Giải hệ (1) và (2) ta được v = 5 và a = 54
Vậy vận tốc xe lửa là 5m/giây (hay 18 km/giờ)
Chiều dài xe lửa là 54m.
a)Hình khai triển của mặt xung quanh của hình nón có đỉnh tại A , đường sinh l = 3,6dm =AB là hình quạt tâm A , bán kính AB.Mặt xung quanh này có diện tích lớn nhất khi góc ở tâm của hình quạt bằng 900 +Diện tích hình quạt cũng là diện tích xung quanh của hình nón có bán kính đáy là r , nên:
DẠYKÈMQUYNHƠNOFFICIAL
6
22
3604 0,9 4 xq ll Srl l rdm Do đó thể tích của hình nón được tạo ra là : 222 22223 111.3,14.0,9.3,60,92,96 333 Vrhrlrdm
b)Trên đường chéo AC, vẽ đường tròn tâm I bán kính r = 0,9 (dm) ngoại tiếp cung quạt tròn tại E , IH và IK là các đoạn vuông góc kẻ từ I đến BC và CD Ta có CI = AC - AI = 22 3,64,853,60,91,54dm Vì IH // AB 0,910,9 HICI ABAC ABCI IHdmrdm AC Tương tự : IK > r = 0,9 ( dm) Vậy sau khi cắt xong mặt xung quanh , phần còn lại của tấm thiếc ABCD có thể cắt được mặt đáy của hình nón 0,5
.90
0,5
TTa xem đề bài như hình vẽ Khi đó chiều dài cây lúc ban đầu là BC + AC = BC + BC sin�� = 3.(1+ 1 ������400)≈7,67(��)


8 a) Chứng minh tứ giác ADHE nội tiếp được trong một đường tròn. Vì BD, CE là các đường cao của tam giác ABC nên: 090 BDACEA hay 090 HDAHEA Tứ giác ADHE có 0180 HDAHEA nên nội tiếp được trong một đường tròn. b) Chứng minh: HD = DC. Do tứ giác ADHE nội tiếp nên EADDHC (cùng bù DHE ) Mà 045 EAD (gt) nên 045 DHC . Tam giác HDC vuông ở D, 045 DHC nên vuông cân. Vậy DH = DC. c) Tính tỉ số DE BC : Tứ giác BEDC có 090 BECBDC nên nội tiếp được trong một đường tròn.
0,75 0,75
DẠYKÈMQUYNHƠNOFFICIAL 7
1,0
Suy ra: ADEABC (cùng bù EDC ) Xét ADE và ABC có ADEABC , BAC chung nên ADE ABC (g-g) Do đó: DEAE BCAC Mà 0 2 osA=cos45 2 AE c AC (do tam giác AEC vuông ở E và 045 EAC ) Vậy: 2 2 DE BC
DẠYKÈMQUYNHƠNOFFICIAL
0,5
QUẬN 8 - ĐỀ SỐ 3
Câu 1: (1,5 điểm)
ĐỀ THAM KHẢO TUYỂN SINH 10 NĂM HỌC 2022 – 2023 MÔN TOÁN Thời gian làm bài: 120 phút (không kể thời gian phát đề)
a) Cho đồ thị (P) của hàm số : 2 2 x y và đồ thị (d) của hàm số y = x – 4 trên cùng một hệ trục tọa độ.
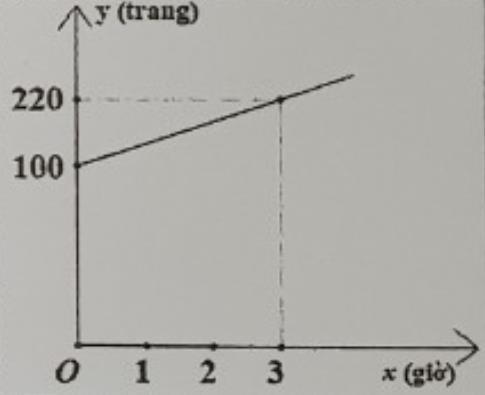
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép toán.
Câu 2: (1,0 điểm)
Cho phương trình: 6x2 + 6x – 13 = 0 có hai nghiệm là 12,.xx Không giải phương trình, hãy tính giá trị của biểu thức: A= x1 x2 1 x2 + x2 x1 1 x1 Câu 3: (0,75 điểm) Để tìm hàng chi của một năm ta dùng công thức: Mã số của hàng CHI bằng số dư trong phép chia 4 12 Năm cộng 1 Rồi đối chiều kết quả với bảng sau: Hàng CHI Tý Sửu Dần Mão Thìn Tỵ Ngọ Mùi Thân Dậu Tuất Hợi Mã số 1 2 3 4 5 6 7 8 9 10 11 12
OFFICIAL
a) Ngày 30/04/1975 Giải phóng miền Nam, thống nhất đất nước có hàng CHI là gì?
b) Ta đã biết ngoài Dương lịch, âm lịch người ta còn ghi theo hệ thống CAN CHI, chẳng hạn Nhâm Ngọ, Ất Dậu…Chữ thứ nhất chỉ hàng CAN của năm. Có 10 can là: Hàng CAN Giáp Ất Bính Đinh Mậu Kỷ Canh Tân Nhâm Quý Mã số 1 2 3 4 5 6 7 8 9 10 (0) Muốn tìm hàng CAN của một năm ta dùng công thức sau (Nếu chữ số tận cùng của năm dương lịch nhỏ hơn 3 thì ta mượn thêm 10) Đối chiếu với bảng trên, em hãy cho biết năm 1930 Đảng Cộng Sản Việt Nam ra đời có hàng CAN CHI là gì? Câu 4: (0,75 điểm) Hôm qua, bạn Phương đã đọc được 100 trang đầu một cuốn sách. Hôm nay, trong 3 giờ bạn đọc thêm 120 trang. Gọi x (giờ) là thời gian đọc sách trong ngày hôm nay, y (trang) là số trang sách đã đọc được trong x (giờ) (số trang sách đọc được mỗi giờ là không thay đổi). Mối liên hệ giữa y và x là một hàm số bậc nhất: y = ax + b có đồ thị như hình bên.
Mã số của hàng CAN = Chữ số tận cùng của (năm dương lịch - 3)
DẠYKÈMQUYNHƠN
a) Xác định các hệ số a , b.

b) Nếu quyển sách 380 trang thì bạn Phương cần thêm bao nhiêu giờ để đọc hết quyển sách trên.
Câu 5: (1,0 điểm) Một cửa hàng bán trái cây nhập khẩu 500 kg Cam với giá 40 000đ/kg. Phí vận chuyển của chuyến hàng là 4 000 000 đồng. Giả sử rằng 10% số kg Cam trên bị hư trong quá trình vận chuyển và số kg Cam còn lại được bán hết. Hỏi giá bán của mỗi kg Cam là bao nhiêu để công ty có lợi nhuận 20% so với tiền vốn ban đầu?
Câu 6: (1,0 điểm) Một cốc nước hình trụ có chiều cao 15cm, bán kính đáy là 3cm và lượng nước ban đầu trong cốc cao 12cm. Thả chìm hoàn toàn vào cốc nước 3 viên bi thủy tinh hình cầu có cùng bán kính là 2cm thì nước bị tràn ra ngoài. (Giả sử độ dày của thành cốc và đáy cốc không đáng kể)
a) Tính thể tích nước bị tràn ra ngoài (làm tròn đến chữ số thập phân thứ hai). Cho biết công thức tính thể tích hình trụ: V = πR2 h trong đó R là bán kính đáy và h là chiều cao hình trụ, thể tích của hình cầu được tính theo công thức �� = 4 3 .π.��3 với r là bán kính hình cầu. b) Thể tích nước tràn ra ngoài bằng bao nhiêu phần trăm của khối nón có chiều cao bằng chiều cao của hình trụ, bán kính đáy bằng đường kính hình cầu? Biết công thức tính thể tích hình nón là V = 1 3 π(2r)2 h
OFFICIAL
Câu 7: (1,0 điểm) Một siêu thị A có các mặt hàng giày dép đồng giá, các mặt hàng quần áo đồng giá. Tổng giá tiền niêm yết của một đôi giày và một bộ quần áo là 850 000 đồng. Biết giá tiền niêm yết của 2 bộ quần áo ít hơn giá tiền niêm yết của 3 đôi giày là 50 000 đồng. Hỏi giá tiền niêm yết của một bộ quần áo, một đôi giày là bao nhiêu?
Câu 8: (3,0 điểm) Từ điểm A ở ngoài đường tròn (O), vẽ tiếp tuyến AB với (O) (B là tiếp điểm), vẽ cát tuyến ACD (điểm C nằm giữa A và D, tiếp tuyến AB và cát tuyến ACD ở hai phía đối với AO). Vẽ dây cung BE vuông góc với AO tại K. a) Chứng minh: AE là tiếp tuyến của đường tròn (O). b) Gọi H là trung điểm của CD. Chứng minh: tứ giác BOHE nội tiếp. c) Chứng minh: AC. AD = AK. AO và ���� ���� =(���� ����)2
DẠYKÈMQUYNHƠN
HƯỚNG DẪN CHẤM TUYỂN SINH 10 MÔN: TOÁN
DẠYKÈMQUYNHƠN OFFICIAL
��2 2 =��
⇔ ��2 2 ��+4=0 ⇔[ �� =2 �� =
��=
Vậy tọa
2 6x2 +
=
Theo
�� = ��1 +��2 = �� �� = 1 �� =��1��2 = �� �� = 13 6 Ta có: �� = ��1 ��2 1 ��2 + ��2 ��1 1 ��1 �� = ��1 2 ��1��2 ��1 +��2 2 ��1��2 ��2 ��1��2 �� = ��2 4�� �� �� �� = 1+26 3 +1 13 6 = 64 13 0,25 0,25 0,25 0,25 3 a) Mã sô của hàng CHI = dư của 1975 4 12 +1=4 Ngày 30/04/1975 Giải phóng miền Nam, thống nhất đất nước có hàng CHI là Mão b) Hàng CHI = dư của 1930 4 12 +1=7 Vậy Năm 1930 Đảng Cộng Sản Việt Nam ra đời có hàng CAN CHI là Canh Ngọ Hàng CAN = Chữ số tận cùng của năm dương lịch - 3 = 10 – 3 = 7 0,25 0,25 0,25 4 y = ax + b
Câu Nội dung Điểm 1 a) Bảng giá trị và đồ thị (P) đúng Bảng giá trị và đồ thị (d) đúng b) Phương trình hoành độ giao điểm của (P) và (d) là:
4
4⇒[��= 2
8
độ giao điểm là (–4; –8) và (2; –2) 0,5 0,25 0,25 0,25x2
6x – 13
0
hệ thức Vi-ét, ta có:
a) Thay x = 0, y = 100 ta được pt: 0a + b = 100 (1)
Thay x = 3, y = 100 + 120 = 220 ta được pt: 3a + b = 220 (2)
Giải hệ pt tìm được a = 40, b = 100
Vậy y = 40x + 100 b) Thay y = 380 vào hàm số ta được: 40x + 100 = 380 ⇔ x = 7 giờ Vậy bạn Phương cần thêm 7giờ
5 Tổng số tiền vốn bỏ ra là: 500. 40 000 + 4 000 000 = 24 000 000 đồng
Tổng số tiền phải bán được là: 24 000 000. (1 + 20%) = 28 800 000 đồng Số kg cam bán ra được là: 500. (1 – 10%) = 450 kg Giá bán 1kg cam là: 28 800 000 : 450 = 64 000 đồng
0,25 0,25 0,25
OFFICIAL
0,25 0,25 0,25 0,25
0,25 0,25 0,25 0,25 7 Gọi x, y (đồng) lần lượt là giá tiền niêm yết của một đôi giày và một
hơn
DẠYKÈMQUYNHƠN
bộ quần áo ĐK: x, y > 0 Giá tiền niêm yết của một đôi giày và một bộ quần áo là 850 000 đồng, ta có phương trình: x + y = 850 000 (1) Giá tiền niêm yết của 2 bộ quần áo ít
giá tiền niêm yết của 3
là 50 000 đồng, ta có phương
6 a) Thể tích cốc nước hình trụ: ��.32.15=135��(����3) Thể tích nước trong cốc: ��.32.12=108��(����3) Thể tích 3 viên bi: 3 4 3 �� 23 =32��(����3) Thể tích nước tràn ra ngoài là: (32 ��+108�� 135�� = 5�� =15,71 (cm3) b) Thể tích của khối nón: 1 3 π42 .15 = 80 π (cm3) So với khối nón thì thể tích nước tràn ra ngoài chiếm: 5�� 80�� 100%=6,25% 3x – 2y = 50 000
đôi giày
trình:
(2) 0,25 0,25
a) Chứng minh: AE là tiếp tuyến của (O)
Chứng minh được BÔK = EÔK
Chứng minh được △AOE = △AOB (cgc) ⇒������ ̂ =������ ̂ =900 ⇒ AE vuông góc OE tại E ⇒ AE là tiếp tuyến của (O)
b) Chứng minh: tứ giác BOHE nội tiếp. Chứng minh OH vuông góc CD Chứng minh tứ giác ABOE nội tiếp đường tròn đường kính AO Chứng minh △vuông AHO nội tiếp đường tròn dường kính AO
5 điểm A, B, O, H, E cùng thuộc đường tròn dường kính AO Vậy tứ giác BOHE

DẠYKÈMQUYNHƠN OFFICIAL
Từ (1) và (2) ta có hệ phương trình 850000 3–250000 350000 500000 x xy xy y
Vậy giá tiền niêm yết của một đôi giày là 350000 đồng, giá tiền niêm yết của một bộ quần áo là 500000 đồng. 0,25 0,25 8
nội tiếp đường tròn. c) Chứng minh: AC. AD = AK. AO và ���� ���� =(���� ����)2 Chứng minh được: △ABC đồng dạng △ADB (gg) ⇒ AB2 = AC. AD Mà AB2 = AK. AO (Htl trong △ vuông ABO) ⇒ AC. AD = AK. AO Kẻ BN vuông góc AD △ABC đồng dạng △ADB (cmt) ⇒ ���� ���� = ���� ���� = ���� ���� ⇒ ��△������ ��△������ =(���� ����)2 0,25 0,25 0,25 0,25 0,25 0,25 0,25 0,25 0,25 0,25 0,25
⇒
DẠYKÈMQUYNHƠN OFFICIAL ⇒ 1 2 �������� 1 2 �������� =(���� ����)2 Vậy ���� ����
���� ����)2 0,25
=(
(Nếu học sinh có cách giải khác, giám khảo vận dụng thang điểm trên để chấm) .
nghiệm là 12 , xx . Không giải phương trình, hãy tính giá tr
a bi
11
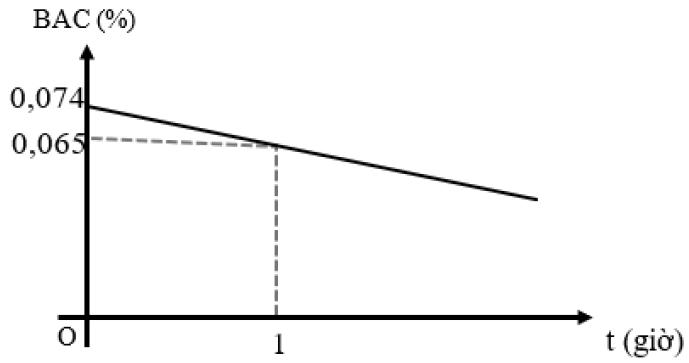
th
3: (1,0 điểm) Nồng độ cồn trong máu (BAC) được định nghĩa là phần trăm rượu (rượu ethyl hoặc ethanol) trong dòng máu của một người. BAC 0,03% có nghĩa là có 0,03 gam rượu trong 100ml máu. Càng uống nhiều rượu bia thì nồng độ cồn trong máu càng cao và càng nguy hiểm khi tham gia giao thông. Nồng độ BAC trong máu của một người được thể hiện qua đồ thị sau:
a) Viế
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10
--------------------
2
a) Vẽ P và d
ột hệ trục tọa độ. b)
tọa độ
điểm của P và d
ằ
2
xx có
PHÒNG GD & ĐT QUẬN 10 NĂM HỌC 2022-2023 ĐỀ THAM KHẢO MÔN : TOÁN 9
Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Quận 10 – 3 Thời gian: 120 phút (không kể thời gian phát đề) Câu 1: (1,5 điểm) Cho parabol
1 : 2
Pyx và đường thẳng
:4
dyx
trên cùng m
Tìm
giao
b
ng phép tính. Câu 2: (0,75 điểm) Cho phương trình
2450
hai
ị củ
ểu
ức 12 21
22 xx T xx Câu
ứ
được tính theo bảng bên dưới. Hỏi sau 2 giờ
ếu
ằng
ẽ bị xử phạt ở mức nào? Mức 1: Nồng độ cồn chưa vượt quá 50 /100 mgml máu 0203 triệu đồng (tước bằng lái xe từ 1012 tháng) Mức 2: Nồng độ cồn vượt quá 50 mg đến 80 /100 mgml máu 04 – 05 triệu đồng (tước bằng lái xe từ 16 – 18tháng) Mức 3: Nồng độ cồn vượt quá 80 /100 mgml máu 06 – 08triệu đồng (tướ
1
t công thức biểu thị mối quan hệ giữa nồng độ cồn trong máu (BAC) sau t giờ sử dụng. b) Theo nghị định 100/2019/NĐ – CP về xử phạt vi phạm hành chính, các m
c phạt (đối với xe máy)
, n
người này tham gia giao thông b
xe máy thì s
c bằng lái xe từ 10 – 12tháng) Câu 4: (0,75 điểm) Phương tiện vận chuyển công cộng phổ biến hiện nay ở thành phố Hồ Chí Minh là xe buýt. Bác Nam mỗi ngày đi làm bằng xe buýt 2 lượt đi và về, trung bình mỗi tháng bác Nam đi làm 26 ngày. Giá vé xe buýt trên tuyến đường bác Nam thường đi là 6000 đồng/lượt và 135000đồng/
p 30 vé. Nếu bác Nam mua tập 30 vé trên thì giảm được bao nhiêu phần trăm chi phí đi xe buýt hàng tháng so với trường hợp không mua vé tháng? (làm tròn đến chũ số thập phân thứ nhất).
Câu 5: (1,0 điểm) Một ông chủ đã mua 100 cái điện thoại với giá 5 triệu đồng mỗi cái. Ông đã bán 70 chiếc với giá 6,5 triệu đồng một cái. Sau đó ông giảm giá để bán số điện thoại còn lại. Vậy mỗi chiếc điện thoại còn lại ông phải bán với giá bao nhiêu tiền để có lợi nhuận (tiền lời) là 27% (so với tiền vốn bỏ ra). Câu 6: (1,0 điểm) Hai trụ điện có cùng chiều cao h được dựng thẳng đứng hai bên đối diện một đại lộ rộng 80m. Từ một điểm M trên đường nằm giữa hai trụ điện người ta nhìn thấy đỉnh hai trụ với góc nâng lần lượt là 60 và 30 (như hình vẽ). Tính chiều cao trụ điện? (Làm tròn đến chữ số thập phân thứ hai).
Câu 7: (1,0 điểm) Một cái thùng hình trụ có đường kính 60cm . Người ta đổ vào thùng một lượng nước cao 80cm . Sau đó người ta thả vào thùng một quả cầu sắt có đường kính bằng đường kính của thùng, lúc này mực nước trong thùng dâng lên, cách miệng thùng 30cm . Tính thể tích của thùng (làm tròn đến chữ số hàng đơn vị).
Câu 8: (3,0 điểm) Cho ABC nhọn ABAC nội tiếp O có ,, ADBECF là 3 đường cao cắt nhau tại H . Tia AH cắt O tại M . Kẻ AK là đường kính của O G là giao điểm của AK và FE
a) Chứng minh tứ giác CDHE và tứ giác BCEF nội tiếp. b) Chứng minh OAEF và tứ giác DHGK nội tiếp. c) Gọi I là trung điểm của AH . Qua I kẻ đường vuông góc với IB cắt AC tại N . Chứng minh tứ giác BIEM nội tiếp và // ONBC
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 78 -
ậ
OFFICIAL
t
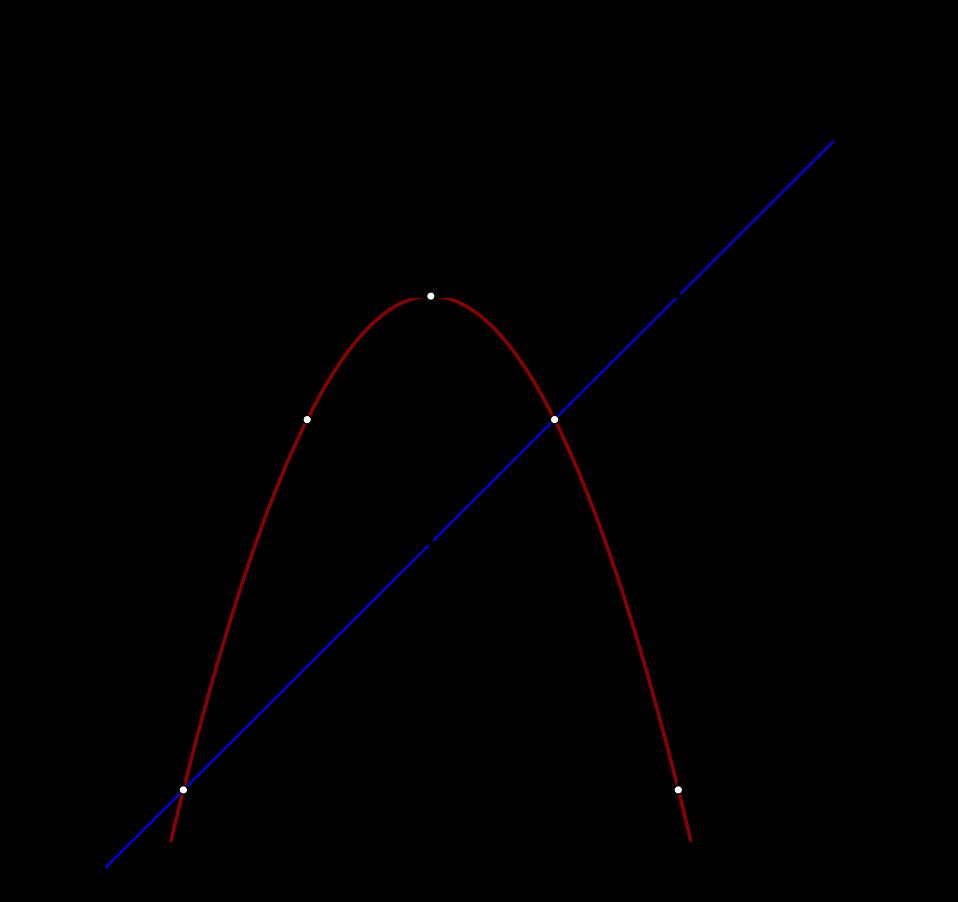
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI Câu 1: Cho parabol 2 1 : 2 Pyx và đường thẳng :4 dyx a) Vẽ P và d trên cùng một hệ trục tọa độ. b) Tìm tọa độ giao điểm của P và d bằng phép tính. Lời giải a) Bảng giá trị x 0 4 4 yx 4 0 x 4 2 0 2 4 2 1 2 yx 8 2 0 2 8 b) Phương trình hoành độ giao điểm giữa 2 1 : 2 Pyx và :4 dyx là: 22 1 4280 2 xxxx 1890 Suy ra phương trình trên có hai nghiệm phân biệt 1 13 4 1 x và 2 13 2 1 x 111448 xyx 222242 xyx Vậy d cắt P tại hai điểm 4;8 và 2;2 . Câu 2: Cho phương trình 2 2450 xx có hai nghiệm là 12 , xx . Không giải phương trình, hãy tính giá trị của biểu thức 12 21 11 22 xx T xx .
u trong 100ml máu. Càng uống nhiều rượu bia thì nồng độ cồn trong máu càng cao và càng nguy hiểm khi tham gia giao thông. Nồng độ BAC trong máu của một người được thể hiện qua đồ thị sau:
a) Viết công thức biểu thị mối quan hệ giữa nồng độ cồn trong máu (BAC) sau t giờ sử dụng.
b) Theo nghị định 100/2019/NĐ – CP về xử phạt vi phạm hành chính, các mức phạt (đối với xe máy) được tính theo bảng bên dưới. Hỏi sau 2 giờ, nếu người này tham gia giao thông bằng xe máy thì sẽ

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 80Lời giải Phương trình 2 2450 xx có hai nghiệm 12 , xx . Theo hệ thức Vi-et, ta có: 12 2 xx ; 12 5 2 xx Do đó 2 22 11221212121212 12 21121212 11112 22222 xxxxxxxxxxxxxx xx T xxxxxxxx 2 5 222 24527 2555 2 Vậy 7 5 T Câu 3: Nồng độ cồn trong máu (BAC) được định nghĩa là phần trăm rượu (rượu ethyl hoặc ethanol) trong dòng máu của một người. BAC 0,03% có nghĩa là có 0,03 gam rượ
ị
ử phạt ở mức nào? Mức 1: Nồng độ cồn chưa vượt quá 50 /100 mgml máu 0203 triệu đồng (tước bằng lái xe
ừ
tháng) Mức 2: Nồng độ cồn vượt quá 50 mg đến 80 /100 mgml máu 04 – 05 triệu đồng (tước bằng lái xe
ừ
– 18tháng) Mức 3: Nồng độ cồn vượt quá 80 /100 mgml máu 06 – 08triệu đồng (tước bằng lái xe từ 10 – 12tháng)
giả
b
x
t
1012
t
16
Lời
i
ta được BAC0,009.20,0740,056
(g) 56
(mg).
ậy sau 2 giờ, nếu người này tham gia giao thông bằng xe máy thì sẽ bị xử phạt ở mức 2.
4: Phương tiện vận chuyển công cộng phổ biến hiện nay ở thành phố Hồ Chí Minh là xe buýt. Bác Nam mỗi ngày đi làm bằng xe buýt 2 lượt đi và về, trung bình mỗi tháng bác Nam đi làm 26 ngày. Giá vé xe buýt trên tuyến đường bác Nam thường đi là 6000 đồng/lượt và 135000đồng/1 tập 30 vé. Nếu bác Nam mua tập 30 vé trên thì giảm được bao nhiêu phần trăm chi phí đi xe buýt hàng tháng so với trường hợp không mua vé tháng? (làm tròn đến chũ số thập phân thứ nhất). Lời giải Nếu không mua vé tháng thì số tiền bác Nam mua vé trong 26 ngày là:
6000.2.26312000 (đồng). Như vậy so với việc không mua vé tháng thì mua tập 30 vé sẽ giảm được: 312000135000 100%56,7% 312000
Câu 5: Một ông chủ đã mua 100 cái điện thoại với giá 5 triệu đồng mỗi cái. Ông đã bán 70 chiếc với giá 6,5 triệu đồng một cái. Sau đó ông giảm giá để bán số điện thoại còn lại. Vậy mỗi chiếc điện thoại còn lại ông phải bán với giá bao nhiêu tiền để có lợi nhuận (tiền lời) là 27% (so với tiền vốn bỏ ra). Lời giải
Số tiền vốn bỏ ra để mua 100 cái điện thoại với giá 5 triệu đồng một cái là: 100.5500 (triệu đồng).
Doanh thu cần đạt được để có lợi nhuận là 27% so với tiền vốn bỏ ra là: 50027%500635 (triệu đồng). Số tiền thu được sau khi bán 70 cái điện thoại với giá 6,5 triệu đồng một cái là: 70.6,5455 (triệu đồng).
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 81a) Công thức biểu thị mối quan hệ giữa nồng độ cồn
(
) sau t giờ sử dụng có dạng: BAC atb Từ đồ
ị đề
.
trong máu
BAC
th
bài cho, ta được hệ phương trình 0,074.0 0,065.1
ab ab Giải hệ phương trình này ta tìm được 0,009 0,074
a b
Vậy BAC0,0090,074 t b) Với 2
t
V
Câu
.
Câu
Hai trụ điện có cùng chiều cao h được dựng
ện
ột
ộ
ộ
một điểm M trên đường nằ
ữ
60
30
Như vậy, số tiền còn thiếu để đạt lợi nhuận 27% là: 635455180 (triệu đồng). Do đó, trong 30 cái điện thoại còn lại cần phải bán mỗi cái với giá: 180 6 30 (triệu đồng).
6:
thẳng đứng hai bên đối di
m
đại l
r
ng 80 m. Từ
m gi
a hai trụ điện người ta nhìn thấy đỉnh hai trụ với góc nâng lần lượt là
và
(như hình vẽ). Tính chiều cao trụ điện? (Làm tròn đến chữ số thập phân thứ hai).
Lời giải
Xét ABM ta có : cot60 BMh
Xét DCM ta có : cot30 CMh .
Chiều dài của đại lộ là: 80cot60cot30cot60cot30 BCBMCMhhh
Chiều cao của trụ điện là: 80 20334,64 cot60cot30 h (m).
Câu 7: Một cái thùng hình trụ có đường kính 60cm . Người ta đổ vào thùng một lượng nước cao 80cm Sau đó người ta thả vào thùng một quả cầu sắt có đường kính bằng đường kính của thùng, lúc này mực nước trong thùng dâng lên, cách miệng thùng 30cm . Tính thể tích của thùng (làm tròn đến chữ số hàng đơn vị).
Bán kính của thùng là: 60 30 2 (cm).
Thể tích lượng nước trong thùng là: 2 308072000 ( 3 cm ).
Thể tích của quả cầu sắt là: 3 4 3036000 3
Thể tích còn lại là: 2 303027000 ( 3 cm ).
( 3 cm ).
tích của thùng là: 720003600027000135000424115
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 82 -
OFFICIAL
của O . G là giao điểm của AK và FE. a) Chứng minh tứ giác CDHE và tứ giác
ộ
ếp. b) Chứng minh OAEF và tứ giác
ộ
ế
c) Gọi I là trung điểm của AH .
kẻ đường
ớ
IB
ắ
ạ
ứ
giác BIEM nội tiếp và // ONBC . Lời giải
Thể
( 3 cm ). Câu 8: Cho ABC nhọn ABAC nội tiếp O có ,, ADBECF là 3 đường cao cắt nhau tại H . Tia AH cắt O tại M . Kẻ AK là đường kính
BCEF n
i ti
DHGK n
i ti
p.
Qua I
vuông góc v
i
c
t AC t
i N . Ch
ng minh tứ
a) Chứng minh tứ giác CDHE và tứ giác BCEF nội tiếp.
Do ,, ADBECF là 3 đường cao cắt nhau tại H của tam giác ABC nên 90 CDHHECBFCBEC
Suy ra 180 CDHHEC và 90 BFCBEC

Suy ra các tứ giác CDHE và BCEF nội tiếp.
b) Chứng minh OAEF và tứ giác DHGK nội tiếp. Do AK là đường kính của O nên 90 ACK (góc nội tiếp chắn nửa đường tròn)
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 83 -
OFFICIAL
Suy
Mặt khác AKCABC (cùng chắn AC ) và ABCAEF (do
ứ giác BCEF
ộ
ếp) Do đó, ta suy ra 90 KACAEF Suy ra OAEF . AEGAKCgg (do EAGKAC và 90 AGEACK ) Suy ra AEAG AEACAGAK AKAC (1). AHEACDgg (do HAECAD và 90 AEHADC ) Suy ra AHAE AEACAHAD ACAD (2). Từ (1) và (2) ta suy ra AHAG AHADAGAK AKAD Suy ra AGHADKcgc do GAHDAK và AHAG AKAD
ra 90
KACAKC
t
n
i ti
Suy ra AGHADK , suy ra tứ giác DHGK nội tiếp.
c) Chứng minh tứ giác BIEM nội tiếp và // ONBC
I là trung điểm AH mà 90 AEH nên IAIEIH . Suy ra EIH cân tại I .
Suy ra IEHIHE mà tứ giác CDHE nội tiếp nên IHEECD.
Do đó IEBIHEACB . Mà IMBACB (cùng chắn AB ) nên IEBIMB
Suy ra tứ giác BIEM nội tiếp.
Mặt khác tứ giác BIEN nội tiếp ( 90 BINBEN ) nên 5 điểm ,,,, BIENM cùng thuộc một đường tròn. Suy ra tứ giác MIEN nội tiếp.
Suy ra IMNIEA . Mà IEAIAE (do IAE cân tại I ) nên NMANAM
Suy ra NAM cân tại N . Suy ra NANM mà , OAOMAMO nên ON là đường trung trực của AM Suy ra ONAM . Suy ra // ONBC (vì BCAD).
OFFICIAL
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 84 -
m phân biệt.
Bài 2:(1đ) Cho phương trình : – x2 + 2(m – 1)x + 1 = 0 (m là tham số; x là ẩn) (1) a) Chứng minh phương trình (1) luôn có hai nghiệm trái dấu với mọi m b) Gọi x1, x2 là hai nghiệm phương trình (1). Tìm m thỏa điều kiện : 33 12xx = 0 Bài 3 (1đ) Để ước tính tốc độ s (dặm/giờ)của một chiếc xe, cảnh sát sử dụng công thức 30 sfd , ở đó d là độ dài vết trượt của bánh xe tính bằng feetvà f là hệ số ma sát.
)a Trên một đoạn đường (có gắn bảng báo tốc độ bên trên) có hệ số ma sát là 0,73 và vết trượt của một xe 4 bánh sau khi thắng lại là 49,7 feet. Hỏi xe có vượt quá tốc độ theo biển báo trên đoạn đường đó không? (Cho biết 1 dặm = 1,61 km).
)b Nếu xe chạy với tốc độ 48km/giờ trên đoạn đường có hệ số ma sát là 0,45 thì khi thắng lại vết trượt trên nền đường dài bao nhiêu feet?


DẠYKÈMQUYNHƠNOFFICIAL PHÒNG GIÁO DỤC VÀ ĐÀO TẠO Q11
Trường THCS Lê Anh Xuân ĐỀ THAM KHẢO TUYỂN SINH 10 ( NĂM HỌC 2022_2023) Môn : Toán 9 Thời gian : 120p ( không kể thời gian phát đề) Bài 1 (1,5đ) )a Vẽ đồ thị P của hàm số 2 1 2 yx trên mặt phẳng tọa độ. )b Cho đường thẳng :54 Dyxm . Tìm điều kiện của m để P và D cắt nhau tại hai điể
p(mmHg)
Càng lên cao không khí càng loãng nên áp suất khí quyển càng giảm. Ví dụ ở khu vực thành phố Hồ Chí Minh đều có độ cao sát mực nước biển nên có áp suất khí quyển là p = 760mmHg, còn ở thành phố Puebla ở Mexico có độ cao h = 2200 m thì có áp suất khí quyển là p = 550,4 mmHg. Với những độ cao không lớn lắm thì ta có công thức tính áp suất khí quyển tương ứng với độ cao so với mực nước biển là một hàm số bậc nhất p = ah + b có đồ thị như hình bên
a) Xác định hệ số a và b ?
760 O
550,4 2200 650 h(m)
b) Hỏi cao nguyên Lâm Đồng có độ cao 650 m so với mực nước biển thì có áp suất khí quyển là bao nhiêu mmHg ? (Làm tròn đến chữ số thập phân thứ nhất)
Bài 5 (0,75đ) Hộp phô mai có dạng hình trụ, hai đáy là hai hình tròn bằng nhau có đường kính là 12,2 cm và chiều cao của hộp phô mai là 2,4 cm. Giả sử trong hộp phô mai chứa 8 miếng phô mai bằng nhau được xếp nằm sát nhau vừa khít bên trong hộp và mỗi miếng được gói vừa khít bằng loại giấy bạc đặc biệt.

a) Biết công thức thể tích hình trụ là �� = ��.ℎ (S là diện tích đáy, h là chiều cao). Tính theo cm3 thể tích của mỗi miếng phô mai bên trong hộp (làm tròn đến hàng đơn vị).
b) Biết công thức diện tích xung quanh hình trụ là ������ =��.ℎ (C là chu vi đáy, h là chiều cao). Tính theo cm2 phần diện tích phần giấy bạc gói 8 miếng phô mai trong hộp (làm tròn đến hàng đơn vị).
DẠYKÈMQUYNHƠNOFFICIAL Bài
4 (0,75đ)
Bài 6 : (1đ) Bác Bảy mua một con nghé và một con bê. Sau đó bác bán lại cho người bạn con nghé với giá 18 triệu, để hỗ trợ bạn, bác nói: “ tôi bán cho anh lỗ mất 20% rồi đấy!!!”. Ít hôm sau ông bán con bê cho ông Ba xã bên với giá 18 triệu, Bác thầm nghĩ: “bán đi con này mình lời 20% so với giá ban đầu!!!”. Hỏi sau khi bán hai con bác lời hay lỗ so với số tiền bác dùng để mua hai con?
Bài 7: (1đ) Một vé xem phim có giá 60.000 đồng. Khi có đợt giảm giá, mỗi ngày số lượng người xem tăng lên 50%, do đó doanh thu cũng tăng 25%. Hỏi giá vé khi được giảm là bao nhiêu? Bài 8 (3đ)Từ điểm S nằm ngoài đường tròn O vẽ tiếp tuyến SA ( A là tiếp điểm) và cát tuyến SBC đến đường tròn O ( A thuộc cung nhỏ BC ). Gọi H là trung điểm

DẠYKÈMQUYNHƠNOFFICIAL
của BC . a) Chứng minh 2 . SASBSC và tứ giác SAHO nội tiếp. b) Kẻ đường kính AK của O . Tia SO cắt CK tại E . Chứng minh EKBHABOK . c) Tia AE cắt O tại D . Chứng minh ba điểm B , O , D thẳng hàng. ĐÁP ÁN ĐỀ THI THỬ TS 10 NĂM HỌC 2022_2023 Bài 1 Điểm 1,5đ a) Đúng bảng giá tri Vẽ đúng (P) )b Phương trình hoành độ giao điểm của 2 1 : 2 Pyx và :54 Dyxm là: 22 1 541080 1 2 xxmxxm P cắt D tại hai điểm phân biệt 1 có hai nghiệm phân biệt 0 0 a 10 25 2580 8 m m . Vậy 25 8 m thì P cắt D tại hai điểm phân biệt. 0,25 0,5 0,25 0,25 0,25
DẠYKÈMQUYNHƠNOFFICIAL Bài 2 1đ Cho phương trình : – x2 + 2(m – 1)x + 1 = 0 a) a.c = 1 . (- 1) = - 1 < 0 => pt luôn có 2 nghiệm trái dấu với mọi m b) Theo đl Viet ta có: 12 12 2(1) .1 b Sxxm a c Pxx a 33 12 22 121122 2 0 .0 2122310 10 1 xx xxxxxx mm m m Vậy m = 1 thỏa đk 0,25 0,25 0,25 0,25 Bài 3 1đ )a Tốc độ xe 4 bánh là: 3030.0,73.49,733sfd (dặm/giờ) 53,13 (Km/giờ). Mà theo biển báo thí xe 4 bánh chỉ được chạy tốc độ
Bài 7 1đ Gọi x là số lượng khán giả đi xem phim lúc chưa giảm giá (x* ) số tiền thu được lúc chưa giảm giá là 60000x (đồng) Số lương khán giả sau khi giảm giá là: x.150% Số tiền thu được sau khi giảm giá là: 60000x.125% Vậy giá tiền số vé lúc giảm: 60000x.125% 50000 x.150% (đồng) 0,5 0,25 0,25 Bài 6 1đ Gọi (đơn vị triệu đồng) lần lượt là giá tiền bác Bảy mua con nghé và con bê. ,0xy Bán nghé 18 triệu, lỗ 20% nên: 80%1822,5 xx Bán bê 18 triệu, lời 20% nên: 20%181,21815yyyy Tổng số tiền mua là: 22,51537,5 xy (triệu đồng) Tổng số tiền bán: 18 t + 18 t = 36 t Vậy bác Bảy lỗ Bài 4 a) Thay h = 0, P = 760 vào công thức P = ah + b 0,25
50Km/h . Vậy xe đã vượt quá tốc độ )b Có 48 s (Km/giờ) 4800 161 (dặm/giờ). Xét 4800 3030.0,45.13,5.888,965,8feet 161 sfdddd 0,5 0,5 Bài 5 0,75đ a)Thể tích một miếng pho mai V = (6,12 .2,4): 8 35 cm3 b)Diện tích giấy bạc gói 8 miếng pho mai: 8( 2,4.12,2. 8 + 2.6,1.2,4 + 2. 12.2..6.1 8.2 ) 560 cm2 0,25 0,25 0,25 0,25
0,75đ
b = 760 P = ah + 760
Thay P = 550,4 , h = 2200 vào công thức P = ah + 760
a = 131 1375 . Vậy a = 131 1375 và b = 760

b) Thay h = 650 vào công thức P = 131 1375 h + 760
P 698. Vậy cao nguyên Lâm Đồng có độ cao 650 m so với mực nước biển thì có áp suất khí quyển là 698 mmHg ?
0,25 0,25 0,25
a) Xét SAB và SCA có S chung và SABSCA (góc nội tiếp và góc tạo bởi dây cung cùng chắn cung AB ), suy ra SAB ~ SCA (g-g) nên 2 SASB SASBSC SCSA . Ta có 90 SAO (vì SA là tiếp tuyến). Do H là trung điểm BC nên 90.OHBCSHO Từ đó ta có tứ giác SAHO nội tiếp (2 góc bằng nhau cùng nhìn 1 cạnh).
DẠYKÈMQUYNHƠNOFFICIAL
Bài
8 3đ
Ta
ABHOKE Xét ABH và
: BHAKOE OKEABH ABH ~ EKO (g-g) .. ABBH ABOKEKBH EKOK . c) c) Gọi I là giao điểm BK và SE d) Chứng hai tam giác KOE và AHC đồng dạng e) Suy ra O là trung điểm IE f) AIKE là HB hành g) Góc K = 900 h) =>B, O, D thẳng hàng i) 0,25 0,25 0,5
b) Tứ giác SAHO nội tiếp nên SHASOA mà SOAKOE (đối đỉnh), suy ra KEOBHA
có
AKCABC (cùng chắn cung AC ) nên
OEK
DẠYKÈMQUYNHƠNOFFICIAL
bởi hàm số 11 50 8 R C (trong đó C là giá bán, đơn vị tính bằng đồng; R là bán kính của đáy ấm, đơn vị tính bằng cm). Bạn Mai mua hai cái ấm có bán kính của đáy ấm lần lượt là 24 cm và 32 cm. Khi đi mua hàng, Mai mang theo 200000 đồng. Hỏi Mai có đủ tiền để trả không?
Bài 4: Cứ 4 năm có một năm nhuận có 366 ngày (thêm ngày 29/2). Năm 2000 là năm nhuận và ngày hạ chí 21/6/2000 là ngày thứ tư. Hỏi từ 21/6/2000 đến 21/6/2020 có bao nhiêu ngày? Ngày 21/6/2020 là ngày thứ mấy?
Bài 5: Anh Tân dự định mua vé máy bay hạng thường đi từ thành phố Hồ Chí Minh ra Đà Nẵng về quê ăn tết với số hành lý dự trù từ 12 kg đến 25 kg. Biết rằng:
Hãng A: Tiền vé cho mỗi khách hàng ở khoang thường là 900000 đồng và quy định mỗi hành khách chỉ được mang 7 kg hành lý. Nếu số lượng hành lý vượt quá quy định, mỗi khách hàng cần phải trả thêm 40000 đồng/kg hành lý.
Hãng B: Tiền vé cho mỗi khách hàng ở khoang thường là 120000 đồng và quy định mỗi hành khách chỉ được mang 12 kg hành lý. Nếu số lượng hành lý vượt quá quy định, mỗi khách hàng cần phải trả thêm 20000 đồng/kg hành lý.
a) Hãy lập hàm số biểu diễn số tiền anh Tân phải trả cho mỗi hãng theo khối lượng hành lý dự trù x . b) Hỏi với 23 kg, anh Tân nên lựa chọn đi hãng nào cho tiết kiệm chi phí?
Bài 6: Ở trường A, đầu năm học số học sinh nam và nữ bằng nhau. Cuối học kỳ I, trường nhận thêm 15 học sinh nữ và 5 học sinh nam nên số học sinh nữ lúc này chiếm 51% tổng số học sinh. Hỏi đầu năm học trường có bao nhiêu học sinh?
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GD & ĐT QUẬN 12 NĂM HỌC 2022-20232 ĐỀ THAM KHẢO MÔN :
9 -------------------- Đề thi gồm 8 câu hỏi tự luận MÃ ĐỀ : Quận 12 – 3 Thời gian: 120 phút (không kể thời gian phát đề) Bài 1: Cho hàm số 2 2 x y có đồ thị là parabol P và hàm số 4 yx có đồ thị là đường thẳng D a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ; b) Tìm tọa độ giao điểm của P và D bằng phép toán. Bài 2: Cho phương trình 2 59140 xx có hai nghiệm 12 ; xx Không giải phương trình hãy tính giá trị biểu thức 12 21 22xx A xx . Bài 3: Giá bán của ấm đun nước được xác định
TOÁN
Bài 7: Có hai cốc thủy tinh hình trụ, cốc thứ nhất phía bên ngoài có đường kính đáy là 30 cm, chiều cao 20 cm đựng đầy nước, cốc thứ hai ở bên trong có đường kính đáy là 40 cm, chiều cao là 12 cm. Hỏi nếu đổ hết nước từ cốc thứ nhất sang cốc thứ hai nước có bị tràn ra ngoài hay không? Tại sao? ( xem như bề dày của đáy cốc không đánh kể) Bài 8: Cho ABC nhọn ( ABAC ) nội tiếp trong đường tròn O . Các đường cao ,, ADBECF cắt nhau tại H. Tia EF cắt tia CB tại K a) Chứng minh tứ giác BFEC nội tiếp và .. KFKEKBKC . b) Đường thẳng KA cắt O tại M . Chứng minh tứ giác AEFM nội tiếp. c) Gọi N là trung điểm của BC . Chứng minh ., MHN thẳng hành.

DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 78 -
OFFICIAL
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI Bài 1: Cho hàm số 2 2 x y có đồ thị là parabol P và hàm số 4 yx có đồ thị là đường thẳng D a) Vẽ đồ thị P và D trên cùng hệ trục tọa độ; b) Tìm tọa độ giao điểm của P và D bằng phép toán. Lời giải a) Hàm số: 2 2 x y Bảng giá trị tương ứng của x và y : x 4 2 0 2 4 2 2 x y 8 2 0 2 8 Đồ thị hàm số là một Parabol đi qua các điểm 4;4 ; 2;1 ; 0;0 ; 2;1 ; 4;4 Hàm số: 4 yx 04xy 04yx Đồ thị hàm số là đường thẳng đi qua 0;4 và 0;4 Vẽ: Bài 2: Cho phương trình 2 59140 xx có hai nghiệm 12 ; xx . Không giải phương trình hãy tính giá trị biểu thức 12 21 22xx A xx Lời giải Ta có: 2 94.5.143610 Vậy phương trình đã cho có hai nghiệm phân biệt 12 ; xx Áp dụng hệ thức Ta – Lét ta có: 12 12 99 55 14 5 b xx a c xx a Ta có: 2 2 22 12 1212 211212 9 2 22222221 5 44 14 ..35 5 xx xxxx A xxxxxx Bài 3: Giá bán của ấm đun nước được xác định bởi hàm số 11 50 8 R C (trong đó C là giá bán, đơn vị tính bằng đồng; R là bán kính của đáy ấm, đơn vị tính bằng cm). Bạn Mai mua hai cái ấm có bán
21/6/2020 là ngày thứ mấy? Lời giải Từ năm 20002020 có 5 năm nhuận là: 2004;2008;2012;2016;2020 (không tính năm 2000 vì bắt đầu tính từ tháng 6) Vậy từ 21/6/2000 đến 21/6/2020 có : 265.15366.57305 ngày. Ta có : 7305:41043 dư 4 vậy tăng thêm 4 ngày : thứ tư tăng thêm 4 ngày là Chủ nhật Vậy 21/6/2020 là ngày Chủ nhật. Bài 5: Anh Tân dự định mua vé máy bay hạng thường đi từ thành phố Hồ Chí Minh ra Đà Nẵng về quê ăn tết với số hành lý dự trù từ 12 kg đến 25 kg. Biết rằng:
Hãng A: Tiền vé cho mỗi khách hàng ở khoang thường là 900000 đồng và quy định mỗi hành khách chỉ được mang 7 kg hành lý. Nếu số lượng hành lý vượt quá quy định, mỗi khách hàng cần phải trả thêm 40000 đồng/kg hành lý.
Hãng B: Tiền vé cho mỗi khách hàng ở khoang thường là 120000 đồng và quy định mỗi hành khách chỉ được mang 12 kg hành lý. Nếu số lượng hành lý vượt quá quy định, mỗi khách hàng cần phải trả thêm 20000 đồng/kg hành lý.
a) Hãy lập hàm số biểu diễn số tiền anh Tân phải trả cho mỗi hãng theo khối lượng hành lý dự trù x b) Hỏi với 23 kg, anh Tân nên lựa chọn đi hãng nào cho tiết kiệm
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 80 -
Lờ
ả
Số tiền khi
ấm
11.2411.32 5050177 88 (đồng) Vậy bạn
4 năm có một năm nhuận có 366 ngày (thêm ngày 29/2). Năm 2000 là năm nhuận và ngày hạ chí 21/6/2000 là ngày thứ tư. Hỏi từ 21/6/2000 đến 21/6/2020 có
nhiêu
kính của đáy ấm lần lượt là 24 cm và 32 cm. Khi đi mua hàng, Mai mang theo 200000 đồng. Hỏi Mai có đủ tiền để trả không?
i gi
i
mua hai cái
có bán kính của đáy ấm lần lượt là 24 cm và 32 cm là:
Mai đủ tiền để mua hai cái ấm. Bài 4: Cứ
bao
ngày? Ngày
Lờ
ải a) Hàm số của hãng A: 90040.762040 yxyx (nghìn đồng) Hàm số của hãng B: 12020.1212020 yxyx (nghìn đồng) b) Với hãng A, anh Tân phải trả: 62040.231540 y (nghìn đồng) Với hãng B, anh Tân phải trả: 12020.23340 y (nghìn đồng) Vậy anh Tân đi hãng B sẽ tiết kiệm hơn. Bài 6: Ở trường A, đầu năm học số học sinh nam và nữ bằng nhau. Cuối học kỳ I, trường nhận thêm 15 học sinh nữ và 5 học sinh nam nên số học sinh nữ lúc này chiếm 51% tổng số học sinh. Hỏi đầu năm học trường có bao nhiêu học sinh? Lời giải
chi phí?
i gi
Gọi x (học sinh) là số học sinh nam ban đầu. * xN
Ta có ban đầu số học sinh nam bằng số học sinh nữ nên số học sinh nữ ban đầu là: x (học sinh)
Cuối học kì I:
Số học sinh nam là: 5 x (học sinh)
Số học sinh nữ là: 15 x (học sinh)
x xx x

Tỷ lệ số học sinh nữ là 51%, ta có phương trình: 15 51% 155 240
Vậy số học sinh đầu năm của trường là : 2.240480 học sinh.
Bài 7: Có hai cốc thủy tinh hình trụ, cốc thứ nhất phía bên ngoài có đường kính đáy là 30 cm, chiều cao 20 cm đựng đầy nước, cốc thứ hai ở bên trong có đường kính đáy là 40 cm, chiều cao là 12 cm. Hỏi nếu đổ hết nước từ cốc thứ nhất sang cốc thứ hai nước có bị tràn ra ngoài hay không? Tại sao? ( xem như bề dày của đáy cốc không đánh kể) Lời giải Thể tích của cốc bên ngoài là: 2 3 1 30 ...2014137,17 4 VShcm
tích
cốc bên trong là:
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 81 -
OFFICIAL
Bài
Cho ABC
(
)
EF cắt tia CB tại K a) Chứng minh tứ giác BFEC nội tiếp và .. KFKEKBKC . b) Đường thẳng KA cắt O tại M . Chứng
tứ
nộ
tiế
c) Gọi N
điểm của BC . Chứ
Thể
của
2 3 2 40 ...1215079,64 4 VShcm Mà 14137,1715079,64 Vậy cốc bên trong có thể chứa được nhiều nước hơn nên sẽ không bị tràn.
8:
nhọn
ABAC
nội tiếp trong đường tròn
O . Các đường cao ,, ADBECF cắt nhau tại H. Tia
minh
giác AEFM
i
p.
là trung
ng minh ., MHN thẳng hành. Lời giải

DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 82 -
nội
ếp ACBKMB (góc
Xét KMB và KCA ,
Kchung KMBKCAcmt KMBKCAGG KMKB KCKA (tỷ số đồng dạng) .. KMKAKBKC KMKAKFKEKBKC KMKF KEKA Xét KMF và KEA , ta
a) Xét tứ giác BFEC ta có: 90 BFCBEC BFEC nội tiếp đường tròn (tứ giác có hai góc kề cùng nhìn một cạnh bằng nhau) ECBKFB (góc ngoài bằng góc đối trong) Xét KFB và KCE , ta có:
Kchung KFBKCEcmt KFBKCEGG
KFKB KCKE
(tỷ số đồng dạng) .. KFKEKBKC b) Ta có ,,, AMBCOAMBC
ti
ngoài bằng góc đối trong)
ta có:
có:
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 83 Kchung KMKF
ằ
Từ
,,
cmt KEKA KMFKEACGC
KMFKEA (cặp góc tương ứng) Xét tứ giác AMFE ta có: ()KMFKEAcmt AMFE nội tiếp đường tròn (tứ giác có góc ngoài bằng góc đối trong). c) Kẻ đường kính AL ta có: 90 ABLACLAML Ta có: // // BHACvCLACBHCL CHABvBLABCHBL BHCL là hình bình hành, mà N là trung điểm của BCN là trung điểm của HL (giao điểm của hai đường chéo) ,, BNL thẳng hàng 1 Xét tứ giác AFHE , có: 9090180 AFHAEH AFHE nội tiếp ( tứ giác có tổng hai góc đối b
ng 180
) Mà AMFE nội tiếp (cmt) ,,,, AMFHE cùng thuộc một đường tròn. AMFH nội tiếp 90 AMHAFH 90,, AMLAMHMHL thẳng hàng 2
1,2,,,MHNL thẳng hàng
MHN thẳng hàng.
Bài 3: (0.75 điểm) Một vật rơi tự do từ độ cao so với mặt đất là 120 mét. Bỏ qua sức cản không khí, quãng đường chuyển động s (mét) của vật rơi sau thời gian t được biểu diễn gần đúng bởi công thức: 2 5 st , trong đó t là thời gian tính bằng giây. a) Sau 3 giây vật này cách mặt đất bao nhiêu mét ? b) Sau bao lâu kể từ khi bắt đầu rơi thì vật này chạm mặt đất ? (Làm tròn kết quả đến chữ số hàng đơn vị)

Bài 4: (0.75 điểm) Mối liên hệ giữa chiều dài y(cm) của một sợi dây xích và số mắt xích x là một hàm số bậc nhất yaxb Biết đoạn xích có 5 mắt xích thì dài 22cm, đoạn xích có 8 mắt xích thì dài 34 cm.

a) Hãy xác định hệ số a; b. b) Hãy tính xem một sợi xích dài 1,5m thì gồm bao nhiêu mắt xích?
Bài 5: (1 điểm) Nhằm để chuẩn bị cho đội ngũ y tế phục vụ công tác phòng chống dịch bệnh Covid – 19, một tổ sản xuất theo dự định phải làm xong 4800 bộ đồ bảo hộ y tế trong một thời gian theo quy định. Thực tế, mỗi ngày tổ đó đã làm nhiều hơn 100 bộ đồ bảo hộ y tế so với kế hoạch đề ra. Vì thế tổ đã hoàn thành xong trước kế hoạch 8 ngày. Hỏi theo kế hoạch, mỗi ngày tổ phải sản xuất bao nhiêu bộ đồ bảo hộ và phải hoàn thành trong bao nhiêu ngày? (Giả định rằng số bộ đồ bảo hộ y tế mà tổ đó làm xong trong mỗi ngày là như nhau)
DẠYKÈMQUYNHƠN OFFICIAL ĐỀ THAM KHẢO TUYỂN SINH 10 TP HỒ CHÍ MINH MÔN TOÁN 9 THI TUYỂN SINH VÀO LỚP 10 1 SỞ GD & ĐT
PHÒNG
ĐT Q.
ÌNH
ĐỀ
2 1 2
3
đồ thị D a) Vẽ đồ thị P và D trên cùng một mặt phẳng tọa độ Oxy . b) Tìm tọa độ giao điểm của P và
TP.HỒ CHÍ MINH
GD &
TÂN B
THCS TRẦN VĂN QUANG
THAM KHẢO TUYỂN SINH 10 NĂM HỌC: 2022 - 2023 MÔN: TOÁN 9 Đề thi gồm 8 câu hỏi tự luận. Thời gian: 120 phút (không kể thời gian phát đề) Bài 1: (1,5 điểm) Cho hàm số yx
có đồ thị hàm số
P và
2 2 yx có
D bằng phép tính. Bài 2: (1 điểm) Cho phương trình xx 2 2510 có hai nghiệm x,x12 . Không giải phương trình, hãy tính giá trị của biểu thức xx A xx 22 12 1222
ĐỀ THAM KHẢO 120m
Bài 6: (1 điểm) Sau kì thi tuyển sinh vào lớp 10 năm học 2020-2021, học sinh hai lớp 9A và lớp 9B tặng lại thư viện trường 738 quyển sách gồm hai loại sách giáo khoa và sách tham khảo. Trong đó, mỗi học sinh lớp 9A tặng 6 quyển sách giáo khoa và 3 quyển sách tham khảo; còn mỗi học sinh lớp 9B thì tặng 5 quyển sách giáo khoa và 4 quyển sách tham khảo. Biết số sách giáo khoa nhiều hơn số sách tham khảo là 166 quyển. Tính số học sinh của mỗi lớp.
OFFICIAL
Bài 7: (1 điểm) Các ống hút nhựa thường khó phân hủyvà gâyhại cho môi trường. Mỗi ngày có 60 triệu ống hút thải ra môi trường gây hậu quảnghiêmtrọng.Ngàynayngười tachủ động sản xuất các loại ống hút dễ phân hủy. Tại tỉnh Đồng Tháp có cơ sở chuyên sản xuất ống hút “thân thiện với môi trường” xuất khẩu ra thị trường thế giới và được nhiều nước ưa chuộng. Ống hút được làm từ bột gạo, các màu chiết xuất từ củ dền, lá dứa, bông sen, bông điên điển, . a) Một ống hút hình trụ, đường kính 12 mm, bề dày ống 2 mm, chiều dài ống 180 mm. Em hãy tính xem để sản xuất mỗi ống thì thể tích bột gạo được sử dụng là bao nhiêu. (Biết thể tích hình trụ: 2 VRh với R là bán kính đáy và h là chiều cao; kết quả làm tròn đến chữ số thập phân thứ 2 với 3,14 ) b) Một hộp đựng ống hút bằng nhựa có dạng hình hộp chữ nhật kích thước 24cmx11cmx18cm thì chứa được tối đa bao nhiêu ống hút như trên?
Bài 8: (3 điểm) Cho tam giác ABC nhọn (AB < AC) nội tiếp (O) có 2 đường cao BE và CF cắt nhau tại H. Tia AH cắt BC tại D. a) Chứng minh góc AFE = góc AHE và tứ giác AFDC nội tiếp.
b) Gọi M là trung điểm của BC, gọi Q là hình chiếu của H trên AM. Chứng minh AF.AB = AH.AD và 4 điểm B, F, Q, M cùng thuộc 1 đường tròn. c) Vẽ đường kính AK của (O), vẽ đường tròn đường kính AH, đường tròn này cắt (O) tại L. Chứng minh M là trung điểm HK và 3 đường thẳng AL, HQ, BC đồng quy. HẾT

DẠYKÈMQUYNHƠN
ĐỀ THAM KHẢO TUYỂN SINH 10 TP HỒ CHÍ MINH MÔN TOÁN 9 THI TUYỂN SINH VÀO LỚP 10 2
DẠYKÈMQUYNHƠN OFFICIAL ĐỀ THAM KHẢO TUYỂN SINH 10 TP HỒ CHÍ MINH MÔN TOÁN 9 THI TUYỂN SINH VÀO LỚP 10 3 ĐÁP ÁN ĐỀ THAM KHẢO TS10
NG THCS TRẦN
BÌNH)
1: a) Lập bảng đúng và vẽ đúng b)
độ
điểm của
: 2 2 11 22 133 220 2222 1 1 2 25 x xxx xy xy Vậy tọa độ giao điểm của (P) và (D) là (1; 1 2 ) và (-2;-5). Bài 2: Cho phương trình xx 2 2510 Ta có: 2 2 b4ac54.2.1330 Phương trình luông có hai nghiệm phân biệt. Theo hệ thức Viet: 12 12 b5 Sxx a2 c1 Px.x a2 Ta có: 22 12 12 22 1221 12 2222 121212 1212 2 12121212 1212 2 22 22 22 22 .24 22. .24 1551 .22. 2222 21 15 2 2.4 22 xx A xx xxxx xx xxxxxx xxxx xxxxxxxx xxxx Bài 3: a) Ta có: 2 5 st Thay t = 3 vào công thức s: 2 s5.345 Vậy sau 3 giây vật này cách mặt đất một khoảng là: 120 – 45 = 75 (m) b) Thay s = 120 vào công thức s: 2 2 1205. 24 245 t t t Vậy sau khoảng 5 giây thì vật rơi chạm mặt đất.
TRƯỜ
VĂN QUANG (Q. TÂN
Bài
Phương trình hoành
giao
(P) và (D)
Bài 4:
a/ Ta có hệ phương trình: 5224 8342 aba abb 42yx
b/ Đổi 1,5m = 150cm Thay y = 150 vào công thức y = 4x +2: 150 = 4x + 2 37 x Vậy sợi xích dài 1,5m có 37 mắt xích
Bài 5: Gọi x (bộ đồ bảo hộ) là số bộ đồ bảo hộ mỗi ngày tổ sản xuất ( x N*)
Ta có: 4800 x (ngày) là thời gian tổ sản xuất theo dự định. 4800 100 x (ngày) là thời gian tổ sản xuất theo thực tế
Theo đề bài, ta có phương trình: 48004800 8 100 480010048008100 xx xxxx
Giải phương trình ta được x = 200 (nhận) Vậy theo dự định mỗi ngày tổ sản xuất 200 bộ đồ bảo hộ.
Và thời gian hàn thành kế hoạch là: 4800 24 200 (ngày)
Bài 6:
Gọi x (học sinh) là số học sinh của lớp 9A (x thuộc N*) y (học sinh) là số học sinh của lớp 9B ( y thuộc N*) ta có : Tổng số sách của hai lớp là 738 quyển: 9.x + 9.y = 738 (1)
Ta có: Số sách giáo khoa nhiều hơn số sách tham khảo là 166 quyển (6x + 5y) - (3x + 4y) =166 6x + 5y - 3x - 4y = 166 3x + y = 166 (2)
Từ (1) và (2) ta có: 9x + 9y = 738 3x + y =166
⇒ x = 42 ; y = 40 ( nhận) Vậy lớp 9A: 42 học sinh; lớp 9B: 40 học sinh.
DẠYKÈMQUYNHƠN
ĐỀ THAM KHẢO TUYỂN SINH 10 TP HỒ CHÍ MINH MÔN TOÁN 9 THI TUYỂN SINH VÀO LỚP 10 4
OFFICIAL
Bài 7:
a) Ta có: Thể tích của ống hút là:
V = π.R2. h = 3,14. 62.180 = 20347,2 (mm3)
Thể tích phần rỗng của ống hút là :
V = π.R1 2. h = 3,14. 42. 180 = 9043,2 (mm3)
Thể tích phần bột gạo để làm 1 ống hút là: 20347,2 - 9043,2 = 11304 (mm3)
b) Đổi: 24cm = 240 mm; 11cm = 110mm ; 18cm = 180 mm
Thể tích của hộp đựng ống hút là: V = 240.110.180 = 4752000 (mm3)
Số ống hút hộp có thể đựng là: 4752000 : 20347,2 = 233,55 (ống)
Vậy hộp có thể đựng tối đa là 233 ống.
Bài 8:
a) Chứng minh tứ giác AFHE nội tiếp.
Suy ra góc AFE = góc AHE
Chứng minh H là trực tâm của tam giác ABC.
Suy ra ADBC tại D
Chứng minh tứ giác AFDC nội tiếp.
b) Chứng minh: AFHADB ∽ (g-g)
AFAHFH ADABDB
Suy ra AF. AB = AH. AD.
Chứng minh được AH.AD = AQ. AM
Suy ra AQ. AM = AF. AB.
Chứng minh: AFQAMB cgc ∽
Suy ra góc AFQ = góc AMB. Suy ra tứ giác BFQM nội tiếp hay 4 điểm B, F, Q, M cùng thuộc 1 đường tròn.
c) Chứng minh được tứ giác BHCK là hình bình hành Mà M là trung điểm của BC nên M là trung điểm của HK. Chứng minh H, K, L thẳng hàng.
Suy ra M, H, L thẳng hàng.
Xét tam giác AHM có: HQ, BC, AL là 3 đường cao nên đồng quy tại 1 điểm.
DẠYKÈMQUYNHƠN
ĐỀ THAM KHẢO TUYỂN SINH 10 TP HỒ CHÍ MINH MÔN TOÁN 9 THI TUYỂN SINH VÀO LỚP 10 5
OFFICIAL
L K Q M E F D H O B C A
Bài 3: (0.75 điểm) Thế giới có 24 múi giờ, vị trí địa lý khác nhau thì giờ ở các địa điểm đó có thể khác nhau. Giờ UTC được xem như giờ gốc. Thế giới có 12 múi giờ nhanh và 12 múi giờ chậm. Cụ thể, kí hiệu UTC 7 dành cho khu vực có giờ nhanh hơn giờ UTC 7 giờ, kí hiệu UTC 3 dành cho khu vực có giờ chậm hơn giờ UTC 3 giờ.
a) Việt Nam thuộc múi giờ UTC 7 . Nếu ở Việt Nam là 20h30p ngày 3/5/2021 thì ở Peru (UTC 5) là ngày giờ nào?

b) Bình đang sống tại Peru, Nghị đang sống ở Malaysia. Nếu thời gian ở chỗ Nghị là 1835hp ngày 9/5/2021 thì ở chỗ Bình là 535hp ngày 9/5/2021. Hỏi múi giờ ở Malaysia là múi giờ nào?
Bài 4: (0.75 điểm) Cước điện thoại y (nghìn đồng) là số tiền mà người sử dụng điện thoại cần trả hàng tháng, nó phụ thuộc vào lượng thời gian gọi x (phút) của người đó trong tháng. Mối liên hệ giữa hai đại lượng này là một hàm số bậc nhất yaxb . Hãy tìm , ab biết rằng nhà bạn Nam trong tháng 3 đã gọi 120 phút với số tiền là 80 nghìn đồng và trong tháng 4 đã gọi ít hơn tháng ba 40 phút với số tiền là 58000 đồng.
Bài 5: (1.0 điểm) Cửa hàng lấy 1 thùng nước ngọt ( 24 lon) của đại lý phân phối với giá 192000đồng và bán lẻ với giá 10000 đồng một lon.
a) Hỏi khi bán hết 1 thùng nước ngọt đó thì cửa hàng thu được lãi bao nhiêu phần trăm so với giá gốc? b) Trong đợt khuyến mãi , do đại lý phân phối giảm giá nên cửa hàng cũng giảm giá còn 9500 đồng một lon và thu được lãi suất như cũ. Hỏi trong đợt này cửa hàng đã mua 1 thùng nước ngọt với giá bao nhiêu?
Bài 6: (1.0 điểm) Cho hình bên là một thúng gạo vun đầy. Thúng có dạng nửa hình cầu với đường kính 50cm, phần gạo vun lên có dạng hình nón cao 15cm
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 77SỞ GD & ĐT TP.HỒ CHÍ MINH ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GD & ĐT QUẬN TÂN PHÚ NĂM HỌC 2022-20232 ĐỀ THAM KHẢO MÔN
9 Đề
MÃ ĐỀ : Quận Tân Phú – 3 Thời
Bài 1: (1.5 điểm). Cho hàm số 2 1 2 yx có đồ thị là parabol P và hàm số 34yx có đồ thị là đường thẳng d a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ; b) Tìm tọa độ giao điểm của P và d bằng phép toán. Bài 2: (1.0 điểm) Cho phương trình 2 2540 xx có hai nghiệm 1x ; 2x . Không giải phương trình, hãy tính giá trị của biểu thức 2 12 12 21 22
: TOÁN
thi gồm 8 câu hỏi tự luận
gian: 120 phút (không kể thời gian phát đề)
xx Mxx xx
a) Tính thể tích phần gạo trong thúng. (Biết thể tích hình nón là 2 1 3 VRh , hình trụ là
và hình cầu là 2 4 3 VRh ) (làm tròn đến dạng 0,1). b) Nhà Danh dùng lon sữa bò cũ có dạng hình trụ (bán kính đáy bằng 5cm, chiều cao 15cm) để đong gạo mỗi ngày. Biết mỗi ngày nhà Danh ăn 5 lon gạo và mỗi lần đong thì lượng gạo chiếm 90% thể tích lon. Hỏi với lượng gạo ở thúng trên thì nhà Danh có thể ăn nhiều nhất là bao nhiêu ngày.
Bài 7: (1.0 điểm) Bạn Vy đi làm thêm ở tiệm café “Take away NT” với hợp đồng lương tính theo ngày, nếu một ngày bán đủ 50 ly thì bạn sẽ nhận được lương cơ bản 150000 đồng, bên cạnh đó với mỗi ly bán vượt chỉ tiêu, bạn sẽ được thưởng thêm 40%so với tiền lời một ly café. Ngày đầu tiên đi làm bạn nhận được 222000đồng. Tính số ly café bạn Vy đã bán được trong ngày đầu tiên đi làm, biết rằng tiền lời một ly café là 6000đồng. Bài 8: (3.0 điểm) Cho đường tròn O , đường kính BC . Trên O lấy điểm A sao cho ABAC . Hai tiếp tuyến kẻ từ A và B của O cắt nhau tại D . Chọn điểm M trên cung nhỏ AB và nằm trong DOB . Đường thẳng DM cắt O tại điểm thứ hai là N ( M khác N )
a) Chứng minh tứ giác DAOBlà tứ giác nội tiếp và 2 DBDMDN b) Gọi H là trung điểm của MN . Chứng minh HD là phân giác của AHB . c) Qua N kẻ đường thẳng song song với DO sao cho đường thẳng này cắt các đường thẳng CB , CM lần lượt tại K và I ( K khác B ). Chứng minh K là trung điểm của NI
DẠYKÈMQUYNHƠN
NHÓM WORD HÓA ĐỀ TOÁN - 78 -
OFFICIAL
2
VRh
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 79HƯỚNG DẪN GIẢI Bài 1: (1.5 điểm). Cho hàm số 2 1 2 yx có đồ thị là parabol P và hàm số 34yx có đồ thị là đườ
ẳ
d
giá trị tương ứng của x và y : x 4 2 0 2 4 2 1 2 yx 8 2 0 2 8 Đồ thị hàm số là một Parabol đi qua các điểm 4;4 ; 2;1 ; 0;0 ; 2;1 ; 4;4 x 0 1 34yx 4 1 Đồ thị hàm số là đường thẳng đi qua 0;4 và 1;1 Vẽ: b) Hoành độ giao điểm của P và D là nghiệm của phương trình: 2 1 34 2 xx 2 68xx 2 680xx 2 31.810 Phương trình có hai nghiệm phân biệt: 1 2 x ; 2 4 x + Với 1 2 x 1 2 y + Với 2 4 x 2 8 y Vậy D cắt P tại hai điểm phân biệt là 2;2;4;8 .
ng th
ng
a) Vẽ đồ thị P và d trên cùng hệ trục tọa độ; b) Tìm tọa độ giao điểm của P và d bằng phép toán. Lời giải:
Hàm số: 2 2 x y
Bảng
vị
địa lý
nhau thì giờ
các địa điểm đó có thể khác nhau.
UTC được xem như giờ gốc. Thế giới có 12 múi giờ nhanh và 12 múi giờ chậm. Cụ thể, kí hiệu UTC 7 dành cho khu vực có giờ nhanh hơn giờ UTC 7 giờ, kí hiệu UTC 3 dành cho khu vực có giờ chậm hơn giờ UTC 3 giờ.
a) Việt Nam thuộc múi giờ UTC 7 . Nếu ở Việt Nam là 2030 h ngày 3/5/2021 thì ở Peru (UTC 5) là ngày giờ nào?
b) Bình đang sống tại Peru, Nghị đang sống ở Malaysia. Nếu thời gian ở chỗ Nghị là 1835hp ngày 9/5/2021 thì ở chỗ Bình là 535hp ngày 9/5/2021. Hỏi múi giờ ở Malaysia là múi giờ nào? Lời giải:
a) Ta có: giờ Việt Nam = UTC 7 20h30p = UTC 7 UTC = 1330hp ngày 3/5/2021
Ta có: giờ Peru = UTC 5 Giờ Peru = 1330hp 5 Giờ Peru = 830hp ngày 3/5/2021
Vậy nếu ở Việt Nam là 20h30p ngày 3/5/2021 thì ở Peru là 8h30p ngày 3/5/2021
b) Ta có: Giờ Peru = UTC 5 5h35p = UTC 5 UTC = 1035hp ngày 9/5/2021
Vì UTC = 1035hp ngày 9/5/2021, mà Nghị đang sống ở Malaysia và thời gian ở chỗ Nghị là 18h35p ngày 9/5/2021 Nên Malaysia nhanh hơn UTC: 183010358 hphph
Vậy múi giờ ở Malaysia là UTC + 8 Bài 4: (0.75 điểm) Cước điện thoại y (nghìn đồng) là số tiền mà người sử dụng điện thoại cần trả hàng tháng, nó phụ thuộc vào lượng thời gian gọi x (phút) của người đó trong tháng. Mối liên hệ giữa hai đại lượng này là một hàm số bậc nhất yaxb . Hãy tìm , ab biết rằng nhà bạn Nam trong tháng 3 đã gọi 120 phút với số tiền là 80 nghìn đồng và trong tháng 4 đã gọi ít hơn tháng ba 40 phút với số tiền là 58000 đồng.
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 80Bài 2: (1.0 điểm) Cho phương trình 2 2540 xx có hai nghiệm 1x ; 2x . Không giải phương trình, hãy tính giá trị của biểu thức 2 12 12 21 22xx Mxx xx Lời giải: Vì phương trình có hai nghiệm 1x ; 2x nên theo Vi-et: 12 12 5 2 4 2 2 Sxx Pxx 222 22 12 2 12 1212 2112 22222 4 xxSP xx MxxxxSP xxxxP 2 2 5 222 52 424 22 M Bài 3: (0.75 điểm) Thế giới
có 24 múi giờ,
trí
khác
ở
Giờ
Bài 5: (1.0 điểm) Cửa hàng lấy 1 thùng nước ngọt ( 24 lon) của đại lý phân phối với giá 192000đồng và bán

giá 10000 đồng một lon. a) Hỏi khi bán hết 1 thùng nước ngọt đó thì cửa hàng thu được lãi bao nhiêu phần trăm so với giá gốc? b) Trong đợt khuyến mãi , do đại lý phân phối giảm giá nên cửa hàng cũng giảm giá còn 9500 đồng một lon và thu được lãi suất như cũ. Hỏi trong đợt này cửa hàng đã mua 1 thùng nước ngọt với giá bao nhiêu? Lời giải:
a) Khi bán hết một thùng nước ngọt đó thì cửa hàng thu được số phần trăm lãi so với giá gốc là: 10000.24192000 100%25% 192000
b) Gọi x (đồng) là giá phân phối 1 thùng nước ngọt của đại lý trong đợt khuyến mãi ( 0 x ) Trong đợt khuyến mãi, do đại lý phân phối giảm giá nên cửa hàng cũng giảm giá còn 9500 đồng một lon và thu được lãi suất như cũ, ta có phương trình: .(125%)24950x 1,2524950 x 182400 x (nhận) Vậy trong đợt này, của hàng đã mua một thùng nước
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 81 -
Lời giải: Thay 120 x và 80 y vào công thức yaxb . Ta có: 80120ab (1) Thay 12040 x và 58 y vào công thức yaxb . Ta có: 5880ab (2) Từ (1) và (2), ta có hệ phương trình: 11 12080 20 8058 14 ab a ab b
Vậy: 11 ;14 20 ab
lẻ với
ngọt với
ng Bài 6: (1.0 điểm) Cho hình bên là một thúng gạo vun đầy. Thúng có dạng nửa hình cầu với đường kính 50cm, phần gạo vun lên có dạng hình nón cao 15cm. a) Tính thể tích phần gạo trong thúng. (Biết thể tích hình nón là 2 1 3 VRh , hình trụ là 2 VRh và hình cầu là 2 4 3 VRh ) (làm tròn đến dạng 0,1).
giá 182400 đồ
b) Nhà Danh dùng lon sữa bò cũ có dạng hình trụ (bán kính đáy bằng 5cm, chiều cao 15cm) để đong gạo mỗi ngày. Biết mỗi ngày nhà Danh ăn 5 lon gạo và mỗi lần đong thì lượng gạo chiếm 90% thể tích lon. Hỏi với lượng gạo ở thúng trên thì nhà Danh có thể ăn nhiều nhất là bao nhiêu ngày.
làm thêm
tiệm café “Take away NT” với hợp đồng lương tính theo ngày, nếu một ngày bán đủ 50 ly thì bạn sẽ nhận được lương cơ bản 150000 đồng, bên cạnh đó với mỗi ly bán vượt chỉ tiêu, bạn sẽ được thưởng thêm 40%so với tiền lời một ly café. Ngày đầu tiên đi làm bạn nhận được 222000đồng. Tính số ly café bạn Vy đã bán được trong ngày đầu tiên đi làm, biết rằng tiền lời một ly café là 6000đồng. Lời giải: Gọi x (ly) là số ly cà phê bạn Vy bán trong ngày đầu tiên đi làm 50 x Số ly cà phê vượt chỉ tiêu là : 50 x (ly)
Tiền thưởng Vy nhận được khi bán vượt chỉ tiêu 1 ly cà phê là: 6000.40%2400 (đồng). Vì tổng số tiền Vy nhận được trong ngày đầu đi làm là 222000 đồng, ta có pt: 15000050.2400222000 x
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 82 -
trong thúng: 23233114114 323323.25.15.2542542,4() RhRcm b) Lượng gạo nhà Danh ăn mỗi ngày: 223) 5 3375 5..100%10%5...15.0,9( 2 Rhcm Với lượng gạo ở thúng trên thì số ngày nhà Danh có thể ăn nhiều nhất là: 3375 42542,4:8,028 2 (ngày) Bài 7: (1.0
m)
Lời giải: a) Bán kính đáy thúng: 50:225cm Thể tích gạo
điể
Bạn Vy đi
ở
O lấy điểm A sao cho ABAC . Hai tiếp tuyến kẻ từ A và B của O cắt nhau tại D . Chọn điểm M trên cung nhỏ AB và nằm trong DOB . Đường thẳng DM cắt O
) a) Chứng minh tứ giác DAOB
tứ
2 DBDMDN . b) Gọi H là trung điểm của MN . Chứng
. c) Qua N kẻ đường thẳng song
CB , CM lần lượt tại K và I ( K khác B ). Chứng
K
NI Lời giải:
80 x (nhận) Vậy bạn Vy bán được 80 ly cà phê trong ngày đầu tiên đi làm Bài 8: (3.0 điểm) Cho đường tròn O , đường kính BC . Trên
tại điểm thứ hai là N ( M khác N
là
giác nội tiếp và
minh HD là phân giác của AHB
song với DO sao cho đường thẳng này cắt các đường thẳng
minh
là trung điểm của
DẠYKÈMQUYNHƠN OFFICIAL NHÓM WORD HÓA ĐỀ TOÁN - 83a) Xét tứ
DAOB
000
(Vì ,
là
tiếp tuyến của O ) Vậy
Xét
và
BDMchung DBMDNB 2 . DBMDNB DBDM
DNDB b) Xét O , ta
OH là một phần bán
H
m MN
MN
OHMN Xét tứ giác HOAD
180 OHDOAD ( OHMN , DA là tiếp tuyến của O ) Vậy : HOAD nội tiếp đường tròn Mà : DAOB nội tiếp đường tròn Nên : ,,,, HOADB cùng thuộc 1 đường tròn. BHDBOD (hai góc nội tiếp cùng chắn cung BD) Mà : AHDAOD ( hai góc nội tiếp cùng chắn cung AD) AODBOD (Tính chất hai tiếp tuyến cắt nhau) Nên : BHD = AHD H I K D O B C A M N
giác
có:
9090180 DBODAO
DADB
các
tứ giác DAOBlà tứ giác nội tiếp
DBM
DNB
có
DBDMDN
có:
kính
là trung điể
(gt)
là dây cung
có:
Suy ra: HDlà phân giác của AHB
c) Ta có : HDOKNH (Hai góc so le trong, // KMDO )
Mà : HBOHDO (hai góc nội tiếp cùng chắn cung HO )
Nên tứ giác BKHN nội tiếp
Suy ra: HKCBND
Mà : BCIBND (hai góc nội tiếp cùng chắn cung BM )
Nên: HKCBCI
Mà hai góc này ở vị trí so le trong
Suy ra: // KHIM
Mà : H là trung điểm MN
Nên : K là trung điểm IN
DẠYKÈMQUYNHƠN OFFICIAL
NHÓM WORD HÓA ĐỀ TOÁN - 84 -
UBND THÀNH PHỐ THỦ ĐỨC ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC: 2022 – 2023 MÔN THI: TOÁN ĐỀ 3 Thời gian làm bài: 120 phút (Không kể thời gian phát đề)
Câu 1. (1,5 điểm)
Cho (P) : 2 x y 2 và (d) : y = x – 4
a. Vẽ (P) và (d) trên cùng hệ trục tọa độ. b. Tìm tọa độ giao điểm của (P) và (d) bằng phép toán.
Câu 2. (1 điểm)
Cho phương trình: 2 2x13x60 . Không giải phương trình, hãy tính giá trị của biểu thức A = (x1 - x2)2 – 4x1x2
Câu 3. (1 điểm)
Gia đình ông Ba là hộ kinh doanh nhà hàng tại một thành phố lớn, nhưng do dịch bệnh covid nên 2 năm nay phần kinh doanh gần như không đáp ứng nhu cầu cuộc sống. Tháng 3 vừa qua ông trở về quê tại Long An dự định làm thêm trang trại. Ông Ba định cải tạo một mảnh vườn hình chữ nhật có chiều dài bằng 2,5 lần chiều rộng. Ông tính rằng nếu đào một cái hồ có mặt hồ là hình chữ nhật thì chiếm mất 3% diện tích mảnh vườn, còn nếu giảm chiều dài 5m và tăng chiều rộng 2m thì mặt hồ là hình vuông và diện tích mặt hồ giảm được 20m2. Hỏi các cạnh vườn nhà ông Ba dài bao nhiêu mét?
Câu 4. (1 điểm)
Một lốc sữa có 4 hộp sữa, một thùng sữa có 12 lốc. Bạn An mang đủ tiền để mua 1 thùng sữa, nhưng đến nơi thì cửa hàng có chương trình khuyến mãi giảm giá 25% trên giá một hộp sữa. Biết rằng với số tiền mang theo thì vừa đủ (không thừa, không thiếu) để An mua thêm được một số hộp sữa nữa so với dự định. Hãy tính số hộp sữa An đã mua?
Câu 5. (1 điểm)
Một viên gạch trang trí nội thất có hoạ tiết như hình vẽ với hai màu tô đen và không tô đen. Em hãy tính diện tích phần không tô đen với các kích thước trên hình vẽ và lấy 3,14
Câu 6. (0,75 điểm)
Một ô tô có bình xăng chứa b (lít) xăng. Gọi y là số lít xăng còn lại trong bình xăng khi ô tô đã đi quãng đường x (km). y là hàm số bậc nhất có biến số là x được cho bởi công thức y = ax + b (a là lượng xăng tiêu hao khi ô tô đi được 1 km và a < 0) thỏa bảng giá trị sau x (km) 60 180 y (lít) 27 21
DẠYKÈMQUYNHƠN
OFFICIAL 4dm 4dm
a) Tìm các hệ số a và b của hàm số bậc nhất nói trên.

b) Xe ô tô có cần đổ thêm xăng vào bình xăng hay không khi chạy hết quãng đường 700 (km) , nếu cần đổ thêm xăng thì phải đổ thêm mấy lít xăng ?
Câu 7. (0,75 điểm)
Một đống cát có dạng hình nón có chu vi đáy là 8 m, biết độ cao của đống cát là 1,7m
Câu
a) Tính thể tích của đống cát (Lấy 3,14 và kết quả làm tròn đến 2 chữ số thập phân)

b) Người ta dùng xe cải tiến để chở đống cát đó đi (biết thùng chở của xe cải tiến có dạng là một hình hộp chữ nhật có kích thước rộng 1m dài 1,2m cao 50cm, và mỗi lần chở người ta chỉ gạt tới miệng xe để cát không bị rơi ra ngoài). Hỏi phải chở bao nhiêu xe cải tiến thì hết đống cát ?
8. (3 điểm)
OFFICIAL
Cho tam giác ABC (AB<AC) có ba góc nhọn nội tiếp đường tròn (O). Đường cao AD của ΔABC cắt đường tròn (O) tại E (E khác A). Từ E vẽ EK vuông góc với đường thẳng AB tại K, qua A vẽ tiếp tuyến xy với đường tròn (O). Từ E kẻ đường thẳng vuông góc với đường thẳng xy tại Q. a/ Chứng minh : Tứ giác AQKE nội tiếp và KQEBCE b/ Tia KD cắt AC tại N. Chứng minh: Tứ giác DECN nội tiếp và EN.QK = ND.EQ.
DẠYKÈMQUYNHƠN
END
HẾT HƯỚNG DẪN CHẤM - ĐỀ 3 Câu Nội dung Điểm 1 Bảng
ị
Tìm
Tọa
(2; -2) 0,5đ + 0,5đ 0,25đ +
c/ Đường thẳng QE cắt BC và AB lần lượt tại I và F. Chứng minh:
EQK S EI SEF
.
giá tr
đúng; Vẽ đúng.
mỗi tọa độ đúng
độ giao điểm là ( -4; -8) và
0,25đ
0,5đ 0,25đ + 0,25đ 0,25đ 0,25đ 3 Gọi chiều dài, chiều rộng của hồ hình chữ nhật là x,y (m) ( x,y > 0) 2510 7 xy xy
0,25đ 0,25đ 0,25đ 0,25đ
4 Gọi x là giá tiền hộp sữa lúc đầu mua (x *N )
Số tiền được giảm là 25%.48.x
Giá tiền của một hộp sữa lúc sau là 75%x (đồng)
Số hộp sữa bạn An mua thêm là: 6 25%.48.x 75%x 1 Vậy Số hộp sữa bạn An mua là 48 + 16= 64 hộp là ¼ hình tròn có bán kính 4dm là: 22 1 444() dm Diện tích phần không tô đen là: 2 4222.3,146,28() dm
5 Diện tích phần tô đen là : 2 2 2. 2() 2 dm Diện tích cả hai hình Vậy công thức liên hệ là 1 yx30 20 b)Ta có x = 700 suy ra 1 y.700305 20 Khi chạy hết quãng đường 700km thì có phải đổ thêm 5 lít xăng
0,25 0,25 0,25
DẠYKÈMQUYNHƠN OFFICIAL
2 Chứng tỏ phương trình luôn có nghiệm Tính tổng và tích đúng S = 13/2 và P = -3 A = (x1 - x2)2 – 4x1x2 = S2 -8P A = 265/4
15 8 x y
Diện tích hồ là 15.8 = 120(m2) Diện tích vườn là 120 : 3% = 4000m2 Gọi a là chiều rộng vườn ta có : 2,5a2 = 4000 => a = 40 ( nhận); a = -40 ( loại) Vậy chiều dài:100(m) ;chiều rộng : 40(m)
0,25đ 0,25đ 0,25đ 0,25đ 0,5đ 0,25đ 0,25đ 6 a)Theo đề bài ta có x = 60 , y = 27 => 27= a.60 + b (1) x = 180 , y= 21 => 21 = a.180 + b (2) Theo đề bài ta có hệ phương trình 27 a.60 b a.60 b27 21 a.180 ba.180 b21 Giải hệ ta được 1 a 20 b30
0,25 0,25 0,25
S D
0,25 0,25 0,25 0,25 b) Chứng minh: Tứ giác DECN nội tiếp và EN.QK = ND.EQ.
Ta có: 090 ADBBKE t/g BDEK nt KBEKDE (cùng chắn cung KE) Mà KBEACE (do ABEC nt) KDEACE T/g DECN nt (…) DENDCN (cùng chắn cung DN),
DCNQAB (cùng chắn cung AB), QABQEK (cùng chắn cung QK)
DENQEK
Lại có: DCEDNE (cùng chắn cung ) KQEDCE (Cmt)
0,25 0,25
DẠYKÈMQUYNHƠN OFFICIAL 7
a) Ta có chu vi 8 C82R8R4(m) 2 Thể tích đống cát là 22311 VRh4.3,14.1,728,47(m) 33
F I
O
C
b) Thể tích của thùng xe là 3 V1.1,2.0,50,6 (m) Số lần chở là 28,47 47,4548 0,6 Vậy phải chở 48 lần mới hết đống cát N
B
A E K Q
8 a) Chứng minh : Tứ giác AQKE nội tiếp và KQEBCE
Ta có: 090 AQEAKE (do EQ xy; EK AB) T/g AQKE nt (…) KQEKAE (cùng chắn cung KE) Mà KAEBCE (cùng chắn cung BE) KQEBCE
OFFICIAL
DẠYKÈMQUYNHƠN
HẾT DNEKQE Xét END và EQK, có: DENQEK , DNEKQE
END EQK .. ENND ENQKNDEQ EQQK 0,25 0,25 c) Chứng minh: END EQK S EI SEF . Ta có: DECAND (do DECN nt), DECxAC (cùng chắn cung AC) ANDyAC , mà 2 góc ở vị trí slt xy // NK mà xy QE NK QE tại S (với S là giao điểm của NK và QE) Áp dụng htl vào các tam giác vuông: KEF, DEI, ta được: 22 .,. KEESEFDEESEI 2 2 DEEI KEEF END EQK S EI SEF 0,25 0,25 0,25 0,25
UBND THÀNH PHỐ THỦ ĐỨC ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC: 2022 – 2023 MÔN THI: TOÁN ĐỀ 4 Thời gian làm bài: 120 phút (Không kể thời gian phát đề)
Bài 1. (1,5đ) Cho hàm số y = 2 x có đồ thị là (P) và đường thẳng (D): 2 yx a) Vẽ đồ thị của hai hàm số trên cùng một hệ trục tọa độ b) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán
Bài 2. (1,5đ) Cho phương trình 0 5 8 2 2 x x không giải phương trình. Tính giá trị biểu thức 2
2 1 53 x x x x x x D
2 1 1
Bài 3. (1đ) Một quyển tập giá 4000 đồng, một hộp bút giá 30000 đồng. Bạn An cần mua một số quyển tập và một hộp bút.
a) Gọi x là số quyển tập An mua và y là số tiền phải trả (bao gồm tiền mua tập và một hộp bút). Viết công thức biểu diễn y theo x. b) Nếu bạn An có 200000 đồng để mua tập và một hộp bút thì tối đa bạn An mua được bao nhiêu quyển tập
Bài 4. (1đ) Một trường THCS tổ chức cho 250 giáo viên và học sinh tham quan biết rằng giá vé vào cổng của giáo viên là 80000 đồng và học sinh là 60000 đồng.Nơi tham quan giảm giá vé cho trường học là 5% cho mổi vé nên nhà trường chi trả là 14535000 đồng .Hỏi có bao nhiêu giáo viên và học sinh tham gia ? Bài 5. (1đ) Một cửa hàng khuyến mãi một sản phẩm bánh kem mua 4 tặng 1. Giá bán 1 bánh là 12 000 đồng. Lan muốn mua 11 bánh, Mai muốn mua 14 bánh. Mai bàn với Lan mua chung sẽ ít tốn tiền hơn từng người mua. Lan hỏi Mai mua chung sẽ đỡ tốn hơn bao nhiêu tiền và mỗi người sẽ chi trả thế nào. Em hãy trả lời giúp Mai hai câu hỏi đó?
DẠYKÈMQUYNHƠNOFFICIAL
Bài 6. (1đ) Các ống hút nhựa thường khó phân hủy và gây hại cho môi trường. Mỗi ngày có 60 triệu ống hút thải ra môi trường gây hậu quả nghiêm trọng. Ngày nay người ta chủ động sản xuất các loại ống hút dễ phân hủy. Tại tỉnh Đồng Tháp có cơ sở chuyên sản xuất ống hút “thân thiện với môi trường” xuất khẩu ra thị trường thế giới và được nhiều nước ưa chuộng. Ống hút được làm từ bột gạo, các màu chiết xuất từ củ dền, lá dứa, bông sen, bông điên điển,…Một ống hút hình trụ, đường kính 12mm, bề dày ống 2mm, chiều dài ống 180mm. Em hãy tính xem để sản xuất mỗi ống thì thể tích bột gạo được sử dụng là bao nhiêu (Biết ≈3,14) Bài 7. (1đ) Lớp 9A có 30 học sinh ,mổi bạn dự định đóng mổi tháng là 70000 đồng để mua quà tăng các trẻ em ở “Mái ấm tinh thương A” và sau 3 tháng đủ tiến để tặng mổi em ở mái ấm là 3 gói quà (giá trị mổi gói quà là như nhau).Khi các học sinh đã đóng đủ thì mái ấm đã nhận chăm sóc thêm 9 em và giá tiến mổi gói quà tăng thêm 5% nên chỉ tặng được mổi em là 2 gói quà.Hỏi lúc đầu có bao nhiêu em ổ mái ấm được tặng quà ?

Bài 8. (2đ) Từ điểm A ở ngoài đường tròn (O;R) vẽ hai tiếp tuyến AB;AC đến (O) (B;C là tiếp đểm).Vẽ đường kính BE của (O);đường thẳng AE cắt (O) tại D;AO cắt BC tại H
a) Chứng minh OA vuông góc BC và AH.AO = AD.AE
b) Chứng minh từ giác OHDE nội tiếp và HC là tia phân giác của góc DHE
c) Vẽ EK vuông góc BC;Gọi M và N là hình chiếu của O lên AE và EH.
Chứng minh MK = NH HẾT---
DẠYKÈMQUYNHƠNOFFICIAL
UBND THÀNH PHỐ THỦ ĐỨC ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC: 2022 – 2023 MÔN THI: TOÁN ĐỀ 4 Thời gian làm bài: 120 phút (Không kể thời gian phát đề)
Bài 1. (1,5đ) Cho hàm số y = 2 x có đồ thị là (P) và đường thẳng (D): 2 yx a) Vẽ đồ thị của hai hàm số trên cùng một hệ trục tọa độ b) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán
Bài 2. (1,5đ) Cho phương trình 0 5 8 2 2 x x không giải phương trình. Tính giá trị biểu thức 2
2 1 53 x x x x x x D
2 1 1

Bài 3. (1đ) Một quyển tập giá 4000 đồng, một hộp bút giá 30000 đồng. Bạn An cần mua một số quyển tập và một hộp bút.
a) Gọi x là số quyển tập An mua và y là số tiền phải trả (bao gồm tiền mua tập và một hộp bút). Viết công thức biểu diễn y theo x. b) Nếu bạn An có 200000 đồng để mua tập và một hộp bút thì tối đa bạn An mua được bao nhiêu quyển tập
Bài 4. (1đ) Một trường THCS tổ chức cho 250 giáo viên và học sinh tham quan biết rằng giá vé vào cổng của giáo viên là 80000 đồng và học sinh là 60000 đồng.Nơi tham quan giảm giá vé cho trường học là 5% cho mổi vé nên nhà trường chi trả là 14535000 đồng .Hỏi có bao nhiêu giáo viên và học sinh tham gia ?
Bài 5. (1đ) Một cửa hàng khuyến mãi một sản phẩm bánh kem mua 4 tặng 1. Giá bán 1 bánh là 12 000 đồng. Lan muốn mua 11 bánh, Mai muốn mua 14 bánh. Mai bàn với Lan mua chung sẽ ít tốn tiền hơn từng người mua. Lan hỏi Mai mua chung sẽ đỡ tốn hơn bao nhiêu tiền và mỗi người sẽ chi trả thế nào. Em hãy trả lời giúp Mai hai câu hỏi đó? Bài 6. (1đ) Các
DẠYKÈMQUYNHƠNOFFICIAL
u ố
ống hút nhựa thường khó phân hủy và gây hại cho môi trường. Mỗi ngày có 60 triệ
ng hút thải ra môi trường gây hậu quả nghiêm trọng. Ngày nay người ta chủ động sản
xuất các loại ống hút dễ phân hủy. Tại tỉnh Đồng Tháp có cơ sở chuyên sản xuất ống hút “thân thiện với môi trường” xuất khẩu ra thị trường thế giới và được nhiều nước ưa chuộng. Ống hút được làm từ bột gạo, các màu chiết xuất từ củ dền, lá dứa, bông sen, bông điên điển,…Một ống hút hình trụ, đường kính 12mm, bề dày ống 2mm, chiều dài ống 180mm. Em hãy tính xem để sản xuất mỗi ống thì thể tích bột gạo được sử dụng là bao nhiêu (Biết ≈3,14) Bài 7. (1đ) Lớp 9A có 30 học sinh ,mổi bạn dự định đóng mổi tháng là 70000 đồng để mua quà tăng các trẻ em ở “Mái ấm tinh thương A” và sau 3 tháng đủ tiến để tặng mổi em ở mái ấm là 3 gói quà (giá trị mổi gói quà là như nhau).Khi các học sinh đã đóng đủ thì mái ấm đã nhận chăm sóc thêm 9 em và giá tiến mổi gói quà tăng thêm 5% nên chỉ tặng được mổi em là 2 gói quà.Hỏi lúc đầu có bao nhiêu em ổ mái ấm được tặng quà ? Bài 8. (2đ) Từ điểm A ở ngoài đường tròn (O;R) vẽ hai tiếp tuyến AB;AC đến (O) (B;C là tiếp đểm).Vẽ đường kính BE của (O);đường thẳng AE cắt (O) tại D;AO cắt BC tại H
a) Chứng minh OA vuông góc BC và AH.AO = AD.AE
b) Chứng minh từ giác OHDE nội tiếp và HC là tia phân giác của góc DHE
c) Vẽ EK vuông góc BC;Gọi M và N là hình chiếu của O lên AE và EH. Chứng minh MK = NH
DẠYKÈMQUYNHƠNOFFICIAL
--HƯỚNG DẪN CHẤM – ĐỀ 4 Câu Nội dung Điểm 1 Bảng giá trị đúng; Vẽ đúng. Tìm mỗi tọa độ đúng Tọa độ giao điểm là ( 1; -1) và (-2; -4) 0,5đ + 0,5đ 0,25đ + 0,25đ 2 c/m : a, c trái dấu. Pt có 2 nghiệm p/b. Ta có: 0,5đ 0,5đ 2 5 4, 2 1 2 1 x x x x
HẾT
b)
V
4 Gọi x là số giáo viên tham gia và y là số học sinh tham gia Ta có hệ phương trình
0,5đ 0,25đ 0,25đ
95%.60000 95%.80000 250
x y x
Tiền phải trả của hai bạn nếu mua riêng là: (9+12).12000 = 252000đồng
Nếu mua chung thì hai bạn phải trả 20 bánh + 5 bánh khuyến mãi
Tiền chỉ trả có: 20.12000 = 240000đồng Vậy đỡ tốn hơn là: 252000 – 240000 = 12000 đồng.
ả
đồ
ng
ủ
DẠYKÈMQUYNHƠNOFFICIAL 5
)
D
82
( 8 2 1 2 2 2 1 2 1
x x x x x x
0,5đ 3 a)
Công thức biểu diễn y theo x là : y = 4000 . x + 30000
Với y = 200000 200000 = 4000. x + 30000 x = 42,5
ậy nếu có 200 000 đồng để mua tập và một hộp bút thì tối đa bạn An mua được 42 quyển tập.
235
15 14535000
y x y
0,25 0,25 0,5 5 Nếu mua riêng thì Lan trả tiền 9 bánh và được 2 bánh khuyến mãi.Nếu mua riêng thì Mai trả tiền 12 bánh và được 2 bánh khuyến mãi (+1 bánh dư không trả tiền)
6 Thể tích ống hút: 223 .6.1806480 VRhmm Thể tích phần lõi rỗng bên trong ống hút: 2 23 .62.1802880 vrhmm Thể tích bột gạo được sử dụng: 3 64802880360011304 Vvmm 0,5đ 0,25đ 0,25đ 7 Gọi giá tiền của mổi gói quà lúc đầu là x (x>0;đồng) Gọi y là số trẻ em ở mái ấm lúc đầu được tặng quà 0,25
Tiền phải trả của Lan là: 240 000 : 25 . 11 = 105600 đồng Tiền phải tr
c
a Mai là: 240000: 25 . 14 = 134400
0,25đ 0,25đ 0,25đ 0,25đ
8
(y nguyên dương)
Số tiền mua quà theo dự định là 3xy
Giá tiền mổi gói quà lúc sau là : 1,05x
Số trẻ em trong mái ấm lúc sau là : y + 9
Số tiền thực tế mua quà 1,05x2(y+9) = 2,1x(y+9)
Ta có 3xy = 2,1x(y+9) giải đúng y = 21
0,25 0,25 0,25
a. C/m: OA ┴BC; AH.AO = AD.AE
AHD ~∆AEO có góc HAE chung N
~∆ AEO(c-g-c) => AEO AHD B D
AH.AO = AD.AE (cmt) nên AO AD AE AH H
Ta có AB = AC (tchtt);OB = OC (bán kính) OAlà trung trực của BC => OA┴ BC
(gnt cc cung) M E K
OHDE nt => ODE OHE O A C
0,5 0,5 b. C/m tứ giác OHDE nội tiếp và HC là tia phân giác góc HDE 0,25 0,25 0,25 c. Chứng minh MK = NH c/m∆ EMO ~∆ EKH (g-g) nên EH EO EK EM c/m∆ EMK ~∆ EOH (c-g-c) => góc EKM = góc EHO 0,25
DẠYKÈMQUYNHƠNOFFICIAL
∆
vì
∆AHE
ˆ ˆ =>T/g
ˆ ˆ
Htl: AB2 = AH.AO; AB2 = AD.AE Do đó AH.AO = AD.AE ∆ODE cân tại O nên OED ODE ˆ ˆ AHD OHE ˆ ˆ => EHC DHC ˆ ˆ (cùng phụ với hai góc bằng nhau) HC là tia phân giác của góc DHE
=> góc MKH = góc NHK(cùng phụ với hai góc bằng nhau) c/m tứ giác EONM nội tiếp(vì góc EMO=góc ENO = 900)
=> góc EOM = góc ENM (cùng chắn cung EM)
mà góc EOM = góc EHK(cmt)
góc ENM = góc EHK =>MN // HK
Tg MNHK là hình thang cân Vậy MK = NH
0,25 0,25
Hết
Lưu ý:
- Khi học sinh giải và trình bày cách khác thì giáo viên dựa trên thang điểm chung để chấm. - Học sinh không vẽ hình bài hình học thì không chấm.
Hết
DẠYKÈMQUYNHƠNOFFICIAL
UBND THÀNH PHỐ THỦ ĐỨC ĐỀ THAM KHẢO TUYỂN SINH 10 PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC: 2022 – 2023 MÔN THI: TOÁN
ĐỀ 5 Thời gian làm bài: 120 phút (Không kể thời gian phát đề)
Câu 1. (1,5 điểm) Cho hàm số 2 1 3 yx có đồ thị (P) và hàm số 2 3 1 yx có đồ thị là đường thẳng (d).
a) Vẽ đồ thị của (P) và (d) trên cùng một hệ trục tọa độ Oxy. b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Câu 2. (1,0 điểm) Cho phương trình 2x2 – 3x – 6 = 0 (1) (m là tham số) a) Chứng minh phương trình (1) luôn có hai nghiệm phân biệt. b) Gọi x1; x2 là hai nghiệm của phương trình (1). Không giải phương trình, hãy tính giá trị của biểu thức: 22 12 22 21
xx A xx Câu 3. (1,0 điểm) Cô Lan chi 116 000 000 (đồng) để nhập 1600 bao gạo và bao ngô. Mỗi bao gạo nặng 10 (kg) và được cô Lan bán ra với giá 120 000 (đồng), mỗi bao ngô nặng 15 (kg) và được cô Lan bán ra với giá 90 000 (đồng). Do thời tiết ẩm ướt, nên 20% số bao gạo và 15% số bao ngô bị hỏng không thể bán. Vì thế, tổng khối lượng gạo và ngô có thể bán lúc này là 15650 (kg). a) Tính số bao gạo và số bao ngô cô Lan nhập về. b) Hỏi sau khi bán hết số gạo và ngô không bị hỏng, cô Lan lời hay lỗ bao nhiêu tiền?
Câu 4. (1,0 điểm) Galilei là người phát hiện ra quãng đường chuyển động của vật rơi tự do tỉ lệ thuận với bình phương của thời gian chuyển động. Quan hệ giữa quãng đường chuyển động y (mét) và thời gian chuyển động x (giây) được biểu diễn bởi công thức y = 4,9x2. Người ta thả một vật nặng từ độ cao 55 (m).
a/ Hãy cho biết sau 2 (giây) thì vật nặng cách mặt đất bao nhiêu mét? b/ Khi vật nặng cách mặt đất 10,9 (m) thì nó đã rơi bao nhiêu giây?
Câu 5. (1,0 điểm) Ông An gửi ngân hàng 2 000 000 000 (đồng) với lãi suất là 6,5%/năm. a/ Sau 2 năm, tổng số tiền vốn và lãi ông An nhận được là bao nhiêu? b/ Ông An dùng số tiền đã nhận (ở câu a) để đầu tư kinh doanh. Biết sau một thời gian đầu tư, số tiền ông An nhận được cả vốn lẫn lãi là 2 608 717 500 (đồng). Hỏi lợi nhuận ông An nhận được trong đợt đầu tư kinh doanh vừa rồi là bao nhiêu phần trăm?
DẠYKÈMQUYNHƠN
OFFICIAL
Câu 6. (1,0 điểm) Một chiếc ly với phần bầu ly có dạng hình nón (như hình vẽ). Sau khi rót vào ly 60 (ml) nước thì chiều cao của lượng nước trong ly bằng 2 3 chiều cao bầu ly ( 2 3 BACA ). Công thức thể tích hình nón là Vnón = 2 1 3 rh (r là bán kính đường tròn đáy, h là chiều cao hình nón). a/ Tính tỉ lệ thể tích của phần nước đổ vào và thể tích bầu ly. b/ Biếu chiều cao thân ly là HA = 5 (cm) và bánh kính miệng ly là CD = 4 (cm). Tính chiều cao của chiếc ly (đoạn CH) (kết quả làm tròn đến hàng đơn vị).
OFFICIAL
Câu 7. (1,0 điểm) Theo âm lịch thì do một chu kỳ quay của Mặt Trăng quanh Trái Đất là khoảng 29,53 ngày nên một năm âm lịch chỉ có khoảng 354 ngày (làm tròn). Do vậy, cứ sau một vài năm âm lịch thì người ta phải bổ sung một tháng (tháng nhuận) để đảm bảo năm âm lịch tương đối phù hợp với chu kỳ của thời tiết, là yếu tố phụ thuộc vào chu kỳ quay của Trái Đất xung quanh Mặt Trời.

Cách tính năm nhuận âm lịch như sau: Lấy số năm chia cho 19, nếu số dư là một trong các số: 0; 3; 6; 9 ; 11; 14; 17 thì năm âm lịch đó có tháng nhuận.
Ví dụ: 2017 là năm nhuận âm lịch vì 2017 chia cho 19 dư 3. 2015 không phải năm nhuận âm lịch vì 2015 chia cho 19 dư 1
a) Em hãy sử dụng quy tắc trên để xác định năm 1995 và 2030 có phải năm nhuận âm lịch hay không?
b) Năm nhuận dương lịch là năm chia hết cho 4. Ngoài ra, những năm chia hết cho 100 chỉ được coi là năm nhuận dương lịch nếu chúng cũng chia hết cho 400.
Ví dụ: 1600 là năm nhuận dương lịch vì 1600 chia hết cho 400 1700 không phải năm nhuận dương lịch vì 1700 không chia hết cho 400 Hỏi từ năm 1895 đến năm 1930, năm nào vừa là năm nhuận âm lịch vừa là năm nhuận dương
DẠYKÈMQUYNHƠN
ịch? Câu 8. (2,5 điểm) Cho tam giác ABC nhọn (AB < AC) nội tiếp ( T ) có tâm O , bán kính R , BC = R√3 . Tiếp tuyến tại B,C của (T) cắt nhau tại P , cát tuyến PA cắt ( T ) tại D (
A ) . Đường thẳng OP cắt BC tại H . a/ Chứng minh : Tam giác PBC đều . Tính PA. PD theo R? b/ AH cắt ( T ) tại E ( khác A ) . Chứng minh : HA.HE = HO.HP và PD = PE c/ Trên AB lấy điểm I , thỏa AI =AC , trên AC lấy điểm J thỏa AJ = AB .Đường thẳng vuông góc với AB tại I và đường thẳng vuông góc với AC tại J cắt nhau ở K . Chứng minh :
BC và AK ⊥ BC . Tính PK theo R? HẾT
l
khác
IJ =
Câu Nội dung
1 Bảng giá trị đúng; Vẽ đúng. Tìm mỗi tọa độ đúng
Tọa độ giao điểm là ( 3;3) và (-1;1/ 3)
2 c/m : a, c trái dấu. Pt có 2 nghiệm p/b. S=3/2; P=-3 Tính A= 89/16
3 Gọi x , y (bao) lần lượt là số bao gạo, bao ngô cô
Lan nhập về. Đk:x,y €N* ; x,y <1600 ta có hpt :{ ��+��=1600 8��+12,75��=15650
x = 1000, y= 6000
Số tiền cô Lan thu được :141 900 000 đ Số tiền cô Lan lời : 25 900 000đ
Điểm
0,5đ + 0,5đ 0,25đ + 0,25đ
0,5đ 0,5đ 0,5đ
0,25 0,25 0,5
4 x=2 (s) => y = 19.6 (m).Sau 2 giây vật cách mặt đất 35,4 (m) y= 44,1 m => x=3. Vật nặng cách đất 10,9 (m) 0,5đ 0,5đ 5 Sau 1 năm Ông An lãnh : 2 130 000 000 đ Sau 2 năm Ông An lãnh : 2 268 450 000 đ
lãi nhận được
DẠYKÈMQUYNHƠN
HƯỚNG DẪN CHẤM – ĐỀ 5
OFFICIAL
��
Thề tích phần bầu ly : 202,5 (cm3) 0,5đ 0,5đ 7 a)1995 chia 19 dư 0 nên là năm nhuận âm lịch 2030 chia 19 dư 16 nên không là năm nhuận âm lịch. b) Các năm nhuận
ch:
Tiền
khi đầu tư :340 267 500 đ Phần trăm lợi nhuận là 15% 0,25 0,25 0,5 6 Thể tích nước đổ vào : ��1 = 1 3 ������2 ����; ��2 =1/3������2 ����
1 ��2 = 8 27 mà V1 = 60 ; V2 =202,5
dương lị
1896, 1904, 1908, 1912, 1916, 1920, 1924, 1928. 1896 : 19 = 99 (dư 15) 1904 : 19 = 100 (dư 4) 1908 : 19 = 100 (dư 8) 1912 : 19 = 100 (dư 12) 1916 : 19 = 100 (dư 16) 1920 : 19 = 101 (dư 1) 0,25đ 0,25 0,25đ
1924 : 19 = 101 (dư 5) 1928 : 19 = 101 (dư 9) Trong đó 1928 chia 19 dư 9 nên cũng là năm nhuận âm lịch Vậy từ năm 1895 đến năm 1930, năm 1928 vừa là năm nhuận âm lịch vừa là năm nhuận dương lịch. 0,25đ
DẠYKÈMQUYNHƠN OFFICIAL
a. H là trung điểm BC
trực BC ) sin ������ ̂ = ���� ���� ⇒������ ̂
0 ⇒△PBC
̂
0 ⇒△PBC
⇒△PBD
⇒ ���� ���� = ���� ���� ⇒
2
��2
b.
) ����2 = HO.HP Xét △ HOA và △ HEP : có ������ ̂ =������ ̂ , ���� ���� = ���� ���� ⇒△ HOA ~ △ HEP (cgc) ⇒������ ̂ =������ ̂ ⇒ Tứ giác AOEP nội tiếp ⇒������ ̂ =������ ̂ ( 2 góc nội tiếp chắn hai cung OA và OE bằng nhau)(1) Lại có PA.PD = ����2 = PH.PO ⇒ ���� ���� = ���� ���� ⇒△ PDH ~ △ POA (cgc) ⇒ Tứ giác OHDA nội tiếp ⇒������ ̂ =������ ̂ =������ ̂ =������ ̂ nên ������ ̂ = ������ ̂ (��ù���� =������ ̂ ) (2) từ (1) và (2) ⇒△ HDP = △ HEP (gcg) ⇒ PD = PE 0,5 0,5 c. △ ABC = △ AJI(cgc)( vì AB = AJ ; ������ ̂ :chung ;AC =AI)⇒ IJ = BC *Gọi : Q = BC ∩ AK Tứ giác : AIKJ nội tiếp đường tròn đường kính AK ( vì ������ ̂ =������ ̂ = 900) ������ ̂ =������ ̂ (��ù���� =������ ̂ , do tứ giác AIKJ nội tiếp và △ ABC = △ AJI) ⇒ Tứ giác BQKI nội tiếp 0,25
8
( PO là trung
= 60
có PB = PC và ������
=60
đều
~ △PAB (gg)
PA.PD = ����
= 3
0,5 0,5
HA.HE = HB.HC ( △HAB ~ △HCE (gg)
⇒ AK ⊥ BC
(������ ̂ =������ ̂ =900)
*vì △ ABC = △ AJI , nên bán kính đường tròn ngoại tiếp của hai tam giác này bằng nhau
Mà AK là đường kính của đường tròn ngoại tiếp
∆������ , nên AK = 2R
△ OCP vuông tại C
⇒����2 = ����2 + ����2 = ��2 + (��√3)2 =4��2
⇒ OP = 2R ⇒ OP = AK
Ta có AK ⊥ BC , OP ⊥���� , nên AK//OP
Tứ giác AOPK có AK//OP và AK = OP , nên AOPK là hình bình hành ⇒ PK = AO = R 0,25
DẠYKÈMQUYNHƠN OFFICIAL