




Editorial.... Pag 3
Equipo de redacción...Pag 4
Procesos estocasticos.... Pag 5
Noción del Proceso.... Pag 6
Tipos de procesos estocasticos.... Pag 7
Procesos estocasticos en las empresas.... Pag 8
Proceso de Markov.... Pag 9
Primer orden.... Pag 10
Cadena de Markov.... Pag 11
Aplicacion en la industria de la cadena de Markov... Pag 12
Tipos de cadenas de Markov.... Pag 13
Gestion de la calidad .... Pag 14
¿Cómo se realiza en la industria?... Pag 15
Tipos de control de calidad en la industria.... Pag 16
Tipos de control de calidad en los proceso profuctivos.... Pag 17
Iso 9001:2015.... Pag 18
Entretenimiento.... Pag 19

En esta edición de nuestra revista de ingeniería, exploramos en profundidad la importancia de integrar la gestión de calidad con los procesos estocásticos para lograr resultados sobresalientes en términos de productividad, rentabilidad y satisfacción del cliente. A través de estudios de caso, entrevistas a expertos y artículos especializados, analizamos las mejores prácticas y estrategias para implementar un enfoque integral que combine la excelencia en la calidad con la optimización de los procesos estocásticos.
En un entorno empresarial cada vez más competitivo y globalizado, es fundamental que las organizaciones inviertan en la mejora continua y la innovación en sus procesos. La gestión de calidad y los procesos estocásticos son herramientas poderosas que pueden marcar la diferencia entre el éxito y el fracaso en un mercado en constante evolución.
¡No te pierdas esta edición especial dedicada a estos temas clave en la ingeniería moderna!







¿Qué
En los procesos estocásticos se representan de los pasos necesarios para la realización de un cierto evento así como también los maneras en que cada uno de los pasos puede ser realizado en términos de las respectivas probabilidades. Por tanto, cualquier proceso en el que se vean involucradas probabilidades de ocurrencia resulta ser un proceso estocástico.
Al describir variables de carácter aleatorio, vinculadas a fenómenos de tipo probabilísticos como lo es el transporte de radiación, es asumido, como premisa implícita por defecto, el hecho de que las características aleatorias permanecen constantes durante el intervalo de tiempo de interés, aunque desde una perspectiva genérica podría no satisfacerse esta asumpción.
En efecto, al incorporar la dependencia (o evolución) de variables consideradas determinísticas, éstas describirán un proceso evolutivo de tipo analítico, mientras que para el caso de variables aleatorias mostrarán una evolución condicionada por el vínculo al fenómeno probabilístico asociado. Entonces, toda función definida a partir de variables aleatorias, como por ejemplo funciones de distribución o funciones de densidad, presentarán dependencia temporal determinada por su carácter aleatorio, dando lugar a la naturaleza estocástica del fenómeno físico involucrado.
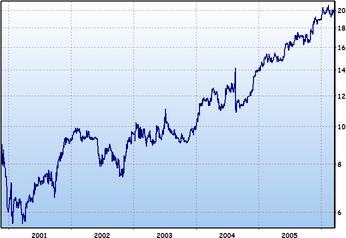
Segun Ruiz, (2012): "Un proceso estocastico, es una colección o familia de variables aleatorias ordenado según el subíndice t que en general se suele identificar con el tiempo.

Muchos campos utilizan observaciones en función del tiempo (o, más raramente, de una variable espacial). En los casos más sencillos, estas observaciones dan lugar a una curva bien definida. En realidad, desde las ciencias de la tierra hasta las humanidades, las observaciones suelen producirse de forma más o menos errática. Por lo tanto, la interpretación de estas observaciones está sujeta a una cierta incertidumbre, que puede reflejarse en el uso de probabilidades para representarlas. Un proceso aleatorio generaliza la noción de variable aleatoria utilizada en probabilidad. Se define como una familia de variables aleatorias X(t) asociadas a todos los valores t ∈ T (a menudo tiempo).
Desde un punto de vista estadístico, consideramos todas las observaciones disponibles x(t) como una realización del proceso, lo que da lugar a ciertas dificultades. Un primer problema se refiere al hecho de que la duración sobre la que se construye el proceso es generalmente infinita, mientras que una realización abarca una duración finita. Por lo tanto, es imposible representar la realidad a la perfección. Una segunda dificultad, mucho más grave, es que, a diferencia del problema de las variables aleatorias, la información disponible sobre un proceso se reduce generalmente a una única realización.





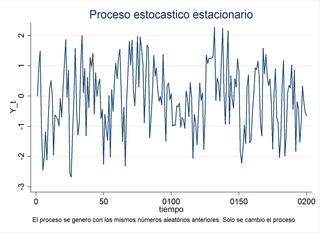
1.Proceso Estacionario:
Un proceso estacionario es aquel cuyas propiedades estadísticas, como la media y la varianza, son constantes a lo largo del tiempo. Se pueden distinguir entre estacionariedad débil (media y covarianza constante) y estacionariedad fuerte (distribución invariante).
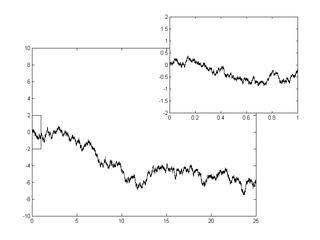
3.Proceso de Wiener (Movimiento Browniano): El proceso de Wiener es un proceso estocástico continuo en el tiempo que describe el movimiento aleatorio de partículas en un fluido. Es un ejemplo importante en la teoría de probabilidad y se utiliza en la modelización de fenómenos físicos y financieros.
Según Abad, (2012): "Un proceso estacionario son aquellos procesos estocasticos que tienen un comportamiento constante a lo largo del tiempo"
2. Proceso de Markov:
En un proceso de Markov, la probabilidad de que el proceso pase a un estado futuro depende únicamente del estado presente y no de los estados anteriores. Este tipo de proceso se caracteriza por tener la propiedad de Markov.
Los procesos estocásticos en una empresa son aquellos que se caracterizan por ser aleatorios o inciertos, es decir, su resultado no puede ser predeterminado con certeza. Estos procesos son de gran importancia porque nos permiten modelar y entender diferentes aspectos del comportamiento de una empresa, como la demanda de productos, los tiempos de entrega, los precios de mercado, entre otros. Para delimitar y medir los procesos estocásticos en una empresa, se pueden utilizar diversos enfoques:
1.Recopilación de datos históricos: Estos datos históricos pueden proporcionar la base para comprender y estimar la variabilidad de los procesos estocásticos.

3.Modelización matemática: Utilizar modelos matemáticos o estadísticos es una forma común de representar y simular procesos estocásticos. Estos modelos pueden variar según el tipo de proceso que se esté estudiando.



2.Análisis estadístico: El análisis estadístico de los datos recopilados puede ayudar a identificar patrones, tendencias y distribuciones de probabilidad asociadas a los procesos estocásticos.

4.Utilización de herramientas informáticas: Existen herramientas y software especializados que pueden ayudar en la delimitación y medición de procesos estocásticos en una empresa.
Por: Daimeris Silva
Un proceso de Markov es un tipo de proceso estocástico en el que la probabilidad de que un sistema pase de un estado a otro depende únicamente del estado actual en el que se encuentra, y no de cómo llegó a ese estado. En otras palabras, la propiedad fundamental de un proceso de Markov es la llamada “propiedad de Markov”, que establece que la evolución futura del sistema solo depende del estado actual y no de la historia pasada.
En un proceso de Markov, se define un conjunto finito o infinito de estados posibles, y se establecen las probabilidades de transición entre estos estados. Estas probabilidades de transición se representan generalmente mediante una matriz de transición, en la que cada entrada indica la probabilidad de pasar de un estado a otro en un solo paso. Los procesos de Markov se utilizan en diversos campos como la economía, la biología, la ingeniería, la informática, entre otros, para modelar sistemas dinámicos que evolucionan en el tiempo de manera aleatoria. Son especialmente útiles para predecir comportamientos futuros basados en el conocimiento del estado actual del sistema.
De acuerdo a González, (2022): "Es un fenómeno aleatorio dependiente del tiempo para el cual se cumple una propiedad específica: la propiedad de Markov"
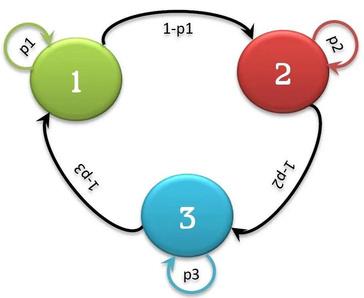



Podemos hablar de diferentes definiciones referentes a los procesos de Márkov de primer orden:
• Estados: Las condiciones en las cuales se encuentra un ente o sucesos posibles.
• Ensayos: Las ocurrencias repetidas de un evento que se estudia.
• Probabilidad de Transición: La probabilidad de pasar de un estado actual al siguiente en un tiempo.
Los procesos de Márkov de Primer Orden, para poder ser usados como modelos de procesos físicos o económicos, deben tener una serie de características:
• Que la probabilidad cumpla con el Principio de Márkov.
• Los ensayos deben ser en períodos iguales.
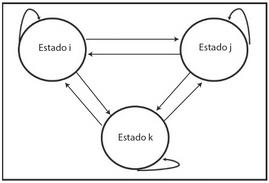

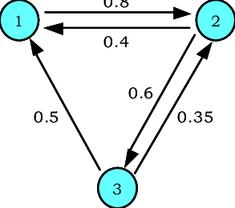
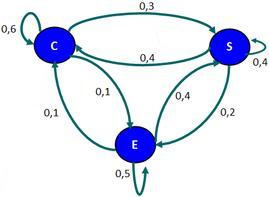
Las cadenas de Markov se representan generalmente mediante un grafo dirigido, donde los nodos representan los estados posibles y las aristas indican las transiciones entre ellos con las probabilidades correspondientes. Estas cadenas se pueden clasificar en dos tipos principales: cadenas de Markov homogéneas, donde las probabilidades de transición no dependen del tiempo, y cadenas de Markov no homogéneas, donde las probabilidades pueden variar en función del tiempo. Las cadenas de Markov son ampliamente utilizadas en diversos campos como la teoría de colas, la modelización de sistemas biológicos, la economía, la ingeniería, la inteligencia artificial, entre otros. Son especialmente útiles para predecir comportamientos futuros de sistemas que evolucionan de manera aleatoria y para analizar la estabilidad y convergencia de estos sistemas en el tiempo.
Segun Pérez, (2003): "Una cadena de Markov es una serie de eventos en la cual la probabilidad de que ocurra un evento depende del evento inmediato anterior".

 Por: Luis Marcano
Por: Luis Marcano
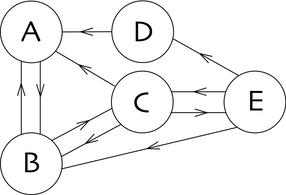
Cadenas irreducibles
Una cadena de Markov se dice irreducible si se cumple cualquiera de las siguientes condiciones (equivalentes entre sí):
- Desde cualquier estado se puede acceder a cualquier otro.
- Todos los estados se comunican entre sí.
Una cadena de Márkov se dice regular (también primitiva o ergódica) si existe alguna potencia positiva de la matriz de transición cuyas entradas sean todas estrictamente mayores que cero.

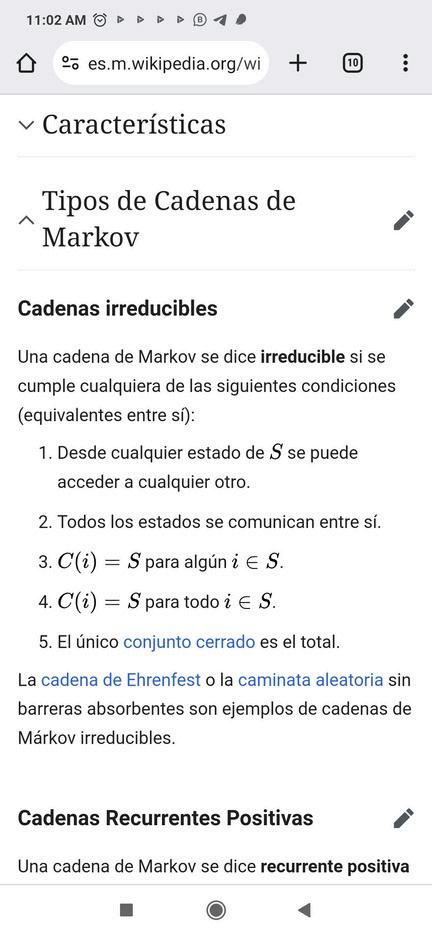
Una cadena de Markov se dice recurrente positiva si todos sus estados son recurrentes positivos. Si la cadena es además irreducible es posible demostrar que existe un único vector de probabilidad invariante y está dado por:

 Por: Luis Marcano
Por: Luis Marcano

1. Análisis de inventarios: Esto permite a las empresas optimizar sus políticas de inventario, minimizar los costos asociados al almacenamiento

3. Análisis de marketing: Esto permite a las empresas diseñar estrategias de marketing personalizadas y segmentar a los clientes en función de su comportamiento.

5. Predicción de demanda: Las cadenas de Markov pueden utilizarse para predecir la demanda de productos o servicios en función de diferentes variables como el comportamiento del mercado.

2. Modelización de procesos de producción: Esto ayuda a identificar cuellos de botella, optimizar los tiempos de producción y mejorar la planificación de la producción.

4. Gestión de proyectos: Las cadenas de Markov se utilizan para modelar y predecir la evolución de un proyecto a lo largo del tiempo, identificando posibles retrasos, riesgos y desviaciones en el plan inicial.

Por: Raúl Odreman

¿Que es?
La gestión de la calidad se define como el acto de supervisar diferentes actividades y tareas dentro de una industria para garantizar que los productos y servicios ofrecidos, así como los medios utilizados para proporcionarlos, son coherentes y adecuados para el propósito de idoneidad.
El inicio del proceso implica el establecimiento de los objetivos de calidad, que se acuerdan con el cliente. A continuación, se lleva a cabo un «proceso de garantía de calidad» y un «proceso de control de calidad» para medir e informar sobre la calidad real de los productos.
Además, como parte del proceso, cualquier problema o incidencia se identifica y se resuelve con rapidez. Después de todo, este proceso te ayudará a mejorar los resultados de tu producción. También te ayudará a implantar un proceso de garantía de calidad para aumentar la confianza en la calidad de los productos o servicios.
Segun Gutiérrez, (2020): "Es un conjunto de acciones y herramientas que tienen como objetivo evitar posibles errores o desviaciones en el proceso de producción y en los productos o servicios obtenidos a través de él"

En resumen, este proceso te ayudará a:
- Establecer los objetivos que debe cumplir tu equipo de producción.
- Definir cómo se medirán esos objetivos.
- Realizar las acciones necesarias para medir la calidad.
Por: Raúl Odreman

1. Obtener el compromiso de los directivos y de los recursos humanos: para llevar a cabo un control eficaz, es necesario el compromiso y la dedicación de todos los miembros del equipo.

3. Determinar las mejores prácticas: decidir cómo evaluar la calidad de los productos que van a elegir, ya sea a través de modelos, normas o manuales

5. Realizar el diagnóstico inicial: antes de realizar el proceso hay que estudiar cómo funciona actualmente la calidad de los productos de tu empresa. Para este paso se pueden utilizar encuestas, cuestionarios o entrevistas.

2. Reconocer las expectativas del cliente: estudiar las necesidades del cliente, saber qué quiere de su empresa y cómo se pueden satisfacer sus necesidades con los servicios o productos que ofrece su sector.

4. Designar un responsable: si se quiere conseguir un control de calidad eficaz, hay que elegir un líder que se encargue de este proceso. Para ello, debes tener en cuenta que esta persona, departamento o grupo sea una persona muy comprometida.
 Por: Raúl Odreman
Por: Raúl Odreman

6. Redactar el manual de calidad: una vez realizados los pasos anteriores, la empresa establecerá las decisiones y compromisos que se llevarán a cabo para evaluar los productos.

8. Establecer registros de calidad: sistematizar todos los registros de los sectores y procesos para realizar los diagnósticos.


7. Redactar el manual de procedimientos: una vez tomadas las decisiones pertinentes para llevar a cabo la evaluación de los productos, ahora se debe establecer cómo se van a cumplir las decisiones tomadas anteriormente.

9. Realizar auditorías periódicas: diagnosticar dónde falla la empresa y dónde hay que hacer correcciones para obtener la calidad que se busca.
Por: Jorge Sarabia
1. Gráfico de barras X: Este gráfico representa si los productos o procesos analizados cumplen las especificaciones previstas y, en caso contrario, el grado en que se apartan de dichas especificaciones.
3. Control de calidad integral:Consiste en examinar y evaluar todas las partes implicadas en la creación de un producto. Para ello, se necesita obtener los datos implicados en el proceso de fabricación y examinar meticulosamente cada elemento.

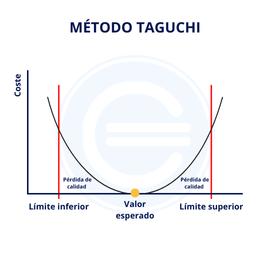
2. Método Taguchi: Presenta un enfoque que hace hincapié en el papel de la investigación, el diseño y el desarrollo del producto para reducir la aparición de defectos y fallos y modos de fallo en materiales.


Por:

1. Six Sigma: Se trata de un conjunto de principios centrados en asegurar que un producto y todas sus características se hayan diseñado para satisfacer las necesidades de los clientes y no presenten defectos.

3. Lean: Lean es una estrategia de mejora de procesos centrada en la planificación y gestión eficaz. Parte de la idea de minimizar cualquier desperdicio y maximizar la eficiencia del producto.


2. Control estadístico de procesos (SPC): Esta técnica se basa en el seguimiento de las métricas de producción mediante la supervisión de la calidad en cada paso. Lo que permite identificar mejor los problemas y resolverlos en etapas iniciales.

4. Mantenimiento productivo total (TPM): Asegura y mejora la integridad de la producción mediante el uso de máquinas, equipos, procesos e innovación en materiales. Al utilizar un enfoque proactivo, los problemas se identifican en las fases iniciales y se eliminan cuanto antes.
Por: Jorge Sarabia
La norma ISO 9001 es un estándar internacional que establece los requisitos para un sistema de gestión de calidad (SGC) en una organización. Esta norma se centra en asegurar que una organización sea capaz de cumplir con los requisitos del cliente, cumplir con la legislación y regulaciones aplicables, y buscar la mejora continua en sus procesos y productos.

La ISO 9001 es aplicable a organizaciones de cualquier tamaño o sector, y su enfoque se basa en una serie de principios de gestión de calidad, incluyendo el enfoque al cliente, el liderazgo, etc.
Al obtener la certificación ISO 9001, una organización demuestra su compromiso con la calidad y la mejora continua.



En la Universidad de Cambridge, específicamente en el departamento de matemáticas aplicada y física teórica se ofrecen programas de postgrado en los que se estudian con profundidad los procesos estocasticos y su aplicación en diversos campos, incluyendo la física, la biología y las finanzas.
En la Universidad de California, Berkeley, específicamente en su departamento de estadística, se destaca la investigación en teoría de probabilidad y procesos estocasticos, así como por ofrecer programas de postgrado que abordan la aplicación de estos conceptos en la ciencia de datos y la ingeniería.


Palabras a encontrar:
Software
Calidad
Producto
Control
Planificacion
Proceso
Estandar Riesgo
¿Sabías qué?

La gestión de calidad comenzó en Japón, por la introducción del sistema productivo de Toyota
Los procesos estocastico son fundamentales en la simulación Monte Carlo, la cual, estima resultados, mediante escenarios aleatorios y es utilizado en la ingeniería.



"La innovación es la que distingue a los líderes de los seguidores"