
Licenciatura en
Administración Marítima y Portuaria
ESTADÍSTICA
Profesora:
MARIA EVA AGUILAR.
Nombres:
Adán Morales
César González
Teoría de las probabilidades conceptos Básicos
Introducción
La teoría de las probabilidades es una rama de las matemáticas que se encarga de estudiar la incertidumbre. Permite cuantificar la probabilidad de que ocurra un evento en un experimento aleatorio. Es una herramienta fundamental en diversas áreas como la estadística, la física, la economía, la ingeniería y muchas otras.

1. Experimento aleatorio: Es un proceso que produce un resultado incierto. Ejemplo: Lanzar una moneda.
2. Espacio muestral: Es el conjunto de todos los resultados posibles del experimento. Ejemplo: Al lanzar una moneda, el espacio muestral es {cara, cruz}.
3. Suceso: Es cualquier subconjunto del espacio muestral. Ejemplo: Sacar un número par al lanzar un dado.

4. Probabilidad: Es la medida de la posibilidad de que ocurra un suceso. Se expresa como un número entre 0 y 1, donde 0 indica que el suceso es imposible y 1 que es seguro.
5. Frecuencia relativa: Es la proporción de veces que un suceso ocurre en un número grande de repeticiones del experimento.
Reglas de la probabilidad
1. La probabilidad de un suceso seguro es 1.
2. La probabilidad de un suceso imposible es 0.
3. La probabilidad de la unión de dos sucesos incompatibles es la suma de sus probabilidades.
4. La probabilidad de la unión de dos sucesos independientes es el producto de sus probabilidades.

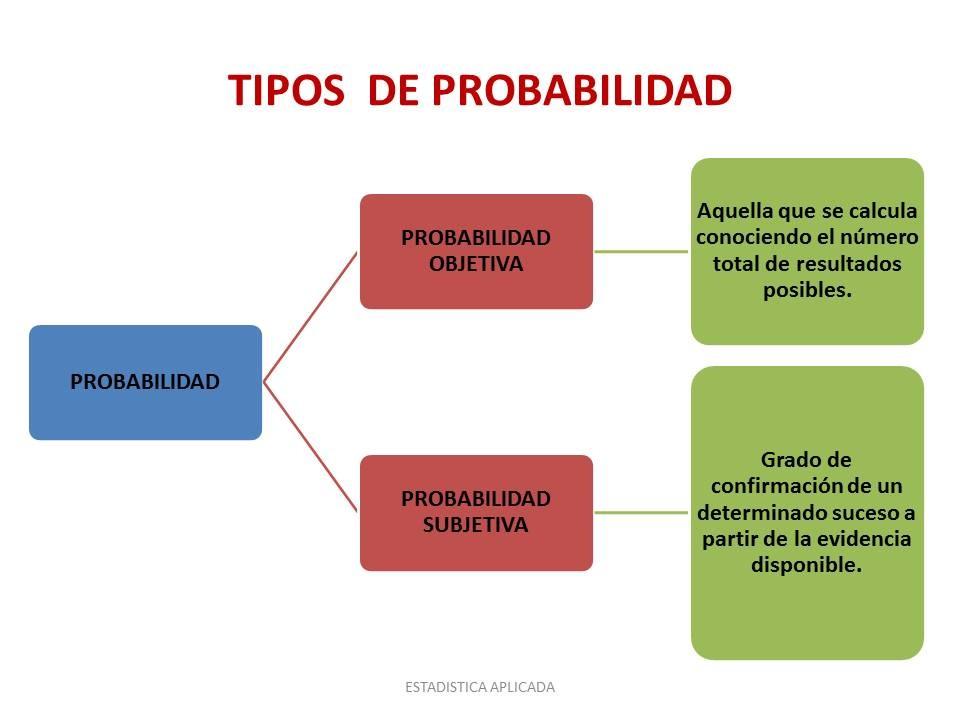
Tipos de probabilidades
1. Probabilidad clásica: Se utiliza cuando todos los resultados del espacio muestral son equiprobables. Ejemplo: Lanzar una moneda.
2. Probabilidad frecuentista: Se basa en la frecuencia relativa de un suceso en un número grande de repeticiones del experimento.
3. Probabilidad subjetiva: Es la probabilidad que una persona asigna a un suceso en función de su propia experiencia y creencias.
Aplicaciones
La teoría de las probabilidades tiene una amplia gama de aplicaciones en diversos campos:
1.Predicción: Permite estimar la probabilidad de que ocurra un evento futuro.
2.Toma de decisiones: Ayuda a tomar decisiones racionales en situaciones de incertidumbre.
3.Análisis de riesgos: Permite evaluar el riesgo asociado a una actividad o evento.
4.Juegos de azar: Se utiliza para calcular las probabilidades de ganar en juegos de azar.

Un ejemplo
Un ejemplo sencillo de la teoría de probabilidades es el lanzamiento de una moneda. Supongamos
que queremos calcular la probabilidad de que salga cara al lanzar una moneda justa.
1.Espacio muestral: El conjunto de todos los posibles resultados del experimento aleatorio, que en este caso es lanzar una moneda. El espacio muestral sería {cara, cruz}.
2.Evento de interés: Queremos calcular la probabilidad de que salga cara. Este evento se denota como A.
3.Probabilidad de un evento simple: Como la moneda es justa, hay igual probabilidad de que salga cara o cruz. Por lo tanto, la probabilidad de que salga cara (P(A)) es 0.5 o 50%.

Este ejemplo ilustra cómo se puede aplicar la teoría de probabilidades para calcular la probabilidad de un evento simple en un experimento aleatorio. En este caso, la probabilidad es intuitiva porque la moneda es justa y los resultados son equiprobables. Conclusión
La teoría de las probabilidades es una herramienta fundamental para comprender y analizar la incertidumbre. Es una herramienta poderosa que se utiliza en una amplia gama de campos.

