Elements of chemical reaction engineering 4th edition fogler solutions manual

Solutions for Chapter 3 – Rate Law and Stoichiometry

P3-2 (b) Exa mp le 3-2 Y es , w ater is alr eady consider ed inert

P3-2 (c ) Exam ple 3-3

The so lution to th e ex amp le at a convers ion of 20 % would remain unchanged For 90 % convers ions of the caus tic soda, the final concen tration of glyceryl sterate is 0 in stead of a neg ative concentration. Therefore 90 % of caus tic soda is poss ible

P3-2 (d) Exa mp le 3-4 !

A + b a B " c a C + d a D

1 / 3 1 = 0.33

P3-2 (e ) Examp le 3-5

For the concentration of N2 to be constant, the vo lume of reactor must be constant. V = VO

So, th e min imum valu e of ΘB = b/a = !

1 / (r a )

160

140

120

100

80

60

X r X X = 20

180 0 0 2 0 4 0 6 0 8 1 1 2 X

40

The r ate of r eaction decreases dras tically with increas e in co nversion at h igher conversions

P3-2 (f) Exa mple 3-6

For a g iven conversion, concentr ation of B is lower in flow r eactor than a constant vo lume batch r eactor

! N 2

!

A

↔ 2 B

2

, e

volum e Batch

flow reactor:

C AO = y AO PO RTO = y AO 0.07176( ) mol / dm 3

Combin ing: For cons tan t volum e b atch:

See Polymath program P3-2-f.pol.

PO LYMA TH Results

NLES Re port (safen ew t)

Nonli near equa tions

[ 1] f(Xeb ) = Xeb - (kc*(1 -Xeb)/(4*Cao ))^0 5 = 0

[

f(Xe f) = Xef - (kc*(1-Xef)*(1+eps*Xef)/(4 *Cao))^0 5 = 0 Exp licit eq uations [ 1] yao = 1

[ 2] kc = 0 1

[ 3] Cao = 0 07174*yao [ 4] eps = yao

rA = k A C A C B

( ( is the requir ed rate law

P3-3 Solu tion is in the decoding algorithm available s eparately from the au thor

P3-4 (a)

Note: Th is problem can hav e m any so lutions as data fitting can be done in m any ways Using Arrhen ius Equ ation

flies: T(in K) 1/T Flashes/ min ln(flashe s/min) 294 0 003401 9 2 197 298 0 003356 12 16 2 498 303 0 003300

See Polymath program P3-4-fireflies.pol.

T(in K) 1/T x103 chrips/ min ln(chirps/ min) 287 2 3 482 80 4 382 293 3 3 409 126 4 836 300 3 333 200 5 298

Plotting ln(ch irps/m in) Vs 1/T, we get a s traight line

Bo th, F iref lies and Crickets d ata follow the Arrhenius Model

ln y = A + B/T , and h ave the same activation energy

See Polymath program P3-4-crickets.pol.

P3-4 (b)

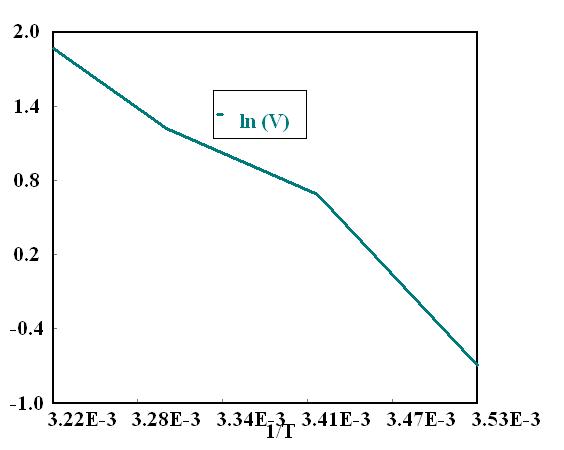
T(in K) 1/T x103 V(cm/s) ln(V) 298 3 356 0 7 -0 357 303 3.300 1.8 0.588 308 3 247 3 1 098

Plotting ln(V) Vs 1 /T, almos t straight line

ln(V) = 44 6 – 1 33E4 /T

At T = 40oC(313K) V = 6 4cm/s

At T = -5oC(268K) V = 0 005cm/s( Bu t bee would not b e alive at th is temper ature)

See Polymath program P3-4-bees pol

P3-4 (c )

For ants :

T(in K) 1/T x103 V(cm/s) ln(V)

283 3 53 0 5 -0 69

293 3 41 2 0 69

303 3 30 3 4 1 22

311 3 21 6 5 1 87

Plotting ln(V) Vs 1 /T, almo st str aight line

See Polymath program P3-4-ants.pol.

So activity of bees, an ts, cr ickets and f iref lies fo llow Arrhenius mod el So activity in creases with an increase in temper atur e Activation en ergies for fireflies and crickets are almos t the same

Insect Activation Energy

Cricket 52150

Firef ly 54800

Ant 95570

Honeybee 141800

P3-4 (d)

There is a lim it to temper atur e for which data for any one of he ins ect can be extr apolate D ata wh ich would be helpful is the m aximu m and th e m inimum temper ature th at thes e insects can endure before death

Therefore, even if ex trapolation g ives us a value that looks reasonable, at certain temp erature it could be useless

P3-5

There are two comp eting eff ects that br ing about th e m aximu m in th e corros ion rate: Temp erature and HCN-H2SO4 concentr ation The corrosion r ate increases w ith incr eas ing temp erature and increasing concen tration of H CN-H2SO4 co mplex. The temper ature in cr eas es as we go from top to bo ttom of the column and cons equently the r ate of corrosion shou ld in creas e How ever, th e H CN concentrations (and the HCN-H2SO4 complex) decrease as we go from top to bottom of the column . There is vir tually no HCN in the bo ttom of th e column Th ese two opposing factors resu lts in the max imum of the corrosion rate somewher e around the m iddle of th e column

P3-6 Antidote d id not d isso lve from glass at low temp eratures

P3-7 (a)

If a reaction rate doubles for an incr eas e in 10°C, at T = T1 let k = k1 and at T = T2 = T1+10, let k = k2 = 2k1. Then with k = A e -E/RT in gener al, 1 / 1 E RT k Ae = and 2 / 2 E RT k Ae = , or

When th e components inside air b ag ar e ignited, follow ing reactions tak e p lace, 2NaN3 → 2N a + 3N2 (1)

+ 2KNO3 → K2O + 5Na2O + N2 ……

+ S iO2 → alkalin e s ilicate glass

etr ic table:

Given w eigh t of N aN3 = 150g

Therefore, no of moles of NaN3 = 2 3

1 moles of N aN3 requ ires 0 2 mo le of KNO3

=> Mo les of B, KNO3 = 0.2(2.3) = 0.46 moles Mwt of KNO3 = 101.1

Therefore, grams of KNO3 requir ed = 0 46 x 101 1 = 46 5 g

1 moles of N aN3 requ ires 0 1 mo le of S iO2

Moles of C, S iO2 = 0 1(2 3) = 0 23 moles Mwt of SiO2 = 60 08

Therefore, grams of SiO2 r equired = 0 23 x 60 08 = 13 8 g

Follow ing proposals ar e giv en to handle all the un-detonated air b ags in cars p iling up in the junkyards:

• Store cars in cool, dry, ventilated areas.

• Avoid Physical damag e of the bag in car

• It is s tab le under ordinary conditions of stor age. Decomposes explos ively upon heating (over 221 ° F or 105 ° C), sho ck, concuss ion, or fr iction

• Conditions to avoid: heat, flam es, ign ition sources and in com patib les

P3-9 (a)

From th e w eb module w e know that (1 ) dX k x dt = and that k is a function of temperature, but not a linear function Th erefore doubling the temper ature will not necessar ily double the reaction r ate, and therefore halve the cooking time.

P3-9 (b)

When you boil the po tato in water , the h eat transf er co efficient is mu ch larger , but the temp erature can on ly be 100°C.

When you bake th e potato , the h eat transf er co efficient is sm aller, but the temp erature can b e mor e than double th at of boiling w ater

P3-9 (c ) No solu tion w ill b e g iven

Stoichiom

To calculate the y ields of b iom ass, you mus t f irst balance the reaction equ ation by find ing th e coefficients

b , c, d , and e. This can be done w ith mass b alances on each elem ent involved in the reaction. Once all the coefficients are found, you can then calculate the y ield coefficien ts by simply assu ming the r eaction

proceeds to completion and calculating th e ending m ass of th e cells

P3-1 4 (a)

Apply mass b alance

For C 6 = 4 4c + e For O 6 + 2a = 1 2c + d + 2 e

For N b = 0 .86c For H 12 + 3b = 7.3 c + 2d

Also for C, 6(2/3) = 4 4c wh ich gives c = 0.909

Next w e solve for e using the other carbon balance

6 = 4 4 (0 909) + e

e = 2

We can solve for b us ing th e nitrogen b alance

b = 0 86 c = 0 86* (0 909)

b = 0.78

Next w e us e the hydrogen balance to solv e for d

12 + 3b = 7.3 c + 2d

12 + 3(0 78) = 7 3(0 909) + 2d

d = 3.85

Finally we solve for a using the oxygen balance

6 + 2a = 1 2c + d + 2e

6 + 2a = 1.2(0.909) + 3.85 + 2(2)

a = 1 .47

P3-1 4 (b)

Assume 1 mo le of gluco se (180 g) r eacts :

Yc/s= mass of cells / m ass of glucos e = mass of cells / 180 g

mass of cells = c*(mo lecular weight) = 0 909 mol* (91 34g /mol)

mass of cells = 83 12 g

Yc/s = 83 12 g / 180 g

Yc/s = 0.46

Yc/o2 = mas s of cells / m ass of O2

If we assum e 1 mole of g lucos e reacted , then 1.47 moles of O2 are n eeded and 83.12 g of cells are produced

mass of O2 = 1 47 mol * (32 g/mo l)

mass of O2 = 47 04 g

Yc/o2 = 83 12 g /47 04 g

Yc/o2 =1.77

P3-1 5 (a)

Isotherm al gas phase reaction

(2) For b atch sys tem, constant volum e

P3-1 6 (a)

Liquid phase reaction  assu me cons tant volum e Rate L aw (rev ersib le reaction):

To find the equilibr ium concen trations , subs titute the equilib rium conversion into the s tio chiom etr ic

Stoichiom etry :

r eaction in a cons tan t pres sure, batch r eactor

Given: Gas phas e r eaction A + B  8C in a b atch reactor f itted with a p iston such that

P3-2 0 No so lution w ill be giv en

CDP3-A

CDP3-B

Polanyi equation: E = C – α(- ΔHR)

We h ave to calcu late E for the reaction

CH3• + RBr  CH3 Br + R•

Given: ΔHR = - 6 kcal/mol

From th e giv en data table, we get

6.8 = C – α(17.5)

and 6 0 = C – α(20)

=> C = 12.4 KJ /mo l and α = 0.32

Using thes e values , and ΔHR = - 6 kcal/mol, w e get E = 10.4 8 KJ/mol

CDP3-C (a)

A  B

rA = kC A

The rate law t high er temp erature must:

1) Satisfy thermodynamics r elationships at equilibriu m, and

2) Redu ce to irrevers ible r ate law when the concentr ation of one or more of th e r eaction products is zero.

Rate law at low temperature: !

Also, We know, !

Rearranging, we get !

K C = C Be C Ae

C Ae " C Be K C = 0

!

!

rA = k A C A C B K C

# $ % & ' (

Also wh en CB = 0, it s atisf ies th e g iven rate law . H ence th e p roposed rate law is correct.

CDP3-C (b)

So, lets assum e r ate law as !

A + 2B  2D

Rate law at low temp eratur e: !

K C = C De 2 C AeC Be 2

rA = kC A 1 / 2C B

C AeC Be 2 C De 2 K C = 0

rA = k A C AeC Be 2 C De 2 K C

# $ % % & ' ( (

But it does not satisfy th e irrevers ible r ate law at low temp er atures Hence it is not correct

rA = k A C Ae 1 / 2C Be C De K C

# $ % % & ' ( (

Which satisfies the irrev ersib le rate law

Hence it is the requir ed rate law.

CDP3-C (c)

K C = C De C Ae 1 / 2C Be , ! !

A + B  C + D

rA ' = kPA PB 1 + K A PA + K B PB

We know,

Hence assume rate law as :

Irreversible r ate law : !

!

PB PA PC PD K P = 0

k PA PB PC PD K P

# $ % & ' (

1 + K A PA + K B PB + K C PC + K D PD

Which satisfies both the above m entioned conditions.

CDP3-D

CDP3-E

CDP3-F

CDP3-G

CDP3-I