Essential Maths Core for the Australian Curriculum 2ed 7 - final pages by cambridge_aused

TEXTBOOK ADVANCE COPY

March 2025

This textbook advance is provided as a sample for course preparation, planning and for use by teachers until the final products is available.

It should not be:

• made available in any other form

• uploaded to any website not affiliated to or authorised by Cambridge University Press & Assessment

• sold, reproduced or otherwise exploited for financial gain

• used in whole or in part to create a derivative work

• edited in any way (this includes the removal or modification of any branding, photographs or illustrations)

These advanced chapters have been provided for use by your school prior to publication of the textbook. The PDF supplied and all downloaded or printed excerpts must be destroyed once the textbook has been released.

For questions related to these instructions, please email copyright@cambridge.org

ShaftesburyRoad,CambridgeCB28EA,UnitedKingdom

OneLibertyPlaza,20thFloor,NewYork,NY10006,USA

477WilliamstownRoad,PortMelbourne,VIC3207,Australia

314–321,3rdFloor,Plot3,SplendorForum,JasolaDistrictCentre,NewDelhi–110025,India

103PenangRoad,#05–06/07,VisioncrestCommercial,Singapore238467

CambridgeUniversityPress&AssessmentisapartoftheUniversityofCambridge.

WesharetheUniversity’smissiontocontributetosocietythroughthepursuitofeducation,learningandresearchatthehighestinternational levelsofexcellence. www.cambridge.org

Firstedition©DavidGreenwood,BrynHumberstone,JustinRobinson,JennyGoodman,JenniferVaughanandStuartPalmer2021

Secondedition©DavidGreenwood,BrynHumberstone,JustinRobinson,JennyGoodman,JenniferVaughanandStuartPalmer2025

Thispublicationisincopyright.Subjecttostatutoryexceptionandtotheprovisionsofrelevantcollectivelicensingagreements, noreproductionofanypartmaytakeplacewithoutthewrittenpermissionofCambridgeUniversityPress&Assessment.

Firstpublished2021

Secondedition2025 2019181716151413121110987654321

CoverdesignbySardineDesign TypesetbydiacriTech

PrintedinChinabyC&COffsetPrintingCo.,Ltd.

AcataloguerecordforthisbookisavailablefromtheNationalLibraryofAustraliaat www.nla.gov.au

ISBN978-1-009-59233-8

Additionalresourcesforthispublicationatwww.cambridge.edu.au/GO

ReproductionandCommunicationforeducationalpurposes

TheAustralian CopyrightAct1968 (theAct)allowsamaximumofonechapteror10% ofthepagesofthispublication,whicheveristhe greater,tobereproducedand/orcommunicatedbyanyeducationalinstitutionforitseducationalpurposesprovidedthattheeducational institution(orthebodythatadministersit)hasgivenaremunerationnoticetoCopyrightAgencyLimited(CAL)undertheAct.

FordetailsoftheCALlicenceforeducationalinstitutionscontact:

CopyrightAgencyLimited Level12,66GoulburnStreet SydneyNSW2000

Telephone:(02)93947600

Facsimile:(02)93947601

Email:memberservices@copyright.com.au

ReproductionandCommunicationforotherpurposes

ExceptaspermittedundertheAct(forexampleafairdealingforthepurposesofstudy,research,criticismorreview)nopartofthis publicationmaybereproduced,storedinaretrievalsystem,communicatedortransmittedinanyformorbyanymeanswithoutpriorwritten permission.Allenquiriesshouldbemadetothepublisherattheaddressabove.

CambridgeUniversityPress&AssessmenthasnoresponsibilityforthepersistenceoraccuracyofURLsforexternalorthird-partyinternet websitesreferredtointhispublicationanddoesnotguaranteethatanycontentonsuchwebsitesis,orwillremain,accurateorappropriate. Informationregardingprices,traveltimetablesandotherfactualinformationgiveninthisworkiscorrectatthetimeofﬁrstprintingbut CambridgeUniversityPress&Assessmentdoesnotguaranteetheaccuracyofsuchinformationthereafter.

CambridgeUniversityPress&AssessmentacknowledgestheAboriginalandTorresStraitIslanderpeoplesofthisnation.Weacknowledgethe traditionalcustodiansofthelandsonwhichourcompanyislocatedandwhereweconductourbusiness.Wepayourrespectstoancestors andElders,pastandpresent.CambridgeUniversityPress&AssessmentiscommittedtohonouringAboriginalandTorresStraitIslander peoples’uniqueculturalandspiritualrelationshipstotheland,watersandseasandtheirrichcontributiontosociety.

4 Algebraictechniques

5A Decimalsandplacevalue CONSOLIDATING

5B Roundingdecimals

5C Additionandsubtractionofdecimals

5D Multiplyinganddividingbypowersof10

5E Multiplicationofdecimals

5F Divisionofdecimals

5G Connectingdecimalsandfractions

5H Connectingdecimalsandpercentages

5I Expressingproportionsusingdecimals, fractionsandpercentages

6A Integers CONSOLIDATING

6B Addingorsubtractingapositiveinteger

6C Addinganegativeinteger

6D Subtractinganegativeinteger

6E Substitutingintegers

6F TheCartesianplane

7B Adjacentandverticallyoppositeangles

7C Transversalsandparallellines

7D Classifyingandconstructingtriangles

7E Classifyingquadrilateralsandotherpolygons

7F Anglesumofatriangle

8A Collectingandclassifyingdata

8B Summarisingdatanumerically

8C Dotplotsandcolumngraphs

8D Linegraphs

8E Stem-and-leafplots

8F Describingchance CONSOLIDATING

8G Theoreticalprobability

8H Experimentalprobability

9E Equationswithfractions

9G Applicationsofequations

Warm-upquiz 564

10A Usingandconvertingmetriclengths CONSOLIDATING 565

10B Perimeter CONSOLIDATING 571

10C Circles, p andcircumference 577

10D Unitsofareaandtheareaofarectangle 584

10E Areaofparallelograms 590

10F Areaoftriangles 595

Progressquiz 601

10G Volumeofrectangularprisms 603

10H Volumeoftriangularprisms 608

10I Capacity CONSOLIDATING 614

10J Massandtemperature CONSOLIDATING 619

Maths@Work:Landscapegardener 624

Modelling 626

Technologyandcomputationalthinking 628

Puzzlesandgames 630

Chaptersummaryandchecklist 631

Chapterreview 635

Semesterreview2 640

AbouttheAuthors

DavidGreenwood istheHeadofMathematicsatTrinityGrammarSchoolinMelbourneand has30+ years’experiencemathematicsfromYear7to12.Heistheleadauthorfor theCambridgeEssentialseriesandhasauthoredmorethan80titlesfortheAustralian Curriculumandforthesyllabusesofthestatesandterritories.Hespecialisesinanalysing curriculumandthesequencingofcoursecontentforschoolmathematicscourses. Healsohasaninterestintheuseoftechnologyfortheteachingofmathematics.

BrynHumberstone graduatedfromtheUniversityofMelbournewithanHonoursdegreein PureMathematics,andhas20+ years’experienceteachingsecondaryschoolmathematics. HewasaHeadofMathematicsfrom2014–2024attwoindependentschoolsinVictoria. Brynispassionateaboutapplyingthescienceoflearningtoteachingandcurriculum design,tomaximisethechancesofstudentsuccess.

JustinRobinson isco-founderof TheWellbeingDistillery,anorganisationcommittedtoenergising, equippingandempoweringteachers.Heconsultswithschoolsgloballyontheﬁeldsof studentandeducatorwellbeing.Priortothis,Justinspent25yearsteachingmathematics, coveringalllevelsofsecondaryeducationincludingteachingVCE,IBandA-Levels.His drivingpassionwasengagingandchallengingstudentswithinasafelearningenvironment. JustinisanHonoraryFellowoftheUniversityofMelbourne’sGraduateSchoolofEducation.

JennyGoodman hastaughtinschoolsforover28yearsandiscurrentlyteachingataselective highschoolinSydney.Jennyhasaninterestintheimportanceofliteracyinmathematics education,andinteachingstudentsofdifferingabilitylevels.ShewasawardedtheJones MedalforeducationatSydneyUniversityandtheBourkePrizeforMathematics.Shehas writtenforCambridgeMATHSNSWandwasinvolvedintheSpectrumandSpectrumGoldseries.

JenniferVaughan hastaughtsecondarymathematicsforover30yearsinNewSouthWales, WesternAustralia,QueenslandandNewZealandandhastutoredandlecturedinmathematics atQueenslandUniversityofTechnology.Sheispassionateaboutprovidingstudentsofallability levelswithopportunitiestounderstandandtohavesuccessinusingmathematics.Shehas hadextensiveexperienceindevelopingresourcesthatmakemathematicalconceptsmore accessible;hence,facilitatingstudentconﬁdence,achievementandanenjoymentofmaths.

StuartPalmer wasbornandeducatedinNSW.Heisafullyqualiﬁedhighschoolmathematics teacherwithmorethan25years’experienceteachingstudentsfromallwalksoflifein avarietyofschools.HehasbeenHeadofMathematicsintwoschools.Heisverywell knownbyteachersthroughoutthestatefortheprofessionallearningworkshopshe delivers.StuartalsoassiststhousandsofYear12studentseveryyearastheyprepare fortheirHSCExaminations.AttheUniversityofSydney,Stuartspentmorethana decaderunningtutorialsforpre-servicemathematicsteachers.

Acknowledgements

Theauthorandpublisherwishtothankthefollowingsourcesforpermissiontoreproducematerial: Cover: © GettyImages/Westend61.

Images: © GettyImages/boggy22,Chapter1Opener/PeterDazeley,p.8/akova,p.9/agrobacter,p.11(1)/PeopleImages, p.11(2)/JoseLuisPelaezInc,p.13/PhotographtakenbyAlanHopps,p.15/feardaused,p.16/Flashpop,p.20/RichVintage, p.21/BusaPhotography,p.22/kevinjeon00,p.24(1)/Wirestock,p.24(2)/kampeepatisena,p.25/BRETTSTEVENS,p.29/Tero Vesalainen,p.31/OscarWong,p.37/LisaMareeWilliams,p.39/SolStock,p.40/JohnW.Banagan,p.42/AlistairBerg,Chapter2 Opener/KriangkraiThitimakorn,p.54/PhynartStudio,p.58(1)/yanikap,p.58(2)/MorsaImages,p.59/ROBERTBROOK/SCIENCE PHOTOLIBRARY,p.61/Flashpop,p.69/ROBERTBROOK/SCIENCEPHOTOLIBRARY,p.70(2)/DSGpro,p.73/k samurkas,p.75/ pixelfit,p.78(1)/baona,p.78(1)/ROBERTBROOK,p.82/VinhTran,p.85/FlavioCoelho,p.88/anusornnakdee,p.90/JohnM LundPhotographyInc,p.94/JoseLuisPelaezInc,p.106/AndriyOnufriyenko,p.112/StanislawPytel,p.113/Al1974ex,p.115/ MartinBarraud,p.117/RobertDaly,p.118/FangXiaNuo,Chapter3Opener/Westend61,p.135/SolStock,p.139/EyeEmMobile GmbH,p.144/Jackyenjoyphotography,p.145/filadendron,p.150/p saranya,p.153(1)/YinYang,p.153(2)/Maskot,p.168(2)/ HenrikSorensen,p.171/SallyAnscombe,p.174/LincolnBeddoe,p.177/PhotobyRafaElias,p.180/PhilBoorman,p.183(1)/ CharleneCollins,p.183(2)/JoosMind,p.184(1)/MartinPoole,p.184(2)/MoMoProductions,p.187/LukeStanton,p.188/ FedotovAnatoly,p.189/JungGetty,p.190/ElyseSpinner,p.192/ozgurdonmaz,p.193/Arctic-Images,p.194(1)/ molchanovdmitry,p.194(2)/FGTrade,p.197/ScottShymko,p.107/DharmendraYadav/500px,p.208/Yuri Arcurs,p.209/ FredFroese,Chapter4Opener/Imgorthand,p.223/PhotographcopyrightEricMeola,p.232(2)/sturti,p.233/DanielGrill, p.235(1)/Westend61,p.236/sihuo0860371,p.237/YuichiroChino,p.242/elenaleonova,p.247/sarayut oat,p.248/MAURO DALLAPOZZA,Chapter5Opener/PeopleImages,p.256/kasto80,p.261(1)/EyeEmMobileGmbH,p.262/FGTrade,p.265(1)/ TomMerton,p.265(3)/hatman12,p.266/HelenKing,p.273/ConnectImages,p.277(1)/stoncelli,p.277(2)/MontyRakusen, p.279/PMImages,p.282/sankai,p.283/kajakiki,p.284/DarrianTraynor/AFLPhotos,p.288/JacobsStockPhotographyLtd, p.295/KenKeifer,Chapter6Opener/AndreSchoenherr,p.322/DanielGrill,p.324/MassimoBorchi/AtlantidePhototravel, p.331/ZU 09,p.341/Maskot,p.346(1)/MichaelH,p.348/malerapaso,p.349/Woodkern,Chapter7Opener/MinaDeLaO, p.361/KarlHendon,p.369/SanghwanKim,p.371/MarioGuti,p.377/AchimThomae,p.384/ReinhardKrull,p.385/Douglas Rissing,p.394/jadaphoto,p.399/DianeMiller,p.403/Warchi,p.427/KittiBoonnitrod,p.436/MartinBarraud,p.438/Trevor Williams,Chapter8Opener/AdamGault,p.464(1)/TimGristPhotography,p.464(2)/SolStock,p.465/TetraImages-Rob Lewine,p.466/BlendImages-MikeKemp,p.469(1)/EricYang,p.476/MorsaImages,p.492(2)/adventtr,p.494/ItziarAio, p.500/TetraImages,p.503/skynesher,p.509/istetiana,p.516(2)/esemelwe,Chapter9Opener/FrancescoCartafotografo, p.532/PhotoAlto/MicheleConstantini,p.540/KanawaStudio,p.550/MattLincoln,p.553/GeraintRowlandPhotography, p.555/MoMoProductions,Chapter10Opener/AlexanderSpatari,p.565/puravida,p.570/lillisphotography,p.576/JoseA. BernatBacete,p.577/PAThompson,p.582/ElenaPopova,p.583/JohnerImages,p.599/ImagetakenbyMayteTorres,p.601/ MintImages,p.607/philly077,p.613/VickiSmith,p.614/manologuijarro,p.618/RundstedtB.Rovillos,p.619/StefaniaPelfini, LaWaziyaPhotography,p.622/kolderal,p.623/FrancescoBergamaschi,p.626/adandr,p.637.

Everyefforthasbeenmadetotraceandacknowledgecopyright.Thepublisherapologisesforanyaccidentalinfringementand welcomesinformationthatwouldredressthissituation.

© AustralianCurriculum,AssessmentandReportingAuthority(ACARA)2009topresent,unlessotherwiseindicated.Thismaterial wasaccessedfromtheACARAwebsite(www.acara.edu.au).ThematerialislicensedunderCCBY4.0(https://creativecommons. org/licenses/by/4.0/).ACARAdoesnotendorseanyproductthatusesACARAmaterialormakeanyrepresentationsastothe qualityofsuchproducts.Anyproductthatusesmaterialpublishedonthiswebsiteshouldnotbetakentobeafﬁliatedwith ACARAorhavethesponsorshiporapprovalofACARA.Itisuptoeachpersontomaketheirownassessmentoftheproduct.

Introduction

Thesecondeditionof EssentialMathematicsCOREfortheAustralianCurriculum hasbeensigniﬁcantlyrevisedandupdatedtosuit theteachingandlearningofVersion9.0oftheAustralianCurriculum.Manyoftheestablishedfeaturesoftheserieshavebeen retained,buttherehavebeensomesubstantialrevisions,improvementsandnewelementsintroducedforthiseditionacrossthe print,digitalandteacherresources.

Newcontentandsomerestructuring

Newcontenthasbeenaddedatallyearlevels.In Year7,thereisnewcontentonratiosandproportions,volumeoftriangular prisms,netsofsolidsandmeasurementrelatingtocircles.Allgeometrytopicsarenowcontainedinasinglechapter(Chapter7).In Year8,thereisnewcontentonorderofoperations,3D-coordinates,operationswithnegativefractions,areasofsectorsand compositeshapes,Pythagoras’theorem,inequalities,similarﬁgures,two-stepexperimentsandtreediagrams.For Year9,thereis newcontentonerrorsinmeasurement,inequalities,factorisation,samplingandproportion,quadraticsexpressionsandparabolas. In Year10,thereisnewcontentoncompositesolids,errorsinmeasurement,networksandlogarithmicscales.

Version9.0placesincreasedemphasison investigations and modelling,andthisiscoveredwithrevisedModellingactivitiesat theendofchaptersanddownloadableInvestigations.Therearealsomanynewelaborationscovering FirstNationsPeoples’ perspectives onmathematics,rangingacrossallsixcontentstrandsofthecurriculum.Thesearecoveredinasuiteofspecialised investigationsprovidedintheOnlineTeachingSuite.

Othernewfeatures

• Technologyandcomputationalthinking activitieshavebeenaddedtotheendofeverychaptertoaddressthecurriculum’s increasedfocusontheuseoftechnologyandtheunderstandingandapplicationofalgorithms.

• Targetedskillsheets –downloadableandprintable–havebeenwrittenforeverylessonintheseries,withtheintentionof providingadditionalpracticeforstudentswhoneedsupportatthebasicskillscoveredinthelesson,withquestionslinkedto workedexamplesinthebook.

• EditablePowerPointlessonsummaries arealsoprovidedforeachlessonintheseries,withtheintentionofsavingthetime ofteacherswhowerepreviouslycreatingthesethemselves.

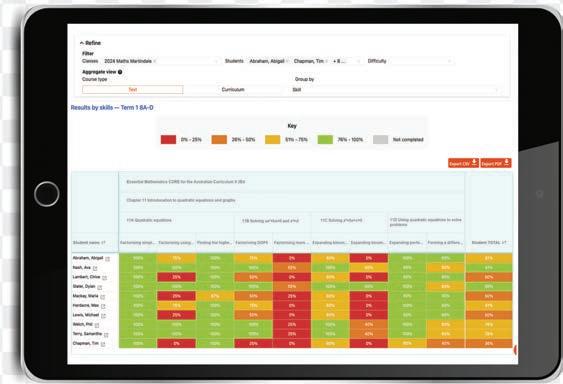
Diagnosticassessmenttool

Alsonewforthiseditionisaﬂexible,comprehensivediagnosticassessmenttool,availablethroughtheOnlineTeachingSuite.This tool,featuringaround10,000newquestions,allowsteacherstosetdiagnosticteststhatarecloselyalignedwiththetextbook content,viewstudentperformanceandgrowthviaarangeofreports,setfollow-upworkwithaviewtohelpingstudents improve,andexportdataasneeded.

Guidetotheworkingprograms

EssentialMathematicsCOREfortheAustralianCurriculum containsworkingprogramsthataresubtlyembeddedintheexercises. ThesuggestedworkingprogramsprovidetwopathwaysthroughthebooktoallowdifferentiationforBuildingandProgressing students.

EachexerciseisstructuredinsubsectionsthatmatchtheAustralianCurriculumproﬁciencystrands(withProblem-solvingand Reasoningcombinedintoonesectiontoreduceexerciselength),aswellas‘Goldstar’( ).Thequestions* suggestedforeach pathwayarelistedintwocolumnsatthetopofeachsubsection.

• Theleftcolumn(lightestshade)showsthequestionsintheBuildingworkingprogram.

• Therightcolumn(darkestshade)showsthequestionsintheProgressingworkingprogram.

Gradientswithinexercisesandproﬁciencystrands

Theworkingprogramsmakeuseoftwo gradientsthathavebeencarefullyintegrated intotheexercises.Agradientrunsthrough theoverallstructureofeachexercise–where there’sanincreasinglevelofsophistication requiredasastudentprogressesthrough theproficiencystrandsandthenontothe ‘GoldStar’question(s)–butalsowithineach proficiencystrand;thefirstfewquestions inFluencyareeasierthanthelastfew,for example,andthefirstfewProblem-solvingand reasoningquestionsareeasierthanthelastfew.

½):completehalfofthepartsfromquestion 10(a,c,e,.....orb,d,f,.....)

• 2–4(½):completehalfofthepartsofquestions2,3and4

• –:completenoneofthequestionsinthissection.

• 4(½),5:completehalfofthepartsofquestion4 andallpartsofquestion5

•

Guidetothisresource

PRINTTEXTBOOKFEATURES

1 NEW Newlessons: authoritativecoverageofnewtopicsintheAustralianCurriculum9.0intheformofnew,road-tested lessonsthroughouteachbook.

2 AustralianCurriculum: contentstrands,sub-strandsandcontentdescriptionsarelistedatthebeginningofthechapter(see theteachingprogramformoredetailedcurriculumdocuments)

3 Inthischapter: anoverviewofthechaptercontents

4 NEW Quickreference: Multiplication,primenumber,fractionwallanddivisibilityrulestablesatthebackofthebook

5 Chapterintroduction: setscontextforstudentsabouthowthetopicconnectswiththerealworldandthehistoryof mathematics

6 Warm-upquiz: aquizforstudentsonthepriorknowledgeandessentialskillsrequiredbeforebeginningeachchapter

7 Sectionslabelledtoaidplanning: Allnon-coresectionsarelabelledas‘Consolidating’(indicatingarevisionsection)or withagoldstar(indicatingatopicthatcouldbeconsideredchallenging)tohelpteachersdecideonthemostsuitablewayof approachingthecoursefortheirclassorforindividualstudents.

8 Learningintentions: setsoutwhatastudentwillbeexpectedtolearninthelesson

9 Lessonstarter: anactivity,whichcanoftenbedoneingroups,tostartthelesson

10 Keyideas: summarisestheknowledgeandskillsforthesection

11 Workedexamples: solutionsandexplanationsofeachlineofworking,alongwithadescriptionthatclearlydescribesthe mathematicscoveredbytheexample.Workedexamplesareplacedwithintheexercisesotheycanbereferencedquickly, witheachexamplefollowedbythequestionsthatdirectlyrelatetoit.

12 Nowyoutry: try-it-yourselfquestionsprovidedaftereveryworkedexampleinexactlythesamestyleastheworkedexample togivestudentsimmediatepractice

Workingprograms: differentiatedquestionsetsfortwoabilitylevelsinexercises

14 Puzzlesandgames: ineachchapterprovideproblem-solvingpracticeinthecontextofpuzzlesandgamesconnectedwith thetopic

15 Gentlestarttoexercises: theexercisebeginsatUnderstandingthenfluency,withthefirstquestionalwayslinkedtothe firstworkedexampleinthelesson

16 Chapterchecklist: achecklistofthelearningintentionsforthechapter,withexamplequestions

17 Chapterreviews: withshort-answer,multiple-choiceandextended-responsequestions;questionsthatare‘GoldStar’are clearlysignposted

18 Maths@Work: asetofextendedquestionsacrosstwopagesthatgivepracticeatapplyingthemathematicsofthechapter toreal-lifecontexts

19 NEW Technologyandcomputationalthinking activityineachchapteraddressesthecurriculum’sincreasedfocusonthe useofdifferentformsoftechnology,andtheunderstandingandimplementationofalgorithms

20 Modellingactivities: anactivityineachchaptergivesstudentstheopportunitytolearnandapplythemathematicalmodelling processtosolverealisticproblems

INTERACTIVETEXTBOOKFEATURES

21 NEW TargetedSkillsheets,oneforeachlesson,focusonasmallsetofrelatedFluency-styleskillsforstudentswhoneed extrasupport,withquestionslinkedtoworkedexamples

22 Workspaces: almosteverytextbookquestion–including allworking-out–canbecompletedinsidetheInteractive Textbookbyusingeitherastylus,akeyboardandsymbol palette,oruploadinganimageofthework.

23 Self-assessment: studentscanthenself-assesstheir ownworkandsendalertstotheteacher.Seethe Introductiononpagexformoreinformation.

24 Interactivequestiontabs canbeclickedonsothat onlyquestionsincludedinthatworkingprogramare shownonthescreen

25 HOTmathsresources: ahugecateredlibraryofwidgets, HOTsheetsandwalkthroughsseamlesslyblendedwith thedigitaltextbook

26 Desmosgraphingcalculator,scientiﬁccalculatorand geometrytoolarealwaysavailabletoopenwithinevery lesson

27 Scorcher: thepopularcompetitivegame

28 Workedexamplevideos: everyworkedexampleis linkedtoahigh-qualityvideodemonstration,supporting bothin-classlearningandtheﬂippedclassroom

29 Arevisedsetof differentiatedauto-marked practicequizzes perlessonwithsavedscores

30 Auto-markedmaths literacyactivitiesteststudents ontheirabilitytounderstandandusethekey mathematicallanguageusedinthechapter

31 Auto-markedpriorknowledgepre-test (the‘Warm-upquiz’oftheprintbook)fortestingtheknowledgethatstudents willneedbeforestartingthechapter

32 Auto-markedprogressquizzesandchapterreviewquestions inthechapterreviewscanbecompletedonline

DOWNLOADABLEPDFTEXTBOOK

33 InadditiontotheInteractiveTextbook,a PDFversionofthetextbook hasbeenretainedfortimeswhenuserscannotgo online.PDFsearchandcommentingtoolsareenabled.

ONLINETEACHINGSUITE

34 NEW DiagnosticAssessmentTool included withtheOnlineTeachingSuiteallowsforﬂexible diagnostictesting,reportingandrecommendations forfollow-upworktoassistyoutohelpyour studentstoimprove

35 NEW PowerPointlesson summariescontainthe mainelementsofeachlessoninaformthatcanbe annotatedandprojectedinfrontofclass

36 LearningManagementSystem withclass andstudentanalytics,includingreportsand communicationtools

37 Teacherviewofstudents’workand self-assessment allowstheteachertoseetheir class’sworkout,howstudentsintheclassassessed theirownwork,andany‘redﬂags’thattheclass hassubmittedtotheteacher

38 Powerfultestgenerator withahugebankof levelledquestionsaswellasready-madetests

39 Revampedtaskmanager allowsteachersto incorporatemanyoftheactivitiesandtoolslisted aboveintoteacher-controlledlearningpathways thatcanbebuiltforindividualstudents,groupsof studentsandwholeclasses

40 Worksheets,Skillanddrill,mathsliteracy worksheets,and twodifferentiatedchapter testsineverychapter,providedineditableWord documents

41 Moreprintableresources: allPre-testsand Progressquizzesareprovidedinprintableworksheet versions

1 Computationwith positiveintegers

Essentialmathematics:whycomputationwithpositive integersisimportant

Skilledworkersinthetechnical,construction,andserviceindustriesneedtoperformaccurate computationsandmakerealisticestimates.

Chefsusemultiplicationordivisionwhenscalingrecipesupordown;forexample,thewhole numberweightofglazedcherriesforfourweddingcakes = 4 × 360 g = 1440 g.

Alandscapegardenerusesdivisiontoﬁndhowmanybagsofmulchareneeded;forexample,the totalgardenareaisdividedbythenumberofsquaremetresthatonebagofmulchwillcover.

Anursecountsthenumberofheartbeatsinaperiodof 20 secondsandmultipliesbythreeto estimateapatient’sheartrateinbeatsperminute.

Rogainingisacompetitionusingmapskillstoﬁndcheckpointsinbushland.Competitorscount stepsandmentallycalculatedistancesrun,ascalculatorsarenotpermitted.

Itismostusefulwhenshoppingtomentallyestimatethetotalwholenumbercostofafewitems.

Inthischapter

1APlacevalue (Consolidating)

1BAddingandsubtracting positiveintegers

1CAlgorithmsforadditionand subtraction

1DMultiplyingsmallpositive integers

1EMultiplyinglargepositive integers

1FDividingpositiveintegers

1GEstimatingandrounding positiveintegers (Consolidating)

1HOrderofoperationswith positiveintegers

AustralianCurriculum9.0

NUMBER

Representnaturalnumbersinexpanded notationusingplacevalueandpowers of 10 (AC9M7N03)

Compare,orderandsolveproblems involvingadditionandsubtractionof integers(AC9M7N07)

Usemathematicalmodellingtosolve practicalproblemsinvolvingrational numbersandpercentages,including ﬁnancialcontexts;formulateproblems, choosingrepresentationsandefﬁcient calculationstrategies,usingdigitaltools asappropriate;interpretand communicatesolutionsintermsofthe situation,justifyingchoicesmadeabout therepresentation(AC9M7N09)

©ACARA

Onlineresources

Ahostofadditionalonlineresources areincludedaspartofyourInteractive Textbook,includingHOTmathscontent, videodemonstrationsofallworked examples,auto-markedquizzesand muchmore.

1 Writedownthelargernumberfromeachpairofnumbers. 9, 11 a 137, 129 b 99, 104 c 10102, 9870 d

2 Foreachofthefollowing,matchthesymbol(A, B, C or D)tothegivenword(a, b, c,and d). add a A subtract b

multiply c

3 Writeeachofthefollowingasnumbers.

ﬁfty-seven a onehundredandsixteen b twothousandandforty-four c eleventhousandandtwo d

4 Whichnumberis:

2 morethan 11? a 5 lessthan 42? b 1 lessthan 100? c

3 morethan 7997? d double 13? e halfof 56? f

5 Completethesepatterns,showingthenextfournumbers.

6 Howmanyequalgroupscan 48 bedividedintoifthesizeofeachgroupis:

7 Givetheresultforeachofthesesumsanddifferences.

8 Givetheresultforeachofthesemultiplicationsanddivisions. 5 × 6

9 Arrangethesenumbersfromsmallesttolargest.

37, 73, 58, 59, 62, 159 a 301, 103, 31, 310, 130 b 29143, 24913, 13429, 24319, 24931 c

10 Whatistheremainderwhenthesenumbersaredividedby 3? 12 a 10 b 37 c

1A 1A Placevalue

Learningintentions

CONSOLIDATING

• Tounderstandhowplacevalueworksinthedecimal(Hindu-Arabic)system.

• Tobeabletoidentifytheplacevalueofdigitsindifferentnumbers.

• Tobeabletowritebasicnumeralsinexpandedformtohighlightplacevalues.

• Tobeabletocomparetwopositiveintegersbyconsideringthedigitsineachposition.

Keyvocabulary: placevalue,digit,decimalsystem,Hindu-Arabicsystem,positiveinteger

Thedecimalsystemisthenumbersystemusedmostoftentoday.ItisalsocalledtheHindu-Arabicsystem. Itusesthedigits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.ThedecimalsystemoriginatedinancientIndiaabout 3000 BCE andspreadacrossEuropethroughArabictextsoverthenext 4000 years.

Lessonstarter:Writethelargestnumber

Writethelargestpossiblenumberusingthesedigits.Digitscannot berepeated.

Explainwhyyournumberisthelargestpossible.

Keyideas

Thesymbols 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 arecalled digits

AFrenchdocumentshowingthe historyoftheHindu-Arabicnumber system.

Thevalueofeachdigitdependsonitsplaceinthenumber. The placevalue ofthedigit 2 inthenumber 3254,forexample,is 200

3254 = 3000 + 200 + 50 + 4

Thebasicnumeral 3254 canbewritteninexpandedformas 3254 = 3 × 1000 + 2 × 100 + 5 × 10 + 4 × 1 orinexpandedformwithindexnotationas 3254 = 3 ×

Symbolsusedtocomparenumbersincludethefollowing. =(equalto) 1 + 3 = 4 or 10−7 = 3

¢ (notequalto) 1 + 3 ¢ 5 or 11 + 38 ¢ 50

> (greaterthan) 5 > 4 or 100 > 37

Å (greaterthanorequalto) 5 Å 4 or 4 Å 4

< (lessthan) 4 < 5 or 13 < 26

Ä (lessthanorequalto) 4 Ä 5 or 4 Ä 4

¥ (approximatelyequalto) 4.02 ¥ 4 or 8997 ¥ 9000

A positiveinteger isawholenumber(greaterthanzero);e.g. 1, 2, 3,...areallpositiveintegers.

Exercise1A

Und er stand ing

1 Forthenumber 5207,writedownwhichdigitisinthe:

Q1Hint:Thetendigitsused inournumbersystemare 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. tensplace a thousandsplace b hundredsplace c onesplace d

2 Writedownthesenumbersusingdigits. forty-six a twohundredandsixty-three b seventhousand,fourhundredandtwenty-one c thirty-sixthousandandﬁfteen d

3 Whichsymbol(A, B, C, D, E or F)matchesthegivenwords(a, b, c, d, e and f)? notequalto a = A lessthan b ¢ B greaterthanorequalto c > C equalto d Å D greaterthan e < E lessthanorequalto f Ä F Fluency

Example1Findingplacevalue

Writedowntheplacevalueofthedigit 4 inthesenumbers. 437 a 1043 b

Solution

a 4 × 100 = 400

b 4 × 10 = 40

Explanation

The 4 hasvalue 4 × 100

The 3 hasvalue 3 × 10

The 7 hasvalue 7 × 1

The 1 hasvalue 1 × 1000

The 0 hasvalue 0 × 100

The 4 hasvalue 4 × 10

The 3 hasvalue 3 × 1

Nowyoutry

Writedowntheplacevalueofthedigit 6 inthesenumbers. 162 a 4628 b

4 Writedowntheplacevalueofthedigit 7 inthesenumbers.

Q4Hint:Writeyouransweras 7, 70, 700, 7000 or 70000 37 a

5 Writedowntheplacevalueofthedigit 3 inthesenumbers.

Example2Writingnumbersinexpandedform

Write 472 inexpandedform.

Write 472 inexpandedformwithindexnotation. b

Solution

a 472 = 4 × 100 + 7 × 10 + 2 × 1

b 472 = 4 ×

Nowyoutry

Write 356 inexpandedform. a

Explanation

Writeeachdigitseparatelyandmultiplyby 100 forthehundredsdigit, 10 forthetensdigit and 1 fortheunitsdigit.

Firstwritethenumberinexpandedform.

Thennotethat 100 = 102 , 10 = 101

Write 356 inexpandedformwithindexnotation. b

6 Writethefollowingnumbersinexpandedform.

7 Writethefollowingnumbersinexpandedformwithindexnotation.

8 Statewhethereachofthesestatementsistrueorfalse.

5 > 4 a

Q8Hint: < lessthan Ä lessthanorequalto > greaterthan Å greaterthanorequalto = equalto ¢ notequalto l

Problem-solving and reasoning

Example3Arrangingnumbers

Arrangethesenumbersfromsmallesttolargest.

29, 36, 18, 132, 1001, 99, 592, 123, 952

Solution

18, 29, 36, 99, 123, 132, 592, 952, 1001

Nowyoutry

Arrangethesenumbersfromsmallesttolargest.

37, 102, 117, 9001, 324, 9, 312, 8413, 799

Explanation

9,109(½),10,11

Thesmallesttwo-digitnumberhasthesmallest numberinthetenscolumn. Thenchoosethenextsmallesttwo-digit, andsoon,beforemovingontothree-digitand four-digitnumbers.

9 Arrangethesenumbersfromsmallesttolargest.

55, 45, 54, 44 a

b 23, 951, 136, 4 c

d 12345, 54321, 34512, 31254 e

, 29, 92, 927,

10 Inthefollowingquestions,digitscannotbeusedmorethanonce,andallthegivendigitsmustbe used.Donotuseadecimalpoint.

a Writethelargestpossiblenumberusingthedigits 2, 7 and 8

b Writethesmallestpossiblenumberusingthedigits 9, 1, 3, 6 and 4

11 Howmanynumberscanbemadeusingthegivendigits?Digitsarenotallowedtobeusedmorethan onceandallthegivendigitsmustbeused. 2, 8 and 9 a 1, 6 and 7 b 2, 5, 6 and 7 c

Largenumbers

12 Thenamesoflargenumbersdependonthenumberofdigitsgroupedintothrees.Forexample, 1000 is 1 thousand, 1000000 is 1 millionand 1000000000 is 1 billion.

a Writethesenumbersusingdigits.

7 thousand i 46 thousand ii 712 thousand iii 5 million iv 44 million v 6 billion vi 437 billion vii 15 trillion viii

b Researchthenumber 1 googol andwriteasentenceexplaining whatitis.

1B 1B Addingandsubtractingpositiveintegers

Learningintentions

• Tounderstandthatnumberscanbeaddedinanyorder,butthatforsubtractionorderdoesmatter.

• Tobeabletousethementalstrategiespartitioning,compensatinganddoubling/halvingtocalculateasumor differenceofpositiveintegersmentally.

Keyvocabulary: partitioning,compensating,mentalstrategy

Theprocessofﬁndingthetotalvalueoftwoormore numbersiscalledaddition.Thewords‘plus’,‘add’and‘sum’ arealsousedtodescribeaddition.

Theprocessforﬁndingthedifferencebetweentwo numbersiscalledsubtraction.Thewords‘minus’,‘subtract’ and‘takeaway’arealsousedtodescribesubtraction.

Lessonstarter:Yourmentalstrategy

Manyproblemsthatinvolveadditionandsubtractioncanbe solvedmentallywithouttheuseofacalculatororwritten working.

Explainyourmentalstrategyforworkingouttheanswerto theseproblems.

132 + 245 • 99 + 35 • 73−41 •

Keyideas

Thesymbol + isusedtoshowadditionorﬁndasum.

Forexample: 4 + 3 = 7

765 +3 4 8 3

• Notethattheorderdoes not matterwithaddition.

Forexample: 5 + 2 = 2 + 5 and 21 + 12 = 12 + 21

Thesymbol isusedtoshowsubtractionorﬁndadifference.

Forexample: 7−2 = 5

76 2 5 8 43

• Notethattheorder does matterwithsubtraction.

Forexample: 5−2 ¢ 2−5 and 21−12 ¢ 12−21

Mentaladditionandsubtractioncanbedoneusingdifferentstrategies.

• Partitioning (Groupingdigitsinthesameposition)

171 + 23 = 194

428−114 = 314

• Compensating (Makinga 10, 100 etc.andthenadjustingorcompensatingbyadding orsubtracting)

46 + 9 = 46 + 10−1

= 55

138−99 = 138 −100 + 1 = 39

Youcanﬁndtheheightdifferenceoftwopeople bysubtractingtheshorterperson’sheightfrom thetallerperson’sheight.

Exercise1B

Und er stand ing

1a Listthreewordsthattellyouwhentouse addition

b Listthreewordsthattellyouwhentouse subtraction

2 Writethenumberwhichis:

2 morethan 5 a 3 morethan 7 b

58 morethan 11 c 5 lessthan 9 d

7 lessthan 19 e 137 lessthan 157 f

3a Addtoﬁndthesumofthesepairsofnumbers.

2 and 6 i 19 and 8 ii 62 and 70 iii

Q1Hint:Choosefromthesewords: minus,add,sum,subtract,plus, takeaway

b Subtract(takeaway)toﬁndthedifferencebetweenthesepairsofnumbers. 11 and 5 i 29 and 13 ii 101 and 93 iii

4 Givetheresultforeachoftheseproblems.

7 plus 11 a 22 minus 3 b thesumof 11 and 21 c 128 add 12 d 36 takeaway 15 e thedifferencebetween 13 and 4 f Fluency

Example4Mentaladditionandsubtraction

Usethesuggestedstrategytomentallyworkouttheanswer.

132 + 156 (partitioning) a 429−203 (partitioning) b 25 + 19 (compensating) c 56−18 (compensating) d

Solution Explanation

a 132 + 156 = 288

100 + 30 + 2 Groupthehundreds, 100 + 50 + 6

Nowyoutry

Usethesuggestedstrategytomentallyworkouttheanswer. 423 + 236 (partitioning) a 758−321 (partitioning) b 46 + 29 (compensating) c 134−28 (compensating) d

5 Mentallyﬁndtheanswerstothesesums.Hint:Usethe partitioningstrategy.

Q5Hint:Workoutthe answerbyadding theones,thenthe tens,andsoon.

6 Mentallyﬁndtheanswerstothesedifferences.Hint:Usethepartitioningstrategy. 29−18 a

b 94−43 c 249−137 d

7 Mentallyﬁndtheanswerstothesesums.Hint:Usethe compensatingstrategy.

Q7Hint:Roundoneofthenumbersto thenearestten,thencompensateby addingorsubtractingthedifference.

+ 52 f

b 19 + 76 c 18 + 115 d 31 + 136 e

8 Mentallyﬁndtheanswerstothesedifferences.Hint:Usethecompensatingstrategy. 35−11 a 45−19 b 156−48 c 244−22 d 376−59 e 5216−199 f

Problem-solving and reasoning

9 Maryhas $101 inherpiggybank.Shetakesout $22 tobuy ajumper.Howmuchmoneyremainsinherpiggybank?

9–12 11–15

10 Garyworked 7 hoursonMonday, 5 hoursonTuesday, 13 hoursonWednesday, 11 hoursonThursday and 2 hoursonFriday.WhatisthetotalnumberofhoursthatGaryworkedduringtheweek?

11 Inabattinginnings,Philhit 126 runsandMariohit 19 runs.How manymorerunsdidPhilhitcomparedtoMario?

12 Mentallyﬁndtheanswerstothesemixedproblems.

13 Matthas 36 cardsandAndyhas 35 morecardsthanMatt. HowmanycardsdoesAndyhave? a Iftheycombinetheircards,howmanydotheyhaveintotal? b

14 Arethesestatementstrueorfalse?

15 Completethesenumbersentences.(Theletters a, b and c representnumbers.)

16 Amagicsquarehaseveryrow,columnandmaindiagonaladdingtothesamenumber,calledthemagic sum.Forexample,thismagicsquarehasamagicsumof 15

Findthemagicsumsforthesesquares,thenﬁllinthemissingnumbers.

1C 1C Algorithmsforadditionandsubtraction

Learningintentions

• Tobeabletoapplytheadditionalgorithmto ndthesumofpositiveintegers.

• Tobeabletoapplythesubtractionalgorithmto ndthedifferenceofpositiveintegers.

Keyvocabulary: borrow,carry,algorithm,placevalue

Toaddorsubtractlargernumberswecanuseastep-by-stepprocesscalledanalgorithm. Addingcaninvolvecarryinga‘one’tothenextcolumn,whilesubtractingcaninvolveborrowinga‘one’ fromthenextcolumn.

Theadditionalgorithminvolvescarryingthe’one’tothenext column.

Lessonstarter:Themissingdigits

Discusswhatdigitsshouldgointheemptyboxes.Givereasonsforyouranswers.

Keyideas

Toaddlargernumbers:

• Arrangethenumbersvertically(aboveeachother)sothatthedigits withsimilar placevalue areinthesamecolumn.

• Adddigitsinthesamecolumn,startingontheright.

• Ifthedigitsaddtomorethan 9, carry the 1 tothenextcolumn.

Tosubtractlargernumbers:

• Arrangethenumbersverticallysothatthedigitswithsimilarplace valueareinthesamecolumn.

• Subtractdigitsinthesamecolumntop-down,startingontheright.

• Ifthedigitssubtracttolessthan 0, borrow a 1 fromthenextcolumn toformanextra 10.

Exercise1C

1 Mentallyﬁndtheresultstothesesimplesums.

2 Mentallyﬁndtheresultstothesesimpledifferences.

3 Whatisthemissingdigitintheseproblems?

Example5Addinglargernumbers

Givetheresultforeachofthesesums.

Addthedigitsvertically. 6 + 6 = 12,socarrythe 1 tothetenscolumn.

b 14139 + 172 611 9 + 2 = 11,socarrya 1 tothetenscolumn. 1 + 3 + 7 = 11,socarrya 1 tothehundreds column.

Nowyoutry

Givetheresultforeachofthesesums.

4 Givetheresultforeachofthesesums.

5 Givetheresultforeachofthesesums.

Example6Subtractinglargernumbers

Givetheresultforeachofthesedifferences.

a 6

b 4 ✁ 511 ✁ 2 16 −138 388

Givetheresultforeachofthesedifferences.

6 Findtheanswerstothesedifferences.

7 Findtheanswertothesedifferences.

Q5Hint:Youwillneedtocarrythe ‘one’twiceinthesequestions.

Borrow 1 from 7 tomake 14−5 = 9

Thensubtract 1 from 6 (not 7).

Borrow 1 from 2 tomake 16−8 = 8.

Borrow 1 from 5 tomake 11−3 = 8 4−1 = 3.

Q6Hint:Forparts c to h,youwill needtoborrowa‘one’fromthe tenscolumn.

Q7Hint:Youwillneedtoborrow

Problem-solving and reasoning

8 FarmerGreenowns 287 sheep,FarmerBrownowns 526 sheep andFarmerGreyowns 1041 sheep.Howmanysheeparethere intotal?

9 Acar’sodometershows 12138 kilometresatthestartofajourneyand 12714 kilometresattheendof thejourney.Howfarwasthejourney?

10 Givetheresultforeachofthesesums.

11 Findthemissingdigitsinthesesumsanddifferences.

12a Whatarethemissingdigitsinthissum? 2 3 + 421

b Explainwhythereismorethanonepossiblesetofmissingdigitsinthesumabove.Givesome examples.

13 Completethesemagicsquares.Rememberthatinamagicsquare,eachrow,columnanddiagonalhas thesamesum.

1D 1D Multiplyingsmallpositiveintegers

Learningintentions

• Tounderstandthecommutativeandassociativelawsformultiplication.

• Tobeabletousementalstrategiesto ndproducts.

• Tobeabletoapplythemultiplicationalgorithmto ndtheproductofasingle-digitnumberbyapositiveinteger.

Keyvocabulary: product,commutativelaw,associativelaw,distributivelaw,algorithm

Themultiplicationoftwonumbersrepresentsarepeatedaddition.Forexample, 4 × 2 couldbethoughtof as 4 groupsof 2 or 2 + 2 + 2 + 2,or 4 × 2 couldbethoughtofas 2 groupsof 4 or 2 × 4 or 4 + 4

× 2

Lessonstarter:Museumtickets

Yourteacherpurchases 21 ticketsat $9 eachforaclassexcursiontothemuseum.Youneedtoworkout thetotalcost.

Lookatthefollowingstrategies.Doanyofthemgivethecorrectanswer?

• 21 × 9 isthesameas 20 × 10,sotheansweris $200

• 21 × 9 isthesameas 21 × 10−1,sotheansweris 210−1 = $209

• 21 × 9 isthesameas 20 × 9 + 1,sotheansweris 180 + 1 = $181

• 21 × 9 isthesameas 21 × 10−21,sotheansweris 210−21 = $189

• 21 × 9 isthesameas 20 × 9 + 9,sotheansweris 180 + 9 = $189

Keyideas

Findingthe product oftwonumbersinvolvesmultiplication. Wesay‘theproductof 2 and 3 is 6’.

a × b = b × a

• Theorderdoes not matterwhenyoumultiplynumbers.Thisisthe commutativelaw Forexample: 2 × 3 = 3 × 2 5 × 11 = 11 × 5

a × (b × c) = (a × b) × c

• Theresultofaddingormultiplyingthreeormorenumbersdoesnotdependonhowtheyare grouped.Thisisthe associativelaw.Forexample: (2 × 3) × 4 = 2 × (3 × 4)

92 4 × 3 = 12 4 × 2 + 1 = 9

Mentalstrategiesformultiplicationinclude:

• Knowingyourmultiplicationtablesoffbyheart.Forexample: 9 × 7 = 63 12 × 3 = 36

• Changingtheorder.Forexample:

15 × 3 = 3 × 15 (3 groupsof 15) = 45

5 × 13 × 2 = 5 × 2 × 13 = 10 × 13 = 130

• Usingthe distributivelaw bymakinga 10, 100 etc.andthenadjustingbyaddingor subtracting.Thedistributivelawmeansthataddingnumbersandthenmultiplyingthetotal givesthesameanswerasmultiplyingeachnumberﬁrstandthenaddingtheproducts.For example:

6 × 21 = 120 +6 = 126 6 × 206 × 1 7 × 18 = 14014 = 126 7 × 207 × 2

• Usingthedoublingandhalvingstrategybydoublingonenumberandhalvingtheother.

5 × 7 × 4 = 10 × 7 × 2 = 70 × 2 = 140 Double the 5Halve the 4

Exercise1D

Und er stand ing

1 Answertrueorfalse. Theproductof 4 and 7 is 21 a

4 × 31 = 4 × 30 + 4 ×

2 Writethemissingnumber.

3 Useyourknowledgeofthemultiplicationtablestowritetheanswer.

Fluency

Example7Usingmentalstrategiesformultiplication

Useamentalstrategytoﬁnd: 3 × 13 a 4 × 19 b 5 × 24 c

Solution

Explanation

a 3 × 13 = 30 + 9 = 39 3 × 13 = 3 × 10 + 3 × 3

Thedistributivelawisbeingused.

b 4 × 19 = 80−4 = 76 4 × 19 = 4 × 20−4 × 1

Thedistributivelawisbeingused.

c 5 × 24 = 10 × 12 = 120 Thedoublingandhalvingstrategyisbeingused.

Nowyoutry

Useamentalstrategytoﬁnd: 5 × 41 a 7 × 19 b 5 × 16 c

4 Findtheresultstotheseproductsmentally.Checkyouranswerswithyourcalculator.

Q4Hint:Forpart a,workout 5 × 20 andthenadd 5 × 1

5 Findtheanswerstotheseproductsmentally.

Q5Hint:Forpart a,workout 3 × 20 andthensubtract 3 × 1 3 × 19 a 2 × 19 b 2 × 29 c 4 × 29 d 5 × 18 e 7 × 18 f 3 × 39 g 4 × 49 h

6 Findtheanswerstotheseproductsmentally.

Q6Hint:Doubleone numberandhalve theother.So 5 × 14 = 10 × 7 = 70

Example8Multiplicationshowingworking

Givetheresultforeachoftheseproducts.

31 × 4

Nowyoutry

Givetheresultofeachoftheseproducts.

7 Givetheresultofeachoftheseproducts,showingworking.

8 Whatisthemissingdigitintheseproducts?

9 Eightticketscosting $33 eacharepurchasedforaconcert.Whatisthetotalcostofthetickets?

10 Acircularracetrackis 240 metreslongandRoryrunssevenlaps.HowfardoesRoryrunintotal?

11 ReggieandAngelocombinetheirpacksofcards.Reggiehasﬁvesetsof 13 cardsandAngelohasthree setsof 17 cards.Howmanycardsarethereintotal?

12 Classifythesestatementsastrueorfalse.

Missingdigits

13 Findthemissingdigitsintheseproducts.

14 Howmanydifferentwayscanthetwospacesbeﬁlledinthisproblem?Explainyouranswer.

1E 1E Multiplyinglargepositiveintegers

Learningintentions

• Tobeabletomultiplybyapoweroften.

• Tobeabletoapplythemultiplicationalgorithmto ndtheproductofanytwopositiveintegers.

Keyvocabulary: product,algorithm,placevalue

Therearemanysituationsthatrequirethemultiplicationoflargenumbers.Forexample,ﬁndingthetotal amountmadefromselling 40000 ticketsat $23 each.Anotherexampleisﬁndingtheareaofarectangular parkwithlengthandwidthdimensionsof 65 metresby 122 metres.Doingsuchcalculationsbyhandrequires anumberofsteps.

Theareaofarectangular-shapedparkcanbecalculatedby multiplyingthepark’slengthbyitswidth.

Lessonstarter:Spottheerrors

Therearethreetypesoferrorsintheworkingshownforthisproblem.Findtheerrorsanddescribethem.

Keyideas

Whenmultiplyingby 10, 100, 1000, 10000 etc.eachdigitmovestotheleftbythenumberofzeros.

2 × 100 = 20041 × 10 = 410279 × 1000 = 279000

Astrategyformultiplyingbymultiplesof 10, 100 etc.istoﬁrstmultiplybythenumberwithout thezerosthenaddthezerostotheanswerlater.

Forexample: 21 × 3000 = 21 × 3 × 1000 = 63 × 1000 = 63000

Tomultiplylargenumbers,dividetheproblemintosmallerproductsandthenaddthetotals.

37 × 12

× 14

37 × 2

× 10

+ 74

× 4

× 10

Exercise1E

Und er stand ing

1 Writethemissingnumber: 10, 100 or 1000 35 × = 350 a 21 × = 2100 b

2 Answertrueorfalse.

6 × 200 = 6 × 2 × 100 a

9 × 3000 = 9 × 3 × 100 c

3 Whichofthefollowingisthecorrectset-upfor 23 × 11?

× =

= 2130 d

Example9Multiplyinglargenumbers

Givetheresultforeachoftheseproducts.

37 × 100 a 21 × 50 b 87 × 13 c

Solution

a 37 × 100 = 3700

b 21 × 50 = 21 × 5 × 10 = 105 × 10 = 1050

c 87 × 13 261

Explanation

Movethe 3 andthe 7 twoplacestotheleftand addtwozeros.

Firstmultiplyby 5,thenmultiplyby 10 21 × 5 105

Firstmultiply 87 × 3 Thenmultiply 87 × 10. Addtheresultstogivetheanswer.

Nowyoutry

Givetheresultforeachoftheseproducts. 53 × 100 a 32 × 40 b 74 × 17 c

4 Givetheresultofeachoftheseproducts.

4 × 100 a

5 Findtheseproducts.

× 20 c

× 30 b

Q5Hint:Firstmultiplyby thesinglenon-zerodigit, thenwritethezeros: 12 × 20 = 12 × 2 × 10 12 × 20 a

6 Findtheseproducts.

Problem-solving and reasoning

7 Mandybuys 28 ticketsat $15 each.Whatisthetotalcostofthetickets?

(½),108,9(½),11,12

9 Findtheanswertoeachofthefollowingproducts(showyourworking).

10 Waldobuys 215 metresofpipeat $28 permetre.Whatisthetotalcostofpiping?

11 Howmanysecondsarethereinoneday?

Q11Hint:Thereare 60 seconds inaminute.

12 Ifbothnumbersinamultiplicationproblemhaveatleastthreedigits,thenmorestepsneedtobe shown.Findtheseproducts.

13 Findthemissingdigitsintheseproducts.

1F 1F Dividingpositiveintegers

Learningintentions

• Toknowthatadivisionoftwonumberscanresultinaquotientandaremainder,andtheresultcanbewrittenasa mixednumberifthereisaremainder.

• Tobeabletousementalstrategiesto ndquotients.

• Tobeabletoapplytheshortdivisionalgorithmtodividepositiveintegers.

Keyvocabulary: quotient,dividend,divisor,remainder

Divisionisusedtoﬁndthenumberofequalgroupsfromagiventotal.Dividing 20 applesamongﬁve peopleordividing $10000 betweenthreebankaccountsareexamplesofwhendivisioncanbeused.

Lessonstarter:Arrangingcounters

Atotalof 24 counterssitonatable.Usingpositiveintegers,inhowmanywayscanthecountersbedivided intoequal-sizedgroupswithnocountersleftover?

• Isitalsopossibletodividethecountersintoequal-sizedgroupsbutwithtwo countersleftover?

• Ifﬁvecountersaretoremain,howmanyequal-sizedgroupscanbeformed andwhy?

Keyideas

Thenumberofequal-sizedgroupsmadebydividingiscalledthe quotient

Thetotalbeingdividediscalledthe dividend.Thesizeoftheequalgroupsiscalledthe divisor. Anyamountremainingafterdivisionintoequal-sizedgroupsiscalledthe remainder 7 ÷ 3 = 2 and 1 remainder

total being divided (dividend) size of equal groups (divisor) quotient

Theorder does matterwhenyoudividenumbers.Youcannot swapnumbersinadivisiontomakethecalculationeasier.Forexample:

6 ÷ 3 ¢ 3 ÷ 6 (10 ÷ 5) ÷ 2 ¢ 10 ÷ (5 ÷ 2)

Useshortdivisiontoworkwithlargernumbers.

• Startbydividingthedivisorintotheﬁrst(left)digit,thencarryanyremainder. Thisexampleshowsthat 413 ÷ 3 = 137 and 2 remainder.

4 ÷ 3 = 1 and 1 rem. 11 ÷ 3 = 3 and 2 rem. 23 ÷ 3 = 7 and 2 rem. ) 3413 137 1 2

So 413 ÷ 3 = 137 and 2 remainder = 137 2 3

Exercise1F

Und er stand ing

1 Findtheremainderwhen 24 isdividedby:

Q1Hint:Theremaindercan bezero.

2 Writethenumberthatismissinginthesestatements.

8 ÷ 2 = 4 isthesameas 4 × ? = 8 a

36 ÷ 12 = 3 isthesameas ? × 12 = 36 b

42 ÷ ? = 6 isthesameas 6 × 7 = 42 c

72 ÷ 6 = ? isthesameas 12 × 6 = 72 d

3 Considerthedivision 83 ÷ 7 = 11 and 6 leftover.Whichnumberis: theremainder a thequotient b thedivisor c thedividend d

Fluency

Example10Usingmentalstrategiesfordivision

Useamentalstrategytoﬁndtheanswer.

(Useyourknowledgefrommultiplicationtables.)

÷ 3 =

Nowyoutry

(Halvebothnumbersrepeatedly.)

Useamentalstrategytoﬁndtheanswer.

4 Useyourknowledgeofmultiplicationtablestoﬁndthequotient.Checkwithacalculator.

5 Findtheanswertotheseusingamentalstrategy.

6 Findtheanswerstotheseusingamentalstrategy.

7 Findtheanswerstotheseusingamentalstrategy.

Q6Hint:Forpart a,remember that 90 ÷ 3 = 30.

Q7Hint:Halvebothnumbers, sincetheyarebotheven.So,

8 Writetheanswerstothesedivisions,whichinvolve 0sand 1s.

Example11Usingshortdivision

Useshortdivisiontoﬁndthequotientandremainder.Thenwritetheresultusingamixednumeral.

Nowyoutry

Useshortdivisiontoﬁndthequotientandremainder.Thenwritetheresultusingamixednumeral. 4 ) 89 a 6 ) 237 b

9 Usetheshortdivisionalgorithmtoﬁndthequotientandremainder.Thenwritetheresultusinga mixednumeral. 3 ) 71 a

Problem-solving and reasoning

10 Writethemissingdigitineachofthesedivisions.

)

11 If 117 foodpacksaredividedequallyamongninefamilies,howmanypacks doeseachfamilyreceive?

12 SpringFreshCompanysellsmineralwaterinpacksofsixbottles. Howmanypacksarethereinatruckcontaining 744 bottles?

Q12Hint:Workout 6 ) 744 13

Astraightfencehastwoendposts.Italsohasotherpoststhatare dividedevenlyalongthefence 4 metresapart.Ifthefenceistobe 264 metreslong,howmanypostsareneeded,includingtheendposts?

14 FriendlyTaxiscantakeuptofourpassengerseach.Howmanytaxisare requiredtotransport 59 people?

15 Piesarepurchasedwholesaleatthreefor $4.Howmuchwillitcostto purchase 153 pies?

Q13Hint:First,considerhow manypostsareneededfor afence 12 metresin length.

16 Shortdivisioncanalsobeusedtodividebynumberswithmorethanonedigit. e.g. 215 ÷ 12 = 17 and 11 remainder.

Usetheshortdivisionalgorithmtoﬁndthequotientandremainder.

17 Inthissquare,everyrow,columnanddiagonalhasaproductof 6720.Findthemissingnumbers.

1 1A Writedowntheplacevalueofthedigit 5 inthesenumbers. 356 a 5103 b 857412 c

2 1A Howmanynumberscanbemadeusingthegivendigits?Digitsarenotallowedtobeused morethanonceandalldigitsmustbeused.

4, 6 and 8 a 1, 2, 3 and 9 b

3 1B Mentallyﬁndtheanswerstotheseproblems.

146 + 332 a 754−531 b 85−19 c 21 + 49−28 d

4 1B Arethesestatementstrue(T)orfalse(F)?

23−17 < 8 a 60−18 + 11 > 50 b

5 1C Givetheresultforeachofthesesumsanddifferences.

6 1D Findtheanswerstotheseproductsmentally. 6

7 1D Givetheresultforeachoftheseproducts.

8 1E Givetheresultforeachoftheseproducts.

1E Jackpurchases 15 basketballticketsat $21 each.Whatisthetotalcostofthetickets?

10 1F Findtheanswertotheseusingamentalstrategy.

11 1F Usetheshortdivisionalgorithmtoﬁndthequotientandremainder.

1G 1G Estimatingandrounding positiveintegers

CONSOLIDATING

Learningintentions

• Tounderstandthatinsomepracticalsituations,anestimateorapproximationisacceptable.

• Tobeabletoroundnumberstoadegreeofaccuracy(e.g.tothenearest 100).

• Tobeabletoestimatenumericalanswerstoarithmeticquestionsbyroundingeachnumberinthequestion.

Keyvocabulary: estimate,approximation,rounding

Often,agoodestimateisenoughtoansweraquestionanditisnotnecessarytoﬁndanexactanswer. Insuchcasesweuseroundingtohelp.Forexample,theapproximatetotalcostof 18 truckloadsofsoilat $54 perloadcouldbeestimatedas 20 × 50 = 1000,sothecostisabout $1000

Lessonstarter:Countingcrowds

Hereisaphotoofacrowdatasportingevent.Describehowyoumight estimatethenumberofpeopleinthephoto.Whatisyouranswer?How differentisyouranswerfromthoseofothersinyourclass?

Howwouldyouestimatethe numberofpeopleinthiscrowd?

Keyideas

An estimate isaninformedguess,an approximation isavalueclosetotherealvalue,and rounding involvesapproximatinganumbertoaspeciﬁedplacevalue.

Estimatesorapproximationscanbefoundbyroundingnumberstothenearest 10,

• Ifthenextdigitis 0, 1, 2, 3 or 4,thenrounddown.

• Ifthenextdigitis 5, 6, 7, 8 or 9,thenroundup.

Leadingdigitapproximationinvolvesroundingtotheﬁrstdigit.Forexample: For 932,roundto 900

For 968,roundto 1000

Thesymbol ¥ means‘approximatelyequalto’.

Exercise1G

1 Havethesenumbersbeenroundedupordown?

2 Thefollowingnumbersaretoberoundedtothenearest 10.Shouldtheyberoundedupordown?

3 Thefollowingnumbersaretoberoundedtothenearest 100.Decideiftheywouldberoundedupor down.

Fluency

Example12Rounding

Roundthesenumbersasindicated.

86 (tothenearest 10) a

Solution

a 86 ¥ 90

b 4142 ¥ 4100

4142 (tothenearest 100) b

Explanation

Thedigitafterthe 8 isgreaterthanorequalto 5,soroundup.

Thedigitafterthe 1 islessthanorequalto 4,sorounddown.

Keepthe 1 andmakethefollowingdigitszero. Nowyoutry

Roundthesenumbersasindicated.

93 (tothenearest 10) a 5851 (tothenearest 100) b

4 Roundthesenumbersasindicated.

59 (nearest 10) a 32 (nearest 10) b

124 (nearest 10) c 185 (nearest 10) d

231 (nearest 100) e 894 (nearest 100) f

96 (nearest 10) g 584 (nearest 100) h

1512 (nearest 1000) i 1492 (nearest 1000) j

7810 (nearest 1000) k 10200 (nearest 1000) l

5 Roundthesenumbersusingleadingdigitapproximation.

Example13Usingleadingdigitapproximation

Q4Hint:Ifthenextdigitis 0, 1, 2, 3 or 4 rounddown. Otherwise,roundup.

Q5Hint:Roundtotheﬁrstdigit ontheleft,so 284 ¥ 300.

Estimatetheanswerstothesequestionsbyﬁrstroundingeachnumbertotheleadingdigit.

42 × 7 a 95 × 326 b

Solution

a 42 × 7 ¥ 40 × 7 = 280

b 95 × 326 ¥ 100 × 300 = 30000

c 302 ÷ 29 ¥ 300 ÷ 30 = 10

302 ÷ 29 c

Explanation

Theleadingdigitin 42 isthe 4 inthe‘tens’column.

Thenearest‘ten’to 95 is 100,andtheleadingdigitin 326 isinthe‘hundreds’column.

302 roundsto 300 and 29 roundsto 30.

Nowyoutry

Estimatetheanswerstothesequestionsbyﬁrstroundingeachnumbertotheleadingdigit. 31 × 8 a

6 Useleadingdigitapproximationtoestimatetheanswer.

÷ 91 c

Q6Hint:Firstroundeach numbertotheleadingdigit beforemakingthecalculation.

Problem-solving and reasoning

7 Youpurchase 59 ticketsat $21 each.Giveanestimateforthe totalcostofthetickets.

8 Adiggercandig 29 scoopsperhourandwork 7 hoursperday. Approximatelyhowmanyscoopscanbedugover 10 days?

Hint:Forquestions 7 to 10,use leadingdigitapproximationto makeyourestimate.

9 Mostofthepensatastockyardarefullofsheep.Thereare 55 pensandoneofthepens has 22 sheep.Giveanestimateforthetotalnumberofsheepatthestockyard.

10 Awholeyeargroupof 159 studentsisroughlydividedinto 19 groups.Estimatethenumberin eachgroup.

11 Forthegivenestimates,decideiftheapproximateanswerisgoingtogivealargerorsmallerresult comparedtothetrueanswer. 58 + 97 ¥ 60 + 100 a 24 × 31 ¥ 20 × 30 b

¥ 130−80 c 267−110 ¥ 270−110 d

12 Itissensiblesometimestoroundonenumberupiftheothernumberisgoingtoberoundeddown. Useleadingdigitapproximationtoestimatetheanswerstotheseproblems.

13 ManyexamplesofAboriginalartincludedotpaintings.Herearetwoexamples.Estimatethenumber ofdotsineachone.

1H 1H Orderofoperationswithpositiveintegers

Learningintentions

• Toknowtheconventionfordeterminingorderofoperationsinanexpressioninvolvingmorethanoneoperation.

• Tobeabletoevaluatearithmeticexpressionsinvolvingmorethanoneoperation.

Keyvocabulary: operation,brackets,multiplication,division,addition,subtraction

Whencombiningtheoperationsofaddition,subtraction,multiplicationanddivision,aspecialorderneeds tobefollowed.Multiplicationanddivisionsithigherintheorderthanadditionandsubtraction.Thisaffects howwemightmakesenseofsimplemathematicalproblemsputintowords. Considerthesetwostatements.

2 groupsof 3 chairsplus 5 chairs

5 chairsplus 2 groupsof 3 chairs

Inbothcases,thereare 2

Thisalsosuggeststhatfor 5 + 2 × 3,themultiplicationshouldbedoneﬁrst.

Lessonstarter:Makeittrue!

Canyouinsertapairofbracketstomakethefollowingtrue?

Discusswhetheryouthinkthefollowingneedbracketstomakethemtrue.

Keyideas

Whenworkingwithmorethanone operation:

• Dealwith brackets ﬁrst.

• Do multiplication and division next,workingfromlefttoright.

• Do addition and subtraction last,workingfromlefttoright.

Exercise1H

Und er stand ing

1 Whichgoesﬁrst?

a Additionormultiplication

b Bracketsordivision

c Subtractionorbrackets

d Multiplicationorsubtraction

2 Whichoperation(addition,subtraction,multiplicationordivision)isdoneﬁrstintheseproblems?

)

Fluency 3(½)

Example14Usingorderofoperations

Useorderofoperationstoﬁndthefollowingvalues.

5 + 10 ÷ 2 a 3 × (2 + 4) b

5 × 2−8 ÷ 4 c

6 × (2 + 10) −24 d 18−2 × (4 + 6) ÷ 5 e

Solution

a 5 + 10 ÷ 2 = 5 + 5 = 10

b 3 × (2 + 4) = 3 × 6 = 18

c 5 × 2−8 ÷ 4 = 10−2 = 8

d 6 × (2 + 10) −24 = 6 × 12−24 = 72−24 = 48

e 18−2 × (4 + 6) ÷ 5 = 18−2 × 10 ÷ 5 = 18−20 ÷ 5 = 18−4 = 14

Explanation

Dothedivisionbeforetheaddition.

Dealwithbracketsbeforemultiplication.

Dothemultiplicationanddivisionbeforethe subtraction.

Dealwithbracketsﬁrst.

Dothemultiplicationbeforesubtraction.

Dothesubtractionlast.

Dealwithbracketsﬁrst.

Dothemultiplicationanddivisionnext,working fromlefttoright.

Dothesubtractionlast.

Nowyoutry

Useorderofoperationstoﬁndthefollowingvalues.

9−2 × 3 a

11 × (8−5) b

20 ÷ 10 + 7 × 3 c

12 ÷ (7−3) + 13 d

4 ÷ (13−11) × 3 + 6 e

3 Useorderofoperationstoﬁndtheanswers.

1 + 2 × 3 a 5 + 7 × 2 b

9−10 ÷ 5 c 4 × (3 + 2) d

21 ÷ (3 + 4) e 18 ÷ (10−1) f

(7 + 2) ÷ 3 g (10−4) × 4 h

(6−5) ÷ 1 i 2 + 3 × 7 j

5 + 8 × 2 k 10−20 ÷ 2 l

22−16 ÷ 4 m 6 × 3 + 2 × 7 n

1 × 8−2 × 3 o 18 ÷ 9 + 60 ÷ 3 p 2 + 3 × 7−1 q 40−25 ÷ 5 + 3 r

63 ÷ 3 × 7 + 2 × 3 s 78−14 × 4 + 6 t

300−100 × 4 ÷ 4 u

4 Useorderofoperationstoﬁndtheanswers.

2 × (3 + 2) a 18 ÷ (10−4) b

(19−9) ÷ 5 c 2 × (3 + 2) −1 d

10 ÷ (3 + 2) + 6 e 13 × (10 ÷ 10) −13 f

(100 + 5) ÷ 5 + 1 g 2 × (9−4) ÷ 5 h

50 ÷ (13−3) + 4 i 16−2 × (7−5) + 6 j

(7 + 2) ÷ (53−50) k 14− (7 ÷ 7 + 1) × 2 l

(20−10) × (5 + 7) + 1 m 3 × (72 ÷ 12 + 1) −1 n

48 ÷ (4 + 4) ÷ (3 × 2) o 20− (3 × 5 + 1) ÷ 4 p

Q3Hint:Rememberthat × and ÷ gobefore + and .Workfrom lefttorightafteryouhavechosen whichoperationgoesﬁrst.

Q4Hint:Dealwithbracketsﬁrst, then × and ÷ then + and .

Problem-solving and reasoning 5–7 7–10

5 Arethesestatementstrueorfalse?

5 × 2 + 1 = (5 × 2) + 1 a 10 × (3 + 4) = 10 × 3 + 4 b 21−7 ÷ 7 = (21−7) ÷ 7 c 9−3 × 2 = 9− (3 × 2) d

Example15Usingorderofoperationsinwordedproblems

Findtheresultif 6 ismultipliedbythesumof 2 and 7

Solution

6 × (2 + 7) = 6 × 9 = 54

Explanation

First,writetheproblemusingsymbolsand numbers.

Usebracketsforthesumsincethisoperationis tobecompletedﬁrst.

Nowyoutry

Findtheresultif 26 isdividedbythedifferencebetween 16 and 3

6 Findtheanswertothesewordedproblemsbyﬁrstwriting thesentenceusingnumbersandsymbols.

Triplethesumof 3 and 6 a

Doubletheresultof 20 dividedby 4 b 44 dividedby 11 plus 4 c 5 morethantheproductof 6 and 12. d

Theresultof 60 dividedby 12 issubtractedfromthe productof 5 and 7 e 15 lessthanthedifferenceof 48 and 12 f

Q6Hint: Sum meansadd. Difference meanssubtract. Product meansmultiply.

Theproductof 9 and 12 issubtractedfromdoubletheproductof 10 and 15 g

7 Adeliveryof 15 boxesofbooksarrives.Eachboxcontainseightbooks.Thebookstoreownerremoves threebooksfromeachbox.Howmanybooksstillremainintotal?

8 Inaclass,eightstudentshavethreeTVsetsathome,fourhavetwoTVsets, 13 haveoneTVsetand twostudentshavenoTVsets.HowmanyTVsetsarethereintotal?

9 Insertbracketsintotheseequationstomakethemtrue.

10 Decideifthebracketsgivenineachequationareactuallynecessary.Thatis,dotheymakeany difference?

2 + (3 × 6) = 20 a (

(5 + 2) = 3

Bracketswithinbrackets 11,12

11 Theseproblemsinvolvebracketswithinbrackets.Makesureyouworkwiththeinnerbracketsﬁrst. (Theﬁrstonehasalreadybeendone.)

2 ×[(2 + 3) × 5−1]= 2 ×[5 × 5−1] = 2 ×[25−1] = 2 × 24 = 48 a

[10 ÷ (2 + 3) + 1]× 6 b

26 ÷[10− (17−9)] c [6− (5−3)]× 7 d

2 +[103− (21 + 52)] (9 + 11) × 6 ÷ 12 e

12 Insertbracketstomakethefollowingtrue.(Youmayneedtousemorethanonepair.)

20−31−19 × 2 = 16 a

50 ÷ 2 × 5−4 = 1 b

25−19 × 3 + 7 ÷ 12 + 1 = 6 c

Stockcontrolleratsportsevents

The2019AFLGrandFinalbetweenthe RichmondTigersandtheGreaterWestern SydneyGiantssawanofﬁcialattendanceof 100014,whichisextremelyclosetothe capacitycrowdof 100024 peoplethatcanﬁt intotheMCG(MelbourneCricketGround).

Atlargesportingeventsandconcerts,there aremanyfoodandbeveragestandsaround thegrounds.Thestockcontrollersneedto predictthecrowdsizeandmakesurethat enoughwaterandfoodisavailableforeach event.

1 Completethetablebelowforthesedifferentstadiumsandevents fromaroundAustralia.Useanallowanceof 1.5 bottlesofwater foreachpersonattendingtheevent.Aftercalculating allanswers,roundtothenearestpositiveinteger.

Q1Hint:Earningsarethe totalamountfromsales, nottheproﬁt. Venue

Suncorp Stadium, Brisbane

MCG,Melbourne CricketGround

BrisbaneRoarvs PerthGlory 35200

Hawthornvs Fremantle 100007

WACA,WA Cricket Association T20 cricketIndia vsAustralia 34527

SCG,Sydney CricketGround

SydneySwans vsWestern Bulldogs 33386

AdelaideOval AdelaideCrows vsWestCoast Eagles 53445

NIBStadium, Perth Wallabiesvs Argentina 16202

DarwinFootball Stadium Brumbiesvs Reds 4600

ANZStadium, Sydney Broncosvs Cowboys 82758

2 Attendancesareoftenroundedforconvenienceofreporting.Fortheeventsinquestion 1,round eachoftheattendancestothenearestthousand.

3 Averageattendanceﬁgureshelpstockcontrollers predicttheneedsofeventsattheirvenues.

Average = Totalattendance Numberofgames

Calculatetheaverageattendanceforeachofthe followingevents:

AFL2019seasonwithatotalattendanceof 7517647 with 198 games.

BigBashLeague2018–19seasonwith 1212596 peopleattending 59 games.

Japanesebaseball2019seasonof 429 gameswitha totalattendanceof 14867071

Majorleaguebaseballwithtotalattendance 68494752 over 2429 games.

4 Listfourfactorsthatcouldcausevariationinattendanceﬁgures.

Usingtechnology

Usethefollowingexampletohelpyouwiththequestionbelow. ForoneMCGcricketevent, 6 bucketsofhotchipsweresoldforevery 10 people.Thefollowing calculationshowshowthestockcontrollerpredictstheamountoffoodrequiredforanevent.

Totalnumberoffooditems = seatingcapacity × numberoffooditems numberofpeople

= 100000 × 6 10

= 60000 bucketsofhotchips

5 Forthefollowingcalculations,you canassumeeachstadiumisﬁlledto capacity.

a Copythetablebelowintoa spreadsheet.Selecttheshaded cells,rightclick,selectFormat Cells/Number/0d.p./OK

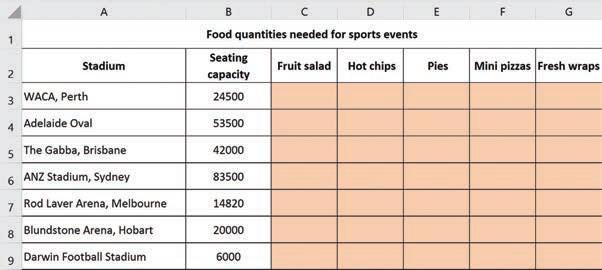
b Insertformulasintotheshadedcellstocalculatethepositiveintegersofservesforeachfooditem inthistable.

Usethesefactstowritetheformulas:

1 in 5 peoplebuyfruitsalad • halfthefansbuyhotchips

3 piesaresoldforevery 2 fans

3 in 8 peoplebuyfreshwraps

2 minipizzasaresoldforevery 5 people

Q5bHint:E3formula

=B3*3/2G3formula =B3*3/8

Cansandchips

Ataschoolfundraisingfair,Mikehasbeengiven $30 tospendon softdrinkandchipsforhimselfandhisfriends.Cansofsoftdrink cost $2 eachandcupsofchipscost $3 each.

Presentareportforthefollowingtasksandensurethatyoushowclearmathematicalworkings, explanationsanddiagramswhereappropriate.

1Preliminarytask

a Findthetotalcostofbuying:

5 cansofsoftdrink i 7 cupsofchips ii

4 cansofsoftdrinkand 3 cupsofchips iii 6 cansofsoftdrinkand 5 cupsofchips iv

b If 6 cupsofchipsand 3 cansarepurchased,ﬁndthechangefrom $30

c DeterminethemaximumnumberofcansofsoftdrinkthatMikecanpurchaseif:

4 cupsofchipsarepurchased i 3 cupsofchipsarepurchased ii

2Modellingtask

Formulate TheproblemistoﬁndthemaximumnumberofcansandcupsofchipsthatMikecanpurchasewith themoneyhewasgiven.

a Writedownalltherelevantinformationthatwillhelpsolvethisproblem.

Solve b Chooseatleasttwocombinationsforthenumberofcansandnumberofcupsofchipssothat thetotalcostislessthan $30.Showyourcalculationstoexplainwhyyourcombinationsare affordable.

c Chooseatleasttwodifferentcombinationsforthenumberofcansandchipssothatthetotal costisequalto $30

d Determinepossiblecombinationscostingupto $30 whichwouldmeanthatMike: i maximisesthenumberofcanspurchased. ii maximisesthenumberofcupsofchipspurchased.

Evaluate and verify

e Determinethemaximumnumberofitems(cansand/orcupsofchips)thatcanbepurchased for $30 orless:

i ifatleast 5 cupsofchipsmustbepurchased. ii iftherearenorestrictions.Describethecombinationsofcansandcupsthatcouldbe boughttogetthismaximumnumber.

Communicate f Summariseyourresultsanddescribeanykeyﬁndings.

3Extensionquestion

g IfMikehad $37,investigatethemaximumnumberofitems(cansofsoftdrinkand/orcupsof chips)thatcouldbepurchasedifatleast 6 cupsofchipsmustbeincluded.

Making100dollars

Keytechnology:Spreadsheets

Youcanimaginethattherearemanywaysinwhichyoucanmake $100 from $10 and $20 notes. Assumingyouhaveenoughofeachtype,youcouldmake $100 usingﬁve $20 andno $10 notesor perhapsthree $20 notesandfour $10 notes,forexample.

1Gettingstarted

a Withoutusingoneofthecombinationsmentionedintheintroduction,listthreedifferentpossible combinationsof $20 and $10 notesthatmakeupatotalof $100

b Canyouﬁndawaytomakeup $100 bycombining $10 and $20 notessothatthereisatotalof sevennotesbeingused?Ifso,describeit.

c Canyouﬁndawaytomakeup $100 bycombining $10 and $20 notessothatthereisatotalof elevennotesbeingused?Explainyouranswer.

2Usingtechnology

Wewilluseaspreadsheettoexplorethenumberofwaysyoucanchoose $10 and $20 notesto form $100

a Createthefollowingspreadsheetusingthegiveninformation.

• Thenumberof $20 notescanvaryandisincellB3.

• TheinformationincellA7 createsthenumberof $10 notesselected.

• TheinformationincellB6 createsthetotalvalueofthe $10 and $20 notesselected.

• TheinformationincellC6 createsthetotalnumberofnotesselected.

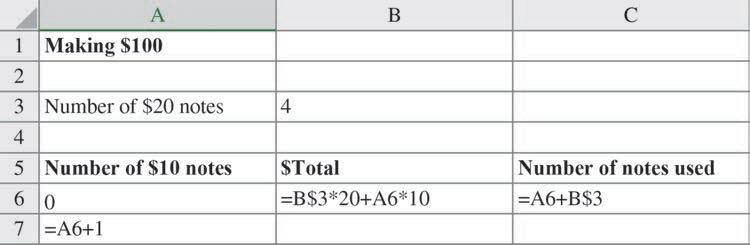
b FilldownatcellsA7,B6 andC6.Filldownuntilten $10 notesareused.Notethatthe $ signincells B6 andC6 ensuresthatthenumberof $20 notesincellB3 isusedforeverycalculation.

Technology and computational thinking

c Seeifyourspreadsheetisworkingproperlybyalteringthenumberof $20 notesincellB3.Allthe valuesshouldchangewhenthiscellisupdated.

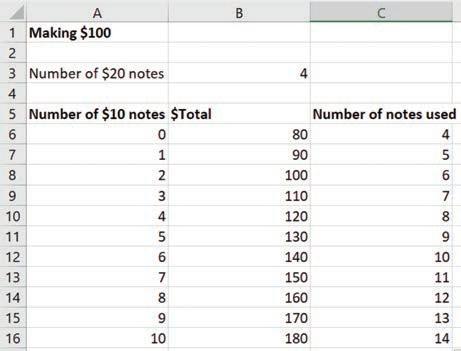
d Choosetwo $20 notesbychangingthecellB3 toequal 2.Readoffyourspreadsheettoanswer thefollowing.

Howmany $10 notesarerequiredtomakethetotalof $100? i Howmanynotesareselectedintotalifyoumake $100? ii Describewhathappensifthenumberof $20 notesincellB3ischangedto 7 iii

3Applyinganalgorithm

a Useyourspreadsheettosystematicallyrunthroughandcountallthewaysyoucanmake $100 using $10 and $20 notes.Applythesesteps.

• Step 1:Choosethesmallestnumberof $20 notespossibleandenterthisnumberintocellB3

• Step 2:Readoffthenumberof $10 notesneededtomake $100

• Step 3:Increasethenumberof $20 usedbyoneandrepeatStep 2

• Step 4:Continueincreasingthenumberof $20 notesuseduntilyoureachamaximum possiblenumber.

b Describethecombinationofnoteswhereatotalof $100 isachievedbutthereareeightnotes intotal.

c Isitpossibletoachieveatotalof $100 usingonlysixnotesintotal?Ifso,describehow.

d Howmanywayswerethereofforming $100 from $10 and $20 notes?

1 Completethesemagicsquares.Eachrow,columnandmaindiagonaladduptothesamemagic total.

2 Decidewherebracketsshouldgotomakeeachstatementtrue.

5 + 2 × 3 = 21 a 16−8 ÷ 10−6 = 2 b

4 + 2 × 7−1 × 3 = 43 c

3 Eachsideonamagictriangleaddsuptothesamenumber,asshowninthisexamplewithasum of 12 oneachside.

a Placethedigits 1 to 6 inamagictrianglewiththreedigitsalongeachsidesothateachside addsuptothegivennumber.

9 i 10 ii

b Placethedigits 1 to 9 inamagictrianglewithfourdigitsalongeachsidesothateachsideadds uptothegivennumber.

20 i 23 ii

Puzzles and games

4 Sudokuisapopularlogicnumberpuzzlemadeupofa 9 by 9 square,whereeachcolumnandrow canusethedigits 1, 2, 3, 4, 5, 6, 7, 8 and 9 onlyonce.Also,eachdigitistobeusedonlyoncein each 3 by 3 square.Solvethesepuzzles.

5 Thesumalongeachlineis 15.Canyouplaceeachofthedigits 1,

and

tomake thiswork?

6 Findallthemissingdigitsintheseproducts.

7 Youdecidetostartcountingbackwardsby 7,startingatthesenumbers.Ifyoustopjustbefore passingzero,whatisyourﬁnalnumber?

205 a 22314 b

Place value

The place value of 3 in 1327 is 300

The place value of 4 in 7143 is 40

2 × 100 + 7 × 10 + 3 × 1 is the expanded form of 273. This can also be written with indices as 2 × 102 + 7 × 101 + 3 × 1

Addition and subtraction

Positive integers

Mental strategies

172 + 216 = 300 + 80 + 8 = 388 98 19 = 98 20 + 1 = 79

Order of operations

Brackets ﬁrst, then × and ÷, then + and from left to right. 2 × (7 + 1) = 2 × 8 = 16

Estimation

955 to the nearest 10 is 960

950 to the nearest 100 is 1000

Leading digit approximation

39 × 326 ≈ 40 × 300 = 12 000

Mental strategies

7 × 31 = 7 × 30 + 7 × 1 = 217 5 × 14 = 10 × 7 = 70

64 ÷ 8 = 32 ÷ 4 = 16 ÷ 2 = 8 156 ÷ 4 = 160 ÷ 4 4 ÷ 4 = 40 1 = 39

Multiplication and division 29 × 13 87 290 377 6 8 3 2025 with 1 remainder Larger numbers 2

Multiplying by 10, 100, …

38 × 100 = 3800

38 × 700 = 38 × 7 × 100 = 26 600

Chapterchecklist

AversionofthischecklistthatyoucanprintoutandcompletecanbedownloadedfromyourInteractiveTextbook.

1A 1

1A 2

1A 3

1B 4

1C 5

Icanwritedowntheplacevalueofdigitswithinanumber. e.g.Writetheplacevalueofthedigit 4 inthenumber 1043

Icanarrangepositiveintegersfromsmallesttolargest.

e.g.Arrangethesenumbersfromsmallesttolargest: 29, 36, 18, 132, 1001, 99, 592, 123, 952.

Icanwritepositiveintegersinexpandedformwithandwithoutindexnotation. e.g.Write 517 inexpandedform.Rewrite 517 inexpandedformwithindexnotation.

Icanusementaladditionandsubtractiontechniqueseffectively. e.g.Mentallyﬁnd 132 + 156 (withpartitioning)and 56−18 (withcompensating).

Icanusetheadditionalgorithm.

e.g.Givetheresultforthissum 439 + 172

1C 6

Icanusethesubtractionalgorithm.

e.g.Givetheresultforthisdifference 526 −138

1D 7

1D 8

1E 9

1E 10

1F 11

1F 12

Icanusementalmultiplicationtechniqueseffectively. e.g.Mentallyﬁnd 4 × 19

Icanusethemultiplicationalgorithmwhenonenumberislessthanten. e.g.Givetheresultof 197 × 7.

Icanmultiplybypowersoftenbyaddingzerostotheendofanumber. e.g.Givetheresultof 37 × 100

Icanmultiplylargernumbersusingthemultiplicationalgorithm. e.g.Find 87 × 13

Icanusementalstrategiestodividepositiveintegers. e.g.Mentallyﬁnd 93 ÷ 3.

Icanusetheshortdivisionalgorithm. e.g.Useshortdivisiontoﬁndthequotientandremainder. 7 ) 195

Giveyouranswerusingmixednumeral.

1G 13

1G 14

1H 15

1H 16

Icanroundpositiveintegerstoapoweroften.

e.g.Round 4142 tothenearest 100.

Icanestimateanswersusingleadingdigitapproximation.

e.g.Estimate 95 × 326 byroundingeachnumbertotheleadingdigit.

Icanuseorderofoperations.

e.g.Findthevalueof 18−2 × (4 + 6) ÷ 5

Icanuseorderofoperationsinwordedproblems.

e.g.Findtheresultif 6 ismultipliedbythesumof 2 and 78

Short-answerquestions

1 1A Arrangethesenumbersfromsmallesttolargest.

317, 713, 731, 371, 173, 137 a 1001, 1010, 199, 999, 1000, 1900, 1090 b 2

1B Useamentalstrategytoﬁndthesesumsanddifferences.

4 1C Findthesesumsanddifferences.

5 1D Useamentalstrategytoworkoutthefollowing.

6 1E/F Showyourworkingtoﬁndeachanswer.

7 1E/F Findthemissingdigitsintheseproblems.

8 1G Roundthesenumbersasindicated.

72 (nearest 10) a

3268 (nearest 100) b 951 (nearest 100) c

9 1G Useleadingdigitapproximationtoestimatetheanswerstotheseproblems.

10 1H Useorderofoperationstoﬁndtheanswerstotheseproblems.

Multiple-choicequestions

1 1A Theplacevalueof 7 in 2713 is:

2 1A Theexpandedformof 372 is

3 1B/D/F Whichofthefollowingis not true?

2 + 3 = 3 + 2 A 2 × 3 = 3 × 2

4 1C Thesumof 198 and 103 is:

5 1C Thedifferencebetween 126 and 29 is:

6 1D/E Theproductof 7 and 21 is:

7 1F Themissingdigitinthisdivision 3

8 1F Theremainderwhen 317 isdividedby 9 is:

9 1G 458 roundedtothenearest 100 is:

1H Theanswerto 4 × 3−26 ÷ 13 is:

Extended-responsequestion

1 Acitytowerconstructionuses 450 tonnesofconcrete.Theconcreteistruckedfromafactorythat is 2 kilometresfromtheconstructionsite.Eachconcretemixercancarry 5 tonnesofconcrete. Theconcretecosts $350 pertruckloadfortheﬁrst 10 loadsand $300 perloadafterthat.

a Howmanyloadsofconcreteareneeded?

b Findthetotaldistancetravelledbytheconcretemixerstodeliverallloads.Theyneedtoreturn tothefactoryaftereachload.

c Findthetotalcostofconcreteneededforthetowerconstruction.

d Ifthepriceofconcreteisalways $350 regardlessofthenumberofloads,howmuchmore woulditcostfortheconcrete?

2 OnenightRickyandhisbrotherMickydecidetohavesomefunattheirfather’ssweetshop. Intheshoptheycollected 3 tinsof 25 jellybeans, 4 packetsof 32 chocbuds, 5 boxesof 10 smartiesand 12 packetsof 5 liquoricesticks.

a Findthetotalnumberofsweets.

b Findthedifferencebetweenthenumberofchocbudsandthenumberofsmarties.

c RickyandMickydecidetodivideeachtypeofsweetintogroupsof 7 andtheneatany remainder.Whichtypeofsweetwilltheyeatthemostofandhowmany?

2 Numberproperties andpatterns

Essentialmathematics:whyunderstandingnumber propertiesandpatternsisimportant

Numberpropertiesandpatternsarewidelyapplied,includingincryptography,engineering, ﬁnance,gamedevelopment,musictheory,science,sportsanalyticsandstatistics.

Asportscoachwith 24 soccerballsand 60 conesusestheHighestCommonFactor(12)tocreate 12 equalsetsoftwoballsandﬁvecones.Iftwobusesarriveevery 15 and 20 minutes,theLowest CommonMultiple(60)tellsustheywillarrivetogether,every 60 minutes.

Squaresandsquarerootsarecomputedwhenapplyingcircleandtriangleproperties,includingby engineers,architects,builders,surveyors,graphicdesignersandanimators.

Verylargeprimenumbersareusedincryptographytoprotectinformationtransmittedoverthe internet.Barcodesystemscanuseprimenumberstoencodeinformation.

Numberpatternrulesaredevelopedbyaccountantsandﬁnancialadviserstoforecastfuture annualincreasinginvestmentvaluesandpropertyprices.

Inthischapter

2AFactorsandmultiples (Consolidating)

2BHighestcommonfactorandlowest commonmultiple (Consolidating)

2CDivisibility

2DPrimenumbersandcompositenumbers

2EIndexform

2FPrimefactors

2GSquaresandsquareroots

2HNumberpatterns (Consolidating)

2IPatternswithshapesandnumbers

2JTablesandrules

2KTheCartesianplaneandgraphs

AustralianCurriculum9.0

NUMBER

Describetherelationshipbetweenperfectsquare numbersandsquareroots,andusesquaresof numbersandsquarerootsofperfectsquare numberstosolveproblems(AC9M7N01)

Representnaturalnumbersasproductsofpowers ofprimenumbersusingexponentnotation (AC9M7N02)

ALGEBRA

Describerelationshipsbetweenvariables representedingraphsoffunctionsfromauthentic data(AC9M7A04)

Generatetablesofvaluesfromvisuallygrowing patternsortheruleofafunction;describeand plottheserelationshipsontheCartesianplane (AC9M7A05)

©ACARA

Onlineresources

Ahostofadditionalonlineresourcesareincluded aspartofyourInteractiveTextbook,including HOTmathscontent,videodemonstrationsofall workedexamples,auto-markedquizzesand muchmore.

1 Find:

10 × 10 × 10 × 10 × 10 × 10 c

2 Find: 20 ÷ 5 a

Warm-up

20 ÷ 1 c 20 ÷ 20 d allthenumbersthatdivideinto 20 withnoremainder e

3 Writethequotientandremainderforthesedivisions.

4 Find: 3 morethan 7 a thedifferencebetween 20 and 16 b thesumof 12 and 7 c 6 multipliedby 4 d theproductof 2 and 9 e 30 dividedby 6 f

5 Listallthefactorsof 24 inascendingorder.

6 Replace with < or > 3 issmallerthan 7 sowewrite 3 7 a 12 isbiggerthan 5 sowewrite 12 5 b

7a Listthenextthreeevennumbers: 2, 4, , , b Listthenextthreeoddnumbers: 1, 3, , ,

8 Find:

9 Copyandcompletethefollowing.

10 Statethemissingnumberinthesefactortrees.

11 Find 33 ÷ 3. a Is 33 divisibleby 3? b Find 32 ÷ 3 c Is 32 divisibleby 3? d

12 Usetheorderofoperationstoﬁndtheanswer. 2 × 10 + 3 a 6 + 3 × 10 b 20 ÷ 2 + 12 ÷ 4 c 3 × (4 × 2−6) d

13 Choosethecorrectsetofnumbers(A to D)thatmatchesthedescription(a to d).

Factorsof 10 a 4, 8, 12, 16, A

Multiplesof 4 b 1, 2, 5, 10 B

Factorsof 16 c 5, 10, 15, 20, C

Multiplesof 5 d 1, 2, 4, 8, 16 D

14 Find: theareaofthissquare a thesidelengthofthissquare b 4 cm 4 cm Area = 36 cm2

2A 2A Factorsandmultiples CONSOLIDATING

Learningintentions

• Tounderstandthatanumberhasin nitelymanymultiples.

• Tobeableto ndfactorsofanumber.

• Tobeableto ndmultiplesofanumber.

Keyvocabulary: factor,multiple,ascending,remainder

Numberpatternscanbequiteuseful whendescribinggroupsofobjectsor relationshipsbetweenquantities.We startthischapterlookingatfactorsand multiples.

Onedozendoughnutsaregenerally packedintobagsorboxeswith 3 rowsof 4 doughnutseach.Since 3 × 4 = 12,we cansaythat 3 and 4 are factors of 12.

Purchasing‘multiple’packsofone dozendoughnutscouldresultinbuying 24, 36, 48 or 60 doughnuts,dependingon thenumberofpacks.Thesenumbersare knownas multiples of 12

Factorsareusefulforsplittingupobjectsevenly,suchasaboxof doughnuts.

Lessonstarter:Usingfactorstoplanaparty

Shaynawantseveryoneatherparty(includingherself)tohavethesamenumberofdoughnuts.

Dad bought 3 boxes of 12 doughnuts for my party!

I hope no-one else comes. That way, we get a whole box each!

If four more people come, can we still share the doughnuts equally?

• What‘partysizes’arepossiblesoeveryonehasthesamenumberofdoughnuts?Forexample, apartysizeof 12 meansthatShaynainvites 11 friendsandeveryonegets 3 doughnutseach (12 groupsof 3 equals 36).

• Listthefactorsof 36 inascending(increasing)order.(Youcouldarrange 36 countersintovariousgroups ofequalsizetoﬁndallthepossiblefactors.)

• IfShaynawantsjustonedoughnut,thenstillwantstheremainingfriendsatthepartytohaveanequal number,howmanyfriendsshouldsheinvite?

Keyideas

Factors ofanumberdivideexactlyintothatnumber.

Forexample: 20 ÷ 4 = 5 exactly,so 4 isafactorof 20

• Factorsof 20 listedinpairs: 1 × 20 = 20, 2 × 10 = 20, 4 × 5 = 20

• Factorsof 20 in ascending order: 1, 2, 4, 5, 10, 20

1 is the smallest factor of any number.

The largest factor of any number is the number itself.

Multiples ofanumberaremadewhenthatnumberismultipliedbywholenumbers.

• Forexample,themultiplesof 5 inascendingorderare 5, 10, 15, 20, ...

• Anotherwaytoﬁndmultiplesof 5 istostartwith 5 andkeepadding 5

+ 5 + 5 + 5

5,10, 15, 20, ...

The smallest multiple of a number is the number itself.

Multiples just keep on getting bigger.

• A remainder isanumberleftoverfromdivision.

Exercise2A

Und er stand ing 1–4 4

1 Thinkaboutarranging 24 countersintoarectanglewith 2 rowsof 12 counters.

Copyandcompletethefactorpairsforthisrectangle.

12 × = 24 or × 12 = 24

Usingall 24 counterseachtime,thinkaboutthreedifferent-sizedrectanglesandwritedownafactor pairforeach.

2 Copyandcomplete:

a 1 × = 5

1 × = 12, 2 × = 12, 3 × = 12

Thefactorsof 12 are 1, , , , , 12

Thefactorsof 5 are , b

1 × = 30, 2 × = 30, 3 × = 30, 5 × = 30

Thefactorsof 30 are , , , , ,

3 Copyandcomplete:

Theﬁrstsixmultiplesof 5 are 5, , 15, , 25, a

Theﬁrstsixmultiplesof 10 are 10, , 30, , , b

Theﬁrstsixmultiplesof 7 are 7, , , 28, , 42 c

Q2Hint:Listthe factorsinascending order(fromsmallest tolargest).

Q3Hint:Tomake multiplesof 5,start with 5 andkeep adding 5.

4 Copyandcomplete:

7 × 6 = 42 so 7 and 6 are of 42 a Tomakemultiplesof 6,multiply 6 bywholenumbers.Forexample:

1 × 6 = 6, × 6 = 12, × 6 = 18, × 6 = 24

Theﬁrstﬁvemultiplesof 6 are 6, , 18, , c

Ifyoustartwith 6 andthenkeepadding 6,youwillproducealistof of 6 d Fluency

Example1Findingfactors

Findthecompletesetoffactorsforeachofthesenumbers.

15 a 40 b

a Factorsof 15 are 1, 3, 5, 15 1 × 15 = 15, 3 × 5 = 15

b Factorsof 40 are: 1, 2, 4, 5, 8, 10, 20, 40. 1 × 40 =

Therearenoothernumbersthatdivideinto 40 withzeroremainder.

Q5Hint:Listthe factorsinascending order(smallestto largest). 10 a 24 b 17 c

Example2Listingmultiples

Writedowntheﬁrstsixmultiplesforeachofthesenumbers.

11 a 35 b

Solution

a 11, 22, 33, 44, 55, 66

b 35, 70, 105, 140, 175, 210

Explanation

Theﬁrstmultipleisalwaysthegivennumber. Addonthegivennumbertoﬁndthenextmultiple. Repeatthisprocesstogetmoremultiples.

Startat 35 (thegivennumber)andrepeatedlyadd 35 to continueproducingmultiples.

Nowyoutry

Writedowntheﬁrstsixmultiplesforeachofthesenumbers. 9 a 21 b

6 Writedowntheﬁrstsixmultiplesforeachofthefollowingnumbers.

Q6Hint:Listthemultiplesin ascendingorder.

7 Fillinthegapstocompletethesetoffactorsforeachofthefollowingnumbers. 181, 2, , 6, 9,

Example3Identifyingincorrectmultiples

Whichnumberisthe wrong multipleinthesequence 7, 14, 20, 28, 35?Writethecorrectsequence.

Solution Explanation 20 isincorrect.

7, 14, 21, 28, 35 14 + 7 = 21 or 3 × 7 = 21 Amultipleof 7 mustbeawholenumbertimes 7

Nowyoutry

Whichnumberisthe wrong multipleinthesequence 8, 16, 24, 34, 40, 48?Writethecorrectsequence.

8 Findthe wrong multipleineachofthefollowing.Writethecorrectsequence.

Problem-solving and reasoning

Example4Findingfactorpairs

Express 96 asaproductoftwofactors,bothofwhicharegreaterthan 6

Solution

Explanation 96 = 8 × 12 Divide 96 bynumbersgreaterthan 6 toﬁndalargefactor.

Nowyoutry

Express 72 asaproductoftwofactors,bothofwhicharegreaterthan 7

9 Expresseachofthefollowingnumbersasaproductoftwofactors, bothofwhicharegreaterthan 4

Q9Hint:Forsome numbers,thetwo factorswillbethe samenumber.

10 ZaneandMattarebothkeenrunners.Zanetakes 4 minutesto jogaroundarunningtrackandMatttakes 5 minutes.Theystart togetheratthesametimeandjog 6 lapsfortraining.

a Copyandcomplete: WhenZanejogged 6 lapsaroundthetrack,hecrossed thestart/ﬁnishlineafter 4, 8, , , and minutes.

Q10Hint:Useadiagramshowing 30 minutes: 012. . .30

i Mattcrossedthestart/ﬁnishlineafter , ,

, and minutes.

b Howmanylapshadeachboyjoggedwhentheycrossedthelinetogether?

c Forhowlonghadtheboysjoggedbeforetheycrossedthelinetogether?

11 Ansonispreparingforhistwelfth birthdayparty.Hehasinvited 5 friendsandismakingeachofthem a‘lollybag’totakehomeafterthe party.Tobefair,hewantstomake surethateachfriendhasthesame numberoflollies.Ansonhasatotal of 67 lolliestoshareamongthelolly bags.

HowmanylolliesdoesAnsonput ineachofhisfriends’lollybags?

HowmanylolliesdoesAnson haveleftovertoeathimself?

Ansonthendecidesthathewantsa lollybagforhimselfalso.

c With 6 lollybags,arethereanylolliesleftover? d

Howmanylollieswillnowgointoeachofthe 6 lollybags?

12 Joannaisavet.Shewantstobuyseveralpensforseparatingsickanimals.Therearesquareorrectangular pensavailable,allwithsidesthatare 1, 2, 3 or 4 metreslong.

a Joannawantstobuyatleasttwoequal-sizedpenstocoveranareaof 12 m2.Twopossibilitiesare shownbelow.FindtheotherfourwaysJoannacouldbuypens.

Option1:Buy 3 squarepens.

Eachpenhas:L = 2 m, W = 2 m,A = 4 m2

Totalarea = 3 × 4 = 12 m2

Option2:Buy 2 rectangularpens.

Eachpenhas:L = 2 m,W = 3 m,A = 6 m2

Totalarea = 2 × 6 = 12 m2

Q12aHint:Usegridpaper anddrawthepens.Note that 2 m × 3 mpensare thesameas 3 m × 2 m pens,sodon’tcountthem twice.

b Workoutthenumberofequal-sized square pensandtheirsizessoallthesepensjoinsidebyside tocoveranareaof:

32 m2 i 54 m2 ii

c Workoutthenumberofequal-sized rectangular pensandtheirsizessoallthesepensjoinsideby sidetocoveranareaof:

32 m2 i 54 m2 ii

d Azoovetwantstobuyseverallarger,equal-sizedpenstocover 150 m2.Findallthepossibilitieswith whole-numbersidesfrom 2 to 25 metres.

CONSOLIDATING

2B 2B Highestcommonfactorandlowest commonmultiple

Learningintentions

• Tobeableto ndthehighestcommonfactoroftwonumbers.

• Tobeableto ndthelowestcommonmultipleoftwonumbers.

Keyvocabulary: factor,multiple,highestcommonfactor(HCF),lowestcommonmultiple(LCM)

Inthelastsection,weworkedwithfactorsandmultiples.Inthissection,welookatcommonfactorsor multiplesthataresharedbytwonumbers.

Itisoftenusefultobeabletoﬁndthehighestcommonfactor(HCF)orlowestcommonmultiple(LCM) andtheseareimportantinhigherlevelsofmathematics.

Lessonstarter:Findingspecialnumbers

My factors are 1, 2, 4, 8, 16.

My factors are 1, 2, 3, 4, 6, 8, 12, 24.

Wesharesomecommonfactors.Whatarethey?

Whichisthehighest(biggest)commonfactorweshare?

My multiples are 10, 20, 30...

Wesharesomecommonmultiples.Whatarethey?

Whatisthelowest(smallest)multipleweshare?

My multiples are 6, 12, 18...

Keyideas

HCF standsfor highestcommonfactor.Itisthelargest factor sharedbythetwoormore numbersbeingconsidered.

• Forexample:FindtheHCFof 24 and 40

Factorsof 24 are 1 , 2 , 3, 4 , 6, 8 , 12 and 24

Factorsof 40 are 1 , 2 , 4 , 5, 8 , 10, 20 and 40

Wecanseethatthehighestcommonfactoris 8 sowewriteHCF = 8

LCM standsfor lowestcommonmultiple.Itisthesmallest multiple thattwoormorenumbers divideintoevenly.

• Forexample:FindtheLCMof 20 and 12

Multiplesof 20 are 20, 40, 60 , 80, 100, 120, 140,

Multiplesof 12 are 12, 24, 36, 48, 60 , 72, 84, 96,

Wecanseethatthelowestcommonmultipleis 60 sowewriteLCM = 60

Exercise2B

1 Copyandcompletethefollowing.

HCFstandsfor a

ToﬁndtheHCF,weﬁrstlistallthe ofeachnumber.

LCMstandsfor c

ToﬁndtheLCM,welist ofeachnumber.

2 Thefactorsof 12 are 1, 2, 3, 4, 6, 12.Thefactorsof 16 are 1, 2, 4, 8, 16

Whatarethecommonfactorsof 12 and 16? a

Whatisthehighestcommonfactorof 12 and 16? b

3 Theﬁrst 10 multiplesof 8 are 8, 16, 24, 32, 40, 48, 56, 64, 72, 80

Theﬁrst 10 multiplesof 6 are 6, 12, 18, 24, 30, 36, 42, 48, 54, 60.

Whataretwocommonmultiplesof 8 and 6? a

Whatisthelowestcommonmultipleof 8 and 6? b

Q1Hint:Lookbackatthe Keyideas

Q2Hint:Commonfactors: numbersinbothlists.

Fluency

Example5Findingthehighestcommonfactor(HCF)

Findthehighestcommonfactor(HCF)of 36 and 48

Solution

Factorsof 36 are:

1 ,

2 , 3 , 4 , 6 , 9, 12 , 18 and 36

Factorsof 48 are:

1 , 2 , 3 , 4 , 6 , 8, 12 , 16, 24 and 48

HCF = 12

Nowyoutry

Explanation

Findthefactorsof 36 (1 × 36 = 36, 2 × 18 = 36, etc.)andlisttheminorder.

Findthefactorsof 48 (1 × 48 = 48, 2 × 24 = 48,etc.)andlisttheminorder.

Circlecommon(shared)factors.Pickthe HCF (highestsharedfactor).

Findthehighestcommonfactor(HCF)of 24 and 32

4 FindtheHCFofthefollowingnumbers.

4 and 5 a 8 and 13 b 2 and 12 c 3 and 15 d 16 and 20 e 15 and 60 f 20, 40 and 50 g 12, 15 and 30 h 5, 7 and 11 i

Example6Findingthelowestcommonmultiple(LCM)

Findthelowestcommonmultiple(LCM)of 6 and 10

Solution

6, 12, 18, 24, 30 , 36, …

10, 20, 30 , 40, LCM = 30

Nowyoutry

Q4Hint:Firstlistthefactorsof eachnumber.

Explanation

Listmultiplesofeachnumber.

Circletheﬁrstcommon(shared)multiple. Thisisthe LCM

Findthelowestcommonmultiple(LCM)of 8 and 12

5 FindtheLCMofthefollowingnumbers.

4 and 5 a 3 and 7 b 5 and 6 c 8 and 10 d 4 and 6 e 5 and 10 f

2, 3 and 5 g 3, 4 and 5 h 2, 3 and 7 i

Q5Hint:Firstlistsomemultiples ofeachnumber.

Problem-solving and reasoning

6 Atrail(line)ofredantsrunsalongsideatrailofblackants. Assumetherearenogapsbetweenantsinatrail.

Q6Hint:Therecanonlybe wholeantsineachtrail!

a Howlongwouldthattrailbe?

Whatisthesmallestnumberofredantsandthesmallestnumberofblackantsthatwould makethetrailsequalinlength?

7 Alineoflargespoonsisnexttoalineofsmallspoons.

Whatisthesmallestnumberofeachtypeofspoonthatwouldmakethelinesequalinlength? a Howlongwouldthatlinebe? b Theanswertopart b iscalledthe of 14 and 21 c

8 Alineofpinkthongsisnexttoalineofgreenthongs.

Q8Hint:RememberthatLCM meanslowestcommonmultiple.

Supposethatthetwolinesofthongsarethesamelength.Howlongcouldeachlinebe?Findthree possibleanswers. a Whichoftheanswersinpart a istheLCMof 20 and 25? b

9 Wendyisaﬂoristwhoismakingupsmallbunchesofrosesforsale.Shehas 36 redroses, 42 pinkroses and 30 creamroses. Wendyusesonlyonecolourforeachbunch.Shewantstousealltheroses. Eachbunchmusthavethesametotalnumberofroses.

WhatisthelargestnumberofrosesWendycanputineachbunch? a Theanswertopart a iscalledthe of 36, 42 and 30 b Howmanybunchesofeachcolourcanshemake? c

10 GiventhattheHCFofapairofdifferentnumbersis 8,ﬁndthe twonumbers:

Q10Hint:Remember,HCFmeans ifbothnumbersarelessthan 20 a whenonenumberisinthe 20sandtheotherinthe 30s b

Cyclinglaps

11 Threegirlsareridingtheirbikesaroundacirculartrack.Theyallstarttogether.

I take 6 minutes to cycle a lap.

I take 4 minutes to cycle a lap.

I take 3 minutes to cycle a lap.

Lillitakes 3 minutestocycleeachlap.(Thatis,shecrossesthestartinglineevery 3 minutes.) Aliyahtakes 4 minutesforeachlapandCiaratakes 6 minutes.

Thisbargraphshowsthetimeeachgirltakesfortheﬁrsttwolaps.

a Ongridpaper,copythegraphandextendittoshowthenumberoflapseachgirlcompletesin 24 minutes.(Drawarectangleforeachlapcycled.)

b Whendoallthreegirlsﬁrstcrossthestartinglinetogether?(Giveyouranswerasthenumberof minutesafterthestart.)

c Howmanyfulllapshaseachgirlcompletedafter 24 minutes?(Countwholelapsonly.)

d Supposethateachgirlrides 15 laps.HowmanyminutesafterLilliwill: Aliyahﬁnish? i Ciaraﬁnish? ii

Ciara Aliyah

Lilli

Ciara Aliyah

2C Divisibility

Learningintentions

• Tounderstandthattestscanbeusedtocheckifanumberisdivisiblebyanothernumberwithoutactuallydividing.

• Tobeabletotestfordivisibilityby 2, 3, 4, 5, 6, 8, 9 and 10

Keyvocabulary: factor,divisible,remainder,divisibilitytest

Itisoftenusefultoknowwhetheranumberisexactlydivisiblebyanothernumber.Forexample, 20 is divisibleby 2 because 20 ÷ 2 = 10 withnoremainder.However, 20 isnotdivisibleby 3 because 20 ÷ 3 = 6 withremainder 2.

Therearesimpledivisibilitytestsforeachofthesingle-digitnumbers,withtheexceptionof 7

Lessonstarter:Exploringremainders

Workwithapartnertosortthesedivisionsintotwogroups:

• Divisionswithnoremainder

• Divisionswitharemainder

Keyideas

Divisibilitytests arewaystoworkoutwhetherawholenumberisdivisiblebyanotherwhole number,withoutactuallydoingthedivision. Allnumbersaredivisibleby 1

Exercise2C

Und er stand ing

1 Writethemissingwordsornumbers.

Wesaythat 24 is by 3 because 24 ÷ 3 = 8 withno a Evennumbersarealldivisibleby b Evennumbersendin , , , or c 432 is by 3 becausethesumofthedigits is + + = and isdivisibleby 3 d 432 isanumberdivisiblebyboth 2 and 3 soitisalso divisibleby e

2 WhoamI?Matcheachcorrectdescription(A to C)toitsclue(a to c). Thesumofmydigitsisdivisibleby 3 a Iamdivisibleby 2 A Iamanevennumber. b Iamdivisibleby 3 B Iamevenandthesumofmydigitsis divisibleby 3 c Iamdivisibleby 6 C

3 Writethemissingwordsornumbers.

Q1Hint:Lookbackatthe Keyideas

Anumberthatendsin 0 isdivisiblebyboth and ,aswellasby 2 a Anumberthatendsin 5 isdivisibleby b Thelasttwodigitsof 316 formthenumber ,and isdivisibleby 4,so 316 isalsodivisible by c Thelastthreedigitsof 5328 formthenumber ,and isdivisibleby 8,so 5328 isalsodivisible by d

4 Writethemissingwordsornumbers.

In 2583,thesumofthedigitsis + + + = a 2583 is by 3 becausethesumofitsdigits, ,isdivisibleby b 2583 isalso by 9 becausethesumofitsdigits, ,isdivisibleby c 2583 isnotdivisibleby 6 becauseitisan number. d

Example7Usingdivisibilitytestsfor 2, 3, 6 and 8

Whichofthenumbers 148, 63, 462, 6387, 7168 aredivisibleby: 2? a 3? b 6? c 8? d

SolutionExplanation

a 148, 462, 7168 Onlyevennumbersaredivisibleby 2.Thenumbers 63 and 6387 areodd.

b 63, 462, 6387 Divisibleby 3 whenthesumofdigitsisdivisibleby 3 For 148: 1 + 4 + 8 = 13 but 13 ÷ 3 = 4 withrem. 1 ✘ For 63: 6 + 3 = 9 and 9 ÷ 3 = 3 ✔ Inasimilarway,test 462 ✔ 6387 ✔ and 7168 ✘

c 462 Divisibleby 6 whenevenandthesumofthedigitsisdivisibleby 3 4 + 6 + 2 = 12 and 12 ÷ 3 = 4 ✔

d 7168 Divisibleby 8 whenthenumberformedfromlast 3 digitsisdivisibleby 8 168 ÷ 8 = 21 ✔

Nowyoutry

Whichofthenumbers 37, 126, 216,and 13914 aredivisibleby: 2? a 3? b 6? c 8? d

Whichofthesenumbersaredivisibleby 2?

3, 6, 13, 14, 8, 17, 21, 54, 22, 34, 33, 50, 18, 35, 46

Whichofthesenumbersaredivisibleby 3?

b Whichofthesenumbersaredivisibleby 6?

12, 14, 18, 20, 22, 30, 27, 23, 54, 50, 36, 42, 13, 24, 43

12, 24, 28, 38, 63, 60, 87, 225, 54, 252, 36, 92, 66, 84, 143

Whichofthesenumbersaredivisibleby 8?

35, 168, 7168, 40, 5032, 9338, 248, 7831, 6400, 9568

Q5Hint:

Divisibilitytests:

2: lastdigiteven

3: sumofdigitsis divisibleby 3

6: divisibleby 2 and 3

8: numberformedfrom last 3 digitsisdivisible by 8 orendsin000.

Example8Usingdivisibilitytestsfor 4, 5, 9 and 10

Whichofthenumbers 540, 918, 8775, 3924 aredivisibleby: 10? a 5? b 4? c 9? d

Solution

a 540

b 540, 8775

c 540, 3924

d 540, 918, 3924, 8775

Explanation

Divisibleby 10 whennumberendsin 0

Divisibleby 5 whennumberendsin 0 or 5.

Divisibleby 4 whenlasttwodigitsdivisibleby 4

For 540: 40 ÷ 4 = 10 ✔

For 918: 18 ÷ 4 = 4 rem.2 ✘

Inasimilarway,test 75 ✘ and 24 ✔

Divisibleby 9 whensumofdigitsdivisibleby 9

For 540: 5 + 4 + 0 = 9 and 9 ÷ 9 = 1 ✔

For 918: 9 + 1 + 8 = 18 and 18 ÷ 9 = 2 ✔

Inasimilarway,test 8775 ✔ and 3924 ✔

Nowyoutry

Whichofthenumbers 62, 570, 2112, 5617 aredivisibleby: 10? a 5? b 4? c 9? d

Whichofthesenumbersaredivisibleby 5?

35, 52, 125, 13, 15, 100, 113, 112, 32, 515, 408, 730, 105 a

Whichofthesenumbersaredivisibleby 10?

20, 64, 800, 98, 290, 610, 85, 265, 590, 52, 39, 90, 160

Whichofthesenumbersaredivisibleby 4?

16, 32, 220, 10, 12, 28, 213, 432, 72, 316, 424, 1836, 135

Whichofthesenumbersaredivisibleby 9?

27, 432, 456, 88, 99, 387, 63, 55, 720, 85, 253, 2799

Example9Applyingdivisibilitytests

Q6Hint:Divisibilitytests: 5:lastdigit 5 or 0

10:lastdigit 0

4:numberformedfromlast twodigitsisdivisibleby 4 9:sumofdigitsisdivisible by 9

Workoutwhetherthefollowingcalculationsarepossiblewithoutleavingaremainder. 54327 ÷ 3 a 765146 ÷ 8 b

Solution

Explanation

a Digitsum = 21 Yes, 54327 isdivisibleby 3. 5 + 4 + 3 + 2 + 7 = 21 21 isdivisibleby 3.

b 8 18 ) 1466 rem. 2 No, 765146 isnotdivisibleby 8

Nowyoutry

Checkwhetherthenumberformedbythelast threedigitsisdivisibleby 8

Workoutwhetherthefollowingcalculationsarepossiblewithoutleavingaremainder. 4168 ÷ 4 a 3142 ÷ 9 b

7 Workoutwhetherthefollowingcalculationsarepossiblewithoutleavingaremainder.

23562 ÷ 3 a 39245678 ÷ 4 b 1295676 ÷ 9 c 213456 ÷ 8 d 3193457 ÷ 6 e 2000340 ÷ 10 f 51345678 ÷ 5 g 215364 ÷ 6 h 9543 ÷ 6 i 25756 ÷ 2 j 56789 ÷ 9 k 324534565 ÷ 5 l 2345176 ÷ 8 m 329541 ÷ 10 n 225329 ÷ 3 o 356781276 ÷ 9 p 164567 ÷ 8 q 2002002002 ÷ 4 r 8

Copythetable.Carryoutthedivisibilitytestsonthegivennumbers, ﬁllinginthetablewithticksorcrosses.

Q7Hint:Applythe divisibilitytests ratherthandoing theentiredivision.

Q8Hint: ✔ ifdivisible. ✘ ifnotdivisible.

by 9

by 10

Problem-solving and reasoning

Giveareasonwhy:

8631 isnotdivisibleby 2 a 31313 isnotdivisibleby 3 b

426 isnotdivisibleby 4 c 5044 isnotdivisibleby 5 d 87548 isnotdivisibleby 6 e 214125 isnotdivisibleby 8 f 3333333 isnotdivisibleby 9 g 56405 isnotdivisibleby 10 h

Givetheremainderwhen:

326 isdividedby 3 a 21154 isdividedintogroupsoffour b 72 isdividedintosixgroups c 45675 issharedintoﬁvegroups d

11 Thegameof‘clusters’involvesagroupgettingintosmaller-sized groups.Playersgetintogroupsasquicklyaspossibleoncethe clustersizehasbeencalledout.Ifayearlevelconsistsof 88 students,whichclustersizeswouldmeanthatnostudentsare leftoutofagroup?Giveallpossibleanswers.

Q9Hint:Thinkabouttherules fordivisibility.

Q10Hint:Theremainderisthe amountleftoverafterthedivision.

Q11Hint:Think: groups of make 88.

12 Blake’sageisatwo-digitnumber.Itisdivisibleby 2, 3, 6 and 9.HowoldisBlakeifyouknowthatheis olderthan 20 butyoungerthan 50?

13 Isthenumber 968362396392139963359 divisibleby 3? a

Manyofthedigitsinthenumberabovecanactuallybeignoredwhencalculatingthedigitsum. Whichnumberscanbeignoredandwhy? b Todetermineifthenumberaboveisdivisibleby 3,onlyﬁveofthe 21 digitsactuallyneedtobeadded together.Findthis‘reduced’digitsum.

c Makealistoflargenumbers.Includesomenumbersthataredivisibleby 3 andothernumbersthat arenot.

Swaplistswithaclassmate.Seehowquicklyyoucanﬁndeachother’snumbersthatare divisibleby 3.

2D 2D Primenumbersandcompositenumbers

Learningintentions

• Tobeabletodeterminewhetheranumberisprimebyconsideringitsfactors.

• Tobeableto ndtheprimefactorsofagivennumber.

• Toknowthat1isneitherprimenorcomposite.

Keyvocabulary: factor,primenumber,compositenumber

Aprimenumberhasonlytwofactors.Forexample, 5 isaprime numberbecauseitscompletelistoffactorsincludesonly 1 and 5 Compositenumbershavemorethantwofactors.Forexample, 9 isacompositenumberbecauseitsfactorsare 1, 3 and 9

Primenumbershavemanyimportantusesineverydaylife, suchasinternetsecurity.Therearesomeinterestingprime numberswithremarkablepatternsintheirdigits,suchas 12345678901234567891.Youcanalsogetprimessuchas 111191111 and 123494321 whicharethesameifyoureadthem forwardsorbackwards.Thesearecalledpalindromicprimes. Belowisapalindromicprimenumberthatreadsthesameupside downorwhenviewedinamirror.

I88808I80888I

Lessonstarter:Findtheprimenumbers

Eliseistryingtodecidewhichofthefollowingareprimenumbers.

Primenumbersareusedininternet securitytoencryptdatalikepasswords.

• Whichnumberscouldsheeliminatestraightaway?Why?

• HowcouldEliseusedivisibilityteststoeliminatesomeoftheother numbers?

• Whichofthenumbersdoyouthinkareprime?

Keyideas

A primenumber isapositivewholenumberthathasonlytwo factors: 1 anditself.

• Thesmallestprimenumbersinclude 2, 3, 5, 7, 11, 13, 17, 19, 23, 29,

Anumberthathasmorethantwofactorsiscalleda compositenumber

Exercise2D

Und er stand ing 1–4 4

1 Copyandcompletethefollowing. A numberhasonlytwofactors:

and . a Anumberthathasmorethantwofactorsisa number.

2 Thefactorsof 12 are 1, 2, 3, 4, 6 and 12.Is 12 aprimenumber?

a Thefactorsof 13 are 1 and 13.Is 13 aprimenumber? b

3a Listtheﬁrst 10 primenumbers.

Q2Hint:Lookatthe Keyideas b

b Listtheﬁrst 10 compositenumbers.

4a Whatistheﬁrstprimenumbergreaterthan 10?

b Whatistheﬁrstcompositenumbergreaterthan 10?

Fluency

Example10Decidingifanumberisprimeorcomposite

Whichofthesenumbersareprimeandwhicharecomposite: 22, 35, 17, 11, 9, 5?

Solution

Prime: 5, 11, 17

Explanation

Composite: 9, 22, 35 5, 11, 17 haveonlytwofactors(1 anditself). 9 = 3 × 3, 22 = 2 × 11, 35 = 5 × 7

Nowyoutry

Whichofthesenumbersareprimeandwhicharecomposite: 7, 25, 39, 43, 58, 73?

5 Labeleachofthefollowingasaprime (P) oracomposite (C) number.

Q5Hint:Aprimenumberhas onlytwofactors: 1 anditself.

Example11Findingprimefactors

Findtheprimenumbersthatarefactorsof 30

Solution Explanation

Factorsof 30 are: 1, 2, 3, 5, 6, 10, 15, 30

Primefactorsare 2, 3 and 5

Findallthefactorpairs: 1 × 30, 2 × 15, 3 × 10, 5 × 6 Determinewhichfactorsareprime. 1 isnotaprimenumber. 2 = 2 × 1, 3 = 3 × 1, 5 = 5 × 1

Nowyoutry

Findtheprimenumbersthatarefactorsof 48

6 Findtheprimenumbersthatarefactorsof:

Q6Hint:Listallthefactorsﬁrst.

7 Listthecompositenumbersbetween:

8 Listtheprimenumbersbetween:

Problem-solving and reasoning

9 Thefollowingarenotprimenumbers,yettheyaretheproduct (×) oftwoprimes.Findthetwoprimes thatmultiplytogive: 15 a 21 b 35 c 55 d 143 e 133 f

10 Whichofthefollowinghasacompletesetoffactorsthatare allprimenumbers,exceptfor 1 anditself? 12, 14, 16, 18, 20

Q10Hint:Firstlistallthefactors ofeachnumber.

11 Twinprimesarepairsofprimesthatareseparatedfromeach otherbyonlyonewholenumber.Forexample, 3 and 5 aretwinprimes. Findthreemorepairsoftwinprimes.

Q11Hint: 3, 4, 5

12 Answerthesequestionsforeachofthearrays(a to h)below. Isitpossibletorearrangethecountersintoarectanglewithtwoormore equalrows? i Ifitispossible,statethedimensionsofthenewrectangle. ii Statethenumberofcountersandwhetherthisisaprimeoracompositenumber. iii

Q12Hint:The‘dimensions’arethe numberofrows andthe number ofcolumns

Playthisgamewithaclassmate.Youwillneedalargesheetofpaper,adieandtwo‘racecars’(counters orerasers).

• Onthesheetofpaper,drawacurvylineforyourracetrack.

• Writethenumbers 1 to 50 alongyourtrackandcirclealltheprimenumbers.Forexample:

• Startwithbothcarson 1.Taketurnstorollthe dieanddriveyourcarthatnumberofplaces alongthetrack.

• Ifyourcarlandsonaprimenumber,itneedsa pitstop(ﬂattyre,lowfuel,etc.)andyoumissa turn.

• Thecarthatwinsreachestheﬁnishlineﬁrst. (Youmustrollthecorrectnumbertoland exactlyon 50.)

2E 2E Indexform

Learningintentions

• Tounderstandwhatanexpressionlike 85 means.

• Tobeabletowriteaproductinindexformiftherearerepeatedfactors.

• Tobeabletoevaluatenumericexpressionsinvolvingpowersusingmultiplication.

Keyvocabulary: base,power,index(plural:indices),expandedform,factorform,indexform,raised

Whenanumberismultipliedbyitself,weoftenwritethat productinindexform.

Forexample:

1000 = 10 × 10 × 10 (expandedform) = 103 (indexform)

For 103 wesay‘10 tothepowerof 3’.

Lessonstarter:Aneasierway

Whatisaneasierwayofwriting:

• 10 × 10 × 10 × 10,otherthan 10000?

• 10 × 10 × 10 × 10 × 10 × 10,otherthan 1000000?

• 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2,otherthan 1024?

Computermemoryandhard-drivestorage aremeasuredinbytes.Doyouknowthe sizeoftheharddriveofyourcomputer atschool?Howmanybytesdoesithave? Copyandcompletethistableofcomputer storageunits.

Keyideas

Usingindexformmakesiteasiertowrite verylargenumberslike 1024

Numberofbytes kilobytekB

Wecanwritetheproductofrepeatedfactorswitha base numberandan index number. Thisiscalledwritinganexpressionin indexform Forexample:

32 768 = 8 × 8 × 8 × 8 × 8 85 number or value expanded form index form index or power = base

The power orindexshowsthenumberofrepeatedfactors.Itisthenumberthatabaseis raised to. 85 reads‘8 tothepowerof 5’.

Numbersinindexformareevaluatedﬁrstintheorderofoperations.

Forexample: 3 + 2 × 42 = 3 + 2 × 16

= 3 + 32 = 35

Notethat 23 = 2 × 2 × 2 = 8.

23 does not mean 2 × 3 = 6

Exercise2E

Und er stand ing 1–4 4

1 Writethemissingwords.

Theproduct 2 × 2 × 2 iscalledthe formof 8. a

23 iscalledthe formof 8 b

23 reads:‘2tothe of 3’. c

In 23,thespecialnameforthe 2 isthe number. d In 23,thespecialnameforthe 3 isthe or e

2 Copyandcompleteeachproductofrepeatedfactors.

32 = 3 × a

24 = 2 × × × b

53 = 5 × × c

85 = × × × × d

3 Copyandcompletethetable.

5 × 5 × 5

Copyandcompletethetable.

Q1Hint:Choosefromthewords: index, expanded, base, power

Fluency

Example12Convertingtoindexform

Simplifytheseproductsbywritingtheminindexform. 5 × 5 × 5 × 5 × 5 × 5 a 3 × 3 × 2 × 3 × 2 × 3 b

Solution

a 5 × 5 × 5 × 5 × 5 × 5 = 56

Explanation

Thefactor 5 isrepeatedsixtimes.

b 3 × 3 × 2 × 3 × 2 × 3 = 22 × 34 2 isrepeatedtwotimes. 3 isrepeatedfourtimes.

Nowyoutry

Simplifytheseproductsbywritingtheminindexform. 7 × 7 × 7 × 7 × 7 a 5 × 2 × 2 × 5 × 2 × 2 × 5 b

5 Simplifytheseproductsbywritingtheminindexform.

Q5Hint:Thebaseis thefactor.Thepower isthenumberof repeats. 3 × 3 × 3

Example13Expandingexpressionsinindexform

Writeeachofthefollowinginfactorformandﬁndthevalue.

Solution

a 24 = 2 × 2 × 2 × 2 = 16

b 23 × 52 = 2 × 2 × 2 × 5 × 5 = 8 × 25 = 200

Nowyoutry

Explanation

Thedigit 2 isrepeatedfourtimes. Calculatethevalue.

Thedigit 2 isrepeatedthreetimes,then multiply 5 by 5 Calculatethevalue.

Writeeachofthefollowinginfactorformandﬁndthevalue.

6 Writeinexpandedfactorformandﬁndthevalue.

7 Copyandcompletethefollowing.

a 3 × 2 = but 32 = × =

b 2 × 4 = but 24 = × × × =

c 5 × 2 = but 52 = × =

d 6 × 2 = but 62 = × =

8 Writeinexpandedform.(Donotﬁndthevalue.)

Example14Evaluatingexpressionswithindexform

Evaluate:

Solution

a 72 −62 = 7 × 7−6 × 6 = 49−36 = 13

b 2 × 33 + 102 + 17

= 2 × 3 × 3 × 3 + 10 × 10 + 1 × 1 × 1 × 1 × 1 × 1 × 1

= 54 + 100 + 1 = 155

Nowyoutry

Evaluate:

9 Evaluate:

Explanation

Writepowersinfactorform.

Domultiplicationbeforesubtraction.

Writepowersinexpandedform.

Domultiplicationﬁrst,thenaddition.

10 Findtheindexnumberforeachofthefollowing.

11 Writeoneofthesymbols <, = or > intheboxtomakethefollowingstatementstrue.

Q11Hint: < meanslessthan. > meansgreaterthan.

12 Fivefriendsreceivethesametextmessageatthesametime.Eachofthefivefriendsthenforwards ittofiveotherfriendsandeachofthesepeoplealsosendsittofiveotherfriends.Howmanypeople doesthetextmessagereach?

Thepowerofemail

13 Achainemailissentto 10 people.Fiveminuteslater,eachofthemsends itto 10 otherpeople.Thatis,after 10 minutes, 110 people (10 + 100) willhavereceivedtheemail.Fiveminuteslater,eachofthemsendsit ontotenotherpeople,etc.

a Howmanypeoplewillhavereceivedtheemailafter: 15 minutes? i 30 minutes? ii

b Iftheemailalwaysgoestoanewperson,howlong wouldittakeuntileveryoneinAustraliahasreceived themessage?(Australiahasapproximately 24.5 million people.)Rounduptothenext 5 minutemark.

c Howlongwouldittakeuntileveryoneintheworld hasreceivedthemessage?(Theworldpopulationis approximately 8 billionpeople.)

Q13Hint:Assume thateveryoneuses emailandeveryone canread!

2F 2F Primefactors

Learningintentions

• Tounderstandthatcompositenumberscanbebrokendownintoprimefactors.

• Tobeabletouseafactortreeto ndtheprimefactorsofanumber(includingrepeatedfactors).

• Tobeabletoexpressaprimedecompositionusingpowersofprimenumbers.

Keyvocabulary: factor,compositenumber,primefactor,factortree

Everycompositenumbercanbewrittenastheproductofprimenumberfactors. Factortreeshelpustoworkouttheprimenumberfactors.Whentherearerepeatedfactors,wewrite thatproductinindexform.

Lessonstarter:Factortrees

Forhomework,JarrodandMatteachdrewafactortree.Thentheirlittlebrotherrubbedoutsomeof thenumbers.

• Canyouﬁndthemissingnumbers?Copyandcompleteeachfactortree.

• Whatwastheboys’homeworkquestion?

• HowisJarrod’sfactortreedifferentfromMatt’s?

• Whatisthesameaboutbothfactortrees?

• Canyoudrawadifferentfactortreethatanswersthehomeworkquestioncorrectly?

Keyideas

Every compositenumber canbewrittenasaproductofits primefactors

Wecanusea factortree orrepeateddivisiontoﬁndtheprimefactorsofacompositenumber. Itisadiagramshowingthebreakdownofanumberintoitsprimefactors.

withprimefactors

Itishelpfultowritetheprimefactorsinascending(increasing)order,usingpowers.

Forexample:

Exercise2F

Und er stand ing

1 Sortthefollowinglistofnumbersintotwogroups: compositenumbersandprimenumbers. 15, 13, 7, 5, 8, 9, 27, 23, 11, 4, 12, 2, 3

2 Copyandcompletethefollowingfactortrees.

3 Copyandcompletetheserepeateddivisionswithprimenumbers.

Q1Hint:Aprimenumberhas twofactors: 1 anditself.

4 Rewritethesewiththeprimefactorsinascendingorder. Thenwriteusingpowers.

Q4Hint:Ascendingmeans smallesttolargest.

Example15Usingafactortreetoﬁndprimefactors

Drawafactortreeforthenumber 120.Thenwrite 120 astheproductofprimefactors.(Use indexform.)

Solution Explanation

Startwith 120.Findanypairoffactors.

Allfactorsarenowprimes. Useindexformforrepeatedfactors. Thepower (3) showsthatthefactorof 2 is repeated 3 times.

Nowyoutry

Drawafactortreeforthenumber 300.Thenwrite 300 astheproductofprimefactors.(Use indexform.)

5 Foreachnumber,useafactortreetowritetheprimefactorisation ofthenumber.

Q5Hint:Writeprime factorsinascending order.Usepowersfor repeatedfactors.

6 Foreachnumber,useafactortreetowritetheprimefactorisation ofthenumber.

Example16Usingrepeateddivisiontoﬁndprimefactors

Userepeateddivisionwithprimenumberstoﬁndtheprimefactorsof 126.Thenwrite 126 asa productofprimefactorswithpowers.

Nowyoutry

Userepeateddivisionwithprimenumberstoﬁndtheprimefactorsof 495.Thenwrite 495 asaproduct ofprimefactorswithpowers.

7 Userepeateddivisionwithprimenumberstoﬁndtheprimefactorsof 96 Thenwrite 96 asaproductofprimefactorswithpowers.

8 Userepeateddivisionwithprimenumberstohelpyouwriteeach ofthesenumbersasaproductofprimefactorswithpowers.

Q7Hint:Youcouldstartby dividing 96 by 2

Problem-solving and reasoning

9 Matchthecorrectcompositenumber(a to d)toitssetofprime factors(A to D).

Q9Hint:Lookforeasywaystomultiply 10 2 × 3 × 5 × 5 15

10 Drawfourdifferentfactortreesthateachshowtheprimefactorsof 24.(Fortwotreestobedifferent, theymustshowdifferentcombinationsoffactors,notjustthesamefactorsinadifferentorder.)

11a Express 144 and 96 inprimefactorform.

b DeterminetheHCFof 144 and 96.Theprimefactorformmayhelp.

12 Onlyoneofthefollowingisthecorrectsetofprimefactorsfor 424

a Whyisoption C wrong?

Explainwhy A and B arewrong.

Showthatoption D isthecorrectanswer.

Q12Hint:Remembertherules fordivisibility.

Fourdifferentprimefactors 13

13 Only 16 compositenumberssmallerthan 1000 havefourprimefactors.Forexample: 546 = 2 × 3 × 7 × 13

Byconsideringtheprimefactorpossibilities,seehowmanyoftheother 15 compositenumbersyoucan ﬁnd.Expresseachoftheminprimefactorform.

2G 2G Squaresandsquareroots

Learningintentions

• Tounderstandthatasquarenumbercanbethoughtofintermsoftheareaofasquare,orthenumberofitemsin asquarearray.

• Tobeableto ndthesquareofanumber.

• Tobeableto ndthesquarerootofaperfectsquare.

Keyvocabulary: squarenumber,squareroot,perfectsquare

Wecanpictureasquarenumberastheareaofasquareorthenumberofobjectsinasquarearray.

Forexample:

Numberofstrawberries = 3 rowsof 3 = 3 × 3 = 32 = 9 9 isasquarenumber. 16 isasquarenumber.

Findingasquarerootofanumberistheoppositeofsquaringanumber.Weusethesymbol √ toshow thesquarerootofanumber.

Thepicturesaboveshowthat √16 = 4 and √9 = 3

Lessonstarter:Shadingsquares

Youwillneedasheetof 1-cmgridpaper.

• Shadeasmanydifferent-sizedsquaresasyoucanﬁtontothepage.

• Writeeachareainindexform.Forexample, 62 = 36, 42 = 16,etc.

• Finally,oneachsquarewritethesidelengthasthesquarerootofthearea.Forexample, 6 = √

Keyideas

Ifyoumultiplyawholenumberbyitself,theresultisa squarenumber

Forexample: 52 = 5 × 5 = 25,so 25 isasquarenumber.

• Squarenumbersarealsoknownas perfectsquares

• Theﬁrst 12 squarenumbersare:

The squareroot ofagivennumbermultipliedbyitselfresultsinthegivennumber.

• Thesymbolforsquarerootis √

• Findingasquarerootofanumberistheoppositeofsquaringanumber.

Forexample: 42 = 16,so √16 = 4.

Wereadthisas‘4 squaredequals 16,so,thesquarerootof 16 equals 4’.

• Wecanlocateanysquarerootbetweentwopositiveintegersbyconsideringitssquare.

Forexample, √31 mustbebetween 5 and 6 because 31 isbetween 52 = 25 and 62 = 36

Orderofoperations

• Squaresarepowers,soevaluateﬁrst.Forexample:

• Squarerootsactlikebrackets.Forexample:

Exercise2G

1 Statethemissingwordornumber.

2 Copyandcompletethistableofsquarenumbers.

3 Copyandcompletethistableofsquareroots.

Example17Findingsquaresandsquareroots

Writethevalueofeachofthese:

42 a 7 squared b (3)2 d 5 tothepowerof 2 c squarerootof 36 e sidelengthofsquarewitharea 64 cm2 f

Solution

Explanation

a 42 = 16 42 = 4 × 4

b 7 squared = 49 7 squaredisthesameas 72

c (3)2 = 9 (3)2 = 3 × 3 = 9

d 5 tothepowerof 2 = 25 5 tothepowerof 2 isthesameas 52 , and 52 = 5 × 5 = 25

e squarerootof 36 = 6 √36 = 6 because 6 × 6 = 36

f sidelength = 8 cm sidelength = √64 and 8 × 8 = 64

Nowyoutry

Writethevalueofeachofthese:

4 Evaluate:

5 Evaluate: √25 a squarerootof 16 b √100 c thesidelengthofasquarethathasanareaof 49 cm2 d

6 Findthevalueof:

Example18Evaluatingsquareroots

Findthevalueof:

a √64 = 8

64 = 8 because 8 × 8 = 64

1600 = 40 because 40 × 40 = 1600

Nowyoutry

Findthevalueof:

7 Findthevalueof:

Example19Locatingsquarerootsbetweenpositiveintegers

Statewhichconsecutivepositiveintegersareeithersideof:

a 6 and 7 62 = 36 and 72 = 49 43 liesbetweenthesquarenumbers 36 and 49, so √43 liesbetween 6 and 7

b 11 and 12 112 = 121 and 122 = 144

130 liesbetweenthesquarenumbers 121 and 144,so √130 liesbetween 11 and 12

Nowyoutry

Statewhichconsecutivepositiveintegersareeithersideof:

8 Statewhichconsecutivepositiveintegersareeithersideof:

Example20Evaluatingexpressionsinvolvingsquaresandsquareroots

Evaluate:

Solution Explanation

Findsquarerootsﬁrst. Thenadd.

Thesquarerootsignislikeabracket:

Multiplyandaddtogive:

Evaluatesquaresandsquarerootsﬁrst.

Nowyoutry

Evaluate:

9 Evaluate:

Q9Hint:Remembertheorder ofoperations

10 Thisarrangementofdotsshowsthat 9 isasquarenumber.

a Show,usingdots,that 16 isasquarenumber.

b Show,usingdots,that 6 is not asquarenumber.

11 Listallthesquarenumbersbetween 50 and 101.

12 Listallthesquarenumbersbetween 101 and 200.Hint:Thereareonlyfour.

13a Showthat 32 + 42 = 52

b Does 52 + 62 = 72?

c Does 62 + 82 = 102?

d Findsomeothertruesumsofsquarenumbersliketheoneinpart a

Numberdotpatterns

14 Foreachofthefollowing:

Copythedotpatternanddrawthenextthreeterms. i Howmanydotsareaddedeachtime? ii Whatpatternsdidyounotice? iii oddnumbers a

1 3 5 evennumbers b

2 4 6 squarenumbers c

1 4 9 triangularnumbers d

1 3 6

15 Canyouseeaconnectionbetweentriangularnumbersandsquarenumbers?

1 2A Findthecompletesetoffactorsforeachofthesenumbers. 20 a 36 b

2 2A Writedowntheﬁrstﬁvemultiplesofeachofthesenumbers. 12 a 21 b

3 2B Findthehighestcommonfactor(HCF)ofthefollowingnumbers. 24 and 40 a 35 and 70 b 18 and 42 c

4 2B Findthelowestcommonmultiple(LCM)ofthefollowingnumbers. 8 and 12 a 11 and 7 b 3, 5 and 10 c

5 2C Whichofthenumbers 75, 14, 141, 52, 88, 1234 aredivisibleby: 2? a 3? b 4? c 5? d

6 2C Workoutwhetherthefollowingcalculationsarepossiblewithoutleavingaremainder. 32689 ÷ 3 a 456336 ÷ 8 b

7 2D Whichofthesenumbersareprime(P)andwhicharecomposite(C)? 15, 23, 31, 39, 51, 80, 91

8 2D Findtheprimenumbersthatarefactorsof:

9 2E Simplifytheseproductsbywritingtheminindexform. 4 × 4 × 4 × 4 × 4 a 6 × 5 × 5 × 6 × 5 × 5 × 6 b

10 2E Writeeachofthefollowinginexpandedformandﬁndthevalue. 34 a 23 × 52 b 62 −23 c

11 2F Writethefollowingnumbersasaproductoftheirprimefactors,usingpowers. 40 a

12 2G Findthevalueof:

2H 2H Numberpatterns CONSOLIDATING

Learningintentions

• Tounderstandwhatanumberpattern(ornumbersequence)is.

• Tobeabletodescribeapatternwherenumbersareincreasingordecreasingbya xedamount.

• Tobeabletodescribeapatternwherenumbersaremultipliedordividedbya xedamount.

Keyvocabulary: pattern,sequence,term,rule,increasing,decreasing

Numberpatternscanbefoundinallsortsofnaturaland artiﬁcialsituations.Forexample,ifbacteriacellsdivideintwo everyhour,thenthenumberofbacteriafollowsthepattern 1, 2, 4, 8, 16, 32, 64, 128,andsoon.Ascientistcouldusethis patterntopredictthenumberofbacteriaafteracertaintime.

Itishelpfultoﬁndtherulethatdescribesanumberpattern. Enteringrulesintoaspreadsheetmakesiteasytoperform calculationswithlargenumbers.Scientists,accountantsandmany otherpeopleusenumberpatternsandrulestohelpthemanalyse dataandmakepredictions.

Lessonstarter:Whichruleiswhich?

Numberpatternsappearallthroughout nature,suchasincelldivision.

• Workwithapartnertomatcheachofthesenumberpatternstothecorrectrule.Discussthethinking youused.

Numberpattern Rule

A 7, 12, 17, 22, 27, P Startwith 96 andkeepdividingby 2

B 96, 48, 24, 12, 6, … Q Startwith 7,add 5,add 6,add 7,etc.

C 96, 92, 88, 84, … R Startwith 7 andkeepadding 5

D 7, 12, 18, 25, 33, 42, … S Startwith 96,add 4,take 10,etc.

E 96, 100, 90, 94, 84, 88, 78, … T Startwith 96 andkeepsubtracting 4

• Makeupsomenumberpatternsofyourown.Thenswappatternswithanothergroup.Seeifyoucan workouteachother’srules.

Keyideas

Alistofnumbersarrangedinorderaccordingtosomeruleiscalledanumber pattern ora sequence

Eachseparatenumberinthesequenceiscalleda term

Toﬁndthetermsofasequence,followthepattern rule.Forexample:therule‘startwith 3 andadd 2 toeachterm’gives 3, 5, 7, 9, 11, ...

Toﬁndthepatternruleforasequence,ask:

• Isthesequence increasing or decreasing byaﬁxedamount? 25, 28,31, 34, ...

+ 3 + 3 + 3 50, 45,40, 35, ... 5 5 5

• Iseachtermbeingmultipliedordividedbythesameamount? 4,12,36, 108, ...

2 ÷ 2 ÷ 2

× 3 × 3 × 3 64, 32, 16,8, ...

Exercise2H

Und er stand ing

1 Writethemissingwords/number.

Whenalistofnumbersfollowsapatternthatcanbe describedbyarule,itiscalleda a

Eachseparatenumberinasequenceiscalleda b

Themissingnumberinthesequence , 2, 4, 6, 8 is c

Themissingnumberinthesequence , 2, 4, 8, 16 is d

2 Listthenextthreetermsineachofthesesequences.

Q1Hint:Lookbackatthe Key ideas

64,32,16,

3 Listtheﬁrstﬁvetermsofthesequenceforeachofthesepatternrules.

Startwith 8 andkeepadding 3 a Startwith 32 andkeepsubtracting 1. b

Startwith 52 andkeepsubtracting 4 c Startwith 123 andkeepadding 7 d

4 Listtheﬁrstﬁvetermsofthefollowingnumberpatterns. Startwith 3 andkeepmultiplyingby 2 a

Startwith 5 andkeepmultiplyingby 4 b

Startwith 240 andkeepdividingby 2 c

Startwith 625 andkeepdividingby 5 d Fluency

Example21Findingpatternsthatchangebyaﬁxedamount

Findthenextthreetermsforthesenumberpatterns.

6, 18, 30, 42, , , a 99, 92, 85, 78, , , b

Solution

a 54, 66, 78

b 71, 64, 57

Explanation

Thesamenumberisbeingaddedtoeachterm. Keepadding 12 toﬁndthenextthreeterms. 6,18,30,42,54,66,

Keepsubtracting 7 toﬁndthenextthreeterms. 99,92,85,78,71,64, 7 7 7 7 7 7 57

Nowyoutry

Findthenextthreetermsforthesenumberpatterns.

3, 7, 11, 15, , , a 126, 115, 104, 93, , , b

5 Findthenextthreetermsforthesesequences.

3, 8, 13, 18, , , a

4, 14, 24, 34, , , b

26, 23, 20, 17, , , c

106, 108, 110, 112, , , d

63, 54, 45, 36, , , e

9, 8, 7, 6, , , f

101, 202, 303, 404, , , g

75, 69, 63, 57, ,

Q5Hint:Lookforaﬁxednumber thatisaddedorsubtracted.

Example22Findingpatternsthatinvolvemultiplicationordivision

Findthenextthreetermsforthefollowingnumberpatterns.

2, 6, 18, 54, , , a 256, 128, 64, 32, , , b

Solution

a 162, 486, 1458

b 16, 8, 4

Explanation

Eachtermisbeingmultipliedbythesamenumber. Keepmultiplyingby 3 toﬁndthenextthreeterms.

2,6,18,54,162,486, × 3 × 3 × 3 × 3 × 3 × 3 1458

Keepdividingby 2 toﬁndthenextthreeterms.

256,128,64,32,16,8,

Nowyoutry

Findthenextthreetermsforthefollowingnumberpatterns.

5, 20, 80, 320, , , a 729, 243, 81, 27, , , b

6 Findthenextthreetermsforthefollowingnumberpatterns.

2, 4, 8, 16, , , a

5, 10, 20, 40, , , b

96, 48, 24, , , c

1215, 405, 135, , , d

11, 22, 44, 88, , , e

7, 70, 700, 7000, , , f

256, 128, 64, 32, , , g

1216, 608, 304, 152, , , h

7 Findthemissingnumbersineachofthefollowingnumberpatterns.

62, 56, , 44, 38, , a

15, , 35, , , 65, 75 b

4, 8, 16, , , 128, c

3, 6, , 12, , 18, d 88, 77, 66, , , , 22 e

2997, 999, , , 37 f

Q6Hint:Iseachterm beingmultipliedor dividedbythesame number?

Q7Hint:These patternscaninvolve + or or × or ÷.

Example23Describingpatternsinwords

Foreachofthesesequences,writethepatternruleinwords.

2, 10, 50, 250, a 6, 10, 14, 18, b 32, 16, 8, 4, c 32, 28, 24, 20, d

Solution

Explanation

a Startwith 2 andmultiplyeachtermby 5 2, 10, 50, 250, ... × 5 × 5 × 5

b Startwith 6 andadd 4 toeachterm. 6, + 4 + 4 + 4 10,14, 18, ...

c Startwith 32 anddivideeachtermby 2 32, 16, 8, 4, ...

d Startwith 32 andsubtract 4 fromeachterm. 32, 28, 24, 20, ... 4 4 4

Nowyoutry

Foreachofthesesequences,writethepatternruleinwords.

3, 12, 48, 192, a 11, 14, 17, 20, b 625, 125, 25, c 123,

, d

8 Usewordstowritethepatternruleforeachsequence.

Problem-solving and reasoning

9 Writethenextthreetermsineachofthefollowingsequences.

a 3, 5, 8, 12, , ,

b 1, 2, 4, 7, 11, , , c 10, 8, 11, 9, 12, , , d 25, 35, 30, 40, 35, , ,

10 Afroghasfallentothebottomofawellthatis 6 metresdeep.

• Ontheﬁrstdaythefrogclimbs 3 metresupthewall ofthewell.

• Ontheseconddayitslidesback 2 metres.

• Onthethirddayitclimbsup 3 metres.

• Onthefourthdayitslidesback 2 metres.

Q9Hint:Lookathowmucheach termincreasesordecreases.

Q10Hint:Drawadiagramof thewell.Usearrowstoshow themovementofthefrog.

Thefrogcontinuesfollowingthispatternuntilitreachesthetopofthewellandhopsaway.

a Writeasequenceofnumberstoshowthefrog’sheightabovethebottomofthewellattheendof eachday.

b Howmanydaysdoesittakethefrogtogetoutofthewell?

11 Foreachofthefollowingsequences,describethepatternrule.

4, 12, 36, 108, 324, a 19, 17, 15, 13, 11, b 212, 223, 234, 245, 256, … c 8, 10, 13, 17, 22, … d 64, 32, 16, 8, 4, … e 5, 15, 5, 15, 5, … f 2, 3, 5, 7, 11, g

12 Copyandcompleteeachofthefollowing.Givethespecialname foreachtypeofnumbers.

1, 4, 9, 16, 25, 36, , , a

1, 1, 2, 3, 5, 8, 13, , , b

1, 8, 27, 64, 125, , , c 2, 3, 5, 7, 11, 13, 17, , , d

4, 6, 8, 9, 10, 12, 14, 15, , , e 121, 131, 141, 151, , , f

Q12Hint: Choosefrom: compositenumbers, cubenumbers,evennumbers, Fibonaccinumbers,negative numbers,oddnumbers,palindromes, primenumbers,squarenumbers, triangularnumbers

13 Whenmakingahumanpyramid,eachrowhasonelesspersonthan therowbelow.Thepyramidiscompletewhenthereisarowofonly onepersononthetop.

Q13Hint:Drawadiagram. Writedownanumberpatternforahumanpyramidwith 10 students onthebottomrow.Howmanypeopleareneededtomakethis pyramid?

2I 2I Patternswithshapesandnumbers

Learningintentions

• Tounderstandthatspatialpatternsarerelatedtonumberpatterns.

• Toknowthataspatialpatternstartswithastartingdesignandhasarepeatingdesign.

• Tobeabletocontinueaspatialpatterngiventhe rstfewshapes.

• Tobeabletodescribeandusearulerelatingthenumberofshapesandthenumberofobjectsrequiredto makethem.

Keyvocabulary: spatialpattern,geometricalshapes,patternrule,numbersequence,tableofvalues

Repeatedgeometricshapesforminterestingspatialpatterns. Architectsoftenusespatialpatternsinthedesignofbuildings. Artistsalsouserepeatedgeometricshapesindesignstobe printedoncurtains,tilesandwallpaper.

Lessonstarter:Stickpatterns

Copytheseshapesusingmatchsticksortoothpicks.Then buildthenextthreeshapesinthepattern.

Patternswithgeometricshapesareused widelyinbuildingdesign.

Howmanystickswouldyouneedtomaketheshapewith:

• 10 triangles?

• 100 triangles?

Ifyouknowthenumberoftriangles,howcouldyouﬁndthenumberofsticks?Discussthiswithapartner andthenwriteyouranswer.

Usesimilarstepstoexplorethenumberofsquaresinthefollowingpattern.

Keyideas

A spatialpattern isasequenceof geometricalshapes.Forexample:

• Thenumberof‘diamonds’ineachtermmakesa numbersequence.

• Thenumberofsticksineachtermmakesanothernumbersequence.

A tableofvalues showsthenumberofshapesandthenumberofsticks.

4 8 12 16 20

A patternrule tellshowmanysticksareneededforacertainnumberofshapes. Forexample:numberofsticks = 4 × numberofshapes

Exercise2I

Und er stand ing

1 Jackusedmatchstickstobeginapatternofrectangles.

diagram 1 diagram 2 diagram 3

Writethemissingwordsornumbersforeachofthese.

a Theshapeoftheﬁrstdiagramiscalleda

b Diagram 1 has rectangle,diagram 2 has rectanglesanddiagram 3 has rectangles.

c Diagram 1 has sticks,diagram 2 has sticksanddiagram 3 has sticks.

d Thesediagramsfollowasequencethatiscalleda pattern.

2 Janeusedmatchstickstomakeaspatialpatternofhouses.

Q2Hint:Howmanyextra sticksareneededtochange 1 houseinto 2 houses? Copyandcompletethistable.

Numberofhouses 1 2

Numberofsticks

3 Drawthenexttwotermsforeachofthesespatialpatterns.

Q3Hint:Whatshapeisbeing addedeachtimetomakethe nextdiagram?

Example24Findingageneralruleforaspatialpattern

a Drawthenexttwoshapesinthisspatialpattern.

b Completethetable.

Numberoftriangles 1 2 3 4 5

Numberofsticks 3

c Completethispatternrule:numberofsticks = × numberoftriangles

d Howmanystickswouldyouneedfor 20 triangles?

Solution

Explanation

a Followthepatternbyaddingonetriangle eachtime.

b Numberoftriangles 1 2 3 4 5

Anextra 3 sticksarerequiredtomakeeach newtriangle.

c Numberofsticks = 3 × numberoftriangles 3 sticksarerequiredpertriangle.

d Numberofsticks = 3 × 20 triangles = 60 sticks 20 triangles × 3 stickseach

Nowyoutry

Drawthenexttwoshapesinthisspatialpattern. a Completethetable.

NumberofLshapes 1 2 3 4 5

b Completethispatternrule:numberofsticks = × numberofLshapes c Howmanystickswouldyouneedfor 30 Lshapes? d

Numberofsticks 2

4a Drawthenexttwoshapesforthisspatialpattern.

b Copyandcompletethistable.

Numberofcrosses 1 2 3 4 5

Numberofsticks

Q4Hint:Forpart c,checkthat yourpatternruleworksforall valuesinthetable.

c Copyandcompletethispatternrule:numberofsticks = × numberofcrosses.

d Howmanystickswouldyouneedfor 10 crosses?

5a Drawthenexttwoshapesforthisspatialpattern.

b Copyandcompletethistable.

Numberofsquares 1 2 3 4 5

Numberofsticks

c Copyandcompletethepatternrule:numberofsticks = × numberofsquares

d Howmanystickswouldyouneedfor 12 squares?

6a Drawthenexttwoshapesforthisspatialpattern.

b Copyandcompletethistable.

Numberofhexagons 1 2 3 4 5

Numberofsticks

c Copyandcompletethepatternrule: numberofsticks = × numberofhexagons

d Howmanystickswouldyouneedfor 20 hexagons?

Q6cHint:Howmanyextra stickswouldyouneedtoadd anotherhexagon?

Problem-solving and reasoning

7 Listtheshapes(A to D)inthecorrectordertomakeaspatialpattern.(Startwiththesmallestshape.) Thendrawthenextshapeinthesequence.

Example25Findingmore-challengingrules

Drawthenexttwoshapesforthisspatialpattern.

Copyandcompletethetable.

Copyandcompletetheruleforthepattern: numberofsticks = 1 +× numberofsquares

c Howmanysticksareneededtomake 30 squaresthisway?

d Howmanysquarescouldbemadefrom 25 sticks?

Solution

c Numberofsticks = 1 + 3 × numberofsquares

d 91 sticks

e 8 squares

Explanation

Add 3 sticksatatimeto completeeachnewsquare.

Countthesquares. Completethecalculations, thencountsticksinthe diagramstocheck.

Thenumberofsticksis 1 morethan 3 timesthe numberofsquares.

Nowyoutry

Drawthenexttwoshapesinthisspatialpattern. a

Copyandcompletethetable.

Copyandcompletetheruleforthepattern: numberofsticks = 1 + × numberofhexagons c Howmanysticksareneededtomake 12 hexagons? d Howmanyhexagonscouldbemadefrom 41 sticks? e

8a Drawthenexttwoshapesforthisspatialpattern.

b Copyandcompletethistable.

Q8Hint:Howmanyextra sticksareneededtomake 1 stickintoatriangle?

c Copyandcompletetheruleforthispattern: numberofsticks = 1 + × numberoftriangles.

d Howmanysticksareneededtomake 12 trianglesthisway?

e Howmanytrianglescouldbemadefrom 81 sticks?

9a Drawthenexttwoshapesinthisspatialpattern.

b Copyandcompletethistable.

c Copyandcompletetheruleforthispattern: numberofsticks = 1 + × numberofshapes

d Howmanysticksareneededtomake 20 shapesthisway?

e Howmanyshapescouldbemadefrom 86 sticks?

Q9Hint:Copythelast shapeandaddmore stickstomakethe nextshape.

10a Drawthenexttwoshapesinthisspatialpattern.

0 fence sections 1 fence section planks 2 fence sections

b Copyandcompletethistable. Numberoffencesections 0 1 2 3 4

1 + =

c Copyandcompletethepatternrule: numberofplanks = 1 + × numberoffencesections.

d Howmanyplankswouldyouneedtomake 9 fencesections?

e Howmanyfencesectionscanbemadefrom 43 planks?

11 Whichrulecorrectlydescribesthisspatialpattern?

A Numberofsticks = 7 × numberof‘hats’

B Numberofsticks = 7 × numberof‘hats’ + 1

C Numberofsticks = 6 × numberof‘hats’ + 2

D Numberofsticks = 6 × numberof‘hats’

12 Whichrulecorrectlydescribesthisspatialpattern?

A Numberofsticks = 5 × numberofhouses + 1

B Numberofsticks = 6 × numberofhouses + 1

C Numberofsticks = 6 × numberofhouses

D Numberofsticks = 5 × numberofhouses

Designyourownspatialpattern 13

13 Designaspatialpatterntoﬁtthefollowingnumberpatterns.

a 4, 7, 10, 13,

b 4, 8, 12, 16,

c 3, 5, 7, 9, …

d 3, 6, 9, 12, …

e 5, 8, 11, 14, …

f 6, 11, 16, 21, …

2J 2J Tablesandrules

Learningintentions

• Tounderstandthataruleconnectstwovaryingquantities.

• Tobeabletocompleteaninput-outputtablegivenarule.

• Tobeableto ndaruleintheforminput=? × output+?foraninput-outputtable.

Keyvocabulary: input,output,tableofvalues,rule,substitute

Inthelastsection,weinvestigatedrulesforspatialpatterns.Rulesarealsousefulformanyother everydaysituations.

Itcanbehelpfultothinkofaruleasa‘machine’.Youfeedinonenumber(theinput),andanother number(theoutput)comesout.Forexample,Marywas 3 yearsoldwhenherbrotherTimwasborn.Ifyou knowTim’sage(theinput),whatisaruleforﬁndingMary’sage(theoutput)?

Showingsomevaluesinatablemakesiteasyto‘see’therule.

Tim’sage(input) 0 1 7 3 + 3

Mary’sage(output) 3 4 10 6

Lessonstarter:What’sthestory?

Rule: Mary’sage = Tim’sage + 3

output = input + 3

Eachofthefollowingstoriestellshowaninputandoutputarerelated.

Story input output

1 Connoris 5 yearsyoungerthan hisbrotherDeclan. Declan’sage Connor’sage

2 Liamearns $5 foreverycarhe washes. numberofcarswashed amount ($) earned

3 Jayceand 4 friendssharesome lolliesequally. totalnumberoflollies numberoflollieseachpersongets

• Whichstorymatchesthefollowingtableofinputandoutputvalues?Howdidyoudecide?

• Howwouldyouﬁndthemissingvalues?

• Pickoneoftheotherstoriesandmakeupyourowntableofvalues.

Keyideas

A rule showstherelationshipbetweentwoamountsthatcanvary.Itisused tocalculatethe output (answer)fromthe input (startingnumber).

A tableofvalues showsinputsandoutputs.Tomakeatableofvalues:

• choosesomeinputvalues

• usetheruletocalculatetheoutputvalues.

Toﬁndtherulefromatableofvalues,trydifferentoperations (+, , ×, ÷) untilyouﬁndarule thatworksfor all thevalues.Forexample:

Togettheoutputsinthetableabove,hasthesamenumberbeen:

• addedtoeachinput?(no)

• subtractedfromeachinput?(no)

• multipliedbyeachinput?(yes)

Theruleis: output = 3 × input

Exercise2J

1 Hereisaspatialpattern.Each‘ﬂower’ismadewith 4 sticks.

1 flower 2 flowers 3 flowers

a Copyandcompletethisrule: output (sticks) = 4 × input ( )

b Copyandcompletethistableofvalues.

Numberofﬂowers(input) 1 2 3 4 5 × 4

Numberofsticks(output)

2 Ebonyis 3 yearsolderthanJos ´ e.

a Copyandcompletethisrule: output ( ) = input (Jos ´ e’sage) + 3

b Copyandcompletethistableofvalues.

Jos ´ e’sage(input) 1 3 7 12 15 + 3

Ebony’sage(output)

3 Jakeearns $8 anhour.

a Copyandcompletethisrule: output (amountearned) = 8 × (hoursworked)

b Copyandcompletethistableofvalues.

Hoursworked(input) 1 2 3 4 5 × 8

Amountearned(output)

4 Useeachruletoﬁndtheoutputwhentheinput = 8 output = input × 2 a output = input −2 b output = input + 2 c output = input ÷ 2 d

Example26Completingatableofvalues

Completeeachtableforthegivenrule.

output = input −2 input 3 5 7 12 20 output a output = (3 × input) + 1 input 4 2 9 12 0 output

Solution Explanation

a output = input −2 input 3 5 7 12 20 output 1 3 5 10 18

b output = (3 × input) + 1

4 2 9 12 0

13 7 28 37 1

Nowyoutry

Completeeachtableforthegivenrule.

Puteach input value,inturn,intotherule.

e.g.When input is 3: output = 3−2 = 1

Puteach input value,inturn,intotherule.

e.g.When input is 4: output = (3 × 4) + 1 = 13

output = input + 5 input 0 1 5 10 12 output a output = (input ÷ 3) + 1 input 93

5 Copyandcompleteeachtableforthegivenrule.

Q5Hint:Substituteeachinput numberintotherule. output = input + 3 input 4 5 6 7 10 output a output = input × 2 input 5 1 3 21 0 output

b output = input −8 input 11 18 9 44 100 output c output = input ÷ 5 input 5 15 55 0 100 output d

6 Copyandcompleteeachtableforthegivenrule.

a output = (input ÷ 2) + 4 input 6 8 10 12 14 output

Q6Hint:Remembertocalculate bracketsﬁrst. output = (10 × input) −3 input 1 2 3 4 5 output

b output = (3 × input) + 1 input 5 12 2 9 0 output

c output = (2 × input) −4 input 3 10 11 7 50 output

Example27Findingarulefromatableofvalues

Findtheruleforeachofthesetablesofvalues.

Solution

Explanation

a output = input + 9 Each output valueis 9 morethanthe input value.

b output = input × 7 or output = 7 × input Byinspection,itcanbeobservedthateach output valueis 7 timesbiggerthanthe input value.

Nowyoutry

Findtheruleforeachofthesetablesofvalues.

7 Statetheruleforeachofthesetablesofvalues.

Q7Hint:Thesame rulemustworkfor eachinput/output pairinatable.

Problem-solving and reasoning

8 Copyandcompletethemissingvaluesinthetableandstatetherule.

Q9Hint:Therulemustbetruefor eachinputnumberinthetable.

9 Matcheachrule(A to D)withthecorrecttableofvalues(a to d).

Rule A: output = input −5

+ 1 Rule C: output = 4 × input

10 WhenZacwasborn,hisgrandfatherplaced $100 inaspecialaccounttosaveforhiseducation. Headds $50 totheaccounteverytimeZachasabirthday.

a CopyandcompletethistableforZac’sbirthdayaccount: Zac’sageinyears(input) 0 1 2 3

Amount($)inaccount(output)

b CopyandcompletethisruleforZac’sbirthdayaccount: output = × input +

c HowmuchwillbeintheaccountwhenZacturns 18?

11 Cindyhas $64 savedsofarfortheschoolskitrip.Shehasjuststartedworkingatthelocalvets,helping tocleanoutpensandfeedtheanimals.Cindygetspaid $8 anhourandsavesallherwages towardstheskitrip.

a CopyandcompletethistableforCindy’ssavings:

Hoursworked(input) 0 2 5 10 Cindy’stotalsavings(output)

b CopyandcompletethisruleforCindy’ssavings: output = × input +

Q11Hint:Forpart c, ﬁrstworkouthow muchmoreCindy needstoearn.

c Cindywantstosave $200 topayfortheskitrip.Howmanyhourswillsheneedtowork?

12 Completethesetwodifferentrulessothattheyeachgiveanoutputof 7 whentheinputis 3

a output = × input +

b output = × input

Findingharderrules

13,14

13 Thefollowingrulesallinvolvetwooperations.Findtheruleforeachofthesetablesofvalues.

= × input

a output = × input +

6 7 8

5 7 9 11 13

= × input

1 2 3 4 5

5 9 13 17 21

c output = input ÷ + input 6 18 30 24 66

10 8 3 1 14

49 39 14 4 69

3 5 7 6 13

e output = × input input 1 2 3 4 5

output = × input + input 4 5 6 7 8 output 43 53 63 73 83

0 4 8 12 16

14 UseaspreadsheettomakeeachofthetablesinQuestion 13.Eachtime,enter aformulasothatthecomputercalculatesalltheoutputvalues. Hereisanexampleoftheformulasfor a above.Tryextendingyour tablesbyusingotherinputnumbers.

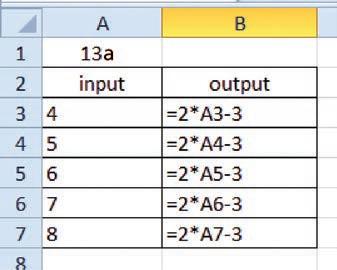
Q14Hint: Whenenteringformulas: – alwaysstartwith = – use*for × – insteadoftyping‘A3’justclick oncellA3 – tocopytheformulaintoother cells,ﬁlldownbydragging.

2K 2K TheCartesianplaneandgraphs

Learningintentions

• Tobeabletointerpretthelocationofapointdescribedbyitscoordinates,e.g. (x, y)(2, 4)

• Tobeabletoplotoneormorepointsgiventheircoordinates.

• Tobeabletodrawagraphofaruleusingatable.

Keyvocabulary: Cartesianplane, x-axis, y-axis,origin,plot,coordinates,input,output

Inearliersectionswelookedatnumbersequencesandspatialpatterns.Weusedrulesandtablesof valuestodescribethem.Anotherwayofshowingapatternisbyplottingpoints.Forexample,wecould useanumberlinetoshowthesimplepattern 3, 6, 9, 12, … 4

However,whenweworkwithtwosetsofvalues(inputsandoutputs)weneedtwodimensions. Insteadofanumberline,weuseanumberplane.

Lessonstarter:Locatingpoints

Thisgridshowsapatternofpointsonanumberplane.

• Describethebehaviourofthe y valuesasthe x valuesincrease.

• Bycontinuingthepattern,whatwouldbethe y valuefor x = 7 or x = 0?

• Howwouldyouwritearulelinking y (theoutput)with x (theinput)?

• Howisthenumberplanelikeastreetmap?Howisitdifferent?

Keyideas

A Cartesianplane isagridfor plotting points.Importantfeaturesofanumberplaneare:

• The x-axis and y-axis:thesearehorizontalandverticalnumberlines.

• The origin:wherethe x-axisand y-axismeetat (0, 0)

the y-axis the x-axis the origin y x

Pointsarelocatedbyagrid-referencesystemof coordinates.

• Thepoint (x, y) means(x unitsacrossfromtheorigin, y unitsup).

• For (2, 4) the x-coordinateis 2 andthe y-coordinateis 4

Toplotthispoint,startattheoriginandgo 2 unitsacross,then 4 unitsup.

Foraruledescribingapatternwith input and output,the x-value isthe input andthe y-valueisthe output

Exercise2K

1 Copyandcompletethefollowingsentences.

a Thehorizontalaxisisknownasthe

b The istheverticalaxis.

c Thepointatwhichtheaxesintersectiscalledthe

d The x-coordinateisalwayswritten

e Thesecondcoordinateisalwaysthe

(2, 4)

Q1Hint:Lookatthe Key ideas

f Theletter comesbefore inthedictionary,andthe -coordinatecomesbeforethe -coordinateonthenumberplane.

2 Matcheachpointonthegridwithitscorrectcoordinates.

Q2Hint:Startat 0 andthen moveacrossandup.

Example28Plottingpointsonanumberplane

Drawanumberplaneandplotthesepointsonit.

A(2, 5) B(4, 3) C (0, 2)

y x

Nowyoutry

Explanation

Drawanumberplanewithbothaxeslabelledfrom 0 to 5 Thenumbersgoonthegridlines,notinthespaces.

Labelthehorizontalaxis x andtheverticalaxis y (2, 5) meansgoacross 2 from 0 (alongthe x-axis)andthen goup 5 units.Plotthepointandlabelit A

B(4, 3) means (4 across, 3 up) C (0, 2) means (0 across, 2 up) so C isonthe y-axis.

Drawanumberplaneandplotthesepointsonit.

A(1, 4) B(5, 0) C (3, 3)

3 Copyandcompletethecoordinatesforeachpointshownonthisnumberplane.

A(5,?) a

B(?, 5) b

C (?,?) c

D(3,?) d

E (?,?) e F (?, 4) f

4 Ongridpaper,drawanumberplane,withthenumbers 0 to 6 markedoneachaxis.Plotandlabel thesepoints:

A(3, 5) B(4, 2) C (0, 3) D(1, 0) E (6, 6)

5 Usegridpaperto drawanumberplanewiththe x-and y-axisnumberedfrom 0 to 10.Ploteachgroup ofpointsandjointheminorder,usingaruler.

(4, 10), (2, 8), (5, 9) a

Namethistypeofangle,lessthan 90°

(2, 6), (4, 6), (4, 3) b Namethistypeofangle,equalto 90°

(6, 8), (8, 8), (8, 5), (6, 5), (6, 8) c Namethisshape.

(5, 1), (6, 4), (7, 1), (5, 1) d

Namethistypeoftriangle.

(0, 0), (0, 3), (3, 0), (0, 0) e Namethistypeoftriangle.

(7, 3), (9, 3), (10, 6) f

Namethistypeofangle,lessthan 180°

6 Drawanumberplanefrom 0 to 8 onbothaxes.Plotthefollowingpointsonthegridandjointhemin theordertheyaregiven.

(2, 7), (6, 7), (

7 Writedownthecoordinatesofeachoftheselabelledpoints.

Q7Hint:Thecoordinatesare (x, y)or(across,up).

Example29Drawingagraph

Fortherule output = input + 1:

Copyandcompletethetableofvalues. a

Listthecoordinatesofeachpoint.

Ploteachpairofpointsonthenumberplane. c

Solution

Explanation

Usetheruletoﬁndeach output valueforeach input value.Theruleis: output = input + 1,soadd 1 toeach input value.

b (0, 1), (1, 2), (2, 3) and (3, 4) Thecoordinatesofeachpointare(input, output). c

Ploteach (x, y) pairasapoint: (x unitsacrossfrom 0, y unitsup).

Nowyoutry

Fortherule output = input −1:

Copyandcompletethetableofvalues. a

Listthecoordinatesofeachpoint. b

Ploteachpairofpointsonthenumberplane. c

8 Forthegivenrule output = input + 2:

a Copyandcompletethegiventableofvalues.

b Listthecoordinatesofeachpoint.

c Ploteachpointonanumberplaneliketheonebelow.

9 Forthegivenrule output = input × 2:

a Copyandcompletethegiventableofvalues.

b Listthecoordinatesofeachpoint.

c Ploteachpointonanumberplaneliketheonebelow.

10 Drawanumberplanefrom 0 to 5 onbothaxes.Placeacross oneachpointwithcoordinatesthathavethesame x valueand y value.

Q8Hint:Coordinatesare (input, output) = (x, y)

11a Whichofthefollowingisthecorrectwaytodescribethepositionof point X ?

A 21

B 2, 1

C (2, 1) D (x2, y1) E (2x, 1y )

b Whichofthefollowingisthecorrectsetofcoordinatesfor point Y ?

A (2, 4)

B 4, 2 C (4, 2)

(2, 4)

a Plotthefollowingpointsonanumberplane.Jointhe pointsintheordergiventodrawthebasicshapeofahouse. (1, 5), (0, 5), (5,

b Drawadoorandlistthecoordinatesofthefourcornersofthedoor.

Q12Hint:Drawanumberplane with 0 to 10 onbothaxes.

c Drawawindowandlistthecoordinatesofthefourcornersofthewindow.

d Drawachimneyandlistthecoordinatesofthefourpointsneededtodrawthechimney.

Secretmessages

13 Agridsystemcanbeusedtomakesecretmessages.

Jakedecidestoarrangethelettersofthealphabetona numberplaneinthefollowingmanner.

a DecodeJake’sfollowingmessage:

b Codetheword‘secret’.

Toincreasethedifﬁcultyofthecode,Jakedoesnotincludebracketsorcommasandheusestheorigin toindicatetheendofaword.

c Whatdothefollowingnumbersmean? 13515500154341513400145354001423114354.

d Codethephrase:‘Behereatseven’.

Computertechnician

Computertechniciansandcomputerengineers arepeoplewholovetechnologyanditsuses. Theirjobsrangeindifﬁculty,hoursandpay. Buttheyallneedtohaveanunderstanding ofpatternsandmathematics.

Thecomputerindustryisalwaysevolving.New devicesandapplicationsrequirelargerand largerstorage.Electronicdataisrepresentedin digitalformusingthedigits 0 and 1,whichare called‘bits’ofdata.A‘byte’is 8 bits,for example,thecapitalletterBis 1 bytestoredas ‘01000010’,whichhas 8 bitsofdata.

• A‘bit’ (1 b) isthesmallestdataunit(eithera 1 or 0 ).

• A‘byte’ (1 B) is 8 bits. Becausethereareonlytwopossiblebits(i.e. 0 or 1),computerstoragedataiscalledbinarydata andcanbewrittenaspowersof 2.Notethat‘bi’meanstwoofsomething,forexample,abicycle has 2 wheels.

1 Rememberingthatabytehas 8 bits,writeeachofthe followinginbytes.

16 bits(i.e. 16 b) a

2 Otherunitsarealsousedinﬁlestorage.Completethetable belowtoﬁndthenumberofbytesforeachofthesestorageamounts.

Q1Hint:numberof bits ÷ 8 = number ofbytes.

3 Useafactortreeorrepeateddivisiontodeterminethefollowingstorageamountsaspowersof 2 64 GB a 512 GB b 2048 GB (= 2TB) c

4 Usethequestion 2 answerstohelpyouwriteeachofthefollowingin kilobytes (kB)

1 MB a 3 MB b

25 MB c 100 GB d

5 Intheearlydaysoftheinternet,downloadspeedswerequiteslow. Adial-upinternetspeedcouldbe 56 kb/s(kilobits persecond).

Determinetheunknownvaluesinthefollowingtableto ﬁndthedownloadtimesforthegivendataﬁles.

Q4Hint: 1 MB = 1048576 1024 = ?kB

Q5Hint:Convert 56 kb/stokB/s 56 ÷ 8 = ?kiloBytes/s

Q5Hint:ConvertMBtokiloBytes 21 MB = 21 × 1024 = ?kiloBytes

Speedin kilobits/s Speed inkB/s (kiloBytes/s) Filesize inMB (MegaBytes) Filesize inkB (kiloBytes) Download timein seconds Download timetothe nearesthour

a 56

26 MBmusic video

b 56 152 MBgame

c 56 740 MBmovie

Usingtechnology

ComputerdownloadtimesdependonthespeedoftheInternetServiceProvider(ISP),thesizeofthe databeingdownload,thetypeandqualityoftheinternetconnection,theamountoftrafﬁcusinga website,etc.

6 Inthisquestion,youwilluseaspreadsheettocalculatethedownloadtimesforvariousBroadband internetspeeds,whicharemeasuredinMb/s(Megabits persecond).

a Setupthefollowingspreadsheet.FormatalltheshadedcellsasNumber/1 d.p.

b IncolumnC,enterformulastocalculateMegabits.Recallthat thereare 8 bitsforeachbyte,so 8 Megabitsforeach Megabyte.

c IncolumnsDtoH,enterformulastocalculatethedownload timesinsecondsforeachdataﬁleforeachofthedifferent speeds.

d Howmuchfaster,inseconds,istheAppdownload timeat 100 Megabits/scomparedto 8 Megabits/s?

e Howmuchfaster,inminutesandseconds,isthemovie downloadtimeat 100 Megabits/scomparedto 8 Megabits/s?

Q6bHint:CellC5 formula = B5*8

Q6cHint:Formulasfordownload times:

Use $ signstoﬁxtheaddressof thespeedcellforeachcolumn.

CellD5formula = C5/$D$3

CellE5formula = C5/$E$3

Toﬁllformulasdownthe column,dragtheﬁllhandle down.

Plungepooltiling

TheAustralianPlungePoolCompanyoffersafreetiledpath aroundeachplungepoolconstructed.Thestandardwidthof eachplungepoolis 2 metres,butthelengthcanvary(itmust beawholenumberofmetres).

Thetilingiscompletedusing 1 metresquaretilesaroundall sidesofthepool.Thisdiagramshowsthetilingforapoolof length 3 metres.

Presentareportforthefollowingtasksandensurethatyoushowclearmathematicalworkings, explanationsanddiagramswhereappropriate.

1Preliminarytask

a Usethediagramabovetocountthenumberoftilesrequiredfora 2 metreby 3 metreplunge pool.

b Drawanaccuratediagramofarectanglewhichis 2 metresby 6 metres.Ifpossibleusegrid paper.

c Onyourdiagram,accuratelydraw 1 metresquaretilesaroundtheoutsideoftherectangle.

d Useyourdiagramtoﬁndhowmanytileswouldberequiredfora 2 metreby 6 metreplunge pool.

2Modellingtask

Theproblemistoﬁndarulerelatingthe numberoftiles requiredtothe lengthofthepool.

a Writedownalltherelevantinformationthatwillhelpsolvethisproblem.

b Usediagramstoillustratethefollowing 4 pools.

i 2 mby 2 m

ii 2 mby 3 m

iii 2 mby 4 m

iv 2 mby 5 m

c Useatableliketheoneshowntosummarisethenumberoftilesrequiredforvaryingpoollengths.

d Ifthepoollengthincreasesby 1 metredescribetheeffectonthenumberoftilesrequired.

e Ifapoolcouldhavealengthofonly 1 metrehowmanytileswouldneedtobeused?

f Determinetherulelinkingthenumberoftilesandthelengthofthepool.

Evaluate and verify

g Usingyourrulefrompart f above,ﬁndthenumberoftilesrequiredforaplungepooloflength: 8 metres i 15 metres ii

h Usingyourrulefrompart f above,ﬁndthelengthofaplungepoolifthenumberoftiles usedis:

22 i 44 ii

i Useyourruletoexplainwhytherewillalwaysbeanevennumberoftilesrequired.

Communicate

j Summariseyourresultsanddescribeanykeyﬁndings.

3Extensionquestions

Supposetheluxuryplungepoolscanhaveawidthof 3 metresinstead of 2 metres.Thelengthcanstillvary,howeveritmustbeawhole numberofmetres.

Useatableliketheoneshownbelowtosummarisethenumber oftilesrequiredforvaryingpoollengthswhenthepoolwidth is 3 m.

Poollength(m) 2 3 4 5 6

Determinetherulelinkingthenumberoftilesandthelengthofthesepools.

Statethedifferencebetweenthisnewruleandtherulefoundwhenthewidthis 2 metres. c

Makingpatterns (Keytechnology:Spreadsheets)

Numberpatternsmightseemlikeaneasythingtogeneratebutdescribingrelationshipswithinpatterns isatthefoundationofalgorithmsandcomplexmathematicalfunctions.Suchalgorithmscanhelpusto writecomputerprogramsandﬁndrulestohelpestimatesolutionstocomplexproblems.Twokeywords usedinthisinvestigationare‘sequence’and‘term’.Thepattern 3, 5, 7, 9, 11,forexample,isasequence ofﬁvetermsandcouldbedescribedasthelistofoddnumbersfrom 5 upto 11.Wewillusetheletter n todescribewhichtermwearetalkingabout.So, n = 2 referstothe 2ndterm,whichinthisexampleis 5

1Gettingstarted

a Thistableshowsninetermsoftheevennumbersequencestartingat 2

Whatisthe 4thterminthesequenceofevennumbers? i Whichtermisequalto 16? ii

b Method1:Onewaytogeneratethesequenceofevennumbersistoadd 2 tothepreviousterm. So,inthissequence,the 6thtermis 12 andsothe 7thtermis 12 + 2 = 14

Usethisideatoﬁndthe 10thterminthesequence. i Whatwillbethe 13thterminthesequence? ii

c Method2:Anotherwaytoﬁndtermsistousearuleandthevalueof n correspondingtothe termyouareﬁnding.Forexample:The 5thtermis 2 × 5 = 10 andthe 7thtermis 2 × 7 = 14 and so,ingeneral,the nthtermisgivenby 2 × n

Usethisideatoﬁndthe 11thterminthesequence. i Whatwillbethe 17thterminthesequence? ii Whatwillbethe 29thterminthesequence? iii

2Applyinganalgorithm

Let’slookatgeneratingthelistofoddnumbersstartingat 1 using Method1 Lookatthisﬂowchartwhichgeneratesthesequence.

a Workthroughtheﬂowchartandwritetheoutputsintothistable

n 1 2 3

Term, t 1

b Whydoesthisalgorithmonlydeliver 5 valuesfor n and t?

c Anotherwayofgeneratingthelistofoddnumbersistousetherule: Term (t) = 2 × n −1.Thisis Method2 asdescribedinpart 1. Checkthisrulebyconfirmingthetermsinthetableabove. i Usethisruletofindthe 8thterm. ii Drawaflowchartthatoutputsthefirst 8 termsoftheoddnumbersequence usingthisrule. iii

3Usingtechnology

Wewilluseaspreadsheettogeneratetheoddnumbersequenceusingbothmethodsdescribed above.

a Createaspreadsheetasfollows.The n valueisincolumnAandthesequenceisgeneratedin columnsBandCusingthetwodifferentmethods.

b FilldownatcellsA5,B5 andD4 togenerate 8 terms.

c Describetheadvantagesanddisadvantagesofbothmethods.

d Nowconstructaspreadsheettogeneratethefollowingsequencesusingbothmethod1and2. Asequencestartingat 1 andincreasingby 3 eachtime. i Asequencestartingat 20 anddecreasingby 2 eachtime. ii

1 Toplay PrimeDrop withapartner,youwillneedanumberchart(withcirclesaroundtheprime numbers,andsquarenumberscolouredin)andadie.

3 WhatnumberamI?

a Readthefollowingcluestoworkouteachmysterynumber. Ihavethreedigits. Iamdivisibleby 5

Iamodd.

Theproductofmydigitsis 15

Thesumofmydigitsislessthan 10 Iamlessthan 12 × 12 i Ihavethreedigits.

Ihavethreedigits.

Iamoddanddivisibleby 5 and 9.

Theproductofmydigitsis 180

Thesumofmydigitsislessthan 20 Iamgreaterthan 302 iii

Thesumofmydigitsis 12

Mydigitsarealleven. Mydigitsarealldifferent. Iamdivisibleby 4

Thesumofmyunitsandtensdigitsequals myhundredsdigit.

b Makeuptwoofyourownmysterynumberpuzzlesandsubmityourcluestoyourteacher.

20: 1, 2, 4, 5, 10, 20 15: 1, 3, 5, 15

20: 20, 40, 60, 80, ... 15: 15, 30, 45, 60, 75, ...

Lowest common multiple LCM = 60 Multiples

5: factors 1 and 5

17: factors 1 and 17

A prime number only has two factors: 1 and itself. Prime numbers

Factor trees

10: factors 1, 2, 5, 10 62: factors 1, 2, 31, 62

Composite numbers are not prime. Composite numbers 0 and 1 are neither prime number nor composite.

Number properties

90 = 2 × 3 × 3 × 5 90 = 2 × 32 × 5

Highest common factor HCF = 5 Factors 10: last digit 0

8 = 2 × 4

9 = 2 × 4 + 1 Division 8 ÷ 2 = 4 no remainder 9 ÷ 2 = 4 remainder 1 243 = 3 × 3 × 3 × 3 × 3 = 35 Powers

Divisibility tests

2: last digit even or 0

3: sum digits ÷ 3 4: last two digits ÷ 4

5: last digit 0 or 5

6: ÷ by 2 and 3

8: last 3 digits ÷ 8 or are 000 9: sum digits ÷ 9

Sequence

A set of numbers ordered according to a rule

2, 4, 6, 8, ...

↑↑↑↑ terms

Spatial pattern: ...

Number pattern: 4 8 12 ...

Pattern rule:

Number of sticks = 4 × number of diamonds

output = 4 × input

Chapterchecklist

AversionofthischecklistthatyoucanprintoutandcompletecanbedownloadedfromyourInteractiveTextbook.

2A 1

Icanlistpairsoffactorsofanumber. e.g.Writethepairsoffactorsfor 18

2A 2 Icanlistthefactorsofanumber.

e.g.Findthecompletesetoffactorsforthenumber 40.

2A 3

2A 4

2B 5

Icanlistthemultiplesofanumber(uptoacertainlimit). e.g.Writedowntheﬁrstsixmultiplesofthenumber 11

Icanidentifyanincorrectmultiplewithinasequence. e.g.Whichnumberisthewrongmultipleinthesequence 7, 14, 20, 28, 35?

Icanlistcommonfactorsandcommonmultiplesoftwonumbers. e.g.aListthecommonfactorsof 8 and 20.bListtwocommonmultiplesof 2 and 3.

2B 6 Icanﬁndthehighestcommonfactor(HCF)oftwonumbers. e.g.Findthehighestcommonfactor(HCF)of 36 and 48

2B 7 Icanﬁndthelowestcommonmultiple(LCM)oftwonumbers. e.g.Findthelowestcommonmultipleof 6 and 10

2C 8 Icandetermineifanumberisdivisibleby 2, 3, 5 and/or 10. e.g.Statewhether 2, 3, 5 and/or 10 arefactorsof 48569412

2C 9 Icandetermineifanumberisdivisibleby 4, 6, 8 and/or 9. e.g.Statewhether 4, 6, 8 and/or 9 arefactorsof 48569412

2D 10 Icandeterminewhetheranumberisprimebyconsideringitsfactors. e.g.Explainwhy 17 isprimebut 35 isnotprime.

2D 11

2E 12

2E 13

2E 14

Icanﬁndtheprimefactorsofanumber. e.g.Findtheprimefactorsof 30

Icanconvertanexpressiontoindexform. e.g.Write 3 × 3 × 2 × 3 × 2 × 3 inindexform.

Icanconvertanexpressiontoexpandedform. e.g.Write 24 inexpandedform.

Icanevaluateexpressionsinvolvingpowersusingtheorderofoperations. e.g.Evaluate 72 −62

2F 15 Icanexpressacompositenumberinprimefactorformusingafactortree. e.g.Drawafactortreeforthenumber 120.Thenwrite 120 astheproductofprimefactorsinindexform.

2F 16 Icanexpressacompositenumberinprimefactorformusingrepeated division.

e.g.Userepeateddivisionwithprimenumberstoﬁndtheprimefactorsof 126.Thenwrite 126 asa productofprimefactorsinindexform.

2G 17 Icanﬁndthesquareofanumber.

e.g.Writethevalueof 42

2G 18 Icanﬁndthesquarerootofanumber.

e.g.Find √64,thesquarerootof 64.

2G 19 Icanlocatesquarerootsbetweenconsecutivepositiveintegers. e.g.Statewhichconsecutivepositiveintegersareeithersideof √43.

2G 20 Icanevaluateexpressionsinvolvingsquaresand/orsquareroots.

e.g.Evaluate √82 + 62

2H 21 Icanﬁndthenexttermsinanumberpatternthatchangebyaﬁxedamount. e.g.Findthenextthreetermsforthenumberpattern 6, 18, 30, 42, …

2H 22 Icanﬁndthenexttermsinanumberpatternthatinvolvemultiplicationor division.

e.g.Findthenextthreetermsforthenumberpattern 256, 128, 64, 32,

2H 23 Icandescribeapatternintermsofthestartingvalueandtheoperationused togetfromeachvaluetothenext.

e.g.Writethepatternruleinwordsforthesequence 2, 10, 50, 250,

2I 24 Icandrawanddescribetermswithinaspatialpattern.

e.g.Drawthenexttwoshapesinthisspatialpatternanddescribetheruleintermsofhowmanysticks arerequiredtomaketheﬁrstterm,andhowmanyareaddedeachtime.

2I 25 Icandescribeandusearuleforspatialpatterns.

e.g.Byfirstdrawingatable,findapatternruleconnectingthenumberofsticksrequiredtothenumberof triangles.Thenusethisruletofindthenumberofsticksfor 20 triangles.

2J 26

Chapter checklist

Icancompleteatableofvaluesforagivenrule.

e.g.Filloutthetablefortherule output = (3 × input ) + 1 input 4 2 9 12 0 output

2J 27 Icanﬁndaruleforatableofvalues.

e.g.Findtheruleforthetableofvaluesshown.

2K 28

Icanplotpointsonanumberplane.

e.g.Plotthepoints

2K 29 Icandrawagraphofarulebycompletingatableofvalues.

e.g.Fortherule output = input + 1,constructatableofvaluesusing input valuesof 0, 1, 2 and 3.Use thetableofcoordinatestoplotagraph.

Short-answerquestions

1 2A Copyandcomplete.

Thefactorpairsof 12 are 1 × = 12, × 6 = 12, × 4 = 12 a

Thefactorsof 12 inascendingorderare: , , , , , b

2 2A

4 2B

Listallthefactorsof 24 inascendingorder.(Hint:Firstwritethefactorpairs.) a

Listtheﬁrst 6 multiplesof 5.(Hint:Startwith 5 andcountinﬁves.) b

Listthefactorsof 16 a

Listthefactorsof 20. b

Circlethecommon(shared)factorsof 16 and 20 c

WhatdothelettersHCFstandfor? d

WritetheHCFof 16 and 20 e

Listtheﬁrstﬁvemultiplesof 6 a

WhatdothelettersLCMstandfor? c

5 2C Writethemissingwordsornumbers.

Listtheﬁrstﬁvemultiplesof 8 b

StatetheLCMof 6 and 8 d

Anumberthatendsin 0 isdivisiblebyboth and ,aswellas 2 a 264 is by 3 becausethesumofthedigitsis + + = and isdivisibleby 3 b 576 is by 9 becausethesumofthedigitsis + + = and is by 9 c 344 is by 4 becausethelasttwodigitsare and is by 4 d

6 2C 206, 48, 56, 621, 320, 85, 63, 14, 312

Fromthelistofnumbersabove,writethenumbersthataredivisibleby: 2

7 2D Answerthesequestions.

Isthenumber 1 aprimenumber? a

Isthenumber 1 acompositenumber? b

5 hasonlytwofactors, 1 and 5.Is 5 aprimenumber? c

Listthefactorsof 10.Is 10 aprimeorcompositenumber? d

Sortthesenumbersintoprimeorcompositenumbers: 2, 3, 8, 7, 11, 15, 20 e

Writethefactorsof 20 intwogroups,primeandcompositenumbers. f

Listtheprimenumbersbetween 15 and 25 g

8 2E/F Answerthesequestions.

For 16 = 42,whatnumberisthebase?Whatnumberistheindexorpower? a

Writetheproduct 5 × 5 × 7 × 7 × 7 inindexform. b Write 23 × 32 infactorformandﬁndthenumbervalue. c

Evaluate: 32 + 52 −3 × 2 (showsteps). d

Findthemissingpowers: 125 = 5 ; 32 = 2 ; 100000 = 10 e

9 2F Foreachnumber,drawafactortree.Thenwritethenumberwithpowersofprimefactors.

50 a 16 b 2400 c

10 2G

Copyandcompleteeachofthesetables.

11 2E/G

Findthevalueof:

12 2H

thesidelengthofasquarethathasarea = 25 cm2 j thesidelengthofasquarethathasarea = 400 cm2 k

Listthenextfourtermsforthesesequences.

Startwith 3 andkeepadding 4 a

Startwith 64 andkeepdividingby 2

13 2I

Drawthenexttwoshapesinthisspatialpattern. a

Copyandcompletethistable.

Numberofsticks 3 b Writethepatternrule. c Howmanystickswouldbeneededfor 12 triangles? d

14 2I Lookatthisspatialpattern.

Copyandcompletethistable.

Copyandcompletetheruleforthispattern: numberofsticks = 1 + × numberofsquares b

Howmanysticksareneededtomake 10 squaresthisway? c

Howmanysquarescouldbemadefrom 82 sticks? d

15 2J

Copyandcompleteeachtableforthegivenrule. output = input + 5 a input 3 5 7 12 20

output = 2 × input + 7 b

16 2J Writethepatternruleforeachofthesetables. output = × input a

3 4 5

15 20 25

= input b

15 20 28

9 14 22

17 2K

Statethecoordinatesofeachpointplottedonthisnumberplane. a Statethecoordinatesoftheorigin. b

Whichaxisispoint (0, 5) on? c Nametheverticalaxis. d

Whichaxisisthepoint (3, 0) on? e

Namethehorizontalaxis. f

Statethecoordinatesofapoint C sothat ABCD isasquare. g

18 2K Fortherule: output = 2 × input −1

Copyandcompletethistableofvalues.

Listthecoordinatesofeachpoint. b Ploteachpointonanumberplaneliketheone totheright.

19 2K Writearule(e.g. output = input × 2)thatwouldgivethesegraphs.

Multiple-choicequestions

1 2A

Whichnumberisthewrongmultipleforthefollowingsequence?

24, 27, 30

2 2A

Whichgroupofnumberscontainseveryfactorof 20?

3 2D

Whichofthefollowingnumbersisaprimenumber?

Whichofthefollowinggroupsofnumbersincludesoneprimeandtwocompositenumbers?

2F Theprimefactorformof 48 is:

2A Factorsof 189 include:

11 2C Whichnumberis not divisibleby 3?

E 12 2K Whichsetofpointsisinahorizontalline? (5, 5), (6, 6), (7, 7) A (3, 2), (3, 4), (3, 11) B (2, 4), (3, 6), (4, 8) C (5, 4), (6, 4), (8, 4), (12, 4) D (1, 5), (5, 1), (1, 1), (5, 5) E

Extended-responsequestions

1 SamisﬁveyearsolderthanhissisterMikaela.

Copyandcompletethisrulefortheirages:Sam’sage = Mikaela’sage + a CopyandcompletethistableshowingSam’sageandMikaela’sageinyears.

Mikaela’sage 0 37

Sam’sage

b Ongridpaper,drawhorizontalandverticalaxesandlabeleachwiththenumbersfrom 0 to 20 (Becarefultomarkthenumbersnexttothegridlines,notinthespaces.)Labeltheaxesas follows.

Sam’s age Mikaela’s age

Onyourgraph,plotthepointsfromthetableabove.(Hint:Mikaela’sagegoes across,Sam’s agegoes up.)

2 AtNorthParkPrimarySchool,theclassroomshavetrapezium-shapedtables.MrsGreenearranges herclassroom’stablesinstraightlines,asshown.

a Copyandcompletethisrule:

Copyandcompletethistableforupto 5 tablesjoinedtogether.

Numberoftables 1 2 3 4 5

Numberofstudents

numberofstudents = × numberoftables +

Checkthattheruleworksforthenumbersinyourtable. Theroomallowsseventablestobearrangedinastraightline.Howmanystudentscansit aroundthetables?

Thereare 80 studentsinGrade 6 atNorthParkPrimarySchool.MrsGreenewouldliketo arrangethetablesinonestraightlineforanoutsidepicniclunch.Howmanytableswillshe need?

3 Fractionsand percentages

Essentialmathematics:whyworkingwithfractionsand percentagesisimportant

Vetsandnursesusefractionskillstodeterminemedicationdosages;forexample,adogneeds 12 1 2 mLofamedicationeveryfourhours.Fora 24-hourperioditrequires: 12 1 2 mL × 6 = 75 mL.

Nursescanusefractionskillstocalculatethetimeneededforanintravenousdriptofullydrain intoapatient’sarm;forexample, 2 3 4

hourperlitre = 5 1 2 hours.

Artists,housepainters,interiordecoratorsandDIYenthusiastscanuseratiostomixdesiredpaint colours.Forexample,mixingyellow:blueintheratio 15 : 1 formsalightshadeofgreen.

Engineersandbuildersworkattimeswithfractionsofaninch,asImperialmeasurementisusedin theUnitedStates.Forexample,aviationengineersandmechanicscalculateprecisemeasurements to 1 1000 ofaninch.

Shoppersusefractionandpercentageskillstocalculatediscountsandﬁndthebestbuy.

Inthischapter

3AIntroductiontofractions (Consolidating)

3BEquivalentfractionsandsimpliﬁedfractions

3CMixednumeralsandimproperfractions (Consolidating)

3DOrderingfractions

3EAddingfractions

3FSubtractingfractions

3GMultiplyingfractions

3HDividingfractions

3IFractionsandpercentages

3JFindingapercentageofanumber

3KIntroductiontoratios

3LSolvingproblemswithratios

AustralianCurriculum9.0

NUMBER

Findequivalentrepresentationsofrationalnumbersand representrationalnumbersonanumberline(AC9M7N04)

Usethe4operationswithpositiverationalnumbers includingfractions,decimalsandpercentagestosolve problemsusingefﬁcientcalculationstrategies (AC9M7N06)

Recognise,representandsolveproblemsinvolvingratios (AC9M7N08)

Usemathematicalmodellingtosolvepracticalproblems involvingrationalnumbersandpercentages,including ﬁnancialcontexts;formulateproblems,choosing representationsandefﬁcientcalculationstrategies,using digitaltoolsasappropriate;interpretandcommunicate solutionsintermsofthesituation,justifyingchoicesmade abouttherepresentation(AC9M7N09)

MEASUREMENT

Usemathematicalmodellingtosolvepracticalproblems involvingratios;formulateproblems,interpretand communicatesolutionsintermsofthesituation,justifying choicesmadeabouttherepresentation(AC9M7M06)

©ACARA

Onlineresources

Ahostofadditionalonlineresourcesareincludedaspart ofyourInteractiveTextbook,includingHOTmathscontent, videodemonstrationsofallworkedexamples, auto-markedquizzesandmuchmore.

1 Inwhichofthefollowingisone-thirdoftheareashaded?

Warm-up

2 Howmanyofthesmallersquareswouldyoushadeforeachgivenfraction?

3 Writethefollowingasfractions.

4 Whichofthefollowingis not equivalentto(thesamevalueas)onewhole?

5 Whichofthefollowingis not equivalenttoone-half?

6 Find:

7 Find:

8 TomeatshalfablockofchocolateonMondayandhalfoftheremainingblockonTuesday. HowmuchchocolateisleftforWednesday?

9 Findthenextthreetermsinthesenumbersequences.

10 Write 1, 3 or 4 ineachboxtomakeatruestatement.

11 Find:

12 Statewhethereachofthefollowingistrue(T)orfalse(F).

3A 3A Introductiontofractions CONSOLIDATING

Learningintentions

• Tounderstandwhatafractionis.

• Toknowwhatthenumeratoranddenominatorofafractionrepresentindifferentsituations.

• Tounderstandhowafractionrelatestotheshadedareaofashape.

• Tobeabletorepresentfractionsonanumberline.

Keyvocabulary: fraction,denominator,numerator,vinculum,properfraction,improperfraction,mixednumber

ThewordfractioncomesfromtheLatinword‘frangere’, whichmeans‘tobreakintopieces’.Fractionsarepartsof awhole.

Weallusefractionseveryday.Theyareusedin cooking,shopping,sportandbuildingconstruction.

Lessonstarter:Whatstrengthdoyoulikeyourcordial?

• Tomuses 40 mLofcordialand 120 mLofwater.

• Sallyuses 40 mLofcordialwith 200 mLofwater.

Manyrecipes usefractions whenlisting ingredients.

• Wholikestheirdrinkthestrongest?Howcanfractionsbeusedtodescribethestrengthsofcordial?

Keyideas

A fraction isanumbermadeupofanumerator(up)anda denominator (down).

Forexample: 3 5 numerator denominator

• The denominator tellsyouhowmanypartsthewholeisdividedupinto.

• The numerator tellsyouhowmanypartswearetalkingabout.

• Thehorizontallineseparatingthenumeratorandthedenominatoriscalled the vinculum

A properfraction hasthenumeratorlessthanthedenominator.

Forexample: 2 7 isaproperfraction.

An improperfraction hasthenumeratorgreaterthanorequaltothedenominator.

Forexample: 5 3 isanimproperfraction.

Wholenumberscanberepresentedasfractions.

Forexample: 1 = 4 4 , 1 = 3 3 , 2 = 8 4

Mixednumbers haveawholenumberandafraction.

Forexample: 1 2 3 isamixednumber.

Wecanrepresentfractionsonanumberline. Thisnumberlineshowsthewholenumbers 0, 1 and 2.Eachunithasthenbeendividedequally intofoursegments,thereforecreating‘quarters’.

Exercise3A

1a Statethedenominatorofthisproperfraction: 2 9

b Statethenumeratorofthisimproperfraction: 7 5

2 Groupthefollowinglistoffractionsintoproperfractionsorimproperfractions.Alsostatewhich onesarewholenumbers.

Q2Hint:

Properfractions: Numeratorislessthandenominator. Improperfractions: Numeratorisgreaterthanorequalto thedenominator.

3 Statethemissingpartsinthefollowingtable.

Thewhole(divided intoequalparts)

Numberofequal partsinthewhole (denominator)

Numberofshaded equalparts (numerator) Fractionshaded Nameoffraction

4 Whatfractionsareindicatedbythedotsonthesenumberlines? a 3 12 0

b 3 12 0

Fluency

Example1Representingfractionsonanumberline

Showthefractions 3 5 and 9

5 onanumberline.

Solution

021 3 5 9 5

Nowyoutry

Showthefractions 3 4 and 5 4 onanumberline.

Explanation

Q4Hint:Writeany improperfractions asmixednumbers ifyouwish.

5–75,6(½),7,8

Drawanumberlinestartingat 0 andmarkonit thewholenumbers 0, 1 and 2

Divideeachwholeunitintoﬁvesegmentsof equallength.Eachofthesesegmentshasa lengthofone-ﬁfth.

5 Representthefollowingfractionsonanumberline.

6 Writethefollowingaswholenumbers.

Q5Hint:Toshowsevenths,rulea 7 cmlineforonewholeandmark eachcmforoneseventh. c

7 Shade 3 4 ofeachofthefollowingdiagrams. a b c d e

8 Writethenextthreefractionsforeachofthefollowingfractionsequences. 3 5 , 4 5 , 5 5 , 6 5 , , , a 5 8 , 6 8 , 7 8 , 8 8 , , , b 1 3 , 2 3 , 3 3 , 4 3 , , , c 11 7 , 10 7 , 9 7 , 8 7 ,,

9 Whatfractionmatcheseachofthedifferentshapes( , and )onthesenumberlines?

Q9Hint:Writeany mixednumbersas improperfractions aswell.

10 Matcheachofthefollowingdiagramstooneofthefractionsintheboxbelow.

11 Foreachofthefollowing,writethefractionthatisdescribingpartofthetotal.

a Afteronedayofa 43-kilometrehike,thestudentshadcompleted 12 kilometres.

b From 15 starters, 13 wentonandﬁnishedtherace.

c Rainfallfor 11 monthsoftheyearwasbelowaverage.

d Oneeggisbrokeninacartonthatcontainsadozeneggs.

e Twoplayersinthesoccerteam(with 11 players)scoredagoal.

f Thelunchstopwas 144 kilometresintothe 475-kilometretrip.

g Sevenmembersintheclassof 20 havevisitedAustraliaZoo.

h Oneofthecartyres(notincludingthespare)iswornandneedsreplacing.

i Itrainedthreedaysthisweek.

12 Whichdiagramhasone-quartershaded?

Adjustingconcentration 13

13a Callumpours 20 mLofwaterintothisbeaker.Whatfractionof 200 mListhat?

b Callumaddsacidtothesamebeakeruntilitholds 200 mL.How muchaciddidheadd?Whatfractionof 200 mListhat?

c Rosahasa 200 mLbeakerthatis 1 4 fullofwater.Howmuchacid willsheneedtoaddtoﬁllthebeaker?

3B 3B Equivalentfractionsandsimpliﬁedfractions

Learningintentions

• Tounderstandwhatitmeansfortwofractionstobeequivalent.

• Tobeabletosimplifyfractions.

Keyvocabulary: equivalentfractions,highestcommonfactor,simplify

Fractionsmaylookverydifferentbutstillhavethesame value.Forexample,inanAFLfootballmatch,‘half-time’is thesameas‘theendofthesecondquarter’.Wecansaythat 1 2 and 2 4 areequivalentfractions.

Consideragroupoffriendseatingpizzasduringa sleepover.Thepizzasarehomemadeandeachpersoncuts uptheirpizzaastheylike.Thegreenshadingshowsthe amounteatenbeforeitistimetostartthesecondmovie.

Bylookingatthepizzas,itiscleartoseethatTrevor, Jackie,TahliaandJaredhavealleatenthesameamount ofpizza.

Thismeansthat 1 2 = 2 4 = 3 6 = 4 8.

Lessonstarter:Oddoneout

• Pickthefractionthatistheoddoneout. 25 100 , 4 16 , 2 8 , 2 5 , 5 20

• Whatcouldwecalltheotherfourfractions?

Keyideas

Equivalentfractions arefractionsthatmarkthesameplaceonanumberline. Forexample: 1 2 and 2 4 areequivalentfractions.

• Equivalentfractionsareproducedbymultiplyingthenumeratoranddenominator bythesamenumber.

• Equivalentfractionscanalsobeproducedbydividingthenumeratoranddenominatorby thesamenumber.

Simplifying fractionsinvolveswritingafractioninits‘simplestform’.Todothis,thenumerator andthedenominatormustbedividedbytheir highestcommonfactor(HCF),thelargestnumber whichdividesintobothnumbers.

• Youshouldusuallywritefractionanswersintheirsimplestform.

Trevor Jackie

Tahlia Jared

Afractionwallcanbehelpfulwhencomparingfractions.

1 UsethefractionwallintheKeyideastoﬁnd: ﬁvefractionsequivalentto(equalto) 1 2 a twofractionsequivalentto 1 4 b threefractionsequivalentto 1 3 c onefractionequivalentto 4

2 Copyandcompletethefollowing.

3 Fillinthegapstoreducethesefractionstotheirsimplestform. a 10 30

HCF = i 10 30 = 1 × 3 × . Therefore, simplestformis 3

Q3Hint: HCF means Highest Common Factor. ii

b 4 18

HCF = i 4 18 = 2 × 9 × Therefore,simplestformis 9 ii

c 4 28 HCF = i 4 28 = 1 × 7 × . Therefore,simplestformis 1 ii

d 9 15

3 bymultiplyingthenumeratoranddenominatorby 2, 3, 4 and 5

Nowyoutry

Writefourequivalentfractionsfor 4 5 bymultiplyingthenumeratoranddenominatorby 2, 3, 4 and 5

4 Writefourequivalentfractionsfor 2 7 bymultiplyingthenumeratorand denominatorby 2, 3, 4 and 5

5 Writefourequivalentfractionsfor 3 4 bymultiplyingthenumerator anddenominatorby 3, 5, 10 and 11

Q4Hint:Showthesteps eachtime.Forexample:

6 Fillinthemissingnumberstocompletethefollowingstringsofequivalentfractions.

7 Copyandcompletetheseequivalentfractions.

numerator(up)and denominator (down)bythesamenumber.

Example3Convertingtosimplestform

Writethesefractionsinsimplestform.

Explanation a 12 20 = 3 × ✁ 41 5 × ✁ 41 = 3 5

TheHCFof 12 and 20 is 4 Boththenumeratorandthedenominatoraredividedby theHCFof 4 4 ÷ 4 = 1

TheHCFof 7 and 42 is 7 The 7 is‘cancelled’(i.e. 7 ÷ 7 = 1)fromthenumeratorand thedenominator.

Nowyoutry

Writethefractionsinsimplestform.

8 Writethefollowingfractionsinsimplestform.

9 Bywritingeither = or ¢ inthebox,statewhethereachpairof fractionsisequivalentornotequivalent.Theﬁrstonehasbeen doneforyou.

Problem-solving and reasoning

10 Ineachgroup,choosethefractionthatisnotinitssimplestform.Whatshoulditbe? 1 3 , 3 8 , 5 9 , 7 14 a 2 5 , 12 16 , 15 19 , 13 37 b 12 19 , 4 42 , 5 24 , 6 61 c 7 63 , 9

11 Whichofthefollowingfractionsareequivalentto 8 20?

12 Afamilyblockofchocolateconsistsof 6 rowsof 6 individualsquares.Taniaeats 16 individualsquares. Whatfractionoftheblock,insimplestterms,hasTaniaeaten?

13 Jason,JoannaandJackaresharingalargepizzafordinner.Thepizzahas beencutinto 12 equalpieces.Jasonwouldlike 1 3 ofthepizza,Joannawould like 1 4 ofthepizzaandJackwilleatwhateverisremaining. HowmuchdoesJackeat?

14 Afractionwhensimpliﬁediswrittenas 3 5 Whatcouldthefractionhavebeenbeforeitwassimpliﬁed? Showyourfractiononadiagram.Isyourfractionthesameasthefractionofthestudentsitting nexttoyou?

3C 3C Mixednumeralsandimproper fractions

CONSOLIDATING

Learningintentions

• Tounderstandwhatimproperfractionsandmixednumeralsare.

• Tobeabletoconvertfromamixednumeraltoanimproperfraction.

• Tobeabletoconvertfromanimproperfractiontoamixednumeral.

Keyvocabulary: properfractions,improperfractions,mixednumerals,wholenumbers,remainder

Aswehaveseeninthischapter,afractionisa commonwayofrepresentingpartofawhole. Forexample,aparticularcartripmayrequire 2 3 ofatankofpetrol.

Onmanyoccasions,youmayneedwhole numbersplusapartofawholenumber. Forexample,alonginterstatecartripmay require 2 1 4 tanksoffuel.Whenyouhavea combinationofawholenumberanda fraction,wecallthisamixednumeral.

Lessonstarter:Pizzafrenzy

Alongcartripmayrequiremorethanonewholetankoffuel.

Tomate 1 1 2 pizzas.Chandraate 3 2 ofapizza.Whoatethemost?Discuss,showingeachperson’spizzas onaseparatediagram.

Keyideas

Anumberissaidtobea mixednumeral whenitisamixofa wholenumber plus a properfraction is

2 3 5

Improperfractions (fractionswherethenumeratorisgreaterthanorequaltothedenominator) canbeconvertedtomixednumeralsorwholenumbers.

Mixednumeralscanbeconvertedtoimproperfractions.

Anumberlinehelpsshowthedifferenttypesoffractions.

Exercise3C

1 Betweenwhichtwowholenumbersdothefollowingmixednumeralslie?

2 Themixednumeral 2 3 4 canberepresentedin‘windowshapes’as 2 3 4 = ++

Representthefollowingmixednumeralsusing‘windowshapes’.

3 A‘windowshape’consistsoffourpanesofglass.Howmanypanes ofglassarethereinthefollowingnumberof‘windowshapes’?

Q1Hint:Drawanumberlineto helpyoudecide.

4 Whatmixednumeralscorrespondtotheletterswrittenoneachnumberline?

Example4Convertingmixednumeralstoimproperfractions

Convert 3 1 5 toanimproperfraction.

Solution

Method1

Explanation

3 1 5 = 1 + 1 + 1 + 1 5 = 5 5 + 5 5 + 5 5 + 1 5 = 16 5 3 1 5 = 3 wholes + 1 5 ofawhole

Method2

3 1 5 = 15 5 + 1 5 = 16 5

Method3

Short-cutmethod:

Step 1:Multiplythewholenumberpartbythe denominator.

Step 2:Thenaddthenumerator: 3 × 5 + 1 = 16

3 1 5 = 3 × 5 + 1 5 = 16 5 5 3 1 5 3 1 5 = This is: 3 × 5 + 1

Step 1: Step 2: Then add 1.

3 × 5

Thedenominatorremains 5,aswearetalking aboutﬁfths.

Nowyoutry

Convert 2 3 4 toanimproperfraction.

5 Convertthesemixednumeralstoimproperfractions.

Example5Convertingimproperfractionstomixednumerals

Convert 11 4 toamixednumeral.

Solution

Explanation Method1 11 4 = 8 + 3 4 = 8 4 + 3 4 = 2 + 3 4 = 2 3 4

3 4 Method2 4 2 ) 11 rem. 3 = 2 3 4

Nowyoutry

Convert 22 7 toamixednumeral.

Dividethebottom(denominator)intothetop(numerator). Theremainderbecomesthefractionpart.

6 Converttheseimproperfractionstomixednumerals.

7 Foreachofthesediagrams,write:

Problem-solving and reasoning

8 10 4 simpliﬁesto 5 2 whichequals 2 1 2

Writethefollowingfractionsintwodifferentways.

9 Copythenumberlineandshowthefractionsonit.

10 Rewriteeachofthesepatterns,usingimproperfractions whereneeded.

11 Fourfriendsorderthreelargepizzasfortheirdinner.Eachpizzaiscut intoeightequalslices.Simonehasthreeslices,Izabellahasfourslices, MarkhasﬁveslicesandAlexhasthreeslices.

a Drawcirclestoshowthethreepizzasordered.

b Howmanypizzaslicesdotheyeatintotal?

Q8Hint:It’seasiertosimplify ﬁrst.

Q9aHint:Thisnumberlineis markedinthirds.

Q9bHint:Thisnumberline showsﬁfths.

Q11Hint:Remember,each pizzahas 8 equalslices.

c Howmuchpizzadotheyeatintotal?Giveyouranswerasamixednumeral.

d Howmanypizzaslicesareleftuneaten?

e Howmuchpizzaisleftuneaten?Giveyouranswerasamixednumeral.

Writingfractions

12 Whatdifferentfractionscanyouwriteusingonlythe digits 1, 2 and 3?Whoinyourclasswrotethemost? Assumethateachdigitcanonlybeusedonce ineachfraction.

Hint:Youcanincludeimproper fractionsandmixednumerals.You don’tneedtouseallthreedigits.

3D 3D Orderingfractions

Learningintentions

• Tobeabletocomparetwofractionsanddecidewhichoneisbigger.

• Tobeabletousethesymbols<or>tocomparetwonumbers.

• Tobeabletoorderalistoffractionsinascendingordescendingorder.

Keyvocabulary: lowestcommondenominator(LCD),equivalentfractions,ascending,descending

Justlikewholenumbers,fractionscanbewritteninorder.Wecanusetheideasfromsection 3Btohelp. Rememberthat > means isgreaterthan and < means islessthan Afractionisgreaterthananotherfractionifitliestotherightofthatfractiononanumberline.

3 4 > 1 2 1 0 1 2 3 4

Lessonstarter:Theorderofﬁve

• Asawarm-upactivity,askﬁvevolunteerstudents toarrangethemselvesinalphabeticalorder,thenin heightorderand,ﬁnally,inbirthdayorder.

• Eachoftheﬁvestudentsreceivesalargefraction cardanddisplaysittotheclass.

Forexample, 1 2 , 1 10 , 2 10 , 10 2 , 2 3

• Therestoftheclassmustthenattempttoorder thestudentsinascendingorder,accordingtotheir fractioncard.Itisagroupdecisionandnoneofthe ﬁvestudentsshouldmoveuntiltheclassagreesona decision.

Keyideas

Toorder(orarrange)fractionswemustknowhowtocomparedifferentfractions.There arethreecasestoconsider.

1 Ifthenumeratorsarethesame,thesmallestfractionistheonewiththelargest denominator,asthewholehasbeendividedupintothemostpieces.

Forexample: 1 7 < 1 2

2 Ifthedenominatorsarethesame,thesmallestfractionistheonewiththesmallest numerator.

Forexample: 3 10 < 7 10

3 Otherwise,use equivalentfractions tomakefractionswiththesamedenominator.(The lowestcommondenominator(LCD) isbest.)Thencomparenumeratorsasabove.

Ascending orderiswhennumbersareorderedgoing up,fromsmallest tolargest.

Descending orderiswhennumbersareorderedgoing down,from largesttosmallest.

Exercise3D

Und er stand ing

1 Statethelargestfractionineachofthefollowinglists.

Q1Hint:Whenthedenominators arethesame,comparenumerators: 6 7 ismorethan 5 7,justas 6 is morethan 5 3

2 Statethelowestcommonmultipleofthefollowingsetsofnumbers.

3 Statethelowestcommondenominatorofthefollowingsetsoffractions.

4 Fillinthegapstoproduceequivalentfractions.

Q3Hint:FindtheLCMofthe denominators.

Fluency

Example6Comparingfractions

Denominatorsarethesame,thereforecompare numerators.

b 1 3 > 1 5

Numeratorsarethesame. Thesmallerfractionhasthelargerdenominator. So 1 3 > 1 5

Nowyoutry

Write < or > ineachboxtomakeatruemathematicalstatement.

5 Write < or > tomaketruestatements.

6 Write < or > tomaketruestatements. 1 4

Example7Comparingfractionsbyusingacommondenominator

Whichislarger, 2 3 or 3 5 ?

Solution Explanation

2 3 = 10 15

3 5 = 9 15

2 3 > 3 5

Nowyoutry

Whichislarger, 3 5 or 4 7 ?

Findacommondenominator. Thelowestcommonmultiple (LCM) of 3 and 5 is 15

Produceequivalentfractionswiththatdenominator.

Comparenumerators:

7 Decidewhichfractionisthelargestineachpair. 1 2 and 2 3 a

and

3 2 and 5 4 d

Example8Orderingfractions

and

Q7Hint:Firstwrite eachpairof fractionswiththe samedenominator. f

Writethefractions 3 4 , 4 5 , 2 3 inascendingorder.

SolutionExplanation

45 60 , 48 60 , 40 60 LCDof 3, 4 and 5 is 60.Produceequivalentfractionswithdenominatorof 60

40 60 , 45 60 , 48 60 Orderfractionsinascendingorder.(Lookatthetopofeachfraction.)

2 3 , 3 4 , 4 5

Nowyoutry

Rewritefractionsbackinoriginalform.

Writethefractions 1 1 3 , 5 6 , 1 1 5 inascendingorder.

8 Placethefollowingfractionsinascendingorder.

Problem-solving and reasoning

9 Placethefollowingcakefractionsindecreasingorderofsize.

Spongecakesharedequallybyfourpeople = 1 4 cake A

Chocolatecakesharedequallybyelevenpeople = 1 11 cake

Carrotandwalnutcakesharedequallybyeightpeople = 1 8 cake C

Q8Hint:Ascendingorderis fromsmallesttolargest.

10 SallyandDionorderedtwolargepizzas. Sallyate 2 3 ofherpizza.Dionate 5 8 ofhispizza.

a Showeachperson’spizzasonaseparatediagram.

b Whoatethemostpizza?

c Shouldtheyhaveorderedonlyonepizza?

11 Rewritethefractionsineachsetwiththeirlowestcommondenominator.Thenwritethenexttwo fractionsthatwouldcontinuethepattern.

12 Writeafractionthatliesbetweenthefollowingpairsoffractions.

13a Foreachofthediagramsshown,workoutwhatfractionoftherectangleiscolouredpurple. ii i

b Createyourownrectangulardesignthatisthree-quarterspurpleoverall.

3E 3E Addingfractions

Learningintentions

• Tounderstandthataddingfractionsrequiresacommondenominator.

• Tobeabletoaddtwofractionsbyconsideringtheirlowestcommondenominator.

• Tobeabletoaddtwomixednumerals.

Keyvocabulary: lowestcommondenominator(LCD),equivalentfractions,simplify

Fractionswiththesamedenominatorcanbeeasilyaddedtogether.

Fractionswithdifferentdenominatorscannotbeaddedtogethersoeasily.

Butwithacommondenominatoritispossible.

+ three-twelfths = seven-twelfths

Lessonstarter:‘Like’addition

Asaclass,discusswhichofthefollowingpairsofnumberscanbesimplyaddedtogetherwithouthaving tochangetheminsomeway.

6 goals, 2 goals a 11 goals, 5 behinds b 56 runs, 3 wickets c 6 hours, 5 minutes d 21 seconds, 15 seconds e 47 minutes, 13 seconds f 15 cm, 3 m g 2.2 km, 4.1 km h 5 kg, 1680 g i 2 7 , 3 7 j

Youcanseethat,whenadding,theunitsneedtobethesame.Withfractions,the‘units’arethe denominators.

Keyideas

Fractionscanbe simpliﬁed usingadditioniftheyare‘like’fractions;thatis,iftheyhavethe samedenominator.

Ifthedenominatorsareequal,addthenumeratorsandretainthedenominator.

Forexample: 3 7 + 2 7 = 5 7

Ifthedenominatorsarenotthesame:

• ﬁndthe lowestcommondenominator(LCD)

• convertfractionsto equivalentfractions usingtheLCD

• addthenumeratorsandretaintheLCD

• simplifytheanswerifpossible.

Forexample: 2 3 + 4 5 = 10 15 + 12 15 = 22 15 or 1 7 15

Exercise3E

1 Copythefollowingsentencesandﬁllinthegaps.

a Toaddtwofractionstogether,theymusthavethe same

b Whenaddingfractionstogether,iftheyhavethesame ,yousimplyaddthe

c Whenaddingtwoormorefractionswherethe aredifferent,youmustﬁndthe

Q1Hint:Choosefrom: denominator, common,lowest,simplify,multiple, numerators,denominators

d Aftercarryingouttheadditionoffractions,youshouldalways youranswer.

2 Usewordstocompletetheseadditions.

one-third + one-third = thirds a one-quarter + two = three-quarters b three-tenths + tenths = seven-tenths c one-ﬁfth + three-ﬁfths = four d half + half = two-halves(onewhole) e

3 Copyandcompletethefollowingbyshadingtheshapeontherightside. a += b += c

4 Answertrue(T)orfalse(F)foreachofthefollowing.

Fluency

Example9Adding‘like’fractions

Addthefollowingfractionstogether.

b 3

Nowyoutry

Addthefollowingfractionstogether.

5 Copyandcomplete.

Thedenominatorsarethesame(‘like’),so simplyaddthenumerators. one-fifth + three-fifths = four-fifths

Denominatorsarethesame,soaddthe numerators.

Weareaddingelevenths.

Converttoamixednumberifrequired.

6 Addthesefractionsandwriteyouranswersusingmixednumbers.

Q6Hint:Whenyou addthesefractions, thedenominator staysthesame. i

Example10Adding‘unlike’fractions

Addthefollowingfractionstogether.

Solution

a 1 5 + 1 2 = 2 10 + 5 10 = 7 10

bc 3 4 + 5 6 = 9 12 + 10 12 = 19 12 = 1 7 12

Nowyoutry

Addthefollowingfractionstogether.

Explanation

LCDis 10

WriteequivalentfractionswiththeLCD. 1 5 × 2 2 = 2 10 1

Denominatorsarethesame,soaddnumerators.

LCDis 12

WriteequivalentfractionswiththeLCD. 3 4 × 3 3 = 9 12 5 6 × 2 2 = 10 12

Denominatorsarethesame,soaddnumerators. Writeasamixednumber,ifrequired.

7 Copyandcompletethefollowingadditions.

8 Addthefollowingfractions.

Q8Hint:Usesimilarstepsto question 7 l

Example11Addingmixednumerals

Simplify:

Solution

a 3 + 4 + 2 3 + 2 3 = 7 + 4 3 = 8 1 3

Alternatively

Explanation

Addthewholenumberpartstogether. Addthefractionpartstogether.

Notingthat 4 3 = 1 1 3,simplifytheanswer.

Firstconverttoanimproperfraction.

Addthenumerators.

Addthewholenumberpartstogether. LCDof 6 and 4 is 12 WriteequivalentfractionswithLCD.

Addthefractionpartstogether.

Notingthat 19 12 = 1 7 12,simplifytheanswer. Alternatively

Firstconverttoanimproperfraction.

ConvertusinganLCDof 12

Addthenumerators. Nowyoutry Simplify:

Problem-solving and reasoning

11 Dadgaveyou 2 5 ofthemoneyforamovieticketandMumgaveyou 1 5

a Whatfractionoftheticketdidyourparentspayfor?

b Whatfractionwasleftforyoutopay?

c Iftheticketcost $10,howmuchdidyoupay?

12 Julieowns 1 3 ofacompanyandSeanowns 1 4

a Whatfractionofthecompanydotheyowntogether?

b Whatfractionofthecompanyisleft?

13 Markspends 1 3 ofthedayatschooland 3 8 ofthedayasleep.

a Whatfractionofthedayhasbeenused?

b Whatfractionofthedayisleftforfun?

c Howmanyhoursoffundoesheget?

14 Toﬁndthenumberineachsquare,addthefractionsinthetwocirclesthatarejoinedtoit. Fillinthefollowingfractionnetworks.

15 Nowﬁndthefractionsinthecircleswithinthefollowingfractionnetworks. 11

3F 3F Subtractingfractions

Learningintentions

• Tounderstandthatsubtractingfractionsrequiresacommondenominator.

• Tobeabletosubtracttwofractionsbyconsideringtheirlowestcommondenominator.

• Tobeabletosubtracttwomixednumerals.

Keyvocabulary: lowestcommondenominator(LCD),equivalentfractions,simplify

Therulesforsubtractingfractionsareverysimilartoaddingfractions.Beforeyoucansubtract,weaimto writethefractionswiththesamedenominator.

Lessonstarter:Subtractiononanumberline

Copythenumberlineanduseittoﬁnd:

Keyideas

Fractionscanbe simpliﬁed easilyusingsubtractioniftheyare‘like’fractionswiththe samedenominator.

Therulesforsubtractingfractionsaresimilartothoseforaddingfractions. Whensubtractingmixednumbers,youmayneedtoborrowawhole. Forexample:

7 1 8 −2 3 8 1 8 isnotbigenoughtohave 3 8 subtractedfromit.

6 9 8 −2 3 8 Therefore,wechoosetoborrowawholefromthe 7 (6 + 1 = 7) Alternatively,ﬁrstconvertthemixednumeralstoimproperfractions.

Exercise3F

Und er stand ing

1 Copythefollowingsentencesandﬁllintheblanks.

a Tosubtractonefractionfromanother,youmusthaveacommon

b TheLCDof 6 and 12 is

c TheLCDof 3 and 5 is

2 Copyandcompletethefollowingsubtractions.

a three-tenths two-tenths = tenth

b three-quarters quarters = one-quarter

c four three-ﬁfths = one-ﬁfth

d onewhole two-ﬁfths = ﬁfths

e ﬁve-eighths two = three-eighths

Example12Subtracting‘like’and‘unlike’fractions

Denominatorsarethesame,thereforewearereadyto subtractthesecondnumeratorfromtheﬁrst.

FindtheLCD,whichis 12 WriteequivalentfractionswiththeLCD.

Wehavethesamedenominatorsnow,sosubtractsecond numeratorfromtheﬁrst.Thedenominatorstaysthesame (twelfths).

Nowyoutry

5 Simplify:

6 Simplify:

Q6Hint:Firstwriteeachfraction usingtheLCD.

Example13Subtractingmixednumerals

Explanation

Amixednumeralsistheadditionofawholenumberand aproperfraction.

Groupwholenumbersandgroupproperfractions. Simplifywholenumbers.

Makedenominatorsthesame.

Borrowingawholewasnotrequired.

Firstconverttoimproperfractions.

FindandusetheLCD.

Subtractthenumerators.

Converttotwentieths:

Borrowawholefromthe 8 sothatthenumeratorscanbe subtracted.

Subtractwholenumbers,subtractfractions.

Firstconverttoimproperfractions.

FindandusetheLCD.

Subtractthenumerators.

7 Simplify:

8 Simplify:

Q7Hint:Forsomeofthese,youwill ﬁrstneedtomakedenominators thesame.

Q8Hint:Youwillneedto‘borrow awhole’forsomeofthese.

Problem-solving and reasoning

9 Afamilyblockofchocolateismadeupof 60 smallsquaresofchocolate.Marciaeats 10 squares,Jon eats 9 squaresandHollyeats 5 squares.Whatfractionoftheblockofchocolateisleft?

10 Threefriendssplitarestaurantbill.Onepays 1 2 ofthebillandonepays 1 3 ofthebill.Whatfractionof thebillmustthethirdfriendpay?

11 Afullcontainerofﬂourweighs 4 5 kg.Theemptycontainerweighs 1

20 kg.Howmuchdoesthe ﬂourweigh?

12 Copyandcompletethesetwosubtractions,whichusetwodifferenttechniques.Statewhich techniqueyouprefer,givingreasons.

Findingfractions 13

13 Twofractionshaveasumof 23 24 andadifferenceof 7 24 Canyouﬁndthetwofractions?

Q13Hint:Startbythinkingoftwo numbersthataddto 23 andhave adifferenceof 7

3G 3G Multiplyingfractions

Learningintentions

• Tounderstandthatmultiplyingfractionsiseasierifyou rstcancelcommonfactorsfromnumeratorsand denominatorsineachfraction.

• Toknowthatawholenumbercanbewrittenasafractionwithadenominatorof 1

• Tobeabletomultiplyfractions,mixednumeralsand/orwholenumbers,givingananswerinsimplestform.

Keyvocabulary: factor,simplify,mixednumeral,improperfraction

Whenwemultiplywholenumberstogether,weendupwithanumberlargerthan(orequalto)theones westartedwith.

2 × 3 = 65 × 7 = 3515 × 1 = 15

Butwhenwemultiplyfractionstogether,thingscanbedifferent.Considerhalfofhalfanapple,forexample, whichresultsinasmallerfractioncomparedtotheoriginalfractions.

Lessonstarter:Partsofacircle

•

Howdoesthisdiagramshowhalfofhalfacircle?

• Whatishalfofthree-quartersofacircle?

Usediagramstoinvestigateotherfractionmultiplications. Whatshortcut(orrule)canyouﬁndtohelpmultiplyfractionstogether?

Keyideas

Fractionsdo not needtohavethesamedenominatortobemultipliedtogether. Tomultiplyfractions,multiplythenumeratorstogetherandmultiplythedenominatorstogether.

• Insymbols: a b × c d = a × c b × d

Ifpossible,‘simplify’or‘cancel’fractionsbeforemultiplying. (Remember,youcanonlycancelnumeratorswithdenominators.)

Mixednumerals mustbechangedto improperfractions beforemultiplying. Finalanswersshouldbewritteninsimplestform.

Exercise3G

Und er stand ing

1 Copythesesentencesandﬁllintheblanks.

a Aproperfractionhasavaluethatisbetween and b Animproperfractionisalwaysgreaterthanorequalto c Amixednumeralconsistsoftwoparts, a partand a part.

2 Copythegridshownhere.

a Onyourdiagram,usebluetoshade 1 3 of thegrid.

b Nowuseredtoshade 1 4 oftheshadedblue.

c Youhavenowshaded 1 4 of 1 3.Whatfractionis thisoftheoriginalgrid?

Q1Hint:Choosefrom: fraction, whole, number, 0, 1,and proper

3 If 1 3 of • = 4,whatis 2 3 of •? a If 1 10 of = 7,whatis 3 10 of ? b If 1 2 of = 4,whatis 3 2 of ? c If 1 5 of 10 = 2,whatis 4 5 of 10? d If 1 100 of 200 = 2,whatis 21 100 of 200? e If 1 10 ofP = 3,whatis 10 10 ofP? f

Fluency

Example14Findingasimplefractionofaquantity

Find 2 3 of 15 bananas.

Solution

2 3 of 15 bananas

= ( 1 3 of 15) × 2

= 5 × 2

= 10 bananas

Nowyoutry

Find 2 5 of 20 cars.

Explanation

Divide 15 bananasinto 3 equalgroups. Therefore, 5 ineachgroup. Take 2 ofthegroups.

Answeris 10 bananas.

4 Usedrawingstoshowtheanswertotheseproblems.

1 3 of 12 lollies a 1 5 of 10 pencils b

2 3 of 18 donuts c 3 4 of 16 boxes d

3 8 of 32 dots e 3 7 of 21 triangles f 1 10 of $20 g 3 5 of 10 kg h

4 7 of 21 triangles i 4 5 of 15 stars

5 Find: 1 3 of 18 a 1

Q4Hint:Thedenominatortellsyou howmanyequalgroupstomake. Thenumeratortellsyouhowmany ofthosegroupstocircle.

Example15Multiplyingproperfractions

Evaluate:

Multiplythenumeratorstogether. Multiplythedenominatorstogether. Theanswerisinsimplestform.

Cancelﬁrst. Thenmultiplynumeratorstogetherand denominatorstogether.

Nowyoutry

Evaluate:

Q6Hint:Wherepossible, cancelﬁrstsothatyou multiplysmallernumbers. Rememberthat‘of’ meansmultiply.

7 Find:

Q7Hint:Multiplyimproper fractionsjustasiftheywere properfractions,thensimplify youranswer.

Example16Multiplyingmixednumerals

Find:

Explanation a

Writetheanswerasamixednumeralifrequired. Convertmixednumberstoimproperfractions. Multiplynumeratorstogether. Multiplydenominatorstogether.

Writetheanswerinsimplestform. Converttoimproperfractions. Simplifyfractionsbycancelling. Multiplynumeratorsanddenominatorstogether.

Nowyoutry

Find:

8 Find:

Q8Hint:Firstconvertmixed numberstoimproperfractions.

Problem-solving and reasoning

9 Atonesecondarycollege, 2 5 oftheYear 7 studentsareboys.

a WhatfractionoftheYear 7 studentsaregirls?

b Ifthereare 120 Year 7 students,howmanyboysandgirlsarethere?

10 Juliewasinjuredduringthenetballseason.Shewasabletoplayonly 2 3 ofthematches.Theseason consistedof 21 matches.HowmanygamesdidJuliemissasaresultofinjury?

11a Blakespends 3 4 ofanhouronhisMathshomework. Howmanyminutesisthis?

b Performthiscalculation: 60 ÷ 4 × 3.Whatdoyou notice?

c Nowﬁndthenumberofminutesin 2 3 ofanhourina similarway.

12 ThediagramshowsaplanofJoel’sgarden.Theshadedsectionisgrass.Therestispaved.

a Whatfractionofthegardenisgrass?

b Ifhalfthegrassisremovedandreplacedwithpavers,whatfractionofthegardenwillremaingrass?

Missingproducts 13

13a Toﬁndthenumberineachsquare,multiplythenumbersinthetwo nearestcircles.

b Challengeyourself.Whatdoes a + b + c equal?Checkusingacalculator.

3H 3H Dividingfractions

Learningintentions

• Tounderstandthatdividingfractionsinvolvesmultiplyingbyareciprocal.

• Tobeableto ndthereciprocalofafractionoramixednumber.

• Tobeabletodividefractions,mixednumeralsand/orwholenumbers,givingananswerinsimplestform.

Keyvocabulary: reciprocal,mixednumeral,improperfraction

Rememberthatdivisionistheoppositeoperationtomultiplication.Thinkingofdivisionas‘howmany’helps ustounderstanddividingfractions.

Forexample,toﬁnd 1 2 ÷ 1 4,think:Howmanyquartersareinahalf?

Considerastripofpaperthatisdividedintofourequalsections.Halfthestripisshaded.

Therearetwoquartersinourhalf.Therefore, 1 2 ÷ 1 4 = 2

Whenitishalf-timeinanAFLgame,youhaveplayedtwoquarters.Thisisanotherwayofshowingthat

Lessonstarter:Usingdivisionpatterns

Usepatternstohelpyouﬁndthemissingnumbers. 20 ÷ 1 = 20

Canyouseeaneasywaytoﬁndthefollowing?

Keyideas

Weusemultiplicationtohelpwiththedivisionoffractions.

• Dividingby 1 2 islikemultiplyingby 2

Forexample: 20 ÷ 1 2 = 40 and 20 × 2 = 40

A reciprocal isafractioninwhichthenumeratoranddenominatorhavechangedplaces.

• Thereciprocalof x is 1 x

• 2isthereciprocalof 1 2 (andviceversa).

• Thereciprocalof 3 5 is 5 3

• Thereciprocalof 1 4 is 4 1 = 4

Findingareciprocaliscalledinverting,ﬂippingorturningthefractionupsidedown. Todividebyafraction,youcanmultiplybyitsreciprocal.

Forexample: 1 2 ÷ 3 4 = 1 2 × 4 3 2 5 ÷ 1 3 = 2 5 × 3 1

Whendividing,orﬁndingreciprocals, mixednumerals mustbechangedto improperfractions

Exercise3H

Und er stand ing 1–4 4

1 Copythesesentences,ﬁllingintheblanksasyougo.

a 10 ÷ 5 isthesameas 10 1 5.

b 24 ÷ 1 4 isthesameas 24 ×

c Toﬁndhalfofanumberyoucan by 2

d The of 3 5 is 5 3

Q1Hint:Choosefrom: ﬂip,divide, 4, ×,reciprocal, improper

e Toinvertafractionyou itupsidedown. f Whendividingfractionswechangeanymixednumeralsinto fractions.

2 Whichofthefollowingisthecorrectﬁrststepforﬁnding

? 3 5 × 7 4 A

3 Copyandcomplete.

Q3Hint:Dividingby afractionisthe sameasmultiplying byitsreciprocal. f

4 Makeeachsentencecorrectbyinsertingtheword more or less inthegap.

a 10 ÷ 2 givesananswerthatis than 10

b 10 ÷ 1 2 givesananswerthatis than 10

c 3 4 ÷ 2 3 givesananswerthatis than 3 4

d 3 4 × 3 2 givesananswerthatis than 3 4

e 5 7 ÷ 8 5 givesananswerthatis than 5 7

f 5 7 × 5 8 givesananswerthatis than 5 7

Example17Findingreciprocals

Statethereciprocalofthefollowing.

2 3 a 5 b 1 3 7 c

Solution

a Reciprocalof 2 3 is 3 2

b Reciprocalof 5 is 1 5

c Reciprocalof 1 3 7 is 7 10

Nowyoutry

Statethereciprocalofthefollowing.

5 Whatisthereciprocalofeachofthefollowing?

Explanation

Thenumeratoranddenominatorareswapped. (Flipthefractionupsidedown.)

Thinkof 5 as 5 1 andtheninvert(ﬂip)it.

Convert 1 3 7 totheimproperfraction 10 7 ,and theninvert.

6 Firstchangeeachofthefollowingtoanimproper fraction,thenﬁnditsreciprocal.

Example18Dividingafractionbyawholenumber Find:

Changethe ÷ signtoa × signandinvert(ﬂip)the 3

Multiplythenumeratorsanddenominators.

Convertthemixednumbertoanimproperfraction. Write 5 asanimproperfraction.

Changethe ÷ signtoa × signandinvertthedivisor. Simplifybycancelling.

Multiplynumeratorsanddenominators. Nowyoutry

Example19Dividingawholenumberbyafraction.

Explanation

Simplify.

8 Find:

Example20Dividingafractionbyafraction

Find:

Solution

Explanation a

Changethe ÷ to × andinvertthedivisor(thefraction after thedivisionsign).

Cancelandsimplify.

Convertmixednumeralstoimproperfractions.

Changethe ÷ signtoa × signandinvertthedivisor.

Cancel,multiplyandsimplify.

Nowyoutry

Find:

9 Find:

Q9Hint:Firstconvertanymixed numberstoimproperfractions.

Problem-solving and reasoning

10 If 2 1 4 leftoverpizzasaretobesharedbetweenthreefriends,whatfractionofpizzawilleach friendreceive?

11 Acartravels 180 kmin 1 1 2 hours.Calculatethiscar’sspeed.Youranswer willbeinkm/h.

12 Ceannacolours 1 4 ofhercirclepink.

Q12Hint: speed = distance ÷ time

Shedividestherestofthecircleintothreeequalsectorsandcoloursthemblue,purpleandgreen.What fractionofthecircleispurple?

Apuzzlingquestion! 13

13 WhydoIlovefractions?

Toﬁndout,workoutthevalueofeachofthese 15 letters.

1 3A Forthefollowinglistoffractions,determineiftheyareproperfractions(P),improperfractions(I) orwholenumbers(W).

2 3B Writethefollowingfractionsinsimplestform.

3 3B Whichofthefollowingfractionsisequivalentto 5 35?

4 3C Convertthesemixednumberstoimproperfractions.

5 3C Converttheseimproperfractionstomixednumbers.

6 3D Decidewhichfractionisthelargestineachpair.

and 5

7 3D Placethefollowingfractionsinascendingorder.

8 3E Addthefollowingfractionstogether.

9 3F Simplify:

10 3G Evaluate:

11 3H Statethereciprocalofthefollowing. 2

12 Evaluate:

3I 3I Fractionsandpercentages

Learningintentions

• Tounderstandthatapercentagecanbethoughtofasafractionwithadenominatorof100.

• Tobeabletoconvertapercentagetoafractioninsimplestform.

• Tobeabletoconvertafractiontoapercentage.

Keyvocabulary: percent,percentage,denominator,equivalentfraction

Percentagesareusedinmanyday-to-daysituationsincludingtest results,discountsandfoodingredients.

Apercentageisanotherwayofwritingafractionwitha denominatorof 100.Forexample, 87 percentsimplymeans 87 outof 100,so:

87%= 87 100

Percentagesofelementsinthe humanbody.

Lessonstarter:Studentranking

FivestudentseachcompletedadifferentMathematicstest.

• Matthewscored 15 outofapossible 20 marks.

• Mengnascored 36 outofapossible 50 marks.

• Mariascored 17 outofapossible 25 marks.

• Marcusscored 7 outofapossible 10 marks.

• Melissascored 128 outofapossible 200 marks.

Changethesetestresultstoequivalentscoresoutof 100,andthereforestatethepercentagetestscorefor eachstudent.Whyarepercentagesusefulinthissituation?

Keyideas

The % symbolmeans percent.ThiscomesfromtheLatin percentum whichmeans ‘outof 100’.

Forexample: 75 percentmeans 75 outof 100.Thatis, 75%= 75 100

Wecanwrite percentages asfractionsbychangingthe % signtoa denominator of 100 (meaningoutof 100)

Forexample: 37%= 37 100

Wecanuse equivalentfractions toconvertfractionstopercentages.

Forexample: 1 4 = 25 100 = 25%

Toconvertanyfractiontoapercentage,multiplyby 100

Forexample: 3 8 × 100 = 3 2 ✁ 8 × ✟✟ 100 25 1 = 75 2 = 37 1 2 Â 3 8 = 37 1 2 % fraction × 100 ÷ 100 percentage

Itisusefultoknowthefollowingcommonpercentagesandtheirequivalentfractions.

1 Changethesetestresultstoequivalentscoresoutof 100,andthereforestatethepercentage.

a 7 outof 10 = outof 100 = %

b 24 outof 50 = outof 100 = %

c 12 outof 20 = outof 100 = %

d 1 outof 5 = outof 100 = %

e 80 outof 200 = outof 100 = %

f 630 outof 1000 = outof 100 = %

2 Copyandcompletethesepatterns. 1

3a If 14% ofstudentsinYear 7 areabsentduetoillness,what percentageofYear 7 studentsareatschool?

b If 80% oftheGeographyprojecthasbeencompleted,what percentagestillneedstobeﬁnished?

Example21Convertingpercentagestofractions

Expressthesepercentagesasfractionsintheirsimplestform. 17% a 36% b 140% c

Solution

a 17%= 17 100

b 36%= 36 100

= 9 × ✁ 4 25 × ✁ 4 = 9 25

c 140%= 140 100

= 7 × ✚✚ 20 5 × ✚✚ 20 = 7 5 = 1 2 5

Nowyoutry

Explanation

Change % signtoadenominatorof 100

CancelHCF.

Answerisnowinsimplestform.

Change % signtoadenominatorof 100

CancelHCF.

Convertanswertoamixednumeralif required.

Expressthesepercentagesasfractionsintheirsimplestform.

5 Expressthesepercentagesasfractionsintheirsimplestform.

6 Expressthesepercentagesasmixednumbersintheirsimplestform.

Example22Convertingtopercentagesthroughequivalentfractions

Convertthefollowingfractionstopercentages.

× 4 × 4

Denominatorisalready 100,thereforesimply writethenumberasapercentage.

Weneedthedenominatortobe 100 Therefore,multiplynumeratoranddenominator by 4 togetanequivalentfraction.

Nowyoutry

Convertthefollowingfractionstopercentages.

7 Convertthesefractionstopercentages,usingequivalentfractions.

Q7Hint:Firstwritewitha denominatorof 100. p

Example23Convertingtopercentagesbymultiplyingby 100

Convertthefollowingfractionstopercentages.

Nowyoutry

Convertthefollowingfractionstopercentages.

Multiplyby 100 SimplifybycancellingHCF.

Convertmixednumeraltoimproperfraction. Cancelandsimplify.

8 Convertthesefractionstopercentagesbymultiplyingby 100

Problem-solving and reasoning

9 Abottleoflemonadeisonly 25% full.

a Whatfractionofthebottlehasbeenconsumed?

b Whatpercentageofthebottlehasbeenconsumed?

c Whatfractionofthebottleisleft?

d Whatpercentageofthebottleisleft?

10 Alemontartiscutintoeightequalpieces.Whatpercentageofthetartdoeseachpiecerepresent?

11 Petrinascores 28 outof 40 onherfractionstest.Whatisherpercentagescore?

12 TheHeathmontHornetsbasketballteamhavewon 14 outof 18 games.Theystillhavetwogamesto play.WhatisthesmallestandthelargestpercentageofgamestheHornetscouldwinfortheseason?

More-challengingconversions 13

13a Copyandcomplete:

b Writeeachofthefollowingpercentagesasfractionsusingtheabovetechnique.

3J 3J Findingapercentageofanumber

Learningintentions

• Tounderstandthat ndingpercentagesofanumbergenerallyinvolvesmultiplyingbyafraction.

• Tobeableto ndapercentageofanumber.

• Tobeabletoapplypercentagestowordedproblems.

Keyvocabulary: percentage,‘of’,fraction

Throughoutlifeyouwillcomeacrossmanyexampleswhereyouneedtocalculatepercentagesofaquantity. Examplesincluderetaildiscounts,interestrates,personalimprovementsandsalaryincreases.

Lessonstarter:Percentagesinyourhead

Itisausefulskilltobeabletocalculatepercentagesmentally.Calculating 10% or 1% isoftenagoodstarting point.Youcanthenmultiplyordividethesevaluestoquicklyarriveatotherpercentagevalues.

Withapartner,andusingmentalarithmeticonly,calculate 10% ofeachoftheseamounts.

Howdidyouﬁnd 10% ofanamountmentally?

Keyideas

Toﬁndthe percentage ofanumber:

1 Expresstherequiredpercentageasa fraction

2 Changethe‘of’toamultiplicationsign.

3 Expressthenumberasafraction.

4 Followtherulesformultiplicationoffractions.

Tomentallyﬁndapercentageofanumber,ﬁndthevalueof 1% or 10% andworkfromthere. Forexample:

Exercise3J

1 Copyandcompletethefollowing.

a Toﬁnd 10% of $20,youcanuse 20 ÷ = 2

b Toﬁnd 25% of $20,youcanuse 20 ÷ 4 =

c Toﬁnd 50% of $20,youcanuse 20 ÷ =

2a If 10% of = 3,ﬁnd 20% of .

b If 1% of = 7,ﬁnd 5% of .

c If 50% of • = 8,ﬁnd 100% of •

3 Usementalstrategiestoﬁnd: 10% of $500 a 1% of $900 b 25% of 84 kilograms c 50% of 7 days d 75% of 84 kilograms e 20% of 35 minutes f

4 Whatis 100% of 8 hours?

Example24Findingthepercentageofanumber

Find:

30% of 50 a 15% of 400 b

Solution

a 30% of 50 = 30 2✟✟ 100 × ✚✚ 50 1 1 = 30 2 = 15

Alternatively

10% of 50 = 5

Explanation

Write 30% asafraction. Theword‘of’tellsustomultiply. Cancelandsimplify.

30% of 50 = 15 10% iseasytoﬁndmentally. Multiply 10% by 3 toﬁnd 30%

b 15% of 400 = 15 1✟✟ 100 × ✟✟ 400 4 1 = 15 × 4 1 = 60

Alternatively

10% of 400 = 40, 5% of 400 = 20

15% of 400 = 60

Nowyoutry

Find:

5 Find:

% of 40 e 25% of

6 Find:

7 Matcheachquestionwiththecorrectanswer. Questions Answers a

Write 15% asafraction. ‘Of’means × Cancelandsimplify.

Find 10% mentally.Halvetoﬁnd 5%.

Add 10% and 5% toﬁnd 15%

Q5Hint: 50% of140 = 50 100 × 140 1 p

8 Find:

30% of $140 a

10% of 240 millimetres b

15% of 60 kilograms c 2% of 4500 tonnes d

20% of 40 minutes e

5% of 30 grams g

80% of 500 centimetres f

25% of 12 hectares h

Q8Hint:Rememberthatthe answersneedtoincludeunits. i

120% of 120 seconds

Problem-solving and reasoning

9 Harryscored 70% onhispercentagestest.Ifthetestisoutof 50 marks,howmanymarks didHarryscore?

10 Inastudentsurvey, 80% ofstudentssaidtheyreceivedtoomuchhomework.If 300 studentswere surveyed,howmanystudentsfelttheygettoomuchhomework?

11 25% ofteenagerssaytheirfavouritefruitiswatermelon.Inasurveyof 48 teenagers,howmanywould writewatermelonastheirfavouritefruit?

12 AtGladesbrookCollege, 10% ofstudentswalktoschool, 35% ofstudentscatchpublictransportand therestaredriventoschool.Ifthereare 1200 studentsattheschool,ﬁndhowmanystudents: walktoschool a catchpublictransport b aredriventoschool c

Percentagechallenge — 13

13a Whichislarger: 60% of 80 or 80% of 60?

b Tomdidthefollowingcalculation: 120 ÷ 4 ÷ 2 × 3.Whatpercentageof 120 didTomﬁnd?

c If 5% ofanamountis $7,whatis 100% oftheamount? i If 25% ofanamountis $3,whatis 12 1 2 % oftheamount?

3K Introductiontoratios

Learningintentions

• Tounderstandthataratiocomparestwoormorerelatedquantitiesinagivenorder

• Tobeabletowritearatiofromadescription

• Tobeabletouseacommonfactortosimplifyaratio

Keyvocabulary: ratio

Ratiosareusedtoshowtherelationshipbetweentwo ormorerelatedquantities.Theycomparequantitiesof thesametypeusingthesameunits.Thenumbersin theratioarethereforewrittenwithoutunits.

Whenreadingorwritingratios,theorderisvery important.Inasport,ateam’swin-lossratioduring theseasoncouldbewrittenas 5 : 2 meaningthata teamhaswon 5 gamesandonlylost 2 games.This isverydifferentfromawin-lossratioof 2 : 5 which wouldmeanthat 2 gameswerewonand 5 games werelost.

Lessonstarter:Impossiblecupcakes

Liamisbakingcupcakesforagroupoffriendsandplanstomake bananacupcakesandchocolatecupcakesintheratio 2 to 3.This meansthatforevery 2 bananacupcakesthereare 3 chocolate cupcakes.

a HowmanychocolatecupcakeswouldLiammakeifhemakesthe followingnumberofbananacupcakes?

4 i 6 ii 8 iii

b HowmanybananacupcakeswouldLiammakeifhemakesthe followingnumberofchocolatecupcakes?

9 i 15 ii 18 iii

c HowmanycupcakeswillLiammakeintotalifhemakes: i 2 bananacupcakes? ii 6 chocolatecupcakes?

d GivenLiam’scupcakeratio,isitpossiblethathecouldmake 7 cupcakes?Explainwhyorwhynot.

Keyideas

A ratio comparestwoormorerelatedquantities.

• Ratiosareexpressedusingwholenumbersinagivenorder.

• Acolonisusedtoseparatethepartsofaratio.

• Ratiosareexpressedwithoutunits.

Aratiocanbesimpliﬁedinasimilarwaytoafraction.

• Thefraction 4 6 canbesimpliﬁedto 2 3 .

Ratio of dark to white = 2 : 3

Asportingteam’swin-lossperformancecouldbe expressedasaratio.

• Theratio 4 : 6 canbesimpliﬁedto 2 : 3

• Aratiocanbesimpliﬁedifthenumbersthatmakeuptheratiohaveacommonfactor.

• Dividingallnumbersinaratiobytheirhighestcommonfactorwillleadtothesimplestform.

Exercise3K

Und er stand ing

1 Ofagroupof 5 counters, 2 ofthemarered and 3 ofthemareblue.

a Whichratiowoulddescribethenumber ofredcounterscomparedtothenumberof bluecounters?

A 2 : 5

B 2 : 3

C 3 : 2

D 3 : 5

E 1 : 2

b Whichratiowoulddescribethenumberofblue counterscomparedtothenumberofred counters?

A 2 : 5

B 2 : 3

C 3 : 2

D 3 : 5

E 1 : 2

c Trueorfalse?Thefractionofredcountersoutofthetotalis 2 3.

d Trueorfalse?Thefractionofbluecountersoutofthetotalis 3

2 Thisrectangleisdividedupinto 12 squares, 4 ofwhichareshaded.

a Howmanysquaresareunshaded?

b Aratiowhichdescribestheratioofshadedtounshaded squarescouldbe:

A 3 : 9

B 4 : 7

C 4 : 8

D 5 : 7

E 4 : 6

c Trueorfalse?Thecorrectratiofrompart b abovecouldalsobewrittenas 8 : 4

d Trueorfalse?Thecorrectratiofrompart b abovecouldalsobewrittenas 1 : 2

e Trueorfalse?Thecorrectratiofrompart b abovecouldalsobewrittenas 2 : 1

Fluency

Example25Expressingasaratio

a Aboxcontains 3 whiteand 4 darkchocolates.Writeeachofthefollowingasaratio.

i theratioofwhitechocolatestodarkchocolates

ii theratioofdarkchocolatestowhitechocolates

b Ashopshelfcontains 2 cakes, 5 slicesand 9 pies.Writeeachofthefollowingasaratio.

i theratioofcakestoslices

ii theratioofcakestoslicestopies

iii theratioofpiestocakes

Solution

ai 3 : 4

ii 4 : 3

bi 2 : 5

ii 2 : 5: 9

iii 9 : 2

Nowyoutry

Explanation

Theorderiswhitetodarkandthereare 3 white and 4 darkchocolates.

Theorderisdarktowhiteandthereare 4 dark and 3 whitechocolates.

Weareonlyconcernedwiththeratioofcakes toslicesandtheorderiscakesthenslices.

Threequantitiescanalsobecomparedusing ratios.Theorderisimportant.

Weareonlyconcernedwithpiesandcakesand theorderispiesthencakes.

a Acontainerhas 2 clearand 5 greymarbles.Writeeachofthefollowingasaratio.

i theratioofclearmarblestogreymarbles

ii theratioofgreymarblestoclearmarbles.

b Acomputershophas 3 laptops, 4 tabletsand 7 phonesonadisplaytable.Writeeachofthe followingasaratio.

i theratiooflaptopstophones

ii theratiooflaptopstotabletstophones

iii theratiooftabletstolaptops.

3a Aboxcontains 5 whiteand 3 darkchocolates.Writeeachofthefollowingasaratio.

i theratioofwhitechocolatestodarkchocolates

ii theratioofdarkchocolatestowhitechocolates

b Atoyshopwindowcontains 3 cars, 7 trucksand 4 motorcycles.Writeeachofthefollowingasa ratio.

i theratioofcarstotrucks

ii theratioofcarstotruckstomotorcycles

iii theratioofmotorcyclestocars

4a Apencilcasehas 8 pencilsand 5 pens.Writeeachof thefollowingasaratio.

i theratioofpencilstopens

ii theratioofpenstopencils

b Acoffeeshopproduces 6 lattes, 7 cappuccinosand 5 ﬂatwhitecoffeesinonehour.Writethefollowingas aratio.

i theratioofcappuccinostoﬂatwhites

ii theratiooflattestocappuccinostoﬂatwhites

iii theratioofﬂatwhitestolattes

5 Eachhour,anewradiostationplanstoplay 3 songsfromthe70s, 4 songsfromthe80s, 7 songsfrom the90sandjustonesongfromthe60s.Writeeachofthefollowingasaratio.

a 80ssongsto70ssongs

b 70ssongsto90ssongs

c 60ssongsto80ssongs

d 70ssongsto60ssongs

e 90ssongsto80ssongsto70ssongs

f 60ssongsto70ssongsto80ssongsto90ssongs

Solution

4 : 10 2 :

3 : 12 : 15

1 : 4 : 5 ÷ 3 ÷ 3

Explanation

Thehighestcommonfactorof 4 and 10 is 2 so dividingbothnumbersby 2 willgivetheratioin simplestform.

Thehighestcommonfactorof 3, 12 and 15 is 3 sodividingallnumbersby 3 willgivetheratioin simplestform.

5 ÷ 5

15 : 10 3 : 2

Nowyoutry

Simplifythefollowingratios.

6 Simplifythefollowingratios. 3 : 6 a 4 : 16 b

Firstusethenumberstowritetheinformation asaratiowithoutunits.Thendivideboth numbersbythehighestcommonfactor 5

7 Simplifythefollowingratios.

8 Simplifythefollowingratios.

Problem-solving and reasoning

9 Writearatioofshadedsquarestowhitesquaresinthesediagrams.Simplifyyourratioifpossible.

10 Findthemissingnumber.

11 Ashadeoforangeiscreatedbymixingyellowandredintheratio 2 : 3.

a Explainwhythisisthesameasmixing 4 litresofyellowpaintwith 6 litresofredpaint.

b Decideifthefollowingratiosofyellowpainttoredpaintwillmakethecolourmoreyellowormore redcomparedtothegivenratioabove:

12 Thefollowingcomparequantitieswithdifferentunits.Writethemusingaratioinsimplestformbyﬁrst writingthemusingthesameunits.

Paintmixing

13 Thethreeprimarycoloursarered,blueandyellow.Mixingthemtogetherindifferentwaysformsa varietyofcolours.Theprimary,secondaryandtertiarycoloursareshowninthischart.

a Thesecondarycoloursareformedbymixingtheprimarycolours.Whatcolourdoyouthinkwillbe formedifthefollowingpairsofprimarycoloursaremixedintotheratio 1 : 1?

i yellowandred

ii yellowandblue

iii redandblue

b Thetertiarycoloursareformedbymixingaprimarycolourandsecondarycolour.Whatcolourdo youthinkwillbeformedifthefollowingpairsofcoloursaremixedintotheratio 1 : 1?

i yellowandorange

ii blueandviolet

iii greenandyellow

3L 3L Solvingproblemswithratios

Learningintentions

• Tounderstandtheconnectionbetweenratios,fractionsandproportions

• Tobeabletosolveproportionproblemsusingratiosandfractions

• Tobeabletodivideagivenquantityinagivenratio

Keyvocabulary: ratio,proportion,fraction

Whenconsideringthemakeupofamateriallike concrete,itisimportanttocorrectlybalancethe proportionsofsand,water,cementandgravel.These ingredientscouldbethoughtofaspartsofthewhole, fractionsofthewholeorasaratio.Youmightsay,for example,thataparticularconcretemixhassand,water, cementandgravelintheratio 3 : 2 : 1 : 4.Thismeansthat outofatotalof 10 parts, 3 ofthemaresand, 2 arewater, 1 iscementand 4 aregravel.Similarly,youcouldsaythat theproportionorfractionofsandinthemixis 3 10 andso ifaloadofconcreteis 40 tonnes,thentheproportionof sandis 3 10 × 40 = 12 tonnes.

Lessonstarter:Makingbread

Durableconcreteneedstohavetherightratioof ingredients.

Thetwomainingredientsinbreadareﬂourandwater.Acommonlyusedratioofﬂourtowateris 5 : 3

• Howwouldyoudescribetheproportionofﬂourinabreadmix?

• Howwouldyoudescribethefractionofwaterinabreadmix?

• Iftheratioofﬂourtowateris 5 : 3,doesthatmeanthatallbreadloavesthataremademusthaveatotal of 8 cupsofingredients?Explain.

• Ifabreadmixconsistedofatotalof 16 cupsofﬂourandwater,describeamethodforworkingoutthe totalnumberofcupsofﬂourorwaterrequired.

• Isitpossibletomakealoafofbreadusingatotalof 12 cupsofﬂourandwater?Describehowyouwould calculatethenumberofcupsofﬂourorwaterneeded.

Keyideas

Ratioscanbeconsideredasacollectionofparts.

Theratioofvinegartowaterforexamplemightbe 3 : 4,whichmeansthatforevery 3 partsof vinegarthereare 4 partsofwater.

Thetotalnumberofpartscanbecalculatedbyaddingupallthenumbersintheratio.

Thetotalnumberofpartsintheexampleaboveis 3 + 4 = 7

Ratioproblemscanbesolvedbyconsideringtheproportionofonequantitycomparedto thewhole.

Theproportionofvinegaris 3 7 andsoa 210 mLbottlecontains 3 7 × 210 = 90 mLofvinegar.

Todivideaquantityintoagivenratio:

• calculatethetotalnumberofparts(e.g. 3 + 4 = 7)

• calculatetheproportionofthedesiredquantity(e.g. 3 7)

• usefractionstocalculatetheamount(e.g. 3 7 × 210 = 90)

Exercise3L

Und er stand ing 1,2 1,2

1 Acordialmixismadeupof 1 partsyrupto 9 partswater.

a Writethecordialtowatermixasaratio.

b Whatisthetotalnumberofpartsintheratio?

c Whatproportionofthecordialmixissyrup?Writeyouranswerasafraction.

d Whatproportionofthecordialmixiswater?Writeyouranswerasafraction.

e If 400 millilitresofcordialmixismadeup,howmuchofitis: syrup? i water? ii

2 $150 istobedividedintotwopartsusingtheratio 2 : 3 forJacobandSally,inthatorder.

a Whatisthetotalnumberofpartsintheratio?

b WhatfractionofthemoneywouldJacobreceive?

c WhatfractionofthemoneywouldSallyreceive?

d Calculatetheamountofmoneyreceivedby: Jacob i Sally. ii

Fluency

Example27Findingamountsgivenaratio

Drymixcementiscombinedwithwaterinagivenratiotoproduceconcrete.

3,4,6,73,5,8

a Ifthedrymixtowaterratiois 3 : 5,writetheproportionofthefollowingasafraction. drymix i water ii

b If 3 7 oftheconcreteisdrymix,writetheratioofdrymixtowater.

c If 8 litresofdrymixisusedusingadrymixtowaterratioof 2 : 3,whatamountofwateris required?

Solution

ai 3 8

ii 5 8

b 3 7 : 4 7 = 3 : 4

Explanation

Thetotalnumberofpartsis 8 andthenumber ofpartsrelatingtodrymixis 3

Thenumberofpartsrelatingtowateris 5 outof atotalof 8

If 3

7 oftheconcreteisdrymix,then 4 7 iswater.

Multiplybothfractionbythecommon denominatortoproducethesimpliﬁedratio. Continuedonnextpage

c × 4 × 4 8 : 12 2 : 3 dry mixwater

Â12 litresofwaterrequired.

Nowyoutry

Multiplybothnumbersintheratioby 4 tosee whatamountofwatercorrespondsto 8 litresof drymix.

Juiceconcentrateistobecombinedwithwaterinagivenratiotoproduceadrink.

a Iftheconcentratetowaterratiois 2 : 7,writetheproportionofthefollowingasafraction. concentrate i water ii

b If 1 5 ofthedrinkisconcentrate,writetheratioofconcentratetowater.

c If 100 mLofconcentrateismixedusingaconcentratetowaterratioof 2 : 9,whatamountof waterisrequired?

3 Powderistobecombinedwithwaterinagivenweightratiotoproduceglue.

a Ifthepowdertowaterratiois 2 : 3,writetheproportionofthefollowingasafraction. powder i water ii

b Ifthepowdertowaterratiois 1 : 5,writetheproportionofthefollowingasafraction. powder i water ii

c Ifthepowdertowaterratiois 3 : 4,writetheproportionofthefollowingasafraction. powder i water ii

4 Flouristobecombinedwithwaterintheratio 4 : 3 toproduce damper.

a Writetheproportionofthefollowingasafraction.

ﬂour i water ii

b If 2 3 ofthedamperisﬂour,writetheratioofﬂourtowater.

c If 60 gramsofﬂourismixedusingaﬂourtowaterratioof 3 : 2,whatamountofwaterisrequired?

5 Anumberofhockeyteamshavevariouswin-lossratiosforaseason.

a TheCatshaveawin-lossratioof 5 : 3.WhatfractionofthegamesintheseasondidtheCatswin?

b TheJetswon 3 4 oftheirmatches.Writedowntheirwin-lossratio.

c TheEagleslost5oftheirmatcheswithawin-lossratioof 2 : 1.Howmanymatchesdidtheywin?

d TheLionshaveawin-lossratioof 2 : 7.WhatfractionofthegamesintheseasondidtheLionslose?

e TheDozerslost 2 5 oftheirmatches.Writedowntheirwin-lossratio.

f TheSharkswon 6 oftheirmatcheswithawin-lossratioof 3 : 2.Howmanymatchesdidtheylose?

Example28Dividinganamountintoagivenratio

Divide 15 kgintotheratio 2 : 1

Solution

Totalnumberofparts = 2 + 1 = 3

Fractionsare 2 3 and 1 3

Amountsare 2 3 × 15 = 10 and 1 3 × 15 = 5

10 kgand 5 kg

Nowyoutry

Divide 60 secondsintotheratio 3 : 1.

6 Divide 24 kgintotheratio 1 : 3

7 Divide 35 litresintotheratio 3 : 4

8 Dividethefollowingintothegivenratios.

$40 intheratio 2 : 3 a

Explanation

Firstﬁndthetotalnumberofpartsintheratio. Calculatetheproportionsforeachnumberin theratio.

Multiplyeachfractionbytheamountgiven toﬁndtheamountscorrespondingtoeach portion.

Answerthequestionwiththeappropriateunits.

intheratio 3 : 7 b 32 kgintheratio 3 : 5 c

Problem-solving and reasoning

9 Mickyismakingupasprayforhisfruitorchardand mixeschemicalwithwaterusingaratioof 2 : 13

a Howmuchchemicalshouldheuseifmakingaspray withthefollowingtotalnumberoflitres?

i 15 litres

ii 45 litres

iii 120 litres

b Ifheuses 20 litresofchemical,howmuchspraywill hemake?

c Ifheuses 39 litresofwater,howmuchchemicaldoes heuse?

9–119,10,12,13

d Ifhemakes 60 litresofspray,howmuchchemicaldidheuse?

10 Mohammadhas $72 todivideamongstthreechildrenintheratio 1 : 2 : 3.

a Howmuchmoneyisgiventotheﬁrstchildlisted?

b Howmuchmoneyisgiventothethirdchildlisted?

11 Theratioofcattletosheeponafarmis 2 : 7.

a Howmanysheeparethereifthereare 50 cattle?

b Howmanycattlearethereifthereare 84 sheep?

c Howmanysheeparethereifthereare 198 cattleandsheepintotal?

d Howmanycattlearethereifthereare 990 cattleandsheepintotal?

12 Maltipsouthiscollectionof 134 onedollarcoinsanddividesthemusingtheratio 2 : 5.WillMalbeable tocompletethedivisionwithoutleavingaremainder?Giveareason.

13 Asportingsquadistobeselectedforatrainingcampwithattacking,midﬁelderanddefenceplayers intheratio 3 : 5 : 2.Currently,thecoachhasselected 4 attackingplayers, 5 midﬁeldersand3defence players.Findtheminimumnumberofextraplayersthecoachneedstoselecttohavethecorrectratio.

Slopesasratios

14 Thesteepnessofaslopecanberegardedastheratiooftheverticaldistancecomparedtothehorizontal distance.Soaslopewithratio 1 : 4 wouldmeanforevery 1 metreverticallyyoutravel 4 metres horizontally.

a Describethefollowingslopesasratiosofverticaldistancetohorizontaldistance.

i vertical 20 metresandhorizontal 80 metres

ii vertical 120 metresandhorizontal 40 metres

b Aslopehasaratioof 2 : 9.

i Findthehorizontaldistancetravellediftheverticaldistanceis 12 metres.

ii Findtheverticaldistancetravelledifthehorizontaldistanceis 36 km.

Buildingconstructionapprentice

TheconstructionindustryinAustraliaishuge, andpropertydevelopersemploymany thousandsofworkers.Apprenticesmust completehoursofon-the-jobtrainingaswell asachieveTAFEqualiﬁcations.Numberand measurementskillsareveryimportant,as constructionworkersapplytheseskillsin everydayprojects.

Fractionsarestudiedbothatschoolandat TAFE.Measuringandcalculatingwithfractions isavitalskillinthebuildingindustry.Many buildingcomponentsarefromtheUnited States,whichstillusesImperialmeasurements, soinchesandfractionsofaninchoftenfeature intheworkplace.

1 Giventhat 1 inchis 25.4 mm,ﬁndthelengthinmillimetresto 1 d.p.forthefollowing.

2 Makeaneat,enlargedcopyofthis 1-inchruleranditsscale.Startbyrulingan 8 cmlineandmark 16 equalspacesonit.Labeltheends 0 and 1 inch,labelthecentre 1

2 inch,thencarefullymarkinallthe otherfractionsofaninchasshownonthisimage.

3 Tapemeasurescanshowunitsinbothinchesandcentimetres.Whatarethefractionalmeasurements ininchesindicatedonthefollowingtapemeasures?

4 TAFEcoursesforconstructionapprenticesincludefractionskills. Writealistininchesforeachofthefollowingsetsofmeasurements:

a Increasinginquartersfrom 10 1 4 inchesto 1 foot.

b Decreasingineighthsfrom 1 footto 11 1 4 inches.

c 3 8 ofaninchlessthaneachof 1 inch, 5 inchesand 1 foot.

d 4 5 16 incheslessthaneachof 1 footand 1 yard.

5 Travis,aﬁrst-yearapprentice,isaskedtocutoffone thirdofa 12-inchpipe.Whatlengthofthepipeinmm isremainingafterhecutsit?

6 Hollyisaskedtocut 8 1 4 inchesfromapipe 41 1 4 inches long.Whatproportionofthepipeiscut(asafraction)?

7 Murrayhaseightlengthsofpipetojointogether.If eachpipeis 4 3 4 incheslong,howmanymmistheﬁnal lengthofpipe?

Usingtechnology

Constructionworkerscalculateandmeasureusing fractions.

8 ManyolderbuildingshavepipesthatwereinstalledbeforeAustraliachangedtothemetricsystem. Thereplacementofoldpipesrequiresexactlythesamelengthofpipemeasuredinmm. Setupthefollowingspreadsheettoaddfractionsandconvert inchestomm.

Selectallthecellsusinginches(columnsA,B,C) andFormat/Fraction/uptotwodigits. Enterformulasintheshadedcells.

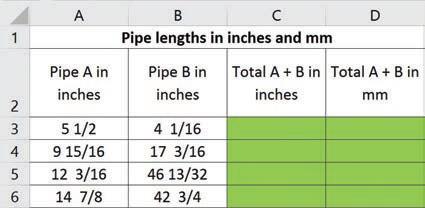
Q8Hint:Totypeafractionintoa spreadsheet,insertaspacebetween thewholenumberandthefraction. e.g. 51/2 means 5 1 2

Pricingplants

Andrewownsanurseryandnormallysellsflowerpotsfor $15 eachandonaveragehesells 100 ofthesepotsperday. Thecosttoproduceeachflowerpotis $5 sotheprofitper potundernormalconditionsis $10 perpot.

Inordertoattractmorecustomerstothenurseryhe considersloweringthepricewithoneofthefollowingdeals.

• Deal 1:Loweringthesellingpriceto $12,wherehe predictshewillsell 1 1 2 timesasmanypotsperday.

• Deal 2:Loweringthesellingpriceto $11,wherehe predictshewillsell 1 4 5 timesasmanypotsperday.

Presentareportforthefollowingtasksandensurethatyoushowclearmathematicalworkingsand explanationswhereappropriate.

1Preliminarytask

1a At $15 each,ﬁndhowmuchincome(revenue)wouldAndrewgetifhesold

10 pots i

50 pots ii

100 pots iii

b CalculatetheproﬁtAndrewwouldmake,undernormalconditions,ifhesells 10 pots i 50 pots ii 100 pots iii

c Evaluate 1 1 2 × 100

d Evaluate 1 4 5 × 100

2a UsingDeal 1,findthefollowing: theprofitmadeoneachpotsold i theexpectednumberofpotstobesold ii theexpectedtotalprofitforAndrew’snurseryforoneday iii

b Comparedtotheproﬁtmadewhenselling 100 potsundernormalconditions,byhowmuch doesAndrewincreasehisproﬁtunderDeal 1?

c Usingtheformula percentageprofit = difference original × 100%,calculatetheprofitincrease asapercentageoftheoriginalprofit.

2Modellingtask

Formulate a TheproblemistocreateadealforAndrewthatwillcausetheproﬁttoincreasebyat least 10%

Writedownalltherelevantinformationthatwillhelpsolvethisproblem.

Solve

Evaluate and verify

b ExamineDeal 2 forthesellingofpotsatAndrew’snursery.Includethefollowinginyour analysis:

i theproﬁtmadeoneachpotsold

ii theexpectednumberofpotstobesold

iii theexpectedtotalproﬁtforAndrew’snurseryforoneday

c ComparedtonormalconditionsbyhowmuchdoesAndrew’sproﬁtincrease,ifheuses Deal 2?Expressyouranswerasapercentageoftheoriginalproﬁtwithnodeals.

Andrewconsidersathirddealwherethesellingpriceisreducedto $8.Itispredictedthatthis willcausethenumberofpotssoldtotripleto 300

d ComparethisDeal 3 tonormalconditions,consideringthetotalproﬁtforaday.

e Byconsideringthedealsabove,comparetheprofitsforoneday’stradeforAndrew’snursery. SortthedealsfrommostprofitabletoleastprofitableforAndrew.

Communicate f Summariseyourresultsintothetablebelow.

% increaseinproﬁtcomparedtonormalconditions

g Usingyourcompletedtable,describeanykeyﬁndings.

3Extensionquestion

Isitpossibleforfindadealthatexactlyproducesa 20% increaseinprofitforAndrew’snursery?Ifso finditandexplainastowhetherornotitisarealisticdealtooffer.

Addingtoinﬁnity

(Keytechnology:Spreadsheets)

Itwouldbenaturaltothinkthatatotalsumwouldincrease toinﬁnityifwecontinuallyaddedonnumberstothetotal, however,thisisnotalwaysthecase.Justlikeinthisimage, wecouldcontinuallyzoominaddingmoreandmore spiralsbutweknowthatthetotalsizeoftheimagenever getslarger.

1Gettingstarted

a Considerasequenceofnumberswhereeachnumberisdoublethepreviousnumberinthe sequence.Thenthetotalsumisobtainedbyaddingeachnewnumbertotheprevioustotal.

i Copyandcompletethistableusingtheabovedescription. Sequence 1 2 4 8 16 32

1 3 7

ii Whatdoyounoticeaboutthetotalsum?Isitincreasingmoreorlessrapidlyasmorenumbers arebeingadded?Giveareason.

b Nowconsiderﬁndingatotalsumfromasequenceofnumberswhereeachnumberisonehalfof thepreviousnumber.

i Copyandcompletethistableusingtheabovedescription.

ii Whatdoyounoticeaboutthetotalsum?Isitincreasingmoreorlessrapidlyasmorenumbers arebeingadded?Giveareason.

iii Whatnumberdoesyoursumappeartobeapproaching?

2Applyinganalgorithm

Hereisanalgorithmwhichﬁndsatotalsumofasequenceof n numbersstartingat 1.Notethat S standsforthetotalsum, t standsfortheterminthesequenceand i countsthenumber oftermsproduced.

a Copyandcompletethistablefor n = 6,writingdownthevalues for t and S frombeginningtoend.

Technology and computational thinking

b Describethissequenceandsumcomparedtothesequencestudiedinpart 1

c Describethepartsofthealgorithmthatmakethefollowinghappen.

i Eachtermisbeinghalvedeachtime.

ii Thesumisincreasedeachtimebyaddingonthenewterm.

iii Thealgorithmknowswhentoend.

d Writeanalgorithmthataddsupallthenumbersinasequencebutthistime:

• thesequencestartsat 2

• thesumisobtainedbyaddingonethirdofthepreviousnumbereachtime.

3Usingtechnology

Wewilluseaspreadsheettogeneratethesumsstudiedabove.

a Createaspreadsheetasshown.

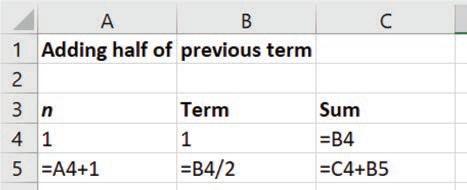
1 ThreecitiesareknownasIndia’sGoldenTriangle.Toﬁndthenamesofthesecities,completethe puzzle.

Matcheachofthefractionsinthemiddlerowwiththeequivalentfractioninthebottomrow. Placetheletterinthecodebelow.

2 Howmanywordswiththreeormoreletterscanyouandapartnermakefromtheword PERCENTAGES?

Youhave 15 minutestocomeupwithasmanywordsasyoucan. Scoreyourresultsasfollows:

• 1 pointforeverythree-letterword

• 2 pointsforeveryfour-letterword

• 3 pointsforeverywordwithﬁveormoreletters

Compareyourlistwiththoseofotherstudentsintheclass.

3 Fractiondicegame

Twodifferent-coloureddicearerequired.Chooseonedieforthenumeratorandonedieforthe denominator.

Forexample: reddieresult bluedieresult = 5 3 or reddieresult bluedieresult = 4 1

Playerstaketurnstothrowbothdiceandrecordtheirfractionresults. Afteranequalnumberofturns,eachplayerthenaddsalltheirresultstogetherandthewinneris theplayerwiththelargestnumber.

4 Inamagicsquare,thesumofthefractionsineachrow,columnanddiagonalisthesame. Findthevalueofeachletterinthesemagicsquares.

proper fraction 3 4

• Same numerator: compare the denominators.

• Same denominator: compare the numerators.

improper fraction 7 5 whole number = 1, = 2 7 7 10 5 mixed number 1 2 5 is less than is greater than

• Different denominators: change to LCD Lowest Common Denominator). Comparing

Adding or subtracting fractions

Number of shaded parts (numerator)

Number of equal parts (denominator)

Fractions

Multiplying fractions

Multiply across the top. Multiply across the bottom. Cancel when you can.

Need a common denominator. A fraction is part of a whole.

Dividing by a fraction

Multiply by its reciprocal.

Reciprocal means to swap the numerator and denominator.

Per cent means 'out of 100'

Percentages

Finding a percentage of a quantity

8% of $70 × = 8 100 $70 = $5.60

Ratios

Simplest ratios use the smallest whole numbers 10 : 4 = 5 : 2. Units must be the same.

$5.20 : 160 cents

520 : 160 13 : 4

Applying ratios

To divide into a given ratio, ﬁnd the

total number of parts.

For example, $60 into the ratio 2 : 1

Total parts is 2 + 1 = 3 so of $60 = $40 and 2 3 of $60 = $20. 1 3

Comparing quantities

Units must be the same.

50 cents out of $2 × 100%

= 50 cents out of 200 cents = 50 200 = 25%

Mental calculations

10% of 300 kg = 30 kg

So 20% of 300 kg = 60 kg

75% of $80 = of $80 3 4 = $60

Chapter checklist

Chapterchecklist

AversionofthischecklistthatyoucanprintoutandcompletecanbedownloadedfromyourInteractiveTextbook.

3A 1

3A 2

Icanidentifythenumeratoranddenominatorofafractiondescribedinwords. e.g.Apizzahasbeencutintoeightpieces,withthreeofthemselected.Writetheselectionasafraction andstatethenumeratoranddenominator.

Icanrepresentfractionsonanumberline. e.g.Representthefractions 3 5 and 9 5 onanumberline.

3B 3 Icanlistfractionsthatareequivalenttoagivenfraction. e.g.Writefourfractionsthatareequivalentto 2 3

3B 4 Icanwritefractionsinsimplestform. e.g.Writethefraction 12 20 insimplestform.

3C 5 Icanconvertmixednumeralstoimproperfractions. e.g.Convert 3 1 5 toanimproperfraction.

3C 6 Icanconvertfromanimproperfractiontoamixednumeral. e.g.Convert 11 4 toamixednumerals.

3D 7 Icancomparetwofractionstodecidewhichisbigger. e.g.Decidewhichof 2 3 and 3 5 isbigger,andwriteastatementinvolving > or < tosummariseyouranswer.

3D 8 Icanorderfractionsinascendingordescendingorder.

e.g.Placethefollowingfractionsinascendingorder: 3 4, 4 5, 2 3

3E 9 Icanaddtwofractionsbyconvertingtoacommondenominatorifrequired.

e.g.Findthevalueof 3 4 + 5 6

3E 10 Icanaddtwomixednumerals.

e.g.Findthesumof 2 5 6 and 3 3 4.

3F 11 Icansubtracttwofractionsbyconvertingtoacommondenominatorif required.

e.g.Findthevalueof 5 6 1 4

3F 12 Icansubtracttwomixednumerals.

e.g.Findthevalueof 5 2 3 −3 1

3G 13 Icanﬁndasimplefractionofaquantity.

e.g.Find 2 3 of 15 bananas.

3G 14 Icanexpressawholenumberasafraction.

e.g.Write 21 asafraction.

3G 15 Icanmultiplyproperfractions.

e.g.Find 3 4 × 8 9.

3G 16 Icanmultiplymixednumbers.

e.g.Find 6 1 4 × 2 2 5

3H 17 Icanﬁndthereciprocalofafraction,wholenumberormixednumber.

e.g.Findthereciprocalof(a) 2 3,(b) 5,and(c) 1 3 7

3H 18 IcandivideafractionbyawholenumberandIcandivideawholenumberbya fraction.

e.g.Find 5 8 ÷ 3 and 24 ÷ 3 4

3H 19 Icandividefractions(properand/orimproperfractions).

e.g.Find 3 5 ÷ 3 8

3H 20 Icandividemixednumbers.

e.g.Find 2 2 5 ÷ 1 3 5

3I 21 Icanconvertapercentagetoafractionormixednumber. e.g.Express 36% asafractioninsimplestform.

3I 22 Icanconvertafractiontoapercentage.

e.g.Convert 11 25 and 3 8 topercentages.

3J 23 Icanﬁndthepercentageofanumber. e.g.Find 15% of 400

3K 24 Icanexpressrelatedquantitiesasaratio. e.g.Aboxcontains 3 whitechocolatesand 4 darkchocolates.Writetheratioofdarkchocolatestowhite chocolates.

3L 25 Icansimplifyaratio. e.g.Write 60 : 24 insimplestform.

3L 26 Icanﬁndanamountgivenaratio. e.g.Iftheratioofdrymixcementtowateris 2 : 3,whatamountofwaterismixedwith 8 litresofdrymix cement?

3L 27 Icandivideanamountintoagivenratio. e.g.Divide 15 kgintotheratio 2 : 1

Short-answerquestions

1 3A Writethefractionofeachcirclethatisshaded.

2 3B Giventhat 24 = 12 × 2 and 36 = 12 × 3,simplifythefraction 24 36

3 3B Writethefollowingfractionsinsimplestform.

4 3C Converteachofthefollowingtoamixednumeralinsimplestform.

5 3D Placethecorrectsymbol(<, = or >) inbetweenthefollowingpairsoffractionstomake truemathematicalstatements.

6 3D Statethelargestfractionineachlist. 3

7 3D Statethelowestcommonmultipleforeachpairofnumbers.

8 3E/F Statethelowestcommondenominatorforeachsetoffractions.

9 3D Rearrangeeachsetoffractionsindescendingorder.

10 3E/F Determinethesimplestanswerforeachofthefollowing.

11 3G Find:

12 3H Determinethereciprocalofeachofthefollowing.

13 3H Performthesedivisions.

14 3I Findthemissingpercentagesandfractions.

15 3J Find 10% of $200. a Find 25% of $840. b

Find 50% of 96 grams. c Find 20% of $150 d

Find 150% of $6 e

16 3K Ashopshelfdisplays 3 cakes, 5 slicesand 4 pies.Writethefollowingasratios. cakestoslices a slicestopies b piestocakes c slicestopiestocakes d

17 3K Expresstheseratiosinsimplestform.

21 : 7 a

3.2 : 0.6 b

$2.30 : 50 cents c

18 3L Divide $80 intothefollowingratios.

7 : 1 a

2 : 3 b

Multiple-choicequestions

1 3A Whichfractionisshownonthenumberline? 2 1

2 3B 3 4 isthesameas:

3 3B 4 5 issmallerthan:

4 3D Whichisthelowestcommondenominatorforthissetoffractions?

5 3A Mariahas 15 redapplesand 5 greenapples.Whatfractionoftheapplesaregreen?

6 3D Whichofthefollowingistrue?

7 3D Whichsetoffractionsisorderedfromsmallesttolargest(ascendingorder)?

8 3E/F/G Whichproblemhasanincorrectanswer?

Whichfractionisgreaterthan 75%?

10 3K $28 to $63 expressedasaratioinsimplestformis: 9 : 4 A

11 3C 60 14 canbewrittenas:

12 3G 17 25 ofametreofmaterialisneededforaschoolproject.Howmanycentimetresisthis?

Extended-responsequestions

1 Aprinterproduces 1200 leaflets.One-quarteroftheleafletsareongreenpaper.Halfthe remainingleafletsareonwhitepaper.Therearesmudgeson 10% oftheleafletsforeachcolour ofpaper.

a Howmanyleaﬂetswereongreenpaper?

b Whatpercentageoftheleaﬂetswere not ongreenpaper?

c Howmanywhiteleaﬂetswereprinted?

d Ofthewhiteleaﬂets,howmanyhadsmudges?

e Howmanyleaﬂetsdidnothaveanysmudges?