

Ma.3.NSO.2.1 – Add and subtract multi-digit whole numbers including using a standard algorithm with procedural fluency.
Objective: Students will learn how to fluently add and subtract whole numbers using knowledge of place value.
Materials: (Per TEACHER)
1 classroom dry erase board
1 dry erase marker
1 dry eraser
Materials: (Per group of 2 students)
1 regular deck of playing cards
1 Write and Wipe holder
1 Adding and Subtracting Worksheet
1 dry erase marker
1 dry eraser
2 numbered bingo chips
2 tens base-ten blocks
Lesson Discussion:
• Review the different terms in place value, such as ones, tens, hundreds, and thousands.
• Teach the students how to perform addition and subtraction using place value. Help the students understand that when adding or subtracting multidigit numbers using place value, always start from the “ones” place value then move left.
• The students will only add and subtract multi-digit whole numbers in this activity.
PART A:
Teacher Preparation:
Step 1: Remove the tens cards and face cards (Jokers, Jacks, Queens, and Kings) from each deck of cards for each group of 2 students.
Step 2: Write the number 10 on 2 bingo chips for each group of 2 students.
Step 3: Place an Adding and Subtracting worksheet into a Write and Wipe holder for each group.
Step 4: Divide the students into groups of 2. Distribute the materials to each group of 2 students.
Procedure:
Step 1: Write the following example on the classroom dry erase board.

Step 2: Explain that the 3 cards in the top row form a three‐digit number, and the 2 cards in the bottom row form a two‐digit number.
Step 3: Ask the students if they know how to find the sum of 537 and 95. Have the students pull the same cards from their deck to follow along with the example. They should put it in the following formation and take out their bingo chips.

Step 4: Explain that to find the sum of multi‐digit numbers, they should add the numbers with the same place value, starting from the ones place and moving left. Tell the students they should treat each place value as an individual addition problem.
Step 5: Have the students find the sum of the numbers in the ones place. Since 7 + 5 = 12 and 12 = 2 + 10, write 2 in the ones place on the dry erase board, and add the 10 to the tens place drawing the bingo chip to represent the 10 being carried over.

Step 6: Have the students go to the next place value and add the numbers in the tens place. While 3 + 9 = 12, we have one 1 tens from the sum of the ones place. So, we have 12 + 1 = 13 for the tens place. Since 13 = 10 + 3, write 3 in the tens place, and add the 10 to the hundreds place, drawing another bingo chip to represent the 10 being carried over.

Step 7: Now have the students to go to the hundreds place value and add the numbers in the hundreds place. Since we only have 5 in the hundreds place, we add the one 1 hundreds from the sum of the tens place to 5. Hence, 5 + 1 = 6.
Step 8: Tell the students that the sum of 537 and 95 is 632.
Step 9: Have the students turn to Part A of their Adding and Subtracting worksheet, return the cards to their deck, and shuffle the cards together.
Step 10: Tell the students that for the 6 problems on Part A of the worksheet, they are to draw 5 cards from their deck, write the numbers that are represented by the cards in the corresponding boxes, and add.
Step 11: Tell the students that whenever the problem calls for them to carry over, they are to indicate it by coloring in the circle next to the number that has the 10 carried over as they indicated with the bingo chip in Step 5 and 6.
PART b:
Step 1: Explain to students that they will be subtracting multi‐digit numbers.
Step 2: Draw the following 5 cards on the dry erase board. Ask the students to pull the same cards from their deck, placing them in the following formation.

Step 3: Explain that when the students start the activity, they will have to draw 1 card at a time. The students cannot have a card with a value of 1 in the tens or hundreds place of the minuend (top number.) They will have to redraw if an Ace is pulled. For the cards pulled to represent the tens and hundreds for the minuend, they must search through their deck to find a card with a value 1 less than the card they drew in an instance where they need to “borrow” when subtracting. For example, if they drew a 2, they will have to find an Ace in their deck to represent 1 and place it behind the 2. In the example below, the card drawn in the tens place was a 5 and the card drawn in the hundreds place is a 2. Therefore, students must find a 4 and place it behind the 5, and an Ace (value of 1) and place it behind the 2.

Step 4: Tell the students to subtract the numbers in the ones place, 3 − 4. Explain that 10 must be borrowed from the tens place in order to subtract. To indicate the borrowing, tell the students to place 1 tens base– ten block next to the 3 to represent 13 − 4, which equals to 9, and remove the 5 card from the tens place to show the 4 in the tens place.
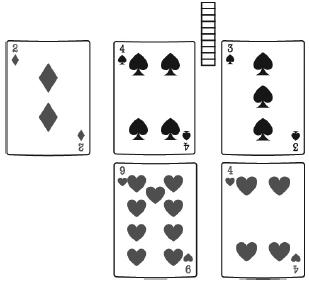
Step 5: Ask the students to subtract the numbers in the tens place, 4 − 9. Explain that 10 must be borrowed from the hundreds place in order to subtract. To show the borrowing, tell the students to place 1 tens base-ten block next to the 4 to represent 14 − 9, which equals to 5, and remove the 2 card from the hundreds place to show the ace in the hundreds place.
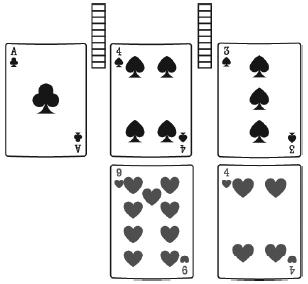
Step 6: Ask the students to subtract the numbers. They should get an answer of 159.
Step 7: Have the students turn to Part B of their Adding and Subtracting worksheet. Tell them to replace the cards in their deck, and reshuffle the deck.
Step 8: Tell the students that for the 6 problems on Part B of the worksheet, they will draw 5 cards from their deck, write the numbers that are represented by the cards into the corresponding boxes, and subtract.
Step 9: Tell the students that whenever the problem calls for them to borrow to solve, they should indicate it by coloring in the tens base-ten block next to the number that needs to borrow the 10 like they indicated with the base-ten block in steps 4 and 5.
Extension Activity
Have the groups take turns coming up to the board to write and solve addition and subtraction problems up to 1,000 that require carrying over and borrowing. Continue until every group has had a turn and is comfortable with the material.
Essential Question for Discussion or Journaling:
Why is understanding place value important when adding and subtracting?














DIRECTIONS: Create place value charts to solve.
Use a place value chart to find the difference of 618 and 543.
Use a place value chart to find the sum of 347 and 245.
Use a place value chart to find the difference of 716 and 698.
Use a place value chart to find the sum of 387 and 416.

Explain what it means to add and subtract.
DIRECTIONS: Use addition and subtraction to solve the questions below.
A company sent 315 emails on Monday, 245 emails on Tuesday, and 196 on Wednesday. How many emails were sent on these 3 days?
Write a word problem that requires you to find the sum, then the difference to solve. 1
It is 485 miles from Point A to Point B and 725 miles from Point A to Point C. What is the distance from Point B to Point C?
The school has 313 students in Grade 3. Of the students, 215 are going on a field trip to the museum. Of the students going on the field trip, only 65 of the students brought their own lunch. How many students will have to buy lunch at the museum?

DIRECTIONS: Solve the following questions.
What is the result if 298 is subtracted from the sum of 245 + 310?
What is the result if 128 is added to the difference of 714 − 454?
What is the result if the difference of 984 − 846 is doubled?
What is the result if the sum of 117 + 245 is doubled?
What is the result if the difference of 626 − 478 is added to 328?

List 2 key words that signal you should subtract and 2 key words that signal you should add in a word problem.

Ma.3.NSO.2.4 – Multiply two whole numbers from 0 to 12 and divide using related facts with procedural reliability.
Ma.3.NSO.2.2– Explore multiplication of two whole numbers with products from 0 to 144, and related division facts.
Objective: Students will learn and understand how to divide a two‐digit whole number by a one‐digit whole number.
Materials:
(Per TEACHER)
1 pair of blank dice
1 permanent marker or dice stickers
1 classroom dry erase board
1 dry erase marker
Materials:
(Per student)
1 standard bingo card from set
10 bingo chips
1 sheet of scratch paper
1 pencil
Lesson Discussion:
• Define the terms “divisor”, “dividend”, and “quotient” for the students. Explain that the “divisor” is the number by which a dividend is divided; “dividend” is the number to be divided; and “quotient” is the result of division.
• Explain the relationship of multiplication and division. Help the students understand that division is the inverse of multiplication.
• The students will be dividing two‐digit whole numbers by one‐digit whole numbers.
PART A:
TEACHER PREPARATION:
Step 1: Label one die 0 through 2 and the other as 0, 1, 2, 3, 4, and 5, using either a permanent marker or stickers that come with the blank dice.
Step 2: Distribute 1 bingo card and 10 bingo chips to each student.
Procedure:
Step 1: Roll the 2 dice at the same time.
Step 2: Read the numbers where the dice landed aloud. Record the numbers on the dry erase board.
Step 3: Tell the students to place a bingo chip on all the numbers on their bingo card divisible by the sum of the numbers on which the dice landed. For example, if one die landed on a 2 and the other landed on a 5, the students must place a bingo chip on all the numbers on their bingo cards that are divisible by 7.
Step 4: Tell the students that the goal of the activity is to be the first to have 10 chips on their bingo card.
Step 5: Instruct the students to shout “Bingo!” if they place 10 chips on their bingo card. The first person to shout out "Bingo!" with the correct answers is the winner. It may be necessary to roll again if no one in the class can find 10 numbers on the first roll.
Step 6: In the event of a draw, the tied players enter a lightning round. Repeat steps 1 and 2, and the first student who finds a number divisible by the product of the numbers on the dice on their bingo sheet and shouts "Bingo!" wins.
Extension Activity
Step 1: Distribute 1 sheet of scrap paper and 1 pencil to each student.
Step 2: Have the students pick any number they choose that was not marked with a bingo chip on their bingo card, and write that number on the front of their paper.
Step 3: Tell the students to write 1 factor pair of that number below it.
Step 4: Have the students write a multiplication and division equation on the back of their paper using the numbers they wrote on the front.
PART B:
Materials: (Per
TEACHER)
1 roll of colored masking tape
1 ruler
1 Operation Trifold
1 Equal Sign Trifold
1 set of Teacher Number Cards
2 dry erase boards
2 dry erase markers
2 dry erasers
1 one-minute timer
Teacher Preparation:
Step 1: At front of the classroom, make 3 squares on the ground measuring 17 × 17 inches with the colored masking tape. Leave about a 6‐inch space in between each square.
Step 2: Create Teacher Number Cards by writing each number below on a separate sheet of paper large enough so the students can see it.
Step 3: Place the Operation Tri‐fold between squares 1 and 2. Make sure that the multiplication sign is facing the students. Place the Equal Sign Trifold between squares 2 and 3 with the equal sign facing the students.
Step 4: Split the class into 5 teams/troops: Troops Black, Red, Yellow, Blue, and Green. Give the first troop to compete 2 dry erase boards, 2 dry erase markers, and 2 dry erasers. These materials will be passed on to the other troops when it is their turn to compete.
Procedure:
Step 1: Stand in the third square with a set of Teacher Number Cards. Hold up any card for each group. Note: A new number should be held for each turn.
Step 2: Flip the timer so the group has one minute to complete their turn.
Step 3: Explain that the students in the troop will have to come up with 2 numbers between 0 and 12 that when multiplied, the product is equal to the number on the Teacher Number Card. Once the troop has come up with the numbers, they will write 1 of the numbers on 1 dry erase board and the other number on the other dry erase board. Example: If the teacher is in the third square and holding a card that says 42, 1 dry erase board should say 6 and the other should say 7.
Step 4: Then, 2 students from the troop will take their places on squares 1 and 2 to make a multiplication equation with the dry erase boards. Example: Student A steps in the first square holding a dry erase board with a 6 and Student B steps in the second square holding a dry erase board with a 7. The equation formed is 6 × 7 = 42.
Step 5: Once the students form the correct equation, the rest of the troop will rearrange you and their teammates to create a related multiplication and a related division equation. Remind students to change the Operation Tri‐fold when necessary to make the equations correct. Example of the related multiplication equation: 7 × 6 = 42. Example of the related division equations: 42 ÷ 6 = 7 or 42 ÷ 7 = 6.
Step 6: If the troop is able to complete the task before the timer runs out, they keep the Teacher Number Card that you are holding. If the troop does not get the equations correct or within the allotted time, the cards will go in the back of the teacher’s deck.
Step 7: Be sure to change the Operation Tri‐fold to show the multiplication sign again and resume position in the third square after each troop has had their turn.
Step 8: Repeat steps 3 to 7 until all the Teacher Number Cards have been dispersed to the winning troops. The troop with the most Teacher Number Cards is the winner.
PART C:
Materials: (Per TEACHER)
1 Fact Family handout
1 pair of scissors
1 clear resealable bag
1 stopwatch or timer
1 classroom dry erase board
1 dry erase marker
Lesson Discussion:
• Explain the relationship between multiplication and division. Help the students understand that multiplication is the “reverse” of division.
• Teach how to identify and create division sentences using a given set of numbers.
• The students will learn how to multiply and divide numbers up to 144.
Teacher Preparation:
Step 1: Cut out the sets of numbers from the Fact Family handout.
Step 2: Place the sets of numbers from the handout inside a resealable bag.
Procedure:
Step 1: Call one student to be the first player.
Step 2: Tell the student to pick 1 set of numbers from the resealable bag but not look at it.
Step 3: Explain to students that they will be timed to see how fast they can determine the 3 numbers from the set that make up a multiplication/division fact family. Then, the student will create the fact families as fast as they can on the classroom dry erase board.
Step 4: Write the Fact Family numbers on the board and set the cut-out aside. Instruct the student to get ready. The student will need to identify the 3 numbers that belong to the same fact family and create fact family equations from the 3 numbers on the classroom dry erase board. For example, if they picked a set of numbers that had 1, 2, 3, and 6, the student would note the relationship between the numbers 2, 3, and 6. These numbers can be used in a multiplication equation (2 × 3 = 6) or a division equation (6 ÷ 3 = 2), so they belong to the same fact family. Once the 3 numbers are identified, the student will make 1 multiplication sentence using the 3 numbers as quickly as possible.
Step 5: Using a timer or stop watch, measure and record how quickly each student completes this task on the classroom dry erase board.
Step 6: When all the sets of numbers have been pulled, place them back in the resealable bag. Repeat steps 4 and 5, but tell the students who haven’t had a turn yet that they will be following the same procedures, but creating a division equation instead.
Step 7: Once all of the students have had a turn, determine which student had the fastest time. That student is the winner of the activity.
PART D:
Materials: (Per group of 4 students)
1 deck of Fact Family Numbers (42 cards)
4 Fact Family Equation templates
4 Write and Wipe holders
4 dry erase markers
4 dry erasers
1 tally sheet
Teacher Preparation:
Step 1: Print 1 Fact Family Numbers template and 4 Fact Family Equation templates for each group of 4 students.
Step 2: Place the Fact Family Equation templates into the Write and Wipe holders and cut out each card from the template so that each group of 4 students has 42 cards.
Procedure:
Step 1: Distribute the materials to each group of 4 students.
Step 2: Ask the students to shuffle their decks of cards.
Step 3: Tell the students to pass out 6 cards to each student. The extra cards will be placed in the middle of the desk so it forms a draw pile that is accessible to all the students.
Step 4: Have the students arrange their cards face up on their desks in front of them. The other students in the group should be able to see their opponents’ cards.
Step 5: Explain to the students that with the cards in their hand, they will try to create as many fact family equations as possible. They will pull the cards for each equation they make and write in the equation on the Fact Family Equation template. For example, if the student had the numbers 6, 5, 30, 2, 4, and 1, the student could pull the 6, 5, and 30 and place them in a pile next to them. They would then write the equation 6 × 5 = 30 or 5 × 6 = 30 and the equation 30 ÷ 6 = 5 or 30 ÷ 5 = 6 on the template.
Step 6: For each correct fact family equation, the student earns 1 point.
Step 7: Once all the students have taken out all the cards that can make a fact family from their hand and written their equations for those cards, the next part of the activity begins.
Step 8: At the beginning of their turn, the Student A will pick 1 card from the draw pile. They will use this card and the remaining cards in their hand to make equations as they did in step 5.
Step 9: The student will have the opportunity to “steal” 1 card from one of their opponents to make fact family equations. Only 1 card may be stolen per turn, and it can only be stolen if it allows an equation to be made. For each correct fact family equation, the student earns 1 point.
Step 10: Students take turns until all the cards have been drawn.
Step 11: The first student to have zero cards left in their hand gets the gold win, but the game continues until all the cards have been drawn.
Step 12: A student can get a silver win if they have the most fact family equations made on their template.
Step 13: In the event of a tie, a bronze win can be won by having the least value of cards in their hand at the end of the game. For example, if Student A has the cards 3, 4, and 7, the value of their cards after finding the sum is 14. If Student B has the 10 and 20 cards, the value of their cards after finding the sum is 30. In this case, Student A will get the bronze win.
Essential Questions for Discussion or Journaling:
(1) Give examples of context clues in text that may be used to help identify the appropriate operations to use in word problems.
(2) If you see an array of objects arranged in rows and columns, how can you tell if it is showing multiplication or division? Can you create your own array to show both a multiplication and division fact?

3, 4, 6, 12
2, 7, 9, 14
2, 7, 9, 18
3, 4, 7, 21
3, 4, 7, 28
2, 3, 6, 12
4, 6, 8, 48
5, 8, 9, 45
6, 7, 9, 54
8, 9, 11, 88
5, 8, 9, 40
4, 6, 12, 48
4, 6, 9, 36
6, 7, 12, 84


DIRECTIONS: Identify whether the following multiplication sentences are TRUE or FALSE.

Explain a strategy that can be used to find the product of 9 and 12.
Name:
LEVELED PRACTICE 2 – MA.3.NSO.2.2
DIRECTIONS: Choose the number sentence that does not belong to the same fact family
1 A 2 × 7 = 14
B 12 ÷ 2 = 6
C 7 × 2 = 14
D 14 ÷ 2 = 7
3 A 3 × 3 = 9
B 12 ÷ 3 = 4
C 3 × 4 = 12
D 12 ÷ 4 = 3
5 A 24 ÷ 3 = 8
B 24 ÷ 4 = 6
C 4 × 6 = 24
D 6 × 4 = 24

2 A 6 × 5 = 30
B 5 × 6 = 30
C 30 ÷ 5 = 6
D 35 ÷ 5 = 7
4 A 6 × 11 = 66
B 66 ÷ 11 = 6
C 77 ÷ 7 = 11
D 11 × 6 = 66
6 A 9 × 8 = 72
B 8 × 9 = 72
C 72 ÷ 9 = 8
D 9 ÷ 9 = 1
Find the product of 6 and 7. Write an equation and draw an array to represent the problem.
Name:
LEVELED PRACTICE 3 – MA.3.NSO.2.4
DIRECTIONS: Use related facts to find the missing numbers that makes the number sentences TRUE

Explain how the product of 4 and 5 is related to the quotient of 20 divided by 4.

MA.3.AR.2.3 – Determine the unknown whole number in a multiplication or division equation, relating three whole numbers, with the unknown in any position.
MA.3.AR.2.1– Restate a division problem as a missing factor problem using the relationship between multiplication and division.
OBJECTIVE: Students will learn how to find the missing factor in a multiplication sentence using division.
MATERIALS: (Per group of 2)
90 bingo chips
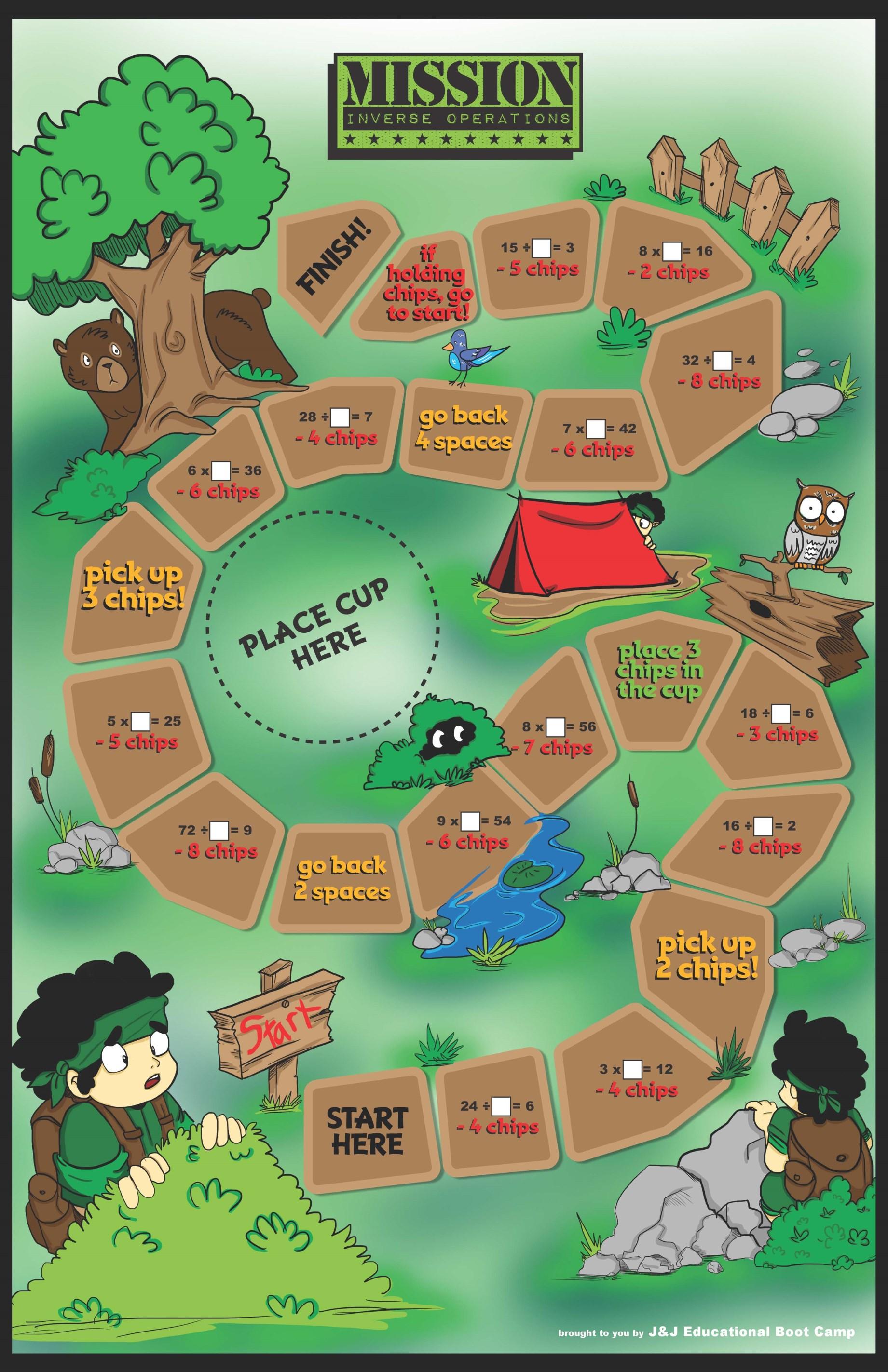
1 Math Mission: Inverse Operations game board
1 Chip Collection cup
2 resealable bags
2 pawns
1 die
LESSON DISCUSSION:
• Review strategies of dividing whole numbers.
• Explain that multiplication and division are inverse operations. Help the students understand that 1 operation can undo the other (i.e., multiplication can undo division, and division can “undo” multiplication).
Teacher Preparation:
Step 1: Print out 1 Math Mission: Inverse Operations game board on an oversized sheet of paper for each group.
Step 2: Count out 30 chips for the Chip Collection cup and 30 chips for each student. Distribute the materials to each group of 2 students.
Procedure:
Step 1: Explain to the students that the objective of the game is to be the first player to land on the finish line with no chips remaining in their bag.
Step 2: Have the students place the Chip Collection Cup on the game board with 30 chips inside of it.
Step 3: Instruct each group to place the pawn they selected on the "Start" section of their game board.
Step 4: Tell each student in the group to roll the die once. The student who rolls the highest number goes first.
Step 5: The first player rolls and moves the amount of spaces indicated.
Step 6: Students follow the instructions written on the tile they land on.
Step 7: When a student lands on an equation tile, they must find the missing value that makes the equation correct. Once the correct answer is verified, the student may deduct the number of chips from their chip bag as indicated on the tile and place them into the Chip Collection cup.
Step 8: The students will continue alternating turns until there is a winner.
Step 9: The winner of the game is the first person to reach the finish line with no chips. If students reach the finish line with chips remaining in their bag, they must return to the start. If after each player has reached the finish line, but still have chips in their cup, the player with the least number of chips is the winner.
Extension Activity
Step 1: Let each student develop a missing factor problem. Remind the students that they should know the correct answer to their problem.
Step 2: Call 1 student at random. Let the student share their missing factor problem with the other students, and let the other students answer the problem.
Essential Questions for Discussion or Journaling:
(1) What are the properties of multiplication?
(2) Describe division in terms of multiplication.
DIRECTIONS: Match each division equation to the question that can help solve the problem
What number multiplied by 6 equals 36?
÷ _____ = 6 What number multiplied by 8 equals 64?
÷ _____ = 3 What number multiplied by 5 equals 25?
÷ _____ = 5 What number multiplied by 2 equals 18?
_____ = 9

÷ 8 = ? 18 ÷ _____ = 2
number multiplied by 3 equals 21?
number multiplied by 9 equals 72?
Which equation below gives you the greater answer? Explain why.
× 9 = ? or
DIRECTIONS: Rewrite the division questions as multiplication equations and solve.

Rewrite the following word problem to be a division equation.
"Samantha buys 5 cans of dog food for each of her 3 dogs. How many cans of dog food does she buy?"
DIRECTIONS: Solve the following word problems.
1 Jesse wants to evenly arrange 21 flower pots into 3 rows in his garden. Write the division equation that could be used to find how many flower pots will be in each row.
2 Julissa volunteers 24 hours a week at the animal shelter, spreading her time across 6 days. She volunteers for the same amount of time each day. Write the division equation that could be used to find the amount of hours she volunteers for each day.
3 Timmy was asked to put 32 eggs into 8 trays. Each tray will have the same number of eggs. Write the division equation that could be used to solve for the number of eggs in each tray.

Write a word problem utilizing the expression 50 ÷ ? = 10 to solve. Give the answer to the word problem you wrote.

