Calculus a complete course canadian 8th edition adams test bank 1

Calculus: A Complete Course, 8e Chapter 9: Sequences, Series, and Power Series

Calculus A Complete Course Canadian 8th Edition Adams

Full download link at:

Test bank: https://testbankpack.com/p/test-bank-for-calculus-acomplete-course-canadian-8th-edition-by-adams-essex-isbn0321880218-9780321880215/

Solution Manual: https://testbankpack.com/p/solutions-manualfor-calculus-a-complete-course-canadian-8th-edition-by-adamsessex-isbn-0321880218-9780321880215/

Chapter 9 Sequences, Series, and Power Series

9.1 Sequences and Convergence

1) Which of the following descriptors apply to the sequence ?

(a) increasing (or ultimately increasing)

(c) positive (or ultimately positive)

(e) bounded below only

(g) bounded

(i) alternating

(k) divergent to ∞

(m) convergent

A) (a), (c), (e), (m)

B) (a), (c), (f), (j)

C) (a), (c), (g), (m)

(b) decreasing (or ultimately decreasing)

(d) negative (or ultimately negative)

(f) bounded above only

h) unbounded above and below

(j) divergent (but not to ∞ or -∞)

(l) divergent to -∞

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

D) (b), (c), (g), (l)

E) (a), (c), (e), (k)

Answer: C

Diff: 1

2) Find the limit of the sequence .

A) 0

B) 1

C) 2

D) 3

E)

Answer: C

Diff: 1

9-2

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

3) Which of the following descriptors apply to the sequence ?

(a) increasing (or ultimately increasing) (b) decreasing (or ultimately decreasing)

(c) positive (or ultimately positive) (d) negative (or ultimately negative)

(e) bounded below only (f) bounded above only

(g) bounded (h) unbounded above and below

(i) alternating (j) divergent (but not to ∞ or -∞)

(k) divergent to ∞ (l) divergent to -∞

(m) convergent

A) (g), (i), (m)

B) (b), (f), (m)

C) (g), (i), (j)

D) (b), (c), (i), (l)

E) (g), (i), (k)

Answer: A

Diff: 1

4) Find the limit of the sequence

A) 0

B) 1

C) 2

D) 3

E) -1

Answer: A

Diff: 1

5) Which of the following descriptors apply to the sequence ?

(a) increasing (or ultimately increasing) (b) decreasing (or ultimately decreasing)

(c) positive (or ultimately positive) (d) negative (or ultimately negative)

(e) bounded below only (f) bounded above only

(g) bounded (h) unbounded above and below

(i) alternating (j) divergent (but not to ∞ or -∞)

(k) divergent to ∞ (l) divergent to -∞

(m) convergent

A) (g), (i), (m)

B) (a), (f), (m)

C) (g), (i), (j)

D) (b), (c), (i), (l)

E) (g), (i), (k)

Answer: C

Diff: 1

9-3

Calculus: A Complete Course, 8e Chapter 9: Sequences, Series, and Power Series

6) Which of the following descriptors apply to the sequence ?

(a) increasing (or ultimately increasing) (b) decreasing (or ultimately decreasing)

(c) positive (or ultimately positive)

(e) bounded below only

(g) bounded

(d) negative (or ultimately negative)

(f) bounded above only

(h) unbounded above and below

(i) alternating (j) divergent (but not to ∞ or -∞)

(k) divergent to ∞ (l) divergent to -∞

(m) convergent

A) (a), (d), (f), (l)

B) (a), (f), (m)

C) (a), (c), (e), (k)

D) (b), (f), (j)

E) (b), (d), (f), (l)

Answer: C

Diff: 1

7) Let an = , n = 1, 2, 3,...

Which of the following statements about the sequence is true?

A) The sequence is decreasing with a lower bound equal to

B) The sequence is increasing with an upper bound equal to

C) The sequence is increasing with a lower bound equal to 0.

D) The sequence is not monotonic and also unbounded.

E) The sequence is decreasing with an upper bound equal to

Answer: E

Diff: 2

8) Find the limit of the sequence .

A) 0

B) 1

C) 2

D) 3

E) 6

Answer: C

Diff: 2

9-4

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

9) The sequence is defined recursively by a1 = , an + 1 = , n = 1, 2, 3,...

Assuming the sequence converges to the real number L, find L.

A) 1

B) -4 or 1

C) -1 or 4

D) -1

E) 4

Answer: E

Diff: 2

10) Find the limit of the sequence {an}, where an = -

A) -54

B) 54

C) -∞

D) 0

E) ∞

Answer: A

Diff: 2

11) Find, if it exists, the limit of the sequence , where k is a positive constant.

A) 0

B) 3

C) 2

D) 1

E) The limit does not exist.

Answer: D

Diff: 2

12) Find the limit of the sequence

A) 0

B) 1

C) 2

D) 3

E) This sequence is divergent.

Answer: A

Diff: 3

9-5

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

13) Find, if it exists, the limit of the sequence {an}, where an = .

A) 0

B) 1

C) 2

D) 3

E) The limit does not exist.

Answer: B

Diff: 3

14) Find the limit of the sequence an = .

A) 0

B) 1

C) 2

D) 22

E) 44

Answer: A

Diff: 2

15) Find the limit of the sequence .

A) 9

B) 3

C) -3

D) 0

E) -9

Answer: A

Diff: 2

16) True or False: If {|an|} converges, then {an} converges.

Answer: FALSE

Diff: 2

17) True or False: If {an} converges, then {|an|} converges.

Answer: TRUE

Diff: 2

18) True or False: If {an} converges, then must diverge.

Answer: FALSE

Diff: 2

19) True or False: If {an} converges and {bn} converges, then must converge.

Answer: FALSE

Diff: 2

Inc.,

9-6

Toronto, Ontario

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

9.2 Infinite Series

1) Sm = is the mth partial sum of an infinite series Find an Determine if the series is convergent or divergent, and if convergent find its sum.

A) a1 = , an = - for n ≥ 2; series converges, sum is 0

B) an = for n ≥ 1; series converges, sum is 1

C) a1 = , an = - for n ≥ 2; series converges, sum is

D) an = for n ≥ 1; series converges, sum is

E) an = for n ≥ 1; series converges, sum is

Answer: A Diff: 1

2) Sm = is the mth partial sum of an infinite series . Find an. Determine if the series is convergent or divergent, and if convergent find its sum.

A) an = , series diverges to ∞

B) an = , series diverges to ∞

C) an = , series converges to 1

D) an = , series converges to 2

E) an = , series converges to 1

Answer: A Diff: 1

9-7

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

3) Sn = is the nth partial sum of an infinite series . Find ak. Determine if the series is convergent or divergent, and if convergent find its sum.

A) ak = , series converges to

B) ak = , series converges to 1

C) ak = , series converges to 2

D) ak = , series diverges to ∞

E) ak = , series diverges to ∞

Answer: A

Diff: 1

4) Find the sum of the series 4 - 1 + - +...

Answer: B

Diff: 2

9-8

A) B) C) D) E)

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

5) On what interval of values of x does the series converge? What is its sum for x in that interval?

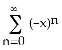
A) (-1, 1), sum =

B) (-1, 1), sum =

C) (-1, 1], sum =

D) [-1, 1), sum =

E) [-1, 1], sum =

Answer: B

Diff: 2

6) Find the sum of the series + + +... + +... = .

A)

B) 1

C) 2

D)

E) ∞ (series diverges)

Answer: B

Diff: 2

7) The geometric series

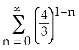
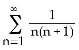
A) converges and its sum is

B) converges and its sum is

C) diverges and hence it has no sum.

D) converges and its sum is 4.

E) converges and its sum is

Answer: B

Diff: 2

9-9

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

8) Find the sum of the series + + +... + +... = A) B)

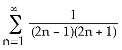
C) 1

D) ∞ (series diverges)

E) none of the above

Answer: A

Diff: 2

9) Find the sum of the series

E) ∞ (series diverges)

Answer: A

Diff: 2

Evaluate

E) series diverges

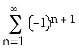
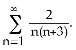
Answer: B

Diff: 2

A) B) C)

D)

10)

A) B) C) D)

11) Evaluate

A) e B) 1 C) D)

E) ∞ (series diverges)

Answer: E Diff: 3

12) Evaluate . A) 4 B) 5 C) 8 D)

E) ∞ (series diverges)

Answer: E

Diff: 3

13) Evaluate

A) -1

B) 0 C) 1 D)

E) no sum, series diverges

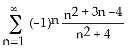
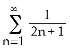
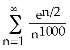
Answer: E

Diff: 3

Calculus: A Complete Course, 8e

Inc.,

9-11

Pearson Canada

Toronto, Ontario

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

14) Find the sum

A)

B)

C) 1

D) ∞ (series diverges)

E) none of the above

Answer: A

Diff: 3

15) Find the sum of the series . A)

E) ∞ (series diverges)

Answer: C

Diff: 2

16) Find the sum of the series

A) 2

B) 3

C) 1

D) 4

E) ∞ (series diverges)

Answer: C

Diff: 3

17) True or False: If diverges to infinity and an ≠ 0 for all n, then converges.

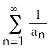
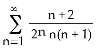
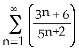
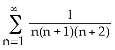
Answer: FALSE

Diff: 2

9-12

B) C) D)

Calculus: A Complete Course, 8e Chapter 9: Sequences, Series, and Power Series

18) True or False: If and both diverge, then also diverges.

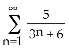
Answer: FALSE

Diff: 2

19) True or False: If converges, then an = 0.

Answer: TRUE

Diff: 2

20) True or False: If an = 0, then converges.

Answer: FALSE

Diff: 2

9.3 Convergence Tests for Positive Series

1) True or False: The series converges.

Answer: TRUE

Diff: 1

2) True or False: The series converges.

Answer: TRUE

Diff: 1

3) True or False: The series converges.

Answer: FALSE

Diff: 1

4) True or False: The series converges.

Answer: TRUE

Diff: 1

9-13

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

5) For exactly what values of the constant p does the series converge?

A) p > 2

B) p ≥ 2

C) p < 1

D) p ≤ 1

E) p > 1

Answer: A

Diff: 2

6) Find all values of the nonzero constant real number p such that the series is convergent.

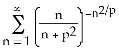
A) p > 1

B) 0 < P ≤ 1

C) 0 < P ≤

D) p < 0

E) p > 0

Answer: D

Diff: 3

7) For exactly what values of the constant p does the series converge?

A) p ≥ 1

B) p > 1

C) p ≥ 2

D) p > 2

E) p > 0

Answer: A

Diff: 2

8) For exactly what values of the constant p does the series converge?

A) -3 < p < 3

B) -3 ≤ p ≤ 3

C) 0 ≤ p ≤ 3

D) 0 < p < 3

E) -3 < p < 0

Answer: A

Diff: 2

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

9) True or False: The series converges.

Answer: FALSE

Diff: 1

10) True or False: The series converges.

Answer: TRUE

Diff: 1

11) True or False: The series converges.

Answer: FALSE

Diff: 1

12) True or False: The series converges.

Answer: TRUE

Diff: 1

13) Use the integral test bounds to estimate the sum of the series using the first three terms.

A) 104

B) 140

C) 119

D) 101

E) 98

Answer: C

Diff: 2

14) What is the largest positive constant K such that if 0 < p < K, then must converge?

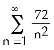
A) 1 B) 2

C) 4 D) 8 E) 9

Answer: C

Diff: 2

9-15

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

15) Give an upper bound for the error when is approximated by the partial sum

A) 0.0004

B) 0.0001

C) 0.00004

D) 0.00001

E) 0.004

Answer: A

Diff: 2

16) Give an upper bound for the error when e = is approximated by the partial sum .

How large should n be taken to ensure that the error is less than 0.001?

A) , n = 7

B) , n = 8

C) , n = 7

D) , n = 8

E) , n = 6

Answer: E

Diff: 2

17) True or False: The series converges.

Answer: TRUE

Diff: 1

18) True or False: The series converges.

Answer: FALSE

Diff: 1

19) True or False: The series converges.

Answer: FALSE

Diff: 1

9-16

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

9.4 Absolute and Conditional Convergence

1) True or False: The series converges.

Answer: FALSE

Diff: 2

2) True or False: The series converges.

Answer: TRUE

Diff: 2

3) True or False: The series converges.

Answer: FALSE

Diff: 2

4) True or False: The series converges.

Answer: TRUE

Diff: 2

5) For what values of x does the series (a) converge absolutely? (b) converge conditionally?

A) (a) x = 0 only, (b) nowhere

B) (a) -1 < x < 1, (b) nowhere

C) (a) -1 < x < 1, (b) x = -1 and x = 1

D) (a) all real x, (b) nowhere

E) (a) -1 < x < 1, (b) x = 1

Answer: A

Diff: 2

6) For what values of x does the series (a) converge absolutely? (b) converge conditionally?

A) (a) x = 0 only, (b) nowhere

B) (a) -1 < x < 1, (b) nowhere

C) (a) -1 < x < 1, (b) x = -1 and x = 1

D) (a) all real x, (b) nowhere

E) (a) -1 < x < 1, (b) x = 1

Answer: D

Diff: 2

9-17

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

7) For what values of x does the series (a) converge absolutely? (b) converge conditionally?

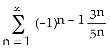
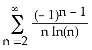
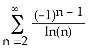
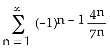
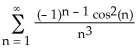
A) (a) on the interval (1, 5), (b) at x = 1

B) (a) on the interval (1, 5), (b) at x = -1 and x = 5

C) (a) on the interval [1, 5], (b) nowhere

D) (a) on the interval [1, 5), (b) at x = 5

E) (a) all real x, (b) nowhere

Answer: A

Diff: 2

8) For what values of x does the series

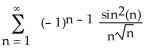
(a) converge absolutely? (b) converge conditionally?

A) (a) on the interval (-2, -1), (b) at x = -2 and x = -1

B) (a) on the interval [-2, -1], (b) nowhere

C) (a) on the interval (-2, -1), (b) for x < -2

D) (a) on the interval (-3, 0), (b) at x = -3 and x = 0

E) (a) on the interval [-2, -1), (b) at x = -1

Answer: A

Diff: 2

9) Which of the three series (i) (ii) (iii) is conditionally convergent?

A) series (iii)

B) series (i)

C) series (i) and (iii)

D) series (ii)

E) All three

Answer: A

Diff: 2

10) Which of the three series (i) (ii) (iii) is absolutely convergent?

A) series (i) and (ii)

B) series (i)

C) series (ii) and (iii)

D) series (i) and (iii)

E) none

Answer: C

Diff: 2

9-18

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

11) For what values of x does the series converge?

A) on the interval [1, ∞)

B) on the intervals (-∞, -1] and [1, ∞)

C) for all x ≠ 0

D) for x = 2 only

E) on the interval (-∞, -1]

Answer: A

Diff: 2

12) For what values of x does the series converge?

A) on the intervals (-∞, -1] and [1, ∞)

B) on the intervals (-∞, -1) and (1, ∞)

C) on the interval [-1, 1]

D) on the interval (-1, 1)

E) on the interval [1, ∞)

Answer: A

Diff: 2

13) For what values of x does the series ln x + + + +... converge?

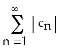
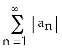
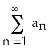
A) < x < e

B) 0 < x < e

C) 1 < x < e

D) 0 < x < ∞

E) 0 < x < 1

Answer: A

Diff: 2

14) True or False: If is conditionally convergent, then must be divergent.

Answer: TRUE

Diff: 1

15) True or False: If is divergent, then must be conditionally convergent.

Answer: FALSE

Diff: 1

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

16) True or False: By possibly rearranging its terms, the series can be forced to have the

sum 17.

Answer: FALSE

Diff: 2

9.5 Power Series

1) Find the radius, centre, and interval of convergence of the series

A) centre 0, radius 1, interval [-1, 1)

B) centre 0, radius 1, interval [-1, 1]

C) centre 0, radius 1, interval (-1, 1)

D) centre 0, radius ∞, interval (-∞, ∞)

E) centre 0, radius 1, interval (-1, 1]

Answer: A

Diff: 2

2) Find the radius, centre, and interval of convergence of the series

A) centre 1, radius , interval

B) centre 1, radius , interval

C) centre 1, radius , interval

D) centre 1, radius , interval

E) centre 1, radius , interval ,

Answer: A

Diff: 2

3) The interval of convergence of the power series is given by [-7, -3).

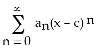
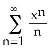
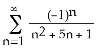
Find the centre c and the radius of convergence R of the power series.

A) c = -10, R = 4

B) c = -5, R = 2

C) c = -4, R = 10

D) c = -2, R = 5

E) c = 2, R = -5

Answer: B

Diff: 1

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

4) Find the centre, radius, and interval of convergence of the series

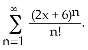
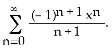
A) centre 0, radius 1, interval [-1, 1]

B) centre 0, radius 1, interval (-1, 1]

C) centre 0, radius 1, interval (-1, 1)

D) centre 0, radius 2, interval (-2, 2)

E) centre 0, radius 1, interval [-1, 1)

Answer: B

Diff: 2

5) Find the centre, radius, and interval of convergence of the series

A) centre 4, radius 3, interval (1, 7]

B) centre 4, radius 3, interval [1, 7)

C) centre 4, radius 1, interval [3, 5]

D) centre 4, radius 1, interval (3, 5)

E) centre 4, radius 1, interval (3, 5]

Answer: C

Diff: 2

6) Find the centre, radius, and interval of convergence of the series

A) centre -3, radius 1, interval [-4, -2]

B) centre -3, radius 1, interval (-4, -2)

C) centre 0, radius ∞, interval (-∞, ∞)

D) centre -3, radius ∞, interval (-∞, ∞)

E) center -3, radius , interval

Answer: D Diff: 2

9-21

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

7) The power series has radius of convergence R = . Assuming exist, find the radius of convergence of the power series .

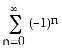
A)

B)

C) ∞

D)

E)

Answer: D

Diff: 3

8) Using the known geometric series representation = , valid for -1 < x < 1, find a power series representation for f(x) = ln in powers of x. On what interval does the series converge to f(x)?

A) f(x) = , for -1 < x ≤ 1

B) f(x) = , for -1 < x < 1

C) f(x) = , for -1 ≤ x ≤ 1

D) f(x) = , for -1 ≤ x < 1

E) f(x) = , for -1 < x ≤ 1

Answer: A Diff: 3

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

9) Using the known geometric series representation = , valid for -1 < x < 1, find a power series representation for f(x) = tan-1(2x) in powers of x. On what interval does the series converge to f(x)?

A) f(x) = , for - ≤ x ≤

B) f(x) = , for - < x <

C) f(x) = , for - 2 ≤ x ≤ 2

D) f(x) = , for - < x ≤

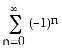
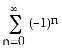
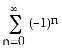
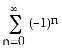
E) f(x) = , for - 2 < x < 2

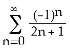
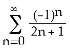
Answer: A Diff: 2

10) Using the known geometric series representation = , valid for -1 < x < 1, find a power series representation for f(x) = in powers of x. On what interval does the series converge to f(x)?

A) f(x) = , for - < x <

B) f(x) = , for - < x <

C) f(x) = , for - < x <

D) f(x) = , for - < x <

E) f(x) = , for -4 < x < 4

Answer: B Diff: 2

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

11) By suitably manipulating the geometric series = , -1 < x < 1, you can calculate the sum of the series . Use this method to evaluate the sum

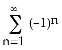
A) 4

B) 6

C) 8

D) 10

E) none of the above

Answer: B

Diff: 2

12) Using the known geometric series representation = xn, valid for -1 < x < 1, find a

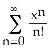
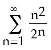
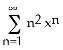
power series representation for f(x) = ln(2 + x) in powers of x - 1. On what interval does the series converge to f(x)?

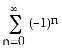
A) f(x) = ln 3 +

B) f(x) = ln 3 +

C) f(x) = ln 2 +

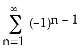
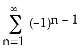
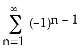
D) f(x) = ln 2 +

E) none of the above

Answer: B

Diff: 2

13) Let f(x) denote the sum of the series wherever the series converges. Where does the series converge? Calculate (x) and f(0). What do these results imply that f(x) actually is?

Answer: Series converges to f(x) for all x, (x) = f(x), f(0) = 1, so f(x) = .

Diff: 2

Copyright

9-24

, for -0 < x ≤ 2

,

for -2 < x ≤ 4

,

for -1 < x ≤ 3

,

for -1 < x < 3

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

9.6 Taylor and Maclaurin Series

1) If f(x) = x, find f(99)(0).

A) -98!

B) 98!

C) -99!

D) 99!

E) 0

Answer: A

Diff: 2

2) Find f(100)(0) if f(x) = . A) B) C) D)

E) 1

Answer: C

Diff: 2

3) Find the Taylor series of f(x) = x2 + 2x + 2 about x = -1. For what values of x does it converge to f(x)?

A) f(x) = 2 + , for all x

B) f(x) = 1 + , for all x

C) f(x) = 1 - , for all x

D) f(x) = 1 + , for all x

E) f(x) = 1 + , -2 < x < 0

Answer: D

Diff: 1

Calculus: A Complete Course, 8e Chapter 9: Sequences, Series, and Power Series

4) Find the MacLaurin series for f(x) = x. For what values of x does it converge to f(x)?

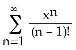
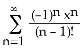
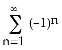
A) f(x) = , for all x

B) f(x) = , for all x

C) f(x) = , for all x

D) f(x) = , for all x

E) f(x) = , for all x

Answer: D

Diff: 1

5) Find the Maclaurin series for f(x) = .

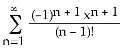
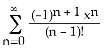
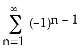
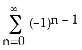
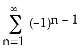
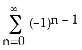
A) f(x) =

B) f(x) =

C) f(x) =

D) f(x) =

E) f(x) =

Answer: A

Diff: 2

6) Find the Taylor expansion of 4 + 3 + 2 + y + 2 in powers of y + 2.

A) 48 + 99(y + 2) + 80 - 29 +4

B) 48 - 99(y + 2) - 80 - 29 + 4

C) 48 + 99(y + 2) + 80 + 29 + 4

D) 48 - 99(y + 2) + 80 - 29 + 4

E) -48 + 99(y + 2) - 80 + 29 - 4

Answer: D

Diff: 2

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

7) Find the Taylor expansion of about x = b.

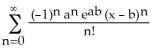
A) B)

C)

D)

E)

Answer: A Diff: 2

8) Find the Maclaurin series for ln . For what values of x does the series converge to the function?

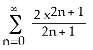
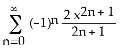
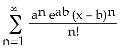
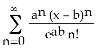
A) , for -1 < x < 1

B) , for -1 < x < 1

C) , for -1 < x < 1

D) , for -1 < x < 1

E) , for all x

Answer: C Diff: 2

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

9) Find the Taylor series for sin x in powers of x - a. A)

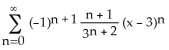
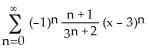
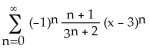
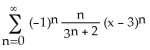
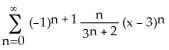
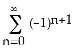
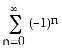
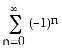
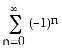
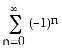
Answer: A Diff: 2

10) Find the Taylor series for f(x) = about x - 3. On what interval does the series converge to f(x)? A) f(x)

E) f(x) = , for 0 < x ≤ 6

Answer: D Diff: 3

B) C) D) E)

,

0

,

0

=

for 0 < x < 6 B) f(x) =

for

< x < 6 C) f(x) =

for

< x ≤ 6 D) f(x) = , for 0 < x < 6

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

11) Find the first three nonzero terms in the Maclaurin series for tan(2x).

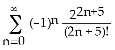
A) 2x + x3 + x5

B) 2x - x3 + x5

C) 2x + x3 + x5

D) 2x - x3 + x5

E) 2x + x3 - x5

Answer: A

Diff: 2

12) Find the sum of the series 1 - + - + -... =

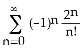
A) e-2

B) cos(2)

C) e-1/2

D) cosh(2) + sinh(2)

E) - e2

Answer: A

Diff: 2

13) Find the sum of the series

A) sin(2) - 1

B) sin(2) -

C)

D)

E) cos(2) -

Answer: B

Diff: 3

9-29

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

14) Find the sum of the series

Answer: A Diff: 2

9.7 Applications of Taylor and Maclaurin Series

1) Find the MacLaurin series for the function F(x) = dt.

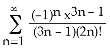
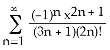
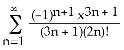
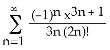
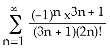
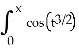
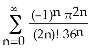
Answer: A Diff: 2

A) B) C) D) E)

cos

A) B) C) D) E)

Calculus: A Complete Course, 8e

2) Calculate the Maclaurin series for the function F(x) = dt and calculate F(1) correct to three decimal

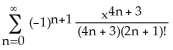
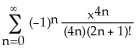
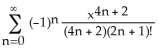
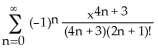
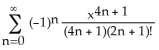
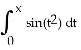
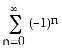
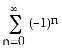
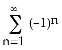
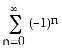
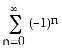
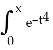
3) Calculate the Maclaurin series for the function G(x) = and calculate G(1) correct to 5 decimal

Chapter 9: Sequences, Series, and Power Series Copyright

places. A) F(x) = , F(1) ≈ 0.991 B) F(x) = , F(1) ≈ 0.844 C) F(x) = , F(1) ≈ 0.863 D) F(x) = , F(1) ≈ 0.842 E) F(x) = , F(1) ≈ 0.873 Answer: B Diff: 2

places. A) G(x) = , G(1) ≈ 0.31025 B) G(x) = , G(1) ≈ 0.31026 C) G(x) = , G(1) ≈ 0.31029 D) G(x) = , G(1) ≈ 0.31031 E) G(x) = , G(1) ≈ 0.31024 Answer: B Diff: 2

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

4) Given f(x) = ln(3x + 1)

(a) Find Taylor's polynomial of degree n = 2 for f about c = 0.

(b) Use part (a) to estimate the value of ln(1.3).

(c) Estimate the maximum absolute error involved in the approximation obtained in part (b) above.

Answer: (a) (x) = 3x - x2 (b) ln(1.3) ≈ 0.255 (c) 0.009

Diff: 3

5) How many nonzero terms of the known Maclaurin series for ln(1 + x) are needed to approximate ln(1.1) correct to 4 decimal places?

A) 2

B) 3

C) 6

D) 9

E) 4

Answer: B

Diff: 2

6) How many nonzero terms of the Maclaurin series for (x) are needed to approximate (0.2) correct to 5 decimal places?

A) 2

B) 3

C) 4

D) 5

E) 1

Answer: B

Diff: 2

7) Assuming that no calculator is handy, what known Maclaurin series would you use to approximate sin(95°) using as few terms as possible, and at what point would you evaluate that series?

A) - cos(x), x =

B) cos(x), x =

C) sin(x), x =

D) sin(x), x =

E) none of the above

Answer: B

Diff: 2

Pearson Canada Inc., Toronto, Ontario 9-32

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

8) Use known Maclaurin series to evaluate .

-

Answer: C Diff: 2

9) Use known Maclaurin series to evaluate

1 Answer: C

2

10) Use known Maclaurin series to evaluate A) -20

B) 20 C) -30

D) 30

E) 10

Answer: A

Diff: 2

11) True or False: The error E in the approximation e ≈ satisfies < .

Answer: FALSE

Diff: 3

D)

E)

A) B) C)

A) B) C) D) E)

Diff:

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

12) True or False: The error E in the approximation ≈ satisfies <

Answer: TRUE

Diff: 3

13) How many terms of the Maclaurin series for are needed to approximate with error less than 0.00005 in size?

A) 4

B) 5

C) 6

D) 7

E) 3

Answer: B

Diff: 3

14) For what range of x can cos x be replaced by the first three nonzero terms of its Maclaurin series to ensure the error is less than 0.00005?

A) ≈ 0.144

B) ≈ 0.072

C) ≈ 0.036

D) ≈ 0.288

E) ≈ 0.575

Answer: E

Diff: 3

9.8 Binomial Theorem and Binomial Series

1) Find the Maclaurin series (binomial series) for

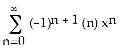
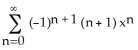
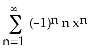
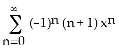
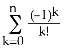
A) , for -1 < x < 1

B) , for -1 < x < 1

C) , for -1 < x < 1

D) , for -1 < x < 1

E) , for -1 < x < 1

Answer: A

Diff: 1

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

2) Find the Maclaurin series (binomial series) for .

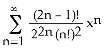
A) 1 - for -1 < x < 1

B) 1 - - for -1 < x < 1

C) 1 - for -1 < x < 1

D) 1 - for -1 < x < 1

E) 1 - + for -1 < x < 1

Answer: B Diff: 1

3) Find the Maclaurin series (binomial series) for (x).

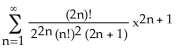
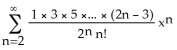
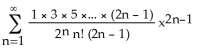
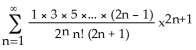
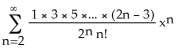
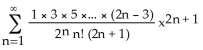
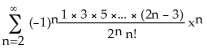
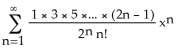
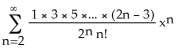
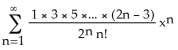
A) x - for -1 < x < 1

B) 1 - for -1 < x < 1

C) x + for -1 < x < 1

D) x + for -1 < x < 1

E) 1 + for -1 < x < 1

Answer: C Diff: 1

4) True or False: (x) = x + for -1 < x < 1

Answer: TRUE Diff: 2

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

9.9 Fourier Series

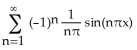
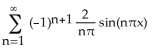
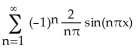
1) Find the Fourier series of the function f having period 2π and defined by f(x) = 0 if -π < x ≤ 0 and f(x) = 1 if 0 < x ≤ π.

A) + sin((2n - 1)x)

B) 1 + sin((2n - 1)x)

C) + sin(2nx)

D) 1 + sin(2nx)

E) + cos((2n - 1)x)

Answer: A

Diff: 2

2) Find the Fourier series of the function f(x) = x defined on the interval [-1, 1]. A) B) C)

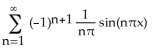
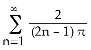
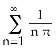
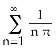
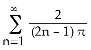
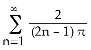
D)

E) none of the above

Answer: B

Diff: 2

Calculus: A Complete Course, 8e

Chapter 9: Sequences, Series, and Power Series

3) Find the Fourier series for f(x) = x2 defined on [- π, π].

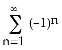
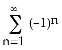
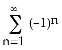
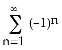
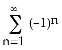
A) f(x) = - cos(nx)

B) f(x) = + cos(nx)

C) f(x) = + cos(nx)

D) f(x) = - cos(nx)

E) f(x) = + sin(nx)

Answer: C

Diff: 2

4) Let [x] denote the greatest integer less than or equal to x, and let f(x) = [x] on the interval [0,3]. To what values will the Fourier series of f converge at (a) x = 1 and (b) x = 2?

A) (a) 1, (b) 2

B) (a) 1, (b)

C) (a) , (b)

D) (a) , (b) 1

E) (a) 1, (b) 1

Answer: C

Diff: 2

9-37

Turn static files into dynamic content formats.

Create a flipbook