Microeconomics An Intuitive Approach with Calculus 1st Edition Nechyba Solutions Manual

2

ChoiceSetsandBudgetConstraints

Solutionsfor Microeconomics:AnIntuitive ApproachwithCalculus

Apartfromend-of-chapterexercisesprovidedinthestudent StudyGuide,these solutionsareprovidedforusebyinstructors. (End-of-Chapterexerciseswith solutionsinthestudent StudyGuide aresomarkedinthetextbook.)

Thesolutionsmaybesharedbyaninstructorwithhisorherstudentsatthe instructor’sdiscretion.

Theymaynotbemadepubliclyavailable.

Ifpostedonacourseweb-site,thesitemustbepasswordprotectedandfor useonlybythestudentsinthecourse.

Reproductionand/ordistributionofthesolutionsbeyondclassroomuseis strictlyprohibited.

Inmostcolleges,itisaviolationofthestudenthonorcodeforastudentto sharesolutionstoproblemswithpeersthattakethesameclassatalaterdate.

•Eachend-of-chapterexercisebeginsonanewpage.Thisistofacilitatemaximumflexibilityforinstructorswhomaywishtoshareanswerstosomebut notallexerciseswiththeirstudents.

•IfyouareassigningonlytheA-partsofexercisesin Microeconomics:AnIntuitiveApproachwithCalculus,youmaywishtoinsteadusethesolutionset createdforthecompanionbook Microeconomics:AnIntuitiveApproach.

• SolutionstoWithin-ChapterExercisesareprovidedinthestudent StudyGuide.

2.1 AnygoodSouthernbreakfastincludesgrits(whichmywifeloves)andbacon(whichIlove).Suppose weallocate$60perweektoconsumptionofgritsandbacon,thatgritscost$2perboxandbaconcosts$3 perpackage.

A: Useagraphwithboxesofgritsonthehorizontalaxisandpackagesofbaconontheverticalto answerthefollowing:

(a) Illustratemyfamily’sweeklybudgetconstraintandchoice set.

Answer:Thegraphisdrawninpanel(a)ofGraph2.1.

Graph2.1:(a)Answerto(a);(b)Answerto(c);(c)Answerto(d)

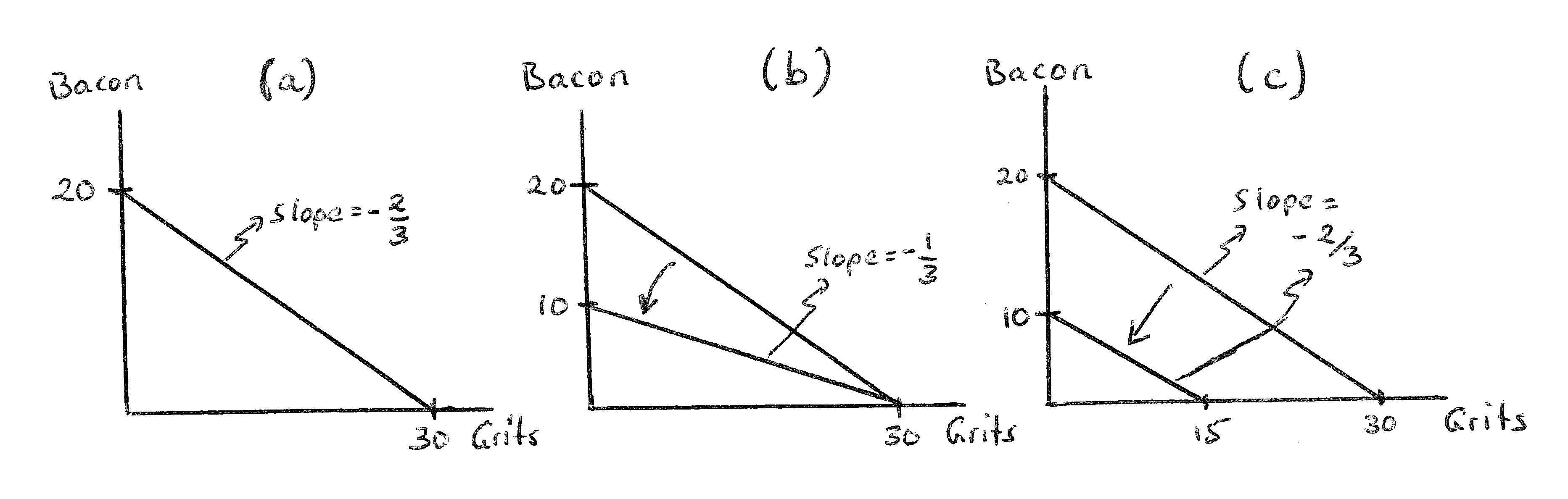
(b) Identifytheopportunitycostofbaconandgritsandrelatethesetoconceptsonyourgraph.

Answer:Theopportunitycostofgritsisequalto2/3ofapackageofbacon(whichisequalto thenegativeslopeofthebudgetsincegritsappearonthehorizontalaxis).Theopportunity costofapackageofbaconis3/2ofaboxofgrits(whichisequaltotheinverseofthenegative slopeofthebudgetsincebaconappearsontheverticalaxis)

(c) Howwouldyourgraphchangeifasuddenappearanceofararehogdiseasecausedtheprice ofbacontoriseto$6perpackage,andhowdoesthischangethe opportunitycostofbacon andgrits?

Answer:Thischangeisillustratedinpanel(b)ofGraph2.1.Thischangestheopportunity costofgritsto1/3ofapackageofbacon,anditchangestheopportunitycostofbaconto3 boxesofgrits.Thismakessense:Baconisnow3timesasexpensiveasgrits—soyouhave togiveup3boxesofgritsforonepackageofbacon,or1/3ofapackageofbaconfor1box ofgrits.

(d) Whathappensinyourgraphif(insteadofthechangein(c))thelossofmyjobcausedusto decreaseourweeklybudgetforSouthernbreakfastsfrom$60 to$30?Howdoesthischange theopportunitycostofbaconandgrits?

Answer:Thechangeisillustratedinpanel(c)ofGraph2.1.Sincerelativepriceshavenot changed,opportunitycostshavenotchanged.Thisisreflectedinthefactthattheslope staysunchanged.

B: Inthefollowing,compareamathematicalapproachtothegraphicalapproachusedinpartA, usingx1 torepresentboxesofgritsandx2 torepresentpackagesofbacon:

(a) Writedownthemathematicalformulationofthebudgetlineandchoicesetandidentifyelementsinthebudgetequationthatcorrespondtokeyfeatures ofyourgraphfrompart2.1A(a).

Answer:Thebudgetequationis p1 x1 + p2 x2 = I canalsobewrittenas x2 = I p2 p1 p2 x1 (2.1)

With I = 60, p1 = 2and p2 = 3,thisbecomes x2 = 20 (2/3)x1 —anequationwithintercept of20andslopeof 2/3asdrawninGraph2.1(a).

ChoiceSetsandBudgetConstraints

(b) Howcanyouidentifytheopportunitycostofbaconandgritsinyourequationofabudget line,andhowdoesthisrelatetoyouranswerin2.1A(b).

Answer:Theopportunitycostof x1 (grits)issimplythenegativeoftheslopeterm(interms ofunitsof x2).Theopportunitycostof x2 (bacon)istheinverseofthat.

(c) Illustratehowthebudgetlineequationchangesunderthescenarioof2.1A(c)andidentifythe changeinopportunitycosts.

Answer:Substitutingthenewprice p2 = 6intoequation(2.1),weget x2 = 10 (1/3)x1 —an equationwithinterceptof10andslopeof 1/3asdepictedinpanel(b)ofGraph2.1.

(d) Repeat(c)forthescenarioin2.1A(d).

Answer:Substitutingthenewincome I = 30intoequation(2.1)(holdingpricesat p1 = 2 and p2 = 3,weget x2 = 10 (2/3)x1 —anequationwithinterceptof10andslopeof 2/3as depictedinpanel(c)ofGraph2.1.

2.2 Supposetheonlytwogoodsintheworldarepeanutbutterandjelly.

A: Youhavenoexogenousincomebutyoudoown6jarsofpeanutbutterand2jarsofjelly.Theprice ofpeanutbutteris$4perjar,andthepriceofjellyis$6perjar.

(a) Onagraphwithjarsofpeanutbutteronthehorizontalandjarsofjellyontheverticalaxis, illustrateyourbudgetconstraint.

Answer:Thisisdepictedinpanel(a)ofGraph2.2.Thepoint E istheendowmentpointof2 jarsofjellyand6jarsofpeanutbutter(PB).Ifyousoldyour 2jarsofjelly(atapriceof$6per jar),youcouldmake$12,andwiththatyoucouldbuyanadditional3jarsofPB(attheprice of$4perjar).Thus,themostPByoucouldhaveis9,theinterceptonthehorizontalaxis. Similarly,youcouldsellyour6jarsofPBfor$24,andwiththatyoucouldbuy4additional jarsofjellytogetyoutoamaximumtotalof6jarsofjelly—theinterceptonthevertical axis.Theresultingbudgetlinehasslope 2/3,whichmakessensesincethepriceofPB($4) dividedbythepriceofjelly($6)isinfact2/3.

(b) Howdoesyourconstraintchangewhenthepriceofpeanutbutterincreasesto$6?Howdoes thischangeyouropportunitycostofjelly?

Answer:Thechangeisillustratedinpanel(b)ofGraph2.2.Sinceyoucanalwaysstillconsumeyourendowment E,thenewbudgetmustcontain E.Buttheopportunitycostshave nowchanged,withtheratioofthetwopricesnowequalto1.Thus,thenewbudgetconstrainthasslope 1andrunsthrough E.Theopportunitycostofjellyhasnowfallenfrom 3/2to1.Thisshouldmakesense:Before,PBwascheaperthanjellyandso,foreveryjarof jellyyouhadtogiveupmorethanajarofpeanutbutter.Nowthattheyarethesameprice, youonlyhavetogiveuponejarofPBtoget1jarofjelly.

B: Considerthesameeconomiccircumstancesdescribedin2.2A andusex1 torepresentjarsof peanutbutterandx2 torepresentjarsofjelly.

(a) Writedowntheequationrepresentingthebudgetlineandrelatekeycomponentstoyour graphfrom2.2A(a).

Answer:Thebudgetlinehastoequateyourwealthtothecostofyourconsumption.Your wealthisequaltothevalueofyourendowment,whichis p1e1 + p2e2 (where e1 isyour endowmentofPBand e2 isyourendowmentofjelly).Thecostofyourconsumptionisjust yourspendingonthetwogoods—i.e. p1 x1 + p2 x2.Theresultingequationis

Graph2.2:(a)Answerto(a);(b)Answerto(b)

ChoiceSetsandBudgetConstraints

Whenthevaluesgivenintheproblemarepluggedin,thelefthandsidebecomes4(6)+6(2) = 36andtherighthandsidebecomes4x1 + 6x2 —resultingintheequation36 = 4x1 + 6x2 Taking x2 tooneside,wethenget

whichisexactlywhatwegraphedinpanel(a)ofGraph2.2—alinewithverticalintercept of6andslopeof 2/3.

(b) Changeyourequationforyourbudgetlinetoreflectthechangeineconomiccircumstances describedin2.2A(b)andshowhowthisnewequationrelatestoyourgraphin2.2A(b).

Answer:Nowthelefthandsideofequation(2.2)is6(6) + 6(2) = 48whiletherighthandside is6x1 + 6x2.Theequationthusbecomes48 =

istakentooneside,

Thisisanequationofalinewithverticalinterceptof8andslopeof 1—exactlywhatwe graphedinpanel(b)ofGraph2.2.

2.3 Considerabudgetforgoodx1 (onthehorizontalaxis)andx2 (ontheverticalaxis)whenyoureconomiccircumstancesarecharacterizedbypricesp1 andp2 andanexogenousincomelevelI.

A: Drawabudgetlinethatrepresentstheseeconomiccircumstancesandcarefullylabeltheintercepts andslope.

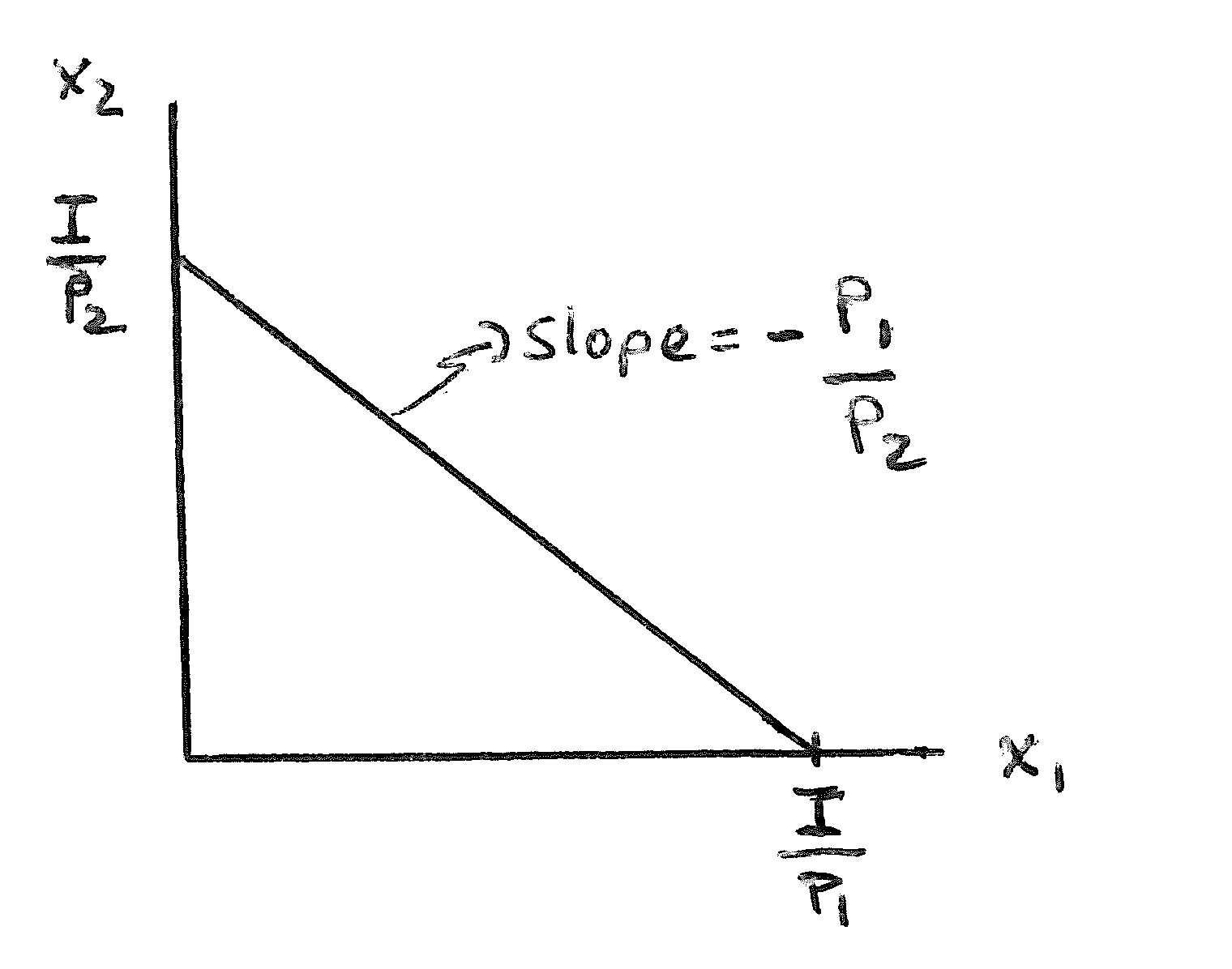
Answer:ThesketchofthisbudgetlineisgiveninGraph2.3.

Graph2.3:Abudgetconstraintwithexogenousincome I

Theverticalinterceptisequaltohowmuchof x2 onecouldbywith I ifthatisallonebought— whichisjust I /p2 .Theanalogousistruefor x1 onthehorizontalintercept.Onewaytoverifythe slopeistorecognizeitisthe“rise”(I /p2 )dividedbythe“run”(I /p1 )—whichgives p1 /p2 —and thatitisnegativesincethebudgetconstraintisdownwardsloping.

(a) IllustratehowthislinecanshiftparalleltoitselfwithoutachangeinI.

Answer:Inorderforthelinetoshiftinaparallelway,itmustbethattheslope p1/p2 remainsunchanged.Sincewecan’tchange I ,theonlyvalueswecanchangeare p1 and p2 —butsince p1 /p2 can’tchange,itmeanstheonlythingwecandoistomultiplyboth pricesbythesameconstant.So,forinstance,ifwemultiply bothpricesby2,theratioofthe newpricesis2p1 /(2p2 ) = p1/p2 sincethe2’scancel.Wethereforehavenotchangedthe slope.Butwehavechangedtheverticalinterceptfrom I /p2 to I /(2p2 ).Wehavetherefore shiftedinthelinewithoutchangingitsslope.

Thisshouldmakeintuitivesense:Ifourmoneyincomedoesnotchangebutallpricesdouble,thenIcanbyhalfasmuchofeverything.Thisisequivalenttopricesstayingthesame andmymoneyincomedroppingbyhalf.

(b) Illustratehowthislinecanrotateclockwiseonitshorizontalinterceptwithoutachangein p2

Answer:Tokeepthehorizontalinterceptconstant,weneedtokeep I /p1 constant.Butto rotatethelineclockwise,weneedtoincreasetheverticalintercept I /p2 .Sincewecan’t change p2 (whichwouldbetheeasiestwaytodothis),thatleavesusonly I and p1 to change.Butsincewecan’tchange I /p1 ,wecanonlychangethesebymultiplyingthem bythesameconstant.Forinstance,ifwemultiplybothby2,wedon’tchangethehorizontalinterceptsince2I /(2p1 ) = I /p1 .Butwedoincreasetheverticalinterceptfrom I /p2 to 2I /p2 .So,multiplyingboth I and p1 bythesameconstant(greaterthan1)willaccomplish ourgoal.

Thisagainshouldmakeintuitivesense:Ifyoudoublemyincomeandthepriceofgood1, Icanstillaffordexactlyasmuchofgood1ifthatisallIbuywithmyincome.(Thusthe unchangedhorizontalintercept).But,ifIonlybuygood2,thenadoublingofmyincome withoutachangeinthepriceofgood2letsmebuytwiceasmuch ofgood2.Thescenario isexactlythesameasif p2 hadfallenbyhalf(and I and p1 hadremainedunchanged.)

B: Writetheequationofabudgetlinethatcorrespondstoyourgraphin2.3A.

ChoiceSetsandBudgetConstraints

Answer: p1 x1 + p2 x2 = I ,whichcanalsobewrittenas

(a) Usethisequationtodemonstratehowthechangederivedin2.3A(a)canhappen. Answer:IfIreplace p

isjustaconstant),Iget

Thus,multiplyingbothpricesby α isequivalenttomultiplyingincomeby1/α (andleaving pricesunchanged).

(b) Usethesameequationtoillustratehowthechangederivedin 2.3A(b)canhappen.

Thus,thisisequivalenttomultiplying p2 by1/β.Solongas β > 1,itisthereforeequivalent toreducingthepriceofgood2(withoutchangingtheotherpriceorincome).

2.4 Supposetherearethreegoodsintheworld:x1,x2 andx3

A: Ona3-dimensionalgraph,illustrateyourbudgetconstraintwhenyoureconomiccircumstances aredefinedbyp1 = 2,p2 = 6,p3 = 5 andI = 120.Carefullylabelintercepts.

Answer:Panel(a)ofGraph2.4illustratesthis3-dimensionalbudgetwitheachinterceptgivenby I dividedbythepriceofthegoodonthataxis.

(a) Whatisyouropportunitycostofx1 intermsofx2?Whatisyouropportunitycostofx2 in termsofx3?

Answer:Onanysliceofthegraphthatkeeps x3 constant,theslopeofthebudgetis p1 /p2 = 1/3.Justasinthe2-goodcase,thisisthentheopportunitycostof x1 intermsof x2 —since p1 isathirdof p2,onegivesup1/3ofaunitof x2 whenonechoosestoconsume1unitof x1.Onanyverticalslicethatholds x1 fixed,ontheotherhand,theslopeis p3/p2 =−5/6. Thus,theopportunitycostof x3 intermsof x2 is5/6,andtheopportunitycostof x2 interms of x3 istheinverse—i.e.6/5.

(b) IllustratehowyourgraphchangesifIfallsto$60.Doesyour answerto(a)change?

Answer:Panel(b)ofGraph2.4illustratesthischange(withthedashedplaneequaltothe budgetconstraintgraphedinpanel(a).)Theanswertopart(a)doesnotchangesinceno pricesandthusnoopportunitycostschanged.Thenewplaneisparalleltotheoriginal.

(c) Illustratehowyourgraphchangesifinsteadp1 risesto$4.Doesyouranswertopart(a) change?

Answer:Panel(c)ofGraph2.4illustratesthischange(withthedashedplaneagainillustratingthebudgetconstraintfrompart(a).)Sinceonly p1 changed,onlythe x1 intercept changes.Thischangestheslopeonanyslicethatholds x3 fixedfrom 1/3to 2/3—thus doublingtheopportunitycostof x1 intermsof x2.Sincetheslopeofanysliceholding x1 fixedremainsunchanged,theopportunitycostof x2 intermsof x3 remainsunchanged. Thismakessensesince p2 and p3 didnotchange,leavingthetradeoffbetween x2 and x3 consumptionunchanged.

B: Writedowntheequationthatrepresentsyourpicturein2.4A.Thensupposethatanewgoodx4 is inventedandpricedat$1.Howdoesyourequationchange?Why isitdifficulttorepresentthisnew setofeconomiccircumstancesgraphically?

Answer:Theequationrepresentingthegraphsis p1 x1 + p2 x2 + p3 x3 = I or,pluggingintheinitial pricesandincomerelevantforpanel(a),2x1 + 6x2 + 5x3 = 120.Withanewfourthgoodpricedat

Graph2.4:Budgetsover3goods:Answersto2.4A,A(b)andA(c)

ChoiceSetsandBudgetConstraints

2.5 EverydayApplication: WatchingaBadMovie: Ononeofmyfirstdateswithmywife,wewenttosee themovie“Spaceballs”andpaid$5perticket.

A: Halfwaythroughthemovie,mywifesaid:“Whatonearthwereyouthinking?Thismoviesucks!I don’tknowwhyIletyoupickmovies.Let’sleave.”

(a) Intryingtodecidewhethertostayorleave,whatistheopportunitycostofstayingtowatch therestofthemovie?

Answer:Theopportunitycostofanyactivityiswhatwegiveupbyundertakingthatactivity. Theopportunitycostofstayinginthemovieiswhateverwewouldchoosetodowithout timeifwewerenotthere.Thepriceofthemovieticketsthatgotusintothemovietheateris NOTapartofthisopportunitycost—because,whetherwestay orleave,wedonotgetthat moneyback.

(b) Supposewehadreadasignonthewayintothetheaterstating“SatisfactionGuaranteed! Don’tlikethemoviehalfwaythrough—seethemanagerandget yourmoneyback!”How doesthischangeyouranswertopart(a)?

Answer:Now,inadditiontogivingupwhateveritiswewouldbedoing ifweweren’twatchingthemovie,wearealsogivingupthepriceofthemovietickets.Putdifferently,bystaying inthemovietheater,wearegivinguptheopportunitytogeta refund—andsothecostof theticketsisarealopportunitycostofstaying.

ChoiceSetsandBudgetConstraints

: SupposemybrotherandIbothgoona week-longvacationinCaymanand,whenwearriveattheairportontheisland,wehavetochoosebetweeneitherrentingacarortakingataxitoourhotel.Rentingacarinvolvesafixedfeeof$300forthe week,witheachmiledrivenafterwardsjustcosting20cents —thepriceofgasolinepermile.Takinga taxiinvolvesnofixedfees,buteachmiledrivenontheisland duringtheweeknowcosts$1permile.

2.6 EverydayApplication: RentingaCarversusTakingTaxis

A: SupposebothmybrotherandIhavebrought$2,000onourtriptospendon“milesdrivenonthe island”and“othergoods”.Onagraphwithmilesdrivenonthe horizontalandotherconsumption ontheverticalaxis,illustratemybudgetconstraintassumingIchosetorentacarandmybrother’s budgetconstraintassuminghechosetotaketaxis.

Answer:ThetwobudgetlinesaredrawninGraph2.5.Mybrothercould spendasmuchas$2,000 onothergoodsifhestaysattheairportanddoesnotrentanytaxis,butforeverymilehetakesa taxi,hegivesup$1inothergoodconsumption.Themosthecan driveontheislandis2,000miles. AssoonasIpaythe$300rentalfee,Icanatmostconsume$1,700inothergoods,buteachmile costsmeonly20cents.Thus,Icandriveasmuchas1700/0.2=8,500miles.

Graph2.5:Graphsofequationsinexercise2.6

(a) WhatistheopportunitycostforeachmiledriventhatIfaced?

Answer:Iamrentingacar—whichmeansIgiveup20centsinotherconsumptionpermile driven.Thus,myopportunitycostis20cents.Myopportunitycostdoesnotincludethe rentalfeesinceIpaidthatbeforeevengettingintothecar.

(b) Whatistheopportunitycostforeachmiledriventhatmybrotherfaced?

Answer:Mybrotheristakingtaxis—sohehastogiveup$1inotherconsumptionforevery miledriven.Hisopportunitycostistherefore$1permile.

B: Derivethemathematicalequationsformybudgetconstraint andmybrother’sbudgetconstraint, andrelateelementsoftheseequationstoyourgraphsinpart A.Usex1 todenotemilesdrivenand x2 todenoteotherconsumption.

Answer:Mybudgetconstraint,onceIpaytherentalfee,is0.2x1 + x2 = 1700whilemybrother’s budgetconstraintis x1 + x2 = 2000.Thesecanberewrittenwith x2 onthelefthandsideas

x2 = 1700 0.2x1 forme,and (2.8)

x2 = 2000 x1 formybrother. (2.9)

Theinterceptterms(1700formeand2000formybrother)aswellastheslopes( 0.2formeand 1formybrother)areasinGraph2.5.

(a) Whereinyourbudgetequationformecanyoulocatetheopportunitycostofamiledriven?

Answer:Myopportunitycostofmilesdrivenissimplytheslopeterm inmybudgetequation —i.e.0.2.Igiveup$0.20inotherconsumptionforeverymile driven.

(b) Whereinyourbudgetequationformybrothercanyoulocatetheopportunitycostofamile driven?

Answer:Mybrother’sopportunitycostofmilesdrivenistheslopeterminhisbudgetequation—i.e.1;hegivesup$1inotherconsumptionforeverymiledriven.

ChoiceSetsandBudgetConstraints

: Onarecentdoctor’svisit,youhavebeentoldthatyou mustwatchyourcalorieintakeandmustmakesureyougetenoughvitaminEinyourdiet.

2.7 EverydayApplication: DietingandNutrition

A: Youhavedecidedthat,tomakelifesimple,youwillfromnowoneatonlysteakandcarrots.A nicesteakhas250caloriesand10unitsofvitamins,andaservingofcarrotshas100caloriesand30 unitsofvitaminsYourdoctor’sinstructionsarethatyoumusteat nomore than2000caloriesand consume atleast 150unitsofvitaminsperday.

(a) Inagraphwith“servingsofcarrots”onthehorizontalandsteakontheverticalaxis,illustrate allcombinationsofcarrotsandsteaksthatmakeupa2000calorieadaydiet.

Answer:Thisisillustratedasthe“calorieconstraint”inpanel(a)ofGraph2.6.Youcanget 2000caloriesonlyfromsteakifyoueat8steaksandonlyfrom carrotsifyoueat20servings ofcarrots.Theseformtheinterceptsofthecalorieconstraint.

Graph2.6:(a)CaloriesandVitamins;(b)BudgetConstraint

(b) Onthesamegraph,illustrateallthecombinationsofcarrotsandsteaksthatprovideexactly 150unitsofvitamins.

Answer:Thisisalsoillustratedinpanel(a)ofGraph2.6.Youcanget150unitsofvitamins fromsteakifyoueat15steaksonlyorifyoueat5servingsofcarrotsonly.Thisresultsinthe interceptsforthe“vitaminconstraint”.

(c) Onthisgraph,shadeinthebundlesofcarrotsandsteaksthat satisfybothofyourdoctor’s requirements.

Answer:Yourdoctorwantsyoutoeatnomorethan2000calories—whichmeansyouneed tostayunderneaththecalorieconstraint.Yourdoctoralso wantsyoutogetatleast150units ofvitaminE—whichmeansyoumustchooseabundle above thevitaminconstraint.This leavesyouwiththeshadedareatochoosefromifyouaregoing tosatisfybothrequirements.

(d) Nowsupposeyoucanbuyaservingofcarrotsfor$2andasteakfor$6.Youhave$26perday inyourfoodbudget.Inyourgraph,illustrateyourbudgetconstraint.Ifyoulovesteakand don’tmindeatingornoteatingcarrots,whatbundlewillyou choose(assumingyoutakeyour doctor’sinstructionsseriously)?

Answer:With$26youcanbuy13/3steaksifthatisallyoubuy,oryoucanbuy13servingsof carrotsifthatisallyoubuy.Thisformsthetwointerceptsonyourbudgetconstraintwhich hasaslopeof p1/p2 =−1/3andisdepictedinpanel(b)ofthegraph.Ifyoureallylikesteak anddon’tmindeatingcarrotsonewayoranother,youwouldwanttogetasmuchsteak aspossiblegiventheconstraintsyourdoctorgaveyouandgivenyourbudgetconstraint. Thisleadsyoutoconsumethebundleattheintersectionofthevitaminandthebudget constraintinpanel(b)—indicatedby(x1, x2)inthegraph.Itseemsfromthetwopanels thatthisbundlealsosatisfiesthecalorieconstraintandliesinsidetheshadedregion.

B: ContinuewiththescenarioasdescribedinpartA.

(a) DefinethelineyoudrewinA(a)mathematically.

2000whichcanbewrittenas

(b) DefinethelineyoudrewinA(b)mathematically.

(c) Informalsetnotation,writedowntheexpressionthatisequivalenttotheshadedareainA(c).

(d) DerivetheexactbundleyouindicatedonyourgraphinA(d).

Answer:Wewouldliketofindthemostamountofsteakwecanaffordintheshadedregion. Ourbudgetconstraintis2x1 + 6x2 = 26.Ourgraphsuggeststhatthisbudgetconstraint intersectsthevitaminconstraint(fromequation(2.11))withintheshadedregion(inwhich casethatintersectiongivesusthemoststeakwecanaffordintheshadedregion).Tofind thisintersection,wecanplugequation(2.11)intothebudgetconstraint2x1 + 6x2 = 26to get 2x1 + 6(15 3x1 ) = 26, (2.13) andthensolvefor x1 toget x1 = 4.Pluggingthisbackintoeitherthebudgetconstraintor thevitaminconstraint,wecanget x2 = 3.Weknowthisliesonthevitaminconstraintaswell asthebudgetconstraint.Tochecktomakesureitliesintheshadedregion,wejusthaveto makesureitalsosatisfiesthedoctor’sordersthatyouconsumefewerthan2000calories. Thebundle(x1, x2)=(4,3)resultsincaloriesof4(100) + 3(250) = 1150,wellwithindoctor’s orders.

ChoiceSetsandBudgetConstraints

: Supposethatyou,afterstudyingeconomicsin college,quicklybecamerich—sorichthatyouhavenothingbettertodothanworryaboutyour16-year oldniecewhocan’tseemtofocusonherfuture.Yourniececurrentlyalreadyhasatrustfundthatwillpay heraniceyearlyincomeof$50,000startingwhensheis18,andshehasnoothermeansofsupport.

2.8 EverydayApplication: SettingupaCollegeTrustFund

A: Youareconcernedthatyourniecewillnotseethewisdomofspendingagoodportionofhertrust fundonacollegeeducation,andyouwouldthereforeliketouse$100,000ofyourwealthtochange herchoicesetinwaysthatwillgivehergreaterincentivestogotocollege.

(a) Oneoptionisforyoutoplace$100,000inasecondtrustfundbuttorestrictyourniecetobe abletodrawonthistrustfundonlyforcollegeexpensesofup to$25,000peryearforfouryears. Onagraphwith“yearlydollarsspentoncollegeeducation”onthehorizontalaxisand“yearly dollarsspentonotherconsumption”onthevertical,illustratehowthisaffectsherchoiceset.

Answer:Panel(a)ofGraph2.7illustratesthechangeinthebudgetconstraintforthistype oftrustfund.Theoriginalbudgetshiftsoutby$25,000(denoted$25K),exceptthatthefirst $25,000canonlybeusedforcollege.Thus,themaximumamountofotherconsumptionremains$50,000becauseofthestipulationthatshecannotuse thetrustfundfornon-college expenses.

(b) Asecondoptionisforyoutosimplytellyourniecethatyouwillgiveher$25,000peryearfor 4yearsandyouwilltrustherto“dowhat’sright”.Howdoesthisimpactherchoiceset?

Answer:Thisisdepictedinpanel(b)ofGraph2.7—itisapureincome shiftof$25,000since therearenorestrictionsonhowthemoneycanbeused.

(c) Supposeyouarewrongaboutyourniece’sshort-sightedness andshewasplanningonspendingmorethan$25,000peryearfromherothertrustfundoncollegeeducation.Doyouthink shewillcarewhetheryoudoasdescribedinpart(a)orasdescribedinpart(b)?

Answer:Ifshewasplanningtospendmorethan$25Koncollegeanyhow,thentheadditionalbundlesmadepossiblebythetrustfundin(b)arenotvaluedbyher.Shewould thereforenotcarewhetheryousetupthetrustfundasin(a)or(b).

(d) Supposeyouwererightabouther—sheneverwasgoingtospend verymuchoncollege.Will shecarenow?

Answer:Nowshewillcare—becauseshewouldactuallychooseoneofthebundlesmade availablein(b)thatisnotavailablein(a)andwouldthereforeprefer(b)over(a).

(e) Afriendofyoursgivesyousomeadvice:becareful—yourniecewillnotvaluehereducation ifshedoesnothavetoputupsomeofherownmoneyforit.Soberedbythisadvice,youdecide tosetupadifferenttrustfundthatwillrelease50centstoyourniece(tobespentonwhatever shewants)foreverydollarthatshespendsoncollegeexpenses.Howwillthisaffectherchoice set?

Answer:Thisisdepictedinpanel(c)ofGraph2.7.Ifyourniecenowspends$1oneducation, shegets50centsforanythingshewouldliketospenditon—so,ineffect,theopportunity costofgetting$1ofadditionaleducationisjust50cents.This“matching”trustfundthereforereducestheopportunitycostofeducationwhereasthepreviousonesdidnot.

(f) Ifyourniecespends$25,000peryearoncollegeunderthetrustfundinpart(e),canyou identifyaverticaldistancethatrepresentshowmuchyoupaidtoachievethisoutcome?

Answer:Ifyourniecespends$25,000onhereducationunderthe“matching”trustfund, shewillgethalfofthatamountfromyourtrustfund—or$12,500.Thiscanbeseenasthe verticaldistancebetweenthebeforeandafterbudgetconstraints(inpanel(c)ofthegraph) at$25,000ofeducationspending.

B: Howwouldyouwritethebudgetequationforeachofthethreealternativesdiscussedabove?

Answer:Theinitialbudgetis x1 + x2 = 50,000.Thefirsttrustfundin(a)expandsthistoabudget of

ChoiceSetsandBudgetConstraints

2.9 BusinessApplication: PricingandQuantityDiscounts: Businessesoftengivequantitydiscounts.Below,youwillanalyzehowsuchdiscountscanimpactchoicesets.

A: Irecentlydiscoveredthatalocalcopyservicechargesoureconomicsdepartment$0.05perpage(or $5per100pages)forthefirst10,000copiesinanygivenmonth butthenreducesthepriceperpage to$0.035foreachadditionalpageupto100,000copiesandto $0.02pereachpagebeyond100,000. Supposeourdepartmenthasamonthlyoverallbudgetof$5,000.

(a) Putting“pagescopiedinunitsof100”onthehorizontalaxis and“dollarsspentonother goods”onthevertical,illustratethisbudgetconstraint. Carefullylabelallinterceptsand slopes.

Answer:Panel(a)ofGraph2.8tracesoutthisbudgetconstraintand labelstherelevant slopesandkinkpoints.

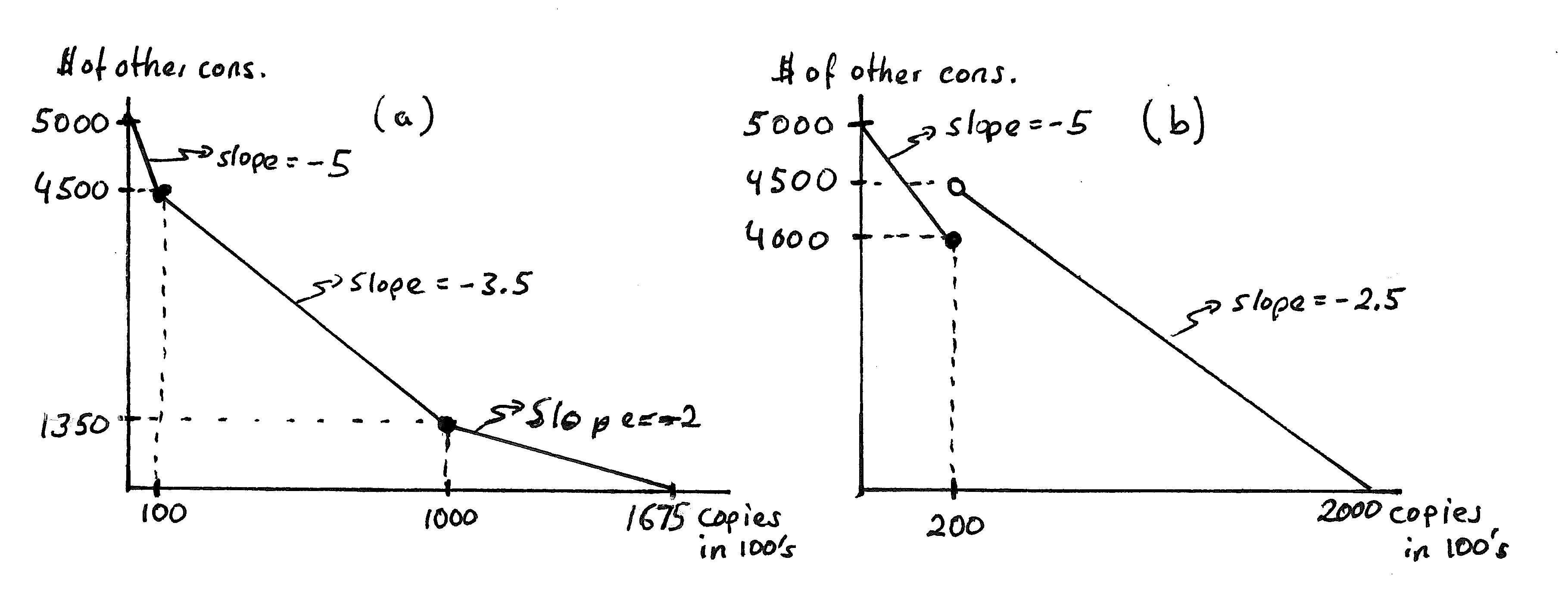
(b) Supposethecopyservicechangesitspricingpolicyto$0.05 perpageformonthlycopyingup to20,000and$0.025perpagefor all pagesifcopyingexceeds20,000permonth.(Hint:Your budgetlinewillcontainajump.)

Answer:Panel(b)ofGraph2.8depictsthisbudget.Thefirstportion (beginningatthe x2 intercept)isrelativelystraightforward.Thesecondpart arisesforthefollowingreason:The problemsaysthat,ifyoucopymorethan2000pages, all pagescostonly$0.025perpage —includingthefirst2000.Thus,whenyoucopy20,000pagespermonth,youtotalbillis $1,000.Butwhenyoucopy2001pages,yourtotalbillis$500.025.

(c) Whatisthemarginal(or“additional”)costofthefirstpagecopiedafter20,000inpart(b)? Whatisthemarginalcostofthefirstpagecopiedafter20,001 inpart(b)?

Answer:Themarginalcostofthefirstpageafter20,000is-$499.975,andthemarginalcost ofthenextpageafterthatis2.5cents.Toseethedifference betweenthese,thinkofthe marginalcostastheincreaseinthetotalphoto-copybillforeachadditionalpage.When goingfrom20,000to20,001,thetotalbillfallsby$499.975.Whengoingfrom20,001to 20,002,thetotalbillrisesby2.5cents.

B: Writedownthemathematicalexpressionforchoicesetsforeachofthescenariosin2.9A(a)and 2.9A(b)(usingx1 todenote“pagescopiedinunitsof100”andx2 todenote“dollarsspentonother goods”).

Answer:Thechoicesetin(a)is

Graph2.8:(a)Constraintfrom2.9A(a);(b)Constraintfrom 2.9A(b)

ChoiceSetsandBudgetConstraints

2.10 BusinessApplication: Supersizing: SupposeIrunafast-foodrestaurantandIknowmycustomers comeinonalimitedbudget.Almosteveryonethatcomesinfor lunchbuysasoft-drink.Nowsuppose itcostsmevirtuallynothingtoserveamediumversusalarge soft-drink,butIdoincursomeextracosts whenaddingitems(likeadessertoranotherside-dish)tosomeone’slunchtray.

A: Supposeforpurposesofthisexercisethatcupscomeinallsizes,notjustsmall,mediumandlarge; andsupposetheaveragecustomerhasalunchbudgetB.Onagraphwith“ouncesofsoft-drink”on thehorizontalaxisand“dollarsspentonotherlunchitems” onthevertical,illustrateacustomer’s budgetconstraintassumingIchargethesamepricepperounceofsoft-drinknomatterhowbiga cupthecustomergets.

Answer:Panel(a)ofGraph2.9illustratestheoriginalbudget,withthepriceperouncedenoted p Thehorizontalinterceptisthemoneybudget B dividedbythepriceperounceofsoftdrink;the verticalinterceptisjust B (sincethegoodontheverticalaxisisdenominatedindollars—withthe priceof“$’soflunchitems”thereforeimplicitlysetto1.

(a) Ihavethreebusinesspartners:Larry,hisbrotherDaryland hisotherbrotherDaryl.The Darylsproposethatwelowerthepriceoftheinitialouncesofsoft-drinkthataconsumer buysandthen,startingat10ounces,weincreasetheprice.Theyhavecalculatedthatour averagecustomerwouldbeabletobuyexactlythesamenumber ofouncesofsoft-drink(if thatisallheboughtonhislunchbudget)asunderthecurrent singleprice.Illustratehowthis willchangetheaveragecustomer’sbudgetconstraint.

Answer:Panel(b)illustratestheDaryls’proposal.Thebudgetisinitiallyshallower(because oftheinitiallowerpriceandthenbecomessteeperat10ouncesbecauseofthenewhigher price.)Theinterceptsareunchangedbecausenothinghasbeendonetoallowtheaverage customertobuymoreofnon-drinkitemsifthatisallshebuys,andbecausethenewprices havebeenconstructedsoastoallowcustomerstoachievethe sametotaldrinkconsumptionintheeventthattheydonotbuyanythingelse.

(b) LarrythinkstheDarylsareidiotsandsuggestsinsteadthat weraisethepriceforinitialounces ofsoft-drinkandthen,startingat10ounces,decreasethepriceforanyadditionalounces. He,too,hascalculatedthat,underhispricingpolicy,theaveragecustomerwillbeabletobuy exactlythesameouncesofsoft-drinks(ifthatisallthecustomerbuysonhislunchbudget). Illustratetheeffectontheaveragecustomer’sbudgetconstraint.

Answer:Larry’sproposalisgraphedinpanel(c).Thereasoningissimilartothatinthe previouspart,exceptnowtheinitialpriceishighandthenbecomeslowafter10ounces.

(c) Iftheaveragecustomerhadachoice,whichofthethreepricingsystems—thecurrentsingle price,theDaryls’proposalorLarry’sproposal—wouldhechoose?

Answer:CustomerswouldsurelyprefertheDaryls’proposal—since thechoicesetitforms containsalltheotherchoicesets.

Graph2.9:(a)OriginalBudget;(b)TheDaryls’proposal;(c)Larry’sproposal

Microeconomics An Intuitive Approach with Calculus 1st

P.S:IfyoudidnotcatchthereferencetoLarry,hisbrotherDarylandhisotherbrotherDaryl, Irecommendyourentsomeoldversionsofthe1980’sBobNewhartShow.

B: Writedownthemathematicalexpressionforeachofthethree choicesetsdescribedabove,letting ouncesofsoft-drinksbedenotedbyx1 anddollarsspendonotherlunchitemsbyx2

Answer:Theoriginalbudgetsetinpanel(a)ofGraph2.9issimply px1 + x2 = B givingachoiceset

IntheDaryls’proposal,wehaveaninitialprice p′ < p forthefirst10ounces,andthenaprice p′′ > p thereafter.Wecancalculatethe x2 interceptofthesteeperlinefollowingthekinkpointin panel(b)ofthegraphbysimplymultiplyingthe x1 interceptof B /p bytheslope p′′ ofthatline segmenttoget Bp′′/p.ThechoicesetfromtheDaryls’proposalcouldthenbewrittenas

Wecouldevenbemorepreciseabouttherelationshipof

10,anditmustthereforebethecasethat

Larry’sproposalbeginswithaprice p′′ > p andthenswitchesat10ouncestoaprice p′ < p (where thesepriceshavenoparticularrelationtothepriceswejustusedfortheDaryl’sproposal).This resultsinthechoiceset

Wecouldagainderiveananalogousexpressionfor