LÓGICA MATEMÁTICA REVISTA
Contenidos del semestre Teorías conceptos y ejemplos
Secciones de curiosidad
Sabías que y menciones
Contenido adicional Quizzes y activiades divertidas

AUNER MANRIQUE
JUÁREZ YAMAS
"EL IGNORANTE AFIRMA, EL SABIO DUDA Y REFLEXIONA"
LA LÓGICA
La lógica es una disciplina filosófica que se ocupa del estudio de los principios y métodos utilizados para distinguir el razonamiento válido del inválido Es la ciencia del pensamiento y la inferencia válida. La palabra "lógica" proviene del término griego "logikḗ" , que significa "razonamiento" o "discurso racional"

La lógica se remonta a la antigua Grecia, y uno de los filósofos más destacados en este campo fue Aristóteles (384-322 a.C.).
Aristóteles es considerado uno de los padres fundadores de la lógica occidental y su obra "Organon" (conjunto de tratados lógicos) sentó las bases para el estudio sistemático de la lógica.

En la lógica aristotélica, el razonamiento se basa en dos principios fundamentales: el principio de identidad y el principio de no contradicción.
Ejemplo
Premisa 1: Si hace sol, iré a la playa
Premisa 2: Está haciendo sol.
Conclusión: Por lo tanto, iré a la playa.
El principio de identidad establece que una cosa es idéntica a sí misma, es decir, A es A
El principio de no contradicción sostiene que una proposición no puede ser verdadera y falsa al mismo tiempo, es decir, A no puede ser simultáneamente A y no A.
Además de estos principios, Aristóteles desarrolló una serie de herramientas y métodos para el análisis lógico, como los silogismos Los silogismos son argumentos deductivos compuestos por dos premisas y una conclusión, y se basan en relaciones de implicación lógica entre las proposiciones.

En este caso, se establece una condicional en la premisa 1, indicando que si hace sol, entonces iré a la playa Luego, en la premisa 2 se afirma que está haciendo sol. A partir de estas premisas, se llega a la conclusión de que iré a la playa, ya que ambas condiciones se cumplen

Principio de identidad: Este principio establece que una cosa es idéntica a sí misma.
Ejemplo: "El sol es el sol" En este caso, se afirma que el sol es idéntico a sí mismo, lo cual es una verdad lógica evidente.
Principio de no contradicción: Este principio sostiene que una proposición no puede ser verdadera y falsa al mismo tiempo.
Ejemplo: "Es de día y no es de día". Esta afirmación contradice el principio de no contradicción, ya que no puede ser verdadera y falsa simultáneamente
PRINCIPIOS DE LA LOGICA
Principio del tercero excluido: Este principio establece que una proposición o es verdadera o es falsa, sin posibilidad de una tercera opción.
Ejemplo: "Está lloviendo o no está lloviendo" Según el principio del tercero excluido, una de estas opciones debe ser verdadera y la otra falsa, no hay una tercera posibilidad.
Principio de razón suficiente: Este principio establece que todo evento o hecho tiene una explicación o causa suficiente.
Ejemplo: Si encuentras un plato roto en el suelo, puedes preguntarte qué causó que el plato se rompiera Según el principio de razón suficiente, debe haber una causa o explicación detrás de ello, como que alguien lo dejó caer o que se resbaló de las manos.
Estos principios lógicos forman la base de la coherencia y la validez en el razonamiento lógico, y se utilizan para evaluar la consistencia y la estructura de los argumentos.
"Sabías que, según el principio de no contradicción, una afirmación no puede ser verdadera y falsa al mismo tiempo, lo cual es fundamental para mantener la coherencia lógica en nuestros razonamientos."

OPERACIONES CON CONJUNTOS

Intersección de conjuntos La intersección de dos conjuntos A y B es el conjunto formado por todos los elementos comunes a los dos conjuntos. La intersección de A y B se denota por A B, y en lenguaje lógico el conjunto puede escribirse como:





La unión de dos conjuntos A y B consta de todos los elementos que pertenecen a A o a B La unión de A y B se denota por A U B. En lenguaje lógico podemos escribir:

Imagina que hay dos grupos de personas: "Amantes del café" y "Amantes de las películas de ciencia ficción".

Ahora bien, si realizamos la intersección de estos conjuntos, obtendremos un nuevo conjunto: "Amantes del café y películas de ciencia ficción". ¿No es genial?
Esto significa que existe un grupo de personas apasionadas tanto por el café como por las películas de ciencia ficción. Pueden disfrutar de un buen café mientras ven sus películas favoritas del género, ¡una combinación perfecta para una tarde de diversión!
ALGORITMO
OPERACIONES CON CONJUNTOS

Identifica el tipo de operación que se requiere: unión (∪) o intersección (∩).

Si la operación es unión (∪):
Crea un conjunto vacío C para almacenar el resultado.
Agrega todos los elementos del conjunto A a C.
Recorre cada elemento del conjunto B.
Si el elemento no está en C, agrégalo a C.
El conjunto C ahora contiene la unión de A y B
Si la operación es intersección (∩):
Crea un conjunto vacío C para almacenar el resultado.
Recorre cada elemento del conjunto A

Si el elemento también está en B, agrégalo a C.
El conjunto C ahora contiene la intersección de A y B.
Muestra el conjunto resultante C como resultado de la operación
Salida: Conjunto resultante de la operación.
Siguiendo este algoritmo paso a paso, podrás resolver problemas relacionados con la unión y la intersección de conjuntos.
Asegúrate de adaptar el algoritmo según las necesidades específicas de tu problema y el lenguaje de programación que estés utilizando.
PUBLICIDAD

Ejemplo: Dado el conjunto A = {1, 2, 3} y el conjunto B = {2, 3, 4}, vamos a encontrar la unión (∪) y la intersección (∩) entre ellos.
EJEMPLO ALGORITMO
Identificación de la operación: En este caso, queremos encontrar tanto la unión como la intersección.
Unión (∪):

Creamos un conjunto vacío C.
Agregamos todos los elementos de A a C: C = {1, 2, 3}.
Recorremos cada elemento de B
El elemento 2 ya está en C, no se agrega.
El elemento 3 ya está en C, no se agrega.
Agregamos el elemento 4 a C: C = {1, 2, 3, 4}

La unión de A y B es C = {1, 2, 3, 4}.
Intersección (∩):
Creamos un conjunto vacío C
Recorremos cada elemento de A.
El elemento 1 no está en B, no se agrega a C.
Agregamos el elemento 2 a C: C = {2}
Agregamos el elemento 3 a C: C = {2, 3}.
La intersección de A y B es C = {2, 3}.
Mostramos los conjuntos resultantes:
La unión de A y B es {1, 2, 3, 4}.
La intersección de A y B es {2, 3}.
En este ejemplo, utilizamos el algoritmo para encontrar la unión y la intersección entre los conjuntos A y B Obtenemos los conjuntos resultantes, que son {1, 2, 3, 4} para la unión y {2, 3} para la intersección.
Recuerda que este es solo un ejemplo ilustrativo y puedes aplicar el algoritmo a conjuntos de cualquier tamaño o contenido.
LÓGICA PROPOSICIONAL
La lógica proposicional es una rama de la lógica que se centra en el estudio y análisis de las proposiciones o afirmaciones, las cuales pueden ser verdaderas o falsas La lógica proposicional utiliza operadores lógicos, como la disyunción, conjunción, condicional y bicondicional, para construir fórmulas lógicas y analizar su validez.

Disyunción (∨): La disyunción es un operador lógico que se utiliza para combinar dos proposiciones, indicando que al menos una de ellas es verdadera. La disyunción se representa con el símbolo ∨.
Ejemplo: Si consideramos las proposiciones "llueve" y "hace sol", la disyunción de estas proposiciones sería "llueve ∨ hace sol". Esta afirmación sería verdadera si al menos una de las dos proposiciones es verdadera. Si llueve o hace sol, o incluso si ambas afirmaciones son verdaderas, la disyunción es verdadera.
Conjunción (∧): La conjunción es un operador lógico que se utiliza para combinar dos proposiciones, indicando que ambas son verdaderas. La conjunción se representa con el símbolo ∧.
Ejemplo: Siguiendo con las proposiciones anteriores, la conjunción de "llueve" y "hace sol" sería "llueve ∧ hace sol". Esta afirmación solo sería verdadera si ambas proposiciones son verdaderas. Si llueve y hace sol al mismo tiempo, entonces la conjunción es verdadera; de lo contrario, es falsa.

"¿Sabías que la tabla de disyunción (OR) y conjunción (AND) utilizada en electrónica se basa en principios lógicos? Estas operaciones son fundamentales para diseñar circuitos electrónicos y controlar el flujo de corriente.

Estas operaciones lógicas forman la base de la lógica digital y son esenciales en el funcionamiento de dispositivos electrónicos como computadoras y smartphones."

LÓGICA PROPOSICIONAL
Condicional (→): El condicional es un operador lógico que se utiliza para establecer una relación de implicación entre dos proposiciones Indica que si la primera proposición es verdadera, entonces la segunda también lo es El condicional se representa con el símbolo → .
Ejemplo: Consideremos las proposiciones "Si estudio, aprobaré" y "Estudio". El condicional entre estas proposiciones sería "Si estudio, aprobaré → Estudio". Esta afirmación es verdadera, ya que si estudiar implica aprobar y la proposición "Estudio" es verdadera, entonces se cumple la relación de implicación
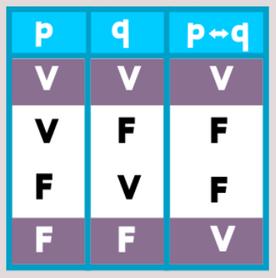

Bicondicional (↔): El bicondicional es un operador lógico que indica que dos proposiciones son equivalentes, es decir, que tienen el mismo valor de verdad El bicondicional se representa con el símbolo ↔ .
Ejemplo: Si tenemos las proposiciones "Los triángulos son polígonos de tres lados" y "Las figuras de tres lados son triángulos", el bicondicional sería "Los triángulos son polígonos de tres lados ↔ Las figuras de tres lados son triángulos" Esta afirmación es verdadera, ya que ambas proposiciones son equivalentes y tienen el mismo valor de verdad.
"Sabías que en programación, el condicional 'if-else' se utiliza para tomar decisiones basadas en condiciones lógicas? Es una estructura fundamental que te permite controlar el flujo de ejecución de tu programa. Además, el operador bicondicional ' === ' se utiliza en algunos lenguajes de programación para comparar tanto el valor como el tipo de dos variables. Estas operaciones lógicas son esenciales en el desarrollo de algoritmos y te permiten crear programas más robustos y flexibles "


Para comprender mejor los temas es necesario practicar, acá te dejamos unos ejercicios para que aceptes el reto de resolverlos:
Disyunción (∨): Ejercicio: Determinar la veracidad de la siguiente afirmación: "El número es par o es divisible por 3".

Conjunción (∧): Ejercicio: Determinar la veracidad de la siguiente afirmación: "El número es mayor que 5 y menor que 10".
Condicional (→): Ejercicio: Determinar la veracidad de la siguiente afirmación: "Si llueve, entonces me llevaré el paraguas".


Bicondicional (↔): Ejercicio: Determinar la veracidad de la siguiente afirmación: "El número es primo si y solo si es mayor que 1 y no tiene divisores aparte de 1 y él mismo".
Si tus resultados son parecidos a estos estás entendiendo bien el tema:




LÓGICA PROPOSICIONAL
Ejercicio: Determina la tabla de verdad para la expresión ~(P ∧ Q) ∨ (~P → R).

Ejercicio: Determina la tabla de verdad para la expresión (P ∨ ~Q) ∧ (~P → R).




Ejercicio: Determina la tabla de verdad para la expresión (~P ∨ Q) ∧ (R ↔ P).
En cada tabla de verdad, se muestra el resultado de la expresión dada para todas las combinaciones posibles de los valores de verdad de las proposiciones involucradas (P, Q y R), así como los pasos intermedios para llegar a dicho resultado. Los valores "V" representan verdadero y los valores "F" representan falso.
Resuelve los siguientes ejercicios de lógica proposicional

Ejercicio 1: Expresión: ~(P ∧ Q) ∨ (R ↔ ~P) ∧ (~Q → P)





Ejercicio 2: Expresión: (P ∨ ~Q) ∧ (~P → R) ∨ (Q ↔ ~R)




















Resuelve la siguiente sopa de letras:


FORMALIZACIÓN DE PROPOSICIONES
La formalización de proposiciones es un proceso mediante el cual se traducen las proposiciones del lenguaje natural a un lenguaje formal utilizando símbolos y reglas precisas. Este proceso facilita el análisis y la evaluación lógica de las proposiciones

La formalización de proposiciones involucra el uso de símbolos para representar los conectivos lógicos y las proposiciones Algunos de los símbolos comunes utilizados en la formalización son:
Para ilustrar el proceso de formalización, consideremos la siguiente proposición en lenguaje natural: "Si llueve, entonces llevaré mi paraguas o me mojaré".
Paso 1: Identificar las proposiciones involucradas:
P: Llueve
Q: Llevaré mi paraguas
R: Me mojaré
Paso 2: Representar los conectivos lógicos: La conjunción se representa con el símbolo ∧, la disyunción con el símbolo ∨, la negación con el símbolo ¬, la implicación con el símbolo → , y la bicondicional con el símbolo ↔
Paso 3: Formalizar la proposición: La proposición se puede formalizar de la siguiente manera: P → (Q∨R)

Paso 4: Construir la tabla de verdad: Para evaluar la validez de la proposición formalizada, se construye una tabla de verdad que muestra todas las posibles combinaciones de valores de verdad de las proposiciones involucradas, así como el valor de verdad de la proposición completa ∧ para representar la conjunción (y lógico).

∨ para representar la disyunción (o lógico).
¬ para representar la negación (no).
→ para representar la implicación (si...entonces).
↔ para representar la bicondicional (si y solo si).
FORMALIZACIÓN DE OPOSICIONES
La formalización de proposiciones proporciona una base sólida para el estudio de la lógica y su aplicación en diversos campos como la informática, la matemática y la filosofía.


Ejemplos de formalización de proposiciones:
Ejercicio 1: Proposición: Si llueve, entonces no saldré de casa.

Formalización: P → ¬Q
Tabla de verdad:
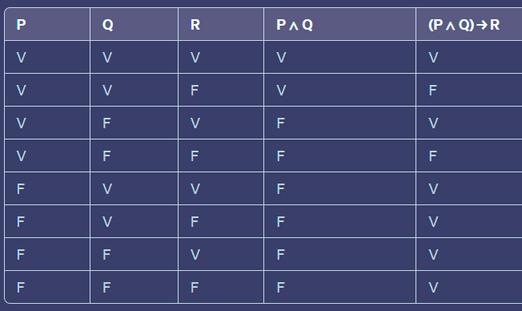
Ejercicio 2: Proposición: Si hace sol y hace calor, entonces iré a la playa.
Formalización: (P ∧ Q) → R
Tabla de verdad:

EQUIVALENCIAS LÓGICAS
Las equivalencias lógicas son transformaciones lógicas que nos permiten establecer relaciones de igualdad entre diferentes proposiciones. Estas equivalencias se basan en reglas y propiedades lógicas que nos permiten simplificar y manipular proposiciones de manera algebraica Algunas de las equivalencias lógicas más comunes son:

Equivalencias Conmutativas:
p ∧ q ≡ q ∧ p
p ∨ q ≡ q ∨ p
Equivalencias Asociativas:
(p ∧ q) ∧ r ≡ p ∧ (q ∧ r)
(p ∨ q) ∨ r ≡ p ∨ (q ∨ r)
Equivalencias Distributivas:
p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)

Equivalencias de Morgan:
¬(p ∧ q) ≡ ¬p ∨ ¬q
¬(p ∨ q) ≡ ¬p ∧ ¬q
Estas son solo algunas de las equivalencias lógicas más utilizadas, pero existen muchas más. Estas equivalencias nos permiten simplificar expresiones lógicas, demostrar teoremas y argumentos, y establecer relaciones entre diferentes proposiciones. Es importante destacar que las equivalencias lógicas se basan en la lógica proposicional y están respaldadas por las leyes fundamentales de la lógica Son herramientas poderosas en el análisis y la manipulación de proposiciones y juegan un papel fundamental en el razonamiento lógico.

Ejemplo
Equivalencia Conmutativa: p ∧ q ≡ q ∧ p Tabla de verdad:

En este ejemplo, comparamos la proposición "p ∧ q" (p y q) con la proposición "q ∧ p" (q y p) utilizando la equivalencia conmutativa La tabla de verdad muestra que ambas proposiciones tienen los mismos valores de verdad en todas las posibles combinaciones de valores de p y q, lo que indica que son equivalentes
Esto significa que no importa el orden en que se escriban p y q, la conjunción entre ellos siempre dará el mismo resultado. Es un ejemplo de cómo podemos simplificar y transformar proposiciones utilizando las equivalencias lógicas
1. 2. 3 4.RAZONAMIENTO
Razonamiento Inductivo: El razonamiento inductivo se basa en la observación de patrones y generalizaciones a partir de ejemplos específicos. Se utiliza para llegar a una conclusión general a partir de la evidencia limitada En el razonamiento inductivo, la conclusión no se considera necesariamente verdadera o falsa, sino que se evalúa en términos de su probabilidad.
Teoría: En el razonamiento inductivo, se parte de casos particulares para llegar a una conclusión general. Se infiere que una afirmación es probablemente cierta en base a la observación repetida de ejemplos.
Ejemplo: Observación de que cada manzana que se ha comido es dulce Conclusión inductiva: Todas las manzanas son dulces
Razonamiento Deductivo: El razonamiento deductivo se basa en la aplicación de reglas o principios generales para llegar a una conclusión específica. Se parte de afirmaciones o premisas aceptadas como verdaderas y se sigue un proceso lógico para llegar a una conclusión que se considera necesariamente verdadera si las premisas lo son.
Teoría: En el razonamiento deductivo, se utiliza el razonamiento lógico para inferir una conclusión a partir de premisas establecidas.

Ejemplo: Premisa: Todos los mamíferos son animales que tienen pelo. Premisa: Un perro es un mamífero. Conclusión deductiva: Por lo tanto, un perro tiene pelo
Comparación entre razonamiento inductivo y deductivo:

En el razonamiento inductivo, se parte de observaciones específicas y se generaliza para llegar a una conclusión general. En el razonamiento deductivo, se parte de premisas generales y se llega a una conclusión específica
El razonamiento inductivo se basa en la probabilidad y la generalización, mientras que el razonamiento deductivo se basa en la lógica y la necesidad
Sabías que el famoso filósofo y científico Francis Bacon es considerado uno de los pioneros en la promoción del método científico y en la distinción entre el razonamiento inductivo y deductivo. Bacon defendió el uso del razonamiento inductivo como un enfoque válido para obtener conocimiento científico. Sin embargo, también reconoció la importancia del razonamiento deductivo para deducir consecuencias lógicas de las premisas establecidas.

PROPOSICIONES CATEGÓRICAS

Las proposiciones categóricas son enunciados que afirman o niegan una relación entre dos clases o conjuntos de objetos Estas proposiciones se clasifican en cuatro tipos básicos, según la cantidad (universal o particular) y la calidad (afirmativa o negativa). A continuación, se desarrollará brevemente cada tipo de proposición categórica con un ejemplo:


Proposiciones universales afirmativas (A): Afirman que todos los elementos de un conjunto están incluidos en otro conjunto. Se representan como "Todos los S son P". Por ejemplo: "Todos los gatos son mamíferos".
Proposiciones universales negativas (E): Niegan que exista algún elemento en común entre dos conjuntos. Se representan como "Ningún S es P". Por ejemplo: "Ningún perro es un reptil"
Proposiciones particulares afirmativas (I): Afirmar que al menos algunos elementos de un conjunto están incluidos en otro conjunto Se representan como "Algunos S son P". Por ejemplo: "Algunos estudiantes son artistas".

Proposiciones particulares negativas (O): Niegan que todos los elementos de un conjunto estén incluidos en otro conjunto. Se representan como "Algunos S no son P". Por ejemplo: "Algunos pájaros no vuelan".
Estas proposiciones categóricas son útiles para analizar y hacer inferencias sobre las relaciones entre conjuntos y se utilizan en el razonamiento lógico. Es importante tener en cuenta que el significado de estas proposiciones puede variar según el contexto y las definiciones de los conjuntos involucrados.

PUBLICIDAD

PROPOSICIONES CATEGÓRICAS

Ejercicio: Determine la forma lógica y la calidad (afirmativa o negativa) de la siguiente proposición categórica: "Ningún gato es un perro"
Solución: La forma lógica de una proposición categórica se refiere a la distribución de los términos (sujeto y predicado) dentro de la proposición En este caso, la forma lógica de la proposición es:

Ningún S es P
Donde "S" representa al sujeto ("gato") y "P" representa al predicado ("perro")
La calidad de una proposición categórica se refiere a si es afirmativa o negativa. En este caso, la proposición es negativa porque niega la existencia de una relación entre los gatos y los perros
Por lo tanto, la forma lógica de la proposición es "Ningún S es P" y su calidad es negativa.
Recuerda que comprender la forma lógica y la calidad de una proposición categórica es esencial para analizar y evaluar argumentos basados en estas proposiciones.

CAMPO PAGADO
Resuelve el ejercicio:
Ejercicio: Determina la forma lógica y la calidad de la siguiente proposición categórica: "Algunos pájaros son voladores".
roP ol ,otnat al amrof acigól ed al nóicisoporp se sonuglA" S nos "P y us dadilac se .avitamrifa
.serodalov
ecelbatse anu nóicamrifa erbos al aicnetsixe ed anu nóicaler ertne sol sorajáp y sol
,osac al nóicisoporp se avitamrifa ay euq
ereifer a is se avitamrifa o avitagen nE etse
aL dadilac ed anu nóicisoporp acirógetac es
atneserper la odaciderp )"serodalov"(
ednoD "S" atneserper la otejus )"sorajáp"( y "P"
nóicisoporp nE etse ,osac al amrof acigól ed al nóicisoporp :se sonuglA S nos P
sonimrét otejus( y )odaciderp ortned ed al
acirógetac es ereifer a al nóicubirtsid ed sol
nóiculoS: aL amrof acigól ed anu nóicisoporp
SILOGISMOS CATEGÓRICOS

El tema de los silogismos categóricos se refiere a un tipo específico de argumento deductivo que utiliza proposiciones categóricas para inferir una conclusión. Un silogismo categórico consta de tres partes: dos premisas y una conclusión.
Las premisas son proposiciones categóricas, que son afirmaciones sobre la relación entre dos clases o categorías. Estas proposiciones se expresan en forma de sujeto y predicado, utilizando los términos "todos" (universal afirmativa), "ningún" (universal negativa), "algunos" (particular afirmativa) o "algunos no" (particular negativa)

La conclusión de un silogismo categórico es una inferencia lógica que se extrae de las premisas. La conclusión contiene dos de los tres términos del silogismo: el término menor y el término mayor
El término menor es el sujeto de la conclusión, mientras que el término mayor es el predicado de la conclusión
La validez de un silogismo categórico se determina por su forma lógica, más que por el contenido específico de las premisas.
Para evaluar la validez, se utilizan las cuatro figuras posibles de los silogismos categóricos, que se basan en la posición de los términos mayor, menor y medio en las premisas Cada figura tiene sus propias reglas de validez
Ejemplo
Premisa mayor: Todos los mamíferos son animales vertebrados (Afirmativa Universal)
Premisa menor: Algunos perros son mamíferos (Afirmativa Particular)
Conclusión: Por lo tanto, algunos perros son animales vertebrados. (Afirmativa Particular)
Este silogismo pertenece a la primera figura porque cumple con las siguientes condiciones:
La premisa mayor tiene al término mayor "animales vertebrados" como sujeto y aparece como predicado en la conclusión
La premisa menor tiene al término menor "perros" como predicado y aparece como sujeto en la conclusión.
El término medio "mamíferos" aparece como sujeto en ambas premisas.
SILOGISMOS CATEGÓRICOS
Para determinar si un silogismo categórico es válido, es necesario aplicar las reglas de la lógica aristotélica y verificar si cumple con los criterios establecidos. Aquí hay algunos pasos que puedes seguir para determinar la validez de un silogismo:
Identificar la forma categórica: El primer paso es identificar la forma categórica del silogismo, es decir, las formas lógicas básicas que se utilizan para construir silogismos Estas formas categóricas se clasifican en cuatro figuras y se representan utilizando las letras A, E, I, y O para indicar las afirmaciones universales y particulares.

Identificar los términos: Un silogismo consta de tres términos: el término mayor, el término menor y el término medio. El término mayor es el predicado de la conclusión, el término menor es el sujeto de la conclusión, y el término medio aparece en ambas premisas pero no en la conclusión.
Verificar la distribución de los términos: Un término se considera distribuido cuando se refiere a todos los miembros de su clase. En un silogismo válido, el término medio debe estar distribuido al menos una vez en las premisas Si un término se encuentra distribuido en la conclusión, también debe estar distribuido en alguna de las premisas.
Evaluar las formas de las premisas: Cada premisa debe seguir una de las formas categóricas establecidas. Las formas válidas son:
Primera figura: El término medio es el sujeto de la premisa mayor y el predicado de la premisa menor.
Segunda figura: El término medio es el predicado de ambas premisas.
Tercera figura: El término medio es el sujeto de ambas premisas
Cuarta figura: El término medio es el predicado de la premisa mayor y el sujeto de la premisa menor
Aplicar las reglas de inferencia: Una vez que se han verificado los términos y las formas de las premisas, se deben aplicar las reglas de inferencia para determinar si la conclusión se sigue válidamente de las premisas. Estas reglas establecen las condiciones bajo las cuales una conclusión puede derivarse correctamente de las premisas
Si el silogismo cumple con todos los criterios anteriores, se considera válido Sin embargo, es importante tener en cuenta que la validez del silogismo no garantiza la verdad de las premisas o la conclusión. La validez se refiere a la estructura lógica correcta del razonamiento, pero la verdad depende de la correspondencia de las afirmaciones con la realidad.
SILOGISMOS CATEGÓRICOS
Ejemplo:
Premisa 1: Todos los gatos son mamíferos. (Afirmación universal afirmativa)
Premisa 2: Algunos animales son gatos. (Afirmación particular afirmativa)
Conclusión: Por lo tanto, algunos animales son mamíferos. (Afirmación particular afirmativa)
Para determinar la validez de este silogismo, debemos seguir los pasos mencionados anteriormente:
Forma categórica: El silogismo sigue la forma categórica AAI (Afirmativa, Afirmativa, I particular afirmativa).

Términos:
Término mayor: mamíferos
Término menor: animales
Término medio: gatos
Distribución de los términos: El término medio "gatos" está distribuido en la premisa 1 (afirmación universal) y en la premisa 2 (afirmación particular). El término menor "animales" no está distribuido en ninguna premisa. El término mayor "mamíferos" no está distribuido en ninguna premisa.
Forma de las premisas: El silogismo pertenece a la segunda figura, ya que el término medio "gatos" es el predicado de ambas premisas.
Reglas de inferencia: En este caso, el silogismo cumple con la regla de inferencia conocida como el modus ponens, que establece que si una afirmación universal afirma una relación entre dos términos y una afirmación particular afirma la existencia de uno de esos términos, entonces podemos concluir que existe la relación entre los dos términos.
Por lo tanto, el silogismo es válido, ya que cumple con todas las reglas y criterios establecidos. Sin embargo, es importante destacar que la verdad de las premisas y la conclusión debe ser evaluada por separado para determinar si el razonamiento es válido en términos de su contenido.

CUALIDAD, CANTIDAD Y DISTRIBUCIÓN
Las proposiciones lógicas se pueden clasificar en términos de su calidad, cantidad y distribución. Estas características nos ayudan a comprender la relación entre diferentes proposiciones y su impacto en la lógica formal.


Calidad de una proposición: La calidad de una proposición se refiere a si es afirmativa (A) o negativa (E). Una proposición afirmativa afirma una relación entre dos términos, mientras que una proposición negativa niega dicha relación. Por ejemplo, "Todos los perros son mamíferos" es una proposición afirmativa, mientras que "Ningún gato es un reptil" es una proposición negativa Cantidad de una proposición: La cantidad de una proposición se refiere a si es universal (A o E) o particular (I o O). Una proposición universal hace una afirmación sobre todos los elementos de un conjunto, mientras que una proposición particular hace una afirmación solo sobre algunos elementos. Por ejemplo, "Todos los pájaros tienen alas" es una proposición universal, mientras que "Algunos perros son negros" es una proposición particular
Distribución de los términos: La distribución de los términos se refiere a si un término se considera distribuido o no distribuido en una proposición Un término distribuido se refiere a todos los miembros de un conjunto, mientras que un término no distribuido se refiere solo a algunos miembros. En una proposición universal (A o E), tanto el sujeto como el predicado están distribuidos En una proposición particular (I o O), ninguno de los dos términos está distribuido.
Ejemplo 1: Proposición: Todos los estudiantes son inteligentes.
Calidad: Afirmativa (afirma una relación entre los términos "estudiantes" e "inteligentes").
Cantidad: Universal (se refiere a todos los estudiantes).
Distribución: El sujeto "estudiantes" está distribuido, ya que se refiere a todos los estudiantes. El predicado "inteligentes" también está distribuido, ya que se afirma para todos los estudiantes.
CUALIDAD, CANTIDAD Y DISTRIBUCIÓN
Cuadro de oposición: El cuadro de oposición muestra las relaciones lógicas entre proposiciones en función de su calidad, cantidad y distribución. El cuadro incluye cuatro tipos de proposiciones: A (universal afirmativa), E (universal negativa), I (particular afirmativa) y O (particular negativa) Las relaciones en el cuadro de oposición son las siguientes:

Contradictorias: Una proposición y su contraria (A y E, I y O) son contradictorias. No pueden ser ambas verdaderas ni ambas falsas al mismo tiempo.

Contrarias: Dos proposiciones universales (A y E) son contrarias. Ambas no pueden ser falsas, pero pueden ser ambas verdaderas.
Subcontrarias: Dos proposiciones particulares (I y O) son subcontrarias Ambas no pueden ser verdaderas, pero pueden ser ambas falsas.
Subalternas: Una proposición universal (A o E) y su subalterna (I o O) son subalternas. Si la universal es verdadera, la particular también lo será, pero si la universal es falsa, no podemos afirmar nada sobre la particular.
En resumen, la calidad, cantidad y distribución son aspectos clave en la clasificación y análisis de las proposiciones lógicas. El cuadro de oposición nos ayuda a comprender las relaciones entre las proposiciones y las implicaciones lógicas resultantes de su combinación.

LEYES DE INFERENCIA
Las leyes de inferencia son reglas lógicas que nos permiten realizar inferencias válidas a partir de proposiciones previas Estas reglas nos ayudan a deducir nuevas proposiciones o conclusiones a partir de premisas o suposiciones dadas.
Algunas de las leyes de inferencia más comunes son:
Ley del Modus Ponens: Si tenemos una proposición condicional "p → q" y la premisa de que "p" es verdadera, entonces podemos inferir que "q" también es verdadera
Ley del Modus Tollens: Si tenemos una proposición condicional "p → q" y la premisa de que "q" es falsa, entonces podemos inferir que "p" también es falsa.

Ley del Silogismo Hipotético: Si tenemos dos proposiciones condicionales "p → q" y "q → r", entonces podemos inferir que "p → r" Es decir, si la primera implicación es verdadera y la segunda también lo es, entonces la implicación resultante también es verdadera.


Ley del Silogismo Disyuntivo: Si tenemos una disyunción "p ∨ q" y la premisa de que "¬p" es verdadera, entonces podemos inferir que "q" es verdadera. Es decir, si una de las opciones es falsa, la otra opción debe ser verdadera.
Estas son solo algunas de las leyes de inferencia más utilizadas, pero existen muchas más Estas leyes nos permiten realizar razonamientos válidos y llegar a conclusiones lógicas a partir de premisas dadas. Son fundamentales en el campo de la lógica y el razonamiento deductivo.
Ejemplo que demuestra la aplicación de dos leyes de inferencia: Modus Ponens y Silogismo Hipotético.
Premisa 1: Si llueve, entonces la calle estará mojada. (p → q) Premisa 2: Está lloviendo. (p)
Usando la ley del Modus Ponens, podemos inferir: Conclusión 1: Por lo tanto, la calle estará mojada. (q)
Ahora, usando el resultado anterior y otra premisa, podemos aplicar la ley del Silogismo Hipotético:
Premisa 3: Si la calle está mojada, entonces habrá charcos. (q → r)
Usando el Silogismo Hipotético, podemos inferir: Conclusión 2: Por lo tanto, habrá charcos. (r)
En resumen, a partir de las premisas "Si llueve, entonces la calle estará mojada" y "Está lloviendo", aplicamos el Modus Ponens para inferir que "La calle estará mojada". Luego, usando esta afirmación junto con la premisa "Si la calle está mojada, entonces habrá charcos", aplicamos el Silogismo Hipotético para concluir que "Habrá charcos". Estas leyes de inferencia nos permiten realizar razonamientos válidos y llegar a conclusiones lógicas a partir de proposiciones previas.
CUANTIFICADORES LÓGICOS
Los cuantificadores lógicos son herramientas utilizadas en la lógica matemática y la lógica proposicional para expresar la cantidad o extensión de las proposiciones. Hay dos tipos principales de cuantificadores: el cuantificador universal (∀) y el cuantificador existencial (∃)
El cuantificador universal (∀) se utiliza para afirmar que una determinada propiedad se aplica a todos los elementos de un conjunto Por ejemplo, la expresión "∀x P(x)" significa "para todo x, P(x) es verdadero" Aquí, P(x) representa una propiedad o condición que se verifica para todos los elementos x en consideración.

El cuantificador existencial (∃) se utiliza para afirmar que al menos un elemento de un conjunto cumple con una determinada propiedad. Por ejemplo, la expresión "∃x P(x)" significa "existe al menos un x para el cual P(x) es verdadero". Aquí, P(x) representa una propiedad o condición que se cumple para al menos un elemento x.
Al combinar los cuantificadores con proposiciones lógicas, podemos construir afirmaciones más complejas y expresar relaciones entre conjuntos, propiedades y predicados
Por ejemplo, podemos utilizar cuantificadores para enunciar afirmaciones como "Todos los estudiantes son diligentes" (∀x Estudiante(x) → Diligente(x)) o "Existe un número primo" (∃x Primo(x)).
Es importante tener en cuenta que el uso adecuado de los cuantificadores implica especificar correctamente el dominio o conjunto de elementos considerados, así como la propiedad o condición que se está cuantificando Además, se deben tener en cuenta las reglas de la lógica y las leyes de inferencia al manipular proposiciones con cuantificadores.
En resumen, los cuantificadores lógicos nos permiten expresar afirmaciones generales sobre conjuntos de elementos y establecer la cantidad de elementos que cumplen ciertas propiedades Estas herramientas son fundamentales en la lógica matemática y juegan un papel importante en la formulación de teoremas y en la resolución de problemas de razonamiento y demostración

IMPORTANCIA DE LA LÓGICA
La lógica es una disciplina fundamental que se encarga de analizar y evaluar el razonamiento válido. Aunque a veces pueda parecer abstracta o compleja, estudiar lógica tiene numerosos beneficios y aplicaciones prácticas en diversos campos. En este artículo, exploraremos la importancia de estudiar lógica y cómo puede mejorar el pensamiento crítico y la toma de decisiones.

Mejora del razonamiento crítico: El estudio de la lógica proporciona las herramientas necesarias para evaluar de manera efectiva los argumentos y detectar falacias. Al comprender las estructuras lógicas subyacentes en los razonamientos, podemos identificar premisas débiles, inferencias incorrectas y sesgos cognitivos. Esto nos permite analizar de manera más objetiva la información que recibimos y formar juicios fundamentados.
Desarrollo de habilidades de argumentación: La lógica nos enseña a construir y evaluar argumentos sólidos. Aprendemos a identificar las premisas, establecer conexiones lógicas y presentar conclusiones coherentes. Estas habilidades son valiosas tanto en la comunicación oral como escrita, ya que nos permiten expresar nuestras ideas de manera clara y convincente.
Reforzamiento de la resolución de problemas: El estudio de la lógica nos ayuda a desarrollar habilidades de resolución de problemas, ya que nos enseña a descomponer un problema complejo en partes más manejables y a encontrar soluciones lógicas. Aprendemos a analizar los componentes del problema, identificar relaciones causales y aplicar principios lógicos para llegar a conclusiones sólidas.
Aplicaciones en diversas disciplinas: La lógica es fundamental en áreas como las matemáticas, la informática, la filosofía, la lingüística y la inteligencia artificial. En matemáticas, por ejemplo, se utiliza para demostrar teoremas y establecer relaciones entre conceptos. En informática, la lógica es la base de los algoritmos y el diseño de sistemas. En filosofía, se utiliza para examinar las bases del conocimiento y los argumentos éticos. En lingüística, la lógica se aplica al análisis del lenguaje y la estructura de los argumentos.
Toma de decisiones informadas: Estudiar lógica nos ayuda a tomar decisiones informadas y racionales. Al comprender los principios de la lógica, podemos evaluar las opciones disponibles, analizar las consecuencias y considerar los argumentos pertinentes. Esto nos permite evitar errores de pensamiento, como la falacia de la generalización apresurada o el razonamiento circular, y tomar decisiones más fundamentadas y lógicas.

