Matemáticas en red: conectando ideas con matrices. by artepormediodelanaturaleza

28 de marzo de 2025

MATEMÁTICASENRED

CONECTANDOIDEASCONMATRICES

Las matemáticas son una disciplina que estudia las propiedades y relaciones de los números, las formas y las estructuras.

Las matemáticas fomentan habilidades analíticas y de resolución de problemas:

La programación y el desarrollo de algoritmos dependen de conceptos matemáticos.

AlbertEinstein,“Lasmatemáticas purasson,ensuforma,lapoesíade lasideaslógicas.”

Las matemáticas no solo son una herramienta académica, sino que también son esenciales para el desarrollo personal y profesional.

Integrantes: Valeria Martínez.

María Medina. Salim Kelzy. Rossielis Fernández.

EDITORIAL Matrices

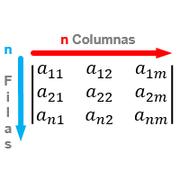
Una matriz es una estructura matemática que consiste en un conjunto de números organizados en filas y columnas

Las matrices nos ayudan a organizar y trabajar con muchos números a la vez.

Determinantes

Un determinante es un número especial que se calcula a partir de una matriz cuadrada.

Los determinantes se utilizan para para resolver sistemas de ecuaciones lineales, calcular áreas y volúmenes, y determinar si una matriz tiene inversa.

Objetivos

Una revista es una publicación periódica que contiene una gran variedad de contenidos, son una fuente importante de información y de entretenimiento que influyen en la sociedad. Los objetivos de esta revista son los siguientes:

• Explicarcontenidos de manera accesible y comprensible para el público en general.

• Mostrar cómo las matemáticas se usan en la vida cotidiana, desde hvideojuegos asta cocinar.

• Aprender de forma sencilla y dinámica a resolver matrices utilizando distintos métodos.

En la revista titulada como Matemáticas en red: conectando ideas con matrices, encontrarás contenido una gran variedad de contenido informático y dinámico para conocer un poco sobre las matrices, estadísticas, entre muchos otros. Te invito a explorar cada sección donde podrás encontrar además de información sección de entretenimiento como memes, pasatiempos, etc. En la siguiente página encontrarás más detalle.

1. Las matemáticas

•¿Cómo se relacionan con la telemática?

2-3. ¿Qué son las estadísticas?

Elementos de la estadística

•¿Para qué se utilizan?

•Características

•Propiedades de las estadísticas

4. ¿Qué són los polinomios?

•¿Para qué se utilizan?

5. ¿Qué son las matrices?

•Tipos de matrices

•Funciones

6. Propiedades de las matrices

•¿Para que se utilizan las matrices en los videojuegos?

7. Matrices en la telemática.

8. ¿Que es el método de Gauss?

•¿Para que se utiliza?

9. ¿Qué es el método de Sarrus o Cramer?

•¿Pará que se utilizan?

10. ¿Quién creo el cubo de Rubik?

• ¿Sé relacionan con la programación?

11. Algoritmo para armarlos

12. Publicidad.

13, 14. Entretenimiento.

15. Conclusión.

16. Agradecimientos.

Lasmatemáticas

Lasmatemáticassonunacienciaqueestudia números,figurasyestructurasabstractas, desarrollándosealolargodelahistoriaen civilizacionescomoMesopotamiayGrecia, dondefilósofoscomoPitágorashicieron contribucionesclave;sedividenenramas comoaritmética,geometríayálgebra,yson esencialesendisciplinascomolafísicayla economía,asícomoenlaresoluciónde problemascotidianos.

¿Cómoserelacionanconla telemática?

Las matemáticas se relacionan con la telemáticaalutilizarseenlateoríade la información para optimizar la transmisión de datos, en criptografía para asegurar la comunicación, en el análisisderedesparamejorarelflujo dedatos,yenalgoritmosyestadística para procesar y evaluar datos, siendo esencialesparaeldiseñoylaseguridad delossistemastelemáticos.

Lasmatemáticasseutilizan en diversas áreas como las ciencias naturales para modelar fenómenos, en ingeniería para diseñar estructuras y tecnologías, en economía y finanzas para realizar cálculos y análisis de datos, en estadística para interpretar información, en informática para desarrollar algoritmos y en medicina para estudios clínicos, además de ser esenciales en la vida cotidianaparalagestiónde finanzas y la resolución de problemas.

Lasmatemáticassonfascinantes,yaquepiesun númeroirracionalcondecimalesinfinitos,elcero fuedesarrolladoenlaIndiaylosnúmerosprimos incluyenunoconmásde24millonesdedígitos.

ElTeoremadeFermatfueprobadotras350años, la Conjetura de Collatz sugiere que cualquier número entero positivo llegará a uno, y la secuencia de Fibonacci y la proporción áurea aparecen en patrones naturales, evidenciando la bellezadelasmatemáticas.

Lasestadísticas

LasEstadísticassónuna ramadelasMatemáticas que,atravésdediversas metodologíasytécnicas,se encargadelarecoleccióny organizacióndedatos acercadepersonas,sucesos ocosas.Asimismo,facilita suanálisiseinterpretación, conelfindeobtener conclusiones.

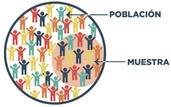
Elementosdelaestadística:

Población:Grupodeindividuos

Muestra: Es un subgrupo de datos extraídosdeunapoblación.

Parámetros: Son medidas que ofrecen información sobre el centro de un conjuntodedatos.

Experimento: Proceso o actividad llevadaacabodeformaintencionalpara obtenerunaseriededatos.

Variable:Lacaracterísticaocualidadde unamuestraopoblación.

Lasestadísticas Lasestadísticas

Usarestadísticasesaccesible graciasaherramientascomo ExcelyR,recursoseducativos enlínea,yplataformasde visualizacióncomoTableau.

Aunquehayunacurvade aprendizaje,elapoyode comunidadesenlíneafacilita suusoendiversasáreas.

Característicasdelasestadísticas:

•RecoleccióndeDatos

•Análisisdescriptivo

•InferenciaEstadística

•Variables

•Visualización

•Aplicabilidad

Lasestadísticasseutilizanpara analizardatos,tomar decisionesinformadas,validar hipótesiseninvestigaciones, entendermercados,evaluar intervencionesensaludy analizarcaracterísticas demográficas,convirtiendo datoseninformaciónútil.

Lasestadísticastienenpropiedades clave como consistencia, invarianza,eficienciaysimplicidad. Son robustas, asumen linealidad y normalidad, y requieren independenciadelosdatosparala validezdemuchastécnicas.

Polinomios

Un polinomio es una expresión algebraica de sumas, restas y multiplicaciones ordenadas hecha de variables, coeficientes y exponentes. Sirven principalmente para representar funciones de formagráficaoparahallarel valor de las variables al igualarelpolinomioacero.

Valor numérico de un Polinomio

Es el valor que toma un polinomio al sustituir la variableporunciertonúmero. Así,dadoelpolinomioP(x)= 2x+5,suvalornuméricopara x=-1es:P(-1)=2(-1)+5=3

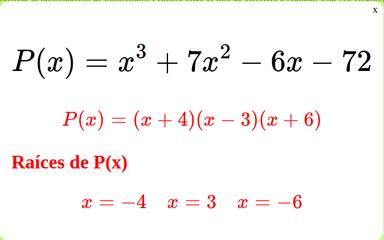
Para resolver, simplificar, sumar o restar polinomios se recomienda agrupar los términos con las mismas variables. Por ejemplo, los términos con la variable " x " se suman o restan, y lo mismo con los términos que no tienenvariables.Es importante fijarse en el signo que está antes del término, pues determinará si suma, resta o multiplica.

Normalmentelos polinomios se escribenordenados segúnlosgradosde sus monomios de mayoramenor.En ocasiones parece que "falta" alguno de los monomios intermedios.Esoes así porque el coeficiente de ese monomioesceroy, por tanto, no se escribe. Si un polinomio tiene todos sus coeficientes iguales a cero, se lo denomina polinomio nulo y carecedegrado.

MATRICES MATRICES

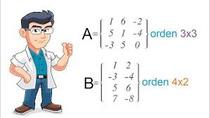
Lasmatricessontablasde númerosordenadasenfilasy columnas. Se utilizan para organizar y trabajar con datos de manera eficiente. Eltamañodeunamatrizse describe por el número de filas y columnas que tiene. Porejemplo,unamatrizde 2x3 tiene 2 filas y 3 columnas.

• Matriz rectangular tiene distintonúmerodefilasque de columnas, su dimensión es mxn , siendo m el numero de filas y n el numerodecolumnas.

• Matriz traspuesta: Dada una matriz A, se llama matriztraspuestadeAala matriz que se obtiene cambiando ordenadamente lasfilasporlascolumnas.

• Matriz cuadrada: tiene el mismonúmerodefilasque de columnas, siendo su dimensión . Los elementos delaforma constituyenla diagonalprincipal.

•Matriz diagonal: En una matriz diagonal todos los elementos que no están situados en la diagonal principalsonnulos.

Las matrices permiten organizar y almacenar grandes cantidadesdedatosde forma estructurada. Por ejemplo, se pueden usar para representar tablas de datos, imágenes digitales o redes sociales.Asuvez,las matrices también son fundamentales para resolver sistemas de ecuacioneslineales.

• Matriz escalar: Una matriz escalar es una matrizdiagonalenlaque los elementos de la diagonal principal son iguales.

•Matrizidentidad:Esuna matrizdiagonalenlaque los elementos de la diagonal principal son igualesa1.

• Matriz opuesta: Es opuesta a otra cuyos elementostienenunsigno contrario a la matriz principal. Es decir, la matriz opuesta a A se denomina-Aytodoslos elementos del conjunto son contrarios a los elementosdelamatrizA.

Las matrices son esencialesenelcálculo númerico, que se utiliza para resolver problemas matemáticos complejos mediante aproximaciones numéricas.

Propiedadesdelasmatrices

Las matrices tienen varias propiedades importantes que son fundamentales en álgebra lineal y en diversas aplicaciones matemáticas.

✓SumadeMatrices

•Conmutativa:(A+B=B+A)

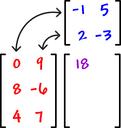
•Asociativa:(A+(B+C)=(A+B)+C)

•Elementoneutro:Existeunamatrizcero(O)tal que(A+O=A)

✓ProductodeMatrices

•Asociativa:(A(BC)=(AB)C)

•Distributiva:(A(B+C)=AB+AC)

•Elementoneutro:Existelamatrizidentidad(I) talque(AI=A)

✓Transposición

•Transposicióndelasuma:(A+B)^T=A^T+ B^T)

• Transposición del producto:(AB)^T = B^T A^T)

✓Determinante

•Determinantedelaidentidad:(det(I)=1)

•Multiplicación:(det(AB)=det(A)cdotdet(B)

✓Inversa

•Inversadelproducto:(AB)^{-1}=B^{-1}A^{-1})

•Elementoneutro:(AA^{-1}=I)

Las matrices son fundamentales en los videojuegos para realizar transformaciones geométricas como traslación, rotación y escaladodeobjetos,así como para convertir coordenadas 3D a 2D mediante proyecciones. También se utilizan para definir la vista de la cámara, calcular animaciones suaves, detectar colisiones entre objetos, simular sistemasdepartículasy en algunos casos, para la inteligencia artificial en el movimiento de personajesnojugables. En resumen, las matrices permiten manipular y representar el espacio tridimensional de manera efectiva, mejorando la experiencia del jugador.

Matricesenlatelematica

Lasmatricespuedenrepresentarlas conexiones entre diferentes dispositivos en una red. Cada elementodelamatrizindicasihayuna conexión entre dos dispositivos y, en caso afirmativo, la intensidad de esa conexión. Esto es útil para analizar y optimizar el funcionamiento de las redes.

Las matrices se utilizan en gráficos por computadora para realizar transformaciones geométricas, como rotaciones, traslaciones y escalados. Esto permite crear imágenes y animacionesen3D.

Lasmatricessonesencialesentelemáticaporquepermitenorganizaryestructurar grandesvolúmenesdedatos,facilitandosuanálisisymanipulaciónenaplicaciones comoelprocesamientodeimágenesyseñales.Sonfundamentalesenalgoritmosde transformaciónyoptimización,modelandoredesdecomunicaciónysimulando sistemascomplejos.Además,seutilizanenelanálisisestadísticoyenelaprendizaje automáticopararepresentardatosyrealizarcálculosalgebraicos.Tambiénjuegan unpapelcrucialenlacodificacióndecorreccióndeerroresyenlacriptografía, garantizandolaintegridadyseguridaddelainformacióntransmitida.

“Las matrices facilitan la codificación y corrección de errores en telemática, garantizando la integridad de la informacióntransmitida."

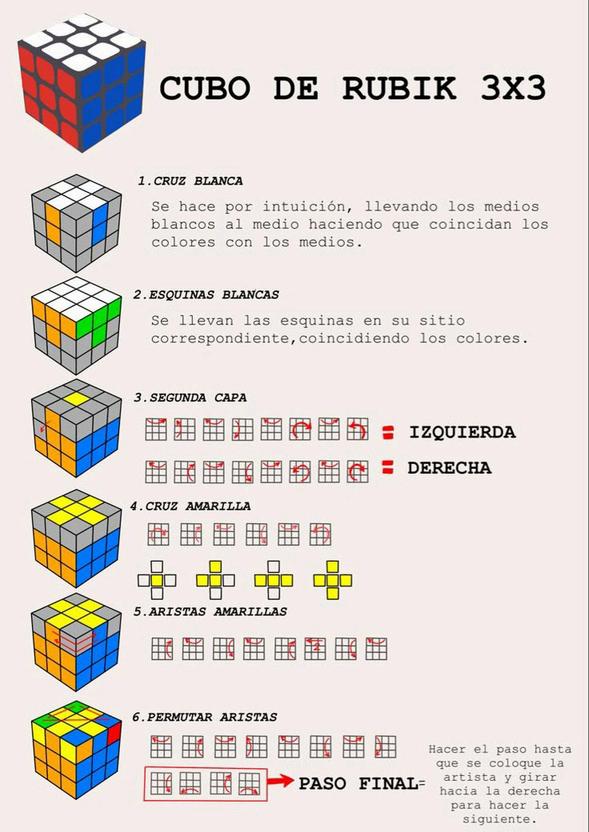
MétododeGauss

Es un método que utiliza operaciones elementales para resolver un sistema de ecuacioneslineales.Elresultaesunsistema triangularequivalentealoriginalquetiene lasmismassoluciones.

El método de Gauss es una técnica matemáticaqueseutilizaprincipalmente para resolver sistemas de ecuaciones lineales. A su vez, se puede utilizar el método de Gauss para simplificar una matriz y facilitar el cálculo de su determinante.

La inversa de una matriz es unamatrizque, al multiplicarse por la matriz original, da como resultado la matriz identidad. El método de Gauss-Jordan, unavariantedel método de Gauss,seutiliza para encontrar la inversa de unamatriz.

¿Sabíasque?

AunquellevaelnombredeCarlFriedrichGauss, unmatemáticoalemándelsigloXIX,lasraícesde estemétodoseremontanalaantiguaChina.Hay evidenciadequematemáticoschinosyautilizaban técnicas similares para resolver sistemas de ecuacioneslinealeshacemilesdeaños.

MétodoSarrus-Cramer

El método de Sarrus calcula el determinante de matrices (3x3) mediante diagonales, mientras que el método de Cramer resuelve sistemas de ecuaciones lineales usando determinantes para encontrarlasincógnitas,aplicablesolosiel determinante de la matriz de coeficientes esdistintodecero.

El método de Sarrus se utiliza para calcular determinantes de matrices(3x3), facilitando la resolución de sistemas de ecuaciones y aplicaciones en geometría, como el cálculo de áreas y volúmenes.

Elmétodode Cramerseutiliza pararesolver sistemasde ecuacioneslineales mediante determinantes, encontrandolas solucionesdelas incógnitasaldividir eldeterminantede matricesmodificadas poreldeterminante delamatrizde coeficientes, aplicablesolosiel determinantees distintodecero.

ElmétododeCramer ySarrusserelacionan con la telemática al resolver sistemas de ecuaciones lineales que modelan problemas de redes, comolaoptimización derutasdedatosyla gestión de tráfico, siendo útil en el análisis de rendimiento y en algoritmos de procesamiento de señales.

El método de Sarrus es un enfoque rápido e intuitivo para calcular determinantes, nombrado por Pierre Frédéric Sarrus. En cambio, elmétododeCrameresútil en optimización y teoría de control, y se enseña en álgebra lineal para mostrar cómo resolver problemas de manerasistemática.

Cubo Rubik Cubo Rubik

ElcuboRubikfuecreadoporelarquitectoy profesorhúngaroErnőRubiken1974. Originalmentelodiseñócomouna herramientaeducativaparaayudarasus estudiantesaentenderconceptosde tridimensionalidad.Sinembargo,elcubose convirtióenunjuguetepopularanivel mundialenladécadade1980.

ElcuboRubikestándarde3x3x3tieneun totalde26piezasvisibles,queincluyen:

-8esquinas(cadaunacon3colores) -12aristas(cadaunacon2colores) -6centros(cadaunocon1color)

Internamente,elcubotieneunmecanismo centralquepermitelarotacióndelascaras, peronotienepiezasadicionalesensuinterior. EltamañodelcuboRubikestándaresde aproximadamente**5.7cm**(2.2pulgadas) delado.

ElcuboRubikse relacionaconla telemáticaatravés delusode algoritmosparasu resolución,queson esencialesen programacióny procesamientode datos.Además,su análisispuede involucrar conceptosdeteoría degrafos,aplicables eneldiseñoderedes telemáticas,yse puedenutilizar modelos matemáticospara estudiarsu resoluciónenel desarrollode softwareeducativo.

Algoritmopara resolverlo

Adivinanzas

1.Tengofilasycolumnasy puedosumaryrestar.¿Quiénsoy?

2.Tengotresladosytres ángulos,ysoyfamosopormi teorema.¿Quiénsoy?

3.Tengoformadeanilloyestoy siempreentero,perosimepartes porlamitad,¡yanovalgodinero! ¿Quiénsoy?

4.Tengounadiagonal principal,llenadeunosy ceros,¿quiénsoy?

“Lavidaescomo unaecuación: ¡tienesque convertirlos negativosen positivos”

Chistes

•¿Quélediceel3al30?: para ser como yo tienes quesersincero.

• ¿Por qué los triángulos son tan buenos amigos?: porque siempre tienen ángulosencomún.

• ¿Por qué el libro de matemáticas se deprimió? porque tenía demasiados problemas.

Entretenimiento

Horóscopodel30/03

Aries: Hoy es un buen día para enfocarte en tus metaspersonales.

Piscis: La empatía serátufuerza.

Acuario: Tú originalidad brillará hoy.

Capricornio: Enfócate en tus responsabilidades.

Sagitario: Las aventuras te llaman. Has algo emocionante.

Escorpio:Reflexiona sobretusemociones.

Géminis: La comunicación será clavehoy.

Tauro: Es un buen momento para fortalecerrelaciones.

1¡AyudaaGaussallegaralotrolado! .

2.Encuentralaspalabrasrelacionadas conlostemasleídos. inversahqinhrp

Libra: Recibirás buenas noticias en el ámbitosocial.

Virgo: La organizació n será tu aliada.

Leo: Tú creatividad estará en un punto más alto.

Cancer: Hoy es un día para cuidar de ti mismo.

Conclusión Conclusión Conclusión

La revista de matemáticas nos invita a explorar la riqueza y la interconexión de conceptos fundamentales como las matrices, las ecuaciones lineales y los polinomios, revelando cómo estos elementos se entrelazan para ofrecer soluciones a problemas complejos. A través de un enfoque analítico y creativo, se destaca la importancia de las matemáticas en diversas disciplinas, desde la ciencia hasta la economía, mostrando que su aplicación va más allá de lo abstracto y se convierte en una herramienta esencial para comprender y modelar el mundo que nos rodea. En este viaje, se celebra la belleza de las matemáticas como un lenguaje universalquenosconectaconlalógicaylaprecisión enlabúsquedadelconocimiento.

Las matemáticas son un lenguaje universal que nos permitecomprenderydescribirelmundodemanera precisa. Fomentan el pensamiento crítico y la resolución sistemática de problemas, revelando patronesyrelacionesenlacomplejidaddelarealidad. Además,estimulanlacreatividadalofrecermúltiples enfoques para cada desafío. En esencia, las matemáticas conectan diversas disciplinas, empoderándonosparaenfrentarlosretosdelfuturo conconfianzayclaridad.

Agradecimientos

Gratos agradecimientos para nuestros padres que fueronpartedeesteprocesomientraslaborabamosesta revista con el objetivo de inspirar y facilitar información, fomentando el aprendizaje a los estudiantes o a las personas que decidan leer de la misma..

Igualmentegraciasalaspersonasquefueronpartede esta laboracion, como lo es la profesora María Chirinos,porlaideadepoderinnovaralgodistintoen eláreadelasmatemáticas..