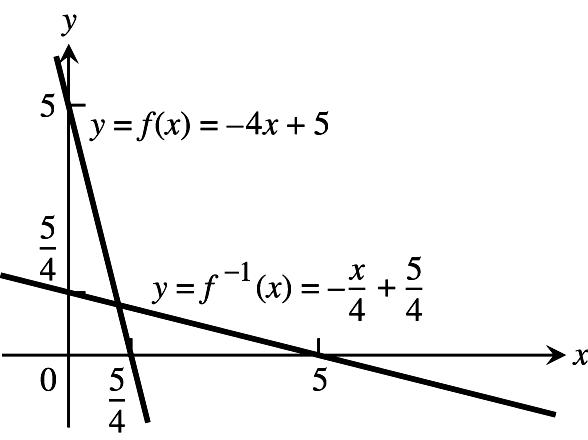University Calculus Elements with Early Transcendentals 1st Edition Hass Solutions Manual

82. We need to show a is constant: a and ks a v œœ œœœÊ œœ dv dvdvdsdvd k dvdsdv dt dtdsdtdsds dsdtds 2s

which is a constant.

œ Ê kkk 2s s ss $Î#

œœœ

# ## È # "" #

œœœœœœœ ˆ‰

w

86. The graph of y(fg)(x) has a horizontal tangent at x1 provided that (fg)(1)0 f(g(1))g(1)0œ‰œ‰œÊœ www either f(g(1))0 or g(1)0 (or both) either the graph of f has a horizontal tangent at ug(1), or the ÊœœÊœ ww graph of g has a horizontal tangent at x1 (or both). œ

ÉÈ

x x, in agreement. Êœ œœ dy dxdx4 xx d x """" ## # $Î%

ÈÈÈ

È È È ˆ‰

É "Î%

1. xyxy6: ## œ

Step 1: x y2xx2y y10Š‹Š‹ ## dydy dxdx œ

Step 2: x 2xy 2xyy ## dydy dxdx œ

Step 3: x2xy2xyy dy dx ab## œ

Step 4: dy2xyy dxx2xy œ # #

xy18xy 3x3y 18y18x

3y18x

Step 1: 2x 2y2y 1 Š‹ dy dydy dx dxdx œ

Step 2: 2x 2y 12y dydydy dxdxdx œ

Step 3: (2x2y1)2y dy dx œ"

Copyright © 2012 Pearson Education, Inc. Publishing as Addison-Wesley University Calculus Elements with Early Transcendentals 1st Edition Hass Solutions Manual Full Download:http://testbanktip.com/download/university-calculus-elements-with-early-transcendentals-1st-edition-hass-solutions-manual/ Download all pages and all chapters at: TestBankTip.com

4. xxyy1 3xyx 3y 0 3yx y3x $$#### œÊ œÊ œ Êœ dydy dy dyy3x dxdx dx dx3yx ab # #

5. x(xy)xy: #### œ

Step 1: x2(xy)1(xy)(2x)2x2y ##

œ dy dy dx dx

Step 2: 2x(xy) 2y 2x2x(xy)2x(xy) œ ## # dydy dxdx

Step 3: 2x(xy)2y2x1x(xy)(xy) dy dx cdcd œ ##

Step 4: dy dx2x(xy)2yyx(xy)xyxy 2x1x(xy)(xy)x1x(xy)(xy) x1xxyx2xyy œœœ cd cd ab ## ### $

### œ x2x3xyxy xyxy $## #$

6. (3xy7)6y 2(3xy7)3x 3y6 2(3xy7)(3x) 6 6y(3xy7) œÊ œÊ œ #

dy dy dydy dx dx dxdx [6x(3xy7)6]6y(3xy7) Ê œ Êœ œ dy dyy(3xy7)3xy7y dx dxx(3xy7)113xy7x # #

7. y 2y # "" œÊœœÊœ x2 x1dx(x1)(x1)dxy(x1) dy(x1)(x1)dy ###

8. x xxyxy 3x2xyxy1y x1y13x2xy y #$ ### ww#w#w œÊ œ Ê œ Ê œ Êœ xy 13x2xy xy x1 ab # # 9. xtan y 1secy cosy œÊœÊœœ ab## " dydy dxdxsecy # 10. xycot xy xycsc(xy)xy xxcsc(xy)ycsc(xy)y œÊ œ Ê œ ab Š‹ dy dy dy dy dx dx dx dx ## # xxcsc(xy)ycsc(xy) Ê œ "Êœœ dy dy y dx dx x ycsc(xy) xcsc(xy) ‘ ‘ ## " " ‘

yxy

y) yx (cos yx) y1 œÊ œ Ê œ Êœ dy dy dy dyy1 dx dx dx dxcos yx

13. y sin1xy ycos(1) sin x y Š‹ ’

"" " " y y ydx ydxdx dy dydy œ Ê œ Ê # cossinxy dy dy y y dxyy y dx cossinxy sincosxy

’“ Š‹Š‹

œ Êœœ """ """ ""

# yyy yy Š‹Š‹

Š‹Š‹

14. e2x2yexy2xy22yxey2xye22yxey2y22xye xy xy2 2xy xy 2xy xy 22 2 222 œ Ê œ Ê œ Ê œ abwwwww w y Êœ w 22xye xe2 xy 2 2xy 2

15. r1 r0 )) "Î#"Î# "Î# "Î# "" " " ## # # œÊ œÊœÊœ œ † dr dr dr dd d r 2rr 2 )) ) ))) ’“ÈÈ ÈÈ ÈÈ

16. r2 œ Ê œ Êœ È ))))))))) 34 dr dr 3d d # #Î$$Î% "Î# "Î$ "Î% "Î# "Î$ "Î% ))

17. sin(r) [cos(r)]r 0 [ cos(r)]r cos(r) , )))))) œÊ œÊœ Êœœ " # ˆ‰ dr dr dr r dd d cos (r ) r cos(r) )) )))) ) cos(r)0 ) Á

Chapter 2 Differentiation

18. cos rcot e sin rcsc er sin rcsc ree œÊ † œ Ê † œ ))))) rr r r dr dr dr dr dddd )) ) ) )))) ##

#

sin re recsc Ê œ Êœ dr dr drrecsc dd d rr esin r )) ) )) ) ) )) # r r ) )

19. xy1 2x2yy0 2yy2x y; now to find , y ## w w w w œÊ œÊœ Êœœ œ dy dy dx y dxdxdxy xd d x # # ab Š‹ y since y y Êœœ œ Êœœœœ ww w ww " " y(1)xy dy yx yyydxyyy yx x yy w# # # ## #$$$

## Š‹ ab x y

20. xy1 xy 0 y x y ; #Î$#Î$ "Î$ "Î$ "Î$ "Î$w "Î$ œÊ œÊ œ Êœœ œ 22 22 x 3 3dx dx3 3 dx x dy dy dy y y ‘

Differentiating again, yww œœ xyyyx xx

xyyx "Î$ #Î$w"Î$ #Î$ "" #Î$#Î$

"Î$ #Î$"Î$ #Î$ "" "Î$ "Î$ ˆ‰ˆ‰ ˆ‰ˆ‰ Œ 33 33 y x

"Î$ "Î$

"" " #Î$ "Î$"Î$ %Î$

xyyx Êœ œ dy y dx3 3 3x3yx # "Î$ # %Î$"Î$#Î$

# w ### x xxx

21. ye2x 2yy2xe2#w œ Êœ ʜʜ xx dydy dxydxy xe1 y2xeexe1y ## # # ##

œœ y2xeexe1 y2xeexe2xe1 yy Š‹Š‹Š‹Š‹ ## # ### #### # #

xxx 2xx2xx xe1 x y 3 † œ ˆ‰ 2xyy2xexe1 y #### 22x2x 3

22. y2x12y 2yy22y y(2y2)2 y(y1); then y(y1)y #w w ww " ww # w " œ Ê œ Ê œÊœœ œ y1 (y1)(y1) y œ Êœœ # " ww " dy dx (y1) # # $

23. 2yxy yy1y yy11 y ; we can

œ Êœ Ê œÊœœœ "Î#w ww "Î# w " dy dx y1 y1 y "Î# È È differentiate the equation yy11 again to find y: yyyy1y0 w "Î# www $Î#w "Î#ww " #

" #

y1yyy y Ê œÊœœœœ

cd"Î#www $Î# ww "" " # # # dy dx y y1 2yy1 1y # #

# $Î# "Î# $Î# "Î# $$ Œ ab ab ˆ‰ È

" "Î# y1

24. xyy1 xyy2yy0 xy2yyy y(x2y)y y; y œÊ œÊ œ Ê œ Êœœ #wwwww www ydy (x2y)dx # #

œœœ (x2y)yy(12y) (x2y)(x2y)(x2y) (x2y)y12 y(x2y)y(x2y)2y ww ###

# ’“’“ Š‹ cd " yy (x2y)(x2y) (x2y)

œœœ2y(x2y)2y2y2xy2y(xy) (x2y)(x2y)(x2y) ## $$$

25. xy16 3x3yy0 3yy3x y; we differentiate yyx to find y:

# ## 2 œÊœœ œ œ œ (2)(1)(0) 44 ˆ‰ " # 27. yxy2x at () and (1) 2y 2x4y 2 2y 4y 22x ##% $ $ œ #ß" #ß Ê œ Ê œ dy dy dydy dx dx dxdx 2y4y22x 1 and 1 Ê œ ʜʜ œ dy dy dy dy dx dxyydx dx x ab ¹¹ $ " # $ (21) (21) ß ß Copyright © 2012 Pearson Education, Inc. Publishing as Addison-Wesley

(b) the normal line is y4(x3) yx œ Êœ 44 33

31. xy9 2xy2xyy0 xyyxy y; ## ##w #w#w œÊ œÊœ Êœ y x

(a) the slope of the tangent line my 3the tangent line is y33(x1) y3x6 œœ œÊ œ Êœ k ¸ w (13)

(b)

(a)

(b)

Š‹

37. y2 sin(xy)y2[cos(xy)]yy[12 cos(xy)]2 cos(xy) œ Êœ Ê œ 111111 ww w † ab y;Êœ w # 2 cos(xy) 1 cos(xy) 11 1

(a) the slope of the tangent line my

cos(xy) 12 cos(xy) 11 1 1 y02(x1) y2x2 œ Êœ 111

the tangent line is œœœÊ

(b) the normal line is y0(x1) y œ Êœ "" ## 111 x 2

38. x cosysin y0 x(2 cos y)(sin y)y2x cosyy cos y0 y2x cos y sin ycos y ## # w#w w# œÊ œÊ cd 2x cosy y ; œ Êœ#w 2x cosy 2x cos y sin ycos y # # (a) the slope of the tangent line my

the tangent line is y

1 (b) the normal line is x0 œ

39. Solving xxyy7 and y0 x7 x7 7 and 7 are the points where the ## # œœÊœÊœ„Ê ß!ß!

curve crosses the x-axis. Now xxyy7 2xyxy2yy0 (x2y)y2xy ## ww w œÊ œÊ œ y m the slope at 7 is m 2 and the slope at 7 is Êœ Êœ Ê ß!œ

m 2. Since the slope is 2 in each case, the corresponding tangents must be parallel.

40. Let p and q be integers with q0 and suppose that yxx. Then yx. Since p and q are integers and œ œœ È q p pqqp Î assuming y is a differentiable function of x, ddyxqypx x dxdx dx dxqyqy qpq1p1 dy dypxp ababœÊœÊœœ† p1 q1q1 p1 xx œ†œ†œ†œ† pppp qqqq xx x x p1ppqpq1 p1 p1 pq q1 ppq Î Î ab abab

41. yyx 4yy2yy2x 22yyy2x y; the slope of the tangent line at %##$ww $w w œ Êœ Ê

42. xy9xy0 3x3yy9xy9y0 y3y9x9y3x y $$ ##ww w# #w œÊ œÊ œ Êœœ ab 9y3x3yx 3y9xy3x ## ##

(a) y and y;kk ww (42) (24)ßß

œœ 54 45

###

Š‹Š‹

(b) y0 0 3yx0 y x 9x0 x54x0 w# $' $ $ œÊœÊ œÊœÊ œÊ œ 3yx y3x333 xxx # #

xx540 x0 or x5432 there is a horizontal tangent at x32. To find the Ê œÊœœœÊœ $$ab È ÈÈ 3 3 3 corresponding y-value, we will use part (c).

#$ $ ÈÈÈÈ

(c) 0 0 y3x0 y3x; y3x x3x9x3x0 dx dy3yx y3x œÊœÊ œÊœ„œÊ œ # #

x63x0 xx630 x0 or x63 x0 or x10834. Ê œÊ œÊœœÊœœœ $ $Î# $Î#$Î# $Î# $Î# ÈÈÈÈ

Since the equation xy9xy0 is symmetric in x and y, the graph is symmetric about the line yx. That is, if $$ œ œ (ab) is a point on the folium, then so is (ba). Moreover, if ym, then y. Thus, if the folium has a ßßœœ kk ww " (ab) (ba)ßß m horizontal tangent at (ab), it has a vertical tangent at (ba) so one might expect that with a horizontal tangent at ßß x54 and a vertical tangent at x34, the points of tangency are5434 and 3454,œœßß ÈÈÈ

33 respectively. One can check that these points do satisfy the equationxy9xy0. $$ œ

33

43. x2xy3y02x2xy2y6yy0y(2x6y)2x2yy the slope of the tangent ##www w œÊ œÊ œ ÊœÊ xy 3yx line my 1the equation of the normal line at (11) is y11(x1)yx2. To find

œœœÊ ß œ Êœ k ¹ w (11) (11) ß ß

xy 3yx where the normal line intersects the curve we substitute into its equation: x2x(2x)3(2x)0 ## œ

x4x2x344xx04x16x120x4x30 (x3)(x1)0 Ê œÊ œÊ œÊ œ #### # ab

x3 and yx21. Therefore, the normal to the curve at (11) intersects the curve at the point (31). Êœœ œ ß ß Note that it also intersects the curve at (11). ß

œÊœ œ dy dy dyy2 dx dx dx1x parallel, the normal lines must also have slope of 2. Since a normal is perpendicular to a tangent, the slope of the tangent is . Therefore, 2y41x x32y. Substituting in the original equation, "" # # y2 1x œÊ œ Êœ y(32y)2(32y)y0 y4y30 y3 or y1. If y3, then x3 and œÊ œÊœ œ œ œ # y32(x3) y2x3. If y1, then x1 and y12(x1) y2x3.

44. xy2xy0 x y20 ; the slope of the line 2xy0 is 2. In order to be œÊ

45. xyxy6 x3y yx 2xy0 3xyxy2xy $# #$# ##$ œÊ œÊ œ Êœ Š‹ ab dy dy dy dyy2xy dx dx dx dx3xyx $ ##

$##$#$## ab ab

; thus appears to equal . The two different treatments view the graphs as functions ʜ dx dx dyy2xydy 3xyx## $

" dy dx symmetric across the line yx, so their slopes are reciprocals of one another at the corresponding points œ (ab) and (ba).ßß

46. xysiny 3x2y (2 sin y)(cos y) (2y2 sin y cos y)3x $### # œÊ œ Ê œ Êœ dy dydy dy dx dxdx dx2y2 sin y cos y 3x#

; also, xysiny 3x 2y2 sin y cos y ; thus œ œ Ê œÊ œ 3x dx dx dx 2 sin y cos y2y dy dy 3x dy 2 sin y cos y2y # #

$### appears to equal . The two different treatments view the graphs as functions symmetric across the line " dy dx yx so their slopes are reciprocals of one another at the corresponding points (ab) and (ba).œßß

47-54. Example CAS commands:

Maple:

q1 := x^3-x*y+y^3 = 7; pt := [x=2,y=1];

p1 := implicitplot( q1, x=-3..3, y=-3..3 ):

p1;

eval( q1, pt );

q2 := implicitdiff( q1, y, x );

m := eval( q2, pt );

tan_line := y = 1 + m*(x-2);

p2 := implicitplot( tan_line, x=-5..5, y=-5..5, color=green ):

p3 := pointplot( eval([x,y],pt), color=blue ):

Mathematica

display( [p1,p2,p3], ="Section 2.8 #47(c)" ); : (functions and x0 may vary):

Note use of double equal sign (logic statement) in definition of eqn and tanline. <<Graphics`ImplicitPlot`

Clear[x, y]

{x0, y0}={1, /4}; 1

eqn=x + Tan[y/x]==2;

ImplicitPlot[eqn,{ x, x03, x03},{y, y03, y03}]

eqn/.{xx0, yy0}ÄÄ

Copyright © 2012 Pearson Education, Inc. Publishing as Addison-Wesley

Chapter 2 Differentiation

D[%, x] Solve[%, y'[x]] slope=y'[x]/.First[%] m=slope/.{xx0, y[x]y0}ÄÄ tanline=y==y0m (xx0) ImplicitPlot[{eqn, tanline}, {x, x03, x03},{y, y03, y0 + 3}]

2.9 INVERSE FUNCTIONS AND THEIR DERIVATIVES

1. Yes one-to-one, the graph passes the horizontal test.

2. Not one-to-one, the graph fails the horizontal test.

3. Not one-to-one since (for example) the horizontal line y intersects the graph twice. œ#

4. Not one-to-one, the graph fails the horizontal test.

5. Domain: 1x1, Range: y

6. Domain: x, Range: y ŸŸ ŸŸ _ _ Ÿ 11 11 ## ##

7. Step 1: yx1 xy1 xy1 œ Êœ Êœ ## È

Step 2: yx1f(x) œ œ È "

8. Step 1: yx xy, since x. œÊœ Ÿ! # È

Step 2: yxf(x) œ œ È "

9. Step 1: yx1 xy1 x(y1) œ Êœ Êœ $ $ "Î$

Step 2: yx1f(x) œ œ $ " È

10. Step 1: yx2x1 y(x1) yx1, since x1 x1y œ Êœ Êœ  Êœ ## ÈÈ

Step 2: y1xf(x) œ œ È "

11. Step 1: y(x1) yx1, since x1 xy1 œ Êœ   Êœ # ÈÈ

Step 2: yx1f(x) œ œ È "

12. Step 1: yx xyœÊœ #Î$ $Î#

Step 2: yxf(x) œœ $Î# "

13. Step 1: yx xyœÊœ & "Î& Step 2: yxf(x); œœ & " È

Domain and Range of f: all reals; "

" "Î& " & & "Î& œœœœ

ff(x)xx and f(f(x))xxabab

14. Step 1: yx1 xy1 x(y1) œ Êœ Êœ $ $ "Î$

Step 2: yx1f(x); œ œ $ " È

Domain and Range of f: all reals; "

ff(x)(x1)1(x1)1x and f(f(x))x11xxababab ˆ‰ ab " "Î$ " $ $ $ "Î$"Î$ œ œ œœ œœ

15. Step 1: y x x œÊœÊœ""" # xyy # È

Step 2: yf(x) œœ " " È x

Domain of f: x0, Range of f: y0; " "

ff(x) x and f(f(x)) x since x0 ab " " "" "" œœœœœœ

" "" È x xx # " #x

16. Step 1: y x x œÊœÊœ""" $ xy y $ "Î$

Step 2: y f(x); œœœ "" $ " x x "Î$ É

Domain of f: x0, Range of f: y0; " " ÁÁ

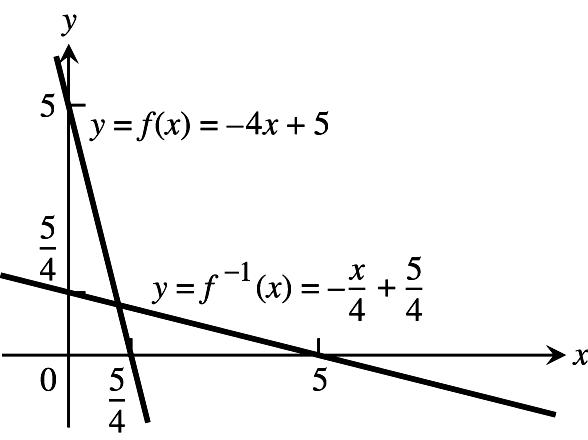
ff(x) x and f(f(x)) x ab

" " "" "" "Î$ " œœœœœœ ab x xxx "Î$ $ "$

17. (a) y2x3 2xy3 œ Êœ x f(x) Êœ Êœ y 3x3 #### "

(c) 2, ¸ ¹ df df dx dx x1 x1 œ

œœ " " #

18. (a) yx7 xy7 œ Êœ"" 55 x5y35 f(x)5x35 Êœ Êœ "

(b)

(b)

œœ " "

(c) , 5 ¸ ¹ df df dx 5dx x1 xœ$%Î&

19. (a) y54x 4x5y œ Êœ x f(x) Êœ Êœ 55 x 44 44 y "

(b)

œ œ " "

(c) 4, ¸ ¹ df df dx dx 4 x1 x3 œÎ# œ

100 Chapter 2 Differentiation

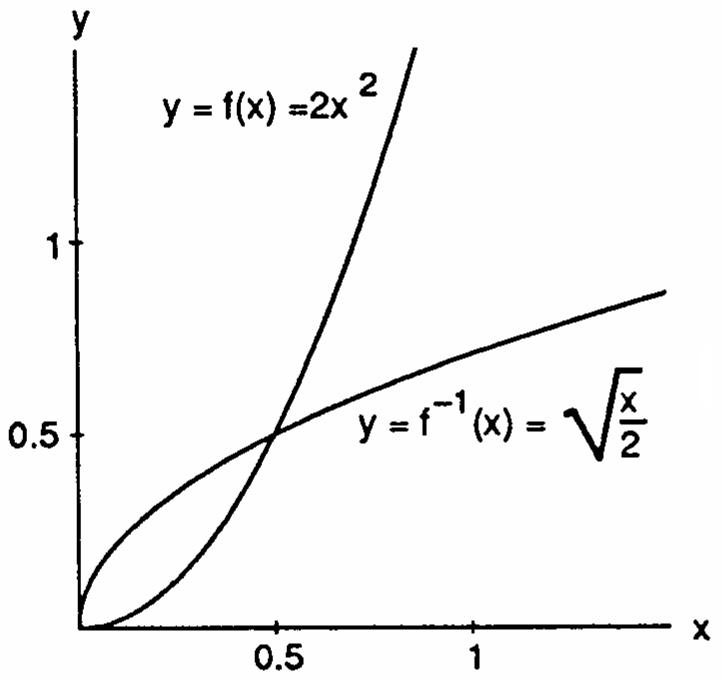
20. (a) y2x xyœÊœ ## " # xy f(x) ʜʜ " " # È 2 x È È

œœ x ¹¹ df dx0 2 " x0 x50 œ& œ (b)

œœ "" # "Î# # È

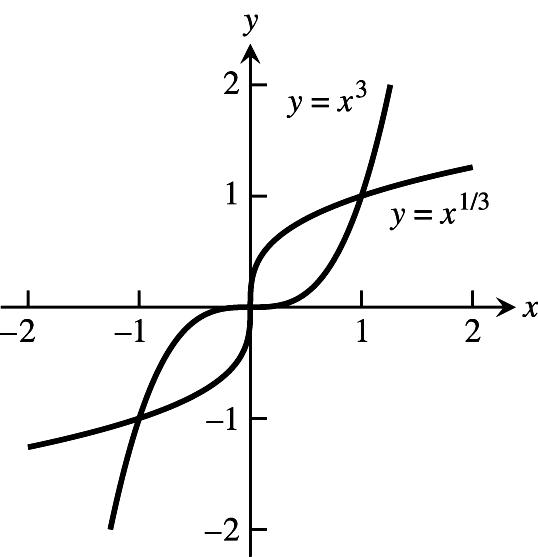
21. (a) f(g(x))xx, g(f(x))xx œœœœ ˆ‰ È È $ $ $ $

(c) f(x)3x f(1)3, f(1)3;w#ww œÊœ œ g(x)x g(1), g(1) w #Î$w w """œÊœ œ 333

(d) The line y0 is tangent to f(x)x at ();œœ!ß! $ the line x0 is tangent to g(x)x at (00)œœß $È

(b)

(c) h(x) h(2)3, h(2)3;www œÊœ œ 3x 4 # k(x)(4x) k(2), k(2) w #Î$w w "" œÊœ œ 4 333

# "

(b) 23. 3x6x 24. 2x4 df df df df dx dx 9 dx dx 6 œ Êœœ œ Êœœ

(b) The graph of yf(x) is a line through the origin with slope . œ " " m

26. ymxb x f(x)x; the graph of f(x) is a line with slope and y-intercept . œ Êœ Êœ y mmmmmm bb b " " ""

27. Let xx be two numbers in the domain of an increasing function f. Then, either xx or "# "# Á xx which implies f(x)f(x) or f(x)f(x), since f(x) is increasing. In either case, "# "#"# f(x)f(x) and f is one-to-one. Similar arguments hold if f is decreasing. "# Á

28. f(x) is increasing since xx xx; 3 #"#" """" Ê œÊœœ3636dx3dx 55dfdf " " ˆ‰ 3

œÊœÊœ

33

81x

30. f(x) is decreasing since xx

31. f(x) is decreasing since xx

32. f(x) is increasing since xx

33. The function g(x) is also one-to-one. The reasoning: f(x) is one-to-one means that if xx then f(x)f(x), so "#"# ÁÁ f(x)f(x) and therefore g(x)g(x). Therefore g(x) is one-to-one as well.

34. The function h(x) is also one-to-one. The reasoning: f(x) is one-to-one means that if xx then f(x)f(x), so "#"# ÁÁ , and therefore h(x)h(x). "" "# f(x)f(x) "#ÁÁ

35. The composite is one-to-one also. The reasoning: If xx then g(x)g(x) because g is one-to-one. Since "#"# ÁÁ g(x)g(x), we also have f(g(x))f(g(x)) because f is one-to-one. Thus, fg is one-to-one because "# "#ÁÁ ‰ xx f(g(x))f(g(x))."#"# ÁÊÁ

36. Yes, g must be one-to-one. If g were not one-to-one, there would exist numbers xx in the domain of g with "# Á g(x)g(x). For these numbers we would also have f(g(x))f(g(x)), contradicting the assumption that "# "#œœ fg is one-to-one. ‰

37. (gf)(x)x g(f(x))x g(f(x))f(x)1‰œÊœÊœ ww

38. The function fxx is diferentiable everywhere, and gxx is the inverse of f, so by Theorem 4 abab œœ n1/n gx x provided x0. w ab œœœœœœÁ

39-46. Example CAS commands:

Maple:

with( plots );#41

f := x -> sqrt(3*x-2);

domain := 2/3 .. 4;

x0 := 3;

Df := D(f); # (a)

plot( [f(x),Df(x)], x=domain, color=[red,blue], linestyle=[1,3], legend=["y=f(x)","y=f '(x)"],

title="#41(a) (Section 2.9)" );

q1 := solve( y=f(x), x ); # (b)

g := unapply( q1, y );

m1 := Df(x0); # (c)

t1 := f(x0)+m1*(x-x0);

y=t1;

m2 := 1/Df(x0); # (d)

t2 := g(f(x0)) + m2*(x-f(x0));

y=t2;

domaing := map(f,domain); # (e)

Chapter 2 Differentiation

p1 := plot( [f(x),x], x=domain, color=[pink,green], linestyle=[1,9], thickness=[3,0] ):

p2 := plot( g(x), x=domaing, color=cyan, linestyle=3, thickness=4 ):

p3 := plot( t1, x=x0-1..x0+1, color=red, linestyle=4, thickness=0 ):

p4 := plot( t2, x=f(x0)-1..f(x0)+1, color=blue, linestyle=7, thickness=1 ):

p5 := plot( [ [x0,f(x0)], [f(x0),x0] ], color=green ):

Mathematica:

display( [p1,p2,p3,p4,p5], scaling=constrained, title="#41(e) (Section 2.9)" ); (assigned function and values for a, b, and x0 may vary)

If a function requires the odd root of a negative number, begin by loading the RealOnly package that allows Mathematica to do this.

<<Miscellaneous `RealOnly`

Clear[x, y]

{a,b} = {2, 1}; x0 = 1/2 ;

f[x_] = (3x2) / (2x11)

Plot[{f[x], f'[x]}, {x, a, b}]

solx = Solve[y == f[x], x]

g[y_] = x /. solx[[1]]

y0 = f[x0]

ftan[x_] = y0f'[x0] (x-x0)

gtan[y_] = x01/ f'[x0] (yy0)

Plot[{f[x], ftan[x], g[x], gtan[x], Identity[x]},{x, a, b}, EpilogLine[{{x0, y0},{y0, x0}}], PlotRange{{a,b},{a,b}}, AspectRatioAutomatic]ÄÄÄ 47-48. Example CAS commands:

Maple:

with( plots );

eq := cos(y) = x^(1/5);

domain := 0 .. 1;

x0 := 1/2;

f := unapply( solve( eq, y ), x ); # (a)

Df := D(f);

plot( [f(x),Df(x)], x=domain, color=[red,blue], linestyle=[1,3], legend=["y=f(x)","y=f '(x)"],

title="#48(a) (Section 2.9)" );

q1 := solve( eq, x ); # (b)

g := unapply( q1, y );

m1 := Df(x0); # (c)

t1 := f(x0)+m1*(x-x0);

y=t1;

m2 := 1/Df(x0); # (d)

t2 := g(f(x0)) + m2*(x-f(x0));

y=t2;

domaing := map(f,domain); # (e)

p1 := plot( [f(x),x], x=domain, color=[pink,green], linestyle=[1,9], thickness=[3,0] ):

p2 := plot( g(x), x=domaing, color=cyan, linestyle=3, thickness=4 ):

p3 := plot( t1, x=x0-1..x0+1, color=red, linestyle=4, thickness=0 ):

p4 := plot( t2, x=f(x0)-1..f(x0)+1, color=blue, linestyle=7, thickness=1 ):

p5 := plot( [ [x0,f(x0)], [f(x0),x0] ], color=green ):

Mathematica:

display( [p1,p2,p3,p4,p5], scaling=constrained, title="#48(e) (Section 2.9)" ); (assigned function and values for a, b, and x0 may vary)

For problems 47 and 48, the code is just slightly altered. At times, different "parts" of solutions need to be used, as in the definitions of f[x] and g[y]

2.10

Clear[x, y]

{a,b} = {0, 1}; x0 = 1/2 ; eqn = Cos[y] == x1/5

soly = Solve[eqn, y]

f[x_] = y /. soly[[2]]

Plot[{f[x], f'[x]}, {x, a, b}] solx = Solve[eqn, x]

g[y_] = x /. solx[[1]]

y0 = f[x0]

ftan[x_] = y0f'[x0] (xx0)

gtan[y_] = x01/ f'[x0] (yy0)

Plot[{f[x], ftan[x], g[x], gtan[x], Identity[x]},{x, a, b}, EpilogLine[{{x0, y0},{y0, x0}}], PlotRange{{a, b}, {a, b}}, AspectRatioAutomatic]

FUNCTIONS

104 Chapter 2 Differentiation

8. (a) lne(sec )(ln e)sec (b) ln ee(ln e)e ˆ‰ ab sec ex x ) œœ œœ )) ab x

(c) lnelneln x2 ln x ˆ‰ Š‹ 2lnx lnx œœœ # #

9. ln y2t4 ee ye 10. ln yt5 ee ye œ ʜʜœ ʜʜ lny2t4 2t4 lnyt5 t5

11. ln(y40)5t ee y40e ye40 œÊœÊ œÊœ lny40)5t 5t 5t Ð

12. ln(12y)t ee 12ye 2ye1 y œÊœÊ œÊ œ Êœ ln12y)t t t e Ð " # Š‹ t

13. ln(y1)ln 2xln x ln(y1)ln 2ln xx lnx ee e œ Ê œÊœÊœÊœ ˆ‰ y1 y1 2x x ln x x # ˆ‰ y1 2x y12xe y2xe1 Ê œÊœxx

14. lny1ln(y1)ln(sin x) lnln(sin x) ln(y1)ln(sin x) ee ab Š‹ # Ð ÑÐÑ " œÊœÊ œÊœ y y1 lny1lnsinx # y1sin x ysin x1 Ê œÊœ

15. (a) e4 ln eln 4 2k ln eln 2 2k2 ln 2 kln 2 2k 2k œÊœÊœÊœÊœ #

(b) 100e200 e2 ln eln 2 10k ln eln 2 10kln 2 k 10k 10k 10k ln 2 10 œÊœÊœÊœÊœÊœ

(c) ea ln eln a ln eln a ln a k1000 ln a k1000 k1000 kk 1000 1000 ÎΜʜʜʜʜ

16. (a) e ln eln 4 5k ln eln 4 5kln 4 k 5k 5k 4 5 ln 4 œÊœÊœ Êœ Êœ " "

(b) 80e1 e80 ln eln 80 k ln eln 80 kln 80 kkk œÊœÊœÊœ Êœ " "

(c) e0.8 e0.8 (0.8)0.8 k1 ÐÞÑln08k ln08 k k œÊœÊœÊœ

ˆ‰

17. (a) e27 ln eln 3 (0.3t) ln e3 ln 3 0.3t3 ln 3 t10 ln 3 Þ Þ$ 03t 03t œÊœÊ œÊ œÊœ

(b) e ln eln 2kt ln eln 2 t kt kt ln 2 k œÊœœœ Êœ " # "

(c) e0.4 e0.4 0.20.4 ln 0.2ln 0.4 t ln 0.2ln 0.4 t ÐÞÑ ln02t ln02 t t t ln 0.4 ln 0.2 œÊœÊœÊœÊœÊœ

ˆ‰

18. (a) e1000 ln eln 1000 (0.01t) ln eln 1000 0.01tln 1000 t100 ln 1000 Þ Þ 001t 001t œÊœÊ œÊ œÊœ

(b) e ln eln 10kt ln eln 10 ktln 10 t kt kt 10 k ln 10 œÊœœœ Êœ Êœ " "

(c) e e2 22 t1 ÐÑ " " " # ln2t ln2 t t œÊœÊœÊœ

23. (a) Let zlog x 4x 2x 2x 2xœÊœÊœÊœÊœ 4 z2zzz ab È #

(b) Let zlog x 3x 3x 3x 9xœÊœÊœÊœÊœ 3 zz2zz ab# ###

(c) log elog 2sin x 22 ln2 sinxsinxab ÐÑ œœ

24.

Let zlog 3x 53x 259xœÊœÊœ 5 zz ab##%

(b) log ex e x ab œ

aln aln bln

yln kx y(k) œÊœœ œÊœœ w w """ ˆ‰ ˆ‰ 1 3xxkxx 29. ylnt (2t)

31.

" 32.

yln ln 10x 10x œœÊœ œ 10 xdx10xx dy " # ""

yln x 3x

(c) t 42. y œÊœœœ " " ln t 1ln tln t tdt tt dy t(ln t)(1) t ˆ‰ " #

ylnt t œÊœœ œÊœœ ab ˆ‰

log a log aln xln xln xln t " ## 43. y y œÊœœœ ln x 1ln xx(1ln x) (1ln x)(ln x) (1ln x) (1ln x) w " ˆ‰ˆ‰ """ xxxxx ln xln x ## # 44. y y 1 œÊœ œœ x ln x ln x 1ln x(1ln x)(1ln x) (1ln x) (x ln x) (1ln x) (ln x)ln x w " ˆ‰ˆ‰ ln xx "" xx #

"" "" #

34.

y(ln x) 3(ln x)(ln x) œÊœœ œÊœœ $# $# " dy dy 3(ln x) dxx x dx dx x 3 d

yt(ln t) (ln t)2t(ln t)(ln t)(ln t)(ln t)2 ln t œÊœ œ œ ## ## dy dt dt t d 2t ln t † 38. ytln tt(ln t) (ln t)t(ln t)(ln t)(ln t) (ln t) œœÊœ œ œ È "Î# "Î# "Î# "Î# "Î# " " ## # dy t(ln t) dt dt t d (ln t) † "Î#

aln aln aln x2 ln x x x# # # œƒœœœ # ## Copyright © 2012 Pearson Education, Inc. Publishing as Addison-Wesley

#

106 Chapter 2 Differentiation

45. yln(ln x) y œÊœœ w """

ln xxx ln x

46. yln(ln(ln x)) y (ln(ln x)) (ln x) œÊœœœ w """" ln(ln x)dxln(ln x)ln xdxx(ln x) ln(ln x) dd

47. y[sin(ln )cos(ln )] [sin(ln )cos(ln )]cos(ln )sin(ln ) œ Êœ )))))))) dy d ))) ‘ "" sin(ln )cos(ln )cos(ln )sin(ln )2 cos(ln ) œ œ )))))

48. yln(sec tan ) sec œ Êœœœ )) ) dy sec (tan sec ) dsec tan tan sec sec tan sec ))))) ))) ))) #

49. yln ln x ln(x1) y œœ Êœ œ œ """ " " ## w xx1 xx12x(x1)2x(x1) 2(x1)x 3x2

50. y ln ln(1x)ln(1x) y (1) œœ Êœ œœ " " """ " " # # # # " w 1x 1x1x 1x 1x1x (1x)(x)1x cd ‘

51. y œÊœœœ 1ln t 2 1ln tdt(1ln t)(1ln t)t(1ln t) dy (1ln t)(1ln t) ˆ‰ˆ‰ " """ t ttttt ln tln t ## #

52. yln tln t ln t ln tln t t œœÊœ œ

"Î# "Î# "Î# "Î# "Î# "Î# "Î# "Î# "" " ## dy dt dt dt dd t"Î# ln t t œœ "" "" ## "Î# "Î# "Î# ˆ‰ t 4tln t "Î#

53. yln(sec(ln )) (sec(ln )) (ln ) œÊœœœ ))) dy sec(ln ) tan(ln ) tan(ln ) dsec(ln )d sec(ln )d dd ))) ))) )) ) "

54. yln (ln sin ln cos )ln(12 ln ) œœ Êœ È sin cos 12 ln dsin cos 1 ln dy cos sin )) )) ) ) ) )) # # # "" ))) ˆ‰ 2 ) cot tan œ " # ’“ )) 4 (12 ln ) ))

#

5205 ## ## "" w & #! œ 53x2 (x1)(x) # # ’“

57. yx(x1)(x(x1)) ln y ln(x(x1)) 2 ln yln(x)ln(x1) œ œ Êœ Êœ Êœ È "Î# " "" # 2y yxx1 w yx(x1)Êœ œœ w """ " # ˆ‰ˆ‰ È xx12x(x1) x(x1)(2x1) 2x 2x(x1) È È 58. yx1(x1) ln ylnx12 ln(x1) œ Êœ Êœ Èabcd ab ˆ‰ ## "" ## # y yx1x1 2x2 w # yx+1(x1) x1(x1) Êœ œ œ w #### " ÈÈ abab ˆ‰ ’“

61. y3(sin )(3) sin ln y ln(3)ln(sin ) œ œ Êœ Êœ È )))))) "Î# """ ##yd(3)sin dy cos ))) ) 3(sin )cot Êœ dy d2(3) )) È ’“ ))) "

62. y(tan )21(tan )(21) ln yln(tan ) ln(21) œ œ Êœ Êœ )))))) È ˆ‰ˆ‰ "Î# """ ### ydtan 1 dy sec2 ))) ) # (tan )21 sec21 Êœ œ dy dtan 1 sectan 21 ))) )) ) )) ))ÈÈ Š‹ ab # " # # È

63. yt(t1)(t2) ln yln tln(t1)ln(t2) œ Êœ Êœ"""" # ydttt1t dy t(t1)(t+2) t(t1)(t2) 3t6t2 Êœ œ œ dy (t1)(t2)t(t2)t(t1) dt tt1t t(t1)(t2)

""" # #

64. y ln yln 1ln tln(t1)ln(t2) œÊœ Êœ " """" # t(t1)(t2)ydttt1t dy Êœ œ dy (t1)(t2)t(t2)t(t1) dtt(t1)(t2)tt1tt(t1)(t) t(t1)(t2) """" " # # ‘

œ 3t6t2 t3t2t # $# #ab

65. y ln yln(5)ln ln(cos ) œÊœ Êœ ) ) )))))) """ 5 sin cos yd5cos dy ))) tan Êœ dy d cos 5 5 ))))) ) ˆ‰ˆ‰ "" )

66. y ln yln ln(sin ) ln(sec ) œÊœ Êœ )) ) ) )))) )) sin cos sec ydsin 2 sec dy(sec )(tan ) È )))""" # ’“ cot tan Êœ dy d sin sec )) )) ) È ˆ‰ "" # ))

"" # # ab y Êœ w " xx1 (x1) xx13(x1) x2 È # #Î$ # ’“

w #

67. y ln yln x lnx1 ln(x1) œÊœ Êœ xx1 y (x1) 2x 2 3 yxx13(x1) È # #Î$

68. y ln y[10 ln(x1)5 ln(2x1)] œÊœ Êœ É (x1) y (2x1) yx12x1 55 # " "! &

w y Êœ w É ˆ‰ (x1) (2x1)x12x1 55 "! &

69. y ln yln xln(x2)lnx1 œÊœ Êœ É cd ab ˆ‰ 3 x(x2) y x1 3 y3xxx1 2x # "" " " # # #

w y Êœ w """ # 3x1xxx1 x(x2) 2x É ˆ‰ 3 ##

70. y ln yln xln(x1)ln(x2)lnx1ln(2x3) œ Êœ É cd ab 3 x(x1)(x2) x1(2x3)3 " # ab # y Êœ w """" # 3x1(2x3)xx1xx12x3 x(x1)(x2) 2x2 É ˆ‰ 3 ab##

71. ylncos 2cossin2tanœÊœ†† œ ab ab 2 dy dcos 1 )) )) )) 2

72. yln3eln 3ln ln eln 3ln 1 œœ œ Êœ ˆ‰)))) " )) )) dy d 73. yln3teln 3ln tln eln 3ln tt 1 œœ œ Êœ œ ab " tt dy dttt 1t 74. yln2e sin tln 2ln eln sin tln 2tln sin t 1 (sin t)1 œœ œ Êœ œ ab

108 Chapter 2 Differentiation

75. yln ln eln1eln1+e 1 1e1 œœ œ Êœ œ œ e de 1e 1e1e1e dy dd ) ) ) )) )

"")))) )) ˆ‰ˆ‰ˆ‰ˆ‰ )

76. yln ln ln1 1 œœ Êœ È ÈÈÈ ) )))))) 1 1 dy dd d dd"" ÈÈÈÈ

Š‹Š‹Š‹Š‹Š‹ ))))

œ œœœ Š‹Š‹Š‹Š‹ """" "" # # # # ÈÈÈÈ Š‹ÈÈ

ÈÈ ab )))) )) )))) )) 1 1 21 1 1 "Î#

Š‹Š‹

77. yeeete ete (cos t)(1t sin t)e œœœÊœ œ Ð Ñ costln tcostlntcostcostcostcost dy dtdt d

78. yeln t1 e(cos t)ln t1eeln t1(cos t) œ Êœ œ sint sint sintsint dy dt t t 22 ab abab ‘ ###

79. ln ye sin x yye(sin x)e cos x ye sin xe cos x œÊœ Ê œ yy yy y yyŠ‹

ab "" www y e cos x y ÊœÊ œ ww Š‹ 1ye sin x ye cos x y 1ye sin x y yy y

80. ln xye ln xln ye y1ye yee œÊ œÊ œ Ê œ xy xy xy xyxy xy y x w w w "" " "

y y ʜʜ ww " "

1ye yxx1ye xe yxe xy xy xy xy ab ab

2 2

82. tan yeln x secyye y œ Êœ Êœ xx xx xe cosy ab#w w " " ab x #

))

œ dy d(sin )(ln 7)(cos )(ln 7)ln 7ln 7ln 7 cos sin ln 2 ))) ))

))

tan 1ln 2)

100.

xe 2x1 ln xln eln 2ln x1 ln 2ln

È

2 2 ln x2ln 2 ln(x1)

ˆ‰ˆ‰ ’“"" " ##

œœœÊœœÊœ œ ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰ È t t tt "Î# Î# ### # # """" Î# tt ln t ydt t dy t Êœ dy dt ln t

t ## "

ˆ‰

" yxÊœ w sinx ’“ sin xx(ln x)(cos x) x

ˆ‰

cd w

113. (a) Begin with yln x and reduce the y-value by 3yln x3. œÊœ

(b) Begin with yln x and replace x with x1ylnx1. œ Êœ ab

(c) Begin with yln x, replace x with x1, and increase the y-value by 3ylnx13. œ Êœ ab

(d) Begin with yln x, reduce the y-value by 4, and replace x with x2ylnx24. œ Êœ ab

(e) Begin with yln x and replace x with xylnx. œ Êœ ab

(f) Begin with yln x and switch x and yxln y or ye.œÊœœ x

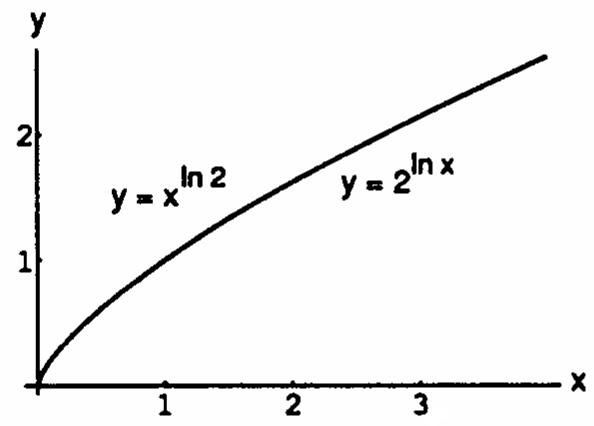
114. The functions f(x)x and g(x)2 appear to œœ ln2 lnx have identical graphs for x0. This is no accident, because xee2. ln2ln2lnxln2 lnx lnx œœœ ab

115. yAsinlnxBcoslnxyAcoslnxBsinlnxAcoslnxBsinlnx œ Êœ† †œ † ababababab abab w 111 xxx yAcoslnxBsinlnx AsinlnxBcoslnx

† † †† ww a ababbababˆ‰ 111 1 xxx x 2 AcoslnxsinlnxBsinlnxcoslnx œ † ab abab abababab 1 x2 xyxyyAcoslnxsinlnxBsinlnxcoslnxAcoslnxBsinlnx

a b a ba ababababbabab AsinlnxBcoslnx