APPLICATIONOFBVP4CINTHEANALYSISOF HYDROMAGNETICFLOWOFMAGNETITEWATER (NANOFLUID)ADAPTEDBUONGIORNOMODEL
IWETAN,PAULANIREJUORITSE 21055131456
B.Sc/EdMATHEMATICS(UNN)
APROJECTSUBMITTEDTODEPARTMENTOFMATHEMATICS, FACULTYOFSCIENCE,LAGOSSTATEUNIVERSITY, INPARTIALFULFILMENTOFTHEREQUIREMENTFORTHEAWARDOF MASTEROFSCIENCEDEGREE(M.Sc)INMATHEMATICS, ATLAGOSSTATEUNIVERSITY,OJO,LAGOS,NIGERIA.
FEBRUARY,2025
AUTHOR: IWETAN,PAULANIREJUORITSE TITLEOFDISSERTATION: APPLICATIONOFBvp4cINTHEANALYSIS OFHYDROMAGNETICFLOWOFMAGNETITEWATER(NANOFLUID)ADAPTED BUONGIORNOMODEL.
DEGREE: MASTERSDEGREE YEAR: 2025
I,IWETAN,PaulAnirejuoritsewithmatriculationnumber210551311456hereby authorizetheLagosStateUniversityLibrarytocopymydissertationinwholeor inpartinresponsetorequestfromindividualresearcherandorganisationsforthe purposeofprivatestudyorresearch. SignatureDate
Certification
Thisdissertationwiththetitle ”APPLICATIONOFBvp4cINTHEANALYSISOF HYDROMAGNETICFLOWOFMAGNETITEWATER(NANOFLUID)ADAPTED BUONGIORNOMODEL,” submittedbyIWETAN,PaulAnirejuoritsewithMatriculationNumber 210551311456 wascarriedoutundermysupervisionatLagosState University,Ojo,Lagos.
MUSTAPHAR.A.(Ph.D.)DATE (Supervisor)
OLUTIMO(Ph.D.)DATE (Ag.Head,MathematicsDepartment) ExternalExaminerDATE
Attestation IherebyattestthatthisresearchworkwascarriedoutattheDepartmentofMathematics;LagosStateUniversity,Ojo,Lagos,Nigeria.
OLUTIMO.(Ph.D)Date Ag.Head,MathematicsDepartment
DEDICATION ThisprojectisdedicatedtotheAlmightywhohasbeenmysustainer,GodAlmighty hasbeenmyguidanceandstrengthfromthebeginningandthroughoutmyprogramme.Hehasbeenafatherandcompanion,leteverythingthathasbreathpraise thelord.Also,tomyevergreenparentsinmemoryoflatefatherMrandMrsIwetan Danielfortheirparentalaffection,IalsothankstomydarlingwifeBelloOmowunmi NimotallahifortheroleheplayedduringmyMscprogramme.Alsotomyprince ’AnirejuoritseNathanielAninoritse’andmyprincess’AnirejuoritseNoraAmajuoritse fordisturbingmeduringthisproject.MyfamilywasawonderfulgiftfromGod.
ThankyouallmayGodblessyou.(Amen)
ACKNOWLEDGMENT AllpraisebetoGodAlmightyforHisunendingmerciesandformakingitpossible formetostartandendthisprogramsuccessively.
IwouldliketoexpressmysinceregratitudetomysupervisorMUSTAPHAR.A. (Ph.D.),forhistimeandeffortsheprovidedthroughouttheyear.Yourusefuladvice andsuggestionswerereallyhelpfultomeduringtheseminarwork.Iamgratefulsir.
Iwouldliketotakethisopportunitytoexpressmygratitudetomycolleagues,Mr. Moshood,MrsHamzatMiss.Basheerah,Mr.Loko,Mr.SegunandMr.Godwinand alsototheentirestaffsofdepartmentofMathematics,LASU.
ABSTRACT ThehydromagneticflowofmagnetiteWaterNanofluidduetoarotatorystretchablediskhasbeeninvestigatednumericallyviaBvp4c.Thenanofluidhasbeen modeledutilizingtheadaptedBuongiornomodelwhichconsiderthevolumefractiondependenteffectivenanofluidpropertiesandthemajorslipmechanismstogetherwith dynamicviscosityandeffective,thermalconductivityaredeployed.Thegoverning equationsaretransformedintoafirst-orderODEsviaasuitablesimilarityvariable calledVonKarman’s,similarityconversions.TheresultingODEsisthensolvedusing anumericaltechniqueknownasBvp4c.Theimpactofpertinentparametersoverthe physicalquantities,nanofluidtemperatureandnanofluidconcentrationisexplained withthehelpofgraphs.Resultsshowthatrisingvolumefractionofmagnetitenanoparticle(NPs)andmagneticfieldtermenhancethedragforce.Itisdetectedthat changesinstretchingparameterareinverselyproportionaltothethermalfield.
Keywords:Nanofliud,Bvp4c,hydromagnetic,magnetitewater,thermophoresis
Chapter1 INTRODUCTION 1.1BackgroundInformation Fluidflowordischargeratehappeninallareasofourspecializedandcharacteristicenvironmentandanybodyseeingtheirenvironmentwithopeneyesandsurveying theirnoteworthinessforthemselvesandtheirindividualcreaturescanpersuadethemselvesofthedistantcomingtoimpactsofliquidstreams.Withoutliquidstreams, lifeasweknowit,wouldnotbeconceivableonSoil,norseemmechanicalformsrun intheframeknowntousandleadtothehugenumberofitemswhichdecidethetall standardoflivingthatwethesedaystakeforallowed.Withoutstreamsourcommon andspecializedworldwouldbediverse,andmightnotindeedexistatall.There, streamsareimperative,asrecognizedby(Franz,2008).Fluidscanbecharacterized asasubstance,suchasafluidorgas,whichcanmovealmostwithopportunityand hasnosettledshape.(Chambers21stcenturylexicon).Commonliquidssuchas water,oil,anddiscussfulfillthedefinitionofaliquidi.e,theywillstreamwhenacted onbytheshearingstress.FluidscanbeclassifiedasCompressibleorIncompressible. Liquidswhosethicknessdoesnotalteressentiallywithalterinweightortemperature areacceptedtobeincompressibleliquids.Whenthereisnoteworthyalterinthe
thicknessoftheliquidwithalterinweightortemperature,atthatpointtheliquid isconsideredtobecompressible.Nanofluidisablendgottenbyblendingnanoparticleswithstandardwarmvitalityexchangeliquidssuchasoil,glycol,water,ethylene glycol,etc.Nanoparticlescanbearrangedonalittlescaleinresearchfacilitiesas wellasonaexpansivescale(inbusinesses).Theregularestimateofnanoparticles liesintherun1–100nm.NanoparticlescanbemadefrommetalssuchasAl,Cu, Au,andAg,metaloxidessuchas Fe3 O4 ,CuO,TiO2 ,andAl2 O3 NitridessuchasSiN andAlN,andcarbidessuchasSiC,etc.Nanometer-sizedparticlescanbeaddedin aminiaturesumtoexpandthewarmvitalityexchangerateduetotheirhugewarm conductivities.Duetonanometer-sizedgeometry,thenanoparticlescaneffectively blendwiththebaseliquid.Theprogressionofwarmgadgetsinbuildingframeworks, theutilizationofnanofluidshasbeenplayingacrucialpartintheprepareofcooling electronicgadgetsandwarmexchangeimprovementinnumerousmechanicalfabricatingforms.Nanofluidiscreatedbyblendingnanosizedmetallicornonmetallic particlesornanofiberparticlesintocustomaryliquidsinarrangetoincrementthe warmpropertiesGuptaetal.Amongdiverseinvestigatesonnanofluids,afewworks havebeencenteredonamodernkindofnanofluidscalledferrofluids.
1.2Statementoftheproblem Severalworkshavebeendoneonthehydromagnetic/magnetohydrodynamics(MHD) ofnanofluidbasedonthesingle-phasemodel.Inthisstudy,weadaptedtheBuogiorno model,whichinvestigatedthetwo-phasenanoparticlemodel.
1.3GoalsandObjectives Thegoalsandobjectivesofthisstudyareto:
1.Investigatethenanofluidflowwithinconcentriccylinders
2.Investigatethefluidonarotatorysheetandderiveasemi-analyticsolution
3.Tostudythenanofluidflowoverastretchingsheet
4.Investigatethecouplestressmagnetite-waterbasednanofluidmotionnearabidirectionalstretchablesurfaceincorporatingtheeffectduetonon-linearthermal radiations
5.Investigatetheheatenergytransferfromthiskindoffluidatastagnationpoint
6.Examinetheaccumulativeeffectsofheatingandmagneticfieldonacoupleof stressfluids(three-dimensionalflow)
7.Effectsontheconvectiveflowinaporousmedium.
8.Employedthetwo-phasenanofluidmodeltoinvestigatethecombinedimpacts ofconvectiveboundaryconditionsandmagneticfieldonthecouplestressfluid three-dimensionalflowonanon-linearenlargedsurface.
1.4Significanceofstudy ToinvestigatehydromageticflowofmagnetiteswaternanofluidusingBuogiorno modelandBvp4ctoexaminetheBrownianmotionandthermophoresisaspects.The equationsgoverntheflowofthenanofluid,heattransfer,nanoparticleconcentration, anddensityofmotilemicroorganisms’fields.
1.5Definitionofterms 1.FluidFlow:FluidFlowisthemovementoffluidinamechanicsanddealswith fluiddynamics.Itinvolvesthemotionofafluidsubjectedtounbalancedforces. Thismotioncontinuesaslongasunbalancedforcesareapplied.
2.Nanoparticle:Ananoparticleorultrafineparticleisusuallydefinedasaparticle ofmatterthatisbetween1and100nanometres(nm)indiameter.Thetermis sometimesusedforlargerparticles,upto500nm,orfibersandtubesthatare lessthan100nminonlytwodirections.
3.Nanofluid:Ananofluidisafluidcontainingnanometer-sizedparticles,called nanoparticles.Thesefluidsareengineeredcolloidalsuspensionsofnanoparticles inabasefluid.Thenanoparticlesusedinnanofluidsaretypicallymadeof metals,oxides,carbides,orcarbonnanotubes.Commonbasefluidsinclude water,ethyleneglycolandoil.
4.Hydromagnetic:Hydromagneticisthestudyofmagneticpropertiesandbehaviourofelectricallyconductingfluids
1.6Nomenclature Thefollowingabbreviationsareused: (u; v; w) Velocitycomponents
DB-Browniandiffusioncoefficient
α -Thermaldiffusivityofnanofluid
Pe-Pecletnumber
Sc -Schmidtnumber,
qw -Heatflux
Nu -Nusseltnumber
p -Pressureisrepresentedby
υ-Kinematicviscosity
DT -Thermophoreticdiffusioncoefficient
Dn -Diffusivityofmicroorganisms
b -Chemotaxisconstant
Pr -Prandtlnumber
Le -Lewisnumber
Sh -Sherwoodnumber
δ -Electricalconductivity
Tw -Surfacetemperature
R∞ -Freestreamtemperature
A1Couplestressparameter
Rex -LocalReynoldsnumber
Cfx -Localskinfriction
τij Stresstensor
dij -Deformationratetensor
∞-Conditionatinfinity
(x,y,, z)-Coordinates
0Referencecondition
η -Similarityvariable
n′ -Couplestressviscositycoefficient
γ Thicknessparameter
λ1 -Viscositycoefficient
knf -Thermalconductivityofthenanofluid
ρnf -Nanofluiddensity
µnf -Nanofluidviscosity
k -Thermalconductivity
T -Fluidtemperature
m -Traceofthecouplestress
v -Kinematicviscosity
µ -Dynamicviscosity
t -Time
cp -Specificheat
R0 -RotationParameter
Rd -RadiationParameter
f -Dimensionlessaxialvelocityx-direction
k -Dimensionlessdrainingvelocityx-direction
S -Dimensionlessinducedvelocityalongy-direction
g -Dimensionlessinducedvelocityalongz-direction
θ -Dimensionlesstemperature
DDS -Drugdeliverysystems
Chapter2 LITERATUREREVIEW 2.1Preamble Inthischapterthepreambleworkwillauditrelatedworksofallthecreatorsandappearthedefenseforthedisplayconsider.Thenanofluidhasappearedafewmarvelous applicationsindifferentbranchesofscience,chemicalandmechanicalinnovation, warmbuilding,atomicbusinessesandbio-mechanics.Amidthefewfinaldecades, thegadgetsinthinmeasurementswithdistinctionexecutioncanbesynthesizedand itcheerstoilluminatingtheelectricgadgetinnovation.Sinceofdroppingthemeasure,tallwarmloadsrequiringsuccessfulandfastevacuationareachievedallthrough theworkperiodofmodestgadgets.Inlateralongtime,thinkaboutofnanofluid isbeingbegunsuccessfullysignificantduetodistinctivecharacteristicstonano-sized molecule,commonlylessthan100nm,blendsinceofthewarmconductivity.The warmconductivityofnanoparticlesismorethanbasefluid’swarmconductivity.
Thenanofluidshasenergeticpartincoolingandwarmingmethods.Thenanofluidshasenergeticpartincoolingandwarmingstrategies.Theconceptofnanofluid
wasatfirstpresentedbyChoiin1995.Afterwardon,Buongiorno(2006)reconnoiterthenanofluidconvectivetransportbypresentingtheBrownianmovementand thermophoresishighlights.Agreeingtothisponder,thesupremespeedofnanofluid canbearticulatedastheentiretyofbothspeedsi.e.baseliquidandrelativeslip.
ConcurringtoBuongiorno’snanofluiddemonstrate,outofsevenslipcomponentsfor warmexchange,Brownianmovementandthermophoresisviewpointsplayaprincipal part.Notatalllikebaseliquids,movementofmotilemicroorganismscanbecarriedoutwiththeofferassistanceBrownianmovementandthermophoresisparameter. ThereareafewresearchersworkedonBuongiorno’snanofluiddemonstratetocomprehendthewarmtradeupgradeinthecharacteristicwarmdisseminationconvection innanofluids.Nanofluidisablendgottenbyblendingnanoparticleswithconventionalwarmvitalityexchangeliquidssuchasoil,glycol,water,ethyleneglycol,etc.
Nanoparticlescanbearrangedonalittlescale(researchfacilities)aswellason aexpansivescale(inbusinesses).Thenormalmeasureofnanoparticlesliesinthe run1–100nm.NanoparticlescanbemadefrommetalssuchasAl,Cu,Au,and Ag,metaloxidessuchas Fe3 O4 ,CuO, TiO2 ,and Al2 O3 ,nitridessuchasSiNand AlN,andcarbidessuchasSiC,etc.Thesenanometer-sizedparticlescanbeincluded inaminiaturesumtoincreasethewarmvitalityexchangerateduetotheirhuge warmconductivities.Duetonanometer-sizedgeometry,thenanoparticlescaneffectivelyblendwiththebaseliquid.Awritingthinkaboutproposesthatthereare twoprimarystrategiestodemonstratenanofluids.Inthetobeginwithsort,the nanoparticlesaredispersedconsistentlyallthroughthehaveliquid.Thenanofluids’ thermophysicalcharacteristicsleadtotheboundary-layerconditions,whichcanbe
utilizedtoponderthenanoparticles’impacts.Ontheotherhand,themodelsmadeto considerthenanoparticles’interactionwiththebaseliquidareknownastwo-phase models,andareknownasthemomentcaseofthenanofluiddemonstrate.Tewari andDas(2007)examinedthesingle-phasedemonstrate,whereasBuongiornohasexploredthetwo-phasenanoparticledemonstrate.Athinkaboutwastooperformedby VajraveluandMukhopadhayay(2015)onasingle-phaseshow.
Theutilizeofnanoparticleschangesfromalittlescaleinresearchfacilitiestoaexceptionallyexpansivescaleinbusinesses.Duetotallwarmconductivities,nanofluids areutilizedforcoolingpurposesintransformers,coolingchambers,andinatomicreactors.Fortherapeuticpurposes,theyareutilizedtoplandiversesurgerygeartomurdertumorcells.Inelectronicmachines,thewarmproducedamidtheiroperationcan toobediminishedbyutilizingdiversenanofluids.TewariandDas’smodel(2007)has beenencourageexaminedbynumerousanalyststoexpandonthewarmhighlightsof diversenanofluids.Theexaminationofwarmvitalityexchangeamidnon-Newtonian liquidstreamonextendedsurfaceshasasoflatepickedupcriticalconsideration. Duetodistinctivesortsofstreamingenuinecircumstances,asingleconstitutiveconnectionwhichrelatestheshearstretchandshearrateisinadequatelytoexplorethe non-Newtonianliquidproperties.
Thereareafewviscoelasticliquidswhichappearpolarimpacts,calledcouple pushliquids,whichrearrangetheconventionalspeculationsforexamination.Forthis kindofliquid,theconstitutiverelationsrelatetheskew-symmetricparcelofthepush tensorwiththeprecisespeed,andthecouplepushwiththeangleinprecisespeed.
Eringen(1966)calledthepolarliquidsmicropolarliquids.Thehypothesisofdipolar liquidswascreatedbyBleusteinandGreen(1967).Ifthepolarliquidisinsuchastate thatthecosseratgroupofthreeisinflexiblyjoinedtothemedium,atthatpointitis knownasacouplestretchliquid.Thepolaranddipolarliquidsareconsideredinthe couplestretchhypothesiswhichStokes(1966)made.TheNavier–Stokesconditions cannotportraysuchliquidsduetotheirpushtensornon-symmetricnature.Cases incorporategreasesthatcontainpolymeradditivetoafewdegree,manufacturedliquids,blood,andelectro-rheologicalliquids.Duetothepertinenceofcouplestretch liquidsinthechemicalexchangeanddifferentmachineries,agreatnumberofanalysts havegivenconsiderationtothethinkaboutoftheirstreamandrelatedproperties. Hayatetal(2013).workedoutthesofteningprepareinexaminingthewarmvitality exchangeforthiskindofliquidatthestagnationpoint.Ramzanetal(2013).Inspectedthecollectiveimpactsofwarmingandattractivefieldonthecouplestretch liquidthree-dimensionalstream.SrinivasacharyaandKaladhar(2012)haveexamined bothDuofourandSoretimpactsontheconvectivestreaminapermeablemedium. Turkyilmazoglu(2016)logicallyexploredtwo-dimensionalstreamonanamplifiedsurface.Besides,Hayatetal(2015).utilizedthetwo-phasenanofluidshowtoexplore thecombinedimpactsofconvectiveboundaryconditionsandattractivefieldonthe couplestretchliquidthree-dimensionalstreamonanon-linearextendedsurface.Pordanjanietal(2019).Examinedtheaffectofradiationandattractivefieldonentropy eraandconvectivewarmvitalitynanofluidstreamratethrougharectangularholder andexploredtheimpactofgermaneparametersonthestreamhighlights.Moreover, Ramzan(2015)hasexploredtheimpactsofJoulewarming,gooeydissemination,and connectedattractivefieldonthe3Dcouplestretchnanofluidstream.
Therearediversecomponentsbywhichvitalitycanexchangefromoneputto another.Indiversefabricatingprocedures,thewarmexchangethroughradiationis moreproductiveanddowntoearththanconvectivewarmexchangewhenthereis ahugetemperaturecontrastbetweentheencompassingliquidandthesurface.To streamlinethecircumstance,thelion’sshareofanalystshaveconnectedtheRosseland estimationtopondertheimpactsofdirectradiation.Jamshedetal(2021).Examined theimpactsofsunpoweredradiationtransportandslipconditionontheconvective warmhighlightsofaninsecurestreamofCassonnanofluid.Sheikholeslam(2017) examinedtheimpactsofstraightwarmradiationsonnanofluidstreamthroughan ellipticbarrel.Sajidetal(2021).
Inspectedtheimpactsofnumerousconvectivesurfaceboundaryconditions,nonlinearwarmradiations,exponentialwarmsource,andgooeydisseminationonincompressiblemicropolarliquidmovementthroughapermeableextendingsurface. Dogonchietal(2017).Utilizedapermeablechanneltothinkabouttheimpactsof warmradiationsonthewarmexchangeamidnanofluidrelocation.Inthelargerpart oftheseexaminations,theanalystsconnectedstraightwarmradiationtermstomake thecircumstancestraightforward.Togetthetotalinformationofthewarmexchange amidnanofluidstream,itisexceptionallycriticaltotakeintoaccounttheimpacts deliveredduetotheincorporationofnon-linearwarmradiations.Thewideextendof applicationsofnanofluidsdependuponthegeometryoftheissuebeneaththought.
Warmexchangeexaminationofthemovementofdistinctivenanofluidshasbeenperformedbynumerousanalystsutilizingdiversegeometries.Devakaretal(2017).Considerednon-Newtonianliquidmovementthroughasquareconduitpastaporous medium.SrinivasacharyaandShafeeurrahman(2017)examinedthenanofluidstream betweenconcentricbarrels.Rashidietal(2009).Examinedtheliquidstreamona rotatorysheet,andinferredasemi-analyticarrangement.KhanandPop(2010)examinedthenanofluidstreamoveraextendingsheet.Thestreamoveraextending sheethaspulledinnoteworthyconsiderationinthefinalfewalongtimeduetoits specialnatureandmechanicalapplications.Diversepondersonextendingsheetscan befoundindetailinthepapers.Goshetal(2018).UtilizedtheTiwariandDas showtoexplorethecouplepushmagnetite–water-basednanofluidmovementclosea bi-directionalstretchablesurfaceconsolidatingtheimpactsduetonon-linearwarm radiations.Lundetal(2020).Examinedthedoubleandsymmetricalarrangement ofcrossovernanofluidstreampastaextendingsurface.Theyanalyzedtheturning frame’saffectonthecrossbreednanofluidstream.Amorelaterstudyofthecrossover nanofluidstreamisexaminedbyAlietal(2020).Thedisplayarticlebargainswith thethree-dimensionalnanofluid(water-based)streamoftheboundarylayerovera turningsurfaceconsideringtheimpactsofbothwarmradiationsandcouplestretch.
Fetecauetal(2017).Examinedthenormalconvectionstreamofnanofluidlimitedby anisothermalmovingsurface.BhattiandRashidi(2016)anticipatedtheBrownian movementandthermophoresisimpactsforWilliamsonnanofluidstreamactuatedby extendedsetup.Venthanetal(2019).InspectedapplicationsofBinghamnanofluids limitedbyconcentricannuliduetoturninginternalbarrel.InBinghamnanofluids, ordinarilywaterisutilizedasthebaseliquidwhichisimplantedwiththesilver(Ag)
andcopper(Cu)nanoparticlescoalescingwithBinghamliquid.Tlilietal(2019).Detailedthewarmexchangehandleincircularbarrelwithutilizationofnanoparticles. AnotherhypotheticalinvestigationwithrespecttonanofluidbasedonBuongiorno’s demonstrateforthirdreviewliquidwasdisplayedbyKhanandShehzad(2019).The nanofluidexaminationforMaxwellbasedmicropolarwithutilizationofslipimpacts andpermeablemediumhasbeenscrutinizedbyWaqasetal(2019).Alietal(2020). impliedthewarmexchangeinCrossnanofluidutilizationinreachingandgrowingbarrelfurthermorehighlightingattractiveconstrain.Lietal(2020).suggestedafewnovel centralityofnanoparticlesincapacityfinnedinmachineofsofteningprepare.Raju etal.LookatthewarmexchangeinvestigationinshakystreamofCarreaunanofluid designedbyacone.Thethermophoreticviewpointsin3-DstreamofCassonliquid innearnessofgraphenenanoparticlesoveradefamingsurfacehasbeeninspected byDurgaprasadetal(2019).Rajuetal(2017).CenteredonslipstreamofCarreau nanofluidcontaininggyrotacticmicroorganismsbeneaththeimpactofattractivefield. Inanotherexamination,Rajuetal(2017).inspectedthecrossdisseminationviewpointsinslipstreamofmagnetizedCarreauliquidinnearnessofwarmassimilation anderahighlights.Zahmatkeshetal(2019)performedbasicexaminationwithrespect towarmviewpointsofnanofluidBuongiorno’sshow.Alsaberyetal(2020).Usedtwophasestreamofnanofluidkeptbyawarmedwavydepression.Thewarmexhibitions ofAg-MgO/waterbasednanoparticlesrestrictedbyapermeablewalledinareahave beentalkedaboutbyMehryanetal(2020).Ghalambazetal(2020).Hypothetically tendedtowarmexchangeinvestigationinapermeablespacebyutilizingtypified stagealtermaterials.
Thehalfbreedupgradeinvestigationbasedoncombinationofcopperfrothand Cu/GOnano-materialswasinvestigatedbyZadehetal(2020).Zadehetal(2020). performedanumericalbasedexaminationwithrespecttoentropyeraapplications innanoparticlesdesignedbyasquarewalledinarea.Rafiqetal(2020).Examined anittygrittyauditandcuriouslyapplicationsofnano-materialsindifferentphysicochemicalframeworks.Mostafazadehetal(2019).Exploredthepropertiesofsingle andtwo-phasenano-materialactuatedbyaverticalchannel.Danialietal(2020). examinedtheutilizationofcopperoxidenanoparticleswithwarmexchangerand thermo-hydraulicapplications.Miretal(2020).Evaluatedthewarminstrumentof silvernanoparticleskeptbybendedminichannel.Karbasifaretal(2018).Atwostage approachfornon-Newtoniannanofluidbytakingaftertwostagenanodemonstrate actuatedbyH-shapeddepthhasbeentalkedaboutbyLietal.(2019).Alrashedetal. (2018)inspectedthestreamofmulti-walledcarbonnanotubeinabackward-facing contractingchannelnumericallybytakingafterlimitedvolumestrategy.Turkyilmazoglu(2012)inspectedthestreamofthickliquidduetoturningunboundeddisk indisplayofattractivedrive.Qayyumetal.(2018)inspectedthethermallycreated streamduetoturningdisk’svariablethickness.Anumericaltakenafterendeavor withrespecttothemicropolarnanofluidstreambetweenmovingdiskwasassessed byRamzanetal.(2017).Hashmietal.(2017)workedonmodelingofOldroyd-Bliquidbetweentwoisothermaldisksinapparatusofchemicalresponse.Afewcuriously arrangementshavebeenanticipatedbyTurkyilmazoglu(2018)whereasanalyzingthe warmexchangecharacteristicsinmovingdisks.Khanetal.(2018)coordinatedthe chemicallyreceptivestreamofMaxwellfluidbetweenextendingdiskswithapplicationsofchemicalresponse.Thewarmsource/sinkimpactsinstagnationpointrate
sortliquidstreaminextendingdiskswerepointedoutbyAhmedetal.(2019).The inclusionofdifferentsliphighlightsinstreamofnanoparticlesstreamduetopermeablepivotingdiskwasinspectedbyWaqasandco-workers(2019).Khanetal.(2020) decidedthestreamofMaxwellfabricbetweentwodisksbyincludingtheblended convectionandwarmabsorption/generationhighlights.Khanetal.(2015)inspected theJoulewarmingandgooeydisseminationimpactsinaxisymmetricstreamofgooey liquidbetweenextendingdisks.
Thestreamdesignedbyextendingandpivotingdiskshasanothercuriousinvestigateregionwhichincludednovelapplicationsinnumerousgenuinelifeissues andbusinesseslikeinfusionmodeling,centrifugalpumps,semiconductorfabricating, controltransmission,lubrications,turbinemotors,compression,polymerhandling, turningwafers,pushedorientation,turningterminals,viscometry,mechanicalcomponentstransitorystacking,airshipmotors,geothermal,outspreaddiffusers,geophysics,biomechanics,oceanography,etc.Forthedevelopmentofliquidbetween extendingdisks,thetemperaturecalculatehastheawesomesignificance.Thereare numerousapplicationsofliquidinsideorinitiatedbyextendingdisks.Fewcasesfor extendinggeometriesaregenerationofglassfiber,plasticandelasticsheetgeneration, ropedrawing,theunusedrolling,expansivemeasuredcoolingplatesinshowertub,car fabricatingindustryandmostvitalinrecuperatingofpetroleumbusinesses.Twistingstreamhascrucialsignificanceoverawiderunoflogicalandbuildingbranches whichworkforitemplanapplication.Thelittleestimateandtallsurfaceregionof nanomaterialspermitthemtoentercellsandconnectedwithbiomoleculeseffortlessly. Progressingretention,bioavailability,andsolidnesscanbeaccomplishedbyutilizing
nanotechnologyinmedicateconveyance,andinthismannerovercomethesurrenders ofcommonDDS.
Intermsofillnessdetermination,treatment,andavoidance,nanomedicineoffers variouspointsofinterest.Bethatasitmay,itmoreoverhasafewdisadvantages, suchasharmfulness,cost,andtroubleswithcontrol,moralquestions,andaneedof knowledge.GrammarCheck
Chapter3 METHODOLOGY 3.1MathematicalFormulationofProblem Hydromagneticrelentlessaxisymmetricandincompressiblestreamofmagnetite-water nanofluidpastacirculardisksituatedat z =0(Fig.1)isconsidered.Thediskis pivotedthroughanprecisespeed(omega).Additionally,thediskisextendedradially atanindeedrate ω.Moreover,thediskisstretchedradiallyatanevenrate s.Let u, v,and w bethevelocitycomponentsalong r, ψ,and z directions.
Also,let T , T1 , TW bethenanofluidtemperature,nanofluidtemperaturedistant fromthedisk,andnanoliquidtemperatureclosethedisk,inthatarrange.Let C, CW , C1 bethenanofluidconcentration,nanoliquidconcentrationclosethedisk,and nanofluidconcentrationdistantfromthedisk,individually.Anoutsidepivotalattractivefieldwithanescalated B0 isutilized.Utilizingthetwo-phaseadjustedBuongiornonanofluidconspireandthepreviouslymentionedsuspicions,theadministering conditionsaremodeledbelow:
3.2GoverningEquations Massconservation:
Momentumequationalongthe r-direction:
Momentumequationalongthe ϕ-direction:
Momentumequationalongthe z-direction:
Conservationofenergy:
Conservationofnanoparticleconcentration:
subjecttothefollowingboundaryconditions:
u = sr,v = γr,w =0,T = TW ,C = CW at z =0;
u → 0,v → 0,T → T1 ,C → C1 as z → 1.
Introducingthefollowingsimilaritytransform: η = r s z,u = rF (η),v = rG(η), w = s γ H(η),p = p1 2γP (η), T = T1 +(TW T1 )Ψ(η),C = C1 +(CW C1 )Φ(η)
(3.7)
(3.8)
Inequations(3.1)–(3.7),thegoverningequationsarereducedto:
where Pr (Prandtlnumber)=(γCP )f /µf , M (magneticfieldparameter)= ρf B 2 0 /(µf γ), eta (effectiveheatcapacityratio)=(CP )p/(CP )f , Nt (thermophoresisparameter) = βDT (TW T1 )/(T1 µf ), Nb (Brownianmotionparameter)= βDB(CW C1 )/µf , Sc (Schmidtnumber)= µf /DB, c (stretchingstrengthparameter)= s/γ,and Re (localReynoldsnumber)= γr2 /µf arethedimensionlessparameters.
ThenanoliquidmodelsforeffectivedynamicviscosityandeffectivethermalconductivityhavebeenderivedfromtheexperimentalworkofSundaretal.[?].The proposedmodelisvalidonlyfor0 <η< 2.0%and20◦C<T< 60◦C.Inaddition,theremainingnanoliquidmodelshavebeenadoptedfromMustafaetal.The consideredmodelsaregivenby:
Effectivespecificheatcapacity:(∆
Thephysicalquantitiesofinterestandtheirreducedform(onintroducingthe similaritytransformations)aregivenby(Mahantheshetal.,Hayatetal.,Sabuetal.) (2019):
Sherwoodnumber:
3.3MethodofSolution 3.3.1Bvp4c
Hereisadraftwrite-uponthebvp4cfunctionforsolvingboundaryvalueproblems incomputationalfluidmechanicsmodelswithsomereferences:
Thebvp4cfunctioninMATLABisvaluablefornumericallytacklingboundary esteemissuesthatemergeincomputationalfluid(liquidorgas)flowandmodeling liquidstream.Particularly,bvp4cexecutesthecollocationstrategyforunderstandingframeworksofTributes(standarddifferentialconditions)subjecttoboundary
conditions(PolyaninandZaitsev,2003).
Somepreferencesofutilizingbvp4cforcomputationalliquidmechanicsmodels include:
ItcanhandlenonlinearODEsandnon-standardboundaryconditionslikeperiodicitylimitations(Shampineetal.,2003).Thisisvitalformodelingcomplexliquid flows.
Ithasversatileworkchoiceandmistakecontrolforpreciselysettlingsoakslopes andboundarylayersinthearrangement(Ascheretal.,1995).Thesearecommon challengesinliquidmechanics.
Thecollocationstrategymergesquicklyandgivessmootharrangementsforwellposedissues(RussellandShampine,1972).Thismakesadifferenceproductively illuminateliquidstreamequations.
Itstraightforwardlygivestheunraveledarrangementworkwhichcanbeutilized foradvanceexaminationwithoutrequiringinterpolation.
Somecasesofutilizingbvp4cforcomputationalliquidelementsissuesincorporate modelingpipestreams,streamlinedprofiles,boundarylayers,andsmoothedmolecule hydrodynamics(LiuandLiu,2003).Thebvp4csolverhasmoreoverbeenutilizedfor fluid-structureinteractionissues(BorkerandAquino,2019).
Overall,bvp4cisastrongboundaryesteemissuesolverwell-suitedfornumericalrecreationofdesigningliquidelementsmodels,givencareistakentoguarantee adjustdetailingandnon-singularityoftheframework.Theversatilepseudo-spectral collocationstrategyequalizationsexactness,smoothnessandefficiency.
X2 (0)= c
X4 (1)=1
X1 (θ)= F0
X1 (θ)=0
X6 (0)=1
X8 (0)=1
X2 (∞)=0
X4 (∞)=0 X8 (∞)=0
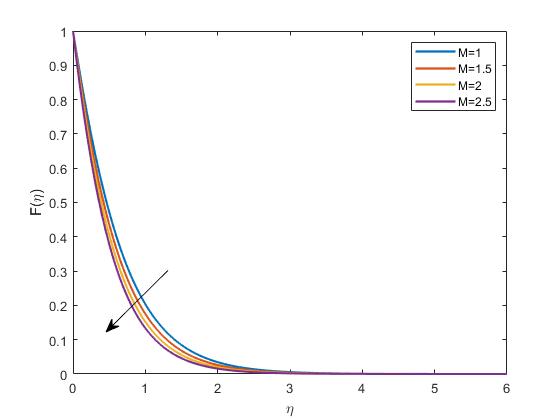
Chapter4 RESULTSANDDISCUSSION Figure4.1: ImpactofMonFprofile
Thefigureaboveshowstheimpactofthepertinentparameter M whilethevalueis variedforM=1,1.5,2,2.5,thisfigureillustrateshowthedimensionlessvelocityprofile
F varieswiththemagneticfieldparameter M .Themagneticfieldexertsadragforce ontheconductingnanofluid,whichwouldtypicallyresultinadecreaseinthefluid
velocityas M increases.ThisisbecausetheLorentzforceactsoppositetotheflowdirection,therebydampeningthevelocity.As M isvaried,thechangeintheprofileof F wouldhighlightthesignificanceofthemagneticfield’sinfluenceontheflowdynamics.
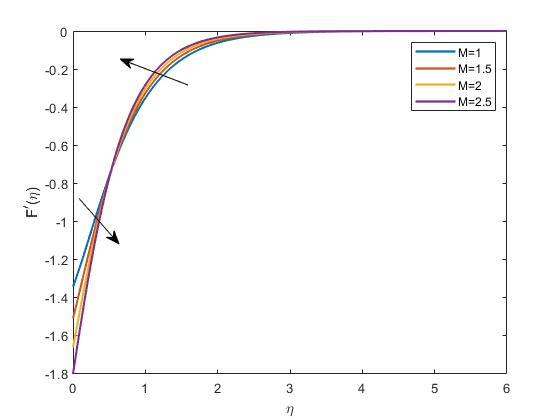
Thederivativeofthedimensionlessvelocityprofile(F ′ ) withrespecttothesimilarityvariable η infigure4.2reflectstheshearrateorvelocitygradientattheboundary layer.Theimpactof M onthisgradientiscrucialbecauseitcanprovideinsightsinto thebehaviorofthefluid’sboundarylayerthicknessandthemomentumtransferrate. Anincreasing M wouldlikelyshowadecreasingtrendin(F ′ ) duetothemagnetic dampingeffect.
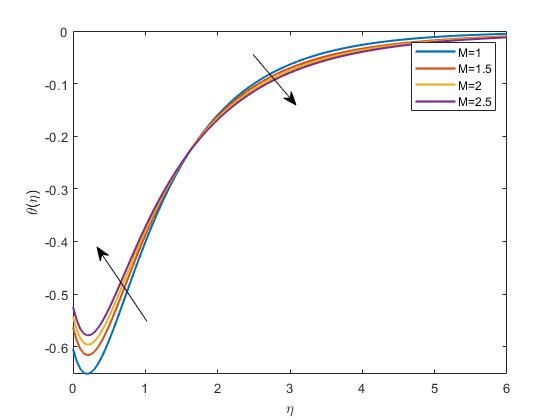
InFigure4.3Thisgraphdisplaytheeffectofthemagneticfieldparameteron
Figure4.2: ImpactofMonF’profile
Figure4.3: ImpactofMontemperatureprofile thetemperaturedistributionwithintheboundarylayerofthenanofluid.Sincethe magneticfieldcaninfluencetheconvectiveheattransfer,variationsin M couldalter thethermalboundarylayer’sthicknessandprofile.Thenanofluid’stemperatureisa criticalaspectofitsheattransfercapabilities,andthisfigurewouldbeanalyzedto understandtheextentofthisimpact.
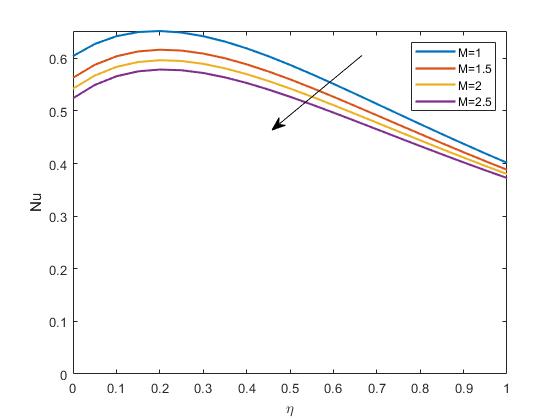
Figure4.4whichistheImpactof M onNusseltnumberprofile,TheNusseltnumber(Nu)isindicativeoftheconvectiveheattransferraterelativetotheconductive heattransfer.Theimpactof M on Nu showhowthemagneticfieldparametermodifiestheheattransferefficiency.Typically,ahighermagneticfieldcouldleadtoa lower Nu ifthemagneticfieldsuppressesthefluidmotionthatcontributestoconvectiveheattransfer.
Figure4.4: ImpactofMonNusseltnumberprofile
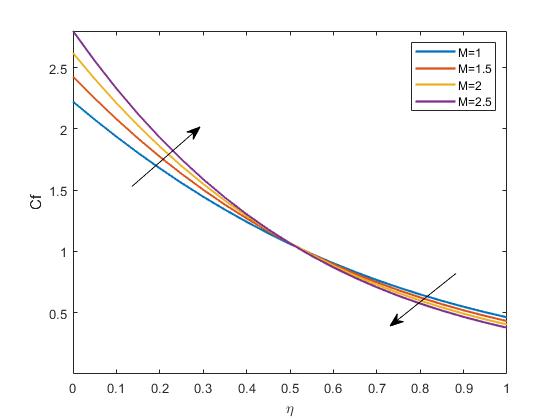
InFigure4.5,Skinfrictionisrelatedtotheresistanceamovingfluidfacesinthe vicinityofaboundary.Thegraphshowingtheimpactof M ontheskinfrictionprofile elucidatehowthemagneticfieldinfluencesthedragexperiencedbythenanofluid.A higher M isexpectedtoincreasetheskinfrictionduetotheincreasedelectromagnetic forceopposingtheflow.
Figure4.5: ImpactofMonSkinfrictionprofile
Table4.1: Resultsof F (0)and G(0)
Physicalquantities Mebareketal Bvp4cresult
F0 (0)
0.5102 0.4898 G0 (0) 0.6159 0.5797
IntegratingtheResultswiththeGraphicalAnalysis:Thedifferencesinthevalues ofphysicalquantities F0 (0)and G0 (0)betweenthebvp4cresultsandthoseobtained byMebareketal.usingtheRunge-Kuttamethodcanbefurthercontextualizedwith thegraphicalresultsexaminedearlier
VelocityProfile F ′andF ′′:Thebvp4cmethodproducedthevelocityprofilesthat wereobservedinthegraphs.Thelower F0 (0)valuefrombvp4ccomparedtoMebarek
etal.suggestsalesspronouncedvelocityattheboundary,whichcorrelatewiththe graphicaltrendswhereareducedvelocityneartheboundarycouldleadtoasteeper velocitygradient(asindicatedbytheshapeoftheF’curve).
TemperatureandConcentrationProfiles:Thegraphsdepictingthetemperature andconcentrationprofilescouldbeinfluencedbythedifferencein G0 (0)values.A higher G0 (0)frombvp4cindicateasharpertemperatureandconcentrationgradientattheboundary,whichreflectedintheshapesoftheconcentrationprofileand temperatureprofilegraphs,particularlyinregionsclosetotheboundary(near=0).
ImpactofMagneticField(M):TheRunge-Kuttamethod,asusedbyMebarek etal.,andthebvp4cresultsshowvariationsinhowthemagneticfieldimpactsthe flowcharacteristics,suchasskinfrictionandNusseltnumber.Thegraphsinthis workdisplaytheimpactofthesephysicalquantitiesunderdifferentmagneticfield strengths.Thediscrepancyinnumericalvaluesmightbeobservedasdifferentslopes orshiftsinthegraphicalprofileswithchangingMvalues.
InfluenceofBrownianMotionandThermophoresis(NbandNt):Thediscrepancy invaluesalsocarriesimplicationsforthegraphsrelatedtoBrownianmotion(Nb) andthermophoresis(Nt).ThegraphsshowingtheSherwoodnumberandconcentrationprofilesfordifferentNbandNtwouldbeimpactedbythenumericaldifferences, potentiallyshowingvarianceinmassandheattransferrates.
NumericalMethodSensitivity:Thesensitivityofthenumericalmethodstoinitialconditionsandparametervaluesishighlightedbythedifferencesinresults.The Runge-Kuttamethodisverysensitivetostepsizeandmightyielddifferentresults ifthestepsizeisnotappropriatelychosen,whilebvp4c’sadaptivemeshingbetter captureboundarybehaviors,aspossiblyseeninthegraphs.
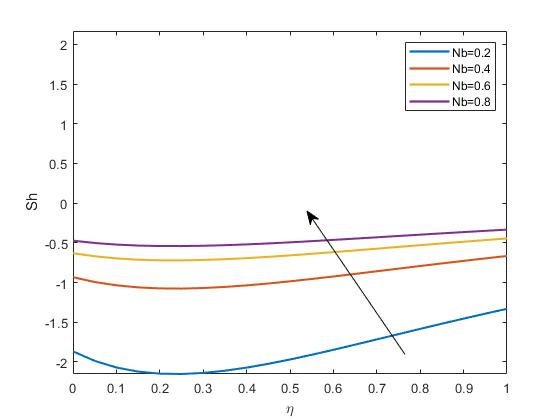
Figure4.6: ImpactofNbonSherwoodnumberprofile
InFigure4.6,theSherwoodnumber(Sh)isadimensionlessnumberdescribingthe masstransferataboundary.ThegraphshowingtheimpactoftheBrownianmotion parameter(Nb)on Sh wouldhighlighttheroleofBrownianmotioninenhancingthe masstransferrate.As Nb increases,theintensificationofnanoparticlemotionmay increasethemasstransfer,reflectedinthe Sh profile.
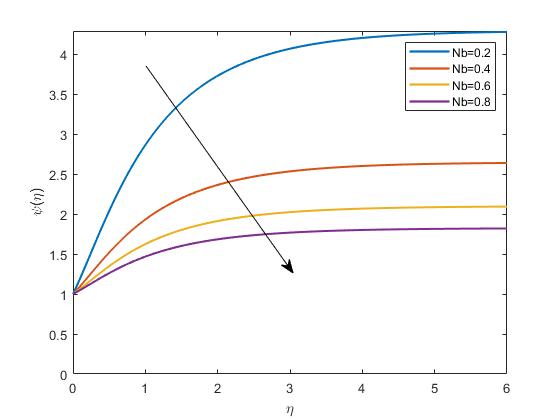
Figure4.7depicttheconcentrationprofileofnanoparticleswithinthenanofluid as Nb isvaried.Anincreasein Nb suggestsstrongerBrownianmotion,potentially leadingtoamoreuniformdistributionofnanoparticlesandachangeintheconcentrationboundarylayer.
Figure4.7: ImpactofNbonConcentrationprofile
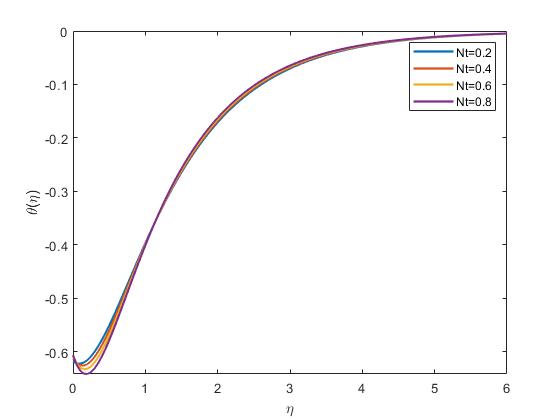
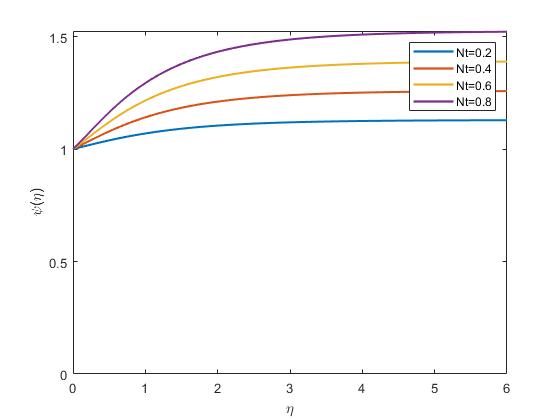
InFigure4.8, Nt representsthethermophoresisparameter,whichaffectsthedistributionofnanoparticlesduetotemperaturegradients.Thegraphillustratehow changesin Nt impactthetemperatureprofilewithinthenanofluid.Thermophoresis caninfluencethenanoparticledistributioninthethermalboundarylayerandthus thefluid’stemperaturedistribution.
InFigure4.9,Thermophoresisaffectstheconcentrationprofileofnanoparticles. Thefigureshowhowvariationsin Nt affectthedistributionofnanoparticleconcentrationacrosstheboundarylayer.Ahigher Nt couldresultinaconcentrationprofile thatindicatesthemovementofnanoparticlesfromhottertocoolerregions.
Figure4.8: ImpactofNtontemperatureprofile
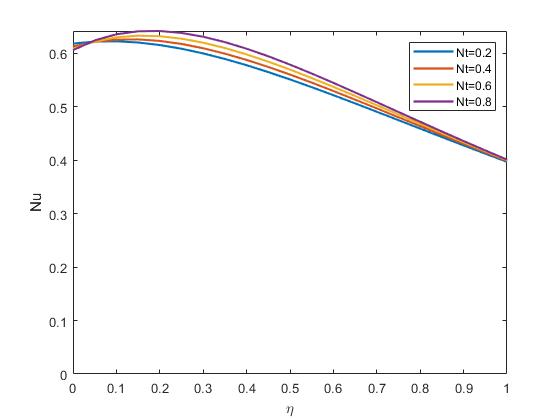
InFigure4.10,thisfigureshowtherelationshipbetweenthethermophoresisparameterandtheNusseltnumber,givinginsightintohowthermophoresisinfluences theconvectiveheattransferofthenanofluid.Sincethermophoresisaffectsparticle distribution,itdoeshaveasignificanteffectontheheattransfercharacteristics,as indicatedbychangesin Nu
Lastly,Figure4.11theimpactof Nt ontheSherwoodnumberrevealtherelationshipbetweenthermophoreticeffectsandtheconvectivemasstransferrate.A variationin Nt couldpotentiallyalter Sh,indicatingchangesinhowthermophoresis affectsthetransportofmassinthepresenceofatemperaturegradient.
ImpactofNtonConcentrationprofile
ImpactofNtonNusseltnumberprofile
Figure4.9:
Figure4.10:
ImpactofNtonSherwoodnumberprofile
Figure4.11:
Chapter5 CONCLUSION ThemodifiedBuongiornoschemeinvolvesconvertingthemathematicallymodeled equationsintoafirst-orderODEsschemeusingVonK´arm´an’ssimilarityconversions andthensolvingthemnumericallyusingthebvp4cmethodinMatlab.Themain conclusionsare:
ChangesinthestretchingstrengthtermaredirectlyproportionaltotheNusselt numberandinverselyproportionaltothethermalfield.
Thevolumefractionofmagnetitenanoparticleshasaconstructiveimpacton theheattransferrateandthethermalfield.
Surfacedragincreaseswithanincreasingmagneticfieldparameterandvolume fractionofmagnetitenanoparticles.
HeattransportratedecreaseswiththermophoresisandBrownianmotionparameters.
ThemagneticfieldandtheSchmidtnumbertermsexhibitadestructiveinfluenceandaconstructiveeffectoverthemasstransportrate,respectively.
References [1]Mebarek-Oudina,FatehPrashar,PreetiaS,SabuVaidya,HanumeshLewis,R Areekara,SujeshMathew,Sr.AlphonsaIsmail,A..(2024).Hydromagneticflow ofmagnetite-waternanofluidutilizingadaptedBuongiornomodel.International JournalofModernPhysicsB.38.2450003.10.1142/S0217979224500036.
[2]B.Mahantheshetal.(2020).J.Therm.Anal.Calorim.141,37.
[3]T.Hayatetal.(2017).Int.J.Numer.MethodsHeatFluidFlow27,221.
[4]A.S.Sabuetal.(2021).Int.Commun.HeatMassTransf.129,105711.
[5]Sheikholeslami,M.;Shehzad,S.(2017)MagnetohydrodynamicnanofluidconvectiveflowinaporousenclosurebymeansofLBM.Int.J.HeatMassTransf.Pg: 113,796–805.
[6]Buongiorno,J.(2006)Convectivetransportinnanofluids.J.HeatTransf.128, 240–250.
[7]TurkyilmazogluM.(2016)Flowofnanofluidplanewalljetandheattransfer.Eur. J.Mech.BFluids;59:18–24.
[8]AliM,SultanF,KhanWA,ShahzadM,ArifH.(2020)Importantfeaturesof expanding/contractingcylinderforCrossmagneto-nanofluidflow.ChaosSoliton Fract;133:109656.
[9]LiF,SheikholeslamiM,DaraRN,AfaryarM,ShafeeA,Nguyen-ThoiT,Li Zh.(2020)Numericalstudyfornanofluidbehaviorinsideastoragefinnedenclosureinvolvingmeltingprocess.J.M.Liq.;297:111939.
[10]RajuCSK,HoqueMM,AnikaNN,MamathaSU,SharmaP.(2017)Natural convectiveheattransferanalysisofMHDunsteadyCarreaunanofluidovera conepackedwithalloynanoparticles.PowderTechnol.;317:408–16.
[11]DurgaprasadP,VarmaSVK,HoqueMohammadMainul,RajuCSK.(2019) CombinedeffectsofBrownianmotionandthermophoresisparametersonthreedimensional(3D)Cassonnanofluidflowacrosstheporouslayersslenderingsheet inasuspensionofgraphenenanoparticles.NNeural.Comput.Appl.;31:6275–86.
[12]RamzanM,ChungaJD,UllahNaeem.(2017)Partialslipeffectintheflowof MHDmicropolarnanofluidflowduetoarotatingdisk:anumericalapproach. ResultsPhys.;7:3557–66.
[13]TliliI,WaqasH,AlmaneeaA,KhanSU,ImranM.2019Activationenergyand secondorderslipinbioconvectionofOldroyd-Bnanofluidoverastretchingcylinder:Aproposedmathematicalmodel.Processes;7(12):914.
[14]FetecaC,VieruD,AzharWA.(2017)Naturalconvectionflowoffractional nanofluidsoveranisothermalverticalplatewiththermalradiation.Appl. Sci.;7:247.
[15]Eringen,A.C.(1966)Theoryofmicropolarfluids.J.Math.Mech.16,1–18.
[16]Lund,L.A.;Omar,Z.;Raza,J.;Khan,I.(2020)Magnetohydrodynamicflowof Cu–Fe3O4/H2Ohybridnanofluidwitheffectofviscousdissipation:Dualsimilaritysolutions.J.Therm.Anal.Calorim.143,915–927.
[17]Devakar,M.;Ramesh,K.;Chouhan,S.;Raje,A.(2017)Fullydevelopedflowof non-Newtonianfluidsinastraightuniformsquareductthroughporousmedium. J.Assoc.ArabUniv.BasicAppl.Sci.23,66–74.
[18]Srinivasacharya,D.;Shafeeurrahman,M.(2017)Hallandionslipeffectson mixedconvectionflowofnanofluidbetweentwoconcentriccylinders.J.Assoc. ArabUniv.BasicAppl.Sci.24,223–231.
[19]Rashidi,M.M.;Dinarvand,S.(2009)Purelyanalyticapproximatesolutionsfor steadythree-dimensionalproblemofcondensationfilmoninclinedrotatingdisk byhomotopyanalysismethod.NonlinearAnal.RealWorldAppl.10,2346–2356.
[20]Khan,W.;Pop,I.(2010)Boundary-layerflowofananofluidpastastretching sheet.Int.J.HeatMassTransf.53,2477–2483.
[21]Ascher,U.M.,Mattheij,R.M.,Russell,R.D.(1995).NumericalSolutionof BoundaryValueProblemsforOrdinaryDifferentialEquations.SIAM.
[22]BorkerandAquino(2019).Fluid–structureinteractionusingbvp4c.MatlabCentralFileExchange.
[23]Liu,G.R.andLiu,M.B.(2003).SmoothedParticleHydrodynamics:AMeshfree ParticleMethod.WorldScientificPubCo.
[24]Polyanin,A.D.andZaitsev,V.F.(2003).HandbookofExactSolutionsforOrdinaryDifferentialEquations.ChapmanHall/CRC.
[25]Russell,R.D.,Shampine,L.F.(1972).Acollocationmethodforboundaryvalue problems.NumerischeMathematik.19,1–28.
[26]Shampine,L.F.,Gladwell,I.,Thompson,S.(2003).SolvingODEswithMATLAB.CambridgeUniversityPress.
[27]M.Mustafaetal.,Int.J.NonlinearSci.Numer.Simul.19,1(2018).