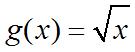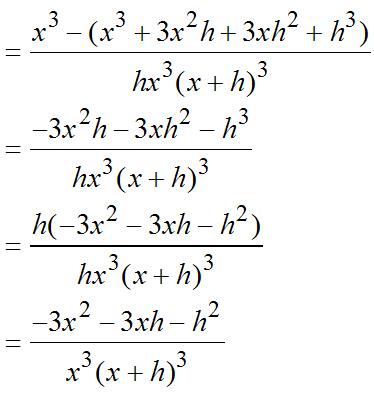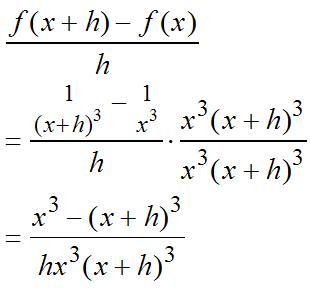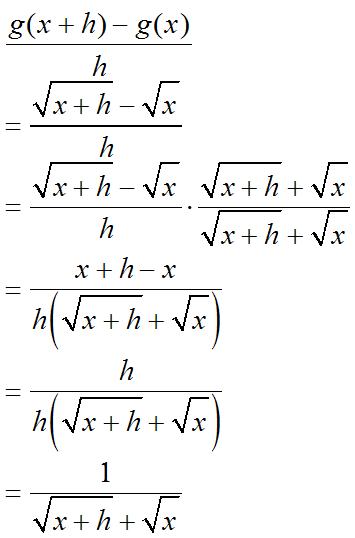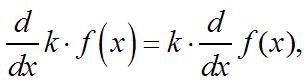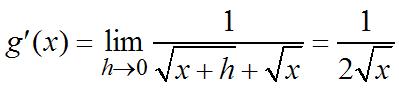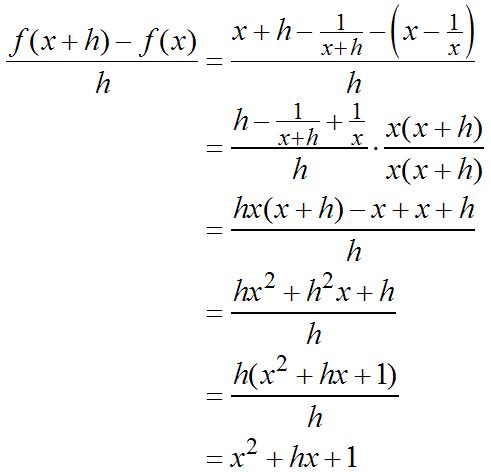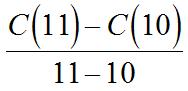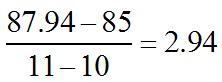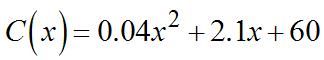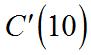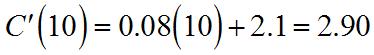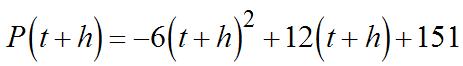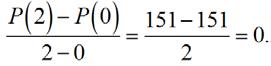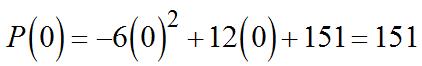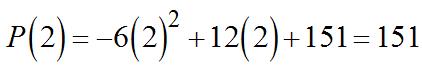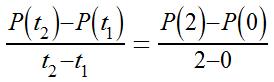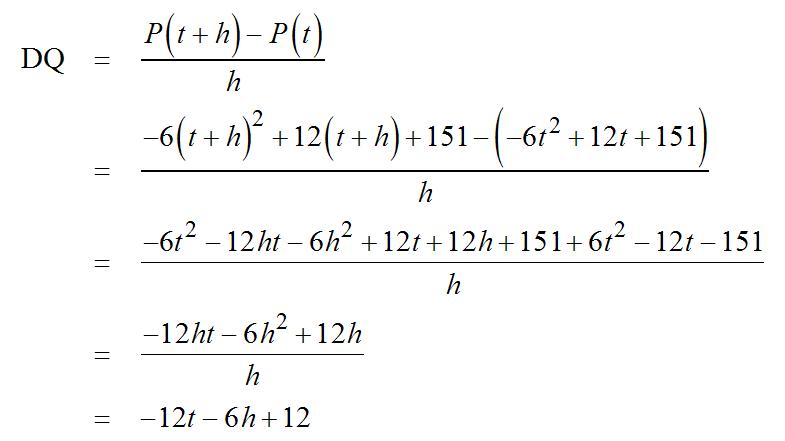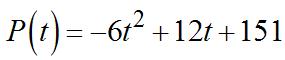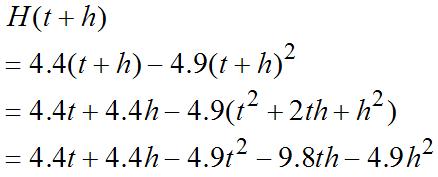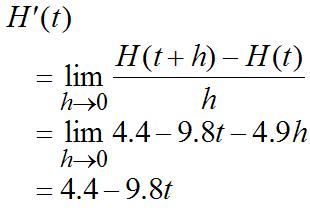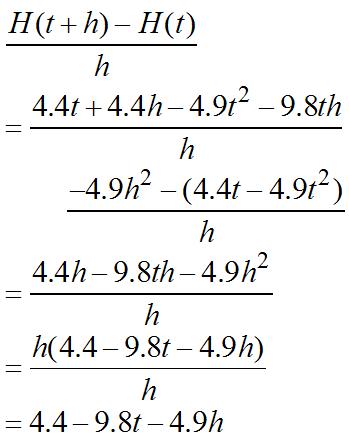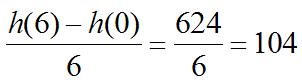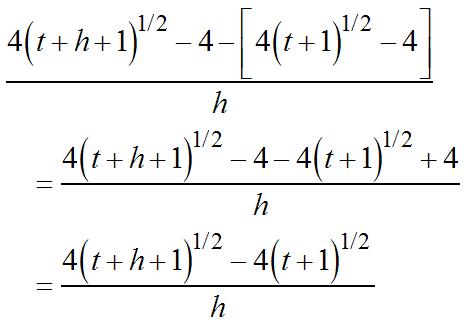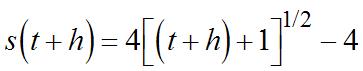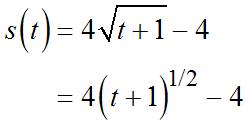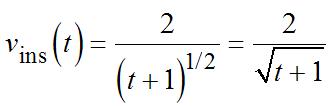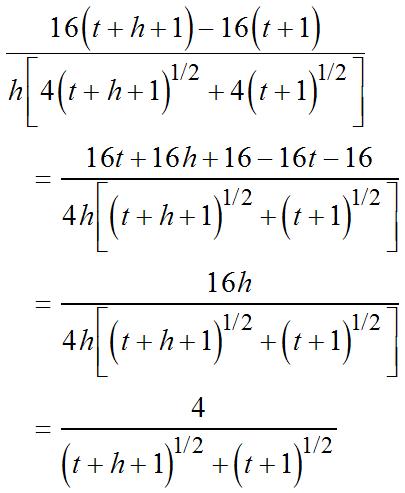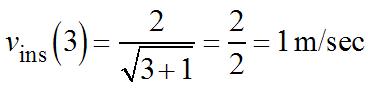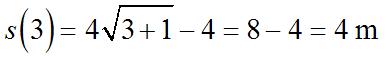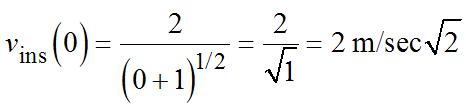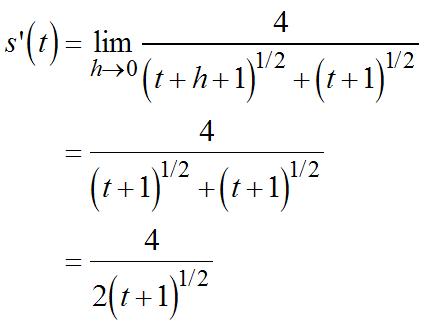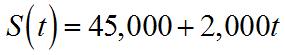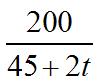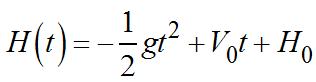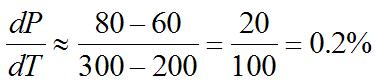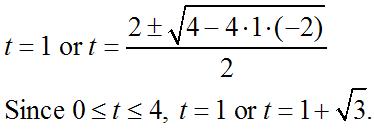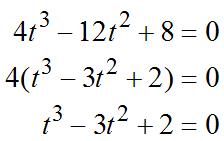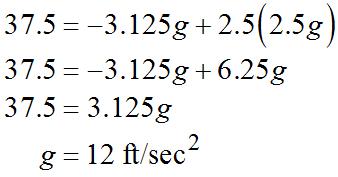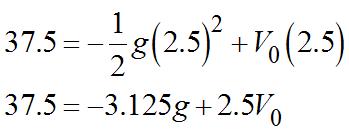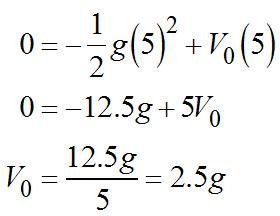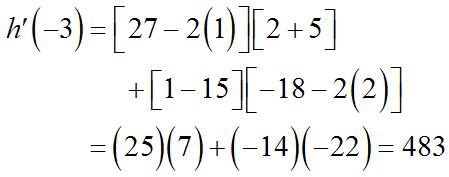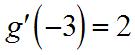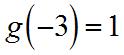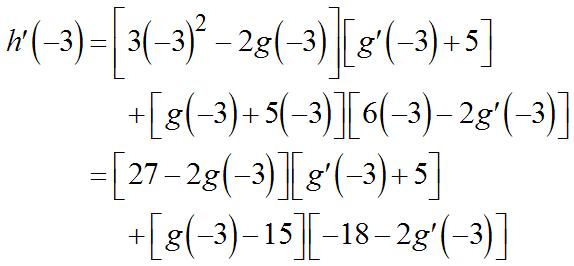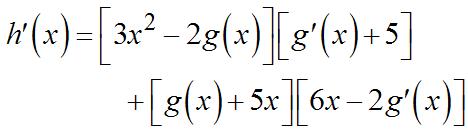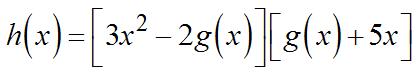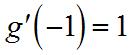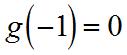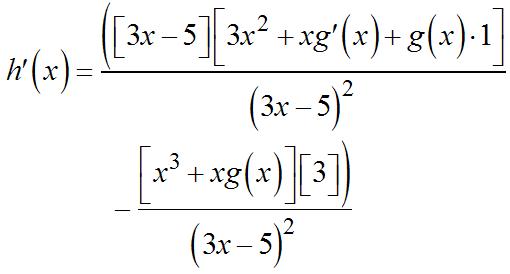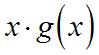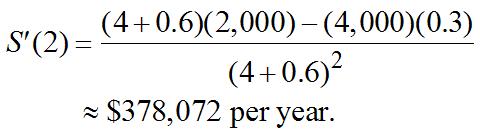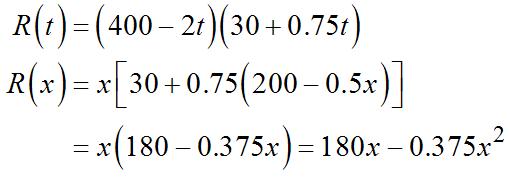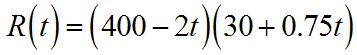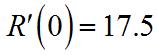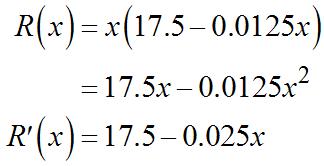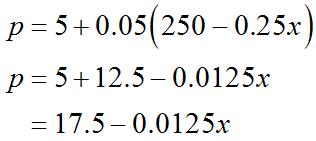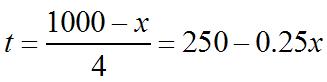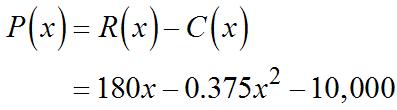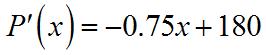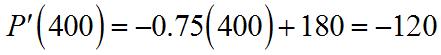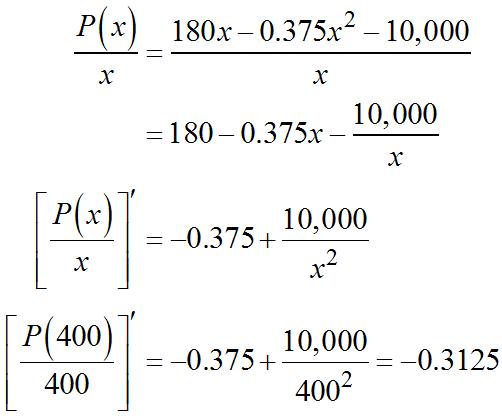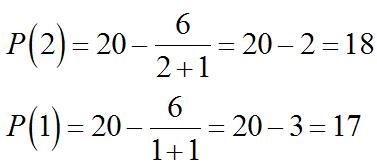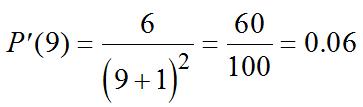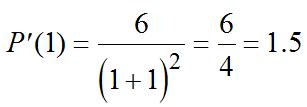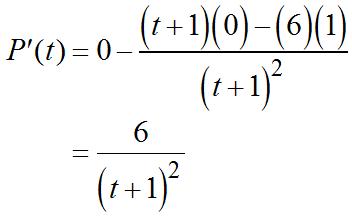Applied Calculus For Business Economics And The Social And Life Sciences 11th Edition Hoffmann Solutions Manual Visit to Download in Full: https://testbankdeal.com/download/applied-calculus-for-busi ness-economics-and-the-social-and-life-sciences-11th-edition-hoffmann-solutions-ma nual/

Chapter 2
Differentiation: Basic Concepts
2.1 The Derivative
1. If f(x)=4,then f(x + h)=4.
Thedifferencequotient(DQ)is ()()440. fxhfx hh +−− == 0 ()lim()()0 h fxfxhfx h →
Theslopeofthelinetangenttothegraph of f at x =1is(1)7. ′ −=− f
+− ′ = =
Theslopeis(0)0. mf ′ ==
2. f(x)=3
Thedifferencequotientis ()()3(3)00 +−−−− === fxhfx hhh
Then 0 ()lim00. → ′ == h fx
Theslopeofthelinetangenttothegraph of f at x =1is(1)0. ′ = f
3. If f(x)=5x 3,then f(x + h)=5(x + h)3.
Thedifferencequotient(DQ)is
5. If2()235, fxxx=−+ then 2 ()2()3()5. fxhxhxh +=+−++
+−++−+ +− = =+− 0 ()lim()()43 h fxfxhfxx h →
[2()3()5][235] 42()3 xhxhxx hh xhhh h xh
+− ′ = =− Theslopeis(0)3. mf ′ ==−
2 ()1
fxhfxxhx hh h h
()()[5()3][53] 5 5
+− ′ = =
+−+−−− = = = 0 ()lim()()5 h fxfxhfx h →
Theslopeis(2)5. mf ′ ==
4. f(x)=27x
Thedifferencequotientis
=− Thedifferencequotientis 22 222 2 ()()(()1)(1) 211 2 2 fxhfxxhx hh xhxhx h hxhxh h +−+−−− = ++−−+ = + ==+
Then
+−−+−− = −−−+ = ==−
fxhfxxhx hh xhx h h h
()()(27())(27)
27727 7 7
Then 0 ()lim(7)7. → ′ =−=− h fx
87
Thedifferencequotient(DQ)is ()() fxhfx h +− 22 2 423
0 ()lim(2)2
of
© 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part. Applied Calculus For Business Economics And The Social And Life Sciences 11th Edition Hoffmann Visit TestBankDeal.com to get complete for all chapters
6.
fxx
h fxxhx → ′ =+= . Theslopeofthelinetangenttothegraph
f at1 x =− is(1)2 f ′ −=−
7. If3()1,fxx=− then
9. If2(),gt t = then2(). gthth += +
10.
11. If 1 (),Hu u = then 1 ().Huh uh +=
88 Chapter2.Differentiation:BasicConcepts
3 22 3223 ()()1 (2)()1 331 fxhxh xxhhxh xxhxhh +=+− =+++− =+++− 32233 223 22 22 ()() 331(1) 33 (33) 33 fxhfx h xxhxhhx h xhxhh h hxxhh h xxhh +− +++−−− = ++ = ++ = =++ 0 22 0 2 ()lim()() lim33 3 h h fxfxhfx h xxhh x → → +− ′ = =++ = Theslopeis2(2)3(2)12. mf ′ ===
Thedifferencequotientis 33 32233 223 22 ()()(())() 33 33 33 +−−+−− = −−−−+ = = =−−− fxhfxxhx hh xxhxhhx h xhxhh h xxhh Then 222 0
→
=−−−=− h fxxxhhx
8. ()3 =− fxx
()lim(33)3.
′
=− f
Theslopeofthelinetangenttothegraph of f at x =1is(1)3. ′
22 22 ()() () () 22() ()() 2 () tht tht gthgt hh tth htth tth htth tth + + +− = + =⋅ + −+ = + = + 02 ()lim()()2 h gtgthgtht → +− ′ = =− Theslopeis18. 2 mg ′ ==−
Thedifferencequotient(DQ)is
2 1 ()fx x = Thedifferencequotientis 22 222 222 222 11 () 11 2 (2) (2) 2 222 222 ()() 2 (2) 2 (2) xhx xhxhx xxhxh xhxhx fxhfx hh h h hxh hxhxhx xh xhxhx + ++ −++ ++ +− = = = = ++ = ++ Then 0222 4 3 2 ()lim (2) 2 2 h fxxh xhxhx x x x → ′ = ++ = =− Theslopeofthelinetangenttothegraph of f at2 x = is 1
f ′ =−
(2)4
© 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
+ Thedifferencequotientis
Then 0 11 ()lim 2 → ′ = = ++ h fx xhxx
Theslopeofthelinetangenttothegraph of f at x =9is 1 (9). 6 ′ = f
13. If f(x)=2,then f(x + h)=2. Thedifferencequotient(DQ)is ()()220. fxhfx hh +−− ==
Theslopeofthetangentiszeroforall valuesof x.Since f(13)=2. y 2=0(x 13),or y =2.
14. For()3 fx = ,
forall x.Soatthepoint4 c =− ,theslope ofthetangentlineis(4)0 mf ′ =−= .The point(4,3)isonthetangentlinesoby thepoint-slopeformulatheequationofthe tangentlineis30[(4)] yx−=−− or 3 y =
15. If f(x)=72x,then f(x + h)=72(x + h).
Thedifferencequotient(DQ)is ()()[72()][72] 2
+− ′ = =−
fxhfxxhx hh +−−+−− = =− 0 ()lim()()2 h fxfxhfx h →
Theslopeofthelineis(5)2. mf ′ ==−
Since f(5)=3,(5,3)isapointonthe curveandtheequationofthetangentline is y (3)=2(x 5)or y =2x +7.
16. For f(x)=3x, 0 0
forall x.Soatthepoint c =1,theslopeof
Chapter2.Differentiation:BasicConcepts 89 ( ) ( ) ( ) ( ) ( ) 11 ()() () 1 uhu fxhfx h uuh huuh uuhuuh huuhuuh uuh huuhuuh h huuhuuh uuhuuh + +− + =⋅ + ++ −+ = + ++ −+ = +++ = +++ = +++ ( ) () () 0 0 ()lim()() 1 lim 1 1 2 1 2 h h Hufxhfx h uuhuuh uuuu uu uu → → +− ′ = = +++ = ⋅+ = =− Theslopeis11 (4). 2(4)416 mH ′ ==−=−
Thedifferencequotientis ( ) ( ) ()() 1 +− +− = +−++ = ⋅ ++ +− = ++ = ++ = ++ fxhfx h xhx h xhxxhx hxhx xhx hxhx h hxhx xhx
12. () = fxx
()lim()()lim00
00
hh fxfxhfx h →→ +− ′ = ==
()lim()()33
00
lim0 hh fxfxhfxhh→→ +−− ′ = ==
()lim()()
+−
= +− = =
fxfxhfx
li333 m 3 → →
′
h h
h xhx h
© 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
thetangentlineis(1)3. ′ ==mf Thepoint (1,3)isonthetangentlinesobythe point-slopeformulatheequationofthe tangentlineis y 3=3(x 1)or y =3x
17. If2 (),fxx = then2 ()(). fxhxh +=+ Thedifferencequotient(DQ)is
Since f(1)=2,(1,2)isapointonthe curveandtheequationofthetangentline is22((1)) 24 yx
Theslopeofthelineis(1)2. mf ′ == Since f(1)=1,(1,1)isapointonthe curveandtheequationofthetangentline is y
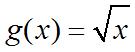
20. For 2()3fx x = , 0 22 0 022 3
forall x.Atthepoint1 c = ,theslopeof thetangentlineis(1)6 mf ′ ==− .The point(1,1)isonthetangentlinesobythe point-slopeformulatheequationofthe tangentlineis(1)6(1) yx−−=−− or 65yx=−+
19. If2(),fx x =− then2(). fxhxh += +
Thedifferencequotient(DQ)is
21. Firstweobtainthederivativeof Thedifferencequotientis
90 Chapter2.Differentiation:BasicConcepts
22 2 ()()() 2 2 fxhfxxhx hh xhh h xh +−+− = + = =+ 0 ()lim()()2 h fxfxhfxx h → +− ′ = =
1=2(x 1)or y =2x 1.
=−
0 22 0 0 ()lim()() lim(23())(23) lim(63) 6 h h h fxfxhfx h xhx h xh x → → → +− ′ = −+−− = =−− =−
18. For2 ()23 fxx
,
22 22 ()() () () 22() ()() 2 () xhx xhx fxhfx hh xxh hxxh xxh hxxh xxh + + +− = + + =⋅ + −++ = + = + 02 ()lim()()2 h fxfxhfxhx → +− ′ = =
=−=
Theslopeofthelineis(1)2. mf ′
yx −=−− =+
()lim()() 33 lim() lim63 ()
h h h fxfxhfx h xhx h xh xhx x → → → +− ′ = + = = + = Atthepoint 1 2 c = ,theslopeofthe tangentlineis 1 48 2 mf ′ ==− .The point 1 ,12 2 isonthetangentlinesoby thepoint-slopeformulatheequationofthe tangentlineis 1 1248 2 yx −=−− or4836 yx=−+
6
© 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
Soatthepoint c =1,theslopeofthe
tangentlineis 1 (1). 2 ′ =− f Thepoint(1, 1)isonthetangentlinesobythepointslopeformula,theequationofthetangent lineis 1 1(1) 2 −=−−yx or 13 22 =−+yx
23. If 3 1 (),fx x = then 3 1 (). () fxh xh += +
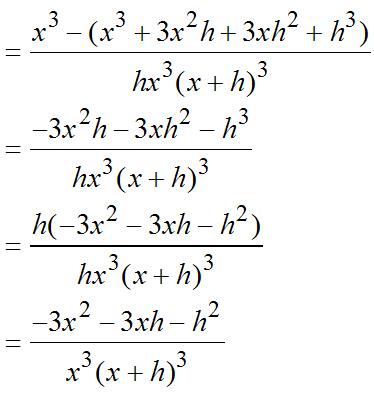
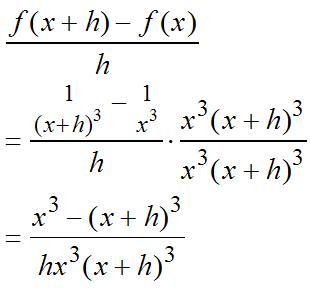
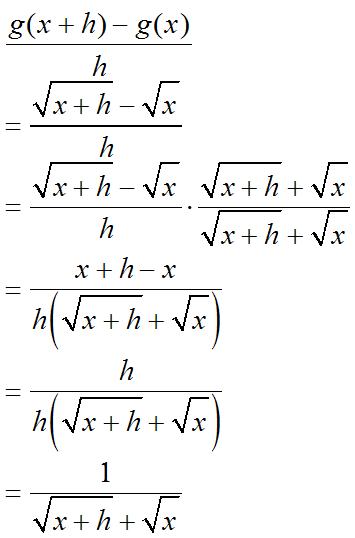
Thedifferencequotient(DQ)is
Theslopeis4
Further, f(1)=1sotheequationoftheline is y 1=3(x 1),or y =3x +4.
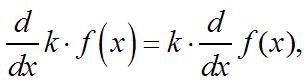
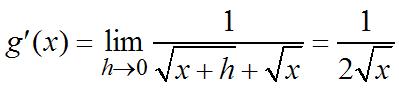
24. FromExercise7ofthissection
()32fxx ′ = .Atthepoint1 c = ,theslope
Chapter2.Differentiation:BasicConcepts 91 Then Nowsince 11 ()2. 2 fx xx ′ ==
mf
equationofthetangentlineis 1 4(4), 2 yx−=− or 1 2. 2 yx=+ 22. For 1 (), = fx x ( ) ( ) () 0 11 0 02 02 02 2 3/2 ()lim()() lim lim lim() 1 lim 1 2 1 2 → + → → → → +− ′ = = −+ = + −+ = +++ = +++ = = h xhx h h h h fxfxhfx h h xxh hxxh xxh hxxhxxh xxhxxh xx x
Theslopeis1(4), 2
′ == f(4)=4,the
0 22 033 2 33 4 ()lim()() lim33 () 3 () 3 h h fxfxhfx h xxhh xxh x xx x → → +− ′ = = + = =−
mf ′ ==−=−
3 (1)3. (1)
© 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
ofthetangentlineis(1)3 mf ′ == .The point(1,0)isonthetangentlinesobythe point-slopeformulatheequationofthe tangentlineis03(1) yx−=− or 33yx=− .
25. If y = f(x)=3,then f(x + h)=3. Thedifferencequotient(DQ)is
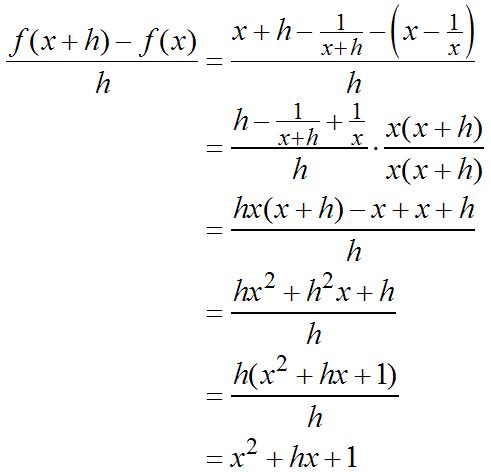
Thedifferencequotient(DQ)is 22 2
26. For f(x)=17, dy dx at014 = x is
+− +−+−− = = =−−
lim()()12 h dyfxhfx x dxh → +− = =−
fxhfx h xhxhxx h hxhh h xh 0
3 dy dx = when x =1.
(1)lim(1)(1) lim((1)2(1))(12(1))
0 2 0
+−++−+ = = =
fxhfxxhx hh h h lim()()lim33
+− = ==
00
3 dy dx = when x =1.
(3)lim(3)(3) lim(62(3))(62(3))
0 0 0
Thedifferencequotient(DQ)is
92 Chapter2.Differentiation:BasicConcepts
()()330.
0 lim()()0
=
0
fxhfx hh +−− ==
h dyfxhfx dxh → +−
=
dy dx = when x =2.
0 0 0 (14)lim(14)(14) lim17(17) lim0 0 → → → +− ′ = = = = h h h
h h
ffhf h
27. If y = f(x)=3x +5,then f(x + h)=3(x + h)+5=3x +3h +5. Thedifferencequotient(DQ)is ()()335(35) 3 3
hh dyfxhfx dxh→→
2 lim 2 h h h ffhf h h h h h → → → +− ′ = −+−− = = =−
28. For()62 fxx =− , dy dx at03 x = is
29. If y = f(x)= x(1 x),or2 (),fxxx =− then2 ()()(). fxhxhxh +=+−+
()() [()()][] 2 12
0
lim 0 → → → +− ′ = +−+−− = = = h h h
30. For2()2, =− fxxxdy dx at01 = x is
22
ffhf h hh h h h
31. If 1 (),yfxx x ==− then 1 (). fxhxhxh +=+− +
© 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
32. For 1 ()2fx x = , dy dx at03 x =− is
33. (a) If2 (),fxx = then2(2)(2)4 f −=−= and2(1.9)(1.9)3.61. f −=−= The slopeofthesecantlinejoiningthe points(2,4)and(1.9,3.61)onthe graphof f
(b) If2 (),fxx = then 222 ()()2. fxhxhxxhh +=+=++ Thedifferencequotient(DQ)is
Theanswerispart(a)isarelatively goodapproximationtotheslopeofthe tangentline.
35. (a) If3 (),fxx = then f(1)=1, 3 (1.1)(1.1)1.331. f ==
Theslopeofthesecantlinejoiningthe points(1,1)and(1.1,1.331)onthe graphof f is
(b) If3 (),fxx = then 3 ()(). fxhxh +=+
Thedifferencequotient(DQ)is
Theslopeofthetangentlineatthe point(2,4)onthegraphof f is tan(2)2(2)4.mf ′ =−=−=−
Theslopeistan(1)3. mf ′ == Noticethatthisslopewas approximatedbytheslopeofthe secantinpart(a).
Chapter2.Differentiation:BasicConcepts 93 0 2 0 2 lim()() lim1 1 h h dyfxhfx dxh xhx x → → +− = =++ =+ When x =1,2
dy dx =+=
(1)12.
0 11 2(3)2(3) 0 0 (3)lim(3)(3) lim 1 lim 5(5) 1 25 h h h h ffhf h h h → −−+−− → → −+−− ′ −= = = =
21 sec 21 3.614 3.9. 1.9(2) yy m xx == =−
is
222 2 ()()2 2 (2) 2
hh xhh h hxh h xh +−++− = + = + = =+ 0 0 ()lim()() lim2 2 h h fxfxhfx h xh x → → +− ′ = =+ =
fxhfxxxhhx
34. (a) () () () 1 2 1 2 1122 22 1 2 3 4 1 2 (0) 0 2(2(0)0) 0 3 2 = = = = ff m
0 2 0 0 (0)lim(0)(0) lim20 lim(2) 2 → → → +− ′ = = =− = h h h ffhf h hh h h
(b)
xx
21 sec 21 1.3311 3.31. 1.11 yy m
===
33 223 22 ()()() 33 33 fxhfxxhx hh xhxhh h xxhh +−+− = ++ = =++ 2 0 ()lim()()3 h fxfxhfxx h → +− ′ = =
© 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
Theanswerinpart(a)isarelatively goodapproximationtotheslopeofthe tangentline.
xx Since f(0)=0and fxfx xx = =− =−
()() . fxfx ()()0 0 13 16 0.8125.
161616256
(b) If2()3, fxxx =− then 2 ()3()(). fxhxhxh +=+−+
39. (a) If1 (), 1 t st t = + theaveragerateof changeof s is21
21
94 Chapter2.Differentiation:BasicConcepts 36. (a) () 1 2 1 2 1 21 111 1 2 1 2 11 32 1 2 (1) (1) 1 3 ff m = = = =− (b) 0 11 1111 0 0 (1)lim(1)(1) lim 1 lim 2(2) 1 4 h h h h h ffhf h h h → −+ −+−−− → → −+−− ′ −= = = =−
2 11113 3,
37. (a) If2()3, fxxx =− theaveragerateof changeof f is21 21 f =−=− 13 21256 1 2116
22 222 2 ()() 3()()(3) 3633 63 631. fxhfx h xhxhxx h xxhhxhxx h xhhh h xh +− +−+−− = + + −−−+ = +− = =+− 0 ()lim(631)61 h fxxhx → ′ =+−=− Theinstantaneousrateofchangeat x =0is(0)1. f ′ =− Noticethatthis rateisestimatedbytheaverageratein part (a). 38. (a) () () () 1 2 ave1 2 11 22 1 2 1 2 (0) 0 120(12(0)) 00 0 ff f = = = = (b) 0 0 0 (0)lim(0)(0) lim(12)0 lim(12) 1 h h h ffhf h hh h h → → → +− ′ = = =− = Theanswerinpartaisnotavery goodapproximationtotheaverage rateofchange.
Thedifferencequotient(DQ)is
tt Since 1 2 1 2 11 3 21 s −==− −+ and 1 2 0131 (0)1,4. 010 s −−+ ==−= + © 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
()()stst
©
+−− +++ +− = Multiplyingnumeratorand denominatorby(t + h +1)(t +1). (1) 1 1 1 2 3
(b) ()
(a) ss s
11 (1)(1) = = = =
shs s h h h hh hh h hh h
h h h h h
→ → → → →
0 0 0 0 0
(1)lim(1)(1) 11 lim 1111 lim 11 11 lim 11 1 lim 11 1 2
+− ′ = +− = +−++ = ⋅ ++ +− = ++ = ++ = Theanswerinpartaisarelatively goodapproximationtothe instantaneousrateofchange.
41. (a) Theaveragerateoftemperature changebetween0 t and0th + hours aftermidnight.Theinstantaneousrate oftemperaturechange0 t hoursafter midnight.
(b) Theaveragerateofchangeinblood alcohollevelbetween0 t and 0 th + hoursafterconsumption.The instantaneousrateofchangeinblood alcohollevel0 t hoursafter consumption.
on
a
for
distribution in any
Chapter2.Differentiation:BasicConcepts 95
22 (1)(1)(1)(1) (1)(1)
2 (1)(1) 2 (1)(1) thttth htht tthtthtthtth htht h htht tht +−+−−++ = +++ +−++−−−−+++ = +++ = +++ = +++ 02 22 ()lim(1)(1)(1) h st thtt → ′ = = +++ + Theinstantaneousrateofchange when 1 2 t =− is ()12 2 12 8. 21 s ′ −== −+ Noticethattheestimategivenbythe averagerateinpart
(b) If1 (), 1 t st t = + then ()1 (). ()1 sthth th +− += ++ Thedifferencequotient(DQ)is 11 ()()11 tht sthsttht hh differs significantly. 40. (a) () 1 4 ave1 4 1 4 3 4 1 2 3 4
(c) Theaveragerateofchangeofthe 30-yearfixedmortgageratebetween 0t and0th + yearsafter2005.The instantaneousrateofchangeof 30-yearfixedmortgagerate0 t years after2005.
42. (a) ...theaveragerateofchangeof revenuewhentheproductionlevel changesfrom0 x to0xh + units. ...theinstantaneousrateofchangeof revenuewhentheproductionlevel is0 x units.
website,
part.
(b) ...theaveragerateofchangeinthe fuellevel,inlb/ft,astherockettravels between0 x and0xh + feetabovethe ground.
2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized
sale or
manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted
in whole or
...theinstantaneousrateinfuellevel whentherocketis0 x feetabovethe ground.
(c) ...theaveragerateofchangein volumeofthegrowthasthedrug dosagechangesfrom0 x to0xh + mg. ...theinstantaneousrateinthe growth’svolumewhen0 x mgofthe drughavebeeninjected.
43. P(x)=4,000(15 x)(x 2)
(a) Thedifferencequotient(DQ)is
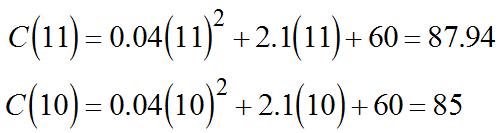
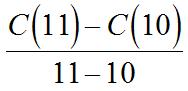
(b) Theaveragerateas q increasesfrom q =0to q =20is 2 (20)(0)[70(20)(20)]0
(c) Theratetheprofitischangingat q =20is(20). ′
(b) ()0Px ′ = when4,000(172x)=0. 17 8.5, 2 x == or850units.
When()0, Px ′ = thelinetangentto thegraphof P ishorizontal.Sincethe graphof P isaparabolawhichopens down,thishorizontaltangentindicates amaximumprofit.
44. (a) Profit=(numbersold)(profitoneach) Profitoneach
=sellingpricecosttoobtain ()(120)(50) =−−Pppp
Since q =120 p, p =120 q. P(q)= q[(120 q)50] or 2 ()(70)70. =−=− Pqqqqq
Since(20) ′ P ispositive,profitis increasing. 45.
(a) As x increasesfrom10to11,the averagerateofchangeis or$2,940perunit.
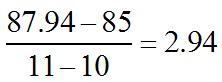
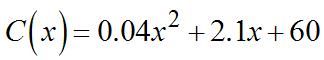
96 Chapter2.Differentiation:BasicConcepts
2 ()() [4,000(15())(()2)] [4,000(15)(2)]
4,000(172) 4,000(172) PxhPx h xhxh h xx h xhxhxx h hxhh h xh +− −++− = −−+−−−− = = =−− 0 ()lim()() 4,000(172) h PxhPx Px h x → +− ′ = =−
4,000[(15)(2)(15)(2)]
2020 $50perrecorder
= PP
=
P Thedifferencequotientis 22 222 2 ()() [70()()][70] 7070270 702 702 +− +−+−− = +−−−−+ = = =−− PqhPq h qhqhqq h qhqqhhqq h hqhh h qh 0 ()lim()()702 → +− ′ = =− h PqPqhPqq h (20)702(20)$30′ =−= P per
recorder.
© 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
Theaveragerateofchangeiscloseto thisvalueandisanestimateofthis instantaneousrateofchange. Sinceispositive,thecostwill increase.
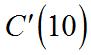
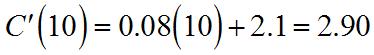

Chapter2.Differentiation:BasicConcepts 97 (b) So,thedifferencequotient(DQ)is or$2,900perunit
46. (a) () ave (3,100)(3,025) 3,1003,025 3,1003,1003,1003,025 75 3,100103155 75 28.01 QQQ = = = ≈ Theaveragerateofchangeinoutputisabout28unitsperworker-hour. © 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
Theinstantaneousrateofchangeis28.2unitsperworker-hour.
WritingExerciseAnswerswillvary.
Theinstantaneousrateofchangeis$80perunitwhen x =4.Theexpenditureisdecreasing
49. When t =30, 65503 50304 dV dt ≈= Inthe“longrun,”therateatwhich V ischangingwithrespecttotimeisgettingsmallerandsmaller, decreasingtozero.
98 Chapter2.Differentiation:BasicConcepts (b) ( ) ( ) 0 0 0 0 0
lim3,1003,0253,1003,025 lim3,1003,025553,02555 3,02555 lim3,100(3,0253,025) 3,02555 lim3,100 3,02555 3,100 110 28.2 h h h h h QQhQ h h h hh hh h hh h → → → → → +− ′ = +− = +− ++ = ⋅ ++ +− = ++ = ++ = ≈
(3,025)lim(3,025)(3,025)
2 ()() (35200) 35200 ExxDx xx xx =⋅ =−+ =−+ (b) ave 22 (5)(4) 54 35(5)200(5)(35(4)200(4)) 125240 115 EE E = =−+−−+ =− =− Theaveragechangeinconsumerexpendituresis$115perunit. (c) 0 22 0 2 0 0 (4)lim(4)(4) lim35(4)200(4)(35(4)200(4)) lim3580 lim(3580) 80 h h h h EhE E h hh h hh h h → → → → +− ′ = −+++−−+ = = =−− =−
47.
48. (a)
when x =4.
© 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
50. Answerswillvary.Drawingatangentlineateachoftheindicatedpointsonthecurveshowsthe populationisgrowingatapproximately10/dayafter20daysand8/dayafter36days.Thetangent lineslopeissteepestbetween24and30daysatapproximately27days.
51. When h =1,000meters,
When h =2,000meters,0C/meter.
Sincethelinetangenttothegraphat h =2,000ishorizontal,itsslopeiszero.
52.
(a) Theaveragerateofchangeis. Since and,
Thepopulation’saveragerateofchangefor2010–2012iszero.
(b) Tofindtheinstantaneousrate,calculate P’(2). sothedifferencequotient(DQ)is
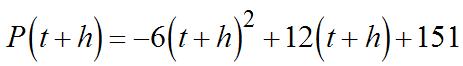
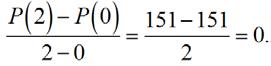
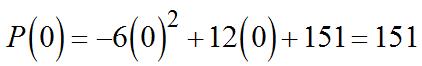
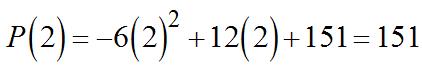
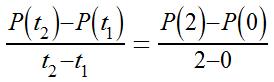
For2012, t =2,sotheinstantaneousrateofchangeis P’(2)=–12(2)+12 =–12,oradecreaseof12,000people/year.
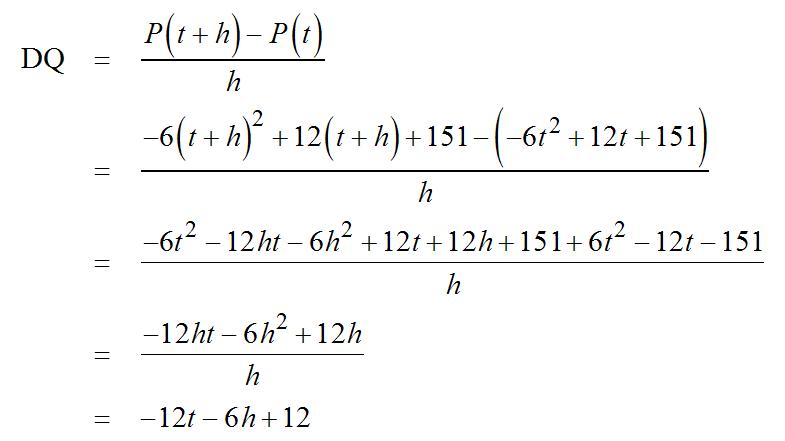
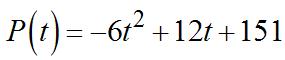
Chapter2.Differentiation:BasicConcepts 99
60 2,0001,000 6 1,000 0.006C/meter dT dh ≈ = =−°
dT dh =°
© 2013
Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any
This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in
or part.
by McGraw-Hill
manner.
whole
53. ()4.44.92 Httt
=−
(a) Thedifferencequotient(DQ)is
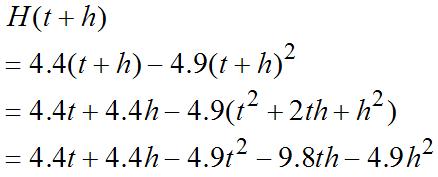
After1second, H ischangingatarateof(1)4.49.8(1)5.4m/sec, H ′ =−=− wherethenegative representsthat H isdecreasing.
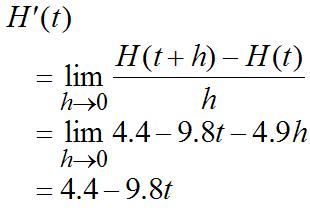
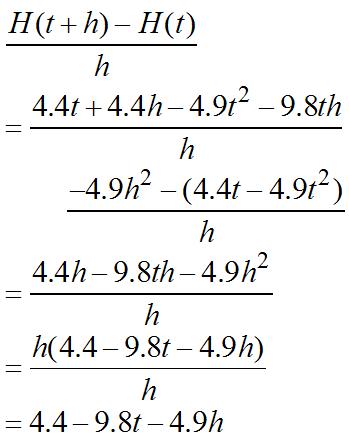
(b) ()0Ht ′ = when4.49.8t =0,or t ≈ 0.449seconds.
Thisrepresentsthetimewhentheheightisnotchanging(neitherincreasingnordecreasing). Thatis,thisrepresentsthehighestpointinthejump.
(c) Whentheflealands,theheight H(t)willbezero(asitwaswhen t =0).
Again,thenegativerepresentsthat H isdecreasing.
54. (a) If P(t)representsthebloodpressurefunctionthen(0.7)80 P ≈ ,(0.75)77 P ≈ ,and(0.8)85 P ≈ Theaveragerateofchangeon[0.7,0.75]isapproximately77806 0.5 =− mm/secwhileon [0.75,0.8]theaveragerateofchangeisabout 8577 16 0.5 = mm/sec.Therateofchangeis greaterinmagnitudeintheperiodfollowingtheburstofblood.
(b) Writingexerciseanswerswillvary.
100 Chapter2.Differentiation:BasicConcepts
2 4.44.90 (4.44.9)0 4.44.90 44 0.898seconds 49 tt tt t t −= −= −= =≈ Atthistime,therateofchangeis 4444 4.49.8 4949 4.4m/sec. H ′ =− =−
© 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
©
55. 2 ()0.00090.1317.81 Dppp =−++
()() . DpDp pp
Since 2 (60) 0.0009(60)0.13(60)17.81
()() DphDp h +− 2 2 22 2 2 [0.0009()0.13() 17.81 (0.00090.1317.81)] [0.00090.00180.0009 0.130.1317.81 0.00090.1317.81] 0.00180.00090.13 0.00180.00090.13 phph pp h pphh ph pp h phhh h ph −+++ + −−++ +++ +−− = −−+ = =−−+ 0 () lim(0.00180.00090.13) 0.00180.13 h Dx ph p → ′ =−−+ =−+ Theinstantaneousrateofchange when p =60is (60)0.0018(60)0.13 0.022mm D ′ =−+ = permmofmercury.Since(60) D ′ is positive,thepressureisincreasing when p =60.
(c) 0.00180.130 72.22mmof mercury
p p −+=
≈
56. (a) Therocketis feetabove ground.
(b) Theaveragevelocitybetween0and 40secondsisgivenby feet/second.
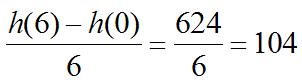
(c) ft/secand ft/sec.Thenegative signinthesecondvelocityindicates therocketisfalling.
57. (a)
So,thedifferencequotient(DQ)is
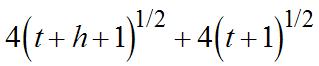
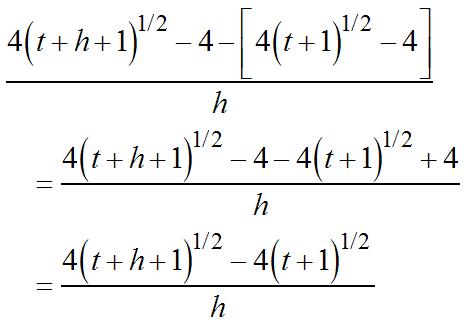
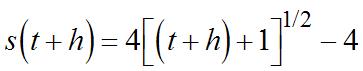
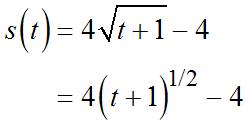
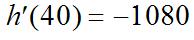
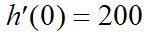
2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
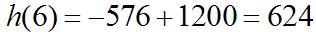
Chapter2.Differentiation:BasicConcepts 101
22.37 D
= and 2
D =−++ =
(a) Theaveragerateofchangeis 21 21 = =
=−++
(61) 0.0009(61)0.13(61)17.81 22.3911,
22.391122.37 6160 0.0211mmpermmofmercury
(b) 2 ()0.0009()0.13 Dphph+=−++ (p + h)+17.81
So,thedifferencequotient(DQ)is
Atthispressure,thediameteris neitherincreasingnordecreasing.
Multiplyingthenumeratorand denominatorby gives
(b) At1 x =− ,3(1)25 y =−−=− and (1,5)isapointonthetangentline. Usingthepoint-slopeformulawith
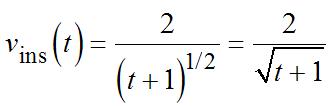
(c) Thelinetangenttoastraightlineat anypointisthelineitself. 59. (a) For2 (),yfxx ==
yx=− isthegraph of2 yx = shifteddown3units.Sothe graphsareparallelandtheirtangent lineshavethesameslopesforany valueof x.Thisaccounts geometricallyforthefactthattheir derivativesareidentical.
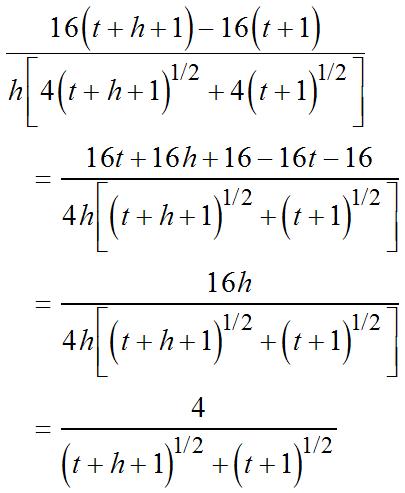
(b) Since25 yx=+ istheparabola 2 yx = shiftedup5unitsandthe constantappearstohavenoeffecton thederivative,thederivativeofthe function25 yx=+ isalso2x.
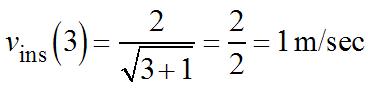
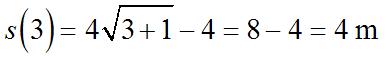
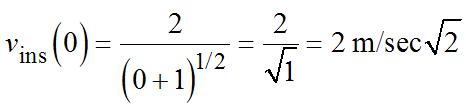
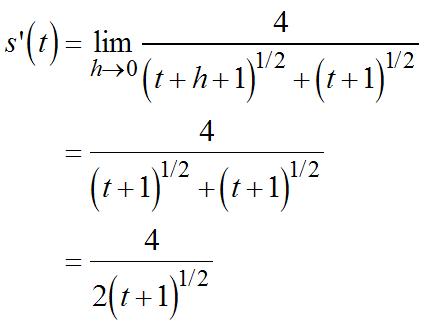
102 Chapter2.Differentiation:BasicConcepts (b) (c) 58.
0 0 ()lim(3()2)(32) lim3 3 h h fxxhx h h h → → +−−− ′ = = =
(a)
3
32yx
m = gives(5)3((1)) yx−−=−− or
=−
2 ()().
22 2 ()()() 2 2 fxhfxxhx hh xhh h xh +−+− = + = =+ 0 () lim()() 2 h dyfx dx fxhfx h x → ′ = +− = = For2()3,yfxx==− 2 ()()3. fxhxh+=+− Thedifferencequotient(DQ)is 222[()3](3)2 2 xhxxhh hh xh +−−−+ = =+ 0 () lim()() 2 h dyfx dx fxhfx h x → ′ = +− = =
fxhxh +=+ Thedifferencequotient(DQ)is
Thegraphof23
©
for
on a website,
2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized
sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted
in whole or part.
60. (a) For2()3 fxxx =+ ,thederivativeis
(c) Thederivativeofthesumisthesum ofthederivatives.
(d) Thederivativeof() fx isthesumof thederivativeof() gx and() hx
(a) For2 (),yfxx ==
For3 (),yfxx == 3
()(). fxhxh +=+
Thedifferencequotient(DQ)is
(b) Thepatternseemstobethatthe derivativeof x raisedtoapower() n x isthatpowertimes x raisedtothe powerdecreasedbyone1(). n nx So, thederivativeofthefunction4
63. When x <0,thedifferencequotient(DQ) is()()()()
When x >0,thedifferencequotient(DQ) is()()()1. fxhfxxhx hh +−+− ==
So, 0 ()lim11. h fx → ′ ==
Sincethereisasharpcornerat x =0 (graphchangesfrom y = x to y = x),the graphmakesanabruptchangeindirection at x =0.So, f isnotdifferentiableat x =0.
Chapter2.Differentiation:BasicConcepts 103
22 0 222 0 0 () lim[()3()](3) lim2333 lim(23)23 → → → ′ +++−+ = ++++−− = =++=+ h h h fx xhxhxx h xhxhxhxx h xhx
22 0 222 0 0 ()lim() 2 lim lim(2) 2 h h h xhx gxh xhxhx h xh x → → → +− ′ = ++− = =+ = Whilefor()3hxx = ,thederivativeis 00 ()lim3()33lim3 hh hxxhxh hh→→ +− ′ = ==
(b) For2 () gxx = ,thederivativeis
61.
2 ()().
Thedifferencequotient(DQ)is 22 2 ()()() 2 2 fxhfxxhx hh xhh h xh +−+− = + = =+ 0 () lim()() 2 h dyfx dx fxhfx h x → ′ = +− = =
fxhxh +=+
33223
hh xxhh +−++ = =++ 0 2 () lim()() 3 h dyfx dx fxhfx h x → ′ = +− = =
22 ()33 33 xhxxhxhh
is3 4 x andthederivativeofthe function27 yx = is2627. x
0 0 0 0 lim[()]() lim lim lim ,aconstant. h h h h dymxhbmxb dxh mxmhbmxb h mh h m m → → → → ++−+ = ++−− = = = =
1
yx =
62. If ymxb =+ then
fxhfxxhx hh h h +−−+−− = = =− So, 0 ()lim11. h fx → ′ =−=−
© 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
©
64. (a) Writeanynumber x as xch =+ .If thevalueof x isapproaching c,then h isapproaching0andviceversa.Thus theindicatedlimitisthesameasthe limitinthedefinitionofthe derivative.Lessformally,notethatif xc ≠ then()() fxfc xc istheslopeof asecantline.s x approaches c the slopesofthesecantlinesapproachthe slopeofthetangentat c
(b)
usingpart(a)forthefirstlimitonthe right.
=−
2 11 1(1)(1) limlim2 11xx xxx xx++ →→ −+ = = 2 11 1(1)(1) limlim2 11xx xxx xx→→ −+ = =−
66. UsingtheTRACEfeatureofacalculator withthegraphof3220.84yxx=−+ showsapeakat0 x = andavalleyat
0.2667 x = .Notethepeaksandvalleys arehardtoseeonthegraphunlessasmall rectanglesuchas[0.3,0.5] × [3.8,4.1]is used.
=−
fxfc fxfc fxfc
→ →→ → =−
xc xcxc xc
65. Toshowthat 21 ()1 x fx x = isnot differentiableat x =1, press y =andinput2(abs(1))/(1) xx for1 y =
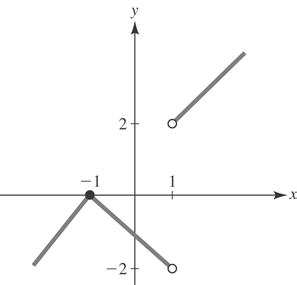
TheabsisundertheNUMmenuinthe mathapplication.
Usewindowdimensions[4,4]1by [4,4]1
67. Tofindtheslopeoflinetangenttothe graphof2()23 fxxxx =+− at x =3.85,fillinthetablebelow.
The x + h rowcanbefilledinmanually. For f(x),press y =andinput
( ) ^22(3) xxx +− for1 y = Usewindowdimensions[1,10]1by [1,10]1.
Usethevaluefunctionunderthecalc menuandenter x =3.85tofind
f(x)=4.37310.
For f(x + h),usethevaluefunctionunder thecalcmenuandenter x =3.83tofind
f(x + h)=4.35192.Repeatthisprocessfor x =3.84,3.849,3.85,3.851,3.86,and 3.87.
The()()
fxhfx h +− canbefilledin
2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
104 Chapter2.Differentiation:BasicConcepts
=
lim()()lim()
= ′ =⋅ =
lim[()()] lim()()() xc xc fxfc fxfc xc xc → →
lim[()()]
()0 0 xc xcxc fxfc fxfc xc xc fc → →→
(c) Usingthepropertiesoflimitsandthe resultofpart(b) 0lim[()()] lim()lim() lim()()
solim()() xc fxfc → = meaning f(x)is continuousat xc =
PressGraph Weseethat f isnotdefinedat x =1.There canbenopointoftangency.
manuallygiventhattherestofthetableis nowcomplete.So, slope(3.85)1.059. f ′ =≈
2.2 Techniques of Differentiation
1. Sincethederivativeofanyconstantis
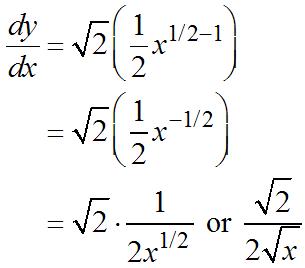
6. 7/3 yx = 7/314/377 33 dy xx dx ==
7. 3.7 yx = 3.712.73.73.7 dy xx dx ==
8.
(Note: y =2isahorizontallineandall horizontallineshaveaslopeofzero,so
Chapter2.Differentiation:BasicConcepts 105 h 0.020.010.001 x + h 3.833.843.849 f(x)4.373104.373104.37310 f(x + h)4.351924.362514.37204 ()() fxhfx h +− 1.0591.0591.059 00.0010.010.02 3.853.8513.863.87 4.373104.373104.373104.37310 4.373104.374154.383684.39426 undefined1.0581.0581.058
zero, 2 0 y dy dx =− =
dy
y =3 0 = dy dx
53
505 yx dydd x dxdxdx dy dx =− =− =−= 4. y =2x +7 2(1)02 =−+=− dy dx 5. 4 yx = 415 5 4 44 dy xx dxx =−=−=−
dx mustbezero.) 2.
3.
(5)(3)
=−−=
=π
=π=π
1.2 1.212.2 4 0(1.2)1.2 =−
yx dy xx dx 9. 2 yr
21 (2)2 dy rr dx
dr ==
221/2yxx ==⋅ 12. 433/422 yxx == 3/411/4 4 333 2 422 dy xx dxx = == 13. 91/2 9 yt t == 1/21 3/2 3/23 1 9 2 1 9 2 99 or 22 dyt dx t tt =− =− =−− © 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
10. 43 π 3 yr = 422 π(3)4π 3 dy rr
11.
14. 2 2 33 22 yt t ==
3 3 33 2(2)dyt dtt =−=
=++
=++
yxx dyddd xx dxdxdxdx dy x dx =+
=−+−
=−+
dy xx dx xx
=−++
=−++ =−+
yxxx dydddd xxx dxdxdxdxdx dy xx dx
512 ()(5)()(12) 9401
fxxx xx
11 ()8610 42 231
′ =⋅−⋅−+ =−−
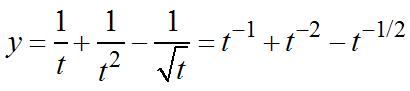
22
()0.02(3)0.30.060.3 fxxx ′ =−+=−+
uu ′ =−+− =−+
32 ()4(0.07)3(1.21)30 0.283.633
106 Chapter2.Differentiation:BasicConcepts
15. 2 2 23 ()(2)(3) 22
16. 53 3496yxxx =−+− 42 42 3(5)4(3)9(1)0 15129
17. 98 98 87
18. 8611 ()2 42 fxxxx=−−+ 75 75
19. 3 ()0.020.3 fxxx =−+ 3 ()(0.02)(0.3) dd fxxx dxdx ′ =−+
32
21. 121/2 11211/21 233/2 233/2 ()()() 1 12 2 1 12 2 121 , 2 dydddttt dtdtdtdt ttt ttt ttt =+− =−+−−− =−−+ =−−+ or233 121 2 ttt −−+ 22. 123 23 3222 32 33 yxxx xxx =−+=−+ 234 234 234 2 (1)(3)(2)(2)(3)3 342 342 dy xxx dx xxx xxx =−−−+− =−+− =−+− 23. 33/23/2 3 1 (), fxxxx x =+=+ 3/23/2 3/213/21 1/25/2 1/2 5/25 ()()() 33 22 33 22 3333 ,or 2222 dd fxxx dxdx xx xx xx xx ′ =+ =+ =− =−− 24. 3 3/21/2 4 ()22 242 ftt t tt =+− =+− 3/211/21 1/23/2 3 31 ()(2)(4)0 22 32 2 3 fttt tt t t ′ =+− =− =− © 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
20. 43 ()0.071.2135.2 fuuuu =−+−
fuuu
28.
=−−+− =−−+
29. 32 2 531 3103 yxxx dy xx dx
At x =1,10. dy dx = Theequationofthe tangentlineat(1,8)is y +8=10(x +1),or y =10x +2.
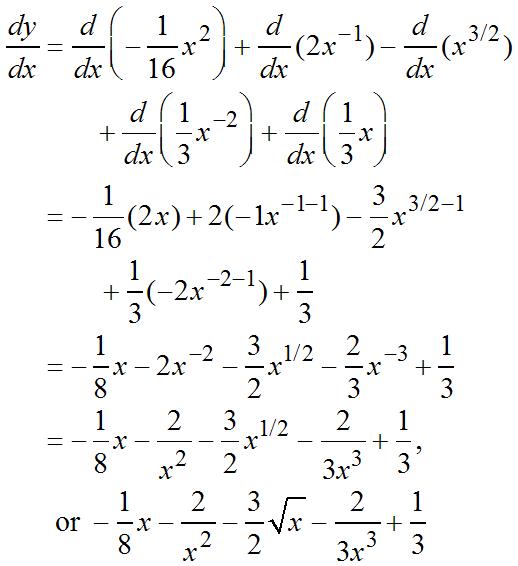
30. Given53352yxxx=−−+ andthepoint (1,5),then42595 dy xx dx =−− andthe slopeofthetangentlineat1 x = is 42 5(1)9(1)59 m =−−=− .Theequation ofthetangentlineisthen (5)9(1)yx−−=−− or94 yx=−+ .
31. 1211/2112 yxx xx =−+=−+ 23/2 23/2 11 dy xx dxxx =−=−
At 7 4,, 4 1 16 dy dx =− Theequationof thetangentlineis71(4), 416 yx−=−− or 1 2. 16 yx=−+
32. Given32 2 16 yxx x =−+ andthepoint (4,7),then3 332 2 2 dy xx dxx =−− andthe slopeofthetangentlineat4 x = is 3 33211 42(4) 22 4 m = −=− .Theequation ofthetangentlineisthen 11
(7)(4) 2 yx −−=−− or 11 15 2 yx=−+
33. 232 2 ()(32)23 623 yxxxxxx dy xx dx
=−+=+− =+−
At x =1,1. dy dx = Theequationofthe
Chapter2.Differentiation:BasicConcepts 107
2
111 2, 1633 xx yx xx xxxxx =−+−++ =−+−++
1.22.1 1.22.1 75 75 yxx xx =+=−+ 1.212.11 2.21.1 1.1 2.2 1.2(7)2.1(5) 8.410.5 8.4 10.5 dy xx dx xx x x =−−+ =+ =+ 27. 52 3 52 33 2 21 4 4 4 4 xx y x xx xx x x xx = =− =− =− 21 11 2 2 ()(4) 24(1) 24 4 2 dydd xx dxdxdx xx xx x x =− =−− =+ =+
25. 2 3/2
213/22 21 163 3
26.
23532 (67)67 yxxxxxx =−+=−+ 42 51814 dy xxx dx =−+
© 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
tangentlineat(1,2)is y 2=1(x +1), or y = x +3.
34. Given43 2 yxx x =−+ andthepoint
(1,4),then32 13 8 2 dy x dxxx =−− andthe slopeofthetangentlineat1 x = is
3 2 8(1)139
2(1)2 1 m =−−= .Theequation ofthetangentlineisthen94(1) 2 yx−=− or 91 22yx=−
'(2)481193 44 mf==+= .Theequationof thetangentlineis19366(4)
1 ()22 2 ()6
fxxxx x fxx x
35. 332 2 2 3
=−+=−+ ′ =−−
At x =1,(1)4. f ′ −=− Further, y = f (1)=3.Theequationofthetangent lineat(1,3)is y 3=4(x +1),or y =4x 1.
36. 432 ()326;2 fxxxxx =−+−=
32 ()494 fxxxx ′ =−+
(2)1624866 f =−+−=− so(2,6)isa pointonthetangentline.Theslopeis
(2)323684 mf ′ ==−+= .Theequation ofthetangentlineis(6)4(2) yx−−=− or 414yx=−
Further,84 (2)4. 33 yf==−+= The equationofthetangentlineat4
40. 3/2 ()(1);4 fxxxxxx =−=−= 3 ()1 2 fxx ′ =−
1 () 2 ()1
fxxxx x fx x
37. 2 2 3
=−=− ′ =+
At x =1,(1)3. f ′ = Further, y = f (1)=0. Theequationofthetangentlineat(1,0)is y 0=3(x 1),or y =3x 3.
38. 3 ();4 fxxxx=+=
()321 2 fxx x ′ =+
(4)64266 f =+= so(4,66)isapointon thetangentline.Theslopeis
(4)844 f =−= so(4,4)isapointonthe tangentline.Theslopeis (4)312. mf ′ ==−= Theequationofthe tangentlineis42(4) yx−=− or 24yx=−
41. 4 3 ()231 ()83 fxxx fxx =++ ′ =+
Therateofchangeof f at x =1is
(1)5. f ′ −=−
42. 3 ()35;2 fxxxx=−+= 2 ()33 (2)3(4)39 fxx f ′ =− ′ =−=
108 Chapter2.Differentiation:BasicConcepts
193 127 4 yx=− . 39. 331/2 2 1/2 11 ()88 33 ()8 2
fxx x =−+=−+⋅ ′ =−+ At x =2, (2)48 22 18 4 22 1 42 2 3. f ′ =−+ =−+ =−+⋅ =−
4 yx−=− or
fxxxxx
2, 3 is 4
3.
33(2),yx−=−− or 22
3 yx=−+
© 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
43. 1/22 2 1/23
fxxxxxx x fx xx
=−+=−+ ′ =−−
1 () 12 ()1 2
Therateofchangeof f at x =1is
3 (1). 2 f ′ =−
48. ()11; =+=+ fxxxx x f(1)=1+1=2
2 2 1 ()11;(1)110 ′′ =−=−=−=fxxf x
At c =1,therelativerateofchangeis (1)00 (1)2
′ == f f
fx x f
′ =+ ′ =+=
44. ()5;4 fxxxx=+= 1 ()5 2 121 (4)52(2)4
45. 1/2
+ = =+ =+ =+ 1/2 1 () 2 fx x ′ =
() 1 1
fxxx x xx xx x x
Therateofchangeof f at x =1is 1 (1). 2 f ′ =
49. 2 1/22 3/22
=+ =⋅+ =+ 1/2 33 ()22 22 fxxxxx ′ =+=+
() fxxxx xxx xx
Therelativerateofchangeis () 3 2 22 ()2234 . ()22 fxxxxx fxxxxxxx + ′ + =⋅= + +
′ + = = +
When x =4, () 2 ()344(4)11 (4)24 2444 fx f
50. 11 ()(4)41; =−=−fxxxx 41 31 ()33 f =−= 24 ()4;(3)9 ′′ =−=−fxxf
46. 2 ();1 fxxxx x =−= 2 ()23 2 (1)237 22
fxx x f
′ =− ′ =−−=−
47. 32 2 ()254 ()610 fxxx fxxx =−+ ′ =−
Therelativerateofchangeis 2 32 ()610 . ()254 fxxx fxxx
′ = −+
At c =3,therelativerateofchangeis 4 9 1 3
′ ==− f f
(3)4 . (3)3
51. (a) 2 ()0.11020 ()0.210 Attt Att =++ ′ =+
Intheyear2008,therateofchangeis
(4)0.810 A′ =+ or$10,800peryear.
(b) A(4)=(0.1)(16)+40+20=61.6,so thepercentagerateofchangeis
(100)(10.8)17.53.
61.6 % =
′ ==− −+
When x =1,(1)6104. (1)254 f f
52. (a) Since32()615 fxxxx =−++ isthe numberofradiosassembled x hours after8:00A.M.,therateofassembly after x hoursis
Chapter2.Differentiation:BasicConcepts 109
©
2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
2 ()31215fxxx ′ =−++ radiosper hour.
(b) Therateofassemblyat9:00A.M. (1 x = )is (1)3121524 f ′ =−++= radiosper hour.
(c) Atnoon, t =4. and.So,Lupeiscorrect: theassemblyrateislessatnoonthan at9A.M.
53. (a) 2 ()2040600 Txxx=++ dollars Therateofchangeofpropertytaxis ()4040dollars/year.Txx ′ =+ Intheyear2008, x =0, (0)40dollars/year. T ′ =
(b) Intheyear2012, x =4and T(4)=$1,080.Intheyear2008, x =0 and T(0)=$600. Thechangeinpropertytaxis T(4) T(0)=$480.
54. 2 ()2,300125517Mx xx =+− 23 ()1251034Mx xx ′ =−+ 23 (9)12510340.125 99 M ′ =−+≈− .Salesare decreasingatarateofapproximately 1/8motorcycleper$1,000ofadvertising.
=
4.0(# 4.0(250)11,200 250 4,8004.0
x x x x = + =+
So,thecostfunctionis 9,800 ()4. Cxx x =+
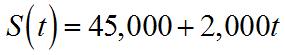
(b) Therateofchangeofthecostis ().Cx ′ 1 2
()9,8004 ()9,8004dollars/miperhr Cxxx Cx x
=+ ′ =−+
When x =40, (40)2.125dollars/miperhr. C ′ =−
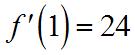
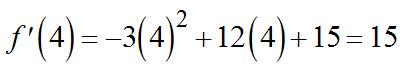
Since(40) C ′ isnegative,thecostis decreasing.
56. (a) Since2()1004005,000 Cttt=++ is thecirculation t yearsfromnow,the rateofchangeofthecirculationin t yearsis
()200400Ctt ′ =+ newspapersper year.
(b) Therateofchangeofthecirculation 5yearsfromnowis
(5)200(5)4001,400 C ′ =+= newspap ersperyear.Thecirculationis increasing.
(c) Theactualchangeinthecirculation duringthe6thyearis
(6)(5)11,0009,500 1,500newspapers. CC−=− =
=
costdriverhrs) mi x x = =
57. (a) SinceGary’sstartingsalaryis$45,000 andhegetsaraiseof$2,000peryear, hissalary t yearsfromnowwillbe dollars.
Thepercentagerateofchangeofthis salary t yearsfromnowis
© 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
110 Chapter2.Differentiation:BasicConcepts
55. (a) Cost=costdriver+costgasoline 20(# 250 20 5,000
costgasoline gals) dollars
(b) Thepercentagerateofchangeafter1 yearis
2 ()18500Nxx ′ =+ commutersper week.After8weeksthisrateis 2 (8)18(8)5001652 N ′ =+= usersper week.
(b) Theactualchangeinusageduringthe 8thweekis (8)(7)15,07213,558 1,514riders. NN−=− =
(c) Inthelongrun,approaches0. Thatis,thepercentagerateofGary’s salarywillapproach0(eventhough Gary’ssalarywillcontinuetoincrease ataconstantrate.)
58. Let G(t)betheGDPinbillionsofdollars where t isyearsand0 t = represents1997. SincetheGDPisgrowingataconstant rate, G(t)isalinearfunctionpassing throughthepoints(0,125)and(8,155)
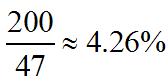
Then
()15512515125125 804 Gttt =+=+ .
In2012,15 t = andthemodelpredictsa GDPof(15)181.25 G = billiondollars.
59. (a) f(x)=6x +582 TherateofchangeofSATscoresis
()6.fx ′ =−
(b) Therateofchangeisconstant,sothe dropwillnotvaryfromyeartoyear. Therateofchangeisnegative,sothe scoresaredeclining.
60. (a) Since3()65008,000Nxxx=++ is thenumberofpeopleusingrapid transitafter x weeks,therateatwhich systemuseischangingafter x weeks is
′ = +
x Px x
=
100(9)100(20) (9)2(9)4(9)5,000
3/2
2 100()200(100)200 ()100 (100) Ptt Ptt t ′ + = = + +
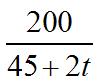
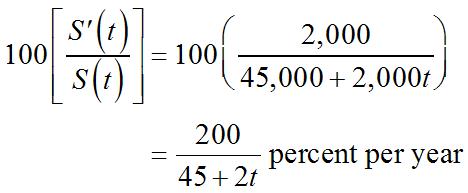
Chapter2.Differentiation:BasicConcepts 111
61. (a) 3/2 ()245,000Pxxx=++ isthe population x monthsfromnow.The rateofpopulationgrowthis 1/2 1/2 ()2432 26peoplepermonth. +
Ninemonthsfromnow,the
populationwillbechangingattherate of1/2(9)26(9)20peopleper P ′ =+= month.
2,000 5,126 0.39
P P
= ++ = =
(b) Thepercentagerateatwhichthe populationwillbechanging9months fromnowis
%.
′
©
Education.
is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any
This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
62. (a) 22 ()20010,000(100) Ptttt =++=+ ()22002(100)Pttt ′ =+=+ Thepercentagerateofchangeis
2013 by McGraw-Hill
This
manner.
(b) Thepercentagerateofchanges approaches0since 200 lim0. 100 tt →∞ = +
63. 331/2()105105 Nttttttt =++=++
Therateofchangeoftheinfected populationis
2 1/2 1 ()305 2 people/day. Ntt t ′ =++
Onthe9thday,(9)2,435people/day. N ′ =
64. (a) 3 43 ()5,175(8) 5,1758 Nttt tt =−− =−+
32 (3)4(3)83(3)108 N ′ =−+⋅= people perweek.
(b) Thepercentagerateofchangeof N is givenby 32 43 100()100(424)
is T(0.442) ≈ 42.8°C.
Thebird’stemperaturestartsat
T(0)=37.1 °C,increasesto
T(0.442)=42.8°C,andthenbeginsto decrease.
66. (a) Usingthegraph,the x-value(taxrate) thatappearstocorrespondtoa y-value (percentagereduction)of50is150,or ataxrateof150dollarsperton carbon.
()5,1758 Nttt Nttt
′ −+ = −+ Agraphofthisfunctionshowsthatit neverexceeds25%.
(c) Writingexerciseanswerswillvary.
65. (a) 32 ()68.0730.9812.52 37.1 Ttttt =−++ + 2
()204.2161.9612.52 Tttt ′ =−++
()Tt ′ representstherateatwhichthe bird’stemperatureischangingafter t days,measuredin °Cperday.
(b) (0)12.52C/day T ′ =° since(0) T ′ is positive,thebird’stemperatureis increasing.
(0.713)47.12C/day T ′ ≈−°
Since(0.713) T ′ isnegative,thebird’s temperatureisdecreasing.
(b) Usingthepoints(200,60)and(300, 80),fromthegraph,therateofchange isapproximately orincreasingatapproximately0.2% perdollar.(Answerswillvary dependingonthechoiceof h.)
(c) Writingexercise–Answerswillvary.
67. (a) 2 ()0.050.13.4 ()0.10.1 PPM PPM/year Qttt Qtt =++ ′ =+
Therateofchangeof Q at t =1is (1)0.2PPM/year. Q ′ =
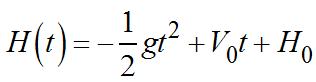
(b) Q(1)=3.55PPM, Q(0)=3.40,and Q(1) Q(0)=0.15PPM.
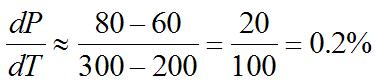
68.
22 441 π π 339 N PNT kTk = = µµ 22 2 2 4π 4π 99 dPNN T dtkkT = −= µµ
tt t t = ≈
(c) Find t sothat()0. Tt ′ = 2 2
=−++ −±−−
0204.2161.9612.52
61.96(61.96)4(204.21)(12.52)
2(204.21)
Thebird’stemperaturewhen t =0.442
2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
112 Chapter2.Differentiation:BasicConcepts
0.442days
(c) Q(2)=0.2+0.2+3.4=3.8, Q(0)=3.4,and Q(2) Q(0)=0.4PPM.
©
69. Since g representstheaccelerationdueto gravityfortheplanetourspyison,the formulafortherock’sheightis Sincehethrowstherockfromground
level,.Also,sinceitreturnstothe groundafter5seconds,
73. (a) 43 ()48 stttt =−+ for0 ≤ t ≤ 4 32 ()4128 vttt=−+ and 2 ()1224 attt =−
(b) Tofindalltimeingivenintervalwhen stationary,
Therockreachesitsmaximumheight halfwaythroughitstrip,orwhen. So, Substituting
So,ourspyisonMars.
70. (a) 2 ()26 sttt=−+ for02 t ≤≤ ()22 ()2 vtt at =− =
(b) Theparticleisstationarywhen ()220vtt=−= whichisattime1 t = .
71. (a) 2 ()325 sttt=+− for0 ≤ t ≤ 1 v(t)=6t +2and a(t)=6
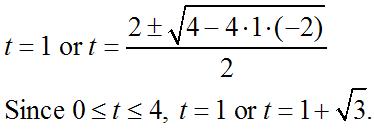
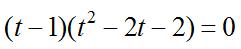
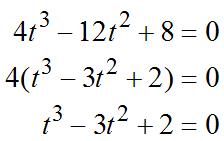
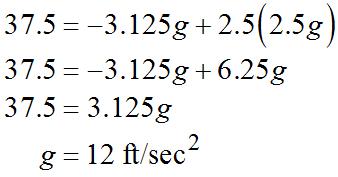
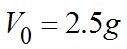
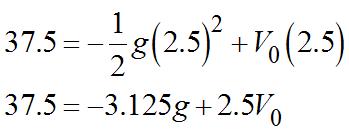
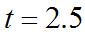
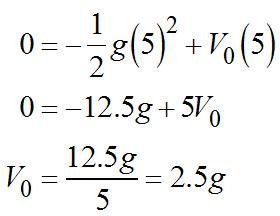
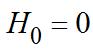
(b) 6t +2=0at t =3.Theparticleisnot stationarybetween t =0and t =1.
72. (a) 32 ()91525 stttt=−++ for06 t ≤≤ 2 ()318153(1)(5) ()6186(3) vttttt attt =−+=−− =−=−
(b) Theparticleisstationarywhen ()3(1)(5)0 vttt=−−= whichisat times 1 t = and5 t =
74. (a) Sincetheinitialvelocityis00 V = feet persecond,theinitialheightis 0144 H = feetand32 g = feetper secondpersecond,theheightofthe stoneattime t is 2 00 2
1 ()2 16144.
=−++ =−+ Thestonehitsthegroundwhen 2 ()161440Htt=−+= ,thatiswhen 29 t = orafter3 t = seconds.
HtgtVtH t
(b) Thevelocityattime t isgivenby ()32 Htt =− .Whenthestonehitsthe ground,itsvelocityis(3)96 H ′ =− feetpersecond.
75. (a) Ifafter2secondstheballpassesyou onthewaydown,then0 (2),HH = where200 ()16 HttVtH =−++ So,2000 16(2)()(2), VHH−++= 0 6420, V −+= or032. sec ft V =
(b) Theheightofthebuildingis0 H feet. Frompart (a) youknowthat 2 0 ()1632. HtttH =−++ Moreover, H(4)=0sincetheballhitstheground after4seconds.So,
Chapter2.Differentiation:BasicConcepts 113
© 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
2 0 16(4)32(4)0, H −++= or 0128feet. H =
(c) Fromparts (a) and (b) youknowthat 2 ()1632128Httt=−++ andsothe speedoftheballis
()3232. sec ft Htt ′ =−+
After2seconds,thespeedwillbe (2)32feet H ′ =− persecond,where theminussignindicatesthatthe directionofmotionisdown.
(d) Thespeedatwhichtheballhitsthe groundis(4)96. ft sec H ′ =−
76. Let(x, y)beapointonthecurvewhere thetangentlinegoesthrough(0,0).Then theslopeofthetangentlineisequalto 0 0 yy xx = .Theslopeisalsogivenby
()24fxx ′ =− .Thus24 y x x =− or 2 24 yxx =−
Since(x, y)isapointonthecurve,we musthave2425 yxx=−+ .Settingthe twoexpressionsfor y equaltoeachother
78. (a) If4 () fxx = then 4 432234
()() 464 fxhxh xxhxhxhh +=+ =++++
32234()()464 fxhfxxhxhxhh +−=+++ and
()()3223 464 fxhfxxxhxhh h +− =+++
gives 22 2 42524 25 5
−+=− = =±
xxxx x x
If5 x =− ,then70 y = ,theslopeis
14andthetangentlineis14yx =−
If5 x = ,then30 y = ,theslopeis6and thetangentlineis6yx = .
77. ()2 fxaxbxc =++
Since f (0)=0, c =0and2(). fxaxbx =+
Since f (5)=0,0=25a +5b
Further,sincetheslopeofthetangentis1 when x =2,(2)1. f ′ =
()2
12(2)4 fxaxb abab ′ =+ =+=+
Now,solvethesystem:0=25a +5b and 1=4a + b.Since14a = b,using substitution
0255(14) 025520 055
aa aa a
= +− =+− =+ or a =1and b =14(1)=5.
So,2()5. fxxx =−+
(b) If() n fxx = then 1221()()(1)... 2 nnnnnn nn fxhxhxnxhxhnxhh +=+=++ +++
1221()()(1)... 2 nnnn nn fxhfxnxhxhnxhh +−=+ +++
114 Chapter2.Differentiation:BasicConcepts
©
material
for
for sale or distribution in any
be
distributed,
2013 by McGraw-Hill Education. This is proprietary
solely
authorized instructor use. Not authorized
manner. This document may not
copied, scanned, duplicated, forwarded,
or posted on a website, in whole or part.
2.3 Product and Quotient Rules; Higher-Order Derivatives
Chapter2.Differentiation:BasicConcepts 115 and 1221()()(1) ... 2 nnnnfxhfxnnnxxhnxhh h +− =++++ (c) Frompart(b) ()()122 (1) 2 fxhfxnnn nn nxhxh h +− =+ ++ Thefirsttermontherightdoesnotinvolve h whilethesecondtermapproaches0as0 h → . Thus1 0 []lim()(). nn h dfxhfx xnx dxh → +− = = 79. ()() fgx ′ + 0 0 0 00 lim()()()() lim()()[()()] lim()()()() lim()()()() lim ()() h h h hh fgxhfgx h fxhgxhfxgx h fxhfxgxhgx h fxhfxgxhgx hh fxgx → → → →→ ++−+ = +++−+ = +−++− = +− +− = + =+′′
1. f(x)=(2x +1)(3x 2), ()(21)(32) (32)(21) (31)(3)(32)(2) 121 d fxxx dx d xx dx xx x ′ =+− +−+ =++− =− 2. ()(5)(12) fxxx =−− ()(5)(12)(12)(5) 2(5)1(12) 114 dd fxxxxx dxdx xx x =−−+−− =−−+− =− © 2013 by
for
not be
distributed, or
on a website, in
or part.
McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized
sale or distribution in any manner. This document may
copied, scanned, duplicated, forwarded,
posted
whole
116 Chapter2.Differentiation:BasicConcepts 3. y =10(3u +1)(15u), ()() 10(31)(15) 10(31)1515(31) 10[(31)(5)(15)(3)] 30020 dy du d uu du dd uuuu dudu uu u =+− =+−+−+ =+−+− =−− 4. 2 400(15)(32)yxx =−− 2 22 2 2 400(15)(32) 400(15)(32)(32)(15) 400(15)(3)(32)(2) 400(9445) dyd xx dxdx dd xxxx dxdx xxx xx =−− =−−+−− =−+−− =−++ 5. 53 53 53 2 42 53 2 11 ()(21) 3 1 (21) 11 3(21)1 1 (56) 411 24 33 3 d fxxxxdxx d xxx xdx xx x xxx x xxx x ′ =−+− +−−+ =−++ +−− =−+++ 6. 3 ()3(525)(2) fxxxxx =−−++ () 32 5/231/2 1/2 1 ()3(525)22(152) 2 10515 12092430 22 fxxxxxx x xxxx x ′ =−−++++− =−−++−− © 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
Chapter2.Differentiation:BasicConcepts 117 7. 1 2, x y x + = 2 2 2 (2)(1)(1)(2) (2) (2)(1)(1)(1) (2) 3 (2) dd dxdx dyxxxx dxx xx x x −+−+− = −−+ = =− 8. 23 54 x y x = + 2 2 2 (54)(23)(23)(54) (54) 2(54)5(23) (54) 23 (54) dd dyxxxx dxdx dxx xx x x +−−−+ = + +−− = + = + 9. 2 (), 2 ftt t = 22 22 2 22 2 22 (2)()(2) () (2) (2)(1)()(2) (2) 2 (2) dd dtdt tttt ft t ttt t t t ′ = = = 10. 1 ()2fx x = 22()(2)(0)1(1)1 (2)(2) fxx xx ′ = = 11. 3 5, y x = + 2 2 2 (5)(3)3(5) (5) (5)(0)3(1) (5) 3 (5) dd dxdx dyxx dxx x x x +−+ = + +− = + =− + © 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
118 Chapter2.Differentiation:BasicConcepts 12. 2 2 1 1 t y t + = 22 2222 (1)(2)(1)(2)4 (1)(1) dyttttt dttt −−+− = = 13. 2 2 ()32, 251 fxxx xx −+ = +− 22 22 22 22 2 22 2 22 2 22 (251)(32) () (251) (32)(251) (251) (251)(23) (251) (32)(45) (251) 11107 (251) d dx d dx xxxx fx xx xxxx xx xxx xx xxx xx xx xx +−−+ ′ = +− −++− +− +−− = +− −++ +− = +− 14. 2 ()(1)(4) 21 xxx gx x ++− = 22 2 32 2 (21)[1(1)(4)(21)](1)(4)(2) () (21) 49611 (21) xxxxxxxx gx x xxx x −−+++−+−++− ′ = −+−− = 15. 2 ()(25)(25)(25) fxxxx =+=++ ()(25)(25) (25)(25) 2(25)(25) 2(25)(5) 2050 10(25) d fxxx dx d xx dx d xx dx x x x ′ =++ +++ =++ =+ =+ =+ 16. 2 2 2 11 ()2 fxxx xx =+=++ 3 2 ()2 fxx x ′ =− © 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
19.
When x =0, y =4and17. dy dx = Theequationofthetangentlineat(0,4)is y +4=17(x 0),or y =17x 4.
20. 2 (31)(2) yxxx =+−−
2 (31)(1)(23)(2) yxxxx ′ =+−−++−
At01 x = ,(3)(1)3 y == and(3)(1)(5)(1)2 y ′ =−+= .Theequationofthetangentlineisthen 32(1)yx−=− or21 yx=+
x y x dy dxx
= + = +
21. 2
23 3 (23)
When x =1, y =1and3. dy dx = Theequationofthetangentlineat(1,1)is
y +1=3(x +1),or y =3x +2.
Chapter2.Differentiation:BasicConcepts 119
tt ++ == ++ ( ) 1/2 1/2 21/2 21/2 2 121/2 2 2 21/251/2 2 21/2 5/23/2 1/22 53 2 (25)() ()(25) () (25) (25)2()(2) (25) 2102 (25)2 42025 2(25) 42025 2(25) d dt d dt t t ttt ttt gt t tttt t tttt tt ttt tt ttt tt ++ −++ ′ = + ++−+ = + +−+ = + +−+ = + +−+ = +
4
hxxx xx =+ −+ 22 2222 22 2222 ()(1)(1)(2)(1)(1)(4)(2) (1)(1) 181 (1)(1) hxxxxxxx xx xxx xx −−+−−− ′ = + −+ =+ −+
17. 221/2 ()2525 tttt gt
18. 22
() 11
(51)(43) 3017 yxx dy x dx =−+ =+
© 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
22. 7 52 x y x + =
2 (52)(1)(7)(2) (52) xx y x −−+− ′ =
At00 x = , 7 5 y = and 2 51419 525 y + ′ ==
Theequationofthetangentlineisthen 719(0) 525 yx−=− or 197 255yx=+
23. () 2 1/22 3(2) (3)(2) yxxx xxx
=+− =+−
23/2 1/2 153 32 2 dy xx dxx =−−++
When x =1, y =4and11 2 dy dx =−
Theequationofthetangentlineat(1,4)is114(1), 2 yx−=−− or 1119 . 22yx=−+
24. 2 ()(1)(87) fxxxx=−−+
fxxxxx xx xx
′ =⋅−++−− =−+ =−−
2 2 ()1(87)(1)(28) 31815 3(1)(5)
()0fx ′ = when x =1and x =5.
2 (1)(11)(1817)0 f =−−⋅+=
2 (5)(51)(5857)32 f =−−⋅+=−
Thetangentlinesat(1,0)and(5,32)arehorizontal.
25. 2 2 2
fxxxx fxxxxx x
()(1)(2) ()(1)(21)(2)(1) 33
=+−− ′ =+−+−− =−
Since() fx ′ representstheslopeofthe tangentlineandtheslopeofahorizontal lineiszero,needtosolve
2 0333(1)(1) xxx =−=+− or x =1,1.
When x =1, f (1)=0andwhen x =1, f (1)=4.So,thetangentlineis horizontalatthepoints(1,0)and (1,4).
120 Chapter2.Differentiation:BasicConcepts
26. 2 2 1 () 1 fxxx xx +− = −+ 22 22 2 22 22 () (21)(1)(1)(21) (1) 24 (1) 2(2) (1) fx xxxxxx xx xx xx xx xx ′ +−+−+−− = −+ −+ = −+ = −+ ()0fx ′ = when x =0and x =2 2 2 (0)0011 001 f +− ==− −+ 2 2 (2)2215 2213 f +− == −+ © 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
Thetangentlinesat(0,1)and 5 2, 3
are horizontal.
=+ =+
31. 2
yx x dyx dxx
3 24 1(24)(0)3(4) (24)
+ = ++ ′ = ++
27. 2 2 22
1 () 1 2 () (1)
fxx xx fxxx xx
Since() fx ′ representstheslopeofthe tangentlineandtheslopeofahorizontal lineiszero,needtosolve 2 22 2
When x =0,2 12 14. (2) dy dx =+=
32. 235yxx=+− 23yx ′ =+
At0,3 xy ′ == sotheslopeofthe
2 0 (1) 02(2)0,2. or
= ++ =−−=−+=−
xx xx xxxxx
When x =0, f (0)=1andwhen x =2, 1 (2). 3 f −=− So,thetangentlineis horizontalatthepoints(0,1)and 1 2,. 3
28. 2 (2)() yxxx =++
21 (2)12 2 dy xxxx dxx
perpendicularlineis 1 3 m =− .The perpendicularlinepassesthroughthe point(0,5)andsohasequation 1 5 3 yx=−−
=+− =+−+−
29. 23 223 (3)(52) (3)(6)(52)(2) yxx dy xxxx dx
When x =1, (13)(6)(52)(2)18. dy dx =+−+−=−
30. 21 35 x y x = + 22 2(35)3(21)13 (35)(35) dyxx dxxx +−− = = ++
At01 x = ,2 1313 864 dy dx ==
33. 11/2 21/2
yxxx x dy dxxx
=−=− =−
2 2 21 2
When x =1, 15 2. 22 dy dx =−−=−
Theslopeofalineperpendiculartothe
tangentlineat x =1is2 5
Theequationofthenormallineat(1,1)is 2 1(1), 5 yx−=− or 23 . 55yx=+
34. ()(3)1 yxx =+− () 1 (3)1 2 yxx x ′ =+−+−
At1,2 xy ′ ==− sotheslopeofthe
perpendicularlineis 1 2 m = .The perpendicularlinepassesthroughthe point(1,0)andsohasequation
11 22yx=−
Chapter2.Differentiation:BasicConcepts 121
=++=
()
=++++
At04 x = , 1 (18)18(6)70.5 4 dy dx
©
is proprietary material
for authorized instructor use. Not authorized for sale or distribution in any
This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
2013 by McGraw-Hill Education. This
solely
manner.
38.
x dyxx
x y = =
When x =1, 2 (23)(5)(57)(3)31. (23) dy dx −−+−
Theslopeofalineperpendiculartothe tangentlineat x =1is 1 . 31
Theequationofthenormallineat (1,12)is112(1), 31 yx+=−− or 1371 3131yx
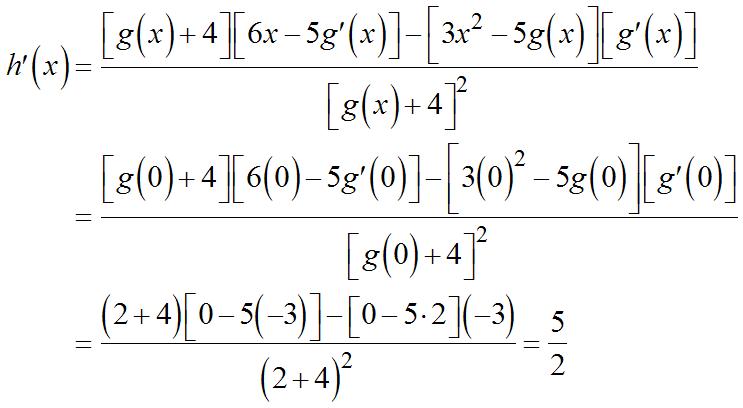
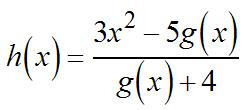
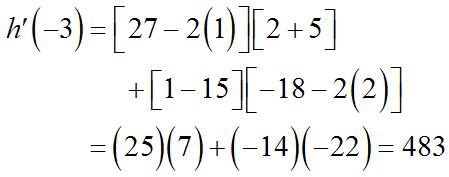
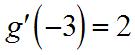
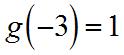
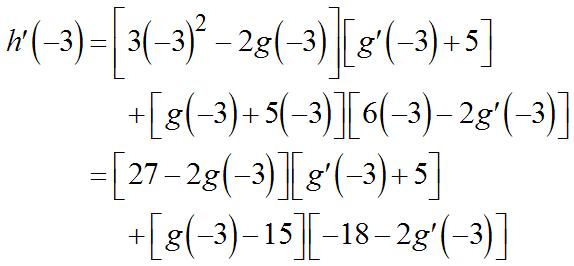
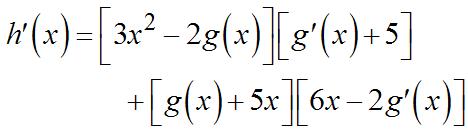
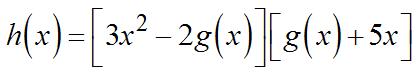
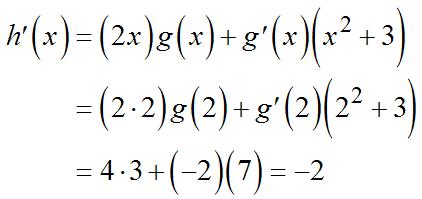
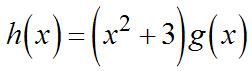
36. 37. Usingtheproductrule,
Sinceand,
122 Chapter2.Differentiation:BasicConcepts
35. 2 dxx
57 23 (23)(5)(57)(3) (23) + = −−+− =
=−−
Substituting x =3,
© 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
Usingthequotientrule,andnotingthatthe derivativeofthenumeratorrequiresthe productrulefortheterm,
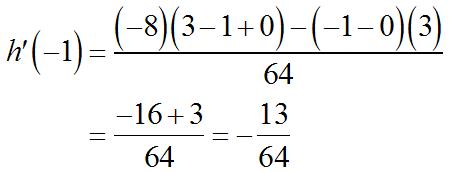
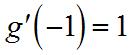
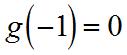
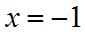
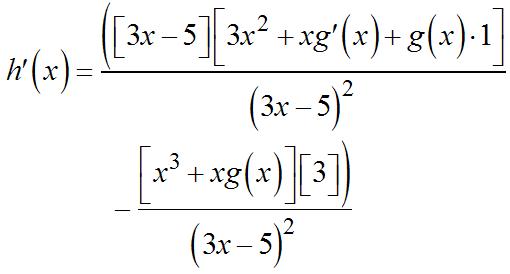
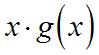
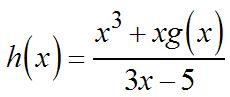
Chapter2.Differentiation:BasicConcepts 123
39.
Substituting, () ()()()()() () ()()() [] () () [] ()() ( () () [] ) () 2 2 3 2 2 2 31531111 1 315 1113 315 8311 1 8 113 8 gg h g gg h g ′ +−−+− ′ −= −+−− ′ −−−+− ′ −= Sinceand, 40. (a) 2 253yxx=−− 45yx ′ =− (b)
=+− (21)(1)(2)(3)45yxxx ′ =++−=− 41. (a) 3 32 6 32 6 4 23 ()(2)(23)(3) 49 49 x y x dyxxx dxx xx x x x = = −+ = −+ = (b) 3 43 4 4 (23)() (23)(3)()(2) 3(23)2 49 yxx dy xxx dx xx x x x =− =−−+ −−+ = −+ = (c) 23 34 34 4 23 49 49 49 yxx dy xx dx xx x x =− =−+ =+ −+ =
105 ()56274 fxxxx =−−+ 94 83 ()503027 ()450120 fxxx fxxx ′ =−− ′′ =− 43.
()4962
()212186 ()82418 fxxxxx fxxxx fxxx =−+−− ′ =−+− ′′ =−+ 44. 2 311 5 32 yx xx =+++ 1/233/251 6 26 dy xxx dx =−− 2 3/245/2 2 3/245/2 51 18 44 5181 44 dy xxx dx xxx =−++ =−++ © 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
(21)(3)yxx
42.
532 42 3 2
5
attherateof (3)15.72 p ′ =− dollarsperthousand calculators.
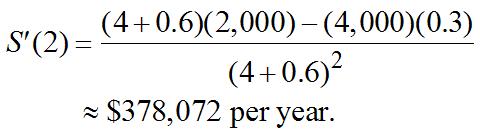
(b) ()() Rxxpx = 222
(3)46.29 R ′ = sorevenueisincreasing attherateof$46.29perthousand
50. (a) Sinceprofitequalsrevenueminuscost andrevenueequalspricetimesthe quantitysold,theprofitfunction P(p)is givenby
Whenthepriceis$12perbottle, (12)1.133 P ′ =− .Theprofitis decreasing.
124 Chapter2.Differentiation:BasicConcepts 45. 11/21/221 22 36 yxxxx =−+− 21/23/2221 2 3212 dy dxy xxx ′ = =−−++ 2 33/25/2 2 33/25/2 421 348 421 348 dy yxxx dx xxx ′′ ==+− =+− 46. 21()2 yxxx x =−− 2 2 2 11 ()2(21)2 641 dy xxxx dxx x xx =−++−− =−− 2 2 124 dy x dx =−
3 (21)(35)yxxx =+−+ 32 32 (21)(3)(35)(32) 1215127 dy dxy xxxx xxx ′ = =+−+++ =+++ 2 2 2363012dy yxx dx ′′ ==++ 48. (a) 2 ()1,000 0.38 px x = + 2 22 22 ()(0.38)(0)1,000(0.6) (0.38) 600 (0.38) xx px x x x +− ′ = + = + whenthelevelofproductionis3,000 (3 x = )calculators,demandischanging
47.
′′=+ = + ++ −+ =
2 22 ()()()(1) 6001,000 (0.38)0.38 3008,000 (0.38) Rxxpxpx x x xx x x
+
t = +
2 ()(40.3)(2000)(2000)(0.3) (40.3) tt St t +− ′ = + Therateofchangeintheyear2010is
Rewritethefunctionas 4 2,000 (). 0.3 t St = + Since40 t → as t → +∞,salesapproach 2,0006,666.67
calculators. 49. ()200040.3 t St
(a)
(b)
0.3 thousand, ≈ or approximately$6,666,667inthelong run.
2 ()()() 500(0.23200) 3 PppBpCp p pp p =− =−++ + (b) 2 2
(3) 1500 0.43 (3) Ppppp p p p +− ′ = + =−− +
()(3)500500(1)0.43
© 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
51. 2 2 ()10055 1030 tt Pt tt
++ = ++ (a)
2 2 22
ttt ttt Pt tt
(1030)(25) ()100(55)(210) (1030)
+++ −+++ ′ = ++
Therateofchangeafter5weeksis
(255030)(105) (5)100(25255)(1010) (255030) P
2
+++ −+++ ′ = ++ (5)4.31%perweek. P ′ =
Since(5) P ′ ispositive,thepercentage isincreasing.
(b) Rewritethefunctionas
Substitutethisintothesecondequation toget Then, Currently,when x =0, or$17.50perunit
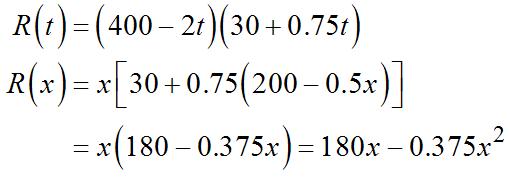
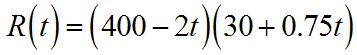
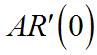
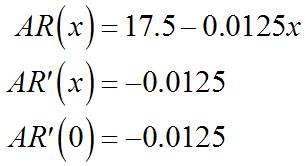
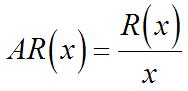
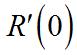
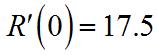
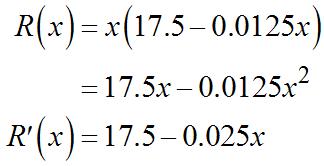
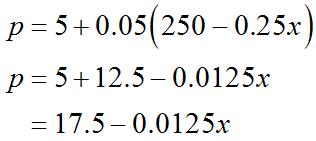
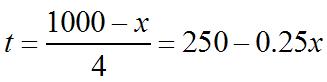
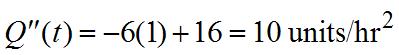
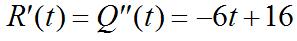
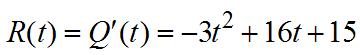
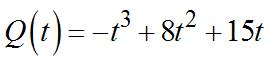
53. (a)
1 ()100. 1 tt tt pt ++ = ++
55 1030
2
Sinceispositive,therevenueis currentlyincreasing.
2
Since25510 ,, tt t and230 t allgotozero as t → +∞,thepercentageapproaches 100%inthelongrun,sotherateof changeapproaches0.
52. (a) (b) Therateofchangeoftheworker’srateis thesecondderivative
(b)
At9:00a.m., t =1and
Revenue=(#units)(sellingprice)
x =#units=10004t,where t is measuredinweeks p =sellingprice=5+0.05t
So,
Tofind R(x),solvethefirstequationfor t
54. (a)
Sinceisnegative,theaverage revenueiscurrentlydecreasing.
Since x isthelevelofproductionattime t, x =400–2t or t =200–0.5x and
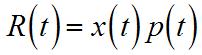
Chapter2.Differentiation:BasicConcepts 125
©
for
2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized
sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
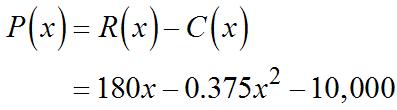
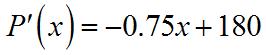
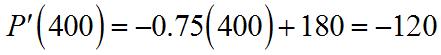
126 Chapter2.Differentiation:BasicConcepts
C(x)=10,000.Therefore, and When t =0, x =400 and Sotheprofitisdecreasingattherateof $120/unit.
Theaverageprofitwillbedecreasingat therateofabout0.31dollarsperunit perunit. 55. 1/2 22()100100 0.0390.039 xx Px xx == ++ (a) ()21/2 1 2 1/2 22 (0.039) (()(0.06) )100 (0.039) xx xx Px x + ′ = + Therateofchangeofpercentagepollutionwhen16milliondollarsarespentis 21/2 1 2 22 1/2 22 (16) [0.03(16)9](16) 100 [0.03(16)9] (16)[0.06(16)] [0.03(16)9] 0.63 P ′ + = + + =− percent Since(16) P ′ isnegative,thepercentageisdecreasing. (b) ()0Px ′ = when 21/2 1/2 1 0(0.039)2 ()(0.06) xx xx =+ or x =10milliondollars. Testingonevaluelessthan10andonevaluegreaterthan10shows() Px ′ isincreasingwhen0 < x <10,anddecreasingwhen x >10. © 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
Weknow
(b)
Chapter2.Differentiation:BasicConcepts 127 56. (a) 2 ()2410 1 t Pt t + = + 2 22 2 22 22 ()(1)(24)(2410)(2) (1) 242024 (1) 4(23)(32) (1) ttt Pt t tt t tt t +−+ ′ = + −−+ = + −+− = + (1)5 P ′ =− sothepopulationisdecreasingat1 t = . (b) Thepopulationrateofchangeis0at 2 3 t = ,positivefor 2 3 t < andnegativefor 2 3 t > .The populationbeginstodeclineafter 2 3 t = or40minutesaftertheintroductionofthetoxin. 57. 123 3()FKMM =− (a) 2 2 1 3(23) 2 3 dF S dM KMM KMM = =− =− (b) 12 (26)2 33 dS KMKM dM =−=− istheratethesensitivityischanging. 58. (a) 2 2 () 316 t Ct t = + 22 2222()()(316)22(6)326 (316)(316) tttt RtCt tt +−− ′ == = ++ R(t)ischangingattherate 22222 2423 ()(316)(12)(326)(2)(316)(6)36(16) (316)(316) ttttttt Rt tt +−−−+ ′ = = ++ (b) (1)26361 C ′ = ,theconcentrationisincreasingatthistime. (c) R(t)ispositiveandtheconcentrationisincreasinguntil()0 Rt = orwhen23260 t −= .This occurswhen42.3 3 t =≈ hours(ignoringthenegativesolution.)Theconcentrationbeginsto declineafterroughly2.3hours. © 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
(d) Theconcentrationischangingatadecliningratewhen
orwhen236(16)0 tt −< (assuming0 t > ).Thisoccurswhen04 t <<
59. ()2061Pt t =− +
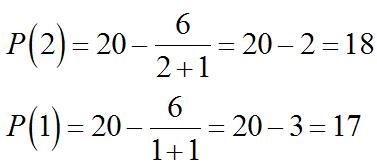
(a)
(b) orincreasingatarateof1,500peopleperyear
(c) Actualchange= P(2)– P(1)
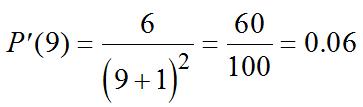
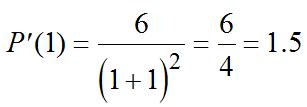
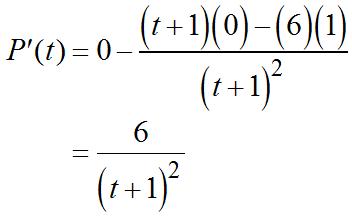
So,thepopulationwillactuallyincreaseby1thousandpeople.
(d) orincreasingatarateof60peopleperyear
(e) Inthelongrun, 2 6 lim()lim0 (1) tt Pt t →∞→∞ ′ = = +
So,thepopulationgrowthapproacheszero.
60. (a) () m Ax px Bx = +
128 Chapter2.Differentiation:BasicConcepts
2 23 ()36(16)0 (316) tt
t
+
Rt
′ = <
1 2 2 ()()()()() () ((1)) () mm m m m BxAAxmx px Bx ABmx Bx +− ′ = + +− = + © 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
AmxmxBm px Bx
−−+
′′ = + ()0px ′′ = when(1) 1 m Bm x m + =
61. (a) 53 ()357 sttt=−− 4242 ()151515() vttttt =−=−
32 ()15(42)30(21) attttt=−=−
(b) a(t)=0when230(21)0, tt −= or t =0and2.
2 t =
62. (a) 43 ()253 stttt=−+−
)=0when6
(b) ()0at = when4 t = 65. 5 ()105 1 Dtt t =+− +
=
5 4
© 2013 by McGraw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.
Chapter2.Differentiation:BasicConcepts 129
(b) 1 3 (1)(1) () ()
mm m
32 ()()8151 vtsttt ′ ==−+ 2 ()()()2430 6(45) atvtsttt tt ′′′ ===− =−
a(t
t +14=0,or 7 3 t =
(b) ()0at = at0 t = and
t
63. 32 ()72 stttt=−+++ (a) 2 ()3141 ()614 vttt att =−++ =−+
(b)
64. (a) 5/22 ()4153 stttt=−+− 3/2 1/2 ()()10301 ()()()1530
vtsttt atvtstt
′ ==−+ ′′′ ===−