Parametric Software Portfolio_DA_BNCA_2019

PARAMETRIC SOFTWARES

Anahita Ghatage

F.Y. Digital Architecture , B.N.C.A

Tutors : Ripple Patel | Mugdha Gandhi

01 Modelling

1.1 Furniture Design

1.2 Lofted Geomteries

1.3 High Rise Structures

1.4 Coal Drops Yard

1.5 Serpentine Sackler Gallery

02 Geometry

2.1 Parametric Star

2.2 Rotating Panels

2.3 Wall Panel

2.4 Parametric Louvers

2.5 Rotating Cylinders

2.6 Fractals - Koch Snowflake

2.7 Mathematical Surfaces

2.8 Recreating Felix Candela’s Shell Structures

03 Manipulation &Transformation

3.1 Single and Multiple Attractor Points

3.2 Attractor Curves

3.3 SDU Facade

About the Author

Anahita Ghatage

Architect | Designer

Student of Digital Architecture

Abstract

Department of Digital Architecture Semester 1_2019-20

This book shall contain basic exercises in Rhino and Grasshopper as an Introduction to 3d modelling and parametric design. The final chapter about the Natural Phenomenon shall speak about logic based diagrams of The Glass Sponge and a few exercises that could be explored based on this logic.

3.4 Hybrid Facade

04 Natural Phenomenon

4.1 Anatomy of the Hexactinellid Deep Sea Sponge

4.2 Structural & Component Logic

4.3 Relationship Between Components

4.4 Exploring Exoskeletons- WeaverBird

4.5 Exploring Mesh and Weave

Chapter 01: Modelling

Creating a Grid according to Anthropometry and Ergonomics

RHINO FURNITURE DESIGN

The Chair has been designed using CURVES FROM TWO VIEWS. This allows us to achieve this type of geometry.

Creating two Curves for the Front and Side Using CURVE FROM TWO VIEWS to achieve the desired item

Creating the Chair using Loft (Selecting curves to create loft)

LOFTED GEOMETRIES

1. Lofted Geometries from 2 curves

2. Lofted Geometries from 3 curves

3. Lofted Geometries from 4 curves

Create Base Curve

Create Secondary Curves for Contours

Create Secondary Curves for Loft & Contours

Process Steps Involved in Modelling the Coal Drops Yard

SERPENTINE SACKLER GALLERY PARK

Process Steps Involved

in Modelling of the Column of Serpentine Sackler Gallery Park

Chapter 02: Geometry

PARAMETRIC STAR

GRASSHOPPER BASICS

Grasshopper is a visual programming language and environment developed by David Rutten at Robert McNeel & Associates, that runs within the Rhinoceros 3D computer-aided design (CAD) application. Programs are created by dragging components onto a canvas.

1. Create Circle

2. Divide Curve

3. Select Alternate Points (Dispatch)

4. Move Selected Points (Vector and Amplitude)

5. Weave

Achieve Different Number of Divisions by Changing Number Slider

Achieve Larger/ Smaller Geometry by Changing Radius of Circle

Use Custom Preview Apply Colour Swatch

RotaTING Panels

Create Rectangle Offset and Range

Rotate 3D

WALL PANEL

Create Subdivisions Divide Domain2 Isotrim

Create Thickness Offset Curve Loft Extrude

Extract Centroid and Extrude Point

Create Loft from 2 Curves

PARAMETRIC LOUVERS

Create Rectangle Contour

Divide Curve

Create Curve Closest Point for Attractor

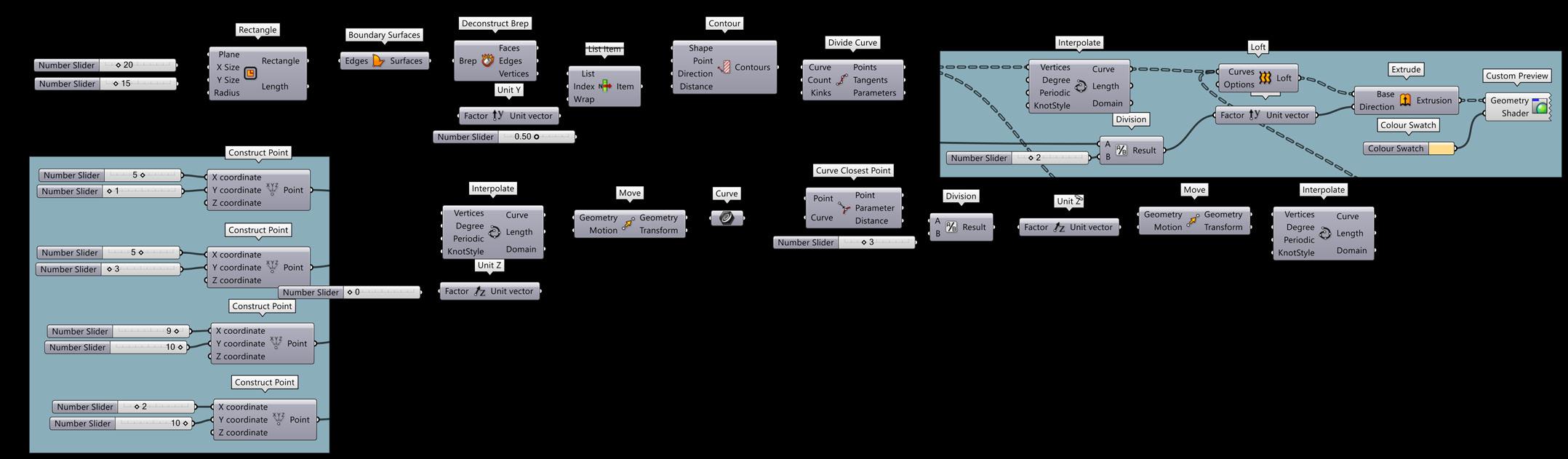
Loft

Create Extrusion

ROTATED CYLINDERS

Create Curve

Perpendicular Frames

Line SDL and Pipe Rotate

FRACTALS THE KOCH SNOWFLAKE

In mathematics, a fractal is a subset of a Euclidean space for which the Hausdorff dimension strictly exceeds the topological dimension. Fractals exhibit similar patterns at increasingly small scales called self similarity, also known as expanding symmetry or unfolding symmetry. Fractal geometry lies within the mathematical branch of topology.

The feature of “self-similarity”, for instance, is easily understood by analogy to zooming in with a lens or other device that zooms in on digital images to uncover finer, previously invisible, new structure. If this is done on fractals, however, no new detail appears; nothing changes and the same pattern repeats over and over, or for some fractals, nearly the same pattern reappears over and over.

The Koch snowflake (also known as the Koch curve, Koch star, or Koch island) is a mathematical curve and one of the earliest fractals to have been described. It is based on the Koch curve, which appeared in a 1904 paper titled “On a Continuous Curve Without Tangents, Constructible from Elementary Geometry” by the Swedish mathematician Helge von Koch.

1. Polygon 2. 3 Segments (Triangle)

3. Divide Segments 4. Perpendicular Frame

5. Deconstruct Plane & Move

6. Join Curves 7. Anemone (Fast Loop Start/End)

Growth Logic at Iteration 01

Equilateral Triangles with each angle as 60 degrees

Image Source: Internet

Growth Logic at Iteration 02

MATHEMATICAL SURFACES

Growth Logic at Iteration 03

Growth Logic at Iteration 04

Reference for Definition: Parametric3d

Source: Internet

In mathematics, a minimal surface is a surface that locally minimizes its area. This is equivalent to having zero mean curvature (see definitions below).

The term “minimal surface” is used because these surfaces originally arose as surfaces that minimized total surface area subject to some constraint. Physical models of area-minimizing minimal surfaces can be made by dipping a wire frame into a soap solution, forming a

soap film, which is a minimal surface whose boundary is the wire frame. However, the term is used for more general surfaces that may self-intersect or do not have constraints.

For a given constraint there may also exist several minimal surfaces with different areas the standard definitions only relate to a local optimum, not a global optimum.

Demonstration of Growth Logic around Base Geometry

Cartesian Coordinate System

Polar/Spherical Coordinate System

Grasshopper Definition

SPIRAL

Mathematical Expression Used For Spiral: (sinh(v)*cos(3*u))/(1+cosh(u)*cosh(v)) (cosh(v)*sinh(u))/(1+cosh(u)*cosh(v)) (sinh(v)*sin(3*u))/(1+cosh(u)*cosh(v))

Domain : -pi to pi

Sine curve

Mathematical Expression Used For Sine Curve: Pi*x sin(u)*(-2+v*sin(u/2)) cos(u)*(-2+v*sin(u/2)) v*(cos(u/2))

TWISTED SPHERE HELICOIDAL

Mathematical Expression Used For Twisted Sphere:

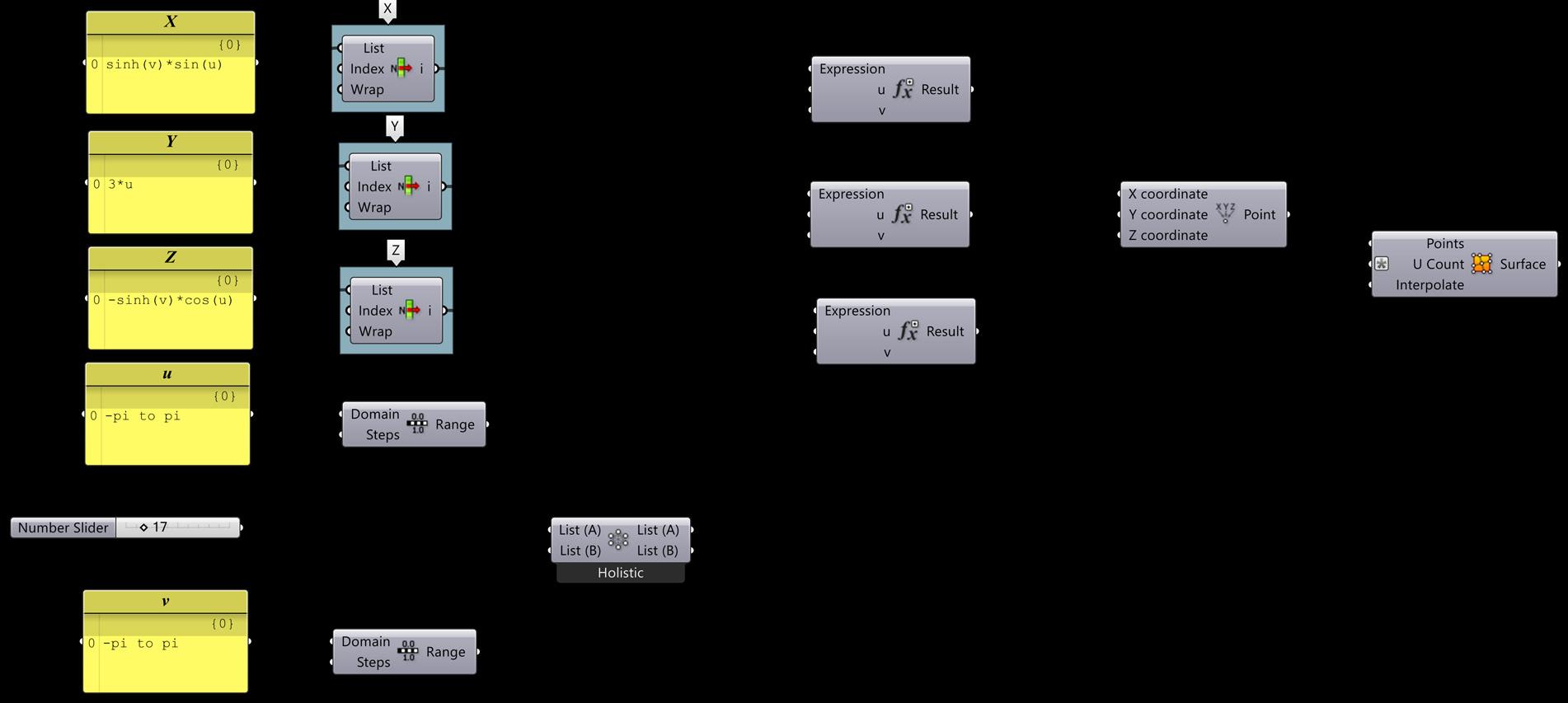
x = a cos(u) cos(v)

y = a sin(v) + b u

z = a sin(u) cos(v)

Domain: -pi to pi

Mathematical Expression Used For Helicoidal: sinh(v)*sin(u)

3*u

-sinh(v)*cos(u)

Domain: -pi to pi

SHELLS

RECREATING FELIX CANDELA’S SHELLS

With the design for Los Manantiales, Felix Candela’s experimental form finding gave rise to an efficient, elegant, and enduring work of structural art. Comprised of four intersecting hypars, a strikingly thin roof surface creates a dramatic dining space. Built as Candela was establishing an international reputation as the foremost shell building, he demonstrated to the world his masterful combination of artistry and techni-

cal virtuoso. Los Manantiales was created as Candela’s mastery thin-shell concrete construction was solidifying. Initially conceived for another client on a different site, the structure found realization as a replacement for a wooden restaurant alongside a floating gardens filled canal in the Xochimilco area of Mexico City.

Image Source: Internet

Grasshopper Definition

Los Manantiales / Felix Candela

Recreating Felix Candela’s SHELL STRUCTURES

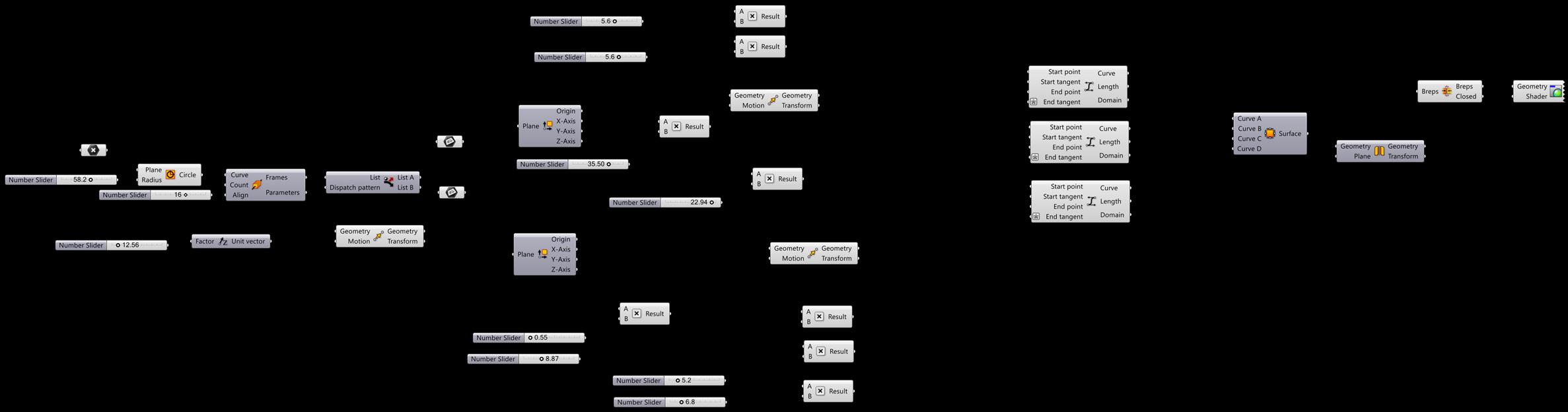
Geometry 01

Base Geometry with Expression: (y2/a2)-(x2/b2)

Geometry 02

Base Geometry with Expression: a(x*y)/b

Geometry 03

Geometry 04

Geometry 05

Base Geometry Derivation Logic

Achieved Shell Geometry

Base Geometry Derivation Logic

Achieved Shell Geometry

Base Geometry Derivation Logic

Achieved Shell Geometry

Base Geometry Derivation Logic

Achieved Shell Geometry

Base Geometry Derivation Logic

Achieved Shell Geometry

Base Geometry Derivation Logic

Achieved Shell Geometry

Base Geometry Derivation Logic

Achieved Shell Geometry

Base Geometry Derivation Logic

Achieved Shell Geometry

Chapter 03: Manipulation and Transformation

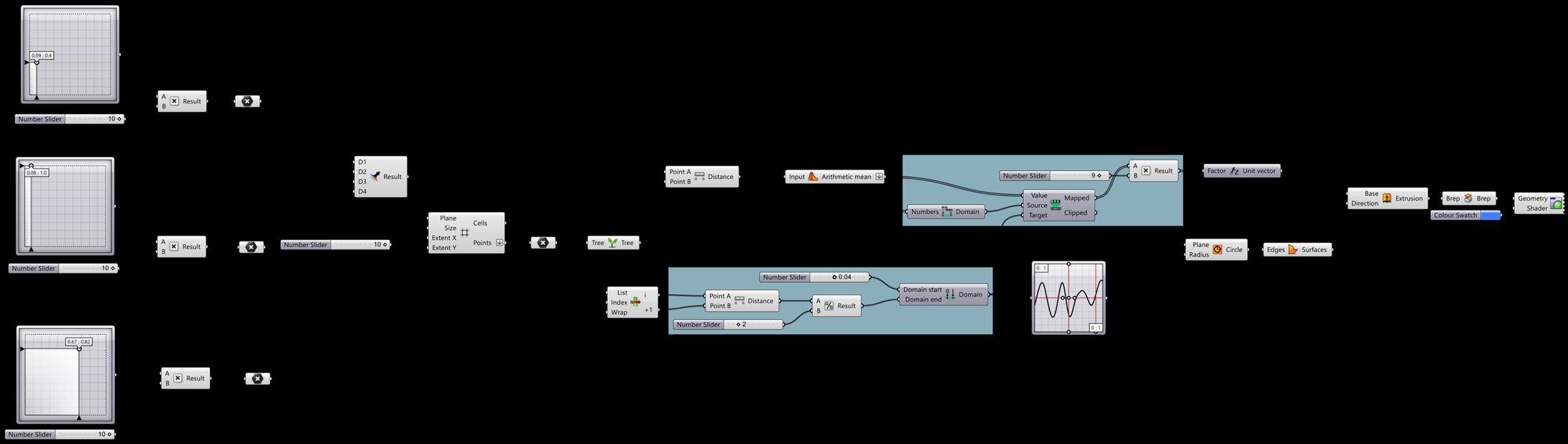
Single Attractor Point

Grasshopper Definition

GRASSHOPPER

ATTRACTORS

Attractors are points that act like virtual magnets - either attracting or repelling other objects. In Grasshopper, any geometry referenced from Rhino or created within Grasshopper can be used as an attractor. Attractors can influence any number of parameters of surrounding objects including scale, rotation, color, and position. These parameters are changed based on their relationship to the attractor geometry.

Multiple Attractor Points

Grasshopper Definition

Attractor CURVE

FACADE

EXPLORING RESPONSIVE FACADE SYSTEMS

Grasshopper Definition

Grid of Cylinders Introduce an Attractor Curve

Resizing of cylinders based on Attractor Curve by Domain

Create Rectangular Surface Divide Domain2 Isotrim to get Facade Segments

Surface Split (Splits Surface into Fragments to Create a Pattern) Dispatch Cull Pattern

SDU FACADE

Henning Larsen Architects aimed to set a benchmark for green design with the Southern Denmark University building in Kolding, Denmark, featuring a climate-responsive kinetic facade and a triangular form

Rotational Logic Remap Numbers Rotate

Grasshopper Definition

Generate Surface Rectangle

FACADE

The research conceives sunscreens as performing a hybrid role: performing environmentally as a shade and glare modulator; while also enabling the façade to operate as a low resolution media screen that can generate income.

Current state of research: A prototype consisting of physical mock-ups and software has been developed and calibrated with simulations to provide an interactive proof of concept.

Step 01

Hybrid Responsive FACADE

Next stage that requires funding: The research will shift to the design and fabrication of a solar powered autonomous panel, and research and testing of low maintenance actuators.

Divide Domain2 and Isotrim (Control U and V values) Create Cull Pattern

Deconstruct Brep and Extract Centroids

Facade Derivation Logic

Polygon From Centroid Boundary Surfaces (Control Radius)

Rotate Module (Using Remap Numbers)

Deconstruct Brep and Extract Vertices

Create Axis of Rotation for each Module from Line SDL using Polygon Centroid

Extrude and Extact Points to Move for Module

Single Module of the Hybrid Facade

Create Hexagonal Grid

Deconstruct and Scale Each Cell

Create Face Each Cell Using Scale NU (Scale Non-Uniform)

Reworking Using HEXGRID

Simplified Grasshopper Definition

Chapter 04: Natural Phenomenon

Anatomy of the GLASS SPONGE

Top Cylinder

Diameter

Bottom cylinder diameter

20-30 cm

GLASS SPONGE

Glass sponges are exclusively marine sponges with mineral skeletons composed of silica (glass) spicules. They have a worldwide distribution but are mainly restricted to deeper waters (200 to > 6000 m) where they grow attached to hard or soft substrates..

Hexactinellid SEA SPONGE

The complex and mechanically robust cage like skeletal system of hexantinellid sponge has proved to be particularly useful model system for investigating structure- function relationships in hierarchically ordered biological components.

Vertical Struts: 36 Horizontal Struts: 70 (Appx

Barbs

1. Anchor Spicules

Lower end of cylinder

Upper end of cylinder

2. Cylindrical cage

3-5 cm

2-3 cm

1:2)

3. Sieve Plate

Structural logic

Quadrate Lattice

Horizontal + Vertical Bundles

Diagonal Bundles Ridge Formation

Fixed node Free node Verticals towards exterior, Horizontals towards interior

Lattice at lower end of cylinder more dense, less porus, overlap = x

Lattice at upper end of cylinder less dense, more porous, overlap = x/2

Relationship between COMPONENTS

Skeleton

Skeletal Walls

Spicule Network

Constituent Spicules

Organic and Inorganic Composites

Inorganic and Organic Components

Cylinderical Skeletal Lattice

Anchoring Apparatus Cap Spiral Ridges Tapered Tube

Partially Ordered Network of Bundled Spicules Diagonally Ordered Spicule Bundles

Vertically and Horizontally Ordered Bundles

Underlying Square Grid of Cruciform Spicules

Basilia (Anchor Spicules)

Other Diactine, Tetractine and Hexactine Spicules Non-Planar Cruciform Spicules

Laminated Cement Laminated Spicules

Consolidated Silica Nanoparticles

Organic Interlayers

Axial Protien Filament

A : External Ridge system and terminal sieve plates

B : Underlying Siliceous cylinderical skeletal lattice.

C : Square grid and ordering of the vertical and horizontal components of the skeletal system

Reference: <Science Direct, Hierarchical assembly of the siliceous skeletal lattice of the hexactinellid sponge

Euplectella aspergillum> Journal of Structural Biology 158 (2007) 93–106

Workshop: AAVS, Biomorph_2016

Reference for Definition: OM.egvo

Create Ellipse Series

Rotate the Ellipse

Loft Mesh Surface Mesh Machine

Creating the Exoskeleton using Weaverbird Components

Reference for Definition: OM.egvo

Create Circle

Perpendicular Frames

Rotate

Create Polygons

Create Closed Loft Mesh Surface

Explode Mesh

Extract Centroid

Remap

Join Meshes and Weld

Grasshopper Definition

Create 2 Circles Use Perpendicular Frames

Evaluate Curve to find Points Interpolate to Join

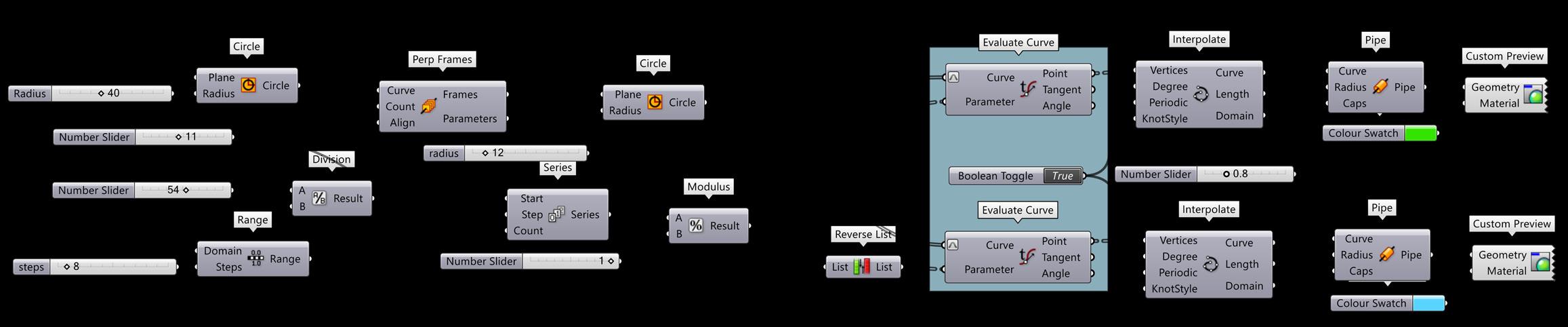
Alter Radius Number Slider to change Geometry

Reference for Definition: Parametric House

Grasshopper Definition

Reference for Definition: Parametric House

Grasshopper Definition

PARAMETRIC SOFTWARES

ANAHITA GHATAGE

anahitaghatage29@gmail.com

DA1905

TUTORS: RIPPLE PATEL | MUGDHA GANDHI