SSM CA Spanish Third Grade Sample

GRADO 3

CALIFORNIA

Muestra de la edición para el maestro

Muestra de la edición para maestros Grado 3

Publicado por Accelerate Learning Inc., 5177 Richmond Ave, Suite 800, Houston, TX 77056. Copyright © 2025, Accelerate Learning Inc. Todos los derechos reservados. Ninguna parte de esta publicación podrá ser reproducida o distribuida en ninguna forma ni por ningún medio, ni almacenada en una base de datos o sistema de recuperación, sin el consentimiento previo por escrito de Accelerate Learning Inc., incluyendo, entre otros, en cualquier red u otro sistema de almacenamiento o transmisión electrónica, o difusión para educación a distancia.

Para obtener más información, visítenos en www.stemscopes.com.

MODELOS DE MULTIPLICACIÓN

ESTÁNDARES CLAVE

Representar y resolver problemas que impliquen multiplicación y división.

• Interpretar productos de números enteros, por ej., interpretar 5 × 7 como el número total de objetos en 5 grupos de 7 objetos cada uno. Por ej., describir un contexto en el que un número total de objetos pueda expresarse como 5 × 7. Por ej., describir un contexto en el que un número total de objetos pueda expresarse como 5 × 7.

ACTIVIDADES DE PARTICIPACIÓN

ACCESO A CONOCIMIENTOS PREVIOS

Los estudiantes explorarán la adición a través de matrices para profundizar su comprensión de los conceptos matemáticos.

• Utilizarán la adición para determinar el número total de objetos en matrices con hasta cinco filas y columnas.

• Escribirán ecuaciones para expresar el total como una suma de sumandos iguales.

• A través de la conversación, los estudiantes evaluarán diferentes oraciones de multiplicación y justificarán su razonamiento.

• La actividad incluye oportunidades para el aprendizaje colaborativo y aborda las lagunas en el conocimiento previo si es necesario.

CAPTAR INTERÉS: RECUERDITOS DE FIESTA

Los estudiantes usan la multiplicación para determinar el número total de recuerditos disponibles para una fiesta de cumpleaños. Se presenta a los estudiantes una situación en la que hay regalitos y se les anima a identificar conceptos matemáticos dentro del contexto.

• Trabajan en grupos para calcular el número total de cada tipo de recuerditos de fiesta a partir de la multiplicación. Se basan en el número de artículos por bolsa y en el número de bolsas.

• Los estudiantes comparten sus métodos y soluciones con la clase, planteando diferentes estrategias para encontrar los totales.

• Como ampliación, los estudiantes calculan cuántas bolsas se necesitan para dar un recuerdito de fiesta de cada tipo para 30 niños.

ACTIVIDADES DE EXPLORAR

EXPLORACIÓN 1: GRUPOS IGUALES

Los estudiantes exploran el concepto de multiplicación a través de la práctica con grupos iguales.

• Trabajan en grupos para representar escenarios de multiplicación usando contadores y platos de papel en varias estaciones.

• Escriben oraciones de multiplicación para representar los grupos iguales e identificar factores y productos.

• Rotan a través de las estaciones, resolviendo problemas y creando escenarios del mundo real para expresiones dadas.

• La lección concluye con una charla matemática para discutir observaciones y reforzar la comprensión de los conceptos de multiplicación.

EXPLORACIÓN 2: COMPRENDER LA MULTIPLICACIÓN CON MATRICES

Los estudiantes exploran la multiplicación a través del uso de matrices para determinar el número total de objetos en un escenario dado.

• Trabajan en grupos para organizar fichas de colores en matrices según las instrucciones de las «tarjetas de exhibidores».

• Cada grupo registra sus hallazgos dibujando modelos de matrices y escribiendo las ecuaciones de multiplicación correspondientes en sus diarios del estudiante.

• La actividad incluye preguntas guiadas para ayudar a los estudiantes a comprender la relación entre filas, columnas y multiplicación.

• Los estudiantes concluyen discutiendo sus estrategias y completando un boleto de salida para evaluar su comprensión.

EXPLORACIÓN 3: MULTIPLICACIÓN CON DIAGRAMAS DE CINTAS

Los estudiantes exploran conceptos de multiplicación utilizando diagramas de cinta para interpretar productos de números enteros.

• Trabajan en parejas para representar escenarios de multiplicación con cubos de enlace y diagramas de cinta.

• Crean y analizan diagramas de cinta para representar problemas de multiplicación, registrando sus hallazgos en los diarios del estudiante.

• La actividad fomenta el debate y la colaboración, con los estudiantes quienes comparten estrategias y observaciones.

• Se utiliza un boleto de salida para evaluar la comprensión de los estudiantes de los conceptos de multiplicación explorados.

EXPLORACIÓN 4: RECTAS NUMÉRICAS Y CONTAR SALTEADO

Los estudiantes exploran la multiplicación con un enfoque colaborativo y práctico a partir de rectas numéricas y múltiplos.

• Trabajan en grupos para simular el embalaje para un viaje de campamento; usan rectas numéricas para resolver problemas de multiplicación.

• Usan varas de medir como rectas numéricas para saltar cuentas y encontrar totales; registran sus hallazgos en los diarios del estudiante.

• La actividad anima a compartir estrategias y observaciones, fomentando una comprensión más profunda de los conceptos de multiplicación.

• Se utiliza un boleto de salida para evaluar la comprensión del material por parte de los estudiantes, y se proporcionan apoyos adicionales para diversas necesidades de aprendizaje.

ALCANCE: IDEAS FUNDAMENTALES

FLEXIBILIDAD NUMÉRICA

HASTA EL 100 CON LAS CUATRO OPERACIONES

USO DE STEMSCOPES MATH

RECURSOS PARA MAESTROS

El alcance y la secuencia sugeridos para cada grado se basan en un calendario escolar de 180 días. La progresión natural de las matemáticas fue el factor más importante a la hora de determinar el orden de los alcances. ¿Tiene su propio alcance y secuencia? No hay problema. Enseñe los alcances en cualquier orden para satisfacer las necesidades de los estudiantes en su aula. Las únicas actividades afectadas son la «Revisión en espiral» y las «Evaluaciones de referencia».

¡Encuentre el alcance y la secuencia en la sección «Recursos del maestro» de su nivel de grado!

CONCEPTOS CLAVE

• Puedo interpretar la multiplicación como el número total de objetos en grupos iguales.

• Puedo encontrar los productos de números con imágenes, objetos, palabras, números y ecuaciones.

• Puedo describir un contexto para objetos expresados como una expresión de multiplicación.

• Puedo usar las palabras producto y factor para describir la multiplicación.

Los estudiantes desarrollan el sentido numérico utilizando matrices, diagramas de cinta y rectas numéricas para representar la multiplicación. Estas estrategias les ayudan a ver la estructura de la multiplicación y a adquirir soltura con las operaciones de menos de 100. Al explorar patrones en la multiplicación y establecer conexiones entre modelos, los estudiantes refuerzan su capacidad de razonar de forma flexible con los números.

PREGUNTAS FUNDAMENTALES

• ¿Qué estrategias y modelos puedo usar para representar la multiplicación?

• ¿Cómo se relacionan los grupos de igual tamaño con la multiplicación?

• ¿Qué contexto podría usar para describir una expresión de multiplicación?

• ¿Qué palabras puedo usar para explicar las partes dentro de un problema de multiplicación?

INICIO: CALENDARIO SUGERIDO

PLANIFICACIÓN

Internalización de la lección

Alcance

• Revise los estándares abordados en el alcance.

• Familiarícese con la forma en que se evalúan los estándares y lo que demuestra el dominio de la materia.

• Revise el documento «Secuencia de aprendizaje» que se encuentra en el elemento «Visión general del alcance» para comprender la secuencia de los conceptos.

• Determine qué recursos se utilizarán para la práctica y la evaluación.

Lección

• Revise las instrucciones para el maestro y los documentos asociados.

• Familiarícese con los modelos, herramientas y estrategias que se usarán en la actividad.

• Considere el propósito de la lección dentro del alcance e identifique lo que los estudiantes deben saber y ser capaces de hacer como resultado.

DÍA 1

Se presenta a los estudiantes una actividad en la que determinan una cantidad total en grupos iguales utilizando modelos de multiplicación. Volverán a realizar la actividad después de haber completado las exploraciones correspondientes.

Los estudiantes expresan opiniones, ideas y sentimientos sobre un problema utilizando frases como «yo noto . . .» y «me pregunto si . . .»

• Enunciado diario de aritmética

• Ciencia de datos

• Identifique las áreas en las que los estudiantes pueden necesitar apoyo o enriquecimiento y planifique cómo responder.

Contenido de apoyo

Contenido desglosado

Visión general del alcance

Manipulativos/materiales

Exploración 1

• 50 fichas de dos colores (por grupo)

• 10 platos pequeños de papel (por grupo)

Exploración 2

• 60 fichas de colores (por grupo)

Exploración 3

• 10 cubos conectables (por pareja)

DÍA 2

Los estudiantes determinan el número total de objetos en un escenario utilizando modelos y ecuaciones.

Exploración 4

• 1 regla de 1 metro (por grupo)

• 1 rollo de cinta de embalar (por grupo)

• 1 sobre de manila (por grupo)

Acceso a conocimientos previos (~15 minutos)

• Completar la semana anterior a este alcance.

Carta para llevar a casa

• Imprima y envíe a casa la semana anterior a este alcance.

• Captar interés (parte 1): Exploración previa

Práctica independiente (del alcance o nivel de grado anterior)

• Constructor de fluidez

Práctica interactiva

Práctica guiada

• Constructor de bases fundamentales

• Conversaciones estructuradas

• Preguntas de facilitación

Los estudiantes utilizan pistas contextuales y ayudas visuales para comprender el lenguaje desconocido usado durante las interacciones y la enseñanza en clase.

• Enunciado diario de aritmética

• Ciencia de datos

DÍA 3

Los estudiantes determinan el número total de objetos en un escenario utilizando grupos iguales.

DÍA 4

Los estudiantes determinan el número total de objetos en un escenario utilizando matrices.

Los estudiantes utilizan tanto el inglés formal como el informal para comunicar su comprensión.

• Enunciado diario de aritmética

• Ciencia de datos

• Habilidades básicas: Use cuentos de problemas escritospara representar la multiplicación

• Comience la «Exploración 1: Grupos iguales»

Práctica independiente

• Refiérase a la sección de «Práctica».

Práctica guiada

• Refiérase a la sección de «Práctica».

• Lista de verificación de la observación

• Preguntas de facilitación

• Folleto del estudiante sobre habilidades básicas

• Continúe la «Exploración 1: Grupos iguales»

• Charla de matemáticas

• Esquema de anclaje: Exploración 1

Práctica independiente

• Refiérase a la sección de «Práctica».

Práctica guiada

• Refiérase a la sección de «Práctica».

• Exploración 1: Boleto de salida

• Muestra lo que sabes (parte 1)

• Lista de verificación de observación

• Preguntas de facilitación

Los estudiantes conectan el vocabulario nuevo con sus experiencias y discusiones informales para mejorar su comprensión.

• Enunciado diario de aritmética

• Ciencia de datos

• Exploración 2: Comprender la multiplicación con matrices

• Charla de matemáticas

• Esquema de anclaje: Exploración 2

Práctica independiente

• Refiérase a la sección de «Práctica».

Práctica guiada

• Parte II: Intervención en grupos pequeños

• Exploración 2: Boleto de salida

• Muestra lo que sabes (parte 2)

• Lista de verificación de observación

• Preguntas de facilitación

INICIO: CALENDARIO SUGERIDO

PRÁCTICA

Práctica independiente

Todos los estudiantes

• Fluidez en los hechos matemáticos: Suma y resta (15-30 minutos)

• Fluidez en los hechos matemáticos: Multiplicación y división (15-30 minutos)

• Explicar: Vocabulario ilustrado (15-30 minutos)

• Explicar: Mis pensamientos de matemáticas (15-30 minutos)

• Elaborar: Conexiones profesionales (15-30 minutos)

• Elaborar: Revisión en espiral (15-30 minutos)

Los que dominan

• Aceleración: Matemáticas de hoy (15-30 minutos)

• Aceleración: Crea el tuyo (30-45 minutos)

• Aceleración: Tablero de opciones (15-30 minutos)

DÍA 5

Los estudiantes interpretan productos de números enteros con diagramas de cinta.

Los que cumplen

• Elaborar: Cuento de matemáticas (30-45 minutos)

• Elaborar: Tarea basada en problemas (30-45 minutos)

• EElaborar: Constructor de fluidez(15-30 minutos)

Los deficientes

• Elaborar: Práctica interactiva(15-30 minutos)

• Evaluar: Prueba de habilidades (3045 minutos)

Práctica guiada

• Intervención: Intervención en grupos pequeños (15-30 minutos)

• Explicar: Conexiones lingüísticas (15-30 minutos)

• Inicio: Guía de instrucción andamiada (30-45 minutos)

EVALUACIONES

D = Diagnóstico F = Formativo S = Sumativo

Acceso a conocimientos previos (D)

Breve actividad de sondeo para evaluar los conocimientos previos antes de abordar el contenido del alcance.

Boleto de salida (F)

Evaluación rápida sobre lo que aprendieron en esta exploración.

Muestra lo que sabes (F)

Tarea de práctica independiente que permite a los estudiantes demostrar su aprendizaje.

Decide y defiende (F)

Evaluación abierta que pide a los estudiantes que razonen matemáticamente y apoyen sus ideas con pruebas.

Lista de verificación de la observación (D, F)

Lista de conceptos y habilidades que el maestro y el estudiante pueden usar para reflexionar sobre el progreso del estudiante y establecer objetivos.

Prueba de habilidades (F, S)

Evaluación basada en estándares para determinar la habilidad para resolver problemas matemáticos de manera eficiente

DÍA 6

Los estudiantes interpretan productos de números enteros con diagramas de cinta.

y precisa.

Evaluación basada en estándares (S)

Evaluación basada en estándares de opción múltiple en la que los estudiantes demuestran el dominio del contenido

Intervención en grupos pequeños: Revisión (F)

Tarea de práctica independiente para evaluar el dominio del contenido después de la intervención en grupos pequeños.

Evaluaciones de referencia (D, S)

Evaluaciones de principio, mitad y final de año que ofrecen datos significativos que pueden informar la instrucción.

Evaluaciones de medición del crecimiento (D, S)

Evaluaciones previas y posteriores diseñadas para realizar un seguimiento del crecimiento de los estándares de nivel de grado desde el principio hasta el final del año.

DÍA 7 DÍA 8

Los estudiantes representan y resuelven problemas de multiplicación con rectas numéricas y múltiplos.

Los estudiantes usan lo que saben para predecir el significado del vocabulario nuevo.

Los estudiantes repiten el nuevo vocabulario escuchado en clase para practicar su uso adecuado.

Los estudiantes crean respuestas escritas utilizando el vocabulario recién adquirido y revisan sus respuestas según sea necesario.

Los estudiantes repiten la actividad en la que determinan una cantidad total en grupos iguales con modelos de multiplicación. Los estudiantes resolverán el problema original ahora que han completado las exploraciones correspondientes.

Los estudiantes intercambian ideas, proporcionan retroalimentación y modifican su trabajo según sea necesario.

• Enunciado diario de aritmética

• Ciencia de datos

• Enunciado diario de aritmética

• Ciencia de datos

• Enunciado diario de aritmética

• Ciencia de datos

• Comience la «Exploración 3: Multiplicación con diagramas de cintas»

Práctica independiente

• Refiérase a la sección de «Práctica».

Práctica guiada

• Refiérase a la sección de «Práctica».

• Lista de verificación de la observación

• Preguntas de facilitación

• Continúe la «Exploración 3: Multiplicación con diagramas de cintas»

• Charla de matemáticas

• Esquema de anclaje: Exploración 3

Práctica independiente

• Refiérase a la sección de «Práctica».

Práctica guiada

• Parte III: Intervención en grupos pequeños

• Exploración 3: Boleto de salida

• Muestra lo que sabes (parte 3)

• Lista de verificación de la observación

• Preguntas de facilitación

• Exploración 4: Rectas numéricas y contar salteado

• Charla de matemáticas

• Esquema de anclaje: Exploración 4

Práctica independiente

• Refiérase a la sección de «Práctica».

Práctica guiada

• Parte II: Intervención en grupos pequeños

• Exploración 4: Boleto de salida

• Muestra lo que sabes (parte 4)

• Lista de verificación de la observación

• Preguntas de facilitación

• Enunciado diario de aritmética

• Ciencia de datos

• Libreta interactiva: modelos diferentes

• Captar interés (parte 2): Posexploración

Práctica independiente

• Refiérase a la sección de «Práctica».

Práctica guiada

• Refiérase a la sección de «Práctica».

• Comprobación de la intervención en grupos pequeños

• Evaluación de habilidades

INICIO: CALENDARIO SUGERIDO

DÍA 9

Los estudiantes demuestran su dominio de los conceptos y habilidades clave del alcance de aplicación a través de una evaluación basada en estándares.

Los estudiantes emplean habilidades de lectura y escritura utilizando lenguaje académico para demostrar su comprensión de los conceptos clave.

• Enunciado diario de aritmética

• Ciencia de datos

Práctica independiente

• Refiérase a la sección de «Práctica».

Práctica guiada

• Refiérase a la sección de «Práctica».

• Decidir y defender

• Evaluación basada en estándares

INICIO: CALENDARIO SUGERIDO

GRADO 3: MODELOS DE MULTIPLICACIÓN

INICIO: CONTENIDO DE APOYO

¿QUÉ ESTOY ENSEÑANDO?

CONTENIDO DE APOYO

Representar y resolver problemas que impliquen multiplicación y división.

Interpretar productos de números enteros; por ej., interpretar 5 × 7 como el número total de objetos en 5 grupos de 7 objetos cada uno. Por ej., describir un contexto en el que un número total de objetos puede expresarse como 5 × 7.

CONOCIMIENTOS PREVIOS

El jardín de infancia y el primer grado forman los cimientos de nuestro sistema de base 10 a través de la representación de objetos en conjuntos, la composición y descomposición de números, la construcción de relaciones de valor posicional y el desarrollo de estrategias y habilidades de suma y resta. En segundo grado se avanza en esta progresión a medida que los estudiantes trabajan con grupos iguales, organizan objetos en conjuntos rectangulares de hasta cinco filas y cinco columnas y escriben ecuaciones para expresar el total como una suma de sumandos. Esto sienta las bases necesarias para que tercer grado desarrolle plenamente la relación entre suma y multiplicación, comprenda patrones, proporcione estrategias basadas en las propiedades de las operaciones y asegure la capacidad de aplicar la multiplicación dentro de un contexto del mundo real.

CONCEPTOS ERRÓNEOS Y OBSTÁCULOS

• Los estudiantes ven las matrices como una colección de unos, no observan el patrón de filas y columnas y no ven las relaciones en grupos iguales.

• Los estudiantes pueden creer que 5 × 2 y 2 × 5 tienen productos diferentes. La construcción de matrices permite a los estudiantes tener visualmente la propiedad conmutativa de la multiplicación.

• Los estudiantes aún no comprenden que el signo igual significa «tiene el mismo valor que»; por lo tanto, pueden pensar que las ecuaciones de multiplicación escritas con el producto al principio no son correctas.

• Las operaciones de multiplicación carecen de situaciones contextuales. Los estudiantes son incapaces de ver la relación o hacer conexiones entre el hecho y cualquier contexto del mundo real.

EN ESTE ALCANCE

Los estudiantes comprenden e interpretan el producto de números enteros cuando se les da un número igual de grupos con un número igual de objetos en cada grupo. El significado y las propiedades de la multiplicación están en el centro de la instrucción. Se usan diversas estrategias para determinar el producto, como la suma repetida, el conteo salteado, las matrices, los modelos de área y los saltos en una recta numérica. Los estudiantes deben ser capaces de describir y contextualizar cualquier problema de multiplicación.

TÉRMINOS CLAVE

• modelo de área: un modelo rectangular de multiplicación o división que representa el total como el área; los factores o cociente y divisor se representan por las longitudes de los lados.

• matriz: objetos o números dispuestos en filas y columnas iguales.

• propiedad conmutativa de la multiplicación: establece que los números se pueden multiplicar en cualquier orden y el producto será el mismo.

• grupos iguales: conjuntos de objetos que tienen la misma cantidad o número, o tienen el mismo valor.

• ecuación: oración matemática que utiliza números, uno o más símbolos de operación y un signo igual.

• factor: un número que se multiplica por otro número para encontrar un producto.

• multiplicación: una forma de crear un producto haciendo grupos iguales, repitiendo sumas o formando matrices.

• producto parcial: multiplicar factores descompuestos y juntar esos productos para obtener un producto final.

• patrón: una disposición de números o formas que se repite.

• modelo pictórico: una imagen o representación de (un) objeto(s) real(es).

• producto: el resultado de multiplicar dos o más números juntos.

• problema del mundo real: una situación hipotética y una pregunta que requieren conocimientos matemáticos, estrategias y una ecuación para ser resueltos.

• estrategia: un plan o forma de resolver un problema o encontrar una respuesta.

• número entero: un valor numérico sin parte decimal o fraccionaria.

INICIO: CONTENIDO DE APOYO

APLICAR LAS PRÁCTICAS MATEMÁTICAS

• MP.1 Dar sentido a los problemas y perseverar en su resolución: Los estudiantes exploran la multiplicación a través de grupos iguales, matrices, diagramas de cinta y rectas numéricas, a partir de escenarios del mundo real tales como exhibiciones en tiendas de comestibles, trabajos de limpieza de ventanas y empacando para un viaje de campamento para determinar las cantidades totales.

• MP.2 Razonamiento abstracto y cuantitativo: Los estudiantes interpretan la multiplicación como suma repetida, conteo salteado y agrupación, conectando expresiones numéricas con representaciones visuales y contextuales.

• MP.3 Construir argumentos viables y debatir el razonamiento de otros: Los estudiantes explican sus estrategias de multiplicación, justifican el uso de diferentes modelos y discuten la efectividad de varios enfoques con sus compañeros.

• MP.4 Representar con matemáticas: Los estudiantes usan herramientas prácticas como contadores, cubos conectables, diagramas de cinta, rectas numéricas y matrices para representar visualmente la multiplicación y desarrollar una comprensión conceptual más profunda.

• MP.5 Utilizar estratégicamente las herramientas adecuadas: Los estudiantes seleccionan y usan herramientas como papel cuadriculado, pizarras de borrado en seco, manipulativos y rectas numéricas para estructurar su pensamiento y resolver problemas de manera efectiva.

• MP.6 Atienden a la precisión: Los estudiantes organizan y etiquetan cuidadosamente sus modelos de multiplicación, asegurando la precisión en sus ecuaciones, diagramas y razonamientos, a la vez que usan un vocabulario matemático preciso.

• MP.7 Buscan y utilizan estructuras: Los estudiantes reconocen patrones en la multiplicación, como sumas repetidas en matrices y saltos iguales en rectas numéricas, aplicando estas estructuras para desarrollar fluidez en la multiplicación.

• MP.8 Buscan y expresan regularidad en razonamientos repetidos: Los estudiantes identifican patrones repetidos en la multiplicación, como el conteo salteado por factores, el uso de diagramas de cinta para modelar grupos iguales y la aplicación de propiedades de la multiplicación a través de diferentes tipos de problemas.

GRUPOS IGUALES

El fundamento de la multiplicación se forma comprendiendo que cuando hay un cierto número de grupos con la misma cantidad en cada uno, se puede hallar el número total de objetos mediante la operación de multiplicación. El signo × simboliza grupos iguales de; 4 × 9 denota 4 grupos iguales de 9. Trabajando con este lenguaje y modelos concretos, los estudiantes adquieren un significado fundacional de factores: número de grupos con la misma cantidad en cada grupo.

Ejemplo: Jill compró 4 paquetes de manzanas con 3 manzanas en cada paquete. ¿Qué modelo representa la compra de Jill?

La opción de respuesta B es la correcta, ya que muestra correctamente 4 grupos iguales de 3 manzanas en cada uno.

INICIO: CONTENIDO DE APOYO

MATRICES

Los estudiantes usarán modelos concretos junto con representaciones pictóricas para desarrollar el concepto de multiplicación utilizando matrices. Generar concretamente cuántos grupos (filas) y cuántos objetos hay en cada grupo (columnas) desarrolla el concepto fundamental de la multiplicación. Las matrices también permiten representar físicamente la propiedad conmutativa de la multiplicación (cambiando la orientación de la matriz), que los estudiantes necesitan para demostrar que, por ejemplo, 6 × 3 tiene el mismo producto que 3 × 6.

Ejemplo: ¿Qué dos oraciones numéricas están representadas en el siguiente modelo?

a 3 × 7

3 + 7

b 7 × 3

3 + 3 + 3

c 7 × 3

3 × 7

d 7 + 7 + 7

3 + 3 + 3

La opción de respuesta c es la correcta. La matriz muestra correctamente 3 grupos (filas de notas musicales) con 7 objetos (columnas de notas musicales) en cada fila. Cuando se cambia la orientación de la matriz, ésta muestra correctamente 7 grupos (filas de notas musicales) con 3 objetos (columnas de notas musicales) en cada fila.

3 × 7 7 × 3

Ejemplo: ¿Qué situación puede representarse mediante la expresión 6 × 7?

a Gina tenía 6 ramos de flores. Se le cayeron 7 ramos.

b Gina compró 6 ramos de flores. Compró 7 ramos más.

c Gina tenía 6 ramos de flores. Había 7 flores en cada ramo.

d Gina vendió 6 ramos de flores. Compró 7 ramos más.

La opción de respuesta c es la correcta. Representa correctamente 6 ramos de flores con 7 flores en cada ramo.

MODELOS DE ÁREA

Los estudiantes usarán modelos concretos junto con representaciones pictóricas para desarrollar el concepto de multiplicación con el modelo de área. Esta estrategia se basa en el valor posicional y las propiedades de las operaciones. Un rectángulo proporciona el espacio de trabajo a medida que se descomponen los factores. Trabajando con 24 × 5, 24 se descompone en 20 (2 decenas) y 4 (4 unidades). El producto de 5 × 20 se coloca en el modelo inferior, que representa el valor de las decenas. El producto de 5 × 4 se coloca en el modelo que representa el valor de las unidades. A continuación, se suman los productos parciales para obtener el producto.

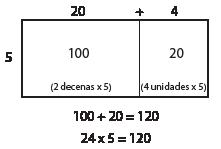
Este modelo se usa con cualquier factor de un dígito por 1, y también cuando ambos factores tienen más de un dígito, como se muestra a continuación.

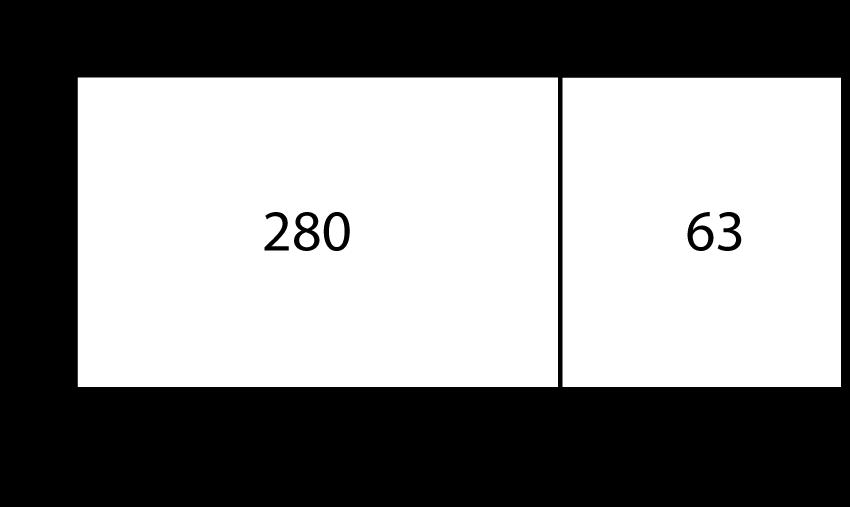
Ejemplo: ¿Qué expresión representa este modelo de área?

a 40 + 9 + 7

b 7 × 40

c 49 × 7

d 7 × 9 + 7 × 4

La opción de respuesta c es la correcta. El número 49 se descompone en 40 (4 decenas) y 9 (9 unidades). Cada producto parcial se multiplica por 7.

RECTAS NUMÉRICAS

Los estudiantes usarán modelos concretos junto con representaciones pictóricas para desarrollar el concepto de multiplicación usando saltos en una recta numérica. El concepto de adición repetida/conteo salteado se refuerza a medida que los estudiantes realizan saltos iguales en una recta numérica.

4 × 3

3 + 3 + 3 + 3

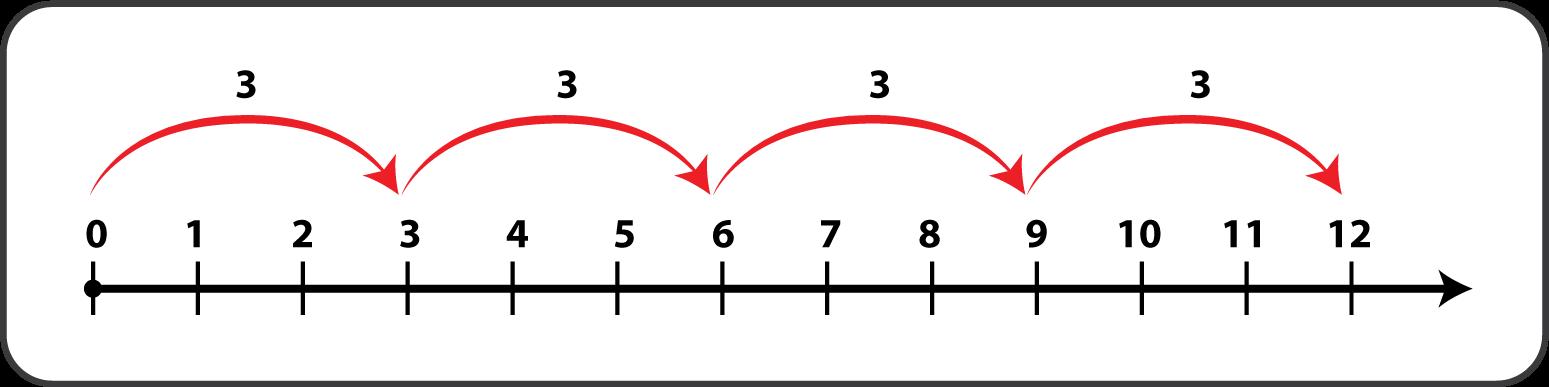
Este modelo representa 4 saltos iguales de 3, dando como resultado un producto de 12.

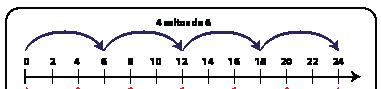
También se puede utilizar una recta numérica para apoyar la propiedad conmutativa de la multiplicación.

4 × 6 = 24

6 × 4 = 24

Ejemplo: ¿Qué problema escrito se puede resolver con la recta numérica de abajo?

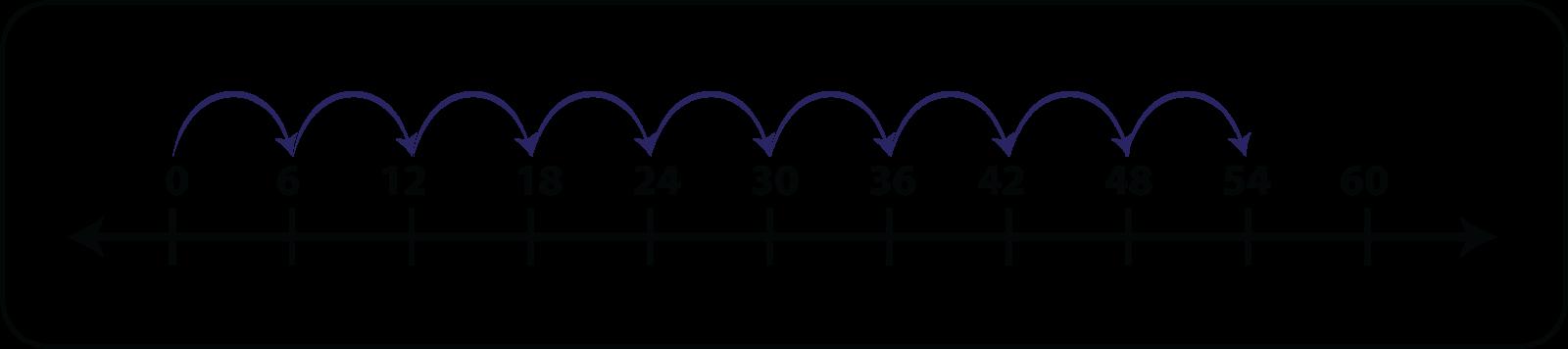
a Yolanda corrió 6 minutos un día y 54 minutos al día siguiente. ¿Cuántos minutos corrió Yolanda los dos días juntos?

b Miguel encontró 6 conchas marinas en la playa cada día durante 9 días. ¿Cuántas conchas encontró durante los 9 días?

c Sandra trabajó 6 problemas de matemáticas en la escuela y 9 problemas de matemáticas en casa el lunes. ¿Cuántos problemas de matemáticas trabajó Sandra el lunes?

d Noah colocó 9 filas de sillas. Colocó 54 sillas en cada fila. ¿Cuál es el número total de sillas que Noé colocó?

INICIO: CONTENIDO DE APOYO

La opción de respuesta b es la correcta. Miguel encuentra 6 conchas marinas cada día durante 9 días. El modelo de abajo muestra 9 saltos iguales de 6. Michael encuentra 54 conchas marinas durante el período de 9 días.

DIAGRAMAS DE CINTA

Los estudiantes han usado esta estrategia en grados anteriores con sumas y restas. Los diagramas de cinta usan modelos visuales en forma de rectángulos que son instrumentales para ayudar a los estudiantes a entender cómo resolver problemas escritos. Al aplicar esta estrategia a un problema de multiplicación, los estudiantes dibujan el modelo para organizar los datos según lo determine el contexto del problema. Etiquetar el diagrama ayuda a los estudiantes a relacionar las partes del diagrama con las partes correspondientes del problema.

Ejemplo: Bob compró 9 cajas de clavos. Había 24 clavos en cada caja. ¿Cuántos clavos compró Bob?

AVANCES

Los estudiantes amplían este concepto de multiplicación en tercer grado a medida que hacen conexiones entre la multiplicación y la división y aplican este conocimiento a problemas de palabras. En cuarto grado, representan enunciados verbales de comparaciones multiplicativas como ecuaciones de multiplicación y resuelven problemas de palabras usando dibujos y ecuaciones con un símbolo para la incógnita, así como resuelven problemas de palabras de varios pasos que involucran la multiplicación. En quinto grado avanza el aprendizaje a través de la evaluación e interpretación de expresiones, incluyendo el uso de paréntesis, corchetes o llaves en expresiones numéricas.

INICIO: CONTENIDO DESGLOSADO

ANÁLISIS PROFUNDO DE LOS ESTÁNDARES

CONTENIDO DESGLOSADO

ESTÁNDARES

Representar y resolver problemas de multiplicación y división.

• Interpretar productos de números enteros; por ej., interpretar 5 × 7 como el número total de objetos en 5 grupos de 7 objetos cada uno. Por ejemplo, describir un contexto en el que un número total de objetos pueda expresarse como 5 × 7.

DESGLOSAR EL ESTÁNDAR

VERBOS: ¿QUÉ DEBERÍAN HACER LOS ESTUDIANTES?

• interpretar: explicar; dar o proporcionar significado.

• describir: contar las características de algo utilizando palabras.

• expresar: representar con palabras.

SUSTANTIVOS: ¿QUÉ PALABRAS CONCRETAS DEBEN CONOCER LOS ESTUDIANTES?

• producto: el resultado de multiplicar dos o más números.

• número entero: valor numérico sin parte decimal ni fraccionaria.

• total: cuántos hay por todo.

• objeto: una cosa que se puede ver, tocar, agrupar, contar y manipular.

IMPLICACIONES PARA LA ENSEÑANZA

• Hasta este punto, los estudiantes han tenido experiencia sólo con la multiplicación como una suma repetida con grupos de números iguales de objetos que se unen.

• Los estudiantes usan objetos concretos, imágenes y matrices como pasos iniciales en la progresión hacia la fluidez y el algoritmo.

• Cuando se trabaja en la multiplicación utilizando grupos iguales, los estudiantes deben entender que cada factor juega un papel diferente: mientras que uno indica el número de objetos en un grupo, el otro indica el número de grupos. Cambiar estos factores puede no cambiar el resultado total, pero sí cambia el aspecto del modelo.

• Las matrices permiten a los estudiantes representar la multiplicación sin dejar de ver cada objeto individual. En las matrices, los factores pueden relacionarse con grupos iguales, siendo las filas el número de grupos y las columnas el número de objetos de cada grupo. Esto facilita la transición, a veces difícil, de los grupos iguales a las matrices.

USO DE STEMSCOPES MATH

PUNTOS DE REFERENCIA

Desde Kindergarten hasta Álgebra I, STEMscopes Math ofrece potentes Evaluaciones de Referencia para controlar al principio, a mediados y al final del año. Elaboradas por expertos de STEMscopes Math, estas evaluaciones están diseñadas con el mismo aspecto que los exámenes estatales estandarizados, lo que proporciona a los estudiantes una práctica auténtica y a los maestros la información que necesitan. GRADO 3:

INICIO: CONTENIDO DESGLOSADO

ALINEACIÓN VERTICAL

GRADO

ESTÁNDAR

2 Usar la suma para encontrar el número total de objetos dispuestos en matrices rectangulares con hasta 5 filas y hasta 5 columnas; escribir una ecuación para expresar el total como una suma de sumandos iguales.

2 Contar hasta 1,000; contar de 5 en 5, de 10 en 10 y de 100 en 100.

3 Interpretar productos de números enteros; por ej., interpretar 5 × 7 como el número total de objetos en 5 grupos de 7 objetos cada uno. Por ejemplo, describir un contexto en el que un número total de objetos pueda expresarse como 5 × 7.

4 Interpretar una ecuación de multiplicación como una comparación; por ejemplo, interpretar 35 = 5 × 7 como una declaración de que 35 es 5 veces más que 7 y 7 veces más que 5. Representar declaraciones verbales de comparaciones multiplicativas como ecuaciones de multiplicación.

4 Aplicar y extender comprensiones previas de multiplicación para multiplicar una fracción por un número entero.

a. Entender una fracción a/b como un múltiplo de 1/b. Por ej., usar un modelo visual de fracción para representar 5/4 como el producto 5 × (1/4), registrando la conclusión mediante la ecuación 5/4 = 5 × (1/4).

b. Comprender un múltiplo de a/b como múltiplo de 1/b, y usar esta comprensión para multiplicar una fracción por un número entero. Por ej., utilizar un modelo visual de fracción para expresar 3 × (2/5) como 6 × (1/5), reconociendo este producto como 6/5. (En general, n × (a/b) = (n × a)/b).

c. Resolver problemas escritos que impliquen la multiplicación de una fracción por un número entero; por ej., usando modelos visuales de fracciones y ecuaciones para representar el problema. Por ejemplo, si cada persona en una fiesta comerá 3/8 de libra de carne asada y habrá 5 personas en la fiesta, ¿cuántas libras de carne asada se necesitarán? ¿Entre qué dos números enteros se encuentra tu respuesta?

5 Explicar patrones en el número de ceros del producto cuando se multiplica un número por potencias de 10, y explicar patrones en la colocación del punto decimal cuando se multiplica o divide un decimal por una potencia de 10. Utilizar exponentes de números enteros para denotar potencias de 10.

5 Interpretar la multiplicación como un escalamiento (redimensionamiento), mediante:

a. La comparación del tamaño de un producto con el tamaño de uno de los factores, basándose en el tamaño del otro factor, sin resolver la multiplicación.

b. Explicando por qué al multiplicar un número dado por una fracción mayor que 1 se obtiene un producto mayor que el número dado (reconociendo la multiplicación por números enteros mayores que 1 como un caso familiar); explicando por qué al multiplicar un número dado por una fracción menor que 1 se obtiene un producto menor que el número dado (y relacionando el principio de equivalencia de fracciones a/b = (n×a)/ (n×b) con el efecto de multiplicar a/b por 1).

5 Relacionar el volumen con las operaciones de multiplicación y adición y resolver problemas matemáticos y de la vida real en los que intervenga el volumen.

a. Hallar el volumen de un prisma rectangular recto con longitudes laterales enteras empaquetándolo con cubos unitarios, y demostrar que el volumen es el mismo que se hallaría multiplicando las longitudes de las aristas, equivalentemente multiplicando la altura por el área de la base. Representar productos de tres números enteros como volúmenes, por ej., para representar la propiedad asociativa de la multiplicación.

b. Aplicar las fórmulas V = l × w × h y V = b × h para prismas rectangulares para encontrar volúmenes de prismas rectangulares rectos con longitudes de arista de números enteros en el contexto de la resolución de problemas matemáticos y del mundo real.

c. Reconocer el volumen como aditivo. Hallar volúmenes de figuras sólidas compuestas por dos prismas rectangulares rectos no superpuestos sumando los volúmenes de las partes no superpuestas, aplicando esta técnica para resolver problemas del mundo real.

6 Sumar, restar, multiplicar y dividir con fluidez decimales de varios dígitos con el algoritmo estándar por operación.

7 Aplicar propiedades de las operaciones como estrategias para multiplicar y dividir números racionales.

INICIO: GUÍA DE INSTRUCCIÓN ANDAMIADA

MONITOREAR Y AJUSTAR

GUÍA DE INSTRUCCIÓN ANDAMIADA

La guía de instrucción andamiada se proporciona para que los maestros puedan planificar los siguientes pasos basándose en el rendimiento de los estudiantes en las evaluaciones de alcance o en los datos de su evaluación de medición de crecimiento MAP. Se trata de una herramienta integrada que lleva a los maestros a buscar materiales basados en las necesidades de los estudiantes. Los materiales sugeridos están organizados por estándares. Dentro de cada estándar, los materiales se clasifican además por el rango de percentiles que mejor se adapta.

Cuando se usa la guía de instrucción andamiada con los datos de su evaluación de medición de crecimiento MAP, cada tabla puede guiar a los maestros a los materiales sugeridos basados en los puntajes del área de instrucción de los estudiantes. Se sugiere a los maestros a permitir que todos los estudiantes experimenten con «Captar interés», «Exploración», «Muestra lo que sabes» y «Pruebas de habilidades». Estos elementos cubren a fondo los estándares incluidos en el alcance.

La guía se divide en cuatro rangos de percentiles para cada estándar.

Refuerzo del grado anterior Nivel de grado con apoyos Nivel de grado

Los estudiantes con puntaje en este rango de percentil necesitan refuerzo del contenido del grado anterior.

Los estudiantes con puntaje en este rango de percentil necesitan apoyo de intervención de nivel de grado.

Los estudiantes con puntaje en este rango de percentil pueden trabajar en contenido de nivel de grado con apoyos de instrucción.

Ampliación del nivel de grado

Los estudiantes con puntaje en este rango de percentil están listos para aplicar su conocimiento del contenido en una variedad de actividades.

Para interpretar y responder al rendimiento del estudiante en las evaluaciones del alcance, complete los siguientes pasos:

1 Revise los datos recopilados a través de la plataforma en línea o el «Mapa de calor» para determinar el rango percentil del estudiante para cada estándar evaluado.

2 Las tablas proporcionadas recomiendan un conjunto de materiales de instrucción para cada rango percentil dentro de cada estándar evaluado. Elija cuál de estos materiales usará para apoyar mejor al estudiante con base en sus datos de evaluación.

3 Haga clic en el enlace directo al material elegido para el estudiante.

Para interpretar y responder al desempeño del estudiante en la evaluación de medición de crecimiento MAP, complete los siguientes pasos:

1. Revise los datos proporcionados para determinar el percentil, el área de instrucción y/o el desglose de estándares para cada estudiante.

2. Encuentre el alcance que incluye los estándares que necesitan enfoque o intervención.

3. Acceda a la «guía de instrucción andamiada» en la sección «inicio» del alcance.

4. Haga clic en el enlace directo al material recomendado para el estudiante.

La guía es un plan sugerido y no se limita a los estándares y actividades incluidos. Además, no todas las actividades sugeridas necesitan ser completadas por cada estudiante.

Área de instrucción: Operaciones y pensamiento algebraico

Todos los estudiantes:

• Captar interés

• Exploración

• Muestra lo que sabes

• Prueba de habilidades

Interpretar productos de números enteros; por ejemplo, interpretar 5 × 7 como el número total de objetos en 5 grupos de 7 objetos cada uno. Por ejemplo, describir un contexto en el que un número total de objetos pueda expresarse como 5 × 7.

0 %25 % (Nivel de grado anterior con apoyo)

25 %50 % (Nivel de grado con apoyo)

2 Matrices

Intervención en grupos pequeños

Constructor de fluidez

• Preguntas y respuestas sobre matrices

• Resolver problemas de matrices

Práctica interactiva

• Patitos en fila

Prueba de habilidades

Mis pensamientos de matemáticas

2 Aprendizaje virtual Números y operaciones

• Representar y describir multiplicaciones

3 Modelos de multiplicación

Acceso a conocimientos previos

Constructor de fluidez

Intervención en grupos pequeños

• Partes 1, 2, 3, 4

3 Aprendizaje virtual Números y Operaciones

• Grupos iguales, adiciones repetidas, matrices, modelos de área, rectas numéricas, y conteo salteado

3 Modelos de multiplicación

Vocabulario ilustrado

Libreta interactiva

50 %80 % (Nivel de Grado)

80 %100 % (Ampliando el Nivel de Grado)

Mis pensamientos de matemáticas

Práctica interactiva

• ¡Enciéndelo!

Constructor de fluidez

• Multiplicación dentro de 100: Modelos y ecuaciones

Ciencia de datos

Conexiones de lenguaje

3 Modelos de multiplicación

Tarea basada en problemas

Conexiones profesionales

Matemáticas de hoy

Cuento de matemáticas

Crea el tuyo

Tablero de opciones

ATRAER: ACCESO A CONOCIMIENTOS PREVIOS

EVALUAR PREVIAMENTE EL CONOCIMIENTO DE LOS ESTUDIANTES

ACCESO A CONOCIMIENTOS PREVIOS

DESCRIPCIÓN

En esta actividad, los estudiantes usarán la adición para encontrar el número total de objetos dispuestos en una matriz y escribirán una ecuación para expresar el total como una suma de sumandos iguales. Esta actividad está diseñada para evaluar el dominio del siguiente estándar:

• Usar la adición para encontrar el número total de objetos dispuestos en matrices rectangulares con hasta cinco filas y hasta cinco columnas; escribir una ecuación para expresar el total como una suma de sumandos iguales.

MATERIALES

IMPRESO

• 1 folleto del estudiante (por alumno, por grupo o por clase)

PREPARACIÓN

• Puede optar por imprimir un folleto del estudiante para cada alumno o grupo o proyectar la página en la pizarra.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Los estudiantes deben leer las respuestas de sus cuatro compañeros.

2. Con compañeros, grupos o toda la clase, los estudiantes deben discutir qué oración de multiplicación es correcta y explicar su razonamiento. Algunos ejemplos de respuestas de los estudiantes son los siguientes:

○ Riya no es correcta. Hay más de dos grupos de cuatro.

○ Gabriel no es correcto. Hay tres grupos, pero cada uno tiene cuatro, no tres.

○ Noa no es correcta. Hay tres filas y cuatro en cada fila, pero no estamos combinando tres y cuatro más.

○ Isaac es correcto. Hay tres grupos iguales de cuatro galletas.

3. Si los estudiantes tienen dificultades para completar esta tarea, realice el ejercicio de construcción de la base para llenar el vacío en los conocimientos previos antes de pasar a otras partes del alcance.

RECUERDITOS PARA FIESTAS

ATRAER: CAPTAR INTERÉS

LECCIÓN PARA CAPTAR INTERÉS

RECUERDITOS DE FIESTA

DESCRIPCIÓN

Los estudiantes usan la multiplicación para determinar cuántos artículos de fiesta tienen.

MATERIALES

IMPRESOS

• 1 juego de tarjetas de recuerditos de fiesta (por clase)

REUTILIZABLES

• 1 fenómeno (por clase)

• 21 bolsas resellables (por clase)

CONSUMIBLES

• 1 hoja de papel (por grupo, opcional)

PREPARACIÓN

• Planee mostrar los fenómenos.

• Planee que los estudiantes trabajen en cuatro grupos para completar esta actividad.

• Imprima el conjunto de tarjetas de recuerditos para fiestas, recórtelas y ponga los artículos similares juntos en las mismas bolsas de la siguiente manera:

◦ 3 giradores inquietos en cada una de las 8 bolsas

◦ 6 yoyos en cada una de las 4 bolsas

◦ 8 linternas para dedos en cada una de las 4 bolsas

◦ 5 pares de gafas de sol en cada una de las 5 bolsas

• Escriba cuántos artículos hay en cada bolsa, similar a lo que encontraría en las bolsas de recuerditos para fiestas en una tienda.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

PARTE I: EXPLORACIÓN PREVIA

1. Presente esta actividad hacia el principio del alcance. La clase retomará la actividad y resolverá el problema original después de que los estudiantes hayan completado las actividades correspondientes a «Explorar»..

2. Muestre los fenómenos. Formule las siguientes preguntas: «¿Qué observan? ¿Dónde puedes ver matemáticas en esta situación?». Permita que los estudiantes compartan todas sus ideas.

3. Explique el escenario a la clase: «Estás planeando una fiesta de cumpleaños y has elegido un montón de recuerditos para regalar a tus amigos. Tienes 8 bolsas con 3 giradores inquietos cada una, 4 bolsas con 6 yoyos cada una, 4 bolsas con 8 internas para dedos cada una y 5 bolsas con 5 pares de gafas de sol cada una. ¿Cuántos regalos tienes de cada tipo?».

4. Deje que los estudiantes hagan preguntas y aclaren el contexto si es necesario. Anímelos a compartir sus ideas y experiencias con la clase con las siguientes preguntas:

a. «¿Has estado antes en una fiesta de cumpleaños?».

b. «¿Recibiste algún recuerdito de fiesta?»

c. «¿Con cuál de estos recuerditos de fiesta has jugado antes?».

ATRAER: CAPTAR INTERÉS

5. Plantee la siguiente pregunta con la clase:

a. DOK-2 «¿Qué información necesitaríamos saber para determinar cuántos recuerditos de fiesta tenemos?». Tendríamos que saber cuántos recuerdos de fiesta hay en cada bolsa y cuántas bolsas de cada recuerdo de fiesta tenemos.

6. Continúe con las actividades de exploración.

PARTE II: DESPUÉS DE LA EXPLORACIÓN

1. Después de que los estudiantes hayan completado las actividades de exploración para este tema, muestre nuevamente los fenómenos y repita la situación.

2. Discuta la siguiente pregunta con la clase:

a. DOK-2 «¿Qué información necesitaríamos saber para determinar cuántos recuerditos de fiesta tenemos?». Necesitaríamos saber cuántos artículos hay en cada bolsa y cuántas bolsas de cada artículo tenemos.

3. Repase el problema y divida a los estudiantes en cuatro grupos.

4. Entregue a cada grupo todas las bolsas con artículos de regalo similares (8 bolsas de giradores inquietos, 4 bolsas de yoyos, 4 bolsas de linternas para dedos y 5 bolsas de gafas de sol). Los estudiantes también pueden necesitar una hoja de papel para realizar sus cálculos.

5. Plantee las siguientes preguntas con la clase:

a. DOK-1 «¿Cómo averiguaste cuántos ______ recuerditos de fiesta tenía tu grupo?». Las respuestas pueden variar. Contamos que teníamos 4 bolsas de yoyos. También vimos que cada una de las bolsas contenía 6 yoyos. Así que sabíamos que teníamos 4 grupos de 6, y 6 + 6 + 6 + 6 = 24. También sabíamos que 4 × 6 = 24. Teníamos 24 yoyos en total.

b. DOK-2 «¿De qué otra manera podrías encontrar el número total de recuerdos de la fiesta?». Las respuestas pueden variar. Vimos que teníamos 5 bolsas de gafas de sol con 5 gafas de sol en cada bolsa, así que nos saltamos contar por múltiplos de 5, contando así: 5, 10, 15, 20, 25. Sabíamos que 5 × 5 = 25.

6. Pida a cada grupo que explique a la clase cuántos recuerditos tenían y que discutan cómo hallaron el total.

7. Proponga la siguiente pregunta a la clase:

a. DOK-3 «¿Pueden pensar en una situación o contexto del mundo real en el que necesitarían hallar el número total usando grupos iguales?». Las respuestas pueden variar. Si quiero saber cuántos marcadores hay en nuestra clase, entonces podría contar cuántas cajas tenemos y cuántos marcadores hay en cada caja.

8. Como extensión, pida a los estudiantes que determinen cuántas bolsas de cada tipo de recuerditos de fiesta necesitarían para tener una de cada tipo para 30 niños.

RECUERDITOS PARA FIESTAS

EXPLORAR: EXPLORACIÓN 1

LECCIÓN INSTRUCTIVA

EXPLORACIÓN 1: GRUPOS IGUALES

Antes de completar esta exploración, haga que los estudiantes completen Habilidades básicas: Use problemas con cuentos para representar la multiplicación para que puedan aplicar la habilidad a este concepto.

Estándar(es)

• Representar y resolver problemas que involucren multiplicación y división. Interpretar productos de números enteros; por ej., interpretar 5 × 7 como el número total de objetos en 5 grupos de 7 objetos cada uno. Por ejemplo, describir un contexto en el que un número total de objetos puede expresarse como 5 × 7.

Ideas fundamentales

Estándares para la práctica matemática

DESCRIPCIÓN

Estándares para la práctica matemática

MP.1 Dar sentido a los problemas y perseverar en su resolución.

MP.2 Razonar abstracta y cuantitativamente.

MP.4 Representar con matemáticas.

MP.5 Usar herramientas apropiadas estratégicamente.

Los estudiantes determinan el número total de objetos en un escenario usando grupos iguales.

MATERIALES

IMPRESO

• 1 diario del estudiante (por alumno)

• 1 juego de tarjetas ¡Muéstrame el producto! (por clase)

• 1 boleto de salida (por estudiante)

REUTILIZABLE

• 50 contadores de dos colores (por grupo)

• 1 marcadores de borrado en seco (por estudiante)

• 1 pizarra de borrado en seco (por estudiante)

• 10 platos de papel pequeños (por grupo)

PREPARACIÓN

• Planifique que los estudiantes trabajen en 6 grupos para completar esta actividad.

• Imprima un diario del estudiante y un boleto de salida por alumno.

• Imprima las tarjetas ¡Muéstrame el producto! para toda la clase. Si lo desea, plastifíquelas para que duren más. Recorte las tarjetas.

• Coloque 6 estaciones en el aula con una tarjeta ¡Muéstrame el producto!, 10 platos de papel y 50 fichas de dos colores en cada estación.

Conexiones de contenido

Motores de investigación

CC2 Explorar cantidades cambiantes

DI1 Dar sentido al mundo (Comprender y explicar)

DI3 Impactar el futuro (Afectar)

• Prepare un marcador borrable y una pizarra de borrado en seco para cada estudiante.

• Para los estudiantes que necesiten más apoyo para recordar información, consulte nuestros elementos de «Ayudas complementarias» que incluyen tapetes para compartir, disponibles en la sección «Intervención».

• ¡Hazlo digital! Haga que los estudiantes exploren o presenten sus soluciones utilizando manipulativos virtuales. Los manipulativos usados en esta lección se pueden encontrar en el menú desplegable de la sección «Explorar» y se pueden asignar digitalmente a los estudiantes. (Contadores de dos colores)

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Ayude a los estudiantes a acceder a la tarea haciendo las siguientes preguntas guía:

a. «Miren alrededor del aula. ¿Qué objetos están en grupos iguales?».

b. «¿Cuáles son otros ejemplos de objetos ordenados o empaquetados en grupos iguales?».

c. «¿Qué sabes ya sobre la combinación de grupos iguales?».

2. Lea la siguiente situación a la clase: «Muchos objetos de nuestro mundo vienen en grupos iguales. Piensa en los paquetes de marcadores, las ruedas de un coche o los dedos de tus manos y pies. Puede que querramos saber el número total de objetos, pero tardaríamos mucho tiempo en contarlos todos. Sigamos el reto de encontrar mejores formas de combinar grupos iguales».

EXPLORAR: EXPLORACIÓN 1

3. Comience combinando fichas en cuatro grupos de tres fichas cada uno. Formule la siguiente pregunta:

a. DOK-1 «¿Qué ves y qué crees que significa?». Las respuestas variarán. Vemos cuatro grupos. Cada uno tiene tres fichas. Todos los grupos son iguales. Si sumamos todas las fichas, obtenemos 12 fichas.

4. Entregue un marcador borrable y una pizarra de borrado en seco a cada estudiante.

5. Pida a los estudiantes que escriban en sus pizarras una frase de multiplicación o de suma que describa el modelo de grupos de fichas y que compartan sus frases. Haga hincapié en cómo cada vez que se suma un grupo, el total aumenta en el mismo número. Haga la siguiente pregunta:

a. DOK-1 «¿Qué operación matemática representa tu frase?». Multiplicación o suma

6. Siga el ejemplo de los estudiantes y escriba un símbolo de multiplicación. Formule la siguiente pregunta:

a. DOK-2 «¿Qué representa este símbolo?». Representa "veces", "multiplicado por", "multiplicación", "suma repetida" y "grupos iguales de".

7. Haga que los estudiantes vuelvan a mirar el modelo. Hágales la siguiente pregunta:

a. DOK-2 «¿Cómo podrías describir el modelo con la frase “grupos de”?». Tres grupos de cuatro

8. Muestre cómo «tres grupos de cuatro» puede escribirse como 3 × 4. Pregunte a los estudiantes cuántos objetos hay en total y complete la oración de multiplicación, 3 × 4 = 12. Marque las partes de la oración de multiplicación y explique que los «factores» son los números que se multiplican y que el «producto» es el número total de objetos.

9. Repita esta actividad tres veces más con diferentes grupos iguales (2 × 3, 3 × 5, 4 × 10). Para cada nuevo grupo de fichas, pida a los estudiantes que escriban lo siguiente en sus pizarras de borrado en seco utilizando sus marcadores:

a. «Esboza el modelo de grupos iguales».

b. «Descríbelo con palabras utilizando "grupos de" (por ejemplo, "dos grupos de tres")».

c. «Tradúcelo en una frase de multiplicación (por ejemplo, 2 × 3 = 6)».

10. Pida a los estudiantes que identifiquen qué números son los factores y cuál es el producto.

11. Entregue un diario del estudiante a cada estudiante.

12. Explique que en cada estación, deben leer el escenario, hacer un modelo del problema con las placas y los contadores, escribir una descripción, registrar la oración de multiplicación y escribir una oración de solución. Para las tarjetas 4 a la 6, también deben escribir problemas del mundo real que podrían representar las expresiones dadas.

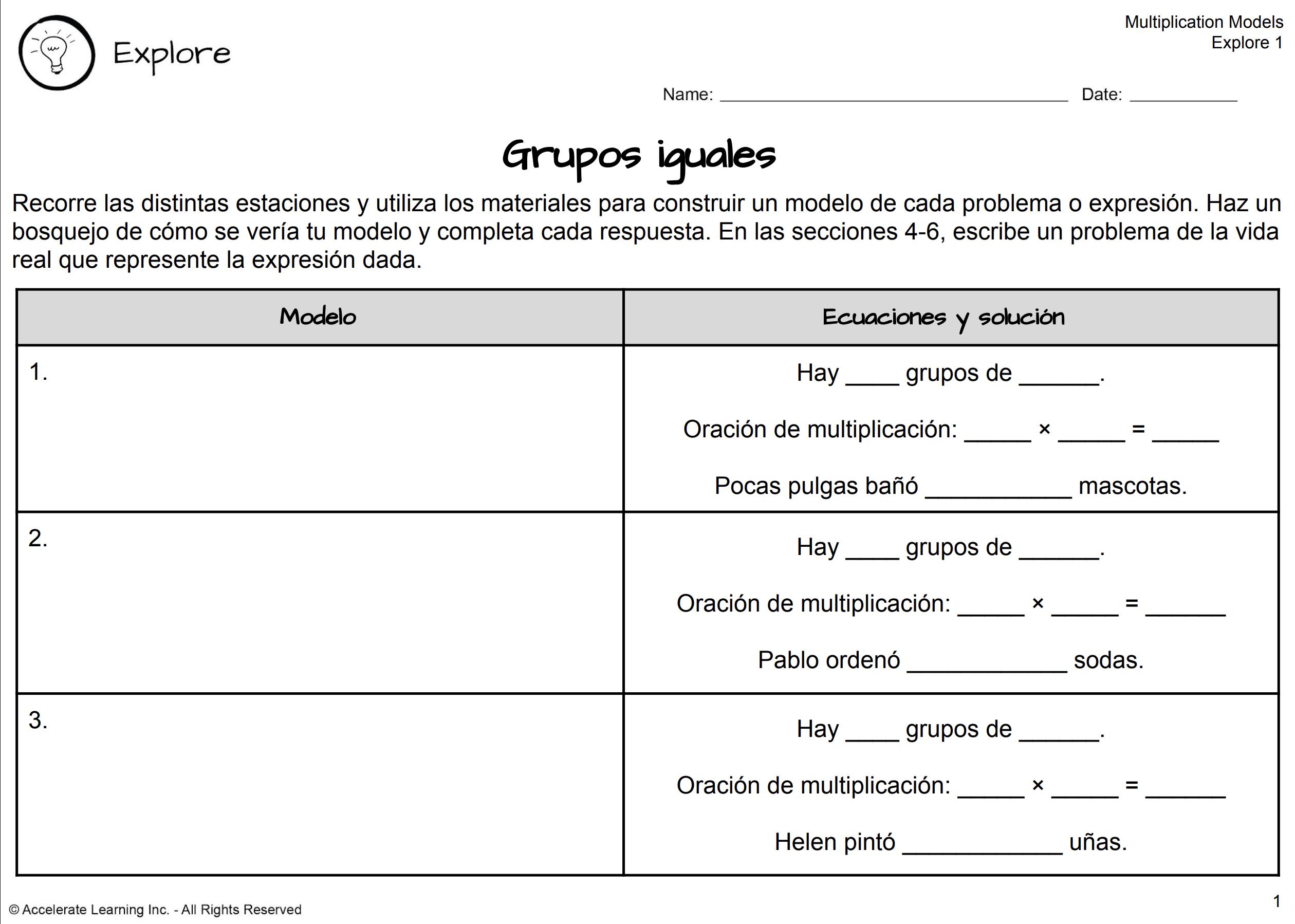
DIARIO DEL ESTUDIANTE

BOLETO DE SALIDA

13. Coloque a los estudiantes en seis grupos y asigne a cada grupo una estación.

14. Cuando hayan terminado en una estación, haga que los estudiantes roten a otra hasta que hayan completado las seis estaciones.

15. Cuando hayan terminado, anime a los estudiantes a conversar y escribir las respuestas a las preguntas de reflexión en sus diarios del estudiante.

16. Supervise y hable con los estudiantes según sea necesario para comprobar la comprensión utilizando las siguientes preguntas guía:

a. DOK-1 «¿Cuántos grupos iguales hay? ¿Cuántos hay en cada grupo?». Las respuestas pueden variar.

b. DOK-1 «¿Cómo describirías tu modelo?». Las respuestas pueden variar.

c. DOK-2 «Crea un problema similar que podría ser representado por la expresión __ × __». Las respuestas variarán.

17. Pida a los estudiantes que compartan sus estrategias y anímelos a que se hagan preguntas y establezcan conexiones. Invítelos a notar las similitudes y diferencias entre las estrategias usadas para multiplicar usando grupos iguales.

18. Después de la exploración, invite a la clase a una charla de matemática para compartir sus observaciones y aprendizajes.

CHARLA DE MATEMÁTICAS

• DOK-1 «¿Qué es la multiplicación?». La multiplicación combina grupos iguales en una cantidad total.

• DOK-2 «¿Por qué crees que usamos la multiplicación?». La multiplicación es útil porque es mucho más rápida que sumar los números uno por uno o contar individualmente.

• DOK-2 «¿Cuáles son algunas maneras en que podemos representar y resolver una oración de multiplicación?». Podemos usar grupos iguales.

• Elige una rutina de conversación estructurada para facilitar la siguiente pregunta:

◦ DOK-2 «¿Cómo se relacionan los modelos y las oraciones de multiplicación?». Los modelos representan directamente los números que se multiplican. Si hay 2 grupos con 5 fichas en cada grupo, el número 5 se está multiplicando por 2. Esto se traduce en multiplicación porque el signo × representa "grupos de". Esto significa que cada vez que aparece un número, ese número representa 1 grupo, por lo que si el número 5 aparece 2 veces, esto significa que hay 2 grupos de 5, que se escribe 2 × 5 = 10 como una oración de multiplicación.

APOYOS PEDAGÓGICOS

1. Al principio de la exploración, cuando se muestren y discutan los grupos iguales de contadores, proporcione un método alternativo para registrar la información auditiva y ofrezca una representación visual de la idea, como un esquema de anclaje. Mientras se organizan los grupos iguales de fichas, registre las conversaciones de los estudiantes sobre lo que notan en el modelo y el símbolo que representa la operación y lo que significa, y relacione la «frase grupos de» con cada modelo.

2. Al principio de la exploración, puede resultarles útil tener un organizador gráfico de las cuatro cosas que se les pide que representen en sus pizarras de borrado en seco. Dibuje un diagrama de ventana para mostrar cómo los estudiantes pueden mostrar el modelo, la descripción y la oración de multiplicación para cada grupo de fichas que se presenta.

3. Antes de pasar a la fase de representación, algunos estudiantes pueden necesitar más oportunidades para practicar con los manipulativos. Concédales tiempo para que trabajen con un compañero y se centren sólo en construir un modelo y usar sus palabras para explicar cómo representa la frase o el escenario de multiplicación. Una vez que los estudiantes entiendan cómodamente cómo un modelo se relaciona con un problema, pase a dibujar una representación del modelo.

4. Anime a los estudiantes a escribir los múltiplos de cada grupo para ayudarles a saltar la cuenta.

5. Al igual que con muchas otras habilidades matemáticas, es importante determinar si los errores de los estudiantes son conceptuales (falta de habilidades prerrequisito) o estratégicos (falta o confusión sobre el análisis de la tarea involucrada en la multiplicación). Si se trata de un error conceptual, es posible que el estudiante deba repasar los conocimientos previos, como el conteo salteado. Si se trata de un error de estrategia, sería útil que el estudiante explicara en voz alta lo que piensa mientras resuelve el problema para poder identificar los errores o las ideas erróneas.

EXPLORAR: EXPLORACIÓN 1

6. Para empezar a construir conocimientos útiles a los que referirse a lo largo de este alcance, pida a la clase que le ayude a crear un muro de palabras interactivo al que los estudiantes puedan referirse durante cada exploración u otras actividades. Muestre el vocabulario clave con los ejemplos correspondientes relacionados con la multiplicación, como grupos iguales, el símbolo de multiplicación ×, grupos de, y oración de multiplicación.

7. Como extensión, desafíe a los estudiantes a trabajar con un compañero para crear su propio modelo de multiplicación utilizando grupos iguales y un escenario del mundo real que podría representar. El compañero puede utilizar ese modelo para crear una frase de multiplicación y determinar una solución.

APOYOS LINGÜÍSTICOS

De ejemplos y aclare lo que significa tener grupos de una cantidad determinada de objetos. Puede ser útil proporcionar un ejemplo visual de esta frase junto con la frase traducida a las lenguas maternas de los estudiantes.

Explique los términos no matemáticos usados para los manipulativos en esta actividad, como contadores y platos, y cómo se utilizará ese vocabulario en las pláticas de los estudiantes sobre los modelos.

Proporcione estructuras de frases para que los estudiantes las utilicen durante la discusión con sus compañeros, así como durante el trabajo en grupo, cuando debatan cómo se representa un modelo:

• «Vemos ____ grupos».

• «Cada grupo tiene ____».

• «El número total de fichas es ____. Lo sé porque ____».

Cuando se pida a los estudiantes que representen diferentes tipos de grupos iguales utilizando sus fichas y platos, muestre un apoyo visual de estos pasos, divida las instrucciones en pasos más pequeños y destaque el verbo o la acción de cada paso poniendo el verbo en negrita:

1. Esboza el modelo de grupos iguales en la pantalla.

2. Describe de forma escrita utilizando "grupos de" (por ejemplo, "dos grupos de tres").

3. Traduzce eso en una frase de multiplicación (por ejemplo, 2 × 3 = 6).

Si es necesario, elabore una lista física de estos pasos en una hoja de papel separada para cada grupo y permita que los estudiantes marquen cada paso a medida que se realiza. Anímelos a repetir cada paso para cada descripción de grupo igual que usted proporcione, centrándose en la acción del verbo a medida que resuelven.

Represente lo que significa escribir una oración de multiplicación. Lea una en voz alta mientras la escribe. Por ejemplo, mientras escribe 5 × 9 = 40, diga «cinco veces nueve es igual a cuarenta» para enfatizar el significado de los símbolos matemáticos. Si los estudiantes necesitan apoyo adicional para representar simbólicamente un modelo con una oración de multiplicación, considere la posibilidad de anotar el modelo de un estudiante con números y modelar cómo los símbolos.

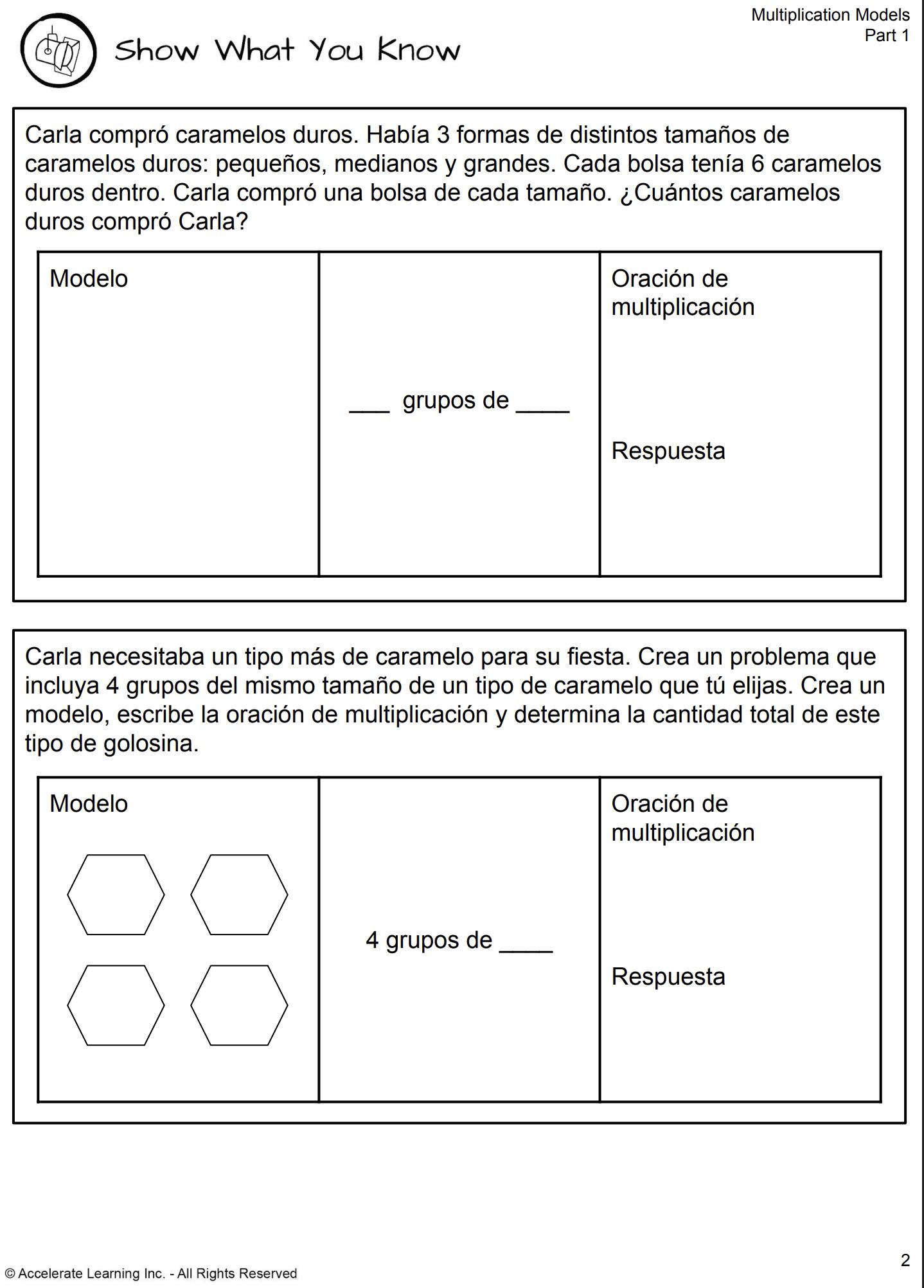
MUESTRE LO QUE SABE (PARTE 1)

EXPLORAR: EXPLORACIÓN 2

LECCIÓN PEDAGÓGICA

EXPLORACIÓN 2: COMPRENDER LA MULTIPLICACIÓN CON MATRICES

Estándar(es)

• Representar y resolver problemas de multiplicación y división. Interpretar productos de números enteros; por ejemplo, interpretar 5 × 7 como el número total de objetos en 5 grupos de 7 objetos cada uno. Por ejemplo, describir un contexto en el que un número total de objetos puede expresarse como 5 × 7.

Ideas fundamentales

Estándares para la práctica matemática

DESCRIPCIÓN

Estándares para la práctica matemática

MP.1 Dar sentido a los problemas y perseverar en su resolución.

MP.2 Razonar abstracta y cuantitativamente.

MP.6 Atender a la precisión.

MP.7 Buscar y hacer uso de la estructura.

Los estudiantes determinan el número total de objetos en un escenario utilizando matrices.

MATERIALES

IMPRESO

• 1 diario del estudiante (por estudiante)

• 1 juego de tarjetas de estación de pasillo (por clase)

• 1 boleto de salida (por estudiante)

REUTILIZABLE

• 60 fichas de colores (por grupo)

• 1 bolsa resellable (por grupo)

PREPARACIÓN

• Planifique que los estudiantes trabajen en 6 grupos para completar esta actividad.

• Imprima un diario del estudiante y un boleto de salida por alumno.

• Imprima el juego de tarjetas de estación de pasillo en cartulina y recórtalas.

• Coloque 60 fichas de colores en una bolsa resellable para cada grupo.

• Coloque 6 estaciones en el aula con una tarjeta de estación de pasillo y una bolsa de 60 fichas de colores en cada estación.

• Para los estudiantes que necesitan más apoyo para recordar información, consulte nuestros elementos de ayuda complementaria de papel cuadriculado y matriz de multiplicación en la sección «Intervención».

Conexiones de contenido Motores de investigación

CC2 Explorar cantidades cambiantes

DI1 Dar sentido al mundo (Comprender y explicar)

• ¡Hazlo digital! Haga que los estudiantes exploren o presenten sus soluciones utilizando manipulativos virtuales. Los manipulativos usados en esta lección se pueden encontrar en el menú desplegable de la sección «Explorar» y se pueden asignar digitalmente a los estudiantes. (Fichas cuadradas de colores)

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Ayude a los estudiantes a acceder a la tarea formulando las siguientes preguntas de orientación:

a. «¿Te gusta ir al supermercado? ¿Por qué sí o por qué no?».

b. «¿Qué imaginas cuando piensas en una tienda de comestibles?».

c. «¿Qué sabes ya sobre la multiplicación?».

2. Lee la siguiente situación a la clase: «Tu jefe en el supermercado Wally World quiere que organices los mostradores del final del pasillo para las próximas rebajas. Cada pasillo tiene un número diferente de estantes y un número diferente de artículos que esos estantes pueden contener, dependiendo de cuán grandes o pequeños son los artículos que estás colocando en los estantes. El gerente le ha dicho qué artículos colocar en los estantes; sin embargo, es su trabajo registrar cuántos estantes hay, cuántos artículos caben en cada estante y cuántos artículos hay en total en toda la exhibición».

3. Coloque a los estudiantes en seis grupos. Dígales que hay fichas de colores que representan artículos de alimentación por toda la sala. Deben colocarlos de acuerdo con las instrucciones de las tarjetas de estación de pasillo.

EXPLORAR: EXPLORACIÓN 2

4. En la estación, deben registrar cada visualización dibujando un modelo de matriz y escribiendo una ecuación de multiplicación, una oración de multiplicación y un enunciado de solución en sus diarios del estudiante.

5. Supervise y hable con los estudiantes según sea necesario para verificar la comprensión usando las siguientes preguntas guía:

a. DOK-1 «¿Cuál es la diferencia entre una fila y una columna?». Una fila es horizontal y una columna es vertical. (Si observa que los estudiantes tienen dificultades para entender la diferencia entre filas y columnas, puede pedirles que imaginen un barco en el que reman con un remo para que se mueva. Se rema horizontalmente por el agua. Con una columna, puede pedirles que imaginen una casa con columnas de arriba abajo que la sostienen. La casa se caería si la columna estuviera horizontal o tumbada en el suelo.)

b. DOK-1 «¿Dónde hay algunas filas y columnas en nuestra habitación?». Las respuestas pueden variar: estanterías, semanas en un calendario, etc.

c. DOK-2 «¿Qué representa una fila en cada situación de la tarjeta de estación de pasillo?». Un estante representa una fila.

d. DOK-2 «¿Qué representa una columna en cada situación de tarjeta de estación de pasillo?». Cada artículo en un estante y todos los artículos directamente encima y debajo de él representan una columna.

e. DOK-1 «¿Cuáles son los números de filas y columnas que tienes que intentar hacer según la tarjeta de estación de pasillo?». Las respuestas pueden variar. Necesito hacer 4 filas con 6 columnas.

f. DOK-2 «¿Cómo se relacionan los grupos iguales y las matrices?». Cada fila tiene el mismo número de elementos, así como en un grupo igual.

g. DOK-1 «¿Cómo podrías encontrar el número total de elementos?». Las respuestas pueden variar. Podría omitir la cuenta por el número de elementos de cada fila. Podría usar la multiplicación porque tengo _____ filas con _____ en cada fila.

h. DOK-1 «¿Cómo se llama un modelo de filas iguales?». Una matriz

6. Al terminar, anime a los alumnos a platicar y escribir sus respuestas en sus diarios del estudiante.

7. Pídales que compartan sus estrategias y anímelos a hacerse preguntas y establecer conexiones. Diga a los estudiantes a que observen las similitudes y diferencias entre las estrategias usadas para construir una matriz y determinar el número total de elementos.

8. Después de la exploración, invita a la clase a una charla de matemáticas para compartir sus observaciones y aprendizajes.

DIARIO DEL ESTUDIANTE

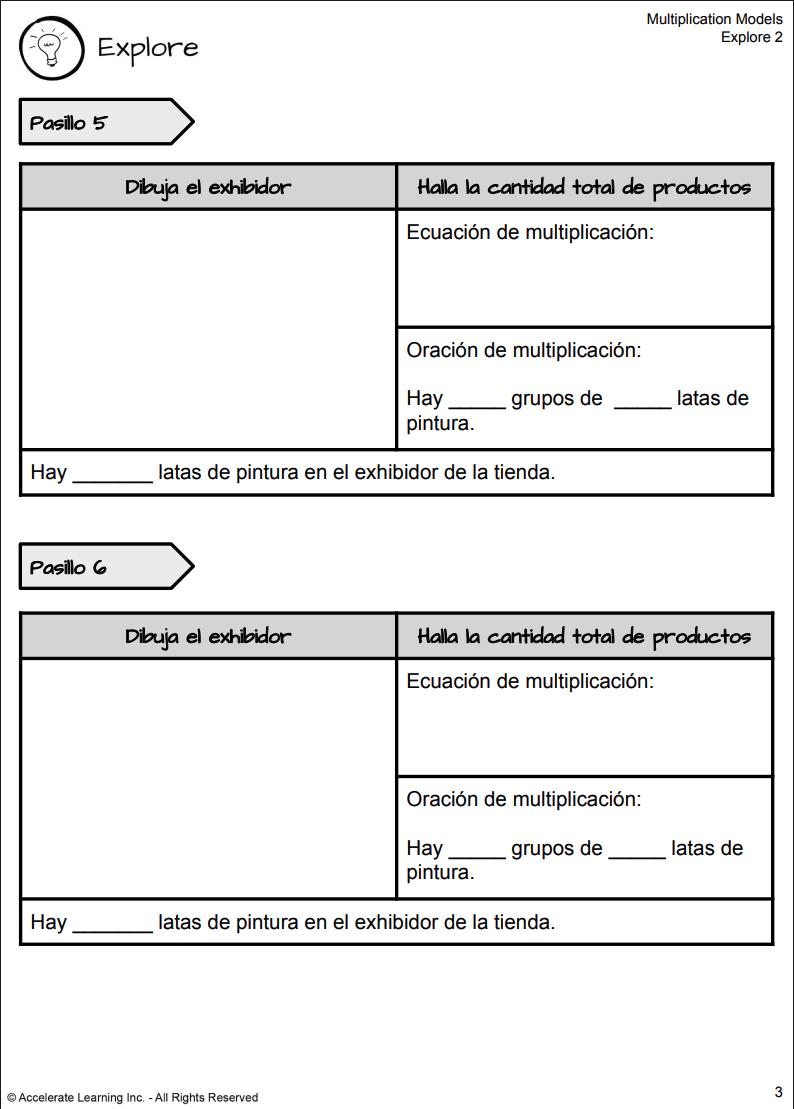
CHARLA DE MATEMÁTICAS

• DOK-2 «¿Qué operación es mejor para encontrar el total de artículos en exhibición sin tener que contar cada artículo? Explica». La mejor operación es la multiplicación porque tienes filas de artículos con el mismo número de artículos en cada fila.

• DOK-2 «¿Cómo tradujiste el modelo de matriz en una ecuación de multiplicación?». El número de filas en el modelo me dio mi primer factor porque cada fila es un grupo. El número de elementos en cada fila me dio el otro factor porque hay el mismo número de elementos en cada fila. El número total de ítems fue el producto.

• Elija una rutina de conversación estructurada para facilitar la siguiente pregunta:

◦ DOK-2 «Cada oración de multiplicación explica su matriz como "grupos de objetos". ¿Cómo muestran las matrices los grupos de objetos?». Cuando haces una matriz, tus objetos deben mostrarse en filas y columnas con un número igual de objetos en cada fila y columna. Esta matriz se explica entonces con cuántos grupos de objetos tiene en filas o columnas.

APOYOS PEDAGÓGICOS

1. Consolide el conocimiento previo de matrices revisando cómo se pueden construir a partir de filas o columnas iguales, y recuerde a los estudiantes que hacer grupos iguales dentro de este modelo está relacionado con la multiplicación.

2. Proporcione ejemplos y no ejemplos de objetos en filas o columnas iguales para una oración de multiplicación dada, como cuatro filas de tres. El uso de imágenes realistas de objetos para modelar filas/ columnas puede ser útil para hacer que el concepto sea más accesible antes de que los estudiantes intenten modelar este concepto por su cuenta.

3. Utilice un muro de palabras interactivo para mostrar vocabulario clave con ejemplos correspondientes relacionados con la multiplicación, como matriz, fila, columna, factor, producto, grupo, y elementos/ objetos.

4. Los estudiantes pueden construir modelos de los elementos en los estantes utilizando una variedad de herramientas, si no hay fichas de colores disponibles. Algunas herramientas posibles son el papel cuadriculado, los cubos conectables, los cubos centimétricos o las fichas de dos colores. DIARIO DEL ESTUDIANTE

EXPLORAR: EXPLORACIÓN 2

5. Para proporcionar una estructura adicional a medida que los estudiantes construyen sus modelos, deles una pizarra de borrado en seco y un rotulador para que puedan dibujar el número dado de estantes en los que colocar las baldosas.

6. Permita a los estudiantes tener un escribano o trabajar con compañeros para ayudar con la parte de dibujo de la exploración. Esto permite aumentar la interacción y elimina la necesidad de dibujar rápidamente. Como alternativa, podrían crear modelos pictóricos de sus matrices con papel cuadriculado.

7. Como ampliación, desafíe a los estudiantes a trabajar con un compañero para crear sus propias matrices. A continuación, otro compañero puede utilizar ese modelo para escribir la frase de multiplicación que representa la matriz.

APOYOS LINGÜÍSTICOS

Durante la exploración, anime a los estudiantes a usar las imágenes de las tarjetas de estación de pasillo para apoyar su comprensión del contexto del escenario de cada estación. Use elementos visuales cuando estén disponibles para evitar que se malinterpreten términos no matemáticos, como estanterías, sillones, puf, DVDs, y pantalla. Si hay estanterías en el aula, relaciónelas con el escenario y cómo sirven para representar el modelo. Ayude a los estudiantes a comprender cada escenario de las tarjetas de estación de pasillo leyendo la raíz del problema (sin la frase de acción) tres veces. Después de la primera lectura, pregunte: «¿De qué trata este escenario?». Escuche y aclare cualquier pregunta sobre el contexto. Después de la segunda lectura, pregunte: «¿Cuáles son los números que vemos en el escenario? ¿Qué representan estos números?». Después de la tercera lectura, aclare: «¿Qué preguntas matemáticas podrían responderse con esta información?». A continuación, pida a los estudiantes que creen un modelo y completen la información restante del escenario.

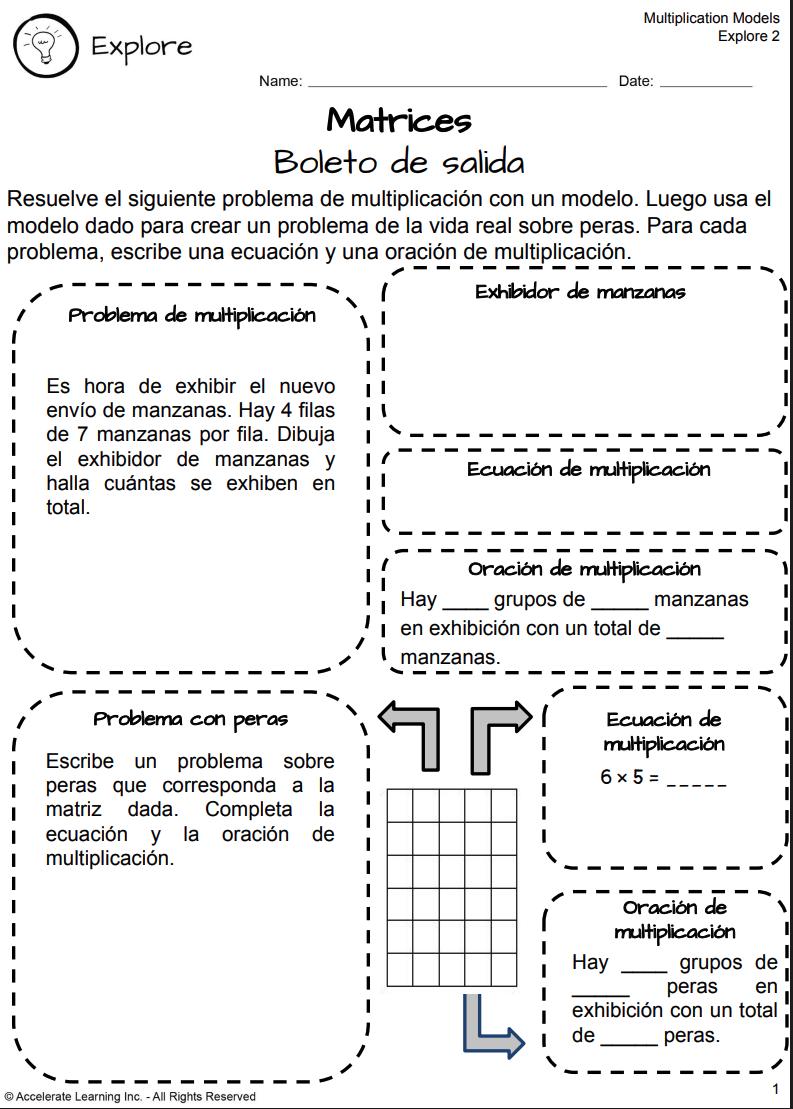
BOLETO DE SALIDA

MUESTRA LO QUE SABE (PARTE 2)

EXPLORAR: EXPLORACIÓN 2

Proporcione estructuras de oraciones para que los estudiantes las usen durante sus debates en grupos:

• «Nuestra matriz debe tener _____ filas y _____ columnas porque ....».

• «Podemos encontrar grupos iguales en nuestro modelo mirando el _____ ».

• «Sé que los _____ son iguales porque ....».

• «Podemos encontrar la cantidad total de elementos por ... ».

• «La cantidad total de elementos es _____».

• «La ecuación de multiplicación es _____».

Represente lo que significa escribir una ecuación de multiplicación. Lea en voz alta cómo se escribe. Por ejemplo, al escribir 6 × 3 = 18, diga «seis veces tres es igual a dieciocho». A medida que los estudiantes trabajan para representar cada situación, controle que representen los valores matemáticos de sus modelos en sus ecuaciones. Si observa que los estudiantes siguen necesitando apoyo adicional para representar la oración de multiplicación y la ecuación de su modelo, considere la posibilidad de anotar el modelo de un estudiante con números y modelar cómo se pueden utilizar los símbolos para representar lo que ocurre con esos valores.

EXPLORAR: EXPLORACIÓN 3

LECCIÓN PEDAGÓGICA

EXPLORACIÓN 3: MULTIPLICACIÓN CON DIAGRAMAS DE CINTAS

Estándar(es)

• Representar y resolver problemas de multiplicación y división. Interpretar productos de números enteros; por ejemplo, interpretar 5 × 7 como el número total de objetos en 5 grupos de 7 objetos cada uno. Por ejemplo, describir un contexto en el que un número total de objetos puede expresarse como 5 × 7.

Grandes ideas

Flexibilidad numérica hasta 100 para las cuatro operaciones

DESCRIPCIÓN

Estándares para la práctica matemática

MP.1 Dar sentido a los problemas y perseverar en su resolución.

MP.4 Representar con matemáticas.

MP.5 Usar herramientas apropiadas estratégicamente.

MP.6 Atender a la precisión

Los estudiantes interpretan productos de números enteros usando diagramas de cinta.

MATERIALES

IMPRESO

• 1 diario del estudiante (por estudiante)

• 1 juego de tarjetas de situación (por pareja)

• 1 boleto de salida (por estudiante)

REUTILIZABLE

• 1 pizarra de borrado en seco (por estudiante)

• 1 marcadorde borrado en seco (por estudiante)

• 10 cubos de enlace (por pareja) CONSUMIBLE

• 1 bolsa resellable (por pareja)

PREPARACIÓN

• Planifique que los estudiantes trabajen en parejas para completar esta actividad.

• Imprima un diario del estudiante y una tarjeta de salida por alumno.

• Imprima el conjunto de tarjetas de situación, recórtelas y colóquelas en una bolsa resellable para cada pareja de estudiantes.

• Prepare materiales de borrado en seco y cubos conectables para cada pareja de estudiantes.

• Para los estudiantes que necesiten más apoyo para recordar información, consulte nuestros elementos de «Ayudas complementarias» que incluyen papel cuadriculado en la sección «Intervención».

Conexiones de contenido Motores de investigación

CC2 Explorar cantidades cambiantes

DI1 Dar sentido al mundo (Comprender y explicar)

• Digitalízate ¡Hazlo digital! Haga que los estudiantes exploren o presenten sus soluciones utilizando manipulativos virtuales. Los manipulativos usados en esta lección se pueden encontrar en el menú desplegable de la sección «Explorar» y se pueden asignar digitalmente a los estudiantes. (Cubos conectables)

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Ayude a los estudiantes a acceder a la tarea haciendo las siguientes preguntas guía:

a. «¿Caminas, conduces o tomas el autobús para llegar a la escuela cada mañana?».

b. «¿Cómo es tu ruta a la escuela?».

c. «¿Qué recuerdas acerca de combinar grupos iguales de objetos?».

2. Lea el siguiente escenario a la clase: «Esta mañana, de camino al colegio, contaste nueve casas en la calle de tu barrio. Te diste cuenta de que todas las casas tienen exactamente seis ventanas. Empiezas a pensar que probablemente podrías ganar algo de dinero lavando ventanas en tu barrio. Te gustaría encontrar una forma de saber cuántas ventanas hay en total sin tener que contarlas individualmente».

3. Plantea a los estudiantes las siguientes preguntas:

a. DOK-2 «¿De qué formas diferentes podemos representar el número total de ventanas que se podrían lavar?». Las respuestas variarán. Podemos multiplicar el número de ventanas por casa por el número de casas usando matrices, grupos iguales, en palabras usando "grupos de", en oraciones de multiplicación, etc.

b. DOK-1 «¿Qué necesitamos encontrar?». Necesitamos encontrar el número total de ventanas.

DIARIO DEL ESTUDIANTE

4. Distribuya una pizarra de borrado en seco y un marcador a cada estudiante.

5. Coloque a los estudiantes en parejas y distribuya los cubos conectables a cada pareja.

6. Pida a los estudiantes que unan nueve cubos conectables. Dígales que estos cubos representan las casas. Formule a los estudiantes las siguientes preguntas:

a. DOK-2 «¿Qué más tenemos que hacer para representar el problema?». Aún necesitamos representar las 6 ventanas de cada casa.

b. DOK-2 «¿Qué podríamos hacer para modelar las 6 ventanas de cada casa?». Las respuestas pueden variar. Podríamos escribir 6 en cada cubo para hacer 9 grupos de 6.

7. Anime a los estudiantes a dibujar sus modelos en las pizarras y a comentar sus observaciones con sus compañeros. Formule las siguientes preguntas:

a. DOK-2 «¿Cómo has encontrado la solución a este problema?». Las respuestas pueden variar. Nos saltamos la cuenta de 6 en 6 porque teníamos 9 grupos de 6.

b. DOK-2 «¿Qué observaciones puedes hacer sobre tu modelo?». Este modelo utiliza un rectángulo para mostrar las partes de una cantidad total. Muestra "grupos de" en un rectángulo. Los grupos o partes del rectángulo que son del mismo tamaño representan el mismo valor. Nos ayuda a escribir una ecuación.

8. Explique que los modelos se llaman diagramas de cinta. Formule las siguientes preguntas:

a. DOK-1 «¿Qué expresión podrías escribir utilizando el diagrama de cinta que has creado para hallar el número de ventanas?». 9 × 6

b. DOK-2 «¿Cómo sabes que la expresión es verdadera?». Vemos 6 nueve veces. Vemos 9 grupos de 6.

9. Distribuya un diario del estudiante por alumno y una bolsa de tarjetas de situación por cada pareja.

10. Anímelos a usar cubos conectables y marcadores borrables para ayudar a construir y discutir un diagrama de cinta que represente cada problema.

11. Explique que los estudiantes registrarán sus diagramas de cinta, oraciones de multiplicación y oraciones de solución en sus diarios del estudiante.

12. Monitoree y hable con los estudiantes según sea necesario para verificar la comprensión usando las siguientes preguntas guía:

a. DOK-2 «¿Cómo te ayuda a dibujar tu diagrama de cinta conocer los "grupos de"?». El número de grupos es el número de secciones en el diagrama de cinta. El número en cada grupo representa el tamaño del grupo.

b. DOK-2 «¿Por qué las partes del diagrama de cinta deben ser del mismo tamaño?». Si representan el mismo valor, entonces deben ser del mismo tamaño.

c. DOK-1 «¿Cómo escribirías la oración de multiplicación?». Las respuestas variarán. Escribiríamos el número de secciones en el diagrama de cinta multiplicado por el número en cada sección.

d. DOK-1 «¿Cuáles son los factores en el diagrama de cinta?». Los factores son el número de secciones y el número en cada sección.

e. DOK-2 «¿Cómo ayuda el diagrama de cinta a encontrar el producto?». Las respuestas pueden variar. Puedes sumar todas las secciones en el diagrama de cinta. Puede saltar la cuenta hasta obtener un producto. Puedes multiplicar el factor en el diagrama de cinta por el número de veces que lo ves. Puedes escribir el hecho de la multiplicación.

13. Si los estudiantes han completado las tarjetas de situación antes de que lo hayan hecho sus compañeros, anímelos a crear sus propios problemas escritos y a que dibujen un diagrama de cinta y una oración de multiplicación para que coincidan.

14. Pida a los estudiantes que compartan sus estrategias y anímeles a que se hagan preguntas y establezcan conexiones. Invítelos a notar las similitudes y diferencias entre las estrategias usadas para interpretar productos de números enteros usando diagramas de cinta.

15. Después de la exploración, invite a la clase a una charla de matemáticas para compartir sus observaciones y aprendizajes.

CHARLA DE MATEMÁTICAS

• DOK-3 «¿Qué situaciones notan en estos problemas que les indican que la operación es la multiplicación?». En cada situación, estamos combinando grupos iguales y hallando el total. Sé que puedo usar la multiplicación para combinar grupos iguales y determinar el total.

• Elige una rutina de conversación estructurada para facilitar la siguiente pregunta:

◦ DOK-2 «¿Cómo se comparan los diagramas de cinta con otros modelos de multiplicación?». Los diagramas de cinta pueden parecer diferentes de los grupos iguales y de las matrices, pero todos representan grupos iguales que se multiplican un cierto número de veces, lo que da como resultado un producto.

• DOK-2 «Explique cómo el modelo de diagrama de cinta representa una ecuación de multiplicación». En un diagrama de cinta, tenemos un número de secciones iguales que representan el número de grupos en un problema. Dentro de cada una de las secciones iguales, hay el mismo número, que representa el segundo factor que se multiplica, o el número de objetos en cada grupo. Multiplicando el número de secciones iguales por el número de cada sección se obtiene el producto.

APOYOS PEDAGÓGICOS

1. Continúe usando un muro de palabras interactivo para mostrar el vocabulario clave con los ejemplos correspondientes relacionados con la multiplicación. Asegúrese de añadir un ejemplo y descripción del diagrama de cinta.

2. Comenzar con un repaso rápido del conteo salteado por múltiplos puede ser muy beneficioso a la hora de resolver problemas de multiplicación. Si, durante la exploración, un estudiante necesita apoyo adicional, recuérdele que estrategias como hacer grupos iguales o crear matrices puede ayudarle a empezar a resolver el problema.

3. Algunos pueden seguir necesitando objetos concretos, como los contadores utilizados en la «Exploración 1», para representar y resolver el problema. Pueden usar fichas para representar el valor de cada cubo conectable y ver cómo los múltiplos se acumulan para representar la situación y cómo se relaciona con la multiplicación. Adicionalmente, anime a los estudiantes a avanzar hacia la etapa abstracta retirando los manipulativos hacia el final de los problemas y trabajando para resolverlos con un modelo del diagrama de cinta.

4. Proporcione flexibilidad a los estudiantes que puedan necesitar tareas reducidas permitiéndoles completar menos tarjetas de escenario.

5. Busque oportunidades para enfatizar lo duro que los estudiantes están trabajando y el beneficio de la lucha productiva cuando se aprende algo nuevo.

6. Como extensión, desafíe a los estudiantes a elegir uno de los escenarios o crear uno propio con cubos conectables, un diagrama de cinta y una oración de multiplicación. A continuación, los estudiantes tomarán fotografías digitales de su representación y las publicarán en un esquema de anclaje o en una presentación digital para que puedan consultarlas a medida que profundizan en su conocimiento de los distintos modelos de multiplicación.

BOLETO DE SALIDA

MUESTRE LO QUE SABE (PARTE 3)

EXPLORAR: EXPLORACIÓN 3

APOYOS LINGÜÍSTICOS

Dedique tiempo a explicar y mostrar un ejemplo de los términos no matemáticos, como cubos conectables, utilizados para los manipulativos en esta exploración y cómo se utilizará ese vocabulario en las discusiones de los estudiantes sobre los modelos.

Ofrezca inicios de oraciones para que los estudiantes los usen durante las conversaciones en grupo:

• «Cada cubo conectable representa _____».

• «El número en el cubo conectables representa _____».

• «Podemos utilizar nuestro modelo para ayudarnos a determinar el total en _____».

• «La cantidad total es _____».

Pida a los estudiantes que se turnen para leer las tarjetas de situación dentro de sus grupos. Los estudiantes que no lean en voz alta deben seguir la lectura. Una vez leída la situación, deben comprobar su comprensión mutua haciendo que cada uno de ellos repita la información dada antes de que el grupo empiece a trabajar en el problema. Asegúrese de que los estudiantes se escuchan atentamente unos a otros y corrigen la información si es necesario.

Cuando determinen una frase de solución para cada situación en sus diarios del estudiante, pídales que se turnen para decir primero sus respuestas en voz alta a un miembro del grupo, recibir comentarios de ese miembro del grupo y, a continuación, escribir sus respuestas en los diarios del estudiante. Los alumnos pueden hacer las revisiones necesarias.

EXPLORAR: EXPLORACIÓN 4

LECCIÓN PEDAGÓGICA

EXPLORACIÓN 4: RECTAS NUMÉRICAS Y CONTAR SALTEADO

Estándar(es)

• Representar y resolver problemas de multiplicación y división. Interpretar productos de números enteros; por ejemplo, interpretar 5 × 7 como el número total de objetos en 5 grupos de 7 objetos cada uno. Por ejemplo, describir un contexto en el que un número total de objetos puede expresarse como 5 × 7.

Grandes ideas

Flexibilidad numérica hasta 100 para las cuatro operaciones

DESCRIPCIÓN

Estándares para la práctica matemática

MP.1 Dar sentido a los problemas y perseverar en su resolución.

MP.4 Representar con matemáticas.

MP.5 Usar herramientas apropiadas estratégicamente.

MP.6 Atender a la precisión.

MP.7 Buscar y hacer uso de la estructura.

Los estudiantes usan rectas numéricas y múltiplos para resolver problemas de multiplicación.

MATERIALES

IMPRESO

• 1 diario del estudiante (por estudiante)

• 1 juego de tarjetas de embalaje (por grupo)

• 1 boleto de salida (por estudiante)

REUTILIZABLE

• 1 regla de 1 metro (por grupo)

• 1 marcador de borrado en seco (por grupo)

• 1 pizarra de borrado en seco (por grupo, opcional) CONSUMIBLE

• 1 rollo de cinta de embalar (por grupo)

• 1 sobre de manila (por grupo)

• 1 pegamento en barra (por clase)

Conexiones de contenido

Motores de investigación

CC2 Explorar cantidades cambiantes

DI1 Dar sentido al mundo (comprender y explicar)

PREPARACIÓN

• Planee que los estudiantes trabajen en grupos de 3 o 4 para completar esta actividad.

• Imprima un diario del estudiante y un boleto de salida para uno.

• Imprima cada grupo de artículos de las tarjetas de embalaje en cartulinas de diferentes colores.

• Recorte y coloque un juego de tarjetas de embalaje en un sobre manila por grupo.

• Pegue un dibujo de la mochila de camping de las tarjetas de embalaje en la parte delantera de cada sobre.

• Cubra la parte delantera de las regla de 1 metro con cinta de embalar para crear una superficie que se pueda borrar.

• Para los estudiantes que necesiten más apoyo para recordar información, consulte nuestros elementos de «Ayudas complementarias» que incluyen: línea numérica abierta en la sección «Intervención».

• Digitalízate ¡Hazlo digital! Haga que los estudiantes exploren o presenten sus soluciones utilizando manipulativos virtuales. Los manipulativos usados en esta lección se pueden encontrar en el menú desplegable de la sección «Explorar» y se pueden asignar digitalmente a los estudiantes. (Rectas numéricas)

4

DIARIO DEL ESTUDIANTE

PROCEDIMIENTO Y PUNTOS DE APOYO

1. Muestre a los estudiantes los sobres. Lea la siguiente situación a la clase: «Nos vamos a acampar. Hay muchas cosas que preparar. Tenemos que hacer la maleta con todo lo necesario. Al comprar las provisiones, nos hemos dado cuenta de que muchos artículos vienen en paquetes. Necesitamos saber cuántos tenemos de cada artículo para asegurarnos de que estamos preparados para nuestro viaje».

2. Ayude a los estudiantes a acceder a la tarea haciéndoles las siguientes preguntas:

a. «¿Has ido a acampar alguna vez? Si es así, ¿cómo fue?».

b. «¿Cuáles son algunas cosas que podrías necesitar para empacar para un viaje de campamento?»

c. «¿Qué has aprendido hasta ahora sobre la multiplicación?».

3. Entregue un diario del estudiante por alumno.

4. Coloque a los estudiantes en grupos. Entregue un sobre de manila, una regla de 1 metro y un marcador de borrado en seco a cada grupo.

5. Desafíe a los estudiantes a usar sus reglas de 1 metro para encontrar el número total de cada artículo y registrar su trabajo en sus diarios del estudiante.

6. Monitoree y hable con los estudiantes según sea necesario para verificar la comprensión usando las siguientes preguntas guía:

a. DOK-1 «¿Cuántos paquetes hay? ¿Cuántos hay en cada paquete?». Las respuestas pueden variar. Hay 2 paquetes de 8 pares de calcetines.

b. DOK-2 «¿Cómo usaron la recta numérica (regla) para representar los paquetes de artículos?». Saltamos contados por el número de artículos en cada paquete. Podíamos saltar esa misma cantidad en la recta numérica cada vez que contábamos un paquete. Por ej., cada paquete de Battery Buddies es un grupo de tres pilas, así que saltamos tres números a la derecha en la recta numérica cada vez que contamos un paquete y contamos de tres en tres.

7. Pida a los estudiantes que compartan sus estrategias y anímelos a que se hagan preguntas y establezcan conexiones. Pida que se fijen en las similitudes y diferencias entre las estrategias usadas para multiplicar con rectas numéricas y el conteo salteado.

8. Después de la exploración, invite a la clase a una charla de matemática para compartir sus observaciones y aprendizajes.

EXPLORAR: EXPLORACIÓN 4

CHARLA DE MATEMÁTICAS

• DOK-2 «¿Cómo podemos mostrar la multiplicación en una recta numérica?». Cada salto en la recta numérica es como un grupo igual, y el número de saltos muestra el número de grupos. Si quiero mostrar 5 grupos de 4, podría saltar 4 espacios 5 veces.

• Elija una rutina de conversación estructurada para facilitar la siguiente pregunta:

◦ DOK-2 «¿Cuál es la relación entre los saltos iguales en una recta numérica y el conteo de saltos?». Cada vez que saltas en una recta numérica, aterrizas en un múltiplo del factor. Aterrizas en los números que dirías si estuvieras contando saltos por ese factor.

• DOK-3 «Comparte un error que hayas cometido durante la exploración. ¿Qué aprendieron tú y tu grupo?». Nos equivocamos al contar las cajas de cerillas. Aprendimos a contar con cuidado y a comprobar nuestro trabajo. También aprendimos que si te equivocas en un múltiplo, el resto de tus múltiplos podrían ser incorrectos, por lo que es importante tener cuidado.

APOYOS PEDAGÓGICOS

1. Continúa utilizando un muro de palabras interactivo para mostrar vocabulario clave con ejemplos correspondientes relacionados con la multiplicación, asegurándote de agregar un ejemplo y una descripción de una recta numérica a esta exhibición.

2. Si es posible, proporciona reglas de medir adicionales para que más estudiantes puedan practicar el conteo en saltos. Los estudiantes pueden comprobar el recuento de los demás y comparar las soluciones.

3. En lugar de la regla de metro, algunos estudiantes pueden preferir una recta numérica abierta y la suma repetida para encontrar los múltiplos para el recuento de saltos.

4. Puede ser útil permitir que los estudiantes usen manipulativos, como cubos conectables, junto a sus rectas numéricas para ayudar a representar su pensamiento. Pueden usar cubos para representar el valor de cada salto en la recta numérica y cómo ese modelo se relaciona con la multiplicación. A modo de ampliación, anime a los estudiantes a pasar a la fase abstracta retirando los manipulativos hacia el final de los problemas y resolviendo utilizando sólo el modelo de la recta numérica.

5. A modo de ampliación, anime a los estudiantes a encontrar grupos iguales de objetos por el aula y a utilizar sus rectas numéricas y el conteo salteado para hallar el número total de objetos.

BOLETO DE SALIDA

LO QUE SABE (PARTE 4)

APOYOS LINGÜÍSTICOS

Para los hispanohablantes, relacionar la palabra number line con recta numérica. Hable de las semejanzas entre otros términos matemáticos en inglés y español relacionados con este explore, como múltiple para múltiple. Incluya a hablantes de todas las lenguas y pregúnteles si notan alguna similitud con sus lenguas maternas en el vocabulario matemático.

Ayude a los estudiantes a identificar los verbos en las instrucciones del diario del estudiante, como «rodea los múltiplos» y «colócalos en la recta numérica», y pregúnteles cómo estos verbos dan dirección en la tarea. Discuta cómo el uso de diferentes verbos significaría diferentes expectativas para las respuestas de los estudiantes.

Proporcione estructuras de oraciones para que los estudiantes las usen cuando debatan con sus grupos cómo se representa un modelo:

• «Hay ____ paquetes en el sobre de la bolsa de acampar».

• «Cada paquete contiene ____».

• «Podemos usar la recta numérica para ayudarnos a determinar el total por ___».

• «La cantidad total es ___».

Cuando verbalice la estrategia de un estudiante, hable en voz alta para crear un lenguaje matemáticamente preciso. Por ejemplo: «Veo que has omitido contar de dos en dos porque has rodeado con un círculo los múltiplos de dos en tu vara de medir. La ecuación de multiplicación que usaste para representar este modelo fue 8 × 2 = 16».

Mientras los estudiantes trabajan y discuten ideas con sus grupos, resuma lo que escucha y repita las ideas y el vocabulario clave a través de la entonación, el habla más lenta y las señales visuales, como grupos iguales, contar salteando, múltiple, multiplicar, y recta numérica. Anote esas palabras y frases con dibujos que las representen y ayude a los estudiantes a utilizarlas.

MUESTRE

EXPLICAR: ESQUEMA DE ANCLAJE

CONSOLIDAR EL APRENDIZAJE DEL ESTUDIANTE

ESQUEMA DE ANCLAJE

DESCRIPCIÓN

Este esquema de anclaje destaca las operaciones de multiplicación por una variedad de métodos, grupos de igual tamaño, matrices, diagramas de cinta y saltos iguales en una recta numérica. También destaca expresiones de multiplicación como comparaciones.

EXPLORACIÓN 1: GRUPOS IGUALES

1. Después de que los estudiantes hayan completado la exploración, dibuje tantos círculos como desee en llos esquemas de anclaje. Coloque la misma cantidad de notas adhesivas pequeñas en cada círculo. Haga las siguientes preguntas a los estudiantes:

a. «¿Cuántos círculos hay en el esquema de anclaje?». Las respuestas variarán en función de cuántos haya dibujado el maestro.

b. «¿Qué observas en el número de notas adhesivas de cada círculo?». Hay el mismo número de notas adhesivas en cada círculo.

c. Pida a un estudiante que complete los espacios en blanco para describir los grupos iguales: «_____ grupos de _____». Las respuestas pueden variar. 4 grupos de 8

d. «¿Qué operación se utiliza para hallar el valor de los grupos iguales?». Multiplicación

e. «¿Qué oración de multiplicación se puede escribir para este modelo? Pida a un estudiante que la escriba en la tabla de anclaje». Las respuestas variarán. 4 × 8 = 32

2. Retire igual número de notas adhesivas de cada círculo y pregunte qué cambió y qué permaneció igual. El número de notas adhesivas en cada círculo cambió, pero el número de círculos (grupos) permaneció igual.

a. «¿Cambiará esto la oración de multiplicación? Explícalo». Sí. Las respuestas pueden variar.

3. A continuación, marque un círculo entero (pero no quite más notas adhesivas de otros círculos). Pregunte qué ha cambiado y qué ha permanecido igual. El número de círculos (grupos) ha disminuido, pero el número de notas adhesivas sigue siendo el mismo.

a. «¿Cambiará esto la oración de multiplicación? Explícalo». Sí. Las respuestas pueden variar.

EXPLORACIÓN 2: COMPRENDER LA MULTIPLICACIÓN CON MATRICES

1. Lea la siguiente situación a los estudiantes: «Jalid está jugando con sus coches de juguete. Coloca los coches en tres filas con siete coches en cada fila». Pida a los estudiantes que debatan cómo representarían esta situación como una matriz. A continuación, pida a un estudiante que vaya a la tabla de anclaje y dibuje la matriz.

a. «¿Cómo podrías resolver este problema por adición?». Sabemos que hay siete coches en tres filas, así que podríamos sumar 7 + 7 + 7 para obtener 21 coches.

b. «¿Cómo puedes expresar esto como grupos de números?». Hay 3 grupos de 7.

c. «¿Cómo podrías resolver este problema por multiplicación?». Como sabemos que hay tres grupos con el mismo número de coches en cada grupo, podemos multiplicar 3 veces 7 para obtener 21 coches.

2. Pregunte cómo el uso de la multiplicación hace que el problema sea más fácil de resolver. No tiene que contar cada uno de los x. Como sabe que hay números iguales en cada fila, sólo tiene que multiplicar las filas por el número de cada fila.

3. Pida a un estudiante que dibuje esta matriz como un modelo de área. «¿Cambia esto el problema de suma o multiplicación?». No. Un modelo de área es sólo otra forma de representar la multiplicación.

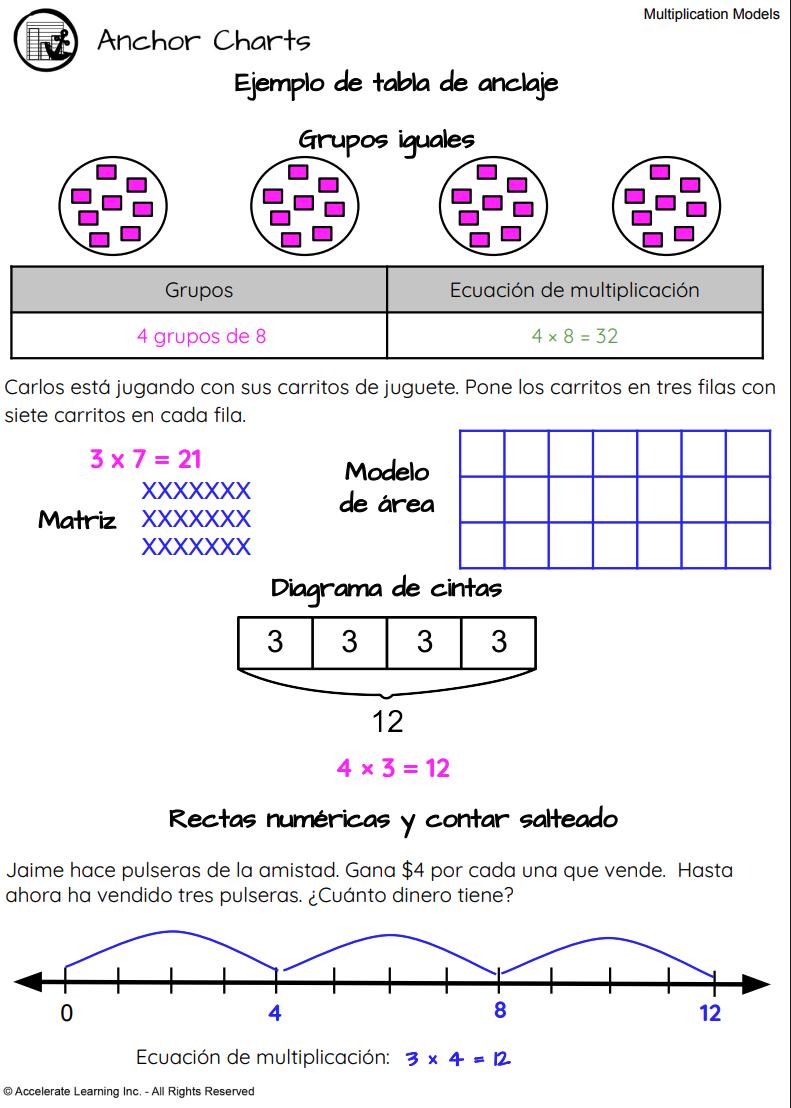
EJEMPLO DE ESQUEMA DE ANCLAJE

EXPLORACIÓN 3: MULTIPLICACIÓN CON DIAGRAMAS DE CINTAS

1. Lea la siguiente situación a los estudiantes: «En cada hornada de bizcochos se usan 3 huevos. «¿Cuántos huevos necesitarás para hacer 4 tandas de bizcochos?».

2. Haga que los estudiantes discutan cómo podrían representar este problema usando un diagrama de cinta. Luego pida a un estudiante que lo dibuje en el esquema de anclaje.

a. «¿Cuál es el valor de cada grupo y qué representa?». Cada grupo tiene un valor de 3 y representa la cantidad de huevos de cada lote.

b. «¿Cuántas unidades hay y qué representan?». Hay 4 grupos, que representan 4 lotes.

c. «¿Cuál es la cantidad total de huevos utilizados en 4 lotes?». 12

d. «¿Qué oración de multiplicación representa la cantidad de huevos en 4 lotes?». 4 × 3 = 12

EXPLORACIÓN

4: RECTAS NUMÉRICAS Y CONTAR SALTEADO

1. Lea la siguiente situación a los estudiantes: «Jayme hace pulseras de la amistad. Gana $4 por cada pulsera que vende. Hasta ahora ha vendido tres pulseras. ¿Cuánto dinero ha ganado?».

2. Pida a los estudiantes que conversen en clase cómo representar esto usando saltos iguales en una recta numérica; luego pídales que lo dibujen en el esquema de anclaje (etiquetando el múltiplo donde cae cada salto).

a. «¿Qué múltiplos usaste para saltar la cuenta?». Jayme ganó $4 por cada pulsera, así que los múltiplos fueron 4, 8, 12.

b. «¿Cómo puedes hacer una ecuación de multiplicación a partir de la recta numérica?». Cada salto representa un grupo o una cantidad. Había tres saltos de $4 cada uno, así que la ecuación sería 3 × 4 = 12.

c. Haga que un estudiante venga a escribir la ecuación en el esquema de anclaje.

EXPLICAR: LIBRETA INTERACTIVA

DOCUMENTAR EL APRENDIZAJE DEL ESTUDIANTE

LIBRETA INTERACTIVA

DESCRIPCIÓN

Los estudiantes toman notas, expresan ideas y/o procesan la información presentada en clase utilizando la actividad y el cuaderno.

MATERIALES

IMPRESO

• 1 folleto del estudiante (por alumno)

PREPARACIÓN

• Imprima una copia del folleto del estudiante (por alumno).

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Prepare una libreta interactiva con un cuadeno de espiral o de composición por estudiante. Así pueden usar las primeras páginas para crear un índice con números de página para llevar un registro de las actividades.

2. Recorte previamente o deje que los estudiantes recorten las piezas de cada material para el alumno según las instrucciones del maestro que aparecen en el recuadro de la primera página.

3. De tiempo a los estudiantes para que completen la actividad y luego peguen las piezas en su libreta interactiva.

4. Las libretas interactivas pueden utilizarse como referencia durante el trabajo independiente y pueden enviarse a casa al final del año como registro del aprendizaje de los estudiantes.

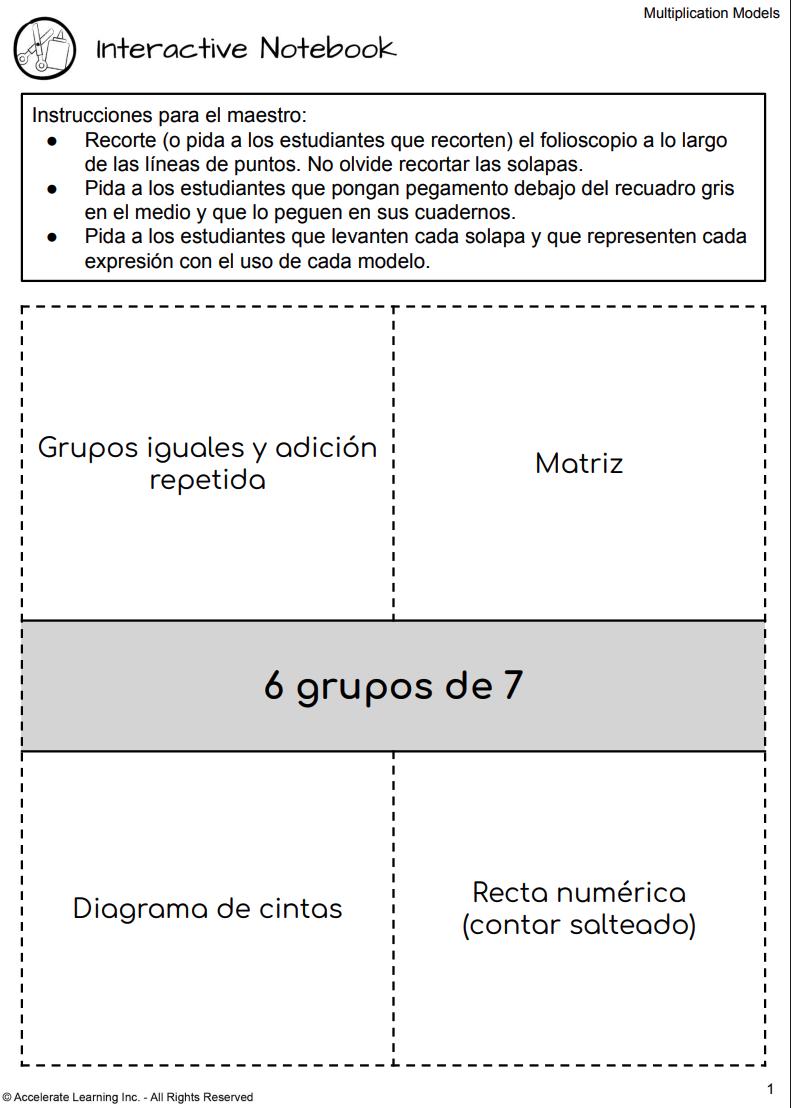
DEL ESTUDIANTE

FOLLETO

DESCRIPCIÓN

Los estudiantes tienen la oportunidad de utilizar sus conocimientos lingüísticos y culturales previos para apoyar las conexiones con nuevas destrezas, vocabulario y conceptos en sus niveles de competencia.

MATERIALES

IMPRESOS

• 1 folleto del estudiante según su nivel de competencia (por alumno)

REUTILIZABLES

• 100 contadores (por estudiante)

PREPARACIÓN

• Determine el nivel de competencia en inglés de cada alumno.

• Imprima un folleto del estudiante por alumno según su nivel de inglés.

• Permita que los estudiantes tengan acceso al vocabulario ilustrado para este alcance.

• Permita que los estudiantes tengan acceso a manipulativos como contadores.

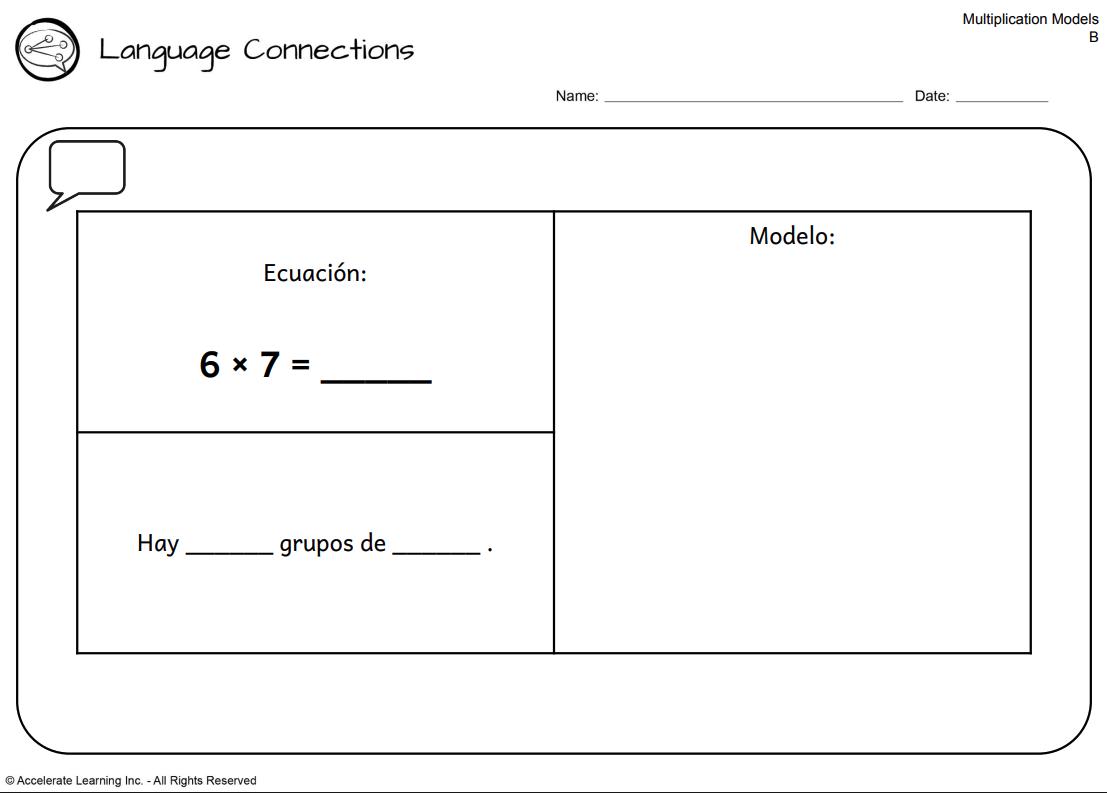
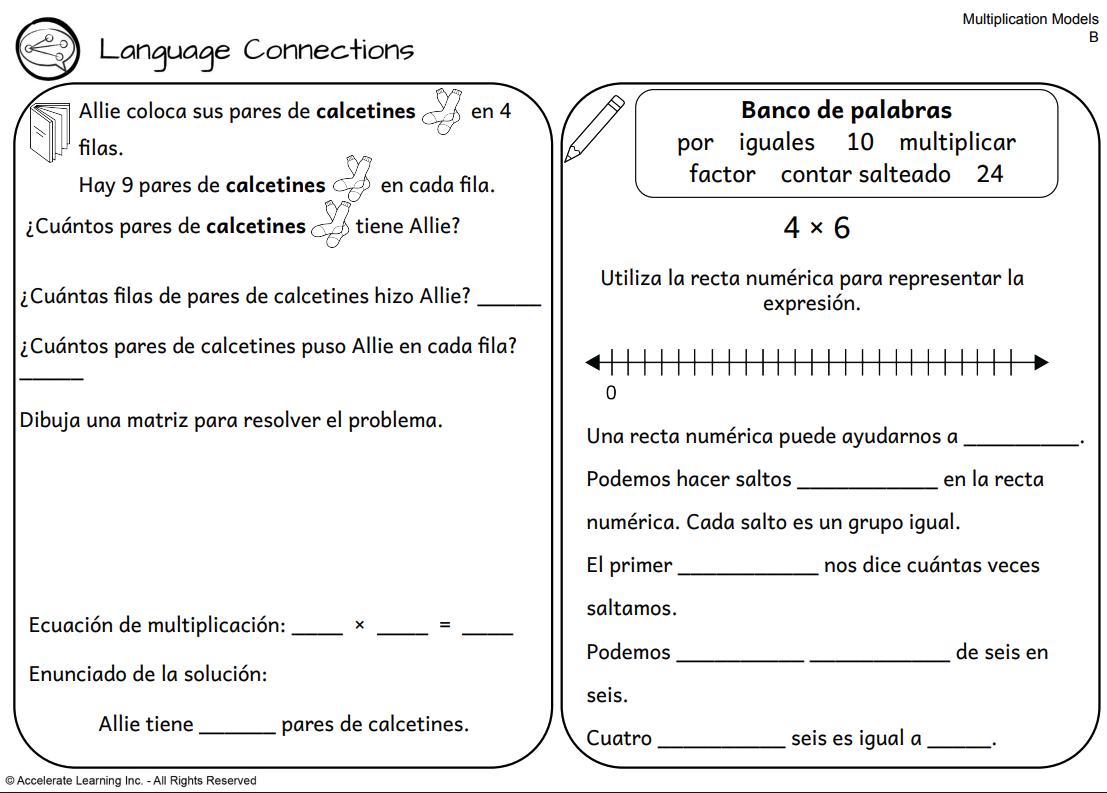
PRINCIPIANTE

DEL ESTUDIANTE

EXPLICAR: CONEXIONES LINGÜÍSTICAS

APOYO PARA ESTUDIANTES MULTILINGÜES

CONEXIONES LINGÜÍSTICAS

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Distribuya un folleto del estudiante según su nivel de competencia para cada alumno.

2. Use las instrucciones para las partes de escuchar, leer, hablar y escribir. Use gestos, señale objetos y elementos visuales, según proceda. Consulte las indicaciones para obtener sugerencias.

3. Conceda tiempo a los estudiantes para que piensen antes de responder.

4. Anímelos a perseverar en su pensamiento y usar herramientas y modelos matemáticos.

5. Invítelos a responder adecuadamente a cada dominio lingüístico.

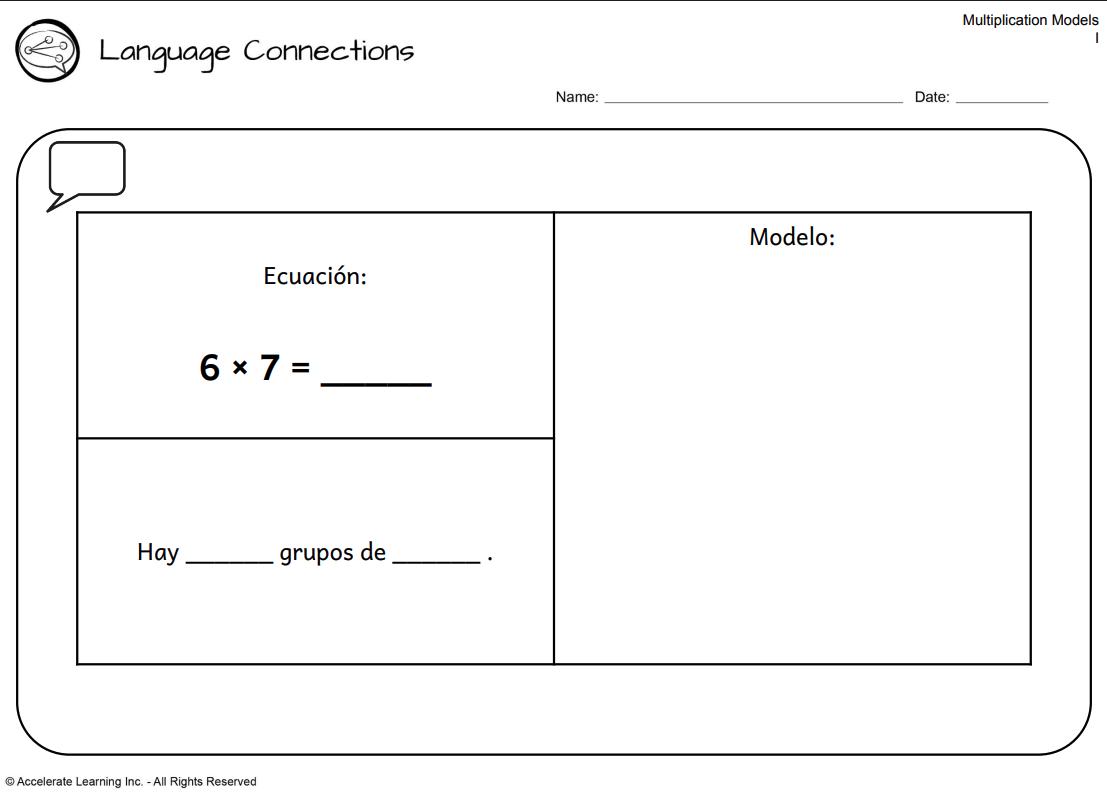
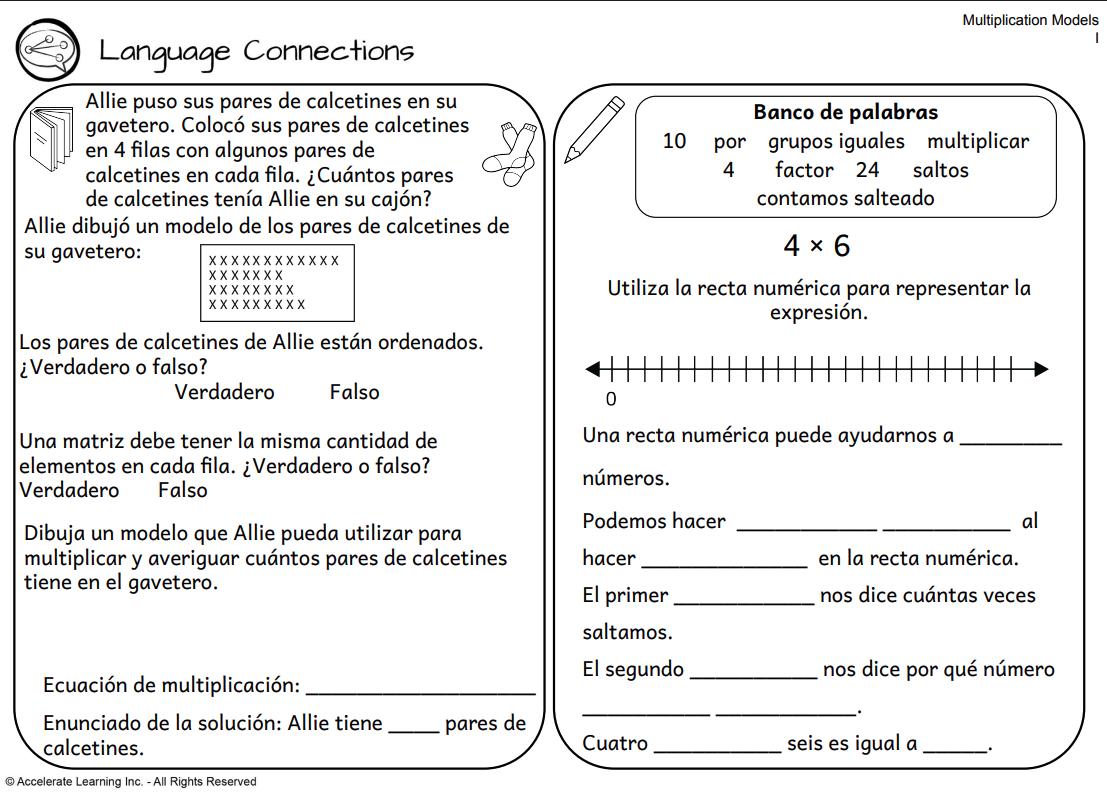
EXPLICAR: CONEXIONES LINGÜÍSTICAS

HABLAR

PRINCIPIANTE

Tenga fichas a mano para que los estudiantes las usen. Lea las siguientes indicaciones de uno en uno.

• Mira la ecuación 6 × 7 = en blanco.(Señale la ecuación).

¿Qué nos dice el símbolo (señale el símbolo de multiplicación) que estamos haciendo con estos dos números? (Pida a los estudiantes que utilicen el siguiente marco de oraciones):

◦ Estamos _______ 6 y 7.

• Miren el modelo que dibujaron. (Señale la maqueta). ¿Cuántos grupos de fichas hay? (Señale cada grupo). (Haga que los estudiantes usen estas frases):

◦ Hay _____ grupos de fichas.

• ¿Cuántas fichas hay en cada grupo? (Señale cada ficha de un grupo). Haga que los estudiantes usen estas frases):

◦ Hay _____ fichas en cada grupo.

• ¿Qué observas en los grupos? (Pida a los estudiantes que utilicen la siguiente estructura de frases):

◦ Todos los grupos tienen un _______ número de fichas.

• ¿Cuál es el producto de 6 multiplicado por 7? (Señale el producto de la ecuación). Pida a los estudiantes que utilicen la siguiente estructura de frases:

◦ 6 por 7 es igual a _____.

• ¿Cómo has encontrado el producto de 6 × 7? (Pida a los estudiantes que usen la siguiente estructura de oración):

◦ Usé los contadores para hacer 6 _____ de 7 para encontrar el producto ______.

LEER

PRINCIPIANTE

Disponga de fichas. Lea en grupo el problema de la historia. Pida a los estudiantes que señalen cada palabra mientras leen. Invíteles a rodear con un círculo las palabras que no conozcan. Revise las palabras entre todos, dando ejemplos cuando sea necesario.

• (Lea cada pregunta y pida a los estudiantes que señalen cada palabra mientras leen). ¿Cuántas filas (señale el problema de la historia) de calcetines hizo Allie? ¿Cuántos calcetines puso en cada fila?

• (Lea las instrucciones y pida a los estudiantes que señalen cada palabra mientras leen). Dibuja una matriz para resolver el problema.

• ¿Qué es una matriz? (Pida a los estudiantes que usen las siguientes frases):

◦ Una matriz tiene objetos dispuestos en ______ y columnas.

◦ Una matriz tiene un _______ número de objetos en cada fila.

Haga eco de los enunciados restantes y anime a los estudiantes a que señalen cada palabra mientras leen. Pídales que se refieran al problema escritos y a sus modelos para encontrar las respuestas haciendo que señalen.

Permítales que usen contadores según sea necesario.

INTERMEDIO

Tenga contadores disponibles para que los estudiantes los usen. Lea las siguientes instrucciones de una en una.

• Observa la ecuación 6 × 7 = en blanco. Comparte con tus compañeros lo que notas sobre la ecuación.

◦ ¿Qué representa cada símbolo?(Señale cada símbolo).

◦ ¿Qué representa cada número?

◦ Para encontrar la respuesta, ¿cuántos grupos dibujaste en tu modelo? ¿Cuántas fichas dibujaste en cada grupo de tu modelo?

• Explica a tus compañeros cómo hiciste tu modelo. (Pida a los estudiantes que usen los siguientes enunciados):

◦ Primero hice...

◦ Luego puse...

• Comenta con tus compañeros cuándo podrías utilizar grupos iguales en la vida real. ¿Cómo facilita esto la comprensión de la multiplicación?

INTERMEDIO

Tenga contadores disponibles para los estudiantes. Haga una lectura coral del problema de la historia. Pida a los estudiantes que señalen cada palabra mientras leen. Invíteles a rodear con un círculo las palabras que no conozcan. Revisen las palabras juntos o en parejas, proporcionando ejemplos según sea necesario.

• Comparte con tus compañeros dos cosas que sepas sobre el problema de la historia. Señala dónde puedes encontrarlas en el párrafo.

• (Coro): lee el enunciado debajo del problema de la historia. Comenta con tus compañeros lo que notas en el modelo que dibujó Allie.

• ¿Qué es una matriz? (Pida a los estudiantes que usen las siguientes oraciones):

• Una matriz tiene objetos organizados...

• Cada fila de un arreglo tiene...

• (Coro): lee las afirmaciones debajo del modelo de Allie. Decide si cada afirmación es verdadera o falsa. Rodea con un círculo la respuesta correcta. Explica tus respuestas a tus compañeros.

• (Lectura coral del resto de las instrucciones). Dibuja tu modelo. Compara tu modelo con el de tu compañero.

• Escribe la ecuación y completa el enunciado de la solución. (Pídales que discutan sus respuestas con sus compañeros).

Permita que los estudiantes usen fichas según sea necesario.

AVANZADO

Tenga contadores a mano para que los estudiantes los usen. Lee las siguientes instrucciones e una en una.

• Comparte con tus compañeros lo que notas sobre la ecuación.

◦ ¿Qué operación matemática estás usando para resolver esta ecuación?

◦ ¿Cuáles son algunas maneras en que podemos modelar y resolver una ecuación de multiplicación?

• Explica a tus compañeros los pasos que seguiste para hacer tu modelo.

• Explica a tus compañeros cómo se relacionan los modelos y las oraciones de multiplicación.

• Busca con tus compañeros ejemplos de grupos iguales y multiplicación en la vida real. ¿Cómo te facilita la vida entender esto?

AVANZADO

Tenga fichas disponibles para los estudiantes. Pida a los estudiantes que lean el problema en parejas. Invítelos a encerrar con un círculo las palabras que no conozcan y a comentarlas con sus compañeros.

• ¿Qué información tienen sobre el problema? Señala dónde puedes encontrarla en el párrafo.

• ¿Qué pide el problema? ¿Cómo lo sabes?

• ¿Qué es una matriz? Discute las características de las matrices con tus compañeros.

Haga que los estudiantes lean en parejas las instrucciones y las preguntas de a una por vez.

Anime a los estudiantes a referirse a la historia y a los modelos para encontrar las soluciones.

Haga que los estudiantes trabajen con sus compañeros para discutir y completar los enunciados. Que hagan una lluvia de ideas en grupo sobre cuándo las matrices son útiles en la vida real.

Permita que los estudiantes usen contadores según sea necesario.

PRINCIPIANTE

Disponga de fichas para los estudiantes. Señale el banco de palabras y léalas en voz alta. Repita los significados de las palabras en grupo. Defina y proporcione ejemplos según las necesidades de los estudiantes.

• Señalemos y leamos la expresión.(Señale la expresión). (Ecolectura de la expresión: 4 por 6).

◦ ¿Qué te dicen los números de la expresión?

◦ ¿Qué te dice el primer número(señale el primer número)?

• ¿Qué te dice el segundo número( señale el segundo número)?

• ¿Cómo podemos usar la recta numérica(señale la recta numérica) para ayudarnos a resolver la expresión?

◦ ¿Cuántos saltos das? Muestra el número de veces en tus dedos. (Levante sus dedos y muévalos).

◦ ¿Cuán lejos está cada salto? (Gesticule haciendo saltos en la recta numérica).

• Usa la recta numérica para representar la expresión.

• ¿Cuál es el producto de la expresión? (Haga que los estudiantes resuelvan la expresión usando la recta numérica).

• Usa el banco de palabras para completar las oraciones.

• (Haga una eco-lectura de cada oración, guiando a los estudiantes al banco de palabras). ¿Cuál de las palabras del banco de palabras (señale el banco de palabras) encaja mejor en el espacio en blanco? (Dé tiempo a los estudiantes para que completen cada espacio en blanco antes de pasar al siguiente enunciado).

Una vez completados todos los enunciados, revíselos en grupo.

PRINCIPIANTE

Tenga fichas a mano para que los estudiantes las utilicen. Lea las siguientes indicaciones de una en una.

Señale la sección de ecuaciones. Señale con el dedo los números y los símbolos a medida que los leean: 6 por 7 es igual a blanco. Señale cada número y símbolo mientras lee la ecuación.

• Piensa cómo puedes crear un modelo para mostrar esta ecuación. (Señala la ecuación). Muéstrame con tus dedos (mueve los dedos) cuántos grupos de fichas (señala las fichas) hay.

• Muéstrame con tus dedos (mueve los dedos) cuántas fichas (señala las fichas) hay en cada grupo.

• Haz un modelo con tus fichas (levanta una ficha) que represente 6 × 7.

• Señala la sección del modelo. Dibuja (gesticula) tu modelo.

• Señala mientras lees la frase. Esta frase dice que hay ____ grupos de ____. Escribe cuántos grupos hay. Señala los grupos de la maqueta y haz el gesto de contarlos.

• Escribe cuántas fichas hay en cada grupo. Señala los puntos de un grupo y haz el gesto de contarlos.

• Escribe la respuesta (señala la línea del producto) de 6 multiplicado por 7.

• Repasa en grupo el modelo, la ecuación y el enunciado.

INTERMEDIO

Tenga contadores a disposición de los estudiantes. (Coro): lea el enunciado y el banco de palabras y pida a los estudiantes que debatan sobre el significado de las palabras con sus compañeros. Defina y proporcione ejemplos según lo necesiten los estudiantes.

• Señalemos y leamos la expresión 4 por 6.

• ¿Qué nos dicen los factores de la expresión?

• ¿Cómo podemos usar la recta numérica para ayudarnos a resolver la expresión?

• ¿Cuál es el producto de la expresión? (Los estudiantes resuelven la expresión utilizando la recta numérica con sus compañeros).

• Usa el banco de palabras para completar las frases.

Diga a los estudiantes que las palabras del banco de palabras se pueden utilizar más de una vez.

• (Haga una eco-lectura de cada oración, guiando a los estudiantes al banco de palabras). ¿Cuál de las palabras del banco de palabras (señale el banco de palabras) encaja mejor en el espacio en blanco? (De tiempo a los estudiantes para rellenar cada espacio en blanco antes de pasar al siguiente enunciado).

• Deje unos momentos a los estudiantes para que comparen y comenten los enunciados completados con sus compañeros.

ESCRIBIR

AVANZADO

Ponga fichas a disposición de los estudiantes. Pídales que lean en parejas la expresión y la pregunta.

• Comparte con tus compañeros lo que notas sobre la expresión y la recta numérica.

• Conversa con tus compañeros lo que representa cada uno de los factores en la expresión.

• Resuelve la expresión con una recta numérica.

• Explica cómo se puede usar una recta numérica para modelar la multiplicación.

Permita a los estudiantes unos momentos para compartir su escritura con sus compañeros.

INTERMEDIO

Tenga fichas a mano para que los estudiantes las utilicen. Lea las siguientes indicaciones de uno en uno.

• (Señale la sección de la ecuación). (Coro): lee la ecuación conmigo: 6 por 7 es igual a blanco. Piensa cómo puedes crear un modelo para representar esta ecuación.

• Muéstrame con tus dedos cuántos grupos de fichas hay.

• Muéstrame con tus dedos cuántas fichas hay en cada grupo.

• Haz un modelo con tus fichas que represente 6 × 7.

• Dibuja tu modelo.

• Señala mientras lees la frase: Hay ____ grupos de ____. Rellena los espacios en blanco para completar el enunciado.

• Escribe el producto de 6 multiplicado por 7 en la sección de la ecuación.

• Repasa tu modelo, ecuación y enunciado con tus compañeros.

ESCUCHAR

AVANZADO

Tenga fichas a mano para que los estudiantes las usen. Lea las siguientes indicaciones de uno en uno.

• Mira la sección de ecuaciones. Escúchame decir una ecuación. Escribe en este recuadro la ecuación que escuchas: 6 por 7 es igual a blanco.

• Piensa cómo puedes crear un modelo para representar esta ecuación.

• Muestra a tus compañeros con los dedos cuántos grupos de fichas hay.

• Muestra a tus compañeros con los dedos cuántas fichas hay en cada grupo.

• Haz un modelo con tus fichas que represente 6 × 7.

• Dibuja tu modelo.

• Completa la oración con la información sobre el número de grupos y fichas en cada grupo.

• Escribe el producto de 6 multiplicado por 7 en la sección de la ecuación.

• Comparte con tus compañeros tu modelo, ecuación y oración.

EXPLICAR: MIS PENSAMIENTOS DE MATEMÁTICAS

ANALIZAR EL PENSAMIENTO DEL ESTUDIANTE

MIS PENSAMIENTOS DE MATEMÁTICAS

DESCRIPCIÓN

Los estudiantes tendrán la oportunidad de escribir sus pensamientos e ideas matemáticas utilizando las siguientes tres vías diferentes:

Imagen Tipo

Contenido

Proceso

Descripción

Escritura sobre conceptos y relaciones matemáticas

Afectivo

Escritura centrada en la resolución de problemas, estrategias y procedimientos

Escritura sobre la actitud, experiencia o mentalidad de un estudiante hacia las matemáticas.

Los iconos de arriba se proporcionan en cada actividad con el fin de darle orientación en cuanto a qué tipo de escritura se utilizará. Los tres tipos se entrelazarán a lo largo del programa para garantizar un enfoque equilibrado de la escritura en matemáticas.

MATERIALES

IMPRESOS

• 1 folleto del estudiante (por alumno)

REUTILIZABLES

• Acceso a herramientas y modelos matemáticos (por clase)

PREPARACIÓN

• Permita que los estudiantes tengan acceso a una variedad de herramientas matemáticas como bloques de valor posicional y círculos de fracciones, y modelos matemáticos como tablas de valor posicional, muros de fracciones, rectas numéricas, etc.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Permita que los estudiantes planteen sus ideas a un compañero antes de escribir sus pensamientos en papel.

2. Anímelos a perseverar en su pensamiento y a usar herramientas y modelos matemáticos según sea necesario.

3. Invite a los estudiantes a escribir sus respuestas en oraciones completas utilizando ortografía, gramática y puntuación correctas.

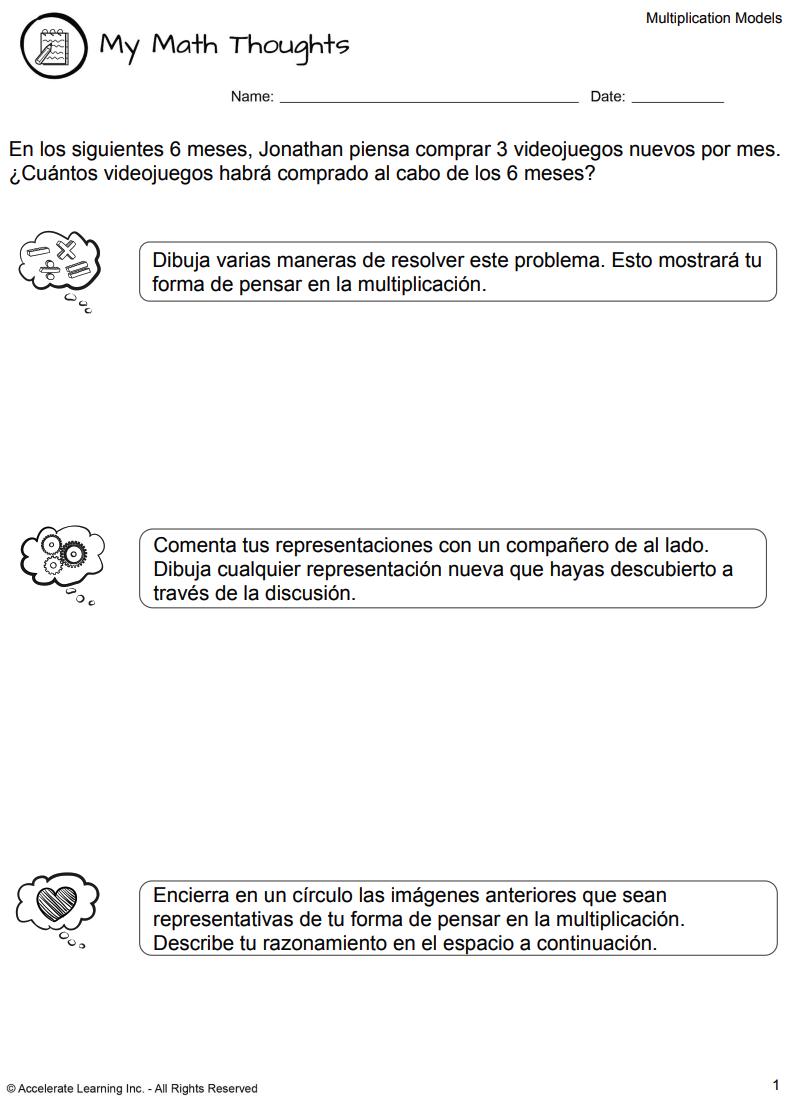
FOLLETO DEL ESTUDIANTE

Matriz

Grupos iguales

Conjuntos de objetos que tienen la misma cantidad o número, o que tienen el mismo valor

Modelo

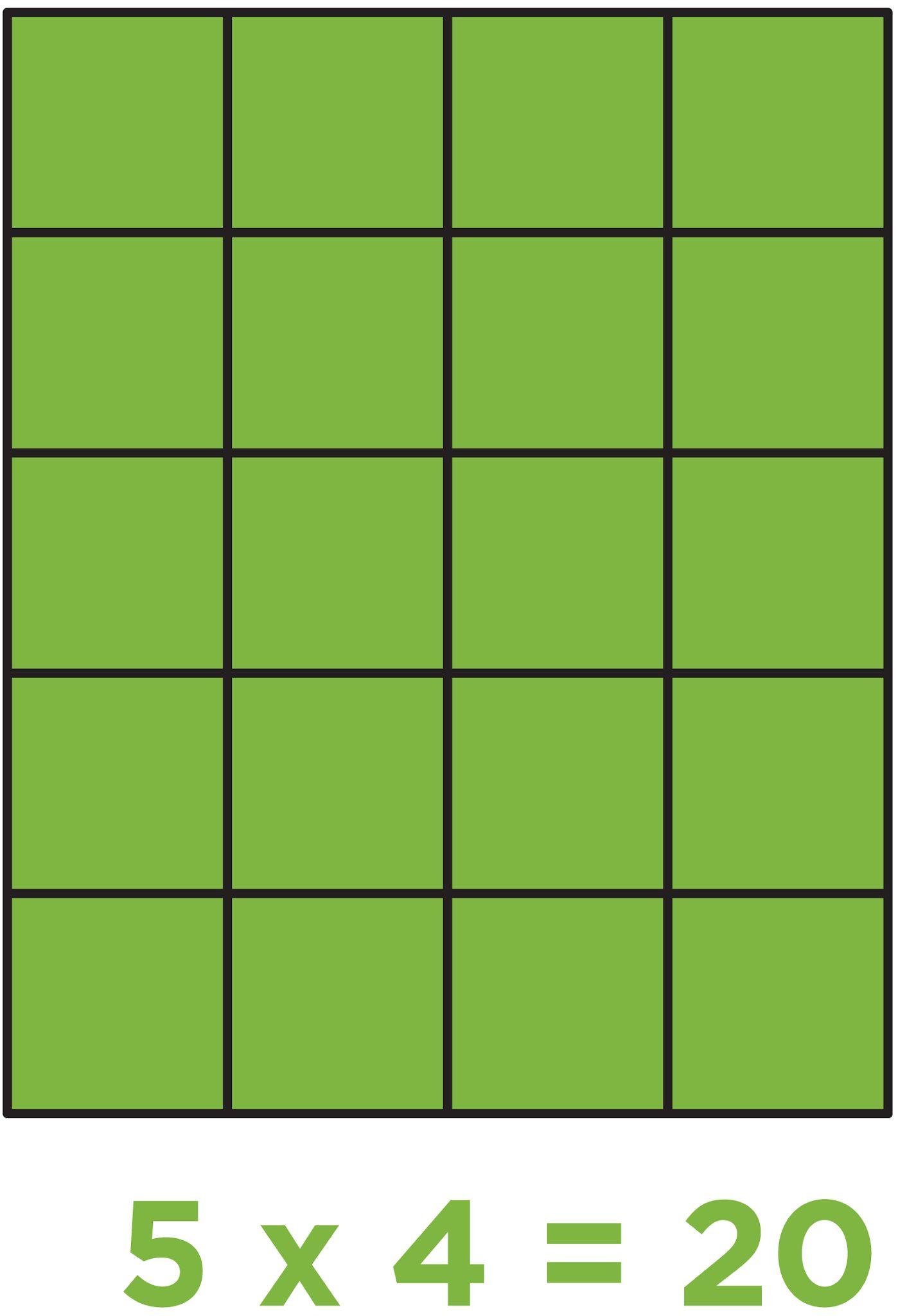
Una representación

Recta numérica

Línea con marcas de graduación espaciadas uniformemente para mostrar la posición de un número en relación con otros números

Objetos o números organizados en filas y columnas iguales

Ecuación

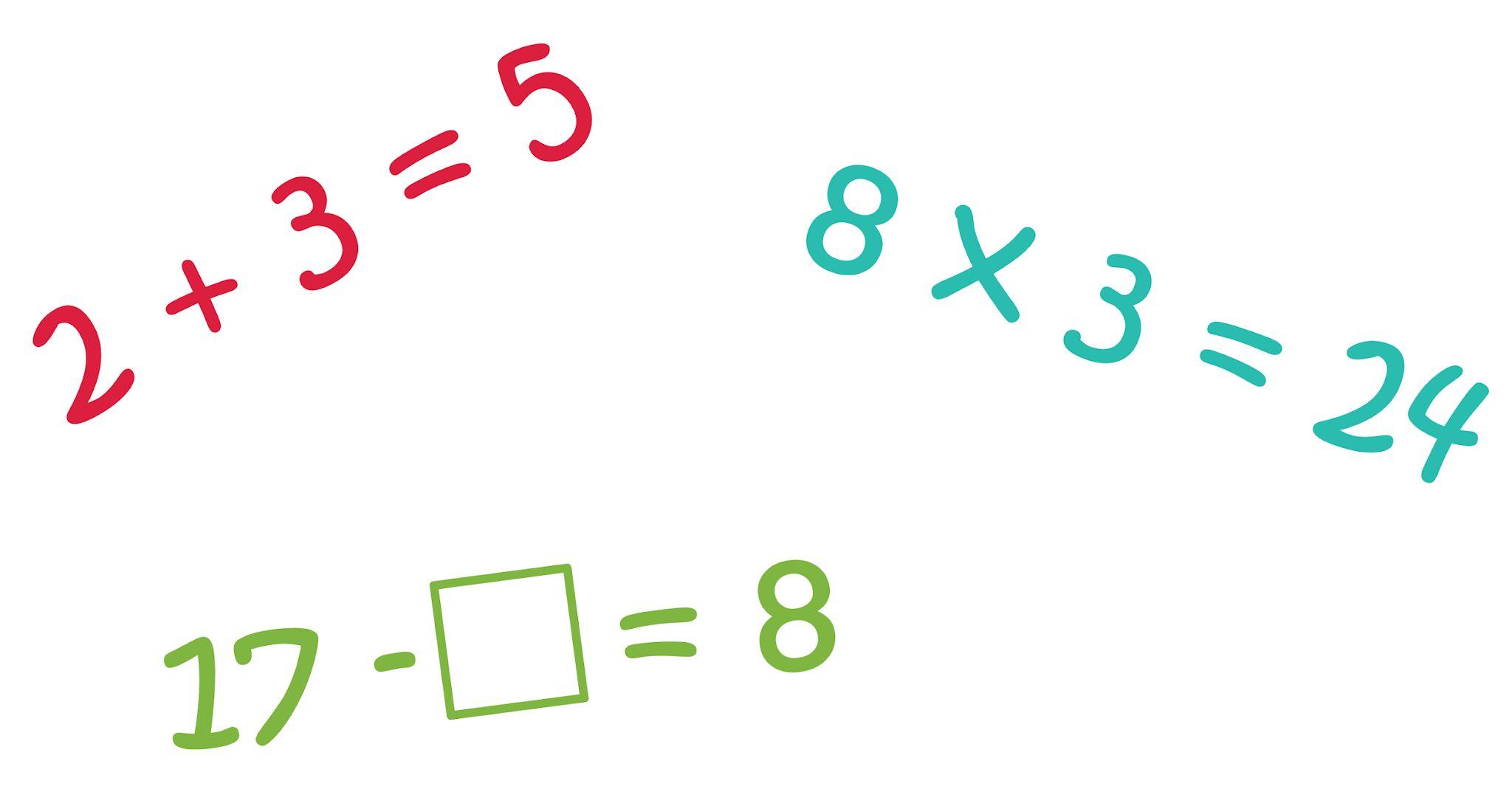
Operación matemática que utiliza números, uno o más símbolos de operación y un signo de igual

Múltiplo

EXPLICAR: VOCABULARIO ILUSTRADO VOCABULARIO ILUSTRADO

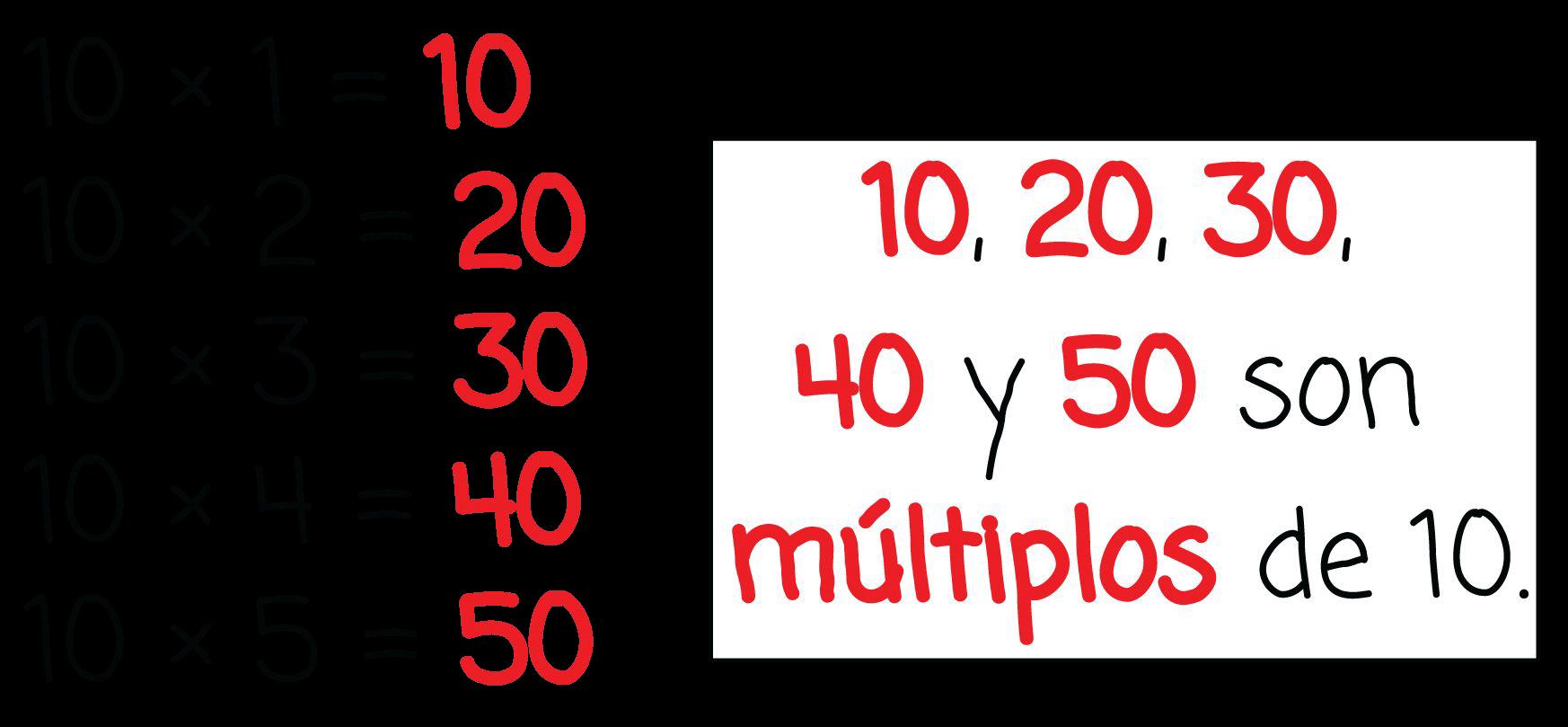
El producto de dos números; un número que se puede dividir equitativamente por otro número

Oración numérica

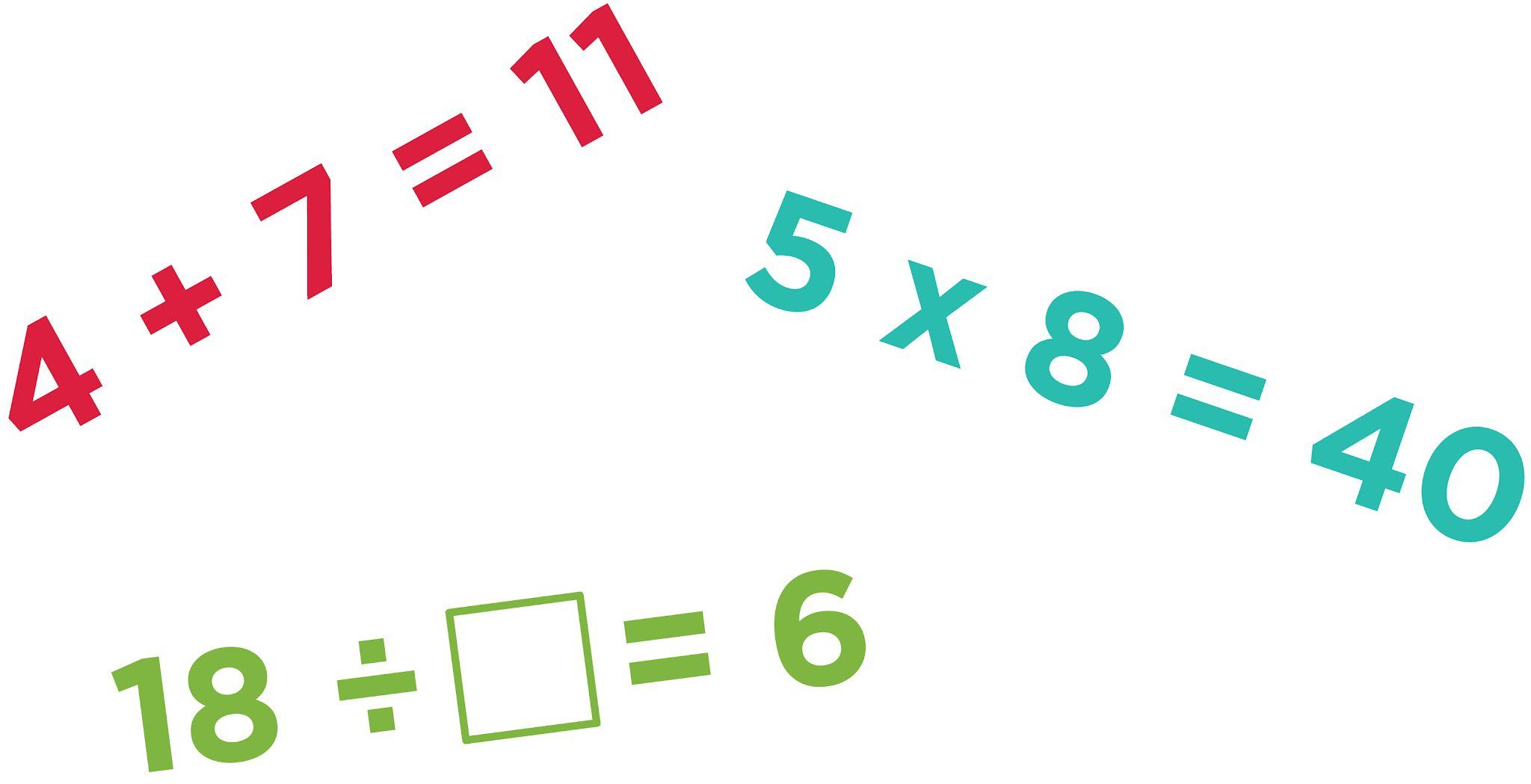
Enunciado matemático escrito usando números; ecuación

QUE HAY QUE CONOCER

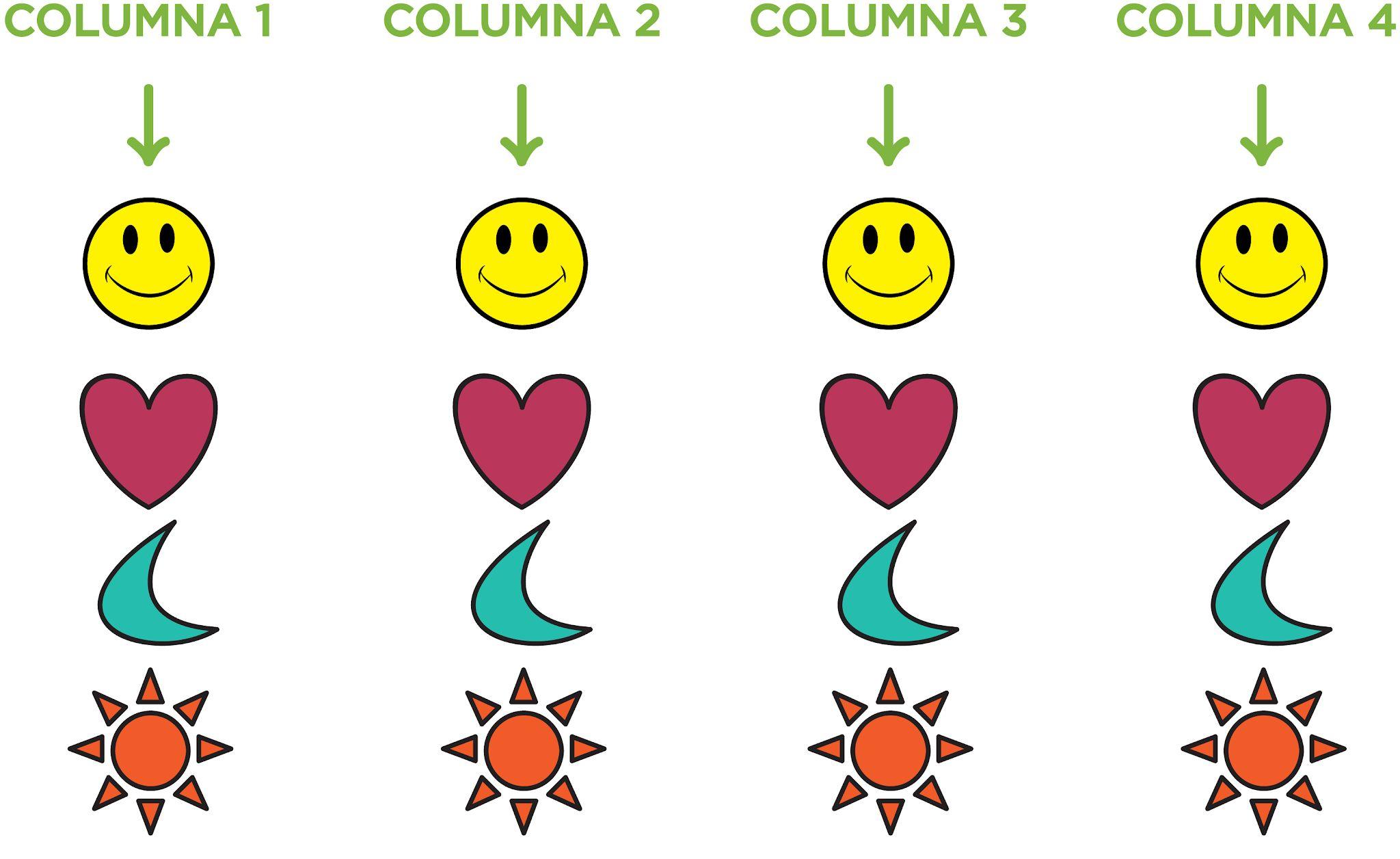
Objetos que están alineados uno encima del otro y debajo del otro; una disposición vertical de objetos

Factor

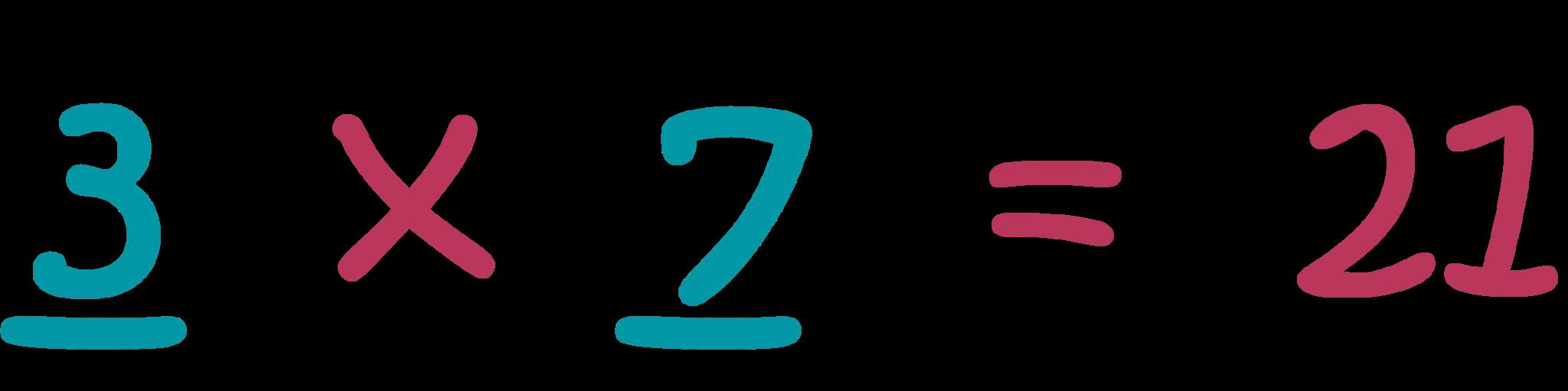
Número que se multiplica por otro número para encontrar un producto

Multiplicación

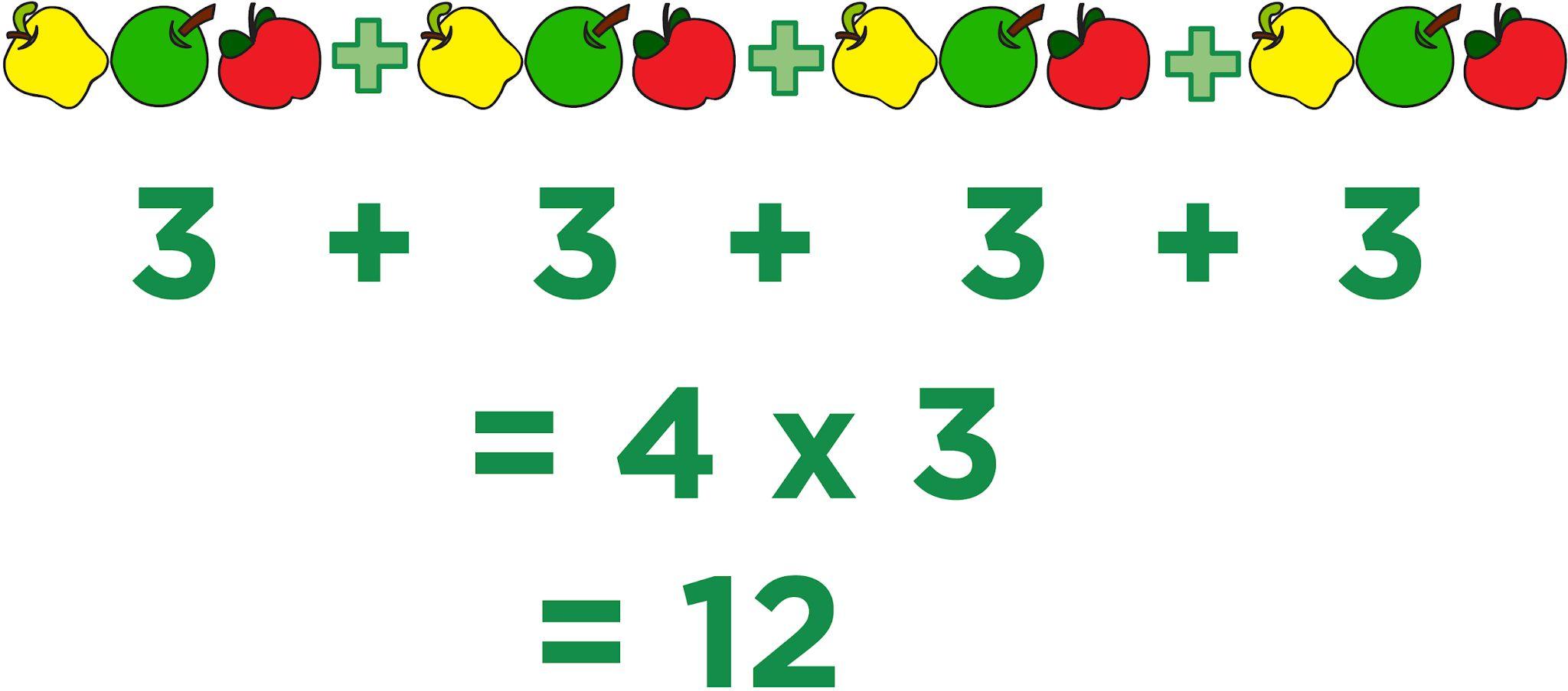
Forma de crear un producto al hacer grupos iguales, sumar repetidamente o formar matrices

Operaciones

Procesos matemáticos, como la adición, sustracción, multiplicación y división

PALABRAS

Columna

EXPLICAR: VOCABULARIO ILUSTRADO

Producto

El resultado de multiplicar dos o más números

Contar salteado

Técnica de conteo en la que se agrega repetidamente el mismo número al número anterior; contar por múltiplos

Suma repetida

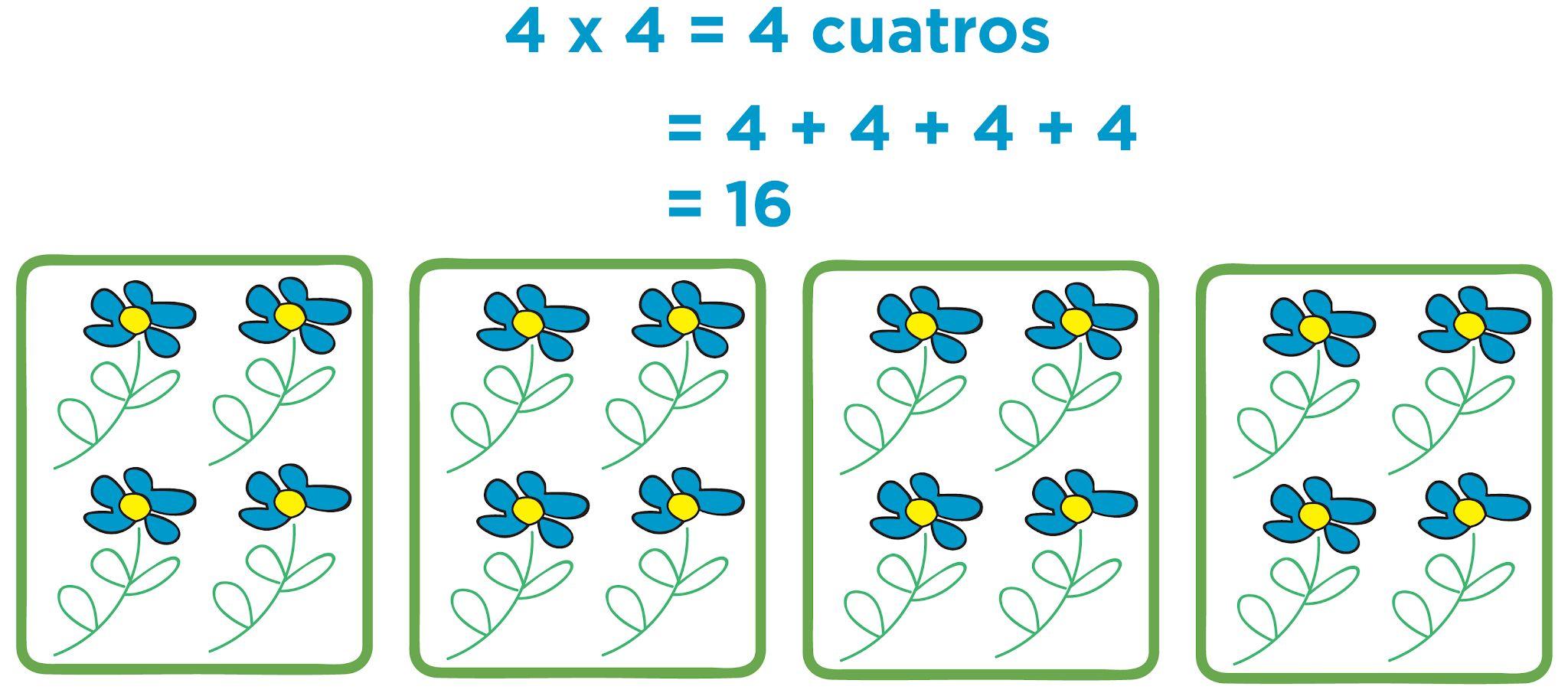
Patrón de sumar el mismo número una y otra vez; se puede representar con una oración numérica de multiplicación

Carácter que se usa para representar un valor o un proceso

Número entero

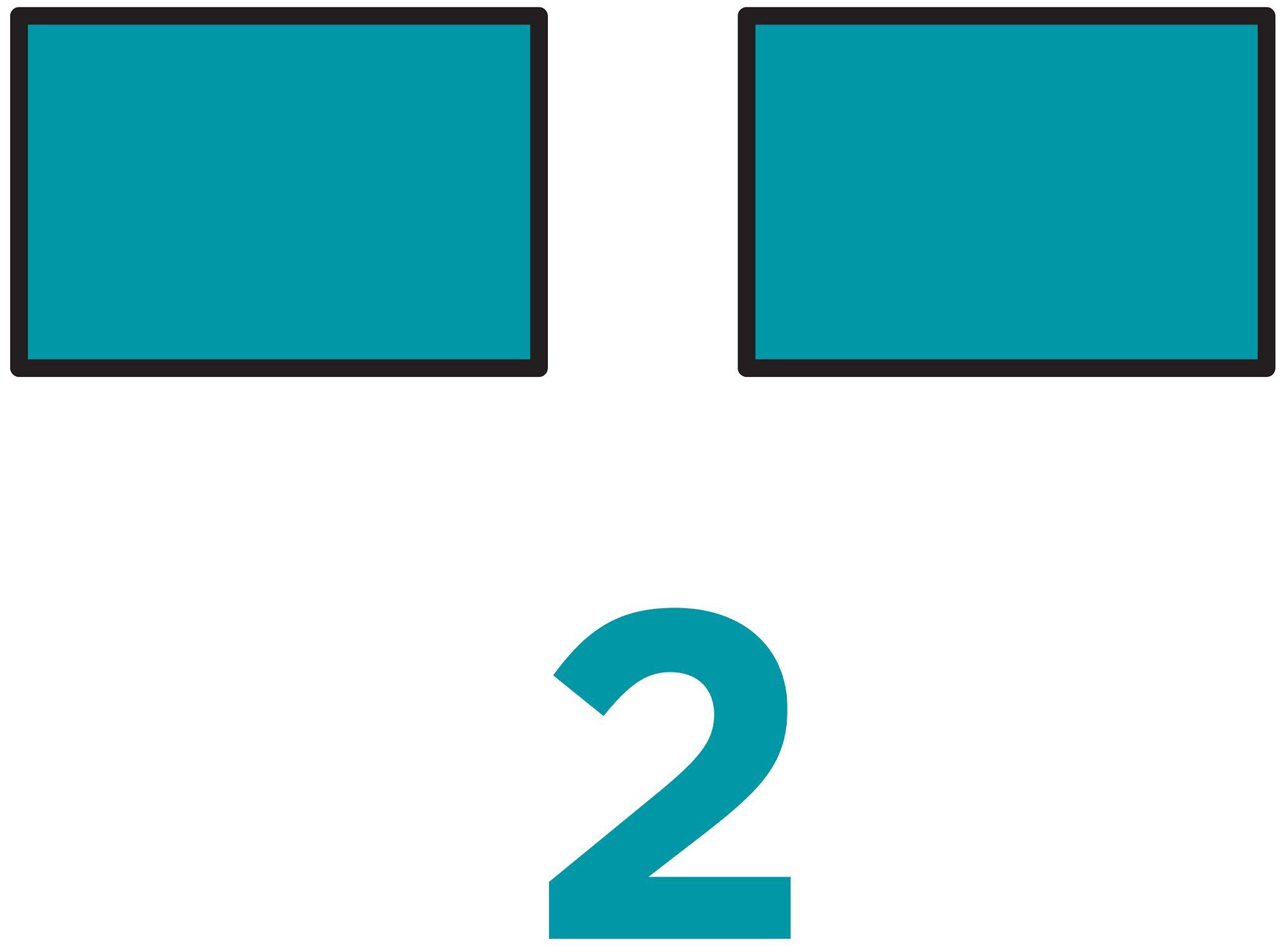
Valor numérico sin partes decimales o fraccionarias

Objetos alineados uno al lado del otro; una disposición horizontal de objetos

Diagrama de cintas

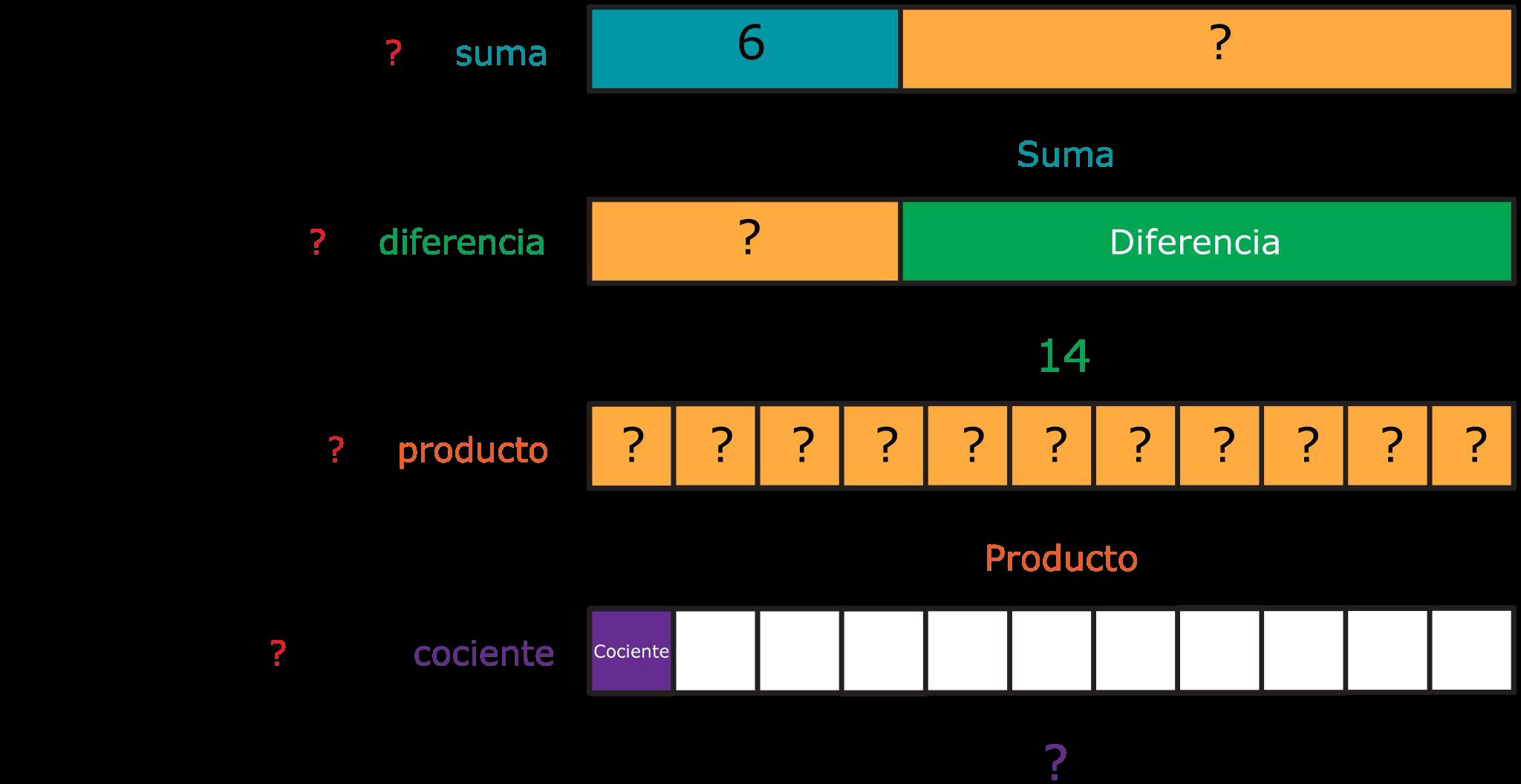
Modelo que se utiliza para resolver problemas escritos, y que muestra la relación entre cantidades conocidas y desconocidas

Fila

ELABORAR: CONSTRUCTOR DE FLUIDEZ

HOJA DE REGISTRO DEL ESTUDIANTE

DESARROLLAR LA FLUIDEZ CONCEPTUAL

CONSTRUCTOR DE FLUIDEZ: MULTIPLICACIÓN HASTA EL 100 CON MODELOS Y ECUACIONES.

DESCRIPCIÓN

Los estudiantes dan la vuelta a dos tarjetas y buscan coincidencias entre las imágenes, los números y/o las palabras.

MATERIALES

IMPRESO

• 1 hoja de instrucciones (por pareja)

• 1 juego de tarjetas de pareo (por pareja)

• 1 hoja de registro del estudiante (por estudiante)

REUTILIZABLE

• 1 sobre o bolsa con cierre (por pareja)

PREPARACIÓN

• Imprima y recorte un juego de tarjetas de pareo para cada pareja. Asegúrese de imprimirlas por las dos caras para que el logotipo del juego aparezca en una cara de cada tarjeta.

• Imprima una hoja de instrucciones para cada juego de tarjetas.

• Considere la posibilidad de plastificar todos los materiales impresos, excepto la hoja de registro del estudiante, para que puedan utilizarse durante mucho tiempo. Puede colocar las piezas más pequeñas en sobres o bolsas con cierre.

• Imprima una hoja de registro del estudiante por alumno.

PROCEDIMIENTO

Y PUNTOS DE AYUDA

1. Muestre cómo barajar las cartas y colocarlas boca abajo en una matriz de 4 × 6.

2. Haga una demostración del juego con un estudiante.

a. El primer jugador voltea dos cartas para intentar encontrar una coincidencia.

b. Si el jugador empareja dos cartas, se queda con el conjunto coincidente y vuelve a jugar.

c. Si no encuentra ninguna coincidencia, vuelve a colocar las cartas boca abajo y es el turno del siguiente jugador.

d. Continúan turnándose hasta que se hayan encontrado todas las coincidencias.

e. Gana el jugador que reúna más cartas.

3. Distribuya los materiales.

4. Pida a los estudiantes que jueguen.

5. Al final del juego, pida a cada jugador que anote dos de las coincidencias que encontró en la hoja de registro del estudiante. Pídales que expliquen por qué las 2 cartas coinciden. Anímelos a compartir sus respuestas con sus compañeros.

ELABORAR: REVISIÓN EN ESPIRAL

REPASAR CONCEPTOS PREVIOS

REVISIÓN EN ESPIRAL:

UNA

SEMANA EN LA PLAYA DESCRIPCIÓN

Los estudiantes repasan el contenido del grado anterior o actual basándose en los puntos centrales establecidos para cada grado.

PREPARACIÓN

• Imprima una copia de la hoja de revisión en espiral para cada estudiante.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Puede que necesite proporcionar ayuda con la lectura para que algunos estudiantes completen esta actividad.

2. Lea la historia en la primera página para despertar el interés antes de pasar a las preguntas.

3. Use este repaso en espiral como calentamiento en clase o envíelo a casa como tarea, pero asegúrese de revisar las respuestas y estrategias con toda la clase.

4. Consulte el estándar en la esquina inferior derecha de cada cuadro de preguntas para evaluar el conocimiento del contenido de los estudiantes o la necesidad de una mayor intervención..

REPASO EN ESPIRAL ENFOQUE POR PREGUNTA

• Pregunta 1

◦ Grado 2: Explicar por qué funcionan las estrategias de suma y resta, usando el valor posicional y las propiedades de las operaciones.

• Pregunta 2

◦ Grado 2: Estimar longitudes usando unidades de pulgadas, pies, centímetros y metros.

• Pregunta 3

◦ Grado 2: Medir para determinar cuánto más largo es un objeto que otro, expresando la diferencia de longitud en términos de una unidad de longitud estándar.

• Pregunta 4

◦ Grado 2: Usar sumas y restas dentro de 100 para resolver problemas escritos que involucran longitudes que están dadas en las mismas unidades; por ejemplo, con dibujos (como dibujos de reglas) y ecuaciones con un símbolo para el número desconocido para representar el problema.

FOLLETO DEL ESTUDIANTE

ELABORAR: TAREA BASADA EN PROBLEMAS

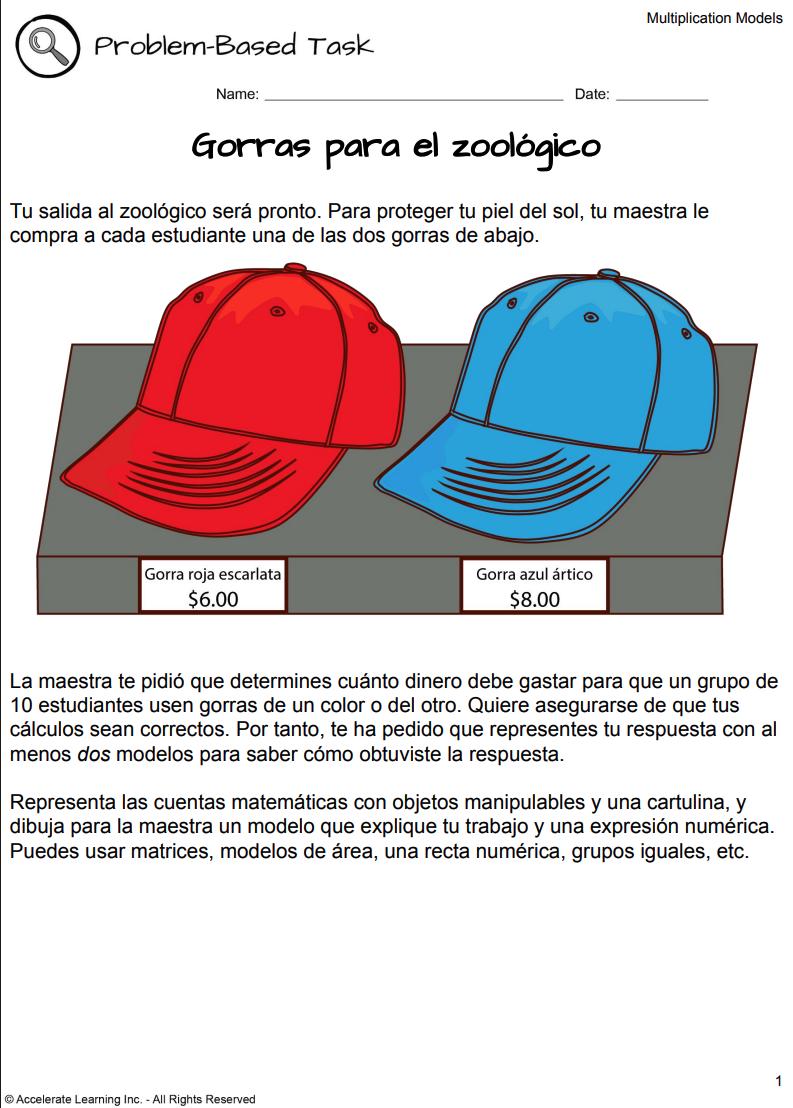
FOLLETO DEL ESTUDIANTE

DESARROLLAR HABILIDADES PARA RESOLVER PROBLEMAS

TAREA BASADA EN PROBLEMAS: GORRAS PARA EL ZOOLÓGICO

DESCRIPCIÓN

Los estudiantes trabajan en colaboración para aplicar los conocimientos y habilidades que han aprendido a un desafío abierto del mundo real.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Permita que los estudiantes trabajen en grupos.

2. Anímelos a consultar sus diarios del estudiante de las actividades de exploración si necesitan repasar las habilidades que han aprendido.

3. Si los estudiantes están atascados, use preguntas orientadoras para ayudarles a pensar sin decirles qué pasos deben dar a continuación. Si el tiempo lo permite, haga que cada grupo comparta su solución con la clase.

4. Vea cómo los diferentes grupos abordaron el reto de diferentes maneras.

RÚBRICA

ELABORAR: CONEXIONES PROFESIONALES

MATEMÁTICAS EN EL TRABAJO

CONEXIONES PROFESIONALES:

JAMES GOSLING

Las conexiones profesionales pretenden ser una vía que introduzca a sus estudiantes en las carreras matemáticas y en las habilidades del siglo XXI necesarias para tener éxito en diversos campos. Éstas incluyen, entre otras, la creatividad y la innovación, el pensamiento crítico, la resolución de problemas y las habilidades tecnológicas.

DESCRIPCIÓN

Este alcance destaca la carrera de James Gosling, creador del lenguaje de programación Java. Los estudiantes considerarán su profesión, las matemáticas utilizadas y el impacto que esta carrera ha tenido en su comunidad.

MATERIALES

IMPRESOS

• Presentación de diapositivas de James Gosling (por clase o por estudiante)

REUTILIZABLES

• Proyector (por clase)

PREPARACIÓN

• Agrupe a los estudiantes para una colaboración y discurso.

• Prepárese para proyectar las diapositivas a la clase. Si no dispone de proyector, puede imprimir la diapositiva para que la utilicen los estudiantes.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Proyecte la diapositiva e invite a un estudiante a leer la biografía de James Gosling.

2. Facilite una conversación con los estudiantes, formulando preguntas como las siguientes:

a. «¿A qué se dedica James Gosling?».

b. «Pensando en lo que ha conseguido, ¿parece difícil o fácil utilizar las matemáticas de esta manera?».

c. «¿Habías pensado antes en las matemáticas de esta manera?».

d. «¿Por qué crees que esta carrera es importante para nuestra sociedad?».

e. «¿Es ésta una carrera que te interesa? ¿Por qué o por qué no?».

f. «¿Cómo utilizó James Gosling sus conocimientos tecnológicos en los modelos de multiplicación?».

PASE DE DIAPOSITIVAS DE JAMES GOSLING

La ciencia de datos consiste en un breve debate en clase sobre un conjunto de datos. Esta actividad no está pensada para ser calificada. La parte I incluye preguntas abiertas para ayudar a los estudiantes a interpretar y analizar los datos. Las partes siguientes son actividades opcionales para ampliar el aprendizaje de los estudiantes en contexto.

DESCRIPCIÓN

Los estudiantes analizan, interpretan y generan conjuntos de datos, además de responder a preguntas basadas en los datos.

MATERIALES

IMPRESO

• 1 folleto para el alumno (por alumno)

• 1 conjunto de datos (por clase)

REUTILIZABLE

• 1 proyector o cámara de documentos (por clase)

• 1 marcador de borrado en seco (por clase)

CONSUMIBLE

• 1 trozo de papel milimetrado (por clase)

PREPARACIÓN

• Prepárese para proyectar el conjunto de datos en la clase.

• Reúna un trozo de papel milimetrado y un marcador de borrado en seco.

• Imprima el folleto del estudiante para cada alumno.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

PARTE I

1. Proyecte el conjunto de datos y prepárese para anotar las observaciones de los estudiantes.

2. Plantee las siguientes preguntas::

a. «¿Qué observas en este conjunto de datos?».

b. «¿Qué representa este conjunto de datos?».

c. «¿Qué categorías se incluyen en este conjunto de datos?».

d. «¿Cuántas ventanas hay en un lado de tu casa? ¿En el edificio de tu colegio? ¿Están dispuestas en forma de matriz?».

e. «¿Qué preguntas tienes sobre los datos?».

ELABORAR: CIENCIA DE DATOS

ANÁLISIS DE DATOS

CIENCIA DE DATOS

PARTE II

1. Repase la multiplicación usando modelos y escriba lo que los estudiantes recuerden en el papel milimetrado.

2. Plantee las siguientes preguntas:

a. «¿Qué expresión puede usarse para encontrar el número total de ventanas en el Edificio H?». 11 × 2 = 22 ventanas

b. «¿Qué expresión se puede utilizar para hallar el número total de ventanas del Edificio F?». 14 × 9 = 126 ventanas

c. «¿Cuántos conjuntos diferentes de ventanas hay en el Edificio B?». Hay tres conjuntos diferentes de ventanas en el Edificio B.

d. «¿Cómo puedes usar la multiplicación para encontrar el número total de ventanas en el Edificio I?». Las respuestas pueden variar. Los estudiantes pueden usar 38 × 2 para hallar el número total de ventanas del Edificio I.

e. «¿La expresión 12 + 12 + 12 se usa para hallar el número total de ventanas de qué edificio?». Escribe una expresión de multiplicación que pueda usarse para hallar el número total de ventanas del edificio. Edificio J; 3 × 12 = 36

PARTE III

1. Entregue a cada alumno una copia del folleto del estudiante.

2. Lea las instrucciones y responda a las preguntas que puedan tener los estudiantes.

3. Conceda tiempo para que los estudiantes completen el folleto el estudiante en clase o la envíen a casa como tarea.

4. Anime a los estudiantes a compartir sus datos con la clase.

FOLLETO DEL ESTUDIANTE

EVALUAR: LISTA DE VERIFICACIÓN DE OBSERVACIÓN

EVALUACIÓN DE HABILIDADES

LISTA DE VERIFICACIÓN DE LA OBSERVACIÓN

DESCRIPCIÓN

Este elemento proporciona un desglose de los conceptos y destrezas clave del alcance de aplicación. Puede utilizarse como evaluación formativa para los maestros y como autoevaluación para los estudiantes.

MATERIALES

IMPRESO

• 1 folleto del estudiante (por alumno)

• 1 materiales para el maestro (por estudiante)

PREPARACIÓN

• Imprima los materiales para el maestro y un folleto del estudiante para cada alumno.

PROCEDIMIENTO Y PUNTOS DE APOYO

1. Distribuya un folleto del estudiante a cada alumno.

2. A medida que los estudiantes trabajen en las actividades explorar y explicar del alcance, evalúe formativamente su progreso tomando notas sobre cómo se observaron los conceptos y habilidades clave. Se pueden plantear preguntas de reflexión para medir el impacto de las actividades tanto en grupo completo como en pequeño grupo.

3. Pida a los estudiantes que reflexionen sobre las formas en que pueden demostrar su comprensión y autoevaluar su progreso en cada concepto o habilidad clave a medida que trabajan tanto en grupo completo como en pequeño grupo.

4. Los estudiantes pueden reflexionar sobre su pensamiento, aprendizaje y trabajo en el alcance; identificar las formas en que han mejorado y establecer nuevas metas de aprendizaje.

5. Quienes brindan apoyo pedagógico a los estudiantes pueden estar equipados con las adaptaciones y modificaciones anotadas en los materiales para el maestro.

6. Las notas anecdóticas proporcionadas en las instrucciones del maestro pueden usarse como documentación para los boletines de calificaciones basados en estándares.

7. Una vez que se hayan recopilado los datos de los estudiantes después de la evaluación, consulte la guía de instrucción andamiada en la sección «Inicio» de este alcance para diferenciar la instrucción para cada estudiante.

EVALUAR: MAPA DE CALOR

ANALIZAR LOS RESULTADOS DE LA EVALUACIÓN

MAPA DE CALOR

DESCRIPCIÓN

Los estudiantes analizan los resultados de su evaluación y determinan qué hicieron bien y en qué pueden mejorar.

MATERIALES

• 1 mapa de calor (por estudiante)

• 1 crayón rojo (por estudiante)

• 1 crayón verde (por estudiante)

PREPARACIÓN

• Determine si los estudiantes analizarán su prueba de habilidades, la evaluación basada en estándares o ambas.

• Imprima un mapa de calor para cada estudiante.

• Reúna un crayón rojo y un crayón verde para cada estudiante.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Distribuya un mapa de calor a cada estudiante junto con los crayones rojo y verde. Los estudiantes deben tener a mano su(s) evaluación(es) corregida(s).

2. Los estudiantes utilizan su(s) evaluación(es) corregida(s) para colorear el mapa de calor. Por cada pregunta contestada correctamente, colorean de verde la casilla correspondiente. Para cada pregunta contestada incorrectamente, los estudiantes colorean la casilla correspondiente en rojo.

3. Anime a los estudiantes a buscar patrones en sus datos, como un determinado estándar que se perdió con más frecuencia o un estándar que han dominado claramente, y utilizar esta información para reflexionar y establecer metas en la tabla proporcionada.

4. Consulte la guía de instrucción andamiadas que se encuentra en la sección «Inicio» para proporcionar extensión o apoyo adicional.

INTERVENCIÓN: INTERVENCIÓN EN GRUPO PEQUEÑO

REFORZAR Y VOLVER A ENSEÑAR

INTERVENCIÓN EN PEQUEÑOS GRUPOS

DESCRIPCIÓN

Los estudiantes determinan el número total de objetos en escenarios que involucran números de un solo dígito usando grupos iguales, matrices, diagramas de cinta, rectas numéricas y conteo salteado como estrategias de multiplicación.

MATERIALES

IMPRESO

• 1 juego de tapetes de trabajo de modelos de multiplicación (por estudiante)

• 1 juego de tarjetas numéricas (por pareja)

• 1 lista de verificación para el maestro (por profesor)

• 1 evaluación de control (por alumno)

REUTILIZABLE

• 4 protectores de plástico para las hojas (por estudiante)

• 10 platos de papel (por pareja)

• 10 cubos conectables (por pareja)

• 100 contadores (por pareja)

• 1 marcador de borrado en seco (por estudiante)

• 1 bolsa pequeña, bolsa resellable (por pareja)

• 1 regla de medir (por pareja)

CONSUMIBLE

• 1 rollo de cinta de embalar (por maestro)

PREPARACIÓN

• Planifique que los estudiantes trabajen en parejas para completar esta actividad.

• Imprima una evaluación de control (por alumno)

• Imprima la lista de verificación para el maestro.

• Imprima un juego de tapetes de trabajo de modelos de multiplicación para cada estudiante. Coloque cada parte en un protector de hojas separado para crear una superficie que se pueda borrar. Como alternativa, los tapetes de trabajo pueden imprimirse por las dos caras y colocarse en dos protectores de hojas.

• De un marcador borrable a cada estudiante.

• Imprima un juego de tarjetas numéricas y recórtelas. Coloque las tarjetas en una bolsa con cierre.

• Prepare manipulativos para cada parte:

◦ Parte I: Grupos iguales

• Contadores para cada par (hasta 100)

• 10 platos de papel para cada par

◦ Parte II: Comprender la multiplicación con matrices

• Contadores para cada par (hasta 100)

◦ Parte III: Multiplicación con diagramas de cintas

• 10 cubos de enlace para cada par

◦ Parte IV: Rectas numéricas y contar salteado

• Cubra el lado del numerado de una regla con cinta de embalaje para crear una superficie borrable para cada par.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

PARTE I: GRUPOS IGUALES

1. Pida a los estudiantes que discutan lo que recuerdan sobre la multiplicación y las estrategias utilizadas para combinar grupos iguales.

2. Distribuya los platos de papel y los contadores por pareja de estudiantes. Distribuya un tapete de trabajo de modelos de multiplicación para la parte I y un marcador de borrado en seco a cada estudiante.

3. Coloque las tarjetas numéricas boca abajo frente al grupo.

4. Señale el escenario en la parte superior del tapete de trabajo y mencione que le falta alguna información. Lea el escenario en voz alta e invite a los estudiantes a compartir lo que notan.

5. Explique que darán vuelta dos tarjetas numéricas y usarán los números para completar las partes faltantes del escenario.

6. Elija a un estudiante para que dé vuelta una tarjeta numérica. Pida a los estudiantes que anoten el número en el primer espacio en blanco.

7. Elija a otro estudiante para que entregue una tarjeta numérica. Pida a los estudiantes que escriban el número en el segundo espacio en blanco.

8. Invite a un estudiante a leer en voz alta la nueva situación. Formule las siguientes preguntas: Las respuestas variarán en función de las tarjetas seleccionadas.

a. «¿Qué información conoces?». Sabemos que María tiene 4 macetas y que hay 3 plantas en cada maceta.

b. «¿Qué necesitas averiguar?». Tenemos que averiguar el número total de plantas que hay en las macetas de María.

INTERVENCIÓN: INTERVENCIÓN EN GRUPO PEQUEÑO

9. Pida a los estudiantes que trabajen con sus compañeros para crear un modelo de grupos iguales que represente las macetas de María utilizando platos de papel y fichas.

10. Formule las siguientes preguntas: Las respuestas variarán en función de las fichas seleccionadas.

a. «¿Qué representan los platos?». Los platos representan el número de macetas o grupos.

b. «¿Qué representan las fichas?». Los contadores representan el número de plantas en cada maceta o grupo.

c. «¿Cómo puedes representar este problema con platos de papel y contadores?». Podemos colocar 4 platos de papel sobre la mesa para representar el número de grupos. Podemos colocar 3 fichas en cada plato para representar cuántas hay en cada grupo.

11. Dé tiempo a los estudiantes para crear sus modelos con sus compañeros.

12. Invite a los estudiantes a compartir sus modelos con el grupo. A continuación, pídales que anoten individualmente su modelo en lel tapete de trabajo. Formule las siguientes preguntas: Las respuestas variarán en función de las tarjetas seleccionadas.

a. «¿Cómo puede ayudarte el modelo a averiguar el producto?». Las respuestas variarán. Podemos contar todas las fichas. Podemos sumar el número de fichas de cada placa para hallar el total.

b. «¿Qué símbolo indica que se están multiplicando números?». El símbolo ×

c. «¿Qué expresión de multiplicación representa este problema?». 4 × 3

13. Pida a los estudiantes que escriban la expresión de multiplicación en sus tapetes de trabajo. Formule las siguientes preguntas: Las respuestas variarán en función de las tarjetas seleccionadas.

a. «¿Cómo se relacionan el modelo y la expresión de multiplicación?». El modelo muestra el número de grupos y el número en cada grupo. Esto se traduce en multiplicación porque el símbolo × representa "grupos de". La expresión de multiplicación representa nuestro modelo.

b. «¿Cuál es el producto de este problema?». El producto es 12.

14. Pida a los estudiantes que completen el enunciado de la solución en la parte inferior de sus tapetes de trabajo.

15. Revise rápidamente la comprensión del trabajo de cada estudiante en sus tapetes de trabajo y oriente a los estudiantes según sea necesario.

16. Después de revisar el trabajo de los estudiantes, indíqueles que borren su tapete de trabajo.

17. Repita la actividad según el tiempo lo permita. EVALUACIÓN

INTERVENCIÓN: INTERVENCIÓN EN GRUPO PEQUEÑO

PARTE II: COMPRENDER LA MULTIPLICACIÓN CON MATRICES

1. Pida a los estudiantes que discutan lo que recuerdan sobre el uso de matrices para ayudar a resolver problemas de multiplicación. Permita que compartan sus conocimientos y comprensión con el grupo.

2. Entregue fichas a cada pareja de estudiantes. Distribuya un tapete de trabajo de modelos de multiplicación para la parte II y un marcador de borrado en seco a cada estudiante.

3. Coloque las tarjetas numéricas boca abajo frente al grupo.

4. Señale el escenario en la parte superior de la alfombra de trabajo y mencione que le falta alguna información. Lea el escenario en voz alta al grupo e invite a los estudiantes a compartir lo que notan en el escenario.

5. Explique que darán vuelta dos tarjetas numéricas y usarán los números para completar las partes faltantes del escenario.

6. Elija a un estudiante para que dé vuelta una tarjeta numérica. Pida a los estudiantes que anoten el número en el primer espacio en blanco.

7. Elija a otro estudiante para que entregue una tarjeta numérica. Pida a los estudiantes que escriban el número en el segundo espacio en blanco.

8. Invite a un estudiante a leer en voz alta la nueva situación. Formule las siguientes preguntas: Las respuestas variarán en función de las tarjetas seleccionadas.

a. «¿Qué información conoces?». Sabemos que Sam llena 4 estantes de la tienda de comestibles con 3 cajas de cereales en cada estante.

b. «¿Qué necesitas averiguar?». Necesitamos encontrar el número total de cajas de cereal en todos los estantes.

c. «¿Qué ecuación de multiplicación puedes escribir para representar este problema?». 4 × 3 = __

9. Pida a los estudiantes que escriban la ecuación en la parte superior del tapete de trabajo. Formule las siguientes preguntas: Las respuestas variarán en función de las tarjetas seleccionadas.

a. «¿Cómo puedes representar este problema con las fichas?». Podemos hacer una matriz de 4 filas de fichas con 3 fichas en cada fila.

b. «¿Qué representa cada ficha?». Cada ficha representa una caja de cereales.

10. Comente que las matrices pueden mostrar problemas de multiplicación usando filas para representar grupos con un número determinado de elementos en cada fila.

11. Pida a los estudiantes que trabajen con sus compañeros para crear una matriz que represente el número total de cajas de cereales. Formule las siguientes preguntas: Las respuestas variarán en función de las tarjetas seleccionadas.

a. «¿Dónde ves grupos iguales en los modelos que acabamos de construir?» Cada fila tiene el mismo número de artículos.

b. «¿Cómo puede ayudarte la matriz a averiguar el producto?» Las respuestas variarán. Podemos contar todas las fichas. Podemos sumar cada grupo. El modelo nos muestra que tenemos 4 grupos de 3. Podemos sumar 3 + 3 + 3 + 3.

c. «¿Cómo puedes hallar el total sin contar cada objeto?» Podríamos multiplicar el número de filas por el número de objetos de cada fila para hallar el producto, o podríamos sumar la cantidad de cada fila o columna para hallar el producto.

a. «¿Cuál es el producto de este problema?». El producto es 12.

12. Invite a los estudiantes a compartir sus modelos con el grupo. A continuación, pídales que anoten individualmente su matriz en el tapete de trabajo.

13. Pídales que completen el enunciado de la solución en la parte inferior de sus tapetes de trabajo.

14. Revise rápidamente la comprensión de la actividad en los tapetes de trabajo y oriente a los estudiantes según sea necesario.

15. Después de revisar el trabajo de los estudiantes, indíqueles que borren su tapete de trabajo.

16. Repita la actividad según el tiempo lo permita.

PARTE III: MULTIPLICACIÓN CON DIAGRAMAS DE CINTAS

1. Pida a los estudiantes que discutan lo que recuerdan sobre el uso de diagramas de cinta para ayudar a resolver problemas de multiplicación. Permita que compartan sus conocimientos y comprensión con el grupo.

2. Entregue los cubos conectables a cada pareja de estudiantes. Distribuya un tapete de trabajo de modelos de multiplicación para la parte III y un marcador de borrado en seco a cada estudiante.

3. Coloque las tarjetas numéricas boca abajo frente al grupo.

4. Explique a los estudiantes que trabajarán con diagramas de cinta y un escenario con partes faltantes. Darán vuelta dos números para representar el escenario y lo resolverán con una estrategia de multiplicación.

5. Lea el escenario en voz alta al grupo e invite a los estudiantes a compartir lo que notan sobre el escenario.

6. Elija a un estudiante para que dé vuelta una tarjeta numérica. Pida a los estudiantes que anoten el número en el primer espacio en blanco.

7. Pida a otro estudiante que entregue una tarjeta numérica. Pida a los estudiantes que anoten el número en el segundo espacio en blanco.

8. Invite a un estudiante a leer en voz alta la nueva situación. Explique que deben crear un diagrama de cinta con cubos conectables o dibujando el escenario en sus tapetes de trabajo.

9. Formule las siguientes preguntas: Las respuestas variarán en función de las tarjetas seleccionadas.

a. «¿Qué información sabes?». Sabemos que hay 9 cajas y que cada caja contiene 6 camisas.

b. «¿Qué necesitas averiguar?». Tenemos que averiguar el número total de camisas que hay en todas las cajas.

c. «¿Cómo puedes representar el número de cajas que aparecen en la situación con los cubos conectables?». Cada cubo de enlace puede representar una caja.

d. «¿Cómo puedes representar el número de camisas de cada caja utilizando los cubos conectables?». Podríamos escribir el número de camisas de cada caja encima de los cubos de enlace con un rotulador de borrado en seco.

e. «¿Qué ecuación puedes escribir para representar tu problema?». 9 × 6 = __

10. Pida a los estudiantes que escriban la ecuación en la parte superior del tapete de trabajo.

11. Dé tiempo a los estudiantes para que trabajen con sus compañeros para crear un diagrama de cinta con sus cubos conectables. Formule las siguientes preguntas. Las respuestas variarán en función de las tarjetas seleccionadas

a. «¿Cuántos cubos conectables usaste para representar las cajas?» Usamos 9 cubos de enlace para representar las cajas.

b. «¿Qué número escribiste encima de cada cubo conectable para representar el número de camisas en cada caja?». Escribimos el número 6 encima de cada cubo de enlace.

12. Invite a los estudiantes a compartir sus modelos con el grupo. Pídales que anoten sus diagramas de cinta en el tapete de trabajo. Formule las siguientes preguntas: Las respuestas variarán en función de las tarjetas seleccionadas.

a. «¿Cómo dibujaste tu diagrama de cinta?». El número de grupos es el número de secciones del diagrama de cinta. El número escrito en cada sección representa el tamaño del grupo.

b. «¿Por qué las partes del diagrama de cinta deben ser del mismo tamaño?». Si representan el mismo valor, deben tener el mismo tamaño.

c. «¿Cuáles son los factores que muestra el diagrama de cinta?». Los factores son el número de secciones en el diagrama de cinta y el número dentro de cada sección.

d. «¿Cómo puedes usar los cubos conectables y el diagrama de cinta para encontrar el producto del número de camisas en todas las cajas?». Podemos contar de 6 en 6. Podemos sumar con sumas repetidas: 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6. Podemos multiplicar 9 veces 6.

e. «¿Cómo sabes que la ecuación es cierta utilizando el modelo del diagrama de cinta?». Vemos 6 9 veces. Vemos 9 grupos de 6.

f. «¿Cuál es el producto de este problema?». El producto es 54.

13. Pida a los estudiantes que completen el enunciado de la solución en la parte inferior de sus tapetes de trabajo. Haga la siguiente pregunta:

a. «¿Cómo se utiliza un diagrama de cinta para representar una ecuación de multiplicación?». En un diagrama de cinta, tenemos un número de secciones iguales que representan el número de grupos en un problema. Dentro de cada una de las secciones iguales, hay el mismo número que representa el segundo factor que se multiplica o el número de objetos en cada grupo.

14. Revise rápidamente la comprensión de la actividad en los tapetes de trabajo y oriente a los estudiantes según sea necesario.

15. Después de comprobar el trabajo de los estudiantes, indíqueles que borren sus tapetes de trabajo y los cubos conectables. Repita la actividad según el tiempo disponible.

PARTE IV: RECTAS NUMÉRICAS Y CONTEO DE SALTOS

1. Pida a los estudiantes que platiquen sobre lo que recuerdan del uso de rectas numéricas para ayudar a resolver problemas de multiplicación. Permita que compartan sus conocimientos y comprensión con el grupo.

2. Entregue una regla de medir a cada pareja. Distribuya un tapete de trabajo de modelos de multiplicación para la parte IV y un marcador de borrado en seco a cada estudiante.

3. Coloque las tarjetas numéricas boca abajo frente al grupo.

4. Lea el escenario en voz alta al grupo e invite a los estudiantes a compartir lo que notan sobre el escenario.

5. Explique que darán vuelta a dos tarjetas numéricas y usarán los números para completar las partes faltantes del escenario.

6. Elija a un estudiante para que dé vuelta una tarjeta numérica. Pida a los estudiantes que anoten el número en el primer espacio en blanco.

7. Elija a otro estudiante para que entregue una tarjeta numérica. Pida a los estudiantes que escriban el número en el segundo espacio en blanco.

8. Invite a un estudiante a leer en voz alta la nueva situación. Explique que deben crear un modelo de recta numérica utilizando su regla de medir. Formule las siguientes preguntas: Las respuestas variarán en función de las tarjetas seleccionadas.

a. «¿Qué información conoces?». La tienda de animales tiene 9 acuarios. Cada uno tiene 6 peces.

b. «¿Qué necesitas averiguar?». Tenemos que averiguar el número total de peces que tiene la tienda de animales.

c. «¿Cómo puedes representar el número de acuarios con la regla de medir?». Cada salto nos dice cuántos acuarios hay.

d. «¿Cómo puedes representar el número de peces de cada acuario con la regla?». El número que saltamos es el número de peces que hay en cada acuario.

e. «¿Qué ecuación puedes escribir para representar tu problema?». 9 × 6 = __

9. Haga que los estudiantes escriban la ecuación en la parte superior del tapete de trabajo.

10. Anime a los estudiantes a practicar el conteo salteado en la recta numérica de la regla de medir para representar el problema. Deben usar el marcador para encerrar con un círculo cada número que digan mientras cuentan saltando.

11. Recuerde a los estudiantes que los números encerrados con un círculo se llaman múltiplos. Como contaron de seis en seis, cada número que dijeron era múltiplo de seis. (Los múltiplos cambian según las tarjetas seleccionadas).

INTERVENCIÓN: INTERVENCIÓN EN GRUPO PEQUEÑO

12. Conceda tiempo a los estudiantes para que trabajen con sus compañeros en la creación de un modelo de recta numérica con sus reglas de medir. Formule las siguientes preguntas: Las respuestas variarán en función de las tarjetas seleccionadas.

a. «¿Cómo puedes utilizar la regla de medir para representar los acuarios?». Podemos contar 9 veces con la vara de medir.

b. «¿Cómo puedes utilizar la regla de medir para representar el número de peces que hay en cada acuario?». En cada salto podemos contar de 6 en 6 y rodear con un círculo el número en el que caemos. Podemos hacerlo 9 veces, ya que hay 9 acuarios.

c. «¿Cómo puedes utilizar la recta numérica para hallar el producto del número de peces de todos los acuarios?». Después de contar 9 veces en grupos de 6, encontramos que el producto es el número final en el que caemos y rodeamos.

13. Invite a los estudiantes a compartir sus modelos con el grupo. Pida que anoten sus modelos de recta numérica en lel tapete de trabajo. Formule las siguientes preguntas: Las respuestas variarán dependiendo de las tarjetas seleccionadas.

a. «¿Cuáles son los factores en el modelo de la recta numérica?». Los factores son el número de saltos y el valor de cada salto.

b. «¿Cómo puedes utilizar tu modelo de recta numérica para hallar el producto del número de peces que hay en todos los acuarios?». Podemos contar de 6 en 6. Podemos sumar con sumas repetidas: 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6. Podemos multiplicar 9 veces 6.

c. «¿Cómo sabes que la ecuación es verdadera utilizando el modelo de la recta numérica?». Vemos 6 9 veces. Vemos 9 grupos de 6.

d. «¿Cuál es el producto de este problema?». El producto es 54.

14. Pida a los estudiantes que completen el enunciado de la solución en la parte inferior de sus tapetes de trabajo. Haga las siguientes preguntas:

a. «¿Cómo usaste el modelo de la recta numérica para representar una ecuación de multiplicación?». Contamos por saltos el número de elementos de cada grupo. Podríamos contar de forma salteada ese número cada vez que tuviéramos un grupo. Por ejemplo, cada acuario tiene 6 peces, así que saltamos 6 más cada vez que contamos un grupo.

b. «¿Cómo podemos mostrar la multiplicación en una recta numérica?». Los factores de una oración de multiplicación nos dicen cuántas veces estamos saltando (el primer factor) y por qué número estamos saltando o saltando la cuenta (el segundo factor). Cada salto en la recta numérica es como un grupo igual.

c. «¿Cuál es la relación entre los saltos iguales en una recta numérica y el conteo saltado?» Cada vez que saltas en una recta numérica, caes en un múltiplo del factor. Aterrizas en los números que dirías si estuvieras contando saltos.

15. Revise rápidamente la comprensión del trabajo de cada estudiante en su tapete y oriénteles si es necesario.

16. Después de comprobar el trabajo de los estudiantes, pídales que borren sus tapetes y reglas de medir.

17. Repita la actividad si el tiempo lo permite.

18. Después, deje tiempo para que los estudiantes completen la comprobación individualmente.

ACELERACIÓN: MATEMÁTICAS DE HOY

CONEXIONES EN EL MUNDO REAL

MATEMÁTICAS DE HOY: PLUMAS DE PAVO REAL

DESCRIPCIÓN

Los estudiantes exploran las conexiones y aplicaciones de las matemáticas y otros contenidos transversales a través de interacciones con eventos auténticos del mundo real proporcionados por Associated Press

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Permita que los estudiantes observen la foto. Pregunte si alguna vez han visto un pavo real de verdad. Deje que los estudiantes compartan sus experiencias.

2. Lea el siguiente pie de foto:

a. Un pavo real muestra las plumas de su cola en el Jardín Botánico Tropical de Lisboa, miércoles 8 de abril de 2015. Los pavos reales macho exhiben y agitan las plumas de la cola para atraer a su pareja. (Foto: AP/Francisco Seco)

3. Pregunte:

a. Deje que los estudiantes compartan las afirmaciones «me doy cuenta...» y «me pregunto...». Debata con los estudiantes cómo se utilizan las matemáticas en esta situación.

b. Hay tres áreas en el Jardín Botánico Tropical con seis pavos reales en cada área. ¿Cuántos pavos reales hay en total? 18

c. ¿Cuáles son dos expresiones diferentes que podrían utilizarse para resolver el problema anterior? 3 × 6 = 18, 6 × 3 = 18, y/o 6 + 6 + 6 = 18

4. Los estudiantes deben completar la hoja del estudiante de forma independiente o con un compañero.

ACELERACIÓN: CREA EL TUYO

ESTABLECER CONEXIONES RELEVANTES

CREA

EL TUYO

DESCRIPCIÓN

Crea el tuyo es una actividad enriquecedora para que los estudiantes puedan crear sus propios inventos, obras de teatro, canciones, aplicaciones tecnológicas, ¡y mucho más!

MATERIALES

IMPRIMIR

• 1 material «crea el tuyo» para el estudiante (por alumno)

• 1 material «crea el tuyo» (para el maestro)

REUTILIZABLE

• Herramientas y modelos matemáticos (por clase)

CONSUMIBLE

• Materiales para crear juegos, obras de teatro e inventos

PREPARACIÓN

Ninguna

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Distribuya un material «crea el tuyo» por estudiante.

2. Deles tiempo para que sean lo más creativos posible. No hay límites para su creatividad en esta actividad.

3. Invite a cada estudiante a presentar o representar su producto ante la clase o el pequeño grupo.

ACELERACIÓN: TABLERO DE OPCIONES

TABLERO DE OPCIONES

OPCIONES PARA EL APRENDIZAJE CONTINUO

TABLERO DE OPCIONES

DESCRIPCIÓN

Los estudiantes exploran las conexiones con el mundo real y las aplicaciones del contenido matemático a través de interacciones con actividades atractivas.

MATERIALES

IMPRESO

• 1 tablero de opciones (por estudiante)

REUTILIZABLE

• Tecnología (si procede)

PREPARACIÓN

• Imprima un tablero de opciones por estudiante.

• Planifique con antelación el uso de la tecnología. Es posible que se necesite acceso a otras actividades dentro del alcance para algunas variaciones del tablero de opciones.

• Esta actividad se puede completar en clase o en casa.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Distribuya un tablero de opciones a cada estudiante.

2. Conceda tiempo a los estudiantes para examinar el tablero de opciones y seleccionar las actividades que les gustaría explorar.

3. Anime a los estudiantes a intentar al menos tres actividades del tablero de opciones.

4. Si el tiempo lo permite, pida a los estudiantes que compartan las conexiones que hicieron al completar las actividades que eligieron.