SSM CA Spanish Sixth Grade Sample

GRADO 6

CALIFORNIA

Muestra de la edición para el maestro

Muestra de la edición para maestros Grado 6

Publicado por Accelerate Learning Inc., 5177 Richmond Ave, Suite 800, Houston, TX 77056. Copyright © 2025, Accelerate Learning Inc. Todos los derechos reservados. Ninguna parte de esta publicación podrá ser reproducida o distribuida en ninguna forma ni por ningún medio, ni almacenada en una base de datos o sistema de recuperación, sin el consentimiento previo por escrito de Accelerate Learning Inc., incluyendo, entre otros, en cualquier red u otro sistema de almacenamiento o transmisión electrónica, o difusión para educación a distancia.

Para obtener más información, visítenos en www.stemscopes.com.

ESTÁNDARES

CLAVE

ÁREA Y VOLUMEN

Resolver problemas matemáticos y de la vida real relacionados con el área, la superficie y el volumen.

• Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales y polígonos mediante la composición en rectángulos o la descomposición en triángulos y otras formas; aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y de la vida real.

• Hallar el volumen de un prisma rectangular recto con longitudes de arista fraccionarias empaquetándolo con cubos unitarios de las longitudes de arista fraccionarias unitarias apropiadas, y demostrar que el volumen es el mismo que se hallaría multiplicando las longitudes de arista del prisma. Aplicar las fórmulas V = lwh y V = bh para hallar volúmenes de prismas rectangulares rectos con longitudes de arista fraccionarias en el contexto de la resolución de problemas matemáticos y de la vida real.

ACTIVIDADES DE EXPLORAR

EXPLORACIÓN 1: DESCUBRIR FÓRMULAS DE ÁREA

Los estudiantes exploran el concepto de área descomponiendo y reordenando varias figuras geométricas para formar rectángulos, lo que les permite conectar y aplicar las fórmulas de área.

• Los estudiantes trabajan en grupos para descomponer triángulos, trapecios y paralelogramos utilizando tangramas y una tapete de trabajo, reordenando estas figuras para formar rectángulos.

• Participan en debates para comprender las propiedades de las figuras bidimensionales y utilizan preguntas orientativas para reforzar su comprensión de los conceptos geométricos.

• A través de la manipulación práctica y la colaboración, los estudiantes descubren y aplican fórmulas de área para rectángulos, paralelogramos, triángulos y trapezoides.

• La actividad concluye con los estudiantes compartiendo sus estrategias y observaciones, mejorando su comprensión de cómo las diferentes formas se relacionan entre sí en términos de área.

EXPLORACIÓN 2: ENCONTRAR EL ÁREA DE CUADRILÁTEROS

Los estudiantes exploran el concepto de encontrar el área de cuadriláteros a través de la descomposición y reordenación de figuras.

• Trabajan en grupos para determinar el área de varios cuadriláteros, como paralelogramos y trapezoides, utilizando cuadrículas y fórmulas.

• Participan en debates guiados para profundizar en su comprensión de las estrategias de cálculo del área y las relaciones entre las diferentes formas.

Aplicar y ampliar los conocimientos previos de multiplicación y división para dividir fracciones entre fracciones.

ESTÁNDARES DE CONEXIÓN

• Interpretar y calcular cocientes de fracciones y resolver problemas de palabras que impliquen la división de fracciones entre fracciones, por ej., usando modelos visuales de fracciones y ecuaciones para representar el problema. Por ej., crear un contexto de historia para 2/3 ÷ 3/4 y usar un modelo visual de fracción para mostrar el cociente; utilizar la relación entre multiplicación y división para explicar que 2/3 ÷ 3/4 = 8/9 porque 3/4 de 8/9 es 2/3. En general, (a/b ÷ c/d = ad/bc). ¿Cuánto chocolate recibirá cada persona si 3 personas se reparten 1/2 libra de chocolate a partes iguales? ¿Cuántas porciones de 3/4 hay en 2/3 de una taza de yogur? ¿Qué anchura tiene una franja rectangular de tierra con longitud 3/4 milla y área 1/2 milla cuadrada?

Calcula con fluidez números de varios dígitos y encuentra factores y múltiplos comunes.

• Dividir con fluidez números de varios dígitos utilizando el algoritmo estándar.

• Sumar, restar, multiplicar y dividir con fluidez decimales de varios dígitos utilizando el algoritmo estándar para cada operación.

ACTIVIDADES

DE PARTICIPACIÓN

ACCESO A CONOCIMIENTOS PREVIOS: NO PERTENECE

Los estudiantes se involucrarán en el pensamiento crítico analizando tablas para identificar qué opción no pertenece. Este ejercicio está diseñado para revelar los conceptos erróneos de los estudiantes y no debe utilizarse como una evaluación sumativa.

• Los estudiantes trabajan individualmente o en pequeños grupos para examinar tablas con cuatro opciones, identificando el valor atípico y explicando su razonamiento.

• La actividad se centra en distinguir entre los conceptos de área y volumen, ayudando a los estudiantes a aclarar estas ideas matemáticas.

• Los maestroes facilitan un debate para abordar cualquier concepto erróneo y reforzar la comprensión de los cálculos de área y volumen.

CAPTAR INTERÉS

Los estudiantes exploran conceptos matemáticos determinando el área de paralelogramos y triángulos y el volumen de prismas rectangulares con dimensiones fraccionarias.

• Se presenta un escenario del mundo real que implica parcelas de jardín y jardineras, animándoles a aplicar conceptos matemáticos para resolver problemas prácticos.

• Participan en debates y exploran las formas y dimensiones de diseños de jardín únicos, centrándose en el cálculo del área y el volumen.

• La actividad retoma los problemas iniciales después de la exploración, permitiendo a los estudiantes aplicar los conocimientos recién adquiridos para determinar el área de trapecios y el volumen de prismas rectangulares.

• Se anima a los estudiantes a identificar y calcular el área y el volumen de varias figuras bidimensionales y tridimensionales de su entorno.

• Los estudiantes registran sus hallazgos en un diario del estudiante y participan en una charla de matemáticas para compartir observaciones y estrategias.

• La actividad concluye con un boleto de salida para evaluar la comprensión y una oportunidad para aplicar el aprendizaje a través de desafíos creativos de diseño de jardines.

EXPLORACIÓN 3: HALLAR EL ÁREA DE TRIÁNGULOS

Los estudiantes explorarán el concepto de encontrar el área de triángulos descomponiendo y reordenando figuras.

• Trabajan en grupos para determinar el área de triángulos en cuadrículas, utilizando su comprensión de figuras bidimensionales como paralelogramos, rectángulos y cuadrados.

• Aplican la fórmula del área de un triángulo para calcular el área de jardines sin utilizar una cuadrícula.

• La actividad incluye preguntas guiadas para facilitar la comprensión y animar a los estudiantes a compartir estrategias y observaciones.

• Los estudiantes completan una boleto de salida y participan en una charla de matemáticas para consolidar su aprendizaje y reflexionar sobre las estrategias usadas.

EXPLORACIÓN 4: HALLAR EL ÁREA DE FIGURAS COMPUESTAS

Los estudiantes exploran el concepto de determinar el área de figuras compuestas a través de la colaboración en grupo y la práctica.

• Los estudiantes trabajan en grupos para analizar y descomponer figuras compuestas en formas más simples utilizando Garden Cards.

• Calculan el área de cada forma utilizando fórmulas apropiadas y registran sus hallazgos en un Student Journal.

• La actividad fomenta el debate y la comparación de estrategias para encontrar áreas, fomentando una comprensión más profunda de los conceptos geométricos.

• Los estudiantes demuestran su comprensión completando un "Boleto de salida" y participando en un "Math Chat" para compartir ideas y estrategias.

EXPLORACIÓN 5: VOLUMEN DE PRISMAS RECTANGULARES

Los estudiantes exploran el concepto de volumen trabajando en colaboración para encontrar el volumen de prismas rectangulares utilizando cubos de unión y fórmulas matemáticas.

• Los estudiantes trabajan en grupos para construir modelos de cajas de cartón utilizando cubos de unión, representando las dimensiones dadas en las tarjetas de cajas de cartón.

• Calculan el volumen de cada cartón en unidades smile multiplicando la longitud, la anchura y la altura, y anotan sus conclusiones en un diario del estudiante.

• A continuación, los estudiantes aplican sus conocimientos para determinar el volumen de cajas de envío utilizando tanto la fórmula para el volumen como el área de la base multiplicada por la altura.

• La actividad concluye con una charla de matemáticas para debatir las observaciones, las estrategias y la relación entre los modelos físicos y los cálculos matemáticos.

ÁREA Y VOLUMEN

ALCANCE: IDEAS FUNDAMENTALES

DISTANCIA & DIRECCIÓN

PLANOS & ÁREA DE SUPERFICIE

GRAFICAR

FIGURAS

GRADO 6: ÁREA Y VOLUMEN

Los estudiantes aplican sus conocimientos sobre el área trabajando con cuadrículas de coordenadas para determinar las dimensiones y calcular el área de figuras geométricas. Analizan la colocación de las formas en un plano, usando los vértices para definir las longitudes de los lados y aplicar fórmulas de área. Estas actividades ayudan a desarrollar su capacidad para interpretar y representar gráficamente polígonos, preparándoles para un trabajo más avanzado en geometría de coordenadas.

CONCEPTOS CLAVE

• Puedo resolver el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales y polígonos mediante la composición en rectángulos o la descomposición en triángulos y otras formas.

• Puedo utilizar cubos unitarios para hallar el volumen de un prisma rectangular recto con longitudes de arista fraccionarias.

• Puedo usar cubos unitarios para demostrar que el volumen de un prisma rectangular recto se puede encontrar multiplicando las longitudes de las aristas del prisma.

• Puedo usar las fórmulas V = lwh y V = bh para encontrar volúmenes de prismas rectangulares rectos con longitudes de arista fraccionarias en el contexto de la resolución de problemas matemáticos y del mundo real.

Los estudiantes trabajan con el razonamiento espacial a medida que descomponen y reorganizan figuras compuestas para hallar el área y el volumen. Esto les ayuda a visualizar las medidas y las relaciones entre las distintas dimensiones, lo que es fundamental para comprender el movimiento y la posición en la geometría de coordenadas.

Los estudiantes exploran las redes y la superficie descomponiendo figuras tridimensionales en sus componentes bidimensionales. Construyen redes a partir de rectángulos y triángulos, las emparejan con los modelos tridimensionales correspondientes y utilizan fórmulas de área para calcular la superficie total. Mediante actividades prácticas, construyen prismas rectangulares y pirámides para comprender cómo se combinan sus caras para formar una figura completa, reforzando la relación entre área y superficie.

PREGUNTAS FUNDAMENTALES

• Describir las diferencias entre el área y el volumen de una figura dada.

• Describir cómo utilizar la composición o descomposición para encontrar el área de formas compuestas.

• Identificar las fórmulas para el área de triángulos, cuadriláteros, trapezoides y paralelogramos.

• Identificar las fórmulas utilizadas para encontrar el volumen de prismas rectangulares.

GRADO 6: ÁREA Y

INICIO: CONTENIDO DE APOYO

¿QUÉ ESTOY ENSEÑANDO?

CONTENIDO DE APOYO

Resolver problemas matemáticos y de la vida real relacionados con el área, la superficie y el volumen.

• Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales y polígonos mediante la composición en rectángulos o la descomposición en triángulos y otras formas; aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y de la vida real.

• Hallar el volumen de un prisma rectangular recto con longitudes de arista fraccionarias empaquetándolo con cubos unitarios de las longitudes de arista fraccionarias unitarias apropiadas, y demostrar que el volumen es el mismo que se hallaría multiplicando las longitudes de arista del prisma. Aplicar las fórmulas V = lwh y V = bh para encontrar volúmenes de prismas rectangulares rectos con longitudes de arista fraccionarias en el contexto de la resolución de problemas matemáticos y del mundo real.

CONOCIMIENTOS PREVIOS

En sexto grado, los estudiantes amplían sus conocimientos previos sobre longitud, área y volumen al resolver problemas aplicando fórmulas para el área de triángulos y paralelogramos y el volumen de prismas rectangulares. Los estudiantes se basan en su trabajo con el área de grados anteriores razonando sobre las relaciones entre las formas para determinar el área, la superficie y el volumen. Los estudiantes siguen entendiendo el área como el número de cuadrados necesarios para cubrir una figura plana. En grados anteriores, los estudiantes calcularon el volumen de prismas rectangulares rectos utilizando aristas de números enteros y entendieron hacerlo como encontrar el número de cubos unitarios (es decir, la unidad cúbica) dentro de una forma sólida. En sexto, amplían este trabajo a cubos unitarios con longitudes de arista fraccionarias.

CONCEPTOS ERRÓNEOS Y OBSTÁCULOS

• Los estudiantes pueden tener dificultades para elegir y aplicar fórmulas para resolver tareas de área y volumen.

• Los estudiantes pueden tener dificultades para calcular el área y el volumen cuando las formas tienen longitudes de arista fraccionarias.

• Los estudiantes pueden demostrar dificultad para descomponer una forma como estrategia para determinar el área o el volumen.

• Los estudiantes pueden mostrar dificultad para aplicar estrategias y fórmulas de área y volumen a aplicaciones del mundo real.

• Los estudiantes pueden tener dificultades para identificar la base y la altura de un paralelogramo y/o triángulo.

ALCANCE ACTUAL

Los estudiantes de sexto grado siguen entendiendo el área como el número de cuadrados necesarios para cubrir una figura plana. Encuentran las áreas de triángulos rectángulos, otros triángulos y cuadriláteros especiales descomponiendo estas figuras, reorganizando las piezas y relacionando las figuras con rectángulos. A medida que los estudiantes componen y descomponen formas para determinar áreas, aprenden que el área se conserva. Por ej., los estudiantes descompondrán trapecios en triángulos y/o rectángulos y utilizarán este razonamiento para obtener fórmulas del área de un trapecio. Los estudiantes hallarán el volumen de un prisma rectangular recto con longitudes de arista fraccionarias empaquetándolo con cubos unitarios de las longitudes de arista fraccionarias unitarias apropiadas y demostrarán que el volumen es el mismo que se hallaría multiplicando las longitudes de arista del prisma.

TÉRMINOS CLAVE

• área: el número de unidades cuadradas que se necesitan para cubrir la superficie bidimensional de un objeto.

• base: la superficie sobre la que se asienta un objeto sólido.

• base de un polígono: el lado del polígono que es perpendicular a la altitud.

• base de un triángulo: el lado del triángulo que es perpendicular a la altitud.

• componer: juntar partes o elementos (por ejemplo, figuras geométricas o números).

• figura compuesta: figura formada por dos o más figuras geométricas.

• descomponer: separar en partes o elementos (por ejemplo, figuras geométricas o números).

• borde: línea en la que termina un espacio o forma, donde se cruzan dos caras de un sólido 3D.

• fórmula: enunciado o regla matemática escrita con símbolos.

• altura: distancia perpendicular desde un vértice al lado opuesto de una figura.

• altura (figura 3D): la distancia vertical desde la parte superior de un objeto o figura hasta su base.

• longitud: la medida de un objeto de extremo a extremo; la distancia de un extremo al otro extremo de un objeto.

• paralelogramo: un cuadrilátero con dos conjuntos de lados paralelos.

• polígono: una figura cerrada que tiene tres o más lados, sin líneas curvas ni intersecciones; una figura cerrada formada por segmentos de línea que se encuentran en sus puntos extremos.

• cuadrilátero: un polígono con cuatro lados y cuatro ángulos.

• prisma rectangular recto: un prisma con seis caras rectangulares donde la arista lateral es perpendicular al plano de la base.

• triángulo rectángulo: un triángulo con un ángulo de 90º.

• trapezoide: un cuadrilátero con un conjunto de lados. paralelo.

• volumen: la cantidad de espacio que ocupa un objeto; la cantidad medida de unidades cúbicas que caben dentro de una figura sólidas

• anchura: cuántas unidades de anchura tiene algo.

INICIO: CONTENIDO DE APOYO

APLICAR LAS PRÁCTICAS MATEMÁTICAS

• MP.1 Dar sentido a los problemas y perseverar en su resolución: Los estudiantes perseveran para determinar las fórmulas y resolver problemas para hallar el área de un paralelogramo, de un trapecio, de un triángulo y de otras figuras compuestas.

• MP.2 Razonan abstracta y cuantitativamente: Los estudiantes razonan sobre las dimensiones de prismas rectangulares y sobre cuántos cubos caben en un prisma.

• MP.3 Construir argumentos viables y criticar el razonamiento de otros: Los estudiantes explican su razonamiento y los pasos seguidos para determinar las áreas y volúmenes de diferentes figuras, colaboran con sus compañeros y proponen ideas para resolver problemas.

• MP.4 Modelar con matemáticas: Los estudiantes modelan descomponiendo y componiendo figuras para determinar las áreas de figuras bidimensionales y los volúmenes de figuras tridimensionales.

• MP.5 Utilizar estratégicamente las herramientas apropiadas: Los estudiantes determinan cómo utilizar adecuadamente los cubos de presión para medir los volúmenes de figuras tridimensionales. Usan tángram para explorar la composición y descomposición de figuras 2D.

• MP.6 Prestar atención a la precisión: Los estudiantes usan unidades de medida correctas en sus cálculos y respuestas finales, realizan cálculos de áreas y volúmenes cuidadosamente y comprueban su trabajo para asegurar la precisión en la aplicación de fórmulas.

• MP.7 Buscan y utilizan estructuras: Los estudiantes buscan patrones y estructuras para resolver problemas. Al descomponer y componer formas para hallar el área y el volumen, hacen uso de la estructura de las formas.

• MP.8 Buscar y expresar regularidad en razonamientos repetidos: Los estudiantes se dan cuenta del uso repetido de la multiplicación en fórmulas de área y volumen y entienden cómo el cambio de una dimensión o forma afecta al resultado. Desarrollan estrategias para hallar las áreas de triángulos basándose en su conocimiento del área de cuadriláteros.

ÁREA

Los estudiantes hallarán el área de triángulos y cuadriláteros especiales componiendo, descomponiendo y reordenando estas formas y relacionándolas con rectángulos. Empiezan sabiendo que un rectángulo tiene una base de b unidades y una altura de h unidades, lo que da un área de bh unidades cuadradas. Los estudiantes descubren que pueden descomponer y reordenar un paralelogramo en un rectángulo para determinar que el área de un paralelogramo es A = bh. Descubren que dos triángulos rectángulos pueden disponerse juntos para formar un rectángulo, por lo que el área de un triángulo es la mitad del área de un rectángulo con el mismo tamaño de base y altura, dando la fórmula A = bh/2. La misma fórmula se cumple al componer un paralelogramo con dos triángulos no rectángulos. Los trapecios pueden descomponerse de varias maneras. Por ejemplo, un trapezoide puede descomponerse en dos triángulos con bases de distinto tamaño, b1 y b2, con lo que la fórmula del área de un trapezoide es A = 1/2(b1 + b2)h.

Ejemplo: ¿Cuáles de los siguientes paralelogramos están etiquetados correctamente? Selecciona todas las respuestas correctas.

INICIO: CONTENIDO DE APOYO

Las opciones de respuesta A, B, y D son correctas. Cualquier lado de un paralelogramo puede ser una base, y la base y su altura correspondiente deben ser perpendiculares entre sí. A veces la altura se dibuja fuera del paralelogramo. La altura es la distancia más corta entre una base y su lado opuesto. Respuesta C no es correcta, porque la base y la altura no son perpendiculares.

Ejemplo: ¿Cuál es el área de este paralelogramo?

a 16 unidades2

b 12 unidades2

c 5 unidades2

d 6 unidades2

La opción de respuesta D es la correcta. Los estudiantes pueden utilizar sus conocimientos de composición y descomposición para crear un rectángulo. Podrían descomponer el triángulo y reordenarlo en el lado opuesto de modo que forme un ángulo recto dentro de un rectángulo. A continuación, los estudiantes realizarían el cálculo de base por altura para llegar a una respuesta de 6 unidades2.

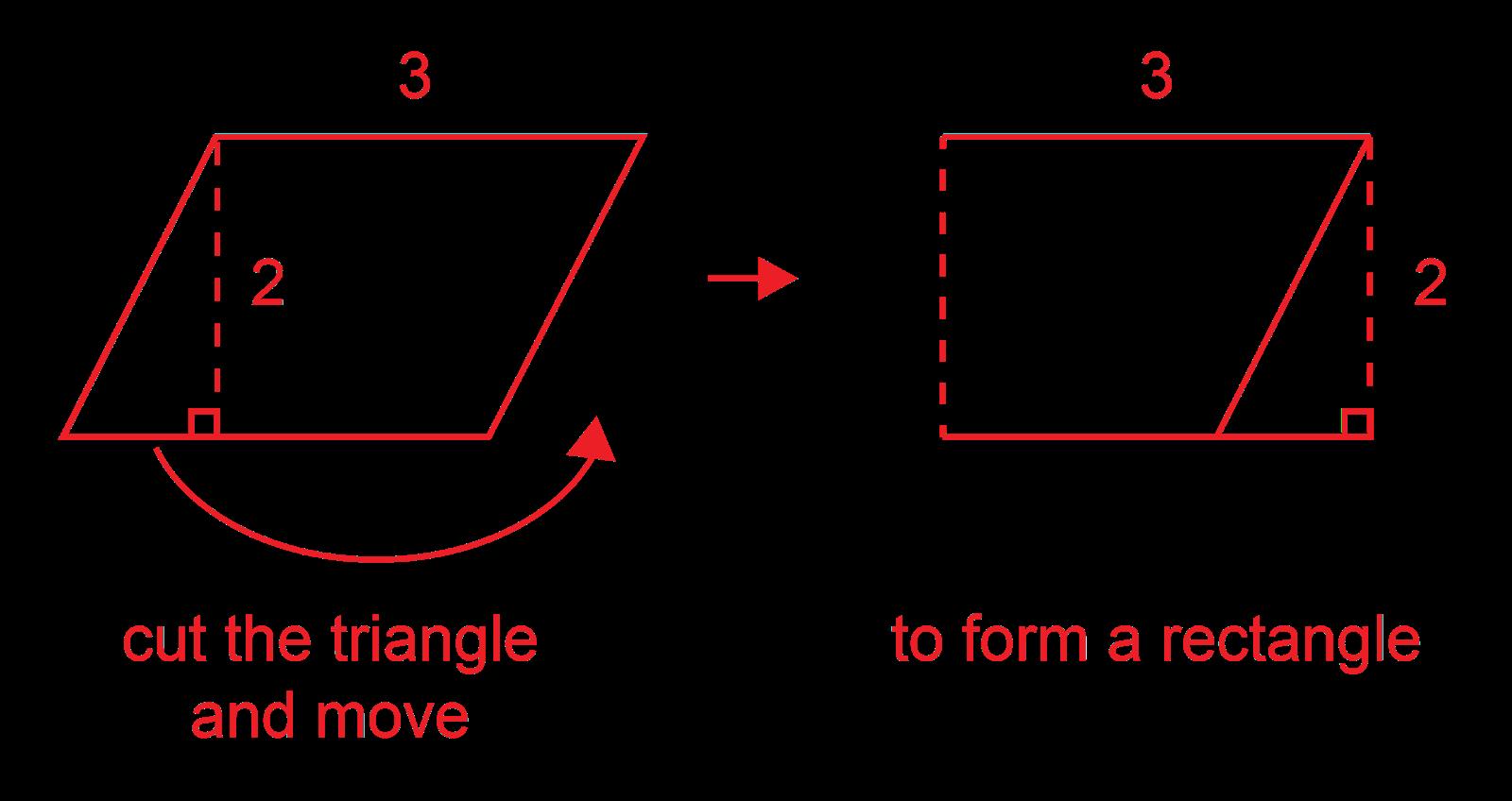
Ejemplo: ¿Cuál es el área del triángulo?

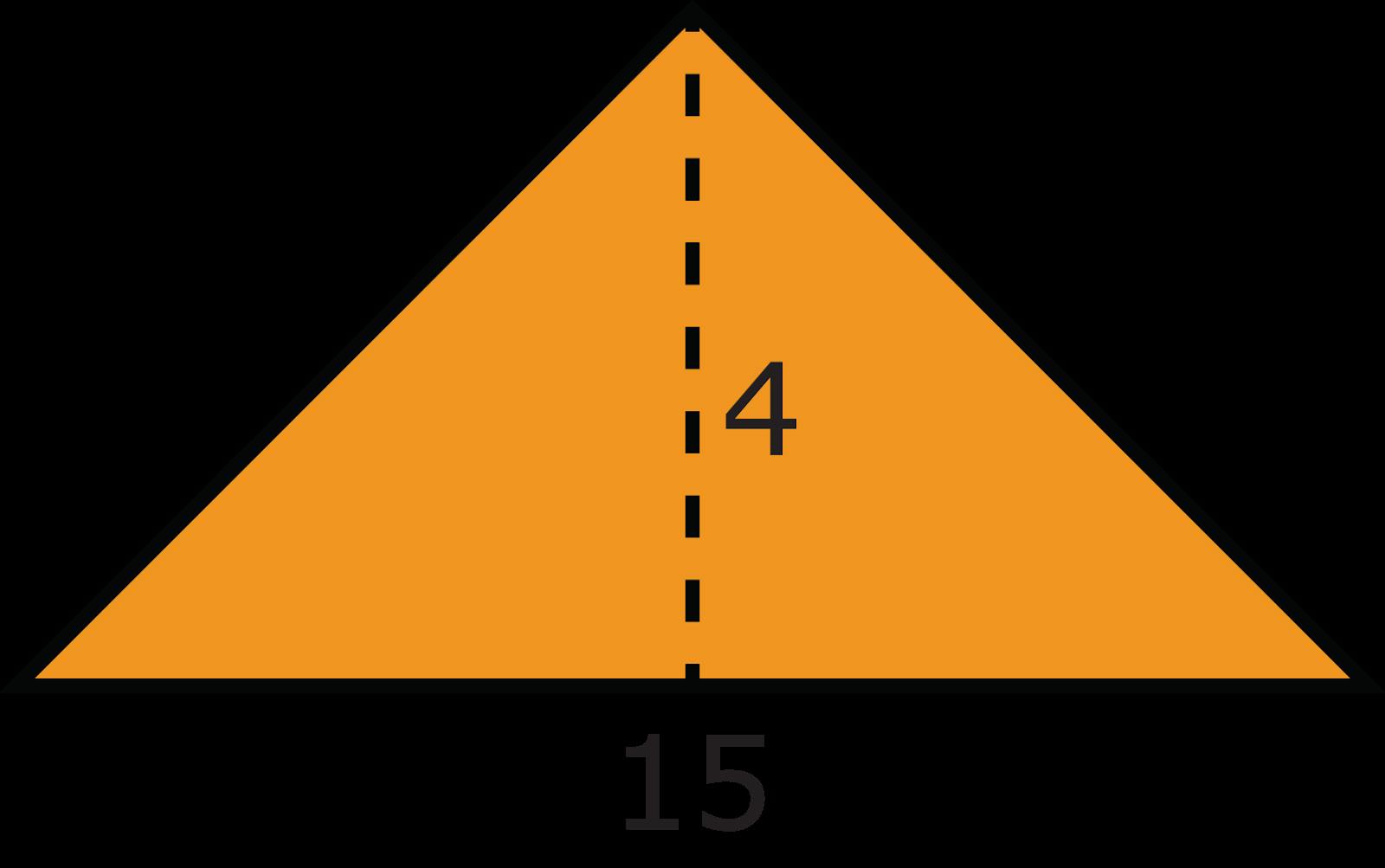
a 15 unidades2

b 30 unidades2

c 60 unidades2

d 120 unidades2

La opción de respuesta B es la correcta. Los estudiantes pueden duplicar el triángulo para crear un paralelogramo. Una vez creado el paralelogramo, los estudiantes pueden utilizar sus conocimientos sobre el área de los paralelogramos. Los estudiantes pueden multiplicar la base, 15 unidades, por la altura, 4 unidades, para obtener 60 unidades para el paralelogramo. Como la figura en cuestión es el triángulo y hay dos triángulos en el paralelogramo, los estudiantes dividirán el área del paralelogramo por 2. 60 dividido por 2 es 30, por lo que el triángulo tiene un área de 30 unidades.

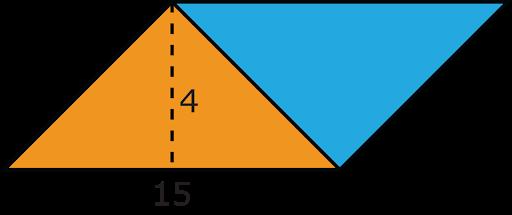
Ejemplo: ¿Cuál es el área de este trapecio?

a 60 unidades2 b 22 unidades2 c 70 unidades2 d 42,5 unidades2

Opción de respuesta D es la opción correcta. Los estudiantes deben utilizar sus conocimientos de descomposición de formas para crear un cuadrado y un triángulo. A continuación, los estudiantes aplicarían la fórmula del área de un cuadrado y del área de un triángulo para hallar las áreas de cada parte descompuesta del trapecio. El área del cuadrado daría una respuesta de 25 unidades cuadradas y el área del triángulo sería de 17.5 unidades cuadradas. Los estudiantes sumarían estas dos partes para obtener el área total del trapecio, 42.5 unidades². Las imágenes siguientes muestran la descomposición y cómo los estudiantes pueden determinar el área.

Ejemplo: ¿Cuál es el área de este trapecio?

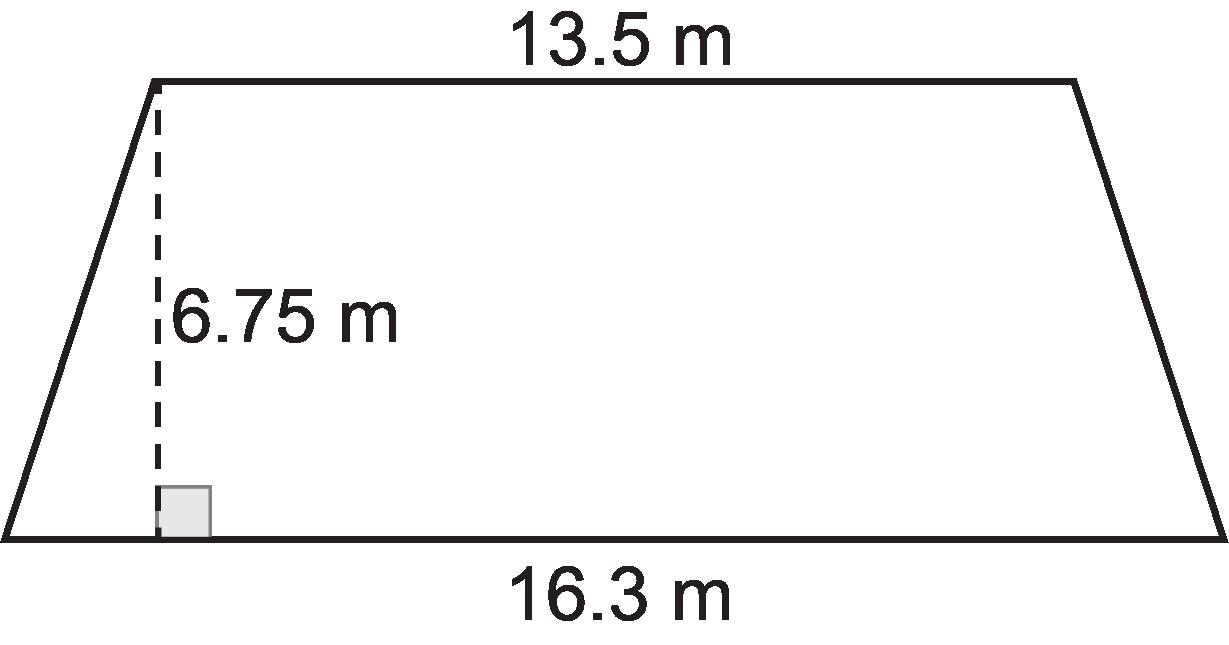
a 201.15 m2

b 371.7 m2

c 182.25 m2

d 100.575 m2

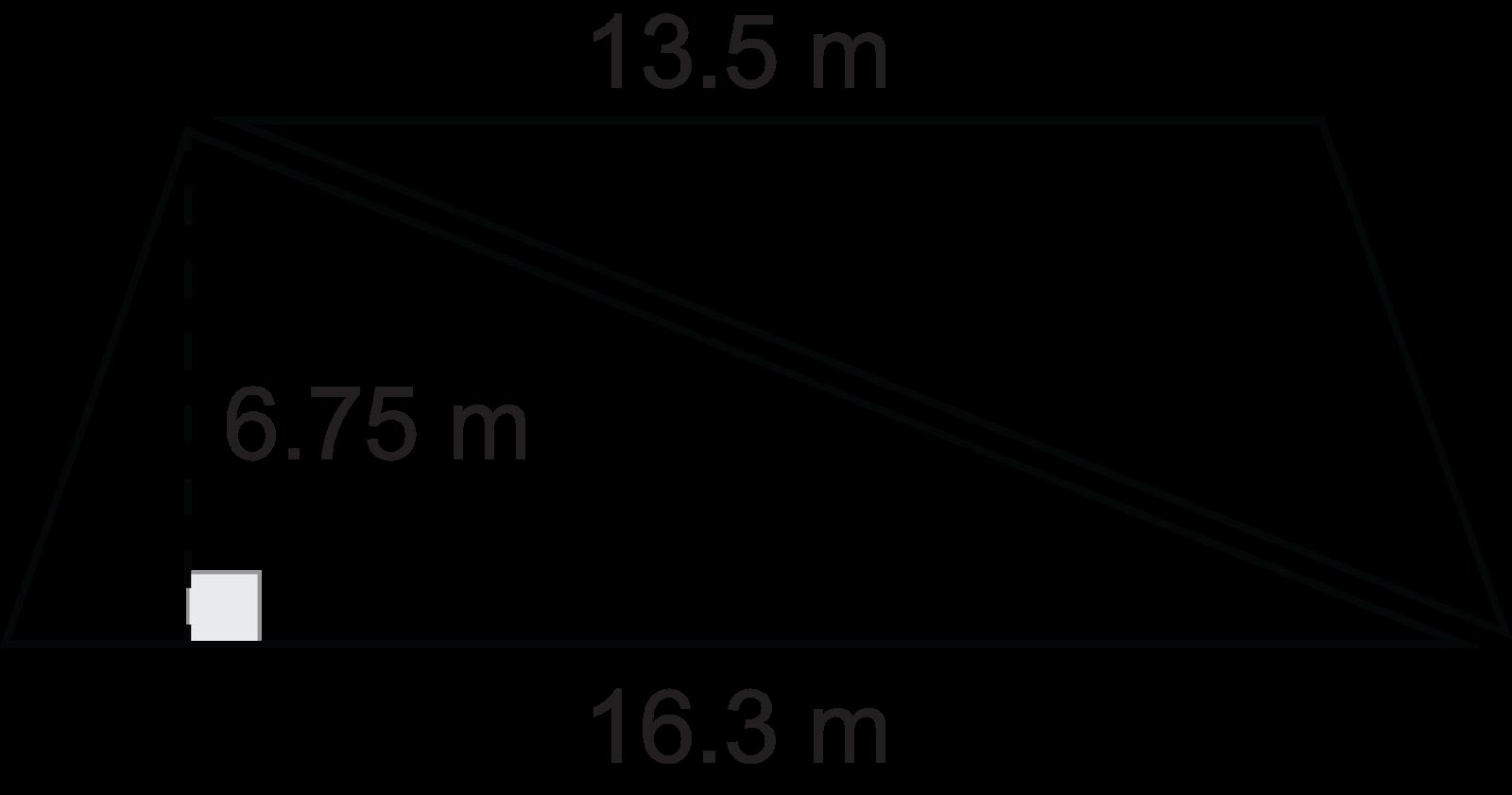
Opción de respuesta D es la opción correcta. Una forma en que los estudiantes pueden determinar el área es utilizar sus conocimientos de descomposición de formas para crear dos triángulos. A continuación, los estudiantes aplicarían la fórmula del área de un triángulo para hallar el área de cada parte descompuesta del trapecio. El área del triángulo de la izquierda sería 55.0125 m2, y el área del triángulo de la derecha sería 45.5625 m2. A continuación, los estudiantes tendrían que sumar las dos áreas para obtener el área total del trapecio, que es 100,575 m2. Las imágenes siguientes muestran la descomposición y cómo los estudiantes pueden determinar el área.

VOLUMEN

INICIO: CONTENIDO DE APOYO

Anteriormente, los estudiantes han aprendido a hallar el volumen de prismas rectangulares rectos empaquetándolos con cubos unitarios. Los estudiantes se basarán en este conocimiento para explorar fórmulas para encontrar el volumen y descubrir que la primera capa del prisma también se llama base. Los estudiantes continuarán su comprensión del volumen de los prismas rectangulares rectos para determinar el volumen cuando se dan dimensiones fraccionarias. Los estudiantes descubrirán la conexión entre la fórmula V = lwh y la fórmula V = bh.

Ejemplo: ¿Cuántos cubos con longitudes laterales de 1 4 pulg. se necesitan para llenar el prisma que se muestra a continuación?

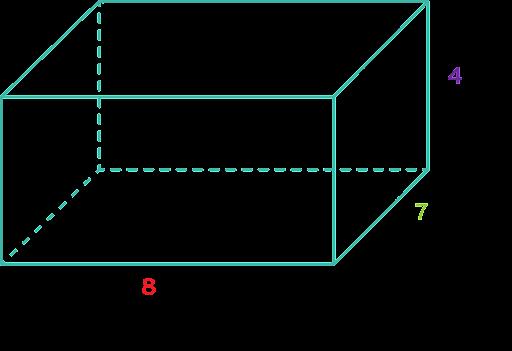
a 896 b 19 c 224 d 56

La opción C es la respuesta correcta. Los estudiantes deben llegar a la conclusión de que la longitud sería de 8 cubos de un cuarto, la anchura sería de 7 cubos de un cuarto y la altura sería de 4 cubos de un cuarto. Luego, los estudiantes multiplicarían para encontrar cuántos cubos de 1/4 pulgada se necesitarían para llenar el prisma.

AVANCES

Después de este alcance, los estudiantes de sexto grado exploran el área de la superficie de las figuras usando redes formadas por rectángulos y triángulos. En séptimo grado, amplían sus conocimientos para resolver problemas de volumen y superficie de objetos bidimensionales y tridimensionales formados por triángulos, círculos, cuadriláteros, polígonos, cubos y prismas rectángulos. Este trabajo conducirá a los próximos conceptos de dibujos a escala, tasas, proporciones y formas similares.

INICIO: CONTENIDO DESGLOSADO

ANÁLISIS PROFUNDO DE LOS ESTÁNDARES

CONTENIDO DESGLOSADO

ESTÁNDARES

Resolver problemas matemáticos y de la vida real relacionados con el área, la superficie y el volumen.

• Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales y polígonos mediante la composición en rectángulos o la descomposición en triángulos y otras formas; aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y de la vida.

• Hallar el volumen de un prisma rectangular recto con longitudes de arista fraccionarias empaquetándolo con cubos unitarios de las longitudes de arista fraccionarias unitarias apropiadas, y demostrar que el volumen es el mismo que se hallaría multiplicando las longitudes de arista del prisma. Aplicar las fórmulas V = lwh y V = Bh para hallar volúmenes de prismas rectangulares rectos con longitudes de arista fraccionarias en el contexto de la resolución de problemas matemáticos y del mundo real.

DESGLOSAR EL ESTÁNDAR

VERBOS: ¿QUÉ DEBERÍAN HACER LOS ESTUDIANTES?

• aplicar: utilizar

• componer: juntar partes o elementos (por ej., figuras geométricas o números).

• descomponer: separar en partes o elementos (por ej., figuras geométricas o números).

• encontrar: descubrir; resolver.

• multiplicar: aplicar la operación matemática consistente en sumar repetidamente (mediante diversas estrategias) para obtener el producto.

• mostrar: representar un número o cantidad; demostrar una conclusión.

• resolver: encontrar un valor que responda a una pregunta y/o haga verdadera una ecuación.

SUSTANTIVOS: ¿QUÉ PALABRAS CONCRETAS DEBEN CONOCER LOS ESTUDIANTES?

• área: el número de unidades cuadradas que se necesitan para cubrir la superficie bidimensional de un objeto.

• base: superficie sobre la que se asienta un objeto sólido.

• borde: una línea en la que termina un espacio o forma, donde se cruzan dos caras de un sólido tridimensional

• fórmula: un enunciado o regla matemática escrita con símbolos

• altura (figura tridimensional): la distancia vertical desde la parte superior de un objeto o figura hasta su base.

• longitud: la medida de un objeto de extremo a extremo; la distancia de un extremo al otro extremo de un objeto .

• problema matemático: un problema que puede ser representado, analizado, y posiblemente resuelto, con los métodos de las matemáticas.

• polígono: una figura cerrada que tiene tres o más lados, sin líneas curvas, y sin intersecciones; una figura cerrada formada por segmentos de línea que se encuentran en sus puntos finales.

• prisma: figura tridimensional que tiene al menos un conjunto de caras congruentes y paralelas (bases) que son polígonos con paralelogramos como caras restantes.

• cuadrilátero: un polígono con cuatro lados y cuatro ángulos.

• problema de palabra real: un problema contextual que puede interpretarse, representarse y analizarse mediante la aplicación de las matemáticas.

• rectángulo: un paralelogramo con lados opuestos iguales y cuatro ángulos rectos.

• prisma rectangular recto: un prisma con seis caras rectangulares en el que la arista lateral es perpendicular al plano de la base.

• triángulo rectángulo: un triángulo con un ángulo de 90º.

• triángulo: un polígono con exactamente tres lados rectos y tres ángulos.

• cubo unitario: un cubo en el que todos los lados tienen una longitud de una unidad.

• fracción unitaria: una fracción en la que el numerador es 1 y el denominador es un entero positivo.

• volumen: la cantidad de espacio que ocupa un objeto; la cantidad medida de unidades cúbicas que caben dentro de una figura sólida.

• anchura: cuántas unidades de ancho tiene algo.

IMPLICACIONES PARA LA ENSEÑANZA

• En grados anteriores, los estudiantes han explorado el área y el perímetro de rectángulos con matrices y relacionando el proceso de contar unidades cuadradas con sumas y restas repetidas. Vieron la ecuación para el área de un rectángulo como una ecuación de multiplicación con un factor desconocido. Los estudiantes utilizaron fórmulas para el área y el perímetro de un rectángulo para resolver problemas matemáticos y del mundo real que implicaban números enteros y longitudes de lado fraccionarias. Exploran el volumen como atributo de una figura tridimensional y miden el volumen de un líquido. Los estudiantes han determinado el volumen de prismas rectangulares rectos con medidas de números enteros empaquetándolos con cubos unitarios y relacionando el proceso con sumas y multiplicaciones repetidas. Además, los estudiantes han utilizado diagramas de cinta, modelos de área y rectas numéricas para multiplicar fracciones por números enteros y fracciones por fracciones.

• En este grado, se espera que los estudiantes encuentren el área de triángulos, cuadriláteros y polígonos. Componen y descomponen y reorganizan partes de polígonos en triángulos y cuadriláteros para hallar el área del polígono. Los estudiantes hallan el volumen de prismas rectangulares con longitudes laterales fraccionarias empaquetándolos con cubos unitarios. Este trabajo lleva a los estudiantes a deducir fórmulas para el volumen de prismas rectangulares. Los estudiantes aplican fórmulas de volumen con longitudes laterales fraccionarias al contexto de problemas matemáticos y del mundo real.

INICIO: CONTENIDO DESGLOSADO

ALINEACIÓN VERTICAL

GRADO

ESTÁNDAR

5 Usar paréntesis, corchetes o llaves en expresiones numéricas y evaluar expresiones con estos símbolos.

5 Aplicar y ampliar la comprensión previa de la multiplicación para multiplicar una fracción o un número entero por una fracción.

a. Interpretar el producto (a/n) × q como a partes de una partición de q en b partes iguales; equivalentemente, como el resultado de una secuencia de operaciones a × q ÷ b

b. Hallar el área de un rectángulo con longitudes laterales fraccionarias embaldosándolo con cuadrados unitarios de las longitudes laterales fraccionarias unitarias apropiadas, y demostrar que el área es la misma que se hallaría multiplicando las longitudes laterales. Multiplicar longitudes laterales fraccionarias para hallar áreas de rectángulos y representar productos de fracciones como áreas rectangulares.

5 Reconocer el volumen como un atributo de las figuras sólidas y comprender conceptos de medición de volumen.

5 Medir volúmenes contando cubos unitarios, utilizando cm cúbicos, pulg cúbicos, pies cúbicos y unidades improvisadas.

5 Relacionar el volumen con las operaciones de multiplicación y suma y resolver problemas matemáticos y de la vida real en los que intervenga el volumen.

a. Hallar el volumen de un prisma rectangular recto con longitudes laterales enteras empaquetándolo con cubos unitarios, y demostrar que el volumen es el mismo que se hallaría multiplicando las longitudes de las aristas, equivalentemente multiplicando la altura por el área de la base. Representar productos de tres números enteros como volúmenes, por ejemplo para representar la propiedad asociativa de la multiplicación.

b. Aplicar las fórmulas V = l×w×h y V = b×h para prismas rectangulares para hallar volúmenes de prismas rectangulares rectos con longitudes de arista de números enteros en el contexto de la resolución de problemas matemáticos y del mundo real.

c. Reconocer el volumen como aditivo. Hallar volúmenes de figuras sólidas compuestas por dos prismas rectangulares rectos no superpuestos sumando los volúmenes de las partes no superpuestas, aplicando esta técnica para resolver problemas del mundo real.

6 Escribir y evaluar expresiones numéricas que involucren exponentes de números enteros.

6 Escribir, leer y evaluar expresiones en las que las letras representan números.

a. Escribir expresiones que registren operaciones con números y con letras que representan números.

b. Identificar partes de una expresión utilizando términos matemáticos (suma, término, producto, factor, cociente, coeficiente); ver una o más partes de una expresión como una entidad única.

c. Evaluar expresiones con valores específicos de sus variables. Incluir expresiones que surjan de fórmulas utilizadas en problemas del mundo real. Realizar operaciones aritméticas, incluyendo aquellas que involucran exponentes de números enteros, en el orden convencional cuando no hay paréntesis para especificar un orden particular (Orden de Operaciones).

6 Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales y polígonos componiendo en rectángulos o descomponiendo en triángulos y otras formas; aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y del mundo real.

6 Hallar el volumen de un prisma rectangular recto con longitudes de arista fraccionarias empaquetándolo con cubos unitarios de las longitudes de arista fraccionarias unitarias apropiadas, y demostrar que el volumen es el mismo que se hallaría multiplicando las longitudes de arista del prisma. Aplicar las fórmulas V = lwh y V = bh para hallar volúmenes de prismas rectangulares rectos con longitudes de arista fraccionarias en el contexto de la resolución de problemas matemáticos y del mundo real.

6 Aplicar las propiedades de las operaciones para generar expresiones equivalentes.

6 Identificar cuándo dos expresiones son equivalentes (es decir, cuando las dos expresiones nombran el mismo número independientemente del valor que se sustituya en ellas).

6 Entender la resolución de una ecuación o desigualdad como un proceso de respuesta a una pregunta: ¿qué valores de un conjunto especificado, si los hay, hacen que la ecuación o desigualdad sea verdadera? Utilizar la sustitución para determinar si un número dado de un conjunto especificado hace que una ecuación o desigualdad sea verdadera.

6 Utilizar variables para representar números y escribir expresiones al resolver un problema matemático o del mundo real; comprender que una variable puede representar un número desconocido o, según el propósito, cualquier número de un conjunto especificado.

6 Representar figuras tridimensionales utilizando redes formadas por rectángulos y triángulos, y utilizar las redes para hallar la superficie de estas figuras. Aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y de la vida real.

7 Resolver problemas que impliquen dibujos a escala de figuras geométricas, incluido el cálculo de longitudes y áreas reales a partir de un dibujo a escala y la reproducción de un dibujo a escala a una escala diferente.

7 Conocer las fórmulas para el área y la circunferencia de un círculo y utilizarlas para resolver problemas; dar una derivación informal de la relación entre la circunferencia y el área de un círculo.

7 Resolver problemas matemáticos y de la vida real relacionados con el área, el volumen y la superficie de objetos bidimensionales y tridimensionales formados por triángulos, cuadriláteros, polígonos, cubos y prismas rectángulos.

8 Explicar una demostración del Teorema de Pitágoras y su inversa.

8 Utilizar los símbolos de raíz cuadrada y raíz cúbica para representar soluciones a ecuaciones de la forma x2 = p y x3 = p, donde p es un número racional positivo. Evaluar raíces cuadradas de pequeños cuadrados perfectos y raíces cúbicas de pequeños cubos perfectos. Saber que √ 2 es irracional.

HS Utilizar formas geométricas, sus medidas y sus propiedades para describir objetos (por ejemplo, modelar el tronco de un árbol o un torso humano como un cilindro).

HS Aplicar métodos geométricos para resolver problemas de diseño (por ejemplo, diseñar un objeto o estructura para satisfacer restricciones físicas o minimizar costes; trabajar con sistemas de retícula tipográfica basados en proporciones).

HS Derivar la fórmula A = 1 2 ab sin(C) para el área de un triángulo trazando una línea auxiliar desde un vértice perpendicular al lado opuesto.

HS Argumenta de manera informal las fórmulas de la circunferencia de un círculo, el área de un círculo, el volumen de un cilindro, una pirámide y un cono. Utilizar argumentos de disección, el principio de Cavalieri y argumentos informales de límites.

INICIO: GUÍA DE INSTRUCCIÓN ANDAMIADA

MONITOREAR Y AJUSTAR

GUÍA DE INSTRUCCIÓN ANDAMIADA

La guía de instrucción andamiada se proporciona para que los maestros puedan planificar los siguientes pasos basándose en el rendimiento de los estudiantes en las evaluaciones de alcance o en los datos de su evaluación de medición de crecimiento MAP. Se trata de una herramienta integrada que lleva a los maestros a buscar materiales basados en las necesidades de los estudiantes. Los materiales sugeridos están organizados por estándares. Dentro de cada estándar, los materiales se clasifican además por el rango de percentiles que mejor se adapta.

Cuando se usa la guía de instrucción andamiada con los datos de su evaluación de medición de crecimiento MAP, cada tabla puede guiar a los maestros a los materiales sugeridos basados en los puntajes del área de instrucción de los estudiantes. Se sugiere a los maestros a permitir que todos los estudiantes experimenten con «Captar interés», «Exploración», «Muestra lo que sabes» y «Pruebas de habilidades». Estos elementos cubren a fondo los estándares incluidos en el alcance.

La guía se divide en cuatro rangos de percentiles para cada estándar.

Refuerzo del grado anterior Nivel de grado con apoyos Nivel de grado

Los estudiantes con puntaje en este rango de percentil necesitan refuerzo del contenido del grado anterior.

Los estudiantes con puntaje en este rango de percentil necesitan apoyo de intervención de nivel de grado.

Los estudiantes con puntaje en este rango de percentil pueden trabajar en contenido de nivel de grado con apoyos de instrucción.

Ampliación del nivel de grado

Los estudiantes con puntaje en este rango de percentil están listos para aplicar su conocimiento del contenido en una variedad de actividades.

Para interpretar y responder al rendimiento del estudiante en las evaluaciones del alcance, complete los siguientes pasos:

1 Revise los datos recopilados a través de la plataforma en línea o el «Mapa de calor» para determinar el rango percentil del estudiante para cada estándar evaluado.

2 Las tablas proporcionadas recomiendan un conjunto de materiales de instrucción para cada rango percentil dentro de cada estándar evaluado. Elija cuál de estos materiales usará para apoyar mejor al estudiante con base en sus datos de evaluación.

3 Haga clic en el enlace directo al material elegido para el estudiante.

Para interpretar y responder al desempeño del estudiante en la evaluación de medición de crecimiento MAP, complete los siguientes pasos:

1. Revise los datos proporcionados para determinar el percentil, el área de instrucción y/o el desglose de estándares para cada estudiante.

2. Encuentre el alcance que incluye los estándares que necesitan enfoque o intervención.

3. Acceda a la «guía de instrucción andamiada» en la sección «inicio» del alcance.

4. Haga clic en el enlace directo al material recomendado para el estudiante.

La guía es un plan sugerido y no se limita a los estándares y actividades incluidos. Además, no todas las actividades sugeridas necesitan ser completadas por cada estudiante.

Área de instrucción: Operaciones y pensamiento algebraico

Todos los estudiantes:

• Captar interés

• Exploración

• Muestra lo que sabes

• Prueba de habilidades

Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales y polígonos mediante la composición en rectángulos o la descomposición en triángulos y otras formas; aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y del mundo real.

0 %25 % (Nivel de grado anterior con apoyo)

25 %50 % (Nivel de grado con apoyo)

4 - Resolución de Problemas de Área y Perímetro

Intervención en grupos pequeños

Constructor de fluidez

• Resolución de problemas con área y perímetro

Práctica interactiva

• Cruce de armadillo

Prueba de habilidades

6 - Area and Volume

Acceso a conocimientos previos

Constructor de fluidez

Repaso y práctica de habilidades

• Evaluación rápida (preguntas 1-4)

• Repaso: Área e los polígonos, en la sección «Área de figuras compuestas».

• Revisión (preguntas 1-9)

6 - Área y volumen

50 %80 % (Nivel de Grado)

Vocabulario ilustrado

Vocabulario interactivo

Libreta interactiva

Constructor de fluidez

• Área y volumen

Conexiones lingüísticas

80 %100 % (Ampliando el Nivel de Grado)

6 - Área y volumen

Tarea de presentación matemática

Tablero de opciones

INICIO: GUÍA DE INSTRUCCIÓN ANDAMIADA

Hallar el volumen de un prisma rectangular recto con longitudes de arista fraccionarias empaquetándolo con cubos unitarios de las longitudes de arista fraccionarias unitarias apropiadas, y demostrar que el volumen es el mismo que se hallaría multiplicando las longitudes de arista del prisma. Aplicar las fórmulas V = lwh y V = bh para encontrar volúmenes de prismas rectangulares rectos con longitudes de arista fraccionarias en el contexto de la resolución de problemas matemáticos y del mundo real.

0 %25 % (Nivel de grado anterior con apoyo)

25 %50 % (Nivel de grado con apoyo)

5 - Aplicar Fórmulas de Volumen

Intervención en grupos pequeños

Constructor de fluidez

• Resolución de problemas con volumen

Práctica interactiva

• Kyoobz

Prueba de habilidades

6 - Área y Volumen

Acceso a conocimientos previos

Constructor de fluidez

Repaso y práctica de habilidades

• Evaluación rápida (pregunta 5)

• Repaso: Volumen de prismas rectangulares)

• Revisión (pregunta 10)

6 - Área y volumen

Vocabulario ilustrado

50 %80 % (Nivel de Grado)

Vocabulario interactivo

Libreta interactiva

Constructor de fluidez

• Área y volumen

Conexiones lingüísticas

Ciencia de datos

80 %100 % (Ampliando el Nivel de Grado)

6 - Área y volumen

¿Qué prefieres?

Tablero de opciones

GRADO 6: ÁREA Y VOLUMEN

ATRAER: ACCESO A CONOCIMIENTOS PREVIOS

EVALUAR PREVIAMENTE EL CONOCIMIENTO DE LOS ESTUDIANTES

ACCESO A CONOCIMIENTOS

PREVIOS: NO PERTENECE

ESTÁNDAR PREVIO

Se dice que una figura plana que puede cubrirse sin huecos ni solapamientos por n cuadrados unitarios tiene un área de n unidades cuadradas.

Halla el volumen de un prisma rectangular recto con longitudes laterales de números enteros empaquetándolo con cubos unitarios, y demuestra que el volumen es el mismo que se hallaría multiplicando las longitudes de las aristas, equivalentemente multiplicando la altura por el área de la base. Representar productos de tres números enteros como volúmenes (por ej., para representar la propiedad asociativa de la multiplicación).

DESCRIPCIÓN

Los estudiantes examinarán una serie de tablas y determinarán qué opción no pertenece al grupo. Este elemento está diseñado para descubrir los conceptos erróneos de los estudiantes; no debe utilizarse como evaluación sumativa.

MATERIALES

IMPRESOS

• 1 documento «No pertenece» (por estudiante o por grupo)

PREPARACIÓN

• Si no asigna el acceso a conocimientos previos digitalmente, imprima un documento «No pertenece» para cada estudiante.

• Planifique dividir la clase en grupos de dos o tres.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Reparta el acceso a conocimientos previos a cada estudiante o grupo.

2. Explique que cada tabla del folleto contiene cuatro opciones. Tres de las opciones van juntas, mientras que una no pertenece.

3. Pida a los estudiantes que determinen qué letra no pertenece a cada grupo y que expliquen lo que piensan.

a. Conjunto 1: B no pertenece porque es la única opción que implica volumen. Las otras opciones implican superficie.

b. Conjunto 2: C no pertenece porque es la única opción que implica superficie. Las otras opciones implican volumen.

c. Conjunto 3: D no pertenece porque describe un área de 18 pulgadas cuadradas, y las otras opciones describen un área de 16 pulgadas cuadradas.

d. Conjunto 4: A no pertenece porque describe un volumen de 60 pulgadas cúbicas, y las otras opciones describen un volumen de 64 pulgadas cúbicas.

4. Concluya dirigiendo una plática.

5. Si los estudiantes tienen dificultades para completar esta tarea, continúe con el constructor de fundamentos para llenar este vacío en el conocimiento previo antes de pasar a otras partes del alcance.

Conjunto 1: No pertenece

Determina qué letra no pertenece en cada grupo y explica tu razonamiento.

A. ¿Cuánto espacio hay sobre una pizza para el queso?

B. ¿Cuánto helado llena el contenedor mediano de plástico?

Area and Volume

C. ¿Cuánto espacio cubre la hierba en el jardín de adelante?

D. ¿Cuánta pintura se necesita para cubrir una pared del dormitorio?

La letra ______ no pertenece porque ____________________________________

Conjunto 2: No pertenece

Determina qué letra no pertenece en cada grupo y explica tu razonamiento.

A.

¿Cuánta agua se necesita para llenar la pecera?

B.

¿Cuánto hielo puede contener esta caja térmica?

Area and Volume

C. ¿Cuánto papel para envolver se necesita para cubrir la parte de afuera de la caja?

D. ¿Cuánto espacio hay dentro de la maleta?

La letra ______ no pertenece porque ____________________________________

NO PERTENECE

IDENTIFICACIÓN DE CONCEPTOS ERRÓNEOS

• Es posible que los estudiantes no se den cuenta de que el área mide el número de unidades cuadradas que cubren la parte superior de una figura bidimensional, y el volumen mide el número de unidades cúbicas que llenan el interior de una figura tridimensional.

• Los estudiantes pueden no saber que el área de un rectángulo es la longitud por la anchura, y el volumen de un prisma rectangular es la longitud por la anchura por la altura.

Jardín único

Longitud de abajo de 11.2 pies

Longitud de arriba de 3 pies

Altura de 3 pies

Caja del macetero

Altura de 1 pulgada

Longitud de 8 pulgadas

Ancho de 5 pulgadas

HUERTOS

DESCRIPCIÓN

ATRAER: CAPTAR INTERÉS

LECCIÓN PARA CAPTAR INTERÉS

CAPTAR INTERÉS

Los estudiantes determinan los lados que faltan en los triángulos rectángulos utilizando el teorema de Pitágoras.

MATERIALES

IMPRESOS

• 1 teorema de Pitágoras (por clase)

REUTILIZABLES

• 1 fenómenos (por clase)

PREPARACIÓN

• Planee mostrar los fenómenos.

• Prepárese para proyectar la diapositiva Parcelas de jardín para que toda la clase la vea.

• Prepárese para presentar el escenario y anime a los estudiantes a pensar en cómo resolverlo.

• Prepárese para presentar el escenario y anime a los estudiantes a pensar en cómo resolverlo. Prepárese para pasar a las actividades de exploración, regresando a la actividad para captar interés con los nuevos conocimientos adquiridos después de que se hayan completado las exploraciones.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

PARTE I: EXPLORACIÓN PREVIA

1. Presente esta actividad hacia el comienzo del alcance. La clase retomará la actividad y resolverá el problema original después de que los estudiantes hayan completado las actividades explorar correspondientes.

2. Muestre los fenómenos. Formule a los estudiantes las siguientes preguntas: ¿Qué observas? ¿Dónde puedes ver matemáticas en esta situación? Permita que los estudiantes compartan todas sus ideas.

3. Explique el escenario a la clase: Sarah está trabajando para crear nuevos estilos de jardín. Quiere que cada uno de sus nuevos jardines tenga una forma única. Incluso ha decidido crear una jardinera alta. Una vez decidida la forma, tendrá que determinar la superficie de los nuevos jardines. También tendrá que determinar el volumen de la nueva jardinera para saber cuánta tierra tendrá que comprar.

4. Deje que los estudiantes hagan preguntas y aclaren el contexto si es necesario. Anímeles a compartir sus ideas y experiencias con la clase con las siguientes preguntas:

a. ¿Habías visto un jardín antes? ¿Qué forma tenía?

b. ¿Por qué Sarah necesitaría saber el área y el volumen de un jardín?

5. Proyecte la diapositiva «Parcelas de jardín».

6. Explique a los estudiantes que Sarah ha decidido las formas de su nuevo y exclusivo jardín y jardinera. Ha compartido sus ideas sobre cuáles deberían ser las dimensiones de cada nueva parcela. Haga las siguientes preguntas a la clase:

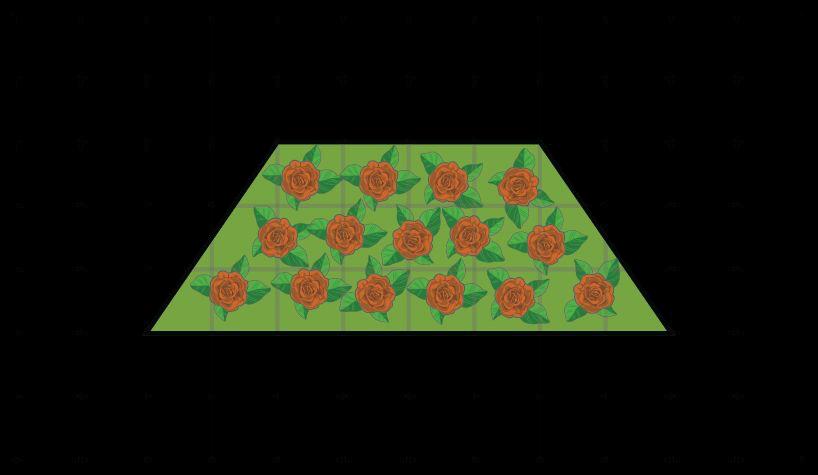
a. DOK-1 ¿Por qué el jardín único puede tener dos medidas de longitud? La parte inferior del jardín es más larga que la parte superior del jardín, por lo que hay dos longitudes de diferente tamaño.

b. DOK-1 ¿Cuál es la forma del jardín único? El jardín único es un trapecio.

c. DOK-1 ¿Qué forma tiene la jardinera? La jardinera tiene forma de prisma rectangular.

7. Continúa con las actividades de exploración.

PARTE II: DESPUÉS DE LA EXPLORACIÓN

1. Después de que los estudiantes hayan completado las actividades de exploración para este tema, muestre nuevamente los fenómenos y repita el escenario.

2. Refiérase a la diapositiva «Parcelas de jardín» y haga las siguientes preguntas a la clase:

a. DOK-1 ¿Por qué el jardín único puede tener dos medidas de longitud? La parte inferior del jardín es más larga que la parte superior del jardín, por lo que hay dos medidas de longitud diferentes.

b. DOK-1 ¿Cuál es la forma del jardín único? El jardín único es un trapecio.

c. DOK-1 ¿Qué forma tiene la jardinera? La jardinera tiene forma de prisma rectangular.

d. DOK-1 ¿Cómo puedes determinar el área del jardín único? El jardín único es un trapecio. Podemos determinar el área del jardín único utilizando la fórmula A = ½ (b1 + b2)(h).

e. DOK-1 ¿Cuál es el área del jardín único? El área del jardín único es de 21.3 pies cuadrados.

f. DOK-1 ¿Cómo puedes determinar el volumen de la jardinera? La jardinera tiene forma de prisma rectangular. Puedo hallar el volumen de la jardinera utilizando la fórmula V = lwh

g. DOK-1 ¿Cuál es el volumen de la jardinera? El volumen de la jardinera es de 60 pulgadas cúbicas.

3. Si dispone de tiempo, anime a los estudiantes a buscar en su entorno representaciones de figuras bidimensionales y tridimensionales, como rectángulos, paralelogramos, trapecios, triángulos y prismas rectangulares, para las que puedan calcular el área y/o el volumen.

EXPLORAR: EXPLORACIÓN 1

LECCIÓN PEDAGÓGICA

EXPLORACIÓN

1: DESCUBRIR FÓRMULAS DE

ÁREA

Estándar(es)

• Resolver problemas matemáticos y de la vida real relacionados con el área, la superficie y el volumen.

Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales, y polígonos componiendo en rectángulos o descomponiendo en triángulos y otras formas; aplicar estas técnicas en el contexto de resolver problemas matemáticos y del mundo real.

Ideas fundamentales Estándares para la práctica matemática Conexiones de pontenido Motores de investigación

Redes y área de superficie

Distancia y dirección

Graficar formas

MP.1 Dar sentido a los problemas y perseverar en su resolución.

MP.2 Razonar abstracta y cuantitativamente.

MP.5 Usar herramientas apropiadas estratégicamente.

MP.7 Buscar y hacer uso de la estructura.

CC3 Desarmar el todo, armar las partes

CC4 Descubrir la forma y el espacio

DI1 Dar sentido al mundo (Comprender y explicar)

DESCRIPCIÓN

Los estudiantes descomponen triángulos, trapecios y paralelogramos y reorganizan sus partes para formar rectángulos. Hacen conexiones con las fórmulas de área de las figuras y la fórmula para el área de un rectángulo y usan esas fórmulas para calcular el área.

MATERIALES

IMPRESO

• 1 diario del estudiante (por estudiante)

• 1 tapete de trabajo de figuras 2D (por grupo)

• 1 formas (por grupo)

• 1 boleto de salida (por estudiante)

REUTILIZABLE

• 1 juego de tángram (por grupo)

• 1 marcador de borrado en seco (por estudiante)

• 1 protector de hojas transparente (por grupo)

• 1 bolsa con cierre (por grupo)

PREPARACIÓN

• Planee que los estudiantes trabajen en grupos de 4 para completar esta actividad.

• Imprima el diario del estudiante y la boleta de salida para cada estudiante.

• Reúne los tangramas y coloca las siguientes formas en una bolsa resellable para cada grupo:

◦ 4 triángulos pequeños

◦ 1 triángulo mediano

◦ 2 cuadrados

• Imprime un juego de figuras para cada grupo. Recorta y coloca cada juego en las bolsas resellables con los tángram. Si lo deseas, imprime en cartulina y plastifícala para utilizarla en el futuro.

• Imprime una tapete de trabajo de figuras 2D por grupo. Colócala dentro de un protector de hojas transparente para que los estudiantes puedan utilizar marcadores de borrado en seco. Si lo desea, imprímala en cartulina y plastifíquela para utilizarla en el futuro.

• Reúna suficientes marcadores de borrado en seco para que cada estudiante tenga uno.

• Tenga preparado un proyector o una cámara de documentos en caso de que los estudiantes necesiten ayuda para descomponer las formas o identificar la base y la altura.

• Para los estudiantes que necesiten más apoyo para recordar información, consulte nuestros elementos de «Ayudas complementarias» que incluyen papel cuadriculado y tángram en la sección «Intervención».

EXPLORAR: EXPLORACIÓN 1

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

PARTE I: DESCOMPONER Y REORGANIZAR FIGURAS CON UN TÁNGRAM PARA EXPLORAR EL ÁREA

1. Lea el siguiente escenario a la clase: La compañía X-traordinary Landscaping trabaja con áreas de diferentes formas para desarrollar hermosos diseños. Las formas de estas áreas no siempre son rectangulares, por lo que los trabajadores deben determinar otras maneras de hallar el área total con la que tienen que trabajar. Hoy ayudarás a los paisajistas a determinar cómo hallar el área de cada espacio.

2. Ayude a los estudiantes a acceder a la tarea formulando las siguientes preguntas orientadoras:

a. ¿Qué sabes ya sobre paisajismo?

b. ¿Qué recuerdan sobre cómo encontrar el área?

3. Entregue a cada grupo un juego de tángram y un tapete de trabajo para figuras bidimensionales.

4. Guíe a los estudiantes a través de un debate para recordarles los términos sobre figuras bidimensionales:

a. DOK-1 ¿Qué son las líneas perpendiculares? Líneas que se encuentran en ángulos rectos

b. DOK-1 ¿Qué es un ángulo recto? Un ángulo que mide 90°

c. DOK-1 ¿Qué son líneas paralelas? Líneas que están siempre a la misma distancia una de otra

5. Explique a los estudiantes que usarán tángram para descomponer y reorganizar figuras para crear otras figuras bidimensionales. Tenga en cuenta que al descomponer y reorganizar figuras, los estudiantes deben entender que 1 cuadrado representa 1 unidad cuadrada. Hay que animar a los estudiantes a explorar diversas formas de crear figuras bidimensionales que les ayuden a comprender el área. Anímelos a crear triángulos, cuadrados, rectángulos, paralelogramos y trapezoides.

6. Supervise y hable con los estudiantes según sea necesario para comprobar la comprensión mediante el uso de las siguientes preguntas orientadoras:

a. DOK-1 ¿Qué figuras bidimensionales se pueden utilizar para descomponer un cuadrado? Las respuestas de los estudiantes variarán. Puedes descomponer un cuadrado usando 2 triángulos pequeños.

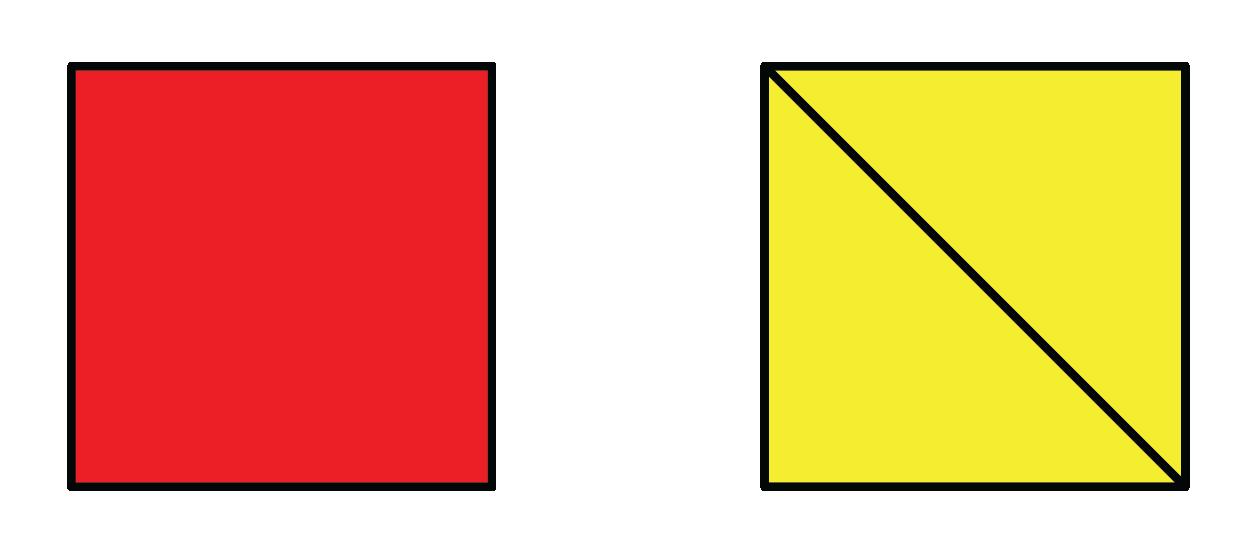
b. DOK-1 ¿Qué figuras bidimensionales se pueden usar para descomponer un rectángulo? Las respuestas de los estudiantes pueden variar. Puedes descomponer un rectángulo usando 2 triángulos pequeños y un cuadrado.

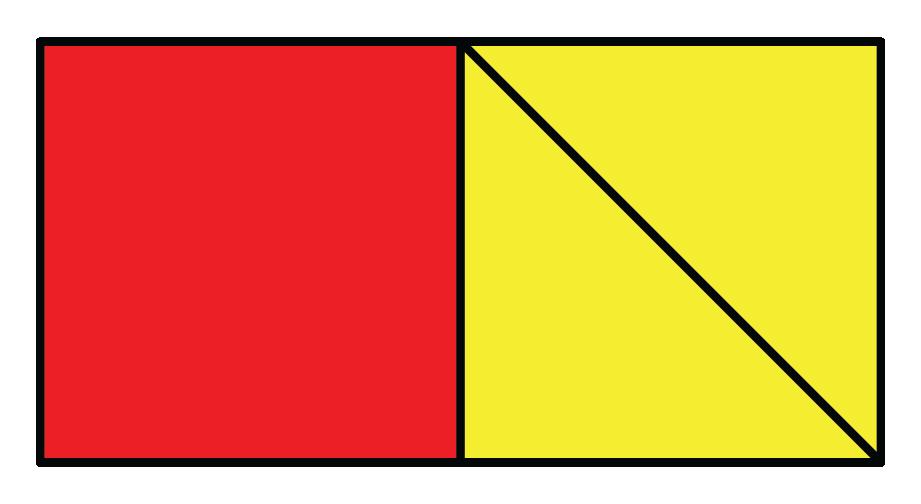
Diseños de paisajismo

Fórmula: Área: Fórmula: Área:

Jardín 2 Jardín nuevo 2

b = ____ unidades h = ____ unidades

¿Cómo puedes encontrar el área de este jardín?

and

b = ____ unidades h = ____ unidades ¿Cómo puedes encontrar el área de este jardín?

Fórmula: Área: Fórmula: Área:

b = ____ unidades h = ____ unidades

¿Cómo puedes encontrar el área de este jardín?

b = ____ unidades h = ____ unidades

¿Cómo puedes encontrar el área de este jardín?

Fórmula: Área: Fórmula: Área:

4 Jardín nuevo 4

b = ____ unidades h = ____ unidades

b₂ = ____ unidades

¿Cómo puedes encontrar el área de este jardín?

b = ____ unidades h = ____ unidades

b₂ = ____ unidades h = ____ unidades

¿Cómo puedes encontrar el área de este jardín?

Fórmula: Área: Fórmula: Área:

DIARIO DEL ESTUDIANTE

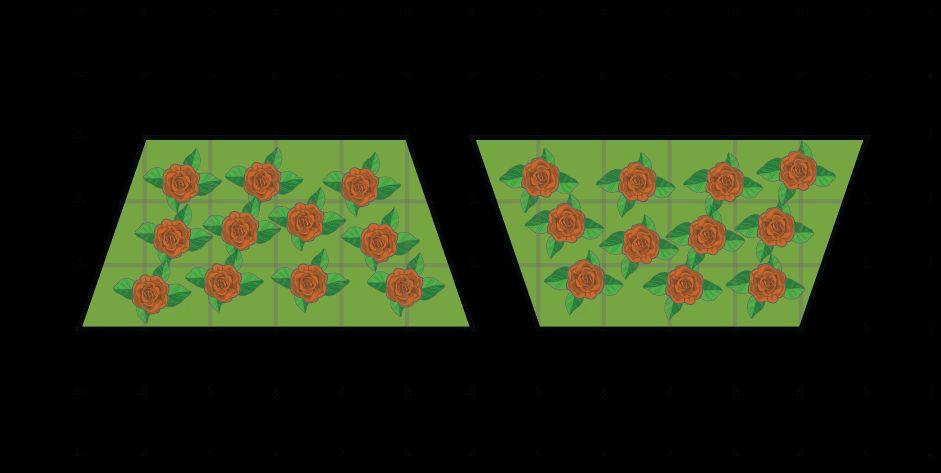
¿Cómo puedes encontrar el área de este jardín?

Fórmula: Área: Fórmula: Área:

Jardín 6 Nuevo jardín 6

¿Cómo puedes encontrar el área de

Fórmula: Área: Fórmula: Área:

Jardín nuevo

¿Cómo puedes encontrar el área de este jardín? ¿Cómo puedes descomponer u ordenar las figuras de este jardín?

Fórmula: Área: Fórmula: Área:

c. DOK-2 ¿En qué se parece o en qué se diferencia tu rectángulo del rectángulo de otro grupo? Las respuestas de los estudiantes variarán. Yo usé 2 triángulos pequeños y un cuadrado para componer un rectángulo, y otro grupo usó 4 triángulos pequeños para componer un rectángulo. Aunque se usaron diferentes figuras bidimensionales para componer un rectángulo, cuando pusimos nuestros rectángulos uno encima del otro, notamos que el largo y el ancho de ambos rectángulos son iguales.

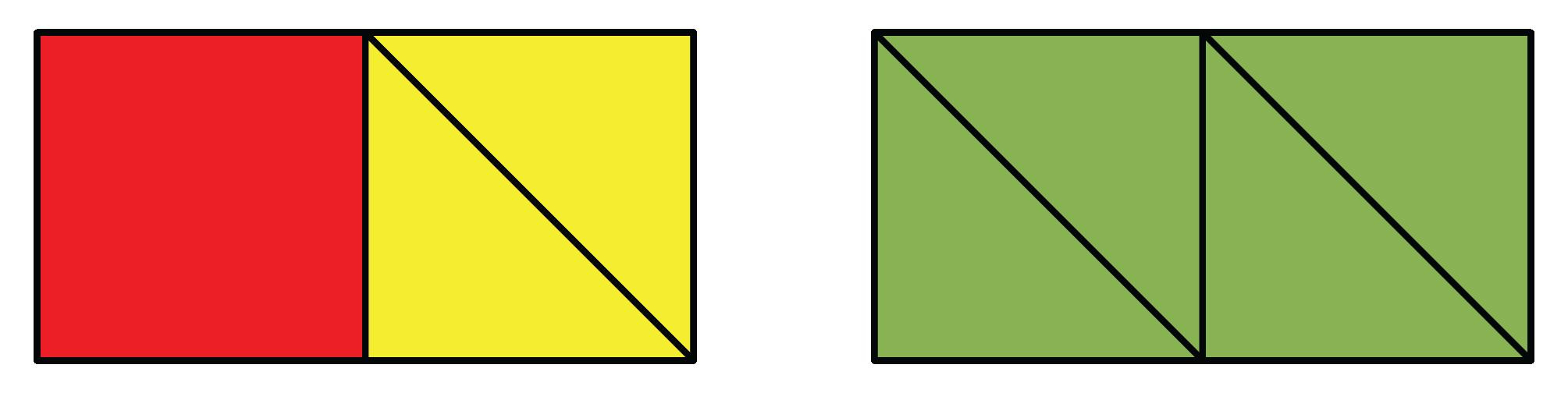
d. DOK-1 ¿Qué es un paralelogramo? Incluya los atributos de un paralelogramo. Las respuestas de los estudiantes variarán. Un paralelogramo es un tipo de cuadrilátero que tiene dos conjuntos de lados paralelos. Un rectángulo es un paralelogramo especial y tiene lados opuestos que son iguales y cuatro ángulos rectos. Un paralelogramo con base b y altura h puede dividirse en un trapezoide y un triángulo rectángulo y reordenarse en un rectángulo

e. DOK-2 ¿Qué figuras bidimensionales pueden usarse para descomponer un paralelogramo? Las respuestas de los estudiantes pueden variar. Puedo descomponer un paralelogramo usando 1 triángulo mediano y 2 triángulos pequeños.

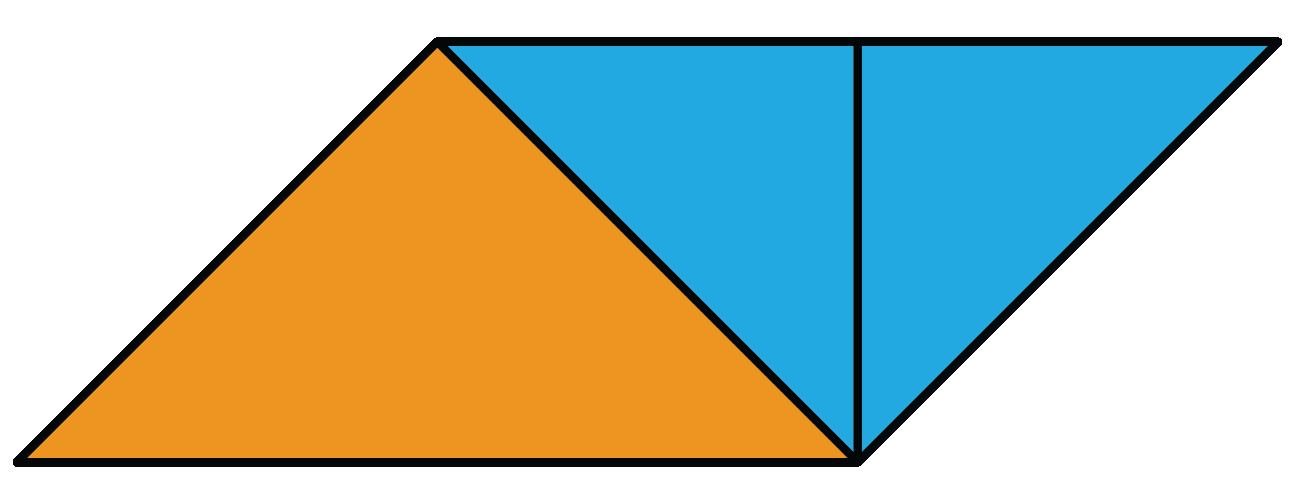
f. DOK-2 ¿Cómo puedes reorganizar el paralelogramo para crear un rectángulo? Las respuestas de los estudiantes pueden variar. Puedo reordenar el paralelogramo para crear un rectángulo moviendo el triángulo mediano al centro y poniendo un triángulo pequeño a la izquierda del triángulo mediano y 1 triángulo pequeño a la derecha del triángulo mediano.

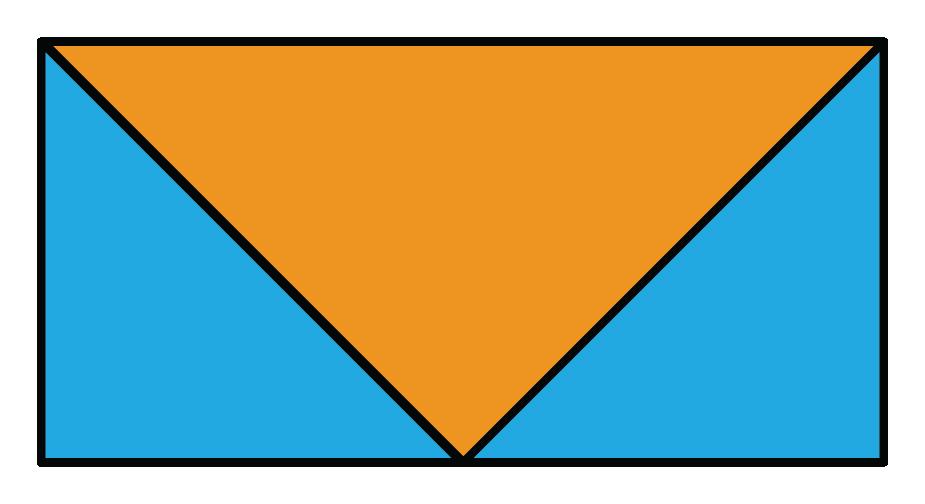
1. ¿Cómo se calcula el área de un rectángulo?

2. ¿Por qué la fórmula del área de un paralelogramo es la misma que

3. ¿Cómo determinaste la fórmula del área de los triángulos?

4. ¿Cómo determinaste la fórmula del área de los trapecios?

g. DOK-2 ¿En qué se parece un paralelogramo a un rectángulo? Las respuestas de los estudiantes variarán. Si descompones un paralelogramo y reordenas las partes, puedes componer un rectángulo. Como el paralelogramo y el rectángulo se pueden componer de las mismas partes, el área es la misma. El paralelogramo y el rectángulo tienen la misma base y la misma altura. Como la base × la altura da el área del rectángulo, podemos usar las mismas medidas del paralelogramo para calcular su área. Si un cuadrado mide 1 unidad cuadrada, entonces tanto el paralelogramo como el rectángulo tienen un área de 2 unidades cuadradas.

h. DOK-2 ¿Qué figuras bidimensionales se pueden usar para descomponer un trapecio? Las respuestas de los estudiantes variarán. Puedo usar un cuadrado y 2 triángulos pequeños para descomponer un trapezoide.

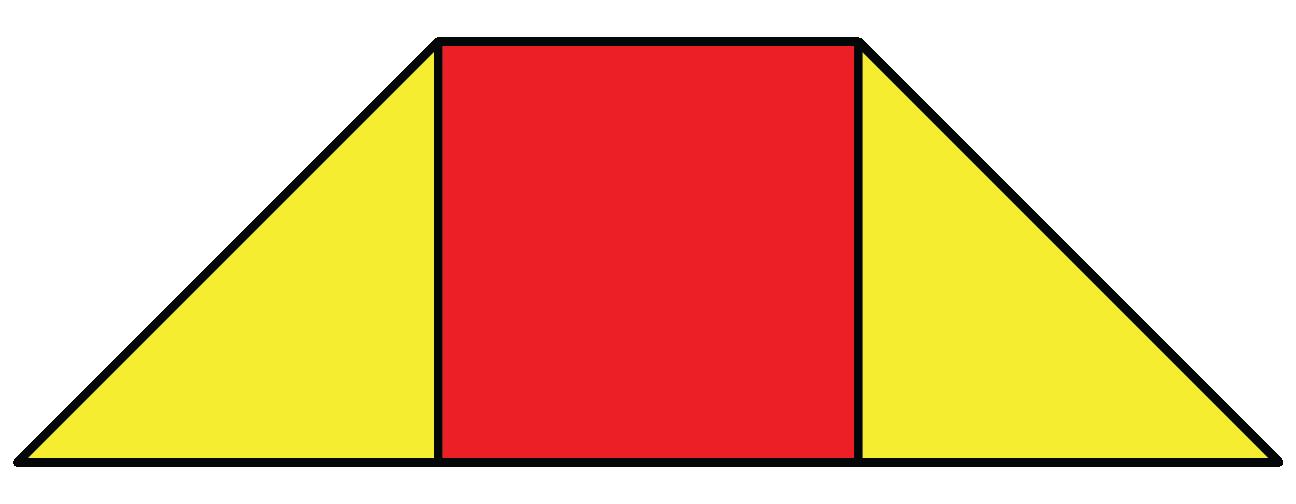
EXPLORAR: EXPLORACIÓN 1

i. DOK-2 ¿Cuántas unidades cuadradas representa el triángulo? Si un cuadrado es 1 unidad cuadrada, entonces un triángulo es 1/2 de una unidad cuadrada porque usé 2 triángulos para componer el cuadrado.

j. DOK-2 ¿Cuál es el área de un trapezoide? Puedo usar 1 cuadrado y 2 triángulos para componer un trapezoide. Como un cuadrado tiene un área de 1 unidad cuadrada, un trapecio tiene un área de 2 unidades cuadradas.

k. Haz que los estudiantes observen sólo los recortes de papel de Shapes.

l. DOK-2 ¿Qué otras figuras bidimensionales se pueden utilizar para descomponer un trapecio? Las respuestas de los estudiantes variarán. Puedo usar dos triángulos para hacer un trapecio.

6. Explique lo siguiente a la clase: «Los matemáticos dicen que en un paralelogramo, la longitud del segmento de corte vertical es también la longitud del lado vertical del rectángulo. La altura es perpendicular (en ángulo recto) a la base, y la altura se puede dibujar fuera de un paralelogramo siempre que se dibuje en un ángulo de 90° con respecto a la base».

7. Después de la parte I de la exploración, invite a la clase a una charla de matemáticas para compartir sus observaciones y aprendizajes.

CHARLA DE MATEMÁTICAS

• Elija una rutina de conversación estructurada para facilitar la siguiente pregunta:

○ DOK-2 ¿Cómo se comparan las áreas del paralelogramo y del trapecio con el área de un rectángulo? Usando los tangramas, noté que tanto un paralelogramo como un trapezoide están compuestos de las mismas partes (figuras bidimensionales) que se pueden usar para componer un rectángulo. Como un paralelogramo y un trapecio están compuestos de las mismas partes (figuras 2D), también tendrán la misma área.

• DOK-2 ¿En qué se parecen la figura descompuesta y las figuras recién creadas? Cada figura descompuesta y cada figura recién creada tienen la misma área.

• DOK-1 ¿Cómo puedes descomponer un triángulo mediano? Puedo descomponer un triángulo mediano usando 2 triángulos pequeños.

• DOK-1 ¿Cómo puedes determinar la base y la altura en un paralelogramo? En un paralelogramo, cualquier lado puede servir como base, pero la altura es siempre perpendicular al lado elegido como base.

• DOK-1 ¿Cómo puedes determinar la base y la altura en un triángulo? La base de un triángulo es uno cualquiera de sus lados, y la altura del triángulo es la longitud de la altura desde el vértice opuesto a esa base. Un triángulo rectángulo tiene tres lados: la hipotenusa, la altura y la base del triángulo. La base y la altura de un triángulo rectángulo son siempre los lados adyacentes al ángulo recto, y la hipotenusa es el lado más largo.

• DOK-1 ¿Cómo puedes determinar la base y la altura en un trapecio? Los lados paralelos representan las bases. La base y la altura de un trapezoide son perpendiculares entre sí. La distancia perpendicular entre los dos lados paralelos de un trapezoide es la altura.

PARTE II: DESCOMPONER Y REORDENAR FIGURAS PARA DESCUBRIR LA FÓRMULA DEL ÁREA

1. Lea el siguiente escenario a la clase: La compañía X-traordinary Landscaping trabaja con áreas de diferentes formas para desarrollar hermosos diseños. Las formas de estas áreas no siempre son rectangulares, por lo que los trabajadores deben determinar otras maneras de encontrar el área total con la que tienen que trabajar. Hoy ayudarás a los paisajistas a determinar cómo hallar el área de cada espacio.

2. Entregue un diario del estudiante y un marcador borrable a cada grupo.

3. Explique que descompondrán y reorganizarán figuras de jardín en una cuadrícula para crear rectángulos. Tenga en cuenta que es importante que los estudiantes utilicen la cuadrícula para determinar la base y la altura y, a continuación, hallar el área. Los estudiantes no deben contar los cuadrados de la cuadrícula para hallar el área de las figuras bidimensionales.

4. Pida que usen la tapete de trabajo de figuras bidimensionales, tángram y un marcador de borrado en seco para crear y etiquetar la base y la altura de cada figura bidimensional. Haga que los estudiantes colaboren con sus grupos para revisar dónde se encuentran los pares base-altura en un paralelogramo. Nota: si los estudiantes tienen dificultades para identificar la base y la altura, proyecte la Tapete de trabajo de figuras bidimensionales y explique a la clase cómo identificar la base y la altura en paralelogramos, triángulos y trapecios.

5. Supervise y hable con los estudiantes según sea necesario para verificar la comprensión utilizando las siguientes preguntas guía: DOK-1 ¿Qué forma tiene el jardín en el Jardín 1? El jardín tiene forma de paralelogramo.

a. DOK-2 ¿Cómo puedes descomponer y reorganizar el Jardín 1 para crear un rectángulo? Las respuestas de los estudiantes variarán. Los estudiantes deben notar que si cortan una pieza triangular de un lado y la agregan al otro lado, entonces tendrán un rectángulo. (Ver imagen abajo.)

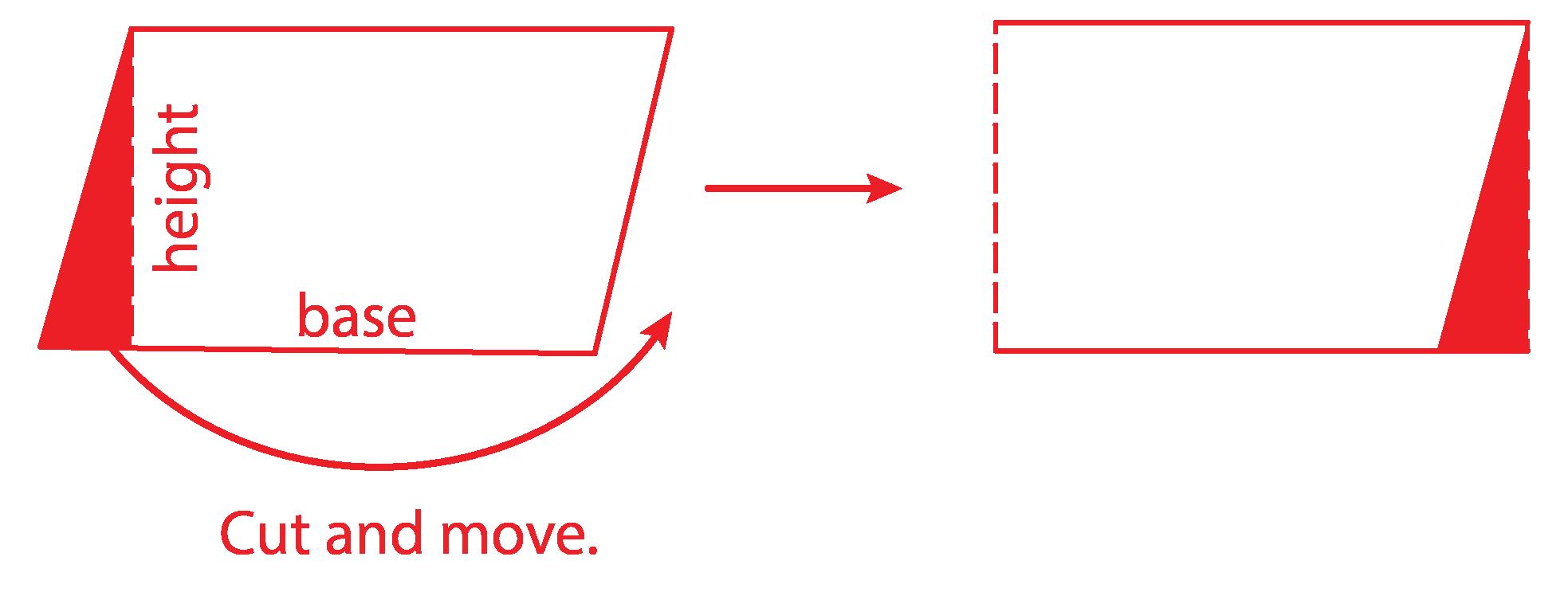
c. DOK-2 ¿Cómo puedes reorganizar el Jardín 2 para crear un rectángulo? Las respuestas de los estudiantes variarán. Los estudiantes deben notar que si duplican el triángulo, entonces pueden hacer un rectángulo.

d. DOK-2 ¿Podría usar más de una forma para hacer un rectángulo o un paralelogramo? ¿Qué tendría que añadir a la fórmula si utilizo más de una? Sí, puedes usar 2 triángulos para hacer un rectángulo/paralelogramo, y puedes usar dos trapecios para hacer un paralelogramo. Tendré que añadir 1/2 a la fórmula si utilizo más de una forma.

6. Explica lo siguiente a la clase: Los matemáticos utilizan las siguientes fórmulas de área para hallar el área de figuras 2D: para un rectángulo, A = l × w o A = bh; para un paralelogramo, A = bh; para un triángulo, A = 1/2bh, y para un trapecio, A = 1/2 (b₁ + b₂).

7. Concede a los estudiantes tiempo suficiente para registrar todo su trabajo para la parte ii de la exploración en sus diarios del estudiante.

8. Pide a los estudiantes que compartan sus estrategias y anímalos a que se hagan preguntas y establezcan conexiones. Anima a los estudiantes a notar las similitudes y diferencias entre las estrategias usadas para encontrar fórmulas de área.

9. Después de la parte ii de la exploración, invita a la clase a una charla de matemáticas para compartir sus observaciones y aprendizajes.

CHARLA DE MATEMÁTICAS

• DOK-1 ¿Cómo calculas el área de un rectángulo? Multiplica la base del rectángulo por su altura.

• DOK-2 ¿Por qué la fórmula del área de un paralelogramo es la misma que la fórmula del área de un rectángulo? Un paralelogramo puede descomponerse para crear un rectángulo sin cambiar la longitud de la base o la altura.

• DOK-3 ¿Cómo determinaste la fórmula del área para los triángulos? Cada triángulo tiene una sola base. Podemos tomar dos triángulos iguales y reorganizarlos para crear un rectángulo. Como estamos usando 2 triángulos para crear un rectángulo, tendremos que hallar la mitad del área del rectángulo para obtener el área del triángulo. Lo mismo ocurre con los triángulos no rectángulos, excepto que formarán un paralelogramo en lugar de un rectángulo. Aún necesitaríamos hallar la mitad del área del paralelogramo ya que está hecho de 2 triángulos y sólo queremos el área de un triángulo no rectángulo.

• DOK-3 ¿Cómo determinaste la fórmula del área para los trapezoides? Los trapezoides tienen dos bases de distinto tamaño. Cuando se duplicaron los trapezoides para crear un paralelogramo, tuvimos que tomar la mitad del área porque hicimos nuestro paralelogramo a partir de dos trapezoides.

• Elige una rutina de conversación estructurada para facilitar la siguiente pregunta:

◦ DOK-2 ¿Qué relación existe entre la fórmula del área de un trapecio y la fórmula de un triángulo? Un trapezoide se puede cortar diagonalmente en dos triángulos. Entonces, se halla el área de cada triángulo, que sumados darían la fórmula de un trapecio, 1/2 (b1 + b2)h

• DOK-2 ¿Cómo ayuda la fórmula del área de un rectángulo a entender cómo se determina el área de otras figuras? Como sabemos que el área de un rectángulo es A = l × w o A = bh y vimos que el rectángulo y el paralelogramo están compuestos de las mismas figuras, entonces también podemos usar A = bh para hallar el área de un paralelogramo.

DESPUÉS DE LA EXPLORACIÓN

1. Haga que los estudiantes completen el boleto de salida para evaluar formativamente su comprensión del concepto.

2. Complete el cuadro de anclaje como clase.

3. Haga que cada estudiante complete su libreta interactiva.

Gardening

X-traordinary Landscaping Company is creating a blueprint of the Tranquility Garden and wants to know the area of the garden. Decompose and rearrange the garden figure to create a new garden in the shape of a rectangle. Label the base and the height of each garden. Find the area in square units of both gardens using the area formula. Each grid square is 1 square unit.

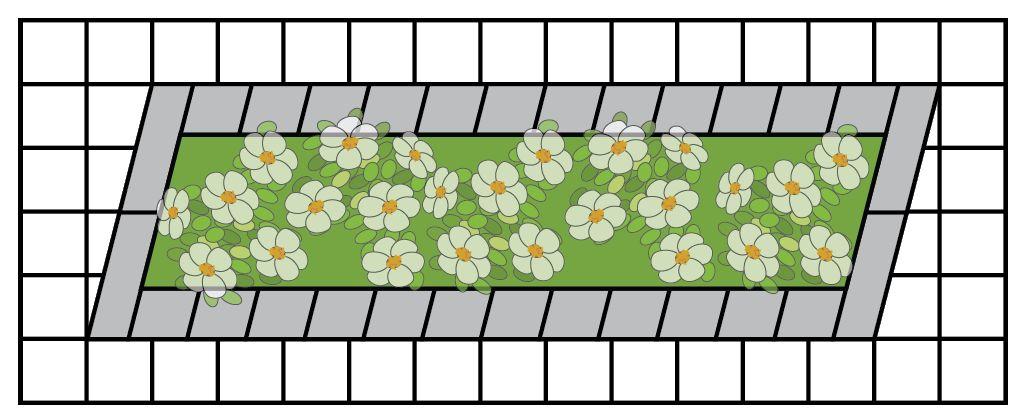
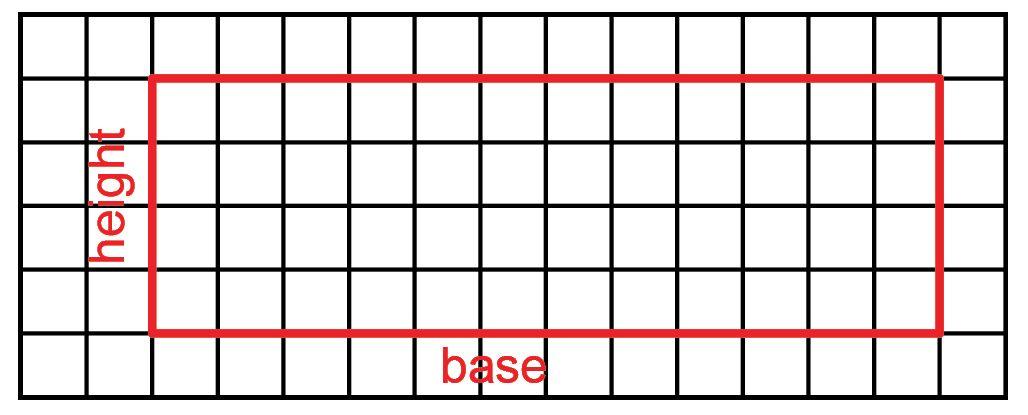
h = _____ units

How can you find the area of this new garden?

This

Formula: A = bh

= 12 × 4 = 48 square units

This garden has been rearranged to be a rectangle. To find the area, you have to multiply the base times the height.

Formula: A = bh

×

BOLETO DE SALIDA

EXPLORAR: EXPLORACIÓN 1

APOYOS PEDAGÓGICOS

1. Antes de la exploración, repase con los estudiantes los términos de vocabulario necesarios. Colocar un esquema de anclaje que muestre diferentes nombres de polígonos, tipos de ángulos y tipos de líneas puede ayudar a los estudiantes a recordar estos términos a lo largo de la unidad.

2. Debido a los diferentes colores de las formas más pequeñas, algunos estudiantes pueden tener dificultades para visualizar la forma más grande que crean las formas más pequeñas. En una hoja de papel aparte, permita a los estudiantes trazar el contorno de la forma descompuesta para que puedan verla con mayor claridad.

3. Para asegurarse de que los estudiantes comprenden el concepto de área por encima de la aplicación mecánica de la fórmula, señale que los cuadrados unitarios también pueden utilizarse para determinar el área porque el área es el espacio cubierto por una forma plana cerrada y se necesitan x cuadrados unitarios para cubrir el espacio. Los estudiantes pueden utilizar la estrategia de contar cuadrados para comprobar su trabajo. Sin embargo, evalúe las limitaciones de esta estrategia, ya que a veces hay cuadrados parcialmente llenos y no obtendrán un área precisa.

4. Si los estudiantes necesitan apoyo adicional para conceptualizar la altura del paralelogramo y del triángulo, dígales que la base y la altura son siempre perpendiculares entre sí. Permítales identificar y marcar con un marcador fluorescente la base y la altura de la figura para ver y comprobar su perpendicularidad.

5. Como ampliación, anime a los estudiantes a crear una canción que les ayude a recordar las distintas fórmulas.

APOYOS LINGÜÍSTICOS

Antes de la exploración, entregue a los estudiantes un organizador gráfico con columnas etiquetadas con nombres de formas específicas (trapecio, triángulo, paralelogramo, rectángulo, etc.). Los estudiantes recorrerán el aula y enumerarán en las columnas correspondientes los objetos que tienen las formas especificadas.

Repasar el significado de las palabras descomponer y reorganizar. Hable de los prefijos utilizados y de cómo ayudan a entender el significado de la palabra. Pida a los estudiantes que compartan ejemplos de otras palabras que empiecen por de- o re- en las que el prefijo ayude a transmitir el significado de la palabra.

Durante la parte II, pídales que se turnen para explicar sus respuestas en voz alta antes de escribir sus respuestas a la pregunta «¿Cómo puedes hallar el área de este jardín?». Explique a los estudiantes que sus respuestas escritas deben usar un lenguaje matemático preciso para que puedan ayudarse mutuamente a modificar sus respuestas según sea necesario.

Descubrir fórmulas de área

Utiliza la cuadrícula detrás de cada figura para determinar su base y altura. Luego, utiliza la fórmula para determinar el área de cada figura. Todos los polígonos se miden en unidades.

Polígono Base Altura Fórmula y espacio para trabajar Área

Áreas de las figuras (unidades²):

total (unidades²):

MUESTRA LO QUE SABES (PARTE 1)

Área

Figura Cuántas

EXPLORAR: EXPLORACIÓN 2

LECCIÓN PEDAGÓGICA

EXPLORACIÓN 2: HALLAR EL ÁREA DE CUADRILÁTEROS

Estándar(es)

• Resolver problemas matemáticos y de la vida real relacionados con el área, la superficie y el volumen. Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales, y polígonos componiendo en rectángulos o descomponiendo en triángulos y otras formas; aplicar estas técnicas en el contexto de resolver problemas matemáticos y del mundo real.

Ideas fundamentales Estándares para la práctica matemática Conexiones de pontenido Motores de investigación

Redes y Área de Superficie

Distancia y Dirección

Graficar Formas

MP.2 Razonar abstracta y cuantitativamente.

MP.3 Construir argumentos viables y criticar el razonamiento de otros.

MP.4 Modelar con matemáticas.

MP.8 Buscar y expresar regularidad en razonamientos repetidos.

CC3 Desarmar el todo, armar las partes

CC4 Descubrir la forma y el espacio

DI1 Dar sentido al mundo (Comprender y explicar)

DESCRIPCIÓN

Los estudiantes usan sus conocimientos de descomposición y reordenamiento de figuras para encontrar el área de los cuadriláteros.

MATERIALES

IMPRESOS

• 1 diario del estudiante (por estudiante)

• 1 boleto de salida (por estudiante)

PREPARACIÓN

• Planea que los estudiantes trabajen en grupos de 4 para completar esta actividad.

• imprime el diario del estudiante y el boleto de salida para cada estudiante.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

PARTE I: DETERMINAR EL ÁREA DE CUADRILÁTEROS EN CUADRÍCULAS

5. Lea el siguiente escenario a la clase: La compañía X-traordinary Landscaping está trabajando con clientes para diseñar jardines. La empresa muestra a cada uno de sus clientes un plano de su jardín con las flores que se plantarán. Hoy ayudarás a los paisajistas a determinar cómo encontrar el área del jardín de cada cliente.

6. Ayuda a los estudiantes a acceder a la tarea planteándoles las siguientes preguntas:

a. ¿Qué sabes ya sobre paisajismo?

b. ¿Qué recuerdas sobre cómo hallar el área de una figura?

1. Entregue un diario del estudiante a cada estudiante.

2. Explique a los estudiantes que encontrarán el área de cuadriláteros en cuadrículas. Tenga en cuenta que los estudiantes encontrarán el área de una variedad de figuras bidimensionales (paralelogramos, trapezoides, rectángulos y cuadrados).

3. Monitoree y hable con los estudiantes según sea necesario para verificar la comprensión usando las siguientes preguntas guía:

a. DOK-2 ¿Cómo determinaste el área de un paralelogramo? Al descomponer y reordenar, moví el triángulo rectángulo de un lado del paralelogramo al otro lado para formar un rectángulo. Esto me mostró la altura del paralelogramo. Sé que puedo usar la altura encontrada aquí para multiplicar por la base y determinar el área de un paralelogramo.

b. DOK-2 ¿Qué estrategia usaste para encontrar el área del jardín de cada cliente? Las respuestas de los estudiantes pueden variar. Primero, hallar el área de todo el jardín, y luego hallar el área de la fuente. Luego, reste el área de la fuente del área de todo el jardín.

4. Conceda a los estudiantes suficiente tiempo para registrar todo su trabajo de la parte i de la exploración en el diario del estudiante.

PARTE II: ÁREA DE LOS CUADRILÁTEROS

1. Explique a los estudiantes que aplicarán sus conocimientos sobre el área de los cuadriláteros para determinar el área de los paralelogramos y trapecios utilizando las fórmulas.

2. Los estudiantes aún deben tener sus diarios del estudiante de la parte i de la exploración.

3. Los estudiantes calcularán el área de paralelogramos y trapecios usando la fórmula y sin la cuadrícula para determinar el área del jardín donde se plantarán flores.

4. Monitoree y hable con los estudiantes según sea necesario para verificar la comprensión usando las siguientes preguntas guía:

a. DOK-2 ¿Cómo identificaste la altura del paralelogramo? Las respuestas de los estudiantes pueden variar. La línea punteada en el paralelogramo me ayudó a determinar que la medida que estaba incluida era la altura.

b. DOK-2 ¿Qué estrategia usaste para encontrar el área de cada jardín? Las respuestas de los estudiantes pueden variar. Utilicé la fórmula del paralelogramo para el área, que es base por altura, para encontrar el área del jardín donde se plantarán las flores. Si el jardín era un trapecio, utilicé la fórmula base uno más base dos por altura dividido por dos. Cuando había más de un área donde se plantarán flores, determiné el área de cada jardín.

5. Conceda a los estudiantes tiempo suficiente para registrar todo su trabajo para la parte ii de la exploración en el diario del estudiante.

6. Pida a los estudiantes que compartan sus estrategias y anímelos a que se hagan preguntas y establezcan conexiones. Anime a los estudiantes a notar las similitudes y diferencias entre las estrategias utilizadas para encontrar el área de un cuadrilátero.

Diseñar nuevos jardines

Parte I Descompón y reorganiza las figuras para encontrar el área. Representa la imagen descompuesta y reorganizada en la cuadrícula. Etiqueta la base y la altura. Encuentra el área y describe la estrategia que usaste para encontrar el área. Representa cómo encontrar el área de cada jardín con el uso de su fórmula de área. Cada cuadrado de la cuadrícula es 1 unidad cuadrada.

Jardín de Janice

Janice diseña su jardín y solo quiere tener flores de manta en su jardín. Encuentra el área de su jardín que incluirá flores de manta. (Cada unidad representa 1 unidad cuadrada).

¿Qué estrategia usaste para encontrar el área?

Área del jardin:

Jardín de Tao Tao diseña su jardín y le gustaría que plantaran margaritas alrededor de su fuente. Encuentra el área de su jardín que incluirá solo margaritas. (Cada unidad representa 1 unidad cuadrada). ¿Qué estrategia usaste para encontrar el área?

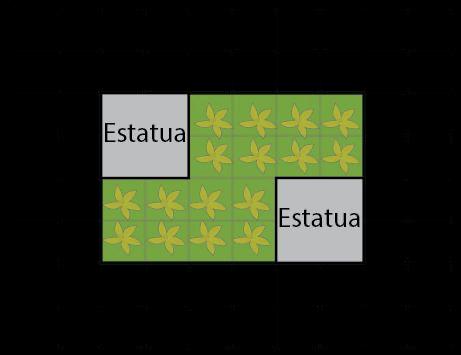
Jardín de Isabel Isabella diseña su jardín y ha comprado rosas. Encuentra el área de su jardín que solo incluirá rosas. (Cada unidad representa 1 unidad cuadrada).

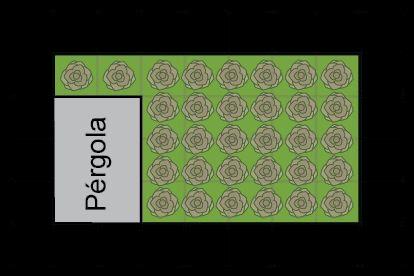
¿Qué estrategia usaste para encontrar el área?

Área del jardin:

Inz diseña su jardín y ha comprado

Jardín de Inz

Parte

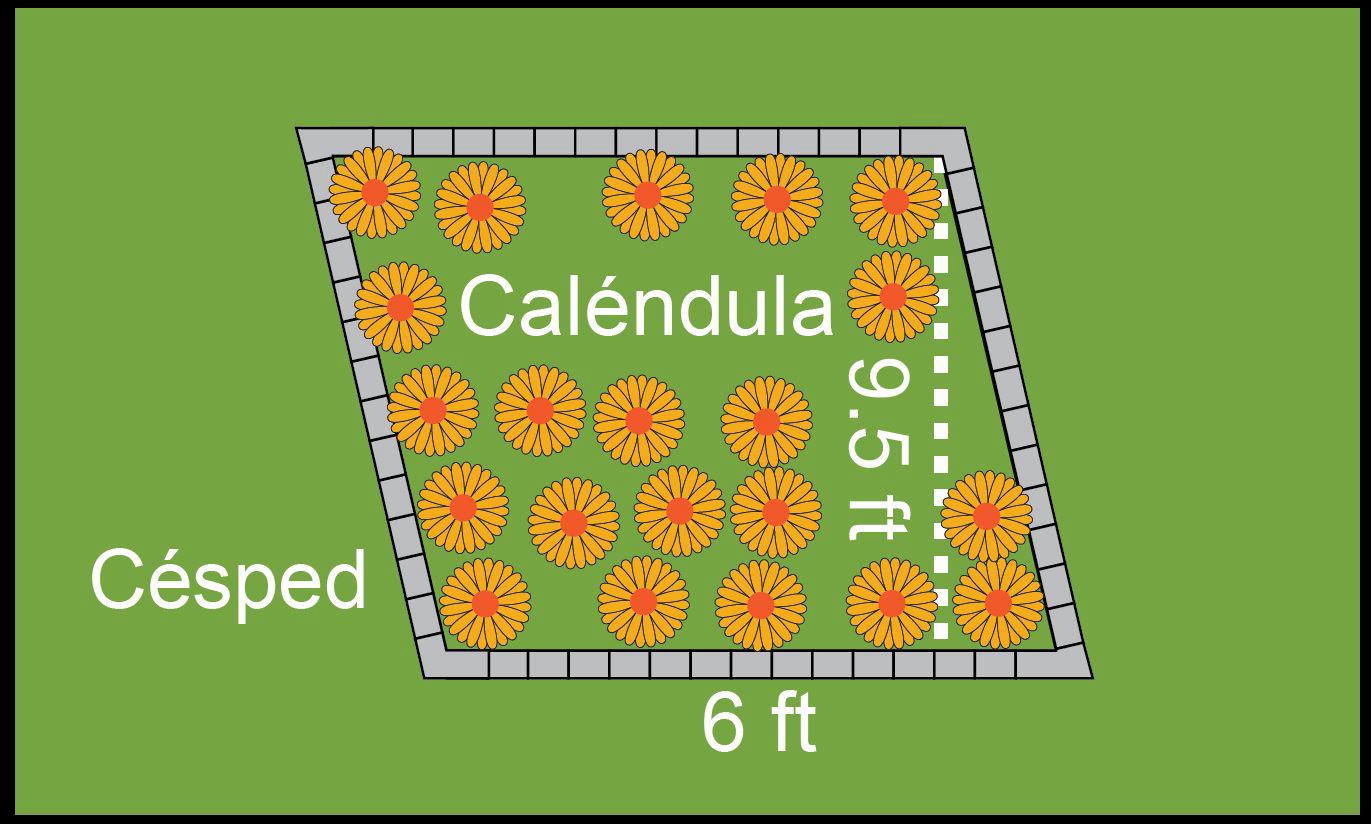
Toscana les gustaría agregar girasoles a los jardines. Tratan de determinar el área que incluirá girasoles.

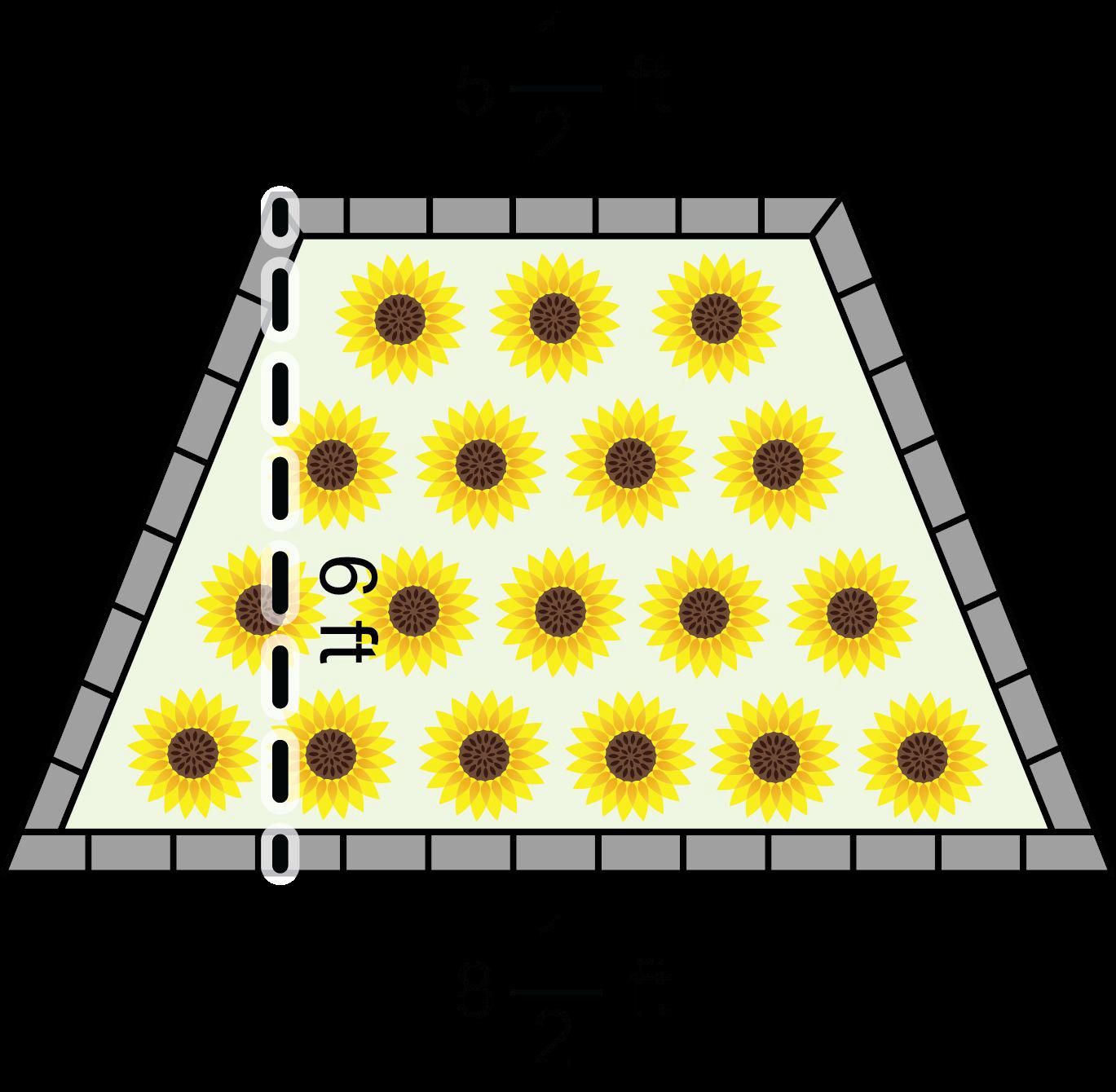
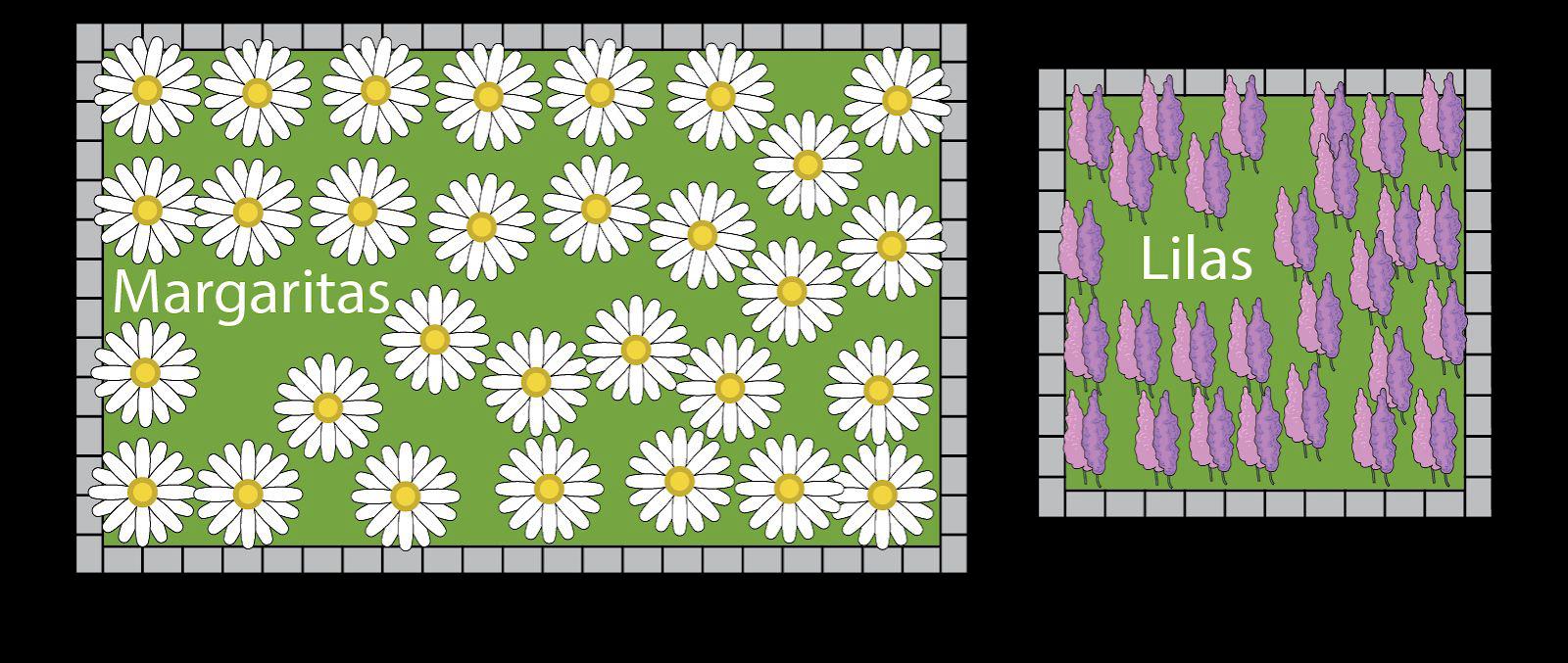
3.

7. Después de la parte ii de la exploración, invita a la clase a un charla de matemáticas para compartir sus observaciones y aprendizajes.

CHARLA DE MATEMÁTICAS

• DOK-3 ¿Qué sucede con el área de un paralelogramo si la altura se duplica pero la base permanece igual? Si la altura de un paralelogramo se duplica y la base permanece igual, el área del paralelogramo también se duplicará.

• DOK-2 ¿Cuál es la relación entre la figura descompuesta y sus nuevas figuras creadas? Cada figura descompuesta y la figura recién creada incluyeron el uso de la fórmula A = bh, la misma fórmula de área que se usa para rectángulos y paralelogramos.

• Elige una rutina de conversación estructurada para facilitar la siguiente pregunta:

○ DOK-2 ¿Cómo te ayuda la fórmula del área de un rectángulo a entender cómo se determina el área de un paralelogramo y un cuadrado? Como un paralelogramo y un rectángulo están compuestos de las mismas partes, se puede usar área = base por altura para calcular el área, que es similar a área = largo por ancho. Puesto que un cuadrado tiene lados que son todos de igual longitud, aún podemos usar área = base por altura para hallar el área de un cuadrado, que es similar a área = lado por lado.

• DOK-2 ¿Importa cuál de las bases del trapezoide se sustituye por b1 y cuál se sustituye por b₂? Explica. No importa qué base del trapecio se sustituya por b1 y b2 debido a la propiedad conmutativa de la suma. La suma de las bases seguirá siendo la misma cantidad.

DESPUÉS DE LA EXPLORACIÓN

1. Pida a los estudiantes que completen el boleto de salida para evaluar formativamente su comprensión del concepto.

2. Completen el esquema de anclaje como clase.

3. Pida a cada estudiante que complete su libreta interactivo.

Determina

Diseñar nuevos jardines

Boleto de salida

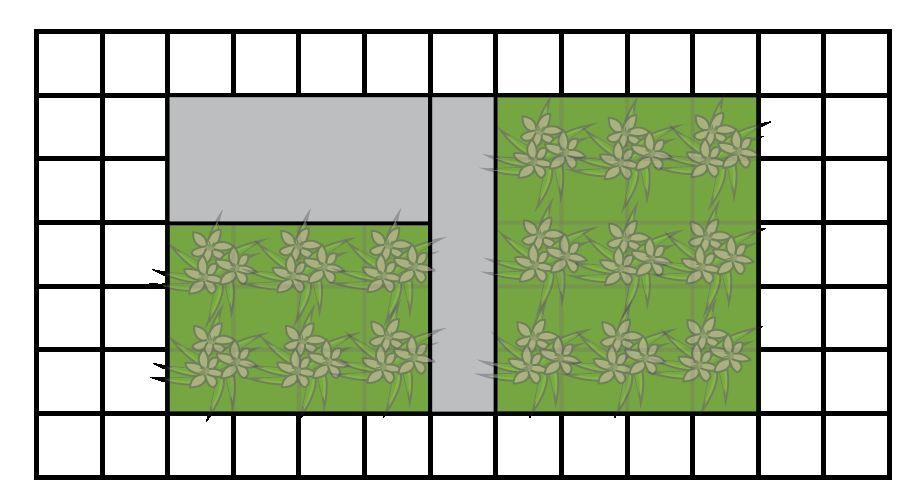
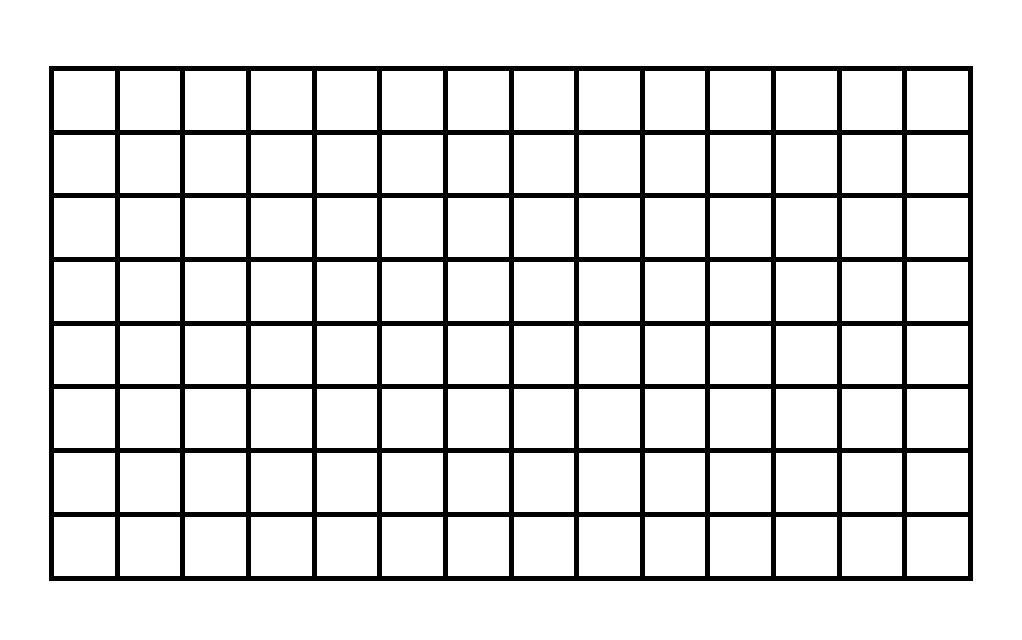
EXPLORAR: EXPLORACIÓN 2

APOYOS PEDAGÓGICOS

1. Revise las fórmulas descubiertas durante la primera exploración de este alcance, y coloque las fórmulas en un lugar donde los estudiantes puedan consultarlas fácilmente.

2. Para asegurarse de que entienden el concepto de área por encima de la aplicación mecánica de la fórmula, señale que los cuadrados unitarios también se pueden utilizar para determinar el área porque el área es el espacio cubierto por una forma plana cerrada y se necesitan x cuadrados unitarios para cubrir el espacio. Los estudiantes pueden usar la estrategia de contar cuadrados para comprobar su trabajo. Sin embargo, hable de las limitaciones de esta estrategia, ya que a veces hay cuadrados parcialmente llenos y no obtendrán un área precisa.

3. Si los estudiantes necesitan apoyo adicional para conceptualizar la altura del paralelogramo y el trapecio, dígales que la base y la altura son siempre perpendiculares entre sí. Permítales identificar y marcar con un resaltador la base y la altura de la figura para ver y comprobar su perpendicularidad.

4. Si los estudiantes necesitan apoyo adicional con el etiquetado de su área como unidades cuadradas, entonces refiérase a la Parte I donde puede contar físicamente el número de cuadrados en la forma. Relaciona el exponente de 2, como ft.², como dos dimensiones multiplicadas (longitud y anchura, o base y altura).

5. Como ampliación, rete a los estudiantes a dibujar jardines con requisitos específicos, como un paralelogramo con un área de 18 unidades cuadradas.

APOYOS LINGÜÍSTICOS

Antes de la exploración, platique sobre la experiencia de los estudiantes con los jardines. Pida a los estudiantes que conversen en grupos lo que les gustaría cultivar en un jardín, como plantas, frutas o verduras concretas. Pregunte a los estudiantes cómo podrían afectar las dimensiones de un jardín al crecimiento de sus plantas. Pida a los estudiantes que colaboren en grupos para crear carteles sobre diferentes cuadriláteros. Deben etiquetar los atributos de su forma, mostrar varios ejemplos de cómo podría ser esa forma e incluir las fórmulas aplicables que conozcan. Permita que los grupos presenten su forma a la clase y anime a todos los miembros del grupo a hablar.

Durante las conversaciones con sus compañeros, anime a los estudiantes a utilizar el vocabulario. Si escucha a los estudiantes referirse a las figuras como «eso» o «la forma», anímeles a utilizar el vocabulario específico. Anímeles a utilizar las palabras del vocabulario haciéndoles preguntas como: «¿El jardín tiene la forma de...?».

Proporcione frases para que los estudiantes las utilicen en su Diario del estudiante y durante los debates:

• El jardín es una _____ (nombre de la forma) porque

• Para encontrar el área, yo ....

Encontrar el área de cuadriláteros

Encuentra el área de cada espacio sombreado.

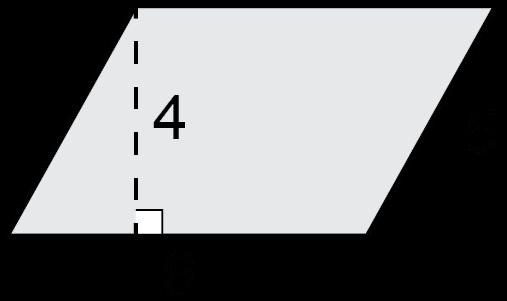
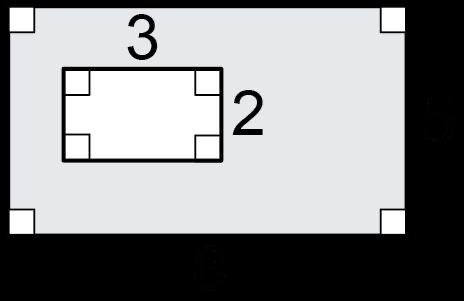
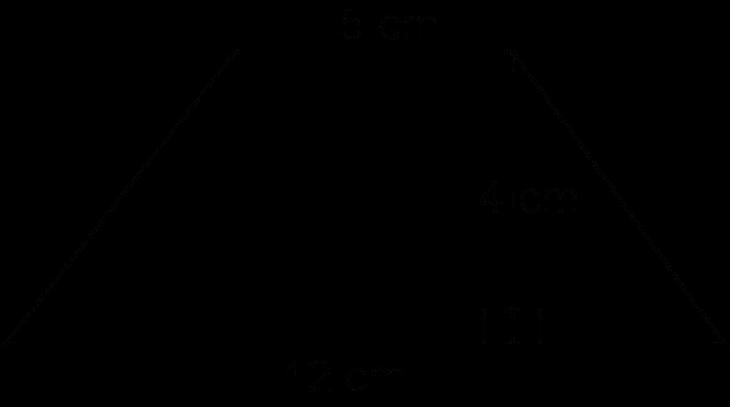
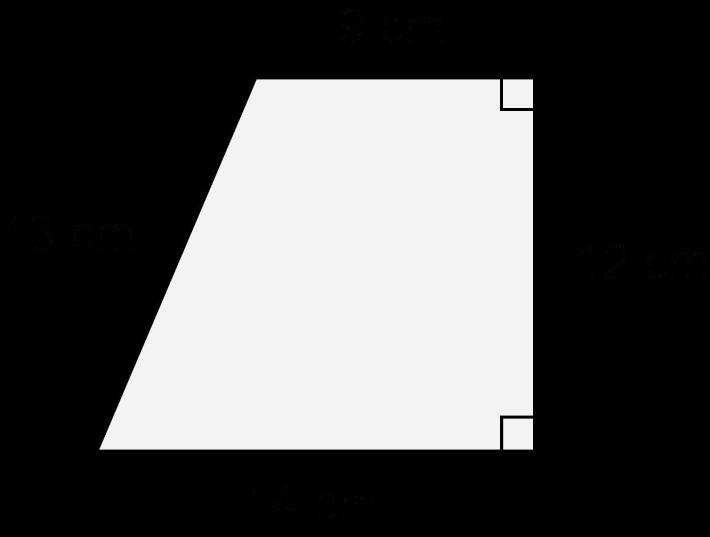
MUESTRA LO QUE SABES (PARTE 2)

Figura Espacio de trabajo Área (unidades)

Figura Espacio de trabajo Área

EXPLORAR: EXPLORACIÓN 3

LECCIÓN PEDAGÓGICA

EXPLORACIÓN 3: HALLAR EL ÁREA DE TRIÁNGULOS

Estándar(es)

• Resolver problemas matemáticos y de la vida real relacionados con el área, la superficie y el volumen. Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales, y polígonos componiendo en rectángulos o descomponiendo en triángulos y otras formas; aplicar estas técnicas en el contexto de resolver problemas matemáticos y del mundo real.

Ideas fundamentales

Redes y área de superficie

Distancia y dirección

Graficar formas

Estándares para la práctica matemática Conexiones de pontenido Motores de investigación

MP.1 Dar sentido a los problemas y perseverar en su resolución.

MP.3 Construir argumentos viables y criticar el razonamiento de otros.

MP.6 Prestar atención a la precisión.

MP.7 Buscar y hacer uso de la estructura.

DESCRIPCIÓN

Los estudiantes usan sus conocimientos sobre descomposición y reordenamiento de figuras para encontrar el área de la figura.

MATERIALES

IMPRESOS

• 1 diario del estudiante (por estudiante)

• 1 boleto de salida (por estudiante)

PREPARACIÓN

• Planee que los estudiantes trabajen en grupos de 4 para completar esta actividad.

• Imprima una copia del diario del estudiante y del boleto de salida para cada estudiante.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

PARTE I: DETERMINAR EL ÁREA DE TRIÁNGULOS EN CUADRÍCULAS

1. Lea la siguiente situación a la clase: La compañía X-traordinary Landscaping está trabajando con la Granja Summerville para crear un mapa de sus huertos. Cada huerto tiene forma de triángulo. Están indicando a los propietarios de la granja dónde se plantarán las hortalizas. Hoy ayudarás a los paisajistas a determinar cómo encontrar el área del huerto de cada cliente.

2. Ayuda a los estudiantes a acceder a la tarea formulando las siguientes preguntas orientativas:

a. ¿Qué sabes ya sobre jardinería?

b. ¿Qué recuerdas sobre los triángulos?

CC3 Desarmar el todo, armar las partes

CC4 Descubrir la forma y el espacio

DI1 Dar sentido al mundo (comprender y explicar)

3. Entregue un diario del estudiante a cada estudiante.

4. Explique a los estudiantes que descompondrán y reorganizarán figuras 2D para hallar el área de triángulos. Tenga en cuenta que los estudiantes encontrarán el área de una variedad de figuras bidimensionales (paralelogramos, rectángulos y cuadrados) y utilizarán esas figuras para encontrar el área de un triángulo.

5. Monitoree y hable con los estudiantes según sea necesario para verificar la comprensión utilizando las siguientes preguntas guía:

a. DOK-1 ¿Cómo puedes identificar la base del triángulo? Las respuestas de los estudiantes variarán. Como cualquier lado puede ser la base, miré las medidas que representan el lado y su longitud.

b. DOK-1 ¿Cómo puedes identificar la altura del triángulo? Las respuestas de los estudiantes variarán. La altura correspondiente de un triángulo es la longitud de un segmento perpendicular desde la base hasta el vértice opuesto a ella.

c. DOK-2 ¿Qué estrategia usaste para hallar el área de cada jardín en la cuadrícula? Las respuestas de los estudiantes pueden variar. Primero determine el número de unidades que representa la base y el número de unidades que representa la altura. Usé la fórmula para el área de un paralelogramo y luego multipliqué la respuesta por 1/2 para obtener la respuesta para el área de un triángulo.

6. Permita a los estudiantes suficiente tiempo para registrar todo su trabajo para la parte I de la exploración en el diario del estudiante.

EXPLORAR: EXPLORACIÓN 3

PARTE II: USO DE LA FÓRMULA PARA EL ÁREA DE TRIÁNGULOS

1. Explique a los estudiantes que aplicarán sus conocimientos sobre el área de triángulos para determinar el área de los jardines sin la cuadrícula.

2. Los estudiantes calcularán el área de triángulos usando la fórmula y sin la cuadrícula para determinar el área del jardín donde se plantarán las hortalizas.

3. Monitoree y hable con los estudiantes según sea necesario para verificar la comprensión usando las siguientes preguntas guía:

a. DOK-2 ¿Qué estrategia usaste para encontrar el área de cada jardín? Las respuestas de los estudiantes pueden variar. Primero hallar el área de todo el huerto y luego hallar el área del huerto que incluirá las hortalizas que se plantarán. Usa la fórmula A = bh para encontrar el área de todo el jardín, y luego toma la mitad del área para obtener el área del triángulo.

b. DOK-1 ¿Qué representa la línea punteada en un triángulo? Las respuestas de los estudiantes pueden variar. La línea punteada representa la altura.

c. DOK-2 ¿Cómo compusiste un paralelogramo para hallar el área del triángulo? Las respuestas de los estudiantes variarán. Agregué un triángulo rectángulo adicional que tenía la misma base y altura y compuse ambos triángulos rectángulos para crear un paralelogramo. Para hallar el área de un triángulo, hallé el área del paralelogramo y luego multipliqué el área por la mitad para hallar el área de un triángulo.

4. Conceda a los estudiantes tiempo suficiente para registrar todo su trabajo para la parte II de la exploración en el diario del estudiante.

5. Pida a los estudiantes que compartan sus estrategias y anímelos a hacerse preguntas y establecer conexiones. Anima a los estudiantes a notar las similitudes y diferencias entre las estrategias usadas para encontrar el área de un triángulo.

6. Después de la parte II de la exploración, invita a la clase a una charla de matemáticas para compartir sus observaciones y aprendizaje.

CHARLA DE MATEMÁTICAS

• Escoge una rutina de conversación estructurada para facilitar la siguiente pregunta:

○ DOK-2 ¿Cómo está conectada la fórmula del área de un paralelogramo con la fórmula del área de un triángulo? Como un triángulo ocupa la mitad del área de un paralelogramo con la misma base y altura, hay una mitad en la fórmula del área de un triángulo.

• DOK-3 ¿Cuántas bases posibles tiene un triángulo? Cada lado de un triángulo puede ser una base, así que hay tres bases posibles.

• DOK-2 En el problema sobre el jardín de guisantes, ¿cómo podemos usar el área de un triángulo sombreado para calcular el área de toda la parte sombreada del jardín? La altura del jardín representa 12 pies, y cada base de los triángulos sombreados representa la mitad de la base del jardín. Para calcular la parte sombreada del jardín, utiliza la mitad de 27 pies, que son 13,5 pies, y multiplícalo por 12 para obtener 162 pies cuadrados. Como la fórmula del área de un triángulo es A = 1/2bh, multiplicarías 162 por 1/2 para obtener 81 pies cuadrados. Luego puedes multiplicar el área de un triángulo por 2 para hallar el área de las partes sombreadas (triángulos).

DESPUÉS DE LA EXPLORACIÓN

1. Haz que los estudiantes completen el boleto de salida para evaluar formativamente su comprensión del concepto.

2. Completa la esquema de anclaje como clase.

3. Haz que cada estudiante complete su libreta interactiva.

APOYOS PEDAGÓGICOS

1. Repase con los estudiantes las fórmulas descubiertas durante las exploraciones anteriores de este alcance y coloque las fórmulas en un lugar donde los estudiantes puedan consultarlas fácilmente.

2. Para asegurarse de que los estudiantes comprendan el concepto de área por encima de la aplicación mecánica de la fórmula, señale que los cuadrados unitarios también pueden usarse para determinar el área porque el área es el espacio cubierto por una forma plana cerrada y se necesitan x cuadrados unitarios para cubrir el espacio. Los estudiantes pueden utilizar la estrategia de contar cuadrados para comprobar su trabajo. Sin embargo, plantee las limitaciones de esta estrategia, ya que a veces hay cuadrados parcialmente llenos y no obtendrán un área precisa.

3. Si los estudiantes necesitan apoyo adicional para conceptualizar la altura del triángulo, dígales que la base y la altura son siempre perpendiculares entre sí. Permítales identificar y marcar con un resaltador la base y la altura de la figura para ver y comprobar su perpendicularidad.

4. Si los estudiantes necesitan apoyo adicional para multiplicar por 1/2, entonces repase que la multiplicación y la división son operaciones inversas, de modo que puedan dividir por 2 para resolver.

5. Como ampliación, desafíe a los estudiantes a dibujar jardines que sean tipos específicos de triángulos con áreas designadas, como un triángulo obtuso con un área de 15 unidades cuadradas.

GRADO 6:

Cultivar huertas

Parte I

Halla el área de las figuras 2D para determinar el área del huerto. Etiqueta la base y la altura. Encuentra el área del paralelogramo y el triángulo. Representa cómo encontrar el área del huerto triangular con el uso de la fórmula A = bh. Describe la estrategia que usaste para encontrar el área. Cada cuadrado de la cuadrícula es 1 unidad cuadrada.

Lechuga

Huerto Área

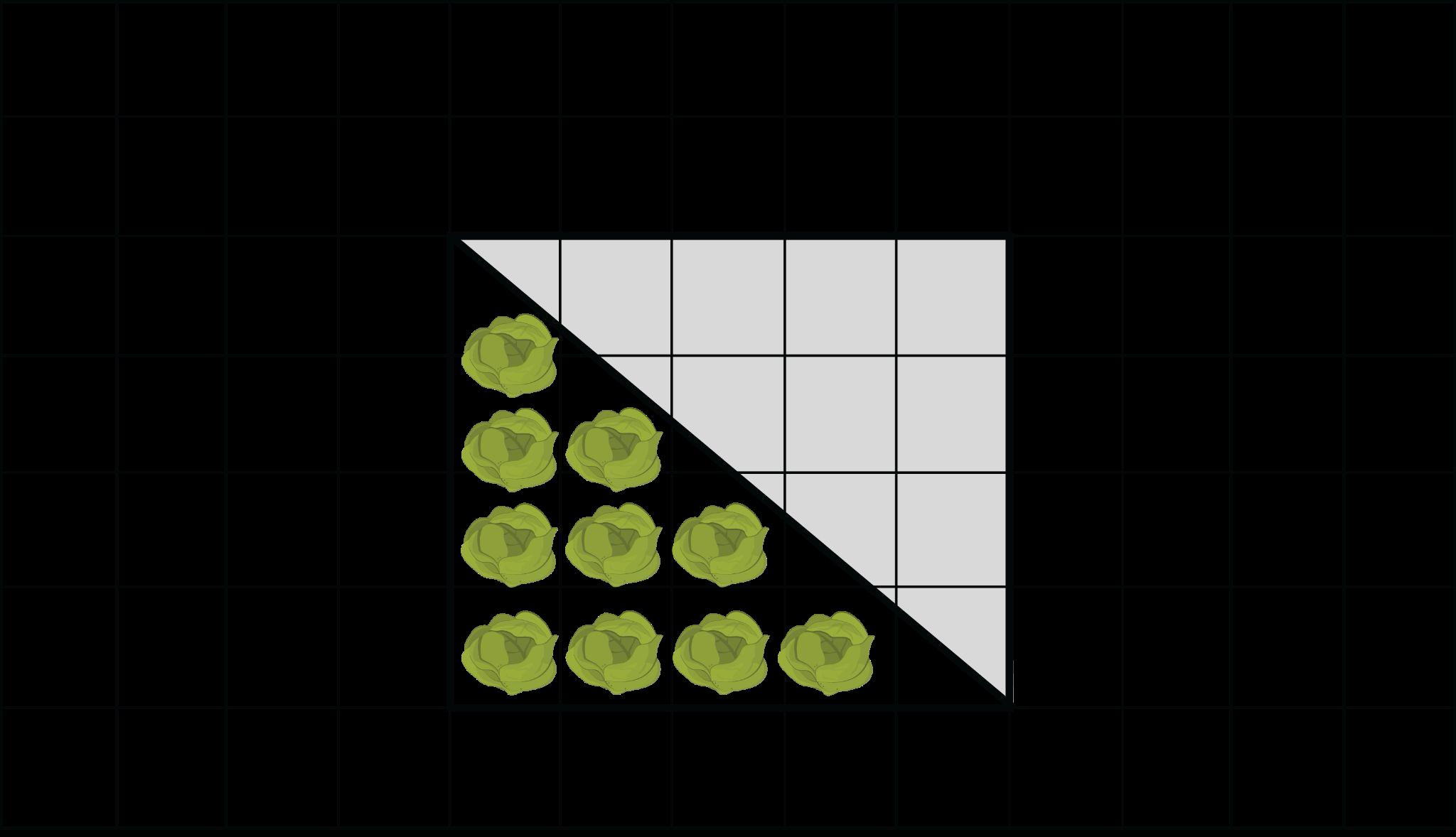
Paralelogramo:

Triángulo:

¿Cómo encontraste el área del huerto que incluirá lechugas?

y rábanos Huerto

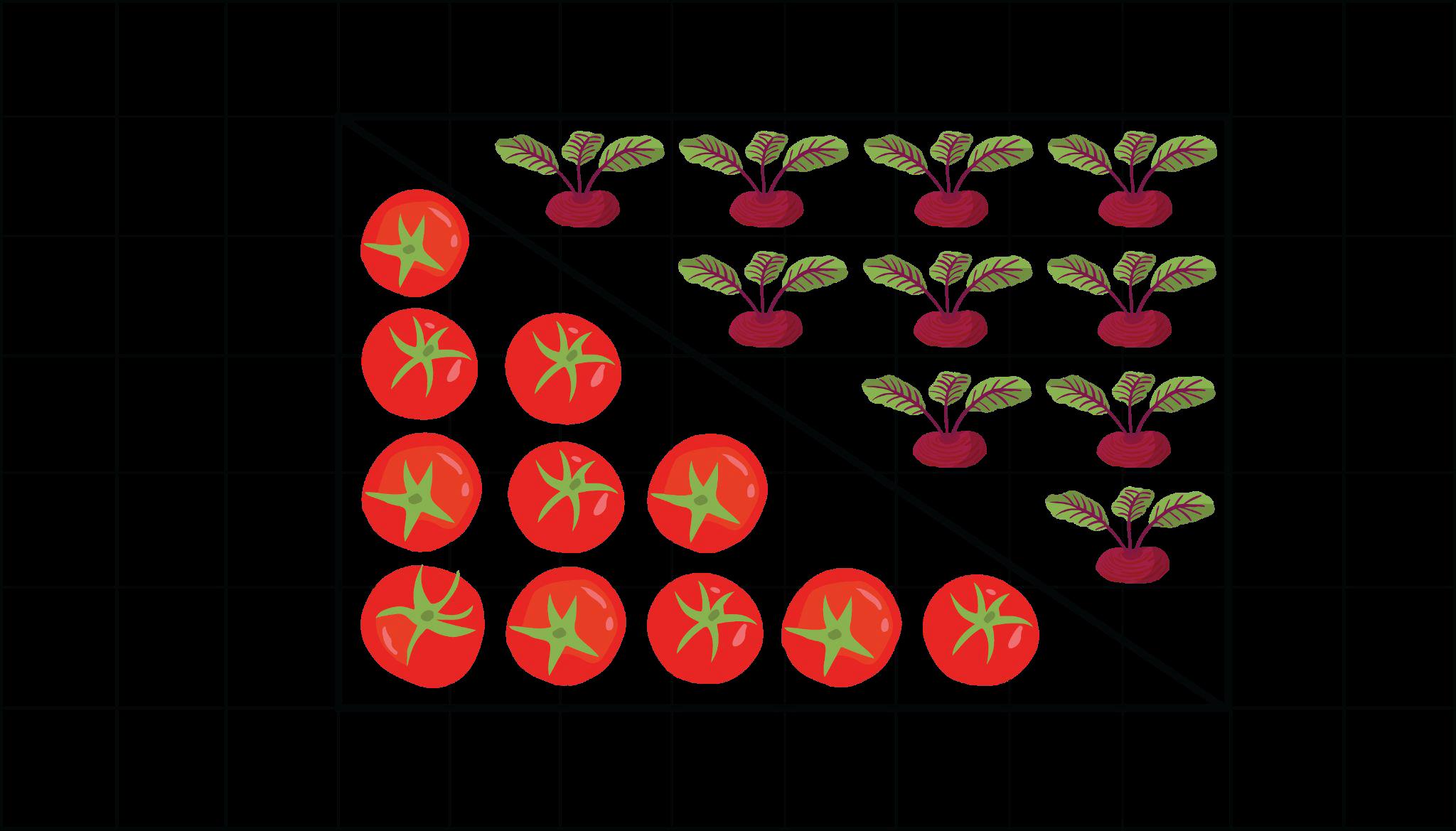
Paralelogramo:

Triángulo:

¿Cómo encontraste el área del huerto que incluirá tomates o rábanos?

Calabacín

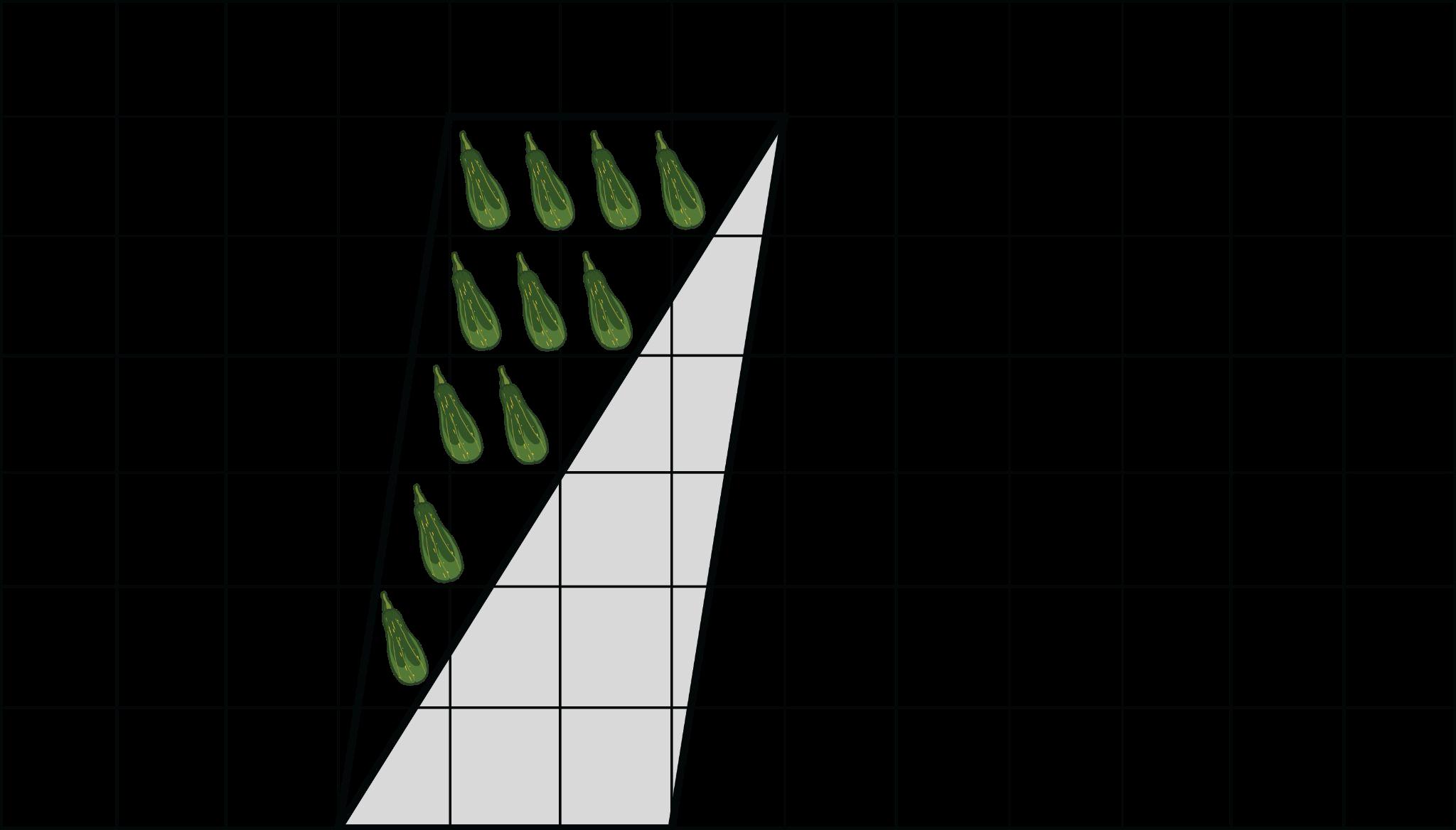
Paralelogramo:

Triángulo: ¿Cómo encontraste el área del huerto que incluirá calabacines?

Zanahorias

¿Cómo encontraste el área del huerto que incluirá zanahorias?

Guisantes

Huerto Área

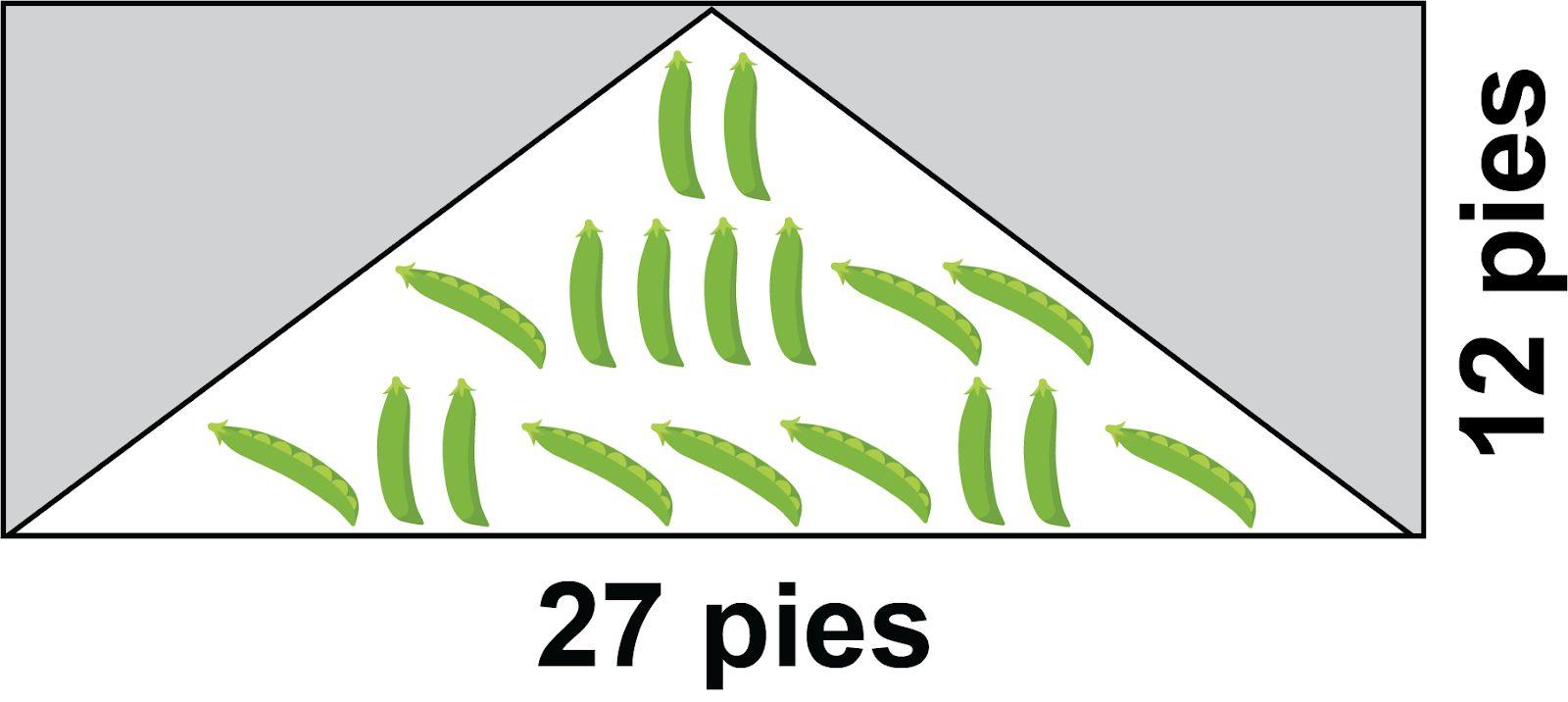
¿Cómo encontraste el área de la huerta que incluirá guisantes?

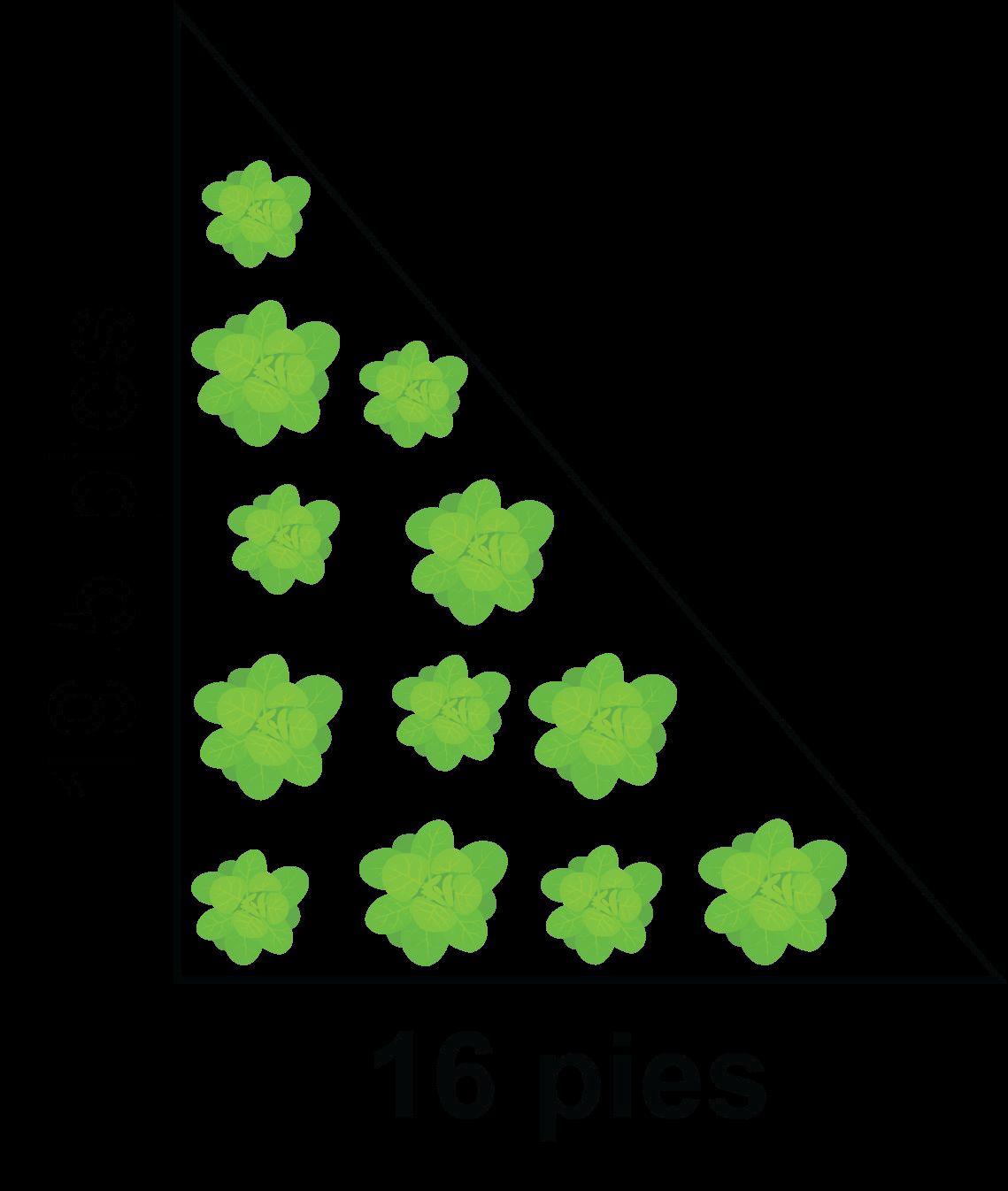
¿Cómo encontraste el área del huerto que incluirá espinacas?

Pimentones

encontraste

Reflexiona

1. ¿Cómo se relaciona la fórmula del área del paralelogramo con la fórmula del área de un triángulo?

2. ¿Cuántas bases posibles tiene un triángulo?

3. En el problema del huerto de guisantes, ¿cómo podemos usar el área de un triángulo sombreado para calcular el área de toda la parte sombreada del huerto?

DIARIO DEL ESTUDIANTE

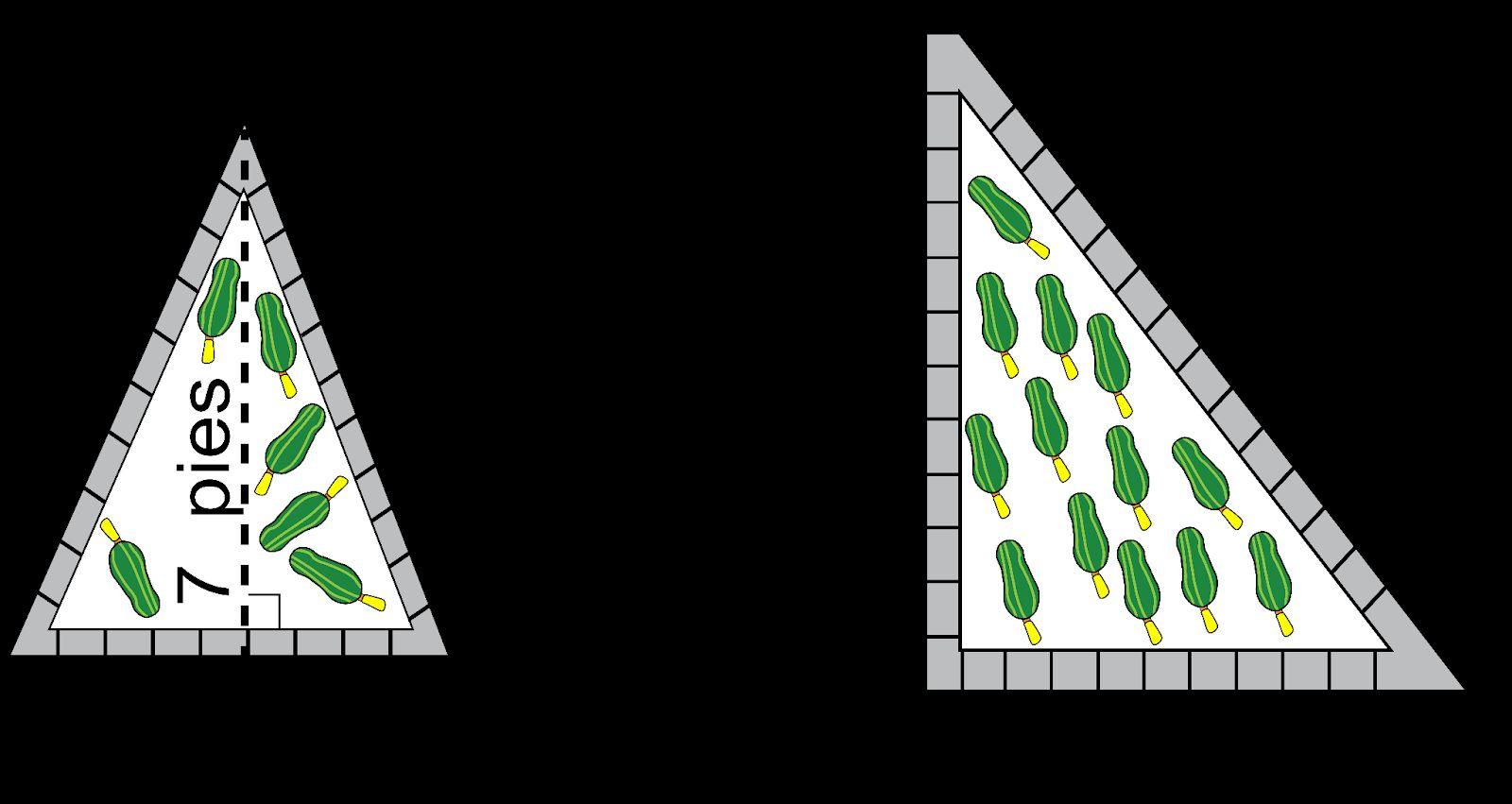
APOYOS LINGÜÍSTICOS

Antes de la Exploración, ponga en fila y etiquete, en la parte delantera de la clase, uno de cada tipo de verdura mencionada en la Exploración: un cogollo de lechuga, un tomate, un calabacín, una zanahoria, un pimiento y un guisante. Levante cada objeto y pida a los estudiantes que repitan el nombre después de usted. Deje que los estudiantes toquen, sostengan, lean la etiqueta y digan el nombre de cada hortaliza. Anime a los estudiantes a compartir su experiencia con cada una de ellas. (¿La han probado antes? ¿Les gusta?)

Presente la palabra triángulo como dos partes de palabras, tri- y -ángulo. Pida a los estudiantes que piensen en otras palabras que utilicen tri- y en su significado, como triciclo

Pida a los estudiantes que elijan un jardín sobre el que hacer un vídeo-respuesta. Pueden mostrar una imagen o un vídeo del jardín y grabarse a sí mismos explicando cómo han determinado la superficie del jardín. Deje tiempo para que los estudiantes preparen su guión, vean y escuchen sus propios vídeos y vuelvan a grabar para hacer los ajustes necesarios.

Encontrar el área de triángulos

Encuentra el área de cada espacio sombreado.

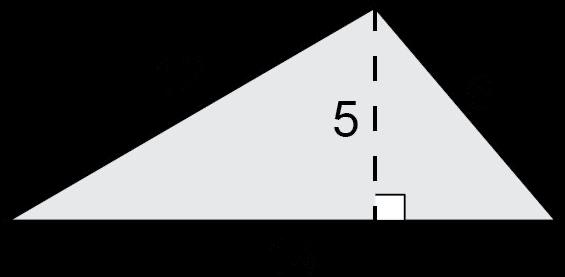
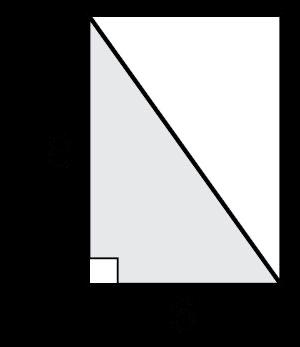
Figura Espacio para trabajar Área (u²)

1. ¿Cuál es el área de un triángulo con una base de 4 pies y una altura de 3 pies?

2. ¿Cuál es el área del triángulo cuya altura es de 8 milímetros y cuya base es de 24 milímetros?

Sembrar pepinos en el huerto Boleto de salida

Determina el área de la huerta de pepinos de Tamika con el uso de las figuras 2D. Encuentra el área de los triángulos al usar la fórmula A = bh. Luego, describe la estrategia que usaste para encontrar el área.

huerta de Tamika Tamika cultiva pepinos en su huerta. Encuentra el área total que incluirá pepinos en su huerta. Resuelve:

¿Qué estrategia usaste para encontrar el área?

Área de la huerta:

BOLETO DE SALIDA

EXPLORAR: EXPLORACIÓN 4

LECCIÓN PEDAGÓGICA

EXPLORACIÓN 4: HALLAR EL ÁREA DE FIGURAS COMPUESTAS

Estándar(es)

• Resolver problemas matemáticos y de la vida real relacionados con el área, la superficie y el volumen. Encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales, y polígonos componiendo en rectángulos o descomponiendo en triángulos y otras formas; aplicar estas técnicas en el contexto de resolver problemas matemáticos y del mundo real.

Ideas fundamentales

Redes y Área de Superficie

Distancia y Dirección

Graficar Formas

Estándares para la práctica matemática Conexiones de pontenido Motores de investigación

MP.1 Dar sentido a los problemas y perseverar en su resolución.

MP.6 Prestar atención a la precisión.

MP.7 Buscar y hacer uso de la estructura.

MP.8 Buscar y expresar regularidad en razonamientos repetidos

CC3 Desarmar el todo, armar las partes

CC4 Descubrir la forma y el espacio

DESCRIPCIÓN

Los estudiantes determinan el área de figuras compuestas.

MATERIALES

IMPRESO

• 1 diario del estudiante (por estudiante)

• 1 tarjetas de jardín (por grupo)

• 1 boleto de salida (por estudiante)

REUTILIZABLE

• 1 bolsa resellable (por grupo)

PREPARACIÓN

• Planea que los estudiantes trabajen en grupos de 4 para completar esta actividad.

• Imprime un juego de tarjetas de jardín para cada grupo. Recorta las tarjetas y colócalas en una bolsa resellable para cada grupo. Si lo desea, imprímalas en cartulina y plastifíquelas para utilizarlas en el futuro.

• Imprima un diario del estudiante y una hoja de salida para cada estudiante.

DI1 Dar sentido al mundo (comprender y explicar)

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Lea el siguiente escenario a la clase: La compañía X-traordinary Landscaping acaba de recibir algunos pedidos recientes de jardines que son figuras compuestas. Esto significa que cada jardín tiene una forma que es una combinación de rectángulos, triángulos y/o paralelogramos. Necesitan que utilices tus conocimientos sobre las fórmulas de área de cada uno de estos polígonos para determinar el área de los jardines con forma de figuras compuestas.

2. Ayuda a los estudiantes a acceder a la tarea planteándoles las siguientes preguntas orientadoras: a. ¿Qué recuerdas sobre las figuras compuestas?

3. Reparte una bolsa de tarjetas de jardín a cada grupo.

4. Haga que los estudiantes propongan sus ideas sobre la definición del término figura compuesta con sus grupos. Explique a los estudiantes que una figura compuesta es una figura formada por dos o más figuras geométricas.

5. Entregue un diario del estudiante a cada estudiante.

6. Explique a los estudiantes que trabajarán con sus grupos para determinar el área de cada uno de los ocho jardines de los clientes. Descompondrán y reorganizarán los jardines en diversas figuras que les ayudarán a determinar la superficie.

7. Pida a los estudiantes que utilicen las tarjetas de jardín para determinar la superficie del jardín de cada cliente. Si las tarjetas jardín están plastificadas, los estudiantes pueden dibujar en ellas con marcadores de borrado en seco para mostrar su descomposición y reordenación de la figura compuesta. Escriben en cuántas figuras bidimensionales se puede descomponer la figura compuesta. También utilizarán las fórmulas de área para determinar el área del jardín de cada cliente.

8. Supervise y hable con los estudiantes según sea necesario para comprobar la comprensión utilizando las siguientes preguntas orientadoras:

a. DOK-2 ¿Cómo puedes descomponer este jardín? Las respuestas de los estudiantes variarán. Para el Jardín A, puedo descomponerlo para hacer dos rectángulos y luego sumar las dos áreas para encontrar el área total del jardín.

b. DOK-2 ¿Por qué necesitas dividir por 2 para encontrar el área de un triángulo? ¿Para un trapecio? Tienes que usar dos triángulos para hacer un rectángulo/paralelogramo, pero sólo necesitas el área de uno, así que encontrarás la mitad del área total. Tienes que usar dos trapezoides para hacer un paralelogramo, pero sólo necesitas el área de uno, así que encontrarás la mitad del área total.

9. Conceda a los estudiantes tiempo suficiente para anotar todo su trabajo en el diario del estudiante.

10. Pida a los estudiantes que compartan sus estrategias y anímeles a hacerse preguntas y establecer conexiones. Anima a los estudiantes a notar las similitudes y diferencias entre las estrategias usadas para encontrar el área de figuras compuestas.

11. Después de la exploración, invita a la clase a un charla de matemáticas para compartir sus observaciones y aprendizajes.

CHARLA DE MATEMÁTICAS

• DOK-3 ¿Qué estrategia puedes usar para hallar el área de una figura compuesta? Puedo descomponer la figura en áreas más pequeñas que puedo encontrar y luego sumar todas las áreas para encontrar el área total. También puedo descomponer la figura en una figura más grande y luego restar la parte que no está en la figura original para hallar el área de la figura dada.

• DOK-2 Describe el proceso que utilizaste para hallar el área del jardín E. Descompuse el jardín E en 2 triángulos y 1 paralelogramo, hallé el área de cada figura y determiné la suma de las áreas.

• Elige una rutina de conversación estructurada para facilitar la siguiente pregunta:

○ DOK-3 ¿Cuál es un ejemplo de por qué necesitaríamos hallar el área de una figura compuesta? Si estuviéramos pintando una casa y pintáramos una pared con ventanas, podríamos ver la pared como una figura compuesta y hallar el área de la figura compuesta.

Flores en abundancia

Mira la figura compuesta de los jardines en cada tarjeta de jardín. Escribe cuántas de cada figura 2D se usan para encontrar el área total de cada figura compuesta. Usa las fórmulas del área para determinar el área del jardín de cada cliente.

Jardín A

_____ rectángulo(s) _____ paralelogramo(s) _____ triángulo(s) _____ trapecio(s)

Resuelve para encontrar el área del jardín.

Área de la figura compuesta:

Jardín B

_____ rectángulo(s) _____ paralelogramo(s) _____ triángulo(s) _____ trapecio(s)

Resuelve para encontrar el área del jardín.

Jardín C

_____ rectángulo(s) _____ paralelogramo(s) _____ triángulo(s) _____ trapecio(s)

Resuelve para encontrar el área del jardín.

Área de la figura compuesta:

Área de la figura compuesta:

Jardín D

_____ rectángulo(s) _____ paralelogramo(s) _____ triángulo(s) _____ trapecio(s)

Resuelve para encontrar el área del jardín.

Jardín E

_____ rectángulo(s) _____ paralelogramo(s) _____ triángulo(s) _____ trapecio(s)

Resuelve para encontrar el área del jardín.

Área de la figura compuesta:

Área de la figura compuesta:

Jardín F

_____ rectángulo(s) _____ paralelogramo(s) _____ triángulo(s) _____ trapecio(s)

Resuelve para encontrar el área del jardín.

Área de la figura compuesta: 3

DIARIO DEL ESTUDIANTE

Jardín G

_____ rectángulo(s) _____ paralelogramo(s) _____ triángulo(s) _____ trapecio(s)

Resuelve para encontrar el área del jardín.

Área de la figura compuesta:

Jardín H

_____ rectángulo(s) _____ paralelogramo(s) _____ triángulo(s) _____ trapecio(s)

Resuelve para encontrar el área del jardín.

Área de la figura compuesta:

Reflexiona

1. ¿Qué estrategia puedes usar para hallar el área de una figura compuesta?

2. Hay varias formas de descomponer figuras compuestas en figuras en las que sabes cómo encontrar el área.

Describe una estrategia para resolver una de las tarjetas de jardín de manera diferente a como la resolviste.

DIARIO DEL ESTUDIANTE

DESPUÉS DE LA EXPLORACIÓN

1. Pida a los estudiantes que completen el boleto de salida para evaluar formativamente su comprensión del concepto.

2. Completen la esquema de anclaje como clase.

3. Pida a cada estudiante que complete su libreta interactiva.

APOYOS PEDAGÓGICOS

1. Si los estudiantes necesitan apoyo adicional para descomponer los jardines en formas, dibuje una línea de puntos para el jardín A que delimite las diferentes formas y pida a los estudiantes que nombren las formas que ven. Repita este proceso para el jardín B. A continuación, pida a los estudiantes que dibujen líneas de puntos e identifiquen las formas de los jardines siguientes. Haga hincapié en que a menudo hay varias maneras de descomponer una forma. Aunque una forma pueda ser menos eficaz, permita que los estudiantes elijan la que les parezca más adecuada. Deje que los estudiantes comparen estrategias para demostrar que, aunque sus áreas parciales no coincidan todas, dependiendo de cómo hayan descompuesto el jardín, sus áreas totales deberían coincidir siempre.

2. Si los estudiantes necesitan apoyo adicional para organizar su trabajo, modele un problema para ellos. Preste mucha atención a la organización del trabajo mostrado y etiquete todo a medida que trabaja. Por ejemplo, escriba los siguientes pasos en orden: Parte 1: Área del 1er. Rectángulo (y luego resolver); Parte 2: Área del 2do. Rectángulo (y luego resolver); y Parte 3: Área total (y luego resolver). Alternativamente, puede etiquetar cada parte del jardín con una letra y luego encontrar el área de la forma A, la forma B, y así sucesivamente.

3. Rete a los estudiantes a pensar cómo se podría hallar el área de una acera con una anchura específica que se instalara alrededor de uno de los jardines.

Jardinería

Boleto de salida

Resuelve para encontrar el área de cada parte de la huerta a continuación. Explica la estrategia que usaste para resolver el problema.

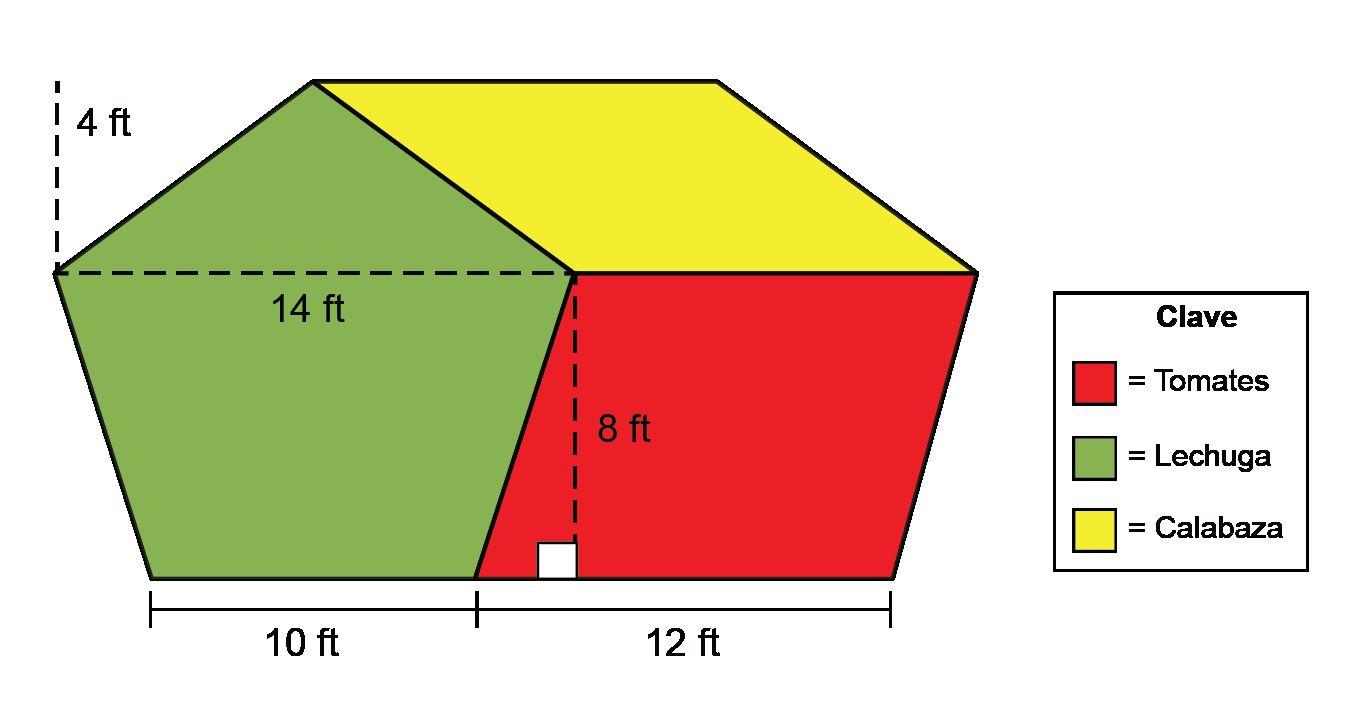
Tomates Lechuga

Estrategia: Estrategia:

Resuelve:

EXPLORAR: EXPLORACIÓN 4

APOYOS LINGÜÍSTICOS

Antes de la exploración, proyecte una imagen en la pizarra y destaque dentro de la imagen algo que tenga una forma específica. Pregunte a los estudiantes (por ejemplo): "¿Cuántas cosas con forma de trapecio podéis encontrar en esta imagen?"

Aclare el significado de la palabra compuesto en este contexto, y conéctelo con el significado en otros contextos. Los estudiantes pueden recordar que un número compuesto tiene varios pares de factores, del mismo modo que una forma compuesta está formada por varias formas.

Mostrar un esquema de anclaje con términos clave, fórmulas y ejemplos para que los estudiantes puedan consultarlos a lo largo de la unidad. Practique la pronunciación de palabras multisilábicas señalando la palabra en la esquema de anclaje, dividiéndola en sílabas y haciendo que los estudiantes repitan después de usted (paralelogramo, cuadrilátero, trapezoide, etc.).

Proporcione varias estructuras de frases para utilizar durante la charla de matemáticas y el diario del estudiante:

• Jardín ____ (letra) puede descomponerse en las formas _____ y _____.

• Para hallar el área de una _____ (forma), yo ....

• El área total es _____ unidades cuadradas.

Encontrar el área de figuras compuestas

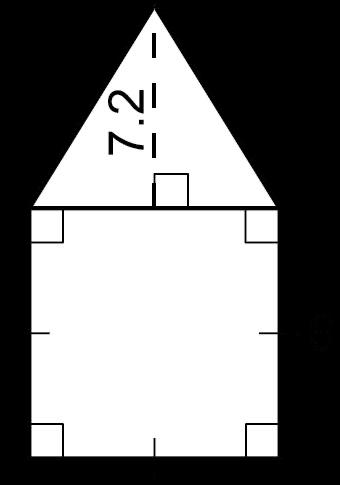
MUESTRA LO QUE SABES (PARTE 4)

EXPLORAR: EXPLORACIÓN 5

LECCIÓN PEDAGÓGICA

EXPLORACIÓN 5: VOLUMEN DE PRISMAS RECTANGULARES

Estándar(es)

• Resolver problemas matemáticos y de la vida real que involucren área, área de superficie y volumen. Hallar el volumen de un prisma rectangular recto con longitudes de arista fraccionarias empaquetándolo con cubos unitarios de las longitudes de arista fraccionarias unitarias apropiadas, y demostrar que el volumen es el mismo que se hallaría multiplicando las longitudes de arista del prisma. Aplicar las fórmulas V = lwh y V = bh para hallar volúmenes de prismas rectangulares rectos con longitudes de arista fraccionarias en el contexto de la resolución de problemas matemáticos y de la vida real.

Ideas fundamentales Estándares para la práctica matemática

Redes y superficie

Distancia y dirección

DESCRIPCIÓN

MP.2 Razonar abstracta y cuantitativamente.

MP.4 Modelar con matemáticas.

MP.5 Usar herramientas apropiadas estratégicamente.

MP.7 Buscar y hacer uso de la estructura.

Los estudiantes hallan el volumen de prismas rectangulares.

MATERIALES

IMPRESOS

• 1 diario del estudiante (por estudiante)

• 1 juego de tarjetas de cartón de frutas y verduras (por grupo)

• 1 boleto de salida (por estudiante)

REUTILIZABLES

• 40 cubos de enlace (por grupo)

• 1 bolsa resellable (por grupo)

PREPARACIÓN

• Planifique que los estudiantes trabajen en grupos de 3 o 4 para completar esta actividad.

• Imprime el diario del estudiante y el boleto de salida para cada estudiante.

• Imprime y recorta un juego de cartones de frutas y verduras para cada grupo. Coloca cada juego de tarjetas en una bolsa con cierre. Si lo deseas, imprime las tarjetas en cartulina y plastifícalas para que duren más.

• Reúne 40 cubos para cada grupo.

Conexiones de pontenido Motores de investigación

CC3 Desarmar el todo, armar las partes

CC4 Descubrir la forma y el espacio

DI1 Dar sentido al mundo (comprender y explicar)

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

PARTE I

1. Lea el siguiente escenario a la clase: The Farmer's Company está revisando su inventario de cajas de cartón de productos agrícolas para actualizar su sitio web. Todos los cartones deberán mostrar la cantidad total de productos que pueden contener. La Farmer's Company utiliza unidades smile para las medidas, por lo que tendríamos que utilizar una balanza para convertir las medidas a unidades smile. ¿Puedes utilizar las medidas de la Farmer's Company para construir un modelo de cada cartón y utilizar el modelo para encontrar el volumen de cada cartón?

2. Ayuda a los estudiantes a acceder a la tarea formulando las siguientes preguntas orientativas:

a. ¿Qué sabes ya sobre el volumen?

b. ¿Qué recuerdas sobre los prismas rectangulares?

3. Entrega a cada grupo un juego de tarjetas de cartón de productos y cubos de enlace.

4. Explica a los estudiantes que los cubos de enlace representan los productos que caben en el cartón. Deben entender que una unidad de sonrisa es una longitud igual a dos cubos de enlace.

EXPLORAR: EXPLORACIÓN 5

7. Pida a los estudiantes que lean juntos la primera tarjeta. Después de leer la tarjeta, dé tiempo a los estudiantes para ver cómo podrían construir un modelo del cartón con su grupo.

a. DOK-1 ¿Cómo puedes crear los cartones de frutas y verduras con los cubos de unión? Puedes conectar el número de cubos necesarios para hacer el largo, ancho y alto de cada uno de los cartones.

8. Pida a los estudiantes que construyan el cartón de frutas y verduras A, un cubo usando 8 cubos de un color. Permita que los estudiantes construyan la primera capa y luego expliquen qué representa la primera capa.

a. DOK-1 ¿Cuántos cubos hay en la primera capa? 4

b. DOK-2 ¿Qué representa la primera capa? La base del cartón de frutas y verduras que tiene forma de cuadrado

c. DOK-2 Mientras construimos el cartón de frutas y verduras A, ¿cómo podemos hallar el área de su base? Podemos multiplicar su longitud por su anchura para hallar el área de la base.

9. Explique a los estudiantes que hallar el área de la base es una parte del proceso que utilizamos para hallar el volumen de un prisma rectangular.

10. Pida a los estudiantes que continúen construyendo el cartón de producción A. Explique a los estudiantes que el cubo que se construyó representa un cubo de la unidad smile. Los estudiantes deben notar que todas las dimensiones de la unidad smile representan 1.

11. Entregue un diario del estudiante a cada estudiante.

12. Pida a los estudiantes que trabajen en colaboración para leer cada tarjeta del cartón de productos. Utilizarán sus cubos de enlace para construir un modelo del cartón utilizando la información de cada tarjeta. Luego dibujarán un modelo de sus cartones y registrarán la longitud, el ancho y la altura en cubos y unidades de sonrisa en el Diario del estudiante.

13. Supervise activamente a los estudiantes mientras trabajan con sus grupos para construir los cartones de productos agrícolas con cubos de enlace. Supervise y hable con los estudiantes según sea necesario para comprobar la comprensión utilizando las siguientes preguntas guía:

a. DOK-1 ¿Qué información se te da sobre este cartón? Me dan la longitud, la anchura y la altura.

b. DOK-1 ¿Cuáles son las dimensiones de este cartón? Las respuestas variarán. Las dimensiones de esta caja de cartón son 2 cubos y 1 unidad de sonrisa para la longitud, la anchura y la altura.

c. DOK-2 ¿Qué estrategia estás utilizando para construir tu modelo de la caja de cartón? Las respuestas pueden variar. Estoy multiplicando las medidas para construir el cubo.

d. DOK-2 Compara el cartón A y el cartón B. ¿Qué cartón crees que contendrá más productos? Las respuestas pueden variar. Creo que en el cartón B caben más productos porque la altura es mayor.

e. DOK-2 ¿Cómo se relaciona la cantidad de cubos que puedes poner dentro del cartón con la longitud? ¿Con la anchura? ¿Con la altura? ¿El total de cubos? El número de cubos que caben en una fila en la parte inferior es la longitud. El número de cubos que caben en una fila de delante hacia atrás es la anchura. El número de cubos que caben en una columna de abajo arriba es la altura. El número total de cubos necesarios para construir la caja es el volumen.

5. Deje tiempo para que los estudiantes construyan modelos y completen el diario del estudiante para todas las tarjetas de cartón de productos restantes. Los estudiantes determinarán el volumen de cada cartón en unidades de smile. Si es necesario, repase brevemente la fórmula para calcular el volumen.

6. Cuando los estudiantes hayan terminado, recoja los cubos de enlace y pase a la parte II.

PARTE II

1. Lea el siguiente escenario a la clase: Ahora que la Farmer's Company ha obtenido su ayuda para construir un modelo de cada caja de cartón y registrar las medidas de cada una, necesitan que encuentren el volumen de diferentes cajas de envío para saber cuánto producto puede contener cada caja.

2. Dirija la atención de los estudiantes a la parte II del diario del estudiante.

3. Explique que trabajarán con sus grupos para determinar el volumen de cada tipo de caja usando la información que se proporciona.

4. Pida a los estudiantes que trabajen en colaboración para utilizar las dimensiones dadas de cada caja para calcular su volumen de dos maneras. En primer lugar, hallarán el volumen utilizando la fórmula de la longitud multiplicada por la anchura multiplicada por la altura. A continuación, calcularán el área de la base de cada caja y usarán esta información para hallar el volumen utilizando la fórmula de la base multiplicada por la altura. Los estudiantes deben comparar ambas respuestas para el volumen de cada caja y ver que son iguales.

5. Supervise y hable con los estudiantes según sea necesario para comprobar la comprensión mediante el uso de las siguientes preguntas guía:

a. DOK-1 ¿Qué necesito hacer para multiplicar medidas fraccionarias? Cambiaré el número mixto para que sea una fracción impropia o cambiaré un número entero para que sea una fracción.

b. DOK-1 ¿Qué significa B en la fórmula V = Bh? Nota, compara ambas fórmulas de volumen para determinar B Al comparar ambas fórmulas de volumen, noté que la longitud por el ancho representa el área de la base, así que B, "big b", es el área de la base.

c. DOK-2 ¿La fórmula l × w × h te dará una solución diferente que la fórmula Bh? ¿Por qué? No, ambas fórmulas te darán la misma solución. B es encontrar el área, que es la longitud por la anchura, y se multiplica el área de la base por la altura.

6. Los estudiantes colaborarán con sus grupos para completar las preguntas restantes en el diario del estudiante.

7. Conceda a los estudiantes tiempo suficiente para completar su trabajo y anotar sus observaciones y reflexiones en los diarios del estudiante.

8. Pida a los estudiantes que compartan sus estrategias y anímelos a hacerse preguntas y establecer conexiones. Anima a los estudiantes a notar las similitudes y diferencias entre las estrategias usadas para encontrar el volumen de prismas rectangulares.

9. Después de la parte II, invita a la clase a una charla de matemáticas para compartir sus observaciones y aprendizajes.

3 2 3

(B). V = Bh

4 Caja de envío de zanahoria

Longitud = 2 pies Ancho = 4 pies Altura = 3 pies

Fórmula de volumen 1 V = × a × h

Fórmula de volumen 2 Encuentra el área de la base (B).

Caja de envío de sandía

V = Bh Area and Volume Explore 5

Longitud = 18 pulgadas Ancho = 24 pulgadas Altura = 5 pulgadas

2 1 8

Fórmula de volumen 1

V = × a × h

Reflexiona

Fórmula de volumen 2 Encuentra el área de la base (B). V = Bh 5 1 4 1 4

1. ¿Cómo se relaciona la cantidad de cubos que puedes poner en la caja con la longitud? ¿El ancho? ¿La altura? ¿El total de los cubos?

2. ¿Qué notas acerca de encontrar el volumen de un prisma rectangular con el uso de cubos conectables frente a usar dimensiones?

3. Explica cómo multiplicar medidas fraccionarias.

EXPLORAR: EXPLORACIÓN 5

CHARLA DE MATEMÁTICAS

• Elige una rutina de conversación estructurada para facilitar la siguiente pregunta:

◦ DOK-2 ¿Cómo se relaciona la cantidad de cubos que puedes poner en la caja con la longitud? ¿Con la anchura? ¿Con la altura? ¿El total de cubos? El número de cubos que caben por el fondo es la longitud. El número de cubos que caben de delante a atrás es la anchura. El número de cubos que caben de abajo arriba es la altura. El número total de cubos es el volumen de la caja de envío.

• DOK-2 ¿Hay alguna diferencia entre hallar el volumen usando cubos de enlace y usando las dimensiones? Cuando encuentras el volumen usando cubos de enlace y cuando encuentras el volumen usando dimensiones, el volumen seguirá siendo el mismo. La única diferencia es el método que se elige para hallar el volumen.

• DOK-1 Explique cómo multiplicar medidas fraccionarias. Para multiplicar medidas fraccionarias, necesito convertir el número mixto a una fracción impropia o cambiar el número entero a una fracción.

DESPUÉS DE LA EXPLORACIÓN

1. Haga que los estudiantes completen el boleto de salida para evaluar formativamente su comprensión del concepto.

2. Complete la esquema de anclaje como clase.

3. Haga que cada estudiante complete su libreta interactiva.

4. Regrese a la sección «Captar interés» e instruya a los estudiantes a usar sus habilidades recién adquiridas para completar exitosamente la actividad.

Una empresa de envíos ofrece 3 opciones de camiones; cada opción tiene

camión de diferentes tamaños. Encuentra el

para determinar qué camión puede contener la mayor cantidad de productos. Muestra tu trabajo.

Camión A Camión B Camión C

Longitud de la caja de camión 9 14 23

Ancho de la caja de camión

de la caja de camión

APOYOS PEDAGÓGICOS

1. Antes de la exploración, revise los atributos de los prismas rectangulares y los cubos con la clase y pida a los estudiantes que compartan cualquier cosa que ya sepan sobre el volumen.

2. Si los estudiantes necesitan apoyo adicional para completar los cálculos de fracciones, entonces revise cómo convertir números mixtos en fracciones impropias y fracciones impropias en números mixtos.

3. Para abordar la idea errónea de que el volumen de un prisma es el área total de las superficies visibles, haga que los estudiantes calculen su versión del volumen, luego presénteles el volumen real y explique las razones de la discrepancia.

4. Para abordar la idea errónea de que el volumen se compone del número total de cubos unitarios visibles cuando se dibujan en papel, haga hincapié en cómo el modelo físico de cubos enlazables se relaciona con el dibujo y cuáles son las implicaciones para el volumen. (Hay cubos que no se ven cuando se dibuja el prisma, pero sabemos que están ahí, sobre todo cuando miramos el modelo físico).

5. Anime a los estudiantes a compartir sus observaciones sobre el volumen. Por ejemplo, los estudiantes pueden observar que la longitud y la anchura se pueden intercambiar y no afecta al volumen total. O un estudiante puede observar que puede multiplicar el número de cubos unitarios de la capa base por la altura para determinar el volumen total.

una caja de

volumen de cada caja de camión

¿Qué

APOYOS LINGÜÍSTICOS

Como actividad previa o posterior a la exploración, pida a los estudiantes que creen un mapa conceptual del área frente al volumen. Incluya un banco de términos y frases que puedan utilizar para completar sus mapas. Los términos y frases pueden incluir bidimensional; teodimensional, espacio total ocupado por una forma tridimensional, y espacio cubierto por una forma plana cerrada

Proporcione a menudo elementos visuales para reiterar la definición de términos clave, como cubo, unidades cúbicas, y volumen. Platique sobre la similitud entre las palabras cube y cubic, y pregunte a los estudiantes si se les ocurren otras palabras que tengan una relación similar. Explique los significados alternativos de volumen para aclarar el significado matemático (como volumen de sonido en la radio o la televisión, volumen en el pelo como se ve en los anuncios de champú).

Invite a los estudiantes a hablar a la clase desde la perspectiva de uno de los cartones de productos agrícolas que construyeron. Por ejemplo, un estudiante que elija el cartón de productos A podría hacer afirmaciones como «Soy un prisma rectangular. Tengo una longitud de 2 cubos, que es 1 unidad de sonrisa». Conceda tiempo a los estudiantes para preparar su breve presentación y deje que los compañeros hagan preguntas al presentador cuando hayan terminado. Ayude a los estudiantes a hablar en primera persona correctamente, así como a utilizar el vocabulario matemático con precisión. A continuación, los compañeros de clase pueden adivinar qué cartón de frutas y verduras fingía ser el estudiante basándose en la información facilitada. Aclare lo que significa utilizar una fórmula en matemáticas. Asegúrese de indicar el sustantivo asociado a cada parte de la fórmula, incluidas las unidades utilizadas, para ayudar a los estudiantes a comprender lo que representan las letras.

EXPLICAR: ESQUEMA DE ANCLAJE

ESQUEMA DE ANCLAJE

DESCRIPCIÓN

Este gráfico de anclaje destaca las ideas principales del alcance. Esta es una herramienta para apoyar la instrucción y anclar el aprendizaje de los estudiantes a lo largo del alcance.

MATERIALES

• 1 hoja de papel cuadriculado

• 1 juego de marcadores multicolores

PREPARACIÓN

● Imprima el ejemplo de esquema de anclaje (opcional).

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. El ejemplo de esquema de anclaje puede usarse como referencia antes de crear el esquema de anclaje de la clase con los estudiantes. La creación de un esquema de anclaje debe estar dirigida por los estudiantes para promover que se apropien de su aprendizaje.

2. A medida que los estudiantes trabajen en el alcance, colaboren para añadir piezas al esquema de anclaje Formule las siguientes preguntas:

a. ¿Qué estrategia utilizamos para resolver este problema?

b. ¿Qué vocabulario necesitamos conocer para poder resolver este problema?

3. Continúe añadiendo habilidades o estrategias importantes aprendidas después de cada exploración para resaltar el contenido importante.

4. Explique a los estudiantes que pueden utilizar este esquema como herramienta de apoyo para su aprendizaje. Los estudiantes también pueden pegar una copia del esquema de anclaje en sus cuadernos para utilizarla como referencia durante todo el año.

5. Algunos esquema de anclaje sólo se mostrarán durante ese alcance o grupo de alcances, mientras que otras permanecerán expuestas durante todo el año escolar. CONSOLIDAR EL

Área de un triángulo

Área = (b h)

Área de un paralelogramo

Área = b h

Área de un trapecio

Área = (b

+ b₂)h 1 2 1 2

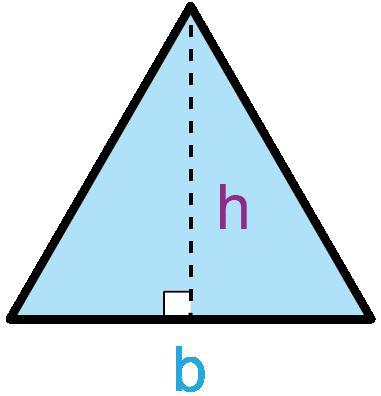
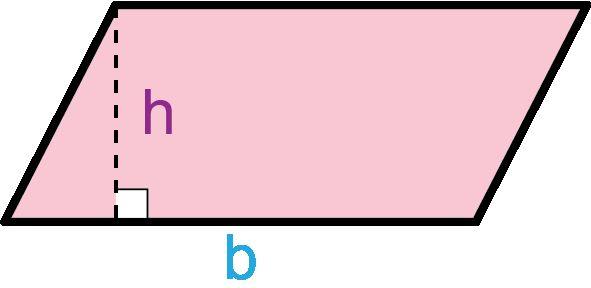
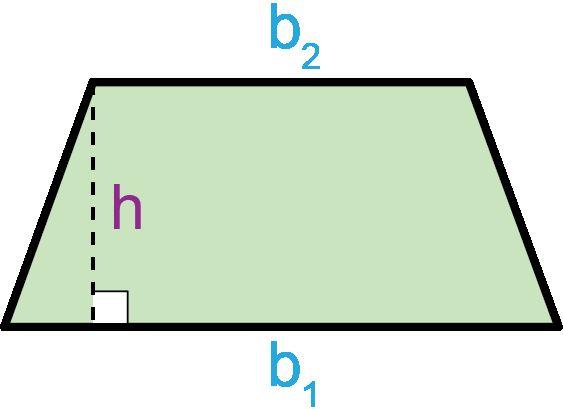
VOLUMEN

Prisma rectangular

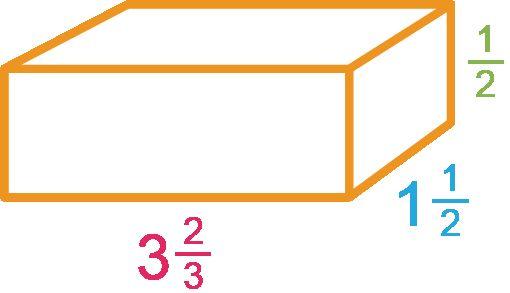
EJEMPLO DE ESQUEMA DE ANCLAJE

Instrucciones

● Recorta por las líneas punteadas.

● Coloca pegamento en la parte de atrás y pégalo en tu cuaderno.

EXPLICAR: LIBRETA INTERACTIVA

● Escribe en tu cuaderno arriba de la tabla: «El área siempre se mide en unidades cuadradas»

● Escribe la fórmula de cada figura a la derecha de tu imagen.

● Resuelve para hallar el área de cada figura. Area and Volume

Área de un triángulo

Fórmula para el área de un triángulo

A =

Inserta las dimensiones para resolver.

A =

Área de un paralelogramo Fórmula para el área de un paralelogramo

A =

Inserta las dimensiones para resolver.

A =

Área de un trapezoide Fórmula para el área del trapezoide

A =

Inserta las dimensiones para resolver.

A =

ANCLAR EL APRENDIZAJE DE LOS ESTUDIANTES

LIBRETA INTERACTIVA

DESCRIPCIÓN

Los estudiantes toman notas, expresan ideas y/o procesan la información presentada en clase utilizando la actividad y el cuaderno.

MATERIALES

IMPRESO

● 1 folleto del estudiante (por estudiante)

PREPARACIÓN

● Imprima una copia del folleto del estudiante por alumno.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Prepare una libreta interactiva con un cuaderno de espiral o de composición para cada estudiante. Los estudiantes pueden utilizar las primeras páginas para crear una tabla de contenidos con números de página para realizar un seguimiento de las actividades.

2. En el folleto del estudiante se ofrecen instrucciones para cada actividad.

Instrucciones

● Recorta por las líneas punteadas.

● Coloca pegamento en la parte de atrás y pégalo en tu cuaderno.

● Completa la información. Area and Volume

Volumen de un prisma rectangular = ________ · _________ · __________

El volumen se mide en _______________________.

Un cubo _______ es un cubo con una arista con una longitud de una unidad.

Halla el volumen del siguiente prisma rectangular.

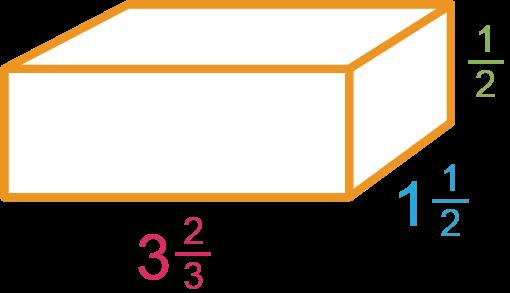
Volumen = _____ ______ = ______ pies cúbicos

FOLLETO DEL ESTUDIANTE

3. Dé tiempo a los estudiantes para que completen la actividad y peguen las piezas en sus cuadernos interactivos.

4. Las libretas ineractivas pueden utilizarse como referencia para los estudiantes durante el trabajo independiente y pueden enviarse a casa al final del año como registro de su aprendizaje.

EXPLICAR: CONEXIONES LINGÜÍSTICAS

APOYO PARA LOS ESTUDIANTES MULTILINGÜES

CONEXIONES LINGÜÍSTICAS

DESCRIPCIÓN

Los estudiantes tienen la oportunidad de utilizar sus conocimientos lingüísticos y culturales previos para apoyar las conexiones con nuevas destrezas, vocabulario y conceptos en sus niveles de competencia.

MATERIALES

IMPRESO

• 1 folleto del estudiante según su nivel de competencia (por estudiante)

REUTILIZABLE

• 1 lápiz o marcador de color rojo (por estudiante)

• 1 lápiz o marcador de color azul (por estudiante)

• 1 lápiz o marcador de color verde (por estudiante)

PREPARACIÓN

• Prepárese para que los estudiantes trabajen con compañeros cuando sea necesario.

• Determine el nivel de inglés de cada estudiante.

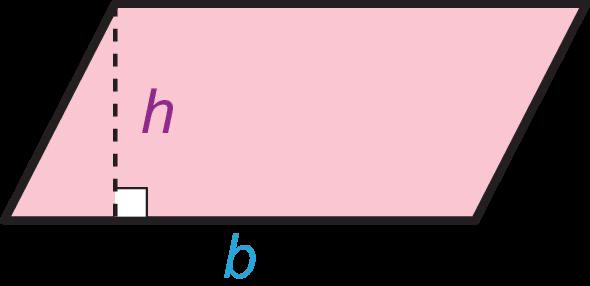
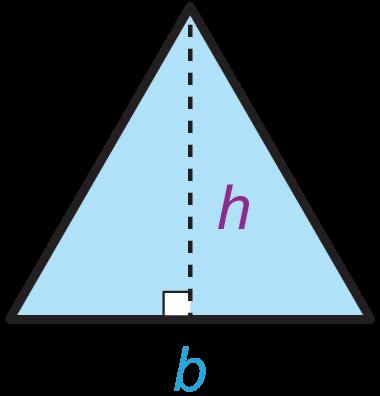
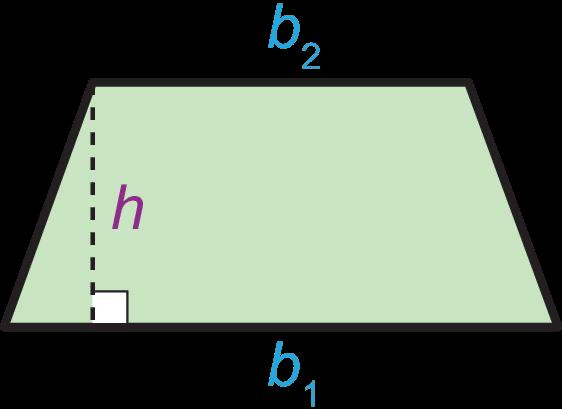
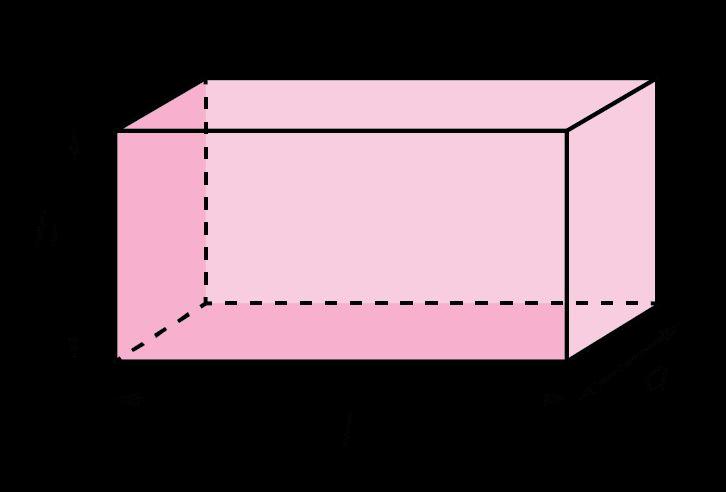
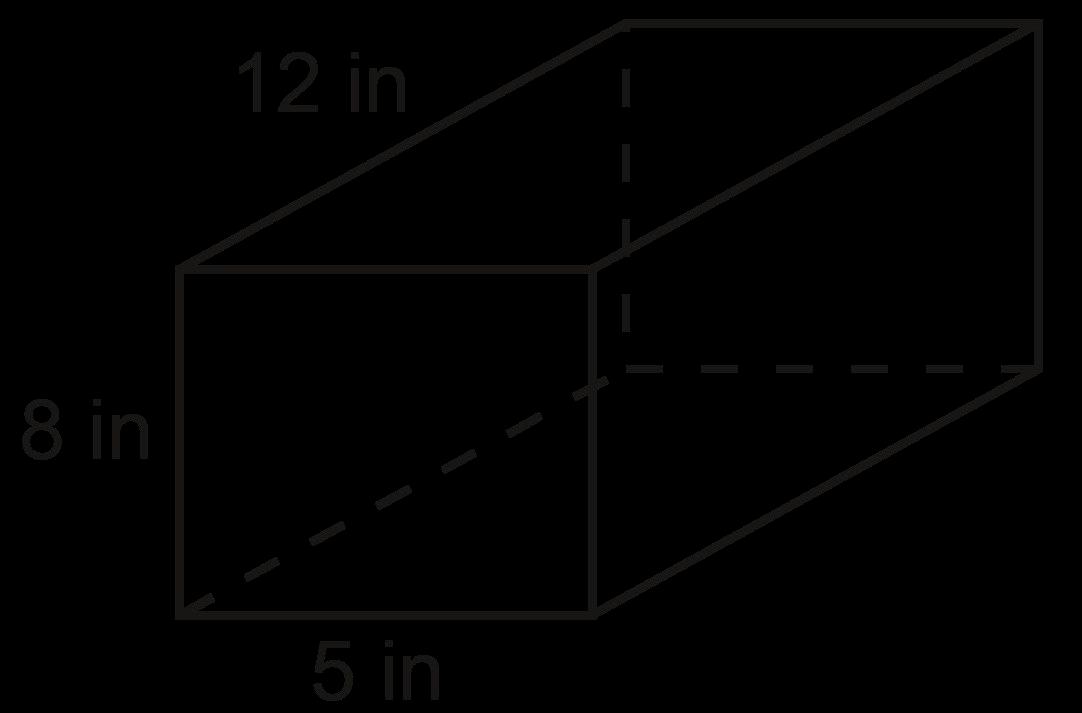
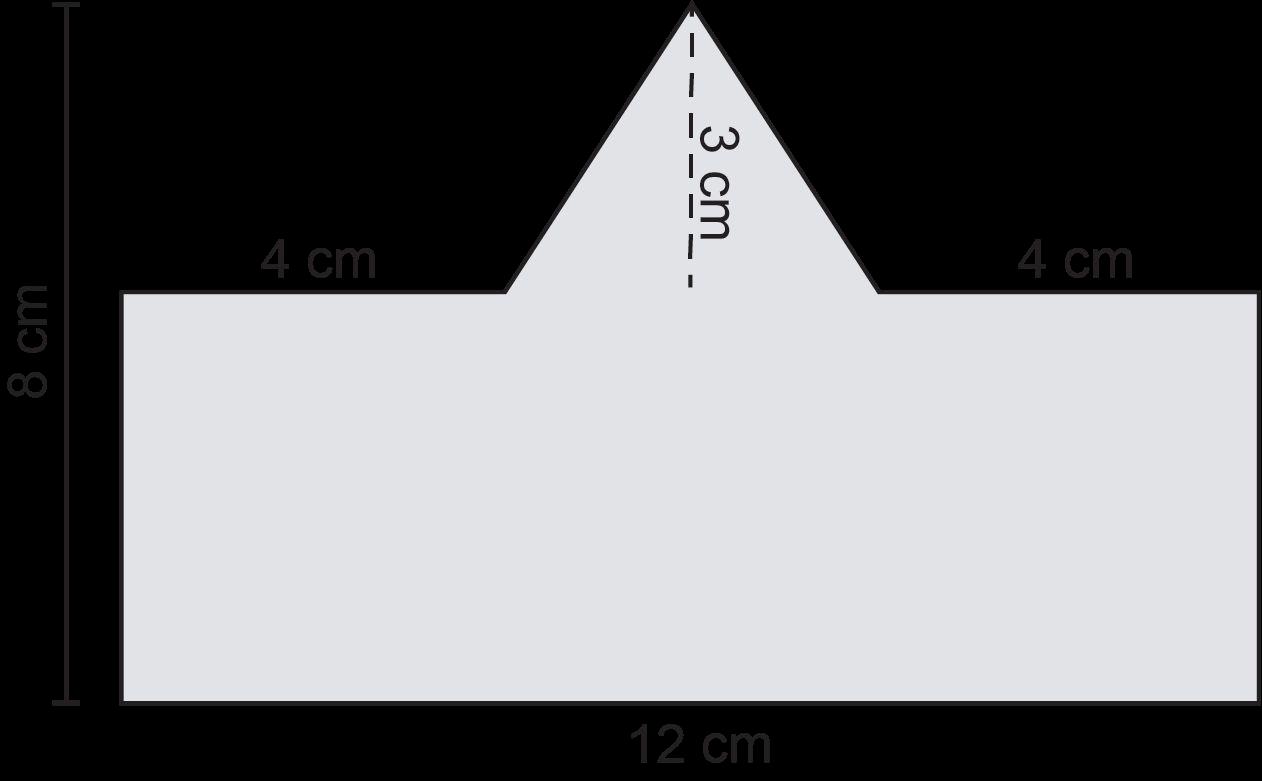
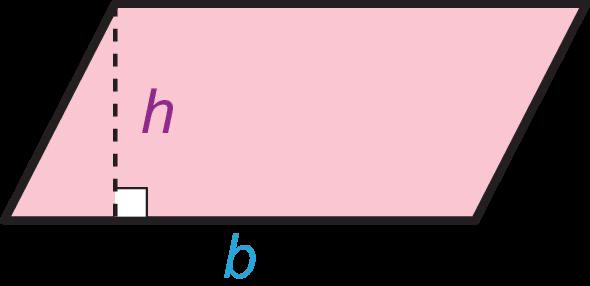
• Imprima un folleto del estudiante para cada estudiante según su nivel de inglés.

• Permita que los estudiantes tengan acceso al vocabulario ilustrado para este alcance.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Distribuya un folleto del estudiante a cada uno según su nivel de inglés.

2. Use las indicaciones para las partes de comprensión auditiva, expresión oral, lectura y escritura. Use gestos, señale objetos y elementos visuales según proceda. Consulte las indicaciones para obtener sugerencias.

3. De tiempo a los estudiantes para que piensen con sus compañeros antes de responder.

4. Anime a los estudiantes a perseverar en su pensamiento y a utilizar herramientas y modelos matemáticos.

5. Invite a los estudiantes a responder adecuadamente a cada dominio lingüístico.

6. Haga que los estudiantes utilicen la página final del folleto del estudiante para formar conexiones entre los conceptos matemáticos y el mundo real.

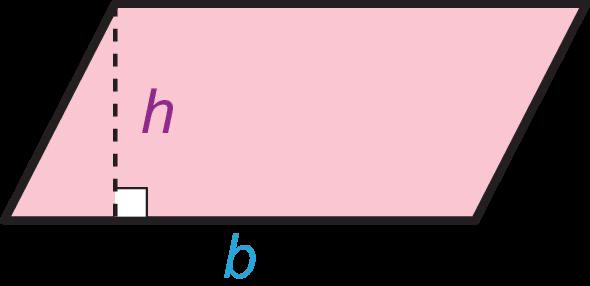
PRINCIPIANTE

PRINCIPIANTE

Leer la historia en grupo. Divida la historia en frases. Pida a los estudiantes que señalen cada palabra mientras leen. Pídales que rodeen con un círculo las palabras que no conozcan. Exponga las palabras a todo el grupo.

• Coral: lea el primer enunciado. ¿Qué forma tiene el acuario de Jacob? ¿Para qué sirve el acuario?

◦ Pida a los estudiantes que utilicen la siguiente estructura de frase: Jacob compró un acuario con forma de _____ para su ____.

• Coro: lea el segundo enunciado. ¿Qué preguntó el dependiente de la tienda sobre el acuario?

◦ Haga que los estudiantes utilicen la siguiente estructura de frases: El empleado de la tienda preguntó por el _____________ del mismo.

• Coral-lea el tercer enunciado. ¿Cómo podemos encontrar el volumen? Mire la primera página, busque la fórmula del prisma rectangular y señálela.

◦ Pida a los estudiantes que utilicen el siguiente marco de enunciado: La fórmula para hallar el volumen del acuario es _____.

• Señala la longitud, que está en el recuadro rojo. Señala la anchura, que está en el recuadro azul. Señala la altura, que está en el recuadro verde.

• Ahora utiliza las dimensiones del prisma rectangular para rellenar los números en el lugar correcto de la fórmula. Completa tu fórmula escribiendo la longitud, la anchura y la altura en el lugar correcto.

• Coral - lee el cuarto enunciado. El primer paso es multiplicar la longitud y la anchura. ¿Cuál es el producto de la longitud y la anchura?

◦ Pida a los estudiantes que utilicen el siguiente marco de frases: El área de la base, la longitud multiplicada por la anchura, es _____ en2

• La longitud multiplicada por la anchura se llama área de la base. En tu prisma rectangular, sombrea la base del prisma rectangular.

• ¿Cuál es la altura del prisma?

◦ Pide a los estudiantes que utilicen el siguiente marco de frases: La altura es ____ pulg.

• Completa el segundo paso de tu fórmula escribiendo el área de la base y la altura. Asegúrate de que los estudiantes obtienen la respuesta correcta al multiplicar la longitud y la anchura antes de proceder a multiplicarla por la altura.

• Coro: lee el quinto enunciado. Para hallar el volumen total, debemos multiplicar el área de la base por la altura.

• Pida a los estudiantes que utilicen el siguiente marco de enunciado: El volumen total es ____________ en3

INTERMEDIO

Lectura coral en grupo. Pida a los estudiantes que señalen cada palabra mientras leen. Pídales que rodeen con un círculo las palabras que no conozcan. Comenten las palabras con sus compañeros. Ten a mano utensilios de escritura rojos, azules y verdes para que los utilicen los estudiantes.

• Comparte con tus compañeros de qué trata la historia.

◦ ¿Qué intenta hacer Jacob con su acuario? Coméntalo con tus compañeros.

• Coro: lee el primer enunciado. Señala la respuesta en la historia antes de marcar la afirmación como verdadera o falsa.

• Coro: lee la segunda afirmación. Señala la respuesta en la historia antes de marcar la afirmación como verdadera o falsa.

• ¿Cómo podrías cambiar esta afirmación para que fuera verdadera?

• Mira la primera página de tu folleto del estudiante y señala la fórmula para un prisma rectangular.

• Compañero - lee la tercera afirmación. Define con tus compañeros y decide si es verdadera o falsa.

• Encierra en un círculo rojo la longitud del prisma rectangular. Rodea la anchura en azul y la altura en verde.

• Ahora, completa tu fórmula escribiendo la longitud, la anchura y la altura en los espacios proporcionados.

• Debate con tus compañeros cuál sería el primer paso para resolver el volumen. ¿Cómo puedes hallar el área de la base?

• Haz que los estudiantes resuelvan el primer paso multiplicando l × w Comprueba que su respuesta es correcta y que la han rellenado en los espacios en blanco correctos del Material para el estudiante.

• Coro: lee el cuarto enunciado. Conversa con tus compañeros para decidir si es verdadera o falsa.

• ¿Esto coincide con lo que calculaste cuando hiciste el primer paso?

• Acuerda con tus compañeros cuál será el próximo paso.

• Compañero-lee la quinta afirmación. Decide con tus compañeros si es verdadera o falsa.

LEER Y HABLAR

AVANZADO

Haz que los estudiantes lean la historia con sus compañeros y señalen cada palabra mientras leen. Invite a los estudiantes a rodear con un círculo las palabras que no conozcan y a comentarlas con sus compañeros.

• Explique a sus compañeros de qué trataba el pasaje.

• Comente lo que Jacob intenta hacer con su acuario.

• Explique a sus compañeros lo que sabe sobre el prisma rectangular a partir de la lectura de la historia.

• Lea cada afirmación y comente sus respuestas con sus compañeros.

ESCUCHAR Y HABLAR

PRINCIPIANTE

Disponga de lápices de colores azul, rojo y verde para que los estudiantes los utilicen. Lee las siguientes instrucciones de una en una:

• Señala el paralelogramo. Señala su base.

• Señala la altura del paralelogramo.

• Para hallar el área de un paralelogramo, multiplicaríamos su altura por la base. Traza una línea que una el paralelogramo con la fórmula correcta.

• Señala el triángulo. Señala su base.

• Señala la altura.

• Para hallar el área de un triángulo, multiplicamos la mitad de su base por su altura.

• Dibuja una línea que conecte el triángulo con su fórmula de área.Señala el trapecio. Los trapecios tienen dos bases. Señala sus dos bases.

• Señala la altura del trapezoide.

• Para hallar el área de un trapezoide, primero calculamos la media de las bases hallando la mitad de la suma de las dos bases. Luego multiplicamos por su altura.

• Dibuja una línea que conecte el trapezoide con su fórmula de área correcta.

• Señala el prisma rectangular. Esta es una forma tridimensional.

• Podemos encontrar el volumen de un prisma rectangular multiplicando su longitud por su anchura por su altura.

• Dibuja una línea que conecte el prisma rectangular con la fórmula para el volumen.

• En la siguiente sección, encontraremos el área o el volumen de las figuras ilustradas.

• Primero, veamos el triángulo.

• Encierra en un círculo la altura del triángulo en azul.

• Encierra en un círculo la longitud de la base del triángulo en rojo.

• Señala la ecuación debajo del triángulo. Señala el número 20. ¿Cómo obtuvimos este producto?

◦ Pida a los estudiantes que utilicen la siguiente secuencia de oraciones: Para obtener el producto de 20, _____.

• Encierra en un círculo verde los dos números que se multiplicaron para obtener el producto de 20.

• En el siguiente paso, tenemos que multiplicar 20 por la mitad. Una forma de multiplicar un número por la mitad es dividirlo por 2.

• Para encontrar la solución, divide 20 por 2 y escribe el producto de 20 por la mitad en el espacio en blanco.

• Mira el prisma rectangular. Señala el prisma rectangular. La anchura es 12. Rodea el ancho en azul.

• El largo es 5. Rodea el largo en rojo.

• Rodea la altura en verde.

• Ahora mira la fórmula del volumen. ¿Qué se multiplicó para obtener 60?

◦ Pida a los estudiantes que utilicen la siguiente secuencia de oraciones: Para obtener el producto de 60, _____.

• Para completar la fórmula, necesitamos multiplicar 60 por 8. Encuentre el producto y escriba su respuesta en el espacio provisto.

INTERMEDIO

Tenga lápices de colores azul, rojo y verde a disposición de los estudiantes. Lee las siguientes instrucciones de una en una:

• El folleto nos da las fórmulas para el área y el volumen de varias figuras bidimensionales y tridimensionales. Señala las fórmulas del área y del volumen.

• Señala las fórmulas del área y léelas.

• Señala la fórmula del volumen y léela.

• Señala el paralelogramo. ¿Qué fórmula corresponde a esta forma? ¿Cómo lo sabes?

◦ Pide a los estudiantes que utilicen la siguiente estructura de frases: La fórmula que corresponde al paralelogramo es _____ porque _____.

• Escribe la fórmula en la línea.

• Señala el triángulo. ¿Qué fórmula corresponde a esta forma? ¿Cómo lo sabes?

◦ Haz que los estudiantes utilicen la siguiente estructura de frases: La fórmula que corresponde al triángulo es _____ porque _____.

• Escribe la fórmula en la línea.

• Señala el trapecio. ¿Qué fórmula corresponde a esta forma? ¿Cómo lo sabes?

◦ Haz que los estudiantes utilicen la siguiente estructura de frases: La fórmula que corresponde al trapecio es _____ porque _____.

• Escribe la fórmula en la línea.Señala el prisma rectangular. ¿Qué fórmula corresponde a esta forma? ¿Cómo lo sabes?

◦ Haz que los estudiantes utilicen la siguiente estructura de frases: La fórmula que corresponde al prisma rectangular es _____ porque _____.

• Escribe la fórmula en la línea.

• Señala el triángulo en la parte inferior del folleto.

• Rodea la altura en rojo y la base en azul.

• Ahora, escribe la fórmula para el área de un triángulo en el espacio proporcionado. En la fórmula, rodea la base en azul y la altura en rojo.

• Escribe las dimensiones del triángulo en la fórmula. Discute con tus compañeros cuál debe ser el primer paso para resolver la fórmula.

• Discute con tus compañeros cuál será el siguiente paso.

◦ Haz que los estudiantes utilicen la siguiente estructura de frases: El siguiente paso es _____ porque _____.

• Completa los pasos para hallar el área del triángulo y escribe la respuesta en el espacio proporcionado.

• Señala el prisma rectangular. Rodea la longitud en azul, la anchura en rojo y la altura en verde.

• Escribe la fórmula para el volumen de un prisma rectangular bajo la forma. En la fórmula, rodea con un círculo la longitud en azul, la anchura en rojo y la altura en verde.

AVANZADO

Ten a mano lápices de colores azul, rojo y verde para que los utilicen los estudiantes. Lea las siguientes preguntas de una en una:

• Señale el paralelogramo.

• Escriba la fórmula del área del paralelogramo bajo la forma.

• Señale el triángulo.

• Escriba la fórmula del área del triángulo bajo la forma.

• Señale el prisma rectangular.

• Escribe la fórmula del volumen del prisma rectangular bajo la forma.

• Señala el trapecio.

• Escribe la fórmula del área del trapecio bajo la forma.

• En la parte inferior de la hoja hay tres problemas resueltos. Todos ellos contienen errores. Examina el triángulo y el trabajo para hallar el área. Señala el paso que contiene el error.

• Pregunta a la persona que está a tu lado dónde encontraron un error.

• Escribe la solución correcta para el área del triángulo.

• Examina el prisma rectangular y el trabajo para encontrar el volumen. Señala el paso que contiene el error.

• Pregunta a la persona que está a tu lado dónde ha encontrado un error.

• Escribe la solución correcta del volumen del prisma.

• Examina el trapecio y el trabajo para encontrar el área. Señala el paso que contiene el error.

• Pregunta a la persona que está a tu lado dónde encontró un error.

• Escribe la solución correcta para el área del trapecio.

ESCUCHAR Y HABLAR (CONTINUACIÓN)

PRINCIPIANTE

• Comprueba que los estudiantes han obtenido la respuesta correcta de 480.

• Ahora, observemos el trapecio. Señala el trapecio. Encierra en un círculo azul las dos bases.

• Encierra en un círculo rojo la altura del trapecio.

• Observa la fórmula del área. ¿Cómo hemos obtenido el número 25?

◦ Pide a los estudiantes que utilicen la siguiente raíz de frase: Para obtener 25, _____.

• El siguiente paso para resolver la ecuación sería multiplicar 25 por 6. Encuentre el producto de 25 por 6 y escríbalo en el espacio proporcionado. Ayúdales si es necesario y asegúrate de que los estudiantes obtienen la respuesta 150.

• El último paso para hallar el área del trapecio es multiplicar 150 por la mitad. Puedes hacerlo dividiendo 150 por 2.

• Encuentra el cociente de 150 y 2, y escríbelo en el espacio provisto.

INTERMEDIO

• Escribe las dimensiones de la forma en la fórmula en los lugares correctos.

• Discute con tus compañeros el primer paso para encontrar el volumen del prisma.

◦ Haz que los estudiantes usen la siguiente estructura de oraciones: El primer paso es _____ porque _____.

• Discute con tus compañeros cuál será el siguiente paso para encontrar el volumen del prisma.

◦ Haz que los estudiantes utilicen la siguiente estructura de frases: El siguiente paso es _____ porque _____.

• Completa los pasos para hallar el volumen del prisma rectangular y escribe la respuesta en el espacio proporcionado.

• Señala el trapecio. Rodea las bases en azul.

• Rodea la altura del trapezoide en rojo.

• Escribe la fórmula para el área de un trapezoide bajo la forma.

• En la fórmula, rodea las bases en azul y la altura en rojo.

• Escribe las dimensiones del trapezoide en los lugares correctos de la fórmula.

• Explica a tus compañeros cuál será el primer paso para resolver el área del trapezoide.

◦ Pide a los estudiantes que utilicen la siguiente estructura de frases: El primer paso es _____ porque _____.

• Haz que tus compañeros te expliquen cuál será el siguiente paso.

◦ Haz que los estudiantes utilicen la siguiente estructura de frase: El siguiente paso es _____ porque _____.

• Complete el último paso para hallar el área y escriba la respuesta en el espacio provisto.

PRINCIPIANTE

Ponga a disposición de los estudiantes tarjetas de vocabulario con imágenes. Lea y comente las palabras del banco de palabras. Defina y ponga ejemplos según las necesidades de los estudiantes. Discuta las siguientes preguntas mientras lee:

• Observe la figura compuesta. ¿Cómo podríamos descomponerla en diferentes figuras para hallar el área de la figura completa?

• ¿Cómo la descompondrías para hacer diferentes figuras?

• Permita que los estudiantes discutan cómo podrían descomponer la figura.

• ¿Cómo podríamos cortar esta figura en sólo dos figuras para hallar el área?

• Haga una eco-lectura de cada enunciado y pida a los estudiantes que consulten sus tarjetas de vocabulario según sea necesario antes de escribir sus respuestas.

INTERMEDIO

Tenga a disposición de los estudiantes tarjetas de vocabulario con imágenes. Coro: lee y comenta las palabras del banco de palabras. Defina y proporcione ejemplos según las necesidades de los estudiantes.

• Pida a los estudiantes que comenten las palabras del banco de palabras con sus compañeros.

• Doble la mitad inferior del papel para que sólo se vea el banco de palabras. Señale una palabra del banco de palabras y, por turnos, explique las palabras con sus compañeros.

• Tome nota de los estudiantes que proporcionan explicaciones matemáticamente precisas de las palabras del banco de palabras.

• A continuación, señale una palabra del banco de palabras cuyo significado necesite aclarar.

• En función de los estudiantes a los que haya oído dar las explicaciones matemáticamente precisas, pida a los estudiantes que ayuden a aclarar las palabras seleccionadas a sus compañeros.Veo que varios estudiantes están pidiendo aclaraciones sobre la palabra ________. (nombre del estudiante) pudo proporcionar una explicación clara de la palabra _________ a su compañero. _____, ¿podrías compartir tu explicación?

• Lee cada enunciado con tus compañeros y utiliza las palabras del banco de palabras para completar cada enunciado. Tenga en cuenta que algunas palabras pueden utilizarse más de una vez o no utilizarse en absoluto.

• Recuerde a los estudiantes que consulten el banco de palabras cuando rellenen los espacios en blanco.

AVANZADO

Ponga a disposición de los estudiantes tarjetas de vocabulario con imágenes. Los estudiantes deben leer en coro las palabras del banco de palabras con sus compañeros. Defina y proporcione ejemplos según las necesidades de los estudiantes.

• Haga que los estudiantes comenten las palabras del banco de palabras con sus compañeros.

• Comente las palabras del banco de palabras con sus compañeros. Cada persona debe dar una explicación o descripción de una palabra y, a continuación, pedir a su compañero que parafrasee el significado de la palabra. Continúa este proceso hasta que hayas discutido todas las palabras del banco de palabras.

• Lee las instrucciones con tus compañeros. ¿Qué plan seguirás para asegurarte de que utilizas el mayor número posible de palabras del banco de palabras en tu redacción? Si no estás seguro de cómo utilizar una palabra, rodéala con un círculo en el banco de palabras. Los estudiantes aún no deben empezar a escribir.

• Esté atento a los estudiantes que tengan dificultades para crear un plan o que marquen con un círculo las palabras del banco de palabras. Ofrezca apoyo y permita que los estudiantes que hayan podido crear un plan lo compartan con la clase.

◦ Veo que varios de nosotros necesitamos aclaraciones sobre la palabra _______. Diríjase a alguien cercano que no sea su compañero y pídale que aclare o defina la palabra ___________.

◦ Veo que varios de nosotros necesitamos ayuda para diseñar un plan que utilice palabras del banco de palabras. Acércate a alguien que no sea tu compañero y pídele que explique cómo piensa utilizar el mayor número posible de palabras del banco de palabras.

• Pide a los estudiantes que escriban sus explicaciones una vez que se hayan aclarado todas las palabras y se hayan compartido los planes.

• Ahora, escribe tu explicación utilizando al menos 5 de las palabras del banco de palabras. Cuando termines de escribir, comparte tu escrito con tus compañeros.

EXPLICAR: VOCABULARIO ILUSTRADO

PALABRAS QUE HAY QUE CONOCER

VOCABULARIO ILUSTRADO

Área

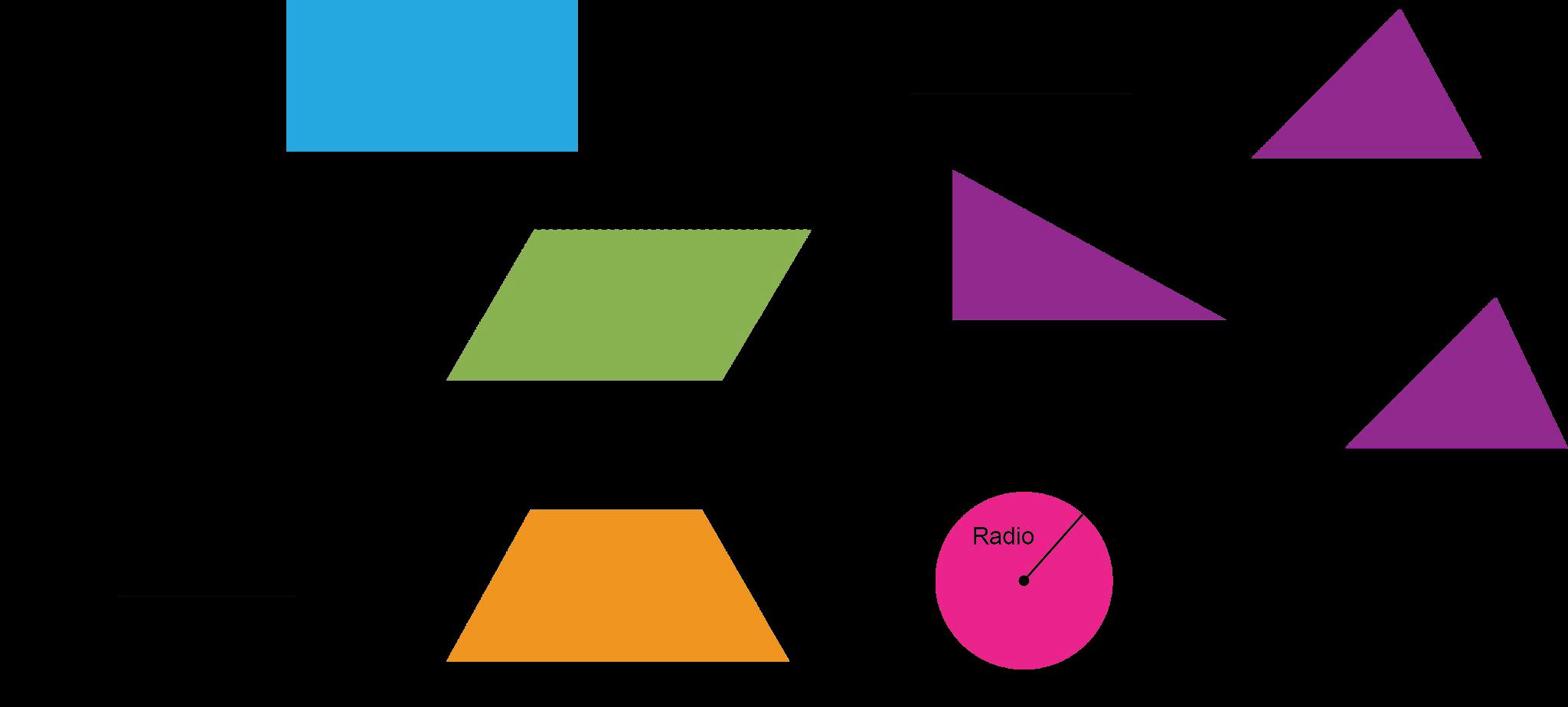
Número de unidades cuadradas que se necesitan para cubrir la superficie bidimensional de un objeto

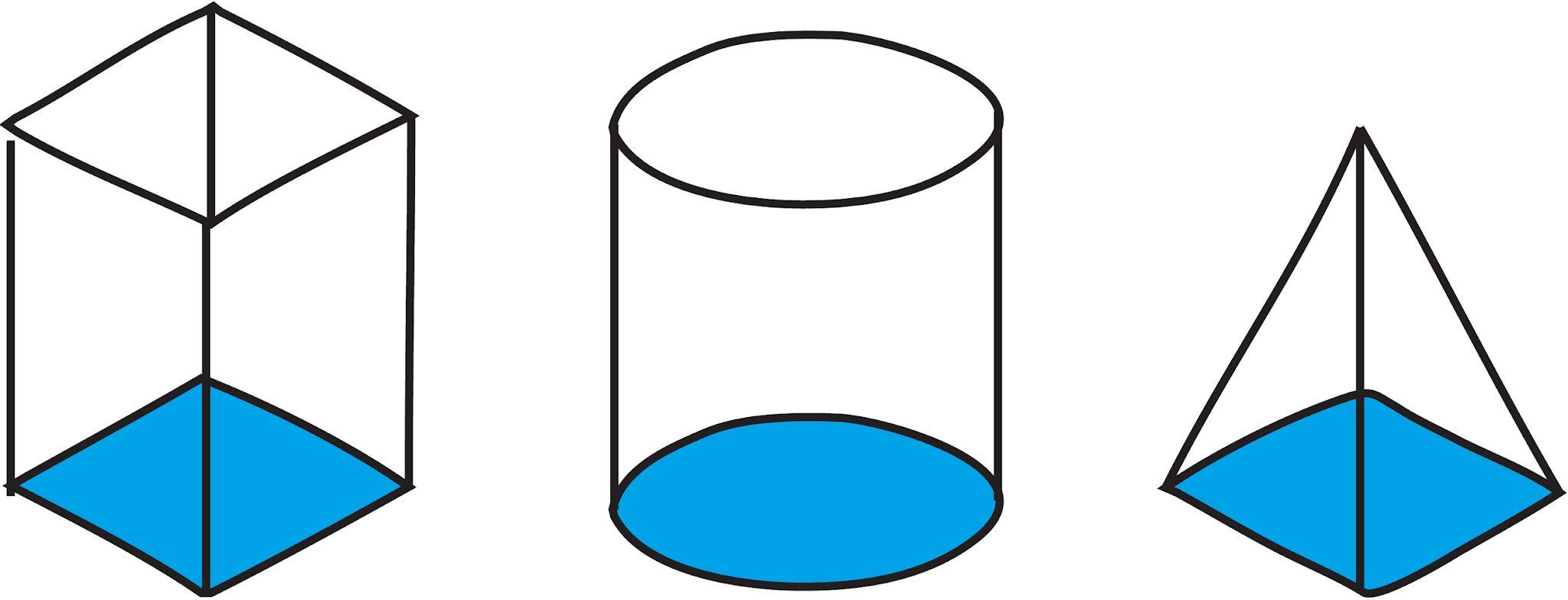
Superficie sobre la que se apoya un objeto sólido

Base de un polígono

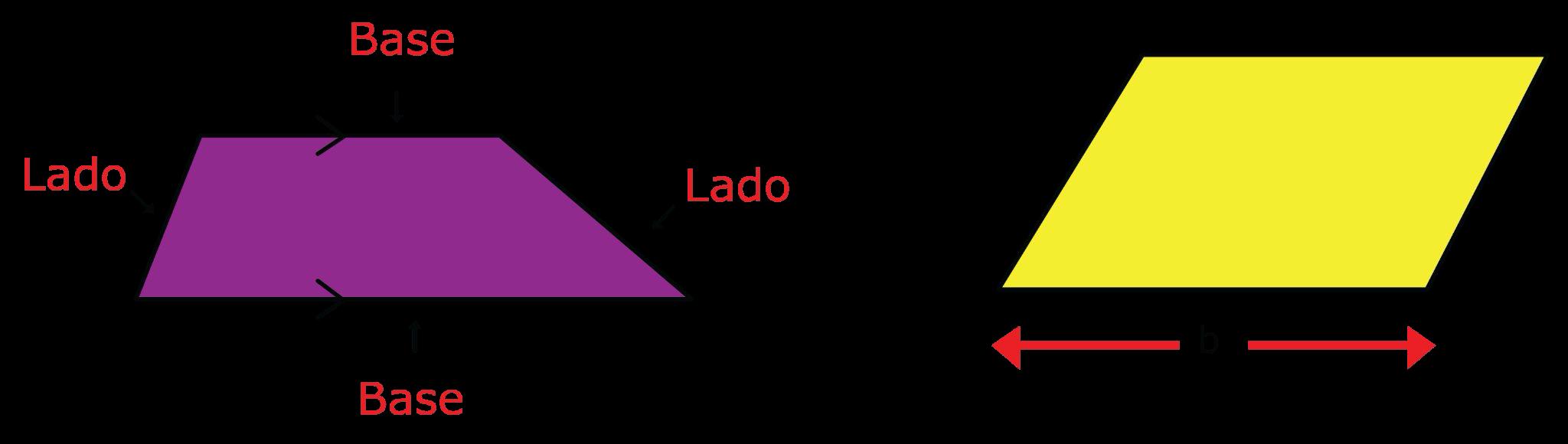
Lado del polígono que es perpendicular a la altura

Base de un triángulo

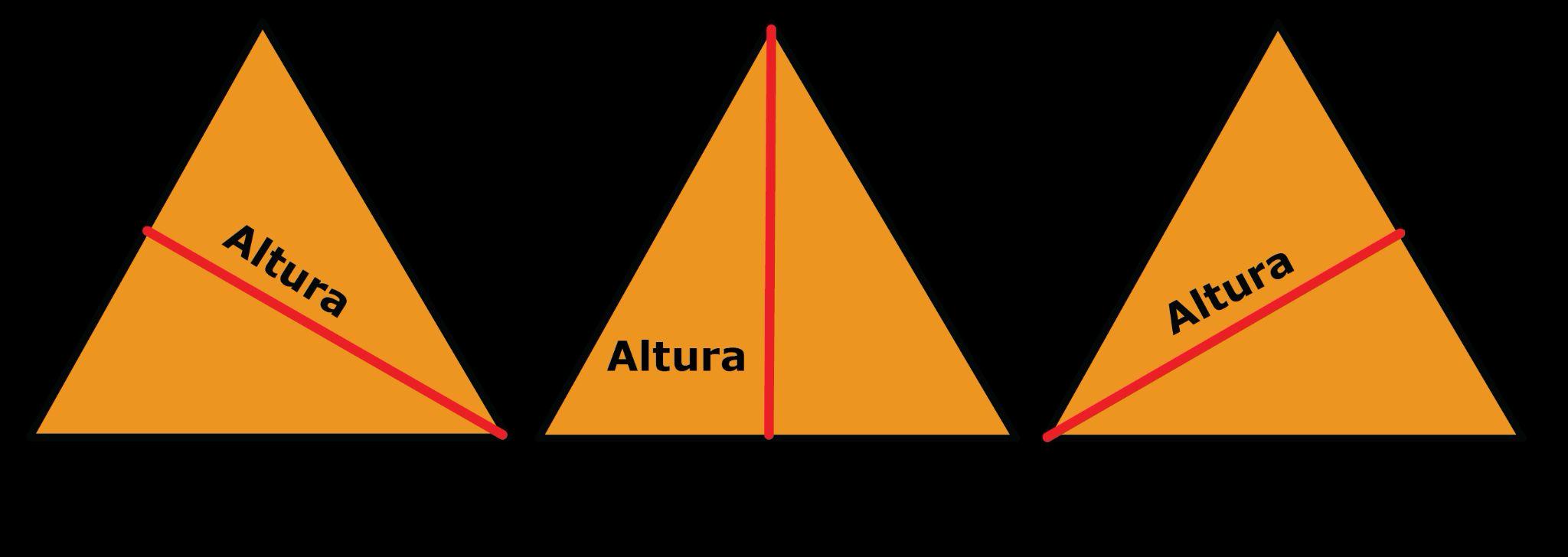
Lado del triángulo que es perpendicular a la altura

Figura compuesta

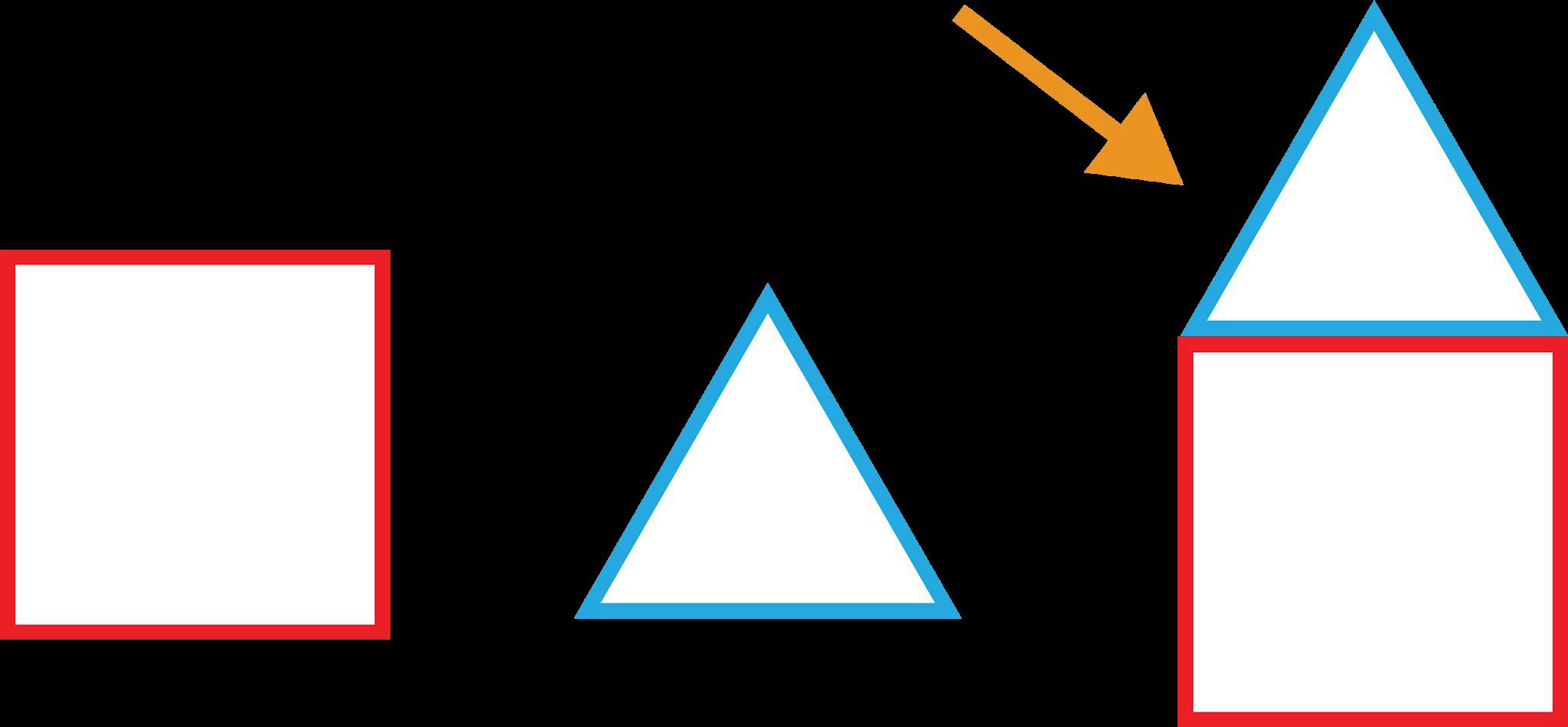
Figura que consta de dos o más formas geométricas

Descomponer

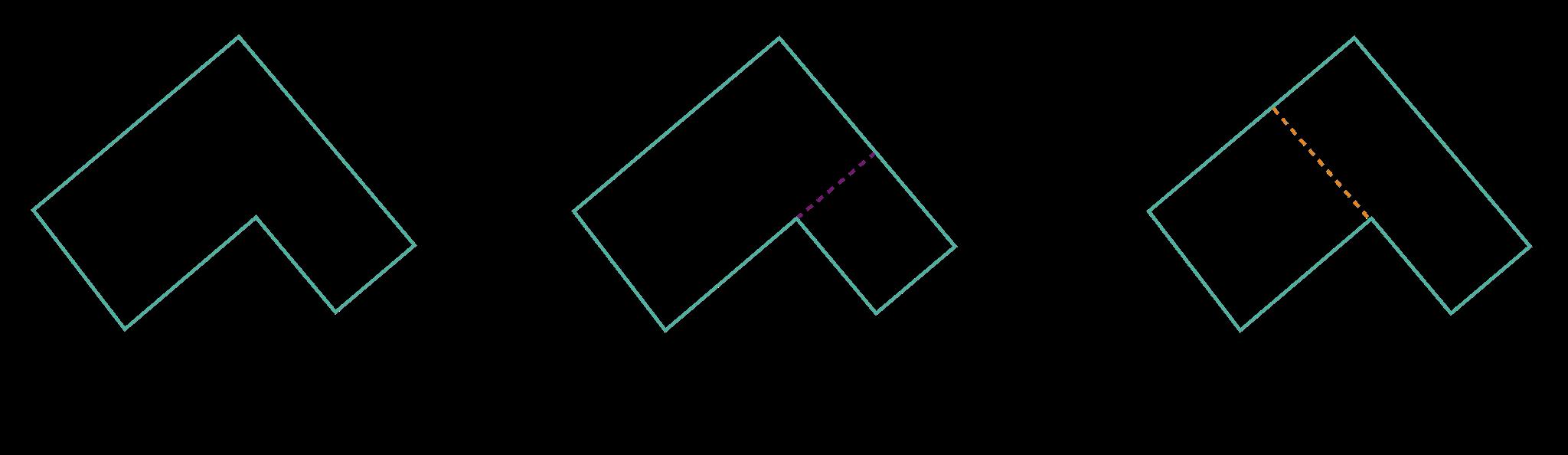
Separar en partes o elementos (por ejemplo, figuras geométricas o números)

Arista

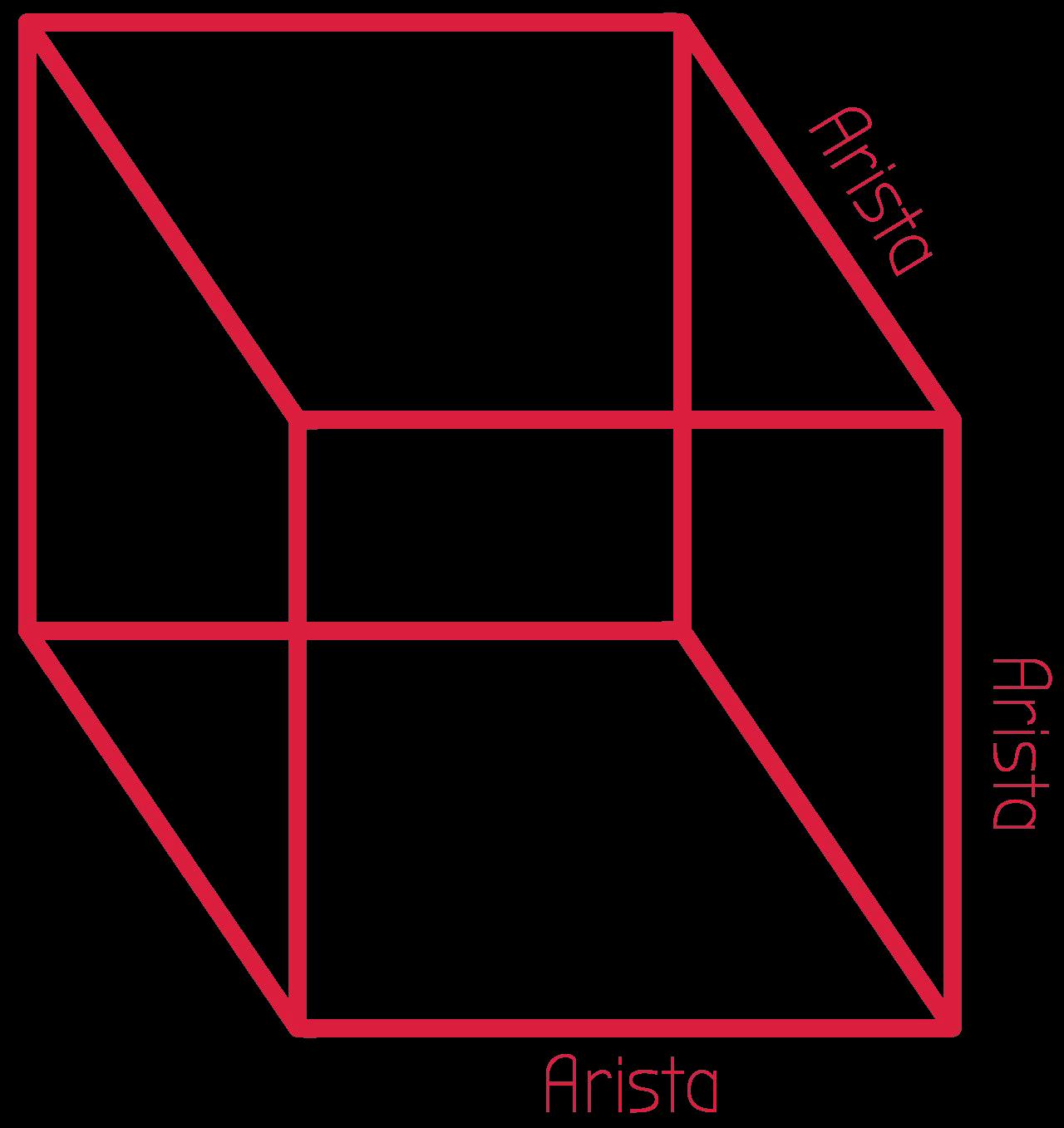
Línea en la que termina un espacio o una forma, donde se cruzan dos caras de un sólido tridimensional

Declaración o regla matemática escrita con símbolos Fórmula

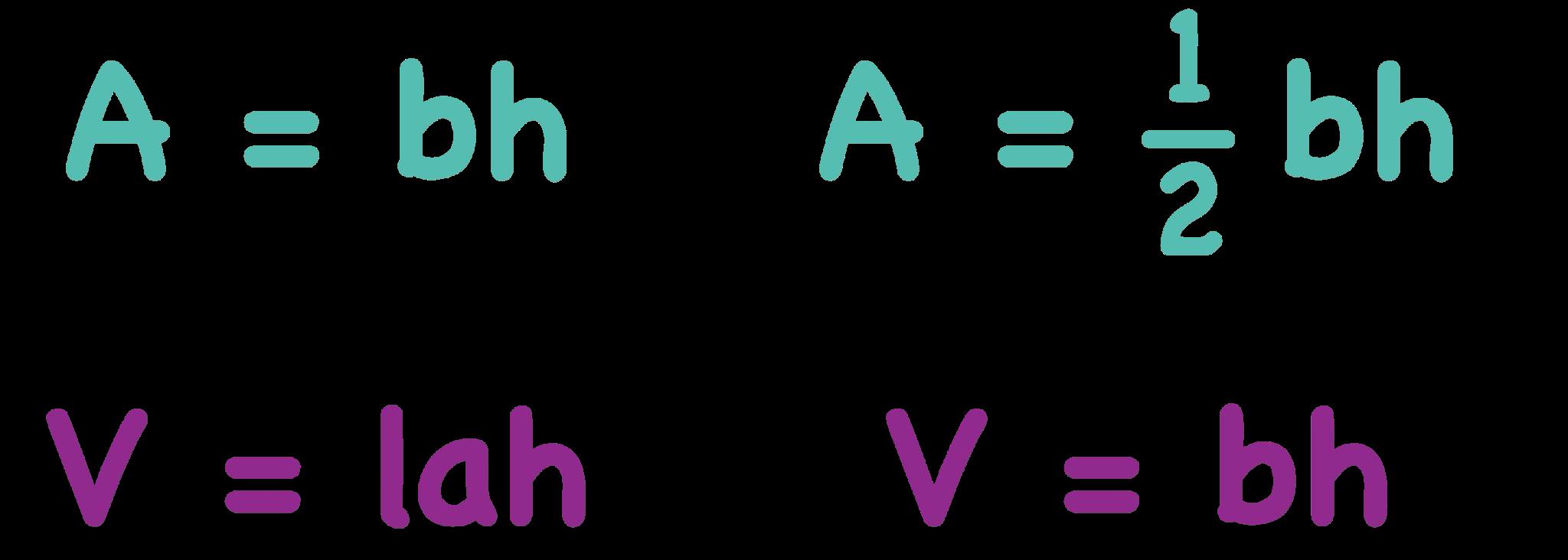
Distancia perpendicular de un vértice al lado opuesto de una figura

EXPLICAR: VOCABULARIO ILUSTRADO

Distancia vertical desde la parte superior de un objeto o figura a su base Altura (figura 3D)

Longitud

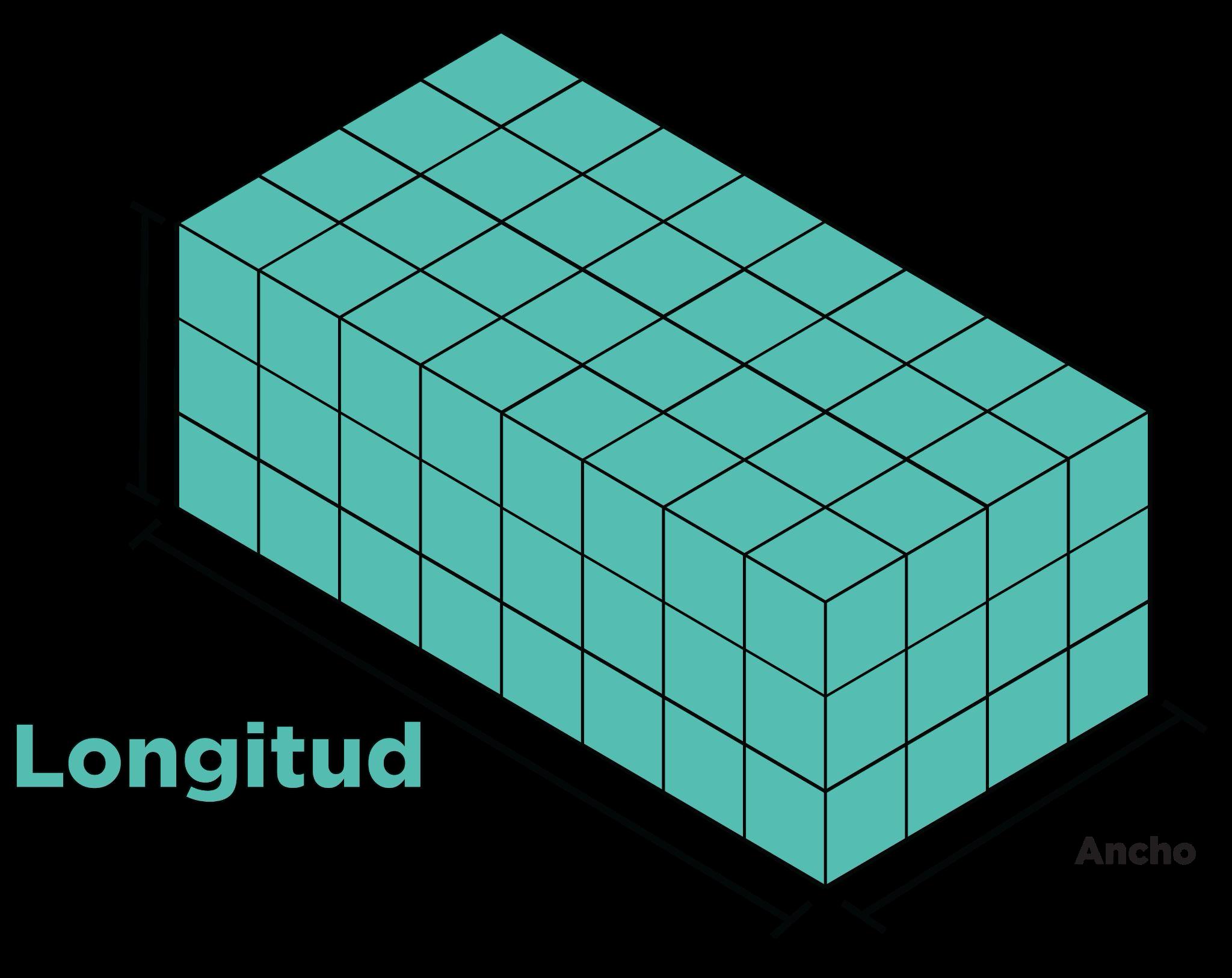
Medida de un objeto de punta a punta; distancia de un extremo al otro extremo de un objeto

Figura cerrada que tiene tres o más lados, sin líneas curvas ni intersecciones; una figura cerrada formada por segmentos de recta que se unen en sus puntos finales

Polígono de cuatro lados y cuatro ángulos

Prisma rectangular recto

Prisma con seis caras rectangulares donde el borde lateral es perpendicular al plano de la base

rectángulo

Triángulo con un ángulo de 90º (triángulo recto)

Cuadrilátero con un conjunto de lados paralelos Trapecio

Volumen

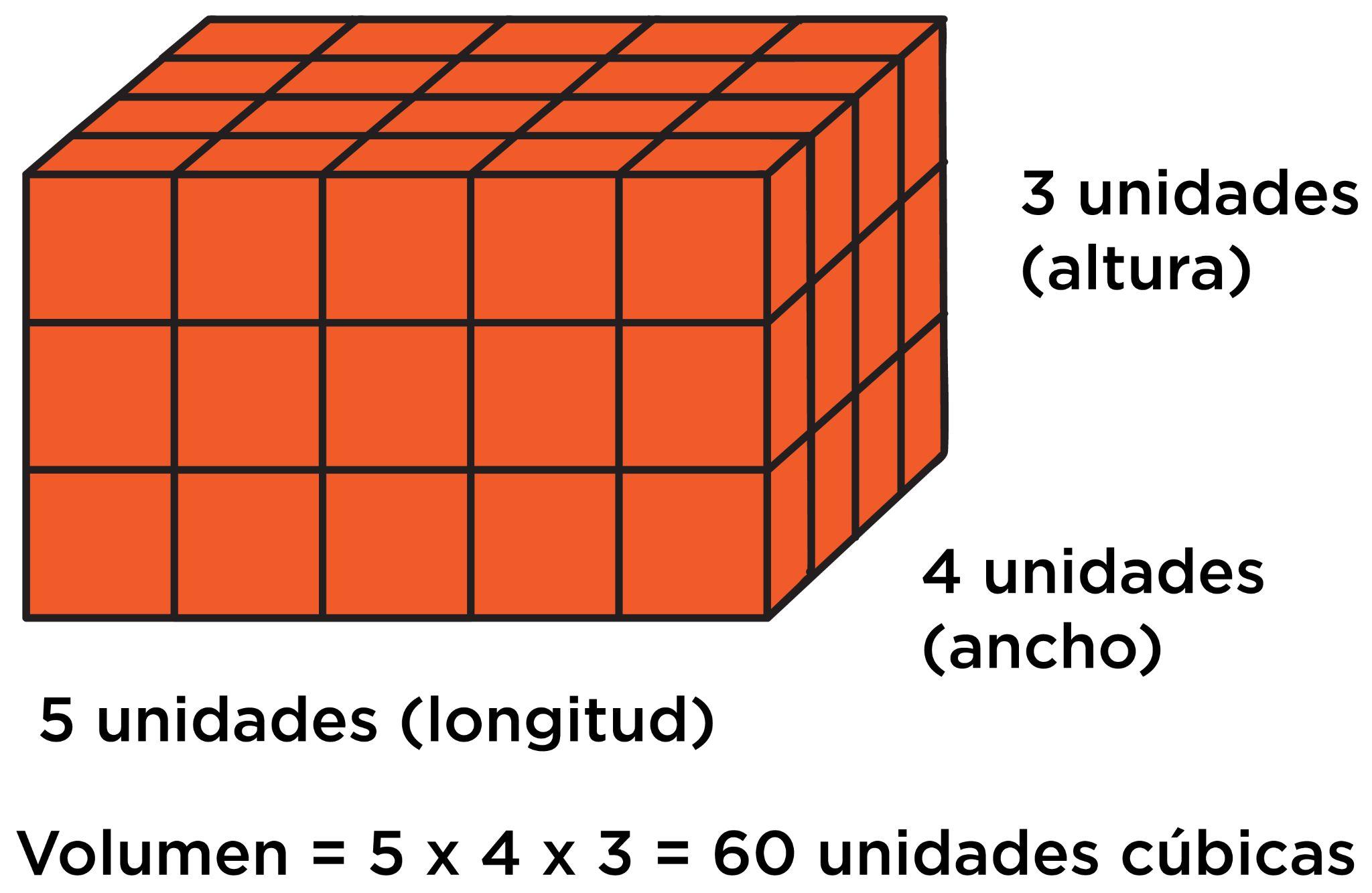
Cantidad de espacio que ocupa un objeto; cantidad medida de unidades cúbicas que caben dentro de una figura sólida

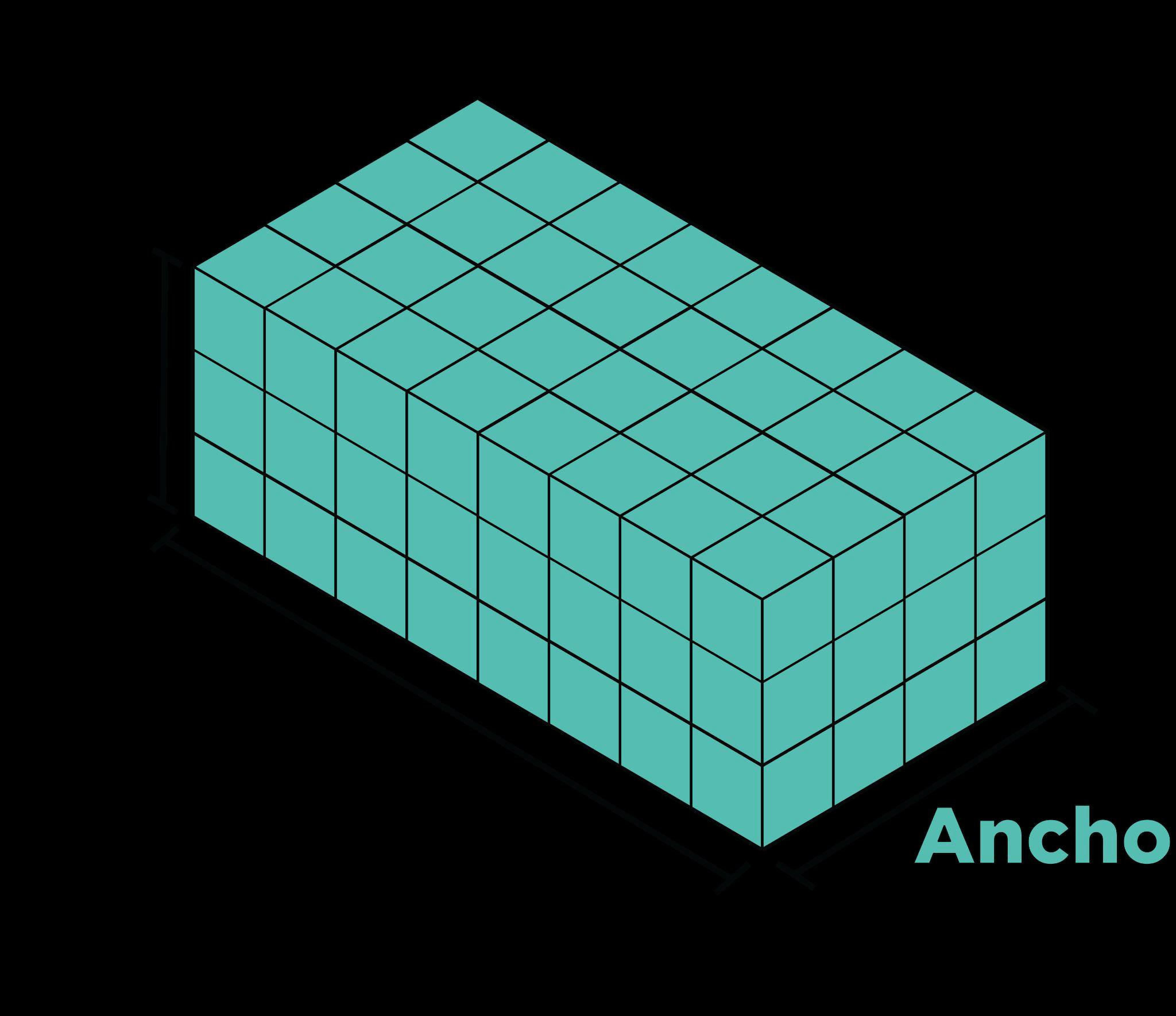
Cuántas unidades de ancho tiene algo

ELABORAR: CONSTRUCTOR DE FLUIDEZ

DESARROLLAR LA FLUIDEZ CONCEPTUAL

CONSTRUCTOR DE FLUIDEZ: ÁREA Y VOLUMEN

DESCRIPCIÓN

En esta actividad, los estudiantes realizarán a un juego de concentración.

MATERIALES

IMPRESOS

• 1 hoja de instrucciones de concentración (por pareja)

• 1 juego de tarjetas de concentración (por pareja)

REUTILIZABLES

• 1 sobre o bolsa (por pareja)

PREPARACIÓN

• Haga copias a doble cara de las tarjetas de concentración.

• Lamínalas para que duren más.

• Recorta las tarjetas individuales y colócalas en un sobre o bolsa para facilitar su distribución y limpieza.

• Coloque a los estudiantes en parejas.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Muestre a los estudiantes cómo barajar las tarjetas y colocarlas boca abajo en una matriz de 4 × 6.

2. Modele cómo jugar el juego con un estudiante.

a. El jugador 1 voltea 2 tarjetas para tratar de encontrar una coincidencia. Una coincidencia es un problema con su respuesta correcta. Será necesario resolver los problemas para determinar las respuestas que coinciden.

b. Si el jugador 1 encuentra un problema con la respuesta correcta, entonces el jugador 1 se queda con el conjunto coincidente y toma otro turno.

c. Si el jugador 1 no encuentra una coincidencia, entonces vuelve a colocar las tarjetas boca abajo y es el turno del siguiente jugador.

d. Los jugadores continúan tomando turnos hasta que se hayan encontrado todas las coincidencias.

e. Gana el jugador que reúna la mayor cantidad de tarjetas.

3. Distribuya los materiales. A continuación, pida a los estudiantes que barajen las cartas y las coloquen boca abajo.

4. Vigile a los estudiantes para asegurarse de que encuentran las parejas correctas.

Hoja de instrucciones de Concentración

Este juega es para jugar en pareja. Necesitarás

1 conjunto de tarjetas del juego Concentración (por pareja)

Instrucciones del juego

2. Barajea las tarjetas y colócalas boca abajo para formar una matriz de 4 × 6.

3. El jugador 1 voltea dos tarjetas para tratar de encontrar un pareo. Un pareo es un problema con su respuesta correcta. Los problemas deberán resolverse para determinar que respuestas respuestas se parean.

4. Si el jugador 1 empareja un problema con la respuesta correcta, entonces el jugador 1 se queda con el conjunto emparejado y toma otro turno.

5. Si el jugador 1 no encuentra ningún pareo, vuelve a colocar las tarjetas boca abajo y es el turno del siguiente jugador.

6. Los jugadores continúan tomando turnos hasta que se hayan encontrado todas los pareos.

7. El jugador que termine con más tarjetas ganará el juego.

HOJA DE INSTRUCCIONES

ELABORAR: REVISIÓN EN ESPIRAL

Mosca en el techo

¡Puede ser molesto cuando hay una mosca en tu casa! Las moscas son difíciles de atrapar porque se mueven rápidamente y pueden ver seis veces más rápido que un humano. ¿Alguna vez has observado una mosca en el techo de tu dormitorio?

René Descartes fue un matemático francés del siglo XVII conocido por inventar el sistema de coordenadas del plano. Cuenta la leyenda que Descartes estaba acostado en la cama y observaba una mosca en su techo. Quería idear un sistema para rastrear la ubicación exacta de la mosca cada vez que aterrizaba. Pensó que podría describir la ubicación en relación con la distancia horizontal y vertical de la mosca desde cada pared. Esto condujo a la noción de coordenadas.

Descartes podría entonces describir cada punto de aterrizaje de la mosca al utilizar un conjunto específico de coordenadas. El sistema de Descartes ayudó a los matemáticos a describir mejor las formas geométricas mediante el uso de coordenadas para describir la ubicación de los puntos a lo largo de cada lado de una forma y para marcar cada vértice de una forma. Los cartógrafos usan las coordenadas cuando construyen mapas, los sistemas GPS usan coordenadas para guiarnos a ubicaciones exactas y el radar usa el sistema de coordenadas para rastrear las ubicaciones de los barcos en el mar.

La próxima vez que veas una mosca en el techo, considera cómo la técnica de descartes para identificar la ubicación de una mosca condujo a un descubrimiento tan importante.

1. Dos moscas están en el techo y están ubicadas a la misma distancia a través de un eje imaginario. Una mosca está ubicada en (–2, 3). ¿Cuál es una posible ubicación de la otra mosca? Seleccione dos respuestas correctas.

A. (3, 2)

B. (2, 3)

C. (–2, –3)

D. (3, –2)

3. Dibuja un punto para mostrar la ubicación de una mosca cuando aterriza en (3, –4).

2. Una mosca aterriza en un eje y imaginario dos veces seguidas. La primera vez que aterriza en (0, 5). La segunda vez aterriza en un punto opuesto al primer lugar de aterrizaje, al otro lado del eje x. ¿Cuál es la coordenada de la mosca cuando aterriza por segunda vez? Explique su razonamiento.

4. ¿Qué ubicaciones incluyen una coordenada x- o y- que es negativa? Seleccione todas las que correspondan.

A. Dos unidades a la derecha y dos unidades hacia arriba

B. Dos unidades a la izquierda y dos unidades arriba

C. Dos unidades a la derecha y dos unidades hacia abajo

D. Dos unidades a la izquierda y dos unidades hacia abajo

FOLLETO DEL ESTUDIANTE

REPASAR CONCEPTOS ANTERIORES

REVISIÓN EN ESPIRAL: MOSCA EN EL TECHO

DESCRIPCIÓN

Los estudiantes repasan el contenido previo o actual del grado para ayudar a apoyar su trabajo en el alcance actual y fortalecer las habilidades necesarias para alcances posteriores.

PREPARACIÓN

• Imprima un folleto del estudiante por alumno.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Entregue un folleto del estudiante a cada alumno.

2. Anime a los estudiantes a tratar de responder a las preguntas de forma independiente sin utilizar regrados externos para ver lo que saben. Invite a los estudiantes a anotar ideas o fragmentos que recuerden sobre los temas que han aprendido previamente. Reconozca que los errores son bienvenidos en esta actividad y en la clase de matemáticas.

3. Utilice las preguntas de repaso en espiral como calentamiento en clase, o envíelas a casa como deberes. Proporcione a los estudiantes comentarios y oportunidades para corregir su trabajo y consolidar aún más sus conocimientos previos.

4. Consulte la sección «Revisión en espiral centrada en la pregunta» para evaluar los conocimientos de contenido de los estudiantes o su necesidad de una mayor intervención. Si es necesario repasar más, utilice los Constructores de fluidez en los alcances apropiados.

5. Capstone incluye una parte del alcance actual para que los estudiantes vean la conexión y relevancia de su aprendizaje previo con el alcance actual.

ELABORAR: CIENCIA DE DATOS

ANÁLISIS DE DATOS

CIENCIA DE DATOS

La ciencia de datos consiste en un breve debate en clase sobre un conjunto de datos. Esta actividad no está pensada para ser calificada. La parte I incluye preguntas abiertas para ayudar a los estudiantes a interpretar y analizar los datos. Las partes siguientes son actividades opcionales para ampliar el aprendizaje de los estudiantes en contexto.

DESCRIPCIÓN

Los estudiantes analizan, interpretan y generan conjuntos de datos, además de responder a preguntas basadas en los datos.

MATERIALES

IMPRESOS

• 1 conjunto de datos (por clase)

REUTILIZABLES

• 1 proyector o cámara de documentos (por clase)

• 1 marcador de borrado en seco (por clase)

CONSUMIBLES

• 1 trozo de papel milimetrado (por clase)

PREPARACIÓN

• Prepárese para proyectar el conjunto de datos en la clase.

• Reúna un trozo de papel milimetrado y un marcador de borrado en seco.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

PARTE I

1. Proyecte el conjunto de datos y prepárese para anotar las observaciones de los estudiantes.

2. Plantee las siguientes preguntas:

a. «¿Qué observas en este conjunto de datos?».

b. «¿Qué representa este conjunto de datos?».

c. «¿Qué categorías se incluyen en este conjunto de datos?».

d. «¿Por qué podría ser útil conocer las dimensiones de un tanque de acuario?».

e. «¿Qué tiendas de tu zona venden tanques de acuario?».

f. «¿Qué preguntas tienes sobre los datos?».

Comprar el mejor acuario

CONJUNTO DE DATOS

PARTE II

1. Repasa la fórmula para el volumen de un prisma rectangular, y escribe lo que los estudiantes recuerden en el papel milimetrado.

2. Haga las siguientes preguntas:

a. ¿Cuál es el volumen del tanque del acuario 1? Para hallar el volumen, multiplico 50 × 28,5 × 20 = 28.500, por lo que el volumen del tanque del acuario 1 es de 28.500 pulgadas cúbicas.

b. ¿Qué estrategias se pueden utilizar para determinar el volumen de los tanques del acuario? Para hallar el volumen, multiplico la longitud por la anchura por la altura del acuario.

c. Si un cliente compra las peceras 3 y 5, ¿cuál es el volumen total de ambas peceras? La pecera 3 mide 30 × 18 × 16 = 8.640. La pecera 5 mide 8 × 8,2 × 9 = 590,4. Después de hallar el volumen de cada tanque, los sumamos (8.640 + 590,4) y hallamos que el volumen total de ambos tanques es de 9.230,4 pulgadas cúbicas.

d. ¿Cuál es la diferencia de volumen entre los acuarios 1 y 4? Primero, calcula el volumen del acuario 1 multiplicando 50 × 28,5 × 20 = 28.500. A continuación, calcula el volumen del acuario 4 multiplicando 50 × 28,5 × 20 = 28.500. A continuación, halla el volumen del tanque 4 multiplicando 50 × 14 × 28 = 19.600. A continuación, resta 19.600 de 28.500 para hallar que la diferencia entre los acuarios es de 8.900 pulgadas cúbicas.

e. ¿Por qué compraría un cliente el acuario 2 en lugar del acuario 3? Las respuestas pueden variar. Tal vez el cliente sólo tiene un pequeño espacio para poner el acuario.

f. Si la tienda de mascotas vende un acuario tanque 6 que tiene un volumen de 1.056 pulgadas cúbicas, ¿cuáles podrían ser las dimensiones del acuario tanque? Basándote en el coste y las dimensiones de los acuarios 1-5, ¿cuál es una estimación del coste del acuario 6? Las respuestas pueden variar. El acuario podría medir 10 × 11 × 9,6 = 1.056 pulgadas cúbicas. Yo lo estimaría en 60 $ porque su tamaño está entre el del acuario 2 y el del acuario 5.

EVALUAR: LISTA DE VERIFICACIÓN DE OBSERVACIÓN

Área y volumen

Habilidad o concepto clave ¿Cómo podrías demostrar que sabes esto?

Puedo encontrar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales y polígonos mediante la composición en rectángulos o la descomposición en triángulos y otras formas; puedo aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y de la vida real.

Para encontrar el volumen de un prisma rectangular recto con longitudes de arista fraccionarias, puedo empaquetarlo con cubos unitarios de las longitudes de arista fraccionarias unitarias apropiadas y demostrar que el volumen es el mismo que se encontraría si multiplico las longitudes de la arista del prisma. Puedo aplicar las fórmulas V = a h y V = b h para encontrar volúmenes de prismas rectangulares rectos con longitudes de arista fraccionarias en el contexto de la resolución de problemas matemáticos y de la vida real.

❏ Represéntalo. ❏ Dibújalo. ❏ Aplícalo.

❏ Habla sobre esto. ❏ Escribe sobre esto.

¿Cómo te calificarías a ti mismo?

¡Lo tengo!

¡Ya casi!

¡Todavía no!

❏ Represéntalo. ❏ Dibújalo. ❏ Aplícalo.

❏ Habla sobre esto. ❏ Escribe sobre esto.

¡Lo tengo!

¡Ya casi!

¡Todavía no!

Estándares para la práctica matemática ¿Cómo te calificarías a ti mismo?

Puedo dar sentido a los problemas y perseverar en resolverlos.

Puedo razonar de forma abstracta y cuantitativa.

Puedo construir argumentos viables y criticar el razonamiento de otros.

Puedo representar con matemáticas.

Puedo utilizar estratégicamente las herramientas adecuadas.

Puedo prestar atención a la precisión.

Puedo buscar y utilizar estructuras.

Puedo buscar y expresar regularidad en razonamientos repetidos.

Reflexiona sobre tu pensamiento, aprendizaje y trabajo en este alcance.

¿Qué objetivos te has propuesto? ¿En qué has mejorado en este alcance?

¿Tienes nuevos objetivos? ¿Dónde quieres mejorar en el próximo alcance?

MATERIAL PARA EL MAESTRO

EVALUACIÓN DE HABILIDADES

LISTA DE VERIFICACIÓN DE LA OBSERVACIÓN

DESCRIPCIÓN

Este elemento proporciona un desglose de los conceptos y destrezas clave del alcance de aplicación. Puede utilizarse como evaluación formativa para los maestros y como autoevaluación para los estudiantes.

MATERIALES

IMPRESO

• 1 folleto del estudiante (por alumno)

• 1 materiales para el maestro (por estudiante)

PREPARACIÓN

• Imprima los materiales para el maestro y un folleto del estudiante para cada alumno.

PROCEDIMIENTO Y PUNTOS DE APOYO

1. Distribuya un folleto del estudiante a cada alumno.

2. A medida que los estudiantes trabajen en las actividades explorar y explicar del alcance, evalúe formativamente su progreso tomando notas sobre cómo se observaron los conceptos y habilidades clave. Se pueden plantear preguntas de reflexión para medir el impacto de las actividades tanto en grupo completo como en pequeño grupo.

3. Pida a los estudiantes que reflexionen sobre las formas en que pueden demostrar su comprensión y autoevaluar su progreso en cada concepto o habilidad clave a medida que trabajan tanto en grupo completo como en pequeño grupo.

4. Los estudiantes pueden reflexionar sobre su pensamiento, aprendizaje y trabajo en el alcance; identificar las formas en que han mejorado y establecer nuevas metas de aprendizaje.

5. Quienes brindan apoyo pedagógico a los estudiantes pueden estar equipados con las adaptaciones y modificaciones anotadas en los materiales para el maestro

6. Las notas anecdóticas proporcionadas en las instrucciones del maestro pueden usarse como documentación para los boletines de calificaciones basados en estándares.

7. Una vez que se hayan recopilado los datos de los estudiantes después de la evaluación, consulte la guía de instrucción andamiada en la sección «Inicio» de este alcance para diferenciar la instrucción para cada estudiante.

EVALUAR: MAPA DE CALOR

ANALIZAR LOS RESULTADOS DE LA EVALUACIÓN

MAPA DE CALOR

DESCRIPCIÓN

Los estudiantes analizan los resultados de su evaluación y determinan qué hicieron bien y en qué pueden mejorar.

MATERIALES

• 1 mapa de calor (por estudiante)

• 1 lápiz rojo (por estudiante)

• 1 lápiz azul (por estudiante)

• 1 lápiz naranja (por estudiante)

PREPARACIÓN

• Determine si los estudiantes analizarán su prueba de habilidades, la evaluación basada en estándares o ambas.

• Imprima un mapa de calor para cada estudiante.

• Reúna lápices de color rojo, azul y naranja para cada estudiante.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Distribuya un mapa de calor a cada estudiante junto con los lápices de color rojo, azul y naranja. Los estudiantes deben tener a mano su(s) evaluación(es) corregida(s).

2. Los estudiantes utilizan su(s) evaluación(es) corregida(s) para colorear el mapa de calor. Para cada pregunta no contestada por error de cálculo, los estudiantes colorean de azul la casilla correspondiente. Para cada pregunta no contestada por una explicación, los estudiantes colorean la casilla correspondiente de naranja. Para cada pregunta omitida por un concepto erróneo, colorean el cuadro correspondiente de rojo.

3. Anime a los estudiantes a buscar patrones en sus datos, como un determinado estándar que se perdió con más frecuencia o un estándar que han dominado claramente, y utilizar esta información para reflexionar y establecer metas en la tabla proporcionada.

4. Consulte la guía de instrucción andamiada que se encuentra en la sección «Inicio» para proporcionar extensión o apoyo adicional.

Consulta tus respuestas en la tabla «Prueba de habilidades». Colorea de verde los cuadros de preguntas correctas y colorea según la siguiente clave los cuadros de preguntas incorrectas.

Prueba de habilidades

Estándares Preguntas

Encuentra el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales y polígonos mediante la composición en rectángulos o la descomposición en triángulos y otras formas; aplica estas técnicas en el contexto de la resolución de problemas matemáticos y de la vida real.

Para encontrar el volumen de un prisma rectangular recto con longitudes de arista fraccionarias, empaqueta con cubos unitarios de las longitudes de arista fraccionarias unitarias apropiadas y demuestra que el volumen es el mismo que se encontraría si multiplicas las longitudes de la arista del prisma. Aplica las fórmulas V = lah y V = bh para encontrar volúmenes de prismas rectangulares rectos con longitudes de arista fraccionarias en el contexto de la resolución de problemas matemáticos y de la vida real. 7 4 10 1

Consulta tus respuestas en la tabla «Evaluación basada en estándares». Colorea de verde los cuadros de preguntas correctas y colorea según la siguiente clave los cuadros de preguntas incorrectas.

Azul: Error de cálculo Naranja: Explicación Rojo: Error de concepto

Evaluación basada en estándares

Estándares Preguntas

Halla el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales y polígonos mediante la composición en rectángulos o la descomposición en triángulos y otras formas; aplica estas técnicas en el contexto de la resolución de problemas matemáticos y de la vida real.

Para encontrar el volumen de un prisma rectangular recto con longitudes de arista fraccionarias, empaqueta con cubos unitarios de las longitudes de arista fraccionarias unitarias apropiadas y demuestra que el volumen es el mismo que se encontraría si multiplicas las longitudes de la arista del prisma.

Aplica las fórmulas V = lah y V = bh para encontrar volúmenes de prismas rectangulares rectos con longitudes de arista fraccionarias en el contexto de la resolución de problemas matemáticos y de la vida real.

Revisión

Reorganiza o descompone cada forma para ayudarte a encontrar el área de la forma original.

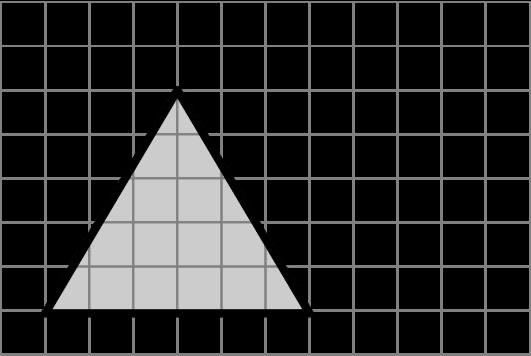
1. Fórmula del área del rectángulo: ___________ Área: _________________________________

2. Fórmula del área del paralelogramo: ________ Área: _________________________________

3. Fórmula del área del rectángulo: ___________ Área: ________________________________

4. Fórmula del triángulo: ___________________ Área: ________________________________

5. Fórmula del área del paralelogramo: ________ Área: _________________________________

6. Fórmula del triángulo: ___________________ Área: _________________________________

7. Fórmula del área del rectángulo: ___________ Área: ________________________________

8. Fórmula del trapezoide: _________________ Área: ________________________________

INTERVENCIÓN: REPASO Y PRÁCTICA DE HABILIDADES

REFORZAR Y VOLVER A ENSEÑAR

REPASO Y PRÁCTICA DE HABILIDADES

DESCRIPCIÓN

Esta actividad está diseñada para repasar los conceptos clave del alcance. Utilícela como repaso o para intervención.

MATERIALES

IMPRESOS

• 1 evaluación rápida (por estudiante)

• 1 repaso (por estudiante)

• 1 evaluación de control (por estudiante)

• 1 lista de verificación para el maestro (por profesor)

PREPARACIÓN

• Imprima una copia de la evaluación rápida, el repaso y la evaluación de control por estudiante.

• Si lo desea, coloque a los estudiantes en grupos de 3 o 4 para completar la revisión.

• Si lo desea, imprima un ejemplo del esquema de anclaje de la sección «Explicar» o pida a los estudiantes que usen la libreta interactiva como regrado.

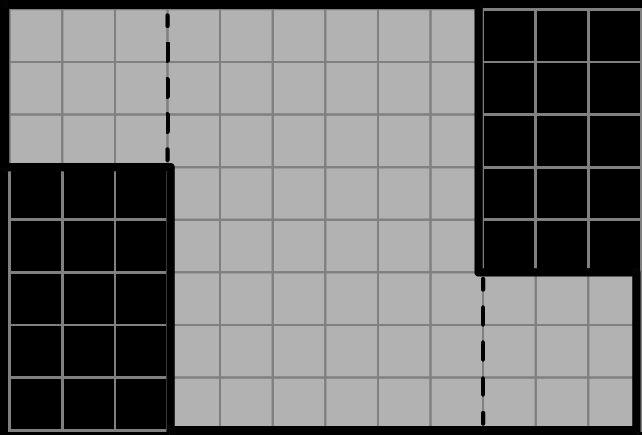
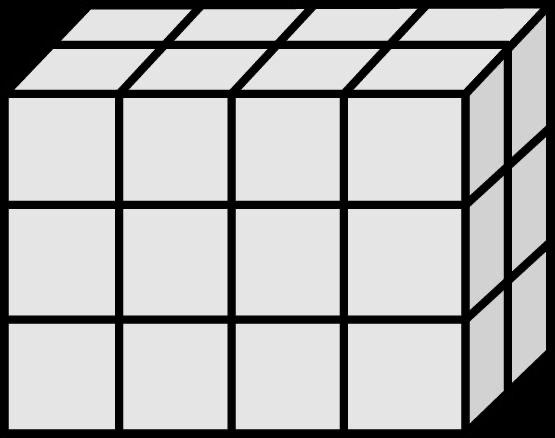
9. Encuentra el área de la figura compuesta sombreada descomponiendo la forma en figuras más pequeñas. Muestra las fórmulas y tu trabajo. Area and Volume

10. Encuentra el volumen del prisma rectangular. Muestra la fórmula y tu trabajo.

EVALUACIÓN DE CONTROL

• Opcionalmente, imprima cualquiera de los materiales de ayuda complementarios para que los estudiantes los utilicen mientras trabajan.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. De una copia de la evaluación rápida a cada estudiante.

2. Cada uno debe completarla de forma independiente.

3. Use la rúbrica de habilidades al final de la evaluación rápida para identificar qué estudiantes necesitan ayuda adicional en las habilidades.

4. Distribuya una copia del repaso a cada estudiante.

5. Cada uno debe completar el repaso como actividad de intervención o como actividad independiente.

a. Si lo desea, reúna a los estudiantes en pequeños grupos para trabajar en las destrezas de repaso. Use el repaso como ayuda para la reenseñanza.

6. Distribuya una copia de la evaluación de control a cada estudiante.

7. Cada estudiante debe completarla de forma independiente.

8. Analice los resultados de la evaluación de control utilizando la lista de verificación para el maestro para identificar a quienes necesitan un repaso adicional y quienes han alcanzado el dominio de los conceptos.

ACELERACIÓN: ¿QUÉ PREFIERES?

RAZONAMIENTO MATEMÁTICO

¿QUÉ PREFIERES?:

PECERAS PARA GOLDFISH

DESCRIPCIÓN

Los estudiantes utilizan el razonamiento matemático y la creatividad para justificar una respuesta.

MATERIALES

IMPRESORA

• 1 folleto del estudiante (por alumno)

• 1 rúbrica (por maestro)

PREPARACIÓN

• Imprima un folleto del estudiante por alumno.

• Planifique que los estudiantes trabajen en parejas para completar esta actividad, si lo desea.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Entregue un folleto del estudiante a cada alumno.

2. Anime a los estudiantes a mirar sus folletos del estudiante de las exploraciones si necesitan repasar habilidades.

3. Invite a los estudiantes a compartir respuestas y justificaciones con sus compañeros.

4. Utilice la rúbrica proporcionada para evaluar las habilidades de comprensión, cálculo y razonamiento de los estudiantes.

Peceras para goldfish

Usa razonamiento matemático y la creatividad para justificar tu respuesta a la pregunta, ¿qué prefieres?

Anaya y su familia están en la tienda de mascotas y buscan peceras para sus goldfish Buscan una pecera que contenga un paisaje con plantas y que sea lo suficientemente grande para que incluya más peces que se añadirán en el futuro. Han reducido sus opciones a la pecera azul y a la pecera gris que se muestran a continuación. ¿Preferirías comprar la pecera azul o la pecera gris? Justifica tu razonamiento con matemáticas.

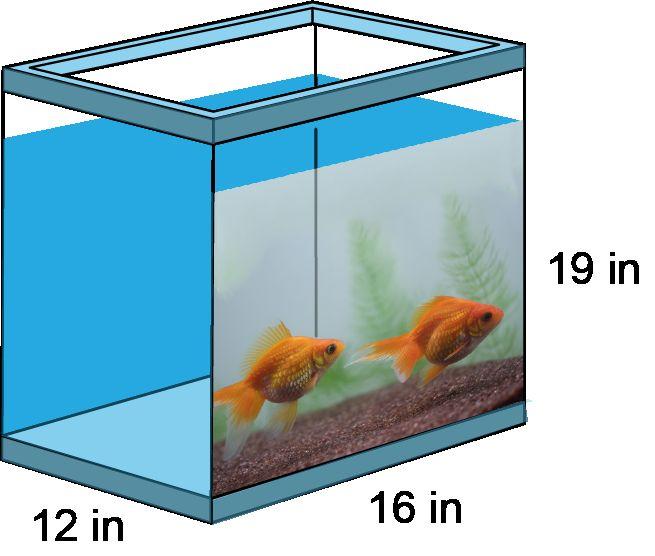
FOLLETO DEL ESTUDIANTE

ACELERACIÓN : TABLERO DE OPCIONES

Área

y volumen

Selecciona una o más actividades de extensión de la siguiente tabla.

Conexión profesional Conexión con el arte

Diseño de interiores

Investiga el campo profesional de diseñador de interiores. La investigación debe incluir la siguiente información: Crea una presentación para compartir la investigación con tu clase.

Arte abstracto

Aprende sobre el artisa Piet Mondrian y crea una obra de arte abstracto con paralelogramos y triángulos.

Analogías Matemáticos en primer plano

Tamaños diferentes

Utiliza las analogías para encontrar las áreas y los volúmenes de diferentes figuras.

Leonhard Euler

Investiga el descubrimiento de Leonhard Euler sobre la relación entre los números de caras, bordes y vértices de un poliedro. Crea un póster informativo, un diorama o un discurso para presentar el trabajo de este matemático relacionado con representación de datos.

Conexión gastronómica Crear algo nuevo

Área de la encimera

Encuentra el área de una encimera de cocina con el uso de dos estrategias diferentes.

Figura compuesta

Crea tu propia figura compuesta en papel cuadriculado y pide a un compañero que determine el área de la figura.

TABLERO DE OPCIONES

OPCIONES PARA EL APRENDIZAJE CONTINUO

TABLERO DE OPCIONES

DESCRIPCIÓN

Los estudiantes exploran las conexiones con el mundo real y las aplicaciones del contenido matemático a través de interacciones con actividades atractivas.

MATERIALES

IMPRESOS

• 1 tablero de opciones (por estudiante)

• 1 juego de hojas de actividades (por estudiante)

• 1 autoevaluación del tablero de opciones (por estudiante)

REUTILIZABLE

• Tecnología (si corresponde)

PREPARACIÓN

• Imprima un tablero de elección y un juego de hojas de actividades para cada estudiante.

• Imprime una autoevaluación del tablero para cada estudiante.

• Planifica con antelación el uso de la tecnología. Puede ser necesario investigar para algunas actividades del tablero de opciones.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Distribuya un tablero de opciones a cada estudiante.

2. Conceda tiempo a los estudiantes para examinar el tablero de opciones y seleccionar las actividades que les gustaría explorar.

3. Anime a los estudiantes a intentar al menos tres actividades del tablero de opciones.

4. Distribuya las hojas de actividades correspondientes según las elecciones de los estudiantes.

5. Al finalizar cada actividad del tablero de opciones, haga que los estudiantes completen una autoevaluación del tablero para revisar su propio pensamiento matemático y sus esfuerzos en su proyecto.