SSM CA Spanish Seventh Grade Sample

GRADO 7

CALIFORNIA

Muestra de la edición para el maestro

Muestra de la edición para maestros Grado 7

Publicado por Accelerate Learning Inc., 5177 Richmond Ave, Suite 800, Houston, TX 77056. Copyright © 2025, Accelerate Learning Inc. Todos los derechos reservados. Ninguna parte de esta publicación podrá ser reproducida o distribuida en ninguna forma ni por ningún medio, ni almacenada en una base de datos o sistema de recuperación, sin el consentimiento previo por escrito de Accelerate Learning Inc., incluyendo, entre otros, en cualquier red u otro sistema de almacenamiento o transmisión electrónica, o difusión para educación a distancia.

Para obtener más información, visítenos en www.stemscopes.com.

ÁREA, SUPERFICIE Y VOLUMEN

ESTÁNDARES CLAVE

Dibujar, construir y describir figuras geométricas y describir las relaciones entre ellas.

• Describir las figuras bidimensionales que resultan de cortar figuras tridimensionales, como en secciones planas de prismas rectangulares rectos y pirámides rectangulares rectas.

Resolver problemas matemáticos y de la vida real que involucren medida de ángulos, área, área de superficie y volumen.

• Resolver problemas matemáticos y de la vida real que involucren área, volumen y superficie de objetos bidimensionales y tridimensionales compuestos de triángulos, cuadriláteros, polígonos, cubos y prismas rectángulos.

Aplicar y ampliar la comprensión previa de las operaciones con fracciones para sumar, restar, multiplicar y dividir números racionales.

• Resolver problemas matemáticos y de la vida real que involucren las cuatro operaciones con números racionales. (Nota: Los cálculos con números racionales extienden las reglas para manipular fracciones a fracciones complejas)

ACTIVIDADES

DE PARTICIPACIÓN

ACCESO A CONOCIMIENTOS PREVIOS: «NO PERTENECE»

Los estudiantes se involucrarán en el pensamiento crítico para identificar qué opción «No pertenece» en una serie de descripciones, con el objetivo de descubrir y abordar conceptos erróneos.

• Los estudiantes reciben un folleto con grupos de cuatro opciones, identificando la que no encaja con las demás.

• Deben analizar cada grupo y explicar su razonamiento para la opción que «No pertenece».

• La actividad se centra en distinguir entre los conceptos de volumen y superficie.

• Un debate final ayuda a aclarar los malentendidos, con apoyo adicional si es necesario.

CAPTAR INTERÉS

Los estudiantes exploran el concepto de superficie resolviendo un problema del mundo real que implica una figura tridimensional compuesta.

• Se presenta a los estudiantes un escenario en el que deben calcular la superficie de un mueble para determinar la cantidad de sellador y papel decorativo necesarios.

• Participan en debates y comparten experiencias personales relacionadas con la restauración de muebles y el uso de conceptos matemáticos en situaciones prácticas.

• A través de la exploración guiada, los estudiantes aprenden a medir y calcular la superficie de varios componentes del mueble, reforzando su comprensión de la geometría.

• Después de completar las actividades de Exploración, los estudiantes vuelven a visitar el escenario para aplicar sus habilidades recién adquiridas y verificar sus soluciones.

ACTIVIDADES DE EXPLORAR

EXPLORACIÓN 1: CORTAR FIGURAS 3D

Los estudiantes exploran la relación entre las formas tridimensionales y sus secciones bidimensionales mediante el corte práctico de prismas rectangulares rectos y pirámides rectas.

• Los estudiantes trabajan en parejas para cortar arcilla de modelar en forma de prismas rectangulares rectos y pirámides rectas, revelando figuras bidimensionales.

• Predicen e identifican las formas bidimensionales que se forman al cortar las figuras tridimensionales tanto vertical como horizontalmente.

• Los estudiantes documentan sus descubrimientos en un diario del estudiante y participan en debates para comparar las estrategias de corte y los resultados.

• La actividad concluye con una charla de matemáticas y un boleto de salida para evaluar la comprensión y fomentar la reflexión sobre el proceso de aprendizaje.

EXPLORACIÓN 2: ÁREA

Los estudiantes exploran el concepto de área realizando tareas prácticas para determinar las áreas de varios polígonos y resolver problemas del mundo real.

• Los estudiantes trabajan en grupos para calcular las áreas de triángulos, cuadriláteros y otros polígonos utilizando las tarjetas de etiquetas de figuras bidimensionales.

• Aplican fórmulas y operaciones matemáticas para resolver problemas de un solo paso y de varios pasos relacionados con el área, centrándose en aplicaciones del mundo real.

• La actividad anima a los estudiantes a dibujar figuras, calcular áreas y expresar los resultados en unidades apropiadas, fomentando la colaboración y el pensamiento crítico.

• Los estudiantes participan en conversaciones para compartir estrategias, reflexionar sobre su aprendizaje y conectar conceptos matemáticos con escenarios prácticos.

EXPLORACIÓN 3: ÁREA DE SUPERFICIE

Los estudiantes exploran el concepto de área superficial a través de tareas prácticas de resolución de problemas que involucran figuras tridimensionales.

• Los estudiantes trabajan en grupos para determinar el área superficial de cubos, prismas rectos y figuras complejas utilizando los materiales proporcionados.

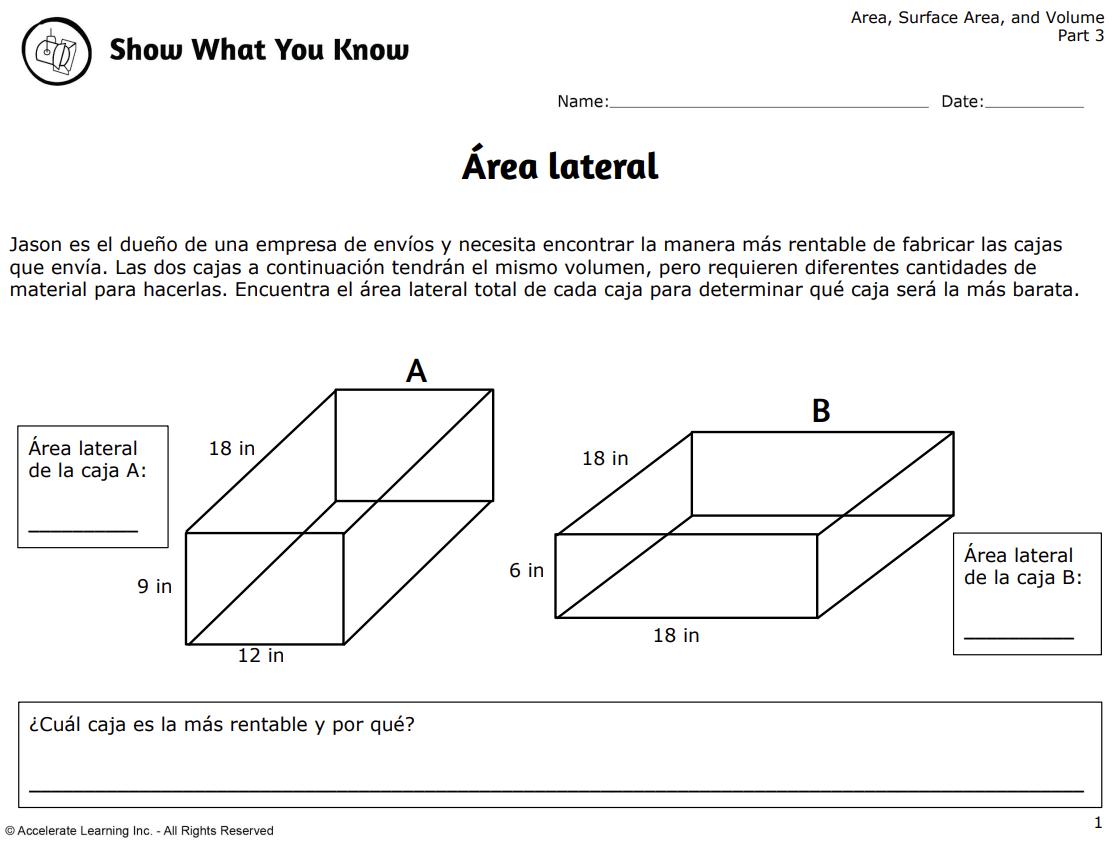
• Resuelven problemas del mundo real calculando la superficie necesaria para impermeabilizar cajas de envío.

• La actividad incluye dibujar, etiquetar dimensiones y aplicar fórmulas para hallar la superficie total.

• Los estudiantes participan en debates para comparar estrategias y reflexionar sobre su aprendizaje, culminando en una charla de matemáticas para compartir observaciones.

EXPLORACIÓN 4: VOLUMEN

Los estudiantes exploran el concepto de volumen participando en tareas prácticas de resolución de problemas relacionados con escenarios del mundo real.

• Los estudiantes trabajan en grupos para determinar el volumen de varias cajas de envío, incluyendo cubos, prismas rectos y figuras tridimensionales complejas.

• Aplican fórmulas de volumen y descomponen formas complejas en componentes más simples para encontrar volúmenes totales.

• Los estudiantes resuelven problemas del mundo real relacionados con el embalaje y el envío, calculando el volumen necesario de cacahuetes de embalaje teniendo en cuenta el espacio ocupado por los artículos enviados.

• La actividad fomenta la colaboración, el pensamiento crítico y la aplicación de estrategias matemáticas a situaciones prácticas.

ALCANCE: IDEAS FUNDAMENTALES

VISUALIZAR POBLACIONES

CONNECCIONES 2D & 3D

POBLACIONES & MUESTRAS

RELACIONES ENTRE ÁNGULOS

MODELOS DE PROBABILIDAD

EN EL MUNDO

Los estudiantes usan las habilidades desarrolladas a través del cálculo de áreas y volúmenes para comprender cómo interactúan los ángulos y las formas geométricas en problemas más complejos. Por ej., en futuras lecciones sobre relaciones angulares, los estudiantes utilizarán su comprensión de las formas para explorar cómo afectan los ángulos al área o al volumen de una figura, como cuando trabajan con prismas triangulares u otras figuras tridimensionales que implican componentes angulares.

DIBUJOS A ESCALA

La comprensión de las propiedades geométricas, como el área y el volumen, ayuda a los estudiantes a visualizar e interpretar datos complejos. Por ej., al considerar el volumen de cajas o embalajes, los estudiantes pueden relacionar este conocimiento con situaciones del mundo real, como determinar cuánto espacio ocupan los distintos elementos de una población o muestra. Este razonamiento espacial ayuda a hacer inferencias visuales sobre los datos.

CONCEPTOS CLAVE

• Puedo describir las figuras 2D que resultan de cortar figuras 2D.

• Puedo describir las secciones planas de prismas rectangulares rectos y pirámides rectangulares rectas.

• Puedo resolver problemas matemáticos y del mundo real que impliquen el área de objetos bidimensionales y tridimensionales.

• Puedo resolver problemas matemáticos y de la vida real que involucren el volumen de objetos bidimensionales y tridimensionales.

• Puedo resolver problemas matemáticos y de la vida real que involucren el área de la superficie de objetos bidimensionales y tridimensionales.

• Puedo resolver problemas matemáticos y de la vida real que involucren el área, el volumen y el área de la superficie que involucren las cuatro operaciones con números racionales.

Los estudiantes usan sus conocimientos sobre el área y la superficie para trabajar con figuras tridimensionales y aplican fórmulas de volumen para calcular el espacio interior de estas figuras. Comprender cómo moverse entre las representaciones 2D y 3D permite a los estudiantes resolver problemas en los que intervienen ambos tipos de formas, lo que resulta crucial en campos como la ingeniería, la arquitectura y el diseño de productos.

Los estudiantes usan las habilidades de cálculo de superficie y volumen para apoyar futuras aplicaciones en el análisis y modelado de datos. Por ej., comprender el volumen de las formas 3D es importante a la hora de analizar datos físicos, como la cantidad de espacio necesario para el almacenamiento o el volumen de los materiales de una muestra. Al aprender a calcular el volumen y la superficie de cajas o recipientes, desarrollan las habilidades necesarias para analizar y criticar datos de muestras relacionados con objetos físicos.

Los estudiantes usan los conceptos de área, superficie y volumen se aplican directamente para resolver problemas del mundo real, como determinar los materiales necesarios para cubrir o llenar una forma geométrica. Por ej., los estudiantes calculan la superficie de una caja para determinar cuánto material de envoltura se necesita, o calculan el volumen de una piscina o recipiente para determinar cuánta agua puede contener. Estas lecciones proporcionan las herramientas necesarias para resolver problemas prácticos relacionados con el mundo físico.

Los estudiantes utilizan el cálculo de áreas, superficies y volúmenes para resolver problemas en los que intervienen dibujos a escala. Por ejemplo, aplican sus conocimientos de figuras geométricas para calcular la superficie o el volumen de modelos a escala, lo que resulta útil a la hora de construir representaciones precisas de objetos o entornos. Esto es crucial cuando se trabaja con modelos de edificios, maquinaria o incluso mapas, en los que la escala es necesaria para mantener la proporcionalidad.

PREGUNTAS FUNDAMENTALES

• Describir las diferencias entre área, volumen y superficie de objetos bidimensionales y tridimensionales compuestos por triángulos, cuadriláteros, polígonos, cubos y prismas rectángulos.

• Explicar el proceso para determinar si se deben utilizar fórmulas de área, volumen o superficie.

• Explicar cómo al cortar una figura tridimensional se puede crear una figura bidimensional.

FIGURAS

INICIO: CONTENIDO DE APOYO

¿QUÉ ESTOY ENSEÑANDO?

CONTENIDO DE APOYO

Dibujar, construir y describir figuras geométricas y describir las relaciones entre ellas.

• Describir las figuras 2D que resultan de cortar figuras tridimensionales, como en secciones planas de prismas rectangulares rectos y pirámides rectangulares rectas.

• Resolver problemas matemáticos y de la vida real que involucren medida de ángulos, área, área de superficie y volumen.

• Resolver problemas matemáticos y de la vida real que involucren área, volumen y superficie de objetos bidimensionales y tridimensionales compuestos de triángulos, cuadriláteros, polígonos, cubos y prismas rectángulos.

Aplicar y ampliar la comprensión previa de las operaciones con fracciones para sumar, restar, multiplicar y dividir números racionales.

• Resolver problemas matemáticos y de la vida real que involucren las cuatro operaciones con números racionales. (Nota: extender las reglas para manipular fracciones a fracciones complejas).

CONOCIMIENTOS PREVIOS

En la escuela primaria, los estudiantes fueron introducidos a las formas geométricas y sus clasificaciones. En 6.º grado, empezaron a calcular las áreas de las formas mediante la composición y descomposición de otras formas. Se centraron en las áreas de triángulos y cuadriláteros junto con el descubrimiento del volumen entre formas tridimensionales más simplistas. Los estudiantes son capaces de ver formas más pequeñas dentro de una forma mayor. Este conocimiento de fondo ayudará a los estudiantes a entender cómo se derivan las fórmulas de área y volumen en este alcance.

CONCEPTOS ERRÓNEOS Y OBSTÁCULOS

• Los estudiantes pueden tener dificultades con las figuras tridimensionales mostradas en un papel bidimensional. Necesitarán practicar viendo qué lados son cuáles para poder etiquetarlos correctamente en la fórmula.

• Pueden encontrar desafiantes las piezas dentro de los problemas de área del mundo real, como la determinación de áreas que tienen que ver con tasas, proporciones y conversiones de unidades.

• Como se ha indicado anteriormente, los estudiantes también pueden confundir el área superficial con el área regular al resolver los problemas. Deben ser conscientes de que el área de la superficie incluye el área de cada lado individual de la figura.

ALCANCE ACTUAL

En este alcance, los estudiantes hallarán el área, el volumen y el área de la superficie de diferentes figuras 2D y 3D. Comprenderán que al cortar figuras 3D se crean figuras 2D. Esto puede ayudar a los estudiantes a decidir qué fórmulas utilizar en qué figuras. Extenderán este pensamiento para resolver triángulos, cuadriláteros, polígonos, cubos y prismas rectángulos en situaciones matemáticas y del mundo real.

TÉRMINOS CLAVE

• área: el número de unidades cuadradas que se necesitan para cubrir la superficie bidimensional de un objeto

• base: la superficie sobre la que se asienta un objeto sólido.

• base de un polígono: el lado del polígono que es perpendicular a la altitud.

• cubo: una figura sólida con seis caras cuadradas congruentes.

• descomponer: separar en partes o elementos (por ejemplo, figuras geométricas o números).

• dimensión: algo mensurable (como longitud, anchura y altura).

• fórmula: enunciado o regla matemática escrita con símbolos.

• altura: distancia perpendicular desde un vértice hasta el lado opuesto de una figura

• altura (figura 3D): distancia vertical desde la parte superior de un objeto o figura hasta su base

• longitud: medida de un objeto de extremo a extremo; distancia de un extremo a otro de un objeto

• perímetro: distancia alrededor del exterior de una figura o forma.

• polígono: una figura cerrada que tiene tres o más lados, sin líneas curvas ni intersecciones; una figura cerrada formada por segmentos de línea que se encuentran en su punto final

• prisma: una figura tridimensional que tiene al menos un conjunto de caras congruentes y paralelas (bases) que son polígonos con paralelogramos como las caras restantes

• cuadrilátero: un polígono con cuatro lados y cuatro ángulos.

• prisma rectangular recto: un prisma con seis caras rectangulares donde la arista lateral es perpendicular al plano de la base.

• triángulo rectángulo: un triángulo con un ángulo de 90º.

• cuadrado: un polígono de 4 lados (una forma plana con lados rectos) donde todos los lados tienen la misma longitud y cada ángulo es un ángulo recto (90º)

• área de superficie: el área total de cada una de las caras y superficies curvas de una figura sólida.

• figura tridimensional: un sólido que tiene tres dimensiones medibles.

• triángulo: un polígono con exactamente tres lados rectos y tres ángulos.

• figura bidimensional: una figura plana con dos dimensiones medibles.

• volumen: la cantidad de espacio que ocupa un objeto; la cantidad medida de unidades cúbicas que caben dentro de una figura sólida

• anchura: cuántas unidades de anchura tiene algo.

INICIO: CONTENIDO DE APOYO

APLICAR LAS PRÁCTICAS MATEMÁTICAS

• MP.1 Dar sentido a los problemas y perseverar en su resolución: Los estudiantes aplican sus conocimientos previos sobre los atributos de los objetos bidimensionales y tridimensionales para ayudar a dar sentido a nuevas figuras desconocidas. Perseveran en la resolución de estos problemas mediante la descomposición.

• MP.2 Razonar abstracta y cuantitativamente: Los estudiantes razonan de forma abstracta sobre cómo al cortar una figura tridimensional con un plano se obtienen formas bidimensionales. Los estudiantes cuantifican situaciones del mundo real y problemas matemáticos que implican medidas tales como ángulos, área, superficie y volumen.

• MP.3 Construir argumentos viables y criticar el razonamiento de los demás: Los estudiantes justifican sus respuestas y trabajan en colaboración con sus compañeros para resolver problemas de área, superficie y volumen.

• MP.4 Modelar con matemáticas: Los estudiantes aplican conocimientos de área, volumen y superficie para resolver problemas del mundo real.

• MP.5 Utilizar estratégicamente las herramientas apropiadas: Los estudiantes utilizan diagramas, bocetos y modelos geométricos para visualizar y analizar las formas bidimensionales resultantes de cortar figuras tridimensionales.

• MP.6 Prestar atención a la precisión: Los estudiantes calculan y comparan con precisión medidas como el área, el volumen y la superficie de objetos bidimensionales y tridimensionales compuestos por triángulos, cuadriláteros, polígonos, cubos y prismas rectángulos.

• MP.7 Buscar y utilizar estructuras: Los estudiantes descomponen estructuras en formas que reconocen. Utilizan composiciones y descomposiciones como apoyo para hallar el área, el volumen y la superficie.

• MP.8 Buscan y expresan regularidades en razonamientos repetidos: Los estudiantes identifican patrones en las formas que se forman al rebanar figuras tridimensionales. Identifican y expresan regularidades en fórmulas y procedimientos matemáticos que involucran área, superficie y volumen.

ÁREA

Los estudiantes resolverán problemas que contengan el área de diferentes figuras. Serán capaces de decidir qué fórmula utilizar para determinadas figuras y comprenderán cómo descomponer figuras en otras más pequeñas y manejables.

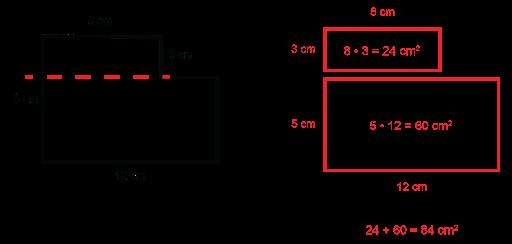
Ejemplo: ¿Cuál es el área de la siguiente figura?

a 2.304 cm2

b 120 cm2

c 100 cm2

d 84 cm2

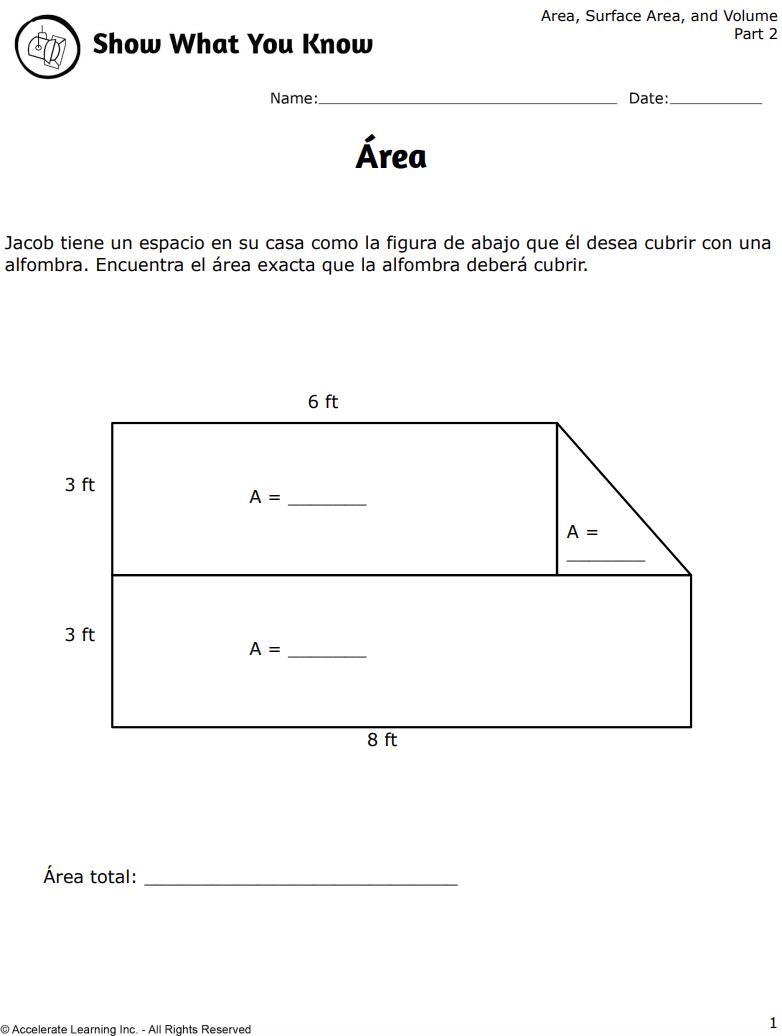
La respuesta correcta es la opción D. Los estudiantes deben descomponer la figura en dos rectángulos. Hay dos formas distintas de descomponer la figura, por lo que los estudiantes deben tener cuidado con las nuevas dimensiones de los rectángulos. Si se descompone en dos rectángulos, uno superior y otro inferior, los estudiantes deben ver que 3 de los 8 cm de anchura se contabilizan en el rectángulo superior. Por lo tanto, sólo quedan 5 cm de la anchura del rectángulo inferior. Ahora tienen dos rectángulos con dimensiones de 8 cm •3 cm y 5 cm •12 cm. Ahora pueden hallar el área de cada uno utilizando la fórmula del área. Encontrarán áreas de 24 cm2 y 60cm2. Tras sumarlas, obtendrán un total de 84 cm2 .

INICIO: CONTENIDO DE APOYO

SUPERFICIE

Los estudiantes resolverán problemas que contengan la superficie de diferentes figuras. Serán capaces de descomponer figuras más grandes en figuras más pequeñas y manejables con el fin de utilizar fórmulas conocidas para resolver estos problemas.

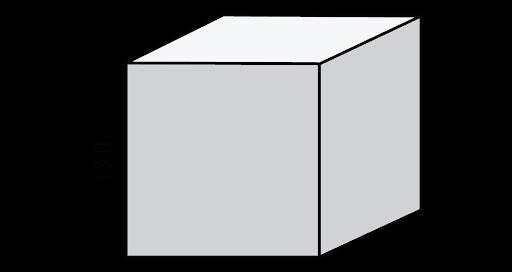
Ejemplo: ¿Cuál es el área de la superficie del siguiente cubo?

a 169 ft.2

b 1,014 ft.2

c 507 ft.2

d 2,197 ft.2

La respuesta correcta es la opción B. Los estudiantes deben saber que el área de la superficie de cualquier figura es la suma del área de todos los lados de la figura. Como la figura es un cubo, eso significa que todos los lados son iguales y, por tanto, la fórmula es SA = 6s2. Al resolverla, los estudiantes obtendrán una respuesta de 1.014 pies.2.

VOLUMEN

Los estudiantes resolverán problemas que contengan el volumen de diferentes figuras tridimensionales. Serán capaces de descomponer figuras más grandes en figuras más pequeñas y manejables con el fin de utilizar fórmulas conocidas para resolver estos problemas.

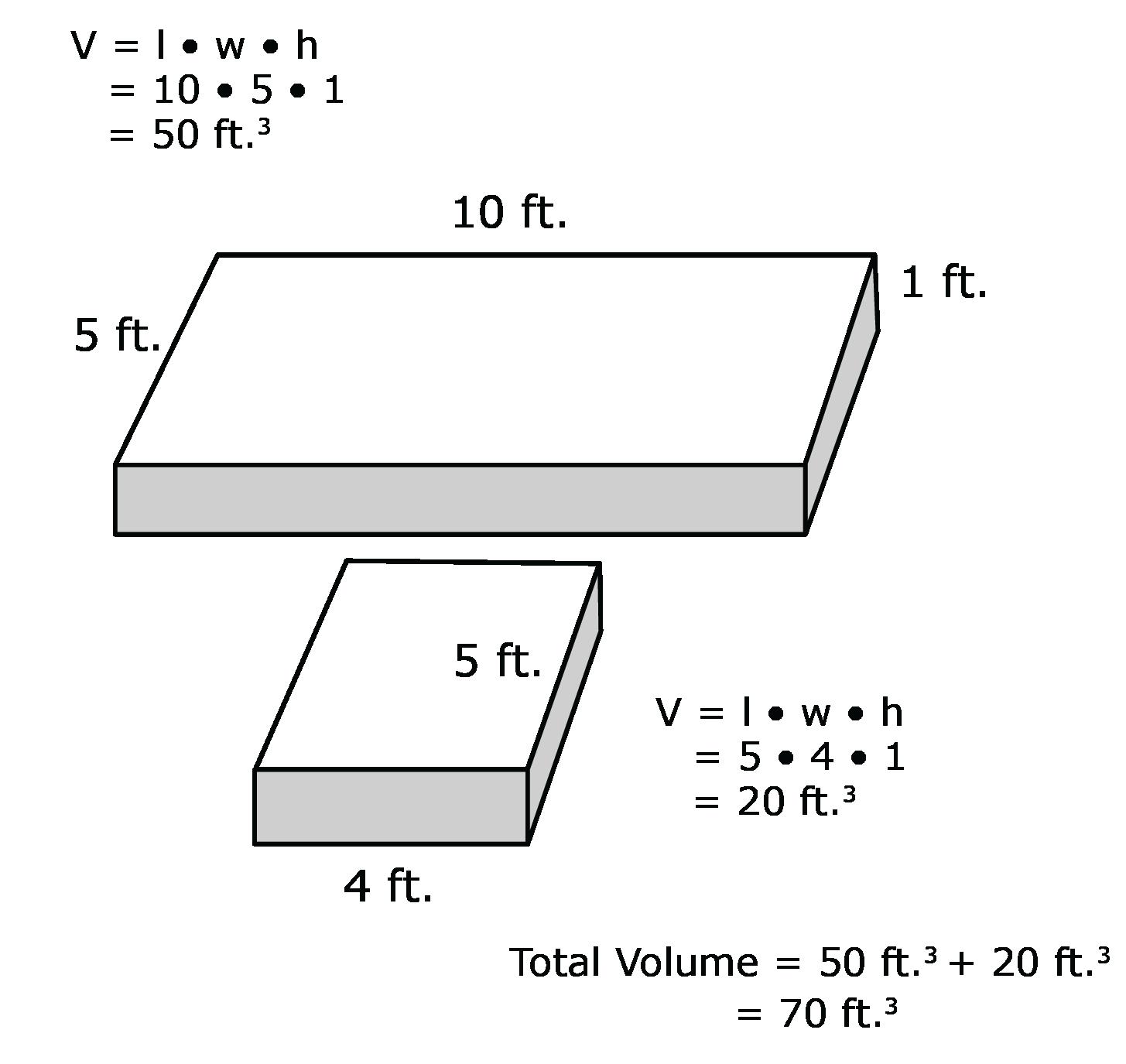
Ejemplo: ¿Cuál es el volumen de la siguiente figura?

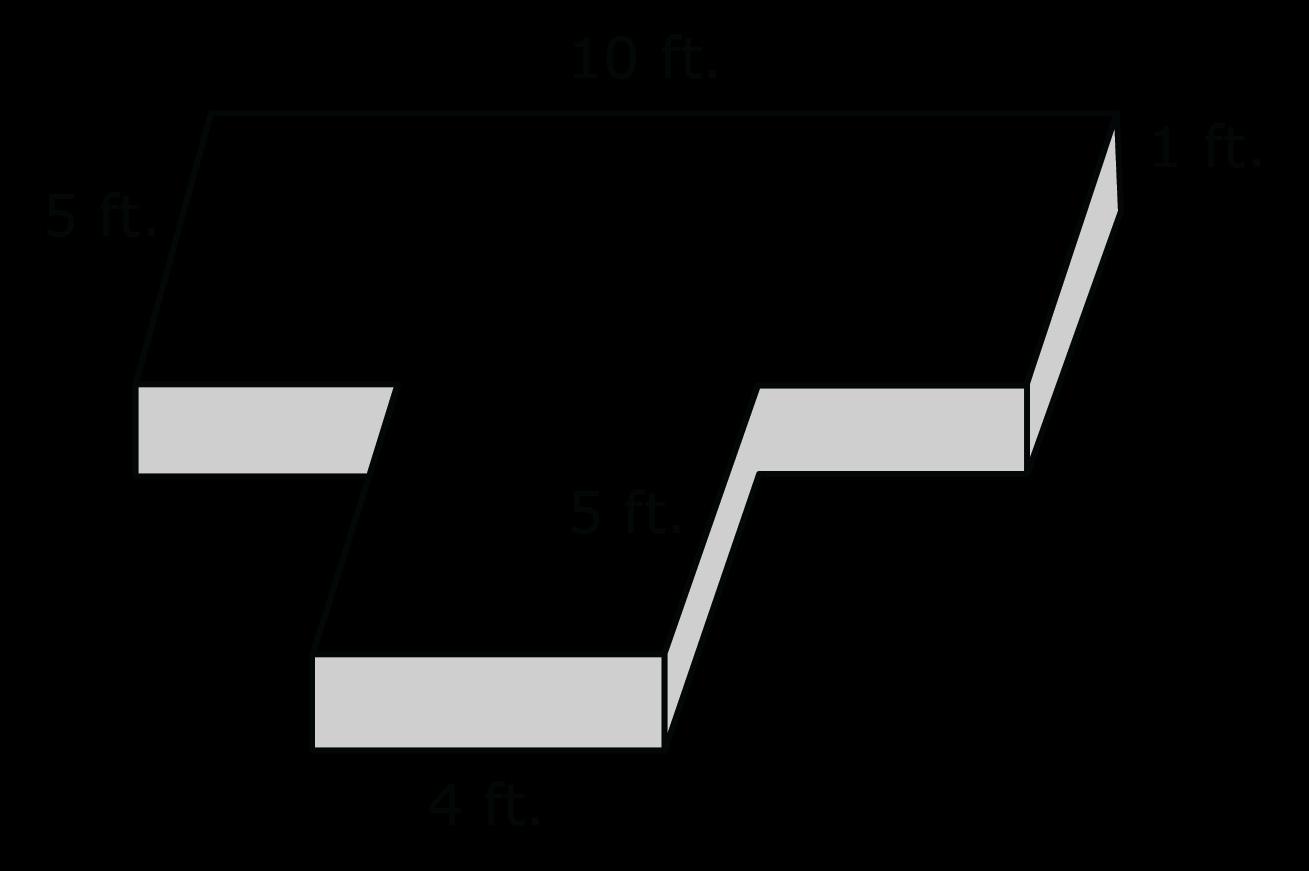
a 20 pies3

b 25 pies3

c 50 pies3

d 70 pies3

La respuesta correcta es la opción D Los estudiantes deben descomponer esta figura en dos prismas rectangulares. Sabiendo que la fórmula para hallar el volumen de un prisma rectangular es V = l • w • h, los estudiantes deducirán las dos ecuaciones V = 10 •5 •1 y V = 4 •5 •1 . Hallarán que los dos volúmenes son 50 pies3 y 20 pies3 respectivamente. Después de sumarlos, su respuesta final será 70 pies3

CORTAR FORMAS TRIDIMENSIONALES

Los estudiantes rebanarán formas tridimensionales en formas bidimensionales. Descubrirán cuáles son las formas resultantes del corte.

Ejemplo: Katie tiene un bloque de queso en forma de prisma cuadrado. Corta el bloque de queso por la mitad. ¿Cuáles son las dos caras bidimensionales que podrían resultar de cortar el queso por la mitad?

a Dos rectángulos

b Dos cuadrados

c Un rectángulo y un cuadrado

d Un triángulo y un rectángulo

La respuesta correcta es la opción C. Los estudiantes deben reconocer que si cortan el bloque de queso horizontalmente obtendrán dos prismas rectangulares con sección transversal en forma de rectángulo.

Si cortan el queso verticalmente, obtendrán dos prismas cuadrados con sección transversal en forma de cuadrado. Por lo tanto, hay dos diferentes caras bidimensionales que podrían ser un resultado.

AVANCES

A medida que los estudiantes avancen a 8.º grado y a la escuela secundaria, utilizarán los conceptos de área, área de superficie y volumen para derivar nuevas fórmulas y demostrar teoremas para figuras tridimensionales más profundas. En geometría, aprenderán a rotar, reflejar y trasladar figuras bidimensionales y tridimensionales, utilizando estas ideas para demostrar la similitud y la congruencia entre las formas.

ESTÁNDARES

Dibujar, construir y describir figuras geométricas y describir las relaciones entre ellas.

• Describir las figuras bidimensionales que resultan de cortar figuras tridimensionales, como en secciones planas de prismas rectangulares rectos y pirámides rectangulares rectas.

Resolver problemas matemáticos y de la vida real que involucren la medida de ángulos, el área, la superficie y el volumen.

• Resolver problemas matemáticos y de la vida real que involucren el área, el volumen y la superficie de objetos bidimensionales y tridimensionales compuestos por triángulos, cuadriláteros, polígonos, cubos y prismas rectángulos.

Aplicar y ampliar la comprensión previa de las operaciones con fracciones para sumar, restar, multiplicar y dividir números racionales.

• Resolver problemas matemáticos y del mundo real que impliquen las cuatro operaciones con números racionales. (Nota: extender las reglas de manipulación de fracciones a fracciones complejas)

DESGLOSAR EL ESTÁNDAR

VERBOS: ¿QUÉ DEBERÍAN HACER LOS ESTUDIANTES?

• sumar: combinar dos o más números para calcular el total (suma).

• aplicar: usar

• construir: construir a partir de dos o más partes.

• describir: escribir o contar los detalles de.

• dividir: separar o agrupar un número en partes iguales o justas.

• dibujar: crear usando información dada.

• extender: hacer que algo continúe más allá de donde se muestra, como continuar una recta numérica para incluir más números.

• manipular: idear una transformación estratégica.

• multiplicar: aplicar la operación matemática consistente en sumar repetidamente (mediante diversas estrategias) para obtener el producto.

• trocear: cortar

• resolver: hallar un valor que responda a una pregunta y/o haga verdadera una ecuación.

• restar: quitar un número a otro para calcular la diferencia.

INICIO: CONTENIDO DESGLOSADO

ANÁLISIS PROFUNDO

DE LOS ESTÁNDARES

CONTENIDO DESGLOSADO

SUSTANTIVOS: ¿QUÉ PALABRAS CONCRETAS DEBEN CONOCER LOS ESTUDIANTES?

• medida del ángulo: la medida del ángulo formado por los dos rayos de un vértice común.

• área: el número de unidades cuadradas que se necesitan para cubrir la superficie bidimensional de un objeto.

• fracción compleja: una fracción en la que el numerador y/o el denominador son fracciones.

• cubo: una figura sólida con seis caras cuadradas congruentes.

• fracción: un número que muestra una parte de un todo o una parte de un conjunto.

• figura geométrica: una figura delimitada por líneas, creada uniendo puntos en un plano.

• problema matemático: un problema que puede ser representado, analizado, y posiblemente resuelto, con los métodos de las matemáticas.

• operación: uno de los procesos matemáticos de suma, resta, multiplicación, división y exponenciación.

• plano: una superficie plana bidimensional que continúa indefinidamente.

• figura plana: una figura bidimensional que es plana y puede estar formada por líneas rectas, líneas curvas o una combinación de ambas.

• polígono: una figura cerrada que tiene tres o más lados, sin líneas curvas y sin intersecciones; una figura cerrada formada por segmentos de línea que se encuentran en sus puntos extremos.

• problema: una pregunta para resolver.

• cuadrilátero: un polígono con cuatro lados y cuatro ángulos.

• número racional: un número que se puede escribir como una fracción de enteros a/b, donde b ≠ 0; un número que se puede escribir como un cociente usando dos enteros.

• problema del mundo real: un problema basado en el contexto que se puede interpretar, representar y analizar mediante la aplicación de las matemáticas.

• relación: la regla en un patrón.

• prisma rectangular derecho: un prisma con seis caras rectangulares donde la arista lateral es perpendicular al plano de la base.

• pirámide rectangular derecha: una figura tridimensional con un rectángulo para la base y caras triangulares que corresponden a cada uno de los lados de la base.

• prisma derecho: sólido compuesto por un polígono como base y caras verticales perpendiculares a la base.

• superficie: superficie total de cada una de las caras y superficies curvas de una figura sólida.

• figura tridimensional: sólido que tiene tres dimensiones mensurables.

• triángulo: un polígono con exactamente tres lados rectos y tres ángulos.

• figura bidimensional: una figura plana con dos dimensiones medibles

• volumen: la cantidad de espacio que ocupa un objeto; la cantidad medida de unidades cúbicas que caben dentro de una figura sólida.

INICIO: CONTENIDO DESGLOSADO

IMPLICACIONES PARA LA ENSEÑANZA

• En grados anteriores, los estudiantes han modelado fórmulas de área para paralelogramos, trapezoides y triángulos descomponiendo y reordenando partes de estas formas. Los estudiantes han escrito ecuaciones que representan problemas relacionados con el área de rectángulos, paralelogramos, trapezoides y triángulos y el volumen de prismas rectangulares derechos donde las dimensiones son números racionales positivos.

• En este grado, se espera que los estudiantes modelen la relación entre el volumen de un prisma rectangular y una pirámide rectangular que tienen bases y alturas congruentes y conecten esa relación con las fórmulas. Deben explicar verbal y simbólicamente la relación entre el volumen de un prisma triangular y una pirámide triangular con bases y alturas congruentes y relacionar esa relación con las fórmulas. Los estudiantes deben usar modelos para determinar las fórmulas aproximadas para la circunferencia y el área de un círculo y conectar los modelos con las fórmulas reales.

ALINEACIÓN VERTICAL

5

5

Sumar, restar, multiplicar y dividir decimales hasta centésimas, usando modelos concretos o dibujos y estrategias basadas en el valor posicional, las propiedades de las operaciones y/o la relación entre la suma y la resta; relacionar la estrategia con un método escrito y explicar el razonamiento utilizado.

Aplicar y ampliar conocimientos previos sobre la multiplicación para multiplicar una fracción o un número entero por una fracción.

a. Interpretar el producto (a/b) × q como a partes de una partición de q en b partes iguales; equivalentemente, como el resultado de una secuencia de operaciones a × q ÷ b

b. Hallar el área de un rectángulo con longitudes laterales fraccionarias embaldosándolo con cuadrados unitarios de las longitudes laterales fraccionarias unitarias apropiadas, y demostrar que el área es la misma que se hallaría multiplicando las longitudes laterales. Multiplicar longitudes laterales fraccionarias para hallar áreas de rectángulos, y representar productos de fracciones como áreas rectangulares.

5 Relacionar el volumen con las operaciones de multiplicación y suma y resolver problemas matemáticos y de la vida real que involucren volumen.

a. Hallar el volumen de un prisma rectangular recto con longitudes laterales enteras embalándolo con cubos unitarios, y demostrar que el volumen es el mismo que se hallaría multiplicando las longitudes de las aristas, equivalentemente multiplicando la altura por el área de la base. Representar productos de tres números enteros como volúmenes, por ejemplo para representar la propiedad asociativa de la multiplicación.

b. Aplicar las fórmulas V = l × w × h y V = b × h para prismas rectangulares para hallar volúmenes de prismas rectangulares rectos con longitudes de arista de números enteros en el contexto de la resolución de problemas matemáticos y del mundo real.

c. Reconocer el volumen como aditivo. Hallar volúmenes de figuras sólidas compuestas de dos prismas rectangulares rectos no superpuestos sumando los volúmenes de las partes no superpuestas, aplicando esta técnica para resolver problemas del mundo real.

6

6

6

Hallar el área de triángulos rectángulos, otros triángulos, cuadriláteros especiales y polígonos componiendo en rectángulos o descomponiendo en triángulos y otras formas; aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y del mundo real.

Hallar el volumen de un prisma rectangular recto con longitudes de arista fraccionarias empaquetándolo con cubos unitarios de las longitudes de arista fraccionarias unitarias apropiadas, y demostrar que el volumen es el mismo que se hallaría multiplicando las longitudes de arista del prisma. Aplicar las fórmulas V = lwh y V = bh para hallar volúmenes de prismas rectangulares rectos con longitudes de arista fraccionarias en el contexto de la resolución de problemas matemáticos y de la vida real.

Representar figuras tridimensionales utilizando redes formadas por rectángulos y triángulos, y utilizar las redes para hallar la superficie de dichas figuras. Aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y de la vida real.

6 Sumar, restar, multiplicar y dividir con fluidez decimales de varias cifras utilizando el algoritmo estándar para cada operación.

7 Describir las figuras bidimensionales que resultan de cortar figuras tridimensionales, como en las secciones planas de prismas rectangulares rectos y pirámides rectangulares rectas.

INICIO: CONTENIDO DESGLOSADO

7 Resolver problemas matemáticos y del mundo real que involucren el área, el volumen y la superficie de objetos bidimensionales y tridimensionales compuestos de triángulos, cuadriláteros, polígonos, cubos y prismas rectos.

7 Aplicar y ampliar la comprensión previa de la suma y la resta para sumar y restar números racionales; representar la suma y la resta en un diagrama de recta numérica horizontal o vertical.

a. Describir situaciones en las que cantidades opuestas se combinan para formar 0.

b. Entender p + q como el número situado a una distancia |q| de p, en sentido positivo o negativo dependiendo de si q es positivo o negativo. Demostrar que un número y su opuesto tienen suma 0 (son inversos aditivos). Interpretar sumas de números racionales describiendo contextos del mundo real.

c. Entender la resta de números racionales como la suma del inverso aditivo, p - q = p + (-q). Demostrar que la distancia entre dos números racionales en la recta numérica es el valor absoluto de su diferencia, y aplicar este principio en contextos del mundo real.

d. Aplicar propiedades de las operaciones como estrategias para sumar y restar números racionales.

7 Aplicar y extender conocimientos previos de multiplicación y división y de fracciones para multiplicar y dividir números racionales.

a. Entender que la multiplicación se extiende de fracciones a números racionales al requerir que las operaciones continúen satisfaciendo las propiedades de las operaciones, particularmente la propiedad distributiva, llevando a productos como (-1)(-1) = 1 y las reglas para multiplicar números con signo. Interpretar productos de números racionales describiendo contextos del mundo real.

b. Comprender que los números enteros pueden dividirse, siempre que el divisor no sea cero, y que todo cociente de números enteros (con divisor distinto de cero) es un número racional. Si p y q son números enteros, entonces -(p/q) = (-p)/q = p/(-q). Interpretar cocientes de números racionales describiendo contextos del mundo real.

c. Aplicar propiedades de las operaciones como estrategias para multiplicar y dividir números racionales.

d. Convertir un número racional en decimal utilizando la división larga; saber que la forma decimal de un número racional termina en 0s o se repite eventualmente.

7 Resolver problemas matemáticos y del mundo real que impliquen las cuatro operaciones con números racionales.

8 Utilizar los símbolos de raíz cuadrada y raíz cúbica para representar soluciones a ecuaciones de la forma x2 = p y x3 = p, donde p es un número racional positivo. Evaluar raíces cuadradas de pequeños cuadrados perfectos y raíces cúbicas de pequeños cubos perfectos. Saber que √ 2 es irracional.

8 Explicar una demostración del Teorema de Pitágoras y su inversa

8 Conocer las fórmulas de los volúmenes de conos, cilindros y esferas y utilizarlas para resolver problemas matemáticos y de la vida real.

HS Dar un argumento informal utilizando el principio de Cavalieri para las fórmulas del volumen de una esfera y otras figuras sólidas.

HS Identificar las formas de secciones transversales bidimensionales de objetos tridimensionales, e identificar objetos tridimensionales generados por rotaciones de objetos bidimensionales.

HS Utilizar formas geométricas, sus medidas y sus propiedades para describir objetos (por ejemplo, modelar un tronco de árbol o un torso humano como un cilindro).

HS Aplicar métodos geométricos para resolver problemas de diseño (por ejemplo, diseñar un objeto o estructura para satisfacer restricciones físicas o minimizar costes; trabajar con sistemas de retículas tipográficas basados en proporciones).

INICIO: GUÍA DE INSTRUCCIÓN ANDAMIADA

MONITOREAR Y AJUSTAR

GUÍA DE INSTRUCCIÓN ANDAMIADA

La guía de instrucción andamiada se proporciona para que el maestro pueda planificar los siguientes pasos basándose en el rendimiento de los estudiantes en las evaluaciones de alcance o en los datos de su evaluación de medición de crecimiento MAP. Se trata de una herramienta integrada que lleva a los maestros a buscar materiales basados en las necesidades de los estudiantes. Los materiales sugeridos están organizados por estándares. Dentro de cada estándar, los materiales se clasifican además por el rango de percentiles que mejor se adapta.

Cuando se usa la guía de instrucción andamiada con los datos de su evaluación de medición de crecimiento MAP, cada tabla puede guiar a los maestros a los materiales sugeridos basados en los puntajes del área de instrucción de los estudiantes. Se sugiere a los maestros a permitir que todos los estudiantes experimenten con «Captar interés», «Exploración», «Muestra lo que sabes» y «Pruebas de habilidades». Estos elementos cubren a fondo los estándares incluidos en el alcance.

La guía se divide en cuatro rangos de percentiles para cada estándar.

Refuerzo del grado anterior Nivel de grado con apoyos Nivel de grado

Los estudiantes con puntaje en este rango de percentil necesitan refuerzo del contenido del grado anterior.

Los estudiantes con puntaje en este rango de percentil necesitan apoyo de intervención de nivel de grado.

Los estudiantes con puntaje en este rango de percentil pueden trabajar en contenido de nivel de grado con apoyos de instrucción.

Ampliación del nivel de grado

Los estudiantes con puntaje en este rango de percentil están listos para aplicar su conocimiento del contenido en una variedad de actividades.

Para interpretar y responder al rendimiento del estudiante en las evaluaciones del alcance, complete los siguientes pasos:

1 Revise los datos recopilados a través de la plataforma en línea o el «Mapa de calor» para determinar el rango percentil del estudiante para cada estándar evaluado.

2 Las tablas proporcionadas recomiendan un conjunto de materiales de instrucción para cada rango percentil dentro de cada estándar evaluado. Elija cuál de estos materiales usará para apoyar mejor al estudiante con base en sus datos de evaluación.

3 Haga clic en el enlace directo al material elegido para el estudiante.

Para interpretar y responder al desempeño del estudiante en la evaluación de medición de crecimiento MAP, complete los siguientes pasos:

1. Revise los datos proporcionados para determinar el percentil, el área de instrucción y/o el desglose de estándares para cada estudiante.

2. Encuentre el alcance que incluye los estándares que necesitan enfoque o intervención.

3. Acceda a la «guía de instrucción andamiada» en la sección «inicio» del alcance.

4. Haga clic en el enlace directo al material recomendado para el estudiante.

La guía es un plan sugerido y no se limita a los estándares y actividades incluidos. Además, no todas las actividades sugeridas necesitan ser completadas por cada estudiante.

Área de instrucción: Operaciones y pensamiento algebraico

Todos los estudiantes:

• Captar interés

• Exploración

• Muestra lo que sabes

• Prueba de habilidades

Describe las figuras bidimensionales que resultan de cortar figuras tridimensionales, como en las secciones planas de prismas rectangulares rectos y pirámides rectangulares rectas.

0 %25 % (Nivel de grado anterior con apoyo)

6 - Área de superficie

Repaso y práctica de habilidades

Constructor de fluidez

• Área de superficie usando redes

Práctica interactiva

• Yangtze.com

Prueba de habilidades

25 %50 % (Nivel de grado con apoyo)

7 - Area, Surface Area and Volume

Acceso a conocimientos previos

Constructor de fluidez

Repaso y práctica de habilidades

• Evaluación rápida (preguntas 1-2)

• Repaso: Secciones «Cortar figuras 3D» «transversal plana, prisma del rectángulo recto» y «prisma triangular»

• Repaso (preguntas 1-3)

50 %80 % (Nivel de Grado)

80 %100 % (Ampliando el Nivel de Grado)

7 - Área, superficie y volumen

Vocabulario ilustrado

Vocabulario interactivo

7 - Área, superficie y volumen

Tablero de opciones

INICIO:

Resolver problemas matemáticos y del mundo real relacionados con el área, el volumen y la superficie de objetos bidimensionales y tridimensionales compuestos por triángulos, cuadriláteros, polígonos, cubos y prismas rectángulos.

6 - Área y volumen

(Nivel de grado anterior con apoyo)

25 %50 % (Nivel de grado con apoyo)

Repaso y práctica de habilidades

Constructor de fluidez

• Área y volumen

Prueba de habilidades

6 - Área de superficie

Repaso y práctica de habilidades

Generador de fluidez

• Área de superficie con redes

Práctica interactiva

• Yangtze.com

Prueba de habilidades

7 - Area, Surface Area and Volume

Acceso a conocimientos previos

Constructor de fluidez

Repaso y práctica de habilidades

• Evaluación rápida (preguntas 3-8)

• Repaso: Secciones «área de superficie» y «volumen»

• Evaluación de control (preguntas 4-10)

7 - Area, Superficie y Volumen

Vocabulario ilustrado

Vocabulario interactivo

Libreta interactiva

50 %80 % (Nivel de Grado)

80 %100 % (Ampliando el Nivel de Grado)

Práctica interactiva

• Hábitat de las criaturas

Constructor de fluidez

• Área de figuras compuestas

• Volumen

• Área de superficie: prismas and cilindros

Ciencia de datos

Conexiones lingüísticas

7 - Area, Área, superficie y volumen

Tarea de representación matemátics

¿Qué prefieres?

Tablero de opciones

Resolver problemas matemáticos y del mundo real que impliquen las cuatro operaciones con números racionales. (Nota: Los cálculos con números racionales extienden las reglas para manipular fracciones a fracciones complejas)

6 - Operaciones con números racionales positivos

Repaso y práctica de habilidades

Generador de fluidez

• Multiplicar y dividir decimales

0 %25 % (Nivel de grado anterior con apoyo)

Práctica interactiva

• Aventura en la mazmorra

• Reino de los dragones

Prueba de habilidades

7 - Suma y resta con números racionales

Repaso y práctica de habilidades

Constructor de fluidez

• Suma y resta números enteros

• Suma y resta números racionales

Práctica interactiva

• Piloto de papel

Prueba de habilidades

25 %50 % (Nivel de grado con apoyo)

50 %80 % (Nivel de Grado)

7 - Área, superficie y volumen

Repaso y práctica de habilidades

• Evaluación rápida (preguntas 3-8)

• Repaso: secciones «área», «área de superficie» y «volumen»

• Evaluación de control (preguntas 4-10)

7 - Área, superficie y volumen

Vocabulario ilustrado

Vocabulario interactivo

Libreta interactiva

Práctica interactiva

• Hábitats de las criaturas

Constructor de fluidez

• Área de figuras compuestas

• Volumen

• Área de superficie prismas y cilindros

Ciencia de datos

Conexiones lingüísticas

80 %100 % (Ampliando el Nivel de Grado)

7 - Área, superficie y volumen

Tarea de represetnación matemática

¿Qué prefieres?

Tablero de opciones

ATRAER: ACCESO A CONOCIMIENTOS PREVIOS

EVALUAR PREVIAMENTE EL CONOCIMIENTO DE LOS ESTUDIANTES

ACCESO A CONOCIMIENTOS PREVIOS: «NO PERTENECE»

ESTÁNDAR PREVIO

Representar figuras 3D con redes formadas por rectángulos y triángulos, y usar las redes para encontrar el área de la superficie de estas figuras. Aplicar estas técnicas en el contexto de la resolución de problemas matemáticos y del mundo real. Encontrar el volumen de un prisma rectangular recto con longitudes de arista fraccionarias empaquetándolo con cubos unitarios de las longitudes de arista fraccionarias unitarias apropiadas, y demostrar que el volumen es el mismo que se encontraría multiplicando las longitudes de arista del prisma. Aplicar las fórmulas V = lwh y V = bh para hallar volúmenes de prismas rectangulares rectos con longitudes de arista fraccionarias en el contexto de la resolución de problemas matemáticos y del mundo real.

DESCRIPCIÓN

Los estudiantes examinarán una serie de descripciones y determinarán qué opción «No pertenece» al grupo. Este elemento está diseñado para descubrir conceptos erróneos; no se debe realizar para obtener una calificación.

MATERIALES

IMPRESO

• 1 «No pertenece» (por estudiante o por grupo)

PREPARACIÓN

• Imprima un documento «No pertenece» por estudiante.

• Puede elegir colocar a los estudiantes en grupos de dos o tres.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Reparta el «No pertenece» a cada estudiante o grupo.

2. Explique que cada descripción de la hoja contiene cuatro opciones. Tres de las opciones van juntas, mientras que una no pertenece.

3. Pida a los estudiantes que determinen qué letra no pertenece a cada grupo y que expliquen lo que piensan.

a Primera tarjeta: B es incorrecta, porque describe superficie y el resto describe volumen.

b Segunda tarjeta: C es incorrecta, porque describe volumen y el resto describe superficie.

c Tercera tarjeta: A es incorrecta, porque describe volumen y el resto describe superficie.

4. Concluya dirigiendo un debate.

5. Si los estudiantes tienen dificultades para completar esta tarea, continúe con el constructor de fundamentos para llenar este vacío en los conocimientos previos antes de pasar a otras partes del alcance.

IDENTIFICACIÓN DE CONCEPTOS ERRÓNEOS

• Los estudiantes pueden no saber cómo usar una fórmula para calcular el volumen.

• Los estudiantes pueden confundir las medidas de una figura sólida al dividirlas en formas netas bidimensionales.

«NO PERTENECE»

ATRAER: CAPTAR INTERÉS

LECCIÓN PARA CAPTAR INTERÉS

CAPTAR INTERÉS

DESCRIPCIÓN

Los estudiantes determinan el área de la superficie de una figura tridimensional compuesta para resolver un problema del mundo real.

MATERIALES

IMPRESOS

• 1 Estantes de exhibición (por clase)

REUTILIZABLES

• 1 Fenómenos (por clase)

PREPARACIÓN

• Planee mostrar los fenómenos.

• Prepárese para proyectar los estantes de exhibición para que toda la clase los vea.

• Prepárese para presentar el escenario y anime a los estudiantes a pensar en cómo resolverlo. Prepárese para pasar a las actividades explorar, regresando a la actividad de «captar interés» con los nuevos conocimientos adquiridos una vez que se hayan completado las exploraciones.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

PARTE I: EXPLORACIÓN PREVIA

3. Presente esta actividad hacia el comienzo del alcance. la clase retomará la actividad y resolverá el problema original después de que los estudiantes hayan completado las actividades explorar correspondientes.

4. Muestre los fenómenos. Formule a los estudiantes las siguientes preguntas: ¿Qué observas? ¿Dónde puedes ver matemáticas en esta situación? Permita que los estudiantes compartan todas sus ideas.

5. Explique el escenario a la clase: «Sheba encontró un pequeño mueble antiguo en un mercadillo. Decidió convertirlo en un expositor para sus trofeos de los diferentes congrados deportivos, musicales y artísticos en los que participa. Lo ha lijado y limpiado. A continuación, sellará la pieza para proteger la madera. Por último, decorará los estantes con papel autoadhesivo decorativo. Tiene que determinar la superficie de toda la pieza para saber cuánto sellador tiene que comprar, y tiene que averiguar la superficie de la parte superior de cada estante para saber cuánto papel decorativo tiene que comprar».

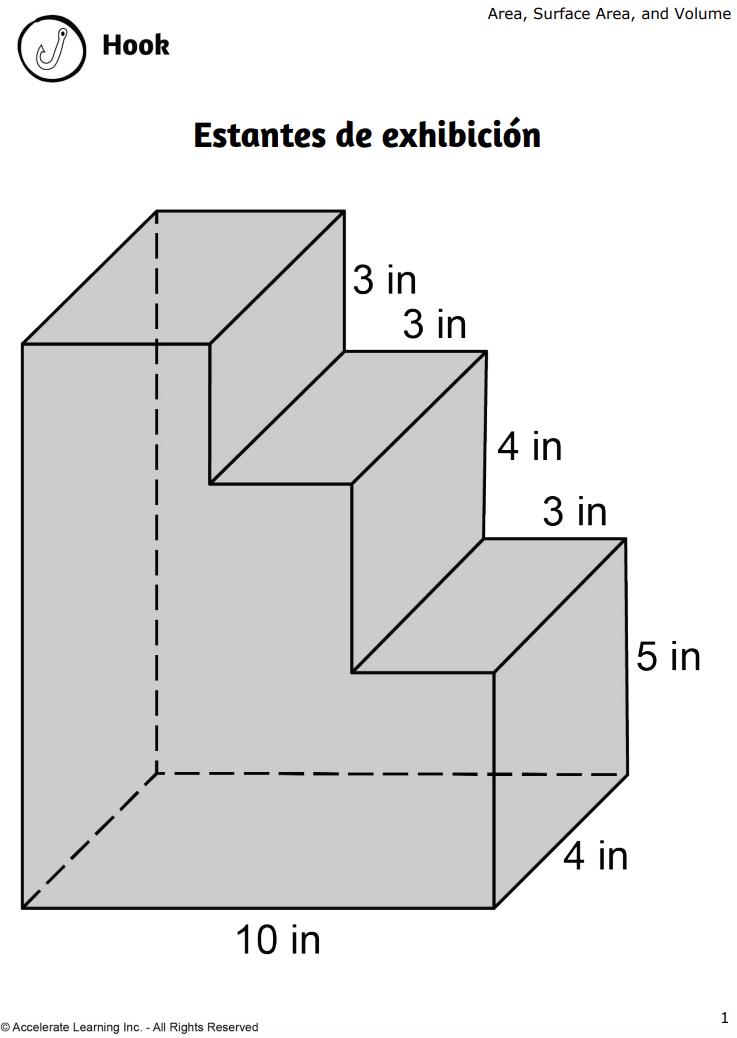
ESTANTERÍAS PARA PRESUMIR

1. Permita que los estudiantes hagan preguntas y aclaren el contexto según sea necesario. Anímelos a compartir sus pensamientos y experiencias con la clase utilizando las siguientes preguntas:

a. ¿Alguna vez ha rehecho un mueble?

b. ¿Ha tenido que sellar un objeto de madera?

c. ¿Ha utilizado papel autoadhesivo decorativo para un proyecto?

d. ¿Qué tipo de matemáticas necesitará utilizar Sheba para terminar su proyecto?

2. Proyecto «Estantes de exhibición».

6. Explique a los estudiantes que Sheba ha medido las dimensiones de su nuevo mueble y las ha registrado en pulgadas. Haga las siguientes preguntas con la clase:

a DOK-1 ¿En qué unidad se medirá la superficie del mueble y la superficie de las estanterías? Pulgadas cuadradas

b DOK-1 ¿Es la superficie de todas las estanterías del mismo tamaño? ¿Cómo puedes saberlo? No, todos los estantes tienen la misma longitud, pero el estante superior es una pulgada más ancho. Puedo saberlo porque la anchura/profundidad de la pieza es de 10 pulgadas. Las dos baldas inferiores miden 5 cm de ancho cada una; 10 - 3 - 3 = 4. La balda superior mide 5 cm de ancho. El estante superior tiene 4 pulgadas de ancho.

c DOK-1 ¿Cómo puedes hallar el área de la superficie de todo el mueble? Tengo que hallar el área de cada cara del mueble y hallar la suma de todas las áreas.

7. Pasa a completar las actividades de explorar.

PARTE II: DESPUÉS DE LA EXPLORACIÓN

2. Después de que los estudiantes hayan completado las actividades explore para este tema, muestre de nuevo los fenómenos y repita el escenario.

3. Refiérase al documento «Estantes de exhibición», y haga las siguientes preguntas con la clase:

a. DOK-1 ¿En qué unidad se medirá el área de la superficie de los muebles y el área de los estantes? Pulgadas cuadradas

b. DOK-1 ¿Es el área de todos los estantes del mismo tamaño? ¿esquema de Cómo puedes saberlo? No, todos los estantes tienen la misma longitud, pero el estante superior es una pulgada más ancho. Puedo saberlo porque la anchura/profundidad de la pieza es de 10 pulgadas. Las dos baldas inferiores miden 5 cm de ancho cada una; 10 - 3 - 3 = 4. La balda superior mide 5 cm de ancho. El estante superior tiene 4 pulgadas de ancho.

c. DOK-1 ¿Cómo puedes hallar el área de la superficie de todo el mueble? Tengo que hallar el área de cada cara del mueble y hallar la suma de todas las áreas.

d. DOK-1 ¿Cuál es el área total de los estantes para que Sheba sepa cuánto papel decorativo autoadhesivo debe comprar? El área total de los tres estantes es 40 pulgadas cuadradas. 3 × 4 = 12; 3 × 4 = 12; 4 × 4 = 16 →12 + 12 + 16 = 40

ATRAER: CAPTAR INTERÉS

a. DOK-2 ¿Cuál es la superficie de todo el mueble para que Sheba sepa cuánto sellador de madera comprar? 356 pulgadas cuadradas

Estantes = 40 3 × 4 = 12; 3 × 4 = 12; 4 × 4 = 16 →12 + 12 + 16 = 40

Parte trasera de los estantes = 48 3 × 4 = 12; 4 × 4 = 16; 5 × 4 = 20 → 12 + 16 + 20 = 48

Parte posterior = 48 4 × 12 = 48

Parte inferior = 40 10 × 4 = 40

Lados = 180 3 × 5 = 15 3 × 9 = 27 4 × 12 = 48 → 15 + 27 + 48 = 90 → 90 × 2 = 180

Superficie total = 356 pulgadas cuadradas → 40 + 48 + 48 + 40 + 180 = 356

1. Según el tiempo disponible, haz que los estudiantes encuentren en clase las dimensiones de una estantería y la cantidad de sellador y papel autoadhesivo que necesitarían para rehacerla.

EXPLORAR: EXPLORACIÓN 1

LECCIÓN PEDAGÓGICA

EXPLORACIÓN 1: CORTAR FIGURAS 3D

Estándar(es)

• Dibujar, construir y describir figuras geométricas y describir las relaciones entre ellas. Describir las figuras bidimensionales que resultan de cortar figuras tridimensionales, como en secciones planas de prismas rectangulares rectos y pirámides rectangulares rectas.

Ideas fundamentales

Formas en el mundo

Conexiones 2D y 3D

Estándares para la práctica matemática

MP.1 Dar sentido a los problemas y perseverar en su resolución.

MP.6 Prestar atención a la precisión.

MP.7 Buscar y hacer uso de la estructura.

Conexiones de pontenido

CC3 Desarmar el todo, armar las partes

CC4 Descubrir la forma y el espacio

Motores de investigación

DI1 Dar sentido al mundo (comprender y explicar)

DESCRIPCIÓN

Los estudiantes cortan prismas rectangulares rectos y pirámides rectas para descubrir qué figuras bidimensionales se revelan como secciones planas.

MATERIALES

IMPRESO

• 1 folleto del estudiante (por estudiante)

• 1 boleto de salida (por estudiante)

• 1 juego de «Cortes 3D» (por pareja)

REUTILIZABLE

• 1 par de tijeras (por maestro)

• 1 cuchillo de plástico o palito de manualidades (por pareja)

CONSUMIBLE

• 1 bolsa con cierre (por pareja)

• 1 libra de plastilina (por pareja)

• 1 rollo de envoltorio de plástico (por maestro)

PREPARACIÓN

• Planifique que los estudiantes trabajen en parejas para completar la actividad.

• Imprima el diario del estudiante y la boleta de salida para cada estudiante.

• Reúne modelos de prismas rectangulares rectos (como cajas, dados, gomas de borrar, libros, fichas de dominó y prismas rectangulares rectos de conjuntos de sólidos tridimensionales). Reúne modelos de pirámides rectas (por ejemplo, modelos de pirámides egipcias, prismas de vidrio y pirámides rectas de conjuntos de sólidos tridimensionales).

• Imprime un juego de tarjetas de situación de corte de figuras tridimensionales para cada grupo. Recorta las tarjetas. Coloca cada juego de tarjetas en una bolsa resellable para cada grupo. Si lo deseas, imprime las tarjetas en cartulina y plastifícalas para utilizarlas en el futuro.

• Obtenga arcilla, divídala en terrones de 1 libra y envuelva cada libra en plástico para cada grupo de compañeros.

• Para los estudiantes que necesiten más apoyo para recordar información, consulte nuestros elementos de «Ayudas complementarias» que incluyen tapetes para compartir, disponibles en la sección: redes tridimensionales y objetos tridimensionales con líneas de puntos en la sección «Intervención».

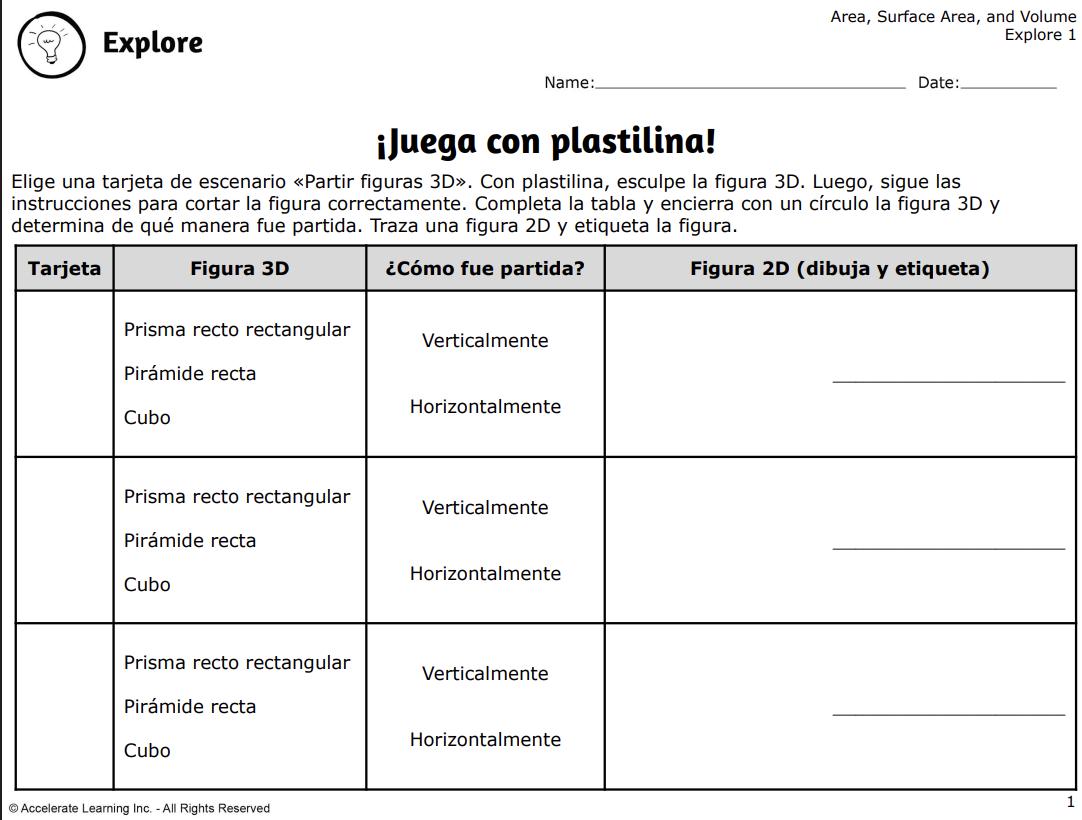
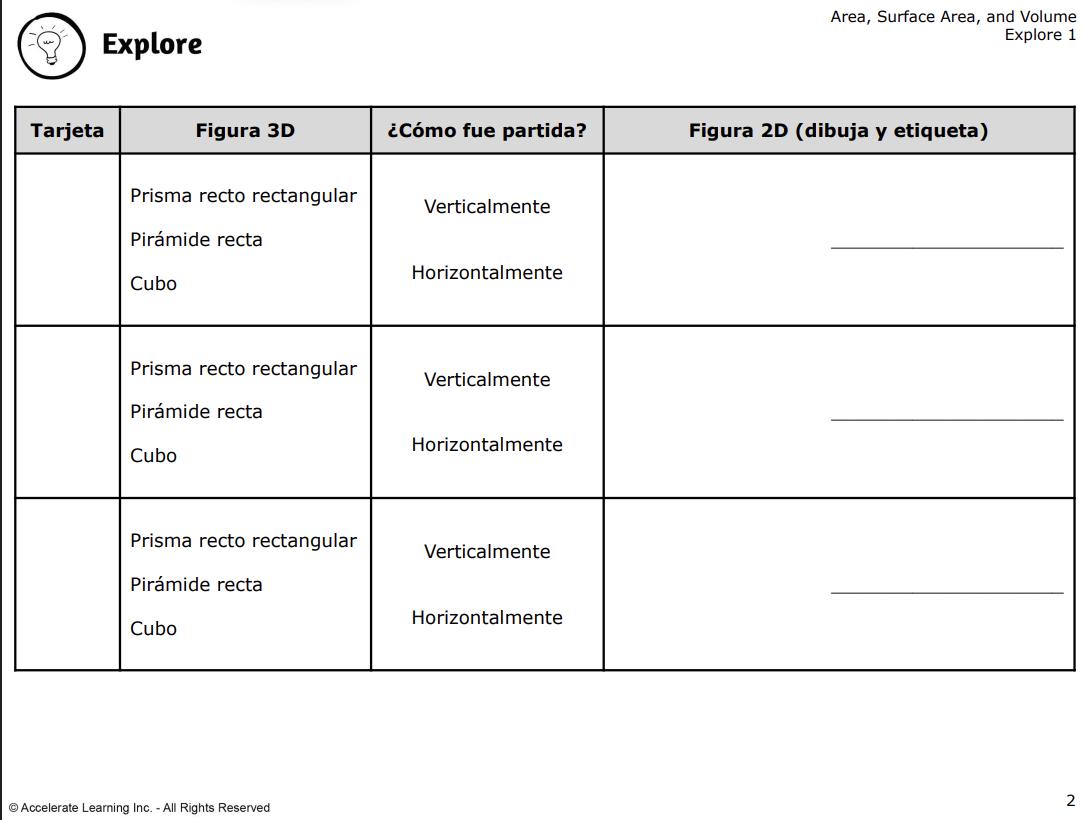
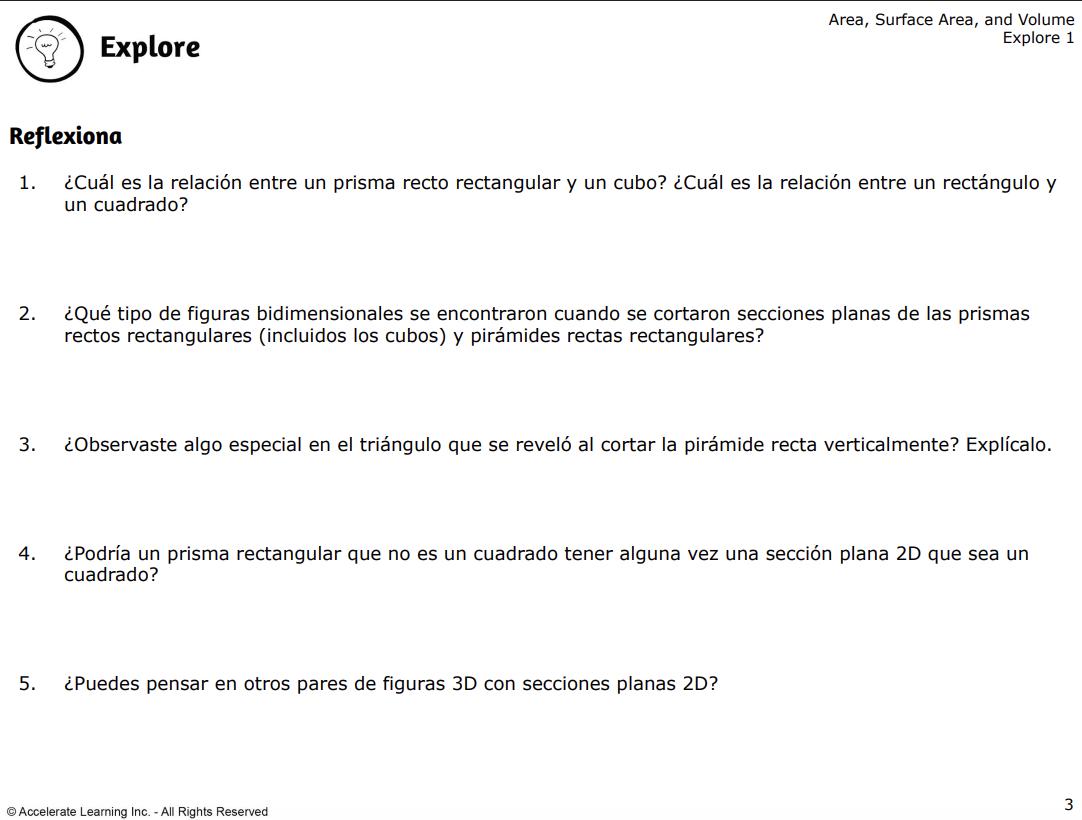
DIARIO DEL ESTUDIANTE

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Lea la siguiente situación a la clase: «Un día, María buscó en el almacén de la tienda de su madre. Encontró envases viejos con figuras de prismas rectangulares rectos y pirámides rectas. La señora López dijo que eran contenedores de transporte reutilizables que ya no usaba. María decidió utilizarlos para un proyecto artístico. Quería poner arcilla dentro de cada contenedor para moldearla con la forma del contenedor. Luego, sacaría la arcilla del interior del contenedor y cortaría secciones planas de la arcilla, ya fuera vertical u horizontalmente. Tu trabajo consiste en ayudar a María a predecir y descubrir qué figuras bidimensionales serán las secciones planas de arcilla. Después, María pintará y cocerá las figuras bidimensionales de arcilla para hacer posavasos y platos coloridos y únicos».

2. Ayude a los estudiantes a acceder a la tarea haciéndoles las siguientes preguntas orientadoras:

a. ¿Qué sabes ya sobre la creación de proyectos de arcilla?

b. ¿Qué recuerdas sobre las figuras bidimensionales?

3. Entregue un diario del estudiante a cada estudiante y una bolsa con tarjetas de escenarios de figuras tridimensionales, un trozo de arcilla y un cuchillo de plástico o un palo de manualidades a cada pareja.

4. Explique a los estudiantes que trabajarán con sus compañeros para determinar las figuras bidimensionales de las secciones planas cortadas de los distintos prismas rectangulares y pirámides rectas. Para ello, primero construirán cada figura tridimensional a partir de las tarjetas de situaciones de corte de figuras tridimensionales y, a continuación, seguirán las instrucciones para cortar la figura correctamente. A continuación, dibujarán la figura bidimensional descubierta.

5. Supervise y hable con los estudiantes según sea necesario para comprobar la comprensión mediante las siguientes preguntas orientativas:

a. DOK-2 ¿Hay más de una forma de cortar una pirámide recta? Sí, se puede cortar vertical u horizontalmente.

b. DOK-1 ¿Qué figura bidimensional se revela con cada forma en que se corta la pirámide recta? Si se corta verticalmente, se ve un triángulo. Cuando se corta horizontalmente, se revela un cuadrado.

c. DOK-2 ¿Hay más de una forma de cortar un prisma rectángulo? Sí, también se puede cortar vertical u horizontalmente.

d. DOK-1 ¿Qué figura 2D se revela con cada forma de corte del prisma rectangular recto? Tanto si se corta vertical como horizontalmente, la figura 2D que se revela es un rectángulo. (Esto también incluye a los cuadrados, que son tipos especiales de rectángulos).

EXPLORAR: EXPLORACIÓN 1

6. Deje tiempo para que los estudiantes completen el diario del estudiante, incluidas las preguntas de reflexión.

7. Pida a los estudiantes que compartan sus estrategias y anímelos a que se hagan preguntas y establezcan conexiones. Anime a los estudiantes a notar las similitudes y diferencias entre las estrategias utilizadas para cortar formas tridimensionales.

8. Después de la exploración, invite a la clase a una charla de matemáticas para compartir sus observaciones y aprendizajes.

CHARLA DE MATEMÁTICAS

• DOK-2 Cuando cortas una pirámide recta horizontalmente en varios lugares diferentes, ¿por qué siempre produce un cuadrado y por qué son de diferentes tamaños? Cortar una pirámide recta horizontalmente siempre produce un cuadrado porque el corte es paralelo a la base, que es un cuadrado. Los cuadrados tienen tamaños diferentes porque una pirámide recta se estrecha hasta un punto en el vértice (parte superior) y se ensancha hasta su cuadrado más ancho en la base. Si cortas cerca de la parte superior, será un cuadrado más pequeño que en la parte inferior, donde será más grande.

• DOK-2 ¿Por qué un prisma rectangular recto sólo produce un tipo de figura 2D (rectángulo) cuando se corta, mientras que una pirámide recta tiene opciones tanto de triángulo como de cuadrado? Un prisma rectangular recto sólo produce rectángulos (incluyendo cuadrados) cuando se corta porque todas sus caras son rectángulos (incluyendo cuadrados). Los rectángulos pueden tener diferentes dimensiones, dependiendo de cómo se corte. Una pirámide recta puede tener un cuadrado o un triángulo porque tiene caras triangulares y cuadradas.

• DOK-2 ¿Notaste algo especial en el triángulo que se reveló cuando la pirámide recta se cortó verticalmente? Explica. Notamos que era un triángulo isósceles. Esto se debe a que el prisma recto se cortó desde el vértice hasta la base y todas las caras triangulares y sus aristas tienen la misma longitud, por lo que se crea un triángulo con lados de la misma longitud.

• Elige una rutina de conversación estructurada para facilitar la siguiente pregunta:

○ DOK-2 En el mundo real, ¿cuándo podría la gente cortar figuras tridimensionales para utilizar las figuras bidimensionales creadas? Las respuestas variarán. Hacemos esto cuando hacemos galletas. Hacemos una figura tridimensional (como un cilindro o un prisma rectangular recto) con la masa de galletas y luego la cortamos en rodajas de un cuarto de pulgada para hornear galletas con forma de círculos, cuadrados o rectángulos.

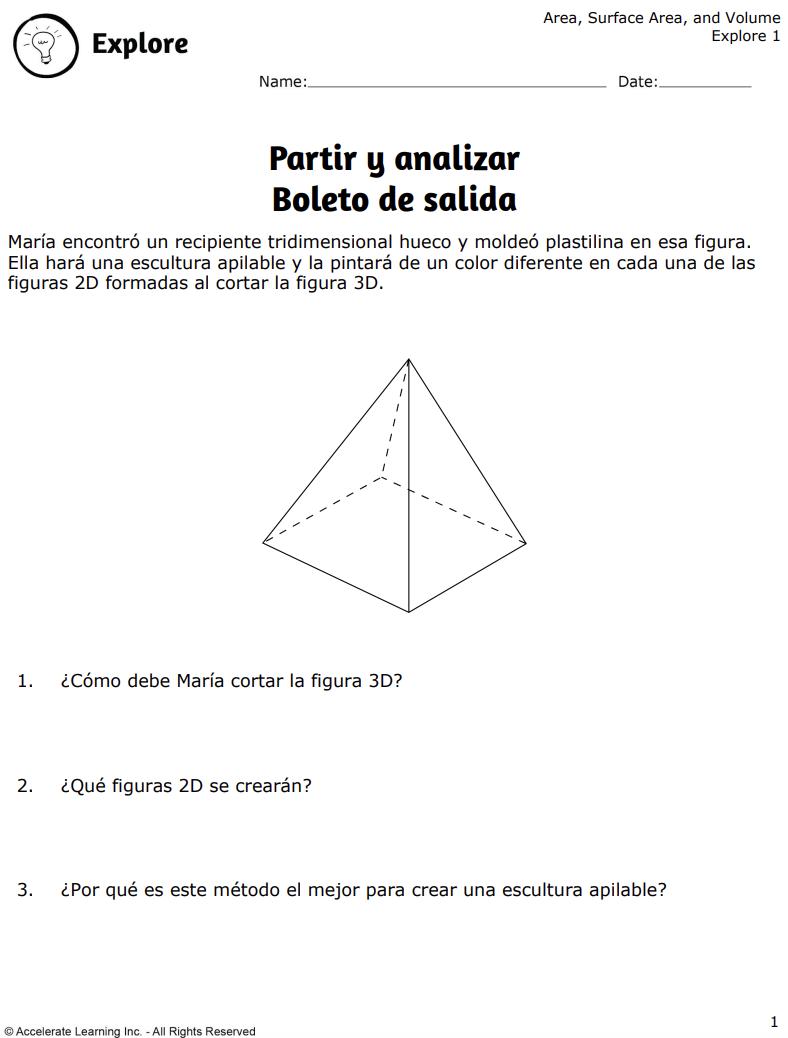
DESPUÉS DE LA EXPLORACIÓN

1. Haga que los estudiantes completen el boleto de salida para evaluar formativamente su comprensión del concepto.

2. Complete el esquema de anclaje como clase.

3. Haga que cada estudiante complete su libreta interactiva.

BOLETO DE SALIDA

EXPLORAR: EXPLORACIÓN 1

MUESTRA LO QUE SABES (PARTE 1)

APOYOS PEDAGÓGICOS

1. Anime a los estudiantes a utilizar el lenguaje académico a lo largo de la lección. Por ejemplo, los estudiantes con dificultades pueden referirse a un prisma rectangular como un rectángulo. Guíeles para que utilicen la terminología correcta. Puede decirles: «Veo que esto se parece a un rectángulo, pero explícame en qué se diferencia». (Un rectángulo es bidimensional, mientras que un prisma rectangular es tridimensional).

2. Puede que a algunos estudiantes les resulte difícil imaginar dibujos bidimensionales como formas tridimensionales. Permítales comparar los modelos de arcilla en 3D con los dibujos, comparando cara con cara, vértice con vértice y arista con arista.

3. Rete a los estudiantes a considerar cómo se podrían deslizar otras figuras en 3D y qué forma tendría la figura en 2D resultante.

APOYOS PARA LA ADQUISICIÓN DEL LENGUAJE

Antes de la Exploración, ayude a los estudiantes a aprender los términos direccionales horizontal y vertical con movimientos de las manos. Realice un juego en el que, cuando se diga un término direccional, tengan que hacer el movimiento de brazos correspondiente. A continuación, proporcione a los estudiantes imágenes de objetos colocados en diagonal, horizontal o vertical. Pida a los estudiantes que identifiquen y anoten tres objetos horizontales y tres verticales.

Utilice una estrategia de pensamiento en voz alta para modelar un lenguaje matemáticamente preciso mientras verbaliza la estrategia de un estudiante. Por ejemplo: «Veo que cortaste la pirámide derecha verticalmente porque cortar desde el ápice hasta la base es un corte vertical. El vértice está en la parte superior de la pirámide. La figura bidimensional que se crea es un triángulo».

Pida a los estudiantes que se turnen para leer en voz alta cada tarjeta de situación de corte de figuras tridimensionales y que lo platiquen antes de trabajar juntos para construir y cortar cada figura tridimensional. Antes de que escriban sus respuestas para las preguntas de reflexión, pida a los estudiantes que se turnen para entrevistarse entre sí, plantear ideas, dar retroalimentación y utilizar los términos matemáticos utilizados durante la exploración. Deja que trabajen juntos para escribir sus respuestas.

EXPLORAR: EXPLORACIÓN 2

LECCIÓN PEDAGÓGICA

EXPLORACIÓN 2: ÁREA

Estándar(es)

• Resolver problemas matemáticos y de la vida real que involucren la medida de ángulos, área, superficie y volumen. Resolver problemas matemáticos y de la vida real que involucren área, volumen y superficie de objetos bidimensionales y tridimensionales compuestos de triángulos, cuadriláteros, polígonos, cubos y prismas rectángulos.

• Aplicar y ampliar la comprensión previa de las operaciones con fracciones para sumar, restar, multiplicar y dividir números racionales. Resolver problemas matemáticos y del mundo real que involucren las cuatro operaciones con números racionales. (Nota: extender las reglas para manipular fracciones a fracciones complejas)

Ideas fundamentales

Poblaciones y muestras

Visualizar poblaciones

Modelos de probabilidad

Dibujos a escala

Formas en el mundo

Conexiones 2D y 3D

Relaciones angulares

DESCRIPCIÓN

Estándares para la práctica matemática

MP.1 Dar sentido a los problemas y perseverar en su resolución.

MP.6 Atender a la precisión.

MP.7 Buscar y hacer uso de la estructura.

Los estudiantes determinan las áreas de triángulos, cuadriláteros y otros polígonos y resuelven problemas del mundo real de un solo paso y de varios pasos que involucran el área.

MATERIALES

IMPRESO

• 1 diario del estudiante (por alumno)

• 1 boleto de salida (por estudiante)

• 1 juego de etiquetas de figuras 2D (por grupo)

REUTILIZABLE

• 1 bolsa resellable (por grupo)

PREPARACIÓN

• Planifique que los estudiantes trabajen en grupos de 4.

• Imprima el diario del estudiante y el boleto de salida para cada estudiante.

• Imprime un juego de tarjetas de figuras bidimensionales para cada grupo. Recorta las tarjetas y coloca cada juego de tarjetas en una bolsa con cierre para cada grupo. Si lo desea, imprima las tarjetas en cartulina y plastifíquelas para utilizarlas en el futuro.

• Para los estudiantes que necesiten más apoyo para recordar información, consulte nuestros elementos de «Ayudas complementarias» que incluyen: Redes tridimensionales y Objetos tridimensionales con líneas de puntos en la sección «Intervención».

Conexiones de pontenido Motores de investigación

CC1 Razonar con datos

CC2 Explorar cantidades cambiantes

CC3 Desarmar el todo, armar las partes

CC4 Descubrir la forma y el espacio

DI1 Dar sentido al mundo (comprender y explicar)

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Lea la siguiente situación a la clase: «La madre de María, la Sra. López, tiene un negocio de empaquetado y envío en su comunidad. A María le encanta ir allí después del colegio y ayudar poniendo etiquetas en los paquetes. La Sra. López ahorra dinero comprando etiquetas y pegándolas en las cajas con pegamento industrial. Hoy la Sra. López quiere que María determine las áreas de sus etiquetas de embalaje de diferentes formas para saber cuánto pegamento debe pedir en función de cuántas etiquetas utiliza al día de media. Tu trabajo es ayudar a María a encontrar el área de cada figura bidimensional de las diferentes etiquetas de envío que utiliza la Sra. López».

2. Ayuda a los estudiantes a acceder a la tarea haciéndoles las siguientes preguntas:

a. ¿Qué sabes ya sobre las etiquetas de embalaje?

b. ¿Qué recuerdas sobre el área?

3. Entrega un diario del estudiante a cada estudiante.

4. Entrega un juego de tarjetas de etiquetas de figuras bidimensionales a cada grupo.

5. Explica a los estudiantes que trabajarán con sus grupos para determinar las áreas de las diferentes figuras 2D de las etiquetas que utiliza la Sra. López. Diga a los estudiantes que, para hallar el área de cada figura, tendrán que dibujar la figura y mostrar cómo han hallado el área. A continuación, escribirán el área en las unidades correctas. (Tenga en cuenta que es importante que los estudiantes presten atención a las unidades).

EXPLORAR: EXPLORACIÓN 2

DIARIO DEL ESTUDIANTE

EXPLORAR: EXPLORACIÓN 2

6. Supervise y hable con los estudiantes según sea necesario para comprobar la comprensión utilizando las siguientes preguntas orientativas:

a. DOK-1 ¿Qué es importante saber sobre las figuras bidimensionales antes de medir para hallar el área? Necesitamos conocer las fórmulas para el área de triángulos, rectángulos, cuadrados y otros paralelogramos. También necesitamos conocer las unidades que se usan para medir la figura.

b. DOK-1 ¿Qué operaciones usas para determinar el área total de un polígono complejo? Usamos la multiplicación para hallar las áreas de figuras bidimensionales. Luego usamos la adición para hallar la suma de las áreas de las figuras bidimensionales, lo que nos da el área total de un polígono complejo.

c. DOK-2 ¿Qué figura bidimensional de etiquetas te pareció más difícil de calcular el área? ¿Por qué? Las respuestas pueden variar. Creo que la figura H fue la más difícil porque tuvimos que dividirla en tres rectángulos diferentes, calcular tres áreas diferentes y luego sumarlas. Nos llevó más tiempo resolver el área de la forma H.

7. Conceda a los estudiantes tiempo suficiente para dibujar cada forma de la etiqueta y calcular su área.

8. Conceda tiempo a los estudiantes para completar el diario del estudiante, incluidas las preguntas de reflexión.

9. Pida a los estudiantes que compartan sus estrategias y anímelos a que se hagan preguntas y establezcan conexiones. Anima a los estudiantes a notar las similitudes y diferencias entre las estrategias utilizadas para determinar las áreas de varios polígonos.

10. Después de la exploración, invita a la clase a una Charla de matemáticas para compartir sus observaciones y aprendizajes.

CHAT DE MATEMÁTICAS

• Elige una rutina de conversación estructurada para facilitar la siguiente pregunta:

○ DOK-2 ¿Cuál fue tu estrategia para hallar el área de los polígonos más complejos? Primero, dividimos los polígonos complejos en figuras simples. Después, hemos calculado el área de cada figura simple. Por último, sumamos las áreas. La suma de las áreas fue el área total del polígono.

• DOK-2 ¿Cambió el área total de un polígono complejo cuando se dividió en figuras simples de diferentes maneras? ¿En qué se parece esto a componer y descomponer un número? No, el área permaneció igual porque no cambió, sin importar cómo lo descompusimos en figuras simples para calcular el área. El número 12 se puede componer de 6 + 6 + 0 o 3 + 3 + 3 + 3 u 8 + 4, pero no importa cómo se componga 12, sigue siendo un total de 12.

• DOK-2 ¿Cómo podrías comprobar tu respuesta al hallar el área de una figura compleja? Podríamos ver si hay una forma alternativa de dividir la figura compleja en formas simples. Luego podríamos hallar el área de esas figuras simples, hallar la suma de esas áreas y ver si el área total es la misma que nuestra respuesta original.

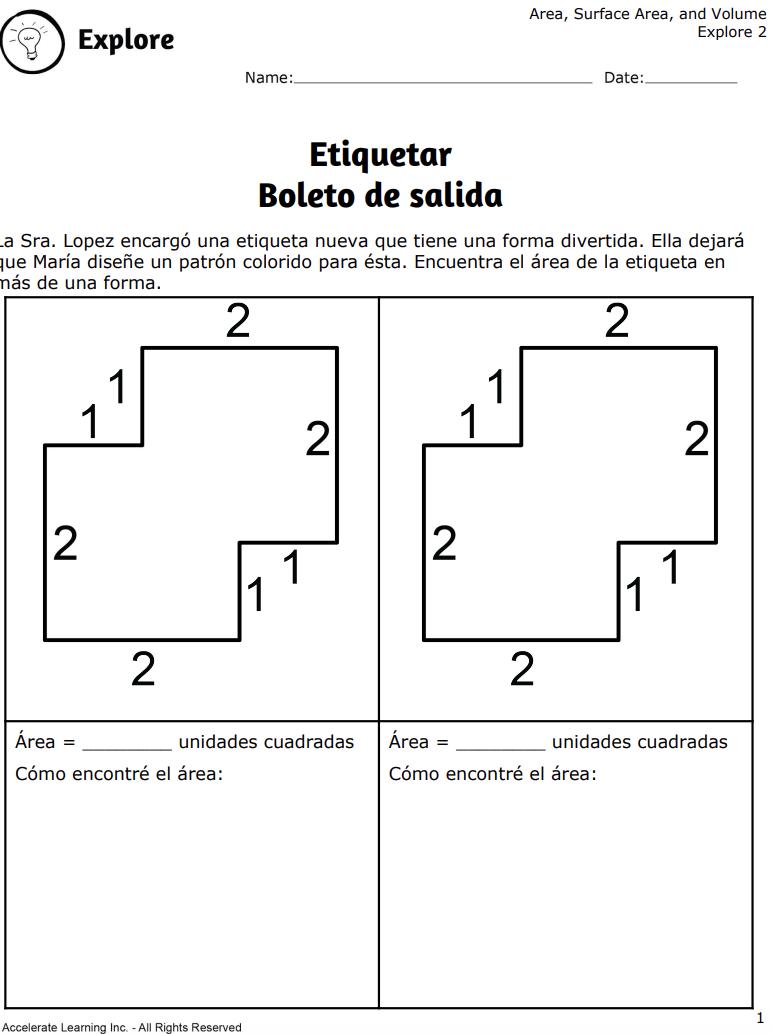
• DOK-2 ¿Cómo cambió el proceso de determinar el área de figuras con longitudes laterales que contienen fracciones? No cambió el proceso general. Añadió pasos adicionales porque a veces tenía que cambiar las fracciones a fracciones impropias.

• DOK-3 ¿Cuándo necesita la gente encontrar el área de figuras complejas en el mundo real, y por qué es importante saber cómo hacerlo? Da ejemplos concretos. Las respuestas pueden variar. Las personas necesitan colocar pisos en áreas que no son formas simples. Tienen que ser capaces de calcular la superficie para poder pedir la cantidad correcta de suelo. Si adivinan, pueden malgastar el dinero pidiendo demasiado suelo o quedarse sin suelo y no poder terminar el proyecto.

DESPUÉS DE LA EXPLORACIÓN

1. Pida a los estudiantes que completen el boleto de salida para evaluar formativamente su comprensión del concepto.

2. Completen el esquema de anclaje como clase.

3. Pida a cada estudiante que complete su libreta interactiva.

BOLETO DE SALIDA

APOYOS PEDAGÓGICOS

1. Para asegurar la comprensión del concepto de área por encima de la aplicación mecánica de la fórmula, señale que los cuadrados unitarios también se pueden utilizar para determinar el área porque el área es el espacio cubierto por una forma plana cerrada y se necesitan x cuadrados unitarios para cubrir el espacio. Los estudiantes pueden utilizar la estrategia de contar cuadrados para comprobar su trabajo. Sin embargo, plantee las limitaciones de esta estrategia porque a veces hay cuadrados parcialmente llenos y no obtendrán un área precisa.

2. Ayude a los estudiantes a conceptualizar la altura del paralelogramo diciéndoles que la base y la altura son siempre perpendiculares entre sí. Permítales identificar y marcar con un resaltador la base y la altura de la figura para ver y comprobar su perpendicularidad.

3. Si los estudiantes necesitan apoyo adicional con la multiplicación por 1/2, entonces repase que la multiplicación y la división son operaciones inversas, por lo que pueden dividir por 2 para resolver.

4. Como extensión, desafíe a los estudiantes a dibujar figuras con requisitos específicos, como un paralelogramo con un área de 18 unidades cuadradas. unidades o un triángulo con un área de 15 unidades cuadradas.

APOYOS LINGÜÍSTICOS

Invite a los estudiantes a presentar una de sus soluciones a la clase y a explicar qué pasos siguieron para resolver un problema y determinar el área de uno de los jardines.

Proporcione a los estudiantes ilustraciones o ejemplos de palabras y frases utilizadas en esta Exploración, como descomponer, paralelogramo, cuadrilátero, fórmula, triángulo, base, altura, y área. Modele la pronunciación correcta de cada frase y pida a los estudiantes que la repitan si es necesario.

Utilice una estrategia de pensamiento en voz alta para modelar un lenguaje matemáticamente preciso mientras verbaliza la estrategia de un estudiante. Por ejemplo: «Veo que has descompuesto la figura en un rectángulo y dos cuadrados».

Mientras los estudiantes trabajan y proponen ideas a sus grupos, resuma lo que oye y repita las ideas clave y el vocabulario mediante la entonación, el habla más lenta y las pistas visuales: descomponer, paralelogramo, cuadrilátero, fórmula, y área

EXPLORAR: EXPLORACIÓN 3

LECCIÓN PEDAGÓGICA

EXPLORACIÓN 3: ÁREA DE SUPERFICIE

Estándar(es)

• Resolver problemas matemáticos y de la vida real que involucren la medida de ángulos, área, superficie y volumen. Resolver problemas matemáticos y de la vida real que involucren área, volumen y superficie de objetos bidimensionales y tridimensionales compuestos de triángulos, cuadriláteros, polígonos, cubos y prismas rectángulos.

• Aplicar y ampliar la comprensión previa de las operaciones con fracciones para sumar, restar, multiplicar y dividir números racionales. Resolver problemas matemáticos y del mundo real que involucren las cuatro operaciones con números racionales. (Nota: extender las reglas para manipular fracciones a fracciones complejas Ideas fundamentales

Poblaciones y muestras

Visualizar poblaciones

Modelos de probabilidad

Dibujos a escala

Formas en el mundo

Conexiones 2D y 3D

Relaciones angulares

DESCRIPCIÓN

Estándares para la práctica matemática

MP.1 Dar sentido a los problemas y perseverar en su resolución.

MP.6 Atender a la precisión.

MP.7 Buscar y hacer uso de la estructura.

Los estudiantes encuentran el área de la superficie de cubos, prismas rectos y figuras tridimensionales complejas. Los estudiantes resuelven problemas del mundo real de un solo paso y de varios pasos que involucran el área de la superficie.

MATERIALES

IMPRESOS

• 1 diario del estudiante (por estudiante)

• 1 boleto de salida (por estudiante)

• 1 juego de tarjetas de caja de envío (por grupo)

REUTILIZABLE

• 1 bolsa resellable (por grupo)

Conexiones de pontenido Motores de investigación

CC1 Razonar con datos

CC2 Explorar cantidades cambiantes

CC3 Desarmar el todo, armar las partes

CC4 Descubrir la forma y el espacio

PREPARACIÓN

• Prevea que los estudiantes trabajen en grupos de 4.

• Imprima el diario del estudiante y el boleto de salida para cada estudiante.

• Imprime un juego de tarjetas de caja de envío para cada grupo. Recorta las tarjetas y coloca un juego de tarjetas en una bolsa con cierre para cada grupo. Si lo desea, imprima las tarjetas en cartulina y plastifíquelas para utilizarlas en el futuro.

• Para los estudiantes que necesiten más apoyo para recordar información, consulte nuestros elementos de «Ayudas complementarias» que incluyenRedes tridimensionales y Objetos tridimensionales con líneas de puntos en la sección «Intervención».

DI1 Dar sentido al mundo (comprender y explicar)

DIARIO DEL ESTUDIANTE

EXPLORAR: EXPLORACIÓN 3

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Lea la siguiente situación a la clase: «La Sra. López recibió comentarios de clientes de que algunas de sus cajas se rompían y se deshacían si se mojaban durante el envío. Para proteger sus cajas y los bienes de sus clientes, creó un producto en aerosol para impermeabilizar sus cajas. Una botella cubre 20.000 pulgadas cuadradas de superficie. La Sra. López pidió a María que le ayudara a determinar la superficie de los seis tamaños diferentes de cajas de envío que vende. La Sra. López puede entonces hacer un seguimiento de las cantidades de cajas que vende mensualmente para saber cuántas botellas de spray impermeabilizante necesita fabricar mensualmente. Tu tarea consiste en ayudar a María a calcular la superficie de cada caja de cartón que vende la Sra. López».

2. Ayude a los estudiantes a acceder a la tarea haciéndoles las siguientes preguntas guía:

a. ¿Qué saben ya sobre el uso de productos en aerosol?

b. ¿Qué recuerdan sobre el área superficial?

3. Entregue un diario del estudiante a cada estudiante.

4. Entregue un juego de tarjetas de cajas de envío a cada grupo.

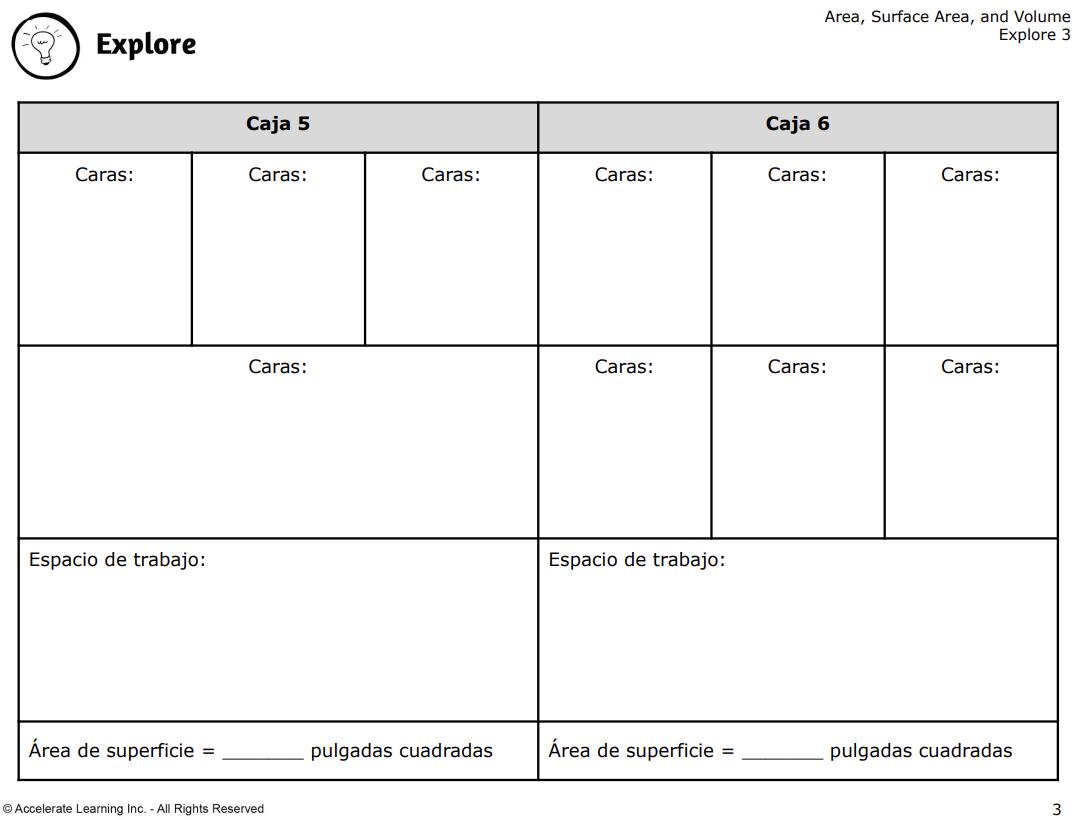
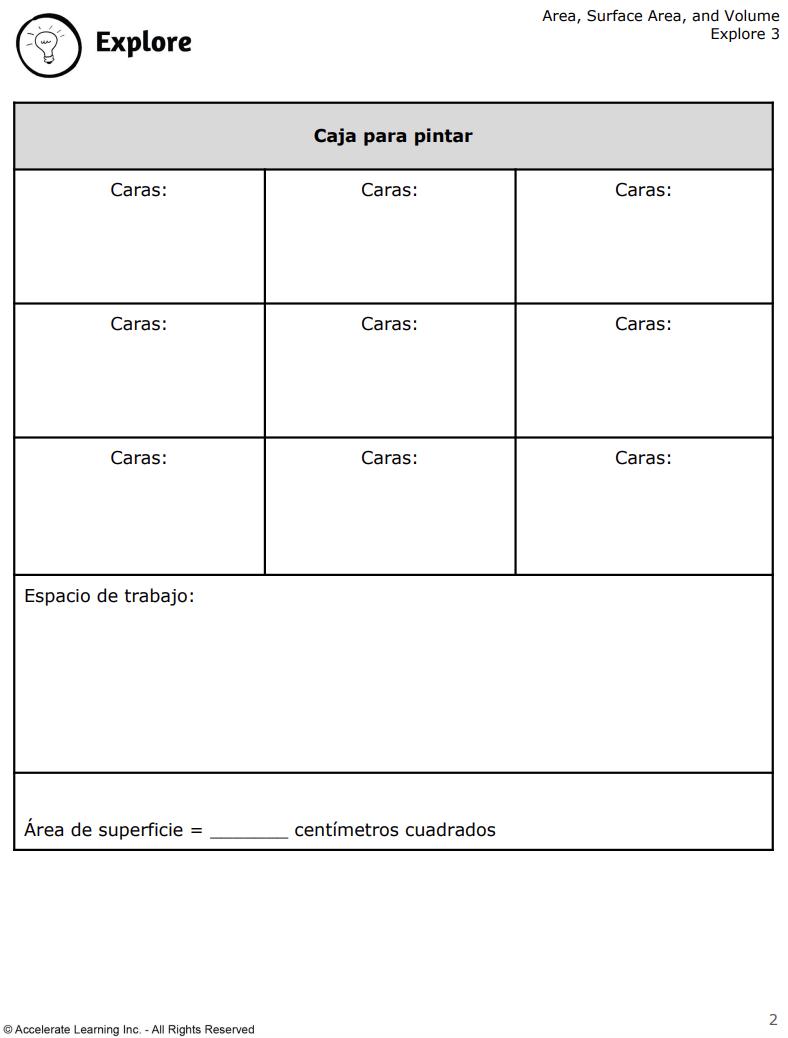
5. Explique a los estudiantes que trabajarán en sus pequeños grupos para determinar las áreas superficiales de las seis cajas de envío diferentes que vende la Sra. López. Diga a los estudiantes que, para hallar la superficie de cada caja, tendrán que dibujar la cara de cada caja, etiquetar las dimensiones y, a continuación, hallar las áreas. Los estudiantes hallarán la superficie total de cada caja combinando las áreas de cada cara.

6. Supervise y hable con los estudiantes según sea necesario para comprobar la comprensión y haga la siguiente pregunta:

a. DOK-1 ¿Cómo afecta el corte al prisma rectangular? No importa cómo se corte, un prisma rectangular siempre mostrará un rectángulo (que también podría ser un cuadrado, que es un rectángulo especial).

7. Dé tiempo suficiente para dibujar cada tipo de cara de caja, calcular su área y determinar el área de superficie de cada caja.

8. Dé tiempo a los estudiantes para completar el Diario del estudiante, incluyendo las preguntas de reflexión.

9. Pida a los estudiantes que compartan sus estrategias y anímeles a que se hagan preguntas y establezcan conexiones. Anime a los estudiantes a observar las similitudes y diferencias entre las estrategias utilizadas para determinar el área de la superficie.

10. Después de la Exploración, invite a la clase a una Charla de matemáticas para compartir sus observaciones y aprendizajes.

EXPLORAR: EXPLORACIÓN 3

CHARLA DE MATEMÁTICAS

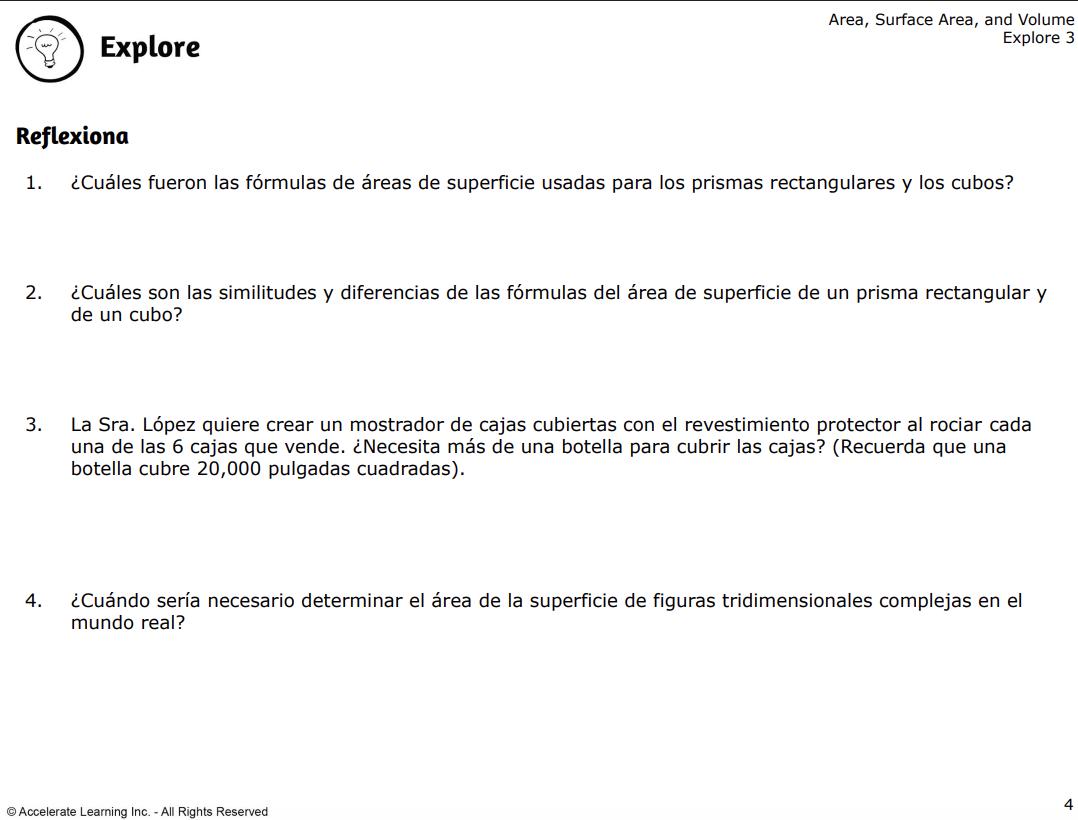
• DOK-1 ¿Cuáles fueron las fórmulas de área de superficie que usaste para prismas rectangulares y cubos? Las estrategias pueden variar. La fórmula del prisma rectangular es 2(base + cara + cara). Cada base o cara es un rectángulo, por lo que la fórmula para hallar el área de cada base o cara es A = lw. La fórmula del cubo es 6s2 .

• Elige una rutina de conversación estructurada para facilitar la siguiente pregunta:

○ DOK-2 ¿Cuáles son las similitudes y diferencias de las fórmulas de área de superficie para un prisma rectangular y un cubo? Ambas fórmulas encuentran la suma del área de las 6 caras. Como todas las aristas y caras de un cubo son congruentes, para hallar el área de la superficie, simplemente eleva al cuadrado la longitud de una arista y multiplícala por seis.

• DOK-2 En el mundo real, ¿cuándo podría la gente necesitar determinar el área de la superficie de figuras tridimensionales complejas? Las respuestas pueden variar. Cuando alguien necesita saber cuánta pintura comprar para pintar juegos tridimensionales, como cubos para escalar o túneles de prismas rectangulares, necesitaría saber cómo determinar el área de la superficie.

DESPUÉS DE LA EXPLORACIÓN

1. Haz que los estudiantes completen el boleto de salida para evaluar formativamente su comprensión del concepto.

2. Completa la tabla de anclaje como clase.

3. Haz que cada estudiante complete su libreta interactiva.

BOLETO DE SALIDA

GRADO

EXPLORAR: EXPLORACIÓN 3

MUESTRA LO QUE SABES (PARTE 3)

APOYOS PEDAGÓGICOS

1. Antes de la exploración, puede ser beneficioso repasar con los estudiantes los conocimientos previos, como la forma de encontrar las áreas de rectángulos (incluyendo cuadrados), círculos y triángulos.

2. Anime a los estudiantes a tomarse su tiempo cuando dibujen cada cara de la caja y etiqueten las dimensiones antes de encontrar el volumen. Anímelos a leer el problema cuidadosamente, dibujar y etiquetar sus diagramas en consecuencia y luego resolver.

3. Si los estudiantes necesitan apoyo adicional para entender que las caras triangulares representan las bases de un prisma triangular, entonces pídales que sombreen o resalten las bases triangulares.

4. Si los estudiantes necesitan apoyo adicional para saber si deben etiquetar sus unidades como pulgadas o pulgadas cuadradas, entonces aborde brevemente este tema durante la charla de matemáticas. Recuérdeles que las unidades cuadradas son para dos dimensiones (como largo por ancho).

5. Como extensión, reúna cajas de diferentes tamaños y haga que los estudiantes encuentren sus áreas de superficie.

APOYOS LINGÜÍSTICOS

Dedique tiempo a repasar lo que los estudiantes recuerdan sobre el área de una figura y cómo se mide. Aborde los diferentes significados de la palabra net, y aclare el significado en el contexto de las figuras y la geometría.

Muestre las siguientes estructuras de frases para que los estudiantes las utilicen a lo largo de la exploración:

• La cara tiene forma de _____, por lo que puedo hallar su área mediante ________.

• La red se puede utilizar para hallar el área de la superficie porque ________.

• La fórmula para el área de un _____ es ________.

Coloque a los estudiantes en grupos de cinco y asigne a cada miembro del grupo una red sobre la que realizar una presentación. Los estudiantes deben escribir frases sobre los atributos y la superficie de sus redes, pedir a un miembro del grupo que revise su trabajo y les ayude a añadir detalles y, a continuación, presentar sus redes a la clase.

EXPLORAR: EXPLORACIÓN 4

LECCIÓN PEDAGÓGICA

EXPLORACIÓN 4: VOLUMEN

Estándar(es)

• Resolver problemas matemáticos y de la vida real que involucren la medida de ángulos, área, superficie y volumen. Resolver problemas matemáticos y de la vida real que involucren área, volumen y superficie de objetos bidimensionales y tridimensionales compuestos de triángulos, cuadriláteros, polígonos, cubos y prismas rectángulos.

• Aplicar y ampliar la comprensión previa de las operaciones con fracciones para sumar, restar, multiplicar y dividir números racionales. Resolver problemas matemáticos y del mundo real que involucren las cuatro operaciones con números racionales. (Nota: extender las reglas para manipular fracciones a fracciones complejas)

Ideas fundamentales

Poblaciones y muestras

Visualizar poblaciones

Modelos de probabilidad

Dibujos a escala

Formas en el mundo

Conexiones 2D y 3D

Relaciones angulares

DESCRIPCIÓN

Estándares para la práctica matemática

MP.1 Dar sentido a los problemas y perseverar en su resolución.

MP.6 Atender a la precisión.

MP.7 Buscar y hacer uso de la estructura.

Conexiones de pontenido

CC1 Razonar con datos

CC2 Explorar cantidades cambiantes

CC3 Desarmar el todo, armar las partes

CC4 Descubrir la forma y el espacio

PREPARACIÓN

Motores de investigación

DI1 Dar sentido al mundo (comprender y explicar)

Los estudiantes encuentran el volumen de cubos, prismas rectos y figuras tridimensionales complejas y resuelven problemas del mundo real de un solo paso y de varios pasos que involucran el volumen.

MATERIALES

IMPRESO

• 1 diario del estudiante (por estudiante)

• 1 boleto de salida (por estudiante)

• 1 juego de tarjetas de cajas de envío (por grupo)

REUTILIZABLE

• 1 bolsa resellable (por grupo)

• Prevea que los estudiantes trabajen en grupos de 4.

• Imprima el diario del estudiante y el boleto de salida para cada estudiante.

• Imprime un juego de tarjetas de caja de envío para cada grupo. Recorta las tarjetas y coloca un juego de tarjetas en una bolsa con cierre para cada grupo. Si lo desea, imprima las tarjetas en cartulina y plastifíquelas para utilizarlas en el futuro.

• Para los estudiantes que necesiten más apoyo para recordar información, consulte nuestros elementos de «Ayudas complementarias» que incluyen Redes tridimensionales y Objetos tridimensionales con líneas de puntos en la sección «Intervención».

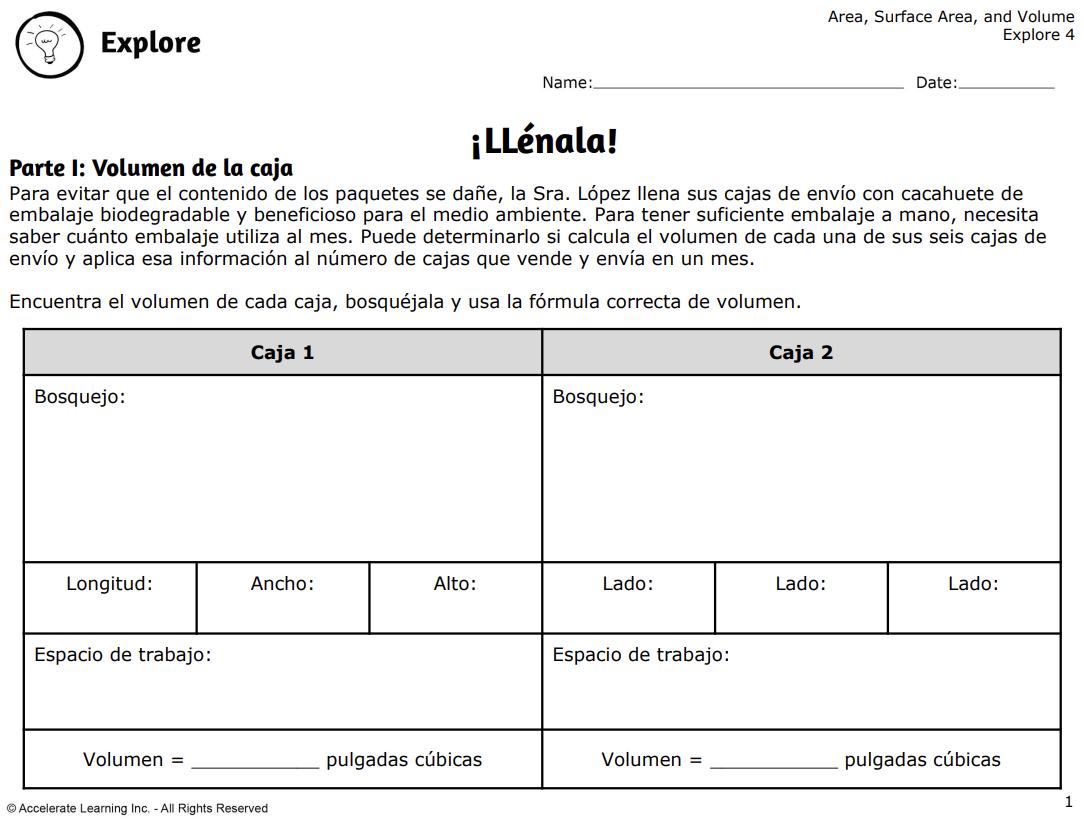
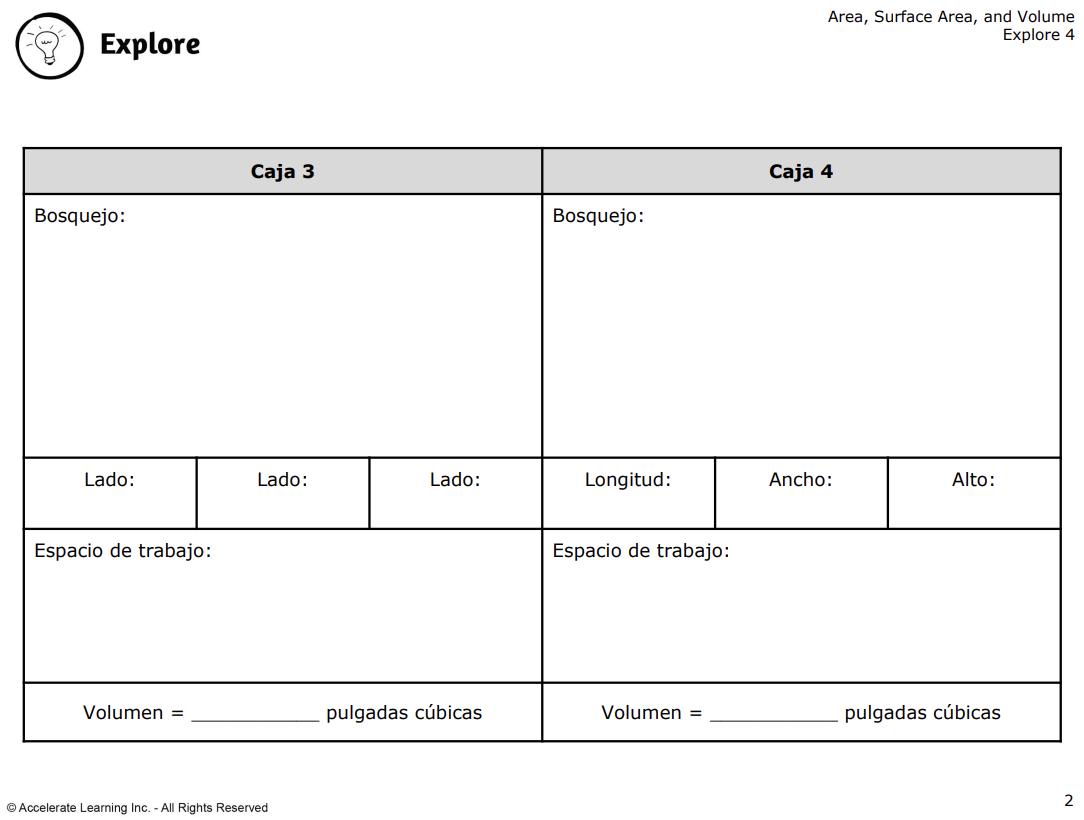
DIARIO DEL ESTUDIANTE

EXPLORAR: EXPLORACIÓN 4

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

PARTE I

1. Lea la siguiente situación a la clase: «Para evitar que se dañe el contenido de los paquetes, la Sra. López rellena sus cajas de envío con cacahuetes de embalaje biodegradables y respetuosos con el medio ambiente. Para hacer un pedido, la Sra. López necesita saber cuántos cacahuetes de embalaje utiliza al mes. Puede determinarlo calculando el volumen de cada una de sus seis cajas de envío y aplicando esos datos al número de cajas que vende y envía mensualmente. Su tarea hoy es ayudar a María a determinar el volumen de cada caja de envío que la Sra. López vende en su tienda».

2. Ayude a los estudiantes a acceder a la tarea haciéndoles las siguientes preguntas:

a. ¿Qué saben ya sobre el uso de cacahuetes de embalaje?

b. ¿Qué recuerdan sobre el volumen?

3. Entregue un diario del estudiante a cada estudiante y una bolsa con las tarjetas de cajas de envío a cada grupo.

4. Explique a los estudiantes que trabajarán en sus grupos para determinar los volúmenes de las seis cajas de envío diferentes que vende la sra. López. Diga a los estudiantes que, para hallar el volumen de cada forma, tendrán que dibujar cada caja, descomponiendo las cajas que son figuras tridimensionales complejas en cubos o prismas rectangulares. Los estudiantes hallarán el volumen total, combinando los volúmenes de las figuras tridimensionales complejas cuando sea necesario. Pueden decidir en grupo cómo realizar mejor esta tarea o probar varios métodos y comprobar sus respuestas.

5. Supervise y hable con los estudiantes según sea necesario para comprobar la comprensión utilizando las siguientes preguntas orientativas:

a. DOK-2 ¿Existen varias formas de hallar el volumen de cajas de envío con forma de cubo? No, s - s - s es exactamente igual que l - w - h ya que todas las aristas son iguales.

b. DOK-1 ¿Te resulta más fácil hallar la superficie de prismas rectangulares o de cubos? ¿Por qué? Un cubo es un tipo de prisma rectangular. Creemos que es igual de difícil porque, sea como sea, estamos multiplicando 3 números, ya sea l - w - h o s - s - s

c. DOK-2 ¿Qué caja o cajas te han parecido más difíciles de calcular el volumen? ¿Por qué? Las cajas 5 y 6 nos parecieron las más difíciles porque eran figuras tridimensionales complejas. Tuvimos que dividirlas en dos figuras tridimensionales y hallar los volúmenes de ambas figuras. Luego tuvimos que calcular la suma de ambos volúmenes. Nos llevó el doble de tiempo porque tuvimos que hacer el doble de pasos.

6. Dé a los estudiantes tiempo suficiente para dibujar cada caja; etiquetar su longitud, ancho y altura; y determinar el volumen de cada caja.

7. Dé tiempo a los estudiantes para completar la parte I del diario del estudiante, incluidas las preguntas de reflexión.

PARTE II

1. Lea la siguiente situación a la clase: «Cuando los clientes entran en la tienda, la Sra. López a menudo tiene que resolver problemas para encontrar la mejor manera de empaquetar los artículos. Debe determinar qué tamaño de caja utilizar y el volumen de cacahuetes de embalaje necesarios. Su trabajo hoy será ayudar a la Sra. López y a María a resolver problemas de embalaje y envío que impliquen volúmenes de cajas y volúmenes de cacahuetes de embalaje».

2. Explique a los estudiantes que trabajarán con sus pequeños grupos para determinar soluciones a problemas complejos que impliquen dimensiones y volúmenes de cajas de embalaje y envío. Utilizarán el sentido común, las fórmulas de volumen, las cuatro operaciones y las estrategias para resolver de la mejor manera posible las solicitudes de los clientes del mundo real.

3. Supervise y hable con los estudiantes según sea necesario para comprobar la comprensión mediante el uso de las siguientes preguntas orientadoras:

a. DOK-2 ¿Por qué encontrar el volumen de una caja de embalaje y envío no es equivalente al volumen de cacahuetes de embalaje necesarios para esa caja? Los cacahuetes de embalaje no llenarán toda la caja porque lo que se envíe ocupará parte del espacio dentro de la caja.

b. DOK-1 ¿Qué estrategia utilizaste? Calculamos el volumen total de la caja de envío. Hallamos el volumen del artículo que se envía. Resté el volumen del artículo enviado del volumen total de la caja. La diferencia era la solución, el volumen de cacahuetes necesarios.

c. DOK-3 ¿Cuándo puede ser difícil calcular el volumen de cacahuetes necesarios para enviar algo en el mundo real? ¿Por qué? Las respuestas pueden variar. Sería difícil calcular el volumen necesario de cacahuetes de embalaje cuando no se puede determinar el volumen del artículo que se envía (como la ropa en una pila blanda).

4. Dé a los estudiantes tiempo suficiente para dibujar cada caja, hallar el volumen de cada una y encontrar la diferencia entre el volumen de la caja de embalaje/envío y el volumen del artículo que se envía.

5. Dé tiempo a los estudiantes para que completen la parte II del Diario del estudiante y sus preguntas de reflexión.

6. Pida a los estudiantes que compartan sus estrategias y anímeles a que se hagan preguntas y establezcan conexiones. Anime a los estudiantes a notar las similitudes y diferencias entre las estrategias utilizadas para determinar los volúmenes de las figuras.

7. Después de la exploración, invite a la clase a una charla de matemáticas para compartir sus observaciones y aprendizajes.

DIARIO DEL ESTUDIANTE

EXPLORAR: EXPLORACIÓN 4

BOLETO DE SALIDA

CHARLA DE MATEMÁTICAS

• DOK-1 ¿Cuáles fueron las fórmulas de volumen que utilizaste para los prismas rectangulares y los cubos?

Prisma rectangular: l - w - h

Cubo: s3 o s - s - s o l - w - h

• DOK-2 María le dice a su madre que calcular el volumen de una caja no explica realmente el volumen de cacahuetes que utilizará una caja cuando se envíe algo dentro de ella. ¿Tiene razón María? Explica lo que quiere decir. María tiene razón. Lo que quiere decir es que cuando algo se envía dentro de la caja, ocupa parte del espacio/ volumen que se habría llenado con los cacahuetes de embalaje, por lo que se necesitan menos cacahuetes de embalaje de los que llenarían el volumen total de la caja.

• Elige una rutina de conversación estructurada para facilitar la siguiente pregunta:

○ DOK-3 ¿Cómo encontrarías el volumen de cacahuetes de embalaje necesarios para una caja grande en forma de prisma rectangular que contiene otra caja más pequeña en forma de cubo? En primer lugar, hallaría el volumen de la caja más grande. l - w - h me da el volumen de una caja en forma de prisma rectangular. A continuación, hallaría el volumen de la caja que se coloca dentro de la caja de envío utilizando s3 o s - s - s. Por último, restaría el volumen de la caja que se envía del volumen total de la caja de envío. La diferencia es el volumen de cacahuetes de embalaje necesarios para llenar la caja de embalaje y proteger el contenido de la caja durante el envío.

• DOK-3 En el mundo real, ¿por qué la gente podría necesitar conocer el volumen de prismas rectangulares o cubos? Las respuestas pueden variar. La gente necesita saber el volumen de una piscina que tiene la forma de un prisma rectangular para saber cuántos pies cúbicos de agua contiene. Es posible que necesiten saber esto para saber cuánto tiempo llevará llenar la piscina o cuánto costará llenarla.

DESPUÉS DE LA EXPLORACIÓN

1. Haga que los estudiantes completen el boleto de salida para evaluar formativamente su comprensión del concepto.

2. Completen el esquema de anclaje como clase.

3. Haga que cada estudiante complete su libreta interactiva.

4. Regrese a la sección «Captar interés» e instruya a los estudiantes para que usen sus habilidades recién adquiridas para completar exitosamente la actividad.

EXPLORAR: EXPLORACIÓN 4

APOYOS PEDAGÓGICOS

1. Antes de la exploración, repase los atributos de los prismas rectangulares y los cubos con la clase y pida a los estudiantes que compartan cualquier cosa que ya sepan sobre el volumen.

2. Aclare a los estudiantes que puedan pensar que el volumen de un prisma es el área total de las superficies visibles pidiéndoles que calculen su versión del volumen, presentándoles el volumen real y evaluando las razones de la discrepancia.

3. Para abordar la idea errónea de que el volumen se compone del número total de cubos unitarios visibles cuando se dibujan en papel, haga hincapié en cómo el modelo físico de cubos que se unen se relaciona con el dibujo y cuáles son las implicaciones para el volumen. (Hay cubos que no podemos ver cuando dibujamos el prisma, pero sabemos que están ahí, especialmente cuando miramos el modelo físico).

4. Anime a los estudiantes a compartir sus observaciones sobre el volumen. Por ejemplo, pueden observar que la longitud y la anchura podrían intercambiarse y no afectar al volumen total, o un estudiante puede observar que puede multiplicar el número de cubos unitarios de la capa base por la altura para determinar el volumen total.

5. Como ampliación, anime a los estudiantes a construir modelos con dimensiones variables y a utilizar esas dimensiones para calcular el volumen de la figura utilizando las fórmulas. A continuación, pueden desmontar sus modelos y compararlos para ver si el número de cubos del modelo coincide con el volumen que encontraron utilizando las fórmulas.

APOYOS LINGÜÍSTICOS

Proporcione ejemplos y aclare lo que significa que un prisma rectangular tenga longitud, anchura y altura.

Al leer las palabras largo, ancho, alto, área, y volumen, usar gestos con las manos para aclarar el significado.

Aclare los significados matemáticos de los siguientes términos clave haciendo hincapié en ellos durante la Exploración: longitud, anchura, altura, área, volumen, y fórmula.

Asigne a cada grupo un problema de cajas de envío para que se conviertan en expertos en él. Haz que los estudiantes preparen una presentación en la que expliquen cómo utilizar la fórmula para hallar el volumen de la caja. Cada estudiante debe tener un turno de palabra. Anima a los estudiantes a utilizar un lenguaje matemático preciso en sus explicaciones. Pueden prepararse escribiendo un guión o anotando sus puntos clave en fichas.

Aclare qué significa utilizar una fórmula en matemáticas. Asegúrese de indicar el sustantivo asociado a cada parte de la fórmula, incluidas las unidades utilizadas, para ayudar a los estudiantes a comprender lo que representan las letras.

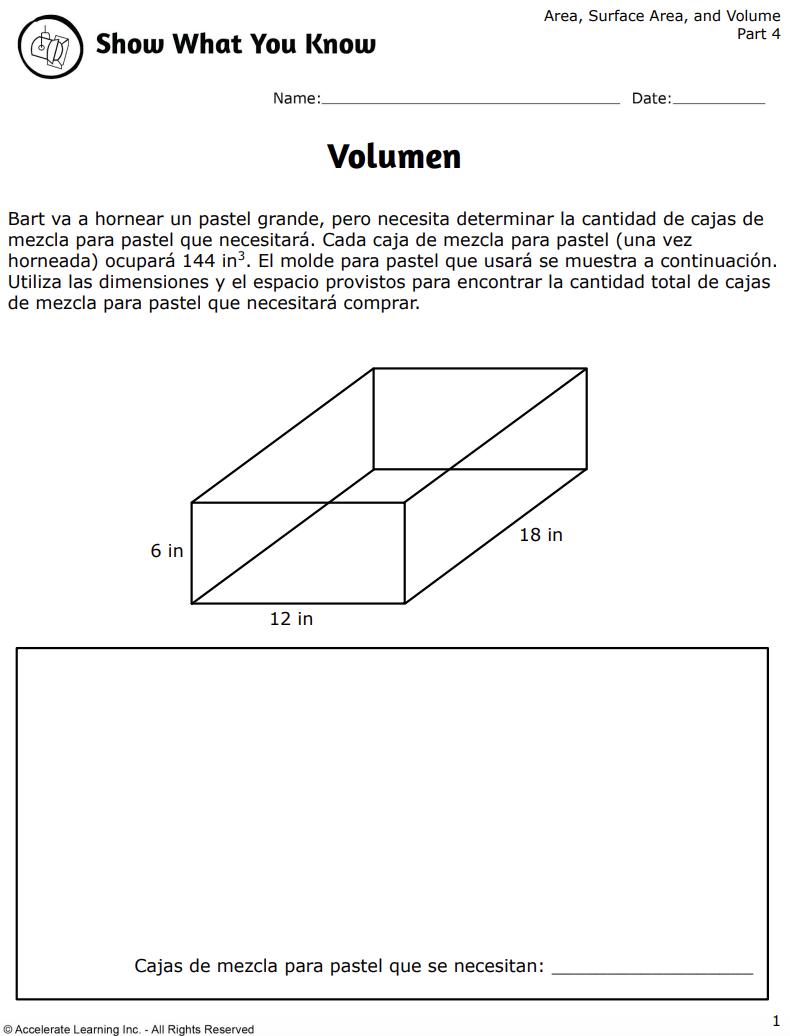
LO QUE SABES (PARTE 4)

MUESTRA

EXPLICAR: ESQUEMA DE ANCLAJE

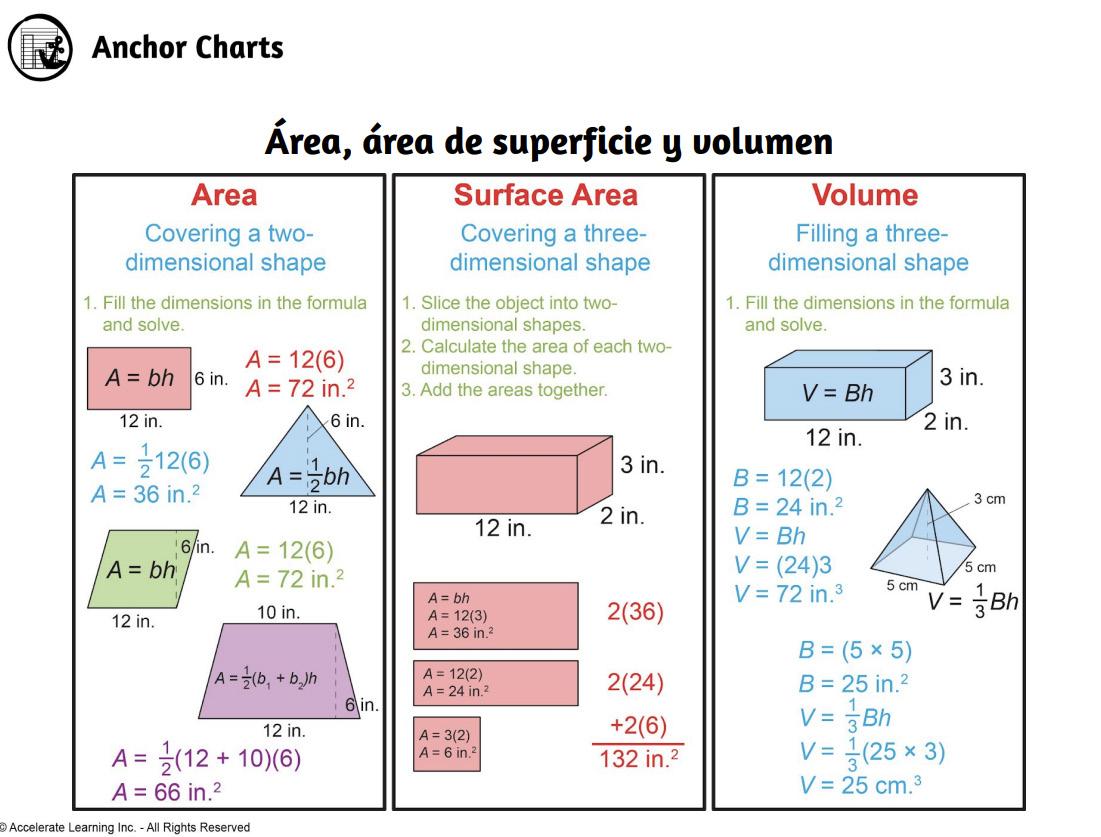
EJEMPLO DE ESQUEMA DE ANCLAJE

CONSOLIDAR EL APRENDIZAJE DEL ESTUDIANTEESTUDIANTES

ESQUEMA DE ANCLAJE

DESCRIPCIÓN

Este gráfico de anclaje destaca las ideas principales del alcance. Esta es una herramienta para apoyar la instrucción y anclar el aprendizaje de los estudiantes a lo largo del alcance.

MATERIALES

• 1 hoja de papel cuadriculado

• 1 juego de marcadores multicolores

PREPARACIÓN

● Imprima el ejemplo de esquema de anclaje (opcional).

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. El ejemplo de esquema de anclaje puede usarse como referencia antes de crear el esquema de anclaje de la clase con los estudiantes. La creación de un esquema de anclaje debe estar dirigida por los estudiantes para promover que se apropien de su aprendizaje.

2. A medida que los estudiantes trabajen en el alcance, colaboren para añadir piezas al esquema de anclaje. Formule las siguientes preguntas:

a. ¿Qué estrategia utilizamos para resolver este problema?

b. ¿Qué vocabulario necesitamos conocer para poder resolver este problema?

3. Continúe añadiendo habilidades o estrategias importantes aprendidas después de cada exploración para resaltar el contenido importante.

4. Explique a los estudiantes que pueden utilizar este esquema como herramienta de apoyo para su aprendizaje. Los estudiantes también pueden pegar una copia del esquema de anclaje en sus cuadernos para utilizarla como referencia durante todo el año.

5. Algunos esquema de anclaje sólo se mostrarán durante ese alcance o grupo de alcances, mientras que otras permanecerán expuestas durante todo el año escolar.

EXPLICAR: LIBRETA INTERACTIVA

DOCUMENTAR EL APRENDIZAJE DE LOS ESTUDIANTES

LIBRETA INTERACTIVA

DESCRIPCIÓN

Los estudiantes toman notas, expresan ideas y/o procesan la información presentada en clase utilizando la actividad y el cuaderno.

MATERIALES

IMPRESO

● 1 folleto del estudiante (por estudiante)

PREPARACIÓN

● Imprima una copia del folleto del estudiante por alumno.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Prepare una libreta interactiva con un cuaderno de espiral o de composición para cada estudiante. Los estudiantes pueden utilizar las primeras páginas para crear una tabla de contenidos con números de página para realizar un seguimiento de las actividades.

2. En el folleto del estudiante se ofrecen instrucciones para cada actividad.

3. Dé tiempo a los estudiantes para que completen la actividad y peguen las piezas en sus cuadernos interactivos.

4. Las libretas ineractivas pueden utilizarse como referencia para los estudiantes durante el trabajo independiente y pueden enviarse a casa al final del año como registro de su aprendizaje.

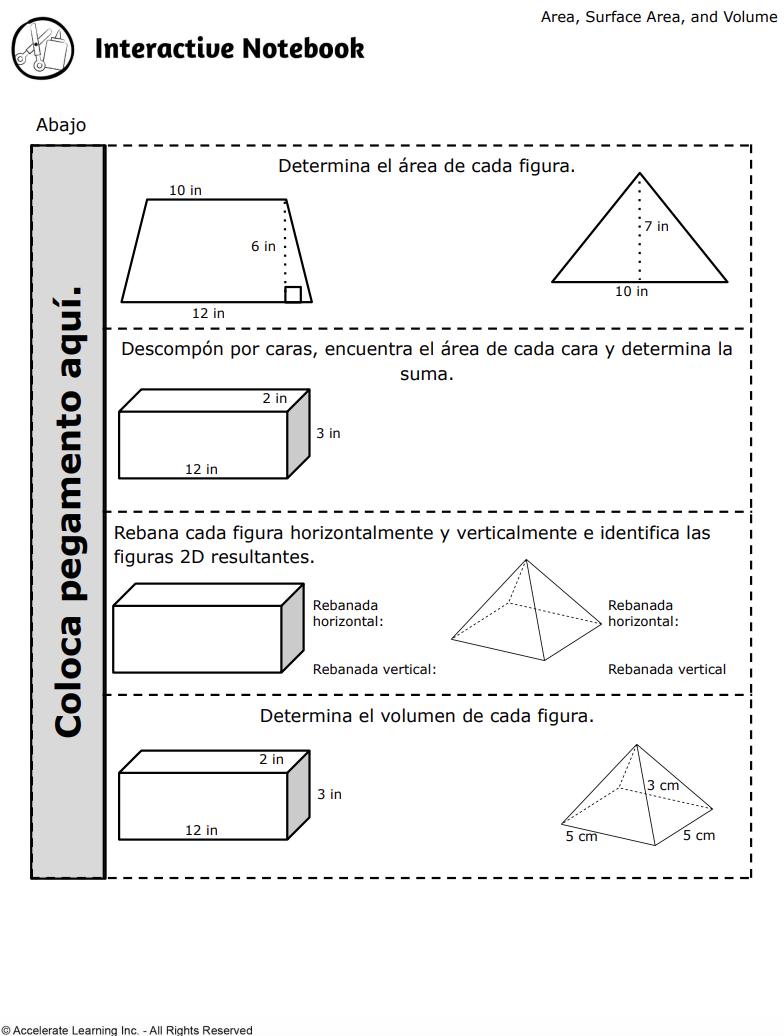
DESCRIPCIÓN

Los estudiantes tienen la oportunidad de utilizar sus conocimientos lingüísticos y culturales previos para apoyar las conexiones con nuevas habilidades, vocabulario y conceptos en sus niveles de competencia.

MATERIALES

IMPRESO

• 1 folleto del estudiante en el nivel de competencia (por estudiante)

PREPARACIÓN

• Prepare a los estudiantes para trabajar con compañeros cuando sea necesario.

• Determine el nivel de competencia en inglés de cada estudiante.

• Imprima un folleto del estudiante para cada estudiante según su nivel de inglés.

• Permita que los estudiantes tengan acceso al vocabulario ilustrado para este alcance.

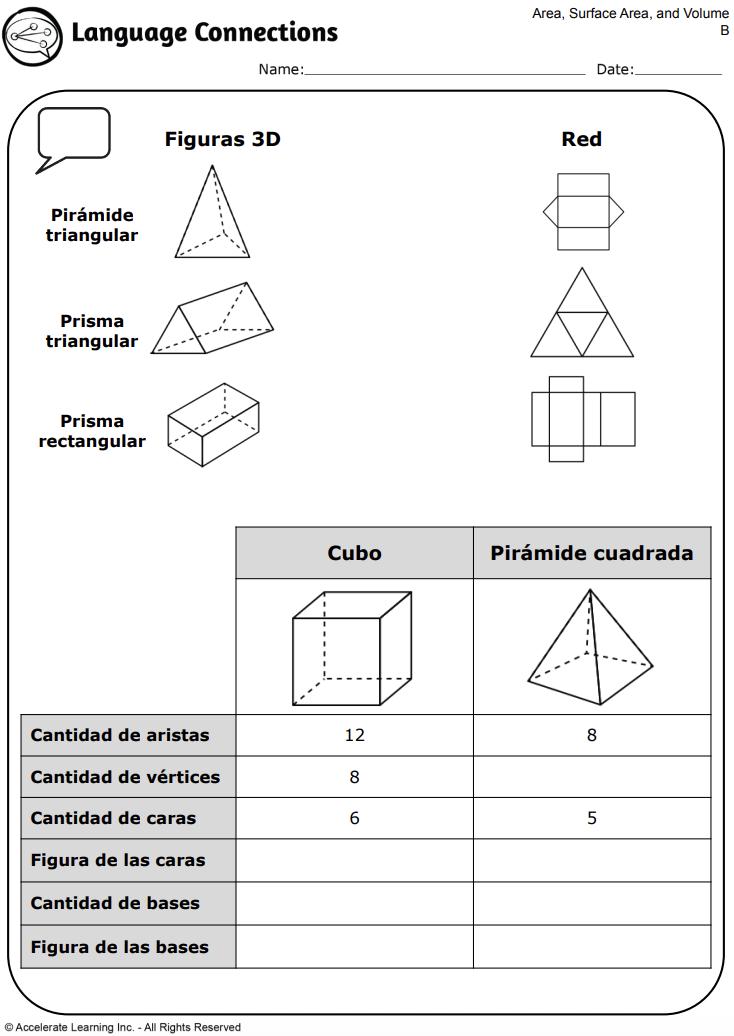
PRINCIPIANTE FOLLETO DEL ESTUDIANTE

EXPLICAR: CONEXIONES LINGÜÍSTICAS

APOYO PARA LOS ESTUDIANTES MULTILINGÜES

CONEXIONES LINGÜÍSTICAS

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

4 Distribuya un folleto del estudiante a cada estudiante según su nivel de inglés.

5 Utilice las instrucciones para las partes de comprensión oral, expresión oral, lectura y escritura. Use gestos, señale objetos y elementos visuales, según proceda. Consulte las indicaciones para obtener sugerencias.

6 Deje tiempo a los estudiantes para que piensen con sus vecinos antes de responder.

7 Anime a los estudiantes a perseverar en su pensamiento y a utilizar herramientas y modelos matemáticos.

8 Invite a los estudiantes a responder adecuadamente a cada dominio lingüístico.

9 Haga que los estudiantes utilicen la página final del folleto del estudiante para formar conexiones entre los conceptos matemáticos y el mundo real.

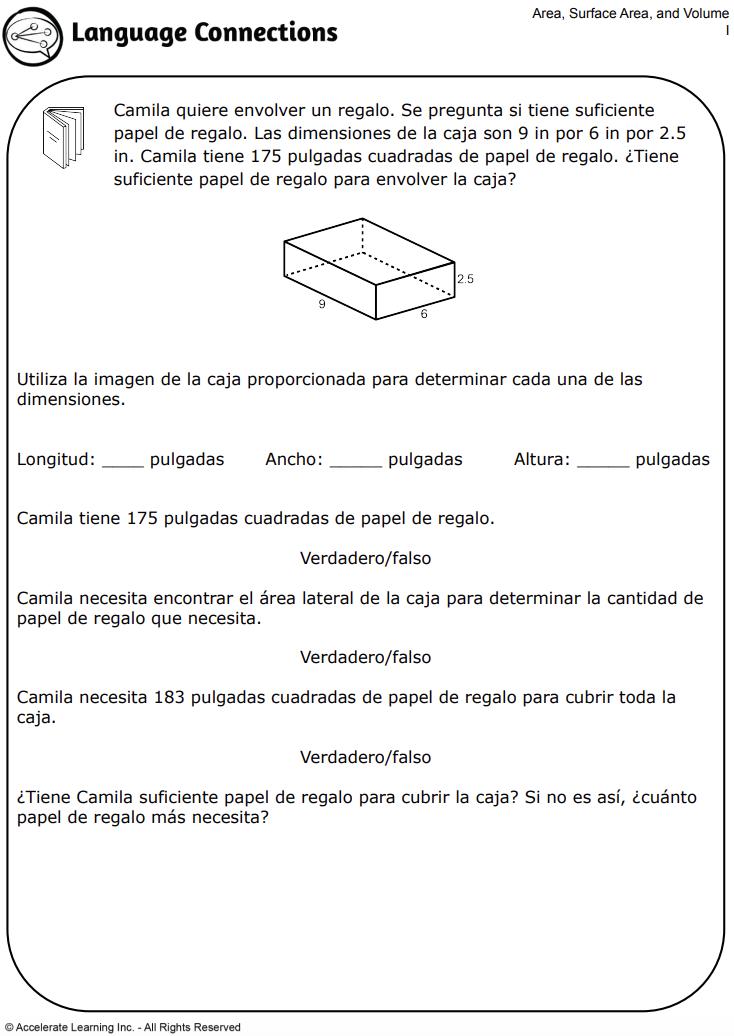
INTERMEDIO MANUAL DEL ESTUDIANTE

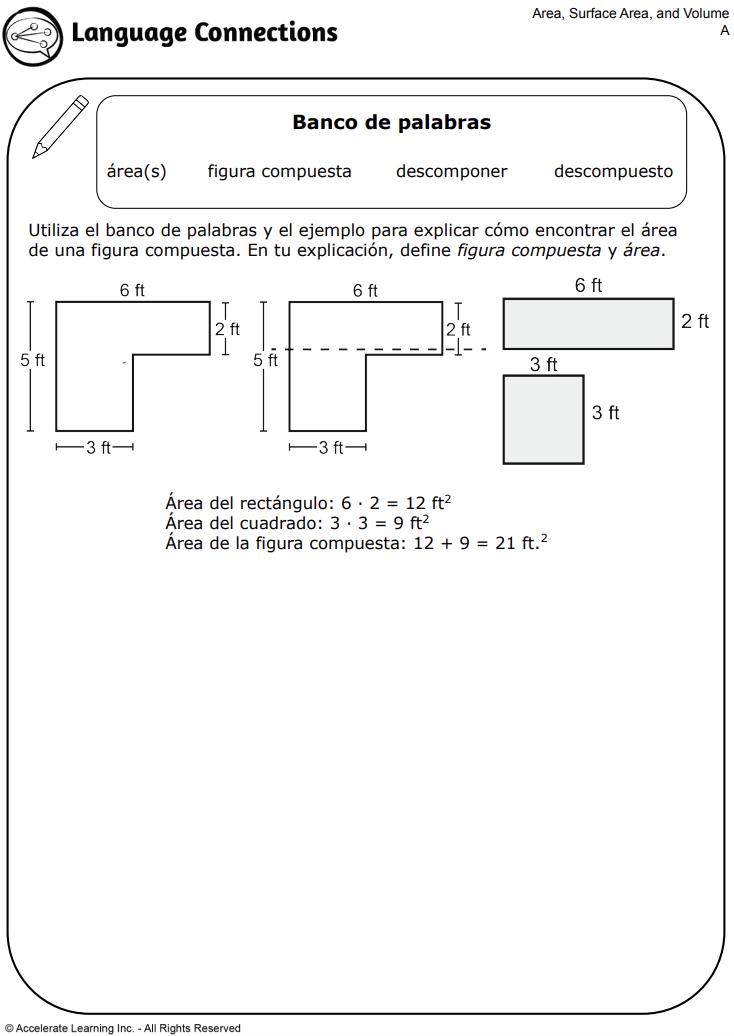
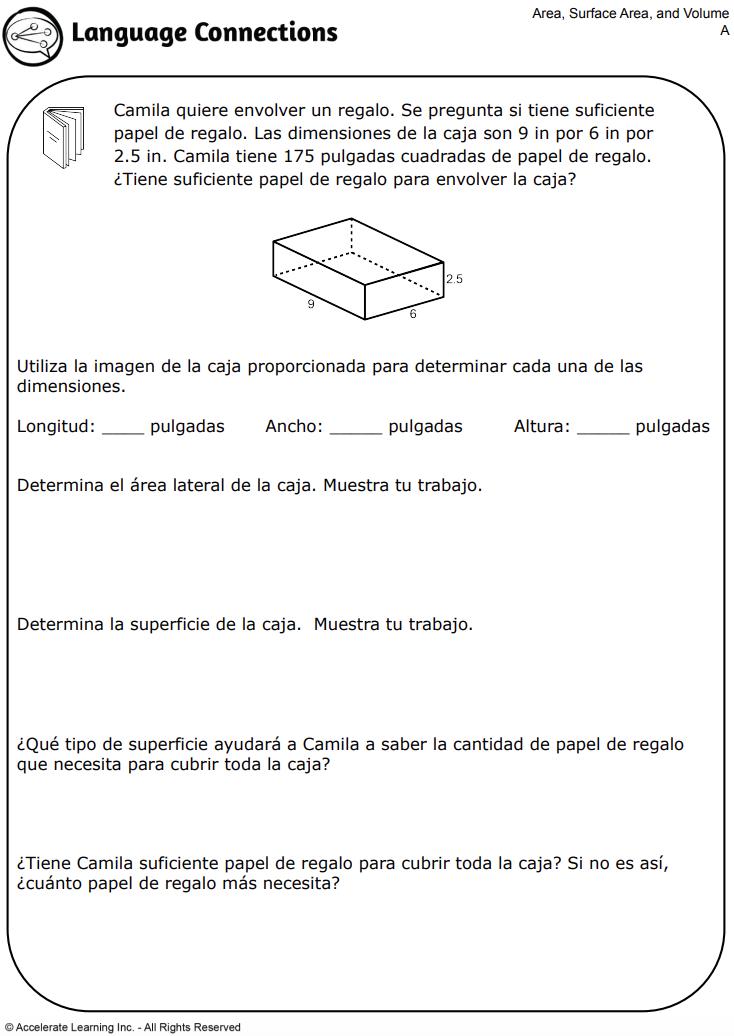
AVANZADO MANUAL DEL ESTUDIANTE

EXPLICAR: CONEXIONES LINGÜÍSTICAS

ESCUCHAR Y HABLAR

PRINCIPIANTE

Ponga a disposición de los estudiantes el vocabulario ilustrado. Lea las siguientes instrucciones de una en una:

• Señale el prisma rectangular.

• Señale la pirámide triangular.

• Señale el prisma triangular.

• ¿Cuántas bases tiene una pirámide?

◦ Pida a los estudiantes que utilicen el siguiente marco de frases: Una pirámide tiene _________ base(s).

• ¿Cuántas bases tiene un prisma?

◦ Pida a los estudiantes que utilicen la siguiente estructura de frases:Un prisma tiene _________ base(s).

• Empareje cada figura tridimensional con su red.

• Explique cómo sabe qué red va con cada figura.

◦ Pida a los estudiantes que utilicen la siguiente estructura de frases:Sé que esta red va con la ____ (nombre de la figura tridimensional) porque ___.

• Señale el cubo.

• Trace con el dedo las aristas del cubo.

• ¿Cuántas aristas tiene el cubo?

◦ Pida a los estudiantes que utilicen la siguiente estructura de frases: El cubo tiene ___ aristas.

• Señale y cuente en voz alta el número de vértices del cubo.

• Señale y cuente el número de caras del cubo.

• ¿Qué forma tienen las caras?

◦ Pida a los estudiantes que utilicen el siguiente marco oracional: Las caras son ____.

• Escriba la forma en la tabla.

• ¿Cuántas bases tiene un cubo?

◦ Pida a los estudiantes que utilicen el siguiente marco oracional: Un cubo tiene ____ bases.

• Escriba el número de bases en la tabla.

• ¿Cuál es la forma de las bases?

◦ Pida a los estudiantes que utilicen la siguiente raíz de oración: La forma de las bases es un ___.

• Escriba la forma en la tabla.

• ¿Qué figura tridimensional es ésta? (Señale la pirámide cuadrada.)

◦ Pida a los estudiantes que utilicen el siguiente marco oracional: Esto es un ___ (nombra la figura tridimensional).

• Completa la tabla para la pirámide cuadrada.

INTERMEDIO

Pon a disposición de los estudiantes el Vocabulario ilustrado. Lea las siguientes indicaciones de una en una:

• Señale la palabra en el banco de palabras mientras la leo en voz alta. Lea en voz alta las palabras del banco de palabras.

• Ahora, utilice el banco de palabras para etiquetar cada figura tridimensional. Supervise a los estudiantes para asegurarse de que etiquetaron las figuras correctamente.

• Señale la pirámide triangular.

• ¿Cuántas bases tiene una pirámide?

◦ Pida a los estudiantes que utilicen el siguiente marco de oraciones: Una pirámide tiene ___ base(s).

• Señale el prisma triangular.

• ¿Cuántas bases tiene un prisma triangular?

◦ Haga que los estudiantes usen el siguiente marco de oraciones: Un prisma triangular tiene ___ base(s).

• Señale el prisma rectangular.

• ¿Cuántas bases tiene un prisma rectangular?

◦ Pida a los estudiantes que utilicen el siguiente marco de frases: Un prisma rectangular tiene ___ base(s).

• Empareja cada figura tridimensional con su red.

• Explica cómo sabes qué red va con cada figura.

◦ Haz que los estudiantes utilicen la siguiente estructura de frase: Sé que esta red va con la ____ (nombre de la figura tridimensional) porque ___.

• Señale el cubo.

• Señale y cuente en voz alta el número de aristas del cubo.

• Señale y cuente en voz alta el número de vértices del cubo.

• Señale y cuente el número de caras del cubo.

• ¿Por qué un cubo es un tipo especial de prisma rectangular?

◦ Pida a los estudiantes que utilicen la siguiente estructura de frase: Un cubo es un tipo especial de prisma rectangular porque ____.

• ¿Qué información de la tabla permite saber que un cubo es un prisma y no una pirámide?

◦ Pida a los estudiantes que utilicen la siguiente raíz de frase: Sabemos que un cubo es un prisma y no una pirámide porque la tabla lo indica ____.

• ¿Qué figura tridimensional es ésta? (Señale la pirámide cuadrada.)

◦ Pida a los estudiantes que utilicen la siguiente raíz de frase: Esto es un ___ (nombre la figura tridimensional).

• Complete la tabla para la pirámide cuadrada.

AVANZADO

Ponga a disposición de los estudiantes el Vocabulario ilustrado. Lea las siguientes preguntas de a una por vez:

• Rotule cada figura tridimensional. (Ayude a los estudiantes con la ortografía según sea necesario.)

• ¿Cuál es la diferencia entre un prisma y una pirámide?

• Empareje cada figura tridimensional con su red.

• Explique cómo decidió qué red va con cada figura tridimensional.

• ¿Qué forma tiene esta figura? (Señale el cubo.)

• Completa la tabla para el cubo.

• ¿Qué forma tiene esta figura? (Señala la pirámide cuadrada.)

• ¿En qué se parece la pirámide cuadrada al prisma triangular y a la pirámide triangular?

• ¿En qué se diferencia la pirámide cuadrada del prisma triangular y de la pirámide triangular?

• Completa la tabla para la pirámide cuadrada.

PRINCIPIANTE

Leer la historia en grupo. Divida la historia en frases. Pida a los estudiantes que señalen cada palabra mientras leen. Pídales que rodeen con un círculo las palabras que no conozcan. Revise las palabras en grupo.

• Revise la situación con los estudiantes. Haga gestos con las manos cuando proceda mientras formula las preguntas.

◦ ¿Has envuelto un regalo antes?

◦ ¿Tienes alguna técnica especial para envolver regalos?

• Pida a los estudiantes que utilicen las siguientes frases:

◦ Sí, he envuelto regalos para _______.

◦ Para envolver un regalo, primero ___. Después, ______.

• Haga eco de la primera afirmación antes de que los estudiantes respondan.

• ¿Qué es el área lateral?

◦ Pida a los estudiantes que utilicen la siguiente raíz de frase: El área lateral es ___.

• ¿Qué es el área superficial?

◦ Pida a los estudiantes que utilicen la siguiente secuencia: El área de la superficie es ___.

• Encierre en un círculo su respuesta.

• Lea el segundo enunciado antes de que los estudiantes respondan. Señala la parte de la figura que es la longitud. Escriba su respuesta.

• Lea el tercer enunciado antes de pedir a los estudiantes que respondan. Señala la parte de la figura que corresponde a la anchura. Luego escriba su respuesta.

• Lea el cuarto enunciado antes de que los estudiantes respondan. Señala la parte de la figura que corresponde a la altura. Luego escribe tu respuesta.

• Haz eco de la quinta afirmación antes de que los estudiantes respondan. ¿Cómo hallarás la respuesta?

◦ Pida a los estudiantes que utilicen la siguiente secuencia de oraciones: Encontraré la respuesta ___.

• Encierra en un círculo tu respuesta.

• Haz eco de la sexta afirmación antes de que los estudiantes respondan. Encierre en un círculo su respuesta.

• Lea la séptima afirmación antes de que los estudiantes respondan. Encierra en un círculo tu respuesta.

EXPLICAR: CONEXIONES LINGÜÍSTICAS

LEER Y HABLAR

INTERMEDIO

Coral: lee la historia en grupo. Pida a los estudiantes que señalen cada palabra mientras leen. Invite a los estudiantes a rodear con un círculo las palabras que no conozcan. Pídales que revisen las palabras con sus compañeros. Comparta con sus compañeros de qué trataba la historia.

• Haga las siguientes preguntas con sus compañeros:

◦ ¿Qué forma tiene el regalo?

◦ ¿La superficie y el área lateral son iguales?

• Eco-lea las instrucciones debajo de la caja. Muestra a tus compañeros la longitud, anchura y altura de la caja antes de escribir tu respuesta.

• Coral-Lee la segunda afirmación. Encierra en un círculo verdadero o falso. Señale la respuesta en la historia antes de marcar la afirmación como verdadera o falsa.

• Coro: lea la tercera afirmación.

• Explique el área lateral a sus compañeros.

◦ Pida a los estudiantes que utilicen la siguiente secuencia de oraciones: El área lateral es ___.

• Explica el área de la superficie a tus compañeros.

◦ Haz que los estudiantes usen la siguiente secuencia de oraciones: El área de la superficie es ___.

• Encierra en un círculo verdadero o falso.

• Lee en pareja el cuarto enunciado. Explica a tus compañeros cómo encontrarías la cantidad de papel de regalo que necesita Camila.

◦ Pide a los estudiantes que utilicen las siguientes frases para comentar sus respuestas:

◦ Yo encontraría la cantidad de papel de regalo que necesita Camila con ___.

◦ Estoy de acuerdo con tu estrategia porque ___.

◦ No estoy de acuerdo con tu estrategia porque ___.

• Lee en pareja la quinta afirmación. Escribe tu respuesta. Compárela con la de sus compañeros.

◦ Pida a los estudiantes que utilicen las siguientes frases para comentar sus respuestas:

◦ Estoy de acuerdo porque ___.

◦ No estoy de acuerdo porque ___.

AVANZADO

Pida a los estudiantes que lean la historia con sus compañeros y que señalen cada palabra mientras leen. Invite a los estudiantes a rodear con un círculo las palabras que no conozcan y a comentarlas con sus compañeros.

• Explique a sus compañeros de qué trataba el pasaje.

• Comente con sus compañeros todos los atributos que observe de la forma.

• ¿Son iguales la superficie y el área lateral?

• ¿Qué sabes sobre cómo envolver un regalo?

• Lea cada enunciado y comente sus respuestas con sus compañeros.

EXPLICAR: CONEXIONES LINGÜÍSTICAS

ESCRIBIR

PRINCIPIANTE

Ponga el vocabulario ilustrado a disposición de los estudiantes. Lea y comente las palabras del banco de palabras. Defina y proporcione ejemplos según las necesidades de los estudiantes. Haga las siguientes preguntas mientras lees:

• Conversa con tus compañeros lo que sabes sobre área, figuras compuestas y formas descompuestas.

• ¿Qué notas sobre el modelo en tus folletos? Compártalo con sus compañeros.

• Lea cada enunciado y pida a los estudiantes que consulten el banco de palabras antes de escribir su respuesta.

INTERMEDIO

Ponga a disposición de los estudiantes el vocabulario ilustrado. Coro: lee y comenta las palabras del banco de palabras. Defina y proporcione ejemplos según las necesidades de los estudiantes.

• Pida a los estudiantes que comenten las palabras del banco de palabras con sus compañeros.

• Doble la mitad inferior del papel para que sólo se vea el banco de palabras. Señale una palabra del banco de palabras y, por turnos, explique las palabras con sus compañeros.

• Tome nota de los estudiantes que proporcionan explicaciones matemáticamente precisas de las palabras del banco de palabras.

• A continuación, señale una palabra del banco de palabras cuyo significado necesite aclarar.

• En función de los estudiantes a los que haya oído dar las explicaciones matemáticamente precisas, pida a los estudiantes que ayuden a aclarar las palabras seleccionadas a sus compañeros. Veo que varios estudiantes están pidiendo aclaraciones sobre la palabra ________. (nombre del estudiante) pudo dar una explicación clara sobre la palabra _________ a su compañero. _____, ¿podrías compartir tu explicación?

• Lee cada enunciado con tus compañeros y utiliza las palabras del banco de palabras para completar cada enunciado. Tenga en cuenta que algunas palabras pueden utilizarse más de una vez o no utilizarse en absoluto.

• Recuerde a los estudiantes que consulten el banco de palabras cuando rellenen los espacios en blanco.

AVANZADO

Ponga a disposición de los estudiantes el vocabulario ilustrado. Los estudiantes deben leer en parejas las palabras del banco de palabras y comentar su significado con sus compañeros. Defina y proporcione ejemplos según lo necesiten los estudiantes.

• Haga que los estudiantes revisen las palabras del banco de palabras con sus compañeros.

• Revisa las palabras del banco de palabras con sus compañeros. Cada persona debe dar una explicación o descripción de una palabra y, a continuación, pedir a su compañero que parafrasee el significado de la palabra. Continúa este proceso hasta que hayas revisado todas las palabras del banco de palabras.

• Lee las instrucciones con tus compañeros. ¿Qué plan seguirás para asegurarte de que utilizas el mayor número posible de palabras del banco de palabras en tu redacción? Si no estás seguro de cómo utilizar una palabra, rodéala con un círculo en el banco de palabras. Los estudiantes aún no deben empezar a escribir.

• Esté atento a los estudiantes que tengan dificultades para crear un plan o que marquen con un círculo las palabras del banco de palabras. Ofrezca apoyo y permita que los estudiantes que hayan podido crear un plan lo compartan con la clase.

◦ Veo que varios de nosotros necesitamos aclaraciones sobre la palabra _______. Diríjase a alguien cercano que no sea su compañero y pídale que aclare o defina la palabra ___________.

◦ Veo que varios de nosotros necesitamos ayuda para diseñar un plan que utilice palabras del banco de palabras. Acércate a alguien que no sea tu compañero y pídele que explique cómo piensa utilizar el mayor número posible de palabras del banco de palabras.

• Pide a los estudiantes que escriban su explicación una vez que se hayan aclarado todas las palabras y se hayan compartido los planes.

• Ahora, escribe una explicación que utilice al menos 5 de las palabras del banco de palabras. Cuando terminen de escribir, compártanlo con sus compañeros.

EXPLICAR: VOCABULARIO ILUSTRADO

QUE HAY QUE CONOCER VOCABULARIO ILUSTRADO

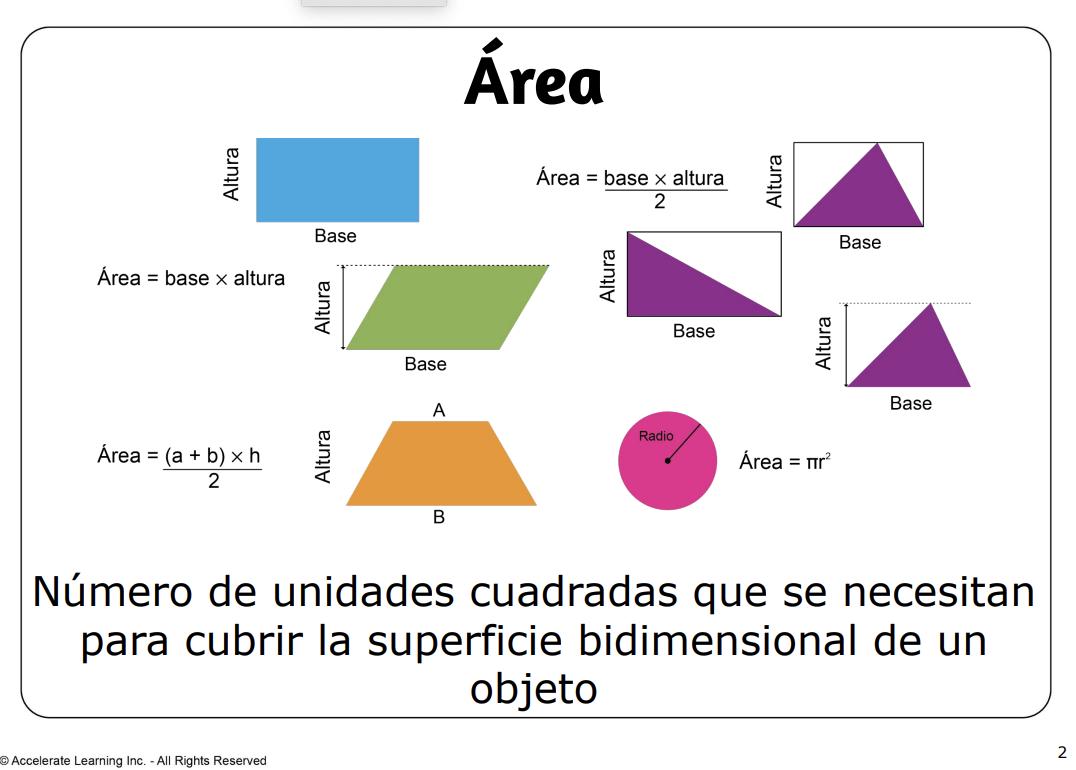
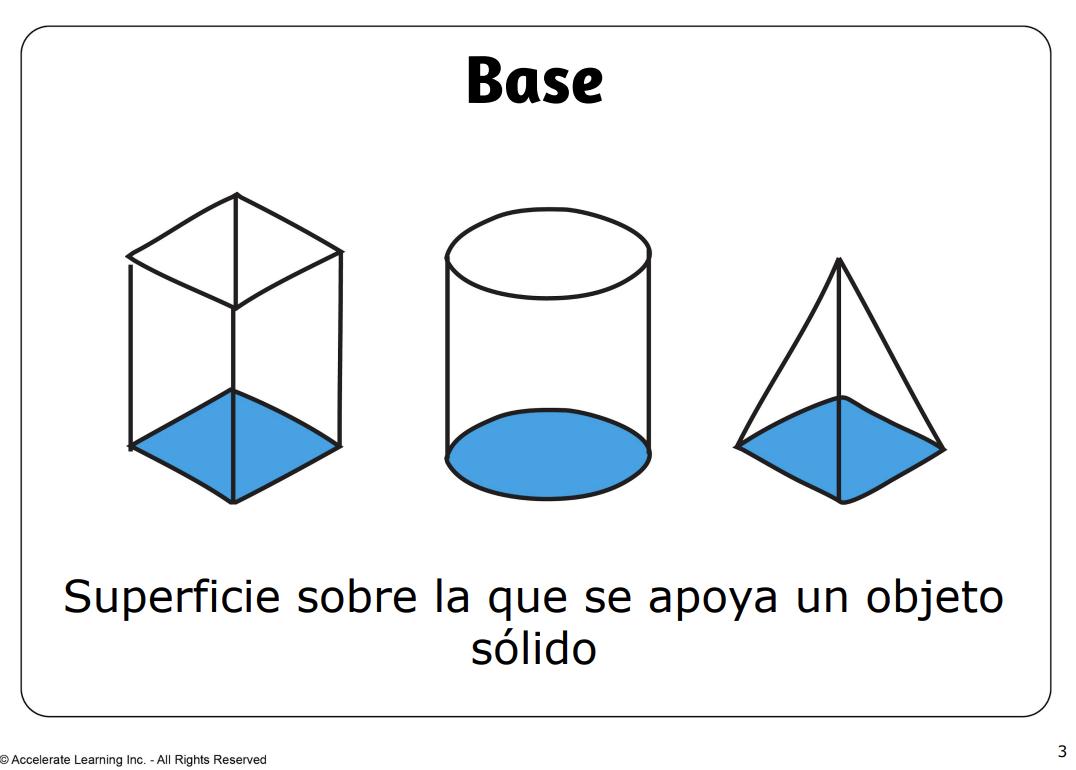
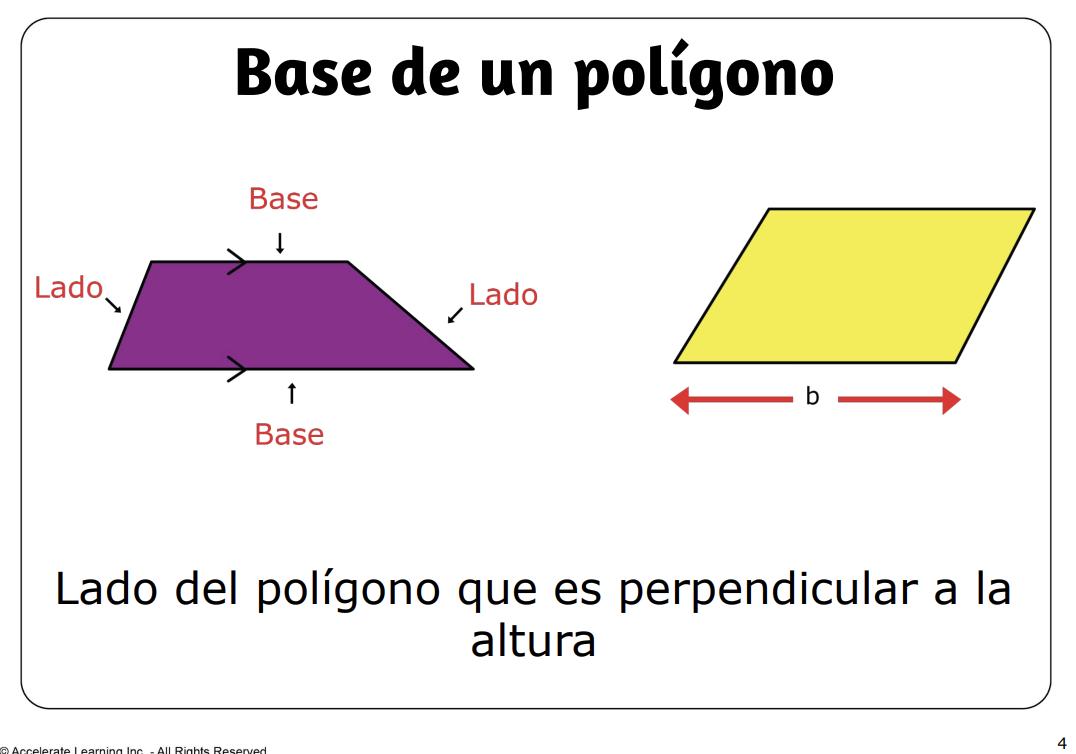
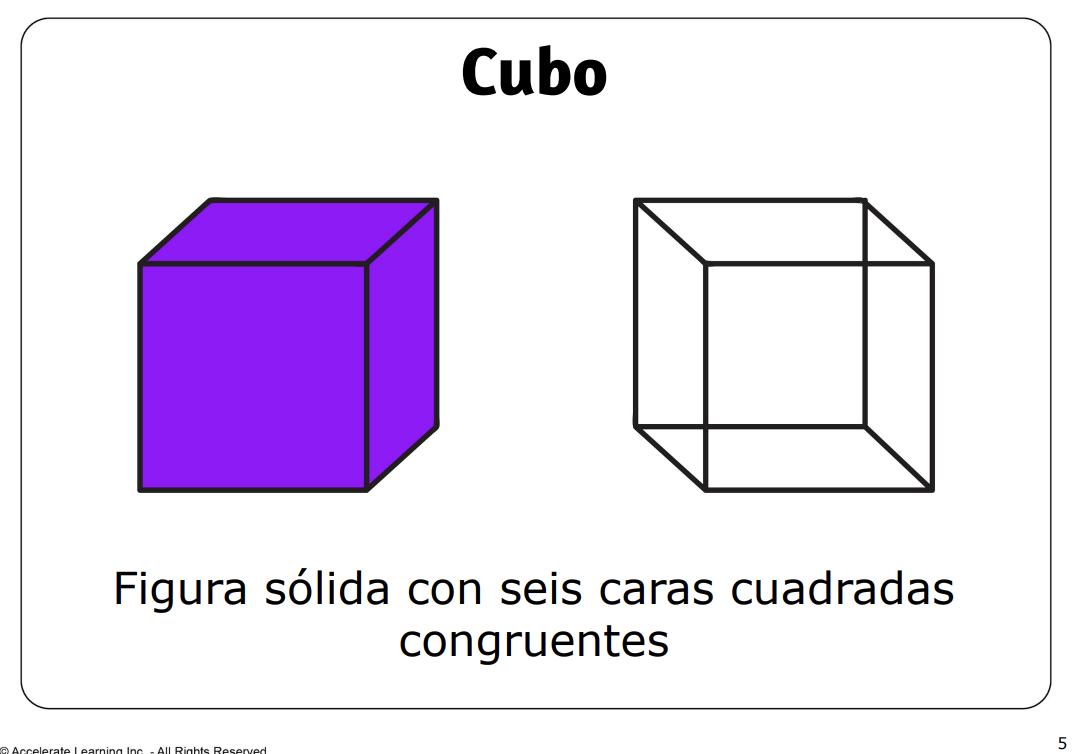
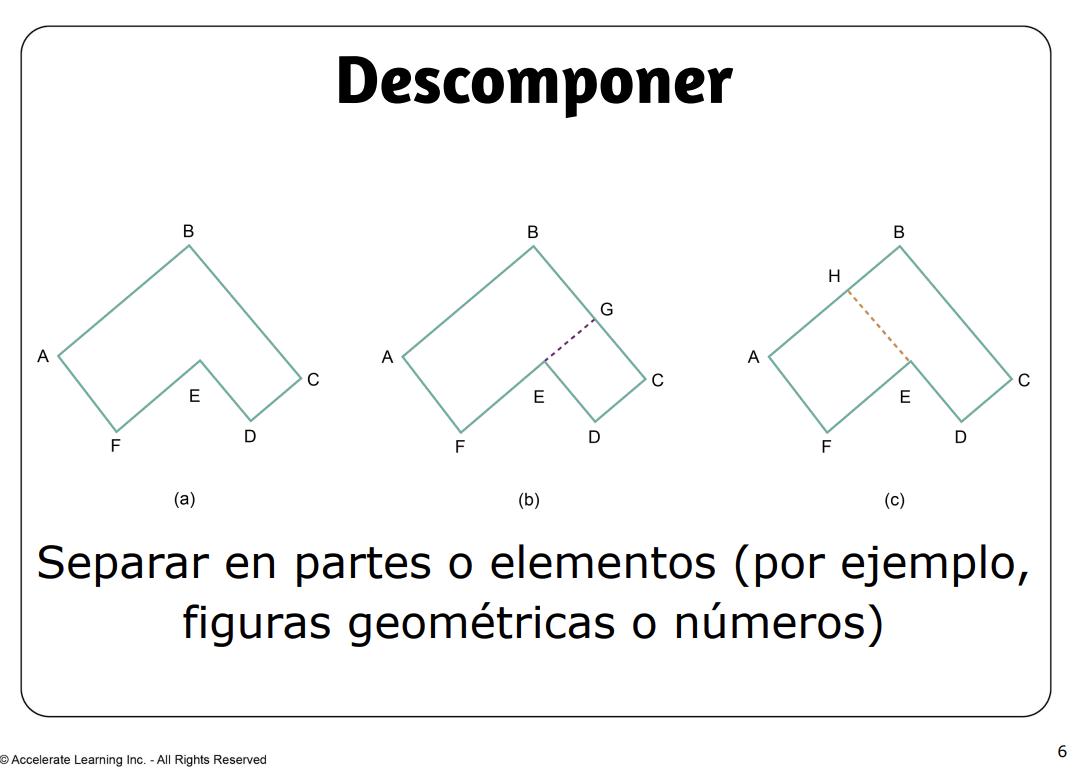
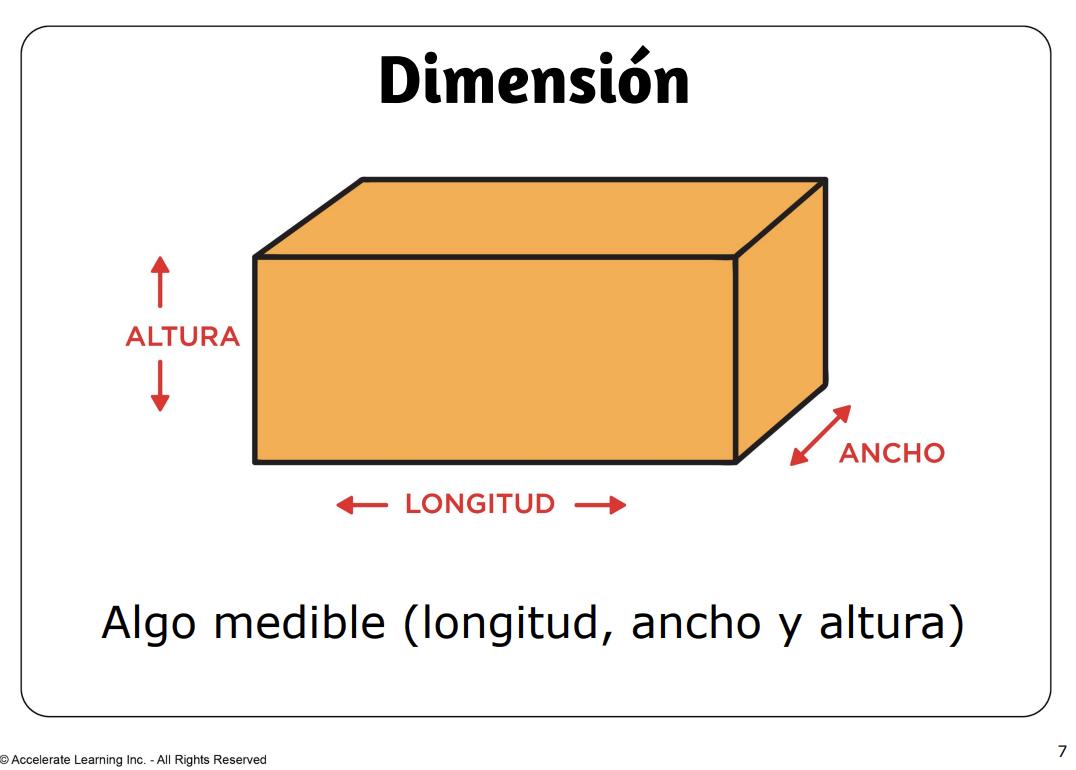
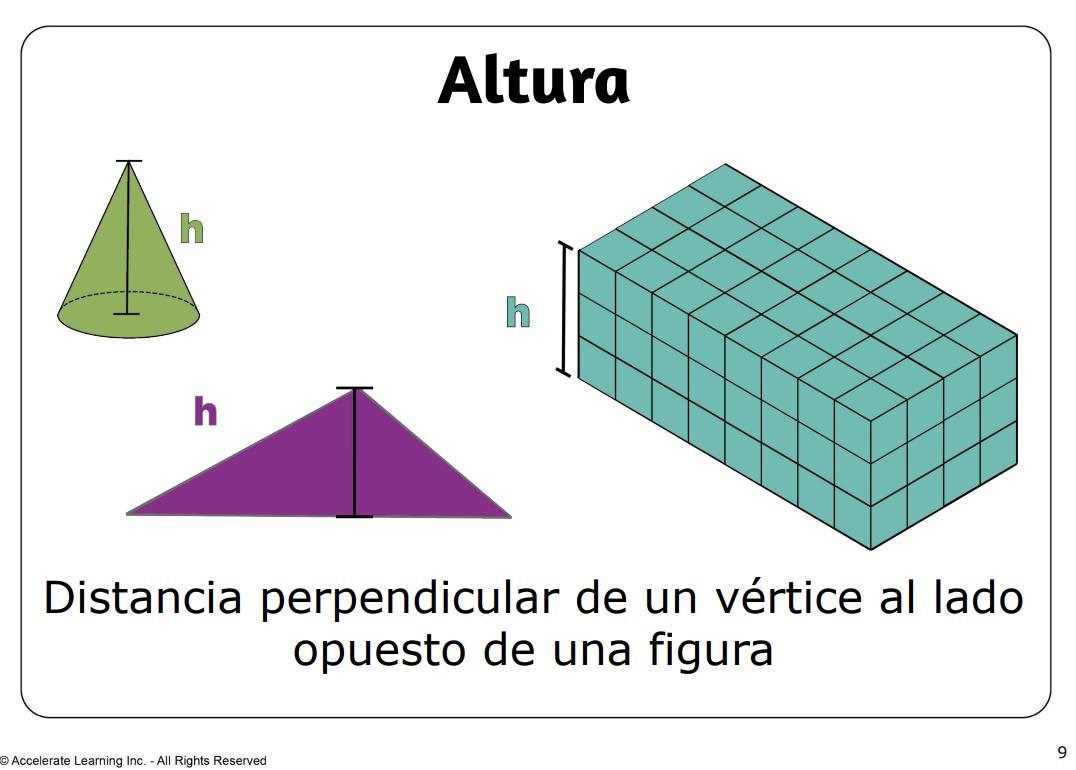
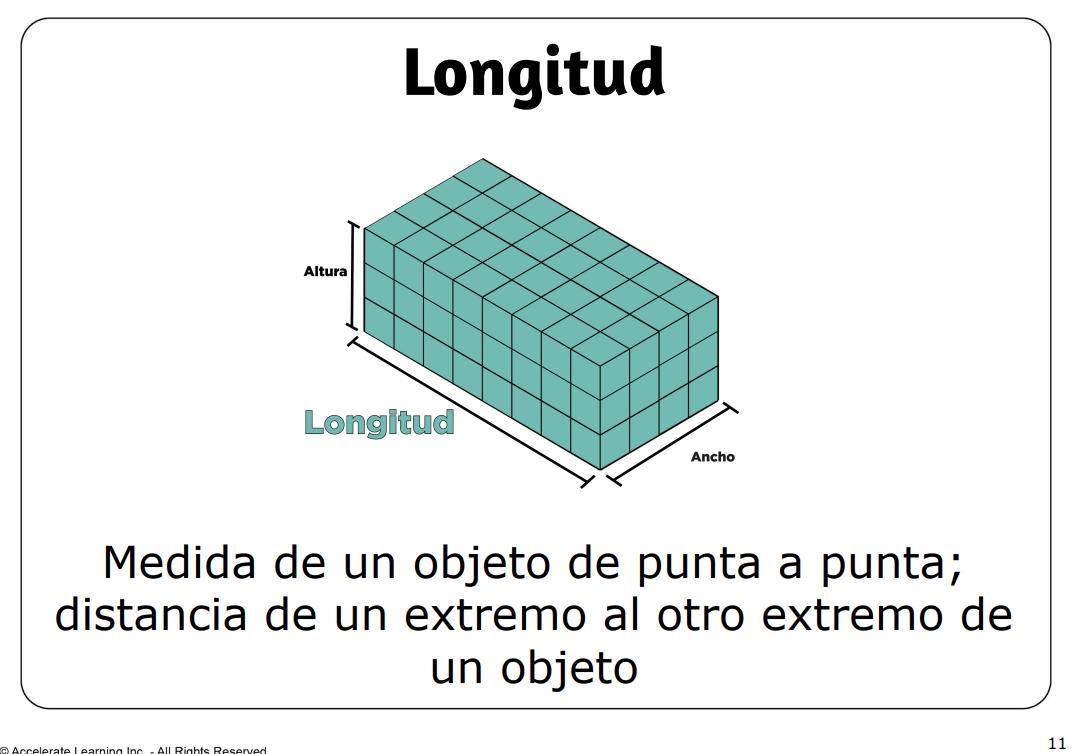
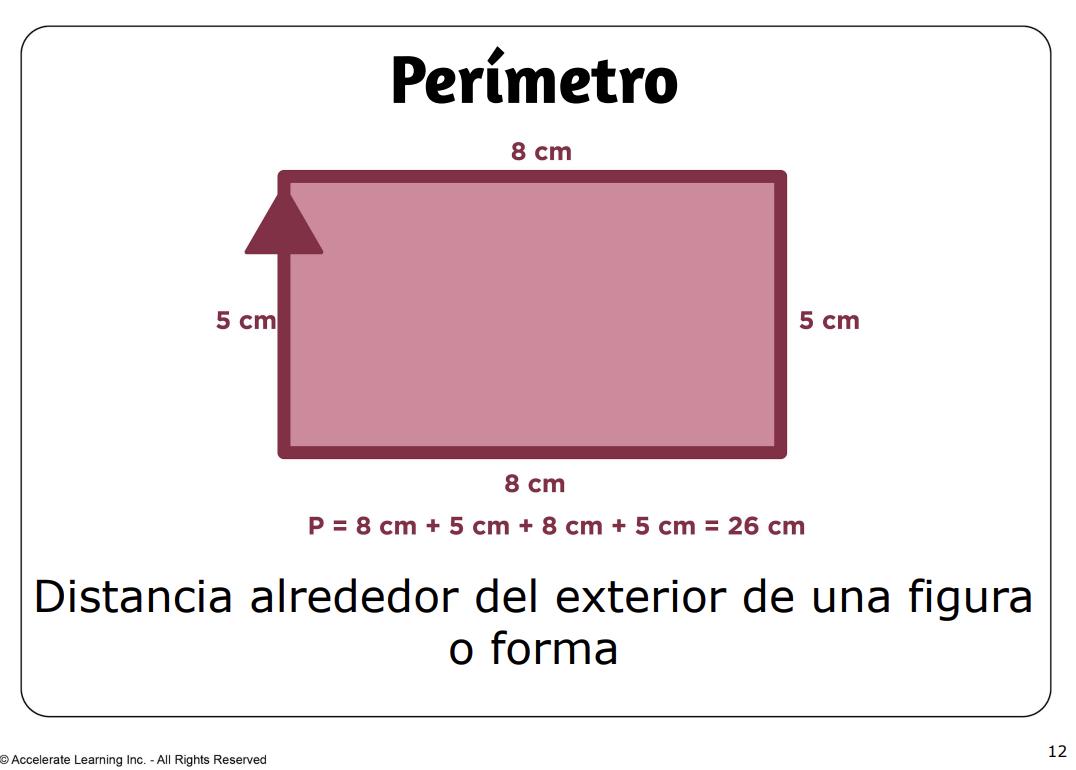
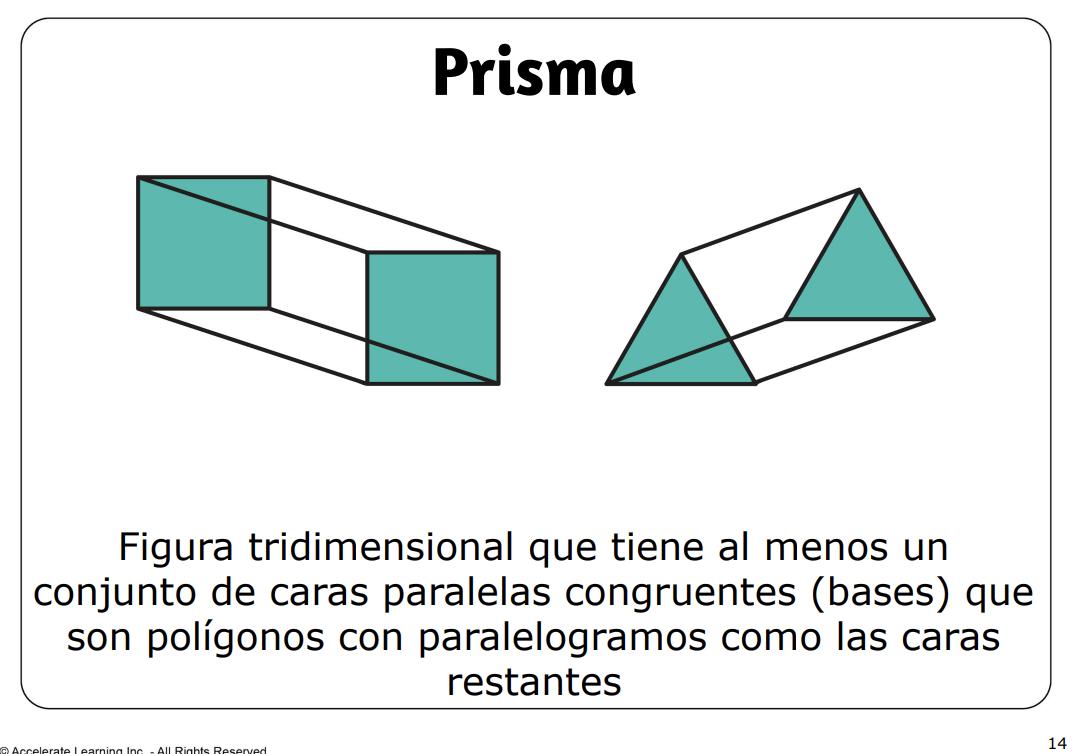
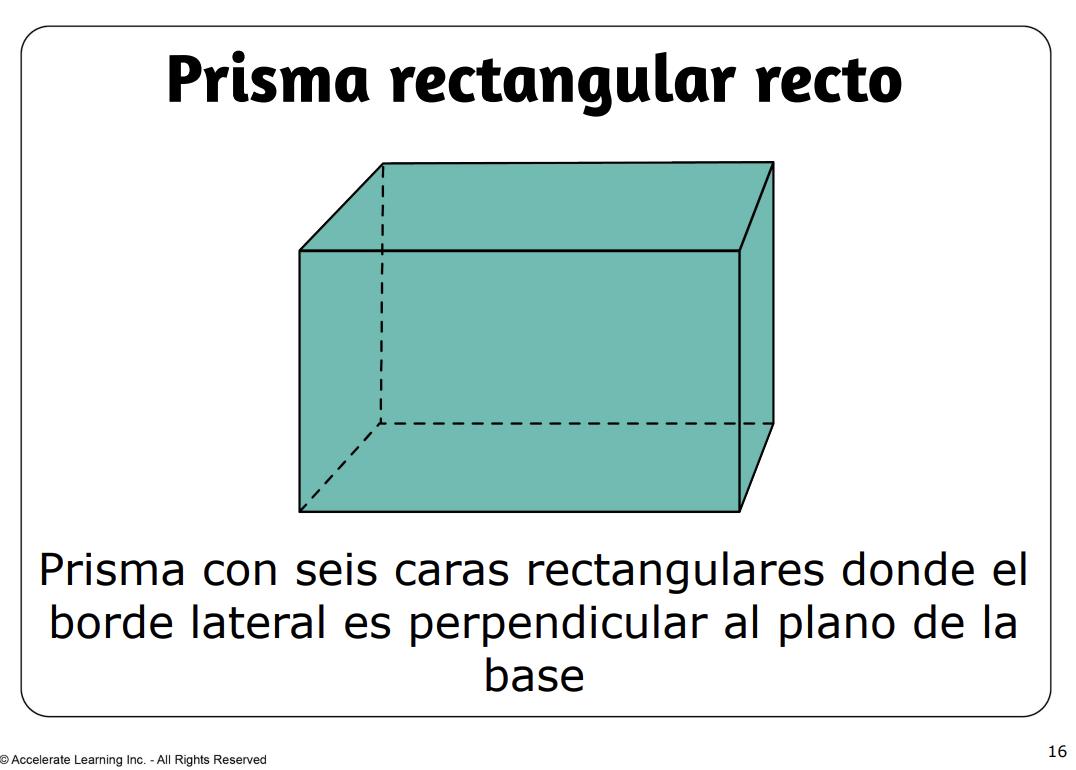
PALABRAS

GRADO

EXPLICAR: VOCABULARIO ILUSTRADO

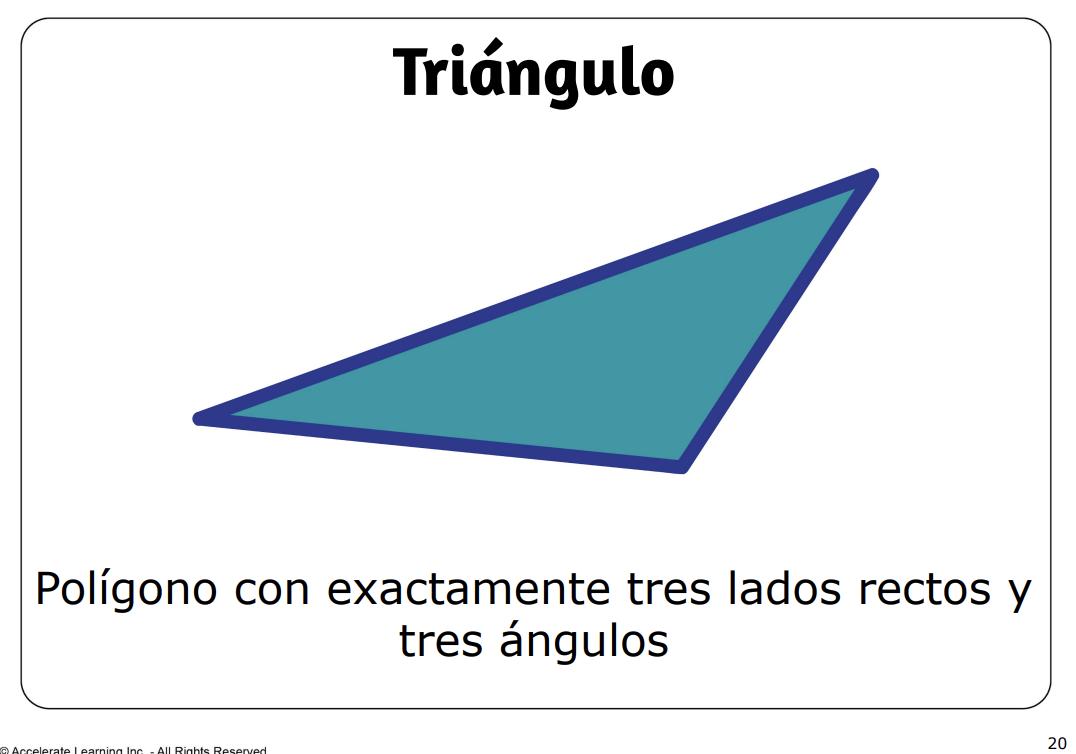
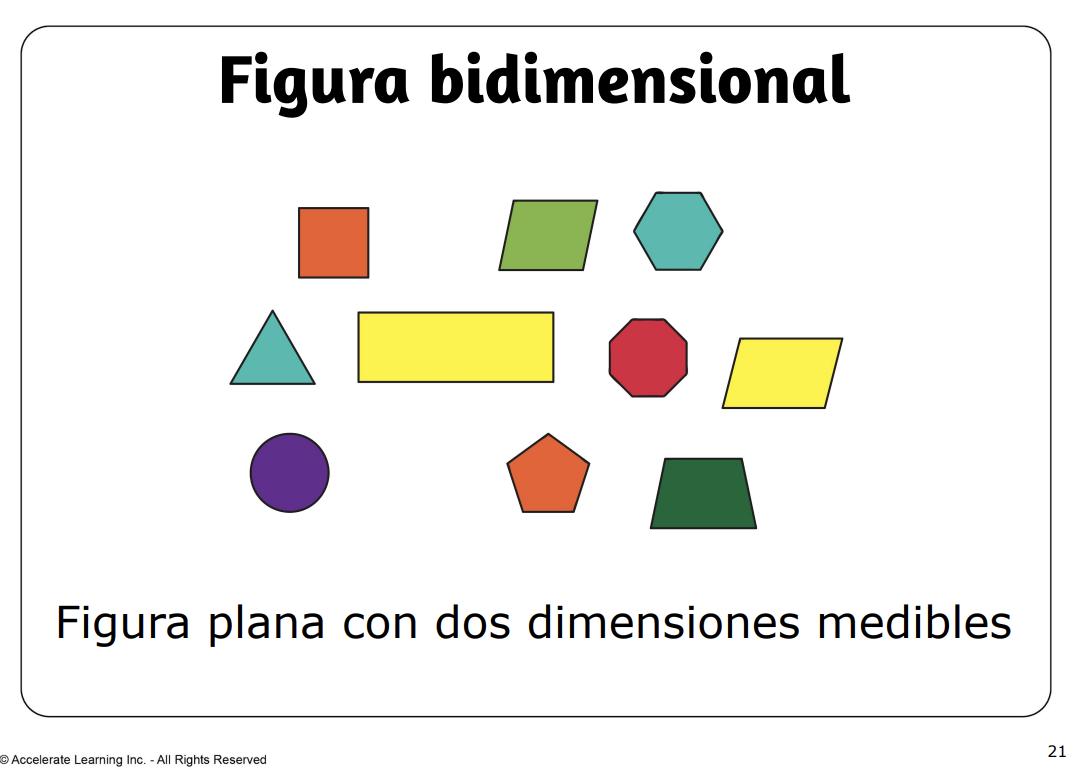
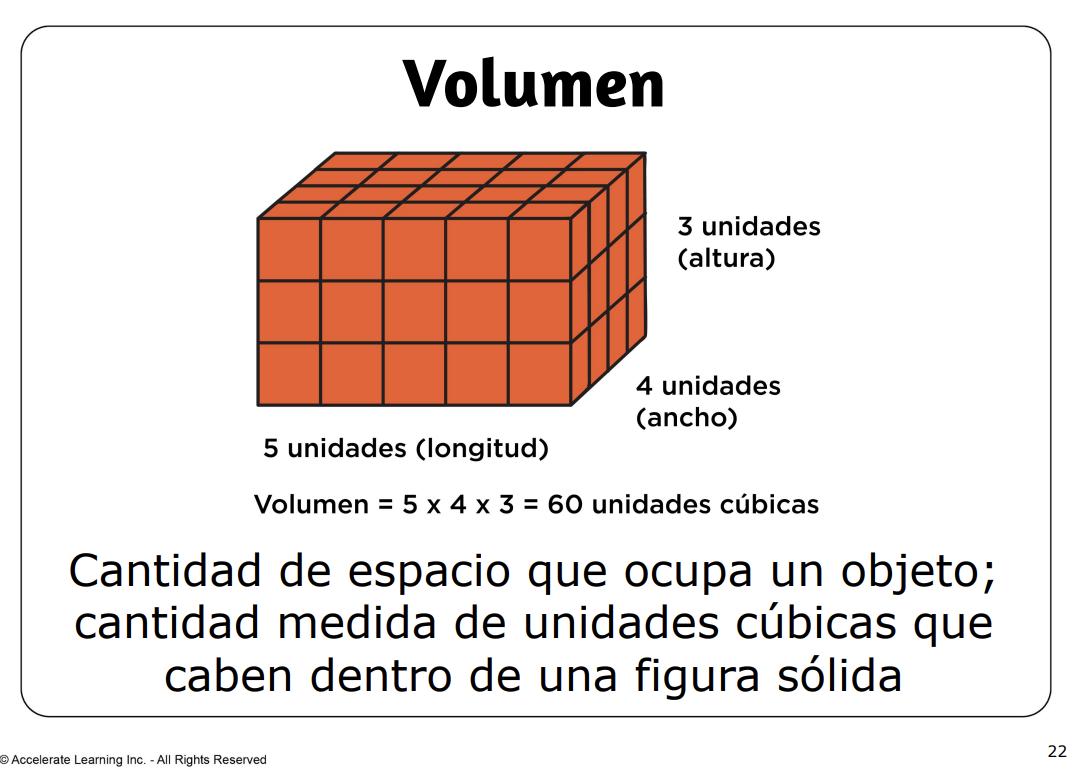
ELABORAR: CONSTRUCTOR DE FLUIDEZ

HOJA DE REGISTRO DEL ESTUDIANTE

PREPARACIÓN

• Haz copias a doble cara de las tarjetas ¡Arregla el error! tarjetas.

• Lamínalas para que duren más.

• Recorta cada una de las tarjetas y colócalas en un sobre o una bolsa con cierre para facilitar su distribución y limpieza.

• Imprime una hoja de registro del estudiante ¡Arregla el error! para cada estudiante.

• Imprime una hoja de respuestas de ¡Arregla el error! para cada pareja de estudiantes. Dobla la clave de respuestas de modo que las respuestas queden cubiertas pero el título aparezca en la parte superior de la página.

• Coloque a los estudiantes en parejas.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Muestre a los estudiantes cómo barajar las cartas y colocarlas boca abajo en una pila.

2. Modele cómo jugar el juego con un estudiante.

a. Baraje las cartas y colóquelas boca abajo en una pila entre los jugadores.

b. El jugador 1 voltea una carta. Ambos jugadores analizan el problema y determinan si la solución proporcionada al problema es correcta y el estudiante que la ha contestado es un experto en matemáticas o si la solución es incorrecta y es necesario corregir el error.

DESARROLLAR LA FLUIDEZ CONCEPTUAL

CONSTRUCTOR DE FLUIDEZ: ÁREA DE FIGURAS COMPUESTAS

DESCRIPCIÓN

En esta actividad, los estudiantes jugarán al juego ¡Arregla el error!

MATERIALES

IMPRESOS

• 1 hoja de instrucciones ¡arregla el error! (por pareja)

• 1 juego de tarjetas ¡arregla el error! (por pareja)

• 1 hoja de registro para el estudiante (por estudiante) hoja de registro del estudiante (por estudiante)

• 1 clave de respuestas de «¡Arregla el error!» (por pareja)

REUTILIZABLE

• 1 sobre o bolsa resellable (por pareja)

c. Los jugadores se turnan para dar la vuelta a una carta cada vez.

d. Los jugadores siguen turnándose hasta que han resuelto todas las cartas.

e. Los jugadores deben rellenar la hoja de registro del estudiante ¡Arregla el error! mientras juegan. (Los jugadores deben rellenar la fila de la hoja de registro del estudiante ¡Arregla el error! que corresponda al número de cada tarjeta).

f. Una vez analizadas todas las tarjetas, los estudiantes utilizan la clave de respuestas de ¡Arregla el error! para comprobar sus respuestas.

g. El jugador con más respuestas correctas es el ganador.

3. Distribuye los materiales del juego. A continuación, indica a los estudiantes que barajen las cartas y las coloquen boca abajo en una pila entre los jugadores.

4. Vigila a los estudiantes para asegurarte de que encuentran y registran las respuestas correctas a cada carta utilizando la Hoja de registro del estudiante ¡Arregla el error!

ELABORAR: CONSTRUCTOR DE FLUIDEZ

DESARROLLAR LA FLUIDEZ CONCEPTUAL

CONSTRUCTOR DE FLUIDEZ:

ÁREA DE SUPERFICIE (PRISMAS Y CILINDROS)

DESCRIPCIÓN

En esta actividad, los estudiantes jugarán al juego ¡Arregla el error!

MATERIALES

IMPRESOS

• 1 hoja de instrucciones ¡Arregla el error! (por pareja)

• 1 juego de tarjetas ¡Arregla el error! (por pareja)

• 1 hoja de registro para el estudiante (por alumno)

• 1 clave de respuestas ¡Arregla el error! (por pareja) REUTILIZABLE

• 1 sobre o bolsa con cierre (por pareja)

PREPARACIÓN

• Haz copias a doble cara de las tarjetas ¡Arregla el error! tarjetas.

• Lamínalas para que duren más.

• Recorta cada una de las tarjetas y colócalas en un sobre o bolsa resellable para facilitar su distribución y limpieza.

• Imprime una Hoja de registro del estudiante ¡Arregla el error! para cada alumno.

• Imprime una hoja de respuestas de ¡Arregla el error! para cada pareja. Dobla la clave de respuestas de modo que las respuestas queden cubiertas pero el título aparezca en la parte superior de la página.

• Coloque a los estudiantes en parejas.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Muestre a los estudiantes cómo barajar las cartas y colocarlas boca abajo en una pila.

2. Modele cómo jugar el juego con un estudiante.

a. Baraje las cartas y colóquelas boca abajo en una pila entre los jugadores.

b. El jugador 1 voltea una carta. Ambos jugadores analizan el problema y determinan si la solución proporcionada al problema es correcta y el estudiante que la respondió es un experto en matemáticas o si la solución es incorrecta y es necesario corregir el error.

c. Los jugadores se turnan para voltear una tarjeta a la vez.

d. Los jugadores continúan turnándose hasta que se hayan resuelto todas las tarjetas.

e. Los jugadores deben completar la hoja de registro del estudiante ¡Arregla el error! hoja de registro del estudiante mientras juegan. (Los jugadores deben rellenar la fila de la hoja de registro del estudiante ¡Arregla el error! Hoja de registro del estudiante que corresponda al número de cada tarjeta).

HOJA DE REGISTRO DEL ESTUDIANTE CLAVE DE RESPUESTAS

f. Una vez analizadas todas las tarjetas, los estudiantes utilizan la clave de respuestas ¡Arregla el error! para comprobar sus respuestas.

g. El jugador con más respuestas correctas es el ganador.

3. Distribuye los materiales del juego. A continuación, indique a los estudiantes que barajen las cartas y las coloquen boca abajo en una pila entre los jugadores.

4. Supervise a los estudiantes para asegurarse de que encuentran y registran las respuestas correctas a cada carta utilizando la Hoja de registro del estudiante ¡Arregla el error! Hoja de registro del estudiante.

HOJA DE REGISTRO DEL ESTUDIANTE

CLAVE DE RESPUESTAS

PREPARACIÓN

• Haz copias a doble cara de las tarjetas ¡Arregla el error! tarjetas.

• Lamínalas para que duren más.

• Recorta cada una de las tarjetas y colócalas en un sobre o una bolsa con cierre para facilitar su distribución y limpieza.

• Imprime una Hoja de registro del estudiante ¡Arregla el error! para cada estudiante.

• Imprime una hoja de respuestas de ¡Arregla el error! para cada pareja de estudiantes. Dobla la clave de respuestas de modo que las respuestas queden cubiertas pero el título aparezca en la parte superior de la página.

• Coloca a los estudiantes en parejas.

PROCEDIMIENTO Y PUNTOS DE AYUDA

1. Muestra a los estudiantes cómo barajar las cartas y colocarlas boca abajo en una pila.

2. Modela cómo jugar al juego con un estudiante.

a. Baraja las cartas y colócalas boca abajo en una pila entre los jugadores.

ELABORAR: CONSTRUCTOR DE FLUIDEZ

DESARROLLAR LA FLUIDEZ CONCEPTUAL

CONSTRUCTOR DE FLUIDEZ: VOLUMEN

DESCRIPCIÓN

En esta actividad, los estudiantes jugarán al juego ¡Arregla el error!

MATERIALES

IMPRESOS

• 1 Hoja de instrucciones ¡Arregla el error! (por pareja)

• 1 Juego de tarjetas ¡Arregla el error! (por pareja)

• 1 Hoja de registro para el estudiante (por estudiante) Hoja de registro del estudiante (por estudiante)

• 1 ¡Arregla el error! Clave de respuestas (por pareja)

REUTILIZABLE

• 1 Sobre o bolsa resellable (por pareja)

b. El jugador 1 da la vuelta a una carta. Ambos jugadores analizan el problema y determinan si la solución proporcionada al problema es correcta y el estudiante que la respondió es un experto en matemáticas o si la solución es incorrecta y es necesario corregir el error.

c. Los jugadores se turnan para dar vuelta una tarjeta a la vez.

d. Los jugadores continúan turnándose hasta que todas las tarjetas hayan sido resueltas.

e. Los jugadores deben completar la Hoja de registro del estudiante ¡Arregla el error! Hoja de registro del estudiante mientras juegan. (Los jugadores deben rellenar la fila de la Hoja de registro del estudiante ¡Arregla el error! que corresponda al número de cada tarjeta).

f. Una vez analizadas todas las tarjetas, los estudiantes utilizan la clave de respuestas de ¡Arregla el error! para comprobar sus respuestas.

g. El jugador con más respuestas correctas es el ganador.

3. Distribuye los materiales del juego. A continuación, indica a los estudiantes que barajen las cartas y las coloquen boca abajo en una pila entre los jugadores.

4. Vigila a los estudiantes para asegurarte de que encuentran y registran las respuestas correctas a cada carta utilizando la Hoja de registro del estudiante ¡Arregla el error! Hoja de registro del estudiante.

ELABORAR: REVISIÓN EN ESPIRAL

REVISIÓN EN ESPIRAL:

REGALOS DE NAVIDAD

DESCRIPCIÓN

Los estudiantes repasan el contenido previo o actual del grado para ayudar a apoyar su trabajo en el alcance actual y fortalecer las habilidades necesarias para alcances posteriores.

PREPARACIÓN

• Imprima un folleto del estudiante por alumno.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Entregue un folleto del estudiante a cada alumno.

2. Anime a los estudiantes a tratar de responder a las preguntas de forma independiente sin utilizar regrados externos para ver lo que saben. Invite a los estudiantes a anotar ideas o fragmentos que recuerden sobre los temas que han aprendido previamente. Reconozca que los errores son bienvenidos en esta actividad y en la clase de matemáticas.

REPASAR CONCEPTOS PREVIOS FOLLETO DEL ESTUDIANTE

3. Utilice las preguntas de repaso en espiral como calentamiento en clase, o envíelas a casa como deberes. Proporcione a los estudiantes comentarios y oportunidades para corregir su trabajo y consolidar aún más sus conocimientos previos.

4. Consulte la sección «Revisión en espiral centrada en la pregunta» para evaluar los conocimientos de contenido de los estudiantes o su necesidad de una mayor intervención. Si es necesario repasar más, utilice los Constructores de fluidez en los alcances apropiados.

5. Capstone incluye una parte del alcance actual para que los estudiantes vean la conexión y relevancia de su aprendizaje previo con el alcance actual.

La ciencia de datos consiste en un breve debate en clase sobre un conjunto de datos. Esta actividad no está pensada para ser calificada. La parte I incluye preguntas abiertas para ayudar a los estudiantes a interpretar y analizar los datos. Las partes siguientes son actividades opcionales para ampliar el aprendizaje de los estudiantes en contexto.

DESCRIPCIÓN

Los estudiantes analizan, interpretan y generan conjuntos de datos, además de responder a preguntas basadas en los datos.

MATERIALES

IMPRESOS

• 1 conjunto de datos (por clase)

REUTILIZABLES

• 1 proyector o cámara de documentos (por clase)

• 1 marcador de borrado en seco (por clase)

CONSUMIBLES

• 1 trozo de papel milimetrado (por clase)

PREPARACIÓN

• Prepárese para proyectar el conjunto de datos en la clase.

• Reúna un trozo de papel milimetrado y un marcador de borrado en seco.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

PARTE I

1. Proyecte el conjunto de datos y prepárese para anotar las observaciones de los estudiantes.

2. Plantee las siguientes preguntas:

a. «¿Qué observas en este conjunto de datos?».

b. «¿Qué representa este conjunto de datos?».

c. «¿Qué categorías se incluyen en este conjunto de datos?».

d. «¿Qué tabla cree que sería más útil? ¿Por qué?».

e. «¿Qué tabla crees que costaría menos hacer? ¿Por qué?».

f. «¿Qué preguntas tiene sobre los datos?».

ELABORAR: CIENCIA DE DATOS

ANÁLISIS DE DATOS

CIENCIA DE DATOS

PARTE II

1. Repasa las fórmulas del área de un triángulo y del área de un rectángulo, así como las fórmulas del volumen de un prisma, y escribe lo que recuerden los estudiantes en el papel milimetrado.

2. Haga las siguientes preguntas:

a. ¿Qué mesa tiene mayor superficie para colocar cosas?

Muestra tu trabajo. La mesa rectangular tiene mayor superficie para colocar objetos.

Mesa rectangular: A = (4 pies)(1.5 pies) = 6 pies.2

Mesa triangular: A = (1/2)(3.25 ft.)(2.81 ft.) ≈ 4.57 ft.2

b. Antes de montar las mesas, hay que teñir cada pieza. Hay 5 piezas para teñir en la mesa rectangular y 4 piezas para teñir en la mesa triangular. La mesa triangular es un triángulo equilátero. ¿Qué mesa necesita más tinte para cubrir su superficie total?

Muestra tu trabajo. La mesa rectangular necesita más tinte porque su superficie total es mayor. Tablero de la mesa rectangular:

SA = 2(4 pies)(1,5 pies) + 2(4 pies)(0.1 pies) + 2(1.5 pies)(0.1 pies) = 13.1 pies.2

Patas de la mesa rectangular:

SA = 4[2(0.15 ft.)(0.15 ft.) + 2(0.15 ft.)(2 ft.) + 2(0.15 ft.) (2 ft.)] = 4.98 ft.2

Superficie total de la mesa rectangular: 13.1 ft.2 + 4.98 ft.2 = 18.08 ft.2

Parte superior de la mesa triangular: SA = 2(1/2)(3.25 ft.)(2.81 ft.) = 9.1325 ft.2

Superficie lateral de la parte superior triangular: LA = 3[(3.25 ft.)(0.15 ft.)] = 1.4625 ft.2

Patas de la mesa triangular:

SA = 3[2(0.2 ft.)(0.2 ft.) + 2(0.2 ft.)(2 ft.) + 2(0.2 ft.)(2 ft.)] = 5.04 ft.2

Superficie total de la mesa triangular: 9.1325 ft.2 + 1.4625 ft.2 + 5.04 ft.2 ≈ 15,64 ft.2

c. Ambas mesas están hechas del mismo tipo de madera. ¿Cuál crees que pesará menos? Explícalo. Las respuestas pueden variar. Creo que la mesa triangular pesará menos. Tiene una superficie más pequeña para colocar cosas y una superficie menor. Por lo tanto, creo que también pesará menos.

d. Calcula el volumen de cada mesa. ¿Cuál pesará menos? Explícalo. La mesa rectangular pesaría menos porque tiene menos volumen.

Parte superior de la mesa rectangular: V = (4 pies)(1.5 pies)(0.1 pies) = 0.6 pies.3

Patas de la mesa rectangular: V = 4[(0.15 ft.)(0.15 ft.)(2 ft.)] = 0.18 ft.3

Volumen total de la mesa rectangular: 0,6 pies.3 + 0.18 pies.3 = 0.78 pies.3

Parte superior de la mesa triangular: V = (4.57 pies.2)(0.15 pies.) = 0.6855 pies.3

Patas de la mesa triangular: V = 3[(0.2 ft.)(0.2 ft.)(2 ft.)] = 0.24 ft.3

Volumen total de la mesa triangular: 0.,6855 pies.3 + 0.24 pies.3 = 0.9255 pies.3

e. ¿Era correcta tu predicción de la parte c? Las respuestas pueden variar.

EVALUAR: LISTA DE VERIFICACIÓN DE OBSERVACIÓN

EVALUACIÓN DE HABILIDADES

LISTA DE VERIFICACIÓN DE LA OBSERVACIÓN

DESCRIPCIÓN

Este elemento proporciona un desglose de los conceptos y destrezas clave del alcance de aplicación. Puede utilizarse como evaluación formativa para los maestroes y como autoevaluación para los estudiantes.

MATERIALES

IMPRESO

• 1 folleto del estudiante (por alumno)

• 1 material para el maestro (por estudiante)

PREPARACIÓN

• Imprima un material para el maestro y un folleto del estudiante para cada estudiante.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Distribuya un folleto del estudiante a cada estudiante.

2. A medida que los estudiantes trabajen en las actividades de «Explorar» y «Explicar» del alcance, evalúe formativamente su progreso tomando notas anecdóticas sobre cómo se observaron los conceptos y habilidades clave. Pueden plantearse preguntas de reflexión para medir el impacto de las actividades tanto en grupo como en pequeño grupo.

3. Haga que los estudiantes reflexionen sobre las formas en que pueden demostrar su comprensión y autoevaluar su progreso en cada concepto o habilidad clave a medida que trabajan en las actividades tanto en grupo como en pequeño grupo.

4. Los estudiantes pueden reflexionar sobre su pensamiento, aprendizaje y trabajo en el alcance; identificar las formas en que han mejorado; y establecer nuevos objetivos de aprendizaje.

5. Los colegas que proporcionan apoyo de instrucción a los estudiantes pueden estar equipados con las adaptaciones y modificaciones señaladas en el Manual del maestro.

6. Las notas anecdóticas proporcionadas en la hoja para el maestro pueden usarse como documentación para los boletines de calificaciones basados en estándares.

7. Una vez que se hayan recopilado los datos de los estudiantes después de la evaluación, consulte la Guía de instrucción de andamiaje en la sección Inicio de este alcance para diferenciar la instrucción para cada estudiante.

Area, Surface Area, and Volume

Skill or Key Concept

Describe the two-dimensional figures that result from slicing three-dimensional figures, as in plane sections of right rectangular prisms and right rectangular pyramids.

Solve real world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.

Solve real world and mathematical problems involving the four operations with rational numbers (extend the rules for manipulating fractions to complex fractions).

❏ Physical modeling ❏ Pictorial modeling ❏ Problem solving ❏ Discussion ❏ Written explanation

❏ Physical modeling

❏ Pictorial modeling

❏ Problem solving

❏ Discussion

❏ Written explanation

❏ Physical modeling

❏ Pictorial modeling

❏ Problem solving

❏ Discussion

❏ Written explanation 1

Standards for Mathematical Practice Notes and Feedback

Make sense of problems and persevere in solving them

Reason abstractly and quantitatively

Construct viable arguments and critique the reasoning of others

Model with mathematics

Use appropriate tools strategically

Attend to precision

Look for and make use of structure

Look for and express regularity in repeated reasoning

Consider these reflection questions in this scope.

● Is this student proficient in the skills addressed in this scope?

○ If so, what is next for them?

○ If not, how can I support them?

● What activities worked well for this student, and what would I do differently next time?

DESCRIPCIÓN

Los estudiantes analizan los resultados de su evaluación y determinan qué hicieron bien y en qué pueden mejorar.

MATERIALES

• 1 mapa de calor (por estudiante)

• 1 lápiz rojo (por estudiante)

• 1 lápiz azul (por estudiante)

• 1 lápiz naranja (por estudiante)

PREPARACIÓN

• Determine si los estudiantes analizarán su prueba de habilidades, la evaluación basada en estándares o ambas.

• Imprima un mapa de calor para cada estudiante.

• Reúna lápices de color rojo, azul y naranja para cada estudiante.

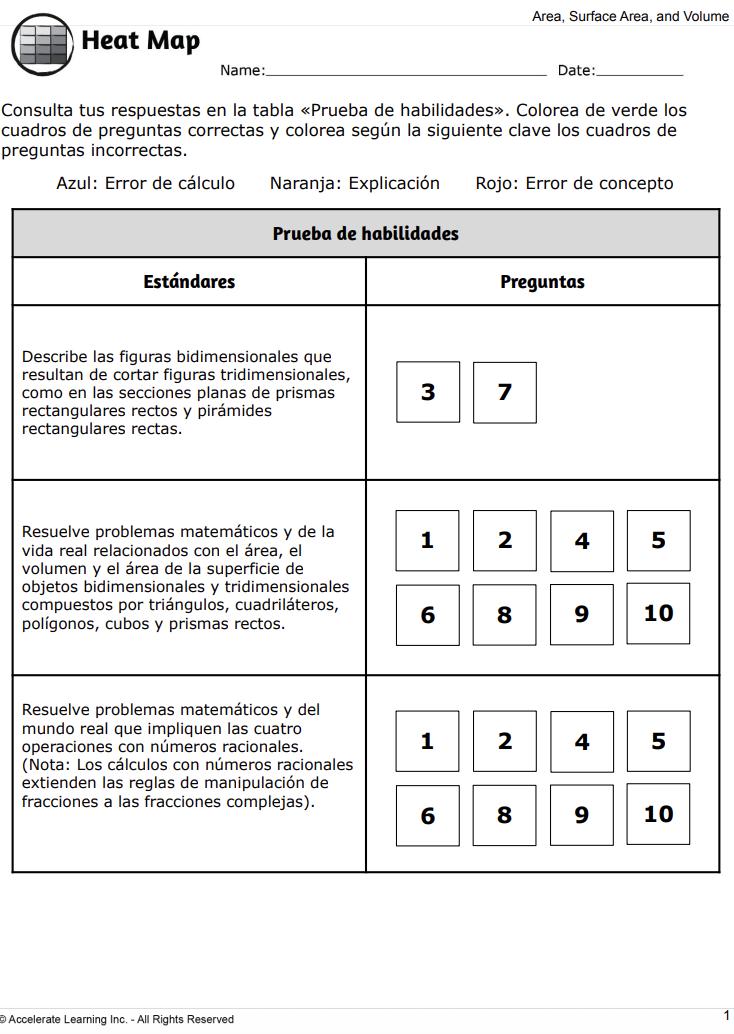
EVALUAR: MAPA DE CALOR

ANALIZAR LOS RESULTADOS DE LA EVALUACIÓN

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Distribuya un mapa de calor a cada estudiante junto con los lápices de color rojo, azul y naranja. Los estudiantes deben tener a mano su(s) evaluación(es) corregida(s).

2. Los estudiantes utilizan su(s) evaluación(es) corregida(s) para colorear el mapa de calor. Para cada pregunta no contestada por error de cálculo, los estudiantes colorean de azul la casilla correspondiente. Para cada pregunta no contestada por una explicación, los estudiantes colorean la casilla correspondiente de naranja. Para cada pregunta omitida por un concepto erróneo, colorean el cuadro correspondiente de rojo.

3. Anime a los estudiantes a buscar patrones en sus datos, como un determinado estándar que se perdió con más frecuencia o un estándar que han dominado claramente, y utilizar esta información para reflexionar y establecer metas en la tabla proporcionada.

4. Consulte la guía de instrucción andamiada que se encuentra en la sección «Inicio» para proporcionar extensión o apoyo adicional.

MAPA DE CALOR

INTERVENCIÓN: REPASO Y PRÁCTICA DE HABILIDADES

REFORZAR Y VOLVER A ENSEÑAR

REPASO Y PRÁCTICA DE HABILIDADES

DESCRIPCIÓN

Esta actividad está diseñada para repasar los conceptos clave del alcance. Utilícela como repaso o para intervención.

MATERIALES

IMPRESOS

• 1 evaluación rápida (por estudiante)

• 1 repaso (por estudiante)

• 1 evaluación de control (por estudiante)

• 1 lista de verificación para el maestro (por profesor)

PREPARACIÓN

• Imprima una copia de la evaluación rápida, el repaso y la evaluación de control por estudiante.

• Si lo desea, coloque a los estudiantes en grupos de 3 o 4 para completar la revisión.

• Si lo desea, imprima un ejemplo del esquema de anclaje de la sección «Explicar» o pida a los estudiantes que usen la libreta interactiva como regrado.

• Opcionalmente, imprima cualquiera de los materiales de ayuda complementarios para que los estudiantes los utilicen mientras trabajan.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. De una copia de la evaluación rápida a cada estudiante.

2. Cada uno debe completarla de forma independiente.

3. Use la rúbrica de habilidades al final de la evaluación rápida para identificar qué estudiantes necesitan ayuda adicional en las habilidades.

4. Distribuya una copia del repaso a cada estudiante.

5. Cada uno debe completar el repaso como actividad de intervención o como actividad independiente.

a. Si lo desea, reúna a los estudiantes en pequeños grupos para trabajar en las destrezas de repaso. Use el repaso como ayuda para la reenseñanza.

6. Distribuya una copia de la evaluación de control a cada estudiante.

7. Cada estudiante debe completarla de forma independiente.

8. Analice los resultados de la evaluación de control utilizando la lista de verificación para el maestro para identificar a quienes necesitan un repaso adicional y quienes han alcanzado el dominio de los conceptos.

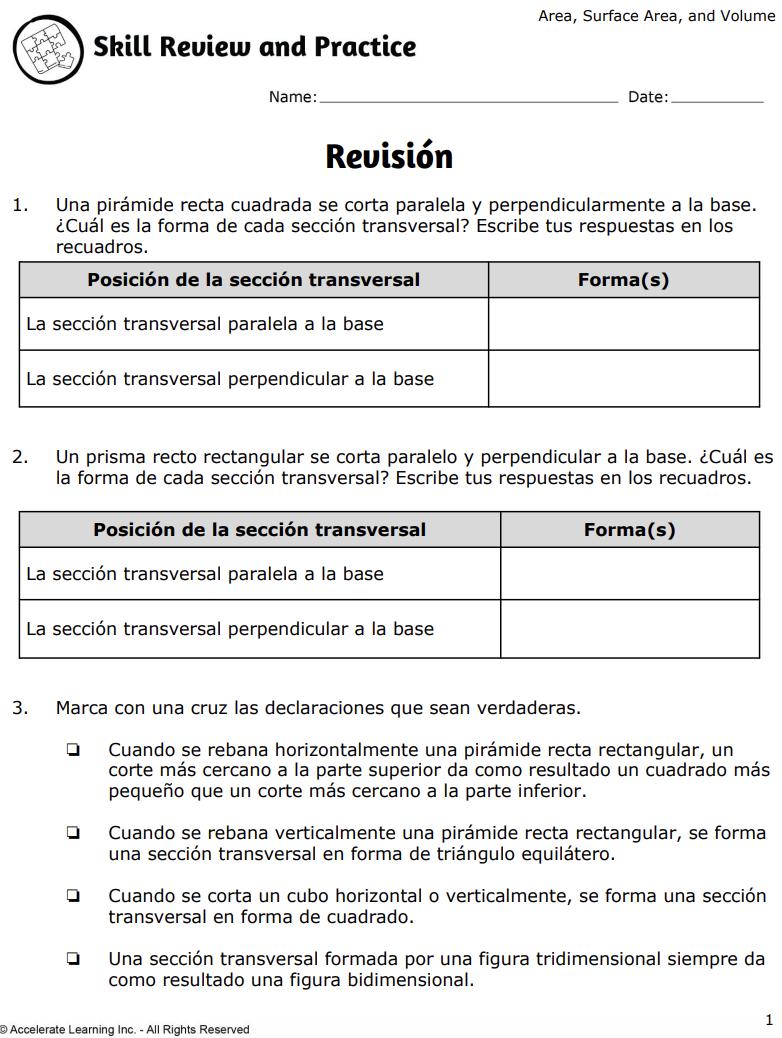
INTERVENCIÓN: REPASO Y PRÁCTICA DE HABILIDADES

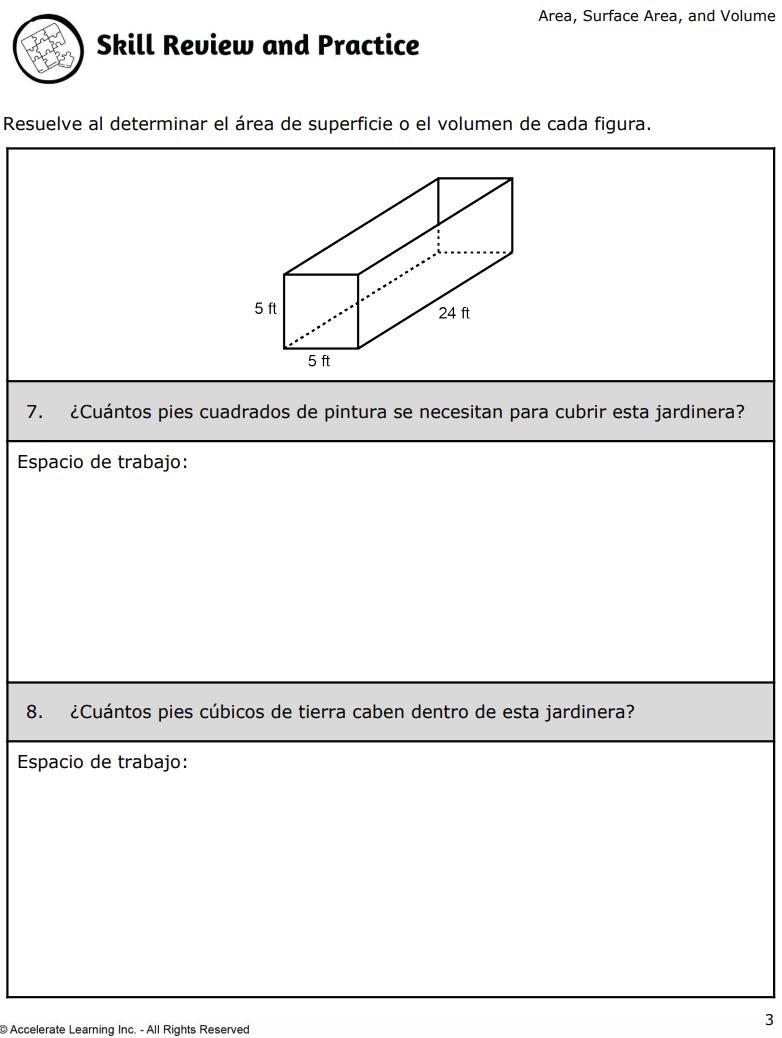
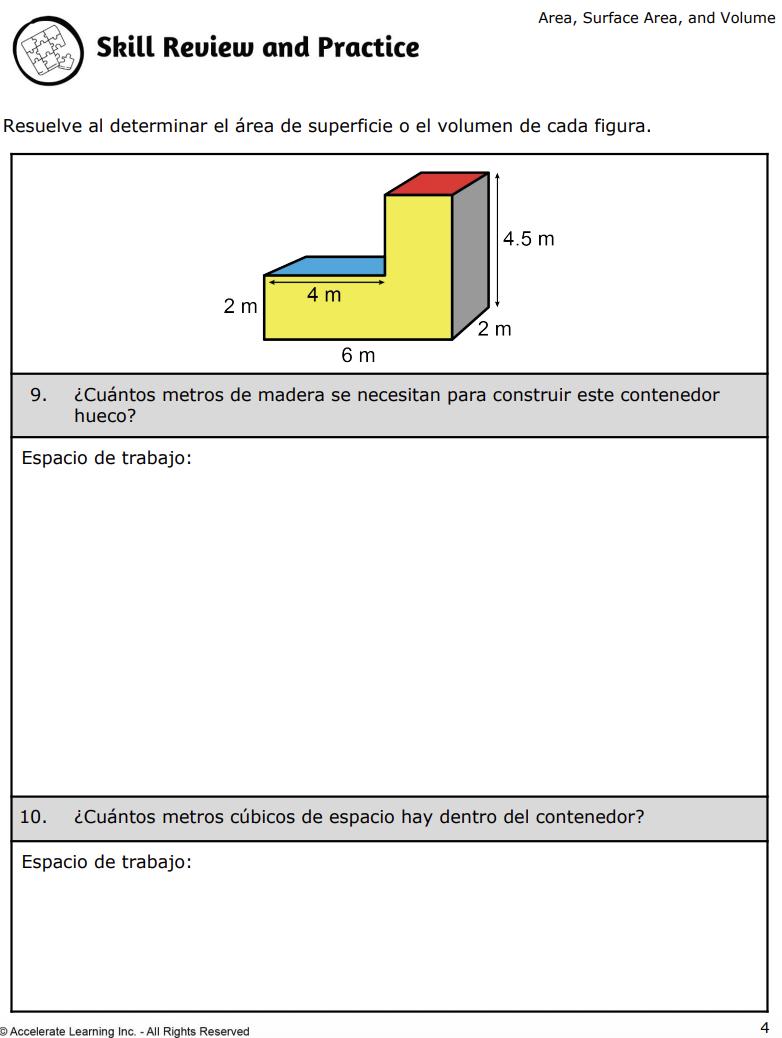
EVALUACIÓN DE CONTROL

ACELERACIÓN: ¿QUÉ PREFIERES?

RAZONAMIENTO MATEMÁTICO

¿QUÉ PREFIERES?: CAJAS DE DONACIÓN

DESCRIPCIÓN

Los estudiantes utilizan el razonamiento matemático y la creatividad para justificar una respuesta.

MATERIALES

IMPRESORA

• 1 folleto del estudiante (por alumno)

• 1 rúbrica (por maestro)

PREPARACIÓN

• Imprima un folleto del estudiante por alumno.

• Planifique que los estudiantes trabajen en parejas para completar esta actividad, si lo desea.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Entregue un folleto del estudiante a cada alumno.

2. Anime a los estudiantes a mirar sus folletos del estudiante de las exploraciones si necesitan repasar habilidades.

3. Invite a los estudiantes a compartir respuestas y justificaciones con sus compañeros.

4. Utilice la rúbrica proporcionada para evaluar las habilidades de comprensión, cálculo y razonamiento de los estudiantes.

FOLLETO DEL ESTUDIANTE CLAVE DE RESPUESTAS

ACELERACIÓN: TABLERO DE OPCIONES

TABLERO DE OPCIONES

OPCIONES PARA EL APRENDIZAJE CONTINUO

TABLERO DE OPCIONES

DESCRIPCIÓN

Los estudiantes exploran las conexiones con el mundo real y las aplicaciones del contenido matemático a través de interacciones con actividades atractivas.

MATERIALES

IMPRESOS

• 1 tablero de opciones (por estudiante)

• 1 juego de hojas de actividades (por estudiante)

• 1 autoevaluación del tablero de opciones (por estudiante)

REUTILIZABLE

• Tecnología (si corresponde)

PREPARACIÓN

• Imprima un tablero de elección y un juego de hojas de actividades para cada estudiante.

• Imprime una autoevaluación del tablero para cada estudiante.

• Planifica con antelación el uso de la tecnología. Puede ser necesario investigar para algunas actividades del tablero de opciones.

PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN

1. Distribuya un tablero de opciones a cada estudiante.

2. Conceda tiempo a los estudiantes para examinar el tablero de opciones y seleccionar las actividades que les gustaría explorar.

3. Anime a los estudiantes a intentar al menos tres actividades del tablero de opciones.

4. Distribuya las hojas de actividades correspondientes según las elecciones de los estudiantes.

5. Al finalizar cada actividad del tablero de opciones, haga que los estudiantes completen una autoevaluación del tablero para revisar su propio pensamiento matemático y sus esfuerzos en su proyecto.