

GRADO 2

CALIFORNIA
Muestra de la edición para el maestro
Muestra de la edición para maestros Grado 2
Publicado por Accelerate Learning Inc., 5177 Richmond Ave, Suite 800, Houston, TX 77056. Copyright © 2025, Accelerate Learning Inc. Todos los derechos reservados. Ninguna parte de esta publicación podrá ser reproducida o distribuida en ninguna forma ni por ningún medio, ni almacenada en una base de datos o sistema de recuperación, sin el consentimiento previo por escrito de Accelerate Learning Inc., incluyendo, entre otros, en cualquier red u otro sistema de almacenamiento o transmisión electrónica, o difusión para educación a distancia.
Para obtener más información, visítenos en www.stemscopes.com.
RESOLUCIÓN DE PROBLEMAS DE ADICIÓN Y SUSTRACCIÓN
ACTIVIDADES DE PARTICIPACIÓN
ACCESO A LOS CONOCIMIENTOS PREVIOS
Los estudiantes resuelven problemas de suma y resta para demostrar su comprensión de los conceptos matemáticos.
ESTÁNDARES CLAVE
Representar y resolver problemas que impliquen sumas y restas.
• Utilizar sumas y restas dentro de 100 para resolver problemas de uno y dos pasos que impliquen situaciones de sumar a, quitar de, juntar, separar y comparar, con incógnitas en todas las posiciones; por ej. con dibujos y ecuaciones con un símbolo para el número desconocido para representar el problema.
Utilizar la comprensión del valor posicional y las propiedades de las operaciones para sumar y restar.
• Sumar y restar dentro de 1,000, a partir de modelos concretos o dibujos y estrategias basadas en el valor posicional, las propiedades de las operaciones y/o la relación entre la suma y la resta; relacionar la estrategia con un método escrito. Comprender que al sumar o restar números de tres cifras, se suman o restan centenas y centenas, decenas y decenas, unidades y unidades; y que, a veces, es necesario componer o descomponer decenas o centenas.
ESTÁNDARES DE CONEXIÓN
Utilizar la comprensión del valor posicional y las propiedades de las operaciones para sumar y restar.
• Sumar y restar con fluidez dentro de 100 con estrategias basadas en el valor posicional, las propiedades de las operaciones y/o la relación entre la suma y la resta.
• Explicar por qué funcionan las estrategias de suma y resta, utilizando el valor posicional y las propiedades de las operaciones.
• Utilizar estrategias de estimación para realizar estimaciones razonables en la resolución de problemas.
Sumar y restar dentro de 20.
• Sumar y restar con fluidez dentro de 20 utilizando estrategias mentales. Al final del segundo grado, saber de memoria todas las sumas de dos números de un dígito. (El dominio de este estándar se desarrolla a en el alcance «Fluidez de los hechos matemáticos: Adición y sustracción»).
• Los estudiantes resuelven problemas de suma y resta dentro de un intervalo de 20, en diferentes situaciones, como sumar, restar y comparar.
• Registran su proceso de resolución de problemas con imágenes y frases numéricas para representar las incógnitas.
• La actividad incluye debates en clase para explorar diferentes estrategias y aclarar conceptos erróneos, que mejoran la comprensión de la suma y la resta.
• Los maestros evalúan el dominio de los estudiantes de la norma y proporcionan apoyo según sea necesario para fortalecer las habilidades fundamentales.
CAPTAR INTERÉS: PUNTAJES DE LANZA Y ANOTA
Los estudiantes se involucran en la resolución de un problema escrito de sustracción con un término desconocido utilizando varios modelos.
• Trabajan en parejas para explorar un escenario del mundo real que implica la sustracción; usan bloques de base diez para representar el problema físicamente.
• Usan modelos de barras o rectas numéricas para representar visualmente y resolver el problema; fomentan diferentes enfoques y comparan soluciones.
• La actividad incluye debates para profundizar en la comprensión de los modelos y el proceso de resolución de problemas, centrándose en la identificación de información conocida y desconocida.
• Los alumnos reflexionan sobre la eficacia de los modelos concretos frente a los pictóricos para resolver el problema, fomentando el pensamiento crítico y la articulación de preferencias.
ACTIVIDADES DE EXPLORAR
EXPLORACIÓN 1: REPRESENTAR Y RESOLVER PROBLEMAS ESCRITOS DE UN PASO
Los estudiantes resuelven problemas escritos de un paso con representaciones pictóricas e identifican modelos para problemas de suma y resta.
• Trabajan en grupos para resolver problemas escritos con temática del zoológico a partir de bloques de base diez y tablas de valor posicional.
• Crean modelos pictóricos y escriben frases numéricas para representar los problemas, centrándose en la identificación de incógnitas.
• En la parte II, los estudiantes analizan diferentes modelos para determinar cuál representa mejor la solución de cada problema.
EXPLORACIÓN 2: REPRESENTAR Y RESOLVER PROBLEMAS ESCRITOS DE VARIOS PASOS
Los estudiantes se dedican a resolver problemas escritos de suma y resta de varios pasos utilizando diversos modelos y herramientas matemáticas.
• Trabajan en grupos para resolver problemas escritos con rectas numéricas o modelos de barras, identificando incógnitas en los problemas.
• Usan bloques de base diez para verificar sus soluciones y registran sus hallazgos en un diario del estudiante.
• La actividad fomenta la resolución colaborativa de problemas y el debate, con los estudiantes compartiendo y comparando diferentes estrategias.
• Se usa un boleto de salida para evaluar la comprensión de los estudiantes y una charla matemática para reflexionar y compartir ideas.
EXPLORACIÓN 3: USAR MODELOS CONCRETOS PARA REPRESENTAR ADICIÓN Y SUSTRACCIÓN HASTA 1,000
Los estudiantes resuelven problemas escritos que implican sumas y restas dentro de 1,000 con objetos concretos. Trabajan en parejas para utilizar bloques de base diez y tablas de valor posicional para representar y resolver problemas.
• Leen y resuelven los planteamientos del documento «tareas de tarjetas coleccionables», y comentan y anotan sus estrategias en el diario del estudiante.
• La actividad incluye preguntas guiadas para ayudar a los alumnos a comprender y aplicar diferentes estrategias para sumar y restar.
• Participan en una charla de matemáticas para compartir y comparar estrategias, y mejoran su comprensión de los distintos métodos de resolución de problemas.
EXPLORACIÓN 4: USAR MODELOS PICTÓRICOS PARA REPRESENTAR LA ADICIÓN Y SUSTRACCIÓN HASTA 1,000 Los alumnos resuelven problemas de sumas y restas dentro de 1,000 a partir de varios modelos pictóricos.
• Trabajan en grupos para resolver problemas con bloques de base diez, modelos de barras y rectas numéricas.
• Anotan sus soluciones en un diario del estudiante, dibujan modelos y escriben frases numéricas para representar los problemas.
• A lo largo de la actividad, propongan estrategias y compartan puntos de vista, comparando diferentes métodos para resolver los problemas.
Los alumnos exploran diferentes estrategias para sumar y restar, como dividir los números en partes de valor posicional, utilizar bloques de base diez y dibujar rectas numéricas. Estas actividades fomentan el pensamiento flexible y los enfoques múltiples para la resolución de problemas, lo que refuerza el uso de estrategias numéricas eficientes.




DÓLARES Y CENTAVOS






ESTRATEGIAS NUMÉRICAS


CONCEPTOS CLAVE
• Puedo usar la adición y sustracción dentro de 100 para resolver problemas escritos de uno y dos pasos que implican sumar a, tomar de, juntar, separar y comparar con incógnitas en todas las posiciones utilizando dibujos.
• Puedo usar sumas y restas dentro de 100 para resolver problemas escritos de uno y dos pasos que involucran sumar a, tomar de, juntar, separar y comparar con incógnitas en todas las posiciones usando ecuaciones con un símbolo para el número desconocido para representar el problema.
• Puedo sumar y restar dentro de 1,000 con modelos concretos y relacionar la estrategia con un método escrito.
• Puedo sumar y restar dentro de 1,000 con dibujos y relacionar la estrategia con un método escrito.
• Puedo sumar y restar dentro de 1,000 a partir de estrategias basadas en el valor posicional y relacionar la estrategia con un método escrito.
• Puedo sumar y restar dentro de 1,000 utilizando las propiedades de las operaciones y relacionar la estrategia con un método escrito.
• Puedo sumar y restar dentro de 1,000 utilizando la relación entre suma y resta y relacionar la estrategia con un método escrito.
• Puedo entender que al sumar y restar números de tres cifras es necesario sumar centenas y centenas, decenas y decenas, y unidades y unidades.
• Puedo entender que al sumar o restar números de tres cifras a veces es necesario componer o descomponer decenas o centenas.
ALCANCE: IDEAS FUNDAMENTALES
Los alumnos siguen la comprensión del valor posicional para practicar la suma y la resta de cantidades de dinero dentro de 1,000 con modelos concretos y representaciones pictóricas. Estas destrezas apoyan el trabajo futuro con los valores monetarios, ya que más adelante conectarán la comprensión del valor posicional con la resolución de problemas relacionados con el dinero.


RESOLUCIÓN DE PROBLEMAS DE MEDIDA



CONTAR SALTEADO HASTA 100

Los alumnos resuelven problemas escritos dentro de 1,000 que implican contextos del mundo real, como tarjetas coleccionables y entradas de máquinas recreativas. Las estrategias de resolución de problemas que practican serán aplicables más adelante en el curso cuando resuelvan problemas de medida de longitud.
Los alumnos aplican sus destrezas de conteo salteado con las rectas numéricas para resolver problemas de suma y resta. Al reconocer patrones en las secuencias numéricas y dividir los números en partes de valor posicional, los estudiantes construyen una base sólida para la fluidez con la suma y la resta de varios dígitos.
PREGUNTAS FUNDAMENTALES
• «¿Cómo puedes usar la adición y sustracción dentro de 100 para resolver problemas de uno y dos pasos que involucran situaciones de sumar, quitar, juntar, separar y comparar, con incógnitas en todas las posiciones, usando dibujos?».
• «¿Cómo puedes usar la adición y sustracción dentro de 100 para resolver problemas de uno y dos pasos que involucran situaciones de adición, sustracción, unión, separación y comparación, con incógnitas en todas las posiciones, usando ecuaciones con un símbolo para el número desconocido para representar el problema?».
• «¿Cómo puedes sumar y restar dentro de 1,000 con modelos concretos o dibujos y relacionar la estrategia con un método escrito?».
• «¿Cómo puedes sumar y restar dentro de 1,000 con estrategias basadas en el valor posicional y relacionar la estrategia con un método escrito?»
• «¿Cómo puedes sumar y restar dentro de 1,000 utilizando las propiedades de las operaciones y relacionar la estrategia con un método escrito?».
• «¿Cómo puedes sumar y restar dentro de 1,000 utilizando la relación entre la suma y la resta y relacionar la estrategia con un método escrito?».
• «¿Cómo puedes comprender que al sumar y restar números de tres cifras, es necesario sumar centenas y centenas, decenas y decenas, y unidades y unidades?».
• «¿Cómo puedes demostrar que comprendes que al sumar o restar números de tres cifras, a veces es necesario componer o descomponer decenas o centenas?». <<NOMBRE DEL ÁMBITO>> <<GRADO>>
INICIO: CALENDARIO SUGERIDO
PLANIFICACIÓN
Internalización de la lección
Alcance
• Revise los estándares abordados en este alcance.
• Familiarícese con la forma en que se evalúan los estándares y lo que demuestra el dominio de la materia.
• Revise el documento «Secuencia de aprendizaje» que se encuentra en el elemento «Visión general del alcance» para comprender la secuencia de los conceptos.
• Determine qué recursos se utilizarán para la práctica y la evaluación.
Lección
• Revise las instrucciones para el maestro y los documentos asociados.
• Familiarícese con los modelos, herramientas y estrategias que los estudiantes utilizarán en la actividad.
• Considere el propósito de la lección dentro del alcance e identifique lo que los estudiantes deben saber y ser capaces de hacer como resultado.
• Identifique las áreas en las que los estudiantes pueden necesitar apoyo o enriquecimiento y planifique cómo responder..
Contenido de apoyo
Contenido desglosado
Visión general del alcance
Manipulativos/materiales
DÍA 1
Se presenta a los alumnos una actividad en la que representan y resuelven un problema de resta en el que la incógnita puede ser cualquiera de los términos del problema. Repiten la actividad después de haber completado las exploraciones correspondientes.
Los estudiantes expresan opiniones, ideas y sentimientos sobre un problema utilizando frases como «Yo noto . . .» y «me pregunto si . . .»
• Numeración diaria
• Fluidez en los hechos matemáticos: Suma y resta
• Ciencia de datos
• Captar interés (parte 1): Preexploración
DÍA 2
Los alumnos dibujan un modelo de barras y una recta numérica basándose en la información dada en un problema escrito.
Exploración 1
• 9 barras de base diez (por grupo)
• 20 unidades de base diez (por grupo) Exploración 2
• 1 conjunto de bloques de base diez (por clase) Exploración 3
• 10 bloques de base diez (por pareja)
• 20 barras de base diez (por pareja)
• 20 unidades de base diez (por pareja) Acceso a conocimientos previos (~15 minutos)
• Completar la semana anterior a este alcance. Carta para llevar a casa
• Imprima y envíe a casa la semana anterior a este alcance.
DÍA 3
Los alumnos utilizan un modelo de resolución de problemas para encontrar la solución a problemas de sumas y restas.
DÍA 4
Los alumnos representan y resuelven problemas escritos de un solo paso de forma pictórica y, a continuación, identifican modelos que representan problemas escritos de sumas y restas.
Los alumnos usan pistas contextuales e ilustraciones para comprender palabras desconocidas.
Los alumnos comentan y resumen textos en pequeños grupos para demostrar su comprensión y entendimiento.
• Numeración diaria
• Fluidez en los hechos matemáticos: Suma y resta
• Ciencia de datos
• Habilidades básicas: Cómo dibujar un modelo pictográfico
• Numeración diaria
• Fluidez en los hechos matemáticos: Suma y resta
• Ciencia de datos
• Habilidades básicas: Modelo de resolución de problemas
Los alumnos utilizan apoyos como modelos e ilustraciones para mejorar su comprensión de vocabulario y conceptos nuevos.
• Numeración diaria
• Fluidez en los hechos matemáticos: Suma y resta
• Ciencia de datos
• Comienza la «Exploración 1»: Representar y resolver problemas escritos de un paso
Práctica independiente (del alcance o nivel de grado anterior)
Constructor de fluidez
Práctica interactiva
Práctica guiada
Constructor de bases fundamentales
Conversaciones estructuradas
Preguntas de facilitación
Práctica independiente
Refiérase a la sección de «Práctica».
Práctica guiada
Refiérase a la sección de «Práctica».
Conversaciones estructuradas
Preguntas de facilitación
Práctica independiente
Refiérase a la sección de «Práctica».
Práctica guiada
Refiérase a la sección de «Práctica».
Conversaciones estructuradas Preguntas de facilitación
Práctica independiente
Refiérase a la sección de «Práctica».
Práctica guiada
Refiérase a la sección de «Práctica».
Conversaciones estructuradas
Preguntas de facilitación
PRÁCTICA
Práctica independiente
• Todos los estudiantes
• Explicar: Vocabulario ilustrado (15-30 minutos)
• Explicar: Mis pensamientos de matemáticas (15-30 minutos)
• Elaborar: Conexiones con la vida (15-30 minutos)
• Elaborar: Revisión en espiral (15-30 minutos)
Los que dominan
• Aceleración: Matemáticas de hoy (15-30 minutos)
• Aceleración: Estación de conexión (15-30 minutos)
• Aceleración: Tablero de opciones (15-30 minutos)
Los que cumplen
• Elaborar: Cuento de matemáticas (30-45 minutos)
• Elaborar: Tarea basada en problemas (30-45 minutos)
• Elaborar: Constructor de fluidez (15-30 minutos)
Los deficientes
• Elaborar: Práctica interactiva (15-30 minutos)
• Evaluar: Prueba de habilidades (30-45 minutos)
Práctica guiada
• Intervención: Intervención en grupos pequeños (15-30 minutos)
• Explicar: Conexiones lingüísticas (15-30 minutos)
• Inicio: Guía de instrucción andamiada (30-45 minutos)
Los alumnos representan y resuelven problemas de un solo paso de forma pictórica y, a continuación, identifican modelos que representan problemas de suma y resta.
Los estudiantes utilizan vocabulario nuevo durante los debates en clase.
• Numeración diaria
• Fluidez en los hechos matemáticos: Suma y resta
• Ciencia de datos
• Continúa la «Exploración 1»: Representar y resolver problemas escritos de un paso
• Charla de matemáticas
• Esquema de anclaje: «Exploración 1»
Práctica independiente
Refiérase a la sección de «Práctica».
Práctica guiada
Parte I: Intervención en grupos pequeños
Exploración 1: Boleto de salida
Muestra lo que sabes (parte 1)
Lista de verificación de observación
Preguntas de facilitación
Los alumnos representan y resuelven problemas de suma y resta de varios pasos en los que la incógnita puede ser cualquiera de los términos del problema, a partir de rectas numéricas o modelos de barras y comprueban las respuestas con bloques de base diez.
Los estudiantes usan un lenguaje matemático preciso cuando participan en los debates en clase.
• Numeración diaria
• Fluidez en los hechos matemáticos: Suma y resta
• Ciencia de datos
• Exploración 2: Representar y resolver problemas escritos de varios pasos
• Charla de matemáticas
• Esquema de anclaje: «Exploración 2»
Práctica independiente
Refiérase a la sección de «Práctica».
Práctica guiada
Parte II: Intervención en grupos pequeños
Exploración 2: Boleto de salida
Muestra lo que sabes (parte 2)
Lista de verificación de observación
Preguntas de facilitación
INICIO: CALENDARIO SUGERIDO
EVALUACIONES
Acceso a conocimientos previos (D)
Breve actividad de sondeo para evaluar los conocimientos previos antes de abordar el contenido del alcance.
Boleto de salida (F)
Evaluación rápida sobre lo que aprendieron en esta exploración.
Muestra lo que sabes (F)
Tarea de práctica independiente que permite a los estudiantes demostrar su aprendizaje.
Mostrar y contar (D, S)
Evaluación rápida en rúbrica individual o pequeños grupos con manipulativos o siguiendo indicaciones del maestro. Lista de verificación de observación (D, F)
Lista de conceptos y habilidades que el maestro y el estudiante pueden usar para reflexionar sobre el progreso del estudiante y establecer objetivos.
Los alumnos representan y resuelven problemas de suma y resta dentro de 1,000 con objetos concretos.
Prueba de habilidades (F, S)
Evaluación basada en estándares para determinar la habilidad para resolver problemas matemáticos de manera eficiente y precisa.
Intervención en grupos pequeños: Revisión (F)
Tarea de práctica independiente para evaluar el dominio del contenido después de la intervención en grupos pequeños.
Evaluaciones de referencia (D, S)
Evaluaciones de principio, mitad y final de año que ofrecen datos significativos que pueden informar la instrucción.
Evaluaciones de medición del crecimiento (D, S)
Evaluaciones previas y posteriores diseñadas para realizar un seguimiento del crecimiento de los estándares de nivel de grado desde el principio hasta el final del año.
Los estudiantes usan apoyos tales como dibujos, modelos y gestos para mejorar su comunicación verbal.
• Numeración diaria
• Fluidez en los hechos matemáticos: Suma y resta
• Ciencia de datos
• Exploración 3: Usar modelos concretos para representar adición y sustracción hasta 1,000
• Charla de matemáticas
Práctica independiente
Refiérase a la sección de «Práctica».
Práctica guiada
Parte III: Intervención en grupos pequeños
Exploración 3: Boleto de salida
Muestra lo que sabes (parte 3)
Lista de verificación de observación
Preguntas de facilitación
Los estudiantes intercambian ideas, proporcionan retroalimentación y modifican su trabajo según sea necesario.
• Numeración diaria
• Fluidez en los hechos matemáticos: Suma y resta
• Ciencia de datos
• Comienza la «Exploración 4»: Usar modelos pictóricos para representar la adición y sustracción hasta 1,000
Práctica independiente
Refiérase a la sección de «Práctica».
Práctica guiada
Refiérase a la sección de «Práctica».
Conversaciones estructuradas
Preguntas de facilitación
INICIO: CALENDARIO SUGERIDO
DÍA 9
Los alumnos representan y resuelven problemas de adición y sustracción dentro de 1,000 con modelos pictóricos, que incluyen el dibujo de bloques de base diez, modelos de barras y rectas numéricas.
DÍA 10
Los alumnos repiten la actividad en la que representan y resuelven un problema de sustracción en el que la incógnita puede ser cualquiera de los términos del problema. Los estudiantes resuelven el problema original ahora que se han completado las exploraciones correspondientes.
DÍA 11
Los estudiantes demuestran el dominio de los conceptos y habilidades clave en este alcance de aplicación a través de una evaluación basada en estándares.
Los estudiantes colaboran para desarrollar respuestas escritas, proporcionan retroalimentación y editan sus respuestas según sea necesario.
Los estudiantes crean respuestas escritas utilizando vocabulario recién adquirido y revisan sus respuestas según sea necesario.
• Numeración diaria
• Fluidez en los hechos matemáticos: Suma y resta
• Ciencia de datos
• Continúa la «Exploración 4»: Usar modelos pictóricos para representar la adición y sustracción hasta 1,000
• Charla de matemáticas
• Esquema de anclaje: «Exploración 4»
• Numeración diaria
• Ciencia de datos
• Libreta interactiva: Modelo de barras y recta numérica
Los estudiantes emplean habilidades de lectura y escritura utilizando lenguaje académico para demostrar su comprensión de los conceptos clave.
Práctica independiente
• Refiérase a la sección de «Práctica».
Práctica guiada
Parte IV: Intervención en grupos pequeños
• Captar interés (parte 2): Posexploración
• Numeración diaria
• Fluidez en los hechos matemáticos: Suma y resta
• Ciencia de datos
• Exploración 4: Boleto de salida
• Muestra lo que sabes (parte 4)
• Lista de verificación de observació
• Preguntas de facilitación
Práctica independiente
• Refiérase a la sección de «Práctica».
Práctica guiada
• Refiérase a la sección de «Práctica».
Práctica independiente
• Refiérase a la sección de «Práctica».
Práctica guiada
• Refiérase a la sección de «Práctica».
• Verificación de la intervención en grupos pequeños
• Prueba de habilidades
• Decidir y defender
• Evaluación basada en estándares
GRADO 2: RESOLUCIÓN DE PROBLEMAS DE ADICIÓN Y SUSTRACCIÓN
INICIO > CALENDARIO SUGERIDO
INICIO: CONTENIDO DE APOYO
¿QUÉ ESTOY ENSEÑANDO?
CONTENIDO DE APOYO
Representar y resolver problemas que impliquen sumas y restas.
• Usar sumas y restas dentro de 100 para resolver problemas escritos de uno y dos pasos que impliquen situaciones de sumar a, quitar de, juntar, separar y comparar, con incógnitas en todas las posiciones; por ej., con dibujos y ecuaciones con un símbolo para el número desconocido para representar el problema.
Usar la comprensión del valor posicional y las propiedades de las operaciones para sumar y restar.
• Sumar y restar dentro de 1,000, utilizando modelos concretos o dibujos y estrategias basadas en el valor posicional, las propiedades de las operaciones y/o la relación entre la suma y la resta; relacionar la estrategia con un método escrito. Comprender que al sumar o restar números de tres cifras, se suman o restan centenas y centenas, decenas y decenas, unidades y unidades; y a veces es necesario componer o descomponer decenas o centenas.
CONOCIMIENTOS PREVIOS
En jardín de infancia, los alumnos explicaron las estrategias que usaron para resolver problemas de suma y resta dentro de 10 con palabras habladas, modelos concretos y pictóricos, y ecuaciones; usaron el proceso de descomposición para encontrar pares de números que sumen una cantidad total. Utilizaron modelos concretos como fichas, cubos conectables y marcos de diez. A medida que se familiarizaban con los modelos concretos, pasaban a crear representaciones pictóricas de fichas y a utilizar marcos de diez. El uso de estos modelos ayudó a los alumnos a ilustrar problemas escritosy a escribir frases numéricas y símbolos cuando pasaron a la fase abstracta de resolución de problemas. En primer grado, los alumnos demostraron fluidez en los hechos al utilizar estrategias tales como contar, hacer diez, descomponer un número que lleva a diez, utilizar la relación entre suma y resta y crear sumas equivalentes pero más fáciles para resolver problemas de suma y resta. Los alumnos resolvieron problemas que requerían la suma de tres números enteros cuya suma era menor o igual a 20. Además, aplicaron estas estrategias para sumar un número de dos cifras y otro de una cifra, sumar un número de dos cifras y un múltiplo de 10, restar múltiplos de 10 de múltiplos de 10 y resolver problemas de suma y resta con un número entero desconocido. En primer grado, los alumnos usaron modelos concretos, como cubos y fichas. Posteriormente, usaron modelos pictóricos como los marcos de diez, los modelos parteparte-entero, los recorridos numéricos, las rectas numéricas, los enlaces numéricos y los modelos de barras para profundizar en su comprensión de cómo usar los procedimientos correctos para resolver problemas.
CONCEPTOS ERRÓNEOS Y OBSTÁCULOS
• Es posible que los alumnos no reconozcan que los sumandos pueden colocarse en cualquier orden (por ejemplo, 3 + 2 = 5 es lo mismo que 2 + 3 = 5).
• Es posible que vean igual como una acción. El signo igual es una relación que muestra equilibrio, y ambos lados tienen el mismo valor.
• Pueden depender de la memorización de la fluidez de los hechos de suma o resta en lugar de explorar y describir estrategias numéricas para esa fluidez.
• Los alumnos pueden centrarse en las palabras clave de un problema escrito a la hora de elegir la operación adecuada para resolverlo, en lugar de comprender realmente el contexto del problema. Deberían representar la acción de los problemas escritos con objetos concretos.
• Los alumnos pueden no darse cuenta de que pueden contar hacia arriba para resolver problemas de resta encontrando la diferencia entre dos números.
• Los alumnos pueden pensar que la resta sólo consiste en separar cuando también puede implicar comparar y distanciar.
• Pueden contar mal si usan modelos concretos para crear un paquete de diez o representar cien.
• Los alumnos pueden cometer errores al usar el modelo de barra para resolver problemas y no hacer que las partes sean proporcionales. Es posible que terminen con una solución poco razonable del problema.
• Es posible que los alumnos no reagrupen correctamente cuando utilicen bloques de base diez.
• Es posible que los alumnos no comiencen en el número correcto cuando utilicen una recta numérica o que salten a números que sean mayores o menores que el número previsto.
EN ESTE ALCANCE
Los alumnos aplican y comunican sus conocimientos sobre tipos de problemas, como sumar a, quitar de, juntar, separar y comparar (dentro de 100). Representarán su pensamiento matemático al resolver problemas de uno y dos pasos mediante una progresión de representaciones concretas, pictóricas y abstractas. Los alumnos sumarán y restarán (hasta 1,000) con modelos concretos como bloques de base diez y cubos conectables. También usarán modelos pictóricos que incluyen dibujos, el uso de rectas numéricas y el modelo de barra. Los alumnos ampliarán su comprensión de la suma y la resta, usando estrategias basadas en el valor posicional, las propiedades de la operación y la relación entre la suma y la resta. Se hará referencia a la composición y descomposición de una decena para que los alumnos puedan utilizar estrategias que impliquen formar una decena, formar una centena y descomponer una decena. No se espera que los alumnos usen el algoritmo estándar en segundo grado.
TÉRMINOS CLAVE
• sumando: un número que se suma a otro.
• adición: combinar dos o más números para obtener una suma o un total.
• modelo de barras: una representación pictórica de un problema en la que se utilizan barras para representar las cantidades conocidas y desconocidas.
• componer: juntar piezas
• modelo concreto: un modelo que utiliza objetos físicos para representar un número o una idea.
• descomponer: romper
• diferencia: la distancia entre dos números; el resultado de restar un número de otro.
• igual a (=): la misma cantidad cuando se compara con otra cantidad.
• ecuación: una oración matemática que usa números, uno o más símbolos de operación y un signo igual.
• problema (escrito) de pasos múltiples: una pregunta matemática escrita con palabras que requiere más de un paso para completarse.
• expresión numérica: una oración que contiene sólo números y los símbolos de las operaciones.
• propiedades de las operaciones: reglas matemáticas que siempre funcionan y te ayudan a resolver ecuaciones.
• resolver: encontrar una respuesta o solución a un problema.
• estrategia: un plan o forma de resolver un problema o encontrar una respuesta.
• sustracción: restar una cantidad a otra mayor; encontrar la diferencia entre dos números.
• suma: la cantidad total; el resultado de la suma.
• incógnita: un dato que falta.
• problemas escritos: una situación y pregunta hipotéticas que requieren conocimientos matemáticos, estrategias y una ecuación para ser resueltas.
INICIO: CONTENIDO DE APOYO
APLICAR LAS PRÁCTICAS MATEMÁTICAS
• MP.1 Dar sentido a los problemas y perseverar en su resolución: Los estudiantes se involucran en tareas de resolución de problemas del mundo real, como el seguimiento de los boletos del salón recreativo, tarjetas de intercambio y los visitantes del parque acuático. Aplican estrategias de suma y resta dentro de 1,000 para resolver problemas de un paso y de varios pasos.
• MP.2 Razonamiento abstracto y cuantitativo: Los alumnos interpretan números en contexto, analizan relaciones parte-entero en problemas y utilizan estrategias de valor posicional para sumar y restar de forma eficiente.
• MP.3 Construir argumentos viables y debatir el razonamiento de otros: Los estudiantes explican sus estrategias de resolución de problemas, justifican la elección de modelos pictóricos o concretos y comparan enfoques con sus compañeros para determinar la precisión.
• MP.4 Representar con matemáticas: Los estudiantes usan bloques de base diez, rectas numéricas, modelos de barras y tablas de valor posicional para representar y resolver problemas de suma y resta, conectando estas representaciones con oraciones numéricas escritas.
• MP.5 Utilizar estratégicamente las herramientas adecuadas: Los estudiantes seleccionan y utilizan herramientas como bloques de base diez, tablas numéricas y pizarras de borrado en seco para representar problemas, ayudar a visualizar la reagrupación y apoyar sus estrategias de resolución de problemas.
• MP.6 Atienden a la precisión: Los estudiantes usan la notación matemática correcta, se aseguran de que sus modelos representan con precisión el contexto del problema dado, y comprueban sus cálculos con operaciones inversas o una estrategia diferente.
• MP.7 Buscan y utilizan estructuras: Los alumnos reconocen patrones en el valor posicional y en las relaciones numéricas, aplicando su comprensión de las centenas, decenas y unidades para sumar y restar con fluidez.
• MP.8 Buscan y expresan regularidad en razonamientos repetidos: Los alumnos aplican estrategias repetidas para resolver problemas de sumas y restas, reconociendo la eficacia de la reagrupación, descomponiendo los números en partes de valor posicional y comprobando las soluciones mediante operaciones inversas.
INICIO: CONTENIDO DE APOYO
RESOLUCIÓN DE PROBLEMAS
Contar hacia adelante y hacia atrás son habilidades muy importantes para los alumnos de segundo grado, y se espera que avancen hacia el dominio de la suma y la resta dentro de 100. Una parte importante del proceso de resolución de problemas es dar a los alumnos la oportunidad de utilizar modelos para representar relaciones matemáticas clave en un problema de palabras para resolver el problema. Los alumnos utilizan modelos para visualizar y dar sentido al problema, organizar su pensamiento y determinar la operación adecuada para encontrar una solución al problema. Mediante el uso de modelos, los alumnos pueden establecer conexiones entre distintos tipos de problemas, como sumar, restar, unir, separar y comparar. Los estudiantes representan su pensamiento matemático a través de una progresión de representaciones concretas, pictóricas y abstractas:
• Concretas: objetos agrupables, como cubos conectables o bloques de base diez.
• Pictóricas: modelos de barras y rectas numéricas.
• Abstractas: expresión numérica o ecuación con un símbolo para representar el número desconocido.
Tipo de problema Resultado desconocido Cambio desconocido Inicio desconocido
Unir (Añadir a)
Separar (Tomar de)
Sherry tiene 58 bloques en su cubo. Su maestro le puso 35 bloques más. ¿Cuántos bloques tiene ahora Sherry?
58 + 35 = ?
Sherry tiene 58 bloques en su cubo. Su maestro le puso algunos bloques más. Ahora hay 93 bloques en el cubo. ¿Cuántos bloques más se colocaron en el cubo?
58 + ? = 93
Hay algunos bloques en el cubo de Sherry. Su maestro le colocó 35 bloques más. Ahora hay 93 bloques en el cubo. ¿Con cuántos bloques empezó Sherry en su cubo?
? + 35 = 93
Tomás tiene 98 estampillas en su colección. Le regaló 47 estampillas a uno de sus amigos. ¿Cuántas estampillas tiene Tomás ahora?
98 - 47 = ?
Tomás tiene 98 estampillas en su colección. Le regaló algunas a uno de sus amigos. Ahora hay 51 estampillas en la colección. ¿Cuántas estampillas le regaló Tomás a uno de sus amigos?
98 - ? = 51
Tomás tiene una colección de estampillas. Ha regalado 47 a uno de sus amigos. Ahora quedan 51 estampillas en su colección. ¿Con cuántas estampillas empezó Tomás su colección?
? - 47 = 51
INICIO: CONTENIDO DE APOYO
UNIR (AÑADIR A)
EJEMPLO
Sherry tiene 58 bloques en su cubo. Su maestro le puso 35 más. ¿Cuántos bloques tiene ahora Sherry?
EJEMPLO DE RESPUESTA A
Usé bloques de base diez para descomponer cada número en decenas y unidades.
• 58 es igual a 5 decenas y 8 unidades.
• 35 es igual a 3 decenas y 5 unidades.
• Combiné las decenas: 50 + 30 = 80.
• Combiné las unidades: 8 + 5 = 13.
• Sumé las decenas a las unidades.
• Sherry tiene 93 bloques en su cubo.



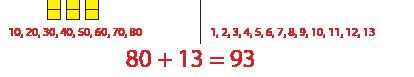
EJEMPLO DE RESPUESTA B
Hice un modelo de barra.
• Dibujé una sección para representar la cantidad de bloques que ella tenía y la etiqueté con el número 58.
• Dibujé una sección más corta para representar la cantidad de bloques que su maestro agregó y la etiqueté con el número 35.
• Necesitaba saber cuánto suman ambas cantidades, así que dibujé una sección debajo que se extendía a lo largo de 58 y 35.
• 58 + 35 = ?
• Sherry tiene un total de 93 bloques en su cubo.

SEPARAR (TOMAR DE)
EJEMPLO
Tomás tiene 98 estampillas en su colección. Le regaló 47 a uno de sus amigos. ¿Cuántas estampillas tiene Tomás ahora?
EJEMPLO DE RESPUESTA A
Usé bloques de base diez para descomponer cada número en decenas y unidades.
• 98 es igual a 9 decenas y 8 unidades.
• 47 es igual a 4 decenas y 7 unidades.
• Resté las decenas: 90 - 40 = 50.
• Resté las unidades: 8 - 7 = 1.
• Puse el número 5 en el lugar de las decenas y el 1 en el lugar de las unidades y obtuve el número 51.
• Tomás tiene 51 estampillas en su colección.
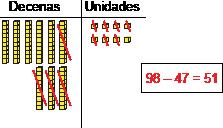
EJEMPLO DE RESPUESTA B
Hice un modelo de barra.
• Dibujé una sección para representar la cantidad total de estampillas que Tomás ya tenía en su colección y lla etiqueté con el número 98.
• Dibujé una sección más corta para representar la cantidad de estampillas que Tomás le dio a su amigo y la etiqueté con el número 47.
• Necesito saber cuántas estampillas quedan en la colección de Tomás, así que dibujé otra sección al lado del 47 con un ?
• 98 - 47 = ?
• A Tomás le quedan 51 estampillas en su colección.

INICIO: CONTENIDO DE APOYO
Los alumnos también resuelven tipos de problemas que implican juntar o separar y comparar cuando se desconoce el total, cuando se desconoce un sumando o cuando se desconocen ambos sumandos.
Tipo de problema Total desconocido Sumando desconocido Ambos sumando desconocidos
Juntar y separar La Sra. Martínez fue a la tienda de jardinería a comprar semillas para plantar rosas y margaritas en su jardín. En su cesta hay semillas para 34 rosas y 38 margaritas. ¿Cuántas semillas hay en la cesta de la Sra. Martínez?
34 + 38 = ?
En la cesta de la Sra. Martínez hay 72 semillas. 34 son de rosas y el resto son de margaritas. ¿Cuántas semillas de margaritas hay en la cesta de la Sra. Martínez?
34 + ? = 72
72 - 34 = ?
Comparar Emilia tiene 56 canicas. Julia tiene 33 canicas. ¿Cuántas canicas más tiene Julia?
33 + ? = 89
¿Cuántas menos tiene Emilia?
89 - 33 = ?
Julia tiene 38 canicas más que Emilia. Emilia tiene 49 canicas.
¿Cuántas canicas tiene Julia?
38 + 49 = ?
Emilia tiene 38 canicas menos que Julia. Emilia tiene 49 canicas.
¿Cuántas canicas tiene
Julia?
49 + 38 = ?
El Sr. Page tiene diez calcomanías. ¿Cuántas puede dar a sus alumnos y cuántas puede guardar en su escritorio?
Puede dar las 10 a los alumnos o guardar las 10 en su escritorio:
10 = 0 + 10 ó
10 = 10 + 0
Puede darle una a un alumno y dejar 9 en su escritorio, o puede dejar 1 en su escritorio y darle 9 a algunos alumnos:
10 = 1 + 9 ó 10 = 9 + 1
El Sr. Page puede dejar 2 en su escritorio y darle 8 a algunos alumnos, o puede darle 2 a algunos alumnos y dejar 8 en su escritorio:
10 = 2 + 8 ó
10 = 8 + 2
Pueden dejar 3 en su escritorio y darle 7 a algunos alumnos, o pueden darle 3 a algunos alumnos y dejar 7 en su escritorio:
10 = 3 + 7 ó
10 = 7 + 3
El Sr. Page puede dejar 4 en su escritorio y darle 6 a algunos alumnos, o pueden darle 4 a algunos alumnos y dejar 6 su escritorio:
10 = 4 + 6 ó 10 = 6 + 4
Pueden dejar 5 en su escritorioy darle 5 a algunos alumno: 10 = 5 + 5
Julia tiene 28 plátanos más que Emilia. Julia tiene 41 plátanos.
¿Cuántos plátanos tiene Emilia?
41 - 28 = ?
Emilia tiene 28 plátanos menos que Julia. Julia tiene 41 plátanos.
¿Cuántos plátanos tiene Emilia?
? + 28 = 41
RESOLUCIÓN DE PROBLEMAS DE DOS PASOS
EJEMPLO
Antonio tenía 16 galletas de queso. Le dio 7 galletas de queso a Melisa. Luego le dio 5 a Aden. ¿Cuántas galletas de queso tiene Antonio ahora?
MODELO CONCRETO
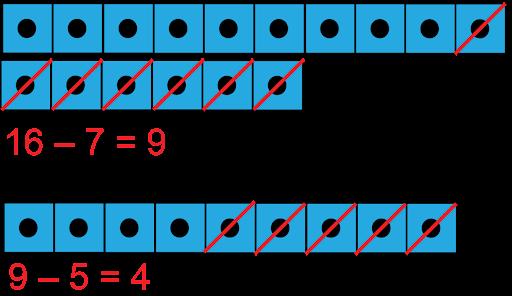
EJEMPLO DE RESPUESTA A
Usé cubos conectables.
• Para el primer paso, empecé con 16 cubos conectables y quité 7 cubos. Después de quitar 7 cubos, me quedaron 9 cubos.
• Para el segundo paso, tenía 9 cubos conectables y quité 5 cubos. Después de quitar 5 cubos, me quedé con 4 cubos.
• Antonio tiene 4 galletas de queso
MODELO PICTÓRICO

EJEMPLO DE RESPUESTA B
Utilicé una recta numérica.
• Empecé con el número 16 y usé una flecha para moverme 7 espacios a la izquierda. Llegué al número 9. Moví la flecha hacia la izquierda 5 espacios más desde el número 9 para aterrizar en el número 4.
• Antonio tiene 4 galletas de queso Contar hacia adelante y hacia atrás en rectas numéricas sirve como modelos mentales para el cálculo.
INICIO: CONTENIDO DE APOYO
SUMAR Y RESTAR DENTRO DE 1,000
Los alumnos suman y restan dos números de 3 cifras con o sin reagrupación. Al principio, utilizan representaciones concretas y pictóricas para apoyar y explicar su trabajo. Con el tiempo, desarrollan estrategias eficaces, como componer o descomponer, compensar, contar hacia adelante o hacia atrás y sumar o restar progresivamente. Los alumnos representan su pensamiento mediante expresiones numéricas o ecuaciones con un símbolo para representar la incógnita.
EJEMPLO
La semana pasada, Marta ganó 275 dólares vendiendo verduras en el mercado de agricultores. Esta semana ganó $142. ¿Cuánto dinero ganó Martha la semana pasada y esta semana?
USANDO BLOQUES DE BASE DIEZ
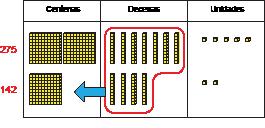
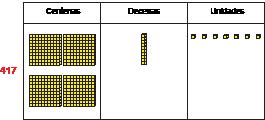
RESPUESTA DEL ESTUDIANTE
275 + 142 = ?
Usé bloques de base diez para representar el número 275. Luego, usé bloques de base diez para representar el número 142 = ?
A continuación, he representado el número 142 con bloques de base diez.
Como tengo 11 decenas, cogí diez de las decenas (barras) y las agrupé en 1 plano, que es 1 centena. Así que ahora tenía 1 centena más en el lugar de las centenas, 1 decena en el lugar de las decenas y 7 unidades en el lugar de las unidades.
275 + 142 = 417
Martha ganó 417 dólares.
INICIO: CONTENIDO DE APOYO
USAR UNA RECTA NUMÉRICA

RESPUESTA DEL ESTUDIANTE
275 + 142 = ?
Usé una recta numérica .
Empecé en 275 y salté 100. Llegué a 375. Luego di 4 saltos de 10, y aterricé en 415. Finalmente, salté 2, y aterricé en 417
275 + 142 = 417
Martha ganó $417.
USAR UN MODELO DE BARRA

RESPUESTA DEL ESTUDIANTE
275 + 142 = ?
Usé un modelo de barra.
Como estoy buscando la cantidad de dinero combinada entre la semana pasada y esta semana, sé que estoy buscando el entero.
Parte + parte = entero. Elentero es mi cantidad desconocida o total desconocido.
Empecé con el número 275, una de mis partes, la cantidad que Martha ganó vendiendo verduras. Luego, incluí 142, mi otra parte, la cantidad que ganó esta semana.
275 + 142 = 417
Martha ganó $417.
AVANCES
En tercer grado, los alumnos encuentran estrategias eficientes para sumar y restar dentro de 1,000. Aplican estrategias basadas en el valor posicional, las propiedades de las operaciones y la relación entre la suma y la resta. Aplican estrategias basadas en el valor posicional, las propiedades de las operaciones y la relación entre la suma y la resta. En tercer grado, resuelven problemas de varios pasos que involucran las 4 operaciones, y representan los problemas usando una ecuación con una variable. Los alumnos evalúan la lógica de las respuestas utilizando el cálculo mental y estrategias de estimación, incluido el redondeo.
En cuarto grado, los alumnos amplían su trabajo con el sistema de base diez para adquirir fluidez y eficacia en el cálculo. Siguen resolviendo problemas de varios pasos e interpretan los restos. Los alumnos empiezan a incorporar el algoritmo estándar como representación de los procesos de suma y resta. En cuarto grado también utilizan su comprensión del valor posicional y las propiedades de las operaciones para representar la multiplicación y la división de números de varios dígitos. En quinto grado, el trabajo con el sistema de base diez se extiende aún más, ya que los alumnos se familiarizan con el algoritmo estándar para la multiplicación con números enteros de varias cifras. También utilizan paréntesis y corchetes para representar problemas de varios pasos en los que se aplican las cuatro operaciones. Los alumnos razonan sobre la división de números enteros con divisores de dos cifras y sobre la suma, la resta, la multiplicación y la división de decimales hasta la centésima.
Los conocimientos adquiridos sobre los patrones de los números de base diez entre el jardín de infancia y el quinto grado constituyen una base fundamental que se utiliza para apoyar el pensamiento algebraico en grados posteriores. Los alumnos de sexto grado llegan a dominar las cuatro operaciones con decimales y fracciones. En 6.º y 7.º, los alumnos empiezan a trabajar con números negativos.
ESTÁNDARES
Representar y resolver problemas que involucren sumas y restas.
• Usar sumas y restas dentro de 100 para resolver problemas escritos de uno y dos pasos que involucren situaciones de sumar a, quitar de, juntar, separar y comparar, con incógnitas en todas las posiciones; por ejemplo, con dibujos y ecuaciones con un símbolo para el número desconocido para representar el problema.
Utilizar la comprensión del valor posicional y las propiedades de las operaciones para sumar y restar.
• Sumar y restar dentro de 1,000, con modelos concretos o dibujos y estrategias basadas en el valor posicional, las propiedades de las operaciones y/o la relación entre la suma y la resta; relacionar la estrategia con un método escrito. Comprender que al sumar o restar números de tres cifras, se suman o restan centenas y centenas, decenas y decenas, unidades y unidades; y que a veces es necesario componer o descomponer decenas o centenas.
DESGLOSAR EL ESTÁNDAR
VERBOS: ¿QUÉ DEBEN HACER LOS ALUMNOS?
• sumar: combinar dos o más números para obtener una suma o un total.
• componer: juntar piezas.
• descomponer: deshacer
• resolver: encontrar una respuesta o solución a un problema.
• restar: quitar una cantidad a otra mayor; hallar la diferencia entre dos números.
• relacionar: establecer una conexión.
• representar: mostrar de alguna manera; representar algo.
• comprender: interpretar o ver de una manera determinada; captar el significado de...
• usar: emplear o utilizar algo para un fin.
SUSTANTIVOS: ¿QUÉ PALABRAS CONCRETAS DEBEN CONOCER LOS ESTUDIANTES?
• problemas escritos: situación hipotética y pregunta que requiere conocimientos matemáticos, estrategias y una ecuación para ser resuelta.
• suma: combinar dos o más números para obtener una suma, o total.
• resta: quitar una cantidad a otra mayor; hallar la diferencia entre dos números.
• incógnita: un dato que falta.
• modelo concreto: modelo que utiliza objetos físicos para representar un número o una idea.
INICIO: CONTENIDO DESGLOSADO
ANÁLISIS PROFUNDO DE LOS ESTÁNDARES
CONTENIDO DESGLOSADO
• dibujo: ilustración (modelo pictórico).
• ecuación: enunciado matemático que usa números, uno o más símbolos de operación y un signo igual.
• valor posicional: el valor de un dígito que depende de su ubicación dentro de un número.
• propiedades de las operaciones: reglas matemáticas que siempre funcionan y ayudan a resolver ecuaciones.
• relación: operaciones opuestas; se deshacen entre sí.
• estrategia: plan o forma de resolver un problema o encontrar una respuesta.
• centenas: valor posicional creado cuando se combina un grupo de 10 decenas; diez veces mayor que el lugar de las decenas, una décima parte del lugar de los millares.
• decenas: valor posicional creado cuando se combina un grupo de 10 unidades; diez veces mayor que el lugar de las unidades, una décima parte del lugar de las centenas.
• unidades: valor posicional creado cuando hay un grupo con un valor de 0-9; una décima parte del valor del lugar de las decenas.
IMPLICACIONES PARA LA ENSEÑANZA
• Los estudiantes se basan en conocimientos previos de jardín de infancia y primer grado en los que trabajan con diversas situaciones de suma y resta con unidades conocidas en todas las posiciones.
• Se espera que los alumnos resuelvan problemas escritos con incógnitas en todas las posiciones.
• Los alumnos deben estar familiarizados con el uso de modelos concretos para demostrar sumas y restas y deben demostrar que entienden cómo usar modelos con incógnitas en todas las posiciones.
• Los alumnos pueden necesitar práctica cuando transfieren estrategias de aplicación de modelos concretos a modelos pictóricos y abstractos, especialmente cuando es necesario reagrupar.
• Los alumnos pueden necesitar andamiaje cuando aplican sumas y restas a problemas escritos de uno y dos pasos.
INICIO: CONTENIDO DESGLOSADO
ALINEACIÓN VERTICAL
GRADO
ESTÁNDAR
J Resolver problemas de suma y resta, y sumar y restar dentro de 10; por ejemplo, con objetos o dibujos para representar el problema.
1
1
Utilizar la adición y sustracción dentro de 20 para resolver problemas escritos que involucren situaciones de sumar a, quitar de, juntar, separar y comparar, con incógnitas en todas las posiciones; por ejemplo, con objetos, dibujos y ecuaciones con un símbolo para el número desconocido para representar el problema.
Sumar y restar dentro de 20, demostrando fluidez para sumar y restar dentro de 10. Utilizar estrategias como seguir contando; formar decenas (por ejemplo, 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); descomponer un número que lleve a una decena (por ejemplo, 13 - 4 = 13 - 3 - 1 = 10 - 1 = 9); utilizar la relación entre suma y resta (por ejemplo, sabiendo que 8 + 4 = 12, se sabe que 12 - 8 = 4); y crear sumas equivalentes pero más fáciles o conocidas (por ejemplo, sumar 6 + 7 creando el equivalente conocido 6 + 6 + 1 = 12 + 1 = 13).
2
2
Utilizar la suma y la resta dentro de 100 para resolver problemas escritos de uno y dos pasos que impliquen situaciones de sumar a, quitar de, juntar, separar y comparar, con incógnitas en todas las posiciones; por ej, con dibujos y ecuaciones con un símbolo para el número desconocido para representar el problema.
3
Sumar y restar dentro de 1,000, utilizando modelos concretos o dibujos y estrategias basadas en el valor posicional, las propiedades de las operaciones y/o la relación entre suma y resta; relacionar la estrategia con un método escrito. Comprender que al sumar o restar números de tres cifras, se suman o restan centenas y centenas, decenas y decenas, unidades y unidades; y que a veces es necesario componer o descomponer decenas o centenas.
3
4
Sumar y restar con fluidez dentro de 1,000 utilizando estrategias y algoritmos basados en el valor posicional, las propiedades de las operaciones y/o la relación entre suma y resta.
Resolver problemas escritos de dos pasos utilizando las cuatro operaciones. Representar estos problemas mediante ecuaciones con una letra que represente la cantidad desconocida. Evaluar la lógica de las respuestas utilizando el cálculo mental y estrategias de estimación, incluido el redondeo.
Resolver problemas de varios pasos planteados con números enteros y que tengan respuestas con números enteros utilizando las cuatro operaciones, incluidos problemas en los que deban interpretarse los restos. Representar estos problemas mediante ecuaciones con una letra que represente la incógnita. Evaluar la lógica de las respuestas con el cálculo mental y estrategias de estimación, incluido el redondeo.
INICIO: GUÍA DE INSTRUCCIÓN ANDAMIADA
GUÍA DE INSTRUCCIÓN
ANDAMIADA
La guía de instrucción andamiada se proporciona para que los maestros puedan planificar los siguientes pasos basándose en el rendimiento de los estudiantes en las evaluaciones de alcance o en los datos de su evaluación de medición de crecimiento MAP. Se trata de una herramienta integrada que lleva a los maestros a buscar materiales basados en las necesidades de los estudiantes. Los materiales sugeridos están organizados por estándares. Dentro de cada estándar, los materiales se clasifican además por el rango de percentiles que mejor se adapta.
Cuando se usa la guía de instrucción andamiada con los datos de su evaluación de medición de crecimiento MAP, cada tabla puede guiar a los maestros a los materiales sugeridos basados en los puntajes del área de instrucción de los estudiantes. Se sugiere a los maestros a permitir que todos los estudiantes experimenten con «Captar interés», «Exploración», «Muestra lo que sabes» y «Pruebas de habilidades». Estos elementos cubren a fondo los estándares incluidos en el alcance. La guía se divide en cuatro rangos de percentiles para cada estándar.
Refuerzo del grado anterior Nivel de grado con apoyos Nivel de grado
Los estudiantes con puntaje en este rango de percentil necesitan refuerzo del contenido del grado anterior.
Los estudiantes con puntaje en este rango de percentil necesitan apoyo de intervención de nivel de grado.
Los estudiantes con puntaje en este rango de percentil pueden trabajar en contenido de nivel de grado con apoyos de instrucción.
Ampliación del nivel de grado
Los estudiantes con puntaje en este rango de percentil están listos para aplicar su conocimiento del contenido en una variedad de actividades.
Para interpretar y responder al rendimiento del estudiante en las evaluaciones del alcance, complete los siguientes pasos:
1. Revise los datos recopilados a través de la plataforma en línea o el «Mapa de calor» para determinar el rango percentil del estudiante para cada estándar evaluado.
2. Las tablas proporcionadas recomiendan un conjunto de materiales de instrucción para cada rango percentil dentro de cada estándar evaluado. Elija cuál de estos materiales usará para apoyar mejor al estudiante con base en sus datos de evaluación.
3. Haga clic en el enlace directo al material elegido para el estudiante.
Para interpretar y responder al desempeño del estudiante en la evaluación de medición de crecimiento MAP, complete los siguientes pasos:
1. Revise los datos proporcionados para determinar el percentil, el área de instrucción y/o el desglose de estándares para cada estudiante.
2. Encuentre el alcance que incluye los estándares que necesitan enfoque o intervención.
3. Acceda a la «guía de instrucción andamiada» en la sección «inicio» del alcance.
4. Haga clic en el enlace directo al material recomendado para el estudiante.
La guía es un plan sugerido y no se limita a los estándares y actividades incluidos. Además, no todas las actividades sugeridas necesitan ser completadas por cada estudiante.
Área de instrucción: Operaciones y pensamiento algebraico y números y operaciones
Todos los estudiantes:
• Captar interés
• Exploración
• Muestra lo que sabes
• Prueba de habilidades
Utilizar la suma y la resta dentro de 100 para resolver problemas de uno y dos pasos que impliquen situaciones de sumar, quitar, juntar, separar y comparar, con incógnitas en todas las posiciones, por ejemplo, utilizando dibujos y ecuaciones con un símbolo para el número desconocido para representar el problema.
1 Resolución de problemas de suma y resta
Intervención en grupos pequeños
• Parte 1 y 2
Constructor de fluidez
0 %25 % (Refuerzo del grado anterior)
• Resolución de problemas y modelos pictóricos
• Emparejar un problema con un modelo pictórico o una oración numérica
Práctica interactiva
• Matemáticas alienígenas
Prueba de habilidades
Habilidades básicas
• Maneras de representar adición y sustracción
Mis pensamientos de matemáticas
1 Aprendizaje virtual
Números y operaciones
• Representar y resolver todo tipo de problemas
2 Resolución de problemas de suma y resta
25 % -
50 % (Nivel de grado con apoyo)
50 %80 % (Nivel de grado)
Acceso a conocimientos previos
Habilidades básicas
Conceptos básicos
• Cómo dibujar un modelo pictórico
Intervención en grupos pequeños
• Partes 1 y 2
2 Resolución de problemas de sumas y restas
Vocabulario ilustrado
Libreta interactiva
• Modelo de barras y recta numérica
Mis pensamientos de matemáticas
Práctica interactiva
• Cuenta tus gallinitas
Constructor de fluidez
• Problemas y representaciones de sumas y restas
• Emparejar una suma o una resta de dos dígitosde con un modelo
Conexiones lingüísticas 80 %100 % (Ampliación del nivel de grado)
2 Resolución de problemas de suma y resta
Conexiones con la vida
Matemáticas de hoy
Estación de conexión
Tablero de opciones
INICIO: GUÍA DE INSTRUCCIÓN ANDAMIADA
Sumar y restar dentro de 1000, utilizando modelos concretos o dibujos y estrategias basadas en el valor posicional, las propiedades de las operaciones y/o la relación entre suma y resta; relacionar la estrategia con un método escrito. Comprender que al sumar o restar números de tres cifras, se suman o restan centenas y centenas, decenas y decenas, unidades y unidades; y que a veces es necesario componer o descomponer decenas o centenas.
1 Resolución de problemas de suma y resta
Intervención en grupos pequeños
• Parte 1 y 2
0 %25 % (Refuerzo del grado anterior)
Constructor de fluidez
• Resolución de problemas y modelos pictóricos
• Emparejar un problema con un modelo pictórico o una oración numérica
Práctica interactiva
• Matemáticas alienígenas
Prueba de habilidades
Habilidades básicas
• Maneras de representar adición y sustracción
Mis pensamientos de matemáticas
1 Aprendizaje virtual Números y operaciones
• Representar y resolver todos tipos de problemas
2 Resolución de problemas de suma y resta
25 %50 % (Nivel de grado con apoyo)
Conceptos básicos de destrezas
• Cómo dibujar un modelo pictórico
Intervención en grupos pequeños
• Partes 3 y 4
2 Aprendizaje virtual Números y Operaciones
• Representar y resolver problemas escritos de un paso
• Representar y resolver problemas escritos de varios pasos
2 Solución de problemas de sumas y restas
50 %80 % (Nivel de grado)
80 %100 % (Ampliación del nivel de grado)
Vocabulario ilustrado
Libreta interactiva
• Modelo de barras y recta numérica
Mis pensamientos de matemáticas
Ciencia de datos
Conexiones lingüísticas
2 Solución de problemas de sumas y restas
Tarea basada en problemas
Conexiones con la vida
Matemáticas de hoy
Cuento de matemáticas
Tablero de opciones
EVALUAR
ATRAER: ACCESO A CONOCIMIENTOS PREVIOS
ACCESO A CONOCIMIENTOS PREVIOS
DESCRIPCIÓN
Los estudiantes resuelven problemas de suma y resta y registran su pensamiento con dibujos y oraciones numéricas. Esta actividad pretende evaluar el dominio del siguiente estándar:
• Usar la suma y la resta dentro de 20 para resolver problemas escritos que impliquen situaciones de sumar a, quitar de, juntar, separar y comparar, con incógnitas en todas las posiciones; por ej., con objetos, dibujos y ecuaciones con un símbolo para el número desconocido para representar el problema.
MATERIALES
IMPRESO
• 1 folleto del estudiante (por alumno)
REUTILIZABLE
• 20 contadores o cubos, según sea necesario (por alumno)
PREPARACIÓN
• Imprima una copia del folleto del estudiante por alumno.
• Prepare contadores o cubos para que estén disponibles para quienes los necesiten.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1 Entregue folleto del estudiante (por alumno).
2 Lea el siguiente problema y pídele a los estudiantes que registren su pensamiento con imágenes y oraciones numéricas.
a «Dani tenía 20 coches. Le dio algunos de ellos a su amiga. Ahora Danni tiene 13 coches. ¿Cuántos coches le ha regalado Dani a su amiga?».
3 Una vez que los estudiantes hayan terminado de registrar su pensamiento para el primer problema, lea el segundo problema en voz alta y pídales que sigan el mismo proceso de registrar su pensamiento con imágenes y frases numéricas.
a «Jake tenía 6 tarjetas intercambiables. Le regalaron más por su cumpleaños. Ahora tiene 19. ¿Cuántas tarjetas recibió Jake por su cumpleaños?».
4 Haga un debate en clase con los problemas resueltos. Esto brinda la oportunidad de comprender los conocimientos previos de los alumnos antes de comenzar las lecciones. Anime a los alumnos a que justifiquen sus respuestas y a que prueben si comprenden o tienen conceptos erróneos. Formule las siguientes preguntas:
a «¿Cuál problema era de suma y cuál de resta?». El problema de Dani era una resta. El problema de Jake era una suma.
b «¿Cómo lo sabes?». Las respuestas pueden variar. Sabía que el problema de Dani era de resta porque regaló algunos de sus coches. Sabía que el problema de Jake era de suma porque consiguió más cartas.

a «¿Qué estrategias usaste para resolver el problema de la suma?». Las respuestas pueden variar. Para resolver el problema de la suma, usé una estrategia de conteo; usé los dedos; hice un dibujo de las tarjetas y marqué las que ya tenía.
b «¿Qué estrategias usaste para resolver el problema de la resta?». Las respuestas pueden variar. Para resolver el problema de resta, dibujé la cantidad total y luego taché el número de coches que regaló; usé los dedos para mostrar cuántos coches tiene y cuántos regaló; volví a contar.
c «¿Cuál es la diferencia entre cómo usaste los modelos pictóricos para resolver el problema de suma y resta?». Las respuestas variarán. Cuando representé el problema de adición, comencé con la cantidad de tarjetas que tenían y saqué más tarjetas hasta llegar a 19. Cuando representé el problema de la resta, saqué el número total de coches y luego taché los que Dani regaló.
d «¿Qué ocurre con el total cuando se suman dos números?». Cuando se suman dos números, el total aumenta.
e «¿Qué ocurre con el total cuando se restan dos números?». Cuando se restan dos números, la cantidad disminuye.
5 Si los alumnos tienen dificultades para completar esta tarea, realice el constructor de bases fundamentales para llenar el vacío de conocimientos previos antes de pasar a otras partes del alcance.
ATRAER: CAPTAR INTERÉS
FOLLETO DEL ESTUDIANTE
LECCIÓN PARA CAPTAR INTERÉS
CAPTAR INTERÉS: ROLL-ANDSCORE-GAME SCORES
DESCRIPCIÓN
Los estudiantes representan y resuelven un problema escrito de sustracción en el que la incógnita puede ser cualquiera de los términos del problema.
MATERIALES
IMPRESOS
• 1 folleto del estudiante (por alumno)
REUTILIZABLES
• 1 fenómenos (por clase)
• 1 conjunto de bloques de base diez, incluyendo 10 planos, 10 barras y 10 unidades (por pareja)
• 1 bolsa resellable (por pareja)
PREPARACIÓN
• Planee mostrar los fenómenos.
• Planifique que los estudiantes trabajen en parejas para completar esta actividad.
• Imprima un folleto del estudiantete por alumno.
• Entregue un juego de bloques de base diez en una bolsa resellable por pareja de estudiantes.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
PARTE I: EXPLORACIÓN PREVIA
1. Presente esta actividad hacia el comienzo del alcance. La clase retomará la actividad y resolverá el problema original después de que los estudiantes hayan completado las actividades correspondientes a «Explorar».
2. Muestre los fenómenos. Formule las siguientes preguntas: «¿Qué observas? ¿Dónde puedes ver matemáticas en esta situación?». Permita que los estudiantes compartan todas sus ideas.
3. Explique este escenario a la clase: «Kayla juega a lanza y anota. En su primera partida, logró 246 puntos. En la segunda, consiguió aún más. Hizo un total de 693 puntos en las dos partidas. ¿Cuántos puntos consiguió en la segunda partida? Usa un modelo de barra o una recta numérica abierta para mostrar tu trabajo».
4. Permita que los alumnos hagan preguntas y aclaren el contexto según sea necesario. Anímeles a compartir sus pensamientos y experiencias con la clase utilizando las siguientes preguntas:
a. «¿Recuerdas alguna vez que hayas estado en un salón recreativo?».
b. «¿A qué juegos te gusta más?».
c. «¿Qué significa conseguir puntos cuando juegas?».
ATRAER: CAPTAR INTERÉS
5. Haga las siguientes preguntas con la clase:
a. DOK-1 «¿Qué información sabemos?». Kayla anotó 246 puntos en su primer partido. Anotó un total de 693 puntos en los dos partidos juntos.
b. DOK-1 «¿Qué información necesitamos averiguar?». ¿Cuántos puntos anotó en su segundo juego?
6. Informe a los estudiantes que no deben resolver el problema en este momento, sino que deben evaluar qué estrategias podrían utilizar para averiguar cuántos puntos anotó Kayla en su segundo juego.
7. Continúe con las actividades «Explorar».
PARTE II: DESPUÉS DE LA EXPLORACIÓN
1. Después de que los estudiantes hayan completado las actividades de «Explorar» para este tema, muestre nuevamente los fenómenos y repita la situación.
2. Plantee las siguientes preguntas con la clase:
a. DOK-1 «¿Qué información sabemos?». Kayla anotó 246 puntos en su primer partido. Anotó un total de 693 puntos en los dos partidos juntos.
b. DOK-1 «¿Qué información necesitamos averiguar?». ¿Cuántos puntos anotó en su segundo partido?
3. Coloque a los estudiantes en parejas y entregue una bolsa de bloques de base diez por pareja. Anime a los estudiantes a usar los bloques de base diez para resolver el problema.
4. Entregue a los estudiantes el folleto del estudiante. Los estudiantes representarán el problema con un modelo de barras o una recta numérica. Anime a los compañeros a probar diferentes enfoques. Luego pídales que comparen sus respuestas.
5. Plantee las siguientes preguntas a la clase:
a. DOK-1 «¿Qué es un modelo de barra?». Es un modelo pictórico de un problema escrito que usa rectángulos para representar las partes y el total del problema.
b. DOK-1 «¿Qué representan los rectángulos en un modelo de barra?». Los rectángulos representan dos cantidades que se combinan para igualar una cantidad total.
c. DOK-1 «¿Qué información usaste para resolver el problema con un modelo de barra?». Usé el total, que fue 693, y su primer puntaje, que fue 246.
d. DOK-2 «¿Qué representa la "?" en tu modelo de barras?». Representa el número de puntos que anotó en su segundo partido, que es la cantidad que estamos buscando.
e. DOK-1 «¿Cuántos puntos anotó en su segundo partido?». 447 puntos
f. DOK-1 «¿Qué es una recta numérica?». Es una línea donde se suman números y marcas como resultado de la información del problema. Se dibujan flechas para indicar las acciones del problema.
g. DOK-2 «¿Qué información usaste para resolver el problema con una recta numérica?». Usé el total, que era 693, y su primer puntaje, que era 246.
h. DOK-2 «¿Hacia dónde apuntó la flecha en tu recta numérica? ¿Por qué?». Las respuestas pueden variar. La flecha apuntó hacia la izquierda para mostrar la resta, o la flecha apuntó hacia la derecha para mostrar la suma.
i. DOK-2 ¿«Qué representa la "?" en su recta numérica?». Representa el número de puntos que anotó en su segundo partido, que es la cantidad que estamos buscando, la incógnita.
j. DOK-1 «¿Cuántos puntos anotó en su segundo partido?». 447 puntos
k. DOK-3 «¿En qué se parecen estas dos representaciones?». Las respuestas variarán. Ambas tienen la primera puntuación y la puntuación total. La puntuación que falta (la segunda puntuación) se representa con un "?" en ambos modelos. Ambos modelos nos llevan a restar para encontrar la segunda puntuación. Ambos nos dan la misma respuesta.
l. DOK-3 «¿Qué es más fácil de usar y entender para ti, los modelos concretos (como los bloques de valor posicional) o los modelos pictóricos (como la recta numérica o el modelo de barras)? ¿Por qué?». Las respuestas pueden variar. Prefiero el modelo concreto porque puedo contar todo y ver que estoy en lo cierto. Prefiero un modelo pictórico porque es más rápido.
6. Como ampliación, permita que los alumnos comparen sus modelos pictóricos y evalúen las similitudes y diferencias.
EXPLORAR: EXPLORACIÓN 1
LECCIÓN PEDAGÓGICA
EXPLORACIÓN 1: REPRESENTAR Y RESOLVER PROBLEMAS ESCRITOS DE UN PASO
Antes de completar esta exploración, pida a los estudiantes que completen Habilidades Básicas: Cómo dibujar un modelo pictórico y Habilidades Básicas: modelo de resolución de problemas para que puedan aplicar la habilidad a este concepto.
Estándar(es)
• Representar y resolver problemas que involucren sumas y restas. Utilizar la suma y la resta dentro de 100 para resolver problemas escritoss de uno y dos pasos que involucren situaciones de sumar a, quitar de, juntar, separar y comparar, con incógnitas en todas las posiciones; por ejemplo, utilizando dibujos y ecuaciones con un símbolo para el número desconocido para representar el problema.
Ideas fundamentales
Resolución de problemas con medidas
Estrategias numéricas
DESCRIPCIÓN
Estándares para la práctica matemática
MP.1 Dar sentido a los problemas y perseverar en su resolución.
MP.3 Construir argumentos viables y criticar el razonamiento de otros.
MP.4 Representar con matemáticas.
MP.6 Atender a la precisión.
Los estudiantes representan y resuelven problemas de palabras de un paso a través de dibujos, y luego identifican modelos que representan problemas escritos de suma y resta.
MATERIALES
IMPRESO
• 1 diario del estudiante (por alumno)
• 1 conjunto de tarjetas de problemas del zoológico (por grupo)
• 1 tabla de valor posicional (por grupo)
• 1 boleto de salida (por estudiante)
REUTILIZABLE
• 1 marcador de borrado en seco (por grupo)
• 2 protectores de hojas de plástico, opcionales (por grupo)
• 9 barras de base diez (por grupo)
• 20 unidades de base diez (por grupo)
• 1 bolsa grande resellable (por grupo)
Conexiones de contenido Motores de investigación
CC2 Explorar cantidades cambiantes
CC3 Desarmar el todo, armar las partes
DI1 Dar sentido al mundo (Entender y explicar)
PREPARACIÓN
• Planifique dividir la clase en grupos de 3 ó 4 para completar esta actividad.
• Imprima un juego de las tarjetas de problemas del zoológico por grupo. Recorte la parte inferior de cada tarjeta. Los estudiantes no usarán esta porción de las tarjetas hasta la parte II de la actividad.
• Coloque las barras y unidades de base diez y un conjunto de tarjetas de problemas del zoológico en una bolsa resellable por grupo.
• Imprima una tabla de valor posicional por grupo y coloque cada página en un protector de hojas de plástico separado, o plastifíquelo para usarlo con un marcador de borrado en seco.
• Imprima el diario del estudiante y la boleta de salida para cada estudiante.
• ¡Hazlo digital! Haz que los alumnos exploren o presenten sus soluciones con manipulativos virtuales. Los manipulativos utilizados en esta lección se pueden encontrar en el menú desplegable «Explorar» y se pueden asignar digitalmente a los estudiantes.
• Para quienes necesitan más apoyo para recordar la información, por favor, consulte nuestra «Ayudas complementarias» que incluyen: línea numérica abierta, base de diez, disponibles en la sección «Intervención».
EXPLORAR: EXPLORACIÓN 1
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
PARTE I
1. Lea el siguiente escenario: «Hoy vamos a tener un día de Zoofari. Vas a pasear por el zoológico para aprender diferentes datos sobre los animales que viven allí. Leerás cada problema y decidirás cómo resolverlo utilizando los manipulativos proporcionados. ¿Puedes usar los bloques de base diez para resolverlo y luego dibujar un modelo pictórico de tu solución?».
2. Divida la clase en grupos de 3 ó 4 y dirija la atención de los estudiantes a las tarjetas de problemas del zoológico, la tabla de valor posicional, el marcador de borrado en seco y los bloques de base diez.
3. Pida a los estudiantes que lean cada problema y lo resuelvan usando los bloques de base diez. Pueden colocar sus bloques en la tabla de valor posicional y escribir cada dígito en el espacio provisto en la parte inferior de la tabla a medida que trabajan.
4. Supervise y hable con los estudiantes, según sea necesario, para verificar la comprensión mediante el uso de preguntas orientadoras.
a. DOK-1 «¿Qué información sabes?». Las respuestas pueden variar. El zoológico tiene 56 serpientes venenosas. Algunas más fueron donadas. Ahora hay 94 serpientes venenosas.
b. DOK-1 «¿Qué información necesitas averiguar?». Las respuestas pueden variar. ¿Cuántas serpientes venenosas fueron donadas?
c. DOK-3 «¿Cómo usarás los bloques de base diez para modelar este problema?». Las respuestas pueden variar. Mostraré el número 56 usando cinco barras y seis unidades. Luego seguiré agregando varillas y unidades hasta llegar al total 94.
d. DOK-2 «¿Qué oración numérica escribirás para describir este problema?». Las respuestas variarán. 56 + ? = 94
e. DOK-2 «¿Dónde está la incógnita en la oración numérica?». Las respuestas pueden variar. La incógnita es el segundo número en la oración numérica.
f. DOK-2 «¿Cómo representarás la incógnita en tu oración numérica?». Las respuestas pueden variar. Escribiré un signo de interrogación para la incógnita.
g. DOK-3 »¿Se trata de un problema de suma o de resta? ¿Cómo lo sabes?». Las respuestas pueden variar. Este es un problema de suma porque tenemos que juntar dos números para igualar el total que se da.
5. Entregue un diario del estudiante por alumno y pídales que dibujen un modelo pictórico de los bloques de base diez que usaron para resolver. Los estudiantes escribirán dos oraciones numéricas: una con un símbolo para la incógnita, y otra con la solución.


DIARIO
EXPLORAR: EXPLORACIÓN 1

PARTE II
1. Continúe con el escenario de la parte I: Cada problema tendrá 4 opciones de modelos para representar el problema. «¿Puedes decidir qué modelo funciona mejor para ayudar al cuidador del zoológico a resolver cada problema?».
2. Distribuya la parte inferior de las tarjetas de problemas del zoológico por grupo.
3. Pida a los estudiantes que utilicen los modelos pictóricos y las oraciones numéricas que crearon en la parte I para determinar qué modelo de barra y qué modelo de recta numérica representan mejor cada tarjeta de problema.
4. Pida a los estudiantes que completen la parte II del diario del estudiante y respondan la pregunta de reflexión. Luego reúna a toda la clase.
5. Después de la «Exploración», invite a la clase a una charla de matemática para compartir sus observaciones y aprendizajes.
CHARLA DE MATEMÁTICAS
• DOK-3 «¿Por qué crees que hubo diferentes representaciones que funcionaron mejor para ciertos tipos de problemas?». Las respuestas variarán. Por ej.: Si el problema se refería a algo que sucede en línea recta, yo usaría una recta numérica. Si estuviéramos comparando algo, entonces usaría un modelo de barra.
• DOK-3 «¿Cómo usó su modelo pictórico y sus oraciones numéricas para ayudarse a elegir el modelo de barra y la recta numérica que mejor describieran cada problema?». Las respuestas variarán. Por ej.: Observé los números y las operaciones que usé en mi modelo pictórico para elegir el mejor modelo de barra y de recta numérica.
• DOK-2 «¿Qué tienen de malo los otros modelos?». Las respuestas variarán. Por ej.: Los otros modelos tienen los números en lugares equivocados, o es la operación equivocada.
• DOK-3 «¿Cuál representación te sientes más seguro de usar?». Las respuestas pueden variar. Por ej.: Me gusta usar la recta numérica porque me ayuda a encontrar la respuesta contando hacia adelante o hacia atrás.
6. Cuando los estudiantes terminen, pídales que completen el boleto de salida para evaluar formativamente su comprensión del concepto.
APOYOS PEDAGÓGICOS
1. Algunos estudiantes pueden sentir que leer los planteamientos en las tarjetas de problemas del zoológico es un desafío. Puede ser beneficioso que un estudiante de cada grupo lea cada problema en voz alta y que el grupo lo revise antes de resolverlo.
2. Puede ser útil determinar si el estudiante está cometiendo un error de estrategia (una falta fundamental de la estrategia, como renombrar o reagrupar) o un error de habilidad de componente (una o más deficiencias en las habilidades previas utilizadas en la estrategia, como la resta de dos dígitos sin renombrar o reagrupar).
3. Si tienen dificultades conceptuales con la resta, puede ser necesario volver a estrategias de resta más simples, como la resta con rectas numéricas o la estrategia del sustraendo faltante.
4. Pueden tener dificultades con la reagrupación. Use bloques de base diez para modelar la reagrupación. Por ej., puede darle a un estudiante 14 bloques de unidades y pedirle que cambie 10 cubos de unidades por una barra. Haga que el alumno ubique bloques de 10 unidades junto a una varilla, si es necesario, para mostrarle que es visualmente equivalente.
5. Si tienen dificultades para escribir oraciones numéricas, use preguntas orientadoras como las siguientes: «¿Qué acción está ocurriendo en tu modelo? ¿Qué símbolo representa esa acción? ¿Qué símbolo representa un total? ¿Qué símbolo podría representar la incógnita?».
6. Si tienen dificultades para decidir qué modelos son correctos en la parte II, deles papel de borrador y anímelos a resolver con cualquiera de los modelos proporcionados de los que no estén seguros.
BOLETO DE SALIDA
EXPLORAR: EXPLORACIÓN 1
ESTRATEGIA DE ADQUISICIÓN DEL LENGUAJE
La siguiente estrategia de adquisición del lenguaje se apoya en esta actividad «Explorar». Consulte las estrategias a continuación para saber cómo apoyar el desarrollo lingüístico del alumno. Al leer en silencio y de forma independiente, los alumnos aumentarán su duración y su capacidad para comprender el texto.
Principiante: Haga una lectura fluida y expresiva mientras los estudiantes lean cada tarjeta de problema del zoológico en pequeños trozos para apoyar la lectura silenciosa posterior.
Intermedio: Ayude a los alumnos a leer en silencio pidiendo a los compañeros que lean la tarjeta del problema del zoológico una vez en voz alta y luego otra vez en silencio.
Avanzado: Forme parejas de estudiantes y pídales que se alternen en la lectura de una tarjeta de problema del zoológico mientras el otro compañero explica el problema con sus propias palabras.


EXPLORAR: EXPLORACIÓN 2
LECCIÓN PEDAGÓGICA
EXPLORACIÓN 2: REPRESENTAR Y RESOLVER PROBLEMAS ESCRITOS DE VARIOS PASOS
Estándar(es)
• Representar y resolver problemas de suma y resta. Usar la adición y sustracción dentro de 100 para resolver problemas de uno y dos pasos que involucren situaciones de sumar a, quitar de, juntar, quitar y comparar, con incógnitas en todas las posiciones; por ej., con dibujos y ecuaciones con un símbolo para el número desconocido para representar el problema.
Ideas fundamentales Estándares para la práctica matemática Conexiones de contenido Motores de investigación
Resolución de problemas con medidas
Estrategias numéricas
MP.1 Dar sentido a los problemas y perseverar en su resolución.
MP.3 Construir argumentos viables y criticar el razonamiento de otros.
MP.4 Representar con matemáticas.
MP.6 Atender a la precisión.
CC2 Explorar cantidades cambiantes
CC3 Desarmar el todo, armar las partes
DI1 Dar sentido al mundo (comprender y explicar)
DESCRIPCIÓN
Los estudiantes representan y resuelven problemas de suma y resta de varios pasos en los que la incógnita puede ser cualquiera de los términos del problema usando líneas numéricas o modelos de barras y comprobando las respuestas con bloques de base diez.
MATERIALES
IMPRESO
• 1 diario del alumno (por alumno)
• 1 conjunto de tarjetas de paseo por el parque acuático (por clase)
• 1 boleto de salida (por alumno)
REUTILIZABLE
• 1 plano de base diez (por grupo)
• 10 barras de base diez (por grupo)
• 20 unidades de base diez (por grupo)
• 1 bolsa resellable (por grupo)
PREPARACIÓN
• Planee dividir la clase en 6 grupos para completar esta actividad.
• Imprima un juego de tarjetas de paseo por el parque acuático (por clase).
• Prepare una bolsa resellable con 1 plano, 10 barras y 20 unidades para cada grupo.
• Imprima el diario del estudiante y la boleto de salida para cada estudiante.
• ¡Hazlo digital! Haga que los estudiantes exploren o presenten sus soluciones utilizando manipulativos virtuales. Los manipulativos usados en esta lección se pueden encontrar en el menú desplegable de la sección «Explorar» y se pueden asignar digitalmente a los estudiantes.
• Para quienes necesitan más apoyo para recordar la información, por favor, consulte nuestra «Ayudas complementarias» que incluyen: línea numérica abierta, base de diez, disponibles en la sección «Intervención».
EXPLORAR: EXPLORACIÓN 2
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Lea la siguiente situación: «Hoy irán de excursión a un parque acuático. Deben visitar todas las atracciones antes de salir del parque. En cada atracción ocurrió algo interesante, pero no se registró toda la información para el parque. ¿Puedes ayudar a los responsables del parque acuático a encontrar la información que falta en cada atracción?».
2. Divida la clase en 6 grupos y coloque a cada grupo ante una tarjetas de paseo por el parque acuático. Dirija la atención de los alumnos a la atracción y al problema presentado.
3. Pida a los alumnos que lean juntos el problema y, a continuación, debatan qué información se da y qué información falta. Anime a los estudiantes a conversar qué modelo pictórico u oración numérica que incluya una incógnita se ajustaría al problema de palabras en cada atracción.
4. Entregue una copia del diario del estudiante a cada uno y pídales que anoten el modelo pictórico o la oración numérica con incógnita para cada atracción. Haga que los estudiantes trabajen con sus grupos para resolver cada problema. Anime a los estudiantes a utilizar bloques de base diez si es necesario.
5. Supervise y hable con los estudiantes, según sea necesario, para comprobar la comprensión mediante el uso de preguntas orientadoras.
a. DOK-3 «¿Cómo decidiste qué estrategia usar cuando sólo se te dio la oración numérica?». Las respuestas pueden variar. Por ej.: Elegí la que me resultó más fácil de resolver. Cuando comparo, me gusta ver las dos barras diferentes para recordarme que debo encontrar la diferencia.
b. DOK-3 «¿Usaste siempre la oración numérica dada para encontrar la respuesta o preferiste una diferente?». Las respuestas pueden variar. Por ej.: A veces tuve que mover los numeros para hacer una nueva oración numérica que me ayudara a resolverlo.
c. DOK-3 «¿Cuáles fueron las diferencias en los tipos de problemas escritos cuando viste que se usaba la recta numérica o un modelo de barras?». Las respuestas variarán. Por ej.: Los problemas de la recta numérica se referían a algo que se podía poner en una línea. Me gusta utilizar el modelo de barras cuando hay dos grupos y un todo.
6. Cuando los alumnos hayan completado todas las tarjetas de paseo por el parque acuático y el diario del alumno, reúna a toda la clase.
7. Después de la exploración, invite a la clase a una charla de matemáticas para compartir sus observaciones y aprendizajes.
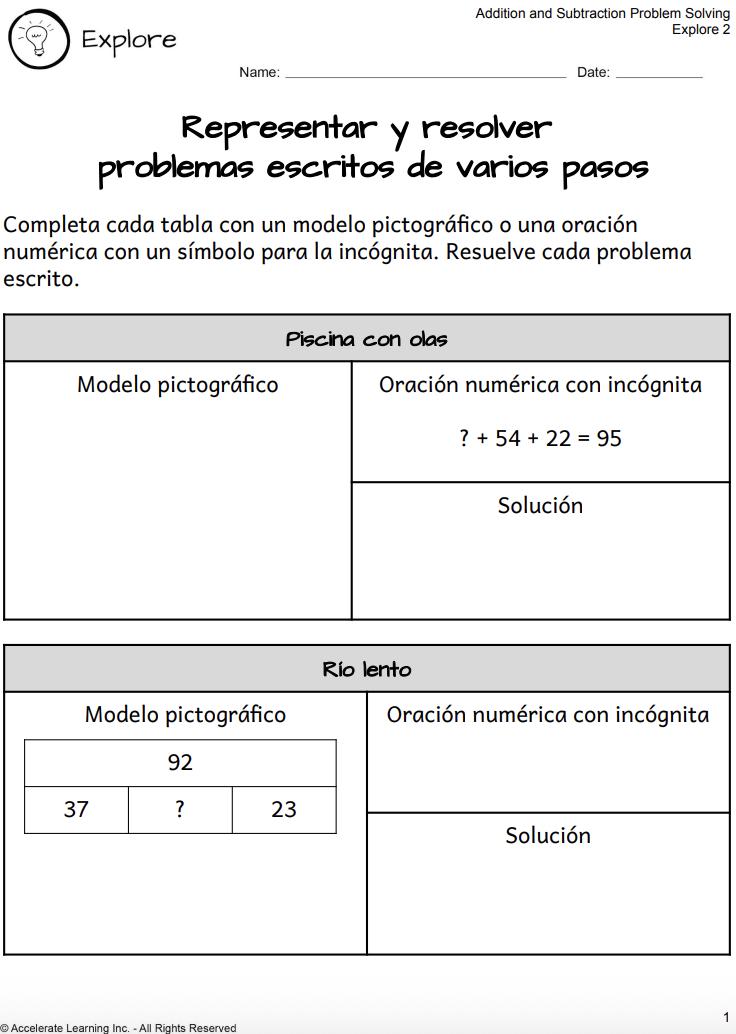
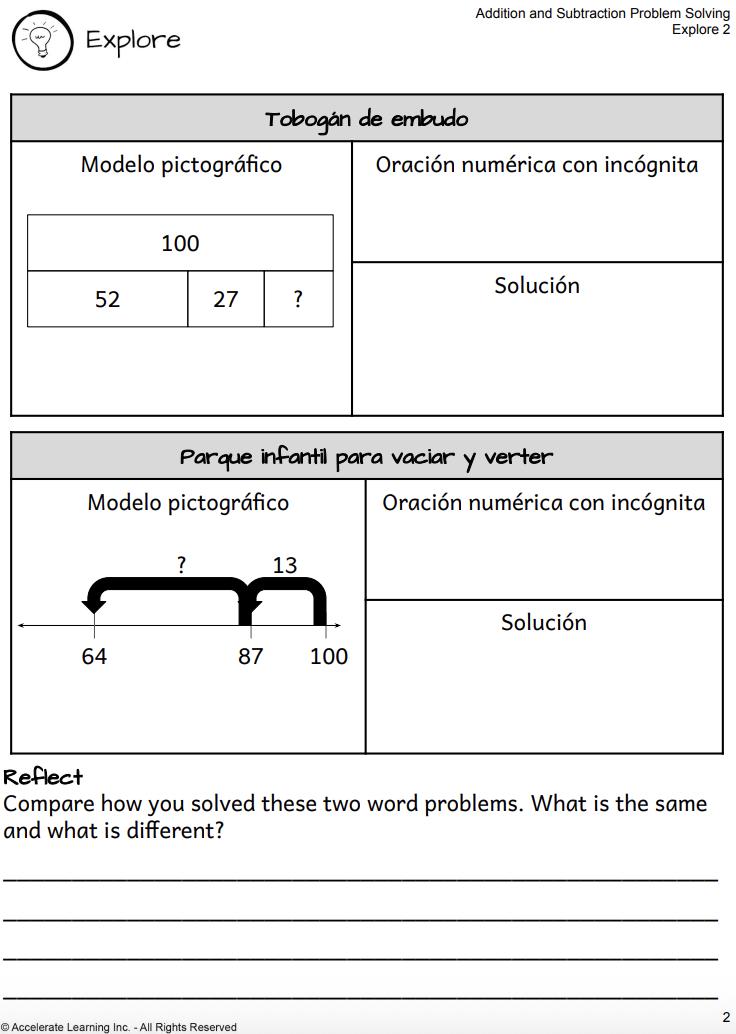
DIARIO DEL ESTUDIANTE
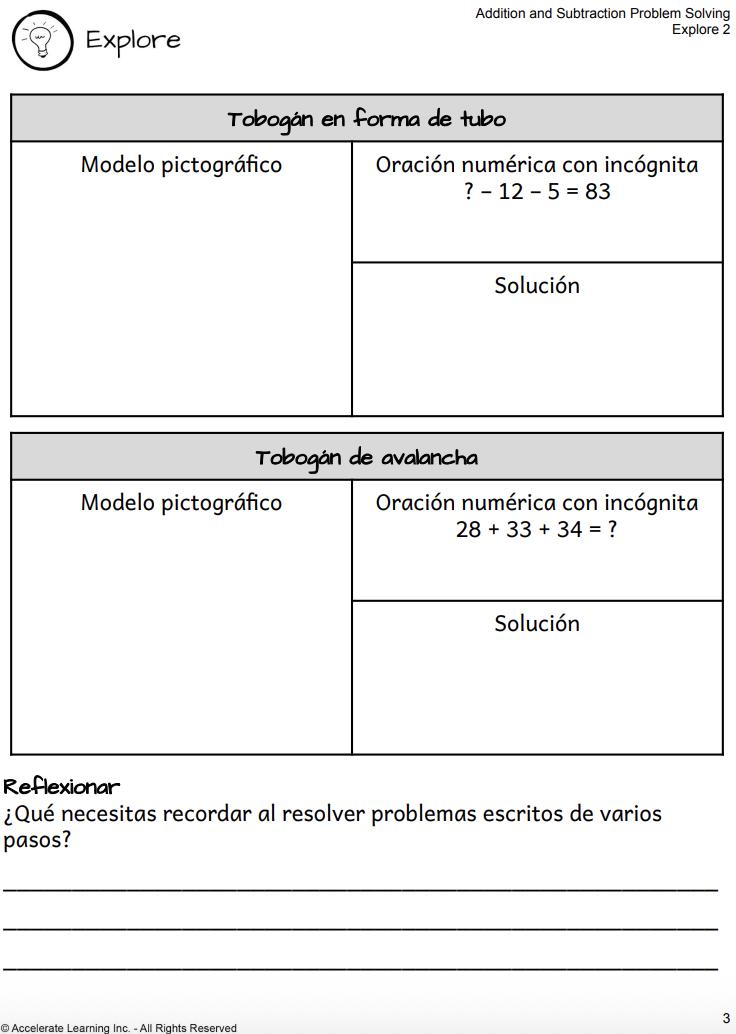
DIARIO DEL ESTUDIANTE
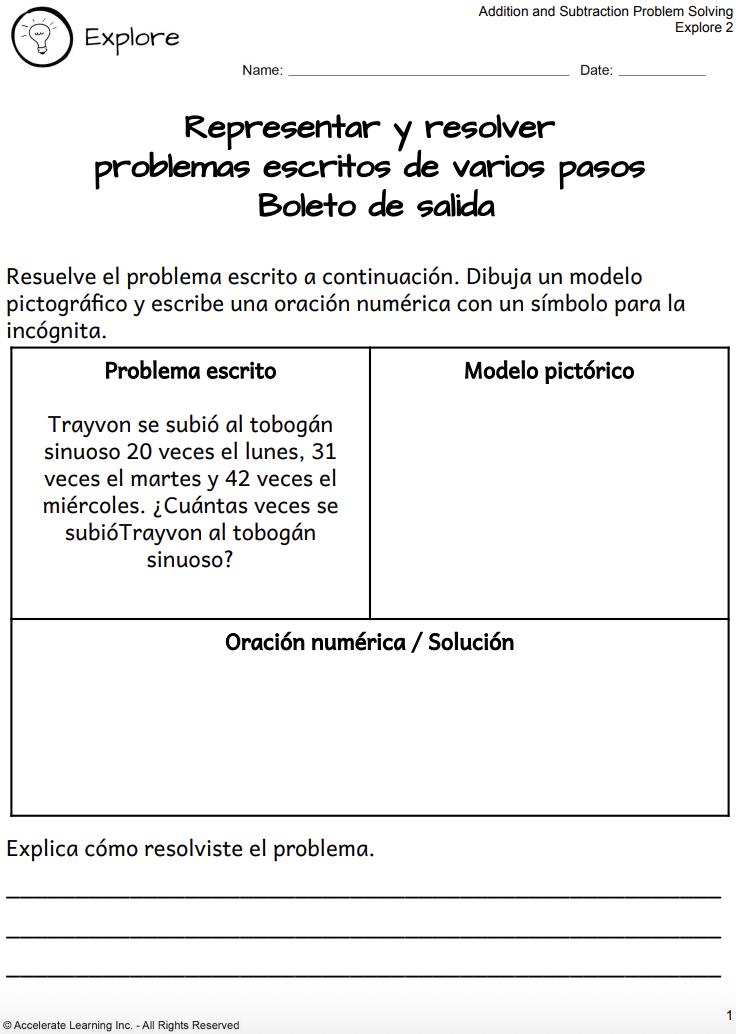
CHARLA DE MATEMÁTICAS
• DOK-3 «¿Qué tipo de problema de palabras resuelves usando un modelo de barra? ¿Por qué?». Las respuestas variarán. Por ej.: Cuando la información está dividida en partes y te falta una parte o el total, se puede usar un modelo de barras para mostrar esa información.
• DOK-3 «¿Qué tipo de problema de palabras resuelves usando una recta numérica? ¿Por qué?». Las respuestas variarán. Por ej.: Cuando está encontrando la distancia entre dos números o se están sumando números, se puede usar una recta numérica para resolver el problema.
• DOK-2 «¿Siempre tiene que restar cuando se le da una oración numérica de resta?». No, puedes sumar hasta el total.
• DOK-3 «¿En qué te ayudaron los bloques de base diez para comprobar tus respuestas?». Las respuestas pueden variar. Por ej.: Para la suma, construiría cada número, sumaría los bloques y reagruparía para encontrar mi respuesta. Para restar, contaría el total y quitaría los bloques, reagrupándolos si era necesario. Luego vería si mi respuesta coincide con la respuesta que obtuve usando un modelo de barra o una recta numérica.
• DOK-2 «¿Qué tienes que recordar cuando resuelves problemas de palabras de varios pasos?». Las respuestas variarán. Por ej.: Tienes que prestar atención a la acción de cada paso y asegurarte de completar todos los pasos.
• DOK-3 «¿Tienes que resolver un problema de suma de varios pasos en cierto orden? Explica». Las respuestas pueden variar. Por ej.: No, puedes mover los números de lugar y aún así obtener la misma respuesta.
• DOK-3 «¿Cuándo podrías necesitar resolver problemas de suma y resta en la vida real?». Las respuestas pueden variar. Por ej.: Cuando pagas facturas, cuando sumas los gastos del supermercado, cuando cuentas tu colección de tarjetas de béisbol.
8. Cuando los estudiantes hayan terminado, pídales que completen el boleto de salida para evaluar formativamente su comprensión del concepto.
EXPLORAR: EXPLORACIÓN 2
APOYOS PEDAGÓGICOS
1. A algunos alumnos les puede resultar difícil leer los problemas escritos de las tarjetas del parque acuático. Puede ser beneficioso que un estudiante de cada grupo lea en voz alta cada problema escrito y que el grupo lo debata antes de resolverlo.
2. Si los estudiantes tienen dificultades para crear una recta numérica, proporcione a cada estudiante una ya hecha con los números de referencia etiquetados.
3. Algunos estudiantes pueden seguir necesitando objetos concretos (al menos al principio) para representar el problema. Anímeles a pasar a la fase abstracta, pero permítales usar objetos manipulativos (como bloques de base diez o fichas para contar) si todavía necesitan apoyo conceptual. Establezca el objetivo de retirar los manipulativos hacia el final de los problemas.
4. Puede que a los estudiantes les resulte mucho más fácil practicar primero una estrategia que funcione de forma fiable que aprender enseguida varias formas diferentes de hacerlo.
5. Si tienen dificultades para utilizar el modelo de barras, etiquete las secciones como "parte", "parte" y "entero" (o "total").
6. Codifique por colores las partes y el total. Por ejemplo, colorea las dos partes en amarillo y azul y el total en verde. Para ayudar a los alumnos a identificar cuáles son los distintos componentes del problema, resáltelos de amarillo, azul o verde. A continuación, los alumnos pueden determinar dónde está representado cada componente del problema en el modelo de barras.
ESTRATEGIA DE ADQUISICIÓN DEL LENGUAJE
La siguiente estrategia de adquisición del lenguaje se apoya en esta actividad de «Explorar». Consulte las estrategias a continuación para conocer las formas de apoyar el desarrollo del lenguaje del estudiante.
A medida que los estudiantes escuchan activamente e interactúan durante la instrucción, adquirirán la estructura del lenguaje, expresiones y vocabulario básico y académico.
Principiante: Lea en voz alta cada problema de palabras mientras los alumnos señalan cada palabra. Haga hincapié en el vocabulario académico.
Intermedio: Enfatice las ideas clave y el vocabulario con señales visuales según sea necesario mientras un estudiante de cada grupo lee el problema escrito.
Avanzado: Pida a un estudiante voluntario que lea cada problema escrito. Amplíe el pensamiento de los alumnos preguntándoles qué ocurre en el problema. Anímelos a debatir utilizando vocabulario académico.


EXPLORAR: EXPLORACIÓN 3
LECCIÓN DIDÁCTICA
EXPLORACIÓN 3: USAR MODELOS CONCRETOS PARA REPRESENTAR ADICIÓN Y SUSTRACCIÓN HASTA 1,000
Estándar(es)
• Utilizar la comprensión del valor posicional y las propiedades de las operaciones para sumar y restar. Sumar y restar dentro de 1,000, a partir de modelos concretos o dibujos y estrategias basadas en el valor posicional, las propiedades de las operaciones y/o la relación entre la suma y la resta; relacionar la estrategia con un método escrito. Comprender que al sumar o restar números de tres dígitos, se suman o restan centenas y centenas, decenas y decenas, unidades y unidades; y a veces es necesario componer o descomponer decenas o centenas.
Ideas fundamentales
Dólares y centavos
Resolución de problemas con medidas
Contar salteado hasta 100
Estrategias numéricas
DESCRIPCIÓN
Estándares para la práctica matemática
MP.1 Dar sentido a los problemas y perseverar en su resolución.
MP.3 Construir argumentos viables y criticar el razonamiento de otros.
MP.4 Representar con matemáticas.
MP.6 Atender a la precisión.
Los estudiantes representan y resuelven problemas escritos que implican sumas y restas dentro de 1,000 con objetos concretos.
MATERIALES
IMPRESO
• 1 diario del estudiante (por alumno)
• 1 juego de tarjetas de tareas «tarjetas coleccionables»(por pareja)
• 1 tabla de valor posicional (por pareja)
• 1 boleta de salida (por alumno)
REUTILIZABLE
• 10 planos de base diez (por pareja)
• 20 barras de base diez (por pareja)
• 20 unidades de base diez (por pareja)
• 1 marcador de borrado en seco (por pareja)
• 3 protectores de plástico para hojas, opcionales (por pareja)
• 2 bolsas resellables (por par)
Conexiones de contenido
CC2 Explorar las cantidades cambiantes
CC3 Desmontar el todo, montar las partes
CC4 Descubrir la forma y el espacio
Motores de investigación
Dar sentido al mundo (comprender y explicar)
PREPARACIÓN
• Planifique dividir la clase en parejas para completar esta actividad.
• Imprima y recorte un juego de tarjetas de tareas «tarjetas coleccionables». Coloque las tarjetas en una bolsa con cierre para cada pareja de alumnos.
• Imprima una tabla de valor posicional para cada pareja. Coloque cada página por separado en su propio protector de hojas de plástico o plastifíquelo para utilizarlo con un marcador de borrado en seco.
• Prepare una bolsa resellable con 10 planos, 20 barras y 20 unidades de base diez para cada pareja de estudiantes.
• Imprima un diario del estudiante y un boleto de salida por alumno.
• ¡¡Hazlo digital! Haga que los estudiantes exploren o presenten sus soluciones utilizando manipulativos virtuales. Los manipulativos usados en esta lección se pueden encontrar en el menú desplegable de la sección «Explorar» y se pueden asignar digitalmente a los estudiantes.
• Para quienes necesitan más apoyo para recordar la información, por favor, consulte nuestra «Ayudas complementarias» que incluyen una base de diez, disponible en la sección «Intervención».
DI1
EXPLORAR: EXPLORACIÓN 3
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Lea la siguiente situación: «Un grupo de alumnos de tu clase colecciona tarjetas deportivas y quiere llevarlas al colegio para intercambiarlas y contarlas durante el recreo. El maestro les ha dicho que pueden traerlas, pero sólo si anotan cómo las intercambian y cuentan en una hoja de registro. ¿Puedes ayudar a los alumnos a registrar cómo intercambian y cuentan las tarjetas en el recreo?».
2. Divida la clase en parejas y dirija la atención de los alumnos hacia los bloques de base diez, la bolsa de tarjetas de intercambio y la tabla de valor posicional. Permita que los estudiantes descubran los manipulativos y experimenten cómo funcionan con sus compañeros.
3. Pida a los estudiantes que lean cada tarjeta de tarea y resuelvan el problema con bloques de base diez. Anime a los estudiantes a evaluar la acción en el problema descrito con sus compañeros mientras lo resuelven juntos. Además, los estudiantes pueden utilizar la tabla de valor posicional para organizar sus bloques de base diez para sus modelos concretos. Pueden usar el marcador de borrado en seco para escribir el total de cada valor posicional después de haber reagrupado.
4. Monitoree y hable con los estudiantes según sea necesario para verificar la comprensión mediante el uso de preguntas orientadoras.
a. DOK-1 «¿Qué información ofrece este problema escrito?». Las respuestas variarán. Por ej.: Fabián y Lucas tienen tarjetas de fútbol. Lucas le dio a Fabian algunas de ellas.
b. DOK-1 «¿Qué información necesitas averiguar?». Las respuestas pueden variar. Por ej.: ¿Cuántas tarjetas tiene Fabián ahora?
c. DOK-2 «¿Qué acción ocurre en este problema escrito?». Las respuestas variarán. Por ej.: Este es un problema de un solo paso aunque hay tres números. Sólo necesitamos sumar el número de tarjetas de fútbol con las que Fabián comenzó y el número de tarjetas que Lucas le dio.
d. DOK-3 «¿Cómo puedes resolver este problema usando bloques de base diez?». Las respuestas pueden variar. Por ej.: Puedo construir 201 usando dos planos y una unidad. Luego puedo añadir 9 barras. Mi respuesta sería 291.
e. DOK-3 «¿Qué tuviste que hacer cuando había diez o más bloques en un valor posicional particular?». Las respuestas variarán. Por ej.: Tuve que reagrupar haciendo un grupo de diez y cambiándolo por un bloque del siguiente valor posicional a la izquierda.
f. DOK-3 «¿Qué tuviste que hacer cuando no había suficientes bloques en un valor posicional para restar?». Las respuestas pueden variar. Por ej.: Tuve que reagrupar cambiando un bloque por diez bloques del siguiente valor posicional a la derecha.
g. DOK-2 «¿Cómo podrías dibujar un modelo pictórico para representar el modelo concreto que acabas de crear?». Las respuestas variarán. Por ej.: Podría dibujar un cuadrado para representar los pisos, una línea recta para representar las barras y un círculo pequeño para representar las unidades.


DIARIO DEL ESTUDIANTE
5. Entregue a cada estudiante una copia del diario del estudiante y pídales que registren un modelo pictórico de los bloques de base diez que utilizaron para resolver el problema. Los estudiantes escribirán una oración numérica y resolverán el problema.
6. Cuando hayan completado todas las tarjetas de tarea y el diario del estudiante, reúna a la clase en grupo.
7. Después de la «Exploración», invite a la clase a una charla matemática para compartir sus observaciones y aprendizajes.

CHARLA DE MATEMÁTICAS
• DOK-1 «¿Cuál es la mejor herramienta para representar y mostrar tu pensamiento para estos problemas escritos?». Bloques de base diez
• DOK-3 «¿Por qué es más eficiente usar bloques de base diez que manipulativos de un solo cuadrado?». Las respuestas pueden variar. Por ejemplo: Puedo representar números más grandes más fácilmente cuando uso bloques de base diez.
• DOK-3 «¿Cómo puedes representar un problema de comparación?». Las respuestas pueden variar. Por ej.: Puedo alinear mis bloques de base diez y ver cuánto más grande es un número que el otro.
• DOK-3 «¿Cómo puedes representar un problema de resta?». Las respuestas pueden variar. Por ejemplo: Puedo construir un modelo del número más grande y restar el número más pequeño de los bloques.
• DOK-3 «¿Cómo puedes representar un problema de suma?». Las respuestas pueden variar. Por ejemplo: Puedo construir un modelo de ambos números y combinarlos para hallar el total.
8. Cuando los estudiantes hayan terminado, pídales que completen el boleto de salida para evaluar formativamente su comprensión del concepto.
APOYOS PEDAGÓGICOS
1. Podría ser útil determinar si el estudiante está cometiendo un error de estrategia (una falta fundamental de la estrategia, como renombrar o reagrupar) o un error de habilidad de componente (una o más deficiencias en las habilidades previas utilizadas en la estrategia, como la sustracción de dos dígitos sin renombrar o reagrupar).
2. Si los estudiantes tienen dificultades conceptuales con la resta, puede ser necesario volver a estrategias más simples, como la resta con rectas numéricas o la estrategia del sustraendo faltante.
3. Los estudiantes pueden tener dificultades con la reagrupación. Utilice bloques de base diez para representar la reagrupación. Por ej., puede darle a un estudiante 14 bloques unitarios y pedirle que cambie 10 cubos unitarios por una barra. Haga que el estudiante alinee los bloques de 10 unidades junto a una barra, si es necesario, para mostrarle que son visualmente equivalentes.
4. Si los estudiantes tienen dificultades para escribir oraciones numéricas, utilice preguntas orientadoras como las siguientes: «¿Qué acción está ocurriendo en tu modelo? ¿Qué símbolo representa esa acción? ¿Qué símbolo representa un total? ¿Qué símbolo podría representar lo desconocido?».
BOLETO DE SALIDA
EXPLORAR: EXPLORACIÓN 3
ESTRATEGIA DE ADQUISICIÓN DEL LENGUAJE
La siguiente estrategia de adquisición del lenguaje se apoya en esta actividad de «Explorar». Consulte las estrategias a continuación para conocer las formas de apoyar el desarrollo del lenguaje de un estudiante.
Los estudiantes internalizarán y construirán vocabulario académico a través del habla utilizando vocabulario de contenido de nivel de grado dentro de un contexto dado.
Principiante: Lea cada problema escrito y pida a los estudiantes que piensen en lo que sucede. Forme parejas con los alumnos para que compartan lo que han entendido.
Intermedio: Proporcione un banco de palabras que incluya elementos visuales para ayudar con el vocabulario básico y académico. Los alumnos también pueden representar el problema para mostrar su comprensión del mismo.
Avanzado: Apoye a los estudiantes proporcionándoles los siguientes marcos de oraciones durante la actividad «Explorar» y «Charla de matemáticas».
Marco de oración 1: «Primero, yo ________, y luego yo ________».
Marco de oración 2: «Decidí resolver usando ________ porque _______».
Marco de la oración 3: «_________ era mejor para resolver porque _________».
Marco de la oración 4: «Otra forma en que puedo resolver es ____________».

MUESTRA LO QUE SABES (PARTE 3)
Estándar(es)
EXPLORAR: EXPLORACIÓN 4
LECCIÓN DIDÁCTICA
EXPLORACIÓN 4: USAR MODELOS PICTÓRICOS PARA REPRESENTAR LA ADICIÓN Y SUSTRACCIÓN HASTA
1,000
• Utilizar la comprensión del valor posicional y las propiedades de las operaciones para sumar y restar. Sumar y restar dentro de 1,000, con modelos concretos o dibujos y estrategias basadas en el valor posicional, las propiedades de las operaciones y/o la relación entre la suma y la resta; relacionar la estrategia con un método escrito. Comprender que al sumar o restar números de tres dígitos, se suman o restan centenas y centenas, decenas y decenas, unidades y unidades; y a veces es necesario componer o descomponer decenas o centenas.
Ideas fundamentales
Dólares y centavos
Resolución de problemas con medidas
Contar salteado hasta 100
Estrategias numéricas
DESCRIPCIÓN
Estándares para la práctica matemática
MP.1 Dar sentido a los problemas y perseverar en su resolución.
MP.3 Construir argumentos viables y criticar el razonamiento de otros.
MP.4 Representar con matemáticas.
MP.6 Atender a la precisión.
Los estudiantes representan y resuelven problemas de palabras que involucran sumas y restas dentro de 1,000 usando modelos pictóricos como el dibujo de bloques de base diez, modelos de barras y rectas numéricas.
MATERIALES
IMPRESO
• 1 diario del estudiante (por alumno)
• 1 conjunto de tarjetas de problemas de la sala de juegos (por clase)
• 1 boleto de salida (por estudiante)
Conexiones de contenido
CC2 Explorar las cantidades cambiantes
CC3 Desmontar el todo, montar las partes
CC4 Descubrir la forma y el espacio
PREPARACIÓN
Motores de investigación
DI1 Dar sentido al mundo (comprender y explicar)
• Planifique dividir la clase en 6 grupos para completar esta actividad.
• Imprima y recorte un conjunto de tarjetas de problemas de la sala de juegos y coloque una en cada estación.
• Imprima un diario del estudiante y un boleto de salida por alumno.
• Para quienes necesitan más apoyo para recordar la información, por favor, consulte nuestra «Ayudas complementarias» que incluyen una línea numérica abierta y una base de diez, disponible en la sección «Intervención».
EXPLORAR: EXPLORACIÓN 4
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Lea el siguiente escenario: «Consigues un nuevo trabajo en el salón recreativo local. Parte de tu trabajo consiste en llevar la cuenta de los boletos que recibe la gente cuando gana los juegos. Tienes que averiguar el número total de boletos que tienen disponibles para gastar en premios, así como cuántos boletos están gastando. Luego tienes que averiguar el número total de boletos que les quedan después de gastarlos. ¿Estás listo para ayudar a contar los billetes?».
2. Divida la clase en seis grupos; asigne a cada grupo una estación y deles un diario del estudiante por alumno.
3. Dirija la atención de los estudiantes al conjunto de tarjetas de problemas de la sala de juegos en su estación.
4. Pídales que lean el problema y creen dos modelos pictóricos de la acción que sucede en la historia: uno de bloques de base diez y otro de un modelo de barra o de una recta numérica. Los estudiantes dibujarán los modelos pictóricos y las acciones que realizaron para resolver el problema en el diario del estudiante.
5. Pídales que escriban una oración numérica que contenga un símbolo que represente la incógnita. Luego, deben utilizar la oración numérica para resolver el problema.
6. Supervise y hable con los estudiantes según sea necesario para verificar la comprensión mediante el uso de preguntas orientadoras.
a. DOK-1 «¿Qué bloques de base diez estás dibujando para crear tu modelo pictórico?». Las respuestas variarán. Por ej.: Hicimos el número ____ dibujando ____ planos, ____ barras y ____ unidades.
b. DOK-3 «Al crear su modelo de barra o recta numérica, ¿cómo decidieron cuál usar?». Las respuestas variarán. Por ej.: Cuando tuve el total pero me faltaba una parte, decidí usar un modelo de barra para poder lo que faltaba.
c. DOK-2 «¿Cómo resolviste este problema?». Las respuestas pueden variar. Preste atención a las conversaciones que tengan los estudiantes para ayudarlos a encontrar un método para mostrar su trabajo que tenga más sentido. (Líneas numéricas abiertas, modelos de barras, etc.).
d. DOK-3 «¿Se te ocurre alguna estrategia diferente que podrías haber usado para resolver este problema?». Las respuestas pueden variar. Anime a los estudiantes a pensar en cómo podrían usar una recta numérica o un modelo de barras para resolverlo.
7. Dé tiempo a los estudiantes para que roten a las estaciones restantes y repitan los pasos 4-6. Cuando hayan completado cada estación y el diario del estudiante, reúna a toda la clase.
8. Después de la «Exploración», invite a la clase a una charla matemática para compartir sus observaciones y aprendizajes.
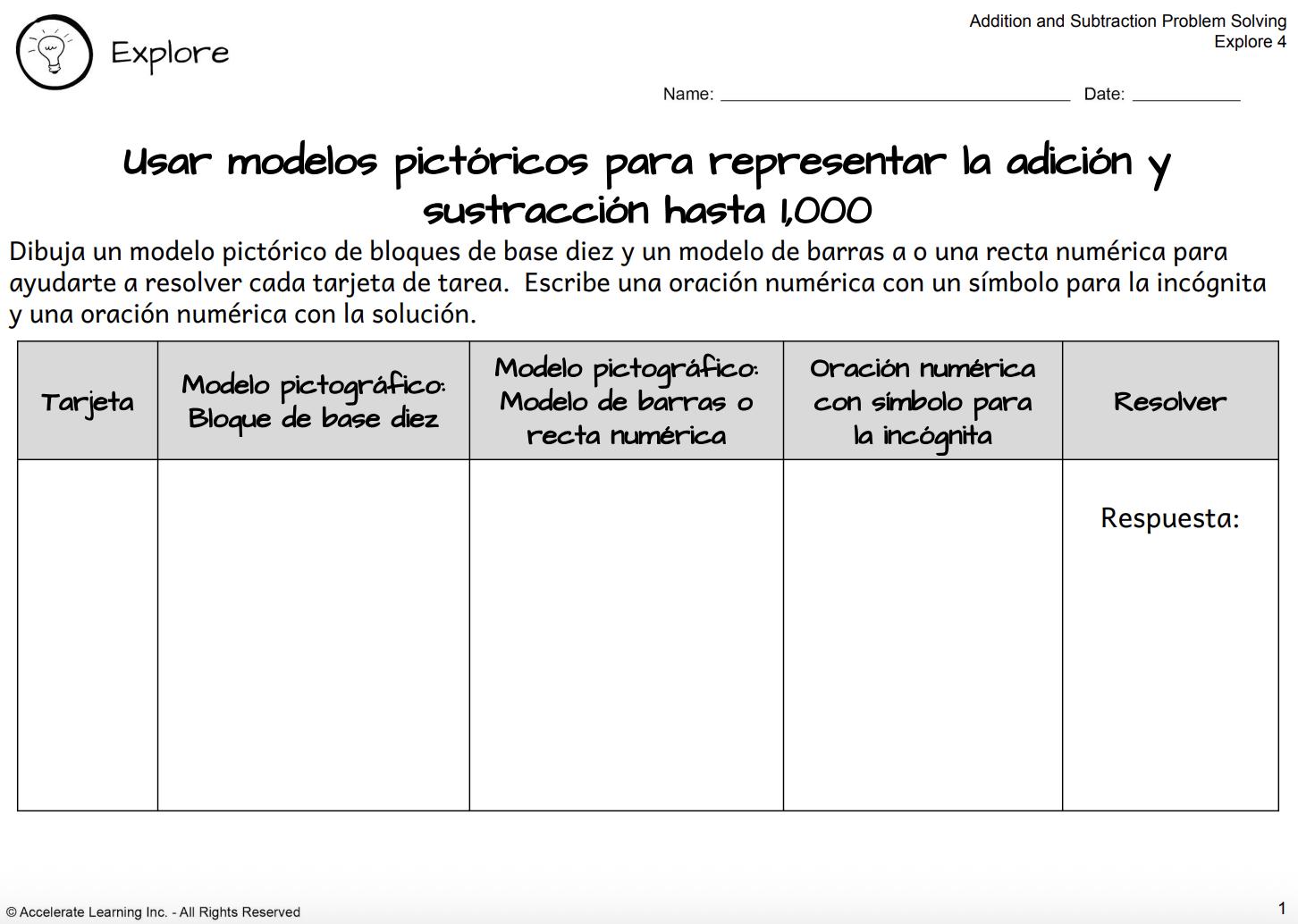
DIARIO DEL ESTUDIANTE
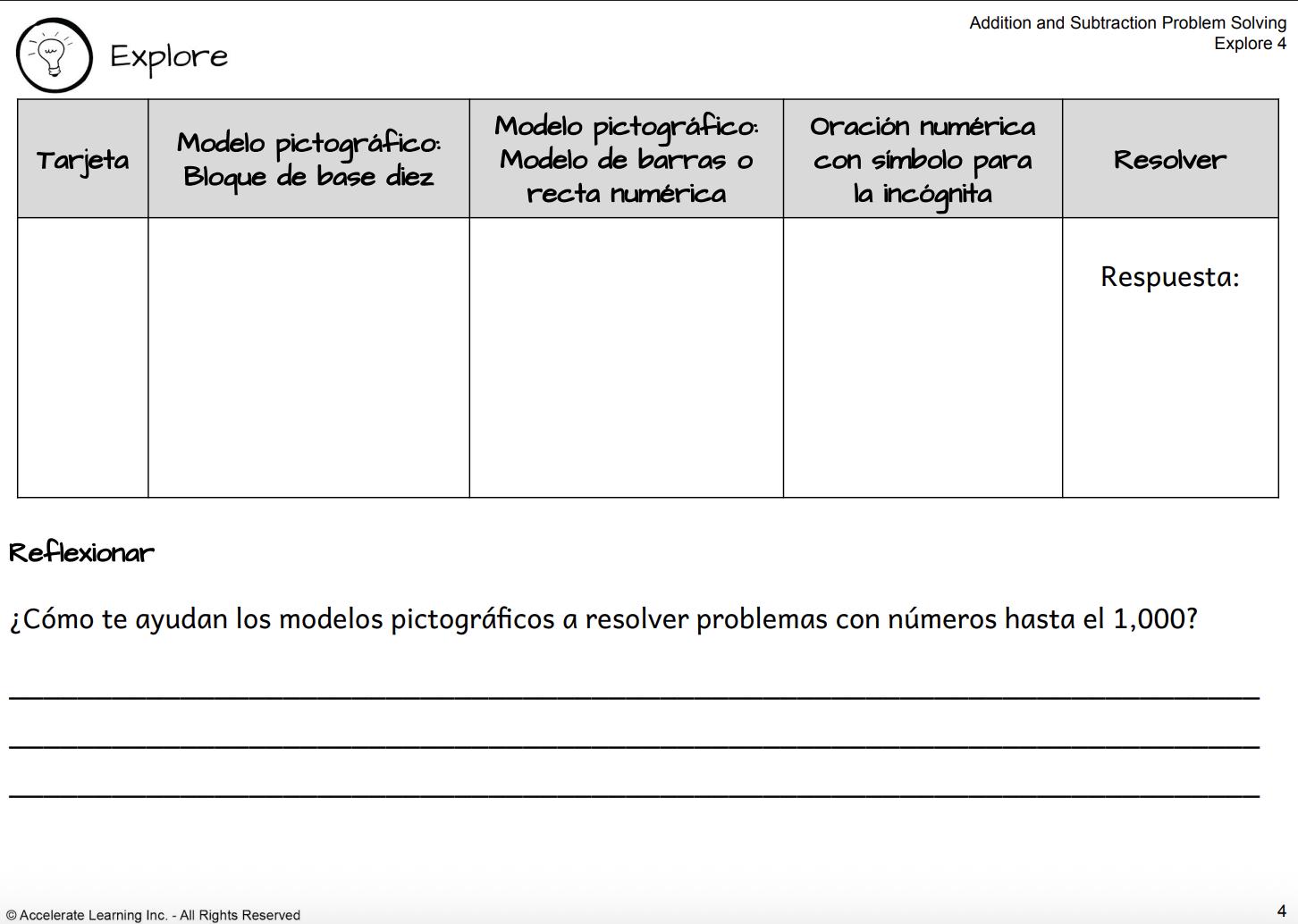
DIARIO DEL ESTUDIANTE
CHARLA DE MATEMÁTICAS
• DOK-3 «¿Cómo decidiste si estabas sumando o restando?». Las respuestas variarán. Por ej.: Leí el problema y visualicé si la persona estaba combinando algo o separando algo.
• DOK-3 «¿En qué se diferenciaba el problema de la tarjeta 6 de las otras tarjetas?». Nos dieron un total pero ninguno de los otros números. Tuvimos que descomponer el total en dos posibles números que pudieran sumarse para igualar el total. Había varias respuestas.
• DOK-2 «Describa la estrategia que utilizó para resolver el problema de la tarjeta 6». Las respuestas variarán. Por ej.: Dibujamos bloques de base diez en diferentes combinaciones. Luego usamos esas combinaciones en modelos de barras.
• DOK-3 «¿Puedes pensar en una estrategia diferente que podrías haber usado para resolver el problema de la tarjeta 6?». Las respuestas pueden variar. Por ej.: Podríamos haber utilizado una recta numérica. Podríamos haber elegido una primera cantidad y luego saltar al total para calcular la segunda cantidad.
• DOK-3 «¿Cómo te ayudó a resolver los problemas dibujar primero un modelo pictórico de bloques de base diez?». Las respuestas pueden variar. Por ej.: Dibujar primero los bloques de base diez me ayudó a visualizar el número. Luego pude ver cómo descomponer el número. O, me mostró dos números que se combinaban para componer un nuevo número. Luego pude usar ese conocimiento para crear mi modelo pictórico adicional.
• DOK-3 «¿Cuáles son algunas cosas que has descubierto que necesitas asegurarte de que estás haciendo bien cuando resuelves problemas?». Las respuestas pueden variar. Por ej.: Necesito leer cuidadosamente, entender si estoy sumando o restando y verificar dos veces mi respuesta revisando ambos modelos pictóricos, etc.
9. Cuando los estudiantes terminen, pídales que completen el boleto de salida para evaluar formativamente su comprensión del concepto.
10. Regrese a la sección de «Captar interés» e instruya a los estudiantes para que usen sus habilidades recién adquiridas para completar exitosamente la actividad.
EXPLORAR: EXPLORACIÓN 4
APOYOS PEDAGÓGICOS
1. Puede ser útil determinar si el alumno está cometiendo un error de estrategia (una carencia fundamental de la estrategia, como renombrar o reagrupar) o un error de habilidad de componente (una o más deficiencias en las habilidades previas utilizadas en la estrategia, como la resta de dos dígitos sin renombrar o reagrupar).
2. Si los estudiantes tienen dificultades conceptuales con la resta, puede ser necesario volver a estrategias más simples, como la resta con rectas numéricas o la estrategia del sustraendo faltante.
3. Los estudiantes pueden tener dificultades con la reagrupación. Utilice bloques de base diez para modelar la reagrupación. Por ej., puede darle a un estudiante 14 bloques de unidades y pedirle que cambie 10 cubos de unidades por una barra. Haga que el estudiante disponga bloques de 10 unidades junto a una barra, si es necesario, para mostrarle que son visualmente equivalentes.
4. Los estudiantes pueden encontrar mucho más fácil practicar primero una estrategia que funcione de manera confiable en lugar de aprender varias maneras diferentes de hacerlo de inmediato.
5. Si tienen dificultades para escribir oraciones numéricas, use preguntas orientadoras como las siguientes: «¿Qué acción ocurre en tu modelo? ¿Qué símbolo representa esa acción? ¿Qué símbolo representa un total? ¿Qué símbolo podría representar lo desconocido?».
ESTRATEGIA DE ADQUISICIÓN DEL
LENGUAJE
La siguiente estrategia de adquisición del lenguaje se apoya en esta actividad «Explorar». Consulte las estrategias a continuación para conocer las formas de apoyar el desarrollo del lenguaje del estudiante.
Los estudiantes utilizarán técnicas de aprendizaje como mapas conceptuales, dibujos, comparaciones, contrastes, memorización y repasos para adquirir vocabulario básico y de nivel de grado.
Principiante: Proporcione un muro de palabras ilustrado utilizando las palabras del diario del alumno. Pida a los alumnos que comparen y contrasten cada palabra para comprenderla mejor.
Intermedio: De tiempo para que los alumnos hagan un dibujo de lo que piensan cuando leen cada palabra en el diario del estudiante. Anímelos a hacer referencia a sus dibujos cuando completen cada modelo pictórico.
Avanzado: Repase el significado de cada palabra utilizada en el diario del estudiante antes de que los alumnos comiencen la exploración. Compruebe la comprensión según sea necesario.
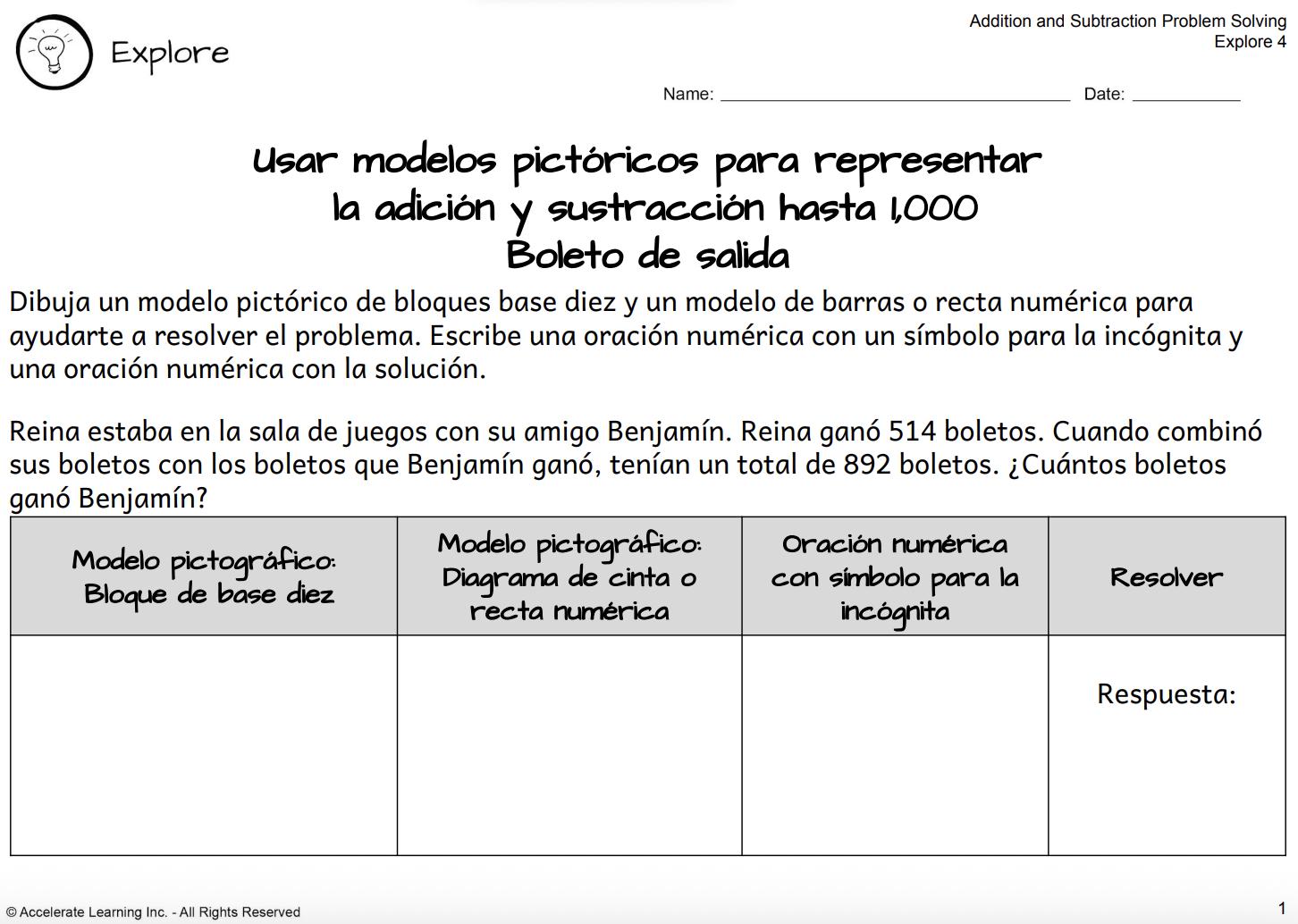

MUESTRA LO QUE SABES (PARTE 4)
BOLETO DE SALIDA
DESCRIPCIÓN
Este esquema de anclaje destaca la representación y las estrategias de solución de problemas de un paso y de varios pasos que implican sumas y restas dentro de 100. También se centra en la resolución de problemas de sumas y restas dentro de 1,000 con modelos concretos y pictóricos.
EXPLORACIÓN 1: REPRESENTAR Y RESOLVER
PROBLEMAS ESCRITOS DE UN PASO
1. Dibuje una tabla con 3 filas en el esquema de anclaje y etiquete la primera casilla como «Suma y resta de un paso». Divida la fila en dos casillas. Escriba una suma y una resta.
2. Lea el siguiente problema escrito: «Alexis tenía 19 boletos. Zach le dio 22 más. ¿Cuántos boletos tiene ahora?».
3. Plantee las siguientes preguntas y anote las respuestas de los estudiantes el esquema de anclaje:
a. «¿Qué información sabemos?». Alexis tenía 19 boletos y Zach le dio 22 boletos más.
b. «¿Qué necesitamos encontrar?». Necesitamos saber cuántos boletos tiene Alexis en total.
c. «¿Se trata de un problema de suma o de resta? ¿Cómo lo sabes?». Es un problema de suma porque el número de boletos aumenta cuando Zach le da más. Estamos hallando el total.
d. «¿Cómo podemos representar este problema escrito con un modelo pictórico?». Podemos dibujar 1 línea y 9 puntos para representar 19. Luego podemos dibujar 2 líneas y 2 puntos para representar 22. Podemos agrupar diez unidades y moverlas al lugar de las decenas para obtener 41 como respuesta.
4. Lea el siguiente problema escrito: «Alexis tenía 92 boletos para gastar en la sala de juegos. Gastó 55 boletos en un peluche. ¿Cuántos boletos tiene Alexis ahora?».
5. Plantee las siguientes preguntas y registre las respuestas de los estudiantes en el esquema de anclaje:
a. «¿Qué información sabemos?». Alexis tenía 92 boletos para gastar y gastó 55 de esos boletos.
b. «¿Qué necesitamos encontrar?». Debemos averiguar cuántos billetes le quedan a Alexis.
c. «¿Se trata de un problema de suma o de resta? ¿Cómo lo sabes?». Se trata de un problema de sustracción porque los billetes desaparecen cuando Alexis los gasta. El número de billetes está disminuyendo.
d. «¿Cómo podemos representar este problema de suma utilizando un modelo de barras?». Podemos dibujar la barra total y etiquetarla con 92. Luego podemos sumar dos partes por debajo. Luego podemos añadir dos partes debajo. Una está etiquetada con 55 y la otra con un signo de interrogación.
EXPLICAR: ESQUEMA DE ANCLAJE ESQUEMA DE ANCLAJE
CONSOLIDAR EL APRENDIZAJE DEL ESTUDIANTE
EXPLORACIÓN 2: REPRESENTAR Y RESOLVER PROBLEMAS ESCRITOS DE VARIOS PASOS
1. Etiquete la segunda fila como «Suma y resta de varios pasos» y divida la fila en dos casillas. Escriba una suma y una resta.
2. Lea el siguiente problema escrito: «DeAndré tenía 15 boletos. Su hermano le dio 36 boletos. DeAndré encontró 22 billetes en el suelo. ¿Cuántos billetes tiene ahora?».
3. Plantee las siguientes preguntas y anote las respuestas en el esquema de anclaje:
a. «¿Qué información sabemos?» DeAndré tenía 15 billetes y su hermano le dio 36 billetes más. También encontró 22 billetes en el suelo.
b. «¿Qué tenemos que averiguar?». Tenemos que averiguar cuántos billetes tiene DeAndré en total.
c. «¿Se trata de un problema de suma o de resta? ¿Cómo lo sabes?». Este es un problema de suma de varios pasos porque el número de boletos aumenta cuando DeAndré recibe algunos de su hermano y encuentra algunos en el piso.
d. «¿Cómo podemos representar este problema de suma usando un modelo de barra?». Podemos dibujar la barra del total y marcarla con un signo de interrogación porque aún no sabemos el total. Luego podemos añadir tres partes debajo. Marqué una con 15, otra con 36 y otra con 22.
4. Lea el siguiente problema escrito: DeAndré tenía 33 boletos. Le dio algunos a Juan. Le dio 3 a Nico. Ahora DeAndré tiene 25. ¿Cuántos billetes le dio a Juan?».
5. Plantee las siguientes preguntas y anote las respuestas de los estudiantes en los esquemas de anclaje:
a. «¿Qué información sabemos?». DeAndré tenía 33 boletos. Le dio algunos a Juan y 3 a Nico. A DeAndré le quedan 25 boletos.
b. «¿Qué tenemos que averiguar?». Tenemos que averiguar cuántos billetes le dio DeAndré a Juan.
c. «¿Se trata de un problema de suma o de resta? ¿Cómo lo sabes?». Este es un problema de sustracción de varios pasos porque el número de boletos disminuye cuando DeAndré le da algunos a Juan y algunos a Nico.
d. «¿Cómo podemos representar este problema con una recta numérica?». Podemos dibujar una recta numérica y empezar por la derecha con 33. Podemos saltar hacia atrás 3 para llegar a 30, y luego saltar 5 para llegar a 25.
EXPLORACIÓN 3: USAR MODELOS
CONCRETOS PARA REPRESENTAR ADICIÓN Y SUSTRACCIÓN HASTA 1,000
No es necesario. El maestro puede usar todas las partes del esquema de anclaje para invitar a los alumnos a usar objetos concretos para resolver cada problema escrito.
EXPLORACIÓN 4: USAR MODELOS PICTÓRICOS PARA REPRESENTAR LA ADICIÓN Y SUSTRACCIÓN HASTA 1,000
1. Etiquete la tercera casilla como «Representación de sumas y restas dentro de 1,000» y divida la fila en dos recuadros. Marque uno con «Suma» y otro con «Resta».
2. Lea el siguiente problema escrito: «Miya tiene 256 barajitas en su colección. Compra un libro de barajitas con su mesada. Ahora, Miya tiene 670 barajitas en su colección. ¿Cuántas barajitas había en el libro que compró con su mesada?».
3. Anime a los estudiantes a usar bloques de base diez para resolver el problema escrito. Permita que los estudiantes compartan cómo resolvieron el problema usando los manipulativos.
4. Plantee las siguientes preguntas y registre las respuestas de los estudiantes en el esquema de anclaje:
a. «¿Qué información sabemos?». Miya tiene 256 barajitas en su colección. Compra más barajitas. Ahora tiene 670.
b. «¿Qué tenemos que averiguar?». Tenemos que averiguar cuántos cromos había en el libro que compró con su mesada.
c. «¿Se trata de un problema de suma o de resta? ¿Cómo lo sabes?». Se trata de un problema de suma porque Miya está recibiendo más barajitas. El número de barajitas está aumentando.
d. «¿Cómo podemos representar este problema con una recta numérica?». Podemos dibujar una recta numérica y empezar por la izquierda con 256. Podemos saltar 400 para llegar a 656, y luego saltar 14 más para llegar a 670. Podemos sumar 400 y 14 para obtener 414 como respuesta.
5. Lea el siguiente problema eacrito: «Miya compró un libro de 500 barajitas. Sacó 321 barajitas del libro y las ha añadido a su colección. ¿Cuántas barajitas quedan en el libro?».
6. Anime a los alumnos a utilizar bloques de base diez para resolver el problema escrito. Permita que los estudiantes compartan cómo resolvieron el problema utilizando los manipulativos.

7. Plantee las siguientes preguntas y anote las respuestas de los alumnos en el esquema de anclaje:
a. «¿Qué información sabemos?». Miya compró un libro de 500 barajitas y sacó 321 barajitas del libro.
b. «¿Qué tenemos que averiguar?». Tenemos que averiguar cuántas barajitas quedan en el libro.
c. «¿Se trata de un problema de suma o de resta? ¿Cómo lo sabes?». Se trata de un problema de sustracción porque se están sacando barajitas del libro. El número de barajitas en el libro está disminuyendo.
d. «¿Cómo podemos representar este problema utilizando un modelo pictórico?». Podemos dibujar 5 cuadrados en el lugar de las centenas para representar 500. Podemos descomponer una centena en 10 decenas y dibujar 10 líneas en el lugar de las decenas. Podemos descomponer una decena en 10 unidades y dibujar 10 puntos en el lugar de las unidades. Entonces podemos tachar 3 cuadrados, 2 líneas y 1 punto para obtener 179 como respuesta.
EJEMPLO DE ESQUEMA DE ANCLAJE
EXPLICAR: LIBRETA INTERACTIVA

FOLLETO DEL ESTUDIANTE
DOCUMENTAR EL APRENDIZAJE DEL ESTUDIANTE
LIBRETA INTERACTIVA
DESCRIPCIÓN
Los alumnos toman notas, expresan ideas y/o procesan la información presentada en clase utilizando la actividad y la libreta.
MATERIALES
IMPRESO
• 1 folleto del estudiante (por alumno)
PREPARACIÓN
• Imprime una copia del folleto del estudiante por alumno.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Prepare una libreta interactiva con un cuadeno de espiral o de composición por estudiante. Así pueden usar las primeras páginas para crear un índice con números de página para llevar un registro de las actividades.
2. Recorte previamente o deje que los alumnos recorten las piezas de cada material para el alumno según las instrucciones del maestro que aparecen en el recuadro de la primera página.
3. De tiempo a los alumnos para que completen la actividad y luego peguen las piezas en su libreta interactiva.
4. Las libretas interactivas pueden utilizarse como referencia durante el trabajo independiente y pueden enviarse a casa al final del año como registro del aprendizaje de los estudiantes.
APOYO PARA ESTUDIANTES MULTILINGÜES CONEXIONES LINGÜÍSTICAS
DESCRIPCIÓN
Los estudiantes tienen la oportunidad de utilizar sus conocimientos lingüísticos y culturales para apoyar las conexiones con nuevas habilidades, vocabulario y conceptos en sus niveles de competencia.
MATERIALES
IMPRESO
• 1 folleto del estudiante según su nivel de competencia (por alumno)
• 1 tabla de valor posicional (por estudiante)
REUTILIZABLE
• 1 conjunto de bloques de base diez (por grupo)
PREPARACIÓN
• Determine el nivel de competencia en inglés de cada estudiante.
• Imprima un folleto del estudiante por alumno según su nivel de inglés.
• Permita que los estudiantes tengan acceso al vocabulario ilustrado para este alcance.
• Permita que los estudiantes tengan acceso a manipulativos tales como bloques de base diez.
• Imprima una tabla de valor posicional en cartulina por estudiante.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1 Distribuya un folleto del estudiante según el nivel de inglés apropiado a cada alumno.
2 Use las indicaciones para las partes de escuchar, hablar, leer y escribir. Utilice gestos, señale objetos y elementos visuales, según proceda. Consulte las indicaciones para obtener sugerencias.
3 Conceda tiempo a los estudiantes para que piensen con sus compañeros antes de responder.
4 Anime a los estudiantes a perseverar en su pensamiento y a utilizar herramientas y modelos matemáticos.
5 Invite a los estudiantes a responder adecuadamente a cada dominio lingüístico.

PRINCIPIANTE

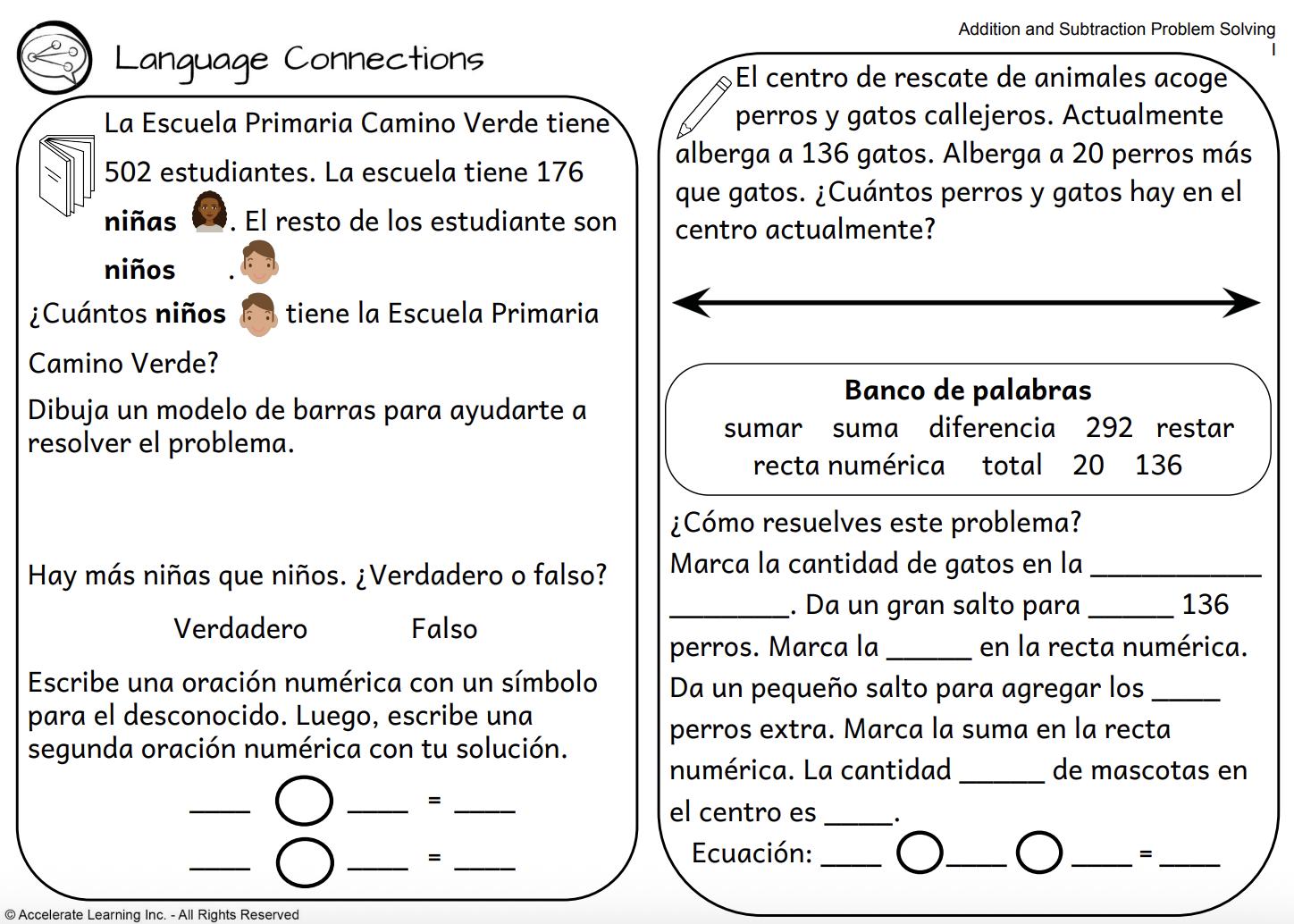

FOLLETO DEL ESTUDIANTE INTERMEDIO FOLLETO DEL ESTUDIANTE



FOLLETO DEL ESTUDIANTE
PRINCIPIANTE
Tenga a mano bloques de base diez y la tabla de valor posicional para que los estudiantes los usen. Lea las siguientes instrucciones de una en una:
• (Señale las palabras mientras lee). Kriti tenía 28 tarjetas de béisbol.Su amigo le dio tarjetas más.Ahora Kriti tiene 62 tarjetas de béisbol. ¿Cuántas tarjetas de béisbol recibió Kriti de su amigo?
• Señala el signo que indica que estamos hallando el número total (junta las manos) de tarjetas de béisbol.
• Señala el signo que indica la parte desconocida para el número de tarjetas de béisbol del amigo de Kriti.
• Usa los bloques de base diez (señale los bloques de base diez) para mostrar con cuántas tarjetas de béisbol comenzó Kriti.
• Usa los bloques de base diez (señale los bloques de base diez) para mostrar cuántas tarjetas de béisbol totales tenía Kriti después de que su amigo le diera algunas.
• Dibuja tu modelo pictórico (señale el folleto del estudiante). Explique que deben dibujar bloques de base diez en la tabla de valor posicional para mostrar su solución.
• (Señale el modelo de barra en blanco). Escribe cuántas tarjetas de béisbol tenía Kriti después de que su amigo le diera algunas más.(Señale la sección superior del modelo de barra). Escribe con cuántas tarjetas de béisbol comenzó Kriti. (Señale la sección inferior izquierda del modelo de barra). Escribe cuántas tarjetas de béisbol le dio el amigo de Kriti. (Señale la sección inferior derecha del modelo de barra).
• Señala la primera oración numérica en blanco. (Señale el número 28 en el problema, luego los bloques de base diez que equivalen a 28 y, por último, la primera casilla de la oración numérica).
• Escribe cuántas tarjetas de béisbol tiene Kriti en total. (Señale el número 62 en el problema, luego los bloques de base diez que equivalen a 62 y, por último, la última casilla de la oración numérica).
• Señala la segunda oración numérica en blanco. Ahora escribe una oración numérica que muestre tu solución. Escribe con cuántas tarjetas de béisbol comenzó Kriti (señale la primera casilla de la oración numérica), cuántas tarjetas de béisbol le dio su amigo (señale la segunda casilla de la oración numérica) y cuántas tarjetas de béisbol tiene ahora en total (señale la tercera casilla de la oración numérica).
INTERMEDIO
Tenga a mano bloques de base diez y la tabla de valor posicional para que los estudiantes los usen. Lea el problema, usando gestos cuando sea necesario, y luego lea las siguientes indicaciones, una a la vez:
• (Haga que los estudiantes conversen lo siguiente con sus compañeros):
◦ ¿Qué está sucediendo en este problema?
◦ ¿Cómo puedes resolver este problema?
• Usa tus bloques de base diez para encontrar la respuesta.
• Dibuja tu modelo de base diez.
• Resuelve el problema usando un modelo de barra.
• Señala la primera oración numérica en blanco. ¿Este problema necesita un signo más o un signo menos? ¿Qué símbolo representa la incógnita?
• Escribe la oración numérica que representa este problema.
• Señala la segunda oración numérica en blanco. Escriba la oración numérica que representa la solución de este problema.
• Señale la solución del problema.
ESCUCHAR
AVANZADO
Tenga bloques de base diez y la tabla de valor posicional a disposición de los estudiantes. Lea el problema. Luego lea las siguientes instrucciones una a la vez:
• (Haga que los estudiantes debatan lo siguiente con sus compañeros):
◦ ¿De qué se trata el problema?
◦ ¿Qué estrategias podríamos usar para resolver este problema?
• Usa tus bloques de base diez para encontrar la respuesta.
• Resuelve el problema con un modelo de barra.
• Escribe la oración numérica que representa este problema usando un símbolo para la incógnita, y luego escriba una oración numérica que muestre su solución al problema.
HABLAR
PRINCIPIANTE
Tenga a mano bloques de base diez y la tabla de valor posicional para que los estudiantes los utilicen. Señale cada palabra mientras lee el problema, utilizando gestos si es necesario. Luego lea las siguientes instrucciones, una a la vez:
• ¿Qué nos pide el problema que hagamos? (Haga que los estudiantes usen la siguiente estructura de oración):
◦ Necesitamos encontrar _____ (cuántas o número de) tarjetas de béisbol obtuvo Kriti de su...
• ¿Cuántos bloques de base diez usaste para modelar el número de tarjetas de béisbol con las que comenzó Kriti? (Haga que los estudiantes usen la siguiente estructura de oración):
◦ Usé ____ barras y ____ unidades para modelar las ____ tarjetas de béisbol con las que comenzó Kriti.
• ¿Cuántas tarjetas de béisbol usaste para representar el número total de tarjetas de béisbol que tiene Kriti después de que su amigo le dio algunas más? (Haga que los estudiantes usen el siguiente marco de oraciones):
◦ Usé ____ barras y ____ unidades para representar el total de ____ tarjetas de béisbol de Kriti.
• ¿Nos falta el total o una parte?
• Para encontrar la parte que falta o la incógnita, ¿cómo decidimos si tenemos que sumar (haga un gesto con el signo más o dibuje un signo más en la pizarra) o restar (haga un gesto con el signo menos o dibuje un signo menos en la pizarra)
◦ Nota: Algunos alumnos pueden decir que restarán. Otros pueden decir que sumarán al número que tenía Kriti hasta llegar al total.
• Explica a tus compañeros cómo usaste el modelo de barra para resolver el problema. (Pida a los alumnos que utilicen los siguientes marcos de oraciones):
◦ En la parte superior (señale la sección superior), escribí _____, el número total de tarjetas.
◦ En la parte inferior izquierda (señale la parte inferior izquierda), escribí _____, el número de tarjetas con las que comenzó.
◦ En la parte inferior derecha (señale la parte inferior derecha), escribí ____, el número de tarjetas que le dio su amigo.
• ¿Cuántas tarjetas de béisbol le dio el amigo de Kriti? (Pida a los alumnos que usen el siguiente marco de oraciones):
◦ El amigo de Kriti le regaló _____ tarjetas de béisbol.
INTERMEDIO
Tenga a mano bloques de base diez y la tabla de valor posicional para que los alumnos los utilicen. Lea el problema, utilizando gestos cuando sea necesario. A continuación, lea las siguientes indicaciones de uno en uno:
• Comparte con tus compañeros lo que observas sobre el problema.
◦ ¿De qué trata el problema?
◦ ¿Qué nos pide que hagamos?
◦ Para encontrar la parte que falta o la incógnita, ¿cómo decidimos si necesitamos sumar o restar?
◦ Nota: Algunos estudiantes pueden decir que restarán. Otros pueden decir que sumarán al número que tenía Kriti hasta llegar al total.
• Explica a tus compañeros cómo usaste los bloques de base diez para encontrar la incógnita. (Pida a los estudiantes que usen la raíz de la oración):
◦ Primero coloqué...
• Explica a tu compañero si colocaste más bloques de base diez o quitaste bloques de base diez. (Use la siguiente oración inicial):
◦ Luego yo...
• ¿Cuántos bloques de base diez le dio el amigo de Kriti? (Pida a los estudiantes que usen siguiente oración inicial):
◦ El amigo de Kriti le dio
• Explica a tus compañeros cómo usaste el modelo de barra para resolver el problema.
AVANZADO
Tenga bloques de base diez y la tabla de valor posicional disponibles para que los estudiantes los usen. Lea el problema. A continuación, lea las siguientes indicaciones de una en una:
• Comparte con tus compañeros lo que observas en el problema.
◦ ¿De qué trata el problema?
◦ ¿Qué pregunta estamos intentando resolver?
◦ ¿Qué diferentes tipos de estrategias podemos utilizar al resolver problemas?
• Explica a tus compañeros qué estrategias serían las mejores para resolver este problema.(Haga que los alumnos utilicen la siguiente estructura de frases):
◦ Una estrategia que puedo utilizar para este problema es __ porque...
• Explica a tus compañeros cómo has utilizado las estrategias de un modelo de base diez y un modelo de barra para resolver el problema.
PRINCIPIANTE
Ponga a disposición de los alumnos bloques de base diez. Repita las palabras con todo el grupo siguiendo el banco de palabras. Defina y proporcione ejemplos según sea necesario.
• Invite a los estudiantes a leer el problema juntos.
• Use la recta numérica (señale la recta numérica) para representar este problema escrito (señale el problemaescrito).
• ¿Alguien puede mostrarnos cómo resolver usando la recta numérica? (Elija un voluntario, o representen juntos si es necesario).
• Permita que los estudiantes conversen con sus compañeros cómo resolvieron el problema.
• Diga a los estudiantes que pueden comprobar su trabajo utilizando bloques de base diez si lo desean.
• Completen las oraciones juntos, utilizando el banco de palabras.
• Escriba una oración numérica que muestre cómo resolvió el problema en la recta numérica.
• De tiempo para que los estudiantes compartan su trabajo con sus compañeros.
PRINCIPIANTE
Tenga bloques de base diez a disposición de los estudiantes. Lea en grupo el problema de la historia. Pida a los alumnos que señalen cada palabra mientras leen. Invítelos a marcar con un círculo las palabras que no conozcan. Explique las palabras en grupo, proporcionando ejemplos cuando sea necesario.
• ¿Cuántos alumnos hay en la escuela? ¿Cuántas niñas hay en la escuela?
• (Lea las instrucciones en voz alta). ¿Tienes que sumar o restar para encontrar el número de niños en la escuela?
• (Señala el modelo de barra.) ¿Qué número va en la casilla entera del modelo de barra? ¿Qué números van en las partes del modelo de barra?
• ¿Cuántos niños hay en la escuela? (Señale el problema de la historia y el modelo.)
• Lea las instrucciones y anime a los alumnos a consultar el problema y el modelo para completar las dos oraciones numéricas. Los estudiantes deben escribir una oración numérica usando un símbolo para la incógnita y luego escribir una oración numérica con su solución.
• Permita que los estudiantes usen bloques de base diez según sea necesario.
INTERMEDIO
Tenga bloques de base diez a disposición de los estudiantes. Haga una lectura coral y use el banco de palabras. Defina y proporcione ejemplos según sea necesario.
• Invite a los estudiantes a leer el problema juntos.
• Use la recta numérica para representar este problema de dos pasos.
• ¿Alguien puede mostrarnos cómo resolverlo usando la recta numérica? (Elija un voluntario).
• Haga que debatan con sus compañeros cómo resolvieron el problema.
• Use el banco de palabras para completar las oraciones que explican los pasos que tomaron para resolver el problema escrito.
• Dé tiempo para que los estudiantes compartan su trabajo con sus compañeros.
ESCRIBIR
AVANZADO
Tenga bloques de base diez disponibles para los estudiantes. Haga que los estudiantes lean la historia en parejas. Defina y proporcione ejemplos según sea necesario.
• Anime a los estudiantes a explicar a sus compañeros cómo resolverán el problema usando la recta numérica.
• Dé tiempo a los estudiantes para resolver el problema con la recta numérica.
• Lea las instrucciones sobre qué escribir.
• Escriba los pasos que siguió para resolver el problema. Asegúrese de escribirlos en el orden en que los hiciste.
• Comparte lo que escribiste con tus compañeros. Escucha lo que han escrito tus compañeros. Debate qué hiciste igual y qué hiciste diferente en ambos escritos.
• Plantea a tus compañeros otras estrategias que podrías haber usado para resolver este problema de dos pasos.
INTERMEDIO
Tenga bloques de base diez disponibles para que los estudiantes los usen. Lea el problema de la historia en grupo. Pida a los alumnos que señalen cada palabra mientras leen. Invítelos a marcar con un círculo las palabras que no conozcan. Explique las palabras, proporcionando ejemplos según sea necesario.
• Comparte con tus compañeros dos cosas que sabe del problema de la historia. Señala dónde puedes encontrarlas en el párrafo.
• Anime a los estudiantes a referirse a la historia.
• Lectura coral de las frases debajo del problema de la historia de una en una.
• Con tus compañeros, debate cómo resolverás el problema.
• Dibuja un modelo de barras para ayudarte a resolver el problema.
• Comparte tu modelo con tus compañeros.
• Hay más niñas que niños. ¿Verdadero o falso? Encierra en un círculo tu respuesta.
• Escribe una oración numérica con un símbolo para la incógnita y luego escribe una segunda oración numérica con tu solución.
• De tiempo a los estudiantes para que compartan con sus compañeros la estrategia que utilizaron para resolver el problema.
AVANZADO
Tenga a mano bloques de base diez para que los estudiantes los utilicen. Pida a los alumnos que lean la historia con sus compañeros. Haga que los estudiantes señalen mientras leen.
• Compartan con sus compañeros la información que conocen del problema de la historia. Señalen dónde pueden encontrarla en el párrafo.
• Anime a los estudiantes a referirse a la historia.
• ¿Qué pide el problema? ¿Cómo lo sabes?
• Debate con tus compañeros cómo resolverás el problema.
• Dibuja un modelo de barra para ayudarte a resolver el problema.
• Comparte tu modelo con tus compañeros.
• Lee las preguntas en pareja y respóndelas.
• Escribe una oración numérica con un símbolo para la incógnita y luego escribe una segunda oración numérica con tu solución.
• De tiempo a los estudiantes para que conversen con sus compañeros la estrategia que usaron para resolver el problema.
ANALIZAR EL PENSAMIENTO DEL ESTUDIANTE
MIS PENSAMIENTOS DE MATEMÁTICAS
DESCRIPCIÓN
Los estudiantes tendrán la oportunidad de escribir sus pensamientos e ideas matemáticas utilizando varias vías diferentes.
PREPARACIÓN
• Imprima una copia del documento «Mis pensamientos de matemáticas» por estudiante.
• Reúna todas las herramientas y modelos matemáticos utilizados en este alcance para ayudar a los estudiantes en el proceso de escritura.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Es posible que algunos estudiantes necesiten ayuda con la lectura para completar esta actividad.
2. Permita que los estudiantes compartir su pensamiento con un compañero antes de escribirlo en papel.
3. Anime a los estudiantes a perseverar en su pensamiento y utilizar herramientas y modelos matemáticos según sea necesario. Recuerde a los alumnos los bancos de palabras que aparecen en la mayoría de los folletos.
4. Invite a los alumnos a escribir sus respuestas con frases completas, utilizando la ortografía, la gramática y la puntuación correctas cuando proceda.
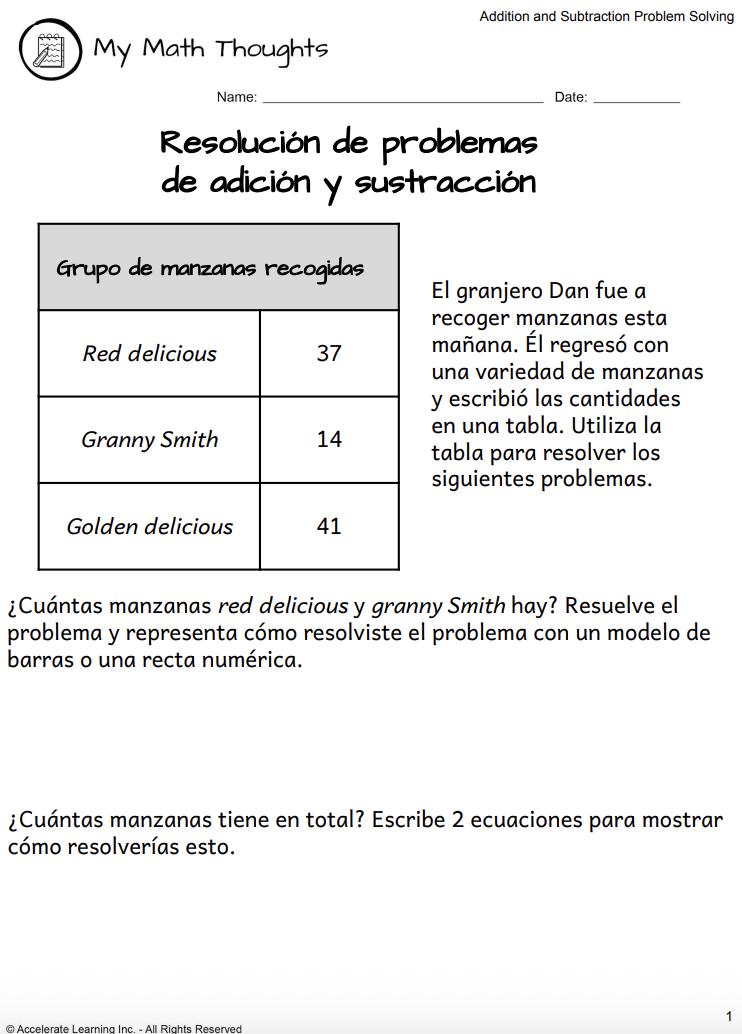

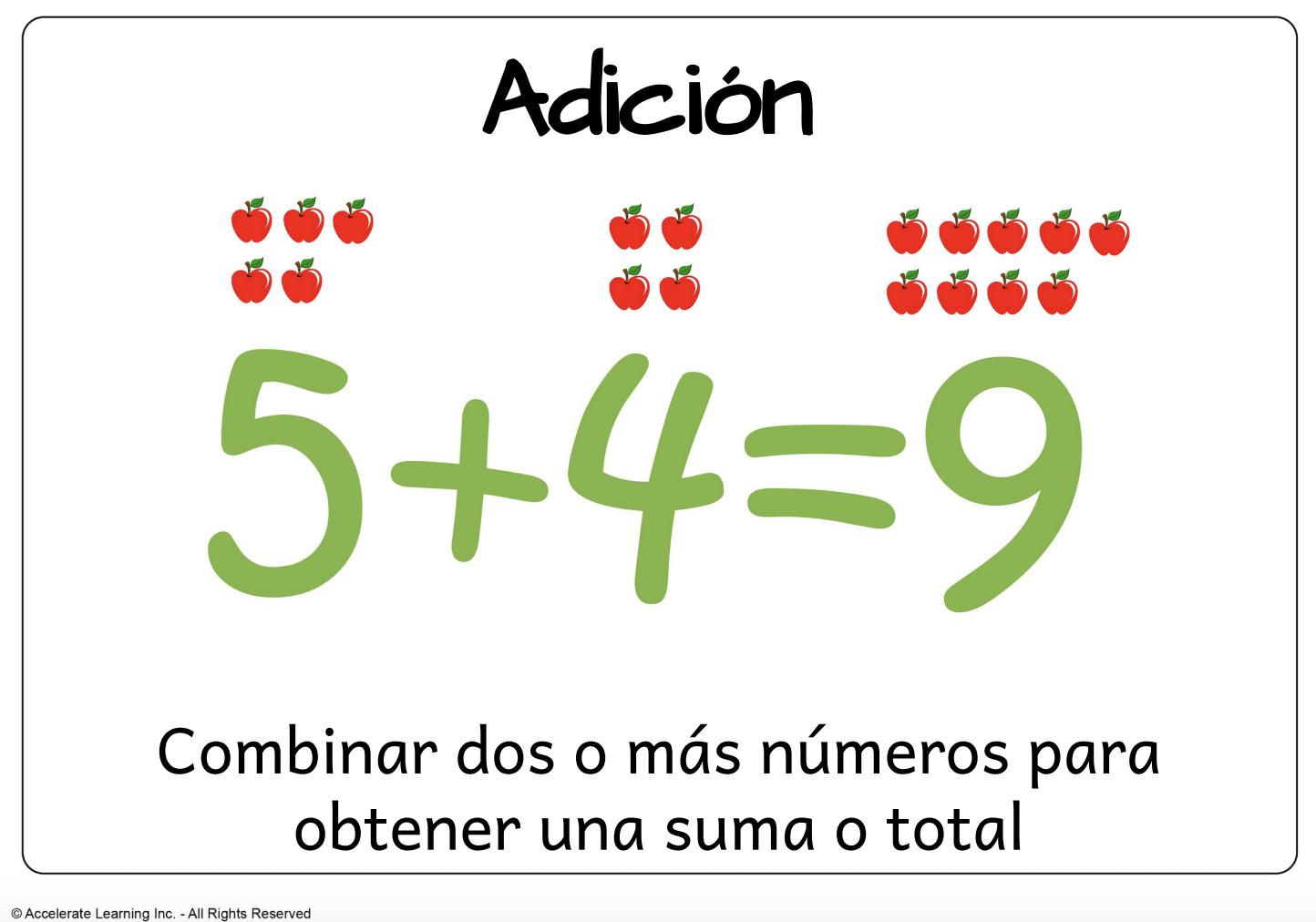
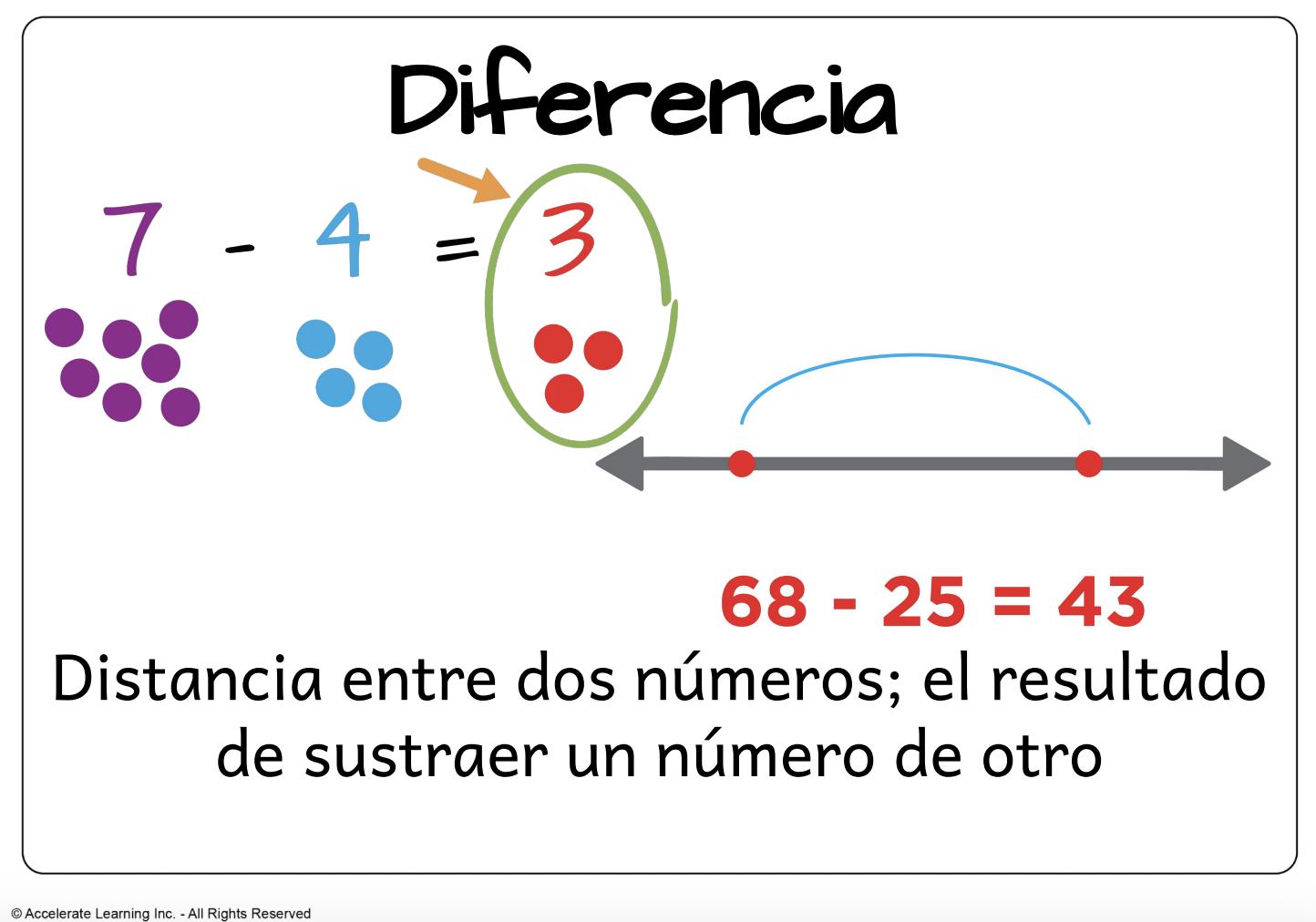
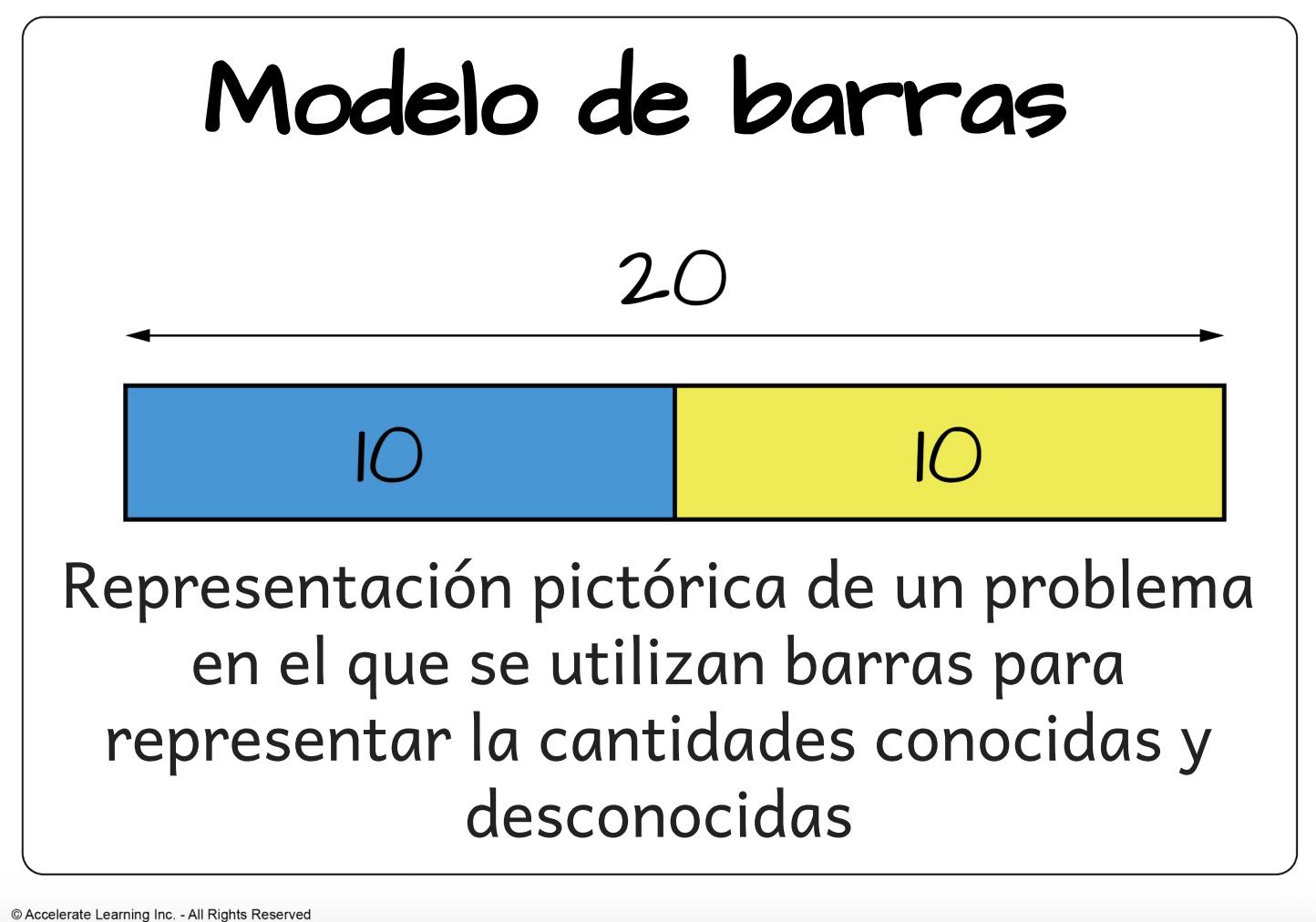
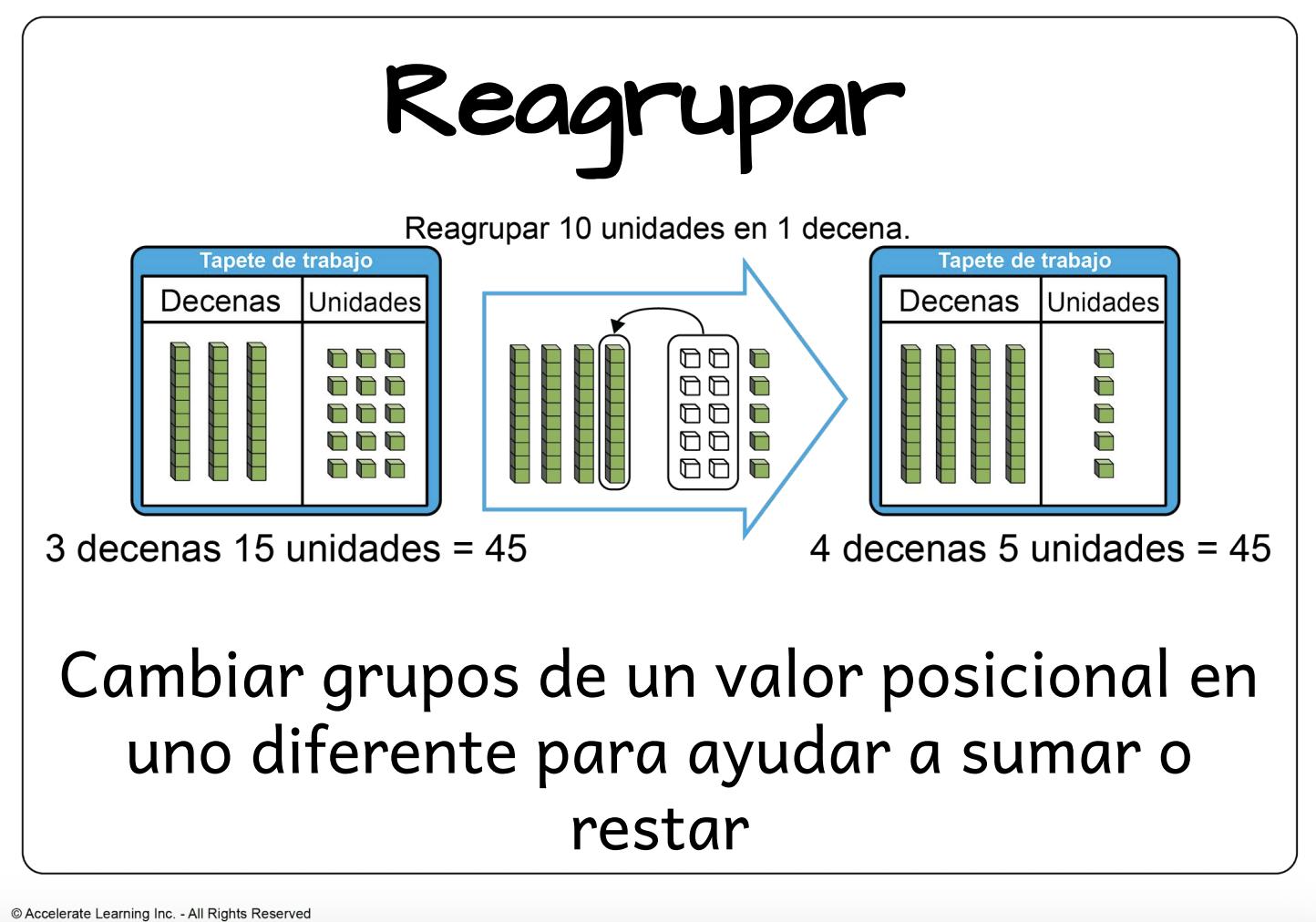
EXPLICAR: VOCABULARIO ILUSTRADO VOCABULARIO
ILUSTRADO
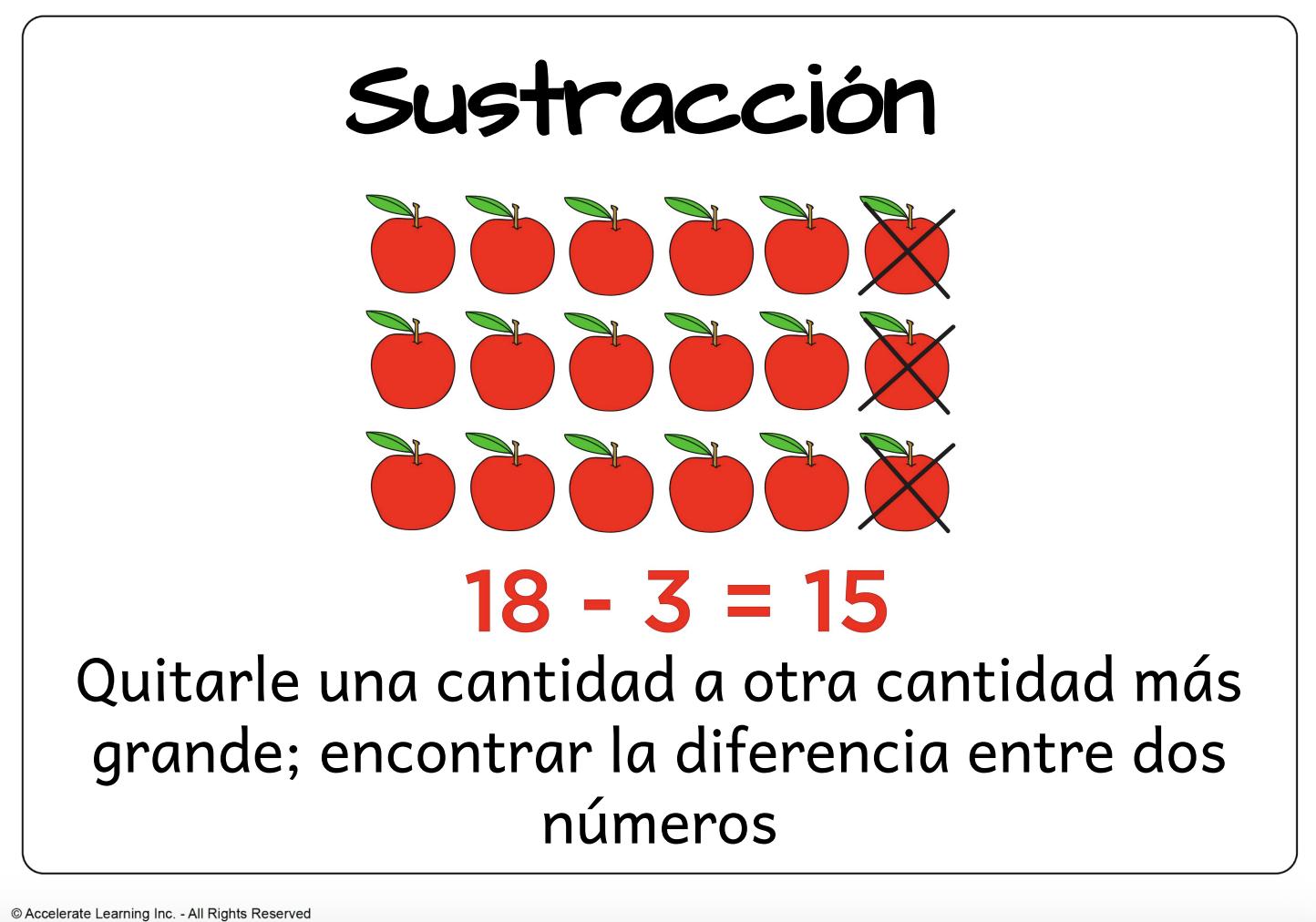

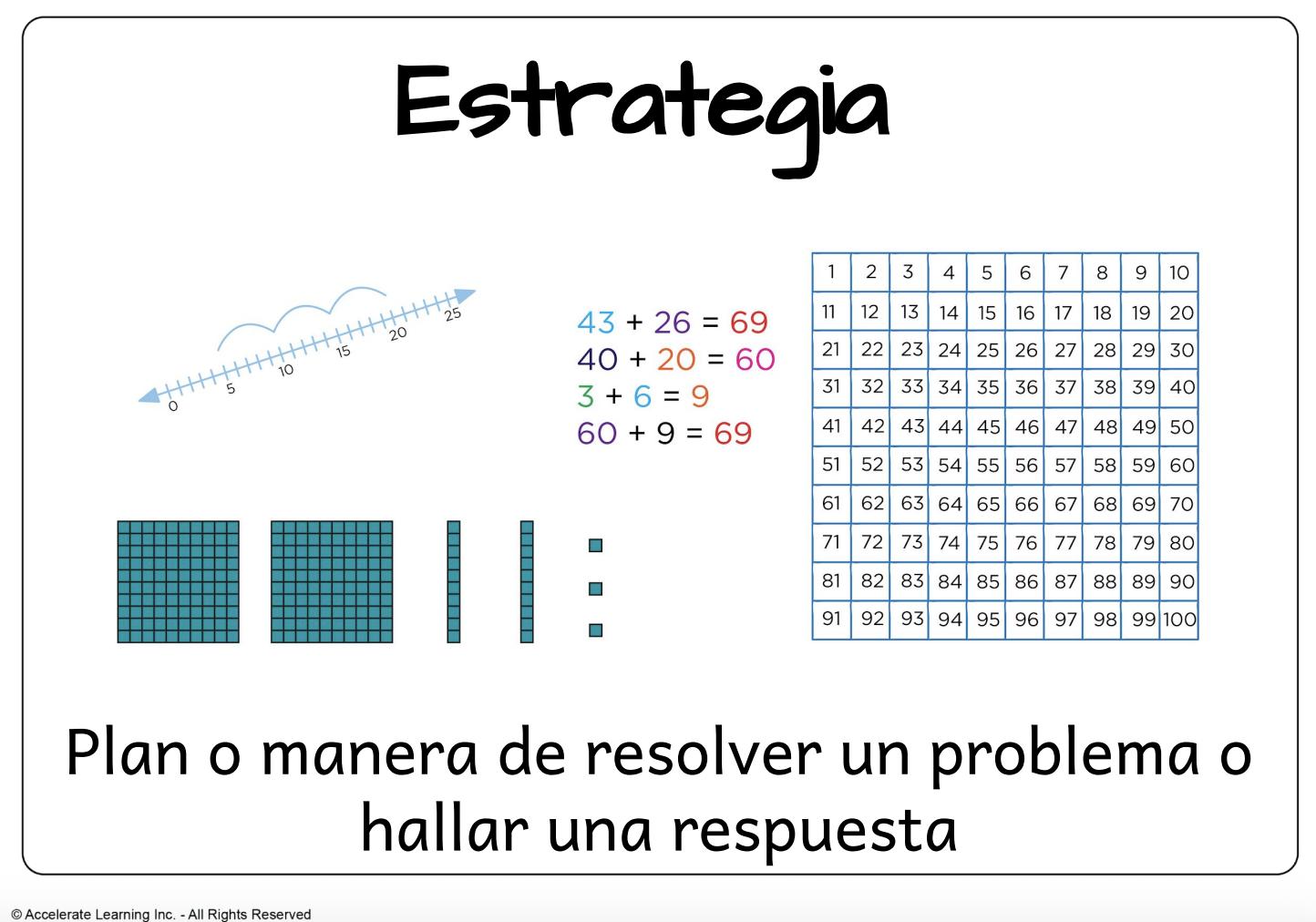
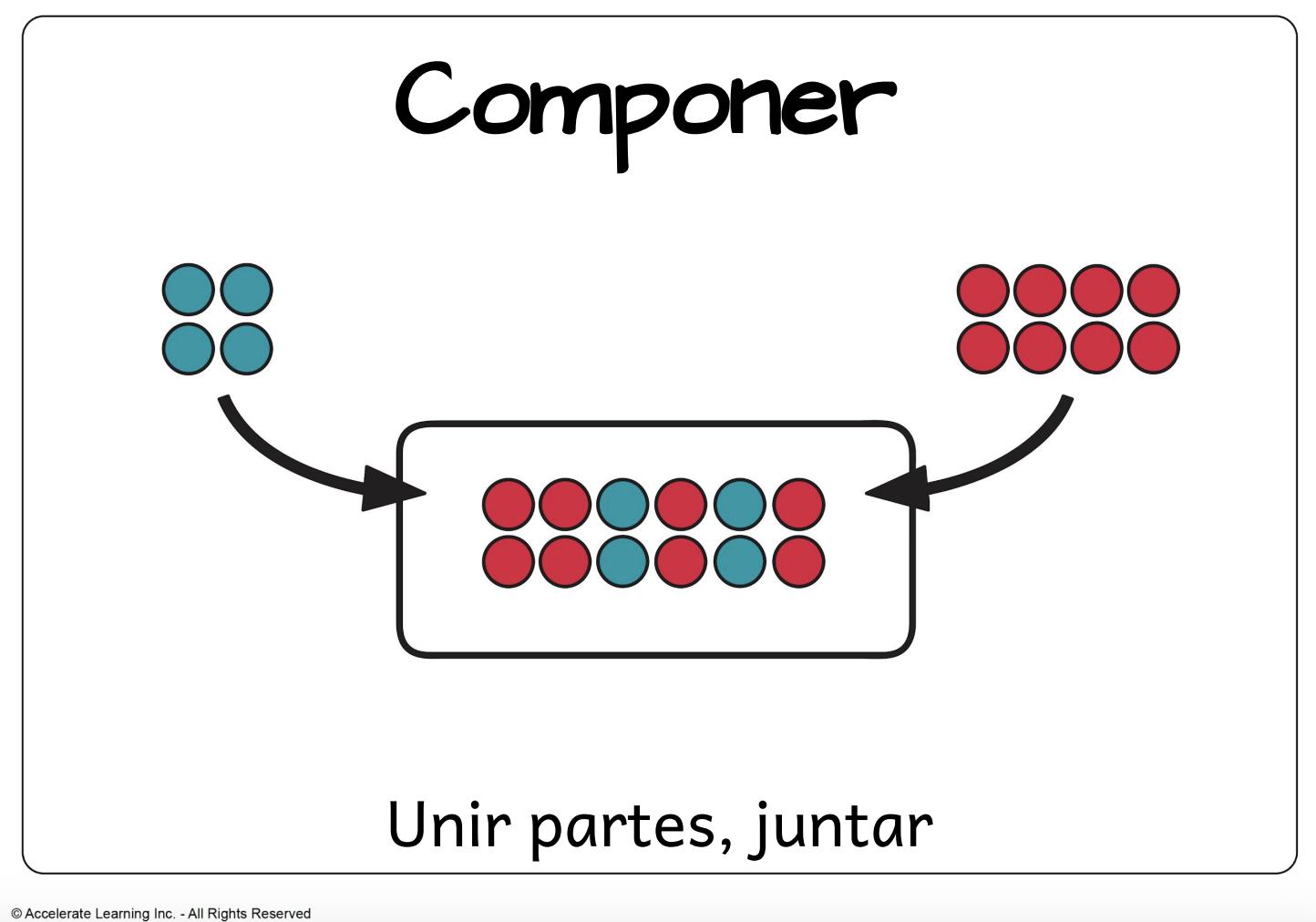


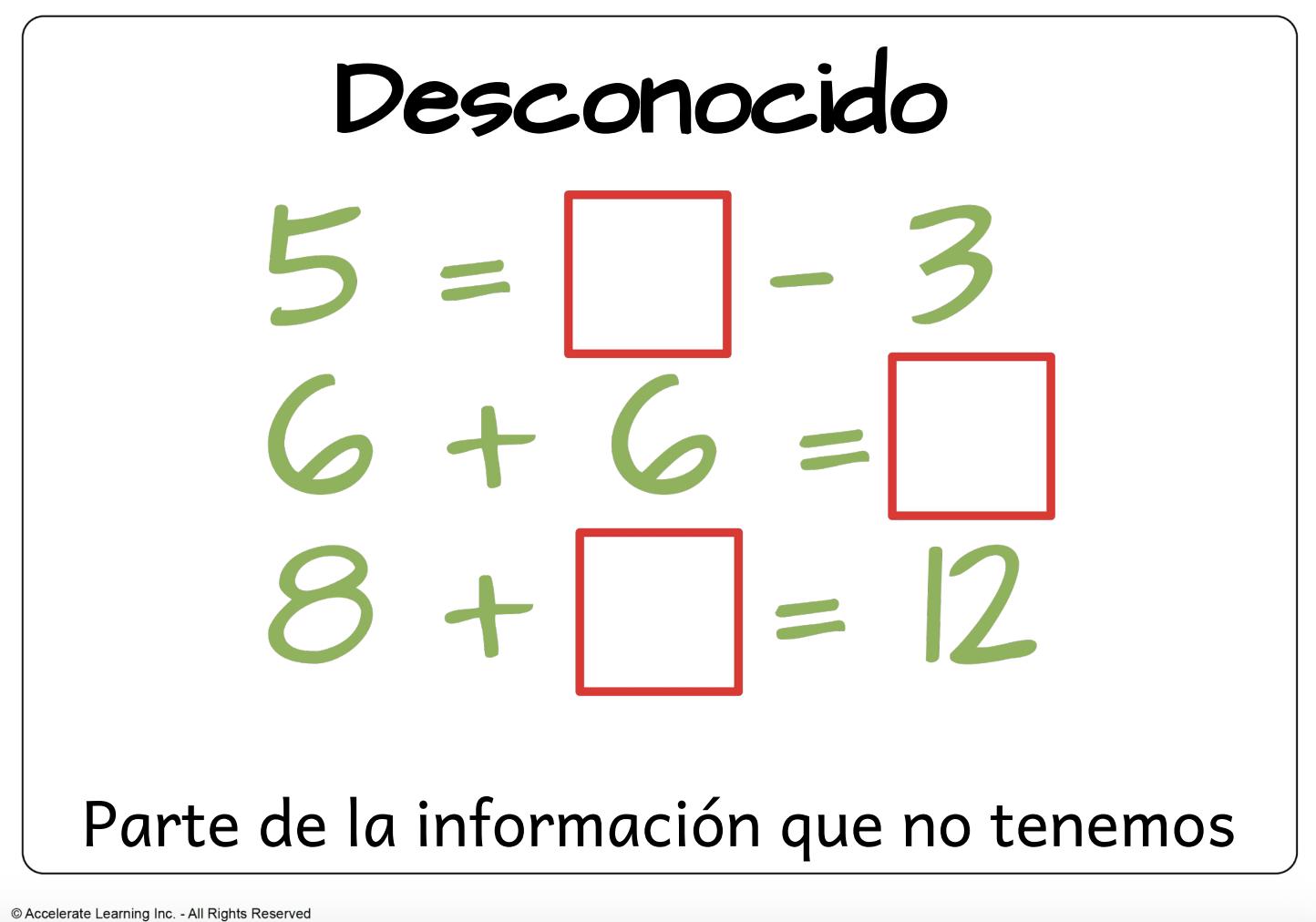
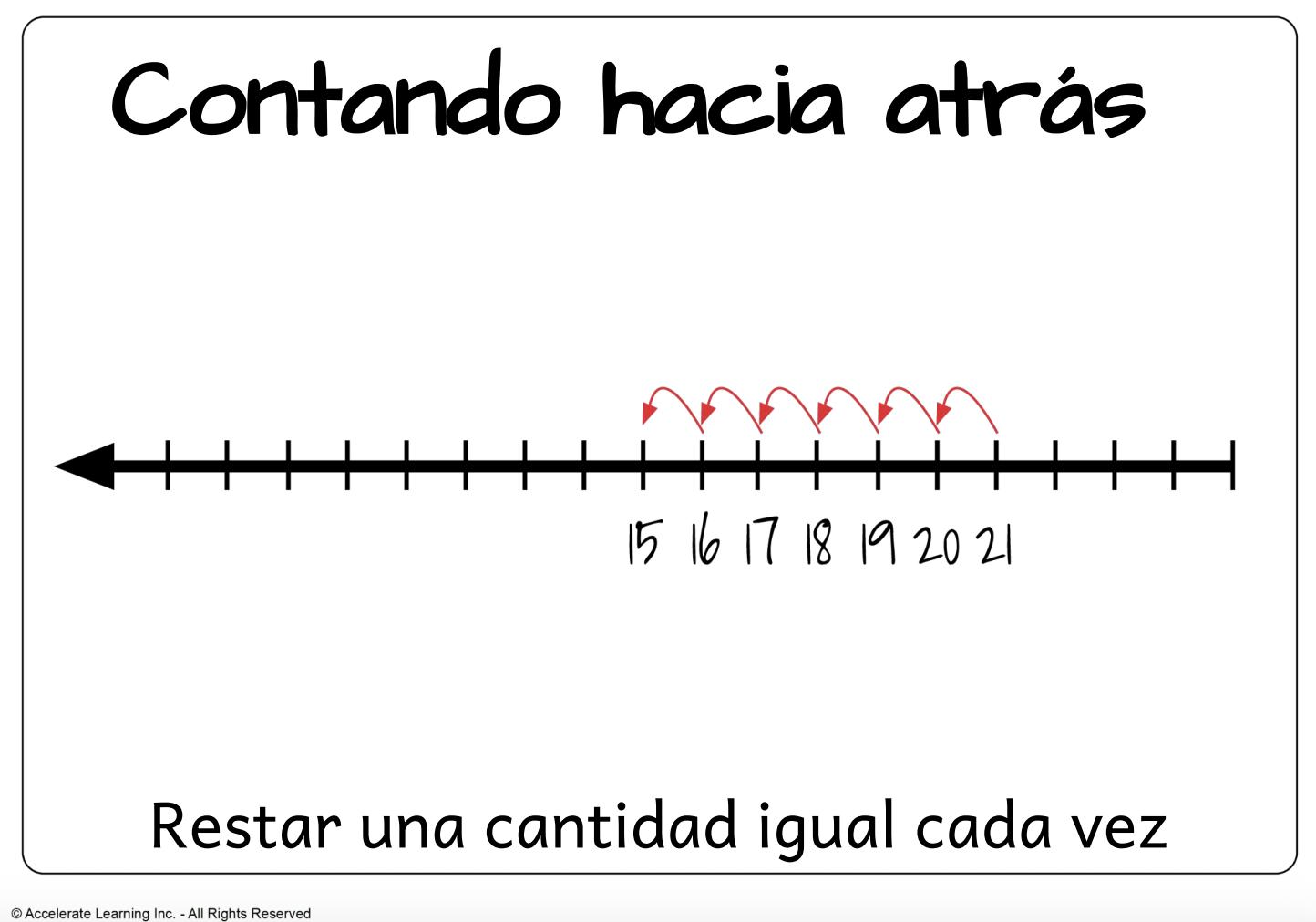
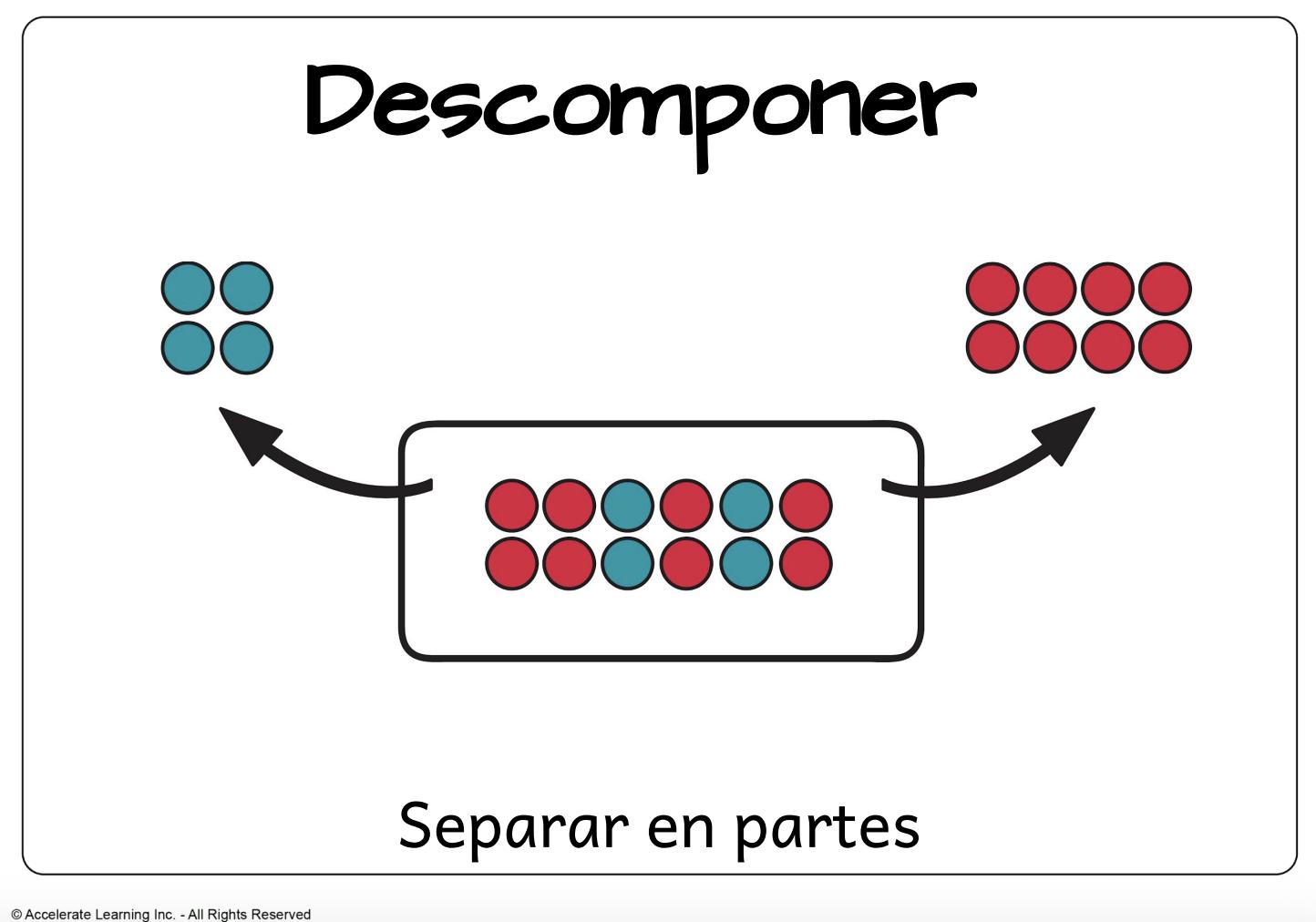
PALABRAS QUE HAY QUE CONOCER
ELABORAR: CONSTRUCTOR DE FLUIDEZ
DESARROLLAR FLUIDEZ CONCEPTUAL
CONSTRUCTOR DE FLUIDEZ:
PROBLEMAS Y REPRESENTACIONES DE SUMAS Y RESTAS
¡DESCRIPCIÓN
Los alumnos trabajan en pequeños grupos para jugar con las cartas de ¡A pescar!
MATERIALES
IMPRESO
• 1 hoja de instrucciones (por grupo)
• 1 conjunto de cartas ¡A pescar! (por grupo)
• 1 hoja de registro del estudiante (por alumno)
REUTILIZABLE
• 1 sobre o bolsa resellable (por grupo)
PREPARACIÓN
• Imprima y recorte suficientes tarjetas de ¡A pescar! para que los alumnos las compartan en pequeños grupos. (Los grupos no deben tener más de cuatro estudiantes.) Cuando imprima las tarjetas, asegúrese de imprimirlas por las dos caras para que el logotipo del juego aparezca en una cara de cada tarjeta.
• Imprima una hoja de instrucciones para cada juego de tarjetas de ¡A pescar!
• Considere la posibilidad de plastificar todos los materiales impresos, excepto la hoja de registro del estudiante, para que puedan utilizarse durante mucho tiempo. Puede colocar los trozos más pequeños en sobres o bolsas con cierre.
• Imprima una hoja de registro del estudiante para cada alumno.

HOJA DE REGISTRO DEL ESTUDIANTE
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Haga una demostración del juego con un grupo de alumnos.
a. El repartidor da cinco cartas a cada jugador y coloca todas las demás cartas boca abajo en un montón.
b. El juego se mueve en el sentido de las agujas del reloj. Cada jugador elige una carta de su mano y pide a otro jugador que la empareje. Las parejas que coinciden también tienen imágenes de peces iguales. Si alguien pide a un jugador una carta que tiene en su poder, el jugador debe dársela. Si el jugador no tiene ese tipo de carta, el oponente debe pescar y tomar una carta del montón boca abajo.
c. Los jugadores ponen boca arriba sobre la mesa las parejas que reciben.
d. El juego continúa hasta que todas las manos estén vacías y no haya más cartas que robar.
e. Cada par de cartas iguales vale un punto. El jugador con más puntos es el ganador..
2. Distribuya los materiales.
3. Haga que los alumnos jueguen.
4. Al final del juego, haga que cada jugador elija una pareja para completar la hoja de registro del estudiante. Pídales que expliquen por qué las 2 cartas coinciden. Anime a los estudiantes a compartir sus respuestas con sus grupos.
ELABORAR: CONSTRUCTOR DE FLUIDEZ

HOJA DE REGISTRO DEL ESTUDIANTE
DESARROLLAR LA FLUIDEZ CONCEPTUAL
CONSTRUCTOR DE FLUIDEZ: EMPAREJAR UN PROBLEMA DE SUMA O RESTA DE DOS CIFRAS CON UN MODELO
DESCRIPCIÓN
Los alumnos dan la vuelta a dos tarjetas y buscan coincidencias entre las imágenes, los números y/o las palabras.
MATERIALES
IMPRESO
• 1 hoja de instrucciones (por pareja)
• 1 conjunto de tarjetas de pareo (por pareja)
• 1 hoja de registro del estudiante (por alumno)
REUTILIZABLE
• 1 sobre o bolsa con cierre (por pareja)
PREPARACIÓN
• Imprima y recorte un juego de tarjetas de pareo por pareja. Al imprimir las tarjetas, asegúrate de imprimirlas por las dos caras para que el logotipo del juego aparezca en una cara de cada tarjeta.
• Imprima una hoja de instrucciones para cada juego de tarjetas.
• Considere la posibilidad de plastificar todos los materiales impresos, excepto la hoja de registro del estudiante, para poder utilizarlos durante más tiempo. Puede colocar los trozos más pequeños en sobres o bolsas con cierre.
• Imprima una hoja de registro del estudiante por alumno.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Enseñe a los alumnos a barajar las cartas y a colocarlas boca abajo en una matriz de 4 × 6..
2. Haga una demostración del juego con un estudiante.
a. El primer jugador da la vuelta a dos cartas para intentar encontrar una coincidencia.
b. Si el jugador encuentra dos coincidencias, se queda con el conjunto coincidente y vuelve a jugar.
c. Si el jugador no encuentra ninguna coincidencia, vuelve a colocar las cartas boca abajo y es el turno del siguiente jugador.
d. Los jugadores continúan turnándose hasta que se hayan encontrado todas las coincidencias.
e. Gana el jugador que reúna más cartas.
3. Distribuya los materiales.
4. Pida a los alumnos que jueguen.
5. Al final del juego, pida a cada jugador que anote dos de las coincidencias que haya encontrado en la hoja de registro del estudiante. Pídales que expliquen por qué las 2 cartas coinciden. Anime a los alumnos a compartir sus respuestas con sus compañeros.
ELABORAR: REVISIÓN EN ESPIRAL
REPASAR CONCEPTOS PREVIOS
REVISIÓN EN ESPIRAL:
FIESTA DE PIZZA
DESCRIPCIÓN
Los estudiantes repasan el contenido del grado anterior o actual basándose en los puntos centrales establecidos para cada grado.
PREPARACIÓN
• Imprima una copia de la hoja de revisión en espiral para cada estudiante.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Puede que necesite proporcionar ayuda con la lectura para que algunos estudiantes completen esta actividad.
2. Lea la historia en la primera página para despertar el interés antes de pasar a las preguntas.
3. Ue este repaso en espiral como calentamiento en clase o envíelo a casa como tarea, pero asegúrese de repasar las respuestas y estrategias con toda la clase.
4. Consulte el estándar en la esquina inferior derecha de cada cuadro de preguntas para evaluar el conocimiento del contenido de los estudiantes o la necesidad de una mayor intervención.
REVISIÓN EN ESPIRAL CENTRADA EN LA PREGUNTA
• Pregunta 1
○ Grado 2 - Dividir círculos y rectángulos en dos, tres o cuatro partes iguales; describir las partes usando las palabras mitades, tercios, mitad de, un tercio de, etc., y describir el todo como dos mitades, tres tercios, cuatro cuartos. Reconocer que partes iguales de enteros idénticos no necesitan tener la misma forma.
• Pregunta 2
○ Grado 2 - Sumar mentalmente 10 o 100 a un número dado 100-900, y restar mentalmente 10 o 100 de un número dado 100-900.
• Pregunta 3
○ Grado 2 - Dividir círculos y rectángulos en dos, tres o cuatro partes iguales, describir las partes usando las palabras mitades, tercios, mitad de, un tercio de, etc., y describir el todo como dos mitades, tres tercios, cuatro cuartos. Reconocer que partes iguales de enteros idénticos no necesitan tener la misma forma.
• Pregunta 4
○ Grado 2 - Sumar hasta cuatro números de dos dígitos utilizando estrategias basadas en el valor posicional y las propiedades de las operaciones.

FOLLETO DEL ESTUDIANTE CLAVE DE RESPUESTAS
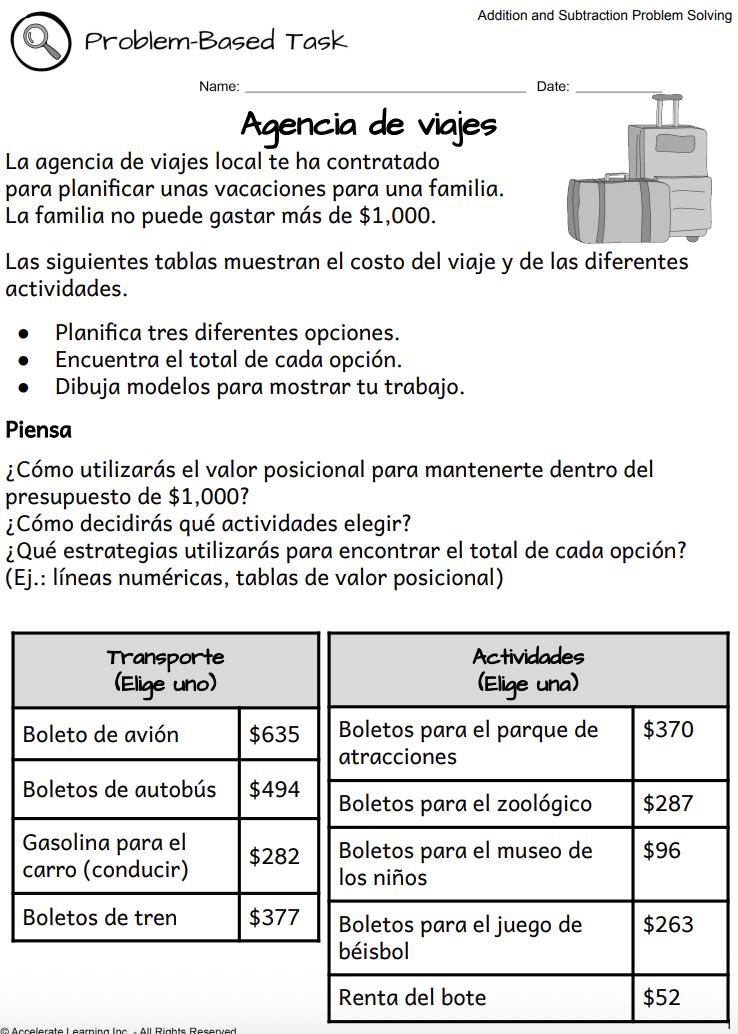

ELABORAR: TAREA BASADA EN PROBLEMAS
DESARROLLAR HABILIDADES PARA RESOLVER PROBLEMAS
TAREA BASADA EN PROBLEMAS: AGENCIA DE VIAJES
DESCRIPCIÓN
Los estudiantes trabajan en colaboración para aplicar los conocimientos y habilidades que han aprendido a un desafío abierto del mundo real.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Permita que los estudiantes trabajen en grupos.
2. Anímelos a consultar sus diarios del estudiante de las actividades de exploración si necesitan repasar las habilidades que han aprendido.
3. Si los estudiantes están atascados, use preguntas orientadoras para ayudarles a pensar sin decirles qué pasos deben dar a continuación. Si el tiempo lo permite, haga que cada grupo comparta su solución con la clase.
4. Plantee cómo los diferentes grupos abordaron el reto de diferentes maneras.

FOLLETO DEL ESTUDIANTE RÚBRICA
ELABORAR: CONEXIONES CON LA VIDA
MATEMÁTICAS DEL MUNDO REAL
CONEXIONES CON LA VIDA
Conexiones con la vida pretende ser una vía que introduzca a sus alumnos en profesiones y experiencias de la vida cotidiana que pongan de relieve los conceptos matemáticos que se aprenden en el aula.
DESCRIPCIÓN
Esta conexión con la vida pone de relieve a un entrenador de baloncesto.
MATERIALES
IMPRESO
• 1 folleto para el estudiante (por grupo)
REUTILIZABLE
• 1 proyector o cámara de documentos (por maestro)
• 1 paquete de lápices de colores y ceras (por grupo)
PREPARACIÓN
• Reúna lápices de colores y ceras para cada grupo.
• Imprima una copia del folleto para el estudiante por grupo.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
PARTE I
1. Muestre el videoclip del entrenador de baloncesto.
2. Organice una conversación con los alumnos haciendo preguntas como las siguientes:
a. «¿Cómo tendría que usar un entrenador la suma y la resta para llevar la cuenta del marcador?».
b. «¿Crees que sería fácil o difícil llevar la cuenta del marcador mentalmente?».
c. «A la hora de elaborar un plan para ganar, ¿qué tipo de resolución de problemas debe hacer el entrenador?».
d. «¿Te interesa esta profesión? ¿Por qué sí o por qué no?».
e. «¿Hay varias maneras de que un equipo marque para ganar un partido cuando va perdiendo?».
PARTE II
1. Divida a los alumnos en grupos de 4. Entrega a cada grupo una copia del folleto del estudiante, lápices y ceras de colores.
2. Facilite un debate:
a. «¿Cuántos puntos se consiguen por una canasta? ¿Y por un tiro libre? ¿Y por un tiro de tres puntos?».
b. «¿Cuántos puntos totales necesitas para ganar al otro equipo?».


FOLLETO DEL ESTUDIANTE
3. Pida a los alumnos que elaboren un plan para anotar suficientes puntos para poder ganar el partido. Pídales que creen un marcador con la puntuación final en la parte inferior de su plan de juego. Anímeles a representar su estrategia de resolución de problemas con un modelo, como una recta numérica o un modelo de barras.
4. Mientras los alumnos trabajan, pasee por la clase y pregúnteles cómo están utilizando la resolución de problemas de suma y resta para crear un plan de juego.
La ciencia de datos consiste en un breve debate en clase sobre un conjunto de datos. Esta actividad no está pensada para ser calificada. La parte I incluye preguntas abiertas para ayudar a los alumnos a interpretar y analizar los datos. Las partes siguientes son actividades opcionales para ampliar el aprendizaje de los alumnos en contexto.
DESCRIPCIÓN
Los alumnos analizan, interpretan y generan conjuntos de datos, además de responder a preguntas basadas en los datos.
MATERIALES
IMPRESO
• 1 folleto del estudiante (por alumno)
• 1 conjunto de datos (por clase)
REUTILIZABLE
• 1 proyector o cámara de documentos (por clase)
• 1 marcador de borrado en seco (por clase)
CONSUMIBLE
• 1 trozo de papel milimetrado (por clase)
PREPARACIÓN
• Prepárese para proyectar el conjunto de datos.
• Reúna un trozo de papel milimetrado y un marcador de borrado en seco.
• Imprime un folleto del estudiante por alumno.

FOLLETO DEL ESTUDIANTE
ELABORAR: CIENCIA DE DATOS CIENCIA
ANALIZAR DATOS
DE DATOS
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
PARTE I
1. Proyecte el conjunto de datos y prepárese para anotar las observaciones de los alumnos.
2. Plantee las siguientes preguntas:
a. «¿Qué observa en este conjunto de datos?».
b. «¿Qué representa este conjunto de datos?».
c. «¿Qué categorías se incluyen en este conjunto de datos?».
d. «¿Te has hospedado alguna vez en un hotel? ¿Dónde quedaba?».
e. «¿Por qué un hotel podría tener diferentes tarifas en diferentes días de la semana?».
f. «¿Qué preguntas tienes acerca de los datos?».
PARTE II
1. Repase la resolución de problemas de suma y resta y escriba lo que los estudiantes recuerden en el papel milimetrado.
2. Plantee las siguientes preguntas:
a. «¿Cuál sería el costo de hospedarse en el hotel un jueves por la noche y un viernes por la noche?». $475 $
b. «¿Cuál es la diferencia de precio entre alojarse en el hotel un lunes por la noche y un sábado por la noche? Escribe una ecuación para el problema.». $250 - $175 = $75
c. «El Sr. Ludwig está tratando de decidir si debe pasar la noche en el hotel un jueves o un viernes. ¿Cuál es la diferencia de precio? Dibuja bloques de base diez para mostrar tu trabajo«. $25
d. «La familia Evans pernocta en el hotel un jueves, un viernes y un sábado. ¿Cuál es el costo total de su estadía en el hotel?». $725
e. «Usa una recta numérica para representar el costo total de la estadía de la familia Evans en el hotel». Las respuestas pueden variar.
f. «La Sra. Mwandia planea pasar la noche en el hotel los miércoles, jueves y viernes. El hotel le ofrece un descuento para personas mayores de $50. ¿Cuál es el costo total de la estadía de la Sra. Mwandia en el hotel?». $600
PARTE III
1. Entregue a cada alumno una copia del folleto del estudiante.
2. Lea las instrucciones y responda a las preguntas que puedan tener los estudiantes.
3. Conceda tiempo para que los estudiantes completen el folleto el estudiante en clase o la envíen a casa como tarea.
4. Anime a los estudiantes a compartir sus datos con la clase.
EVALUAR: LISTA DE VERIFICACIÓN DE OBSERVACIÓN
EVALUACIÓN DE HABILIDADES
LISTA DE VERIFICACIÓN DE LA OBSERVACIÓN
DESCRIPCIÓN
Este elemento proporciona un desglose de los conceptos y destrezas clave del alcance de aplicación. Puede utilizarse como evaluación formativa para los maestros y como autoevaluación para los estudiantes.
MATERIALES
IMPRESO
• 1 folleto del estudiante (por alumno)
• 1 materiales para el maestro (por estudiante)
PREPARACIÓN
• Imprima los materiales para el maestro y un folleto del estudiante para cada alumno.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Distribuya un folleto del estudiante a cada alumno.
2. A medida que los estudiantes trabajen en las actividades explorar y explicar del alcance, evalúe formativamente su progreso tomando notas sobre cómo se observaron los conceptos y habilidades clave. Se pueden plantear preguntas de reflexión para medir el impacto de las actividades tanto en grupo completo como en pequeño grupo.
3. Pida a los alumnos que reflexionen sobre las formas en que pueden demostrar su comprensión y autoevaluar su progreso en cada concepto o habilidad clave a medida que trabajan tanto en grupo completo como en pequeño grupo.
4. Los estudiantes pueden reflexionar sobre su pensamiento, aprendizaje y trabajo en el alcance; identificar las formas en que han mejorado y establecer nuevas metas de aprendizaje.
5. Quienes brindan apoyo pedagógico a los estudiantes pueden estar equipados con las adaptaciones y modificaciones anotadas en los materiales para el maestro.
6. Las notas anecdóticas proporcionadas en las instrucciones del maestro pueden usarse como documentación para los boletines de calificaciones basados en estándares.
7. Una vez que se hayan recopilado los datos de los estudiantes después de la evaluación, consulte la guía de instrucción andamiada en la sección «Inicio» de este alcance para diferenciar la instrucción para cada estudiante.

Addition and Subtraction Problem Solving
Use addition and subtraction within 100 to solve one- and two-step word problems involving situations of adding to, taking from, putting together, taking apart, and comparing, with unknowns in all positions, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem.
Add and subtract within 1000, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method.
Understand that in adding or subtracting three-digit numbers, one adds or subtracts hundreds and hundreds, tens and tens, ones and ones; and sometimes it is necessary to compose or decompose tens or hundreds.
❏ Physical modeling
❏ Pictorial modeling
❏ Problem solving
❏ Discussion
❏ Written explanation
❏ Physical modeling
❏ Pictorial modeling
❏ Problem solving
❏ Discussion
❏ Written explanation
❏ Physical modeling
❏ Pictorial modeling
❏ Problem solving
❏ Discussion
❏ Written explanation
Addition and Subtraction Problem Solving
Mathematical Practice Notes and Feedback
Make sense of problems and persevere in solving them.
Reason abstractly and quantitatively.
Construct viable arguments and critique the reasoning of others.
Model with mathematics.
Use appropriate tools strategically.
Attend to precision.
Look for and make use of structure.
Look for and express regularity in repeated reasoning.
Consider these reflection questions in this scope.
● Is this student proficient in the skills addressed in this scope?
○ If so, what is next for them?
○ If not, how can I support them?
● What activities worked well for this student, and what would I do differently next time? 2

DESCRIPCIÓN
Los estudiantes analizan los resultados de su evaluación y determinan qué hicieron bien y en qué pueden mejorar.
MATERIALES
• 1 mapa de Calor (por estudiante)
• 1 crayón rojo (por estudiante)
• 1 crayón verde (por estudiante)
PREPARACIÓN
• Determine si los estudiantes analizarán su prueba de habilidades, la evaluación basada en estándares o ambas.
• Imprima un mapa de calor para cada estudiante.
• Reúna un crayón rojo y un crayón verde para cada estudiante.
EVALUAR: MAPA DE CALOR
ANALIZAR LOS RESULTADOS DE LA EVALUACIÓN
MAPA DE CALOR
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Distribuya un mapa de calor a cada estudiante junto con los crayones rojo y verde. Los alumnos deben tener a mano su(s) evaluación(es) corregida(s).
2. Los alumnos utilizan su(s) evaluación(es) corregida(s) para colorear el mapa de calor. Por cada pregunta contestada correctamente, colorean de verde la casilla correspondiente. Para cada pregunta contestada incorrectamente, los estudiantes colorean la casilla correspondiente en rojo.
3. Anime a los estudiantes a buscar patrones en sus datos, como un determinado estándar que se perdió con más frecuencia o un estándar que han dominado claramente, y utilizar esta información para reflexionar y establecer metas en la tabla proporcionada.
4. Consulte la guía de instrucción andamiadas que se encuentra en la sección «Inicio» para proporcionar extensión o apoyo adicional.


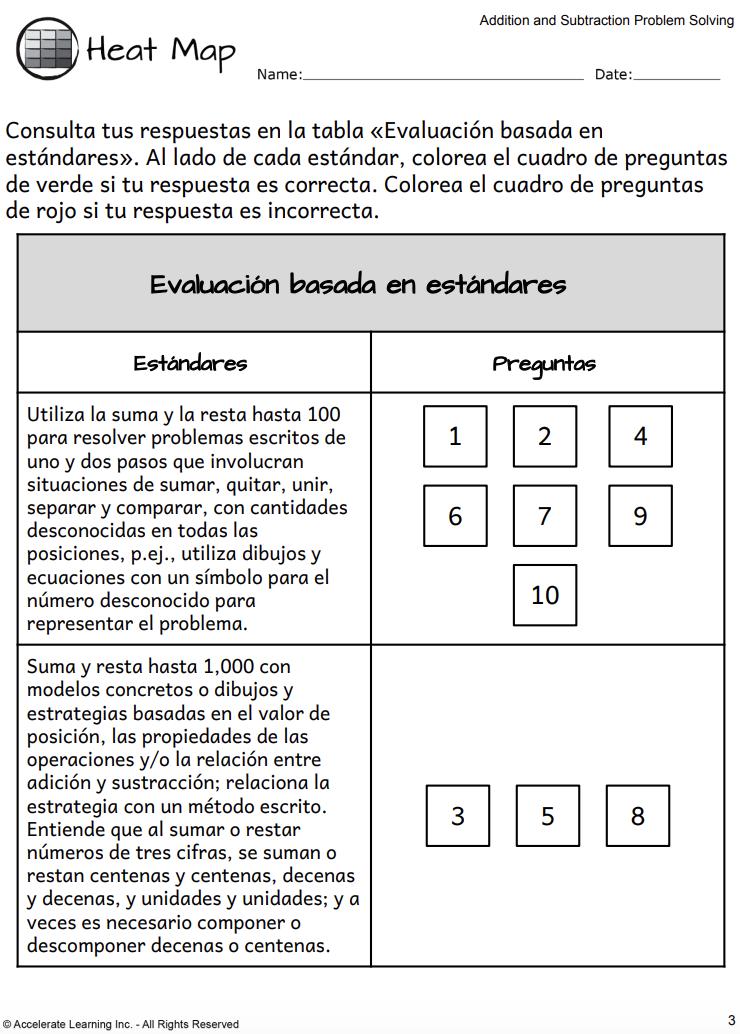
MAPA DE CALOR
INTERVENCIÓN: INTERVENCIÓN EN GRUPO PEQUEÑO
REFORZAR Y VOLVER A ENSEÑAR
INTERVENCIÓN EN PEQUEÑOS
GRUPOS
DESCRIPCIÓN
Los alumnos representan y resuelven problemas de suma y resta de uno y dos pasos dentro de 100 utilizando una variedad de estrategias. Los estudiantes suman y restan dentro de 1,000 usando modelos concretos o dibujos y una variedad de estrategias.
MATERIALES
IMPRESOS
• 1 evaluación de control (por alumno)
• 1 lista de verificación para el maestro (por profesor)
REUTILIZABLES
• 1 pizarra blanca (por alumno)
• 1 marcadorr de borrado en seco (por alumno)
• 10 bloques de base diez (por alumno)
• 20 barras de base diez (por alumno)
• 20 unidades de base diez (por alumno)
PREPARACIÓN
• Prepare juegos de bloques de base diez por alumno.
• Reúna una pizarra y un marcador de borrado en seco por estudiante.
• Imprima una evaluación de control por estudiante.
• Imprima la lista de verificación para el maestro
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
PARTE I
1. Antes de comenzar la actividad, pida a los estudiantes que le digan todo lo que saben sobre los modelos y estrategias usados para resolver problemas escritos de suma y resta. A medida que responden, verifique si comprenden las diferencias entre los modelos de barras y las rectas numéricas. Identifique los conceptos erróneos.
2. Entregue un juego de bloques de base diez, una pizarra blanca y un marcador de borrado en seco a cada estudiante.
3. Lea el siguiente problema escrito: «Candace contó 65 libros en el primer estante de la biblioteca. Contó 26 libros en el segundo estante. ¿Cuántos libros contó en total?».
4. Pida a los estudiantes que primero resuelvan el problema con sus bloques de base diez. Observe cómo construyen cada número. Preste mucha atención a cómo reagrupan los unos y las decenas. Haga las siguientes preguntas:
a. «¿Cuántas unidades contaste en total?». 11
b. «¿Necesitas reagrupar estas unidades?». Sí. «¿Por qué?». Necesito reagrupar porque no puedo tener diez o más en un valor posicional.
c. «Muéstrame cómo reagrupar las unidades. ¿Cuántas unidades sobran?». 1
d. «¿Cuántas barras has contado en total?». 9
e. «¿Necesitas reagrupar estas barras?». No «¿Por qué?». No necesito reagrupar porque no puedo hacer un grupo de diez.
5. Si los estudiantes entienden cómo reagrupar sus modelos concretos, pídales que dibujen un modelo pictórico de este problema de adición en sus pizarras.
6. Guíe a los estudiantes mientras crean una tabla de valor posicional y dibujan sus bloques de base diez. Observe cómo representan la reagrupación en forma de dibujo. Compruebe la exactitud.
7. Lea el siguiente problema escrito: «Candace contó 85 libros en el primer estante de la biblioteca. Contó 26 libros en el segundo. ¿Cuántos libros más contó en el primer estante que en el segundo?».
8. Indique a los estudiantes que primero resuelvan utilizando sus bloques de base diez. Observe cómo construyen el primer número. Preste mucha atención a cómo los estudiantes reagrupan sus decenas y unidades al restar el segundo número. Haga las siguientes preguntas:
a. «¿Necesitas reagrupar estas unidades?». Sí. «¿Por qué?». No puedo restar 6 a 5, así que necesito reagrupar una decena para hacer 15 unidades/unos.
b. «¿Cuántas unidades sobran?». 9
c. «¿Cuántas barras tienes después de reagrupar?». 7
d. «¿Cuántas barras en total has restado?» 2
e. «¿Necesitas reagrupar estas barras?». No «¿Por qué?».
Puedo quitarle 2 a 7
f. «¿Cuál es tu solución?». 59
9. Si los estudiantes entienden cómo reagrupar sus modelos concretos, pídales que dibujen un modelo pictórico de este problema de resta en sus pizarras.
10. Guíe a los estudiantes mientras crean una tabla de valor posicional y dibujan sus bloques de base diez de sólo el primer número. Observe cómo representan la reagrupación en forma de dibujo. Compruebe la exactitud.
11. Haga la siguiente pregunta: a. «Al crear tu dibujo, ¿cómo decidiste qué número(s) construir?». Las respuestas pueden variar. Al sumar, sabía que tenía que construir ambos números con bloques de base diez (decenas y unidades). Al restar, construí el número mayor y mostré mi resta tachando el número menor.
12. Repase los modelos de barras pidiendo a los alumnos que dibujen uno y expliquen qué significa cada parte. Compruebe la exactitud y aborde cualquier concepto erróneo.
13. Lea el mismo problema desde el paso 3 anterior: «Candace contó 65 libros en el primer estante de la biblioteca. Contó 26 libros en elsegundo. ¿Cuántos libros contó en total?».
14. Pida a los estudiantes que resuelvan el problema dibujando un modelo de barras.



COMPROBACIÓN
INTERVENCIÓN: INTERVENCIÓN EN GRUPO PEQUEÑO
15. Mientras los alumnos trabajan, pregúnteles por qué han escrito ciertos números en determinados espacios del modelo de barras. Escuche sus explicaciones. Si su razonamiento es bueno, pase a otro número o haga la misma pregunta a otro alumno. Asegúrese de hacer esta pregunta a cada alumno al menos una vez. Si su razonamiento no es correcto, formule las siguientes preguntas orientadoras:
a. «¿Qué representa el espacio superior de un modelo de barras?». El total
b. «¿Qué representan los dos espacios inferiores de un modelo de barras?». Las partes
c. «¿Qué información conoces del problema?». Las dos partes: 65 y 26
d. «¿Qué información necesitas averiguar?». El total
e. «¿Cómo lo resolverás?». Sumaré los dos números para hallar el total.
16. Compruebe la exactitud de los modelos de barras. Diga a los estudiantes que borren sus pizarras.
17. Anime a los estudiantes a resolver el mismo problema con una recta numérica.
18. Mientras los estudiantes trabajan, pregunte por qué escribieron ciertos números en ciertos lugares de sus rectas numéricas. Escuche sus explicaciones. Si su razonamiento es bueno, pase a otro número o haga la misma pregunta a otro estudiante. Asegúrese de hacer esta pregunta a cada alumno al menos una vez. Si su razonamiento no es correcto, formule las siguientes preguntas orientadoras:
19. «¿Qué información conoces del problema?». Las dos partes: 65 y 26
a. «¿Qué información necesitas averiguar?». El total
b. «¿Qué número marcarás primero en tu recta numérica?». Las respuestas pueden variar. Los alumnos pueden comenzar con cualquiera de los números.
c. «¿Qué representa cada salto?». Las respuestas pueden variar. Los saltos grandes equivalen a 10 y los pequeños a 1.
d. «¿Cómo lo resolverás?». Dibujaré saltos para representar el segundo número y etiquetaré los números en mi recta numérica hasta llegar al total.
20. Verifique la exactitud de las rectas numéricas. Diga a los estudiantes que borren sus tableros.
21. Lea el mismo problema desde el paso 7 anterior: «Candace contó 85 libros en el primer estante de la biblioteca. Contó 26 libros en el segundo estante. ¿Cuántos libros más contó en el primer estante que en el segundo?».
22. Repita los pasos 14-19 con modelos de barras y rectas numéricas para resolver.
INTERVENCIÓN: INTERVENCIÓN EN GRUPO PEQUEÑO
23. Haga la siguiente pregunta:
a. «¿Qué representación le inspira más confianza?». Las respuestas pueden variar. A mí me gusta usar la recta numérica porque creo que es más fácil de resolver dando pequeños saltos al sumar o restar.
PARTE II
1. Haga que los estudiantes trabajen en parejas. Reparta un juego de bloques de base diez a cada pareja. Entregue una pizarra y un marcador de borrado en seco a cada alumno.
2. Lea el siguiente problema de palabras: «Frankie encontró 38 conchas marinas el primer día de sus vacaciones. Encontró 36 conchas el segundo día de sus vacaciones. Se dio cuenta de que 12 conchas de su colección estaban rotas. ¿Cuántas conchas no estaban rotas?».
3. Anime a los estudiantes a trabajar con sus compañeros para resolver el problema escrito.
4. Observe y escuche mientras los estudiantes crean un modelo concreto. Mientras los estudiantes trabajan, pregúnteles qué números están construyendo primero, cómo están reagrupando y qué número están restando. Escuche sus explicaciones. Si su razonamiento es bueno, pase a otra pareja de alumnos con la misma pregunta. Asegúrese de hacer esta pregunta a cada pareja al menos una vez. Si su razonamiento no es correcto, formule las siguientes preguntas orientadoras:
a. «¿Qué información conoces del problema?». Encontró 38 conchas marinas y luego 36 conchas más. Contó 12 conchas rotas.
b. «¿Qué información necesitas averiguar?». ¿Cuántas conchas no estaban rotas?
c. «¿Cuántas acciones ocurren en este problema?». Hay dos acciones en este problema. Tenemos que sumar para encontrar el número total de conchas y luego restar el número de conchas rotas.
d. «¿Qué estrategia usaste para resolver?». Las respuestas pueden variar. Elegí dibujar un modelo de barras. Dibujé una recta numérica.
e. «¿Cómo lo resolverás?». Sumaré los dos primeros números para hallar el total y luego restaré 12.
f. «¿Qué ecuación podría usarse para resolver este problema?». 38 + 36 - 12 = ?
5. Pida a los estudiantes que dibujen un modelo pictórico para mostrar sus soluciones.
6. Verifique la exactitud y guíe a los estudiantes que podrían estar reagrupando incorrectamente.
7. Plantee las siguientes preguntas:
a. «¿Por qué es más eficiente usar bloques de base diez que manipulativos de un solo cuadrado?». Puedo representar números más grandes más fácilmente cuando uso bloques de base diez.
b. «¿Cómo puedes modelar un problema de varios pasos?». Modelo la primera parte del problema y luego modelo la siguiente parte del problema.
8. Lea el siguiente problema escrito: «En el parque para perros hay 87 perros. 12 de ellos son grandes. 28 son medianos. El resto son perros pequeños. ¿Cuántos perros del parque son pequeños?».
9. Pida a los alumnos que lo resuelvan dibujando un modelo de barras.
10. Mientras trabajan, pregúnteles por qué han escrito determinados números en ciertos espacios del modelo de barras. Escuche sus explicaciones. Si su razonamiento es bueno, pase a otro número o haga la misma pregunta a otro alumno. Asegúrate de hacer esta pregunta a cada alumno al menos una vez. Si su razonamiento no es correcto, formule las siguientes preguntas orientativas:
a. «¿Qué representa el espacio superior de un modelo de barras?». El total
b. «¿Qué representan los tres espacios inferiores de un modelo de barras?». Las partes
c. «¿Qué información conoces del problema?». El total y dos partes
d. «¿Qué información necesitas averiguar?». Una de las partes
e. «¿Cómo lo resolverás?». Sumaré las dos partes dadas y restaré del total.
11. Compruebe la exactitud de los modelos de barras.
12. Indique a los alumnos que guarden sus modelos de barras en sus pizarras.
13. Anime a los alumnos a resolver el problema escritos con una recta numérica.
14. Mientras trabajan, pregúnteles por qué escribieron ciertos números en ciertos lugares de sus rectas numéricas. Escuche sus explicaciones. Si su razonamiento es bueno, pase a otro número o hágale la misma pregunta a otro estudiante. Asegúrate de hacer esta pregunta a cada alumno al menos una vez. Si su razonamiento no es correcto, revise la información que se da en el problema y guíe a los estudiantes mientras revisan sus rectas numéricas.
15. Verifique que las rectas numéricas sean correctas.
PARTE III
1. Distribuya bloques de base diez, una pizarra blanca y un marcador de borrado en seco a cada estudiante.
2. Lea el siguiente problema escrito: «Alisha recolectó 218 latas para reciclar. Recogió 387 botellas para reciclar. ¿Cuántas latas y botellas recogió en total?».
3. Indique a los estudiantes que primero resuelvan el problema con sus bloques de base diez. Observe cómo los estudiantes construyen cada número. Preste atención a cómo reagrupan los unos y las decenas. Haga las siguientes preguntas:
a. «¿Cuántas unidades contaste en total?». 15
b. «¿Necesitas reagrupar estas unidades?». Sí. «¿Por qué?». Necesito reagrupar porque no puedo tener diez o más en un valor posicional.
c. «Muéstrame cómo reagrupar las unidades. ¿Cuántas unidades sobran?». 5
d. «¿Cuántas barras en total has contado?». 10
INTERVENCIÓN: INTERVENCIÓN EN GRUPO PEQUEÑO
e. «¿Es necesario reagrupar estas barras?». Sí. «¿Por qué?». Necesito reagrupar porque no puedo tener diez o más en un valor posicional.
f. «Muéstrame cómo reagrupar las barras. ¿Cuántas sobran?». 0
g. «¿Cuántos planos en total has contado?». 6
h. «¿Necesitas reagrupar estos planos?». No «¿Por qué?». Hay 6 planos, que son menos de diez. Puedo tener un 6 en este valor posicional.
i. «¿Qué oración numérica puedes escribir para representar este problema?». 218 + 387 = 605
4. Si los alumnos entienden cómo reagrupar sus modelos concretos, pídales que dibujen un modelo pictórico de este problema de suma en sus pizarras.
5. Guíe a los alumnos mientras crean una tabla de valor posicional y dibujan sus bloques de base diez. Observe cómo representan la reagrupación en forma de dibujo. Verifique la exactitud.
6. Lea el siguiente problema de palabras: «La clase de Saúl recolectó 972 latas para reciclar. La clase de Alisha recogió 681 latas para reciclar. ¿Cuántas latas más recolectó la clase de Saúl que la clase de Alisha?».
7. Indique a los estudiantes que primero resuelvan usando sus bloques de base diez. Observe cómo los estudiantes construyen el primer número. Preste mucha atención a cómo los estudiantes reagrupan sus decenas y centenas cuando restan el segundo número. Haga las siguientes preguntas:
a. «¿Es necesario reagrupar estas unidades?». No. «¿Por qué?». Puedo restar 1 de 2.
b. «¿Cuántas unidades sobran?». 1
c. «¿Necesitas reagrupar las barras?». Sí. «¿Por qué?». No puedo restar 8 a 7.
d. «¿Cuántas barras y planos tienes después de reagrupar?». 17 barras y 8 planos
e. «¿Cuántas barras tienes después de restar?». 9
f. «¿Cómo restas los planos?». Le quito 6 a 8 para que me queden 2 planos.
g. «¿Qué oración numérica puedes escribir para representar este problema?». 972 - 681 = 291
PARTE IV
1. Entregue una pizarra y un marcador de borrado en seco a cada alumno.
2. Lea el siguiente problema escrito: «Jade tenía 368 ladrillos entrelazados. Su hermano le regaló 139 más. ¿Cuántos ladrillos entrelazados tiene Jade ahora?».
3. Pida a los alumnos que creen dos modelos pictóricos de la acción que sucede en la historia: uno de bloques de base diez y otro de un modelo de barra o una recta numérica. A continuación, pídales que escriban una frase numérica que contenga un símbolo que represente la incógnita.
4. Observe cómo dibujan sus bloques de base diez. Preste atención a cómo reagrupan sus unidades y decenas. Haga las siguientes preguntas:
a. «¿Cómo resolviste este problema?». Las respuestas pueden variar. Dibujé los bloques de base diez para cada número y hallé el total. Usé un modelo de barras o una recta numérica.
b. «¿Qué valores posicionales has tenido que reagrupar?». Tuve que reagrupar los unos y las decenas porque no puedo tener diez o más en un valor posicional.
c. «¿Qué oración numérica puedes escribir para representar este problema?». 368 + 139 = 507
5. Cuando los alumnos creen un modelo de barras o una recta numérica, pregúnteles por qué escribieron determinados números en determinados espacios del modelo de barras o de la recta numérica. Escuche sus explicaciones. Si su razonamiento es bueno, pase a otro número o haga la misma pregunta a otro alumno. Asegúrate de hacer esta pregunta a cada alumno al menos una vez. Si su razonamiento no es correcto, formule las siguientes preguntas orientadoras:
a. «¿Qué información conoces del problema?». Las dos partes: 368 y 139
b. «¿Qué información necesitas averiguar?». El total
c. «¿Qué representa el espacio superior de un modelo de barras?». El total
d. «¿Qué representan los dos espacios inferiores de un modelo de barras?». Las partes
e. «¿Qué número marcarás primero en tu recta numérica?». Las respuestas pueden variar. Pueden comenzar con cualquiera de los números.
f. «¿Qué representa cada salto?». Las respuestas pueden variar. Los saltos grandes equivalen a 100, los saltos medianos equivalen a 10 y los saltos pequeños equivalen a 1.
g. «¿Cómo lo resolverás?». Las respuestas pueden variar. Dibujaré saltos para representar el segundo número y etiquetaré números en mi recta numérica hasta llegar al total.
6. Revise los modelos de barras y las rectas numéricas para verificar su exactitud. Diga a los estudiantes que borren sus pizarras.
7. Lea el siguiente problema escrito: «Jade tiene 507 ladrillos entrelazados. Su hermano tiene 468 ladrillos entrelazados. ¿Cuántos ladrillos entrelazados más tiene Jade que su hermano?».
8. Repita los pasos 3-6 con modelos pictóricos de base diez y modelos de barras o rectas numéricas para resolver.
9. Plantee la siguiente pregunta:
a. «¿Qué representación te hace sentir más seguro de usar?». Las respuestas pueden variar. Me gusta usar la recta numérica porque creo que es más fácil de resolver haciendo pequeños saltos al sumar o restar.
10. Haga que los estudiantes completen la verificación.
ACELERACIÓN: MATEMÁTICAS DE HOY
CONEXIONES CON EL MUNDO REAL
MATEMÁTICAS DE HOY: OCTOCAMPEONES DE MATH TODAY
DESCRIPCIÓN
Los estudiantes exploran las conexiones y aplicaciones de las matemáticas y otros contenidos transversales a través de interacciones con medios de comunicación auténticos y del mundo real proporcionados por Associated Press.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Entregue a cada estudiante una copia del folleto del estudiante y lean juntos el pie de foto mientras miran la imagen.
2. Plantee las siguientes preguntas:
a. «Al mirar la tabla de participantes para cada ronda del concurso de ortografía, ¿cómo podemos determinar cuántos estudiantes fueron eliminados de cada ronda?». Las respuestas pueden variar. Los ejemplos pueden ser los siguientes: para ver cuántos estudiantes fueron eliminados, se puede mirar el recuento de estudiantes participantes en la siguiente ronda, y luego restar ese número de la ronda anterior.
b. «¿Por qué crees que el grupo de estudiantes se llama los "Octocampeones"? ¿Dónde más has oído el prefijo octo-?». Las respuestas pueden variar. Los ejemplos pueden ser los siguientes: se llaman los "Octocampeones porque son 8, y octo significa ocho. Los octógonos tienen 8 lados. Los pulpos tienen 8 tentáculos.
3. Pida a los alumnos que completen el folleto para el alumno de forma independiente o con sus compañeros.



ACELERACIÓN: ESTACIÓN DE CONEXIÓN
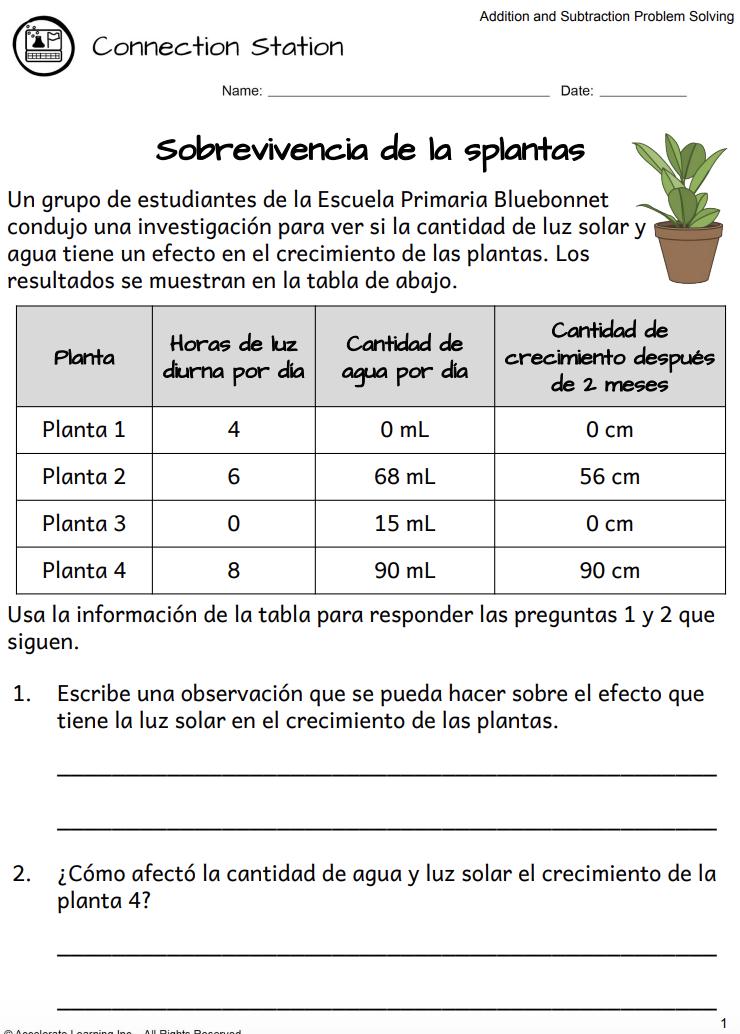

ESTABLECER CONEXIONES RELEVANTES ESTACIÓN DE CONEXIÓN
DESCRIPCIÓN
Los alumnos usan la información de una investigación para realizar un seguimiento al crecimiento que tuvieron las plantas cuando se les dio diferentes cantidades de luz solar y agua. Los alumnos también resuelven problemas de suma y resta sobre los efectos de la luz solar y el agua en el crecimiento de las plantas.
Esta actividad se ajusta al siguiente estándar de ciencias:
Planificar y llevar a cabo una investigación para determinar si las plantas necesitan luz solar y agua para crecer.
MATERIALES
IMPRESO
• 1 folleto del estudiante (por alumno)
PREPARACIÓN
• Imprima una copia del folleto del estudiante (por alumno)
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Haga que los estudiantes trabajen en parejas.
2. Entregue a cada alumno una del folleto del estudiantepor alumno.
3. Pida a los alumnos que lean el párrafo que aparece en la parte superior de la primera página del folleto del estudiante. Explíqueles que usarán la información de la tabla para responder a las preguntas.
4. Pida a los alumnos que respondan a las preguntas de la parte inferior de la primera página del folleto del estudiante.
5. Pida a los alumnos que resuelvan los problemas de suma y resta de la segunda página del folleto del estudiante.
6. Pregunte a la clase: «¿Qué conclusiones puedes sacar de la información de la tabla de la primera página?».
7. Pida a los alumnos que compartan sus respuestas con sus compañeros. Asegúrese de que entienden que las plantas necesitan luz solar y agua para crecer. FOLLETO DEL ESTUDIANTE
ACELERACIÓN: TABLERO DE OPCIONES
OPCIONES PARA EL APRENDIZAJE CONTINUO
TABLERO DE OPCIONES
DESCRIPCIÓN
Los estudiantes exploran las conexiones con el mundo real y las aplicaciones del contenido matemático a través de interacciones con actividades atractivas.
MATERIALES
IMPRESO
• 1 tablero de opciones (por estudiante)
REUTILIZABLE
• Tecnología (si procede)
PREPARACIÓN
• Imprima un tablero de opciones por estudiante.
• Planifique con antelación el uso de la tecnología. Es posible que se necesite acceso a otras actividades dentro del alcance para algunas variaciones del tablero de opciones.
• Esta actividad se puede completar en clase o en casa.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Distribuya un tablero de opciones a cada estudiante.
2. Conceda tiempo a los estudiantes para examinar el tablero de opciones y seleccionar las actividades que les gustaría explorar.
3. Anime a los estudiantes a intentar al menos tres actividades del tablero de opciones.
4. Si el tiempo lo permite, pida a los estudiantes que compartan las conexiones que hicieron al completar las actividades que eligieron.
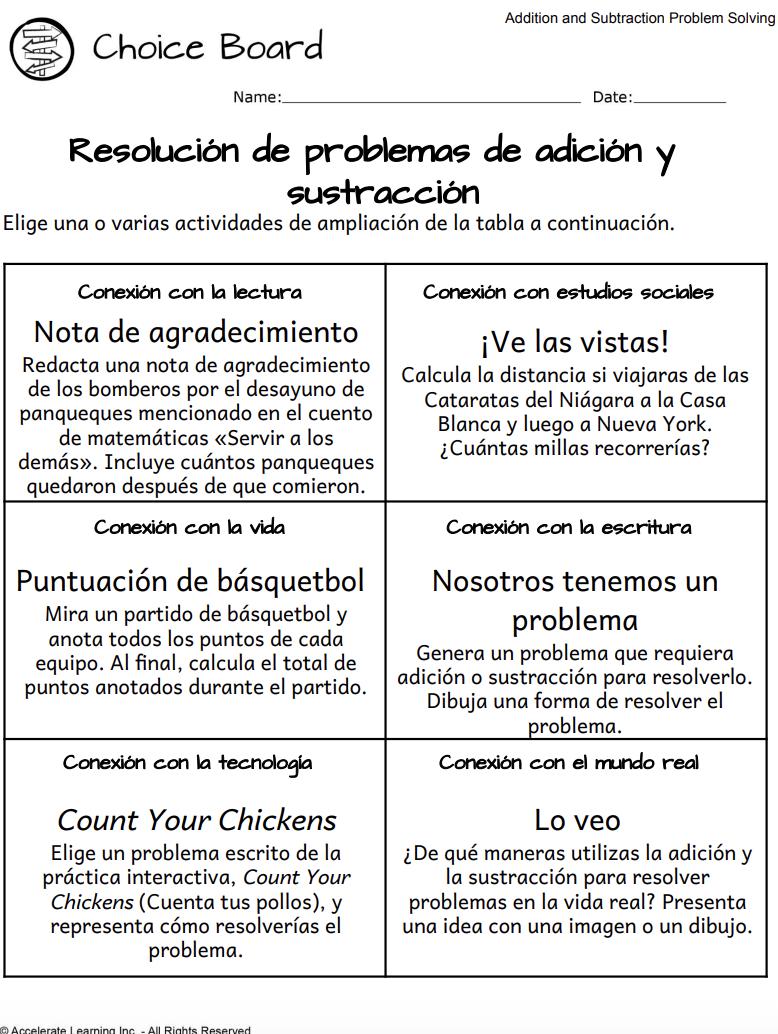
TABLA DE OPCIONES
