

GRADO 4

CALIFORNIA
Muestra de la edición para el maestro
Muestra de la edición para maestros Grado 4
Publicado por Accelerate Learning Inc., 5177 Richmond Ave, Suite 800, Houston, TX 77056. Copyright © 2025, Accelerate Learning Inc. Todos los derechos reservados. Ninguna parte de esta publicación podrá ser reproducida o distribuida en ninguna forma ni por ningún medio, ni almacenada en una base de datos o sistema de recuperación, sin el consentimiento previo por escrito de Accelerate Learning Inc., incluyendo, entre otros, en cualquier red u otro sistema de almacenamiento o transmisión electrónica, o difusión para educación a distancia.
Para obtener más información, visítenos en www.stemscopes.com.
REPRESENTAR Y COMPARAR DECIMALES
ESTÁNDARES CLAVE
Comprender la notación decimal para fracciones y comparar fracciones decimales.
• Utilizar la notación decimal para fracciones con denominadores 10 ó 100. Por ejemplo, reescribir 0.62 como 62/100; describir una longitud como 0.62 metros; localizar 0.62 en un diagrama de recta numérica.
• Comparar dos decimales con centésimas razonando sobre su tamaño. Reconocer que las comparaciones sólo son válidas cuando los dos decimales se refieren al mismo entero. Registrar los resultados de las comparaciones con los símbolos >, =, o ~, y justificar las conclusiones; por ej. con una recta numérica u otro modelo visual.
ESTÁNDARES DE CONEXIÓN
Generalizar la comprensión del valor posicional para números enteros de varios dígitos.
• Reconocer que en un número entero de varios dígitos, un dígito en un lugar representa diez veces lo que representa en el lugar a su derecha. Por ejemplo, reconocer que 700 ÷ 70 = 10 aplicando conceptos de valor posicional y división.
• Leer y escribir números enteros de varios dígitos utilizando numerales de base diez, nombres de números y forma expandida. Comparar dos números de varios dígitos basándose en los significados de los dígitos en cada lugar, utilizando los símbolos >, = y ~ para registrar los resultados de las comparaciones.
ACTIVIDADES DE PARTICIPACIÓN
ACCESO A CONOCIMIENTOS PREVIOS
Los estudiantes se dedican a comparar fracciones para desarrollar una comprensión más profunda de sus tamaños relativos.
• Los estudiantes examinan enunciados y modelos de comparación para determinar cuál compara correctamente dos fracciones con el mismo numerador o denominador.
• Seleccionan la comparación con la que están de acuerdo y justifican su razonamiento utilizando símbolos, palabras o modelos pictóricos.
• La clase participa en debates en los que los estudiantes explican sus elecciones y razonamientos.
• Esta actividad refuerza el concepto de que las comparaciones de fracciones sólo son válidas cuando se refieren al mismo entero.
CAPTAR INTERÉS: COMPARACIÓN DE DULCES
Los estudiantes exploran la relación entre decimales y fracciones, centrándose en décimas y centésimas, y practican la realización de comparaciones razonando sobre su tamaño.
• Los estudiantes comienzan observando un escenario en el que intervienen dos personajes, Jim y Tim, quienes clasifican sus caramelos de Halloween en función de su alergia a los cacahuetes.
• Evalúan y utilizan modelos de fracciones para comparar las cantidades de caramelos que le quedan a cada personaje después de quitar las piezas que contienen cacahuetes.
• La actividad incluye la conversión de fracciones a decimales para facilitar la comparación, especialmente cuando se trata de denominadores diferentes.
• Los estudiantes concluyen resolviendo el problema de forma independiente y presentando sus estrategias y conclusiones a la clase.
ACTIVIDADES DE EXPLORAR
EXPLORACIÓN 1: NOTACIÓN DECIMAL PARA LOS DENOMINADORES DE 10
Los estudiantes exploran los valores decimales hasta las décimas utilizando modelos concretos y visuales, relacionándolos con fracciones y expresándolos de diferentes formas.
• Los estudiantes utilizan bloques de base diez y palitos de manualidades para representar valores decimales y relacionarlos con fracciones.
• Construyen miniesculturas con palitos de manualidades, utilizando bloques de base diez para representarlas y registrarlas como fracciones, decimales y en forma de palabras.
• La actividad fomenta la colaboración en grupo, el aprendizaje práctico y la aplicación de conceptos de valor posicional para comprender los decimales.
• Los estudiantes participan en debates para profundizar su comprensión de la relación entre fracciones y decimales, culminando en una charla de matemáticas para compartir observaciones.
EXPLORACIÓN 2: NOTACIÓN DECIMAL PARA LOS DENOMINADORES DE 100
Los estudiantes participan en tareas prácticas de medición para profundizar su comprensión de los decimales y las fracciones:
• Los estudiantes miden varios elementos del aula utilizando reglas de medir y registran sus medidas tanto en notación decimal como de fracciones a la centésima más cercana.
• Crean rectas numéricas para representar visualmente las medidas, mejorando su comprensión de la colocación y el valor de los decimales.
• A través de la colaboración en grupo, los estudiantes revisan y comparan estrategias para convertir medidas entre formas decimales y fraccionarias.
• La actividad concluye con una charla de matemáticas, donde los estudiantes comparten observaciones y puntos de vista sobre la relación entre decimales y fracciones.
EXPLORACIÓN 3: REPRESENTAR Y COMPARAR DECIMALES Los estudiantes exploran las relaciones de valor posicional para comparar decimales a las centésimas utilizando modelos visuales y símbolos de comparación.
• Los estudiantes trabajan en grupos para analizar y comparar estadísticas de dos parques de atracciones utilizando bloques de base diez y tapetes de valor posicional.
• Representan cada estadística visualmente y escriben enunciados de comparación utilizando >, < o =.
• Los estudiantes participan en debates para profundizar en su comprensión de los valores posicionales decimales y los procesos de comparación.
• La actividad concluye con una charla de matemáticas y una reflexión para consolidar el aprendizaje y compartir estrategias.



ALCANCE: IDEAS FUNDAMENTALES




CÍRCULOS, FRACCIONES & DECIMALES


MODELOS VISUALES DE FRACCIONES




Los estudiantes relacionan la notación decimal con las representaciones de fracciones, en particular con denominadores de 10 y 100. Aplican esta comprensión en contextos del mundo real, como la medición de longitudes en metros y la relación de los valores decimales con el dinero y el tiempo, reforzando la comprensión del valor posicional y de cómo las fracciones y los decimales son representaciones intercambiables.


CONCEPTOS CLAVE
• Puedo leer en voz alta una fracción con un denominador de 10 ó 100, escribirla como decimal y representar cada dígito dentro del decimal en una tabla de valor posicional.
• Puedo trazar y localizar décimas y centésimas en una recta numérica.
• Puedo comparar dos decimales con las centésimas razonando sobre su tamaño.
• Puedo reconocer que las comparaciones sólo son válidas cuando los decimales se refieren al mismo entero.
• Puedo utilizar los símbolos >, = o ~ para registrar comparaciones, y puedo justificar por qué.
Los estudiantes utilizan rectas numéricas, cuadrículas de base diez y modelos de áreas para representar cantidades decimales y escribirlas como fracciones con denominadores de 10 ó 100.
PREGUNTAS FUNDAMENTALES
• ¿Cómo puedo convertir una fracción con un denominador de 10 ó 100 en un decimal y dar sentido al valor posicional de cada dígito dentro del decimal?
• ¿Cómo puedo trazar y localizar décimas y centésimas en una recta numérica?
• ¿Cómo puedo comparar decimales razonando sobre su tamaño?
• ¿Cómo puedo estar seguro de que una comparación es válida?
• ¿Qué símbolos muestran comparaciones entre números, y cómo y por qué se utilizan?
INICIO: CALENDARIO SUGERIDO
PLANIFICACIÓN
Internalización de la lección
Alcance
• Revise los estándares abordados en el alcance.
• Familiarícese con la forma en que se evalúan los estándares y lo que demuestra el dominio de la materia.
• Revise el documento «Secuencia de aprendizaje» que se encuentra en el elemento «Visión general del alcance» para comprender la secuencia de los conceptos.
• Determine qué recursos se utilizarán para la práctica y la evaluación. Lección
• Revise las instrucciones para el maestro y los documentos asociados.
• Familiarícese con los modelos, herramientas y estrategias que los estudiantes utilizarán en la actividad.
• Considere el propósito de la lección dentro del alcance e identifique lo que los estudiantes deben saber y ser capaces de hacer como resultado.
• Identifique las áreas en las que los estudiantes pueden necesitar apoyo o enriquecimiento y planifique cómo responder.
DÍA 1
Se presenta a los estudiantes una actividad que usa la notación decimal para comparar dos decimales hasta las centésimas razonando sobre su tamaño. Volverán a realizar la actividad después de haber completado las exploraciones correspondientes.
Los estudiantes expresan opiniones, ideas y sentimientos sobre un problema utilizando frases como "I notice ..." y "I wonder ...."
• Numeración diaria
• Ciencia de datos
DÍA 2
Los estudiantes utilizan modelos de basediez y una tabla de valor posicional para representar fracciones decimales. Escriben en notación decimal fracciones con denominador 10.
Los estudiantes utilizan apoyos como modelos e imágenes para mejorar su comprensión de vocabulario y conceptos nuevos.
• Numeración diaria
• Ciencia de datos
• Captar interés (parte 1): Preexploración
Práctica independiente (del alcance o nivel de grado anterior)
• Constructor de fluidez
• Práctica interactiva Práctica guiada
• Constructor de bases fundamentales
• Conversaciones estructuradas
• Habilidades básicas: Representar decimales con base diez
• Comenzar la «Exploración 1: Notación decimal para los denominadores de 10».
Práctica independiente
• Refiérase a la sección de «Práctica» Práctica guiada
• Refiérase a la sección de «Práctica»
• ¡PRÓXIMAMENTE! Lista de verificación de observación
• Preguntas para la facilitación
• Hoja para el estudiante sobre habilidades básicas
Contenido de apoyo Contenido desglosado Visión general del alcance Manipulativos/materiales
Explora 1
• 100 palitos de manualidades (por grupo)
• 1 juego de bloques de base diez (por grupo)
• 1 cronómetro (por maestro)
Explora 2
• 2 palitos (por grupo)
Explora 3
• 1 juego de bloques de base diez (por grupo) Acceso a conocimientos previos (~15 minutos)
• Completar la semana anterior a este alcance.
Carta para llevar a casa
• Imprima y envíe a casa la semana anterior a este alcance.
DÍA 3
Los estudiantes escriben en notación decimal fracciones con denominador 10.
DÍA 4
Los estudiantes miden objetos y escriben la notación decimal y la notación de fracción correspondientes a la centésima más cercana. Los estudiantes también trazan una recta numérica con la medida.
Los estudiantes utilizan estructuras de frases variadas para expresar ideas de forma clara y eficaz.
• Numeración diaria
• Ciencia de datos
Los estudiantes utilizan apoyos como dibujos, modelos y gestos para mejorar su comunicación verbal.
• Numeración diaria
• Ciencia de datos
• Siga con la «Exploración 1: Notación decimal para los denominadores de 10».
• Charla de matemáticas
• Esquema de anclaje: Exploración 1
Práctica independiente
• Refiérase a la sección de «Práctica»
Práctica guiada
• Parte I: Intervención en grupos pequeños
• Exploración 1: boleto de salida
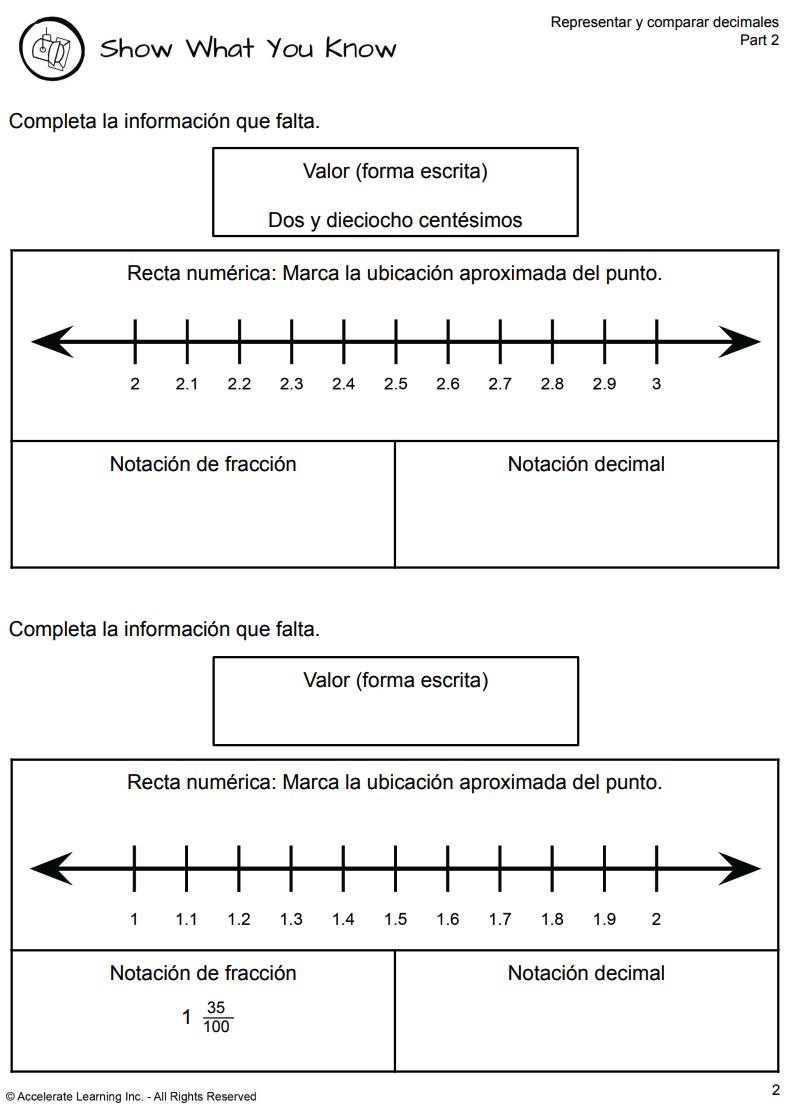
• Muestra lo que sabes (parte 1)
• Lista de verificación de observación
• Preguntas para la facilitación
• Exploración 2: Notación decimal para los denominadores de 100
• Charla de matemática
• Esquema de anclaje: Exploración 2
Práctica independiente
• Refiérase a la sección de «Práctica»
Práctica guiada
• Parte II: Intervención en grupos pequeños
• Exploración 2: boleto de salida
• Muestra lo que sabes (parte 2)
• Lista de verificación de observación
• Preguntas para la facilitación
PRÁCTICA
Práctica independiente
Todos los estudiantes
• Fluidez en los hechos matemáticos: Suma y resta (15-30 minutos)
• Fluidez en los hechos matemáticos: Multiplicación y división (15-30 minutos)
• Explicar: Vocabulario ilustrado (15-30 minutos)
• Explicar: Mis pensamientos de matemáticas (15-30 minutos)
• Elaborar: Conexiones profesionales (15-30 minutos)
• Elaborar: Revisión en espiral (15-30 minutos)
Los que dominan
• Aceleración: Matemáticas de hoy (15-30 minutos)
• Aceleración: Crea el tuyo (30-45 minutos)
• Aceleración: Tablero de opciones (15-30 minutos)
DÍA 5
Los que cumplen
• Elaborar: Cuento de matemáticas (30-45 minutos)
• Elaborar: Tarea basada en problemas (30-45 minutos)
• Elaborar: Constructor de fluidez(15-30 minutos)
Los deficientes
• Elaborar: Práctica interactiva(15-30 minutos)
• Evaluar: Prueba de habilidades (3045 minutos)
Práctica guiada
• Intervención: Intervención en grupos pequeños (15-30 minutos)
• Explicar: Conexiones lingüísticas (15-30 minutos)
• Inicio: Guía de instrucción andamiada (30-45 minutos)
Los estudiantes representan comparaciones con decimales a las centésimas utilizando los símbolos >, ~ y =.
Los estudiantes crean respuestas escritas utilizando el vocabulario recién adquirido y revisane sus respuestas según sea necesario.
• Numeración diaria
• Ciencia de datos
• Libreta interactiva: Notación decimal y de fracciones
• Exploración 3: Representar y comparar decilames
• Charla de matemática
• Esquema de anclaje: Exploración 3
Práctica independiente
• Refiérase a la sección de «Práctica» Práctica guiada
• Parte III: Intervención en grupos pequeños
• Exploración 3: boleto de salida
• Muestra lo que sabes (parte 3)
• Lista de verificación de observación
• Preguntas para la facilitación
INICIO: CALENDARIO SUGERIDO
EVALUACIONES
D = Diagnóstico F = Formativo S = Sumativo
Acceso a conocimientos previos (D)
Breve actividad de sondeo para evaluar los conocimientos previos antes de abordar el contenido del alcance.
Boleto de salida (F)
Evaluación rápida sobre lo que aprendieron en esta exploración.
Muestra lo que sabes (F)
Tarea de práctica independiente que permite a los estudiantes demostrar su aprendizaje.
Decide y defiende (F)
Evaluación abierta que pide a los estudiantes que razonen matemáticamente y apoyen sus ideas con pruebas.
Lista de verificación de la observación (D, F)
Lista de conceptos y habilidades que el maestro y el estudiante pueden usar para reflexionar sobre el progreso del estudiante y establecer objetivos.
Prueba de habilidades (F, S)
Evaluación basada en estándares para determinar la habilidad para resolver problemas matemáticos de manera eficiente y precisa.
DÍA 6
Los estudiantes vuelven a realizar la actividad que utiliza la notación decimal para comparar dos decimales a las centésimas razonando sobre su tamaño. Los estudiantes resolverán el problema original ahora que se han completado las Exploraciones correspondientes.
Los estudiantes colaboran para desarrollar respuestas escritas, proporcionan retroalimentación y editan sus respuestas según sea necesario.
• Numeración diaria
• Ciencia de datos
• Libreta interactiva: Comparar decimales
• Captar interés (parte 2): Posexploración
Práctica independiente
• Refiérase a la sección de «Práctica» Práctica guiada
• Refiérase a la sección de «Práctica»
• Comprobación: Intervención en grupos pequeños
• Prueba de habilidades
Evaluación basada en estándares (S)
Evaluación basada en estándares de opción múltiple en la que los estudiantes demuestran el dominio del contenido
Intervención en grupos pequeños: Revisión (F)
Tarea de práctica independiente para evaluar el dominio del contenido después de la intervención en grupos pequeños.
Evaluaciones de referencia (D, S)
Evaluaciones de principio, mitad y final de año que ofrecen datos significativos que pueden informar la instrucción.
Evaluaciones de medición del crecimiento (D, S)
Evaluaciones previas y posteriores diseñadas para realizar un seguimiento del crecimiento de los estándares de nivel de grado desde el principio hasta el final del año.
DÍA 7
Los estudiantes demuestran el dominio de los conceptos y habilidades clave en el alcance de aplicación a través de una evaluación basada en estándares.
Los estudiantes emplean habilidades de lectura y escritura utilizando lenguaje académico para demostrar su comprensión de los conceptos clave.
• Numeración diaria
• Ciencia de datos
Práctica independiente
• Refiérase a la sección de «Práctica» Práctica guiada
• Refiérase a la sección de «Práctica»
• Decidir y defender
• Evaluación basada en estándares
INICIO: CONTENIDO DE APOYO
¿QUÉ ESTOY ENSEÑANDO?
CONTENIDO DE APOYO
Comprender la notación decimal para fracciones y comparar fracciones decimales.
● Utilizar la notación decimal para fracciones con denominadores 10 ó 100. Por ejemplo, reescribir 0.62 como 62/100; describir una longitud como 0.62 metros; localizar 0.62 en un diagrama de recta numérica.
● Comparar dos decimales con centésimas razonando sobre su tamaño. Reconocer que las comparaciones sólo son válidas cuando los dos decimales se refieren al mismo entero. Registrar los resultados de las comparaciones con los símbolos >, =, o <, y justificar las conclusiones, por ejemplo, usando un modelo visual.
CONOCIMIENTOS PREVIOS
Desde kindergarten hasta tercer grado construyeron una base firme con números enteros. Segundo grado divide diferentes formas en mitades, cuartos y cuartos. Tercer grado desarrolla una comprensión de las fracciones como números, estando compuestas de fracciones unitarias. Empiezan a utilizar fracciones para resolver problemas, comprendiendo que el tamaño de una parte fraccionaria es relativo al tamaño del entero. El Grado 4 desarrolla el concepto de notación decimal para fracciones con denominadores de 10 o 100. Además, los estudiantes aprenderán a comparar dos decimales con centésimas cuando los decimales se refieren al mismo entero.
CONCEPTOS ERRÓNEOS Y OBSTÁCULOS
● Los estudiantes leen una fracción decimal como si fuera un número entero, ignorando el punto decimal.
● Los estudiantes no entienden la colocación de un cero en una fracción decimal, por ejemplo, algunos pueden creer que 2,04 es lo mismo que 2,4.
● Los estudiantes piensan que cuanto más largo es el número, mayor es el número.
● Los estudiantes tienen dificultades para razonar sobre el tamaño del número decimal.
● Los estudiantes pueden pensar que colocar ceros al final de un número decimal cambia el valor del número en lugar de usarse como marcador de posición.
● Los estudiantes tratan los decimales como números enteros al comparar.
● Algunos estudiantes pueden encontrar difícil representar decimales con bloques de base diez, ya que les cuesta cambiar los valores representados de los bloques.
EN ESTE ALCANCE
El grado 4 introduce los decimales, adquiriendo y utilizando la notación decimal para fracciones con denominadores de 10 o 100. La comprensión conceptual de los estudiantes se amplía a medida que adquieren la capacidad de comparar dos decimales con centésimas razonando sobre su tamaño. Los resultados se registran utilizando los símbolos >, < o =. Los estudiantes justifican sus conclusiones utilizando modelos visuales.
TÉRMINOS CLAVE
• decimal: un número que utiliza un punto decimal seguido de dígitos que muestran un valor menor que uno en potencias de diez que disminuyen
• forma decimal: un número que utiliza un punto decimal seguido de dígitos que muestran valores menores que uno
• fracción: una o más partes iguales de un entero
• lugar de las centésimas: el segundo dígito a la derecha del punto decimal, representa las partes del todo que están fuera de 100
• valor posicional: el valor numérico que tiene un dígito basado en su posición dentro de un número
• décimo: el primer dígito a la derecha del punto decimal, representa las partes del todo que están fuera de 10
INICIO: CONTENIDO DE APOYO
APLICAR LAS PRÁCTICAS MATEMÁTICAS
• MP.2 Razonar abstracta y cuantitativamente. Los estudiantes entienden que los decimales representan una cantidad específica. Son capaces de razonar y conectar la notación fraccionaria con denominadores de 10 ó 100 con la notación decimal. Considerarán todos los valores implicados al comparar decimales, dando sentido a las cantidades y determinando su relación dentro del contexto del problema.
• MP.4 Modelar con matemáticas. Se utilizan modelos concretos y pictóricos para ayudar a los estudiantes a comprender la notación decimal y las comparaciones de decimales. Los estudiantes son capaces de explicar diferentes representaciones y cómo se conectan con el problema decimal que se está resolviendo.
• MP.5 Utilizar estratégicamente las herramientas adecuadas. Los estudiantes elegirán cuidadosamente las herramientas necesarias para apoyar su capacidad de representar, escribir y comparar decimales. Las tablas de valor posicional, los cuadrados decimales, los discos decimales, las rectas numéricas y los dibujos son algunos de los recursos utilizados para promover la competencia. Los estudiantes deben establecer conexiones entre fracciones y decimales, adquiriendo la capacidad de comparar valores decimales. Los modelos visuales, como los cuadrados decimales, son la puerta de entrada a esta comprensión conceptual. Es imprescindible que los estudiantes trabajen con el modelo, coloreando físicamente los valores (representación), lo que conduce a la capacidad de comparar valores decimales. Las herramientas utilizadas ayudan a desarrollar la magnitud de un decimal y a construir el sentido numérico decimal de los estudiantes. Los estudiantes son capaces de evaluar sus soluciones y dar sentido al problema.
• MP.6 Atender a la precisión. Es esencial comprender la relación entre los decimales y un punto en una recta numérica. Esto proporciona precisión al localizar un decimal en una recta numérica. Los estudiantes son claros con el lenguaje académico utilizado al representar decimales y son capaces de comunicar el significado de cualquier símbolo utilizado para determinar comparaciones.
• MP.7 Buscar y utilizar estructuras. Los estudiantes buscan patrones en el sistema numérico base-diez, observando que el valor de cada posición de valor posicional es 10 veces el valor de la posición a su derecha y una décima parte del valor de la posición a su izquierda. También se establecen conexiones cuando los estudiantes transfieren la estructura de la notación fraccionaria con denominador de 10 o 100 a la notación decimal.
ESCRIBIR DE LA NOTACIÓN DE FRACCIÓN A LA NOTACIÓN DECIMAL
Los estudiantes necesitan múltiples oportunidades para construir una comprensión conceptual de los decimales. La comprensión del sistema de valor posicional decimal es fundamental en este proceso. El uso de la notación decimal para fracciones con denominadores de 10 o 100 puede representarse de varias maneras. Es vital que los estudiantes generen notación decimal en los modos de cuadrados decimales, discos de centenas y rectas numéricas. Estas formas de representación proporcionan a los estudiantes experiencias prácticas visuales. Una tabla de valor posicional es una herramienta más abstracta. Se sugiere que una tabla de valor posicional se introduzca después de que los estudiantes hayan alcanzado la capacidad de determinar y explicar claramente la relación entre fracciones con denominadores de 10 o 100 y un decimal utilizando cuadrados decimales, discos de centésimas y rectas numéricas.
RESOLUCIÓN DE NOTACIÓN DECIMAL CON CUADRADOS DECIMALES
Ejemplo: ¿Cuál es la forma decimal para 7/10?
a 0.007
b 7
c 0.73
d 0.7
Opción de respuesta d es la opción correcta. Utilizando un cuadrado decimal, 7 de las 10 partes iguales están sombreadas.

INICIO: CONTENIDO DE APOYO
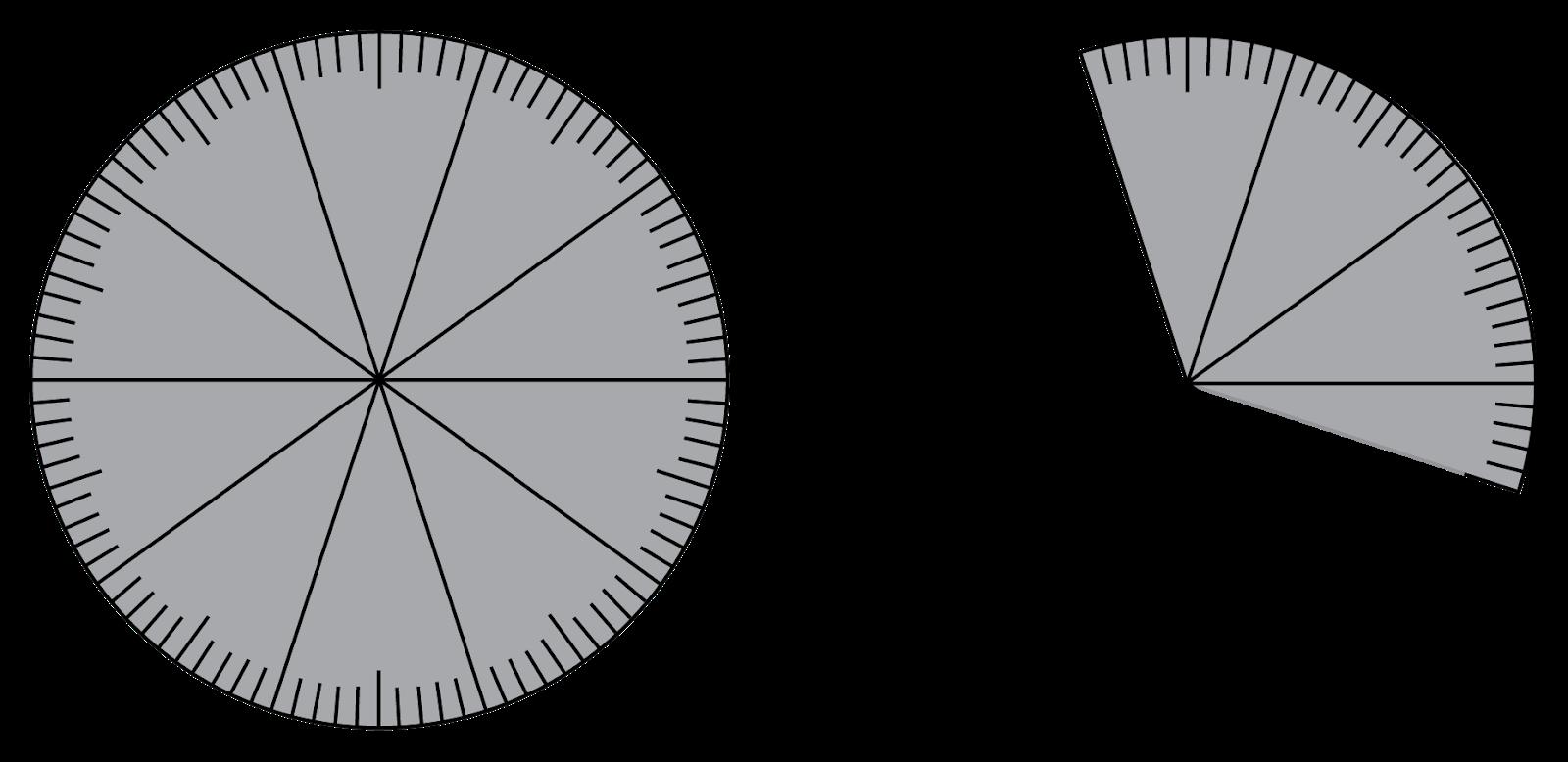
RESOLUCIÓN DE NOTACIÓN DECIMAL CON DISCOS DE CENTÉSIMAS
Ejemplo: ¿Cuál es la forma decimal para 135/100?
a 0.135
b 1.035
c 1.35
d 13.5
Opción de respuesta c es la respuesta correcta. Los discos de abajo representan un entero y 35 centésimas del entero siguiente. Observa que los enteros son del mismo tamaño. Al introducir los discos de centésimas, es importante que los estudiantes adquieran experiencia en la comprensión de la herramienta. Deben contar cada una de las marcas para estar seguros de que son 100. También deben contar de 10 en 10. También deben contar de 10 en 10 para saber que el disco puede representar décimas. Concédales tiempo para practicar y encontrar diferentes cantidades decimales.
RESOLUCIÓN DE NOTACIÓN DECIMAL CON UNA RECTA NUMÉRICA
PARA DÉCIMOS
Ejemplo: ¿Cuál es la forma decimal para 4/10?
a 0.4
b 4.1
c 1.4
d 1.04
Opción de respuesta a es la respuesta correcta. Utilizando la recta numérica, los estudiantes pueden relacionar el concepto familiar de dividir un entero en partes fraccionarias iguales con las notaciones decimales. En este caso, un entero se divide en 10 partes iguales. La notación fraccionaria de cuatro décimas señala la cuarta de diez partes iguales.

RESOLUCIÓN DE NOTACIÓN DECIMAL UNA
TABLA DE VALOR POSICIONAL
Ejemplo: ¿Cuál es la forma decimal para 135/10?
a 0.135
b 1.035
c 1.35
d 13.5
La opción de respuesta c es la respuesta correcta. Los dígitos pueden colocarse en una tabla para que los estudiantes determinen la solución. Una tabla de valor posicional es una herramienta abstracta que los estudiantes pueden utilizar. Es aconsejable utilizar esta herramienta sólo cuando los estudiantes tienen una comprensión conceptual profunda de los valores de cada dígito en un decimal, que se ha ganado a través de otros modelos prácticos como cuadrados decimales, rectas numéricas y discos de centésimas.
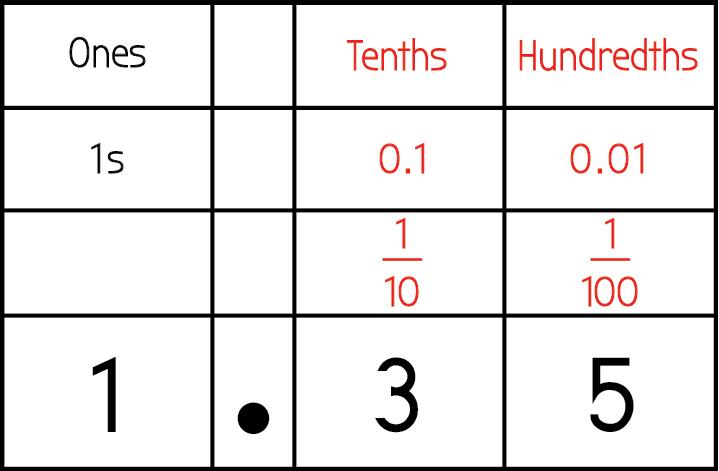
COMPARACIÓN DE DOS DECIMALES CON CENTÉSIMAS
La comprensión del sistema de valor posicional decimal precede a la capacidad de comparar decimales con centésimas de forma eficaz y eficiente. Los decimales que se comparan deben referirse al mismo entero. Deben utilizarse modelos visuales como cuadrados decimales, discos de centésimas y rectas numéricas para desarrollar la comprensión de los estudiantes a medida que se realizan las comparaciones. Dado que una tabla de valor posicional es una herramienta más abstracta para los estudiantes, se introduce después de que éstos hayan alcanzado la capacidad de explicar claramente las comparaciones utilizando los modelos visuales.
COMPARACIÓN DE DOS DECIMALES CON CUADRADOS DECIMALES
Ejemplo: Arrastra y suelta el símbolo en el recuadro para comparar los dos números.
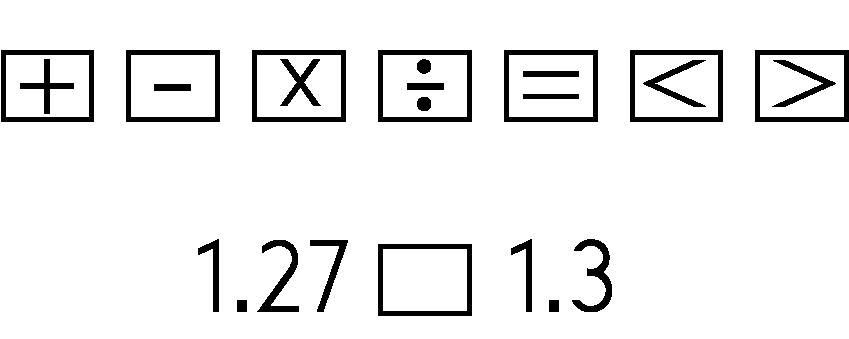
Respuesta: 1.27 < 1.3. Se pueden usar cuadrados decimales para representar visualmente esta comparación.
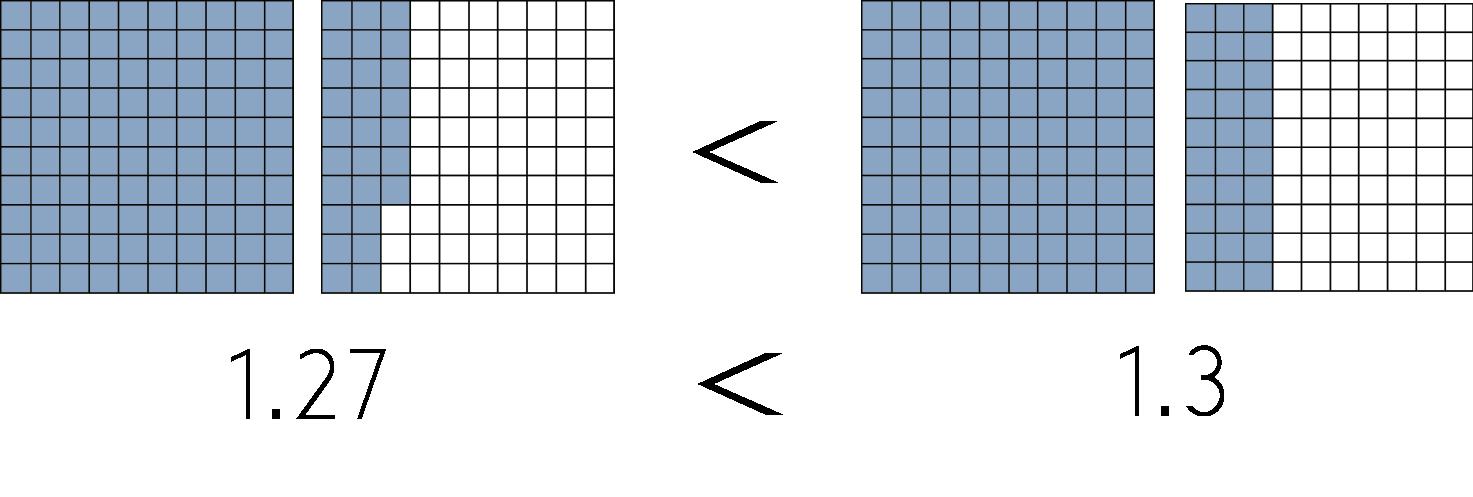
COMPARACIÓN DE DOS DECIMALES CON DISCOS DE CENTÉSIMAS
Ejemplo: ¿Qué comparación es correcta?
a 0.45 > 0.54
b 1.67 < 1.7
c 0.90 = 0.9
d 4.71 > 4.8
La opción de respuesta c es correcta. Se pueden utilizar discos de centésimas para demostrar que estos dos decimales son equivalentes. Los estudiantes podrán ver que añadir un cero en la centésima no cambia el valor del decimal.
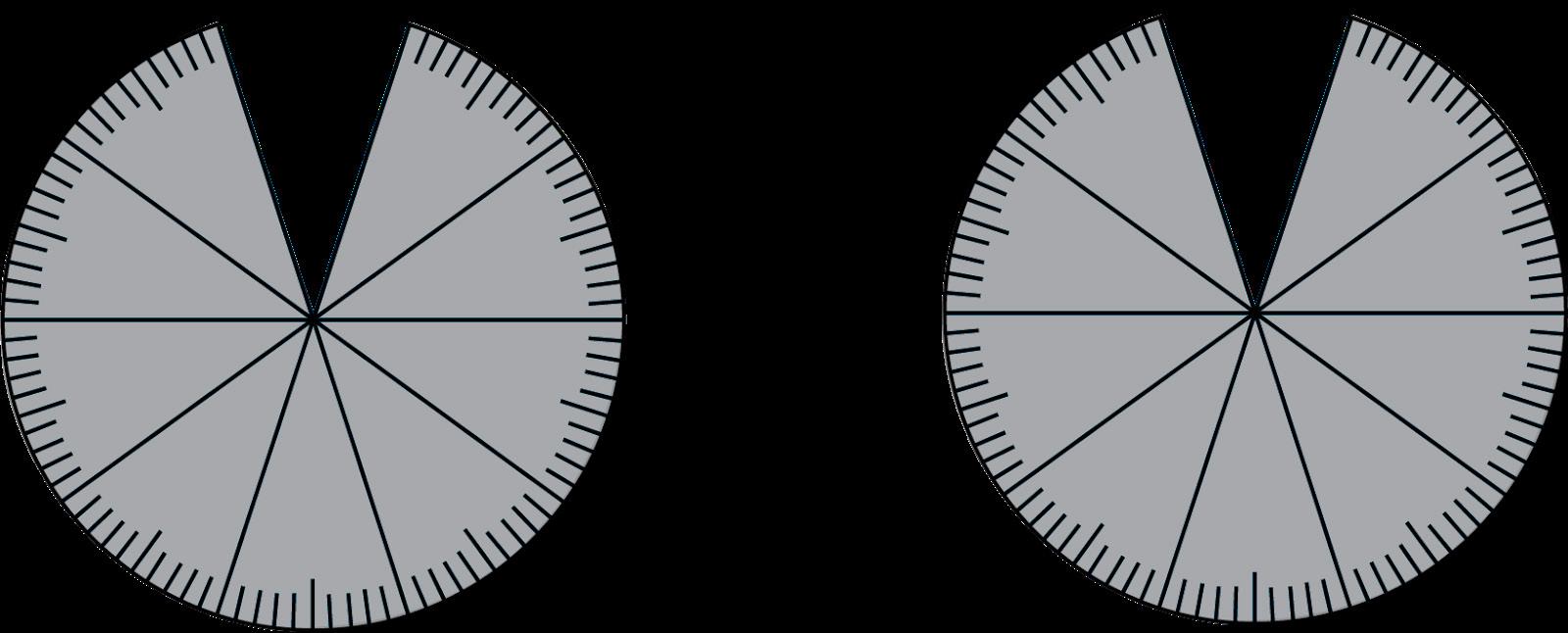
COMPARACIÓN DE DOS DECIMALES CON RECTAS NUMÉRICAS
Ejemplo: Arrastra y suelta el símbolo en el cuadro para comparar los dos números.
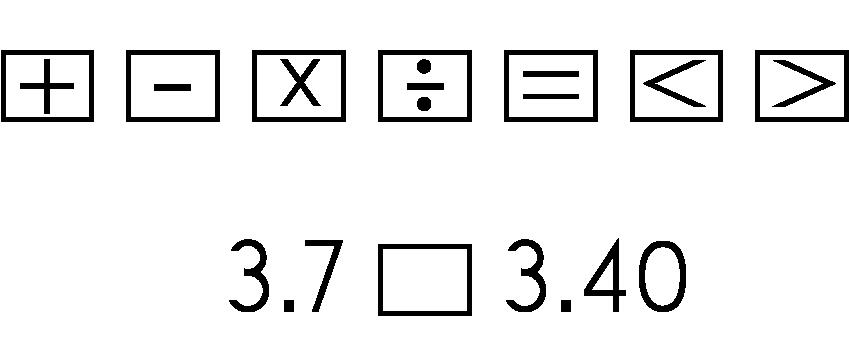
Respuesta: 3.7 > 3.4. Usando una recta numérica, los estudiantes pueden contar por décimas para colocar cada decimal en la recta numérica para representar visualmente la comparación.
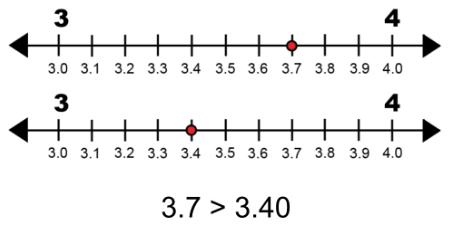
COMPARACIÓN DE DOS DECIMALES CON UNA TABLA DE VALOR POSICIONAL
Ejemplo: ¿Qué comparaciones son correctas? Selecciona tres respuestas correctas.
a 5.89 = 5.9
b 4.5 > 4.45
c 63.1 < 63.01
d 10.5 > 10.50
e 32.62 < 32.8
f 81.3 = 81.30
INICIO: CONTENIDO DE APOYO
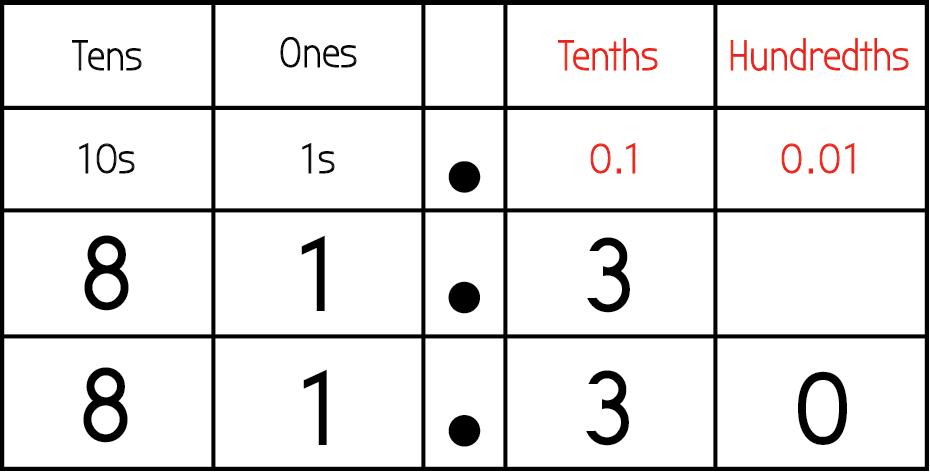
La opción de respuesta b es una comparación correcta. Colocando los dígitos en una tabla de valor posicional se muestra la comparación. Si se añade un cero en la centésima con el número 4,5, la comparación puede verse más fácilmente.
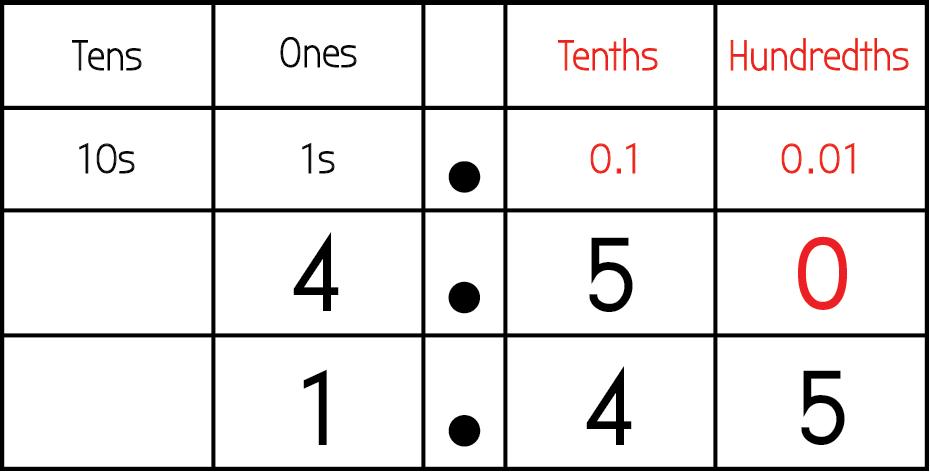
La opción de respuesta e es una comparación correcta. Colocar los dígitos en una tabla de valor posicional muestra la comparación. Se puede añadir un cero en el lugar de las centésimas con el número 32,8 para que la comparación sea explícitamente visible.
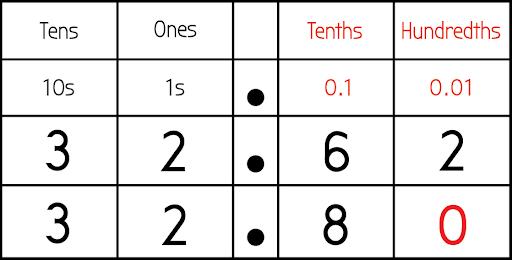
La opción de respuesta f es una comparación correcta. La colocación de los dígitos en una tabla de valor posicional muestra la comparación. El cero no siempre es necesario si los estudiantes comprenden los valores de cada dígito y pueden comparar con un conocimiento sólido del valor posicional.
AVANCES
Los estudiantes de quinto grado leen, escriben y comparan decimales hasta las milésimas. La comprensión del valor posicional se utiliza para redondear decimales a cualquier posición. Se espera que los estudiantes resuelvan problemas con números enteros de varios dígitos y decimales hasta las centésimas basándose en el valor posicional y las propiedades de las operaciones. Los estudiantes de sexto grado sumarán, restarán, multiplicarán y dividirán con fluidez decimales de varios dígitos utilizando el algoritmo estándar para cada operación.
INICIO: CONTENIDO DESGLOSADO
ANÁLISIS PROFUNDO DE LOS ESTÁNDARES
CONTENIDO DESGLOSADO
ESTÁNDARES
Comprender la notación decimal para fracciones y comparar fracciones decimales.
• Utilizar la notación decimal para fracciones con denominadores 10 ó 100. Por ejemplo, reescribir 0.62 como 62/100; describir una longitud como 0.62 metros; localizar 0.62 en un diagrama de recta numérica.
• Comparar dos decimales con centésimas razonando sobre su tamaño. Reconocer que las comparaciones sólo son válidas cuando los dos decimales se refieren al mismo entero. Registrar los resultados de las comparaciones con los símbolos >, =, o <, y justificar las conclusiones, por ejemplo, utilizando la recta numérica u otro modelo visual.
DESGLOSAR EL ESTÁNDAR
VERBOS: ¿QUÉ DEBERÍAN HACER LOS ESTUDIANTES?
• usar: emplear o utilizar para un fin.
• reescribir: escribir de nuevo.
• localizar: encontrar el lugar de algo.
• comparar: determinar semejanzas o diferencias entre dos o más objetos o números.
• reconocer: identificar a partir de un conocimiento o experiencia previos.
• registrar: escribir
• justificar: explicar su pensamiento.
SUSTANTIVOS: ¿QUÉ PALABRAS CONCRETAS DEBEN CONOCER LOS ESTUDIANTES?
• notación decimal: forma de un número que utiliza el punto decimal en el lugar correcto.
• fracción: parte de un grupo de objetos, un número o un entero.
• denominador: el número inferior de una fracción; representa el número total de partes iguales en un entero.
• recta numérica: recta con marcas de graduación espaciadas uniformemente para mostrar la posición de un número en relación con otros números.
• diagrama: información mostrada en un gráfico o en forma de imagen.
• decimal: fracción con un denominador que es una potencia de 10 y se escribe con dígitos a la derecha del punto decimal.
• centésimas: valor posicional que está dos lugares a la derecha del decimal.
• comparación: proceso o resultado de buscar similitudes y/o diferencias entre conjuntos de objetos o números.
• símbolo: carácter utilizado para representar un valor o un proceso.
• conclusión: un juicio o inferencia
• modelo: una representación
IMPLICACIONES PARA LA ENSEÑANZA
• Los estudiantes no han representado decimales antes de este nivel de grado, ni han experimentado los decimales como parte del sistema de valor posicional.
• Los estudiantes hacen conexiones entre los decimales 0.10 y 0.100 y los valores posicionales décimos y centésimos.
• A medida que exploran con la versión fraccionaria de los decimales, los estudiantes también deben hacer la conexión de que estas fracciones pueden descomponerse y expandirse en décimas y centésimas.
• Este es el primer grado en el que los estudiantes han comparado decimales. Los estudiantes deben empezar utilizando modelos concretos. Entender cómo se pueden componer, descomponer y reagrupar los decimales proporcionará una base para comparar decimales. Por ejemplo, los estudiantes deben comprender que 0.6 puede expresarse como "seis décimas" o "60 centésimas" y, por lo tanto, es mayor que 0.06, que se expresa como "6 centésimas".
• Una idea errónea que tienen los estudiantes es que el decimal con más cifras es siempre el número mayor. Esto no es cierto. Otro concepto erróneo que tienen los estudiantes es que el decimal más corto siempre es mayor. Por ejemplo, los estudiantes pueden afirmar que 0.4 es mayor que 0.97 porque una décima es mayor que una centésima. En lugar de ello, los estudiantes deben fijarse en el valor de cada dígito para determinar si es mayor.
• Los estudiantes suelen confundirse si hay un cero en la posición de las décimas. Algunos estudiantes ignoran el cero al comparar, lo que hace que comparen incorrectamente los decimales. Los estudiantes deben utilizar modelos para comprender que no se debe ignorar el cero en la posición de las décimas.
INICIO: CONTENIDO DESGLOSADO
ALINEACIÓN VERTICAL
GRADO
4
4
5
ESTÁNDAR
Utilice la notación decimal para fracciones con denominadores 10 ó 100. Por ejemplo, reescribir 0.62 como 62/100; describir una longitud como 0.62 metros; ubicar 0.62 en un diagrama de recta numérica.
Comparar dos decimales con centésimas razonando sobre su tamaño. Reconocer que las comparaciones sólo son válidas cuando los dos decimales se refieren al mismo entero. Registrar los resultados de las comparaciones con los símbolos >, =, o <, y justificar las conclusiones, por ejemplo, utilizando un modelo visual.
Leer, escribir y comparar decimales hasta las milésimas.
a. Leer y escribir decimales hasta las milésimas utilizando números de base diez, nombres de números y forma expandida, por ejemplo 347,392 = 3 × 100 + 4 × 10 + 7 × 1 + 3 × (1/10) + 9 × (1/100) + 2 × (1/1,000).
b. Comparar dos decimales a milésimas basándose en los significados de los dígitos en cada lugar, usando los símbolos >, = y < para registrar los resultados de las comparaciones.
5 Utilizar la comprensión del valor posicional para redondear decimales a cualquier posición.
6 Sumar, restar, multiplicar y dividir con fluidez decimales de varios dígitos utilizando el algoritmo estándar para cada operación.
7 Resolver problemas matemáticos y del mundo real que impliquen las cuatro operaciones con números racionales.
8 Realizar operaciones con números expresados en notación científica, incluyendo problemas en los que se utilicen tanto la notación decimal como la científica. Utilizar notación científica y elegir unidades de tamaño apropiado para mediciones de cantidades muy grandes o muy pequeñas (por ejemplo, utilizar milímetros por año para la extensión del fondo marino). Interpretar notación científica que ha sido generada por la tecnología.
HS Utilizar unidades como una forma de entender problemas y para guiar la solución de problemas de varios pasos; elegir e interpretar unidades consistentemente en fórmulas; elegir e interpretar la escala y el origen en gráficos y visualizaciones de datos.
MONITOREAR Y AJUSTAR
GUÍA DE INSTRUCCIÓN ANDAMIADA
La guía de instrucción andamiada se proporciona para que los maestros puedan planificar los siguientes pasos basándose en el rendimiento de los estudiantes en las evaluaciones de alcance o en los datos de su evaluación de medición de crecimiento MAP. Se trata de una herramienta integrada que lleva a los maestros a buscar materiales basados en las necesidades de los estudiantes. Los materiales sugeridos están organizados por estándares. Dentro de cada estándar, los materiales se clasifican además por el rango de percentiles que mejor se adapta.
Cuando se usa la guía de instrucción andamiada con los datos de su evaluación de medición de crecimiento MAP, cada tabla puede guiar a los maestros a los materiales sugeridos basados en los puntajes del área de instrucción de los estudiantes. Se sugiere a los maestros a permitir que todos los estudiantes experimenten con «Captar interés», «Exploración», «Muestra lo que sabes» y «Pruebas de habilidades». Estos elementos cubren a fondo los estándares incluidos en el alcance.
La guía se divide en cuatro rangos de percentiles para cada estándar.
Refuerzo del grado anterior Nivel de grado con apoyos Nivel de grado
Los estudiantes con puntaje en este rango de percentil necesitan refuerzo del contenido del grado anterior.
Los estudiantes con puntaje en este rango de percentil necesitan apoyo de intervención de nivel de grado.
Los estudiantes con puntaje en este rango de percentil pueden trabajar en contenido de nivel de grado con apoyos de instrucción.
Ampliación del nivel de grado
Los estudiantes con puntaje en este rango de percentil están listos para aplicar su conocimiento del contenido en una variedad de actividades.
Para interpretar y responder al rendimiento del estudiante en las evaluaciones del alcance, complete los siguientes pasos:
1 Revise los datos recopilados a través de la plataforma en línea o el «Mapa de calor» para determinar el rango percentil del estudiante para cada estándar evaluado.
2 Las tablas proporcionadas recomiendan un conjunto de materiales de instrucción para cada rango percentil dentro de cada estándar evaluado. Elija cuál de estos materiales usará para apoyar mejor al estudiante con base en sus datos de evaluación.
3 Haga clic en el enlace directo al material elegido para el estudiante.
Para interpretar y responder al desempeño del estudiante en la evaluación de medición de crecimiento MAP, complete los siguientes pasos:
1. Revise los datos proporcionados para determinar el percentil, el área de instrucción y/o el desglose de estándares para cada estudiante.
2. Encuentre el alcance que incluye los estándares que necesitan enfoque o intervención.
3. Acceda a la «guía de instrucción andamiada» en la sección «inicio» del alcance.
4. Haga clic en el enlace directo al material recomendado para el estudiante.
La guía es un plan sugerido y no se limita a los estándares y actividades incluidos. Además, no todas las actividades sugeridas necesitan ser completadas por cada estudiante.
Área de instrucción: Operaciones y pensamiento algebraico
Todos los estudiantes:
• Captar interés
• Exploración
• Muestra lo que sabes
• Prueba de habilidades
Utilizar la notación decimal para fracciones con denominadores 10 ó 100. Por ejemplo, reescribir 0.62 como 62/100; describir una longitud como 0.62 metros; ubicar 0.62 en un diagrama de recta numérica.
3 - Fracciones en una recta numérica
0 %25 % (Nivel de grado anterior con apoyo)
Intervención en grupos pequeños
Generador de fluidez
• Fracciones en una recta numérica
Práctica interactiva
• Dragon DNA Lab
Prueba de habilidades
Mis pensamientos de matemáticas
3 - Aprendizaje virtual Números y operaciones
• Determinar un punto dado
4 - Representar y comparar decimales
25 %50 % (Nivel de grado con apoyo)
Intervención en grupos pequeños
• Partes 1 y 2
4 - Aprendizaje virtual Números y operaciones
• Representar décimas y centésimas con notación expandida
• Decimales en una recta numérica
• Fracciones y decimales en una recta numérica
4 - Representar y comparar decimales
Vocabulario ilustrado
• Libreta interactiva
• Notación decimal y de fracción
50 %80 % (Nivel de Grado)
80 %100 % (Ampliando el Nivel de Grado)
Mis pensamientos de matemáticas
Práctica interactiva
• Línea de ensamblaje de robots
Constructor de fluidez
• Emparejar modelos decimales con números decimales
Ciencia de datos
Conexiones lingüísticas
4 - Representar y comparar decimales
Tarea basada en problemas
Matemáticas de hoy
Cuento de matemáticas
Crea el tuyo
Tablero de opciones
Comparar dos decimales con centésimas razonando sobre su tamaño. Reconocer que las comparaciones sólo son válidas cuando los dos decimales se refieren al mismo entero. Registrar los resultados de las comparaciones con los símbolos >, =, o <, y justificar las conclusiones, por ejemplo, utilizando un modelo visual.
3 - Comparar fracciones
Intervención en grupos pequeños
0 %25 % (Nivel de grado anterior con apoyo)
25 %50 % (Nivel de grado con apoyo)
Generador de fluidez
• Comparar fracciones unitarias
Práctica interactiva
• Desafío de paintball
Prueba de habilidades
Mis pensamientos de matemáticas
3 - Fracciones con el aprendizaje virtual
• Fracciones con denominadores iguales
• Comparación de fracciones con numeradores iguales
4 - Representar ycomparar decimales
Acceso a conocimientos previos
Constructor de bases fundamentales
Intervención en grupos pequeños
• Parte 3
4 - Aprendizaje virtual
Comparar y Ordenar Decimales
4 - Representar y comparar decimales
Vocabulario ilustrado
• Libreta interactiva
• Comparar decimales
50 %80 % (Nivel de Grado)
80 %100 % (Ampliando el Nivel de Grado)
Mis pensamientos de matemáticas
Práctica interactiva
• Cazador de gangas
Constructor de fluidez
• Comparar decimales: Décimas y centésimas
Ciencia de datos
Conexiones lingüísticas
4 - Representar y comparar decimales
Tarea basada en problemas
Conexiones profesionales
Matemáticas de hoy
Cuento de matemáticas
Crea el tuyo
Tablero de opciones
ATRAER: ACCESO A CONOCIMIENTOS PREVIOS
EVALUAR PREVIAMENTE EL CONOCIMIENTO DEL ESTUDIANTE
ACCESO A CONOCIMIENTOS PREVIOS
DESCRIPCIÓN
En esta actividad, los estudiantes eligen al estudiante que utiliza correctamente símbolos, palabras o modelos pictóricos para comparar dos fracciones con el mismo numerador o denominador. Esta actividad pretende evaluar el dominio del siguiente estándar:
• Comparar dos fracciones con el mismo numerador o el mismo denominador razonando sobre su tamaño. Reconocer que las comparaciones sólo son válidas cuando las dos fracciones se refieren al mismo entero. Registrar los resultados de las comparaciones con los símbolos >, = o <, y justificar las conclusiones, p. ej, utilizando un modelo visual de fracciones.
MATERIALES
IMPRESOS
• 1 hoja para el estudiante (por alumno, grupo o clase)
PREPARACIÓN
• Puede elegir entre imprimir una hoja de comparación de fracciones para cada estudiante o grupo o proyectar la página en la pizarra.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
Pida a los estudiantes que observen el enunciado de comparación y el símbolo o modelo pictórico de cada estudiante.
1. Los estudiantes deben elegir la comparación con la que estén más de acuerdo.
2. Pida voluntarios que justifiquen sus elecciones.
3. Facilite un debate en clase mientras los estudiantes razonan sus elecciones.
• Estoy de acuerdo con Ángel. Cuatro es mayor que tres, así que 1/4 sería mayor que 1/3.
• Estoy de acuerdo con Monique. Su dibujo muestra que1/4 y 1/3 tienen exactamente el mismo tamaño. Por lo tanto, son iguales.
• Estoy de acuerdo con Rocky. 1/3 van a ser mayores que los trozos de 1/4 , así que1/4 va a ser menor que 1/3.

FOLLETO DEL ESTUDIANTE
DESCRIPCIÓN
Los estudiantes relacionan decimales con fracciones que nombran décimas y centésimas y hacen comparaciones decimales razonando sobre su tamaño.
MATERIALES
IMPRESO
• 1 folleto para el estudiante (por estudiante)
REUTILIZABLE
• 1 fenómeno (por clase)
• 1 proyector (por clase)
• 1 lápiz de color (por estudiante)
PREPARACIÓN
• Planee mostrar los fenómenos.
• Planee que los estudiantes trabajen independientemente para completar esta actividad.
• Imprima el folleto para el estudiante para cada estudiante.
• Reúna un lápiz de color para cada estudiante.
ATRAER: CAPTAR INTERÉS
LECCIÓN PARA CAPTAR INTERÉS
CAPTAR INTERÉS: COMPARACIÓN DE DULCES
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
PARTE I: EXPLORACIÓN PREVIA
1. Presente esta actividad hacia el comienzo del alcance. La clase retomará la actividad y resolverá el problema original después de que los estudiantes hayan completado las actividades Explorar correspondientes.
2. Muestre los fenómenos. Formule a los estudiantes las siguientes preguntas: ¿Qué observas? ¿Dónde puedes ver matemáticas en esta situación? Permita que los estudiantes compartan todas sus ideas.
3. Explique el escenario a la clase: Jim y Tim recibieron cada uno 100 caramelos de Halloween este año. Sin embargo, ambos son alérgicos a los cacahuetes, por lo que cada uno tuvo que sacar una fracción de sus caramelos. 33/100 de los caramelos de Jim tenían cacahuetes. 3/10 de los caramelos de Tim tenían cacahuetes. Después de quitar los caramelos con cacahuetes, a Jim le quedaban 67/100 de sus caramelos y a Tim le quedaban 7/10 de sus caramelos. ¿Quién tuvo que sacar más caramelos y a quién le quedaron más caramelos para comer?
4. Permita que los estudiantes hagan preguntas y aclaren el contexto según sea necesario. Anímeles a compartir sus pensamientos y experiencias con la clase utilizando las siguientes preguntas:
a. ¿Cuál es tu caramelo favorito?
b. ¿Has tenido que ordenar alguna vez los caramelos?
c. ¿Puedes pensar en alguna ocasión en la que comparaste la cantidad de caramelos que tenías con otra persona?
5. Haga las siguientes preguntas a la clase:
a DOK-1 ¿Qué información tenemos? Sabemos que Jim y Tim tenían 100 caramelos cada uno, 33/100 de los caramelos de Jim tenían cacahuetes, y 33/10 de los caramelos de Tim tenían cacahuetes.
b DOK-1 ¿Qué nos pide que resolvamos? Necesitamos saber quién tenía que sacar más caramelos. Necesitamos saber a quién le quedaban más caramelos para comer después de haber sacado los caramelos con cacahuetes.
c DOK-2 ¿Qué estrategia podríamos utilizar para comparar sus caramelos? Podríamos dibujar modelos de fracciones que sean del mismo tamaño para poder compararlos más fácilmente.
d DOK-2 ¿Cambiar las fracciones a decimales te ayudaría con la comparación? Creo que sí, ya que las dos fracciones tienen denominadores diferentes. Puede ser difícil comparar fracciones con denominadores diferentes.
6. Continúa con las actividades de explorar.
PARTE II: DESPUÉS DE EXPLORAR
3. Después de que los estudiantes hayan completado las actividades de exploración para este tema, muestre de nuevo los Fenómenos y repita el escenario.
4. Haga las siguientes preguntas con la clase:
a DOK-1 ¿Qué información tenemos? Sabemos que Jim y Tim tenían 100 caramelos cada uno, 33/10 de los caramelos de Jim tenían cacahuetes, y 3/10 de los caramelos de Tim tenían cacahuetes.
b DOK-1 ¿Qué nos pide que resolvamos? Necesitamos saber quién tenía que sacar más caramelos. Necesitamos saber a quién le quedaban más caramelos para comer después de haber sacado los caramelos con cacahuetes.
c DOK-2 ¿Qué estrategia podríamos utilizar para comparar sus caramelos? Podríamos dibujar modelos de fracciones que sean del mismo tamaño para poder compararlos más fácilmente.
d DOK-2 ¿Cambiar las fracciones a decimales te ayudaría con la comparación? Creo que sí, ya que las dos fracciones tienen denominadores diferentes. Puede ser difícil comparar fracciones con denominadores diferentes.
5. Distribuya a cada estudiante una hoja de trabajo y un lápiz de color.
6. Dé tiempo a los estudiantes para resolver el problema.
1. Haga las siguientes preguntas con la clase:
e DOK-1 ¿Cómo representó la cantidad de caramelos que Jim y Tim necesitaban sacar? Sombreé tres columnas, o tres décimos, en el primer modelo y escribí la fracción 3/10 y el decimal 0.3. En el segundo modelo, sombreé treinta y tres cuadrados, o treinta y tres centésimas, y escribí la fracción 33/100 y el decimal 0.33.
f DOK-1 ¿Qué símbolo de comparación escribiste entre los modelos? ¿Quién tuvo que sacar más caramelos? Escribí < entre los modelos. Puedo ver que 3/10 < 33/100 mirando el área sombreada en cada modelo. Jim tuvo que sacar la mayor cantidad de caramelos.
g DOK-3 ¿Por qué se escriben tres décimas como 0.3 en lugar de 0.03? Si escribo 0.03, estoy colocando el 3 en el lugar de las centésimas. Escribí 0.3 para que el 3 estuviera en el lugar de las décimas.
h DOK-2 ¿Quién tenía más caramelos para comer después de deshacerse de los caramelos con nueces? A Tim le quedaban más caramelos porque 7/10> 67/100 y 0.7 > 0.67.
2. Esta actividad podría ampliarse haciendo que los estudiantes crearan un nuevo escenario y utilizaran una recta numérica para hacer la comparación.
EXPLORAR: EXPLORACIÓN 1
LECCIÓN PEDAGÓGICA
EXPLORACIÓN 1: NOTACIÓN DECIMAL PARA LOS DENOMINADORES DE 10
Antes de completar esta exploración, pida a los estudiantes que completen Habilidades básicas:Representar decimales con base diez para que puedan aplicar la habilidad a este concepto.
Estándar(es)
• Comprender la notación decimal para fracciones y comparar fracciones decimales. Utilizar la notación decimal para fracciones con denominadores 10 ó 100. Por ejemplo, reescribir 0.62 como 62/100; describir una longitud como 0.62 metros; ubicar 0.62 en un diagrama de recta numérica.
Ideas fundamentales
Modelos Visuales de Fracciones
Círculos, Fracciones y Decimales
DESCRIPCIÓN
Estándares para la práctica matemática
MP.2 Razonar abstracta y cuantitativamente.
MP.4 Modelar con matemáticas.
MP.6 Prestar atención a la precisión.
MP.7 Buscar y hacer uso de la estructura.
MP.8 Buscar y expresar regularidad en razonamientos repetidos
Los estudiantes representan valores decimales hasta las décimas utilizando modelos concretos y visuales. Los estudiantes relacionan sus modelos con fracciones y nombran los valores usando notación de fracciones, notación decimal y forma de palabras.
MATERIALES
IMPRESO
• 1 diario del estudiante (por alumno)
• 1 boleto de salida (por estudiante)
REUTILIZABLE
• 100 palitos de manualidades (por grupo)
• 1 juego de bloques de base diez (por grupo)
• 1 cronómetro (por maestro)
Conexiones de contenido Motores de investigación
CC3 Desarmar el todo, armar las partes
CC4 Descubrir la forma y el espacio
DI1 Dar sentido al mundo (comprender y explicar)
PREPARACIÓN
• Planee que los estudiantes trabajen en grupos de 3-4 para completar esta actividad.
• Imprima el Diario del Estudiante y un Boleto de Salida para cada estudiante.
• Reúna 100 palitos de manualidades para cada grupo.
• Reúna un juego de bloques de base diez para cada grupo.
• Prepare un cronómetro para la clase.
• Para los estudiantes que necesiten más apoyo para recordar información, consulte nuestros elementos de «Ayudas complementarias» que incluyen: base de diez, cuadrícua de base diez y tapete para valor de posición decimal en la sección «Intervención».
• ¡Hazlo digital! Haga que los estudiantes exploren o presenten sus soluciones utilizando manipulativos virtuales. Los manipulativos usados en esta lección se pueden encontrar en el menú desplegable de la sección «Explorar» y se pueden asignar digitalmente a los estudiantes. (Bloques de base diez)
EXPLORAR: EXPLORACIÓN 1
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Ayude a los estudiantes a acceder a la tarea formulando las siguientes preguntas orientadoras:
a. ¿Qué es una escultura?
b. ¿Qué recuerdas sobre los bloques de base diez?
c. ¿Qué recuerdas sobre las fracciones?
2. Entregue un Diario del estudiante a cada estudiante.
3. Entrega a cada grupo un juego de bloques de base diez. Explica a los estudiantes que en las exploraciones anteriores han utilizado los bloques de base diez para representar números enteros. Ahora van a utilizar bloques de base diez para representar cantidades menores que un entero. Haga las siguientes preguntas:
a. DOK-1 Si este piso se utiliza para representar un entero, ¿qué podemos predecir sobre el valor de la barra y el cubo unitario? Tanto la barra como el cubo valdrán menos que un entero porque son más pequeños.
b. DOK-1 Sostenga un piso y una barra. Si el piso se considera un entero, ¿cuál es el valor de la barra? La barra es un décimo porque se necesitan 10 de ellas para hacer el piso.
i. Explica que las cantidades inferiores a un entero pueden escribirse como fracciones o como decimales. Explique que el punto decimal seguirá al número entero para señalar que estamos pasando de enteros a partes.
c. DOK-1 Sostenga un piso y un cubo pequeño. Si el piso se considera un entero, ¿cuál es el valor del cubo unitario pequeño? El cubo pequeño es la centésima parte porque se necesitan 100 de ellos para hacer un piso.
4. Entregue un paquete de 100 palitos de manualidades a cada grupo. Explique a los estudiantes que van a montar miniesculturas que se pueden pintar y utilizar para decorar dormitorios, salas de juegos, oficinas, etc.
5. Muestre a los estudiantes cómo construir una escultura. Cada escultura debe construirse con 10 palitos de manualidades y colocarse como se muestra, con cinco capas de dos palitos.
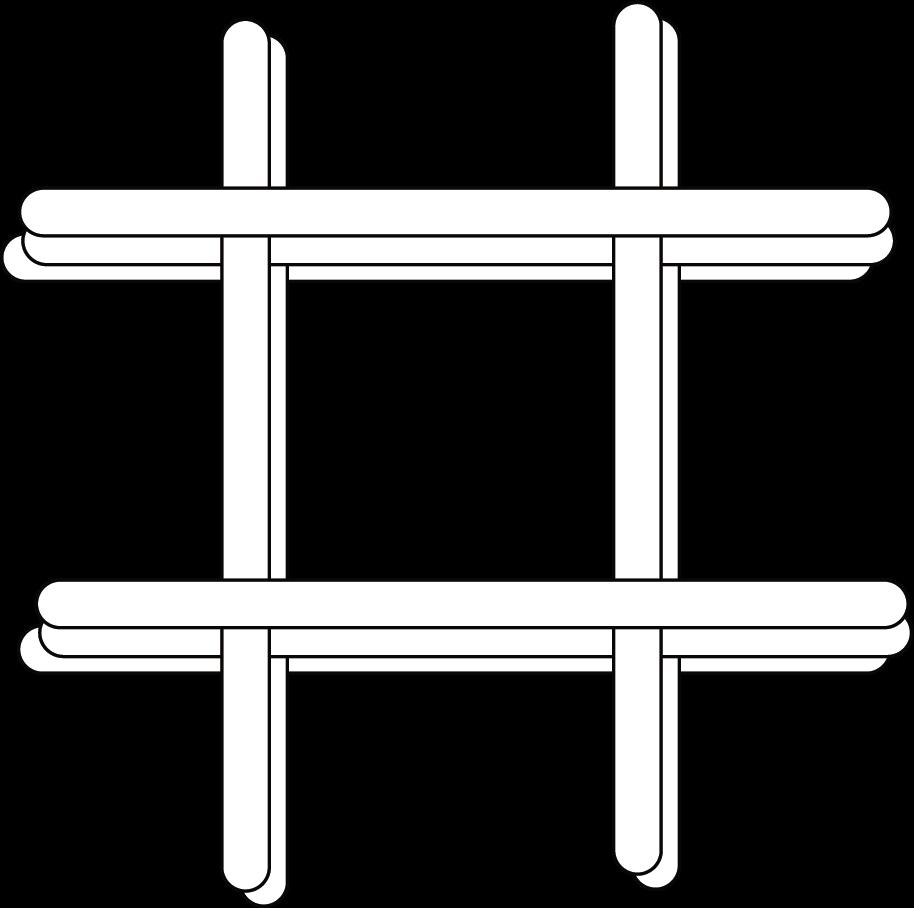
6. Ponga el cronómetro en 30 segundos. Pida a los grupos que construyan tantas esculturas como puedan en 30 segundos. Dígales que todo el grupo debe trabajar en una escultura a la vez.
7. Cuando suene el cronómetro, haga que los estudiantes dejen de construir sus esculturas.
8. Desafíe a los estudiantes a relacionar sus bloques de base diez con cuántas esculturas fueron capaces de construir usando el plano como un entero y la barra como una décima parte de un entero. Indique a los estudiantes que coloquen un plano sobre la mesa cerca de cada una de sus esculturas terminadas; por cada escultura incompleta, colocarán el mismo número de barras de base diez como palitos de manualidades cerca de la escultura incompleta.
1. Después de que los estudiantes hayan relacionado sus palitos de manualidades con bloques de base diez, indíqueles que representen sus modelos sombreando las cantidades en sus Diarios del estudiante. A continuación, los estudiantes anotan su número de esculturas como fracción, como decimal y en forma de palabra. Muestre a los estudiantes cómo ambas formas de mostrar el número se leen de la misma manera. Por ejemplo, uno y dos décimos pueden escribirse como 1 2/10 o 1.2.
2. Supervise a los estudiantes y compruebe la comprensión según sea necesario utilizando las siguientes preguntas orientadoras: (Las respuestas variarán).
a DOK-2 ¿Cómo se relacionan sus esculturas completadas con un plano de base diez? Un plano base-diez representa un todo. Como completamos una escultura entera en 30 segundos, podemos representar esa cantidad con una base-diez entera.
b DOK-2 ¿Cómo se relacionan tus esculturas incompletas con las barras de base-diez? Una barra base-diez representa la décima parte de un entero. Cada escultura necesita 10 palitos de manualidades para considerarse completa, igual que un entero necesita 10 barras, o 10 décimas partes, para estar completo. Como hay dos palitos de manualidades en la escultura incompleta, necesitamos 2 barras para representar este valor.
c DOK-2 ¿Cómo se relaciona tu notación de fracciones con tu modelo? La escultura entera representa el número entero de nuestra notación de fracción o número mixto. La escultura incompleta representa la fracción en nuestro número mixto. Como usamos 2 de 10 palitos de manualidades en la estructura incompleta, podemos representar la fracción como 2/10. La notación de fracción para nuestro modelo es 1 2/10.
d DOK-2 ¿Cómo se relaciona tu notación decimal con tu modelo? La escultura entera representa el número entero de nuestra notación decimal. El punto decimal va entre el número entero y la parte de un entero. La escultura incompleta representa el valor decimal. Como las esculturas se construyen con 10 palitos de manualidades, el valor decimal se representará en las décimas. Como completamos una escultura entera y usamos 2 de 10 palitos de manualidades en la estructura incompleta, podemos representar el decimal como 1.2.
e DOK-2 ¿Cómo se relaciona la forma de las palabras con la notación de fracciones y decimales? Leemos la notación fraccionaria o decimal de izquierda a derecha. Comenzamos escribiendo el número entero en forma de palabra. Luego, cuando llegamos a la fracción o al decimal, escribimos la palabra y. El valor de la fracción o decimal se escribe en forma de palabra seguida del término décimas porque el denominador es diez y el decimal está en la décima. Esto significa que nuestra forma verbal es "uno y dos décimos".
3. Comprueba rápidamente la exactitud del diario del estudiante de cada grupo y corrige cualquier malentendido.
4. Haga que los estudiantes desarmen sus esculturas y vuelvan a colocar sus palitos de manualidades en la pila de 100 palitos.
5. Repita el mismo proceso mientras cronometra a los estudiantes durante 45 segundos. Pida a los estudiantes que anoten su trabajo en sus diarios del estudiante.
EXPLORAR: EXPLORACIÓN 1


DIARIO DEL ESTUDIANTE
9. Pide a los estudiantes que compartan sus estrategias y anímales a que se hagan preguntas y establezcan conexiones. Anime a los estudiantes a notar las similitudes y diferencias entre las estrategias utilizadas para representar decimales hasta las décimas.
10. Después de la Exploración, invite a la clase a un Chat de Matemáticas para compartir sus observaciones y aprendizajes.
CHARLA DE MATEMÁTICAS
• DOK-1 ¿Qué nos dice el punto decimal? Separa los enteros de las partes de un todo. Cualquier cosa a la derecha del decimal es parte de un todo.
• DOK-2 ¿Qué notaste sobre el valor del lugar representado después del punto decimal? Noté que el primer lugar después de un decimal representa décimos porque tiene un valor de un décimo de un entero.
• Elija una rutina de Conversación Estructurada para facilitar la siguiente pregunta:
◦ DOK-2 ¿Cómo se relacionan las esculturas con las fracciones y los decimales? Las esculturas están relacionadas con las fracciones y los decimales porque utilizamos grupos de décimas y centésimas para representar estas estructuras. Si completábamos una escultura entera, ésta representaba el número entero de nuestra fracción o decimal. Si representábamos parte de una estructura, esto representaba la fracción o el decimal.
• DOK-2 ¿Cuál es la relación entre la notación de fracciones y la notación decimal? La notación fraccionaria y la notación decimal son formas diferentes de escribir la cantidad representada en el modelo base-diez. Ambas notaciones se leen de la misma manera.
• DOK-3 ¿Cómo puedes aplicar tu conocimiento de una fracción para representar un valor decimal? Una fracción representa parte de un entero, igual que un decimal representa parte de un entero. Los decimales sólo representan décimas y centésimas, mientras que una fracción puede tener varios denominadores. Cuando una fracción tiene un denominador de 10 o 100, podemos convertir ese valor en un decimal.
• DOK-3 ¿Cómo puedes aplicar tu conocimiento de las relaciones de valor posicional para escribir cantidades en notación decimal? Sé que cada valor posicional tiene un valor 10 veces menor que el lugar a su izquierda. Esto significa que el valor posicional directamente después del punto decimal tiene que valer un décimo tanto como el lugar de las unidades, por lo que lo llamamos el lugar de los décimos.
EXPLORAR: EXPLORACIÓN 1
DESPUÉS DE EXPLORAR
1. Pida a los estudiantes que completen el boleto de salida para evaluar formativamente su comprensión del concepto.
2. Completen la Tabla de anclaje como clase.
3. Pida a cada estudiante que complete su Cuaderno interactivo.
APOYOS PEDAGÓGICOS
1. A medida que revisa los bloques de base diez, puede ser útil crear una tabla de anclaje que represente un plano y una barra y sus valores como un entero y un décimo, respectivamente. Los estudiantes pueden consultarlo a lo largo de la exploración.
2. Para que los estudiantes relacionen con éxito fracciones y decimales, deben tener una comprensión sólida de las fracciones. En la actividad con palitos de manualidades, puede que algunos estudiantes necesiten centrarse únicamente en la cantidad fraccionaria de una escultura que han construido. Podría hacerles practicar la creación de un modelo utilizando bloques de base diez y relacionarlo únicamente con un valor fraccionario. Una vez que los estudiantes comprendan cómo se relacionan los bloques con una fracción, puede mostrarles cómo su fracción o número mixto puede representar un decimal.
3. Si los estudiantes necesitan ayuda para relacionar sus bloques de diez bases con sus palitos de manualidades, repase los valores de los bloques de diez bases y cómo se relacionan con los valores decimales. Compara estos valores con las esculturas y cómo se necesitan 10 palitos de manualidades para hacer una escultura completa, al igual que se necesitan 10 barras para hacer un piso completo.
4. Si los estudiantes necesitan ayuda para sombrear sus modelos de base diez, relaciona los bloques de base diez que representan las esculturas con el modelo. Diez unidades representan una décima parte o una barra.
5. Si los estudiantes necesitan ayuda para representar un modelo con una fracción, un decimal o una forma de palabra, puede ser beneficioso crear una tabla de anclaje para que la clase la consulte a lo largo de la Exploración como recordatorio de cómo es cada representación.
6. Si los estudiantes necesitan apoyo adicional para escribir los números en notación decimal, revise cada valor posicional y la importancia del punto decimal. Haga hincapié en cómo los valores decimales se describen como décimas, y relaciónelo con la forma en que se leen las fracciones.
7. Puede ser beneficioso hacer que los estudiantes usen un marcador para escribir encima de cada modelo de bloque de base diez en el diagrama en sus Diarios del Estudiante. Por ejemplo, en la primera ronda de 30 seg. ronda, si un estudiante sombreó dos cuadrados enteros más cuatro barras en el tercer cuadrado, pídales que escriban 10/10 = 1 encima del primer cuadrado, y 4/10 encima del tercer cuadrado. Del mismo modo, pueden escribir los equivalentes decimales encima de cada uno (1,0. 1,0 y 0.4, respectivamente). Observando los componentes de esta forma, los estudiantes pueden determinar más fácilmente la fracción y el decimal finales de cada modelo.
8. Como ampliación, pida a los estudiantes que observen los números que han encontrado para ambas rondas. Pídales que discutan con un compañero cuántas esculturas creen que serían capaces de hacer si les dieran un minuto o un minuto y medio.

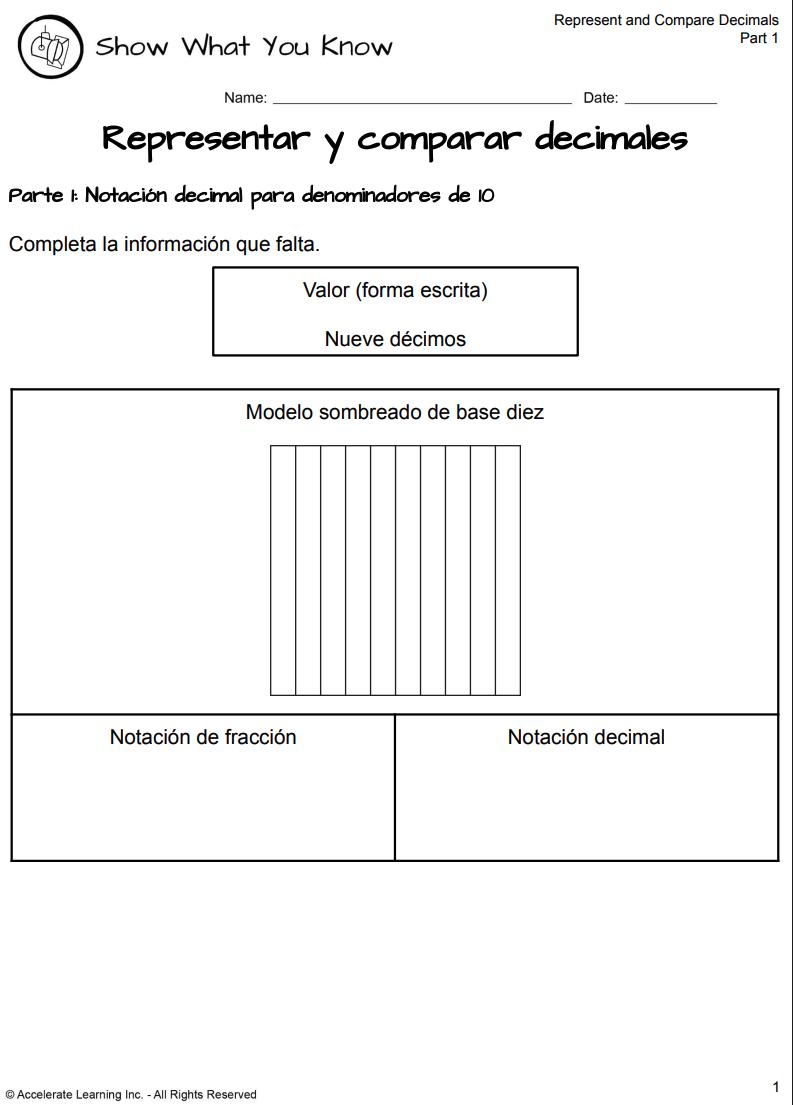
MUESTRA LO QUE SABES (PARTE 1)
BOLETO DE SALIDA
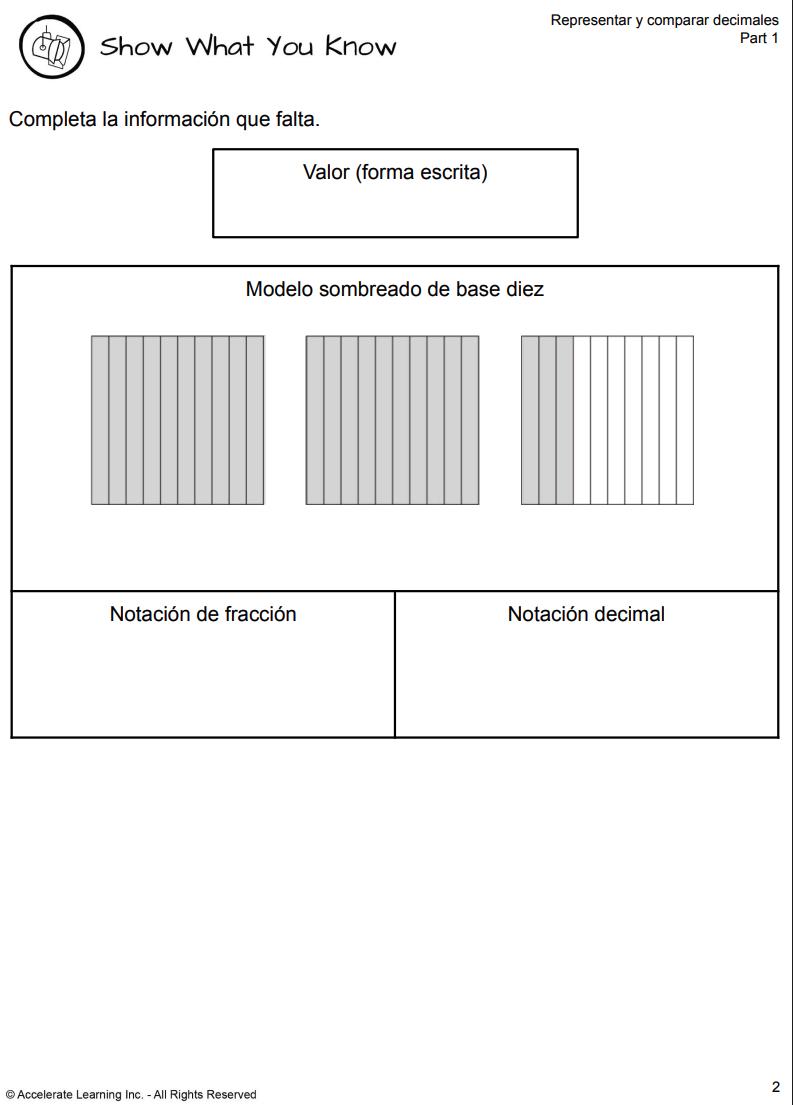
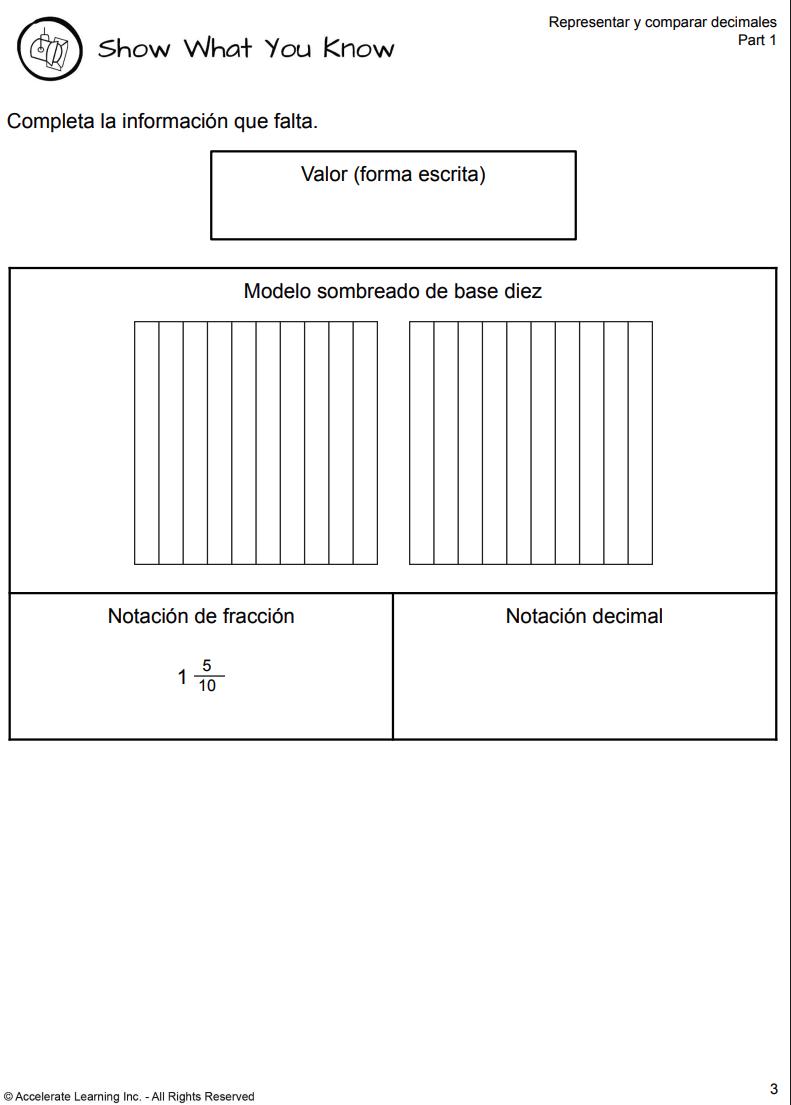
APOYOS LINGÜÍSTICOS
Para los hispanohablantes, relacionar la palabra representa con representa. Plantee la semejanza entre otros términos matemáticos en inglés y español en esta lección, como decimal para decimal, que es el mismo en ambos idiomas. Incluya a hablantes de todas las lenguas y pregúnteles si notan alguna similitud en los términos matemáticos con sus lenguas maternas.
Escriba los números 10, 20, 30 y 0.1, 0.2, 0.3 en la pizarra. Señale cada número en cada secuencia y demuestre la pronunciación correcta de cada número, haciendo hincapié en diez frente a décimos. Pida a los estudiantes que repitan. Asegúrese de que prestan atención a la diferencia al final de la palabra y a su relación con el punto decimal y los valores del número.
Proporcione estructuras de frases para que los estudiantes las utilicen durante el trabajo en grupo:
• Me fijé en _____.
• Construimos ____ esculturas enteras.
• Construimos ____ de la última escultura, que podría describirse como ____(fracción).
• Esa cantidad escrita como decimal sería ____.
Invite a los estudiantes a presentar sus esculturas a la clase y a explicar las formas de fracción, decimal y palabra de sus modelos utilizando imágenes o dibujos. Anime a los estudiantes a ser un buen público y a proporcionar comentarios constructivos.
EXPLORAR: EXPLORACIÓN 2
LECCIÓN PEDAGÓGICA
EXPLORACIÓN 2: NOTACIÓN DECIMAL PARA LOS DENOMINADORES DE 100
Estándar(es)
• Comprender la notación decimal para fracciones y comparar fracciones decimales. Utilizar la notación decimal para fracciones con denominadores 10 ó 100. Por ejemplo, reescribir 0.62 como 62/100; describir una longitud como 0.62 metros; ubicar 0.62 en un diagrama de recta numérica.
Ideas fundamentales
Modelos visuales de Fracciones
Círculos, fracciones y decimales
DESCRIPCIÓN
Estándares para la práctica matemática
MP.2 Razonar abstracta y cuantitativamente.
MP.4 Representar con matemáticas.
MP.5 Usar herramientas apropiadas estratégicamente.
MP.6 Prestar atención a la precisión.
MP.7 Buscar y hacer uso de la estructura.
Los estudiantes miden objetos en el aula y escriben la notación decimal y la notación fraccionaria correspondientes a la centésima más cercana. Los estudiantes también dibujan una recta numérica con la medida.
MATERIALES
IMPRESO
• 1 diario del estudiante (por alumno)
• 1 juego de tarjetas de situación (por grupo)
• 1 boleto de salida (por estudiante)
REUTILIZABLE
• 2 reglas de metro (por grupo)
• 1 bolsa resellable (por grupo)
PREPARACIÓN
• Planifique que los estudiantes trabajen en grupos de 3 o 4 para completar esta actividad.
• Imprime el diario del estudiante y una tarjeta de salida para cada estudiante.
• Imprime y recorta el conjunto de tarjetas de situación para cada grupo. Coloca cada juego en una bolsa resellable.
• Para los estudiantes que necesiten más apoyo para recordar información, consulte nuestros elementos de «Ayudas complementarias» que incluyen: rectas numéricas surtidas, cuadrícula base diez y tapete de valor posicional decimal en la sección «Intervención».
• ¡Digitalízate! Haga que los estudiantes exploren o presenten sus soluciones utilizando manipulativos virtuales. Los manipulativos utilizados en esta lección se pueden encontrar en el menú desplegable Explorar y se pueden asignar digitalmente a los estudiantes. (Rectas numéricas)
Conexiones de contenido
CC3 Desarmar el todo, armar las partes
CC4 Descubrir la forma y el espacio
Motores de investigación
DI1 Dar sentido al mundo (comprender y explicar)
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Entregue a cada estudiante un diario del estudiante.
2. Entregue a cada grupo un juego de tarjetas de escenarios y 2 reglas de medir.
3. Diga a los estudiantes que miren sus reglas de medir. Permita que los estudiantes hablen sobre su pensamiento con su compañero de codo antes de exponerlo con todo el grupo.
g DOK-1 ¿Cuántos centímetros hay en un metro? Hay 100 centímetros en un metro.
h DOK-1 ¿Qué fracción de un metro es 1 centímetro? 1 cm es 1/100 de un metro.
i DOK-2 Si quisieras dividir un metro en 10 partes iguales, ¿cuántos centímetros habría en cada parte? ¿Cómo lo calcularías? Cada una de las secciones tendría 10 centímetros; podríamos dividir 100 entre 10, lo que nos daría 10.
j DOK-1 ¿Qué fracción de metro son 10 centímetros? Cada sección de 10 centímetros es igual a 1/10 de metro.
k DOK-1 ¿Cómo podrías contar de 10 en 10 cada sección de 10 centímetros? Podríamos contar de 10 en 10. 10, 20, 30, 40, 50, 60, 70, 80, 90, 100
4. Lee la siguiente situación a la clase: En 2019, el sultán Kösen era el hombre más alto del mundo. Con sus 2,46 metros de altura, ¡el turco mide más de 2 metros! Hoy vamos a ver cómo se mide en comparación con el Sultán Kösen.


5. Ayude a los estudiantes a acceder a la tarea formulando las siguientes preguntas orientativas:
a. ¿Cómo se miden las alturas?
b. ¿Qué sabes ya sobre los decimales?
c. ¿Qué recuerdas sobre las décimas?
6. Empiece utilizando la altura del Sultán Kösen, 2.46 metros. Formule las siguientes preguntas:
a DOK-1 ¿Cuántos metros mide el hombre más alto del mundo? Más de 2
b DOK-1 ¿Mide 3 metros? ¿Cómo lo sabes? No; si miras el decimal, ves que hay un 2 en el lugar de las unidades, lo que significa que mide al menos 2 metros, pero no 3.
c DOK-1 ¿Entre qué dos números enteros se encuentra la altura del sultán Kösen? Entre 2 y 3
d DOK-1 ¿Cómo escribiríamos su altura en forma de fracción? 2 46/100
iv Explica que, como las centésimas son la décima parte de las décimas, son el siguiente valor posicional a la derecha de la décima. Por lo tanto, la fracción 2 46/100 puede escribirse en notación decimal como 2,46.
5 Dibuje una recta numérica en la pizarra. Formule a los estudiantes las siguientes preguntas:
a DOK-1 ¿Qué números enteros deberían estar en los extremos para trazar 2,46 metros? Entre 2 y 3
b DOK-1 ¿Qué números deberían estar en las marcas? Las respuestas pueden variar: por décimas, centésimas, etc.
c DOK-1 ¿Dónde marcaríamos 2,46? Las respuestas pueden variar: entre 2,4 y 2,5, entre 2,45 y 2,47.
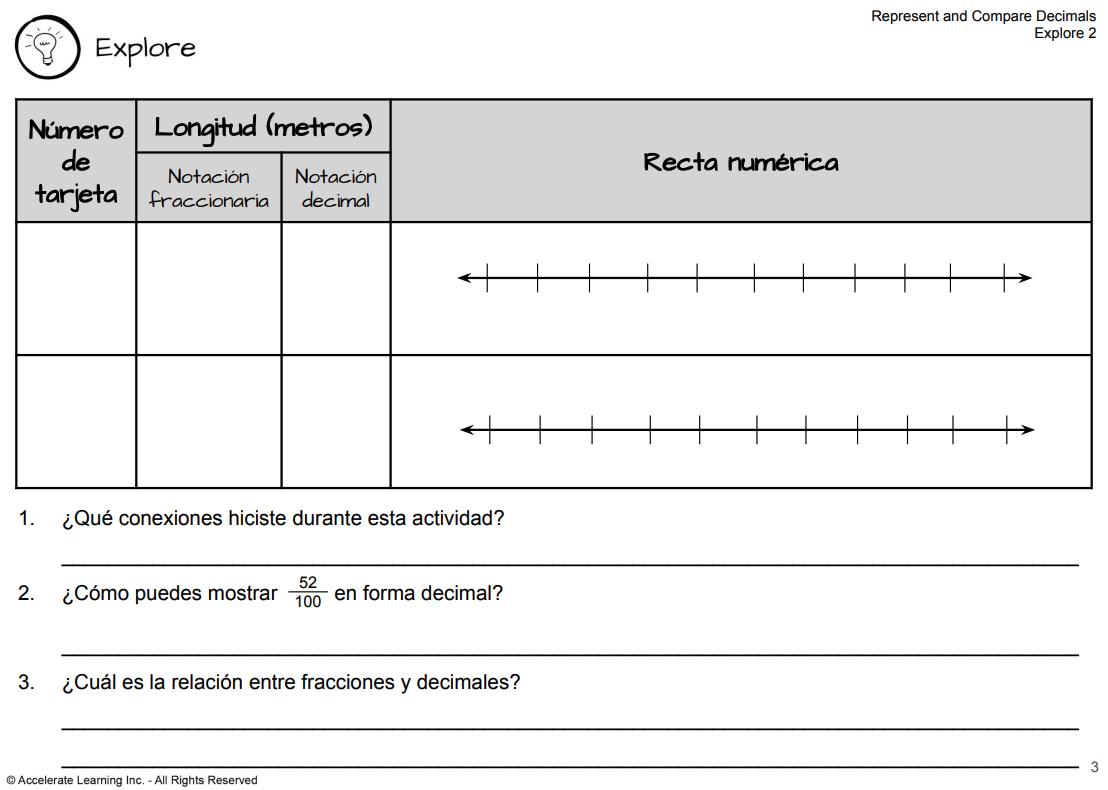
7. Diga a los estudiantes que van a trabajar en equipo para medir varios elementos de la clase, como se indica en cada tarjeta de situación. Deben medir con una precisión de centésimas de metro (o centímetros).
8. Una vez que hayan medido el elemento de la Tarjeta de situación, deben completar su Diario del estudiante con la longitud escrita en notación fraccionaria y decimal. También deben trazar una recta numérica que represente la longitud que han medido. Deben trabajar en colaboración con sus compañeros para completar los elementos de acción para la exactitud, así como el Diario del Estudiante.
9. Monitoree a los estudiantes y verifique la comprensión según sea necesario utilizando las siguientes preguntas guía: (Las respuestas variarán).
a. DOK-2 ¿Cómo usaste tu regla de medir para medir ____? Nos aseguramos de que la regla de medir estuviera colocada de forma que la marca 0 estuviera al principio de la distancia. Luego marcamos en la regla de medir dónde terminaba la longitud y determinamos el centímetro más cercano.
EXPLORAR: EXPLORACIÓN 2
b. DOK-2 ¿Cómo escribiste la medida utilizando la notación fraccionaria? Primero, buscamos entre qué 2 números enteros estaba la longitud y escribimos el menor de los 2 números enteros. Luego localizamos el centímetro más cercano en la regla de medir y escribimos esa cantidad como el numerador de una fracción con un denominador de 100.
c. DOK-2 ¿Cómo escribiste la medida utilizando la notación decimal? Usando la notación de fracción, pusimos el número entero en el lugar de las unidades y el numerador de la fracción después del punto decimal, terminando en el lugar de las centésimas.
d. DOK-2 ¿Cómo podrías registrar una cantidad decimal menor que una décima, como cuatro centésimas? Pondríamos un 0 en el lugar de las décimas y un dígito en el lugar de las centésimas para mostrar el número de centésimas, como 0.04.
10. Pida a los estudiantes que compartan sus estrategias y anímeles a que se hagan preguntas y establezcan conexiones. Anime a los estudiantes a notar las similitudes y diferencias entre las estrategias usadas para representar decimales hasta el lugar de las centésimas.
11. Después de la Exploración, invite a la clase a una Charla Matemática para compartir sus observaciones y aprendizajes.
CHARLA DE MATEMÁTICAS
• DOK-3 ¿Cuál es la relación entre el lugar de las décimas y el lugar de las centésimas? El lugar de las décimas es 10 veces mayor que el lugar de las centésimas, por lo que el lugar de las centésimas es una décima parte del lugar de las décimas. El lugar de las décimas está justo después del punto decimal, y el lugar de las centésimas está dos lugares después del punto decimal.
• Elija una rutina de Conversación Estructurada para facilitar la siguiente pregunta:
◦ DOK-3 ¿Cuál es la relación entre la notación de fracciones y la notación decimal? Las fracciones y los decimales representan partes de un todo. Se leen de la misma manera. Ambos muestran la misma cantidad de diferentes maneras.
• DOK-2 ¿Cuáles son algunas maneras diferentes en las que podrías representar un valor hasta la centésima? Podrías escribir la cantidad en notación decimal, en notación fraccionaria, en forma de palabra, usando una recta numérica, usando bloques de base diez, sombreando un modelo de cuadrícula, etc.
DESPUÉS DE EXPLORAR
1. Haz que los estudiantes completen el Boleto de salida para evaluar formativamente su comprensión del concepto.
2. Completa la Tabla de anclaje como clase.
3. Haz que cada estudiante complete su Cuaderno interactivo.
APOYOS PEDAGÓGICOS
6. Antes de la Exploración, puede ser necesario hacer un repaso rápido sobre cómo medir con precisión al centímetro más cercano utilizando una regla de medir.
7. Como se utilizan bloques de base diez, puede ser útil crear una tabla de anclaje que represente un plano, una barra y un cubo unitario y sus valores como un entero, un décimo y un centésimo, respectivamente. Los estudiantes pueden consultarlo a lo largo de la Exploración.

1. Para los estudiantes que necesiten ayuda para escribir los números en notación decimal, repase cada valor posicional y la importancia del punto decimal. Enfatice cómo los valores de lugar decimal se describen como décimas y centésimas, y relacione eso con cómo se leen las fracciones. Repase que a medida que se desplaza hacia la derecha, cada valor posicional tiene un valor de una décima parte del valor posicional anterior.
2. Algunos estudiantes pueden encontrar útil una tabla de valores posicionales con cada valor decimal etiquetado hasta que adquieran confianza con la ubicación de cada valor posicional.
3. Si los estudiantes necesitan apoyo para representar la ubicación de un decimal en una recta numérica, puede ser útil proporcionarles una recta numérica con números de referencia ya etiquetados. Las Rectas numéricas surtidas están disponibles como un elemento de Ayuda complementaria en la sección Intervención del alcance.
4. Proporcione flexibilidad a los estudiantes que necesitan una carga de trabajo reducida haciéndoles completar menos problemas.
5. Como un desafío adicional, haga que los estudiantes conversen en parejas un escenario en el que observan decimales en la vida cotidiana. Los estudiantes pueden usar bloques de base diez o dibujar una recta numérica para representar este escenario como modelo.
BOLETO DE SALIDA
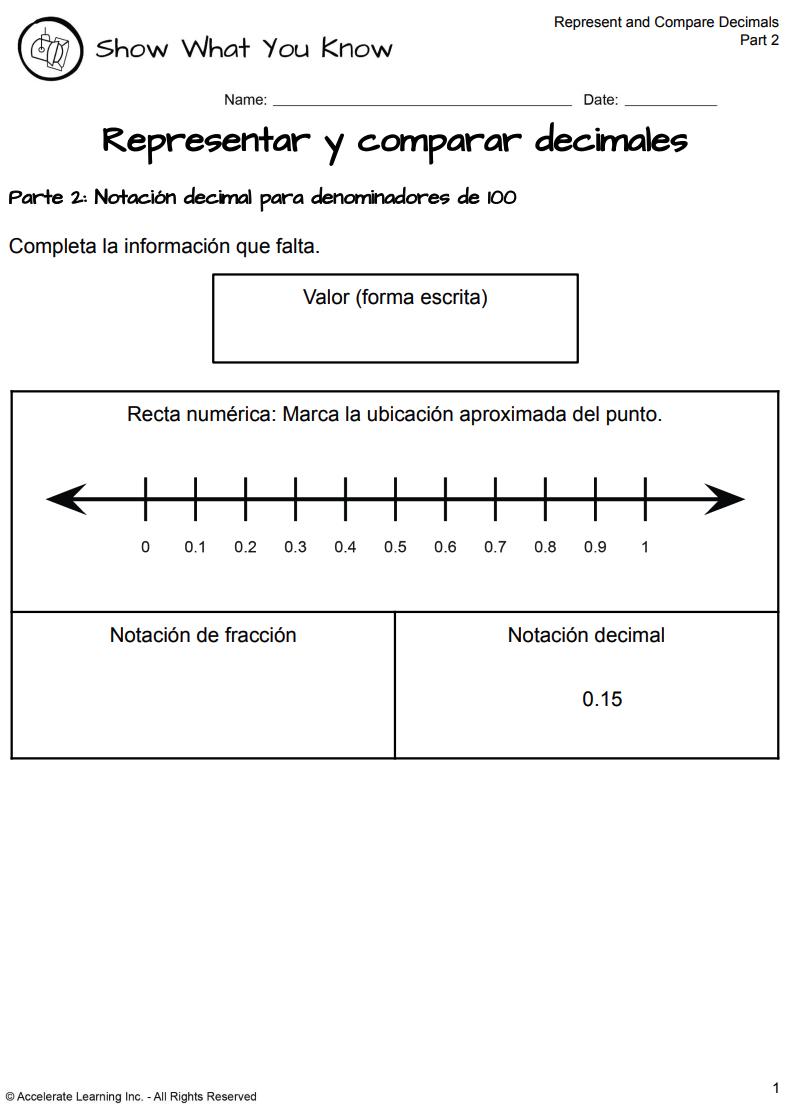
MUESTRA LO QUE SABES (PARTE 2)
APOYOS LINGÜÍSTICOS
Ayude a los estudiantes a identificar verbos en las instrucciones del Diario del estudiante, como medir, y pregúnteles cómo estos verbos dan dirección a la tarea. Pregunte cómo diferentes verbos significarían diferentes expectativas para las respuestas de los estudiantes. Pida a los estudiantes que se turnen para leer en voz alta las Tarjetas de situación antes de que trabajen juntos para medir y crear sus rectas numéricas.
Mientras los estudiantes trabajan y proponen ideas con sus grupos, resuma lo que escucha y repita las ideas clave y el vocabulario a través de la entonación, el habla más lenta y las señales visuales. Las ideas y palabras que deben escucharse incluyen décimas, centésimas, valor posicional, y decimal
Escriba los números 100, 200, 300 ... y 0.01, 0.02, 0.03 ... en la pizarra. Señale cada número en cada secuencia y demuestre la pronunciación correcta de cada número, haciendo hincapié en cien frente a centésimas. Pida a los estudiantes que repitan la pronunciación. Asegúrese de que los estudiantes escuchan la diferencia al final de la palabra y cómo ésta se relaciona con el punto decimal y los valores del número. Cuando llegue el momento de escribir, asegúrese de que los estudiantes añaden los -ths al final de los valores decimales.
Anime a los estudiantes a participar en el discurso matemático durante el trabajo en grupo. Pídales que hablen sobre la relación entre fracciones y decimales antes de responder a la última pregunta del Diario del estudiante.
Forme parejas de estudiantes y pídales que se turnen para explicar sus rectas numéricas. Cada vez que un estudiante explica su trabajo, su compañero debe reformular lo que ha dicho el estudiante y añadir sus propias ideas. Las siguientes estructuras oracionales pueden ayudar a los estudiantes en este intercambio de ideas:
• Te he oído decir _______. ¿Es correcto? ¿Es correcto?
• Te he oído decir _______. Estoy de acuerdo porque
• Te he oído decir _______. No estoy de acuerdo porque ....
EXPLORAR: EXPLORACIÓN 3
LECCIÓN PEDAGÓGICA
EXPLORACIÓN 3: REPRESENTAR Y COMPARAR DECIMALES
Estándar(es)
• Comprender la notación decimal de las fracciones y comparar fracciones decimales. Comparar dos decimales con centésimas razonando sobre su tamaño. Reconocer que las comparaciones son válidas sólo cuando los dos decimales se refieren al mismo entero. Registrar los resultados de las comparaciones con los símbolos >, =, o <, y justificar las conclusiones, por ejemplo, usando la recta numérica u otro modelo visual.
Ideas fundamentales
Modelos visuales de fracciones
Desarmar enteros, armar partes
Descubrir la forma y el espacio
Estándares para la práctica matemática
MP.2 Razonar abstracta y cuantitativamente.
MP.3 Construir argumentos viables y criticar el razonamiento de otros.
MP.4 Modelar con matemáticas.
MP.5 Utilizar estratégicamente las herramientas adecuadas.
MP.6 Atender a la precisión.
MP.7 Buscar y utilizar estructuras.
Conexiones de contenido Motores de investigación
CC3 Descomponer y recomponer
CC4 Descubrir la forma y el espacio
DI1 Dar sentido al mundo (comprender y explicar)
DI2 Predecir lo que podría ocurrir (predecir)
DESCRIPCIÓN
Los estudiantes usan su comprensión de las relaciones de valor posicional entre dígitos para representar comparaciones con decimales hasta las centésimas usando modelos visuales y los símbolos >, < y =.
MATERIALES
IMPRESO
• 1 diario del estudiante (por estudiante)
• 1 comparación de parques de atracciones (por grupo)
• 1 tapete de valor posicional (por grupo)
• 1 boleto de salida (por estudiante)
REUTILIZABLE
• 1 juego de bloques de base diez (por grupo)
• 1 protector de hojas transparente (por grupo)
• 1 marcador de borrado en seco (por grupo)
PREPARACIÓN
• Planifique que los estudiantes trabajen en grupos de 4 para completar esta actividad.
• Imprime el Diario del estudiante y un Boleto de salida para cada estudiante.
• Imprime el documento Comparación de parques de atracciones para cada grupo.
• Imprime el tapete de valor posicional en cartulina para cada grupo. Colócala en un protector de hojas para crear una superficie que se pueda borrar.
• Prepara un juego de bloques de base diez y un marcador de borrado en seco para cada grupo.
• Para los estudiantes que necesiten más apoyo para recordar información, consulte nuestros elementos de «Ayudas complementarias» que incluyen: rectas numéricas variadas, decenas base y cuadrícula base diez, disponibles en la sección «Intervención».
• ¡Hazlo digital! Haga que los estudiantes exploren o presenten sus soluciones utilizando manipulativos virtuales. Los manipulativos usados en esta lección se pueden encontrar en el menú desplegable de la sección «Explorar» y se pueden asignar digitalmente a los estudiantes.(Bloques Base Diez y Rectas numéricas)
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
5. Lea la siguiente situación a la clase: Dos parques de atracciones quieren abrir en su zona de la ciudad. Sin embargo, la ciudad dice que sólo se puede construir uno de los parques. En un esfuerzo por ser elegidos, los propietarios de ambos parques dan a los funcionarios de su ciudad algunas estadísticas sobre sus parques. La ciudad ha decidido someterlo a votación.
6. Ayude a los estudiantes a acceder a la tarea planteándoles las siguientes preguntas orientadoras:
a. ¿Cómo describirías un parque de atracciones?
b. ¿Cuáles son las características importantes de un parque de atracciones?
c. ¿Qué sabes ya sobre la comparación de números enteros o fracciones?
d. ¿Qué recuerdas sobre las relaciones de valor posicional entre las cifras de números enteros de varias cifras?
7. Entregue un juego de bloques de base diez a cada grupo y tenga una breve discusión para establecer el piso de base diez como un entero, la barra de base diez como un décimo y la unidad de base diez como una centésima.
8. Entregue un Diario del estudiante a cada estudiante.
9. Entregue la Comparación del parque de diversiones, un tapete de valor posicional y un marcador de borrado en seco a cada grupo.
10. Pida a la clase que analice y debata sobre lo que notan sobre sus Comparaciones del parque de diversiones y Tapetes de valor posicional. Haga las siguientes preguntas:
a. DOK-2 ¿Qué notan acerca de las cantidades en la Comparación del Parque de Diversiones? Observo que los valores tienen diferentes unidades: millas, dólares y minutos. Observo que algunas cantidades incluyen dígitos en el lugar de las centésimas y otras no.
b. DOK-2 ¿Qué observas en el tapete de valor posicional? Observo que hay dos lugares delante del decimal y dos lugares después del decimal. Los números enteros se llaman unidades y decenas, y los valores decimales se llaman décimas y centésimas. Hay una línea para doblar el tapete después de la décima.
i. Explique que los estudiantes pueden doblar el tapete para ocultar la centésima si los números que se comparan no llegan a ese valor posicional. Alternativamente, pueden anotar un cero en este lugar para mostrar que hay cero centésimas en el número.
c. DOK-3 ¿Por qué crees que no hay un lugar "onésimo"? Creo que no hay un lugar "oneths" porque los unos representan un entero. Se necesitan 10 décimas para hacer un entero y 100 centésimas para hacer un entero. Si hubiera 1 onésimo para hacer un entero, entonces uno y onésimo serían lo mismo.
11. Explique a los estudiantes que compararán las características de ambos parques utilizando el folleto Comparación de parques de atracciones y decidirán qué parque quieren en su ciudad basándose en las estadísticas.
1. Pida a los estudiantes que lean cada fila de la tabla en el folleto Comparación de parques de atracciones y que utilicen sus tapetes de valor posicional para representar cada estadística. Empezando por el valor posicional más alto, utilizarán sus bloques de base diez para representar y evaluar el valor de cada dígito en el tapete.
2. Pida a los estudiantes que completen el modelo sombreado o la recta numérica en sus Diarios del estudiante para cada estadística y utilicen los modelos, junto con el tapete de valor posicional, para hacer una comparación. Pida a los estudiantes que escriban en sus Diarios del estudiante dos enunciados de comparación para cada escenario utilizando >, < o =.
3. Supervise a los estudiantes y verifique la comprensión según sea necesario utilizando las siguientes preguntas guía: (Las respuestas variarán).
a. DOK-2 ¿Cómo puedes representar las estadísticas dadas en las cuadrículas sombreadas? Puedo ver qué dígito está en cada valor posicional y sombrear la cantidad correspondiente en la cuadrícula, con 1 cuadrícula completa representando 1 entero, 1 columna representando 0.1, y 1 cuadrado pequeño representando 0.01.
b. DOK-2 ¿Cómo puedes representar las estadísticas dadas en una recta numérica? Puedo ver entre qué 2 números enteros están mis cantidades y hacer que esos sean mis números enteros finales en la recta numérica. Luego puedo usar marcas de graduación para dividir el entero en partes y colocar las cantidades en el lugar correcto.
c. DOK-1 ¿Cómo puedes utilizar los bloques de base diez para modelar cada número? Puedo usar los bloques de base diez para representar el número entero, las barras de base diez para construir las décimas y las unidades de base diez para construir las centésimas.
d. DOK-2 ¿Qué proceso podrías seguir para comparar las estadísticas? Podríamos mirar primero el valor posicional mayor y mirar sólo los enteros. Si los dígitos son diferentes, podemos decir qué número es mayor basándonos en ese dígito. Si son iguales, miramos el siguiente valor posicional a la derecha y usamos esos dígitos para comparar.
e. DOK-1 Explica cómo sabes qué parque está a mayor distancia del centro de la ciudad. Ambos están a algo más de 3 km. Splashing Wild está a 46 centésimas de milla, y Screaming Good Time está a sólo otras 46 centésimas de milla. Cuarenta y seis centésimas son más que 36 centésimas, así que Splashing Wild está un poco más lejos. Puedo ver esto en mi modelo porque hay más bloques para Splashing Wild.
f. DOK-1 ¿Cómo podríamos registrar esta comparación usando símbolos? Podríamos escribir 2.46 > 2.36.
g. DOK-1 ¿Hay otra forma de escribirlo? Sí, podríamos escribir 2.36 < 2.46 porque significa lo mismo.
h. DOK-1 ¿Cómo podríamos leer esta afirmación? 2.46 es mayor que 2.36; 2.36 es menor que 2.46.
4. Después de que los estudiantes resuelvan cada comparación, compruebe su trabajo y guíeles en caso de malentendidos.
EXPLORAR: EXPLORACIÓN 3
12. Da tiempo a los estudiantes para que trabajen juntos y registren su trabajo y las respuestas a las preguntas de reflexión en sus diarios.
13. Pida a los estudiantes que compartan sus estrategias y anímales a que se hagan preguntas y establezcan conexiones. Anime a los estudiantes a notar las similitudes y diferencias entre las estrategias usadas para representar y comparar decimales hasta el lugar de las centésimas.
14. Después de la exploración, invite a la clase a una charla de matemática para compartir sus observaciones y aprendizajes.
CHARLA DE MATEMÁTICAS
• DOK-2 ¿Cómo cambia el valor de un dígito a medida que se mueve hacia la izquierda o hacia la derecha en el tapete de valor posicional? Cada lugar que mueves un dígito a la izquierda aumenta su valor 10 veces. Cada lugar que mueves un dígito a la derecha disminuye su valor en 1/10.
• DOK-2 ¿Qué proceso podrías usar para comparar dos decimales? Podría mirar primero el número de unos. Si es el mismo, entonces podría mirar el número de décimas y centésimas. Si uno tiene más décimas que el otro, entonces sé que ese número es mayor. Si los décimos son iguales, puedo usar centésimos.
• DOK-1 ¿Por qué cada comparación puede mostrarse usando dos enunciados? Los dos enunciados dicen lo mismo. Sólo cambiamos el orden de los números. Cuando hacemos eso, el símbolo cambia.
• DOK-2 ¿Cómo puede un modelo ayudarte a probar que tu comparación es correcta? Un modelo puede representar ambos números para mostrar cuál es mayor o menor. Si hay más parte del modelo sombreada o el valor está a la derecha en la recta numérica, ese número es mayor que el otro.
• Elige una rutina de conversación estructurada para facilitar la siguiente pregunta:
◦ DOK-3 ¿Qué parque elegirías construir? Explica. Construiría Screaming Good Time porque está más cerca del centro de la ciudad, cuesta menos entrar y tiene un tiempo de espera más corto.
DESPUÉS DE EXPLORAR
1. Haga que los estudiantes completen el boleto de Salida para evaluar formativamente su comprensión del concepto.
2. Completen la tabla de anclaje como clase.
3. Haga que cada estudiante complete su libreta interactiva.
4. Regrese a la sección «captar interés» e instruya a los estudiantes para que usen sus habilidades recién adquiridas para completar exitosamente la actividad.
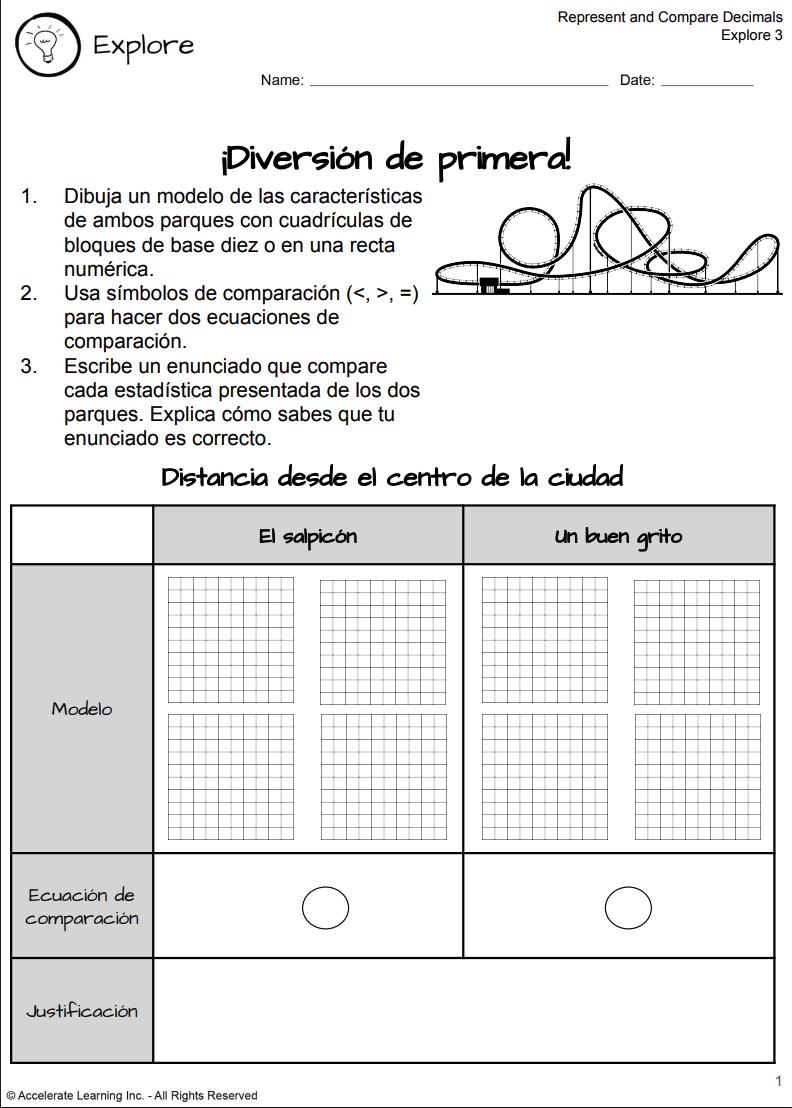
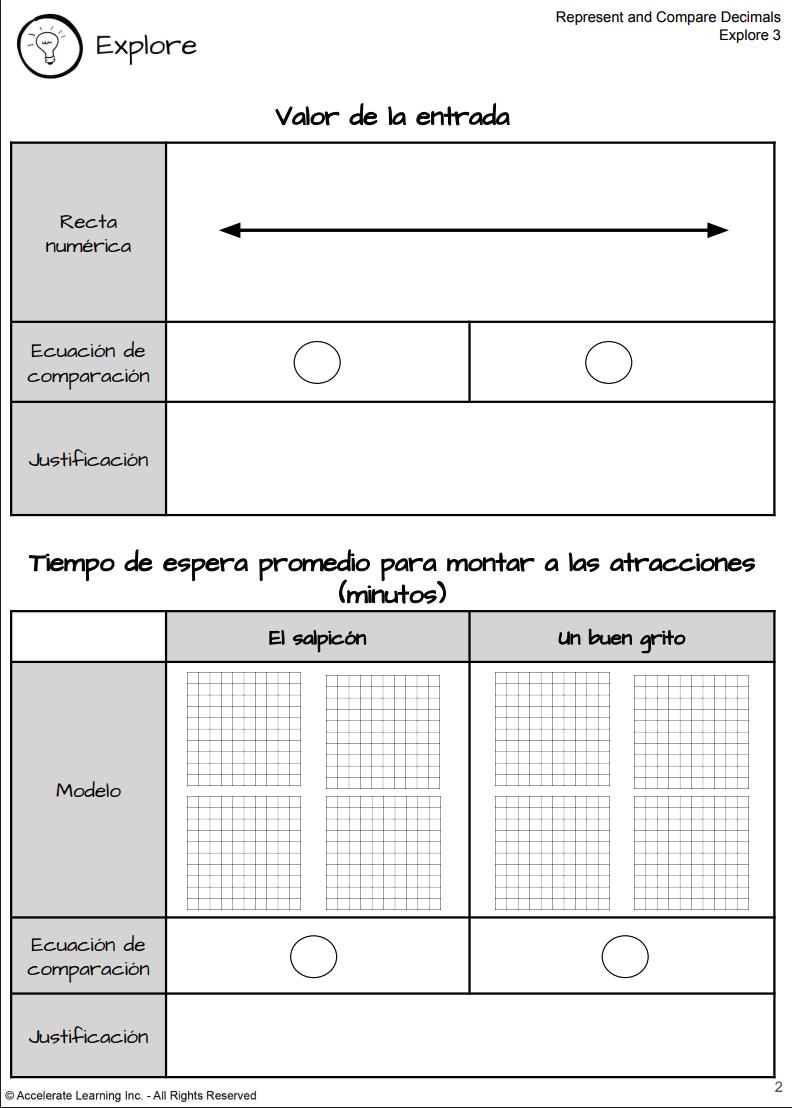
DIARIO DEL ESTUDIANTE
EXPLORAR: EXPLORACIÓN 3
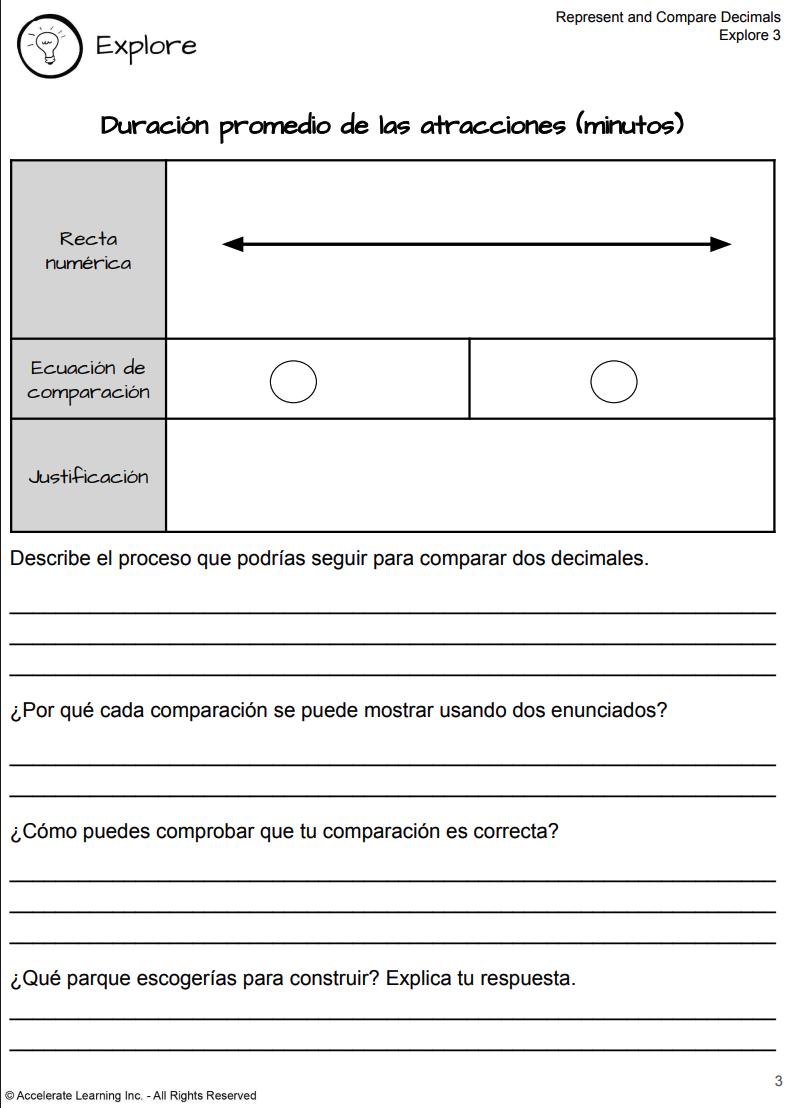
DIARIO DEL ESTUDIANTE

BOLETO DE SALIDA
APOYOS PEDAGÓGICOS
1. Si los estudiantes necesitan ayuda para representar las cantidades con bloques de base diez, guíelos para que ordenen sus bloques de base diez en montones colocando los bloques de base diez correspondientes sobre el valor posicional relacionado en el tapete de valor posicional. Luego, cuando se da un valor, los estudiantes pueden contar el número designado de bloques para ese valor posicional y colocarlos en el tapete.
2. Si los estudiantes necesitan ayuda relacionada con la representación del modelo, aliéntelos a sombrear primero los pisos. A continuación, pueden contar el número de décimas, o barras de base diez, que han representado y sombrear el mismo número de columnas en el siguiente modelo. A continuación, los estudiantes pueden contar el número de centésimas, o unidades de base diez, que han representado y sombrear la misma cantidad de unidades en el mismo modelo en el que sombrearon las décimas.
3. Para los estudiantes que necesiten ayuda con los enunciados de comparación, revise los símbolos de comparación y cree un gráfico de anclaje si es necesario.
4. Cuando los estudiantes comprueban el valor posicional, es posible que olviden moverse de izquierda a derecha. Ayúdeles a hacer la conexión que esta misma dirección se aplica al leer el texto. Para ayudar a mantener un registro de cada posición de valor posicional, haga que los estudiantes tachen o cubran los dígitos de valor posicional de izquierda a derecha a medida que se compara cada dígito.
5. Si los estudiantes necesitan apoyo para representar la ubicación en la recta numérica, puede ser útil proporcionar una recta numérica con números de referencia ya etiquetados. Las Rectas numéricas surtidas están disponibles como un elemento de Ayuda complementaria en la sección Intervención del alcance.
6. Si los estudiantes necesitan apoyo adicional con el proceso de comparación de decimales, entonces pida a los estudiantes que cubran cada valor posicional con una hoja de papel y trabajen de izquierda a derecha. Asegúrese de que los estudiantes comprendan que los puntos decimales siempre deben estar alineados verticalmente para que cada valor posicional esté alineado correctamente. Proporcione papel cuadriculado, disponible como elemento de ayuda complementaria en la sección Intervención del alcance de aplicación, según sea necesario para ayudar a los estudiantes a organizar sus valores para la comparación.
7. Puede ser necesario recordar a los estudiantes que si un decimal sólo tiene un valor en la décima, significa que hay un 0 en la centésima. Esto puede ser útil si están tratando de alinear decimales para comparar.
8. Busque oportunidades para enfatizar lo duro que los estudiantes están trabajando y el beneficio de la lucha productiva cuando se aprende algo nuevo.
9. Como extensión, pida a los estudiantes que creen su propia estadística de comparación de parques de atracciones y luego utilicen la alfombrilla de valor posicional para comparar. Anímales a comparar los valores de sus tarjetas sin sus bloques de base diez. Pueden colgar sus tarjetas para compartirlas con la clase o intercambiarlas con sus compañeros.
EXPLORAR: EXPLORACIÓN 3
APOYOS LINGÜÍSTICOS
Antes de que los estudiantes construyan sus modelos y resuelvan, pídales que se turnen para leer en voz alta las estadísticas de comparación del parque de atracciones.
Utiliza gestos con las manos para enfatizar el tamaño. Por ejemplo, cuando digan "mayor que", abran bien los brazos y cuando digan "menor que", junten bien las manos.
Escuche las conversaciones dentro de los grupos de estudiantes y recoja el lenguaje que utilizan mientras revisan la información de las tarjetas. Anote las palabras y frases con dibujos que representen esos términos y ayude a los estudiantes a utilizarlos. Algunas palabras que podría escuchar son las siguientes: mayor que, menor que, igual a, décimas, centésimas, punto decimal, diez veces, y una décima
Cree estructuras de frases para ayudar a los estudiantes en su comunicación escrita y verbal durante la Exploración:
• Sé que ____ es ____(mayor/menor) que ____ porque ____.
• Puedo ver en mi modelo, ____.
• ___ es igual a ____ porque ____.
Invite a los estudiantes a presentar uno de sus modelos a la clase y a explicar los pasos que siguieron para resolver la comparación.
A medida que los estudiantes responden a las preguntas de reflexión, pídales que se turnen primero para decir sus respuestas en voz alta a un compañero, para recibir comentarios de su compañero y luego para escribir sus respuestas en sus Diarios del estudiante. Los estudiantes pueden revisar sus respuestas si es necesario.
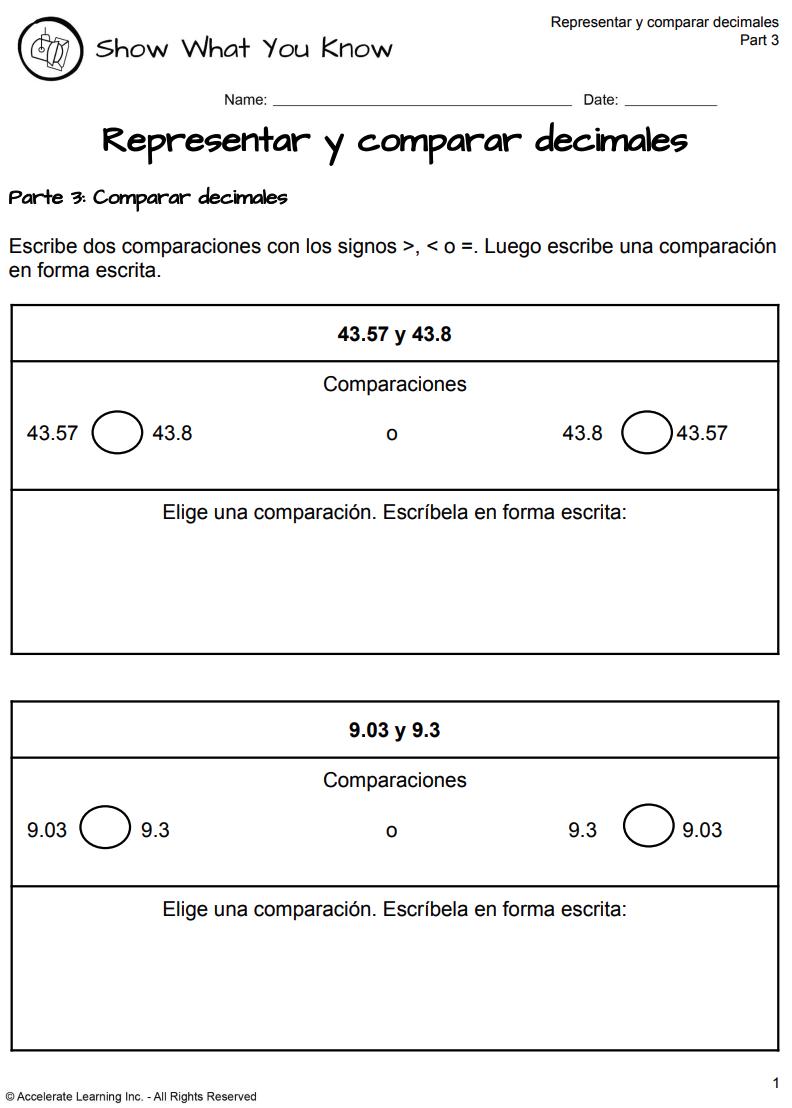
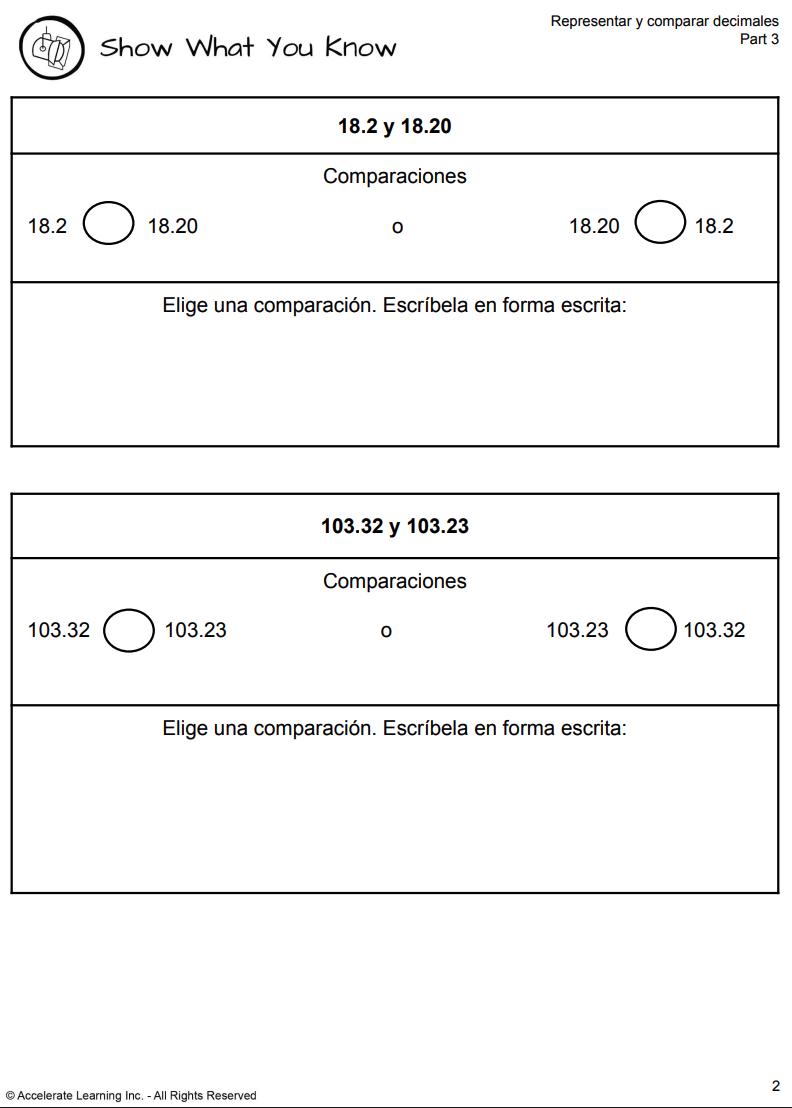
MUESTRA LO QUE SABES (PARTE 3)
DESCRIPCIÓN
Los estudiantes tienen la oportunidad de utilizar sus conocimientos lingüísticos y culturales para apoyar las conexiones con nuevas habilidades, vocabulario y conceptos en sus niveles de competencia.
MATERIALES
IMPRESO
• 1 Folleto del estudiante en el nivel de competencia (por estudiante)
• 1 Tabla de valor posicional (por estudiante)
REUTILIZABLE
• 1 Juego de bloques de base diez, incluyendo 9 centenas, 9 decenas y 9 unidades (por estudiante)
PREPARACIÓN
• Determine el nivel de competencia en inglés de cada estudiante.
• Imprima un Folleto para el estudiante para cada nivel de inglés.
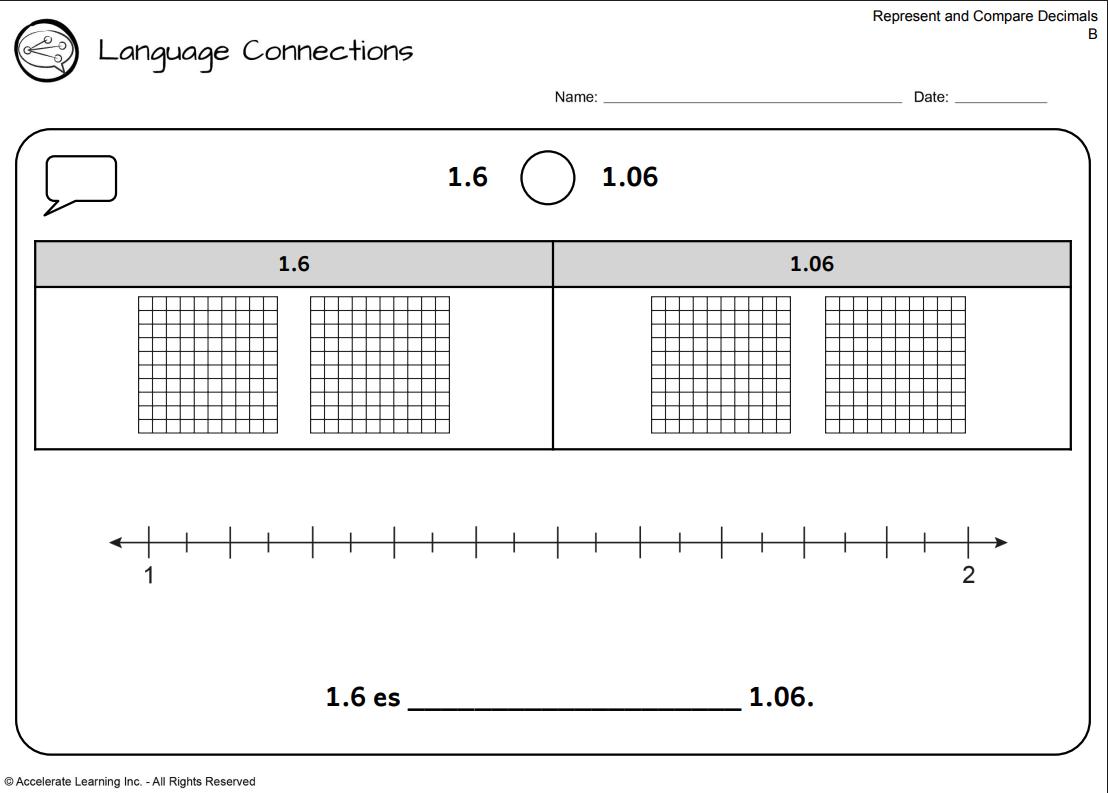


PRINCIPIANTE
FOLLETO DEL ESTUDIANTE
EXPLICAR: CONEXIONES LINGÜÍSTICAS
APOYO PARA ESTUDIANTES MULTILINGÜES
CONEXIONES LINGÜÍSTICAS
• Imprima la Tabla de valor posicional para cada estudiante.
• Permita que los estudiantes tengan acceso al Vocabulario ilustrado para este alcance.
• Permita que los estudiantes tengan acceso a materiales manipulativos, como bloques de base diez.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1 Distribuya un Folleto para el estudiante con el nivel de competencia adecuado a cada estudiante.
2 Utilice las instrucciones para las partes de comprensión auditiva, expresión oral, lectura y escritura. Utilice gestos, señale objetos y elementos visuales, según proceda. Consulte las indicaciones para obtener sugerencias.
3 Conceda tiempo a los estudiantes para que piensen con sus vecinos antes de responder.
4 Anime a los estudiantes a perseverar en su pensamiento y a utilizar herramientas y modelos matemáticos.
5 Invite a los estudiantes a responder adecuadamente a cada dominio lingüístico.
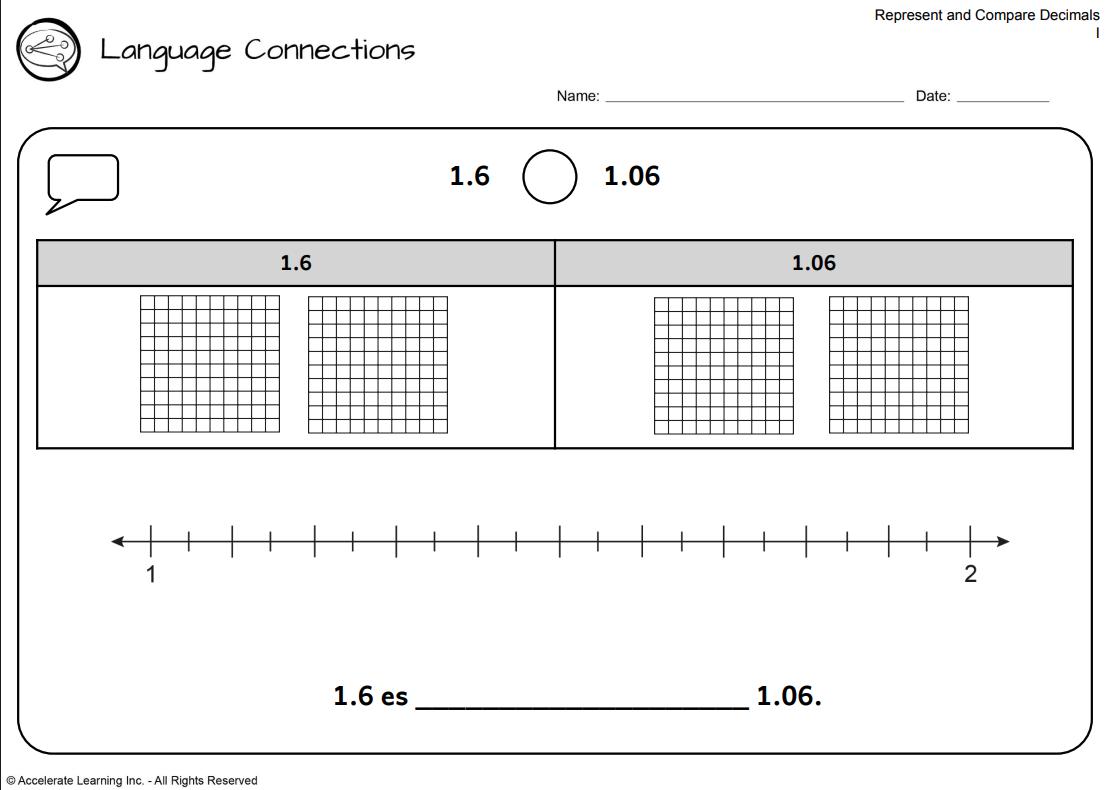
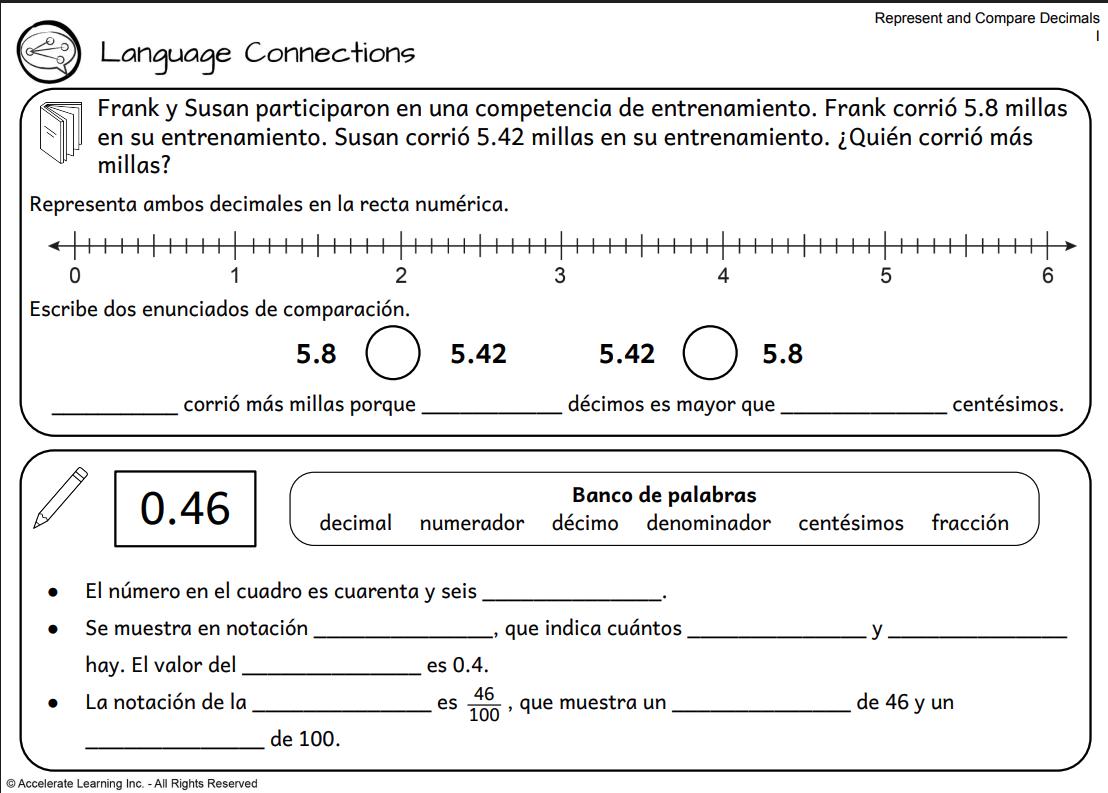

INTERMEDIO FOLLETO DEL ESTUDIANTE
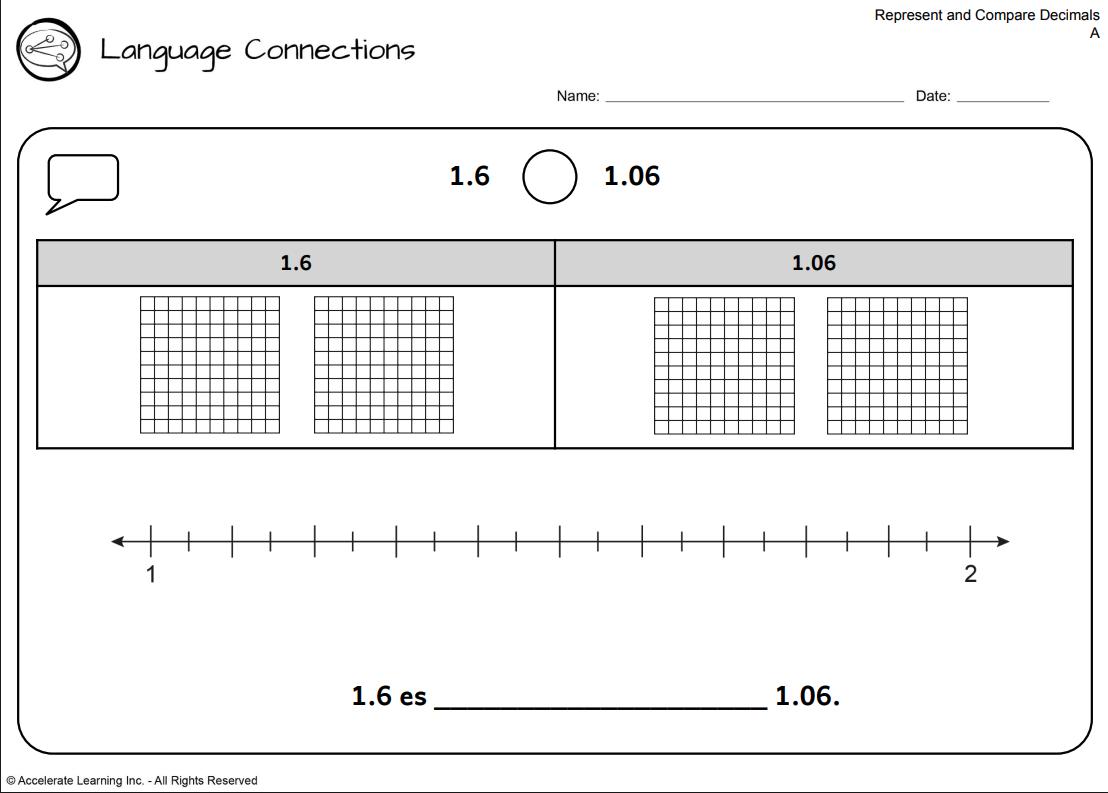

AVANZADO FOLLETO DEL ESTUDIANTE
ESCRIBIR
PRINCIPIANTE
Ponga a disposición de los estudiantes tablas de valor posicional y bloques de base diez. Leer el número de la casilla (señalar el número). Lea y comente las palabras del banco de palabras. Defina y proporcione ejemplos según sea necesario.
• Invite a los estudiantes a leer cada enunciado con usted.
• Plantee los enunciados para asegurarse de que los estudiantes entienden las oraciones.
• Guíe a los estudiantes hacia el número en el recuadro y el banco de palabras.
◦ ¿Cuál de las palabras en el banco de palabras (señale el banco de palabras) se ajusta mejor al espacio en blanco?
INTERMEDIO
Tenga a disposición de los estudiantes Tablas de valor posicional y bloques de base diez. Lectura coral del número de la casilla. Coro: lea y comente las palabras del banco de palabras. Defina y proporcione ejemplos según sea necesario.
• Coro: lea cada enunciado y las preguntas, y permita que los estudiantes debatan con sus compañeros. ¿Cómo se pueden utilizar las palabras del banco de palabras para rellenar los espacios en blanco y responder a las preguntas?
• Dé tiempo a los estudiantes para que rellenen los espacios en blanco de cada enunciado.
• Revise sus respuestas en grupo o invite a los estudiantes a debatirlas con sus compañeros.
AVANZADO
Tenga a disposición de los estudiantes tablas de valor posicional y bloques de base diez. Pida a los estudiantes que lean el número de la casilla a sus compañeros. Asegúrese de comprobar la exactitud mientras leen el número.
• Dé tiempo a los estudiantes para que respondan a las preguntas con sus compañeros.
• Invite a los estudiantes a debatir las preguntas con sus compañeros.
• ¿Cómo puedes añadir o mejorar una de tus respuestas?
• Dé tiempo a los estudiantes para que modifiquen sus respuestas basándose en los comentarios de sus compañeros.
PRINCIPIANTE
Disponga de tablas de valor posicional para que los estudiantes las utilicen. Lea en grupo el problema de la historia. Pida a los estudiantes que señalen cada palabra mientras leen. Invite a los estudiantes a marcar con un círculo las palabras que no conozcan. Revisen las palabras entre todos, proporcionando ejemplos cuando sea necesario.
• Haga las siguientes preguntas, animando a los estudiantes a consultar la lectura para encontrar las respuestas.
◦ ¿Por qué corrían Frank y Susan?
◦ ¿Cuántas millas corrió Frank?
◦ ¿Cuántas millas corrió Susan?
• Señale la recta numérica y lea las instrucciones. Trace, o ponga un punto, donde está cada decimal en la recta numérica.
• ¿Quién corrió más millas? Señale el problema de la historia.
• Lea el resto de las instrucciones, alentando a los estudiantes a referirse al problema para encontrar las respuestas pidiéndoles que señalen.
• Permita que los estudiantes usen tablas de valor posicional según sea necesario.
INTERMEDIO
Tenga tablas de valor posicional disponibles para que los estudiantes las usen. Coro: lea el problema de la historia en grupo. Pida a los estudiantes que señalen cada palabra mientras leen. Invite a los estudiantes a marcar con un círculo las palabras que no conozcan. Revisen las palabras juntos o en parejas, proporcionando ejemplos según sea necesario.
• Comparta con sus compañeros dos cosas que sepa sobre el problema de la historia. Señale dónde puede encontrarlas en el párrafo.
• Coro: lea las instrucciones debajo del problema de la historia de a uno por vez.
• Aliente a los estudiantes a consultar el problema de la historia con sus compañeros para encontrar las respuestas.
• Permita que los estudiantes utilicen tablas de valor posicional según sea necesario.
AVANZADO
Tenga tablas de valor posicional disponibles para que los estudiantes las utilicen. Anime a los estudiantes a leer la historia con sus compañeros. Pídales que rodeen con un círculo las palabras que no conozcan. Revisen las palabras juntos o en parejas, proporcionando ejemplos según sea necesario.
• ¿Qué información tienes sobre el problema? Señala dónde puedes encontrarla en el párrafo.
• ¿Qué pide el problema? ¿Cómo lo sabes?
• Haga que los estudiantes lean las instrucciones en parejas.
• Anime a los estudiantes a referirse al problema para responder a las preguntas.
• Permita que los estudiantes utilicen tablas de valor posicional y manipulativos según sea necesario.
PRINCIPIANTE
Tenga bloques de base diez y tablas de valor posicional a disposición de los estudiantes. Lea las siguientes instrucciones de uno en uno:
• Señale el decimal 1.6. ¿Cómo se dice este número? Pida a los estudiantes que se hagan eco de usted o que utilicen la siguiente secuencia de frases:
◦ Este decimal es...
• Señale el decimal 1.06. Pida a los estudiantes que utilicen la siguiente secuencia de frases. Pida a los estudiantes que le hagan eco o que utilicen la siguiente secuencia de frases:
◦ Este decimal es...
• Describa el modelo sombreado de 1.6 que aparece en su folleto.
◦ ¿Cuántos enteros hay? ¿Cuántas décimas hay? Pida a los estudiantes que utilicen los siguientes marcos de frases:
• He sombreado _____ enteros.
• He sombreado _____ décimos.
• Describa el modelo sombreado para 1.06 en su hoja.
◦ ¿Cuántos enteros hay? ¿Cuántos centésimos hay? Pida a los estudiantes que usen los siguientes marcos de oraciones:
• Yo sombreé _____ enteros.
• Yo sombreé _____ centésimos.
• ¿En qué se parecen o son iguales estos decimales? Pida a los estudiantes que usen la siguiente secuencia de oraciones:
◦ Los decimales son similares porque...
• ¿En qué se diferencian estos decimales?
◦ Los decimales son diferentes porque...
• ¿Dónde trazaste los decimales en la recta numérica?
◦ Tracé el 1.6...
◦ Tracé el 1.06...
• ¿Qué te dice esto? Pida a los estudiantes que usen el siguiente marco de oraciones:
◦ Esto me dice que _____ es mayor que
INTERMEDIO
Tenga bloques de base diez y tablas de valor posicional disponibles para que los estudiantes los usen. Lea las siguientes instrucciones de uno en uno:
• Observen los decimales 1.6 y 1.06.
• Compartan con sus compañeros lo que notan acerca de los decimales.
◦ ¿Cuál es el valor posicional del 6 en el decimal 1.6?Pida a los estudiantes que utilicen la siguiente secuencia:
• En 1.6, el 6 se encuentra en...
◦ ¿Cuál es el valor posicional del 6 en el decimal 1.06? Pida a los estudiantes que utilicen la siguiente secuencia:
• En 1.06, el 6 se encuentra en...
• Señale el decimal 1.6. ¿Cómo se lee este decimal? ¿Cómo se lee este decimal? Pida a los estudiantes que utilicen la siguiente secuencia:
◦ Este decimal se lee...
• Señale el decimal 1.06. ¿Cómo se dice este decimal? Pida a los estudiantes que utilicen la siguiente secuencia:
◦ Este decimal es...
• Describa a sus compañeros el modelo sombreado para 1.6 que aparece en su hoja de trabajo. Pida a los estudiantes que utilicen los siguientes marcos de frases:
◦ He sombreado _____ enteros.
◦ He sombreado _____ décimos.
• Describe a tus compañeros el modelo sombreado para 1.06 en tu hoja de trabajo. Haz que los estudiantes usen los siguientes marcos de oraciones:
◦ Sombreé _____ enteros.
◦ Sombreé _____ centésimos.
• Explica a tu compañero en qué se parecen y en qué se diferencian estos decimales.Pida a los estudiantes que usen los siguientes marcos de oraciones:
◦ Ambos decimales tienen...
◦ Estos decimales son diferentes porque...
• Explique a sus compañeros cómo se trazan ambos números en la recta numérica.
• Compare estos decimales de dos maneras usando palabras.Pida a los estudiantes que usen los siguientes marcos de oraciones:
◦ ____ es mayor que ____.
◦ ____ es menor que ____.
AVANZADO
Tenga bloques de base diez y Tablas de valor posicional disponibles para que los estudiantes los usen. Lea las siguientes instrucciones de uno en uno:
• Fíjese en los decimales 1.6 y 1.06. Comparte con tus compañeros lo que observas en los decimales.
• ¿Cómo se leen en voz alta ambos decimales? Comparte con tus compañeros.
• Explica a tus compañeros cómo sombreaste tu modelo para mostrar el decimal 1.6.
• Explica a tus compañeros cómo sombreaste tu modelo para mostrar el decimal 1.06.
• Explica a tus compañeros en qué se parecen y en qué se diferencian estos decimales.Pida a los estudiantes que utilicen los siguientes enunciados:
◦ Ambos decimales tienen...
◦ Estos decimales son diferentes porque...
• Explique a sus compañeros cómo se trazan ambos números en la recta numérica en relación con el otro.
• Compare estos decimales de dos maneras utilizando palabras.
ESCUCHAR
PRINCIPIANTE
Ponga a disposición de los estudiantes bloques de base diez y tablas de valor posicional. Lea las siguientes instrucciones una a la vez:
• Lea los números en la parte superior de la página conmigo. Señale los decimales.
• Use sus bloques de base diez (señale los bloques de base diez) para hacer modelos de los decimales.
• Sombree 1.6 (punto) y 1.06 (punto) en los modelos de base diez (punto).
• Mire la recta numérica. Señale la recta numérica.
◦ Trace, o ponga un punto, donde se encuentran ambos decimales.
◦ Rotule los decimales sobre el punto.
• Use los modelos(punto) y la recta numérica(punto) para comparar ambos números.
◦ Compare los números escribiendo el símbolo mayor que, menor que o igual a.Señale dónde escribirán la comparación.
• Termine el enunciado de comparación(punto) usando menor que, mayor que o igual a.
INTERMEDIO
Tenga bloques de base diez y Tablas de valor posicional disponibles para que los estudiantes los usen. Lea las siguientes instrucciones una a la vez:
• Lea los números en la parte superior de la página con un compañero.
• Use sus bloques de base diez para hacer modelos de los decimales.
• Sombree 1.6 y 1.06 en los modelos de base diez.
• Mire la recta numérica.
◦ Trace, o ponga un punto, donde se encuentran ambos decimales.
◦ Etiquete los decimales sobre el punto.
• Use los modelos y la recta numérica para comparar ambos números.
◦ Compare los números escribiendo el símbolo mayor que, menor que o igual a. Señale dónde escribirán la comparación.
• Termine la comparación usando menor que, mayor que o igual a.
AVANZADO
Tenga bloques de base diez y tablas de valor posicional disponibles para que los estudiantes las usen. Lea las siguientes instrucciones una a la vez:
• Lea los números en la parte superior de la página con sus compañeros.
• Use sus bloques de base diez para crear modelos de los decimales.
• Sombree 1.6 y 1.06 en los modelos de cuadrícula en su folleto.
• Mire la recta numérica.
◦ Traza y rotula ambos decimales en la recta numérica.
• Usa los modelos y la recta numérica para comparar ambos números.
◦ Compara los números escribiendo el símbolo mayor que, menor que o igual a.
• Termina el enunciado de comparación usando menor que, mayor que o igual a.
USO DE STEMSCOPES MATH
RECURSOS PARA MAESTROS
El alcance y la secuencia sugeridos para cada grado se basan en un calendario escolar de 180 días. La progresión natural de las matemáticas fue el factor más importante a la hora de determinar el orden de los alcances. ¿Tiene su propio alcance y secuencia? ¡No hay problema! Enseñe los alcances en cualquier orden para satisfacer las necesidades de los estudiantes en su aula. Las únicas actividades afectadas son el «revisión en espiral» y las evaluaciones de Referencia. ¡Encuentre el alcance y la secuencia en los Recursos del Maestro de su nivel de grado!


FOLLETO DEL ESTUDIANTE
EXPLICAR: MIS PENSAMIENTOS DE MATEMÁTICAS
ANALIZAR EL PENSAMIENTO DEL ESTUDIANTE
MIS PENSAMIENTOS DE MATEMÁTICAS
DESCRIPCIÓN
Los estudiantes tendrán la oportunidad de escribir sus pensamientos e ideas matemáticas utilizando las siguientes tres vías diferentes:
Imagen Tipo Descripción



Contenido Escritura sobre conceptos y relaciones matemáticas
Proceso Escritura centrada en la resolución de problemas, estrategias y procedimientos
Afectivo Escritura sobre la actitud, experiencia o mentalidad de un estudiante hacia las matemáticas.
Los iconos de arriba se proporcionan en cada actividad con el fin de darle orientación en cuanto a qué tipo de escritura se utilizará. Los tres tipos se entrelazarán a lo largo del programa para garantizar un enfoque equilibrado de la escritura en matemáticas.
MATERIALES
IMPRESOS
• 1 folleto para el estudiante (por estudiante)
REUTILIZABLES
• Acceso a herramientas y modelos matemáticos (por clase)
PREPARACIÓN
• Permita que los estudiantes tengan acceso a una variedad de herramientas matemáticas, como bloques de valor posicional y círculos de fracciones, y modelos matemáticos como tablas de valor posicional, muros de fracciones, rectas numéricas, etc.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Permita que los estudiantes planteen su pensamiento a un compañero antes de escribirlos en papel.
2. Anime a los estudiantes a perseverar en su pensamiento y a utilizar herramientas y modelos matemáticos según sea necesario.
3. Invite a los estudiantes a escribir sus respuestas en oraciones completas utilizando ortografía, gramática y puntuación correctas.
EXPLICAR: VOCABULARIO ILUSTRADO
PALABRAS QUE HAY QUE CONOCER
VOCABULARIO
ILUSTRADO

Comparar
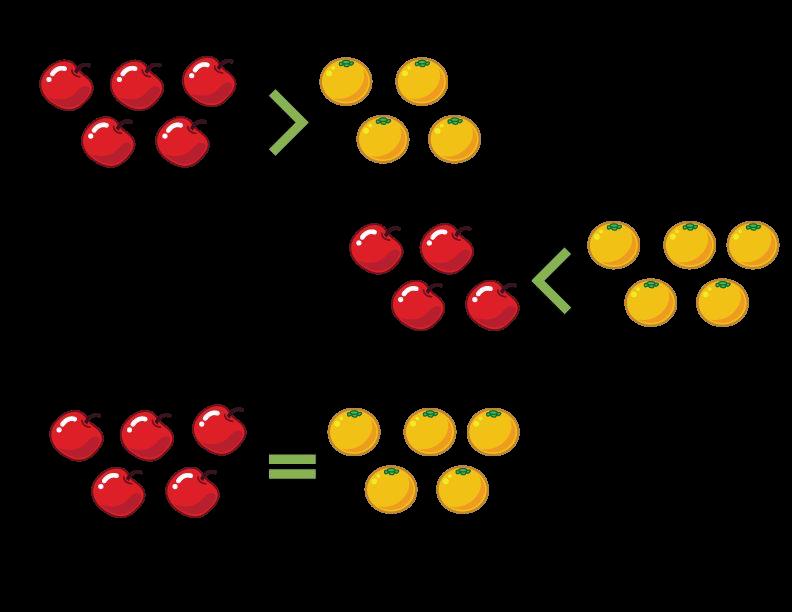
Determinar similitudes o diferencias entre dos o más objetos o números

Punto decimal

El punto entre un número entero y una parte de un número entero

Equivalente
La misma cantidad o valor

Menos que

Menor que; que muestra una relación entre números; <

Valor de posición
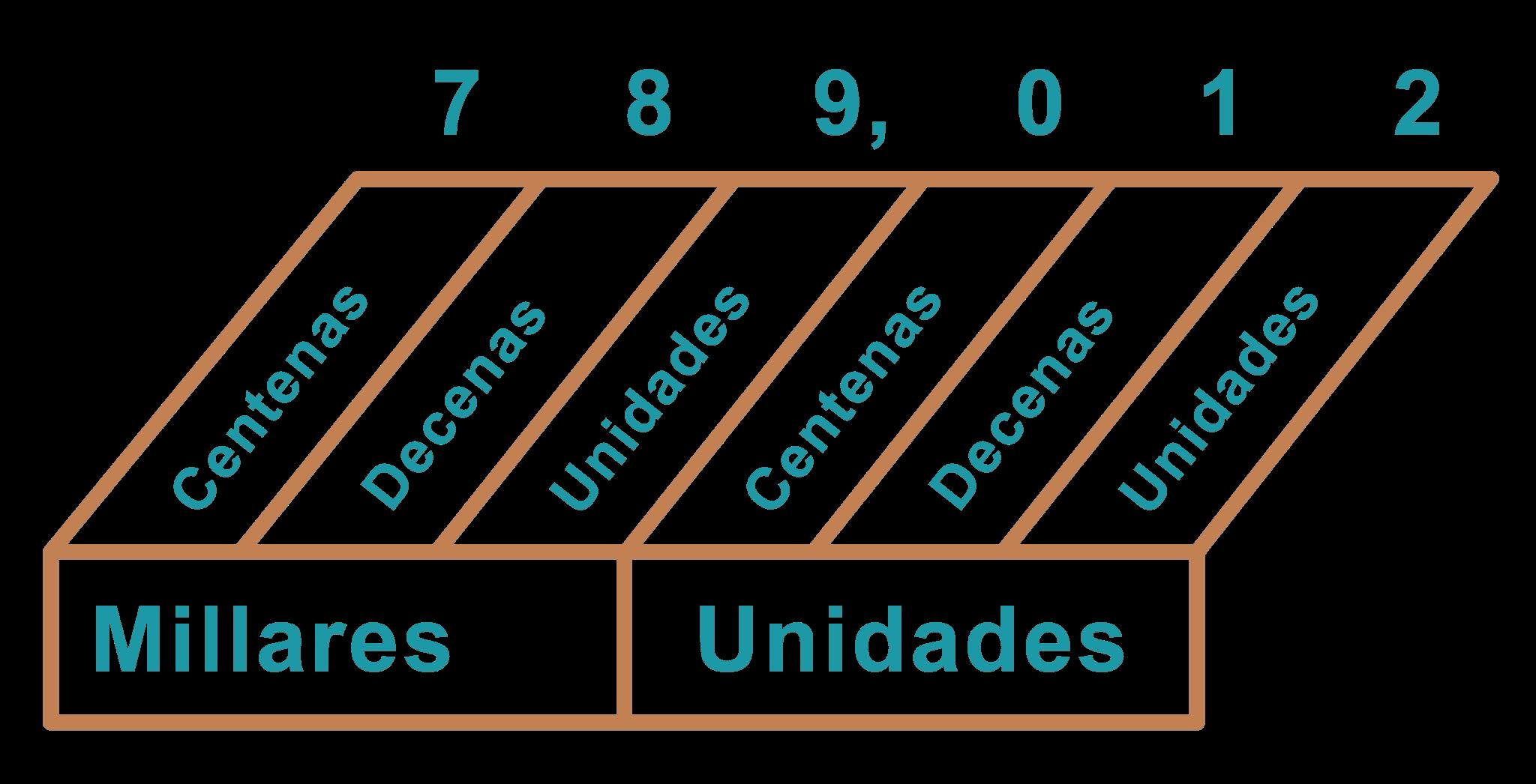
El valor de un dígito que depende de su ubicación en un número
Valor
Decimal
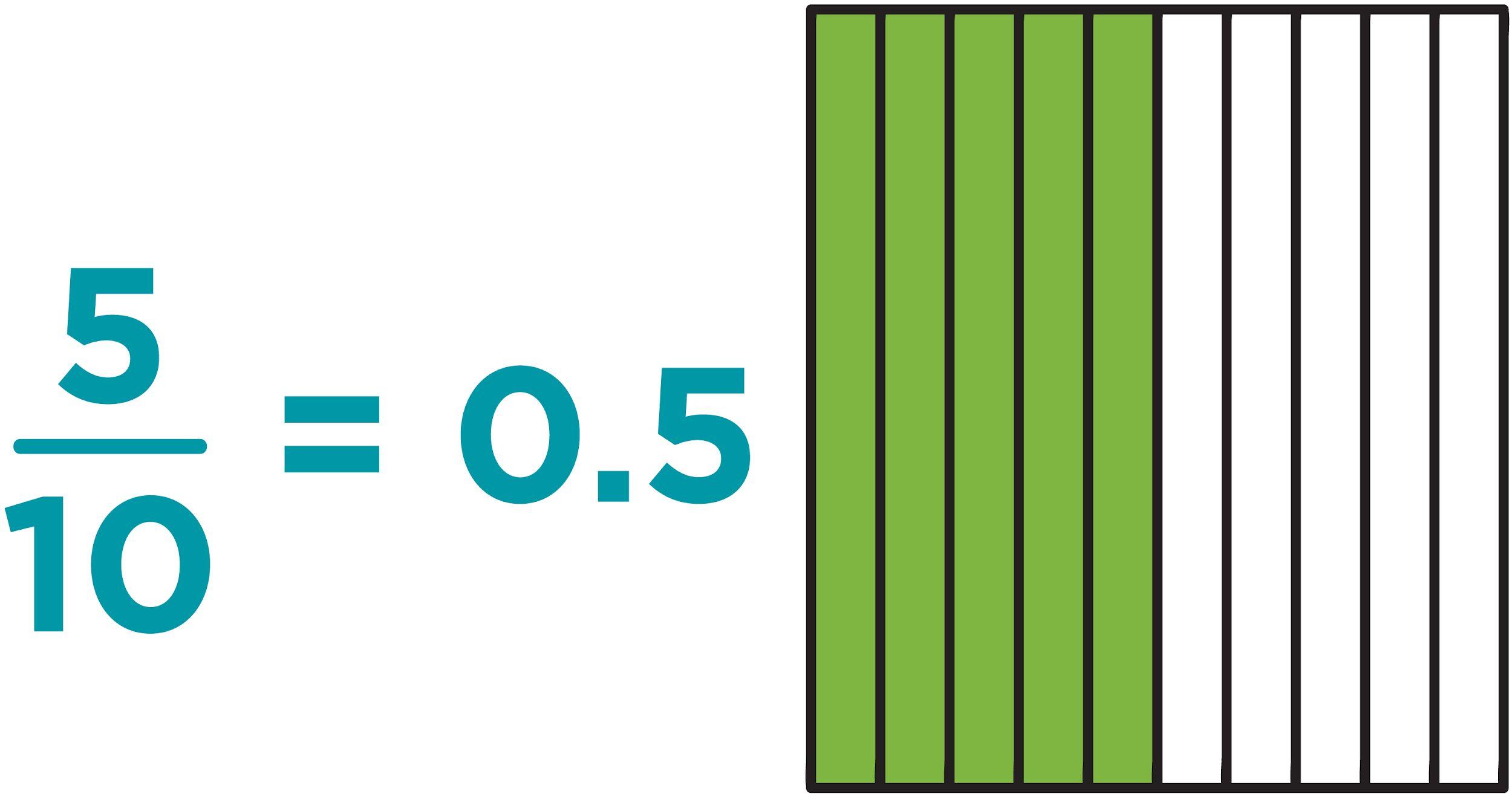
Fracción con un denominador que es una potencia de 10 y que se escribe con dígitos a la derecha del punto decimal


Denominador
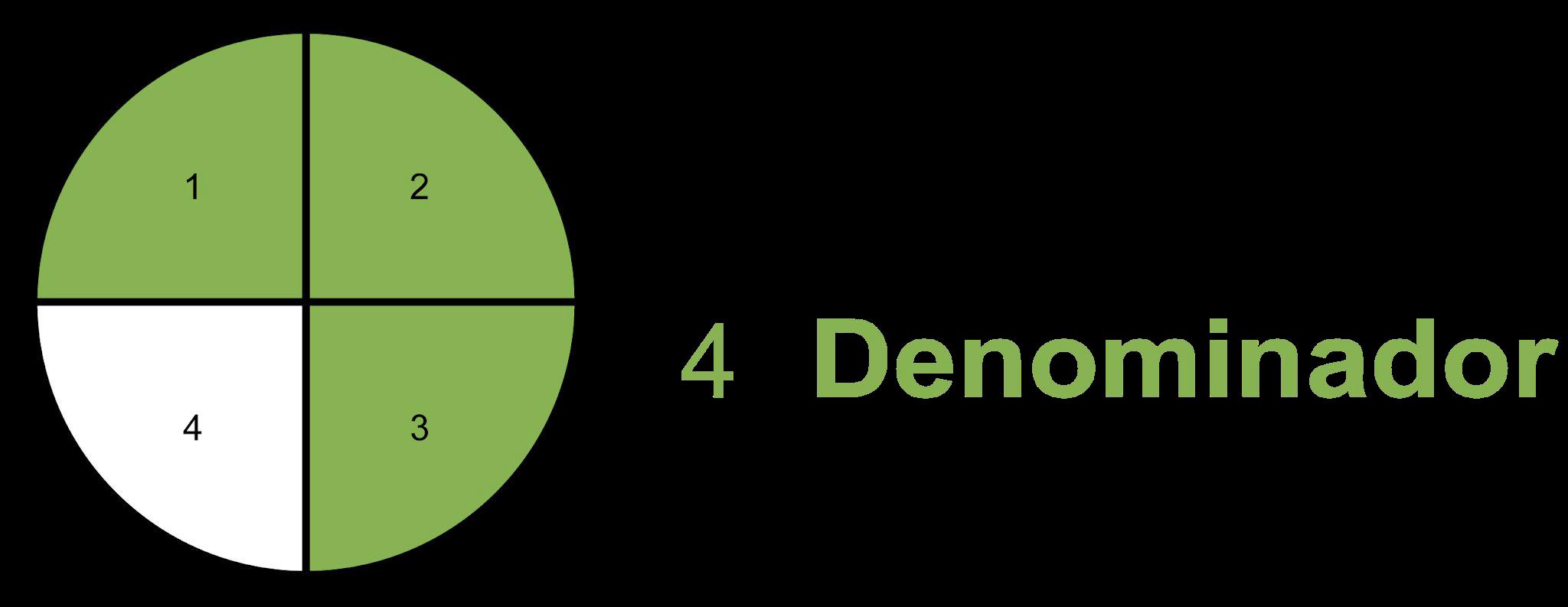
Número inferior de una fracción; representa el número total de partes iguales en un todo

Fracción

Una parte de un grupo de objetos, de un número o de un entero

Recta numérica
Línea con marcas de graduación espaciadas uniformemente para mostrar la posición de un número en relación con otros números

Representar
Mostrar de alguna manera; simbolizar algo

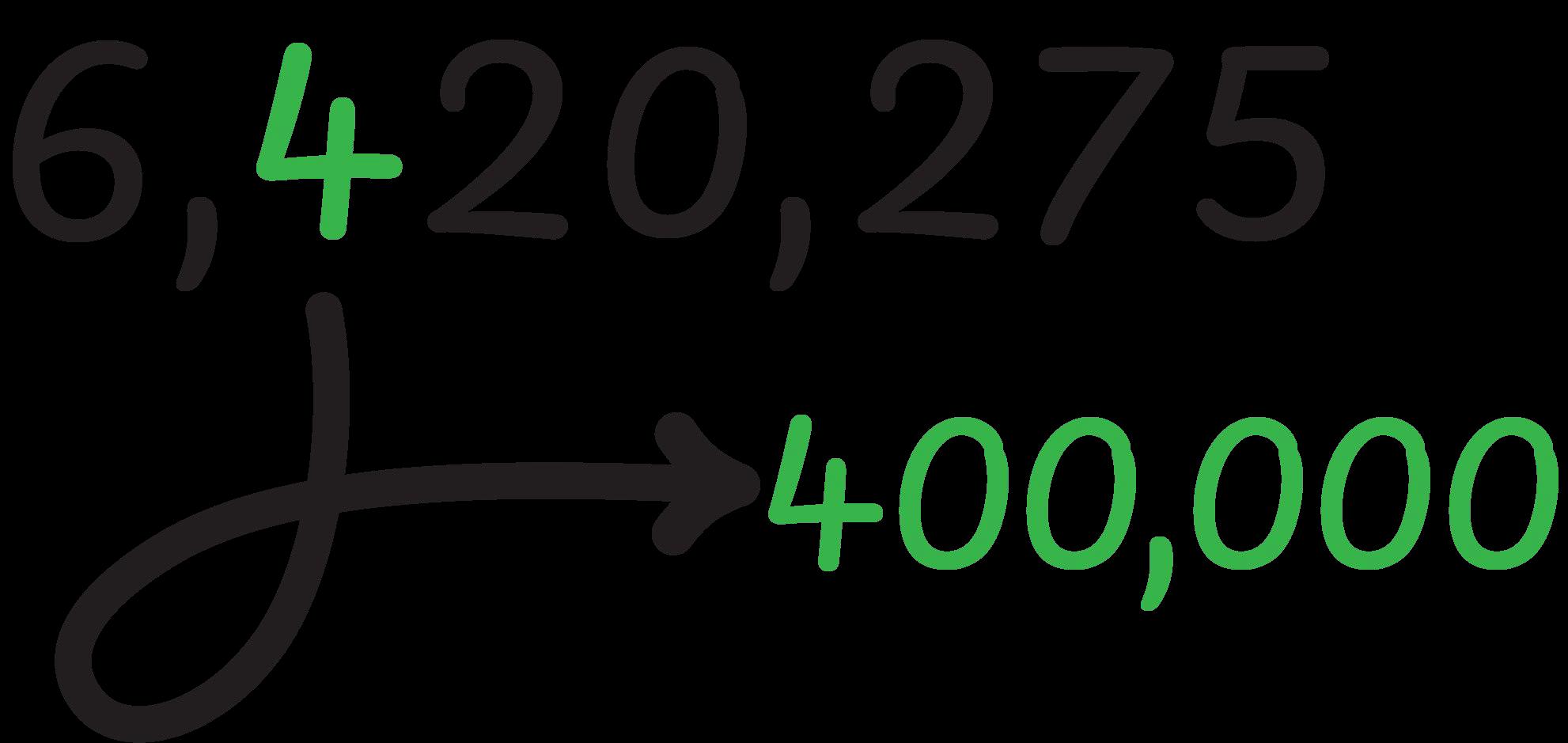
Cantidad total de algo; cuánto vale algo
Fracción decimal
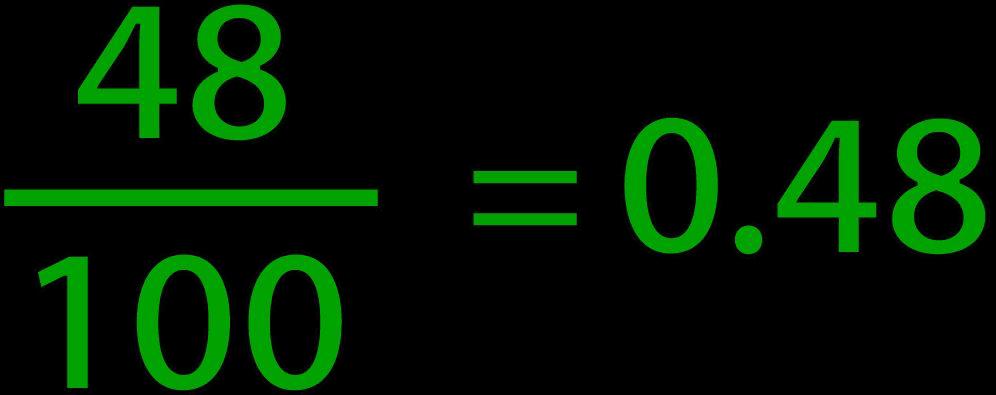
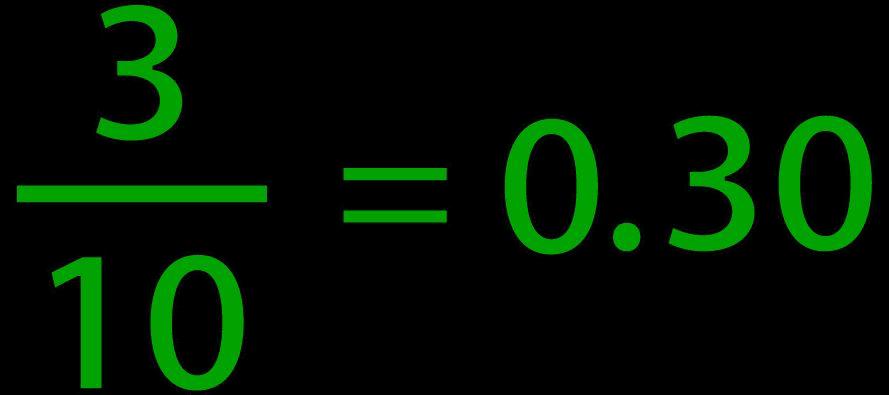
Fracción en donde el denominador es una potencia de 10, como 10 o 100


Dígito
Cualquier número del 0 al 9

Mayor que

Más que; que muestra una relación entre números; >

Numerador

Número superior en una fracción; representa parte de un todo

Signo

N t ión d i l

Número que utiliza el punto decimal en el lugar correcto

Igual a

La misma cantidad en comparación con otra cantidad

Centésimos
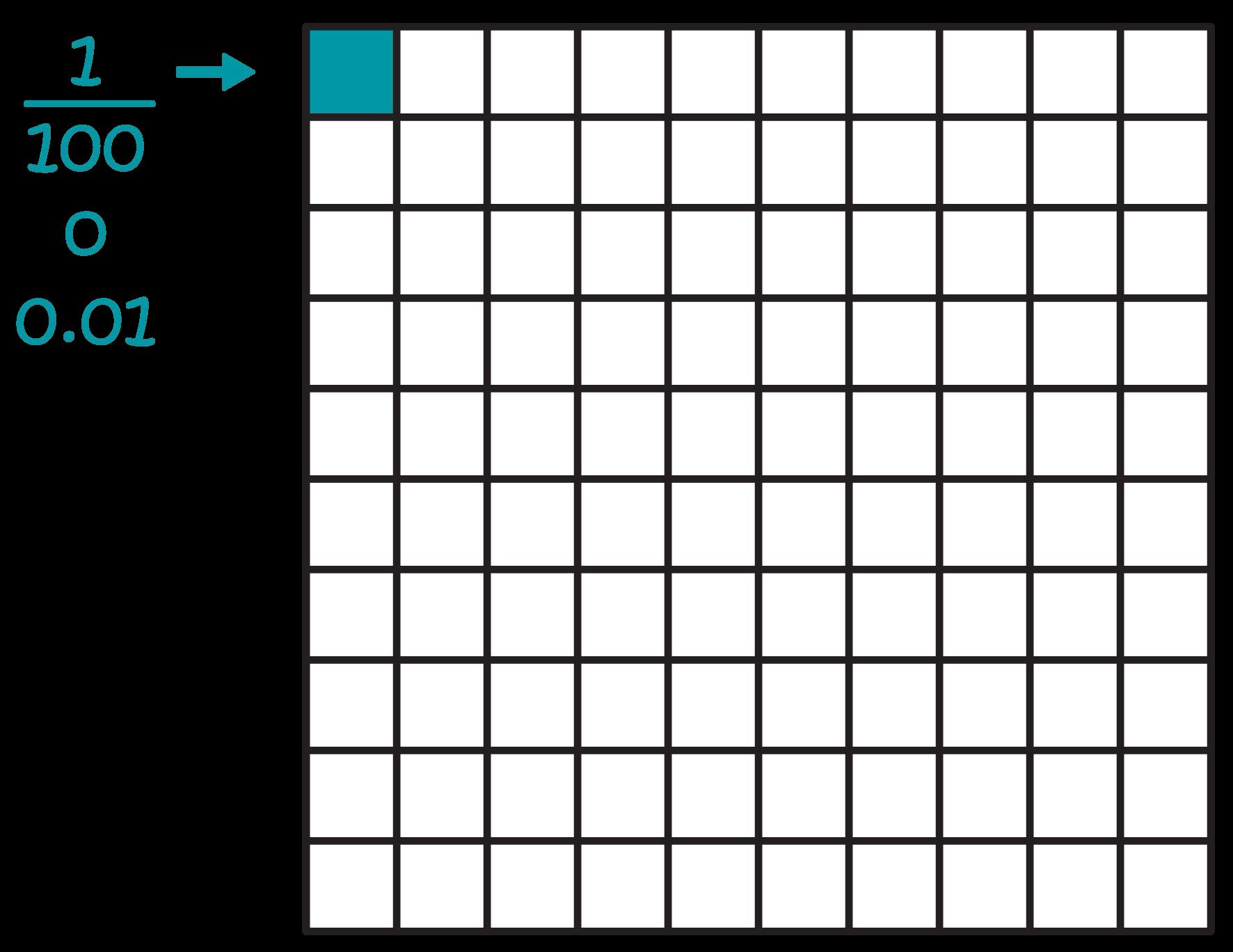
Una parte de un entero que está seccionado en 100 piezas iguales
Unidades
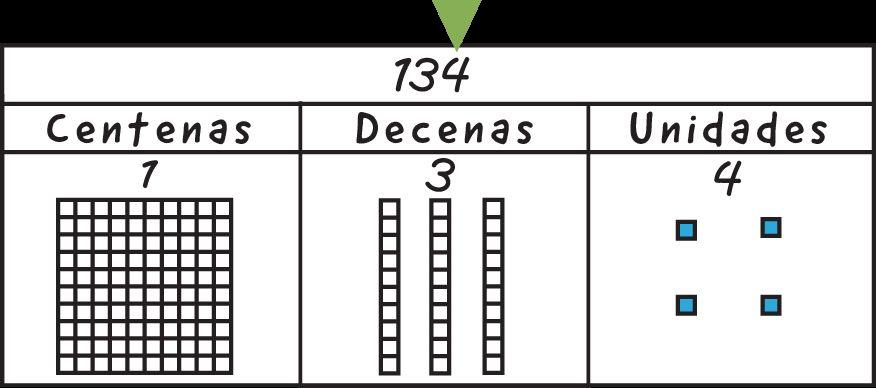
Valor de posición creado cuando hay un grupo con un valor del 0 al 9; la décima parte del valor de la decena

Décimos
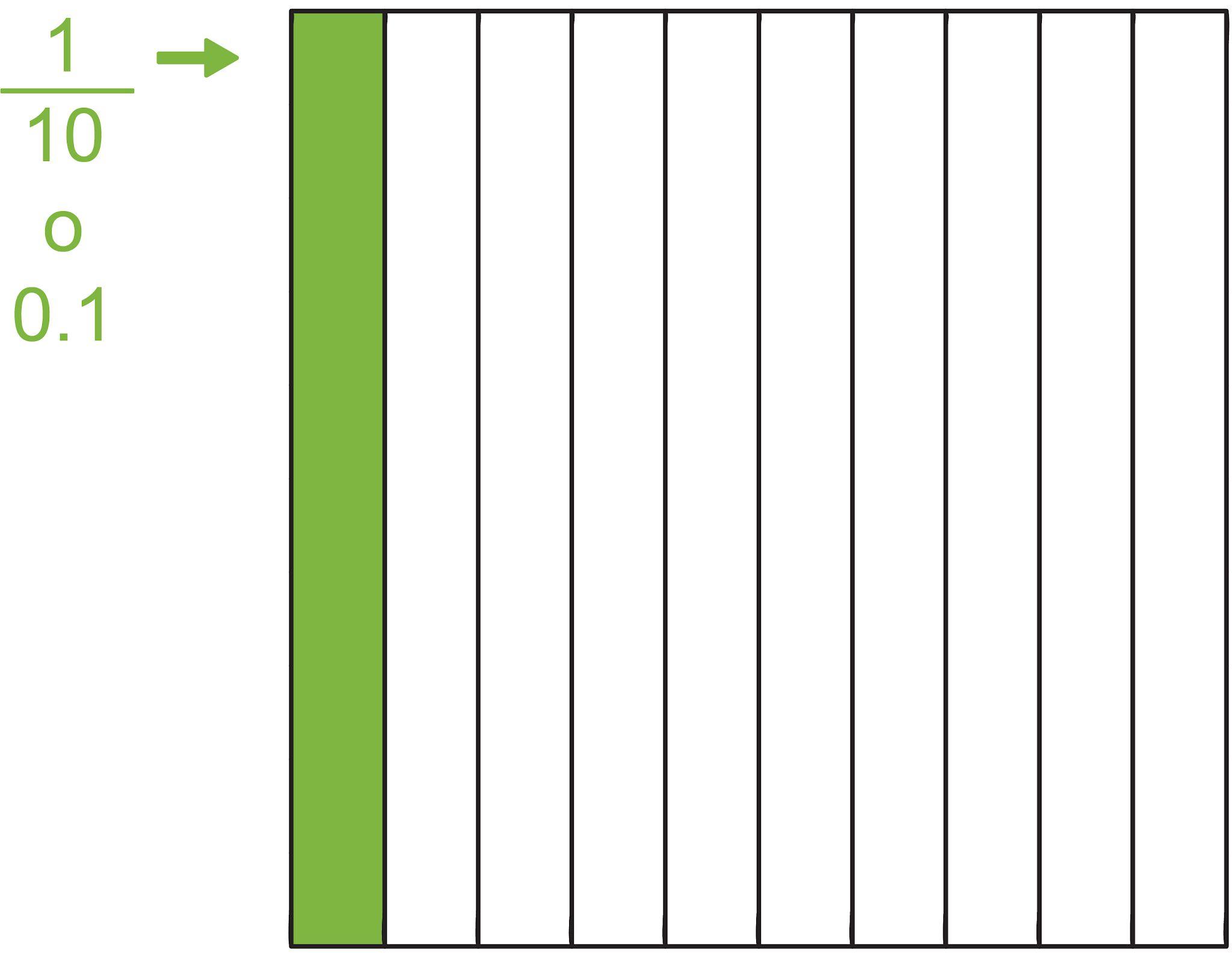
Carácter que se usa para representar un valor o un proceso

Número entero
Valor numérico sin partes decimales o fraccionarias

Una parte igual de un grupo de 10

Forma escrita
Representación de un número en palabras
DESCRIPCIÓN
Esta tabla de anclaje destaca la comprensión de los decimales hasta la centésima. Los estudiantes pueden determinar cómo se relacionan las décimas y las centésimas. También explora la comparación entre decimales y fracciones ya que representan partes de un todo.
EXPLORACIÓN 1: NOTACIÓN DECIMAL PARA
LOS DENOMINADORES DE 10
1. Prepare una tabla de valor posicional. Imprime 3 modelos de cuadrados decimales grandes que muestren décimas sombreadas para mostrar dos y tres décimas, y pégalos en la tabla. No complete todavía las demás secciones de la tabla (véase el ejemplo).
2. Después de que los estudiantes completen la Exploración, pídales que hablen con un compañero sobre qué decimal está representado en el modelo visual. A continuación, plantee lo siguiente a toda la clase:
a. ¿Cómo se dividen los cuadrados decimales? Están divididos en décimos.
b. ¿Cuántas partes forman un entero? 10
c. ¿Cuántos cuadrados enteros están sombreados? 2
d. ¿Cuántas décimas están sombreadas? 3
e. ¿Qué decimal representa el modelo? Dos y tres décimos
f. Para escribir esta cantidad utilizando la notación fraccionaria, ¿qué denominador se utiliza? 10
g. Invite a un estudiante a anotar la notación fraccionaria en la tabla.
h. Para escribir esta cantidad utilizando la notación decimal, ¿dónde irá el punto decimal? Irá después del número entero, que es 2.
i. ¿Qué dígito se colocará después del punto decimal y qué valor representa? Coloque un 3 después del punto decimal para representar tres décimos, que es sólo una parte de otro cuadrado entero.
j. Invite a un estudiante a registrar la notación decimal en la tabla.
CONSOLIDAR EL APRENDIZAJE DEL ESTUDIANTE
EXPLICAR: ESQUEMA DE ANCLAJE ESQUEMA DE ANCLAJE
EXPLORACIÓN 2: NOTACIÓN DECIMAL PARA LOS DENOMINADORES
DE 100
1. Prepara una tabla de valor posicional. Imprime 4 modelos de cuadrados decimales grandes que muestren centésimas sombreadas para mostrar tres y cincuenta y seis centésimas, y pégalos en la tabla. No completes todavía ninguna sección de la tabla. Dibuja una recta numérica en la última sección de la tabla marcada con un intervalo de 3 a 4 con 9 incrementos espaciados uniformemente entre ellos. No etiquetes todavía los incrementos (véase el ejemplo).
2. Después de que los estudiantes completen la Exploración, pídales que hablen con un compañero sobre qué decimal está representado en el modelo visual. A continuación, plantee lo siguiente con toda la clase:
a. ¿Cómo están divididos los cuadrados decimales? Están divididos en centésimas.
b. ¿Cuántas partes forman un entero? 100
c. ¿Cuántos cuadrados enteros están sombreados? 3
d. ¿Cuántas centésimas están sombreadas? 56
e. ¿Qué decimal representa el modelo? Tres y cincuenta y seis centésimas
f. Para escribir esta cantidad utilizando la notación fraccionaria, ¿qué denominador se utiliza? 100
g. Invita a un estudiante a anotar la notación fraccionaria en la tabla.
h. Para escribir esta cantidad utilizando la notación decimal, ¿dónde irá el punto decimal? Irá después del número entero, que es 3.
i. ¿Qué dígitos se colocarán después del punto decimal y qué valor representan? Coloca un 5 y luego un 6 después del punto decimal para representar 56 centésimas, que es sólo una parte de otro cuadrado entero.
j. Invite a un estudiante a anotar la notación decimal en la tabla.
3. Remita a los estudiantes al modelo de recta numérica. Pídales que hablen con un compañero sobre cómo utilizamos los incrementos marcados para representar la ubicación de 3.56. A continuación, plantee lo siguiente a toda la clase:
a. ¿En cuántas secciones está dividida la recta numérica y qué representan? Hay diez secciones y cada una representa una décima parte.
b. Invite a un estudiante a etiquetar los incrementos. Comience con 3.1 y etiquete cada incremento hasta 3.9.
c. ¿Entre qué 2 incrementos podemos aproximar la ubicación de 3.56, y cómo lo sabes? La ubicación de 3.56 estará entre 3.5 y 3.6, porque 3.56 es mayor que 3.5 pero menor que 3.6.
d. ¿A qué distancia entre 3.5 y 3.6 debemos marcar la ubicación de 3.56? Explica tu razonamiento. Estará situado un poco más de la mitad entre 3.5 y 3.6, porque cincuenta y seis centésimas es un poco más que cincuenta centésimas.
e. Invita a un estudiante a marcar un punto en el lugar de 3.56.
EXPLORACIÓN 3: REPRESENTAR Y COMPARAR DECIMALES
2. Prepare una tabla de valores posicionales con centésimas, décimas, unidades y decenas. Incluye dos filas de dígitos que se utilizarán para formar y comparar un conjunto de números decimales. Incluya un espacio para registrar dos desigualdades, una comparación mayor que y una comparación menor que, e incluya una recta numérica que vaya del 21 al 22 con 9 incrementos espaciados uniformemente entre ellos. No etiquetes los incrementos todavía. (ver ejemplo).
3. Después de que los estudiantes completen la Exploración, pídales que observen los números representados en la tabla de valor posicional y que piensen en los valores de cada número. Comente lo siguiente:
a. ¿Qué símbolos utilizamos para comparar números? Mayor que >, menor que < e igual a =
b. ¿Cómo leemos en voz alta el primer número? Veintiuna y sesenta y una centésimas
c. ¿Cómo leemos en voz alta el segundo número? Veintiuna y sesenta y ocho centésimas
4. Remita a los estudiantes a la recta numérica. Pídeles que hablen con un compañero sobre cómo podemos utilizar la recta numérica para comparar los dos números. A continuación, plantee lo siguiente con toda la clase.
a. ¿En cuántas secciones está dividida la recta numérica y qué representan? Hay diez secciones, y cada una representa una décima.
b. Invite a un estudiante a etiquetar los incrementos. Comience con 21.1 y etiquete cada incremento hasta 21.9.
c. ¿Entre qué 2 incrementos podemos aproximar las ubicaciones de estos números, y cómo lo sabes? Ambos estarán situados entre 21.6 y 21.7, porque ambos son mayores que 21.6 pero menores que 21.7.
d. ¿A qué distancia entre 21.6 y 21.7 deberíamos marcar la ubicación de 21.61? Explica tu razonamiento. Ejemplo de respuesta: Estará situado un poco más allá de 21.6, porque sesenta y una centésimas es un poco más que sesenta centésimas.
e. Invite a un estudiante a marcar un punto en el lugar de 21.61.
f. ¿A qué distancia entre 21.6 y 21.7 debemos marcar el lugar de 21.68? Explique su razonamiento. Ejemplo de respuesta: Estará a más de la mitad y casi a la marca de 21.7, porque sesenta y ocho centésimas es más que cincuenta centésimas, y también está muy cerca de setenta centésimas.
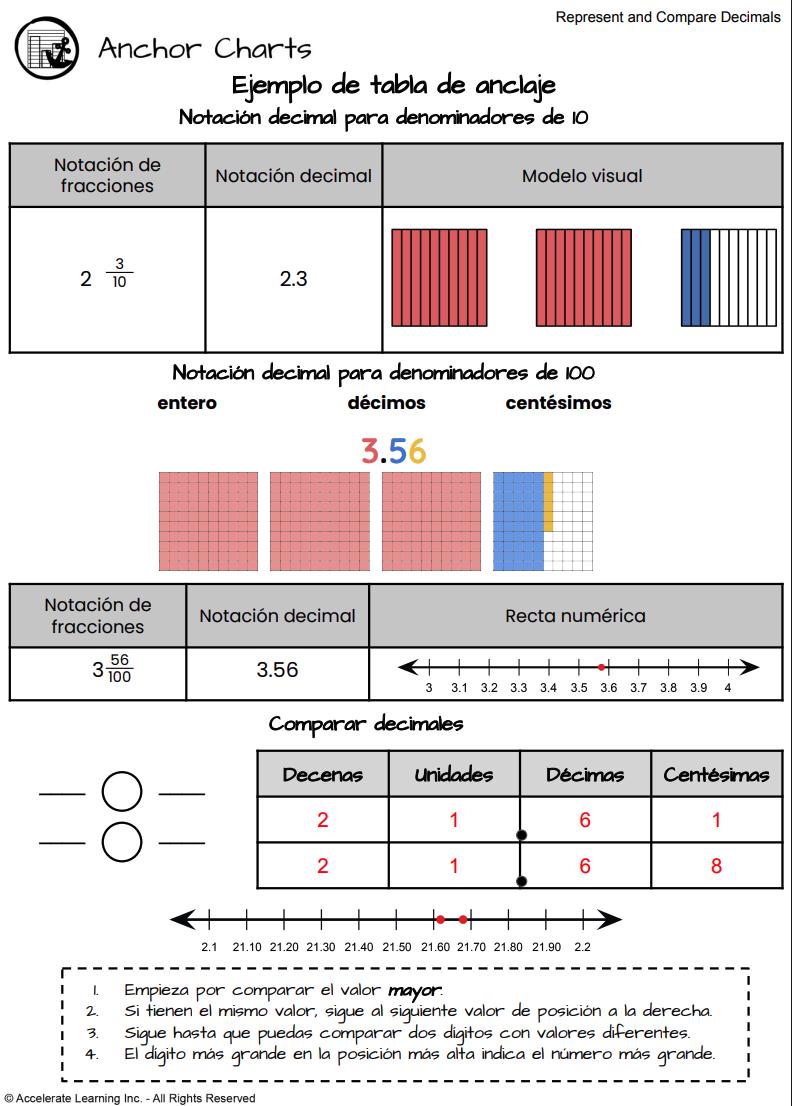
EJEMPLO DE ESQUEMA DE ANCLAJE
1. Pida a los estudiantes que hablen con un compañero sobre cómo podemos utilizar los dígitos del valor posicional para determinar qué número tiene mayor valor. A continuación, coméntelo con toda la clase. Ejemplo de respuesta: Nos fijamos en el lugar más grande de ambos números, que es el lugar de las decenas. Como son iguales, miramos el siguiente lugar a la derecha. Seguimos mirando hasta que los valores posicionales sean diferentes. El valor posicional es el mismo hasta la centésima. Si nos fijamos en las centésimas, ocho centésimas son mayores que una centésima. Por lo tanto, 21.68 tiene un valor mayor.
a. Registra estos pasos en la tabla de anclaje (ver ejemplo).
i. ¿Cómo podemos completar la comparación mayor que en la tabla? 21.68 es mayor que 21.61. Invite a un estudiante a completar la primera desigualdad en el carro.
ii. ¿Hay otra forma de hacer una comparación entre estos dos números? Sí, también podemos decir que 21.61 es menor que 21.68. Invita a un estudiante a completar la segunda desigualdad del carrito.
iii. ¿Se pueden hacer siempre dos comparaciones diferentes entre números? Sí, siempre que los números tengan un valor diferente. Si los números tienen un valor igual, entonces la única forma de compararlos es con un signo igual.
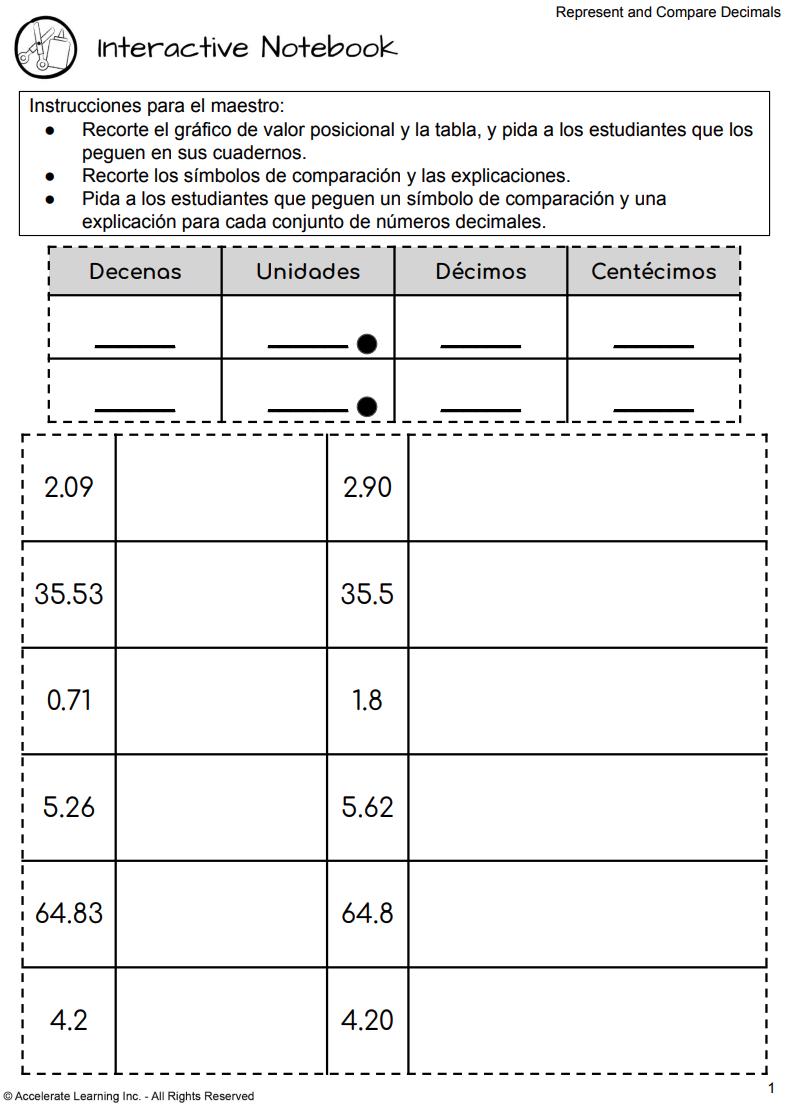

FOLLETO DEL ESTUDIANTE (COMPARAR DECIMALES)
EXPLICAR: LIBRETA INTERACTIVA
DOCUMENTAR EL APRENDIZAJE DEL ESTUDIANTE
LIBRETA INTERACTIVA
DESCRIPCIÓN
Los estudiantes toman notas, expresan ideas y/o procesan la información presentada en clase utilizando la actividad y el cuaderno.
MATERIALES
IMPRESO
• 1 folleto del estudiante (por alumno)
PREPARACIÓN
● Imprime una copia del folleto del estudiante por alumno.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Prepare una libreta interactiva con un cuadeno de espiral o de composición por estudiante. Así pueden usar las primeras páginas para crear un índice con números de página para llevar un registro de las actividades.
2. Recorte previamente o deje que los estudiantes recorten las piezas de cada material para el alumno según las instrucciones del maestro que aparecen en el recuadro de la primera página.
3. De tiempo a los estudiantes para que completen la actividad y luego peguen las piezas en su libreta interactiva.
4. Las libretas interactivas pueden utilizarse como referencia durante el trabajo independiente y pueden enviarse a casa al final del año como registro del aprendizaje de los estudiantes.

FOLLETO DEL ESTUDIANTE (NOTACIÓN DECIMAL Y DE FRACCIONES)
ELABORAR: CONSTRUCTOR DE FLUIDEZ
DESARROLLAR LA FLUIDEZ CONCEPTUAL
CONSTRUCTOR DE FLUIDEZ:
COMPARAR NÚMEROS DECIMALES (DÉCIMAS Y CENTÉSIMAS)
DESCRIPCIÓN
En este juego de cartas, las parejas de estudiantes utilizan su comprensión de mayor que y menor que para comparar.
MATERIALES
IMPRESO
• 1 hoja de instrucciones (por pareja)
• 1 juego de tarjetas de mayor que y menor que (por pareja)
• 1 juego de tarjetas de comparación (por pareja)
• 1 hoja de registro del estudiante (por estudiante)
REUTILIZABLE
• 1 sobre o bolsa con cierre (por pareja)
PREPARACIÓN
● Imprima la hoja de registro del estudiante.
● Imprima y recorte los juegos de tarjetas de comparación y tarjetas de juego.
● Imprima una hoja de instrucciones para cada juego de tarjetas de comparación y tarjetas de juego.
● Considere plastificar todos los materiales impresos, excepto la hoja de registro del estudiante, para su uso a largo plazo. Puede colocar las piezas más pequeñas en sobres o bolsas con cierre.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
5. Pida un estudiante voluntario y haga una demostración de un par de rondas del juego. Asegúrate de justificar qué cartas de juego se ajustan mejor al valor comparativo.
a. Baraje las cartas de Comparación y colóquelas en una pila entre los jugadores. Baraje las cartas de juego y repártalas equitativamente entre los jugadores.
b. El jugador uno saca por turno una carta de comparación y la muestra boca arriba. Diga a los estudiantes que las cartas de comparación deben permanecer apiladas sobre la mesa después de cada turno.
c. Cada jugador elige una carta de su mano que crea que tiene más probabilidades de coincidir con la carta de comparación y la coloca boca abajo sobre la mesa.
HOJA DE REGISTRO DEL ESTUDIANTE
a. Ambos jugadores dan la vuelta a sus tarjetas de juego y determinan qué tarjeta muestra la cantidad mayor que o menor que se indica en la tarjeta de comparación. Diga a los estudiantes que el ganador coge las dos Cartas de Juego y las coloca en una pila delante de ellos. Si los valores de las tarjetas son iguales, ninguno de los estudiantes se queda con el juego.
b. Después de cada turno, los estudiantes deben hacer una pausa y anotar la comparación en sus Hojas de registro del estudiante.
c. Ahora el jugador dos roba por turno una carta de comparación y la muestra boca arriba. El juego continúa como se indica en los pasos c a e.
1. Agrupe a los estudiantes por parejas.
2. Distribuya los materiales.
3. Haga que los estudiantes jueguen hasta que se hayan jugado todas las Cartas de Juego. Gana el jugador que tenga más cartas.
4. Mientras los estudiantes trabajan, compruebe que siguen las instrucciones y que comparan con precisión.
ELABORAR: CONSTRUCTOR DE FLUIDEZ

HOJA DE REGISTRO DEL ESTUDIANTE
PREPARACIÓN
● Imprima y recorte suficientes tarjetas de ¡A pescar! para que los estudiantes las compartan en pequeños grupos. (Los grupos no deben tener más de cuatro estudiantes.) Cuando imprima las tarjetas, asegúrese de imprimirlas por las dos caras para que el logotipo del juego aparezca en una cara de cada tarjeta.
● Imprima una hoja de instrucciones para cada juego de tarjetas de ¡A pescar!
● Considere la posibilidad de plastificar todos los materiales impresos, excepto la hoja de registro del estudiante, para que puedan utilizarse durante mucho tiempo. Puede colocar los trozos más pequeños en sobres o bolsas con cierre.
● Imprima una hoja de registro del estudiante para cada alumno..
DESARROLLAR LA FLUIDEZ CONCEPTUAL
CONSTRUCTOR DE FLUIDEZ: EMPAREJAR MODELOS DECIMALES CON NÚMEROS DECIMALES
¡DESCRIPCIÓN
Los estudiantes trabajan en pequeños grupos para jugar con las cartas de ¡A pescar!
¡MATERIALES
IMPRESO
• 1 hoja de instrucciones (por grupo)
• 1 conjunto de cartas ¡A pescar! (por grupo)
• 1 hoja de registro del estudiante (por alumno)
REUTILIZABLE
• 1 sobre o bolsa con cierre (por grupo)
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Haga una demostración del juego con un grupo de estudiantes.
a. El repartidor da cinco cartas a cada jugador y coloca todas las demás cartas boca abajo en un montón.
b. El juego se mueve en el sentido de las agujas del reloj. Cada jugador elige una carta de su mano y pide a otro jugador que la empareje. Las parejas que coinciden también tienen imágenes de peces iguales. Si alguien pide a un jugador una carta que tiene en su poder, el jugador debe dársela. Si el jugador no tiene ese tipo de carta, el oponente debe pescar cogiendo una carta del montón boca abajo.
c. Los jugadores ponen boca arriba sobre la mesa las parejas que reciben.
d. El juego continúa hasta que todas las manos estén vacías y no haya más cartas que robar.
e. Cada par de cartas iguales vale un punto. El jugador con más puntos es el ganador.
2. Distribuya los materiales.
3. Haga que los estudiantes jueguen.
4. Al final del juego, haga que cada jugador elija una pareja para completar la hoja de registro del estudiante. Pídales que expliquen por qué las 2 cartas coinciden. Anime a los estudiantes a compartir sus respuestas con sus grupos.
ELABORAR: REVISIÓN EN ESPIRAL
REPASAR CONCEPTOS PREVIOS
REVISIÓN
EN
ESPIRAL: SHELBY Y LOS TIBURONES DE SPRINGFIELD
DESCRIPCIÓN
Los estudiantes repasan el contenido del grado anterior o actual basándose en el trabajo principal establecido para cada grado.
PREPARACIÓN
● Imprima una copia de la hoja de repaso en espiral para cada estudiante.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Es posible que necesite proporcionar ayuda con la lectura para que algunos estudiantes completen esta actividad.
2. Lea la historia en la primera página para despertar el interés de los estudiantes antes de pasar a las preguntas.
3. Utilice este repaso en espiral como calentamiento en clase o envíelo a casa como deberes, pero asegúrese de comentar las respuestas y las estrategias con toda la clase.
4. Consulte la norma que aparece en la esquina inferior derecha de cada cuadro de preguntas para evaluar los conocimientos de contenido de los estudiantes o la necesidad de una mayor intervención.
REVISIÓN EN ESPIRAL CENTRADA EN LA PREGUNTA
● Pregunta 1
○ Grado 4: Utilizar la comprensión del valor posicional para redondear números enteros de varios dígitos a cualquier lugar.
● Pregunta 2
○ Grado 4: Reconocer que en un número entero de varios dígitos, un dígito en un lugar representa diez veces lo que representa en el lugar a su derecha. Por ejemplo, reconocer que 700 ÷ 70 = 10 aplicando conceptos de valor posicional y división.
● Pregunta 3
○ Grado 4: Leer y escribir números enteros de varios dígitos usando numerales de base diez, nombres de números y forma expandida. Comparar dos números de varios dígitos basándose en los significados de los dígitos en cada lugar, usando los símbolos >, = y < para registrar los resultados de las comparaciones.
● Pregunta 4
○ Grado 4: Sumar y restar con fluidez números enteros de varios dígitos usando el algoritmo estándar.


FOLLETO DEL ESTUDIANTE
ELABORAR: TAREA BASADA EN PROBLEMAS
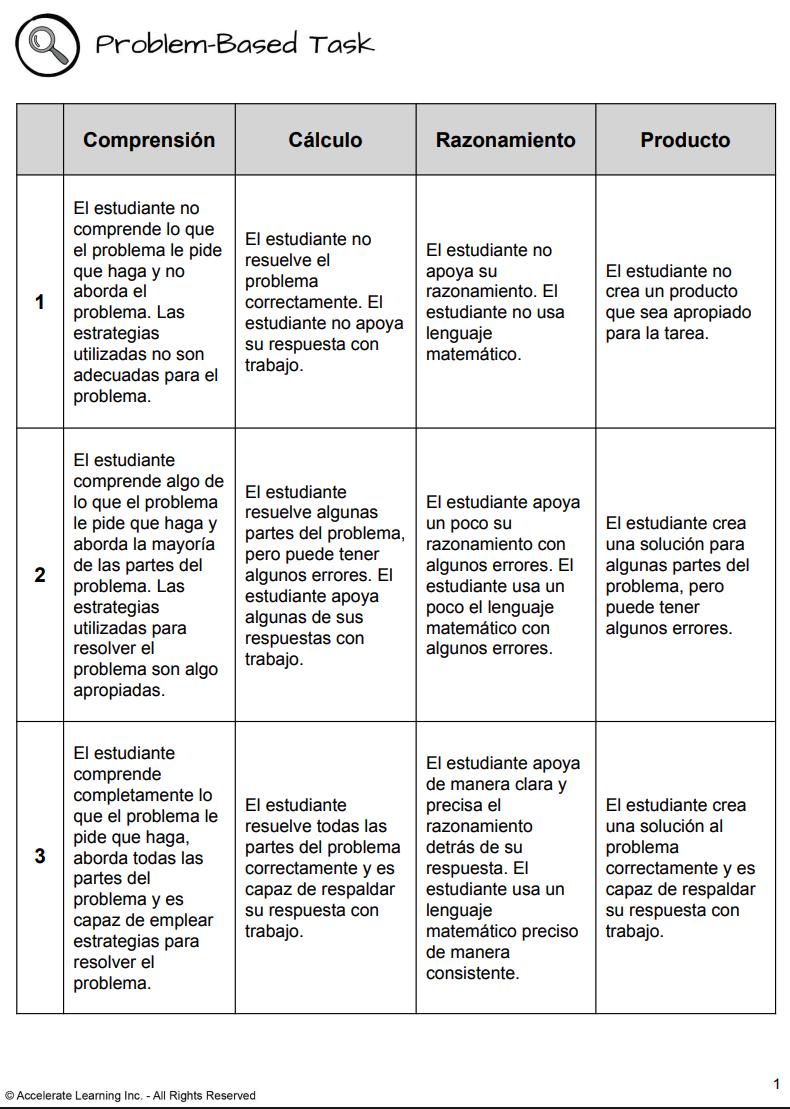
RÚBRICA
DESARROLLAR HABILIDADES PARA RESOLVER PROBLEMAS
TAREA BASADA EN PROBLEMAS: EL ARTISTA
DESCRIPCIÓN
Los estudiantes trabajan en colaboración para aplicar los conocimientos y habilidades que han aprendido a un desafío abierto del mundo real.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Permita que los estudiantes trabajen en grupos.
2. Anime a los estudiantes a revisar sus fiarios del estudiante de las actividades exploración si necesitan repasar las habilidades que han aprendido.
3. Si los estudiantes están atascados, utilice preguntas orientadoras para ayudarles a pensar sin decirles qué pasos deben dar a continuación. Si el tiempo lo permite, permite que cada grupo comparta su solución con la clase.
4. Exponga cómo los distintos grupos abordaron el reto de maneras diferentes.


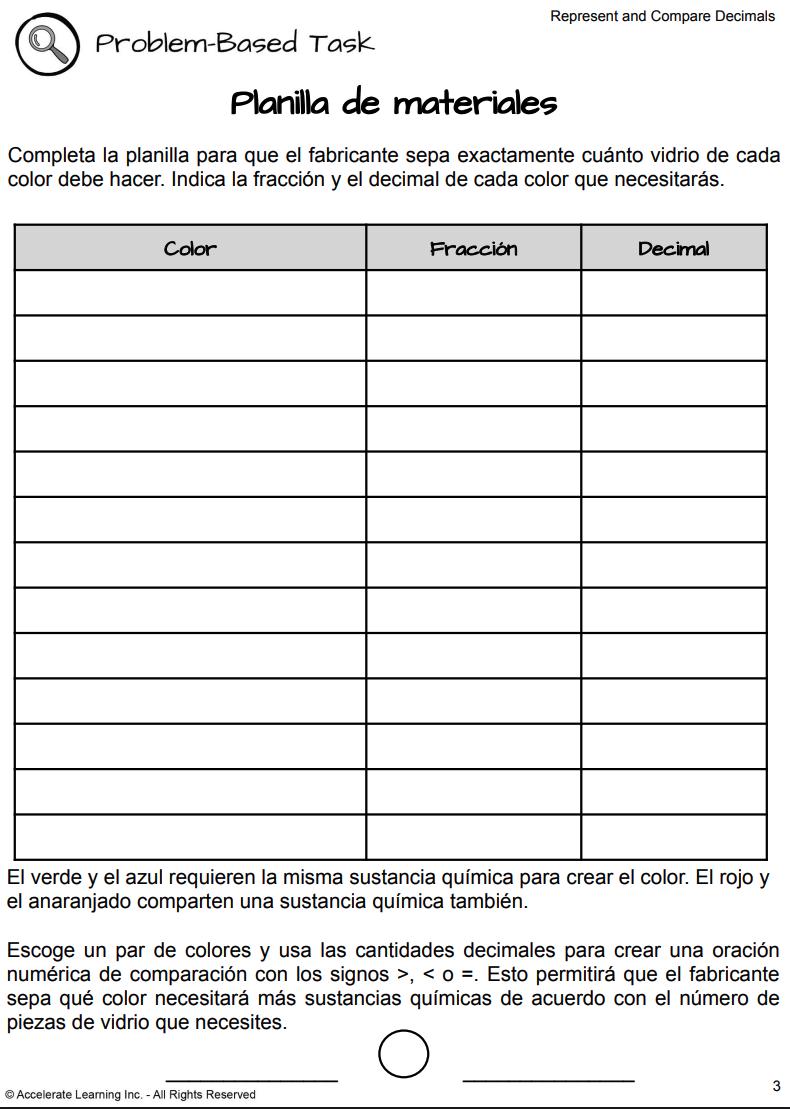
FOLLETO DEL ESTUDIANTE
ELABORAR: CONEXIONES PROFESIONALES
MATEMÁTICAS EN EL TRABAJO
CONEXIONES PROFESIONALES:
MELVIL DEWEY
Las conexiones profesionales pretenden ser una vía que introduzca a sus estudiantes en las carreras matemáticas y en las habilidades del siglo XXI necesarias para tener éxito en diversos campos. Éstas incluyen, entre otras, la creatividad y la innovación, el pensamiento crítico, la resolución de problemas y las habilidades tecnológicas.
DESCRIPCIÓN
Este alcance destaca la carrera de Melvil Dewey, el inventor del sistema de clasificación decimal Dewey. Los estudiantes considerarán su profesión, las matemáticas utilizadas y el impacto que esta carrera ha tenido en su comunidad.
MATERIALES
IMPRESOS
• Presentación de diapositivas de Melvil Dewey (por clase o por estudiante)
REUTILIZABLES
• Proyector (por clase)
PREPARACIÓN
● Agrupe a los estudiantes para una rica colaboración y discurso.
● Prepárese para proyectar la presentación de diapositivas de Melvil Dewey a la clase. Si no dispone de proyector, puede imprimir las diapositivas para que las utilicen los estudiantes.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Proyecte la presentación de diapositivas e invite a un estudiante a leer la biografía de Melvil Dewey.
2. Organice una conversación con los estudiantes, formulando preguntas como las siguientes:
a. ¿Qué carrera tuvo Melvil Dewey?
b. Pensando en lo que ha conseguido, ¿te parece difícil o fácil utilizar las matemáticas de esta manera?
c. ¿Habías pensado alguna vez en las matemáticas de esta manera?
d. ¿Por qué crees que esta carrera es importante para nuestra sociedad cotidiana?
e. ¿Es ésta una carrera que te interesa? ¿Por qué o por qué no?
f. ¿Cómo utilizaba Melvil Dewey la creatividad, la innovación y la capacidad de resolver problemas?
Melvil Dewey
Inventor of the Dewey Decimal Classification System

v Dewey Inventor of the Dewey Decimal Classification System
Melvil Dewey attended Amherst College in Massachusetts. While attending school there, he held a job as a student assistant in the college’s library. Dewey often became frustrated with the disorganized way the books were catalogued and shelved. He researched ideas and experimented with ways to better organize the books. He wanted it to be easier to locate books as well as more efficient to return and shelve them.
Dewey’s research led to him inventing the Dewey decimal classification system. This system focuses on putting nonfiction books into categories and using decimals to organize them by subjects. When shelving books, librarians compare decimals and place books on shelves in order from the decimal with the least value to the decimal with the greatest value. His method brought his love of both order and math together to create a system that libraries still use today to organize books.

Me
PRESENTACIÓN DE DIAPOSITIVAS DE MELVIL DEWEY
La ciencia de datos consiste en un breve debate en clase sobre un conjunto de datos. Esta actividad no está pensada para ser calificada. La parte I incluye preguntas abiertas para ayudar a los estudiantes a interpretar y analizar los datos. Las partes siguientes son actividades opcionales para ampliar el aprendizaje de los estudiantes en contexto.
DESCRIPCIÓN
Los estudiantes analizan, interpretan y generan conjuntos de datos, además de responder a preguntas basadas en los datos.
MATERIALES
IMPRESO
• 1 folleto para el estudiante (por estudiante)
• 1 conjunto de datos (por clase)
REUTILIZABLE
• 1 proyector o cámara de documentos (por clase)
• 1 marcador de borrado en seco (por clase)
CONSUMIBLE
• 1 trozo de papel milimetrado (por clase)
PREPARACIÓN
• Prepárese para proyectar el conjunto de datos para la clase.
• Reúne un trozo de papel milimetrado y un marcador de borrado en seco.
• Imprime el Folleto para el estudiante para cada estudiante.

FOLLETO DEL ESTUDIANTE
ELABORAR: CIENCIA DE DATOS
ANALIZAR DATOS
CIENCIA DE DATOS
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
PARTE I
1. Proyecte el conjunto de datos y prepárese para anotar las observaciones de los estudiantes.
2. Haga las siguientes preguntas:
a. ¿Qué notas sobre este conjunto de datos?
b. ¿Qué representa este conjunto de datos?
c. ¿Qué categorías están incluidas en este conjunto de datos?
d. ¿Qué notas sobre los tamaños de los lagos?
e. ¿Puedes contarme sobre alguna vez que hayas estado en un lago?
f. ¿Qué preguntas tienes sobre los datos?
PARTE II
1. Repase la representación y comparación de decimales y escribe lo que los estudiantes recuerden en el papel cuadriculado.
2. Haga las siguientes preguntas:
a La clave muestra cómo se compara el área de cada lago con el área total de los Grandes Lagos. ¿Cuál es el decimal mostrado para el Lago Superior como fracción? 34/100
b ¿Qué decimal mostrado en la clave puede escribirse con un denominador de 10? Lago Erie = .10
c El lago Hurón tiene aproximadamente 2,32 veces el tamaño del lago Erie. ¿Cuál es el decimal 2,32 como número mixto? 2 32/100
a. ¿Qué dos lagos tienen aproximadamente el mismo tamaño? Explícalo. El lago Hurón y el lago Michigan tienen aproximadamente el mismo tamaño porque la cantidad de área es la misma.
b. Compara los decimales que se muestran en la clave para el lago Ontario y el lago Michigan. Utilizando símbolos, ¿cuál es el enunciado de la comparación? .08 < .24
c. ¿Dónde trazarías cada decimal mostrado en la clave en una recta numérica? Las respuestas variarán.
PARTE III
1. Entrega a cada estudiante una copia del folleto para el estudiante.
2. Lee las instrucciones y responde cualquier pregunta que los estudiantes puedan tener.
3. Deje tiempo para que los estudiantes completen ldel folleto para el estudiante en clase o envíela a casa como tarea.
4. Anime a los estudiantes a compartir sus datos con la clase.
EVALUAR: LISTA DE VERIFICACIÓN DE OBSERVACIÓN
EVALUACIÓN DEL DESEMPEÑO
LISTA DE VERIFICACIÓN DE LA OBSERVACIÓN
DESCRIPCIÓN
Este elemento proporciona un desglose de los conceptos y destrezas clave del alcance de aplicación. Puede utilizarse como evaluación formativa para los maestroes y como autoevaluación para los estudiantes.
MATERIALES
IMPRESO
• 1 folleto del estudiante (por estudiante)
• 1 Apunte para el maestro (por estudiante)
PREPARACIÓN
● Imprima un Apunte para el maestro y un Apunte para el estudiante para cada estudiante.
PROCEDIMIENTO Y PUNTOS DE APOYO
1. Distribuya un folleto del estudiante por alumno.
2. A medida que los estudiantes trabajen en las actividades Explore and Explain (Explorar y explicar) del alcance, evalúe formativamente su progreso tomando notas anecdóticas sobre cómo se observaron los conceptos y habilidades clave. Pueden plantearse preguntas de reflexión para medir el impacto de las actividades tanto en grupo como en pequeño grupo.
3. Haga que los estudiantes reflexionen sobre las formas en que pueden demostrar su comprensión y autoevaluar su progreso en cada concepto o habilidad clave a medida que trabajan en las actividades tanto en grupo como en pequeño grupo.
4. Los estudiantes pueden reflexionar sobre su pensamiento, aprendizaje y trabajo en el alcance; identificar las formas en que han mejorado; y establecer nuevos objetivos de aprendizaje.
5. Los colegas que proporcionan apoyo de instrucción a los estudiantes pueden estar equipados con las adaptaciones y modificaciones señaladas en el Manual del maestro.
6. Las notas anecdóticas proporcionadas en la hoja para el maestro pueden usarse como documentación para los boletines de calificaciones basados en estándares.
7. Una vez que se hayan recopilado los datos de los estudiantes después de la evaluación, consulte la Guía de instrucción de andamiaje en la sección Inicio de este alcance para diferenciar la instrucción para cada estudiante.
DESCRIPCIÓN
Los estudiantes analizan los resultados de su evaluación y determinan qué hicieron bien y en qué pueden mejorar.
MATERIALES
• 1 mapa de calor (por estudiante)
• 1 crayón rojo (por estudiante)
• 1 crayón verde (por estudiante)
PREPARACIÓN
• Determine si los estudiantes analizarán su prueba de habilidades, la evaluación basada en estándares o ambas.
• Imprima un mapa de calor para cada estudiante.
• Reúna un crayón rojo y un crayón verde para cada estudiante.
EVALUAR: MAPA DE CALOR
ANALIZAR LOS RESULTADOS DE LA EVALUACIÓN
MAPA DE CALOR
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Distribuya un mapa de calor a cada estudiante junto con los crayones rojo y verde. Los estudiantes deben tener a mano su(s) evaluación(es) corregida(s).
2. Los estudiantes utilizan su(s) evaluación(es) corregida(s) para colorear el mapa de calor. Por cada pregunta contestada correctamente, colorean de verde la casilla correspondiente. Para cada pregunta contestada incorrectamente, los estudiantes colorean la casilla correspondiente en rojo.
3. Anime a los estudiantes a buscar patrones en sus datos, como un determinado estándar que se perdió con más frecuencia o un estándar que han dominado claramente, y utilizar esta información para reflexionar y establecer metas en la tabla proporcionada.
4. Consulte la guía de instrucción andamiadas que se encuentra en la sección «Inicio» para proporcionar extensión o apoyo adicional.



MAPA DE CALOR
INTERVENCIÓN: INTERVENCIÓN EN GRUPO PEQUEÑO
REFORZAR Y VOLVER A ENSEÑAR
INTERVENCIÓN EN PEQUEÑOS GRUPOS
DESCRIPCIÓN
Los estudiantes utilizan la notación decimal para fracciones y números mixtos con denominadores 10 ó 100. Los estudiantes comparan y registran los resultados de la comparación de dos decimales a las centésimas.
MATERIALES
IMPRESO
• 1 tapete de valor posicional (por estudiante)
• 1 recta numérica (por estudiante)
• 1 lista de verificación para el maestro (por profesor)
• 1 1 evaluación de control (por alumno)
REUTILIZABLE
• 1 pizarra blanca (por pareja)
• 1 marcador de borrado en seco (por estudiante)
• 1 juego de bloques de base diez (por pareja)
• 3 protectores de hojas (por estudiante)
• 1 regla de metro (por pareja)
CONSUMIBLE
• 1 rollo de cinta de embalar transparente (por maestro)
3 fichas (por maestro)
PREPARACIÓN
• Planifique que los estudiantes trabajen en parejas para completar esta actividad.
• Imprima un folleto del estudiante para cada alumno
• Imprime la lista de verificación del maestro.
• Prepara un juego de bloques de base diez para cada pareja de estudiantes y un marcador de borrado en seco para cada estudiante.
PARTES I Y II
• Imprima el tapete de valor posicional en cartulina para que cada estudiante la pueda utilizar durante más tiempo. Coloca cada tapete en un protector de hojas para crear una superficie borrable. Une las hojas con cinta adhesiva en la línea designada en la primera página.
PARTE II
• Prepare un metro para cada pareja de estudiantes. Cubre la regla de medir con cinta de embalar transparente para crear una superficie que se pueda borrar.
• Reúne 3 fichas y escribe un 0, 1 y 2 en cada una de ellas.
PARTE III
• Imprima la recta numérica en cartulina para que cada estudiante la pueda utilizar durante más tiempo. Coloca la línea en un protector de hojas para crear una superficie que se pueda borrar.
• Prepara una pizarra blanca para cada pareja.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
PARTE I: NOTACIÓN DECIMAL PARA LOS DENOMINADORES DE 10
1. Haga que los estudiantes compartan lo que saben sobre los decimales. Haga las siguientes preguntas:
a. ¿En qué se diferencia un número decimal de un número entero? Un número decimal representa una parte de un entero.
b. Cuando escribimos un número decimal, ¿en qué se diferencia de un número entero? La coma decimal va después de la unidad y separa el número entero del decimal. La cantidad decimal viene después de la coma.
c. El primer valor decimal a la derecha del decimal es la décima. ¿Qué son las décimas? Si tomas un entero y lo divides en 10 partes iguales, obtienes 10 décimos.
d. (Sostén una base plana y una barra). Si esta base plana representa un entero, ¿qué representa una barra? ¿Cómo lo sabes? La barra representa la décima parte de un entero. Si dividimos el todo (plano base diez) en 10 partes iguales, obtendremos 10 barras. Cada barra es una décima parte del piso.
2. Distribuye un tapete de valor posicional y un marcador de borrado en seco a cada estudiante.
3. Entregue un juego de bloques de base diez a cada pareja de estudiantes.
4. Pida a los estudiantes que coloquen un piso y una barra en la columna de valor posicional correspondiente de su tapete. Formule a los estudiantes las siguientes preguntas: a Si hay 10 barras en un entero, ¿qué fracción crees que representa esta barra? Si cada barra es una décima parte (o 1 de cada 10), la fracción debería ser 1/10
6 Pida a los estudiantes que escriban 1/10 debajo de la barra. Recuerde a los estudiantes que pueden escribir este mismo número como decimal. Para representar la décima parte, pueden escribir 0.1. Pida a los estudiantes que escriban 0.1 junto a la fracción. A continuación, formule la siguiente pregunta: a ¿Cómo se lee 0.1? Una décima
5. Pida a los estudiantes que modelen 0.4 utilizando bloques de base diez. Pida a los estudiantes que comenten lo que saben sobre el 0.4.
6. Discuta qué número escrito representa 0.4 ahora. Pídales que compartan sus observaciones sobre los cambios.
7. Trabajen juntos en otro ejemplo que muestre cantidades mayores que 1.
INTERVENCIÓN: INTERVENCIÓN EN GRUPO PEQUEÑO


EVALUACIÓN DE CONTROL
8. Pida a los estudiantes que modelen 3 7/10 con bloques de base diez. Formule las siguientes preguntas:
a. ¿Qué valores de posición se utilizarán en nuestra tapete para representar esta cantidad? Las unidades y las décimas porque tenemos 3 unidades y 7 décimas.
b. ¿Qué bloques se pueden utilizar para representar el número entero? Podemos usar 3 bemoles porque cada bemol representa un entero, y nuestro número tiene tres enteros.
c. ¿Cómo podemos representar la fracción? Podemos usar 7 barras, porque cada barra representa una décima, y nuestro número tiene 7 décimas.
d. ¿Cómo podemos escribirlo como decimal? 3.7
e. ¿Cómo leemos 3.7? Tres y siete décimos
9. Dé a los estudiantes algunas fracciones más con denominadores de 10 para modelar y escribir en forma de fracción y decimal.
10. Observe el trabajo de los estudiantes, aborde los conceptos erróneos y proporcione orientación según sea necesario. Documente el progreso y la comprensión de los estudiantes a lo largo de la actividad.
PARTE II: NOTACIÓN DECIMAL PARA LOS DENOMINADORES DE 100
1. Entregue un tapete de valor posicional y un marcador de borrado en seco a cada estudiante.
2. Entregue un juego de bloques de base diez a cada pareja de estudiantes.
3. Pida a los estudiantes que trabajen con sus parejas para elegir y colocar un plano y una barra donde crean que pertenecen en la Tapete de valor posicional y escriban lo que representa cada bloque de base diez en forma fraccionaria y decimal. Mientras los estudiantes trabajan, observe y corrija los conceptos erróneos y haga las siguientes preguntas:
a ¿Qué bloque representa un entero? El piso representa un entero.
b ¿Qué bloque representa una décima parte? ¿Cómo lo sabes? La barra representa una décima parte. Se necesitan 10 barras para igualar un entero, así que una barra es un décimo.
c ¿Cómo puedes escribir un décimo usando fracciones y decimales? 1/10 o 0.1
4. Explica que el segundo decimal a la derecha del decimal es la centésima. Haga las siguientes preguntas:
a. ¿Qué son las centésim as? Si tomas un entero y lo divides en 100 partes iguales, obtienes 100 centésimas.
b. (¿Qué representa una unidad en este caso? ¿Cómo lo sabes? Una unidad de bloque representa la centésima parte de un entero. Hay 100 unidades en un entero (plano). Esto significa que cada unidad es la centésima parte del piso.
c. Si hay 100 unidades en un todo, ¿qué fracción crees que representa esta unidad? Si cada unidad es una centésima (o 1 de cada 100), la fracción debería ser 1/100
INTERVENCIÓN: INTERVENCIÓN EN GRUPO PEQUEÑO
16. Pida a los estudiantes que escriban 1/100 debajo de la unidad. Recuerde a los estudiantes que pueden escribir este mismo número como decimal. Para representar esta centésima, pueden escribir 0.01. Pida a los estudiantes que escriban 0.01 junto a la fracción y, a continuación, formule la siguiente pregunta:
a. ¿Cómo se lee 0.01? Una centésima
17. Modele 62 centésimas (0.62) con bloques de base diez, e invite a los estudiantes a compartir lo que notan y se preguntan sobre el modelo. Deben darse cuenta de que usted ha modelado un valor posicional más allá de las décimas. Hay bloques más pequeños que, al juntar 10, forman una décima. Hay 100 de los bloques más pequeños en un entero.
18. Pida a los estudiantes que escriban el número que representa cada valor posicional en su tapete de valor posicional con un marcador de borrado en seco. Formule a los estudiantes las siguientes preguntas:
a (Señale las décimas en el modelo). ¿Cuántas décimas hay en el número? ¿Cómo escribirías ese número como decimal? ¿En fracción? Hay 6 décimas; 0.6; 6/10
b (Señala las centésimas en el modelo). ¿Cuántas centésimas hay en el número? ¿Cómo lo escribirías como decimal? ¿En fracción? Hay 2 centésimas; 0.02; 2/100
c (Señala el modelo completo). ¿Cómo dirías el número completo? ¿Cómo lo escribirías como decimal? ¿Cómo fracción? 62 centésimas; 0.62; 62/100
19. Si es necesario, muestre cómo, si tuviera que descomponer todas las unidades que componen el modelo de base diez para el número, terminaría con 62 bloques individuales de centésimas.
20. Invite a los estudiantes a practicar modelando, diciendo y escribiendo algunos números más (algunos incluyendo números enteros).
21. Explique que los estudiantes practicarán la representación de decimales en una recta numérica. Entregue una regla de medir, preparada con cinta de embalar transparente, a cada pareja de estudiantes. Deje un tiempo para que las parejas de estudiantes hablen de lo que observan y establezcan conexiones entre los decimales y las rectas numéricas. Formule las siguientes preguntas:
a. ¿Qué observas en la regla de medir? Las respuestas pueden variar. Los números llegan hasta 100 cm. Los múltiplos de 10 están en negrita. Esto nos recuerda a una recta numérica. Esto nos recuerda a un todo dividido en partes iguales. Tienen incrementos de 10, y una regla de medir entera mide 100 centímetros.
b. Si quisiéramos encontrar 0.1 o 1/10 en la regla de medir, ¿qué haríamos? Tenemos que encontrar la forma de dividir toda la regla de medir en 10 partes iguales y detenernos en el primero de los 10 trozos.
5. Rete a los estudiantes a localizar 1/10, o 0.1, en la regla de medir. Observe a los estudiantes mientras acuerdan cómo hacerlo con sus compañeros y asegúrese de que relacionan que cada incremento de 10 en negrita representa una décima parte. Formule a los estudiantes la siguiente pregunta:
a. ¿Cómo sabemos dónde está el 0.1 en la regla de medir? Observamos que hay un total de 10 incrementos de 10 en negrita en una regla de medir de 100 centímetros. Esto significa que cada 10 centímetros representa una décima parte.
i. Indique a los estudiantes que etiqueten el lugar tanto como 0.1 como 1/10
6. Pida a los estudiantes que encuentren y etiqueten otras tres cantidades hasta la décima en notación decimal y fraccionaria.
7. Haga hincapié en la relación entre las décimas y las partes de un todo.
8. Repita la operación con las centésimas, facilitando la conversación para que los estudiantes marquen los centímetros como centésimas. Formule a los estudiantes la siguiente pregunta
a. ¿Los incrementos de las centésimas van a ser menores o mayores que las décimas? ¿Cómo lo sabéis? Tienen que ser más pequeños. Siguen dividiendo un todo del mismo tamaño, sólo que en más trozos, por lo que esos trozos tienen que ser más pequeños.
9. Pida a los estudiantes que etiqueten el lugar como 0.01 y 1/100
10. Pida a los estudiantes que encuentren y etiqueten otras tres centésimas diferentes en notación decimal y fraccionaria.
11. Haga hincapié en la relación entre las centésimas y las partes de un todo.
12. Compruebe el trabajo de los estudiantes, asegurándose de que los números se han identificado y etiquetado correctamente.
13. Pida a los estudiantes que borren su cinta transparente y que trabajen en pequeños grupos para la siguiente parte.
14. Coloque dos reglas de medir una al lado de la otra. Invite a los estudiantes a compartir lo que observen. Hay dos metros enteros. Hay 2 grupos de 10 décimas y 100 centésimas.
15. Distribuya las tres fichas etiquetadas con 0, 1 y 2. Diga a los estudiantes que estos números representan números enteros. Diga a los estudiantes que estas cifras representan números enteros. Rete a las parejas de estudiantes a que coloquen los números enteros en los lugares adecuados de los dos metros. Formule a los estudiantes las siguientes preguntas:
a. ¿Cuántos números enteros tenemos? 2
b. ¿Qué números están representados en la primera regla de medir? Partes fraccionarias de 1 entero
c. ¿Qué números están representados en la segunda regla de medir? Números entre 1 entero y 2 enteros
d. Si quisiéramos representar 1.38 en las barras, ¿en qué barra se representaría el número? ¿Por qué? En la segunda regla de medir; como el 1 está a la izquierda del punto decimal, es un entero. Los números a la derecha del punto decimal son partes de un segundo entero. Los números de la primera regla de medir no son iguales a un entero hasta el final de la regla. Los números de la segunda barra están comprendidos entre un entero y dos enteros.
22. Proporcione a los estudiantes varios números para que los localicen en las barras, incluyendo números mixtos hasta 2. Los estudiantes pueden trabajar juntos para etiquetar cada cantidad o simplemente señalar el lugar correcto. Algunos números sugeridos son 0.83, 1 23/100, 32/100 , y 1.45.
23. Observe el trabajo de los estudiantes, aborde los conceptos erróneos y proporcione orientación según sea necesario. Documente el progreso y la comprensión de los estudiantes a lo largo de la actividad.
PARTE III: REPRESENTAR Y COMPARAR DECIMALES
5. Invite a los estudiantes a compartir lo que entienden sobre comparar. Pídales que hablen con sus compañeros y luego compartan con el grupo. Haga las siguientes preguntas:
a. ¿Qué es comparar? Es cuando analizamos el valor de dos números por su valor posicional y determinamos cuál es mayor y cuál es menor.
b. ¿Cambia la comparación cuando comparamos decimales en lugar de números enteros? No debería ser diferente. Sigue habiendo decimales que son mayores o menores que otros decimales.
6. Escriba los números 1.08 y 1.8 para que los estudiantes los vean.
7. Entregue una recta numérica y un marcador de borrado en seco a cada estudiante.
8. Entregue un juego de bloques de base diez y una pizarra blanca a cada pareja de estudiantes.
9. Explique que un plano representará un entero e invite a los estudiantes a construir ambos números utilizando los bloques de base diez.
10. Pida a las parejas de estudiantes que coloquen la pizarra entre ambos modelos. El número 1.08 se construirá a la izquierda de la pizarra y el 1.8 a la derecha. Mientras los estudiantes construyen, formule la siguiente pregunta:
a ¿Cómo determinaste qué bloques de base diez utilizar para construir cada número? Si un entero está representado por un plano, significa que tuve que analizar qué bloques representaban 1/10 y 1/100. Decidí utilizar barras para las décimas porque hay 10 barras en un todo, lo que hace que cada una 1/10 del todo. Para modelar una centésima, he utilizado una unidad porque hay 100 unidades en un todo. Esto hace que cada uno 1/100 del todo.
11. Una vez que los estudiantes hayan construido sus números, pídales que tracen ambos números en la recta numérica. Formule las siguientes preguntas:
a. ¿Qué modelo de base diez muestra el número decimal con mayor valor y cuál muestra el número decimal con menor valor? Podemos ver que 1.8 es mayor que 1.08 porque tiene un entero y ocho décimas. El otro modelo tiene un entero y ocho centésimas.
b. ¿Qué proceso podrías seguir para comparar números? Podríamos fijarnos primero en el valor posicional más alto. Si los dígitos son diferentes, podemos decir qué número es mayor basándonos en ese dígito. Si son iguales, tenemos que mirar el siguiente valor posicional a la derecha y usar esos dígitos para comparar.
c. ¿Cómo te ayudó la recta numérica a comparar los dos números? Pudimos ver que 1,08 está más cerca de 0 en la recta numérica, y 1.8 está más lejos de 0, por lo que 1.08 es menor que 1.8.
INTERVENCIÓN: INTERVENCIÓN EN GRUPO PEQUEÑO
a. ¿Cómo podemos utilizar un símbolo para representar esta comparación? Como sabemos que 1.8 es mayor, el símbolo estará abierto por ese lado. Por otro lado, como 1.08 es menor que 1.8, el símbolo estará cerrado por ese lado.
1. Pide a los estudiantes que escriban el símbolo de menor que en sus pizarras. Se muestran ejemplos de la recta numérica y del modelo de base diez.
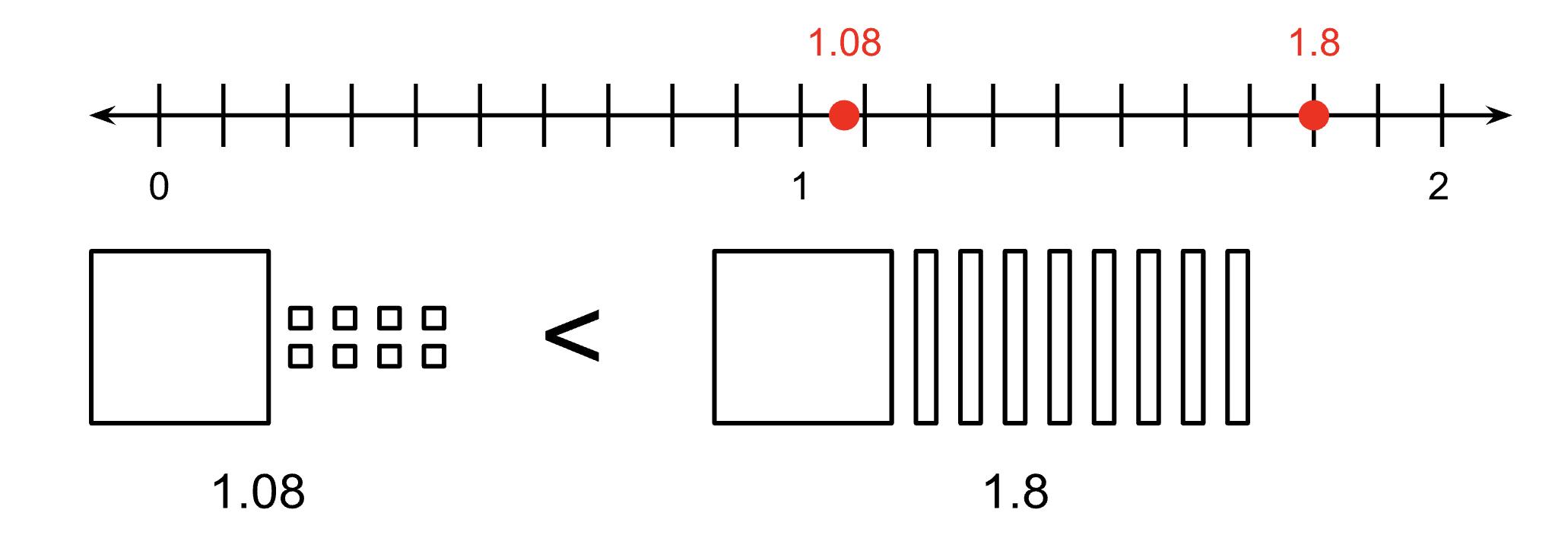
2. Formule las siguientes preguntas:
a. ¿Cómo podemos escribir dos enunciados de comparación utilizando números y un símbolo? Podemos escribir 1.08 < 1.8 o 1.8 > 1.08.
b. ¿Cómo se leen estas comparaciones? 1.08 es menor que 1.8, o 1.8 es mayor que 1.08.
3. Repita el cuestionamiento y el razonamiento para desafiar a los estudiantes a comparar otros pares de decimales.
4. Después, deje tiempo para que los estudiantes terminen la comprobación individualmente.
ACELERACIÓN: MATEMÁTICAS DE HOY
CONEXIONES CON EL MUNDO REAL
MATEMÁTICAS DE
HOY: ¿OTRA TIERRA?
DESCRIPCIÓN
Los estudiantes explorarán las conexiones y aplicaciones de las matemáticas y otros contenidos transversales a través de interacciones con medios auténticos del mundo real proporcionados por Associated Press
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Permita que los estudiantes lean el artículo. Explique brevemente que el telescopio espacial Kepler de la NASA se especializa en encontrar planetas y exoplanetas más allá de nuestro propio sistema solar. Este telescopio permite a los científicos conocer mejor el universo que nos rodea. El telescopio espacial Kepler ha descubierto recientemente Kepler-452b, un planeta que es el más cercano que los científicos han encontrado nunca a nuestro planeta Tierra. Similar a la Tierra, Kepler-452b orbita su estrella aproximadamente a la misma distancia a la que nuestra Tierra orbita el Sol.
2. Discusión:
a. Deje que los estudiantes compartan sus afirmaciones "me doy cuenta..." y "me pregunto...". Cuestione cómo se utilizan las matemáticas en esta situación.
b. Kepler-452b es un 60 % mayor que la Tierra en diámetro. Este porcentaje se escribe como 0.60 como decimal. ¿Cuál es el valor posicional del 6? Décimas
c. Un año en Kepler-452b dura 385 días. Comparado con el año terrestre, esta diferencia es igual a 0.95. En nuestro propio sistema solar, Venus es el más parecido a la Tierra con una órbita de 225 días, una diferencia igual a 0.62. Registra esta comparación utilizando <,=, o >. 0.62 < 0.95
3. Los estudiantes deben completar la hoja del estudiante de forma independiente o con un compañero.


GRADO 4: REPRESENTAR Y COMPARAR DECIMALES
ACELERACIÓN: MATEMÁTICAS DE HOY


FOLLETO DEL ESTUDIANTE
ACELERACIÓN: ESTACIÓN DE CONEXIÓN
ESTABLECER CONEXIONES RELEVANTES
CREA EL TUYO
Crea el tuyo es una actividad enriquecedora para que los estudiantes puedan crear sus propios inventos, obras de teatro, canciones, aplicaciones tecnológicas, ¡y mucho más!
MATERIALES
IMPRIMIR
• 1 material «crea el tuyo» para el estudiante (por estudiante)
• 1 material «crea el tuyo» (para el maestro)
REUTILIZABLE
• Herramientas y modelos matemáticos (por clase)
CONSUMIBLE
• Materiales para crear juegos, obras de teatro e inventos
PREPARACIÓN
Ninguna
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Distribuya un material «crea el tuyo» por estudiante.
2. Deles tiempo para que sean lo más creativos posible. No hay límites para su creatividad en esta actividad.
3. Invite a cada estudiante a presentar o representar su producto ante la clase o el pequeño grupo.


ACELERACIÓN: TABLERO DE OPCIONES
TABLERO DE OPCIONES
OPCIONES PARA EL APRENDIZAJE CONTINUO
TABLERO DE OPCIONES
DESCRIPCIÓN
Los estudiantes exploran las conexiones con el mundo real y las aplicaciones del contenido matemático a través de interacciones con actividades atractivas.
MATERIALES
IMPRESO
• 1 tablero de opciones (por estudiante)
REUTILIZABLE
• Tecnología (si procede)
PREPARACIÓN
• Imprima un tablero de opciones por estudiante.
• Planifique con antelación el uso de la tecnología. Es posible que se necesite acceso a otras actividades dentro del alcance para algunas variaciones del tablero de opciones.
• Esta actividad se puede completar en clase o en casa.
PROCEDIMIENTO Y PUNTOS DE FACILITACIÓN
1. Distribuya un tablero de opciones a cada estudiante.
2. Conceda tiempo a los estudiantes para examinar el tablero de opciones y seleccionar las actividades que les gustaría explorar.
3. Anime a los estudiantes a intentar al menos tres actividades del tablero de opciones.
4. Si el tiempo lo permite, pida a los estudiantes que compartan las conexiones que hicieron al completar las actividades que eligieron.
